Текст
ЭЛЕМЕНТАРНАЯ АЛГЕБРА
КУРСЪ СИСТЕМАТИЧЕСКІЙ
ВЪ ДВУХЪ ТОМАХЪ.
МОСКВА. ‘
Типо-литографія Т-ва И. Н. Кушнеревъ и К°, Пименовская улв| соб. дожъ, 1ѲОЗ.
О ГЛ А В Л Н Н I Е.
ОТДѢЛЪ ПЕРВЫЙ.
Алгебраическія дѣйствія.
Предисловіе..........
Глава I.
Стр, .
, V Глава IX.
Алгебраическія дроби * .
107
Предварительныя понятія и опредѣленія ............................. 1
Глава II.
Положительныя и отрицательныя количества........................ 10
Глава Ш.
Цѣль алгебраическихъ дѣйствій.— Законъ Ганкеля.— Сложеніе и вычитаніе ............................ 17
Глава ІѴ.
Умноженіе ..................... 34
Глава V.
Дѣленіе ....................... 51
Глава VI.
Разложеніе на множителей.—Умноженіе и дѣленіе многочленовъ съ буквенными коэффиціентами ...... 69
Глава ѴП.
О дѣлимости на биномы х а. — Основаніе способа неопредѣленныхъ коэффиціентовъ ................... 77
Глава ѴШ.
Общій наивысшій дѣлитель и наин. кратное............................93
Глава X. Возвышеніе въ степень............120
Глава XI.
Извлеченіе корня (общія правила) . 126 Глава ХП.
Извлеченіе квадратнаго корня изъ чиселъ и многочленовъ..............130
Глава XIII.
Извлеченіе кубичнаго корня изъ чиселъ и многочленовъ ............. 159
Глава XIV.
Объ ирраціональныхъ числахъ. . . 170
Глава XV.
Объ ирраціональныхъ выраженіяхъ . 186 Глава XVI. Степени и корни съ дробными и отрицательными показателями . . . 199
Глава XVII.
Замѣчательныя формы алгебраическихъ выраженій.................. 209
ОТДѢЛЪ ВТОРОЙ.
Уравненія и неравенства первой степени.
Глава XVIII.
Уравненія первой степени съ одппмъ неизвѣстнымъ .....................221
Глава XIX.
Уравненія первой степени съ двумя неизвѣстными......................245
Глава XX.
Рѣшеніе системы трехъ уравненій съ 3 неизвѣстными.......... . . 258
Глава XXI.
Рѣшеніе системы уравненій первой степени съ какий^ъ угодно числомъ неизвѣстныхъ......................266
Глава XXII.
Составленіе уравненій со многими неизвѣстными......................277
Глава XXIII. Теорія пропорцій.................283
Глава XXIV. Неравенства первой степени. . . . 300
Глава XXV. Изслѣдованіе уравненій первой степени съ однимъ неизвѣстнымъ. , . . 331
Глава XXVI.
Изслѣдованіе уравненій первой степени съ 2 неизвѣстными ...... 359
Глава XXVII.
Неопредѣленный анализъ первой степени.......................... 385
ОТДѢЛЪ ТРЕТІЙ,
Уравненія и неравенства второй и высшихъ степеней.
Стр.
Глава XXVIII.
Мнимыя величины и дѣйствія надъ ними ............................ 414
Глава XXIX.
Геометрическое представленіе мнимыхъ величинъ................... . 421
Глава XXX.
Рѣшеніе квадратныхъ уравненій . . 432
Глава XXXI.
Связь между коэффиціентами и корнями квадратнаго уравненія.........460
Глава XXXII.
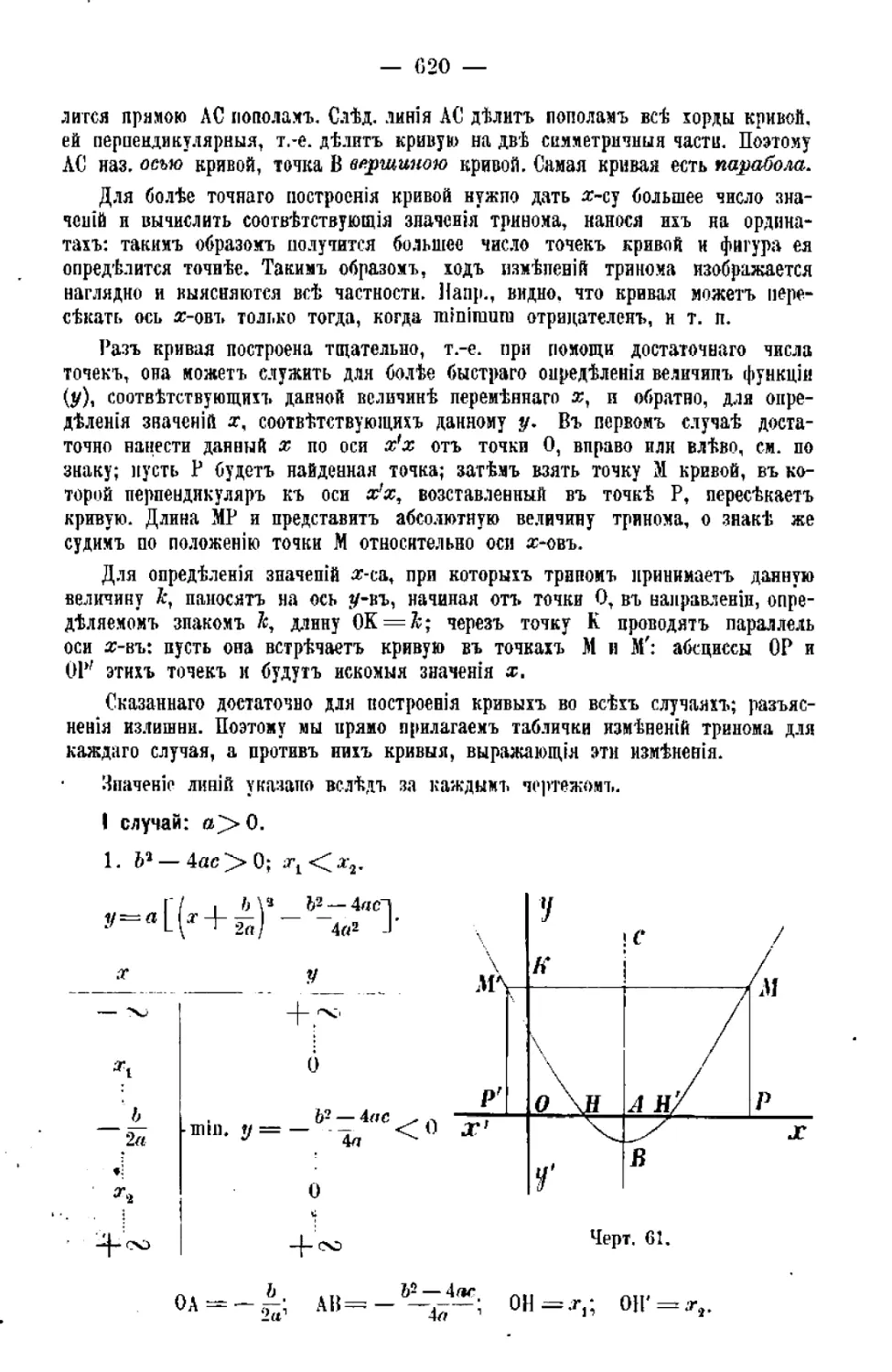
Квадратный триномъ................4Я
Глава XXXIII.
Сіпр. Глава XXXV.
Раціональныя уравненія, приводимыя къ квадратнымъ (продолженіе). . 538 Глава XXXVI.
Ирраціональныя уравненія .... 552 Глава XXXVII.
Системы уравненій высшихъ степеней 578 Глава XXXVIII.
Неравенства высшихъ степеней и прраніонаіьныя .......... 502
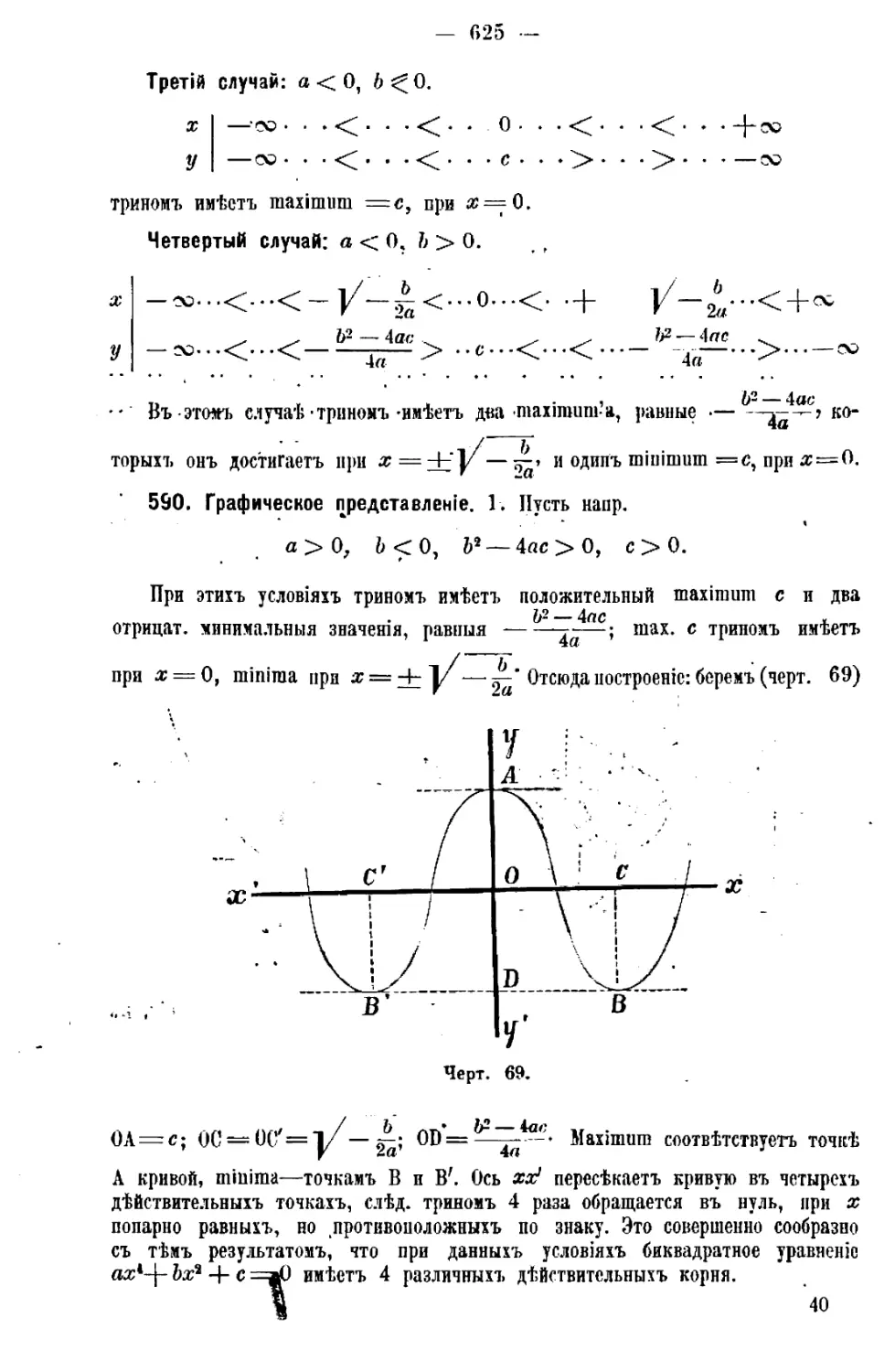
Глава XXXIV, Раціональныя уравненія, приводимыя къ квадратнымъ.................524
Уравненія; кубичное и четвертой степени.............................594
Глава XXXIX.
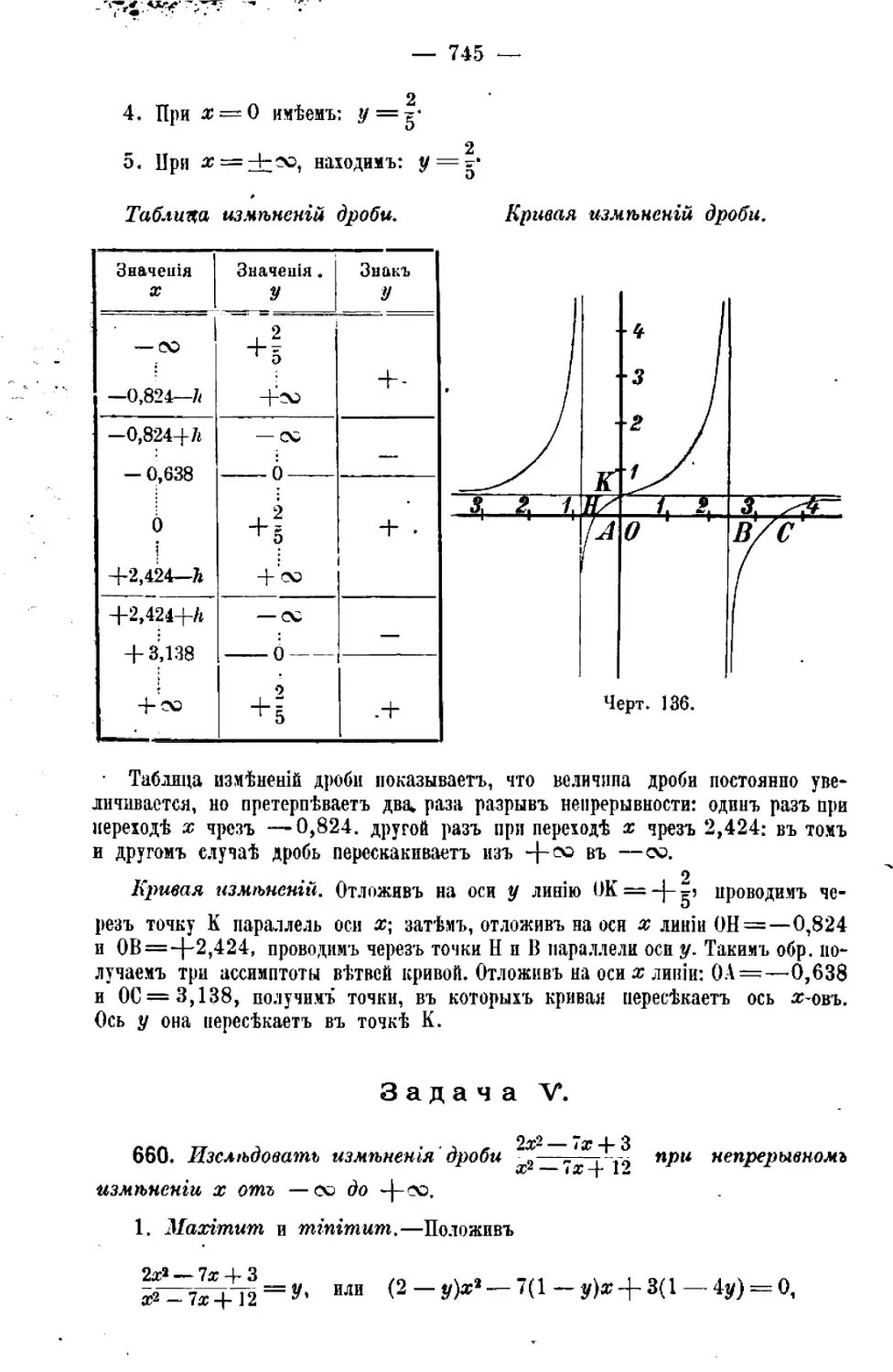
' Численные вопросы высшихъ степеней 604 і Глава ХЬ.
Изслѣдованіе измѣненій нѣкоторыхъ функцій ♦...........................609
1 Глава ХЫ.
; Образцы изслѣдованія вопросовъ : второй степени (24 задачи).........634
і Глава ХЫІ.
| Махіта и тіпіта въ задачахъ . . 709
ОТДѢЛЪ ЧЕТВЕРТЫЙ.
Анализъ соединеній и его приложенія.
Глава ХЫП. Глава ХЫѴ.
Соединенія безъ повтореній и съ по- Биномъ Ньютона..........790
втореніями............. 778
ОТДѢЛЪ ПЯТЫЙ.
Теорія рядовъ и логариѳмовъ.
Глава ХЬѴ.
Прогрессія ариѳметическая .... 810 Глава ХЬѴІ,
Прогрессія геометрическая . . - . 814 Глава ХЬѴІІ.
Элементарная теорія рядовъ . . . 834 Глава ХЬѴІІІ.
Формула бинома для всякаго показателя ............................852
Глава ХІЛХ.
Логариѳмы............... • . . 866
Глава Ь.
Вычисленіе логариѳмовъ посредствомъ рядовъ................... 876
Глава Ы.
О десятичныхъ логариѳмахъ,—Таблицы .............................885
Глава ЫІ.
Приложеніе логариѳмовъ къ рѣшенію показательныхъ уравненій и къ финансовымъ операціямъ..............896
ОТДѢЛЪ ШЕСТОЙ.
Непрерывныя дроби и ихъ приложенія.
Глава ЬПІ.
Непрерывныя дроби. .
Глава ЫГ,
. . 922
Неопредѣленный анализъ второй степени........................ 950
ПРЕДИСЛОВІЕ.
Выпуская вл свѣтъ 2-е изданіе своею курса элементарной алгебры. авторъ позаботился тщательно исправитъ всякіе случайные недосмотры и промахи, почти неизбѣжные въ первомъ изданіи. Весь курсъ снлонгь былъ внимательно пересмотрѣнъ, причемъ, введены всѣ усовершенствованія и всѣ новинки, какія успѣли накопиться со времени появленія 1-ю изданія. Изложенію, при полной ею ясности и простотѣ,, авторъ старался придать совершенную научную строгость, съ устраненіемъ всякихъ мнимыхъ доказательствъ и недомолвокъ, обычныхъ въ нашихъ ходовыхъ курсахъ. Подъ мнимыми доказательствами мы разумѣемъ такіе пріемы, какъ, напримѣръ, выводъ разложеніи функцій въ безконечные ряды но способу неопредѣленныхъ коэффиціентовъ и т. п. Къ, особенностямъ курса, отличающимъ сю отъ другихъ аналогичныхъ явленій, принадлежитъ широкое развитіе одной стороны дѣла, весьма существенной и, несмотря на то, обыкновенно почти игнорируемой учебниками, именно изслѣдованія вопросовъ 1-й и 2-й степени. Въ связи съ этимъ дано и болѣе широкое развитіе статьямъ о неравенствахъ и объ измѣненіи простѣйшихъ функцій, куда примыкаютъ и элементарные способы нахожденія максимальныхъ н минимальныхъ значеній функцій. Благодаря этому, въ нашемъ курсѣ элементарная алгебра приведена въ болѣе тѣсную связь съ аналитическою геометріею и съ высшимъ анализомъ', читатель исподволь подготовляется къ этимъ высшимъ частямъ математики. Что касается новинокъ, введенныхъ во 2-е изданіе, но і.зъ числа ихъ важнѣе другихъ усовершенствованія въ менадахъ изслѣдованія вопросовъ 2-й степени: я разумѣю яла-
VI
ны Ніирода, и особенно Тартэнвилля. Расположеніе изслѣдованія, предложенное Тартэнвиллемъ, вноситъ- въ это нелегкое дгьло необыкновенную ясность, стройность, порядокъ и относительную простоту. Изъ числа другихъ новинокъ стоитъ упомянутъ: объ особомъ методѣ разложенія на множители симметричныхъ функцій; о новыхъ пріемахъ для отличенія паразитныхъ корней резольвента ирраціональнаго уравненія отъ корней, удовлетворяюгцихъ этому уравненію; о безукоризненно строгихъ доказательствахъ теоремы о тахітипі’ѣ произведенія, данныхъ Дарбу и Гурза; о преданномъ было забвенію, но возстановленномъ въ новыхъ курсахъ» Эйлеровомъ доказательствѣ формулы Ньютонова бинома и т. д. Кромѣ того, прибавлены двѣ новыя главы, изъ коихъ въ одной разсматривается ргьшеніе полныхъ уравненій 3-й и 4-й степени. въ другой—рѣшеніе неопредѣленнаго ур—нІя 2-й степенгг съ двумя перемѣнными.
Количество задачъ значительно увеличено введеніемъ тамъ и сямъ задачъ новыхъ типовъ и, кромѣ того, прибавленіемъ 400 смѣшанныхъ задачъ, носящихъ Характеръ болѣе трудныхъ» упражненій, на которыхъ могутъ пытать свои силы болѣе успѣвающіе и болѣе талантливые учащіеся старшаго возраста.
Такъ какъ авторъ имѣлъ въ виду не только учениковъ, обучающихся въ учебныхъ заведеніяхъ, гдѣ они всегда найдутъ опору въ своихъ наставникахъ, но и такихъ лицъ, которыя обстоятельствами вынуждены готовишься дома, гдгь они по большей части лишены опытныхъ руководителей,—въ виду этого, въ настоящемъ изданіи всѣ задачи снажбены отвѣтами, а болѣе трудныя—и полными рѣшеніями; вслѣдствіе этого, пришлось весг» матеріалъ задачъ соедингітг» въ особыіг томъ. Такимъ образомъ, весг» курсъ раздгьленъ на два тома: I—Теорія; 11—Задачи.
Въ видахъ удобства покупателей каждый томъ продается огпдпільно.
Составы ніел і».
Одесса,
I ноября Х902
. ОТДЪЛЪ ПЕРВЫЙ.
I
АЛГЕБРАИЧЕСКІЯ ДѢЙСТВІЯ.
ГЛАВА I.
Предварительныя понятія и опредѣленія.
1. Ньютонъ назвалъ алгебру ариѳмепшкой*.
Называя ее ариніетикой, онъ хотѣлъ этимъ выразить, что предметъ алгебры тотъ же, что и ариѳметики,—изученіе чиселъ, слѣдовательно, что алгебра есть какъ бы продолженіе ариѳметики. Называя ее всеобщей, онъ этпмъ самымъ указалъ, что цѣль алгебры заключается въ обойлияш какъ самихъ вопросовъ о числахъ, такъ и способовъ ихъ рѣшенія.
Возьмемъ задачу: найти два числа, которыхъ сумма равна 105, а разность 15? *
Рѣшая эту задачу а/жбисеетшческгбнв мы стали бы разсуждать
такъ: если бы оба искомыхъ числа были равны, то мы нашли бы ихъ, раздѣливъ пополамъ ихъ сумму. Но мы можемъ уравнять меньшее съ большимъ, если къ первому придадимъ 15, и если эту прибавку сдѣлать къ суммѣ обоихъ чиселъ, то результатъ 105 -р 15, иля 120, будетъ ни что пное, какъ удвоенное большее число, которое и найдемъ, раздѣливъ 120 на 2. Итакъ, большее число = 120:2, или 60; а слѣдовательно, меньшее найдемъ, уменьшивъ 60 на 15, что дастъ 45.
Для повѣрки достаточно числа 60 и 45 сложить, чтобы убѣдиться, составитъ ли ихъ сумма 105; повѣрка по отношенію къ разности (15) не нужна, такъ какъ меньшее число найдено вычитаніемъ этой разности изъ большаго.
Можно бы было идти ииымъ путемъ: приравнивая большее число меньшему, можно уменьшить для этого большее число на 15. Если уменьшить 15-ью сумму, то результатъ, 105 — 15 = 90, представлялъ бы удвоенное меньшее число; п слѣдовательно, раздѣливъ 90 пополамъ, нашли бы въ результатѣ меньшее число — 45; а придавъ къ нему 15, нашли бы большее.
Рѣшеніе задачи значительно і/яуэосяшяіся, если искомыя мы обозначимъ буквами, что сокращаетъ рп>чь, а дѣйствія будемъ обозначать зяатлш, что сокращаетъ письмо. Этого рода сокращенія допускаетъ и ариѳметика.
Итакъ, обозначимъ меньшее число буквою х; тогда большее число будетъ
__ о ____
#-р!5, а оба вмѣстѣ составятъ #4-#4-15, или, короче, 2#4-15, что* по условію, равно 105; записываемъ
2# 4" = 105.
Неизвѣстное слагаемое (2#) опредѣляется вычитаніемъ изъ суммы (105) извѣстнаго слагаемаго (15); слѣд. 2# = 105 —15 = 90. Отсюда # — 90:2 = = 45. Придавъ 15 къ 45, найдемъ большее число.
Отсюда видно, какимъ образомъ введеніе знаковъ для обозначенія дѣйствій, и буквы # для обозначенія искомаго соіфаиюетв и письмо, н этимъ самымъ ускоряетъ рѣшеніе задачи. Чѣмъ сложнѣе задача, тѣмъ важнѣе введеніе этихъ, сокращающихъ запись и рѣчь, знаковъ.
2. Окончательные результаты, полученные нам при рѣшеніи задачи, т.-е. числа 45 и 60, не носятъ на себѣ слѣда данныхъ чиселъ и тѣхъ дѣйствій, путемъ которыхъ эти результаты найдены. Въ самомъ дѣлѣ, по мѣрѣ выполненія дѣйствій, данныя числа замѣнялись новыми; потому-то найденные результаты не даютъ никакого понятія о томъ, какія дѣйсшя и въ какомъ порядкѣ нужно совершить надъ данными числами для полученія искомыхъ. Чтобы это было видно, нужно только обозначать дѣйствія знаками, воздерживаясь отъ всякихъ вычисленій. Поступая такъ въ предыдущей задачѣ, мы нашли бы для меньшаго числа выраженіе
изъ котораго можно заключить, что для нахожденія меньшаго числа нужно изъ заданной суммы вычесть данную разность и остатокъ раздѣлить на 2. Но чтобы такая формула служила отчетливымъ выраженіемъ правила
для рѣшенія даннаго вопроса, нужно, чтобы она удовлетворяла нѣкоторымъ требованіямъ. Необходимо: 1) чтобы данныя величины были выражены небольшими числами, иначе формула будетъ не достаточно я/юсяш; 2) чтобы числа эти были разнообразны: иначе формула будетъ* лишена яснястм. Но если эти условія и будутъ удовлетворены, то все-таки неизбѣжное выполненіе нѣкоторыхъ дѣйствій (каково, нанр», было соединеніе вмѣстѣ нѣсколькихъ #—совъ) можетъ ввести въ формулу числа одинаковыя съ' данными, а вслѣдствіе этого формула потеряетъ совершенную ясность. Неудобства подобныя этому, очевидно, будутъ возрастать вмѣстѣ съ сложностью задачъ. Но они легко устранимы. и легко видѣть—какими средствами.
Наша цѣль состоитъ въ томъ, чтобы достичь возможности выражать формулами правила для рѣшенія сколькихъ угодно задачъ одного рода, т.-е. разнящихся не условіями, а лишь числовыми значеніями данныхъ въ задачѣ величинъ. Пусть, напр., мы хотимъ найти правило для рѣшенія задачи: иаймш два числа по даннымъ суммѣ ихъ и разности, каковы бы ни были &та сумма и эта разность. Легко видѣть, что такое общее рѣшеніе для всѣхъ задачъ одного рода найти возможно* Въ самомъ дѣлѣ, дѣйствія, которыхъ требуетъ рѣшеніе задачи, зависятъ адсодечит&ияо отъ соотношеній между данными въ задачѣ числами, но никоимъ образомъ ‘ не отъ частныхъ значеній этихъ чиселъ. А слѣдовательно, эти данныя числа можно обозначить й/кгалш; но буквы не могутъ сливаться, не могутъ исчезать, замѣняясь другими; дѣйствія надъ ішмн можно только обозначать, но не выполнять; сл. полученное выраженіе будетъ ясно указывать, какія дѣйствія и въ какомъ порядкѣ нужно совершать надъ данными для нахожденія искомыхъ во всѣхъ задачахъ одного рода.
Итакъ, пусть данная сумма равна а, а данная разность гё. Пусть, далѣе, меньшее число = #; большее будетъ по условію, = идя
2x^(1 = $, откуда 2# = $— и слѣд.
5 & /1 \
Х = ^~. . . (1)
$ (I
Формула (1) опредѣляетъ меньшее число, большее число будетъ ——рг?, или-----—г или, наконецъ,
Ч-- •
Формулы (1) и (2) ясно показываютъ правило: для нахожденія большаго числа надо къ данной суммѣ придать данную разность и результатъ раздѣлить на 2; а для нахожденія меньшаго числа слѣдуетъ изъ данной суммы вычесть данную разность и остатокъ раздѣлить на 2.
Разъ такія буквенныя формулы найдены, мы при ихъ помощи можемъ рѣшать какія угодно задачи, однородныя съ данною; стоитъ только вмѣсто буквъ подставлять числа и выполнять указанныя дѣйствія.
Такъ, если данная сумма = 500, а разность 200, то, подставивъ 500 вмѣсто 5 и 200 вмѣсто (7, найдемъ, что:
500 — 200 большая часть =---------
500—200
а меньшая часть = -—~---
700
350,
Преимущества буквенныхъ формулъ передъ числовыми, какъ видно изъ вышеизложеннаго, заключаются въ слѣдующемъ:
1) Подъ буквами можно разумѣть какія угодно числа, поэтому рѣшеніе, выраженное буквенною формулою, пригодно для всѣхъ однородныхъ задачъ: буквенная формула даетъ общее рѣшеніе цѣлаго класса задачъ.
2) Алгебраическая формула даетъ наиболѣе ясное рѣшеніе задачи, ибо въ ней наиболѣе ясно изображаются порядокъ и послѣдовательность дѣйствій, которыя надо совершить надъ данными для нахожденія искомыхъ; между тѣмъ какъ въ ариометической формулѣ эта ясность, какъ мы видѣли, иногда теряется.
3) Результатъ, представленный алгебраическою формулою, выражается обык
новенно коротко и потому дозволяетъ легко удержать въ памяти правило рѣшенія вопроса.
Но это еще не все. Алгебраическая формула, указывая связь между количествами задачи, позволяетъ вывести рядъ другихъ формулъ, дающихъ рѣшенія ряда другихъ задачъ, если брать послѣдовательно за неизвѣстное каждое изъ количествъ, входящихъ въ формулу. Для примѣра выведемъ общую формулу, которая давала бы рѣшеніе всѣхъ вопросовъ о простыхъ процентахъ.
Найти прибылъ, приносимую капиталомъ а, помѣщеннымъ на I лѣтъ по ^дъ, считая простые проценты?
100 руб. даютъ въ годъ прибыль руб.; слѣд. 1 р. дастъ въ то же время прибыль во 100 разъ меньшую, или р., а капиталъ а р. дастъ прибыль въ
а разъ большую, или
ар 100
* Это есть прибыль, приносимая капиталомъ « въ
1 годъ; прибылъ въ і лѣтъ будетъ въ і разъ больше, такъ что, назііівая эту прибыль Л получимъ соотношеніе
•-?Й- О)
Это равенство связываетъ 4 количества: а, г и даетъ рѣшеніе 4 задачъ, позволяя по даннымъ тремъ количествамъ вычислить четвертое. Формула (1) позволяетъ находить прибыль, когда извѣстны—капиталъ, время и проценты.
Разсматривая а какъ одинъ изъ сомножителей, мы его найдемъ, раздѣливъ произведеніе (») на другого сомножителя так’ обр.
. рі 100»
а=':іоб’ или а = ^Г
Формула (2) даетъ рѣшеніе задачи: какой капиталъ надо помѣститъ по р* е на * лп»тэ7 что&ы яолумпть і руб. прибыли?
Подобныхъ хе образомъ, щншмхая въ формулѣ (1) за неизвѣстное А мы найдемъ этотъ сомножитель, раздѣливъ произведеніе (») на другой сомножитель аі
100*
. аі 100»
Р=,:іоб’ или2’ = -^- • (3)
аі
Формула (3) даетъ рѣшеніе задачи: На какіе проценты надо помѣститъ капиталъ а, чтобы онъ въ і лѣтъ далъ .прибыль і руб.?
Принимая, наконецъ, въ равенствѣ (1) за неизвѣстное і, найдемъ
і = . (4)
ар 7
Такова формула, по которой рѣшается вопросъ: на сколько лѣтъ надо отдать капиталъ а по чтооь» онъ принесъ і да#. прибы.ш?
Подставляя въ формулы (1), (2), (3) н (4) вмѣсто буквъ числа, мы можемъ рѣшить любую числовую задачу на простые проценты. Напрл «а сколько % надо яожлапить капшпалъ 3000 р., чтобы въ 4 года получитъ 360 р. прибыли?
Положивъ въ формулѣ (3)
а —3000, * = 4, І =360, найдемъ
_ КЮ X 360 _
Р 3000X4 — 3'
Такимъ образомъ возможно обобщеніе какъ самыхъ вопросовъ, такъ н способовъ ихъ рѣшенія.
Наука,* занимающаяся обобщеніемъ вопросовъ о числахъ и способовъ ихъ /тѣшенія, называется алівброю.
3. Знаки, употребляемые въ алгебрѣ, частью тѣ же самые, что и въ ариѳметикѣ, частью другіе. Ихъ можно раздѣлить на три группы: 1) знаки, употребляемые для изображенія чиселъ; 2) для изображенія дѣйствій надъ числами^ п 3) для изображенія соотношеній между числами.
1. Знаки для изображенія чиселъ. Числа изображаются въ алгебрѣ не цифрами, какъ въ ариѳметикѣ, а буквами; это обозначеніе было введено фран
цузскимъ математикомъ второй половины XVI вѣка Въетомъ (1540—1603). Вьетъ употреблялъ большія литеры; малыя буквы введены англійскимъ математикомъ Томасомъ ]\ярріотомъ (1560—1621).
Для обозначенія извѣстныхъ чиселъ употребляются первыя буквы латинской азбуки: а, 5, с, й, е, для обозначенія неизвѣстныхъ — послѣднія буквы: и, у, х, я, ...
Иногда при буквахъ ставятъ значки или указатели (индексы), когда хотятъ сохранить въ обозначеніи аналогію, существующую между изображаемыми количествами.
Такимъ образомъ пишутъ: а1, а11, аПІ, аІѴ,или: а1,
<!ъ тою же цѣлью употребляютъ еще буквы греческаго алфавита, соотвѣтствующія латинскимъ: а, [3, 7, 5, е, ...
Числа, изображенныя буквами, называются общими числами, нотому-что подъ каждою буквою разумѣютъ не одно какое-либо число, но какія-угодно числа.
2. Знаки для изображенія дѣйствій.
Сложеніе обозначается знакомъ Ц- (плюсъ); такъ а + Ъ означаетъ сумму количествъ а и Ъ.
Вычитаніе обозначается знакомъ — (минусъ); такъ а — 5 означаетъ разность между а и 6.
Знаки — и — введены во всеобщее употребленіе нѣмецкими математиками XV столѣтія. Полагаютъ, что первый началъ ихъ употреблять ІТурбахъ (1423—1461). Въ «Алгебрѣ* напечатанной въ 1525 г. подъ
заглавіемъ «Со8>>, і въ «Агійппеііса іпіегтаэ напечатанной въ
1544 г., примѣнены уже эти знаки.
обозначается знакомъ X* или • (точкою), пли же между сомножителями не ставится никакого знака; такимъ образомъ а X - Ь, и аЬ одинаково означаютъ произведеніе а на 6.
Нужно замѣтить, что знакъ умноженія нельзя опускать, когда числа изображены цифрами; произведеніе 4 иа 7 нельзя представить въ видѣ 47, такъ какъ 47, по принятому способу изображенія чиселъ, означаетъ не произведеніе 4 на 7< а число сорокъ семь.
Опущеніе всякаго знака умноженія между различными факторами произведенія впервые встрѣчается у Стифеля (АгііЬтеііса 1544); знакъ X (косой крестъ) введенъ Ойшредолго (Он^Ьіге^), въ сочиненіи Сіаѵіз шаПіет. 1631; знакъ • (точка) введенъ Лейбницемъ во второй половинѣ XVII столѣтія.
Дѣленіе обозначается пли двоеточіемъ, или чертою; такъ а: Ь и ~ одинаково означаютъ частное отъ раздѣленія а на Ь.
Полагаютъ, что знакъ : введенъ во всеобщее употребленіе Лейбницемъ; знакъ — (черта) встрѣчается уже въ сочиненіи Фибоначчи Пизанскаго (1202 г.)
3. Знаки соотношеній. Соотношенія между величинами могутъ быть двоякаго рода: двѣ величины могутъ быть или равны между собою, или неравны одна другой. Для изображенія равенства двухъ количествъ употребляется знакъ =; такъ, выраженіе
А —В означаетъ: А равно В.
Знакъ равенства (=) введенъ англійскимъ математикомъ Рекордомъ, который въ первый разъ употребилъ его въ своемъ сочиненіи «Брусокъ для ума*
(ТЬе ЖіеЫопе о( ѴѴіі), изданномъ въ 1557 г. Во всеобщее употребленіе знакъ этотъ вошелъ сто лѣтъ спустя.
Слово оолыае изображается’знакомъ >, слово .меямае знакомъ <. Такъ а _> Ь означаетъ: а больше Ь; а < 6 означаетъ: а меньше Ь.
Когда ютятъ выразить, что два количества не равны, не указывая, которое изъ нихъ больше, ихъ отдѣляютъ знакомъ такъ означаетъ, что а неравно &. Вмѣсто этого также пишутъ
Чтобы выразить, что а не меньше Ь, пишутъ а >6.
Такимъ же образомъ означаетъ, что а не больше Ъ,
Знаки > и <С введены англійскимъ математикомъ Гарріоточъ.
Коэффиціентъ. — Если какое-нибудь произведеніе, напрнм., аЬ, требуется повторить слагаемымъ нѣсколько разъ, напрім.. ^ліъ. то сумма будетъ аЬаЪаЬаЬ ~ аЪ. Очевидно, что тзт іі Хъ г? Сраженія суммы неудобенъ, когда число слагаемыхъ велико: письмец у- г суммы заняло бы въ этомъ случаѣ много времени и И ъѴ* Л-? _ - 2_лЪІі ь -граненія такого
неудобства ввели сокращенное обозначеніе стхш ч.тш слагаемыхъ, усло-
вившись слагаемое писать одинъ разъ, а перех^ ставить число, показы-
вающее. сколько разъ взятое выраженіе повторяется слагаемымъ. Такимъ образомъ наша сумма сокращенно выразятся въ видѣ 5аЬ.
Число 5. показывающее. сколько разъ слѣдующее за нимъ выраженіе повторяется слагаемымъ, называется коэффиціентомъ пли юредв-тояадыла. Коэф-
фиціенту можно дать и другое опредѣленіе. Въ самомъ дѣлѣ, повторить аЬ пять разъ слагаемымъ,—это все равно, что аЬ умножить на 5; слѣд. коэффиціентъ есть числовой множитель, стоящій передъ буквеннымъ выраженіемъ.
Такъ, въ выраженіяхъ 7аЬ,
множители 7 и суть, коэффиціенты.
Иногда и буквенные производители разсматриваются какъ коэффиціенты по отношенію къ слѣдующимъ за ними произведеніямъ; такъ, въ выраженіи аЬс можно а считать коэффиціентомъ произведенія Ьс. Если произведеніе состоитъ изъ однихъ буквенныхъ сомножителей, то коэффиціентъ его есть 1; вапр. коэффиціентъ произведенія аЬс есть 1, такъ какъ это произведеніе можно написать въ видѣ 1. аЪс.
Степень, — Степенью называется произведеніе равныхъ множителей.
Если число берется множителемъ два раза, то произведеніе называется второю степенью пли квадратомъ этого числа; такъ 5)-/5 иди 25 есть . квадратъ пяти. Когда число берется множителемъ три раза, то произведеніе называется третъею степенью или кубомъ этого числа; такъ 5.5.5 или 125 есть кубъ пяти. Произведеніе четырехъ равныхъ множителей паз. четвертою степенью; папр. а.а.а.а есть четвертая степень числа а. — Очевидно, что если число равныхъ множителей велико, то письменное изображеніе степени займетъ много времени и мѣста. Для устраненія этого неудобства введено слѣдующее сокращенное изображеніе степени: перемножаемое само на себя количество пишутъ одинъ разъ, а надъ нимъ справа ставятъ число, показывающее, сколько разъ это количество берется множителемъ. Согласно этому условію, квадратъ количества а, т.-е, произведеніе а. а, сокращенно пишется въ видѣ: а*; кубъ а, т.-е. произведеніе а.а.а, сокращенно изображается въ видѣ: а3; четвертая степень а, т.-е. а.а.а.а — въ видѣ а* и т. д. — Каждый изъ равныхъ множителей называется основаніемъ степепи; такъ въ формулѣ основаніе есть а — Числа 2, 3, 4 и т. д., стоящія надъ основаніемъ, называются показателями
степени. Итакъ, яолчттель степени есть число, которое ставится надъ буквою и означаетъ, сколько разъ эта буква берется множителемъ.
Показатель 1 не пишется, а подразумѣвается; такъ, вмѣсто 51 пишутъ Ь.
На основаніи сказаннаго, произведеніе ааааЬЪЪсаІ сокращенно пишутъ въ видѣ Обратно, а253 есть сокращенно написанное произведеніе ааЬЬЬЬЬ.
Дѣйствіе нахожденія степени даннаго числа называется возвышеніемъ въ степень. Такъ, возвысивъ 7 въ кѵбъ, т.-е. взявъ 7 множителемъ
I 1
три раза, получимъ 343. Возвысивъ -у въ четвертую степень, т.-е. взявъ у
1 множителемъ четыре риза, найдемъ и т. д.
Полезно зпатъ на намять квадраты и кубы, по крайней мѣрѣ, первыхъ десяти чиселъ, которые мы и помѣщаемъ въ слѣдующей таблицѣ:
Числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Квадраты: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
Кубы: 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000.
Корень. — Корнемъ второй степени или квадратнымъ изъ даннаго числа называется такое число, квадратъ котораго равенъ данному числу. Такъ, квадратный корень изъ 9 равенъ 3, потому что квадратъ трехъ даетъ 9.
Кубическимъ корнемъ изъ даннаго числа называется такое число, котораго кубъ равенъ диплому числу. Напр., кубическій корень изъ 64 равенъ 4, пото-му-что кубъ четырехъ равенъ 64.
Корнемъ четвертаго порядка изъ даннагд числа называется такое, четвертая степень котораго равна данному числу. Такъ, корень четвертаго порядка изъ 16 равенъ 2, ибо 24 = 16.
Вообще, корнемъ п-іо порядка изъ даннаго числа наз. такое число, котораго п-ая степень равна данному числу. Такимъ образомъ корень п-го порядка изъ ад есть а. _
Для обозначенія корня употребляютъ знакъ , подъ которымъ ставятъ данное число, называемое поэтому подкореянм.нъ тшело.мь. Въ отверстіе этого знака ставятъ число, которое показываетъ, въ какую степень должно возвысить корень для полученія даннаго числа: его называютъ корня.
Такъ, чтобы обозначить письменно, что корень четвертаго порядка изъ 16 равенъ 2, пишутъ: |/16 = 2; здѣсь 2 есть самый корень, 16 — подкоренное число, 4 — показатель корня.
Если показатель корня равенъ 2, то его не пишутъ, а подразумѣваютъ. Такъ, для обозначенія, что квадратный корень изъ -у- равенъ пишутъ: і X—±
4 2 _
Коренной знакъ (К ) называется также рай«кало.н&. Дѣйствіе нахожденія корня называется извлеченіемъ корня.
Первые слѣды употребленія показателей находятся у Лароша (Агізшеііцие еі (іоотеігіе, 1520); онъ употребляетъ показатели 1, 2, 3. — Знакъ ]/ находимъ впервые у Христіана Рудольфа (1524).— Окончательно же эти знаки введены Деяар/но.иь. — Знакъ есть ни что иное, какъ искаженная буква г начальная буква слова гшііх — корень).
Скобки.—Для обозначенія дѣйствій употребляютъ еще особые знаки, называемые скобками. Имъ даютъ видъ: ( )т иля [ ], илп { }, Скобки
перваго вида называютъ — простыла, второго — ксайраягпыла, третьяго — і/шгдакыла.
Такъ, для обозначенія, что разность а~Ь нужно умножить на с, пишутъ:
(а — Ь). с
Если это выраженіе написать безъ скобокъ, т.-е. въ видѣ
а — Ь . с.
то смыслъ его былъ бы иной, именно: оно выражало бы требованіе — вычесть изъ а произведеніе Ь на с, между тѣмъ какъ требуется раяосп» а — Ь умножить на с.
Если бы требовалось сумму а -4- Ь воівькггь въ кубъ і результатъ умножить на разность с — то слѣдуетъ сказанныя дѣісткіі обозначить такъ:
(а — — й).
Если опустить скобки, т,-е, написать ♦
— с/,
то смыслъ новаго выраженія но былъ бы согласенъ съ требованіемъ, потому что послѣднее выраженіе означало бы слѣдующее требованіе: къ а придать произведеніе куба Ъ па с п изъ полученной суммы вычесть й.
Скобокъ не ставятъ всякій разъ, когда и безъ нихъ обозначеніе дѣйствій не представляетъ недоразумѣній, или когда для обозначенія дѣйствій вводится особый знакъ, устраняющій необходимость скобокъ. Напр., если бы требовалось выраженіе а2 -р (а — Ь)с раздѣлить на т2 — я2, то, обозначая дѣленіе знакомъ двоеточія, необходимо п дѣлимое и дѣлитель заключить въ скобки, написавъ:
[а2 (а -— Ь) с]: (т2 — п2).
Но если вмѣсто двоеточія знакомъ дѣленія взять черту, проведя ее подъ всѣмъ дѣлимымъ, то она устранитъ необходимость заключенія дѣлимаго и дѣлителя въ скобки; частное изобразится въ такомъ случаѣ въ видѣ
дЗ + (« —Ь)С
Точно также для обозначенія, что изъ выраженія а Ъ — с надо извлечь кубичный корень, слѣдуетъ данное выраженіе заключить въ скобки, написавши:
У'іаЦ-Ь — с).
Но если протянемъ горизонтальную черту радикала надъ всѣмъ даннымъ выраженіемъ, то послѣдняя устранитъ необходимость заключенія выраженія — с въ скобки; дѣйствіе изобразится слѣд. обр-:
з,___________
— с.
I
Употребленіе скобокъ въ первый разъ встрѣчается въ сочиненіи Ллъберта Жирара: «Іпѵепііоп поѵеііе <іапя ГаІ^еЬге еісл, изданномъ въ іѴмстердамѣ въ 1629 г.
4. Классификація алгебраическихъ формулъ.—Лліебраичшшлп шряже-яіачк или формулою называютъ совокупность буквъ, чиселъ и знаковъ, указывающую рядъ дѣйствій надъ числами, которыя иодразумѣваются подъ данными буквами. Такимъ образомъ:
8д2 —4^
а* — 63
3 /
6’(Р/а+ Гс)
суть алгебраическія выраженія или формулы*
Всякое алгебраическое выраженіе, ие содержащее корней изъ буквенныхъ выраженій, называется раціональнымъ; оно называется если
содержитъ буквенные радикалы. Первыя два изъ вышеприведенныхъ выраженій раціональны, третье — ирраціональное. Нужно замѣтить, что выраженіе можетъ быть раціонально относительно нѣкоторыхъ буквъ, и ирраціонально относительно другихъ буквъ. Такъ, выраженіе раціонально по отношенію къ а
н .г, но ирраціонально относительно Ь.
Раціональныя выраженія раздѣляются на цлиыя и гіробныя; цѣлымъ называютъ раціональное выраженіе, пе содержащее буквенныхъ дѣлителей; дробнымъ, — выраженіе, содержащее буквенныхъ дѣлителей. Такъ, выраженія
ІаѢ + ІаЬ* -!а*Ь*, 19а‘ — А „зЬ । &
1 1 і ’ 3 1 о
суть алгебраическія цѣлыя, хотя второе и третье и содержатъ числовыхъ дѣлителей: выраженія же
а -|- 6 Яа2 — 4аб + ЗЬ2
а — а3 — 63
алгебраически дробныя, такъ какъ имѣютъ буквенныхъ дѣлителей.
Одночленомъ называютъ такое выраженіе, въ которомъ послѣднее дѣйствіе есть умноженіе, дѣленіе, возвышеніе въ степень илн извлеченіе корня, но не сложеніе и не вычитаніе. Такъ выраженія
/аЬс’ 4^+7р* (а2 — Ь8) (с + <0, (х —у+*)‘, ра?» — у2
суть одночлены.
Многочленомъ наз. выраженіе, соединенныхъ знаками -|- или —.
Такъ, выраженія
состоящее изъ нѣсколькихъ одночленовъ,
а«~3«^ + 3аб2 —Ь3,
Зя*|/Ь _ 7а^ баідас
с 4с- 3
суть многочлены.
Одночлены, составляющіе многочленъ, называются его чдеяалш. Зпакъ, предшествующій одночлену, считается составною частью члена; такъ, члены перваго многочлена спь
4-а3, — За2Ь, +Зй&2,
Если передъ первымъ членомъ не поставлено знака, то нужно подразумевать
Многочленъ, состоящій изъ двухъ членовъ, напр. «2 —Ь2, наз. бнноліожь или двучленомъ; состоящій изъ трекъ членовъ, какъ а2 — — трино-
момъ или трехчленомъ; если же число членовъ больше, то многочлену не даютъ особаго названія. і
Измѣреніе. — Число буквенныхъ множителей цѣлаго одночлена называется его ш-клреяі'елъ; такъ, одночленъ 4а3Ь2с будетъ шести измѣреній, потому что, представивъ его въ видѣ іаааЬЪс, видимъ,* что онъ содержитъ шесть буквенныхъ множите лей. Сложивъ показателей, получимъ 3 —2 —|—1 или 6; сл. для опредѣленія измѣренія цѣлаго одночлена нужно взять сумму показателей его буквъ.
Цѣлый многочленъ. состоящій изъ членовъ одинаковаго измѣренія, называется однороднымъ: измѣреніе каждаго члена такого многочлена называется также измѣреніемъ самого многочлена. Напр., выраженіе а* — За-6-^ЗаЬ2 — Ь3 есть однородный многочленъ третьяго измѣренія ілі трехъ измѣреній. Многочленъ, которого члены не*-инаковаго измѣренія. иаз. напр. многочленъ
а* — За1 — аЛ1 — с — разнородныя.
Степенью многочлена относительно одной какой-либо буквы называется высшій показатель этой буквы въ многочленѣ. Такъ
Зах* - 2а2#2 Ц- ?а3;27 Н~
есть многочленъ третьей степени относительно буквы х.
5. Числовое значеніе формулы. — Числовымъ значеніемъ формулы называется то число, которое получится, если буквы замѣнимъ числами и выполнимъ указанныя знаками дѣйствія.
Такъ, если требуется вычислить числовое значеніе выраженія
2а* +
Зс
при а = 4, Ь = 3 и с =х1, то, подставивъ вмѣсто буквъ данныя числа, пай демъ
2 X 42 4-/4’2 + 3*2 = 2 X 16 + /16 -/9 _ 32 + /25 3X1 — 3 “ 3
12— и есть числовое значеніе данной формулы.
О
ГЛАВА II.
Положительныя и отрицательныя количества.
6. Изображеніе количествъ буквами вмѣсто цифръ не составляетъ еще существеннаго отличія алгебры отъ ариѳметики: и ариѳметика, при доказательствѣ теоремъ и при рѣшеніи задачъ, также пользуется для изображенія чиселъ буквами, хотя въ ней употребленіе буквъ и не такъ систематично какъ въ алгебрѣ. Существенная разница между этими науками состоитъ въ томъ, что въ разсмотрѣніе величинъ алгебра вводитъ идею о направленіи, совершенно чуждую ариѳметикѣ.
Все, что можетъ увеличиваться или уменьшаться я быть измѣряемо, вазы-вается ,-ма-те.мат«ческою величиною, .Такъ — вѣсъ, объемъ, время, темпера-
тура, скорость, сила и т. п. суть величины.
Измѣритъ веля чину значитъ сравнить ее съ другою однородною съ нею величиною, называемою при этомъ едшшцею. лпъры; точнѣе говоря, это значитъ найти кутное отношеніе измѣряемой величины къ единицѣ мѣры. Такъ, измѣряя вѣсъ тѣла, мы узнаемъ, сколько въ немъ содержится единица вѣса (пудъ, Фунтъ і т. п.), пли какая-нибудь доля ея. Поэтому результатомъ измѣренія всегда является число отялсчекяое. Цѣлое или дробное отвлеченное
число, измѣряющее данную величину, называется абсолютнымъ числомъ; вмѣстѣ
съ названіемъ е
ГП !•
лл мѣры оно дастъ намъ точное понятіе о разсматриваемой
величинѣ, ёгл ш опредѣленія величины достаточно знать только ея размѣры.
Величины. <ъ которыми имѣетъ дѣло вполнѣ опредѣляются,
какъ скоро г-в&лі* мхъ отношеніе къ 1-цѣ мѣры и самая эта единица; таковы — плошадѵ «йьеть. вѣсъ, капиталъ и т. и. Ихъ называютъ абсолютными
величиначи йххж>ы».
Но есть піл величины. для полнаго опредѣленія которыхъ недостаточно зпать. каково жгъ -тжшеніе къ единицѣ мѣры н какова самая эта единица. Такъ, ес.и я тт находясь сначала у двери, я отошелъ отъ нея на 4 аршнна. то >тмтъ м ** положеніе относительно двери еще не будетъ вполнѣ онреНме; і указать — егг> какую сторону относительно
двери я удалился: и въ такую-то комнату, или вышелъ изъ нея. Еще
примѣръ. Если мы кдх-іъ. что часы измѣнили свой ходъ въ теченіи сутокъ на 2 минуты, іѵ та ве даетъ ьпчлиѣ яснаго понятія о величинѣ измѣненія; въ саиьмъ дѣлѣ, ш должны указалъ еце направленіе измѣненія, т.-е. сказать, ускорили іл замедлили часы евмй іодъ на 2 минуты. Третій примѣръ. Если мы скажетъ, что температура воздуіа измѣнилась на 10 градусовъ, то этимъ мы не опредѣлимъ еще вполнѣ это измѣненіе; для полнаго опредѣленія измѣненія температуры надо указать —повысилась она на 10 градусовъ или понизилась. т.-е. опять надо указать направленіе измѣненія.
Большинство величинъ, существующихъ въ природѣ, имѣютъ два противоположныя направленія, и потому называются противоположными величинами;
таковы — зре.ия, которое можно считать въ направленіи будущаго и прошедшаго относительно даннаго момента; пространство. проходимое прямолинейно движущимся тѣломъ; ускореніе и замедленіе движенія; температура, потому что она можетъ быть выше нуля и ниже пуля; п/жоыль и убытокъ, ибо они измѣняютъ капиталъ въ двухъ противоположныхъ направленіяхъ; суммы иосшу-ншомря въ кассу банкира и суммы выдаваемыя кассою; наконецъ мм’м, наносимыя на неограниченной прямой отъ нѣкоторой постоянной точки, называемой
началомъ.
Такого рода величины, взятыя въ одномъ направленіи, называются юоложм-а въ противоположномъ — отрицательными. Отъ насъ зависитъ, въ какомъ направленіи считать противоположныя величины положительными и въ какомъ — отрицательными; если условимся считать положительными: ^разстояніе вправо отъ начала, 2) время будущее, 3) ускореніе, 4) прибыль, 5) капиталъ, 6) температуру высшую нуля, то противоположныя этимъ величины, т.-е. разстояніе влѣво отъ начала, время прошедшее, замедленіе, убытокъ, долгъг температуру ниже нуля, нужно принимать отрицательными.
7. Существуютъ два способа изображенія противоположныхъ величинъ—графическій и а.иебраичеекйі.
1<- Условимся каждую единицу разсматриваемой величины изображать прямой линіей опредѣленной длины, напри*. линіей аЪ (черт. 1); отложивъ линію <іЬ на неограниченной прямой столько разъ, сколько въ разсматриваемой вели-
Черт. 1.
чинѣ находится единицъ, мы и получимъ графическое изображеніе абсолютнаго значенія этой величины.
Для изображенія противоположныхъ величинъ, какого бы рода онѣ ни были, условимся представлять нхъ прямыми, наносимыми на неограниченной прямой (называемой осью) хх\ начиная отъ нѣкоторой точки о (^е называютъ ло.иь); при чемъ положительныя величины будемъ наноситъ въ направленіи отъ хг къ х; а отрицательныя въ направленіи отъ х къ х’. т.-е. въ противоположную сторону (черт. 2).
Черт. 2.
Итакъ, абсолютныя значенія противоположныхъ величинъ можно представлять длинами извѣстныхъ линій, а направленія — положеніе.^ этпхъ линій относительно начала.
При такомъ представленіи противоположныхъ величинъ каждая изъ ннхъ имѣетъ опредѣленное начало и конеиа. Отрѣзки прямой, конечныя точки которыхъ играютъ различную роль, одна — начала, другая — конца, называются векторами.
Примѣчаніе. Графическимъ представленіемъ противоположныхъ величинъ пользуются при доказательствахъ тамъ, гдѣ чисто алгебраическіе методы трудно примѣнимы. Къ преимуществамъ графическихъ методовъ принадлежитъ ихъ наглядность, позволяющая легко усвоятъ истины весьма отвлеченнаго характера. Ниже мы воспользуемся этимъ методомъ при доказательствѣ теоремъ, относящихся къ свойствамъ суммы.
2. Для изображенія противоположныхъ величинъ, очевидно, можно поступать еще такъ. Взявъ ариеметическое число, выражающее абсолютное значеніе взятой величины, можно снабдить это число какимъ-либо условнымъ значкомъ, который служилъ бы указаніемъ направленія величины. На первый взглядъ кажется, что такой значокъ можно бы было выбрать произвольно; для указанія температуръ, напрнм., можно бы было, обозначивъ число градусовъ цифрою, ставить возлѣ этой цифры букву в для обозначенія градусовъ выше нуля, и букву н для обозначенія градусовъ ниже нуля. Такимъ образомъ, обозначало бы 8 градусовъ выше нуля, а обозначало бы 5 градусовъ ниже пуля. Можно бы было условиться обозначать градусы выше нуля знакомъ ударенія, градусы ниже нуля—двумя такими значками; при такомъ условіи вышеуказанныя температуры были бы выражены знаками: 8' и 5". Однако, болѣе глубокое изученіе вопроса привело къ заключенію, что изъ всѣхъ различительныхъ знаковъ, которыми можно пользоваться для обозначенія направленія противоположныхъ величинъ, всего лучше служатъ этой цѣли, и даже почти необходимы, знаки -|-и —, которыми въ ариеметикѣ указывается сложеніе и вычитаніе, при чемъ по-
ложительпыя величины обозначаютъ знакомъ -р, а отрицательныя—знакомъ —. Такимъ образомъ. вмѣсто того чтобы писать „8 градусовъ выше нуля“ или «8д> пишутъ 8 градл и произносятъ шлюсь $ градусовъ». Вмѣсто вы-раженія «5 градусовъ ниже нуля» или «5,<» пишутъ <— 5 гр.», произнося $ минусъ 5 Точно также, вмѣсто того чтобы писать «5 футовъ
вправо» пишутъ <-р 5 фут.», произнося «гмюеь 5 </»-»; вмѣсто выраженія «семь лѣтъ тому назадъ», пишутъ <— 7 лѣтъ», говоря: «зшн^сь 7 4>ьят, и т. п.
Въ отвѣтъ на вопросъ: почему для обозначенія направленія величинъ взяты знаки: — и —, т.-е. знаки дѣйствій сложенія и вычитанія, замѣтимъ пока слѣдующее. Положительныя величины одного рода слѣдуетъ разсматривать какъ слагаемыя между собою; дѣйствительно, имѣя какую-нибудь прибыль, мы всякую новую прибыль будемъ прикладывать къ прежней, такъ какъ опа служитъ къ увеличенію уже имѣющейся прибыли; если точка, находящаяся на прямой, перемѣщена вправо, то всякое новое перемѣщеніе вправо будетъ прикладываться къ прежнему в т. д. Потому-то положительныя величины, какъ слагаемая между собою, и сопровождаются знакомъ плюсъ. Отрицательныя величины одного рода, по отношенію къ положительнымъ, слѣдуетъ разсматривать какъ вычитаемыя. Дѣйствительно, имѣя капиталъ, мы всякій долгъ будемъ изъ него вычитать, такъ какъ долгъ служитъ къ уменьшенію капитала. Всякій проигрышъ, служа къ уменьшенію капитала, должно разсматривать какъ вычитаемое. Всякое перемѣщеніе точки влѣво, служа къ уменьшенію существующаго перемѣщенія вправо, есть вычнтамое и т. д. Потому-то отрицательныя величины, какъ вычитаемыя по отношенію къ положительнымъ, и сопровождаютъ знакомъ минусъ. Нулю также иногда приписываютъ тотъ или другой знакъ, когда въ изслѣдованіи задачи нужно, чтобы оставался какой-нибудь слѣдъ, показывающій происхожденіе этого нуля. Наприм., когда температура низшая нуля увеличивается, дѣлаясь наконецъ нулемъ, то, очевидно, нужно ее обозначить знакомъ (— 0), Тригонометрія представляетъ множество примѣровъ этого рода.
8. Мы обобщили понятіе объ ариѳметическомъ количествѣ, введя въ это понятіе новый элементъ--яаяраоемге, при чемъ самое обобщеніе вывели изъ разсматриванія величинъ. Но къ тому же обобщенію можно придти еще другимъ путемъ—изъ разсмотрѣнія дѣйствій надъ числами.
Пусть изъ нѣкотораго числа а требуется вычесть Ь: разность выразится формулою а — Ь. Здѣсь слѣдуетъ разсмотрѣть три случая:
1) Когда « больше Ь, то-есть уменьшаемое больше вычитаемаго^ то вычитаніе такое всегда возможно. Такъ, если а =10 и 4, то численная величина разности а — Ь равна 6,
2) Если а=?\ т -е. вычитаемое равно уменьшаемому, то вычитаніе снова возможно, потому что отъ а всегда можно отнять столько единицъ, сколько ихъ въ немъ находится; но остатокъ вычитанія уже не представляетъ никакого числа: онъ есть нуль, выражающій отсутствіе всякой величины. Однако, уже и въ ариѳметикѣ принято н нуль называть числомъ.
3) Когда а<^6, т.-е. вычитаемое больше уменьшаемаго, то вычитаніе не всегда возможно; разсмотримъ, когда оно возможно п когда пѣтъ.
Разсмотримъ сначала величину ариѳметическую, т.-с. такую, для которой не существуетъ противоположной. Различныя состоянія такой величины можно представлять графически разстояніями точекъ прямой, неограниченно простирающейся '• иько въ одну сторону отъ своей начальной точки, наприм., отъ точки О і~: іво (по направленію О.г).
Вычитаніе Ъ изъ а выразится графически нанесеніемъ линіи а вправо отъ точки О — въ направленіи возрастающихъ разстояній, а вычитаемой линіи Ъ отъ конца М линіи 0М = а въ направленіи, противоположномъ направленію возрастающихъ разстояній, т.-е. влѣво отъ М (черт. 3). Самое построеніе показы-
О м И н--_----------------------------------х
Ъ
Черт. 3.
ваетъ: что вычитаніе возможно до тѣхъ поръ, пока Ь —Если же Ь больше а, то построеніе укажетъ яеоо&ножяость дѣйствія. потому что конецъ линіи МХ — Ь упадетъ въ этомъ случаѣ влѣво отъ точкя 0. такъ ска-
зать, въ пустоту, ибо линія Ол, простираясь только
точекъ влѣво отъ 0.
Пусть а = 5, 6 = 7; тогда
а — 6 = 5 — 7;
разность 5 — 7 можно выразить однимъ числомъ; въ самомъ -7 изъ 5 все равно что сперва вычесть 5, а затѣмъ 2, слѣд.
дѣлѣ, вычесть
о і — о — 5 2;
но 5 — 5 = 0, слѣд. 5 — 7 = 0 — 2; опуская О, получимъ въ остаткѣ —2. Разность выражается отрицательнымъ числомъ — 2; во это отрицательное число въ данномъ случаѣ ничего не представляетъ, не имѣетъ никакого реальнаго значенія.
Но если разсматриваемая прямая простирается не только вправо, но п влѣво отъ точки 0, представляя такимъ образомъ величины, имѣющія два противоположныя направленія, то дѣйствіе вычитанія большаго числа изъ меньшаго, бывшее въ первомъ случаѣ невозможнымъ, теперь становится возможнымъ, ибо ли-
М о'р “ г::>.. М
6
Черт. 4.
нія л’х имѣетъ точки влѣво отъ 0, и разность &—Ъ = — 2 имѣетъ совершенно реальное значеніе, представляя линію ОМ, лежащую влѣво отъ начала 0.
Итакъ, при вычитаніи большаго числа изъ меньшаго получается отдогде-. желъноя число; оно не имѣетъ никакого реальнаго значенія въ случаѣ абсолютныхъ величинъ и, напротивъ, имѣетъ совершенно реальное значеніе въ случаѣ величинъ противоположныхъ.
Самое правило вычитанія большаго числа изъ меньшаго легко видѣть изъ приведеннаго примѣра
именно: нужно изъ большаго числа вычесть меньшее и передъ остаткомъ поставить знакъ (—).
Въ противоположность отрицательнымъ числамъ, числа, получаемыя при всегда возможномъ вычитаніи меньшаго числа изъ большаго, называются положительными п обозначаются знакомъ -|—
Такъ, если а = 5. с = 3; то
а — с = 5 — 3 = 4~--
Легко видѣть на чертежѣ, что значеніе положительнаго числа противоположно
значенію отрицательнаго: въ то время какъ отрицательное число а — Ъ = — 2
ОХ,_ лежащую влѣво отъ точки О, положительное число
означаетъ
С
а — с = —2. выражаетъ линію Ор, лежащую вправо отъ начала (черт. 4).
9. Алгебраическое количество.—Количество, состоящее изъ двухъ элементовъ: 1) изъ численной величины, которая можетъ быть цѣлая или дробная, и 2) знака і —) или (—), указывающаго направленіе величины, и называется собственно аліебраическгімъ количествомъ. Такъ
5, -6, +а, -а, +3а*, -5а*
суть количества алгебраическія.
Если къ количествѣ отбросить знакъ, то получится ариѳметическое число, которое называется абсолютнымъ или ч-ислоодлса зяаченіе-иь, также—модулемъ количества. Такъ, количества -{-8 н - имѣютъ абсолютными значе-с 1 ніями ын модулями числа Ь и у.
Для обозначенія абсолютнаго значенія или модуля числа ставятъ это число между двумя вертикальными чертами. Такъ, | а | означаетъ абсолютное значеніе нл модуль алгебраическаго числа а. Такимъ же образомъ:
| -|-5 | =5; | — 3 | =3,
Иногда ставятъ число въ квадратныя скобки; такъ [а] означаетъ модуль числа а.
10. Выгоды, происходящія отъ, введенія отрицательныхъ количествъ.— Введеніе отрицательныхъ количествъ въ алгебру имѣетъ чрезвычайно большое значеніе, такъ какъ оно даетъ математическимъ выводамъ ту общность, которая безъ отрицательныхъ величинъ была бы недостижима. Пояснимъ это примѣрами.
Примѣръ I. Купленъ товаръ за а руб., а проданъ за Ь руб. Какое измѣненіе произошло отъ этого оборота въ капиталѣ?
Для опредѣленія измѣненія капитала вычтемъ изъ Ъ руб. а руб., найдемъ
Ъ — а.
Здѣсь могутъ быть три случая.
1) Если Ь > а, то разность Ь — а будетъ положительная и выразитъ собою побылъ, полученную при продажѣ товара, потому что цѣна (Ь), за которую проданъ товаръ, больше цѣны (а), за которую онъ купленъ.
2) Если Ъ = а, то разносгь Ь — а равна 0 и означаетъ, что при продажѣ не получено ни прибыли, ни убытка, что очевидно.
3) Если Ь < а. то разность Ь — а будетъ отрицательная и выразитъ
убытокъ, полученный при продажѣ товара, потому что цѣна (&), которую купецъ беретъ, продавая товаръ, меньше цѣны (а), которую онъ самъ заплатилъ за товаръ*
Итакъ, всѣ частные случаи, которые могутъ встрѣтиться при рѣшеніи данной задачи, можно соединить въ одной формулѣ: 6 — », которая и выражаетъ собою измѣненіе капитала во всѣхъ случаяхъ, при чемъ положительный результатъ означаетъ прибыль, а отрицательный—-убытокъ. Правда, мы могли бы избѣжать полученія отрицательныхъ выводовъ, еслибы при Ъ<а стали дѣлать вычисленіе по формулѣ.» — й; но такое дробленіе задачи и формулы на нѣсколько отдѣльныхъ задачъ и формулъ соотвѣтственно частнымъ значеніямъ буквъ не соотвѣтствовало бы духу алгебры, стремящейся обобщать какъ самые вопросы, такъ и ихъ рѣшенія.
Примѣръ II, Нѣкоторое событіе случилось спустя і лѣтъ послѣ Р. Х,^ а другое событіе п годами раньше. Хоіда имѣло мѣсто второе событіе?
Время второго событія найдемъ, вычтя я ки> ?: сдѣь ов»» выразится фор- * мглою
/ — я.
Здѣсь опять возіомы три случая:
1) Если * > я, разность і — п положительная; папр., если первое событіе имѣло мѣсто спустя 600 лѣтъ послѣ Р, X.. а второе 400 годами раньше, то подставивъ въ формулу < — я вмѣсто / число 600 п 400 вмѣсто п, найдемъ
— я = 600 — 400 = + 200,
Очевидно, этотъ положительный результатъ означаетъ, что второе событіе имѣло мѣсто черезъ 200 лѣтъ послѣ р, X.
2) Если 2 = п,’то разность і — п = 0. Нулевое рѣшеніе, очевидно, означаетъ, что второе событіе совершилось въ самое Р. X.
3) Если, наконецъ., *О, то разность / — п будетъ отрицательная. Если положимъ, что первое событіе совершилось спустя 600 лѣтъ послѣ Р. X., а второе за 800 лѣтъ до перваго, то подставляя въ формулу і — п этп числа, найдемъ
і— п = 600 — 800= — 200 л.
Ясно, что отрицательный результатъ означаетъ, что второе событіе совершилось за 200 л. до Рг X,
Итакъ, замѣтивъ, что положительный результатъ означаетъ время послѣ Р. X., а отрицательный — время до Р. X,, мы въ формулѣ і— я имѣемъ рѣшеніе всѣхъ частныхъ случаевъ данной задачи. И здѣсь мы могли бы избѣжать отрицательнаго вывода, если бы вторую задачу рѣшили по пной формулѣ: ю — I; но такое дробленіе задачи и формулы не соотвѣтствовало бы духу общности, составляющей отличительный характеръ алгебры.
Итакъ, введеніе отрицательныхъ количествъ даетъ возможность какъ самые вопросы давать въ совершенно общей формѣ, такъ п рѣшенія всѣхъ частныхъ случаевъ выводить изъ одной общей формулы.
11. Свойства положительныхъ и отрицательныхъ количествъ. — Если имѣемъ нѣсколько примѣровъ вычитанія, въ которыхъ уменьшаемыя равны, то остатки будутъ тѣмъ меньше, чѣмъ больше вычитаемыя. Такъ, вычитая изъ 5 послѣдовательно 1, 2, 3,..., получимъ остатки
5 — 1 = 4~ 4
5 —2=4-3
5 —3 = + 2 5 —4 = 4-1 5 — 5 = О
5 — 6 = — 1 5 —7 = —2
5 — 8 = — 3 и т. д.
величина которыхъ становится все меньше и меньше. Сравнивая между собою остатки. іаіодимъ такимъ образомъ, что
— 4
слѣдуетъ, что:
1) Всякое положительное количество больше нуля;
2) Изъ двухъ положительныхъ чиселъ то больше, - у котораго модуль боль»:
3) Всякое отрицательное количество меньше нуля;
4) О составляетъ границу, отдѣляющую положительныя количества отъ отрицательныхъ;
5) Изъ двухъ отрицательныхъ количествъ то больше, котораго абсолютное значеніе меньше.
Въ поясненіе выводовъ — третьяго и пятаго приведемъ слѣдующіе при-мѣры. Пусть изъ двухъ лицъ, А и В, первое ничего не имѣетъ (ни имущества пи долга), а второе, не имѣя никакого имущества, имѣетъ долгъ въ 50 руб. Долгъ и имущество величины противоположныя, при чемъ, согласно съ вышеприведеннымъ условіемъ, долгъ есть величина отрицательная, а имущество — положительная. Такимъ образомъ, состояніе А равно 0, состояніе В равно — 50 р. Лицо, имѣющее только долгъ, имѣетъ менѣе лица, ничего не имѣющаго, поэтому мы въ правѣ сказать, что отрицательное имущество В (— 50 р.) меньше пулеваго имущества А: отрицательное количество меньше нуля. Положимъ теперь, что А и В не имѣютъ никакого имущества, но А имѣртъ долгу 30 р+, а В — 80 р.; состояніе перваго выразится отрицательнымъ числомъ —30 р., второго—отриц. числомъ —80 р. Очевидно, что лицо, имѣющее долгу 30 р., богаче лица, долгъ котораго равенъ 80 р., слѣд. —30 р, >—80 р.: шъ двухъ отрицательныхъ количествъ то больше, котораго численное значеніе меньше. ч
ГЛАВА III
Цѣлъ алгебраическихъ дѣйствій.—Законъ Ганкеля.—Свойства суммы и разности.—
Свойства полинома. —Сложеніе и вычитаніе
12. — Цѣль ариѳметическихъ дѣйствій состоитъ въ нахожденіи окончательно результата. Иное дѣло въ алгебрѣ. Количества, выраженныя буквами, не жгутъ сливаться, поэтому никакое алгебраическое дѣйствіе не можетъ быть до-до копца. Такимъ образомъ, алгебраическія дѣйствія имѣютъ цѣлью: указать знаками производимыя дѣйствія и преобразоеатъ полученный ре-сз тѣмъ. чтобы сдѣлать выраженіе его болѣе короткимъ
илм болѣе яснымъ. Въ самомъ дѣлѣ, очевидно, что далѣе идти нельзя. При этомъ, такъ какъ алгебраическое количество состоитъ изъ двухъ элементовъ—абсолютной величины и знака, то и правило каждаго алгебраическаго дѣйствія должно состоять изъ двухъ частей- правила абсолютныхъ величинъ и правила знаковъ.
13. — Приступая къ какому-либо дѣйствію, надо прежде всего опредѣлить смыслъ его. При этомъ, уже въ ариометикѣ мы видѣли, что обобщеніе понятія о числѣ ведетъ къ обобУцемзю опредѣленій самыхъ дѣйствій, въ тѣхъ видахъ, чтобы избѣжать накопленія частныхъ случаевъ и всѣ эп случаи соединить въ одно общее выраженіе. Такъ, опредѣленіе дѣйствія умноженія расширяется при переходѣ отъ цѣлыхъ чиселъ къ дробнымъ. При этихъ послѣдовательныхъ обобщеніяхъ могутъ иногда утратиться тѣ или другія сдойст дѣйствій. Такъ, мы увидимъ далѣе, что извлеченіе корня. — дѣйствіе. ар^еігтеекомъ смыслѣ дающее одинъ результатъ, въ алгебраическомъ смыслѣ ”і<»«іггъ жъ нѣсколькимъ различнымъ результатамъ; въ данномъ случаѣ, слѣ^еательн-?. обобщенное дѣйствіе теряетъ свойство давать ойкні результатъ.
Но если, въ видахъ обобщенія, и можно откинуть то или другое свойство операціи, необходимо условиться не прибавлять никакихъ новыхъ свойствъ къ тѣгь. которыя имѣли мѣсто для дѣйствій надъ количествами менѣе общими, и это въ тѣхъ видахъ, чтобы всякое правило, установленное для обобщеннаго дѣйствія, было приложимо и къ менѣе общему случаю, содержа въ себѣ, какъ частный случай, правило, найденное ранѣе для дѣйствія, разсматриваемаго въ болѣе узкомъ смыслѣ, совершенно такъ же, какъ менѣе общій видъ количествъ содержится какъ частный случай въ количествахъ обобщенныхъ.
Это начало, которое слѣдуетъ соблюдать при обобщеніи опредѣленій количествъ и дѣйствій надъ ними, названо Ганкелемъ началось постоянства правилъ вычисленія. Въ силу этого начала всякое правило, относящееся къ количествамъ обобщеннымъ, должно прилагаться п къ количествамъ низшаго порядка, такъ какъ обобщеніе не вводитъ новыхъ свойствъ, а стало быть п не даетъ мѣста такимъ правиламъ, которыя не вытекали бы уже изъ свойствъ ранѣе принятыхъ.
14. — Установленіе правилъ вычисленія зависитъ единственно отъ свойствъ дѣйствій; отсюда необходимость предварительнаго изученія этихъ свойствъ. Ознакомимся прежде всего съ фундаментальными свойствами суммы и разности.
При выводѣ этихъ свойствъ мы будемъ означать противоположныя величины — каждую одною буквою; такимъ образомъ подъ буквами: а, с, гі, ... будемъ представлять противоположныя величины, т.-е. абсолютныя значенія съ сопровождающими ихъ знаками.
Свойства суммы.
15. Понятіе о сложеніи есть основное, а потому и не поддается никакимъ опредѣленіямъ.
Мы видѣли, что каковы бы ни были противоположныя величины (скорости, времена, температуры), ихъ всегда можно представлять прямыми линіями, наносимыми на неограниченной прямой въ томъ пли другомъ направленіи. Поэтому, если мы желаемъ сложить нѣсколько вели чипъ, то должны помѣстить пхъ одну за другой, каждую въ направленіи, опредѣляемомъ ея знакомъ, т.-е. начало второй помѣстить въ концѣ первой, нанося ее въ направленіи, указываемомъ ея знакомъ, и т. д. Суммою будетъ разстояніе отъ начала первой до конца послѣдней. Это геометрическое представленіе сложенія полезно какъ облегчающее средство при доказательствѣ нѣкоторыхъ изъ нижеслѣдующихъ теоремъ.
Теорема. 1. — Придать къ данному количеству послѣдовательно ^сколько другихъ—все равно, что придать ихъ сумму; т.-е,
а —|— Ъ —р- с = а 4~ (Ь —с).
Этою теоремою выражается такъ называемый законъ сочетательный въ сложеніи.
Доказательство.—Пусть, напр., а — -}-я, Ъ = — р, с = + у, гдѣ а, 5 і у суть абсолютныя величины. На линіи х'х отъ точки 0 вправо нанесемъ «ачала а: придемъ въ нѣкоторую точку М. Затѣмъ наносимъ — р, сообразно съ лакомъ этого количества, влѣво отъ точки М: придемъ въ точку И. Наконецъ,
.__________________О М -А М Р
X----—-------------------------------7^------7^------------
Черт. 5. « «гь точки К вправо наносимъ отрѣзокъ у: приходимъ въ точку Р. Сумма а 4“ + Ь с выразится линіей ОР отъ начала перваго слагаемаго до конца третьяго.
Но &4“с составляетъ въ то же время сумму МР, ибо М есть начало слагаемаго Ь, а Р — конецъ слагаемаго с; сл. представляя линію ОР суммою ОМ 4~ МР» і замѣчая, что 0М = а, а МР = Ь4“С, имѣемъ:
0Р = а4-(&4-с)‘...(1),
А раньше мы нашли, что
0Р = а4~^4“с (2)-
Изъ (1) и (2) заключаемъ, что
а4“Ь"Ьс = а4” Ф + СХ
такъ какъ оба эти выраженія представляютъ одну и ту же линію ОР.
Теорема П.— Сумма не измѣнится отъ перемѣны порядка слагаемыхъ. Ь- сО
Этою теоремою выражается законъ перемѣстительный въ сложеніи.
Доказательство. — I. Докажемъ эту теорему сначала для двухъ сла-гэемыхъ, т.-е. что
а 4“" Ь =г= 6 4~
Доказательство это, въ свою очередь, распадается на нѣсколько случаевъ, смотря по знакамъ количествъ а и Ъ.
о ...С о м р
X-----------------------------------------------------&
» "а .......а‘
Черт. 6. с
I * Пусть а и Ь — положительныя количества. Наносимъ а по линіи Оя, нкш отъ точки 0: придемъ въ точку ,М. Затѣмъ, отъ точкй М въ томъ же
2*
направленіи наносимъ Ъ, и такимъ образомъ приходимъ въ точку Р. Сумма равна линіи ОР отъ начала перваго слагаемаго до конца второго:
а-}-Ь = 0Р...(1).
Если теперь на линіи ОР отложимъ часть 0($ = Ь, то остальная ея часть <}Р будетъ равна а; слѣдов. линію ОР можно разсматривать также какъ сумму .линій Ь и а:
6-|-а —ОР... (2).
Изъ (I) и (2) слѣдуетъ, что । а —1"“ Ъ Ь в.
2) Составимъ сумму полагая, что а положительно и равно -|-а, а Ь отрицательно и равно — положимъ сверхъ того, что а > 3-
Нанесемъ а на линію Оя: придемъ въ точку М: отъ точки М наносимъ ли-, нію 6, сообразно съ ея знакомъ, влѣво: придемъ въ точку Р* Сумма а^-Ъ выразится линіей ОР отъ начала перваго до конца второго слагаемаго:
а + Ь = 0Р.........(3).
X
Черт., 7.
, Нанесемъ теперь Ь, сообразно съ знакомъ этой линіи, влѣво отъ 0: придемъ въ точку ф очевидно, что линія (}Р = ОМ (ибо каждая состоитъ изъ 6, сложеннаго съ ОР); а потому, нанося а отъ точки вправо, придемъ въ точку Р, и сумма & + « выразится линіей ОР отъ начала слагаемаго Ъ до конца а,
Ь-4-а^ор..........(4).
Изъ равенствъ (3) и (4) находимъ опять, что
ибо та и другая сумма выражаетъ одну и ту же линію ОР-
Пусть Нанеся а на линію О# вправо отъ начала, придемъ въ точ-
О Р О -----------------------м
X -------4------------------Ч-ГТТ7--------------------------------------------
Черт* 8.
ку М; отъ точки М папосимъ Ь въ направленіи Оа/; такъ какъ 8 > я, то придемъ въ нѣкоторую точку Р, лежащую влѣво отъ 0. Сумма выразится линіей ОР, отъ начала перваго до конца второго слагаемаго:
а + й = ОР. . . . : (5).
Отложимъ отъ точки 0 влѣво линію — МР ~ Ь; очевидно, что <^Р
рапа ОМ или а. Слѣд., линія ОР будетъ выражать сумму линій: — Ь і = -1- а, т.-е.
Ь-|~а = ОР........(6).
??ъ равенствъ (5) и (6) заключаемъ:
О- —&----Ъ —(2.
3» Есл бы количества а и Ъ были оба отрицательны, то доказательство йі то же самое, что и въ случаѣ, 1-мъ, только обѣ линіи пришлось бы <^пщмать влѣво отъ начала.
Втакъ. теорема доказана для двухъ слагаемыхъ.
П- Докажемъ теперь, что если имѣемъ сумму трехъ слагаемыхъ, то можно
ть порядокъ двухъ послѣднихъ. Въ самомъ дѣлѣ, на основаніи теоремы
л 1
. пгѣемъ:
а Ь + с = а -|- (і + с);
мгѣигь въ скобкахъ порядокъ слагаемыхъ, отъ чего, по теоремѣ II для двухъ сотыхъ, сумма ихъ не измѣнится, находимъ
а4-Ь4-с = а + (с + 1>);
замѣняя, на основаніи теоремы I, выраженіе а 4~ (с 4“ равнымъ ему « — *4-6, получаемъ
а4-г>4-с = а4-с + Ь.
Ш. Въ суммѣ, состоящей изъ сколькихъ угодно слагаемыхъ, можно измѣнить медокъ двухъ послѣднихъ. Въ самомъ дѣлѣ, такую сумму можно разсматри-вп какъ состоящую изъ трехъ слагаемыхъ.
П\ Во всякой суммѣ можно перемѣнить мѣста двухъ послѣдовательныхъ сла-тнпъ, гдѣ бы они ни находились.
Въ самомъ дѣлѣ, на основаніи пункта III имѣемъ
о 4- Ь + с 4- == а 4- д 4“ $ 4-
отбавляя къ равнымъ величинамъ поровну (по і), получимъ равныя, слѣд.
а 4~ ь 4- с 4~ $ + &== а + ~Н $ ~Н & 4~
•жада такимъ же образомъ
а4-ь4"с4~^4“б +/"=а4~^4'^“Ьс4~е+А «л д.
V. Можно измѣнить какъ угодно мѣста слагаемыхъ въ суммѣ.
Въ самомъ дѣлѣ, перемѣщая два послѣдовательныхъ члена одинъ на мѣсто можно всякое слагаемое помѣстить на какомъ угодно мѣстѣ.
Тморей а III. сколько «лаш&мът ложно суммою
чкжпи ее), и наоборотъ—одно слагаемое можно замѣнитъ нѣскѳлъ-которыхъ сумму оно представляетъ.
іоказательств о.—I. Помѣстимъ въ началѣ всѣ слагаемыя,,которыя мы ъ*евгъ суммировать; вычислимъ ихъ сумму, сообразно съ нхъ знаками; наконецъ, жетгаый результатъ помѣстимъ тамъ, гдѣ хотимъ. Эти преобразованія, закончись догорыхъ выше доказана, доказываютъ первую часть теоремы.
X Помѣстимъ на первомъ мѣстѣ слагаемое, которое желаемъ разложить; уяпвжпгъ его на части, сумму которыхъ оно составляетъ; наконецъ, размѣ
стимъ какъ угодно эти части въ данной суммѣ. Всѣ эти преобразованія, которыя по вышедоказанному всегда можно сдѣлать, служатъ доказательствомъ второй части теоремы.
Свойства разности.
16. Опредѣленіе вычитанія.—Вычитаніе есть дѣйствіе обратное сло- • жепію, Вычесть изъ первой величины вторую значитъ найти такую третью величину, которая будучи сложена со второю, давала бы первую, Итакъ, вычитаніе служитъ для рѣшенія слѣдующей задачи: «по данной суммѣ а двухъ количествъ и одному изъ нихъ Ъ найти другое*.
Дѣйствіе вычитанія и результатъ его, называемый остатка#^ или разностью, обозначается слѣдующимъ образомъ:
а — Ъ,
Назвавъ остатокъ буквою по опредѣленію вычитанія имѣемъ
а = Ь—
Теорема I.—Вычитаніе какой угодно величины всегда можно замѣнить приданіемъ величины ей противоположной (т.-е. противоположнаго знака).
Доказательство. Замѣтимъ сначала, что сумма двухъ количествъ а и а*) одинаковой абсолютной величины, но противоположныхъ знаковъ, равна нулю, т.-е.
а-}-а = 0.
Въ самомъ дѣлѣ, пусть, наприм., а есть количество положительное и выражается отрѣзкомъ ОМ; придать а значитъ отъ точки М влѣво отложить линію МО; придемъ въ точку 0. Такнмъ образомъ сумма, т.-е. разстояніе отъ начала перваго до конца второго слагаемаго, равна 0. (См. черт. 3.)
Состояніе лица, имѣющаго 5 р. капитала и 5 р. долга, очевидно, равно нулю, сл. -|” 5 р. + ( — 5 р.) = 0; и т. и.
Пусть теперь изъ а нужно вычесть I). По опредѣленію вычитанія, это значитъ: найти такое третье количество, которое, будучи сложено съ Ьт давало бы а. Такимъ свойствомъ обладаетъ количество а4-Ь; въ самомъ дѣлѣ:
а4“&4“^ = а4~І^4“М
I
по теоремѣ 1 свойствъ суммы. Но, въ силу только^что сдѣланнаго замѣчанія, количество въ скобкахъ равно нулю; слѣд.
а — Ь = &4~^
что и требовалось доказать.
Теорема И.— Уяіо&д вычесть кужяо вычесть послѣдова-
тельно всѣ ея члены.
Доказательство.—Въ самомъ дѣлѣ, пусть нужно вычислить выраженіе
М — (д 4- Ъ + с — сі)*.
*) Въ этой теоремѣ и въ теоремѣ ГѴ* мы обозначаемъ равныя, по противопс* ложныя количества одинаковыми литерами разныхъ начертаній.
разность буквою 8, мы, по опредѣленію вычитанія, имѣемъ равенство 5 —|— (<х —|— Ь с —
Лт
. по теоремѣ I свойствъ суммы,
К = 8 —р а —р & —с с?1
і перемѣнивъ мѣста слагаемыхъ:
Х = а-|-5-|-й-|-с4-Ь, ши, по той же теоремѣ:
И (5 —[- й —|- с —|-
Здѣсь И есть сумма, 8-|~^4“сЧ“^~одно слагаемое, а—другое; по опредѣленію вычитанія (по данной суммѣ Й и одному слагаемому, а, другое опредѣляется вычитаніемъ) имѣемъ:
К —— а = 8 —|- б? —с Ь,
Такимъ же точно разсужденіемъ изъ послѣдняго равенства находимъ послѣдовательно:
И — а — Ъ = с (5 <0»
К — а — Ь — €= 5 Л;
К -— а — Ъ — с — сі — і.
Подставивъ вмѣсто 8 равную ему величину, находимъ
К — + = — а— Ъ — с —
что и требовалось доказать.
Принципъ, выражаемый этою теоремой, служитъ, между прочимъ, основаніемъ теоріи вычитанія цѣлыхъ чиселъ: изъ уменьшаемаго послѣдовательно отнимаютъ всѣ части вычитаемаго, разсматривая его какъ сумму единицъ, десятковъ, сотенъ и т. д.
Теорема Ш.-—Чтобы придать разность^ нужно придать уменьшаемое и изъ результата отнять вычитаемое.
Доказательство/—Пусть будетъ дана разность
а — Ъ = 8;
по опредѣленію вычитанія, имѣемъ
(і = с Ъ.
Придавая равныя къ равнымъ, получимъ равныя величины (приданіе 8 -|- Ь означаемъ скобками); сл.
Н4-а = Я-|-(8 + Ь);
отсюда, по теор. I св. сум., имѣемъ:
К -р а = И + 8 + Ь,
а во опредѣленію вычитанія:
или,* замѣнивъ 2 его величиною, получаемъ
Х-І-а —Ь = К + —6), что и требовалось доказать.
Теорема IV.— Чтобы вычесть разность, нужно вычесть уменьшаемое и къ результату придать 'вычитаемое.
Доказательство.—Изъ равенства
а — 6 = 8, имѣемъ
а = Ь + Ъ,
Придавая къ обѣимъ частями по Ь, имѣемъ:
а4_Ь = ? + Ь + Ь = 8; вычитая равныя изъ равныхъ, получимъ:
Х-(а^Ь) = Х-г;
отсюда, по теор. П св. рази., имѣемъ
X — а — Ь = X — 8
но вычесть Ь — то же самое, что придать 6; слѣд.
К_а-4_Ь = Х-§ = Х_(а —Ь), что и требовалось доказать.
Слѣдствіе. Придавая или вычитая разность, всегда можемъ измѣнить порядокъ двухъ производимыхъ дѣйствій.
Доказательство. — Чтобы доказать теорему для случая приданія разности, напишемъ равенство
Х4”а — 6 = а Ц- X — 6, справедливое потому, что въ суммѣ К-ра можно перемѣнить порядокъ слагаемыхъ.
Вторую часть равенства, на основаніи теоремы III св. разн., можно представить въ видѣ: а 4- (К — 6); слѣд.
Х4-а — 6 = а + (Х-6);
перемѣнивъ снова мѣста слагаемыхъ во второй части, получимъ х 4"* & — 6 ^=5 (х — 6)
опустивъ скобки, такъ какъ и безъ нихъ смыслъ дѣйствій ясенъ, имѣемъ
И -I- а — Ь = И — Ъ а. »
Для случая вычитанія разности, па основаніи случая приданія прямо имѣемъ: X — а Ц- Ъ = X’ Ъ — а.
Теорема V. — Разность не измѣнится, если къ уменьшаемому и вычитаемому придать или изъ нихъ вычесть одно и то же количество.
I
Доказательство. — Въ самомъ дѣлѣ, изъ равенства
а — Ь = 5,
♦
ж опредѣленію вычитанія, имѣемъ
а = 8 Ь.
Предавая къ равнымъ поровну, получимъ количества равныя, слѣд.
а 4- ~ 8 Ц- Ь 4*
ни по теоремѣ 1 св. суммы:
а т= 2 Ц- (Ь -|~ т)-
Отсюда по опредѣленію вычитанія,
(а 4“ т) — (Ъ т) = 8,
ли, замѣнивъ 8 его величиною, имѣемъ
(а 4* т) — (Ъ т) = а — 6.
Совершенно аналогичнымъ пріемомъ докажемъ, что
(а — т) — (Ь — т) — а — Ь.
Слѣдствіе. — Всякая разность ртвна обращенной разности, взятой со знакомъ минусъ.
Доказательство. — Имѣя разность а — Ь, мы не измѣнимъ ее, вычтя изъ обоихъ членовъ ея по а; поэтому
а — Ь = (а — а) — (Ъ — а); ли
а — Ь = О — (Ь — а);
опустивъ ноль, получимъ окончательно
а — Ъ = — (Ь — а). >
Теорема VI. — Количество не измѣнится, если къ нему придать и затѣмъ вычесть одну и ту же величину,
Доказательство. — Въ1 самомъ дѣлѣ, по теоремѣ ІП о приданіи разности имѣемъ:
р_)_а _ а ==Р-4(«-«) = ₽ + О = Р.
Свойства полинома.
17. Выраженіе вида
а-\-Ъ — — е
газывающее рядъ сложеній и вычитаній, называется полиномомъ или многочле-шлъ, Члены, предшествуемые знакомъназываются положительными, а ^едшествуемые знакомъ—, отршдетелъяылш. Если передъ первымъ членомъ ж иходится никакого знака, надо подразумѣвать -р. Члены полинома суть жтетва, которыя сами по себѣ могутъ быть или положительныя, или отри-
дательныя. Отдѣльный членъ, называемый одночленомъ или лонялола, всегда можно разсматривать какъ двучленъ или биномъ; въ самомъ дѣлѣ:
а = а О = О а — а — О.
18. Теорема.'—Во всякомъ полиномѣ можно какъ угодно измѣнятъ порядокъ членовъ^ сохраняя передъ ними ихъ знаки: величина полинома отъ этого не измѣнится.
Доказательство. — I. Сначала докажемъ, что можно измѣнить порядокъ двухъ послѣднихъ членовъ; т.-е., назвавъ совокупность предшествующихъ членовъ буквою Р, докажемъ справедливость равенствъ:
р^а_р = Р„Ь —
Р — а — Ь — Р — Ь — а.
Р -к а — Ь = Р — Ь — а. ] » л
. Въ самомъ дѣлѣ, по теоремѣ П свойствъ суммы, величина суммы не измѣнится отъ перемѣны мѣстъ слагаемыхъ: слѣд. 1-е равенство доказано.
Для доказательства второго припомнилъ, что на основаніи теоремы II свойствъ разности имѣемъ
Р — а — Ь = Р — (а 4- &);
измѣнивъ въ суммѣ мѣста слагаемыхъ, получимъ
Р — а — 6 = Р — (і а);
отсюда, основываясь опять на теор. II св. разн., вторую часть замѣняемъ формулою Р — Ъ — а, послѣ чего окончательно находимъ
Р — а— 6 = Р— Ь— а.
Наконецъ, на основаніи слѣдствія теоремы IV св. разн., прямо имѣемъ
Р + а — Ъ = Р — Ъ -|- а ,
и третье равенство доказано.
II. Докажемъ теперь, что можно измѣнить порядокъ двухъ послѣдовательныхъ (рядомъ стоящихъ) членовъ полинома.
Въ самомъ дѣлѣ, всякіе два рядомъ стоящіе члена суть послѣдніе члены полинома, составленнаго изъ нихъ и имъ предшествующихъ членовъ; а по 1 пункту нашей теоремы такіе два члена могутъ быть переставлены одинъ на мѣсто другого.
III. Можно измѣнить какъ угодно порядокъ членовъ. Въ самомъ дѣлѣ, пере-. ставляя два послѣдовательные члена одинъ на мѣсто другого, можно какой , угодно членъ полинома перевести постепенно на какое угодно мѣсто.
19. Приведеніе подобныхъ членовъ полинома. — Два члена, состоящіе изъ одинаковыхъ буквъ и надъ одинаковыми буквами имѣющіе одинаковыхъ показателей, а коэффиціенты и знаки которыхъ могутъ быть какіе угодно, называются подобными. Короче, гсойооншш называются такіет у кото-
рыхъ буквенная частъ одинакова. Такъ, ЗоЧі3с и — 7а3Ь®с — подобны; также 4 (х — у)2#3 н — у (х — у)3#3 — подобны между собою.
Когда многочленъ содержитъ подобные члены, его можно упроститъ, соеди-
шъ подобные члены въ одинъ. Соединеніе подобныхъ членовъ въ одинъ назы-пется приведеніемъ.
При выводѣ правилъ приведенія нужно разсмотрѣть слѣдующіе случаи.
1) Знака подобныхъ членовъ одинаковы. Пусть данъ двучленъ, состоящій «п> положительныхъ членовъ, напр., ЗааЬ-|-5«я&. Знакъ подразумеваемый жредъ членомъ ЗааЬ, показываетъ, что слѣдуетъ придать Заа6; 4~ передъ ггорымъ членомъ означаетъ, что придается 5а*&; но придать За*й, а затѣгь
— все равно что сразу придать 8а2Ь, слѣдовательно
Зайі ~р 5а4Ь — 8а3Ь.
Возьмемъ двучленъ — 4аЬ3— 5аЬ3. Знакъ (—) передъ первымъ членомъ иѵказываетъ, что нужно отнять 4аЬ3; тотъ же знакъ передъ вторымъ членомъ означаетъ, что нужно отнять 5аЬ8; но отнять 4аЬ3 и затѣмъ 5аЬ® — все равно что сразу отнять 9аЬ3; итакъ
— 4аЬ3 — 5аЬ3 = — 9а63й
Отсюда правило: ее-ш знаки подобныхъ членовъ одинаковы, то для приве-аенія членовъ въ одинъ нужно буквенное выраженіе оставитъ безъ перемѣны, коэффиціенты сложить, а знакъ поставитъ общій,
2) Знаки приводимыхъ членовъ различны. Возьмемъ выраженіе, состоящее изъ двухъ подобныхъ членовъ съ разными знаками, напр., 5а*Ь3 — За3Ь3. Знакъ (-}-), подразумѣваемый передъ первымъ членомъ, означаетъ, что нужно придать 5аЧ3; (—) передъ вторымъ членомъ показываетъ, что нужно вычесть ЗааЬ®. Придать 5 разъ а2і3, а затѣмъ вычесть 3 раза а*Ь3 — все равно что придать 2 раза а263; сл.
5ааЬ3 _ = + 2айЬ3.
Въ выраженія: —5а3Ь3-|-2а*Ь3 заакъ (—) передъ первымъ членомъ показываетъ, что нужно 5 разъ вычесть а2й3; (+) передъ вторымъ члепомъ показываетъ, что нужно придать 2 раза а2Ь3; по это — все равно что отнять 3 рана аа&3, Слѣд.
— 5а2Ь3 -к 2аЧ>3 = — За3Ь3.
<)тсюда правило: /ми да знаки подобныхъ членовъ разные, иго для соединенія членовъ въ одинъ нужно — буквенное выраженіе оставить безъ измѣненія, изъ большаго коэффиціента вычесть меньшій и передъ разностью поставитъ знакъ большаго коэффиціента,
Можетъ случиться, что подобные члены имѣютъ одинаковые коэффиціенты, но разные знаки, напр., ^-1— 2а — 2«; очевидно, что такіе члены взаимно уничтожаются, т.-е. даютъ въ результатѣ ноль. Слѣд.
4~ 2а — 2а — О.
При помощи этихъ правилъ можно дѣлать приведеніе подобныхъ членовъ по-лнома, сколько бы ихъ ни было. Въ самомъ дѣлѣ, примѣняя первое правило, іы соединимъ въ одинъ членъ всѣ подобные члены, имѣющіе одинаковые знаки; і’ <лѣ этого придется сдѣлать приведеніе членовъ съ разными знаками, примѣ-Аіл второе правило. Пусть, напр., данъ полиномъ
7а6 — 5аЧ>2 + 5аЧ>* — За162 + 8а*63 - 13а*Ьа+ а4Ь3 - Ь6.
Членъ 7а®, не имѣющій себѣ подобнаго, остается неприводимымъ. Члены: — 5а4Ьа и 5а46я, какъ подобные члены съ разными знаками и равными коэффиціентами, взаимно уничтожаются. Затѣмъ: —За4і* и —13а*Ь3 даютъ, по первому правилу, — 16а46*; члены: и по тому же правилу, лаютъ Члены: — 16аЧ>3 и по второму правилу, даютъ
— 7а*№. Наконецъ — 6®, какъ не имѣющій себѣ подобнаго, остается не приводимымъ. Такимъ образомъ данный полиномъ приводится къ слѣдующему сокращенному виду:
7а® — ІаЧ)* — Ъ'.
20. Расположеніе многочлена по степенямъ главной буквы. — Когда показатели нѣкоторой буквы въ послѣдовательныхъ членахъ идутъ постоянно уменьшаясь или увеличиваясь, то говорятъ, что полиномъ расположенъ по степенямъ этой буквы, которая въ такомъ случаѣ называется моеной.
Такъ, полиномъ
3 — 5х -Ь 6-г1 — х* — х1
расположенъ по возрастающимъ степенямъ буквы х. Многочленъ
62 6’5
расположенъ по убывающимъ степенямъ буквы х.
Многочленъ
$ах*у — 14 4- 7«вх2^в
расположенъ одновременно по убывающимъ степенямъ буквы х и по возрастающимъ буквы у.
Многочленъ называется полнымъ, если показатели главной буквы идутъ увеличиваясь или уменьшаясь постоянно на единицу и если имѣется членъ, не содержащій главной буквы. Таковъ, наприм., многочленъ
ах1 -|- Ьх1 сх* + Лг 4“ *
это есть полный многочленъ относительно буквы х.
Если же нѣкоторыхъ степеней главной буквы недостаетъ, многочленъ называется неполнымъ, Наприм., 3^4-2х-рі
есть неполный многочленъ четвертой степени относительно буквы х: въ немъ недостаетъ члена, содержащаго
Сложеніе.
21, Сложеніе полиномовъ. Теорема. — Чтобы придать полиномъ къ какому-нибудь количеству, надо всѣ члены полинома приписать къ этому количеству — каждый съ тѣмъ знакомъ, какой передъ нимъ находится.
Первое доказательств о.—Опо основано па правилѣ приданія суммы или разности. Пусть требуется къ Р придать полиномъ а — Ъ с — й; дѣйствіе обозначаемъ, заключивъ многочленъ въ скобки:
Разсматривая й какъ .количество вычитаемое изъ а — обозначаемъ хго дѣйствіе, заключивъ «— Ь-|-с въ новыя скобки; такимъ образомъ полупимъ:
Р 4- (а — Ь с —(?) = Р + [(« — Ь 4" с) —1 й].
Разсматривая а — Ъ с какъ одинъ членъ разности, а (I какъ другой, и припоминая, что по теор, III св. разы., дли приданія разности надо придать первый членъ и отнять второй, найдемъ:
Р 4- (а — 6 4“ с — й) = Р 4~ О* — Ь 4- с) — й.
Разсматривая а — Ь какъ одинъ членъ суммы, а с какъ другой, что обозначаемъ соотвѣтствующими скобками, имѣемъ:
Р -р (4 — Ъ 4- с — й) = Р 4~ [(« — Ь) 4~ С1
На основаніи теоремы III св. суммы можно членъ [(«— Ь)4*с] замѣнить уммою составляющихъ его членовъ; так. обр.
Р 4- (а — 6 4“ г — (?) = Р 4~ (а — Ь) 4“ с
Наконецъ, по теоремѣ о приданіи разности получимъ окончательно
р 4“ (4 — Ь 4" с —й) — Р 4“ а — Ь 4" *с —
Второе доказательство, — Оно проще перваго. Разсматривая прида-яьемый полиномъ какъ одинъ членъ, мы, перемѣняя мѣста слагаемыхъ, можемъ шисать:
Р -1- (а — 6 4~с— й) = (а — — (?)4~Р-
Вторая часть равенства означаетъ, что изъ а надо вычесть Ь, затѣмъ прилить с, вычесть й и, наконецъ, придать Р: но тотъ же смыслъ будетъ имѣть выраженіе, если въ немъ опустить скобки; сл. имѣемъ право написать
Р 4~ (« — Ь 4~ е — (I) = а — Ь 4~ * — й 4- Р.
Переставивъ затѣмъ послѣдній членъ второй части па первое мѣсто, полу-«гь окончательно
Р4~(4 — &4“с — й) = ?4^а —
Итакъ, для сложенія многочленовъ надо члены одного многочлена приписать «ъ другому, каждый съ тѣмъ знакомъ, какой передъ нимъ находится, и, еслп сдѣлать приведеніе. Па практикѣ, для удобства приведенія, пишутъ чле-ж одного многочлена подъ другимъ, наблюдая, чтобы подобные члены пахо-шоиь въ одномъ вертикальномъ столбцѣ. Такъ, пусть требуется сдѣлать сло-
•г* — 5аЪг 4" 7я#2 — а3 4“ (^а3 — х2 4“ — ЗЛг) 4“ — 2яа 4“
Располагая многочлены сказаннымъ образомъ, имѣемъ:
Г 4я3
I «з
— 5л^4“ 7 л#*— — ЗаЪ; — 4а.г4^-
8а3
а3
Слагаемыя < — я3 — За*я
Сѵмма. . , *
х3 — 4~ 11 “р 8а3
или, располагая члены по убывающимъ степенямъ буквы а:
8а® — 4аЪ?4“ Пси?1-(-о?®.
22. Сложеніе мономовъ.—Правило этого дѣйствія можетъ быть выведено на основаніи правила сложенія полиномовъ, такъ какъ всякій мономъ можно разсматривать какъ биномъ.
Пусть къ какому-нибудь количеству Р, подъ которымъ будемъ подразумѣвать или полиномъ, или мономъ, требуется придать -[--а* Разсматривая 4~а какъ биномъ 0 4- а, иа основаніи правила сложенія полиномовъ, получимъ
Р4-(4-в)=Р+(о-Н)=Р+о-Н;
опуская 0, имѣемъ: Р^(-|-а) = Р + а............................(1).
Разсматривая —а какъ биномъ о — а, подобнымъ же образомъ найдемъ:
Р + (— а) = Р — (0 — а) = Р4-0-а = Р-а...........(2).
Итакъ. одночленъ надо приписывать къ данному коли-
честву съ ею знакомъ.
Такъ, наприм.
(— 11а®ЬЪ?) = 5а3Ьия —11а8^вх;
по приведеніи же найдемъ: — 6а863хф
Такимъ же образомъ найдемъ:
1. -|- 5 4’(4"7) = 4~ 5 4~ 7 — 4“ 12, ибо 5 положительныхъ единицъ да 7 такихъ же единицъ даютъ 12 положительныхъ единицъ или 4“ 12.
2. — 5 4~(— 7) = — 5 — 7 5= — 12, ибо 5 отрицательныхъ да 7 отриц. единицъ даютъ всего 12 отрицательныхъ единицъ или —12.
3. 4-8 4-(—5) = 4-8 — 5 = 4~ 8, ибо 8 положительныхъ да 5 отриц. единицъ даютъ въ совокупности 3 положительныхъ единицы или 4“3-
Примѣчаніе, — Изъ послѣднихъ примѣровъ заключаемъ, что съ алгебраическимъ сложеніемъ не всегда соединяется понятіе объ увеличеніи: приданіе положительнаго числа означаетъ увеличеніе, приданіе отрицательнаго — уменьшеніе.
Теорема. — Всякій полиномъ можно разсматривать какъ сумму членовъ, ею составляющихъ.
Такимъ образомъ:
а —Ь4-с-Л = (-}-«) + ( —6) 4-(+ с) + (—й).
Въ самомъ дѣлѣ, примѣняя правило сложенія мономовъ ко второй части равенства, найдемъ выраженіе, стоящее въ первой его части; заключаемъ, что преобразованіе, указываемое этимъ равенствомъ, законно.
Вычитаніе,
23. Вычитаніе многочленовъ. Теорема.— Чтобы вычесть мноючленъ изъ какого-нибудь количества, надо къ этому количеству приписать всѣ члены вычитаемаго съ обратными знаками.
Первое доказательство. — Оно основано на правилахъ вычитанія
тупы пли разности. Пусть требуется изъ Р вычесть многочленъ а — 6 с — оГ; гкігтвіе обозначаемъ, заключивъ вычитаемое въ скобки:
Р — (а~ Ь4~с — ^).
Разсматривая (I какъ количество, вычитаемое изъ а — Ь с, обозначаемъ тѣйствіе этого вычитанія, заключивъ а—>Ь-|-е въ скобки. Такимъ образомъ
Р — (а — Ь с — — Р — [(а — Ъ с) — Л]. ,
Разсматривая а —&4~с какъ одинъ членъ разности, а какъ другой, на стованіи теоремы IV св. разности, имѣемъ:
Р — [(а — & 4“ с) — <4 = Р — (а — Ь 4* с) +
Выраженіе въ скобкахъ разсматриваемъ какъ сумму двухъ слагаемыхъ, изъ вторыхъ одно=а—й, а другое с; обозначая это соотвѣтствующими скобками, пемъ второй части послѣдняго равенства видъ
Р-[(а-Ь) + с] + (/.
Это выраженіе примѣненіемъ теоремы II св. раза, преобразовываемъ въ слѣдующее:
Р — (а — Ь) — с 4-
Примѣняя сюда теорему IV свойствъ разности, находимъ
Р — а + Ь — <? 4-
Итакъ, указанныя преобразованія приводятъ къ равенству:
Р — (а — & 4~с — ^) = Р — а4~&~ +
то и требовалось доказать*
Второе доказательство.—Эту теорему можно доказать иначе, осно-шваясь на опредѣленіи вычитанія и на правилѣ сложенія многочленовъ.
Вычесть изъ Р многочленъ а — Ь 4~ с — й, значитъ найти такой многочленъ, задавъ къ которому вычитаемое, нашли бы уменьшаемое Р. Полиномъ, имѣю-жіі такое свойство, есть
Р — а 4“ Ь с 4“
гь самомъ дѣлѣ, придавая къ нему данное вычитаемое, для чего надо всѣ члены ькдѣдняго приписать съ ихъ знаками, паходимъ
Р — а 4~Ь — с + й + а — Ь 4“ € — Ф
'Хілавъ въ этомъ выраженіи приведеніе, находимъ въ результатѣ Р. Стало дѣйствительно Р — а4”& — с 4" есть остатокъ вычитанія многочлена
* — Ь4~с — & изъ Р, т*-е.
Р — (а — Ь 4~ с — (1) = Р — а 4~ Ъ — с 4- й.
Итакъ, для вычитанія многочленовъ надо къ уменьшаемому приписать члены сжигаемаго съ обратными знаками и, если можно, сдѣлать приведеніе.
На практикѣ, для удобства приведенія, пишутъ члены вычитаемаго подъ жи^Ььзаеіымъ, наблюдая, чтобы подобные члены находились въ одномъ верти-и^ъ-ть столбцѣ.
Такъ, пусть требуется сдѣлать вычитаніе:
(5а36а _ 7аз6з Ь5) _ (2а36* — 7аѢ* + Заі4 — 66й).
Располагая многочлены сказаннымъ образомъ и перемѣняя въ вычитаемомъ знаки на противоположные (измѣненные знаки поставлены на верху), имѣемъ:
Уменьшаемое. .... 5а362 —7а263 + 8а&4— Ь5
Вычитаемое............—2а362 + 7а263 ч- ЗяЬ4 Ч- 663
Остатокъ................ За362 + баб4 + 56я
24. Вычитаніе мономовъ.—Правило вычитанія одночленовъ можно вывести на основаніи правила вычитанія многочленовъ, такъ какъ всякій одночленъ можно разсматривать какъ двучленъ.
Пусть изъ какого-нибудь количества Р, подъ которыхъ можно подразумѣ-вать или многочленъ, или одночленъ, требуется вычесть — а. Разсматривая + а какъ биномъ на основаніи правила вычитанія многочленовъ находимъ
Р — (—а) = Р — (О —а) = Р — О —а;
опустивъ О, имѣемъ:
Р —(+«) = Р —а. . . . (1).
Разсматривая — а какъ биномъ О — а, подобнымъ же образомъ найдемъ:
Р —(— а) = Р—(О —а) = Р — 0 + « = Р + а . . .(2).
Такимъ образомъ, вычитаемый одночленъ надо приписывать къ уменьшаемому съ обратнымъ знакомъ.
Напримѣръ
5а362с — (— 2а362с) = 5а361*с + 2а36'2с = 7а363с.
Такимъ же образомъ найдемъ:
1) 3 —(4-5) = 3 — 5 = — 2.
2) з — (— 5) = 3 + 5 =4-8.
Замѣчая, что остатокъ перваго вычитанія (—2) меньше уменьшаемаго, между тѣмъ какъ остатокъ второго (+8) больше уменьшаемаго, заключаемъ, что съ алгебраическимъ вычитаніемъ не всегда соединяется понятіе объ уменьшеніи: вычесть положительное число—значитъ уменьшить, вычесть отрицательное—значитъ увеличить.
Примѣчаніе.—Правило вычитанія одночленовъ можно бы было вывести непосредственно, основываясь на опредѣленіи этого дѣйствія; такой выводъ ничѣмъ не отличается отъ второго доказательства правила вычитанія многочленовъ, потому мы его и опускаемъ.
Употребленіе скобокъ.
25. Если многочленъ пли нѣсколько его членовъ заключены въ скобки, то можно ихъ опустить, написавъ многочленъ безъ скобокъ. Дѣйствіе это назыв. раскрытіемъ скобокъ, а правила его непосредственно вытекаютъ изъ правилъ сложенія п вычитанія многочленовъ. При этомъ слѣдуетъ разсмотрѣть два случая. V
1. Если передъ скобками стоитъ знакъ +, то можно опустить скобки вмѣ--гі съ знакомъ, который передъ нями находится, переписавъ члены, стоявшіе жъ скобкахъ, съ ихъ знаками. Такъ, выряженіе
а -|- (— Ь -}- с — -|- е), в» раскрытіи скобокъ, дастъ, по правилу сложенія, а — 6 4~ с —
2. Если многочленъ или часть его заключены иъ скобки, передъ которыми Т'<гь знакъ —, то можно опустить скобки вмѣстѣ съ знакомъ, который имъ і^ішествуетъ, перемѣнивъ знаки у всѣхъ членовъ, стоящихъ въ скобкахъ. Такъ, мзогочленъ
а —& — (—₽ + /•—А),
•• гласно съ правиломъ вычитанія, по раскрытіи скобокъ дастъ: а — Ь € — /’4~ Л.
Если многочленъ содержитъ нѣсколько паръ скобокъ, то ихъ можно уничто-вть послѣдовательно, начиная или съ внутреннихъ, или съ наружныхъ, руко-згитвуясь каждый разъ вышеприведенными правилами. Такъ, въ выраженіи х —[6 4"(С — Ф] раскрывъ сперва наружныя скобки, найдемъ •
а— Ь — (с —’ Й), пенимая на время с — за одинъ членъ. Раскрывая оставшіяся скобки, нахо-итъ окончательно
а — Ъ — с + й.
Наоборотъ, раскрывая сначала внутреннія скобки, т.-е. вида ( ), въ выжженіи
а —I——(<? — е)]|, вотчимъ
а - | - Ь + [с —
шарывъ затѣмъ квадратныя скобки, найдемъ
а — | — Ь 4“ с —- (7 4~ & 11
шаривъ, наконецъ, фигурныя скобки, получимъ окончательно: а 4- Ъ — <? 4-
Наоборотъ, можно многочленъ или часть его заключитъ вг> скобки, такъ чвмі передъ иими былъ опредѣленный знакъ. Здѣсь опять надо разсмотрѣть ж случая.
1. Если многочленъ или часть его желаемъ заключить въ скобки со зна-жп — передъ ними, то у членовъ, вносимыхъ въ скобки, слѣдуетъ сохранить къ жаки. Такъ въ выраженіи а4~Ь—с — внося три послѣдніе члена * скобки со знакомъ 4~ передъ ними, получимъ
а4~^“Ь(——е);
этого преобразованія подтверждается тѣмъ, что. раскрывъ скобки, вввнгъ іанное выраженіе а-\-Ь — с 4* — е.
2. Если же многочленъ или часть его требуется заключить въ скобки со знакомъ — передъ ними, то у членовъ, заключаемыхъ въ скобки, надо знаки перемѣнить на обратные. Такъ, если три средніе члена многочлена а — Ь-}-/— — А 4- к нужно заключить въ скобки со знакомъ -— передъ ними, то найдемъ:
(Ъ — /*4“ А) —к;
справедливость преобразованія доказывается тѣмъ, что, раскрывъ скобки, находимъ данное выраженіе
а — Ь —|— / — А —к.
Можно въ данный многочленъ вводить и нѣсколько паръ скобокъ. Такът наприм.. многочленъ а— 6-|-е — й4"е—/* можно написать въ видѣ
Л —[ — Ь 4“ С — — О 4*/)]'
ГЛАВА IV*
Умноженіе,
Опредѣленіе.—Правило знаковъ.—Законъ перемѣстительный. — Умноженіе одночленовъ.—Умноженіе многочлена на одночленъ и обратно.—Умноженіе многочленовъ.— Замѣчательные случаи умноженія.
26. Опредѣленіе. — Если для умноженія даны два ариѳметическія цѣлыя числа, иапр. 5 и 4, то умножить первое на второе значитъ взять первое сла-
» 4
гаемымъ 4 раза. Но если бы требовалось умножить о на -у, то данное опредѣленіе теряетъ смыслъ въ примѣненіи къ этомѵ случаю, потому что нельзя
4 "
взять 5 слагаемымъ у раза. Такимъ образомъ, опредѣленіе дѣйствія умноженія, въ случаѣ умноженія на дробь, должно быть измѣнено, но такъ, чтобы оно не противоречило опредѣленію умноженія на цѣлое число. Умножая 5 на 4. мы повторяемъ множимое слагаемымъ четыре раза, т.-е. составляемъ изъ множимаго новое число такъ, какъ множитель составленъ изъ единицы. Распространяя такое понятіе объ умноженіи па случай дробнаго множителя, т.-е.
г 4 ,
понимая подъ умноженіемъ наприм. э па у —составленіе изъ э новаго числа такъ, какъ у составлено изъ единицы, мы даемъ такое опредѣленіе умноженія. которое, осмысливая случай умноженія на дробь, не противорѣчитъ въ то же время опредѣленію дѣйствія умноженія на цѣлое число. Распространяя это опредѣленіе и на алгебраическія количества, Лакруа даетъ слѣдующее общее опредѣленіе умноженія: умножитъ одно количество на другое значитъ— изъ множимаго составить новое количество такъ, какъ множитель составленъ изъ положительной единицы.
27, Правило знаковъ. — Примѣнимъ это опредѣленіе къ выводу правила знаковъ при умноженіи.
Пусть требуется положительное количество (4~ 5) помножить на положительное количество (4-4). Это значитъ: изъ -|-5 составить новое количество такъг какъ множитель 4“ 4 составленъ изъ положительной единицы. Но для составле-
ал — 4 изъ 4" 1 надо 4' 1 повторить слагаемымъ четыре раза; въ самомъ лл (4-1) 4“ (“Ь і) А- (4* 0 4* (4~ 0=+14" 14~14~1 = 4~ п по-^ку для нахожденія произведенія надо и 4"5 взять слагаемымъ четыре раза. Ъд~дімъ
5 .(+4) = (+5)4-(+5) + (^г5) + (+о) = + 5 + 5 + 5 + 5=х + 20 . . .(1).
Пусть требуется (—5) помножить на (Н-4), По опредѣленію, это значитъ іх~> і — 5) составить новое количество такъ, какъ (4~ 4) составлено изъ поло-хтт*льной единицы, т.-е. надо (— 5) повторить слагаемымъ четыре раза. На-
— 5і . (4-4) = (—5) + (— 5) + (— &) + (— 5) = —5 —5 — 5 — 5 = — 20. . .(2).
Дано: помножить на (— 4). По опредѣленію, надо изъ (4" 5) госта-
«в новое количество такъ, какъ (—4) составлено изъ (4 1). По для соста-ояія (—4) изъ (4~ О нужно у (4“1) перемѣнить знакъ на обратный, я съ тжъ измѣненнымъ знакомъ взять ее слагаемой четыре раза; дѣйствительно: - в-|_(_ і) + (_ 1)_|_(_ 1) = -4.
'Свершая надъ множимымъ тѣ же дѣйствія, что и надъ (4~1), должно: у — 5) перемѣнить знакъ на обратный, вслѣдствіе чего получимъ (—5), а за-"Лжъ — 5 повторить слагаемымъ четыре раза. Найдемъ
- .(-4)-(~5) + (-5) + (—5) + (— 5) = — 5 5 — 5-5 = —20. . . (3).
Пусть, наконецъ, требуется (— 5) помножить на (— 4). Согласно опредѣ--ря». нужно у ( — 5) перемѣнить знакъ на обратный, и съ этимъ измѣненнымъ жкдгь взять его слагаемымъ четыре раза. Получимъ
— 5 • * (— 4) — (+ 5) + (+ о) 4- (+ 5) + (Н- 5) —|- 5 + 5 }- 5 -(- 5 = |- 20 . . . (4).
Результаты: (1), (2), (3) и (4) приводятъ къ слѣдующему правилу: при ѵлхаженіи двухъ количествъ надо перемножитъ ихъ абсолютныя вели-«мы и передъ результатомъ поставитъ знакъ 4~> есл*{ множимое и лвь+зеителъ имѣютъ одинаковые знаки, и (—), если оба сомножителя знаки разные.
При выводѣ этого правила мы брали числа цѣлыя. Возьмемъ теперь дробію жда; пусть, паприм., требуется уѴ Но опредѣленію умно-
ж’яьг надо изъ I — уі составить новое количество такъ, какъ
ілм» взъ (4'0- Но Для составленія уизъ (+1) надо: 1) 4~ 1 раздѣлить ян _ вслѣдствіе чего получимъ 14" у)? въ самомъ дѣлѣ, помноживъ на
* повторивъ слагаемымъ 7 разъ, найдемъ \4"у)4~(4"уу 4“ ’ ’ ' =Н”у ля—1; 2) затѣмъ слѣдуетъ (“Ьу) повторить слагаемымъ пять разъ; сдѣ-мі тгв. найдемъ —у; н 3) въ результатѣ перемѣнить знакъ на обратный,
і летъ Поступая съ І~уу| такъ,екакъ сейчасъ мы поступали
2 2
• >—-1дѣлимъ, во-первыхъ. —у на 7, вслѣдствіе чего находимъ —;
соста-
х 2 > 2X5
повторяемъ, затѣмъ, — ^слагаемымъ пять разъ, что даетъ —3-77-?; нако
нецъ, въ результатѣ перемѣняемъ знакъ и находимъ
Итакъ:
/ П / _.2 1
3 / Д 7 / —3* ‘ 7
что согласно съ вышеприведеннымъ правиломъ.
Такимъ образомъ, обозначая буквами а и абсолютныя числа, цѣлыя или дробныя, имѣемъ:
(+а) • (4“ = 4" н*
а). (+?) = — 2-?• (+ а).(— =І) = — а.?. (— з).(— =і) = 4-я.>.
28. Обобщеніе правила знаковъ — Пусть о и Ь будутъ два количества, которыя сами по себѣ представляютъ числа положительныя или отрицательныя; и распространимъ правило знаковъ и на этотъ случай. Докажемъ, напр., что каковы бы ни были знаки а и б, всегда (—а), (—й) =-|-яЬ. Разсмотримъ четыре случая:
1. Пусть а —-|-а, гдѣ а и —числа абсолютныя, цѣлыя или
дробныя. Въ такомъ случаѣ: — а = — (4~ а) = — а, — Ъ = ~ (-{- }) = — ^ слѣдовательно
(— а). (— Ь) = -- а. —
Съ другой стороны
аЬ = -{* (+ * * 4” ?) = 4“ (+ °Ф) = 4“ яЗ.
Итакъ, количества (—а)(—б) и 4“^Л какъ равныя порознь одному и тому же количеству -р равны между собою, слѣд.
(—• (—&) = + а^
II. Пусть а =— а, Ь — + ^, гдѣ а и рі числа абсолютныя.
Въ этомъ случаѣ: —а = -(— а) = 4~я, и —Ь = — (4“?) —— слѣд.
(— а) . (— &) = + я • —? = —-а?-
Съ другой стороны
-I- аЬ — + (—і. 4- — + (-а?) = — д?.
Заключаемъ опять, что и въ этомъ случаѣ
(— а) . (— 1)) = -}-аЬ.
Ш. Пусть а — + а, Ь — — отсюда: — а = — (-(- а) = — а, и — Ъ = = — (— ?) =+ ?; слѣд. (— а) . (—&) = — а . + ^ = — зф.
Но 4-аЬ = + (4-а. -?) = + (-!>) = -а?-
Опять находимъ, что
( — а) . (—* Ь) =
?т Пусть, наконецъ, а= — а, Ь = — въ такомъ случаѣ:
— а = — (— 1) — + 7; — 6 = — (— 3 — + 3? СЛѢД.
(—а) . (— Ь)=-|~а • + ?= +а?-
Я> і —а/, = + (~а . — 2)= + (+а?)==-Н2-
•'та имѣемъ
(— л) • (— =+«6.
Итакъ, каковы бы пи были знаки количествъ а и &, всегда имѣемъ:
(— а) . (— 6) — а/л
Такимъ же точно образомъ можно убѣдиться, что вышедоказаиное правило жы<*въ распространяется и на три остальные случая; такъ что, каковы бы ни Чии количества а и Ь — положительныя или отрицательныя, и каковы бы ни •*л игъ абсолютныя величины — цѣлыя пли дробныя, всегда имѣемъ:
(+ а) • 0+ Ь) — + (“ а) • (+&) = — (+«) . (— Ь)=^аЬ;
(— а) , (— 6) = -}“
Правило знаковъ при умноженіи, въ сокращенной формѣ, выражаютъ такъ:
-«хшитяе знаки даютъ въ произведеніи плюсъ, а разные — минусъ.
Слѣдствія. — Укажемъ нѣкоторыя слѣдствія правила знаковъ:
1) Произведеніе положительныхъ количествъ всегда положительно; такъ.
(-1- 2) . (+ 3) . (4- 4) = + 24.
-) Знакъ произведенія отрицательныхъ множителей зависитъ отъ числа ихъ, иенно: если число ихъ четное, то произведеніе будетъ положительное, потому ттѵ въ такомъ случаѣ его можно разбить на нары, изъ которыхъ каждая даетъ яакъ (+); еели же число отрицательныхъ множителей нечетное, то произведете будетъ отрицательное, такъ какъ въ этомъ случаѣ будетъ одинъ отрица-’-іьный множитель, для котораго пѣтъ нары. Такъ:
1) (+ 8) . (- 5). (- 2) = (~ 40) . (- 2) = + 80;
2) (+ 8) . (- 5) . (- 2) . (- 3) = (+ 80) . (- 3) = - 240;
3) (-}-8).(~5).(— 2) . 3) , (— 7^ = (— 240) .(-7) = +1680 и
под.
Примѣчаніе. — Правило знаковъ встрѣчаемъ уже у Діофанта (365 по ?. X.), но безъ' доказательства. Знаменитый Эйлеръ въ своей алгебрѣ даетъ лііующее доказательство: (—а) . (—Ъ) равно или + + или —аЬ, третьяго ^ультата быть не можетъ. Этимъ результатомъ не можетъ быть —аЬ, потому что такое произведеніе происходитъ илп Отъ (—а)(+Ь). или отъ — &).(+я). Поэтому, произведеніе будетъ = + «/>. Очевидно, это доказа-т-иіггво, какъ и доказательство Крампа. не выдерживаетъ критики. Крампъ гъ своей Всеобщей Аргюметикѣ говоритъ: «Теорема, въ силу которой два от-жіательные множителя даютъ произведеніе со знакомъ, противоположнымъ лш-•ку, и слѣд. положительное, сводится къ извѣстному правилу грамматики: шмеі пеШіо аГіігтаЬ.
29. Теорема.'— Произведеніе не измѣняется отъ перемѣны порядка сомножителей. Эта теорема составляетъ такъ называемый законъ перемѣстительности въ умноженіи. Докажемъ ее:
1) для цѣлыхъ положительныхъ сомножителей;
2) для дробныхъ положительныхъ производителей;
3) для отрицательныхъ, цѣлыхъ или дробныхъ производителей.
1. Имѣемъ два цѣлыхъ положительныхъ числа а и Ъ; умножить а на Ь1 значитъ повторить а слагаемымъ Ь разъ; сл.
а # Ъ — Я1 4~~ а ~I- я 4~ а —, но а — 1 -р 1 4~ 1 4~ 1 ,
д . Ъ = 1 4” 1 1 1 4”
— (1 4“ 1 + 1 ~~ 1 4~
+ (і + і-н + і +
. (6 разъ):
. (а разъ); слѣд.
... а разъ)
... Ш)
... й)
... И) )
Число горизонтальныхъ строкъ = 6.
Приходится составить сумму единицъ, содержащихся въ этигь Ь строкахъ. Это можно сдѣлать двоякимъ образомъ^
1) Складывая единицы въ каждыхъ скобкахъ, число которыхъ равно Ь9 мы получимъ Ъ слагаемыхъ, изъ которыхъ каждое = я; такимъ образомъ нужно я повторять Ъ разъ слагаемыхъ, что и даетъ намъ произведеніе я.Ь,
2) Можно взять сумму единицъ, составляющихъ первый вертикальный рядъ и равняющуюся Ь; затѣмъ сумму единицъ второго вертикальнаго ряда, равную также Ь, и т. д., а какъ всѣхъ вертикальныхъ рядовъ а, то приходится Ъ повторить я разъ слагаемымъ: найдемъ.
й 4“ & 4“ Ь 4““ • - (а разъ) = Ь. я.
Итакъ, сумма одного и того же числа единицъ можетъ быть представлена произведеніями а . Ь и Ь , я; т.-е.
аЬ = Ьа.
Возьмемъ теперь произведеніе нѣсколькихъ цѣлыхъ положительныхъ сомножителей и назовемъ буквою Р произведеніе всѣхъ ихъ, кромѣ двухъ послѣднихъ; можно доказать, что въ произведеніи Ршп можно перемѣнить мѣста двухъ послѣднихъ множителей, не измѣняя этимъ величины произведенія, т.-е. что Ртпв ~ Въ самомъ дѣлѣ
Рт = р р 4- Р -|- . . . (т разъ\
1 а . ?
’Л
Произведеніе Ря»я- представляетъ сумму п ждое — Рш или, что тоже, = Р 4~ Р 4" Р Ч- *
слагаемыхъ, изъ. которыхъ ка-. . (т разъ); слѣдовательно
Ртн = (р 4- Р 4- р 4- .
. (т разъ) ій) И)
Число горизонтальныхъ строкъ = п.
Эту сумму можно вычислить двоякимъ образомъ:
I) Въ каждыхъ скобкахъ имѣемъ ж слагаемыхъ, изъ которыхъ каждое
= ?: поэтому каждыя скобки даютъ Риі; это количество повторяется слага-мйкхъ п разъ, сл. сумма = Рти.
2) Иначе: въ каждомъ вертикальномъ ряду имѣемъ п слагаемыхъ, изъ кожъ каждое — ₽; сл. каждый вертикальный рядъ даетъ Ри; а какъ всѣхъ вер-чаиальныхъ рядовъ т, то общая сумма = Рпт, Итакъ
Ртп =рпт
Основываясь на этомъ выводѣ, докажемъ, что если дано произведеніе изъ гѴколькихъ цѣлыхъ положительныхъ' чиселъ, то каждое изъ нихъ можно помѣ-"гтть на каждомъ мѣстѣ.
Такъ, имѣя произведеніе аЬссІе^ можемъ, на основаніи предыдущей теоремы, замѣнить его произведеніемъ аЪсесі. Затѣмъ, разсматривая сіи какъ два по-лѣдніе множителя произведенія аЪсе, замѣняемъ послѣднее равнымъ ему произведеніемъ аЪес, такъ что аЬсеЛ ~ аЬес(і. Разсматривая Ь и е какъ два по-<^ѣдніе множителя произведенія дЬе, замѣняемъ послѣднее равнымъ ему произведеніемъ аеЬ, такъ что аЬесгі—аеЬсй, Наконецъ, перемѣняя мѣста множителей произведенія не, находимъ аеЪссІ — еаЪгіІ. Такимъ образомъ, послѣдовательно имѣемъ
аЬссІе =*= а Ъсесі = аЬеаІ — аеЪссІ = еаЬсЗ,
ъкуда видимъ, что множитель # можетъ быть поставленъ на каждомъ мѣстѣ произведенія, ие измѣняя величины его.
. Это справедливо относительно каждаго множителя; слѣд. въ произведеніи цѣлыхъ положительныхъ множителей можно каждаго изъ нихъ помѣстить послѣ-ховательно па каждое мѣсто, не измѣняя этимъ величины произведенія.
II. Пусть множители будутъ положительныя дроби. Означая буквою Р про-взведеніе, предшествующее двумъ послѣднимъ множителямъ -- и нрипоми-іхя правило умноженія дробей и замѣчая, что правило знаковъ доказано и для дробныхъ множителей, находимъ
Такимъ образомъ и здѣсь произведеніе не измѣняется отъ перестановки двухъ послѣднихъ множителей. А отсюда, примѣняя вышеприведенныя разсужденія, находимъ, что
а
Ь
с е к т а с е т к а с е к
(і [ і п Ь сі г ѣ і Ь & п ? і
___ д т с е к_____________________т д с е к
Ь п ' <і * 7 ♦* і п' Ь ' (Г [ і
т.-е. въ произведеніи нѣсколькихъ дробныхъ положительныхъ множителей можно послѣдній изъ нихъ помѣстить на какомъ угодно мѣстѣ произведенія, не взмѣняя величины послѣдняго. Правило это справедливо и для всѣхъ дробныхъ юдожительныхъ множителей. *
III. Если множители произведенія будутъ отрицательные, дробные или цѣлые, то произведеніе, по абсолютной величинѣ, равно будетъ произведенію тѣхъ же множителей, но взятыхъ съ положительными знаками. Но. по доказанному, гь произведеніи положительныхъ множителей можно измѣнять порядокъ ихъ какъ угодно, не измѣняя этимъ величины произведенія. Поэтому абсолютная величина
нашего произведенія не измѣнится отъ перемѣны мѣсгь множителей. Слѣдовательно, если измѣненіе порядка множителей можетъ оказать какое-нибудь вліяніе на величину произведенія, то это вліяніе можетъ простираться только на его знакъ. По выше было показано (§ 28, р. 2), что знакъ произведенія отрицательныхъ множителей зависитъ только отъ ихъ числа, но не отъ порядка, въ которомъ они размѣщены; а какъ число ихъ при производимыхъ перестановкахъ остается то же самое, то и знакъ произведенія всегда будетъ одинъ и тотъ же. Итакъ, измѣняя порядокъ множителей въ произведеніи отрицательныхъ чиселъ, мы этимъ не измѣнимъ ни величины, ни знака произведенія.
С л ъ д с т в і я [. Чтобы умножить данное количество на произведеніе нѣсколькихъ другихъ, нужно его послѣдоватЛьио умножить на множители этого произведенія. Это—такъ-пазываемый законъ сочетательный въ умноженіи.
Въ самомъ дѣлѣ:
т(аЪс) = (о&срн,
по закону перемѣстительному: выраженіе во второй части показываетъ, что а нужно умножить на Ъ> произведеніе на с, и новое произведеніе на лГ; опустивъ, для сокращенія скобки, найдемъ
т(«6с) = абст,
но по закону перемѣст., аЬсш = юш&с, сл. окончательно
лЦабс) = таЬс. •
II- Чтобы умножить произведеніе на нѣкоторое количество, нужно на это количество помножить одного изъ производителей.
Въ самомъ дѣлѣ:
(аЬсЛ)т = аЬаІт (опустивъ скобки)
= стаМ (по закону перемѣстительности) = (ст)аЪ(1 (цо смыслу скобокъ) — аЬ(ст)(1 (по закону перемѣст.).
ІИ. Во всякомъ произведеніи можно: нѣсколько множителей запѣнить ихъ • вычисленнымъ произведеніемъ и обратно, какой угодно множитель другими, которыхъ произведенію онъ равенъ.
Въ самомъ дѣлѣ:
1) Всегда возможно разсматриваемые множители перемѣстить такъ, чтобы они стояли рядомъ; составить затѣмъ ихъ произведеніе; и помѣстить послѣднее куда угодно какъ множителя.
2) Всегда возможно множителя, который желаемъ разложить, помѣстить на первомъ мѣстѣ; замѣнить его сомножителями, произведеніи» которыхъ онъ равнялся бы; и наконецъ расположить этихъ множителей, какъ угодно.
30. Правило показателей. — Разсмотримъ умноженіе степеней одного и того же основанія. Пусть, напр., требуется умножить л1 на а3. Мы знаемъ, что а* = а.а,а.а.а и а5 = а.а.а; слѣдовательно аѴ —а.а.«.а,а.«д.а = а8. Отсюда заключаемъ, что произведеніе имѣетъ то же самое основаніе^ а показатель его равенъ суммѣ показателей множителей. Пусть вообще дано помножить ат на гдѣ а какое-нибудь количество: а т и и — числа цѣлыя и положительныя.
Замѣчая, что ам = а.а.а . . . гдѣ « повторяется множителемъ т разъ, и аи = алі.аа . . . . гдѣ а берется множителемъ п разъ,
находимъ, что т разъ » ризъ
ат,аи = а.а.а ....... а.а.а • • . . =
— а.а. а......................=ат-г*г
роп
Итакъ: а^.а" — ат+л. Слѣд. имѣемъ правило:
Произведеніе двухъ степеней одного и тою же основанія есть другая степень тою же самаго основанія^ которой показателъ равенъ суммѣ показателей сомножителей.
31. Умноженіе одночленовъ. — Пусть дано перемножить одночлены
:; 6а562с3</4 X эа*Ь*ср.
Перемѣнивъ порядокъ множителей 6,а\д2,с3/?\5,аа и т. д., отъ чего величина произведенія не измѣнится, даемъ произведенію видъ
6.5.а\а2.ЬѴАс8.сл/4./^;
4 «
примѣняя сюда правило показателей 30), имѣемъ
6.5.а7Ь8с4йу2.
> №Ь*с9(1' X 5»*ЬV2 = 30а ѴсМУ2.
Отсюда вытекаетъ слѣдующее правило умноженія одночленовъ:
1) перемножить.
2) Затмись яаписать одну за другою вегъ различныя буквы, входящія въ оба одночлена, и при каждой поставитъ показателъ, равный суммѣ показателей этой буквы въ сомножителяхъ; если же буква вхо- дитъ только въ одинъ изъ сомножителей, ее пишутъ въ произведеніи съ тѣмъ показателемъ, какой она имѣетъ.
Примѣръ. Умножить: —7ж”*удя2(и— я)8 на | — ѵ)3. ।
Замѣчая, что знакъ произведенія долженъ быть (—), и примѣняя найденное правило, получимъ въ произведеніи
Умноженіе многочлена на одночленъ.
32. Пусть требуется умножить — с на с7, гдѣ подъ буквами а, Ь и с можно разумѣть какія угодно числа. Что же касается множителя (I, то слѣ-іуетъ различать нѣсколько' случаевъ.
1. Пусть <1 есть цѣлое положительное число, напр., б/~4. Припоминая •шредѣленіе умноженія и замѣчая, что 4 составлено повтореніемъ положительной
единицы, какъ слагаемаго, четыре раза, заключаемъ, что и множимое надо повторить слагаемымъ столько же разъ* Получимъ
(а —Ь — с). 4 = (д 6 — с) —|— (а —|— Ь — с) (а -|— Ь — с) —(а —|" & — с) =
= 4а 46 — 4с.
4 Результатъ показываетъ, что для умноженія многочлена на цѣлое положительное число нужно каждый членъ множимаго отдѣльно помножить на это число, соблюдая правило знаковъ.
3
2. Пусть сі равно нѣкоторой положительной дроби, напр. По опредѣле-
нію, умножить а 4- Ь — с на — значитъ изъ множимаго составить новое коли-і 4
честно такъ, какъ множитель составленъ изъ 4-1. Но для составленія А изъ 4-1, і! * • ; । і
надо отъ взять четверть, вслѣдствіе чего получимъ 4~"ра затѣмъ + у
' 3
помножить на 3, что и даетъ дѣйствительно 4--^- Итакъ, мы должны: 1) взять четверть отъ а 4~6 — с и 2) полученный результатъ умножить на 3.
Можно доказать, что для раздѣленія многочлена а 4~6 — с на 4 нужно каждый его членъ раздѣлить на 4, удерживая передъ каждымъ изъ отдѣльныхъ частныхъ тотъ знакъ, какой имѣетъ дѣлимый членъ, т.-е. что
а + 6 — с а । Ь с
- «__.«• •» « ф
4 4’4 4
Для доказательства помножимъ частное на 4; по извѣстному уже правилу ум-. ноженія многочлена на цѣлое положительное число найдемъ:
(Л_1_ А_ 4 = — . 44-^ ‘4— — • 4.
\4 ’ 4 4 / 4 4*4*’
п » а 1 . . 4
Замѣчая, что д- или -д-а, умноженная на 4, даетъ -*-а или а и т. д., находимъ, что
. _ 4-^ — -^.4 = а4~Ь — с.
Итакъ, помноживъ частное на дѣлителя, мы нашли въ результатѣ дѣлимое, а потому дѣйствительно
Это выраженіе надо умножить на 3. По извѣстному уже правилу умноженія на цѣлое положительное число получаемъ
/ 1-а4-1Ь — -У • 3 = 1я • 3 + 4-і • 3 - -{-с . 3,
\ 4 1 4 4/ 4 4 4 т
или, относя з множителемъ къ А, найдемъ окончательно:
*ж
• /17 \ з ___ 3 । 31 3
(а 4- ь _ С). _ = _.а_|_ — тс,
I X
т.-е. для умноженія многочлена на положительную дробь нужно каждый членъ множимаго умножить отдѣльно на эту дробь, соблюдая правило знаковъ.
3. Пусть Л равно нѣкоторому отрицательному цѣлому числу, напр., = — 3. По опредѣленію умноженія, нужно съ множимымъ поступать такъ, какъ съ —Р 1 при составленіи изъ нея —3, т.-е. перемѣнить у множимаго знакъ, что даетъ — (« —|—6— с), и затѣмъ повторить это выраженіе слагаемымъ три раза. Итакъ
(а-|- Ъ — с) . —3 = — — с) — (« + Ь — с) — (а-|-Ь — с).
По раскрытіи скобокъ и по приведеніи, находимъ
{а + Ь — с) . —3 — — За —3& + 3с.
Результатъ этотъ приводитъ къ тому же заключенію, какъ и два первые случая. 2
4. Пусть наконецъ д=— т.-е. отрицательной дроби. Замѣтивъ, что
2 2 ѵ і
— у = у X — 1 > имѣемъ:
(а4-ь — с). - Л =[(а4-г>—с). — 1.
Отсюда видно, что иуждо а-1-Ь — с умножить сперва на положительную дробь 2
у> а затѣмъ результатъ п отрицательное цѣлое число — 1. Производя эти двѣ операціи, для которыхъ иравила уже найдены, находимъ послѣдовательно (а-р_с)._|=[(в_^б — = — |с). - 1 =
~ 3е Т* ‘ 3€‘
Отсюда тоже заключеик. что и прежде.
Итакъ, каково бы п было имѣемъ
откуда правило: для умноженія многочлена на одночленъ нужно каждый членъ множимаго помножитъ на множителя, соблюдая правило знаковъ. -
Этимъ правиломъ выражается законъ распредѣлительный.—
Примѣръ I. Ь* — 4с2-Д?а^ -з). — |а4с = — Ь4 V |а»е-|-
4“ 4с2 X ъа*с — "аеР X 3 . ~а2с = — а*Ъ*с -4~ $ а2сэ1 — -4-
о э о 1 □ 1 а Іо ’
-|- 2а4с.
Примѣръ И. {а*(г»-|-1)₽ — За(ж»4-1)>-1 + 5(х1-{-1)Р-г| X
—2ая(а;»-|-1)>+3=—2а»+г(а;»-|-1 )2Р4-84-6а“+І(х44-1 )4р+4— 10а"(х4-|-1)4Р+1.
4
Умноженіе одночлена на многочленъ.
33. Пусть требуется одночленъ умножить на многочленъ: <2 на а — Замѣчая, что отъ перемѣны мѣстъ производителей произведеніе не измѣняется, имѣемъ:
д(а — Ь-|-с) = (а —
— 44 —
На основаніи § 32, (ы — . д — а<1 — Ьд-\-с<1; измѣняя въ каждомъ
членѣ этого произведенія порядокъ сомножителей, получимъ
с?(а — Ь -]- с) = да — дЬ
откуда правило: йлл ужяожея/я одмочлеил на многочленъ надо одночленъ помножитъ на каждый «ленъ многочлена, соблюдая правило знаковъ.
Такъ.
^2р-т-4-1 ,
Умноженіе многочлена на многочленъ.
34. Пусть требуется умножить а — на р — </+>'. Представивъ себѣ на время, что буквы множителя замѣнены опредѣленными числами, и выполнивъ указанныя въ немъ дѣйствія, мы представимъ множителя нѣкоторымъ числомъ. Означивъ это число буквою V, приводимъ вопросъ къ умноженію многочлена на одночленъ, н ло извѣстному уже правилу находимъ:
(а — & с) . V — аѴ — ІА’ *-|-сѴ.
Подставляя сюда вмѣсто V данное выраженіе р — <[ г, имѣемъ:
(а — Ь-\-с)(р — (? + »•) = «(/* — з + Н — Ъ(Р — 7 + 0 + ^/’ — 2 + г).
Но по правилу § 33 имѣемъ:
г)= ар— Ь(р— ц-^г) = Ьр — с(р—^-Н*) =
= ср — су ег.
Слѣдовательно
(а — —?Ч~Г) = ар — а$-]-аг—(Ьр—Ьу-\-йг)-\-(ср — с«/ -р сг) =
= ар — ау -|- 6^ — />г-р ер — сд сг.
Разсматривая составъ произведенія, замѣчаемъ, что первые три члена его представляютъ произведеніе перваго члена множимаго на каждый членъ множителя, слѣдующіе три члена — произведеніе второго члена множимаго ва каждый членъ множителя, а три послѣдніе — произведеніе третьяго члена множимаго на множителя. Полное произведеніе состоитъ, слѣдовательно, изъ частныхъ произведеній каждаго члена множимаго на каждый членъ множителя, составленныхъ съ соблюденіемъ правила знаковъ; такъ членъ сг, представляющій произведеніе членовъ, имѣющихъ одинаковые знаки, является въ произведеніи съ знакомъ а членъ — — произведеніе членовъ, имѣющихъ разные знаки, является въ произведеніи со знакомъ —. Итакъ, имѣемъ
Правило, — Для умноженія многочлена на многочленъ нужно каждый членъ множимаго помножитъ на каждый членъ множителя, соблюдая правило знаковъ, и если окажется возможно, сдѣлать приведеніе, —
Существенное въ этомъ правилѣ то, что каждый членъ множимаго слѣдуетъ помножить на каждый членъ множителя съ соблюденіемъ правила знаковъ; порядокъ же частныхъ умноженій члена на членъ остается совершенно произвольнымъ.
Но во избѣжаніе ошибокъ (повтореніи или пропусковъ) соблюдаютъ опредѣленный порядокъ, поступая двоякимъ образомъ:
і. Дѣлаютъ умноженіе въ томъ порядкѣ, па который мы натолкнулись при Кммдѣ правила, т.-е, умножаютъ сначала первый членъ множимаго на каждый множителя, затѣмъ второй членъ множимаго па каждый членъ множите-ж і т. д, Или
2. Умножаютъ каждый членъ множимаго сначала на первый, затѣмъ па вто-ін<. и т. д. члены множителя.
Если многочлены содержатч> одну и ту же букву, то для облегченія приве-міз подобныхъ членовъ удобнѣе расположить оба многочлена или по убынаю-
возрастающимъ степенямъ этой буквы. Затѣмъ, подписываютъ
или по
м» »
изъ многочленъ подъ другимъ, проводятъ горизонтальную черту, умножаютъ в»-жнчое на первый членъ множителя и подписываютъ это частное произведете подъ чертою.
Умножаютъ множимое на второй членъ множителя, и второе частное произ-жіеніе пишутъ подъ первымъ такъ, чтобы подобные члены находились въ одномъ ^тикальномъ столбцѣ.
Составляютъ и располагаютъ такимъ же образомъ и другія частныя произ-біенія; наконецъ, дѣлаютъ приведеніе.
Примѣръ І-. Умножить
— ЗаЛг2 — 2аЗя -р Зах3 4- а1 на 2л.г2 7а3 — 6а’2л\
Расположивъ оба сомножителя по убывающимъ степенямъ буквы ж, и со-•Сражаясь съ сказаннымъ, производимъ умноженіе такъ:
Ізожимое:
Іяожнтель:
8.Г1 За#3 — 5а2#*— 2аЪЦ-а4 2а#2— 6 а2# 4- 7а3
__йт2
30а4#8--12а*#2— ба6# 21а 4#3—35ая#2—14а®#4-7 а7
части, произв. 16а#в4- ба2#5—10а3#4— 4а4#84- 2айх
--ое части, произв. —48а3#5— 18а3#1-
*-ье части, произв. 4-56а3#4-
І-лное произв. 16а#6 — 42а2#я-|-28а3#4-‘-47а4#8—21а5#2—20ае#4-7а7
3 4 5 9
Примѣръ И. Умножить —^а3# -|--а2#2 ~4#4 — ^а#3 на #й4~
Располагаемъ оба сомножителя по возрастающимъ степенямъ главной буквы ' н производимъ дѣйствіе слѣдующимъ образомъ:
II р и м г р ъ III. Умножить — За3^2 — 5а4я а5 на 7я2 — -р °2*
Располагая дѣйствіе такимъ же образомъ какъ и въ предыдущихъ примѣ’ рахъ, оставляя пустое мѣсто тамъ, гдѣ во множимомъ должны* бы были находиться члены, содержащіе и лт\ имѣемъ:
8#п — ЗаАг2 — 5а*л; -р а5
7#2 —• 8ая -р а2
56.г7 21а3х1 — ЗЗа1^3^ 7а5х2
— 64ахк ч- 24а — 40а эх'2 — 8авх
4~ йа’2^:і — За3х2 — 5а*я а1
56я7 — 64ая° 8а2#5 — 2 Іа3?1 — 1 Іа*^ — 44а5х2 — 1 За6#-^- а7.
Свойства произведенія двухъ полиномовъ.
35. І. Число членовъ произведенія. — Умножая множимое на первый членъ множителя, получаемъ первое частное произведеніе, имѣющее столько членовъ, сколько ихъ и во множимомъ. Произведеніе множимаго на второй членъ множителя содержитъ опять столько членовъ, сколько имъ во множимомъ, и т. д, Поэтому. если частныя произведенія не содержатъ подобныхъ членовъ, то число членовъ произведенія равно будетъ произведенію числа членовъ множимаго на число членовъ множителя. Напр., если множимое имѣетъ 7 членовъ, а множитель 5, то въ произведеніи будетъ 7 X или 35 членовъ.
Но произведеніе двухъ многочленовъ можетъ содержать члены подобные; вслѣдствіе соединенія нѣсколькихъ подобныхъ членовъ въ одинъ, число членовъ произведенія можетъ уменьшиться, но никогда не можетъ сдѣлаться меньше двухъ. Въ самомъ дѣлѣ, легко доказать, что въ произведеніи двухъ полиномовъ, содержащихъ одну п ту же букву всегда есть по крайней мѣрѣ два члена, которые не имѣютъ себѣ подобныхъ между другими членами произведенія, и потому неприводимы. Для доказательства замѣтимъ, что всякій членъ произведенія происходитъ отъ умноженія какого-либо члена множимаго на одинъ изъ членовъ множителя; и показатель главной буквы въ немъ равенъ суммѣ показателей той же буквы въ членахъ множимаго и множителя, отъ которыхъ онъ произошелъ. Слѣдовательно, помноживъ высшій относительно главной буквы членъ множимаго па высшій членъ множителя, мы получимъ членъ произведенія. въ которомъ показатель главной буквы будетъ равенъ суммѣ наибольшихъ показателей той же буквы, какіе имѣются въ сомножителяхъ; очевидно, что такой членъ произведенія будетъ имѣть главную букву съ показателемъ большимъ ея показателей въ другихъ членахъ произведенія; поэтому означенный членъ не можетъ имѣть себѣ подобныхъ между остальными членами произведенія и слѣд. есть членъ неприводимый. — Помножая низшій относительно главной буквы членъ множимаго на низшій членъ множителя, получимъ членъ произведеніи, въ которомъ главная буква будетъ имѣть показатель, равный суммѣ наименьшихъ показателей той же буквы въ сомножителяхъ, слѣд. показатель главной буквы этого члена будетъ меньше чѣмъ въ другихъ членахъ произведенія, а потому это будетъ также членъ неприводимый. Заключаемъ, что произведеніе двухъ многочленовъ содержитъ, по меньшей мѣрѣ, два неприводимыхъ члена — высшій низшій относительно главной буквы. Итакъ:
наибольшее число членовъ произведенія равно произведенію числа членовъ множимаго на число членовъ множителя, наименьшее же — два члена.
Примѣчаніе, Когда множимое и множитель расположены по нисходящимъ ш «сходящимъ степенямъ главной буквы, то неприводимые члены (высшій и нежеіі занимаютъ крайнія мѣста произведенія.
Нжжеслѣдующій примѣръ представляетъ одинъ изъ случаевъ, когда произве-мл имѣетъ только два члена,
х* 4-* хз -]“#2 -}~х "Ь і
х5 4~ х* 4” 4- $
— ХІ~Х3 — Х1 — X-1
X3 — 1
II Свойство произведенія однородныхъ многочленовъ. — Произведеніе двухъ однородныхъ многочленовъ есть многочленъ однородный, а измѣреніе его равно суммѣ измѣреній множителей. Въ самомъ дѣлѣ, произведеніе двухъ какихъ-нибудь членовъ множимаго и множителя имѣетъ измѣреніе равное суммѣ показателей перемножаемыхъ членовъ; но оба многочлена однородны, слѣд. эта сумма во всѣхъ членахъ произведенія будетъ одинакова, т.-е. произведеніе само будетъ однородно, а его измѣреніе равно суммѣ измѣреній сомножителей.
Такъ, многочленъ аІ4-а8#4-«2яа4“ад?3_кй'< есть однородный многочленъ четырехъ измѣреній; а — х есть однородный двучленъ одного измѣренія; произведеніе же ихъ а$ — х5—однородное выраженіе пяти измѣреній.
Замѣчательные случаи умноженія.
36. Разсмотримъ нѣкоторые часто встрѣчающіеся особенные случаи умноженія.
I. Пусть требуется сумму а 4"^ возвысить въ квадратъ. Для этого надо в помножить само на себя:
а 4- Ь
а 4“ Ь аа 4" 4“ аі 4~ Ъ'2
аа 4"2ай 4- Ь*.
Итакъ: («4" й)а = аі4~ 2а64“^, т.-е.
квадратъ суммы двухъ количествъ равенъ: квадрату перваго члена, 4“ удвоенное произведеніе перваго члена на' второй, 4" квадратъ второго.
Наприм., (5й?а 4“ = (5ха)'2 4“ 2 . Зя1.2у4_(2#)а = 25х<4“20;Л/4’^2‘
11. Возвысимъ въ квадратъ разность а— Ь* т
а — Ь а — Ь а3 — аЬ
—- && 4-аа — 2а& 4“ ’ лѣдовательно: (а — == а* — 2аЬ 4- т.-е.
квадратъ разности двухъ количествъ равенъ квадрату перваго члена, — удвоенное произведеніе перваго на второй, 4~ квадратъ второго.
Напр. (О,За.?*—я2)2=ЦО,Зая)2— 2 . От3ая # л?3-|-(ж2)2—
Ш. Умножить сумму двухъ количествъ а и Ь на ихъ разность:
н-[-Ь
х а — Ъ
а2 -[-аЪ
— аЪ — Ь*
а*
Итакъ: (а ~4 &)(а — />) = а2 — т-е.
произведеніе суммы двухъ количествъ на ихъ разность равно разности ихъ квадратовъ.
Напр. (4х2у тг Ху*#-!.*1# — і я#2) = (4х*у)2 — (І ху*Ѵ=16х>*—і х^у*.
IV. Найдемъ кубъ суммы а 4- Ь. Замѣчая, что (а 4" &)3 = (а ”Ь &)*.(« 4~ &), 'и что, (а 4“ ^4 — а‘2а&4"^ мы найдемъ искомый результатъ, умноживъ а2 4“ 4; № на а 4 Л:
а*4-2аЛ 4-йа а 4"^ ,
а8—2а'21>—а№
ч . 4- а*& + 2аЬ24-Ь3
а84-3а^4-3а6а4-63, • Слѣдовательно: (а 4~ &)3 = а34* Зл26 4" 4" т-‘е-
кубъ суммы двухъ количествъ равенъ: кубу перваго члена, 4” утроенное произ-' веденіе квадрата перваго члена на второй, 4" утроенное произведеніе перваго члена на квадратъ второго, 4~ кубъ второго.
Напр. (2а2 4- 4/?2)3 = (2а2)3 + 3 . (2а2)2.46* 4- 3 . (2а2)(4Л2)2 4- (4Ь2)3 = = 8а€ 4-48а*62 + 96а2Ь* 4-646е.
V. Такимъ же образомъ найдемъ (а — Ь)8, умноживъ (а — Ь)2 или а2 — 2а&4~ 4~ Ь* на а — 6:
а2 — 2аЬ 4-а — Ь
а3 — 2а2Ь ~р аЬ2
— а2/; — 2ай& — Ь3
аЗ-^За26 + За62_Ь\
Слѣдовательно: (а — &)3 = а3 — За26 — Заі2 — Ь3Т т.-е.
кубъ разности двухъ членовъ равенъ кубу перваго члена, минусъ утроенное произведеніе квадрата перваго члена на второй, 4“ утроенное произведеніе перваго члена на квадратъ второго, минусъ кубъ второго члена.
Напр. — 3x4= (4)’— 3. |дГ- +:} • | | “
9 ,
— -г х24~ я* — 27іс8.
4 1 2
37. Формула № II можетъ битъ выведена изъ формулы № I, если ~ въ по-<гимей положить Ь — — V; находить
। [а 4_(_Ь')]»==аі 4-2а (-&')+(-&')»•
I
г Замѣтивъ, что а (— Ь')—а — У; затѣмъ, что 4“ М— &*) = — 2аУ, и что
I —У)* = + имѣемъ
Г (а — У)« = а’ — 2аУ-|-У».
І Такимъ же образомъ, подставляя въ формулу № IV вмѣсто 5 количество — Ь', і случаемъ
I + (“ ь')13 = а3 + За2(— Ю + За (- У)2 (— У)«.
Замѣчая, что а -{•(— У) = а — Ь\ что 4- За2( —У) = — За’У, что За(—У)1 = 4~ЗаУ2 и что (—У)3 =— У3, имѣемъ
(а — У) * = а* — За2У + ЗаУ2 - У«.
Приложенія.
38. Приложимъ формулы § 36 къ нѣсколькимъ примѣрамъ.
Примѣръ I. Возвысить 79 въ квадратъ.
По формулѣ Л? I имѣемъ:
79’ = (70 -|- 9)* = 4900 + 1260 + 81 = 6241.
Примѣръ II. Возвысить 97 въ квадратъ.
По формулѣ № II имѣемъ:
97’ = (100 — 3)3 = 10000 — 600 + 9 = 9409.
Примѣръ ІП. Помножить 103 на 97.
По формулѣ № III находимъ:
103 X 97 = (ЮО + 3)(Ю0 - 3) = 10000 — 9 = 9991.
Примѣръ IV. Преобразовать:
(За2 — 2ай + ЗЬ2) (За2 + 2аЬ — ЗЬ2).
Первый множитель можно представить въ видѣ За2 — (2аЬ — ЗЬ2); второй въ видѣ За2-|-(2аЬ— ЗЬ2); примѣняя формулу № Ш, получимъ:
(За2)2 — (2аЬ-3&2)2,
или, выполняя дѣйствія:
9а4 — 4а262 + 12аЪ* — 9М.
Примѣръ V. Умножить — * на + у
Представивъ данныя выраженія въ видѣ
(«+») + (* —О П («4-у) — (в — і)
и примѣняя формулу № III, находимъ
(ау-ру)» —(ж — 0».
4
Прилагая сюда теоремы I и II, получимъ
(ж5 2жу + у4) — (г4 — 2гІ 4- і3), или. раскрывъ скобки;
х2 4“ 2яу 4“ У® — #2 4-
Примѣръ VI- Составить произведеніе
(д + & 4~ с) (& 4г ’ ^)(а—ь Н-* ^)(— 4~^ 4~ с) *
Первые два множителя можно представить въ видѣ
(о + ь) 4- с и ихъ произведеніе =
(а4“^)а — с2 или а*-|-2и6 4_^2 — с3». (1).
V
Третій и четвертый множители
ІГ.ІИ
емъ въ видѣ
с 4- (а — і) и с — (а — 6);
ихъ произведеніе равно
с2— (а — 6)2 или с2 -—а®4’2а6 — й2... (2). * -
Представивъ (1) и (2) въ формѣ
2аЬ 4~ (а2 + Ь2 — ^2) и 2аЬ — (а2 4~ &® — с2) 1
и перемноживъ эти выраженія! имѣемъ:
(2аЬ)2 — (а2 4- Ь2 — с2)2 или 4а2Ь2 — (а8 + &2 — с2)2.
Чтобы триномъ а2-|~Ь2—й® возвысить въ квадратъ, разсматриваемъ на-время а24"&3 какъ одинъ членъ; положивъ, что а24-Ь2 = $, имѣемъ:
(а2 4- Ь* — = (,9 — С2)3 = 52 — 2зс* 4- <Л
Подставляя вмѣсто 5 его величину а24-&\ получимъ
з2 — 2л . с2 + с* = (а2 4- Ь2)2 — 2(а2 4- Ь2)с24~ = а* 4~ 2а%2 + &< — — 2аѴ — 2&2е24-е4.
Итакъ, искомое произведеніе равно
4а2Ь2 — а1 — 2аЧ>2 —4“ 2а2с24’ 2Ь2с2— с4, или 2а*Ь24' 2а2с2 4“ 2Ь2с2 — — а1 — Ъ* — с4.
Примѣръ VII. Возвысить въ квадратъ многочленъ 1 4~х — ^3 + гг3-
Въ предыдущемъ примѣрѣ намъ пришлось возвышать въ квадратъ триномъ ая4“Ьа — с2; для этого мы обозначили двучленъ а2 4“ 6® одною буквою и черезъ это получили возможность примѣнить къ данному случаю формулу квадрата бинома. Вообще указанный пріемъ можно съ удобствомъ примѣнять при возвышеніи многочленовъ въ квадратъ и кубъ. Такъ, въ данномъ выраженіи положимъ на время 14~х — #® = 5; данный многочленъ приметъ видъ $4"#8; возвышая въ квадратъ, получимъ
($ 4~ #а)® = “Ь 25. ж® 4- — (1 4” % — я2)2 4“ 2(1 4“ х — #2)#а ^6*
Полагая въ членѣ (1-р^ — х2)2 на время = найдемъ:
.14-я — х2)2 = (І — х2)2 = Г2 — 2^а 4-з* = (1 + з)2 — 2 (1 4-л>24-— х* = I 4- 2з 4- з2 — 2х* — 2з34~^‘- Слѣд., данное выраженіе равно I 4“ 2з 4“ х* — 2я2 — 2з3 4“ з14“ -•г3 4~ 2з* — 2зй -|- хс, или 1 4” 2з — — х14" Зя* — 2зв + з6.
ГЛАВА V.
Дѣленіе.
опредѣленіе.—Правило знаковъ.—Правило показателей; значеніе символовъа~ѵ и а6.— .Дѣленіе одночленовъ; признаки невозможнаго дѣленія ихъ.—Дѣленіе многочлена на пноч ленъ.—Дѣленіе многочлена на многочленъ.—Признаки невозможнаго дѣленія многочленовъ.—Дѣленіе полинома послѣдовательно на нѣсколько данныхъ полиномовъ.—Замѣчательные случаи дѣленія (теорема Безу).
39. Опредѣленіе. — Раздѣлить одно количество на другое значитъ найти такое третье количество, которое, будучи умножено на второе, дало бы въ про-юведеніи первое.— Первое данное количество называется дтьлгисьма, второе — Лълителеліз, а искомое количество—часткыль.
Если дѣлимое есть А. дѣлитель В, а частное Ч, то, по опредѣленію дѣйствія, связь между этими тремя количествами выразится равенствомъ:
40. Правило знаковъ.—Основываясь на опредѣленіи дѣленія и на правилѣ знаковъ при умноженіи, легко найти правило знаковъ при дѣленіи.
Пусть требуется (4-«) раздѣлить па (4" Ь)* По опредѣленію дѣленія, част-юе, умноженное на дѣлителя, должно давать дѣлимое; но только количество, предшествуемое знакомъ 4“» при умноженіи на (-|-Ь) можетъ дать (4~а)* Слѣдов.
(“Ь а): (“К — 4"
При дѣленіи (—а) на (4“Ь), въ частномъ должно быть (—®), потому что только количество, предшествуемое знакомъ —, при умноженіи на (-|-6) можетъ дать (—а). Итакъ
(— а):(+ Ь) = —2-
Дѣля (+«):(—Ь), мы ищемъ количество, которое, будучи умножено на — Ь), давало бы (4~“); но какъ только количество со знакомъ —, при умноженіи на (—6), можетъ дать (-|-а), то
(+«):(— 6) = —2-
Наконецъ, припоминая, что при умноженіи (—) на (-{-) даётъ (—), наіо-имъ:
(—а);(—Ь) = -}-д.
Итакъ:
(~Ь а): (“1“ — “Ь 2-(— а): (+ Ь) = — 2-(+«):(— Ь) = — д_. (—а): (—*) = + 2-
Отсюда вытекаетъ правило* при дѣленіи количествъ съ одинаковыми знаками, въ частномъ получается (~р), при дѣленіи же количествъ съ разными знаками (—).
Правило это — совершенно общее: оно относится и къ тому случаю, когда знаки предшествуютъ абсолютнымъ значеніямъ количествъ, и къ тому — когда а и Ь сами суть количества положительныя или отрицательныя. Въ самомъ дѣлѣ, выводъ правила основанъ на правилѣ знаковъ при умноженіи, а это послѣднее правило доказано для какихъ угодно количествъ.
41. Правило показателей.—Разсмотримъ дѣленіе степеней одного итого же основанія: пусть требуется раздѣлить а'п на а" гдѣ а — какое угодно количество, а т н п — числа цѣлыя и положительныя. Замѣтивъ, что въ частномъ должна получиться нѣкоторая степень буквы а, назовемъ неизвѣстнаго показателя этой степени буквою -е, такъ что частное выразится формулою ах:
а :а =а ... (1).
По опредѣленію дѣленія, частное, умноженное ва дѣлителя, должно давать дѣлимое, слѣд.
а*. а* — а";
но, по правилу показателей при умноженіи, аг.ап = ах+я, слѣд. имѣемъ равенство:
(Г-И = аш.
Но степени одного и того же основанія тогда будутъ равны, когда показатели ихъ равны, а потому должно быть
Чтобы по извѣстной суммѣ (т) и извѣстному слагаемому (п) найти другое слагаемое (#), нужно изъ суммы вычесть извѣстное слагаемое. Итакъ
х — т — п.
Подставляя въ равенство (1) вмѣсто & найденную величину, имѣемъ:
ат; ап = ... (2).
Отсюда правило: при дѣленіи степеней одною и тою же основанія нужно: основаніе въ частномъ написать то же самое, а изъ показателя дѣлимою вычесть показатель дѣлителя.
Изслѣдованіе. — Формула (2) даетъ мѣсто слѣдующимъ случаямъ:
1) т > я; 2) т = п; 3) т < н.
1-й случай, — Если т > п, то разность т — п даетъ положительное (цѣлое) число, и частное подходитъ подъ вышеданное опредѣленіе степени какъ произведенія равныхъ количеству « множителей. Такъ, если т = 8, а п = 5, то ат :ап = а*-* = а3, т.-е. «.а. а., и т. д. Этотъ случай не представляетъ, слѣдовательно, ничего особеннаго.
2-й случай. Если т = п, то разность т — п равна нулю, и частное принимаетъ видъ а0. Выраженіе само но себѣ не имѣетъ никакого смысла, т.-е, его нельзя разсматривать въ смыслѣ степени, ибо показатель долженъ означать, сколько разъ основаніе берется множителемъ. Значеніе символа а9 откроется,
если мы обратимъ вниманіе на его происхожденіе. При т = я дѣлимое аЛІ н дѣлитель а" дѣлаются равными, а частное отъ раздѣленія количества самого на себя есть 1; поэтому
а°=1,
а такъ какъ а означаетъ какое угодно количество, то заключаемъ, что всякое количество въ нулевой степени даетъ единицу.
Такимъ образомъ: 7° = 1; гг°— I; (а2 — ??2)а = 1 и т. п.
Здѣсь самъ собою возникаетъ вопросъ: если мы знаемъ, что а"*: ат есть ни что иное какъ 1, то для чего замѣняютъ 1 особымъ символомъ я®, имѣющимъ только видъ степени, но не имѣющимъ смысла какъ степень? Это дѣлается для того, во-первыхъ, чтобы въ правилѣ показателей не дѣлать исключенія для случая юд = и, другими словами, — въ видахъ обобщенія этого правила; и, во-вторыхъ, чтобы имѣть возможность сохранить въ частномъ букву а, которая иначе не вошла бы въ частное, ибо была бы замѣнена единицею.
3-й случай. — Если ш < п, то разность т — и отрицательна; напр: если п превышаетъ т на д единицъ, то т — п = — д, и частное имѣетъ видъ Выраженіе а~ч опять не имѣетъ значенія степени, ибо а нельзя взять множителемъ отрицательное число разъ. Чтобы выяснить значеніе символа а-’, постараемся частное въ случаѣ т<п выразить въ иной формѣ.
Полагая, что « больше т на ? единицъ, т.-е. п = т-|-д, можемъ частное ат: а* представить въ видѣ ат: Обозначивъ его буквою х* имѣемъ
ат : — я.
По опредѣленію дѣленія, имѣемъ отсюда
= ат.
Раздѣливъ обѣ части этого равенства на а™, находимъ:
х‘а»*-Н__ат
ат ~ ат*
Замѣтивъ, что частное -7-^ равно (ибо, умноживъ его на дѣлителя
X* ам находимъ въ результатѣ дѣлимое и что—^ = 1, получаемъ равенство
а
ж . а?= 1, откуда
1 х = -=•
Но то же самое частное было представлено въ формѣ а-*: поэтому
Такъ какъ а означаетъ какое угодно количество, то заключаемъ, что всякое количество съ отрицательнымъ показателемъ равно единицѣ, дѣленной на то же количество съ положительнымъ показателемъ.
Такимъ образомъ:
О"’ = І; («а — и т. п.
Отрицательные показатели введены для того, чтобы: во-первыхъ, въ правилѣ показателей не дѣлать исключенія для того случая, когда показатель дѣлимаго меньше показателя дѣлителя, т.-е. въ видахъ обобщенія этого правила; и, во-вторыхъ, чтобы имѣть возможность дробь (какъ^ изображать безъ знаменателя, т.-е. въ формѣ цѣлаго алгебраическаго выраженія.
Итакъ, вводя показатели — нуль и отрицательный, іы можемъ всѣ случаи дѣленія степеней одного и того же основанія совершать по одному общему правилу: основаніе писать въ частномъ безъ перемѣны, а надъ нимъ показателя, равнаго разности показателей дѣлимаго и дѣлителя.
Дѣленіе одночленовъ.
42. Пусть требуется раздѣлять ва — 9а4Ь5с. Знакъ частнаго
долженъ быть (—), потому что дѣлимое і дѣятель ммѣжть разные знаки. По опредѣленію дѣленія, въ частномъ должно быть талое количество, которое, будучи умножено на дѣлителя, дажак* бы дѣлимое: слѣд., коэффиціентъ частнаго есть такое число, которое, по умноженіи на 9. давало бы 63; такое число мы найдемъ, раздѣливъ 63 на 9: получимъ 7. Далѣе, чтобы въ произведеніи имѣть а*, надо а1 умножить на а5: слѣд. буква а войдетъ въ частное съ показателемъ равнымъ разности показателей этой буквы въ дѣлимомъ и дѣлителѣ. Такимъ же точно образомъ убѣдимся, что буква Ь войдетъ въ частное — съ показателемъ 3. а буква с — съ показателемъ 4. Наконецъ, чтобы въ произведеніе вошло с?2, необходимо, — такъ какъ буквы Л нѣтъ въ дѣлителѣ, — чтобы опа вошла въ частное съ тѣмъ показателемъ, какой она имѣетъ въ дѣлимомъ. Итакъ
63а°6Ѵгі2; — 9^1б5с = — 7а5б3сМ2
Отсюда имѣемъ
Правило. — Чтобы найти частное отъ раздѣленія одного одночлена па другой, нужно: 1) коэффиціентъ дѣлимаго раздѣлитъ на коэффиціентъ дѣлителя; 2) а затѣмъ написать всѣхъ множителей дѣлимаго — каждаго съ показателемъ, равнымъ разности его показателей въ дѣлимомъ и дѣлителѣ.
Въ частномъ случаѣ, если какой-либо множитель находится только въ дѣлимомъ, онъ входитъ въ частное безъ измѣненія показателя; если же какой-либо множитель имѣетъ въ дѣлимомъ и въ дѣлителѣ одинаковаго показателя, то въ частное войдетъ ^съ нулевымъ показателемъ. Напримѣръ
4а2Ьэс5: 2аЬ3с — 2айѴ.
Но, какъ = I, то можно частное представить въ видѣ 2ос*, Примѣняя это правило, найдемъ, что:
1) 9 2а3Ь Г,х2у9: 2 За2Ь *х2у ” = ѢаЪу \
2) 35а3іа(й?-|“у)1(л? — 2у)3:—7а2(л:-|-у)э(#— 2у)=—5аі2(ж-|-у)(#—2у)2.
3) — 24а8М(а* — 4. Зу)*: — 86^ + Зу)2 = За>(а* — Ь*)(х + Зу)3.
43. Признаки невозможнаго дѣленія одночленовъ. — Дѣленіе цѣлыхъ одночленовъ называется возможнымъ, если частное можетъ быть выражено цѣлого формулою, т.-е. не содержащею буквенныхъ дѣлителей; въ противномъ случаѣ,
у.-т. когда частное получается въ формѣ алгебраической дроби, дѣленіе считает-
Изъ самаго опредѣленія невозможнаго въ алгебраическомъ смыслѣ дѣленія *л г дуетъ, что если не дѣлятся другъ на друга только численные коэффиціенты, то дѣленіе слѣдуетъ считать алгебраически возможнымъ* Напр. дѣля 4а®5*с на 4
За*Ь, получимъ въ частномъ у аЪс— выраженіе алгебраически цѣлое, такъ какъ оно не содержитъ буквенныхъ дѣлителей.
Дѣленіе одночленовъ невозможно въ слѣдующихъ двухъ случаяхъ:
1) Когда показатель хотя одной буквы дѣлителя больше показателя той же буквы въ дѣлимомъ. Такъ дѣленіе 6а3Ь* на 2аЪ* невозможно, потому что на какой бы цѣлый одночленъ пи умножили дѣлителя, всегда въ произведеніе буква Ь войдетъ съ показателемъ, большимъ 2: частное не можетъ быть, поэтому, выражено цѣлымъ одночленомъ.
Въ такомъ случаѣ дѣленіе только обозначается, и получается дробь
6«3?>2
2аЬ*'
послѣдняя, какъ будетъ показано далѣе, можетъ быть упрощена сокращеніемъ.
2) Когда дѣлитель содержитъ такую букву, которой пѣтъ въ дѣлимомъ; напр. 4а3Ь не дѣлится на За2М\ Въ самомъ дѣлѣ, на какой бы цѣлый одночленъ мы ни умножили дѣлителя, въ произведеніе непремѣнно войдетъ буква с?, которой нѣтъ въ дѣлимомъ, а слѣд. частное не можетъ быть представлено цѣлымъ одночленомъ.
Обозначая дѣленіе, получимъ дробь
4а?д Заадг
которая также подлежитъ сокращенію.
Дѣленіе многочлена на одночленъ.
44. Пусть требуется раздѣлить многочленъ а—6-рС—<7 на одночленъ т. Частное не можетъ быть одночленомъ, потому что умноживъ одночленъ на одночленъ (т), въ произведеніи найдемъ одночленъ, между тѣмъ какъ должны получить многочленъ а —— & Итакъ, частное должно быть—многочленъ, для нахожденія котораго имѣемъ слѣдующее
Правило. — Чтобы найти частное отъ раздѣленія многочлена на одночленъ, нужно каждый членъ дѣлимаго раздѣлитъ на дѣлителя, соблюдая привило знаковъ.
Это правила доказывается а ровіегіогі. Мы говоримъ, что
а — Ь-\-с — (і а 6 । с
т т т'т т
Для доказательства умножаемъ частное многочлена на
на дѣлителя: по правилу умноженія
одночленъ находимъ:
а
т
о । с а \ а
----Н---------------- . — яі 1 т-------------------т т
. т— . т.
т
Но частное умноженное на дѣлителя т, даетъ дѣлимое, слѣд. ш — а;
точно такъ же: • т = Ь; — • т = с; и ~~ - т = Л. Такимъ образомъ
Я4 т/І
--------и------ — . юг = а — 6 4- с — а. т т 1 т ш / 1
т.-е. частное, умноженное на дѣлителя, воспроизвело дѣлимое, слѣд. это частное составлено вѣрно, и правило доказано.
Примѣры:
1) (8а»Ь’ — За8Ь*4-12ааЬ‘): 4а*Ь»=2а’ — |аЬ-}-ЗЬ».
2) {28а*Ь’(ж — у)’+ 12аяЬ’(ж* — у*)— 8вЬ’(х-|-у)(я:*—у1)’} ;
4аЬ8 (х — у) — 7аЬ (х — у)1 -|- За’ (х4" У)1 ~ 2(Л+?)*(* — У). «
Дѣленіе многочлена на многочленъ.
45, Частное отъ раздѣленія нѣкотораго многочлена А на многочленъ В есть выраженіе алгебраически дробное, вида
А в'
Въ большинствѣ случаевъ такое выраженіе нельзя замѣнить другимъ — простѣйшимъ. Но когда цѣлые многочлены А и В содержатъ одну и ту же букву, то возможенъ такой третій многочленъ С, цѣлый относительно той же буквы, который, будучи умноженъ на дѣлителя, даетъ дѣлимое. Въ такомъ случаѣ говорятъ, что дѣленіе полинома А на В возможно.
Укажемъ, какъ въ этомъ исключительномъ случаѣ находятъ частное.
Допуская, что многочленъ
8*в4- ІО*1 — 31**4* 22*'2 — 29* + 12
дѣлится на многочленъ
4** — 5*® 4“ Зя — 4, постараемся опредѣлить члены частнаго.
Написавъ дѣлитель справа отъ дѣлимаго, отдѣляютъ ихъ вертикальною чертою; затѣмъ, дѣлителя отдѣляютъ горизонтальною чертою отъ частнаго, котораго члены, по мѣрѣ ихъ нахожденія, и пишутъ подъ этою чертою.
Дѣлимое... 8*в4“^іС<—31*84~22*а—29*4-12 4*1—5*34~^—4... дѣлитель
—8*в4-1О*і=ь 6*84- 8*3 2*‘2-45* —3,.ф частное
1-й остатокъ . .. 20**—37*84”ЗО*3—29*4“ 12
—20*4=25*4= 15*4=20*
2-й остатокъ .....—12*84”1^2— 9*4-12
4=12**4=15*4= 9*4=12
О
По опредѣленію, дѣлимое есть произведеніе дѣлителя на частное.
Но по свойству произведенія двухъ многочленовъ 35), высшій членъ про-
дежи происходитъ.
безъ п^жвеЭенУя,
отъ умноженія а
высшихъ членовъ со-
иььхжтелей, т.-е. въ нашемъ случаѣ отъ умноженія высшаго члена дѣлителя на мкжіі членъ частнаго. Поэтому, назвавъ высшій членъ частнаго буквою ?, имѣ->-с3 = 4я3 Х Ъ откуда, замѣчая, что неизвѣстный сомножитель (?) опредѣляется дѣленіемъ произведенія (8$5) на извѣстнаго сомножителя (4а?3), на-
і-іжігь:
? — 8#я: 4а:3 — 2а:2.
Итакъ, чтобы найти высшій членъ частнаго, нужно высшій членъ дѣлимаго раздѣлить на высшій членъ дѣлителя.
Для нахожденія слѣдующаго члена частнаго руководствуемся такими соображеніями. Дѣлимое есть произведеніе дѣлителя на всѣ члены частнаго; а потому если изъ дѣлимаго вычесть произведеніе дѣлителя на первый членъ частнаго, то остатокъ будетъ представлять произведеніе дѣлителя на сумму остальныхъ членовъ частнаго- Умноживъ дѣлителя на высшій членъ частнаго и вычтя произведеніе 8х5— ІОя14- 6$3— В#2 изъ дѣлимаго, находимъ остатокъ, равный 20л1 — 37а;34“ ЗОл2 — 29$ 4" Такъ какъ этотъ остатокъ есть произведеніе дѣлителя на всѣ члены частнаго, начиная со второго, то его высшій членъ (20$*) произошелъ безъ приведенія отъ умноженія высшаго члена дѣлителя (4а:3) на высшій изъ ненайденныхъ членовъ частнаго. Называя послѣдній буквою ?\ имѣемъ такимъ образомъ: 2О$* = 4$8. откуда
?' = 20$1: 4$3 = 4- 5л.
Итакъ, для нахожденія второго члена частнаго нужно высшій членъ перваго остатка раздѣлить на высшій членъ дѣлителя.
Замѣчая, что первый остатокъ есть произведеніе дѣлителя ва всѣ члены частнаго, начиная со второго, заключаемъ, что если вычтемъ изъ этого остатка произведеніе дѣлителя на второй членъ частнаго, то новый (второй) остатокъ будетъ представлять произведеніе дѣлителя на всѣ члены частнаго, начиная съ третьяго. Умноживъ въ самомъ дѣлѣ дѣлителя на второй членъ частваго и вычти произведеніе изъ перваго остатка, находимъ второй остатокъ: —12$3--415о?3—9$-{-12. По свойству произведенія, высшій членъ этого остатка произошелъ безъ приведенія отъ умноженія высшаго члена дѣлителя на высшій изъ ненайденныхъ членовъ частнаго. Слѣдоват., если назовемъ послѣдній буквою то найдемъ равенство: — 12$3 — 4х3, откуда д" = — 12$3: 4$3 — = — 3. Отсюда заключаемъ, что для нахожденія третьяго члена частнаго надо высшій членъ второго остатка раздѣлить на высшій членъ дѣлителя.
Такими же разсуженіями какъ и прежде убѣдимся, что для нахожденія четвертаго члена частнаго, въ предположеніи что онъ существуетъ, надо дѣлителя умножить на третій членъ частнаго и произведеніе вычесть изъ второго остатка. Сдѣлавъ это, находимъ въ новомъ остаткѣ 0. Это значитъ, что дѣленіе окончено, и послѣдній членъ частнаго равенъ —3. Все же частное равно 2$а 4" — 3.
Что частное найдено вѣрно, въ этолт» убѣждаемся, помноживъ дѣлителя на частное: въ произведеніи получается дѣлимое.
Припоминая ходъ дѣйствія, заключаемъ, что для отысканія послѣдовательныхъ членовъ частнаго намъ приходилось дѣлить высшіе члены дѣлимаго и каждаго остатка на высшій членъ дѣлителя. Чтобы имѣть эти высшіе члены всегда на первомъ мѣстѣ, а также для удобства приведенія, до начала дѣйствія располагаютъ дѣлимое и дѣлителя по нисходящимъ степенямъ главной буквы.
Соображая все сказанное, приходимъ къ слѣдующему правилу дѣленія многочлена на многочленъ:
Правило.—Когда частное отъ раздѣленія двухъ цѣлыхъ полиномовъ можно представитъ въ формѣ цѣлаго полинома, члены частнаго находимъ слѣдующимъ образомъ:
Располагаемъ дѣлимое и дѣлителя по нисходящимъ степенямъ главной буквы.
Первый членъ дѣлимаго дѣлимъ на первый членъ дѣлителя: получаемъ первый членъ частнаго.
Вычитаемъ изъ дѣлимаго произведеніе дѣлителя на первый членъ частнаго и получаемъ первый остатокъ.
Первый членъ этою остатка дѣлимъ на первый члент* дѣлителя: находимъ второй членъ частнаго.
Вычитаемъ изъ порвало остатка произведеніе дѣлителя на второй членъ частнаго и получаемъ второй остатокъ.
Дѣлимъ первый члена огтшлкл на яг/жын члена (йълнтедя; находимъ третій членъ частнаго, и т, д., продолжая до тѣхъ поръ, пока въ остаткѣ получится налъ.
Вотъ еще примѣръ:
— 12лН: 15аей^21 аа62^24аі&3гЬ27а^1
-20а^- За^+54а*Ь3+ 29а^і-н7^Я-ЗІаДО+Зб^
Эа^нЖзб^Ъ^НЗ 1 аЬН 3657
____
:Ч6^+20«э&»+28а2&я--32адН36&’
±І 6аЧ^2^з^і^28й2&5±:32ог^36^
О
4а5а8^—7дД6Д+8аЬЗ—9Ь4
За®—оа^Ь—7аб®-- 4Ь®
(Измѣненные знаки вычитаемыхъ членовъ поставлены сверху).
46. Такъ какъ низшій членъ дѣлимаго есть также членъ неприводимый и происходитъ отъ умноженія низшихъ членовъ дѣлителя и частнаго, то можно начать дѣйствіе съ опредѣленія низшаго члена частнаго, который мы найдемъ, раздѣливъ низшій членъ дѣлимаго па низшій членъ дѣлителя.
Далѣе, дѣля низшій членъ перваго остатка на низшій членъ дѣлителя, най-демъ нисшій изъ ненайденныхъ еще членовъ частнаго и т. д. Однимъ словомъ, дѣленіе многочленовъ можетъ быть выполнено въ порядкѣ, обратномъ вышеизложенному, т.-е. начиная съ низшаго и восходя послѣдовательно до высшаго члена частнаго.
Приводимъ примѣръ такого расположенія дѣйствія:
6 —15я4-13і;*4-54я3 — 67а4-р&г— 9я6—56х7 3—4ха-|-5х3 —7.г*
—6 4г 14я* 2—5# 4“7гг2-|-7,т3
— 15^21л:»+44^3 —33і%38л:5— 9я* —56.т7
±15х 4=20а;3+25^І4:з5д?в _______
21х2-р24а:3“28х<-р 3#й— 9я6—56л:7
— 21х* Ч-28хІ4=35а;й-(-49хв
24я3 —32я54-4бяв'—56х7
— 24ж3 ± 3 2#П=Р 40л6 ± 5 6я7
..О
47. Когда дѣлимое есть многочленъ неполный, т.-е. содержитъ не всѣ степени главной буквы, то сохраняютъ мѣста недостающихъ членовъ, чтобы можно было писать подобные члены одинъ подъ другимъ.
Примѣръ. Раздѣлить 14х8 -|- 54х8 — 39х* — 7х 2 на 2#1 -|- 8х3 — — 5** —Зх+1.
Въ дѣлимомъ недостаетъ членовъ, содержащихъ ж3 и сохраняя мѣста, на которыхъ должны бы были находиться эти члены, располагаемъ дѣйствіе такъ:
14л76 —{— 54хк — 39#1 — 7х Ц- 2 і 2#18л:3—5я2 — Згг-|~ 1
— + + + 7х2 7я*~ X +~2
— 2ггв — 4-я* -[- 21х3 — 7я*—7х-1- 2
Ч- 2#8-4- 8л:4 н- 5г3^р 3.таЧ- х
4я* +16ж3 — 1 Ох2— 6л: + 2
— 4ж1н=16г3і:10а:2±6жн=2 - —
Признаки невозможнаго дѣленія многочленовъ.
48. Когда частное отъ раздѣленія одного цѣлаго многочлена на другой можетъ йпъ шражеде цѣлымъ многочленомъ относительно входящихъ въ него бпагк. т» гин^іігь. «ого жѣмное возможно: если же частное нельзя представить гъ фвржѣ кѣлаги пвгѵтвежж, дѣлеае называется невозможнымъ.
Ізго мю а ртіогі питъ, совершается дѣленіе нацѣло, или нѣтъ; въ йлжпсгаі же случаевъ узиатъ этого нельзя, не совершая ня самомъ дѣлѣ дѣленія.
I. Если дѣлитель содержитъ букву, которой нѣтъ въ дѣлимомъ, то на какой бы цѣлый многочленъ ни умножили дѣлителя, эта буква остается въ произведеніи, которое поэтому никогда не будетъ равняться дѣлимому. Значитъ, въ этомъ случаѣ частное не можетъ быть представлено въ формѣ цѣлаго многочлена. и дѣленіе невозможно. Напримѣръ.
8а* 4~ ^аЪ —
не можетъ раздѣлиться нацѣло на 4 «4-^. Такъ какъ дѣлитель содержитъ букву с, которой пѣтъ въ дѣлимомъ. Частное изображаютъ въ видѣ дроби, означая дѣленіе горизонтальною
чертою:
8а2 4- 5аЬ — Ь2
4а + Ьс
II. Когда дѣлимое есть одночленъ, а дѣлитель — многочленъ, то частное не можетъ быть выражено ни цѣлымъ одночленомъ, пи цѣлымъ многочленомъ. Одночленомъ оно не можетъ быть выражено потому, что произведеніе многочленнаго дѣлителя на одночленное частное дало бы многочленъ, между тѣмъ какъ дѣлимое одночленъ. Многочленомъ оно не можетъ быть выражено потому, что произведеніе многочлена — дѣлителя на многочленъ — частное содержитъ по меньшей мѣрѣ два неприводимыхъ члена, между тѣмъ какъ дѣлимое—-одночленъ.
Такъ, дѣленіе а2 на а-|-Ь невозможно, и частное имѣетъ видъ дроби
III. Если возможенъ цѣлый полиномъ (частное), который, будучи умноженъ на дѣлителя, давалъ бы дѣлимое, то высшій членъ дѣлимаго долженъ быть произведеніемъ высшихъ членовъ дѣлителя и частнаго, а низшій членъ дѣлимаго— произведеніемъ ихъ низшихъ членовъ. Поэтому, высшій членъ частнаго долженъ равняться частному отъ раздѣленія высшаго на высшій, а низшій членъ частнаго “частному отъ раздѣленія низшаго на низшій членовъ дѣлимаго и дѣлителя. Отсюда прямо слѣдуетъ, что если не дѣлятся нацѣло высшій членъ дѣлимаго па высшій членъ дѣлителя, или низшій на низшій, то дѣленіе невозможно.
Такъ, многочленъ
8х: — 6я64" &г3 — 4г4 — 2Н — "х* не дѣлится на
5х* — 2х4
потому что низшій членъ 7х* дѣлимаго не іѣлгтея на низшій членъ х* дѣлителя.
Точно такъ же многочленъ
не дѣлится на
X4 -р Д72-[- 1,
такъ какъ высшій членъ дѣлимаго (Зж3) не дѣлится на высшій членъ (я4) дѣлителя.
IV. Но если высшій членъ дѣлимаго дѣлится на высшій членъ дѣлителя и низшій на низшій, то изъ этого еще никакъ не слѣдуетъ заключать, что дѣленіе возможно. Совершая въ этомъ случаѣ дѣленіе и продолжая его достаточно далеко, всегда можно открыть—возможно оно или нѣтъ.
При этомъ слѣдуетъ различать два случая:
1. Дѣлимое и дѣлитель расположены по нисходящимъ степенямъ главной буквы.
Въ этомъ случаѣ степень высшихъ членовъ послѣдовательныхъ остатковъ идетъ понижаясь. Для возможности дѣленія необходимо, чтобы высшій членъ каждаго остатка дѣлился на высшій членъ дѣлителя; поэтому, если дойдемъ до остатка, въ которомъ высшій членъ содержитъ главную букву въ меньшей степени чѣмъ высшій членъ дѣлителя, и слѣдовательно не дѣлится на высшій членъ дѣлителя, то заключаемъ, что дѣленіе невозможно.
Такъ, пусть требуется раздѣлить
2х4 4~ я3 — ж2 -|- 4
на
х2 — х 4-1 й
Высшій членъ дѣлимаго дѣлится на высшій членъ дѣлителя и низшій на низшій. Попробуемъ, не совершается ли дѣленіе на-цѣло:
2^*4" х3— #а4"’7хг4"4 — 2^4 +
Зз* — 4“ 4
— Зіг® -4" Зх2 4^ Зя
2х2 4- Зя
Высшій членъ второго остатка не дѣлится на высшій членъ дѣлителя: заключаемъ, что дѣленіе невозможно.
Иногда, прежде чѣмъ дойдемъ до такого остатка, можно ранѣе убѣдиться, возможно дѣленіе или пѣтъ. Въ самомъ дѣлѣ, предполагая, что дѣленіе возможно, можно напередъ опредѣлить—каковъ долженъ быть низшій членъ частнаго. Именно, если дѣленіе возможно, то дѣлимое будетъ произведеніемъ дѣлителя на частное, а потому низшій членъ дѣлимаго долженъ быть произведеніемъ низшихъ членовъ дѣлителя и частнаго; слѣдовательно, раздѣливъ низшій членъ дѣлимаго на низшій членъ дѣлителя, мы узнаемъ, каковъ долженъ быть низшій членъ частнаго. Совершая дѣленіе, пусть мы дошли въ частномъ до члена той степени, какую мы ранѣе нашли для послѣдняго члена частнаго; для того чтобы дѣленіе было возможно, необходимо: 1) чтобы членъ, найденный нами въ частномъ, былъ равенъ частному отъ раздѣленія послѣдняго члена дѣлимаго на послѣдній членъ дѣлителя; 2) чтобы слѣдующій остатокъ былъ равенъ нулю. Если хотя одно изъ этихъ условій не осуществляется, заключаемъ, что дѣленіе невозможно.
Приводимъ примѣры.
Раздѣлить х7 — Зх® — 4хя 4“ 2х4 на х* — 5х -|“ 1.
Высшій членъ дѣлимаго дѣлится на высшій членъ дѣлителя и низшій на низшій; при этомъ, если дѣленіе возможно, то послѣднимъ членомъ частнаго долженъ быть: 4“ 2х* ; 1 = 4"
Совершаемъ на самомъ дѣлѣ дѣленіе:
х1 — Зх® — 4х5 -4- 2х*, х4 —5х 4^ І — х~ -4- 5хв 4г х3 х* Ч- 2х*
2хе— ох3—2-г1
— 2х*— 10г5 = 2 х*
Раздѣлимъ жысѵіі члегь іерваго остатка на высшій членъ дѣлителя, находить -^-Зх1. т.-е. икъ разъ такой членъ, какимъ долженъ быть послѣдній членъ частшл»: но какъ слѣдующій остатокъ не равенъ нулю, то заключаемъ, что дѣленіе невозможно.
Другой примѣръ: раздѣлить
8х*4“ 10х“-— 32х4 — Зх8-р$4хЧ— 20х на 4х34“5х2 — 2х.
Первый членъ дѣлимаго дѣлится на первый членъ дѣлителя, и послѣдній на послѣдній; притомъ, частное отъ этого послѣдняго дѣленія есть — 20х; — 2 х или 4“ Ю- Членъ 4” Ю долженъ быть послѣднимъ въ частномъ, если дѣленіе совершается нацѣло, -
Выполняемъ дѣйствіе:
8х«-[-10хя -32х4 — Зх3 + 54ха —20х 4х34-5ха —2х
— 8х® 1 Ох5 =4 4х4 "зхв _7Ж"47з
- 28х* —~~ЗхГ+ 54х2 — 20х~
~Ь 28х* Ч- 35х3 4- 14х *
32х34-40х^ 20х”
— 32х3 Ч2 40хя Ч- 16х
Членъ частнаго, несодержащій буквы х, оказывается равнымъ 4"®і а не 10, какъ должно бы быть при возможномъ дѣленіи: заключаемъ, что дѣленіе невозможно. Вычтя изъ второго остатка произведете (4л34~Зл2—2х), 8, находимъ послѣдній остатокъ: — 4х*
2. Дѣлимое и дѣлитель расположены по восходящимъ степенямъ главной буквы.
Въ этомъ случаѣ степень низшаго члена послѣдовательныхъ остатковъ идетъ постепенно увеличиваясь, а потому низшіе члены остатковъ всегда будутъ дѣлиться на низшій членъ дѣлителя. Невозможность дѣленія открываемъ слѣдующимъ образомъ. Раздѣливъ высшій членъ дѣлимаго на высшій членъ дѣлителя, мы узнаемъ, каковъ долженъ быть высшій членъ частнаго, въ предположеніи, что дѣленіе возможно. Если, дойдя въ частномъ до члена, содержащаго главную букву въ степени, равной избытку показателя главной буквы въ послѣднемъ членѣ дѣлимаго надъ ея показателемъ въ послѣднемъ членѣ дѣлителя, найдемъ, что этотъ членъ отличенъ отъ члена, получаемаго дѣленіемъ послѣдняго члена дѣлимаго на послѣдній членъ дѣлителя, или если этотъ членъ будетъ и = указанному частному, но слѣдующій затѣмъ остатокъ не будетъ О, то дѣленіе— невозможно.
Пусть, напри*.. требуется раздѣлить
4 — Зх4“5ха-(-^а—19л1 на 1 — 2л — л2.
Здѣсь первый членъ дѣлимаго дѣлится на первый членъ дѣлителя и послѣдній членъ дѣлимаго на послѣдній дѣлителя.
Если дѣленіе возможно, послѣднимъ членомъ частнаго долженъ быть
(— 19^1) ; ( — д;2) = 19^
4 — 3x4“ 5л34~ л3 — 19л1 1—‘2л — х*
— 4 4=83? 4л2 4-р5а?Ц-19#2
5 л9х24“ х3 — 19а4
— 5л + Юл2 =Н 5л8
19л2 + 6х3 — 19 л1
— 19л2 ± 38л3 =Ь 19л1
44л3
Третій членъ частнаго дѣйствительно =-|-19х2, но затѣмъ остатокъ не есть ноль: заключенъ, что дѣленіе невозможно*
Еще примѣръ: раздѣлить
— 2 4~ я — 5х3 4- 4л1 на —* 1 — 2л -|- л2.
Если дѣленіе возможно, послѣднимъ членомъ частнаго долженъ быть 4“ 4л2,
— 2л — 5 л8 Ц- 4л1 —1—2л+
+ 2 + 4л=ь 2х2 _ ~ 2 —5х'фі2х2
5х — 2л2 — 5л3 4- 4л1
— 5 л 4" Юл2 + 5л3
— 12л2 + 4л1
+ 12л2 ± 24л3 =р 12л*
івѣгтъ находимъ въ частномъ + 12яа; кромѣ того, соотвѣтствую-яй «татокъ долженъ бы быть нулемъ, а онъ равенъ 24х3— 8х4. Значитъ, .Йкѵж невозможно.
і*э4енность случая дѣленія цѣлыхъ полиномовъ, расположенныхъ но воз-рк-амимъ степенямъ главной буквы (при соблюденія условія дѣлимости край-К5 діеновъ дѣлимаго на крайніе члены дѣлителя), заключается въ возмож-жнш полученія въ частномъ неограниченнаго числа цѣлыхъ членовъ. Обусло-мвается это тѣмъ, что степени низшихъ членовъ остатковъ идутъ, постоянно мышаясь. Такъ, въ послѣднемъ примѣрѣ, продолжая дѣленіе, получили бы ^тьертый членъ — 24т8 и т. д.
49. Когда частное отъ раздѣленія цѣлыхъ относительно х полиномовъ однога п другой не можетъ быть въ точности выражено цѣлымъ полиномомъ съ копеч-шхъ чцеломъ членовъ, то оно можетъ быть представлено въ видѣ суммы, состоящей изъ нѣкотораго цѣлаго относительно х полинома (когда таковой су-шествуетъ и не сводится къ нулю), и дроби, имѣющей числителемъ одинъ изъ остатковъ, а знаменателемъ — дѣлителя.
Въ самомъ дѣлѣ, пусть А и В будутъ два цѣлые по буквѣ х полинома, расположенные или по восходящимъ, пли но нисходящимъ степенямъ буквы т, — въ послѣднемъ случаѣ пусть степень А не ниже степени В, — и положимъ, что въ частномъ получился цѣлый по буквѣ # многочленъ Ц, а въ остаткѣ В. Замѣчая, что остатокъ К происходитъ послѣ вычитанія изъ А произведенія В<і, находимъ:
Н —А —В(),
или, выражая уменьшаемое посредствомъ вычитаемаго и остатка, находимъ а=вч+в...(і), отсюда, раздѣливъ обѣ части на В, имѣемъ
В = Ч+е-<2)-
Различаемъ теперь два случая: 1) А и В расположены по восходящимъ степенямъ буквы х\ 2) А и В расположены по нисходящимъ степенямъ я-са.
Въ первомъ случаѣ преобразованіе, указанное равенствомъ (2), возможно выполнить безчисленнымъ множествомъ способовъ. Въ самомъ дѣлѣ, число цѣлыхъ но буквѣ х остатковъ въ этомъ случаѣ неограниченно, и мы можемъ остановиться на какомъ угодно изъ нихъ. Такъ, дѣля 1 на 1 — я, и, останавливаясь послѣдовательно на 2-мъ, на 3-мъ, на 4-мъ и т. д, остаткахъ, найдемъ преобразованія:
Пусть теперь полиномы А и В расположены но нисходящимъ степенямъ буквы х, и пусть степень А не ниже степени В; то число преобразованій, выражаемыхъ равенствомъ (2), будетъ ограниченное. Степени послѣдовательныхъ остатковъ въ этомъ случаѣ идутъ, все понижаясь, и обыкновенно останавливаются па томъ остаткѣ, котораго степень по крайней мѣрѣ на 1-цу ниже степени дѣлителя. Пусть К ц будетъ такой именно остатокъ, а — цѣлая часть частнаго; при этомъ ограниченіи преобразованіе, указанное равенствомъ (2),
— 64
возможно исполнить только однша единственна^ способомъ; т*-е* при огра-X пиченіи, что степень К нвже степени В, существуетъ только одна пара цѣлыхъ полиномовъ Ч и К, дающихъ равенство (2), или, что то же (1). Чтобы доказать сто, допустимъ, что существуетъ другая пара цѣлыхъ по буквѣ х полиномовъ, Ц' и К\ гдѣ степень IV ниже степени В, такихъ, что
*
А = ВЦ' + К';
если это такъ, тополиному ВЦ -4 И и ВЦ'4^ IV, какъ равные одному и тому же полиному Ат должны быть совершенно одинаковы, или. какъ говорятъ, тождественны:
ВЦ + В = В<І' -4- К\
т-е* что, по выполненіи указанныхъ дѣйствій, по обѣ стороны знака = • должны получиться совершенно одинаковые полиномы, откуда, вычитая отъ равныхъ равныя К ВЦ', найдемъ ВЦ — ВЦ' = В' — В. что можно написать въ видѣ В(Ц — Ц')= = В'— К. Но такое равенство возможно только тогда, когда Ц = Ц' и вмѣстѣ съ тѣмъ К = К'; ибо въ противномъ случаѣ Ц — Ц', будучи цѣлымъ но буквѣ х полиномомъ или, въ крайнемъ случаѣ, будучи независимымъ отъ .г числомъ, по умноженіи на В дастъ полипомъ степени или высшей, или, по меньшей мѣрѣ, равной степени полинома В, между тѣмъ какъ К и В', будучи по степени лг-са ниже В, дадутъ въ разности полиномъ необходимо низшей степени, чѣмъ степень В; и такимъ образомъ полиномы В(Ц — Ц') ц К' — В были бы неодинаковой степени и, слѣдовательно, не могли бы быть тождественны между собою.
Итакъ, необходимо должно быть Ц' тождественно съ Ц и IV тождественно съ К; и потому при указанныхъ условіяхъ преобразованіе, представляемое равенствомъ (1), а слѣдовательно и (2), возможно выполнить только однимъ способомъ *
Такъ, если А = бх1 -|- 5#3 — 14~ 25% 4^ 4, В = •—2я -|-1, то
полное частное отъ раздѣленія А па В будетъ
Л « । о л । 14^4-8
4“ Зя 4 4“ Зх4 _ 2^ р
п, по доказанному, выразить полное частное въ такой формѣ (т.-е. въ формѣ цѣлаго полинома 4^ дробь) возможно только однимъ этимъ способомъ, если желаемъ, чтобы степень остатка была ниже степени дѣлителя.
Такимъ же образомъ найдемъ:
въ иной формѣ преобразованіе и не можетъ быть выполнено, если хотимъ, чтобы степень остатка была ниже степени дѣлителя*
50. Раздѣлить полиномъ X послѣдовательно на полиномы В, С, О,... значитъ раздѣлить А на В, потомъ частное иа С, затѣмъ частное этого новаго дѣленія на В и т* д*
Теорема* Если полиномъ А раздѣлить послѣдовательно на полиномы В, С, I),... (не необходимо различные между собою), то послѣднее полученное частное есть вмѣстѣ съ тѣмъ частное отъ раздѣленія А на произведеніе ВСВ.
Въ самомъ дѣлѣ, полагая, что полиномы расположены по убывающимъ степенямъ главной буквы, имѣемъ тождества:
А — Яр
Чі = ($а 4-ма = п+к3*
причемъ всѣ полиномы Вп К?, В3, необходимо, низшей степени сравнительно съ В, С, И. Подставляя въ первое тождество вмѣсто равное ему выраженіе С9а4“В-а, имѣемъ
А-ВСС^ + В^ + В.,
а сюда вмѣсто подставляя П(?а -|—В3, найдемъ
А = В[С(В(4 + В3) + К2]+Вр
ИЛИ А = Ю ,<І3 + (ВСВЭ 4-ВВз-НВ,).
Легко убѣдиться, что степень полинома въ скобкахъ ниже степени произведенія ВСИ. Слѣдовательно, послѣднее тождество показываетъ, что, раздѣляя А на ВСП, находимъ въ частномъ и въ остаткѣ ВСН3-|-’ ВВ24* ®і5 теорема доказана. Если послѣдовательныя дѣленія совершаются на-цѣло, то, значитъ, А дѣлится на ВСВ, и частное отъ раздѣленія А на ВСО есть послѣднее полученное частное. Обратно, если А = ВСВ. Ц, то А дѣлится на В, и въ частномъ получится СІКН это частное, въ свою очередь, дѣлится па С, и частнымъ этого новаго дѣленія будетъ ТК|: это частное дѣлится на В, и частнымъ этого третьяго дѣленія будетъ <}.
Слѣдствіе. — Основываясь на этомъ, если требуется узнать, дѣлится ли полиномъ А на (х — а)р (гдѣ р — цѣлое положительное число), можно поступать такъ. Дѣлимъ А на х— а; пусть дѣленіе совершается безъ остатка; частное этого дѣленія дѣлимъ опять на х — а и т. д. Если всѣ р дѣленій совершаются безъ остатка, то заключаемъ, что А дѣлится на (ж — а)р, и частное послѣдняго дѣленія будетъ частнымъ отъ раздѣленія А на (я? — а)р.
Замѣчательные случаи дѣленія.
51. Приведемъ нѣкоторые частные случаи дѣленія, заслуживающіе особаго вниманія вслѣдствіе частаго ихъ примѣненія.
I. Разность одинаковыхъ степеней двухъ количествъ дѣлится безъ остатка на разность основаній.
Пусть требуется раздѣлить х'п — ат па я —а. Совершая дѣленіе, имѣемъ: хт — ат х — а
— хт -4-а#"*-1 я”1-1 ...
аз™-1 — ат
—ахт~} -4- а2#”*-2
а2д;т-2---ат
— а2х™ 4? а3#™"3
аЗдмм-з — агл
— ат
— а^1х ат
О
Расположивъ дѣлимое и дѣлителя по убывающимъ степенямъ буквы я, дѣлимъ первый членъ дѣлимаго па первый членъ дѣлителя и находимъ первый членъ частнаго, въ которомъ показатель буквы какъ равный разности показателей той же буквы въ дѣлимомъ и въ дѣлителѣ, будетъ —т — 1. Первый членъ частнаго есть т*'1. Умноживъ его на дѣлителя и вычтя произведеніе изъ дѣлимаго, получаемъ первый остатокъ: ажт 1 — а". Раздѣливъ аят-1 на а?, находимъ второй членъ частнаго: а#”1-2. Умноживъ его на дѣлителя и вычтя произведеніе изъ перваго остатка, получимъ второй остатокъ: а2х”*-2 — ат. Подобнымъ же образомъ найдемъ, что третій членъ частнаго <Лгт”3, а третій остатокъ а3#"1-3 — ат.
Не продолжая дѣйствія, разсмотримъ законъ (.оставленія послѣдовательныхъ остатковъ, Сравнивая ихъ между собою, замѣчаемъ, что всѣ остатки—двучлены, которыхъ вторые члены одинаковы и равны —а" первые же члены представляютъ произведенія степеней буквъ а и х. при четь показатели буквы а идутъ послѣдовательно увеличиваясь на 1, а показатели буквы х уменьшаясь на 1, сумма же обоихъ показателей всегда равна ш. Изъ этого слѣдуетъ, что, продолжая дѣленіе, мы непремѣнно дойдетъ до такого остатка, первый членъ котораго будетъ имѣть букву а съ показателемъ т—' 1, а слѣдовательно букву х съ показателемъ 1. такъ какъ сумма показателей должна равняться т. Этотъ остатокъ будетъ слѣдовательно: а"-1 я — а"1. Дѣля первый его членъ на я, найдемъ въ частномъ членъ а"1-1; а умноживъ этимъ членомъ дѣлителя и вычтя произведеніе изъ остатка, находимъ, что слѣдующій остатокъ есть 0: значитъ. х1*— а** дѣлится безъ остатка на х— а.
Мы не могли выполнить всѣхъ частныхъ дѣленій вслѣдствіе неопредѣленности числа т; мѣста, гдѣ надо подразумѣвать промежуточные остатки и члены частнаго, обозначены точками.
Законъ частнаго. — Всматриваясь въ составъ частнаго, замѣчаемъ, что оно имѣетъ слѣдующія свойства:
1. Всѣмъ его членамъ предшествуетъ знакъ (-р), потому что они происходятъ отъ дѣленія первыхъ членовъ остатковъ, предшествуемыхъ знакомъ (-1-), па первый членъ дѣлителя, имѣющій тотъ же знакъ.
2. Первый членъ частнаго есть послѣдній «гл-1; что же касается промежуточныхъ членовъ, то они представляютъ произведенія степеней обѣихъ буквъ х н а, причемъ показатели буквы х идутъ послѣдовательно уменьшаясь на 1, а показатели буквы а— послѣдовательно увеличиваясь на 1; такъ что сумма показателей въ каждомъ членѣ равна —1. Если въ первомъ членѣ подразумѣвать множителемъ а0, а въ послѣднемъ х°, то можно сказать, что члены частнаго расположены по убывающимъ степенямъ буквы я, которой показатели идутъ, уменьшаясь на I, начиная съ — 1 и кончая нулемъ; и но возрастающимъ степенямъ буквы а, которой показатели идутъ, увеличиваясь на 1, начиная съ О и кончая — 1.
3. Число членовъ частнаго равно я», т.-е. степени дѣлимаго.
Въ самомъ дѣлѣ, показатели буквы а, наприм., идутъ послѣдовательно увеличиваясь на 1, начиная съ О и кончая ш — 1; но послѣдовательныхъ цѣлыхъ чиселъ отъ О до — 1 включительно ровно т. Столько же членонч, и въ частномъ.
При помощи выведенной нами формулы
іТт-1
4-ахт~2
Ц- ... 4~ ат~2х 4“
..ДА)
(12Хт~~^
4-а3я™~4
можно прямо писать частное отъ раздѣленія разности одинаковыхъ степеней двухъ количествъ па разность основаній. Вотъ примѣры:
3. Раздѣлить, по формулѣ (А), 125а3 — 863 на 5а — 26.
Замѣчая' что 125а3 = 5.5.5.а.а,а = 5а. 5а. 5а = (5а)8, и что 863= = 2.2.2.6. Ь. Ъ = 26.26.26 = (26)э, имѣемъ:
(5 5а=2І~ = (5а)“ +(5а) •(2Ь) + (26)3 = 25а* + 10а6+ 4Л1-
4. Подобнымъ же образомъ найдемъ;
— т4 = а* 4- а3™ -|-1 а*т* + І ат3 4" ***.
Слѣдствія. — Такъ какъ х і а означаютъ какія угодно количества, то можно положить а =—а'. Подставмвъ въ формулу (А) вмѣсто а количество—а', м замѣтивъ, что дѣлимое обращается въ лГ — ( — а*)"*, а дѣлитель въ х — (— а') или въ находимъ:
4~ (— а')хт~2 4- (— а')*#т*3 4" ... 4- (— а')м-Лг 4^
4-(-а')”-1.
Изъ правила знаковъ при умноженіи заключаемъ, что (—а')*=(—а').(—а')= = + а'*; ( д')а = (-«>(- а') = (+ а'*)( - а')=-а'3; (-а')4 = ^а'\— — а'= 4-а'4 и т. д. Однимъ словомъ: четныя степени количества—а' даютъ знакъ 4^ а нечетныя—знакъ —. Замѣтивъ это, различаемъ два случая: т— четнаго и т— нечетнаго.
1. ш — число четное. — Въ такомъ случаѣ будетъ: т — 1 — число нечетное, т — 2 •— четное, т — 3 — нечетное п т. д. А потому найдемъ, что: (—а)т = 4»аУт; (—а')т“1 = — а^”1; ( - а')”—2 = а'м~2 и т. д. При-
нимая это въ соображеніе, найдемъ, что послѣднее равенство принимаетъ видъ
М4
Отсюда заключаемъ, что разность одинаковыхъ четныхъ степеней дѣлится безъ остатка и на сумму основаній, при чемъ законъ составленія частнаго отличается отъ вышеуказаннаго только чередованіемъ знаковъ.
Напримѣръ, хв —а3 дѣлится не только на х — а, но и на #4“аі причемъ частное будетъ
2. т — число нечетное. — Въ такомъ случаѣ, т — 1 будетъ число четное, т — 2 — нечетное и т. д. Поэтому: (— а')щ — — сл. Дѣлимое будетъ хт — (— а,щ) = а?” а"Л; затѣмъ, (— а')"1-1 будетъ — -р а'”1”1; (— а')т-2= = — а'*1-2 и т. дм и мы получимъ:
---У г- = г*1-1 — ахт~2 я -|- а
а*хт~3 — а'Ъ?™-4— ат~2х а'1”-1... (С),
Равенство (С) показываетъ, что сумма одинаковыхъ нечетныхъ степеней двухъ колгічествъ дѣлится безъ остатка на сумму основаній,•причемъ въ частномъ знаки чередуются.
Напримѣръ:
II. Сумма одинаковыхъ степеней двухъ количествъ не дѣлится безъ остатка на разность этихъ количествъ.
Пусть требуется раздѣлить сумму яш-|-аад на х — а:
мт ( _т „
х -|- а х — а
— &т ± а#”-1 #т—1 ад?т*-2а2#1”-3 ... -|- а”**1
ахт~1 -|- а”1
— ахт Ч~ а2я:т“2
— аЪ;т~-2 Ч- а8д;го~3
а8#"1”3 Ч- а” ♦
I
V ѵ * « •
с » * * * Ф • ат-1я: -]“»** — ат—хх Ч— ат
2а”
Дѣленіе будетъ возможно, если, найдя въ частномъ членъ — ат-\ получимъ въ остаткѣ 0; но совершая дѣленіе, мы нашли въ частномъ членъ Ц-а”-1 и затѣмъ въ остаткѣ 2а”: заключаемъ, что дѣленіе не совершается безъ остатка. Что касается цѣлой части частнаго, то она составлена совершенно по тому же закону, какъ и въ первомъ случаѣ. Полное частное будетъ
х— а
— ж1"'1 а^‘“2
2ат я—а
... (0).
Слѣдствія. — Полагая въ этой формулѣ а = — а\ находимъ
4- Г
~г -а' ==ж"~1 + (~а>и,-2+ (- ^“-3+...+(-аГ-Ч“Ч4^
Іц ь* . «и •“ I ^“14 !
Разсмотримъ опять два случая: т — четнаго и т — нечетнаго.
1-й случай. — т — число четное» Въ этомъ случаѣ «я» і „гт ч-ля
—а'^ + Д—, ...(Е).
Я? | (К
Откуда заключаемъ, что сумма одинаковыхъ четные степеней двухъ количествъ не дѣлится на сумму тѣхъ же количествъ, и что остатокъ равенъ удвоенному второму члену дѣлимаго.
Такъ, г4-г я4 . , т * о I 2а*
—;— = х1 — ах3 + а*х — €г -4- —;— • я 1 1 а? + а
2-й случай. — т — нечетное число. Въ этомъ случаѣ
Xм-ДГ1" х Ц-а'
— — алхет“2 Ч-а'3#**-3 —... -4- а'*”-1
2а,от х + а'
(Р).
Слѣдовательно, разность одинаковыхъ нечетныхъ степеней двухъ количествъ не дѣлится на сумму этихъ количествъ, и остатокъ равенъ удвоенному второму члену дѣлимаго.
Такъ, х5 — а5 * » । » о я । * 2ав
—, — = х* — ах3 ч- а 2х3 — а Зх + а4--------=
х + а ’ 1 х + «
Выдѣляя изъ разсмотрѣнныхъ случаевъ тѣ, когда дѣленіе совершается безъ остатка, приходимъ къ слѣдующему выводу: раз«ос?п& одг/яакояът степеней двухъ количествъ всегда дѣлится на разность основаній; разность одинаковыхъ четныхъ степеней дѣлится 9 кромѣ того, и на сумму основаній; сумма же одинаковыхъ нечетныхъ степеней — на сумму основаній.
Теорема, доказанная въ этомъ параграфѣ, извѣстна подъ именемъ теоремы Везу (Вегопі).
ГЛАВА VI-
Разложеніе алгебраическихъ выраженій на множители.—Умноженіе и дѣленіе многочленовъ съ буквенными коэффиціентами"
52. Разложить выраженіе на множители — значитъ представить его въ формѣ произведенія, иначе говоря, въ формѣ одночлена. Опредѣленнаго неизмѣннаго правила для такого преобразованія нѣтъ; знаніе теоремъ и навыкъ въ преобразованіяхъ позволяютъ въ нѣкоторыхъ случаяхъ открыть, каковы множители даннаго выраженія.
Естественно, первое, что нужно сдѣлать — это выдѣлить множителя, общаго всѣмъ членамъ даннаго выраженія, если таковой имѣется. Затѣмъ, дальнѣйшее разложеніе совершается примѣненіемъ одного изъ слѣдующихъ трехъ пріемовъ: 1) формулъ замѣчательныхъ случаевъ умноженія в дѣленія; 2) метода опредѣленной группировки членовъ; 3) метода двухчленныхъ дѣлителей. Откладывая взлаженіе послѣдняго метода до слѣдующей главы, ознакомимся въ этой главѣ съ остальными изъ указанныхъ пріемовъ.
53. Вынесеніе за скобки общаго множителя членовъ даннаго многочлена. — Пусть всѣ члены многочлена имѣютъ общаго множителя, напр,,
АВ — ВБ + СП;
замѣтивъ, что величина многочлена не измѣнится, если мы его помножимъ и раздѣлимъ на одно и то же количество, множимъ и дѣлимъ на В; находимъ
АВ — ВО 4- СО = |)^АВ-ВВ.+ср),
Выполнивъ дѣленіе АВ — ВВ —[— СВ на В по правилу дѣленія многочлена на одночленъ, найдемъ въ частномъ А — В + С; слѣд.
АБ — ВВ + СВ = В(А — В + С).
Отсюда видимъ, что если всѣ члены многочлена имѣктъ общаго множителя, то этотъ множитель можно вынести за скобки, написавъ въ скобкахъ частное отъ раздѣленія даннаго многочлена на общій множитель его членовъ.
Такъ, всѣ члены многочлена 356М — 76с3ййЦ- 49а/?<?й4~34363с3 имѣютъ общимъ множителемъ 76са, который и выносимъ за скобки; въ скобкахъ же пишемъ частное отъ раздѣленія многочлена на 7/и?; такимъ образомъ найдемъ:
356 V — 7/>сМ* + 49а/?<Л?+ 3436Ѵ = 76с2(56с2 — есР + 7аМ + 49/?с).
Иногда выраженіе, получившееся въ скобкахъ, бываетъ способно къ дальнѣйшему разложенію, либо къ другимъ преобразованіямъ, могущимъ его упростить. Напр., 14а8/? — 28а4/?-|- І4аЧ>\ по вынесеніи за скобки общаго множителя 14а3/?, приводится къ виду 14аЧ?(аа— 2а6&2); замѣчая затѣмъ, что а2 — 2а6 /? = (а — Ь)*. замѣняемъ данное выраженіе простѣйшимъ
14а3/?(а — 6)2.
54, Методъ примѣненія замѣчательныхъ формулъ умноженія и дѣленія.— Можно иногда съ успѣхомъ примѣнять къ разложенію на множители формулы замѣчательныхъ случаевъ умноженія и дѣленія.
Простѣйшая изъ этихъ формулъ есть
А3 — В2 = (А + В)( А — В)... (1).
Замѣтивъ далѣе, что
^в!=а*+ав+в’ и ^Нг = а’-ав+в»,
и опредѣляя изъ того и другого равенства дѣлимое но дѣлителю и частному, имѣемъ:
А» — В* = (А— В)(А* + АВ + В’)... (2)
А» + В* = (А-Ь В)(А8 - АВ 4- В»)... (3)
Затѣмъ имѣемъ:
А* -В»=(А8)8~(В8)8=(А8+В8) (А8 -В8)=(А»+В’)(А 4~ В)(А - В)...(4).
А» — В* = (А8)8 — (В8)8 = (А8 + В8) (А8 — В8) — = (А + В) (А - В) (А8 + АВ + В8) (А8 — АВ 4- В8)... (5). .
Вотъ примѣры примѣненія этихъ формулъ:
1) 4х8 — 9у8 = (2л)8 - (Зу)8 = (2«4- Зу) (2х - Зу).
2) (а + Ь — с)*— (а — 2Ь 4~ Зс)8 = (2а — Ь 2с) (ЗЬ — 4с).
3) а8—Ь8=(«‘)8—(6‘)8=(а‘-Н>‘)(а‘—6‘)=(а8-|-д‘) (а8-|-Ь8) (а-|-Ь) (а—6).
4) Вж8-|- 27у8 = (2х)8 + (Зу)8 = (2л 4 Зу) (4л8 — бжу + 9у8).
5) 8л8 — 27у8 = (2ж)8 — (Зу)8 = (2л - Зу) (4х8 -|- бжу 4~ 9у8).
6) Разложить на множители
2а8Ь8 -(- 2Ь8с8 -|- 2а8с8 — а* — (>* — с*.
Придавъ къ этому выраженію и вычтя изъ него 2а8Ь8, находимъ:
АаѢ* — 2а868 268с8 -|- 2а8с8 — а‘ — — с* =
(2аЬУ — (а* 4- 2аѢ* 4~ 6‘) 4~ 2 (а8 4- 6») с8 - - с‘ =
(2аі)8 — (а8 4- 68)8 4- 2 (а8 4- 6») с2 - с‘
(2аі)8 — {(а8 4- 68)8 — 2 (а8 -}- Ь8) с8 4- с*} =
(2а/>)8 — I (а8 4- і8) — с8|8 = (2аЬ 4~ а8 4- Ь8 — с8) (2аЬ — а^ — Ь^ с8) = [(а 4- Ь)' - с8] [ — (а — Ь)* 4- с8] =
= (а 4"" 4~ № “І” — е) (а — Ъ 4~ с) (—* а 4~ & с).
Разсмотримъ еще разложеніе выраженій А‘4-В‘, А*4-В* 4-А8В8, А‘4“ 4- В* — &А8В8
Придавая къ первому изъ этихъ выраженій и вычитая изъ него 2А8В8, находимъ:
А« 4- В* = А‘ 4- 2А8В8 4- В‘ — 2А^В8 = (А8 4~В8)8 — (УІ. АВ)8 = = (А8 4- В8 4- АВ У2) (А8 4- В8 — АВ У2).
Такимъ же образомъ найдемъ:
А* 4- В* 4- А8В8 = (А8 4- В8)8 - А8В8 =(А2 4- В8 4- АВ) (А8 4~В8 — АВ).
А‘ 4- В‘ - *А8В8 = (А8 4- В8)8 — (к 4- 2) А8В8 = = (А8 + В8 + АВ }/* + 2) (А8 4-В8 - АВ + 2).
55. Методъ группировки членовъ. — Если всѣ члены многочлена не имѣютъ общаго множителя, то иногда возможно бываетъ разбить иіъ на группы такъ, чтобы*всѣ группы имѣли общаго множителя, который и. выносится за скобки. Общихъ правилъ для такихъ преобразованій нѣтъ; какъ ихъ совершать, укажутъ нижеслѣдующіе примѣры.
1. Разложить на множителя выраженіе а*-\-Ьс — ас — аЬ. Разбиваемъ многочленъ на двѣ группы: а2 —ас и -рбс — аЬ; вынося въ первой группѣ за
скобки а, находимъ а(а—с); вынося во второй группѣ—6, получимъ —6(а—с). Слѣд. данное выраженіе = а(а — с) — Ь (а — с); вынося здѣсь за скобки а — с, получаемъ окончательно (а — с) (а — Ь).
2. Взявъ трипомъ х2 4" (а 4“ Ь) х4" раскроемъ скобки и сгруппируемъ
члены попарно; найдемъ
х* 4“ ах 4~ Н-* = х Iх Н~ а) Н- Ь (х 4“ а) = 4" а) &)•
Подобно этому, найдемъ
(х — а) (х — Ь) = х* — (а 4~ Ь) х 4~ а&, (х— а) (^4” Ь) = ха4^(—а + — ай.
Отсюда заключаемъ, что всегда можно перейти отъ тринома вида ха4^Р^4^ къ произведенію двухъ биномовъ (#4“а) (х4“ &)• какъ скоро удастся подыскать два такихъ числа а и 6, произведеніе которыхэ равнялось бы а алгебраическая сумма давала бы р. Вотъ примѣры.
Пусть нужно разложить триномъ х5— 10x4“ 24, Пробуемъ, нельзя ди свободный членъ -|-24 разложить на два такихъ множителя, — эти множители должны быть одинаковаго знака, — алгебраическая сумма которыхъ давала бы коэффиціентъ при первой степени х, т.-е. —10. Во 24 можно разложить на слѣдующія пары множителей:
+ ІХ + 24, — 1 X—24,
2Х 12, ЗХ 8, 4Х О,
— 2Х”12т ~ЗХ — 8, —4X^6.
Изъ нихъ только послѣдняя пара даетъ въ суммѣ — 10. Такимъ образомъ прямо'находимъ, что искомые множители будутъ
х— 4 и х — 6; слѣд., х2 — 10х-|- 24 —(х — 4) (х — 6).
Пусть еще требуется разложить триномъ х2 -4- 2х — 35. Такъ какъ передъ свободнымъ членомъ стоитъ знакъ —то пытаемся, нельзя ли разбить — 35 на два такихъ множителя съ противоположными знаками, чтобы ихъ произведеніе было —35, а алгебраическая сумма -|-2. Множители—35 будутъ: +1 н + 35, + 5 и требованію удовлетворяютъ: 4”? и —5. Слѣд., искомые множители будутъ:
#4“ 7 и х— 5, и х‘24-2х — 35 = (х — 5) (х 4" 7).
3. Взявъ асх2-\-(а(1-^Ьс)х-\-Ъс11 раскрывъ скобки и сгруппировавъ члены по два, имѣемъ
асх* 4- адх 4“ Ьсх -\-Ь(1=ах(сх-\- (I) 4“ Ь (сх 4- =(ах 4- Ь) (сх 4^ <0-
Отсюда видно, что разложеніе тринома рх2(?х 4~ ** на множители вида их-\-Ь и сх4-с? будетъ возможно, какъ скоро удастся разложить р па два множителя а и с, а г — на два множителя Ь и (I такъ, чтобы средній коэффиціентъ ц равнялся а<і~\-Ьс.
Пусть, напр., требуется разложить трипомъ Зх24~7х — 6. Коэффиціентъ 3 разлагается только на 1 и 3. Послѣдній членъ — 6 можетъ быть произведеніемъ: — 6 на 1. 4~г* на — 1. —2 на-4" + - на —3. Составляемъ те-
перь множители ая-|-Ь и причемъ для коэффиціентовъ а и с при х
должно брать комбинаціи разложенія 3, а для Ъ и д— комбинаціи разложенія — 6, Такимъ образомъ испытываемъ комбинаціи:
(Зя+еНя + І), (За?Ч=1)(л±6),(Зя? + 2)(я;±3), (Зя + 3) (х ± 2).
Изъ этихъ комбинацій даетъ 4"?х для средняго члена —третья, если взять въ ней верхніе знаки; требуемое разложеніе будетъ, слѣдовательно,
(За; —2) (а; 4-3)
Триномы вида ая2 4“ 4“€ можно иногда легко разлагать способомъ дополненія первыхъ двухъ членовъ до полнаго квадрата, съ тѣмъ чтобы привести выраженіе къ разности двухъ квадратовъ. Вотъ примѣры.
Найти множители х2-|-7а:4_ 12. Обращаясь къ формулѣ (а6)2 = а2 4" 4~ 2аЬ-|-Ь2, замѣчаемъ, что х2 можно разсматривать какъ квадратъ перваго члена пока неизвѣстнаго бинома; помноживъ и раздѣливъ 7х на 2, что даетъ
2.x. —, мы можемъ іх разсматривать какъ удвоенное произведеніе перваго
члена (я) искомаго бинома на второй, который, слѣд., равенъ у Отсюда пря-
&
мо видно, что если къ данпомѵ трипому придать квадратъ этого второго члена. /7 V
[у) , при чемъ, понятно, нужно и вычесть столько же, т.-е. если написать данный трмвогь въ видѣ
то первые три члена даютъ квадратъ бинома а?4“Ѵ* такъ что данный триномъ можно написать въ видѣ
I і 7Ѵ /49 I । 'V /IV
2/ \4 1 ИЛИ \ + 2/ \2/ д
а это, по формулѣ а2 — 62 = (а 4” &) (а “ равно
Еще примѣръ, легко рѣшаемый этимъ способомъ: разложить.
(а:2 4- 7х + 6) (я2 4- 7х + 12) — 280.
Раскрывая произведеніе, причемъ х24-'/^ считаемъ за одинъ членъ, имѣемъ
(х2 4- 7а?)* 4-18 (я2 4- 7л) + 72 — 280.
Замѣтивъ, что второй членъ можно написать въ видѣ 2. (а?24^7#) • на-юдимъ, что для требуемаго преобразованія надо придать и вычесть 92, и тогда выраженіе будетъ
(х2 + 7я4-9)а+72—280 —81=(г34-7я?+9)2 - 289 = (л2 +7x4-9)* — — (17)а = (ха4-7^ + 26)(х24-7х — 8) = (ж* + 7я4-26) (х— 1)(а?4-8).
4, Иногда разложеніе группировкой удается, если расположить данное выраженіе по убывающимъ степенямъ одной и той же буквы. Такъ, въ выраженіи
а® (/> — с) 4- (с — а) + (а — Ь) мы не замѣчаемъ общаго множителя; но, расположивъ по убывающимъ степенямъ а, находимъ
а2 (& — с) — а (Ь2 — с*) + Ьс (і — с), откуда прямо виденъ множитель Ь — с. Вынося его за скобки, получимъ (Ь — с) [аа — а (Л Ц- е) + Ьс] = (Ь — с) [(а* — аЬ) — (ас — 1>с)] = = (& — с) [а (а — Ъ) — с (а — Ь)] = (Ь — с) (а — Ь) (а — с).
5. Разложить па множители (а — 6) — аѴ(а — с) 4- Ь2с2 (Ъ — с). Можно бы было начать такъ, какъ указано въ предыдущемъ примѣрѣ. Но можно идти еще такимъ путемъ.
Имѣемъ послѣдовательно:
{6я (о — Ь) - е*0і —е)}4-іѴ(Ь- е)
= а2 \аІ>* — асэ + с> — М| + ЬѴ (Ь - с)
—- аа ] а (Ь2 — с2) — (6* — с*)| 4- Ъ2с* (Ь — с)
= а2 {а (6 — с) (Ь 4~ с) — (Ь — с) (Ь* 4“ ^с2 (6 — с)
= ая (& — с) {а (Ь 4” с)— (^3 + + ^2)} + с)
= (Ь — с) (а3 (Ь + с) ~* я1 0* 4" + ^) +
= 0—с) {а*6(а — /;)4~л'Ма — й) + #2 № — а*)|
= (6 — с) (а — Ь) \а2Ь 4- а2с — ся 4 + Ь)}
= (& — е) (а — 6) {Ь(аа — са) + ас(а С)І
= (Ь — с) (а — 6) (а — с) (аЬ 4" +ас)-
6. Разложить на множители ах+* — аѵ//' + 46Л— Ь*+|Г.
Замѣчая, что показатели складываются при умноженіи степеней одной и той же буквы, замѣняемъ 1-й и 4-й члены произведеніями ах. 4 и ЬХЬУ, послѣ чего данное выраженіе приметъ видъ ахау — аУЪ9 4~ а^*х — ЪХЬ\ или ау (ах — Ьѵ) 4“ 4- Ьх (а* — &ѵ). и наконецъ (ах — 4 (а* 4“ &*).
7. Разложить на множители ж3 + 4я;* + я;— ®- Представивъ второй членъ въ видѣ Зх2 4- я2, а третій — въ видѣ Зх — 2х, получаемъ выраженіе
х3 4“ Зя* + я2 + Зя — 2х — 6 = а;2 4 + 8) + я 4 + 3) — 2 4 4“ 3) = = 44-3) 424’Л? и 2) = 44- 3) 424“2^—х—2) _ 44- з) 4 4+2)“ — 44-2)1 =4 + 3) {4 +2) 4- 1)1=4 + 3)44-2)4—1).
Умноженіе и дѣленіе многочленовъ съ буквенными коэффиціентами.
56. Если въ данныхъ для умноженія многочленахъ встрѣчаются члены,
содержащіе одинаковыя степени главной буквы, то такіе члены разсматриваютъ
х 4 + 3) — 2 4 + 3) =
...ЛЧ^-т^ЛКЙМЪ
Пусть, напр.,
. х3 + Зя2 + х2 + Зл; — 2х — 6 = а;2 4 + 8)4
образомъ полученный, считаютъ коэффиціентомъ этой степени, требуется умножить
36* на
ах3 6я3 — а‘4‘2 + а3х — Забл2 — - + /Д& — а1 -н
ах* + а2х — Ь2х — Ьх2 -4- а3 — 24
Сдѣлавъ вынесеніе за скобки, представимъ первый многочленъ въ видѣ
(а + Ь)я3 - (а* + ЗаЬ + + (а* + Ь8)я — а* ЗЬ\
а второй въ видѣ
(а — 6)х2 4“ (а* — 6а)ж-(“ а3 — 2б3.
Разсматриваемъ первый многочленъ какъ четырехчленъ, а второй какъ трехчленъ; а -|-&т и а:іЦ-63—какъ коэффиціенты при степеняхъ х
перваго многочлена. —а44~^^4 какъ свободный членъ этого многочлена: а — Ь и а* — Ь1 — какъ коэффиціенты, и а3 — 27/ — какъ свободный членъ второго многочлена.
Чтобы многочлены уписались въ одной строкѣ, скобки замѣняютъ вертикальною чертою, справа отъ которой пишутъ степень буквы х, а слѣва одинъ подъ другимъ члены коэффиціента, каждый съ его знакомъ. Дѣйствіе располагаютъ слѣдующ. образ.
о* о о- а ж3 — а8 — Заб — Ъ1 х* 4-а1 — 6» х* -|-а* 4-6* х 4-а» — 2Ь* . х — а1 4-36* . * й « * « • множимое множитель
а» — Ь* 1 1 х* — а* — 2а*й -|-2а6’ 4-6» +“* 4-а«Ь — аЬ* — Ъ* х* -а‘ ’ — аѢ • -г-аЬ* — а* — За3Ь 4-Заб* Ха‘ 4-а3/? — 2а68 — 2Ь* X3 — а* ’ Ч-а'Ь । 4-Заб1 - 368 4“ а3 — а3//2 1 -4 а263 — а3 — За4/; —а36* 4^2а363 -|- баб* 4-26* х3 — а* -!-а‘Ь» ' За3М — 36* 4-«* — а863 — 26* ] X — а’) - 2а*63 - За*6* — 66" Произведеніе до приведенія.
а’ -6* х* — а*Ъ 4~аЬа х* -4- а‘ — За36 4-2а63 — 26* х3 — а” — 2а*6 — 2а363 + За363 і 4-9а6* і — 26я 1 х34-а‘63 ' - а*6’ ; 4-За*6‘ — 56* 1 X 1 — а71 - 2а*Ь3 - За8// — 6// 1 'X' і и и 1 *=с *=с 1 ф У и я □ ® ® я с-Ы о
Сперва умножаютъ всѣ члены множимаго на ах2, потомъ на — 6х2, затѣмъ на 4“^ и т. д., располагая и произведеніе вертикальными колоннами по степенямъ буквы х; соединивъ, наконецъ, подобные члены въ каждой колоннѣ, получаютъ окончательное произведеніе.
57. Пусть требуется раздѣлить многочленъ съ многочленными коэффиціентами на другой такого же рода. Дѣйствіе располагаютъ какъ обыкновенно, съ тою разницею, что вмѣсто скобокъ употребляютъ вертикальныя черты. Дѣленія
коэффиціентовъ совершаютъ отдѣльно, называя эти дѣйствія частными дѣленіями. Все это указано въ нижеслѣдующемъ примѣрѣ.
і I
X*
х* -ф-4а» і х -|-4а1
-|-10а6« I — 96»
а* -ф-а»6» ' '"/ +&*; а' -ф- а«6» + ь‘ х» -4-4а* -ф-ІОаб* 4~5а26 — 5а&2 ; Н-ЗЬЭ х — 9Ь* X
ч • 2а3 — 5аЧ -1- 5а&2 — 36* 2а3 — 5а2Л х -|-4а* — 96» ♦ і х -4-4а» — 96»
-|- 5а6»
— 36»
О.
Частныя дѣленія, служащія для опредѣленія
1-ое частное дѣленіе.
а* — а
— а»6» + аЬ* — 6* — а»6«
коэффиціентовъ частнаго:
2-ое частное дѣленіе.
6‘ а2 — аЬ ~|- 6а а* ' +6* а2—аЪ-\~Ь*
а» —6» а4—
-аб» — 6* б
аѢ -4-6'
а»6-а»6»4-а6* ______ I
а*6»—а6»-|-6* а*6»—аб»
Ъ*
О
3-ье частное дѣленіе. 2а» - 5а»6 -ф- 5а6» — 36» а»
і
2а —36
_3а»г,_|_3а6»_ 36» — За»6—Заб» — 36»
О
ГЛАВА VII.
О дѣлимости на биномы вида х а. — Основанія способа неопредѣленныхъ коэффиціентовъ.— Различныя приложенія предыдущихъ теоремъ.
58. Теорема I,— Если раціональный цѣлый относительно буквы х полиномъ, расположенный по убывающимъ степенямъ этой буквы, раздѣлимъ на биномъ х — а, то въ остаткѣ получимъ результатъ подстановки въ этотъ полиномъ буквы а вмѣсто х.
Приводимъ доказательство д'Аламбера.
Всякій полипомъ, цѣлый и раціональный относительно -с, можно представить въ видѣ
А,Х" + 4- 4-... + А,®* 4- А,® 4- А„.
разумѣя подъ т какое-нибудь цѣлое положительное число, а подъ А,н, Ат-і, ... АІГ Ао— нѣкоторые коэффиціенты, т.-е. выраженія, не содержащія буквы х. Если такой многочленъ раздѣлить на х — а, то окончательный остатокъ долженъ быть выраженіемъ, но содержащимъ буквы х; въ самомъ дѣлѣ, если допустить, что остатокъ содержитъ букву х хотя только въ первой степени, то можно бы было продолжать дѣленіе, потому что дѣлитель содержитъ также букву х въ первой степени. Означивъ этотъ, не содержащій буквы я, окончи-тъііныз остатокъ черезъ К, постараемся опредѣлить К, Назвавъ для этого част-эое. которое, какъ і дѣтое, должна быть многочленомъ, расположеннымъ но иисходящііъ стхпейжгь буквы х, черезъ 9, и замѣтивъ, что дѣлимое = произведенію дѣлителя на частное, сложенному о> остаткомъ, получимъ
А^х*Ат_ >л?ж 1 ... А|іК-|— Ао = (х—&). у-|—В.
Замѣчая, что обѣ части этого равенства представляютъ лишь различныя формы одного и того же выраженія, убѣждаемся этимъ, что равенство наше есть ничто иное какъ тождество, т.-е. равенство, справедливое при всякой величинѣ входящихъ въ него буквъ. Слѣдовательноѵ оно будетъ справедливо и тогда, когда, въ частности, положимъ х = а, Но при такой подстановкѣ первая часть приметъ видъ
А„«"‘ 4- Ап,-іап‘-1 + - + М 4- Ао ... (1).
и слѣд. не будетъ содержать буквы х, такъ какъ и коэффиціенты Ат,,.., Ап Ао не содержатъ х, Что касается второй части, то въ выраженіи 9 буква х также исчезнетъ; разность х—а, при подстановкѣ а вмѣсто х, обратится въ а — а, или въ ноль, а слѣд. и произведеніе котораго одинъ мно-
житель равенъ О, также обратится въ 0. Во второй части останется, поэтому, только выраженіе К, которое не измѣнится отъ указанной подстановки, такъ какъ совсѣмъ не содержитъ буквы х. Итакъ, дѣлая х=а. мы вмѣсто прежняго равенства получимъ слѣдующее
АХ' + А™-^"'-1
Аі« + Ао — В,
которое и доказываетъ, что остатокъ имѣетъ форму даннаго многочлена, въ которомъ буква х замѣнена буквою а.
59. Если бы дѣлитель былъ х то этотъ случай легко привести къ
разсмотрѣнному, замѣтивъ, что можно представить въ видѣ разности — а). Отсюда прямо вытекаетъ
Теорема П, служащая дополненіемъ первой: родгональ-
кым относительно буквы х полинома раздѣлимъ на биномъ х + а, то въ остаткѣ получимъ результатъ подстановки въ этотъ полиномъ буквы (—а) вмѣсто х.
Примѣры. I. Найти остатокъ отъ раздѣленія многочлена
Зх5 — 4х4 — 2х2 -р 7 на я — 2.
Подставляя въ данный полиномъ 2 вмѣсто х. находимъ окончательный остатокъ
Н = 3.25— 4.21- 2.22 +7 = 96 — 64 — 8 + 7 = 31.
II, Найти остатокъ отъ раздѣленія тринома
х1 — 8х + 15 на х+5.
Подставляя въ данный триномъ (— 5) вмѣсто х, получимъ (— 5)2 — 8 . (— 5) + 15 = 25 + 40 + 15 = 80. Окончательный остатокъ = 80.
60. Изъ доказанныхъ теоремъ вытекаютъ такія слѣдствія:
Слѣдствіе і. — Если многочленъ обращается въ ноль послѣ замѣны въ немъ буквы х буквою а, то онъ дѣлится на х — а; если многочленъ обращается въ ноль послѣ замѣны буквы х буквою ( - а), то онъ дѣлится на х-|-а.
Въ самомъ дѣлѣ, многочленъ, полученный послѣ замѣны буквы х буквою а или (— а)тесть ни что иное какъ окончательный остатокъ отъ раздѣленія даннаго многочлена въ первомъ случаѣ на х— а, во второмъ — на # + а. Но если оковчат. остатокъ равенъ нулю, то это значитъ, что многочленъ дѣлится безъ остатка — въ первомъ случаѣ на х — а, во второмъ на х + а.
Слѣдствіе II, обратное предыдущему. Если многочленъ дѣлится па х — а или иа х + а, то результатъ подставки въ него — въ первомъ случаѣ буквы а, а во второмъ (—а) вмѣсто х—долженъ быть равенъ нулю.
Въ самомъ дѣлѣ, такъ какъ, по условію, многочленъ дѣлится на х — а или то остатокъ въ обоихъ случаяхъ долженъ быть равенъ нулю; но этотъ остатокъ есть результатъ подстановки вмѣсто х буквы а или (— а); стало быть, этотъ результатъ долженъ быть равенъ нулю.
II р и м ѣ р ы. I. Трехчленъ х- — 2х + 1 обращается въ 0, если вмѣсто х подставить 1; слѣд. онъ дѣлится на х — 1.
ТІ. Многочленъ 4ах3—7а*х2— ба^ + ^а1 обращается въ 0 при х = а. а потому онъ дѣлится на х—-а.
Ш. Триномъ х* + 5х + 6 обращается въ 0 при х^— 3, слѣд. онъ дѣлится на х + 3,
61, Законъ составленія частнаго отъ раздѣленія цѣлаго относительно буквы х полинома на биномъ х — а.
Легко вывести законъ, но которому составляется частное дѣленія многочлена
А„/м + +... + А+ + + Аа на х — а.
Въ самомъ дѣлѣ, совершая дѣленіе, найдемъ:
Рх*-|- А *_ і 1+Ал_2^і-3+„ .
— РхЧ-ра#*"1
я^Н-А*-^*-2-)-,,.
Найдя первые три члена частнаго, замѣчаемъ, что частное есть полиномъ степени т — 1, при чемъ:
Коэффоіектъ перваго члена частнаго равенъ коэффиціенту 1-го члена дѣтаго:
Коэффиціентъ 2-го члена частнаго равенъ произведенію предшествующаго коэффиціента на а, сложенному со вторымъ коэффиціентомъ дѣлимаго;
Коэффиціентъ третьяго члена частнаго равенъ произведенію предшествующаго коэффиціента на лц сложенному съ третьимъ коэффиціентомъ дѣлимаго.
Докажемъ, что этотъ законъ общій. Пусть, слѣдуя обыкновенному правилу дѣленія, мы нашли въ частномъ членъ Рх*”1. Онъ получился отъ раздѣленія перваго члена соотвѣтствующаго остатка на х; сл. первый членъ остатка есть Рх\ а потому весь остатокъ будетъ РяЛ + Аь-ія*”1 + Лі-г#*”2 -р... Умножая членъ частнаго Ря;*-*1 на дѣлителя и вычитая это произведеніе изъ сказаннаго остатка, въ новомъ остаткѣ получимъ
(Ра + А*-і)ж*“1 -ф- А*_2^2 + ...
Раздѣливъ первый членъ этого остатка па находимъ слѣдующій членъ частнаго
(Р« +#*-2.
* 4
Коэффиціентъ его равенъ произведенію предшествующаго коэффиціента на а, сложенному съ коэффиціентомъ того же порядка дѣлимаго. Общность закона коэффиціентовъ такимъ образомъ доказана.
Если окажется, что дѣлимый полиномъ неполный, т,-е. въ немъ недостаетъ членовъ съ какими либо промежуточными степенями главной буквы, то для приложенія предыдущаго правила слѣдуетъ возстановить недостающіе члены, внося ихъ съ коэффиціентомъ 0.
62. Если дѣлитель будетъ то разсматривая его какъ х— (—а)*
заключаемъ, что для нахожденія частнаго нужно только въ частное § 61 вмѣсто а подставить (— а); сдѣлавъ это, найдемъ
Атят”1 —Аота .тт“2 + Ата® . .тт“а . . .
+ Лт~1 ; -—Ат-1&
+ Ат—2
62- Примѣры. I. Найти частное и остатокъ отъ раздѣленія
5х* — 23#* + 3я: — 58 на х—2.
Дополняя данный полиномъ членомъ съ х\ имѣемъ 5х4 Ц- 0 + х* — 23х« — Зх —58.
Коэфф. 1-го чл/частнаго = 5 а 1-й чл. частнаго = 5х3
» 2-го > » ~ 5.2 + 0 т.-е. -р 10 > 2-й » > + 10х3
» 3-го » > + Ю.2 — 23 т.-е. — 3 > 3-й > » —— Зх
» 4-го » > = (—3).2-|- 3, — 3 > 4-й > > =— 3
Искомое частное, поэтому. = 5-г3 + ІОх* — Зх — 3.
Остатокъ В = 5 . 2* — 23.2*+3 . 2 — 58 = 80 — 92 + 6— 58 = — 64.
Итакъ: ^Аг-^ + Зх-эв = 5д.а ] Оал _ За. _ 3 .тіД X *— х ’ X —- х
П. Такимъ же образомъ найдемъ
= дЛ _ 2жа -4- 2х — 2 Н-------
4~ 1 1 1 х -р 1
III. Найти частное и остатокъ отъ раздѣленія
х3 — Зха+2х — 1 на 2х—3.
Для приложенія нашего правила нужно дѣлимое расположить по степенямъ 2х, разсматривая 2х какъ главную букву. Множа и дѣля первый членъ на 8, изображаемъ его г въ видѣ (2л:)8; множа и дѣля второй членъ на 4, пишемъ 3
его въ видѣ д (2х)а. Дѣлимое так. обр. будетъ
§(2*)» —|(2*)»+(2*)-1.
Затѣмъ, прилагая правило, найдемъ
п
,г*-~3.г2 + 2я —1 _ х?_3 1 8
2ж — 3 ~ 2 Iх 8 2.г —3
63. Обобщеніе теоремы § 58. ~ Способомъ, указаннымъ въ § 58, докажемъ, что остатокъ отъ раздѣленія цѣлаіо по буквѣ х полинома на биномъ вида рх±у есть результатъ подстановки въ этотъ полиномъ • ‘такою значенія х, кояго/хьнь биномъ рх^у обращается въ ноль.
Разсмотримъ, наприм., случай дѣленія на да + д, и пусть частное будетъ <і> а остатокъ, который не будетъ содержать буквы х* пусть будетъ В; имѣемъ
+ Ат-1*”*-14- • • • + Ао = (Рж+«) • 4 + В’
Дадимъ ж-у значеніе—при которомъ + з обращается въ ноль; при лтомъ В. какъ не содержащій буквы х, останется безъ измѣненія, и получимъ
тѣть теорема и доказывается. Подобнымъ же образомъ докажемъ теорему и для сіучм. когда дѣлителемъ будетъ рл' —
Слѣдствія. — Отсюда непосредственно вытекаетъ: 1) если полиномъ обра-шстсі въ ноль по замѣнѣ въ немъ буквы х количествомъ —то онъ дѣ--итсі на и 2) если полиномъ дѣлится на то результатъ под-
ошавки въ него количества вмѣсто х равенъ нулю.
64. Теорема III, — Для того чтобы цѣлый относительно х поли-я**хъ дѣлился на х — а или на #4"^; необходимо, чтоды низшій (свободный) членъ его дѣлился на а.
Въ самомъ дѣлѣ, если полипомъ 1* дѣлится, наприм., на х— а, то
Р = (2г —а) , ч(
гдѣ Ч — цѣлый относительно х полиномъ; изъ этого равенства слѣдуетъ, что низшій членъ полинома Р, какъ произведенія, равенъ произведенію а на низшій членъ частнаго Ч» а слѣд. долженъ дѣлиться на а.
65. Теорема IV.—Нели полиномъ Р, цѣлый относительно х, дѣлится на каждый изъ биномовъ х — а, х— Ъ, х — с, гдѣ а, Ъ и с неравны между собою, то онъ дѣлится и на ихъ произведеніе.
По условію, полиномъ Р дѣлится на х — а: пусть частное будетъ Ч, гдѣ Ч есть также цѣлый относительно х полиномъ; въ такомъ случаѣ
Р= (я —а) , Ч . . . (1).
Но полиномъ Р, по условію, дѣлится и на х — Ь, слѣдов. при х = б онъ обращается въ ноль. Итакъ, если въ предыдущее равенство вмѣсто х подставимъ Ь, то первая часть его обратится въ ноль; слѣдов. и вторая, при подстановкѣ въ нее Ь вмѣсто х, должна обратиться въ ноль, т.-е. должно быть
(Ь — а). Чь = 0, .
гдѣ Чд означаетъ выраженіе Ч, въ которомъ х замѣненъ буквою Ь. Мы имѣемъ произведеніе двухъ множителей: Ь — а и Чм равное 0; для этого необходимо, чтобы по крайней мѣрѣ одинъ изъ нихъ былъ нулемъ. Но множитель Ь — а не есть 0, ибо, по условію, Ь неравпо слѣд. Чъ должно быть нулемъ. Итакъ, Ч обращается въ поль при х — Ь, слѣд. оно дѣлится па х — Ъ. Означивъ частное этого дѣленія черезъ Ч\ гдѣ Ч* есть цѣлый относит. х полиномъ, имѣемъ
Ч = (Я-Ь). Ч'. . .(2).
Вставляя вмѣсто Ч его величину въ равенство (1), получаемъ
Р = (я —а)(я —Ь)Ч'. . • (3).
По условію, Р дѣлится на х — с, слѣд. полиномъ Р, при х=с, обращается г» ишь; поэтому и вторая часть равенства (3)тпри# = с, должна обращаться п жиь, т.-е. должно быть:
(с — а) (с — Ь) Ч'с = 0.
гт /. *-ть значеніе полинома Ч" при х — с. Но разности с — а и с — Ъ пе-ъаж» ібо, по условію, а, Ь и с различны, слѣдов. чтобы произведеніе
было нулемъ, нужно чтобы было —0. Это значитъ, что <}' дѣлится на я — с; обозначивъ частное этого дѣленія черезъ имѣемъ
<Г= (* - с) . (Г
Внося величину. Ц' въ равенство (3), получаемъ
р = — а) (а? — Ь) (х — с). Ч".
Теорема такимъ образомъ доказана.
Примѣр ъ. Доказать, что полиномъ
+ Лсг — — уѴ — №
дѣлится на произведеніе (# — у) (-г — г) (у — г
Подставляя въ данный полиномъ у вмѣсто т, находимъ, что онъ обращается въ 0; слѣдоват. онъ дѣлится на х— у. Такимъ же образомъ убѣждаемся, что какъ при = такъ и при у —л полиномъ обращается въ 0; слѣдов. дѣлится какъ па х — такъ и на у — Дѣлясь на каждый изъ биномовъ х — у, х — з, у - г въ отдѣльности, онъ, въ силу теоремы IV, дѣлится и на ихъ произведеніе.
66. Предыдущія теоремы служатъ для нахожденія цѣлыхъ дѣлителей вида х — а нѣкотораго даннаго цѣлаго относительно х полинома. При помощи теоремы III можно опредѣлить, какіе цѣлые биномы этого вида лсогушь ймь дѣлителями, а при помощи теоремы П, слѣдствіе I. опредѣляемъ тѣ изъ нихъ, которые въ самомъ дѣлѣ служатъ дѣлителями даннаго полинома.
Очевидно, что число дѣлителей полинома не можетъ превышать его степени; иначе, въ силу теоремы IV, онъ долженъ бы былъ дѣлиться на полиномъ, котораго степень выше его собственной, а это невозможно.
Приводимъ примѣры.
1. Найти всѣхъ цѣлыхъ двучленныхъ дѣлителей полинома
.г1 - 17.г3 + 98я?« — 232л:
192.
если таковые имѣются.
Находимъ дѣлителей числа 192; это будутъ числа 2, 3, 4, 6, 8 н т. д. По теоремѣ третьей, искомые дѣлители, если только они существуютъ, будутъ вида #±2, # + 3. я + 4т #±6, . . .
Подставляя въ данный полиномъ вмѣсто я число 2, легко убѣдимся, что полиномъ обращается въ ноль; стало быть онъ дѣлится на х—2,
Подставляя вмѣсто я число — 2, убѣдимся, что полиномъ не обращается въ ноль; слѣд. #-|-2 не есть его дѣлитель.
Подставляя вмѣсто х число 3, убѣдимся, что полиномъ обращается въ ноль; слѣд. дѣлится на х — 3.
Подставивъ вмѣсто х число — 3, замѣтимъ, что поликомъ не обращается въ ноль; слѣд. не дѣлится на я^З,?
Продолжая такимъ же образомъ, найдемъ, что данный полиномъ имѣетъ дѣлителями х— 4 и я — 8.
Мы уже нашли четыре дѣлителя: х — 2, х — 3^ х 4, .с —8; другихъ цѣлыхъ дѣлителей не можетъ быть, такъ какъ данный полиномъ — четвертой степени.
II. Найти цѣлыхъ двучленныхъ дѣлителей полинома
хэ — (а -|- Ь 4- с) х* -р (аЬ 4~ «с 4~ М х — аЬс,
еси таковые существуютъ.
Въ силу теоремы III, искомыми дѣлителями могутъ быть только
х — а, — Ь, х— с; я 4” ^4“ 4“ с.
Но при х = а полиномъ обращается въ
а3 — (а Ь 4~ с)а* 4" (а& 4“ ас 4“ М а —
что, какъ легко видѣть, приводится къ нулю. Слѣдоват. х— а есть искомый дѣлитель.
Такимъ же образомъ убѣдимся, что х — Ъ и х — с также суть дѣлители даннаго полинома.
Нашъ полиномъ — третьей степени; мы нашли трехъ дѣлителей; другихъ не можетъ быть; слѣд. задача рѣшена.
67. Такимъ же образомъ, какъ мы доказали теорему IV, докажемъ, что если полиномъ дѣлится въ отдѣльности на каждый изъ биномовъ рх
/ г / і // « . о а и'1
рх-]-$, р , при условіи, что значенія х : — уь при кото-
рыхъ эти дѣлители обращаются въ ноль, .всѣ различны, то онъ дѣлится и на ихъ произведеніе.
68. Слѣдствія теоремы IV.
1* Если полиномъ Р, цѣлый относительно х. т-й степени:
4" Ат-і^-14- . . . 4" М + Ао
обращается въ ноль при т различныхъ значеніяхъ буквы х : а, 6, с, . . . А, А, то онъ можетъ быть представленъ въ видѣ
Ат (я — а) (я — А) (я — с) , . . (я — і) (я —А).
Въ самомъ дѣлѣ, пусть полиномъ четвертой степени
Р — + Аэя3 4“ А*#* 4- ^х 4“ Ав
обращается въ ноль при четырехъ различныхъ значеніяхъ я: а, с и й. Въ такомъ случаѣ, по теоремѣ IV» онъ дѣлится на произведеніе
(х — и) (х — Ъ) (х — с) (х — й),
которое само четвертой степени; стало быть частное не содержитъ я и есть нѣкоторое число; пусть это число будетъ А. Данный полиномъ равенъ произведенію А (я — а) (я — Ъ) (х — с) (х — й). Если выполнить умноженіе и расположить члены во убывающимъ степенямъ то полученный многочленъ долженъ быть тождественъ заданному, т.-е. состоять изъ совершенно такихъ же членовъ, і потому и высшіе члены обоихъ должны быть равны, т.-е. А^1 ~ Ах\ откуда А = А|: теорема доказана, и
Р — А4 (х — а) (# — Ъ) (х — с) (я — е?).
И_ Опредѣленіе. Если цѣлый относительно х полиномъ обращается въ ноль ~тл ютомъ значеніи х^ то говорятъ, что онъ тождественно равенъ нулю.
6*
Докажемъ, что если цѣлый относительно х .полиномъ, «т-ой степени, обращается въ ноль нри нѣсколькихъ значеніяхъ х, число которыхъ превышаетъ иі, то онъ тождественно равенъ нулю (т.-е. равенъ нулю при всякомъ я).
Пусть, наприм., полиномъ
Р = А^1 + А3х* Аах2 + + А0
•
обращается въ ноль при пяти различныхъ значеніяхъ х: а, б, с, е, Мы доказали, что если полиномъ Р обращается въ ноль при четырехъ значеніяхъ х: а, Ь, с и то онъ беретъ видъ
Р = А4 (х — а) (х — 6) (х — с) (х — й) . . . (1).
Но. по условію,’Р обращается въ ноль также и при х=.е; слѣдов, А4 (е — а) (е — 6) (е — с) (<? — гі) = О;
но какъ множители е— а* е — &, . . . отличны отъ нуля, то чтобы произведеніе равнялось нулю, необходимо, чтобы А4 равнялось нулю. Но если А4 = От то изъ (1) видно, что каково бы пи было х, всегда будетъ Р = О.
Итакъ, Р равно О при всякомъ х, т.-е. тождественно равняется нулю.
69. Теорема V. цѣлый относительно х полиномъ [ (х) йіь-лится въ отдѣльности на (х —- а)1, (х — 6/, (х — с)\ . . . а, М . . , неравныя между собою числа* то онъ дѣлится и на произведеніе
(х — а)1. (х — &)?. (х — с)ч
Пусть /* (х) = (х — а)1. ср (х) и /Дх) = (х — 6)?. ф (х), гдѣ и (х) и ф (х) частныя отъ раздѣленія /Дх) на (х — а)а и (х — Ь)?. Имѣемъ
(х — а)1 «р (х) = (х — &)?ф(х) , . , (1).
Замѣнивъ въ атомъ тождествѣ х буквою Ъч получимъ
(6-а)*ф(6) = О
и какъ Ь — а, по условію, не есть О, то должно быть ф (6) = 0; другими словами, результатъ подстановки буквы Ъ вмѣсто х въ ф (х), обращаетъ эту’функ-цію въ О, слѣд. ср(х) дѣлится на нѣкоторую степень/^' разности (х — Ь), такъ что должно быть
? (х) = (х — &)₽' . (х), . . .
съ условіемъ Докажемъ, что Для этого подставимъ въ\тождество (1) (х — />)? (х) вмѣсто ^(х); найдемъ
(х — а)а (х — б)? (х) ~ (х — б)? ф (х). •
Если бы было то обѣ части можно бы было раздѣлить на (х— и положивъ въ частныхъ х = 6, нашли бы
(Ь - а)* (&) = О,
но это невозможно, такъ какъ ни (Ъ — а)1, ни (6) не равны нулю. Заклю
чаемъ, что нельзя допустить, чтобы [Г было меньше Подобнымъ же образомъ докажемъ, что не можетъ быть и больше Слѣдовательно [*' ~ я потому
? (ж) = (х—г»)? (х),
п слѣдовательно
/(я:) = (х ~ а)’ (х — Ь)? (®).
Продолжая подобныя же разсужденія, докажемъ, что (я) дѣлится на (х — е)?, а слѣд. Дл?) на (я — а)а (я—6)?(я — с)? и т. д. Теорема доказана.
70. Теорема VI. Чтобы цѣлый относительно х полиномъ тождественно (т-е. при всякомъ значеніи х) равнялся нулю, необходимо и достаточно, чтобы всѣ коэффиціенты его равнялись нулю.
Пусть данный полиномъ будетъ
Р = дж4 + Вл:« + С^4 В# + Е.
Такъ какъ этотъ полиномъ долженъ быть равенъ нулю при всякомъ х; стало быть, въ частности, онъ долженъ быть равенъ нулю и при х — 0. Но при х = О всѣ члены, содержащіе х, обращаются въ 0, слѣд. равенство
Кх* 4* в#3 -р с#2 -|- в = о . . „. (і) обращается въ
Е~0 . . . (И).
Откинувъ въ равенствѣ (І)Е, какъ количество, равное 0, а въ остальныхъ членахъ вынеся за скобки х, получимъ равенство
1> = ^Ая3 4-Вя24-{& + !>) = 0.
I
Для того, чтобы Р равнялось 0 при всякомъ я, необходимо, чтобы одинъ изъ его сомножителей всегда равнялся нулю; но х равняется нулю не всегда, а только при х = 0, слѣдовательно, необходимо, чтобы второй множитель всегда равнялся нулю. Такъ какъ Ля3 4" Вж*4“Са:Ч~® долженъ быть равенъ 0 при всякихъ значеніяхъ х, то онъ долженъ быть нулемъ и при я = 0. Но положивъ въ немъ х = Ъ, обратимъ его въ В, а равенство Лх34“В#*-4Ся:4" 4-1) — 0 въ
0 = 0. . . (III).
Откинувъ въ полиномѣ Р члены І)я и Е, какъ равные 0, а въ остальныхъ вынеся за скобки х8, получимъ произведеніе
Р = х4А^4-Вх + С),
которое должно быть равно 0 при всякомъ х. Отсюда, подобно предыдущему, докажемъ, что
0 = 0 . . . (IV)
і т. д. Такимъ образомъ всѣ коэффиціенты полинома Р должны быть равны 0. Доказали, что это условіе необходимо. Но оно и достаточно, потому что если всѣ коэффиціенты равны 0, то и полиномъ Р равенъ нулю.
71. Теорема VII. Если два цѣлые относительно х полинома остаются равными при всякомъ значеніи х, то они тождественны.
Пусть полиномы
Ах5 4~ В#4 С#3 4* О#* 4“ Ея -^Р и о#3 -|- Ъх* -|" "4 е
имѣютъ одинаковую численную величину при всякомъ тогда ихъ разность будетъ тождественно равна нулю. Но эта разность есть
Ая*-4 В#14- (С — а)#3 4“ (° — 4" (Е Н“ (Е — *):
слѣд., по теоремѣ V", имѣемъ:
А —О; В = О; с = а; О = Ь; Е — й; ? = С;
Изъ того, что А = О и В —О, заключаемъ, что члены Ахя и Вг4 исчезаютъ, такъ что число членовъ въ обоихъ полиномахъ одинаково; а какъ С = а, И = Ь, Е = й и Е = е, то коэффиціенты при одинаковыхъ степеняхъ х равны. Оба полинома ничѣмъ не отличаются одинъ отъ другого, или, что тоже, тождественны.
Примѣчаніе. Теоремы VI и VII служатъ основаніемъ способа неопредѣленныхъ коэффиціентовъ, имѣющаго многочисленнѣйшія и разнообразнѣйшія приложенія въ алгебрѣ. Изобрѣтеніе этого способа приписываютъ знаменитому французскому математику и философу Декарту (Сагіеяіь).
Различныя приложенія предыдущихъ теоремъ.
72. Приложеніе /.—Выведемъ условія дѣлимости суммы или разности одинаковыхъ степеней двухъ количествъ на сумму или разность основаній.
1. Пусть требуется раздѣлить хт— ат на х— а. Подставивъ въ дѣлимое букву а вмѣсто х, найдемъ окончательный остатокъ; онъ будетъ = а™ — ат или О, откуда заключаемъ, что дѣленіе совершается безъ остатка*
Для нахожденія частнаго представляемъ дѣлимое въ видѣ полнаго многочлена иг-ой степени;
хт 4- О . я"1'1 4- О . +
4- О . х — а”1.
По правилу § 61, высшій членъ частнаго равенъ я”*-1. Второй членъ частнаго содержитъ ж®1’2; а коэффиціентъ его найдемъ, помноживъ коэффиціентъ перваго члена частнаго на а, что дастъ а, и придавъ сюда второй коэфф. дѣлимаго т.-е. О; итакъ, второй членъ частнаго ~ ахт~\ Продолжая такимъ образомъ, найдемъ
а.'М _
——— = Xя*"14~ал;т_24^ аЪ?та"34~ * * , 4^”’’ - . (1)*
2* Раздѣлить хт4“аШ па х — а, Подставляя въ дѣлимое вмѣсто х букву а, найдемъ окончательный остатокъ 4~ = 2аи. Отсюда заключаемъ, что
дѣленіе не совершается безъ остатка. Составляя частное по предыдущему, получимъ
4-«т-1
2ат
х — а
- (2).
3. Раздѣлить хт— ат на #4~а’ Подставивъ въ дѣлимое вмѣсто а? коли-
чество (— а), найдемъ окончат, остатокъ. Онъ будетъ: а)1 при ш четномъ равенъ (—«)т— ат = ат — а™ = 0. Частное же будетъ въ этомъ случаѣ
---------= .-рат’2ж-а’п-1 . . . (3).
при т нечетномчэ остатокъ = (— я)ш — ыИІ = — ам — ат = — 2аш; частное же
= ят-1
2дт
-г -|-д
(4).
4. Раздѣлить «” + °™ ва ® + «. Подставляя въ дѣлимое вмѣсто х букву (— а), найдемъ окончательный остатокъ. Онъ будетъ: і) при т четномъ: (—а)“ 4" а"* — а"*-|-а"*= 2а“, такъ что
ггпі і цы 9лгм
—-±- = 4- — - . . ат-2^ — 4- ——•. , 45).
х + а 1 х -р
р) при т нечетномъ: ( — а)" — а“ = — = 0; слѣдов, дѣленіе совер-
шается безъ остатка я частное
. +ат-1 , . . (6).
Отсюда заключаемъ, что 1) — аш всегда дѣлится на # — а; 2) а?л — ат
дѣлится на + если т четное; 3) никогда не дѣлится наж — а,
но дѣлится па а? + а ПРИ т нечетномъ. Такимъ образомъ нашли тѣ же выводы, какіе получили раньше непосредственнымъ дѣленіемъ. Новый пріемъ далъ тѣ же результаты быстрѣе.
73. Приложеніе II.—Мы видѣли, что — а™ всегда дѣлится на % — а; но ври четномъ дѣлится еще на Слѣдовательно, когда т четное, хт — а”\ дѣлясь на биномы + « и я —а, дѣлится, по теоремѣ 1Ѵ\ и на ихъ произведеніе (ж — а) (я -|- а), т,-е. на я* — Итакъ: разность одинаковыхъ четныхъ степеней двухъ количествъ дѣлится безъ остатка па разность квадратовъ тѣхъ же количествъ. Частное будетъ
__
—— — - = я™-2 4“ 4“
74. Приложеніе III. — 1, При какомъ численномъ значеніи К полиномъ
дѣлится безъ остатка на х — 3?
Чтобы полиномъ дѣлился на я — 3, нужно, чтобы результатъ подстановки въ него 3 вмѣсто х обращался въ пуль, т.-е, чтобы
З3—3 ф За+5.3 4-К = О, или 15 + К = О,
Послѣднее равенство возможно только при К = — 15.
2. При какомъ значеніи К полипомъ
дѣлится на ^4-3?
гг3 — Зя2 4“ 4“ К
Нужно, чтобы результатъ подстановки въ этотъ полиномъ числа (— 3) вмѣсто х былъ равенъ нулю, т.-е. чтобы
(— з)3-3 , 3)» + 5. (-3) + К = О, или — 69-)-К = О;
а это возможно только при К = 69.
3, При какомъ значеніи К полиномъ
я3 — 3:сй —5 а: —|— К
раздѣлится на Зг — 2?
На оси, § 63, Слѣдств., заключаемъ, что необходимо, чтобы результатъ 2
подстановки въ данный полиномъ числа вмѣсто х былъ нулемъ, т.-е, чтобы-
ѵ 62
а это возможно только при К = —
75. Приложеніе IV.—Теорема IV, § 65 можетъ быть примѣнена къ разложенію многочленовъ на множители. Методъ разложенія, на ней основанный, называется методомъ двучленныхъ дѣлителей и состоитъ въ слѣдующемъ. Расположивъ многочленъ по степенямъ какой-либо буквы, # напримѣръ, стараются открыть двучленныхъ дѣлителей х— а, х — Ь, , . . , я—А; составляютъ изъ нихъ произведеніе (я —а) (я — Ь) . . . (я — &); дѣлятъ на него данный полиномъ Р, и если въ частномъ получается выраженіе то
р = — д) (я; — Ь) , , . (# — &),($.
Разложеніе такимъ образомъ будетъ совершено.
Впрочемъ, слѣдуетъ замѣтить, что этотъ методъ не такъ удобенъ въ практическомъ отношеніи, какъ выше указанные методы разложенія; потому что въ случаѣ большого числа возможныхъ дѣлителей придется дѣлать слишкомъ много вычисленій, чтобы выбрать тѣ изъ нихъ, которые дѣйствительно служатъ дѣлителями даннаго полинома. Поэтому онъ употребляется лишь въ рѣдкихъ, исключительныхъ случаяхъ; такъ, наприм., онъ весьма удобенъ для разложенія смль метричныхъ выраженій.
Круговая перестановка. — Разсмотримъ выраженіе Ъс-\-еа~\- аЬ- членъ, несодержащій буквы а, поставленъ на первомъ мѣстѣ, а остальные члены можно получить послѣдовательно круговою перестановкою буквъ, т.-е, перемѣною а на Ь, Ь па с и с на а *). Такое же расположеніе буквъ легко видѣть и въ выраженіи — а)-|-с3(а— Ь); въ самомъ дѣлѣ, изъ а2(Ъ — с)
*) Если а, Ъ и с поставить на окружности крута (черт. 9) и, выходя отъ нѣкоторой буквы, а, двигаться по окружности крута въ направленіи, указанномъ'стрѣл-конл то мы будемъ слѣдовать въ циклическомъ порядкѣ аЬс, Ьса, саЪ, Слѣдованіе атому порядку, важно въ задачахъ, гдѣ имѣютъ дѣло съ разностями трехъ буквъ. Такъ, когда мы пишемъ Ь—- с, е — а, а - мы слѣдуемъ циклическому порядку; но нарушаемъ этотъ порядокъ, когда пишемъ Ь — с, а — с, а — 6 или а — с, 6 — а, Ь — с. Если съ самаго начала слѣдовать циклическому порядку, то вычисленія сокращаются и дѣлаются легче.
крумж перестановкою получаемъ Ъ*(с—а), а отсюда снова круговою пере-спмбою выводимъ с*{а — 6). Тоже самое замѣчаемъ въ выраженіи
(у-я) (я —ж) (я —у).
Симметричныя выраженія.—Выраженіе, которое не измѣняется отъ пе-і*твовки какой угодно пары буквъ, въ него входящихъ, одной на мѣсто дру-г*с_ называется смлсчетрычяыль выраженіемъ. Такъ, выраженія «6, в’ — аа-|-аЬ-Ь&1, а& + &а — суть симметричныя выраженія изъ двухъ
**хгь: а-|-Ь-|-с, Ьс-^са -^аЬ, а3 — 63с3 — Завс—симметричныя вира-жшя изъ трехъ буквъ; потому что, наприм., аЬ — Ьа, а* &2 = Ьа -ф- аа; а — & -|-с = а-|-с4-й = с-ЬаН“Ь=. . . Но а — 6, яР, очевидно, не-лмметричны, ибо, наприм., а — Ъ неравно Ь — а, и т. д. Замѣтимъ, что единственная симметричная функція первой степени относительно а, Ъ, с есть М(а -|- Ъ 4- с), гдѣ М—числовой коэффиціентъ.
Выраженія, которыя остаются безъ измѣненія величины при круговой перестановкѣ входящихъ въ нихъ буквъ, называются циклически^симметричными. Таково, наприм., выраженіе (Ь — с) (с — а) (а — 6), ибо величина его не измѣняется, если на мѣсто а поставить 6. с на мѣсто 6, и а на мѣсто с.
Очевидно, произведеніе, или частное двухъ симметричныхъ выраженій симметрично; ибо если ни то, ни другое не измѣняется при перестановкѣ двухъ буквъ одной на мѣсто другой, то и произведеніе, и частное останутся безъ измѣненія при такой перестановкѣ.
Ясно также, что произведеніе, или частное двухъ циклически-симметричныхъ выраженій суть также выраженія циклпчески-симметричныя.
Послѣ этих'р предварительныхъ указаній переходимъ къ примѣрамъ.
Примѣръ 1. Разложить на множители
а\Ь — с)-^~й3(с — а)4-с3(а — і) . . -(1).
Положивъ въ этомъ выраженіи Ь = с, убѣдимся, что оно обращается въ воль; слѣдов. Ь — с есть множитель этого выраженія. Такимъ же точно образомъ докажемъ, что и с — а, и а — Ъ суть множители даннаго выраженія. Слѣдовательно, оно содержитъ множитель (&—с)(с — а) (а — Ь).
По данное выраженіе есть выраженіе четвертой степени, слѣдоват., кромѣ трехъ найденныхъ множителей, оно должно содержать еще одного множителя первой степени. Кромѣ того, этотъ множитель долженъ быть симметричнымъ выраженіемъ относительно буквъ а, Ь и с. Заключаемъ, что этотъ множитель долженъ быть = а “Ь
Итакъ, данное выраженіе должно быть —
ЦЬ —с)(с —а)(а —й)(а-|-г> + с) . . .(2),
гдѣ Ь есть нѣкоторое ч^сло, остающееся безъ всякаго измѣненія, каковы бы ни были зпаченія О и с
Чтобы найти И, замѣтимъ, что (1) и (2) тождественны, а слѣдов. коэффиціенты, наприм.. при а3, должны быть равны. Въ (1) этотъ коэффиціентъ есть Ь — с; во (2) онъ есть—Ь(Ь — с); слѣдов. Ь = — 1; а потому выраженіе (1) разлагается въ формѣ
— (6 — с) (с — и) (а — Ь) (а; Ь 4- с).
Для нахожденія Ъ можно еще дать частныя значенія буквамъ а, & и е. Положивъ, наприм,, а = 0, &=1, с = 2; (1) обратится въ —6, а (2) въ 61; слѣдов. 61 = — 6, откуда Ь = —1.
Примѣръ П. Разложить (у — #)в + (# — х)3 + (я — ^)\
Убѣждаемся, что данное выраженіе обращается въ 0 при у = я, слѣдоват. у — я есть множитель даннаго выраженія. Такимъ же точно образомъ убѣдимся, что множителями его будутъ я— х и х— ул А какъ данное выраженіе есть выраженіе 5-й степени и циклически-симметрично, то оно должно быть — (у — в)(г — х}(х — у) )Ь(жа + + + + . .(I)
гдѣ въ фигурныхъ скобкахъ написана самая общая форма циклически-симметрич-наго выраженія второй степени.
Для опредѣленія Ь, безъ труда найдемъ, что коэффиціентъ при хЧ/ въ данномъ выраженіи есть —5, а въ (1) это будетъ —Ь, слѣдов. 1 = 5.
Для нахожденія М, полагаемъ х = 0. у = * = 2, п сравниваемъ данпое
выраженіе со (2); найдемъ
-1+32- 1=(- 1).2.( 1)[5.5 + 2М].
откуда М = —5. Искомое разложеніе будетъ
5(у — я) (я — х) (х (х2 + ^ + #2 - -уя —ях— ху).
П р и м ъ р ъ1III. Разложить на множители
а(Ь —• с)5 + 5(с — а)3 + с(а — &)ь.
Легко убѣдиться, что 6—с, с а, а - -Ь служатъ множителями, Слѣдоват. данное выраженіе, будучи симметричнымъ выраженіемъ 6 степени. =
{Ъ — с)(с~а)( а —Ь) | Е(а3 + &3 + +
+ М|я3(^ + сО + ?Лс + а) + с^(а + ^)]4_^аМ • - • ( +
Остается опредѣлить числовые коэффиціенты 1, М и X.
Коэффиціентъ при въ данномъ выраженіи равенъ —1, а въ (I) равенъ —Ь; слѣдов. 1=1.
Коэффиціенты при въ данномъ выраженіи 0. а во (2) есть 1— М;
слѣдов. 1 — М = О, 1 = М = 1.
Чтобы найти X, положимъ а=1, Ъ — 2. с = 3; сравнивая данное съ (1), находимъ
_ 1 + 64 — 3 = 2 (1 + 8 +27+ 5 + 16 4-27 + 6ЬТ),
откуда М = — 9. Итакъ, данное выраженіе —
(Ь-*— с) (с — а) (а — і)*{а3 + 5® + еа + + а2(Ь + с) + Ь\с + а) + с2(а + 1>) — 9аЬс}. *
Примѣръ IV. Разложить полиномъ
р = а2Ь2с2(а — 6) (а —>с) (Ь — с) — а2ЪЫ2(а — Ь) (а — <?) (Ь — сі) + —- с) (а — й) (с - - г?) — - йй с2 — е) (5 — й)(с - : й). *
Легко убѣдиться, что полиномъ Р обращается въ ноль при а•=+ а = а = г?, Ь = с и т. д.; потому онъ дѣлится на а 6, а - с, « с/, Ь — с и
т. д, Попытаемся выдѣлить этихъ множителей. Вынося изъ первыхъ двухъ чле-новъ а*Ь*(а—&), а изъ двухъ другихъ с^й2^- -й), полупимъ:
Р = д2&2(д — Ь) | с2(д — с) (Ь — с) — й*(д — с?) (& — й)}
4~ с2Й2(с —й) {д2(я- с) (а й) 62(й - с) {Ъ — й)І,
Располагая первый членъ въ первыхъ фигурныхъ скобкахъ по убывающимъ степенямъ сЛ а второй по убывающимъ степенямъ буквы й; затѣмъ, первый членъ во вторыхъ фигурныхъ скобкахъ—по убывающимъ степенямъ буквы «, а второй—буквы Ь, имѣемъ:
р = дЧа(д — Ь) [с4 — ся(д 4" Ь) -|- с?аЬ - - й4 4 й3(д -|- Ъ) (РаЪ І 4-с3й2(с — й)|д* а3(с— й)-]-аасй — 64-|- бэ(с~{-й) 6ѴЙ| или
р ^=_ д3/?а( д 6) 5 с* — й4 — (с3 —> йа) (а 6) 4“ (с3 - йа {
+ с3й2(с - й) |д4 - V (а3 Ь3) (с + й) + (а4— Ь3)сй{
Теперь видно, что въ первыхъ фигурныхъ скобкахъ имѣется множитель с — й, а во вторыхъ а— 6; выиоея ихъ, имѣемъ:
р=(а—Ъ) (с — й) І (са+й2) (с й) — (йг-|-сй-4- й3) (а 4~ Ь) 4~ аЬ (с й) |
-|- с2й2 (с—й)(а — Ь)) (а34~ Ь3) (а Ь) — (а*4“ 4“ ^а) (с 4“Ф “р сй (а !
Вынося теперь за скобки (а — Ъ) (с—й), и означивъ третій множитель буквою Р\ положимъ
Р = (а-6)(с-й),Р';
гдѣ
р' = | (С2 + й2) (с + й) — (с3 + сй 4- й2) (д + Ь) 4- аЬ (с 4- й) (
4~ с*й3;(д3— №) (а— Ъ) — (а* — аЪ— Ь2) (е -|-й) -|- сй(д -|-й)}
= дйЬ*{(с3 + й3) (с - а) 4- й(с3 +Й3)—Ь(с2 4 й*)— сй(а4-і)+ай(с ^й) |
-р С2Й2{(а2—Й3) (д—с) — &2)—й(«24”&2)-- «&(с — Й) 4^Й(Й6) 5 = а3Л3|(а — с) (Ьс^-^й — с2 — й2 —-сй)4~й2(й—,Ь)|
4- с2й2{(а — с) (а2 4- аЪ + Ь* - ай— Ьй) — Ь2(й — Ь)]
= (а — с) |а3Ь*(Ас“Ьй — с2 — й2 — сй) 4^ЛЙа* ^4 62—ай — М)}
4-Ь2й2(й-6)(аа — с3).
Вынося а — с, положимъ
Р' = (« - с)Р", гдѣ
р'^а2^|с(&~с) + й(Ь —с)|_а2Ь2й^4- с^а^с3^{а(Ъ ^-й)4-6(Ь-й)!
4-62й2(й— Ь) (д4-с)
= (с-^й) —с^-Ьс’й2^- й)(а-Ьі)-Ь63й2(й—&) (а^с)
= а*(Ь — с){Ь2(с4^Ф — <^(Ь-|-с)І 4-Й46 — й)5с2(д-4&) 63(а4"с)!
= О2(Ь _ с); с(Ъ* — й2) 4- &й(& — й) I + й2(6 — й) Iа (с* — Ь2) 4~ Ьс(с — 6) |.
Здѣсь мы можемъ вынести за скобки (Ь — с) (Ь — й); полагаемъ
р" = (^^с}(6-й)Г\
гдѣ
р”' = д2{с(Ь 4- й) 4-М| — Й^я^ + с) +^с|
- - й‘) -|- д сй( д - й) 4 (л — й) — (д — й) (лЛг4- и й'Н’ асй4 .
Итакъ, окончательно
Р = (а — 6) (а — с) (а — й) (6— с) (6 —чі) (с— й) (абс + «с^4“ Ъссі).
76. Приложеніе Г. При какихъ значеніяхъ буквъ а и Ъ полиномъ гг3-*-+ Ц- 5л; — а дѣлится безъ остатка на х* 4“ — Ъ?
Вопросъ можно рѣшить двоякимъ путемъ.
1-й методъ. Онъ состоитъ въ томъ, что совершаютъ на самомъ дѣлѣ дѣленіе, доводя его до остатка, степень котораго была бы ниже степени дѣлителя; затѣмъ выражаютъ, что остатокъ долженъ быть тождественно равенъ нулю.
Выполняемъ дѣленіе:
ж3 4" — а 4~ — &
— х3 -р Згс® + Ъх х ~р~ 5
5 | х — а
4~ 6
— 15л: + 56
Ь х — а
Чтобы дѣленіе совершалось безъ остатка, остатокъ долженъ быть тождественно равенъ нулю; а для этого, по теоремѣ VI, § 70, необходимо и достаточно, чтобы
6—10 = 0. . . (1) и 56 — а = 0, . .(2).
Равенство (1) возможно только при 6=10.
Подставляя 10 вмѣсто 6 въ равенство (2), имѣемъ
50 — а = 0,
что возможно только при а = 50,
Итакъ, искомыя значенія а и 6 суть: а = 50, 6=10.
Не трудно провѣрить, что я8 + 8яа 4” &х — 50 дѣлится безъ остатка на я«4-зя—ю.
2-й методъ (неопредѣленныхъ коэффиціентовъ). Выражаютъ, что дѣлимое равно произведенію дѣлителя на цѣлый полиномъ, котораго степень равна разности степеней дѣлимаго и дѣлителя, ибо такова должна быть степень частнаго.
Такимъ образомъ пишемъ:
я3 4- 8д;2 -{-5л; — а
(х5-|-3а; —і) (рх' + д),
такъ какъ общій видъ цѣлаго полинома первой степени есть до 4" Располагая вторую часть по степенямъ имѣемъ тождество
х3 4~ 8ягя -{-^ 5л; — & =.р - х* 4" 3-Р
2
Отсюда, ло теор> ѴП, § 71, приравнивая между собою коэффиціенты при одинаковыхъ степеняхъ буквы имѣемъ четыре условія для опредѣленія а, 6. р и а именно:
р=і;
3^ 4-д = 8;
— 6 .р
Здг=5;
Ъд = а.
Подставляя во второе равенство 1 вмѣсто р9 находимъ: 3 4“ $ = 8, откуда г; =5. Подставивъ въ третье равенство вмѣстои д ихъ величины, имѣемъ:
I
— Ь15 = 5, что.возможно только при 6 = 10. Наконецъ, вставляя въ четвертое равенство вмѣсто Ь и $ ихъ величины, находимъ: а = 50.
Итакъ: а = 50; Ь = 10; р = 1 и — 5.
Стало быть дѣленіе безъ остатка возможно только при а = 50 и‘ Л= 10; а частное есть
77. Приложеніе 1/. Въ какомъ случаѣ Xм —а** дѣлится на хр~а^ Выполняемъ дѣйствіе, чтобы найти законъ образованія послѣдовательныхъ
остатковъ:
хт — ат хр — ар____________________
хіп Ч— архт~? хт~р —ард;т—2р
р — ат
— архт~р Ч~
а2Ртт_2р — ат
„ 2р дЗРдЛі—Зр
а’^-зр — ат
Итакъ, если А означаетъ нѣкоторое цѣлое число, одинъ изъ остатковъ будетъ имѣть видъ
д^т-Ар _ а«
Поэтому, необходимо и достаточно, чтобы существовала такая цѣлая величина Л, при которой этотъ остатокъ тождественно равнялся бы нулю.
Онъ имѣетъ видъ многочлена, расположеннаго по убывающимъ степенямъ буквы я, и условія тождественности остатка нулю будутъ различны въ зависимости отъ того, будетъ ли т— кр равно 0, или отлично отъ нуля.
Если т — кр отлично отъ нуля, то коэффиціенты при степеняхъ х должны быть равны нулю, т.-е.
акр = 0 и а’" = 0;
это возможно только при а — 0. Но такой выводъ не соотвѣтствуетъ задачѣ.
Если т— кр = <\ то хт-Ар = 1; и остатокъ обратится въ ноль, когда акр = ат, т.-е. когда т = к . р.
Итакъ, необходимо и достаточно, чтобы т было кратнымъ числа р.
Въ такомъ случаѣ: и
. - у = хт-р 4* архт-іі> 4- а*рхт-3р 4" • • • 4- а“_2р«р 4“ ат-І>-
ГЛАВА VIII.
Общій наивысшій дѣлитель и наинизшее кратное алгебраическихъ выраженій. *
78. Дѣлителемъ цѣлаго алгебраическаго выраженія называется такое другое цѣлое выраженіе, на которое первое дѣлится на-цѣло. Такъ, есть дѣлитель выраженія 48.г8у*я; я— I есть дѣлитель тринома х* — 2я-|-1; х*— а* имѣетъ дѣлителями х— а, — а2 и
Общимъ дѣлителемъ двухъ или нѣсколькихъ цѣлыхъ выраженій называется такое цѣлое выраженіе, которое дѣлитъ данныя на-цѣло или безъ остатка. Такъ, ^ураженія (а — 6)2 и а2— 62 имѣютъ общимъ дѣлителемъ а— Ь. Взявъ выраженія а3 4“— а№ — Ъ\а3 — ЗаЬ3 4- 263 и а3 — 2а26 — аЬ3 4^ 26е, и разложивъ ихъ на множители, находимъ:
а3 4“ а*Ъ — аЬ'1 — 63 — (а -)- Ь)2 (« — 6);
а3 — ЗаЪ3 4- 263 = (а — Ъ)3 (а + 26);
а3 _ 2а^ _ аъ* + 263 — (а + 6) (а — 6) а — 26);
откуда видно, что данные многочлены имѣютъ общимъ дѣлителемъ биномъ а—6.
Цѣлыя выраженія, не имѣющія никакихъ общихъ дѣлителей, называются первыми между собою или взаимно простыми. Такъ, а-\-Ъ и а — Ь— выраженія взаимно простыя.
Общимъ наивысшимъ дѣлителемъ цѣлыхъ алгебраическихъ выраженій называется произведеніе всѣхъ простыхъ дѣлителей, общихъ даннымъ выраженіямъ. Такъ, въ предыдущемъ примѣрѣ общій наивыстій дѣлитель есть а — 6, потому что иныхъ общихъ дѣлителей данныя выраженія и не имѣютъ. Взявъ выраженія х*— а* и #84-2ал;2- а3х — 2а3 и разложивъ ихъ на множители, находимъ:
х4 — а4 = (я 4~ а) — а) (^2 4" и2);
х3 4- 2ах3 — а3х — 2а3 — (я4~а) (# — й) (х 2«);
замѣчаемъ, что простые дѣлители, общіе этимъ выраженіямъ, суть: #4“а н х — а; ихъ произведеніе х3 — а3 и есть общій наивысшій дѣлитель двухъ данныхъ выраженій.
Очевидно, что если данныя выраженія раздѣлимъ на ихъ общаго наивысшаго дѣлителя, то черезъ это изъ нихъ исключатся общіе ихъ дѣлители, а потому частныя не будутъ имѣть уже никакихъ общихъ дѣлителей, т.-е. будутъ первыя между собою. Отсюда вытекаетъ другое опредѣленіе общаго наивысшаго дѣлителя: ото есть такой общій дѣлитель, по раздѣленіи на который данныхъ выраженій, получаются частныя первыя между собою. Такъ, въ предыдущемъ примѣрѣ, раздѣливъ выраженія я*—а4 и ^84~2ах2 — а2д?—2а3 на общаго дѣлителя х3 — а8, получаемъ частныя #2 4“ и х 4” 2а — первыя между собою. Заключаемъ, что, по опредѣленію, я2 — а2 и будетъ общій наивысшій дѣлитель данныхъ выраженій.
Примѣчаніе I.—Между алгебраическимъ общимъ наивысшимъ дѣлителемъ и общимъ наибольшимъ дѣлителемъ чиселъ (въ ариѳметикѣ) есть существенное различіе. Общій наибольшій дѣлитель чиселъ есть такой ихъ общій дѣлитель, который по величинѣ больше всѣхъ другихъ общихъ дѣлителей. Отсюда и названіе его — наибольшій. Но общій наивасшій дѣлитель алгебраическихъ выраженій, какъ содержащій произведеніе всѣхъ общихъ дѣлителей, очевидно, будетъ по степени выше другихъ общихъ дѣлителей; но изъ этого еще не слѣдуетъ, чтобы онъ былъ больше но величинѣ: такъ а3 не необходимо больше а; папр.. если а есть положительное число меньшее 1, то «2 меньше а.
Примѣчаніе II.—Для краткости слова: общій дѣлитель будемъ означать начальными буквами о. д.; также слова: общій наивысшій дѣлитель — буквами о. н. д.
Переходимъ къ изложенію способовъ опредѣленія общаго напвысшаго дѣлителя алгебраическихъ выраженій.
79. Способъ разложенія на множителей.—Пусть требуется найти о. н. а. одночленовъ
65а5Ь*с, ЗОаЧ® и 45а<Ьпй,
т.-е. такихъ выраженій, которыя пряно даны въ формѣ произведеній.
Согласно съ первымъ опредѣленіемъ, нужно составить произведеніе всѣхъ общихъ простыхъ дѣлителей — численныхъ и буквенныхъ. Произведеніе общихъ простыхъ числовыхъ дѣлителей есть о. н. д. коэффиціентовъ и = 5. Что касается буквенныхъ производителей, то нужно взять только общія буквы съ наименьшими показателями; общія буквы суть а и Ь; наименьшій показатель буквы а есть 4, буквы Ь—2, сл. о. н. д. = 5а*Ьа,
Выраженіе, такимъ образомъ составленное, удовлетворяетъ и второму ^опредѣленію общаго наиб. дѣлителя; въ самомъ дѣлѣ, раздѣливъ на него данные одночлены, получаемъ частныя: ІЗас, 6а3Ь и 9Ь9й — первыя между собою. Отсюда Правило. Для составленія о. н. д. одночленовъ нужно къ общему наив. дѣлителю коэффиціентовъ приписать всѣ общіе буквенные множители съ наименьшими показателями.
Что касается многочленовъ, то, когда онп легко разлагаются на множителей, и употребляютъ способъ разложенія на производителей, или, что то же, превращаютъ многочлены въ одночлены и прилагаютъ къ нимъ предыдущее правило. Вотъ примѣры.
I. Найти о. и. д. многочленовъ
9а2х* — 36 и 12а3х* 4> 48ая + 48.
Разлагая на множители, найдемъ:
9а*.г2 —36 = 3*. (ах 4= 2) (ах — 2);
12а^2 4-48а^-|-48 = 4,3(ал?+2)\
Взявъ произведеніе общихъ простыхъ множителей, найдемъ о. н. д. = 3 (аз -|- 2).
П. Найти о. и. д. многочленовъ
х'у3 — 3#3уа 4~ 2л;4у4 п х*у3 —
Разлагая на множители, находимъ:
.г4у* — Зт3у3 4” 2.г*у4 = #2у®(# — 2у) (я —у), — 4л V = л?ау*(х 4- 2у) (я — 2у);
слѣд. о. н. д. = #3у*(я:—2у).
Ш. Найти о. н. д. полиномовъ
х3 4~ 1 и х3 -|“ тх3 4- тх 1.
Разложивъ на множители, получимъ
#’4~ 1 — (#4“ 1)(#а —#4“ 1)-
х3 4~ тх3 4“1 ~ (^4- і)(#*—»-|-тх4~ О;
слѣд., о. н. д. = #4~ 1.
IV*. Найти о. н. д. полиномовъ ♦
Зх*у — За?8 Згу — Зхз п
I эх'*!/ — ЗОа?уя Ц- 15я*у — 15а;3 -|- 30а?ах? — 15хгЛ
Но разложеніи на множителей, найдемъ, что
1-й полиномъ = 3(а?а (у — а?),
2-й полиномъ = 3 . 5(у — а?) (а; — я)2.
Отсюда: о. п. д. = 3(# — а?).
80. Способъ послѣдовательнаго дѣленія.—Такъ какъ многочлены только въ рѣдкихъ случаяхъ легко поддаются разложенію па простыхъ множителей, то и предыдущій способъ прилагается съ успѣхомъ только въ исключительныхъ случаяхъ. Вообще же, для опредѣленія о. н. д., полиномовъ пользуются общимъ способомъ, который носитъ названіе способа послѣдовательнаго дѣленія. Нахожденіе о. н. д, этимъ способомъ основывается на слѣдующихъ теоремахъ.
81. Теорема I. — О. н. д. двухъ выраженій не измѣнится, если одно изъ нихъ помножимъ или раздѣлимъ на количество, первое съ другимъ.
Въ самомъ дѣлѣ, о. н. д. есть произведеніе множителей, общихъ тому и другому выраженію, а потому если введемъ (умноженіемъ), или уничтожимъ (дѣленіемъ) въ одномъ изъ нихъ множителя, не входящаго въ составъ другого выраженія, то отъ этого прибавится къ первому, или уничтожится въ немъ множитель, котораго нѣтѣ во второмъ, а слѣд. общіе множителп останутся тѣ же; значитъ не измѣнится н о. н. д.
Эта теорема облегчаетъ вычисленія, позволяя избѣгать дробныхъ коэффиціентовъ въ частныхъ.
82. Теорема II.— О. н. д. у дѣлимаго и дѣлителя служитъ общимъ дѣлителемъ у дѣлителя и остатка.
Пусть данные многочлены суть М и Я; обозначивъ частное отъ раздѣленія М на И буквою а остатокъ К, и замѣтивъ, что дѣлимое=произведенію дѣлителя на частное, сложенному съ остаткомъ, имѣемъ
М = ^Х9 + И . . . (1).
Обозначивъ общаго дѣлителя многочленовъ М и К буквою А, раздѣлимъ на А обѣ части полученнаго равенства, найдемъ:
М
А
-уХУ + ѵ
Но, по условію, А есть общій дѣлитель многочленовъ М и X, слѣд. частныя М X . и - , V/
д и у суть выраженія цѣлыя; обозначивъ ихъ соотвѣтственно черезъ М и л , представимъ послѣднее равенство въ видѣ
М' = К'Х94-К, откуда 5 = М' —УХЧ-
Это равенство показываетъ, что *д есть выраженіе цѣлое, иоо равно цѣлому выраженію М' — У X Ч, значитъ, К дѣлится на-цѣло на А,
Итакъ, мы доказали, что всякій дѣлитель, общій дѣлимому и дѣлителю,
сііхггь общимъ дѣлителемъ у дѣлителя в остатка; а слѣд. и общій наив. дѣ-дѣлимаго и дѣлителя служитъ также общимъ дѣлителемъ у дѣлителя и •гзаста.
33. Теорема III, обратная. О* н. Э. у дѣлителя и остатка служитъ шгоге общимъ дѣлителямъ у дѣлимаго и дѣлителя.
Пусть \ будетъ общимъ дѣлителемъ выраженій X и К. Раздѣливъ обѣ ча--т равенства (1) па Лр получимъ
. Хт . К г
по условію, у есть цѣлое выраженіе, равно какъ и у; обозначивъ ихъ буі вами И' и В' нолучимъ
М ІТ, . .
М
Это равенство показываетъ, что т- равно суммѣ двухъ цѣлыхъ выраженій; значитъ, есть дѣлитель многочлена М.
Итакъ, мы доказали, что всякій дѣлитель, общій дѣлителю и остатку, слу
житъ также общимъ дѣлителемъ у дѣлимаго и дѣлителя; а слѣд. и общій наив. дѣлитель дѣлителя и остатка служитъ общимъ дѣлителемъ у дѣлимаго и дѣли-
теля.
Изъ этихъ двухъ теоремъ выводится слѣдующая
84. Теорема IV.—О. н. Э. ЭжАЫлам м джлмтіля равенъ о. м. дѣлителю дѣлителя и остатка.
Обозначимъ о. и. х жэогѵяжиовъ М 5 (т.-е. дѣлимаго и дѣлителя) буквою П: а о. х ъ у X і К у дѣлителя и остатка) буквою В'. Въ силу теоремы ІЕ шражесе Ь д быть общимъ дѣлителемъ многочленовъ X и й,
слѣд. іи» дѣлпъ бт остатка выраженіе 1)' — общаго наив. дѣлителя
5 і К А. во теоремѣ III, выраженіе П' должно дѣлить на-цѣло «лгати I і -Ѵ а слѣд. и ихъ общаго наив. дѣлителя И. Такимъ образомъ В і IV должны дѣлить другъ друга на-цѣло; но это возможно только тогда, евсв ош равны. Итакъ
И = І)', теорема доказана.
85, На послѣдней теоремѣ и основанъ способъ послѣдовательнаго дѣленія.
Пусть данные многочлены суть М и X. Ихъ общій наив. дѣл. можетъ содержать производителей одночленныхъ и многочленныхъ. Начинаютъ съ того, что отдѣляютъ въ многочленахъ М и X одночленныхъ производителей отъ многочленныхъ. Одночленный производитель многочлена М есть общій множитель всѣхъ членовъ этого многочлена; вынося его за скобки и означая черезъ а. а многочленъ, заключающійся въ скобкахъ, черезъ А, имѣемъ:
М —а. А.
Такъ же точно, вынося за скобки общаго множителя всѣхъ членовъ многочлена X и обозначая выраженіе, заключающееся въ скобкахъ, буквою В, получимъ:
х=?. в.
Производители — одночлены, общіе многочленамъ М и X, заключаются въ і и {І; а производители—многочлены, общіе многочленамъ М и X, содержатся въ А и В. Такъ какъ о. н. д. многочленовъ М и X есть произведеніе всѣхъ ихъ общихъ простыхъ множителей или дѣлителей, то очевидно, мы его найдемъ, если общаго наив. дѣлителя количествъ а и помножимъ на о. н. д. многочленовъ А и В. Обозначимъ о. н. д. многочленовъ М и X буквою А; о. н. д. одночленовъ а и [і—буквою п о. и, д. многочленовъ А и В—буквою И. На основаніи сказаннаго имѣемъ:
А = гі. П.
Пусть, напримѣръ:
М = 9аба#п — 30аЬа#3 45а6а# 4" 24а7А
X = ^аіЬісхй — 12(1^4^— ЖаіЬ2схі 4^ 24а46ас#34“ 78а46ас#а 4“
Вынося изъ всѣхъ членовъ перваго многочлена за скобки Заб®, а изъ всѣхъ членовъ второго 6а*&®сл:, получимъ:
М = ЗаЬа(Зх5 — ІО#3 -р 15# -1- 8),
X = 6а46ас#(#* — 2#4 — 6#3 4#а 4~ 13# А).
Общ. н. д. й одночленовъ За6® п 6а*6асл есть За/А Теперь намъ слѣдуетъ опредѣлить Л, т.-е. о. н. д. многочленовъ
д — З.г5 — ІО#3 15# 8 и
В = #5 — 2#4 — 6#3 -|^ 4#а 4“ ІЗя + 6.
I
- Раздѣлимъ А на В. Если бы А раздѣлилось на В безъ остатка, то В и было бы о. н. дм потому что тогда всѣ производители В содержались бы въ А. Но если бы А не раздѣлилось на В безъ остатка, то все-таки рѣшеніе вопроса подвинется впередъ. Въ самомъ дѣлѣ, пусть дѣленіе А на В даетъ частное и остатокъ В; въ такомъ случаѣ
А = Вх(і + К . . . (I).
причемъ степень главной буквы остатка будетъ ниже чѣмъ въ дѣлителѣ В. Замѣтивъ теперь, что, по теоремѣ IV, о. н. д. многочленовъ А и В равенъ о. н. д. многочленовъ В и К, заключаемъ, что вопросъ сводится къ отысканію о. н. д. между прежнимъ дѣлителемъ и остаткомъ, т,-е. между многочленами съ меньшими степенями главной буквы, и слѣд, болѣе простыми. Если бы принтомъ В раздѣлилось на В, тогда В и было бы искомымъ общимъ наив. дѣлителемъ. Но пусть при дѣленіи В на К получается въ частномъ У' и въ остаткѣ IV; тогда
В = 3'ХН4-К'< * »(2)
Хотя дѣленіе В на В и не привело къ окончательному нахожденію о. п. д., но рѣшеніе задачи опять упростилось. Дѣйствительно, мы знаемъ, что о. н. д. между В и Н равеніі о. п. д. между Н и К', такъ что вопросъ приведенъ къ нахожденію о. н. д. между многочленами К и Н\ болѣе простыми, ибо показатель главной буквы въ В' меньше показатели ея въ В.
Пусть В дѣлится безъ остатка на Н' и даетъ въ частномъ такъ что
К = Ч"ХК' . . . (3).
Не трудно провѣрить, что послѣдній дѣлитель IV и есть искомый о. и. д. многочленовъ А и В. Въ самомъ дѣлѣ, равенство (3) показываетъ, что IV есть о. н. д. для самого себя и К; но о* н. д. остатка и дѣлителя (равенство (2)) ровенъ о. н. д. дѣлимаго и дѣлителя, т.-е. многочленовъ В и К; а отсюда, въ -•цт равенства (1) заключаемъ, что ІГ, будучи о. и. д. для В и В, служитъ вмѣстѣ съ тѣмъ (по теор. IV) и общ. каив, дѣлителемъ для А и В, что и требовалось доказать.
При послѣдовательныхъ дѣленіяхъ, здѣсь указанныхъ, возможны два слу-ш: 1) или мы дойдемъ до остатка равнаго нулю; въ такомъ случаѣ, какъ до-шаио, послѣдній дѣлитель и будетъ искомымъ о. п. д. многочленовъ А и В; іл 2| послѣ нѣсколькихъ послѣдовательныхъ дѣленій, дойдемъ до остатка, ко-не содержа главной буквы, не будетъ, однакоже, нулемъ. Что такой лучіі возможенъ, объясняется тѣмъ, что степень главной буквы въ послѣдо-«тельныхъ остаткахъ постоянно понижается; слѣд, непремѣнно дойдемъ до ос-тжтъх іе содержащаго главной буквы. Легко доказать, что если этотъ остатокъ ж еггъ воль^ то слѣдуетъ заключить, что многочлены А и В не имѣютъ обща-шх дѣлителя. т.-е. первые между собою. Дѣйствительно, мы видѣли, что * ь ь тѣжгъ остатки послѣ каждаго дѣйствія, а потому онъ долженъ бы Литъ і «сидокъ. ж содержащій главной буквы. Для этого о, н. д, самъ не малъ сыфпхь іляѵі буквы: но въ такомъ случаѣ, чтобы онъ могъ раз-Гі ііи 6» «ві кштоиесы А и В. онъ долженъ дѣлить каждый коэффи-гъ цж <лнжадъ гпг>і4 буквы въ этихъ полиномахъ, а это невозможно, жй уже исключены (они заключаются въ а и ^).
Іп^мжзчг* примѣру. Дѣлимъ А на В (могли бы.
Литъ ? к* і -тг- къ данномъ случаѣ полиномы—едина-~**ЗгЗЗ ЛЪ Г.
і — —-1 — і аг — х х* — 2л4 — 6л4 + 4л* 4-1 Зх-|-6=В
- -1Н= 6л4 —1>л*=12л*4=39л4=18'3
ІУ ъл* — ъл3—12л*—24л —10
Въ <тлткѣ степень буквы х ниже чѣмъ въ дѣлителѣ, поэтому первое дѣ-ж* окончено: оно показываетъ, что В не есть о. н. д.
слѣдуя теорій, теперь нужно дѣлителя раздѣлить па первый остатокъ. Но, ^мѣш. что члены остатка имѣютъ общаго множителя 2, перваго съ новымъ іЛ-шымъ. мы на основаніи теоремы 1 можемъ сократить этотъ остатокъ на 2, » измѣняя этимъ о. н. д. Черезъ это новый дѣлитель упростится и будетъ равенъ
. Зл4 4л8 — 6л:2 — 12л — 5.
Для избѣжанія дробныхъ коэффиціентовъ въ частномъ и въ остаткахъ, множитъ новое дѣлимое на 3, что возможно, такъ какъ 3 есть количество первое съ Зл*4-4л3 — 6х2—12л— 5, Совершаемъ дѣленіе
Злг>—6л1- 18л3 + 12^ + 39^+ 18
— Злп 4- 4л:1 + 6л3 + 12л*5л
— 10л* — 12л8 4“ 24л3 4“ 44л— 18 .
— 5л:4— 6л3 4“ 12л2--22л-- 9 , . — 15л*— 18л3 -|- 36ля--66л — 27 . , Ч- 15л* + 20 л3 4- 30л 60л 25
2І’4-^‘6л34Г 6л -РУ
Зл4 4л3 — 6л3 — 12л — 5 л\ — 5 . остатокъ
. остатокъ, но раздѣленіи иа 2 . остатокъ, но умноженіи на 3 ь
Степень главной буквы въ первомъ остаткѣ не ниже чѣмъ въ дѣлителѣ, а это даетъ возможность продолжать дѣленіе. Но такъ какъ коэффиціентъ перваго члена остатка не дѣлится на коэффиціентъ перваго члена дѣлителя, то мы условимся считать второе дѣленіе законченнымъ, и полученный остатокъ—окончательнымъ въ этомъ дѣленіи. Теперь, слѣдуя теоріи, мы должны искать о. н. д. между За? + 4д?— 6л?— 12$ — 5 и полученнымъ остаткомъ; принтомъ, остатокъ принимаемъ за дѣлимое, а дѣлителя оставляемъ прежняго. Приступая къ новому дѣленію, сокращаемъ дѣлимое па 2 и умножаемъ его на 3, что позволительно, потому что ни 2, ни 3 не входятъ множителями въ дѣлитель. Чтобы не переписывать дѣлителя, продолжаютъ дѣленіе въ томъ же столбцѣ, только членъ частнаго (— 5) отдѣляютъ отъ частнаго прежняго дѣленія запятою, чтобы этимъ показать, что — 5 не принадлежитъ къ числу членовъ одного и того же частнаго, а есть частное новаго, особаго, дѣленія.
Это дѣленіе даетъ остатокъ 2о?4-6л?4“&г4_ и вопросъ приведенъ къ отысканію о. н. д. между этимъ остаткомъ и дѣлителемъ. Во избѣжаніе дробныхъ коэффиціентовъ въ частномъ и остаткахъ, сокращаемъ дѣлителя на 2, и дѣлимъ
3^*4- 4г1— 6о?—12х—5 о4р За?-|- 3^4-1 — Зл?4-9я?нн 9а?4- За; ~3х — 5.
— 5а? — 15х’2 — 15а; — 5 — 5а? — 15а? — 15а:— 5
О
Послѣдній дѣлитель а? 4“ За? 4“ За; 4" 1 и есть о, н. д. многочленовъ А и В.
Итакъ, мы нашли, что а I) = а? 4- За? 4- За; 4" 1; сл. о. п, д.
данныхъ многочленовъ М и К, или
А = & I) = Заі?(а? 4- Зл? + За?+ ] )=ЗаЪ*х*+$аЪ№ 4» ѴаЪ*х 4> Эаб*.
86. Приводимъ еще примѣры.
Г Найти о. н. д, многочленовъ:
М = 2а*а? — 28аяа? + 142а Ѵ — 308а2д? 4~ 240ааа; и К = Зао? —ЗОоа? 87ао; — 60 а,
Выносимъ за скобки общихъ множителей членовъ каждаго многочлена:
М = 2ааа?(х1 — 14л? + 7 Іа? — 154а;4- 120), И = За(я? — 10а? 4- 29ж — 20).
Отсюда имѣемъ: сІ — ал
Ищемъ о. н. д. многочленовъ, заключенныхъ въ скобки.
Первое дѣленіе.
а? —14а?4^71а?—154а:4-120 я? — 10а? + 29а: — 20
— а? + І Оа? + 29а? + 20а: а; — 4
— 4я?4-42я? - 134а; + 120 ± 4а? + 40л? ± 116а: 4= 80 .
1
Сокративъ остатокъ па 2, принимаемъ я2 — 9#4~20 за дѣлителя слѣдующаго дѣленія.
Второе дѣленіе.
ж’_ 10х’4-29х —20 #а — 9х 4“ -0
#3 4з в#2 нР 20# # — 1
— _ у/р 20
— #2 4- 9# — 20
/о
Заключаемъ, что #2 — 9#4" 20 есть о. н. д. многочленовъ, содержащихся жъ скобкахъ. Итакъ.
Д = гі. В — а(#2 — 9я 4“ 20) = ах* — 9а# -|- 20а.
II. Найти о. н. д. многочленовъ
М— #3 — 8#113#357#2—198#4~135 и
Х = 2г’~ 15#*4“37х ™ 15.
*к жп глувк. гі = 1. Постараемся опредѣлить 0. Умноживъ предвари-яя» шгг-ѵгі 1 в 1 іѣлимъ:
Первое дѣленіе.
ДН— Івх* —114?- 396г4- 27012#*— 15#24-37х - 15
— 1т3 — 15х* —37х* — 15#1 #2,— #, — 37
— г* — 11#1 — 129#’— 396#4~ -70, умноживъ на 2:
— 2-г1 — 22#»+258#а— 792#-р 540
4г 2#<=г15#’ Ч- 37#2=р 15#
— 37#* + 295#2 — 807#~4 540, умноживъ на 2: _74хз_^5до#»— 1614#+ 1080
Ч- 74#8^ 555#2Ч- ІЗбЭ^Ч2 555
35#2— 245#4~ 525
Сокративъ остатокъ на 35, дѣлимъ
2#3— 15#*4~37я —15
—7#4“ І5
2і — 1
Итакъ, I) —#а — 7#4" 15.
Д = й, Г) — #2—7#4“15.
111. Найти о. н. д. многочленовъ
М= 4” 2#8 — З#24- 5# * 12. в -— 4#8 4“ — 6# 4~ 5.
Умноживъ предварительно М на 4, дѣлимъ
4** 4“ &г8 — 1 2*2 4“ 20* — 48 к4*э 4~ 6*3 — (ія 4~
— 4*4 4“ б^3 + б*2 + 5* - Н“ 1
2*3— 6*2+15*~ 48, умноживъ на 2:
4*3 — 12*2 + 30* — 96
—4а;3 4- 6*2Ч- 6*4-
— 18*2 + 36* — 101
Умноживъ дѣлителя на 9, дѣлимъ его на послѣдній остатокъ:
36х8 4" э4*2— 54* + 45
36*3— 7 2*2 4^20 2а;
4~ 126а?2 — 256*4“ ^5
126*2— 252*+ 707
— 4* — 662
— 18*9 + 36* — 101
^^2*~— 7
Раздѣливъ остатокъ на (— 2), дѣлимъ
18*2 — 36* + 101 2* + 331
— 18 4= 2979* 9*2 — 3015
— 3015* + 101, умноживъ на 2:
— 6030* + 202
- 6030* — 997965
+ 998167
При послѣднемъ дѣленіи мы нашли остатокъ, не содержащій главной буквы, не равный нулю, то заключаемъ, что данные многочлены не имѣютъ никакого общаго дѣлителя.
IV. Найти о. н. д. многочленовъ
а3(Ь2 + 2Ъс + с2) — ааЬ( 2Ьа + 36о + с2) + аЬ3(6 + с) и а2(Ь2 — с2) - «5(26* + Ьс — о2) + Ь3(Ь + с).
Принявъ а за главную букву, посмотримъ, не имѣютъ ли коэффиціенты каждаго многочлена общихъ множителей; и для этого разложимъ коэффиціенты на множителей. Имѣемъ
62 + 2Ья+с2 = (Ь + с)2;
2^+36с+с2 = 2/>2+2Ьс+&с+с2=2Ь(Ь+с)4-с(^+с) = (Ь+е)(2Ь+с); Ь2 — с2 = (& + с)(й — с);
2Ь2 + йс- с2=Ь2+^+&с—с2=Ь(& + с)+(&+с)(6 — с) = (й+с)(26 - с).
Такимъ образомъ находимъ, что всѣ члены перваго многочлена имѣютъ общаго множителя а(& + с), всѣ члены второго: (& + с); слѣд. можемъ представить многочлены въ видѣ:
а(?> + с)| (Ь + с)а2 — 6(26 + с)а Ь3| и (б с){(6 — с)а2— Ь(25 — с)а — 68|.
отсюда видно, что ^=й-|-с. Затѣмъ, сокративъ первый мноі’очленъ на «/6-гс), второй на Ь-рс, л помноживъ всѣ члены перваго на Ъ—с, дѣлимъ
— Ь3с
+ Ъ*\а*±2Ь*а^Ъ1
4-е? 4- йас і 4^ Ь8с
-р Ьс'2 I
26?с. а — 268с, или, по сокращеніи на 26?с: а— Ь
Затѣмъ, дѣлимъ
— с
Итакъ, І)=а — Ь. А потому
Д = гі. В = (Ь-Нс)(а- Ь).
87. Изъ сказаннаго выводимъ слѣдующее
Правило,— Чтобы найти о. м. д. двухъ многочленовъ, нужно*. Сначала исключитъ общіе одночленные множители каждаго многочлена; причемъ, если случится, что означенные множители имѣютъ о. п, д,< то послѣдній слѣдуетъ впослѣдствіи ввести множителемъ въ составъ искомаго об, н. д.
Затѣмъ высшій многочленъ дѣлятъ на низшій, преобразовавъ предварительно днлимое такъ, чтобы первый членъ его (предполагая, что многочлены расположены по степенямъ одной буквы) дѣлился на первый членъ дѣлителя.
Въ полученномъ отъ дѣленія остаткѣ сокращаютъ всѣхъ множите-общихъ коэффиціентамъ главной буквы, и дѣлятъ прежняго дѣлителя на этотъ остатокъ, поступая попрежнему.
Затѣмъ дѣлятъ первый остатокъ на второй и т, д., продолжая *ти послѣдовательныя дѣленія до тѣхъ поръ, пока: илгі получится остатокъ нуль,— и тогда послѣдній дѣлитель есть искомый о. н. д,; или въ остаткѣ получится выраженіе, не содержащее главной буквы, — м ндоба данныя вы/іаж?ен/я суть кол^честйі ліежгіу собою, еелде
не имѣютъ общаго множителя, независящаго отъ главной буквы, и не открытаго егце въ началѣ дѣйствія.
При выполненіи послѣдовательныхъ дѣленій слѣдуетъ умножать промежуточные остатки на такихъ множителей, чтобы, первые члены ихъ дѣлились на первый членъ дѣлителя,
88. Иногда процессъ нахожденія о* и. д. можно ускорять на основаніи слѣдующей теоремы.
Теорема, О. «. д, гівіда ишішоліояа А и В, содержащихъ главную букву х, тотъ же, что и о, н. д. выраженій ^А-р^В г/ гД-рзВ, гйп> р, г/, г, я—мзшоторьгл или отрицательныя количества,
независящія отъ х.
Во-первыхъ, очевидно, что всякій множитель общій полиномамъ А и В, будетъ также общимъ множителемъ н выраженій рА-р^В и гЛ-р$В.
Во-вторыхъ, очевидно, что всякій множитель, общій выраженіямъ ^А-р<уВ и гА-|-зВ, служитъ также множителемъ выраженія $СрА-р*?В) — д(гА + $В), пли выраженія (яр~^г)А. А какъ — дг не содержитъ я, то всякій множитель, общій выраженіямъ рА-р^В и гА — гВ. долженъ быть множителемъ полинома А, если только не будетъ лр — ?г = 0. Подобно этому, всякій множитель, общій выраженіямъ у?А + я г А -р $В. будетъ татсже множителемъ и выраженія г(рА -р^В) “ р(гА + 3В) т.-е. выраженія (гд—ря)Вт и слѣд. полинома В,
Такимъ образомъ доказано, что всякій множитель, общій полиномамъ А и В, служитъ общимъ множителемъ и для />Л-р^В и гА-р«В, и обратно, о, м. двухъ послѣднихъ выраженій будетъ также общимъ множителемъ и для А и В; а сл. и о. н. д. у А и В таковъ же какъ и у рА-рдВ и **Л“рзВ.
Примѣръ. Найти о. н. д. полиномовъ
Зяэ4- 10я2 -р7ж - 2 . . . (1) и 3х3+13^+ 17яг-Р6 . . .(2)
. Вычитая (1) изъ (2), имѣемъ ІОаг-Р 8 . . . (3)
Помноживъ (1) на 3 и сложивъ со (2), получимъ
х(12я2-Р43я~Р 38) ... (4)
Слѣд. искомый о. н. д. тотъ же, что у (3) и у 1 4Зг38 , . . (5)
Помноживъ (3) на 4 п вычтя изъ (4), имѣемъ 3(я-р2). Слѣд., пск. о. я. д. = о. н. д. (3) и я-р2.
Но (3) при х = — 2 обращается въ О, слѣдоват., искомый о. н. д. = х-р 2,
89. Общій наивысшій дѣлитель нѣсколькихъ многочленовъ. — Пусть требуется найти о. н. д. нѣсколькихъ многочленовъ Р, Ч, К и 8. Найдемъ о. н. д. между какими-нибудь двумя изъ данныхъ многочленовъ, напр. Р и Ч, и назвавъ его буквою И, замѣчаемъ, что I) есть ничто иное, какъ произведеніе всѣхъ множителей, общихъ многочленамъ Р и Ч- — Если теперь найдемъ о. н. д. между В и К, то, назвавъ его буквою В', замѣчаемъ, что В' есть произведеніе всѣхъ множителей, общихъ В и Й; а какъ В есть произведеніе всѣхъ множителей, общихъ Р и Ч, то В' есть произведеніе всѣхъ множителей, общихъ Р, Ч и К. Найдя затѣмъ о. и. д. для В' и 8,—пусть онъ будетъ В",—убѣдимся, что онъ будетъ = произведенію всѣхъ множителей, общихъ многочленамъ Р, Ч< К и 8. Поэтому В" и будетъ о. п. д. данныхъ многочленовъ.
Отсюда
Правило.— Чтобы найти о. и. д. нѣсколькихъ многочленовъ, находятъ его сперва между какими-нибудь двумя многочленами; потомъ
лежоу найденнымъ о. н. д. и третьимъ даннымъ многочленомъ; затѣмъ лежду вновь найденнымъ о. н. д. и четвертымъ многочленомъ и т. д. П+елъдній о. н. д. и будетъ требуемый.
Примѣръ. Найти о. и. д. многочленовъ
Р = &са— 12#2у ~ Югед
Ц = 6яа-|-12я2 — Зх^у—18#у, К = 6я2 — 1 Ззд бу*. 8=4^э„
0, н. д. многочленовъ К и 8 равенъ 2я — 3^; о. н. д. многочленомъ Р и ±г — Зу есть 2д?— Зу- наконецъ о. н, д, для Ц и Зу есть также 2х — Зу. Слѣдов. о. и. д. всѣхъ четырехъ мнегочленовъ есть 2х — Зу.
90. Наинизшее кратное алгебраическихъ выраженій. — Ііратнымъ даннаго цѣлаго выраженія наз. такое другое цѣлое выраженіе которое на данное дѣлится ващѣло. Такъ 12а4ж2у есть кратное выраженія 2а2х. Очевидно, что ’для даннаго выраженія существуетъ безчисленное множество кратныхъ.
Такъ, для х — у кратными будутъ: (я — у)*, (я — #)3, (я — у)\ . , . я2—Уэ, ф3™^3, — у1 и т. д.
кратнымъ двухъ или нѣсколькихъ цѣлыхъ алгебраическихъ выраженій наз. такое, которое на всѣ данныя дѣлится безъ остатка. Такъ, если данныя выраженія суть:
2а26, 3(а - &)2, а2 - />3;
то общими кратными ихъ будутъ:
6а 2Ь (а “ &)2(а4~&);
12»463(а — Ь)4(а -|- &);
72а46*(а—і)3(а^-Ь)2 и т, д.
Очевидно, что для данныхъ выраженій существуетъ безчисленное множество общихъ кратныхъ.
Наинизшимъ кратнымъ данныхъ выраженій, расположенныхъ по степенямъ одной буквы, называется ихъ общее кратное, низшей степени относительно этой буквы.
Когда данныя выраженія — одночлены, то для составленія яаинизшаго кратнаго нужно перемножить всѣ простые множители, взявъ каждый изъ нихъ съ наибольшимъ показателемъ. Такъ, если даны одночлены 10ай6\ 12а^\ 6а4ЬсМ, то, взявъ всѣхъ простыхъ мпожит. въ высшихъ степеняхъ, т.-е, 2* 3, 5, а\ ѣэ, с2 и с?, найдемъ и. кр, 22.3,5.ай.&3.сі.^ или 60авЬ3сМ.
Такимъ же образомъ составляется и наинизшее кратное многочленовъ, когда послѣдніе легко разлагаются на множителей. Приводимъ примѣры,
I. Найти н. к. для — аа и Л73—-а1.
#2 — а2 = (я а)(# — а); х3 — а3 = (я — а)(#2 -|-.ш -|- а2)»
«
Н, кр. = (# + а)(ж — а)(#2 + ха -|- а1) = х* -|- — а*г —а\
П. Найти и. кр. полиномовъ:
х3 2х-і/ — ху* — 2у3 и Л’3 — 2ла// — ху2 -|- 2?/3й
По разложеніи на множители, первый даетъ
_ у*) 4. 2і/(жа — у2) = (д ; Ц- 2//)(яа — у2); а второй
— у2) — 2у (х2 — у2) = (я —• 2*/)(#2 — у2).
Наин. кр. ™ (#а — з/2)(я 4- 2у)(я — 2у) — (х2 — уа)(я* — 4у2).
91. Если разложеніе многочленовъ па множители представляетъ затрудни ніе, то можно пользоваться слѣдующимъ пріемомъ.
Пусть А и В — данные многочлены, а 0 —ихъ о. н. д. Назвавъ частныя отъ раздѣленія многочленовъ А и В на В буквами А' и В', получимъ: А = А'И и.В = В'Ь. По свойству о. н. дѣлителя. А' и В' суть выраженія первыя между собою, а слѣд. ихъ наин. кр. = А'В'. Очевидно, что выраженіе наименьшей сте-' пени, дѣлящееся на А'П и ВІ), есть А'В'И. Итакъ, наин. кр. многочленовъ А и В есть А'В'П - - . (1). Это выраженіе можно также представить въ видѣ Л'В, если ВЧ) замѣнить черезъ В; или, въ видѣ В'А, замѣнивъ А'П черезъ А. Наконецъ, перемноживъ: А = А'В и В = В'Э найдемъ, А'В'В2=АВ; раздѣливъ
АВ
обѣ части на И, получимъ: А'В'І)=-^-* Итакъ, наин. кр. можетъ быть представлено въ каждой изъ слѣдующихъ формъ:
А'ВТ, АВ', ВА' и
Отсюда вытекаетъ слѣдующее правило нахожденія наинизшаго кратнаго двухъ многочленовъ: находятъ ихъ о. н. д.; дѣлятъ на него одно изъ данныхъ выраженій, и полученнымъ частнымъ умножаютъ другое; пли: произведеніе данныхъ многочленовъ дѣлятъ на ихъ о. н. д.; или: о. н. д. множатъ на частныя, происходящія отъ раздѣленія данныхъ многочленовъ на этого наив. дѣлителя.
Примѣчаніе I Раздѣливъ и. к. А'В'В на АФ (или А), находимъ въ частномъ В\ а раздѣливъ на В'И (или В), въ частномъ получаемъ А'; но А' и В' выраженія первыя между собою, сл. .можно дать наименьшему кратному такое опредѣленіе: это есть такое кратное данныхъ выраженій, которое по раздѣленіи на нихъ, даетъ частныя первыя между собою.
Примѣръ. Найти и. к. многочленовъ
а2 — аб — 1263 и “Н 663.
0. н. д. ихъ = а 4” 36. Раздѣливъ первое выраженіе на а 4- 36, находимъ въ частномъ а — 46. Умноживъ второе выраженіе на это частное, найдемъ искомое н. к.
Итакъ, н. к. = (а2-|-5а6-|-662)(а—46) — а1!) — 14а62 — 2463.
Примѣчаніе II Мы нашли, что наин. кр. для А н В равно отсюда, назвавъ наин. кр. буквою Ь, имѣемъ
Ь.Й = А.В,
фшзѵсОснге двухъ данныхъ выраженій равно произведенію ихъ наин. ф. « наив. дѣлитель,
Ж. Бел М есть н. к. для А и В, то очевидно, что всякое кратное колк-1 есть общее кратное для А и В.
53 Всякое общее кратное двухъ алгебраическихъ выраженій есть снявши ихъ наимизшаго кратнаго.
Ітгь А и В—два данныя выраженія, М—чіхъ н. к., и пусть К озна-«п какое-либо общее кратное. Допустимъ, если возможно, что при дѣленіи X * 1 волучается остатокъ В (при частномъ У). Въ такомъ случаѣ В = X — 9<М. 1* X і М дѣлятся на А, сл. и В дѣлится на А; X и М дѣлятся на В, сл. и 1 іѣлтся на В (§ 81), Но К есть выраженіе степени чѣмъ М; сл.
♦смывается общее кратное количествъ А и В низшей степени, чѣмъ ихъ н. к. >> — нелѣпость: сл. остатокъ К не существуетъ, т.-е. X есть кратное количества М.
94. Пусть требуется найти н. к. нѣсколькихъ многочленовъ, напр., трехъ: 1 В и С. Найдемъ н. к* двухъ изъ нихъ, напр. А и В: пусть опо будетъ М. Затѣмъ найдемъ н, к, для М и 0: пусть оно будетъ Ь, Докажемъ, что Ь и будетъ служить н. к. для А, В и С.
Назовемъ н. кр. А, В и С буквою х. Всякое общее кратное количествъ М і С есть общее кратное и для А, В и С (§ 92); слѣд, Ь должно дѣлиться на хЛ Всякое общее кратное А и В есть кратное и для М (§ 93); сл. всякое об-• щее кратное А, В и С есть общее кратное и для М и С; слѣд. .г должно дѣлиться на ѣ.
Итакъ, Ь должно дѣлиться на а х на Ь; поэтому х = Ь, и правило доказано.
Примѣчаніе. — Нахожденіе наин. кр, имѣетъ приложеніе въ приведеніи дробей къ общему знаменателю. 0. н. д. въ элементарной алгебрѣ прилагается къ сокращенію дробей; въ Высшей Алгебрѣ онъ имѣетъ другія, важнѣйшія примѣненія, именно въ теоріи уравненій.
ГЛАВА IX.
Алгебраическія дроби.
Опредѣленіе.—Основное свойство алгебраической дроби. —Сокращеніе алгебраическихъ дробей и приведеніе къ общему знаменателю.—Четыре основныя дѣйствія надъ дробями,
95. Опредѣленіе. — Мы видѣли, что когда дѣленіе одного алгебраическаго выраженія на другое невозможно, то дѣйствіе только обозначается: дѣлителя пишутъ подъ дѣлимымъ, отдѣляя ихъ горизонтальною чертою. Такимъ образомъ частное отъ раздѣленія А на В изображается въ формѣ
А _ № В
Такое выраженіе называется алгебраическою дробью, причемъ дѣлимое получаетъ названіе ’шедоямм, а дѣлитель—зяалеиатіля» Итакъ: алгебраическая дробь есть частное отъ раздѣленія числителя на знаменателя.
Между дробями — ариѳметическою и алгебраическою есть существенная разница: въ самомъ дѣлѣ, числитель и знаменатель ариѳметической дроби суть числа цѣлыя и абсолютныя, между тѣмъ какъ члены алгебраической дроби могутъ быть какъ цѣлыми, такъ и дробными, какъ положительными, такъ н отрицательными, и вообще какими угодно алгебраическими выраженіями. Такимъ образомъ, понятіе объ алгебраической дроби обилье, нежели объ ариѳметической, а отсюда вытекаетъ необходимость вывода свойствъ алгебраической дроби и доказательства правилъ дѣйствій надъ этими дробями независимо отъ вывода этихъ свойствъ и правилъ для дроби ариѳметической.
Выводъ упомянутыхъ свойствъ и правилъ долженъ вытекать изъ самого опредѣленія алгебраической дроби какъ частнаго отъ раздѣленія числителя на знаменателя.
96. Основное свойство алгебраической дроби состоитъ въ томъ, что величина ея не измѣнится, если числителя в знаменателя умножимъ или раздѣлимъ на одно и то же количество. Докажемъ это.
Пусть величина дроби равна У:
В=Ч - - .(О-
Замѣчая, что дѣлимое = произведенію дѣлителя па частное, имѣемъ
А = В . Ч.
Означивъ буквою М какое-ниб. количество, умножимъ на него каждую изъ равныхъ величинъ А и В . Ц, вслѣдствіе чего получимъ и произведенія равныя:
АМ = В^М;
или, перемѣнивъ мѣста производителей () и М во второй части,
АМ = ВМ X
Это равенство показываетъ, что (}, будучи умножено на ВМ, даетъ въ произведеніи АМ; слѣд. Ч есть частное отъ раздѣленія АМ на ВМ; такимъ образомъ:
ВМ
Но Ч есть ничто иное какъ [см. (I)]; слѣд.
АМ ,_. А
ВМ — В
П ✓ А.М , , .
Это равенство показываетъ, что дробь эдд можетъ быть замѣнена дробью т.-е. что величина дроби не измѣнится, если числитель и знамена* шелъ раздѣлимъ на одно, и то же количество.
На этомъ свойствѣ основано упрощеніе дроби сокращеніемъ, .
А
Равенство (2) показываетъ также, что, наоборотъ, дробь можетъ быть
АМ
шівв дробью іэдр т.-е. что величина дроби не измѣнится, если числи- » игш • знаменатель помножимъ на одно и то же количество.
>гомъ свойствѣ основано приведеніе дробей къ общему знаменателю.
57- Сокращеніе.—Для сокращенія дроби нужно ея числителя и знамена-тм мздѣ лить на ихъ общаго наивысшаго дѣлителя: отъ этого величина ея аг йѣтатся, но дробь будетъ приведена въ простѣйшій видъ, такъ какъ част-вд *п> раздѣленія ея членовъ на ихъ о. н. д. будутъ количества первыя Ж23Т СОбОЮ.
Приводимъ нѣсколько примѣровъ.
Е Сократить дробь
48а»б8Л
’бба^я6 ‘
0. н. д. числителя и знаменателя есть 12а8Ьх4. Раздѣливъ па это коли-*<тво оба члена дроби, имѣемъ: • *
И. Сократить дробь
Зба’б2 — 36а»Ь»
54аЧ>з _ іО8дЗЬ» + 54а’Ь» ’
Когда ч. и з. суть многочлены, легко поддающіеся разложенію на множители, то о. н. д. для нихъ находимъ этимъ способомъ:
36«Ч>» — 36а2Ь‘ _ 36аа62(а2 — Ь2) _ 18а2Ь2(а—б).2а(а + Ь)
54а‘б3 — 108«’Ь‘ + 54аЧН> — 54а2Ь»(а2 — 2аб + Ь2) ~ 18аЧ>2(«~ ?>) ЗЬ(а — Ь)' *
Замѣчая, что о. н. д. членовъ дроби равенъ 18а2бя(а— Ь), мы, раздѣливъ на него числителя и знаменателя, получимъ:
2а(а + б)
$Ь(а — Ь)'
НЕ Сократить дробь
я18 + а12
я1 -рах4 а*х + а5
Знаменатель = л;4(х 4~ а) 4“ 4" а) = 4" а)(#4 4- а4).
Числитель = (х4)3 4“ (а<)’ = (ж< ~Ь а<)[(л;4)2 — х4а4-- (а4)8] = = (х4 4- а*)(#8 — х4а4 4- дв)*
По раздѣленіи обоихъ членовъ дроби на о. н. д. х44-а\ находимъ:
х® — х4а4 + а8 х 4- а
Въ этомъ примѣрѣ о. н. д. былъ л44“а\ ибо я®— х4а4-^а8, не обращаясь въ ноль при х =— а, не дѣлится на х4~а*
IV. Сократить дробь
бс(б — с) — <м?(л - е) 4~ аЬ(а — б)
Ь'№(Ь — с) — бАЯ(а — с) 4- а868(а — 6) ’
Числитель — с) — а(а — с)§ 4~ &) = с(а — 6)(с — а — Ь)-|-
-^аЬ(а — ?>)—(а — 7>)|с(с — а)—&е-|- а/?} = (а — &)(а — с)(Ь — с).
Въ § 54, 5, мы видѣли, что знаменатель = (а— Ь)(а—с)(Ъ—с)(а&-|-ас4--|- Ьс). Итакъ, видно, что о. н. д. числителя н знаменателя есть (а—Ь)(а— с):
раздѣливъ на него оба члена дроби, получимъ
______1 * аЪ + ас + бг’
V. Сократить дробь
Оба члена числителя и оба члена знаменателя дѣлятся на раздѣ-
ливъ ихъ на этотъ биномъ, получимъ дробь
+ //)‘ — (г4 — дДу + ду — ту»
0й + У)2 — -г У2)
Раскрывъ скобки въ числителѣ и знаменателѣ и сдѣлавъ приведеніе, найдемъ
5«Л/ 4- 5л^2 + 5ту®
—--------о г~~—? или, сокративъ на
I (^ + «3/ + у4)-
VI. Сократить дробь
2г» — 15л*+ 37® — 15
®» — 8®‘ + 13а* + 57а* — 198л | 135 '
Въ этомъ примѣрѣ, разложеніе числителя и знаменателя на множители пред-ставляетъ затрудненія; поэтому опредѣляемъ о. и. д. способомъ послѣдовательныхъ дѣленій. Такимъ образомъ найдемъ, что о. н. д = т3 — 7#-]-15. Сокративъ дробь, найдемъ
2л;— I
— я2 — 9а? + 9
98. Приведеніе дробей къ общему знаменателю.—Здѣсь слѣдуетъ различать тѣ же случаи какъ и въ ариѳметикѣ:
1. Если каждые два знаменателя суть выраженія взаимно-простыя, нужно числителя и знаменателя каждой дроби помножать на произведеніе знаменателей прочихъ дробей. Черезъ это общимъ знаменателемъ всѣхъ дробей будетъ произведеніе всѣхъ знаменателей или ихъ наинизшее кратное, т.-е- общій знаменатель будетъ имѣть простѣйшую форму. -
Поступая сказаннымъ образомъ надъ дробями
3 т п
2а 36® И «-Н/
знаменатели которыхъ—количества взаимно-простыя, найдемъ:
. я . З.ЗЬ»(а + 0 9Ь»(«+6).
вмѣсто иервой дроби №^:б~у или -6аМ(я+ьг
х ш. 2«(а 4“ Ь) 2ат(а + 6).
вмѣсто второй дроби ^2_2й(д-|-5)’ или вой®(« + ьу
, я , п.2а.№ ЧаИ'-п
вмѣсто третьей дроби 2я-^о Ь), или
1- Когда знаменатели данныхъ дробей имѣютъ общихъ множителей, то наи-ѵнмве кратное знаменателей опять принимаемъ за общаго знаменателя; затѣмъ гт это наим. кр. на знаменателя, каждой дроби и полученнымъ частнымъ и пп числителя и знаменателя соотвѣтствующей дроби. Приводимъ примѣры.
к Привести къ общему знаменателю дроби:
а Ь с 4 4(1—^)’ 8(1—0!)’ 2(1 + х)' Г+^‘
Разлагая знаменателей на простые множители, получимъ:
4(1 —жа) = 2». (1—®)(1-|-а:); 8(1 — ж) = 23. (1 — х);
«гольные два знаменателя остаются въ данной формѣ. Ндм. кр. знаменателей, нлн об, знам. =
= 23. (1 -1-о;) (1—или 8(1—я4).
Раздѣливъ об, зн. на знаменателя первой дроби и умноживъ полученнымъ частнымъ 2(1-{-&*) оба члена первой дроби, получимъ:
2а(і + г3) 8(1 —г4)
Раздѣливъ об. зн. иа знаменателя второй дроби и помноживъ полученнымъ частнымъ (1 +#)(1 оба члена ея, найдемъ
6(1 + з)(1 + %2) 8(1—а?*) *
Поступая подобнымъ же образомъ съ двумя остальными дробями, вмѣсто иигь получимъ:
4<1 —#)(1+^2) 8^(1 — я?)
8(1— х') 11 8(1—я1)
11. Привести къ общему знаменателю дроби:
1 1 _ 1
- 41 — За?-р^2’ я* + За?-р2
Разлагая знаменателей на множители, найдемъ:
х2 — 4 = О4~2) (я— 2);
х2 — Зл? 2 = (л? — 2) (# — 1) ^Ц-3^4-2=(а? + 2)(ж+1). I
Наин. кратное знаменателей = (а; 4“ 2) (я — 2) (я -(--І) (я— 1) или (я?1—4) — 1). Поступая какъ въ примѣрѣ I, найдемъ слѣдующія, соотвѣтственно равныя даннымъ, дроби: •
я2 — 1 (д? 4- 2) (ж + 1) (аз —- 2) (а? — 1)
4) (Э~Г/ ^ — 4) (я2— !)’ (ж^ —4) (^ —1)' «в
ПК Привести къ общему знаменателю дроби: *
а Ъ с (1
Ьі (а - с) (а—4) (6—с}(Ь—4) (6 - а/ (с—гі) (с—а) (с—-а) (гі—6) (гі—с)'
Здѣсь знаменатели уже дани въ формѣ произведеній простыхъ множителей. Замѣтивъ, что « — Ь, а — с, а — Л и т. д. получаются изъ Ъ — а, с—а, (і — а, . . . умноженіемъ на —1, замѣняемъ данныя дроби слѣдующими:
а _______ _____— Ь________ с ____ —<2
(«—Ь) (а—с) (а—гі)’ (6—с) (я - &)’ (с—<0 (а—с) (д—
Общій знаменатель = (а — Ь) (а — с) (а — Л) (Ъ — с) (Ъ — й) (с — гі). Дѣля его на знаменателя каждой дроби поочередно, и умножая частнымъ оба члена соотвѣтствующей дроби, найдемъ искомыя дроби:
а(6-с)(д—ф(с—ф___________. ____ — Ыа—с)
' (а—Ь) (а—с) (а—й) (6—с) (Ь—гі) (с—4)’ («—*) (а—с) (а—Ф (с—
_______с(а—Ь) (а—ф (Ь—4) _______>_______—6) (а—с) (Ь—с)
(а—6) (г?—с) (а—А) (Ь—с) (&—ф (о—чі)’ (а—Ъ) (а—г) (а—гі)”ф—<0 (6 - </) (с - ф ’ *
НЕ Можетъ случиться, что одинъ изъ знаменателей дѣлится на всѣхъ остальныхъ, т.-е. служитъ наин. кратнымъ всѣхъ знаменателей; онъ и будетъ общимъ знаменателемъ.
Примѣръ. Привести къ общему знаменателю дроби:
а Ъ с
4- &2’ «<—М‘
Замѣчая, что а1 — Ь* = (а2 Ь2) (а* — Ь2), находимъ, что знаменатель
третьей дроби есть наин. кр. всѣхъ знаменателей; онъ и будетъ общимъ знаменателемъ. Третью дробь, какъ уже имѣющую общаго знаменателя, оставляемъ безъ перемѣны, а первыя двѣ приводимъ къ общему знаменателю пріемомъ, указаннымъ въ пунктѣ 2. Такимъ образомъ найдемъ, что данныя дроби могутъ быть замѣнены слѣдующими:
а(„2 — Ъ(а* + 62) с 0І_ &Г’ «4— М ’ «4—
39. Сложеніе и вычитаніе дробей.—Различаемъ два случая:
1. Сложить или вычесть дроби съ равными знаменателями:
а . Ь с т т т
Положимъ, что а_________________________ Ъ______ __
т т ж
Зная, что дѣлимое — произведенію дѣлителя на частное, имѣемъ
а = тд^ с = тц3.
Придавая къ равнымъ (а и равныя количества (& и получимъ и суммы равныя; слѣд.
а 4- Ь = • вычитая изъ равныхъ (а-|-Ь и *и#і4“7П^) равныя, найдемъ и остатки равные; слѣд.
а 4~ Ь — с = 4- тд* —
кж. авва за скобки т,
«+& — с = ($ -{- — &) . т-
ніСііЛіЛ Л3і
Залѣжия д2 и Ц3 ихъ величинами, находимъ: а г Ъ__________________________с___а-\-Ь— с
т т т т
-т^вда правило: чтобы сложитъ или вычесть дроби съ равными зна лшялелями, надо сложить или вычесть числители и подъ результа-ш; «т подписать общаго знаменателя *
— Когда данныя дроби имѣютъ различныхъ знаменателей, то сперва при-адп ихъ къ общему знаменателю, а затѣмъ поступаютъ по предыдущему*
Примѣры. I. Найти сумму дробей
а2 — аЬ а2 4~ аЬ д* — Ъ* а^-д ‘ а — Ъ ' а *
В» приведеніи къ общему знаменателю, имѣемъ
(д2—дд) (а—5) «-|-(ав-РаЬ) (д*-|~&) —Ь2) (#+&) (а—&)
(а+Ь)(а—Ъ)а
яі_2лзг>+^2+(лі+2д^+д^2) + (а*”2«2&2+дІ) Зд<+М
(а2—&2)а — да-ад2’
И. Выполнить дѣйствія: е
X 1 | 1
(х — 1) (д: + 2) (я — 3) ~ Я2 — I ‘ (я—2)(я—3)‘
Во приведеніи къ общему знаменателю (#а — 1) (х2— 4) (# — 3), имѣемъ шоѣіовательно:
х(х + 1) (я — 2) — (я2 —4) (я — 3) + (я2 — 1) (а?-|-2) _ (я2 — 1)02 — 4) (я — 3) ~
Н — х® — 2г — (я® — Зя2 — 4я 4~ 12) + (я® + 2я2 — х — 2) __ я3 + 4я2 -|-я —14 Оа— 1) 02 — 4) 0 — 3) — — (де2— 1 )(^— 4) (ж—3)'
Числитель не обращается въ ноль при х= 1, —1, -р2, —2 и +3, -ь ж дѣлится ни на одного множителя знаменателя, а потому результатъ не ъцежжтъ дальнѣйшему упрощенію.
Ш. Упростить выраженіе о®_____________________।_______________।_____с3
(д — 6) (а — с) ' (& — а) (Ь — с) (с — а) (с — &)‘
• *«іі знаменатель = (а — Ъ)(Ь — с) (с — а); дѣля его на каждаго изъ зна-по порядку, получаемъ частныя:
— (Ь —с), — (с — а), —(а —6).
По приведеніи къ общему знаменателю, получимъ
— л3ф — с) — 6а(с — а) — ^(а — 6) (а — Ъ) (Ь — ё) (с — а)
Полагая въ числителѣ послѣдовательно а = Ъ* Ъ = с и с — а, замѣчаемъ, что онъ въ каждомъ случаѣ обращается въ ноль, а потому дѣлится на (а — І) (Ь — с) (с — а). Это произведеніе открываемъ въ числителѣ разложеніемъ 'на множители: ’ __
а*с— а’і — Ьас-|-аЬ3’— с3(а — с(а3—Ь*) —аЬ(а* — Ьа) — с3(а — Ь) =
— (а — Ь)|с(а2-|-аі-|-Ьа) — а6(а-[“ Ь) —са| =
= (а — Ь)|(а8—с*)е — а6(а — с) — 6а(а — е)} =
— (а — 6) (а — с))(а — с)с — аЬ — Ьа| —
= (а - Ь) (а - с)|аф - Ь) + (& + с)(с - Ь)| =
— (а — Ь) (а —с)(е —&)(аН“Ь + <?) = (а —*} СЬ — с) (с — а) (а-НЬ-|-с).
Итакъ, данное выраженіе равно
(д-6)ф —с)(г —а) ф + 6 + е) _ і , । (л — &) (Ь —е) (с —л)
IV, Упростить выраженіе
4І>+<І=М
1 а
Если дробь соединена (плюсомъ или минусомъ) съ цѣлымъ выраженіемъ, то, помноживъ цѣлое и раздѣливъ на знаменателя дроби, получимъ сумму или разность двухъ дробей. Такъ, данное выраженіе умноженіемъ и дѣленіемъ 46 на а превращаемъ въ
4д6 (а—Ь)?_______6)а 4 дб+аа—-2_ а2-1-2аЬ-(-6* _ (а+6)а
а ' а а ~ а а ~ а
100. Умноженіе дробей,— Перемножить дроби и
Положивъ а с
д=* и ^ = д, имѣемъ отсюда *
а = Ьр и с —
Помноживъ равныя количества а и Ър па равныя с и найдемъ и произведенія равныя; слѣд.
ас = Ьр . гй/.
Перемѣнивъ во второй части мѣста сомножителей, получимъ
ас = М . 2^,
откуда
ас
Р-* = ы'
а , с ,
іл, подставивъ у вмѣсто А и вмѣсто
__ ас ~Ы '
•О).
Отсюда правило: чтобы умножитъ дробь на дробь* надо числителя «ервоы фобы полжожытъ на числителя второй. знаменателя первой на знаменателя второй* и первое произведеніе раздѣлитъ на второе.
Если въ равенствѣ *(1) положимъ 1, оно обратится въ
а ч / с__ ас
Ь’/М ~Гхѵ
замѣтивъ, что у есть тоже, что с, а Ъ X 1 равно 5, имѣемъ:
Итакъ, чтобы умножить дробь на цѣлое выраженіе, надо числителя умножить на ото цѣлое* и произведеніе раздѣлитъ на знаменателя *роби.
Положимъ въ равенствѣ (1) Ъ= 1, получимъ
вс с ас
тХ7=1X3’ или ЙХ й = г
гтіуда правило: для умноженія выраженія на дробь, надо цѣлое
^множитъ на числителя дроби, и произведеніе раздѣлить на ея знаменателя.
п , л* — 64 ѵ/ а — 6 («* — О4)(а —• 6) _
Цримѣры. 1. 2аЬ^. & А аі аЬ (а’ — 2аЬ 4- 6») (дЗ -|- аЬ) ~
62)(а-кб) (а — 6) (а - 5) л ✓ г і іл / тл«
-----' Сокративъ дробь на (аЪ) (а — Ъ)\ получимъ
ггоюе произведеніе:
а*+& а
п- П2_г>2X(а + °) — (а^.ъ)(а—Ь) а — Ъ'
ш. (о. _ і.) х =_
\ / / х д2 ^2 би _|_ ^2
= (а2 — . 2а,
Примѣчаніе.—Доказанное правило распространяется на какое угодно чнс-» іробей; такъ
г а ч / е ас ’ . е
и дѣлѣ, по доказанному: = умноживъ эту дробь на -у
найдемъ помноживъ эту дробь на четвертую у, найдемъ окончательное произведеніе
. асед ЪсІПГ Примѣръ. Вычислить
х8 + У3 х—у \/ (х4~у)5—х5—у5
х3— Зх2у— Згу2
Прилагая предыдущее правило, найдемъ
(х3+у3) (х—у) [(х+у? — х* — уі.
(я* — У3) (х + у) (&г*у — Зху2)
Замѣтивъ, что (х-|“У)3— х5 — у5 = (х-|-у)5— Сг54~у3) = (^+у)(5х3у4-5хѴ + 5ух,) = (х + у) . эху . (х2 + ху + уа),
представляемъ произведеніе въ видѣ
5ху(х* + У3) (х —у) (х + У) (х* + ху +у*)
Зху(х3 —уЗ) (ж + у) (х —у) л
откуда, до сокращеніи, найдемъ
Б^ + уВ)
3(х - у) *
101. Дѣленіе дробей.—Пусть требуется раздѣлить
Положимъ у =7? и у = 7; имѣемъ отсюда
а = Ър и с = &р
Раздѣливъ равныя величины (а и Ьр)*на равныя (с и гід), получимъ равныя; слѣд.
а___Ър
~с~йд
Умноживъ обѣ части этого равенства на у, найдемъ
агі_Ър&
сЪ '
Сокративъ вторую дробь на Ь<7, найдемъ
_____р Ьс /
Подставивъ вмѣсто р и д ихъ величины, получимъ а с
Отсюда правило: чтобы раздѣлитъ дробь на дробь, надо числителя первой дроби умножитъ на знаменателя второй, а знаменателя пер~
«мі ш числителя второй, и первое произведеніе раздѣлитъ на вто/юе. Слагая въ равенствѣ (1) гі=1, найдемъ
а с а X1 а а
~7“ г ~і~ — " і_'_ НЛП ’т ~ * С ч ’
О 1 ОС О ОС
Отсюда слѣдуетъ, что для раздѣленія дроби на цѣлое выраженіе надо: чьсмтеля раздѣлитъ на произведеніе знаменателя на цѣлое выраженіе.
Положивъ въ равенствѣ (1) Ь —1, получихъ
а с ай
Г ; ” Гх<?
с
ЯЛН а : -д-
Слѣд., чтобы уа^ьлитъ цѣлое выраженіе на дробь* надо цѣлое умножатъ на знаменателя дроби и произведеніе раздѣлитъ на числителя.
Примѣчаніе I.—Двѣ величины А и В называются взашеко-о^атяшш, «ли ихъ произведеніе равно 1. Итакъ, когда А.В = 1, то А есть количество кратное величинѣ В, а В обратно количеству А, Изъ равенства АВ=1 нахо-ижъ
И Ь = 4-" А
откуда заключаемъ, что обратная данной величины равна частному отъ раздѣ* ленія 1 на эту величину.
Очевидно, что дроби -4 и -у взаимно-обратны, потому что
А В АВ
В X А — АВ ~
Имѣя въ виду это замѣчаніе, можемъ правило дѣленія на дроби выразить въ слѣдующей формѣ. Изъ правила умноженія дробей слѣдуетъ, что и
можно представить въ видѣ произведеній: уХ“ и °Х_; а потому равен-0 с с
ства (1) и (2) можно написать въ видѣ:
а с а ч / д с (I
т:т=Т"Х““ и «:-э- = «Х—; о а о с а ' ' с
отсюда видно, что для раздѣленія цѣлаго или дробнаго выраженія на дробь надо дѣлимое умножить па величину обратную дѣлителю.
Примѣчаніе нашли, что
а с асі
— -- *
Ь * д~Ьс
Величина дроби не измѣнится, если ш сдѣлавъ это, найдемъ:
числителя и знаменателя раздѣлимъ
ад ед
а с
« с __ __
Ъс~ Т
сй д
Слѣд. при дѣленіи дроби на дробь можно поступать еще слѣдующимъ образомъ: числителя первой дроби раздѣлить на числителя второй, а знаменателя первой на знаменателя второй, п первое частное раздѣлить на второе.
Очевидно, что этотъ- пріемъ слѣдуетъ примѣнять только тогда, когда числнт. и знамен. дѣлимаго дѣлятся нацѣло на числ. и знам. дѣлителя.
т 2а(аЪ — №) , « .съ — 6) 26
Примѣры. I. :а<а ъ ) — (а4-Ь)«а(а—6)(« + &)!(«4-6)»'
іт 14&# _7.5а#б0________56//
1Е х : ~5Ъу~ ~ТйшГ-1Г
„У я? — а2 (я? -|- «)2___(# — п)!(# + а) _ (# — а)2
я? — — а)3 (ж — + а)2 ж-|-а
а34~~За2# + За#24~х3 (а-г#)2 ___ (а-|~#)3______ . (а4~#)2
я3—+ (я — у)(х* + #0 + ’ ^-ря^+02’
Здѣсь числитель и знаменатель первой дроби дѣлятся соотвѣтственно на числ. и знам. второй, с.і. частное =
(я +#)3 : (я + я)2 ___а 4“ 37
[(# — 0) (#2 + #0 + У2)]: (я* + #// + 0'2) — х — У
102. Приводимъ еще нѣсколько примѣровъ дѣйствій надъ дробями. I. Упростить выраженіе
а — Ь а— і;—?
а(а
Умножаемъ прежде всего числителя и знаменателя данной дроби на 1 -р °^ч * чтобы привести ихъ къ цѣлому виду; сдѣлавъ это, найдемъ:
а(1 + (іЬ) — (а — 6) 1 4~ аб + я(а — 6)
Раскрывъ скобки въ числителѣ и знаменателѣ и сдѣлавъ приведеніе, найдемъ
аѢ + 6 6(1 + а2)
Т+й*1 ЙЛИ “Г+^Г’ ИЛЙ
Данное выраженіе равно, слѣдовательно, 1>.
II. Упростить выраженіе
/ 2 а» +
11 а - - - т
а Д а + Ъ )
а -\-Ъ
Чтобы привести оба члена дроби къ цѣлому виду, множимъ ихъ на а(а-|-Ь); при чемъ въ числителѣ первый множитель умножаемъ на а, второй на а-[-Ъ. Такимъ образомъ найдемъ
(д2 — &2)(аЭ + — а3 Д&2)
а{а + 6) —
(«2 — &2)а6(а— 6) /
= к-----~ = («’—ЬЧ(« — ь).
119 —
II]. Помножить
Д.г3^2 Зл2уЗ 2ду1 у* 5л3 “ 2Й26 і“ Зоба ~“/7«
2х2у Зху2 Зу3
За* ЬаЬ 262
гдѣ оба сомножителя расположены по нисходящимъ степенямъ х>
4аЯР'___ Зэ^у* і 2яу* у*
эа3 "“ 2а^7 За№~&
2&У _ 3^2 _ З//3
За2 5аЪ 2Ь2
л4у4 । Іх3?/5 2х2у*
15а* ' 9а^ “ ЗаФ /
__12#4// । 9л*у* 2х*у* । Зху1
25й*Ь ’ 10а362 5а2/Я ’ 5а&4
Г2л'У . Эя4#6 ху1 । Зу*
___ — ТбаФ ‘ ~‘2/7*
8г*?/3 37я4у4 I 13#у . 71 ^у6 Яку1 . Зу8 15й* 2аа*6 “Г Э67ДО ‘ ЙТда — 5оМ Т 2/3*
IV, Провѣрю юдученный результатъ: это будетъ примѣръ дѣленія дробинъ »тмцл. рас&хюженныіъ по степенямъ главной буквы.
ІЗ^5 23а Ч 71хУ ѲОаЗЗ Зой4 , ЗИ 4т*у2 "2б> 5а3 Зт2//3 2«2б 2ау* ‘ Заб2 Ъ3
15о* — а*5 — 4х*у* “^ЭяЧіі — ЗаѢ* а^у 3«г _?Г^ 5аЪ Зу» да’
12д*у» 25а46 . 12^4у4 — 25а46 ; ау । ЮаѢ^ ' — Эя’У1 . + Юа’Л2.— 37я2//> гада 2.г2у« _ 2я^ 5абі Злу7 баЬ1 Г
• &Е*уВ , 5а%ч ’ ”г &»Ѵ і 5«3?;2 ' 4?да ѲѵГ2//* 4а‘2/Я аЬ1 уу1 аЬ1 І_3у* г 2/>» 1 Зу8 । а» 4
О
Опредѣленіе членовъ частнаго:
. 8^3 л 4я%2 _ 8зауа 4л4у2_________________ 2л2у
15а^ ’ 5а3 15а5 : 5а3 За-
9 12я**у2 . 4а,4у* ___12л;1?/1 : 4я3у1 Злу2
25а1/? ‘ 5а3 25а4б : 5а3 . 5аб”
~ в#3#5 ; 4а?//3 вя^З : 4л%2 Зу3
5а3І>2 * 5л3 5а3Ь2 : 5о3 2б\
ГЛАВА X.
Возвышеніе въ степень.
Опредѣленіе.—Правила: знаковъ и показателей.—Степень произведенія и дроби.— Возвышеніе одночлена въ степень.—Квадратъ п кубъ многочлена.
103. Опредѣленіе.—Въ этой главѣ мы разсмотримъ возвышеніе въ цѣлую положительную степень.
Возвысить количество ірьлую положительную степень значитъ повторитъ еіо множителемъ столько разъ, сколько въ показателѣ степени находится единицъ.
Такъ: а^ — а.а^ а3 = а . а . а; а" = а . а . а . . . (и разъ).
Такимъ образомъ, возвышеніе въ степень есть частный случай умноженія,— случай, когда всѣ производители равны. Количество, возвышаемое въ степень, . пазываетая оежтяіела степени. Такъ, въ формулѣ а8, а есть основаніе; въ выраженіи хл основаніе есть х.
104. Правило знаковъ. Правило знаковъ при возвышеніи въ степень вытекаетъ непосредственно изъ правила знаковъ при умноженіи; но послѣднее остается одинаковымъ, будутъ ли производители даны съ ихъ окончательными знаками, или же окончательные ихъ знаки неизвѣстны, поэтому и правило знаковъ при возвышеніи въ степень въ обоихъ случаяхъ будетъ одно и то же.
1, Случай возвышенія въ четную степень. Пусть требуется количества -[-а и — а возвысить въ четную степень 2п; это значитъ — то и другое основаніе надо повторить множителемъ 2п разъ. -|-а, взятое 2п разъ множителемъ, дастъ взявъ (—а) множителемъ 2п разъ, можемъ все произведеніе
разбить на п паръ, изъ которыхъ каждая дастъ знакъ +, а потому и искомая степень имѣетъ знакъ
(—«)(—«) . (— а)(— а) . (— а)(— а) . . . (-а)(—а),
слѣд. (— а)2" = 4- а2в. Итакъ
(4- а)2п = -|-а2", т.-е. четная степень всегда даетъ знакъ будетъ ли передъ основаніемъ знакъ иля —.
2* Случай возвышенія въ нечетную степень. Если передъ основаніемъ находится знакъ+, то изъ правила знаковъ при умноженіи прямо слѣдуетъ, что и произведеніе будетъ имѣть тотъ же знакъ, слѣд.
(_^а)й«+1=_|_а.2п+1 . . .(1)
Если передъ основаніемъ будетъ знакъ —, то возвышая — а въ нечетную степень 2«—|—1, мы получимъ произведеніе 2п-|-1 множителей, изъ которыхъ составится п паръ, дающихъ знакъ и останется одинъ множитель (— &), вслѣдствіе чего произведеніе будетъ имѣть знакъ — :
(—«)(—а) . (—а)(—а) . (—а)(—а) . . . (—«)(—а) . (—а),
італ (— = — а2п+1 ... (2),
2гь (1) и (2) слѣдуетъ, что мечетная степень имѣетъ такой же знакъ сягі м основаніе.
Примѣры. (—3)3 = -|-9; (-(-5)4 = 625; (4'4)3 = + 64; (—4)3 =
— М; (±^)1 = + «4; (Ч-0)® = Ч~а5; (— а)3 = — ай, и т. д.
105. Правило показателей, — Пусть требуется ам возвысить въ степень2>, гіѣ а —какое угодно количество, а т и р— числа цѣлыя и положительныя. Возвысить аш въ степень значитъ повторить это выраженіе множителемъ р разъ; слѣд.
(ат)р = ат . ат . а™ . ат . . . а”4 (р разъ).
По при умноженіи показатели складываются, слѣд. вторую часть равенства можно представить въ видѣ ата+га+т»+* гд^ т берется слагаемымъ р разъ; яі, повторенное слагаемымъ р разъ, даетъ юр; слѣд.
(ага/ = а”*
Отсюда правило: для возвышенія степени въ новую степень нужно показателя возвышаемаго количества помножить на показателя новой степени.
Такъ: (а4)5 — а20; (ат-1)вд+1 = ат,_І и т. д.
* 106. Возвышеніе произведенія въ степень. — Пусть требуется произведеніе аЪс возвысить въ т-ую степень; это значитъ — повторить аЬс множителемъ т разъ; слѣд.
(айс)т = «Ьс . аЬс . аЬс . . . абс (гдѣ аЬс взято т разъ): перемѣняя мѣста производителей, имѣемъ
аЪс . аЬс . . . аЬс = ааа . . . а X ЬЬЪ , . . Ь X . с;
здѣсь каждая изъ буквъ а, Ъ и с берется множителемъ т разъ. слѣд. послѣднее выраженіе въ сокращенномъ видѣ = атЬтст. Итакъ
(аЬс)т = аТс".
Отсюда правило: чтобы возвысить въ степень произведеніе должно каждало множителя отдѣльно возвысить въ требуемую степень и результаты перемножить.
107. Возвышеніе въ степень дроби. — Пусть требуется дробь ~ возвы-снть въ ш-ую степень: это значитъ — дробь & повторить множителемъ т разъ. По правилу умноженія дробей имѣемъ
_ ааа а ѵ_______________________а.а.а . . . а(пі разъ)_а,я
~ Ъ ' Ъ ' Ъ І^разъ; —Ё разъу —
Итакъ т =^>
т.-е. для возвышенія дроби въ степень слѣдуетъ возвысить въ данную степень числителя и знаменателя отдѣльно, и степень числителя раздѣлить на степень знаменателя.
,, /ЗѴ 3* 9 /3\з 33 27
По этому правилу найдемъ: ІуІ 4/ = п т’ [1’
108. Возвышеніе одночлена въ степень. — Пусть требуется одночленъ 2а3/?Л? возвысить въ пятую степень. Для этого надо каждаго изъ множителей 2, а3, Ц и <1 возвысить въ данную степень и результаты перемножить, причемъ при возвышеніи степени въ данную степень — показателей перемножить. Такимъ образомъ, послѣдовательно найдемъ:
(2а36йсѴ)5 = 2й, (а3)3. (6Й)« . (с"У. <1* = 32а156аМ'^\
Итакъ, чтобы возвысить въ степень одночленъ, должно возвысить въ данную степень ею коэффиціентъ, а показателя каждаго изъ буквенныхъ множителей умножить на показателя степени.
При возвышеніи въ степень дроби нужно такимъ образомъ поступать съ числителемъ и знаменателемъ. Такъ, напр., послѣдовательно получимъ «
4аЗЬ'2сія—2\3 (4а!ОД»ш-2)3 6
7й/‘ ) ~— 7"$*? = 343^/15“ ’
109. Для возвышенія многочлена въ какую угодно степень служитъ особая формула, извѣстная подъ именемъ формулы Ньютона. Оиа будетъ выведена впослѣдствіи; въ этой главѣ мы ограничимся выводомъ чаще употребляемыхъ формулъ квадрата и куба многочлена.
110, Квадратъ многочлена—Мы видѣли, что каковы бы ни были количества а н Ь по знаку, всегда имѣемъ
(а -р 6)а = а2 -р 6й 4^ 2а6,
Взявъ триномъ а 4* 6 -1- с и разсматривая на время а-рб какъ одинъ членъ, найдемъ послѣдовательно
(бі + 64-с)я = [(а + б) + с]2 = (а + і)‘і4-2(а + Ь)с + с1 =
= а2 4~ Ъ* 4^ 2а6 4“ 2ас 4“ 26с 4“ с2 = а2 Ь2 4" с2 4“ 4“ 4” ^/С-
Послѣдняя формула показываетъ, что квадратъ тринома состоитъ изъ алгебраической суммы: квадратовъ всѣхъ его членовъ п удвоенныхъ произведеній каждаго члена на каждый, за нимъ слѣдующій. Докажемъ общность этого закона, т.-е. что онъ справедливъ для многочлена, состоящаго изъ сколькихъ угодно членовъ; а для этого, допустивъ, что законъ вѣренъ для многочлена, состоящаго изъ п членовъ, докажемъ, что окэ останется вѣренъ и для многочлена, содержагцаю однимъ членомъ больше.
Итакъ, допускаемъ, что замѣченный для квадрата тринома законъ вѣренъ для полинома а4_^4^4'^4--------Ь*4”^ состоящаго изъ п членовъ^ и возьмемъ полиномъ а~Р^4“с4-лН------4“ Ч содержащій п4~1 членъ.
Принявъ на время сумму а 4” Ь4“*”4’®4’^ нервыхъ п членовъ за одинъ членъ, а весь многочленъ а + Ъ 4---1- і 4" 4" за Двучленъ, по формулѣ квадрата бинома напишемъ: [(^ 4~ 4“ с 4“ 4----4 г 4~ О + Ч*==
= (а4-?>4'^4-^ + ^’+; + Ча4’2(^4'Ь + сН----------|-І-рЛ)й4-АЛ
Но, по допущенію, (а-^----------І-гЦ-АР состоитъ изъ: 1) суммы
квадратовъ всѣхъ членовъ отъ а до А включительно, т.-е. изъ а2 -|- Ь* с2 -р — й2-|_,*‘“Н-а Ч-^3; я -) суммы удвоенныхъ произведеній каждаго изъ чле-новъ Ъ, с, . . . г, А на каждый, за нимъ слѣдующій, т.-е. 2а& -^2ас-|-^2ай4’^^шЧ“2аАЧ_-^сЧ““^^Ч“***Ч_-1^ Всѣ эти члены написаны во второй части равенства (А) влѣво отъ вертикальной черты. Прибавивъ сюда 2(а-^&4"***4“ т.-е. алгебраическую сумму удвоенныхъ произведеній пер-
выхъ п членовъ на добавленный членъ А, и квадратъ ?ѵ3 этого новаго члена, получимъ:
(А) (<х—|—Ъ—с—б? -| -
ЛѴ| •— ІЛг Ы Г *-> ] Ч-Ѵ | ’ ’ * I «' I г* 1 I „ ч '-*/
-|~2а??-|~ 2ас—2а/?—*»*—~ 2аА|Ц~2аА. ..^)
-|-2іЛ Ч-2/А 7.)
^Ч- «аа X)
Отсюда видно, что квадратъ новаго многочлена, содержащаго н-]-1 членъ, состоитъ: 1) изъ суммы квадратовъ всѣхъ его членовъ отъ перваго до послѣдняго включительно (строка а): 2) изъ алгебраической суммы удвоенныхъ произведеній — перваго члена па каждый за нимъ слѣдующій (строка ^). второго члена на каждый, слѣдуэл^іій лз нимъ (;р........третьяго члена отъ конца на
оба. стоящіе за имъ т>. и п^дп-хлѣдняго на послѣдній (а)- Однимъ словомъ, №> вто{ь>й часті умі>2<7ьл іЛі находятся алгебраическая сумма квадратовъ всѣхъ я — 1 иевокъ новаго многочлена п удвоенныхъ произведеній каждаго его члена нл каждый за нимъ слѣдующій.
Такихъ образомъ, допустивъ, что законъ вѣренъ для многочлена, содержащаго я членовъ, мы доказали, что онъ вѣренъ п для полинома, имѣющаго однимъ членомъ больше. Но вначалѣ мы видѣли, что законъ вѣренъ для трехчлена, слѣд., по доказанному, онъ вѣренъ и для четырехчлена; а будучи вѣренъ для четырехчлепа, онъ вѣренъ, по доказанному, и для пятичлена и т. д. — однимъ словомъ, для всякаго многочлена. Итакъ: явафат многочлена }>авенъ алгебраической суммѣ квад/штовъ всѣхъ его членовъ и удвоенныхъ произведеній каждаго члена на каждый за нимъ слѣдующій.
Новый методъ доказательства, съ которымъ мы здѣсь впервые встрѣтились, называется сиособола заключенія отъ п ка п -(-1; у англійскихъ математиковъ онъ извѣстенъ подъ именемъ метода математической или дамонсюумс-тивной индукціи., Изъ предыдущаго видно, что методъ этотъ состоитъ въ слѣдующемъ: сначала справедливость доказываемаго закона подтверждается на частномъ примѣрѣ, какъ напр. у насъ на трехчленѣ; затѣмъ,—и это существенная часть доказательства по этому способу, — доказывается, что если теорема вѣрна для какого-лпбо случая (папр. для п—члена), то она вѣрна и для ближайшаго случая (въ нашей теоремѣ—для нЦ-1—члена); отсюда слѣдуетъ, что будучи вѣрна въ одномъ случаѣ, она вѣрна въ ближайшемъ кіі нему, затѣмъ въ случаѣ —ближайшемъ къ послѣднему и т. д.; слѣдовательно, теорема вѣрна и для всѣхъ случаевъ, слѣдующихъ за тѣмъ, съ котораго мы начали.
Изобрѣтеніе этого способа приписываютъ швейцарскому математику
111. Сгруппировавъ члены квадрата полинома иначе, можемъ дать ему слѣдующій видъ:
(аЦ-1* + с + й-|-Н + Л)* = а2 + 2аЬ-р^ + 2(а + Ь)е + са+2(а +
4“ ь 4- <0^ Ч- 4~ -(й “Р & +сЧ-“Ь Ч-Ч ^2*
Откуда видно, что квадратъ многочлена равенъ: квадрату 1-го члена, 4“ удвоенное произведеніе 1-го члена на 2-й, 4“ задрать 2-го, 4“ удвоенное произведеніе суммы первыхъ двухъ членовъ на 3-й, 4“КІіаДРатъ 3-го, Ч~ удвоенное произведеніе суммы первыхъ трехъ членовъ на 4-й, 4~ квадратъ четвертаго и т. д.
Въ этой формѣ квадратъ многочлена примѣняется при извлеченіи квадратнаго корня изъ многочлена.
112. Примѣръ. Найти (4а*я3—7 аЗх2— 6а*г4’Д3)2.
Примѣняя первую формулу» найдемъ
16аЪг*4- 49а*^ + 36а*г»4- а10 — 56а3яга — 48а "хе1 4~ 8а’х3 4~ 84а\г® — 14а8#2
— 12а^;
сдѣлавъ приведеніе и расположивъ члены по убывающимъ степенямъ буквы получимъ
ІбаѴт*— 56«’Ъ’Г) ~4 4“ 92а7#3Ч“ 22а8ж*— 12аЗ.г4«10.
Примѣчаніе. Если сумму квадратовъ членовъ полинома изобразить сокращенно знакомъ -а2, а въ суммѣ удвоенныхъ произведеній вынести за скобки 2, выраженіе же въ скобкахъ, равное алгебраической суммѣ произведеній каждаго члена на каждый, за нимъ слѣдующій, изобразить въ формѣ ЕаЬ, то формулу квадрата многочлена можно представить въ сокращенной формѣ такъ:
(а 4^ 4” с Ч-----р і 4” Л)2 = 4“
113, Кубъ многочлена. — Въ § 36, IV мы нашли, что (а-4&)3 = я8 + ’ 4- За2&4'3аѣ24“&3- На основаніи этой формулы, взявъ триномъ «4“^ + ° и принявъ на время а -]-Ъ за одинъ членъ, имѣемъ:
(а-4г? + с)а = [(а + г?)4-с]3 = (а4»Ь)3 + 3(а4-Ь)2с4-3(а + Ь)с2 + е3 = а3 4- ЗаЧ 4~ ЗаЪ* + Ь3 + (За* 4~ 6а& + зг,*)с + Зас2 4- ЗЬс* + с3 = а3 4~ Ьа 4” с3 Ч~ За2Ь 4- За2с 4- 4~ ЗЪ2с 4” Зс2а 4~ Зс2Ь -4 6аЬс.
Такимъ же образомъ, взявъ четырех членъ и возвысивъ его въ кубъ, кашли бы:
(а 4“ & 4“ е 4“ ^)3 = а3 + &3 4“ сЭ "Ч- с^3
- За2Ь - -За2с - НЗа’й
-З^а- -ЗЬ2с - -Зі»»<7
- - Зс2а - -Зс2Ь - -Зс»й
к 7 - З^а- - Згі2Ь - гЗй2с
№ *_ • - баЬс - - 6аМ - - баей
- 6 Ьсг7
Изъ этихъ частныхъ случаевъ видно, что куб> взятыхъ въ нихъ полиномовъ -стоитъ изъ алгебраической суммы/ кубовъ всѣхъ членовъ, утроенныхъ произволеній квадрата каждаго члена на каждый , изъ остальныхъ, и ушестеренныхъ і^изведеній этихіі членовъ, взятыхъ но три.
Докажемъ теперь, что если этотъ законъ вѣренъ для полинома объ п чле-виъ а4-^4_<?_Р^Н------р^ + ^-рЛ, то онъ будетъ вѣренъ и для ноли-
>«13 объ п 4“ 1 членахъ а Ц- Ъ 4~ с 4~ с? р -р * -р А + й. Принявъ на фш а~р&-рсН--------рі4~^ за одинъ членъ, по формулѣ куба бинома по-
луляіъ
** — Ь~Р с.-р ---р^~р^ ~Р ^~р й)3 = (а-р & + с-р^^Р”'4мЧ_й)аН“
— 3(а-Р& + е-{---рЛ)аі 4- 3(а + & + с + ^4-рг‘-рЛ)^ +
Іьпо допущенію, (а — Ъ~с-рс?-------------!-і-рЛ)> состоитъ изъ: 1) сумма ку-
^гъ всѣхъ -ъ отъ а до А включительно. 2) суммы утроенныхъ произве-
квалра?* і-^діго члена а, Ь, , .., А на каждый изъ остальныхъ, н
гттт
3» уѵестерешгь крокзведеній этихъ членовъ, взятыхъ по три. Всѣ эти члены
пшпп ккасе влѣво отъ вертикальной черты; вправо же отъ нея прибавлены шжрытыл ^жжлешя:
«“И* й !Ѵ’
, «іркмп получимъ:
рі —р ь 4“ с 4~ 4- * 4“ $ 4- ® ~Р ”Р ’
м 4~ с®4“” -4^3+7і3 і
— ’.лЧ — Заас 4~ *
— Зс*а 4- Зс2А
• * - 4~ За3А - . .~рзь2л * - + ЗСЧ
— к*
— За*к
— З&к
4- Зс*к
“) ?) V)
4- ЗЬ’а 4- ЗКѢ 4-.........4- Зк*і
4~ 6аЬс 4- ЪаЪ(14“.......4~
— 3/ЛЬ х)
— ЗА*а-рзіЬ2&4-3^с-|-----РЗА2Л X)
4* 6аЬА4-6асА-р • 4” и)
Отсюда видно, что кубъ новаго многочлена объ п 4~ 1 членахъ содержитъ: 1) сумму кубовъ всѣхъ членовъ отъ а до і включительно (строка а); 2) алгебраическую сумму утроенныхъ произведеній квадрата каждаго члена отъ а до к на каждый изъ остальныхъ (строки у,. .., X); 3) алгебр. сумму ушестеренныхъ произведеній всѣхъ членовъ а, Ь, с, ... , А, А, взятыхъ по три. Однимъ словомъ, законъ, предположенный вѣрнымъ для многочлена объ п членахъ, оказывается вѣрнымъ и для многочлена, имѣющаго однимъ членомъ больше.
Но прямое возвышеніе въ кубъ показало, что онъ вѣренъ для четырехчлена, слѣд. онъ вѣренъ и для пятичлена; а потому и для шестнчлена и т, д. Общность закона такимъ образомъ доказана.
Сокращенно законъ этотъ выражается формулою:
(а + Ь4-с4-^4--рг4-Л + ^3 = 2а34-3^4-6Ѵа&с,
114. Сгруппировавъ иначе члены второй части, можно написать: (а4^^4_с_р.._рг’_рА-рЛ:)а = а3-рЗа^4-За64 5 + ^4-3(а-рАрс4-4- з(а 4- ъу 4- с3 4- з(а 4- ъ -р ом 4-------р А3.
Въ этой формѣ теорема примѣняется при извлеченіи кубичныхъ корней изъ многочленовъ.
115. Примѣръ. Найти (5#8— За#2-|-2а2#— а8)8.
Примѣняя правило § 113, найдемъ:
125#9 — 27а3#6 Ц- 8а6#3 —а9
— 225а#5 150а2#7 — 75а8#8
— 135а2#7— 54а4#3 — 27а8#4
— 60а4#8 — 36а8#4 — 12а7#2
«У 15а6#3 — 9а7#2 -|- 6а#8 — 180а3#6 + 90а4#8 — 60а8#4 36а6#3.
Сдѣлавъ приведеніе и расположивъ члены по убывающимъ степенямъ буквы #, получимъ:
125#9— 225а#8™]- 285а2#7 — 282а8#6-|- 204а1#8— 123а5#1 -|~ 59а6#3 — — 2 Іа7#2 -ф- 6а8# — а9.
ГЛАВА XI.
Извлеченіе корня.
Опредѣленіе—Правило знаковъ.—Правило показателей.—Корень изъ произведенія и дроби.—Извлеченіе корня изъ одночленовъ.
116. Опредѣленіе. — Мед видѣли, что корне.о п № порядка изъ Л называется такое количество г, которое, будучи возвышено въ сте-п.—
пенЪ) даетъ Л. — Выражая это количество знакомъ ‘У А, ‘имѣемъ; по опредѣленію, два равенства:
... уА = Г и г" = А, имѣющія одинаковое значеніе.
Символъ |/ называется .расколола порядка п; п—показателемъ корня» если показатель п равенъ 2, его не пишутъ.
Дѣйствіе нахожденія корня называется извлеченіемъ корня.
Въ этой главѣ мы займемся выводомъ основныхъ правилъ извлеченія корня шьлаю положительнаго порядка.
117. Правило знаковъ. — Слѣдуетъ разсмотрѣть 4 случая, смотря по тому, будетъ ли подкоренное количество положительное или отрицательное, а показатель корпя — четный или нечетный.
1. Коренъ четнаго порядка изъ положительнаго количества имѣетъ два значенія, одинаковыя по абсолютной величинѣ, но противоположныя по знаку.
Такъ квадратный корень изъ -|-9 имѣетъ два значенія: и —3. То
и другое удовлетворяетъ данному выше опредѣленію корня, потому что какъ (4~ З)2 = 9, такъ и (—3)2 = + 9. Такимъ образомъ можно написать, что
)/-|-9 = ±3 (читается: квадр. корень изъ Ц- 9 равенъ плюсъ или минусъ 3).
Біфеяь четвертаго порядка изъ -р 16 также имѣетъ два значенія: + 2 и — 1 ь^гоиу что какъ (-]- 2)4 = 4“ 16, такъ и (— 2)4 = -^ 16. Итакъ + 1® = — Вообще
/+^-=4-0.
что и (4“а)2н = -г#2"« и (—а)-п = ^а2п.
/Гореяь нічдопяшо до/мижа кл положительною количества есть
якъ ип> — 125. Очевидно, что первый корень не можетъ равняться
— Іа второ! — 5. эти числа не удовлетворяютъ опредѣленію корня; въ ов«ъ іЫ —2і — 5. будучи возвышены въ кубъ, даютъ —8 и — 125.
чт’ »—іі*—1 = 4'й2п+1; между тѣмъ какъ (— а)2^1 =— а2п-К
Хде» мечетнаго порядка изъ отрицательнаго количества есть мел^чяал три м отельная.
’ьп і —8 =— 2, потому что (—2)® = — 8; —64 =— 4, ибо
— =— 64. Вообще
і • : — а)2*1 = — дгм+1; между тѣмъ какъ (4“ а)2п+] = 4~
4. Коренъ четнаго порядка изъ отриггательнаго количества есть величина мнимая.
Въ самомъ дѣлѣ, пусть требуется извлечь )/—25. Искомый корень, если бы онъ былъ возможенъ, по абсолютной величинѣ долженъ быть равенъ 5; но нп -|-5, ни —5, будучи возвышены въ квадратъ, не даютъ —25, такъ что у/— 25 не можетъ быть выраженъ никакимъ положительнымъ я никакимъ отрицательнымъ числомъ. Такія величины называютъ лютшылш. Въ противоположность имъ, обыкновенныя положительныя и отрицательныя количества, съ которыми мы до сихъ моръ имѣли дѣло, называютъ дѣйствительными.
Изъ предыдущаго слѣдуетъ, что правило знаковъ при извлеченіи корня можетъ быть выражено такъ:
Коренъ нечетнаго порядка имѣетъ знакъ подкоренною количества; корень четнаго порядка изъ положительнаго количества имѣетъ двойной знакъ (+); корень четнаго порядка изъ отрицательнаго колггчества есть величина мнимая.
118. Относительно двойного знака необходимо замѣтить, что его слѣдуетъ ставить только тогда, когда происхожденіе подкоренного количества остается неизвѣстнымъ. Напр., а2—2а&4“&а можетъ явиться какъ результатъ возвышенія въ квадратъ или разности а — 5, иди 5 — а, такъ что |/аа — 2аЬ 4~ = 4- (а— &)* Но если требуется извлечь квадратный корень изъ (а — 6)2, то не должно полагать ]/(а — Ь)2 = 4т (а — Ь), но приписывать ему только одно значеніе а — Ъ, Точно такъ же: |/(4~а)а = только 4" а |/(—а)* только —а.
Относительно правила знаковъ при извлеченіи корня слѣдуетъ еще замѣтить, что данное нами въ предыдущемъ § правило—далеко неполное. Въ главѣ XXIX будетъ доказано, что корень изъ какого угодно числа имѣетъ столько различитъ алгебраическихъ значеній, сколько единицъ въ показателѣ корня; такъ, кубичный корень имѣетъ три различныхъ значенія, корень четвертаго порядка’— четыре и т. д.
Примѣчаніе. Въ предстоящемъ намъ изложеніи преобразованій корней мы будемъ разсматривать только такъ называемыя ариѳметическія величины корней, т. е. какъ подкоренныя количества, такъ и салше корни будемъ брать положительные.
119. Правило показателей. —Пусть требуется извлечь корень порядка изъ ар, гдѣ а — нѣкоторое положительное количества, а м и сверхъ того, числа цѣлыя. Искомый корень долженъ представлять нѣкоторую степень буквы а; назвавъ неизвѣстнаго показателя этой степени черезъ х, имѣемъ равенство
По опредѣленію корня, послѣдній, будучи возвышенъ въ степень, изобра жаемую показателемъ корня, даетъ подкоренное количество, а потому
(а1)'1 =
или по правилу возвышенія степени въ степень:
ахл = ар.
Чтобы это равенство было возможно, необходимо, чтобы показатели обѣихъ частей были равны, т.-е. р, откуда
_ ₽_ Итакъ у/аР = ап.
Отсюда правило: Лія извлеченія корня изъ степени должно показателя степепи раздѣлитъ на показателя корня.
Такъ напр. ]/а* = а3; = У (а -|- Ь)й = (а -р Ь)1; и т. Д-
120. Корень изъ произведенія. — Пусть требуется извлечь корень порядка изъ произведенія АВС. Докажемъ, что для этого должно извлечь корень даннаго порядка изъ каждаго производителя отдѣльно и результаты перемножитъ, т.-е. что
/ІВС = X "/в X /с. • •(!)
Дѣйствительно, если окажется, что вторая часть равенства, будучи возвышена въ пжу*° степень, даетъ АВС, то, согласно съ опредѣленіемъ корня, этимъ и будетъ доказано, что она въ самомъ дѣлѣ представляетъ корень порядка изъ АВС. Итакъ, возвышаемъ }/а X В X въ я’*® степень; замѣтивъ, что для этого каждаго производителя отдѣльно нужно возвысить въ степень н результаты перемножить, найдемъ
(І/ Л X /в X І/С)"=(я/ а)" - (в)" • (/ СГ.
Но, по опредѣленію корня, (^а) = А, (^^В) =В и (]/с)** = С, слѣд. (]Хахі/вХ?с)"=авс,
тігь справедливость теоремы (1) и доказана.
Очевидно, что способъ доказательства не зависитъ отъ числа множителей, а зотому теорема доказана для какого угодно числа множителей подкореннаго сраженія.
121- Корень изъ дроби. Пусть требуется извлечь корень порядка изъ дмбя -р» Докажемъ, что для извлеченія корня изъ дроби должно извлечь « отдѣльно шв числителя и знаменателя, и первый раздѣлитъ на іяырой, т.-е. что
Если окажется, что степень второй части равенства равна , — этимъ «зраведливость равенства будетъ доказана. По правилу возвышенія въ степень т?оби имѣемъ
вк. ш гтлт ьдеь (" -Т)" = А. (|/В)" = В, слѣд. въ самомъ дѣлѣ
А
В’
к испытуемое равенство доказано.
Теоремы о корнѣ изъ произведенія и дроби доказаны не прямымъ путемъ— способомъ повѣрки. Впрочемъ, что касается второй теоремы, то она можетъ быть доказана и прямымъ путемъ. Въ самомъ дѣлѣ, пусть
возвысивъ обѣ части въ и-®" степень, имѣемъ
А В“ Х'
откуда
А = В . Хп;
извлекая изъ. обѣихъ частей корень и40 порядка и примѣняя ко второй части теорему § 12(1, найдемъ
/а = ^В./Рі, или ^А = 7в.®.
Послѣднее равенство показываетъ, что х есть частное отъ раздѣленія на */в, сл.
Подставляя вмѣсто х въ равенство (1) его величину, находимъ
122. Извлеченіе корня изъ одночлена.—Цѣлый одночленъ есть произведеніе, а потому для извлеченія изъ него корня нужно извлечь корень изъ каждаго производителя и результаты перемножить. Такъ
ь* & - У)«=|Г«ИХ
Отсюда правило: извлечь корень изъ одночлена, должно извлечь
его изъ коэффиціента, а показателей всѣхъ буквенныхъ множителей раздѣлитъ на показателя корня.
При извлеченіи корня изъ дроби слѣдуетъ, примѣняя это правило, извлечь требуемый корень отдѣльно изъ числителя к знаменателя и первый раздѣлить на второй. Такъ
5/32я»Ь» _ /З2аі"бм _ 2д»і>»
. у — /(еа_й4)І
ГЛАВА XII.
Извлеченіе квадратнаго корня изъ чиселъ и многочленовъ.
Опредѣленія; предварительныя теоремы.—Извлеченіе квадратнаго корня: изъ цѣлаго
числа и изъ дроби съ точностью до 1 и до —.— Сокращенный способъ.— Извлечс-п
ніе квадратнаго корня изъ многочленовъ; приложенія.
123. Когда число есть квадратъ другого числа, то первое называется точнымъ квадратомъ^ а второе точнымъ- квадратнымъ корнемъ изъ перваго.
Такъ, 49 есть точный квадратъ 7-ми; число же 7 — точный квадратный корень изъ 49.
124. Теорема. Когда цѣлое число не есть точный квадратъ, то квадратный коренъ изъ него нельзя выразитъ точнымъ образомъ не только въ цѣлыхъ единицахъ, но и ни въ какихъ доляхъ единицы.
Пусть даниый неточный квадратъ будетъ И. Такъ какъ цѣлое число М не есть квадратъ другого цѣлаго числа, то очевидно, что квадратный корень изъ К не можетъ быть равенъ ни какому цѣлому числу. Посмотримъ, нельзя ли вы-
точно нѣкоторою дробью у, которую всегда можно представлять г -із^іенною къ виду несократимой дроби. Допустивъ возможность равенства
г* завысивъ обѣ его части въ квадратъ, нашли бы
и , а» а.а х
Но дробь = сл. числитель ея содержитъ только тѣхъ множителей, добрые находятся въ а, а знаменатель —только тѣхъ, которые заключаются въ Ь; »*- а и Ъ суть числа первыя между собою, слѣдовательно а2 и Ь® не имѣютъ д2
Мехъ множителей, а потому дробь несократима, Такимъ образомъ, допуще-яе. выражаемое равенствомъ (1), привело къ ложному заключенію, что цѣлое
А равно несократимой дроби -р, а потому это допущеніе невозможно.
Итакъ, квадратный корень изъ числа, не представляющаго точнаго квадрата, эиьзя точно выразить пи повтореніемъ цѣлой единицы, ни повтореніемъ какой-
ея доли. Такіе корни называютъ иесоизжьршшлш са единицею, въ •тхічіе отъ цѣлыхъ чиселъ и конечныхъ дробей, которыя можно точно выра-жать въ частяхъ единицы, и которыя называются поэтому сь
-лвммиею.
Такъ, квадратные корни изъ чиселъ 2, 7, 10 и т. п. суть корни несоизмѣримые. Далѣе мы увидимъ, что такіе корни можно вычислять съ какою угодно "частью. Когда приближенный корень разнится отъ истинной величины мень-к чѣмъ на 1, то онъ называется точкы.м?, до единицы.
125. Опредѣленія. Квадратный коренъ изъ цѣлаго числа, точный до «йввагмы, есть яорень шь наибольшаго квадрата, заключающагося въ аваша числѣ, или этотъ коренъ, увеличенный на 1.
Пусть К есть неточный квадратъ, и А’— наибольшій квадратъ, заключаю-жйігж въ этомъ числѣ; въ такомъ случаѣ, очевидно, X будетъ содержаться «яду двумя послѣдовательными квадратами: А8 и (А-рІ)2, т. е.
(А + 1)*>К>А\
•чиж. переходя къ корнямъ, находимъ:
А4-1 >і/х >А.
разность между А -р 1 и А равна единицѣ; а потому разности между В $ ж А. съ одной стороны, и между А^-1 и |/Й^съ другой, меньше 1; а^лкт^дьно, какъ А, такъ и АЦ-1 выражаютъ )/Х съ точностью до 1. Но а х&адратный корень изъ А®, т.-е. изъ наибольшаго квадрата, содержа-Жъ? -л тг X. а А+1 есть этотъ корень, увеличенный на 1: этимъ данное оправдывается.
о ък.ывается квадратнымъ корнемъ изъ X — точчм.мг до 1 по недостат-г» . — 1 — по избытку.
Такъ, замѣчая, что наибольшій квадратъ, содержащійся въ 109, есть 100, заключаемъ, что квадратный корень изъ 109, точный до 1 по недостатку, есть 10, а по избытку—11.
126. Остаткомъ квадратнаго корня называютъ разность между даннымъ числомъ и квадратомъ его корня, точнаго до 1 по недостатку. Такъ, въ предыдущемъ примѣрѣ остатокъ корня будетъ
109 — 10» или 9.
Вообще, если данное число есть X и корень изъ него, точный до 1 по недостатку, равенъ А, а остатокъ В, то, по опредѣленію остатка, В = Х— А2, откуда
Х = А* + В.
Въ частномъ случаѣ, когда число есть точный квадратъ, остатокъ корня равенъ нулю.
Теорема. Остатокъ корня не больше удвоеннаго квадратнаго корня изъ даннаго числа, точнаго до 1 по недостатку.
Въ самомъ дѣлѣ, пусть А есть квадратный корень изъ И, точный до 1 по недостатку. Въ такомъ случаѣ X содержится между А2 и (А 4“1)2, а потому разность между К и А2 меньше разности (А +1)2 — А2 или 2А + 1; слѣд.
X —А2<2А4~1
или X— А2 <2 А,
ибо X — А2 — число цѣлое. Но X — А2 есть ничто иное какъ В; слѣд.
К^2А.
Слѣдствіе. — Если между цѣлыми числами X, А и В илсіьюпій ллъсяго соотношенія:
К = А2 4“ и К <2А,
то это значитъ} что А есть квадратный коренъ изъ X, точный до 1 «о недостатку, и чиго’В есть остатокъ этою корня.
Въ самомъ дѣлѣ, равенство доказываетъ, что А2 содержится въ X, а неравенство доказываетъ, что X не содержитъ въ себѣ (А-{-1)3т ибо Н не составляетъ 2 А-1- 1.
Извлеченіе квадратнаго корня изъ цѣлаго числа съ точностью -до единицы. .
127. Теорію этого дѣйствія мы подраздѣляемъ на три случая.
Первый случай. Данное число меньше 100.
Въ этомъ случаѣ квадратный корень находятъ при помощи таблицы квадратовъ первыхъ девяти чиселъ.
Числа: 1234 5 6 7 8 9
Квадраты: 1> 4 9 16 25 36 49 64 81.
Пусть, напр., требуется найти квадратный корень изъ 58 съ точностью до 1.
I ' таблицы квадратовъ видимъ, что 58 содержится между 49 и 64, сл. і ' • заключается между 7 и 8, поэтому искомый корень, точный до 1 по не-і равенъ 7, а остатокъ = 58 — 49 или 9.
128. Второй случай. Данное число содержится между 100 и 10000.
Пусть данное число будетъ 7865; оно содержится между 100 и 10000, или в*жлу ІО3 и 100я, а потому квадратный корень изъ 7865 заключается между - і 100. Но между этими предѣлами находятся двузначныя числа, а потому чый корень, точный до 1, состоитъ изъ десятковъ и единицъ: пусть число >- ггковъ его будетъ й, а простыхъ единицъ и; искомый корень выразится *:<улою 10Л-(-и, и если остатокъ корня назовемъ буквою В, то. замѣчая, кі «снованіи § 126, что данное число равно квадрату своего корня, точнаго : 1 по недостатку, Ц-остатокъ, получимъ:
7865 = (1О^+и)2 + В=ІОО^ + 2.10й.н + ^4-Е.,Д1)
Чтобы найти цифру (й) десятковъ корня, замѣчаемъ, что слагаемое 100й'\ слкъ цѣлое число, оканчивающееся двумя нулями, есть цѣлое число сотенъ, я ’-тому должно содержаться въ 7800 суммы, а слѣд. (і* содержится въ 78. Докажемъ, что квадратный корень изъ наибольшаго квадрата, заключающагося гъ 78, и дастъ намъ й. Въ самомъ дѣлѣ, изъ таблицы квадратовъ видимъ, что 78 заключается между 64 и 81, или между 8а и 92:
8*<78<92.
Помножая эти числа на 100, мы не измѣнимъ неравенствъ, сл.
802 < 7800 < 902
Если въ 7800 прибавимъ 65, то этимъ не измѣнимъ смысла неравенствъ. Въ самомъ дѣлѣ, такъ какъ 802 меньше 7800, то оно и подавно будетъ меньше 7865. Но 7865 будетъ также меньше 902. Дѣйствительно, 7800 и 9О3 (или 8100) суть два цѣлыя числа сотенъ; и какъ второе больше перваго, то оно превосходитъ первое, по крайней мѣрѣ, на одну сотню. Слѣд., прибавляя къ первому 65 — число меньше 100, получимъ результатъ, во всякомъ случаѣ, меньшій 90а. Итакъ
802 < 7865 < 902,
а отсюда, переходя къ корнямъ, получимъ:
80 < /7865 < 90.
Эти неравенства показываютъ, что искомый корень больше 8 десятковъ, но меньше 9 десятковъ, т.-е. что онъ содержитъ кгшш десятковъ 8 и, можетъ быть, нѣсколько простыхъ единицъ, число которыхъ никакъ не больше 9 (ибо величина корня меньше 9 десятковъ). Такимъ образомъ й = 8, т.-е. цифра десятковъ корня равна квадратному корню изъ наибольшаго квад-рата, содержащагося въ чмслть Лзкшпо числа.
Подставляя въ равенство (1) 8 вмѣсто с/, найдемъ:
7865 = 6400 + 2.80ы + и* -(- И,
.а вычтя изъ обѣихъ частей по 6400:
1465 = 2.80и + 4-В.. .(2)
Постараемся теперь опредѣлить цифру и единицъ корня* Для этого замѣтимъ, что слагаемое 2.80.м суммы 1465, т.-е* удвоенное произведеніе 8 десятковъ на простыя единицы « корня, есть цѣлое число, оканчивающееся нулемъ и потому представляющее цѣлое число десятковъ. Число 2.80« заключается, поэтому, необходимо, въ 146 десяткахъ суммы. Но въ составъ этихъ 146 десятковъ могутъ входить также десятки отъ слагаемаго (квадрата единицъ корня) и отъ возможнаго остатка К. Въ виду этого мы не можемъ утверждать, что членъ 2.80м равняется 1460: онъ можетъ быть и меньше числа 1460. Итакъ:
2 . 80« < 1460.
Сокративъ на 10 и раздѣливъ обѣ части на 2 V 8. получимъ
164 м<2.8'
Цифра единицъ к есть число цѣлое, а потому изъ послѣдняго неравенства заключаемъ, что, раздѣливъ 146 на 2.8 и взявъ цѣлую часть частнаго, мы найдемъ число равное цифрѣ единицъ корня, либо ее превышающее,—однимъ словомъ, найдемъ высшій предѣлъ цифры единицъ корня. Замѣтивъ, что число 1465 называется первымъ остаткомъ, выводимъ изъ сказаннаго слѣдующее правило для нахожденія цифры единицъ корня: отдѣливъ въ первомъ остаткѣ правую цифру запятой и раздѣливъ находящееся влѣво отъ запятой число на удвоенную цифру десятковъ корня, вь цѣлой части частнаго будемъ имѣть высшій предѣлъ цифры единицъ корня.
Въ данномъ случаѣ цѣлая часть частнаго отъ раздѣленія 146 на 16 есть 9; заключаемъ, что цифра единицъ корня будетъ или 9, или число меньшее 9. Чтобы испытать, годится ли 9, мы должны корень 89 возвысить въ квадратъ и вычесть изъ даннаго числа: если вычитаніе будетъ возможно, то цифра 9 будетъ -требуемая; въ противномъ случаѣ, т, е* если окажется, что 392 больше 7865, надо уменьшить цифру 9 на единицу и испытать цифру 8, п т. д. до тѣхъ поръ, пока вычитаніе будетъ возможно. Но
89* = (804-9)»=80* 4~2.80.94-9»;
мы уже вычли изъ даннаго числа 80* и въ остаткѣ нашли 1465; остается изъ этого остатка вычесть 2 . 80.9 + 9®. Но, вынеся въ этой суммѣ за скобки 9, получимъ
(2.80+ 9) . 9, или 169X9*
откуда замѣчаемъ, что число, подлежащее вычитанію изъ перваго остатка, сокращенно составляется такъ:' удвоивъ цифру десятковъ корня (что даетъ 16), приписываютъ справа испытуемую цифру единицъ и составленное такимъ образомъ число множатъ па эту же цифру; выполнивъ вычисленіе, найдемъ
169X9 = 1521,
результатъ, превышающій первый остатокъ, откуда заключаемъ, что цифра 9 велика*
Взявъ 8 вмѣсто 9, составляемъ такимъ же образомъ
(2.80 + 8) X 8, т.-е, 168.8= 1344.
Полученное число меньше перваго остатка, слѣд. 8 и есть истинная цифра единицъ корня, ибо она ни слишкомъ велика, ни слишкомъ мала. Итакъ, искомый корень = 88, причемъ остатокъ
Н = 1465 — 1344 = 121.
Вычисленіе располагаютъ такимъ образомъ:
1/78,65 = 88 64
168 146.5
Х8 134 4
12 1
Для повѣрки дѣйствія, руководясь § 126, слѣд., сравниваемъ остатокъ съ удвоеннымъ корвеп: такъ какъ въ данномъ случаѣ 121 <2X88, то заклюемъ. чт’- 98 есть дѣйствительно квадратный корень изъ 7865, точный до 1 2 59 е-ть корень, точный до 1 по избытку.
129. Ип туелнітжаго выводимъ слѣдующее правило вычисленія дву.шач-^/--ділгь дли»* чвсдѵ на двѣ грана отъ правой руки къ лѣвой, по гфры въ каждой пани (въ лѣвой грани можетъ быть и одна цифра), и і:.л.ггів>^еъ квадратный корень изъ наибольшаго квадрата. содержащагося въ вервой грани (слѣва): полученная цифра будетъ цифрой десятковъ корня. Квадратъ цифры десятковъ вычитаемъ изъ первой грани и къ остатку сносимъ вторую грань; въ полученномъ остаткѣ отдѣляемъ послѣднюю цифру справа запятой, а оставшееся влѣво отъ запятой число дѣлимъ на удвоенную цифру десятковъ корня: частное дастъ высшій предѣлъ цифры единицъ корня. Для повѣрки къ удвоенной цифрѣ десятковъ корня приписываемъ справа цифру единицъ и образовавшееся число умножаемъ на испытуемую цифру единицъ. Если произведеніе не превышаетъ остатка, то испытуемая цифра единицъ есть истинная. Въ противномъ случаѣ ее уменьшаютъ на 1, п т. д., поступая такимъ образомъ до тѣхъ поръ, пока составленное вышеуказаннымъ способомъ произведеніе не будетъ числомъ, не превышающимъ перваго остатка. Если во второмъ остаткѣ получится ноль,—это будетъ означать, что корень извлекается точно; въ противномъ случаѣ—приближенно, съ ошибкою меньшею 1.
130. Приводимъ нѣсколько примѣровъ.
Примѣръ I.—Найти 1/1369. Руководясь сказаннымъ правиломъ, имѣемъ
/13,69 = 37.
9
67 46,9
(7 46 9
0~
Полученіе нуля въ остаткѣ показываетъ, что квадратъ 37-о въ точности равенъ 1369, т.-е. что 37 есть точный квадратный корень изъ даннаго числа.
Примѣръ И.—Найти }/б341.
/63,41 = 79. 49
149 Д44,Г
Х9 |134 1
100
При опредѣленіи цифры единицъ пришлось дѣлить 144 на 14, причемъ въ цѣлой части частнаго получилось 10; но какъ цифра единицъ не можетъ быть больше 9, то испытываемъ прежде всего эту цифру. Полученіе остатка показываетъ, что цифра единицъ корня дѣйствительно равна 9.
Примѣръ ПІ.—Извлечь |/5038;
|/50^8 49
14 |ТО
70
Дѣля 13 на 14, находимъ въ цѣлой части частнаго 0; сл. цифра единицъ корня равна 0, и самый корень = 70. Удвоенное произведеніе десятковъ на единицы и квадратъ единицъ корня составляютъ 0,. поэтому остатокъ дѣйствія есть 138; онъ меньше удвоеннаго корня, сл. 70 есть корень точный до 1 по недостатку.
Корень точный до 1 по избытку равенъ поэтому 71.
131. Третій случай.—Это есть общій случай, который приводится къ двумъ предыдущимъ при помощи слѣдующей теоремы.
Теорема. Число десятковъ квадратнаго корня точнаго до 1 по недостатку изъ даннаго цѣлаго числа равно квадратному корню изъ наибольшаго квадрата, содержащагося в?> числѣ сотенъ этого числа^
Пусть данное число будетъ 78658143, и пусть наибольшій квадратъ, содержащійся въ 786581, т.-е. въ числѣ сотенъ его, будетъ а3.
Если число 786581 есть точный квадратъ, то оно равно а3, если неточный, то будетъ больше аа; но въ томъ и другомъ случаѣ будетъ меньше квадрата слѣдующаго за а цѣлаго числа, т.-е. меньше (аД-1)2.
И такъ
«3^786581<(а+ I)3;
Помножая эти три числа на 100, найдемъ:
(10а)3^ 78658100 < [(а-/ 1). ІО]3.
Придавъ къ среднему числу 43, мы этимъ нарушимъ возможное равенство, обративъ его въ неравенство (Юа)3 < 78658143, усилимъ первое неравенство, увеличивъ его большую часть, и, наконецъ, не нарушимъ второго неравенства. Послѣднее обстоятельство объясняется тѣмъ, что 78658100 и [(а —1). ІО]3 суть цѣлыя числа сотенъ, и какъ второе больше перваго, то оно превосходитъ первое по меньшей мѣрѣ на одну сотню; слѣдовательно, увеличивъ меньшее число на 43, т.-е. менѣе чѣмъ на сотню, получимъ результатъ все-таки меньшій [(а-рі). Ю]3. Такимъ образомъ имѣемъ
(10а)3 < 78658143 < [(а + 1) . ІО]3,
пи. з^еіодя къ корнямъ, найдемъ
10а < /78658143 <(«+1). 10.
неравенства доказываютъ, что искомый корень, будучи больше а десят-і -Гз- одержитъ въ себѣ эти а десятковъ и однако же не содержитъ а -|- 1 іг лтіи такъ какъ онъ меньше этого числа десятковъ (въ силу второго нера-Слѣдовательно, опредѣляемый корень состоитъ изъ а десятковъ и, > асггь быть, нѣсколькихъ простыхъ единицъ, число которыхъ не больше 9; •опъ словомъ, десятковъ въ немъ будетъ а. Замѣтивъ же, что а
- ~ квадратный корень изъ а4, т.-е. изъ наибольшаго квадрата, содержаща-п въ числѣ сотенъ даннаго числа, заключаемъ, что теорема доказана*
132* Итакъ, число десятковъ квадратнаго корня изъ
78658143
есть квадратный корень изъ наибольшаго квадрата, заключающагося въ числѣ сотенъ этого числа, или, что то же,—квадратный корень, точный до 1 по недостатку, изъ 786581.
Число десятковъ этого корня, или, что все равно, число сотенъ перваго, есть, на основаніи теоремы § 131, квадратный корень, точный до 1 по недостатку, изъ 7865*
Число десятковъ этого корня, т.-е. число тысячъ перваго, по той же теоремѣ, есть квадратный корень, точный до 1 по недостатку, изъ 78.
Такимъ образомъ, отдѣляя отъ правой руки къ лѣвой по двѣ цифры, мы убѣдились, что искомый корень состоитъ изъ четырехъ цифръ, что для нахожденія старшей его цифры нужно извлечь, съ точностью до 1 по недостатку, квадратный коренъ изъ первой грани слѣва, и что число граней равно числу щіфръ искомаго корня.
Прилагая теорему § 131, мы видимъ, что число сотенъ искомаго корня равно точному до 1 по недостатку квадратному корню изъ 7865; находимъ этотъ корень по правилу Й 129:
78,65 | 8143 ] 88
64
168 146,5
Х8 134 4
12 1
88 есть число десятковъ квадратнаго корня изъ 786581; чтобы найти цифру единицъ этого корня, или, что то же, цифру десятковъ искомаго корня, нужно изъ 786581 вычесть квадратъ 880. Вычитаніе это, по частямъ сдѣланное, дало въ остаткѣ 12100—|— 81 или 12181—число, которое находимъ, снеся 81 къ остатку перваго корня* Этотъ остатокъ заключаетъ, слѣдовательно, удвоенное произведеніе 88 десятковъ на единицы и квадратъ единицъ корня изъ 786581 * Совершенно такимъ же образомъ, какъ было указано въ § 128, можно доказать, что, раздѣливъ число десятковъ 1218 новаго остатка на удвоенное число десятковъ, т*-е* на
2.88, или на 176,
чійіемъ въ цѣлой части частнаго высшій предѣлъ цифры единицъ корня і ' ТзбэЗЬЭтотъ предѣлъ есть 6; для испытанія этой цифры удвоиваемъ 88,
къ 176 приписываемъ справа 6 и множимъ 1766 на 6. Произведеніе 1766 X Х6= 10596 не превышаетъ 12181, а потому цифра 6 годится.
Итакъ, цифра десятковъ искомаго корня есть 886. Остается найти цифру ----------------------------------------------------------2
единицъ. Для этого изъ заданнаго числа слѣдуетъ вычесть 8860. Вычитаніе 880 десятковъ въ квадратѣ сдѣлано и дало въ остаткѣ 1218100, который въ совокупности съ 43, составляетъ 1218143. Вычитая отсюда остальныя двѣ части -----2
8860 т.-е. 10596 сотенъ, находимъ 158543.
Въ этомъ остаткѣ заключается удвоенное произведеніе 8860 на простыя единицы искомаго кория и квадратъ единицъ. Раздѣливъ число десятковъ этого остатка или 15854 на 2.886= 1772, въ цѣлой части этого частнаго будемъ имѣть высшій предѣлъ для цифры простыхъ единицъ искомаго корня. Предѣлъ этотъ есть 8; для испытанія цифры 8. приписываемъ ее къ 1772 и множимъ 17728 на 8. Произведеніе 141824 можно вычесть изъ 158543, сл. 8 есть дѣйствительно цифра единицъ искомаго корня. Итакъ, корень = 8868, а остатокъ =
158543 —141824 = 16719.
Дѣйствіе располагается слѣдующимъ образомъ:
/78,65 81,43 = 8868 64
168 146,5 ............. 1-й частный остатокъ.
/8 1344
1766 "І218,1 ..........2-й
Х6 10596
17728“58Щ................3-й > »
Х$ 141824
16719..........окончательп. остатокъ.
Окончательный остатокъ меньше 2X8868 = 17736, слѣдовательно 8868 есть дѣйствительно корень изъ даннаго числа, точный до 1 по недостатку.
Отсюда выводимъ
133. Правило извлеченія квадратнаго корня точнаго до 2 по недостатку изъ цѣлаго числа.
Раздѣляютъ данное число на грани по двѣ цифры, отъ правой руки къ лѣвой (послѣдняя гранъ можетъ имѣть ы одну цифру)', число граней'*равно числу цифръ корня.
Чтобы найти первую цифру корня, извлекаютъ квадратный коренъ изъ наибольшаго квадрата, заключающагося въ первой грани (слѣва).
Чтобы найти вторую цифру корня, вычитаютъ изъ первой грани квадратъ первой цифры корня и къ остатку сносятъ слѣдующую гранъ: получаютъ такъ называемый первый частный остатокъ. Отдѣляютъ въ немъ одну цифру справа запятой, а стоящее влѣво отъ запятой число дѣлятъ на удвоенную первую цифру корня; частное дастъ или вторую цифру корня, или больше ея. Для повѣрки приписываютъ эту цифру съ правой стороны дѣлителя и полученное число умножаютъ на ту же цифру; если произведеніе возможно вычесть изъ перваго частнаго остатка, то испытуемая цифра ц будетъ второю цифрою
корня; п яр&тивномъ случаѣ ее уменьшаютъ на 7, и дѣлаютъ новую «йодж> шжпгмг же точно образомъ, какъ и первую; продолжаютъ та-шп <Хмэсл^ до тѣхъ поръ, пока вычитаніе сдѣлается возможнымъ.
Зжс* найти третью цифру корня, къ остатку послѣдняго вычи-мш ек&слтъ третью гранъ, и получаютъ второй частный остатокъ; «шм іііывиж^ въ немъ одну цифру справа запятой, а оставшееся влѣво кшк ляпшшой число дѣлятъ на удвоенное число, образуемое первыми шфрами корня: частное дастъ высшій предѣлъ для третьей аеуи горня. Провѣряютъ цифру частнаго такимъ же образомъ, какъ в ж случая,.
Гіжмль образомъ продолжаютъ поступать до тѣхъ поръ, пока не снесены всѣ храни, и не будетъ опредѣлена послѣднимъ дѣле-цифра простыхъ единицъ корня и окончательный остатокъ.
134. Примѣры.
1. Найти /28164249. /28,16,42,49 = 5307
25
11. Извлечь /583749876429.
/58 37,49,87,64 29 = 764035 т < 9 г Г <
103 31,6
ХЗ 30 9 1060 74,2
Хоооо
1060717424,9
X 717424 9 О
93,7 87 6 “біТ^ 609 6
146 Х6 1524 X*
152803
Хз 1528065
X
5 3876'4
4 5840 9
—8035 529
7640 325
395 20 4
Такъ какъ остатокъ меньше удвоеннаго корня, то 764035 есть корень точный до 1 по недостатку; слѣд. 764036 есть корень, точный до 1 по избытку.
135. Опредѣлимъ, который изъ двухъ корней, точныхъ до 1, — корень по недостатку, или по избытку, точнѣе выражаетъ истинную величину несоизмѣримаго корня. Можно доказать, что если, найдя корень точный до 1 по недостатку, окажется, что остатокъ корня не болѣе самаго корня, то этотъ корень ошибоченъ менѣе чѣмъ па -у; если же остатокъ окажется больше корня, то корень по избытку будетъ ошибоченъ менѣе чѣмъ на -І--м'
Пусть данное число есть К; корень, точный до 1 по недостатку, пусть будетъ а; остатокъ выразится разностью К — а3.
Первый случай. — Имѣемъ
а3<К<(а-Н)*;
1
по условію, остатокъ Ь — а3<а; слѣд. К — откуда
9 1 г I I I IV но а + гту) * а потому
Итакъ
откуда
1
Такъ какъ разность между крайними величинами равна -а-, то разность & г^~ 1 1
между у И на меньше у- Слѣд. а есть корень, точный до у по недостат-
ку, т.-е. истинная величина (/Й" отличается отъ а менѣе, чѣмъ отъ
Второй случай. Если окажется, что
Я — а3-> а,1
1
то заключаемъ отсюда, что X — а4 > а у, потому что (X — а3) есть число
цѣлое; слѣд.
і1 ѵ I і 1
Я>а2Ч-а + -г или К> « + -
4 \ ’ і /
Итакъ
а + у <а4-1.
откуда
Но разность между крайними числами равна -9-, слѣд. разность между (а0 и меньше у* Заключаемъ, что а-|-1 отличается отъ корня изъ X меньше нежели на 4"» т.-е. этотъ корень ближе лежитъ къ а-(-1, чѣмъ къ а.
Изъ сказаннаго слѣдуетъ, что выгоднѣе братъ коренъ по избытку только тогда, когда остатокъ превышаетъ величину ко/тя, взятаго по недостатку.
Такъ, въ примѣрѣ II, § 134, получился остатокъ меньшій корня но недостатку, и потому 764035 точнѣе выражаетъ величину искомаго корня, чѣмъ число 764036. Въ примѣрѣ § 132 остатокъ больше найденнаго корня, и потому число 8869 ближе къ истинной величинѣ корня, чѣмъ число 8868.
ь я
Извлеченіе квадратнаго корня изъ дробей съ точностью до 1.
»
136. Теорема. Коренъ квадратный изъ несократимой дроби несоизмѣримъ * если его нельзя извлечь отдѣльно изъ числителя и знаменателя.
Пусть у есть данная несократимая дробь; равенство
Ѵт=‘.
гдѣ й— число цѣлое, невозможно, потому что, возвысивъ обѣ части въ квад-?агь, нашли бы '
т.-е. что несократимая дробь равна цѣлому числу. Итакъ, квадратный корень хзъ несократимой дроби не можетъ быть выраженъ цѣлымъ числомъ* Посмотримъ, нельзя ли его выразить дробью, т.-е. не будетъ ли возможно равенство
л і/ а с
гдѣ подъ у- всегда ыж разумѣть дробь несократимую. Возвысивъ обѣ части испытуемаго равенства къ квадратъ, найдемъ
а с2
~Ь~ Т2'
гдѣ есть др«4& «^«301201. тш какъ. по условію, с и а — числа вза-
имно-первыя- Вт гті дроби могутъ быть равны только тогда,
когда числител егь зал когда а = с* і і = і*
в ѴЕКлу оНм. а знаменатели—между собою *), т.-е. іимік что а и Ь должны быть точными квад-
ратами. Инги ішрктхый жзъ несократимой дроби только тогда можетъ бытъ тию® мй4Х?п дробью, когда оба члена данной дроби суть точ-
ные квадраты Въ ^агввкгь случаѣ корень изъ дроби нельзя точно выразить
ни ііжп мвскіъ. Еі дробнымъ; поэтому онъ будетъ число несоизмѣримое.
что 64 и
гі
корень изъ извлекается точно, потому
1 — точные квадраты. Имѣемъ
а «1 *
*) Пусть -у и у будутъ двѣ несократимыя дроби, и посмотримъ условіяхъ возможно равенство
а о1
У — у " ‘ С1)- >
при какихъ
м
Опредѣляя а, имѣемъ: а = -у-; такъ какъ а — число цѣлое, то а1& должно дѣлиться на &1; но а1 есть число первое съ Ь1, сл. Ъ должно дѣлиться на Ы. Опредѣ-аМ
ля я изъ (1) а1, имѣемъ: а1 = -у-, откуда такимъ же то чао образомъ заключаемъ, что М должно дѣлиться на Ъ. Но два числа только тогда могутъ дѣлить взаимно другъ друга, когда они равны; слѣд. 6 — &і. Но въ такомъ случаѣ изъ равенства (1) слѣдуетъ, что и а = а<. Итакъ, чтобы двѣ несократимыя дроби были равны, необходимо, чтобы числители ихъ были равны и знаменатели. Это условіе, очевидно, есть я вполнѣ достаточное.
— несоизмѣримы, потому что у первой дроби знаменатель, у второй — числитель, а у третьей — оба члена суть неточные квадраты.
137. Теорема. — Квадратный корень шь дробнаго числа* точный до 1, есть квадратный корень изъ наибольшаго квадрата* заключаю* щагося въ цѣлой части даннаго числа* или этотъ коренъ, сложенный съ 7.
Пусть данное дробное число будетъ а -|- Ь, гдѣ а — цѣлое число, и Ъ — правильная дробь. Разсмотримъ два случая.
Первый случай: а — точный квадратъ, напр. а — г2; тогда очевидно, что
а Ь > г2.
Съ другой стороны: а, будучи — меньше (г 4” 1)*; но если изъ двухъ неравныхъ цѣлыхъ, (г-рі)2 н а, первое больше второго, то оно больше его, по меньшей мѣрѣ, на 1. сл. (г-рі)2 —а>Ь, или (гЦ-1)2^> Итакъ:
(г + 1)*>а + Ь>г*;
откуда, переходя къ корнямъ, находимъ:
г + 1 > \/а 4~ Ь > г.
Разность крайнихъ чиселъ: г-рі й г равна 1, а потому
|/а4~^“”Г<С1 и (ГЧ~1)—|/а4“&<1?
слѣд. какъ г, такъ и г 4-1 выражаютъ величину съ ошибкою, мень-
шею 1; но г есть квадратный корень изъ а, а г4“1—этотъ корень 4~1і сл. для этого случая теорема доказана.
Второй случай:* а — неточный квадратъ, и пусть наибольшій квадратъ, содержащійся въ а, будетъ г3; въ такомъ случаѣ
< г2<а<(г4“1Л
ш
По первому неравенству: а потому и подавно
а 4- Ь
Въ силу второго неравенства, изъ двухъ цѣлыхъ чиселъ: (г1)3 и а, первое больше второго, сл. оно больше, по крайней мѣрѣ, на 1; а потому разность ихъ больше правильной дроби
(г 4" I)2 — откуда
(г+ 1)3>«4”ь*
Итакъ, имѣемъ:
1)’ > И 4-Ь > »’;
переходя къ корнямъ, находимъ:
(г-|-1) >}/а-|-Ь>г,
’ттда опять заключаемъ, что числа г н г +1 выражаютъ \/ а-\-Ь съ ошиб-з>ш- іея>шею І.Но г есть корень изъ цѣлой части а числа а-рЬ, точный до 1 і‘ «достатку, а — этотъ корень —1,. слѣд. теорема доказана и для случая. Отсюда
ІЛ- Правило. Для извлеченія квадратнаго корня изъ дробнаго числа як*«еж 4о I, слѣдуетъ отбросить дробь и извлечь, съ точностью до 7,. мп цѣлой части. , '
Примѣчаніе. Такъ какъ у правильной дроби цѣлая часть равна нулю, то
>^нв мзъ предыдущаго, что квадратный корень изъ такой дроби, точный до Е «еп: 0 — по недостатку, и 1 — по избытку.
/ 41
Птіміры: I. Найти 1/72^ точно до 1.
* О—
дробь, извлекаемъ |/72 съ точностью до 1; находимъ, что ко-рвъ жтъ и-= * дроби. съ требуемою точностью, равенъ: 8 — по недостатку, и > —Г* ПЙИ іу.
_ у 7<1_±15 іиіикпю до Е
( :ді я г>—»- | 761 съ требуемою точностью.
) 7Л1—27 4
47 ЗбТ
X ‘ | 329
32
' ііИівтуть. что искомый корень равенъ: 27 — но недостатку, и 28 — по
ЯИНІТГ- 1
_ _ . ' ./3417,31
- зііп. съ точностью до 1, 1 —ктко1
Імкм всего нужно выполнить указанное дѣленіе, ограничиваясь наіожде-аип гѣмй части частнаго, н извлечь изъ нея корень съ точностью до 1. 1“^*впяе располагаютъ такъ:
3417310
3164
2533
2260
2731
2712
190
452
75,60 = 86.
64
166 1160
X 996
164
Итакъ, искомый корень равенъ: 86 — но недостатку, и 87 — по избытку.
Извлеченіе квадратнаго корня изъ цѣлыхъ чиселъ и изъ дробей 1 съ точностью до —•
Тѵ
139. Извлечь квадратный корень изъ цѣлаго или дробнаго числа А съ точ-ностью до — значитъ найти такую приближенную величину для искомаго корня, которая отличалась бы отъ его истинной величины менѣе чѣмъ на
Пусть требуется извлечь і/А, гдѣ А — цѣлое или дробное число, представляющее неточный квадратъ, съ точностью ’до при чемъ дробь называется степенью приближенія. Помноживъ и раздѣливъ ]/Л на я, мы не измѣнимъ его величины, слѣд.
,/Т —
1 А~—
Но п — у/п*; поэтому числителя можемъ представить въ видѣ или, по правилу извлеченія корня изъ произведенія, въ видѣ у^Ая3.
Такимъ образомъ
/А = ^-
гдѣ Ап3 — неточный квадратъ, потому что таково А. Извлекаемъ, по извѣстнымъ уже намъ правиламъ, |/Аи3 съ точностью до 1; найдемъ двѣ величины— г по недостатку, и у -р 1 по избытку, такъ что
г —1 > г.
|/Ая^ /—
Раздѣливъ эти три числа на п н замѣтивъ, что-----------= уА, найдемъ
71
|/А
Г
п
п Л Г + 1 Г 1 х
Разность между крайними числами, — -----—> равна слѣдов. каждая изъ
. разностей: у А-’ — и| —------у А, меньше —; это значитъ, что каждая изъ
дробей: и Г \ выражаетъ величину |/А съ ошибкою, меньшею
Отсюда выводимъ
440. Правило. Чтобы изъ даннаго цѣлаго или дробнаго числа извлечь квадратный коренъ съ точностью до нужно умножитъ это число на квадратъ знаменателя степени приближенія, ша полученнаго произведенія извлечь квадратный коренъ съ точностью до 1 и раздѣлитъ его на знаменателя степени приближенія.
Примѣры. 1. Найти у 32 съ точностью до Дк-~ Іо Ліо
7
По правилу должны 32^ умножить на (273)*, что даетъ 2425059; извлечь
въ этого числа квадратный корень съ точностью до 1, и раздѣлять его на 273. Квадратный корень изъ 2425059, точный до 1 по недостатку, есть 1557, а по избытку — 1558; раздѣливъ тотъ и другой на 273, найдемъ: _ 192 .193
^ВЭ273'
заключается
192 193
между числами 5^ и 59^, отли-
шсь отъ каждаго изъ нихъ менѣе чѣмъ на
3- Найти }/3 съ точностью до 0,001.
Н осивъ 3 на 1 0002, извлекаемъ )/3000000 до 1; получимъ числа 1732 і 1753, Раздѣливъ каждое на 1000, найдемъ
1,732 и 1,733.
шмжэеть }/3 съ точностью до 0,001
7» » Ж> избытка
V
по недостатку, вторая—
3,1415926
іі.'О* г 100*. хзвлекаемъ квадратный корень
~ г? 1. Цѣлая часть частнаго есть 59275, а корень
жз» «. !-:• 1 по недостатку, есть 243, а по избытку 244. Раздѣливъ
вжкй ихъ ихъ ка 100, получимъ для искомыхъ приближеній, точныхъ до 1
2,43 (по пед.) и 2Л44 (по изб.)
Сокращенный способъ извлеченія квадратнаго корня.
141 - Предыдущія правила показываютъ, что извлеченіе квадратнаго корня кхгм приводится къ извлеченію его изъ цѣлаго числа съ точностью до 1. Это вклѣднее дѣйствіе дѣлается тѣмъ сложнѣе, чѣмъ больше цифръ содержитъ под-ю^еявое число; въ такихъ случаяхъ дѣйствіе значительно упрощается при по-»«и такъ называемаго сокращеннаго способа.
Пусть будетъ А цѣлое число, изъ котораго требуется извлечь квадратный іѵ-ренъ съ точностью до 1* Искомый корень можетъ имѣть или ^четкое, или чт«ое число цифръ.
7-й случай: коренъ имѣетъ нечетное число цифръ. Пусть въ немъ находится 2п -|- 1 цифръ; найдемъ обыкновеннымъ способомъ больше половины его цифръ, въ данномъ случаѣ м —|— 1 цифръ, и буквою а обозначимъ число, образуемое этими цифрами, сопровождаемыми столькими нулями, сколько цифръ осталось найти, т.-е* п нулями (папр., если корень долженъ содержать 5 цифръ и найденныя три первыя его цифры будутъ 234, то буквою а мы обозначаемъ
число 23400); такимъ образомъ, а будетъ число (2я-|-1) — злачное. Далѣе, назовемъ буквою х то, что слѣдуетъ придать къ а, чтобы получить истинный корень (я состоитъ изъ цѣлой части, имѣющей « цифръ и, можетъ быть, еще изъ несоизмѣримой десятичной дроби); полный корень выразится суммою Наша цѣль—дать правило для вычисленія цѣлой части я-а, т.-е. для нахожденія х съ точностью до 1 сокращеннымъ путемъ.
По опредѣленію корня имѣемъ:
А = (а4“ж)а =
гдѣ а уже извѣстно; вычтя а2 изъ обѣихъ частей и раздѣливъ ихъ на 2а найдемъ
А~~ а*_ и / ♦ \
^Г=х—ъГ • -(І)-
А — а2 есть остатокъ послѣ нахожденія части а корня (назовемъ его буквою К); раздѣливъ его, какъ указываетъ формула, на 2а, назовемъ частное этого дѣленія буквою а остатокъ—г, такъ что
Е । г
2й=®+2а
подставимъ это выраженіе въ первую часть равенства (1); найдемъ:
। г і
д —г— — х Ч-*
* 1 2а 1 2а
откуда г X1
Х~^ = 2а~2а
Докажемъ, что д и выражаетъ величину х съ ошибкою, меньшею 1. Такъ какъ , г х
разница между х и д выражается формулою то и слѣдуетъ доказать,
что
Г X*
2а 2а
Дѣйствительно, такъ какъ г есть остатокъ дѣленія, въ которомъ 2а есть дѣлитель, а остатокъ меньше дѣлителя, то < 1. Съ другой стороны, въ цѣлой части х находится п цифръ, а потому х меньше наименьшаго (п-|-1) — знач-наго числа 10н; а слѣд. а?а< 102п; затѣмъ, а есть (2п-|-1)—значное число, слѣд. оно >102и; а слѣд. 2а >2 . 102\ Составивъ двѣ дроби
102*
2а И 2 X 10»"
и замѣчая, что числитель первой меньше числителя второй, а знаменатель первой равенъ или больше знаменателя второй, заключаемъ, что первая дробь меньше второй: Я2 102п 1
2а < 2 X102"’ или 2а < 2‘
Итакъ, каждая изъ дробей разности
X2
меньше
1, слѣд. и самая раз-
ность < 1, т.-е. ошибка, происходящая отъ замѣны х частнымъ д, если только
т>п т существуетъ, непремѣнно меньше 1, такъ что есть величина тдемія до 1*
I—і случай: корень имѣетъ четное число цифръ 2ж Найдемъ опять *%і>«оыіъ способомъ больше половины всѣхъ цифръ корня, т-е. п-1-1 —і"к ♦’тзется найти п— I цифръ. Въ цѣлой части я>са находится (к— 1)— і мш. число, а потому х меньше наименьшаго м — эпичнаго числа, т.-е. х откуда х* < ІО2"-2; а есть 2п — значное число, слѣд. оно = или >
—2п — значнаго числа, т.-е. а>102м-1, откуда 2а>2.102"-1.
гй^УХ ІО2"-1’ ИЛИ 2а 2 X ю’
• явлиеше относительно $ прежнее.
Ѣсп цѣлая часть корня, состоя изъ четнаго числа цифръ, имѣетъ первою дою 5 или больше 5, то достаточно обыкновеннымъ способомъ найти ровно всѣхъ цифръ корня. Въ самомъ дѣлѣ, въ этомъ случаѣ х < 10й, а ж^<у х* ІО2"; съ другой стороны а, какъ 2п— значное число, начинаю-ш цифрою 5 или большею, будетъ > упятереннаго наименьшаго 2п — знач-аг- ждя, т.-е, 10Ьі-1, откуда 2а^10, ІО2"”1, или 2а^102л, а
оі>тте.іьно
х* 102п 1
2 а ІО2”’ Яли 2а < *♦
І^хжиее заключеніе относительно и здѣсь имѣетъ мѣсто.
Ізъ сказаннаго выводимъ слѣдующее
Правило. — Для извлеченія квадратнаго корня изъ цѣлаго числа съ шчжстью до 1 сокращеннымъ способомъ, находятъ обыкновеннымъ спо-ийгі ооліъе половины всѣхъ цифръ корня, іш же ровно половину, если, чгаяоліз корня, первая его цифра не меньше 5; остапъ-
цифры найдемъ, раздѣливъ полный остатокъ на удвоенную найден-часть корня.
’42. Примѣръ, Найти квадратный корень съ точностью до 1 изъ числа
7316723456713.
ѵ^ень имѣетъ семь цифръ; находимъ четыре первыя прямымъ путемъ:
/7, 31, 67, 23, 45, 67, 13 2704
33,1
32 9
5404 2672,3
Х4 21616
5107456713 | 5408000
48672000 944
24025671
21632000 ”23936713
21632000
2304713
а = 2704000;
2? = 5107456713.
д = 944.
г =2304713.
Найдя первыя четыре цифры корня (2704), находимъ съ точностью до 1 частное отъ раздѣленія полнаго остатка 5107456713 на удвоенный найденный корень 2704000, т.-е. на 5408000. Это частное = 944; слѣд. искомый корень, точный до 1, есть
2704944.
143- По величинѣ частнаго <2 и остатка г дѣленія можно всегда узнать, будетъ ли найденный корень точный, или приближенный; и въ послѣднемъ случаѣ — опредѣлить, будетъ ли онъ ошибоченъ по недостатку, или по избытку.
Въ самомъ дѣлѣ, мы имѣемъ равенство
А — а2 = К, откуда А = аа-}~В;
но К = 2а# слѣдовательно
А = а* 4” 2ад 4~ г.
Съ другой стороны
(а “к “И
Отсюда:
1) Если то
а* -р 2а# г а2 ~к ~к или
А > (а + З)4, откуда
/а > а
т.-е. &~к? будетъ приближеніе, точное до 1 по недостатку.
2) Если г = #4, то
а2 4~ 2а# ~к г = “к 2а# 4“ или
А = (а + з)4, откуда
т.-е. «~к# есть точный корень изъ А.
3) Если, наконецъ, то
а2 -|- 2ад 4~ ** <С яа 4" -а(І ”к или
А < (а + #)2, откуда
}/А <Са4~Зл
и потому а4~0 есть приближеніе, точное до 1 но избытку.
Итакъ: корень а 4” будетъ приближенный по недостатку, точный, или же приближенный по избытку, смотря по тому, будетъ ли остатокъ г дѣленія больше, равенъ или меньше квадрата частнаго.
Такъ, въ предыдущемъ примѣрѣ остатокъ 2304713 больше квадрата числа 944; поэтому корень 2704944 ошибоченъ менѣе чѣмъ на 1 по недостатку.
•ч^еіѣлим’ь такъ называемый остатокъ кормя, предполагая, что для здрня примѣняется сокращенный способъ; при этомъ различаемъ два і-этвл. 'т/т|я по тому, имѣетъ ли найденный этимъ способомъ корень приближу > «достатку, или по избытку.
_ л — 5 есть приближеніе по недостатку. Обыкновенный способъ далъ Ш ** » величину, а потому, называя остатокъ корня буквою р, получимъ
? = А—(а-Н)8. ^гтттаъ, что
д — аа_(-2а^-]-г, и (а4"3)2~а*4"'М4"в\
і^ѵы второе равенство изъ перваго, найдемъ:
А — (а + в)2 = г —
р — г —
*
Втш, въ разсматриваемомъ случаѣ: остатокъ корня расеяъ мммд отъ дѣленія надъ квадратомъ частнаго.
.1. а 4" 7—приближеніе по избытку. Обыкновенный способъ далъ бы для мнл величину
«4"3—К
йхѣя равенства
А = а2+2^-1-г, и (« + « — I)2 — а8 + 2а(д — 1) + («— I)2,
*ілп. что остатокъ отъ обыкновенной операціи былъ бы
р = А — (а -\-д — I)8 = г-|-2а — д1-}’ -3 — 1
= **+2(а + з)-(д84-1).
>к_*чемъ, что -въ данномъ случаѣ остатокъ корня найдется, если къ остатку ілмагія придать удвоенный найденный сокращеннымъ способомъ корень, • «35 результата вычесть сумму квадрата частнаго съ единицей.
145. Сокращенный способъ, вмѣстѣ съ указанными замѣчаніями, даетъ сред-находить сколько угодно цифръ корня. Пусть, напр., требуется найти 1/2 ~ Неограниченнымъ приближеніемъ. Напишемъ справа отъ 2 вдвое больше ну-:-ч чѣмъ сколько желаемъ найти десятичныхъ знаковъ, и вычислимъ три пер-і..л імфры корня обыкновеннымъ способомъ.
2.00.00.00.00.00.00.00.00.00.00.00.00,00.00.00.00 1
?4 10,0
4 96
281 400
X» 281
119
1,41
Іи иапля 141 въ корнѣ и 119 въ остаткѣ. Такимъ образомъ, 141 суть
—м грмпя цифры корня изъ 200000000; двѣ слѣдующія находимъ сокращен
нымъ способомъ. Для этого нужно полный остатокъ, равный 1190000, раздѣлить на удвоенную найденную часть корня, т.-е. на 28200,
119000.01 28200
112800 : 42
62000
56400
5600
. — 1764
3836
42 X 42
84 168 1764
Находимъ въ частномъ 42 и въ остаткѣ 5600. Чтобы узнать, въ какую сторону ошибоченъ корень 14142, нужно полученный остатокъ сравнить съ квадратомъ частнаго: 5600 >42’, слѣд. 14142 есть приближеніе но недостатку, и потому послѣднюю его цифру (2) уменьшать не слѣдуетъ.
Имѣя пять цифръ корня, можно сокращеннымъ способомъ найти слѣдующія четыре цифры. Для этого надо знать остатокъ, который дала бы обыкновенная операція послѣ нахожденія части 141420000 корня изъ 20000000000000000, т.-е. остатокъ корня р. Такъ какъ и-|-д' = 14142 есть приближеніе по недостатку, то р = г—д’ = 5600— 1764 = 3836. Приписавъ сюда 8 нулей, дѣлимъ полученное число на 2а =282840000
38360000. | 0000
28284і =і
100760ІІ
84852ІІ
159080І
141420^
176600
169704
68960000
— 1838736
67121264
28284 | 0000
1356
1356
1356
8136
6780
4068 1356 1838736.
Находимъ въ частномъ 1356, а въ остаткѣ 68960000. Такъ какъ этотъ остатокъ больше 1356’, корень снова ошибоченъ по недостатку: онъ равенъ 141421356.
Зная девять цифръ корня, можемъ сокращеннымъ способомъ найти слѣдующія восемь; для этого опредѣляемъ остатокъ корня:
р = 68960000 — (1356)’ = 67121264.
Приписавъ къ остатку корня 16 нулей, а къ удвоенному найденному корню 8 нулей, дѣлимъ
6712126400000000100000000| 282842712 | 00000000
1055272160 І НІИ 23730950
2067440240іИ = =
875412560= ? = і
2688442400 И
1428579920;
143663600
Въ частномъ мы нашли 23730950, и какъ остатокъ дѣленія больше квадрата частнаго, найденный результатъ ошибоченъ по недостатку; имѣемъ
/2 = 1,4142135023730950,
съ точностью до 1 шестнадцатаго десятичнаго мѣста. Очевидно, можно продолжи* такимъ образомъ находить сколько угодно новыхъ цифръ корня.
146. Извлеченіе квадратнаго корня изъ числа, мало разнящагося отъ 1.
> результатъ, мало разнящійся отъ 1 4“ ъ если е есть весьма малая дробь; откинувъ юхучимъ приблизительное равенство ІІ-ру) — 14^, откуда, извлекая бъ обѣихъ частей квадратный корень, найдемъ:
рйіііііі и по. Опредѣлимъ предѣлъ погрѣшности этого приближенія, т.-е
Івшь и жкхілвъ я» шуатеніе на сумму
1 * а 1 1 *»
*
Откинувъ въ знаменателѣ малыя дроби у и в (подъ знакомъ корня), мы угить знаменателя уменьшимъ, а слѣдов. выраженіе второй части увеличимъ, такъ что будетъ
г*
а <Г—;или ‘+^ 8
Отсюда заключаемъ, что для извлеченія квадратнаго корня изъ числа мало превышающаго 1л достаточно прибавитъ къ 1 полотну избытка е: найдемъ результатъ, точный до по избытку. о
Примѣръ. Найти приближенно у/1,000694.
По правилу имѣемъ:
)/1,000694= к_}_ 9^2^694 = ! 000347
72 . . 1 п
съ точностью до 8 1с8 или до цр Заключаемъ, что ошибка не вліяетъ на послѣдній десятичный знакъ прнближнія 1,000347.
147. Признаки неточныхъ квадратовъ.—Въ заключеніе укажемъ нѣкоторые признаки неточныхъ квадратовъ.
1. (2я)3 = 4п\ т.-е. квадратъ всякаго четнаго числа (2п) дѣлится на 4, а слѣд. обратно, четное число только тогда можетъ бытъ квадратомъ, когда оно дѣлится на 4. Само собою разумѣется, что изъ этого не слѣдуетъ, чтобы всякое число, дѣлящееся на 4, было необходимо точнымъ квадратомъ; такъ, 40 есть неточный квадратъ.
2* (2п4~ 1)а = 4и24“4м-|-1, т.-е. всякое нечетное число имѣетъ квадратъ вида 4п-4п-|- 1, т.-е. такой, который, будучи уменьшенъ на ^дѣлится на 4; слѣд. обратно, нечетное число только тогда можетъ быть точнымъ квадратомъ, когда оно, уменьшенное на 1, дѣлится на 4.
3. Изъ умноженія цѣлыхъ чиселъ извѣстно, что произведеніе двухъ такихъ чиселъ оканчивается тою же цифрою, какою и произведеніе ихъ простыхъ единицъ. Но квадраты чиселъ 1, 2, 3, .... 9 оканчиваются цифрами 1, 4, 5, 6, 9, но не оканчиваются цифрами 2, 3, 7 и 8. Изъ этого слѣдуетъ, что всякое цѣлое число, оканчивающееся одною изъ цифръ: 2, 3, 7 и 8, не можетъ быть точнымъ квадратомъ. Здѣсь опять слѣдуетъ замѣтить, что если число оканчивается одною изъ цифръ: 1, 4, 5, 6 и 9, то оно не есть необходимо точный квадратъ; такъ, 825 есть точный, а 15—неточный квадратъ.
4. Если число оканчивается 5-ю, его квадратъ долженъ оканчиваться 25-ю. Въ самомъ дѣлѣ, разсматривая число какъ сумму десятковъ и простыхъ единицъ, находимъ, что квадратъ десятковъ оканчивается двумя нулями, удвоенное произведеніе десятковъ на единицы, въ данномъ случаѣ, будетъ оканчиваться также двумя нулями, слѣд. квадратъ числа, оканчивающагося 5-ю, необходимо оканчивается 25-ю. Слѣд., всякое число, оканчивающееся 5-ю, котораго предпослѣдняя цифра не есть 2, не можетъ быть точнымъ квадратомъ.
5. Квадратъ числа, оканчивающагося нулями, имѣетъ нулей вдвое больше, т.-е. четное число ихъ. Слѣд., число, оканчивающееся нечетнымъ числомъ нул§й? не есть точный квадратъ.
Извлеченіе квадратнаго корня изъ многочлена.
148. Корень изъ многочлена только въ исключительныхъ случаяхъ извле-комъ, т.-е. можетъ быть выраженъ въ формѣ раціональнаго многочлена.
Для возможности извлеченія квадратнаго корпя изъ многочлена, послѣдній долженъ содержать не менѣе трехъ неприводимыхъ членовъ. Въ самомъ дѣлѣ, если данный многочленъ есть двучленъ, то корень изъ него не можетъ быть выраженъ точно ни одночленомъ, пи мпогоченомъ, потому что квадратъ одночлена есть одночленъ, а квадратъ простѣйшаго многочлена — двучлена, содержитъ три неприводимыхъ члена.
Пусть данный многочленъ будетъ точный квадратъ:
25а*#6 ~ 20а а#й 7 4а*#1 — 48а5#3 57а6#2 — 28а'# -|- 4а8,
расположенный по убывающимъ степенямъ главпой буквы #0 и пусть
Р + 2 + г + *+-
будетъ квадратный корень изъ него, также расположенный по убывающимъ сте
пенямъ х. Данный многочленъ, какъ квадратъ своего корня, будетъ = (#4”*? ”Ь "г4“5г|”‘* * * А ил1,і раскрывъ этотъ квадратъ, получимъ равенство
ЗоаАг6—20л3л*5+7 4а —48аМ+57аМ—28аЪ' 4- 4а8 = рз + +д14*
+ 2Ср+д)г+г*
+ 2(р + дг4-г)5+$*+...(1)
Вторая часть этого равенства, по раскрытіи скобокъ и по приведеніи, должна давать первую часть, поэтому равенство это есть тождество, а слѣдов. высшіе члены въ обѣихъ частяхъ должны быть равны. Но вторая часть есть произведеніе (р + ^4”* * * )» а потому высшій членъ ея равенъ
произведенію высшихъ членовъ сомножителей, т.-е. =р,р или Итакъ р2 = = 25а2хв, откуда
р ~ ]/25а2яА
Слѣдов. чтоб'ы найти высшій членъ корня, нужно извлечь квадратный корень изъ высшаго члена даннаго полинома.
|/25а’х* = + 5ах3. Возьмемъ для р его значеніе со знакомъ -рі т-*е- поло-жжгь р = — 5лх*. Вычтя изъ первой части равенства (1) 25а2#6, а изъ вто-МЙ р\ ІІДКГЪ ТмЖІгГГВО
— ------ 2р^4~2а4" 2(Р “Н/У 4“ГМ--(2),
шм яггту тт р 1 < суть высжіе члены корня. Слѣдоват.
і_я. р = 5ах* то: 10ах3.^= — 20а3дА откуда
. Чши-іг-і'
5 = — 20а’х5: ІОах® — — 2а-дА
Отсюда: чтобы второй членъ корня, нужно вычесть изъ дан-
юк полинома квадршпь перваго члена корня, и высшій членъ перваго илшка раздіълить на удвоенный первый членъ корня.
Вычтемъ изъ обѣихъ частей тождества (2) до
2рдг -|- 52, или (2р
т.-е. въ данномъ случаѣ
(Юах* — 2а2х2) (— 2а2х3) = — 20а3х5 Ц- 4а4х4;
найдемъ тождество
70а4#4—48а5х3-|-^7а6х2-|-*- •=2(2?-4^)гЧ‘г8~г-й’_Н!_Ьг)5Ч_^2_[_* ‘ *(3)«
Высшіе члены обѣихъ частей его должны быть равны; но высшій членъ второй части есть 2рг, слѣдов. 2рг = 70а1х1; а какъ р = 5ах3, то
1 Оах3. г = 70а4х\ откуда г 70а4#4: Юох’ = 7а8х,
Отсюда заключаемъ: чтобы найти третій членъ корня, нужно вычесть изъ перваго остатка произведеніе втораго члена на алгебраиче
скую сумму удвоеннаго перваго члена со вторымъ, и высшій членъ второю остатка раздѣлитъ на удвоенный первый членъ корня *
Вычтемъ изъ обоихъ частей тождества (3) по
2(2?4“^)г+ т.-е. (2/? —2 г/—|—г). г,
нлп въ данномъ случаѣ
(10а#3 — 4а2#2 4" 7а3#). 7 а3# = 70а1#1 — 28а5#3 4" 49а6#2.
Сдѣлавъ это, получимъ тождество
— 20а5#3 4- 8ав#а — 28а7# 4“ 4а8 = 2(2? 4" у 4“ 0* 4~ 4~ - - • (4).
Высшіе члены обѣихъ частей должны быть равны, и какъ высшій членъ второй части есть 2^, то 2рз = — 20а5#3, или Юа#а. $ = — 20а3#3. откуда 5 = — 20а5#3:10а#3 = — 2а4.
Отсюда: чтобы найти четвертый членъ корня, нужно вычесть изъ второю остатка произведеніе третьяго члена корня на алгебраическую сумму удвоенныхъ первыхъ двухъ членовъ корня съ третьимъ, и высшій членъ третьяго остатка раздѣлить на удвоенный первый членъ корня.
Вычтемъ изъ обѣихъ частей тождества (4) но
2(2> + 2 + *’)« + «8, т.-е ’(2р + 2з + 2г 4-в). в,
или въ данномъ случаѣ
(10а#3 — 4а2#2 4-14а3#—2а*).(—2а1) = — 20а5#3-[- ^а6#2—28а7# 4^ 4а8;
въ первой части тождества получается въ остаткѣ ноль, слѣд. данный полиномъ есть квадратъ полинома р 4^ 74*“ г 4~ т.-е. въ данномъ случаѣ корень въ точности равенъ 5а#3 — 2аа#24~7а3#— 2а\
Дѣйствіе располагаютъ слѣдующимъ образомъ:
25а2#«—20а3#4+ 74а1#1—48аяя3-(-57 а6#2—28а“#+4а81 5а#3—2а г#2+ 7а3#—2а1
2±20аМір 4аМ______________;_________(Гба^2аад)(^2а2#3)
2-й ост. . . . 70а1#1—48а5#3+57а5#'2—28а7#+4а8 |
(10а#3—4а2#24-7а3#). 7а3#
—7 ОаМ 28ая#3=г 49аМ
3-й ост...............—20а*#3-!- 8а6#2—28а7#-р4а8
±і20айА^ 8ай#2^:28а‘7#ц^4а8
(10а#3- 4а2#2+14а3#-2а9(- 2а1)
149- Правило. — Чтобы извлечь квадратный корень изъ цѣлаго по буквѣ # ко-шноліа, представляющаго точный квадратъ, располагаютъ полиномъ но убывающимъ степенямъ буквы ‘#; извлекая квадратный коцепь изъ перваго члена полинома, найдемъ первый членъ корня.
Вычтя изъ даннаго полинома квадратъ перваго члена корня, и раздѣливъ первый членъ остатка па удвоенный первый членъ корня, получимъ второй членъ ею,
Чтобы найти третій членъ корня, вычитаютъ изъ перваго остатка произведеніе второю члена корня на алгебраическую сумму удвоеннаго перваго члена корня со вторымъ, и дѣлятъ первый членъ второю остатка на удвоенный первый членъ корня: частное и будетъ третьимъ членомъ корня.
Для нахожденія четвертаго члена корня вычитаютъ изъ второго остатка произведеніе третьяго члена корня на алгебраическую сумму удвоенныхъ первыхъ двухъ членовъ корня съ третьимъ^ и дѣлятъ первый членъ третьяго остатка на удвоенный первый членъ корня: частное этого дѣленія и даетъ четвертый членъ корня.
Продолжаютъ эти дѣйствія до тѣхъ поръ, пока въ остаткѣ не получится НОЛЪ.
Это правило безъ измѣненія прилагается и къ тому случаю, когда данный полиномъ будетъ расположенъ по возрастающимъ степенямъ главной буквы.
150. Примѣчанія. —1* Степень корня, очевидно, вдвое меньше степени полинома.
П* Для перваго члена корня (§ 148) мы могли бы взять: —5ая3; изъ формулъ для д, г и з видно, что въ такомъ случаѣ нашли бы: #
г = — 7а3я, $ — 2а*; слѣд. второе значеніе корня будетъ: — 5ая3 2аV* — 7а3ж-р2а*. Оно отличается отъ перваго только знакомъ. Итакъ, искомый корень имѣетъ два значенія:
+ (5ая3— 2а*&* -р 7а3х — 2а4)*
151. Выводя правило § 149, мы предполагали, что существуетъ многочленъ съ конечнымъ числомъ членовъ, квадратъ котораго равенъ данному полному Р- Н - обыкновенно напередъ неизвѣстно, существуетъ ли такой многочленъ д? — - * • — Е т.-е- будетъ ли Р точный квадратъ* Чтобы
ополнить прашкч іуж* . :і!і . сказать. чтѵ. примѣняя его, всегда послѣ ограныченмаъо числа съйстъй можно узнать, будетъ ли Р точный квадратъ, жл нѣтъ. Въ ? <1 ? 14>. когда оно существуетъ, если полиномъ Р
і убывающимъ степенямъ главной буквы, низшій членъ
• Г*) кшркп ъ э? имѣя себѣ подобныхъ, съ которыми могъ бы быть сое-жнп іэ»гЕт. долженъ равняться низшему члену,—назовемъ его Е,—
птаи ? -ззома. т.-е, должно быть ^ = Е, откуда 2 = ±]/Е. Слѣдовательно,
корня можетъ быть непосредственно найденъ извлеченіемъ корня
шъ ххз»го члена даннаго полинома. Поэтому, показатель главной буквы члена Е долженъ быть числомъ четнымъ. Пусть это такъ и есть, и пусть это число = 24. Когда, выполняя дѣйствія, мы дойдемъ въ корнѣ до члена степени 4, жлідя. наприм., что этотъ членъ = то, чтобы данный полиномъ былъ точилъ квадратомъ, необходимо: во-1-хъ, чтобы было (Па^)й = Е, и, во-2-хъ, ютобы слѣдующій остатокъ былъ нулемъ. Эти условія, будучи необходимы, очевидно, вмѣстѣ съ тѣмъ и достаточны.
Тѣ же разсужденія приложимы и къ случаю, когда оба полинома расположены по восходящимъ степенямъ главной буквы: стоитъ только вездѣ слово «пизшій» замѣнить словомъ «высшій >*
Когда указанныя условія не имѣютъ мѣста, то данный полиномъ не есть точный квадратъ*
Пусть, въ такомъ случаѣ, данный многочленъ есть Р, остатокъ, который долженъ бы быть нулемъ—В, а корень—П; такъ какъ остатокъ получился по вычитаніи изъ Р всѣхъ членовъ квадрата многочлена П, то Р — ІР = К, откуда
р=іі*4-к.
Эта формула и служитъ для преобразованія неточнаго квадрата.
Примѣръ I. Возьмемъ полиномъ, расположенный по убывающимъ степенямъ главной буквы, наприм.
9а2#* 1 — 24а3#3 46а1#2 — 20ав# 1 За6.
Если этотъ многочленъ есть тонный квадратъ, то низшій членъ корня долженъ быть равенъ }/13а3, а слѣдующій затѣмъ остатокъ долженъ быть нулемъ. Если оба эти условія окажутся невыполненными, то должно заключить, что данный полиномъ не есть точный квадратъ. Примѣняемъ правило § 149.
9а2#* г— 24а3#3 46а1#2 -— 20ай# -р 1 За6
Ч- 24а3#3 4= 16а1#2
30а1#2 — 20ав#+ 1 За6
— 30а*#2 + 40а 3#Ч- 25а3
20а’# — 12а3
За#3 — 4а3# 5а3
(6а#2 — 4а2#) (— 4а2#) (6а#2 — 8а2# -|- 5а3), 5а8
Найдя въ корнѣ членъ -рэа3, и замѣчая, что: 1) онъ не равенъ }/13а6, а 2) что слѣдующій остатокъ не есть 0, заключаемъ, что данный полиномъ не есть точный квадратъ. Примѣняя формулу Р = можемъ его представить
въ видѣ
(За#2 — 4а2# 5а3)2 20а3# — 12а6,
Примѣръ II. Пусть данный полиномъ расположенъ по восходящимъ степенямъ главной буквы, наприм.
1 — 5# 4#2 — 6#3 4” 8#Ч
Если этотъ многочленъ—точный квадратъ, то дойдя въ корнѣ до члена, содержащаго #2, и получивъ затѣмъ остатокъ неравный 0, должны заключить, что данный полиномъ есть неточный квадратъ.
Разница этого случая отъ предыдущаго заключается въ томъ, что степени главной буквы въ послѣдовательныхъ остаткахъ повышаются, а это ведетъ за собою возможность полученія въ частномъ неограниченнаго числа членовъ цѣлыхъ относительно главной буквы, такъ что разложеніе многочлена по формулѣ Р = П24-К, гдѣ П и В—цѣлыя относительно # выраженія,—неопредѣленно.
152- Д» іджеяія. — I. Найти условіе, необходимое и достаточное
для тоъ*. квадратный триномъ
%• лялодъ. Найдемъ остатокъ квадратнаго корня изъ даннаго тринома.
— 4а
&а
С'—Т" 4а
Іюбы триномъ былъ точнымъ #гь былъ равенъ нулю, т.-е.
п
с — ^ = 0,
4а ’
л»еягоЛ>. Положивъ
Ь
2Ѵа
квадратомъ, необходимо и достаточно, чтобы чтобы
или Ь2 — 4ас = О.
і раскрывъ вторую часть, найдемъ тождество
Ь
2 Ѵа
ах1-|- Ьх -|- с = оЛг2 4“ 21^ ^2;
приравнивая коэффиціенты при одинаковыхъ степеняхъ я, найдемъ три условія:
а = а2; Ь = 2я^; с = ^2.
Эти три условія должны существовать совмѣстно, а потому величины а и Эг выведенныя изъ 1-го и 3-го, должны удовлетворять второму.
Такимъ образомъ найдемъ: Ь = 4= 2 |/а . или Ь2 = 4ас.
Примѣчаніе. Если бы а равнялось нулю, то изъ условія Ь2 = 4ас, слѣдуетъ, что и Ь должно =0; триномъ приводится въ этомъ случаѣ къ с: это есть квадратъ количества |/с. Поэтому можно сказать, что каково бы пи было а. искомое условіе есть Ъ*—іас = 0,
И. Найти условіе, необходимое и достаточное для тою, чтобы триномъ
ах'2 -р 2Ьху 4“ су*
былъ точнымъ квадратомъ.
Различаемъ два случая: 1) а = 0; 2) а не равно 0.
Когда а = 0, то, какъ триномъ не можетъ имѣть высшею степенью х— первую, необходимо положить и Ъ = 0. Это условіе, будучи необходимымъ, вмѣстѣ съ тѣмъ и достаточно; ибо, если оно выполнено, то триномъ приводится къ су\ а это есть точный квадратъ количества }/с. у.
Пусть а не равно нулю. Извлеченіе корня даетъ:
а#2 2Ъху -|*
2
о Ь1 б2 ас гч
Заключаемъ, что если — — с, или —-— не равно нулю, т.-е. если о— ас отлично отъ нуля, .триномъ не есть точный квадратъ. Итакъ, необходимо* чтобы Ъ2 — ас равнялось нулю. Этого условія, вмѣстѣ съ тѣмъ, и достаточно; ибо равенство
ахі + 2Ъху су* = Н'а. х 4~ ~=у
показываетъ, что какъ скоро Ьа = ас, данный триномъ превращается въ точный квадратъ количества
+ —-і/, или - - у-к а У а
Ш. Найти условія, необходимыя и достаточныя для того, чтобы полиномъ
ах2 а'у2 -|- а"я* %Ъуг -|- 4“ 2Ь"яу
былъ точнымъ квадратомъ.
Къ этому примѣру можно приложить общій методъ, которымъ мы пользовались въ двухъ предыдущихъ примѣрахъ. Но мы выведемъ искомыя условія изъ условій, найденныхъ въ предыдущемъ примѣрѣ.
Различаемъ опять два случая: а = 0 и а не.равно 0.
Первый случай. Когда а = 0, то, какъ данный полиномъ, чтобы быть точнымъ квадратомъ, не долженъ содержать членовъ съ первою степенью я, мы должны при всякихъ у И 2 имѣть
6'^4-Ь"у = 0,
откуда, извѣстнымъ уже путемъ, заключаемъ, что
Ь' = 0 и 6" = 0.
Полиномъ приводится къ
а*у2 2Ъуз а”#2.
Изъ предыдущаго примѣра знаемъ, что триномъ этого вида будетъ точнымъ квадратомъ при условіи
а'а" —й« = 0.
Итакъ, искомыя условія суть:
V = 0, б" = 0, а'а" - = 0.
- Второй случай. Пусть а не равно 0. Дадимъ полиному видъ
ая* + 2 (Ь"у + 6'я) # + 2^ 4~ а' *
Его можно разсматривать какъ квадратный относительно х триномъ, котораго первый коэффиціентъ а отличенъ отъ нуля. Прилагая сюда доказанное въ предыдущемъ примѣрѣ условіе, найдемъ
(Ь"у -|- Ъ'я)2 = а(а'у2 -|- 2Ьу^ -|- а"яа).
Такъ какъ это равенство должно быть тождествомъ, оно должно имѣть мѣсто »уэм всяяолс у и при всякомъ откуда извѣстнымъ образомъ найдемъ условія:
Ь"* = ааг; ѴЬ" = аЬ; Ь9* = аа".
Этиіъ условій, вмѣстѣ съ тѣмъ, и вполнѣ достаточно. Въ самомъ дѣлѣ, изъ нихъ имѣемъ:
№
-
Ідоиш этм значенія а', а" и Ь въ данный полиномъ, дадимъ ему видъ
* , 26'6"ѵя . । ЛѴ,
•г* ---------------— -—— 2о ях + 26 хи =
• в а 1
«А”* — йгу — ЬѴ — Э6Ѵу? 4- 2а6^ 4- 2аЪ”ху________
« ат — Уу — 6'г\* \ Iх® /
Отсюда видно, что при найденныхъ условіяхъ данный полиномъ есть полный квадратъ количества
ах + Ъ"у 4- ЬЪ
Г а
ГЛАВА XIII.
Извлеченіе кубичнаго корня изъ чиселъ и многочленовъ.
Ожредѣленія; предварительныя теоремы.—Извлеченіе кубичнаго корня изъ цѣлыхъ и дробныхъ чиселъ съ точностью до 1 и до —.— Сокращенный способъ.—Извлеченіе кубичнаго корня изъ многочленовъ.
153. Когда число есть кубъ другого числа, то первое называется точнымъ кубомъ, а второе — мочныла кубичнымъ корнемъ изъ перваго. Такъ 125 есть точный кубъ 5-ти, а 5 — точный кубичный корень изъ 125.
154. Разсужденіями, приведенными въ § 124, докажемъ, что:
Когда цѣлое число не есть точный кубъ, то кубичный корень изъ нею, не выражаясь точно въ цѣлыхъ единицахъ, не можетъ быть точно выраженъ и ни въ какихъ доляхъ единицы.
Такіе корни называются несоизмѣримыми съ единицею: такъ» кубичные корни изъ чиселъ: 3, 10, 15 и т. д. суть числа несоизмѣримыя.
155. Опредѣленія.—Кубичный коренъ изъ цѣлаго числа, точный до единицы, есть корень изъ наибольшаго куба, заключающагося въ этомъ числѣ, или этотъ корень -}~ 1 -
Первый называется корнемъ точнымъ до 1 по недостатку, второй — по избытку. Такъ, замѣчая, что наибольшій кубъ, заключающійся въ 70, есть 64, заключаемъ, что кубичный корень изъ 70, точный до 1 но недостатку, есть 4, а по избытку — 5.
156. Остаткомъ кубичнаго корня изъ цѣлаго числа называется избытокъ этого числа надъ кубомъ его корня, точнаго до 1 по недостатку. Напр., остатокъ кубичнаго корня изъ 70 есть разность 70—64 или 6.
Вообще, если данное число есть X, кубичный корень изъ него, точный до 1 по недостатку, равенъ А, а остатокъ—К. то, по опредѣленію остатка, В = Х— А3, откуда
х = а34-в.
Въ частности, когда X есть точный кубъ, остатокъ корня равенъ нулю.
Теорема. — Остатокъ кубичнаго корня не больше утроеннаго произведенія корней изъ даннаго числа, точныхъ до 1 по недостатку и по избытку.
Въ самомъ дѣлѣ, пусть А есть кубичный корень изъ X, точный до 1 по недостатку; въ такомъ случаѣ X содержится между А3 и (А -|-1)3, и слѣд. разность между X и А3 меньше разности (А—I)3 — А3 или ЗА(А-}-1)4"Ь т.-е.
В <2 ЗА(А 4~ 1) 4~ 1 •
Но К и ЗА(А +1)4-1 суть числа цѣлыя, и К — меньше изъ нихъ, то оно меньше второго по крайней мѣрѣ на 1, т.-е.
й<ЗА(А4-1).
Слѣдствіе. Условія, необходимыя и достаточныя для того, чтобы А было кубичнымъ корнемъ изъ X, точнымъ до 1 по недостатку, суть:
К = А84-В и К<ЗА(А4-1).
Въ самомъ дѣлѣ, равенство выражаетъ, что кубъ числа А содержится въ X, а неравенство означаетъ, что X не заключаетъ въ себѣ куба числа А +1.
Извлеченіе кубичнаго корня изъ цѣлаго числа съ точностью до 1.
Эту теорію подраздѣляемъ на три случая.
157. Первый случай. Данное число меньше 1000.
Въ этомъ случаѣ кубичный корень находятъ прямо при помощи таблицы кубовъ первыхъ девяти чиселъ
Числа: 1 2 3 4 5 6 7 8 9
Кубы: 1 8 27 64 125 216 343 512 729.
г
Ьгтъ требуется извлечь кубичный корень* съ точностью до 1, изъ 427. ігѵ палицы кубовъ видно* что это число содержится между 343 и 512, слѣд.
кубъ, въ немъ заключающійся, есть 343; поэтому искомый корень — * а остатокъ есть 427 — 343 или 84.
158. Второй случай. Данное число содержится между 1000 и 1000000.
Ітсть дано число 341254; оно больше 1000 или 10®, но меньше 1000000 о 100®, а потому кубичный корень изъ него больше 10, но меньше 100, т. состоитъ изъ десятковъ и единицъ; пусть число его десятковч» будетъ л якхтыіъ единицъ — »; искомый корень будетъ 10^4“ м> и если возможный ♦г-пг'.гь назовемъ буквою К, то получимъ равенство:
41254=( 10Л-р«)®-рК= 1ОООбР + 3 Л 00 й3. и^-3.1 Ой. ... (1).
Чтобы найти цифру десятковъ корня, замѣчаемъ, что слагаемое 1000с?®
«зъ жѣлое число тысячъ, а потому необходимо содержится въ 341000 суммы, а оід. (Р заключается въ 341. Докажемъ, что кубичный корень изъ наиболь-« куба, заключающагося въ 341, и дастъ намъ (2. Въ самомъ дѣлѣ, изъ
іи
кубовъ замѣчаемъ, что 341 содержится между 216 и 343, или между
•*2 і 7*:
63 < 341 < 73.
Помножая этн числа на 1000, мы не измѣнимъ неравенствъ, такъ что: —з —з
60 < 341000 < 70 .
Прибавивъ къ 341000 число 254, мы усилимъ первое неравенство. Что ка-октгя второго, то какъ 341000 и 70 суть цѣлыя числа тысячъ и первое «Бше второго, то оно меньше его но крайней мѣрѣ на 1000; слѣд,, увели-чвъ первое на 254 — число, меньше 1000, получимъ результатъ, во всякомъ з
лучаѣ, меньшій 70 , такъ что и второе неравенство не нарушится. Итакъ ---------------------------3 —3 60 < 341254 <70 ,
т^тда, переходя къ корнямъ, имѣемъ:
60 < ^341254 <70.
Эти неравенства доказываютъ, что искомый корень больше 6 десятковъ, но т- заключаетъ въ себѣ 7 десятковъ, т.-е. что онъ содержитъ 6 цѣлыхъ де-л г ко въ, и, можетъ быть, нѣсколько простыхъ единицъ, число которыхъ не боль-
9. Итакъ, й = 6, т.-е. корня равна кубичному кор-
ню изъ наибольшаго куба, содержащагося въ числѣ тысячъ даннаго числа.
Подставивъ въ равенство (1) 6 вмѣсто й, получимъ:
341254 =216000 4-3 , 3600 , и + 3.60 . и24-«3-)-К.. .(2) изъ обѣихъ частей по 216000, найдемъ
125254 = 3.3600 . »-}-3.60 . и*4-и3-]-Н.
162 —
Для нахожденія цифры и единицъ корня замѣчаемъ, что слагаемое 3.3600л/ ость цѣлое число сотенъ, а потому необходимо заключается въ 1252 сотняхъ суммы* Но въ составъ этихъ сотенъ суммы могутъ входить сотни и отъ остальныхъ членовъ ея (т.-е. отъ 3 . 60 . и2, «3 и К). Поэтому, членъ 3 , ЗбООи или равенъ, или меньше 125200. Итакъ
3 . 3600* < 125200,
откуда
^1252
<3.36*
и
Но цифра единицъ и есть число цѣлое, а потому, раздѣливъ 1252 на 3.36, и взявъ цѣлую часть частнаго, найдемъ высшій предѣлъ цифры единицъ корня. Замѣтивъ, что 125254 называется первымъ остаткомъ, выводимъ изъ сказаннаго слѣдующее правило для нахожденія цифры единицъ корня: опиливъ аа первомъ остаткѣ двѣ цифры справа запятою и раздѣливъ оставшееся влѣво отъ запятой число на утроенный квадратъ цифры десятковъ корня, въ цѣлой части частнаго будемъ имѣть высшій предѣлъ цифры единицъ корня.
Въ данномъ случаѣ, цѣлая часть сказаннаго частнаго есть 10; слѣд., цифра единицъ корня будетъ 9 или меньше 9. Для испытанія цифры 9, мы должны составить сумму 3 . 3600.9 —3 . 60.9а —9В и вычесть ее изъ перваго остатка: если вычитаніе будетъ возможно, то цифра 9 будетъ требуемая; въ противномъ случаѣ ее надо послѣдовательно уменьшать на 1 до тѣхъ поръ, пока вычитаніе сдѣлается возможнымъ* Сумму, подлежащую вычитанію, можно написать такъ:
[3 X 3600 + (3 X 60 4- 9) X 9] X 9.
3X3600=10800; 3X604-9=189; 189X9 = 1701; 10800 4-1701 = = 12501; 12501 X 9 = 112509, что меньше 125254.
Итакъ, цифра единицъ равна 9; искомый корень = 69, а остатокъ корня = 125254 — 112509 = 12745.
Дѣйствіе располагаютъ слѣдующимъ образомъ:
у'341,254 216
10811252,54 1125 09
12 745
69
189
Х9
1701
4-10800
12501
Х9 112509
159. Общій случай. — Этотъ случай приводится къ двумъ предыдущимъ при помощи слѣдующей теоремы.
Теорема. —> Число десятковъ кубичнаго корня изъ даннаго числа равно кубичному корню изъ наибольшаго куба, содержащагося въ числѣ тысячъ этого числа. -
Пусть данное число будетъ 495864349, и пусть а8 будетъ наибольшій кубъ, содержащійся въ числѣ тысячъ этого числа, т.-е* въ 495864; въ такомъ случаѣ имѣемъ:
а3 <495864 < (а+ I)8;
откуда, умноживъ всѣ числа на 1ООО, получимъ:
(10а)а < 495864000 < [10 («+1)]®;
или. придавай къ среднему числу 349, что' не измѣнитъ смысла неравенствъ, но обратитъ возможное равенство въ неравенство:
(10а)3 < 495864349 < [10 (а 4~1)]\
Отсюда, переходя къ корнямъ, найдемъ:
10а < ^495864349 < (а +1). 10.
Итакъ, искомый корень заключается между а десятками и а 1 десяткомъ, а потому содержитъ а десятковъ, и нѣкоторое число единицъ, не большее 9. Теорема такимъ образомъ доказана.
160. Мы нашли, что число десятковъ кубическаго корня изъ числа 495864349 есть корень кубичный изъ 495864; число же десятковъ этого послѣдняго корня, или число сотенъ перваго, равно кубическому корню изъ 495 (по той же теоремѣ). Отсюда заключаемъ:
1. Чтобы найти цифру высшаго разряда кубичнаго корня изъ цѣлаго числа, достаточно раздѣлитъ его на грани, отдѣляя по три цифры отъ правой руки къ лѣвой, и извлечь кубичный коренъ изъ первой грани слѣва.
2. Число цифръ корня, точнаго до 1 по недостатку, изъ цѣлаго числа равно числу сказанныхъ граней.
161* Извлечемъ кубичный корень изъ 495864349.
Извлекая кубичный корень изъ 495864 такъ, какъ указано въ § 158, найдемъ число десятковъ искомаго корня: оно будетъ 79. Назвавъ цифру единицъ корня буквою и и возможный остатокъ черезъ К, имѣемъ:
—з —2
495864349 = 79 . 10004-3 . 79 . 100 . и-{-3 . 790 . и*4-ыа4-В.
—з
Вычитая изъ обѣихъ частей этого равенства по 79 . 1000, получимъ:
—2
2825349 = 3 . 79 . 100 . ^4-3 . 790 . ««4-и84-В.
Отсюда, извѣстными разсужденіями убѣдимся, что высшій предѣлъ цифры единицъ * найдемъ, опредѣливъ цѣлую часть частнаго отъ раздѣленія 28253 на
3 . 79 , т.-е. на 18723. Цѣлая часть этого частнаго равна 1; поэтому цифра
единицъ корня будетъ или 1 или 0.
Для испытанія 1, составляемъ остальные три члена куба корня, т.-е. ---2
3 . 79 . 100 Х1 + 3 . 790 XI4 * * * 4- 470 Даетъ 1874671; такъ какъ это
число не превышаетъ остатка 2825349, заключаемъ, что цифра единицъ корня есть 1, самый корень = 791, а остатокъ корня =2825349 — 1874671,
или 950678.
Дѣйствіе располагаютъ слѣдующимъ образомъ:
}/ 495,864,349 343
147 9 '1528,64
' 1500 39
18723 1 ~| 28253,49
18746 71
9506 78
791
49 X 3 = 147^ 219 X 9 = 1971
14700
+ 1971
1667] X 9 = 150039
~ ” 1971 “ ’ .
16671
81 _____ __2 18723 = 3X79 , 2371X1 = 2371. 1872300
2371
1874671 X1
Отсюда выводимъ:
162. Правило извлеченія кубичнаго корня съ точностью до 1 изъ цѣлаго числа.
Раздѣляютъ данное число на грани по три цифры отъ правой руки къ лѣвой, при чемъ первая гранъ слѣва можетъ имѣть и двѣ цифры и даже одну.
Первую цифру корня найдемъ, извлекая кубичный коренъ изъ первой грани слѣва.
Чтобы найти вторую цифру, вычитаютъ изъ первой грани кубъ первой цифры корня, и къ остатку сносятъ вторую гранъ: такимъ образомъ получается первый частный остатокъ. Отдѣляютъ съ правой стороны его двѣ цифры, а оставшееся влѣво отъ запятой число дѣлятъ на утроенный квадратъ первой цифры корня: цѣлая частъ частнаго дастъ высшій предѣлъ для второй цифры корня.
Чтобы узнать, годится ли эта цифра, приписываютъ ее справа къ утроенной первой цифрѣ корня, и умножаютъ полученное число на испытуемую цифру; къ произведенію придаютъ утроенный квадратъ первой цифры корня (служившій сейчасъ дѣлггтелемъ), приписавъ къ нему справа два нуля, и умножаютъ полученную сумму на испытуемую цифру. Если это произведеніе не превыгиаетъ перваго остатка, испытуемая цифра годится; въ противномъ случаѣ уменьшаютъ ее на 1 и снова исполняютъ указанное испытаніе, и т. д., пока испытаніе не дастъ произведенія, не превышающаго первый частный остатокъ. Найденную цифру приписываютъ справа отъ первой цифры корня.
Для нахожденія третьей цифры корня, вычитаютъ составленное произведеніе изъ перваго остатка, и къ разности сносятъ третью грань: получится второй частный остатокъ. Съ правой стороны его отдѣ-. ялюли йвіъ цифры, и дѣлятъ оставшееся влѣво отъ запятой число на утроенный квадратъ числа, найденнаго въ корнѣ: цѣлая часть частнаго будетъ представлять высшій предѣлъ третьей цифры корня: испытываютъ эту цифру вышеуказаннымъ способомъ.
Такимъ образомъ продолжаютъ до тѣхъ поръ, пока будутъ снесены всѣ грани.
Извлеченіе кубичнаго корня изъ дробей съ точностью до 1.
163. Теорема. /Губмчный корень изъ несократимой дроби несоизмѣримъ, если его нельзя извлечь отдѣльно изъ числителя и знаменателя. То же доказательство какъ въ § 136.
8
Такъ, члены дроби ^5 — точные кубы, поэтому кубичный корень изъ нея извлекается точно:
7/а =?.
У 125 ^125 5
8 3
Кубичные корни изъ дробей ттг и
9 «
3
— несоизмѣримы.
164. Теоре м а. ~ Кубичный коренъ изъ дробиі точный до 1, есть корень изъ наибольшаго куба, заключающагося въ цѣлой части даннаго числа* или этотъ корень -}- 1*
Доказательство аналогично § 137. Отсюда
Правило, Чтобы извлечь кубичный коренъ изъ дроби точно до 1, надо отбросить дробную частъ, и извлечь кубичный корень изъ цѣлой части точно до 1,
Примѣръ. Извлечь кубичный корень изъ 2896,75 съ точностью до 1.
Откидывая дробь, извлекаемъ, съ указанною точностью, корень изъ 2896; находимъ результаты: 14 —по недостатку и 15 — по избытку.
Извлеченіе кубичнаго корня изъ цѣлыхъ чиселъ и изъ дробей съ точностю до -* п
165. /Троило, Ѵтпооод извлечь кубичный коренъ изъ цѣлаго или изъ 1
дробнаго числа съ точностью до нужно умножитъ это число на кубъ знаменателя степени приближенія, изъ произведенія извлечь коренъ точно до 1, и раздѣлитъ ею на знаменателя степени приближенія.
Доказательство такое же какъ н въ § 139. 3/- 1
Примѣръ. Вычислить у 3 съ точностью до
Для этого надо извлечь кубичный корень изъ 3)^ 100\ т.-е. изъ 3000000 съ точностью до 1; и раздѣлить результатъ на 100.
3/3,000,000
34 | 20,00
17 44 | 2560,00.
2419 84
140 16
1
Искомый корень = 1,44—
144
34X4 = 186
300
136
436 Х4 = 1744
136 424 Х4= 1696
436
16
’58800
1696
60496X4 = 241984
недостатку, и 1,45 — но избытку.
Сокращенный способъ извлеченія кубичнаго корня.
166. Пусть требуется извлечь кубичный корень съ точностью до 1 изъ цѣлаго числа А — случай, къ которому приводятся всѣ остальные. Положимъ, что корень имѣетъ 2т 4* 1 цифръ, и что обыкновеннымъ способомъ найдено т -|-1 цифръ, т.-е. больше половины всѣхъ цифръ корня, а остается найти послѣднія т цифръ. Обозначимъ буквою а число, составленное найденными т-|-1 цифрами, сопровождаемыми т нулями, а буквою х остальную часть корня, которая вообще есть число несоизмѣримое: истинный корень выразится суммою Итакъ:
А = (а 4” х)8 = аа За2# За#2 4“ откуда
А—а3____ ।
~3а» -:Г' « За7:'
Найдемъ цѣлую часть ? частнаго отъ раздѣленія А — а3 на За3, и пусть остатокъ дѣленія будетъ г; слѣд. получимъ равенство:
А—а* За»
Приравнивая два выраженія частнаго
найдемъ:
откуда
Докажемъ, что абсолютная величина разности 4"^] меньше 2,
и что слѣд. д_ выражаетъ величину х съ ошибкою, меньшею 2 единицъ.
Замѣтивъ, что г есть остатокъ дѣленія, въ которомъ дѣлитель равенъ За2, заключаемъ, что 1. Затѣмъ, въ цѣлой части х находится т цифръ, поэтому х меньше наименьшаго (т4~1) значнаго числа, т.-е. #<1От, а потому х* < 1О2т; съ другой стороны а состоитъ изъ 2т 4“ 1 Цифръ, слѣд. а^ІО2™;
% 1
а потому — < 1. Наконецъ, За> 3 . ІО2”*, а потому < з ^т* Отсюда вид-но, что I 4“ < 2, и слѣдовательно
а?3 /. । а: \ а \ За/
. г #3 /. । х \ п
а значитъ и абсолютная величина раности —а ѵ ' За/ также меньше 2.
Отсюда вытекаетъ слѣдующее заключеніе:
чтобы извлечь, съ точностью до 1, кубичный корень изъ цѣлаіо числа, находятъ обыкновеннымъ способомъ больше половины всѣхъ цифръ корня; затѣмъ остальныя, съ точностью до 2, находятъ, раздѣливъ полный
гмдтока яа утроенный квадратъ найденной части корня (т-е. числа, еюлоящаго изъ т-|-1 ж/юыяь съ т ж/лялш^-
Слѣдуетъ замѣтить, что лишь въ исключительныхъ, рѣдкихъ, случаяхъ при-<^женіе будетъ ошибочно болѣе чѣмъ на 1; обыкновенно же, ошибка бываетъ
ньше 1; во всякомъ случаѣ, найдя указаннымъ сокращеннымъ способомъ ко-
мъ, слѣдуетъ прямо вычислять предѣлъ разности
167. Можно всегда опредѣлить, будетъ ли корень, вычисленный сокращен-югъ способомъ, т.-е. а 4- 5 — точный, или приближенный; а въ послѣднемъ случаѣ — въ какую сторону сдѣлана ошибка.
Въ самомъ дѣлѣ, назовемъ остатокъ по нахожденіи части а корня буквою К; имѣемъ равенство:
А — а’ = К, откуда А = <ъ3—К.
Раздѣливъ Н на За*, въ частномъ получимъ 0, и въ остаткѣ г; слѣд.
В За*. 0 4*
а потому
Отсюда:
А = а® Ц- За*д 4“
I) Если г > (За 4-0)0*, то А>(а-[“#)3і я слѣд. будетъ приближеніе по недостатку.
2) Если —(За4“5)52, то А = («4-®)®, слѣд. а 4*0 будетъ точный корень.
3) Если же г<(За4-0)02, то А<(а4”0)\ а слѣд. а 4*0 будетъ приближеніемъ по избытку.
168. Извлечь кубичный корень изъ 96428639457679. Первыя три цифры опредѣляемъ обыкновеннымъ способомъ.
96,428,639,457,679
324,28
5303639
356727
458
4800 125 607500 1358
625 5 10864 8
5425 618364
25 64
6075 629292
Находимъ 458. Остатокъ К=356727457679; а=45800; За2=6292920000. ' ѵігѢ-гивъ В на За*, находимъ въ частномъ 56. Искомый корень = 45856.
Вычисляемъ предѣлъ разности I 4~ V Такъ какъ а > 4.10\ и
- < !0\ то — < 7* Затѣмъ, За > 12 , ІО1 сл. а 4 7 ’ 3«
т
< 1 ~ плда Отсюда: 1 +з5/ <41 + Ила») < Е Сл- и У
^1—^)<1. Корень 45856 ошибоченъ меньше чѣмъ на 1, и какъ легко убѣдиться— по недостатку.
Извлеченіе кубичнаго корня изъ многочленовъ.
169. Пусть требуется извлечь кубичный корень изъ многочлена
— 125а9#12 4“ 150а8#114~ 165а7#16 — 172ай#й — 99ап#84~ ^^а1#7 Ц- 27а3#6, расположеннаго по убывающимъ степенямъ буквы х, которую мы принимаемъ за главную. Допуская, что многочленъ этотъ есть точный кубъ, и что корень изъ него, также расположенный по убывающимъ степенямъ буквы есть 4’^4“
г 4"3“Ь ’ •, замѣчаемъ, что данный многочленъ долженъ быть равенъ кубу своего корня, т.-е. (^4~ Г-Н5-Ь •*)* Такимъ образомъ имѣемъ тождество:
— 125аэ#,24’ 15Оа8#114~165а7#10— 172а6#9 — 99а5#84-54а4#74-27а3#6= р* -|“ ^Р2? 4“ Зр#2 4“ 7* 4“ ?)*г “Ь ^Ср 4“ “Ь г* 4“ * ‘ (1 )•
По свойству тождества, высшіе члены обѣихъ частей должны быть равны, а потому р* =—125а°#Іа, откуда
р= і/—125а9#12 = —5а3#1.
Отсюда заключаемъ: сЬья нахожденія высшаго члена корня нужно извлечь кубичный коренъ изъ высшаго члена даннаго многочлена^
Вычтя изъ первой части тождества (1)—125а9#12, а изъ второй — равное ^тому количество р8, найдемъ тождество:
150а8#п 4” 165а7#10— 172а8#9— 99а5#8-}- 54а1#7 4~ 27а3#6 = Зр2#4“ 4- зр$*+г?3 + зСр+оУ*г+зср4~ ?)г2+ГЧ— (2)’
а потому высшіе по буквѣ # члены обѣихъ частей должны быть равны, т.-е.
З^а д = 150а8#11, или, такъ какъ = — 5а8#1, то 3.25а6#8. ц = 150а8#11, откуда
ц = 150а8#11 : 75а6#8 = 2аа#3.
Отсюда заключеніе: чтобы найти второй членъ корпя, нужно изъ даннаго полинома вычесть кубъ перваго члена и высшій членъ перваго остатка раздѣлитъ на утроенный квадратъ высшаго члена корпя.
Вычтемъ изъ второй части тождества (2) 3/>ядг4"3^324_?3і а изъ первой равное этому выраженіе: 3,{—5а3#1)а.2а2#34_^(—5а8#1)Д2аа#в)а4~(2а2#3)3 ил и 150а 8#н — 6 Оа7#1 * 4~ чай де мъ т ож дес тв о
225а7#10— 180а6#9 — 99аг,#84~ 54а1#7 4~ 27а3#6 3(^4_<?)2г4-+ 3(Р + д)г* + Г» 4-.. .(3).
Приравнивая снова высшіе члены обѣихъ частей, получимъ равенство
Зр3г = 225а7#10, или 3.25а6#\ г = 225а7#10, откуда г = 225а7#10: .75а6#8 = За#8
Отсюда заключаемъ: чтобы найти третій членъ корня, нужно изъ перваго остатка вычесть утроенное произведеніе квадрата 1-го члена корня на 2-й “I* утроенное произведеніе перваго члена на квадратъ второго и кубъ второго, а первый членъ второго остатка раздѣлитъ на утроенный квадратъ 1-го члена корня.
Вычтемъ изъ второй части тождества (3) выраженіе 3(р-|-д)Ѵ-]-3(р-|-<2) г3-]-г3, а изъ первой равное емѵ количество: 3(—5а3#*-р2аа#3)а. За#2-^-3(— 5аа#*+2а2#а).(3а#а)я+(3а#й)3=225а7#19— 180аМ-^36а*а:8— 135аѴ -|= 54а*#7 — 27а3#6 = 225а7#16 — 180а6#3 — 99а3#8 -|- 54а*#7-|- 27а3#6, Но вычитаніи въ остаткѣ въ 1-й части получается ноль; поэтому, данный полиномъ есть точный кубъ, и искомый корень = — 5а3#*-р 2а2#3За#2.
Дѣйствіе располагаютъ слѣдующимъ образомъ:
— 125а9# 12+150а»#1 4-1 65а7#1®—172аМ—99а’#8-ь5^і1#Н 27а3#8 - 5а3#4 ^аЗД+Зая* ± 125а9#12 75ав#»
+Т50аВДН 165а7#10—І72д^^д3д^ - 5а^). 4а*а^4-( 2а'9Р)
—150а»#11 -р 60а7#1® 8а»#9 7 5а6#»
225а7#19—180а’#9—Э9а^4-54а1#7+27а5#»:3(—5аЗЛ<(_2а^ ^За^Ч-
—225аЗД9±180а«^^Ж(МТ54а^^27аЗ^'+3(—5аЗдГі_|_2а2#з).9а'#*Ч=27аз#9 ±135а5.г8
------------------б----------------
Отсюда выводимъ слѣдующее
170. Драяімя. Распо^оэса^ъ полиномъ по убывающимъ степенямъ главной буквы, извлекаемъ кубичный коренъ изъ перваго его члена: получаемъ первый членъ корня.
Вычтя кубъ его изъ даннаго полинома, найдемъ первый остатокъ: раздѣливъ первый членъ этого остатка на утроенный квадратъ перваго члена корня, въ частномъ получимъ второй членъ корня.
<* Вычтя изъ перваго остатка утроенное произведеніе квадрата пер*
ваго члена корня на второй, утроенное произведеніе перваго члена на квадратъ второго и кубъ второго члена корня, получимъ второй остатокъ. Раздѣливъ первый его членъ на утроенный квадратъ перваго члена корня, получимъ въ частномъ третій членъ корня.
Вычтя гізъ второго остатка утроенное произведеніе квадрата суммы первыхъ двухъ членовъ корня на третій, утроенное произведеніе суммы первыхъ двухъ членовъ на квадратъ третьяго а ят/бг> третьяго члена, найдемъ третій остатокъ. Раздѣливъ .первый его членъ на утроенный квадратъ перваго члена корня, получимъ въ частномъ четвертый членъ корня и т. д.
Дѣйствіе продолжаютъ до тѣхъ поръ, пока въ остаткѣ получится ноль. *
171. Когда неизвѣстно, представляетъ ли данный полиномъ точный кубъ г или нѣтъ, примѣняютъ къ нему предыдущее правило, замѣчая, что будетъ ли поли-
номъ расположенъ по нисходящимъ, пли но восходящимъ степенямъ главной буквы, всегда можно предвидѣть степень послѣдняго члена корня, въ предположеніи, что данный многочленъ есть точный кубъ; она должна быть втрое меньше степени послѣдняго члена его. Когда данный полиномъ есть точный кубъ, послѣдній членъ корня долженъ равняться кубичному корню изъ послѣдняго члена полинома, а слѣдующій остатокъ долженъ быть нулемъ. Въ противномъ случаѣ данный многочленъ не есть точный кубъ.
ГЛАВА XIV.
Объ ирраціональныхъ числахъ.
Происхожденіе ирраціональныхъ чиселъ.—Несоизмѣримыя величины въ геометріи.— Способъ предѣловъ. — Распространеніе основныхъ законовъ дѣйствій на числа несоизмѣримыя.
172, Изученіе обратныхъ дѣйствій служитъ источниковъ для открытія новыхъ разрядовъ величинъ. Такъ, три прямыя ариѳметическія дѣйствія надъ цѣлыми числами, т.-е. сложеніе, умноженіе, которое есть только частный случай сложенія и возвышенія въ степень — частный случай умноженія, даютъ въ результатѣ всегда только цѣлыя числа. Прн изученіи же трехъ обратныхъ дѣйствій — вычитанія, дѣленія и извлеченія корня, открываются новые роды величинъ, а именно: вычитаніе приводитъ къ открытію отрицательныхъ величинъ, дѣленіе — къ открытію дробныхъ, а извлеченіе корня приводитъ къ двумъ но-вымъ разрядамъ величинъ — несоизмѣримыхъ и мнимыхъ* Въ этой главѣ мы займемся изученіемъ чиселъ несоизмѣримыхъ или ирраціональныхъ.
173. Происхожденіе ирраціональныхъ чиселъ при извлеченіи корня.
Обобщимъ теоремы 124, 136, 154 и 163 для корня какого-угодно по-
рядка.
Теорема I. Если цѣлое число А есть неточная п-ая степень корень п-ю порядка изъ нею — несоизмѣримъ,
*Въ самомъ дѣлѣ, такъ какъ лаго числа, то і/А не можетъ же, что этотъ корень равняется можность равенства
то
цѣ-
А не есть точная «-ая степень другого равняться никакому цѣлому числу. Допустивъ
X X Р
несократимой дроби
т.-е. допустивъ воз-
рп
имѣли бы отсюда, что
Но р есть число первое съ слѣд. рп — первое съ д’1, а потому не но-жетъ равняться цѣлому числу А, и допущенное равенство невозможно. Итакъ, корень п-го порядка изъ цѣлаго числа, не представляющаго точной п-ой степени, несоизмѣримъ съ единицею.
Таковы; /7, /32, /53, и т. д.
Теорема II. Корень п-ю порядка изъ несократимой дроби песо-измѣримъ, если его нельзя извлечь отдѣльно изъ числителя и знаменателя.
** /а
Въ самомъ дѣлѣ, равенство 1/ — = Р, гдѣ Р— число цѣлое, невозможно, \ в ,
ибо оно приводитъ къ равенству у = Рп, выражающему, что несократимая дробь
равна цѣлому числу. Такимъ образомъ, искомый корень не можетъ быть выраженъ цѣлымъ числомъ. Но онъ не можетъ быть точно выраженъ и конечною
«/л С С
* дробью. Въ самомъ дѣлѣ, допустивъ равенство т/ — =~, Г) — не~ ж А Сп , *
сократимая, имѣемъ: 3 = цні гдѣ вторая часть — также дробь несократимая.
Равенство этихъ дробей возможно .только тогда, когда А = СП, и В = В", т.-е.
„ м / А
когда А и В суть точныя я-ыя степени; если же этого нѣтъ, то 1/ — нельзя
точно выразить ни въ цѣлыхъ единицахъ, ни въ доляхъ единицы, слѣд. корень * этотъ будетъ несоизмѣримъ.
Таковы: р/Ч |/? и т. д.
174. Хотя ирраціональныя числа нельзя вычислять точно, но всегда можно ихъ опредѣлять съ какою-угодно степенью точности.
Пусть, напр., требуется вычислить УА, гдѣ А есть цѣлое число, не представляющее точной я-ой степени, съ ошибкою меньшею гдѣ р—какъ угодно большое цѣлое число. Умноживъ и раздѣливъ данный корень на получимъ (подведя множителя р подъ знакъ корня):
"/т _ Р _ ѴАрп
* Р Р
Если наибольшая я-ая степень, содержащаяся въ Арм, будетъ цѣлое число гп, то »• + 1 >’/аР > г, откуда, раздѣливъ всѣ три' числа на р и замѣтивъ, что
* = у"А, найдемъ
Г+1 >,/А>Г. ₽ г Р
, г г-4-1 /-
откуда прямо слѣдуетъ, что какъ такъ и - выражаютъ к А приближенно, съ ошибкою меньшею : требуемое доказано.
* /а а
Точно такъ же, если "| / гдѣ — дробь несократимая, нельзя вычислить точно, то можно найти его съ какимъ-угодно приближеніемъ. Въ самомъ дѣлѣ, помноживъ числ. и знам. на Вп“\ найдемъ:
"/а _ ”/ав*-і _ /аі>2 у В~|/ ВЛ в“;
но, по предыдущему, всегда можно найти двѣ
пусть эти дроби будутъ -
дроби, разнящіяся
А -4-1 и -----, такъ что
Р ’
меньше чѣмъ
на ~ Р
п______
отъ і/ІВ*”1;
раздѣливъ всѣ три числа на В, найдемъ,
у-і ВР
откуда заключаемъ, что крайнія дроби выражаютъ искомый корень съ ошибкою, меньшею о * '
175, Несоизмѣримыя величины въ геометріи. Геометрія также представляетъ примѣры несоизмѣримыхъ величинъ; извѣстнѣйшія изъ нихъ: окружность круга и,діаметръ, діагональ квадрата и сторона. Чтобы показать, какимъ образомъ можно убѣдиться геометрически въ несоизмѣримости двухъ линій, докажемъ а ргіогі,—сравненіемъ на самомъ дѣлѣ этихъ линій, что діагоядль квадрата несоизмѣ2)има съ ею стороной.
Черт. 10,
Проведемъ діагональ АС квадрата АВСВ и продолжимъ ее ?а точку А. Изъ А, какъ изъ центра радіусомъ АВ опишемъ полуокружность, которая пересѣчетъ діагональ и ея продолженіе въ точкахъ М и К. Для доказательства, что АС несоизмѣрима съ АВ, постараемся измѣрить первую изъ этихъ линій помощію второй.* *
Итакъ, составимъ отношеніе
АС
АВ
Мы имѣемъ: АС = АМ МС = АВ МС. откуда
АС _ . д_ МС _ 1
АВ “ 1 АВ “ 1 "і" АВ * *
МС
АВ
Вопросъ приводится къ опредѣленію отношенія Замѣчая, что СВ есть касательная, а СИ — сѣкущая къ окружности имѣемъ:
ав = св = смхс^
откуда
АВ _ Сі\т
МС — АЙ', а • — X
Но Сй = ЙА-|- АМ —|—МС == 2АВ + МС, поэтому
АВ _ 2АВ + МС . о । МС _ о . 1
МС““ АВ “ । АВ — ~ ' АВ"
МС ‘
Внося эту величину въ равенство (1), находимъ
АС _ т । 1
АВ ~ 1
“+/АВ'\ \мс)‘
Итакъ, снова приходится опредѣлять отношеніе Но эта величина намъ извѣстна: она опредѣляется равенствомъ (2); такимъ образомъ снова мы вве-АВ
демъ которое опять нужно будетъ замѣнить его величиною изъ (2), и т. д.
Такія когда АВ МС’
подстановки будутъ продолжаться неограниченно, такъ что дѣйствіе ни-не можетъ бытъ закончено. потому что всегда будемъ получать отношеніе Итакъ, отношеніе представляется въ видѣ
ЛС- 1 _г ]_
АВ ~ ' 2 + 1
2 + 1
2+ -
такъ что оно никогда не можетъ быть вычислено съ точностію: линіи АС и АВ — суть, слѣдовательно, линіи несоизмѣримыя.
176. Дѣйствія надъ несоизмѣримыми числами подчинены тѣмъ же законамъ, какъ и дѣйствія надъ числами соизмѣримыми. Доказательство этого положенія основано на особомъ способѣ, называемомъ способомъ предѣловъ, съ начальными основаніями котораго намъ необходимо, поэтому, теперь же ознакомитыя-
Способъ предѣловъ.
177. Количество называется постояннымъ, если въ данномъ вопросѣ оно м-* измѣняетъ своей величины. Такъ: радіусъ въ данномъ кругѣ есть величина иклоянная, также сумма угловъ треугольника и т. и.
Количество наз. перемѣннымъ, если оно не имѣетъ одной опредѣленной млкчіны, но измѣняется въ болѣе или менѣе широкихъ границахъ. Напр», углы треугольника, хорда крута, и т. п.
Если перемѣнная величина, измѣняясь, приближается къ нѣкоторой постоянной^ такъ что разность между ними можетъ быть сдѣлана какъ угодно малою, то постоянная называется предѣломъ перемѣнной. Для выясненія понятія о предѣлѣ приводимъ слѣдующіе примѣры.
Примѣръ I.—Разсмотримъ выраженіе 1-р"* въ которомъ буквѣ х будемъ послѣдовательно давать цѣлыя положительныя значенія: 1, 2, 3,...; тогда будетъ принимать величины: 1 + р 1-р^ !+§»••• постепенно уменьшающіяся и приближающіяся къ 1.
Слѣд. 14“ - будетъ количество перемѣнное, приближающееся къ постоян-•Г
ному числовому значенію—къ 1.
При этомъ, разность между перемѣннымъ 1-|““ и постояннымъ 1 выра-. 1
жается дробью - которая можетъ быть сдѣлана какъ угодно малою; въ са-момъ дѣлѣ, желая, чтобы эта разность была меньше нужно только ^-су дать величину, большую 1ООООО.
і- । і
Заключаемъ, что предѣломъ перемѣнной въ данномъ случаѣ, будетъ 1.
Слово предѣлъ означаютъ буквами Ііт (отъ франц. слова Іітііе—предѣлъ), такъ что можемъ предыдущій результатъ письменно выразить такъ:
Лт
1.
Примѣръ П. — Разсмотримъ еще величину а, выраженную линіей АВ.
Раздѣлимъ эту .линію пополамъ, потомъ одну изъ половинъ еще пополамъ и т. д. до безконечности, и разсмотримъ рядъ
іВ
Черт. 11.
состоящій изъ безконечнаго числа членовъ. Это будетъ величина перемѣнная, увеличивающаяся съ возрастаніемъ п и все болѣе и болѣе приближающаяся къ а. Если взять въ этой суммѣ п первыхъ членовъ, то она будетъ меньше а на чѣмъ больше будетъ п, тѣмъ эта разница будетъ ближе къ нулю, никогда, однако, его не достигая. Итакъ « есть предѣлъ перемѣнной при
неограниченномъ увеличеніи п.
178. Замѣтимъ, что одного приближенія перемѣнной величины къ постоянной еше недостаточно для того, чтобы постоянную принять за предѣлъ пе-
ремѣнно*: необходимо, чтобы разность между ними могла быть сдѣлана какъ угодно Такъ періодическая дробь 0,9898 - *., по мѣрѣ увеличенія числа і- ^’ичныіъ знаковъ, увеличивается, приближаясь къ 1, но 1 не лесть
предѣлъ >т <й дроби, ибо разность между 1 и данною дробью, сколько бы въ послѣтжі ни взяли десятичныхъ знаковъ, всегда больше Предѣлъ данной
дрси.і
179, Выясняя понятіе о предѣлѣ, мы встрѣтились съ особаго рода вели-'ГйЕдті: перемѣнными, имѣющими свойство неограниченно уменьшаться, приблп-хді-:ь къ пулю. Перемѣнная величина, неограниченно приближающаяся къ нулю п •’.гѣтпвательпо имѣющая предѣломъ нуль, получаетъ названіе .калой. если ее разсматривать въ состояніи близкомъ къ нулю. Такъ, разность м-хіу перемѣнною и ея предѣломъ, когда перемѣнная приближается къ своему :*-іѣлу, есть безконечно-малая величина.
Нужно остерегаться смѣшивать понятія — #езконечно-лшлое и </есъл<а л/</-лле: эти понятія не имѣютъ ничего общаго между собою. Названіе весьма-малой примѣняется къ постоянной величинѣ, настолько малой, что она ускользаетъ > тъ оцѣнки ея нашими чувствами. Напротивъ, безконечно-малая, будучи существенно перемѣнною, не имѣетъ опредѣленной величины, и слѣд. величпна ея ничѣмъ не связана съ нашими физическими средствами оцѣнки величинъ. Сущность безконечно-малой заключается въ томъ, что она имѣетъ свойство неограниченно уменьшаться, становясь какъ угодно близкою къ нулю.
180. величиною наз. такая перемѣнная, которая
можетъ быть сдѣлана болѣе всякой напередъ заданной величины, какъ бы послѣдняя ни была велика.
Примѣромъ безконечно-болыпой величины можетъ служить дробь -, *гдѣ х безконечно-малая величпна. Въ самомъ дѣлѣ, можетъ быть сдѣлана больше всякой заданной величины: желая, напр., сдѣлать эту дробь больше 100000, достаточно взять х меньше 0,00001.
Понятіе о безконечно-большой величинѣ не слѣдуетъ смѣшивать съ понятіемъ о весъла большой величинѣ. Такъ, 1000000 верстъ есть величина весьма большая, но не подходитъ подъ понятіе о безконечно-большой величинѣ. Названіе весьма большой дается величинѣ постоянной; напротивъ, безконечно-большая — есть величина существенно перемѣнная.
Не слѣдуетъ также смѣшивать понятіе о безконечно-большомъ съ абсолютною безконечностью, взятою въ обыкновенномъ смыслѣ. Абсолютная безконечность исключаетъ всякую идею ограниченія и численнаго опредѣленія, и потому не іожегь служить предметомъ математическаго изслѣдованія.
181. Свойства безконечно - малыхъ. — I. Сумма безконечно- малыхъ, взятыхъ въ числя^ есть величина безконечно-малая.
Возьменъ п безконечно-малыхъ величинъ: аят..., ап; требуется
•}ѵ доказать, что сумма ихъ можетъ быть сдѣлана меньше всякой произвольно малой величины а. Такъ какъ і1э і2,... суть величины безконечно-малыя.
то каждая изъ нихъ можетъ быть сдѣлана меньше поэтому имѣемъ рядъ не-
равенствъ:
21
і н
а к
а
П
Сложивъ ихъ, пайдемъ
такъ какъ берется слагаемымъ га разъ; или
а
«< *
и требуемое доказано
'* га
й можетъ быть сдѣлана меньше а,
•II. Ралностъ гіаудъ бешжечно-.малыхь есть величина безконечномалая.
Дѣйствительно, если зц н л5 суть величины безконечно-малыя, то уменьшивъ на о*, получимъ разность — аа меньшую ап а потому и подавно безконечно-малую.
111. Произведеніе нѣсколькихъ безконечно-малыхъ, взятыхъ въ опредѣленномъ числѣ, есть величина безконечно-малая.
Возьмемъ п безконечно-малыхъ: аа, з3, ..., ай и докажемъ, что про-
изведеніе ихъ можетъ быть сдѣлано меньше произвольно малаго количества а. ап — будучи безконечно-малыми, могутъ быть сдѣланы меньше поэтому имѣемъ:
аі < Перемноживъ эти неравенства, найдемъ:
аа < /а . а3 ... < і/я |/а - — ’/а,
или а1.аа.а3...ап<(^)я;
но, но опредѣленію корня, (|/Гй)Л = ^ слѣд.
. <2а * ... Л,
что п требовалось доказать.
Слѣдствіе. Такъ какъ степень есть произведеніе равныхъ множителей, то изъ предыдущей теоремы прямо слѣдуетъ, что степень съ конечнымъ цѣлымъ положительнымъ показателемъ безконечно-малой есть величина безконечно
малая.
IV. Произведеніе безконечно-малой на величину конечную—безконечно мало.
Пусть аг—безконечно-малое, а « — конечное количество; доказать, что можетъ быть сдѣлано меньше произвольно малаго количества а. Такъ какъ . а а
безконечно-мало, то всегда можно положить < — откуда , «у или
< а.
V. Частное отъ раздѣленія безконечно-малой величины на конечную есть безконечно-малая величина.
Въ <ммгъ іілк если безконечно-мало, то всегда можно сдѣлать &!< па, гдѣ •—вмрѵь. а а — произвольно мало; а отсюда — < а.
1Т Лрегь еъ конечнымъ цѣлымъ положительнымъ показателемъ изъ безявшвшп-лллбй величины есть величина безконечно-малая,
<4рші прежнія обозначенія, имѣемъ: сц < ап, ибо сц безконечно-мало; а га»ш кмрень п-ой степени изъ обѣихъ частей, найдемъ і/зц < а.
1С- Сжеобъ находить постоянную величину, служащую предѣломъ пере-тім<, вливается способомъ предѣловъ, Онъ основавъ на нижеслѣдующихъ
РгМФСКП.
1ШХ Теорема I. — Если постоянная величина К заключается ме-перемѣнными и и ѵ (т.-е. если м<К<^у, или п "> К >> г), /идиютші которыхъ безконечно-мала, то К служитъ общимъ предѣломъ лереляшмыхъ и и ѵ.
омомъ дѣлѣ, такъ какъ К заключается между и и у, то разности К — « н К — у численно меньше разности и — ѵ, т.-е. безконечно-малой, а вт‘«у также безконечно-малы; отсюда, на основаніи опредѣленія предѣла, за-итееп. что К служитъ общимъ предѣломъ перемѣнныхъ и и ѵ.
Примѣръ. Окружность круга заключается между периметрами правиль-езъ одноименныхъ многоугольниковъ описаннаго и вписаннаго, разность между і^т^ыми при неограниченномъ удвоеніи числа сторонъ становится безконечно-вкюю: заключаемъ, что окружность есть общій предѣлъ для обоихъ пери->гтровъ.
184. Теорема П. .Если лерелпькная величина ѵ заключается между перемѣнною и и ея предѣломъ К, то ѵ имѣетъ тотъ же предѣлъ К.
Въ самомъ дѣлѣ, К есть но условію предѣлъ перемѣнной и7 слѣд, разность К — и есть величина безконечно-малая; но ѵ заключается между и и К, слѣд. разность К — у численно меньше разности К — п, т.-е. и подавно безконечномала, а потому К есть предѣлъ перемѣнной у.
185. Теорема ПК Если двѣ перемѣнныя величины іг и у связаны между собою такъ, что при всѣхъ измѣненіяхъ остаются равны между собою, или же разнятся одна отъ другой на безконечно-малую величину; если, притомъ, одна изъ нихъ стремится къ опредѣленному предѣлу, то и другая перемѣнная стремится къ тому же предѣлу.
Дѣйствительно, пусть и и у будутъ двѣ перемѣнныя, разность между которыми равна нулю или безконечно-малой, тогда
и = у-|- 5,
гдѣ 3 равно 0 или безконечно-мало; пусть, кромѣ того, и стремится къ предѣлу К; тогда, по опредѣленію предѣла, можпо положить
и К Е,
гдѣ н безконечно-мало. Сравнивая оба выраженія имѣемъ
Вторая часть равенства, какъ разность двухъ безконечно-малыхъ, безконечно-мала, слѣд. такова же и первая часть: значитъ ѵ имѣетъ предѣломъ К — ту же постоянную, что и «.
186* Теорема IV, Если двѣ перемѣнными и я «жгають общій предѣлъ К, »іо всякая посмѣнная заключающаяся между и и ѵ, «лгать тотъ же предѣлъ.
Въ самомъ дѣлѣ, если К служитъ предѣломъ для « п г, то
« К -|- 5 и # К —
гдѣ 5 и е безконечно-малы. Вычитая второе равенство изъ перваго* имѣемъ:
и — ѵ = о — з,
т.-е* «— г? есть безконечно-малая величина* Но ю заключается между « и ѵ, слѣд* разности и м? — г численно меньше безконечно-малой 3 — а, а
потому также безконечно-малы. Значить, перемѣнныя « и м?—съ одной стороны, и ѵ и го — съ другой, связаны между собою такъ, что разнятся между собою на безконечно-малую величину, а потому, по теор* III, заключаемъ, что ю имѣетъ тотъ же предѣлъ, что и и т*-е. К.
187. Теорема V. Предѣлъ суммы конечнаго числа перемѣнныхъ равенъ суммѣ ихъ предѣловъ.
Пусть имѣемъ п перемѣнныхъ (гдѣ п— конечное число): «2,„*, «п, которыхъ предѣлы соотвѣтственно равны: Ки Ка,*.., Кп. По опредѣленію предѣла имѣемъ:
Кх —1^ = 0^ Здѣсь оц, а2, аа.„ безконечно-малы* Складывая эти равенства, Кі “ = з2 находимъ:
— «$ = (^Ч-К^+К^Ч----ЬКИ)—(«іЧ-«аЧ— •Ч-И^=а1Чйа3+- * •Ч-ян.
К»— «п ” а» называетъ, что «і —и„ • * явная &! 4- Щі
Вторая часть этого равенства, какъ сумма конечнаго числа і безконечно-малыхъ, безконечно-мала, слѣд. равенство это по-разность между постоянной ^4-^4*-------------НКге и перемѣнной
— ил безконечно-мала, а слѣд* по опредѣленію предѣла, посто-------р Кп служитъ предѣломъ перемѣнной «! 4^ * - • + «л1
Примѣчаніе. Въ теоремѣ оговорено, что число слагаемыхъ должно быть и опредѣленное: безъ этого ограниченія теорема не имѣетъ мѣста*
Пояснимъ это примѣромъ*
Черт* 12.
Раздѣлимъ прямоугольникъ АВСП па нѣкоторое число равныхъ частей прямыми параллельными АП (черт* 12)* Если число дѣленій неограниченно увеличивать,
то каждый изъ малыхъ прямоугольниковъ, ВСКЕ и т* д., становится безконечно-малымъ, стремясь къ предѣлу—нулю. При конечномъ числѣ слагаемыхъ сумма предѣловъ была бы равна нулю; въ данномъ же случаѣ эта сумма предѣловъ равна прямоугольнику АВСІ), Слѣд., при неограниченномъ числѣ слагаемыхъ теорема не имѣетъ мѣста.
188. Теорема VI. Предѣлъ суммы перемѣнной и постоянной равенъ суммѣ постоянной и предѣла перемѣнной.
Пусть перемѣнная и имѣетъ предѣлъ К; по опредѣленію предѣла имѣемъ: « —К = а, гдѣ а—безконечно-малая величина. Прибавивъ а вычтя въ первой части постоянную а, найдемъ: («4-а) ~ (К-|-а) = 2* Это равенство показываетъ, что разность между перемѣнною и + а н постоянною К а безконечно мала, а потому К-ра есть предѣлъ перемѣнной иЦ-а, и теорема доказана*
189. Теорема ѴІЕ Предѣлъ разности двухъ перемѣнныхъ равенъ разности ихъ предѣловъ.
Пусть перемѣнныя и ия имѣютъ предѣлы К! и К2; по опредѣленію пре-тѣла имѣемъ:
«і — Кз = и щ — Ка =
а безконечно-я алы. Вычитая 2-е равенство изъ 1-го, имѣемъ:
ІЦ ) (К| К.) -—- оц — сц.
Вф Ц —\ безконечно-малая: отсюда, по опредѣленію предѣла,
заключаемъ. что перемѣнная и| — «ц имѣетъ предѣломъ — 1ц, и теорема доказана.
190. Теорема ѴПЕ Предѣлъ разности между перемѣнной и постоянной равенъ разности между предѣломъ перемѣнной и постоянною.
Если перемѣнная и имѣетъ предѣломъ К, то, по опредѣленію предѣла, и — К = а, гдѣ а—безконечно-мало. Вычтя и придавъ къ 1-й части равенства постоянную а, имѣемъ: (и — а) — (К — а) = а. Этимъ равенствомъ и доказывается, что предѣлъ величины и— а равенъ К — а*
191. Теорема IX. Предѣлъ произведенія конечныхъ перемѣнныхъ, взятыхъ въ конечномъ числѣ, равенъ произведенію ихъ предѣловъ.
Пусть двѣ перемѣнныя и1 п ия имѣютъ предѣлы и ІЦ; въ такомъ случаѣ: шІ=К1+а1 и и2 = К24”2і7 гдѣ оц и безконечно-малы. Перемножая оба равенства, имѣемъ
и1 . =з (ІЦ 20 (Ка Я2) з= К1 . Ка • К2 -|— 2^ , ІЦ -|- * ЗЦ.
Произведенія а,*К2 и сц.ІЦ, въ силу пункта IV § 181, ааі*сц—въ силу «•- ІП того же §, безконечно-малы, а потому послѣднее равенство показываетъ, что перемѣнная ил. и2 разнится безконечно мало отъ постоянной І^іц, сл. эта постоянная и есть предѣлъ перемѣнной ы1иа.
Теорема справедлива для сколькихъ угодно множителей; это можно доказать, разсматривая произведеніе нѣсколькихъ перемѣнныхъ какъ одну перемѣнную и прилагая сюда теорему о двухъ перемѣнныхъ* Такимъ образомъ найдемъ:
авд. (м1м1ыам|) = пред. (МіМі«з) • пРеД- иі = пред. (мі«з) • пред. «»’ “РеД- “* = пред. и,. пред. м,. пред. и3. пред. «4.
Примѣчаніе. Теорема справедлива только для случая, когда число множи-
1 V’*
телей конечно. Напримѣръ, въ случаѣ выраженія (1-р-у , при т = со каждый множитель имѣетъ предѣломъ 1, между тѣмъ какъ произведеніе имѣетъ предѣломъ не 1, которая, повидимому, должна бы была составлять произведеніе предѣловъ, а число е (2,71828...), какъ это будетъ доказано въ главѣ ХЫХ,
192* Теорема X. Предѣлъ произведенія перемѣнной на постоянную равенъ произведенію этой постоянной на предѣлъ перемѣнной,
Пусть « есть перемѣнная, предѣлъ которой = К, в а™данная постоянная.
По опредѣленію предѣла имѣемъ и — К - х гдѣ а — безконечно-мало. Помноживъ обѣ части равенства на а, получимъ: м. л = Ка-^а. а* но аа есть величина безконечно-малая 180. IV), сл. Ка разнится безконечно-мало отъ иа, а потому пред. (ш) = К. а* и теорема доказана.
193* Теорема XI- -Если гдер&шънгіыя при всѣхъ своихъ измѣненіяхъ сохраняютъ постоянное^ конечное, отношеніе^ то и предѣлы ихъ имѣютъ то же самое отногаеніе.
Пусть и двѣ перемѣнныя, отношеніе которыкъ всегда остается равнымъ постоянному т, т.-е. = т- Отсюда: иТ = и2. т; но по предыдущей теоремѣ:
пред. («і) = т X пред. (и2), откуда и теорема доказана.
* Пред. ѵ*91
194. Теорема XII. Предѣлъ отношенія двухъ конечныхъ перемѣн* их и и^ равенъ отношенію ихъ предѣловъ к\ и К2.
Пусть “і=#1 откуда Изъ этого равенства, на осн. теор. III
$ 184 и теор. IX. § 190 имѣемъ: пред, («]) = пред. (и3) .пред. (я)< а отсюда, раздѣливъ обѣ части на пред, («*), получимъ Пред = пред, (#) иля =
Іні\
иред* И*
195. Теоерма ХІП. Предѣлъ частнаго отъ раздѣленія перемѣнной на конечную постоянную равенъ частному отъ раздѣленія предѣла перемѣнной на эту постоянную.
Пусть предѣлъ перемѣнной « равенъ К, а постоянная = т* Положимъ откуда « = гдѣ # — перемѣнная* По теор* Ш § 184 и теор. X К
§ 191 имѣемъ иред. (и) или К = т* пред. (я), откуда пред* (ж) — —, или пред* (— = —, что и требовалось доказать*
196. Теорема XIV’. Предѣлъ частнаго отъ раздѣленія конечной постоянной на конечную перемѣнную равенъ частному отъ раздѣленія этой постоянной на предѣлъ перемѣнной.
Пусть данная постоянная = а, перемѣнная = щ и пусть гдѣ х перемѣнная; отсюда а = их Пусть пред* («) = К, а пред. (х) = Ь; по опредѣленію орЛѣла: « = К + = гдѣ 2 и =!—безконечно-малы. Пере-
множая <ги равенства, имѣемъ: и. х — (К + а) (Ь + !) = КЪ + Ья ±. Три послѣдніе члена, представляя алгебраическую сумму безконечно-малыіъ, могутъ давать въ результатѣ или безконечно-малую, или нуль. Въ первомъ случаѣ
вторая часть была бы перемѣнная величина» а этого не можетъ быть, потому что первая часть (ш?) равна постоянной а; слѣдовательно
отражается въ ноль, а потому яя = К.Е, или, замѣняя их равной сй величиной а. находимъ: а = К.Ь, откуда Ь = ^, что и треб. доказать.
197. Теорема XV, Предѣлъ степени перемѣнной равенъ той же іжеяеэш нрейииа атой нерел?ьнмо«? полагая показатель цѣлымъ и по-лпжпжелънымъ числомъ.
Пусть и**1 есть данная степень; при т цѣломъ положительномъ она пред-сшиетъ произведеніе т перемѣнныхъ множителей если пред.
то но теор. IX § 190 имѣемъ: пред. (*ш... и) =А. к... &, или пред. (м* і=к*.
198. Теорема XVI. Предѣлъ корня съ цѣлымъ положительнымъ по-кпжпелемъ изъ перемѣнной равенъ корню того же порядка изъ предѣла зшяй перемѣнной.
Пусть имѣемъ Й*Л/, гдѣ и—перемѣнное и т— цѣлое положительное число. Здхѣтмжъ. что и = [7(г/)]Л по предыдущей теоремѣ имѣемъ: пред. («) = (Т7**)]"*; извлекая изъ обѣихъ частей корень ?п-го порядка, находимъ:
пред. ("/») = "/пред. (и).
ттѵ я трейшось юказать.
Распространеніе основныхъ законовъ на нееоизмѣрииыя числа.
199. Мы видѣли, что есть такія, называемыя несоизмѣримыми. количества, которыя нельзя точнымъ образомъ выразить ни въ цѣлыхъ единицахъ, ни въ какихъ доляхъ единицы. Однако и между такимъ количествомъ и единицею существуетъ извѣстное отношеніе. Это-то отношеніе мы и попытаемся опредѣлить; выяснимъ, что слѣдуетъ разумѣть, напр., подъ і/2.
Извѣстнымъ способомъ нахожденія приближенныхъ квадратныхъ корней, можемъ вычислить сколько угодно десятичныхъ знаковъ корня кв. изъ 2; сдѣлавъ это, разсмотримъ рядъ чиселъ
1 1,4 1,41 1,414, 1,4142,.,.
которыя выражаютъ наибольшее число цѣлыхъ единицъ, десятыхъ, сотыхъ, тысячныхъ, квадраты которыхъ меньше 2.
Разсмотримъ затѣмъ другой рядъ чиселъ,
2, 1,5 1,42 1,415, 1,4143...
показывающихъ наименьшее число цѣлыхъ единицъ, десятыхъ, сотыхъ..., которыхъ квадратъ больше 2. Эти числа получаются прибавленіемъ 1-цы къ послѣдіе* цыфрѣ чиселъ перваго ряда.
Затѣмъ, взявъ неограниченную прямую ОХ
м нѣкоторый отрѣзокъ О А принявъ за 1, нанесемъ, начиная отъ точки 0, отрѣзки
ОА, ОА', ОД", ОА"\**-, равные 1; 1,4; 1,41;...; а затѣмъ, отрѣзки ОВ, ОВ\ ОВ", ОВ'",... равные 2; 1,5; 1,42; 1,415,... Отрѣзки О А, ОА', ОА",... идутъ возрастая, но при этомъ всегда остаются меньше нѣкоторой опредѣленной длины; напр., они всегда будутъ меньше ОВ. Но когда перемѣнное количество постоянно
01
—!--1 1—I——Ч- Ь-< 1 Н
А Л'ХГ В'В'В 'В
Черт. 13.
возрастаетъ и, однако, остается всегда меньше нѣкоторой опредѣленной величины, то очевидно, оно стремится къ нѣкоторому предѣлу. Слѣд. и перемѣнные отрѣзки ОА, 0А\ 0А",« •• увеличиваясь, стремятся къ нѣкоторому предѣлу; пусть этотъ предѣлъ будетъ ОМ.
Съ другой стороны, перемѣнныя количества 08, ОВ'. ОВ",... постоянно уменьшаются и однако всегда остаются больше нѣкоторой опредѣленной величины; напр., они всегда больше ОА; сл. и этотъ рядъ уменьшающихся отрѣзковъ стремится къ нѣкоторому предѣлу. Легко видѣть, что этотъ предѣлъ будетъ тотъ же, что и для перваго ряда, т.-е. = ОМ. Въ самомъдѣлѣ, составивъ разности между 1-ми значеніями того и другого ряда, затѣмъ между вторыми ихъ значеніями, потомъ между третьими, и т. д., замѣчаемъ, что эти разности суть 1; 0,1; 0,01; 0.001;... т.-е. постоянно убываютъ; заключаемъ, что разность между перемѣнными, ОВП — ОАН, есть величина безконечно-малая; а слѣд. ОВП стремится къ тому же предѣлу какъ и ОАП (§ 185), т.-е. къ предѣлу ОМ.
Итакъ, оба ряда значеній стремятся къ одному п тому же предѣлу, и квадратъ этого предѣла есть число 2; въ с. д. квадратъ этого общаго предѣла не м. б. ни больше 2, ни меньше 2, потому что онъ служитъ общимъ предѣломъ и чиселъ меньшихъ 2, и чиселъ большихъ 2.
Этотъ-то общій предѣлъ и называется квадратнымъ корнемъ изъ и обозначается символомъ |/2.
Совершая дѣйствія надъ несоизмѣримыми числами, необходимо дать этимъ дѣйствіямъ опредѣленія, ибо точный смыслъ дѣйствій извѣстенъ только въ отношеніи соизмѣримыхъ чиселъ. Достаточно дать опредѣленія сложенія и умноженія; за обратными дѣйствіями мы сохранимъ ихъ общія опредѣленія.
200. Опредѣленіе суммы. Пусть требуется опредѣлить, что слѣдуетъ разумѣть подъ суммою несоизмѣримыхъ чиселъ г и }/2.
т> 111
Взявъ ихъ приближенныя величины точныя до '
статку и по избытку, получимъ:
по недо-
3,1 < я < 3,2
3,14 < - < 3,15 3,141 < л < 3,142
1,7 <]/3 <1,8 1,73 </3< 1,74 1,732 <]/3 <1,733
Отсюда, взявъ суммы, найдемъ два ряда (А) п (В):
3,2+ 1,8
3,15+ 1,74
3,142 + 1,733
*уімы группы (А) идутъ постоянно увеличиваясь, но всегда оставаясь конечными, ибо ихъ слагаемыя конечны; слѣд. эти суммы стремятся къ нѣкоторому предѣлу. Суммы группы (В) идутъ уменьшаясь, но оставаясь конечными, ибо мхъ слагаемыя конечны; слѣдовательно суммы и этой группы стремятся къ опредѣленному предѣлу. Каковы же эти предѣлы? Взявъ разность двухъ суммъ въ группахъ (А) и (В), соотвѣтствующихъ приближенію находимъ, что эта
2 -
разность равна слѣд. при неограниченномъ возрастаніи п, она стремится къ нулю. Это значитъ, что оба сказанные предѣла равны. Этотъ общій предѣлъ группъ (А) п (В) и называютъ суммою несоизмѣримыхъ * м |/3+ изображаютъ ее въ видѣ т:-|-]/3.
201. Свойства суммы. I. <7дол<а несоизмѣримыхъ чиселъ не измѣняется отъ перемѣны порядка слагаемыхъ.
По опредѣленію суммы несоизмѣримыхъ чиселъ имѣемъ
- + |/2 = пред. (а + Ь),
называя буквою а — приближенную величину числа * а буквою 5 — числа ]/2; точно такъ же _
|/2 + Ги = пред. (Ь-(- а). , .
Но приближенія а и Ь суть числа соизмѣримыя, слѣд. по теор. II § 15, а-|-& всегда равно 6-)- а; если же перемѣнныя величины при своихъ измѣненіяхъ остаются равными, то по теор. Ш § 184 и предѣлы ихъ равны; слѣд.
и + ]/2 = |/24-~-
П. Придать сумму двухъ несоизмѣримыхъ чиселъ—все равно что придать послѣдовательно каждое изъ нихъ.
По опредѣленію суммы несоизмѣримыхъ чиселъ имѣемъ:
|/5 + (т^ + у/2) = пред. [« + {Ь + с)],
гдѣ а. Ь и с суть приближенныя величины чиселъ: |/5, ' и /2.
Точно такъ же *
)/5-|“" + 1/2 = пред. (а —Ь —с);
т . а. Ь и с соизмѣримы, то всегда
а —(Ъ —с) = а —|— Ь с;
предѣлы же равныхъ перемѣнныхъ равны, слѣд.
/5 (к~|- /2) = /5 Ч~“ +А
202. Опредѣленіе произведенія. Опредѣлимъ произведеніе "ХА Для /— 11
этого составимъ произведенія приближеній чиселъ т и у 3, точныхъ до уур щу ГббОт'" ‘ па неД°статкЬ а также по избытку; такимъ образомъ получимъ двѣ группы произведеній:
(А)
ЗД X 1,7 3,14 XI,73 3,141 X 1.732
3,2 X 1,8 3.15 X 1,74 3.142X1-733
Произведенія ъруішы (А) постепенно увеличиваются; но, оставаясь конечными, стремятся къ нѣкоторому предѣлу. Произведенія груішы (В) идутъ уменьшаясь, но какъ онѣ остаются конечными, то приближаются также къ нѣкоторому предѣлу. Докажемъ, что предѣлъ обоихъ произведеній одинъ и тотъ же.
Въ самомъ дѣлѣ, взявъ для * и приближенія, точныя до найдемъ
Перемножая, получимъ:
Разность между этими приближенными произведеніями равна
1 Р і И і 1 іо*иоп+’іоп/-' І0*«
Членъ по мѣрѣ неограниченнаго возрастанія и, стремится къ нулю, сумма стремится къ ” у/3, т.-е. остается конечною, множитель же
1 1 / а । а \
Уфп стремится къ нулю, а потому произведеніе ІГо’1 + стремится къ нулю. Итакъ разность между перемѣнными приближенными произведеніями стремится къ нулю, а слѣд. сказанные предѣлы равны.
Этотъ общій предѣлъ рядовъ А и В и называютъ произведеніемъ к на |/Зф
203. Свойства произведенія. I. йедяъ кесокздгърыжът
чиселъ не измѣняется отъ перемѣны мѣстъ сомножителей.
Въ самомъ дѣлѣ, по опредѣленію произведенія несоизмѣримыхъ чиселъ, имѣемъ:
т:. |/ 2 = пред. (а. Ь) и У 2 . к = пред. (Ь . а)
гдѣ а и Ъ соизмѣримыя приближенія чиселъ т: и Но, по свойству произведенія соизмѣримыхъ чиселъ всегда аЬ = Ъа; сл. и предѣлы этихъ перемѣнныхъ равны, т.-е.
т:.р/2 = р/2 .и.
II. Чтобы умножить на произведеніе двухъ множителей, достаточно умножитъ послѣдовательно на каждый изъ нихъ.
Въ самомъ дѣлѣ, по опредѣленію (§ 201), имѣемъ:
]/5 . (-]/ 2) = пред. [а (Ьс)]; и также
. т;. = пред. (аЬс).
Но а, 6 и с соизмѣримы; слѣд. а(Ьс) = аЬс, а потому и предѣлы этихъ перемѣнныхъ равны, т.-е.
|/5(^}/2) = }/5.-.)/2.
III. Въ произведеніи сколькихъ угодно несоизмѣримыхъ множителей можно какъ угодно измѣнятъ порядокъ ихъ.
Докажемъ сперва, что можно измѣнить порядокъ двухъ послѣднихъ. Пусть а есть произведеніе всѣхъ множителей, за исключеніемъ двухъ послѣднихъ: ^2 и ]/ 5. Полное произведеніе будетъ
а.р 2.) 5,
или. въ силу пункта II,
а. (И2. }/5);
но, въ силу п. I, это выраженіе =
а. (]/5 . рх2),
а, на оси. п. II, это произведеніе равно
а.]/5. У 2.
Итакъ:
а . ]/2 . "|/5 = а)/5 ,)/2,
т.-е. можно измѣнить порядокъ двухъ послѣднихъ множителей.
Отсюда слѣдуетъ, что можно измѣнить порядокъ всякихъ двухъ смежныхъ множителей, ибо ихъ можно разсматривать послѣдними въ произведеніи, составленномъ изъ нихъ и имъ предшествующихъ.
Изъ этого слѣдуетъ, что переставляя послѣдовательно смежные сомножители, можно каждый изъ нихъ помѣстить на какомъ угодно мѣстѣ произведенія. Слѣд. порядокъ сомножителей не вліяетъ па величину произведенія.
IV*. Чтобы умножитъ данное число на сумму двухъ несоизмѣримыхъ чиселъ, нужно умножитъ его на каждое слагаемое отдѣльно и результаты сложить.
Въ самомъ дѣлѣ, по опредѣленіямъ, имѣемъ
5. (я+]/2) = пред. [а(Ь-Н)];
съ другой стороны:
|/ 5, т: -1- |/ 5.^2 = пред. [аб ос] = пред. [а(Ь -|- <0]-
Слѣдовательно
1/5 . (к + Ѵ'2) - 1^ . ~ +1<5.1/2.
Итакъ, вообще, основные законы дѣйствій, доказанные для соизмѣримыхъ чиселъ, распространяются и на несоизмѣримыя.
ГЛАВА XV.
Объ ирраціональныхъ выраженіяхъ, а
Происхожденіе ирраціональныхъ выраженіи. — Преобразованіе ихъ и дѣйствія надъ ними, “ Ирраціональныя дроби.— Примѣры.
к
204» Происхожденіе ирраціональныхъ выраженій. — Дѣйствіе извлеченія корня изъ алгебраическихъ выраженій не всегда возможно. Такъ, когда показатель подкореннаго количества не дѣлится на показателя корня, то извлеченіе корня можно только обозначитъ, но нельзя выполнивъ на самомъ дѣлѣ, напр. а7, и т. д. Точно такъ же, корень изъ многочлена, не представляю-
щаго точной степени, не можетъ быть извлеченъ, а потому его только обозначаютъ при помощи знака |/ ; примѣромъ можетъ служить )/а24-Ь2. Подоб-
наго рода выраженія, которыя нельзя привести къ раціональному виду, называютъ ирраціональными, также радикальными или коренными.
Не слѣдуетъ смѣшивать ирраціональныхъ выраженій съ несоизмѣримыми числами: ирраціональное выраженіе можетъ представлять и соизмѣримыя и несоизмѣримыя числа, смотря по числовому значенію входящихъ въ нето буквъ. Такъ, ]/а представляетъ'соизмѣримое число 3 при а = 9, и несоизмѣримое число ]/7 при а = 7; точно такъ же, представляетъ соизмѣримое число 5 при
а = 3и& = 4, и несоизмѣримое число при а=1 и Ь =
Впослѣдствіи мы увидимъ, что |/А имѣетъ т различныхъ значеній, имѣю- • щиіъ одну и ту же абсолютную величину; въ этой главѣ мы изучимъ преобразованіе корней, ограничиваясь разсмотрѣніемъ ихъ абсолютныхъ значеній.
205. Преобразованіе ирраціональныхъ выраженій помощью выведенія множителей изъ - подъ знака корня и введенія множителей подъ коренной знакъ.
Е Если въ выраженіи А подкоренное количество Л разлагается на такіе два множителя, шь которылъ одинъ представляетъ точную степень съ показателемъ^ равнымъ показателю корня, но этотъ множитель — извлеченіемъ изъ нею корня — можетъ быть вынесенъ изъ-подъ знака корня.
Пусть А = Рт X Чі гдѣ Ч уже не есть точная т-ая степень; въ такомъ случаѣ
”і/а = 1/ГМ;
примѣняя правило извлеченія корня изъ произведенія, и замѣчая, что |/Рт = Р, найдемъ:
р/А = |/‘РМ X Ч = "/р™ X Уч=Р X ’кч-
Примѣры. 1* Упростить, выведеніемъ множителя изъ-подъ знака корня, выраженіе |/ 50а“Ь10.
Подкоренное количество разлагается на два множителя 25а8йІ0Х2а, изъ которыхъ первый есть квадратъ 5а*63; слѣд.
|/50а*і10 = у"25БЬі0Х2а = ]/(5«46Ф X = 5а4&3 • И 2а.
2. Подобнымъ же образомъ получимъ:
^128а176^са = ^64а«6»Х2а2<?3 = ^(40*6% 2аМ = 4а56*. ^2а»с*.
3. Точно -такимъ же образомъ:
4. к ѴЧН№Ч^)(®4-у)(®-у)=
+у)3 («’ -Н у2) * (®—у) = (®+у)(®*+у а) Vх — у
Г/«"Н-зь»ч+5 _ ' а^Ь'1 ?/(№
V С-тг^тг-і V с"‘г<І'“г<І V С^ПГ(І1ПГ ‘ (І Сг'}г У ГІ
>
И. Если передъ радикаломъ находится множитель, то этотъ множитель можно внести подъ знакъ корня, возвысивъ въ степеньу изображаемую показателемъ корня.
Требуется доказать, что_Р’|Хч = |/рот * Ч*
Замѣтивъ, что Р = что, по правилу извлеченія корня изъ произведенія (§ 120): |[/А.В = ^/АХ откуда обратно: ’^А .р^В ™ ^АВ, имѣемъ:
рх/ч=^х^=^і^іігхч*
требуемое, такимъ образомъ, доказано.
Примѣры. Сдѣлать внесеніе множителей подъ знакъ корня въ примѣрахъ:
1. (а-Ь) У= }/(« + Ь)(а-Ь) = Ѵ^-Ъ*.
"• *+^ г ^—2.ту+^ г (а-—— К 1®~ГУД® У) — V х У •
Дѣйствія надъ ирраціональными выраженіями.
206. Подобныя ирраціональныя выраженія; ихъ приведеніе. — Два ирраціональныя выраженія называются подобными, если у нихъ показатели корня и подкоренныя выраженія одинаковы; такъ напр. 2і]/ас и—Зх|/ ас суть иррац. выраженія подобныя; а 2^7&2с и |/2ас— неподоб-ны. Иногда корни, кажущіеся на первый взглядъ неподобными, могутъ быть приведены къ виду подобныхъ ирраціональныхъ выраженій: для этого ихъ надо упростить, сдѣлавъ, гдѣ возможно, вынесеніе множителей изъ-подъ знака корня. Напр. выраженія р/27а4х3 и р 12а2х\ имѣющія одинаковыхъ показателей корня, но неодинаковыя подкоренныя количества, кажутся на первый взглядъ не-подобными; но сдѣлавъ въ нихъ вынесеніе изъ-подъ знака корня, приведемъ ихъ къ виду
За2хр Зх и 2ах2| Зх,—
подобныхъ выраженій. Множители За2х и 2ах2 при радикалахъ называются козффиціен томи.
Соединеніе нѣсколькихъ подобныхъ ирраціональныхъ выраженій въ одно называется ихъ приведеніемъ. Дѣйствіе это состоитъ въ томъ, что коэффиціенты подобныхъ иррац. выраженій заключаютъ въ скобки, къ которымъ и приписываютъ множителемъ общій корень. Примѣры:
I. Выраженіе: р27а4х3— рі2аѴ4“р75а6х приводится къ
За2х| Зх — 2ах2р Зх 4~ 5а3|/Зх;
вынося въ немъ общій корень и а за скобки, получимъ:
(Зах — 2х2 -р 5а2)а |/ Зх.
II. Сдѣлать приведеніе въ выраженіи
|/10Гз _р р/20у — у'Ьу + уіОх3 — /8бу.
Вынесеніемъ множителей изъ-подъ радикаловъ выраженіе приводится къ виду
х р ІОхр/бу -** V 5? -Н 2х р іОх—4 рбу;
приводя подобные члены, получимъ
Зх ІОх *— 3 р^бу*
207. Сложеніе и вычитаніе. При сложеніи иррац. выраженій ихъ пишутъ рядомъ съ тѣми знаками, какіе они имѣютъ; при вычитаніи же приписываютъ къ уменьшаемому члены вычитаемаго съ обратными знаками; затѣмъ члены суммы или разности приводятъ къ простѣйшему виду, и, если окажутся въ числѣ ихъ подобные члены, дѣлаютъ приведеніе.
Примѣры. I. + (“У6^)
« э/т^ г л 4 з/, . я/— । тп2 ъ/— з/г*’ _ 3 Ѵ-Х
= тяа р/ -|- 3 тп* эу — 4иш* у эу -|—9 у ъу-------------— у лу = — тп* у іуу.
208. Умноженіе. Въ § 120 было доказано, что
У А . В . С=’/а . Ув . У С: написавъ это равенство въ обратномъ порядкѣ, найдемъ:
X V В X V С = У ГГвТс;
Отсюда правило: насколько ирраи, выраженій
одинаковаго порядка, надо перемножитъ подрадикалъныя количества и изъ произведенія извлечь коренъ того же порядка.
Примѣры I. ^2ахуіу^у^а9ху3 ==]/12аіх*у1 = 2а?ху*\/Зу.
II. ]/л# -|- я*/|/Ъх — у/(лж-|- л2)(аЬ Ц“ Ьх) = = («-}" х)
ПІ. а +]/а2 — б’Х^« — ]/о®“Ь’=г/аГ::Т«1‘— Ъ3)=^Ъ3=Ь.
IV. (а|/а — Уа*-|- За3|/а,)Х(—6)/а®) = — 6а|/д* 4~3а2|/а6 —
— 18а*/а1^ — 6в84-3ав — 18а».
209. Дѣленіе. Въ § 121 было доказано, что
у А
іиг
Написавъ это равенство въ обратномъ порядкѣ, имѣемъ:
Отсюда правило: чтобы /уаздѣлитъ одинъ на другой два корня съ одинаковыми показателями^ надо первое подрадикалъное количество раздѣлитъ на второе, и изъ частнаго извлечь коренъ того же порядка.
— 4а2 }/аЬ -|-
+ 4а2 ]/ аЬ Ч-й
м ІО
“о”
1) Вычисленіе 1-го
2 ,/ ’ Заг а-
2) Вычисленіе 2-го *
3) Вычисленіе 3-го
члена частнаго: —4а2|/а6 ; 2а )/а ~ — 2а }/Т. члена частнаго: |айі: 2а|/а = |аЬ]/а*: 2а)/а =
210. Возвышеніе въ степень. Пусть требуется |/а* возвысить въ ^р-ую степень, гдѣ т, к и р—цѣлыя положительныя числа. Это значитъ — данный корень взять множителемъ р разъ; слѣд.
($акУ* = ^/а*Х|/®*Х • • - (всѣхъ множителей р);
но, по правилу перемноженія корней (§ 208), вторая часть равна
Итакъ:
|/а*.а*.а*. , . . (р разъ)= |/(а*)р.
т.-е. чтобы коренъ возвыситъ въ степень, нужно въ эту степень возвыситъ подрадикалъное выраженіе, и изъ результата извлечь коренъ даннаго порядка.
Примѣры: I. (^гЪ/3#)8 =
За* в/^Г— 51 3/^! — 81я^Н5 3
5?/ ‘ 1/ I ‘ 625?/* '•!/ узо 625^10 ’ 1/
211. Извлеченіе корня. Пусть требуется извлечь корень йі-го порядка изъ ^А: положимъ, что результатъ этого дѣйствія будетъ т.-е. что
. (1).
Возвышая обѣ части равенства въ степень йг и замѣчая, что извлеченіе р/т
корня етг-го порядка изъ у А и возвышеніе результата въ йі-ую степень, какъ два противоположныя дѣйствія, взаимно уничтожаются, найдемъ:
?І=хт.
Возвышая обѣ части этого равенства въ степень р, получимъ
А=«и,?;
а извлекая изъ обѣихъ частей корень порядка тр, найдемъ:
7а=®.
Подставивъ эту величину вмѣсто х въ равенство (1), получимъ:
ІР'Та^Ѵа . . .(2).
Отсюда правило: чтобы шоечъ корень изъ корня, нужно подкоренное количество оставитъ безъ перемѣны и извлечь изъ него коренъ, котораго показатель = произведенію показателей данныхъ когтей.
Примѣры. I. V^/2ахі = |/2ах\
II. Ѵэа^аЬ5 = За’^аЬ*.
Если равенство (2) прочесть въ обратномъ порядкѣ, то найдемъ, что извлеченіе корня, показатель котораго разлагается на множители, можно замѣнить послѣдовательнымъ извлеченіемъ корней, которыхъ показатели равны этимъ множителямъ. Напр.
1) ^64=^)/б4 = ,/8 = 2.
2) 1^4096а’*і*®* = V /)/Ж96аа‘6‘а;8 = У]/біайЪ*х* — =
= 2а'2
212. Теорема. Величина корня не измѣнится, если показателъ подкоренного количества и показателъ корня помножитъ или раздѣлитъ на одно и то же число.
Мы видѣли, что если у^а* возвысить въ степень р. то получится жзвлекая изъ полученнаго выраженія корень порядка у, на оси. § 211 найдемъ *і о*. Такъ какъ надъ выраженіемъ |/а* мы произвели два противоположныя г!>ггш, то величина его не измѣнилась, а потому
^=Уа*?.
Итакъ: 1) данное выраженіе можно замѣнить равнымъ ему: т.-е. ве-
личина ирраціональнаго выраженія не измѣняется отъ умноженія показателей корня подкоренного количества на одно и то же число; 2) обратно, "У'а1*’ равенъ слѣд. величина корня не измѣнится отъ раздѣленія показателей корня и подкоренного количества на одно и то же число.
Слѣдствія I.—На первомъ изъ зтпгь свойствъ основано приведеніе ирраціональныхъ количествъ къ общему показателю корня. Для этого нужно составить паим. кратное всѣхъ показателей корней; оно и будетъ общимъ показателемъ; послѣдній дѣлятъ на показателей каждаго корня и соотвѣтствующими частными множатъ показатели корней и подкоренныхъ количествъ. При этомъ могутъ быть тѣ же случаи, какъ и при приведенія дробей къ общему знаменателю.
1. Всѣ показатели корней числа взаимно первыя, напр.
Общій показатель = 2Х^ХЛ — 30; раздѣливъ его поочередно на 2, на 3 и на 5, множимъ показатели корней и подрадикальныхъ выраженій: перваго—на 15, второго—на Ю, третьяго—на 6; найдемъ:
“ 3* (2а6*)10 = ^210. а1 бЧ
У уі&а) У \2е*сі/ У
2. Одинъ изъ показателей—число кратное для остальныхъ, напр.
^2А, >^с.
Общій показатель корня =12; имѣемъ:
^2А = *^(2А)‘ = У ГбА4.
12/—
у С остается безъ перемѣны.
3. Показатели корней имѣютъ общихъ множителей; напр. ’^А, ’^В, ѴС.
Общій показатель —180; получимъ:
1^А = 15Л^/А^ = 1^дТ2. 1^й = 12Л^вП = 1^зіі. 36/(1 _3€^/см =
Примѣчаніе. Правила, данныя въ §§ 208 и 209 для умноженія и дѣленія корней, относятся къ случаю корней съ одинаковыми показателями; если же показа
тели корней различны, то ихъ сначала приводятъ къ общему показателю, а затѣмъ уже производятъ умноженіе и дѣленіе по упомянутымъ правиламъ.
Примѣры. Ь Составить произведеніе: ]/аЁЛ?Х X
Приведя корни къ общему показателю 6, получимъ:
X X УаЧЮ=
^ав61а Ха’&с’^ай2 . у'Х/Гс5.
„ Ѵа&с п
П. Составить частное Приведя корни къ общему показателю, по-
Ш. Вторая часть теоремы этого § даетъ возможность сокращать ирраціональныя выраженія; для этого нужно показателя корня и показателей подкореннаго выраженія раздѣлить на ихъ общаго паиб. дѣлителя.
Такъ: Vа^с”4 аѢс4’, ^16а‘Ь»= ^2аГ».
Ирраціональныя дроби.
213. Когда числитель, или знаменатель, или оба — ирраціональны, дробь зазывается «рраиідяа-ѵьяото. Въ видахъ упрощенія вычисленій, дроби съ знаменателями ирраціональными выгодно замѣнять равными имъ дробями, но имѣю-жижи раціональные знаменатели. Такъ, если бы требовалось вычислить величину лроби
х— ~ 1
ГЗ-
то, пайдя (/3 = 1,732 и |/ 2 ~ 1,412 .. ., мы должны бы были раздѣлить 1 на приближенное число 0,320... Понесли умножимъ предварительно числителя и знаменателя дроби на (/3 + (/2, то найдемъ
Х= |/3 4-/2,
и простое сложеніе чиселъ ‘1,732 . . . и 1,412 ... дастъ величину а?,
#=3,144...
Такимъ образомъ дѣйствіе дѣленія приведено къ простѣйшему дѣйствію — сложенію; другая выгода указаннаго преобразованія состоитъ въ томъ, что найденная для х величина 3,144 ... допускаетъ непосредственное опредѣленіе предѣла погрѣшности, которая меньше 0,002, потому что каждое слагаемое ошибочно менѣе чѣмъ на 0,001.
Уничтоженіе ирраціональности въ знаменателѣ дроби безусловно всегда возможно. Не останавливаясь па доказательствѣ этого предложенія и на вытекаю-13
щемъ изъ него общемъ методѣ (о чемъ рѣчь будетъ ниже), разсмотримъ здѣсь частные случаи этой задачи, важные въ практикѣ.
214* Укажемъ пріемы, которыми можно уничтожить ирраціональность въ знаменателѣ, содержащемъ только квадратные корни.
1. ——• лмпожая числитель и знаменатель па у с, получимъ:
Ь V с
а __ аУс____аУс
ьѴс ~ Ь (» а) ~ Ье
2. Умножая числитель и знаменатель на }/ Ь — ]/ с, найдемъ:
а _____ а (у Ь — I с)_____ а (У б — У с) _а (У6 ~ У <0 е
У 5 + У с “ о Б + Уё)(»г — Уё) О7*)* — (У с)* Ь — С
3. —Умножая чясл. и знам. на ш получимъ:
тѴЬ—пУс
а _____ а(тІ У с) __ д (тУЙ-Ь п 1 с)
тI б—я! с (тУ?)3—(я Уё)2 т26—п*с
4* у&^ )ё__|_) 5 ^множая числ* 0 знам. на і/б-І-р^— найдемъ: а ___________________«(УЬ-рУс—УЗ) _ «(уб^-У с-—Угі)_______
Уб+Ус+УЭ^ (Уд+Ус+У5)(і/&+Уё-УЭ)^~ (УЬ + Уё)3—
_ а(у'дЦ-Ус—У5) Ъ + с — (І + 2 У бё*
умножая оба члена этой дроби на — 2|/йс, получимъ:
а а (уб+Уё—У2)(&+с—&—2 У де)
Уб -Ь У с+ УЭ (6 + с—йр - 4бс
Общій способъ исключенія изъ знаменателя квадратныхъ корней, каково бы ни было ихъ число, заключается въ слѣдующемъ. Если )/ к есть одинъ изъ радикаловъ, который мы хотимъ исключить, выносимъ его за скобки изъ всѣхъ членовъ, его содержащихъ; знаменатель приметъ видъ Р4“9 р^, гдѣ Рн<і— раціональныя или ирраціональныя выраженія, не содержащія )/&. Если теперь умножимъ оба члена дроби на Р — () )/А, то новый знаменатель Р*— уже не будетъ содержать |/А. Такъ какъ произведенное умноженіе не вводитъ новыхъ радикаловъ, то очевидно, что примѣняя указанный пріемъ послѣдовательно къ каждому изъ нихъ, мы исключимъ всѣ радикалы.
Этотъ именно способъ мы и прилагали въ предыдущихъ примѣрахъ; приложимъ его еще къ дроби, содержащей въ знаменателѣ пять радикаловъ:
___ т _______
У а + У 6 + У с+УЗ -у У ё
Умноживъ оба члена ея на 4“ V & Н- 4" — У7 получимъ но-
вый знаменатель, въ которомъ /* есть раціональная часть:
ЛЬ 2(|/а/6 + ]/а/с + у ь ]/с) 4-2(/а 4-+/с)• • - О)
Умножая оба члена долученной дроби на выраженіе» выведенное изъ (1) перемѣною на — )/й, получимъ новый знаменатель, въ которомъ д представляетъ раціональную часть:
^4(/4-2с-2(?)ѵ/оі/Ь+4К/+2г>-2<гу а-Н/+2а—2й)|/Ь]|/с . . . (2).
Помножая оба члена новой дроби на выраженіе, выведенное изъ предыдущаго перемѣною на — }/с, получимъ новый знаменатель, котораго раціональная часть обозначена буквою А:
А-р[8^(/ + 2с—2Л) —32с(/4-2а—2й)(/ + 2&-2Л)]|/аЬ . . , (3),
Умножая, наконецъ, оба члена послѣдней дроби на выраженіе, выведенное изъ предыдущаго перемѣною на — 1/аЬ, и означая числителя новой дроби буквою А, найдемъ
А
Л2 — І&р (Н-'2с — 2й) — 32с (/'+ 2а — 2й) (/ + 2Ь - 2й)|*, аЬ
Дробь, которой знаменатель раціоналенъ. Примѣчаніе I, Взявъ, напр,, дробь ________________________________________ ~/2+ИЗ + Ѵо
и примѣняя къ ней указанный пріемъ, мы должны начать исключеніе съ большаго корня, такъ какъ вычисленія при этомъ будутъ проще. Умножая, поэтому, оба члена на + — 1^- найдетъ:
Гяш Иа это* дробя на получимъ окончательно:
_ гП+ѵ'Тв—г зб
12
Прѵлманіе І1Г Нерѣдко можно значительно упрощать вычисленія, пользу» слѣдующимъ замѣчаніемъ, _ _
Выраженіе “Ь с состоящее изъ четырехъ радикаловъ, разлагается на два множителя вида ]/А -|- уПВ, если числа а, Ь, с и й составляютъ кратную пропорцію.
- Въ самомъ дѣлѣ, пусть напр.
Л Ь 7 У □ I' 6 /-у / /— Л— у--
откуда н сл^д‘ у а—у с.ук в уЪ=уЛ.ук.
Знаменатель приметъ видъ
= (^+Ѵ^)(1+^)
или’7= (]/с + |/й) (]/^4-р/с).
V с
Примѣнимъ это замѣчаніе къ дроби _ 1__________________________________________
Х ”П0+ КІ5 + Н4 + КП *
Такъ какъ 10X21 = 15X 14, то, согласно сказанному, найдемъ:
1
Ж~(і/2-+-1/3)(і/о+Ѵ/7)’
умноживъ числ. и знам. на (]/3 — ]Л2)(і/7 —1/5), сразу уничтожимъ ирраціональность въ знаменателѣ, и найдемъ: •
(КЗ-К2)(К7—Ко)
, __ •
215. Пусть знаменатель содержитъ только радикалы кубичные.
1. А - Положивъ: и —у, имѣемъ: а —Ь
Взявъ разложеніе я> + У3^(^ + У)0с2вя;У + 2/2), и подставивъ вмѣсто хну ихъ величины, найдемъ:
а-]-Ь= (^а+ №>) фа' — УаЪ + ^Ь»),
откуда видно, что отъ умноженія знаменателя дроби на уа*—онъ обращается въ раціональное выраженіе, равное а-}-Ь. Итакъ, умноживъ числ. и знам. на указанный триномъ, получимъ:
2. Подобнымъ же образомъ, пользуясь разложеніемъ: я8 — у3 =
($ — у) (#а яу 4~ У*)> найдемъ:
а — Ъ
‘ Положивъ въ равенствѣ
8 — Зяуя = (я -|- У + ^)(#2 + ув + — ху — хг — уг) я — у = я= у/с, найдемъ:
а 4-Ь+с - 3 ^аЪс = (^аЪ— ^ас— ^Ьс);
отсюда, умноживъ числителя и знам. данной дроби на ^2_І_ аЬ — ^ас— ^с?
А А(У^+ Уъ* + - ѴаЪ-.753- МЬ)
найдемъ: а + ь + ё- з^яй
Если аЪс есть точный кубъ, то преобразованіе окончено: новый знаменатель радмжмеяъ; если же лЬс не есть точный кубъ, то представивъ знаменатель въ
4" Ь с)а — 27аЪ(^
^«нпъ вопросъ къ предыдущему случаю.
4- ^+^4^+^ СЪ УСЛ0ВІеМЪ’ 470 «=5‘ Не трудно что знаменатель можно представить въ видѣ произведенія двухъ ілл и + ^ѵ, и вопросъ приводится къ примѣру 1.
216. Если знаменатель дроби есть сумма или разность двухъ
убѣдиться, множителей
радикаловъ
ыкого угодно порядка, то ихъ можно привести къ общему показателю корня; такимъ образомъ знаменатель будетъ вида ’р/а + Отсюда два случая:
I. Положивъ у/а = % и *уЬ = У, откуда а = хт и Ь =
м замѣчая, что при всякомъ т — четномъ или нечетномъ, имѣемъ:
~ = (я — у) (я™”1 -р хт~2у
* 4-#ут-24_УИ1^1)*
подставивъ сюда вмѣсто х и у ихъ величины, найдемъ:
« — Ъ =( ра—’і/&)(Р'а’-’+р'а"-’Ь4-р/ав>-3Ьа ... +р'аЬв-г+^^Г1).
Это равенство показываетъ, что если числит. и знам. данной дроби помно-жимъ на і/а"*”1 -|- ^ат-2Ъ то знаменатель обратится въ
раціональное выраженіе а — Ь; такимъ образомъ получимъ:
а-д~
Если ш—число четное, то замѣчая, что разность одинаковыхъ
четныхъ степеней двухъ количествъ дѣлится безъ остатка на сумму первыхъ степеней, имѣемъ:
хт " у,п = 4~ у) — хт~2у ^"“яу2 "4
Подставляя сюда |/а вмѣсто я, и вмѣсто у, дадимъ равенству видъ:
4^6 = 4- фЪ) — ^“2І + —
— ^>-4
Отсюда видно, что для уничтоженія ирраціональности въ знаменателѣ дроби » четномъ, надо оба члена ея помножить на — |/ат-Ч) 4“ • * • — Сдѣлавъ это, найдемъ:
А Аф'а"-! — у/а«-2^4- . , #
Если т — число нечетное, то припомнивъ, что сумма одинаковыхъ нечетныхъ степеней двухъ количествъ дѣлится на сумму первыхъ степеней, имѣемъ равенство:
+ Ут = (# + — . . . + У1"”1);
т/ т/7 *
положивъ въ немъ я = у а и у=уо, имѣемъ:
а 4- Ь = 0/а^1 — ^-Ѣ + І/а"-3Ь’ - . . . -|- ^6—’).
Отсюда слѣдуетъ, что для уничтоженія ирраціональности въ знаменателѣ данной дроби, при т нечетномъ, надо оба ея члена умножить на |/ата-1 — — сдѣлавъ это, найдемъ:
1
Примѣръ,-^—Приводя корни къ общему показателю 6, полу-і/ я —|- а/ ь
чимъ дробь
Множитель, обращающій знаменатель въ выраженіе раціональное, въ данномъ случаѣ есть
^(а^— ^(а’)‘Ь*+ ^(а»)’(Ь«)’ — ^Ѵ(Ь»)» + ^а»(Ь®)* — ^)®, или — . ^ — аЬ-^-Уа . —
Умноживъ имъ числитель и знаменатель дроби, получимъ:
1 —аа 0]/5 , —«^ + -|/а.б^5—
)АЧ- а’ — Ь1
чч»-
217- Въ заключеніе этой главы приведемъ нѣсколько примѣровъ дѣйствій надъ ирраціональными выраженіями.
1. Провѣрить равенство:
У—і—+]/ —2— = >/»+ А
Провѣрка равенства двухъ данныхъ выраженій, которыя > О, приводится къ провѣркѣ равенства ихъ квадратовъ, т.-е. что
а + +2 _ а +^}
пли что а + « -р 1/^*
Но это равенство вѣрно; слѣд. вѣрно и предложенное.
2. Упростить выраженіе:
|/3-Н
Это выраженіе можно представить въ видѣ
яли (^-(^+ № - '
3/— 3/~,
или, по сокращеніи на / х — у у.
х3^х — Уу) №х+&у)№хЧ~№—Уху)
т.-е.
X + у
3. Разложить на множители выраженіе:
, '~аѢ* + к'ЬѴ -|- ’ЛЛІ* — ( */б*ё» 4- ^0*0* 4- ^а*Ьг).
Назвалъ это выраженіе буквою Р, имѣемъ послѣдовательно:
Р - (’/'ьі _ _р */? - ^Г‘) 4- ^‘.(^ — ^а»)
= (^ — ^7Г») {^((/аа4-^) — ^аѢ3 — )/<?}
= — ^/7а){ ус3 (^Га — ^с2) }
= (^а> — ^Г») (^6® — (у'с® — ^)-
к
Примѣчаніе. Индусамъ уже были извѣстны методы извлеченія корней — квадратнаго п кубичнаго. — Олсора Ллкахійялем (средина XI вѣка) доказалъ точность этиіъ методовъ и указалъ пріемы для нахожденія корней высшихъ порядковъ. Правила дѣйствій надъ коренными количествами находимъ уже въ ариѳметикѣ Алъкалъцади (-|- 1477).
ГЛАВА XVI.
Степени н корни съ дробными и отрицательными показателями.
Дробные показатели.
218. Происхожденіе с^пепеней съ д/}обными показателями.—Для извлеченія корня изъ степени надо показатель подкореннаго количества раздѣлить на
__ 15
показателя корня; такимъ образомъ: /а13= а8 = адй Но если показатель под-
кореннаго количества не дѣлится на показателя корня, какъ напр. въ случаѣ _ 2
то, примѣняя указанное правило, мы найдемъ выраженіе а3, пе имѣющее смысла степени какъ произведенія множителей, равныхъ основанію въ самомъ дѣлѣ, очевидно, что нельзя а повторить множителемъ у раза» Однако, вполнѣ нозволительно допускать подобныя выраженія, если только подъ ними разумѣть ничто иное какъ новый особый способъ изображать ирраціональныя
2 _ ^2
выраженія. Такимъ образомъ пишутъ: а3 вмѣсто а2 вмѣсто а5 тл
вмѣсто н т. д. Вообще, выра-жекге ап есть ничто иное какъ и называется количествомъ съ дробнымъ показателемъ. Итакъ: количество съ дробнымъ показателемъ есть корень, показатель котораго равенъ знаменателю дробнаго показателя, изъ количества въ степени^ равной числителю дробнаго показателя.
условное обозначеніе ирраціональныхъ выраженій въ видѣ дробныхъ степеней, распространяя правило показателей при извлеченіи корпи и на тотъ случай, когда показатель подрадикальпаго количества не дѣлится на показателя корня, т-е. обобщая это правило, вполнѣ соотвѣтствуетъ духу алгебры, стремящейся къ обобщеніямъ.
Разсматривая правила дѣйствій падъ дробными степенями, мы придемъ къ тому важному заключенію, что правила эти остаются тѣми же самыми, какія мы нашли раньше для показателей цѣлыхъ. Обстоятельство это, говоритъ Лакруа въ своей алгебрѣ, «служитъ однимъ изъ замѣчательнѣйшихъ примѣровъ пользы знаковъ, когда они удачно выбраны. Чѣмъ дальше мы подвигаемся въ алгебрѣ, тѣмъ болѣе узнаемъ безчисленныя выгоды, какія повело за собою введеніе показателей...»
Дробные показатели были введены Ньютономъ.
219, Теорема, Двѣ дробныя степени равны,
если
показатели изъ
равны*, т.-е.
т
то ап
р
а4.
т р если - =
Дѣйствительно, по опредѣленію степени съ дробнымъ показателемъ имѣемъ:
т р
Приводя корни къ общему показателю, найдемъ
т р
а» = ра* = . (1) и «’ = ^а1’ = .
• (2);
но изъ условія имѣемъ: «15=слѣд. вторыя части равенствъ (1) и (2) равны, а потому равны и первыя. Итакъ
«I р
220. Умноженіе. Умножить имѣемъ
т р
ап на Но опредѣленію дробныхъ степеней
т а =
_ р __
и а" = а*;
* р ________ _ __
откуда а'ха'1- ^а,нХ^а^=^/апи1Хп^/аІГр (по приведеніи корней къ общему показателю). Такъ какъ и пр—числа цѣлыя и положительныя, то пригоняя правила—умноженія корней и степеней, доказанныя для такихъ показателей. получимъ: 4
’у/а^Х ”і/а’гр=іу/ а"ч'.а,'^='‘Уав,’+я<>.
Такъ какъ пц и 4“^^ Цѣлыя положительныя числа, то раздѣливъ въ П’<-гѣхнемъ выраженіи показатель подкореннаго количества на показателя корня. найдемъ:
тд-}'ІІР тЧ пр т р 4
а—а^+"»=а" '
Итакъ: я» р яі р ^Ха?=а" + < . .(1).
Положивъ въ этомъ равенствѣ сперѣа п = 1, потомъ ? = 1 (на что имѣетъ право, такъ какъ п и $—цѣлыя положительныя числа) иайдемъ, въ первомъ случаѣ:
Г т+' атХа*=а ®. . . (2). а во второмъ т т
а5 *Хл”=а" . . .(3).
Равенства (1), (2) и (3) показываютъ, что: будутъ ли оба показателя (робкые^или одинъ цѣлый, а другой дробный, при умноженіи степеней одною и тою же основанія показатели складываются.
1 1 Д + ± и 1 з+А И
Такъ: 1) а5Ха3=я3 2=а10; 2) а®Х&5=а 5—а5.
т р
221. Дѣленіе. Раздѣлить а№ на а*, полагая, что “ >
Послѣдовательно имѣемъ:
т ’р
а*: а« = = У а"4: апр = *^а’лі-"г.
приведеніи обѣихъ частей неравенства
»»
Я "'Я
къ общему знаменателю,
По
откуда: а слѣдовательно разность тд—пр поло1
жктелып. Но при цѣлыхъ положительныхъ показателяхъ имѣемъ
явд—яр тд пр я» р
Итакъ
т р я» р
. (1).
Положивъ я —1, находимъ изъ этого равенства:
р т р
— я» — —
а : 7 , .
(2)-
Р х
порядка^, т.-е. опредѣлить
Положивъ въ равенствѣ (1) д = 1, найдемъ: гп т
а*: аѵ — а^~Р . . .(3)
Равенства (1), (2) и (3) доказываютъ, что правило показателей при дѣленіи, доказанное первоначально для цѣлыхъ показателей, остается справедливымъ и тогда, когда оба или одинъ изъ показателей — числа дробныя,
3_ 5_ _5 4^ 2
Примѣръ:#2 :а*=аа в=а 0=а1. /
222. Возвышеніе въ степень. Пусть требуется ап возвысить въ степень т\ у
#пр. Замѣняя каждую изъ степеней съ дроб-
нымъ показателемъ — корнями, получимъ: иі\ р у
Такъ какъ показатели пу и тр— числа цѣлыя и положительныя, то тр т у а7* = а “ ‘ «. Слѣд.
(ш\ р й* у а“)« = а" . (I).
Полагая сперва д— 1, а затѣмъ н=1, найдемъ: т р р
а~к) =а!і'Р: .(2); и (ат)^ = ат^. . .(3). •
Отсюда слѣдуетъ, что правило показателей при возвышеніи въ степень, выведенное въ § 104 для показателей цѣлыхъ, распространяется и на тѣ случаи, когда одинъ или оба показателя — дробные.
I -1\2_ _1 - 5 _5
Примѣръ. ^а4]в=а4 *=а8.
223. Возвышеніе въ дробную степень произведенія и дроби.
। і'а\< -,7/аѴ -.7^ А’ »
к\В7 = у \в) ~у в? = =—• Заключаемъ, что для возвыше
нія дроби въ дробную степень нужно отдѣльно возвысить въ данную степень числителя и знаменателя и первый результатъ раздѣлить на второй: то же самое правило, что и для возвышенія дроби въ цѣлую степень.
р___________________ __________ р р
2. (А.В)^= ^/(АВУ=^А/’.Вір= ^Р7.^/Вр= АУ.В^, слѣд. правило возвышенія произведенія въ дробную степень —такое же какъ и въ цѣлую степень.
224. Извлеченіе корня. Пусть р
ПЧ М
а* т.-е. найти V а*1. Распространяя опредѣленіе корня и на этотъ случай,
требуется извлечь корень порядка - изъ
т уэдишсся подъ корнемъ порядка ~ кзв ам разумѣть такое количество,
т
жммрее, будучи возвышено въ степень порядка ^давало бы а*. Согла-оэя лому опредѣленію, назвавъ искомый корень буквою т -е. положивъ
^ан=х . . . (1)
р >н
Аймяъ, что ха = а‘\ откуда, возвышая обѣ части
рф тд т р
х°=ам, или х = ал Подставивъ въ равенство шраженіе, получимъ:
г
^-1
У / т »і р
V а7* = а* 1« . . . (2).
я
въ степень
(I) вмѣсто #
получимъ:
найденное
Полагая здѣсь сначала д — 1, а потомъ н = 1
?/ т т Р р
Уая=а"''Р. . . (3); 2/(?г=аИ‘!»
имѣемъ:'
: Р
. . (4)
Такимъ образомъ, будутъ ли показатели — корня и подкореннаго количества оба дробные, или одинъ — цѣлый, а другой — дробный, надо для извлеченія корня — показатель подрадикальнаго количества раздѣлить на показатель корня: то » самое, что к для цѣлыхъ показателей.
3 -1 1?
Примѣръ. * а7 =а7 3=ан.
225. Корень дробнаго порядна изъ произведенія, дроби я корня съ дробнымъ показателемъ.
1. /а.В = ^(АВ)‘ = (АВ)1' *(§ 224,4) = (АВ)Р = А* . В₽(§ 223, 2)
1 ; Г 1 : * Ѣ Р. _
= А “ . В ' * = ^А X И* (§ 224, 4).
Заключаемъ, что правило извлеченія корня дробнаго порядка изъ произведенія— такое же точно какъ и корня съ цѣлымъ показателемъ.
и въ этомъ случаѣ для извлеченія корня изъ корня нужно показатели корней перемножить.
Итакъ, всѣ правила, доказанныя для показателей цѣлыхъ, распространяются я на дробные показатели. Замѣняя радикалы дробными показателями, мы получаемъ возможность совершать преобразованія ирраціональныхъ выраженій по тѣмъ же правиламъ, какія имѣемъ для выраженій раціональныхъ, а это ведетъ къ упрощенію вычисленій и болѣе быстрому полученію результатовъ.
226. Приводимъ примѣры преобразованій выраженій съ дробными показателями.
I. Упростгітъ выраженіе
I А —♦ Л А\_1 \Д2 _|_д 86 8 ) ф ф ,
_4 4^
Вынося въ первыхъ скобкахъ общаго множителя а а во вторыхъ Ь3» имѣемъ:
возвышая каждаго множителя отдѣльно въ степень находимъ:
/ Л ® V
взявъ общимъ множителемъ имѣемъ
или, выполнивъ умноженіе:
II. ‘Провѣритъ равенство
_іг — ПГ -П- - 3
22Ьа-}-(а2 — &2)2 Ла— (а* — Ь2)2Ъ ^=(а + &)2 — (а — Ь)2.
Для облегченія повѣрки положимъ:
х = а -1- Ъ . . . (1) п ~ — Ь. . .(2).
Сложивъ эти равенства, получимъ:
X -4- у 2а = я-|"2/>а отсюда а— —
перемноживъ (1) со (2), найдемъ
а2 — Ь2 = ху, откуда (а2 — Ь*)2 = (я$)3.
Первая часть даннаго равенства послѣ подстановки приметъ видъ:
2е .Ссу-|-(ху)4].
я + у + —у4) ]’
А 2.
(а + Ь)4-(а-&)4,
что и требовалось найти.
Отрицательные показатели.
227. Въ § 41 мы нашли, что а~т = ^ но тамъ формула эта установлена была для случая т цѣлаго. Если въ равенствѣ
т р т р
« “ ; а* = а " ~ ®,
доказанномъ въ > 221 пра условіи — > с условимся не дѣлать послѣдняго » = О ™ Л обратятся въ а* или въ 1, а самое ра-
* Итакъ
а«
«
т.-е. степень съ отрицательнымъ дробнымъ показателемъ равна единицѣ, дѣленной на то же основаніе съ положительнымъ показателемъ, равнымъ по абсолютной величинѣ отрицательному. Такимъ образомъ, будетъ ли т— цѣлое или дробное, всегда имѣемъ:
Отрицательные показатели даютъ возможность изображать дробь въ формѣ цѣлаго выраженія (безъ знаменателя). Такъ дробь можно написать въ вигѣ: 5а*Ь3- ~5 • замѣтивъ, что —с’5 и ^ = с?-7, найдемъ, что
= 5л263с~5 Д”7.
Такимъ образомъ, чтобы дробь представить безъ знаменателя, надо всѣ множители знаменателя перенести въ числитель съ отрицательными показателями.
Наоборотъ, всѣ множители числителя можно перенести въ знаменатель, написавъ игъ съ отрицательными показателями; въ самомъ дѣлѣ, напр.
_ 1
а'2 о
1
Перейдемъ теперь къ изученію дѣйствій надъ количествами съ отрицательными показателями.
228. Умноженіе. I. Пусть требуется помножить ар на замѣтивъ, что
= получимъ:
П д р 1 ЯР
такъ какъ р и 2—числа положительныя, то, будутъ ли они цѣлыя или дробныя, нужно при раздѣленіи ар на а? вычесть $ изъ слѣд.
— лр_'7 = слѣдовательно
ар .
т.-е. показатель произведенія равенъ алгебраической суммѣ показателей множимаго и множителя.
2. Пусть оба показателя—отрицательны; найдемъ:
а_р . —-Д - Ду — = а_(р-Н) = а-Р-?=а-р+(-?):
то же самое заключеніе, что и въ предыдущемъ случаѣ.
229. Дѣленіе. I, Пусть будетъ одинъ изъ показателей — положительный, а другой — отрицательный.
а~р : ад — Д7:а9= а = -^г:і — а~(Р^) = а-Р~і= а-р-(+ч\
ар а? . а? шЖг ѵ 7 \
т.-е. изъ показателя дѣлимаго вычитается показатель дѣлителя.
2. а_р:а~г = ^Д: = а~р-Н = а-л-(-я); то же заключеніе.
/ I Ѵл 1
230. Возвышеніе въ степень. 1. (^ш)” = І-ж) = по правилувоз-. X1* і /
1 I
вышенія дроби въ положительную степень; далѣе: ^р — = ”.
(а")-" = - а = а- • - «.
Всѣ три результата приводятъ къ общему заключенію: при возвышеніи степени въ новую степень показатели перемножаются, будутъ ли они цѣлые или дробные, положительные или отрицательные.
231. Возвышеніе въ отрицательную степень произведенія и дроби.
1 1 Ч і“ж— 1 —- - 1 1 V -— иі т>—т
*- (ДВ)т Ат. Вт Ат ВНІ Л ’п
что Дзія возвышенія въ отрицательную степень (цѣлую или зрУдун и?жведенія нужно отдѣльно возвысить въ эту степень каждаго мно-жтгео і результаты перемножить.
. V— 1 I Вт А-т . ,и
-- А"*^ А™~ В27™’ 00 перенесеніи А въ числителя, а
ІТГ) В"1
Р—гь аиенателя. Заключеніе: для возвышенія дроби въ отрицательную сте-в - * въ эту степень возвысить отдѣльно числителя и знаменателя, и пер-
іті -тульгатъ раздѣлить на второй.
232. Извлеченіе корня. I. Пусть требуется извлечь корень положительнаго іять степени съ отрицательнымъ показателемъ: )/а~р, гдѣ ши р —цѣ~ _ дробныя числа. Имѣемъ:
г
Т 1 1 -- —
р=—= — = а м = ат , т.-е. показатель подкореннаго ко-га” а"*
лгчрггва нужно раздѣлить на показатель корня.
2. Разсмотримъ теперь извлеченіе корня съ отрицательнымъ показателемъ.
дѣленіе корня, данное для цѣлаго положительнаго показателя и распростра-т—затѣмъ на корень дробнаго порядка, распространяютъ и на корни от-тщательнаго порядка. Такимъ образомъ, корнемъ минусъ ш-го порядка изъ А вызываютъ количество, которое по возвышеніи въ минусъ *п-ую степень даетъ А; согласно этому опредѣленію:
«ли ”|/а = В, то К“ш = А.
Докажемъ, что
1
7^»
—т
т.-е. что коренъ съ отрицательнымъ показателемъ равенъ единицѣ, раздѣленной на коренъ съ тѣмъ же по величинѣ, но положительнымъ по знаку? показателемъ.
Въ самомъ дѣлѣ, пусть” |р/А = я; по опредѣленію корня найдемъ: — А,
1 і
или^й — А, откуда х =-т, а извлекая изъ обѣихъ частей корень т-го (по-ложительнаго) порядка, получимъ:
ад /Т 1
= и требуемое доказано.
Пусть теперь требуется извлечь корень (—т)-ой степени изъ ар, гдѣ р— юйжжтельно; въ силу только что доказаннаго предложенія имѣемъ:
т.-е. и въ этомъ случаѣ
показатель под-
растпігътаго і^личества надо раздѣлить на показатель корня.
Пусть, наконецъ, оба показателя отрицательны; найдемъ, что ____ _____1__ ___________
Г/ «-р=^/^Т7р; но |Уа-*’ = а м (§ 232,1); слѣдовательно
а ’р = —р = а'н = а"ІЛ* прежнее заключеніе.
Итакъ, во всѣхъ случаяхъ, при извлеченіи корня нужно показателъ подрадикалънаю количества дѣлитъ на показателъ корня, будутъ ли оба показателя — цѣлые или дробные, положительные или отрицательные.
Напр. У а 4=а 4
233. Извлеченіе корня отрицательнаго порядка изъ произведенія, дроби и корня съ отрицат. или положит. показателемъ.
1
Ні
1
гп. Но, но доказанному,
туг— н слѣд.
т.-е. для извлеченія корня отрицательнаго порядка изъ произведенія нужно извлечь его отдѣльно изъ каждаго производителя и результаты перемножить.
і
(по §§ 231,2 и 232,2). Итакъ
т.-е. для извлеченія корня отрицательнаго порядка изъ дроби нужно извлечь его отдѣльно изъ числителя и знаменателя, и первый раздѣлить на второй.
3. Пусть, наконецъ, требуется извлечь корень (—т)-го порядка изъ —™ ।
г д-р—А р Ш = = = т.-е. пока-
затели корней слѣдуетъ перемножать.
Итакъ, всѣ правила, относящіяся къ вычисленіямъ надъ количествами съ положительными показателями, относятся и къ отрицательнымъ показателямъ.
Отрицательные показатели были введены раньше дробныхъ; ихъ введеніе приписываютъ Михаилу Стифелю (1509—1567),
ГЛАВА XVII.
Замѣчательныя формы алгебраическихъ выраженій.
0 т т сс О
Формы: —> —> —»
1 т 0 со т О
—, со — (X?.— Раскрытіе неопредѣленностей.
234. Въ силу общности алгебраическихъ формулъ онѣ могутъ представлять замѣчательныя формы при частныхъ предположеніяхъ относительно количествъ, входящихъ въ составъ ихъ. Займемся изученіемъ этихъ особыхъ, замѣчательныхъ формъ.
т а 0
235. Численная величина алгебраическаго выраженія равна нулю, если оно является въ видѣ частнаго отъ раздѣленія нуля на конечное количество отличное отъ нуля. Такимъ образомъ, если т есть конечное количество, отличное отъ нуля, то
°=0 т
Въ самомъ дѣлѣ, по опредѣленію частнаго, оно есть такое количество, которое, по умноженіи на дѣлителя, даетъ дѣлимое; но только нуль, умноженный на количество отличное отъ нуля, можетъ дать въ произведеніи нуль.
Примѣръ. — Дробь
.г* + —10
х* -|- 5
при х = 2 обращается въ нуль; въ самомъ дѣлѣ, подставляя вмѣсто х число о 0 А
2. находимъ у» т.-е. 0.
П. Форма:
236. Численная величина алгебраическаго выраженія равна безконечности, если оно является подъ видомъ частнаго отъ раздѣленія числа отличнаго отъ нуля на нуль.
Въ самомъ дѣлѣ, взявъ дробь которой числитель т есть нѣкоторое ко
нечное число отличное отъ нуля, станемъ уменьшать ея знаменателя, неограниченно приближая его къ нулю: дробь будетъ безпредѣльно возрастать.
— = 1 Такъ, дѣля 1 послѣдовательно на 1, на • • •
= 10 будемъ въ частномъ получать: 1, 10, 100, 1000,..., т.-е. числа
1 4100
= 100
возрастающія, такъ что когда численная величина знаменателя
—-1 000 1/іооо
и т. д.
велика.
будетъ менѣе всякой величины, т.-е. О, то численная величина дроби будетъ больше всякой величины, т.-е. будетъ безконечно-
Такъ какъ безконечность не можетъ быть выражена никакимъ числомъ, то для письменнаго изображенія ея необходимъ особый знакъ; такимъ знакомъ служитъ сс. Итакъ
т___
СГ
если т отлично отъ нуля.
Знакъ сс предложенъ Валлисомъ въ XVII столѣтіи.
Примѣчаніе. Иногда говорятъ, что есть символъ невозможности; это нужно понимать такъ, что невозможно найти никакого конечнаго числа^ которое, будучи помножено на нуль, давало бы т. И въ самомъ дѣдѣ, всякое конечное число, помноженное на 0, дастъ нуль.
Примѣръ. Дробь
а^Н-1
х* — За? — 4
обращается въ сѵ, если положить х — 4; въ самомъ дѣлѣ, тогда получимъ 17
-0 или сс.
Когда числитель и знаменатель дроби имѣютъ одинаковые знаки, то при постепенномъ уменьшеніи численной величины знаменателя до нуля дробь будетъ оставаться положительною, и потому она стремится къ положительной безконечности. Если же числитель и знаменатель имѣютъ разные знаки, то по мѣрѣ приближенія знаменателя къ нулю дробь стремится къ отрицательной безконечности. Положительная безконечность изображается знакомъ -р сс, _|_ 2
отрицательная—знакомъ — сс. Такъ, если въ дроби я, будучи больше 3, приближается къ 3, то х — 3 будетъ оставаться величиною положительною; а потому, когда я, въ концѣ своего измѣненія, обратится въ 3, дробь обратится въ -[-сс. Если же будучи меньше 3, приближается къ 3, то раз-
ность х— 3 все время будетъ оставаться отрицательною; а потому, когда & достигнетъ своего предѣла 3, дробь обратится въ —ес. Но дробь будетъ ли х приближаться къ 1 уменьшаясь, или увеличиваясь, въ обоихъ случаяхъ при х = 1 обращается въ -р ос, потому что и въ томъ и въ другомъ случаѣ ея числитель и знаменатель остаются положительными.
III. Формы: —
т
и
237. Частное отъ раздѣленія безконечности на конечное количе ство—есть безконечность; т.-е.
ОС т
если т конечно.
Въ самомъ дѣлѣ, но опредѣленію частнаго,— это послѣднее, будучи умножено на конечное количество яц должно дать безконечность; но никакое конечное .количество, умноженное на конечное т, не можетъ дать безконечности; поэтому частное—безконечно велико.
238. Частное отъ раздѣленія конечнаго количества на безконечно-большое равно нулю; т.-е.
если т конечно.
Въ самомъ дѣлѣ, если дѣлимое конечно, то при неограниченномъ возрастаніи дѣлителя частное неограниченно приближается къ нулю, сл. при безконечно-большомъ дѣлителѣ численная величина частнаго будетъ нуль.
239. Частное отъ раздѣленія нуля на безконечность есть ноль, а частное отъ раздѣленія безконечности на нуль есть безконечность; т.-е.
Въ самомъ дѣлѣ, — есть 0 по двоякой причинѣ: съ одной стороны по-тому, что числитель =0 (§ 235), съ другой потому, что знаменатель равенъ безконечности (§ 238). — Подобнымъ же образомъ убѣдимся и въ томъ, что оэ О —
240. Теорема. Численная величина цѣлаго по буквѣ х полинома съ конечными коэффиціентами, — конечна при х конечномъ, и безконечно-велика при х безконечномъ.
Пусть имѣемъ полипомъ
а#4 + Ья3 -р сх* -|- Лх о,
цѣлый относительно я, съ конечными коэффиціентами а, Ь, с, е, причемъ а отлично отъ нуля; понятно, что при всякомъ конечномъ значеніи х каждый членъ полинома конеченъ, а алгебраическая сумма конечнаго числа конечныхъ слагаемыхъ конечна.
Пусть теперь х будетъ безконечно-велико; вынеся л4 за скобки, дадимъ полиному видъ
Ч* х = каждый изъ членовъ въ скобкахъ, содержащій х въ знаменателѣ, обратится въ 0 (§ 238), такъ что въ скобкахъ останется а; поэтому произведете т.-е. данный полиномъ, обращается въ т.-е. представляетъ про-
изведете конечнаго числа а, отличнаго отъ нуля, на безконечность; а такое провзведеніе, очевидно, есть безконечность. Очевидно, знакъ этой безконечности будетъ такой, какой имѣетъ членъ ах* — высшій членъ полинома.
іѵ А 0 П . Форма: -д*
241. Выраженіе разсматриваемое сахо-по-себѣ, означаетъ какое угодно число. Въ самомъ дѣлѣ, раздѣлить 0 па 0 значитъ найти такое число, которое, будучи умножено на О, давало бы 0; но всякое конечное число имѣетъ это свойство (такъ: 5X0 = 0, —2X0 = 0 и т. д.), слѣд. означаетъ не
л іт О
одно какое-либо число въ частности, но какія угодно числа. Поэтому -д называютъ символомъ неопредѣленности.
Изъ этого слѣдуетъ, что если два количества А и В равны третьему С, то нельзя еще заключить, что А = В, не увѣрившись предварительно, что С не О есть д-*
242. Теорема, Когда алгебраическая дробь, которой числитель и знаменатель суть цѣлые раціональные относительно х полиномы, принимаетъ при нѣкоторомъ частномъ значеніи х неопредѣленную форму
—эта неопредѣленность—только кажущаяся, на самомъ же дѣлѣ дробь имѣетъ совершенно опредѣленную величину.
Въ самомъ дѣлѣ, пусть будетъ дробь которой числитель и знаменатель обращаются въ ноль при х — а; это доказываетъ, что н А и В дѣлятся на х — а (§ 60). Пусть частное отъ раздѣленія А на х — а будетъ А'; въ такомъ случаѣ
А = (х — а)А';
цѣлый относительно х полиномъ А' можетъ также обращаться въ нуль при х — а; тогда онъ будетъ имѣть видъ
А' = (я— а)А", а слѣд.
А = (я — а)эА".
А”, въ свою очередь, также можетъ обратиться въ нуль при х = а и т. д. Такимъ образомъ можно написать:
А = (я—а)т.Р,
гдѣ Р есть цѣлый относительно ' х полиномъ, не обращающійся въ нуль при х = а; онъ можетъ быть и нулевой степени, т.-е. вовсе не содержать буквы х. Такимъ же образомъ можемъ написать:
В = (я— а)р . Ч,
гдѣ У — цѣлый относительно х полиномъ, который можетъ быть и нулевой степени, не обращающійся въ ноль при х = а. Данная дробь имѣетъ, такимъ образомъ, видъ:
(я —
Изслѣдуемъ всевозможные случаи, полагая послѣдовательно:
т <^р.
Первый случай. т>р. Положимъ х = а, найдемъ, что дробь обращается въ ’д” Но сокративъ ее на (я — а)р, дадимъ ей видъ
* (я—а)1"—*’.?
гдѣ т—р — положительно; положивъ я = а, найдемъ, что (я — а)т-г = 0. а Р и Ч — отличны отъ нуля; поэтому, истинная величина дроби при я=а есть ноль.
Примѣръ. Дробь
(*-- 3)4*+ 1)
(* + 2)
при х=3 принимаетъ видъ но, сокративъ ее на (* — З)3, найдемъ
(*-3)^+1)
(* + 2) ’
и, положивъ ж = 3, найдемъ
0X4 п
—^— или 0.
Второй случай. т=р. Положивъ х = а, найдемъ, что дробь обращается въ — * а сокративъ ее иа (# — а)щ = (* — а)\ получимъ
А Р
В —
а гакъ Р в Ч не обращаются при х — а въ ноль, то представляетъ нѣ-которое овредѣіеиЕ^ чмо«.
Прімірк Дробь
іг— -н 3)
ця х= 1 ібрщіетті въ но, по сокращеніи на (х— 1)3Т она обращается
2
#+ 3 з
Положивъ въ этой дроби я — 1, найдемъ вполнѣ опредѣленное число Третій случай, т <,р. Положивъ я = а, найдемъ но если предварительно сократимъ дробь на (а? — а)т, то найдемъ
' А = __2^_;
В (ж —
такъ какъ р — ш — положительно, то при х = а знаменатель обратится въ воль; а какъ числитель отличенъ отъ нуля, то дробь обратится въ ео.
Примѣръ. Дробь
(яН-1)«(я — 2)
(я-Н)*бг —3)
при х = — 1 обращается въ но, по сокращеніи на (я-|-1)3, принимаетъ видъ
х__2
_з
Доживъ я = —1, найдемъ Такимъ образомъ, истинное зиа-
«пе дроби при х = — 1 есть безконечность
243. Первый способъ опредѣленія истиннаго значенія неопредѣленности О
вида уу.
Изъ предыдущаго § слѣдуетъ, что для опредѣленія истиннаго значенія неопредѣленности, или, какъ говорятъ, для раскрытія неопредѣленности, надо въ числителѣ и знаменателѣ дроби выдѣлить общаго множителя, обращающагося при сдѣланномъ частномъ предположеніи въ ноль, сократить дробь па этого множителя и потомъ ввести сказанное предположеніе.
Примѣръ I. Найти истинное значеніе дроби
' а2-За 4-2
а2—а—6 при а — 2.
Замѣняя а числомъ 2, получаемъ т.-е. неопредѣленность; тѣмъ не менѣе, мы утверждаемъ, что при а = 2 данная дробь имѣетъ совершенно опредѣленную величину. Въ самомъ дѣлѣ, мы знаемъ уже, что если числитель и знаменатель обращаются при а = 2 въ пуль, то они дѣлятся на а — 2, откуда находимъ, что дробь можно представить въ видѣ
(а— 2)<а—1).
(а - 2)(«+3)*
сокративъ па а — 2, находимъ
а — 1
положивъ здѣсь а = 2, найдемъ, что истинная величина дроби равна
2-1 1
2 4-3 или 5*
Примѣчаніе. 0 данномъ предметѣ нельзя составить себѣ вполнѣ яснаго представленія, не обращаясь къ теоремамъ о предѣлахъ. Здѣсь мы имѣемъ двѣ перемѣнныя величины:
а2—За 4- 2 а—1 а — 2 «2 + а—6 11 «4-3 ' а —2*
которыя, если а приближать къ 2, будутъ при всякомъ значеніи а оставаться равными. Но мы знаемъ, что въ такомъ случаѣ, въ силу теоремы III, § 184, и предѣлы этихъ перемѣнныхъ, при а = 2, будутъ равны? такъ что
Ііш
/а2 —Зя + 2\____р /а — 1 х а — 2\
Пт\л+"3Ха — 2)
при а = 2.,.(І).
Но, но теоремѣ XI, § 190,
Ііш
(а— —2\ ѵ Іа—1\ М—2\
|,ГрзХ^—2,1- 1,гаІ5=з) • іт\а^2/і при а =2.
Но Ііш (д-ц-'з)» >ФИ «— 2, равенъ Что касается Ііш то, по теор. XI, § 192. этотъ предѣлъ =1. Подставляя въ (1), имѣемъ
— 215 —
Ііш(^»--у) =Ь<| = А.
\ Я2-{-<7 — 6 /а=2 5 5
1
при а = 2, есть *
т.-е. что истинное значеніе данной дроби,
Примѣръ II. Найти истинное значеніе дроби
я* — 4зг — 4^2 + 24а; — 9 я! — а?2 — 21я + 45
при х~ 3.
Подставляя 3 вмѣсто х, замѣчаемъ, что оба члена нуль; слѣд, они дѣлятся на х— 3. Совершивъ дѣленія, х* — я* — 7х “|- 3 и — 15, такъ что дробь
видѣ
(дт — 3)(л^ — х^ — 4- 3)
(х —3)(^4-2х —15) 1
дроби обращаются въ найдемъ въ частныхъ: можно представить въ
или. по сокращеніи на х— 3:
яг» — х2 — ~х + 3
• + 2х —15
Для нахожденія истиннаго значенія нужно теперь положить х ~ 3» Сдѣ-лавъ это, находить, что новая дробь также обращается въ это значитъ, что оба чма ея дѣлятся снова на х — 3, такъ что дробь можно представить въ
(х —ЗХя*Ч-2г —1) . я«+2т~1
^-ЗХг + 5)-» ™ сокращеніи, -^5—
п О 14
Положивъ х = 3, находимъ ложенной дроби при х=3.
і
или -ц-’ это и ость истинное значеніе пред-
а
__ьт
Примѣръ III, Найти величину дроби ~р~"р ПРИ а — &•
При а = Ь оба члена дроби дѣлаются нулями; слѣд. они дѣлятся на а—6; по сокращеніи на а — дробь принимаетъ видъ
ат—і -|- 4" а1"-*^2 -Н.. 4* аЬ”»—- 4"
а₽—14- 4- ор-3&2 4-... 4“
положивъ а = Ъі находимъ или “ ’а р: это и есть истинное зна-
ченіе данной дроби при а = 6.
О
244. Второй способъ нахожденія истиннаго значенія неопредѣленности д*
Пусть дробь принимаетъ неопредѣленный видъ д при я? = а. Положивъ х = а + А, подставимъ въ данную дробь вмѣсто х> получимъ дробь Ірі сдѣлавъ въ ней приведеніе, найдемъ, что числитель и знаменатель ея бу* дутъ содержать общимъ множителемъ Л. Въ самомъ дѣлѣ, данная дробь при-шімаетъ видъ при х = а, сл. оба члена ея содерасатъ общій множитель х — а, т.-е. Л (ибо изъ равенства я=а-}-к9 слѣдуетъ х — а = к). Сокра-
щаемъ дробь на А, и если по сокращеніи количество Ь еще будетъ находиться въ дроби, нужно положить А=О: полученный результатъ и будетъ представлять истинную величину данной дроби при я = а, ибо изъ равенства я = а + Л слѣдуетъ, что положить Л = О — то же самое, что въ данной дроби положить х = а.
Способъ этотъ принадлежитъ Рушё (КопсЬё).
Примѣръ. Найти истинную величину дроби
іг3 — х2 — х 4-1 — я? — 3^- — 2
при х= 1. . О „
Положивъ х=1, найдемъ, что дробь принимаетъ видъ Подставляемъ въ нее вмѣсто х биномъ 1 + Л; находимъ
(1 ЛЛ)»-(1-НМ* — (1 + Л) + 1 _ 2Л*Ч- Л®
(1 + Л)4^(і ц_ ;оз_з(і + Л)2 _|_ 5(і +*) —2 ЗА®+ Л*‘
Сокративъ на А2, получимъ а положивъ здѣсь Л = О, найдемъ
0 или <х>. Итакъ, истинное значеніе данной дроби при х = 1 есть ес.
V. Форма: 0Х<х.
245. Если въ равенствѣ АХ^ = -^ положить: А=О и В = О, то получится ОХд = д» или 0Хс^=д- Итакъ, символъ ОХ<х, разматриваемый самъ по себѣ, означаетъ неопредѣленность.
Эта неопредѣленность можетъ быть только кажущеюся: ею можетъ маскироваться совершенно опредѣленная величина. Напримѣръ:
хл X = Зя; при х = О получаемъ: 0X^ = 0.
4
з
я* X = 3: при х = 0 получаемъ: О X = 3.
при ж = 0 получаемъ: 0Хс^ = сс.
• Итакъ, подъ видомъ неопредѣленности О х сс можетъ являться и 0, и конечное число, и безконечность.
246. Изъ сказаннаго вытекаетъ, что если одинъ изъ сомножителей произведенія равенъ нулю* то мы не вправѣ утверждать, что и произведеніе равно нулю, не убѣдившись предварительно, что ни одинъ изъ остальныхъ сомножителей не есть безконечность.
247. Такимъ образомъ, когда алгебраическое выраженіе принимаетъ видъ ОХ^Ѵ при частномъ значеніи какой-либо буквы, то является вопросъ объ опредѣленіи истинной величины этого выраженія.
Примѣръ. Найти истинную величину выраженія
(ж»4-5® + 6) X ів+^2 при х = — 2.
Подставивъ (— 2) вмѣсто а?, находимъ: О х Представивъ данное выраженіе въ видѣ * •
3(^+5а?Ч-6) ^4-3^4:2 ’
О о
приводимъ вопросъ къ раскрытію неопредѣленности при # — — 2.
Примѣняя пріемъ § 243, находимъ:
3(я + 2)(я + 3) _ 3(^ + 3) (г + 2)(я"+1) #+1
Истинное значеніе будетъ: 3( —2 + 3) 3 „
-ТТ2--+1- или
VI. Форма:
1
__ »
А. в
248. Если въ равенствѣ положить А = О и в —О, то полу-
В 1
О О сс О л . со
чимъ: —р- — -0- влп — = -ф~* Слѣдовательно, символъ —, разсматрнвае-
“0
мый самъ по себѣ, означаетъ неопредѣленность.
Неопредѣленность эта можетъ быть только кажущеюся. Такъ:
1 \ о Л со
1) --г- = 2ж; положивъ я ~ со, найдемъ: = оэ.
2) —^-=‘2; положивъ 'л; = ос, найдемъ въ этомъ случаѣ, что
2я: 2 X Л А
3) — = —; положивъ я = ес, въ этомъ случаѣ найдемъ: — =0.
Итакъ, подъ видомъ неопредѣленности можетъ скрываться пли <х, или конечное количество, или нуль. Отсюда задача о раскрытіи неопредѣленности разсматриваемаго вида.
249. Въ § 240 мы видѣли, что величина цѣлаго раціональнаго по буквѣ х полинома равна безконечности при х = сс, если коэффиціенты его конечны. Отсюда слѣдуетъ, что алгебраическая дробь, числитель и знаменатель которой суть цѣлые относительно х полиномы, обращается въ — при х — со. Докажемъ. что истинная величина такой дроби при х безконечномъ равна: яіулю.
если степень знаменателя выше степени числителя; безконечности — если, наоборотъ, степень знаменателя ниже степени числителя; и частному отъ раздѣленія коэффиціентовъ при высшихъ степеняхъ буквы х, если степень знаменателя равна степени чгіслителя.
Первый случай. Найти истинную величину дроби
при я = сс.
Дробь принимаетъ видъ ность, раздѣлимъ числ. и знам.
чтобы раскрыть эту кажущуюся неопредѣлеп-• 4
на высшую степень х, въ данномъ случаѣ на х3. Найдемъ
Если положить х = (Хі, каждый членъ, содержащій х въ знаменателѣ, обра-тится въ нуль, а дробь въ 2 или въ О.
Второй случай. Найти истинное значеніе дроби г
За?+2х — 1 - ,
5жЗ —2х»+3 при х = <х. ,
Дробь принимаетъ видъ Раздѣливъ оба члена ея на высшую степень х, въ данномъ случаѣ на х\ найдемъ:
2 12 3
При х = сѵ дроби: — и обращаются въ пуль, и данная дробь
3' равна у, т.-е. отношенію коэффиціентовъ при высшихъ степеняхъ х.
1'ретій случай. 'Найти истинное значеніе дроби
ж3—я-}-1 *
— 2^ + 6 ’ *
при х=<х>.
Раздѣливъ числителя и знаменателя на х\ получимъ:
При х = сіс числитель обращается въ 1, а знаменатель въ ОХ — 2 или въ—0, истинная величина дроби = —
VII. Форма: сс— со.
250. Сумма двухъ безконечностей одного знака, очевидно, равна безконечности съ тѣмъ же знакомъ; разность двухъ безконечностей съ противоположными знаками равна безконечности; но разность двухъ безконечностей одного знака и сумма двухъ безконечностей противоположнаго знака суть формы неопредѣленныя.
Въ самомъ дѣлѣ, если въ равенствѣ ~положимъ и
ИЛя110 1 0
В = 0, то найдемъ: п — 7т = тгі или сс — = — -
ѵ У М «О
Укажемъ, какъ раскрывать кажущуюся неопредѣленность этого вида.
П р и м ѣ*р ъ I. Найти истинное значеніе выраженія
При # = -|-сс данная разность принимаетъ видъ сс— ос. Вынося я3 за скобки, мы дадимъ ей видъ: #3 (1 — —), что приа? = 4-^> обращается въ 4-сс, При х = — сс данное выраженіе = ~ ес — сю = — сю.
Примѣръ II. Найти истинное значеніе разности
(х 4- 1) — )/2ха — Зх-|- 1
при я = + сс+
При х = — ос данная разность обращается въ — ес — ес или въ —
При = равняется 4~^ равно какъ и 2х2 — Зх-|~Ъ сл.
мы получаемъ разность двухъ положительныхъ безконечностей — выраженіе не опредѣленное. Чтобы раскрыть эту кажущуюся неопредѣленность, множимъ и дѣлимъ данное выраженіе па сумму’ х 4* 1 -{-(/Яя:3 — За? -(- 1, и получаемъ
(.т + 1——Зж+1)(а?4-1 + —Здг + 1)
х +1 +
или
(х -Н)3—(2^ — 4-1) х +1 +V2й^ —Зх + 1
или
л® 5а:
х +1 — Зя + 1
Раздѣливъ числ. и знам. на я;2, находимъ
или
Положивъ здѣсь # = наюдимъ
Примѣръ III. Найти истинное значеніе разности
х 2 — рЛг2 — 5х + 1 при = > *
При я — — находимъ — При разность принимаетъ неопредѣленный видъ —
Чтобы раскрыть неопредѣленность, множимъ и дѣлимъ данное выраженіе на х 4~ 2 4- }/#3 — 5^4^ 1; находимъ:
_______9* + 3
х 4- 2 + — 5 я +1
или
Раздѣливъ числителя и знаменателя на я, получаемъ
п _г 9
Положивъ + со, находимъ -—
I “Ь г 1
. 9
даннаго выраженія, ври я~ 4^°°» равна
или
* Итакъ, истинная величина
ОТДЪЛЪ ВТОРОЙ.
УРАВНЕНІЯ и НЕРАВЕНСТВА ПЕРВОЙ СТЕПЕНИ.
ГЛАВА ХѴШ.
Уравненія первой степени съ однимъ неизвѣстнымъ.
Опредѣленія: равенство, тождество, уравненіе.—Уравненія эквивалентныя.—Преобразованія уравненія'въ другое ему эквивалентное. —Рѣшеніе уравненія первой степени съ однимъ неизвѣстнымъ.—Примѣры. „
Опредѣленія.
251. Соединеніе двухъ равныхъ количествъ знакомъ = (знакъ равенства) называется равенствомъ. Такъ 7 = 5-|-2 есть равенство; общій видъ равенства есть ♦
А = В.
Количество А, находящееся влѣво отъ знака равенства, наз. первою частью, количество же В, стоящее вправо отъ этого знака, второю частью равенства. Равенства бываютъ двоякаго рода: тождества и уравненія.
Всякое очевидное равенство называютъ тождествомъ.
Такъ, равенства
5 = 5; 10 = 7 + 2 + 1; (а + й)а = (<* +
суть тождества.
Тождествомъ называютъ также всякое равенство двухъ буквенныхъ выраженій.* вѣрное при всѣхъ, какихъ угодно, значеніяхъ входящихъ въ нею буквъ. Такимъ образомъ, равенства
(а + к)2 = а2 -|- 2ай -|- 62, а2 — 62 = (а -|- 6) (а — 5), ат X ап — ат+*
суть тождества.
Но есл возьмемъ равенство 2 г—10 = 0, то легко убѣдимся, что оно будетъ вѣрю не при всякихъ частныхъ значеніяхъ буквы х; въ самомъ дѣлѣ, чтобы первая часть была нулемъ, нужно чтобы 2х равнялось 10, а это воз-
можно только при х равномъ 5, н ни при какомъ другомъ значеніи буквы х. Точно такъ же равенство #* = 16 возможно не нри всякомъ значеніи буквы х, а лишь при двухъ частныхъ значеніяхъ этой буквы, именно: при ж = и
при х = — 4; въ самомъ дѣлѣ, какъ (4~4)2=16, такъ и (—4)а = 16.
Такія равенства у которыя вѣрны не при всѣхъ, а лишь при нѣкоторыхъ частныхъ значеніяхъ входящихъ въ нихъ буквъ, называются уравненіями.
Тѣ буквы, которымъ нужно дать особыя значенія для того, чтобы существовало равенство между обѣими частями ур—пія, иначе говоря, тѣ буквы, при частныхъ значеніяхъ которыхъ уравненіе въ самомъ дѣлѣ обращается въ тождество, называются неизвѣстными количествами уравненія, или просто неизвѣстными. Прочія же количества, входящія въ уравненія, паз.
Такъ, если мы ищемъ, при какомъ значеніи х равенство
а-\~Ь = 2х — с
будетъ справедливо, т.-е. обратится въ тождество, то # будетъ неылянісишыла этого уравненія. Легко видѣть, что ур. это обратится въ тождество, если л>су
' * а I/ “4“ С и ѵ
дать значеніе —Нр2—; въ самомъ дѣлѣ, вторая часть обращается при этомъ въ 2 X 2 — с ІІЛИ въ а 4“ & ~Ь с что равно а 6; ур—піе же
дѣйствительно дѣлается тождествомъ
л -’І— Ъ = а —Ъ.
Тѣ частныя - значенія неизвѣстныхъ, при которыхъ ур—ніе обращается въ тождество, называются рѣшеніями или корнями уравненія. Въ вышеприведенныхъ примѣрахъ:
ур—ніе 2д?— 10 = 0 имѣетъ одинъ корень' =5;
ур—піе я* =16 имѣетъ два корпя: -р4 и —4;
ур—піе и фо = — с имѣетъ одинъ корень: — 2 - *
Рѣшить уравненіе значитъ найти ого корни, т.-е. тѣ значенія для неизвѣстныхъ, которыя обращаютъ уравненіе въ тождество.
Принято говорить, что коренъ удовлетворяетъ уравненію; этимъ сокращенно выражаютъ, что уравненіе обращается въ тождество, если замѣнить въ немъ неизвѣстныя корнями.
Для отличія неизвѣстныхъ количествъ ур-пія отъ извѣстныхъ, принято неизвѣстныя обозначать послѣдними буквами азбуки: х, у, и, ѵ, . . , ; извѣстныя же первыми: а, Ь, с, т, п, . . .
Такъ, въ уравненіи а-\-Ъ = 2х — с неизвѣстное есть х, извѣстныя же: а, Ь и с.
252. Классификація уравненій-—Уравненіе наз. алгебраическимъ, если въ немъ надъ неизвѣстными -не совершается иныхъ дѣйствій кромѣ сложенія, вычитанія, умноженія, дѣленія, возвышенія въ степень и извлеченія корня.
Во всѣхъ другихъ случаяхъ ур. называется
Такъ уравненіе 10х = 8 есть трансцендентное; оно называется нымъ, ибо въ немъ неизвѣстное является показателемъ.
Всѣ алгебраическія уравненія раздѣляются на два класса: на раціональныя и ирраціональныя.
Алгебраическое ур. называется раціональнымъ, если въ немъ неизвѣстныя не входятъ подъ знакомъ корня; если же въ уравненіи неизвѣстныя встрѣчаются подъ знакомъ корня, то оно наз. ирраціональнымъ.
Такъ, уравненіе
есть раціональное, ибо въ немъ неизвѣстное не встрѣчается подъ знакомъ корня. Уравненіе же
}/ 5х — 1 = — 3
есть ирраціональное, ибо членъ |/ 5л;-^1 содержитъ неизвѣстное подъ знакомъ корня.
Раціональныя уравненія, въ свою очередь, раздѣляются на цѣлыя и дробныя.
Цѣлымъ паз. такое раціональное ур., которое не содержитъ неизвѣстное въ знаменателѣ; напр. уравненія
— 4 = 0, —10 = 5л;—1 и х — х 1/2 = 6
суть цѣлыя.
Если же уравненіе содержитъ неизвѣстныя въ знаменателѣ, то оно назыв. дробнымъ. Уравненіе
3 — 5<г
есть ур. дробное.
Такимъ образомъ обѣ части цѣлаго алгебраическаго уравненія суть полиномы цѣлые относительно неизвѣстнаго.
Степенью цѣлаго уравненія съ однимъ неизвѣстнымъ называется высшій показатель при неизвѣстномъ въ этомъ уравненіи. Такъ:
ур—ніе ~ 0 есть ур—ніе первой степени;
ур—ніе аяа4-^ + с —0—второй степени;
ур—ніе 4л;8 — 2ая2 -|- 5я — 1 ~ 0— третьей степени.
Если же цѣлое ур. содержитъ нѣсколько неизвѣстныхъ, то степенью его наз. наибольшая сумма показателей при неизвѣстныхъ въ одномъ и томъ же членѣ.
Такъ, ур—ніе
ах Ъу + ея = &
есть ур. первой степени съ тремя неизвѣстными (я, у и ^)*
4л; — эху — У = 4у — 11х
есть гтчргі степени съ двумя неизвѣстными, ибо наибольшая сумма пока-итежі ф «жвѣстныхъ равна 2 (въ членѣ — 5л$).
Ур.
х3у1 4* у4 4- -|~ ]/ с = 2
есть ур. седьмой степени, такъ какъ наибольшая сумма показателей при неизвѣстныхъ въ одномъ и томъ же членѣ равна 7 (въ первомъ членѣ).
Понятно, что нельзя говорить о степени ур^нія, если оно не есть раціональное цѣлое. Такъ мы не можемъ говорить о степени ур—пій
ибо они содержатъ члены пли дробные, идя ирраціональные относительно неизвѣстныхъ.
Уравненія раздѣляютъ еще на численныя и буквенныя; численнымъ ур—мъ называютъ такое, коэффиціенты котораго суть опредѣленныя числа, а буквеннымъ такое, коэффиціенты коего суть буквенныя выраженія. Такъ
ур—ніе — у2 -р 5 = О есть численное;
. а <Х ~Р б л л т
ур — ніе а2х---------х1 — 2 = а есть ур. буквенное.
Если два ур— нія имѣютъ одинаковые корни, то они наз. эквивалентными ур—ми. Итакъ, уравненія
А = В . . . (1) н А' = В' ... (2)
будутъ эквивалентны, если всякій корень ур—-нія (1) удовлетворяетъ (2), и обратно, каждый корень (2) удовлетворяетъ (1).
Такъ напр.. ур—нія
2^4-1 —7 ... (1) и 2^ + 4 = 10 ... (2)
эквивалентны, ибо какъ то, такъ и другое удовлетворяются однимъ и тѣмъ же корнемъ, равнымъ 3.
253. Процессъ рѣшенія ур—нія заключается въ томъ, что отъ даннаго уравненія, путемъ послѣдовательныхъ преобразованій, стараются придти къ та-* кому уравненію, первая часть котораго есть само неизвѣстное; понятно, что вторая часть такого ур—нія и будетъ искомымъ корнемъ, если послѣднее эквивалентно данному.
Сказанныя преобразованія основаны на слѣдующихъ началахъ.
254. Первое начало. — Придавая къ обѣимъ частямъ уравненія поровну ? или отнимая отъ обѣихъ частей равныя количества ? получимъ уравненіе эквивалентное данному.
Пусть данное уравненіе будетъ
А = В ... (I)
гдѣ А и В суть нѣкоторыя алгебраическія выраженія, содержащія одно или нѣсколько неизвѣстныхъ. Пусть будетъ, далѣе, М нѣкоторое произвольное ко-
лпчество, содержащее пли не содержащее неизвѣстныя. Требуется доказать, что уравненіе
А + М = В + М . . . (2)
эквивалентно данному. Это значитъ, нужно доказать, что всякій корень ур—нія (1) служитъ также корнемъ и для (2), и обратно—всякій корень ур—нія (2) удовлетворяетъ и ур—нію (1). Въ самомъ дѣлѣ:
1. Пусть х = 5 будетъ корнемъ ур—нія (1); это значитъ, что при подстановкѣ числа 5 вмѣсто а? въ уравненіе (1) количества А и В дѣлаются равными; но такъ какъ М всегда остается равнымъ самому себѣ, то очевидно, что при х = 5, и Л + М будетъ равно В-рМ, т.-е. подстановка 5 вмѣсто х въ уравненіе (2) обращаетъ его въ тождество, а это и значитъ, что 5 есть корень уравненія (2). Такимъ образомъ, мы доказали, что всякій корень уравненія (1) удовлетворяетъ необходимо и уравненію (2).
2. Наоборотъ: пусть х — а, будетъ корнемъ уравненія (2), т.-е. что при подстановкѣ количества а вмѣсто х въ уравненіе (2), А М дѣлается равнымъ В4-М; но какъ М всегда равно самому себѣ, то равенство суммъ А-рМ и В4~М требуетъ равенства выраженій А и В. Итакъ, при х~ъ имѣемъ А=В, т.-е. х = а. служитъ корнемъ ур—нія (1).
Итакъ, доказано, что уравненія (1) и (2) эквиваленты.
Если отъ обѣихъ частей ур—нія (1) отнять по М, то уравненіе Л—М=В—М также эквивалентно уравненію А = В. Въ самомъ дѣлѣ, отнять М все равно что придать (— М) къ обѣимъ частямъ даннаго ур—нія; но уже доказано, что приданіе равныхъ количествъ къ ^обѣимъ частямъ уравненія приводитъ къ уравненію, эквивалентному данному.
255. Слѣдствіе I.— Всякій членъ уравненія можно перенести изъ одной части уравненія въ другую, написавъ ею въ этой другой части съ обратнымъ знакомъ.
Въ самомъ дѣлѣ, пусть данное уравненіе будетъ
ах — Ь = (I . , . (1)
ідош гь обѣимъ частямъ по — сх, имѣемъ
ах — сх — Ь = сх — или ах — сх — Ь = -\-сІ . . . (2)
причемъ, на основаніи доказаннаго начала, ур. (2) эквивалентно (1)-му. Придавая, затѣмъ, къ,обѣимъ частямъ ур. (2) по + &, находимъ
ах — сх—= или ах — с$= Ь-\- А . . . (3),
причемъ это ур. эквивалентно (2)-му, а слѣд. и (1)-му.
Сравнивая ур. (3) съ (1), замѣчаемъ, что членъ сх перешелъ въ первую часть съ знакомъ —, между тѣмъ какъ во второй части ур. (1) этотъ членъ имѣлъ знакъ -|-, членъ Ъ перешелъ во вторую часть съ знакомъ между тѣмъ какъ въ первой части уравненія этому члену предшествовалъ знакъ —. Отсюда выводится заключеніе: перенося члены изъ одной части уравненія въ другую, слѣдуетъ у переносимыхъ членовъ мѣнять знаки на противоположные.
256. Слѣдствіе П, — Всякое уравненіе можно привести къ виду
Р = О.
Въ самомъ дѣлѣ, перенеся всѣ члены изъ второй части уравненія въ первую, очевидно, будемъ имѣть во второй части О.
Напримѣръ, уравненіе
' 4я2 — 7« + 2 = 3х — 6
эквивалентно уравненію
4^2 _ Юж + 8 О, ।
. Если имѣемъ уравненіе первой степени съ однимъ неизвѣстнымъ, 'то перенеся всѣ члены въ первую часть и сдѣлавъ приведеніе, дадимъ такому ур—нію видъ
= О,
гдѣ а и Ь суть выраженія, не содержащія Это и есть, слѣд,, самый общій видъ уравненія первой степени съ однимъ неизвѣстнымъ.
Точпо такъ же уравненіе ах* -(- с = О,
въ которомъ а, 6 и с не зависятъ отъ я, есть самый общій видъ ур—нія второй степени съ однимъ неизвѣстнымъ.
Уравненіе
-р -|- сл; -|- = О
представляетъ общій видъ ур^—нія третьей степени съ однимъ неизвѣстнымъ.
Наконецъ, уравненіе
Ктхт4- Ат-і X"-1 + А„_2 ж“~2 Н---------І-Л^’ + + Ао = О
есть общій видъ ур—нія ш-ой степени съ‘ 1 неизвѣстнымъ.
257. Слѣдствіе ПК — Можно перемѣнить знаки у всіьхъ членовъ уравненія на обратные.
Въ самомъ дѣлѣ, пусть дано уравненіе
19 — 7# = 5 — . (1)
Замѣтимъ прежде всего, что всегда можно переставить части уравненія, т.-е. написать вторую часть уравненія влѣво отъ знака равенства н наоборотъ; ибо очевидно, что ур—ніе Л] = №, эквивалентно ур—нію $ = М*). Сдѣлавъ это, найдемъ •
5 — 4л; = 19 —7 л;.
Затѣмъ перенесемъ члены второй части въ первую и наоборотъ; получимъ
‘ ‘ — 19 + 7л:= — 5-}-4я . , . (2).
• <
Сравнивая это ур. съ (1), замѣчаемъ, что оно отличается отъ (1) знаками при всѣхъ членахъ.
і) Дѣйствительно, всякое значеніе неизвѣстнаго, дѣлающее М равнымъ К, дѣлаетъ, наоборотъ, и Ы равнымъ М.
258. Второе начало. Помноживъ обѣ части уравненія на одно и то же количествоЛ полг/чижь уравненіе эквивалентное данному? если только взятый множитель не есть ни нуль? ни безконечность? и не содержитъ неизвѣстнаго.
Пусть дано уравненіе
А = В . . . (1),
М— количество, не равное ни 0, ни со и не «вращающееся ни въ 0, ни въ со. Требуется доказать, что при такомъ ограниченіи относительно М, уравненіе
АЛІ = В.М . . . (2)
эквивалентно уравненію А — В, т.-е. что всякій корень перваго удовлетворяетъ второму и наоборотъ.
Для удобства доказательства замѣнимъ уравненія (1) и (2) имъ эквивалентными
А —В = 0. . . (I) и (А —В).М = О. . * (II)
ур. (I) эквивалентно (1)-му и (II) (2)-му, ибо перенесеніе членовъ изъ одной части въ другую приводитъ всегда къ ур—мъ эквивалентнымъ даннымъ. * Итакъ, докажемъ, что (I) эквивалентно (П)-му.
1. Пусть я = а будетъ однимъ изъ корней уравненія (I); это значитъ, что при подстановкѣ а вмѣсто х въ ур. (I), это ур, обращается въ тождество, т.-е. А — В — въ нуль. Подставимъ теперь а вмѣсто х въ ур. (II); при этомъ А—В, какъ уже знаемъ, обратится въ 0; а произведеніе двухъ множителей: А —В и М, изъ коихъ одинъ равенъ нулю, само равняется 0, если только другой множитель не обращается въ оз; но, по условію, М не есть и не обращается въ со, сл. произведеніе (А — В) М, при ж = ат дѣйствительно обращается въ 0, а ур. (II) въ тождество 0=0, Значитъ х = а служитъ корнемъ ур—пія (И).
2. Пусть я = есть одинъ изъ корней ур—нія (И); это значитъ, что при подстановкѣ ? вмѣсто х въ ур-піе (II) произведеніе (А — В)М дѣлается нулемъ; но чтобы произведеніе двухъ множителей было =0, необходимо, чтобы одинъ изъ множителей равнялся 0, и какъ М, по условію, не есть 0, то А—В должно обращаться въ нуль. Итакъ, при подстановкѣ вмѣсто х. выраженіе А —В обращается въ 0, а сл. служитъ корнемъ и (1) уравненія.
Итакъ, мы доказали, что при сдѣланномъ ограниченіи относительно М, всякій корень 1-го уравненія служитъ корнемъ и втораго, и паоберотъ; а слѣд. ур^кія (I) и (II) эквивалентны, и одно изъ нихъ можетъ быть замѣнено дру-ліъ.
259. Можно раздѣлить обѣ части ур—нія на одно и то же количество М, ііжгь бы оно не было = ни нулю, ни безконечности; полученное ур* будетъ .гігЕалентно данному.. Въ самомъ дѣлѣ, раздѣлить на М — все равно что по-хжтъ ка но если М не есть 0 или со, то не есть ни со, ни 0; а гін і у?<жггель. по доказанному, приводитъ къ эквивалентному съ даннымъ * «
260. П р 11 о ж е а і е. На этомъ началѣ основано уничтоженіе дробей въ
уравненіи, когда знаменатели этихъ дробей не содержатъ неизвѣстныхъ. Пусть, напр,, требуется освободить отъ дробей уравненіе
I? _ ?____1 ] | X
8 4 — 6 і 12 * "
Для этого нужно помножить обѣ части ур—нія, или, что то же, всѣ члены ур—нія на наименьшее кратное знаменателей, м затѣмъ въ каждомъ членѣ сократить общихъ множителей числителя и знаменателя; такъ какъ каждый знаменатель входитъ множителемъ въ составъ наименьшаго кратнаго, то очевидно, что указаннымъ сокращеніемъ всѣ дробные члены будутъ приведены къ цѣлому виду.
Наименьшее кратное знаменателей ур—нія (1) есть 23ХЗ = 24; умножаемъ всѣ члены на 24; имѣемъ
7л? X 24 _ З Х 24 _ 24 । 5* X 24
8 4 " 6 ‘ 12
или. сокращая первую дробь на 8, вторую на 4, третью па б и четвертую на 12. находимъ
7.г X 3 — 3 X б = 4 X 2, или, наконецъ
21я— 18 = 44-1^ . . . (2).
Это ур. (2), но доказанному, эквивалентно (1)-му, ибо множитель въ данномъ случаѣ не содержалъ неизвѣстнаго, поэтому онъ не могъ измѣнять своей величины, а слѣдовательно и не могъ обратиться ни въ 0, ни въ сѵ: это была конечная величина 24.
Возьмемъ еще примѣръ: освободить отъ дробей уравненіе
х +« . х — Ь___ х х
Ъ ' а ~ а —Ъ
Наименьшее кратное знаменателей = (а — Ъ) (а 4 6); умноживъ на него всѣ члены уравненія, получимъ:
(а; 4 а)ав(а — 6) (п + 6) < {х— Ъ)аЬ(а — б) (а + 5)_(а — Ь) (а 4- 6)
‘Ь ' а ~ а — Ъ
хаЬ(а — 6) (а + &) а + Ь
Сокративъ дроби, по порядку, на Ь. а, а — Ь и &4^ получимъ:
(#4а)а (а* — &2)-\-(х — Ь)Ь(а2 — Ьа) = х.аЪ(а4~&) — ха^ (а — ^).
Такъ какъ множитель въ данномъ случаѣ = аЬ(а“— Ь2)^ т-е. количеству, не зависящему отъ неизвѣстнаго, то послѣднее ур. эквивалентно данному.
261. Случаи, когда множитель равенъ, безконечности, нулю или же содержитъ неизвѣстное.
При доказательствѣ предыдущей теоремы мы сдѣлали ограниченіе относительно величины множителя М, разумѣя подъ М количество опредѣленное, не равное ни 0, ни сс, и не зависящее отъ неизвѣстнаго. При такомъ ограниченіи
уравненіе, полученное по умноженіи на М, всегда эквивалентно данному. Разсмотримъ теперь случаи: М = со, М = О, М содержитъ неизвѣстное.
Случай: М = со. — Въ этомъ случаѣ уже нельзя утверждать, что всякій корень ур—нія (!) удовлетворяетъ и 11-му, потому что, ютя іѴ—В и равно О, но (А — В) . М, принимая теперь видъ О X не необходимо равно нулю. Но всякое рѣшеніе ур—нія (II) необходимо будетъ удовлетворять и І-му; въ самомъ дѣлѣ, (А — В) . М должно быть нулемъ, но какъ М = со, то необходимо, чтобы было А —В = О.
Случай: М = О. — Въ этомъ случаѣ всякій корень ур — нія (I) необходимо удовлетворяетъ ІІ-му, такъ какъ при А — В = О, первая часть ур—нія (И) обращается въ О X 0. Но не всякій корень ІІ-го ур. будетъ необходимо удовлетворять и І-му, потому что (А — В) . О равно О, хотя бы А — В и не было нулемъ.
Случаи, когда М зависитъ отъ неизвѣстнаго. — Если множитель М есть выраженіе, содержащее неизвѣстное, то при нѣкоторыхъ частныхъ значеніяхъ послѣдняго оно можетъ обращаться или въ О, или въ напримѣръ, если М |- 2, то при я = — 2, М дѣлается нулемъ; если М = ^—р то при х — 1, М обращается въ со. Разсужденія, служившія намъ при доказательствѣ теоремы, опять становятся неприложимыми, и мы не въ правѣ утверждать, что по умноженіи будемъ имѣть уравненіе эквивалентное данному. Вопросъ этотъ требуетъ, поэтому, особаго изслѣдованія, которое, въ видахъ ясности, подраздѣляемъ та трі случая.
I. Выраженія А —В и М —цѣлыя относительно неизвѣстнаго.— Кромѣ тлпх значенія х. обращающія М въ нуль, пусть не обращаютъ въ нуль А — В.
Доказать, что ур—нія
А — В = О ... (1) и М(А —В) = О ... (2)
не эквивалентны одно другому.
Здѣсь прежде всего необходимо замѣтить, что ур. Р = О, гдѣ Р — цѣлый относительно а? многочленъ съ конечными коэффиціентами, не можетъ имѣть безконечнаго корня, ибо цѣлый отн. я многочленъ съ конечными коэффиціентами обращается при # = оо въ оо, а не въ нуль, какъ требуетъ ур. Р = О. Слѣдоват., уравненіе (1) имѣетъ конечные корни; въ частности, нѣкоторые изъ нихъ могутъ быть нулями. Переходимъ къ доказательству теоремы.
Всякій корень ур—нія (1). обращая А — В въ нуль, дѣлаетъ нулемъ множителя А—В въ ур—ніи (2); выраженіе же М, какъ цѣлое относительно х, при корняхъ ур—нія (1), какъ конечныхъ количествахъ, не можетъ обратиться въ а будетъ конечнымъ количествомъ. Поэтому, произведеніе М (А — В) обратится въ нуль, а ур. (2) въ тождество 0 = 0.
Итакъ, всякій корень ур—нія (1) удовлетворяетъ и ур—нію (2).
Но корни ур—нія (2) не необходимо удовлетворяютъ и ур—нію (1). Въ самомъ дѣлѣ, кромѣ значеній я, обращающихъ А — В въ нуль, ур — ніе (2) удовлетворяется еще такими значеніями А при которыхъ М обращается въ пуль, ібо эти значенія, какъ неравныя не могутъ обратить А — В въ сс, Н, значенія х, обращающія въ нуль выраженіе М, по условію, не обращаютъ въ нуль количество А — В. Значитъ, этотъ второй родъ корней ур—нія (2) не удовлетворяетъ первому уравненію^ такъ что ур—ніе (2) имѣетъ большее чнгло корней нежели (1), и слѣдовательно, ему пе эквивалентно.
Заключаемъ, что въ разсматриваемомъ случаѣ умноженіе ур—пія на множитель, зависящій отъ неизвѣстнаго, приводитъ къ уравненію, имѣющему лишніе корни сравнительно съ даннымъ, при чемъ эти лишніе корни суть тѣ значенія неизвѣстнаго^ при которыхъ множитель М обращается въ нуль.
Примѣръ, — Пусть дано ур—ніе
2х — 4 = 3& — 6
корень котораго есть х = 2. Умноживъ обѣ части на х—1, найдемъ новое уравненіе
(2я - 4) (х — 1) = (За? - 6) (х - 1).
Значеніе х = 2, удовлетворяющее первому, удовлетворяетъ п второму ур—'Нію/ ибо обращаетъ обѣ его части въ 0. Но легко видѣть, что второе ур—ніе обращается въ тождество н при #=1, слѣд., имѣетъ еще корень =1, не удовлетворяющій первому. Заключаемъ, что второе ур-—ніе не эквивалентно первому.
11. А — В — выраженіе цѣлое относительно неизвѣстнаго, М — дробное.— Въ этомъ случаѣ уравненія
д-В = 0...(1) и М(А-В) = О . . . (2)
не необходимо эквивалентны: ур—ніе (2) лсожета яв удовлетворя/яься нѣкоторыми корнями ур—нія (1).
Въ самомъ дѣлѣ, пусть х = а будетъ одипъ изъ корней ур—пія (1). Обращая, при подстановкѣ во (2), множителя А — В въ пуль, корень этотъ можетъ обратить М въ со; тогда первая часть ур—нія (2) приметъ видъ с^ХО, по это выраженіе можетъ и пе быть пуломъ. Такимъ образомъ, умноженіе ур—пія можетъ въ разсматриваемомъ случаѣ повести къ потерѣ нѣкоторыхъ корней; эяш теряемые корни суть тѣ значенія неизвѣстнаго, которыя обращаютъ множителя въ безконечность.
Примѣръ I. — Пусть данное ур. будетъ
(х-1)(Ж+2) = 0.. .(1).
Корни его, какъ легко видѣть, суть: ж'=1 и х” = —2. Помноживъ 1 ур—ше па ——г, получимъ «V 1
Ь-1-(.г-1)(Ж4-2) = 0...(2).
Подставивъ въ это ур—ніе 1 вмѣсто замѣчаемъ, что оно принимаетъ видъ
оо X 0 = 0.
Если теперь истинное значеніе неопредѣленности ооХО, при я=1, будетъ О, то я=1 будетъ служить корнемъ ур—нія (2); въ противномъ случаѣ, ур. (2) не имѣетъ корня равнаго 1.
й /дн.— 1 /ф г
Для раскрытія неопредѣленности ~:. сокращаемъ дробь на х—1
я затѣмъ въ полученномъ выраженіи я-|-2 полагаемъ #=1: въ результатѣ находимъ 3. Значитъ ур. (2), при я=1, боретъ видъ
3 = 0,
и потому я = 1 не есть его корень.
Но х =—2 служитъ корнемъ и ур—нія (2). Итакъ, вслѣдствіе умноженія на М дробное, ур—ніе потеряло одинъ изъ корней, равный тому значенію неизвѣстнаго, при которомъ множитель обращается въ
Примѣръ II.— Пусть данное ур—ніе будетъ
я2 12 = 7#,
имѣющее корни х =3 и а/ =4. I
Умноживъ обѣ части на 5,
находимъ
х2 + 12_ 7®
’ г-:Г’г —3’
или & = °’ или х Ц X (* — 3) (® — 4) = 0.
Это ур—ніе удовлетворяется значеніемъ #=4. Но подставивъ х = 3, находимъ сс X 0 = 0; и какъ истинное значеніе неопредѣленности ес X О, при х=3, есть —1, то второе ур. не имѣетъ корня =3. Здѣсь опять отъ умноженія на ^73 ур—піе потеряло коренъ 3, т.-е. равный тому значенію неизвѣстнаго, которое обращаетъ множителя въ оі.
Ш, А — В —выраженіе дробное относительно неизвѣстнаго, М — цѣлое.
Мы видѣли, что когда въ случаѣ М цѣлаго было и А — В — цѣлое относительно х, то ур—ніе М(А— В) = 0 имѣло больше корней чѣмъ ур—піе А — В = 0, и этими лишними корнями были тѣ значенія неизвѣстнаго, при которыхъ М обращалось въ нуль. По если, при цѣломъ М, А — В будетъ дробное, то уже нельзя утверждать, чтобы ур—піе М(А — В) = 0 удовлетворялось и всѣми корнями ур—нія М = 0; ибо можетъ случиться, что нѣкоторые изъ корней ур—нія М = 0 обратятъ А — В въ ес, и тогда произведеніе М(А — В) не необходимо будетъ нулемъ, по можетъ быть и отличнымъ отъ нуля. Это значитъ, что умноженіе на М, въ данномъ случаѣ, можетъ и не ввести постороннихъ рѣшеній; иначе говоря, можетъ получиться ур. эквивалентное данному.
262. Случай дробнаго ур—нія и цѣлаго множителя особенно важенъ, ибо онъ встрѣчается при освобожденіи ур—нія отъ дробей; поэтому мы должны разсмотрѣть съ особеннымъ вниманіемъ всѣ представляемыя имъ обстоятельства.
Приэтомъ, для большаго удобства, предположимъ, что всѣ члены перенесены въ первую часть, приведены къ общему знаменателю и соединены въ одпу Р
дробь ту гдѣ Р я — цѣлые относительно х полиномы. Ур. приметъ видъ
ояо всегда м. б. приведено къ этому виду.
Рѣшить это уравненіе — значитъ найти для неизвѣстнаго такія значенія, р
при которыхъ дробь обратилась бы въ нуль; но дробь можетъ обратиться въ нуль только при слѣдующихъ обстоятельствахъ:
1. Если числитель обращается въ нуль, а знаменатель при этомъ остается отличнымъ отъ нуля.
2. Если знаменатель обращается въ безконечность, а числитель не дѣлается безконечностью.
3. Если числитель и знаменатель обращаются: оба въ нуль, или же оба въ СО, но истинная величина полученныхъ неопредѣленныхъ формъ равна О.
Разберемъ эти обстоятельства.
1. Во-первыхъ, числитель обращается въ нуль при значеніяхъ равныхъ корнямъ ур—нія Р = 0. Поэтому, приравнявъ числителя нулю, опредѣляемъ всѣ корни уравненія Р = О. Затѣмъ, каждый изъ найденныхъ корней подставляемъ въ знаменателя Ч: всѣ корни ур—нія Р = О, не обращающіе знаменателя Ч въ нуль, обращаютъ въ нуль дробь поэтому удовлетворяютъ данному урав-
ненію 0 ~ 0; если же при какомъ-либо корнѣ я* = і ур—нія Р = О и знаме-натель 9 обратится въ О, такъ что дробь приметъ неопредѣленный видъ нужно будетъ найти истинное значеніе этой неопредѣленности; если это истинное значеніе будетъ нуль, то х = а удовлетворяетъ данному ур—нію; если же истинная величина неопредѣленности,* при будетъ отлична отъ нуля,
корень а слѣдуетъ отбросить.
2. Во-вторыхъ, такъ какъ знаменатель Ц есть полиномъ цѣлый по буквѣ х, то онъ можетъ обратиться въ оэ только лри я = ес; но при этомъ и числитель, какъ цѣлый полиномъ относительно также обратится въ дробь же приметъ видъ истинная величина этой неопредѣленной формы будетъ нулемъ только тогда, когда степень знаменателя выше степени числителя. Въ р
этомъ, и только въ этомъ случаѣ, ур. ^ = 0 будетъ имѣть безконечный корень.
Это изслѣдованіе приводитъ къ слѣдующему заключенію: для рѣшенія ур— нія, содержащаго неизвѣстное въ знаменателяхъ дробей, собираемъ всѣ члены въ первую часть, приводимъ ихъ къ общему знаменателю и соединяемъ въ одну дробь; приравнявъ числителя этой дроби нулю, рѣшаемъ уравненіе Р = 0, Если окажется, что ни одинъ изъ корней этого ур. не обращаетъ знаменателя Ч въ нуль, то заключаемъ, что ур. Р = 0 эквивалентно данному, если оставить въ сторонѣ безконечные корни.
Если же окажется, что какой-либо изъ корней ур—нія Р = 0 обращаетъ л > Р
и знаменателя Ч въ нуль, то истинная величина дроби при этомъ частномъ значеніи х покажетъ, слѣдуетъ ли его удержать пли отбросить.
Приведемъ нѣсколько примѣровъ въ поясненіе этого правила.
Примѣръ I. Рѣшить уравненіе 4
(дг— ір (х-ь 2)(а;—-3) _ 0 , п
(ж — 1)(а?Ч-2)»(жН-3)®
Приравнивая числителя пулю, рѣшаемъ уравненіе:
(х- 1)«(ж+2)(я — 3) = 0 . . .(2) «
Произведеніе (.г—I)2. (я 4“ 2) (я— 3) обращается въ О при .т—1, при х = — 2 и при я = 3. Слѣд, (2) имѣетъ три корня,
^=1; У' = —2; #"' = 3.
Подставляемъ каждый изъ нихъ, поочередно, въ знаменателя. При ж=1 знаменатель обращается въ О» а вся первая часть въ д; по сокративъ дробь на х — 1, и положивъ затѣмъ х = 1, находимъ, что истинная величина первой части ур—нія (1) есть О* Заключаемъ, что а/=1 есть одинъ изъ корней ур—нія (1),
При х =— 2, знаменатель снова обращается въ О, а первая часть ур—нія (1) въ но истинная величина этой неопредѣленности, при х=2, есть со, слѣд. корень х" =— 2 не удовлетворяетъ данному ур—нію.
Наконецъ, корень ./" = 3, обращая числителя въ О, знаменателя;—дѣлаетъ конечнымъ, а потому удовлетворяетъ ур—нію (1).
•Замѣчая, наконецъ, что степень знаменателя ур. (1) выше степени числителя (числитель 4-й степени относительно я, а знаменатель 6-й), заключаемъ, что данное ур. имѣетъ еще безконечный корень.
Итакъ, данное ур. имѣетъ три корня:
1, 3 и со.
Примѣръ II. Рѣшить уравненіе
Собравъ всѣ члены въ 1-ую часть и соединивъ ихъ въ одну дробь, найдемъ уравненіе
^~7іС+-6 = О;
1 —X *
пли. разложивъ числитель на множители и умноживъ обѣ части на —1, получимъ
(ж-1)(ж-6) _п
(®-1)
Приравнивая числитель нулю, находимъ уравненіе (я—О (%—6) = О, которое имѣетъ, какъ легко видѣть, два корня: #'=1 и я" =6. Изъ нихъ второй, какъ обращающій знаменателя въ конечную величину 5, удовлетворятъ и данному уравненію. Первый же, т-е. 1, обращаетъ дробь ----}--------БЪ о:
истинная величина этой неопредѣленности, при х=1, есть не 0, а —5, сл. корень х=1 не удовлетворяетъ предложенному уравненію*
Наконецъ, данное ур. не имѣетъ безконечнаго корпя, ибо степень числн-х а-2 — 7 а? 4-6 теля дроби ———р— выше степени ея знаменателя.
‘ Итакъ, данное ур. имѣетъ одинъ корень: д? = 6.
Рѣшеніе уравненій 1-й степени съ однимъ неизвѣстнымъ.
263. Доказанныхъ началъ совершенно достаточно для рѣшенія уравненіи первой степени съ однимъ неизвѣстнымъ. Механизмъ рѣшенія укажемъ на нѣсколькихъ примѣрахъ.
Примѣръ 1. Рѣшить уравненіе
1 — 5 — 4___— • • • (П
' 6 4 3 1 Л
Освобождаемъ уравненіе отъ дробей, умножая обѣ части его на общаго знаменателя 12; получимъ
7X12 я?хі2 .ч/11 5л*Х12
—6---------4- = 4Х12-----------з ’
или, по сокращеніи,
14 Зя = 48 —20я . . .(2).
Перенеся, затѣмъ, неизвѣстные члены въ первую часть, а*извѣстные во вторую, найдемъ ур.
20я —Зя = 48 — 14;
« сдѣлавши приведеніе въ той и другой части,
17^ = 34; . . . (3);
наконецъ, раздѣливши обѣ части па коэффиціентъ 17 при неизвѣстномъ, имѣемъ:
или #=2 . , ф (4).
Уравненія (I), (2), (3) и (4) всѣ эквивалентны между собою: въ самомъ дѣлѣ, каждое изъ нихъ мы выводимъ изъ предыдущаго или умноженіемъ, или дѣленіемъ обѣихъ частей на одно и то же число, или перенесеніемъ членовъ изъ одной части въ другую; а всѣ этн преобразованія не измѣняютъ корней ур—нія. Но ур—ніе (4), очевидно, можетъ быть удовлетворено лишь величиною х равною 2; слѣд, 2 служитъ и корнемъ уравненія (1), эквивалентнаго (4).
Изъ предыдущаго выводимъ слѣдующее:
Общее правило. Для рѣшенія уравненія первой степени съ однимъ неизвѣстнымъ нужно:
1. Освободитъ ур-ніе отъ дробей, если таковыя имѣются;
2. Перенести всѣ членъ}, содержащіе неизвѣстное* въ одну частъ* а всѣ извѣстные члены въ другую;
3. Сдѣлать приведеніе подобныхъ членовъ, т.-е. всѣ члены* содержащіе неизвѣстное, соединитъ въ одинъ членъ* а также и члены извѣстные;
4. Раздѣлить обѣ части полученнаго так. обр. уравненія на коэффиціентъ при неизвѣстномъ* частное и будетъ корнемъ предложеннаго уравненія.
* г * — 235 —
Примѣръ П. Рѣшить уравненіе .
Ц-1+^+2>=16 -
ъУ '
Умноживъ обѣ части на 12—общаго знаменателя дробей, получимъ • ‘д& .
’ 6(^+1) + 4 (я 4-2) = 192 — 3(я 4-3);
раскрывъ скобки, найдемъ
&х4- 6 4- 4я + 8 = 192 — Зх — 9; сдѣлавъ приведеніе въ каждой части уравненія, получимъ болѣе простое ур—ніе 10^4-14=183 — Зя;
по перенесеніи членовъ, имѣемъ Юя4-3я= 183 — 14, по приведеніи: 13а? = 169.
* Отсюда, раздѣливъ обѣ части на 13, имѣемъ х= 13.
Повѣрка. Подставивъ вмѣсто х въ данное ур. 13, получимъ
44(1-4-2) =16-1(13 + 3), или 7 + 5 = 16-4, пли 12=12.
Слѣд. пайденпое рѣшеніе въ самомъ дѣлѣ удовлетворяетъ данному уравненію.
Примѣръ III. Рѣшить уравненіе • 5ж —9 —^ = 7ж— 19.
О Освободивъ отъ дробей, получимъ 15я —27 — 4я = 21я—57;
по перенесеніи членовъ имѣемъ: ♦
15я— 4я— 2 Ія = 27— 57; по приведеніи: • — Юя = — 30.
Умноживъ обѣ части на —1, найдемъ
Юя = 30;
откуда
х = 3.
Повѣрка не представляетъ никакого затрудненія.
Примѣръ IV. Рѣшить уравненіе ч
—|— 7 2^ — 2 2я 1 /іх
“15 77^6“ “7Г“ * • ’
Умножаемъ обѣ части на 15(7я —6) и рѣшаемъ полученное уравненіе; если найденный корень не обращаетъ въ нуль знаменателя, то онт> удовлетворяетъ данному уравненію. Но знаменатель 15(7х—6) обращается въ нуль при 6
& = сл. если корень освобожденнаго отъ дробей уравненія будетъ отличенъ 6 отъ онъ удовлетворяетъ предложенному ур—нію.
Освобожденное отъ дробей ур—ніе есть
(6х + 7)<7ж — 6) — (2х— 2) 15 = 3 (2я -Ь- 1)(7я — 6)
или, собирая всѣ члены въ первую часть и въ двухъ изъ нихъ выводя за скобки 7я— 6, находимъ
(7х—6) . 4 — 30 (г— 1) = О, или
2&г — 24 —- ЗОгг 30 = 0, или
— 2гг = — 6, откуда
х~ 3.
Итакъ, данному уравненію удовлетворяетъ значеніе х, равное 3, въ чемъ не трудно убѣдиться повѣркою.
Примѣръ V, Рѣшить уравненіе
1 । 2г । х ___ . 9 “I- 4л? / ч \
х2 4* 3$ + 2 ‘ г2 + 4х + 3 • х2 -|- 5ж 6 х 4- 3 '
Для нахожденія общаго знаменателя, разлагаемъ на множителей знаменатели первой части уравненія; находимъ:
я2 4* 3Ж-[-2 = (а?+ 1)(я4"2);
^4-4я + 3 = (#+1)(я4-3):
х2 -|- 5я + 6 — (х + 2)(я+ 3);
общій знаменатель = (х + 1)(я 4" 2)(я 4“ 3)-
Умноживъ обѣ части на общаго знаменателя и сдѣлавъ надлежащія сокращенія въ дробныхъ членахъ, имѣемъ:
л:+3+244?+2)4-^+іг=4(^+і)(л:+2)(^+3)—(9 + 4х)(^+1)(ж^2), или
Зяа + 6х + 3 = 4я3 4- 24яа 4- 44х 4> 24 — 4я3 — 21 — 35я — 18,
или, по приведеніи во второй части и по отнятіи отъ обѣихъ частей по Зга, имѣемъ:
6^4-3 =9г'4-6 . . . (2).
Это уравненіе не необходимо эквивалентно данному, такъ какъ оно получено умноженіемъ даннаго на выраженіе (#4” 1)(#4” 3), содержащее неиз-
вѣстное. Но если корень (2) не обращаетъ въ нуль общаго знаменателя, то онъ удовлетворяетъ и ур—нію (1); общій же знаменатель обращается въ О при значеніяхъ я, равныхъ —1, ~2 и ~3; поэтому, если корень ур—нія (2) не равенъ ни одному изъ этихъ чиселъ, то онъ необходимо уд—тъ данному ур—нію; если же равенъ одному изъ этихъ чиселъ, то необходимо дальнѣйшее изслѣдованіе.
Рѣшая ур. (2) имѣемъ:
б# — Эя = 6 — 3 или
— 3я=3, откуда
х = ’— 1.
Перенеся всѣ члены даннаго ур—нія въ первую часть и соединивъ ихъ въ одну дробь, имѣемъ
— Зя —3 - 3(^+1)
(а: + 1)(яГ+2)(ж + 3) ИЛИ (*+ 1)(х + 2)(^ + 3) “
Первая часть, при х =— 1, обращается въ но, сокративъ на я?4~Ь и положивъ затѣмъ х —— 1, найдемъ
— 3
—что не = Ѵ,
слѣд. — 1 не есть
— 3(д? +1)
(я 4- 1)(л* + 2)(я -р 3)
корень даннаго ур—нія. Но какъ степень знаменателя дроби
выше степени числителя, то данное ур. имѣетъ корень
Примѣръ VI. Рѣшить уравненіе
. । х + а 2а + Ь ~~ ’ 2а — Ъ *
Умноживъ обѣ части на общаго знаменателя (2а-|-Ь)(2а — />)т найдемъ (2я + 76)(2а — Ь) = (2а Ь)(2а — 6) -|- (ж 4- а)(2а 4- 6),
или, выполнивъ указанныя дѣйствія,
4ал 4“ 14га6 ~ 2&с — 7№ = 4а3 — № 4- 2а^ 4~ 2а3 4^
а нѵ перенесеніи членовъ,
4ах— 2Ьх — 2ах — Ьх — 4а3 — 63 4~ 2а3 4”— 14аЬ 4~ 763, или (2а — 3&) х = ба3 — 1 Заб 4~ откуда
6а2 — ІЗаЬ + 662
Х~ 2а— ІЪ
Г
Совершивъ дѣленіе, найдемъ окончательно
х = '3а— 26.
Если значенія, данныя буквамъ а и 6, обращаютъ одного изъ знаменателей въ нуль, тогда мы уже не имѣли бы права умножать ур. на произведеніе (2а-|-6)(2а— 6), какъ равное 0; но въ этомъ случаѣ самое ур., содержа дробь съ знаменателемъ равнымъ 0, не имѣло бы никакого смысла.
Примѣръ VII. Рѣшить уравненіе
1 ’ 2 1 Аг------------------— = 0 . . . (1).
х—2а х—а х 7
х— 6а
Приводя къ общему знаменателю, имѣемъ:
(#4-За)(&—2а)(а?—а)-{-2(#—6а)(л?—2а)(х—а)4-3{х—6а) (-г-)-За) (я—а)—6(,г—6а) (а?4-3а) (а;—2а) (я?—6а)(лг4-ЗаХд‘—2а)(а;—а)
Числитель м. б. упрощенъ; вынося въ первыхъ двухъ членахъ общій множитель (#—2а)(#— а), а въ двухъ послѣднихъ 3(ж— 6а)(ж-|-3а), найдемъ
(х—2а) (я — За-т--^—12а]4-3(я?—6а) (я За) [# — а — 2х-[-4а]=
(# “ 2а)(х — а)(3*г — 9а) -р 3(я — 6а) (я За)(— х За) = 3(х — 2а) (я — а)(гг — За) — 3(# — 6а)(я -|- За)(я — За) =
3(ж — За)[(ж— 2а)(я — а) — (я — 6а)(я За)] = 3(х — За) X 20а*-
Уравненіе принимаетъ, поэтому, видъ
__________60а2(ж — За)__________, ,9*
(д? — 6а)(яг + За)(*г — 2аХ^ — а) ' ' -
Числитель обращается въ 0 только при х = За; и какъ это значеніе я не обращаетъ въ нуль знаменателя, то оно уд-—тъ и ур—нію (I). Кромѣ того, данное ур. имѣетъ еще безконечный корень, ибо степень знаменателя выше степени числителя. Итакъ, ур. имѣетъ два корня
х — За, и я” = сс.
Повѣрка. Подставляя За вмѣсто х въ данное ур*, находимъ
1,2,3 6 п
— К- + Н------о" — О, или
За • 6а 1 а 2а *
- = 0, а ’
что вѣрно*
Подставивъ вмѣсто х, замѣчаемъ, что каждый членъ цервой іцстн обращается въ 0, сл. ур* также обращается въ тождество 0 = 0.
Задачи, приводящія къ уравненіямъ 1-й степени съ однимъ неизвѣстнымъ.
264. Рѣшеніе задачи средствами алгебры состоитъ изъ четырехъ частей:
1) составленія уравненій пли неравенствъ изъ условій, связывающихъ данныя величины съ неизвѣстными;
2) рлшеяія полученныхъ эдшянеиш или неравенствъ;
3) дезджЬваиія задачи, т.-е. а) опредѣленія условій, которымъ должны удовіетворжть данныя (предполагая, что они изображены буквами), для того чтобы задача была возможна; Ь) опредѣленія числа рѣшеній въ случаяхъ воз-клюоі задачи, и с) разсмотрѣнія всякихъ представляемыхъ ею особенностей. Слѣдуетъ замѣтить, что пе всякая задача даетъ матеріалъ для изслѣдованія;
4» амидо# найденныхъ рѣшеній, служащей удостовѣреніемъ въ правиль-мп рѣшетя задачи.
Въ этой главѣ мы займемся рѣшеніемъ только такихъ задачъ, которыя жрподггь къ уравненіямъ первой степени съ однимъ неизвѣстнымъ; а изслѣдо-шкжъ рѣшеній займемся въ отдѣльной главѣ, по касаясь пока этого вопроса.
Что касается составленія уравненій изъ условій задачи, то па этотъ счетъ мѣтъ никакихъ общихъ правилъ; все, что можно сказать по этому предмету, оодмтся къ слѣдующему: назвавъ неизвѣстное (мы ограничиваемся здѣсь случаемъ одного неизвѣстнаго) буквою обозначаютъ при помощи этой буквы и данныхъ задачи всѣ дѣйствія, какія должно бы было произвести надъ ними для повѣрки рѣшенія, предполагая, что неизвѣстное найдено; такимъ образомъ получатся выраженія, которыя, по условію задачи, должны быть равны: соединяя дъ знакомъ равенства, и получимъ искомое уравненіе.
Укажемъ примѣненіе этого правила на нѣсколькихъ вопросахъ.
265. Первая задача. Часовая и минутная стрѣлка находятся вмѣстѣ, показывая полденъ. Въ которомъ часу произойдетъ слѣдующая ихъ встрѣча ?
Составленіе уравненія. Циферблатъ часовъ раздѣленъ па 60 равныхъ , частей, каждую изъ которыхъ большая стрѣлка проходитъ въ минуту времени, и пусть отъ полудня до встрѣчи стрѣлокъ малая стрѣлка прошла х такихъ дѣленій. Минутная стрѣлка, чтобы догнать часовую, должна обойти весь циферблатъ, т.-е. пройти 60 дѣленій, да еще х дѣленій, пройденныхъ часовою, всего 60 + х дѣленій. По въ то время какъ часовая проходитъ 5 дѣленій (отъ XII до I), минутная стрѣлка проходитъ 60 такійгь дѣленій, сл. въ 12 разъ большее число ихъ. Изъ этого слѣдуетъ, что въ одно и то же время путь, пройденный минутною стрѣлкою, въ 12 разъ больше пути, пройденнаго часовою, т.-е. 60 -\-х въ 12 разъ больше х.
Итакъ, имѣемъ уравненіе
60 -|“ я — 12х.
Рѣшеніе уравненія. Перенеся # во вторую часть, находимъ >
60 = 1Ія;
откуда
60 .5
11 — 0 Г]
Слѣд., до встрѣчи стрѣлокъ часовая должна пройти 5^ минути. дѣленій, 5 встрѣча произойдетъ въ 1 ч. 5^ мнн.
Посѣрка. Пространство, пройденное минутною стрѣлкою, должно быть въ 12 разъ больше разстоянія, пройденнаго часовою; и въ самомъ дѣлѣ
5 с 5 720 60
65П:5П = Т1 :И
266. Вторая задача. Въ трехзначномъ числѣ цифра десятковъ вдвое больше цифры сотенъ, цифра же единицъ втрое больше цифры сотенъ; если къ искомому числу придать 396, найдемъ число обращенное, т.-е. составленное тѣми же цифрами какъ и искомое, но написанными въ обратномъ порядкѣ. Опредѣлить неизвѣстное число?
Составленіе уравненія. Пусть цифра сотенъ искомаго числа будетъ тогда цифра десятковъ выразится черезъ 2х, а цифра единицъ формулою Зх.
Все число единицъ въ искомомъ числѣ будетъ
1 ООх + 20х + Зх.
Число единицъ въ обращенномъ числѣ будетъ
ЗООх 20х
Придавъ къ первому 396, найдемъ число обращенное; слѣдов.
1 ООх 20х —|— Зх —1“ 396 ЗООх —20х ~|— х.
*
Рѣшеніе уравненія. Отнявъ отъ обѣихъ частей по 20х, собравъ неизвѣстные члены въ одну часть и сдѣлавъ приведеніе, получимъ
396 = 198х, откуда
_ 396 _ 9
л ~ І98 — /
Итакъ, число сотенъ искомаго числа равно 2; слѣд. число десятковъ = 4, а число единицъ 6. Поэтому искомое число есть 246.
Повѣрка. Придавъ къ найденному числу 396т должны получить обращенное число, т.-е. 642; и дѣйствительно
246 + 396 = 642,
267. Третья задача. Два капитала составляютъ въ совокупности 167280 руб. Первый, помѣщенный на 7°/й, въ 3 м. при-
быль вдвое большую той, какую можетъ принести второй капиталъ* помѣщенный на 5%, въ 7 мѣсяцевъ. Опредѣлитъ оба капитала?
Составленіе уравненія. Пусть первый капиталъ = х; тогда второй будетъ = 167280 — х руб. Каждая сотня перваго капитала, принося въ 1 годъ 4 4 3
4 руб- прибыли, дастъ въ 1 мѣсяцъ въ 3 мѣсяца - или 1 руб.; слѣд.
каждый рубль
перваго капитала принесетъ руб. прибыли, а х рублей —
07
ІбО'
Такимъ же точно образомъ найдемъ, что капиталъ 167280 —х р., при 5%, дастъ въ 7 мѣсяцевъ
(167280 — а;) X 5 X 7 (167280 — ^X35
100X12 “ЛИ 100X12 р. прибыли.
4
Но условію, первая прибыль вдвое больше второй, слѣд.
л* (167280 —я) X 35 X 2
100— 100X12
Рѣшеніе уравненія. Освободивъ это ур. отъ дробей, имѣемъ
12х = 167280 X 70 — 7(Ч
12гН- 70л:— 167280 X ™ ,
82л: = 167280 X "О , 167280X70 1 4оепп
х—------—= 142800 р.
Итакъ: капиталъ, помѣщенный на 4%, =142800 р.; капиталъ, помѣщенный на 5%, =167280— 142800 = 24480 р.
тт тт „ 142800X3X4
Повѣрка. Прибыль, приносимая первымъ капиталомъ, равна —= = 1428 р.; вторымъ — х * =714. Дѣйствительно, 1428 больше 714 въ 2 раза.
268. Четвертая задача. Лисица, преслѣдуемая собакою, находится впереди послѣдней на 60 своихъ скачковъ^ и дѣлаетъ 0 скачковъ въ то время, въ какое собака дѣлаетъ только 6; но 3 скачка собаки равны 7 скачкамъ лисицы. Сколько скачковъ должна сдѣлать собака, чтобы д&інать лисицу?
Когда въ задачѣ рѣчь идетъ о разстояніяхъ, полезно изображать иіъ линіями; этимъ путемъ мы яснѣе представимъ себѣ зависимость между величинами і скорѣе съумѣемъ составить ур—піе.
Предложенная задача представляетъ примѣръ этого рода.
Составленіе уравненія. Пусть X (см. черт. 3) означаетъ мѣсто, въ которомъ находится собака; 0 — мѣсто, въ которомъ въ тотъ же самый моментъ сходится лисица; М — точка, въ которой собака настигаетъ лисицу. Пусть, затѣмъ, собака должна сдѣлать х скачковъ, чтобы догнать лисицу, т.-е. чтобы і робѣ жать разстояніе ХМ.
Выразимъ черезъ х число скачковъ, которое должна сдѣлать лисица на эдгтмяніи ОМ. Въ то время какъ собака дѣлаетъ 6 скачковъ, лисица дѣлаетъ иъ Ч. сл. пока собака дѣлаетъ 1 скачекъ, лисица дѣлаетъ или скачка;
ютожѵ, въ то время какъ собака дѣлаетъ х скачковъ отъ X до И, лисица 3 Зл?
'ііллетъ х разъ 2 или скачковъ отъ 0 до М.
Итакъ, на одномъ и томъ же разстояніи ХМ, собака дѣлаетъ х скачковъ, Зя:
а лжяцж 60-]--^ (60 скачковъ на разстояніи отъ X до 0).
принятыхъ
П’оеиъ скачекъ лисицы за единицу мѣры; тогда разстояніе ХМ, выра-жъ этихъ единицахъ, будетъ 1
<4 другой стороны, 3 скачка собаки равны 7 скачкамъ лисицы, ,7 г 7х
чекъ собаки =х скачка лисицы; а потому ж скачковъ собаки =-н-
сл. 1 ска-принятымъ
единицамъ: это дрѵгая формула, выражающая разстояніе ХМ въ тѣхъ же еди-ницахъ, какъ и формула 60
&
Приравнивая одну формулу другой, имѣемъ ур—ніе
Рѣшеніе уравненія* стей на 6, получаемъ
Освобождая ур. отъ дробей умноженіемъ обѣихъ ча~
5л: = 360, 360
Итакъ, собака сдѣлала 72 скачка, чтобы догнать лисицу.
Повѣрка не представляетъ затрудненій.
269. Пятая задача. Два выходятъ одновременно со станцій
А к В и идутъ на встрѣчу другъ другу; первый все разстояніе АВ можетъ пройти въ 4 ч. 20 м*; второй на прохожденіе того же пути употребляетъ 3 ч. 30 м. Разстояніе отъ А до В равно 211 верстамъ. На какомъ разстоянія отъ А оба поѣзда 'встрѣтятся, полагая, что каждый движется все время съ одинаковою скоростью?
Составленіе уравненія. Пусть будетъ х искомое разстояніе, т.-е. число верстъ отъ А до мѣста встрѣчи; разстояніе отъ мѣста встрѣчи до В равно, поэтому, 211—х, Такъ какъ оба поѣзда выходятъ со станцій одновременно, то до встрѣчи они находятся въ дорогѣ одинаковое время; выразивъ эти времена и приравнявъ полученныя выраженія, и найдемъ искомое уравненіе.
Первый поѣздъ въ 4 ч. 20 м. или въ 260 м. можетъ пройти 211 верстъ, сл. чтобы пройти одну версту, времени нужно мин., а для прохожденія х 260* т гл х
верстъ мин. Такимъ же разсужденіемъ убѣдимся, что второму поѣзду для
. Л 210(211—о-) л
прохожденія 211—х верстъ потребуется —91]---------- мин. Сл. ур—ніе есть
260ж _ 210 (211 — д-)
211 — 211
Рѣшеніе уравненія. Освобождая отъ дробей, имѣемъ
260л?= 210(211 — х);
выполняя умноженіе и перенося члены:
260x4-210л = 44310;
470х= 44310;
44310 п,із х=^- = 94й версты.
Итакъ, встрѣча произойдетъ въ разстояніи версты отъ А.
Провѣрить рѣшеніе нетрудно.
270. Шестая задача. Раздѣлитъ 5600р. между пятью лицами такъ, 2-е имѣло вдвое больше 1-ю и еще 200 р.; 3-е втрое больше Т-» безъ 400 руб.; 4-е полусумму частей 2-го и З-іо и еще 150 р.; мжвдеда, 5-е четверть суммы остальныхъ четырехъ и еще 475 руб.
Составленіе уравненія. Пусть будетъ х часть перваго; часть второго вы-разжгся формулою 2х4- 200;—3-го Зх—400.
Четвертый получитъ
2х + 200 4- Зх — 400 2
Ц-150
5х-|-100 или —--------
Сумма частей четырехъ первыхъ лицъ =
х 4- 2х + 200 + Зх — 400 4-
или
17х —300
Пятый получитъ
17х — ЗСИ1
17-г 4- 3500 т.-е. -------т;------
По условію задачи части всѣхъ пяти лицъ въ совокупности составляютъ 5600 р.; отсюда уравненіе
П^-ЭДО 2
17х + 3500 8
= 5600,
Рѣшеніе уравненія. Освобождая уравненіе отъ дробей, находимъ
68х — 1200 4- 17х4- 3500 = 44800;
85х = 44800 4-1200 — 3500, -
85х = 42500,
42500 -АЛ х= - оѵ— = эОО.
8о
Птакъ: часть 1-го =500 р.; часть 2-го = 1200; 3-го =1100; 4-го = 1300; 5-го =1500 р.
Повѣрка. Дѣйствительно, сумма 500 1200 4~ 1ЮО 4~ 1300 4~ 1500 =
= 5600.
Примѣчаніе. Задача эта приведена какъ примѣръ, указывающій, насколько кжо сокращать и приводить въ простѣйшій видъ сложный результатъ, прежде тѣшь иереходпть къ слѣдующему.
Яраѵіимъ примѣры съ буквенными данными.
27К Седьмая задача. Число а раздѣлитъ на двѣ части7 которыя (іитпямп бы между собою какъ т : п?
Составленіе уравненія. Пусть первая часть = х; тогда вторую можно шраяпъ зри иомощи х изъ пропорціи
х : второй части = т ; п.
откуда
Отсюда уравненіе
пх
вторая часть = — *
Рѣшеніе уравненія. Умноживъ обѣ части на ж, найдемъ •
тх -|- = апі;
ат
Вторая часть = —х=-г т т
та _ па ш -г п т + л
/
Повѣрка. Обѣ части должны въ суммѣ составлять а, И дѣйствительно
ли, < па _____________та 4- па_______(ш ’-ь п)«
т + п ’ т п т + п т -+• п
272. Восьмая задача. .И/ьюло долженъ уплатить своему заимодавцу нѣсколько суммъ въ различные сроки, а именно: з руб. черезъ т мѣсяцевъ, $' руб. черезъ т* мц.? з” руб* яо истеченіи т" мѣсяцевъ, наконецъ в'" руб. черезъ тгг/ мѣсяцевъ. Заимодавецъ желаетъ получить всю сумму разомъ. Черезъ сколько мѣсяцевъ должна быть произведена эта уплата, чтобы ни та ни другая сторона не потерпѣла убытка?
Составленіе уравненія. Допустимъ, что каждые сто руб. приносятъ заимодавцу р % въ мѣсяцъ; тогда прибыль, которую заимодавецъ получилъ бы съ перваго капитала при уплатѣ его черезъ т мѣсяцевъ, составляетъ р.; при-1. чЛЛ быль, доставляемая вторымъ капиталомъ, при уплатѣ его черезъ т’ мѣсяцевъ* з'рт' з”рт" з'”рт"' х Л .
равна ; третьимъ----------; и четвертымъ ; слѣдов. общая прибыль*
зрт і з'рт* । з"рт” . которую долженъ получить заимодавецъ, составляетъ юд Н—іоо”*”
-]—р. Время, по истеченіи котораго вся сумма а-|-зЦ-должна быть уплачена разомъ, должно быть таково, чтобы вся сумма давала прибыль равную вышеозначенной. П^сть это время =х мая капиталомъ по истеченіи
мѣсяцамъ; прибыль, доставлявъ этого времени, составляетъ
(«-Ь а +$" +
100
руб..
Поэтому, уравненіе будетъ
(з + з* 4" &,г ”1“ 5 ^) .Рх ЗРПі ^Рт' і 8ггртгг I
Ібб ІОО “1“ ІѲСГ “г 100 “I Гбо
Рѣшеніе уравненія. Сокращая обѣ части на общаго множителя на*
Ѵ’ІЮГЬ
откуда
($+$+-$ Т'? ) #= зт—(-5 Л? +- т т* < «
+ 5'шГ 4“ 3^" +
, Х ~ в"+ 8' -+- 5" + в'" ’
Повѣрка не представляетъ затрудненій.
ГЛАВА XIX.
1
Уравненія первой степени съ двумя неизвѣстными.
Опредѣленія.—Начала п методы.
273. Опредѣленія. Одного уравненія со многими неизвѣстными недостаточно для опредѣленія этихъ неизвѣстныхъ.
Въ самомъ дѣлѣ, пусть два неизвѣстныя х и у связаны однимъ уравненіемъ, наприм. •
4# — оу = 12.
Выражая отсюда я, имѣемъ
12 + 5^
откуда видно, что величина я-са зависитъ отъ у. самый же у остается вполнѣ произвольнымъ, такъ что ему можемъ давать какія угодно значенія; такъ, по
ложивъ
„ 12 + 5X0 □
у — О, находимъ, что я — —------= о.
У = 1; . . *
у = 2, »
»
п.
4 ’
11
9 >
И т. д.
/ Итакъ, одно ?//). съ 2 неизвѣстными имѣетъ безчисленное множество ѣаръ рѣшеній* и слѣд. неопредѣленно.
Если уравненіе содержитъ три неизвѣстныя, то двумъ изъ нихъ можно дать ^«вольныя значенія, а третье неизвѣстное получитъ совершенно опредѣленное зжічаіе; ур. будетъ имѣть опять безчисленное множество рѣшеній. Вообще, одно умвяеше съ нѣсколькими неизвѣстными имѣетъ безчисленное множество рѣшеній т читается поэтому неопредѣленнымъ.
Свстена совмѣстныхъ уравненій. Когда нѣсколько неизвѣстныхъ должны умаетафять одновременно нѣсколькимъ уравненіямъ, то совокупность ур—ніп ожтазляетъ то. что называется смсшелою совмѣстныхъ уравненій.
Простѣйшую систему составляютъ, очевидно, два уравненія съ двумя непз-
Рѣшитъ систему нѣсколькихъ уравненій со многими неизвѣстными значитъ найти значенія неизвѣстныхъ, удовлетворяющія одновременно всѣмъ уравненіямъ. Такъ, система
4х — 3$ — 8,
7я-(- 2у = 43
имѣетъ рѣшеніемъ х = 5, у = 4, потому что при этихъ значеніяхъ неизвѣстныхъ и то и другое уравненія обращаются въ тождества.
Двѣ системы уравненій называются эквивалентными, если они принимаютъ одни и тѣ же рѣшенія.
Начала и методы.
274. Начало первое. Если р, / і суть количества конечныя, т.-е. неравныя ни 0, ни оо, если притомъ ру—р'д неравно нулю, то системы
А = 0 | в=о; <4 и
р А + ?В = О |
р'А + д'В = О ) эквивалентны.
Доказательство. Въ самомъ дѣлѣ:
1) Пусть х = а и суть рѣшенія системы (1): это значитъ, что при подстановкѣ въ А и В вмѣсто х количества а и вм. у количества [і, А и В обращаются въ нули; но какъ р, у, р1 и у\ но условію, конечны, а произведеніе конечнаго количества на нуль равно 0, то при тѣхъ же значеніяхъ х и у выраженія рА 4" дВ и р'А + обращаются въ нули. Слѣд. х —а п У = ?» удовлетворяютъ системѣ (2),
2) Пусть теперь х = а и у = Ь будутъ рѣшенія системы (2), т.-е. пусть при этихъ величинахъ х и у выраженія рА^-дВ и р'А -|-д'В обращаются въ нули; въ такомъ случаѣ и выраженіе
$'(рА Д- дВ) — д(р'А -И' В) • • • (3 ),
въ которомъ и { конечвы, а рА дВ и р'А д'В равны нулю, обращается въ нуль; но выраженіе (3) равно
(рд' —.р'дІА;
слѣд. и это послѣднее равно кулю; но по условію ру' — р'у отлично отъ нуля, слѣд. А должно быть равно нулю при х = а и у = Ь, Но тогда и рА = О, а котому ур. рА + уВ = О обращается въ дВ = 0; а какъ у конечно, то должно быть В = О. Итакъ рѣшенія системы (2) удовлетворяютъ уравненіямъ системы (1).
Мы доказали, что системы (1) и (2) эквивалентны.
Па этомъ началѣ основанъ
275. Методъ уравниванія коэффиціентовъ при неизвѣстныхъ или методъ сложенія и вычитанія.
Пусть имѣемъ систему двухъ уравненій съ двумя неизвѣстными
7х-^ 4у = 76
1 Ія ~ 9у = 43
Исключимъ изъ этихъ уравненій неизвѣстное яг; для этого помножимъ обѣ части 1-го ур. на коэффиціентъ 11 при я во второмъ уравненіи, а обѣ части 2-го ур. на —7, т.-е. на взятый съ обратнымъ знакомъ коэф. при х въ первомъ ур—ніи, и полученныя уравненія сложимъ. Такимъ обр. получимъ
77х -)- 44у — 836
77х 63у = — 301
107^“ 535.
Для исключенія у изъ системы (1), множимъ обѣ части перваго ур—нія на 9, а обѣ части втораго на 4 и складываемъ почленно полученныя уравненія:
63л + Збу = 684
44х— Збі/ = 172
107х =856.
Па основаніи доказаннаго начала, система ур—ній
107^ = 535 и 1О7х = 856. . .(2)
эквивалентна данной системѣ; поэтому рѣшенія системы (2) будутъ удовлетворять и (1). Рѣшая ур—нія (2), находимъ
Нетрудно провѣрить, что рѣшенія
х = 8 и у = 5
дѣйствительно удовлетворяютъ даннымъ уравненіямъ.
Отсюда
Правило. Для нахожденія одного изъ неизвѣстныхъ* напр. х* умно* жаемъ данныя уравненія на такія количества^ чтобы коэффиціенты яри Оруюмъ неизвѣстномъ (у) сдѣлались равными, но имѣли бы про-тивоположные знаки; затѣмъ полученныя новыя ур--нія почленно скла-дываемъ. Такимъ обр. неизвѣстное у исключите# приведеніемъ и получится ур—ніе съ однимъ неизвѣстнымъ х, которое уже легко опредѣлитъ. Подобнымъ же образомъ найдемъ у, исключивши х.
На практикѣ нужно пользоваться всѣми обстоятельствами, ведущими къ упрощенію вычисленій. Пояснимъ это примѣрами.
1. Рѣшить уравненія
5х — 12у — 17 Зх -|- 8у = 71.
Для исключенія у замѣчаемъ, что нѣтъ надобности множить первое ур. на 8, а второе на 12, Въ самомъ дѣлѣ, наим. кратное чиселъ 12 и 8 есть 24, и для того чтобы коэффиціенты при у сдѣлались равными 24, достаточно первое ур. помножить на 2, а второе на 3. Сдѣлавъ это, найдемъ:
10* — 24 г/ 34 9*4-24// = 213;
сложивъ почленно оба ур—нія, найдемъ
откуда
Умноживъ 1-ое ур. на 3, а второе на — 5. имѣемъ
15г—36//= 51
— 15* — 40у = — 355;
сложивъ эти уравненія, получимъ
*— 7 бу = — 304, откуда
—304 .
' * # _ 76
2. Рѣшить уравненія
5* + 2у = 40
11*—4у = 4.
Для исключенія у достаточно первое ур, умножить на 2, а второе оставить безъ перемѣны (или, что то же, умножить на 1); найдемъ
10*-)- 4у = 80
11* — 4у = 4;
сложивъ эти уравненія, получимъ
21*= 84, откуда * = 4.
Умноживъ первое ур. на 11, а второе на —5, находимъ ♦
55*4*22// = 440
— 55* 20у = — 20;
сложивъ, имѣемъ:
42у — 420, откуда у =* 10.
3. Рѣшить ур—нія
4*4 9у = 127
8* — Зу = 23.
Умноживъ второе ур. на 3 и сложивъ съ первымъ, найдемъ 28л: = 196, откуда х = 7,
Умноживъ первое на —2 и сложивъ со вторымъ, полупимъ — = —231, откуда ^=11. .
4. Рѣшить уравненія
х-±у = а х — у = Ь.
Рѣшеніе этой системы встрѣчается на каждомъ шагу, и весьма просто. Складывая почленно оба ур— нія, получимъ
2х^аф6, откуда х = ^~;
вычитая изъ перваго второе, имѣемъ: - ’
2у = а — Ь, откуда у=——
5, Рѣшить систему уравненій
(а "Р 6) х 4~ (а — 6) у — а1 4~ 2аб — Ь* (а3 4~ б3) х (а3 — Ь3) у — а1 — Ьк-\-аЪ (а2 ^>*)*
Для исключенія у замѣчаемъ, что а3 — Ь* — (а — 6)(а2 -к аб -|~ б2). откуда видно, что достаточно первое ур. помножить на а2 -|-4“ второе на 1, и изъ перваго вычесть второе.
Сдѣлавъ это, найдемъ
! (а + Ь)(а2 4- аЬ 4^*) — (а3 4~ 63) } х = (а2 + 2аб — б2)(а2 4~ аЬ 4- б2) -{а1 — г>*4^(а*+Ь2)}
или %
2аЪ (а 4- 6) х = 2а?Ь (а 4^ б),
откуда
х — а.
Для исключенія х, т.-е. для нахожденія у, замѣчаемъ, что а34~б3 — = (а 4~ б)(а4 — «6 4“ й слѣд. достаточно, умноживъ первое уравн. на а2 — аЬ 4" б1, а второе на 1, вычесть второе изъ перваго. По упрощеніи, найдемъ ч
у~Ъ.
6. Рѣшимъ общія уравненія
ах-[~Ъу =с , . . (1) а'х — Ъ'у = с’ . . , (2).
Для исключенія у умножаемъ 1-е ур, на а второе на — би складываемъ почленно; так. обр. найдемъ е
(аѴ — а'Ъ^х — сІ}1 — Л, ... (3)
откуда
сЬ' — сЪ
«Л—а Ь
Для исключенія х, съ цѣлію опредѣлить у, умножимъ 1-ое ур. на —а', второе на сложивъ почленно оба ур., найдемъ
(аі/ — а*Ъ) у = ас — а'с, ... (4) откуда
___ас* — «'с аЪ'— аЪ'
Уравненія (3) и (4) эквивалентны уравненіямъ (1) и (2); въ самомъ дѣлѣ, множители д, 2 имѣютъ здѣсь частныя значенія
< 4-а;
поэтому, эквивалентность обѣихъ системъ имѣетъ мѣсто всякій разъ, когда аЬг—а'б неравно нулю* Итакъ: если (аУ — аЬ) отлично отъ нуля, система ур—кій
ах 4- Ьу = с |
ах-\-Ъгу —- с' |
илпьеиіь единственное конечное и опредѣленное рѣшеніе:
__сЪ* — с*Ъ __ас' — а'с
Х аЪ*—аЪ' & аЪ'— агЬ'
276. Начало второе, .Если р и ц суть количества конечныя и отлич-ныя отъ нуля, то ур—ніе
2> А — </В — О
.ножеиг© замѣнить одно изъ ур — нІй
Л-07 В-0;
шо-ест системы
А = 0 1 а = 0 1
В = о)^ “ рА + ?В = 0 | эквивалентны.
Доказательство. Дѣйствительно:
I. Всякое рѣшеніе системы (1), обращая А и В въ нули, обращаетъ рХ и ?В въ нули, ибо р н $ конечны, а слѣд. удовлетворяетъ системѣ (2).
2. Всякое рѣшеніе системы (2), обращая А въ нуль, тѣмъ самымъ удовлетворяетъ первому ур—нію системы (1); но если А обращается въ 0, то и рА равно нулю, а какъ сумма ^А 4" дБ, которой одно слагаемое равно 0, также обращается въ нуль, то должно, и. другое слагаемое ?В обратиться въ 0; но д конечно, слѣд. В должно равняться 0. А этимъ доказано, что всякое рѣшеніе системы (2), удовлетворяетъ и второму ур—нію системы (1), Эквивалентность системъ (1) и (2) такимъ образомъ доказана.
На этомъ началѣ основаны методы: пойстаяоялеяія, сравненія величинъ неизвѣстныхъ и методъ неопредѣленныхъ множителей или методъ Безу (Вегоиі).
277. Методъ подстановленія. Пусть даны уравненія
| бгх —|— Ьу =с . . . (1) | ах'-^-Ь'у = с' . . . (2)
Опредѣлимъ изъ ур —нія (1) х, принимая на время у за извѣстное; находимъ х=с^і. . .(3) а
Подставляя эту величину въ ур—ніе (2), находимъ ур.
а'К-ъУ\^ъ'у=2С-
которое и рѣшаемъ:
ас — а'Ъу -|- аЬ'у — ас
(аЬ' — аЪ)у — ас—а'с . . .(4)
у~~аЪ’— аЪ '
Подставляя эту величину у-ка въ формулу (3), получимъ , ас' — а'с
_саЬ’ — Ьа’с — Ьа<?
<і{аЬ' - а’С) ’
,__ а(с6' — </6)_сЬ — сЪ
Х <7(а6' —а’6) аб* — а'Ь"
Нужно доказать, что найденныя такимъ образомъ величины х и # удовлетворяютъ предложенной системѣ (1) и (-).
Въ самомъ дѣлѣ, перенесеніемъ ах и Ьу Ѵь другую часть замѣняемъ ур.
(1) эквивалентнымъ ему ур—емъ
— ах 4“ (с — Ъу) = О
н слѣд. вмѣсто системы (1) и (2) можемъ взять ей эквивалентную:
— ах+(с — Ьу) = 0. . .(Г)
а'х -р Ъ'у~ с' . . . (2).
а'
Помножая обѣ части ур—нія (1) на а (2) на 4-1 и складывая почленно, имѣемъ
[— ах -{- (с — Ьу)] а'х Ъ'у = с';
или
а'(с^Иь'у=с'-
А потому, на основаніи начала втораго, можемъ систему (!'), (2), а сл, к данную, замѣнить системою
• ах Ьу = с
(6>- •Ів'(^)+6'У=С',
которая и даетъ искомыя рѣшенія,
Ур—нія (6) позволяютъ формулировать слѣд, правило: Выводимъ изъ одного изъ предложенныхъ ур—ній величину одного изъ неизвѣстныхъ, ярмяилая другое за извѣстное, и подставляемъ эту величину во второе уравненіе. Изъ полученнаго так. обр. уравненія опредѣляемъ то неизвѣстное, которое въ немъ содержится; а внеся найденное неизвѣстное въ первое, ур^ получимъ изъ него величину и втораго неизвѣстнаго.
Нужно* впрочемъ, замѣтить, что (4) можно замѣнить ур—мъ (5) лишь тогда, когда аі)—
Приводимъ примѣры,
1* Рѣшить систему уравненій « — 51/ = 2
-У — ”
Рѣшая первое ур—ніе относительно при чемъ у принимаемъ на время за извѣстное* находимъ:
х = . (1))
Подставляя эту величину х во второе уравненіе, имѣемъ:
4 Ц^4-2у = 7 . . . (2). О
Такимъ образомъ получаемъ систему уравненій (1) и (2), которая, по доказанному, эквивалентна данной. Рѣшая ур. (2), находимъ
1.
• У
*
подставляя вмѣсто у въ ур, (1), получаемъ
3
Х~ 2"
2. Рѣшить систему уравненій
(а’ _ 4- Зу) = 2а&(4а — і) ... (1)
а*у----^-4_(а_|_&4-е)Ьа:=^4-аЬ(а + 26) . . .(2).
Выводимъ изъ перваго ур—нія принимая на время у за извѣстное;
находимъ
__2ай(4а — 6) — 3(я2 —62}у 4
Подставляя это выраженіе х въ ур—ніе (2), имѣемъ:
+ ,г + > + еХ..|^1->,^-ЭД = + + эд
Освобождаемъ это ур. отъ дробей, помножая обѣ его части на 5 (а2—62); найдемъ
5а2 (и2—— 5аЬ2с (а — Ь) -|- 2аЬа (а Ь -|- с) (4а—Ь) — 3 (а2 — Ь2) (а -ЬЬ
с) Ъу = 5, (а2 — &2) Ь^у ЪаЪ (а 4" 2Ь)(а2 — б2).
Перенося неизвѣстные въ первую часть, а извѣстные члены во вторую и вынося за скобки, найдемъ
[5а2(а2 — &*) — 3 (а2 - &2)(а + Ь^-с)Ь — 5 (а2 — Ь2) Ь2] . у =
5аЬ (а -р 2Ь)(а2 — &) (а — Ь) — 2аЬ2 (а-{- 6 -р с)(4а — і), жди
(а2—Ь2)[5а2—8Б2“ ЗаЬ—36с]^=а&(5а34“2а*і— 1 ІаІ2—За&с*—8й3—ЗЬ^с) откуда
Внося эту величину у въ формулу для я, найдемъ
278. Методъ сравненія величинъ,неизвѣстныхъ. Пусть требуется рѣшить уравненія
ах-^ Ьу “С ... (1)
а'х-[-Ь'у=с' . . ..(2).
Выражая изъ каждаго уравненія одно неизвѣстное черезъ другое, напр. х черезъ у. найдемъ:
с — Ъу /пч с'—Ъ'і) /о
• • • (3) и « = -а,- • • • (4)
Вставивъ въ (4) на мѣсто х его величину изъ (3), находимъ уравненіе
е-Ьу=с^# . .(5) а а '
которое вмѣстѣ съ (3) и составитъ систему, эквивалентную данной. Рѣшая (5)т найдемъ у; а подставивъ величину у въ (3), опредѣлимъ х.
Итакъ, надо доказать, что система уравненій (3) и (5) эквивалентна системѣ (1) и (2). Въ самомъ дѣлѣ,- перенеся Ьу и Ъ’у во вторыя части данныхъ ур—ній, найдемъ имъ эквивалентныя:
ах— с — Ьу . . . (Г) а'х = с'— Ь'у . . , (21).
Помноживъ (1') на и (2') на —и сложивъ, получимъ
с— Ъу______— Ь'у
а а'
(6).
а это ур. вмѣстѣ съ (Г), на основаніи начала втораго, можетъ замѣнить систему (Г) и (2'). а слѣдовательно данную. Умноживъ обѣ части ур—нія (Г) на 1 •
получимъ
с'— Ъ'у л
а перенеся--------—- изъ второй части ур—нія (6) въ первую, находимъ
Сѵ
— Ь'у _ с —Ьу а' а
ур—нія, эквивалентныя ур—мъ (Г) и (6). Такимъ образомъ данная система эквивалентна системѣ
с— бу
----~ И
а
с — Ьу сг — Ьгу а а'
требуемое доказано.
Примѣненіе этого метода, согласно началу II, требуетъ, чтобы а и а' были количества конечныя, отличныя отъ нуля; а рѣшеніе ур—нія (5) требуетъ кромѣ того, чтобы аѴ — а'Ь было отлично отъ нуля.
Изъ сказаннаго выводимъ третій пріемъ рѣшенія:
Выводимъ изъ обоихъ данныхъ ур—ній величину одною и того же неизвѣстнаго, напр. х и полученныя выраженія сравниваемъ; такимъ образомъ получаемъ одно ур. съ однимъ неизвѣстнымъ у, которое и опредѣляемъ. Внеся найденную для у величину въ одну изъ формулъ для х. находимъ и ото неизвѣстное.
Примѣръ. Рѣшить систему
5(4»+30=Й
Освобождаемъ ур—нія отъ дробей, и для этого множимъ обѣ части перваго на 4, а второго на 10. Находимъ: •
4лт-|- 2 (Згс —у — 1) = 1 4- 3 (V — 1),
2 (4я 4 Зу)= СУ + ’-О*
По перенесеніи членовъ и по упрощеніи, имѣемъ
ІО.г—0, или 2х — у = 0,
8х — у = 20.
Опредѣляя изъ каждаго ур—нія у, получаемъ:
у = 2х и у = &г—20. ♦
Сравнивая оба выраженія для- у, находимъ
2х = 8х — 20, или — 6х = — 20; откуда
20 10 О1
Ж=-6 = 3-=33-
Вставляя найденное для х число въ формулу у = 2х, найдемъ и— А 3 — з з
279. Методъ Везу. Этотъ методъ по существу одинаковъ съ методомъ уравниванія коэффиціентовъ или сложенія и вычитанія. Онъ состоитъ въ слѣдующемъ. Помноживъ одно изъ данныхъ уравненій на произвольнаго множителя, складываютъ съ нимъ или вычитаютъ изъ него другое, и получаютъ такимъ образомъ уравненіе, содержащее оба неизвѣстныя и произвольный множитель. Произволомъ послѣдняго пользуются для исключенія одного изъ неизвѣстныхъ, и слѣд. для полученія одного уравненія съ однимъ неизвѣстнымъ.
Приложимъ этотъ методъ къ системѣ
6а;+7# = 46. , .(1)
5х-|- 3?/ = 27 . . . (2).
Помножимъ первое ур. на произвольнаго множителя т и изъ полученнаго ур—нія вычтемъ второе (или, что тоже, придадимъ (2), помноженное на —1); получимъ
Ътх — 5х -|=- 7 ту — Зу = 46т — 27, или
(6 т — 5)х — 3)у = 46т — 27.
Это ур., въ'соединеніи съ однимъ изъ данныхъ, напр. съ (2), составляетъ, въ силу начала втораго, систему, эквивалентную данной. Такимъ образомъ вопросъ приводится къ рѣшенію ур—ній *
(6т — 5)х-р(7т — 3)у —— 27. . . (3) и
5.г-|-3і/ —27 . . . (4).
Произволомъ количества т воспользуемся для исключенія одного изъ неизвѣстныхъ, напр. у. Для этого опредѣлимъ т подъ условіемъ, чтобы коэффиціентъ при у обратился въ нуль, т.-е. чтобы
7т — 3 — 0 . . . (5).
Но значеніе т, обращающее 7т —3 въ нуль, есть корень ур—нія (5);
его найдемъ, рѣшивъ это ур.:
* 3
Подставивъ въ ур—ніе (3) ? вмѣсто т, получимъ ур. съ однимъ неизвѣстнымъ я, именно:
(6 • - — 46 • 3 _ 27, оТКуда а- — 3.
і
Подставивъ найденную для х величину въ ур. (4), найдемъ
5.34“3у— 27, откуда ^ = 4.
Приложимъ способъ Везу къ рѣшенію системы деухъ уравненій въ общемъ видѣ:
ах — Ьу — с ,
а'х -{- Ъ‘у ~ с\
Множимъ первое уравненіе на произвольнаго множителя т и вычитаемъ изъ него второе уравненіе; найдемъ
(ат — а') х 4“ (Ьт — Ь') у ~ ст —- с'.
Для исключенія у положимъ Ьт— 6' = 0, откуда т = у-Вставивъ это'значеніе т въ предыдущее уравненіе, получимъ
умноживъ обѣ части на Ь, находимъ:
(аЪ'~ а'Ъ)х=сЬ' — с'Ь, откуда х=^2.аЪ‘ а' а1
Для исключенія х, полагаемъ ат — а1 = 0, откуда величину т въ то же самое ур., имѣемъ:
вставивъ эту
умноживъ обѣ части на — а, получимъ:
(аЬ' — а'Ъ)у = ас’ — а'с, откуда у^
Полученныя формулы для х и у имѣютъ одинаковаго знаменателя, который легко получить, не рѣшая ур—ній, слѣдующимъ искусственнымъ пріемомъ: выписываемъ коэффиціенты при неизвѣстныхъ изъ перваго уравненія, и подъ ними пишемъ коэффиціенты втораго ур—нія:
Черт. 14.
затѣмъ перемножаемъ эти коэффиціенты на-крестъ, какъ указываютъ стрѣлки, причемъ въ произведеніи, взятомъ слѣва" на право, не измѣняемъ знака (это ука-
зииетеі шкогь а въ произведеніи вправо на лѣво перемѣняемъ знакъ на іртгшый (это указано знакомъ минусъ). Такимъ образомъ составится вы-ражею
аЬ’ — аЪ,
преістжЕЛжщее общаго знаменателя корней. Изъ знаменателя легко составить чи^гт-г-нй: для этого нужно только въ знаменателѣ коэффиціенты опредѣляема -совѣстнаго замѣнить извѣстными членами изъ соотвѣтствующихъ ур —ній; т.-. ті? составленія числителя неизвѣстнаго х нужно вмѣсто а в а* подста-вжтъ е в с', а для составленія числителя у, надо въ знаменателѣ буквы Ь и Ь' загѣммп» соотвѣтственно буквами с и Это правило составленія знаменателя чжлжтелей и извѣстно подъ именемъ правила Крамера (1704 — 1752).
Такъ, если имѣемъ ур—нія
7х -р 5у ~ 60
1&г—11у=10,
г* знаменатель рѣшеній найдемъ, составивъ табличку,
Черт. 15.
изъ которой имѣемъ: 7 , (—11) — 5^13.
Подставивъ въ это выраженіе вмѣсто 7 и 13 соотвѣтственно 60 и 10, и вмѣсто 5 и “И числа 60 и 10, найдемъ числителей: для х: 60. (—11)—5ХЖ а для у: 7.10 — 60X13. Итакъ: /
_60.(-Н) —5.10_ —660—50__ —710__ -
Х~ 7.(—М)—5.13- — 77—65“ —142 — Э’ — 7^0-60.13 _70-780 _ —710
У“7.(-И)—5.13“ —142 ~~- П2 —'"*
280. Всѣ четыре метода рѣшенія ур —ній имѣютъ одну и ту же цѣль: изъ двухъ уравненій съ двумя неизвѣстными исключитъ одно изъ неизвѣстныхъ и получить такимъ образомъ одно уравненіе съ однимъ неизвѣстнымъ, поэтому всѣ четыре методы суть методы исключенія.
Изъ всѣхъ четырехъ способовъ исключенія — способа уравниванія коэффиціентовъ самый удобный и всего чаще употребляемый; онъ ведетъ къ болѣе симметричнымъ вычисленіямъ; но неудобенъ, когда коэффиціенты при неизвѣстныхъ выражаются большими числами или десятичными дробями. Въ послѣднемъ случаѣ удобнѣе примѣнять способа этотъ же способъ удобопрп-
мѣнимъ и тогда, когда коэффиціентъ при одномъ изъ неизвѣстныхъ равенъ единицѣ, такъ какъ въ этомъ случаѣ выраженіе неизвѣстнаго черезъ другое не имѣетъ знаменателя. Способъ сравненія неизвѣстныхъ имѣетъ то неудобство, что, какъ и предыдущій способъ, вводитъ въ уравненія дроби; но при большомъ числѣ неизвѣстныхъ имѣетъ то преимущество, что дѣлаетъ рѣшеніе уравненій однообразнымъ. Наконецъ, способъ Везу имѣетъ скорѣе теоретическое, нежели практическое, значеніе.
ГЛАВА XX.
Рѣшеніе системы трехъ уравненій съ тремя неизвѣстными.
Опредѣленія. — Начала и методы.
281. Опредѣленія. Всякое ур. первой степени съ тремя неизвѣстными можно привести къ виду
ах 4~ Ьу — сх =
гдѣ а, М н суть нѣкоторыя цѣлыя количества. Если х^ у м должны удовлетворять только одному уравненію, то очевидно, что такое ур. будетъ неопредѣленно, потому что двумъ неизвѣстнымъ можно давать совершенно произвольныя значенія. Тоже самое будетъ и въ томъ случаѣ, когда три неизвѣстныя должны удовлетворять двумъ уравненіямъ. Такъ, система
ах + Ьу 4~ ся = (I
а'х 4- Ъ'у -\-с'г = <Г
неопредѣленна, потому что одному изъ неизвѣстныхъ можно давать произвольныя значенія: тогда система послужитъ для опредѣленія остальныхъ двухъ неизвѣстныхъ.
Но если неизвѣстныя должны удовлетворять тремъ уравненіямъ
ах -]- Ъу сг = И
ах Ь'у4”— $
+ =
то существуетъ, вообще, одна система рѣшеній, удовлетворяющихъ этимъ ур—мъ.
Двѣ системы называются эквивалентными, если онѣ удовлетворяю тся одними и тѣми же рѣшеніями.
282. Начало I. Система трехъ уравненій
А=О, В = О, С = О . . . (1)
эквивалентна системѣ ♦
А = О, рА + зВ = 0, УА4-^С = О . . . (2)
если количества р? ц, р1, конечны и отличны отъ нуля*
Въ самомъ дѣлѣ: 1) значенія неизвѣстныхъ, удовлетворяющія системѣ уравненій (1), обращаютъ каждое изъ выраженій А, В и С въ нуль; стало быть эти значенія обратятъ въ нуль и произведенія рА, #В, р'А и д'С, ибо р, д, р' и ц' конечны; слѣдовательно, величины неизвѣстныхъ, удовлетворяющія системѣ (1), удовлетворяютъ и системѣ (2).
2) Значенія неизвѣстныхъ х^ у, я, удовлетворяющія уравненіямъ (2), обращая въ пуль выраженіе А, обрятятъ въ ноль и рА и р'А, такъ какъ р ир' конечны; но эти значенія обращаютъ въ нуль суммы рАЦ-дВ и р'А 4-9^, а слѣд. они обращаютъ въ ноль и и #'С; но д н </ отличны отъ нуля, слѣд. В и С обращаются въ нули при сказанныхъ значеніяхъ неизвѣстныхъ. Итакъ, корни системы (2) удовлетворяютъ уравненіямъ системы (1).
Примѣчаніе, Можно выбрать ® и д7 такъ* чтобы уравненія
.рА + дВ = О и рА + д'С = О
содержали только два изъ трехъ неизвѣстныхъ; т.-е* люзюно исключитъ одно изъ трехъ неизвѣстныхъ изъ одного изъ данныхъ ур—нІй и каждаго изъ двухъ остальныхъ.
На этомъ началѣ основаны способы исключенія: чрезъ уравниваніе коэффиціентовъ* чрезъ нодстановлѳніе и чрезъ сравненіе величинъ неизвѣстныхъ*
283. Способъ уравниванія коэффиціентовъ* Пусть требуется рѣшить ѵр—нія
Зя — 2у + ^ = 13 - - * (1)
* 5х-|-4у — 3^ = 25 . . . (2)
Пя —бу —&г =24 * . * (3)
удобнѣе исключить изъ этихъ уравненій у* Для исключенія у изъ (1) и (2), множимъ
<2), множеннымъ на получимъ:
первое на 2 и складываемъ со
11*4-7^ = 51 . . . (4).
Вк/еымъ же образомъ* для исключенія у изъ (1) и (3)* множимъ (1) на — 3. (3) & — 1 и складываемъ: находимъ:
2х —23г = —15 • . . (5).
На освѵшіі начала I* система уравненій (1), (4) и (5) эквивалентна даи-ж<; и какъ уравненія (4) и (5) содержатъ только два неизвѣстныхъ я и то и опредѣляемъ изъ нихъ эти неизвѣстныя* Для этого множимъ (4) па 2, (5) на —11 и складываемъ; получаемъ
откуда
267# = 267,
2= 1.
Подставивъ вмѣсто 2 найденную величину въ ур- (5), имѣемъ
2а?—23= — 15, откуда 2х = 23 — 15 = 8, и слѣд*
х = 4.
Подставивъ въ ур* (1) найденныя для # и 2 величины, имѣемъ
12 — 2у-4-5 = 13, ^ткѵда
У = 2.
Итакъ, искомыя рѣшенія суть:
Я = 4; у=2; ^=1.
Легко убѣдиться прямою подстановкою ихъ въ ур—нія, что они дѣйствительно удовлетворяютъ даннымъ уравненіямъ.
— 2«0 —
284. Способъ подстановленія. Пусть требуется рѣшить уравненія
ат Ъу сг = сі.........(1)
а'х Ц- Ъ'у с'г = .... (2)
а''х 4- Ъ”у + с"з = Г . . . (3).
Принимая на-врсмя у и г за извѣстныя, рѣшаемъ ур. (1) относительно х:
а—Ъу — сг
л - - —8 1 -
а
. (4).
Подставивъ вмѣсто х это выраженіе въ уравненія (2) и (3), получаемъ: іу -сг) = . .(5)
а’’\а-ьі-^} +ъ„у с„г = й„. . _
РѣшаемъТуравненія (5) и (6) относительно у и 0. Освободивъ* ихъ отъ дро-бей и отъ скобокъ, имѣемъ:
* а'Л — а*Ьу — 4“ -|- = а&
а” (I— а"Ьу — а"с# Ч~ ас или
(аЬг — а'Ь)# 4" (ас — аф = — аг(1
(аЬ” — а"Ъ)у 4- (ас" - а"с> = аГ — а”<1 * Примѣняя формулы § 275, 6, имѣемъ:
__(шГ — а'ф (ас" — а"с) — (асР' — (ас* — а'с) ~ (а&* — а'б) (ас*' — а"с) — (аЪ** — а*Ъ) (ш/ — а'с)
(а&* — а'б)(ас" — а'*с) - (аЪ" — анЬ) (ас1 — а'с)
Раскрывая скобки въ знаменателѣ и въ обоихъ числителяхъ, получаемъ: для знаменателя выраженіе:
а2Ус" — ааЪс" - ™"Ь'с + М'Ьс - аѢ"с 4~ оаѴ + аа'Іі'с — а'а'Ьс; по приведеніи п по вынесеніи за скобки общаго множителя а, этотъ многочленъ принимаетъ видъ
а(аЪ'с” — а'Ьс" - а"6'с - <>Ъ'гс' 4- а"Ъс' 4- а'Ь''с) . . . (7).
Для числителя формулы у находимъ
а*с"Л* — аас'сі — аа"с& -|- — аРс'сГ 4~ 4” —* а*а^сс?т
или, вынося за скобки а:
а(ас"<? — а’с"(1 — « - ас'Г Цг а"с'гі + а'сй") . . .(8).
Раскрывъ скобки въ числителѣ форм у л ед получимъ:
аѢ'сГ _ аа'Ъ(Г — аа"ЬУ + а'Л — аѢ"(Т + аа”№ 4~ аагУ\1 ~ Мі,
или, по приведеніи и по вынесеніи за скобки а:
а(аЬ'<Г — а'Ы" — а"Ъ'а - аУ\Г аѴ + аТ/7?) . . . (9),
Внося выраженія (7), (8) и (9) въ формулы лля у н и сокращая па а, найдемъ:
__ас”(Іг — аѴ'</ — а^сЛ1 — а&А” + -(-а ’сй**
V ~ а&с" — (і'Ъс” — а%>с — аУ’сг + «,7Ь<У +
_ «У#' - а*Ъ&* — а(,№і — + а*'Мг +
* “ ’аЬГ — а'Ьс" — аѢ'с аЪ V + а"Ьс' + а’Ъ'1с *
Подставляя найденныя для у и выраженія въ уравненіе (4), находимъ
, Ь(ле"гі'—аѴТ/ - ае7Г+«'Ѵ^+а^Г) _ с^Ь'^^- а№г^агѴд—аЪ"аг +«''М'+д'Ь'^
__- аЬѴ-й'Ъс’+аТЛ;«Ь'с"—аЬ?<^^с—дЬ^^+а'Ьс^+лЪ^с
а
аЪ*с"(І—аЪс"<і—- ой"с'с^-Рб?7іс(<^а7УЧ'(і—йЬс'7Г+«'Ьс"гі Л-д'ЪЫ?
_ 4а6е'<Г'—а”№<1 - йб/^"-Н^ей"+а'г,ей-ьа6^Ы/- а"Ъс&— а'У'ей
~ а(а^г'- аЪс''^'ЪЪ—аб Ѵ+ а'Ъе'-ННГс)
Сгѣшъ яроекнй? і сокративъ на а, получимъ:
_ Ъ'с"(і — ІШ — 6<""сГ + ЬсТГ — 6гаГ + Ь”аГ Х ~ аУ е” - - а Ьс" — а'Ѵс — аЬ"с' + а"ЬУ -ь а'Ь"с ‘
285, Докажемъ теперь, что уравненія (4), (5) и (6) эквивалентны даннымъ.
Уравненіе (4) получено изъ (1) перенесеніемъ членовъ Ьу и во вторую
часть и дѣленіемъ обѣихъ частей на а, которое предполагается отличнымъ отъ
нуля; сл, это уравненіе эквивалентно (1)-му.
Помножая уравненіе
<і — Ъц — с^г ---------- = ІЕ а
на а' и складывая со (2), найдемъ, по упрощеній:
— Ьу — с^) 4- Ь^у -|- с #
Умножая то же самое ур, на а' и складывая съ (3), по упрощеніи найдемъ
(Л —Ьу —^) + Ь>+с^=й';
А, въ силу начала I, эти три ур—нія эквивалентны даннымъ: требуемое доказано.
286. Способъ сравненія величинъ неизвѣстныхъ.
Пусть требуется рѣшить уравненія:
5х - 2у + &г = 35 ... (1)
8 г 7у — 5^ — 67 . , . (2)
9т Зу4-2^ = 5Я. . .(3).
Опредѣляя изъ каждаго ур—нія причемъ я и у на-время считаемъ из-
вѣстными, найдемъ
лг =
. .(4)
—67-р8а?4-7у
5 і
58 — 9® -|- Зу
• (6).
Приравнивая первое выраженіе г поочередно — второму и третьему, получимъ:
35 — + 2у___— 67+8.г-|-7у 35 — 5®4“2у__58 — 9®-(-Зу
з — 5 3 — 2
уравненія съ двумя неизвѣстными х и у.
Докажемъ, что система уравненій: (4), (7) и (8) эквивалентна данной. Съ этою цѣлью перенесемъ въ данныхъ уравненіяхъ всѣ члены, за исключеніемъ содержащихъ лг, во вторую часть; такимъ образомъ найдемъ:
Зя = 35 — 5а? —|— 2у — 5^ = 67 — 8гг — 7у
2я = 58 — 9я -|- Зу.
Помножая первое изъ этихъ ур—ній на второе на и третье на — и сложивъ первое сначала со вторымъ, а потомъ съ третьимъ, имѣемъ:
Р_35 — 5я + 2у 67 — 8® — 7у
и“ 3 ”1 5
Л___35 — 5® + 2у 58 — 9® + Зу
° ~ 3 2 ’
или, по перенесеніи:
35 — 5® + 2у___— 67 Ц- 8® -н 7у 35 — 5®+ 2у______58 — 9® Зу
3 5 " 3 ~ 2
Эти два ур—нія, вмѣстѣ съ (4), па оси. начала I, составляютъ систему, эквивалентную данной. Освобождая ур—пія (7) и (8) отъ дробей, перенеся извѣстные члены въ одну часть, а неизвѣстные въ другую, и сдѣлавъ приведеніе, дадимъ имъ видъ *
— 49а;—Ну = — 376; 17ж —5у = 104.
Рѣшивъ эти ур—нія, найдемъ: х=7, а у = 3. Подставивъ эти числа въ ур. (4), найдемъ: 0 = 2.
287. Начало II. Система уравненій
А = О, В = О, С = О . . . (1)
эквивалентна системѣ
А = 0
В = 0
т X 4“ иВ 2>С = 0...........(2)
м?л т, п и ^“Яоличсстаа конечныя, отличныя оть нуля.
Въ самомъ дѣлѣ: 1) Всякое рѣшеніе системы (1), обращая въ ноль выраженія А, В и С, обратитъ въ нуль и выраженія тА, пВ и рС, такъ какъ множители т, п и р конечны; слѣд. рѣшеніе первой системы удовлетворяетъ второй.
2) Обратно: всякое рѣшеніе второй системы, обращая А и В въ нули, удовлетворяетъ первымъ двумъ уравненіямъ системы (1). Затѣмъ, при А = 0 и В — 0, произведенія тА и Вн также обращаются въ нули, потому что ш и п—кончены; но какъ разсматриваемое рѣшеніе обращаетъ въ нуль выраженіе тЛ 4~ пВ 4”РС, котораго два первые члена — пули; то и ^>С должно обращаться въ ноль; но р конечно, поэтому С должно обращаться въ ноль; т.-.е. рѣшеніе системы (2) удовлетворяетъ и третьему ур—нію системы (1).
На этомъ началѣ основанъ способъ Везу.
288. Способъ Безу. Способъ этотъ состоитъ въ употребленіи множителей, которые затѣмъ опредѣляютъ подъ условіемъ исключенія двухъ какихъ-нибудь изъ трехъ неизвѣстныхъ. Приложимъ этотъ способъ къ общей системѣ:
ах Ьу 4“ ••♦(!)
а'# 4~ Ь'у 4“ = * • • (2) а''^Ь''у4-с'^ = й'', . .(3).
Помноживъ ур. (1) па произвольный множитель X, ур. (2) на ц, а третье на 4“ Ъ сложимъ ихъ почленно; получимъ ур.
рл4_)ха/4“а^)ж4'0^4"іхЬ*4"^/)у4"0-с4_іхс,4“сг')-зг=*^+рі^,4’^ • • (^)-
Это ур., въ силу начала П § 287, можетъ замѣнить въ данной системѣ одно изъ трехъ уравненій.
Располагаемъ произвольными множителями X и и такъ, чтобы исключить изъ ур—нія (4) неизвѣстныя у и хг. Для этого, очевидно, надо, чтобы коэффиціенты при у и 2 обращались въ пули, т.-е. надо положить:
ХЬ + иЬ' + Ь" = О кЬ+рЛ' = -Ь"
АС 4-рс'4-С/' =0 ИЛИ АС -|- |іс' = — с" |
Значенія X и и, удовлетворяющія ур—мъ (5) найдемъ, рѣшивъ эти уравненія относительно X и и; примѣняя правило § 279, получимъ:
. _ Ъ’с” — сЧ»" _ сЪ" — Ъс"
к~ Ъс' — сЪ'1 И “ Ъс' — *
Подставляя эти значенія X и ц въ ур. (4), мы исключимъ этимъ самымъ у и я, и получимъ- ур—ніе съ однимъ неизвѣстнымъ х:
/Ь1с''—сЪ" . еЪ”-Ъс" , . ,Л Ъ'с" - сЪ" , . сЬн-Ъсг' г , 3„
\ Ъс — 1 Ъс — со ‘ / Ъс — сЬ' 1 ОС — сЬ 1 ’
откуда
Ф'С" — с'Ь") гі'+ (ей" - Ьс") (I' + {Ьс’ - сЬ')Л" х — (6'с" — с'Ь") а + (сЪ" ~ Ьс") а' + (Ьс' — сЬ')а"'
или, по раскрытіи скобокъ:
_ Же" — — Ы'сгт + е&ТГ
# аЪ'с** — са{Ьн — Ьа'<?г Ьс'а" — сЬ'л" *
Приравнивая въ ур—ніи (4) коэффиціенты при и пулю, найдемъ у; а опредѣливъ для а и ц такія значенія, при которыхъ обращаются въ нуль коэффиціенты при х и у. найдемъ г:
_ а(Гс” — ас’<і" н- сМ” -Ыс" + гіе'а" — сгі'а"
У ~ аЪ’с” — исЪ” + саѴ — Ъа+ Ма” — сЬ’а”'
а№ — — Ьа'<і''+Ь<і'а"— Ма"
аЬ’<Г - асЬ” + еа'Ъ" - Ъа'с" + Ъс'а" — сКа” *
289- Разсмотрѣніе общихъ формулъ предыдущаго параграфа приводитъ къ слѣдующему правилу механическаго рѣшенія трехъ ур—ній съ 3 неизвѣстными (такъ называемое правило Со/гроса).
Для составленія общаго знаменателя неизвѣстныхъ, выписываютъ коэффиціенты при неизвѣстныхъ изъ всѣхъ трехъ уравненій, и подъ ними еще разъ коэффиціенты изъ двухъ первыхъ ур ній; такимъ образомъ получается табличка:
Затѣмъ перемножаютъ выписанныя буквы наклонно: сначала слѣва направо, не измѣняя знаковъ этихъ произведеній (что указывается знакотъ 4“), а потомъ справа на лѣво, перемѣнивъ при каждомъ произведеніи знакъ (что указывается знакомъ — X Такимъ образомъ получается общій знаменатель искомыхъ рѣшеній:
аЪ'с" -р а'Ь”с + а”Ъс' — сЬ'а" - с'К'а - сѢа'.
Для полученія числителей пользуемся правиломъ Крамера: 1) для полученія числителя неизвѣстнаго х — нужно въ знаменатель вмѣсто коэффиціентовъ этого
- 265 —
О
неизвѣстнаго т.-е. вмѣсто а, а' а" подставить извѣстные члены изъ соотвѣтствующихъ ур—пій, т.-е. Л, сГ и <Г'; 2) неизвѣстнаго у—вмѣсто его коэффиціентовъ: 6, V и Ь” подставить гі' и 3)2наконецъ, неизвѣстнаго з — вмѣсто с, с и с" подставить А' и
II р и м ѣ р ъ. Примѣнимъ этотъ механическій пріемъ къ рѣшенію системы:
4х — 5у г = 6
1х— 11у 4“ 2^— 9 х-\- у-|-3г=12.
Общій знаменатель О составляемъ указаннымъ способомъ при помощи таблички:
Черт. 17. найдемъ:
В = 4.(—11).3-|-7.1.1+Н— 5).2 -1.(— 11).1—2.1.4—3.(—5).7
= -132-4-7 —Ю-р 11 -84-105 = —27.
Назвавъ числителей неизвѣстныхъ х, у и г, соотвѣтственно буквами К,, Я и найдемъ:
^ = 6(—11).349.1.1.4-12.(—5).2—12.(—11).1—2.1.6-3.(—5).9
= — 198-^9— 1204-132'— 12 4-135=— 54.
Хм=4.(9).3 4- 7.12.1 4-1.6.2 — 1.9.1 — 2.12.4 — 3.6.7
”= 108 4-844- 12 — 9 —96 — 126 = —27.
И.= 4(—11).12-}-7.1.6-|-1.(—5).9—1.(—11).6—9.1.4—12.(—5).7
‘=—5284-42 —45 4-66 —36 4-420= —81.
Итакъ:
И, —54.. ___Кт»_ — 27, —81 „
х~ I) ~ — 27 ’ О - — 27~1; г~ О 27 '3'
ГЛАВА XXI.
Рѣшеніе системы уравненій первой степени съ какимъ угодно числомъ неизвѣстныхъ.
Общій методъ.—Методъ Безу*Жергонна.—Случаи упрощенія; искуственные пріемы.— О системахъ ^уравненіи, въ которыхъ число неизвѣстныхъ но равно числу уравненій: случаи несовмѣстности (условныя уравненія) н неопредѣленности.
Общій методъ.
290. Начало. Пустъ дана система р уравненій первой степени съ р неизвѣстными:
А = 0, В —0, С — 0, і> = 03 , . , К —0т . . . (1)
тя, »я, . . . , Мр-і суть количества конечныя и отличныя отъ пуля, то система р уравненій
А —О, ’
г?г1А-)-м1В = О, паС = О,
тр-}А Пр_іЬ — О
эквивалентна данной, •
Въ самомъ дѣлѣ: 1) рѣшенія системы (1), какъ обращающія въ нули выраженія А,Г_В, С, . . . , К, Ь, обращаютъ въ нули и произведенія т^, пгр, тяА, п3С, ♦ . . , ир-]Ь, такъ какъ количества т^ м1, . . . конечны; слѣд. эти^рѣшепія удовлетворяютъ системѣ (2).
2) Рѣшенія системы (2), обращая въ нуль А и (ю^А обращаютъ въ нуль и В, такъ какъ конечно, и отлично отъ пуля; такимъ же образомъ они обратятъ въ нуль и С, I), . . . Ь; слѣд. эти рѣшенія удовлетворяютъ [системѣ (1).
291. Методъ. Количества тЛ, , тР-і, выбираютъ такимъ
образомъ, чтобы исключить одно и то же неизвѣстное изъ (р — 1) уравненій, напр. изъ послѣднихъ; такимъ образомъ данная система (1) замѣняется новою:
А —0, Ві=0, С\=О, В1 = 0, . . .,^ = 0,^=0. . . (3)
эквивалентною съ (1); но въ ней ур. А = 0 содержитъ всѣ неизвѣстныя, а остальныя р — 1 уравненій содержатъ только р — 1 одинаковыхъ неизвѣстныхъ.
Подобнымъ же образомъ систему (3) замѣняютъ системою
А = 0, В1=О, Ся = 0, , Кя—О, ЬЯ = О ... (4)
эквивалентною съ (3), а слѣд. и съ (1); по въ этой новой системѣ уравненіе А = (У1 содержитъ всѣ неизвѣстныя. ВА — О только р—1 неизвѣстныхъ, а остальныя уравненія содержатъ однѣ и тѣ же неизвѣстныя въ числѣ р~ 2.
Продолжая такимъ же образомъ, достигнемъ наконецъ того, что данная система будетъ замѣнена новою, ей эквивалентною системою
А —О, В, =ОТ Са = 0, Й3“0..........нр-з = 0, Кр_2 = О, Ьр-і^О,
въ которой уравненіе Ьр_х = О содержитъ только одно неизвѣстное, Кр_г = 0 содержитъ это же самое неизвѣстное и еще одно, Пр_з = О содержитъ эти два неизвѣстныя и новое, и т. д., наконецъ ур. А = 0 содержитъ всѣ неизвѣстныя.
Рѣшивъ ур. Ьр-і = О, опредѣлимъ то неизвѣстное, которое въ немъ содержится. Внеся его величину въ ур. = 0, найдемъ изъ него еще одно неизвѣстное. Внеся величины этихъ двухъ неизвѣстныхъ въ ур. Нр_з=0, найдемъ третье неизвѣстное, и т. д. Всѣ неизвѣстныя будутъ послѣдовательно найдены.
Примѣръ. Рѣшить уравненія
1)
2)
3)
4)
5)
Зж — 4у-|-Зя + Зѵ — 6ы=11
Зя — -р 2я — 4« — 11
ІОу -- Зя—2ѵ 4^ Зе* = 2
— 2л? ♦ 4’ 5^ 2и 4“ 4« “ 3
— 2у — -р 6м = 6
Исключаемъ изъ данныхъ уравненій неизвѣстное для этого комбинируемъ ур. (1) съ каждымъ изъ остальныхъ, за исключеніемъ (3)т которое уже не содержитъ х. Вычтя (2) изъ (1). находимъ:
1/4^4 ~ О-
%
Помноживъ (1) на 2, а (4) на 3, и сложивъ ихъ, имѣемъ
—► -р 12і? =31.
Наконецъ, умноживъ (1) на 4, а (5) на —3, и сложивъ, получимъ:
— 10^4- 12-аг — 42«-|- 211? = 26.
Такимъ образомъ, на основаніи общаго начала, замѣняемъ данную • систему ей эквивалентною:
1) Зж— 4і/4“ *^4~ 6м = 11
2) ^4“ я 4“ -— 2^=0
3) _ 8у + 21^4- 12ѵ =31
4) — 10р-Рш4-2й —42и=26
5) Юу— 3#<— 2^4“ Зі*= 2
п.
Исключаемъ теперь у изъ (2) уравненія системы II и каждаго за нимъ слѣдующаго; для этого множимъ ур. (2) на 8 и складываемъ съ (3); затѣмъ множимъ (2) на 10 и складываемъ съ (4); наконецъ, помноживъ (2) на 10, вы-
читаемъ изъ него (5), Такимъ образомъ найдемъ систему III, эквивалентную II. а слѣдовательно и предложенной:
♦ Зл? — 41/ 4~ з* 4 - З у 6« “ 11
у Ч- *4 Зѵ — 2я = О
29г ч -36ѵ- 16« — 31
22*4" ^Ір — 62н = 26
ІЗгЧ Р32с — 23» = о
ПІ.
Исключая я изъ трехъ послѣднихъ уравненій, найдемъ:
Зх — 4^ "Р 3* 4~ Зг — би — 11
у -|- * + Зу — 2» = О
13*-}- 32г?— 23м . = — 2 IV.
— 46Оѵ + 459м = 461
41г-|-300» = —382 ;
систему, эквивалентную данной*
Исключая наконецъ « изъ послѣднихъ двухъ уравненій системы IV, находимъ эквивалентную ей систему:
I) 3^—41/4" 3*4"
2) $/4“ Зѵ
3) 13*4“ 32ѵ
4) 4-41ѵ
5)
— 6и= 11
— 2м — О
— 23» = — 2 V.
4- зоо»=
— 382
156819ѵ = — 313638
Послѣднее ур. этой системы прямо даетъ: ѵ =— 2. Подставляя вмѣсто ѵ число —2 въ ур. (4), находимъ: « = —I. Подставляя найденныя для и и ѵ величины въ ур. (3), находимъ: * — 3. Наконецъ, изъ втораго и перваго ур. получаемъ: і/=1 и х=2.
Методъ Бѳзу, измѣненный Жергонномъ.
292. Начало. Если 2, у, . . . , л суть количества конечныя и отличныя отъ нуля, то уравненіе
оі А + В 4" уС 4* ‘ “Ь ~ ®
можетъ замѣнитъ одно изъ п уравненій системы
А=О, В = О, С = О, . . . , Ь = О, т.-е. системы
А = О я А 4" гН уС 4" - * ’ "і“ = о
В—о ‘ ‘ В = О
с = о
І О II
ь = о давндемеятиы.
Въ самомъ дѣлѣ: 1) всякое рѣшеніе системы I удовлетворяетъ уравненіямъ системы II, такъ какъ В, С, . . . , Ь, а также и сумма аА4?^4 * . * 4*^ обращаются въ нули; 2) обратно, всякое рѣшеніе системы П, обращая въ нуль выраженія В, С, * . • Ь, удовлетворяетъ всѣмъ уравненіямъ системы 1, кромѣ ур—пія А = О; а обращая въ пуль, вмѣстѣ съ выраженіями В, С, . . . , Ь, также и выраженіе аА 4 ?В 4? уС 4 - * • 4*^» приводитъ первое ур, системы II къ виду зА = 0, откуда и Л = 0, ибо а отлично отъ нуля,
293. Примѣняя это начало, Везу употреблялъ столько неопредѣленныхъ множителей. сколько неизвѣстныхъ безъ одного; так, обр. для рѣшенія п уравненій съ п неизвѣстными онъ бралъ я — 1 множитель (такъ, въ случаѣ двухъ ур —ній вводилъ 1 множитель, въ случаѣ трехъ ур—ній — 2 множителя и т. д.). Жергоннъ вводитъ столько множителей, сколько неизвѣстныхъ. При этомъ, вычисленія остаются такія же какъ и у Везу; но, приравнивая нулю п —1 коэффиціентъ, получаемъ п—1 ур—ній, которыя служатъ для опредѣленія уже не самихъ множителей, а отношеній п — 1 множителей къ какому-либо одному изъ нихъ.
Въ этомъ Жергонновскомъ варіантѣ способа Везу вычисленія симметричнѣе; кромѣ того, пользуясь этнмъ методомъ, легко избѣгаемъ такихъ случаевъ, когда способъ Везу оказывается непримѣнимымъ. Вотъ примѣры.
Примѣръ I. Рѣшить систему
4 Зу — я — 9 4л'4 бу — 3^— 14 5х— 2у-|-2я=И2.
Попробуемъ сперва примѣнить методъ Везу. Помноживъ І-е ур. на X, 2-е на р, сложимъ ихъ съ 3-мъ; получимъ
(2). 4" 4"И 4 4- — -) У — 0' + — 2) & — 9), 4“ 14)1 4~ і •
Приравнивая нулю коэффиціенты при % и у, имѣемъ
(1) 2к + 4?і + 5 = О, (2) 31 + би - 2 = 0, и (3)
Для опредѣленія X и |і. рѣшаемъ ур—нія (1) и (2), и для этого уравниваемъ коэф-ты при X; так. обр. найдемъ
6Х-]-12р=—15 и 6а4-12|а = 4,
а это — система несовмѣстная, ибо первыя части равны, а вторыя различны. П однако, данныя ур—нія представляютъ систему совмѣстныхъ уравненій.
Примѣнимъ теперь способъ Жергонна, умноживъ и 3-е ур—ніе на найдемъ:
(3) 214-4-1 + 5^ = 0, (4) 31 + 6^1-2ѵ = 0 и (5)
Изъ ур—ній (3) и (4) найденъ отношенія т и у; имѣемъ
= — 2- 6^—2* = — 3, откуда ? = — 1 и т —О,
А * А А А 7 11 А 4 А 7
и слѣдовательно
Подобнымъ образомъ найдемъ: а? =2, у = 3-
Здѣсь, какъ легко видѣть, способъ Жергопна сводится къ перестановкѣ множителей Везу въ другія строки; но какъ вначалѣ нельзя предвидѣть невозможности, которая обнаруживается вычисленіями лишь впослѣдствіи, то понятно, что пользованіе варіантомъ Жергопна имѣетъ преимущества. Въ самомъ дѣлѣ, легче перемѣнить множителя, по отношенію къ которому ищемъ отношенія другихъ множителей, нежели, слѣдуя методѣ Везу, начинать сънзнова всѣ вычисленія.
Примѣръ П. Рѣшить систему уравненій:
а:—[—2у-|— 3*4"4« = 27 (1) Злг ——|— 7я-|“ ы = 48 (2) 5х -|- 8у + — 2и = 65 (3)
7л?—бу—|— 5^-|-4и = 53 (4).
Помноживъ первое ур. на т, второе на п, третье на р, четвертое на д и сложивъ ихъ, найдемъ:
(т4“3и4"5р4-7д)д;-|-(2?п-|-5м-|“82) 4“ 6^)у 4“ (Зт 4“ 1п Юр -|- 5д)я 4~ — 2р4~4д')«= 27т-|-48пЦ-65р-|-53<? . . . (5).
Приравнивая пулю коэффиціенты при х, у и я. находимъ первую вспомогательную систему уравненій:
(6)
(7)
т Зн 4~ 5р 7# = О 2ж 4~ —|— “|— 6*2 И Зт4~ 7п4~ Юр 4“ = О
г
И
27т + 48н + 65р 53д
4ш 4- п — 2р4~ 4д
Опредѣлимъ отношенія р и д къ п. Система (6) дастъ:
т_____ 17 р______~ ___1
п 8 ’ п 1 п 8
Подставивъ эти величины въ уравненіе (7), получимъ: м =2.
Подставивъ найденную для и величину въ первыя три изъ данныхъ уравненій, найдемъ систему уравненій съ тремя неизвѣстными:
л?4"2у4“ Зя= 19 (8)
Зх 4~5у4- 7^=46 (9)
5я?4-8у 4- 10^ = 69 (10).
Умноживъ первое изъ этихъ уравненій на г, второе на 5, третье на і и сложивъ ихъ, имѣемъ:
(г4_3^4.5^4_(2г4-5я+8^)у4-(Зг4-754-100^=19г4-4б54-69С . . (11).
Приравнивая нулю. коэффиціенты при х и у, получаемъ другую вспомогательную систему уравненій:
г 4-35 4-5^ = 0
(12) 2г -|- 5л 4- 84 = О
и
_ 19г 4-465 + 694
* ~ “374-75 + 104
Опредѣляя изъ системы (12) отношенія т и находимъ: ^ = 1, у= — 2.
Подставляя эти значенія и въ формулу для находимъ: # = 4.
Подставивъ найденную для я величину въ у—нія (8) и (9), имѣемъ
х-)- 2у = 7 . 3#-|- 5у = 18 .
.(14)
. (15).
Умноживъ (14) на «, (15) на ѵ и сложивъ ихъ. имѣемъ
(іі-ф-ЗгО^Ч- (2«Ч-5іг)у = 7 и Ч~ 18ѵ.
іі > «у п л и
Положивъ « —Зс = 0, откуда - — — 3, и подставивъ это значеніе - въ
7.-—" 18
ур—« У= *-------------, найдемъ: у = 3.
2.“4- 5 г ♦
ІЬктавявъ 3 вмѣсто і/ въ уравненіе (14), найдемъ: х= I, ’ •
294, Случаи упрощенія. Изъ предыдущаго видно, что процессъ рѣшенія опин уравненій вообще довольно сложенъ, особенно если число неизвѣстныхъ у Но иногда его можно упростить; случаи для упрощенія ф представляются тв. когда не всѣ неизвѣстныя входятъ въ каждое уравненіе, или же когда ууожжія представляютъ нѣкоторую симметрію по отношенію къ неизвѣстнымъ.
Когда не всѣ уравненія содержатъ всѣ неизвѣстныя, тогда начинаютъ съ жименія того неизвѣстнаго, которое входить въ наименьшее число уравненій, й тѣ уравненія, въ которыя это неизвѣстное не входитъ, можно считать рѣ-зтіьтатажи его исключенія.
Примѣръ I. Рѣшить систему уравненій >
2х —5я-|-4м = 7
— уЧ~ б# — з# = з
— 7^4'4!/ =10
— 5я Ч-* = -0.
Исключая и, которое входитъ только въ первыя два уравненія, получаемъ ур—ніе
— 4у Ч- — зз,
которое вмѣстѣ съ уравненіями
— У Ч- З'И~ 3
— 7#Ч“ 4у = 10
— 5ж -}- 6я =20
составляетъ систему, эквивалентную данной.
Исключая во второй системѣ у изъ перваго и третьяго уравненій, получаемъ систему
— у -|~ 6* — Зы = 3
— х + 9л =43
— 7х Ч~ 4у =10
— эх -4" 6л =20
эквивалентную второй, а слѣд. и данной.
Исключая въ ней х изъ втораго и четвертаго уравненій, находимъ эквивалентную данной систему:
— уЧ" — Зм= 3
— 7^ + 4у -= 10
— я 9я =43
394? =195.
Изъ послѣдняго^уравненія находимъ: я ~ 5. Вставивъ вмѣсто я его. величину въ третье уравненіе, найдемъ: х = 2; затѣмъ изъ втораго урав. получимъ: у = 6; наконецъ, изъ перваго: « = 7.
Примѣръ II. Рѣшить систему уравненій
х-^-2у= 5. у-рЗг = 11. ^-|”4«= 19. м-|-5* =29.
-|- 6х = 11.
Выражая изъ пятаго уравненія і черезъ х, имѣемъ: I = 11 — 6х. Вставляя вмѣсто і его величину въ четвертое ур., получимъ: и — 29 — 5(11 — 6х) = — 26ЗОх. Вставляя вмѣсто и полученную величину въ третье ур., найдемъ: ^“ 123— 120я. Подобнымъ же образомъ, изъ второго ур. имѣемъ: у = — 358 + 360а?. Вставивъ вмѣсто у найденное выраженіе въ 1-е ур., найдемъ изъ него: а?=1. Всѣ остальныя неизвѣстныя выражены черезъ а потому ихъ легко теперь вычислить. Найдемъ: у = 2, #=3, «=4 и ^=5.
Примѣръ III, Рѣшить систему уравненій:
х ч~ у ч~ Ч- ® у -[ Ч* * 4“ * я ч-иЧ~* Ч”а;=с н Ч~ Ч- Ч~ у $ і ч~яЧ”У Ч-=€>
Въ этой системѣ неизвѣстныя входятъ симметрично ~ каждое одинаковое число разъ; это обстоятельство позволяетъ найти сумму всѣхъ неизвѣстныхъ: для этого стоитъ только сложить всѣ уравненія и результатъ раздѣлиться 4, Такимъ образомъ получимъ
। і . । _а “і- Ъ с ”4” е 1 ч
* + у + + * = —І7Г--- Л1)'
А какъ въ каждое‘уравненіе не входитъ по одному только неизвѣстному, то, вычитая изъ уравненія (1) послѣдовательно каждое изъ данныхъ, опредѣлимъ всѣ неизвѣстныя. Получимъ:
, 6 4-с + й + е — За
г =-------------------?
а с-ь+ е — 36 ___ ~ •
а ч-д 4- — Зс
——1 *
4
а + с ~Н
4
и =
а + 6 + с + <і — Зе
“ 4
Здѣсь сумма всѣхъ неизвѣстныхъ, съ опредѣленія которой мы начали, пред-сгажша вспомогательное неизвѣстное^ позволившее скорѣе опредѣлить каж-ж неизвѣстное въ отдѣльности. Вотъ еще примѣры употребленія вспомогательныхъ неизвѣстныхъ.
Примѣръ IV. Рѣшить систему уравненій
а । Ъ
—і----------=с
я? + у 1 х — у
-т- + —= Г-
X + у 1 X — у 1
Освобождая уравненія отъ дробей, мы нашли бы уравненія, въ которыхъ иѣжгглрые члены содержали бы вторыя степени неизвѣстныхъ; но легко избѣ* жжтъ полученія уравненій второй степени, введя вспомогательныя неизвѣстныя, и иеннэ полагая:
X + у ’ X — у
Ішшя уравненія примутъ видъ:
ам-{- ді/ = с,
(Іи -[-еѵ = /.
Рѣши ихъ, найдемъ:
се — Ы а[— с(і
—А и ѵ= - -т/
ае—Ъа ае —Ьа
Подставивъ вмѣсто и о игъ выраженія черезъ а; и у, найдемъ
1 ___се —
х-\-у~ ае — Ы и
откуда
ае — М се — Ь/'
<іе — ЬЛ
И # — у = —г-------------у
17 «/ — €</
Сначала складывая, а потомъ вычитая эти ур — нія, найдемъ:
___1 ( ае — Ьі.1 । ле — і ____________1 / л<? — Ь*1 ае — Ъ(1 I
Х 21 се — Ь[ + а/ — аі І и 21 ее — Ъ/ а/ — еЛІ
Примѣръ V. Рѣшить систему уравненій
ах + т{у + # + и) = 1
Ьу 4~ -|- и -|- #) =
сз -|- ?п(и 4" х 4" ,Ѵ) — 7 (іи 4- ~4 У 4“ =
Введемъ вспомогательное неизвѣстное, положивъ: #4“?/4“^Ч_ и — §; дкн-ныя уравненія примутъ видъ:
ах ~4^ (8 — я) =а
Ьу + ?п(8 — у) = ег 4~т(8 — 4) =7
4- мг($ — и) = Й.
Выводя изъ перваго ур—нія я, изъ второго у и т. д., найдемъ:
а — ж8
Х =-------э
а — ш
7 — эті8 е —
Складывая почленно эти уравненія и замѣчая, что въ первой чается я4-'у4'^~Ни вли найдемъ*
части полу-
а — ж8 _|_ ? — г Т “* < — м8
а — м ' Ь — т -"г е — т еі — ж
Изъ этого уравненія, первой степени относительно 8, найдемъ это вспомогательное неизвѣстное; зная его, изъ уравненій (1) найдемъ у, я и и.
Приведемъ еще примѣры искусственныхъ пріемовъ, облегчающихъ рѣшеніе уравненій.
Примѣръ VI. Рѣшить систему травпсчіГі:
___1.
ау-\-Ьх с ’
ах + га
1 ___сс/
я “ у ле — М'
р — пі8 Ь— и* ’
и =
о —
(і — ш
1
6^ су а
Обращая дроби, найдемъ:
Складывая эти уравненія й обозначая, для краткости, сумму черезъ 28, находимъ '
а ।. Ь . с_____$
Вычитая отсюда поочередно
каждое изъ предыдущихъ уравненій, находимъ:
ттіа
а Ъ с
&"— о ~ — о ? л? —- ~ *
о /Т о 0 л — с
(
Примѣръ VII. Рѣшить систему уравненій:
4~ ау -|- ~р а3 = 0. я 4” Ъу 4~ -|- Ь3 = 0.
-|- су сЪ; —|— с® = 0.
Можно бы было рѣшить эти уравненія способомъ исключенія черезъ сложе-ше і іычѵтше, во проще употребить слѣдующій искусственный пріемъ, предло-анні Бшж (17^6—1856). Данныя уравненія выражаютъ, что полиномъ
х> + хх’4- ух-н
ііцтігтгі къ нуль врі подстановкѣ вмѣсто X количествъ М н с; слѣд. онъ Литсм на проізведевіе (X — а) {X — 6) (X — с), причемъ частное равно 1, •ктммт что первый членъ дѣлителя есть X3. Итакъ, имѣемъ тождество:
Хэ +^Х2 4-уХ -р г = (X — а) (X — 6) (X — с),
кж. во раскрытіи произведенія:
X* 4“ “Ь ^х Ц- = X3 — (а 4^ Ъ с)Х2 4“ (а& 4“ ас 4” аЬс,
гтхуда, приравнивая коэффиціенты при одинаковыхъ степеняхъ X, находимъ:
— (« + &4"€’); у“аі4”ас4“^ & — ~аЬс.
295. О системахъ уравненій, въ которыхъ число неизвѣстныхъ не равно числу уравненій. Когда число уравненій равно числу неизвѣстныхъ, то система имѣетъ, вообще, одно опредѣленное рѣшеніе. Разсмотримъ теперь случаи, когда число неизвѣстныхъ не равно числу уравненій.
296. Теорема. Система уравненій, которыхъ число меньше числа неизвѣстныхъ, неопредѣленна.
Пусть имѣемъ т уравненій, содержащихъ т 4-р неизвѣстныхъ. Можно дать произвольныя значенія р неизвѣстнымъ; тогда получится система ш уравненій, взъ которой опредѣлятся остальныя *и неизвѣстныхъ. Слѣд., система имѣетъ безчисленное множество рѣшеній, что выражаютъ однимъ словомъ, говоря, что система неопредѣленна.
297. Теорема. Система уравненій, число которыхъ больше числа неизвѣстныхъ, вообще невозможна.
Пусть число уравненій превышаетъ число неизвѣстныхъ; пусть, напр., имѣемъ т -\~р уравненій съ т неизвѣстными. Взявъ т изъ числа данныхъ уравненій, въ которыя входили бы т неизвѣстныхъ, и рѣшивъ ихъ, опредѣлимъ эти т неизвѣстныхъ. Если окажется, что найденныя величины удовлетворяютъ и остальнымъ р уравненіямъ, то заключаемъ, что система имѣетъ одно опредѣленное рѣшеніе. Если же окажется, что значенія, найденныя для т неизвѣстныхъ, не удовлетворяютъ остальнымъ р уравненіямъ, это будетъ значить, что система не имѣетъ рѣшеній; въ такомъ случаѣ говорятъ, что она невозможна, или что уравненія несовмѣстны.
Примѣръ I. Рѣшить систему трехъ уравненій съ двумя неизвѣстными:
3&4- 2у — 5=0 7х — Зу 4~ 2 = 0 — х -|- 7 у — 12 = 0.
Рѣшаемъ послѣднія два уравненія и находимъ, что имъ удовлетворяютъ: 11 41 „ .
х = 23 и ~ ^3* Вставивъ эти величины въ первое уравненіе, замѣчаемъ,
что оно обращается въ тождество. Слѣд. система возможна и имѣетъ рѣшеніе:
11 41
х~ 23? у 23*
Примѣръ П. Рѣшить систему
6# -|- 7 у = 46
4~ Зу = 27 х— 2у = 14.
Первыя два уравненія имѣютъ рѣшеніе: ж = 3, у = 4. Но эти значенія не удовлетворяютъ третьему уравненію, слѣд. предложенная система несовмѣстна.
Когда число уравненій превышаетъ число неизвѣстныхъ, и ур—пія имѣютъ буквенные коэффиціенты, то можно предложить себѣ вопросъ: при какой зависимости между коэффиціентами найденныя для т неизвѣстныхъ величины будутъ удовлетворять и остальнымъ уравненіямъ? Эти р условій обыкновенно называютъ условными уравненіями.
Примѣры:!. 4^ 7^ — 46, 5#4-Зу = 27, ах-{-2у = 14.
Первыя два уравненія удовлетворяются при х=3 и у = 4.
Для того чтобы всѣ три уравненія были совмѣстны, необходимо, чтобы тѣ же значенія х и у удовлетворяли и третьему уравненію, т.-е. чтобы существовало тождество
За8 = 14, откуда а =2.
Итакъ, система совмѣстна при а = 2.
II. ах 4- Ьу 4~ с — 0; а'х Ь'у 4~ с/ = Ф а"х 4- 4“ с” = О*
Рѣшая первыя два уравненія, найдемъ:
____Ъс' — сЬ' ______са1— ас' Х аЪ'— Ъа’3 У аЬг—Ъаг
Для того чтобы система была совмѣстна, необходимо, чтобы тѣ же рѣшенія обращали въ тождество и третье уравненіе, т.-е. чтобы (по освобожденіи отъ знаменателя)
а"(Ьс' — сЬ') + Ъ"(са' — ас') + с"(аЬ' — Ьа') - - О, или
аЪ'с" — ас’Ь" + са'Ь” - Ьа'с” + Ъса" — сЪ’а” = О.
Легко видѣть, что первая часть этого условія есть ничто иное какъ знаменатель значеній неизвѣстныхъ, удовлетворяющихъ тремъ уравненіямъ съ 3 неизвѣстными въ общемъ видѣ.
III. Пусть даны шесть уравненій съ 3 неизвѣстными:
* + у-\- г= 9
Зл: — у -\-2#= 10
7у — 3^ = 8
ах— Ьусг = 20
ах Ьу + = 44
Юах 4- ЗЬу — сг = 26
и требуется опредѣлить, при какихъ значеніяхъ коэффиціентовъ а, Ь и с эти шесть уравненій будутъ удовлетворены одними и тѣми же значеніями неизвѣстныхъ.
Рѣшивъ первыя три уравненія, не содержащія а, Ъ и с, найдемъ: х=1, і/ = 3, ^ = 5. Эти величины должны удовлетворять тремъ послѣднимъ уравненіямъ, т.-е. должны существовать равенства
а — ЗЬ 4~ 5с = 20
а -|- ЗЬ -|“ 5с = 44
10а -|- 9Ь — 5с = 26.
Рѣшивъ эти уравненія относительно а, Ь и с, находимъ, что они удовлетворяются при а = 2, Ь = 4, с = 6; при этихъ значеніяхъ коэффиціентовъ шесть предложенныхъ уравненій совмѣстны.
ГЛАВА XXII.
Составленіе уравненій со многими неизвѣстными.
298. Когда задача требуетъ нахожденія нѣсколькихъ неизвѣстныхъ, то для рѣшенія ея нужно имѣть столько различныхъ условій, сколько есть неизвѣстныхъ. Обозначая каждое неизвѣстное особою буквою, и выражая каждое изъ условій особымъ уравненіемъ, мы получимъ систему опредѣленныхъ уравненій, рѣшивъ которую и найдемъ искомыя неизвѣстныя,
Когда въ подобныхъ задачахъ встрѣчается нѣсколько неизвѣстныхъ, то при составленіи уравненій можно поступать двоякимъ образомъ: или можно привести задачу къ составленію одного уравненія съ однимъ неизвѣстнымъ, выражая всѣ неизвѣстныя черезъ одно, или къ нѣсколькимъ уравненіямъ, если каждое ненз-вѣстное обозначить особою буквою. Выражая всѣ неизвѣстныя черезъ одно, мы въ сущности дѣлаемъ въ умѣ исключеніе нѣсколькихъ неизвѣстныхъ; но этотъ пріемъ, сокращая вычисленія, усложняетъ и затрудняетъ составленіе уравненія. Въ виду этого, за исключеніемъ самыхъ простыхъ вопросовъ, слѣдуетъ каждое изъ неизвѣстныхъ обозначать особою буквою и каждое условіе выражать отдѣльнымъ уравненіемъ. Приводимъ примѣры.
Примѣръ I. Изъ трехъ слитковъ, сплавленныхъ изъ золота, серебра и мѣ^и:
первый содержитъ 50 гр. золота, 60 гр. серебра и 80 гр. мѣди;
второй ѵ 30 > » 5о » » 70 > з>
третій > ,75 » » 65 » » » »
По сколько нужно взять отъ каждаго слитка, чтобы составить четвертый, который содержалъ бы 79 ф, золоти, 118 гр. серебра и 162 гр. мѣди?
Пусть отъ перваго слитка нужно взять ф гр., отъ второго у, а отъ
третьяго я.
Первый слитокъ, согласно первому условію, содержитъ всего 50 -|- 60 80
или 190 гр. На эти 190 граммовъ приходится 50 гр. золота; слѣд, на 1 гр.
50 5
сплава приходится у^д или грамма золота, а стало быть въ х граммахъ, взя-тыхъ отъ перваго слитка, содержится уд х гр. золота. На тѣ же 190 гр. слит-ка приходится 60 гр. серебра, слѣдов. на 1 гр. слитка приходится у^д или уд , 6 , грамма серебра, а въ х граммахъ этого слитка содержится уд х гр. серебра.
Такимъ же точно образомъ убѣдимся, что въ я гр., взятыхъ отъ перваго слитка, г. 8
мѣди содержится уд х граммовъ.
По второму условію, второй слитокъ содержитъ 150 граммовъ, въ томъ числѣ 30 гр. золота, 50 гр, серебра и 70—мѣди. Разсужденія, подобныя вышеприведеннымъ, покажутъ, что въ у граммахъ, взятыхъ отъ этого слитка, содержится
3 5 , 7 ,
гр. золота, у^у гр. серебра и у~у гр. мѣди.
Наконецъ, согласно третьему условію, третій слитокъ содержитъ 190 гр., изъ которыхъ: 35 гр. золота, 65 гр. серебра и 90—мѣди; слѣд., въ я граммахъ, взятыхъ отъ этого слитка, содержится
35 65 . 90 г
Уэдя гр. золота, удд^ гр. серебра, у^д^ гр. мѣди.
Все количество золота, входящаго въ сбставъ четвертаго слитка, выражается формулою
5 । 3 , 35
15^ ‘190 * г₽>:
полное количество серебра—формулою 6 I 5 । 65
19^^ 15 190^ Гр<;
а количество мѣди равно + + гр-
Но по условію, четвертый слитокъ долженъ содержать 79 гр, золота, 118— серебра и 162—мѣди; такимъ образомъ имѣемъ три уравненія:
5 » 3 । 35 ____
• І9б*— /9>
6 । 5 I 65 1,о
19 ж + І5 У + ]90*“118,'
Ніи, по освобожденіи отъ дробей:
50-г —38у-[“ 35^= 15010, 36x4- 38^4- 39г = 13452, 120х +1 ЗЗу 4- 135г = 46170.
Исключивъ изъ первыхъ двухъ уравненій получимъ ур.:
7х— 2г = 779,
а исключивъ у изъ второго и третьяго: »• 4х4~ 2 = 608.
Рѣшая эти уравненія, находимъ
хе = 133, 2 = 76 гр.
Подставивъ эти величины въ первое уравненіе, получимъ:
•х у — 150 гр.
Примѣръ II. Въ бассейнъ проведены три трубы:
1-я и <2-/^ будучи открыты вмѣстѣ, наполняютъ бассейнъ въ 12 час.
х?-я и 3-я ? * > > > > » 20 »
3-я ы І-Яд > » > » > > 75 »
♦
Во сколько часовъ всѣ три трубы? открытыя одновременно* напол нятъ бассейнъ ?
Въ такомъ случаѣ
1 ч. наполнитъ - часть бассейна; Л" г
Пусть первая труба, будучи открыта одна, наполняетъ бассейнъ въ % часовъ: вторая, дѣйствуя также отдѣльно, наполняетъ бассейнъ въ у час., а третья — въ з часовъ.
1-я труба въ
2-я »
3-я >
слѣдовательно, всѣ три трубы, дѣйствуя вмѣстѣ, наполнятъ въ 1 часъ часть бассейна, равную ' - *
1 » » - » »
У
1 г
а потому весь бассейнъ наполнится во столько часовъ, сколько разъ дробь 1 । 1 . 1 з
- + + - включается въ х 1 у 1 г необходимое для наполненія
объемѣ цѣлаго бассейна, т.-е. въ 1. Итакъ, время, бассейна тремя трубами, выражается формулою:
это и есть искомое задачи.
Для его опредѣленія мы изъ условій задачи имѣемъ три уравненія
і+і=і, х^у 12
1 і 1 _ 1
у + г ~ 20’
1 + 1 = 1.
я ' х 15
Складывая пхъ, находимъ:
1
9
откуда
а потому
Для наполненія бассейна нужно 10 часовъ, что нетрудно провѣрить.
Примѣръ 111. Опредѣлитъ время изобрѣтенія Гуттенбергомъ книгопечатанія на 'основаніи слѣдующихъ данныхъ: 1) цифра десятковъ іода, въ который совершилось это событіе, вдвое меньше цифры единицъ; X) цифра тысячъ равна разности между цифрою сотенъ и циф
рою десятковъ 3) сумма всѣхъ четырехъ цифръ искомаго числа равна 14; 4) если увеличитъ искомое число на 4905, то получится число обращенное.
Обозначимъ, шълорядку, цифры'единицъ, десятковъ, сотенъ и тысячъ буквами х, у, г, Первыя три условія прямо даютъ слѣдующія уравненія:
2у = х ... (1)
і = з — у ... (2) ®4-у4-г4-і=14 ... (3)
Искомое число изображается формулою: а?+ ЮОг-}- 10004; обращенное число—формулою 1000х-|~ ЮОу 4- 10г-|-4. Четвертое условіе выражается уравненіемъ
ж + 10у ЮОг + ЮООі Ц-4905 = ІОООж + 100у + 10г + <, или, короче:
ИЬ^-Юу—10г—1112 = 545 . . . (4). .
Вычтя (2) изъ (3), находимъ
х + у4-г= 14 - г + у, откуда
х= 14 — 2г*
Въ такомъ случаѣ ур. (1) дастъ
2у — х = 14 — 2г, откуда
У = 7 — г; а слѣдов.
2 = г — у = 2г — 7. и
♦
Подставивъ въ ур. (4) вмѣсто х, у и і ихъ выраженія черезъ г, находимъ:
111(14 — 2г)4~ Ю(7—г)— 10г - 111 (2^ — 7) = 545, откуда
лг = 4;
а потому: ж = 6, у = 3, 2=1. Итакъ, книгопечатаніе изобрѣтено было въ 1436 году.
ІІ р и мѣръ IV. Два свѣчныхъ завода конкуррируютъ другъ съ другомъ. Второй открытъ 40 днями позже перваго, и на немъ работаетъ 70 человѣкъ по 12 ічасовъ въ день, между тѣмъ какъ на первомъ только 60 рабочихъ, занятыхъ по 10 часовъ въ день. Черезъ сколько дней оба завода приготовятъ одинаковое число свѣчей, полагая, что каждый рабочій на той и другой фабрикѣ изготовляетъ одинаковое число свѣчей въ часъ ?
Пусть искомое число дней, считая со времени открытія перваго завода, будетъ я; пусть, кромѣ того, каждый рабочій изготовляетъ въ часъ у свѣчей. 60 рабочихъ перваго завода, работая по 10 часовъ въ день, изготовятъ въ х дней у. Ю. х. 60 свѣчей; 70 рабочихъ второго завода, работая по 12 часовъ въ день, изготовятъ въ я — 40 дней у. 12. (я— 40).70 свѣчей. По условію, оба числа свѣчей равны, слѣд. получается уравненіе съ двумя неизвѣстными:
у. 1О.я.60 = у. 12 .(х — 40) .70.
Обѣ части уравненія дѣлятся на произведеніе у. 10.12; это дѣленіе позволительно, такъ какъ у, по смыслу задачи, отлично отъ пуля. Сокративъ, найдемъ
5х — 7(х — 40). откуда л= 140.
Примѣчаніе. Для составленія уравненія пришлось ввести вспомогательное неизвѣстное у, котораго величина остается неопредѣленною.
Приводимъ еще одну задачу, въ которой составленіе уравненій требуетъ введенія двухъ негдевмтхыдо; это — исторически извѣстная
задача Ньютопа.
Примѣръ V. Задача Ньютона. Площади трехъ луговъ равны соотвѣтственно: 5 4 десятинамъ, 10 и 24 десятинамъ; причемъ на всѣхъ <5
трехъ лугахъ трава имѣетъ одинаковую высоту и растетъ равномѣрно съ одинаковою быстротою. Первый лугъ прокор лилъ 12 быковъ въ продолженіе четырехъ недѣлъ, второй—21 быка въ теченіе 9 недѣль. Сколько быковъ можетъ прокормить третій лугъ въ теченіе 18 недѣль?
Пусть искомое число быковъ равно Для облегченія составленія уравненій нужно ввести два вспомогательныхъ неизвѣстныхъ, именно: высоту травы на каждомъ лугу, которую обозначимъ буквою у, и скорость, съ которою трава растетъ, т.-е. количество, на которое увеличивается ея высота въ недѣлю; пусть это неизвѣстное будетъ
На первомъ лугу количество травы вначалѣ было уХ'^з или у У, а ПРИ” ростъ ея въ 4 недѣли равенъ ^Х^дХ^, или Полное количество травы, съѣденной 12-ю быками въ 4 недѣли, равно
10 . 40
3 з
или
10 (у+ 4*).
" 3 ’
слѣд. одинъ быкъ въ 1 недѣлю съѣдалъ
10(у + 4я) 3X4X12’
или
5 (у + 4я)
72
Подобнымъ же образомъ найдемъ, что количество травы, съѣденной однимъ быкомъ въ одну недѣлю на второмъ лугу, равно
Й1И 10^ + 91).
или 18д ,
а на третьемъ,оно равно
24 (у + 18г)
18Х® ’
ИЛИ
4 (у + 18г) Зз
Выражая, что количество травы, поѣдаемой на каждомъ лугу однимъ быкомъ въ одну недѣлю, одно и то же, получимъ уравненія:
5(# + 4х?)_ 10(у + &0
72 189 ’
5 (// + 4г)__4 0/ 4-18#)
72~^ ~ За*
Такимъ образомъ получили два уравненія съ тремя неизвѣстными, сл. имѣемъ случай неопредѣленности; но здѣсь неопредѣленны только у и между тѣмъ какъ главное неизвѣстное # имѣетъ величину вполнѣ опредѣленную, Въ самомъ дѣлѣ, два полученныя уравненія даютъ возможность опредѣлить отно-у
шеніе вспомогательныхъ неизвѣстныхъ и главное неизвѣстное я, Дѣйстви-тельпо, раздѣливъ обѣ части каждаго уравненія па г и положивъ - = «, найдемъ два уравненія съ двумя неизвѣстными зс и
5(и-|-4)_1О(и + 9)
72 — 189
5(«+4) _4(и+ 18) 72 — Зх ’
изъ которыхъ и можно опредѣлить эти неизвѣстныя. Изъ перваго ур, найдемъ: — 12; вставивъ вмѣсто « его значеніе во второе, найдемъ: .г = 36.
Слѣд., третій лугъ могъ прокормить 36 быковъ въ теченіе 18 недѣль.
ГЛАВА ХХШ.
Теорія пропорцій.
Пропорція ариѳметическая, — Пропорція геометрическая; производныя и' сложныя пропорціи; свойства ряда равныхъ отношеній. — О пропорціональности величинъ.— Гармоническая пропорція,—Приложенія,
299. Въ этой главѣ мы займемся изученіемъ особаго вида равенствъ, называемыхъ пропоргііями; изученіе свойствъ этихъ равенствъ важно въ виду многочисленныхъ и разнообразныхъ ихъ примѣненій.
Пропорція ариѳметическая.
300. Разность двухъ количествъ а и Ъ называется разностнымъ или ариѳметическимъ ихъ отношеніемъ; письменно оно выражается такъ: а—Ъ. Количества а и Ъ называются членами отношенія: а—предыдущимъ^ Ь- послѣдующимъ; числовая величина а — Ь наз. разностью отношенія,
Если два ариѳметическія отношенія а — Ь и с — д равны, то соединяя ихъ знакомъ равенства, получимъ равенство
а — & — с — <7Т
называемое іжзностядео или ариѳметическою пропорціею.
Пропорція читается такъ: а относится къ 6, какъ с къ й. Количества «, Ь, с и І называются членами пропорціи: а —первымъ, Ь~ вторымъ, с— третьимъ, гі—четвертымъ; кромѣ того, а и й называются хряйнызеы, Ъ и с— средними.
301. Главное свойство ариѳметической пропорціи. Если въ равенствѣ
« — Ъ = с — сі
перенесемъ въ первую, а Ь во вторую часть, то получимъ а —(і = & — с,
т.-е. во всякой ариѳметической пропорціи сумма крайнихъ членовъ равна суммѣ среднихъ.
Обратно: взявъ равенство
= Ь-|-с
и перенеся Ь въ первую, а й во вторую часть, найдемъ а — Ь = с — гі.
т.-е. если сумма двухъ количествъ равна суммѣ двухъ другихъ^ то эти четыре .количества ариѳметически пропорціональны.
302. Опредѣленіе неизвѣстныхъ членовъ. Перенеся въ пропорціи
а — Ь = с — д
членъ Ъ во вторую часть, найдемъ:
а = (Ь4-с) — (I . . , (1).
Опредѣляя изъ той же пропорціи 6, находимъ
Ъ = (а-\-д) — с . . , (2).
Равенство (1) показываетъ, что крайній членъ ариѳм. пропорціи равенъ суммѣ среднихъ безъ другою крайняго; а равенство (2), что средній членъ равенъ суммѣ крайнихъ безъ другою средняго.
303. Непрерывная пропорція. Ариѳметическая средина. Если въ ариѳметической пропорціи равны оба крайніе, или оба средніе члена, то пропорція называется непрерывною. Таковы напр. пропорціи: 5 — 3 = 7 — 5; 2 — 10 = = 10—18; вообще
а~Ь = 6—с и р—д=г—р
суть пропорціи непрерывныя. Въ первой а во второй называются а/л<ѳ.ѵе* тическими срединами двухъ другихъ членовъ.
Примѣняя главное свойство къ одной изъ этихъ пропорцій, напр. къ первой, находимъ:
2Ь — а-[-с, откуда
т.-е. ариѳметическая средина между двумя количествами равна ихъ полусуммѣ.
Обобщая этотъ выводъ, называютъ ариѳметическою срединою нѣсколькихъ количествъ - сумму ихъ, дѣленную на число ихъ.
Такимъ образомъ, если имѣемъ п количествъ
«и «з, - , Йн-Ь
то ариѳметическая средина ихъ будетъ
Лі Яд “1“ “Ь * • * Н~ —X ”1“
— —— „
Опредѣленіе ариѳметическихъ срединъ весьма важно для наблюдательныхъ наукъ. Пусть, напр., опредѣляя угломѣрнымъ приборомъ нѣкоторый уголъ въ нѣсколько пріемовъ, нашли: при первомъ измѣреніи 28*52'36", при двухъ слѣдующихъ 28*51'52" и при четвертомъ измѣреніи 28°5Г24". Какова величина угла? Такъ какъ всѣ четыре измѣренія не согласуются между собою, то остается одно средство—взять среднюю величину.
28<>52'36" + 28<>5Г52" X 2 + 28*5Г2Г
28*51'56".
Пропорція геометрическая. *
304. Частное отъ раздѣленія двухъ количествъ наз. кратнымъ или гео-метрическимъ отношеніемъ а къ Ь; численная величина отношенія наз. зна-менателемъ отношенія.
Равенство двухъ геометрическихъ отношеній называется кратною или геометрическою пропорціею, напр.
305. Главное свойство геометрической пропорціи. Во всякой геометрической пропорціи произведеніе крайнихъ членовъ равно произведенію среднихъ.
Въ самомъ дѣлѣ, приведя въ вышенаписанпой пропорціи дроби къ общему знаменателю и откинувъ его, найдемъ
аА= Ъс . . . (2).
Наоборотъ, если произведеніе двухъ количествъ равно произведенію двухъ друіихъ количествъ, то такія четыре количества пропорціональны.
Въ самомъ дѣлѣ, раздѣливъ обѣ части равенства а<1 — Ъс на М, найдемъ: а_________________________________с
306. Опредѣленіе неизвѣстныхъ членовъ. Если обѣ части равенства (2), вытекающаго изъ пропорція (1), раздѣлимъ па Л, то найдемъ:
а=а-..(3).
Раздѣливъ же обѣ части (2) на с, находимъ
Равенство (3) показываетъ, что всякой геометрической пропорціи крайній членъ равенъ произведенію среднихъ, дѣленному на- другой крайній; а равенство (4), что неизвѣстный средній равенъ произведенію крайнихъ } дѣленному на другой средній.
Опредѣленіе неизвѣстнаго члена, когда остальные три члена извѣстны, называется рѣшеніемъ пропорціи.
307. Непрерывная пропорція. Геометрическая средина. Когда равны оба крайніе, или оба средніе члена, пропорція называется непрерывною; напр. 12:6 = 24:12, или 2 : 4 = 4 : 8.
Каждый изъ равныхъ членовъ непрерывной пропорціи наз. среднимъ геометрическимъ между двумя другими. Приравнявъ въ непрерывной пропорціи а : б = б : й произведеніе среднихъ произведенію крайнихъ, получимъ Ъ2 — ад, откуда * _
слѣд, геометрическая средина двухъ количествъ равна квадратному корню изъ ихъ произведенія.
По аналогіи съ этимъ выводомъ, среднимъ геометрическимъ нѣсколькихъ количествъ называютъ корень порядка, равнаго ихъ числу, изъ ихъ произведенія. Потому, геометрическая средина п количествъ: а3, . . . , будетъ
«/ ~ у
308. Производныя пропорціи. Если пропорція получается изъ другой пропорціи посредствомъ нѣкоторыхъ преобразованій, то первая называется производною отъ второй. Ознакомимся съ различными видами производныхъ пропорцій.
I. Взявъ пропорцію
ь а
приравняемъ въ ней произведеніе крайнихъ произведенію среднихъ, и раздѣлимъ полученное равенство ад^Ьс послѣдовательно на: сс^аЬ и ас; по сокращеніи найдемъ:
а і) уѵ (і с , (і б / л\
- = -...2) -------(3) -=------(4).
с <7 ' 7 б а А 7 о а 4 7
Переставивъ въ каждой изъ этихъ четырехъ пропорцій самыя отношенія, найдемъ еще четыре пропорціи:
а Ъ а с чл а Ь \7 а с
Такимъ образомъ въ каждой пропорціи можно перемѣнятъ мѣста: среднихъ членовъ,, крайнихъ, и тѣхъ и другихъ вмѣстѣ. Чрезъ ото всякую пропорцію можно представить въ восьми различныхъ видахъ,
II. Придавъ къ обѣимъ частямъ равенства = ... (1) по 1, а потомъ вычтя по 1, получимъ по приведеніи каждой части къ общему знаменателю:
«4^==Ц^..,(2) н «=* = ЦЛ..(3).
О а ѵ л о а ' 7
Пропорціи (2) и (3) показываютъ, что: суллей ши разность членовъ первою отношенія относится къ своему послѣдующему такъ, какъ сумма «ли разнотъ *숫овь втораго отношенія къ своему послѣдующему.
Раздѣливъ почленно каждую изъ пропорцій (2) и (3) на (1), найдемъ:
•••(4) и
’ лим клм разжхж* «декою перваго отношенія относится къ пре-'ьшдутлму ятя же втмагяемія такъ, какъ сумма или разность членовъ гт и* о ііредыйуыделу пшю же отношенія.
жъ мроаоршяхъ (2), (3), (4) и (5) мѣста среднихъ членовъ, ІГѢгГі:
т.-е_ сумма или разность членовъ перваго отношенія относится къ суммѣ ллм разности членовъ втораго отношенія такі, какъ предыдущій къ вр&ндущему или послѣдующій къ послѣдующему.
Раздѣливъ пропорцію (2) на (3), найдемъ
>
•(10)
т.-е. сумма членовъ перваго отношенія относится къ ихъ разности* какъ сумма членовъ втораго отношенія къ ихъ разности.
Перемѣнивъ въ пропорціи (1) мѣста среднихъ членовъ и примѣнивъ къ новой пропорціи - = д преобразованія, указываемыя равенствами (2), (3) и т. д., найдемъ:
^ = ^(12), с а 4 ” с а 4
"_±с_ ?П5\
6 + <і — <Гіг>>’
Изъ сравненія же (15) съ (16) имѣемъ
«4-е___а — с
Ъ + Ь — 4’
откуда
и -|-с
а — с ~ Ь — сГ
Результаты, выражаемые этими равенствами, нетрудно выразить словесно.
309. Сложныя пропорціи. Пропорція, выводимая изъ нѣсколькихъ другихъ пропорцій, называется сложною.
I. Посмотримъ, при какихъ условіяхъ возможно почленное сложеніе или вычитаніе двухъ пропорцій. Пусть данныя пропорціи будутъ
I-а __ с а* Ъ~а “ ь'~<г;
изслѣдуемъ, при какихъ условіяхъ возможна пропорція
л — аг
с(
(I)
гдѣ знакъ (-|-) относится къ почленному сложенію, а (—) къ почленному вычитанію. Преобразуемъ испытуемое равенство, приравнявъ произведеніе крайнихъ членовъ произведенію среднихъ; сдѣлавъ это, найдемъ:
(а + о ) (^ + с?) = (Ь + У) (с + е').
Выполняя умноженіе и замѣчая, что верхніе знаки надо брать съ верхними, а нижніе съ нижними, находимъ:
а(1 + л'Й + а'й' = Ьс + Ь'с ± Ь& 4"
Но изъ данныхъ пропорцій имѣемъ: аД = Ьс и а'Лг = Ь'с'; отнявъ по-ровпу изъ обѣихъ частей, найдемъ
Ч- а'с? з+і аЛ* = + Ь'с + Ьс*.
Здѣсь совокупно написаны два равенства: въ одномъ членамъ предшествуетъ знакъ 4", въ Другомъ — всѣмъ членамъ предшествуетъ (—); помноживъ обѣ части втораго на (—1), увидимъ, что оно ничѣмъ не отличается отъ перваго, такъ что оба равенства приводятся къ одному
а'(14~ а<1' — Ь'с 4~ Ьс',
а это значитъ, что почленное сложеніе и почленное вычитаніе двухъ пропорцій возможны при однихъ и тѣхъ же условіяхъ. Затѣмъ, пользуясь Жданными пропорціями, исключимъ изъ послѣдняго равенства сі и й', чтобы уменьшить этимъ число входящихъ въ него буквъ и такимъ образомъ упростить его. Съ этою цѣлью опредѣлимъ изъ данныхъ пропорцій й и й' и ихъ выраженія подставимъ въ предыдущее равенство; такимъ образомъ найдемъ:
а'Ъс । аЬ’с? а ' а1
— Ь'с 4~ Ьс',
пли. освободивъ отъ дробей,
а'*Ъс а*Ъ'с' = ааЬ'с Ц- аа'Ьс'.
Перенеся всѣ члены въ первую часть и вынося за скобки въ 1-мъ и 3-мъ* членахъ а'с, а во 2-мъ и 4-мъ ас\ найдемъ
4>
а‘с(а'Ъ—а?/)—асг(а'Ъ—аУ) = 0, или (а'Ь—аУ) (а'с—ас')=0 . . . (2).
Это равенство замѣняетъ собою испытуемое, а потому при какихъ условіяхъ возможно (2), при такихъ же условіяхъ возможно и (1).
Но равенство (2) требуетъ, чтобы произведеніе двухъ множителей равнялось нулю; а это возможно только тогда, когда одинъ изъ нихъ равенъ нулю, поэтому слѣдуетъ положить
или а'Ь — аі/ — О, пли а'с — асг — О. ’ »-
Обративъ ихъ въ пропорціи, имѣемъ
а!_н
Ѵ~Ъ
а' _ а
илялгнвое сложеніе или вычитаніе двухъ пропорцій возможно только ѵ Ингъ удовлетворено или первое, или второе изъ этихъ равенствъ.
и гутъ з^зжнател отношеній данныхъ пропорцій, заклю-
’г < іі*г» е-миг*жіе или вычитаніе двідо пропорцій возможно
х гж« ізижынчм отношеній удоны. Замѣчая, что р и " суть зпа-
♦тмя^ііі пропорцій, выведенныхъ изъ данныхъ перемѣщеніемъ сред-шь вжякъ. заключаемъ, что искомое преобразованіе возможно еще тогда, ляамяатели отношеній равны въ пропорціяхъ, выведенныхъ изъ перемѣщеніемъ среднихъ членовъ. /
Ісли зсаженатели отношеній данныхъ пропорцій равны, то, назвавъ общую шв велпжиу буквою д, имѣемъ
а а 7 / 7,
/; = 7 и ~ <Ь откуда: а == Ъ$ и а — Ь у.
Складывая или вычитая эти равенства, находимъ:
а + а' — (Ь + й') откуда
л ~ а' аг о 1Г^17~ 6' = Ь’
<*ігюда слѣдуетъ, что (какъ есть зи. отн. сложной пропорціи 1 зна-леявтелъ отношенія сложной пропорціи, порученной чрезъ почленное слежгніе или вычитаніе двухъ пропорцій, имѣющихъ равныхъ знамена-шелпі отношеній, равенъ знаменателю отн. дан. пропорцій.
п г т *ц 10 30 5 15
Примѣръ I. Такъ изъ пропорцій: п ^ = ’б" ІЮЛУчаемъ чрезъ
очленное сложеніе: = а чрезъ почленное вычитаніе: | = у — пропорціи. имѣющія такого же знаменателя отношенія какъ и данныя.
тт II іі -Ч 10 30 7 21
Примѣръ II. Изъ пропорційи получаемъ чрезъ по-
членное сложеніе и вычитаніе вѣрныя пропорціи:
17 _ 5[
6" 18
3 9
“ 2~б'
И. Можно перемножать почленно какія-угодно пропорціи; знаменатель отношенія полученной сложной пропорціи будетъ равенъ произведенію знаменателей отношеній данныхъ пропорцій.
Пусть даны пропорціи
а с которой знаменатель отношенія равенъ
аг с'
б7-З5
а"__с"
*
Перемножая почленно эти
> >
> »
равенства по правилу а,аг,п" ___с.с'л*'
» д"
умноженія дробей, найдемъ
Знаменатель отношенія этой пропорціи равенъ
«а'а"____л
ЬЬ'Ъ'' ~ Ь
а" і и
#=9- д'з".
т.-е. произведенію знаменателей отношеній данныхъ пропорцій.
ПІ. Можно пропорцію раздѣлитъ почленно на друіую; знаменатель отношенія сложной пропорціи будетъ равенъ частному отъ раздѣленія
знаменателей отношеній данныхъ пропорцій.
Раздѣливъ пропорцію =
на
а'_
Ѵ~
по правилу дѣленія
дробей най-
демъ:
а'Ъ с'д
Раздѣливъ оба члена первой части на а!Ь\ а оба члена второй на сѴ, получимъ
а : аг_с : с'
Знаменатель отношенія полученной пропорціи равенъ
: а'_аЪ* _ а 6'___а, аг___
ЬТЪ,~"(ёЬ~Б^'а,~Ь' Ъ' — У’-Ѵ’
если знаменатели отношеній данныхъ пропорцій обозначить соотвѣтственно буквами 7 и
IV. Если въ двухъ пропорціяхъ предыдущіе члены равны, то изъ послѣдующихъ чожно составить пропорціи; если же послѣдующіе равны, то предыдущіе пропорціональны.
Въ самомъ дѣлѣ, если въ пропорціяхъ
а__с а_______с
ь~2 и Ь'~Л'
перемѣнамъ мѣста среднихъ, то найдемъ
откуда
а _ Ъ а Ъ'
с Л И с
Ь Ъ' ъ а
(і~а' или ѵ~Л’‘
Такимъ же образомъ, взявъ двѣ пропорціи съ равными послѣдующими членами
а__с а*_______с*
ь~а и ь~7і
и перемѣстивъ въ нихъ средніе члены, найдемъ
а Ь а' Ь с~3 и 7 “ 5’
откуда
а а'
с с*
или
а с аг с?
V. Еслш «мтежа рядъ равныхъ отношеній, то сумма всѣхъ преды-ммлмскаі гя о суммѣ всѣхъ послѣдующихъ, какъ любой изъ пре-
Лвеущыхъ къ сюелу послѣдующему.
Пусть даны равныя отношенія
01 _#2_^3__ _____ап,
61 — 6*— 63
«л назовемъ общаго знаменателя этихъ отношеній буквою д, то:
«3
а^, Ьн
9
Выражая дѣлимое чрезъ дѣлителя и частное, имѣемъ:
<»і =М; <Ч = Ь,«; ааз=Ь,® . ., ая = Ъп$ . . , (1).
Сложивъ почленно эти равенства и во второй части вынеся за скобки ?, пДдеиъ:
*
аі + аі + аз 4-----Н а»= (&і + +»3 4--------Ь
Раздѣливъ обѣ части на 4“ 4“ * - * 4“ и сокративъ вторую часть на я2 это выраженіе, получимъ во второй части или у. у и т. д.:
Ч~ ~Ь * + ^2 Ч~ ^3 •
* Н~ __0^___
• +ьп—д—ъі-ьі—‘
что и требовалось доказать.
ѴЕ Если имѣемъ рядъ равныхъ отношеній, то сумма всѣхъ предыдущихъ, умноженныхъ на какія-угодно количества, такъ относится къ суммѣ всѣхъ послѣдующихъ ч умноженныхъ соотвѣтственно на тѣ же самыя количества, какъ любой изъ предыдущихъ относится къ своему посл ѣдую щему,
Умноживъ равенства (1),пункта V’ соотвѣтственно на т.п а затѣмъ поступая по предыдущему, найдемъ:
+ ^3 + • > - + _ «1 «2 __
+ Ъ$т2 + Мъ + - • * + ^нтн
ѴІЕ Возвысивъ равныя отношенія
а । Лу
&2
въ »»-ую степень,
найдемъ
«іт _ _ д8ш___ _ «/"
Ьіт~ь.ііп Ь3Ш —‘ ’ * V1’
откуда (на оси. V), получаемъ
а,” + а2т + «з™ 4-6“ + Ь2"‘ + Ьіт +
• + й»я‘ _ . аГ _ °»т __
. + 6н-* — 6/“ ~ Ь2»‘~ ‘
а но извлеченіи корня т-го порядка:
4
О пропорціональности величинъ.
310. Опредѣленія. I, Когда двѣ величины А и В зависятъ одна отъ другой такъ, что отношеніе двухъ какихъ угодно значеній первой равно отношенію соотвѣтствующихъ значеній второй, то такія величины называются прямо пропорціональными или просто пропорціональными.
Согласно этому опредѣленію, если изобразимъ буквами а. а', а", а'", ... послѣдовательныя значенія величины А, а буквами Ь, Ьг, Ъ", Ъ”\ ... соотвѣтствующія значенія величины В, то А и В—прямо пропорціональны, если
а & а ________ Ъ а _______ Ь а___
а'~Ъ’' <ё'~ V’' ‘ ИЛИ Ъ ~ V — Ь* ~
Примѣры. Цѣна провизіи пропорціональна ея вѣсу; жалованье рабочаго пропорціонально времени его работы; окружность круга пропорціональна его діаметру: вѣсъ однороднаго тѣла пропорціопаленъ его объему; пространство, проходимое равномѣрно движущимся тѣломъ, пропорціонально времени движенія; и т. п.
И. Когда двѣ величины А и В находятся въ такой зависимости одна отъ другой, что отношеніе двухъ какихъ-либо значеній первой равно обратному отношенію соотвѣтствующихъ значеній второй,—такія величины называются обратно пропорціональными,
Согласно этому опредѣленію, если буквами а, а\ а'\ а'", . . . назовемъ нѣкоторыя значенія величины А, а буквами Ь, Ь\ Ь’\ У", . . . соотвѣтствующія значенія величины В, то А и В обратно пропорціональны, если
Л (I Й Ь*** / г і г г? 1.*^ іа і.
, = і т = ~7г, = ^-э , ,. или а . Ь = а . & = а , Ь = а . Ъ = •
а 6 а* о «г/ о
Примѣры, Время, необходимое для окончанія нѣкоторой работы, вообще обратно пропорціонально числу рабочихъ; скорость равномѣрнаго движенія обратно пропорціональна времени, необходимому для прохожденія опредѣленнаго разстоянія; объемъ газа, при постоянной температурѣ, обратно пропорціоналенъ давленію. подъ которымъ газъ находится; и т. п*
311. Какимъ образомъ доказывается пропорціональность величинъ, Въ нѣкоторыхъ случаяхъ пропорціональность величинъ очевидна, или принимается за таковую, напр. пропорціональность капитала и прибыли, платы рабочаго н вреяеп. въ теченіе котораго онъ работалъ. Затѣмъ, пропорціональность нѣко-т^нп величинъ строго доказывается въ тѣхъ наукахъ, къ которымъ величины уя принадлежатъ: такъ въ геометріи доказывается пропорціональность
‘-торовъ подобныхъ треугольниковъ, пропорціональность окружно-гхт :а±у-ажк і т. в.; въ физикѣ доказывается пропорціональность плот-
Г-Лі 1 1 Т- В-
Б лз рх>«ітріваемыхъ величинъ не подлежитъ спеціально ни-
каткѣ. і. ?-л іхъ пр^фяйві^ьності (прямой или обратной) убѣждаются
ІГУТІТЬ 5’ЖЪ-
Е Еслм • Блтхтсм. чр» въ то время какъ величина А принимаетъ значенія гь т. трв. четыре, .... разъ большія или меньшія, другая величина В, ^туѣтственво этому, принимаетъ значенія также въ два. три, четыре.........
мл большія или меньшія, то величины А и В прямо пропорціональны.
Въ гамомъ дѣлѣ, пусть соотвѣтственно значеніямъ А, равнымъ а, 2а, За, 1 1 *
- ^а, а, . . . . величина В принимаетъ значеніе 6, 2&э 3&, . . . .
м о
к ...........; требуется доказать, что если А приметъ значеніе равное
*
г» соотвѣтствующее значеніе В будетъ^Ъ, Для доказательства можно прп-5
жягк. что А получаетъ значеніе равное у а въ два пріема, т.-е. что сперва изъ « обращается въ у а. а затѣмъ изъ у а превращается въ у а. Но, по условію, сиза А получаетъ значеніе у а, въ 7 разъ меньшее а, то В получаетъ зна-«>е у Ь. въ 7 разъ меньшее 6. Затѣмъ, опять по условію, когда А изъ ^а жревращается въ у а. увеличиваясь въ □ разъ, то В увеличивается во столько 1 5
же разъ, и слѣд. изъ обращается въ уЬ. Такимъ образомъ теорема дока-аьа для всѣхъ случаевъ, когда одна изъ величинъ измѣняется въ
ото разъ. Но если величина А изъ а обращается въ а. )/2. измѣняясь въ пе-<ч»ізіѣримое число разъ, то легко доказать, что соотвѣтственно этому и В изъ & ‘•братмтся въ Ь. |/2; въ самомъ дѣлѣ, замѣняя ]/2 приближенными соизмѣримыми дробями (1, 4; 1, 41: 1, 414 и т. д.) неограниченно приближающимися
къ предѣлу у/2, каждый разъ разъ будемъ находить, что во сколько разъ измѣняется А, во столько же разъ в В; это заключеніе вѣрно, слѣд,, и въ предѣлѣ.
П. Если окажется, что соотвѣтственно значеніямъ А, равнымъ а, 2а, За, 11 п
-а, ^а, ..., величина В принимаетъ значенія, во столько же разъ меньшія о
или большія, т.-е. 6, ^6,
26. 36.. . . , то величины А и В обратно
пропорціональны.
Требуется доказать, что если А приметъ значеніе то соотвѣтствующее значеніе В будетъ ^6. Въ самомъ дѣлѣ, когда А, вначалѣ имѣвшее величину а, обращается въ | а, т.-е. уменьшается въ 7 разъ, то В, по условію, во столько же разъ увеличивается, и слѣд. изъ Ъ превращается въ 76; затѣмъ,' когда А изъ обращается въ -у а, увеличиваясь въ 5 разъ, то В, соотвѣт-
ственно этому, уменьшается въ 5 разъ, и потому изъ 76 превращается ?6. Теорема такимъ образомъ доказана для всѣхъ случаевъ, когда отношеніе соизмѣримо; а отсюда, по способу предѣловъ, легко заключить, что она распространяется и на случай отношеній несоизмѣримыхъ
Примѣры: 1 • Если принять, что для исполненія работы въ два, три, четыре и т. д, разъ большей или меньшей нужно рабочихъ въ два, три, четыре и т. д* разъ больше или меньше, то заключаемъ, что и во всѣхъ случаяхъ количество исполненной работы пропорціонально чнелу рабочихъ.
2. Въ физикѣ доказывается, что когда давленіе, подъ которымъ газъ находится, увеличивается или уменьшается въ два, три и т. д. разъ, объемъ газа уменьшается или увеличивается во столько же разъ; заключаемъ, что во всѣхъ случаяхъ объемъ газа обратно пропорціоналенъ давленію.
312. Пусть будутъ X и I двѣ прямо-пропорціональныя величины, напр., вѣсъ товара и цѣна его. Пусть будутъ, затѣмъ, г и два частныя значенія первой, а у' и уи два частныя значенія второй величины, соотвѣтствующія я/ и яР. По опредѣленію прямо пропорціональныхъ величинъ, отношеніе двухъ какихъ-либо значеній первой величины равно отношенію соотвѣтствующихъ значеній второй, слѣд.
_ У
х" у'1'
перемѣнивъ мѣста среднихъ членовъ, имѣемъ
х*__#2
Такъ какъ разсматриваемыя значенія совершенно произвольны, то можно сказать, что отношеніе двухъ какихъ угодно соотвѣтственныхъ значеній пропорціональныхъ величинъ постоянно, Обозначивъ эту постоянную величину буквою К, имѣемъ
X
У = К, откуда X = К. Т,
-< «3$ величинъ одна равняется дру~
»»<. рлшожмной на постоянное количество, называемое коэффиціен-жш шрстаргаоиалъяясйш.
"удѣливъ изъ опыта или наблюденія два соотвѣтственныя частныя зна-чекі разсматриваемыхъ величинъ, и взявъ ихъ отношеніе, найдемъ коэффи-ыгтъ пропорціональности, т.-е. числовую величину отношенія, связывающаго ізЛ величины.
Если X и V — величины обратно - пропорціональныя, то, по опредѣленію, имѣемъ
х' _ $'* у’
ш, приравнявъ произведеніе крайнихъ произведенію среднихъ:
37 * у = X , у .
Такъ какъ взятыя значенія произвольны, то можно сказать, что нрошяе-двухъ какихъ угодно соотвѣтственныхъ значеній двухъ обратно-пропор-і>-вАльныхъ величинъ — постоянно. Обозначивъ это постоянное буквою К. имѣетъ
X. У = К, откуда X = у,
т.-е* іш йедяг обратно - пропорціонал ьныхъ величинъ одна равна по-иному коэффиціенту, дѣленному на другую.
Коэффиціентъ опредѣляется опытомъ или наблюденіемъ.
Разсмотримъ теперь нѣсколько величинъ. Когда измѣненіе величины зависать отъ измѣненія нѣсколькихъ другихъ величинъ, то, говоря, что разсматри-5«і2 величина прямо пли обратно пропорціональна другой, разумѣютъ при утъ. что всѣ другія величины въ моментъ сравненія двухъ взятыхъ величинъ спж/тся* постоянными.
Примѣръ I. Говоря, что простыя проідотныя прямо - про-регіональны капиталу и времени обращенія, разумѣютъ подъ этимъ, что озейтныя деньги, приносимыя въ опредѣленйое время, измѣняются въ томъ -увопіеніи, какъ и капиталъ, и что процентныя деньги, приносимыя однимъ і гѣгь же капиталомъ, измѣняются въ томъ же отношеніи какъ продолжитель* жть обращенія его.
Примѣръ И. Говоря, что объемъ газа прямо пропорціоналенъ его вѣсу » биному расширенія и обратно пропорціоналенъ давленію, разумѣютъ і» іъ этнмъ, что: при данныхъ—температурѣ и давленій объемъ газа измѣняется гъ г гь же отношеніи какъ его вѣсъ; при данныхъ — температурѣ и вѣсѣ газа находится въ обратномъ отношеніи къ давленію; наконецъ, при плохъ давленіи и данномъ вѣсѣ, объемъ газа прямо пропорціоналенъ биному хь "ЗНАНІЯ.
«Значимъ разсматриваемыя величины буквами х, А, В, Р и 9, и пусть - ізхім пропорціоналенъ А и В и обратно пропорціоналенъ Р и Пусть два _ і_ -•тмѣтственныхъ частныхъ значеній этпхъ величинъ будутъ
а\ ?/, р', а”, Ъ\ р".
и выразимъ У* черезъ остальныя величины.
Разсматривая величины и А, полагаемъ, что остальныя величины остаются безъ перемѣны, т.-е* въ то время какъ о А измѣняются, тѣ величины сохраняютъ неизмѣнныя значенія 6', р? и д'* Въ то время какъ А изъ а* переходитъ въ величина х переходитъ изъ %' въ такую величину X, которая удовлетворяетъ равенству
X я" ѵ , /п
хг = аг' откуда Х = —(О
ибо х и А прямо пропорціональны.
Ври измѣненіи х и В другія величины сохраняютъ значенія р' и д'; при переходѣ В изъ въ х переходитъ изъ X. соотвѣтствующаго количеству Ь\ въ такое значеніе Х\ которое удовлетворяетъ пропорціи
X' Л" Л"
откуда Х'=у’Х. . , (2),
такъ такъ х и В прямо пропорціональны.
Разсмотримъ х и Р. Другія величины сохраняютъ значенія а”, Ь\ при переходѣ Р изъ р* въ р", х перейдетъ нзъ а , соотвѣтствующаго р\ въ X"— удовлетворяющее пропорціи
X" р' V" 1'Г ѵ'
Х'=-^? ^куда Х = ^‘Х * '
ибо х и Р обратно пропорціональны.
Наконецъ, разсмотримъ х и у, при чемъ остальныя величины сохраняютъ значенія аг\ Ь'\ р”. При переходѣ У изъ </ въ х переходитъ изъ X" въ такую величину х*\ которая соотвѣтствуетъ ряду а\ р?\ у". Эта величина х^ удовлетворяетъ пропорціи
X ___ Ц іі (3 '-.гц /
откуда. ®" = ^і-Х . • . (О, ибо х и У величины обратно пропорціональныя*
Для исключенія вспомогательныхъ неизвѣстныхъ X, X', X'', перемножимъ почленно равенства (1), (2), (3) и (4); найдемъ
ѵ V' V'' д/'___V V
Сокративъ на X * X'. Х'\ получимъ
а" Ъ" рг </
“ * 77 ' р" * д"’
Положивъ
х\р*.д'
= к,
гдѣ я/, У, р' и представляютъ рядъ соотвѣтственныхъ частныхъ значе ній разсматриваемыхъ величинъ, найдемъ
Такъ какъ это равенство относится къ ряду какихъ угодно соотвѣтственныхъ значеній взятыхъ величинъ, можно замѣнить эти частныя значенія общими символами, и написать
ѵ АВ х—КРЗ‘
Опредѣливъ изъ опыта или наблюденія рядъ частныхъ соотвѣтственныхъ значеній данныхъ величинъ, найдемъ численную величину коэффиціента К, связывающаго данныя величины.
Если бы разсматриваемыя величины были только о?, А и В, то имѣли бы
х = К. АВ,
т.-е. если величина прямо пропорціональна нѣсколькимъ другимъ, то она равна ихъ произведенію, умноженному на постоянный коэффиціентъ.
Если бы взяты были только величины я, Р и у, то имѣли бы
К Рі/
т.-е. величина, обратно пропорціональная нѣсколькимъ другимъ, равна постоянному коэффиціенту, дѣленному на произведеніе этихъ величинъ.
Наконецъ, изъ формулы
ѵ АВ х ~ к • ру
»
слѣдуетъ, что величина, прямо-пропорціональная ряду нѣкоторыхъ величинъ, и (кратно-пропорціональная ряду другихъ величинъ, равна постоянному коэффиціенту. мопожевноиу на произведеніе ряда первыхъ величинъ, и дѣленному на жришд?» ряда вторыхъ величинъ.
Гармоническая пропорція.
313. Если три количества «, Ь и с удовлетворяютъ пропорціи а чс — (а — Ь): (Ь — с),
т,-е, есл первое такъ относится къ третьему, какъ разность между первымъ и лімрцит къ разности между вторымъ и третьимъ, то они называются гармони-ъеежи-проплрціоналъными; при этомъ Ъ называется гармоническою срединою между а и с.
Приравнявъ произведеніе крайнихъ произведенію среднихъ, найдемъ аЬ — — ас = ас — Ьс; а раздѣливъ обѣ части этого равенства на аЪс. найдемъ
_ 1 _ 1 _ і с Ь~ Ь а
откуда
1 1 /1 । М
— . — I |— — 1 • е
б 2 \а ’ с)
Изъ этого слѣдуетъ, что если Ь есть гармоническая средина между а и с, 1 ’ 11
то есть ариѳметическая средина между д и -•
314. Теорема. іеоліеигрігческая и гармоническая
средины двухъ какихъ-нибудь чиселъ составляютъ непрерывную геометрическую пропорцію.
Пусть х, у і\ я будутъ: гармоническая, геометрическая и ариометичеткая средины чиселъ а и 6; т.-е,
а‘Ь = (а—я) ;(&—/>); у* = аЪ; м>
Приравнявъ въ первой произведеніе крайнихъ произведенію среднихъ, находимъ
ах — аЬ = аЪ — Ъх;
прибавивъ къ обѣимъ частямъ по Ьх-[-аІ^ находимъ
ах Ь.г = 2а6: пли или ли? = «/’,
откуда
х:у=^у
’ Примѣчаніе. Поводомъ къ названію разсматриваемой пропорціи гармониче-4 2
скою послужило замѣчаніе, что числа 1, и представляющія длины струнъ, дающихъ совершенный аккордъ т% зоі), удовлетворяютъ этой пропорціи.
Приложенія.
315. I. Раздѣлить число А на части пропорціональныя даннымъ числамъ а, Ъ, с?
Это значитъ найти три такія числа, которыхъ сумма равнялась бы А, и которыя удовлетворяли бы равенствамъ
х у я а Ь с
По свойству равныхъ отношеній имѣемъ:
X____у 2 X + У 4- 2.
а Ь с а -Ь Ь + с1
НО Х-\-у-\-2 = А, слѣд. для
опредѣленія я, і/ и 2 имѣемъ три равенства
откуда
х А у А 2 А _ — —. ----------• 1 -------- - _______ * —г — ------------------------
а а -у Ъ с* Ь а + б + с а 4- Ь 4- с
П. Три купца внесли для общей торговли капиталы: А, А' и А'', находившіеся въ оборотѣ: первый—і лѣтъ, второй—2', третій—^ лѣтъ. Сколько каждый купецъ долженъ получить изъ общей прибыли В?
4
Части каждаго должны быть прямо пропорціональны капиталамъ и временамъ ихъ обращенія; а слѣд. эти части должны быть пропорціональны произведеніямъ капиталовъ на соотвѣтствующія времена; итакъ, имѣемъ
я Ч~ У В и X? ~ А7'~ А'Т7’
откуда, подобно предыдущему, найдемъ
_ ВлѴ _ О.А'Г В.А"Г
х ~ А^Н- ЛГ 4- А'Т” У ~ АГ+ АТ + А"Г * ~ АГ+ А'Г +
III. Рѣшить уравненія
ах Ьу сл? = Л,
и
Р
Умноживъ оба члена перваго отношенія на а. второго на Ь, третьяго на с, получимъ ста; Ъу __ сх ат ~ Ъп~ ер
Отсюда, по свойству равныхъ отношеній, выводимъ:
х у г_ ах -\-Ъу 4- се <1___
т п р от-]-Ьп-^ср апі^Ъп-\-ср~
а отсюда:
__ __ сір жж — Ья—ср $ ат-\-Ъп-\~ср* & от4~б^4-ср
IV. Ріжжтъ систему уравненій
Уравненія (1) можно представить въ видѣ
Но въ ряду равныхъ отношеній сумма всѣхъ предыдущихъ членовъ относится къ суммѣ послѣдующихъ, какъ одинъ изъ предыдущихъ къ своему послѣдующему; такимъ образомъ, замѣчая, что въ силу ур—нія (2), сумма послѣдующихъ членовъ равна получимъ:
а + & + с4-^ а б с д
1 х у х и
откуда
^=(а + й + с + Ф^
г = (« + ь + с + а) *"
“ = (а -|- Ь -|- с гі)
V. Рѣшить уравненіе
Ѵа 4 д 4^3— гс 6
Г а 4я— }'а— х с
Во всякой пропорціи сумма членовъ перваго отношенія относится къ ихъ разности такъ, какъ сумма членовъ второго отношенія къ ихъ разности; слѣдовательно
|4 4 я___6 4
Га — # & с ‘
Возвысивъ обѣ части въ квадратъ, для освобожденія неизвѣстнаго изъ-подъ радикала, получаемъ
а 4 х.... № + ^)2
« — х (6 — с)2
Примѣнивъ снова то же самое свойство пропорцій, найдемъ
а = + с)г + (й —е)2 _ & 4_^
і ~ {Ь 4 с)2 —~ — ср 26с ’
откуда
бЯ^2’
ГЛАВА XXIV.
Неравенства первой степени.
Опредѣленія.—Общія начала,—Начала, относящіяся къ совмѣстнымъ неравенствамъ.— Провѣрка неравенствъ.—Доказательство нѣкоторыхъ замѣчательныхъ неравенствъ.— Рѣшеніе неравенствъ первой степени съ однимъ и со многими неизвѣстными.
Опредѣленія.
316. Если разность двухъ количествъ а и Ь равна положительному числу то изъ равенства а — находимъ: а = 6-|-р, откуда видно, что количество а превышаетъ Ь на р единицъ.
Если же разность между а и Л равна отрицательному числу — 2?, то изъ условія а — Ь ——р наюдимъ: а = 6 — откуда видно, что а меньше Ъ на р единицъ*
Отсюда вытекаетъ опредѣленіе: количество а считается большимъ каковы бы ни были ихъ знаки, если размоетъ а—Ь положительна; наоборотъ, « считается меньшимъ Ь, если разность а — б отрицательна.
Обратно: если а больше &, то это значитъ, что а равно Ь, сложенному съ положительнымъ числомъ р: а = Ъ-\-р^ откуда а — Ъ=р; если а меньше і», то это значитъ, что а равно й безъ нѣкотораго положительнаго числа р, т*-е. а = Ь~р. откуда а — Ь =— р.
Итакъ: каковы ом ни были знаки количествъ а и Ь, если а больше разность а — Ь положительна, если же а меньше Ь, эта разность отрицательна .
Слѣдствія* Изъ данныхъ опредѣленій можно вывести всѣ свойства относительно сравнительной величины положительныхъ и отрицательныхъ чиселъ*
1. Изъ двухъ положительныхъ чиселъ то больше, котораго абсолютная ве-чина больше*
Такъ, -|- 10 больше -|-6, потому что разность + Ю—(+ 6) равна положительному числу -|-4.
2. Всякое положительное число больше нуля.
'Гакъ, 4~ 5 > 0, потому что разность -р 5 — 0 равна положительному числу -(-5.
3* Всякое положительное число больше всякаго отрицательнаго*
Такъ, 4“ 2 > — А ибо разность 4- 2 —(— 7) положительна и равна + 9*
4. Изъ двухъ отрицательныхъ чиселъ то больше, котораго абсолютная величина меньше.
Напр* — 3 больше —8, ибо разность — 3—(—8) равна положительному числу 4-5.
5* Ноль больше всякаго отрицательнаго числа*
Такъ, О> — 4, ибо разность 0 — (—4) равна +4, числу положительному*
Отсюда вытекаетъ, что если написать рядъ положительныхъ и отрицательныхъ чиселъ, такъ чтобы ихъ абсолютныя величины шли возрастая въ обѣ стороны отъ нуля:
-^, . * * , 4, — 3, — 2, — 1, 0, 1, 4~ 2, 4-3, 4” * , * 4" »
то любое число, взятое въ этомъ ряду, больше каждаго числа, находящагося влѣво отъ него, и меньше каждаго числа, стоящаго справа отъ него.
Если по дразу мѣнять въ этомъ ряду между цѣлыми числами и дроби и несоизмѣримыя числа, то получимъ всевозможныхъ дѣйствительныхъ чиселъ.
Такъ какъ всякое положительное число больше нуля, а всякое отрицательное меньше нуля, то желая выразить, что число а положительно, пишутъ, что но больше пуля:
а желая выразить, что число Ь отрицательно, пишутъ, что оио меньше нуля:
317. Соединеніе двухъ неравныхъ величинъ знакомъ неравенства называется неравенствомъ; такъ
7 > 5, а <^Ъ
суть неравенства. Выраженія, находящіяся по ту и по другую сторону знака неравенства, называются частями неравенства: находящееся слѣва отъ этого знака, называется первою частью неравенства, а стоящее справа — второю частью его.
Подобно равенствамъ, неравенства бываютъ двоякаго рода: одни, какъ напр. а2 > 2ай, имѣютъ мѣсто при всякихъ частныхъ значеніяхъ буквъ, въ нихъ входящихъ; другія, каково напримѣръ 2ах* ~Ь с > имѣютъ мѣсто только при нѣкоторыхъ частныхъ значеніяхъ этихъ буквъ.
Такимъ образомъ, по отношенію къ неравенствамъ подлежатъ рѣшенію два вопроса: 1) провѣрка такихъ неравенствъ, которыя справедливы при всѣхъ значеніяхъ буквъ; и 2) опредѣленіе тѣхъ значеній неизвѣстныхъ, которыя удовле-. творяютъ неравенству, имѣющему мѣсто при частныхъ значеніяхъ буквъ.
Рѣшеніе этихъ вопросовъ основано на слѣдующихъ началахъ.
Общія начала.
318. Опредѣленіе. Два неравенства называются оквивалентнылш одно другому, если второе есть слѣдствіе перваго, и обратно—первое есть слѣдствіе второго.
319. Начало 1. Неравенства
А>В . . . (1) и А —В>0 . . . (2)
эквивалентны, каковы бы ни были знаки количествъ А и В.
Въ самомъ дѣлѣ: і) если А больше В, то разность А — В положительна, т.-е. больше нуля; слѣд. неравенство (2) вытекаетъ изъ (1); 2) обратно, если разность А — В больше нуля, т.-е. положительна, то количество А больше В: значитъ, неравенство (1) есть слѣдствіе неравенства (2). Эквивалентность неравенствъ (1) и (2) доказана.
Подобнымъ же образомъ доказывается, что неравенства
а <^ Ь и а — Ь < О эквивалентны, каковы бы ни были знаки количествъ а и Ь.
320. Начало II. Придавая оа/ьи.иь чатш неравенства одно и то же количество, положительное или отрицательное, и не перемѣняя знакъ неііавенства, получимъ новое не2)авенство, эквивалентное данному.
То-есть, если данное неравенство есть
А>В. . .(I)
и М—произвольное количество, положительное или отрицательное, то требуется доказать, что неравенство
А-ЬМ>В-|-М . . .(2) эквивалентно (1). Въ самомъ дѣдѣ;
1) Если дано, что
А>В,
то это значитъ, по опредѣленію, что разность А —В положительна, и слѣдов., жзъ (1) вытекаетъ неравенство
А — В>0;
прибавивъ къ первой части М и вычтя изъ нея М, мы не измѣнимъ разности А — В, а потому и
(А + М)-(В + М)>О,
откуда, по опредѣленію, имѣемъ
а+м>в + м.
Итакъ, неравенство (2) есть слѣдствіе перваго.
2) Если дано, что
а+м>в+м,
т* развесть между первою и второю суммою положительна, т.-е.
(А + ІЫВ-НОХ),
А —В>0,
А > В.
*ярмкв» іII есть слѣдствіе второго.
яізкжптстъ веравеиствъ (1) н (2) доказана.
1-З’йнп » образовъ доказали бы, что вычтя изъ обѣихъ частей одно и ш ж ь»лпсстт»>. найдемъ неравенство эквивалентное данному.
Слѣдствіе I. Можно переноситъ члены изъ одной части неравен* л Оругую, перемѣняя у переносимыхъ членовъ знаки.
Тагъ. имѣя неравенство
ах — Ь > сх г/ . . . (1)
ѵ ірідавъ къ обѣимъ частямъ его по — сх-\-Ъ, найдемъ
ах —Ь — сх -|- Ъ > сх -р Л — сх 6,
или, по приведеніи подобныхъ членовъ,
ах — сх > г/ Ъ . . . (2).
Но доказанному, неравенство (2) эквивалентно (1) и слѣд. можетъ его замѣнять. Сравнивая ихъ, замѣчаемъ, что членъ — Ь перешелъ изъ первой части во вторую со знакомъ а членъ сх изъ второй части въ первую со знакомъ —. Такимъ образомъ, правило перенесенія членовъ изъ одной части неравенства въ другую ничѣмъ не отличается отъ правила перенесенія членовъ изъ одной части уравненія въ другую,
Слѣдствіе П. 7?сяко<? неравенство можно привести къ виду
А>0, т.-е. къ неравенству, вторая часть котораго есть нуль.
Въ самомъ дѣлѣ, достаточно для этого всѣ члены собрать въ первую часть. Такъ, неравенство
5ха — ~х -}- 1^> 2х* -|- Зг -|- 4 эквивалентно неравенству
Зх* — Юх — 3 > 0.
321. Начало III. Помножая обѣ части неравенства на одно и тоже количество—существенно положительное, и не перемѣняя знакъ неравенства, получимъ новое неравенство, эквивалентное данному.
Требуется доказать, что неравенство
А>В. . .(1) эквивалентно неравенству ,
АМ > ВМ . * (2) при условіи: М > 0.
Въ самомъ дѣлѣ: 1) неравенство А>В эквивалентно неравенству
А —В>0; I
помноживъ положительное количество А — В на положительное количество Мд получимъ и произведеніе положительное, слѣд.
(А — В) М > 0, или АМ — ВМ > О, откуда
ЛМ > ВМ.
Итакъ, доказано, что изъ неравенства (1) слѣдуетъ (2).
2) Обратно: перенеся въ неравенствѣ АМ > ВМ вторую часть въ первую, найдемъ
АМ —ВМ>0, или (Л-В)М>0;
но множитель М положительнаго произведенія (А — В)М положителенъ, слѣд. и другой множитель долженъ быть положителенъ, т.-е.
А — В > 0, откуда А > В;
т.-е. изъ неравенства (2) вытекаетъ (1).
Эквивалентность неравенствъ (1) и (2) такимъ образомъ доказана.
Слѣдствіе I. Помножая обѣ части неравенства на одно и то же существенно-отрицательное количество и перемѣнивъ знакъ неравенства, получимъ новое неравенство, эквивалентное данному.
Т.-е. неравенство
эквивалента неравенству при условіи: 1 < 0.
АМ<ВМ. . .(2)
Въ с»чп> дѣлѣ, если М отрицательно, то на начала III, помноживъ обѣ части
— М положительно, а потому, неравенства (I) на — М и со-
хра
г тэтъ же знакъ, получимъ неравенство
— АМ > - ВМ . . . (3)
«таитное (1-му). Перенеся въ (3) члены изъ одной части въ другую, да-іжгъ *лу видъ
ВМ > АМ. или АМ < ВМ.
Заключаемъ, что неравенство (1) эквивалентно (2-му).
Слѣдствіе II. Умножая обѣ части неравенства на такою множился*, котораго знакъ неизвѣстенъ, получимъ неравенство, котораго елплслъ неизвѣстенъ, т.-е. неизвѣстно — больше ли его первая часть сторой, или меньше.
Это очевидно, потому что знакъ неравенства сохраняется, когда множитель Положителенъ, и измѣняется въ противный, когда множитель отрицателенъ.
Итакъ: нельзя умножать обѣ части неравенства на такого множителя, котораго знакъ неизвѣстенъ.
Слѣдствіе III. Раздѣливъ обѣ части неравенства на одно и то же количество М, и не перемѣнивъ знакъ неравенства при М^>0, и перемѣнивши его знакъ при М < 0, найде.иа неравенство, эквивалентное данному.
Въ самомъ дѣлѣ, раздѣлить на М — все равно что помножить на а для случая умноженія теорема доказана.
322. Приложеніе. Начало III съ вытекающими изъ него слѣдствіями имѣетъ важныя приложенія при вычисленіяхъ надъ неравенствами, а именно при сокра-щенги неравенствъ и при освобожденіи ихъ отъ дробей.
Пусть, напр., требуется освободить отъ дробей неравенство
Р К
8 *
. .(1)
Собравъ его члены въ первую часть, найдемъ эквивалентное ему неравенство
Р ІК п Р8-ЧЕ. п
' или • - со-
Умножить обѣ его части на (|8 нельзя, когда знаки количествъ 4 и 8 не- івіпки. потому что въ такомъ случаѣ неизвѣстенъ и знакъ произведенія (}8. На бы пи были знаки 4 и 8, квадратъ произведенія 48 всегда будетъ встзжтеленъ. а потому умноживъ обѣ части неравенства (2) на 4282 и сохранитъ знакъ неравенства, найдемъ
^8І(РфГ^->0’ или уй)>0,
неравенство —эквивалентное (1)-му н представленное въ цѣломъ видѣ.
Пользуясь слѣдствіемъ ІП, ложно сокращать неравенство, дѣля обѣ части его на общаго множителя; но эта операція возможна, когда -извѣстенъ знакъ того множителя, на который сокращаемъ. Такъ напр. если въ неравенствѣ замѣчаемъ множителя, имѣющаго видъ квадрата или суммы, квадратовъ, такихъ множителей можно сократить, не измѣняя знака неравенства; въ самомъ дѣлѣ, квадратъ всякаго количества и положительнаго и отрицательнаго—всегда положителенъ, а слѣд. и сумма квадратовъ такова же. Такъ, имѣя неравенство
8(я3 — 2)(я2 4- 2х 1)(& — 5) 0.
Замѣчаемъ, что множитель а;3-!-2x4^1 есть ничто иное какъ (я4-1)*, и потому существенно - положителенъ; затѣмъ, множитель #2 — 2л; 4- 2 равенъ (я2— 2х + 1)4~1> или (я — 1)24~Ъ т.-е, представляетъ сумму двухъ квадратовъ, а потому, прн всякомъ а?, существенно-положителенъ. Заключаемъ, что и произведеніе 8(я2 — 2х-1- 2)(л:2 4~ 2х~4 1), при всякихъ значеніяхъ существенно-положительно; сокративъ на него данное неравенство, замѣнимъ его простѣйшимъ неравенствомъ
х — 5 0.
Имѣя неравенство
— 5а2(ж — 2) < О,
и замѣчая, что какъ квадратъ, всегда положителенъ (каковъ бы знакъ ни имѣло количество а), заключаемъ, что —- 5а3— существенно-отрицательно; а потому, раздѣливъ неравенство на — 5а* и перемѣнивъ знакъ <С на >, найдемъ неравенство
х— 2 > О, эквивалентное данному, но имѣющее простѣйшій видъ.
323. Начало IV. об7ь части неравенства положительны, то возвышая ихъ въ одинаковую цѣлую положительную степень и не перемѣняя знакъ неравенства, получимъ неравенство эквивалентное данному.
Разсмотримъ сначала простѣйшій случай — возвышенія въ квадратъ. Если дано неравенство
А > В, . . . (1)
въ которомъ А > 0 и В > 0, то доказать, что неравенство
А3>В2. . .(2) эквивалентно данному.
Въ самомъ дѣлѣ: 1) Изъ неравенства (1) выводимъ:
А — В > 0;
но какъ А и В положительны, то и
А 4- в о.
Перемноживъ два положительныя количества, найдемъ и произведеніе положительное, слѣд.
(А — В)(А + В)> 0, или А2 —В“>0,
откуда
А2 > В2.
2) Обратно, если А2 > В2, то
А2 - В2 > 0, или (А + В)< А — В) > 0;
слѣдовательно, оба множителя: А -}- В и А — В должны быть одного знака; но какъ А + В положительно (ибо А > 0 и В > 0), то и А — В > 0, откуда
А > В.
Эквивалентность неравенствъ (1) и (2) доказана.
Слѣдствіе I. Если обѣ части неравенства отрицательны, то возвысивъ ихъ въ квадратъ и измѣнивъ знакъ неравенства, получимъ неравенство , эквивалентное данному.
То-есть, если дано неравенство
А > В, . . .(1)
причемъ А < 0 и В < 0, то доказать, что неравенство
А2 < В* . . . (2) эквивалентно данному.
Въ самомъ дѣлѣ, умноживъ обѣ части (1) на — 1, найдемъ ему эквивалентное неравенство
— А <—В,
гдѣ уже — А и — В положительны, а потому, но доказанному, возвысивъ въ квадратъ и не измѣнивъ знака неравенства, получимъ
А2 < В2,
жвивалентное неравенству — А < — В, а слѣд. и нор—ву А > В.
Слѣдствіе II. Если обѣ части неравенства имѣютъ противополож-пн знаки, то нельзя ихъ возвышать въ квадратъ, не зная ихъ числен-вй величины.
Въ самомъ дѣлѣ, пусть имѣемъ неравенство
А > В,
гті А 3> 0 и В < 0, и требуется доказать, что результатъ возвышенія въ квад-жжетъ быть нли А2 > В2, или А2 = В2, или А2 < В2.
Питательно:
А2— В2 — (АВ)(А — В);
ра уемхж: А > 0 и В < 0 будетъ А — В положительно; но мы не знаемъ зпа супы А — В. а потому неизвѣстенъ и знакъ разности А2 — В2; поэтому не можемъ сказать, будетъ ли А2 > В2, или А2 = В2, или А2 < В2.
Напримѣръ:
неравенство -р 3 > — 2 приводитъ къ + 9 > + 4;
» 3 > — 5 » > ”|- 0 < 25;
» з > __ з * » 4- 9 = + 9.
Слѣдствіе 111. Нельзя возвышать въ квадратъ такое неравенство, въ которомъ знаки частей неизвѣстны,
Это непосредственно очевидно изъ предыдущаго.
324. 'Обобщеніе. Если обѣ части неравенства положительны, то возвышая ихъ въ одинаковую цѣлую положительную степень и неизмѣ-ня я при этомъ знакъ неравенства, получимъ* неравенство эквивалентное данному.
Требуется доказать, что если А>0иВ>0, а т — цѣлое положительное число, то неравенства
. А> В. . • (1) и Ат>іГ . . . (2) эквивалентны.
Въ самомъ дѣлѣ, такъ какъ В > 0, то раздѣливъ обѣ части на В, найдемъ
что означаетъ, что есть неправильная дробь; но тая степень неправильной дроби есть также дробь неправильная, слѣд.
откуда, множа обѣ части на положительное количество В*\ находимъ
АЛ1 > В’".
Обратно, изъ неравенства (2) можно вывести (1). Въ самомъ дѣлѣ:
Ат — В”* = (А - ВХА”1-1 + А”1”2 В + - * • + В™"1).
Въ силу неравенства (2) это произведеніе > 0; но второй множитель, какъ сумма положительныхъ членовъ, положителенъ, слѣд. и А — В > 0, откуда
А > В.
Слѣдствія. 1. .Если количества А и В оба отрицательны, то возвышая обѣ части неравенства X В въ цѣлую положительную степень т, и не измѣняя знакъ неравенства при т нечетномъ, и напротивъ измѣняя его при т четномъ, получимъ неравенство, эквивалентное данному.
Дано неравенство
въ которомъ А < О и В < 0, Положивъ А = — А' и В = — В\ гдѣ уже А' В* ноложительны, помножимъ обѣ части неравенства (1) на — 1; найдемъ
— А < — В, или А' В'.
Такъ какъ А' и IV положительны, то по предыдущей теоремѣ имѣемъ
В'ш
Изъ равенствъ А = — А* и В = — В' имѣемъ: А'=(—1).А и ]р—(—1).В, •ггкуда. по возвышеніи въ т-ю степень, находимъ: А'”1 = (— 1 )ИІАт и 1Г*' — (— Подставляя въ послѣднее неравенство, получимъ
Если ш—четное, то (—1)т есть число положительное; а потому, раздѣливъ на него послѣднее неравенство, не должны перемѣнять знакъ неравенства; напротивъ, при нечетномъ. (— 1)т<0 и дѣленіе неравенства на это число поведетъ за собою перемѣну знака неравенства. Такимъ образомъ, неравенство (1), въ которомъ А < 0 н В <С 0, эквивалентно нер—ву
при т—четномъ; и нер—ву
Аш > В"1 при «і—нечетномъ,
II. Когда части неравенства имѣютъ различные знаки, то слѣдуетъ различать два случая:
1) когда возвышаемъ неравенство въ начетную степень, то степени сохранятъ тѣ знаки, какіе имѣли части неравенства, а потому и знакъ неравенства сохранится. Напр.
изъ Н~2> — 7 слѣдуетъ (4- 2)3 > (— 7)\ или 4~ 8 > — 343.
2) Когда возвышаемъ неравенство въ четною степень, то нельзя дать никакого правила: знакъ неравенства можетъ измѣниться или же сохраниться, или даже неравенство можетъ перейти въ равенство. Такъ:
+ 3^ > — 2 приводитъ КЪ (4-3)* > (- 2)‘, ИЛИ 4-8і > 4 Н 16;
4-2 > — о » / ’ (+2)‘< (- 5)‘, или 4-іб<я |-625;
1 “ > — 2 > > (+2)‘ = (- 2)‘, или - 416 = 4 Н 16.
Ш. Если обѣ части неравенства положительны, то возводя ихъ въ чллую отрицательную степень и перемѣняя знакъ неравенства^ полу-неравенство эквивалентное данному.
Требуется доказать, что если
А > В, . . . (1)
гтіА>0іВ>0, то неравенство
А~Л < В-”
Такъ какъ н—число положительное, то неравенство А* > В* . . \ (3)
эквивалентно (1). Раздѣливъ обѣ части на положительное количество Ап . В“, найдемъ неравенство
или В”п > А”и. или, наконецъ,
А”” <В"\
эквивалентное (3), а потому и (1)-му.
325. Начало V. I. Каковы бы ни были знаки обѣихъ частей неравенства, извлекая корень нечетнаго порядкал должно сохранятъ знакъ неравенства.
Это есть прямое слѣдствіе правила знаковъ при извлеченіи корня.
Такъ:
Изъ неравенства Ц-27 >-(- 8 имѣемъ; ^4“ 2?' > ^4“ или 4~3>4~-:
» » -|- 27 > — 8 » і/ + 27 > — 8, или 4“®>—2;
> > _ 8>-27 > ~8 > у' —27, или — 2>—3.
2. Если же показатель корня — четный, то, во-первыхъ, необходимо, чтобы обѣ части неравенства были положительны (въ противномъ случаѣ корни были бы мнимые, и не могло бы быть рѣчи о ихъ сравненіи); въ такомъ случаѣ каждый корень имѣетъ два значенія, равныя по величинѣ, но противоположныя по знаку; и неравенство сохраняетъ знакъ, или измѣняетъ его, смотря по тому, беремъ ли положительныя, или отрицательныя значенія корней. Такъ: неравенство 4“ 49 > 4~
даетъ
или
или
Но если взять корни съ различными знаками, то очевидно, что отрицательный корень всегда'будетъ меньше. Такъ
неравенство 4* 49 > 4^ 25
| V 49 > — }425, или 4" 7 > —
даетъ { , 1
| —уЧэ <4~ к 25, или — 7<4~5.
Начала, относящіяся къ совмѣстнымъ неравенствамъ.
326. Если въ двухъ или нѣсколькихъ неравенствахъ первыя части больше вторыхъ, или первыя части меньше вторыхъ, то они называются неравенствами одинаковаго смысла. Такъ, неравенства
3 > — 2 и а > Ь
суть два неравенства одинаковаго смысла.
Если же въ одномъ неравенствѣ первая часть больше второй, а въ другомъ первая меньше второй части, то ихъ называютъ неравенствами противоположнаго..смысла, Таковы
а > Ь и с < гі,
327. Начало VI* Складывая почленно два или нѣсколько неравенствъ одинаковаго смысла, получимъ неравенство того же еліьим-а; «о оно не можетъ замѣнитъ одною изъ данныхъ.
Пусть данныя неравенства будутъ
А > В и А' > В'.
Изъ пихъ слѣдуетъ, что разности А — В и А' — В' положительны, а потому и сумма ихъ положительна; слѣд.
А —В-НА' —В'>6,
откуда, перенеся — В и — Вг во вторую часть* найдемъ
а+а'>в+в\
Но это неравенство не можетъ замѣнить одного изъ данныхъ, иначе говоря, система:
не имѣетъ слѣдствіемъ:
А'>В\
Въ самомъ дѣлѣ, изъ неравенства
А —А* В В , перенесеніемъ членовъ въ первую часть выводимъ: (А - В) + (А' - В') > 0;
и хотя изъ условія А > В мы и знаемъ, что А — В > 0, однако отсюда нельзя заключить, чтобы к
А' — В' > 0.
Слѣдствіе. Нельзя почленно складывать два неравенства различнаго смысла, ибо нельзя предвидѣть, которая сумма будетъ больше. Дѣйствіе въ этомъ случаѣ возможно только въ численныхъ примѣрахъ. Такъ
О
2)
3
328. Начало VII. Можно сдѣлать почленное вычитаніе двухъ нера-★ венствъ различнаго смысла: полученное неравенство будетъ одинаковаго смысла съ первымъ^ но оно не можетъ замѣнить одного изъ данныхъ.
Пусть данныя неравенства суть:
А > А' и В < В\
Мы заключаемъ изъ нихъ, что разности: А — А' и В' — В обѣ положительны, а потому и сумма ихъ положительна; слѣд.
А- А'Ч-В'-В>0,
или
Но система
не имѣетъ необходимымъ слѣдствіемъ В < В' и потому не необходимо эквивалентна данной.
Въ самомъ дѣлѣ, изъ неравенства А — В > А' — В' имѣемъ .
(А-А') + (В' —В)>0, \
и хотя знаемъ, что А — А' > 0, но отсюда нельзя заключить, чтобы необходимо было и В' — В > 0.
Слѣдствіе. Нельзя дѣлать почленнаго вычитанія двухъ неравенствъ одинаковаго смысла, ибо нельзя напередъ знать относительную величину разностей; такъ
329. Начало VIII. Перемножая почленно два или нѣсколько неравенствъ одинаковаго смысла, части которыхъ положительны, получимъ неравенство того же смысла*, но оно не можетъ замѣнить одною изъ данныхъ.
Пусть данныя неравенства суть:
А>В н А'>В',
причемъ: А, А', В, Вг—положительны. Изъ данныхъ неравенствъ имѣемъ:
А —В>0 и А' —В'>0.
а такъ какъА' и В положительны, то и
(А-В)А'>0 и (А'~В')В>0;
складывая, находимъ
(А — В) А'(А'— В') В > О, или АА' —ВВ’>0, откуда
АА'>ВВ'.
Но изъ того, что
А>В 1
И АА' > ВВ' )
нельзя заключить, что и А'>В', ибо сумма (А — В)А'Н-’(А"—В')В можетъ быть положительна, хотя бы А' — В' и было отрицательно’.
Эта теорема справедлива для какого угодно числа неравенствъ.
Пусть, напр., имѣемъ р неравенствъ
А| > Вр
А.2 > В2,
Примѣнимъ новый пріемъ доказательства, который полезенъ намъ будетъ и впослѣдствіи. Пріемъ этотъ основанъ на томъ замѣчаніи, что неравенство А В всегда можно замѣнить равенствомъ А = В4-а\ гдѣ я>0; въ самомъ дѣлѣ, это равенство означаетъ, что А больше В на Итакъ, данныя неравенства можемъ замѣнить равенствами
А। В| , А2 = В2-|-#2, * . . , Ар Вр |г
Перемноживъ ихъ, имѣемъ:
А,А, . . . А/, = (Ві+ж1)(В8+жі) . . . (1^4-жД ,
или, раскрывъ скобки и перенеся членъ ВіВ2 . . . Вр въ первую часть, имѣемъ: Ма • * . Ар“В|В3 . . . В„ = 2 ^((В2 -(-Жг) * * . (Вр + .
г Такъ какъ вторая часть, какъ сумма положительныхъ членовъ, положительна, то и заключаемъ, что
А4А2 * . Ауі В1В2 . . . В^.
Примѣчаніе^ Для другихъ случаевъ нельзя формулировать никакого об-
330. Начало IX. Можно раздѣлитъ почленно одно на другое .два не-до&аѵгмм разнаго смысла, если всѣ четыре части положительны, со-хр - такой знакъ неравенства, какъ въ дѣлимомъ; но новое неравен-еш- ле лгожегиг замѣнитъ одного изъ данныхъ.
Пусть іаиы неравенства
А>В .и С<1),
гдѣ А, В, С ь —положительны. Помноживъ А > В на В > С, но предыду-гореаѣ ваДіеп:
АО > ВС;
~ 314 -
откуда, раздѣливъ обѣ части на положительное количество СВ, имѣемъ;
Другое доказательство* Замѣнивъ первое изъ данныхъ неравенствъ равенствомъ: Л = В-р^ а второе равенствомъ С = П—3/, гдѣ #>О и ^>0, и раздѣливъ первое равенство на второе, имѣемъ:
С“ О -
вычтя изъ обѣихъ частей по р, получимъ;
А В В+л В
—- Н- - -- «
с о о —і/ і»'
А В 1)ж + В// с Г) ‘ “сТГ ~
А , В ~ іітитпп —
Вторая часть положительна, слѣд. больше
Примѣчаніе, Для другихъ случаевъ нельзя формулировать общаго правила.
Провѣрка заданныхъ неравенствъ.
331. Для провѣрки данныхъ неравенствъ не существуетъ никакого общаго правила; укажемъ методы наиболѣе употребительные.
I. Методъ возвышенія въ степень. Если въ подлежащемъ провѣркѣ неравенствѣ встрѣчается радикалъ, его изолируютъ и затѣмъ возвышаютъ обѣ части неравенства въ степень, изображаемую показателемъ корня. Пусть, напр., требуется доказать, что среднее ариѳметическое двухъ положительныхъ количествъ « и Ь больше ихъ средняго геометрическаго, т.-е* что
Такъ какъ обѣ части неравенства положительны, то, возвысивъ ихъ въ квадратъ и сохранивъ знакъ неравенства, замѣнимъ данное неравенство ему эквивалентнымъ
или, умноживъ обѣ части на 4 и собравъ всѣ члены въ первую часть:
(а &)2 — 4а& > 0, или (а — Ьр О*
Такъ какъ квадратъ всякаго дѣйствительнаго количества положителенъ, то послѣднее неравенство вѣрно; поэтому вѣрно и эквивалентное ему данное неравенство.
332* II. Методъ разложенія на множителей. Переносятъ всѣ члены въ одну часть и разлагаютъ полученный полиномъ на множителей; справедливость провѣряемаго неравенства дѣлается очевидною.
Пусть, напр., требуется доказать, что при всякихъ значеніяхъ а, положительныхъ или отрицательныхъ,
По перенесеніи въ первую часть, по раскрытіи скобокъ и по приведеніи замѣняемъ данное неравенство ему эквивалентнымъ:
2а4 - 2а3 —2а-]-2 > О,
или, по разложеніи на множителей, неравенствомъ:
2(а — 1)а (ай Ц- -р 1) > О;
или, придавъ къ триному а2 -|~ а 4~ 1 и вычтя изъ него найдемъ
2(а-1)’{(а+-’У+1(>0.
2(а — I)2, очевидно, положительно; биномъ (а ~Н 2) +4’ сУмма двухъ положительныхъ количествъ, также положителенъ, а отсюда справедливость послѣдняго неравенства, а потому и эквивалентнаго ему перваго, очевидна.
333. III. Методъ превращенія полинома въ сумму квадратовъ. Переносятъ всѣ члены въ одну часть и разлагаютъ полученный полиномъ въ сумму квадратовъ: справедливость неравенства дѣлается очевидною.
Примѣръ I. Доказать справедливость неравенства
а2 _|_ ^2 _[_ с2 — . ас _* । >0.
Его можно представить въ видѣ:
~ (а4 - 2аЬ 4- Ь*) 1 (М - 2Ьс + с») +1 (с4 — 2ас а4) + 1 > О, или
1 (а _ + ’ (Ь _ С)Я +1 (с _ а)і > о,
что очевидно.
Примѣръ II. Доказать, что если Ь2 — 4ас < 0, то справедливо неравенство
|ЬЬ' - 2(са' 4-а<?'){2 — (Ь2 — 4ас) (6'2 — 4аV) > 0.
Раскрывая и располагая по степенямъ количества Ь', можемъ этому неравенству дать видъ:
асЪ1* — Ь(са‘ 4- 4” (са^4“^)а 4” — 4ас) > О,
или
+ лс*') і * . (4ас— Ь2) , , м
ас <Ь-----—тг~—-} + л - (еа — ас)3 > О,
I 2ас I 1 4ас 4 7
*
Изъ даннаго условія Ьа— 4ас<^0 выводимъ, что 4ас>5\ а потому ас>0, равно и 4ас—&2>0; отсюда видно, что первая часть послѣдняго неравенства положительна, и стало быть оно вѣрно; поэтому вѣрно и эквивалентное ему заданное неравенство.
334. IV, Неравенства симметричныя относительно данныхъ буквъ. Когда неравенство симметрично относительно нѣкоторыхъ буквъ а, Ь, с, то предварительно условливаются въ относительной величинѣ этихъ буквъ; пусть, напр., а есть наименьшее изъ третъ данныхъ количествъ: въ такомъ случаѣ і и с можно представить въ видѣ: Ь = а-\-х, с — гдѣ и ^>0.
Пусть, наприм.. требуется доказать, что если а, і, и с положительны, то имѣетъ мѣсто неравенство:
аЬс (а 4“ Ь — с) (Ь 4~ с — а) (а 4“ е — 6).
Положивъ 6 = а-|“# и с = а~4у, и подставивъ въ испытуемое неравенство, приводимъ задачу къ провѣркѣ неравенства
а(а-|-ж) (а-|-і/) > (а + х — у) (а -}~ х у) (« + У — «), или
а{а’-|-в(а;-}-у)4-з:у* — *аа — (х — у)2| (а-|-а:-|-у)>О, или
«лу-Ь (“+®+у)(®-у)’>о;
справедливость этого неравенства очевидна, такъ какъ оба его члена положительны.
335. V. Иногда справедливость заданнаго неравенства можно доказать, показавъ, что оно есть слѣдствіе равенствъ или перавенствъ уже доказанныхъ или легко доказуемыхъ.
Примѣръ. Доказать, что если а, Ь и с положительны, то имѣетъ мѣсто
неравенство
с3 4” 4~ с3 Зайе.
Такъ какъ а, Ь н с входятъ въ это неравенство симметрично, то мы могли бы примѣнить къ нему предыдущій способъ. Но можно доказать справедливость данпаго неравенства, исходя изъ неравенствъ:
а24-^>2«Ь (1), Ь24-с3>26с (2), <?*+а*>2ас (3).
Справедливость этихъ неравенствъ легко обнаружить; въ самомъ дѣлѣ, изъ очевиднаго неравенства (а — &)а^>0 или а2 4“^— 2аЬ > О прямо имѣемъ + Такимъ же образомъ докажемъ (2) н (3).
Сложивъ неравенства (1), (2) и (3), получимъ:
а/> 4~ Ьс + ас;
помноживъ обѣ части этого неравенства на положительное количество а+ найдемъ, по упрощеніи:
а8_р.&8_рсз -> Забе,
что и требовалось доказать.
336. VI. Методъ заключенія отъ п къ я 4^1 и наоборотъ. Пусть требуется доказать, что если'<4 н й положительны, всегда имѣютъ мѣсто неравенства
2 +
2Ма3~Н3)>(а + йА
2\(а* + М) >(« + &)<,
и вообще
гдѣ п— цѣлое положительное число.
Первое неравенство доказать не трудно; въ самомъ дѣлѣ, перенеся въ первую часть, раскрывъ скобки и сдѣлавъ приведеніе, найдемъ:
а'1 — 2аЬ > О или (а — &)2 > О, что вѣрно.
Второе неравенство приводится къ виду
4(а* -[“ &’) — (а 4" > О* или. замѣтивъ, что
а*4”Ъ* = (а 4“&) (а- —- и (а-]-Ь)3 = (а -)-(а34“ 2а/>-р62),
даемъ неравенству видъ
4(а 4- 6) (а» — аЬ 4- Ъ*) — (а 4~ Ь) (а* 4» 2аЬ 4» Ь9) > О, или
3(а 4~ Ь) (а9 — 4” &*) >
или
3(а 4- &) (а — Ь)2 О, что очевидно.
Чтобы доказать общность закона, выражаемаго этими неравенствами, допустимъ, что онъ вѣренъ для показателя п, т.-е. что неравенство
2"-1(а“4-Ьй) >(« + &)" • - *(1)
I справедливо, и докажемъ, что въ этомъ предположеніи будетъ вѣрно и неравенство для показателя п 4- 1, т.-е.
2я(ам+14’Ьп'н)>(®Ч-Ь)Л+1 . . . (2).
Въ самомъ дѣлѣ, умножая обѣ части (1) на положительное количество ®4"^ найдемъ
2п-і(д« 4- Ьп) {а + Ь) > (а + Ь)
Слѣдовательно, достаточно показать, что
2*0 -+1 _|_ Ь «+!) > 2 + И (« + Ь)-
Ііо сокращеніи на 2П“\ но раскрытіи скобокъ во второй части и по упрощеніи, получимъ или
а«(а — 6) — 6"(а — Ь) > О, или
и («_*>)> О,
неравенство очевидное, потому что оба множителя, ап — Ъп и а — Ь, всегда имѣютъ одинаковые знаки.
Итакъ, какъ скоро неравенство (1) провѣрено для нѣкотораго значенія п, мы можемъ заключить, что оно также вѣрно и для величины м, на единицу большей. Но мы доказали, что оно вѣрно для п = 2, слѣд. оно вѣрно и для п = 3; будучи же вѣрно для п = 3, оно вѣрно и для « = 4 и т. д.
Доказанное неравенство можпо написать въ видѣ
въ этой формѣ оно показываетъ, что ариѳметическая средина п-хъ степеней дхухъ чиселъ больше п-ой степени ариѳметической средины этихъ чиселъ.
Можно распространить эту теорему на какое угодно число р положительныхъ количествъ а, 6, с, Д, . . . й, I.
Взявъ четыре количества а, 6, с, имѣемъ тождество:
/а 4- Ь , с 4- н
4 2 /
и слѣд. по предыдущей теоремѣ имѣемъ:
/п 4- 6У* I /<? + ^у1 й/4-&4-с4-<^“ \ 2’ / ,
\ 4 7 2 ~
но мы имѣли:
м-ну «й + ьи /с4- сп4-гін \ 2 / 2 И \ 27 < 2 ;
слѣдовательно
Іа + Ь + г 4- а" + *>м + с" 4"
\ 4 / < 4
Такимъ же точно образомъ докажемъ, что предложеніе вѣрно для 8, 16,..., 2* положительныхъ количествъ. Чтобы доказать справедливость теоремы вообще, употребимъ пріемъ, впервые введенный французскимъ математикомъ Лоши; пріемъ этотъ разнится отъ пріема Бернулли тѣмъ, что дѣлается заключеніе не отъ р къ а обратно: отъ р + 1 къ р. Итакъ, допустивъ, что теорема справедлива для />4-1 чиселъ, докажемъ, что она будетъ вѣрна и для р чиселъ.
Имѣемъ тождество
і,. , ... ^±1(а+6-НЯ-... +») «+&+<?+. ,+Л+п+6+с+- • '+ІІ
, «4^+с4-. . »4л\ _ Р ___________'__1 ________р
\ р Р 4-1 р +1
слѣдовательно
/ । к і । । । । о-НН-с-|- - . . 4-ЛА*
.і*і і і * х к ! . 4^+ —------—-------।
д+Ь+с+*«»+М* _ р I . . . (3).
Р / \ Р + I /
Но, по допущенію, теорема вѣрна для р 1 количествъ; поэтому вторая часть равенства (3) меньше
Р
5
а слѣд. и
5
а потому и
/д -{-&•+ • + М* . г? -|- 6* + с* + . . 4- Л*
\ Р I р
337. Доказательство нѣкоторыхъ замѣчательныхъ неравенствъ. Приведемъ доказательство нѣкоторыхъ теоремъ, имѣющихъ примѣненіе къ элементарной математикѣ, или же представляющихъ интересъ въ самомъ способѣ иіъ доказательства. *
338. I. Полусумма двухъ чиселъ, каковы бы ни были ихъ знаки, всегда заключается между этими числами.
Пусть данныя числа будутъ а и Ь, и пусть
а<Ь . . (I).
Придавая къ обѣимъ частямъ по а, найдемъ:
2а < а -|- 6, откуда
. а 4- Ь а<--
Придавая къ обѣимъ частямъ (1) по Ь, получимъ
#ауи
«-|-Ь ।
—<ь-
тусИоме дешш). Эта теорема имѣетъ обширныя приложенія въ изслѣдо-вашм вдвоожъ 2-й степени.
II. Если дано нѣсколько дробей % % г’* * * ’г’ У которыхъ всѣ О| О2 О3 0п
знаменатели имѣютъ одинъ и тотъ же знакъ, то дробь, которой числитель = суммѣ всѣхъ числителей, а знаменатель=суммѣ всѣхъ знаменателей, содержится между наименьшею и наибольшею изъ нихъ.
Пусть наименьшая изъ данныхъ дробей будетъ ш, а наибольшая М, тогда, по условію, имѣемъ
т<^<М, т^<М................... .(1).
Пусть Ьѵ Ь...., \—всѣ>0; въ такомъ случаѣ умноженіе на Ь^Ь*,...
не измѣнитъ смысла неравенствъ и мы получимъ
Ьіт^.аі^.Ь^ , . . , \т^адСЬнМ, а складывая почленно эти неравенства, найдемъ I»
т(^і +&іЧ 4* М яі 4~ “іі+аз 4-----------Н ап 4-^4- • •• И- ья).
Дѣленіе на положит. колич. Ь, -\-Ь9 4“ • • • +"&, не измѣнитъ смысла неравенствъ, и мы найдемъ
"^М . . .(2). I»
Пусть теперь , 6М—всѣ<СО; въ такомъ случаѣ умноженіе не-
равенствъ (1) на эти количества измѣнитъ смыслъ всѣхъ неравенствъ, и получится
а3 > Ь2М, * * ♦,
откуда почленное сложеніе дастъ:
77і(&і —|— Ь. —• * ♦ —' &н) —|— а^ 6Ц
Н * ‘+а« (&і + +‘ ’ ‘ Н”
Такъ какъ теперь + &2-|-***-|-6п < 0, то дѣленіе на эту сумму измѣнитъ смыслъ неравенствъ, и получится
4“ ^2 4~ аз Ч~
-Н * »
Такимъ образомъ снова получилось соотношеніе (2), и теорема доказана.
Напр., если даны дроби
1—53—4
з’ 6 ’ 4’ 25 * Т<)
6
4 —6—1
-5’ —15’ —8’ то
Также, если даны дроби —
4 1—3 + 4 — 6 —1 3
-5 '—3 — 7 — 5 —15-8 < — 1
339- III. Теорема Коши/ Среднее ариѳметическое п положительныхъ количествъ ан аа, а3, * . . которыя «е всн> роемы леж?Л/ со-/Гоад, больше ихъ средняго геометрическаго.
Для двухъ количествъ теорема уже доказана выше; слѣд* •
Затѣмъ, имѣемъ тождество
у а1а3аіаі = Ѵу'а1аі.у'а3аі слѣдовательно
‘____* .— .— 4“ . । ~Ь
^а.а^а.а. - Иаіаа+ V аз"і 2 ‘ 2
2 . . 2
итакъ: Ѵ“------ Лі Ч- о? -н а3 +
• Г < - 4
* * ’ * « 4 >
Такимъ же образомъ, замѣчая, что
--*і/|/вввва7Л8Т
докажемъ, что теорема вѣрна для 8 количествъ; и вообще, что она справедлива для 2* чиселъ-
Чтобы доказать, что теорема справедлива для какого угодно числа данныхъ количествъ, Коши доказываетъ, что если теорема вѣрна для р +1 количествъ, то она вѣрна и для р количествъ*
Имѣемъ тождество:
1Л - р4~і/
р /
- Г ма
ио, по условію, теорема вѣрна для р +1 количества
слѣдовательно
Р7
*
ар^1а1.
-------*
р
Замѣчая, что первая часть = ... ар, наюднмъ:
Г Л1Л8а!»
-р
Р/---------
— 01+
- «р< —
•а
Р1
р
чт> -гліювало доказать.
Эмрои-іь, обобщеніе теоремы для случая, когда число п данныхъ количествъ іе есть сте®?яь двухъ, можетъ быть сдѣлано инымъ пріемомъ. Пусть % будетъ ѵілое число, которое надо прибавить къ п, чтобы получить степень двухъ* 21
' Обозначимъ арнометич. средину *** данныхъ п чиселъ бук-
вою Ъ. Присоединивъ къ этимъ числамъ о, чиселъ', изъ которыхъ каждое равнялось бы Й, получимъ чиселъ:
^1» «31 *
~*_|1 1 з п
Такъ какъ число «4"^ есть степень двухъ, то по доказанному
+ - * + вя+<г*ь
п-н ~
аі^йа3
• ЯП.Ь* т»
Но «і 4- аз + аз 4“ * ' - 4* — п • Ъ; подставивъ въ послѣднее неравенъ ство, найдемъ;
лб 4“ <уЬ «44/ ~ ' іо" г я-Н/ іа-
п^'п > у • • -ан‘Ь і ИЛИ і> Ѵаі% • ‘
откуда
> «Н . Ь’,
а по сокращеніи на Ь7, по замѣнѣ Ъ его величиною и по извлеченіи изъ обѣихъ частей я-го корня, находимъ:
’ а 1 4~ в» + аз + • • "Ь ап «/----——
;--------г------->Г«іМ» . . . ап.
340. IV* Формула дѣленія при цѣломъ положительномъ т:
= ат_і а,л_2& аМ_ЗЬ2 аг,»»-г
позволяетъ вывести слѣдующія неравенства. Если а > Ъ > 0, то, подставивъ во вторую часть вмѣсто Ь количество а, мы этимъ вторую часть увеличимъ; слѣд*.
ат — Ьш тв1
----=— < тат 1 а — Ъ
. (1)-
*
Напротивъ, подставивъ во второй части Ь вмѣсто а, мы ее уменьшимъ, и
получимъ
ат_^т а — Ъ
т,Ь*”1
.(2).
Помноживъ неравенство (1) на положительное количество а — Ъ и вынеся за скобки а”"1, найдемъ:
[а — т(а — Ъ^а"-'<ЪМ . . . (3).
Подобныхъ же образомъ изъ неравенства (2) найдемъ:
°м > [Ь + ™(«— Ь)] Ь’"-1 . . . (4).
Если а — т(а — Ь) будетъ количество положительное, то, раздѣливъ нера-жвктво (3) на а — ж(а— Ь), найдемъ:
ът ____-______ а — т(а—Ъу
аідовательно это неравенство возможно при условіи
, ' а>т(а —&), или
Положивъ т —пЦ-1, получимъ:
а
• -(5).
п
-г-і • а
Воспользуемся неравенствомъ (3), въ которомъ а > Ь, для вывода слѣдую-даго неравенства:
я \к
1-2.3.4. . .к
гдѣ г произвольное, а і—цѣлое положительное число.
Положивъ въ (3): а —и Ь = найдемъ:
тт, откуда 1—
Подставляя сюда вмѣсто т послѣдовательно 2, 3, 4. . —1, имѣемъ:
Перемножая эти неравенства, получимъ
откуда, по извлеченіи квадратнаго корня, находимъ:
У*)‘ < 1 . 2.3.4 . . .к.
1
Отсюда ясно, что
1.2.3.
“ЛИ 1.2.3... .
4
Рѣшеніе неравенствъ первой степени съ однимъ неизвѣстнымъ.
341. Нерѣдко случается, что неизвѣстное вопроса, по свойству самой задачи, должно заключаться между извѣстными предѣлами, и слѣд. должно удовлетворять нѣкоторымъ неравенствамъ. Отсюда задача о рѣшеніи неравенствъ.
Рѣшитъ неравенство значитъ найтп предѣлы, между которыми должны заключаться значенія неизвѣстнаго, для того чтобы неравенство было удовлетворено.
342. Рѣшеніе одного неравенства первой степени съ однимъ неизвѣстнымъ. Всякое неравенство первой степени съ 1 неизвѣстнымъ, по уничтоженіи дробей, по перенесеніи извѣстныхъ членовъ въ одну часть, а неизвѣстныхъ въ другую и по приведеніи, можетъ быть представлено въ видѣ
(1).
Чтобы найти отсюда предѣлъ значеній я, нужно обѣ части раздѣлить на а, а при этомъ нужно знать знакъ коэффиціента а. Отсюда два случая:
I. Если а>0, то раздѣливъ обѣ части на а, слѣдуетъ сохранить знакъ неравенства; такимъ образомъ найдемъ
Заключаемъ, что въ этомъ случаѣ неравенству (1) удовлетворяютъ всѣ значенія х, большія а потому называется низшимъ предѣломъ неизвѣст-(л (I
наго х.
П. Если а<0, то раздѣливъ обѣ части неравенства (1) на отрицательное количество а, должны перемѣнить -смыслъ неравенства; найдемъ
т.-е. что неравенству удовлетворяютъ всѣ значенія я, меньшія въ этомъ
случаѣ “ будетъ бысшиліь предѣломъ неизвѣстнаго. а
Приводимъ примѣры:
Примѣръ I. Какъ нужно взять х^ чтобы удовлетворить неравенству:
Для освобожденія неравенства отъ дробей множимъ обѣ части на положительное число 24: знакъ неравенства отъ этого не измѣнится и мы получимъ
32я—6 —|—72 < 120л=——456, или
32л + 66 < 119г—456.
По перенесеніи членовъ и по приведеніи, найдемъ:
522 < 87г,
откуда, раздѣливъ обѣ части на* положительное число 87^ имѣемъ * « « ”
Л > 6ф
Итакъ, всѣ числа большія 6 удовлетворяютъ данному неравенству.
Примѣръ II. Рѣшить неравенство х а х Ъ А
а-\-Ъ а — а — Ь
Для уничтоженія дробей нужно* бы было умножить обѣ части неравенства на (а + &)(а — 6) или а1 — Ь1; но какъ мы не знаемъ знака этого количества, то помножить обѣ части на (а1 — 6*)а, т.-е. на положительное количество; при этотъ звать неравенства не перемѣнится, и иы получимъ: .
(а1—6*)(а—Ъ)х—а(аі—Ь*)(а+&)> (а®—Ь*)(а+Ь)я—Ь(аа—68)(а—6).
Перенеся неизвѣстные члены въ первую часть, а извѣстные во вторую и сдѣлавъ надлежащія упрощенія, найдемъ:
— 26 (а® — Ъ*)х > (а2 * * — 68) (а2 + 62).
! Далѣе приходится дѣлить обѣ части на коэффиціентъ при я, а при этомъ надо знать знакъ количества 6 (а8— 62); отсюда два случая:
1) Если 6(аа— 6а)<СО, то —26 (а2 — 68) будетъ количество положительное, п слѣдов. дѣля на него обѣ части неравенства, слѣдуетъ сохранить знакъ неравенства; такимъ образомъ получимъ
(«г - 6®)(^ + 6>) Х> — 26(а1 —Ь2) ’
или, по сокращеніи дроби на аа— 6а:
а2 4- 6« 26
2) Если Ъ(аі — Ь»)>0, то раздѣляя обѣ части неравенства на отряда-
тельное количество —26 (а*— 6а), нужно измѣнить смыслъ неравенства, такъ
что въ этомъ случаѣ, по сокращеніи, найдемъ:
Провѣримъ найденные для #-предѣлы на самомъ неравенствѣ.
Мы нашли, что при условіи: 6 (а2 — 6*) < О неравенству удовлетворяютъ всѣ значенія #, большія------; слѣд. для повѣрки должны положить
26
гдѣ Л > О, и это значеніе найдемъ:
х подставить въ данное неравенство. Сдѣлавъ это,
а а — Ь
26____
сі — Ъ
к’ • • • (1)
или:
— (а2 ч- 62) + 266___________а — (<,* + 62) + 2Ьк _ Ъ
26(а + 6) а — Ъ %Ь(а — 6) б + 6’
помноживъ обѣ части на количество 2Ь(а-\-Ъ)(а — 6), по условію, меньшее нуля, найдемъ по упрощеніи
— 2&Ч<4-2Ь8Л. . .(2).
Но Л и Ь* положительны, слѣд. — 2Ь*Л отрицательно, а -|-262Л положительно, и потому неравенство (2), а слѣд. и эквивалентное ему (1) вѣрно.
Такимъ же образомъ убѣдимся, что при условіи Ь(а*— 6*)>О данному х . * • а2+ 6»
неравенству удовлетворяютъ всѣ значенія х, меньшія--—
343. Рѣшеніе нѣсколькихъ неравенствъ первой степени съ однимъ неизвѣстнымъ.
Пусть, наприм., имѣемъ два неравенства первой степени съ однимъ неизвѣстнымъ:
ах > Ъ и а'х > Ь*.
1. Пусть мы нашли: изъ перваго: # > я», а изъ второго: &>р*
Если, при этомъ, то очевидно, что даннымъ неравенствамъ удовлетворяютъ всѣ значенія #, большія р; такимъ образомъ р есть низшій предѣлъ#.
2. Если, рѣшая неравенства, найдемъ х<^т и х<^р.
и если то очевидно, что всѣ значенія #, меньшія р, удовлетворяютъ
даннымъ неравенствамъ, ибо такія значенія будутъ меньше и юг. Въ этомъ случаѣ р есть высшій предѣлъ неизвѣстнаго.
3. Если найдемъ
х>т и #<.р,
то когда р>т, очевидно, что даннымъ неравенствамъ удовлетворяютъ всѣ значенія #, заключающіяся между т нр; т есть низшій, а р высшій предѣлъ для #.
4, Если же, найдя - . ч а * . •
х^>т и х<^р, окажется, что т>р, то предѣлы.будутъ противорѣчащіе; а это значитъ, что не существуетъ такихъ значеній х, которыя удовлетворяли бы совмѣстно даннымъ неравенствамъ. Самыя неравенства въ такомъ случаѣ называются яесо-умѣстными. .
344. Нетрудно обобщить этотъ способъ. Пусть дана система « неравенствъ 1-й степени съ однимъ неизвѣстнымъ
, а^х > Ьа, Ь8.
• • °я» > Ъя.
Рѣшить иіъ — значитъ найти всѣ значенія я, удовлетворяющія всѣмъ заданнымъ неравенствамъ совмѣстно. Для этого рѣшимъ каждое неравенство отдѣльно, т.-е. найдемъ изъ него предѣлъ для х. При этомъ могутъ имѣть мѣсто 3 случая.
1) Можетъ случиться, что. рѣшая неравенства, мы найдемъ, что х долженъ превышать извѣстные предѣлы: напр.
х Л .
Если наибольшее изъ я чиселъ Ли . Лл будетъ Л, то очевидно, что всѣ неравенства будутъ удовлетворены, если мы возьмемъ
х"> Л:
въ этомъ случаѣ существуетъ, слѣдов., для неизвѣстнаго х*
2) Можетъ случиться, наоборотъ, что, рѣшая каждое изъ данныхъ неравенствъ, мы найдемъ, что х должно быть меньше нѣкоторыхъ предѣловъ;.напр., что '
х , х <^кп.
Въ такомъ случаѣ^ очевидно, мы удовлетворимъ даннымъ неравенствамъ, взявъ гдѣ А—наименьшее изъ чиселъ /. . , Это к дастъ <?ыс-шій предѣлъ неизвѣстнаго. ч
3) Наконецъ, можетъ случиться, что, рѣшивъ заданныя неравенства, мы найдемъ, что % неравенствъ покажутъ; что х должно быть больше 5 чиселъ:
х > Л3, . .
, ®>Лв;
а остальныя и — д неравенствъ дадутъ для х высшіе предѣлы, напр.
ж <С
Если наибольшее въ ряду чиселъ Л17 Ла, Л3, . въ ряду йр іа, й3, . . . будетъ Л, то очевидно,
. . будетъ Л, а наименьшее что мы должны взять:
- Л х <
т.-е. даннымъ неравенствамъ удовлетворяютъ всѣ числа, большія к, но въ то же время меньшія к, При этомъ:
а) если й < й, то такія числа существуютъ, и слѣд., данныя неравенства совмѣстны;
Ь) если Л Л, то, очевидно, нѣть чиселъ, удовлетворяющихъ данной системѣ неравенствъ, которыя, поэтому, несовмѣстны.
Рѣшеніе совмѣстныхъ неравенствъ первой степени съ нѣсколь кими неизвѣстными.
345. Когда имѣемъ нѣсколько неравенствъ первой степени съ нѣсколькими неизвѣстными, то не всегда можно найти предѣлы для каждаго* неизвѣстнаго.
Для нахожденія этихъ предѣловъ употребляютъ или методъ сравниванія величинъ неизвѣстныхъ, или методъ уравниванія коэффиціентовъ при одномъ и томъ же неизвѣстномъ.
346. Методъ сравненія величинъ неизвѣстныхъ. Пусть требуется рѣшить два неравенства съ двумя неизвѣстными:
5я— Зу>4,
8#-|~ 2у > 25,
Выводя предѣлы для х, находимъ: изъ перваго неравенства
и изъ второго
Такъ какъ получились.два низшіе предѣла для неизвѣстнаго, то нельзя сказать, который изъ нихъ больше, и нельзя такимъ образомъ исключить я. Если же рѣшимъ неравенства относительно у, то найдемъ:
25— &?
2
*<~з----О) и у>
. .(2)
и исключеніе у возможно. Въ самомъ дѣлѣ, первая дробь, какъ большая количества у, очевидно, больше второй дроби, какъ меньшей того же самаго у; слѣдов.
5я? — 4 25 — 8л?
* 2
Рѣшивъ это неравенство, находимъ
*1 о
Давая х какое угодно значеніе, большее 2 найдемъ,' что каждому изъ нихъ соотвѣтствуютъ два предѣла для у, изъ неравенствъ (1) и (2). Такъ, взявъ х=3, найдемъ, что
„2 . 1
у<3§, но у>$ » л
Взявъ я = 4, найдемъ , • , . ’
\ оі *
У<5^ но у> — 3-
Такимъ образомъ, данныя неравенства могутъ быть удовлетворены безчислев* нымъ множествомъ значеній х и у. . .
Пусть требуется рѣшить три неравенства съ 3-мя неизвѣстными: \
2х— у + 1 > О,'!
х-|-2і/ — г — 2 <0, I (і)
За: -2у— г— 1 > 0. I
Рѣшивъ иіъ относительно х, находимъ:
(2)
Очевидно, что 4” 2 — 2у, какъ выраженіе большее я, больше каждой изъ дробей, меньшихъ х; слѣд. у и г удовлетворяютъ двумъ неравенствамъ:
Рѣшая эти два неравенства относительно у, найдемъ:
3 ^4* э 2^4-э
’ и у < —у- • • . (4)
Давая 2 произвольное значеніе, напр. # = 0, изъ послѣднихъ неравенствъ находимъ:
у<1 и у<г, *
взявъ теперь какое угодно значеніе, меньшее 1, для у, положивъ, напримѣръ, У = — 1, мы удовлетворимъ неравенствамъ (4).
Внося въ систему (2) у = —1 и л = 0, найдемъ
“х> — 1, ж<4, ®>1.
Слѣдов., взявъ 1 < х < 4, мы удовлетворимъ этимъ тремъ неравенствамъ. Такъ, напр. 1
Х = 2. у = —1, #=0; Ж=2|, у=— 1, ^ = 0; #=3, у~ — 1, # = 0;
и т. п. удовлетворяютъ даннымъ неравенствамъ.
347. Методъ уравниванія коэффиціентовъ. Пусть требуется рѣшить неравенства:
5л;— Зу> 4,
8^4“ > 25,
Желая исключить х, мы должны умножить первое неравенство на 8, а второе на 5, послѣ чего получимъ
40я— 24у > 32 ' и 40з+ Юу >125.
Затѣмъ слѣдовало бы вычесть одно неравенство изъ другого; но такъ какъ мы не имѣемъ права вычитать неравенства одинаковаго смысла, то и нельзя этимъ пріемомъ исключить х, Но можно исключить у, помноживъ первое неравенство на 2, а второе на 3, и сложивъ ихъ. что позволительно; такимъ образомъ найдемъ:
34л: >83, откуда #>2^|-
Затѣмъ, продолжаемъ такъ, какъ указано въ § 346.
Когда предложенныя неравенства противоположнаго смысла, можно методомъ уравниванія коэффиціентовъ исключить неизвѣстное, имѣющее въ обоихъ неравенствахъ одинаковый знакъ. Такъ, имѣя неравенства
2л:Зу > 23,
Зя-1- 2у < 22.
можно исключить х, умноживъ первое на 3, второе на 2 и вычтя второе изъ перваго. Такимъ путемъ найдемъ
5. *
Давая у какое угодно значеніе, большее 5, напр. 7, найдемъ два предѣла для х:
х > 1, л; < 2 з*
Подобнымъ образомъ можно бы было исключить и у; вычитая утроенное второе изъ удвоеннаго перваго неравенства, нашли бы
х < 4.
Затѣмъ, для х < 4, можно изъ данныхъ "неравенствъ найти предѣлы для у.
Примѣчаніе. Не всякую систему неравенствъ можно рѣшить.
Пусть, напр., даны неравенства * «
Зл:-4 5у > 7, 4#-}“5у>9‘
' Замѣчаемъ, во-первыхъ, что нельзя исключить у, такъ какъ непозволительно дѣлать почленное вычитаніе неравенствъ одинаковаго смысла. Также непримѣнимъ въ данномъ случаѣ и способъ подстановки, потому что рѣшивъ, напр.,
первое неравенство относительно найдемъ низшій предѣлъ дляа замѣнивъ у этимъ предѣломъ въ выраженіи 4я-|-5у, мы послѣднее уменьшимъ, а слѣд* останется неизвѣстнымъ, будетъ ли оно необходимо больше 9. Такимъ же точно образомъ убѣдимся, что нельзя исключить и х*
Вообще, можетъ случиться, что нельзя найти предѣловъ ни для одного неизвѣстнаго; или же можно найти предѣлъ для одного неизвѣстнаго, или, наконецъ, и для обоихъ.
ГЛАВА XXV.
Изслѣдованіе уравненія первой степени съ однимъ неизвѣстнымъ.
Рѣшенія: положительныя, отрицательныя, нулевыя, безконечныя, неопредѣленныя. — Примѣры изслѣдованія буквенныхъ вопросовъ.
348. Выразивъ условія задачи уравненіемъ и рѣшивъ это уравненіе, найденное рѣшеніе изслѣдуютъ. При этомъ надо различать два случая.
1. Когда задача дана въ числахъ, т.-е. въ формѣ частной задачи, то полученное рѣшеніе, удовлетворяя уравненію, не всегда представляетъ вмѣстѣ съ .этимъ и отвѣть на вопросъ, алгебраическимъ выраженіемъ котораго служитъ уравненіе. Такъ, напр., если въ задачѣ требуется опредѣлить число людей, и
3 мы, составивъ уравненіе и рѣшивъ его, найдемъ, что искомое число равно иди 10^, то подобныя числа, удовлетворяя уравненію, никоимъ образомъ не могутъ служить отвѣтомъ на предложенную задачу, ибо число людей можетъ выражаться только цѣлыми числами. Другой примѣръ. Если въ задачѣ требуется опредѣлить сторону треугольника, и рѣшивъ уравненіе, вытекающее изъ условій задачи, мы найдемъ, что длина стороны треугольника равна (—Зф.),то подобное рѣшеніе, удовлетворяя ур—нію, очевидно, не можетъ выражать длину стороны треугольника. Подобныя рѣшенія, не соотвѣтствующія смыслу задачи, указываютъ на ея невозможность. Розысканіе—гдѣ кроются причины невозможности вопроса, составляетъ задачу изслѣдованія.
Затѣмъ, иногда искомыя рѣшенія являются въ особыхъ формахъ — нуля, безконечности или неопредѣленности. Изслѣдованіе значенія подобныхъ формъ по отношенію къ задачѣ также составляетъ предметъ шслмідоеакая.
2. Когда данныя вопроса выражены буквами, т,-е. задача предложена въ общемъ видѣ, то значенія неизвѣстныхъ выразятся формулами, составленными изъ этихъ буквъ. Опредѣленіе условій, которымъ должны удовлетворять данныя, для того чтобы задача была возможна, а также изученіе всѣхъ замѣчательныхъ обстоятельствъ, какія можетъ представить разсматриваемая формула при всевозможныхъ предположеніяхъ относительно данныхъ, составляетъ также предметъ изслѣдованія*
349. Если задача приводитъ къ уравненію первой степени съ однимъ неизвѣстнымъ, то это ур., по освобожденіи отъ дробей, по перенесеніи членовъ и по приведеніи, всегда можетъ быть приведено къ виду
ах = Ъ . . . (1),
Для рѣшенія его, мы должны обѣ части раздѣлить на коэффиціентъ а при х* Если а есть количество конечное и отличное отъ нуля, то сказанное дѣленіе позволительно, и мы получимъ ур.
эквивалентное (I). Такъ какъ ур. (2) удовлетворяется только при х=~, то
СЕ заключаемъ, что и эквивалентное ему (1) имѣетъ въ данномъ случаѣ одно
единственное рѣшеніе, равное которое можетъ быть или положительное, или отрицательное, смотря по тому, будутъ ли а п Ь имѣть знаки одинаковые или разные. При 6 = 0 это рѣшеніе обращается въ 0.
Но если положитъ а = 0, то мы уже не имѣемъ права множить обѣ части ур—нія (1) на дробь которая въ этомъ случаѣ равна со, ибо мы не можемъ утверждать, что новое уравненіе будетъ въ данномъ случаѣ необходимо эквивалентно данному. Цѣль изслѣдованія—розыскать, каково будетъ рѣшеніе уравненія (1) въ частномъ случаѣ а = О, при чемъ 6 можетъ быть или отлично отъ нуля, или также равно нулю*
Пзъ сказаннаго заключаемъ, что намъ предстоитъ разсмотрѣть слѣдующіе случаи:
I) а и Ь конечны и имѣютъ одинаковые знаки;
•2) а п 5 конечны и имѣютъ противоположные знаки;
3) а — конечно* 5 = 0;
4) а = 0, 6 — конечно;
^) « = 0 и & = 0.
350* I. Положительныя рѣшенія* Когда а п 6 конечны и имѣютъ одинако-
Ъ * * '
вые знаки, то я = какъ частное отъ раздѣленія двухъ конечныхъ количествъ одинаковаго знака, означаетъ конечное жмвжительное число* Это же самое непосредственно видно и изъ ур. (1); въ самомъ дѣлѣ, будутъ ли а и 5 оба положительны или оба отрицательны, выраженія ах и 5 могутъ быть уравнены только выборомъ опредѣленнаго положителънаіо значенія для а?.
По отношенію къ задачѣ положительныя значенія, получаемыя для неиз-вѣстнаго, въ большинствѣ случаевъ представляютъ вполнѣ опредѣленный и ясный отвѣтъ на нее. и этимъ самымъ показываютъ возможность задачи. Подтвержденіемъ этому служатъ всѣ задачи, рѣшенныя нами въ §§ 265—272.
Но есть случаи, когда положительныя рѣшенія, удовлетворяя уравнешю, по представляютъ, однако, удовлетворительнаго отвѣта на задачу и этимъ обнаруживаютъ ея невозможность. Это бываетъ именно тогда, когда неизвѣстное вопроса, по самому смыслу задачи, должно удовлетворять такимъ условіямъ, которыя не могутъ быть выражены уравненіемъ; напр*, когда неизвѣстное должно быть цѣлымъ числомъ, пли не должно выходить изъ опредѣленныхъ предѣловъ. Въ такихъ случаяхъ положительное рѣшеніе, не удовлетворяющее этимъ особымъ условіямъ, укажетъ намъ, что задача невозможна.
Въ поясненіе приводимъ слѣдующіе примѣры*
Примѣръ I. Партія рабочихъ, состоящая изъ мужчинъ и женщинъ, въ числѣ 50 человѣкъ, заработала въ 6 дней 170 руб., при челъ каждый получалъ въ день по 1 рублю, а каждая женшина по 50 копѣекъ* Сколько было мужчинъ и женщинъ?
Пусть мужчинъ было а?; слѣд. число женщинъ равнялось 50 — я?; каждый мужчина получалъ въ день 1 р., слѣд. х мужчинъ въ 6 дней заработали р.; 50—я женщинъ, получая въ день по і р* каждая, въ 6 дней [получили 6 * ^ . (50 — х) или 3(50 — х) руб* По условію задачи:
6я? + 3(50 — я?) = 170*
Рѣшая ур*, найдемъ, что число мужчинъ
а число женщинъ
50 —о: = 43.ѵ <5
, Изслѣдованіе. Эти дробныя рѣшенія суть единственныя рѣшенія, удовлетворяющія уравненію; но уравненіе представляетъ точное и полное выраженіе условія задачи. Слѣд. другихъ рѣшеній задача не можетъ имѣть. Но по смыслу задачи рѣшенія должны быть числами цѣлыми; а какъ уравненіе дало дробныя рѣшенія, то заключаемъ, что задача невозможна.
О невозможности задачи можно судить по самымъ условіямъ; въ самомъ дѣлѣ, суммы, заработанныя мужчинами и женщинами, суть числа кратныя 3. слѣд. я 'полная сумма должна выражаться числомъ кратнымъ 3; между тѣмъ 170 не имѣетъ этого свойства. Въ этомъ и состоитъ несообразность условій, выразившаяся полученіемъ дробныхъ рѣшеній.
Примѣръ II. СлрАЪьлшяь двузначное число, въ которомъ сумма цифръ равна 14, если извѣстно, что придавъ къ числу 7Д яам&меь число обро;/(с^ное.?
Пусть цифра единицъ равна и, тогда цифра десятковъ выразится формулою 14 —и, самое же число формулою (14 — и). 10 +и; обращенное будетъ: 10и + (14 — и). По условію:
(14 — и) . 10 + н + 72 = Юи + 14 — «.
Рѣшая уравненіе, найдемъ: и =11, = 3
Изслѣдованіе. Это цѣлое положительное рѣшеніе есть единственное рѣшеніе. тд ндегвсряющее уравненію: слѣд. задача не можетъ имѣть другого р Ѵт-нія. Н : ейство вопроса требуетъ, чтобы искомыя числа не превышали 9; в Ылъ ідг: г;ъ нжхъ превышаетъ этотъ предѣлъ, то заключаемъ, что задача Ег*- 1-МчХХЖК.
О ЗЁ9ОЗМО28ОСН задачи можно сулить по самымъ условіямъ. Въ самомъ дѣлѣ, датжачвое число, котораго сумма цифръ равна 14, можетъ быть: или 59, пли 68, лж 77, иля 86, идя 95. Къ какому бы изъ этихъ чиселъ ни придали 72, никогда не получимъ обращеннаго числа, такъ какъ каждый разъ будутъ получаться числа трехзначныя.
351 • И. Отрицательныя рѣшенія. Когда а и д’конечны^и имѣютъ^противо-. Ь .
ноложные знаки, то формула х = - для неизвѣстнаго конечное отрица-а
телъное число. Это непосредственно видно и изъ уравненія ая = Ь; въ самомъ дѣлѣ, пусть напр. а>’0, а&<0: очевидно, что ур. не можетъ быть удовлетворено никакимъ положительнымъ значеніемъ х, ибо произведеніе положительныхъ чиселъ а и х не можетъ дать отрицательнаго числа; но обѣ части могутъ быть уравнены выборомъ отрицательнаго значенія для х, ибо произведеніе положительнаго а на отрицательное ж дастъ отрицательное количество д, при опредѣленномъ числовомъ значеніи х.
По отношенію къ отрицательнымъ рѣшеніямъ докажемъ слѣдующую теорему, примѣненіе которой тотчасъ же найдетъ себѣ мѣсто.
352. Теорема. Два уравненія а» однмлга нензвіъстныАсь, разнящіяся между собою только знаками членовъ, содержащихъ неизвѣстное, имѣютъ рѣшенія равныя по величинѣ, но противоположныя по знаку.
Въ самомъ дѣлѣ, возьмемъ два уравненія
ая* + д = сх + гі . . .(1) и — а# + Ь = —сх + ^. . . (2).
Рѣшая первое, найдемъ *
рѣшая второе, имѣемъ:
(I — 6 а — с'
Сравнивая обѣ формулы для я, замѣчаемъ, что онѣ имѣютъ одинаковую величину, но противоположные знаки, такъ что если рѣшеніе 1-го ур. положительно, то рѣшеніе 2-го отрицательно, и наоборотъ.
Итакъ, если уравнвЕіІѳ 1-й степени съ однимъ неизвѣстнымъ имѣетъ отрицательное рѣшеніе, то такое же точно по абсолютной величинѣ рѣшеніе, но взятое съ положительнымъ знакомъ, удовлетворяетъ уравненію, которое получается изъ перваго уравненія перемѣною х на — х.
353. Перейдемъ теперь къ разсмотрѣнію вопроса о томъ, какое значеніе можетъ имѣть отрицательное рѣшеніе по отношенію къ задачѣ, отвѣтомъ на которую оно служитъ* Разборъ нижеслѣдующихъ задачъ покажетъ намъ, что отрицательное рѣшеніе всегда служитъ указаніемъ на одно изъ слѣдующихъ обстоятельствъ: 1) или на нѣкоторую несообразность въ условіяхъ задачи,—несообразность, которую, впрочемъ, можно исправить; 2) или на неправильную постановку вопроса; 3) или на неправильное предположеніе, сдѣланное при составленіи уравненія изъ условій задачи и обусловленное не вполнѣ опредѣленною формою вопроса; или, наконецъ, 4) на абсолютную невозможность задачи.
354* п р и м ъ р ъ I* 2/аши цѣну одною фунта нѣкотораго товара, зная, что цѣна 3 фунтовъ ею, уменьшенная 5-ю рублями, равна цѣнѣ 7 фунтовъ, увеличенной двумя рублями?
Пусть цѣна фунта будетъ х руб* Изъ условія задачи непосредственно получаемъ уравненіе
Зл? — 5 7х 4- 2, рѣшивъ которое, получаемъ
7
Изслѣдованіе. Получили отрицательное рѣшеніе; но искомая величпна— цѣна фунта товара, по существу своему, положительна; заключаемъ, что отрицательное рѣшеніе должно указывать на несообразность въ самыхъ условіяхъ задачи* Въ данномъ случаѣ эта несообразность прямо бросается въ глаза: въ самомъ дѣлѣ, цѣна 3 фунтовъ, уменьшенная 5-ю рублями, никакъ не можетъ равняться большей цѣнѣ (7-ми ф.), да еще увеличенной 2-мя рублями.
Попытаемся исправить несообразныя условія задачи; и для этого замѣтимъ, что если въ уравненіе, составленное по этимъ условіямъ, вмѣсто я подставимъ — я, то новое уравненіе
— Зх— 5 ——7а? + 2,. . .(1)
будетъ имѣть рѣшеніе, по абсолютной величинѣ равное прежнему, а по знаку положительное, т*-е* новому ур-нію удовлетворяетъ
Оно будетъ представлять прямой отвѣтъ на задачу* соотвѣтствующую измѣненному ур—нію (1); поэтому, если окажется возможнымъ слегка измѣнить условія данной задачи, не измѣняя численной величины данныхъ, такъ чтобы новая задача соотвѣтствовала ур—нію (1), то положительное рѣшеніе и будетъ служить прямымъ отвѣтомъ на измѣненную задачу* Помноживъ обѣ части ур—нія (1) на — 1, дадимъ ему видъ
За; 4-5 = 7$— 2,* , .(2).
Такъ какъ здѣсь къ 3$ придается 5, а не вычитается 5, какъ было въ первоначальномъ ур—ній; затѣмъ изъ 7х вычитается 2, а не придается, какъ въ перво-
начальномъ ур—ніи, то очевидно, что ур. (2) есть алгебраическое выраженіе условій слѣдующей задачи:
„найти цѣну фунта нѣкотораго товара, зная, что цѣна 3 фунтовъ его, увеличенная 5-ю рублями, равна цѣнѣ 7 фунтовъ, уменьшенной 2-мя рублями?"
Отвѣть: 1 р. 75 к. удовлетворяетъ этой задачѣ, какъ нетрудно убѣдиться повѣркою.
Возможность исправленія задачи въ данномъ случаѣ обусловливалась тѣмъг что хотя искомое и есть здѣсь величина положительная, но данныя (5 р. и 2 р.) могутъ быть принимаемы въ двухъ противоположныхъ значеніяхъ — въ смыслѣ придаваемыхъ и вычитаемыхъ величинъ.
Примѣръ II. Найти лѣта нѣкотораго лица, экая, что если изъ пять разъ взятаго числа его лѣтъ вычесть удвоенный возрастъ, который оно имѣло 20 лѣтъ тому назадъ, то въ остаткѣ получится число лѣтъ, какое оно будетъ имѣть черезъ 12 лѣтъ?
Пусть будетъ х— требуемый возрастъ. Изъ условій задачи непосредственно получаемъ уравненіе
5л — (# — 20) . 2 = # + 12 . . .(1).
Рѣшивъ уравненіе, находимъ
х = —14.
Изслѣдованіе. Искомая величина — число лѣтъ лица, по существу своему, полоалгтельца; а потому отрицательное рѣшеніе указываетъ на невозможность задача. Эту невозможность легко обнаружить слѣдующимъ образомъ. Если изъ упятереннаго числа лѣтъ лица вычесть удвоенное число дѣтъ, которое лицо зто имѣло 20 лѣтъ тому назалъ, то получится 5х — (х — 20). 2 или Зх + 40; при положительномъ #, каково это количество и должно быть по существу своему, За?+ 40 никоимъ образомъ не можетъ равняться # + 12, т.-е. условія задачи невозможны. Попытаемся теперь измѣнить условія задачи, не измѣняя величины данныхъ, такъ, чтобы задача сдѣлалась возможною и имѣла рѣшеніемъ положительное число 14. Съ этою цѣлью измѣнимъ въ уравненіи (1) х въ —г; найдемъ:
— 5г — (—я — 20)2 = — # + 12,
или, помноживъ обѣ части на —1: і
5х — (а? + 20)2 — # — 12.
По извѣстной теоремѣ, рѣшеніе этого ур—пія есть х = + 14; оно представляетъ прямой отвѣтъ на задачу, соотвѣтствующую этому ур—нію. Задача этау очевидно, такова:
„Найти возрастъ лица, зная, что если изъ упятереннаго числа его лѣтъ вычесть удвоенное число лѣтъ, какое оно будетъ имѣть черезъ 20 лѣтъ (а не: какое оно имѣло 20 х тому назадъ, какъ было въ условіи данной задачи), то въ остаткѣ получится число лѣтъ, какое это лицо имѣло 12 л. тому назадъ (вмѣсто: будетъ имѣть черезъ 12 л., какъ дано было въ условіи задачи).
Легко провѣрить, что число 14 удовлетворяетъ условіямъ этой измѣненной задачи.
Примѣръ ІП. Отцу 40 лѣтъ, а сыну 13; черезъ сколько лѣтъ отецъ будетъ вчетверо старше сына?
Положимъ, что черезъ х лѣтъ отъ настоящаго времени отецъ будетъ вчетверо старше сына; слѣд. отцу будетъ 40+ #, а сыну 13+ # лѣтъ; и по условію задачи имѣемъ ур—ніе
40 + х = 4(13 + #) . , .(1),
х
4.
Изслѣдованіе. Прямымъ отвѣтомъ на вопросъ должно бы было служить положительное рѣшеніе; отрицательное рѣшеніе указываетъ, что вопросъ невозможенъ въ томъ смыслѣ, въ какомъ онъ заданъ. Невозможность вопроса можно обнаружить слѣдующимъ образомъ. Отношеніе лѣтъ отца къ лѣтамъ сына въ на-
«поящее время выражается неправильною дробью у*, которой величина лгеяьшс 4, и требуется узнать, сколько нужно придать къ числителю и знаменателю, чтобы дробь сдѣлалась равна 4, т.-е. чтобы она увеличилась. Но легко видѣть, что отъ приданія по-ровну къ членамъ неправильной дроби величина ея не увеличивается,
а
а уменьшается; въ самомъ дѣлѣ, взявъ неправильную дробь (гдѣ, слѣд., а>Ь),
* «+«*
и придавъ къ членамъ ея по пц получимъ дробь ; приведя обѣ дроби къ
О -+-ІЛ
общему знаменателю, найдемъ, что первая — а вторая
впивая числителей и замѣчая, что такъ какъ а>д,
дробь дѣйствительно уменьшилась. Итакъ, постановка вопроса впльно, что и обнаружилось въ рѣшеніи полученіемъ отрицательнаго отвѣта.
°Ра' находимъ, что сдѣлана непра-
Это отрицат. рѣшеніе указываетъ вмѣстѣ съ тѣмъ, какъ слѣдуетъ правильно поставить вопросъ, именно, что слѣдуетъ спросить: сколько лѣтъ тому назадъ отецъ былъ вчетверо старше сына?
Что вопросъ долженъ быть измѣненъ въ этомъ смыслѣ,—это показываетъ и тотъ пріемъ, который служилъ для исправленія несообразныхъ условій въ двухъ предыдущихъ задачахъ. Подставивъ въ ур. (1) —я? вмѣсто аг, найдемъ ур.
40 — ж = 4(13 — я), которое, очевидно, служитъ алгебраическимъ выраженіемъ условій вопроса:
„Въ настоящее время отцу 40, а сыну 13 лѣтъ; сколько лѣтъ тому назадъ отецъ былъ вчетверо старше сына?* Положительное рѣшеніе ж = 4 и служитъ прямымъ отвѣтомъ на эту задачу, какъ легко убѣдиться въ этомъ повѣркою.
Примѣръ IV, Изъ двухъ игроковъ АмВ илоьет 400 р., а второй
120 р,; послѣ нѣсколькихъ игръ у А оказалось втрое болѣе, чіьль у В. Сколько выигралъ А?
Пусть А выигралъ х рублей; ур—ніе будетъ
откуда
400 + ^ = 3(120 —ж), х = — 10.
Изслѣдованіе. Прямымъ отвѣтомъ на вопросъ служило бы положительное рѣшеніе; отрицательное рѣшеніе показываетъ, что вопросъ невозможенъ въ томъ смыслѣ, въ какомъ онъ заданъ* Невозможность вопроса легко обнаружить* Лицо А, имѣя до начала игры больше чѣмъ втрое лица В, послѣ выигрыша, очевидно, не можетъ имѣть втрое больше денегъ чѣмъ у В. Поэтому, вопросъ: „сколько выигралъ А“ поставленъ неправильно. Отрицательный знакъ рѣшенія указываетъ — какъ должно правильно поставить вопросъ, именно, что нужно спросить: „сколько руб. А проигралъ?* Къ тому же заключенію приведетъ и указанный выше пріемъ истолкованія отрицательныхъ рѣшеній; въ самомъ дѣлѣ, подставивъ въ ур—ніе —х вмѣсто я?, найдемъ:
400 — х = 3(120+- а);
положительное рѣшеніе гг = + 10 этого ур—нія и служитъ прямымъ отвѣтомъ на вопросъ, ему соотвѣтствующій: „изъ двухъ игроковъ А имѣлъ 400 руб., В — 120 руб*; послѣ нѣсколькихъ игръ у А оказалось втрое болѣе чѣмъ у В. Сколько проигралъ А?“
Примѣръ V. Два поѣзда идутъ равномѣрно въ одномъ направленіи къ станціи, отстоящій ши а лпъстл выхода перваго поѣзда на 200 верстъ, а отъ мѣста выхода второю на 90 верстъ. Первый поѣздъ проходитъ 25 верстъ въ часъ, второй 14 верстъ. Опредѣлитъ разстояніе точки встрѣчи поѣздовъ отъ станціи, полагая, что оба поѣзда выходятъ въ одно время?
Черт. 18*
Пусть поѣзда выходятъ изъ Л и В и ѣдутъ къ станціи С; такъ какъ нельзя заранѣе сказать» встрѣтятся ли поѣзда но доѣзжая станціи С, или проѣханіи и т* ее, то для составленія уравненія необходимо сдѣлать то или другое допущеніе. Итакъ, предположимъ, что точка встрѣчи находится въ разстояніи ж верстъ не доѣзжая до станціи С, въ нѣкоторой точкѣ II. Первый поѣздъ, выходящій изъ Л, проходитъ разстояніе АК, равное 200 — х вер., дѣлая по 25 верстъ въ часъ, а потому пройдетъ все разстояніе АК въ —*2бГ“ часовъ; второй, дѣлая въ часъ
90___х
по 14 в.» пройдетъ разстояніе ВВ = 90 — х в., въ —у— час. Выходя со станцій Л и В въ одно время, они употребляютъ на прохожденіе разстояній АВ и ВК одинакоиое число часовъ, а потому
200 — х __ 90 — х ~25 — 14 * *
откуда х = — 50 верстамъ.
Изслѣдованіе. Прямымъ отвѣтомъ на вопросъ служило бы положительное рѣшеніе; посмотримъ, какъ объяснить въ данномъ случаѣ происхожденіе отрицательнаго отвѣта? Обращаясь къ условіямъ задачи, не находимъ въ нихъ никакой несообразности: поѣздъ, выходящій со станціи А, двигаясь скорѣе поѣзда, выходящаго изъ В, долженъ догнать его гдѣ-нибудь вправо отъ точки В. Слѣд., не въ условіяхъ задачи должно искать источникъ отрицательнаго отвѣта. Обращаясь затѣмъ къ вопросу, замѣчаемъ, что онъ поставленъ не вполнѣ опредѣленно, такъ какъ въ немъ не указано, гдѣ искать точку встрѣчи—не доѣзжая ’і станціи С, или за нею. Въ виду этой неполной ясности требованія, пришлось > при составленіи ур—нія сдѣлать одно изъ двухъ предположеніи: или что поѣзда встрѣтятся влѣво отъ С, или что встрѣча ихъ произойдетъ вправо отъ С. Мы . сдѣлали первое предположеніе, и получили отрицательный отвѣтъ, который и Iуказываетъ, что слѣдовало сдѣлать противное этому предположеніе. ІІредполо-|живъ, что встрѣча произойдетъ вправо отъ С, въ нѣкоторой точкѣ отстоящей |отъ С на х верстъ, получимъ ур—ніе 4 ' 2004-я 90 +я?
; -25“ = —4“’• • •(2)
сотораго положительное рѣшеніе я? = + 50 и служитъ прямымъ отвѣтомъ на во-іросъ: „въ какомъ разстояніи за станціей С оба поѣзда встрѣтятся?" Замѣтимъ, гто н здѣсь ур. (2) получается пзъ (1) перемѣною х въ — х.
Въ данномъ примѣрѣ отрицательное рѣшеніе получилось не отъ несообраз-і>:т> задачи, но отъ ложнаго предположенія, сдѣланнаго при составленіи ур—нія. Убсолж тая вели чипа отриц. рѣшенія, взятая съ положительнымъ знакомъ, пред-гъ -’л-^тъ отвѣтъ на задачу, но представляетъ неизвѣстное съ значеніемъ, прямо фсттт л .жнымъ тому, какое ему придавали при составленіи уравненія.
Ппііръ VI. точки А, С находятся на одной прямой, причемъ мочжа В лсжШ/ фэдшлгн; ралсмоян/е АВ — АС = 5 ф. На
продолженіи прямой, соединяющей точки А и С, мшпи такую точку М, коюо-рой разстояніе отъ точки В било бы среднимъ пропорціональнымъ между ея разстояніями отъ точекъ А и
м’
м
—I—
Черт, 19.
9
Точка М можетъ находиться пли вправо отъ точки С, пли влѣво отъ точки А, п а ргіогі нельзя сказать, какое изъ этихъ двухъ положеній она должна занимать* Допустимъ, что она должна находиться вправо отъ С, и обозначимъ разстояніе ея отъ А буквою а*. Уравненіе задачи будетъ
(т — 2)2 ——5). . . (1).
Рѣшивъ уравненіе, найдемъ: т = — 4.
Изслѣдованіе. Прямымъ отвѣтомъ на вопросъ было бы положительное рѣшеніе; затѣмъ, такъ какъ условія задачи не содержатъ никакой несообразности, то заключаемъ, что отрицательное рѣшеніе обусловливается единственно ложнымъ предположеніемъ, сдѣланнымъ при составленіи уравненія. Поэтому, положимъ, что искомая точка находится влѣво отъ А, и обозначимъ по прежнему разстояніе АМ буквою х. Уравненіе задачи будетъ въ этомъ предположеніи такое:
Сг4-2)2 = а^ + 5). . • (2).
По если въ ур. (1) перемѣнимъ х въ —х, то найдемъ
(— х — 2)2 = — а* — 5), или (я + 2Я = + 5\
т.-е. ур. (2). Изъ этого прямо^заключаемъ, что корень ур—нія (2) отличается отъ корня ур—нія (1) только знакомъ, и котому равенъ Н- 4. Итакъ, искомая точка находится влѣво отъ А, въ разстояніи =4 ф. отъ этой точки,
Такимъ образомъ и въ этой задачѣ отрицательное рѣшеніе указывало только на ложное предположеніе, сдѣланное относительно положенія искомой точки при составленіи уравненія.
Примѣръ VII. Имѣемъ двухъ сортовъ чай: въ 5 руб. и го <9 руб. фунтъ. Сколько нужно взять каждаго сорта, чтобы составить 6 фунт. цѣною въ 10 р. за фунтъ?
Если перваго сорта возьмемъ х ф., то второго нужно взять 6—х ф. Цѣна перваго будетъ Зх р., цѣна второго 8(6 — л?) р., цѣна всей смѣси 5х-(-8(6— л*); по условію:
ох -|- 8(6 — я) = 60, откуда
х —— 4.
Изслѣдованіе. Искомое датпюй задачи есть величина существенно положительная, а потому отрицательное рѣшеніе здѣсь не имѣетъ смысла. Измѣнивъ въ ур—ніи х па —х, найдемъ ур., котораго рѣшеніе будетъ +4, но’ подобрать задачу, соотвѣтствующую измѣненному ур—нію, и однородную съ лапной, въ этомъ случаѣ нельзя. Обстоятельство это указываетъ на то, что задача абсолютно невозможна. И дѣйствительно, изъ двухъ сортовъ чаю — въ 5 и въ 8 р. за фунтъ нельзя составить смѣси, цѣна одного фунта которой превышала бы эти цѣны.
Примѣръ ѴПІ. За входъ въ музей взимается плата двоякаго рода, а именно: постоянная въ 20 коп., назначаемая на содержаніе боіадзъльни, « тре-мѣнная, пропорціональная числу часовъ, въ музеѣ*
чель за каждый часъ берется по 5 копл этотъ сборъ назначается на новыя пріобрѣтенія. О'диіжды 60 человѣкъ вошли въ музей въ полдень, и вышли всѣ &а оііно время. Во сколько часовъ они оставили музей, если весь ео<)^а была равенъ 9 рублямъ?
Пусть я —будетъ число часовъ отъ полудня до момента выхода посѣтителей изъ музея. Сборъ равенъ, съ одной стороны» 900 кои., а съ другой (20-)-5л?) . 60 к. Уравненіе задачи есть
(20 + 5х). 60 = 900, откуда
х = — 1.
Изслѣдованіе* Хотя неизвѣстное въ данной задачѣ есть время, которое можно считать въ двухъ противоположныхъ направленіяхъ (до полудня и по-по-луднн), но очевидно, что въ предложенной задачѣ рѣчь идетъ объ абсолютномъ количествѣ часовъ, проведенныхъ посѣтителями въ музеѣ. Поэтому задача требуетъ положительнаго рѣшенія. Подставивъ въ ур—ніе —.т вмѣсто х, мы конечно получимъ ур—ніе, которое будетъ имѣть положительное рѣшеніе -г = -|-1; но измѣнить задачу такъ, чтобы она соотвѣтствовала измѣненному ур—нію, оказывается невозможнымъ. Такимъ образомъ, отрицательное рѣшеніе указываетъ, въ данномъ случаѣ, па абсолютную невозможность задачи. Невозможность задачи состоитъ въ томъ, что полный сборъ (9 руб.) меньше даже суммы, получаемой отъ одного 20-ти копеечнаго сбора со всѣхъ 60 лицъ, составляющей 12 р., а это, очевидно, нелѣпо.
355. Заключеніе* Разобранные примѣры приводятъ къ тому заключенію, что полученіе отрицательныхъ рѣшеній указываетъ: или I) па несообразность самыхъ условій задачи, какъ въ примѣрахъ I и 11; пли 2) на неправильную постановку вопроса, какъ въ примѣрахъ III и IV; или 3) на неправильное предположеніе, сдѣланное при составленіи ур—нія, какъ въ примѣрахъ V и VI; или, наконецъ, 4) на абсолютную невозможность задачи (примѣры VII и VIII).
Для истолкованія смысла отрицательнаго рѣшенія всегда употребляется одинъ и тотъ же пріемъ: въ уравненіе, вытекающее изъ условій задачи, вмѣсто х подставляютъ —х, и получаютъ такимъ образомъ новое ур—ніе, корень котораго имѣетъ прежнюю абсолютную величину, но положительный знакъ* Затѣмъ пытаются, шлтнля численною значенія данныхъ, подобрать задачу, которая соотвѣтствовала бы измѣненному уравненію* Если эта попытка будетъ имѣть успѣхъ, то слѣдуетъ заключить, что отрицательное рѣшеніе означало только нѣкоторую неправильность въ условіяхъ, либо въ постановкѣ вопроса, либо въ предположеніи при составленіи ур—нія, и положительное рѣшеніе измѣненнаго ур—нія будетъ служитъ прямымъ отвѣтомъ на исправленную задачу. Если же сказанная попытка будетъ безуспѣшна, то слѣдуетъ заключить, что задача абсолютно невозможна.
356. III* Нулевыя рѣшенія. Когда а конечно, аЬ = 0, тогда т=-і а такъ какъ частное отъ раздѣленія нуля на конечное количество есть нуль, то
ж = 0.
Обращаясь къ уравненію, находимъ, что при Ь = 0, оно принимаетъ видъ алг=0; но чтобы произведеніе двухъ множителей, одинъ изъ которыхъ конеченъ, равнялось 0, необходимо, чтобы другой множитель равнялся 0; итакъ, ур. не можетъ быть удовлетворено никакимъ инымъ значеніемъ неизвѣстнаго, кромѣ нуля. Такое рѣшеніе называется нулевымъ.
Если по смыслу задачи неизвѣстное можетъ быть нулемъ, то нулевое рѣшеніе дастъ удовлетворительный отвѣтъ на вопросъ; если же искомое, по смыслу вопроса, означаетъ число не равное нулю, то полученіе нулевого рѣшенія укажетъ на невозможность задачи.
Примѣръ Е йнодо 57 липна, а сыну 19; чергза сколько лѣтъ отецъ будетъ втрое старше сына?
Означивъ искомое буквою я, будемъ имѣть ур—ніе
57 4-я=3(19
или
57 4- # = 57 + Зт, или 22 = 0, откуда 2=0.
Отвѣтъ .этотъ даетъ удовлетворительное рѣшеніе вопроса, показывая, что уже въ настоящее время отецъ втрое старше сына; дѣйствительно: 57 = 19X3.
7
Примѣръ II. Знаменатель дроби равенъ § ея числителя; если же къ числи-
телю придать 5, а къ знаменателю 10, то дробь обратится въ Найти дробь?
Означивъ числителя искомой дроби буквою х, имѣемъ ур—ніе
Л '1' - = 1, откуда х — 0.
5*4-10 2 О
Этотъ отвѣть обнаруживаетъ, что такой дроби, какъ требуется въ задачѣ, не существуетъ.
357. IV. Безконечныя рѣшенія. Если а = 0, 6^0, общая формула принимаетъ видъ
Ь
х = - — со;
0 *
это значить, что х безконечпо-велико; обращаясь къ уравненію, находимъ, что оно въ данномъ случаѣ принимаетъ видъ
0X^ = 5,
и требуетъ нахожденія такого числа, которое, будучи умножено на пуль, давало бы конечное произведеніе 6. По мы знаемъ, что нуль, умноженный на конечное количество, даетъ всегда нуль; а между тѣмъ вторая часть ур—нія отлична отъ нуля, и слѣд. невозможно удовлетворить уравненію никакимъ конечнымъ значеніемъ аг. Итакъ, безконечныя рѣшенія служатъ признакомъ невозможности удовлетворить ур—нію коночнымъ значеніемъ неизвѣстнаго.
По не всегда такія рѣшенія означаютъ невозможность задачи. Когда, по смыслу задачи, неизвѣстное должно быть конечнымъ количествомъ, то безконечное рѣшеніе укажетъ невозможность задачи.
Г1 р и м ѣ р ъ. Найти число, котораго половина, сложенная съ его третью, превышала бы на 6 единицъ пять разъ взятый избытокъ четверти этою числа надъ ею двѣнадцатою долею.
Называя искомое число буквою х, получимъ уравненіе
Освобождая это ур. отъ дробей, находимъ
102 = ІОх + 72, или (10 —10)2 = 72, откуда 2 = . < ій = 77 “ 00• Л. А*
Полученное безконечное рѣшеніе означаетъ невозможность задачи. О невозможности задачи можно заключить й ргіогі, измѣнивъ нѣсколько форму заданія.
1 41 5
Въ самомъ дѣлѣ, - и х какого-нибудь числа составляютъ вмѣстѣ н его; а избы-о о «
токъ 7 надъ 75 числа составляетъ х этого числа; а потому задача можетъ быть * 1 V
о о
выражена гакъ: „наити число, котораго превышаютъ на 6 единицъ - того же
числа?4
Въ этой формѣ нелѣпость задачи становится очевидною.
Когда неизвѣстное есть величина вс помогаш<мы<ая, то случается, и именно въ вопросахъ геометрическихъ, что безконечное значеніе х не указываетъ невозможности задачи. 'Гакъ, когда для опредѣленія положенія прямой, удовлетворяющей различнымъ геометрическимъ условіямъ, принимаютъ за неизвѣстное разстояніе между точкою пересѣченія этой прямой съ данною прямою и точкою, взятою на этой второй прямой, то очевидно, что безконечное значеніе неизвѣстнаго укажетъ на параллельность обѣихъ прямыхъ.
Примѣръ. Къ двумъ кругамъ, которыхъ радіусы равны К и г, провести общую внѣшнюю касательную (черт, 23),
Задача будетъ рѣшена, если мы опредѣлимъ положеніе точки Т, въ которой искомая касательная встрѣчаетъ линію центровъ. Примемъ за неизвѣстное разстояніе точки Т оть центра 0; изъ подобія треугольниковъ ОАТ и оаТ имѣемъ пропорцію
ТО : То = О А : оа,
или, положивъ: О А — В, оа = г, Оо = <1 и ОТ = х:
х : (.г — а) — К : г, откуда х — ----•
Сдѣлавъ К — г, найдемъ: х = = ?о. По это безконечное рѣшеніе отнюдь
не означаетъ невозможности задачи: оно показываетъ только, что при данномъ условіи (К = г) точка Т удалилась въ безконечность, иными словами, что общая касательная приняла особое положеніе относительно линіи центровъ, а именно: сдѣлалась параллельна этой линіи. И въ самомъ дѣлѣ, при К —г, фигура АОоа обращается въ прямоугольникъ, и слѣдовательно линія Ла дѣлается параллельна Оо.
358. V. Неопредѣленныя рѣшенія. Приа = 0 и Ь = О общая формула принимаетъ видъ
О
*=б’
означающій неопредѣленность. Обращаясь къ ур—нію, находимъ, что оно беретъ видъ: 0 / і = 0. Какова бы ни была- величина я, первая часть всегда равна нулю, а слѣд. ур—ніе обращается въ тождество при всякомъ х, а потому оно дѣйствительно неопредѣленно.
Неопредѣленныя рѣшенія указываютъ на неопредѣленность задачи, т.-е. па’ то, что условія вопроса не ограничиваютъ произвола неизвѣстнаго.
Примѣръ. Найти возрастъ лица, зная, что если ихъ утроеннаго числа его лѣтъ вычесть удвоенное число лѣтъ, какое лица это будетъ имѣть черезъ 10 лѣтъ, то въ результатѣ получится то число лѣтъ, какое лицо имѣло 20 лѣтъ тому назадъ.
Обозначивъ искомое число лѣтъ буквою х, прямо имѣемъ ур—ніе
Зх — 2(я;+ 30) = а? — 20,
или а* — 20 = д; — 20, или (1 — 1)я? = 20 ~ 20, откуда ж =
Это рѣшеніе указываетъ на полную неопредѣленность задачи; въ самомъ дѣлѣ, легко видѣть, что условія данной задачи—только кажущіяся и не ограничиваютъ произвола неизвѣстнаго. Дѣйствительно, такъ какъ За; — 2(лт —|—10), по упрощеніи, обращается въ а? — 20, то задачу можно выразить тахы „найти возрастъ лица, зная, что число лѣтъ, какое это лицо имѣло 20 л. тому назадъ, равно возрасту, какой оно имѣло 20 л. тому назадъ*. Очевидно, что этому условію удовлетворяетъ всякое число, и что задача ничѣмъ не ограничиваетъ величину неизвѣстнаго.
Если въ формулѣ я — ~ выраженія а и & суть цѣлые полиномы относительно одной и той же буквы то можетъ случиться, что при нѣкоторомъ частномъ значеніи этой буквы полиномы Ъ и а обращаются въ нули; тогда я; предста-вится подъ видомъ неопредѣленности По отсюда не слѣдуетъ заключать, что въ этомъ частномъ случаѣ задача неопредѣленна. Неопредѣленность эта, какъ мы уже знаемъ, только кажущаяся, и зависитъ отъ того, что въ уравненіе ах = Ъ введенъ множитель, обращающійся въ нуль въ разсматриваемомъ частномъ случаѣ, вслѣдствіе чего окончательное ур-ніе, изъ котораго выведенъ х* не эквивалентно первоначальному уравненію. Поэтому нужно вернуться къ первоначальнымъ вычисленіямъ и уничтожить этотъ обращающійся въ нуль множитель, прежде чѣмъ будетъ сдѣлано частное предположеніе.
Впрочемъ, можно это сдѣлать и въ самой формулѣ я, т.-е. раскрыть ея не-’ опредѣленность. Мы знаемъ, что если Ъ обращается въ 0 при # = у', то оно дѣлится па у — у/, такъ что можно его представить въ видѣ: (у—У). полагая, что 6' уже не обращается въ 0 при у=уг'і точно такимъ же образомъ а=(#—у'} . а*, гдѣ уже а' не содержитъ множителя у — у. Такимъ образомъ
-(у^у'Р &
(у — у')а’ а'"
Положивъ теперь у — уТ9 мы и найдемъ истинное значеніе кажущейся не* опредѣленности формулы я?.
Если бы оказалось, что Ь и а содержатъ у— у' въ степени высшей первой, то должны бы были выдѣлить эту степень въ обоихъ членахъ дроби, сдѣлать сокращеніе п потомъ уже положить у — у1.
Примъръ. Вычислитъ площадь трапеціи, которой основанія ровны соопе вѣтственно а и 6, а высота —к, імзсматри-гч вая ее какъ разность площадей двухъ треуголъ-
никовъ* составляемыхъ основаніями трапеціи и продолженными до пересѣченія непараллельными ея боками.
Обозначивъ искомую площадь буквою 8, имѣемъ:
Изъ подобія треугольниковъ ВЕС и АЕВ находимъ
ЕО а ЕЕ 4-й о Ък .
ЕЕ = 5’ ,,Л1* ' ЁЕ~ = Ь' 0ТКуда ЬЬ ’
слѣд.
Ьк а — 6
а — Ь
ц2 - 62
« — 6
Пока а отлично отъ Ь, эта формула даетъ для площади трапеціи вполнѣ опредѣленную величину. Но если положить а = 6, формула принимаетъ видъ
8 = и задача, повидимому, дѣлается неопредѣленною. Но эта неопредѣленность только кажущаяся, и зависитъ отъ того, что числитель и знаменатель 8 содержатъ общаго множителя а — б, который въ частномъ предположеніи а — Ь д2_____________________________________________________&2
обращается въ нуль. Сокративъ предварительно дробь ——на а—6, найдемъ
8 = (а 6); положивъ, затѣмъ, а — Ь, найдемъ 8 = ак — величину вполнѣ опредѣленную. II дѣйствительно, при а = Ь трапеція превращается въ параллелограммъ. котораго площадь равна аЛ.
359. Заключеніе. Уравненіе первой степени съ однимъ неизвѣстнымъ:
ах = Ъ
имѣетъ единственное и конечное рѣшеніе, когда а отлично отъ нуля; когда а —О, а Ь 0, уравненіе невозможновъ томъ смыслѣ^ что оно не имѣетъ конечныхъ рѣшеній; наконецъ, когда а^Ь — 0, уравненіе неопредѣленно, при чемъ неопрсдѣ* лен ноетъ можетъ бытъ или дѣйствительная, или только кажущаяся.
Методъ изслѣдованія вопросовъ 1-й степени.
360. При изслѣдованіи вопросовъ 1-й степени полезно держаться слѣдующаго порядка:
1) Дѣлаютъ всевозможныя предположенія относительно знака знаменателя: знаменатель положительный, отрицательный, равный нулю-
2) Къ каждому изъ этихъ предположеній относительно знаменателя присоединяемъ всевозможныя предположенія относительно числителя, лишь бы они не противорѣчили взятому предположенію о знаменателѣ.
Так. обр. мы разсмотримъ всевозможные случаи относительно знака неизвѣстнаго или неизвѣстныхъ.
3) Слѣдуетъ дать истолкованіе отрицательныхъ значеній неизвѣстныхъ.
4) Если, какъ въ вопросахъ геометріи, свойство задачи налагаетъ на неизвѣстныя тѣ или другіе предѣлы, нужно подвергнуть разсмотрѣнію н это обстоятельство.
5) Наконецъ, нужно построить неизвѣстное, пользуясь его формулою; послѣднее, очевидно, имѣетъ мѣсто въ случаѣ задачъ геометрическихъ.
Первый примѣръ изслѣдованія.
361. Отцу а, а сыну Ъ лѣтъ; черезъ сколько лѣтъ отецк будетъ въ п разъ старше сына?
Пусть это случится черезъ х лѣтъ отъ настоящаго времени; уравненіе задачи, очевидно, будетъ:
а + х — п(Ь 4- ж);
откуда
Изслѣдованіе, п есть число большее I; слѣд. знаменатель всегда отличенъ отъ нудя и положителенъ. Относительно числителя возможны три предположенія: а 2> а = «6; а < иб.
1) При этомъ условіи и числитель, а слѣд. и х, положителенъ.
Это положительное значеніе х даетъ прямой отвѣтъ на вопросъ, т,-е, что яь
будущемъ, по истеченіи числа лѣтъ, выражаемаго формулою х, отецъ будетъ въ п разъ старше сына. И въ самомъ дѣлѣ, отношеніе лѣтъ отца къ лѣтамъ сына въ настоящее время равно ~ (непр. дроби); требуется чтобы это отношеніе умець-
шилось, ибо изъ условія, а>ио находимъ «<^; но отъ приданія поровну къ членамъ неправильной дроби величина ся дѣйствительно уменьшается.
2) а = Въ этомъ случаѣ числитель формулы я обращается въ нуль, а вмѣстѣ съ этимъ и х = 0. Это рѣшеніе показываетъ, что искомое событіе имѣетъ мѣсто въ настоящее время, что очевидно, такъ какъ изъ даннаго условія имѣемъ
— п, т.-е. что уже теперь отношеніе лѣтъ отца и сына имѣетъ требуемую величину п.
3) а < ліь Числитель .г, а слѣд. и х въ этомъ случаѣ отрицателенъ.
Отрицательное рѣшеніе означаетъ, что вопросъ въ прямомъ смыслѣ невозможенъ. Въ самомъ дѣлѣ, въ настоящее время отношеніе лѣтъ отца и сына равно
изъ условія же имѣемъ, что п> т.-е* требуется, чтобы это отношеніе увеличилось; очевидно, что это невозможно въ будущемъ, потому что отъ приданія поровну къ членамъ непр. дроби ея величина не увеличивается, а уменьшается.
Абсолютная величина отрицательнаго рѣшенія удовлетворяетъ уравненію, полученному изъ первоначальнаго перемѣною я на —-г, т.-е. ур—нію:
а — х = н(6 — .г),
а потому служитъ прямымъ отвѣтомъ на задачу: „отцу а, а сыну Ь лѣтъ; сколько лѣтъ тому назадъ отецъ былъ въ н разъ старше сына?"
Въ этоп формѣ, при данномъ условіи: и > р задача возможна, потому что отъ вычитанія поровну изъ членовъ неправ. дроби величина ея дѣйствительно увеличивается.
Заключеніе. Изъ предыдущаго слѣдуетъ, что если дать предложенной задачѣ наиболѣе общую форму: „отношеніе лѣтъ отца къ лѣтамъ сына есть опредѣлить эпоху, въ которую это отношеніе имѣетъ величину п?“ то формула (1) дастъ для всѣхъ случаевъ рѣшеніе задачи, если найденное число лѣтъ считать: въ будущемъ, когда оно полйжмтелі'но, и въ прошедшемъ, когда оно отріи{аж<мьяо.
Второй примѣръ изслѣдованія.
362. Три точки А, В и С лежатъ на прямой, при чемъ точка В находится между двумя другими; разстояніе АВ = а, АС = 6. Найти на продолженіи прямой АС шбш/ю точед М? кожорок разстояніе отъ точки В было бы средни.чъ пропорціональномъ между ея разстояніями отъ точекъ А и С? (черт. 19 и 21.)
Обозначимъ разстояніе АМ буквою х в положимъ, что искомая точка лежитъ вправо отъ С; въ этомъ предположеніи уравненіе будетъ
(я — а)2 — — 6) . . . (1).
Предполагая же, что точка М находится влѣво отъ А, получимъ ур. (я + а)3 = + 6) . . .(2).
Ур. (2) выводится изъ (1) перемѣною х въ — а?; слѣд. можно ограничиться рѣшеніемъ ур—нія (1), помня, что если оно имѣетъ отрицательный корень, то
этотъ корень, по перемѣнѣ у него знака, будетъ корнемъ ур—нія (2), и слѣд. дастъ точку, лежащую влѣво отъ А; однимъ словомъ, корень ур —нія (1) всегда представляетъ разстояніе искомой точки отъ А, при чемъ это разстояніе нужно брать вправо отъ А, если корень я о дарителемъ, и вл/ыю отъ А, если онъ отрицателенъ.
Сдѣлавъ эти подготовительныя замѣчанія, рѣшаемъ ур. (1) и находимъ
а*
Изслѣдованіе. Формула я даетъ мѣсто слѣдующимъ случаямъ:
2а — б > 0; 2а — 6 < 0‘ 2а — 6 — 0.
1) Если 2а — корень ур—нія положителенъ, а потому искомая точка находится вправо отъ А; но задача требуетъ кромѣ того, чтобы эта точка была вправо и отъ С, т.-е. чтобы величина а; была больше 6, Итакъ, нужно разсмотрѣть, удовлетворяется ли неравенство
такъ какъ 2а — 6 положительно, то умножая обѣ части неравенства на 2а — Ъ и не перемѣняя знакъ неравенства, замѣняемъ послѣднее ему эквивалентнЫхМЪ
а2 > 2а6 — 62, иля а2 — 2аб + № > 0, пли (а — 6)2 > 0;
послѣднее неравенство всегда удовлетворено, потому что квадратъ всегда положителенъ; слѣд. справедливо и эквивалентное ему первое неравенство? Такимъ образомъ, при условіи 2а — Ь >0, ур—ніе имѣетъ положительный корень большій 6, опредѣляющій точку М вправо отъ С, какъ того требуетъ заданіе.
2) Если 2а — Ь<0, корень ур—нія (1) отрицателенъ, и согласно вышесказанному, опредѣляетъ точку, находящуюся на продолженіи линіи АС, влѣво отъ точки А и въ разстояніи отъ ноя, равномъ
3) Наконецъ, если 2а — 6 = 0, количество а? обращается въ оо. Это значитъ, что х неограниченно возрастаетъ по мѣрѣ того какъ Ь приближается къ 2а; точка М удаляется отъ А, и когда Ь дѣлается равнымъ 2а, точка М дѣлается безконечно далека отъ А, и задача о нахожденіи такой точки невозможна.
м
Черт. 21.
Построеніе. Пусть 2а —6 >0. Отложивъ отъ точки В линію ВП = а, найдемъ, что длина линіи СВ = 2а — Ъ, Проведя подъ произвольнымъ утломъ къ прямой АС линію АН, от-ложихмъ на ней АГ = 2а —6 и А И = а; соединивъ затѣмъ точки Е и В, проводимъ изъ точки И прямую НМ И ГВ; точка М будетъ требуемая. Въ самомъ дѣлѣ, подобіе ДА АВЕ и АМН даетъ:
АЕ : АП — АВ : АМ, или (2а — 6):а = а;АМ, откуда а2
2а— Ъ
Примѣчаніе. Если 2а — 6 уменьшать, приближая къ нулю, линія ВЕ приближается къ совпаденію съ ВА, а линія ПМ — къ параллельности съ АВ;
вслѣдствіе этого точка М удаляется отъ С, и когда 2а— Ь обратится въ О, І1М сдѣлается параллельна АВ, и точка М удалится въ безконечность.
Третій примѣръ изслѣдованія.
363. Задача 0 фонтанахъ. Два фонтана наполняютъ бассейна.* персын, дѣйствуя одинъ, ложет наполнить бассейнъ въ а часовъ; друюй, будучи открытъ одинъ, наполнитъ бассейнъ въ Ь часовъ. Кранъ, находящійся въ днѣ, можетъ опорожнить бассейнъ въ с часовъ. Во сколько часовъ бассейнъ, вначалѣ пустой, будетъ наполненъ, если оба фонтана и кранъ будутъ открыты одновременно?
Пусть бассейнъ наполняется въ х часовъ. Первый фонтанъ, наполняя бассейнъ въ а часовъ, въ 1 часъ наполнитъ « часть бассейна, а въ х час. -а а
частей его.
х
Другой фонтанъ въ то же самое время наполнитъ частей бассейна. Наконецъ, кранъ выпуститъ въ х час. ? частей бассейна. Такъ какъ разность между приходомъ воды и ея расходомъ въ х часовъ, по условію, равна емкости бассейна, то имѣемъ уравненіе
а ' Ь с~
откуда
а^~ 6 с
Изслѣдованіе. Здѣсь слѣдуетъ разсмотрѣть три случая:
1 11. 1^ 1 1, 1 + 1 = 1, а а 6 с’ и с
111
1) Когда - 4~г> величина х конечна и положительна. Это значитъ, что «ОС
задача возможна, т.-е. что бассейнъ черезъ нѣсколько часовъ дѣйствительно будетъ наполненъ. Въ самомъ дѣлѣ, - + г есть часть бассейна, наполняемая въ
1 часъ обоими фонтанами, а-------количество воды, уносимой въ 1 ч. краномъ;
с
такъ какъ первое количество, по условію, больше второго, то очевидно, что по истеченіи нѣсколькихъ часовъ бассейнъ наполнится.
Сверхъ того, если увеличивать с, т.-е. уменьшать отверстіе крана, величина х также будетъ уменьшаться, стремясь къ предѣлу ------р котораго она дости-
а + Ь
гаегь при с со, т.-е. когда кранъ будетъ закрытъ. 1 1 1
2) Когда - + величина я становится отрицательной. Это отрицательное рѣшеніе означаетъ невозможность задачи, т.-е. что бассейнъ не можетъ на-полниться. Въ самомъ дѣлѣ, неравенство означаетъ, что количество-
воды, доставляемое въ 1 часъ обоими фонтанами, меньше количества воды, которое отводящій кранъ можетъ унести въ часъ. Очевидно, слѣд., что бассейнъ не можетъ быть наполненъ: задача невозможна въ томъ смыслѣ, въ какомъ она
предложена. Для истолкованія отрицательнаго рѣшенія, перемѣняемъ я въ - въ уравненіи задачи, и получаемъ.
11,11 11 И* И 1
--= -+т—пли " + г (1), откуда # = 3-—т,-гг.
х а'Ь с’ я с \а 1 Ъ) 4 л 3 /1 И
с \а^~ Ь/
Ур. (1) соотвѣтствуетъ слѣдующей задачѣ: бассейнъ наполняется краномъ, который, дѣйствуя отдѣльно, наполнилъ бы бассейнъ въ с часовъ; изъ двухъ «р«-мозъ, находящихся въ днѣ бассейна, одинъ будучи открытъ, можетъ опорожнить бассейнъ въ а часовъ, а другой, дѣйствуя отдѣльно, въ Ь часовъ. Во сколько часовъ наполнится бассейнъ, вначалѣ пустой, если будутъ открыты всѣ три крана? Такимъ образомъ, для исправленія задачи слѣдуетъ предположить, что питательные краны становятся опоражнивающими, и наоборотъ.
3) Если - 4- г “ то і и задача невозможна* Въ самомъ дѣлѣ, 7 а 1 о с 0 *
1 . 1 1 « равенство - + ~ означаетъ, что количество воды, приносимой въ часъ обоими
фонтанами, равно количеству воды, уносимой въ то же самое время краномъ, слѣд* бассейнъ никогда не можетъ наполниться: задача абсолютно невозможна.
Четвертый примѣръ изслѣдованія.
364. Вакое число нужно прибавить къ четыремъ даннымъ числамъ а, Ъ, с, (I, чтобы составить кратную пропорцію?
Пусть искомое число будетъ я; ур—ніе будетъ, очевидно:
д + дс __ с + # т
рѣшая его, находимъ:
_______Ъс — ай_____
~(а + гі)—(6 + е) ‘
Члены искомой пропорціи суть:
I
а |.а._(я-ЬИ<»-< ь с , д- (Д-с) (<>-<*). Л і
н-|-й-(Ь+с)’ а+<МН-с)’ * «+<*-(&+€)’ +
Изслѣдованіе. Слѣдуетъ различать два главные случая: знаменатель формулы х отличенъ отъ нуля, или же этотъ знаменатель равенъ пулю; и въ каждомъ изъ этихъ главныхъ случаевъ дѣлать возможныя предположенія относительно числителя.
1. Если а + ^>д-|-с и при этомъ Ьс>агі, или же а + ^<ЬН-с и при этомъ Ьс<^ад, то для х найдемъ величину положительную, которою вопросъ рѣшается въ прямомъ смыслѣ.
П. Если а -|- > Ь + с и Ъс<і «4, или же а + <Ь + с и Ьс>ай, то для я получается величина отрицательная, представляющая, очевидно, отвѣть на вопросъ; какое число нужно вычесть изъ чиселъ а, 6, с и й, чтобы остатки образовали кратную пропорцію?
111. Если а 4- с? Ь 4" 110 — Ъс, то х = 0.
Но условіе агі = Ъс то же, что пропорція: — откуда имѣемъ теорему: если четыре числа составляютъ пропорцію, то нѣтъ такого числа, которое, будучи придано къ каждому изъ нихъ, дало бы пропорцію.
IV* Если а + й — 6 + с и > абІ) то я — — со и задача невозможна, т.-е* не существуетъ конечнаго числа, рѣшающаго вопросъ. Въ самомъ дѣлѣ, для того чтобы четыре числа Ъ-^-х, сЦ~А + # составляли пропорцію, необходимо, чтобы произведеніе крайнихъ равнялось произведенію среднихъ, т.-е. чтобы
(а 4- х){іі + х) = (Ъ + аг)(с + *) пли
а<і 4~ (а + = 6с + (6 + с)#*
Но, по условію, ай отличію отъ 6с, а асі — Ъ с, слѣд. ни при какомъ конечномъ значеніи х равенство невозможно.
V* Если, наконецъ, а + <1 — Ь -у с и ай = Ъе, то я = т.-е. задача неопре-
дѣленна. Въ самомъ дѣлѣ, для того чтобы четыре числа « + Ъ + гс, с 4- х и 4 4- х составляли кратную пропорцію, необходимо, чтобы произведеніе крайнихъ равнялось произведенію среднихъ; т.-е. какъ выше указано, чтобы
а<1 (а + = Ъс + (6 + С)*П
по какъ 06? — Ьс и а + <і = Ь -|-е, это уравненіе есть тождество, а потому удовлетворяется при всякомъ значеніи х: неопредѣленность полная.
Неопредѣленность задачи при данныхъ условіяхъ можно обнаружить еще слѣдующимъ образомъ.
Изъ условія о 4 имѣемъ <і = Ь 4- с — а; подставляя эту величину (1
въ другое условіе асі = Ъс или а<1 — Ьс = 0, имѣемъ: а(Ь + с — а) — Ъс — 0, или
а2 — а(Ь -|- с) 4~ 6с — О, или (а — Ъ)(а — с) = О.
Этому равенству можно удовлетворить двояко: пли положивъ а = 6, или а = с. При а = 6, имѣемъ с/ — с, и искомая пропорція беретъ видъ
а 4- я? <2 + а 4- х — <1 4- х'
При а = с имѣемъ & = Ь\ и искомая пропорція будетъ
а 4~ Д 4"^
(і4~ # сі 4-&
И та, п другая пропорція — ничто иное какъ тождества, и стало быть удовлетворяются при всякомъ х.
Пятый примѣръ изслѣдованія*
365. Задача 0 курьерахъ. Два курьера выѣхали въ одно время изъ мѣстъ А и В, разстояніе между которыми равно (1 верстамъ, и ѣоутъ равномѣрно въ направленіи АВ, при чемъ первый дѣлаетъ ѵ верстъ, второй ѵ' верстъ въ часъ. Въ какомъ разстояніи отъ точки А они встрѣтятся?
Черт. 22.
Пусть точка встрѣчи находится на разстояніи х верстъ отъ А. Такъ какъ, по условію, курьеры выѣзжаютъ изъ точекъ А и В одновременно, то время, въ
которое первый проѣзжаетъ разстояніе АС, равно времени, въ которое второй проѣзжаетъ ВС. Первый, дѣлая ѵ верстъ въ часъ, про ѣдетъ разстояніе ЛС =? х въ - часовъ: второй, проѣзжая по ѵ' верстъ въ часъ, на проѣздъ всего разстоя-
д»__
ніяВС —х —<7, употребитъ часовъ. Уравненіе будетъ
X_X— (I
— * • • ф
V V
откуда
х — (I
V
•(2).
V — ѵ' *
Изслѣдованіе* Замѣтивъ, что какъ разстояніе между двумя точками, есть величина положительная, могущая въ частномъ случаѣ равняться нулю, заключаемъ, что между данными величинами могутъ быть слѣдующія соотношенія:
1)гі>0, ѵ>ѵ'; 3) = 0, 1? 5*4) > 0, я == і/;
5) (і = 0, ѵ — «Л
т (ІѴ
1. Когда <і>0 и оба члена дроби -----; положительны, сл. и х
-у—«г
есть величина положительная; кромѣ того, потому что сі умножается на дробь большую 1, ибо ѵ > ѵ — іЛ Это положительное и большее сі значеніе х означаетъ, что встрѣча курьеровъ произойдетъ вправо отъ точки В, т.-е. оно даетъ прямой отвѣтъ па вопросъ. И въ самомъ дѣлѣ, оба курьера выѣзжаютъ изъ точекъ Л и В одновременно и догоняющій ѣдетъ быстрѣе передняго (#>ѵ'), слѣд. первый непремѣнно догонитъ второго.
11. Когда <?>0 п ѵ<гЛ числитель гіу>0, а знаменатель ѵ —я'<0, слѣд. величина х отрицательна. Это отрицательное рѣшеніе указываетъ на то, что при данныхъ условіяхъ задача невозможна въ томъ смыслѣ, въ какомъ она предложена, т.-е. что встрѣча не можетъ произойти въ направленіи АВ (вправо отъ В). Дѣйствительно, такъ какъ оба курьера выѣзжаютъ въ одно время и первый ѣдетъ медленнѣе второго, то онъ никогда не догонитъ послѣдняго.
Чтобы исправить задачу, подставимъ въ ур. (1) — х вмѣсто х; найдемъ:
—х _ — х — (і ѵ ~ ѵ
х х + й или - = —Ц— . . . у ѵ'
Рѣшеніе уравненія (3) по абсолютной величинѣ таково же какъ и (1), но по знаку положительно, и потому даетъ прямой отвѣтъ на вопросъ, соотвѣтствующій ур—нію (3). Но послѣднее можетъ служить алгебраическимъ выраженіемъ слѣдующихъ двухъ задачъ.
1. х есть разстояніе, проѣзжаемое курьеромъ А; х + & — курьеромъ В, такъ что второй проѣзжаетъ <1 верстами больше перваго. Это возможно, если предположить, что оба ѣдутъ не въ направленіи АВ, а въ направленіи ВА, такъ что курьеръ, выѣзжающій изъ В, догоняетъ курьера, выѣзжающаго изъ А. Обозначивъ точку встрѣчи буквою С* и положивъ АС'=х, найдемъ ур. (3), котораго корень и будетъ служить отвѣтомъ па новую задачу.
Дѣйствительно, такъ какъ то при движеніи въ направленіи ВА,
курьеръ В и догонитъ курьера А въ нѣкоторой точкѣ С', лежащей влѣво отъ А. Такимъ образомъ, для истолкованія отрицательнаго рѣшенія, мы измѣнили направленіе движенія курьеровъ.
2. Но легко видѣть, что ур. (3) можно также разсматривать какъ выраженіе условій задачи, отличающейся отъ данной не направленіемъ движенія, а допущеніемъ, что движеніе имѣетъ мѣсто неопредѣл. время, и что встрѣча произойдетъ не въ будущемъ, а что она уже имѣла мѣсто раньше того момента, въ который курьеры проѣзжаютъ — одинъ черезъ А, а другой чрезъ В, въ нѣкоторой
точкѣ С', отстоящей влѣво отъ А на х = -7---- ве^стъ* Т^то за,лача н въ этомъ смыслѣ возможна, прямо слѣдуетъ изъ того, что при ѵ' > я, курьеръ В, догнавъ А въ точкѣ С', обгоняетъ послѣдняго и ѣдетъ впереди его*
\ 0 X я
НЕ Когда й = 0 п іХ < то х ~ = 0.
Такъ какъ й —0, то оба курьера выѣзжаютъ изъ одного мѣста, притомъ одновременно; но они ѣдутъ съ разными скоростями слѣд. одинъ по-
стоянно будетъ впереди другого, такъ что никакая точка пути, кромѣ мѣста выѣзда, не можетъ быть ихъ общимъ мѣстомъ. Это и выражается рѣшеніемъ х = 0.
IV. Когда > 0, а ѵ — то х = - = 'XX
Безконечное рѣшеніе служитъ въ данномъ случаѣ признакомъ полной невозможности задачи, т.-е, невозможности встрѣчи курьеровъ. Дѣйствительно, они выѣзжаютъ одновременно изъ двухъ разныхъ точекъ и ѣдутъ съ одинаковою скоростью; понятно, что разстояніе между ними всегда — и слѣд. встрѣча ихъ невозможна,
V, При чі — О и ѵ = ѵ' 0 . ѵ 0
Это рѣшеніе означаетъ полную неопредѣленность задачи. Дѣйствительно, условія а — 0 и <’ = ѵ' означаютъ, что курьеры выѣзжаютъ изъ одного мѣста (одновременно) и ѣдутъ съ одинаковою скоростью: очевидно, что они всегда будутъ вмѣстѣ: каждая точка пути будетъ служить мѣстомъ встрѣчи.
Примѣчаніе. Еслп положить, что курьеры ѣдутъ не въ одну сторону, а навстрѣчу другъ другу, то направленія скоростей будутъ противоположны; слѣд. если одну изъ нихъ, напр.будемъ считать положительною, то другую слѣдуетъ принять за отрицательную; обозначивъ ее черезъ —і/, найдемъ
__ сіѵ ______ (Іѵ ~ ѵ—(—#') ѵ + я'’
Не трудно было бы вывести эту формулу и непосредственно. Заключаемъ, что формула (2) прилагается и къ этому случаю, а потому она — вполнѣ общая.
Шестой примѣръ изслѣдованія,
366. Лровтнм обш^ю касательною яь
А. Проведеніе общей внѣшней касательной.
Пусть разстояніе ОТ точки встрѣ-_______д чн общей внѣшней касательной съ линіей центровъ отъ центра О пер-ваго круга будетъ ж; радіусъ О А = К;
——А_____ оа=Іѵ; Оо— <і. Изъ подобія тре-
/ Лі у- угольниковъ ОАТ и ояТ находимъ
|X ♦КО ) * пропорцію: ОТ : оТ — О А : оа или
\ и /х Т 4—7 х : (я — гі) — В : Е\ откуда
і=іг-н'' •
Черт. 23.
Изслѣдованіе подраздѣляется на три главные случая, смотря по тому, будетъ ли знаменатель К —В' положителенъ, отрицателенъ иди равенъ нулю.
I. К—Н/>0, или К>ВГ. Величина я въ этомъ случаѣ положительна, конечна и >4, потому что ** > 1» а слѣд. точка Т находится на продолженіи іѵ—іѵ
лпніп Оя. Сверхъ того, необходимо, чтобы э’^й-рВ', иди Такъ
какъ К — К' >0, то, умножая обѣ части на эту разность, мы не измѣнимъ знака неравенства, слѣд. гіК (гі + В')(Н — откУДа
К —В'.
Неравенство удовлетворяется, когда: 1) круги расположены одинъ внѣ другого, не имѣя общихъ точекъ, ибо тогда <1 > даже К + В'; 2) круги имѣютъ внѣшнее касаніе; 3) они пересѣкаются. Равенство же удовлетворяется яри внутреннемъ касаніи; въ послѣднемъ случаѣ ж = ~ и точка Т совпа-
даетъ съ точкою касанія круговъ.
Когда IV — 0, т.-е. малая окружность сводится къ своему центру, условіе возможности приводится къ гі^В, а х — гі,—результаты сами собою понятные.
И. К—К' <0, или К<1Ѵ. Въ этомъ случаѣ х отрицателенъ, слѣдовательно точка Т находится влѣво отъ 0. Въ этомъ случаѣ безполезно повторять изслѣдованіе, приведенное выше; ибо для опредѣленія различныхъ положеній точки Т, очевидно, достаточно перевернуть предыдущій чертежъ, такъ чтобы меньшій кругъ помѣщался влѣво отъ большаго.
III. В —В' = 0, или К=В\ т.-е. оба круга равны. При этомъ возможны слѣдующіе случаи:
л) Если х = — со, т.-е. точка Т удаляется въ безконечность. Въ
самомъ дѣлѣ, въ этомъ случаѣ линіи О А и оа равны и параллельны, слѣдоват. прямая Лл ]| Оо и не встрѣчаетъ ее. Безконечное рѣшеніе означаетъ, такимъ образомъ, параллельность общей касательной линіи центровъ. Разсматривая вопросъ съ другой точки зрѣнія, можно замѣтить, что если бы радіусы, будучи сначала неравными, разнились бы незначительно, точка Т находилась бы на очень большомъ разстояніи отъ точки О, и что если радіусы будутъ стремиться къ равенству, разстояніе ОТ будетъ неограниченно возрастать; слѣд. когда радіусы будутъ строго равны, точка Т удалится въ безконечность и х — со.
Ь) Если, при В — IV — 0, и — 0, тогда х — и задача становится дѣйствительно неопредѣленною. Въ самомъ дѣлѣ, оба круга имѣютъ въ этомъ случаѣ общій центръ и равные радіусы, сл. они сливаются; ни линія Аа, ни Оо не имѣютъ въ такомъ случаѣ опредѣленнаго положенія, а потому и точка ихъ встрѣчи абсолютно неопредѣленна.
с) Наконецъ, если К = НГ —0, х также принимаетъ неопредѣленный видъ^* Неопредѣленность—опять дѣйствительная, и легко объясняется: оба круга приводятся къ своимъ центрамъ, линія Аа сливается съ Оо и точка Т можетъ быть взята произвольно на линіи Оо.
Построеніе. Формула (1) даетъ пропорцію: (К — В'): В — й : х, изъ которой видно, что х есть четвертая пропорціональная къ тремъ линіямъ В — IV, В и Проведя произвольный радіусъ (Ж въ кругѣ центра О, откладываемъ на немъ линію КМ = В'; получимъ ОМ = В—В'. Соединивъ точку М съ о, проводимъ линію КТ И Мо: точка Т будетъ требуемая. Проведя изъ нея касательную ТА къ кругу О, убѣдимся, что эта линія коснется и круга о.
В. Проведеніе общей внутренней касательной.
Обозначивъ разстояніе ОТ" буквою я, изъ подобія треугольниковъ ОВТ' и обТ имѣемъ: откуда
х = ТГ+К' • •
Изслѣдованіе. Такъ какъ < 1, то всегда х<гі, т.-е. точка Т' находится между центрами. Кромѣ того, разстояніе точки Т' отъ О но должно
быть <В, т.-е. должно имѣть ;>К, откуда Й^К + К\ т.-е. окружности должны быть одна внѣ другой. Въ крайнемъ случаѣ, т.-е. при внѣшнемъ касаніи;
<1 = В + ІЦ и я = К, т.-е. точка Т' совпадаетъ съ точкою касанія круговъ.
Когда К' — О, х — т.-е. точка Т совпадаетъ съ центромъ о, къ кото-
рому, въ данномъ случаѣ, приводится второй кругъ.
Наконецъ, если К = IV = 0, х = точка Т' неопредѣленна, и въ самомъ дѣлѣ, въ этомъ случаѣ прямая Да совпадаетъ съ линіей центровъ.
Построеніе аналогично предыдущему.
Седьмой примѣръ изслѣдованія.
367. Въ точкѣ А, дайкой круглаго билліарда, помѣшенъ упругій
шарикъ. .Къ иаколге направленіи нужно сто пустиит, чтобы, отразившись три раза отъ бортовъ, онъ возвратился снова въ точку А?
„ По закону отраженія, уголъ
В * паденія равенъ углу отраженія, при
чемъ угломъ паденія будетъ уголъ, составленный направленіемъ паденія (напр. АВ) съ радіусомъ, проведеннымъ въ точку В, а угломъ отраженія—уголъ, образуемый направленіемъ ^отраженнаго движенія (ВС) съ тѣмъ же радіусомъ. Зная это, и замѣчая, что фигура расположена симметрично отяосн-тельно діаметра ВС, проходящаго черезъ точку А, усматриваемъ, что задача приводится къ слѣдующей: въ какомъ направленіи надо пустить шарикъ А, чтобы, отра-лившись отъ борта* онъ ударился въ конечную точку С діаметра І)С.Р Пусть ОС — К, О А = а, В — искомая точка; проведя хорду ВВ' перпендикулярно къ діаметру ВС, замѣчаемъ, что какъ скоро извѣстно
Черт. 24. будетъ разстояніе 10 этой хорды
отъ центра, то будетъ извѣстно и положеніе искомой точки В. Поэтому за неизвѣстное принимаемъ 01 = я. Углы: паденія А ВО, и отраженія—О ВС, равны, слѣд. ОВ есть биссектриеса угла АВС треугольника АВС; по свойству ея, имѣемъ пропорцію:
АВ_АО. ВС “ ОС’
возвысивъ обѣ части въ квадратъ, находимъ:
АВ _ о*.
—а к»’
ВС
затѣмъ, на основаніи теоремъ о квадратѣ стороны треугольника, имѣемъ:
АВ*= АО2-І-ВО2 —2А0.01 № —
ВС2 = 0С2 + 0В2 + 20С.01 = 2В2 + 2К.я:;
подставивъ эта величины въ предыдущую пропорцію, находимъ:
й* + К2 — 2лх _ «2 2К2 + 2Ка: — К2 *
- - О)
изъ этого у;—нія, по сокращеніи сначала на Н, а затѣмъ на К—а, имѣемъ:
х =
К(В— а) 2а *
Изглъдованіе. Такъ какъ а < К (точка А находится внутри круга 0), то яреіжхущее выраженіе даетъ для х всегда величину положительную; но для вазждкжхти [задачи этого недостаточно: необходимо еще, чтобы было х < К, млі
-Цч----откуда а>-=-
Ипкъ, чтобы задача была возможна, нужно, чтобы а имѣло величины въ между К и слѣд. задача невозможна, когда шарикъ А находится круга, концентричнаго билліарду и описаннаго радіусомъ, равнымъ трети рълуса билліарда.
Когда а измѣняется непрерывно отъ К до х измѣняется непрерывно отъ О к» К; въ частности:
при а = К, гс = О: шарикъ опишетъ половину контура квадрата;
К К
при а——, 2 = —: шарикъ опишетъ полупериметръ равносторонняго треугольника;
при а = ”, ж = шарикъ опишетъ діаметръ ЬС.
Построеніе. Формула х даетъ пропорцію:
а : — = (К — а): х,
такъ что нужно построить четвертую пропорціональную къ тремъ линіямъ: а, — и К — а. Взявъ на діаметрѣ ОЕ, перпендикулярномъ къ ОА, часть О А' — К*
= 0А = «, и 0Е = ^, затѣмъ на діаметрѣ БС часть 01)' —АО —Е— а, соеди-нимъ точки I)' и А' и черезъ точку Е проведемъ линію ЕІ параллельную АЪ':
• эта линія и дастъ искомую точку 1. Въ самомъ дѣлѣ, изъ подобія треугольниковъ А'ОЙ' и Е01 имѣемъ:
ОА': ОЕ = 013': 01, иди а: — (К — а): 01» откуда и видно, что 01=я.
Обобщеніе задачи. Когда шарикъ А находится внѣ круга, напр. въ А' (черт. 25) задача будетъ возможна, если удалить матеріальную полуокружность Е*Ггб\ обращенную своею выпуклостью къ шарику. Въ самомъ дѣлѣ, въ такомъ случаѣ шарикъ А* можетъ удариться въ такую точку В' другой половины круга, что по отраженіи попадетъ въ точку С, а слѣдовательно отсюда, по симметріи
фигуры относительно линіи А'С, возвратится въ А'. Для опредѣленія точки В' положимъ О1' = а/; въ таком> случаѣ, подобно предыдущему, найдемъ ур.
«з + Ш _ о*
. ,2В* —2Вя' "”Ва* * *
отличающееся отъ (1) только перемѣною % на —а потому корень его отличается отъ корпя ур—нія (I) только знакомъ; итакъ
, Кч. л—К Н Л Щ ------------= -а”П------г -2 а 2 а1 •
Чтобы х' было положительно, необходимо, чтобы было или ’«>К;
слѣд, л можно измѣнить отъ В до При этомъ х> будетъ измѣняться отъ О до
Черт. 25.
2» т.-е. по мѣрѣ того какъ точка А* удаляется отъ точки Ь', точка паденія В' приближается къ точкѣ В", отстоящей на 60° отъ точки С.
Итакъ, ур. (1) всегда даетъ рѣшеніе задачи, когда шарикъ находится внѣ круга, а знакъ —, предшествующій корню, указываетъ ту область, которая заключаетъ точку паденія.
Построеніе аналогично предыдущему и указано па чертежѣ.
Восьмой примѣръ изслѣдованія.
368. Радикальная ось двухъ круговъ. Даны двѣ окружности радіусовъ И и. г; разстояніе между ихъ центрами пустъ =гі. Найти на плоскости такую точку М, чтобы касательныя, проведенныя изъ нея къ даннымъ окружностямъ, были равны между собою. Геометрическое- мѣсто этихъ точекъ.
Рѣшеніе. Ищемъ, нѣтъ ли на линіи центровъ точки, удовлетворяющей требованію задачи. Если такая точка существуетъ, гто пусть она будетъ М; въ такомъ случаѣ касательныя МА и МА' равны. Примемъ за нецявѣстное разстояніе точки М отъ центра О, положивъ ОМ=я;; будетъ МО' = с/ — х. Прямоугольные треугольники АОМ и А'О'М —2 —2
дадутъ: ЛМ^я2—К*, А'М=(М2^; по условію, х* — № = (б/ — ІГ)2 — г2, откуда
Черт. 26.
X- . .(1).
Этой формулой и опредѣляется разстояніе искомой точки отъ центра круга О.
Ищемъ, нѣтъ ли также внѣ линіи центровъ точекъ, удовлетворяющихъ требованію задачи. Пусть одна изъ такихъ точекъ будетъ Р. Опустивъ перпендикуляръ РМі на линію цент-
ровъ. замѣчаемъ, что точка Р будетъ найдена, какъ скоро будутъ извѣстны: разстояніе ОУЦ перпендикуляра РМ| отъ центра О и отрѣзокъ МГР, показывающій разстояніе точки Р отъ линіи центровъ. Пусть и РМі=#.
Проведя касательныя РІ и РГ, линіи РО, РО', 01 и ОТ, изъ прямоугольныхъ
—2 —2 —2
треугольниковъ РОІ и РОТ найдемъ: РІ = РО —В*, пли, какъ Р0=я'* + у2. то РІ = ->-у2— К5. Подобно этому, найдемъ РГ = (<і —+ — га. По требованію задачи, имѣемъ ур—ніе
я/2 _|_ у'1 — Ц2 = ((/ — 4- ^2 — г’2, откуда х' — —- . (2).
Сравненіе (1) со (2) показываетъ, что х = &і т.-е. что всякая точка искомаго геометрическаго мѣста пролагается въ точку М, а это значитъ, что всѣ искомыя точки находятся на одной и той же прямой — на перпендикулярѣ къ линіи центровъ, разстояніе котораго отъ центра 0 опредѣляется формулою бР —I— К,2 -----. Этотъ перпендикуляръ и есть, слѣд. геометрическое мѣсто такихъ точекъ плоскости, что касательныя, проведенныя изъ каждой къ даннымъ кругамъ, равны между собою.
Изслѣдованіе. I. Данные круги неравны между собою, и пусть К>г. Разберемъ задачу для всякихъ относительныхъ положеніи данныхъ круговъ.
1) гі > В 4- г: круги лежатъ одинъ внѣ другого, не имѣя общихъ точекъ. Сравнимъ х съ В: не будетъ ли, напр., а?>В? Отвѣтъ найдемъ, испытавъ, вѣрно ли будетъ неравенство
^2-4X2 — г2 2(1 ‘
К.
Освободивъ отъ знаменателя, легко найдемъ: ^ + К2 — га > 2гіК, или <₽ — 2ЛК + № > г2, или (<і —- В)* > г2, откуда іі — К > г, н, наконецъ, К-Ь г. Каждое преобразованіе приводило къ неравенству, эквивалентному предшествующему, какъ послѣднее совпадаетъ съ условіемъ, которое намъ дано, то заключаемъ, что испытуемое соотношеніе вѣрно, и х > К. Сравнимъ теперь х съ отрѣзкомъ ОІД или гі —г, и посмотримъ, не будетъ ли —г, т.-е. испытаемъ неравенство
2 с?
сі — г.
Послѣдовательно имѣемъ: й* — 2гіг + г®>К2, или (<і—г)2>К2, откуда д — г > К, и наконецъ, д > К + г — что намъ дано. Заключаемъ, что г>я> Кг т.-ѳ. радикальная ось проходитъ между данными кругами, пересѣкаетъ линію центровъ на отрѣзкѣ ЫЛ
Остается разсмотрѣть, къ какому изъ обоихъ круговъ она ближе, и для этого надо сравнить ЬМ^ съ Ь'Мі, пли я — К съ а — х — г. Не будетъ ли, напр., л — К, < — х — г, или, что то же, 2я < + В — г, или, наконецъ,.
Провѣрка этого неравенства приводится къ провѣркѣ неравенства гі’+К* — — г2 < -р гі(В, — г), или (К + г)(К — г) < (В — г), или К + г < с?, а это намъ дано. Итакъ:
Черт. 27.
Когда круги лежатъ одинъ внѣ другого, не имѣя общихъ точекъ, то раои-кальная осъ гіхъ проходитъ между обои-ми кругами, ближе къ большему кругу.
2) <і = К+г: круги и мѣютъ внѣшнее касаніе.
Подставивъ въ формулу (1) К + г вмѣсто А, найдемъ
а?==:К.
Это значитъ, что въ данномъ случаѣ радикальная ось отстоитъ отъ центра круга 0 на разстояніе = его радіусу. Слѣдовательно:
Въ случаѣ внѣшняго касанія радикальная ось сливается съ общею внутреннею касательною къ даннымъ кругамъ.
3) В — г < <С Н + г: круги пересѣкаются.
Въ треугольникѣ 0Р0' имѣемъ: г2 — В^ + сЯ2— 2^. ОМ, откуда
Сравнивая это выраженіе съ (1), находимъ: ж —ОМ. Слѣдовательно, въ данномъ случаѣ додимммая ось совпадать съ общею хордою круговъ, что можно было предвидѣть, ибо точки Р и очевидно, принадлежать искомому мѣсту.
4) <і = К — г: круги имѣютъ внутреннее касаніе*
Вводя В —г вмѣсто (I въ формулу (1), находимъ
Заключаемъ, какъ и во 2-мъ случаѣ, что радикальная ось совпадаетъ съ общею касательною данныхъ круговъ.
5) < В — г: меньшій кругъ находится внутри большаго, не имѣя съ нимъ -общихъ точекъ.
Въ этомъ случаѣ опять имѣемъ х > К: въ самомъ дѣлѣ, провѣрка неравен-X І{2 _ г2
ства В<-----приводитъ послѣдовательно къ: г3<(В—г<В — сі,
</<Е— г, а это намъ дано. Въ разсматриваемомъ случаѣ, значитъ, рпд. ось расположена внѣ обоихъ круговъ. Здѣсь само собою очевидно, что она ближе къ большему кругу*
Такимъ образомъ, въ двухъ послѣднихъ случаяхъ, когда одинъ кругъ находится внутри другого, замѣчаемъ, что рад.ось не встрѣчаетъ разстоянія центровъ, т.-е* отрѣзка 00', а пересѣкаетъ линію центровъ на продолженіи его, при чемъ разстояніе точки М отъ 0, бившее сначала = К, дѣлается затѣмъ > К: значитъ, точка пересѣченія М движется въ направленіи воображаемой точки, которая перемѣщалась бы отъ центра большаго круга къ центру меньшаго.
6) <і = 0: окружности концентричны. Находимъ
Е*— 0
т.-е* по мѣрѣ сближенія центровъ х растетъ, рад, ось болѣе* и болѣе удаляется вправо, и при б?==0 отбрасывается въ безконечность.
II. Пусть круги равны между собою: Е —г. Формула (I) даетъ
Значить, рлд* ось перпендикулярна къ разстоянію центровъ въ его (рединѣ.
Если при этомъ положить б? = 0, то окружности совпадутъ, при этомъ- а? — 0* Это значить, что рад. ось проходитъ чрезъ общій центръ, и положеніе ея ничѣмъ 45олѣе не опредѣляется; неопредѣленность эта очевидна, ибо изъ какой бы точки внѣ круговъ нн провести касательной къ одному кругу, она вмѣстѣ съ тѣмъ будетъ касательна и къ другому*
Частные случаи. 1) Если кругъ г обращается въ точку, г = 0, то
Х “ 2 а :
но условію задачи, эта формула опредѣляетъ разстояніе отъ 0 проэкціи такой точки М, чтобы было ,
АЛІ —М0\ или МО —К2=МО', или МО — МО' = К4,
слѣд», рад. ось круга 0 и точка 0' есть геометрическое мѣсто такихъ точекъ^ что разность квадратовъ ихъ разстояній отъ центра даннаго круга и отъ данной точки (У равна квадрату К2.
2) Если г = 0 и К = 0, тогда т*'е’ РаДикальная ось двухъ точекъ О и 0' есть перпендикуляръ въ срединѣ прямой 00'.
Девятый примѣръ изслѣдованія.
369. Тллф, состоящее изъ двухв призмъ, сложгниьт осмовляАя.мм*
погружено въ ванну, состоящую также изъ двухъ жидкостей, находящихся одна поверхъ другой. Спрашивается, въ какомъ разстояніи надъ поверхностью раздѣла жидкостей находится площадь соприкосновенія призмъ? Плотности и высоты призмъ равны: въ верхней призмѣ О и Н, въ нижней О' и Н1; плотность верхней жидкости равна а, нижней аг.
Пусть требуемая высота будетъ х. По закону Архимеда: „вѣсъ плавающаго тѣла равенъ вѣсу вытѣсненной Жидкости", Зная это и припоминая, что Р=ІЮд (гдѣ Р —вѣсъ тѣла, Е —его объемъ, В —плотность и $ — вѣсъ кубической единицы воды), мы, обозначивъ буквою 8 площадь основанія каждой призмы, имѣемъ уравненіе
8(ПО+Н'О') = 8(П + ^ + 8(Н' —ж)^',. . .(1) откуда
- О) + ІГ(<Г — Б')
Изслѣдованіе. Величина х можетъ быть пли положительною, или отрицательною: если она положительна, то можетъ быть рѣшеніемъ предложенной задачи, если же отрицательна, то дастъ отвѣтъ на слѣдующій вопросъ: „въ какомъ разстояніи подъ поверхностью, . . в?
Съ другой стороны, никогда количество я, по абсолютной величинѣ, не можетъ быть больше
Н', если х положительно, и
Н, если х отрицательно:
иначе тѣло не погружалось бы заразъ въ обѣ жидкости, и ур—ніе (1) не было бы уже уравненіемъ задачи.
Наконецъ, по законамъ равновѣсія жидкостей, а* не можетъ быть меньше гі, такъ что относительно знаменателя можетъ быть только два предположенія:
—гі>0 и — гі = 0. Итакъ:
I. аг — <і>0. При этомъ относительно числителя возможны 3 предположенія:
1) — Б) + Н'(бГ — 0')>0, Въ этомъ случаѣ, для того чтобы величина а?
дѣйствительно служила рѣшеніемъ задачи, необходимо, чтобы она была Н\ слѣд., нужно чтобы
Щгі — Е) + — И') — ф,
т.-е.
НЕ + Н'Е' > (И + Н%
2) 11(гі — Г)) 4- — Ь') < 0. Въ этомъ случаѣ х отрицателенъ, и для того,
чтобы онъ служилъ рѣшеніемъ задачи, необходимо чтобы абсолютная величина его была И, т.-е. чтобы
д' - а
или
1Ш + НТИ< (И + ну.
3) — И) + Н'(<Г — Р') — 0. Въ такомъ случаѣ и площадь сопри-
косновенія призмъ совпадаетъ съ поверхностью раздѣла жидкостей.
т
ІИ (I*— (? = 0. Если при этомъ числитель не =0, то х = эта форма означаетъ дѣйствительную невозможность: тѣло не можетъ быть въ равновѣсіи внутри жидкости.
Если же НВ + ІГВ' = ^(Н+ !!')» то ж = Эта форма означаетъ дѣйствительную неопредѣленность: такъ и должно быть, ибо въ данномъ случаѣ тѣло будетъ въ равновѣсіи въ какомъ угодно положеніи.
ГЛАВА XXVI-
Изслѣдованіе уравненій первой степени съ двумя неизвѣстными.
Изслѣдованіе двухъ уравненій съ двумя неизвѣстными въ общемъ видѣ. — Примѣры изслѣдованія буквенныхъ вопросовъ.
370. Рѣшая два уравненія первой степени съ двумя неизвѣстными
ах ч- Ъу = с 1 и'х-+-Уу=с* ( мы нашли формулы:
___с// — Ъс* _ггс—са' Х~ «6'-6а' “ ^аб'-ба' •
предполагая, что коэффиціенты а и а*, пли Ъ и У отличны отъ нуля, н что при этомъ: аУ — Ъа* отлично огь нуля. Цѣль изслѣдованія заключается въ томъ, чтобы показать, во всѣхъ ли случаяхъ эти формулы дадутъ рѣшенія ур—ній, или же, напротивъ, есть такіе случаи, когда онѣ непримѣнимы.
Мы должны разсмотрѣть два случая, смотря по тому, будетъ ли знаменатель въ формулахъ х и у: 1) отличенъ отъ нуля, или: 2) равенъ нулю, при чемъ или одинъ изъ числителей, или оба — равны нулю.
Это раздѣленіе основывается на слѣдующихъ свойствахъ биномовъ сУ— Ъс' и ас*— са'.
Первое свойство. Если коэффиціенты при одномъ и томъ же неизвѣстномъ, или свободные члены с и с? не равны нулю одновременно, и если два изъ биномовъ аУ — сУ — Ъс* и «с' — са', рлбчш нулю, то и третій равенъ нулю.
Пусть сУ — Ъс' =0 и ас*— са'~0; отсюда сЪ'~Ъс' и ае1 —са': перемноживъ эти равенства, найдемъ аУсс* “ я'Ьсс', или («6' — Уб)сс' = 0; если с и с' не равны нулю, то должно бытъ аУ — а'Ъ = Ь. Если же с=О, въ такомъ случаѣ, по условію, с'<0; а потому изъ равенствъ сУ~Ъс* и ас' = саг имѣемъ: а = 0,
Ъ — о, к слѣд. а/У—*/я/'=0. Вслѣдствіе того, что всѣ три бинома симметричны относительно «, Ь и с, это свойство доказано, какіе бы да бинома ни были равны нулю.
Второе свойство. Условія и досиіашочиыя оля тою, чтобы два
изъ этихъ биномовъ были нулями, а третій былъ бы отличенъ отъ нуля, состоятъ въ томъ, чтобы буквенныя количества, общія этимъ двумъ биномамъ, были нулями.
Очевидно, что этихъ условій достаточно; затѣмъ, если имѣемъ сЬ'— Ьс' — О, ас’— <хУ = О, и аіз—Ьа'^О, то равенства даютъ: сс'(^6'— 6л') = О, а слѣд. ссг — 0. Пусть с —0, тогда Ьс* = 0 и лс'^=0, а потому и с' = 0: ибо, положивъ е'^0, 6—0 и л=0, нашли бы аЬ9—Ьа(—$, что противно условно: аЬ'—бп'^0.
371. 1. Общій знаменатель аЬ' — Ьа' отличенъ отъ нуля.
Въ этомъ случаѣ система ур—«ім плотна конечное и онре^Иіленное ръшеніе, иредтавллел(0в дбор.иулл.хи (1).
Въ самомъ дѣлѣ, эти рѣшенія составляютъ систему эквивалентную данной» потому что дѣлитель аЬ’— Ьа' не есть нуль.
Въ случаѣ, когда числитель ас' — са' равенъ нулю, что возможно при одномъ а с
изъ трехъ условій: седи ^, = -; или если л = 0 и с —0; или С —0 и с' = 0 (предположеніе « = 0 и а’ — 0 повело бы къ: аЬ'—Ьа' — О, что противно условію), замѣчаемъ, что у обращается въ нуль; а при третьей группѣ условій, именно при с —0 и с1 = 0, и а; дѣлается нулемъ.
Примѣчаніе. Въ сиду второго свойства, условія необходимыя и достаточныя для того, чтобы оба неизвѣстныя были нулями: л? —О н у=0, суть с — О и с' = 0.
Итакъ, когда общій знаменатель аЬг — Ьа' отличенъ отъ нуля, система имѣетъ конечное опредѣленное рѣшеніе; принтомъ или оба неизвѣстныя будутъ положительны, или оба отрицательны, или одно положительно, а другое отрицательно; наконецъ, или одно, или оба могутъ быть нулями. Послѣднее имѣетъ мѣсто только въ томъ исключительномъ случаѣ, когда свободные члены — оба нули.
Положительныя рѣшенія въ большинствѣ случаевъ даютъ прямой отвѣтъ на вопросъ; отрицательныя же или служатъ признакомъ невозможности задачи, или неправильной постановки ея. Истолкованіе отрицательныхъ рѣшеній основано на теоремѣ, аналогичной той, которая была доказана для ур-нія съ однимъ неизвѣстнымъ.
372. Т е о р е м А. Двѣ системы двухъ ур—ній съ двумя неизвѣстными, отличающіяся только знакомъ при одномъ ши при обоихъ неизвѣстныхъ, имѣютъ» рѣшенія: равныя по абсолютной величинѣ, но разнящіяся знаками — для тѣхі, неизвѣстныхъ, знаки при которыхъ въ обѣихъ системахъ различны; іе рѣшенія, одинаковыя по величинѣ и по знаку—для неизвѣстныхъ, пііедщеетвуемыхъ обшим» знакомъ о&ыдо системахъ.
Въ самомъ дѣлѣ, сравнимъ системы:
ах + Ьу~с ) . ах — Ьу = с |
а*х-ь-Ь‘у=.с* і * а'х — Ь*у — ъ* I “
разнящіяся только знакомъ при у; докажемъ, что эти системы имѣютъ одинаковое рѣшеніе для аг, и рѣшенія, равныя по абсолютной величинѣ, но противоположныя по знаку, для у.
Въ самомъ дѣлѣ, положивъ —у = я, система (2) обратится въ
пл* + Ь? — с і , р 4-6'2 — 1 "
Замѣчая, что система (2') ничѣмъ не отличается отъ (1), заключаемъ, что рѣшенія системы (1): аг' и / удовлетворяютъ и (2'); такъ что система (‘2') имѣетъ рѣшенія: х = г' и г=#'; пли, такъ какъ я = — то (2Г), а потому и (2) имѣетъ рѣшенія:
х = у = — зА
Примѣръ, Куплено нѣсколько аршинъ матеріи по опредѣленной цѣнѣ. Если бы было куплено 3 аршинами больше, а за аршинъ было заплачено 1 руб. меньше, то на всю покупку издержали бы 11 рублями меньше. Если же было бы куплено 8 аршинами меньше, а за аршинъ платили бы 2 рублями дороже, то издержали бы 12 рублями больше. Сколько аршинъ куплено и сколько платили за аршинъ?
Пусть было куплено х арш. по у руб. за аршинъ. Получаемъ ур—нія:
(а‘4-3)(у-1)=.ту-11
(.г — 8)(?/ -Н 2) = ху -4- 12; откуда
т = —10; у = — 6.
Слѣд. задача невозможна въ томъ смыслѣ, какъ она- дана.
Подставивъ въ ур—нія: —я? вмѣсто а?, и — у вмѣсто у, найдемъ:
— 3)(рч-1) = .г>/ —11 (а? + 8)(у-2)=^-н12;
которымъ, на осн. доказанной теоремы, удовлетворяютъ рѣшенія: х 10, у = 6. Они служатъ прямыми отвѣтами на слѣдующую задачу:
„Куплено извѣстное число аршинъ матерій по опредѣленной цѣнѣ. Если бы было куплено тремя аршинами меньше, а за аршинъ было заплачено 1 рублемъ дороже, то на всю покупку издержали бы 11 руб. меньше. Если же было бы куплено 8-то аршинами бо.шне, а за аршинъ платили бы 2 рублями .немыке, то издержали бы 12 рублями больше. Сколько аршинъ куплено и сколько платили за аршинъ?*
373. II. Общій знаменатель аЪ' — Ъа'=0, а одинъ изъ числителей, напр.
— Ьс'^О.
Равенство аЬ'— 6а'= 0 можетъ имѣть мѣсто при слѣдующихъ обстоятельствахъ:
1) = = 2) п=0, Ь=О; 3) а = 0, а' = 0.
Предположеніе Ь = 0, 6' = 0, обращающее также въ нуль биномъ аб' — Ъа', слѣдуетъ устранить, потому что при немъ обращается въ нуль и числитель сЬ* — Ъс1, по условію, неравный нулю.
Первый случай. = Оба неизвѣстныя представляются въ этомъ случаѣ м подъ видомъ или с©:
Докажемъ, что представляютъ единственно возможное
рѣшеніе системы въ разсматриваемомъ случаѣ.
Такимъ образомъ нужно доказать, что въ данномъ случаѣ уравненія не допускаютъ конечныхъ рѣшеній; а затѣмъ, что безконечныя рѣшенія дѣйствительно удовлетворяютъ системѣ.
тг а Ъ , а'Ь
Изъ условія — имѣемъ: а — подставивъ въ первое ур*, находимъ:
а'Ь , , сЪ'
р- а? 4- Ъу — с, или а х 4- Ъу =
Но второе ур, есть
а'х 4- Ъу' = с';
по условію же сЪ' — Ъс ^0, откуда ~^с'.
Отсюда видно, что система состоитъ изъ двухъ ур-пій, которыхъ первыя части одинаковы, между тѣмъ какъ вторыя неравны; очевидно, слѣдовательно, что всякія конечныя значенія х п*у, обращающія въ тождество одно изъ ура* вненій, не могутъ обратить въ тождество и другое. Такія ур—нія. которыя не имѣютъ общихъ конечныхъ рѣшеній, называютъ несовмѣстными (противорѣча-щими одно другому).
Покажемъ теперь, что безконечныя значенія х и у удовлетворяютъ системѣ, и для этого разсмотримъ два случая, смотря по тому, имѣютъ ли коэффиціенты а и & одинаковые знаки, или противоположные.
Пусть а и Ь имѣютъ одинаковые знаки; пусть, при этомъ, сЪ'—Ъс'^О, и аЬг—Ьа', уменьшаясь, стремится къ нулю; въ такомъ случаѣ
Умноживъ обѣ части неравенства сб' > Ъс1 на — количество положитель* ное, получимъ -у-> ле; но = а , слѣд. ас > «г, или ас^ — ас < 0; поэтому
у = — се.
Замѣтивъ, ‘что видимъ, что а' и 6' также имѣютъ одинаковые знаки; слѣд., подставивъ въ ур—нія вмѣсто х и у ихъ величины, найдемъ
т.-е-
а . се — Ъ . се=с а' - со — // . со = с', со — сс-=с и ее— со = с',
что возможно, потому что разность двухъ безконечностей можетъ быть какимъ угодно количествомъ.
Если а и & имѣютъ противоположные знаки, напр. а>0 и &<0, то, оставивъ остальныя предположенія безъ измѣненія, найдемъ
х — 4- се.
Умноживъ обѣ части неравенства сЪг>Ъс' на —р количество положитель* аЪ'е , аЪ’ , . , л
ное, получимъ:----> — ас*, но , слѣд. — ас> — ас, или ас ' — а'с>0;
а потому и ^/ = 4- со.
Замѣтивъ, что а' и имѣютъ противоположные знаки, подставивъ вмѣсто х и у ихъ значенія, получимъ:
а . со — (—?/). 00 = с,’ а'. оо — (— &'). се — с\
или се — се“ с и се — се• = с', — тождества.
Второй случай. а = 0, 6 = О* И въ этомъ случаѣ: # = ео и */ —оэ; значенія эти приличествуютъ уравненіямъ. Въ самомъ дѣлѣ, подставляя, имѣемъ:
О . соч-0 . сс — с
«', сс -ь Ь'. = с\
Но произведеніе 0 . оо есть символъ неопредѣленности, сл. первое равенство можемъ разсматривать какъ тождество. Что касается второго, первая часть его есть разность двухъ безконечностей; ибо
откуда
гі/ — с«'
* = "О"’ а * = -о-’
а'х-Ь Ъ’у — а'Ь'с /д — дк
и равенство аЪ'с (сс — сх>) = с, есть тождество.
Съ другой стороны, очевидно, что всякая иная система значеній т и у не можетъ соотвѣтствовать ур—мъ:
О.ж-ьО.^ = с и а'#Ч“Ь'у =с\
Третій случай. а=0, а' = 0. Формулы ж и у принимаютъ видъ:
Итакъ, а? безконеченъ, а $ неопредѣлененъ. И въ самомъ дѣлѣ, очевидно, что никакая система конечныхъ значеній х и у не можетъ удовлетворять уравненіямъ
О . х -4- Ъу = е, 0 . а* -н Ъ'у = с',
с сг ибо ПО условію т о о
Съ другой стороны, если вмѣсто х подставимъ со, то какъ 0 . оэ изображаетъ количество неопредѣленное, усматриваемъ, что существуетъ безчисленное множество значеній у, удовлетворяющихъ.заразъ предыдущимъ уравненіямъ, въ которыхъ 0 . х замѣненъ количествами а и а, лишь бы произвольныя количества
, . . С — а с' — а'
а и і удовлетворяли [соотношенію: —•
Примѣчаніе I. Если кромѣ а~0 и —0 было бы и 6=0, у имѣло бы сг
опредѣленную величину ибо тогда слѣдовало бы положить а = с и а' = 0.
Примѣчаніе II. Въ разсмотрѣнныхъ трехъ случаяхъ, если уравненія вытекаютъ изъ условій задачи, нужно еще разсмотрѣть, можетъ ли быть истолковано чисто алгебраическое рѣшеніе уравненій; если да — это будетъ единственно возможное рѣшеніе задачи; если нѣтъ — задача нешз.чожиа; невозможность эта, во всякомъ случаѣ, будетъ зависѣть отъ несовмѣстности данныхъ между собою и съ неизвѣстными. Потому-то и говорятъ, какъ и по отношенію къ ур —мъ съ 1 неизвѣстнымъ, что символъ сх, есть признакъ невозможности задачи.
371. III. Знаменатель и оба числителя — нули.
аЬ1 — аЪ — 0, сб' — с'Ь — 0, ас' — а'е = 0.
Эти равенства могутъ имѣть мѣсто при слѣдующихъ обстоятельствахъ:
1) -, = р= с,; 2) а = 0, 6 = 0, с = С; 3) « = 0, а' = 0, сЬ' —Ьс' = О.
„ л а о с о . -
Первый случай. — _ — — Значенія іг и у берутъ видъ
О О
* = б’ У = б‘
Неопредѣленность эта — дѣйствительная. Въ самомъ дѣлѣ, назвавъ общую величину равныхъ отношеній буквою А*, т.-е. положивъ = р = р = имѣемъ
отсюда: а = а'&, Ъ = Ь,кі с = с'к; подставивъ въ первое ур., получимъ к
к(а’х + Ъ'у) = кс' или агг-ь&*у = с\
Такимъ образомъ, первое ур—ніе ничѣмъ не отличается отъ второго, такъ что въ сущности два неизвѣстныя связаны однимъ уравненіемъ, которое принимаетъ безчисленное множество рѣшеній: неопредѣленность дѣйствительная. Однако же, значенія х и у не вполнѣ произвольны, такъ какъ, въ силу того, что они связаны уравненіемъ ах -ь бу = с, произвольному значенію одного неизвѣстнаго соотвѣтствуетъ вполнѣ опредѣленное значеніе другого.
Примѣчаніе. Если бы было с—О, а потому и с'—О, а™ и у были бы неопре-дѣленны, какъ и прежде, съ тѣмъ отличіемъ, что отношеніе ихъ - сохраняло бы постоянную величину, равную —что прямо видно изъ уравненія <кгч-бу=0, къ которому въ этомъ случаѣ приводятся оба ур—нія.
Второй случай, а—0, 6=0, с=0, Въ этомъ случаѣ
О О
Х~ 0’ і,~о'
Но первое ур. обращается въ тождество 0=0, слѣд. система сводится къ одному ур—нію съ двумя неизвѣстными: неопредѣленность дѣйствительная.
Третій случай. д=0, «г=0, еЪ*—6с'=0. Оба неизвѣстныя опять принимаютъ неопредѣленный видъ а система
0 . х -н бу = с, 0 . .т -к б'у = с',
показываетъ, что х въ самомъ дѣлѣ неопредѣлененъ, но у — т.-е. имѣетъ
вполнѣ опредѣленную величину. Но это противорѣчіе между результатами, получаемыми изъ формулъ для неизвѣстныхъ, и результатами, непосредственно выводимыми изъ уравненій, только кажущееся; оно зависитъ отъ того, что дробь, дающая значеніе у:
ас'—еа' У__аЬг— бп'’
въ данномъ случаѣ содержитъ въ числителѣ и знаменателѣ общаго множителя, обращающагося въ нуль при данныхъ предположеніяхъ. Въ самомъ дѣлѣ, вынося за скобки: въ числителѣ с, а въ знаменателѣ б, имѣемъ
сг Ъг
но изъ условія сЬ' — с'Ь=О имѣемъ — = —; слѣд.
/аЪ' Л С -т-----
__ \ Ъ / с
У . /аЬ' А Ь
Ь -------а
Если бы сб'—бс'=О имѣли вслѣдствіе предположеній 6^0, б'=0, то нашли 0
бы: * = у=№; эти рѣшенія отвѣчали бы ур—мъ, ибо, какъ 0 . со есть сим-
волъ неопредѣленности, то равенства
0 н- 0 . сс — с и 0 ч- 0 . оо = с' суть тождества.
375. Примѣчаніе. Раскрытіе неопредѣленности дроби, принимающей видъ при частныхъ значеніяхъ нѣсколькихъ буквъ, въ нее входящихъ, можно дѣлать д
еще слѣдующимъ пріемомъ. Если дробь въ составъ которой входятъ коли-
чества я?,#, е, . . . принимаетъ видъ при х=а, у—Ь^ . .то, положивъ
а? = ан-Л, у = Ъ-+-р!і, г — с-і-дк,. . .
подставляютъ эти величины въ числит. и знай, и, сокративъ дробь, полагаютъ
А=0: тогда и получится истинное значеніе дроби при а^=а, .
Оно можетъ быть или опредѣленно или неопредѣленно, см. по тому, будетъ ли независимо отъ р, 3, • - . или же, послѣ всевозможныхъ упрощеній, будетъ еще содержатъ одно или нѣсколько изъ этихъ количествъ, располагая которыми произвольно, можно дать дроби какую угодно величину.
Такъ, мы видимъ, что при а—0, а'^0 и с6г—6^=0, дроби
сіУ — Ъс' _____ас'—еа/
аіУ—Ъа* И $ иіУ—Ъа*
0 гт принимаютъ видъ -• Полагаемъ
а = Л аг =р/і^ с' = -г-о
находимъ
ЫУд
сл. х дѣйствительно неопредѣлененъ, потому что, выбирая извѣстнымъ образомъ р и д, можно ему давать произвольныя значенія.
Для у находимъ
ЛЛ'—
сокративъ на Л, а потомъ положивъ Л—0:
Ь(Ь1 — Ър) Ъ
— величину вполнѣ опредѣленную.
376, Сдѣланное изслѣдованіе можно резюмировать такъ: скст&иа двухъ уравненій первой степени съ двумя неизвѣстными имѣетъ одно рѣшеніе конечное пли безконечное, если из?> треоъ бино.иоеа
аЬ'— Ъа\ сЬ'— Ъс\ ас' — са'
обращается въ нуль не болѣе одною; рѣшеніе неопредѣленно, если два гізъ низъ дѣлаются нулями, за исключеніемъ случая, когда: с=0, с'=0.
Приводимъ нѣсколько задачъ съ полнымъ изслѣдованіемъ;
Первый примѣръ изслѣдованія.
377. Два курьера ѣдутъ равномѣрно и въ одну сторону, отъ І<" къ И, но прямой ху, со скоростями ѵ и ѵ'; еа данный льхмеюна одинъ находится въ А, другой въ А', въ разстояніяхъ ОА=й « ОА'^бГ отъ точки 0. Сюртоелеп/ая: въ какомъ разстояніи отъ точки 0 и черезъ сколько часовъ отъ даннаго момента произойдетъ встрѣча?
(Г к о _к---—4-
г
А’ Ч--
Черт, 31.
Пусть встрѣча произойдетъ въ будущемъ, т.-е, вправо отъ А' на разстояніи отъ 0, равномъ ОЕ— аг, и черезъ і часовъ отъ даннаго момента. Уравненія задачи будутъ слѣдующія: 0Е=0Ач-АК, ОК=ОАг-ьА'К или
я*=сі-нгіі I
х—(і'+ѵЧ I
Если допустить, что встрѣча имѣетъ мѣсто между О и А, въ нѣкоторой точкѣ В/, т.-е, вправо отъ О, но до того момента, когда курьеры проѣзжаютъ— одинъ черезъ А, другой черезъ А\ то уравненія, при сохраненіи прежнихъ обозначеній, будутъ: 0К'=0А —Е'А, ОЕ'=ОА'—Е'А', или
а?—еі—ѵі I х~<І’— ѵгі /
(2)-
Такъ какъ эта система отличается отъ первой знакомъ при і, то заключаемъ обратно, что если система (1) дастъ положительное рѣшеніе для х и отрицатель-* ноѳ для /, это служитъ признакомъ того, что встрѣча имѣла мѣсто вправо отъ 0, но раньше даннаго момента, и что время, протекшее отъ встрѣчи до этого момента равно абсолютной величинѣ отрицательнаго рѣшенія.
Наконецъ положимъ, что встрѣча имѣла мѣсто въ точкѣ Е", влѣво отъ точки О; уравненія, при сохраненіи прежнихъ обозначеній, будутъ: Е"О=В"А—-ОА, В"О=Е"А' — ОА\ или х—ѵі—я?=ѵ'е—4', пли
— ті 1
-х=(і'-ѵ'І ) 1 Ь
Эта система выводится изъ (1) перемѣною ж и і на — # и —Слѣдовательно, обратно, если система (1) даетъ отрицательныя значенія для г и /, это будетъ признакомъ того, что встрѣча имѣла мѣсто влѣво отъ О, въ разстояніи, равномъ абсолютной величинѣ х, и что время, протекшее отъ момента встрѣчи, равно абсолютной величинѣ С
378. Изслѣдованіе. Послѣ этого предварительнаго изслѣдованія рѣ*
таемъ систему (1): _ѵЗг—Зуг — (і Я* V — г' 7 V — V* 3
Дѣлаемъ всевозможныя предположенія относительно общаго знаменателя; эти предположенія суть:
ѵ<ѵ'.
При этомъ, такъ какъ числители могутъ получать какія угодно величины, разложимъ каждый изъ предыдущихъ случаевъ на три другіе случая:
Отсюда уже вытекаютъ опредѣленныя предположенія относительно другого числителя:
Въ самомъ дѣлѣ, если: при возьмемъ то отсюда необходимо вытекаетъ, что но не можетъ быть: ни ѵгі'—і/гі, ни Но если
при взять то другой числитель даетъ три возможныя предположенія
Ыг=
Поступая такимъ образомъ, получаемъ комбинацій, въ числѣ тринадцати:
слѣдующую таблицу всевозможныхъ
ѵЗ'>Зи'
Г €<?>(&'
1'3'=3ѵ'
I гЗ'<Зѵ*
ѵЗ’>Зѵ’ ѵЗ'=Зѵ' ѵЗ'<^Зѵ'
ѵЗг>Зѵ' ѵЗ'=Зі;' ѵЗ[<Зѵ'
гЗг<^Зѵ'
ѵЗг<СЗѵ' г
Изслѣдуемъ поочередно каждый изъ этихъ случаевъ.
Первый случай.
Формулы для неизвѣстныхъ даютъ конечныя, опредѣленныя и положительныя значенія для х и означающія, что встрѣча будетъ имѣть мѣсто въ будущемъ (считая отъ даннаго момента) и, слѣд., вправо отъ точки О и отъ А\
Этотъ результатъ можно было предвидѣть: въ самомъ дѣлѣ, такъ какъ ѵ>іА т.-е. догоняющій курьеръ ѣдетъ скорѣе передняго, слѣд. долженъ необходимо встрѣтиться съ нимъ вправо отъ А\
Второй случай^ 3'=3, ьчГ>ЛА
Формулы даютъ
Это значить, что встрѣча имѣетъ мѣсто въ данный моментъ, что совершенно очевидно* Въ самомъ дѣдѣ, при (і—сГ оба курьера въ разсматриваемый моментъ находятся въ одной точкѣ (напр. А), а какъ ѵ>г/, т.-е. скорости ихъ неравны, то они только въ этотъ моментъ и будутъ вмѣстѣ, а затѣмъ одинъ будетъ постоянно впереди другого.
Третій случай.
Формулы даютъ:
®>0, і<0.
Положительное значеніе а? показываетъ, что встрѣча имѣетъ мѣсто вправо отъ 0; отрицательное і означаетъ, что она произошла раньше того момента, когда одинъ курьеръ проѣзжаетъ черезъ А, другой черезъ А', въ нѣкоторой точкѣ К' (подставивъ въ систему (1) вмѣсто і. . . — находимъ систему (2), относящуюся къ точкѣ К').
Это можно видѣть изъ условій, при помощи чертежа:
Такъ какъ то курьеръ, ѣдущій со скоростью находится въ данный моментъ ближе другого къ точкѣ 0; сл, курьеръ, ѣдущій со скоростью ѵ, долженъ былъ встрѣтить другого раньше даннаго момента, т.-е. влѣво отъ точки А'; затѣмъ, неравенство даетъ
сГ ѵ'
а
V
а это значитъ, что курьеръ (г?') ѣдетъ верстъ большее время, чѣмъ курьеръ (у) проѣзжаетъ сі верстъ; значитъ послѣдній проѣхалъ черезъ точку О послѣ перваго, и какъ въ данный моментъ онъ обогналъ перваго, то и долженъ былъ встрѣтить его вправо отъ точки 0.
Четвертый случай. ѵ>-ѵг,
Формулы даютъ: 2<0.
Эти рѣшенія означаютъ, что встрѣча имѣла мѣсто въ точкѣ О раньше разсматриваемаго момента. И въ самомъ дѣлѣ, равенство ѵсІг=<1ѵг даетъ
т.-е. времена, употребленныя на прохожденіе разстояній ОА' и О А, равны (предыд* черт.), слѣд. оба курьера прошли черезъ точку О въ одинъ и тотъ же моментъ.
Пятый случай.
Формулы даютъ: ж<0, $<0.
Рѣшенія эти означаютъ, что встрѣча имѣла мѣсто раньше даннаго момента и влѣво отъ точки 0 (см. систему (3) уравненій).
Въ самомъ дѣлѣ, такъ какъ курьеръ, находящійся впереди, въ А, двигается съ большею скоростью (и >я'), — то встрѣча уже имѣла мѣсто. Затѣмъ, изъ неравенства имѣемъ: —а это значитъ, что курьеръ, ѣдущій
•ѵ ѵ
скорѣе, прошелъ черезъ точку О раньше другого, слѣд. встрѣча его съ другимъ уже была влѣво отъ точки О.
Шестой случай. ѵ—ѵ\
Формулы даютъ: /—х>.
Эти рѣшенія служатъ признакомъ дѣйствительной невозможности. Въ самомъ дѣлѣ, въ данный моментъ курьеры находятся въ различныхъ точкахъ, скорости же ихъ движенія равны, слѣд. разстояніе между нпмн всегда будетъ одинаково, и потому они не могутъ встрѣтиться.
ОеЭьлош случай. (Г—сІу ѵй'==$’<%.
Формулы даютъ: # = 0, — о:
неопредѣленность дѣйствительная; въ чемъ не трудно убѣдиться и изъ самыхъ условій. Въ самомъ дѣлѣ, въ данный моментъ курьеры находятся вмѣстѣ ѣдутъ они съ одинаковою скоростью (ѵ—у')» с-іѣд. постоянно они будутъ находиться вмѣстѣ.
Восьмой случай. ѵ=ѵ\
Формулы даютъ: х=со, і=эо, что объясняется такимъ же точно образомъ, какъ и въ случаѣ шестомъ.
Девятый случай.
Формулы даютъ: я?<0, ^<0. <
Рѣшенія эти означаютъ, что встрѣча уже имѣла мѣсто влѣво отъ 0 (черт. 33).
Черт. 33.
Въ этомъ убѣждаемся разсужденіями, аналогичными приведеннымъ въ пя-
томъ случаѣ.
Деежжим случай. ѵа!'=Лс'.
Формулы даютъ: #=0, /<0.
Это значитъ, что встрѣча имѣла мѣсто въ точкѣ О; въ чемъ убѣждаемся такимъ же образомъ, какъ и въ четвертомъ случаѣ.
Одиннадцатый случай. ѵ<ѵ\ Ѵ(Г<Діѵ\
Формулы даютъ: я>0, ^<0.
Встрѣча имѣла мѣсто вправо отъ точки О, но раньше настоящаго момента. Объясненіе то же самое, что для третьяго случая.
Двѣнадцатый случай.
Формулы даютъ: х—(і=(Іг; і—о.
Встрѣча имѣла мѣсто въ настоящій моментъ. Какъ и во второмъ случаѣ.
Тринадцатый случай. г?<ѵ\
Формулы даютъ величины конечныя, опредѣленныя и положительныя; слѣд. встрѣча имѣетъ мѣсто въ будущемъ. Какъ въ первомъ случаѣ.
379. Примѣчаніе. Уравненія
і А
х — Л' •+- ѵ'і I ' '
были выведены въ томъ предположеніи, что оба курьера ѣдутъ въ одну сторону, именно въ направленіи отъ х къ у. Легко видѣть, что эти же уравненія могутъ служить и для другихъ задачъ, аналогичныхъ первой, если только условиться подъ ѵ и ѵ' разумѣть отрицательныя количества, если направленіе движенія будетъ отъ у къ я*, а подъ сі и & отрицательныя числа, если линіи О А и О А' будутъ находиться влѣво отъ О.
Такъ напр., если1 курьеры ѣдутъ но направленію отъ т/ къ л?, и при составленіи уравненіи мы допустимъ, что точка встрѣчи К лежитъ вправо отъ О, то уравненія будутъ
х=а’-ѵ'і ( { '
Очевидно, что ту же задачу можно выразить и уравненіями (А), если только подъ буквами с и ѵ' въ системѣ (А) разумѣть отрицательныя числа.
О
н
-+-
Черт. 34.
Если бы курьеръ, выѣзжающій изъ А, ѣхалъ въ направленіи ат/, а выѣзжающій изъ А'—въ направленіи мы имѣли бы систему
х=<г-ьѵ/ | Х=Л'-ѵЧ I (С)‘
I
Вмѣсто нея мы могли бы взять также систему (Л), разумѣя въ ней подъ ѵ'— количество отрицательное.
Точки А и А', въ которыхъ находились курьеры въ настоящій моментъ, помѣщались вправо отъ точки 0; задача будетъ еще общѣе, если дать этимъ точкамъ какія угодно положенія на линіи ху, считая & и гГ положительными, когда эти точки расположены вправо отъ О, и отрицательными, если точки А и А' находятся влѣво отъ 0.
Такимъ образомъ, разумѣя подъ и сі' абсолютныя количества, для чертежа (35) найдемъ уравненія
} (О)-
А для чертежа (36) уравненія
♦
л' л о -і--------1----------------1----
Черт. 36.
7?
—+
х——а + ѵі ) х=-а' + ѵ'і / (Е)і
Очевидно, что система (А) можетъ замѣнить собою каждую изъ системъ (О) и (Е). если только въ первомъ случаѣ будемъ разумѣть въ системѣ (А) подъ а число отрицательное, а во второмъ—условимся подъ й и іі* разумѣть отрицательныя числа.
Итакъ, уравненія
X — (I 4-
X = еГ -+-
пмѣіція рѣшеніями:
—<2*/ __с?' —
я х ѵ — ѵг ’ і; — ю' ’
служатъ выраженіемъ слѣдующей совершенно общей задачи:
Два курьера ѣдутъ равномѣрно но прямой со скоростями, равными, по величинѣ и по знаку, количествамъ ѵ и я'; въ настоящій моментъ они находятся отъ точки О, лежащей на этой прямой, въ разстояніяхъ, изображаемыхъ, по величинѣ и по знаку, буквами и Найти разстояніе точки 0 до точки встрѣчи, и время встрѣчи*
При этомъ, разстоянія считаются положительными — вправо отъ О, отрицательными — влѣво отъ О; скорости — положительными въ направленіи отрицательными въ направленіи да; времена — положительными, когда они слѣдуютъ за даннымъ моментомъ, отрицательными — когда предшествуютъ этому моменту*
Числовой примѣръ. Два курьера, ѣдущіе равномѣрно по прямой, находятся въ настоящій моментъ: одинъ въ точкѣ А, отстоящей отъ 0 влѣво на 20 верстъ, другой въ А'—въ разстояніи, равномъ 35 верстамъ, вправо отъ О. Они движутся навстрѣчу другъ другу, первый со скоростью 4, а второй 6 верстъ въ чадя». Опредѣлить разстояніе точки встрѣчи отъ О и время встрѣчи.
Для рѣшенія задачи нужно только въ формулы
ічі(—, (іг — б х =------------------у
ѵ — іг ѵ — V
подставить: вмѣсто сі число — 20, вмѣсто число ч- 33; затѣмъ: н-4 вмѣсто с — 6 вмѣсто Найдемъ:
.г=2 вер.; /—4 час. 30 мин.
Слѣд. кяка мтрѣчм находятся вправо отъ О на 2 версты, а время встрѣчи черезъ 4 час- 30 яжи_ отъ настоящаго момента.
Второй примѣръ изслѣдованія.
380. Ял двдаз етмавт серебра, пробы хонюрыаъ рааяы соототьтсягееамо а ѵ 6, составитъ р фунтовъ новаго сплава пробы с. Сколько яужяо
опта каждаго сплава?
Пусть отъ перваго сплава нужно взять х, отъ втораго у фунтовъ. Но условію, имѣемъ уравненіе
«+?/=р- .(О-
Въ одномъ фунтѣ перваго сплава находится а золотниковъ чистаго серебра, слѣд. въ х фунтахъ его будетъ эох; въ у фунтахъ второго сплава Ьу зол.; слѣд. въ яч-у или въ р фунтахъ новаго сплава содержится зол., а въ
. ах 4- Ьу ,
одномъ фунтѣ —2—— зол* чистаго серебра, что равно с; поэтому второе ур.
будетъ
агЧ-бу —ср. . .(2).
Рѣшивъ уравненія (1) и (2), найдемъ №
с — Ь а — с
х—------1 * р, у=----— . р,
і а — Ъ * у а — Ь *
Изслѣдованіе. По свойству вопроса, а? и у не могутъ быть ни безконеч-інп, п отрицательными, поэтому рѣшенія такого рода будутъ служить призна-вмо абсолютной невозможности задачи при тѣхъ условіяхъ, которыя ведутъ къ
рѣшеніямъ этого рода. Въ этомъ и заключается особенность разсматриваемой задачи; изъ всѣхъ значеній а? и у, какія допускаютъ найденныя формулы для этихъ количествъ, слѣдуетъ удерживать только значенія конечныя, опредѣленныя и положительныя.
Относительно общаго знаменателя возможны 3 предположенія:
а >6, а = «
Каждое изъ этихъ предположеній соединяемъ со всевозможными предположеніями касательно одного изъ числителей, напр., перваго:
с>6, с = Ь,
Относительно второго числителя нужно дѣлать такія предположенія, которыя были бы совмѣстны съ прежде взятыми. Такъ, еслп возьмемъ предположеніе а > Ъ и с > 6, то его можно сочетать съ каждымъ изъ трехъ возможныхъ предположеній относительно другого числителя: л < с. Но если взять
комбинацію « = 6 и то ее можно соединить только съ предположеніемъ а<с, такъ какъ с, будучи больше 6, не можетъ быть ни равно, ни меньше количества а, равнаго 6. Такимъ путемъ мы получаемъ слѣдующую таблицу изслѣдованія:
Первый случай. с>Ъ, а > с.
Формулы даютъ для х и у рѣшенія конечныя, опредѣленныя и положительныя; слѣд. задача возможна. Это слѣдуетъ и изъ условій: въ самомъ дѣлѣ, проба с искомаго сплава, по условію, больше низшей пробы 6, по меньше высшей пробы а; очевидно, такой сплавъ всегда можно составить.
Второй случай, а > 6, с > Ъ, а — с.
Формулы даютъ: у — 0.
Это значитъ, что вегѣ р фунтовъ должны быть взяты отъ сплава пробы а, и ничего не нужно брать отъ сплава пробы 6. Это очевидно а ргіогі, ибо проба с составляемаго сплава должна равняться, по условію, пробѣ а.
Третій случай. а^Ъ* с > Ь, а<с.
Формулы даютъ: х > 0, у < 0.
Заключаемъ, что задача невозможна. Это видно й ргіогі: въ* самомъ дѣлѣ, проба требуемаго сплава должна быть больше не только низшей пробы 6, но и высшей а данныхъ сплавовъ; очевидно, что сплавляя послѣдніе, нельзя получить пробы с.
Четвертый случай. а^>Ъ9 с — Ь, а > с.
Формулы даютъ: ^ = 0, у — р.
Это значить» что всѣр фунтовъ должны быть взяты отъ сплава пробы Ъ, что очевидно, ибо искомый сплавъ и долженъ имѣть пробу Ь (условіе с = б).
Пятый случай, а > с < 7>, а > с.
Формулы даютъ: т<0, $>0.
Отрицательное значеніе ,т указываетъ па невозможность задачи. II въ самомъ дѣлѣ, .задача невозможна, потому что проба искомаго сплава должна быть меньше не только л, но и низшей пробы Ь одного изъ данныхъ сплавовъ.
Шестой случай, а — 6, с > 6, а < с.
Формулы даютъ: /у — со.
Задача невозможна; п въ самомъ дѣлѣ, составляющіе сплавы — одинаковой пробы (а = 6), проба же требуемаго сплава с должна быть больше пробы а = 6, что невозможно.
Седьмой случай. а = 1) — с.
Яг 0 0
Формулы даютъ: .г—^ = 0-
Это значитъ, что задача неопредѣленна, въ томъ смыслѣ, что можно взять число фунтовъ, не превышающее отъ одного изъ данныхъ сплавовъ, а недостающую до р часть изъ другого. Результатъ этотъ очевиденъ а ргіогі, по-тому что всѣ три сплава—одинаковой пробы.
Восьмой случай, а = Ь, с < Ь, а > с.
Формулы даютъ: х — у =
Задача невозможна, какъ и въ шестомъ случаѣ.
Девятый случай, а с > 6, а < с.
Формулы даютъ: й*<0, ?/>0; отрицательное значеніе а? указываетъ на невозможность задачи, подобно пятому случаю.
Десятый случай, а < б, с —6, л < с.
Формулы даютъ: о? = О, у =р, какъ въ четвертомъ случаѣ.
Одиннадцатый случай, а <6, с < б, а > с.
Формулы даютъ: #>0, #<0; задача невозможна, какъ и въ третьемъ случаѣ, . .
Двѣнадцатый случай, а с а = с.
Формулы даютъ: !/ —0* какъ и во второмъ случаѣ.
Тринадцатый случай. а<^Ъ, с < б, а < с.
Формулы даютъ: для х и у величины конечныя, опредѣленныя и иоложитель-Задача, слѣд., возможна, какъ въ первомъ случаѣ.
Третій примѣръ изслѣдованія.
381. 2?ъ АВС, котораго основаніе равно Ь, а высота 7і, впи*
- прямоугольникъ даннаго периметра 2^.
Птяоугольникъ называется вписаннымъ въ треугольникѣ, когда двѣ его находятся на одной сторонѣ треугольника, а двѣ другія вершины на л ’зутихъ сторонахъ; таковъ прямоугольникъ ІІЕЕО. Если же эти двѣ по-і^;чижны находятся не на самыхъ сторонахъ, а на ихъ продолженіяхъ, •умдьникъ называютъ внѣ-вписаннимъ; таковы прямоугольники й'Е'Е'О' П * X * .
вписанный прямоугольникъ.
ЗІ2 г тъ задача рѣшена и ЭЕЕ6 есть требуемый прямоугольникъ; озна
чимъ сторону ПЕ буквою х, сторону ЕЕ буквою ?/, основаніе АС буквою д» высоту ВП треугольника буквою Л. Во-первыхъ имѣемъ ур—ніе
Въ подобныхъ треугольникахъ АВС и ВІ)Е основанія относятся какъ высоты, слѣдовательно
или
БЕ__ ВТ
Аѓ²Г
х к — у Ь~~к
Рѣшая ур—нія (1) и (2), находимъ
х-~к=іГ
церт 37 Изслѣдованіе. Во-
первыхъ замѣтимъ, что х и ?/ не могутъ быть одновременно отрицательными, потому что сумма ихъ, въ силу ур—нія (1), равна положительному количеству но одно изъ этихъ количествъ можетъ быть отри-
цательнымъ; причемъ отрицательныя значенія ж или «/, въ данномъ случаѣ, не могутъ быть отбрасываемы, какъ невозможныя, но подлежать истолкованію слѣдующимъ образомъ.
Если для у получается отрицательное рѣшеніе, и слѣд. для х положительное, то для истолкованія этого отрицательнаго рѣшенія перемѣнимъ въ уравненіяхъ (1) и (2) у на — у\ найдемъ:
х Ѣ-+-У < \
а? — ъ=~1і '
Первое изъ этихъ уравненій означаетъ, что дается не сумма сторонъ прямоугольника, а разность между его основаніемъ и высотой. Второе уравненіе отвѣчаетъ прямоугольнику ІУЕТ'б', котораго основаніе В'Е' находится подъ основаніемъ АС треугольника; въ самомъ дѣлѣ, назвавъ ІЭ'Е' буквою а? и ЕТ' буквою у* изъ подобія треугольниковъ І)ВЕ' и АВС прямо находимъ ур—ніе (т). Впрочемъ, непосредственно видно, что высота ГН этого прямоугольника имѣетъ, по отношенію къ АС, положеніе противоположное, высотѣ 1Н перваго прямоугольника. Итакъ, отрицательное значеніе для у соотвѣтствуетъ слѣдующему видоизмѣненію даннаго вопроса: построить внѣ-вписанныгі прямоугольникъ, котораго двѣ вершины находились бы на продолженіяхъ сторонъ ВА « ВС треугольника подъ ею основаніемъ, если извѣстна разность между основаніемъ и аы-сотою прямоугольника.
Рѣшеніе, соотвѣтствующее этому новому условію, будемъ называть рѣшеніемъ второго рода, называя рѣшеніе въ точномъ смыслѣ даннаго вопроса рѣшеніемъ ясреаій рода.
Если отрицательное рѣшеніе получится для я, то для истолкованія его перемѣнимъ въ уравненіяхъ (1) и (2) а? на —т; найдемъ:
- х к — у х у — к 1Г~^к ПЛИ Ъ~ к
Первое изъ этихъ уравненій означаетъ, что дается разность между высотою и основаніемъ искомаго прямоугольника. Второе ур—ніе отвѣчаетъ прямоугольнику 1)"Е"Р"О"І котораго основаніе Е"1)" находится надъ вершиною В треугольника; въ самомъ дѣлѣ, сохранивъ прежнія обозначенія, изъ подобія треугольниковъ 1)"ВЕ" и АВС тотчасъ находимъ уравненіе (и). Впрочемъ, къ такому истолкованію отрицательнаго значенія х можно придти еще такимъ образомъ: проектируя сторону Е'Т)" на линію основанія тр—ка посредствомъ прямой ЕѴ', параллельной АВ, замѣчаемъ, что отрѣзокъ Ае" имѣетъ положеніе отрицательныхъ аъовъ (положительные я>сы СЕ к проектированные подобнымъ же образомъ на АС, займутъ положеніе вправо отъ точки А). Итакъ, всякій разъ, когда будетъ получаться для ж отрицательное значеніе, мы его будемъ истолковывать какъ рѣшеніе слѣдующаго вопроса: построить оннгвнншнный прямоугольникъ, котораго высота превышала бы основаніе на р, и двѣ вершины котораго лежали бы на продолженіяхъ сторонъ АВ СВ за вершину треугольника. Назовемъ это рѣшеніе рѣшеніемъ третьяго рода.
Послѣ этого подготовительнаго изслѣдованія, составляемъ таблицу всевозможныхъ случаевъ, какіе могутъ представить формулы х и у. Во-первыхъ, относительно общаго знаменателя этихъ формулъ можно сдѣлать три предположенія: к > 6, к<^Ьч к = Ъ. Каждое изъ этихъ предположеніи можно комбинировать съ каждымъ изъ трехъ предположеній относительно числителя формулы я?:
Л>Р» к=р, к<р.
Такимъ образомъ составится 9 комбинацій. Относительно второго числителя придется дѣлать такія предположенія, которыя не находились бы въ противорѣчіи съ вышеуказанными. Такъ, взявъ 7*>Ь и 7і>р, можемъ это предположеніе комбинировать съ каждымъ изъ слѣдующихъ трехъ: р > А, р=^Ь, р < 6; а взявъ комбинацію Л = 7>, А—р, можемъ относительно второго числителя положить только р = А, Поступая такимъ образомъ, имѣемъ слѣдующую таблицу изслѣдованія:
[А>р, к—Ъ / к=р , р—Ь
| Л<р , р>7л
Первый случай. к> I), Л >р > 7;.
Въ этомъ случаѣ: к — Ь > 0, к —р > 0 и р — Ь > 0; а слѣд.
х > 0 и у > 0.
По чтобы эти алгебраическія положительныя рѣшенія дали внутренній вписанный прямоугольникъ, надо еще, чтобы было а? < Ъ, у <^к. Въ данномъ случаѣ х * - Л —Р р—б
такъ и есть, ибо каждая изъ дробей у—г и 5 —. меньше 1. Л — О А — о
Такимъ образомъ, при данныхъ условіяхъ имѣемъ рѣшеніе перваго рода.
Второй случай. к^>Ъ, к^р, р = Ъ.
Здѣсь имѣемъ: Л — А > О, 7; — р > О, р — Ъ = 0; слѣд, я* = Ь, г/ —О;
т>е. прямоугольникъ сливается съ линіей ЛС, обращается въ прямую
Третій случай. к > Ь, А > р <6,
Въ этомъ случаѣ: А — 6 > О, к — р > О, р — А < О; слѣд, я* > О (и > Ь), р<0;
*
это рѣшеніе', какъ уже знаемъ, даетъ нішмоугольнпкъ яторам р<х)а,
Четвертый случай. р = А > А,
Здѣсь имѣемъ: к — 6 > 0, к—р = 0, р — 6 > 0; слѣд.
а<=0, у = А,
и прямоугольникъ обращается въ прямую ВН.
Пятый случай, р >дА > А,
Это условіе даетъ: к — р < О, 7г — Ь > 0, р — Ь > 0; а потому
х < 0, у > О
1 Г- X Р-----
А, ибо Дробь д——
Получаемъ рѣшеніе шриньяіо рода, т.*е. прямоугольникъ 0”Е"Р"6", въ которомъ разность между линіями Е'Т" и Е"О" равна р.
Шестой случай, р <к<Ъ.
Въ такомъ случаѣ: к — к < 0, к — р > 0, р —6 < 0; а потому
' #<0, ?/>0 (и больше А).
Имѣемъ, какъ и въ пятомъ случаѣ, рѣшеніе жрежаяіо рода.
Седьмой случай. р = к<^Ъ.
Въ этомъ случаѣ: к — б<0, к—р = О, р — А<0; слѣд.
^ = 0, Р = А;
прямоугольникъ сливается съ высотою треугольника.
Восьмой случай. р^>Ъ^>к.
Въ этомъ случаѣ: к — Ь < О, А — р < 0, р — Ъ > 0.
х > 0 (и больше 6), # < 0: получаемъ рѣшеніе отпорно ро<Эл, какъ въ третьемъ случаѣ. Девятый случай, к <р^Ъ.
Здѣсь имѣемъ: к — Ъ < 0, к —р < 0, р — Ъ — 0; а потому
я? = А, у — 0:
Прямоугольникъ сливается съ основаніемъ треугольника.
Десятый случай, к <ір<ІЪ.
Въ этомъ случаѣ: к — А < О, Л — р < 0, р — Ъ < 0; а потому
х > 0 и у > 0, при чемъ х < 7», а у < к:
имѣемъ рѣшеніе перваго рода, какъ въ первомъ случаѣ,
- 377 —
1
Г
_ Одиннадцатый случай. р < Ъ — Л. Находимъ:
г
Эти рѣшенія означаютъ невозможность задачи. Въ самомъ дѣлѣ, положивъ въ уравненіи (2) имѣемъ: .т = Л — г/, откуда а*ч-у — Л, т.-е. когда въ треугольникѣ основаніе равно высотѣ, полупериметръ впнсан. нрям—ка долженъ равняться высотѣ; слѣд. какъ скоро р не равно Л-, задача невозможна.
Двѣнадцатый случай. к = Ь=р. Въ этомъ случаѣ:
к — Ь — Л — р =р — 6 = 0, слѣд.
О О а, = б’ *=о
Эта неопредѣленность дѣйствительная; въ самомъ дѣлѣ, тотчасъ мы видѣли, что при 6—Л полу пери метръ всякаго вписаннаго прямоугольника долженъ равняться Л; слѣд. если будетъ дано, какъ и есть въ данномъ случаѣ, р=А, всякій вписанный прямоугольникъ будетъ требуемый, и задача имѣетъ безчисленное множество рѣшеній.
Тринадцатый случай. р^к^=Ъ. Въ этомъ случаѣ
х—'хэ, у—
задача невозможна, какъ въ одиннадцатомъ случаѣ.
Примѣчаніе I. Изслѣдованіе показало намъ, что рѣшеніе перваго рода получается въ томъ случаѣ, когда полу пери метръ искомаго прямоугольника заключается между основаніемъ и высотою треугольника, т.-е. прп Л>6 если имѣемъ: 6>р>6 ^первый случай), а при А <6, если дано, что Л<р<6 (десятый случай). Эти условія можно найти и геометрически. Проведя 1)К параллельно ВС, найдемъ КС=ІЭЕ, и слѣд.
р=ОЕ ч-1)6=СК-ь Б6.
По вслѣдствіе подобія треугольниковъ АВС .и АЭК, необходимо имѣемъ
при Л>6 и 1)6 >АК, а потому р>СК-И АК илир>6; а при к <6 и В6<АК, а потому р<СКч-ЛК или р<6.
Съ другой стороны
р=ВОЧг-ВЕ=НІч—ОЕ*
Но изъ подобія треугольниковъ ВВЕ и ВАС необходимо имѣемъ
при к >6 и ВІ>ВЕ, а слѣд. р<Шч-ВІ или р<Л; а при к<6 и В1<БЕ, а слѣд. р>Шч-В1 или р>Л.
Итакъ, для того чтобы рѣшеніе перваго рода имѣло мѣсто, необходимо и достаточно, чтобы полу периметръ прямоугольника заключался между основаніемъ и высотою даннаго треугольника.
Примѣчаніе II* Когда р мало отличается отъ к, получается прямоугольникъ весьма растянутый въ направленіи высоты ВН; напротивъ того, если р близко къ 6, прямоугольникъ получается сплюснутый; а измѣняя непрерывно р между этими предѣлами, получимъ всѣ промежуточныя формы: слѣд. можетъ получиться, между прочимъ, и кепгірлть; и для этого необходимо, чтобы было
а?=?у, илн ЦЛ—р)=Л(р—6), откуда
2Ьк
^~6-+-Л*
Въ такомъ случаѣ, имѣя въ виду уравненіе .т4-ѵ=р, получимъ
Ьк
Построеніе. Легко построить найденныя величины для я? и у; построимъ, напр., у въ случаѣ: Л<_р<Ь. Изъ формумы У=—с^?~ имѣемъ пропорцію:
Черт. 37.
Внѣ-вписанный прямоугольникъ.
(6—к): (6—р)=к :у\ такимъ образомъ, слѣдуетъ построить четвертую пропорціональную къ тремъ линіямъ: Ь—к, Ь—р и к. Нанеся на АС отрѣзки АМ=Л, АЬ=р, имѣемъ
6— Л=СМ, 6—р=СЬ
Изъ точки С возставляемъ перпендикуляръ СХ къ АС, равный Л, соединяемъ М съ X и проводимъ ЬО параллельно МХ; легко видѣть, что ОС~#. Проведя изъ О линію ОЕ) параллельно АС, получимъ верхнее основаніе І)Е прямоугольника, а опустивъ перпендикуляры ІЯ? и ЕС, и самый прямоугольникъ.
383. I. Когда вершины I) и Е прямоугольника находятся подъ основаніемъ треугольника, имѣемъ прямоугольникъ ІУЕ'Е'6'. Пусть требуется построить такой прямоугольникъ по данному периметру 2р. Называя сторону І)'Е' буквою д? и Е'Е' буквою у, имѣемъ уравненія:
-ь=-^ •••(*) откуда
Изслѣдованіе. Такъ какъ знаменатель въ этихъ формулахъ не можетъ быть нулемъ, то х и у не могутъ быть ни безконечными, ни неопредѣленными; кромѣ того, х всегда положителенъ, а у можетъ быть или положительнымъ, или отрицательнымъ, или нулемъ, что зависитъ отъ знака разности р—Ъ. Итакъ:
1. р>6. Въ этомъ случаѣ: а?>0 и р>0; и кромѣ того, такъ какъ дробь то Итакъ, въ данномъ случаѣ существуетъ внѣ-вписанный прямоугольникъ съ даннымъ периметромъ 2р, имѣющій такое положеніе какъ Б'ЕТ'О'.
2. р=6. Въ этомъ случаѣ: а?=Ь,-у=О, и разсматриваемый прямоугольникъ сливается съ основаніемъ треугольника.
3. р<6. Въ этомъ случаѣ &>0, но <6; у<0.
Вставляя въ уравненія (4) —у вмѣсто уі получаемъ
я—3/=Р,
х_к—у
Ъ~~7Г'
Легко видѣть, что эти уравненія соотвѣтствуютъ вписанному прямоугольнику ОЕЕО, въ которомъ разность между основаніемъ и высотой равна р.
Примѣчаніе. Чтобы въ разсматриваемомъ случаѣ прямоугольникъ былъ квадратомъ, надо, чтобы было а*=у, или б(р4-Л)=Л(р—6), откуда
2Ьк _ Ьк
и слѣд-
Такъ какъ р—величина положительная, то к не можетъ быть <6; такимъ образомъ нельзя получить внѣ-вписапнаго квадрата водъ основаніемъ треугольника, если 6>А.
Построеніе. Сдѣлаемъ построеніе для случая р>А. Изъ пропорціи (&Ч-Л):(р — Ъ)—к:у
видно, что построеніе у сводится къ нахожденію четвертой пропорціональной къ тремъ даннымъ линіямъ А, р—6 и Л; для чего беремъ ВМ=Л-, ВЬ~р, и слѣдов.
и СЬ=уз—&.
Соединяемъ М съ М и изъ Ь проводимъ линію ЬО, параллельную МК: точка
Черт. 38.
О опредѣляетъ сторону Б'Е' искомаго прямоугольника, а вмѣстѣ съ гЬмъ и самый прямоугольникъ.
384. П. Когда вершины внѣ-вписаннаго прямоугольника находятся на продолженіяхъ сторонъ ВА и ВС за вершину В, имѣемъ прямоугольникъ □"Е"Е"6", для опредѣленія котораго послужатъ уравненія
г+У=Р, • • (5)
въ которыхъ х означаетъ основаніе, а у—высоту новаго прямоугольника. Изъ нихъ имѣемъ:
, р—Л ,
®=ь<—,, у=к.
Изслѣдованіе. 1. р>Л; въ этомъ случаѣ: а*>0, ?/>0 и >Л. Это рѣшеніе даетъ прямоугольникъ съ периметромъ 2р, имѣющій такое положеніе какъ О"Е"Г"С".
2. р=к; въ этомъ случаѣ: я=0, у=Л’, и разсматриваемый прямоугольникъ сливается съ высотою треугольника.
3. р<А; въ этомъ случаѣ: а?<0, #>0, но <Л. Подставивъ въ ур—нія (5) — х вмѣсто х, получимъ
х А—у
у-х=р,
легко видѣть, что эти уравненія соотвѣтствуютъ вписанному прямоугольнику ИЕЕО, въ которомъ разность между высотою и основаніемъ равна данной линіи р.
Примѣчаніе, Чтобы прямоугольникъ былъ квадратомъ, надо, чтобы было х—у^ т.-е. А(р— Л)=А(6-ь-р), откуда
’ 2Ък _ Ък
нельзя, слѣд,, получить внѣ - вписаннаго квадрата въ разсматриваемъ случаѣ, если будетъ Ь<ік.
Построеніе. Для построеніи # беремъ на продолженіи основанія АС линіи АМ~Л, АЬ=р; тогда
СМ Ъ 7а, СЬ ~Ъ-4яр*
Соединивъ М съ проводимъ ОЬ параллельно МИ; затѣмъ изъ точки О —
Черт. 39.
параллель къ линіи АС, которая и дастъ вершины Б" и Е" искомаго прямоугольника.
385. Заключеніе. Обозрѣвая изслѣдованіе, не трудно усмотрѣть, что никогда всѣ три рода прямоугольниковъ, имѣющихъ данный периметръ 2р, не появляются совмѣстно па одномъ и томъ же чертежѣ, т.-е. въ одномъ и томъ же треугольникѣ, но являются попарно; а именно:
1) Если р меньше меньшаго изъ количествъ Ь и Л, задача не имѣетъ рѣшенія* ?
2) Если р заключается между Ъ и 7/, то внутренній прямоугольникъ является совмѣстно съ однимъ изъ внѣшнихъ, а именно: съ 1 ври и со II при Ъ > к. . . .
3) Если р больше большаго изъ количествъ Ъ и 7/, то внутренній прямоугольникъ невозможенъ, но являются совмѣстно два внѣшнихъ*
Четвертый примѣръ изслѣдованія.
Черт* 40,
386. Дамы два прямоуіолъяика: АВСР « ЕЕОН, имѣющіе измѣренія: первый Ъ и /?, при чемъ Ъ^>к, второй т и й, ярмчслсъ т > я. Вписать въ первый гіэъ нить прямо-уюлъникъ Р(^К8 подобный второму.
Вершины Р, К и 8 искомаго прямоугольника могутъ лежать или на самыхъ сторонахъ прямоугольника А ВС О, или на ихъ продолжено/' ніяхъ: въ первомъ случаѣ получается 1У внутреине-вписаннъійпрямоу гол ьнпкъ, / во второмъ внѣ-вписанный,
387* I. Для построенія прямоугольника Р<^К8 достаточно знать разстоянія: АР=іг, А8=?/ точекъ Р и 8 отъ вершины А. Такъ какъ
уголъ 8Р(}, прямой, то углы АР8 и ВР<І дополнительны и тр—кн А8Р и ВР(^ подобны, а потому сходственныя ихъ стороны пропорціональны:
т.-е.
ЛР_А8_Р8 вф 'вр—ріг*
а? __ у ___п
к—у Ъ—х т
Приравнивая каждое изъ двухъ первыхъ отношеній третьему, находимъ два уравненія съ двумя неизвѣстными:
тх-ъ-пу^пк . . . (1)
пх+ту=пЪ ... (2) откуда
п(пік—яб) п(тЪ—пк)
слѣдовательно
№=ь-г=^^.!й
т(тЛ — яЬ) ~ ;
т г или. положивъ — =л:
кк—Ь . к(кЬ—к)
6-ж=-А2—Г
_кЬ—к
У~ №—1
Изслѣдованіе. Если данные прямоугольники не квадраты, то достаточно ограничиться разсмотрѣніемъ предположеній: 6 >7/ и ш>п, такъ что изслѣдованію подлежать случаи:
г і
Ъ
&7Т7-, при Ъ—/к
, т Ъ , । , т
к — — >^* Изъ итого неравенства находимъ, что ЛЛ>6. что й, будучи больше больше и дроби /которая <
Первый случай.
Затѣмъ, замѣчаемъ, а слѣдовательно и изъ послѣднихъ двухъ неравенствъ слѣдуетъ, что іг<6 и у <А. Такимъ образомъ, вершины искомаго прямоугольника находятся на самыхъ сторонахъ прямоугольника АВСИ, т.-е. РЦК8 представляетъ дѣйствительно внутренній вписанный прямоугольникъ.
ѵ . т Ъ .
Условіе —показываетъ, что всѣ вписанные прямоугольники имѣютъ форму болѣе удлиненную, нежели прямоугольникъ АВСР.
Второй случай, к——Это условіе даетъ: Л7і—слѣд.
П Л
г~0, у=Л;
это значитъ, что вершины Р и К совпадаютъ—первая съ А, вторая съ С; а вер-шины 8 н — первая съ Б, вторая съ В, а потому прямоугольникъ РЦК8 съ
Третій случай. Изъ этого слѣдуетъ, что а потому #<0
и #<0 пли //>/*; такимъ образомъ: я отрицателенъ, а у положителенъ и больше 7г. Этн результаты означаютъ, что вершина Р должна находиться влѣво отъ точки А на продолженіи стороны ВА, а вершина В — вправо отъ точки Б на продолженіи стороны БС; вершина 8 — вверхъ отъ С на продолженіи АС, а вершина О—внизъ отъ В на продолженіи БВ; т.-е. получается прямоугольникъ Р'У'1Г8\ обнимающій АВСБ.
Если составить уравненія для этой новой задачи, положивъ АТ'—х и А'8'=у, найдемъ:
х ___ у ___п
у—А хч-Ь яГ
и эти уравненія мы получаемъ прямо изъ ур—ній предшествующихъ перемѣною х на —я. Итакъ, первоначальныя уравненія всегда даютъ отвѣтъ па предложен-
Черт, 42,
ную задачу: этимъ отвѣтомъ служитъ внутренне-внисанныіі прямоугольникъ РЦК8, если ЕЕСН болѣе удлиненъ чѣмъ АВСБ, п внѣ-вписапяый прямоугольникъ Р'у/Г1'8' ічерт. 42), если ЕЕ6Н менѣе удлиненъ нежели АВСБ.
Слѣдуетъ замѣтить, что взявъ БР' = АР и Б8^А8 (черт. 41), получимъ второй прямоугольникъ РЧ^'К/8', удовлетворяющій условіямъ вопроса, но какъ онъ равенъ РС^Кй, то мы и не будемъ считать его новымъ рѣшеніемъ. То же замѣчаніе относится къ внѣ-вписанному прямоугольнику Р"(}"Е"8", равному Р'(}'Е'8' (черт. 42)*
Четвертый случай, к—1 и 6>Л. Находимъ:
я——се, */=со.
Условіе Л—1 означаетъ, что прямоугольникъ ЕЕОН есть квадратъ; а полученное рѣшеніе, въ которомъ ж<0, означаетъ, что для даннаго прямоугольника никогда но можетъ быть полученъ внѣ-вписанный квадрать, но что внѣ-вписанный прямоугольникъ, какъ Р'ф'Е'8', тѣмъ болѣе приближается къ формѣ квадрата, чѣмъ больше становятся его размѣры.
Нятый случай. Если к=1 и 6— Л, т.-е. данные прямоугольники АВСБ и ЕЕСН—квадраты, формулы даютъ:
О о
эти рѣшенія означаютъ дѣйствительную неопредѣленность, потому что въ квадрать можно вписать безчисленное множество квадратовъ; въ самомъ дѣлѣ, легко доказать, что если нанести на каждой сторонѣ квадрата, начиная отъ каждой вершины, одну н ту же произвольную длину, получимъ вершины новаго квадрата.
Примѣчаніе. Здѣсь умѣстно сдѣлать слѣдующее замѣчаніе. Когда, какъ въ данномъ случаѣ, неопредѣленность получается отъ нѣсколькихъ предположеній относительно частныхъ значеній буквъ, нужно всѣ эти предположенія вводить заразъ: иначе могла бы ускользнутъ изъ виду дѣйствительная неопредѣленность. Такъ, положивъ въ формулахъ х и заразъ 1 и 6—А, тотчасъ обнаружимъ неопредѣленность; к если бы мы захотѣли найти истинное значеніе ж и у, положивъ
то, упростивъ формулы и положивъ затѣмъ а=0, нашли бы к—д А-ьр
выраженія, вслѣдствіе присутствія въ нихъ произвольнаго количества р, дѣйствительно неопредѣленныя.
Но если бы оба предположенія мы ввели не совмѣстно, а положивъ сперва Ь=к, что позволяетъ удалить общаго множителя А—1, а затѣмъ А=Д въ упрощенныхъ уже формулахъ
__ Ьк ____ Ък
Х~к+Ѵ к+Ѵ
нашли бы опредѣленныя величины Ь Ъ
а!—2' У=2;
слѣдовательно, мы удалили бы неопредѣленность, на дѣлѣ существующую.
Примѣчаніе это весьма важно, и его всегда слѣдуетъ имѣть въ виду при изслѣдованіи вопросовъ, когда приходится дѣлать не одно частное предположеніе.
Если будемъ к неограниченно увеличивать, приближая его къ со, х и у будутъ стремиться къ нулю. Въ самомъ дѣлѣ, при имѣемъ:
для раскрытія этихъ неопредѣленностей раздѣлимъ числителя и знаменателя формулъ з? и у на А2, что дастъ
а жхюжжвъ і—^с. находимъ «г=0 и #=0: прямоугольникъ Р(^Н8 обращается жъ діагональ АС, что совершенно понятно.
Построеніе. Величины я и к—у можно представить въ видѣ
и построить при помощи четвертыхъ пропорціональныхъ. Во-первыхъ, чтобы получить линію
тк -----= т — п ’
достаточно взять (черт. 40) на продолженіи НЕ линію ЕК—А, затѣмъ на линіи ЕЕ нанести ЕСГ—ЕС—п; соединивъ точки (Г м К и проведя черезъ точку Е линію ЕЬ параллельно 6'К, найдемъ
ЕС' ЕК т— п к
ЕЕ -ЁЁ’ т,‘е’ “ІІГ"~ЁЪ’ откуда ЕЬ = ЙГ^я—
Такимъ же образомъ: чтобы построить отрѣзокъ
пЬ ------= т — п
беремъ ГО —А, ЕІГ — ЕН — п; соединивъ точки И' и О, проводимъ изъ точки О' параллель 6Т, и получаемъ
НТ го т—п 6 пЪ
6 Г ГТ’ п ГТ т—п
Нанеся ГТ отъ Ь до V, получимъ
ЕѴ=ЕЬ—ЬѴ=я —м,
и выраженія х и А—у примутъ видъ
и
т т-^-п
ХЕѴ.
Итакъ, для опредѣленія з* нужно взять Г(}"=ЕО=:н, провести прямую 6"Ѵ и черезъ точку IV ей параллельную П'Х; для полученія А—у проводимъ черезъ точку Г линію ГУ параллельно ѴС"; найдемъ: ЕХ — х и ЕУ — А—у.
Нанеся на стороны прямоугольника АВСІ)
АР=ЕХ, 08 —ѴЕ, получимъ и прямоугольникъ РфК8. *
Фигура Р'СуВ'8' (черт. 42). строится такимъ же образамъ, ибо въ этомъ случаѣ
П і ч , ч
х ~ ~ г- (и — у — Л = ------(и — ^).
ш ч- п гл ч-я
388. п. Вершины Р и 8 могутъ находиться въ Р" и 8" на продолженіяхъ сторонъ ВА и СЛ; виѣ-вписанный прямоугольникъ приметъ положеніе (черт. 43)* Положивъ
л”
\П
н
•»
откуда
изъ подобія найдемъ:
Черт. 43.
АР"—яэ А8"=у,
треугольниковъ Р"А8" и Р"Вф"
пи‘—
ту—пх=Ъп\
рѣшивъ ихъ, находимъ:
я(шАч-яА) __к(шАч-иА)
’ У—-т2~~пі~^
или
АА —I— А АА ч~ А
Изслѣдованіе* Задача всегда возможна, какова бы ни была величина А въ предѣлахъ отъ сх> до 1; то же самое замѣчаніе, что и прежде, прилагается п къ случаю А—1.
Что касается выраженій х и Л-+-у, ихъ строимъ такимъ же образомъ какъ и въ первомъ случаѣ, приведя къ виду
4- м),
»і ч- &
ХЕѴ, А-у-х
ш
т ч~ н
Я «
гдѣ г и и имѣютъ вышеуказанныя значенія; сверхъ того, построенія, уже исполненныя при нахожденіи х и Л—у или х и //—Л, позволяютъ быстрѣе построить х и кч-у, опредѣляющія новое рѣшеніе
Заключеніе. Итакъ, задача, взятая въ самомъ общемъ смыслѣ, всегда имѣетъ два рѣшенія: 1) прямоугольникъ яию-впысанным, какъ Р"О''В/'8" (черт, 43); 2) прямоугольникъ такой какъ (черт. 41), или какъ Р'ф'Н/8' (черт. 42) смотря по тому, будетъ ли — больше, или меньше т-
ГЛАВА XXVII.
Неопредѣленный анализъ первой степени.
Рѣшеніе одного уравненія съ 2-мя неизвѣстными, въ цѣлыхъ числахъ.—Рѣшеніе системы уравненій, въ которой число неизвѣстныхъ однимъ больше числа уравненій.—
Рѣшеніе одного ур—нія съ 3-мя неизвѣстными*
1. Рѣшеніе въ цѣлыхъ числахъ одного уравненія съ 2-мя неизвѣстными.
389. Когда число неизвѣстныхъ больше числа уравненій, послѣднія имѣютъ безчисленное множество рѣшеній и называются поэтому неопредѣленными. Простѣйшій случай представляетъ одно ур. съ двумя неизвѣстными, напримѣръ, х — Зу = 5. Овредііяя взъ вето л?, находимъ
х = 3#-}-5.
Эго ур. показываетъ, что х зависитъ отъ у, самый же у остается совершенно произвольнымъ; поэтому мы можемъ давать ему какія угодно значенія. Такъ, полагая
у = — 2, находимъ: х = — 1,
У= 0, * 5,
у = 4, > х = 17 ит*д.
Иногда вопросъ, приводящій къ неопредѣленному уравненію, требуетъ, чтобы неизвѣстныя были числа цѣлыя; а нерѣдко къ этому присоединяется еще требованіе, чтобы онл были и положительныя (напр., если я и у означаютъ числа лицъ въ извѣстномъ обществѣ, или цифры искомаго числа и т. п.); такимъ образомъ является задача: изъ безчисленнаго множества рѣшеній цѣлыхъ м дробныхъ, положительныхъ и отрицательныхъ, выдѣлить только цѣлыя и по-лсжмтелъныя: такое ограниченіе значительно уменьшаетъ число рѣшеній.
Всякое неопредѣленное ур. съ двумя неизвѣстными, по освобожденіи отъ дробей, по перенесеніи неизвѣстныхъ въ одну часть, а извѣстныхъ въ другую и по приведенія можетъ быть представлено въ видѣ:
ах-\-Ъу = с,
гдѣ а, Ъ и с—числа цѣлыя. Прежде всего мы должны рѣшить вопросъ о томъ, всегда ли подобное ур. можетъ быть рѣшено въ цѣлыхъ числахъ? Отвѣтомъ на это служатъ слѣдующія двѣ теоремы.
390. Теорема 1. Если въ уравненіи ах~\-Ъу = с коэффиціенты а м Ъ при неизвѣстныхъ имѣютъ общаго множителя, не содержащагося въ извѣстномъ членѣ с, то уравненіе не имѣетъ цѣлыхъ })ѣгиеній.
Пусть а и Ъ имѣютъ общаго дѣлителя т, который «е дѣлитъ числа с; въ тикомъ случаѣ, по раздѣленіи а п Ъ на т, получимъ нѣкоторыя цѣлыя числа а и У.
а: = а', Ь:т = У; откуда а = и Ь —жЬ'.
Подстановка въ уравненіе дастъ
а'тх Ь'піу — с,
откуда
а'х-\-Ъ'у =
с
” ? т
гдѣ —з по условію, дробь. Допустивъ, что ж и у могутъ быть цѣлыми числами, г/4
мы получили бы въ первой части послѣдняго уравненія цѣлое число, тогда какъ вторая часть его—дробь: равенство было бы невозможно. Итакъ, ур. не можетъ быть рѣшено въ цѣлыхъ числахъ.
Примѣромъ можетъ служить ур. 15л? —{— 21г/ = 29, въ которомъ коэффиціенты 15 и 21 имѣютъ общаго множителя 3, на который 29 не дѣлится.
Если всѣ три коэффиціента аі Ь и с имѣютъ общаго множителя, то по сокращеніи на него уравненія можетъ оказаться: или, что коэффиціенты а и‘ Ь имѣютъ общаго множителя, пли что а и Ь — числа первыя между собою. Въ первомъ случаѣ, по предыдущей теоремѣ, ур. не имѣетъ цѣлыхъ рѣшеній. Что же касается второго случая, то можно доказать, что ур. необходимо имѣетъ цѣлыя рѣшенія.
391. Теорема II. Аснда коэффиціенты а и Ъ суть числа первыя между собою у то ур, ах-^Ьу = с имѣетъ цѣлыя рѣшенія.
Рѣшивъ ур. относительно напр., получимъ
„ с —
X = ------
а
Докажемъ прежде всего, что если въ эту формулу вмѣсто у будемъ под* ставлять всѣ послѣдовательныя цѣлыя числа меньшія а, т.-е. О, 1, 2, 3^. .. а—1Л и каждый разъ совершать дѣленіе, то всѣ а остатковъ будутъ различны. Въ самомъ дѣлѣ, подставимъ вмѣсто у какія-нибудь два числа у' и у” меньшія а (изъ ряда 0, 1, 2, . . .а—-1); получимъ два выраженія
Выполнивъ каждое дѣленіе и означивъ частныя буквами ф и ф\ а остатки г' и г", найдемъ:
г—Ьу ' і
а х 1 а
г" = 2" + -1 а
С.-_ЪМ1 : а
Допустивъ, что остатки г' и г" могутъ быть равны, найдемъ по вычитаніи второго равенства изъ перваго:
С — Ъу' __ С - Ъу" _ ._ „
а а " *
или
иу'-.й
а * *
Такъ какъ какъ разность цѣлыхъ чиселъ, есть число цѣлое, то и
первая часть должна быть цѣлымъ числомъ, а потому Ъ(у”— уг) должно нацѣло дѣлиться на а. Но Ъ н а—числа первыя между собою, слѣдов. ун—у* должно дѣлиться на а, т.-е. разность двухъ чиселъ, изъ которыхъ каждое меньше'а, должна бы дѣлиться на а, что невозможно. Невозможно, поэтому, и допущеніе, что могутъ быть равные остатки.
Итакъ, мы доказали, что если вмѣсто у подставлять всѣ послѣдовательныя цѣлыя числа отъ О до а — 1 включительно, и каждый разъ совершать дѣленіе с — Ъу на а, то мы получимъ а остатковъ, которые всѣ различны и каждый меньше а (какъ дѣлителя). Но всѣ цѣлыя числа меньшія а, различныя между собою, число которыхъ а, суть, очевидно, числа
* . О, 1, 2, 3, . . . а—1.
Слѣд. въ числѣ остатковъ будетъ непремѣнно одинъ и только одинъ, равный нулю. Значеніе у^ подстановка котораго въ выраженіе —- даетъ оста-
с — Ъѵ ж <
токъ О, обращаетъ х =—~ въ цѣлое число: цѣлому у соотвѣтствуетъ цѣ-лый х. Итакъ, когда а и ,Ь первыя между собою, уравненіе дѣйствительно допускаетъ цѣлыя рѣшенія, что и требовалось доказать.
392. Первый способъ рѣшенія ур—нія ах-\-Ъу=с въ цѣлыхъ числахъ. Вышеприведенное доказательство даетъ также средство находить одну пару цѣлыхъ рѣшеній. Пусть, напр., дано уравненіе;
7# + = 232.
Такъ какъ коэффиціенты при х и у суть числа первыя между собою, то ур—ніе допускаетъ цѣлыя рѣшенія. Для опредѣленія * одной пары ихъ рѣшаемъ ур. относительно, напр., У; находимъ
232—7^ У=——
Поіггшяемъ сюда вмѣсто х послѣдовательно цѣлыя числа, меньшія 5, т.-е О. 1, 2, 3. 4: находимъ:
при з = О, У=-~- =46 + -
Итакъ, подстановка 1 вмѣсто х даетъ для у цѣлое число 45; сл. я = 1 и у = 45 представляютъ одну пару цѣлыхъ рѣшеній, что не трудно провѣрить.
Замѣтимъ, что въ видахъ ограниченія числа возможныхъ подстановокъ слѣдуетъ всегда рѣшать уравненіе относительно неизвѣстнаго, имѣющаго меньшій коэффиціентъ.
Какъ скоро найдена одна пара цѣлыхъ рѣшеній, то легко найти сколько угодно такихъ рѣшеній при помощи формулъ, къ выводу которыхъ теперь й переходимъ.
393. Тео ре м а III. Если какимг-нибудь способомъ найдена одна пара цѣлыхъ рѣшеній: х = а, = т0 вс*ь цѣлыя
рѣшенія заключаются въ формулахъ
х = а-\^Ы, у = $ — аі)
гдѣ і—произвольное цѣлое число.
Такъ какъ х=а и # = по условію, суть рѣшенія даннаго уравненія, то подстановка ихъ въ это уравненіе дастъ тождество
= с.
Вычтя это тождество изъ даннаго уравненія, имѣемъ:
• а(х — а) + &(у— ?) = 0, откуда
х-а=«і=ЛІ, а
а слѣдовательно 1 а
Т> ’ л. > * 6(3 —
Выраженіе х состоитъ изъ: цѣлаго числа а и дробнаго выраженія —
Поэтому х только тогда можетъ быть цѣлымъ числомъ, когда 6(3 — у) дѣлится на но Ь и а—числа первыя между собою, слѣд. чтобы — у) дѣлилось на-цѣло на а, необходимо, чтобы — у дѣлилось на а; поэтому для у
* * 5 #
можно брать только такія цѣлыя числа, при которыхъ обращается въ
произвольное цѣлое число і, т.-е. условіе того, чтобы х былгГцѣлымъ, есть
. >
Р —У _ X а ’ или
у = аІ, или
У = ? — а въ такомъ случаѣ х = а
Выраженія: х — й даютъ сколько угодно цѣлыхъ рѣ-
шеній; стоитъ только вмѣсто I подставлять какія угодно цѣлыя числа.
Такъ какъ I подчинено только одному условію, что оно должно быть цѣ’ лымъ, то въ формулы х и у можно вмѣсто і подставить —Си тогда онѣ примутъ видъ:
х — а— Ы, у =
Возьмемъ ли группу формулъ:
или
х = а -|- &С
х = а — ЬС
У = р —аС
замѣчаемъ, что вторые -члены ихъ суть произведенія неопредѣленнаго цѣлаго С* па коэффиціентъ при у въ формулѣ х, и на коэффиціентъ при х въ формулѣ у, при чемъ одинъ изъ этихъ коэффиціентовъ берется съ тѣмъ знакомъ, какой онъ имѣетъ въ уравненіи, а другой—со знакомъ противоположнымъ тому, какой онъ имѣетъ въ уравненіи. Зная это правило, можно тотчасъ опредѣлить всѣ цѣлыя рѣшенія уравненія, какъ скоро найдена одна пара такихъ рѣшеній.
Примѣръ I. Выше мы нашли, что одна пара цѣлыхъ рѣшеній уравненія 7гг —5 т/ = 232 есть: х=1, у = 45; слѣд. всѣ цѣлыя рѣшенія заключаются въ формулахъ:
я=14-5С у = 45 —7С
или въ формулахъ:
я=1— 5С ж = 45-|-7С
Взявъ, напр., вторую группу формулъ, и давая въ ней I какія угодно цѣлыя значенія, положительныя и отрицательныя, найдемъ сколько угодно паръ цѣлыхъ рѣшеній; такъ
‘ при і = О имѣемъ: х = 1, Э =45;
і = 1 4, У = 52;
і = 2 X = 9, У = 59, и т. д.
> І = — 1 * X = 6Л У = 38,
І = — 2 X — 11, у — 31, и т. д.
Примѣръ II. Рѣшить въ цѣлыхъ числахъ уравненіе
8я — 13у=159.
Опредѣляя х, имѣемъ:
13//+ 159 х 8 ;
7 11
грі у = О. имѣемъ: «=19^; при у=1, х = 215; при у — 2, х — 23
3 3
при у = 3, х = 24^: при у = 4, х = 26 при у = 5, # = 28.
Общія формулы цѣлыхъ рѣшеній суть:
я = 284-Ш, у = 5 + 8^; или же
х — 28—ІЗі, у=5—8і.
Примѣчаніе. Изъ самаго доказательства теоремы III слѣдуетъ, что въ формулахъ: х = а-[*Ы' у = )— аі содержатся всѣ цѣлыя рѣшенія уравненія ах Ьу = с; непосредственною же повѣркою можно доказать, что эти выраженія дѣйствительно удовлетворяютъ данному уравненію* Въ самомъ дѣлѣ, подстановка даетъ:
а(а-|“ Ьі) 4“ Ь(^— лі) = с, пли а2-[~^ = с;
а это есть тождество, потому .что, по положенію, 2 и ? удовлетворяютъ данному уравненію.
Указанный способъ рѣшенія неопредѣленныхъ уравненій въ цѣлыхъ числахъ очень простъ, и его слѣдуетъ употреблять всякій разъ, когда коэффиціенты при неизвѣстныхъ, или, по крайней мѣрѣ, одинъ изъ нихъ — числа небольшія. Въ противномъ случаѣ, могло бы потребоваться большое число подстановокъ для нахожденія одной пары цѣлыхъ рѣшеній, н способъ этотъ отнималъ бы -много времени. Поэтому для рѣшенія ур—ній съ большими коэффиціентами предпочтительнѣе употреблять
394. Второй способъ рѣшенія уравненія ах-\-Ьу = съъ цѣлыхъ числахъ.
Сперва разсмотримъ два частныхъ случая:
1. Пусть одинъ изъ коэффиціентовъ заключается множителемъ въ извѣстномъ членѣ, напр., пусть с = уравненіе будетъ
ах Ьу = откуда
та — Ьі/ Ьу
х = - = т------*
а а
Чтобы х было цѣлымъ числомъ, необходимо (такъ какъ т—цѣлое число), чтобы Ьу дѣлилось на а; но Ъ н а—числа первыя между собою, слѣд. необходимо у должно быть кратнымъ а, т.-е. должно быть
У = аі,
гдѣ і—какое угодно цѣлое число: тогда х выразится цѣлою формулою
# = т — Ьі.
Формулы: х = т — Ьі, ^ = аі, гдѣ і—произвольное цѣлое число, п даютъ всѣ цѣлыя рѣшенія предложеннаго уравненія.
2. Если одинъ изъ коэффиціентовъ равенъ 1, напр. а —1, то ур.,
х*-\-Ьу = с
даетъ х = с — Ьу\ давая у какія угодно цѣлыя значенія, будемъ и для х получать каждый разъ цѣлыя же величины. Рѣшеніе такого уравненія, слѣдоват., весьма просто.
На этомъ замѣчаніи и основанъ общій способъ рѣшенія неопредѣленнаго уравненія въ цѣлыхъ числахъ. Въ самомъ дѣлѣ, если бы намъ удалось привести рѣшеніе уравненія ах-\-Ьу — с къ такому уравненію, въ которомъ одинъ изъ коэффиціентовъ равенъ 1, то задача была бы рѣшена. Но когда а и Ъ числа первыя между собою,—такое приведеніе всегда возможно. Пусть, напр., дано ур—ніе '
4 + іЗу = 159 . . , (1).
Коэффиціенты 8 и 13 числа первыя между собою, слѣд. уравненіе можетъ быть рѣшено въ цѣлыхъ числахъ. Опредѣливъ то неизвѣстное, у котораго коэффиціентъ меньше, находимъ':
159 — 13г/
8 ;
исключая цѣлыя числа изъ
159
8
соединяя дробные члены въ одну дробь,
И
получимъ:
х — 19— у-|-
7 — 5у. 8
Выраженіе х состоитъ изъ двухъ частей: 19—-у, которая будетъ цѣлою г 7 — 5// у х
при всякомъ цѣломъ у, п —8“^’ имѣющей дробный видъ; для того чтобы х было цѣлымъ числомъ, необходимо между всѣми значеніями у выбрать такія, при которыхъ —8^ равнялась бы нѣкоторому цѣлому числу і. Итакъ, нахожденіе цѣлыхъ значеній для х приводится къ рѣшенію въ цѣлыхъ числахъ уравненія 9
Въ такомъ случаѣ будетъ
х = 19 — у •
.(а).
Замѣтимъ, что въ уравненіи (2), или все равно, 5у 4“ = 7, меньшій
коэффиціентъ есть остатокъ отъ раздѣленія большаго коэффиціента въ данномъ ур—ніи на меньшій; а большій коэффиціентъ равенъ меньшему коэффиціенту даннаго ур—нія; вслѣдствіе этого ур—ніе (2) проще даннаго. Кромѣ того, коэффиціенты его 5 и 8 числа первыя между собою: это необходимо вытекаетъ изъ того, что если дѣлимое (13) и дѣлитель (8) первые между собою, то остатокъ (5) будетъ первый съ дѣлителемъ; такимъ образомъ ур—ніе (2) имѣетъ необходимо цѣлыя рѣшенія. Опредѣляя изъ него неизвѣстное, имѣющее меньшій коэффиціентъ, получимъ:
Чтобы цѣлому I соотвѣтствовалъ цѣлый у, необходимо, чтобы выраженіе *__%
— было числомъ цѣлымъ; обозначивъ это цѣлое число буквою находимъ
У = 1 + Л . .(/)
причемъ
2 — 3^
Такимъ образомъ нахожденіе цѣлыхъ значеній у приводится къ рѣшенію въ х 2 — 3^ ,,
цѣлыхъ числахъ уравненія —— = г, или
3<4-5Г = 2 . . . (3).
Выводя изъ него неизвѣстное съ меньшихъ коэффиціентомъ, имѣемъ
Разсуждая по предыдущему, убѣдимся, что нахожденіе цѣлыхъ значеній для і приводитъ къ рѣшенію въ цѣлыхъ числахъ ур—нія
или 2і'+ Зі'1 = 2 . . . (4), причемъ
Рѣшая ур. (4) относительно имѣемъ
Чтобы і' было цѣлымъ, необходимо, чтобы было цѣлымъ положивъ
і,г
у = і"\ гдѣ —неопредѣленное цѣлое, имѣемъ
Г' = 2Г . . . (5) причемъ 1 л" л'"
» Итакъ, мы пришли къ ур-—нію (5), въ которомъ коэффиціентъ при ін есть I; давая Г' какія угодно цѣлыя значенія, будемъ каждый разъ получать и для і” цѣлыя значенія.
Такимъ образомъ мы нашли рядъ соотношеній
I) #=19 — 2/“Ь^
2) =
3) / = — г-Н”,
4) Г=1—Г—Г,
5) Г=2Г.
Давая произвольное цѣлое значеніе количеству іп\ мы изъ ур. (5) получимъ цѣлое же значеніе и для Г. Цѣлыя значенія і" и і"’, подставленныя въ ур. (4), дадутъ цѣлое значеніе для I'. Цѣлыя значенія і" и Г, подставленныя
въ (3), дадутъ цѣлое значеніе для Эти цѣлыя значенія I и подставленныя въ (2), дадутъ цѣлое значеніе для у- Наконецъ цѣлыя значенія і и у, подставленныя въ (1), дадутъ соотвѣтствующее цѣлое значеніе я. Но во избѣжаніе неудобства, представляемаго такими послѣдовательными подстановками, выражаютъ х и у непосредственно чрезъ произвольное количество Гг. Подставляя въ (4) вмѣсто і” его величину 2^"', найдемъ
е = 1 — 2Г
подставляя это выраженіе I' и вмѣсто і” его величину въ (3), получимъ: і = — 1 + ЗГ + 2Г" = — 1 + 5Г;
подстановка значеній і к I' во (2) дастъ:
у = 1 4- 1 — 5Г' + 1 — ЗГ" = 3 — 8Г;
наконецъ, подстановка найденныхъ выраженій для у и і въ (1) дастъ:
х = 19 — 3 + 8Г — 1 + 5Г = 15 -|- ІЗГ.
Итакъ, общія формулы цѣлыхъ рѣшеній нашего ур. суть:
X = 15 + 13Г, У = з — 8ГС
Онѣ имѣютъ совершенно тотъ же составъ, какой указанъ въ~§ 393.
395. Докажемъ, что указанный въ предыдущемъ § пріемъ рѣшенія ур—нія всегда мрмводвтъ къ полученію цѣлыхъ рѣшеній. Въ самомъ дѣлѣ, мы получили рцъ уравненій:
1) 8#4-13у =159,
2) 5»/+ 8* = 7,
3) Зі 4- 51’ = 2,
4) 2^4- ЗГ= 2,
5) Г— 2Г= О,
при чемъ во (2) меньшій коэффиціентъ 5 есть остатокъ отъ раздѣленія большаго коэффиціента даннаго ур. 13 на меньшій 8. Въ ур—ніи (3) меньшій коэффиціентъ 3 есть остатокъ отъ дѣленія 8 па 5, т.-е. дѣлителя на первый остатокъ. Въ ур—ніи (4) меньшій коэффиціентъ 2 есть остатокъ отъ дѣленія 5 на 3, т.-е. перваго остатка на второй и т. д. Изъ этого видно, что процессъ рѣшенія приводитъ въ данномъ случаѣ къ такому же ряду дѣйствій, какой пѣлъ бы мѣсто при нахожденіи общаго наиб. дѣлителя между коэффиціентами даннаго уравненія. Но какъ эти коэффиціенты—числа первыя между собою, то въ указанномъ рядѣ дѣленій непремѣнно дойдемъ до остатка равнаго 1, который и явится коэффиціентомъ при одномъ изъ неизвѣстныхъ въ одномъ изъ уравненій [въ нашемъ примѣрѣ — коэффиціентомъ при I" въ ур. (5)]. Такимъ образомъ, цѣль будетъ достигнута.
Для полученія цѣлыхъ рѣшеній въ опредѣленныхъ числахъ стоитъ только произвольному цѣлому I'" давать какія угодно цѣлыя значенія—положительныя или отрицательныя: О, 1, 2, 3, . . , —1, —2, —3, . . .
]1риГ= |О 1' 2| 3
я= 15-(-13Г"= 15 28' 41 54
у = 3— 84’" = 3’— 5—13—21
— 2’— 3'— 4' . —11—24—37
27 35 =
396. Упрощенія общаго способа. При рѣшеніи неопредѣленнаго уравненія слѣдуетъ пользоваться всѣми обстоятельствами, которыя ведутъ къ упрощенію вычисленій и слѣд* къ скорѣйшему Достиженію цѣли. Укажемъ эти упрощенія.
1. Рѣшая уравненіе 19х-{-15у = 23, находимъ
8 — 4 т
15
4 Приравнявъ і дробный членъ, получили бы уравненіе съ коэффиціентами 4 и 15; но можно получить ур. съ меньшими коэффиціентами, замѣтивъ, что 8 — 4(2 — х)
——— = _і__' и СЛѢД.
Іо іо * .
очевидно, что у будетъ цѣлымъ при такомъ цѣломъ х, который обращаетъ —рг
I о въ цѣлое число /; поэтому нолагаемъ
откуда
2— х =15/, и я = 2—15/; затѣмъ
' у = 1—л;-р4/~1 —2-|-15/-к4/ = — 1 -1- 19/.
Указанный пріемъ быстро привелъ къ цѣлыхъ формуламъ для х и у.
2. Упрощеніе рѣшенія всегда возможно въ томъ случаѣ, когда одинъ изъ коэффиціентовъ при неизвѣстныхъ и извѣстный членъ имѣютъ общаго множителя. Пусть дано ур—ніе
6х—-5у = 21;
раздѣливъ обѣ части на общаго множителя 3 чиселъ 6 и 21, получимъ:
Такъ какъ 2л и 7—числа цѣлыя, то 5у должно дѣлиться на 3; но 5 и 3 суть числа первыя между собою, слѣдовательно ? должно быть цѣлымъ. Обо-о
У і значивъ это цѣлое буквою у\ имѣемъ: | ~ у\ откуда = 3/, и данное ур. принимаетъ простѣйшій видъ
2х— 5/=7;
рѣшая его, послѣдовательно наюдичъ:
Э УГ 4- І -к / ГІ Г V 4“ 1 V Ч- 1- і I -т гА 1 г -» I ГА *
= = +3 + =<-2—; ^у-=г: у'4-1 = 2І; у'= — 1 + 2<;
х = 2у4~ 3 +1 ~ 2 + 4і + 3 4-I ~ 1 4- 5і; и наконецъ
у^3/ = 3(—1 + 2$) = — 3 + 6^
3. Однимъ изъ полезнѣйшихъ упрощеній служитъ введеніе отрицательныхъ остатковъ* Такъ, рѣшая ур—ніе
имѣемъ
7х —[— 26^/ = 111,
111 —-26^ 1 - . 6 л 5у
—7—" = 1э +-7 — Ьу—у-
Здѣсь каждый изъ остатковъ: 6 и 5 отъ дѣленія 111 и 26 на 7 больше половины дѣлителя; во ихъ можно уменьшить, если каждое изъ частныхъ увеличить на 1. Взявъ при дѣленіи 111 па 7 въ частномъ 16, получимъ отрицательный остатокъ —-1, численная величина котораго меньше 6; точно такимъ же образомъ, взявъ при дѣленіи 26 на 7 въ частномъ 4, найдемъ отрицательный остатокъ —2, численно меньшій прежняго остатка. Формула х приметъ видъ
16— 1— (4у — у) = 16 — 4у4*^у~;
2ѵ — 1 полагая — = Л имѣемъ:
х —16— 4у + ^.
о
; полагая
имѣемъ
Наконецъ
у = 3^ + Г, г = — 14- 22'.
у = — 3 + 7і\ х = 27 — 26Г.
397. Рѣшеніе въ цѣлыхъ положительныхъ числахъ. Иногда вопросъ, приводящій къ неопредѣленному уравненію, требуетъ не только цѣлыхъ, но вмѣстѣ съ зтимъ и положительныхъ рѣшеній. Слѣдующая теорема позволяетъ, при одномъ взглядѣ на. уравненіе, опредѣлить, имѣетъ ли уравненіе ограниченное число цѣлыхъ положительныхъ рѣшеній, или неограниченное, или совсѣмъ не имѣетъ такихъ рѣшеній.
398. Теорема. Уравненіе аг + Ьу = с имѣетъ ограниченное число рѣшеній въ цѣлыхъ положительныхъ числахъ, или совсѣмъ не имѣетъ такихъ рѣшеній когда коэффиціенты а и Ь имѣютъ одинаковый знакъ; напротивъ^ оно имѣетъ неограниченное число сказанныхъ рѣшеній, когда а и Ь имѣютъ противоположные знаки.
4
Мы видѣли, что цѣлыя рѣшенія уравненія = с выражаются фор-
мулами
х ~ а Ы, у = — а2,
гдѣ а и 3 представляютъ одну пару цѣлыхъ рѣшеній, а і произвольное цѣлое число, положительное или отрицательное.
Условившись коэффиціентъ а считать всегда положительнымъ (еслибъ было «<А то умноживъ все уравненіе на —•!, мы сдѣлали бы коэф. при л? положительнымъ), и обозначая абсолютныя величины количествъ а, Ь п с буквами а'т Ь' и с', убѣдимся, что въ отношеніи знаковъ ур. а#“|“Ьу = с можетъ представлять только слѣдующіе случаи:
а'х Ь'у — с'
= — с' . . . (2).
а'х — Ь'у = ±с . . , (3).
I. Цѣлыя рѣшенія ур—нія (1) изображаются формулами:
я — я У — $— а'2;
чтобы х и у были положительны, цѣлое I должно удовлетворять неравенствамъ:
рѣшая эти неравенства, находимъ:
* > < а'5
т.-е. ограничивающіе предѣлы для Если между этими предѣлами находятся адълыя числа, то уравненіе имѣетъ столько паръ цѣлыхъ положительныхъ рѣшеній, сколько существуетъ такихъ цѣлыхъ значеній 2; если же между продѣ-а Й
лами — и нѣтъ цѣлыхъ чиселъ, то ур—ніе совсѣмъ не имѣетъ цѣлыхъ положительныхъ рѣшеній. Вотъ примѣры:
1. Рѣшая ур, 8х-р ІЗу = 159, мы нашли
15—[— 13/т у = 3 —8/;
рѣшая неравенства 15-|-132 > О и 3 — 82 > О, находимъ:
Между предѣлами — 1 и заключаются только два цѣлыя числа: — 1 л 0; полагая 1 = — 1, находимъ: 2, у — П; положивъ 2 = 0, получимъ:
#=15, у = 3. Данное ур. допускаетъ, такимъ образомъ, только двѣ пары цѣлыхъ положительныхъ рѣшеній.
2. Рѣшая ур. 2х -р Зу = 1, находимъ
х = —1 + 3*, у=1 — 2^
откуда находимъ предѣлы для і: і > у, По какъ между и - нѣтъ
цѣлыхъ чиселъ, то заключаемъ, что данное уравненіе не имѣетъ цѣлыхъ положительныхъ рѣшеній. Это видно изъ самаго уравненія; въ самомъ дѣлѣ, сумма коэффиціентовъ при х и у больше извѣстнаго члена, а потому даже при самыхъ малыхъ цѣлыхъ положительныхъ значеніяхъ неизвѣстныхъ, при х = 1 н у = 1, первая часть уравненія больше второй. Вообще, если въ уравненіи ах Ъ’у = с' имѣемъ а' —Ь' > с', оно не имѣетъ цѣлыхъ положительныхъ рѣшеній.
II. Уравненіе а'х-}-Ъ'у —— с', въ которомъ коэффиціенты при неизвѣстныхъ положительны, а извѣстный членъ отрицателенъ, не имѣетъ положите.!ь^ пыхъ рѣшеній, ни цѣлыхъ, ни дробныхъ, ибо сумма положительныхъ чиселъ не можетъ равняться отрицательному числу.
ПІ. Цѣлыя рѣшенія уравненія а'х— Ьгу = с, гдѣ с^О, выражаются формулами:
х = а “Н У — ? +
чтобы выбрать изъ нихъ только положительныя, надо рѣшить неравенства
а-4-Ь7>0, ? + О,
откуда
отсюда очевидно, что всякое цѣлое значеніе большее большей изъ дробей— — Р и — —, дастъ цѣлыя положительныя рѣшенія; а такъ какъ такихъ значеній I безконечно много, то ур. допускаетъ безчисленное множество цѣлыхъ положительныхъ рѣшеній.
Примѣръ. Выше мы нашли, что цѣлыя рѣшенія уравненія 6х— 5у = 21 выражаются формулами:
а предѣлы для I опредѣляются неравенствами •»
1-р5*>0, — 3 4-6^>О, откуда
Заключаемъ, что всѣ цѣлыя числа, большія т.-е. 1, 2, 3, 4, . . * до + даютъ цѣлыя положительныя значенія х и у. *
399. Примѣчаніе. Когда число цѣлыхъ положительныхъ рѣшеній ограниченное. его можно опредѣлить, съ точностью до 1, пе рѣшая уравненія.
Этотъ случай представляется тогда, когда а п Ь имѣютъ одинаковые знаки, для і получается два предѣла—низшій и высшій, именно
и
1* а’
откуда видно, что уравненіе = имѣетъ столько цѣлыхъ положитель-
ныхъ рѣшеній, сколько есть цѣлыхъ, положительныхъ или отрицательныхъ, чн-а ?
селъ между .— н
I случай. Числа — ~ и ~—бровныя.
Пусть будутъ — у — / ’ п д “I” Л цѣлыя числа, изъ которыхъ первое меньше — второе больше • Между двумя цѣлыми числами — — /* и -7 + /1 содержится столько, послѣдовательныхъ цѣлыхъ чиселъ, сколько единицъ *€* безъ одной заключается въ ихъ разности. Слѣд. число п цѣлыхъ положительныхъ рѣшеній уравненія будетъ
Ь аЪ
Но какъ а н суть рѣшенія даннаго ур—нія, то число аа-\-Ь$ равно с, н потому
Пусть цѣлая часть частнаго равна а дополнительная дробь /*2; тогда
и=з+/Ч-А+/і~1 • - О)-
Такъ какъ, по положенію, — и — не цѣлыя числа, то и суть
числа положительныя, отличныя отъ нуля, и меньшія 1, а потому число
—1, будучи цѣлымъ, можетъ равняться только О или 1, такъ что п равно у или в+І.
Л Й
II случай. Одно изъ чиселъ: — т и — гми оба—грыыя.
* о а
Если —у число цѣлое, то можно взять і равнымъ — и х будетъ равенъ нулю, между тѣмъ какъ у будетъ имѣть величину положительную и цѣлую, равную частному отъ раздѣленія о на Ь. Въ такомъ случаѣ при доказательствѣ беремъ цѣлое число, предшествующее — т.-е. полагаемъ /* = 1.
3
Подобное же замѣчаніе относятся и къ случаю, когда — будетъ цѣлое чясло; и тогда, при этихъ новыхъ условіяхъ, формула (1) всегда примѣнима.
Полагая, что только одно изъ чиселъ —и — — цѣлое, цѣлое число / 4“ /і + /і — 1 приводится къ суммѣ двухъ чиселъ, отличныхъ отъ нуля п меньшихъ, каждое, единицы; оно равно» слѣд., 1, а потому число рѣшеній будетъ д+1- , •
а Й
Пусть, затѣмъ, оба числа: — и ~ цѣлыя. Числа / и будутъ оба равны 1, и легко показать, что равно 0. Въ самомъ дѣлѣ, какъ сказано выше, — т- есть цѣлое число, слѣд. с дѣлится на і; — есть цѣлое число, О €і
слѣдовательно, с дѣлится на а, а потому и на аЬ. Такимъ образомъ — О, /’=/і = 1> слѣд. /'+/І+/І—1 равно 1, и п = ц-\- 1. Итакъ, число цѣлыхъ положительныхъ рѣшеній уравненія ах-\-Ьу = с равно Я или д-]-1, называя буквою з цѣлую часть частнаго отъ раздѣленія с на аЬ. (При этомъ О принимается числомъ положительнымъ.)
Напр., для ур—ній 5х -1- Зу = 2 п 7я + 5у = 39 число рѣшеній =д; для уравненій 4я-[- Зу = 11 и 7я:-|-3у = 61 оно равно ^4~1.
* й
400. Для примѣненія изложенной теоріи рѣшимъ слѣдующія три задачи.
I задача. Выдать 78 рублей одними 5-ти и 3-хъ рублевыми биле-тами9 не имѣя никакихъ другихъ.
Положимъ, что для этого нужно выдать пятирублевыхъ билетовъ х, а трех-рублевыхъ—у; уравненіе, очевидно, будетъ:
5х — Зу = 78.
Задача требуетъ цѣлыхъ положительныхъ рѣшеній; и по коэффиціентамъ при х н у видно, что ур—ніе имѣетъ цѣлыя рѣшенія. Раздѣливъ все ур—ніе на 3, находимъ
х
полагая к- — і, гдѣ I—цѣлое число, тотчасъ имѣемъ:
х — Зі, у = 26— 51.
Чтобы з. и у были положительными, необходимо, чтобы
3/0 (если 0 включить въ
число положит. чиселъ);
26 —5і>0, откуда или 5^-
Итакъ, полагая
/= О, 1, 2, 3, 4, 5, находимъ
ж= О, 3, 6, 9, 12, 15,
у = 26, 21, 16, 11, 6, 1.
Отсюда видно, что выдать 78 рублей требуемымъ различными способами, именно:
образомъ можно шестью
1) Давая 26 билетовъ въ 3 рубля и ни одного въ 5 рублей; или
2) * 21
3) » 16
4) > 11
5) » 6
6) > 1
> » » »
» > > » > » » »
» > > >
» 3 билета
>6 »
>9 »
> 12 »
» 15 >
> » > ; или
> » » ; или
> > > ; или
«
* ъ > ; или
> » >
II задача. Извѣстно, что пріемами элементарной геометріи (т.-е. посредствомъ циркуля и линейки) можно раздѣлитъ окружность какъ на 6, такъ и на 5 равныхъ частей. Какъ и сколькими способами можно съ помощью этихъ частей найти — частъ окружности?
Очевидно, что нужно найти такія двѣ дроби съ знаменателями 5 и 6, которыхъ разность и у, имѣемъ:
равнялась бы назвавъ числители этихъ дробей буквами х
5 = 1 (2)
5 6 15 ' ’
Рѣшаемъ ур. (1); по освобожденіи отъ знаменателей имѣемъ:
5л;— бу = 2;
раздѣливъ обѣ части на 2 и положивъ получимъ ур—ніе
5я' — Зу = 1,
откуда х' = — 1 -|- 3^, а слѣд.
х= — 2<Ц-6^
затѣмъ
. у = — 2 —5/1
1 2
Чтобы х и у были >0, нужно, чтобы было: С>*гг Полагая
находимъ:
<=1, 2, 3, . . .
х=4, 10, 16, . . .
У=3, 8, 13, . . .
Итакъ, наименьшія значенія х.и у, дающія простѣйшее рѣшеніе задачи, ' о 4 2 3
суть: х = 4 и у = 3, т.-е.: отъ или окружности нужно отнять у ея, и
1
остатокъ дастъ окружности.
Рѣшая ур—ніе (2), или, по освобожденіи отъ дробей, уравненіе: бу — 5#=2, находимъ:
х = 2 — 62,
у = 2 —52.
предѣлы для I суть: і < -Ь
о
т- Полагая
2 = 0, -1, - 2, - 3,. . .
имѣемъ:
х =2, 8, 14, 20,...
У = 2, 7, 12, 17, . . ,
Итакъ, при этомъ способѣ, простѣйшее рѣшеніе задачи будетъ а? = 2 и 9 1
у = 2, т.-е. вычтя изъ дуги, равной у окр. дугу =у окр., получимъ въ
остаткѣ 15 окружности.
Ш задача. Зубчатое колесо съ 17-ю зубцами захватываетъ зубцы другого колеса съ 13-ю зубцами. Сколько оборотовъ должно сдѣлать каждое изъ нихъг чтобы каждый зубецъ перваго побывалъ въ каждомъ промежуткѣ второго?
Пусть первое колесо должно сдѣлать х оборотовъ, а второе у. Когда первое обернется одинъ разъ, его 17 зубцовъ зацѣпятъ послѣдовательно столько же промежутковъ второго; слѣд. при х оборотахъ 17л? зубцовъ зацѣпятъ ІЗу промежутковъ между зубцами второго. Но при х оборотахъ каждый зубецъ долженъ зацѣпить каждый промежутокъ, слѣд.
17гг = ІЗу, откуда: х = 132, у =172.
Чтобы х и у были положительны, нужно і давать всѣ цѣлыя значенія, начиная съ 1. Такимъ образомъ, требуемое будетъ имѣть мѣсто черезъ 13 оборотовъ (вообще 132) перваго, или 17 (вообще 172) оборотовъ второго.
2. Рѣшеніе системы уравненій, въ которой число неизвѣстныхъ однимъ больше числа уравненій.
4С1. Возьмемъ 2 ур—нія съ 3-мя неизвѣстными:
. ах -|- Ъу Ц- сз = а'х 4~ Ъ’у с'я == (Г
.(1)
• (2)-
Есл въ каждомъ изъ нихъ или въ одномъ всѣ четыре коэффиціента имѣютъ общаго множителя, то предварительно на него сокращаютъ уравненіе; пусть это сдѣлано, и оба уравненія приведены въ простѣйшій видъ.
Чтобы эти уравненія принимали цѣлыя рѣшенія, необходимо, чтобы въ
каждомъ всѣ три коэффиціента: при а?, у и я были первые между собоют т.-е. а, Ъ и с—первые между собою, и а', Ьг и с'—между собою. Въ самомъ дѣлѣ, пусть, напр. а, 6 и с имѣютъ общаго множителя «г, на который не дѣлится; въ такомъ случаѣ частныя
будутъ цѣлыя; отсюда
а = а"т, Ъ = Ъ”т, с = с' 'т.
Подставляя въ ур/ (1) и сокращая на т, найдемъ
а"х-\-Ь”у-\-с"г — —' *
1^1 т
При цѣлыхъ ж, у п з первая часть представляетъ число цѣлое, тогда какъ вторая есть дробь; слѣд. ур—ніе не имѣетъ цѣлыхъ рѣшеній.
Рѣшая одно ур—ніе съ 2-мя неизвѣстными: ах Ьу = с, мы видѣли, что когда а п Ъ — числа первыя между собою, ур—ніе необходимо имѣетъ цѣлыя рѣшенія; слѣд. условіе, что для цѣлыхъ рѣшеній коэффиціенты а и 6 должны быть первыми между собою, было въ этомъ случаѣ условіемъ необходимымъ и достаточнымъ.
Что же касается взятой системы 2-хъ ур —ній съ 3-мя неизвѣстными, то въ каждомъ ур—ніи коэффиціенты могутъ быть числами первыми между собою, а * ур—нія могутъ не шстьтъ цѣлыхъ рѣшеній; слѣд. условіе это для данной системы, будучи необходимымъ, можетъ быть еще недостаточнымъ (см. далѣе случай П).
4-02. Пріемъ рѣшенія состоитъ въ исключеніи одного изъ неизвѣстныхъ^ исключивъ, напр., з, найдемъ:
(ас' — а*с)х~І~ (Ьс* — Ъ*с)у = Ас1 — і'с. , . (3).
При этомъ могутъ представиться слѣдующіе 3 случая:
403. Первый случай. Если коэффиціенты при х п у въ ур—ніи (3)— числа первыя между собою, то, какъ извѣстно, ур—ніе это необходимо имѣетъ цѣлыя рѣшенія. Если одна пара этихъ рѣшеній будетъ а и то всѣ цѣлыя ' рѣшенія выразятся формулами:
х = — Ь'с).(,
г/ = — (ас*—а'с).
Подставивъ ихъ въ ур. (1), найдемъ
сз — с(аЬг:—= аа — іф.
Первая часть дѣлится на с; если раздѣлится и вторая часть, то ур. будетъ имѣть цѣлыя рѣшенія, въ противномъ случаѣ—нѣтъ. Пусть дѣленіе Л—аі— на с совершается безъ остатка и пусть
^=^=Т....(4>
тогда
откуда
я — (аЪг — Ъа*)І = у, = у _|1 (ау _ Ьа’)і,
[Изъ (4) имѣемъ: а а + + гу = <?, т.-е. а, [5 и у обращаютъ 1-е ур—ніе
въ тождество, а потому составляютъ систему цѣлыхъ рѣшеній этого ур—нія].
Итакъ, имѣемъ симметричныя формулы
х = а + (Ьс’ — Ь'с). /, у = р + (са' — ас%
•' г = у4" (а^ — Ьа')і-
ф ‘ 1 ' • 4
• • • *
цѣлыя і дадутъ цѣлыя же значенія и для х, у,и з.
Положивъ для краткости:
Ъс’ — Ъ'с—р, са'— ас' = ц, аЪг — а,Ъ = г1 найдемъ
Х = а^-‘рі; у = $ + г^=у-\-гІ.
Если бы по смыслу задачи требовалось найти для я, у, з цѣлыя положительныя числа, то пришлось бы рѣшить совмѣстныя неравенства
я+^>0, ?+»•*> о,
которыя дадутъ три предѣла для і.
Если всѣ эти предѣлы одного смысла, то: 1) когда всѣ они низшіе, то нужно давать і всѣ цѣлыя значенія, большія большаго изъ нпхъ; 2) если всѣ три предѣла высшіе, то надо давать і всѣ цѣлыя значенія, меньшія меньшаго изъ нихъ; въ томъ и другомъ, случаѣ ур—ніе имѣетъ безчисленное множество цѣлыхъ положительныхъ рѣшеній. Если предѣлы не всѣ одного смысла, то нужно давать I всѣ цѣлыя значенія, содержащіяся между этими предѣлами: число цѣлыхъ положительныхъ рѣшеній будетъ, слѣдовательно, ограниченное. Наконецъ, если предѣлы получатся противорѣчащіе, то ур—нія не имѣютъ цѣлыхъ положительныхъ рѣшеній.
Примѣръ. Рѣшить ур—нія
15а: Зэу 35& = 385, 6а: -|~ 9у-|~ 8^=104.
Всѣ коэффиціенты перваго ур—пія имѣютъ общаго множителя 5, на который и сокращаемъ это ур—ніе, послѣ чего получимъ систему
Зя4-7уЦ-7/= 77,
6х-|-9у-|- 8^=104. ѵ
Въ каждомъ изъ этихъ ур—ній въ отдѣльности коэффиціенты при неизвѣстныхъ числа первыя между собою; стало быть, возможно, что ур—нія имѣютъ цѣлыя рѣшенія. Предварительно сдѣлаемъ нѣкоторыя упрощенія. Въ пер-
26*
вомъ ур—ніи коэффиціенты 7, 7 п 77 дѣлятся на 7; раздѣливъ обѣ части на это число, найдемъ ур—ніе
замѣчая, что у должно быть цѣлымъ, полагаемъ у=х\ откуда х = 7я\
а уравненіе принимаетъ видъ
За/у# — 11 • • • (1)*
Во второмъ уравненіи коэффиціенты 6, 8 и 104. дѣлятся на 2; по сокращеніи на это число, получимъ
3Ж4_^_|_4^=52:
такъ какъ | должно быть цѣлымъ, то положивъ 5 =У',откуда у—2у', имѣемъ
’ Зх-|-9у'-|-4.г = 52 . . . (2') г
Внося въ ур. (V) 2у' вмѣсто у, а во (2') 7х( вмѣсто х, найдемъ:
Зх'-|“2у' + # = П, 21ж'-}-9у'4-4я = 52. с
Умноживъ первое изъ этихъ ур—ній на 4 н вычтя второе, мы исключимъ е и получимъ (по умноженіи на — 1):
Эя'-}-у' = 8, откуда у' = 8— 9я'.
Отсюда видно, что всякому цѣлому хг соотвѣтствуетъ цѣлый у'. Внося эту величину у' въ ур—ніе Зхг-\-2у'-р^ = И, наюдимъ
— 15я' -г =— 5, откуда
—5Н-15х',
слѣд. цѣлому я' соотвѣтствуетъ и цѣлый 2. Такимъ образомъ, у* и 2 выражены черезъ х\ самый же х' произволенъ. Находимъ теперь формулы для я, у, онѣ будутъ
х = 7х\ у —16 — 18я\ — 5 15 х\
гдѣ х'—произвольное цѣлое число.
Если надо имѣть цѣлыя положительныя величины неизвѣстныхъ, то рѣшаемъ неравенства
7я'>0, 16 —18я'>0 и — 5 + 15я'>0/
откуда
О,
х'
8
9’
X
Предѣлы одного свойства должно быть/
1\ -
I приводятся къ одному: слѣдовательно
8 п« 9’
а какъ между этими предѣлами нѣтъ цѣлыхъ чиселъ, то заключаемъ, что уравненія не допускаютъ цѣлыхъ положительныхъ рѣшеній,
404, Второй случай. Если коэффиціенты ас' — саг и Ъс' — сЪ\ имѣютъ общаго множителя й, который не дѣлитъ <№— сИ\ ур. (3) не будетъ имѣть цѣлыхъ рѣшеній, а слѣд. и данныя уравненія не будутъ ихъ имѣть.
Примѣръ. Такъ, уравненія
5х4-4і/ —3^=11, 4х 4” 4” = 26
имѣютъ, каждое, коэффиціенты при х, у, # первые между' собою, но не допускаютъ цѣлыхъ рѣшеній. Въ самомъ дѣлѣ, умноживъ первое на 3 и сложивъ со вторымъ, найдемъ
19х4“13у = 59,
въ которомъ коэффиціенты при х п у имѣютъ общаго множителя 19, на который 59 не дѣлится.
Точно также не имѣютъ цѣлыхъ рѣшеній и ур—нія, выводимыя изъ данныхъ исключеніемъ х пли у. Первое было бы
19у4~57хг=86, или у4-3л = ^;
а второе
19х — 57я= — 27, /или
оба неразрѣшимы въ цѣлыхъ числахъ.
405. Третій случай. Если всѣ три количества ас’—са', Ъс*— сЬ' и <іс’ — сЛ' имѣютъ общаго множителя й, то раздѣливъ все ур—ніе на й и назвавъ частныя отъ раздѣленія этихъ количествъ па й буквами т, п и р, получимъ ур—ніе
тх-\-пу =р^
Если т и п—числа первыя между собою, то найдемъ цѣлыя рѣшенія для х и у вида:
х = а — пі, у = Э + і
Подставляя въ одно изъ данныхъ уравненій, напр., въ 1-е, получимъ ур—ніе въ * и если оно допускаетъ цѣлыя рѣшенія, они будутъ вида:
Подставляя выраженіе для І въ формулы % и у, выразимъ всѣ три неизвѣстныя черезъ і’; итакъ
а; =ж= (а — п5) — «>
У = (? +»»?)+ тгг';
*=т+#'.
Цѣлыя значенія і' дадутъ таковыя же п для х, у и г.
Примѣръ. Пусть даны ур—нія
6я — 7у + 2^=21 . . .(I)
8л* 4“ 5у -|-6^ = 49 . . . (2),
Исключивъ я, находимъ —
10х — 26]/ = 14.
или, по сокращеніи на 2:
5 а? — ІЗу = 7, откуда:
я = 4 — ІЗі, у = 1— 5/.
Подстановка въ (1) дастъ:
— 43^ + 2^ 4,
Положивъ у = і\ откуда I = 2Г, получимъ
— 43/' 4~ & -- 2: слѣдовательно
г = 2-|-43і’, і = '2і’.
Окончательно:
ч
х = 4 — 26Г, у = 1 — 2 4- 43К
Легко видѣть, что данная система не допускаетъ цѣлыхъ положительныхъ рѣшеній.
406. Задача. Найти число, которое при раздѣленіи на 11, на 17 и на 23, давало бы послѣдовательно остатки 4, 9 « 10.
Обозначивъ частныя соотвѣтственно буквами у п а искомое число буквою К, имѣемъ:
М . 4 К і 9 I* іЛ
И-37 I 11’ 17~’УТп’ 23“ ' 23’
или - 1
К = 11й?4^4, К = 17у-р^! Ьт = 23^4“ Юі *
откуда получаемъ два уравненія:
11^-1-4 = 171/+ 9 и 1 Іх + 4---23^Ц- 10,
которыя можно представить въ видѣ:
Ш —17і/=5 . . (1) 11х- 23я=6 . . . (2).
Изъ (1) имѣемъ:
х = Ц Щ = 2у + = 2у+51,
полагая 1 = і, откуда у = 1 — Ш.
• г
Подставляя вмѣсто*у его величину въ выраженіе а?, получимъ
а?“2 —17/, и
у = 1 — ІИ.
Подставляя выраженіе х въ ур. (2), находимъ
11(2 — 170 — 23^ = 6, пли 187^4-23^=16. . .(3).
Л 16 — 187/ , 16 — 3/ .
Отсюда я ——— = — 8/4-------------23— = — 8^4*$»
полагая ^3—= Г, ' или. 32 4~ 232' = 16, откуда
, 16 — 23*' _ 1+і' 14-Г '
і ~ —3— = 5 — 8/4----------з- = 5 — 8/ -|- 2 , полагая —— = I •
Изъ послѣдняго ур—нія имѣемъ: 2' =— 14^32", Обратная подстановка даетъ послѣдовательно:
і = 5 — 8(— 14- 32") 4- Г = 13 — 232";
я = — 8(13 - 23/") — 1 + Ы" = — 105 + 1872"*
Остается х и у выразить въ зависимости отъ 2"; получимъ:
-ж = — 2194-3912", у = — 142 4-2532", = —105 4-1872".
Взявъ для К одну изъ трехъ формулъ этого числа, напр. М = 11я?—[—4 и подставивъ вмѣсто х найденное выраженіе, имѣемъ:
К = 11(— 219 + 3912") 4- 4 = — 2405 + 43012"*
Это и есть общая формула всѣхъ чиселъ, имѣющихъ то свойство, что при дѣленіи на 11,17 и 23, они даютъ остатки, соотвѣтственно равные 4, 9 к 10. Полагая 2" = 0, 1, 2, . . . , — 1, — 2, . . , находимъ цѣлый рядъ чиселъ этого свойства. Такъ:
I = 0 даетъ К = — 2405;
/=1 даетъ X = 1896 и т. д.
Если бы требовалось найти наименьшее положительное число даннаго свойства, то оно соотвѣтствовало бы наименьшему цѣлому Г, дающему для И—-положительное значеніе. Такое і" опредѣляется изъ условія:—24054-4301 2">0, и есть 2"=1; соотвѣтствующая'величина К, равна 1896.
407* Подобнымъ же образомъ рѣшается всякая система ур—ній, въ которой число неизвѣстныхъ однимъ больше числа уравненій, потому что послѣдовательныя исключенія неизвѣстныхъ всегда приведутъ къ одному ур—нію съ 2 неизвѣстными. Пусть для примѣра дана
Задача. Найти число, которое при раздѣленіи на 6, 7 и 8 давало бы послѣдовательные остатки 5, 1, 0 и 5.
Обозначивъ искомое число буквою X, а частныя по порядку буквами х, у, з и и, находимъ:
Х = 5^4-3, Х = 6у + 1, Я = 7*, Х = 8«4-5;
откуда 3 ур—нія
1. 5х—6у =— 2,
2. 5х — 7я= — 3, 3. 5х — 8и=2.
Въ данномъ случаѣ нѣтъ даже надобности въ исключеніи неизвѣстныхъ, ибо и безъ того каждое ур—ніе содержитъ только два неизвѣстныя.
Рѣшая ур—ніе-5х— 6у =— 2, находимъ:
у = 24^52, я; =24^ 62.
Вставляя я=24“62 въ уравненіи (2), получаемъ ур—ніе
7-5— 302= 13, изъ котораго находимъ
я = — 11 4- 302', 2 = — 34-72'.
Выразивъ хну черезъ *', имѣемъ
х—— 16 + 42*', у = — 13+ 35*'. *
Вставляя вмѣсто х его выраженіе черезъ *' въ ур. (3), имѣемъ
210*' —8м = 82, откуда:
*'=1 + 4*", м= 16 + 105*”; ’
Выражая и остальныя неизвѣстныя черезъ *'', получаемъ
.г = 26 + 168*", у = 22 + 140*”, г = 19 + 120*”, и= 16 4~ Ю52".
Вычисляя X, проще всего по формулѣ = 7-гг, находимъ: Х = 133 + 840/".
Итакъ, искомыя числа имѣютъ видъ 133+ 840/; изъ нихъ наименьшее положительное = 133.
3. Рѣшеніе въ цѣлыхъ числахъ уравненія, содержащаго болѣе двухъ неизвѣстныхъ. '
408. Ограничимся разсмотрѣніемъ случая одного уравненія съ 3-мя неизвѣстными.
Пусть будетъ ах-\-Ъу + <?л = 4 такое ур., въ которомъ а, Ь, с и й—-числа цѣлыя. Прежде всего необходимо, чтобы коэффиціенты а, Ь и с не имѣли такого общаго множителя, который не заключается въ <?; иначе ур. не могло бы быть рѣшено въ цѣлыхъ числахъ. Если же эти коэффиціенты имѣютъ общаго множителя, содержащагося въ Л, то его удаляютъ сокращеніемъ; затѣмъ могутъ представиться два случая: 1) изъ трехъ коэффиціентовъ а, Ь и с, по крайней мѣрѣ, два — первые между собою (или а и &, пли а и с, или Ь и с), какъ напр. въ ур—ніи 12^+11у+15-г= 141, гдѣ 12 и 11—числа первыя между собою; 2) или каждые два коэффиціента имѣютъ общаго множителя, такъ что . нѣтъ ни одной пары коэффиціентовъ первыхъ между собою; таково ур—ніе
12л?+ 15у + 20^= 181,
въ которомъ 12 и 15 дѣлятся на 3; 12 и 20—на 4, а 15 и 20—иа 5.
409. Первый случай. Пусть а и Ь—числа первыя между собою; перенесемъ сз во вторую часть и приложимъ къ ур—нію
а# + Ьу = Л — с-г
пріемъ § 394, принимая на время -г за извѣстное; такпмъ образомъ мы найдемъ формулы ,
х = і— Ь/, у = [} + «/,
въ которыхъ а и 3—цѣлые относительно з полиномы первой степени. Давая -г и / произвольныя цѣлыя значенія, найдемъ цѣлыя значенія п для х н у.
Если неизвѣстныя должны быть, сверхъ того, положительными, то даемъ -г произвольное, но цѣлое и положительное, значеніе, и полагаемъ
а — 6/ > 0 и ? + а/ > О,
откуда получимъ для / два предѣла; смотря по тому, будутъ ли эти предѣлы одного смысла или разнаго, согласные между собою или противорѣчащіе, получится неограниченное число цѣлыхъ положительныхъ рѣшеній для х и у, или же ограниченное, или же такихъ рѣшеній совсѣмъ не будетъ. Такимъ образомъ поступаютъ по отношенію ко всякому цѣлому положительному значенію
Примѣръ. Пусть дано ур—ніе
5х+ 8у— 12л? = 41.
Такъ какъ 5 и 8 числа первыя между собою, то указанный пріемъ примѣнимъ къ этому уравненію. Итакъ
5гг —8у = 41 + 12^ откуда
х = 41+Ш-^г = 8 + 2а _ 2у +1±.2? + 2,. о о
ИЛИ
х — 8 + 2^ — 2у 4-
полагая или 2у— 5 / = — 1 — 2я. Отсюда
полагая —5— = или і = 1 + 2Г.
Это значеніе, подставленное въ дастъ
у = — #4” 2 4’4^-|-й/ или у ——
Подставляя найденныя для у и I величины въ формулу 2, получимъ
2 = 84-2^4-2^ —4—10Г4-1+2Г = 5-р4^~ 8Г.
Если ищемъ для 2, у и 2 только дѣляя предѣлы для і\ получимъ
положительныя цѣлыя значенія, то опре-
я— 2 “Г
^8
41 ✓
—19’ а какъ для % беремъ только по-1 ш
л л 4я4-5^* — 2 х
Отсюда: —— > —— > слѣд. я о о
ложительныя значенія, то, включая сюда н 0, имѣемъ:
я = 0, 1,2. . . до 4"
2
При # = 0 находимъ ^г>> —и О
Г = 0, что дастъ: 2 = 5 и ?/ = 2.
При # = 1 имѣемъ > — і и V < О
І' < слѣд. можно положить только
1$; сл. можно взять ^' = 0 и і'= 1,
что дастъ:
5
При г —2 находимъ 4'>0 и ^<1^; слѣд. условіе Г>0 не исключаетъ равенства) п =
При Іг = 0 имѣемъ: */ = 0, 2=13;
» ^=1 х> ^ = 5, ‘ 2= 5.
можно взять Г = 0 (ибо
При я = 3 получаемъ і' > и < 2 э слѣдов. можно взять: і' = 1 и ^ = 2, что дастъ:
Г=1, а .у = 4, х = 9; ^ = 2. . .у — 9, а= 1.
Продолжая такимъ образомъ, получимъ сколько угодно системъ цѣлыхъ положительныхъ рѣшеній.
410. Второй случай. Положимъ теперь, что между тремя коэффиціентами нѣтъ нп одной пары взаимно-первыхъ. Назовемъ буквою Н общаго наиб. дѣлителя, напр., для а и д; п пусть а" и Ъ' будутъ* частныя отъ раздѣленія а и 6 на к. Ур—ніе будетъ
Аа' х -|- ІіЬ'у -(- ся = откуда
а'х-\-Ъ'у=~^-
Полагая, что первая равнялась цѣлому числу,
часть есть число цѣлое, необходимо, чтобы и вторая напр. въ такомъ случаѣ
а'х-{-Ъ'у — / . . . (1)
и или сз -|- кі = с? . . . (2).
г
Но а* и і' первыя между собою, какъ частныя отъ раздѣленія а и Ъ на нхъ общ. напб. дѣл. А; а потому ур. (1) имѣетъ цѣлыя рѣшенія вида:
я=а — Ъгі' и у = ^-|-а7' . . .(3)
гдѣ а п суть цѣлые полиномы первой степени относительно I.
Затѣмъ, замѣчая; что с и А—первыя между собою’ числа, потому что множитель А, будучи общимъ для а и А,, не дѣлитъ с; усматриваемъ, что ур. (2) имѣетъ цѣлыя рѣшенія вида
я = у — кі" н і = 3 -|- сІ'( . . . (4),
Подставляя эту величину I въ формулы х и у, мы представимъ эти неизвѣстныя цѣлыми полиномами первой степени въ I” и Г; между-тѣмъ какъ я зависитъ только отъ
Если вопросъ требуетъ еще, чтобы х, у и я были положительными, то должно выразить, что' величины' ихъ больше нуля? Въ ’ полученныхъ неравенствахъ нужно стараться изолировать і' и I" п такимъ образомъ получить предѣлы для этихъ неопредѣленныхъ; однако, изъ теоріи неравенствъ мы знаемъ, что это не всегда возможно.
Примѣръ. Пусть дано ур—ніе
6я—10^^15^ = 37.
Замѣчая, что 6(и 10 имѣютъ общаго дѣлителя 2, даемъ ур—нію видъ:
о _ 37 - 15я
З# — 5у = —------->
и полагаемъ, что . -ь
Зл;— 5$ = I и —= / или 15^ + 22 — 37-&
Изъ- перваго находимъ
у = 1— 31г и х = 2/— 5/'.
Изъ второго имѣемъ
г==1—.2/" и / = 11 + 15/''.
Вставляя эту величину і въ выраженія у п х, получимъ у =11+ 15/"— ЗГ и а; = 22+ 30/" —5/'; *
достаточно дать іг и /" какія угодно цѣлыя значенія, и такимъ образомъ получатся цѣлыя значенія х, у и
Чтобы выдѣлить только положительныя, полагаемъ
1 —2<">О; 114-15Г —Зі'>0; 22 + ЗОГ—5Г>0.
Первое даетъ /"<--• Два другія можно написать такъ:
3/' — 15/" <11 и 5/' — 30/" < 22,
или, умноживъ первое на 2:
6/' — 30/" <22 и 5/' —30/" <22.
Изъ условія 2/"<1 имѣемъ 30/" <15. Складывая это неравенство съ каждымъ изъ двухъ предыдущихъ, находимъ условія 6/'<37 и 5/'<37,
изъ которыхъ второе заключается въ первомъ. Итакъ, количеству /' можно давать только значенія
+ 6, + 5, + 4, . . . до —
Изъ неравенствъ въ V и /" находимъ 6/'—22 5/'— 22
1 >-зб~ и 1 >—зб-
При положительныхъ /' первый предѣлъ больше второго, поэтому нужно удержать первый предѣлъ. При отрицательныхъ і'—наоборотъ, при чемъ для I” слѣдуетъ брать только величины между 0 и этимъ вторымъ предѣломъ.
Такимъ образомъ, находимъ: г
Для /' = 6, 5, 4,—нѣтъ соотвѣтствующихъ значеній для
При:
і' = 3 имѣемъ:
Г= 2 1 » » • « • * • • і'=— 2 »
» і'=г — 3 »
»
Г = —8 »
»
»
И т. д.
і" = 0; откуда х
І" = 0; »
7; у= 2; г=1.
12; 5; 1.
Г = 0; » X
-1;
0;
— 1 »
Г = 0; > Х
— 1; »
— 2: »
32; у=17; Я == 1.
2; 0. -» 3.
37; 20; 1.
5; 3.
62; у =35; г= 1.
32; 20; 3.
2; 5; 5.
ОТДЪЛЪ ТРЕТІИ.
УРАВНЕНІЯ и НЕРАВЕНСТВА ВТОРОЙ п ВЫСШИХЪ СТЕПЕНЕЙ.
ГЛАВА XXVIII.
Мнимыя величины и дѣйствія надъ ними.
411. Происхожденіе мнимыхъ количествъ* Мы видѣж что извлеченіе корня привело къ открытію двоякаго рода новыхъ величинъ—несоизмѣримыхъ п мнимыхъ. Съ величинами перваго рода мы уже ознакомились; переходимъ къ изученію величинъ второго рода—мнимыхъ.
Пусть требуется извлечь ]/— 49; очевидно, что по абсолютной величинѣ этотъ корень равняется 7; по онъ не можетъ быть равенъ ни + 7, ни — 7, ибо и(4^7)ац (—7)а даютъ +49. Такимъ образомъ, квадратный корень изъ отрицательнаго числа не м. б. выраженъ никакимъ положительнымъ и никакимъ отрицательнымъ числомъ. Къ тому же заключенію придемъ и относительно /—81, /—"17, вообще относительно 2/— а2\ Итакъ, вообще: корень четной степени изъ отрицательнаго числа не м. б* выраженъ ни положительнымъ, ни отрицательнымъ числомъ, и представляетъ поэтому новый разрядъ величинъ: ихъ называютъ мнимыми, въ отличіе отъ обыкновенныхъ положительныхъ и отрицательныхъ чиселъ, называемыхъ дѣйствительными.
412. Приведеніе мнимаго количества къ виду а.у/— 1. Всякое мнимое количество приводится въ зависимость отъ простѣйшаго мнимаго выраженія: /— !• Въ самомъ дѣлѣ, имѣя мнимое выраженіе /—49 п разложивъ —49 па множители 49\(—1, а затѣмъ примѣнивъ правило извлеченія корня изъ произведенія, послѣдовательно найдемъ:
= |/49у—’і = ^/49хі =±7 • /—И
и вообще
Отсюда видно, что всякое мнимое количество .можно представить подъ видомъ произведенія изъ/—1 па нѣкоторое положит. или отрицат. (соизмѣримое или несоизм.) число; слѣд. мнимое число составляется изъ /— 1 точно такимъ же образомъ, какъ дѣйствительное число изъ положительной или отрицат. единицы, Поэтому /— 1 разсматриваютъ какъ нѣкоторую новую, особаго рода, единицу, п называютъ ее мнимою единицею* Гауссъ предложилъ обозначить ее буквою г. Знакъ і Коши называлъ ключей.
Такимъ образомъ, вмѣсто 5|/—1 пишутъ 5г; вмѣсто 4=^/—1 пишутъ і
413. Общій видъ всякаго числа. Мнимое выраженіе вида а 4“ Ъі, состоящее изъ дѣйствительной части а н чистаго мнимаго члена Ы, называется коль плекснымъ количествомъ (т.-е, составнымъ) пли просто колплексолп; въ немъ а и Ь — дѣйствительныя количества, причемъ Ь называется коэффиціентомъ при мнимой единицѣ. Два комплексныя количества: и а — Ц различаю-
щіяся только знаками коэффиціента Ь, называются сомряжеямылги.
Комплексное количество есть самая общая форма чиселъ: въ немъ заключаются дѣйствительныя и чистыя мнимыя числа какъ частные случаи. Въ самомъ дѣлѣ, полагая Ь=О, получаемъ дѣйствительное количество а; полагая же а=О, находимъ чистое мпнмое количество Ьі.
Модуль. Абсолютная величина квадратнаго ‘ корпя изъ суммы квадратовъ дѣйствительной, части и коэффиціента при мнимомъ знакѣ т.-е. /а2 4~ иаз. модулемъ комплекснаго выраженія. Такимъ образомъ:
модуль комплекса 3 — 4і равенъ /3*4-4* = 5;
> э 7 —8і > /7* 4> 82 =/113?
Еси въ выраженіи положить Ь = О, то^ комплексъ дастъ дѣйствительна количество а: модуль же обратится въ /а2 = а, т.-е. модулъ дѣй-етвытелъмаю количества равенъ ею абсолютной величинѣ.
414. Степени і. Прежде всего мы должны разсмотрѣть возвышеніе въ степень мнимой единицы і. . '
1. Очевидно,, /= (/-— 1)1 = /— 1.
2. і* = (/—I)2; нахожденіе результата можетъ повести въ данномъ случаѣ къ нѣкоторымъ недоразумѣніямъ, и потому требуетъ разъясненія. По опредѣленію корня имѣемъ (/—1)2 =—1; съ другой стороны: (/~1)2 = /~ 1.у—1=/4*1=4=1; спрашивается, что же брать для і2: — 1 или
1? Ёезу разъяснилъ это недоразумѣніе, замѣчая, что когда мы не знаемъ происхожденія подкореннаго количества въ формулѣ /а2, то должны брать для корня двойной знакъ, т.-е. полагать = но когда знаемъ происхожденіе подкореннаго количества, т.-е. знаемъ, получилось ли а2 отъ умноженія (4-й)(-^а), или же отъ умноженія (—а)(—а), то корень слѣдуетъ брать съ однимъ знакомъ: въ первомъ случаѣ съ второмъ съ —. Этотъ случай, очевидно, относится къ выраженію (/—1)2=/— I./—1=/(—1)*=/4-1: здѣсь подкоренное число -/1 получилось отъ возвышенія въ квадратъ —1, а не 4-1, а потому для /4-1 данномъ случаѣ надо брать значеніе: — 1. Этимъ всякое недоразуменіе устранено. Итакъ, і2 =— 1.
3. р = г2 . і = — 1 . ]/ — 1 — — ]/ — 1, или — і.
4. Р = Р —1 х —1=4-1.
Возводя затѣмъ і въ слѣдующія высшія степени, найдемъ прежнія значенія степеней. Такъ:
р=р . . г=4“гі Р=і* . • —1 = -—1; г’=ге . г=—і;
Р = Р . Р — 1 и т* д.
Можно доказать, что и при дальнѣйшемъ увеличеніи показателей будутъ періодически повторяться все тѣ же четыре" значенія степеней, т.-е. 4-і, —1, — г и +1. Въ самомъ дѣлѣ, по отношенію къ дѣлителю 4 всѣ цѣлыя числа можно разбить на четыре группы: 1) числа, дѣлящіяся на 4 безъ остатка; 2) числа, дающія при дѣленіи на 4 въ остаткѣ 1; 3) числа, дающія при дѣленіи на 4 въ остаткѣ 2; 4) дающія при дѣлителѣ = 4, остатокъ 3. Всѣ они заключаются, поэтому, въ четырехъ формулахъ: 4и, 4п~рі, 4п-|~2, 4п-|-3, гдѣ п—какое угодно цѣлое положительное число/
Давая показателю каждую изъ этихъ четырехъ формъ, получимъ послѣдовательно:
Отсюда заключаемъ: всѣ четныя степени і дѣйствительны, и равны: -}-1, когда показатель есть число кратное 4, и когда четный показатель не дѣлится безъ остатка на 4; всѣ нечетныя степени і мнимы, и равны: -р Ъ когда показателъ при дѣленіи на 4 даетъ оста- ' токъ 1, « —і, когда рпи дѣленіи показателя на 4 получается остатокъ 5.
Напр., при дѣленіи 17 на 4 остатокъ =1, слѣд. Р7 = -рг, и т. д.
415. Теорема. Зіиобы комплексъ а-\-Ы равнялся нулю, необходимо и достаточно, чтобы дѣйствительная часть и коэффиціентъ при і равнялись нулю, т.-е. чтобы а = О и Ъ = О.
Въ самомъ дѣлѣ, равенство а + Ъі = О даетъ а = — Ы, откуда, возвышая обѣ части въ квадратъ, и замѣчая, что
Р = —1, имѣемъ: а2 = 5*.— 1, или а2 =— Ь2, откуда а8-4 Ь* = 0.
Но сумма квадратовъ двухъ дѣйствительныхъ количествъ а и Ъ тогда только можетъ равняться нулю, когда каждое количество отдѣльно равно нулю; слѣд. а = 0 и Ь = 0.
Обратно, если а = 0 и Ь = 0, то оба члена комплекса обращаются въ О, и слѣд. а-{-Ьі = О.
416. Теорема. Чтобы два комплекса были равны, необходимо и достаточно, чтобы дѣйствительныя части и коэффиціенты при і были отдѣльно равны между собою.
Въ самомъ дѣлѣ, изъ уравненія
а 4- Ы = а 4~ рі
по перенесеніи всѣхъ, членовъ* въ первую часть и по вынесеніи і за скобки, имѣемъ
(« — а)-}-(Ь — ^)і = 0, • • • • • л
откуда по предыдущей теоремѣ имѣемъ: , »
а — а = О и Ь — — О, или а^а и 6=^. "
Слѣд- сказанное условіе необходимо. Оно и достаточно, ибо при а = х и Ь = оба комплекса становятся тождественными.
Дѣйствія надъ комплексными выраженіями.
• «
417. Условившись правила, найденныя нами для дѣйствій надъ дѣйстви-телышж количествами, распространять и на мнимыя, мы придёмъ къ тому замѣчательному выводу, что результатъ всякаго дѣйствія надъ комплексами ярысодитъ къ выраженіямъ того же вида.
1. Сложеніе. Пусть требуется сложить а 4-6/ съ с4-Л’* Прилагая сюда равно сложенія дѣйствительныхъ количествъ, найдемъ: (а-|-Ьі)-Р (с-{-<й) = = а 4" Ъі Ч~с или, перемѣняя порядокъ членовъ и выводя і за скобки,
ю лучимъ:
(«4"^г) 4~(с4“^0 = 4" •»,
выраженіе того же вида какъ и слагаемыя.
Примѣръ. (5 4-4г) 4“ (—?— 90 = — 2— 5**
Примѣчаніе. Сумма двухъ сопряженныхъ комплексовъ есть величина дѣй-ствтельная; въ самомъ дѣлѣ: ’ 1
(а Ц— Ъг) 4~ (а — 6г) “ 2а. *
2. Вычитаніе. Вычитая с4“Л’ изъ а-^-Ы, имѣемъ
(а4“ &0 — (с 4“ <?0 = а 4“ — с — & ~ (а — с) + (Ь — Л)г,
шражешв того же вида, что и данныя.
3. У вношеніе. Примѣняя правило умноженія многочленовъ, данное для дѣй-спвтелыонъ количествъ, и замѣчая, что г3 = — 1, найдемъ:
< а—Ы) (с—<К)=ас-{-Ьсі 4" а&і 4" = ас-]- Ьсі 4" — Ь<1 = (ас—Ь&) 44
4~ (Ьс 4- сгсі) . г,
выраженіе того же вида, какъ и сомножители.
ТО,
Такъ какъ произведеніе двухъ комплексовъ есть выраженіе того же вида,
тмио 4
въ это произведеніе на третій комплексъ, получимъ снова выраженіе
комплексной формы и т. д. Слѣд. теорема справедлива для какого угодно числа
^.1
мнимыхъ множителей.
Примѣръ. (3 + 5»)(4 — 7І)= 12 + 20І — 2Ь’4-35 =47 - і.
Примѣчаніе. Взявъ сопряжеиные комплексы, имѣемъ:
(а 4- Ъг)(а — Ы) = а* — &’ . і2- - аа 6’, т.-е. произведеніе двухъ сопряженныхъ комплексовъ есть дѣйствительное положительное количество, равное квадрату ихъ общаго модуля.
4. Дѣленіе. Пусть требуется раздѣлить а4~Ьі па Изображая част-, ное въ видѣ дроби, имѣемъ
а + Ьі с + ді ’
Для уничтоженія мнимости знаменателя множимъ числителя я знаменателя на с — <1І (выраженіе, сопряженное съ знаменателемъ), и находимъ послѣдовательно:
а -\-Ъі_(а 4- &г)(с — &і)_(дс -|- &гі) 4- (Ъс — асЦі_ас + [ 5с — ай .
с + йі ™ (с + — йі) о2 + йа сй + й2 еа 4“
,т 10+15» (10 + 150(1-20 40—5» й .
Примѣръ. ------------------5— - 5 =8-*.
5. Возвышеніе въ степень. Такъ какъ возвышеніе въ положа-
тельную степень совершается рядомъ послѣдовательныхъ умноженій, а произведеніе комплексовъ есть выраженіе того же вида, то и степень комплекса имѣ-етъ тотъ же видъ* Слѣд.
(а 4~ Ь(Г — (а Ьг)(а 4- 5і) . . * (а 4“ Ьі) = Р 4“
гдѣ Р и 0—дѣйствительныя количества.
Примѣры. I. (а 4~ &02 = а2 4“ 4" = 4"
п. (і—/з . і)3=і — з. /з. &4-з . (/з (/з. І)3
= 1 — 3/3 . і — 9 4-3/3 . І = —8.
Если показатель степени—цѣлое отрицательное число, то
, . , я I 1 р /а — М + № _________________пій;
(а Ь») — _[_6^ — — (аі_|_б2)й ~
слѣд. степень имѣетъ тотъ же видъ.
6. Извлеченіе корня; Пусть требуется извлечь квадратный корень изъ комплекса а-\-Ыг Докажемъ, что результатъ дѣйствія и въ этомъ случаѣ будетъ комплексъ того же вида, т.-е. что
= . (1).
Предложеніе это будетъ доказано, если окажется возможнымъ найти для х н у такія дѣйствительныя значенія, которыя удовлетворяли бы этому равенству. Возвысивъ обѣ части въ квадратъ для освобожденія первой части отъ радикала, нолучпмъ ур.
—^34_2х,#і> * - (2).
Мы знаемъ (§ 416), что такое равенство возможно только тогда, когда дѣйствительныя и мнимыя количества отдѣльно равны между собою; слѣд. ур. (2) распадается на два:
х* — у2 = а и 2ху — (3).
Такимъ образомъ неизвѣстныя х и у должны удовлетворять двумъ уравне- • ніямъ второй степени, изъ которыхъ они всегда могутъ быть опредѣлены. Для этого возводимъ оба ур—нія въ квадратъ и складываемъ:
я* 4~ У1 ~ 2хгу^ 4я3#3 — а2 + или (я3 у3)3 = а3 4“ Ъ\
Извлекая изъ обѣихъ частей квадратный корень, имѣемъ
4~ У3 = ]/а2 4“
Передъ радикаломъ надо брать одинъ знакъ 4~, потому что первая часть, какъ сумма квадратовъ дѣйствительныхъ количествъ, всегда положительна. Такимъ образомъ, система ур—ній (3) замѣняется слѣдующею
я3 4* у~ — 4“ 6* - и я2 — у* =
Складывая сначала, а потомъ вычитая эти ур—нія, находимъ
откуда
2х3 — а 4~ 4“"
2у2= — а4-/а*4-62,
Такъ какъ абсолютная величина }/а24-Ь2 больше абсолютной величины а или — а, я корень этотъ находится подъ верхнимъ радикаломъ со знакомъ 4”» то подкоренная величина въ выраженіяхъ дну положительна, а потому я и у—дѣйствительны. Такимъ образомъ, всегда можно найти для х и для у дѣйствительныя количества, удовлетворяющія ур—нію (1), а потому преобразованіе, выражаемое этимъ ур—емъ, всегда возможно.
Уравненіе 2ху = Ь показываетъ, что когда Ь положительно, х н должны имѣть одинаковые знаки, когда же Ь отрицательно, знаки х и у должны быть разные. Поэтому, разумѣя подъ Ь—абсолютное число, и слѣдов. знаки при Ь— окончательными, имѣемъ двѣ формулы:
/—ГГ- і Гі/а + 1'7/2 । 1/— а + V л* + О2
уа4-йі = ± р . *
ш іи
П р н м ъ г ы: I. Пусть требуется преобразовать |/5 -р 1-^ Полагая въ формулѣ (I) а = 5, Ъ = 12, найдемъ:
|/э 4~* І 2 г = —[—
П. Извлечь квадратный корень изъ 3 — 4/
Полагая въ формулѣ (И) а = 3 и Ъ = 4, найдемъ:
Здѣсь мы разсматривали только квадратные корни изъ отрицательныхъ чи-селъ и изъ комплексовъ. Далѣе будетъ указало, что и корни какого угодно порядка представляютъ комплексы того же вида, т.-е. а 4~Ьг.
418. І^шложенія, Приводимъ нѣкоторыя приложенія, съ цѣлью показать, какимъ образомъ употребленіе комплексныхъ выраженій даетъ возможность безъ труда достигать результатовъ, выводъ которыхъ безъ помощи этого рода выраженій представлялъ бы значительныя трудности.
Теорема ]. Если данное число есть сумма двухъ квадратовъ, то и квадратъ ею также есть сумма двухъ квадратовъ.
Пусть к есть число, равное суммѣ двухъ квадратовъ а2 и У2, т.-е.
« — а2 -4- Ь2.
Я , ( ;
Замѣтивъ, что а24~Ь2 есть произведеніе двухъ мнимыхъ сопряженныхъ выраженій «4”^ » замѣняемъ это выраженіе слѣдующимъ:
п — (а (я — Ьі).
Возвышая обѣ части въ квадратъ, имѣемъ:
п2 = (а 4“ Ьг)2 • (а ““ Ь*)* — (а2 — Ь2 4~ 2лЬі)(а2 — Ьа — 2аЫ) = = (“* — Ь2)24-4а2Ь2 = (а2 - 62)2 4-(2аЬ)*,
т.-е. п* есть сумма квадратовъ количествъ: а2— Ь2 и 2аУ Такимъ образомъ, не только теорема доказана, но полученная формула указываетъ и самый способъ разложенія- п2 на сумму двухъ квадратовъ.
Пусть, наприм., п = 5. Это число есть сумма двухъ квадратовъ: 22—|— 1-. Полагая а = 2 и Ь —I, но найденной формулѣ имѣемъ: гг (22—1-)"4~ (2.2.1)2, или 25 = 32 + 4*.
Положимъ теперь п = 25, а = 4, Ь = 3. по той же формулѣ найдемъ: 252 иди 625^(42 —32)2-4(2.4.3)2 = 734-242; и т. д.
Теорема II. двухъ чиселъ, изъ которыхъ каждое есть
сумма двухъ квадратовъ, также суммѣ двухъ квадратовъ.
Пусть даны четыре комплекса: а'-ф-Ц а — Ы, «'4^4 а' — Ь'і попарно сопряженные; взявъ произведеніе
(а + Ьі)(а — Ьі)(а' 4“ У 0(а< — ^0»
помноживъ перваго множителя на второй н третьяго на четвертый, найдемъ: (а2 + 62)(а'24-Ь'2). Если же помножимъ перваго на третій и второго на четвертый, получимъ [аа' — ЪЬ' 4~ (аУ 4” . [си/ — ЬУ — («У 4- 6с/)*1 или
(аа — ЬУ)2 4“ (аѴ 4“ Ьс/)2. Слѣд.
(а* + Ьа)(а'2 + У*) = (аа'— 6У)2 + (аУ 4-Ьа')2 , , .(1)
Если умножимъ перваго на четвертый и второго на третій, то произведеніе приметъ видъ: [аа*4“ Ьд'-|-(а'6 — аЬ')г] . [аа'-|- 6Ь' — (&'& —* аУ)г], или (аа' + ЬЬ')34" — аЬ')2. Такимъ образомъ имѣемъ другую формулу:
(а* ьі)(а'і 4- у2) = (о»' 4- ЬЬу 4- (а'Ь — аЬ')2 . . . (2)ь
Формулы (1) и (2) доказываютъ предложенную теорему, показывая вмѣстѣ съ тѣмъ, что разложеніе взятаго произведенія на сумму двухъ квадратовъ можетъ быть исполнено двоякимъ образомъ. Эта теорема была найдена Леонардомъ Пизанскимъ.
Теореи III. Произведеніе двухъ чиселъ, изъ коихъ каждое есть сумма четырехъ квадратовъ, также равно суммѣ четырехъ квадратовъ.
Взявъ тождество
1______1 _ / I_________1_\ । /_1________1_\
а—Ъ а—гГ \а — 6 а — с/'\а — с а—а}
выполнимъ въ немъ три указанныхъ вычитанія и освободимъ его отъ знаменателя; найдемъ
(Ь — Л)(а — с)’= (Ь — с)(а — (7) 4“ (<? — й)(а — Ь).
Положивъ теперь
замѣнимъ въ предыдущемъ тождествѣ а, Л, с и Л ихъ мнимыми выраженіями; волѵчимъ »
гр14- 4~4- 52)Ср'2++г'2 4~ ^*)= (рр' 4" м! 4"гг' 4“ 4"
рч — г5' чр'—5гТ 4~ 4- 8(і’ — ч$г—гр')* 4- (р3’ 4” —3рг— гч Л
что и требовалось доказать.
Теорема эта принадлежитъ Эйлеру. Приведенное доказательство ея проще ірехніго доказательства, даннаго Эрмитомъ и основаннаго также на употре-бдекіі комплексовъ.
ГЛАВА XXIX.
Геометрическое представленіе мнпиыхъ величинъ. — Обобщеніе» основныхъ алгебраическихъ законовъ. — Предметъ Алгебры.
419. Мы уже видѣли, что если взять неограниченную прямую х'х, на пей иѣстную точку О принять за начало, и условиться длинами, откладываемыми вправо отъ О, представлять числа положительныя, то длины, отсчитываемыя влѣво отъ 0. будутъ служить геометрическимъ представленіемъ чиселъ отрицательныхъ. Таіп>, если отрѣзокъ О А будетъ представлять единицу, то отрѣзки, отложенные вправо отъ 0: ОЛ, ОА', О А",... будутъ представлять числа ч-І, ~н2, —3,..-. отрѣзки ОВ, ОВ', ОВ",.., отложенные влѣво отъ 0, изобразятъ отрицательныя числа — 1, — 2, —3,... Точка 0 представляетъ 0. Такимъ образомъ линія л-'л* будетъ представлять всевозможныя дѣйствительныя числа—положительныя и отрицательныя; она называется поэтому осью <тйствителъныхъ< чиселъ, или Онт-стеительною осью.
Спрашивается, какъ представить геометрически чистыя мнимыя п комплексныя (составныя) числа? Проведя черезъ точку 0 прямую уу' перпендикулярно
♦ У
р- '(-Ь+І і 1 +51 < АІ
с 1* 1 /ѣ< г 6
у»* -4 3 -2 -г +1 +2 +5 +4
В" В' в в 0 -і А'х А" А"'
-2і ^““4 Р'(з ;2і)
Р'. 1і) -51 1
к 1 I- - ч -4/
- У'
Черт. 44*
къ опишемъ изъ точки 0 радіусомъ, равнымъ единицѣ длины, окружность; радіусъ ОС будетъ среднею пропорціональною между отрѣзками О А = -+- ] и
— 2
ОВ = — 1 діаметра; слѣд, ОС = (ч-1) . (— 1) = — 1, откуда ОС = I — 1, т,-с* ОС=/. Итакъ, чистыя мнимыя числа і, 2?, 3/,... должно отсчитывать на перпендикулярѣ уу* вверхъ отъ О, а числа — —2/, — 3/,... на томъ же перпендикулярѣ внизъ отъ 0. Поэтому прямая у у' называется осью мнимыхъ чиселъ, пли лооілюю осью.
Пусть требуется теперь представить геометрически комплекс-ное число лч-йі. Для этого на дѣйствительной оси откладываемъ число <7, вправо отъ О, если оно положительно, и влѣво, если отрицательно. Потомъ на мнимой оси откладываемъ число Ы вверхъ отъ 0, если оно положительно , и внизъ, если отрицательно. Изъ точекъ а и Ъі возставляемъ перпендикуляры къ осямъ: пересѣченіе этихъ перпенди
куляровъ и дастъ точку, которая геометрически представляетъ число « + Напр., точка Р представляетъ число Зч-2і, точка Р— число 3 —2г, Р"—число — 4 -|- Зі, и Р'"— число — 3 — Зі. Согласно этому, комплексныя количества изображаются точками, наполняющими всю плоскость по обѣ стороны дѣйствительной оси; отсюда названіе латеральныхъ количествъ, данное /«//ссолга комплекснымъ числамъ. Точку Р называютъ аффиксомъ комплекса Зч-2«; точку Р' — аффиксомъ комплекса 3 —2г и т* д*
Пусть комплексъ а-і-Ъі опредѣляетъ точку М; соединивъ ее съ началомъ и назвавъ ОМ буквою г, изъ треугольника МКО получимъ: ОМ — г—И«2ч-Слѣд., модуль комплекса есть длина линіи ОМ, соединяющей точку М съ началомъ* Одной линіи ОМ недостаточно для опредѣленія точки М, ибо всѣ точки плоскости, лежащія па окружности, описанной изъ 0 радіусомъ г, будутъ находиться отъ начала па разстояніи г. По если вмѣстѣ съ длиною линіи г данъ будетъ уголъ, составляемый ею съ осью оя, то этихъ двухъ данныхъ достаточно для опредѣленія точки М. Такимъ образомъ, абсолютная длина линіи ОМ—г и направленіе ея, выражаемое угломъ а, составляемымъ этой линіей съ вполнѣ опредѣляютъ точку М, такъ что положеніе этой точки можетъ быть представлено какъ комплексомъ а 4- Ъі, такъ и комплексомъ г&| которые и называются поэтому піриче-ски-равними. г называется также комплекса г , и есть количе-
ство существенно положительное; уголъ а наз* аргументомъ комплекса: онъ считается въ направленіи яоМ, обратномъ движенію часовой стрѣлки. Согласно этому, комплексный символъ г можно разсматривать условно какъ сумму ко-личествъ а п Ъі, каждое изъ которыхъ можетъ имѣть только два противоположныя направленія; такъ, на нашемъ чертежѣ будемъ имѣть
Аргументъ можно увеличивать или уменьшать па цѣлое число окружностей 2кт., ибо направленіе линіи ОМ не измѣнится, если поворотить эту линію на 4, 8,... прямыхъ угловъ; сл.
га = га + 2Я = Га + 4Я=- ' '
Если линію ОМ повернуть до совпаденія съ О.г, то уголъ а обратится въ нуль, и комплексъ приметъ видъ г0. Но отрѣзокъ полуоси ох представляетъ дѣйствительное положительное количество; сл. послѣднее можетъ быть изображено символомъ г0, гдѣ г — его абсолютная величина. Увеличивъ уголъ а до г., получимъ комплексы , представляющій, слѣд,, дѣйствительное отрицательное число. Знаки 0 и я играютъ роль знаковъ 4" и —- Чистое мнимое количество Ы изобразится комплексомъ Ъ~; мнимое —6І комплексомъ
2 "2
Примѣчаніе. Вычисленіе мнимыхъ вида о + Ъі было впервые изложено Бом-белли въ его алгебрѣ (1579); но заслуга введенія въ обычай употребленія въ анализѣ мнимыхъ величинъ принадлежитъ знаменитому Эйлеру (1707—1783). Первая попытка геометрическаго представленія этихъ количествъ принадлежитъ члену Петербургской Академіи Наукъ Генриху Кюну (1690—1769) и относится къ 1750 году. Аббатъ Бюэ (Виее) первый предложилъ, въ 1806, представлять мнимыя единицы на оси перпендикулярной къ дѣйствит. оси. Въ томъ же году Робертъ Аріандъ, изъ Женевы, приложилъ новую теорію къ доказательству нѣкоторыхъ теоремъ. Но усовершенствованіе этой теоріи принадлежитъ Гауссу, и ему же обязаны комплексныя количества правомъ гражданства въ наукѣ. Благодаря этимъ количествамъ, ученикъ Гаусса Рнліпимь пришелъ къ весьма важнымъ открытіямъ. Развитію теоріи мнимыхъ количествъ также много способствовали Копіи, Лежандръ, Абель, Якоби и Вейериітрассъ,
420. Обобщеніе основныхъ алгебраическихъ законовъ. Опредѣленія дѣй-ствій остаются прежнія; но какъ понятіе о комплексѣ шире понятія объ обык-
новенныхъ положительныхъ и отрицательныхъ количествахъ, то и дѣйствія надъ комплексами должны получить болѣе широкій смыслъ.
421. Сложеніе комплексовъ. Такъ какъ всякій комплексъ опредѣляется длиною нѣкоторой линіи и ея направленіемъ, то подъ сложеніемъ комплексовъ разумѣютъ слѣдующую операцію: сложить нѣсколько комплексовъ значитъ помѣстить начало втораго въ концѣ перваго, давая второму направленіе, опредѣляемое его аргументомъ; начало третьяго въ концѣ втораго и т. д. Суммою будетъ лихія, соединяющая начало перваго комплекса съ концомъ послѣдняго. Очевидно, это представленіе сложенія есть не болѣе какъ обобщеніе понятія о сложеніи противоположныхъ величинъ, заключая въ себѣ послѣднее, а равно и ариѳметическое сложеніе,
Черт. 45.
какъ частные случаи.
Такъ, если требуется сложить два комплекса аа и Ь^, чертимъ линію 0М=а подъ угломъ а съ положительнымъ направленіемъ оси х'х, затѣмъ наносимъ отъ точки М линію МК — Ъ подъ угломъ съ тою же осью, и соединяемъ точки О и К: линія ОК по величинѣ и направленію и выразитъ искомую сумму.
Три точки О, М и К, вообще, лежатъ не на одной прямой, образуя треугольникъ М0К; замѣчая, что въ треугольникѣ одна сторона меньше суммы двухъ другихъ, но больше ихъ разности, находимъ, что: модуль суммы двухъ комплексовъ меньше или равенъ суммѣ модулей слагаемыхъ, и больше или равенъ
ихъ разности.
Черт. 46.
Поступая такимъ же образомъ съ нѣсколькими комплексами л , да, с^ наЙ-демъ ихъ сумму, выражаемую по величинѣ и направленію линіей ОС, соединяю- * щей начало 1-го комплекса съ концомъ послѣдняго. (Черт. 45).
Когда всѣ вершины многоугольнаго контура ОАВС находятся не на одной прямой, то ОС, инкъ прямая, будетъ меньше ломаной ОАВС; если же всѣ вершины О, А, В, С, будутъ на одной прямой, то ОС будетъ меньше или равна суммѣ сторонъ контура. Итакъ модуль суммы нѣсколькихъ комплексовъ равенъ или меньше суммы модулей слагаемыхъ.
422. Законъ перемѣстительный въ сложеніи. Возьмемъ тѣ же три комплекса «а,
с^. Чтобы построить сумму + проводимъ послѣ-довательно прямыя О А — л, АВ —6, ВС —с полъ углами
р и 7 съ ОХ. Сумма выразится линіей ОС. Чтобы построить сумму
проведемъ пзъ точки А прямую А1), равную и параллельную ВС, и соединимъ й съ С; изъ равенства и параллельности сторонъ Ай и ВС слѣдуетъ, что фигура АОСВ есть параллелограмъ, сл. йС и АВ равны и параллельны; такимъ образомъ, прямая Ай представляетъ комплексъ с^,а йС—комплексъ 6^. Видимъ, что конецъ послѣдняго слагаемаго суммы находится въ той же точкѣ С, какъ и
конецъ послѣдняго слагаемаго суммы а '
а+^ + <у обѣ суммы, слѣдоват*, равны.
Черт. 47.
423. Законъ сочетательный въ сложеніи. Разсмотримъ тѣ же три комплекса: а& — ОА, —АВ и с^=ВС. (Черт.46). Ихъ сумма равна ОС. По АС = Ьд + с., и ОС можно разсматривать какъ сумму комплексовъ О А и АС. Слѣд.
т.-е. кшжгы сочетшкедьмы ея
сложеніи.
самомъ дѣлѣ, сумма двухъ противоположныхъ трудно убѣдиться, равна нулю. Слѣдов.
424. Вычитаніе комплексовъ. Вычитаніе опредѣляется какъ дѣйствіе, обратное сложенію. Легко видѣть, что вычитаніе комплекса сводится къ приданію противоположнаго комплекса а . . Въ а —т:
комплексовъ а и а . , какъ не а а г?
т -I- а । и а +
4-а — т + (а » +а)—т 4-0 = т .
к ' а (д і ' а 4“ Н И
Такимъ образомъ, ость результатъ вычитанія гг, потому
что этотъ результатъ, сложенный съ «а> даетъ т .
Пусть (черт. 47) изъ комплекса ОМ = а* нужно вычесть комплексъ ОМ'=6^. Согласно вышеприведенному правилу вычитанія, должно къ ОМ придать комплексъ, противоположный комплексу ОМ', т.-е. отъ точки М провести линію МІІ, параллельную ОМ' и равную 6, но въ противоположномъ направленіи. Сумма ОМ и МЙ, т.-е. ОК и представитъ искомую разность.
Изъ этого построенія слѣдуетъ, что т. к. точки О, М, В, вообще, составляютъ треугольникъ, то: модулъ разности двухъ комплексовъ не больше суммы модулей обоихъ комплексовъ и не меньше ихъ разности.
425. Умноженіе комплексовъ. Распространяя опредѣленіе умноженія на комплексы, мы должны разумѣть подъ этимъ дѣйствіемъ слѣдующее: умножить комплексъ нл ад значима произвести надъ множимымъ тѣ же дѣйствія, шія нужно произвести надъ положительной единицей для составленія изъ нея множителя. Но чтобы изъ 4-1 или изъ 10 составить а^, надо: 1) помножить
абсолютную единицу на а и помѣстить а на ОХ, вслѣдствіе чего получится н0;
2) повернуть л0 на уголъ а. Слѣд., чтобы умножить на нужно сначала помножить модуль множимаго на а, вслѣдствіе чего получится затѣмъ этотъ комплексъ повернуть на уголъ а, т.-е. къ аргументу множимаго придать аргументъ множителя. Итакъ: перемножитъ комплексы значитъ перемножитъ ихъ модули и сложитъ аріумеиты: Іц . аа— (Ьа)« < .
Въ этомъ опредѣленіи заключаются, какъ частные случаи, опредѣленія умноженія абсолютныхъ чиселъ и противоположныхъ. Такимъ образомъ, имѣемъ:
(+ о) • (4~ й) — Л* . Ьф — (<з^)е = -{- лб;
(— а) . 6) — а, . (аЪ)_ _р — (^Ь)_— — аЬ;
(+ о) . (— б) = . Ь_ = (а&)_ = — ад;
«ъ <
(— а) . (— &) — . 6, — (аЪ)ъ_ = (а7>)0 = + аЪ.
4 Ф 4 ѵ а < ѵ*
426. Свойства Произведенія. Изъ опредѣленія умноженія комплексовъ прямо выводимъ:
Е аа . ^ = (ад)а+ ноад = &а и а + ^^а, слѣд.,(аЬ)а+
пли, по опредѣленію умноженія, . аа. Итакъ
т.-е. произведеніе двухъ множителей не измѣняется отъ перемѣны ихъ порядка. п. йа (у7) = «я + ? 7 =
т.-е. і/.иноженія яаломексл а на произведеніе двухъ другихъ, Іѵ и , ш/.жно а р і
аа умножить послѣдовательно на каждый изъ комплексовъ и Въ этомъ заключается сочетательный въ умноженіи. и
Основываясь на этихъ двухъ положеніяхъ, не трудно доказать законъ перемѣстительный для какого угодно числа множителей.
ІИ. Докажемъ равенство - '
а (Ьг.-ъс Ь^Ч-а с
1 ? . 7 а Р а г
выражающее законъ распредѣлительный въ умноженіи. Комплексы и с^, подлежащіе сложенію, образуютъ между собою нѣкоторый уголъ у — дополнительный до г къ углу А треугольника ОАВ. Послѣдній вполнѣ опредѣляется этимъ угломъ и сторонами Ь и с. Третья сторона выражаетъ по величинѣ и направленію ихъ сумму
Если каждую изъ величинъ 5^ и помножимъ на то модули ихъ умножатся па а и сл. сохранятъ то же самое численное отношеніе. Аргументы 0 п 7 получатъ одно и то же приращеніе а, слѣд., сохранятъ ту же разность. Поэтому, если составить сумму частныхъ произведеній аД+ад> то по-а а 1 сх
лучится треугольникъ ОА'В' подобный ОАВ, такъ какъ углы*А и А' равны и заключающія ихъ стороны пропорціональны. Слѣд. ОВ' будетъ имѣть модулемъ ОВ, умноженное на а, аргументъ же комплекса ОВ' будетъ — А'ОХ + ВО А = АОХ 4-
— пронзве-
прежнему аргументу, сложенному съ а. Итакъ, денію «а (Ь^ + с ).
IV. а . 0 = а О =(в.0)„. = 0=0. а а о а+о а
Слѣд., произведеніе двухъ комплексовъ равно нулю, равенъ нулю.
V. а . 1 =а . 10 = (л . 1) =а . 1 а ц 4 'а <і
Слѣд., умноженіе комплекса на 1 не измѣняетъ его.
427* Дѣленіе. Сохраняя прежнее опредѣленіе этого дѣйствія, находимъ, что частное отъ раздѣленія а : Ъ* равно
когда модуль одного изъ нихъ
К
Въ самомъ дѣлѣ, умноживъ это частное на дѣлителя, имѣемъ:
т.-е. дѣлимое. Итакъ: чтобы раздѣлить одинъ комплексъ па другой, надо: лоф/ль дѣлимаго раздѣлитъ на модуль дѣлителя, а изъ аргумента дѣлимаго вычесть аргументъ дѣлителя.
428. Возвышеніе въ степень. Пусть показатель степени п —число цѣлое и положительное; по опредѣленію возвышенія въ степень имѣемъ:
а*. . . а* (п разъ); отсюда, по правилу умноженія:
ап — (а.а . . . а)_ , л , . „ =а* •
а ' 'яН—я-г- . . • Н— 1 ля
Пусть показатель степени будетъ цѣлое отрицательное число ~ По свойству такого показателя, имѣемъ:
Итакъ: чтобы возвыситъ комплексъ въ цѣлую степень, нужно модуль возвысить въ мну степень, а аріументъ умножить на показателя степени.
429. Извлеченіе корня. Пусть требуется извлечь корень порядка т (гдѣ ш — цѣлое положительное число) изъ кокплекса г , и пусть искомый корень выра-
женъ комплексомъ ₽ , такъ что Г О)
По опредѣленію корня, мы должны имѣть г* =(р<о)іл>иля г =? . Этому ра-
венству удовлетворимъ, полагая, что модули обѣихъ частей равны, а аргументы разнятся на число кратное 2г, такъ что для опредѣленія р и ш имѣемъ ур—нія:
— г, тш = 2кг. н- а,
гдѣ і —цѣлое положит. или отрнцат. яисло; но г есть число положительное, а какъ и существенно положительно, какъ модуль, то оно равно ариѳметическому корню изъ г. Такимъ образомъ имѣемъ:
Итакъ
тн т
Опредѣлимъ, сколько различныхъ значеній получится для Если въ формулѣ (11 дать А; два какія-нибудь значенія, разнящіяся между собою на число кратное м, то получимъ два угла, разнящіеся кратнымъ 2^; но поворотъ комплекса на уголъ кратный 2к не измѣняетъ величины комплекса. Слѣд. чтобы получить всѣ значенія достаточно числу А дать т цѣлыхъ послѣдовательныхъ значеніи, напр. значенія
О, 1, 2, 3, . * , , пі — 1.
Такимъ образомъ получимъ корни, которыхъ аргументы будутъ
а —» т
а
т'
о
м *
Ш «і
т т
крайніе углы разнятся на (т — т.-е. менѣе чѣмъ на 2я, слѣд. два какіе
угодно изъ этихъ аргументовъ имѣютъ разность, меньшую 2я, и потому даютъ различные комплексы. Отсюда заключаемъ, что
количество, даменнштельное «ли лшилгое, имѣетъ т различныхъ корней іп-іо порядка, дѣйствительныхъ или мнимыхъ, и только т.
Представимъ эти ш корней геометрически. Возьмемъ перпендикулярныя оси х*х и у'у, и опишемъ изъ начала 0, какъ центра, окружность радіусомъ раннымъ линейной единицѣ; пусть А будетъ точка пересѣченія этой окружности съ
положительною частью Ох оси х'х. Отложимъ на этой окружности, начиная отъ точки А, въ приличномъ направленіи, дугу АМ0, равную до величинѣ н по знаку а
дугѣ —? затѣмъ, отъ раздѣлимъ окружность на т равныхъ частей; пусть Мй,
Мр М2,,»., Ми-і будутъ точки дѣленія* Если соединить начало О съ этими точками дѣленія, то т радіусовъ ОМЙ, ОМ-,».,, ОМт—і будутъ комплексы модуля =1, а аргументы этихъ комплексовъ будутъ
а
т
а
т
2-
-т
т
9-
т' *
а
т
2 ,
т т
Затѣмъ, на каждомъ изъ этикъ радіусовъ отложимъ, начиная отъ точки 0, длину равную |/г; новые комплексы ОХЙ, 0Х1г.м ОХш-і представятъ т корней т-го порядка изъ даннаго количества г , а изъ построенія видно, что ихъ концы рас-
т/ е
положены па окружности центра 0 и радіуса у г, образуя на этой окружности вершины .правильнаго т—угольника.
Изъ этого построенія непосредственно видно, что при т четномъ, т корней попарно равны и противоположны по знаку, и что не можетъ быть больше двухъ дѣйствіи тельныхъ корней, и только при т четномъ»
ІЬс.тдоваше. I. Пусть данное количество будетъ д&Лсмотгшслъное и по./о-жи/мелькой; оно будетъ равно своему модулю г, аргументъ же, какъ кратный 2г, всегда можно принять равнымъ 0. Такимъ образомъ
т
Черт» 48.
Чтобы получился дѣйствительный положительный корень, необходимо, чтобы аргументъ ра-
внялся четному кратштму
2&Я , т ,
г, т.-е, —=2Лг, откуда к = атакъ какъ & положптельпо п меньше т, то ?н
необходимо, чтобы А=0, и слѣд,, чтобы А=0; стало быть въ числѣ корней будетъ одинъ положительный, и только одинъ,
Чтобы получился корень дѣйствительный отрицательный, нужно, чтобы аргу-2кг. .
ментъ —- равнялся нечетному кратному отъ г, т.-е. чтобы
2Ь , (2*4-1)™.
—=(27л- 1 )я, откуда к=---я— - >
но А —цѣлое, 2Д +1 — нечетное число, сл, при ш нечетномъ равенство невоз-• можно. Если же ш — четное, то какъ к меньше т, необходимо, чтобы А было
нулемъ, и тогда Л — слѣд. при т четномъ, и только въ атомъ случаѣ, имѣется дѣйствительный отрицательный корень, но абсолютной величинѣ равный дѣйствительному положительному корню.
ІТ г 2Лт. 2к'г.
Чтобы два корня аргументовъ — и гдѣ 7г отлично отъ я, были со-пряженны, необходимо и достаточно; чтобы; сумма ихъ аргументовъ равнялась четному кратному отъ к,
2к'ъ і , іі
----1----— 2Л-, откуда кч-к — т/і, т т
а такъ какъ к и кг положительны, различны и меньше т, необходимо, чтобы к равнялось 1, и чтобы
Отсюда видно, что всякому значенію к9 за исключеніемъ нулевого и равнаго т ,*
если т четное, т.-е. за исключеніемъ случая дѣйствительныхъ корней, сог отвѣтствуетъ значеніе к* отличное отъ к; слѣд., всѣ лгян.мые корни — попарно сопряженіи*!.
Итакъ: Если т—нечетно, всякое дѣйствительное положительное количество имѣетъ одинъ, и только одинъ, корень т-ю порядка положительный, и т—І-т-хъ корней мнимыхъ попарно сопряженныхъ.—Если т—четно, всякое дѣйствительное положительное количество имѣетъ два корня тло порядка дѣйсттстельныхъ, равныхъ и противоположныхъ по знаку, и т—2 корня мнимыхъ попарно соіція-женнихъ.
Геометрическое представленіе этихъ т корней ін-го порядка непосредственно приводить къ предыдущимъ результатамъ. Въ самомъ дѣлѣ, гакъ какъ а = 0, то вершина Мо совпадаетъ съ точкой А; точка Хо находится, поэтому, на Иг, и слѣд. существуетъ дѣнст. положнт. корень О_\т0. Если т четно, то будетъ другой дѣй-ствит. корень, отрицательный, равный предыдущему, но съ противоположнымъ знакомъ, но такого корня не будетъ при ш нечетномъ; въ обоихъ случаяхъ всѣ остальные корни мнимы; и какъ многоугольникъ симметриченъ относительно Оя, эти мнимые корни попарно сонряжеішы.
II. Пусть данное количество будетъ но <т;рицаті.шо; оно
равно своему модулю, но съ противоположнымъ знакомъ; всегда можно положить, что его аргументъ а равенъ тг, такъ что количество это будетъ гг или —г, и
т
Чтобы могъ быть дѣйствительный положительный корень, необходимо, чтобы его аргументъ мылъ равенъ четному кратному отъ гс, т.-е. чтобы — —^-=2//тг, т
откуда 27г 1 — 2тк, что невозможно, потому что 2к + 1 нечетно, 2 т к четно;
и такъ, въ данномъ случаѣ, не существуетъ ни одного дѣйствит. положнт. корня.
Чтобы могъ быть дѣйствительный отрицательный корень, нужно, чтобы его (21'4-1)- , (2Л4- Пг.
аргументъ —- оылъ равенъ нечетному кратному отъ п, -—— (27* + 1)^ откуда 2к + 1 = (27і + 1)ш; это равенство невозможно, если т четно; слѣд. при четномъ ж не существуетъ ни одного дѣйствіи. отрицат. корня.
Положимъ, что ш нечетно; въ этомъ случаѣ, такъ какъ к меньше т, нужно ]
чтобы к было нулемъ, и тогда & = —; слѣд., если ш нечетно, будетъ одинъ дѣйствіи, отрицат. корень, и только одинъ.
тг г (2&4-1)л (2&'4-1)гс А т,
Чтобы два корня аргументовъ *—--• , отлично отъ А;,
были сопряженны, необходимо и достаточно, чтобы сумма ихъ аргументовъ равнялась четному кратному отъ яг,
(2& -Р 1)^ (2А' + 1)*
откуда
А; ч- к' = тк — 1,
а такъ какъ А и к* положительны, различны и меньше ж, необходимо, чтобы Л равнялось 1, и сл, чтобы
к -|- к’ = «і — Ь
Отсюда видно, что всякому значенію й, кромѣ ~у— ПРИ ™ нечетномъ, соотвѣтствуетъ одно значеніе к* отличное отъ к, и только одно; слѣд. всѣ мнимые корни попарно сопряженкы.
Итакъ: Ійшг т нечетно, то дѣйствительное отрицательное количество имѣетъ одинъ т-й отрицательный корень, и только одинъ, и т—1 т-хъ корней мнимыхъ попарно сопряженныхъ. Если т четно, дѣйствительное отрицательное количество не имѣетъ дѣйствительныхъ т*хъ корней, но имѣетъ т различныхъ корней т-ю порядка мнимыхъ и попарно сопряженныхъ.
Геометрическое представленіе корней приводитъ къ тѣмъ же заключеніямъ;
въ самомъ дѣлѣ, въ этомъ случаѣ — = ~, и каждое дѣленіе МрМрМі М2> • • -т ЛІ
2-
равно а потому вершины и Мш—і симметричны относительно діаметра я?Ш; точки Ыо и Км—і имѣютъ тоже свойство, и вершины Хо, К2,,.м Хт-і попарно симметричны относительно я'Оя; отсюда видно, что корни — мнимы и попарно сопряженны.
Затѣмъ, на положительный полуоси Ол? не м. б. ни одной вершины, на отрицательной же полуоси 0я' будетъ вершина только при т нечетномъ; сл. если «і — четно, то не существуетъ ни одного дѣйствительнаго ж-го корня; ври т— нечетномъ есть одинъ дѣйствительный корень отрицательный; всѣ же мнимые корни попарно сопряженны.
III, Пусть, наконецъ, данное количество г—мнимое; аргументъ его уже не будетъ кратнымъ к. Легко видѣть, что ни одинъ ж-й корень изъ не м. б. дѣйствительнымъ; въ самомъ дѣлѣ, для этого нужно бы было, чтобы
2&^ а / т п 7 \
—- + — = /іг., откуда а = (гиЛ—2л)к,
т.-е. нужно, чтобы а было кратнымъ и слѣдовательно, чтобы данное количество было дѣйствительнымъ.
Затѣмъ, не м.б. двухъ мнимыхъ сопряженныхъ корней, ибо для этого нужно, чтобы сумма ихъ аргументовъ была четнымъ кратнымъ к, т.-е. чтобы
«
4-----Н- —Н- —2/іт., или а — — к — к)~,
т т т т
а это требуетъ, чтобы данное количество было дѣйствительнымъ.
Слѣдовательно: велкш кем<плекс*ь «.шьешь ш ритмичныхъ корней ж-ю порядка также комплексныхъ и не сопряженныхъ.
Геометрическое, представленіе корней показываетъ, что въ этомъ случаѣ ж корней суть ж радіусовъ правильнаго полигона, не имѣющаго ни одной вершины на оси я/0х, и не имѣющаго радіусовъ симметричныхъ относительно х'Оя; а этимъ снова доказывается, что ж корней комплексны и не сопряженны.
7/рп.і^чаяіе. Если взять два мнимыхъ сопряженныхъ комплекса гд и г
— а»
то каждый изъ нихъ, какъ мы видѣли, имѣетъ т различныхъ корней ж-го порядка, комплексныхъ и не сопряженныхъ. Можно показать, что ш корней ж-го порядка изъ соотвѣтственно сопряженіи! т корнямъ ж-го порядка изъ г_а. Въ самомъ дѣлѣ:
т т
Но очевидно, для того чтобы два комплекса были солряженны, необходимо и достаточно, чтобы модули ихъ были равны, а сумма аргументовъ была кратна . , гяЛ т/
2п; по всѣ величины у гд и г г„7 имѣютъ одинъ и тотъ же модуль, слѣд. до-
24я статично показать, что аргументу —
2к'~___а_
т т
1 * г-
-4----какого-нио. ж-го корпя изъ г соот-
1 т 1 а
вѣтствуетъ аргументъ
ж-го
корня изъ г такой, что
24т: а 24'~ а т т іѣ т
или что 4'4-4 = жЛ; но если давать 4 и 4' только значенія 0, 1,.„, ш—1, то нужно взять 4=1, и тогда 4' = ж —4. Отсюда видно, что всякому значенію 4 соотвѣтствуетъ только одпо значеніе 4'; слѣд.: если два комплекса сопряженны, то т корней тло порядка перваго соотвѣтственно сопряженны т корнямъ т-ю порядка втораго,
430. Изъ предыдущаго видно, что всѣ дѣйствія надъ комплексами приводятъ къ выраженіямъ того же вида; поэтому весь количественный матеріалъ алгебры, надъ которымъ она производитъ дѣйствія и въ формѣ котораго получаетъ результаты, выражается въ слѣдующей общей формѣ:
а -н Ъі или г ,
частными видами которой являются: -|- а (или ец), —а (или а_), (или аг),
2
— си (или а3„), гдѣ а и Ь — числа дѣйствительныя, цѣлыя, дробныя или ирра-
ціональныя. Существенный характеръ этихъ величинъ тотъ, что полное опредѣленіе ихъ требуетъ знанія но только ихъ .мвді/лсй, но еще и яап?ххамжгя. Потому ихъ называютъ также величинами директивными. Однѣ изъ этихъ величинъ имѣютъ только два противополоясныя направленія, вслѣдствіе чего геометрически онѣ представляются прямыми, наносимыми на неограниченной оси, отъ нѣкотораго постояннаго начала, то въ одну, то въ другую сторону, смотря по нхъ направленію. Ихъ называютъ поэтому діогіами, Другія величины могутъ быть изображаемы прямыми, проводимыми на плоскости изъ начала въ какомъ угодно направленіи. Ихъ называютъ плоскими поліадами; діоды—ихъ частный случай. Наконецъ, есть величины, въ представленіе о которыхъ не входитъ идея направленія; поэтому ихъ изображаютъ прямыми, наносимыми на оси въ одну сторону отъ начала. Ихь называютъ .мояодалш (изученіемъ нхъ занимается ариѳметика). Всѣ эти величины подчиняются тѣмъ основнымъ законамъ, обобщенію которыхъ н была посвящена эта глава.
Въ виду сказаннаго, цѣль алгебры можно опредѣлить такъ: это есть наука, занимающаяся изученіемъ дѣйствій надъ плоскими поліодами, и рѣшеніемъ вся-ыгъ задачъ, относяшился къ этимъ величинамъ.
Величины, имѣющія въ пространствѣ какое угодно направленіе (какъ силы въ механикѣ, прямыя, воображаемыя въ пространствѣ) не подчиняются тѣмъ же законамъ, какъ плоскіе поліолы, въ правилахъ умноженія и дѣленія; поэтому нхъ изученіе выходитъ изъ рамокъ алгебры.
. ГЛАВА XXX. *
Рѣшеніе квадратныхъ уравненій,—Изслѣдованіе корней,—Вычисленіе корней уравненія ах- Ц- /аг -н с — 0, когда коэффиціентъ .« весьма .надъ,
431. Опредѣленія, Уравненіе навивается если, будучи ра-
ціональнымъ и ижшлі» относительно неизвѣстнаго, не содержитъ членовъ съ степенями неизвѣстнаго, высшими второй. Такое ур, имѣетъ троякаго рода члены: съ квадратомъ, неизвѣстнаго, съ первою степенью его и, извѣстные члены; общій • видъ его будетъ, слѣдовательно,
ая2 4- йг 4"с = О*
гдѣ а, бис суть нѣкоторыя числа, положительныя или отрицательныя; бис могутъ быть вмѣстѣ или порознь нулями, и тогда ур, называется неполнымъ; когда а, Ъ и с отличны отъ нуля, оно называется поли-ылга.
432. Рѣшеніе неполныхъ ур—ній. I. Когда Ь = О, уравненіе будетъ
аяа-|-с = 0.
Раздѣливъ обѣ части на и положивъ для краткости —“=А> можемъ дать этому ур—кію видъ
х2— А = 0.
Замѣчая, что А = получимъ:
х* — (|/Л)* = 0, или А)(я 4- =0’
Но чтобы произведеніе двухъ множителей равнялось нулю, необходимо и достаточно, чтобы одинъ изъ нихъ былъ равенъ нулю. Приравнивая перваго множителя нулю: х—|/а = 0, находимъ отсюда # = -|-)/а, прячемъ второй множитель обращается въ конечное количество 2)/а. Приравнявъ второго множителя нулю: х' +/А ~ 0, имѣемъ отсюда х — — ]/а, причемъ другой множитель даетъ конечную__величину — 2}/А. Итакъ, имѣемъ два рѣшенія: #/ = 4’Ѵ^і — У А; ихъ условились, ради краткости, писать вмѣстѣ:
х = + ]/ А
и читать: х равенъ плюсъ или минусъ }/А.
• Если А > 0, оба корня дѣйствительны; при А 0, оба мнимы. Примѣры. 1. Рѣшить уравненіе З#2 — 75== О,
Перенеся 75 во вторую часть, и раздѣливъ обѣ части на 3, получимъ ур.: я2 = 25, откуда # —±р/25 = ±5, Итакъ:
: л/ = 4- 5; х” =— 5.
2, Рѣшить уравненіе За24“^ = в*
Выводимъ изъ него: — 25; откуда х = + ]/—25 = 4-5/,
т.-е.
х' = 4' 5г; я" = — 5Л
II. Положивъ въ уравненіи ах2~р <? = О извѣстный членъ с=О, получаемъ уравненіе
ах* Ц- 6х = О.
Выводя х за скобки, дадимъ ур—нію видъ х (ах-|’ Ь) = 0. Приравнивая перваго множителя нулю, т.-е. полагая х — О, и замѣчая, что при этомъ второй множитель обращается въ конечную величину 6, заключаемъ, что одинъ изъ корней ур—нія равенъ 0. Полагая затѣмъ ах -|- Ъ = О, откуда х = — замѣчаемъ, что и при этомъ значеніи х ур—ніе обращается въ тождество.
Итакъ, ур—ніе ал2-|-&х = 0 имѣетъ два корня
х' = О, х” = — - • а
Примѣчаніе. Если бы, въ видахъ упрощенія, мы сократили первоначально ур. на х, то, рѣшивъ полученное ур—ніе, нашли бы только одинъ корень х = — другой корень х = 0 потеряли бы при сокращеніи. По едва ли не лишнее снова напоминать, что не позволительно дѣлить ур. на множителя, который можетъ обратиться въ нуль.
Примѣръ. Рѣшить уравненіе Зх2 — 7х = 0.
Давъ ему видъ х(3х — 7) = 0, по предыдущему, находимъ два корня:
х' = 0; =
й
III. Если 6 = с = 0, то ур. принимаетъ видъ
ах* = 0.
Такъ какъ а отлично отъ нуля, то произведеніе ах* можетъ обратиться въ нуль только при х = 0. И въ этомъ случаѣ можно сказать, что ур. имѣетъ два корня
х' = 0 и х" = О, равныхъ между собою.
433. Рѣшеніе полнаго квадратнаго уравненія. Рѣшимъ теперь квадратное уравненіе общаго вида
ах*-|- Ьх-4 с = 0 . . . (1).
Первый пріемъ. Принимая & отличнымъ отъ нуля, выносимъ а за скобки, вслѣдствіе чего получимъ ур.
а (х*4-- - х4- =0 . . . (2)
\ 1 а а) 4 7
Замѣчая, что - . я можно представить въ видѣ 2 _ . я, разсматриваемъ
> п Ь
я2 какъ квадратъ перваго члена х нѣкотораго бинома, а 2 * я . какъ удвоенное произведеніе перваго члена (я) искомаго бинома на второй, который равенъ, поэтому, Д* Такимъ образомъ, если въ скобкахъ ур—нія (2) прибавимъ ми
и вычтемъ квадратъ второго члена бинома, то составимъ Іур—ніе эквивалентное (2):
I 9 . о Ъ . Ь3 &я । с\ А
а I х^ —Н 2 - - х + -г—„ —-- —I— | = О
\ 2а * 4а2 4а2 ~ а/
г Ь „ Первые три члена въ скобкахъ составляютъ квадратъ бинома Поэтому послѣднее ур. можно написать въ видѣ:
« Г(„+ »у_<^к]=о . . .(3). Ц 1 2а/ 4а2 -I ' '
Каковъ бы ни былъ знакъ разности Ьа — 4ас, мы всегда можемъ разсма-
тривать “4Яа " какъ квадратъ дроби ——» и Дать уравненію (3) видъ
а
(Ѵб3— 4оеѴ
\ 2а /
или, по разложеніи на множители, видъ
Ь ѴЪ2 — 4ас\І » 6 і ѴЬ2 — 4ос\
2а 2а )\ '2^** 4а /
Но какъ а отлично отъ нуля, то, чтобы первая частъ была нулемъ, необходимо и достаточно, чтобы тотъ или другой изъ остальныхъ двухъ множителей былъ нулемъ. Итакъ, послѣднему, а потому и эквивалентному ему данному уравненію, мы удовлетворимъ, положивъ
. „ , Ь ѴЬ* — 4ас п 060 ж+2в- ' 2а ’=0’ , — Ъ -4- ГЬ» — 4ас откуда х = 2а ,
Ь । 4ас п либо х + -4-._^-. = 0, „ —Ъ — 1 д2— 4а€ откуда х =
Итакъ, квадратному ур—нію удовлетворяютъ два значенія неизвѣстнаго, два корня. Для краткости оба корня пишутъ въ одной формулѣ:
— Ь — ѴЪ2 — 4ас х —------ , ------»
2а
изъ которой выводимъ слѣдующее
Правило. Чтобы найти значенія неизвѣстнаго^ удовлетворяющія полному квадр. ур—нію, нужно: выраженіе> составленное изъ коэффиціента при неизвѣстномъ въ 1-й степени, взятаго съ обратнымъ зна-комЪ) плюсъ или минусъ квадратный коренъ изъ квадрата того же коэф-
фиціента безъ учетвереннаго произведенія крайнихъ коэффиціентовъ^ раздѣлитъ на удвоенный первый коэффиціентъ^
Примѣръ. Рѣшить уравненіе 99#*— 37#—10 = 0.
Сравнивая это уравненіе, которому можно дать видъ *
99жа 4- (— 37)л: + (— 10) = О
съ общимъ, замѣчаемъ, что нужно положить
а = 99, Ь =—37, с = —10. *
Вставляя въ общую формулу эти числа, найдемъ:
37 1/(-н 37)2 — 4.99 . (—10) _ 37 ± 175329 _ 37 * 73
Х~ 2.99 ’ 198 — 198 ’
и наконецъ:
,_37 + 73_5. „_ 37 — 73 _ 2
Х~ 198 “ 9’ Я — 198 — 1Г
434. Второй пріемъ. Умножая обѣ части уравненія (1) на 4а, что позволительно, если а не равно нулю, получимъ уравненіе
4а*#1 4аЛх -р 4ас = О, хишектвэе іаен мт; жл. перенеся *4ое во вторую часть:
4а *х* -|- 4 а Ь# = — 4ас.
Разсматривая 4а*#т и 4а^# какъ два первые члена квадрата бинома, у котораго первый членъ = 2ах, а второй Ъ, и придавая къ обѣимъ частямъ ур - нія по Ь5, находимъ уравненіе 4а2#9 -|- 4аЬх -|- Ь9 = Ьа — 4ас, котораго первая часть есть ничто иное какъ (2а#Приведя такимъ образомъ ур. къ виду
(2о# -|- Ъ)* = Ь* ~ 4ас,
замѣчаемъ, что 2а# Ъ есть алгебраич. квадр. корень изъ &’ — 4ас, т.-е.
2ах-|- Ъ ~ —4ас,
откуда _______
— & — 4ас
формула, совершенно одинаковая съ найденной въ § 433.
435. Третій пріемъ. Найдемъ формулу корней при помощи введенія неопредѣленнаго количества. Имѣя ур.
ах* -|- Ъх -|- с = О,
положимъ х = 2 гдѣ новое неизвѣстное, а к нѣкоторое произвольное количество, и подставимъ въ ур. вмѣсто х сумму {- й. Найдемъ ур —ніе
а (# —А?)2 *-{-* Ь —р &) —р с = О
раскрывъ въ немъ скобки и расположивъ по степенямъ получимъ ая24~ (2я&-р 6) #“Ь с “ О * • - (2)
Воспользуемся произволомъ количества к для того, чтобы уничтожить членъ съ первою степенью (2ай-|-Ь)л и получить такимъ образомъ неполное уравненіе; очевидно, для к надо выбрать такое значеніе, чтобы 2а7с Ъ = О, от-ъ ь
куда ^ = ~2І-
Подставивъ это значеніе к къ ур. (2), имѣемъ
’ \ 2а) 1 \ 2а) 1 1
или
откуда я* =
№ — 4ас
4а2 ’
и слѣд. я =
— 4ас
2а
- -|- с = О, 4а ’ '
т х „ „ , 7. Ъ . кб2 — 4ас —- & :± кЪ2 — 4ас Такимъ образомъ: х = я Ч- к = — =—н ----------------=-------------------
г ‘ 2а — 2а 2а
Этотъ способъ, состоящій въ уничтоженіи 2-го члена, предложенъ Карданомъ (1501—1576).
436. Замѣчанія относительно примѣненія предыдущихъ формулъ.
1. Когда коэффиціенты а, Ь и с числа цѣлыя и Ь — число'четное, формула корней допускаетъ упрощеніе. Въ самомъ дѣлѣ, полагая Ъ~2Ь\ имѣемъ
_ - 25/ _ - 2?/^ 2 — ас _ — Ъ'± уЬ^—ас
Я 2а 2а а ’
по сокращеніи на 2. Напр., если дано уравненіе
77я2 + 50л? + 8 = О,
то, полагая въ послѣдней формулѣ а = 77, 6'— 25 и с = 8, найдемъ
откуда
2. Когда коэффиціентъ при х^ равенъ 1, и ур. имѣетъ видъ
х2 до д = О,
то, полагая въ общей формулѣ а = 1, Ь~р я"с = ц. получимъ
_ — —Ір2 —
г
Если при этотъ р— четное число, то для удобства вычисленій выгоднѣе этой формулѣ дать видъ
Напримѣръ. въ уравненіи я* — 10&Ц-21 =0 имѣемъ: р = — 10, слѣд. = — 5, и 5= 21; примѣняя послѣднюю формулу, найдемъ
х = 5 Ч-|/ 25— 21=5 + 2; слѣд. #'=7, х" = 3.
437. Приводимъ еще нѣсколько примѣровъ на примѣненіе выведенныхъ формулъ.
1. Рѣшить уравненіе Зя2 — 1х—2 = 0,
Примѣняемъ первую формулу, полагая въ ней а = 3, Ъ = — 7, с =— 2, і находимъ
7 ѵ'49+14 7 I 73
Х~ 6 6 *
откуда
= = 2,591, съ точностью до 0,001 по избытку;
х" ——— = “ 0,257, съ точностью до 0,001 по недостатку.
2. Рѣшить уравненіе лЬ-г2 — (а2 + 62) # + аб = 0. Примѣняя первую формулу, находимъ
Я2 ^2 4- 4д^і _ аГ-Ь ±2 /«4 — 9^2
2аЪ ~ 2аЪ
_ й2-ь ±Г _ Д2 ч- ^2 (Д2 &>)
2аЪ — 2аЬ
Отдѣляя корни, имѣемъ
_^4^2 4-„2—1/1 _ а 62 __6
*2аЪ Ъ1 Х 2аЪ ~ а*
3. Рѣшить уравненіе
Перенеся 3 влѣво, напишемъ:
“ИЛИ
или
X | X | X х ч- а ' х ч- Ь ~ х ч- с
Приравнивая нулю 1-й множитель, имѣемъ
я' = О . . . (2).
Приравнивая нулю 2-й множитель, по приведеніи къ общему знаменателю и по упрощеніи числителя, найдемъ •
Зя2 -ь 2(« ч- Ъ ч- е)яч-йс + га+я6_~
(я ч- «)(я + 6)(а?ч-с) ** *
Приравнявъ числителя нулю, имѣемъ: ур.
Зяа~Н 2 (а-|-Ь4-с)а:-|-Ьс4-са-1-аЬ = О . : .(4)
корни котораго будутъ требуемые, если убѣдимся, что они не обращаютъ знаменателя въ 0; въ противномъ случаѣ, ихъ слѣдуетъ принять только тогда, когда истинное значеніе неопредѣленной въ которую обратится 1-ая часть ур—нія (3), будетъ = О, Корни (4) суть
-—[а Н" Ч- — Ъс — си — аЬ] . . , (5).
О
Они не обращаютъ въ нуль + удовлетворяютъ
ур—нію (3), а слѣд. и (4), которое так. обр. имѣетъ три корня: (2) и (5).
Оба корня (5), какъ легко видѣть, дѣйствительны, такъ какъ подрадикальное выраженіе приводится къ виду
1[{6 _ е). + (С _ в)« + (а - Ь)*].
4. Рѣшить уравненіе 2________________________________1 _ я — 2
1 я(я — I) 1)’
Собравъ всѣ члены въ первую часть, приведя къ общему знаменателю я(я-|-1)(я — 1) и сдѣлавъ приведеніе въ числителѣ, дадимъ уравненію видъ
— я^4-4я —3 я(яч- 1)(я—1)
Приравнявъ числителя нулю, рѣшаемъ ур—ніе
— —3-0,
и находимъ, что корни его суть: х’ = 3 и х" — 1 *
Первый корень не обращаетъ знаменателя въ нуль, а потому удовлетворяетъ данному уравненію. Второй же, обращая знаменателя въ нуль, даетъ первой части уравненія (1) видъ д Опредѣляя истинное значеніе этой неопредѣленности, имѣемъ
- ггз 4- 4д’ — 3 _ (^ — 1)(3 — = 3 —д-
* д,(а?4-1)(д’— 1) (о?— 1)о?(іг-ь 1) -ьі)’
эта дробь при я=1 обращается въ 1, а ур—ніе (1) въ 1 = 0. Заключаемъ, что корень я" = 1 не удовлетворяетъ данному ур—нію.
Кромѣ корня, равнаго 3, данное ур—ніе имѣетъ еще корень = оо, ибо степень знаменателя выше степени числителя.
438. Рѣшая квадратное уравненіе, мы нашли два корня; болѣе двухъ корней оно имѣть не можетъ: въ самомъ дѣлѣ, если бы ур—ніе аж24~ О
имѣло болѣе двухъ различныхъ корней, оно было бы тождествомъ, такъ какъ цѣлый по буквѣ х квадратный полиномъ, обращающійся въ нуль болѣе нежели при двухъ различныхъ значеніяхъ х, тождественно равенъ нулю.
Изслѣдованіе корней квадратнаго уравненія.
439. Рѣшая общее уравненіе мы нашли два корня:
, — Ъ ь I №— 4ас ,, — Ь — ѴЪ2 — Аас
Х = -—•—=----------, хг =-------------------
2а 2а
Вычисленіе корней зависитъ, такимъ образомъ, отъ извлеченія квадратнаго корня изъ разности Ь2 — 4ас, которая можетъ быть положительною, нулемъ, или отрицательною. Опредѣленіе природы корней въ каждомъ изъ этихъ случаевъ; указаніе, что значенія корней въ каждомъ случаѣ соотвѣтствуютъ формѣ уравненія, которому они удовлетворяютъ; наконецъ, опредѣленіе знаковъ дѣйствительныхъ корней,—все это составляетъ кгалъ шоиъдоеаягя корней.
Относительно разности Ь2 — 4ас, которую будемъ называть уравненія, можетъ быть три предположенія: она можетъ быть положительною, жуиъ и отрицательною:
Ъ* — 4ас>0, Ь2— 4ас = 0, Ь2— 4ас<0.
Прм этомъ условимся коэффиціентъ а считать положительнымъ; когда а < О. то умноживъ уравненіе на — 1, сдѣлаемъ этотъ коэффиціентъ положите льнмть.
440. Первый случай:
Въ формулахъ корней подрадикальное количество будетъ, такимъ образомъ, положительное, слѣдовательно, оба корня дѣйствительные, Вычитая изъ перваго второй, найдемъ
такъ какъ при данномъ условіи выраженіе это отлично отъ нуля, то заключаемъ, что корни не между собою.
Далѣе замѣчаемъ, что количество Ь2 — 4ас представляетъ или сулшу или разность ариѳметическую} смотря по тому, будетъ лн с отрицательно или положительно,
1 . с>0.
Такъ какъ по условію и а > 0, то 4ас > 0; вычитаніе положительнаго количества ведетъ къ уменьшенію, слѣд.
Ъ* — 4ас < в3,
а потому ариѳметическая величина |/ — 4ас меньше ариѳмет. величины
или количества Ь, Означимъ абсолютную величину коэффиціента 6 буквою [і; въ такомъ случаѣ:
Если Ь>0, то Ь = + и корни можно написать въ видѣ:
— 62 — 4ас
'----- - —-—,
а — {І — 1— 4ас.
“ 2а 5
такъ какъ а > 0, то знаки корней зависятъ отъ числителей; второй числитель, какъ состоящій изъ двухъ существенно-отрицательныхъ членовъ, отрицателенъ; въ первомъ—абсолютная величина отрицательнаго члена больше чѣмъ положительнаго, слѣд. и этотъ числитель отрицателенъ. Значитъ при Ъ положительномъ оба корня отрицательны.
Если Ь<07 то Ь= — и корни будутъ
-Нр — рЪ* ^4ас
2а
Первый числитель, какъ состоящій изъ двухъ существенно-положительныхъ членовъ, положителенъ; во второмъа—бсолютная величина положительнаго члена больше, нежели отрицательнаго, слѣд. п второй — положителенъ. Такимъ образомъ, при Ь отрицательномъ оба корня положительны.
Итакъ: при с>0 йш/стяшпелъные кярш илиьктіз знаки окаковые, противоположные знаку коэффиціента Ь,
2 . с<0.
Тогда какъ а>0, то 4ас<0; отсюда заключаемъ: во-первыхъ, что при я<0 выраженіе Ь2— 4ас представляетъ количество существенно-положительное, д слѣд. корни безусловно дѣйствительны; во-вторыхъ, что
и слѣд. абсолютная величина )/Ьа — 4ас больше абсолютной }/Ь*, т.-е. абсолютной величины количества Ь.
Если Ъ > О, т.-е. Ь = -р то
х ~
— + * Ьа —'
2а ’
— * —
7о”
Отсюда видно, что первый числитель имѣетъ большій по абсолютной величинѣ членъ—положительный, слѣд. #'>О; во второмъ числителѣ оба члена существенно отрицательны, слѣд, #"<0. Итакъ: знаки корней различны. При этомъ абсолютная величина числителя корня х’ есть разность
у/Ь2 — 4ас —
абсолютная величина числителя корня х* есть сумма
у/62 — 4яс 4“ ?
тѣхъ же количествъ, и слѣд. больше абс, вел. числителя корня так. обр. большую абсолютную величину имѣетъ тотъ коренъ, знакъ котораго противоположенъ знаку Ъ.
Если Ь < 0, то Ь = — }, и
Г6?_ 2а
Первый числитель, очевидно, положителенъ, слѣд. х' > 0; у второго отрицательный членъ имѣетъ большую абсолютную величину, чѣмъ положительный, слѣд. х” < 0; знаки корней опять различны. При этомъ, абсолютная величпна числителя положительнаго корня равна суммѣ
|/іа — 4ас4~ а отрицательнаго—разности тѣхъ же количествъ, — 4ас —
т.-е. опять большую абсолютную величину имѣетъ тотъ коренъ, котораго знакъ противоположенъ знаку коэффиціента Ь.
Резюмируя сказанное, заключаемъ, что: когда Ъ* — ±ас'>0, уравненіе имѣетъ корни дѣйствительные и неравные; при этомъ (полагая а > 0). если свободный членъ положителенъ, знаки корней одинаковы и противоположны знаку коэффиціента Ь; если же свободный членъ отрицателенъ, знаки корней различны, и знакъ ко])ня, большаго по абсолютной величинѣ, противоположенъ знаку Ъ.
441. Примѣ ры. I. Изслѣдовать корни ѵр—нія 8жа4"^"гс4_Ю= О* -------------------2
Такъ какъ Ь* — 4ас = 57 — 320 = 4~2929>0, то корни дѣйствительные и неравные; прн а>0 здѣсь и с>0, сл. знаки корней одинаковы; Ь>0, слѣд. оба корня отрицательны.
И. Наслѣдовать корни ур—нія 57х — 10 = О.
Здѣсь при а>0 имѣемъ с<0, слѣд*, но составляя разности Ь* — 4ас, заключаемъ, что. корни — дѣйствительные и неравные; знаки ихъ различны, ибо с < 0; большій корень, имѣя знакъ противоположный коэффиціенту Ь, положителенъ.
442, Докажемъ теперь, что при условіи Ъ*— 4ас>0 изъ самой формы уравненія вытекаетъ, что оно можетъ быть удовлетворено двумя различными дѣйствительными значеніями х.
Выводя въ ур —ніи а за скобки, имѣемъ:
Изъ условія Ь* — 4а€ > 0 имѣемъ 4ас < Ь2, откуда, раздѣливъ обѣ части неравенства на существенно-положительное количество 4а2, находимъ:
с , с Ь2
и СлѢд‘ а = 4^~К ’
гдѣ К2 должно быть существенно-положительнымъ количествомъ, и слѣд. К — дѣйствительнымъ. Ур—ніе принимаетъ видъ
а Р + |Ж+Й~К’} = ()’ или «{(®+^)в-К4} =0, или, наконецъ» разложивъ выраженіе въ скобкахъ на множители:
Такъ какъ а отлично отъ нуля, то этому,уравненію удовлетворимъ, полагая или — К = 0, откуда —^Ц-К;
или х-|-^ + К = 0, откуда # = —
откуда и видно, что ур—ніе удовлетворяется двумя дѣйствительными неравными значеніями х.
443. Второй случай.
Ь* — 4ас = 0.
При этомъ условіи подрадикальноѳ количество въ формулахъ корней обращается въ нуль, слѣд. радикальные члены исчезаютъ, и получается
т.-е. оба корня дѣйствительные и равные, а общая величина ихъ'есть __ Ъ_
Хотя въ данномъ случаѣ ур—ніе имѣетъ только одинъ корень, но говорятъ* что оно имѣетъ два, но равныхъ между собою корня. Чтобы оправдать такое условное выраженіе, достаточно предположить, что количество Ь2— 4ас сначала положительно, и что оно постепенно уменьшается до нуля; тогда неравные корни будутъ болѣе н болѣе приближаться къ равенству, и наконецъ, когда
разность ихъ, выражаемая формулою — — , дѣлается нулемъ, оба корня становятся равными.
Примѣръ. Уравненіе 9,г2“]-12.г~|-4 = 0 имѣетъ корни дѣйствительные равные, ибо Ь'1— ас=&2— 9X4 = 0; а общая величина ихъ равна
Ѵ = _6__ 2 а~ 9— 3*
444. Что равенство корней при условіи Ь*— 4ас = 0 обусловливается самою формою ур—нія, легко обнаружить слѣдующимъ образомъ. Давъ ур^нію видъ
а .г*------х 4- - = О,
\ а а I ?
и замѣчая, что изъ условія Ь2 — 4ас = 0 сперва имѣемъ 4ас=&2, а затѣмъ, а С С
раздѣливъ обѣ части на 4а2, получаемъ - — подставивъ вмѣсто - его а 4а а
величину въ ур—ніе, найдемъ
Такъ какъ а отлично отъ нуля, то очевидно, что атому ур—нію можно удовлетворять единственнымъ способомъ, положивъ
« + = откуда х= — ~
445, Третій случай-
Ь2— 4ас< 0.
Такъ какъ квадратный корень изъ отрицательнаго количества Ь*—4ас есть выраженіе мнимое, то изъ самой формулы корней видно, что оба корня будутъ мнимые.
Имъ можно дать видъ Въ самомъ дѣлѣ, Ь2 — 4ас — (4ас—62).
(—1); слѣд. — 4ас = 1^4ас — Ь2. ]/—1=)/4ас — І2. і, гдѣ количество ]/4ас дѣйствительно, такъ какъ 4ас— Ь2 >0.
Корни берутъ видъ *
, _ ь ,Ѵіас — & . Ь ѴАас - 6а .
2а'> 2а ’ 2а 2а *’
откуда видно, что это—мнимыя сопряженныя количества.
Примѣръ. Рѣшить ур—ніе 7х2— ЗхЦ-2 = О.
Ь2 — 4ас За — 4 X ? X 2 = — 47, слѣдов. корни—лпшлше. По предыдущимъ формуламъ имѣемъ:
г
446. Покажемъ изъ самой формы ур—нія, что при условіи Ь* — 4ас<0 ему нельзя удовлетворить никакимъ дѣйствительнымъ значеніемъ х.
т» у ѵ . т а. . л ж С *
Въ самомъ дѣлѣ, изъ условія о* — 4ас<^ѵ имѣемъ а эт0 неРа’
сЬ2
венство можно замѣнить равенствомъ “ = -р К2, гдѣ К^—существенно по-
ложительное количество, не могущее обратиться въ нуль. Внося это выраженіе , с
вмѣсто а въ уравненіе
а я2 *4- - - = Оч
\ 1 а 1 а]
даемъ ему видъ
Отсюда очевидно, что ур—ніе не м. б. удовлетворено никакимъ дѣйствительнымъ значеніемъ я, потому что сумма двухъ положительныхъ количествъ можетъ обратиться въ нуль только тогда, когда каждое изъ нихъ въ отдѣльности обращается въ нуль, но мы знаемъ, что К2 не м. б. нулемъ.
Изъ формулъ корней видно, что въ данномъ случаѣ ур. м. б. удовлетворено мнимыми значеніями неизвѣстнаго.
447. Задача. Опредѣлитъ параметръ I такъ* чтобы ур—яіе
х2 — 4Ъх 4- 4аЬ 4- і2 — 21х = О
«лиьло корни равные.
Написавъ ур—ніе въ видѣ
х2— 2 (2Ь 0$ 4“ 4а&Х і2 = О,
замѣчаемъ, что должно быть V2 — ас — 0, т.-е. (2Ь 4^ г)2 — (4аЬ 4“И = или Ь 4~ —а = 0, откуда і — а — Ъ.
448. Задача. В& уравненіи 5х2— 4#Ха = 0 опредѣлитъ параметръ А така, чтобы первая частъ уравненія представляла:
1) сумму двухъ квадратовъ;
2) разность двухъ квадратовъ;
3) точный квадратъ.
1) Первое требованіе равносильно условію 6'а —ас<0, или 4 —5л<0, 4 . 4
откуда ^>5* Слѣдовательно, когда А больше^ первая часть ур—нія представляетъ сумму двухъ квадратовъ; корни ур—нія будутъ мнимые.
2) Второе требованіе равносильно условію Ъ'*— найдемъ: и корни ур—нія будутъ дѣйствительные неравные.
3) Третье требованіе равносильно условію У3—ас=0, откуда ^ = з’ л ур—ніе будетъ имѣть равные корни.
449. Теорема. Если уравненіе ах2 X Ьх X с = О, въ которомъ коэффиціенты а, Ь и с соизмѣримы, удовлетворяется несоизмѣримымъ корнемъ а 4“ И юго другой ею корень будетъ несоизмѣримое количества а — )Х? сопряженное первому.
Въ самомъ дѣлѣ, но условію, а X ? есть корень даннаго уравненія, слѣд. имѣемъ тождество
«(^ + /?)в + Ь(а+/?) + с=О,
или, раскрывъ скобки и собравъ въ отдѣльныя группы соизмѣримые и несоизмѣ рнмые члены, найдемъ
(аиаХа?Х^аХс)Х(-ааХ^)У^? — О - • - (!)
Первая часть этого тождества имѣетъ видъ М X К }Х> гдѣ М и Н соизмѣримы. Въ силу (1) это выраженіе должно равняться нулю; во можно доказать, что оно можетъ равняться нулю только.тогда, когда М = О и К = О.
Въ самомъ дѣлѣ, пока И отлично отъ нуля, мы можемъ обѣ части раздѣлить па К и отъ этого получимъ равенство
. .(2)
*
*
эквивалентное ур—нію М4-№|/у=О; но равенство (2) невозможно, ибо оно выражаетъ, что несоизмѣримое количество рХ равно соизмѣримому —Итакъ, необходимо, чтобы К было нулемъ; но тогда изъ равенства М X № = О слѣ-
дуетъ, что и М = О.
Такимъ образомъ, тождество (1) ведетъ за собою слѣдствія
аа3 X Х^1 X с~ О \ /о\ 4
2аа + Ь = 0 ( ( )
Есл теперь въ триномѣ ах2Х^Хс замѣнимъ х выраженіемъ а — ]/Х то жШеіъ
X X Ьа X е) — (2ааХ&)]/ Р’
м это выраженіе, въ силу (3), равно нулю, т.-е. триномъ обращается въ нуль пре х=і— уХ слѣдов., послѣднее выраженіе служитъ корнемъ даннаго ура-в&еніі.
450. Теорема. Если ур—ніе ах3 X Xс = которомъ а, Ь и с ЧЫС.Ш цж4ыя, м.юьеть соизмѣримый коренъ, выражающійся въ видѣ
несократимой дроби то а служить (ЪълителеліЬ с, лсмъ а.
а р—Лълмтс-
Въ
самомъ дѣлѣ, если & есть корень даннаго уравненія, то имѣемъ тожде-
ство
°4і+г’-Нс=0’
или
да9 -|- с^3 = О.
Но аа*4“&2? дѣлится на а, слѣд, и с^а должно дѣлиться на а; но а есть число первое съ и ^3, слѣд. с должно дѣлиться на а. Такимъ же образомъ докажемъ, что 3, будучи дѣлителемъ суммы ЬлЭ4“с?2» дѣлитъ непремѣнно и а.
Слѣдствіе. Уравненіе я*-[-рх-]-$= О, въ которомъ р и д—числа цѣлыя, не можетъ имѣть соизмѣримыхъ дробныхъ корей.
Въ самомъ дѣлѣ, допустивъ, что ур—ніе имѣетъ такой корень на осно
ваніи предыдущей теоремы нашли бы, что цѣлое число дѣлитъ коэффиціентъ при я3, т.-е. 1.
Изъ этого слѣдуетъ, что наше уравненіе можетъ имѣть дѣйствительные корни: или цѣлые, и тогда оба они цѣлые, или же оба несоизмѣримые.
451. Теорема. 2Гсли уравненіе аяа4-Ь#4”с~^ въ которомъ коэффиціенты а, Ь и с дѣйствительны} имѣетъ мнимый коренъ, то другой ею корень есть мнимое количество^ сопряженное Аъ первымъ.
Въ самомъ дѣлѣ, пусть а 4~ 3* есть коренъ даннаго уравненія; въ такомъ случаѣ имѣемъ тождество
а(а 4“ & (а + 30 4“ с = О»
или, группируя дѣйствительные и мнимые члены, находимъ:
(ааа — а^-Р^а + с) + (-а23 + ^?Х = О . . .(1)
Первая часть имѣетъ видъ А 4“ Вг, гдѣ А и В дѣйствительны; но такое выраженіе можетъ равняться нулю только тогда, когда одновременно А = О и В —О. Итакъ, два. условія необходимыя и достаточныя для того, чтобы а 4“ было корнемъ даннаго уравненія, суть
аа» — а^ + Ья4-с = О 1
2сиф + ЬЗ = ° |
Замѣняя въ триномѣ алл4~^4“с количество % выраженіемъ а — найдемъ (аз2 — а^3 4“ 4“ с) “ (2аа^ 4“
а въ силу условій (2) это выраженіе обращается въ нуль. Итакъ, предложенное уравненіе, въ которомъ коэффиціенты дѣйствительны, имѣя мнимый корень а 4~ имѣетъ и сопряженный ему корень а — {Іі.
Изслѣдованіе частныхъ случаевъ.
452. До сихъ поръ мы предполагали, что коэффиціенты отличны отъ нуля. Положимъ теперь, что: /
Е Коэффиціентъ а равенъ нулю. При рѣшеніи квадратнаго уравненія намъ приходилось или дѣлить, или множить уравненіе на выраженіе, содержащее а; но мы знаемъ, что это дѣйствіе непозволительно, когда а = О, ибо можетъ повести къ уравненію, неэквивалентному данному. Поэтому является необходимость въ изслѣдованіи, представляютъ ли найденныя формулы для я? и х” рѣшенія уравненія и въ случаѣ когда а = О,
Обращаясь къ формуламъ корней:
/ — Ь + ѴЬ* — 4ас ________— Ъ —} — 4лс
2а 2а
и полагая въ нихъ а —О, найдемъ:
, —ъ + ѵ'& „ — ь — ГБ»
----0—’ х =—б---------------
дѣ есть абсолютное значеніе числа Ь. Слѣдовательно, различаемъ два лѵчая.
I. Ь > О, Имѣемъ: |/&а= | Ъ | =6. При а = О найдемъ:
— & + & О О — О’
Такихъ образомъ, первый корень принимаетъ неопредѣленный видъ, а второй обращается въ со. Чтобы раскрыть неопредѣленность, множимъ числителя и знаменателя дроби я/ на —Ь —]/ба—4ас, количество сопряженное числителю, и находимъ:
___(— Ь + — 4ш?)(— Ъ — —4а&) _ Ъ2 — (&а — 4ас) _ 2а(— Ь —Ѵь*— 4ш?) 2а(— Ь — 1—4ас)
___ 4ас_____________
—И^4аё)
Отсюда видно, что неопредѣленность корня х' зависитъ отъ присутствія въ числителѣ и знаменателѣ общаго множителя 2а, который при а = О обращается въ нуль. Сокративъ на 2а, имѣемъ
_______ 2<?
— 6 —— 4ас
и, положивъ здѣсь а = О, найдемъ:
,__ 2і_____ с
~ ^2& —
количество опредѣленное.
. Ь<0* Имѣемъ: [ 6 | — — Ь, При а = 0 будетъ
слѣд» когда а приближается къ О, корень х* стремится къ со. Что касается я", то числитель этого корпя при а = О есть — Ь 4- Ь = О, и х>г принимаетъ форму Для опредѣленія истиннаго значенія этой неопредѣленности поступаемъ
по предыдущему и находимъ хг,= 2с
— 6 +І/6‘3 — 4<н‘
что при а = О даетъ
с
слѣд. въ этомъ случаѣ второй корень — — а первый обращается въ со.
Итакъ, я/ж а — О одинъ изъ корней обращается въ с©, а другой равенъ корню уравненія первой степени Ъх 4~ с = О* въ которое обращается квадратное уравненіе при а= О.
453. Обратимся теперь къ самому уравненію, и посмотримъ, что оно даетъ при а = О.
Уравненію можно дать видъ
Ьх с = — ах-;
и какъ оно не удовлетворяется при х = О, ибо обращается въ с = 0, между тѣмъ какъ с отлично отъ нуля, то можно раздѣлить обѣ части на х2, вслѣдствіе чего получимъ уравненіе, эквивалентное данному:
с I
Такъ какъ, по условію, а = 0, то произведеніе множителей Ь“Г“ и — должно быть нулемъ; а для этого необходимо, чтобы либо тотъ, либо другой множитель обращался въ нуль. Положивъ ♦
ь + 5 = °, откуда X = —
1 Ь
равенъ—т.-е. конеченъ.
замѣчаемъ, что при этомъ другой множитель
Поэтому х = —есть корень даннаго уравненія.
Положивъ
1 п
- ~ О, откуда х=со, V
находимъ, что другой множитель обращается въ 6, и слѣд. конеченъ. Поэтому х = с© есть также корень уравненія. Эти результаты вполнѣ согласуются съ
выводомъ, полученнымъ изъ формулъ корней; поэтому, послѣднія приложимы и къ случаю а = О.
Примѣръ. Во что обращаются корни ур—нія
(«« _ _ 2(2а» — Ьа)я + 4а2 — Ь* = О
при а = Ь?
Такъ какъ при а = Ь коэффиціентъ при х3 обращается въ нуль, то одинъ 4д2__________________________________________________________________52
изъ корней обращается въ со, а другой принимаетъ значеніе дроби при а = &, т.-е. =-^. &
Эго можно провѣрить и общими формулами корней, которыя даютъ
_ 2а — Ь _ 2а + Ь
Л? — , * «Я/ ~ -3 г- •
а — Ъ а-\-Ь
454. II. Коэффиціенты а и & одновременно равны нулю. Обращаясь къ формуламъ корней, находимъ, что при а = Ь=О оба корня принимаютъ не-х Л О опредѣленный видъ ду.
Чтобы раскрыть неопредѣленность, преобразуемъ формулы корней такимъ же точно образомъ, какъ въ предыдущемъ случаѣ; найдемъ:
_______
— 6 — V 62 — 4ас — Ъ -р'І2 — 4ас
Положивъ здѣсь а = О и Ь = О, имѣемъ
, 2с 2с
ж=_ = СОі а/ =- = «>.
Итакъ, при а = Ь = $ оба корня безконечны. Обращаясь къ уравненію, даемъ ему видъ
ілк. такъ какъ а = Ь = 0, видъ
А=о.
Такъ какъ с конечно, то этому ур—нію можно удовлетворить единствен нымъ способомъ, ПОЛОЖИВЪ я—со.
Примѣръ. Каковы корни уравненія
(а + — (ч3 - аЬ - 2Ь3)а; (2аа - ЗаЬ + 6®) = О
при а = — Ь?
I
Когда а = — 6, коэффиціенты (а -ф- 6)2 и (а2 — аЬ —26*) при х* и х обращаются въ нули, между тѣмъ какъ свободный членъ въ 662; заключаемъ, что при а = — Ь оба корня безконечны.
То же можно видѣть и изъ формулъ корней; рѣшая данныя ур—нія, имѣемъ
а — Ь 2п — Ъ
сдѣлавъ а = — Ь, имѣемъ
— 26 О
— 36 О
455. III. Всѣ три коэффиціента а, Ь и с равны нулю. Изъ формулъ корней убѣдимся, что онѣ представляютъ дѣйствительную неопредѣленность.
Обращаясь къ уравненію, замѣчаемъ, что оно принимаетъ видъ ох^+ох^4-о = о, и слѣдовательно удовлетворяется всякимъ значеніемъ это—тождество.
ь|
Вычисленіе корнёй уравненія + когда коэффиціентъ
а весьма малъ.
456. Когда коэффиціентъ а весьма малъ, то изъ предыдущаго изслѣдованія (§ 452) видно, что одинъ изъ корней будетъ, по абсолютной величинѣ, весьма великъ, другой же близокъ къ —Общія формулы корней
— Ъ +і Ь2 — 4«с ,, — Ъ — ѴЬ2 — 4ае
-------------Т X = -------—Л~------
въ данпомъ случаѣ будутъ неудобны для вычисленій- Въ самомъ дѣлѣ, № — 4ас
вообще не есть точный квадратъ, и слѣд. }/б* — 4ас придется вычислять при-
близительно. Ошибку, сдѣланную при вычисленіи —4ас нужно будетъ раз-
дѣлить на _ 5 “100000’
2а для нахожденія ошибки х' или
то 2а=іоббб’ а П0Т0МУ
ошибка а,
и если а весьма мало, напр. сдѣланная при вычисленіи
)/ба — 4ас, поведетъ за собою погрѣшность, равную 10000г въ величинахъ х' и х"г Такъ что, если бы мы пожелали вычислить корни уравненія съ точностью до уфй' то должны бы были |/б* — 4ас найти съ точностью до іродоХТоп*
т.-е. съ 4 лишними десятичными знаками.
Отсюда понятно, что сложность вычисленій будетъ тѣмъ значительнѣе, чѣмъ меньше а.
Несравненно легче, при маломъ а, вычислять корни особымъ способомъ, называемымъ методомъ послѣдовательныхъ приближеній. Этимъ способомъ достаточно вычислить одинъ изъ корней; въ самомъ дѣлѣ, сумма корней извѣстна
и равна —— (въ чемъ убѣдимся, сложивъ формулы я?' и и если будетъ вычисленъ корень х\ то другой найдемъ, вычтя изъ суммы извѣстный корень:
Нужно разсмотрѣть два случая: корни одинаковаго знака, и корпи разнаго знака. Если черезъ а, Ь и с означимъ абсолютныя числа, то уравненіе съ положительными корнями будетъ вида: ах*— Ьх-^-с = 0; съ отрицательными: ах* -р Ъх 4* = 0- Достаточно указать вычисленіе положительныхъ корней, т.-е. ур—нія ах2 — Ъх с “ 0; ибо, если оба корня отрицательны, то перемѣнивъ у Ь знакъ 4“ на получимъ ур—ніе съ положительными корнями, вычисливъ которые и перемѣнивъ у нихъ знакъ, получимъ корни ур—нія «л:а-|-^4"С=0.
457. 1-й случай. Знаки корней одинаковы. Итакъ, разсмотримъ уравненіе съ положительными корнями, т.-е. вида
ах*— Ъх-^-с = О, . . . (1)
гдѣ а, & и с—абсолютныя часла, и слѣд. знаки окончательные.
Меньшій корень этого уравненія есть
_ ?> - >Ъг — 4ас _ (& — ) + Ѵ&2—4ас) _ 2с <
Х ~ 2а 2а(6 + У^“4аё) — Ъ + ‘ - ’
Этотъ корень мы и вычислимъ.
Рѣшая ур. (1) относительно Ьяг, находимъ
Ъх = с 4’
«ТЕТЦ
Т. к. а весьма мало, Ь величина конечная, х представляетъ въ этой формулѣ меньшій корень, имѣющій также конечную величину, то и ^х* будетъ весьма мало. Поэтому, откинувъ членъ мы сдѣлаемъ небольшую ошибку, п слѣд. первымъ приближеніемъ корпя хг будемъ ‘имѣть
с • — О
Это приближеніе меньше настоящей величины х, ибо откинули положительный а 2 членъ -
Если теперь въ формулѣ (3) замѣнимъ во второй части х величиною * меньшею чѣмъ х, то получимъ второе приближеніе
которое опять меньше настоящей величины х\ по больше чѣмъ ж, па
Замѣнивъ снова въ ур. (3) во второй части & черезъ #я, найдемъ третье приближеніе
^=сь + аь^>
снова меньшее истинной величины х\ ибо меньше х’. Но #3 будетъ больше я2; въ самомъ дѣлѣ, мы видѣли, что я2 >а^; возвысивъ обѣ части послѣдняго а с
неравенства въ квадратъ, помноживъ на & и придавъ по получимъ
к+к(^>к+?(^
то-есть > г2 и т. д.
Итакъ, послѣдовательныя приближенія идутъ все увеличиваясь, но всегда остаются меньше х\ сл. они приближаются къ яЛ Докажемъ теперь, что разница между х’ и приближеніями стремится къ нулю, и сл, можетъ быть сдѣлана какъ угодно малою.
Разность, между х' и первымъ приближеніемъ я?п т.-е. яоірь гадость перваго приближенія мы выразимъ изъ уравненія (3), которое даетъ (замѣтивъ, с V что ^ = ^):
| (®'Л
Но на основаніи (2), равняется
2с
& + Рб2 — 4ас
и слѣд.
г 2с.
х меньше
написавъ неравенство
г х
2с
Т’
возвысивъ обѣ его части въ квадратъ и умноживъ на найдемъ
& ь А
замѣнивъ первую часть равною ей величиною х' — х^ которую обозначимъ черезъ еІТ имѣемъ:
Эта формула даетъ предѣлъ погрѣшности 1-го приближенія. Вообще, погрѣшность «-го приближенія
— ъ *^л —^Х*^* _і)’
Но
х — ^Л_! = ед_і; а х* 4- < 2х
, 2с п / 4с •
ибо но ж <у, откуда 2х <-&-, а потому и подавно
*
Слѣдовательно
. 4ас
е« ~де' е*—1
4с Ъ *
Дѣлая въ этой формулѣ послѣдовательно п = 2, 3, 4, . писавъ формулу для 1-го приближенія, имѣемъ
, П и при-
4а<? ч / с
6і < X ъ
Аас^, /Хгі
де
де /х ей — і
Перемножая почленно эти неравенства., сокращая обѣ части на общаго множителя
’ получимъ
/4ас\" с епЛЬ^/ ’ Г
Но корни дѣйствительные, слѣд.
откуда
Ъ*— 4ас> 0.
4ас .
Ъ* <
Если количество, меньшее 1, возвышать въ возрастающія степени, то сте-/ 4ос\п
пени эти приближаются къ нулю, если же І-р-І приближается къ нулю, то
С п
і произведеніе его па конечную величину также стремится къ О.
Итакъ, количеству п всегда можно датъ' такую величину, чтобы ея бшо какъ угодно мало.
Итакъ, указаннымъ способомъ всегда можно найти приближенную величину мшаго корня съ какою угодно точностью; причемъ, останавливаясь на при-я*, дѣлаемъ ошибку меньшую
4ас\ну, с
Этотъ способъ приложимъ всякій разъ, когда т.-е. когда корни
, ,с^ . Ц . . *
4ас .
дѣйствительные; но практически пригоденъ тогда, когда весьма малая дробь сравнительно съ 1, ибо только въ этомъ случаѣ хх> достаточно
быстро приближаются къ х\
Примѣръ. Дано ур.
Зл* - 7640л; 4- 400 = 0.
Имѣемъ:
а = 3; Ъ = 7 640; с=400.
4ш?_4ХЗХ400__ 4800 _ 48 ш
6* — 58369600 — 58369600 — 583'696’ ’ ’ ’
если бы имѣли дробь ^^обо • - . (V), то по сокращеніи она дала бы но (1) имѣетъ такого же числителя какъ (V), но большаго знаменателя, слѣд. (1) или
4ос 1
’ 7^ < 10000'
Эта дробь весьма мала сравнительно съ 1, слѣд. наша метода приложима. Первое приближеніе для меньшаго корня есть
_ с _ 400 _ 40 — Ъ ~ 7640 — 764’ .
его ошибка
4аг ѵ / с
4ас I с > . ' >
но < іоооо? а по обращеніи въ десятичную дробь, даетъ
2 = 0,05235002. . . слѣд.
2 <0,06. О 1
•Поэтому ѵ 6 ___6_
Бі< 10000^ ЮО1 ИЛИ 51 < 1000000
сл. Е| навѣрное меньше
Слѣд., взявъ для х' число 0,05235, получимъ меньшій корень'съ ошибкою, 1
итакъ
меньшею
100000;
хі = 0,05235.
Вычислимъ еще второе приближеніе; оно будетъ
л л л ~ л 4ас . 1
Ошибка этого приближенія е2 но мы видѣли, что іоооо* а
6‘ < 1000000;
значитъ
с
6я<- 10000000000
«
С О [ \2
Вычисляя & и съ 10-ю дес. знаками, имѣемъ
р = 0,0523560209 . 7 . Ь '
| Ма= 0,0000010763 . . .
0,0523570972.
Сохраняя 9 десятичныхъ мѣстъ, имѣемъ:
—0,052357097
съ ошибкою
Чтобы вычислить другой корень, нужно изъ суммы корней, равной
7640 __4-
вычесть найденный; взявъ въ
7^40 х .
—девять десятичныхъ мѣстъ, имѣемъ: о
2546,666666666
— 0,052357097
2546,614309569, съ точи, ДОу^*
458. 2-й случай. Знаки корней различны.
Если знаки корней различны, что будетъ, когда с отрицательно, то, назвавъ абсолютныя величины коэффиціентовъ черезъ а, Ь и с, уравненіе будетъ одного изъ слѣдующихъ видовъ:
ах2 -}- Ъх — с = 0, ах* — Ъх — с ~ 0.
Въ первомъ уравненіи меньшій корень положителенъ, во второмъ отрицателенъ; но если во второе вм. х подставимъ —я, то превратимъ его въ первый видъ, т.-е. меньшій корень сдѣлаемъ положительнымъ.
Поэтому разсмотримъ, какъ найтк положит. корень уравненія
ах* -|- Ъх — с = О
но способу послѣдовательныхъ приближеній.
Опредѣляя Ъх, находимъ
Ъх — с — ах2, а отсюда
Послѣдовательныя приближенія будутъ:
С С а / \л С ® / X Ф @ Л- / \ л
і = Ъ * “ Ь = Ъ ’
и вообще
Искомый меньшій корень
выражается формулою
с я ^ь-ь'*
. ДО
Очевидно, что
Возвышая обѣ части а найдемъ
этого неравенства въ квадратъ и
затѣмъ умножая на
а > I (О3;
вычитая это неравенство
с с
изъ равенства = нолуч.
с
Ь
С (а
Ъ~Ь'Х ;
первая часть есть ж2, а
вторая есть х\ слѣд.
Возвышая обѣ части этого неравенства въ квадратъ, имѣемъ
затѣмъ умножая на 1 №
. с с
вычитая это неравенство изъ равенства & = & имѣемъ:
с
Ъ
Ъ Ь{х) 9
первая часть есть х3, а вторая =л?\ слѣд.
3
и т. д.
Продолжая такимъ образомъ, убѣдимся, что всѣ приближенія нечетнаго порядка больше настоящей величины х\ а четнаго — меньше х'.
' 4э7 ~
Кромѣ того, если выпишемъ всѣ четныя, затѣмъ всѣ нечетныя приближенія, получимъ два ряда: *
с
хі ь
х»~ь ь
ж5 = Ь
х* = ъ~ъ ж* ~ ъ — ь ь ~~ ь
Разсматривая первую пару нечетныхъ приближеній, замѣчаемъ, что, очевидно: х~ < х<.
Обращаясь затѣмъ къ первой парѣ четныхъ приближеній, в взявъ ихъ разность, имѣемъ
ф (*^1 * Я'з*), НО ^3 < > СЛѢД.
хі > я?8.
Переходя ко второй парѣ нечетныхъ приближеній и взявъ .нхъ разность, находимъ:
^8 ' = й Я'З*)» НО *^4 > СЛѢд*
Взявъ разность второй пары четныхъ приближеній:
- - #1 = (V но х$ х^ слѣд-
И т. д.
Заключаемъ, что приближенія нечетнаго порядка, оставаясь всегда больше ж', идутъ постепенно уменьшаясь и слѣд. приближаются къ а/; приближенія же четнаго порядка, всегда оставаясь меньше х\ идутъ увеличиваясь, и слѣд. также приближаются къ х'.
Докажемъ, что разность между тѣми и другими приближеніями и х' стремится къ нулю, и слѣд. м. б. сдѣлана какъ угодно малою.
Возьмемъ приближеніе нечетнаго порядка , которое больше х\ и назовемъ погрѣшность этого приближенія, т.-е. разность между нимъ и х\ черезъ имѣемъ:
Но, по (2), % а сл. и подавно
с НЛП
Л пли
какъ приближеніе четнаго порядка, меньше
итакъ
* <Ь
^ 6" складывая, имѣемъ
2е
Ь
е 2ас 2р-Н<
сі
а г»
Ь'Х ’
но
ь> сл.
слѣд.
Кромѣ того
поэтому
о а С*
или множа и дѣля вторую часть на 2:
• п
„ 2ас , с
'і< уХ 26’
Выразимъ теперь предѣлъ погрѣшности приближенія четнаго порядка, напримѣръ хір. Имѣемъ
Но ^2Р-і и х меньше хі или г, сл.
2 а с , < ДО ’ 1
Итакъ, предѣлъ погрѣшности четнаго и нечетнаго порядка выражается одинаково: произведеніемъ на погрѣшность предшествующаго приближенія. Слѣд., будетъ ли п четное или нечетное, всегда
Полагая въ этой формулѣ п = 2, 3, 4, . . . , п, получимъ формулы по-
грѣшностей 2-го, 3-го, . . . приближеній; присоединивъ сюда формулу погрѣшности 1-го приближенія, имѣемъ:
1
2ас ух с
?1 < Ь2 X
2ас у/ / \ еі
*
2«с х, е3 < /\ е2
Перемножая и
сокращая общихъ множителей, найдемъ
/2«б\Лх/ с е«<(ьГІ А^'
Отсюда видно
что если
будетъ < 1, или, 2с
что все равно, если
то всегда можно ваять п достаточно большимъ, чтобы сдѣлать кг Хад г \ СЯ / ' ѵ 20
меньше данной величины; н сл* чтб,- погрѣшность и подавно, была меньше той же величины.
Но и въ этомъ случаѣ метода удобна только тогда, когда будетъ чипгельно меньше 1, ибо только при такомъ условіи #2, х3, , . . будутъ быстро приближаться къ искомой величинѣ. Останавливаясь на приближеніи нечетнаго порядка, получимъ величину ошибочную по избытку; останавливаясь на приближеніи четнаго порядка, имѣемъ величину съ ошибкою по недостатку; въ обоихъ случаяхъ высшій предѣлъ сдѣланной погрѣшности узнаемъ, вычисливъ
і'2«еукч / с
[&) ^2Ь
Примѣръ, 5^3-|-140х — 7 = 0, Здѣсь
а = 5; Ь = 140; С=7;
2ас 70 1
~ 140*= 280’ это число значительно <1, поэтому метода приложима* Первое приближеніе
С 7 1 пп-
140 20
Погрѣшность этого приближенія, еп будетъ меньше о^Хтн =
О* 20 2оОЛ
= 11200' а С1, 11 подаБК0’ <10ббб' .
Второе приближеніе
ж, = - — - «^ = 0,05 — ЛХ 0,0025 =0,0499107.
Л , „ „ /2вс\а ч, с . I ч, 1 1
Ошибка е8 <Ц Хэді или < ^280)2 X 40 “ 3136000’ а ПОТОМУ и п0~
давно меньше §Х ]000000-
Значитъ, положительный корень, съ ошибкою меньшею одной полу-милліонной, равенъ
0,049911,
Сумма корней = — 28, сл. отриц. корень, съ тою же точностью, равенъ
— 27,950089.
ГЛАВ А XXXI.
Связь между коэффиціентами и корнями квадратнаго уравненія.—Приложенія.—Построеніе корней квадратнаго уравненія*
459. Теорема. Каковы бы на были коря# уравненія
ах* 4~ с = 0-
1) ихъ сумма равна взятому съ обратнымъ знакомъ частному отъ раздѣленія втсрого коэффиціента на первый* т.*е.
а’
2) а произведеніе равно частному отъ раздѣленія третьяго коэффиціента на первый* т.-е.
с
а
Повѣрка. Мы знаемъ, что во всѣхъ случаяхъ корни даннаго уравненія выражаются формулами
складывая которыя, находимъ
а‘ перемножая, наюдпмъ
, „__(— Ь + Ѵ&— 4ас) (— Ъ — Ѵб3— 4ас).
X , X ——’ ~ 5 а - --- У
4аа
замѣчая, что числитель представляетъ произведеніе суммы двухъ количествъ на ихъ разность, и слѣд. равенъ разности ихъ квадратовъ, имѣемъ:
, (— 6)2 — а 62 — 4ас)2 _ 63 — (63 —4ас) ' с
Х‘Х~ 4 а*' — 4вз — а
Первое доказательство. Такъ какъ корни х’ и х\ при подстановкѣ въ уравненіе, обращаютъ его въ тождество, то имѣемъ два тождества
ах1'* 4- Ъх + с = О, ах”* + ЪзГ + с = О.
Принимая за неизвѣстныя—коэффиціенты а, 6 и с, видимъ, что они удовлетворяютъ двумъ ур—мъ, и потому задача объ ихъ нахожденіи неопредѣленна.
Но если оба равенства раздѣлимъ на а:
X .6с .
то, принимая за неизвѣстныя—отношенія - и находимъ, что эти отношенія должны удовлетворять двумъ уравненіямъ, и потому задача объ ихъ нахожде-нш опредѣленна. Эти два ур—нія и дадутъ намъ величины - и - въ функціи а а
корней. Для исключенія ; вычитаемъ 2-е ур—ніе изъ 1-го и находимъ (1>
Положимъ, что х'^х”' въ такомъ случаѣ позволительно сократить ур—ніе на количество х’— х" (какъ неравное нулю), и получится
ж'4~^” 4“ ~ = 0, откуда х’-\-х’’=—
Внеся вмѣсто равную ему величину — (х 4- ж”) въ первое уравненіе, найдемъ
дУ3 — (х* х")х’ = или — х'х* + ^ = О,
откуда х!х" = --а
Теорема доказана; но опредѣленіе | сдѣлано въ предположеніи, что корни неравны. Остается доказать, что теорема справедлива и въ случаѣ равныхъ корней. Мы знаемъ, что если корни равны, то каждый изъ нихъ = — слѣд., 6 г г, С
ихъ сумма ——а отсюда, какъ и выше, найдемъ, что жж =-• с» а
Второе доказательство. Такъ какъ х' и хІГ суть корни уравненія гіх2 Ъх -|- с — О, то триномъ ая* -{- -|- с обращается въ нуль при под-
становкѣ въ него х’ и я” вмѣсто я, и слѣд, дѣлится какъ на я— х\ такъ и на х — я"; слѣд., если х( но равно х’\ то этотъ триномъ, на основ, теоремы § 65, дѣлится и на произведеніе (я — я/) (я — х"), а какъ дѣлитель—одинаковой степени съ дѣлимымъ, то частное будетъ нулевой степени относительно хі и потому приводится къ одному члену, именно къ частному отъ раздѣленія перваго члена, ах\ дѣлимаго на первый членъ я2 дѣлителя, что даетъ Итакъ
или, раскрывъ вторую часть и расположивъ по степенямъ буквы я, находимъ тождество
ах2 Ъх с = ля2 — а(х’ 4“ х” Ч- ах'х1'*
а отнявъ отъ обѣихъ частей по ах2
Ъх 4- с = — й(я'4~#/)а:Ч_ал:
Отсюда, по теоремѣ § 71, имѣемъ
Ь — — а(х' 4“ п с = ало/';
выражая изъ 1-го равенства я?'Ч“*", а изъ 2-го х'х”, находимъ:
И это доказательство предполагаетъ, что Но нужно замѣтить, что
осли найденныя соотношенія вѣрны, когда корни различны, то они приложимы п тогда, когда корни разнятся между собою какъ угодно мало, а потому справедливы и для равныхъ корней,
460, Примѣчаніе. Если уравненіе имѣетъ видъ
то, чтобы перейти къ нему отъ уравненія агс24~^4^с"^' надо положить: а= 1, & = р, с = ,
Тогда формулы соотношеній примутъ видъ:
х’ . х" = ? = а;1-|~ж" = — у = —/>;
слѣд., сумма корней уравненія х2рхд — О равна коэффиціенту при первой степени неизвѣстнаго^ взятому съ обратнымъ знакомъ^ а произведеніе корней равно извѣстному члену.
461. Слѣдствія. I, Вычислить разность корней уравненія ая*4-Ья4~ 4-е = 0, не рѣшая уравненія.
Обозначивъ разность корней буквою можемъ выразить в* по суммѣ и произведенію корней; въ самомъ дѣлѣ:
2* — (&' — #")2 = 4“ я:"* — = х'* я"2 2^^" — 4а?'я" =
откуда
= (і. + И1-4Л" = Х-? = ^
= Г62—~4оё, а
Тотъ же результатъ нашли бы и прямымъ вычитаніемъ корней.
II , Когда извѣстенъ одинъ изъ корней квадратнаго уравненія, то другой можно найти, не рѣшая уравненія, а: 1) раздѣливъ произведеніе корней М) на извѣстный корень, пли: 2) вычтя извѣстный корень изъ суммы корней, т.-е.
б изъ
Примѣръ. Рѣшить уравненіе ~4~д.^ — ^4~^ц_~7/ Прямо видно, что уравненіе имѣетъ корень х = а, ибо при ж — а обѣ части дѣлаются тож
дественными. д
Для нахожденія второго корня приводимъ уравненіе къ цѣлому виду:
(2а + Ъ)х* + (Ь2 — 2«*)я — аЬ(а + Ь) = О:
. . „ аЪ(а -|- ?>)
и раздѣливъ произведеніе корней---------.
на извѣстный корень а, найдемъ
другой корень
б(а —|- 6)» 2а -|- Ь
Можно рѣшить это ур—ніе и другимъ пріемомъ; напишемъ его въ видѣ
1 — 2 г а
= О, или (а — х) [(а? 4“ &)(а 4” 4“ — О.
Приравнивая пулю первый множитель, находимъ одинъ корень = приравнивая нулю второй множитель, получаемъ ур—иіе первой .степенп
в (х + Ь)(а 6) + ах = О,
откуда и найдемъ второй корень.
III . коэффиціенты уравненія соизмѣримы, то дѣйствительные корни или оба соизмѣримы, или оба несоизмѣримы, потому что нхъ сумма, напр., соизмѣрима; и когда они несоизмѣримы, то сопряженны.
IV .—Когда-коэффиціенты ур—нія дѣйствительны, то или оба корня дѣйствительны, или оба мнимы, ибо ихъ сумма дѣйствительна, и когда они мнимы, то сопряженны.
Переходимъ къ изученію приложеній теоремы § 459.
462. Приложеніе 7. Изслѣдованіе, а ргіогі, корней квадратнаго уравненія. Опредѣленіе,—Изслѣдовать а ^ггоп' коафатяое доаонеяге
не рѣшая его* опредѣлить* будутъ ли корни его дѣйствительные или мнимые* когда они дѣйствительны* узнать—равные они* или неравные; въ случаѣ ихъ равенства* указать ихъ общую величину* въ случаѣ же неравенства указать—одинаковаго они знака* или имѣютъ знаки противоположные; если имѣютъ общій знакъ* то указать—какой именно; если же знаки корней различны* то указать знакъ корня* имѣющаго большую абсолютную величину.
I. Если окажется, что
Ь2 — 4ас < О,
то корни уравненія будутъ жянліые сопряженные,
II. Если
Ъ* — 4ас = О,
то мы знаемъ, что корпи уравненія дѣйствительные равные* и общая величина иіъ есть
Ъ
~ 2а'
откуда видно, что оба корня положительны, когда < О, оба отрицатель-и
ни, когда ~>0, и оба равны нулю* когда ^ = 0.
ПІ. Наконецъ, если окажется, что
&2 — 4ас > О,
то заключаемъ, что ур—ніе имѣетъ корни дѣйствительные неравные. При этомъ слѣдуетъ замѣтить, что для опредѣленія знака разности Ъ2 — 4ас не всегда необходимо вычислять эту разность, а именно если ас < О, т.-е. а и с имѣютъ знаки противоположные* то разность Ь2— 4ас необходимо положительна. Въ самомъ дѣлѣ, еслиао<О, то можно положить 4ас = — а2, гдѣ — а2 количество существенно - отрицательное, и слѣд. Ь2 — 4ас = Ь2 — (— а2) = Ь2 4~ я2» а сумма квадратовъ дѣйствительныхъ количествъ существенно положительна. Значитъ, при ас<.0 корни уравненія безусловно дѣйствительны.
Когда уравненіе имѣетъ корни дѣйствительные и неравные, то:
1) Если ^>0, произведеніе корней положительно, оба корня имѣютъ о^накоеме знаки. Но если знаки корней одинаковы, то общій ‘знакъ будетъ такой, какъ у ихъ суммы, которая равна —
Отсюда:
Если Ъ > 0, то - будетъ количество отрицательное* и слѣд. оба кор-до Я
пя отрмдателъяы.
Если - < 0, то — — положитолько* и потому оба корня положительны. а а
Предположеніе = 0 невозможно, ибо изъ него слѣдовало бы, что корни до
равны и противоположны по знаку, что противно предположенію О, которое требуетъ, чтобы знакъ корней былъ одинаковъ.
2) Если — <0, т.-е. произведеніе корней отрицательно, то знаки корней противоположны. Но въ такомъ случаѣ сумма ихъ имѣетъ такой знакъ, какой у корня съ большею абсолютною величиной. Отсюда:
Если " > О, то сумма корней —будетъ отрицательна, и слѣд. боль-шій, по абсолютной величинѣ, корень отргіцателенъ.
Если - < О, и слѣд. — - > О, то большій, по абсолютному значенію, корень положителенъ.
Наконецъ, если ~ ~ О, то сумма корней = пулю, сл. корни равны по величинѣ и противоположны по знаку.
3) Если - = О, то одинъ корень = нулю. Что касается другого, то: а
Когда > О, сумма корней отрицательна, а, слѣд., другой корень отри-Я
цателенъ.
Когда' - < О, сумма положительна, и другой корень положителенъ, а
Гипотеза ^ = 0 не имѣетъ мѣста, ибо въ этомъ случаѣ выходилобы & —О, с = 0, а слѣдовательно вышло бы в Ь* — 4ас = 0, что противорѣчивъ условію 6* — 4ас > 0.
Изслѣдованіе можно резюмировать такъ:
I. № — 4ас < 0, корни уравненія мнимые сопряженные.
Первую часть уравненія можно представить въ формѣ суммы двухъ квадратовъ.
II. № — 4ас — 0. Корни дѣйствительные равные.
корни положительны.
корни отрицательны.
корни равные нулю.
Первую часть уравненія можно представить
->0 . . . р <0, а | а ’
Знаки корней | 6 . п одинаковы Р *
111. Ь*~ 4ас>0.
Корни дѣйствнтель- > ные неравные.
- < о . . а
знаки корней а
различны
;>0’ ь - О,
- = 0, а ’
въ формѣ полнаго квадрата.
оба корня положительны.
оба корня отрицательны.
корень съ большою абсолютною величиною отрицателенъ.
большій по абсолютн. величинѣ корень положителенъ.
корни равны и противоположны по знаку.
“ = 0 . . * - < 0, другой корень положителенъ.
одинъ корень ! Ь л
=пѵчю I л Другой корень отрицателенъ*
Первую часть уравненія можно представить въ формѣ разности двухъ квадратовъ*
Примѣры, I. Лзс.тдоватъ корни уравненія
7я3-{” 4” 5 = О;
въ’данномъ случаѣ Ьа — 4ос = 32— 4Х^Х^~— 131, т.-е. количеству отрицательному, слѣд. корни—мнимые,
II. Изслѣдовать корни уравненія
9х*4- 12x4-4 = 0.
Такъ какъ коэффиціентъ при х четный, то составляемъ разность Ъ'* — ас; имѣемъ № — ас = 62— 9У4 = 0т а потому корни ур—нія
Ь' 6 2
ные равные. Общая величина ихъ = — — — —
III. Изслѣдовать корни уравненія
Зх* — 8х 4~ 4 = 0;
6'2 — ас = 42 — 3 X 4 = 4~ 4, слѣд. корни й/ьастшпелъныс Про-
изведеніе корней = + д« т.-е. положительно, слѣд. знаки корней одинаковы.
। 3 .
Сумма корней =4“ т.-с. >07 слѣд. оба корня положительны.
IV. Изслѣдовать корни уравненія
8 л;3 4- 57ж-{-10 = 0;
Ь* — 4ас = 573 — 4 X 8 X Ю = + 2929, количеству положительному,поэтому корни—(Ьъисяшіягелъяые неравные, Произведеиіеихъ, равное 4~ положитель-
57
но, слѣд. знаки корней одинаковы. Сумма корней, равная —отрицательна, слѣд. оба корня отрицательны.
V. Изслѣдовать корни уравненія
Зх2 — 8х — 3 = 0;
а и с имѣютъ знаки противоположные, слѣд. корни—дѣйствительные неравные. Произведеніе ихъ, равное — 1, отрицательно, потому знаки корней различны. Сумма корней, равная 4*31 положительна, слѣд. большій по абсолютной величинѣ корень положителенъ.
VI. Изслѣдовать корни уравненія
; Зха + 8х — 3 = 0;
а и с — разнаго знака, сл. опять корни ур —нія дѣйствительные, неравные
и разнаго знака. Сумма игъ, равная —отрицательна, слѣд. большій но абсолютной величинѣ корень отрицателенъ.
463. Приложеніе II. Составленіе квадратнаго уравненія по даннымъ корнямъ.
Пусть требуется составить квадратное уравненіе, корнями котораго были бы количества а и р. Искомое ур—ніе должно быть вида
х1-Н = 0;
нужно опредѣлить коэффиціенты р н з; соотношенія между коэффиціентами н корнями даютъ:
Р — — (* + ?), 3 = а-?;
искомое ур—ше такимъ образомъ есть
X4 — (а ?|)х 5$ = 0.
2 3
Примѣры. I. Составить ур—ніе3 котораго корни были бы: и —д*
Исковое ур—ніе должно быть вида <- «
арпегь должно быть:
__ /2_3\_ 7_ _2 /_3\ _6у
\5 4/ 20’ 2 — 5 \ 4/ “ 20*’
I
слѣд- вскомое ур—ніе будетъ: <
—^х = 0, илл 20х3-і-7л7 — 6 = 0.
П. Составитъ ур—ніе9 корнями котораго были бы & и -д ; Исковое ур—ніе должно быть вида
х2 + рх % = О,
, ___(а I & \_________________________ а ______6 __ дЛ
Г ” \а-|-6 । а — б) 4 а3 — а — Ь а2 —
слѣд. ур—ніе будетъ
х1 - или (а8 — г»*)х4 — (а* -|- Ь!)я аЬ = 0.
III. Составить квадратное уравненіе, съ соизмѣримыми коэффиціентами, которое имѣло бы корень 5 — 3|/7.
— 4€8 -
Искомое ур—ніе должно быть вида
яа4-до + #= О;
такъ какъ, по условію^ и % должны быть и мы доказали, что
ур—ніе съ соизмѣримыми коэффиціентами, имѣющее корень 5—Зр'Т, имѣетъ другой корень сопряженный съ первымъ; слѣд. второй корень будетъ 5 -1- 3)/7; поэтому
г = _ (5 —3|/7-|_5-рз/7) = —10;
^ = (5-3/7) (5 + зѴ?) = -38;
слѣд. искомое уравненіе есть
я* — Юя— 38• = 0.
Примѣчаніе.— Задача эта опредѣленна только тогда, когда существуетъ условіе, чтобы коэффиціенты искомаго уравненія были соизмѣримы; если этого требованія нѣтъ, то задача неопредѣленна, ибо существуетъ безчисленное множество квадратныхъ уравненій, имѣющихъ данный корень; такъ, уравненія, имѣющія корень 5 — 3]/7 (называя другой корень буквою к), суть
я* - (к + 5 - 3 / 7)я+к (5 — 3 у/7) = О,
гдѣ 1—произвольное количество*
Въ § 449 мы видѣли, что условіе, чтобы квадратное ур—ніе сг соизмѣримыми коэффиціентами удовлетворялось несоизмѣримымъ значеніемъ а -р (/3 неизвѣстнаго, выражалось двумя соотношеніями между коэффиціентами. Взявъ эти соотношенія, мы имѣли бы два ур—пія, изъ которыхъ могли бы получить уже найденныя значенія для р и <1.
IV. Составитъ квадратное ур—ніе, съ дѣйствительными коэффиціента ми^ имѣющее коренъ 2 4“3г.
Искомое ур—ніе имѣетъ видъ
я3 4-^ +2 — 0;
для опредѣленія р т замѣчаемъ, что ур. съ дѣйствительными коэффиціентами, имѣющее корень 2 4" Зі, имѣетъ другимъ корнемъ мнимое сопряженное выраженіе 2 — Зі* Отсюда
р= — (2 4-ЗІ-Р2 — Зг) = — 4, (2-НО (2 — Зі)= 13;
и искомое ур—ніе будетъ — 4x4^13 = 0*
Примѣчаніе. Задача эта опредѣленна потому только, что на коэффиціенты наложено ограниченіе, чтобы спи были дѣйствительны. Если этого ограниченія нѣтъ, задача неопредѣленна; называя буквою к совершенно произвольное количество, дѣйствительное или мнимое, получимъ уравненіе
;Г2 — (к 4-2 + 30^4-Ч2 + 30 = °
необходимо имѣющее одинъ изъ корней, равный 2 4~3г'.
Еслибы мы прямо выразили ,что 2-^Зг удовлетворяетъ ур—пію 4~д = 0, то (си. § 451) въ случаѣ дѣйствительныхъ р и д пашли бы два ур—нія для опредѣленія р я д, именно:
4- 9^д-}-2р = О, 12 + = О,
откуда нашли бы р = — 4, $ = 13,
464. Приложеніе ІІГ. Преобразованіе корней квадратнаго уравненія.
Задача I. Дано квадратное уравненіе а.г2с = О- сотавыть другое уравненіе, котораго корни отличались бы отъ корней даннаго только знаками.
Искомое уравненіе будетъ вида
^+/>с-|-7 = О,
«ли юрнп даппаго ур—пія обозначимъ буквами х' и ж", то корпи новаго долхны равняться —%' и —яЛ подъ этимъ условіемъ и нужно опредѣлить р в д. Итакъ
р = — (— — д/) = #'-|-#" = — д = (—х'} , (— х”) = т'.т" = -•
Слѣд. искомое уравненіе будетъ
4- - = 0 или -4- с = О.
а 1 а 1
Легко видѣть, что мы ею получимъ прямо изъ даннаго, подставивъ въ послѣднее —х вмѣсто х.
другое ур—ніе, Пусть корни
Дано квадратное ур—ніе ш;2Ц-с = 6; составитъ корни котораго были бы обратны корнямъ даннаго, даннаго уравненія будутъ я' и я". Мы хотимъ составить урав-1 1
-д = 0, корнями котораго были бы и слѣдовательно
__1 ___1_____1 , с_а
$ х''х"—~х*х" *а с*
Такимъ образомъ, искомое ур—піе будетъ
я;2 -|~ х -|- = 0, или сха -|“ а = 0. -
Этотъ хе результатъ мы найдемъ, если въ данное ур—ніе подставимъ - вмѣсто х; въ самомъ дѣлѣ, подстановка эта даетъ
54_~4~с=о1 или с#2-р Ья-|-а=0. ОС
Итакъ: уравненіе съ обратными величинами корней выводится изъ даннаго замѣною х обратнымъ ему количествомъ -•
Задача ІП. По данному уравненію ах* -{- Ъх с = 0 составитъ другое, корни котораго равнялись бы корнямъ даннаго, сложеннымъ съ даннымъ количествомъ А.
Пусть корни даннаго уравненія будутъ хг и я"; требуется составить уравненіе = О? корни котораго были бы #-рХ п я/'-РХ- Слѣдова-
тельно
Р = - (*' + + 21) = - (- \ + 21) = Р 21; '
5 = X) = х'х” -|- (&' -}- X") А + ~ X 4~ а*.
Требуемое уравненіе есть, слѣдовательно,
—2Йя4-(а3 --Х+ -)=О,
1 \а / 1 \ а 1 а/ ’
ИЛИ
ая2 (& — 2ал)х 4“ С*2'2 — Ы -|- с) = 0.
Этотъ результатъ мы нашли бы, если бы въ данное ур—ніе вмѣсто х подставили я —І; въ самомъ дѣлѣ, подстановка эта даетъ
а{х — а)2 -(у —а) -|" с = О,
или, раскрывая скобки и приводя члены въ порядокъ, а#2 _р (й _ 2яа)я 4“ (аХя — Ъ\ 4= с) = 0.
Итакъ: эдэавнеше съ корнями даннаго, сложенными съ X, выводится изъ даннаго замѣною х биномомъ х—X.
Примѣръ. Составитъ уравненіе, котоваго корки были бы больше корней ур—нія Зл?2 — 5а: — 4 = 0 на
Замѣнивъ въ данномъ уравненіи я? разностью х — 2, имѣемъ:
3(я — 2)* — 5 (я— 2) — 4 = О, или Зя3 — 17я 4-18 = 0.
465. Эта задача важна по своему отношенію къ слѣдующимъ двумъ вопросамъ, встрѣчающимся при изслѣдованіи задачъ второй степени.
Вопросъ I. Выразить, что оба корня квадратнаго уравненія
ах* 4~ 4~ с ~ О
больше даннаго количества X.
Если корни уравненія назовемъ буквами х> и х>\ то, по условію, должно быть
хг>\ и хн >Х, или, что то же, х' — Х>0 и х” — Х>0 . . . (1).
Если теперь по давнему уравненію мы составимъ такое, котораго корни равнялись бы х*— X и х"—X, то найдемъ требуемыя условія, выразивъ, что корни новаго уравненія должны быть положительны (въ силу 1).
Для составленія новаго уравненія нужно въ данномъ замѣнить х суммою х-|~Х; сдѣлавъ это, найдемъ:
= 0 • • -(2)
Чтобы корни этого ур—нія были положительны, необходимо, чтобы: 1) ихъ произведеніе было положительно; 2) ихъ сумма была положительна. Итакъ, требуемыя условія будутъ:
. ѵ 4- 6Х 4- с. Л х9
1) —!—>о, или, умноживъ обѣ части на а3:
а(аХ9 -(- Ъ\ —с) > 0;
2) _ —> 0, пли, умноживъ обѣ части на — а*:
* а(Ь-|~2ал) <0.
Примѣчаніе. Чтобы выразить, что корпи даннаго ур—нія оба меньше X, необходимо выразить, что корни ур—нія (2) оба отрицательны; сдѣлавъ это, получимъ условія:
а(аХ* ЬХ + с) > 0; а(Ъ 2аХ) > 0.
Вопросъ II. Выразитъ > что данное количество \ заключается между корнями ур—нія ах* -р Ъх 4- с = 0.
Пусть корни даннаго уравненія будутъ х' и х'\ причемъ х'<х”.
По условію должно быть:
х' <Х и ж">Х, или х' —1<0 и х"— а>0 . . (1)
Ур—ніе, имѣющее корни х< — X и х" — X, есть
’ ах* + (6 4- 2а\)х 4~ (аХ* 4" ЬХ 4“ с) —
Въ ежлу неравенствъ (1) корни этого ур—нія должны имѣть противополож-ве жш, слѣд., необходимо и достаточно, чтобы ихъ произведеніе было отри-кишм т.-е. чтобы
< 0, или а(аХ2 ^Х 4“ с) < 0. к
466. Приложеніе IV. Найти соотношеніе между коэффиціентами квадратнаго уравненія подъ условіемъ, чтобы между корнями уравненія существовала данная зависимость.
Задача I. Какая связь должна существовать между коэффиціентами у]>авненія ах* -(- Ъх с = 0, чтобы его корни х' и х" удовлетворяли условію рх' — дх" — г?
Рѣшивъ данное уравненіе и подставивъ найденные корни въ равенство рх' — ухц = г, найдемъ требуемое условіе. Ио обыкновенно требуется дать искомое условіе, не рѣшая ур—-нія; этого достигнемъ слѣдующимъ пріемомъ.
Говоря, что хг и яУ суть корни даннаго ур—-нія, мел выражаемъ этимъ, что они удовлетворяютъ ур—ямъ:
г I ГГ Ь . I/ С
X 4- ІГ =-------и & Я =
1 а «’
и наоборотъ. Слѣд., задачу можно формулировать такъ:
Какова должна бытъ связь между коэффиціентами даннаю ур—нія, чтооы хг и хг* удовлетворяли тремъ ур^ямъ.
, ч / I гі Ь і п С
рх—дх =>', # -|-Л? = — -1 XX =
Очевидно, рѣшивъ два изъ отъ ур—ній (и проще первыя два, какъ ур—нія 1-й степени), мы найдемъ требуемое условіе, подставивъ найденныя рѣшенія въ З-о. Первыя два даютъ:
аг — Ьд _______ Ър +
«(?+<?)’ х ~ «(р+з)’
подставляя въ третье, найдемъ:
“ ^4Й+7І^ = а’ вли (вг—М(«»- + Ьр) + ас(р + ?)’ = 0.
Это и есть требуемое соотношеніе.
Задача II* Опредѣлитъ X такъ, чтобы корни хг и х” уравненія ч
(2Х—1)лгН- (Зк-|- 1) =0
илоьли отношеніе
Согласію условію, корни должны удовлетворять уравненіямъ
",
2СТ’ г'Ж" = 2СТ-
Рѣшая первыя два, находимъ
Х'~ 5ф—О’ Х"~ 5(2І— 1)’
ч внося въ третье, уравненіе, имѣемъ
^Г=ТГ» = ІІ=Г или С(5Ч-Оа-25 (Зл-|-1)(2Х- 1) = 0
это и есть соотношеніе, которому должно удовлетворять І; располагая по стс-пенямъ а, имѣемъ
31=0,
откуда
31
Провѣримъ, дѣйствительно ли эти значенія 1 суть требуемыя.
Во-первыхъ, посмотримъ, каковы корпи даннаго ур—нія прп Х = для этого выносимъ X за скобки:
# - 0 *’+(5+О*+(3+і)]=0;
отсюда видно, что когда к приближается къ безконечности, корни данннаго ур—нія стремятся къ предѣламъ, удовлетворяющимъ ур—нію 2я2 5x4-3 = 0 откуда %*= — | и х" = —1; отношеніе я : а" дѣйствительно = 3 : 2.
31
Во-вторыхъ, при Х = —данное ур—ніе беретъ видъ 147я24“ 7О.г-|“ 2 4
4-8 = 0, откуда х' = — х” = — —; дѣйствительно : я" = 3 : 2.
467, Приложеніе V. Какому условію должны удовлетворять коэффиціенты двухъ квадратныхъ уравненій
ах--\-Ъх + с= 0 , . , (1) а'ят24~Ь'я4“= 0 - * . (2),
чтобы эти ур—нія имѣли одинъ общій корень?
Первое рѣшеніе. Пусть корпи ур—пія (1) суть а и ур — нія (2) я и [і/, гдѣ а—общій корень; мы имѣемъ 4 уравпепія
«+?=-4-. -(з)
«? = Д...(4)
*-Н'=~'- ' -(5>
• • (6)
Докажемъ, что для того, чтобы данныя ур—нія имѣли одинъ общій корень, необходимо и достаточно, чтобы ур—пія (7) съ тремя неизвѣстными а, р п имѣли по крайней мѣрѣ одно общее рѣшеніе. Въ самомъ дѣлѣ:
1) Если ур—нія (1) и (2) имѣютъ общій корень а, то ур—пія системы (7) будутъ удовлетворены этимъ корнемъ а и двумя не общими корнями и р'.
2) Если ур—нія (7) имѣютъ общее рѣшеніе (а, ₽ и р'), то: корпи а п р, удовлетворяя ур—мъ (3) и (4), служатъ корнями (1), а а и удовлетворяя (5) и (6), будутъ корнями ур—нія (2); т.-е. а и будетъ общимъ корнемъ данныхъ ур—ній.
Итакъ, искомое условіе есть условіе, при которомъ система (7) имѣетъ общее рѣшеніе; это условіе найдемъ, исключивъ а, $ и изъ ур—ній системы (7). Комбинируя (3) и (5), имѣемъ
□, = аЪ'-Ъа'
Р аа’ ’
-(8),
комбинируя (4) съ (6), получимъ
Отсюда:
__са' — ас'
Я аЬ'— Ъа'*
Слѣд. изъ (4) имѣемъ
0 = с(а//— Ьа') «(сл'— ас1}'
Подставляя эти величины въ (3), и найдемъ искомое условіе:
са' — а/?' । с(лд' — ?>лЛ) Ь лЬ' — Ьаг ' а(гл' — ас') * а ~~ ’
что не трудно привести къ виду ►
(са' — ас')3 — (аЪг — Ъа')(Ъѵ — сЪ') = О.
Второе рѣшеніе. Полагая а й а' отличными отъ нуля и умноживъ ур. (1) на а', а (2) на а, замѣнимъ игъ двумя слѣдующими, икъ эквивалентными: • •
аа'я9 “И — О • • (Ю)і аа'я;*-р аЬ'л-|-ас'= О, . . . (11),
изъ которыхъ тотчасъ выводимъ слѣдующія замѣчанія:
1) Если аУ — Ьа' = О, то ур—нія не могутъ имѣть никакого общаго рѣшенія, если въ то же время не будетъ и ас’ — са' = 0; но въ такомъ случаѣ оба ур—нія дѣлаются тождественными, иначе говоря, имѣютъ два общихъ корпя.
2) Если ас' — са1 = О, то ур—нія не могутъ имѣть ни одного общаго корня, если при этомъ не будетъ и аЪг — Ьа' = 0; но тогда опять оба ур—нія будутъ тождественны.
3) Изъ сопоставленія этихъ замѣчаній выводимъ то заключеніе, что если два квадратныя ур—нія имѣютъ ойинь только общій корень, то разности аЬ'— Ъа' и ас’ — са' отличны отъ нуля; слѣд. по крайней мѣрѣ одно изъ чиселъ с и с' не есть нуль.
Зная это, вычтемъ изъ (10) ур—ніе (11); найдемъ
(аЬ'— Ьа') я — са' = 0, . . . (12).
По извѣстному принципу, система (1) и (2) эквивалентна системѣ (1) и (12); слѣд., общій'корень м. б. найденъ изъ послѣдней системы; а какъ ур. (12) есть ур—ніе 1-й степени и слѣд. имѣетъ только одинъ корень, значитъ, если данныя ур—нія имѣютъ общій корень, онъ долженъ быть
__ ас' — са'
Х аЬ' —Ьа'
Будучи общимъ корнемъ системы (1) и (12), онъ долженъ удовлетворять
ур—нію (1); такъ что искомое условіе найдемъ, подставивъ найденное для х значеніе въ у^—піе (1), Итакъ
а(ас' — агс)2 Ъ(ас* — л'с) . _ ~
ТаЬ'—«ър + С “
что легко привести къ виду
(а€'—а'<?)3 — (аЪг — а'Ь^Ъс* — Ъ'с) = Ог . - - (13),
Соотношеніе ото просто, симметрично и легко удерживается въ намяти.
Его можно представить въ другой формѣ. Раскрывъ скобки и умноживъ всѣ члены на 4, найдемъ:
4с*а'3 — 8аса'с' — — 4Ьа'сЬ'-|- 4Б2а'с' 4Ь'аас = ОЛ
«
или, придавъ и вычтя можемъ дать ему видъ:
+ 4аѴй + 4сѴ2 — 4ЬЬгас' - 4ЬЬ'са' + Зас'са* — №>’* 4ай'а +
4а'с'6* — Ібаса'с' — О, НЛП
(6Ь' — 2ас' — 2са')а — (&3 “ 4ае)(Ь'а — 4а V) — 0 . . . (14).
Лриюьчанге I, Общій корень раціоналенъ; слѣд., онъ не м. б, мнимымъ, Слѣд., когда два квадратныя ур—нія имѣютъ одинъ общій корень, всѣ игъ корни дѣйствительны и потому
Ь3 — 4ас >0 н Ь'* — 4а'С' > О,
Это же можно видѣть и непосредственно. Если квадратное ур—піе имѣетъ корень ато другой его корень будетъ а—₽»; а слѣд. если два ур—нія имѣютъ одинъ общій мнимый корень, то опи имѣютъ два общихъ корня и слѣд, тождественны.
Примѣчаніе II. Мы замѣтили, что два квадратныхъ ур—нія не могутъ имѣть общаго корня, если ас' — с& — 0, и прямомъ аЬ‘ — Ъа* отлично отъ нуля. Слѣдуетъ прибавить: исключая случая, когда с = с' = 0.
Въ самомъ дѣлѣ, въ этомъ случаѣ ас' —са' = 0 и ур—нія будутъ №
а#а Ц- Ъх = 0, а'#3 -{- Ъ(х = 0;
очевидно, что онп имѣютъ общій корень ж = 0 и что два другіе корня, опредѣляемые ур—ми
а#-|-Ь = О, а'#4^ = 0
различны, ибо, по положенію, аЬ' — Ьа' не равно нулю. «
Замѣтимъ, что соотношеніе (13) удовлетворяется и при с —с'“0; слѣд., оно обадее и примѣнимо и къ исключительному случаю, р которомъ идетъ рѣчь-
468. Приложеніе VI. Условіе, при которомъ два квадратныхъ у -—нія имѣютъ два общихъ корня.
I. Называя общіе корни уравненій аяа4“ Ъхф~с = О и — О
буквами а и будемъ имѣть
іа Ь 15 V а + ? = —«’ а + г = —
откуда необходимо, чтобы
Ъ У „ с с'
а а а а
что можно представить въ видѣ
д'_е а~ Ъ с
(1)
Эти условія, будучи необходимы, вмѣстѣ съ тѣмъ и достаточны, ибо, какъ скоро они выполнены, то, называя общую величину равныхъ отношеній (^буквою К, имѣемъ: а' = аКт Ь/ = дК1 с' = сКи потому второе уравненіе беретъ видъ К(а#24“ Ь#-[-с) = 0 или ах2 Ц- -|- с = 0, т.-е. ничѣмъ не отличается отъ перваго, а слѣд. имѣетъ тѣ же корни, какъ и первое. Итакъ:
Чтобы два квадратныхъ уравненія имѣли два общихъ корня, необходимо и достаточно, чтобы ихъ коэффиціенты были пропорціональны.
И. Можно это условіе вывести иначе. Выше мы видѣли (§ 467), что, полагая & и аг отличными отъ пуля, можно одно изъ данныхъ уравненій замѣнить ур—ніемъ
(аЬ' ~ Ъа*)х — са') = 0.
Слѣдоват., если данныя ур—нія имѣютъ два общихъ корня, то полиномъ (аЬ' — Ьа')#Н“ будучи первой степени, долженъ обращаться въ
пуль при двухъ различныхъ значеніяхъ х, а потому (§ 68) онъ долженъ быть тождественно равенъ нулю, а для этого (§ 70) необходимо и достаточно, чтобы его коэффиціенты равнялись нулю, т.-е. чтобы
аѴ — Ьа' = О и асг — са* = 0, откуда
_ ъг _ е а Ь с
469. Приложеніе VII. Найти два числа, зная ихъ сумму 8 и произведеніе Р.
Очевидно, искомыя числа суть корни уравненія
— Зж-рр —0 . . . (1);
въ самомъ дѣлѣ, сумма корней этого ур—пія равна 8, а произведеніе Р.
Примѣръ. Найти два числа, которыхъ сумма равнялась бы 13, а произведете 40.
Искомыя числа суть корни ур—нія х* — 13я -[-40 = 0; рѣшая его, находимъ: х* = 8, я" = 5, И въ самомъ дѣлѣ: — 13, 8)<(5 = 4О.
Чтобы задача была возможна, необходимо, чтобы ур. (1) имѣло корни дѣйствительные, т.-е- чтобы разность 8я — 4Р была положительна или нуль:
$2—4Р>0; отсюда
т.-е. наибольшая величина (пшішиш) тсрошеедешя чмгелг, положи-, гсюъиыхь ыл« шиімоидо* постоянную сумму, равна
квадрату ихъ полусуммы.
Если бы требовалось найти два числа^ зная ихъ разность 3 и произведеніе Р, то задачу эту можно бы было свести къ предыдущей. Въ самомъ дѣлѣ, если искомыя числа будутъ хг и у\ то по условію задачи имѣемъ
х' — = і и —Р;
по положивъ — у' = я", дадимъ этимъ ур—ямъ видъ
я'4-я" = 5, я/а;" = —Р,
слѣд. х* и суть корни уравненія
— 5х — Р — 0.
«
Если 3 подожшпелъио, слѣд. а/ — у' 0, то для нужно взять большій корень ур—нія, а другой корень, взятый съ обратнымъ знакомъ, дастъ у\ Если 8 отрицательно, нужно сдѣлать наоборотъ.
Условіе возможности задачи выразится слѣдующимъ образомъ:
?+Р>0,
т> X I Г»
откуда видно, что при Р положительномъ задача всегда возможна, ибо + Е
будетъ представлять сумму двухъ существенно положительныхъ количествъ.
470. Приложеніе VIII. Найти сумму одинаковыхъ степеней корней квадратнаго уравненія ахя4"^1?4"с = ^- ‘
Пусть корни будутъ а?! и яа; требуется вычислить яѴ’4-^"*, не рѣшая ур—нія. Сумму эту для краткости будемъ обозначать знакомъ 8т.
I. Во-первыхъ, мы имѣемъ
81 = 4" #2 ~
II. Чтобы найти 83, возьмемъ тождества
ах1і-\-Ъх1 4-е = 0 . . .(1), = * * -(2),
сложивъ ихъ, найдемъ
+ 2с = 0» откуда 8, =
Этотъ результатъ можно найти иначе, замѣчая, что
III. Чтобы найти 83, помножимъ ур. (I) на ур. (2) на и сложимъ игъ почленно, что дастъ:
а83 + Ь82с8, = О, откуда 83 ~ .
или, замѣняя 8а и 81 ихъ величинами:
с __ 6(6- — Зас)
Этотъ результатъ можно найти иначе, замѣчая, что
'г’ = (X Н“ -|-яа) =
63
а3
36с а2 *
IV. Помножая тождества (1) и (2) соотвѣтственно на я/ и и складывая, найдемъ
а84 683 -|“ — О»
6* — 406*0 + 2аМ
откуда 84 =------------4-------
Иначе найдемъ этотъ результатъ, замѣчая, что
. . . /6^ ?с\а 2е*
* + V = 01е + «.Т- 2(*Л)’= - тг) - 7^
Вообще, легко найти 8ОТ, зная суммы 8да~і и 8т^а; ибо, помноживъ тождества: (I) на ^т-3, (2) на и сложивъ, имѣемъ соотношеніе
#8т —Н I -|- с8щ—2 — О,
въ которомъ и содержится общее рѣшеніе задачи: при ея помощи можно но порядку вычислять 8а, 83, 84, . . .
Такъ, полагая т = 2, имѣемъ уравненіе а8а-|^^і = 0, въ кото-
ромъ 8і = — 8е =#/-(-0:/= I-р 1 = 2; слѣд.
с _ 2с
‘ ~ а* а ’
Положивъ т = 3, имѣемъ а83Ь8а= 0, откуда
6 о ___Со __ 6 /62 2с\ с 6\___ 63 . 36с
~а * (Л““ аХ\дз «/ лХ\ а)^ а* а*
471- Пусть требуется найти сумму одинаковыхъ степеней обратныхъ величинъ корней квадратнаго уравненія.
Называя эту сумму черезъ 8_л, имѣемъ
И \т _ , л _ I____________। 1_ = я?!™ + _ _8т
\ Хл) "Г \ ЗР2/ ~ 2’1™ Я’з*1 Яіт#2ПІ / с\ т
а —— Ч
-т ‘ %'
Такъ, напр,, отсюда найдемъ:
1 г 1 Ъ 1 і 1 _№ — 2ас I । 1 ВДЗ—ЗМ
Л'х ‘ #2 С* Я^2 Са ’ Х^ #2* с3 ’
472, Построеніе корней квадратнаго уравненія.
Рѣшая геометрическій вопросъ съ помощью алгебры, всегда получаемъ уравненія однородныя, если только всѣ линіи вопроса изображены буквами, а не числами. Такія ур—нія мы и будемъ разсматривать
1. Уравненіе вида х’ = тл даетъ пропорцію т : х = х : п; слѣд,, построеніе линіи ж приводится къ нахожденію средней пропорціональной между линіями т и к*
2, Полное уравненіе. Обозначая буквами р и й отношенія двухъ данныхъ линій къ линейной единицѣ, а буквою х отношеніе къ той же единицѣ линіи искомой, имѣемъ четыре вида ур—ній:
я2-]--ря4“йа=0; я2—да-|-Аа = О; 7г2=О; х2—рх—й2 = 0.
Такъ какъ, первое выводится изъ второго, а третье изъ четвертаго перемѣною х на — я, то достаточно построить корни 2-го и 4-го.
Представивъ 2-е въ видѣ х(р—х)=к\
замѣчаемъ, что вопросъ приводится къ &
построенію сторонъ х и р — я; прямо- —г——
угольника, равновеликаго квадрату сто- I
ропы &, зная сумму измѣреній прямо- .........X.........2\В
угольника. ’ ? Л і \
Для этого на прямой АВ=р опи- \/ і : \
сывасмъ полуокружность; въ точкѣ А / ! I \
возставляемъ къ линіи АВ перпендикуляръ АЕ = і и черезъ точку Е проводимъ прямую ЕВ параллельно АВ, пересѣка-
Л с
о
Черт, 50,
В
ьшѵю окружность въ В и Г. Легко ви-
гѣтъ, что прямая ЕЕ = АС изображаетъ одинъ корень ур — нія, а линія
0Е = ВС—другой. Въ самомъ дѣлѣ:
АС4ВС = АВ-хр, АС X ВС = СЕ2 = АЕа =
Для возможности задачи необходимо, чтобы прямая ЕВ встрѣчала окружность; слѣд,, задача невозможна, когда АЕ>ОС = -^ или когда по
тому что при этомъ условіи ЕВ не встрѣчаетъ окружности, Когда АЕ = 00 = или й— ?» прямая ЕВ касается окружности въ точкѣ 0, и корни получаются равные, АО " ОВ — Наконецъ, когда АЕ < 00 = или А <|> прямая ЕВ пересѣкаетъ окружность, и корни получаются неравные; АС и СВ. Все это вполнѣ согласно съ тѣмъ, что при условіи корни уравненія мнимы, при — дѣйствительные равные, а при &*< — дѣйствительные неравные.
Четвертое ур—ніе приводится къ виду = и соотвѣтствуетъ во-
просу: построить измѣренія прямоугольника, равновеликаго данному квадрату, по
ур—ніе 4-е, имѣя свободный членъ ные корни.
разности р этихъ измѣреній. На прямой АВ =к какъ на діаметрѣ, описываемъ окружность; въ точкѣ А проводимъ къ ней касательную АЕ = к и изъ точки Е проводимъ сѣкущую ЕСВ черезъ центръ. Имѣемъ
ЕІ) = < ЕС=— ибо
ВЕ-СЕ = ВС = АВ = р,
ЕС X ЕВ = АЕа = 7Л
Очевидно, построеніе всегда возможно, такъ какъ точка Е всегда будетъ находиться внѣ круга; и это обстоятельство вполнѣ согласно съ тѣмъ, что отрицательный, всегда имѣетъ дѣйствитель-
Другой пріемъ. Если ур—пія 2-е и 4-е имѣютъ видъ
—2лг-|-т , п = 0 . . .(2) х*—рх — т.п~0. . -(4),
то для примѣненія указаннаго пріема слѣдовало бы предварительно найтп среднюю пропорціональную к между т и п; нижеслѣдующее построеніе позволяетъ избѣжать этого предварительнаго построенія,
давая, къ тому же, способъ, примѣнимый во всѣхъ случаяхъ.
Для построенія корней ур—нія (2) беремъ АВ въ точкѣ А возставляемъ къ ней перпендикуляръ АВ = т, въ точкѣ В перпендикуляръ ВС = я, проводя ихъ въ одну сторону отъ прямой АВ.
Проведя прямую СВ, описываемъ на ней, какъ на діаметрѣ, окружность, которая, вообще, пересѣчетъ АВ въ двухъ точкахъ Е, Е; искомыя линіи будутъ
АЕ и ЕВ, илп АЕ и ЕВ, Въ самомъ дѣлѣ, изъ подобія треугольниковъ ВАЕ и
ЕСВ имѣемъ: АЕ : СВ = АВ : ЕВ, откуда АЕ X ЕВ = ?п , п; кромѣ того, по
построенію, АЕ 4~ ЕВ = АВ —р.
Перпендикуляръ, опущенный изъ средины 0 линіи ВС на АВ, пересѣкаетъ хорду ГЕ въ ея срединѣ Н; отсюда выходитъ, что АР = ЕВ и, слѣд,, АЕ=РВ.
Для возможности задачи нужно, чтобы окружность СЛ встрѣчала АВ, а это СО требуетъ, чтобы ОН было не больше -у-
Но ОН = + С№ = СК*-}~0К2 = АВа-р(*п — я)2; отсюда легко ви-
/р\3 дѣть, что условіе возможности будетъ •
Примѣчаніе. Если я» = п, СВ будетъ параллельна АВ, АВ — карательна къ окружности въ В, и перевернувъ чертежъ, найдемъ обыкновенное построеніе. Для построенія корней (4), къ АВ, равной данной разности возставляемъ въ точкахъ А и В перпендикуляры АВ = яі и ВС = « по разныя стороны отъ АВ; на прямой СВ, какъ ва діаметрѣ, описываемъ окружность, пересѣкающую прямую АВ въ точкахъ Е и Е. Корни будутъ
х = АЕ, х" = - ВЕ.
Въ самомъ дѣлѣ, разность абсолютныхъ величинъ этихъ линій (или ихъ алге
брапческая сумма) есть АЕ — ВЕ = АВ=^, подобные треугольники АІ)Е и ВСЕ даютъ: АВ : АЕ = ВЕ ; ВС, или АЕ X ВЕ = = АВ X ВС = ш , п.
Задача всегда возможна, ибо всегда имѣетъ мѣсто пересѣченіе прямой АВ съ окружностью ЛС, так;ь какъ послѣдняя, по самому построенію, имѣетъ точки С и В по обѣ стороны прямой АВ,
Такимъ образомъ, измѣняя направленіе перпендикуляра, соотвѣтствующаго тому изъ множителей т и я, который отрицателенъ, мы тѣмъ же самымъ построеніемъ находимъ оба корня ур—нія, при
а произведепіе ихъ — т . я, ибо
чемъ отрицательный корень приходится на Черт. 54.
продолженіи АВ; противоположности въ
знакѣ соотвѣтствуетъ противоположность направленія.
Примѣчаніе. Если я» и я равны, средина прямой АВ будетъ въ центрѣ окружности; если па АВ, какъ на діаметрѣ, описать окружность концентричную первой, ВС будетъ касательною къ ней, и какъ ОС = ОЕ, найдемъ обыкновенное построеніе.
ГЛАВА XXXII.
Квадратный триномъ: разложеніе его на множители первой степени; теорема объ измѣненіи знака.—Приложенія.
473. Квадратный триномъ. Если въ полиномѣ ах2 -|- ЪхЦ- с подъ а, Ь п с разумѣть постоянныя количества, а подъ % —перемѣнное, измѣняющееся въ области дѣйствительныхъ чиселъ (отъ — со до О, и отъ О до —|— "№), то
полиномъ этотъ, называемый квадратнымъ триномомъ* будетъ измѣняться по величинѣ и знаку. Такъ, при я=О онъ =с; при &=1, равенъ а4“&+<?; при х= — 10, равенъ 100а —10Ь-|-с; и т. д. Между этими величинами однѣ могутъ быть положительны, другія отрицательны. Тѣ значенія х* при которыхъ триномъ обращается въ нуль, называются корнями тринома; ихъ мы найдемъ, приравнявъ триномъ нулю и рѣшивъ квадратное ур—ніе
ах* -}- Ьх 4- с = 0.
Квадратный триномъ обладаетъ замѣчательными свойствами, изъ числа которыхъ въ этой главѣ мы изучимъ: 1) разложеніе тринома на множители; 2) измѣненіе его знака, и затѣмъ займемся приложеніями этихъ свойствъ.
Разложеніе квадратнаго тринома на множители первой степени.
474. Теорема. Квадратный триномъ равенъ произведенію .коэффиціента при х* на два двучленныхъ множителя, равныхъ разностямъ между х и каждымъ изъ корней тринома.
Первое доказательство. Обозначивъ триномъ буквою у и вынеся за скобки а, найдемъ
__ о 1 I)
дополнимъ квадратъ бинома, первые два члена котораго суть: я* д х; при-
пимая х за первый членъ бинома, второй найдемъ, раздѣливъ -х на 2я, что (I
даетъ 2^; прибавляя въ скобки и вычитая получимъ
г/ । И2 Ь2 і сл г/ у = а х — -4- акг — —-----------—— .
* Ц 1 2а/ 4а2 1 ал І_\ 2а/ 4а2 -I
Различаемъ три случая: й2— 4ас>0, Ь2 —4ас = 0, Ь*— 4ас<0.
I. Ь2 — 4ас>0. Въ этомъ случаѣ дробь ~^2~ положительна, а потому величина дѣйствительная; триномъ беретъ видъ
. 17 । И2
ѵ = а —
Ц 1 2а/
ІѴ& — 4ас\2 \ 2а /
Примѣняя сюда формулу разложенія А2 — В2 — (А 4" В)(А — В), найдемъ:
П* — 4ас\ {
Ъ — 4ас
2а 2а
причемъ ясн три множителя дѣйствительны.
Этому разложенію можно дать видъ:
— & — I — 4ас\ / — 6 -4- ѴЬ* — 4(КІ
— ---------------| {де —. -—— ------------!
2а / \ 2а ;
и замѣчая, что
— Ъ + Ѵ&3 — 4 г/г — & — Г62 — 4ас
“ “&Г И 2а“
суть корни ур—нія а^а4-Ь^ + с = оі илпі что тоже, корни тринома, можемъ, назвавъ эти корни черезъ &' и дать триному видъ
у = а(х - х)(х — У) , . . (Г),
гдѣ всѣ множители дѣйствительны.
II. Ь* — іас = 0. Триномъ (форм* 1) приводится къ виду
/ . Ъ V
у = а^+—) -
Замѣтивъ, что х 4- , и что —
равныхъ корней при условіи Ь* — 4ас = О, мы, назвавъ можемъ дать триному видъ
есть общая величина эту величину буквою
Таково разложеніе тринома въ случаѣ дѣйствительныхъ равныхъ корней.
III. Ь*— 4ас < 0. Яри этомъ условіи триномъ имѣетъ корни мнимые; ему можно дать такой же видъ, какъ и при дѣйствительныхъ неравныхъ корняхъ, т.-е. (1) или (Г), но оба двучленные множители будутъ мнимые.
Впрочемъ, для дальнѣйшихъ изслѣдованій удобнѣе дать триному въ этомъ случаѣ иной видъ. Замѣтивъ, что изъ неравенства Ъ*— 4ас<0 слѣдуетъ а т» л 4аС“-Ь2 .
4ас— і^>0, такъ что дробь —4й2 - будетъ положительная, представимъ у въ видѣ
Ъ V 4«с — & 2а] "I" 4а2
и замѣтимъ* что въ квадратныхъ скобкахъ находится сумма двухъ существенъ но-поло жательныхъ количествъ.
475* Второе доказательство. Представивъ триномъ въ видѣ
I а । Ъ । с, у = а - іт
замѣчаемъ, что =ж") и — х\х\ гдѣ х1 и я" суть корни тринома. Подстановка дастъ
у = — ($' х'х'1] ^а[#а — хгх — х”х 4- .
Вынося въ первыхъ двухъ членахъ за скобки х, а въ двухъ остальныхъ — я", послѣдовательно имѣемъ
у = а[(ж — х')х— х”(х — ж')] = — х!1).
Такъ какъ соотношенія между коэффиціентами и корнями, на которыхъ основано это доказательство, существуютъ и для дѣйствительныхъ и для мнимыхъ корней, то и полученное разложеніе имѣетъ мѣсто для тѣхъ и другихъ.
Когда дѣйствительные корни равны между собою, то, положивъ въ преды-дущей формулѣ х* = хг\ найдемъ
у = а(я — хУ — (я ~ а/)]\
триномъ представляетъ точный квадратъ выраженія ]/а(4— *').
476. Третье доказательство. Если я” и хг‘ будутъ корни тринома ая* 4* Ъх 4- с, то, предполагая, что они различны, замѣчаемъ, что триномъ обращается въ нуль при подстановкѣ въ него двухъ различныхъ значеній х* и х" вмѣсто х; а потому онъ дѣлится на произведеніе биномовъ х — ж' и ;Г — я"; слѣд.
ах* 4~ Ъх 4* с = (х — — #") * Ч- +
есть цѣлое относительно х частное нулевой степени, ибо дѣлитель одинаковой степени съ дѣлимымъ; слѣд. найдемъ, раздѣливъ высшій членъ аяа дѣлимаго на высшій членъ дѣлителя; слѣд. (^ = а; и потому * ах* 4~ Ъх 4~ с = а(х — — я").
Примѣчаніе. Доказательство предполагаетъ, что х' и х" неравны; но если теорема вѣрна для х' и х” неравныхъ, то она остается вѣрна, какъ, бы мала ни была разность между х и я"; значитъ она вѣрна и въ предѣльномъ случаѣ, когда корни равны.
Впрочемъ, для случая равныхъ корней можно дать самостоятельное доказательство теоремы. Въ самомъ дѣлѣ, при равныхъ корняхъ Ь* = 4ас, откуда с 6* ,
а 4а«; СЛѣл>
I I Ъ \ I г & \ \ 1 2л/ \ 1 2а
но каждый изъ равныхъ корней = — такъ что и въ данномъ случаѣ
ах* 4" Ъх 4~ с “ а(х — хг) (х —
только здѣсь х' = х" =
477. П р и м ѣ р ы.—I. Разложить па множители триномъ */= — Зх2-|-5х-|-8.
Рѣшивъ ур—ніе —Зха4-5х+8 = 0, находимъ корни тринома: — 1,
н _ 8 *
X слѣд.
У ~— 3 (я + 1) = — (#4~ 1) (З# ~ 8)«
II. Разложить на множители триномъ у = 49х2— 70x4*25.
Рѣшивъ уравненіе 49х2— 70x4-25 = 0, находимъ равные корни: х' = х" = І; слѣд.
у = 49 Іх — = (7х — 5)*.
III. Разложить триномъ у = — 9х2 4* 6х+1.
т. Г 1+12
Корни тринома равны: х =—,
IV. Разложить триномъ і/ = 4х2—12x4-13.
і’ 3 — 2> „ 3 4" 2і -
Корни тринома суть: х = —, х = —~; слѣд.
У = 4 (х — З—І’) — -+-) = {2х — 3 4- 2і) (2® — 3 — 2і).
Такъ какъ корни тринома мнимые, то его нужно представить въ иной формѣ—въ видѣ суммы квадратовъ; найдемъ:
у = (2х-3)2^4.
478. Приложенія.—I. Составленіе квадратнаго уравненія по даннымъ корнямъ.
„ . 3
Пусть требуется составить квадратное ур—ніе съ корнями хг =—
х” = Оно должно быть вида (х~х')(х— Хг)=0; слѣд.
найдемъ пли
А п । 2х 21 А
= 0, или х +15 “75 = °
75х24^ Ю® — 21=0.
II. Часто можно примѣнять разложеніе квадратнаго тринома на къ сокращенію дробей.
Пусть требуется сократить дробь 4х3 __ 9д, * Разложивъ на числителя, получимъ
множители
множители
6 (х - I) [х + I) = (2х - 3) (3® + 2);
знаменатель = х(4ха — 9) ~ х(2#+ 3)(2х — 3).
Сокративъ дробь на 2х—3, найдемъ
Другой примѣръ: сократить дробь
і9^ + 11Вх- 245
Зх’2 —ЗЯс + 119
Разлагая на множителей знаменателя, найдемъ
За:» —38л + 119 = 3(4:— 7) (х — У = (л— 7) (Зх—17);
I 1 ъл /
для сокращенія дроби надо попытаться, не дѣлится ли числитель на х — 7 или на Зх —17; найдемъ
— 19я2 +119я — 245 — — 12^4- 35) (а; - 7);
. „ , я? — 12x4-35
сокращая дробь на х — 7, получимъ дробь '—з^Гіу—1 не подлежащую дальнѣйшему упрощенію.
Измѣненія знака квадратнаго тринома.
479, Теорема, іьоійа корни тринома -чмі/.чме, т.-е.
коійа Ь*— 4а<?<С0, то при всѣхъ дѣйствительныхъ значеніяхъ х, триномъ неизмѣнно сохраняетъ знакъ коэффиціента а, Когда корни тринома дѣйствительные равные, т.-е. когда Ь2— 4ас = 0, триномъ сохраняетъ знакъ коэффиціента а при всякомъ кромѣ х= — при каковомъ значеніи х триномъ обращается въ нуль. Наконецъ, если корни тринома дѣйствительные неравные, т.-е. если Ь1 — 4ас>0, то при всѣхъ значеніяхъ перемѣннаго х, лежащихъ внѣ корней (т.-е, меньшихъ меньшаго, а также большихъ большаго корпя), охь сохраняетъ знакъ коэффиціента а; при всѣхъ же значеніяхъ х, лежащихъ между корнями, знакъ тринома противоположенъ знаку коэффиціента а.
I. Когда Ь3 — 4ас < 0, триномъ имѣетъ мнимые сопряженные корни; слѣд. х' == д -|~ X ~а — гДѣ а и —количества дѣйствительныя. Разложеніе будетъ:
о#2-|-Ь#-рс = а(# — а — —-Л + = а [(я — а)2 + н2]’
Изъ этой формы тринома видно, что при всякомъ дѣйствительномъ значеніи я, положительномъ или отрицательномъ, выраженіе въ скобкахъ, какъ сумма квадратовъ дѣйствительныхъ количествъ, всегда положительно, а стало быть произведеніе этого выраженія на а всегда будетъ имѣть знакъ количества а, каково бы ни было Итакъ, если а > 0, триномъ будетъ всегда положителенъ; если а < 0, онъ всегда будетъ отрицателенъ.
Можно дать другое доказательство. Изъ неравенства 6* — 4ас<0 имѣемъ 4ас > а раздѣливъ обѣ части на существенно-положительное количество 4а\ находимъ: Слѣдовательно, можно положить = гдѣ К дѣй-
ствительно и отлично отъ нуля. Триномъ беретъ видъ
а#24-- с = а(ж2-|“ - я 4“ т^-Ь К3) = а[ Ш*4” ^аТ 1 1 1 а 1 4а1 1 1 2а) 1 л
аналогичный уже найденному. Далѣе доказательство ведется вышеуказаннымъ способомъ,
II. Пусть Ь2 — 4ас = 0: корни тринома дѣйствительные равные; означая общую величину ихъ буквою я', имѣемъ
ах2 4“ Ьх 4- с = а(х — я')2.
Произведеніе неизмѣнно сохраняетъ знакъ а, каково бы ни было дѣйстви-
тельное значеніе х, ибо факторъ (я—я')* положителенъ при всякомъ дѣйствительномъ х; н только при # = ж' оно обращается въ нуль.
Можно вести доказательство еще такъ: изъ Ь2—4ас=0 имѣемъ 4ас=/>2; раздѣливъ обѣ части на 4аа, находимъ ~ = Представивъ триномъ въ ви-
с Ъ2
и замѣнивъ - дробью получимъ
а#2 -}— Ьа? —с = а (я; -4—
2а] ’
откуда очевидно, что триномъ неизмѣнно сохраняетъ знакъ коэффиціента « при всякомъ дѣйствительномъ я.
Ш. Пусть, наконецъ, Ь2—4ас>0: триномъ имѣетъ корни дѣйствительные неравные; пусть они будутъ х' и х'\ причемъ ж'<ж". Триномъ можно представить въ видѣ
а(ж — а/)(я — я").
Разобьемъ скалу возрастающихъ значеній х на три области: 1) отъ —за до меньшаго корня 2) отъ меньшаго корня хг до большаго ж"; 3) отъ большаго корня х" до 4“°°’
Когда х остается въ первой области, т.-е. меньше меньшаго корня л/, а слѣдоцательно и подавно меньше х*\ обѣ разности ж—х' и х—х" будутъ отрицательны; произведеніе ихъ положительно, а потому все произведеніе «(я— ж')(я — я") сохраняетъ знакъ коэффиціента а.
Когда х находится во второй области, т.-е. больше ж\ но меньше х'\ тогда х — х' > О, а х—я''<0; произведеніе разностей отрицательно, а потому все произведеніе а(я— ж')(ж— ж") имѣетъ знакъ, противоположный знаку коэффиціента
Наконецъ, когда х лежитъ въ области (3), т.-е. больше ж'', а потому и подавно больше х\ оба бинома х — & и х — х" положительны; ихъ произведеніе положительно, а потому все произведеніе а(ж— ж')(ж —я") имѣетъ знакъ коэффиціента а.
Такимъ образомъ при измѣненіи х отъ — со до триномъ два раза мѣняетъ знакъ; причемъ перемѣнѣ знака предшествуетъ обращеніе тринома въ нуль (прп ж = ж' и при я =
Резюме,
у — а#« -|_ Ъх 4~ с,
(я' и я"— корни тринома, причемъ я'<я")-
I- Ь2— 4ас О .....................,у имѣетъ знакъ 4^й*
( х<х'...............у имѣетъ знакъ 4~*а-
П. Ь2 — 4ас>0 । ж'<ж<ж"..............имѣетъ знакъ -—а.
( і'Ух'1 ...... у имѣетъ знакъ 4~а-
480. Примѣры.—I. Триномъ хг —г 2х 3 имѣетъ корни мнимые, ибо 2І—— 3<0; црнэтомъ коэффиціентъ при положителенъ, слѣдов. при всѣхъ значеніяхъ х отъ — со до -р со триномъ остается неизмѣнно положительнымъ.
П. Триномъ —4х2 р 12х— 9 имѣетъ корни дѣйствительные равные, ибо /7*~ас = 6‘2 — (—4) . (—9) = 0; приэтомъ коэффиціентъ при отрицателенъ, слѣд. при всѣхъ х отъ —ос до -|-сс трипомъ остается неизмѣнно отрицательнымъ.
Ш. Триномъ х2 —6х~|-5 имѣетъ корни дѣйствительные неравные: &'=-]-1 • и #'' = -[-5. Слѣд. при всякомъ значеніи х отъ — со до а также при всѣхъ я-хъ отъ до -{-со триномъ положителенъ; при всѣхъ значеніяхъ х, лежащихъ между —|— 1 и —|— 5, онъ отрицателенъ.
IV. Корни тринома 15-{-2л;— 8х2 суть — и го’ слѣд. при всѣхъ х 5 . з ,
между — оо и — а также между н і онъ отрицателенъ; при вся-
_ , 5 I 3
комъ х между предѣлами — и положителенъ.
481. Слѣдствія.—1. ЬЬш тргглоль ах2 -={- Ъх -{- с лиьяяет знакъ при подстановкѣ въ нею послѣдовательно вмѣсто х сначала количества а, яояголи уравненіе
«.н/ъемъь корни дѣйствительные неравные и одинъ изъ нихъ, и только одинъ, заключается между а м
Во-первыхъ, уравненіе имѣетъ корни дѣйствительные неравные, ибо въ противномъ случаѣ триномъ при всякомъ х сохранялъ бы знакъ коэффиціента а, что протнворѣчитъ условію.
Во-вторыхъ, обозначивъ корни черезъ х' и х" и полагая х'<^х”, имѣемъ слѣдующую скалу дѣйствительныхъ значеній х;
Пусть, напр. при х=^а триномъ имѣетъ знакъ коэффиціента а, то а заключается внѣ корней, т.-е. или въ (1) или въ (3) области; при трп-помъ, мѣняя злакъ, получить знакъ —а иотому [5 содержится между корнями, т.-е. во (2) области. Такимъ образомъ, если а находится въ (1) 'области, то между а и р заключается корень я'; если же а лежитъ въ области (3), то между а и ? будетъ корень х”.
Обратно^ _Ес*лм ліслсЛ/ с?ет/-н.я числами а і/ р заключается коренъ ур—нія ах2-р6х-|-с = О, й только одинъ, то знаки, принимаемые пер-вою частью ур—нія при подстановкѣ вмѣсто х чиселъ а и противоположны .
По условію, между а и {I заключается только одинъ корень: пусть это будетъ меньшій корень х\ и пусть тогда скала дѣйствительныхъ значеній х будетъ
а .... х' х” .
откуда видно, что при х = а, какъ лежащемъ внѣ корней, триномъ имѣетъ знакъ +аі а ПРП ж = какъ лежащемъ между корнями, знакъ — а, противоположный первому.
II. Когда триномъ ах2 4“ + с сохраняетъ одинъ и тотъ же знакъ
при подстановкѣ вмѣсто х количествъ а и то между а и заключается четное число (0 ши 2) корней уравненія ах* 4^ Ьх с — 0.
Въ самомъ дѣлѣ, триномъ имѣетъ два корня, слѣд., между а н могутъ заключаться 0 или 1, или 2 корня; по въ данномъ случаѣ между а и не можетъ содержаться только одинъ корень, ибо въ этомъ предположеніи, на оси. слѣд. I, обр., результаты подстановокъ а и ? вмѣсто х имѣли бы разные знаки, что противоречитъ условію. Слѣд. пли между а и р заключаются оба корня, пли нп одного не содержится.
Приложенія.
482. I. Когда ас < 0, корни ур—нія с = 0 — дѣйстви-
тельные, неравные и имѣютъ противоположные знаки.
Въ самомъ дѣлѣ, подставивъ вмѣсто х нуль, замѣчаемъ, что триномъ обращается въ с, а слѣд. знакъ его противоположенъ знаку коэффиціента а. Слѣд. ур. имѣетъ корпи дѣйствительные, неравные, и такъ какъ 0 заключается между этими корнями, они имѣютъ противоположные знаки.
А В
483. II. Когда А и В имѣютъ одинаковые знаки, ур—ніе - —I-- ~ С
х «— а 1 х — р илоьетг корни дѣйствительные неравные, и одинъ изъ нихъ, и только одинъ, заключается между а и
Дадимъ ур—нію цѣлый видъ, собравъ всѣ члены въ первую часть; сдѣлавъ это, найдемъ:
К(х — 3) + В(^ — д) ~ С(я — а) (я — = 0.
Замѣнивъ х сначала количествомъ а, потомъ [і, получимъ результаты: А(а— 3)* В(3 — а); такъ какъ А и В — одного знака, разности же а—и ?— а имѣютъ знаки противоположные, то заключаемъ, что оба результата имѣютъ противоположные знаки, а потому: уравненіе имѣетъ корни дѣйствительные неравные, и одинъ, и только одинъ изъ нихъ, содержится между а и
Рѣшимъ теперь два вопроса, имѣющіе обширное т приложеніе въ изслѣдованіи задачъ 2-й степени, въ виду чего совѣтуемъ читателю изучить эти два вопроса возможно тщательнѣе.
484. Вопросъ I*—Не рѣшая уравненія ах1 Ъх 4- с = 0, расположить корни этого уравненія (когда они дѣйствительные и неравные) и данное число X въ порядкѣ возрастающихъ значеній.
Это значитъ, не рѣшая уравненія, опредѣлить, будетъ ли данное число X меньше меньшаго корня, или оно будетъ заключаться между корнями, или, наконецъ, будетъ больше большаго корня. Приэтомъ для сокращенія письма первую часть ур—нія, т.-е. триномъ аха4~^4”с будемъ обозначать символомъ /(х) (читается: функція я>са), такъ что [(х) = ах* 4^ Ьх 4~ с; результатъ же подстановки въ трипомъ числа X вмѣсто х будемъ обозначать знакомъ такъ что ДХ) = а)? 4" 4" с- Напр. Д2) будетъ означать 4а 4~2Ь4~С: ДО) будетъ означать с и т. п.
Переходимъ къ рѣшенію вопроса. Подставимъ X вмѣсто х въ первую часть ур—нія и вычислимъ ака + ЬХ-|“с или /ѴЭ; такимъ образомъ мы будемъ знать знакъ /\Х). Во-первыхъ, если окажется, что /\Х) равняется нулю, то это будетъ значить, что X есть одинъ изъ корней уравненія; и можно непосредственно узнать, будетъ ли X большій, или это будетъ меньшій корень уравненія: стоитъ
* &
только сравнить А съ полусуммою корней, — которая заключается между корнями. Если Х>““? то X есть большій корень, въ противномъ случаѣ, X будетъ меньшій корень.
Если окажется, что знакъ /(X) противоположенъ знаку коэффиціента а, т.-е. если а . /*(Х) < 0, то это будетъ служить вѣрнымъ признакомъ того, что-корни тринома дѣйствительные и неравные, и что число X содержится между корнями. Въ самомъ дѣлѣ, въ случаѣ дѣйствительныхъ равныхъ и въ случаѣ мнимыхъ корней триномъ всегда имѣетъ знакъ одинаковый съ а, слѣд. въ этихъ случаяхъ всегда будетъ аДХ)>0. Значитъ, разъ а/*(Х)<0, корни дѣйствительные и неравные; а въ этомъ случаѣ знакъ ДХ) противоположенъ знаку а только для х, лежащихъ между корнями, слѣд. X содержится между корнями» Назвавъ корни чрезъ х' и х”, полагая х* <х", будемъ имѣть слѣдующее расположеніе чиселъ х\ х1' и X на скалѣ дѣйствительныхъ чиселъ:
, . . хт . < . X . < а? . . . .
Если же окажется, что знакъ ДХ) одинаковъ со знакомъ а, т.-е. если -а . ДХ)>0, то мы не знаемъ напередъ, будутъ ли корни дѣйствитеіьные, или' они мнимые; поэтому нужно опредѣлить знакъ реализанта (Ь* — 4ас): пусть ‘ будетъ — 4ас > 0. Тогда корни ур—нія будутъ дѣйствительные и неравные; назовемъ ихъ, попрежнему, х и хн* полагая я?'<х\ Число X теперь уже не будетъ находиться между корнями; для X между корнями было бы а /*(X) < 0. Значитъ, X находится внѣ корней, т.-е. либо X < я/, либо X > х”. Чтобы рѣшить, какой изъ этихъ случаевъ имѣетъ мѣсто, нужно сравнить X с& какимъ-нибудь числомъ* лежащимъ между корнями; одно такое число всегда намъ извѣстно, это—полусумма корней, —Д (см. § 358). Если окажется при этомъ, что
Х<— то, находясь внѣ корней, X будетъ меньше меньшаго корня, и расположеніе чиселъ на скалѣ восходящихъ дѣйств. чиселъ будетъ такое:
— со . . . X . . . х’ . . . я/' . . . -}“
1 б
Если же окажется, что X > — то, будучи внѣ корней, X будетъ больше большаго корня, и распорядокъ чиселъ х’1 и X будетъ таковъ:
Примѣчаніе, Когда корни различны по знаку, то 0 будетъ заключаться между корнями. Слѣдов., если X есть число положительное, то оно будетъ больше большого корня; если же X < 0, то оно будетъ < меньшаго корня.
Примѣръ 1. Дано уравненіе х2— 22х-1-80 = 0. Требуется расположить въ порядкѣ возрастающихъ значеній корни х’ и х1' и число 12?
Подставляя въ первую часть число 12 вмѣсто находимъ: /(12) = 12а — 22 X 1280 = — 40: результатъ подстановки имѣетъ знакъ противо
I
положный знаку коэффиціента при х*-, заключаемъ, что корни ур—нія дѣйствіи тельные и неравные (пусть х' <х') и что 12 заключается въ иптерваллѣ корней:
. , . х’ < 12 <х" . . .
Примѣръ 2. Расположитъ въ порядкѣ возрастающихъ значеній корни х’ и х’ (полагая тою же ур—нія и число 20*
Подстановка 20 вмѣсто х даетъ /(20) = 203 — 22 X 20 4- 80 > 0, т.-е. одинаковаго знака съ первымъ коэффиціентомъ. Отсюда нельзя заключить, будутъ ли корни дѣйствительные или мнимые; вычисляемъ реализантъ; для даннаго ур—нія беремъ Ь'* —ас=(11)3—1.80, что >0, слѣд* корня дѣйствительные неравные. Такъ какъ /(20) > 0, то 20 находится внѣ корней. Далѣе: 20 > полусуммы корней (11), слѣд. 20 больше большого корня. Итакъ:
х1 . . . < . . . х" . . . < . 20. ♦
Примѣръ 3. Пересѣчь шаръ радіуса К плоскостью такъ, чтобы объемъ сферическаго сегмента АМВ бьыь равновеликъ объему цилиндра, имѣющаго тоже основаніе* а высоту равную разстоянію центра шара отъ этою общаго основанія, (Черт. 55).
Пусть МС = я; ур—ніе задачи будетъ
^(ЗК—я)=т:(В—х) . АС =~(В—^)а?(2К—я).
Одинъ изъ корней, я=0, очевиденъ й ргіогі; раздѣливъ ур.‘ на тсс, получимъ
3(К — а?)(2В - я) — я(ЗВ —я) = 0, или
2я3 — 6Вя 4- ЗВ3 = 0. «
Чтобы рѣшеніе этого ур—нія служило отвѣтомъ
на задачу, нужно, чтобы оно было дѣйствительнымъ, Черт. 55. положительнымъ и <В.
V2 — ас = (ЗК)3— 6В3 = ЗК\ — количеству положительному: слѣдоват., корни дѣйствительны. Ихъ произведеніе, равное ^В3, положительно, слѣд. оба корня имѣютъ одинаковые знаки; сумма ихъ, равная ЗК, положительна: сл. оба корня положительны. Подставивъ въ первую часть К вмѣсто х* находимъ въ результатѣ —К3: слѣд, К заключается между корнями, т.-е., называя корни буквами х' и я", и полагая я'<я", имѣемъ
заключаемъ, что одинъ изъ корней меньше В, другой больше В.
Такимъ образомъ задача имѣетъ одно рѣшеніе, выражаемое меньшимъ корнемъ
< = К(3 —/3)
Примѣръ 4. Описать около шара такой конусъ, чтобы отношеніе его полной поверхности къ поверхности шара было равно данному числу т.
Легко видѣть, что если за неизвѣстное принять высоту конуса я, уравненіе задачи будетъ
х* — 4шВл; 8?пН3 = 0.
Чтобы х, выведенный изъ этого ур—нія, представлялъ рѣшеніе данной задачи, необходимо, чтобы онъ былъ количествомъ дѣйствительнымъ, положительнымъ н > 2К. Корпи будутъ дѣйствительны, если (2Кт)2 — 8ІР?п> 0, пли т(т — 2)^0, или, наконецъ, такъ какъ ш>0, если ш$>2. Пусть это условіе удовлетворено. Произведеніе корней положительно, слѣд. они имѣютъ одинаковые знаки; сумма иіъ (4тЕ) положительна, сл. оба они положительны. Остается разсмотрѣть, какова ихъ величина сравнительно съ 2В. Подстановка 2К вмѣсто х въ первую часть даетъ +/П3, т.-е. результатъ одинаковаго знака съ коэффиціентомъ при заключаемъ, что 2В. лежитъ внѣ корней; слѣд. или оба корня < 2К, пли оба > 2К. Полусумма корней = 2»іВ, а какъ т>2, то она не меньше 4Н; но 2Н меньше этой величины, сл. оба корня больше 2В, и задача имѣетъ 2 рѣшенія.
485. Вопросъ П.—Не рѣшая уравненія ах2-|-Ьхс — 0, распредѣлитъ въ порядкѣ возрастаюгцихъ значеній корни (если они дѣйствительные неравные) м числа X и рц полагая X < р.?
Подставляемъ въ триномъ ах'2Ьхс вмѣсто сначала X, потомъ рі, и вычисляемъ результаты /(X) и / (и) этихъ подстановокъ. Здѣсь нужно различать два случая: 1) /(X) и /(и) имѣютъ одинаковый знакъ; 2) эти числа имѣютъ противные знаки.
1) Пусть /(X) и /(и) имѣютъ знаки разные, что можно записать въ видѣ /"(X) . /(*і)<0. По § 481 мы знаемъ, что это—вѣрный признакъ, что уравненіе имѣетъ корни дѣйствительные и неравные (&'<&")? л что только одинъ изъ ынхъ заключается между X и н; слѣд. будетъ одно изъ двухъ:
либо X < х* < < х\ либо хг < X < я/' < |1.
Первое будетъ тогда, когда а , /(X) > 0; второе имѣетъ мѣсто тогда, когда а./(Х)<0. Впрочемъ, о томъ, имѣетъ ли мѣсто первое расположеніе, или второе, можно судить и иначе. Такъ какъ (идя слѣва направо) числа X, рі п корни расположены въ порядкѣ возрастанія ихъ значеній, то, очевидно, въ первомъ случаѣ X-1- р. <х'~х\ т.-е. <—во второмъ же случаѣ Х-{-И
Заключаемъ, что если Х-^и меньше —то имѣетъ мѣсто первый случай: если же Х-|-Н больше —то имѣетъ мѣсто второй случай,
2) Пусть /(X) и /(рі) имѣютъ одинаковые знаки, что можно записать такъ: / (X) , / (ц) > 0. Этотъ случай, въ свою очередь, подраздѣляется на два другіе, смотря потому, имѣетъ ли / (X) знакъ одинаковый съ а, или имѣетъ знакъ противоположный знаку а.
Если а . / (X) < то УР* имѣетъ корни дѣйствительные неравные, и оба числа, X н ц, находятся между корнями:
ж' , . , а . , . |і. . . я".
Если а./(Х)>0, то еще нужно убѣдиться, имѣетъ ли ур. дѣйствительные неравные корпи, и для этого надо опредѣлить знакъ реализавта Ь2 —4ас. Пусть оказалось, что Ь* — 4ас>0, и слч ур. имѣетъ дѣйствительные неравные корни (пусть я'<я"). Ни X, ни и не содержатся между корнями. Слѣд., возможно одно изъ слѣдующихъ трехъ распредѣленій:
либо либо
х' . . . я?" . . . X . . . ц;
X . . . х . , . хи . . . |і;
*. * '/ А . . . И . . . X . . . X . . .
Когда имѣетъ мѣсто то, пли другое, или третье распредѣленіе, легко рѣ-Ъ
шается сравненіемъ данныхъ чиселъ съ полусуммою корней, — которая всегда содержится между корнями. Если —^<Х, но имѣемъ 1-е распредѣленіе; если X < — “ < р, то имѣетъ мѣсто 2-е распредѣленіе, а если и < — то, очевидно, имѣемъ дѣло съ третьимъ.
Примѣръ. Указать расположеніе чиселъ'-—1 и 4 относительно корней уравненія — х3 4~ Зх 4" 2 = 0.
Такъ какъ первый и третій коэффиціенты имѣютъ знаки противоположные,, то корни ур—нія дѣйствительные и неравные.
Подставляя вмѣсто х послѣдовательно данныя числа, имѣемъ /(—1) = —, /(4) = —: знаки одинаковые; при этомъ а . /(X) или —1 . /(—1) 3> 0, заключаемъ, что числа — 1 и 4” 4 не находятся между корнями. Полусумма корней, 4“ о-, больше ~1, но меньше 4~4? заключаемъ, что меньшій корень больше — 1, а большій коренъ меньше 4, и распредѣленіе корней и чиселъ — 1 и +4, въ восходящемъ порядкѣ, будетъ таково:
. . . — 1 . . . х' . . . X'’ . . . + 4 - • <
486. Задача. Дать общую форму условій, необходимыхъ и достаточныхъ для того^ чтобы корпи уравненія
ах3 Ъх с ~ О, предполагая, что они дѣйствительны, были оба больше, или оба меньше даннаго количества X.
Во-первыхъ, согласно требованію, необходимо, чтобы X лежало внѣ корней, а потому подстановка этого числа на мѣсто х въ триномъ ах3 4~ Ъх 4~ с должна
• ' давать результатъ одинаковаго знака съ а, т.-е. должно быть
а (аХ* 4- ЬХ
с) > 0.
Это условіе выражаетъ только, что X не содержится между корнями; остается выразить, что:
1) въ первомъ случаѣ оба корня больше X, т.-е.
I Лр" а,
#'>Х и я">Х, откуда х'-1- аг"> 21, пли ——> X, или, наконецъ,
_ А \ *
2л
Итакъ, условія, необходимыя для того, чтобы оба корня были больше а, таковы:
,а(ал2-|-&к-|_с)> О и —~>4, или короче, а . /*(Х)>0 и —Л> X.
Будучи необходимы, они вмѣстѣ съ тѣмъ н достаточны, ибо какъ скоро они выполнены, то изъ перваго слѣдуетъ, что X не содержится между корнями, а изъ второго должно заключить, что X меньше каждаго изъ корней, ибо, допустивъ, что корни меньше X, имѣли бы
2) Такимъ же образомъ найдемъ, что условія «еойгод«.чыл и достаточныя для того, чтобы-оба корня были меньше X, будутъ:
а (аХа + 6Хс) > О и —? <Х, И-1И <*-/(Х)>0 и —^:<Х. * Х.С* вгС*
е-
487. Задача. Дать общую форму условія, необходимаго и достаточнаго для того, чтобы данное количество X содержалось между корнями ур—нія алл-{- Ъх 4- с = О.
Необходимо и достаточно, чтобы результатъ подстановки числа X на мѣсто х въ триномъ ая24~^ + с имѣлъ знакъ, противоположный знаку а.
Каковъ бы пи былъ знакъ а, это условіе будетъ
а (аХ2 4* ЬХ 4" с) < О, или а . /*()) < 0.
488. Задача. Датъ общую форму условій, необходимыхъ и достаточныхъ для .тога, чтобы, квадратный триномъ сохранялъ неизмѣнно одинъ и тотъ же знакъ, каковы бы ни были дѣйствит. значенія х?
Триномъ не можетъ сохранять одинаковый знакъ при всякомъ х, если корни его будутъ дѣйствит. неравные» ибо въ этомъ случаѣ онъ дважды мѣняетъ знакъ при измѣненіи х отъ —со до 4~ когда корни его дѣйств. равные, то онъ -сохраняетъ знакъ а при всякомъ я, кромѣ х = — ибо тутъ онъ обращается въ 0; п только въ одномъ случаѣ знакъ его неизмѣнно всегда будетъ одинъ и тотъ же: когда корни его—мнимые. Итакъ:
1) Триномъ всегда, при всякомъ х, будетъ положителенъ, если
Ъ* — 4ас <0 и вмѣстѣ съ тѣмъ а > 0;
2) Триномъ всегда, при всякомъ х, будетъ отрицателенъ, если
Ь2— 4ос<0 и вмѣстѣ съ тѣмъ а<0.
Очевидно, что это и суть необходимыя и достаточныя условія, при которыхъ требованіе задачи будетъ удовлетворено.
489. Задача. Теорема о знакѣ кввдратнаго тринома .можетъ служить для послѣдовательнаго вычисленія сколькихъ угодно десятичныхъ цифръ несоизмѣримаго корня* Пусть, напр., дано уравненіе я2-|-3х —7 = 0, котораго одинъ изъ корней заключается между 1 и 2. Очевидно, цѣлая часть этого корня есть 1.
Для вычисленія перваго десятичнаго знака положимъ Цѣлая
часть у-ка, очевидно, будетъ первымъ десятичнымъ знакомъ х. Подстановка дастъ
(1-Ью)’+3 (1+ю)“7 = 0’ пли У’+ 500-300 = 0 . . .(1).
Подставляемъ вм. у, послѣдовательно, О, 1, 2, 3,... до тѣхъ поръ пока не получимъ двухъ послѣдовательныхъ результатовъ съ противоположными знаками. Т. о. найдемъ, что положительный корень ур —нія (1) содержится между 5 и 6. Цѣлая часть у-ка равна, слѣд*, 5: это и есть первый десятичный знакъ корня х.
, Зная это, положимъ теперь У = 5 т гдѣ цѣлая часть # будетъ первымъ десятичнымъ знакомъ у, и слѣдов., вторымъ десятичнымъ знакомъ х. Ур. въ я будетъ
(5 + ^)І + 50(5 + к))“300 — °’ плп «’ +600^ — 2500 = 0.
Подобно предыдущему найдемъ, что это ур. имѣетъ корень', содержащійся между 4 и 5. Второй десятичный знакъ корня х равенъ, значитъ, 4. Итакъ, предложенное ур. имѣетъ корень ^ = 1,54, съ точи, до 0,01. Продолжая указаннымъ путемъ, можемъ найти сколько угодно дальнѣйшихъ знаковъ.
490. Задача. Сравнитъ корни .двухъ уравненій, изъ которыхъ одно— квадратное, другое — первой степени.
Пусть /*(х) = а#2 Ьл; -р с = 0 и а (а?) = а'# V = 0 — два данныхъ уравненія. Пусть дѣйствительные корни перваго суть хх и я*2 (полагая, что и корень второго. Полагаемъ ц а'^О.
Чтобы опредѣлить положеніе числа относительно чиселъ и нужно знать знакъ результата подстановки числа въ/Х#). Замѣчая, что — имѣемъ
ГЫ=д-Е«Ь'2- Ьа'і-Н-са'»],
или. положивъ, для краткости, аЬ'* — ЪаѴ «Г1 = Д (Д называется ^езулъ-тантонъ -данныхъ ур—ній), можемъ написать
Такъ какъ всегда положительно, ибо коэффиціенты предполагаются дѣйствительными, то заключаемъ, что /(^) имѣетъ тотъ же знакъ, что и Д; откуда прямо слѣдуетъ, что:
Если аД < Оі заключается между корнями ур—нія / (а?) = О, и расположеніе трехъ корней таково:
Если аА = О, т.-е. если А = О, то /(;>) = О, а это значитъ, что равно одному изъ корней квадратнаго ур—нія, и слѣд., имѣетъ мѣсто одно изъ слѣдующихъ распредѣленій:
или ч = л:, < х^ или . < ФI,
Наконецъ, если аА > О, находится внѣ иптервалла корней квадратнаго ур—нія, и слѣд. распорядокъ корней будетъ
либо ^<^08, либо • * - П.
г- л ^1+^2
Если замѣтимъ, что — всегда заключается между корнями квадратнаго ур—нія, то тотчасъ усматриваемъ, что въ строкахъ I п II расположенія, указанныя слѣва, имѣютъ мѣсто, если окажется, что < д?1^а?а, а расположенія, 4М>
паписанныя справа, имѣютъ мѣсто, если будетъ >• *
&
Замѣняя и — иіъ значеніями въ коэффиціентахъ, найдемъ, что лѣвымъ распорядкамъ отвѣчаетъ соотношеніе
~а'<~й' ИЛИ ^>2^’ ИЛП ЙО(Ш —Ь“)>°. а правымъ — соотношеніе
— ^> — 25’ ИЛИ -^2 < 2^’ пли аа (2аЬ — йах°-
Это изслѣдованіе можно резюмировать въ формѣ слѣдующей таблицы:
Если ♦ т 0
аД < о, • - •» « ж1’ <#2
Г аа' (2аЬ' — Ьа') <0 . . . .т. <1^2 {
аА== о, । аа'(2аУ — Ъа') = 0 . . . ж, = =
аа (2аЬг — Ьа') >0 . . . <.т4
аД > о, — Ъа') <0 . . . '1
и 6» — 4ас> 0, і аа'(2аЪ’ — Ьа') >0 . . . -1 <ж, <Жа і
Примѣчанія, і. Эта таблица показываетъ, что когда аЛ^О, корни квадратнаго ур—иія дѣйствительны. Но можно и прямо показать, что если аЛ<^0, то Ъ*—4ас не можетъ быть отрицательнымъ. Въ самомъ дѣлѣ, написавъ «А въ видѣ
і [(2аУ — Ьа')* — (&’ — 4ас) а'»], »
непосредственно усматриваемъ, что при Ь3 — 4ас<0 было бы аЛ>0.—Изъ этого выраженія легко видѣть еще, что если аЛ = О и 2аЬ' — Ъа' = О, то необходимо должно быть Ъ* — 4ас = О, что показываетъ и таблица. Наконецъ, если аЛ > О и корпи и дѣйствительны, то не можетъ быть 2аЬ'—Ьа1 — 0, II. Если аД>0, корни и могутъ и не быть дѣйствительными; но если они мнимы, то необходимо аЛ^>0.
491. Задача. Сравнить лежду собою корни Эвухь квадраткъдо уравненіи.
Пусть имѣемъ квадратныя ур—нія
[(х) = а#а-|-&С’[-с=О, ф(.т)=а'а?2-|” -р с' ~ О,
въ которыхъ а 4^0 и а'фО; и пусть дѣйствительные корпи перваго будутъ х1 и х* а второго и (4 С М-
Чтобы опредѣлить положеніе корней 4 и относительно и х3, разсмотримъ знаки подстановокъ и въ /(х), и для этого вычислимъ нроизве-Деніе /(;,) . Г(У и сумму /(^) + /(ч).
1) Произведеніе / (;,) . / (^) = (а^2 -|- -|~ с) {а\3 -(- -р с)
= а« V + аЫ1(6, 4- 5,) + ас (V + V) + + Мч 4Л) + ^
или, подставивъ вмѣсто 5^, и — вмѣсто имѣемъ
/•/> X х^ч «2<^ аЬе'Ь' і 6'г —2й'с' . №?'» М>' , 9 /(я) • /(ч) =-^Г „^- + “с—---------------—+ с’
= (а2с'2 — аЬс’Ъ' + асЪ’3 — 2аса'с' 4- Ь’с'3 — Ъса'Ь' 4- а'3с31
= [аМ2 — 2аса'с/ 4~а,3с3 — аЬс'Ѵ 4~асЬ'3 -|- 62<У2 — Ъса'Ь’]
= Д-» [(«с* — са1)3 — (аЬ' — Ъа’) {Ъс1 — сѴ)] = Д-, • Д,
называя буквою А скобочное выраженіе (результантъ данныхъ ур—ній).
2) Сумма ЛЕі.)+/(ч) = в(Ѵ + Ѵ) + ^+^) + 2с
= в
б'2 — ЪЬ( । ___аЬ * — 2аа'с' — ЪЪ'аг 2са,і1
__Ь' (аЬ1 — Ъа') — 2а' (ас' — са')_ 1 р
“ а* ~а^' Гѵ
называя буквою Р выраженіе & (аѴ — Ьа') — 2а' (ас? — са').
Итакъ, знаки произведенія /(^). Г(^)* и суммы / (^і) —Н Л’«) “ соотвѣтственно тѣ же, что и знаки А и Р.
Подобнымъ же образомъ нашли бы, что знаки и гИ^і) + —
соотвѣтственно тѣ же, что и выраженій Д и 9, гдѣ Ч = 2а (ас' — са') — — 1)(а& — Ьаг),
Теперь можемъ приступить къ сравненію корней данныхъ ур—ній.
Л. Случай? когда данныя уравненія не имѣютъ общаго корня. Въ этомъ случаѣ въ самомъ дѣлѣ, если бы было Д = 0, т.-е. было бы
/&)•/&) = 0, то одинъ изъ этихъ множителей былъ бы нулемъ; если бы, напр., было /(^) = 0, то ^—корень ур — нія = 0 обращалъ бы и/(^) въ нуль, слѣд., былъ бы общимъ корнемъ. Д, отличное отъ нули, можетъ быть или < 0, или > 0. Пусть, во-первыхъ:
а) Д < 0. Легко видѣть, что Д можно представить въ формахъ
4Д = (2ас' + 2са' — ЪЬ')* — (Ъ* — іас)(Ь'* — 4аѴ) . . . (то) 4а2Д = (Ь2 — 4ас) (ай' — 6а')2 — [2а (ас' — са) — Ъ (аЬ* — 6а')]2 4а'2Д = (6'2- 4а'с')(аУ - 6а')2 — [2а'(ас' - са')- Ь'(а7/- 6а')]2 . . . (р).
Тождество (т) показываетъ, что 62— 4ас и У2—4а'с' не могутъ быть ни противоположны по знаку, ни нулями. Тождества (п) и (р) показываютъ, что эти выраженія могутъ быть положительны, либо отрицательны.
Слѣдовательно, когда А<СО, то или оба уравненія имѣютъ корни дѣйствительные, или оба имѣютъ корни мнимые. Пусть будетъ 62— 4ас^>0; въ такомъ случаѣ будетъ V2 — Ѣа'с' 0; и будутъ корпи дѣйствительные неравные.
Такъ какъ /(^) . отрицательно, то множители имѣютъ знаки противоположные; слѣд., одно изъ чиселѣ и заключается между корнями ур—нія /(#) = 0, другое внѣ этихъ корней: между и заключается только одинъ изъ корней ур—нія /(#) = 0, и корни будутъ представлять одно изъ распредѣленій:
(1) хг х^ либо
(2) <С Хг ч3
Первое распредѣленіе имѣетъ мѣсто, если будетъ -р второе—
когда будетъ + 5а Оі
Итакъ: распорядокъ (1) имѣетъ мѣсто, если
— или аа1 (аЬг — Ьаг) 0;
распорядокъ (2) имѣетъ мѣсто, если
— 7, < — Ьп, или аа' (аЬ' — Ьа') > 0. а а 7
₽) Пусть А>0, Тождества («) и (/?) показываютъ, что выраженія 6’3—4ас и У® — 4а'с' не могутъ быть ни отрицательными, ни нулями. Слѣд., корпи того и другого ур—нія всегда дѣйствительные и’ неравные.
Такъ какъ произведеніе /(^) .. положительно, его множители имѣютъ одинаковый знакъ. Опредѣляемъ этотъ знакъ посредствомъ суммы ДНЛ-/(^)-
Но знакъ этой суммы одинаковъ съ Р. Если аР<0, и отрицательны, и корни и лежатъ между и имѣетъ мѣсто распорядокъ
(3) 3*1 <С ^2 Жі'
Если аР>0, а/(^) и а/(^) положительны, и корни и лежатъ впѣ интервалла корней и можетъ имѣть мѣсто троякое распредѣленіе корней:
либо либо либо
(4)
(5)
(6)
Когда имѣетъ мѣсто то, или другое, или третье?
Такъ какъ Д>0, . <₽(х2) > 0; въ первомъ случаѣ х, и нахо-
дятся между и слѣд., а'? (а:,) и а'<р (я,) отрицательны, а потому ихъ сумма а’ [ (ж,) 4~ ф (А) ] = а'9 отрицательна.
Въ случаяхъ распредѣленій (5) и (6), очевидно, а'9>-0.
Для (5) Н-я, < $!-[-5,, и слѣд. аа'(аЪ' — Ъа'Х$\
для (6) а?і -|-ж, >5, + =2, и слѣд. аа' (аЪ' — Ъа) > О.
Такимъ образомъ отличаемъ распредѣленіе (5) отъ (6).
В. Случай, ком)а данныя уравненія имѣютъ, по крайней мѣрѣ^ одинъ общій корень.
Въ этомъ случаѣ 1 = 0. Тождества (м) и (р) показываютъ, что если будетъ аЪ' —г Ьа1 = 0 вмѣстѣ съ Р = 0 или 9 = 0, то реализанты Ь2 — 4а/? и У3 — 4а'с' могутъ быть положительны, нули, либо отрицательны: при этомъ — одновременно, ибо также и ос — са'=0, и оба уравненія должны либо имѣть общіе корни, либо не имѣть дѣйствительныхъ корней. Если же аЬг— Ьа* 4=0, Ъ* — 4ас и Ь'8 — 4а'<г не могутъ быть отрицательны: уравненія имѣютъ корни дѣйствительные.
а) Пусть Ь8 — 4ас > 0 ц 6'2 — 4а*с' > 0.
Ни одно ур—ніе не имѣетъ равныхъ корней.
Если аЬг — Ьа* = 0, то, какъ 1 = 0, будетъ и ас* — са' = 0, коэффиціенты ур—ній пропорціональны, и, слѣд., корни одного ур—нія одинаковы съ корнями другого:
(7) л\=^<>ч = ^.
Если аЬ* — Ьа'=Ь0, ур—нія имѣютъ лишь одинъ общій корень.. Въ этомъ случаѣ одно изъ количествъ /(^), равно нулю; другое имѣетъ знакъ суммы /(М“кГ т’’е' знакъ Р.
Точно такъ же, одинъ изъ результатовъ подстановки ^(^), ?(#а) равенъ нулю, а другой имѣетъ знакъ суммы т.-е. знакъ 9.
Отсюда слѣдуетъ, что если аР <С0, одинъ изъ корней содержится между и и имѣетъ мѣсто одно изъ распредѣленій
(8) Ж1 ч*
(9) -------#1 <С ^2 Я'і*
Первое изъ нихъ имѣетъ мѣсто, если <С Ц- т.-е. если
аа'(аЬ*—Ьа')<$; второе, если т.-е. если аа'(аЬ'—6а')>0.
Если аР>0, одинъ изъ корней $п лежитъ внѣ интервалла (^, я3). Въ этомъ случаѣ возможны 4 распорядка:
(10)
(11) = ж( <Ся:і с -
(12) г <Т1 р жя,
(13) ж. ’і -
Если «^<0, одинъ изъ корней лежитъ меясду и слѣд., имѣетъ мѣсто распорядокъ (10), либо (И), а именно: (10), если аа'(аЪ'— и
(11), если аа'(аЬ' — 6а') >0.
Если «'Ч>0, имѣетъ мѣсто распредѣленіе (12), либо (13): первое, если аа'(а&' — Ъа') < 0, второе, если аа' (аЬ' — Ъа') > 0.
р) Пусть Ъ2 — 4ас4:0, Ь'а — 4а'с< = 0.
Слѣдовательно, Возможны распорядки:
(14) а?! <4 — ^2 — ^2»
(15) а;1 = $1 = $я<;ха:
(14) — если аа(аѴ — Ъа') 0;
(15) — если аа' (аЪг — Ъа') 0.
у) Пусть Ьа — 4<эс = О, Ъ'2 — 4а'с'±0.
Въ этомъ случаѣ хг=х^. Возможны лишь распорядки:
(16)
(17)
/
(16) — если аа'(а6' — Ъа') <^0; (17) — если аа'(аЪ' — Ъа) >0.
2) Пусть, наконецъ, 62 — 4ас — Ь'* — 4а'с' = О.
Въ этомъ случаѣ и имѣетъ мѣсто только одно распре-
дѣленіе:
Рѳзюмѳ. Результантъ данныхъ уравненій:
А = (ас1 — са')2 — (аб' — 6а') (6с' — сЪ'),
= 5 [(2ас + 2са' — ЪЪ')* — (Ь* — 4ас) (Ь'« — 4а'с')],
А»С(^5 — 4ас) (аЪ' — Ъа')* — |2а(ас' — са') — Ъ(аЬ' — Ъа’) }*],
= [(Ь'а - 4а'с') (аЪ' — Ъа)* — {2а'(ас' - са') - Ъ'(аЬ' — Ьа')|»]
= «'2 . / (і() . / &) = а* . <р (ж,) у (.«,).
р = Ь'(аЪ' — Ъа') - 2а' (ас' - са') 1 а* [/ (;,) + / (^)].
Ч = 2а (ас' — са') — Ъ (аЬ' — Ъа') = а» (^) -}- -р(жа)].
ж„ жа корни ур—нія аж8Ьж4~ с = 0, (Ж|<Сж2).
;3 » > а'х* 4" 4"с' ~ 0» (ч ^)*
Ь2 — 4а<? = 5, Ъ'2 — 4аѴ =
Нижеслѣдующая таблица резюмируетъ вышеприведенное изслѣдованіе
Примѣчаніе. Эта таблица должна научить, какъ располагать изслѣдованіе въ каждомъ частномъ вопросѣ. Попятно, что иногда можетъ потребоваться построеніе только части этой таблицы.
9 Необходимо, чтобы было* & — 4ас>0, что влечетъ за собою и Ь'2—4а'с'>0.
2) Корня ур—ній въ этомъ случаѣ всегда дѣйствительные неравные, поэтому нѣтъ надобности опредѣлять знаки о и
3) Въ этотъ случаѣ корни ур—ній всегда дѣйствительны; слѣд., разсмотрѣнію подлежатъ только случаи, когда 3 и V положительны или нули.
ГЛАВА ХХХШ.
I
Рѣшеніе неравенствъ: квадратныхъ» высшихъ степеней» ирраціонаіьныхъ.— Приложенія.
Цѣлое квадратное неравенство.
492» Цѣлыя квадратныя неравенства могутъ быть двоякаго вида:
ая* 4“ “Ь с > 0, или ах* Ьх с <0;
но умноживъ второе на —- 1, приведемъ его къ виду перваго; слѣд. съ теоретической точки зрѣнія достаточно указать рѣшеніе неравенства
си?2Ьх4“ с > 0 ,..(!)
Слѣдуетъ различать два случая: — 4ас^0 и Ь*— 4ас>0.
1-й случай: №—
При этомъ условіи корни тринома будутъ дѣйствительные равные, или мнимые; а извѣстно, что какъ въ томъ, такъ и въ другомъ случаѣ, при всѣхъ дѣйствительныхъ значеніяхъ ж отъ —-оэ до Ц-со триномъ сохраняетъ неизмѣнно знаки коэффиціента я. Поэтому надо различать случаи: а > 0 и а < О,
Если а > 0, триномъ всегда останется положительнымъ, и слѣд. неравенству
(1) удовлетворяютъ всѣ дѣйствительныя значенія х
(за исключеніемъ значенія
2а
въ случаѣ № — 4ас^0).
Если же а<0, триномъ всегда останется отрицательнымъ: неравенство не можетъ быть удовлетворено никакимъ дѣйствительнымъ значеніемъ х*
2-й случай: № — 4ас > О,
Въ этомъ случаѣ триномъ имѣетъ корни дѣйствительные неравные; мы ихъ найдемъ, рѣшивъ ур. ая* 4~ 4” с = пусть они будутъ х и я", и пусть х' < хт\
Если а>0, то триномъ, сохраняя знакъ перваго члена при всѣхъ значеніяхъ х, лежащихъ внѣ корней, останется при всѣхъ этихъ значеніяхъ положительнымъ; слѣд. неравенству будутъ удовлетворять, съ одной стороны, всѣ значенія меньшія меньшаго корня а', съ другой, всѣ ж-сы, большіе большаго корня х”:
х < хг и х > х”.
Если а < 0, то триномъ, сохраняя знакъ противоположный первому члену при всѣхъ значеніяхъ х, лежащихъ между корнями, будетъ положителенъ при
Нижеслѣдующая табличка резюмируетъ рѣшеніе квадратнаго неравенства тою и другого вида, при томъ или другомъ знакѣ коэффиціента.
Если Рѣшеніе перав. ах* Ъх 4~ с > 0
0 а <С0
- Нѣтъ дѣйств. значеній х
Ь* — 4ас <С 0 Всякое значеніе
удов—хъ нер—ву.
& — 4ас = 0 Всякое значеніе кромѣ Ь Нѣтъ дѣйств. значеній я,
2а * удов—хъ нер—ву.
Всякое значеніе я, лежащее Всякое значеніе х, лежащее
о — ъас ѵ внѣ корней: х<^х' и х^>х". между корнями:
а<^ 0 а^>0
♦ Рѣшеніе нерав. ал:4-|-^4-с<С0
493. Примѣръ Ь Рѣшитъ неравенство: — Зх4-|-“х — 5 <0. «
Здѣсь Ь* — — 7^-4 (— 3) . (— 5) = — 11, слѣд. корни тринома
мнимые, а потому при всѣхъ дѣйствительныхъ значеніяхъ сохраняя знакъ перваго члена, онъ будетъ отрицателенъ; такъ что неравенство удовлетворяется всякимъ дѣйствительнымъ значеніемъ перемѣннаго.
Примѣръ И. Рѣшитъ неравенство Зх4 — 1 Ож 3 > 0.
Здѣсь Ъ1*—ас = о2 — 3.3 = 16: корни тринома дѣйствительные нерав-, 1 Н Л
ные, именно: ж ж =3.
Неравенство требуетъ, чтобы триномъ былъ положителенъ, т.-е. имѣлъ знакъ перваго члена, а это имѣетъ мѣсто при всѣхъ значеніяхъ лежащихъ внѣ корней. Поэтому неравенству удовлетворяютъ всѣ
а также #> 3.
Примѣръ ІП. Рѣшитъ неравенство 4ж* -|- 5ж — 19 < 0.
Здѣсь Ь'1— 4ас = 54 — 4.4. (— 19) ~ 329: корни тринома дѣйствительные неравные, именно:
Неравенство требуетъ, чтобы знакъ тринома былъ противоположенъ знаку перваго члена, и потому х должно заключаться между корнями, т.-е.
—5-4-Ѵ329 - 5 - 1'329
-----8-----
__5
Примѣръ IV. Рѣшитъ неравенство 7------------> О»
।' о?
Чтобы частное было положительно, нужно, чтобы дѣлимое и дѣлитель имѣли одинаковые знаки, или, что то же, надо, чтобы произведеніе ихъ было положительно, т.-е. чтобы
(За — 5) (7 — ж)> 0, или — Зх2+26л: — 35 > 0.
Отсюда, какъ въ примѣрѣ Ш, найдемъ, что
Примѣръ V. Рѣшить неравенство я3 -|- 2ах — а3 > 0.
Крайніе члены противоположны по знаку, слѣд. корни тринома дѣйствительные неравные; а именно, найдемъ, что
#'=0(1/2— 1)т я"= — а(|/2 4“1)*
Неравенство требуетъ, чтобы триномъ сохранялъ знакъ 1-го коэффиціента, а въ случаѣ дѣйствит. неравныхъ корней это имѣетъ мѣсто при всѣхъ значеніяхъ лежащихъ внѣ корней.
Отсюда:
1) Если а>0, и слѣд. неравенству удовлетворяютъ всѣ значенія
я>а(|/2— 1), а также всѣ х<^— а(]/2-[“1)*
2) Если «<С0, и слѣд. неравенству удовлетворяютъ
всѣ х<^а (р/‘2 — 1), а также всѣ &/>— а(|/2-р1).
Примѣръ VI. Рѣшитъ неравенство
(п^ 3)(п — 4) я3 — 8а(и^3)я — 12а*>0.
Находимъ корни тринома; для этого рѣшаемъ ур.
(п 3) (п — 4) — 8а (и — 3) х — 12а2 = О,
изъ котораго
х „ 4а (п — 3) ± Иба« (и — 3)з + 12а2 (и — 3) (и —Т) (п — 3)(*г — 4)
Подрадикальное количество = 4а* (я — 3) |4(га — 3) -|- 3 (п — 4) | = 4а* (п — 3) (7га — 24); такимъ образомъ иайдемъ
, _ 2а[2(га - 3)+|/(м-3)(7«—24)1 * „ 2а[2(я—3)—У(п-ЗХ7и-24)]
(я—3) (я—4) ’ Х ~ (я—3)(я—4)
Знакъ тринома зависитъ какъ отъ знака коэффиціента (п — 3) (п — 4), такъ и отъ природы корней, слѣд. отъ подрадикальнаго количества, а потому нужно разсмотрѣть нѣсколько случаевъ, давая п всѣ значенія въ слѣдующихъ интерваллахъ:
Первый интерваллъ.—Давая п значенія въ первомъ интерваллѣ, т.-е» меньшія 3, будемъ имѣть: я — 3 <А 7и — 24 < 0, п — 4 <С 0; слѣд. коэффиціентъ при я2 больше 0; подрадикальное количество >0, и корни дѣйствительные. Неравенству будутъ удовлетворять значенія я, лежащія внѣ корней; нужно, слѣд., сравнить корни. Пишемъ наугадъ неравенство
2а [2 (п —3) 4-1 (та — Зк7я — 24)] 2а (2 (п—3) — И(п — 3) (7м — 24)|
(п — 3) (п — 4) ' (п — 3) (п — 4)
Такъ какъ (а З (п — 4) > 0, то можемъ откинуть знаменателя, не измѣняя знака неравенства; затѣмъ, сокращаемъ на 2, откидываемъ отъ обѣихч> частей общіе члены 2а(п —3), сокращаемъ на полож. количество 2}/(п —3)(7г? —24) и получимъ такимъ образомъ эквивалентное (1)-му неравенство
а 4> — а или 2а > 0.
Если а>0, это неравенство, а слѣд. и испытуемое, вѣрно; слѣд. будетъ х'\ Если же а 0, то п 2а < 0, а потому въ испытуемомъ неравенствѣ первая часть должна быть меньше второй, т.-е. х'<^х”г Заключаемъ, что при а^>0 неравенству удовлетворяютъ
всѣ ж^х1', а также х>х';
при а <С 0 ему удовлетворяютъ
всѣ а также всѣ
24
Второй интерваллъ. Для значеній п, большихъ 3, но меньшихъ 4г, будетъ: я—3>0, 7п— 24 < О, « — 4<^0. Слѣд. (я — 3) (п — 4)<0; подрадикалъное количество < 0, значитъ, корни мнимые, а потому триномъ будетъ отрицателенъ, и данному неравенству, которое требуетъ, чтобы триномъ былъ положителенъ, удовлетворить нельзя.
24 г*
Третій интерваллъ. Для у<л<^4 будетъ: п— 3>0, 7п — 24 > 0, п — 4 < 0; слѣд. коэффиціентъ при х* отрицателенъ, а корпи дѣйствительные. Неравенство требуетъ, чтобы триномъ имѣлъ знакъ противоположный коэффиціенту при .г2, а этому требованію удовлетворяютъ всѣ значенія я, лежащія между корнями.
Для сравненія корней пишемъ неравенство (1); умножая обѣ его части на отрицательное количество (п—3)(н—4), должны измѣнить знакъ неравенства; откинувъ, затѣмъ, общіе члены и сокративъ на полож. количество 2}/(н—3)(7п—24), найдемъ . .
а <Г — а. или 2а <4 0. •
Если а>0, это неравенство невѣрно, а потому смыслъ испытуемаго неравенства надо измѣнить, слѣд. будетъ я' < ж". Если а <С 0, то и 2а <\0, а поэтому испытуемое неравенство вѣрно; и слѣд. Заключаемъ, что'*"
при а>0, неравенству удовлетворяютъ всѣ х> большія я', но меньшія я”:
х
х
X';
при а < 0, значенія ’х заключаются въ предѣлахъ X Х^> X .
Четвертый интерваллъ. Когда п ^>4, то будетъ: «— 3^>0/ 7п —24 > 0, « ~ 4 > 0; (я — 3) (« — 4) О, а корни дѣйствительные.
Неравенство требуетъ, чтобы триномъ имѣлъ знакъ перваго коэффиціента, что имѣетъ мѣсто для х, лежащихъ внѣ корней.
Сравненіе корней въ этомъ случаѣ покажетъ, что при а^>0 будетъ хг\ при а<0 будетъ Заключаемъ, что
при а^>0 данному неравенству удовлетворяютъ
а также
х < Я".
при а < О ему удовлетворяютъ
х
х1
х"
и
Примѣръ VII Рѣшитъ неравенство
з* + х — 6 2а 4-1
я6 (2а — 1),
Общій знаменатель =2а-[-1; но какъ знакъ его неизвѣстенъ, то мы не можемъ, въ видахъ освобожденія неравенства отъ дробей, множить обѣ его части на не.сдѣлавъ предварительно того пли другого предположенія о знакѣ
этого двучлена. Итакъ, нужно разобрать два случая: 2с* —1~ 1 >0 и 2а 4“ 1 <0.
Первый случай: 2а 4~ 1 0, или а
Въ такомъ случаѣ, умноживъ обѣ части на 2а 4-1 и не перемѣняя смысла неравенства, получимъ эквивалентное данному неравенство:
х24-я — 6>(2а+ 6 (2а — 1) (2а 4-1)
или
х* — 2ах — 24а2 0;
корни тринома первой части дѣйствительные неравные, именно: —- 4а и 4" Неравенство требуетъ, чтобы триномъ имѣлъ знакъ одинаковый съ коэффиціентомъ при х\ сл. х должно содержаться внѣ корней ~~ 4а и 4~ 6а. Такимъ образомъ, нужно знать, который изъ этихъ корней больше, а это зависитъ отъ знака а. Но а, будучи > —можетъ имѣть значенія отъ —до 0 * (отрицательныя), и отъ 0 до 4“^° (положительныя). Когда а<^0, то очевидно — 4а > 6а; при а > 0, наоборотъ ~ 4а < 6а. *
Такимъ образомъ
1/ а<С0..................я<^6а, а также — 4а.
2 I а>0....................Х<С~ 4а, а также #>6а.
Второй случай. 2а-|- 1 <0, или а< —у
Умножая обѣ части неравенства на отрицательное количество 2а 4~ 1 и измѣняя смыслъ неравенства, придемъ къ слѣдующему неравенству, эквивалентному данному:
— 2аг — 24а2<0.
Оно требуетъ, чтобы триномъ первой части имѣлъ знакъ/ противоположный коэффиціенту при я4, а этому требованію удовлетворяютъ значенія я, лежащія между корнями — 4а и 4- 6а тринома.
Такъ какъ а, будучи <—отрицательно, то —’4а>-]-6а, и потому значенія х, удовлетворяющія неравенству при
а < — суть ба < я < — 4а+
Примѣчаніе. Можно бы было получить тѣ же результаты, умноживъ обѣ части предложеннаго неравенства на положительное количество (2а-[-1)\
494. Приложеніе I. При какихъ условіяхъ О будетъ заключаться между корнями уравненія
х(х— 1) — 1) — 2/^ = 0?
Необходимо и достаточно, чтобы результатъ подстановки нуля вмѣсто х имѣлъ знакъ, противоположный знаку коэффиціента при я2, т.-е. чтобы
1) — — или (р-Н?)2— (р+?)>0 или, наконецъ,
. (р + <і)(р +$ — 0>°-
А этому неравенству можно удовлетворить двояко, полагая: или или р < 0.
495. II. Какимъ условіямъ должно удовлетворять коли-
чество а для югоіо, чтобы “4-, содержалась между корнями уравненія
Х(*+ 1) (я2 + За + 3) 4- я2 = 0.
Необходимо и достаточно, чтобы результатъ подстановки —1- вмѣсто х въ первую часть былъ отрицательный, т.-е чтобы было
~5(я24-Зя + 3) + я2<0, иля я2-а-1 <0.
Этому неравенству удовлетворимъ, взявъ
496. Приложеніе III. Какимъ условіямъ должны удовлетворятъ коэффиціенты полинома
г = А#* 4- 2В"#і/ 4- АУ* + 2В'я 4" 2В^ + А"
для того, чтобы онъ оставался положительнымъ при всякихъ значеніяхъ х и у?
Первое условіе состоитъ въ томъ, что А должно 6ыть'>0, ибо при А<0, если корпи ур—нія въ х
Ая2 + 2В''^ + Л'^4-2В'я+2Ву + А'' = О , . , , (1)
будутъ дѣйствительны, полиномъ з будетъ отрицателенъ при тѣхъ значеніяхъ х, которыя лежатъ внѣ корней, а если мнимы, то з постоянно будетъ отрицателенъ; слѣд. онъ не былъ бы положителенъ при всякомъ х. •
Если А>0, то полиномъ з будетъ всегда положителенъ, если корни ур— нія (1), рѣшеннаго относительно х, будутъ мнимыми, что ведетъ къ неравенству:
(В"а - АА'й1 + 2(8^“ АВ)у + В'* - ІА" < 0;
а этотъ квадратный относительно у триномъ будетъ постоянно отрицателенъ, если
‘ В"* —АА'<0 и (В'В" — АВ)* — (В"* - АА')(В'* — ЛА") < 0.
Слѣд., искомыя условія таковы:
А > О, В"2 — АА' < 0 и (В'В" - ЛВ)2 - (В"2 - АА')(В'* — АА") < 0.
497. Приложеніе IV. Изслѣдовать корни ур—нія
х* — 2Ь + Р + 21 — 3 = 0?
Ищемъ критическія значенія >.*
1. Дѣйствительность корней. Корпи будутъ дѣйствительны, если
—т.-е. Р — 1(1*-|-21~3)>О пли
2. Знаки корней. Произведеніе корней 4? 21 — 3; корпи этого тринома дѣйствительны и суть \ = 4~ 1, Ч = — 3, потому произведеніе корней = (1 ~ 1) (а —р 3), и, сл* будетъ > 0, если А>1, или — 3; и будетъ <^0, если —3<д<1. і
Сулема корней = 21, сл. сумма > 0, если 1 > 0, и сумма < О, если 1 < 0.
Расположивъ значенія 1 въ восходящемъ порядкѣ, имѣемъ скалу:
— гю . . . . —3 . . . О . . - +1 • •
Разсмотримъ теперь каждый изъ четырехъ иптервалловъ значеній А, при которыхъ корни дѣйствительны.
1) 1< — 3. Здѣсь произведеніе корней >0, слѣд. знаки ихъ одинаковы; сумма корней <0; сл. оба корня отрицательны.
2) 1 = —3. Произведеніе корней —0; сл. одинъ корень—,0; сумма корней =— 6; сл. другой корень = — 6.
3) — 3</. <0. Произведеніе корней < О, сл. знаки ихъ различны; сумма ихъ < 0, сл» большій но абс. зн. корень отрицателемъ.
4) ). = 0. Знаки противоположны; а какъ сумма = 0, то оба корня по абс. значенію равны (х = 4“Ѵ^ х" = — |/з).
5) О < к < 1. Такъ какъ произв, < 0, то знаки корней противоположны; сумма >0, сл. большій по абс. зн. корень положителенъ.
6) ). = 4-1, Произв. корней = 0; сл. одинъ корень = 0; а какъ сумма >0, то другой корень положителенъ.
3
7) Н-1 <А<СН~ 9* Такъ какъ произведеніе корней > 0, то знаки корней «ІВІ
одинаковы; сумма >0; оба корня положительны.
• 3
8) Корни равны и положительны.
3
Корни мнимые.
Изслѣдованіе можно резюмировать въ слѣдующей таблицѣ:
і< — 3: два отриц. корня.
1= — 3 : одинъ корень = 0; другой = — 6.
— 3 <і < 0 : большій по абс. знач. корень отрицателенъ, меньшій полож.
1 = 0: равные корни съ против. знаками (+1/3 и —)/ 3).
1: большій по абс. знач. корень положителенъ, меньшій отрицателенъ.
1 : одинъ корень — 0, другой положит.
3 ' ’
*: два положит. корня не равныхъ.
3
два положит. корня равныхъ.
3
: корни мнимые.
498. Приложеніе Г. Изслѣдовать корни уравненія (к—1)х2 — 2(к— — 2)#—7). — 1=0 при измѣненіи і отъ —со до 4“^ и оюред/мшпъ, сколько око «.ніьтъ корней въ каждомъ изъ интерваловъ:
отъ — оо до — 1, отъ — 1 до -|“ 1, отъ -}" 1 До 4“ сс.
Находимъ замѣчательныя значенія а.
1. Дѣйствительность корней. Прежде всего, корни должны быть дѣйствительными; сл. должно быть
(к — 2)*4-(а— 1)(714- 1)> 0 или 8к* — Юа4-3,>0.
Такъ какъ реализантъ этого тринома положителенъ, то корни его дѣйстви-1 3
тельные и неравные; они равны: \ = 2? ^=4* Слѣд. триномъ будетъ оста-
ваться > 0 для всѣхъ X внѣ корней, т.-е, для X между — со и —ц между
Ай
2. Знаки корней. Произведеніе корней тораго тотъ же, что и произведенія
— выраженію, знакъ ко-
(7).+ 1)(1-л),
а это произведеніе отрицательно для значеній X, лежащихъ внѣ корней этого выраженія, т-е* для 1<—у и для Х>1; и положительно для всѣхъ иначе-1
ній А, лежащихъ между —у и +1.
2 Л — 9)
Сумма корней — ; _ р — выраженію, знакъ котораго тотъ же, что и произведенія (X—2) (X—1), которое будетъ >0 для всѣхъ X, лежащихъ внѣ корней, т.-е. для X, лежащихъ между — со и + 1, и между -|-2 и Н-со; оно <10 для X, лежащихъ между корнями, т.-е. для
1
2.
3. Ищемъ знакъ подстановокъ — 1 и 1 вмѣсто % въ первую часть ур—нія. Имѣемъ:
Д + 1)~ а— 1 — 2(1 - 2) - П— 1 = - 81 + 2;
отсюда видно, что будетъ Д-р1)>0, если — 81 -|-2>О, т.-е. если X и будетъ 1) если 8X4" 2 <СО, т 'е* когда Х> |-
Подстановка — 1 дастъ
Д— 1) = Х^1 + 2(Х— 2) — 7Х —1 = — 41 — 6,
откуда заключаемъ, что при Х<—будетъ Д—1)>0; при Х> — будетъ Д-1)<0.
4. Затѣмъ, 1-й коэффиціентъ = X—1; онъ будетъ >0 при Х>1, и будетъ <0 при 1< 1.
5. Находимъ корни при X + со; вынося въ данномъ ур—ніи X за скобки, даемъ ему видъ
Если абсолютное значеніе X увеличивать неогранич., то необходимо, чтобы выраж. въ квадр. скобк. стремилось къ 0; т.-е. при Х = + оо х должно удовлетворять -ур—нію х* — 2х — 7 = 0; откуда Хд = 1 — 2 }Л2, х3 = 1 + 2]/2-
Итакъ, замѣчательныя значенія X, расположенныя въ восходящемъ порядкѣ, будутъ:
3 1 1 1 3 1 9 і
~ 9* 4’ .у 1, 2 и +СЧ
которыя въ этомъ порядкѣ и наносимъ въ первую горизонтальную строку нижеслѣдующей таблицы: получимъ скалу возрастающихъ значеній к; подъ ними располагаемъ, для каждаго интервалла, знаки: реализанта, произведенія корней, ихъ суммы, знаки Д-[-1), Д— 1) и перваго коэффиціента ур—нія.
Скала значеній 1 + 0О 1^ Ю1 —' 1^ 1 СО 1>1 1 2 і
Реади зайть — —|— — 1
Произведеніе корней. — + 9 1 ‘ -—- ——
Сумма корней. -р —|— 1 —і-
Ц+1) / — —*
Г(-І) — — —
1-й коэф. — — — — — —
Имѣя таблицу знаковъ, легко опредѣлить знаки корней ур—нія для всякаго интервалла.
1) Х<С— 2* Произведеніе корней отрицательно, сл. знаки корней различны; сумма корней положительна, сл. большій по абсол. знач. корень положителепъ. /*(— I) и Д-[-1) положительны, тогда какъ 1-ый коэффиціентъ отрицателенъ, сл. — 1 и -р 1 находятся между корнями х и хч (называя, какъ всегда, х*— менып. кор., х”—большій кор.). Итакъ
— ОС, —1, +1, х",
3
2) /. = — 2* Въ этомъ случаѣ Д—1) = О;сл. х'—— 1; другой корень— между +1 и-р^'
3 1
3) — Произведеніе корней отрицательно, а сумма ихъ поло-
жительна, сл. знаки корней различны; и большій по абс. велич. корень положителенъ; Д—р между тѣмъ какъ 1-ый коэф. сл. -р 1 — между корнями; затѣмъ, знакъ Д— 1) одинаковъ со знакомъ 1-го коэф. сл. —1 внѣ корней. Расположеніе корней, сл., таково:
— оэ . . . — 1 . . . л/ . . . —1 . . . х" . . ,
4) ). — — Произведеніе корней проходитъ чрезъ 0, сл. одинъ корень —0; расположеніе же корней таково, какъ только что указано.
5) Произведеніе и сумма корней положительны, сл. я'>0 п
/'>0. Знакъ Г(“Ь 1) противоположенъ знаку 1-го коэф., а знакъ /(—1) одинаковъ со знакомъ 1-го коэф,, сл. 4~ 1 между корнями, — 1 внѣ корней; расположеніе корней таково:
— со . . , — 1 . . . х' . . . + 1 . . . я/' . . . со.
6) л = обращается въ 0; сл. одинъ корень = 4-1; другой же
находится между 4“ 1 и ибо, по предыдущему случаю, онъ больше 4~1-
7) Оба корня положительны, /(-р 1) имѣетъ одинаковый знакъ съ
1-нъ коэф., сл. -рі внѣ корней. Сравнимъ ее съ полусуммою корней, которая равна ___2 __о
не будетъ ли <зту2>1? Такъ какъ ). <О, то 1—2<^).— 1, или — 2 — 1, что вѣрно. Итакъ: 4" 1 вн^ корней и меньше ихъ полусуммы,
сл. меньше меньшаго корня. Расположеніе таково:
А.' А." 1 АЛ
. 4 . X . , . х . , . -р- СО.
8) Х = ()- Реализантъ обращается въ нуль ц корни дѣлаются равными: я' = У' = 3.
9) Реализантъ дѣлается отрицательнымъ: корни—мнимые.
3
10) 1 = -- Реализантъ снова обращается въ нуль; ур. имѣетъ равные корни: х' = х"~5г
з
11) Произведеніе и сумма корней >0: оба корня положительны.
/(4*1 )<.Ѳ и 1-ый коэф. <^0; сл. +1 внѣ корней; сравнимъ ее съ полусуммой кор-
1 — 2
ней, положивъ, напр., у—|->1, откуда X — 2<Ч—1, или —2<^ —1, что вѣрно, сл. 4~ 1 меньше меньшаго корпя, и потому
4-1 . . . . .х” . . . +*).
4
12) ).= 1. Коэффиціентъ при я3 обращается въ 0, сл. одинъ корень = со, другой удовлетворяетъ ур—нію 2х— 8 = 0, откуда х = 4.
13) 1 <4л<^2. Произв. и сумма корней отрицательны, сл. знаки иіъ различны и большій по абс. знач. корень отрицателенъ. Д-|- 1) и /(— 1) имѣютъ знакъ противоположный 1-му коэф., сл. 4“ 1 и “ между корнями. Имѣемъ:
— со. . . я' . . .—1. . . 4~1 • - • У - .'.4“^<
14) л = —|— 2. Сумма корней=0, сл. корни равны и противоположны по знаку: а? = -Ь |/І5,
15) Х>‘4-2. Знаки корней противоположны; большій по абс. величинѣ корень положителенъ; — 1 и 4" 1 между корнями, сл.
— со , . . а/ . . . — 1 . . . 4" 1 • - * х" . . . 4“
Резюме изслѣдованія.
Примѣчаніе.— Когда изслѣдованіе корней, какъ въ только что разсмотрѣнной задачѣ, нѣсколько сложно, полезно предварительно составить таблицу знаковъ: это даетъ возможность почти непосредственно читать въ ней искомые результаты. Планъ изслѣдованія, указанный въ этомъ §, лишь слегка (въ расположеніи таблички знаковъ) разнится отъ плана, предложеннаго Тартзнвил* лемъ.
Раціональныя дробныя неравенства,
499. Когда неизвѣстное входитъ въ неравенствѣ въ знаменателя, то мы можемъ уничтожитъ знаменателя, если онъ представляетъ количество существенно-положительное. Во всѣхъ остальныхъ случаяхъ приводятъ., всѣ члены неравенства къ одному знаменателю и собираютъ ихъ въ первую часть. Такимъ образомъ получается неравенство вида
гдѣ Р и Ч суть полиномы, содержащіе Замѣчая, что по правилу знаковъ при умноженіи и дѣленіи, произведеніе количествъ Р іНІ всегда имѣетъ тотъ же знакъ, какъ и игъ частное, можно предыдущія неравенства замѣнить эквивалентными имъ:
РЗ>0, или РЧ<0.
Къ тому же результату мы пришли бы, умножая обѣ части того или другого неравенства на существенно-положительное количество
Затѣмъ разлагаютъ полиномы Р и на множители 1-й степени относительно х, и получаютъ неравенство вида:
А(х — а)(х — 3)(х — у)(х — 3) , . . > О,
гдѣ А не содержитъ Затѣмъ распредѣляютъ количества а, у, . . . въ порядкѣ возрастающихъ величинъ. Пусть, напр., будетъ
— со < а < 3 С у • - . <С + с0*
Очевидно, каждый двучленный множитель будетъ сохранять неизмѣнный знакъ до тѣхъ поръ, пока х, увеличиваясь, не перейдетъ значеніе, обращающее этотъ множитель въ нуль. Такимъ образомъ можно указать знакъ произведенія для всякаго отдѣльнаго интервалла, и сл. указать тѣ интерваллы, въ которыхъ произведеніе сохраняетъ требуемый неравенствомъ знакъ.
500. Примѣръ I. какахъ нужно измѣнятъ х, чтобы
удовлетворить неравенству
Дх2— 5я — 1 -
2x2 _ 5я + з >
Перенеся 1 въ первую часть и приведя къ общему знаменателю, получимъ неравенство
—.>0. 2а'2 —5ж+3^
Умноживъ обѣ части на существенно-положительное количество (2х2—5х~р З)2, найдемъ неравенство, эквивалентное предложенному.^
2(х2 — 2)(2х2 — 5х + 3) > О,
или, по разложеніи х2—-2 и 2х2— 5х-}-3 (триномовъ, имѣющихъ корни дѣйствительные неравные, и сл. измѣняющихъ знакъ при измѣненіи х) на множители 1-й степени:
4 (х +/2) (х — /2) (х — 1) [х — > 0.
Будемъ давать х значенія въ слѣдующихъ интерваллахъ, въ которыхъ величины, обращающія каждый биномъ въ нуль, расположены въ возрастающемъ порядкѣ:
Если давать х значенія меньшія (—}/2), то каждый множитель будетъ отрицателенъ; а какъ ихъ четное число, то все произведеніе будетъ оставаться положительнымъ.
Если давать х значенія, большія (—}/2), но меньшія 4~1, а сл. и по’ давно меньшія |/2 и 9» то множитель ^4”}^ - будетъ положителенъ, оста ль* ные же биномы отрицательны, и такъ какъ число отрицательныхъ множителей нечетное, все произведеніе будетъ отрицательно.
Давая х значенія, большія 4-1, но меньшія 4“ѴХ находимъ, что два множителя: и х — 1 будутъ положительны, а два: х —]/2 и х — |
отрицательны; сл. произведеніе положительно. И такъ далѣе.
Убѣдимся, что данному неравенству удовлетворяютъ значенія х; опредѣляемыя нижеслѣдующими предѣлами:
х<— у/2; Н-1<«<+|/2;
501. Примѣръ П. Рѣшитъ неравенство
5*5 — 2* + 3
(х — — За?-|- 1)
Это неравенство эквивалентно слѣдующему;
(5х* — 2х — ЗХх - 1)(х* - Зх 4-1) < 0.
Замѣчая, что для транома 5ха — 2x4-3 имѣемъ: 1—5.3< 0, т.-е. что' корни его мнимые, заключаемъ, что онъ всегда будетъ сохранять знакъ перваго коэффиціента, т.-е. всегда положителенъ. Поэтому данное неравенство эквивалентно еще слѣдующему простѣйшему: * !і_|
(х — 1)(х2 — Зх-]-1)<0.
или
Даемъ х послѣдовательно значенія въ интерваллахъ:
Когда х < —9“’ всѣ три множителя, а сл. и произведеніе, будутъ отри-3—15 . . . „
цательны. При—9— <х<1, первый множитель положителенъ, два другіе
3 4- У5
отрицательны, сл. произведеніе положительно. При 1 < х < -—9, первые два
3 -к)/ 5
множителя >0, третій < 0, сл. произведеніе С 0. Наконецъ, при х > —9— *
всѣ множители, а съ ними и произведеніе > О. Итакъ, неравенству удовлетворяютъ:
502. Примѣръ III. Рѣшить неравенство
2ах + 36 эЪх — 4«
Приведя къ общему знаменателю, имѣемъ
2 (а — 106)ж —]— 36 16л 0
56я — 4л 1
что эквивалентно неравенству
[2 (а — 106> 4- ЗЪ +16а](56я — 4а) < О,
или, по вынесеніи изъ первыхъ скобокъ 2(а—105), а изъ вторыхъ 55:
Относительно коэффиціента 10(а —106)5 могутъ быть предположенія
[а< 105 |а<10&
Ь<°|а>10Ь’ Ь>°|а>10Ь'
Первый случай: Ь<^0, а<^\ОЬ. •
Произведеніе 10(а—106)Ь положительно; сл. неравенство эквивалентно съ
/ । ЗЬ + 16а \ / . Л
X + ы—Нпіл ® < 0.
\ 1 2 (а— 106)/\ об /
сл.
Трпномъ долженъ имѣть знакъ противоположный коэффиціенту при лА 36 -ъ 16а 4а х должно заключаться между —п
Нужно знать, который изъ этпхъ предѣловъ большій. Положимъ наугадъ — 2(а — 106) > В5* такъ какъ ' Ю5)Ь > 0, мы можемъ умножить обѣ части на это произведеніе, и не измѣняя смыслъ, неравенства, получимъ ему эквивалентное: — (35 Ц- 16а)55 4а. 2(а —105), или — 1562 — 8а2 > О,
что невѣрно, ибо первая часть существенно отрицательна.
п 35 + 16а 4а
Заключаемъ, что — 9(а — 106) < 5б’ а ПОТОМУ х -НУЖНО взять такъ, чтобы
36 + 16а ^4а
2(^2По6)< х<бГ
Второй случай: 6<0, а>106.
Произведеніе 10(а— 106)6 отрицательно, сл. предложенное неравенство эквивалентно неравенству
/ - 36 + 16а \ / 4а\ . Л
\ 2^а—106)/\ э5/ ’
36 +16л 4л а потому х не должно заключаться между корнями тринома: — и
Посмотримъ, который изъ нихъ больше. Допустивъ, что —5^11и замѣчая, что 1О(а — 106)Ь<0, умножаемъ допущенное неравенство па это
произведеніе и перемѣняемъ смыслъ неравенства; найдемъ эквивалентное ему неравенство — 1563— 8а1*<0, что вѣрно.
Заключаемъ, что предположеніе было правильно, а потому данному неравенству удовлетворяютъ два ряда значеній х:
36 + 16л 2(« —106)
и
Третій случай: Ь>0, а <106.
Оперируя такимъ же образомъ, найдемъ, что предложенному неравенству удовлетворяютъ:
36 + 16л 2(д -106)
Четвертый случай: 6+>0~ а >*106.
Вышеуказаннымъ способомъ придемъ къ результату:
4л
56'
2(л - 106) *
Итакъ, чтобы удовлетворить предложенному неравенству, надо:
56
При (а — 106). Ъ > 0 брать: — 2(«— 106)
При (а — 106).Ъ<0 брать: х > — или
4л
56’
Рѣшеніе ирраціональныхъ неравенствъ.
503. Когда неизвѣстное встрѣчается подъ знакомъ квадратнаго корня, то, вообще говоря, нужно бываетъ освободить его изъ-подъ знака корня, а для этого нужно изолировать радикалъ въ ту или другую часть неравенства. Затѣмъ, слѣдуетъ разсмотрѣть знакъ другой части неравенства, изслѣдуя, остается ли онъ неизмѣннымъ, пли же зависитъ отъ предположеній относительно буквъ, входящихъ въ эту часть. Если знакъ этотъ не одинаковъ со знакомъ, стоящимъ передъ радикаломъ, слшслъ неравенства очевиденъ, Если же — одинаковъ, то нужно возвыситъ обѣ части въ квадратъ, сохраняя или перемѣняя смыслъ неравенства, смотря потому, будетъ ли этотъ общій знакъ-р «ли —,
504. Примѣръ I. Рѣшитъ неравенство |/(я — 1)(я — 2) > я — 3, Чтобы 1)(я — 2) былъ дѣйствителенъ, надо, чтобы подрадикальное количество было >0: этому требованію удовлетворяютъ всѣ х отъ —со . . . до 1, и отъ 2 до 4-со. Затѣмъ, очевидно, неравенство будетъ удовлетворено всѣми значеніями х, которыя, не содержась между 1 и 2, будутъ меньше 3, ибо въ этомъ случаѣ вторая часть будетъ отрицательна. Итакъ, во-первыхъ, для х можно брать всѣ числа отъ —со до 4~1, и отъ <2 до 4-3.
Пусть теперь будетъ обѣ части будутъ положительныт а потому, возвысивъ въ квадратъ и сохранивъ знакъ неравенства, ищемъ числа, удовлетворяющія неравенству
х2— Зх+2>л?2— 6х 4” 9, пли х—|>О.
Это неравенство удовлетворяется всѣми значеніями большими 3.
Итакъ: предложенному неравенству удовлетворяютъ всѣ значенія я? отъ — до +1 н отъ + 2 до + ео.
505. Примѣръ II. Рѣшитъ неравенство |/ая — х*-^]/2ах— л2>а, въ котоузоліъ а^>0.
Сначала ищемъ, какъ взять х, чтобы оба радикала были дѣйствительны, иначе, чтобы подкоренныя количества были положительны. Разсматривая а*—я?2 какъ неполный квадратный триномъ, замѣчаемъ, что онъ будетъ положителенъ, если х взять между его корнями, т.-е. если —(1). Такимъ же образомъ убѣдимся, что второй радикалъ будетъ дѣйствителенъ при 0<^х<^2а - - . (2). Изъ сопоставленія (I) со (2), заключаемъ, что оба радикала будутъ дѣйствительны, если
а>х>0 . . . (3).
Зная это, перенесемъ первый членъ неравенства во вторую часть; найдемъ: |/2аж — х2^>« — |/а2— х\ Такъ какъ вторая часть положительна, какъ и первая, то, возведя въ квадратъ и не перемѣняя смысла неравенства, получимъ эквивалентное данному неравенство: 2ах^> 2а* — 2а]/а* — ж*, или, раздѣливъ обѣ части на положительное количество 2а и изолировавъ радикалъ: )/а*—х* >а—х. Въ силу (3), сл. а—*г>0, а потому вторичное возвышеніе въ квадратъ дастъ: х*-—ах<^0. По смыслу этого неравенства х должно заключаться между корнями первой части; сл.
а
О,
что не отличается отъ условія дѣйствительности.
506. Примѣръ ІП. Рѣшить неравенство -Д> -- (1), вг
Vх* 4- а2 -|- Ь*
котсороль а и Ъ положительны и а^>Ъ,
Пусть сначала #4“Ь>0, т.-е. —&. Изъ условія а>Ь слѣдуетъ,
что х-^-а^х-^Ь^ а потому и Обѣ частй предложеннаго нера-
венства положительны, а потому, возвысивъ ихъ въ квадратъ и сохранивъ смыслъ неравенства, получимъ эквивалентное данному неравенство (по отнятіи 1 отъ обѣихъ частей):
Изъ числа значеній х, большихъ —6, возьмемъ сперва положительныя; тогда л а* Ъ
сокращеніе на положит. количество 2л? дастъ: > гутги* или* по осво-
божденіи отъ дробей, ал?2-р а?? > Ьх2-рили *2(а— &)>аЬ(а — &). Сокративъ на положительное количество а — 6, дадимъ этому неравенству видъ (х 4-* (#— у/аб)>0, и какъ первый множитель >0, то необходимо,
чтобы было
Разсмотримъ теперь величины х, содержащіяся между О и — Ь, отрицатель' ныя; въ этомъ случаѣ сокращеніе (2) на 2л- дастъ: или
(.гЦ-у/аб) (х — ]/од)<0, а какъ второй множитель <СО, то необходимо, чтобы __
х^> — |/ «6.
Но откуда а&^>Ь3 и а сл. —<^~Ъ; такимъ об-
разомъ условіе х>—|/оЬ содержится въ условіи — іо
Пусть теперь или х<і—Ь, т.-е. содержится между —Ь и
— го. Дадимъ сначала я значенія между —& и — аг т.-е. положимъ х> — а, откуда х4~л>0; въ такомъ случаѣ первая часть предложеннаго неравенства будетъ положительна, между тѣмъ какъ вторая отрицательна, и потому неравенство (1) будетъ удовлетворено всѣми значеніями х между — Ь и — а.
Давъ х значенія <С — будемъ имѣть х а < 0; а какъ и х + Ь<0, обѣ части даннаго неравенства будутъ отрицательны, а потому возводя въ квадратъ, должны измѣнить смыслъ неравенства; найдемъ
2о# 2Ъх
откуда, сокративъ на 2х < О и т. д., получимъ
(а? 1/ (.г — |/аб) > О;
второй множитель для разсматриваемыхъ значеній х отрицателенъ, сл. необходимо, чтобы и х Ц-]/«Ь < О, откуда
— уаК;
такъ какъ это условіе удовлетворено само собою, то неравенство (1) удовлетворяется всѣми отрицательными величинами хг меньшими — а.
Итакъ: предложенному неравенству удовлетворяютъ всѣ отрицательныя значенія х, и положительныя, большія и стало-быть неудовлетворяютъ только значенія х содержащіяся между О и -{-у/аЬ.
507. Примѣръ IV. Ргьшѵшъ неравенство
і/'Зл? + а * х — а
а — 1
і
а данное дѣйствительное количество,
Во-первыхъ
долженъ быть дѣйствительнымъ; а для этого надо,
чтобы было (Зя4-а)(я — а) > От т.-е. чтобы х не содержалось между —к о
и а. Отсюда видно, что надо различать два случая: а<0 и а>0_
Если а < 0, надо брать # такъ, чтобы было: х < а, или х > — при а > 0 должно брать: или х > а, или х < —
Но если а < 0, то и сх — 1 < 0, и неравенство становится невозможнымъ * ибо оно будетъ требовать, чтобы положительное количество было меньше отрицательнаго.
Итакъ, необходимо должно положить а>0; затѣмъ необходимо еще, чтобы было а>1; тогда обѣ части будутъ положительны; возвысивъ ихъ въ квадратъ и сохранивъ смыслъ неравенства, получимъ эквивалентное ему
пли
х— а
Зл* + а — (а — 1)26г — <0 я — а
а по умноженіи обѣихъ частей на — а)®:
(я? — а) [— (а® — 2а — 2) х -|” (°а — 2а -|- 2) а] < О,
» что можно представить въ видѣ
(а1 — 2а — 2) (х — а} (х — . а} > 0.
Во-первыхъ, должно быть а — 1 > 0; во-вторыхъ, я можно давать только такія значенія, которыя: или <; — нли >а.
Разсмотримъ, каковъ будетъ знакъ коэффиціента а2— 2а— 2; корпи этого тринома, какъ видно & ргіогі, дѣйствительные и неравные, одинъ положительный, другой отрицательный; замѣняя въ триномѣ а единицей, находимъ въ результатѣ — 3, сл. 1 находится между корнями, и слѣд. положнт* корень >1; вычисливъ его, находимъ а! = 1-|-)/3. Мы можемъ давать а только значенія, большія единицы; но эти значенія могутъ быть или «С, или ^І-^Ѵ^З*.
Такимъ образомъ, различаемъ два случая:
Первый случай: 1 < < 1 —)/3*
Такія значенія а лежатъ между корнями тринома а® — 2а— 2, а потому онъ отрицателенъ; значитъ и произведеніе двухъ другихъ множителей д. 6. отрицательнымъ, а потому величины ж, удовлетворяющія неравенству, должны лежать междѵ
I а2 — 2а+ 2 а “ ~і~а2 — 2а~ 2 ’а;
нужно знать сравнительную величину этихъ предѣловъ.
Но триномъ а® — 2а 2, имѣя корни мнимые, положителенъ при всякомъ а; а® — 2а—2, при взятыхъ значеніяхъ а, отрицателенъ; слѣд.
а® — 2а 4- 2
а > а* — 2а^2 ‘ ®’ и потому должно взять а2 — 2а 4- 2 . .
—о—Ні ' а < х < а.
а3— 2а — 2 %
Съ другой стороны, для дѣйствительности радикала, находящагося въ неравенствѣ, 'х нужно брать иля > а, пли <-—.>• Поэтому сравнимъ предѣлы
«2 _ 2а + 2
и на_2а — 2‘а’
допустивъ, напр., что
а а2 — 2а + 2
а'
Въ разсматриваемомъ случаѣ: а > О и а4 — 2а — 2 < О; слѣд. умноживъ ,. (,і — 2а — 2 ' , . *
обѣ части на ------------ и перемѣнивъ смыслъ неравенства, найдемъ ему экви-
валентное
— а24- 2а 2 < За2 — 6а^6, или 0<4а3—8а-|-4, или 0<(2а —2)2,
что вѣрно; слѣд. вѣрно и допущеніе. Такимъ образомъ, необходимо п достаточно взять х такъ:
а2 — 2« 4- 2
—. а < х
а2 — 2а — 2
Второй случай. а> 1 4“1^3-
Множитель а2 — 2а — 2 въ этомъ случаѣ > 0; сл. необходимо и достаточно, чтобы произведеніе двухъ другихъ множителей было положительно, слѣд. х можетъ принимать всѣ значенія, не содержащіяся между
а и
а2 — 2а + 2
а3 — 2а — 2
а.
Для сравненія этихъ предѣловъ допустимъ, напр.:
п2 — 2а 4- 2 а2— 2а —2
а < а.
Такъ какъ въ изслѣдуемомъ случаѣ а и а2 — 2а — 2 положительны, замѣ наемъ это неравенство ему эквивалентнымъ
а3— 2а~р2<а3 — 2а — 2, или 4 < О,
что. невѣрно;
а3 — 2а + 2 .
и потому —п--------о а > а; такъ что должно взять
а* —а *-
или х а, или
а2 — 2а 4- 2
— 2а — 2 " а'
Комбинируя эти результаты съ предѣлами, найденными й ргіогі, находимъ
. а а3 — 2а + 2
ж < з» пли х > я2 21 2а — 2 ’
Итакъ:
при а < 1 предложенное неравенство невозможно; при 1<а<1-|-}/3 ему удовлетворяютъ:
а3 — 2а 4- 2 а.
й2_2а —2 а < —
при а > 1 4“ ]/3 ему удовлетворяютъ:
или х < —
508, Примѣръ V. Рѣшить
иЭм» а д&бствіш&мяое количество.
9
Чтобы оба радикала были дѣйствительны, нужно, чтобы было и
. я х > з: во
одно изъ этихъ условій содержитъ въ себѣ другое, а именно: необходимо и достаточно, чтобы было ^>5;
9
необходимо и достаточно взять
при а<0
при а>0
Первый случай: а < 0.
Нужно знать знаки обѣихъ частей, н для этого сдѣлать предположенія относительно знаковъ я-]-а и
1) тогда и подавно обѣ части неравенства отри-
цательны, а потому, возвысивъ обѣ части въ квадратъ, съ перемѣною смысла неравенства, и уничтоживъ положительный знаменатель, получимъ:
(За;— 2а)(д;-]-5а)а — (Зя — а)(#4-а)а<СД илп 23а#*-|-54а3я— 49а3<^0,
или, сокративъ на а<0:
23я3 — 49аа > О,
і
Триномъ первой части, какъ видно & ргіогі, имѣетъ корни дѣйств. неравные съ противоположными знаками; слѣд. чтобы сдѣлать его > 0, необходимо п достаточно дать х значенія, лежащія внѣ корней. Корпи его суть
ѵЧѲобН-ЗТ „ , VI856 —27
------!---/т ѵг —— -X- ----------
и какъ а«С0, то очевидно Слѣдовательно, должно взять
11856 — 27 Vх 1856 + 27
<г . ----л, или -т --------------——=-
Г
Подставляя въ трп-расноложены относи
тельно корней я/ и я" такъ:
ИРГв —27 . /1858 + 27 .
-=° • ---------23----“* ‘ ’З* ‘ --------93 й ' ' ’ + °°
' 23 ’ 27
Но мы видѣли,' что х должно быть и <С —а. . номъ (— а) и н вмѣсто х. убѣдимся, что эти величины
и слѣд. невозможно удовлетворить неравенству, если
2) —а<^х<^— 5а, т.-е. #-)-а и противоположны по знаку;
первая часть неравенства >0, вторая <0; и какъ неравенства удовлетворено.
3) х-|-5а>0; и подавно Обѣ части неравенства положи-
тельны, и потому, возвышая въ квадратъ и сохраняя смыслъ неравенства, найдемъ:
23л2 + 54лг — 49а2 < О,-
и слѣд. . ...
11856 — 27 . . /Пйб + 27
----^—а<х<--------------аз— «•
Кромѣ того, должно быть: и что приводится къ х>— 5а;
а какъ порядокъ величинъ
^1856 — 27
-- ...-----------П •
таковъ
Ѵ1856 + 27 —---------а
а
— эа
— а •
то очевидно, что неравенству удовлетворить нельзя.
Итакъ: когда а<0, чтобы удовлетворить неравенству, надо взять
— а<б х<б — 5а.
Второй случай: а>0.
2
Чтобы радикалы были дѣйствительны, надо чтобы было: я>-а. Слѣд.
о
будетъ: и т4-5а>0; а потому, возвысивъ въ квадратъ и сохра-
нивъ смыслъ неравенства, находимъ эквивалентное данному неравенство (по сокращеніи на а>0):
23я* 54аж — 49аа 0;
откуда заключаемъ, что х нужно взять внѣ интервалла корней. А какъ порядокъ величинъ въ данномъ случаѣ таковъ:
Ѵ1856-—27
то: когда а^>0, ягобяоди.мо и достаточно взятъ
х
У 1856 —
23
27
— а.
ГЛАВА XXXIV.
Раціональныя уравненія, приводимыя къ квадратнымъ. — Биквадратное ур—ніе; ПЗ’ слѣдованіе его корней.—Разложеніе биквадратнаго тринома иа множители первой и второй степени.—Преобразованіе сложныхъ ради каловъ :}/а Н-І^в, у А. 4- /В и т. п.
*
509. Рѣшеніе биквадратнаго уравненія. Уравненіе четвертой степени называется биквадратнымъ, коіда оно содержитъ только четныя степени неизвѣстнаго > Слѣдовательно, общая форма его есть
ах1Ьх* 4“ с = 0 • • • (!)•
Его рѣшеніе приводится къ рѣшенію квадратнаго уравненія. Въ самомъ дѣлѣ, примемъ за неизвѣстное положивъ
& = у. . .(2).
Ур—ніе (1) приметъ видъ
«Уа + ^ + с = О. . .(3).
Это ур—ніе называютъ разрѣшающимъ (резольвентомъ) ур—нія (1).
Рѣшивъ его, найдемъ два корня
г — Ъ + Ѵ62 — 4ас „ — Ъ — 162 — 4ас
2а * 2а
Подставляя въ ур—ніе (2) вмѣсто у сначала у', потомъ у", находимъ *
„ „а „у „2__.//
X* — у * X* = у
откуда
или ______ _____ _ ___
, 1 /— Ъ -|- тТ)®— 4ае . і/ — Ь — /б2—* 4ас
х = -+- К --Н,-------- х = + г ’——й———
— г 2а — г 2а
Итакъ, биквадратное ур—ніе имѣетъ четыре корня, попарно равные и противоположные по знаку.
510. Изслѣдованіе корней. Мы знаемъ, что корни ур—нія ах4+&х*-|-с=0 суть корни уравненія
ж* = у,
въ которомъ у означаетъ одинъ изъ корней уравненія
ау24-Ьу4-с = 0.
Слѣдовательно: всякому дѣйствительному и положительному значенію у соотвѣтствуютъ два дѣйствительныя значенія х, равныя по величинѣ * и противоположныя по знаку; каждому дѣйствительному и отрицательному значенію у соотвѣтствуютъ два значенія х мнимыя сопряженныя; наконецъ, каждое мнимое значеніе у даетъ деа леям.мыя значенія для х. *
Итакъ, приходимъ къ слѣдующему изслѣдованію:
I. Ь2 — 4ас > 0. Корни ур—пія ау2 Ъу -|- с — 0 дѣйствительные не-. с
равные: одного знака, если ихъ произведеніе - положительно, и съ протнвопо-ложными знаками, если - отрицательно.
->0|, оба корня положительны, если ихъ сумма
— - положительна, я отрицательны, если — - отрицательно. Если оба значенія у положительны, всѣ четыре значенія х дѣйствительны; если оба значенія у отрицательны; вгѣ четыре значенія х мпимы. Во второмъ случаѣ два
значенія у иропвоволожиы по знаку, поэтому два значенія х дѣйствительны* два другія жимы- Въ частномъ случаѣ, когда с = 0, одинъ корень резольвента нуль, другой = — *: слѣд. х* = 0, ж3 ~ Первое даетъ х = х" = 0; второе даетъ х — —) —(два корня дѣйств., если |<0, два мпим., если
а/
И, Ь* — 4аг = 0. Корни уравненія ау2 Ьу + с = 0 дѣйствительные равные: игъ обжал величина = — —•
Слѣд. бомдратное ур. имѣетъ четыре корня, попарно равные:
они дѣйствительны, если - < 0, и мнимы, если ->0.
1 05 ? ’ 65 ।
Если Ь = 0, то условіе 62— 4ас = 0 ведетъ къ с = 0; ур. въ х будетъ ах* = 0, т.-е. у у, имѣетъ 4 ко/жя ш/лад.
Ш. Ъ*— 4ас<0. Корпи ур^нія ау3-[“^ + с~ ® мнимые, слѣд. и всѣ четыре корня биквадратнаго ур—нія мнимые, ибо квадратный корень изъ есть мнимое выраженіе того же вида.
Результаты этого изслѣдованія можно резюмировать въ видѣ слѣдующей -таблицы:
- < 0 . . ,4 корня дѣйствительные, попарно равные и противоположные ио знаку.
> 0 . . .4 корня мнимые.
Ь'2 — 4ас > О
-=0 а
2 корня дѣйствительные, равные и противоположные по знаку; 2 корня мнимые.
[дѣйств., если
• 0; Хд* — ~4~~
ь п ь
- <С0; мнимые, если -
а
О
і1 — 4а с = О
. 4 корня дѣйствительные, попарно равные і і / Ь і / Ь
ХІ—хі~ +1' ~2«; хз~ хі— — 1 — 2«-
. 4 корпя мнимые.
. = ІГ4 — о.
Ь2 — 4ас <0...................4 корня мнимые.
Примѣчаніе, Отсюда видно, что нужны три условія для того, чтобы всѣ четыре корня биквадратнаго ур—нія были дѣйствительны; именно:
Ь* — 4ас>0, ->О, - <0;
’ а а ’
н одно условіе, чтобы два корня были дѣйствительны, а два мнимы; именно:
511. Примѣры: I. Рѣшить уравненіе 64я4 — 244.x2-|-225 = 0.
Положивъ #2=^, находимъ квадратное ур—ніе
64у2 —244^ + 225 = 0;
въ немъ: Ь'3 — ас = 1223 — 64X 225 =^484>0; 0; —< 0; сл.
оба значенія у дѣйствительныя, неравныя и положительныя, а потому биквадратное ур—ніе имѣетъ всѣ четыре корня дѣйствительные. Находимъ:
122 /1222 — 64 X 225 122 22
64 64 ’
/ 9 г 25 г
^=4’ Тб;
откуда:
И. Рѣшить уравненіе бх1 + 12#2 + 4 = 0.
Положивъ #а = у, находимъ ур—ніе 5у2 + =0; въ немъ
У2 —ас = 36 — 5Х*= 16 >0;
*=Л>0; * = ^>0, а о ’ а э
Слѣд. корни его дѣйствительные, неравные, оба отрицательные; а потому данное ур—ніе имѣетъ всѣ четыре лшилшт Находимъ
6 — 1 16 *— 6 — 4 »“-----§----= —5—;
У—— у" = —2-
Слѣдовательно
^ = +)/|-*, = *з= + /2Ч «, = —
III. Рѣшитъ уравненіе Зх* — 26ха — 9 = 0.
Положивъ х2 = у, находимъ ур—нге Зу2— 26у — 9=0. Въ немъ: Ь'2 — ас= 13*4-3.9 = 169 4-27 = 196 > 0;
слѣд. оно имѣетъ корни дѣйствительные неравные, съ противоположными знаками, а потому предложенное ур—ніе имѣетъ два дѣйствительныхъ корня и два мнимыхъ.
13=^/196 13=1=14.
У~ 3 ~ 3 ’
откуда
у' =+9; У" = —
слѣдовательно
IV. Рѣшитъ уравненіе х1 — 10х*4“61 =0.
Положивъ х2 = у, получимъ ур—ніе у2 — 1 Оу 4“ 61= О, въ которомъ Vе* — ас — 25 — 61— — 36; слѣд. оба значенія у мнимы, и потому данное ур—ніе имѣетъ четыре лямжыха корня. Находимъ
у = 5 +12г, у' = 5 — 12г.
Слѣдовательно
х = + )/5 ± 12г\
Преобразовавъ это выраженіе по способу § 417, найдемъ:
х1 = 34“2г, ха = 3— 2г\ хэ = — 3 — 2г, х4 =— 3 4“ 2г.
V. Рѣшитъ уравненіе х*—10х24“28 = 0.
Положивъ х* = у, имѣемъ ур—ніе у2 — 10у4~28 = 0, въ которомъ
6'2 — ас = 25 — 28 = — 3 < 0;
слѣд. корни его мнимые, именно
. Слѣд. четыре мнимые корня предложеннаго заключаются въ формулѣ х = ± ± / 3.г. .
Примѣняя къ ней преобразованіе, указанное въ § 417, найдемъ:
Такимъ образомъ:
512. Приложеніе,—Доказать,
* л*2 ।
что уравненіе _ —-
имѣетъ всѣ четыре корня дѣйствительные, каковы бы ни были дѣй
ствительныя количества а и Ь.
Помноживъ обѣ части на (а?3— а2) (я2— 62), дадимъ ур—нію цѣлый видъ
х2(я2 — Ь2) -р #2(х3 — а2) —'4(ж2 — а2)($2 — 62) = 0.
Положивъ #2 = у, получаемъ квадратное относительно у ур.
у(у — + УІУ “ а2) — — а2) (У — &2) = О-
Подставляя въ первую часть вмѣсто у сперва а2, потомъ Ь\ замѣчаемъ, что результаты этихъ подстановокъ: а2(а2—•&“) и 62{63—а2) имѣютъ противоположные знаки; слѣд, корни относительно у дѣйствительные и неравные, и одинъ изъ низъ содержится между а2 и Ь2. Далѣе: коэффиціентъ при у3 отрицателенъ {= — 2); подстановка же 0 намѣсто у даетъ —4а2Ь2; слѣд. О находится внѣ корней, и слѣд. меньше обоихъ корней, ибо мы уже знаемъ, что одинъ изъ корней положителенъ. Итакъ, оба корня: у' и у4 дѣйствительны п положительны, каковы бы ни были а и Ѣ, а слѣд. всѣ четыре корпя даннаго ур—нія дѣйствительны.
Къ этому заключенію можно придти и иначе. Ур—ніе относительно у приводится къ виду:
2у* _ з(да „|_ ь2)у + 4а2Ь2 = 0.
Подрадикальное количество формулы корней есть
9(а2-Н2)2 — 32а3Ь2, или 9а1— 14а*Ь*4-9Ь*.
Но этотъ квадратный относительно а3 триномъ имѣетъ корни мнимые, ибо 496*—8слѣд, при всякихъ а и Ъ знакъ его одинаковъ со знакомъ 9, т.-е. положителенъ. Поэтому оба значенія у дѣйствительны. Ихъ произведеніе 3
2а262 показываетъ, что они одного знака, а сумма ихъ -(а24“62) показыва-етъ, что оба они положительны. Слѣд. четыре корня предложеннаго ур—нія всегда дѣйствительны.
513. Теорема, Сумма корней биквадратнаго ур—нія равна нулю, произведеніе ихъ равно а су.кліа квадратовъ ихъ равна —
Въ самомъ дѣлѣ, четыре корня хэ, #3, попарно равны и противоположны но знаку, слѣд. сумма ихъ =0. Во-вторыхъ, (+1/У)24~(— ]/У)а + (+ ]/у")2 + (— ]/у'Т — (У 4“у"); но 4" УИ* какъ сУмма корней
квадр. ур—нія а«/*4’^4~с = 0» равна —слѣд* сумма квадратовъ корней даннаго ур—нія = — Наконецъ, произведеніе
=Л"=<Т
514. Разложеніе биквадратнаго тринома ах* 4“с на множители первой степени.
Триномъ ахк Ъх* 4~ с, обращаясь въ нуль прп каждомъ изъ четырехъ своихъ корней а?1, я2, л;3, я4, дѣлится на каждый изъ биномовъ х— #4, х — х^ х — а:а, х — х^ а потому и на ихъ произведеніе; такъ какъ дѣлимое и дѣлитель—одинаковой степени относительно то частное будетъ нулевой степени, и потому приводится къ частному отъ раздѣленія высшаго члена, дѣлимаго на высшій членъ хк дѣлителя. Итакъ:
ах4 4” Ъх* -}- с = а (я — — яа)(я — ^3)(^ — ^)-
Примѣ? ы.—I. Разложитъ триномъ 5#4 — 5О*г2 45.
Корни его суть: ±3, ±1; слѣд.
5а1 — 5Ох2 45 = 5 (х — 3)(з + 3)(ж — 1)(ж + 1).
ІЕ Разложитъ триномъ 2л?14“ 7^34”
Корни его суть: Ез Ѵ^2 • »’, =Е ) і * » Слѣд. *5*-
2х‘ + 7х* 6 = 2 (х -) 2 . ) 2.0(*“ Г I • *) (*+ И • О-
НЕ Рахммплпь тиноли —х14_І0х2—169.
Корни его суть: 3±2/, — 3 + 2і\ Слѣд.
— г4—10л** — 169 = — (х— 3 — 2г)(У— 34-2г)(л*4«3 — 2г)(* 4" 3+20.
515. Разложеніе биквадратнаго тринома съ дѣйствительными коэффиціентами на дѣйствительные квадратные множители.
Пусть триномъ ах1 -4- Ъх* 4~ с имѣетъ корпи а, —а, въ такомъ
случаѣ его можно представить подъ видами:
ах* 4~ + с ~ а [(я " а)(^ 4“ — ?)(^ 4" ?)] - • • (1)
= а [(х — а)(х — а)(х + ЙІ • . • (2) = в [(х — з)(х + })][(.г + а)(х — ?)] . . . (3)
Когда четыре корня а, — а, ;Е — ? дѣйствительны, всѣ три разложенія дадутъ дѣйствительные квадратные множители.
» Если два изъ этихъ корней мнимы, то квадратные множители будутъ дѣйствительны только въ одномъ изъ этихъ разложеній, именно въ томъ, гдѣ для составленія одного и того же множителя соединены два сопряженные корня.
Наконецъ, если четыре корня мнимы, то опять существуетъ только одно разложеніе на дѣйствительные квадратные множители, то именно, въ которомъ каждый изъ квадратныхъ множителей происходитъ отъ сочетанія сопряженныхъ корней. Отсюда
Теорема. Биквадратный триномъ съ дѣйствительными коэффиціентами всегда можно разложить, по крайней мѣрѣ, однимъ способомъ, • на произведеніе дѣйствительныхъ квадратныхъ множителей.
Чтобы получить это разложеніе, нужно вычислить корни тринома; это вычисленіе усложняется вспомогательнымъ вычисленіемъ въ томъ случаѣ, когда всѣ четыре корня мнимы, т.-е. когда — 4ас<^0. Въ этомъ послѣднемъ случаѣ значительно быстрѣе найдемъ требуемое разложеніе слѣдующимъ пріемомъ. Пусть имѣемъ триномъ
/ І 1 б О 1 С\
ѵ ~ а а?1 + - 4-
* “ а 1 а;
въ которомъ предполагается Ь2— 4ас<0. Разсматривая х1 и какъ крайніе члены квадрата, дополнимъ его, прибавляя и вычитая
; найдемъ
Но какъ 4ас<0т то слѣд. и а потому У ~ — ко-
<личество дѣйствительное. Далѣе, раздѣливъ обѣ части неравенства Ь2—4ас<4) на положительное количество а2, находимъ
Но оба эти множителя не могутъ быть отрицательными, ибо пхъ сумма, равная 4|/^+, положительна, слѣд, оба они положительны, и потому
2ъ4_?>0.
г а а
Итакъ, триномъ можно представить въ видѣ произведенія двухъ дѣйствительныхъ факторовъ:
>=«Р+р'!+-|/ м+Г
Примѣръ. Разложитъ на два дѣйствительные множителя триномъ у =гг4 — 1О.г2-{- 28.
Имѣемъ,
у = (і’ + 2 / 7)2 — (4 /7 +?10) л»
= (х* + х /4/7 4-10 + 2 >/7}(.гг — х У4/7 + 10 + 2 |/ 7).
516. Преобразованіе сложнаго радикала /А + /В. Корна биквадратнаго ур—нія выражаются формулою вида } Л + у В; п когда В не есть точный квадратъ, т.-е. /В несоизмѣримъ, формула эта весьма невыгодна для пріг
блаженнаго вычисленія. Попытаемся, если окажется возможно, замѣнить выраженіе этого вида другимъ, которое не содержало бы извлеченія корпя изъ несоизмѣримаго числа. Но предварительно докажемъ слѣдующую лемму.
517. Лемма, і&ш а, 6, а* и Ьг суть числа соизмѣримыя, а ]/б и у/Ь* несоизмѣримы, то равенство ,
а }/& = а1 -}- }/б' . . * (1)
возможно только тогда, когда а = а' и Ь = Ѵ.
1
Въ саномъ дѣлѣ, изъ равенства а-\~уь = а' + ]/&' выводимъ
/і'= (а — а'),4- |/Ь,
или, возвышая обѣ части въ квадратъ:
Ь' = (а — а')» + 2 (а — а') у/б Ъ,
или
(Ь' — Ь) — (а — а')1 = 2 (а — а') ]/Ь.
Доауаам, тге а не равно а', мы нашли бы отсюда нелѣпый выводъ
* -Ъ)-(а— а?
) 6 =
х.-і, та юпгіуом несло равно соизмѣримому. П такъ а = а', а тогда * жп <1/ егііуетѵ. что 6 = 6’.
Зшая т. мипаенся найти такія два соизмѣримыя числа х и у, которыя
;іми імріті бы равенству
)/А+/В = /^4-/у . . .(1)
гдѣ А ж В положительныя соизмѣримыя числа, а ]/В несоизмѣримъ. Возвысятъ обѣ части въ квадратъ, найдемъ ч
А-|-}/В = гг2у/яу . . ,'(2)
] ^ху долженъ быть несоизмѣримъ; въ самомъ дѣлѣ, допустивъ противное п напасавъ ур—ніе (2) въ видѣ
+ А + 2 ѴХУ^
нашли бы, что несоизмѣримое число равно соизмѣримому. Примѣняя къ ур—нію (2) предыдущую лемму, наіодимъг *
іі В.
ж-|-у = А и ху — -^і ъ
и это—единственно возможное условіе существованія равенства (2) при х и у 34*
I
соизмѣримыхъ. Послѣднія уравненія показываютъ, что х и у суть корни квадратнаго уравненія
*. । В Л
откуда
А+УА2»В А ——в
ж- ъ 5 3^ л ’
• -(3)
Видимъ, что преобразованіе ) А-|-]/В въ выраженіе гдѣ я?
и у были бы соизмѣримы, возможно только тогда, когда А5 — В есть точный квадратъ; дѣйствительно, въ этомъ^ случаѣ, положивъ А2 — В = К2, гдѣ К— соизмѣримо, имѣемъ: ,
И такъ, если это условіе выполнено, искомое преобразованіе возможно и выражается тождествомъ
и это—единственно возможная форма преобразованія въ разсматриваемомъ случаѣ, ибо ур—ніе (2) распалось на два ур—нія съ 2 неизвѣстными, вслѣдствіе чего и получились опредѣленныя рѣшенія для х и у.
Желая подобнымъ же образомъ преобразовать ]/А — ]/в, не можемъ положить )/л — |/в = ибо это повело бы къ нелѣпому слѣдствію:
—/В = 2]/^/;
но можно положить равенство
откуда, подобно предыдущему, найдемъ:
По если бы мы искали два количества х и у, удовлетворяющія ур—нію
)А± УВ = /ж±|/у,
не дѣлая ограниченія относительно соизмѣримости х и у, то задача, очевидно, была бы неопредѣленна. Возвышая обѣ части въ квадратъ, мы пашли бы уравненіе
А + /» = « + </ ±2 ужу,
которому можно удовлетворить, полагая
ж-|-у = А, жу = |,
откуда нашл^ бы прежнюю форму преобразованія
ѵ/ГТи. і/^-5±і/л^Т-В'- •(»
но можно бы было удовлетворить ур—нію и иначе; что дало бы другія значенія для х я у; рѣшеніе (1) было бы однимъ изъ безчисленнаго множества рѣшеній неопредѣленнаго ур—нія Г7 А±/В = /« ± Уу.
518. Примѣчаніе. Опредѣляя жну, удовлетворяющія ур—нію * •
1/а/в —/#4~• - • (1)
мы должны были возвысить это ур. въ квадратъ и рѣшать ур—ніе
А Ц-/І = яН“ 2/гу . . .(2).
Но ур—ніе (2) могло бы получиться и изъ ур—нія
Ѵа+/в=—/«—/у;
такъ что нужно удостовѣриться, что найденныя значенія для х и у дѣйствительно удовлетворяютъ преобразованію /#4~/у-
И въ самомъ дѣлѣ, преобразованіе V А 4” }^В = — у/іс — /у не можетъ имѣть мѣста прі дѣіствмтельиытъ х к у; слѣд. тождество (4) § 517 въ самомъ дѣлѣ отвѣчаетъ искомому преобразованію.
Примѣры.—I. Преобразовать И6Ч-/Г1*
Здѣсь А = 6, В = 11; слѣд. А2— В = 25 = 52; а потому
/в+?п =УФ+Ѵф=+и=ч +О.
/в-)/П=!^(/ІІ —1).
П. Преобразовать /17 Ч- 2 /70.
Въ данномъ случаѣ А =17; подводя 2 подъ знакъ корня, имѣемъ 2/70 = /4770 = ]/280, слѣд. В = 280; А2 —В = 17*— 280 = 9 = 3*. Такимъ образомъ:
/17 + 2/70 = /Щ^ 4-/1++ = /10 + /7; и
Ѵ17 — 2/70 = /10 — /7.
ІП. Преобразовать
«2 — — 4 т*
2
Это выраженіе можно представить въ видѣ ----
П х і Й2 тъ ЙЛ I і-1 п /а* л ,
Здѣсь А = В = ——яг; А3 — В—-т- — -7- — т1 = т1; слѣд.
* 6і ‘Л к * /
— Ш1 |
2 = 9
[ Ѵа«+2т2 4_ у/аэ_ 2тя].
519. Приложенія.—I* Опредѣлитъ условія которымъ должны удовлетворятъ коэффиціенты биквадратнаго уравненія ах1 ~р + с — О, для того чтобы ею корни можно было выразить въ видѣ алгебраической суммы двухъ простыхъ радикаловъ.
/
Корни биквадратнаго ур—нія можно представить въ видѣ
Ь . -]/& — 4ас. 2а± г ” 4«2
слѣд.
п Ь2 — 4ас х * а п 4яс <?
в = —4-2-> и слѣд. А1 —В=^ = --
Заключаемъ, что когда есть точный квадратъ, преобразованіе возможно, и получается формула
Пусть, наприм., дано ур—ніе 18х4 — 45.Г1 -|- 2 = 0. Здѣсь = указанное условіе имѣетъ мѣсто, и слѣд. корни можно представить въ видѣ
(/57±>/33).
Г ИѣЗ
6Ѵ'2
Еще примѣръ. Въ уравненіи ау4-]-2 (а —’2^)у3-І-а = 0 отношеніе 3-го коэффиціента къ 1-му, равное — или 1, есть точный квадратъ, и слѣд. корни можно преобразовать въ сумму простыхъ радикаловъ; преобразованіе дастъ
у = 4-у/Ь — а.
II. Въ геометріи доказывается, что если а означаетъ сторону правильнаго, вписаннаго въ кругъ радіуса В, многоугольника, а Ь—сторону прав. впис. многоугольника съ.двойнымъ числомъ сторонъ, то
Ь = І2К2 —}/К*(4ВА—а4).
~~ о 3 о
Это выраженіе можно превратить въ сумму простыхъ радикаловъ; въ самомъ дѣлѣ, А = 2Е3, В = К*(4К- — а2), слѣд. А* — В = «2К2, и потому
, -і/2Н2+аВ 1/2К2*-аВ і/в/р । і хр/р «I
V ---у-----) ----2- -- = К^+^— ] ГЦВ — 2ф
Пусть, наприм., а = К; первый многоугольникъ будетъ правильный шестиугольникъ, второй—правильный двѣнадцатиугольникъ; получимъ
520. Въ заключеніе этой главы рѣшимъ еще три вопроса, относящіеся къ преобразованію квадратнаго п биквадратнаго корней.
Первый вопросъ. Представитъ въ формѣ
V*+Ѵу+Ѵ^-_________________________
Положивъ / а -{-/ Ъ -/ ]/~с /^—]/я -|-1/ у -(~ Ѵ~^і в возвысивъ въ
квадратъ, имѣемъ
а + 1/ь + )/ ^4-1^ = ^ + ^+ ^ + 20п/-|- 20^ + 2)/^
Если удастся найти соизмѣримыя числа х, ут г. удовлетворяющія ур—ямъ
20п/ = ;/’Ь. 20хг = ]/с? = . (1)
и если, вмѣстѣ съ тѣмъ, найденныя значенія х, $/, я, удовлетворяютъ ур—нію + я = а . (2), то указанное преобразованіе выполнимо.
Слѣд., соотношеніе между а, 6, с, Л, при которомъ искомое преобразованіе возможно, мы найдемъ, исключивъ х, у и з изъ ур—ній (1) и (2).
Ур—нія (1) даютъ:
Ъ с 3.
перемножая и извлекая квадратный корень, имѣемъ:
откуда дѣленіемъ находимъ:
подставивъ во (2), найдемъ:
таково искомое соотношеніе.
Пусть, напр., нужно найти
Приравнявъ это ]/^4“Ѵ4/— ]/4 и возвысивъ въ квадратъ, имѣемъ
16~2у/2О— 2}/28 4“2)/35 = Д?4-у-р * 4" 2]Лгу — 2|/^ — 2у/уя.
Положивъ
у/ху = |/35, ]/ хз = |/2О, у/уя “ |/28, имѣемъ
•гуя=140, слѣд. уЛгуя = 2}/35; откуда
Ѵ^ = 1/5; )/у = у/7; |/г=2.
Эти значенія .г, _у, г удовлетворяютъ ур—нію х у -Н я 16; слѣд.
искомый коренъ = |/ 5 4~ У^і — 2.
Второй вопросъ. Представитъ выраженіе
V = 1 а -р |/ Ь -р }/с -р |/ сі
въ видѣ произведенія двухъ сомножителей вида у*—Доказать,
что преобразованіе возможно только при условіи, когда а~(і = Ьс, и что оно выгодно только тогда, когда а*~Ъ и а3— с суть точные квадраты.
Въ самомъ дѣлѣ, равенство
]/» 4~ 4“ У (]/#4“У4/) (У^ + У^)’
но возвышеніи въ квадратъ, даетъ
а4-у^4_УЛ^+И + ®4”2/и»).
Этому ур—нію удовлетворимъ, положивъ
а ~ (х 4- у) (а 4~ ѵ); 4~ с = 4” — і бху«у.
Эти у])—нія, какъ легко видѣть, несовмѣстны, если не имѣется соотношенія а3й=Ье. Когда это условіе удовлетворено} система неопредѣленна. Эта неопредѣленность объясняется при помощи тождества
9
имѣющаго мѣсто при всякомъ а; этимъ доказывается, что разложеніе можетъ быть произведено безчисленнымъ количествомъ способовъ. Неопредѣленность эта даетъ возможность допустить между двумя количествами произвольное соотношеніе. Положимъ, напр., Тогда первыя два ур—нія обратятся въ
. ъ /
и + ѵ — а. —
1 4
откуда
Внося этп величины въ третье, имѣемъ ху- зная, кромѣ того, что найдемъ
Изъ этихъ формулъ видно, что если а*— Ь и а2— с будутъ точные квадраты, то и, ѵ, х й у будутъ раціональны, и слѣд., преобразованіе выгодно, ибо оно представляетъ произведеніе двухъ множителей, изъ которыхъ каждый есть сумма простыхъ радикаловъ.
Такъ, если П=Ѵ 14~ 1 / 2 +11^6, то а=1, Ь=|?
" X О О У
а2 — Ь = 7? а2 4
Л = х; условіе аМ = Ъс удовлетворено;
Итакъ
(ѵ 2+1) (ГЗЧ- 3)
6
Третій вопросъ. Полагая, что В не есть точный квадратъ, представитъ
Ѵ = ^А + /В
яодь видомъ суммы двухъ квадратныхъ корней: Указать
условія, необходимыя и достаточныя для того, чтобы преобразованіе было выгодно, что можетъ имѣть мѣсто въ двухъ различныхъ случаяхъ: когда х и у имѣютъ видъ когда эти количества соизмѣ-
римы*
Положивъ
/а /в=/ зл
н возвысивъ въ четвертую степень, получимъ
А + /в = (х 4- у)2 + іху + 4{х + у) /ху,
откуда
(я? + у)*4-4.гу = А, 16.гу(х4~у)8 = В.
Отсюда видно, что и суть корни ур—нія
- А/+1 = 0;
и какъ разность 4л*у = (х— у)2, т.-е. существенно положительна,
такъ какъ х и у предполагаются дѣйствительными, мы должны большій корень ур—нія въ і принять за (-#—{—у)2, меньшій за 4ггу. Такимъ образомъ
или, вычитая второй результатъ изъ перваго
(я —і/)2=/а3 —В.
Не трудно теперь найти % и у.
Чтобы разсматриваемое преобразованіе было выгодно, нужно, чтобы ж ила у не содержали биквадратныхъ радикаловъ; слѣд. необходимо, чтобы А3 — В=К\ гдѣ К—число раціональное. Тогда
(х 4- у)' = (ж —у)а = К.
Въ этомъ случаѣ я и у имѣютъ, вообще, видъ суммы двухъ простыхъ радикаловъ. Но если одно изъ чиселъ, — или К, будетъ точнымъ квадратомъ, выраженіе представится въ видѣ суммы двухъ квадратныхъ корней изъ выраженій вида Если, наконецъ, оба числа: - и К — точные квадраты,
выраженіе приметъ видъ двухъ простыхъ радикаловъ.
П р пмъры.—І, 1^6>/2О; найдемъ: А = 6, К = 4; слѣд.
(#+у)а = О—у)2 ^4.,
Потому
И. И=к7-|-/48; найдемъ: А = 7; К—1; слѣд.
Отсюда
(.г-|-і/)’ = 4
ГЛАВА XXXV.
Раціональныя уравненія, приводимыя къ квадратнымъ: продолженіе. — Возвратныя * уравненія. — Двучленныя уравненія. — Трехчленныя уравненія. — Уравненія вида Р.(}.К~0 н нѣкоторыя другія.
Возвратныя уравненія четвертой степени.
• 521, Опредѣленія. Уравненіе налагается возвратнымъ перваго рода, если обратная величина каждаго корня уравненія служитъ также кср-немъ этого уравненія.
Уравненіе называется возвратнымъ второго рода, если обратная величина каждаго корня, взятая съ противоположнымъ знакомъ, удовлетворяетъ также уравненію.
• ' -
522, Лемма, Если два цѣлыя уравненія съ однимъ неизвѣстнымъ^ т-й степени, приведенныя къ виду А = 0, имѣютъ т различныхъ общихъ корней, то коэффиціенты ихъ пропорціональны.
Въ самомъ дѣлѣ, пусть два уравненія
ах1 4“ Ьх3 -|- сх-4“ сіх 4~ е =0 . ,
.(1)
а'х1 Ь’х* сх2 д’х + е' = О
имѣютъ 4 общихъ корпя, т,-е, первыя части ихъ обращаются въ нуль при 4-хъ различныхъ значеніяхъ х; тогда и многочленъ
а'(ах4 4“ Ьх8 4* бх2 4~ 4" е) — аіа'х*4“ &'#а 4* 4“ 4“
обратится въ нуль при тѣхъ же значеніяхъ а;; но этотъ многочленъ,
(Ьа' — аЬ')^а “4 ~ ас')х2 4~ 0^ —6 $)х ~Ь (еа —ае) ?
есть многочленъ третьей степепи относительно х; слѣд, (§ 68, II) онъ тождественно равенъ нулю; а потому всѣ его коэффиціенты равны нулю. Отсюда
Л'_— 1' —
а Ъ с <і е
523, Условія, необходимыя и достаточныя для тою, чтобы уравненіе было возвратнымъ первою рода.
Составимъ ур—ніе, котораго корни были бы обратны корнямъ даннаго, До-і
статочно вмѣсто х подставить -• Сдѣлавъ подстановку н приведя къ цѣлому виду, получимъ
ех1 + Лг* + с-т* 4" ^х 4“ а = 0 • * * (2).
Если (1) есть возвратное перваго рода, то (2) будетъ имѣть тѣ же корни. Въ самомъ дѣлѣ, если корни перваго будутъ а, то корни 2-го будутъ і* а, Ь [к Оба уравненія имѣютъ общіе корни, слѣдоват., на основаніи леммы
§ 522, имѣемъ
а_ Ъ _ ,_д__ е
— і — Ъ^а'
откуда
а = е, Ь = Д,
т.-е. коэффиціенты членовъ, равноудаленныхъ отъ крайнихъ, равны и имѣютъ одинаковые знаки. Итакъ, возвратное уравненіе четвертой степени перваго рода имѣетъ видъ
ах1 ± -Ь схй + Ьх 4~ Д — 0>
Примѣчаніе I. Если средній коэффиціентъ разсматриваемаго уравненія равенъ 0, с = 0, то уравненія
ах4 4~ 4- йх + е = 0 и ех14“ 4“ 4“ а = О
дадутъ а Ъ (і е е й Ь 7ё
отсюда:
а = € и 6 = 4“^' или а — — е и Ъ = ~й;
ур—ніе будетъ въ первомъ .случаѣ
ах14" Ъх 3 4~ Ъх ~4 а = о,
во второмъ
ах14~ Ъх* — Ьх — а = О,
Легко видѣть непосредственно, что ур—нія эти возвратныя. Въ самомъ дѣлѣг раздѣливъ первое на х* и положивъ х -4 найдемъ два ур—нія
въ каждомъ произведеніе корней равно 1, слѣдоват. въ каждомъ одинъ корень обратенъ другому.
Написавъ второе въ видѣ
(42 —
замѣчаемъ, что каждый изъ корней 4~ 1 я — 1 равенъ своему обратному; въ уравненіи ат24“&г + а = 0 произведеніе корней равно 1, слѣд., корни его также обратны одинъ другому.
Примѣчаніе II. Такимъ же образомъ найдемъ, что ур. третьей степени возвратное перваго рода есть
а.т34-Ьл'а + Ь^4г0 • * * (1)
причемъ верхній знакъ берется съ верхнимъ, нижній съ нижнимъ.
524. Чтобы рѣшить уравненіе ох14“ + + + а “0, раздѣлимъ
обѣ части на х* (на это имѣемъ право, ибо ур—ніе не имѣетъ корня, равнаго нулю, слѣд. х2 не обращается въ нуль); найдемъ, сгруппировавъ члены, равно удаленные отъ концовъ:
Положивъ х4-= у, имѣемъ отсюда: гга4“^ = У3— демъ
+ + — 2а) = 0 . . .(2)
подставляя, най-
Отсюда найдемъ два значенія для у: у' и у". Подставляя поочередно эти зна-і 1 А
ченія въ ур—ніе + которое можно написать въ видѣ
найдемъ всѣ четыре значенія я*. Такимъ образомъ рѣшеніе ур—нія (1) сводится къ рѣшенію системы (2) и (3).
525, Изслѣдованіе, Чтобы величины л?, выводимыя изъ (3),были дѣйствительны* необходимо, во-первыхъ, чтобы коэффиціенты этого ур—пія были дѣйствительны, т,-е. чтобы у было дѣйствительно; затѣмъ необходимо, чтобы разсматриваемое значеніе у удовлетворяло условію
У2 — 4^0,
т.-е. чтобы у находился внѣ интервала отъ — 2 до 4’2, иначе, чтобы абсо-• лютная величина у была больше 2, Очевидно, что этихъ условій достаточно, і а ѵ
526, Примѣры, I, Рлмшиіъ ур—ніе 2 л?4 4“**—11тв4-л*_Ь2 = О, Напишемъ его въ видѣ
V Г \ ”* *
Положивъ х-|-- = у, наіоінмъ ур—ніе 2у’-|-у — 15 = 0, откуда X
Внося эти величины въ ур—ніе х — ~~У* имѣемъ ур—нія:
х*—5Х4-1=О, х’-НЗдг; 1 0;
откуда:
о 1 — З + Ѵ'5 —С5
— 2, , 2 2
Легко удостовѣриться*, что* , *т4 = !♦ • •
II. Изслѣдовать корни уравненія .г1-|-2Х*г34-(Х4”1)^аН-2)нг4-1 =0 при измѣненіи л *отг> — оѵ до 4~
Вышеуказаннымъ пріемомъ приводимъ рѣшеніе этого ур—нія къ рѣшенію системы
ж« —уж-|-1 =0 . . .(1), з/а + 2лу + (А —1) = 0 . . .(2). №
Чтобы корни (1) были дѣйствительны, необходимо, во-первыхъ, чтобы у было дѣйствительно, и затѣмъ, чтобы
Каждое значеніе у] удовлетворяющее этимъ двумъ условіямъ, дастъ дѣйствительныя значенія для х.
Ур. (2) даетъ слѣдующее условіе дѣйствительности
і4-1>0,
условіе, всегда существующее, ибо ур, Iй — X 4- 1 = 0 имѣетъ корни мнимые,
Второе условіе: — 4 О — 2 и 4“ 2» т.-е. должно быть вм. у въ первую часть ур—нія
означаетъ, что у не должно содержаться между или < — 2, или >~42. Подстановка (—2) (2) даетъ
подстановка (4~2) даетъ
разсмотримъ скалу значеній X, содержащую значенія, обращающія эти .биномы
въ нуль:
о
2
Если X давать величины въ интервалѣ (1), то результатъ подстановки (— 2) оказывается > О; слѣд. — 2 находится внѣ корней ур. (2); но полусумма корней, равная — X, положительна; слѣд. оба корня больше (— 2). Результатъ подстановки (4-2) отрицателенъ, сл. Ц-2 содержится между корнями ур—нія (2). Итакъ, для значеній X, лежащихъ въ (1) области, расположеніе корней у' и (полагая у1 у”) и чиселъ — 2 и -р 2 таково:
Итакъ: одинъ корень (у") дастъ два дѣйствительныя значенія для я; другой (у9~два мнимыя значенія.
Для X, содержащихся во (2) области, результаты подстановокъ (—2) и (4-2) положительны, сл. (—2) и (4~2) лежатъ внѣ корней; приэтомъ полусумма корней, равная — X, больше — 2, но меньше 4“ 2; сл. расположеніе корней и чиселъ — 2 и 4“ 2 таково:
. . - —2 » . . у' . • . у” • - . 4“2;
заключаемъ, что 4 значенія я мнимы.
Для X, содержащихся въ (3) области, результатъ подстановки (—2) отрицателенъ; слѣд. (— 2) содержится между корнями ур. (2); результатъ подстановки (+ 2) положителенъ; слѣд. + 2> находясь внѣ корней, больше у". Такимъ образомъ, одинъ корень (у') дастъ два дѣйств. значенія я, другой (у”)— два мнимыхъ значенія х.
527. Условія, необходимыя и достаточныя для тою, чтобы уравненіе было возвратнымъ второю рода,
• Пусть дано ур—ніе четвертой степени
а#і4-Ь#34^с*г*4“^*г4'“в = О • • (1)
Составимъ ѵр—ніе, корни котораго были бы обратны корнямъ (1) и имѣли 1 противоположные имъ знаки; достаточно вм. я подставить у = — сдѣлавъ X подстановку п приведя къ цѣлому виду, получимъ ур—ніе.
ех* — сіх*“4— Ьх-]-а = $ , . .(2)
Если (1*) есть возвратное 2-го рода, то (2) будетъ имѣть тѣ же корни. Въ самомъ дѣлѣ, пусть корни (1) суть я, то корни (2)-го
будутъ
а _1 о.
“і рі г»
слѣд. оба тр—нія имѣютъ одинаковые корки, а потому
а___ 6 _ і___ (I____е
е ~ Ь "а’
откуда
а = е, Ь = — г/.
Слѣд- о^идея форма возвратнаго ур—нія четвертой степени второе о рода такова
ах1 + &;г8 -|- сх* 4= Ьх -|- а = 0.
Примѣчаніе I Если бы средній членъ равнялся нулю, то ур. было бы воз-жратктъ второго рода въ двухъ слѣдующихъ случаяхъ:
ах1 Ьх1 -4- Ьх -н д = 0.
ірашь жржіі знакъ надо брать съ верхнимъ, нижній съ нижнимъ.
Ьгхі ур—віе имѣетъ видъ ах14*^*“кЬх — а =0, его можно написать
а (х4— 1) Ьх (х* 1) — О
іл
(х*+1)[а(х*-1) + К| = 0, *
«пуха ицно, что оно имѣетъ два мнимыхъ корня: 4^ 11
Примѣчаніе II. По предыдущему легко убѣдиться, что уравненіе не-степени съ дѣйствительными коэффиціентами не м. б. возвратнымъ вто-р» дома.
52в, Чтобы рѣшить уравненіе дхІфЬх84-сх*— Ьх-[-Д = 0, раздѣлимъ €<ѣ его части на х2 и напишемъ его въ видѣ:
я4+4+6(ж — 1)+с=0, • 0);
2; подстановка въ (1) дастъ
ауа + Ьу + (с + 2д) = 0 . . .(2)
Отсюда найдемъ два значенія*/. Подставляя каждое въ ѵр. * * *ѵ
которое можно представить въ видѣ:
х2 — ух — 1 = 0 . , . (3),
найдемъ четыре корня предложеннаго’ ур—нія.
Изслѣдованіе. Если корни ур—нія (2) будутъ дѣйствительны, то и всѣ четыре корня даннаго будутъ дѣйствительны, потому что корни (3) будутъ дѣйствительны. Итакъ, условіе дѣйствительности всѣхъ четырехъ корней даннаго ур. выражается неравенствомъ
Ь* — 4а(с + 2а)^0.
И ри мѣ ръ. — Ргьшшиъ —кіе а?*—3(л Ц-1) — 2кхЦ-1=О.
Это есть возвратное ур—ніе 2-го рода. Раздѣливъ его на #а н положивъ 1 х — “ = или, что то же,
• лг2 — у# — 1 = О,
рѣшаемъ ур—ніе
у* -|— 2),у — (За 1) 0.
Условіе дѣйствительности всѣхъ корней предложеннаго будетъ
^0,
откуда заключаемъ, что ). не должно содержаться между
Двучленныя уравненія.
529. Двучленнымъ уравненіемъ называется ур—ніе вида
ал:т + Ь = О.
б
Раздѣливъ обѣ части на а и положивъ — - = А, можемъ представить это ур—ніе въ видѣ /
ят-А = 0, или жш = А.
Рѣшитъ это уі>—ніе значитъ найти такое количество я, «п-ая степень котораго равнялась бы А; иначе говоря, значитъ: найти всѣ значенія корня т-ю порядка изъ А.
530. Теорема. Рѣшеніе ур—«вя хт — А = 0 приводится къ рѣшенію ур—нія ут 1 = 0.
Въ самомъ дѣлѣ, пусть а будетъ ариѳметическій корень ги-го порядка изъ А, если А > 0, и изъ (—А), если А<СО. Ур—ніе ят —А приметъ одинъ изъ видовъ: = а”*, хт = — аш, Положивъ а? = ау и подставивъ это выраженіе
въ каждое изъ послѣднихъ ур—ній, по сокращеніи на ато, найдемъ
= или Г = ~1*
Такимъ образомъ, чтобы рѣшить ур—віе я”1—А. = О, нужно: 1) найти абсолютное значеніе равное а; 2) найти всѣ корни у\ у”, уГІ\ . . . ур—нія углЧ- 1 —0; 3) каждый изъ нихъ помножитъ на а.
531. Переходимъ къ рѣшенію ур—нія ушЧк 1=0: элементарная алгебра даетъ средства рѣшать это ур—ніе лишь въ нѣкоторыхъ частныхъ случаяхъ.
I. т=2; ур—нія суть: у2—1=0; у2 4-1=0.
Рѣшеніе ихъ - извѣстно; корни перваго суть: у' = 4~1, у"== — 1; корни Г 1 Н
второго: > ?= + », у = — *
II. т = 3; ур—нія: у® — 1 = 0; у3 4~ 1 = С.
Первое ур—ніе можно представить въ видѣ: (у — 1 )(у* Ц- у 1) = О
оно распадается на два: у — 1 = 0, у34“У 4~ =^-
и л іі — 1 =ь ГЗ. ?
Первое имѣетъ корень 4~ 1; второе — два корня —------------; такъ что
трп корня даннаго ур—нія суть:
Это значитъ, что кубичный коренъ изъ 4~ 1 имѣетъ три значенія: одно дѣйствительное и два мнимыхъ.
Легко видѣть, что каждый изъ мнимыхъ корней изъ 4“ 1 равенъ квадрату другого. Въ самомъ дѣлѣ, назвавъ эти корни черезъ а и В, и замѣчая, что они удовлетворяютъ уравненью у2 + У +1 = О, находимъ: = 1; но і‘3=1, слѣд. = или = Слѣд., если а есть одинъ изъ мнимыхъ кубичныхъ корней изъ 1, то три корня будутъ: а, а8.
Можно и прямымъ возвышеніемъ въ квадратъ убѣдиться, что у" — у'"* и у " — у"\
Прямѣе» ъ.—Рѣшитъ ур—ніе х* — 343 = 0.
По доказанному, надо ариѳметическое значеніе ^343, т-е* 7, помножить на каждое изъ трехъ значеній кубичнаго корня изъ +1. Найдемъ:
Переходить къ рѣшенію ур—нія у3Ц-1 = 0. Его можно представить въ . видѣ (у 4“(У*— У + 1) = 0; а это уравненіе распадается на два: у +1 —О и у2 —у+1=0-
1
Первое имѣетъ корень = — 1; второе —два корня: —/-такъ что три корня даннаго суть:
1 -13 .
Эти корни и представляютъ три значенія кубичнаго корня изъ —1.
—— э 4Ь
і
Примѣръ,—Рѣшитъ ур—ніе х,34“8 = 0.
Корни его найдемъ, помноживъ ариѳметическое значеніе ^8 или 2 на каждый изъ кубичныхъ корней изъ — 1; слѣд.
—2; = . і; У" = 1 — /3 . і.
Ш. т ~ 4;* уравненія: у* — 1 = 0; у4 -|- 1 = 0.
Уравненіе у1 — 1 — 0 можно представить въ видѣ (у2 — 1) (У2 4~ 1) — 0; оно распадается на два ур—нія: у*— 1 = 0 и #а4“ I =0. Первое имѣетъ корни: уі и — 1, второе: 4“* и — такъ что ур—ніе у*—1 = 0 имѣетъ четыре корня:
<6=44 = —1, у3= 44 3/і= — і-
Чтобы рѣшить ур—ніе #44~1 = ^ дополнимъ первую часть его до полнаго квадрата, прибавивъ къ ней и вычтя 2^а; найдемъ:
г/і4“2^4_ 1 — 2ув —0, или (?/2+I)2 — (/2 . г/)2 = 0, или (у» + /2 .У + 1)(у’-/2.У + 1)=0.
Это ур—ніе распадается на два квадратныхъ: у24-у1— /І2 . у-|_І=О- Рѣшивъ игъ, найдемъ 4 корня:
>/ 2 .у 1 = 0 и
Уі І_Ѵ2
Уз\~ *
Уз I
Уз Г 2
1±0.
о
Уравненіе у*41 = 0 можно рѣшить-иначе, разсматривая его какъ возвратное, въ которомъ коэффиціенты трехъ среднихъ членовъ равны нулю. Раз* дѣливъ его на 4 имѣемъ у2 4“ Л = 0; положивъ у 4- - == Л у
у* 4~ — 2; слѣд. я* — 2 = 0, откуда / = 4~ и
ТТ / ’ • ' I 1
Подставляя поочередно оба значенія я въ ур—піе у4”«—
У ур —-нія у * — |/2 . у 4- 1 = 0 п 4” - У 4- 1 кс
выше.
имѣемъ отсюда:
получаемъ два
Примѣръ I.—Уравненіе х* — 81 = 0 имѣетъ 4 корня, которые найдемъ, умноживъ ариѳметическое значеніе ^8І, т.-е. 3, на четыре значенія корня четвертаго порядка изъ 4~1; именно
— 3, = 4~ = — Зі.
Примѣръ 11.—Ур—ніе #*4-16 = 0 имѣетъ четыре мнимыхъ корня, которые найдемъ, умноживъ четыре значенія корпя 4-го порядка изъ — 1 па ариѳм. значеніе |/І6, т.-е. на 2. Получимъ:
Л= /2(1+ 0і л’а=/2(1 — -г3 = /2(—14-»), ^ = /2 (— 1 -- г).
IV. т = 5; ур—нія: х5—1=0 и х3 4-1=0,
Первое ур. можно представить въ видѣ: (х —= оно распадается на два ур—нія
аг—1=0. ф . (1) и г* —|—□г3 —|—аг* —|—-Г —1 =0 . , ф (2)
изъ которыхъ первое даетъ = 4* 1. Второе же есть возвратное ур. перваго рода, ибо коэффиціенты членовъ, равноудаленныхъ отъ крайнихъ, равны; слѣд. рѣшеніе его приводится къ рѣшенію системы двухъ уравненій:
х2 — у.гЦ-1 — 0 и у* 4“ У — 1 = 0.
Корни ур—нія въ у дѣйствительные, неравные и противоположны по знаку; необходимо и достаточно, чтобы эти корни не заключались между - 2 и 4-2, чтобы корни ур—нія (2) были дѣйствительны. Но 2*4~ 2 — 1 >0, слѣд. положительный корень содержится между 0 и 4"2- Точно такъ же (—2)а4“(—2) —1>*0, слѣд. отрицательный корень содержится между 0 и (—2). Слѣд. всѣ четыре корня ур—нія (2) мнимы. Для нахожденія ихъ рѣшаемъ сначала ур. въ у; оно даетъ
- 1=Ы 5
У=~ 9-------
Рѣваж ур—ніе въ л имѣемъ
. — 1 +1 о . 1 + Iх 5
подставляя сюда вмѣсто у сперва --» затѣмъ — —получимъ еще
четыре корня, такъ что всѣ пять корней ур-нія .г5 — 1 = 0 суть:
•г, = 1;
— І4-/54/1042/5 .г — 1 4/5-/1042/5 . !
— 4 > ~ ~ 4 ’
1 — /5 +/10 —2/5 . і _-1 —/5 — /10 — 2/5.»
~ 4 ” ; 4 *
Чтобы рѣшить ур. .г54~1 = От разлагаемъ первую часть на множители и получаемъ уравненіе (# 4" І) С1*4 “ *г9 4~х* — х 4“ М = распадающееся на два ур—нія: я 4“ 1=0 и ж4 — .тэ4-^а — #4-1 = 0, рѣшеніе которыхъ аналогично вышеуказанному. Впрочемъ, легко доказать, что корни ур—нія #!і4“1=0 отличаются отъ корней ур—нія #5—1 = 0 только знаками; въ самомъ дѣлѣ, положивъ въ данномъ ур—ніи х = — х\ получимъ ур—ніе #'в—1=0, тождественное съ рѣшеннымъ, слѣд. для х* имѣемъ 5 вышенаписанныхъ формулъ; а какъ х = — У, то перемѣнивъ въ этихъ формулахъ знаки, прямо имѣемъ пять корней ур—нія лгя4“1—0. Это замѣчаніе относится ко всѣмъ'двучленнымъ ур—ніямъ х'п—1=0 и .г™4-1=0, въ которыхъ т нечетно.
V. т = 6: ур—нія: —.1=0 и <гѳ4~^”^*
Первое ур. можно представить въ видѣ (я3 —1)(я'34-1) = О; сл. оно разлагается на два кубичныхъ ур—нія: х3 — 1 — О и я3 4~ 1 = О, рѣшенія которыхъ уже извѣстны, такъ что .г® —1=0 имѣетъ шесть корней:
— і4-»із — і— ііз 1 і—і И*
----X----: ..хл = — 1: .г. = —і
Уравненіе я® 4" 1 = О можно представить въ видѣ (л:1)3 -|- 1 — 0, т.-е.
4~ 1)(^4 — 4“*) = оно распадается на два: квадратное ур. ^4"1 — и биквадратное х* — ял4- 1 = 0, рѣшеніе которыхъ извѣстно.
VI. т = 7. Уравненія дг1 Ч-1 — О неразрѣшимы средствами элементарной алгебры.
ѴП. т = 8; ур—нія а?8—1=0 и
Первое можно написать въ видѣ (я4 — 1) (#44~ 1) 0; оно распадается
на два: г4—1 = 0 и «г44- 1 = 0, корни которыхъ уже найдены въ пунктѣ III.
Ур—ніе ;г84“1“О можно написать въ видѣ (^<4~ О2 — 2^* = 0 или (я4-|- |/2 . ;г24~ Ъ 4й — ’ ,гй4“1)“0; оно распадается на два биква-
дратныхъ ур—нія: я4 4-1/2 . ^4- 1 = 0 и т* — |/2 . .г2 4-1 = 0, рѣшеніе которыхъ извѣстно.
Подобнымъ образомъ могли бы рѣшить элементарно еще нѣкоторыя двучленныя ур—нія.
На частныхъ примѣрахъ'мы видѣли, что число значеній корня, или рѣшеній двучленнаго ур—нія всегда оказывается равно показателю корня или степени ур—нія. Общее доказательство этрй истины дано въ главѣ XXIX, § 429.
Трехчленныя уравненія.
532. Всякое трехчленное уравненіе
ахѵ 4~ Ьхч 4~ схг = О
можетъ бытъ рѣшено посредствомъ уравненія второй степени и уравненій двучленныхъ въ случаѣ, если показатели р, г связаны соотношеніемъ р— у = <1— г, т.-е. образуютъ непрерывную ариѳметическую пропорцію.
Въ самомъ дѣлѣ, если д — г=т, то д = т-[-г, р = ц-^т = 2т-{-гч и уравненіе будетъ оіг2т+г 4~ Ь.гт+Г 4" г,гГ ~ или, по вынесеніи #г:
^[а^«4-Ь.гш4-с] = О.
Отсюда видно, что оно имѣетъ, во-первыхъ, г корней, равныхъ нулю, а затѣмъ удовлетворяется всѣми корнями уравненія
а.т2,Л 4“ Ьхт 4“ о = 0.
Рѣшеніе послѣдняго приводится къ рѣшенію квадратнаго уравненія п столькихъ двучленныхъ, сколько корней имѣетъ квадратное.
Въ самомъ дѣлѣ, положивъ = и слѣд. получаемъ ур—ніе
ау* + Ьу + е = 0, имѣющее два корня: # = и у = у"; подставляя эти значенія у въ ур—ніе хт = уч получаемъ два двучленныхъ ур—нія
;гш = У* И я™ =
изъ коихъ каждое имѣетъ т корней, такъ что предложенное ур—ніе имѣетъ 2т корней.
Очевидно, биквадратное ур. есть частный случай трехчленнаго.
II в н м ѣ р ъ—Рѣшитъ ур—ніе ІООО.г® — 6119х3 -|- 9261 = 0.
Положивъ = имѣемъ ур. ІОООу3 — 6І19^—|— 9261 = От откуда
6119 ± Г37442161 — 37044000 _ 6119 ± 631 #
2000 2000 ;
слѣд.
_ 5488 _ 343
У “2000“ 8; $ “2000 “125*
Вопросъ приводится къ рѣшенію двухъ двучленныхъ ур — ній
и
3____
.г
343
125
изъ которыхъ и находимъ шесть корней предложеннаго:
Уравненія вида р.у.Н —0 и нѣкоторыя другія. »
533. Какова бы ни была степень уравненія, вторая часть котораго равна нулю, но если окажется возможнымъ разложить первую часть его на множители первой или второй степени, или вида ах1 -|- Ъх* с, или а./1 Ь.гя + сх* + + Ь.г-р а, то ур—ніе возможно рѣшить средствами элементарной алгебры. Въ самомъ дѣлѣ, чтобы произведеніе множителей было нулемъ, необходимо и достаточно, чтобы одинъ изъ нихъ было нулемъ; слѣд. рѣшеніе уравненія Р(|К = О приводится къ рѣшенію отдѣльно ур—ній Р = 0, ф = 0, К = ОТ которыя, по предположенію, разрѣшимы элементарными средствами-.
Приводимъ примѣры,
I. Рѣшитъ ур—ніе ах3 4“ Ь#2 ~Ь сх = 0.
Написавъ его въ видѣ с) = 0, заключаемъ, что его корни
суть корни ур—ній: .г = 0, а.г3Ц~Ь.т 4~с = 0; т.-е.
- Ъ + — Ь^ Ѵ&—
П *Г '- П
2л 2а
И. Рѣшитъ ур—ніе 7х* — 5 г2 — 4х -|- 2 = 0.
Непосредственно видно, что ур* удовлетворяется при *т=1; слѣд* первая часть его, обращаясь при х = 1 въ нуль, дѣлится на х — 1; выполнивъ дѣленіе, дадимъ ур—нію видъ (я — 1) (7#а4~2л: — 2) = 0, откуда видно, что оно распадается на два ур—нія: х —1=0 и 7*га-|-2^ — 2 = О,
Рѣшая ихъ, получаемъ:
III. Рѣшитъ ур—ніе: (Здт1— 7дл~|-4)г — (2х4— 5#а 4" 2)2 = О, Разложивъ на множители, получимъ
(5ж4 — 12^4-6) — 2.г*+ 2) = О,
ур—ніе* распадающееся на два биквадратныхъ, изъ которыхъ найдемъ
534. Уравненія «9’4” &94"с = и а9* 4“ЭД*4~С = ГД^ М есть квадратный или биквадратный по буквѣ х полиномъ, заключаютъ въ себѣ четыре типа ур—ній:
а(гх2 -|“ 4^0* 4“ (гг3 з-г 4- о = 0;
а(г.г44-зг2 4~ 024~^ГХІ 4~^4" 0 4“6 = а (г#2 -4 14“ -4 4~ 024-с =
а (гх* &г2 + і)4 4” 6(гх4 4"я#8 4~ О2 +с =
Чтобы рѣшить такого рода ур—нія, полагаемъ, смотря по случаю: пли г^2*4 з.г4-^ = 9, или гг44“5‘г*4- = 4* • • • (а) рѣшая ур—нія въ 9, найдемъ для 9 два или четыре значенія; внося каждое изъ значеній 9 въ вспомогательныя ур—нія (а), найдемъ соотвѣтствующія значенія х,
535. Слѣдующіе четыре типа уравненій:
аР2 4- &РР' + сГ2 = О; а92 + &99' 4- = 0;
аР4 4- ЬРТ* + сР'4 = 0 и а94 4- ЭД Vя + <* = О,
въ которыхъ Р и Р' суть триномы вида г^2 -[“5д: 4“ а 9 и 9' — вида гх*-|-&г-4~ рѣшаются помощію двухъ квадратныхъ, либо двухъ биквадратныхъ ур—ній.
Для рѣшенія ихъ полагаемъ, смотря по случаю;
Р р 0 у
р, = К или о7 = 1ч
приходится затѣмъ рѣшать квадратное, либо биквадратное ур. въ Н, которое дастъ для К два, либо четыре значенія; внося значенія К во вспомогательное ур,. найдемъ соотвѣтствующія значенія х.
536, Примѣры,—I. Рѣшитъур. (х — а)(х — За)(т — 8а)(я--к4а) = = Ь4 — 35а*52.
Послѣдовательныя преобразованія даютъ:
(т3 — 4ая? -|- За2) (т* — 4ат — 32а*) = М — 35а*5*, (;г* — 4а;г)* — 29а*(.га — 4а.т) — (96а* 4- М — 35а*5*) = 0.
Принявъ гг2 —4а.т за вспомогательное извѣстное, находимъ
.г* _ 4а г =
29а2 + (35а® — 2№)
2 :
рѣшая каждое изъ этихъ квадратныхъ ур—ній, найдемъ всѣ 4 корня предложеннаго.
И. Рѣшитъ ур. (х* — —10<г*(я:2— #4~ 1)24~ — 0.
Раздѣливъ обѣ части па о*4 (что, замѣтимъ, не поведетъ за собою уничтоженія нѣкоторыхъ корней, ибо при х = 0 ур. не удовлетворяется), дадимъ ур—нію видъ
откуда
Такимъ образомъ имѣемъ 4 ур—нія
изъ которыхъ находимъ:
г = I т :г = 4: Л х = 2 + |/з, х = — I.
тіт п (я* “Н ая + 1)* , х , (а — 6) (а — с)
ІИ. Рѣшить ур. + Ъх + })^ + сх^} = ^ гдѣ й = — й----------------
Послѣдовательныя преобразованія даютъ:
б7|х*4-ах+1 —(а—Ь)х | |я24“ 1 ” (а— с)Х1 + 1)2= О,
(д—І)(^’+адг-^1)а — <7(2а — Ъ—с)(^24“^гЧ_Оя:_І_^(а—6) (а—е)т*=0#
откуда, раздѣливъ на
п принявъ за неизвѣстное — ------------, имѣемъ:
іг® + ах 1 _ б?(2а — Ь — с) ±ѴсР(2а — і> — с)? — {(Г— 1) (а — 6) (а — с)
і ~ —2 (сі — 1) “ ' - ’
& + ах + 1 _ гі(2а — Ъ — с) ± ѴЭ(6— е)2 + (а — 5) (а — с)
Но, по условію,
<)= слѣд.
<7*(Ь — с)*4“4(7(а — й) (а — с) = №(64“е)*т
откуда
т.-е.
з2 4- ая +1_{2« — 6— с (Ь -Ь с)}
X — “ 2(й—Т)
^ 4- ^4-1 __ (а — &) (« — й) 2а — Ъ — с ± (&+_«)_} х 2а (а — I) — д)
Итакъ, нахожденіе % приводится къ рѣшенію ур—ній
;г2_+й^2±1 — (а — Ь) (а — <0 х а — Ъ^с
4- яя ~М____(а — (а — с)
х а
что не представляетъ уже затрудненій.
ГЛАВА XXXVI.
Ирраціональныя уравненія.
537. до—ели называется такое, въ которомъ неизвѣст-
ныя входятъ подъ знакомъ одного или нѣсколькихъ радикаловъ. Рѣшеніе такихъ ур—пій требуетъ освобожденія неизвѣстныхъ изъ-подъ радикаловъ. Можно доказать, что всякое ур—ніе можетъ быть освобождено отъ радикаловъ, каковы бы ни были ихъ показатели. Доказательство этой теоремы и основывающійся на ней общій методъ рѣшенія ирраціональныхъ ур—ній мы помѣщаемъ въ концѣ этой главы. Предварительно же разсмотримъ другой пріемъ, болѣе элементарный, приложимый лишь въ нѣкоторыхъ случаяхъ, обыкновенно встрѣчающихся въ практикѣ элементарныхъ вычисленій/Онъ состоитъ въ томъ, что изолируютъ радикалъ н затѣмъ возводятъ ур—ніе въ степень, изображаемую показателемъ изолированнаго корня. Такимъ образомъ освобождаютъ ур—ніе отъ ирраціональности того члена, который былъ отдѣленъ. Повторяя эту операцію столько разъ, сколько нужно для уничтоженія всѣхъ радикаловъ, приводятъ такимъ образомъ ур—ніе къ раціональному виду. Но нужно помнить, что этотъ методъ приложимъ лишь въ нѣкоторыхъ исключительныхъ случаяхъ. Такъ, этимъ способомъ можно освободить ур—ніе отъ квадратныхъ корней, каково бы ни было ихъ число.
Теорема. Всякое до—ніе можно освободить отъ радикаловъ второй степени, каково бм было ихъ число, возвышеніемъ въ квадратъ обѣихъ частей нѣсколько разъ.
Докажемъ эту теорему. Пусть будетъ тотъ радикалъ, который желаютъ уничтожить. Для того приведемъ ур—ніе къ виду Р —|— к & = гдѣ Р ц ((— количества раціональныя или ирраціональныя, но ие содержащія Ѵ&. Изолируя членъ во второй части и возвышая обѣ части въ квадратъ, получимъ ур—ніе Р2^^2^ уже не содержащее радикала Такимъ же образомъ можно освободить ур—ніе отъ другого, третьяго,... квадратныхъ корней, сколько бы ихъ ни было.
Освободивъ такимъ образомъ ур—ніе отъ радикаловъ, рѣшаемъ полученное раціональное ур—ніе вышеизложенными пріемами. Во легко доказать, что оно можетъ имѣть постороннія рѣшенія, не удовлетворяющія данному ур—нію.
538. Теорема. Если обѣ части уравненія возвыситъ въ одинаковую степень, то получится уравненіе, вообще, не эквивалентное данному: оно необходимо удовлетворяется всѣми корнями даннаго ур—нія, но можетъ имѣть и постороннія рѣшенія.
Въ самомъ дѣлѣ: I. Пусть дано ур—ніе
А = В . . .(1).
Возвысивъ обѣ его части въ квадратъ, найдемъ ур—ніе
Аа = В2, пли (А — В)(А + В) = О . . . (2).
Всякій корень уравненія (1), дѣлая А равнымъ В, обращаетъ разность (А — В) въ нуль, и слѣд. удовлетворяетъ ур—нію (2).
Но послѣднее ур—ніе удовлетворяется еще тѣми значеніями неизвѣстнаго, при которыхъ А —В обращается въ нуль, т.-е. корпями новаго ур. А =— В. Такимъ образомъ не всѣ корни ур—нія (2) необходимо удовлетворяютъ и (1).
Итакъ, рѣшивъ ур—кіе (2), необходимо еще удостовѣриться, удовлетвори* ютъ ли полученныя рѣшенія ур—нію (1), т.-е, обращаютъ ли эти рѣшенія А и В въ количества одинаковаго знака.
Корни ур—нія А = — В называютъ посторонними или паразитными рѣшеніями, введенными возвышеніемъ въ квадратъ.
II. Возвышая обѣ части ур—нія А = В въ кубъ, найдемъ: А® = В3; но это ур—ніе не эквивалентно данному, ибо содержитъ корни трехъ ур—ній
А = В, А = Ва, А = Ва\
гдѣ а одинъ изъ мнимыхъ кубичныхъ корней изъ единицы.
ІИ Возвысивъ ур — ніе А = В въ четвертую степень, найдемъ ур —ніе А* = В\ которое опять общѣе даннаго, ибо удовлетворяется корнями четырехъ уравненій:
А = В, А= —В, А = Ві, А = —Ві. №
IV. Вообще, возвысивъ ур—ніе А = В въ т-ую степень, получимъ ур—ніе:
Аш = Вт, или (А - В)(А™"1 + А™"2 В + • • • + В'”"1) = О, которое кромѣ корней даннаго ур—нія удовлетворяется еще корнями ур—нія
А”—1 + Ат-2В-|- • • -^-Вт-1 = О.
Можетъ оказаться» что это послѣднее не содержитъ рѣшеній, отличныхъ отъ корней ур—нія А = В: но такой случай исключителенъ.
Покажемъ на нѣсколькихъ примѣрахъ примѣненіе этого метода, причемъ главнымъ образомъ обратимъ вниманіе на ур—нія, содержащія радикалы второго порядка.
539. Разсмотримъ сначала простѣйшій случай, когда ур—ніе содержитъ только одинъ радикалъ. Такое ур—ніе можно представить въ видѣ
В + /Ч = О. .(1)
если буквою К обозначить совокупность раціональныхъ членовъ, а буквою 9— подрадикальное выраженіе.
Изолируя радикалъ, напишемъ ур—ніе (1)*въ формѣ /9 = —В, и возвысимъ обѣ части въ квадратъ; найдемъ: (^ = К\ или
В2 — 9 = 0, . . . (2)
что можно написать такъ: (В 4= /9)(В — /9) = 0.
. Ур —ніе (2) раціонально и его корни удовлетворяютъ либо ур—нію (1), либо сопряженному ему ур—нію
В —/9 = 0 . . , (Г)
Взявъ одинъ изъ корней ур—нія (2), подставимъ его въ это ур—ніе; и пусть при этомъ К и 9 принимаютъ значенія В' и 9', такъ что получается тождество
Н'2 — 9' = 0.
Оно доказываетъ, что 9' есть количество положительное, и слѣд. / 9' Дѣйствителенъ. Если, теперь, В' положительно, то разсматриваемое рѣшеніе не можетъ удовлетворять ур—нію (1), ибо сумма двухъ положительныхъ чиселъ не можетъ равняться нулю; оно, сл., удовлетворяетъ сопряженному съ (1) ур—пію (Г). Если же Н' отрицательно, то наше рѣшеніе не можетъ удовлетворять ур—нію (Г); слѣд., оно удовлетворяетъ (І)-му. Отсюда заключаемъ, что всегда легко отличить тѣ рѣшенія ур—нія (2), которыя удовлетворяютъ данному ур—пію: это будутъ тѣ корни (2), которые, будучи подставлены въ В, обращаютъ В въ количество отрицательное.
Пусть, наприм., В есть полиномъ 1-й степени въ а 9—квадратный полиномъ, наприм.
В = — а), 9 = ах1 Ьх 4“ е.
Ур—ніе (2) будетъ въ этомъ случаѣ квадратное:
(</#2 4~ Ьл 4~ с) — — я)2 = 0:
рѣшая его, найдемъ два корня а/ и х". Чтобы удостовѣриться, удовлетворяютъ ли они данному ур—нію, нужно поочередно подставить въ функцію В вмѣсто х сначала х\ потомъ х?' и смотрѣть, удовлетворяется ли условіе
к(х — а) < 0;
т.-е.
при к > 0, будетъ ли х < а, а при к < 0, будетъ ли
Приводимъ примѣры.
540. Примѣръ I. уравненіе 2х + |/5^' — 4 — 12.
Изолируя ирраціональный членъ, имѣемъ:
/57^4 = 12 — 2т.
Возвысивъ въ квадратъ и приведя въ порядокъ члены, получимъ квадратное ур—ніе
4т5 —33.?+ 148 = 0 . . \ (1). *
корни котораго необходимо удовлетворяютъ одному изъ уравненій
/5,г-4 = 12 — 2х . , , (2) —/5г —4= 12 —2,г . . .(3),
такъ какъ п то и друтое, по возвышеніи въ квадратъ, одинаково даетъ ур—ніе (1). Но во (2), которое эквивалентно данному, передъ радикаломъ находится знакъ +, слѣд. и вторая часть его должна быть положительна; въ ур—ніи же (3) передъ радикаломъ находится —, слѣд. и вторая часть его должна быть отрицательна. Слѣд., если въ числѣ дѣйствительныхъ корней ур—нія (1) имѣется корень, удовлетворяющій неравенству 12 — 2х>0, или л?<+ то онъ будетъ удовлетворять данному ур—нію, а если имѣется корень, удовлетворяющій условію 12 — 2іе<0, или онъ удовлетворяетъ ур—нію (3), со-
пряженному со (2).
Рѣшивъ ур—ніе (1). находимъ: = х” = 4.
х* нужно отбросить и удержать х\ искомое рѣшеніе: х = 4.
Въ данномъ примѣрѣ легко найденные результаты провѣрить прямою подстановкою, хотя это не необходимо,
'Подстановка х — 4 въ предложенное ур—ніе даетъ:
/5^4 — 4=12— 2X 4, пли 4=4.
Подстановка я, = 9^ въ ур—ніе (3) даетъ:
- )/5Х?-4= 12 - 2 Х^’ или
13_ _13
9 — 9 ’
Дрхгой пріемъ. Можно рѣшить данное уравненіе иначе, введеніемъ вспомогательнаго неизвѣстнаго. Преобразуемъ ур—ніе такъ, чтобы имѣть въ немъ 5
раціональный членъ 5л* — 4; для этого множимъ обѣ части на^а- потомъ вычитаемъ изъ нихъ по 4. Такимъ образомъ, получаемъ эквивалентное данному уравненіе
— 4+ ~ |/5л‘ — 4 = 26.
Положивъ |/5а* — 4=і/ . . . (1), даемъ этому ур—нію видъ
4 I О Лр / 13 А
У +оУ = 26, откуда 1/ =—у =4.
— 556 <— *
Но буквою у обозначенъ радикалъ положительный, поэтому отбрасываемъ у* и удерживаемъ у" — 4. Подставляя въ вспомогательное ур—ніе (1) вмѣсто у число 4, получаемъ ур—ніе —4 = 4, затѣмъ 5 г—4 = 16, откуда
.г =4.
Этотъ способъ позволяетъ безъ труда отличать значенія .г, удовлетворяющія ур—нію, отъ паразитныхъ корней.
541. Примѣръ II. Ршаитиь уравненіе х — 1 = |/3г — 5.
Возведя обѣ части въ квадратъ и приведя въ порядокъ, получаемъ
г2 — 5* +6 = 0. . . (1).
Корни этого уравненія удовлетворяютъ одному изъ двухъ уравненій: данному, либо я — 1= — — 5 . . . (2), данному—если эти корни больше 1, и
ур—нію (2)—если они меньше 1. Рѣшивъ ур—ніе (1), находимъ корни:
У = 2, ;г" = 3;
оба корпя больше 1, слѣд., оба удовлетворяютъ данному, но не удовлетворяютъ ур—нію (2), которое, такимъ образомъ, не имѣетъ рѣшеній.
542. Примѣръ Ш. Рѣшитъ уравненіе х /а* — я2 = Ь, <?а кшно-ролкъ а и Ъ —дѣйствительныя и положительныя количества.
Изолируя радикалъ, имѣемъ
|/а2 — л;2 = Ь—х . . . (1).
Возвышая обѣ части въ квадратъ, находимъ
а’2 — ,г2 = (Ь — .г)2. . , (2) или 2л,а—25.г-|-(М —а2) = 0 . . . (3),
изъ котораго
х =-------~2------• • • (4) и я = ———2--------- . . . (э).
То же самое ур—ніе (3), а слѣд. и тѣ же самые корни (4) и (5) нашли
бы и для уравненія
— а2 — х2 = Ъ — х . . . (б)»
отличающагося отъ (1) знакомъ при радикалѣ. Замѣчаемъ, что дѣйствительные корни ур—нія (3), удовлетворяющіе ур—нію (1), отличаются отъ корней, удовлетворяющихъ ур—иію (6), тѣмъ признакомъ, что они должны еще удовлетворять условію
х < Ъ.
Корни ург-нія (3) будутъ дѣйствительны, если будетъ
б8— 2(Ь8— а8)^0. или Ь8 — 2а'1 ^0.
Разсматривая № — 2а* какъ квадратный относительно Ъ триномъ, находимъ, что онъ будетъ отрицателенъ, когда 6 будетъ заключаться между его корнями а^2 п — а^/ІІ, изъ коихъ первый положителенъ, а второй отрицателенъ, такъ какъ, по условію, а > О. Но какъ и то заключаемъ, что необходимое п достаточное условіе дѣйствительности корней будетъ
Ъ ^а|Л2,
Знакъ -корней зависитъ отъ ихъ произведенія и суммы. Произведеніе корней, 6*—а*, будетъ положительно, если Ь>а, в отрицательно, если Ъ <а. Сумма корней, будучи =6, всегда положительна. Значитъ, при Ъ^>а оба корня положительны, а при Ъ <а знаки ихъ противоположны, причемъ большій корень положителенъ. ___
Что касается величины корней, то, во-первыхъ, дѣйствительность І^а* — .т* [ур—ніе (1)] требуетъ, чтобы разность а2 —я* была >0. „о дѣйствительные корни ур—нія (3), въ силу того, что они удовлетворяютъ ур—нію (2), необходимо дѣлаютъ разность аа— я* положительною.
Окончательно приходимъ къ такому заключенію: при соблюденіи условія оба корня уравненія (3) будутъ дѣйствительны, но данному ур—нію они будутъ удовлетворять только тогда, когда будутъ < 6.
Нужно, поэтому, изслѣдовать, какимъ образомъ располагается число Ъ относительно корней тринома 2х2— 2Ьх-[-52— а*. Для этого надо знать результатъ подстановки въ этотъ триномъ буквы Ь вмѣсто Этотъ результатъ есть
/(Ь) = Ьа — а*.
гдѣ Ь п а положительны. Очевидно, что если 5>а, что не противорѣчитъ условію Ь^а|Л2, то результатъ этотъ положителенъ, т.-е. одного знака съ первымъ членомъ; если же Ь<1а, то /(6)<0, т.-е. знакъ ея противоположенъ первому коэффиціенту. Критическими значеніями Ь будутъ, слѣдовательно, а н а/2.
' Легко составить слѣдующую таблицу знаковъ.
Скала значеній Ь 0 а -П-СО
» Реалнзантъ —|— —1“ “——
Произведеніе корней — 1
Сумма корней
IV») 1 —
1-Іі коэффиц. —
Изъ этой-таблицы прямо видно, что если:
1) 6 = 0, то (хотя освобожденное отъ радикала ур—ніе даетъ корни . о Ѵ2 х ! а 1/2 .
Ч——* но) данному ур—нпо удовлетворяетъ 1 корень — : задача имѣ-
етъ 1 рѣшеніе.
2) і О. Корни дѣйствительны и противоположны по знаку, причемъ большій корень положителенъ. Такъ какъ /(6) имѣетъ знакъ противоположный 1-му коэффиціенту, то Ъ заключается между корнями
слѣд., одинъ корень <6, другой > Ь; и какъ задачѣ уд—тъ только первый, то задача имѣетъ одно рѣшеніе, выражаемое отрицательнымъ корнемъ
У = 0,
3) Ь = а. Корни будутъ
х * = а
4) а<^Ь<^а^2. Корни дѣйствительны; произведеніе и сумма ихъ ^>0. слѣд, оба корня 5>0. Знакъ /(6) одинаковъ съ 1-мъ коэффиціентомъ, слѣд. 6 находится внѣ корней. Чтобы знать положеніе Ь относительно корней, сравни-> и Ь 7^6
ваемъ о съ полусуммою корней, равною такъ какъ о > то расположеніе чиселъ х\ У' и Ь таково:
Ь
О
т.-е. оба корня < 6, и потому задача имѣетъ 2 рѣшенія:
, 6 — ^ 2 - 62 „
X =------------» х = —1--------
5) 6 = «|/2. Уравненіе имѣетъ равные корни:
/ // Ь ЛI 2
х — х = : 1 рѣшеніе.
б) 6>а|/2. Корни мнимые; задача не имѣетъ дѣйствит. рѣшеній.
Резюме.
Ь<^а ...............1 рѣш. отриц. У = ------------
Ъ = а ..............2 корня: У — О» У' = а.
а<о<аі/2,...............2 иолож. корня:х = - - — — •
г
, ’ п / П «^2
6=а}/2 .........2 равныхъ корня: я = я' = *
6 7>а|/2 ...........Корни мнимые.
Въ разсматриваемомъ случаѣ (а > О, Ь > 0) можно дать нашему ур—нію геометрическую интерпретацію, которая наглядно покажетъ, въ какомъ случаѣ допустимо то или другое рѣшеніе.
Наше уравненіе есть переводъ на языкъ алгебры требованій задачи: на окружности круга, построеннаго на діаметрѣ АВ =а, найти такую точку В, сумма разстояній которой отъ концовъ діаметра равнялась бы данной линіи Ъ:
АВ4-Т)В = 6.
Въ самомъ дѣлѣ, если искомая точка есть В, и АВ = то ВВ = |/а2 — д’2, слѣд. ур—ніе задачи будетъ
х + = 6.
на окружности АСВ требуемую
Корни его и дадутъ искомую линію АВ.
Геометрически задача рѣшается такъ. На продолженіи линіи АВ возьмемъ отрѣзокъ І)Е — ВВ и соединимъ В съ Е. Въ равнобедренномъ треугольникѣ ВИЕ уголъ В = 90°, слѣд. < АЕВ ~ 45°. Поэтому конецъ Е прямой АЕ = 6 находится на дугѣ АНЕВ, вмѣщающей уголъ 45° и описанной на хордѣ АВ = а. Центръ С этой дуги есть конецъ радіуса, перпендикулярнаго къ АВ.
Если дуга, описываемая изъ А радіусомъ = Ь, встрѣчаетъ нижнюю часть искомой окружности въ В\ то на данной окружности полу; чаемъ точку К'. Такъкакъ < АВ'В = 135°, то <ВВ'Е'=45*=<О'ВЕ', откуда В'Е'=Е'В, и слѣд. АЕ' —1ГЕ' = АЕ' —Е'В = Ь, такъ что нижняя дуга даетъ точки, для которыхъ разность разстояній отъ А н В равна 6, и не отвѣчаетъ задачѣ въ прямомъ смыслѣ заданія.
Итакъ, для рѣшенія' задачи описываемъ на АВ сегментъ, вмѣщающій 45°, и изъ А, какъ изъ центра, радіусомъ Ь описываемъ дугу, которая пусть встрѣчаетъ дугу АНВ въ нѣкоторой точкѣ Е: соединивъ А съ Е, найде» точку В.
Чтобы задача была возможна, нужно, чтобы дуга, описываемая радіусомъ Ь изъ точки А, какъ изъ центра, встрѣчала дугу АНВ; для этого должно быть
—- а
2, такъ какъ АС= 9 *
Когда & < а, наше изслѣдованіе показало, что значеніе .г, удовлетворяющее ур—нію, отрицательно. Что касается геометрической задачи, приводящей къ тому же ур—нію, то ей могутъ удовлетворять только положительныя значенія Заключаемъ, что полученіе отрицательнаго рѣшенія должно указывать на невозможность задачи. И дѣйствительно, на окружности нѣтъ такихъ точекъ, сумма разстояній которыхъ отъ концовъ діаметра была бы меньше діаметра.
Пусть Ъ = а. Существуютъ 2 точки, обладающія тѣмъ свойствомъ, что сумма
ихъ разстояній отъ А п В равна а ‘ это точки А и В, что и указывается корнями х' = 0, х" = а.
Когда а с Ь<а)Л2 или АВ < Ъ < АН, очевидно, дуга, описанная изъ А радіусомъ Ь, встрѣтитъ дугу ЛНВ въ двухъ точкахъ Е и Е", дающихъ двѣ точки В и В" на дугѣ АСВ. Это вполнѣ согласуется съ результатомъ алгебраическаго изслѣдованія, что въ данномъ случаѣ задача имѣетъ 2 положительныхъ корня.
При Ъ — а/2 или АН, точка встрѣчи одна, Н, и искомая точка на данной окружности одна, С, что согласуется съ результатомъ алгебраическаго изслѣдованія, съ полученіемъ въ этомъ случаѣ двухъ сливающихся корней.
Наконецъ, результатъ алгебраическаго изслѣдованія, что при Ь>а|/2 ур—ніе имѣетъ мнимые корни, согласенъ съ геометрическимъ указаніемъ невозможности задачи при этомъ условіи: въ самомъ дѣлѣ, дуга, описанная изъ А радіусомъ, большимъ & |/2, не встрѣтитъ дуги ЛНВ.
543. Примѣръ IV. Возьмемъ теперь примѣръ нѣсколько сложнѣе.
Пусть дано рѣшить уравненіе
2л + = ЗЬ . . . (1).
Во-первыхъ, замѣчаемъ, что какъ вторая часть ур—нія дѣйствительна, то и первая должна быть такова же, и для этого должно быть а2 — 0, откуда
— а
Изолируя радикалъ, получаемъ ур—ніе
— дт* = ЗЬ —. .(2),
которое, по возвышеніи въ квадратъ, даетъ ур—ніе
а2 —.г2 = (ЗЬ— 2^)а, или 5#3—12Ь#-|-9Ь2 — а2 = 0 . . . (3).
Но то же самое раціональное ур—ніе (3) мы получили бы и изъ ур—нія
2я — а2 — х* = ЗЬ, или — |/а3 — я*3 = ЗЬ —
Слѣд., дѣйствительные корни (3), чтобы удовлетворять' (2) или (1), должны еще удовлетворять требованію
ЗЬ — 2я > 0, или а; <С - Ь. А
Переходимъ теперь къ изслѣдованію корней ур—пія (3), которые выражаются формулою
6Ь V 9Ь* X =---------і------•
о
Эти корни будутъ дѣйствительны, когда будетъ удовлетворено условіе
5а’ — 9б2 О, или (а ^5-}- ЗЬ)(а |Л5 — Зі)^О,
а какъ а и о > О, то должно быть о < •
Когда по условіе удовлетворено, то корни ур—нія (3) будутъ дѣйствительны.
Но когда х дѣйствительно, то вторая часть ур—нія (2) будетъ дѣйствительна. слѣд„ и равная ей первая также будетъ дѣйствительна, а потому условіе — а < х а будетъ удовлетворено.
Выразитъ теперь, что корни (3), чтобы удовлетворять данному ѵр—нію,
ДОЛЖНЫ быть «и
Подставляя въ триномъ (3) вмѣсто ж* • • имѣемъ
Л суть V
результатъ, который мѣняетъ знакъ при
г « 12 ь н 96*^ а* х
Супа корней, т-р, всегда >0; произведи корней, ——мѣняетъ о о
Ь 1 звать при о = ^а.
Тавлъ образомъ критическія значенія
1 2
3^’ зй и
научается слѣдующая таблица знаковъ:
Скала значеній 6 0 5я 5я 'з0® 130
Реализантъ 1 -г
Произведеніе корней -—“ —р- + Л- » ѵѵ-
Сумма корней —|— —1“ нн
гО со іечі * 1
1-й коэффиц. •р ™|— + '
Разсмотримъ каждый интерваллъ. / V
I
2 /3, \
1) 5 <^а: корни дѣйствительны; Ц2 т- е'заакъ ея противоположенъ знаку коэффиціента при слѣд. заключается между корнями:
Въ этомъ интерваллѣ только одинъ корень уд—тъ данному ур.; это —меньшій
корень ур—нія (3), который, пока 5 <С а - отрицателенъ; при Ь = ^а равенъ О, а при —положителенъ.
2 /3 \ 3
2) / 1-51 = 0, сл. есть одинъ изъ корней. Который это ко -
рень, покажетъ слѣдующій случай*
Полусумма корней
’ / сл- находится внѣ
6, Зъ
— -о, что меньше ^о: расположеніе
корней. •
корней относи-
Зі
тельно 7)Ь таково:
_// з> л: , . ~уО.
з
Заключаемъ, что оба корня меньше ^Ъ: задача имѣетъ 2 рѣшенія.
з
Отсюда же заключаемъ, что въ предыдущемъ случаѣ «Ъ былъ большій
корень.
4) &=:—< ур—ніе имѣетъ равные корни: ченіе то задача имѣетъ 1 рѣшеніе.
МІ
5) о > —н-: корни мнимые.
г ________6 1
х =х = 55; какъ это зна-
Резюме.
л , 65 — Ѵ5л2-9$
О < о < : 1 корень . . . х — --------
0 = ^:2 корня ... # ~1(г’ = <А
2 . , а. рЪ о 65 — Р 5а2 — 95’
за<о<—: 2 корня . . . х=--------- ~5
5 = -^- : 2 равныхъ корня . , . х —х =^о.
, аѴ5
о>—3- : Корни мнимые*
544. Перейдемъ къ случаю, когда ур—ніе содержитъ два квадратныхъ корня: пусть это ур—ніе будетъ /Р + Д + К —0. Изолируя ихъ въ первой части, возвышаемъ ур—ніе въ квадратъ; изолируемъ, затѣмъ, единственный оставшійся радикалъ, снова возвышаемъ ур—ніе въ квадратъ; въ результатѣ получимъ ур—ніе раціональное. Можно поступать еще такъ: изолируя одинъ изъ радикаловъ, возвышаемъ ур—ніе въ квадратъ; изолируемъ остающійся послѣ этого радикалъ и снова возвышаемъ ур—ніе въ квадратъ: получаемъ раціональное ур—ніе.
Возьмемъ сначала частный примѣръ: рѣшить ур—ніе
/40 + х = /18 + 2х 4-1.
Возвысивъ въ квадратъ, находимъ
40 + х = 18 + 2.г+ 2 /18 + 2x4-1
или, изолируя радикалъ и сдѣлавъ приведеніе, находимъ:
21 — .г = 2 /І 8 4- 2х~
Возвысивъ это ур—ніе въ квадратъ, по приведеніи въ порядокъ, найдемъ ур—ніе х2—50х + 369 = 0, откуда х' = 9, х" = 41. Эти корни не необходимо удовлетворяютъ данному ур—нію; они могутъ удовлетворять одному изъ уравненій:
/40+7= /18 + 27+1. . .(1)
/40 + х = — /18+"27+1 . . .(2)
— /40+7= /18+2х+1 . . . (3)
— /40+ х = — /18 + 2ж + 1 . . . (4).
Во-первыіъ, устраняемъ ур—ніе (2), ибо, написавъ его въ видѣ
/40 + х+/18 + 2х= 1,
замѣчаемъ, что при положительномъ х (а таковы а/ и х") первая часть всегда больше 1. Затѣмъ, ур—ніе (3) не можетъ быть удовлетворено никакимъ дѣйствительнымъ значеніемъ х, ибо первая часть его <0, вторая же Такимъ образомъ, найденные корни могутъ удовлетворять только ур—мъ (1) и (4). По ур—нію (1) разность / 40 + х— /18+2х, какъ равная +1, должна быть > 0; по ур—нію (4), она должна быть < 0. Слѣдовательно, необходимо, чтобы было: /40+ х^>/18 + 2.с или 40 + х^>18 + 2х, или х<22. Слѣдовательно, данному ур—нію удовлетворяетъ корень х' = 9; х7' — 41 удовлетворяетъ ур—нію (4). Легко подтвердить то и другое прямою подстановкою.
Постараемся теперь формулировать общія для разсматриваемаго случая правила, которыя позволяли бы отличать тѣ изъ корней раціональнаго резольвента, которые принадлежатъ данному ур—нію, отъ корней, ему не удовлетворяющихъ.
Комбинируя всѣми возможными способами двойные знаки передъ радикалами уравненія ± /р±А+« = 0, получимъ ур—нія
/р+/ч + К = о. . .(1).
/р—/Ч + К = О . . . (2), -/р+/9 + « = о. -(3), — /р— /Ч + В=О . . . (4).
Перемноживъ- ихъ почленно, найдемъ ч
(/Н'/й+кХ/р- /Н-В)( -/р+/у+Ю( - /р - /о+вХ=о...(5)
ур—ніе, необходимо раціональное. Въ самомъ дѣлѣ, его можно написать въ формѣ
[в» - (/р+Ач [в2—(/г—А-И=0 или
(В« —Р—ч —2/ШВ2—Р—Ч+2/РЧ)=0, или
(Вя~Р-4)«-4Р<1 = 0 . . .(6),
которое также нашли бы и по двукратномъ возвышеніи въ квадратъ способомъ, указаннымъ выше.
Всякій коренъ ур—нія (6), въ силу (5), будетъ рѣшеніемъ одного изъ уравненій (1), (2), (3) и (4).
Комбинируя различнымъ образомъ множителей ур—нія (5), можно это ур. представить еще въ формахъ
[(к+А)’ - [(К - А)’ - <М = о,
или
(В’ + Р-<І)» —4В*Р = 0 . . .(&).
Также
(К3 + <і — Р)а — 4Н*Ч = 0 . . .(6").
Ур—нія (6') и (6") показываютъ, что всякій корень резольвента (6) дѣлаетъ полиномы Р и Ч пожительными. Зная это, посмотримъ, какимъ образомъ рѣшенія (6) распредѣляются между ур—ми (1), (2), (3) и (4).
Корни ур—нія (6) принадлежатъ тому или другому изъ ур—ній
В» —Р-Ц-2 Ач = 0 . . .(7),
К» — Р — 4+2 А = 0 . .'.(8).
Тѣ, которые принадлежатъ (7), должны удовлетворять неравенству
В«_р-4>0 . . . (т),
* . - , -
а тѣ, которые принадлежатъ (8), должны удовлетворять соотношенію
К2 — Р — Ч<0 . , . (и).
Но (7) можно написать въ видѣ
(К 4- |/р + у7|)(К - |/р - V Ч) = 0;
слѣд. корни (7) удовлетворяютъ либо (1), либо (4): (1)-.іу? если они дѣлаютъ К 0; (4)-му, если они дѣлаютъ К > О,
Ур—ніе (8) можно написать въ видѣ
[Н + (/р - V Ч)] [К. — ()/₽ — |/Ч)] = 0;
его корпи удовлетворяютъ либо (2)-му, либо (З)-му, а именно: (2)-му, если они сообщаютъ В и уТ—У^ противоположные знаки, т.-е. если они удовлетворяютъ неравенству
В(]/р - Ѵч) < 0;
(З)-му, если удовлетворяютъ неравенству
В(1/р—Ѵ/Ч)>о.
Эти ирраціональныя соотношенія можно сдѣлать раціональными, помноживъ первыя ихъ части на положительное количество ]/ Р -р |/ У, что даетъ
К(Р-Ч)<0_ . . (р\
К(Р-<і»о. . .
Резюмируя сказанное, находимъ, что рѣшеніе резольвента будетъ принадлежать:
уравненію (1), если оно уд—тъ К2— Р — <| > О,
> (2), я » » Н2 —Р —{|<(\
> (Я), > » » К2— Р — (|<0,
> (4), » * » ГР —Р —Ч>(\
Н<0;
Н(Р - 9) < 0;
К(Р - <і) > 0;
Н>0.
545. Прпмъръ. Рѣшитъ уравненіе
|/т.77 Ь = с . , >(1),
еь «отороли т 1.
По двукратномъ возвышеніи въ квадратъ или по перемноженіи четырехъ УР“НІЙ съ различной комбинаціей знаковъ при радикалахъ, найдемъ резольвентъ
(т— І)(а—Ь-с2) — 2ся>+(а — &— с2)й— 46с*=О , . Д2),
Данное ур—ніе, написанное въ видѣ )/яи: 4~ а + /ж 4~ — с = О, подходитъ подъ форму (4); слѣд., чтобы тотъ или другой корень резольвента удовлетворялъ ему, необходимо, чтобы было В2 — Р — и ВО, или
с2—(тх-{"а) — (ж4~Ь)>*0Ф . ДЗ) и с>0. . . (4).
Чтобы корни резольвента были дѣйствительны, необходимо, чтобы было
яіс24’ (т — 1) (тЪ — я) Э* О*
Когда тпЬ — а > О, это условіе удовлетворено; если же Ыі — а < О, то должно быть
л (т — 1) (а — жй)
С 1 " ™ *
Затѣмъ, неравенство (3) требуетъ, чтобы было
«
Итакъ, данное ур—ніе будетъ имѣть столько корней, сколько резольвентъ имѣетъ дѣйствительныхъ корней меньшихъ ——Чтобы знать, какъ корни резольвента расположены относительно этого числа, нужно знать результатъ подстановки этого числа вмѣсто х въ ур—ніи (2), Найдемъ:
М— а —
+ I /
4тс* 4” 4(т — 1) (а — Ьт)с2 4~ 4 (а — іоя)2
. (5).
Корни этого квадратнаго въ с2 тринома суть а— тЪ и -• Когда с2
т.*е. того
//е2 —а—М . . л
заключается между этими значеніями, то ' будетъ >0,
же знака, какъ коэффиціентъ при я2 въ ур—ніи (2). Значитъ, бу-
детъ лежать внѣ корней этого ур—нія; слѣдов., чтобы ур—ніе (2) имѣло корень меньшій этой дроби, необходимо, чтобы полусумма его корней была меньше е2 — а *— Ь ----_Гі~ ’ что ведетъ къ условію
2ягс2 4“ (т — 1) — а) О,
которое противорѣчивъ условію дѣйствительности корней ур—нія (2).
Итакъ, необходимо, чтобы с2 не находилось въ интерваллѣ корней тринома (5), а лежало бы внѣ этого интервалла. Отсюда необходимость различать 3 случая:
1) Если а — тЬ<^0^ то О» и какъ положительно, то если
тЬ— а г/с2 — а —.
взять с2>———’ знакъ /I будетъ отрицателенъ, и слѣдовательно
л2 — 0 — 6 . •
будетъ лежать между корнями ур—нія (2), и потому одинъ изъ нихъ будетъ меньше этой дроби: задача имѣетъ 1 рѣшеніе.
2) Если а — тпЬ > 0, то <С Й. Взявъ с* а — тб, опять найдемъ, что задача имѣетъ 1 рѣшеніе.
3) Если а — п?Ь = О данное ур—ніе приметъ видъ
^х-\-Ь (1 4" /т) = с,
и всегда имѣетъ одинъ корень,
Остается разсмотрѣть, будутъ ли значенія обоихъ радикаловъ, і/і-р Ь и дѣйствительны. Достаточно разсмотрѣть одинъ изъ нить, такъ какъ въ силу дѣйствительности с, если одинъ радикалъ дѣйствителенъ, то дѣйствителенъ и другой; если мнимъ одинъ, то мнимъ и другой. Чтобы )/&-]-& былъ дѣйствителенъ, должно быть х^>— &. Подстановка —Ъ вмѣсто х въ триномъ (2) даетъ
/(—Ь) = (с2 Ц- Ьт — а)2,
количество положительное; слѣд., — Ъ находится внѣ интервалла корней этого ур—нія, и потому, чтобы х было > — Ъ, полусумма корней
2с2 — (ш— 1) (« — Ъ-&) (іи - ір
должна быть > — Ь,
что даётъ условіе (тп —Р 1)сэ —(ттг — 1)(Ьш — а)>0, всегда выполненное, разъ условіе дѣйствительности корней резольвента удовлетворено.
546. Пусть уравненіе содержитъ три радикала:
±/Р±/ч±/к = о.
Если перемножить уравненія
/?+/ч+/»=о. . .(I) ѴР4-/Ч—/К = О. . .(.2) /р —= . (3)
-/Р + /Ч+/К = О. • .(4),
то получимъ резольвентъ въ формѣ
р*4-(}5»4-п2 —2рд —2РВ —2дв=о . . . (З),
откуда легко заключить, что для всякаго корня этого ур—нія всѣ три количества Р? Ч и В одновременно положительны, или всѣ отрицательны. Въ са
момъ дѣлѣ: не можетъ быть одновременно Р>0, Ц>-0 п К<0; ибо, положивъ К= — К\ первая часть ур. (5) была бы
1>а + Ча + — 214} + 2РК' + 2(}К' = (Р + К' - ())* + 4(}П',
а это, при пашемъ предположеніи, есть количество положительное.
Также, нельзя имѣть Р > О, <^<0, К<;0; ибо, положивъ 9 = —
К = — К', первая часть (5) будетъ
Р2 (р + К'2 + 2 РЦ' + 2 РН' — 21}К' = (у' — К)2 + Р3 + 2Р^' + 2РК',
количество существенно-положительное.
Итакъ достаточно провѣрить, дѣлаетъ ли какой-либо корень ур—нія (5) одно изъ количествъ Р, У, К, положительнымъ.
Замѣтивъ, что ур. (1) не можетъ имѣть рѣшеній, ибо сумма положительныхъ количествъ не можетъ быть нулемъ, остается разсмотрѣть, какому изъ множителей (2), (3), (4) принадлежитъ тотъ пли другой корень резольвента.
Разсмотримъ, напр., при какихъ условіяхъ нѣкоторый корень ур. (5) обратитъ въ нуль множитель /р-Ь /ч—/в?
Если этотъ корень удовлетворяетъ ур—нію (2), то онъ удовлетворяетъ и ур—нію
(/р + /ч+/к)(/р+/ч-/к) = о . . .(6), первый множитель котораго не обращается въ нуль ни при какомъ дѣйствительномъ значеніи х. И обратно, всякій корень (6) удовлетворяетъ и ур—нію (2).
Но ур. (6) можно написать такъ
р-Н—К+2/РЧ=0 . . .(7).
Всякій корень ур—нія (2), удовлетворяя (7)-му, долженъ удовлетворять условію
Р + Ч„К<0, . .(8).
Подобнымъ образомъ убѣдимся, рять ур—нію
что корень ур—нія (5) будетъ удов.іетво-
/р —/ц +/Й = О, если Р-4-К — 4<о. . .(9),
и уравненію
— |/р|/ц= 0, если —Р-(-К-|-Ч<^0 . . .(10).
Но какой-либо изъ корней ур—нія (5) служитъ корнемъ (2), (3) или (4); слѣд., необходимо, чтобы одно изъ неравенствъ (8), (9) или (10) удовлетворялось, т.-е. чтобы для одного изъ дѣйствительныхъ корней резольвента одно изъ положительныхъ количествъ Р, 9, В было больше суммы двухъ другихъ. Оче-
— 569 —
видно, что таково будетъ только одно изъ нихъ, и корень ур—нія (5) удовлетворяетъ
уравненію ^ + /^4 — |/К = О, если Р-1- 9<К; > —/"Ч+|/К = О, если Р-|“И<СЧ;
> - /р + /ч + /Н=о, если 9-рВ^Р*
Уравненіе же /^4“ /ЧЧ“ /В = О не можетъ имѣть дѣйствительныхъ корней.
547, Примѣръ. Тушитъ уравненіе
/а і ^СЧ" = О,
а, 5, с—нѣкоторыя дѣйствительныя количества. I
Въ этой формѣ записи содержатся 4 уравненія:
/а /б-р& + О . . . (т),
+ = . . (и),
4~#+ = О . . . (р),
/а 4“я— + — О . . . (д).
Перемножая эти уравненія, найдемъ резольвентъ
Зх22(а“|“ Ь4“ <0®—(а24“^2Ч-с2 — 25с — 2са— 2«Ь) = О . . . (1).
Условіе дѣйствительности корней этого уравненія будетъ
(а -рЬ-р^)2 + 3(а3 + 5а + с2— 25с — 2са — 2а5) ^0,
или
а3 4~ 52 + с3 -— (Ьс 4~~ са 4~ Э- О,
или еще, расположивъ по степенямъ с, напр.,
с*— (а 4“ 5)с 4- а2 4~ 52 — «5^0.
Но корни тринома въ с мнимы, ибо его реализантъ
'(а + ^)2 " 4(а* + Ь2 — аЬ)
приводится къ —3(а*—5)2; слѣд., при всѣхъ значеніяхъ буквъ а, 5, с триномъ положителенъ, и корни ур—нія (1) всегда дѣйствительны.
Посмотримъ теперь, какіе знаки даютъ эти корпи подрадикальнымъ количествамъ уравненій (м) (п) . . . Подставимъ —а вмѣсто х въ первую часть ур—нія (1); эта подстановка дастъ въ результатѣ: —(5 — с)а; слѣд., одинъ изъ корней >— а, другой <С — а* Для перваго, слѣд., ж4“°Ч>0, для второго я4-а<0. На основаніи вышеизложеннаго анализа заключаемъ, что мень-
шій корень, х', будетъ меньше меньшаго изъ количествъ — а, — Ь, — с, и дѣлаетъ всѣ три радикала мнимыми; большій корень, я/', больше большаго изъ количествъ — а, — 5, — с, и дѣлаетъ всѣ три радикала дѣйствительными.
Разсмотримъ сначала большій корень а/'. Во-1-хъ, онъ не можетъ удовлетворять ур—нію (т). Чтобы онъ удовлетворялъ ур—нію (п), необходимо, чтобы было (а 4'я) 4" Ф+с4"или я<С с — а — Подстановка въ ур. (1) с — а — Ь вмѣсто я, какъ легко видѣть, даетъ результатъ:
4(с — а) (с — &).
Пусть а>Ь>с, что нисколько не вредитъ общности заключеній; въ такомъ случаѣ, этотъ результатъ положителенъ, и. слѣд., с — а—Ь лежитъ внѣ интервалла корней резольвента, и чтобы корень х" былъ меньше с — а- — Ь, необ-л 4- Ъ -р с . 7
юдимо, чтобы полусумма корней^ равная —’ была меньше с—а—О, ѵ л . п -ь 6 _ ’ *
откуда легко найдемъ, что должно быть: * или, что То же, с > а,
с>Ь,
Сдѣлавъ подобное же изслѣдованіе по отношенію къ ур—мъ Ср) и (<?), убѣдимся, что корень х” будетъ удовлетворять
уравненію (п), если
уравненію (р), если уравненію (д), если а->с*
Перейдемъ къ корню х\ который дѣлаетъ всѣ три радикала мнимыми. Чтобы этотъ корень удовлетворялъ одному изъ ур—ній (яі), (>0 . . ., необходимо, чтобы коэффиціентъ при }/—1 былъ нулемъ, т.-е. должно быть
|/—а —# + —Ь — —с—&=0. . .(2).
откуда снова четыре ур—нія. Составляя резольвентъ, получимъ снова ур. (1), котораго корень х\ дѣлающій радикалы ур. (2) дѣйствительными, необходимо удовлетворяетъ одному изъ ур-—ній (2). Очевидно, что никакое значеніе х не можетъ удовлетворять ур—нію (т'). Корень х* будетъ удовлетворять ур —нію если будетъ
т.-е. если
«
6;
с
этотъ корень удовлетворяетъ
уравненію (р'Х если
(9'), если
<
Резюмируя сказанное, заключаемъ, что:
ур—ніе (т) не имѣетъ рѣшеній;
ур—нію (я) удовлетворяетъ корень: если и =г", если
» (р) » » х\ > Ъ а и > Ъ
» ($) * > » я/, > а < и х\ > а
548. Что касается провѣрки корней, то иногда ее можно дѣлать и другими пріемами* Пусть, напр., требуется рѣшить ур-ніе.
р/а — дт = |/а.
Возвышая первый разъ въ квадратъ, найдемъ: 2|/а2— х* =— а; возвы-3 сивъ въ квадратъ другой разъ, получимъ: 4а* — 4#* = ая или #* = ^а*, откуда я —|/3- Подставляя иго или другое значеніе я въ данное ур., одинаково находимъ, по сокращеніи на /а:
У'+'-І+у/ і-^=і.
Такъ какъ обѣ части этою равенства положительны {то для провѣрки его можемъ и.гъ возвысить въ квадратъ; находимъ 1 1 -[- 1 == 1, что не-
вѣрно, слѣд* ни одинъ изъ корней не удовлетворяетъ данному ур-нію. Но если въ немъ передъ вторымъ радикаломъ взять —, то получится 1 — 1-|-1 = Ъ что вѣрно. Заключаемъ, что найденные корни принадлежатъ ур-нію
а 4- х — а — х = |/а.
549. Для провѣрки рѣшеній можно иногда съ успѣхомъ примѣнять преобразованіе сложнаго радикала въ алгебраическую сумму простыхъ радикаловъ. Пусть требуется рѣшить ур-ніе.
а
и провѣрить рѣшенія. Изолируя радикалъ, имѣемъ /х = а — а возвышая въ квадратъ, получаемъ
х* — (2а 4- 1) ж а* = О.
Корни этого ур-вія, которое общѣе даннаго, дѣйствительны при условіи (2а 4* 1)а — 4а*> О или Полагая это условіе выполненнымъ, нахо-
димъ 2 дѣйствительныхъ корня:
Нависавъ предложенное ур-ніе въ видѣ ^х= а — х, подставляемъ первый корень я'; въ первой части получается сложный радикалъ, который разлагаемъ на два простыхъ:
2а±1 + »^в±2 = 1 /2а_|_ і + 2 /а’Н-і /2а+1 — 2 |/а»
Когда а > О н равно -|~ а, то = + а; если же а <С О ц равно — а, то — — з; но легко видѣть, что въ обоихъ случаяхъ
/^±1 + і^+1 = 1+',/^+7.
Вторая же часть а — х ур-нія обращается въ
I
заключаемъ; что V, не дѣлая обѣ части ур-нія ^х = а — х равными, не удовлетворяетъ этому ур-нію; но легко видѣть, что этотъ корень удовлетворяетъ ур-нію х — /х = а.
Постановка второго корня х'1 даетъ въ первой части ур-нія ^х=а—х:
|/ ?«. + 1 + 1 = 1 / 2а 4- 1 4- 2 /а* — 1 / 2а +1 — 2 /а».
______
При а>0 это выраженіе приводится къ —>/4а-|-1; при а<0 къ между тѣмъ какъ вторая часть, а — лг, даетъ —5 +
^|/4а-|-и заключаемъ, что хц удовлетворяетъ предложенному ур-нію только при а > О. Итакъ: і
, 1 при <т<С—корни ур-нія мнимы;
при — | < а < О ур-ніе не имѣетъ рѣшеній;
П л. 1 н “I” I — 4л -р 1
при оно имѣетъ 1 корень, равный---------------9-----—
550. При рѣшеніи ирраціональныхъ ур-ній, какъ и всегда, слѣдуетъ пользоваться всѣми средствами, ведущими къ упрощенію вычисленій; въ этомъ отношеніи съ успѣхомъ примѣняются иногда и нѣкоторые искусственные пріемы.
1. Такъ для рѣшенія ур-нія
і^5х—4 —1/5 — а? кдя — 1
примѣняемъ свойство пропорціи (§ 308, II, (10)), и тотчасъ получаемъ, по со-
. л V 5л? — 4 /7-
кращеніи на 2: — = і/4я, откуда, по возвышеніи въ квадратъ и по осво-
|/5— х
вожденіи отъ знаменателя: 5х—4=20іг—4л*2, или 4я2 — 15л:—4 = 0. Легко провѣрить, что оба корня этого ур-нія: х = 4, = — - удовлетворяютъ
данному ур-нію.
2. Рѣшить ур-ніе я2— 1х~\-^х*— 7х-^-18 = 24.
Примѣняя пріемъ, указанный въ § 540, прибавляемъ къ обѣимъ частямъ ур-нія по 18, и въ ур-ніи
х» -л. 7а:_|_ 18 4- /х4 — 7x4-18 = 42
полагаемъ /х4 — 7х4~ 18 = у; рѣшивъ • ур-ніе въ у
У* + У— 42 = 0,
находимъ корни: у{ = 6, у"= —7. Отбрасывая второй, ибо въ данномъ ур-нів передъ радикаломъ стоитъ знакъ -р, получаемъ ур-ніе: х*— 7 а; 4" 18 = 6, откуда х* — ~х — 18 = 0. Легко видѣть, что корпи этого ур-нія: х'= 9, х" = — 2 удовлетворяютъ данному ур-нію.
♦
3. Пусть требуется рѣшить ур-ніе
(X 4-2)4 4-2/х(х 4-2) — 3/7= 46 4-2т;
это ур. легко привести къ виду: х* 4~ 4- 2х -|- |/х = 42 или
< і
!
(.г 4~ /я*)2 + Ф + /я) = 42...............................(а)
Положивъ /х = у, получаемъ ур-ніе у2 + у— 42 = 0, имѣющее корни у'=6, у"=—7. Затѣмъ рѣшаемъ ур-нія: .т-|-^Лг=6, или, освободивъ отъ радикала, х* — 13#4” 36 = 0; и х 4” х = — 7, или, по освобожденіи отъ ра-
дикала, я213я-|“49 = 0. Первое имѣетъ корни 9 и 4; второе —
Повѣрка покажетъ, что изъ пихъ ур-нію (а) удовлетворяютъ только 4 и _ 13 4-31/3.»
2
и • тт л 13 4-31/3. і
Ііримѣчалпе. Для провѣрки корня — ----- преобразовываемъ
/]3 . Зі/З . , Л к 31/3+» -
1/ у 4—г по формулѣ § 417,6, въ —2~- ?
/ 134-ЗГЗ . і 31/3 . і — Г
ъно, |/---------— въ---------2 — , и подставляемъ въ
4. Прежде освобожденія ур-нія отъ радикаловъ, въ нѣкоторыхъ случаяхъ,
полезно изслѣдовать, нѣтъ ли общаго множителя, на который можно бы было сократить уравненіе. Такъ, въ примѣрѣ
х* — 7ах -|“ 10а2 — >/х* 4“ ах — 6а2 = х — 2а,
разложивъ подрадикальные триномы на множителей, находимъ
/(х — 2а) (я — 5а) — /(х — 2а) (х За) = х — 2а.
Сокративъ на общаго множителя всѣхъ членовъ, ]/х —2а, найдемъ
^х — 5а — -|- За = ^х — 2а
и, по освобожденіи отъ радикаловъ, получаемъ ур. Зг*— %ах — 60а* = 0# изъ котораго х ~ 6а, х” = — Приравнявъ нулю множителя ^х — 2а, имѣемъ еще корень: х'" = 2а.
Повѣрка покажетъ, что изъ числа найденныхъ корней, 6а не удовлетворяетъ предложенному уравненію, которое, такимъ образомъ, имѣетъ два корпя: 10а Л ----д- и 2а.
Этимъ же пріемомъ упрощаемъ рѣшеніе уравненій
(1) /2х* — 9 с4-4 4-3/2х^Л = 21 х — 11,
(2) |/4х* — 7х — 15 — /х* — Зх = /х* — 9,
удаливъ изъ перваго предварительно общ. множ. >/2х —1, а изъ второго-/х— 3, Рѣшеніе(І) приводится такимъ образомъ къ рѣшенію пары: /2х — 1=0-и >/х— 4 4^3 = |/х—|—11, а второго—пары: >/х—3 = 0 и >/4x4-5—>/х = /х4-3. Найдемъ, что ур-нію (1) удовлетворяютъ корни: 5 и -у, а ур-ніиь ' (2): 1 и 3.
5. Вотъ еще полезный искуственный пріемъ. Пусть имѣемъ ур-ніе /2х*4~5х ~2 — ^2х*4”5х — 9 = 1,..(1)
Имѣемъ тождественно
(2х* + 5х — 2) — (2х* + 5х — 9) = 7.. .(2)
‘Раздѣливъ (2) на (1), получимъ
/2х* + 5х~— 2 4- /2х* 4- 5х~ 9 = 7... (3)
(2) есть тождество, вѣрное для вслнкха значеній х, тогда какъ (1)» есть уравненіе, вѣрное лишь для нѣкоторыхъ значеній х; слѣд., и (3) есть, ур-ніе, вѣрное для тѣхъ же значеній х. Складывая (1) съ (3), имѣемъ
4 2х* 4” 5х — 2 = 4,
э/а —
откуда
г =2, = —4|.
Рѣшая этимъ пріемомъ ур-нія
(1) /з®*—2®-|-9
(2) >/2І8 — 7^-[- 1
4- /Зі«_2х— 4 = 13, — >/2.га — 9х4~4 = 1,
(3) /З.г2 - 7х — 30 — |/2.с« — 7х — 5 = х — 5,
пользуемся тождествами:
для (1): (Зх3 — 2х Ц-9) — (Зх* - 2х — 4) = 13
для (2): (2хя — 7x4-1) — (2®* — 9х-|-4) = 2х — 3,
для (3): (Зл-Я — 7л — 30) — (2.га — 7х— 5)=х* — 25,
и находимъ корни:
(1) 4.-^; (2) 0 и 5; (3) 6 и
551. Приводимъ, въ заключеніе, примѣры на ирраціональныя ур-нія, содержащія радикалы выше второго порядка.
1. Рѣшить ур. 4“ х -Ь — і* =
Возвышаемъ обѣ части въ кубъ, примѣняя формулу («4"^)*=
Зію(и4-е); получаемъ:
в— х4~<*—а3 — х*(-]-X-4 —-я) = 2а.
Прмв&ія і замѣчая, что выраженіе въ скобкахъ, въ силу' даннаго ур., рав-> 2*і. вносимъ ур.
а* — .г1, ^2а^=0, или ^а3 — х3~0, откуда а'2 —жа = 0, слѣд.
= 4- а.
Оба кормя удовлетворяютъ предложенному ур—нію.
а -»4/1
4 _і_
4 Лгі— а-14
1 —т
Сокративъ дробь второй части на 1 4" а?
. > V1 + X 1
и слѣд. у получаемъ ур—ніе
откуда
Такимъ образомъ получаемъ ур. въ х:
или
откуда я
1 —ж__
1 + *
Корень этотъ удовлетворяетъ предложенному ур—нію.
3, Рѣшить ур—ніе
Выполнивъ умноженіе въ первой части, освободивъ ур. отъ знаменателя и приведя въ порядокъ, находимъ:
97х 3 +1296 = 0.
Это ур—ніе — квадратное относительно х* — даетъ: х* =81, я’ = 16, откуда:
х' = 813 = (Э*)3 = (3я/ = 27*; х* = 163 = (2*)3 = (23)* = 8*.
Рѣшивъ оба двучленныя ур—нія четвертой степени, находимъ 8 корней:
±27; ±271; ±8; ± 8і.
552. Въ заключеніе этой главы докажемъ теорему, что возможно всякое ирраціональное ур—ніе освободить отъ радикаловъ.
Теорема. Всякое ирраціональное ур. можетъ бытъ освобождено отъ радикаловъ* каковы бы они ни были и сколько бы ихъ ни было.
Пусть данное ур. содержитъ радикалъ гдѣ я — выраженіе, содержащее неизвѣстныя. Обозначивъ буквою х и замѣнивъ различныя степени степенями х, всегда можемъ привести ур. къ виду ур—нія раціональнаго относительно х. Освободивъ его отъ дробей, получимъ ур. вида:
Ао ± А4х ±к^х* ±
= о..Ді),
гдѣ Ао, Ар... не содержитъ |/я, но могутъ содержать другіе радикалы. Если здѣсь окажутся члены съ степенями х — са, большими т* то въ такихъ членахъ можно степени х сдѣлать ниже. Въ самомъ дѣлѣ, пусть имѣемъ членъ съ гдѣ раздѣливъ к на т и обозначивъ цѣлое число въ частномъ буквою а остатокъ г, напишемъ:
Ар?* = = аХ"9*
но 2 = хѵ\ откуда: яг™9 —я9; слѣд.
А* %к = Аа # #г, гдѣ г < т. а коэффиціентъ при хг не содержитъ радикала рЧг.
Понизивъ такимъ образомъ всѣ степени я, въ которыхъ показатели и собравъ члены съ одинаковыми степенями х, получимъ ур.
А0 + Л|Х-рА^1+ - . . +Ат^1Д?,"^1 = 0._(2).
Умножая это ур* сначала на я, потомъ на я?Ѵ., на ^ГЛ“г, и понижая каждый разъ степени высшія или равныя т-ой, получимъ «г—1 ур— пій:
А0^4”Аі^а4”^і‘г8_Н • • 4^А™—і# = О
Ао х*-]-Лі яэ + А4 4- * . . 4- АЯІ-2#4“ Ат-і= О
І
* * « • * В « в V
Ао я"1^3 4“ м+ Аа^ +
. * 4-ли_і/хт-э = о.
Эти ур—нія, вмѣстѣ со (2), даютъ систему т уравненій съ т — 1 количествами: х, ят”\ которыя и можно исключить изъ этой системы;
въ результатѣ исключенія получится одно ур*, не содержащее буквы я, т.-е. свободное отъ радикала ||/7. И т. д.
Примѣръ. Освободить по этому
способу отъ радикаловъ ур—ніе
«4-5 — 2 ^//лЧ = О.
Положивъ у^х = и сл. уЧг3 = иа, найдемъ
« 4“ 5ы — 2и2 = 0.,. (1).
Помно
зъ сперва на м, потомъ на «Ч получимъ:
аи 4“ 5«а — 2«в = О аи* 4~ 5н3 — 2 а1 ~ О,
Но «3 = х, і44 = их; слѣд* послѣднія 2 ур. будутъ вида
аы4"5и3— 2х=^О_.(’2) «иа4“ 5х —2нх = О..ДЗ).
Исключая изъ ур. (1), (2) и (3) количество и, найдемъ 8ха — 125а: — ЗОая — а3 = О,
Освобожденіе ур—нія (2) отъ радикаловъ можно" еще выполнить такъ. Умножимъ обѣ части его на полиномъ
В, + В1х + іѴ2+ . * . +Вж-2^-а+^м-1,
гдѣ коэффиціенты на время оставляемъ неопредѣленными* Умноженіе даетъ
АЛ + (АЛ4-Мі)ж+ • • .+Ат_ія*"-2 = 0.
Понизивъ степени я, гдѣ онѣ >т, полупимъ ур*
Со + С^ + С^Ч-. * . Сиі-і#"*”1 = О , . .(4),
гдѣ Се, Сі . - * суть 1-й степени относительно коэффиціентовъ В. Пользуясь неопредѣленностью послѣднихъ, полагаемъ
С,=О, С2 = О . ; .С™-і=От
откуда найдемъ всѣ т—1 коэффиціентовъ В0! Ві * * * Вж-2. Подставивъ ихъ въ ѵр. (4), получимъ
с; = о
ур—ніе, не содержащее радикала
Примѣчаніе, Этотъ способъ уничтоженія ирраціональности въ ур—ніяхъ умноженіемъ на нѣкоторый полиномъ, очевидно, можно прилагать и для уничтоженія ирраціональности въ знаменателяхъ дробей: для этого нужно только умножить числителя и знаменателя на прилично выбранный многочленъ.
ГЛАВА XXXVII.
Системы уравненій второй степени и высшихъ степеней, приво димыя къ квадратнымъ.
Системы уравненій, изъ которыхъ одно второй, остальныя — первой степени. — Системы двухъ уравненій второй степени. — Системы уравненій второй степени болѣе чѣмъ съ двумя неизвѣстными.—Системы уравненій высшихъ степеней, приводимыя къ квадратнымъ.
553. Уравненіе второй степени съ двумя неизвѣстными х и у есть цѣлое раціональное ур-ніе, содержащее члены: съ квадратами обоихъ неизвѣстныхъ,, съ ихъ произведеніемъ, съ первыми степенями неизвѣстныхъ, и члены, независящіе отъ неизвѣстныхъ; слѣд. это есть ур—ніе вида
А.г* + В^ + Су* + 0х4-Еу + Е=0.
Подобно этому, общій видъ ур—нія второй степени съ тремя неизвѣстными есть
Ах* -|7 Ву* 4“ № +1**!/ + Ех? + Н“ +„Ну + К? 4“ Ь = о и т. д.
Сатглоад уравненій второй степени съ двумя или нѣсколькими неизвѣстными называютъ такую систему, въ которой по крайней мѣрѣ одно ур—ніе— второй степени, а остальныя—первой или второй степени.
I. Системы ур—ній, изъ которыхъ одно— второй степени.
554. Система ур—ній съ двумя неизвѣстными, изъ которыхъ одно—второй, а другое—первой степени, имѣетъ видъ:
। А^ + В^ + С^2 + Па?+Еі/ + Е=О....................(1)
| Ьх + Му + Х = 0..................................(2)
Выражая изъ (2) у въ зависимости отъ я, имѣемъ
Внося это знаменіе въ ур. (1). получимъ:
А М ‘ ' М ‘ г — *
Выполняя дѣйствія, располагая члены по степенямъ х и полагая для краткости
Р = АМ2 - ВЬМ + СЬ2, 4 = — ВМЯ + 2СЬК + ЭМ2 — ЕЬМ,
К = С№ — ЕМХ + ні2, замѣняемъ данную систему ей эквивалентною: і»*»+4*4-8=о,
Первое ур—ніе дастъ для х два значенія: а/ и я"; внося ихъ поочередно во второе ур., найдемъ соотвѣтствующія значенія для у: у' и у". Итакъ, данная система ур—ній имѣетъ двѣ системы рѣшеній:
х = а/, у = у' и х = у = у".
Эти рѣшенія будутъ мнимы, если 42 —4І1Е<0; представятъ двѣ дѣйствительныя системы при О2 — 4РК > 0; и сливаются въ однѵ систему рѣшеній при 42—4РК = О.
Примѣръ. Рѣшить систему
5х* ~ 8ху -|~ 4" эу -± 4 = О,
6х — у — 4 = 0.
Изъ второго ур—нія имѣемъ: у = 6х — 4; подставляя это значеніе у въ первое урм находимъ: 7х2 — 7х = О, откуда: х' = 0, х” ~ 1. При х* = О имѣемъ у' = — 4; при х" — 1 получаемъ у = 2. Итакъ, находимъ двѣ системы рѣшеній:
^ = 0, = — 4; х"=1, у"=2.
555, Пусть дана система п ур—ній съ п неизвѣстными, и пусть одно изъ этихъ ур—ній — второй степени, а остальныя — первой. При помощи п — 1 ур—ній первой степени можно п — 1 неизвѣстныхъ выразить черезъ н-ое; такимъ образомъ получится н—1 новыхъ ур—ній 1-й степени вида
у = ах 4~ Ь г = ах 4- Ь' и = а"х+ Ъ”
Внося всѣ эти значенія въ ур—ніе второй степени, получимъ квадратное ур, съ неизвѣстнымъ х; изъ него найдемъ для х два значенія: х' и х". Каждому изъ этихъ значеній соотвѣтствуетъ своя система значеній неизвѣстныхъ у, «,... Данныя ур—нія имѣютъ двѣ системы рѣшеній, г
Примѣръ. Рѣшитъ систему
х2 4“ Зл2 -2уя—1 Оху — 2л; 4" 5у— 25= О, 5х4-22у4-7^= 4, 21х— 7у4“ я = 31.
Выражая изъ двухъ послѣднихъ ур—ній у и я черезъ х, имѣемъ у = 2х—3, з =— 7x4-10;
внося въ первое ур—ніе, находимъ квадратное ур. въ х;
х2 — Зх4~ 2 = О,
откуда: х'=1, х" = 2. Слѣд, рѣшенія предложенной системы будутъ:
Xх = 1, у'= — 1. ? = 3; и х"= 2, у,г= 1, /'= — 4.
556. Разсмотримъ рѣшеніе нѣкоторыхъ замѣчательныхъ системъ, прилагая особые искуственные пріемы, болѣе изящные, нежели указанный общій пріемъ.
I, Рѣшитъ систему х-[-у=а 1 ху = М |
Такъ какъ здѣсь дается сумма и произведеніе неизвѣстныхъ, то послѣднія опредѣлятся какъ корни квадратнаго ур—нія, имѣющаго коэффиціентомъ при первой степени неизвѣстнаго количество —а, а извѣстнымъ членомъ I*2:
г2 — аз + Ь2 = О,
откуда ______
г в 4 — 46® « а —- |/ а2 —462
-----’ =“-----9----
Одно значеніе з принимаемъ за х, двѣ системы рѣшеній:
, _ а + Vха2 — 46®
— - §
д 1/д2 — 462
У =--------о —
другое за у; такимъ образомъ получаемъ
„ а — Ра2— 46® х = —----„— —
2
„ а 4-/а2— 4&2 у = —......
Что такъ должно быть, понятно а ргіогі, ибо х и у въ данныя уравненія входятъ одинаковымъ образомъ.
Другой пріемъ. Возвысивъ первое уравненіе въ квадратъ, имѣемъ: х2 -1- 2ху у1 — а?*, помноживъ второе ур.'на 4 и вычтя изъ предыдущаго, находимъ: х* — 2ху 4~ у® = а2 — 46\ или (х — у)2 = а2 — 46а; откуда х — у==Чк|/аа — 46а. Такимъ образомъ, предложенная система можетъ быть замѣнена двумя ей эквивалентными:
\ х — у ~ ]/ а1 — 46® Н х •— у — —а?— 4а®.
Рѣшая ту и другую, найдемъ прежнія двѣ системы рѣшеній. II. Рѣшитъ систему
х — у = а
, ху = Ь2.
Легко эту систему привести къ предыдущей: стоитъ только положить Ѵ = — у', Такимъ образомъ получимъ ур—нія
а? 4*/ = а, ху'=— Ьа,
изъ которыхъ видно, что х и у1 суть корни ур—нія г2 — _ ь2 = О,
слѣд., вторая система имѣетъ рѣшенія:
а — ^#2 + 4д‘2
, а + ѵ'а^-і-АЬ* У=----------‘
Подставляя сюда у вмѣсто—у’, найдемъ рѣшенія предложенной системы:
а — І^а2 4- 462
Другой пріемъ. Возводя первое изъ данныхъ ур—ній въ квадратъ, , умножая второе на 4 и складывая, получаемъ
= 45й, откуда ж 4~ У = + р/а24~4Ь3.
Такимъ образомъ предложенная система замѣняется двумя:
|х—у = а |х—
і ж +1/= +/^«4-463 " 1 х-|-у=-/а» + 4І’*,
изъ которыхъ и находимъ прежнія двѣ системы рѣшеній.
III. Рѣшить систелі/
-и,,
Возвысивъ въ квадратъ обѣ части второго ур—нія, имѣемъ жа4-2^-)-!/2=Ьа: вычитая изъ этого ур—нія почленно первое, имѣемъ: 2ху~5- —а2, откуда
Такимъ образомъ извѣстны: сумма Ь и произведеніе —— неизвѣстныхъ X И У; слѣд. я и у суть КОрНИ ур—НІЯ
= 0.
Итакъ, имѣемъ двѣ системы рѣшеній: . ।
Ь + Ѵ2а2^^ ( Ь — /2а2^52
2 Х =--------2------
, ____- и \ .------
Ъ — Ѵ2ла - б2 5 + і/2а* — 52
2 I V 2 *
№
IV. Рѣшить систему
х — у = Ъ.
Рѣшеніе этой системы приводится къ предыдущей; ибо, положивъ у == — у\ получаемъ систему
л24-у'* = аа, #4-/ = ^
откуда прямо можемъ написать обѣ системы рѣшеній:
V. Рѣшитъ систему х2 — у2 = а2 •С +у =ь.
Исключивъ у, найдемъ ур—ніе 2Ьх— —первой степени; изъ него
««4-6’ . Ь2-а«
х — .' ; и слѣдовательно У = —
Можно рѣшить эту систему еще такъ: замѣчая, что1 х*—уі—(х^гу)(х~у], мы, раздѣливъ первое ур. на второе, найдемъ ур.
Л2
Х~У = 7^
комбинируя это ур—ніе съ ур—нъ х-р # = найдемъ х и у.
Подобнымъ же образомъ рѣшается система
х2— у* = а* х — у
II. Система двухъ уравненій второй степени съ двумя неизвѣстными.
557. Вообще, система двухъ ур—ній второй степени съ двумя неизвѣстными приводитъ къ полному ур—нію четвертой степени.
Пусть данная система будетъ:
ш?* 4” Ъху 4~ су2 -|“ "Ь €У / " 0 . . . (1)
а'л:24’ 2^4” СѴЧ“ ^4~ ^у-\~Г= 0 . . . (2)
Исключимъ сначала умноживъ ур. (1) на с\ (2) на с и вычтя почленно одно ур. изъ другого; найдемъ ур—ніе
(ас? —- са')#а 4“ “ сй')яу 4“ — 4" (ее?г — се9^ — СЛ =
или, обозначивъ каждый изъ коэффиціентовъ одною буквою:
&2 4~ 4“ 4~И/ 4" 9 " О ’ ’ • (^)*
Это ур—ніе, въ сочетаніи съ однимъ изъ данныхъ, напр. съ (1), составитъ но-
вую систему, эквивалентную данной. Изъ ур. (3) находимъ
_____ІхѴ-^пх-}- д
& тх 4- р 1
подставивъ это значеніе у въ ур. (1), получимъ
ахі __ пх + д) . с(№ + пх -И д)2 =
Освободивъ это ур. отъ дробей, выполнивъ всѣ вычисленія п приведя въ порядокъ, получимъ, вообще, яолное ур. четвертой степени:
Аа* + В.т> + Сг» 4- 4- К = О . . . (4).
которое, въ соединеніи съ (3), составляетъ систему, эквивалентную данной Полное ур. четвертой степени (4) въ общемъ видѣ, хотя и можетъ быть рѣшено средствами элементарной алгебры, но обыкновенно не вводится въ кругъ ур— ній, разсматриваемыхъ въ низшихъ отдѣлахъ алгебры; элементарная алгебра занимается рѣшеніемъ ур—нія 4-й степени только * въ нѣкоторыхъ частныхъ случаяхъ, когда напр. оно биквадратное, или возвратное, или степень его понижается до второй; въ такихъ случаяхъ безъ особаго труда найдемъ четыре значенія для х- подставивъ каждое изъ нихъ въ ур. (3), получимъ четыре соотвѣтствующія значенія для у.
Такимъ образомъ, данная система принимаетъ, вообще, четыре рѣшенія.
Примѣръ. Рѣшитъ систему
я*4~2яі/— 8у* — 6#4“ ~ 7 = О . . . (1)
2х2— эху — Юу* — 3^4“ 4“ 7 — О . . .( 2).
Исключивъ у\ получимъ ур—ніе
х*— 10^4-6л; — 18у+ 21 — 0 •
(3),
изъ котораго
х2 4~ + 21
10г+18 ~
• • • (3').
Подставивъ найденное для у выраженіе (3') въ ур. (1), находимъ
х' — Ю^4Г9 = О ... (4)
ур—ніе, составляющее съ (3) систему, эквивалентную предложенной. •
Но ур. (4) — биквадратное; рѣшивъ его, получимъ для х четыре значенія
Вычисливъ по формулѣ (3'), соотвѣтствующія значенія у, найдемъ
Уі = 1, у* = 2, ?/8 = 1, у4 = —1. *
Итакъ, данная система имѣетъ четыре рѣшенія:
• [ х.= 1 [ х9 = — 1 ( А = 3 ( х. = — 3
Ѵі=і Ѵ»= 2 ) =1 Оі=—
558. Когда одно изъ ур—ній разлагается на два раціональныхъ множителя первой степени, то рѣшеніе всегда можно привести къ квадратнымъ ур—мъ.
Въ самомъ дѣлѣ, выразивъ изъ ур—нія (1) § 557 у по я, имѣемъ
— (6й? 4-е) — і/ (Ьас + е*2 — 4 г? (аа# + 4- Г)
Расположивъ подрадикальное выраженіе по степенямъ х, получимъ (Ь2 — 4ас)&* 4“ -(^е 2оі)х + е2 — 4с/;
оно будетъ точнымъ квадратомъ при условіи
(Ье — 2сД)2 = (&а — 4ас)(е* — 4с/);
какъ скоро это условіе существуетъ, значенія у будутъ раціональны:
— Ъх — е ± (Рйс 4“ V)
У = ------------- >
гдѣ Р#-|-(і есть изъ подрадикальнаго выраженія; имѣемъ
(Р — Ь)#4- 9 “с ---------------
у" =
слѣд. ур. (1) можно представить въ видѣ с(у — у')(У — У") = 0; слѣд. это У Р-будетъ удовлетворено, во-первыхъ, значеніями х и у, удовлетворяющими ур—нію
, а во-вторыхъ, такими значеніями, которыя, обращая въ нуль у — у'\ удовлетворяютъ ур—нію
У------(Р + ЗД. + О + . . . . (4).
такъ что вопросъ сводится къ рѣшенію двухъ системъ: (2), (3) и (2), (4); каждая изъ нвхъ составлена изъ ур—нія 1-й ст. и ур—нія 2-й ст,, а потому приведетъ къ ур—нію 2-й ст. въ я, для котораго и получится 4 значенія; подставляя ихъ въ ур—нія (3) и (4), найдемъ соотвѣтствующія значенія у.
Примѣръ. Рж&шпь систему
2я4 — 5а;т/ 4“ Зу2 —За? — 2у — 5=0,
4” я#— #а4~ х— # — 6 = 0.
Изъ перваго имѣемъ
5.т 4- 2 — іЛеЯ — 16а -к 64 5#4~ 2 ± (я — 8)
=----------------------=----------
откуда
Подставляя вмѣсто у его величину х — 1 во второе данное ур—ніе, получаемъ: х2 -ря •— 6=0, откуда = 2, = — 3; а соотвѣтствующія значенія
У: Уі =Ъ У» = —4.
Для у —^ л”-- имѣемъ ур—ніе &—2х—94=0, изъ котораго ха=3,015 и х\ = — 2,834; а соотв. значенія ]/3 = 3,677 и у1 = — 0/224. Итакъ данная система имѣетъ рѣшенія:
(^=2 |я:а=—3 |іСа = 3,015 н = — 2,834
|Уі=і’ (Уа=—4’ Ѵз = 3>6'7 (#4 = ’-°і224.
559. Когда одно изъ ур—ній оЗмо/мміяо по отношенію къ х п у, можно пользоваться слѣдующимъ пріемомъ. Пусть, напр., ур, (1) § 557 однородно, т.-е. приводится къ
ах* -|- Ьху су2 ~ О,
то, раздѣливъ всѣ его члены на дадимъ ему видъ:
\У/ 1
Рѣшая это квадратное относительно ф два значенія: у = т\ откуда
х . . -г
— ур—ніе, найдемъ для отношенія — у У
х — ту* х = ту,
Комбинируя каждое изъ этихъ ур—ній со (2), получимъ двѣ системы, изъ коихъ каждая состоитъ изъ одного ур—нія 1-й ст. и одного 2-й степени.
Примѣръ. Рѣшитъ систему
3,г2 -4- 13.гу — 1 Оу'2 = 0 . . . .(1)
2^-^^ — + — 34 = 0. . .(2).
о
Ур. (1) даетъ: х — ~ у и х= — 5у. Комбинируя первое изъ этихъ ур—ній со (2), находимъ два рѣшенія
^1 = 2, Уі = 3 я ^ = — 4, Уі = ~ 6.
Рѣшая систему, образуемую ур—мъ (2) съ х = — 5і/, находимъ еще два рѣшенія
= 5. і/3 = — 1 и #4 = — 5, у4 = 1
Не остановливаясь далѣе на этихъ частностяхъ, не имѣющихъ, къ тому же, большихъ приложеній въ начальной алгебрѣ, перейдемъ къ рѣшенію нѣкоторыхъ замѣчательныхъ простыхъ системъ, часто встрѣчающихся въ прило-женіяхъ.
560. Рѣшитъ систему
+ У* = а, = Ь.
Умноживъ второе на 2 и сложивъ съ первымъ, а потомъ вычтя изъ перваго, наюдимъ
х2 + 2ху + У* = а + 26, или и я2 — 2яі/ -|- у* = а — 26, или
О + у)2 = а-р26 , . . (1) (я— у)* = а — 26 , . .(2).
Изъ ур—пій (I) и (2) находимъ
X “Р у = 4^ 4“ 26, X — У ---26.
Отсюда, складывая, а потомъ вычитая, имѣемъ
х = V « + 26+ ]/а — 26], у = ^[+ ]/<* + 26 =й |/а — 26І
Комбинируя знаки всевозможными способами, получимъ четыре значенія для х и столько же для у\ чтобы изъ нихъ составить системы рѣшеній, удовлетворяющихъ даннымъ ур—мъ, достаточно замѣтить, что произведеніе х на у, въ силу второго ур—нія, должно давать 6. Легко убѣдиться, что это требованіе будетъ выполнено, если въ формулахъ х и у передъ первымъ радикаломъ возьмемъ одинаковые знаки, а передъ вторымъ противоположные. Такпмъ образомъ получимъ 4 системы рѣшеній:
[ х* []/а+ 26 +р'а— 26] I ха = |[/а+26—/а —26]
I » I ь
к \
I Уі =|[р/“+ 2Ь~ 26] | & = |[/“+2&+/а — 2&]
| Уа = і}[—/«+26—/а—26] | у, = | [—/«+26 +/а—26].
Другой способъ- Возвышая въ квадратъ второе данное ур., замѣняемъ данную систему болѣе общею
ж*+у* = «, л*у4 = 6* . - .(а)
Зная сумму а и произведеніе Ъ* количествъ х4 и у4, найдемъ ніъ какъ корни квадратнаго ур—нія
я2 — ая + 62 = 0:
= 1 + у4 = |+^-Ь4.
Извлекая квадратные корни, получимъ:
откуда легко составить прежнія комбинаціи соотвѣтствующихъ значеній а? и у. Легко ихъ привести къ прежнему виду. Возьмемъ, напр., формулу х и приложимъ къ ней преобразованіе сложнаго радикала
имѣя
А = ^> В = у — і2, А2 — в=ь2.
Найдемъ
±|/|+Ѵ т-ь*=^М»/й7й+/г-г2’ьЬ
Такимъ же образомъ преобразуемъ и у, » -
561. Рѣшитъ систему
х2 -{- + У* — ах — ау = О, я3 — 2ги/ 1/2 — Ь# 4" Ьу —
Эту систему можно написать въ видѣ:
(х+У)2 — а(х+у) = О, (X — у)2 — Ь(х — у) = О, пли:
(ж-|-у)(ж + у — а) = 0, (ж —у)(ж —у — Ь)=0.
Рѣшеніе данной системы распадается на четыре другія:
|^4~?/ = О, |^4~Ѵ = 0' = |#4-у— 0 = 0,
"[х —# = 0, — у — Ъ = 0^ — « = 0, ^я?—-у — Ь = 0,
изъ которыхъ получаемъ:
III. Системы уравненій второй степени болѣе нежели съ двумя неизвѣстными.
562. Примѣръ I. Рѣшитъ систему
х(х + у4-+ + = Хя4^4"^) = с*-
Складывая и вынося за скобки я?4~у4“^ получаемъ
(^4“У+ ^)2 = °2 + Ь2 + ^ откуда #4“У+
Замѣняя въ каждомъ изъ данныхъ ур—ній его величиною, по-
лучимъ двѣ системы рѣшеній, 'взявъ передъ радикаломъ сперва потомъ — :
/ а*
— —.— . ..
________Ь2
* У ~ /а2 4- Ь'Н-’йі и й»
2 = —_______
/а» + г>2 4- /Я
— Я2
Г—- — -------—
|/а* + &* + с«
____ — Ъ\
У ~ /Й2 ф Ь2 +”2
— й2
2 — —— -
' і/а24-624-^
563. Примѣръ II. Рѣшитъ систему
х'-\-уг — с (1)
у2 4“ хг = с (2) з*
ху = а . . . (3)
Вычитая (2) изъ (1), находимъ
(«—у)(®4- У) — 2(х—у) = О,
или (х — у)(х-\~у— г) = О.
Данная система распадается на двѣ:
х — У = О (2)
у'14- хз = с (2) г2 4_ ху = а (3)
дт4~у —я = О (3)
п у24-аи = с (2)
г24“ ху = а. (3)
Рѣшимъ, напр., вторую.
Приравнивая значенія г изъ (?) и (2), получаемъ
х 4- у.— С — । или х* + у2 4~ ху = с, или (х 4~ у)2 — ху = с,
или, такъ какъ изъ (^) имѣемъ ^4“?/ = ^, то
в* — ху — с.
Это ур. вмѣстѣ съ (3) даетъ
» а 4- с /а + с а — с
г* = откуда = ± |/ —и ху = —2~-
Такимъ образомъ 0 'найдено; для опредѣленія х и у замѣчаемъ, что нз- / вѣстны: сумма # + равная т.-е* + и произведеніе ху, равное
~т^- Сл. х ъ у опредѣляются какъ корни ур—нія
• х+4^ = о,
откуда:
а 4~ с і |/а с а — с Ѵ7а -Н? тг Ѵ5с — За 2^2
8
2
5
Каждое значеніе я даетъ намъ двѣ лично м. б. взято равнымъ X' или X", получимъ 4 системы рѣшеній:
системы значеній х и у, ибо х безраз-и слѣд. у равнымъ X' или X*. Итакъ,
і/а с + і/5с — За
IV. Системы уравненій высшихъ степеней, приводимыя къ квадратнымъ.
564. Примѣръ I. Рѣшитъ систему
х-\-у = 17 . . , (1) #84“У3 = 1343 . . . (2).
Возвысивъ ур. (1) въ кубъ, находимъ
^’ + г/’ + З-г^(ж-|-«/) = 4913 . . . (3).
Это ур—ніе общѣс ур—нія (1); именно, мы знаемъ, что если обозначить одинъ изъ мнимыхъ кубичныхъ корней изъ 1 бюквою а, то ур—нію (3) удовлетворяютъ значенія я и у, повѣряющія каждое изъ ур—ній: (Ж’-|-у)=17а, о?-|-у=17а\ х~\-у~ 17а8. Но если мы замѣнимъ въ немъ числомъ 17, то этимъ мы выразимъ, что корни его удовлетворяютъ ур—нію (1), и слѣд. паразитные корни будутъ устранены. Итакъ, замѣнивъ въ ур—ніи (3) х^у числомъ 17, подставляемъ вмѣсто него ур—ніе #3-р^3Ч“5иу = 4913, или, въ силу ур—нія (2):
51#у = 4913— 1343, или ху = 70.
Зная сумму и произведеніе х и у, найдемъ эти количества, какъ корни квадратнаго ур—нія
и2 — 17^ + 70 = 0,
- откуда:
я'= 7, у7 =10, или а?" =10, у" = 7.
Кромѣ того, данная система имѣетъ третью систему рѣшеній, образуемую безконечными и противоположными по знаку величинами х и у.
Другой способъ* Можно бы было употребить еще слѣдующій методъ* Ур—ніе (2) можно представить въ видѣ:
— 1343, пли, замѣнивъ #4~^ числомъ 17:
і я* —яу4^* = 79.
Прибавимъ къ обѣимъ частямъ по Зху, помчимъ:
(х -|- ,ѵ)" == 79 -р и;іи 239 = 79 4“ или ХУ = "9.
Далѣе вычисленіе окончивается какъ выше указано.
565. Примѣръ П. Рѣшитъ систему
х-\-у = а . . * (1) .т34”’ (2)
Возвысивъ въ пятую степень обѣ части ур—нія (1) и сгруппировавъ извѣстнымъ образомъ члены, получимъ:
• I
4“!/54“ 5эд(^а4“<ѵ*)4" іо#2#а(#4"^) ~ а*і или
я54~Уя + 5дл/[(й;4“2/)3*“ 3($4“#)^] +1°(я4-$)яу = ав . - . (3) *
Это ур. не эквивалентно (1): если обозначимъ буквою а одинъ изъ мнимыхъ корней 5-го порядка изъ 1, то ур—нію (3) удовлетворяютъ корпи каждаго изъ уравненій:
г
хА-у = аа, #4“У = яа^ = яя8, ^4'У==ад4т х-\-у ==(№*.
Но если мы замѣнимъ въ немъ #4~?/ количествомъ а, то этимъ самымъ исключимъ изъ него рѣшенія четырехъ паразитныхъ уравненій, и останется уравненіе
г3 4- у5 4-5ху(а3—Заху) 4“ ІО^У = а8 . . . (4).
которое со (2) образуетъ систему, эквивалентную данной.
Ур. (4) можно представить въ видѣ
эа(ху)1 — 5а*(л?у) 4~ — Ьй = 0.
Будучи квадратнымъ относительно яу, оно дастъ два значенія для каждое изъ нить комбинируемъ съ ур—мъ х4^У = а- Такимъ образомъ получимъ четыре системы рѣшеній: пятую систему составятъ значенія х и у безконечныя по величинѣ и противоположныя по знаку.
566. Примѣръ ПІ. Рѣшитъ систему
* = а®. ,,(3).
Возвысивъ обѣ части ур—нія (1) въ квадратъ, полу чаемъ
х8 4~ У3 4" Н- 2(жу 4“ хг -}- уг) = а3,
или, по причинѣ ур—нія (2):
ху -|- хг + уг = О . . .(4) откуда ху = — з(х -|- у) , . .(5).
Возвысивъ ур. (1) въ кубъ, получимъ: '
** 4- (х 4- у)3 -|- Зх(х + у)(х 4- у 4- х) = а8,
или, принимая во вниманіе ур—кія (1) и (3):
Зху(х 4* У) + + У) = О,
*
а, въ силу соотношенія (4),
ху(х 4- у) — аху = О, или ®у(ж4"У — “)= 0 • • • (5)-ч
Это ур—ніе требуетъ, чтобы было: или жу=О, или = Есл. то должно быть: пли или да=О. При я=0, ур—ніе (4) дастъ уе— О Слѣд* необходимъ еще, чтобы было: или у— 0, или ^=0, причемъ при у = 0 будетъ 2= а, а при -г = 0 имѣемъ у = а* Итакъ имѣемъ систему
I
у' — 0, я' = а;
х"= 0, /'= а, я"= 0.
Если х-^-у — а, тогда ^ = 0; и по причинѣ (4) нужно еще, чтобы было х=а п у —0; или ж = 0 и у = а. Отсюда третья система рѣшеній:
= у'" = 0, У" = 0.
Иначе, необходимо и достаточно, чтобы два изъ неизвѣстныхъ были нули, а третье а*
567. Примѣръ IV. Рѣшитъ систему
хи = да, # 4“ У “Ь я Н“ и ~
х2 у2 И- я2 4~ № = 4" у14~ 4’и*~ о1,
*
Примемъ за вспомогательныя неизвѣстныя: произведенія хи = уг =у, и суммы х-]-и = і п у-\-з = ѵ. Такимъ образомъ прямо получимъ:
і-^ѵ — а. . .(1) і’4-а2 — кі = Ь2 . . .(2)
+1>‘ - 4д(<8 4- ѵ3) + 4?3 = с‘ . . . (3)
Выразивъ 2 изъ ур—нія (2) и подставивъ въ (3), имѣемъ
4(^4 4- ®8) — 4(<8 4- ѵ3)(і3 4- »3 — Ь3) 4- + «’ — 63)3 = 4с‘,
или
— 8г V + 4&*(/2 + ѵ*) 4- р + V* — Ь2)2 = 4с\
Подставивъ сюда вмѣсто ^24“ѵ8 его величину а2 —2ѵ/, выведенную изъ (1)» и обозначивъ ѵі буквою 8, для опредѣленія 8 имѣемъ ур—ніе
482 + 4(а* + Ь2)8 + 4с1 — (а2 + 62)2 = О.
Найдя корни 8' и 8" этого ур., найдемъ ѵ и і изъ ур—ній
X2 — аХ + 8х = О, X2 — »Х + 8" = О.
Первое дастъ для ѵ и і систему У, второе—систему ѵ", 2"; изъ ур—нія (2) найдемъ соотвѣтствующія значенія для д: и Наконецъ, найдемъ двѣ системы значеній для х и и изъ ур—ній
X2 — ГК + д' = О, X2 — Г X + = О,
и двѣ соотвѣтственныя системы значеній для у и я изъ ур—ній
У2 _ г/у 4- О, У2 — ѵ"У -И" - О.
568- Примѣръ V. Рѣшить систему
^4-у1 —яѴ = я(я+у)* • . - (і) у)2 = , .(2).
1-й способъ. Помноживъ (2) на 4 и сложивъ съ (1), получимъ:
(л; + у)<~15хѴ = (а + 4^)(х + у)2 . - . (3). *
Положивъ х-|-у = ^, ху = і\ дадимъ ур—мъ (2) и (3) видъ
#(м2 — 4я) = Ъи\ и1 — 15ѵа = (а 4" 4б)«2,
исключивъ и\ получимъ квадратное ур. относительно ѵ.
2-й способъ (неопредѣленныхъ коэффиціентовъ).— Помножимъ ур—нія (1) и (2) соотвѣтственно на неопредѣленные коэффиціенты а и р., затѣмъ опредѣлимъ а и рі такъ, чтобы первая часть новаго уравненія, которое, однородно по отношенію къ х и у, дѣлилась бы, какъ и вторая часть, на #4зл Зта пеР" вая часть, очевидно, есть а(я<4-#4 — ^э^)4'—у)2; и какъ она должна быть нулемъ при замѣнѣ въ ней х количествомъ —у, то имѣемъ условіе: а — 4р = 0. Можно взять и равнымъ 1, тогда а = 4, т.-е.: чтобы выдѣлить множителя въ первой части новаго ур—нія, нужно помножить на 4 обѣ части ур—нія (1) и сложить со (2). Найдемъ:
(а;4-уУ(4лі + 4у* — ~ху) = (4а -|- Ъ)(х у)’:
итакъ, множитель (ж-[-у), и даже его квадратъ, обнаруженъ въ первой части предыдущаго ур—нія. Приходимъ такимъ образомъ къ рѣшенію системъ
а:-|-у = О, ®у(ж —У)’ = Ь(ж+у)г;
4(жа Уа) — ?«У 4а жу(« — У)’ = 4“ у)’.
Первая система даетъ х=у — О. Для рѣшенія второй полагаемъ гс-{-^ = 2^, х— у = 21. Затѣмъ получаемъ выраженія ^’э + у3 и ху въ § и /, и подставляя ихъ въ оба предыдущія ур—нія, получаемъ два ур—нія въ 5 и кото-фыя рѣшить не трудно.
569. Примѣръ VI. Рѣшить систему:
(х» + у*)(® + у)‘— а(х2 + 2/*).. .(1) ж‘ 4-у* — Зху = у*).. ,{2).
Множа данныя ур—пія соотвѣтственно на к и |і накладывая почленно, находимъ въ первой части полиномъ
> .(®,4-у*)(®+у)4-и(«*+»*”ЗлѴ). • .(3).
к
Опредѣлимъ к и И такъ, чтобы полиномъ (3) дѣлился на ?аз"
сматривая какъ произведеніе комплексовъ х-^уі^ х—уі, посмотримъ,
каково д. б. соотношеніе между к и р, чтобы полиномъ (3) дѣлился на уі. Для этого надо, чтобы результатъ подстановки уг вмѣсто х въ этотъ полиномъ былъ нулемъ. Находимъ условіе: 2кЦ-5р = О. Подстановка дала бы тотъ же результатъ; слѣд., при к и р, удовлетворяющихъ этому условію, полиномъ (3) раздѣлится на -р у3. Можно взять, напр. к ~ 5 и и = — 2. Итакъ, умноживъ ур—нія*( 1) и (2) соотвѣтственно на 5 и — 2 и сложивъ ихъ, получаемъ
-|- у*) -|- 5яу] = к(5а — 2Ь)О* у2).
Вопросъ приведенъ къ рѣшенію двухъ системъ:
* . + + ^ + ^=0;
я1 -|- у1 — Зх'У = + $/3), 3(.г2 т/2) эху = 5а -— 26.
Первая система даетъ: = у —О. Для рѣшенія второй полагаемъ:
= ху = ѵ, и выражаемъ и черезъ и и ѵ; такимъ
обр. получаемъ два ур—нія
— /т2-—2(2иг— Ь)ѵ —ѵ2 = 0, Зк2—ѵ = 5а — 26; -исключивъ изъ нихъ ѵ, найдемъ биквадратное ур. въ «.
ГЛАВА XXXVIII.
Уравненія: кубичное и четвертой степени.
Рѣшеніе полнаго кубичнаго уравненія.
570. Выводъ формулы корней. Всякое кубичное уравненіе дѣленіемъ на коэффиціентъ при & всегда можно представить въ видѣ
.Г3 4- Я4Г2 4~ + с = 0.
Въ такомъ ур. всегда можно уничтожить членъ съ квадратомъ неизвѣстнаго, тѣмъ самымъ пріемомъ, какимъ уничтожали второй членъ въ квадратномъ ур—ніи. Въ самомъ дѣлѣ, подставивъ вмѣсто х въ наше ур—ніе у + к, гдѣ новое неизвѣстное, а Л — пока совершенно произвольное количество, и расположивъ члены по степенямъ у, найдемъ
у3 -Н (ЗА 4“ а№ 4* (ЗА* 4- 2ак Ч- Ь)у А3 4"-ь Ьк 4- с=0.
Пользуясь неопредѣленностью количества А, распорядимся имъ такъ, чтобы коэффиціентъ при у* обратился въ ноль; именно, положимъ ЗА-ьа = 0, откуда А — — подставивъ въ послѣднее ур—ніе — вмѣсто Л, и положивъ для крат-о о
кости
а« , 2,1,,
— — чуй’— + с =
получимъ ур—ніе
У’ + РУ + 2=° •••(!)
которое и будемъ считать нормальною формою кубичнаго ур—нія.
Чтобы рѣшить это ур—ніе, положимъ
у = и + ѵ,
гдѣ и и ѵ пока произвольныя количества, связанныя только однимъ условіемъ, что сумма ихъ даетъ корень ур—нія (1). Подстановка въ это ур-ніе дастъ
или
(и и- г)3 Ч- р(и ч-1;) 4- = О,
к3-+-і4-ь(и4' ѵ) (рн-Зиѵ) -ьд = О , . .(2),
т.-е. одно ур—ніе съ двумя неизвѣстными, которое, поэтому, имѣетъ безчисленное множество рѣшеній: давая і? какое-нибудь частное значеніе, получимъ ур. съ неизвѣстнымъ и, которое дастъ соотвѣтственное значеніе этого неизвѣстнаго. Изъ безчисленнаго множества способовъ удовлетворить этому ур-нію выберемъ слѣдующій, которымъ вопросъ приводится къ рѣшенію квадратнаго ур—нія и двухъ кубичныхъ.
Обратимъ въ нуль членъ (и + ѵ) (р4~3иі>). Въ этихъ видахъ нужно положить либо и-ь г?=0, либо рч-Зги; =0. По первое невозможно, такъ какъ въ этомъ случаѣ было бы и #=0, и ур—ніе (I) обратилось бы въ <2—0, между тѣмъ какъ $ отлично отъ нуля. Итакъ, должно положить р-+-Зиг=0, или иѵ—— а слѣд.
ур—ніе (2) дастъ ?(3-ыЯ —— Такимъ образомъ рѣшеніе ур —нія (1) мы * привели къ рѣшенію совмѣстныхъ ур—ній
иѵ ——- и и3-і-г3— о
найдя отсюда и г?, останется внести ихъ значенія въ формулу у = нч- которая и дастъ у.
Чтобы рѣшить систему ур—ній съ неизвѣстными и и ѵ, возвысимъ первое въ кубъ, такъ что получимъ
• . - и3 ’
«з . гЗ — _ гі3 4- с3 — — г/,
откуда и3 и г?3 найдемъ какъ корни квадратнаго ур—нія , 1 - • I
I
^=о. . .(3) ЗЬ‘
которое называется резолмеитолп (разрѣшающимъ) ур—нія (1) *); одно значеніе I ластъ «э, другое зЛ Такимъ образомъ, рѣшая (3), найдемъ:
«=-1+)/?+І-• •« •”=-Ь/?+й- <*>
и слѣд, у, равный и + будетъ
Въ этой формулѣ, называемой формулой Кардана, и заключается рѣшеніе кубичнаго ур—нія. Названіе Кардановой присвоено ей вслѣдствіе того, что впервые обнародована была этимъ ученымъ, въ 1545 г., но найдена была Таршалъиіу впрочемъ, есть основанія къ предположенію, что рѣшеніе кубичнаго ур—нія найдено было еще ранѣе, въ 1505 г., Сципіономъ Ферре о.
Въ правой части ур—нія (6) указана сумма двухъ кубичныхъ корней. Но мы знаемъ, что кубичный корень изъ даннаго числа имѣемъ 3 различныхъ значенія; слагая каждое значеніе перваго куб. корня съ каждымъ значеніемъ 2-го, мы, повидимому, должны найти 9 значеній для у, тогда какъ ур—ніе 3 степени не можетъ имѣть больше трехъ корней. Но это такъ и есть. Въ самомъ дѣлѣ, въ силу ур—шяиі?= — и и ѵ нужно комбинировать въ такія пары, чтобы про-
о
изведеніе ихъ давало —Эти пары можно найти такъ.
Если правую часть ур—нія (4) назовемъ для краткости А3, то три значенія и, опредѣляемыя кубичнымъ ур—мъ и3 = А3, будутъ
А, шА, Мд ш3А,
гдѣ А есть одинъ какой-либо изъ кубичныхъ корней числа А3, а ш п ш*—два мнимые кубичные корня изъ 1. Точно также, если правую часть ур—нія (5) назовемъ В3, и одинъ изъ кубичныхъ корней числа В3 назовемъ В, то будемъ имѣть
Ѵі = В, = г?з = ш*В.
Если, теперь, одна пара значеній и и г, дающая въ произведеніи —будетъ А и В, то другою нарою будетъ: о А и потому что произведеніе шА . шаВ = ш3АВ = АВ“ —", ибо ш3—1; третья же пара будетъ юаА и шВ, ибо О
. юВ == ш3АВ = АВЛегко видѣть, что никакія другія сочетанія не о р * с
дадутъ въ произведеніи —и сл. должны быть отброшены.
Итакъ, три корня кубичнаго ур—нія (1) будутъ
= А + В у" = іоА + у'" = + (гіВ,
гдѣ Л и В суть два кубичныхъ корня изъ А3 и В3, произведеніе которыхъ да-етъ —х*
*) Ряз(шветіт4імъ даннаго ур—нія называютъ ур—ніе, обладающее слѣдующими свойствами: 1) корпи^его могутъ быть найдены; 2) разъ эти корни найдены, можно вычислить и корни^даннаго.
—— о97 —“
571. Примѣръ. Рѣшить ур—ніе я?3 +12® + 63 = 0. Положивъ х = и -имѣемъ
и3 + ѵ3 + 3 (и + р) +4) + 63 = 0.
Положивъ иѵ' + 4 = 0, или «3г® = — 64, имѣемъ «3 г3 — — 63.
Слѣдов., и3 и г3 будутъ корнями ур—нія #-|- 634 — 64 = 0, изъ котораго
Г = 1, Г = — 64; слѣд. и* = 1, я» = — 64. Итакъ:
^ = 1 -4 = —3,
< 2 —1+^3 4
#2 — 1 — 4 , ш3 — - -4 .
&
— 1—<ѴЗ з + бу'з.і.
2 “ 2
10 4 3 — 513 * і
— 1 . — 4 . ш = ------
2
Примѣчаніе. Вышеизложенный методъ рѣшенія кубичнаго ур—нія, принадлежащій Пшісіе, примѣнимъ ко всякому кубичному ур—нію, будутъ ли коэффиціенты р и д числа дѣйствит. или мнимыя.
572. Изслѣдованіе корней кубичнаго ур—нія для случая, когда коэффиціенты р и д дѣйствительны.—Нужно различать 3 случая, въ зависимости отъ Ч2 і знака количества
4 *
ді «3 . / „3
I Ч- + ^>9* Въ этомъ случаѣ!/ 4-+4? — количество дѣйствительное, 4 27 р 4 27 7
слѣд. и3 и ѵ3 также дѣйствительныя количества, а потому для и и ѵ существуетъ по одному дѣйствительному значенію: назовемъ ихъ А и В. Такъ какъ произве-• р
деніе ихъ даетъ —то они образуютъ пару; и если замѣнить ш и о»3 ихъзна-о
ченіями. то получатся слѣдующія 3 значенія для я;:
(А — В))/3 .
2 * ’
Значеніе х' — дѣйствительно. Что касается двухъ остальныхъ значеній я, то они—мнимы и притомъ сопряженны, такъ какъ А — В не есть нуль; иначе А® и В3 были бы равны, что противно условію. Итакъ: когда ^ + ^у>0, одинъ корень ур—нія #®-|-р# + 5=0 дѣйствителенъ, два другіе—мнимые сопряженные.
II Когда ^"+о^ — 0? и дѣлаются равными, слѣд. и дѣйствительныя
значенія кубичныхъ корней изъ нихъ, А и В, равны, и именно
слѣд.
А какъ А —В, то, два другіе корня, также дѣйствительные, равны, между собою:
е" = ж"' =
Итакъ, въ данномъ случаѣ веѣ три корня кубичною ур—нія дѣйствительны, причемъ два изъ нихъ равны между собою, «9 «3 ді
Ш. —+ Такъ какъ есть количество положительное, то данный 4 27 4
случай требуетъ, чтобы 41 было количествомъ существенно отрицательнымъ,' и л*2
численное значеніе = было бы больше Въ этомъ случаѣ и3 и г*3 предста-Л і д
вляются подъ видомъ мнимыхъ сопряженныхъ выраженій, А и В также—мнимы, слѣд. всѣ три корня, выражаемые Кардановой формулой, являются въ формѣ сложныхъ мнимыхъ выраженій. Но легко видѣть, что возможно такое кубическое ур—ніе, всѣ т^и корня котораго были бы дѣйствительные и неравные между собою. Таково, напр., кубичное ур—ніе (ж— 1) (ж + 3) (ж—-7) = 0, корни котораго: я/ —1, =— 3 и а?" = 7— дѣйствительные и неравные. А какъ изъ двухъ раз-
смотрѣнныхъ случаевъ въ первомъ только одинъ корень дѣйствителенъ, а во второмъ, хотя всѣ корни дѣйствительны, но два изъ нихъ равны между собою, то нужно ожидать, что дѣйствительные неравные корни должны получаться Имейлѣ р3
но въ случаѣ + 27 < О* хотя формула Кардана и даетъ ихъ въ видѣ мнимыхъ выраженій. Въ самомъ дѣлѣ, можно показать, что мнимость эта — только кажущаяся. Пусть будутъ
а + Ы, (а + Ьг) . ю, (« + бі) . ш*
три мнимыхъ кубичныхъ корня изъ и3. Такъ какъ іЯ есть выраженіе мнимое, сопряженное выраженію и3, то по § 429, примѣчаніе, кубичные корни изъ ѵ3 будутъ
а— Ьі, (а — 6/)о, (а — ?л) . а>2.
Сочетать значенія перваго ряда съ значеніями второго нужно такъ, чтобы произведеніе сочетаемыхъ значеній было дѣйствительно; слѣд., можно а-|-5і сочетать съ а— Ьі, и такимъ образомъ три значенія х будутъ
Іл/ — А В = 2а
я?" = А<о-|-Вю* = — «+ ЬѴЗ, х"' — Аш'і + Вш = — а — Ъ ѴЗ;
всѣ они—дѣйствительны. Кромѣ того, легко видѣть, что въ числѣ ихъ нѣтъ равныхъ. Во-первыхъ, нельзя положить 2а =— а±б кЗ, ибо отсюда послѣдовательно имѣли бы: б —іар'З, А = а(1±ОЗ), и А3 = а3(1 ±(ѴЗ)3 — равенство невозможное, потому что первая часть, по предположенію, мнима, вторая же есть число дѣйствительное. Затѣмъ, нельзя имѣть — а — Ъ кЗ = — « + ІИЗ, ибо отсюда вышло бы 6 = 0, что невозможно, такъ какъ мнимое количество н3 ие можетъ имѣть дѣйствительнаго кубичнаго корня 429, Ш). Итакъ:
«2 «3
Когда + лсга »/ри корня ур—нія л3 + ргг/= О—числа
& і •
тельныя и неравныя.
Вычисленіе корней кубичнаго УР—НІЯ.—Формула Кардана имѣетъ весьма су-«2 Р3
щественные недостатки. Во-первыхъ, въ случаѣ 4- + “=>0 дѣйствительный ко-рень выражается посредствомъ радикаловъ даже тогда, когда опъ соизмѣримъ. Такъ, если взять Эйлеровъ примѣръ, ур-*-ніе л*3 — &г —40 —0, то дѣйств. корень
ёго, какъ легко видѣть, равенъ 4, тогда какъ по Кардановой формулѣ онъ выразится въ видѣ ^/20 + 141^2-|-|/20 — 14 Iх 2* Но еще важнѣе тотъ недостатокъ П3 -
формулы Кардана, что при условіи + она даетъ корни въ мнимой формѣ, тогда какъ въ этомъ случаѣе всѣ 3 корня дѣйствительны. Если бы отъ этой мнимости мы захотѣли освободиться алгебраическими средствами, т.-е. алгебраически вычислить количества л и 6, которыхъ значенія-позволяютъ вычислить х по формуламъ (7), то пришлось бы рѣшить кубичныя ур—нія того же вида какъ и предложенное; ихъ дѣйств. корни, какъ и у даннаго ур-нія, были бы осложнены мнимыми количествами. Поэтому Сличай этотъ и названъ
мымъ. Но если мы предложимъ себѣ вычислить корни тригонометрически, то значенія х легко будетъ получить іЛсредствомъ логариѳмовъ. Итакъ, рѣшимъ ур—ніе тригонометрически, въ предположеніи —+ ^<0. Здѣсь р количество существенно отрицательное; если буквами р и </ обозначитъ абсолютныя величины • коэффиціентовъ, то ур—ніе будетъ
— о, ' . _ '
. ю* я3
гдѣ уже знаки окончательные, и д"и * • '
Для рѣшенія ур—нія съ 4- передъ положимъ ?/~г . зіп^, гдѣ г и пока неизвѣстны; ур-ніе будетъ (по раздѣлѣніи на г5):
8>п3? —7?!- віи?+^г = О. . .(8)
' . *
Какъ скоро можно будетъ для т и ? найти дѣйствительныя величины, удовлетворяющія этому ур—нію, то вопросъ будетъ рѣшенъ, ибо извѣстно будетъ и 7/ = г8Іп«. Но такія значенія г и найти не трудно. Взявъ формулу, связывающую синусъ тройной дуги съ синусомъ простой:
» . • ’ *
3 1
8ІП 3? -т 5ІП ? + 7 5ІП 3® = О,
4 4
усматриваемъ, что ур—ніе (8) будетъ удовлетворено, если взять
Первое изъ этихъ ур—ній даетъ значеніе г:
г = 2|/|-- -(9).
Изъ второго имѣемъ
8іпз?=^=і/5' *(іо)’
и какъ изъ даннаго условія имѣемъ 27^ < 4;Я, то зіп 3? выражается правильною дробью, и потому всегда можно найти уголъ 3?, котораго синусъ равенъ (10). Такимъ, образомъ извѣстны будутъ г и а слѣд. и у. По одинаковый синусъ имѣютъ "безчисленное множество угловъ: во-первыхъ, острый уголъ 0, & Затѣмъ, углы
3--&, . . . ; 25,4-Л 4п + Ѵ . .
а слѣд. для будемъ имѣть п, и затѣмъ О
к— о’ з- —а 2л+ & 4л+& 3 ’ 3 ’ ' * ’ 3 ’ 3
Но легко видѣть, что различныхъ значеній
для ?/ получится только 3.
“ г . зіп
В - / 0\
3> Уг — г . втівв» — И,
В
= —г
или
21 = 2
, &
Е1П
2і/<.8ш(б0»-|), у, = -
Итакъ, вычисляемъ острый уголъ 0 по формулѣ (10), беремъ его треть и вносимъ въ послѣднія 3 формулы, которыя и дадутъ искомые 3 дѣйствительныхъ корня.
Въ случаѣ ур—нія у*— — 7 —"0, найдемъ для г ту же формулу, а для
угла Л ур—ніе
я:п
II Оу---^3’
откуда для 3? найдемъ отрицательное значеніе, слѣд, и корни получатся по абсолютному значенію тѣ же какъ и прежде, но знаки ихъ будутъ противоположны.
Примѣръ. Рѣшить ур—ніе у3 — 39у + 70 — 0.
Въ данномъ случаѣ р = 39, д — 70; слѣд., г = 2УІЗ и 8ІвЗ^=-^—.
Таблицы дадутъ
1о^ 5Іп 3? = 9,8731529, откуда 3? = 48°18'22",77 = О,
и слѣд.,
~ = 16°в'7'\59, О
60» — — 43в53'52,,,41
О
60» + ~ — 76°6'7",59.
Найдя въ таблицахъ логариомы синусовъ получимъ
этихъ трехъ угловъ, также 1о§ г,
1о^ Уі — 0.3010299, 1о^у2 = 0,6989700, Іов (— Уз) — 0,8450980,
— + 2; -
#2 ~ + 5;
Ь = —
Повѣрка. Для повѣрки достаточно сложить корпи: сумма должна давать ноль, что въ данномъ случаѣ и имѣетъ мѣсто.
Указанный способъ повѣрки основывается на соотношеніи между коэффиціентами и корнями, къ разсмотрѣнію котораго и переходимъ.
573. Соотношенія между коэффиціентами и корнями кубичнаго уравненія =
Такъ какъ кубичное ур—ніе имѣетъ 3 корня, то его можно представить въ
видѣ а(х — а?!) (а? — (я *-- аг3) = 0, откуда, раскрывъ скобки и сравнивая СЪ
даннымъ ур—мъ, найдемъ соотношенія
а
а
т.-е. сумма всѣхъ корней = взятому съ обратнымъ знакомъ частному отъ раздѣленія второго коэффиціента на 1-й; сумма парныхъ произведеній корней равна частному имъ раздѣленія третьяго коэффиціента на первый; а произведеніе всѣхъ корней = минусъ частному отъ раздѣленія послѣдняго коэффиціента на первый. Функціи корней, здѣсь разсматриваемыя, относятся къ такъ называй’ мымъ симметрическимъ функціямъ, характеризующимся тѣмъ свойствомъ, что величина такихъ функцій не измѣняется отъ перестановки входящихъ въ нихъ буквъ одной на мѣсто другой, послѣдовательно, комбинируя нхъ попарно. Легко, въ самомъ дѣлѣ, провѣритъ, что ни величина, ни знакъ этихъ функцій не перемѣняется отъ перемѣны на на и т. д.
Рѣшеніе полнаго уравненія четвертой степени.
574, Предложено было нѣсколько способовъ рѣшенія ур—нія 4-й степени; и во всѣхъ этихъ методахъ нахожденіе корней ур—нія 4-й степени зависитъ отъ предварительнаго рѣшенія кубичнаго уравненія. Впервые общее рѣшеніе ур—нія 4-й степени найдено было Феррари^ ученикомъ Кардано, и это рѣшеніе, равно какъ и рѣшеніе, данное Декартомъ, принадлежатъ къ простѣйшимъ.
575. Способъ Феррари.—Чтобы рѣшить ур—ніе і «
4-^х3 гх + з = 0, придадимъ къ обѣимъ частямъ (аа?4~&)3> вслѣдствіе чего найдемъ
4~ + (<? + (г + 2аЪ)х н- е -+- д3 = (шг + Ь)3,
и опредѣлимъ а и Ь такъ, чтобы 1*я часть сдѣлалась точнымъ квадратомъ нѣкотораго тринома + Сравненіе коэффиціентовъ покажетъ, что это бу-
детъ достигнуто, какъ скоро будутъ удовлетворены ур—нія
2к -+- = ц + а3, ра - г 4- 2аЬ и і* = 5 4- Ь3.
4
Исключая а и Ъ, получимъ для опредѣленія X кубичное уравненіе
8а3 — 4д . а3 + 2 (рг — 4$)Х — 4“ 4^з — г- — 0,
которое всегда, какъ извѣстно, имѣетъ, по крайней мѣрѣ, одинъ дѣйствительный корень; найдя этотъ корень, мы будемъ знать а и Ь. Такимъ образомъ найдемъ уравненіе
(а* + ^- + >)’ = («г- + Ь)3, откуда
аг3 + ,т + > = ± (я*т 4~ б),
Гдѣ а, Ь, ) извѣстны, и слѣд* всѣ 4 корня а? найдены “будутъ изъ квадратныхъ ур—ній
+ = + & и аг2 + “^ + л= — а.т — Ъ,
&
г
и задача рѣшается вполнѣ.
Примѣръ. Рѣшить уравненіе л4 — 2^ —-|- 10г — 3 — 0.
Придавая къ обѣимъ частямъ (я# + найдемъ
<т4 — 2а*3 + (я3 — а)#2 + 2(а& + 5)е + № — 3 = (ал* 4- &)2.
Приравнявъ первую часть (я4 — #4~*)3, сравненіемъ коэффиціентовъ при . одинаковыхъ степеняхъ х получимъ
< а*-6 = 2А, аЬ + 5 = — 1, ^ — 3 = ^,
откуда, исключивъ а и &, имѣемъ
2\з _р — 7—0;
испытаніе +1 и — 1 покажетъ, что 1 —— 1; отсюда
аа^=4, а& — — 4, Ь'2 —4;
такъ что можно положить
: . (^ —я —1)з = (2л* —2)*, или а« — х — 1 =± (2л* — 2).
Рѣшая полученныя два квадратныхъ уравненія, имѣемъ
г
Л1=і(з+кЗ), 3-5.= 1(3-15), ъ= 1 (- 1 + »/Тз), ».= !(- 1-143). ш і лл &
576- Способъ Декарта,—Въ 1637 году Декартъ. далъ слѣдующій способъ рѣшенія ур—нія 4-й степени, подобно предыдущему основанный также на способѣ неопредѣленныхъ коэффиціентовъ, имъ же изобрѣтенномъ. Освободивъ отъ коэффиціента при .г1 и отъ члена съ кубомъ а*, т.-е, приведя ур—ніе къ виду
’‘ ' я4-р?лг* + 0^'+**—‘ ‘ ’
предположимъ, что оно рѣшено и что первая часть разложена на двучленные множители. Если соединить эти множители попарно, то можно представить себѣ первую часть приведенною къ произведенію
(я? 4- 4" ”) (-Ѣ2 4-я/а? + я0*
Приравнивая коэффиціенты при одинаковыхъ степеняхъ з\ найдемъ для опредѣленія неопредѣленныхъ коэффиціентовъ ш, п, т', и' ур—нія
• • О) ?пт'+я4~я,=ЗР * * * (2) жп'-| т*я—. - (3) ян'=г , - . (4).
*
Подставляя шг — — т въ остальныя *ур—нія, получимъ * ‘ -
ч
— шя4-я+я — Р * * * (5) —и) =9 . . , (Н) ігпг—г - - . (7),
Изъ (5) и (6) имѣемъ
и внеся въ (7), получаемъ
![(>”’+о’-&]='
ИЛИ * 4
ш6 + 2риг* + — 4г)т* — = 0,
третьей степени отн, ті Рѣшивъ это ур., найдемъ тп, а затѣмъ п.и п\ послѣ чего останется рѣшить два- квадратныхъ ур—шія: а* 4” + п = 0 и х* 4- т'#+ 4-и' —0т которыя и дадутъ*4 искомыхъ корня предложеннаго.
Примѣръ. Рѣшить ур^аіа — 12о* + 21а: —10 = 0.
Поступая указаннымъ образомъ, найдемъ, что разрѣшающее кубичное ур. будетъ (положивъ ’?ла = я): .
хг»~24^+ 184гг — 441 = 0,
или, положивъ для уничтоженія члена съ — & + Л, найдемъ
’ЛЗ-8& + 7=0 и Л = 8>
Это куб. ур., очевидно, имѣетъ корень А=+1; слѣд. я—9, откуда п?— ±3. Взявъ т — 3, найдемъ т’ = — 3, п = — 5, н' — 4“ 2. Такимъ образомъ, квадратныя ур—нія, на которыя распадается данное, будутъ
,т2 + За? — 5 = 0 и а^ — 3:г + 2 — 0.
Мшая ихъ» найдемъ всѣ '4 корня
предложеннаго ур—нія:
0*1 — 1, — 2, 3 4~ V 29^ * Яд —- 3 — 29^ •
577. Соотношенія между коэффиціентами и корнями уравненія 4-й степени.—Ур—ніе 4-й степени имѣетъ 4 корня, слѣд. его можно представить въ формѣ
«(л- — — дъ)(г — Я4) — 0.
Раскрывъ скобки и сравнивая съ даннымъ ур— кіемъ
найдемъ
ах* 4" 4“ 4?€ ~ О,
Ь а
. . ^4- ^ + 0:34-0*4 = —
л
+ Л*Ч4~ + г&і 4“ “
4- -Н 'ПО’з^і 4- ” а*
е а
Таковы соотношенія между коэффиціентами и корнями ур—нія 4-Й степени. Легко замѣтить ихъ аналогію подобнымъ же свойствамъ для ур—ній квадратнаго и кубическаго, и нетрудно выразить эти соотношенія словами.
578. Теор ема. Во всякомъ ур—нІи съ дѣйствительными коэффиціентами мнимые корни входятъ попарно,
Пусть данное ур. съ дѣйствительными коэффиціентами есть /'(о*) = 0, и положимъ, что оно имѣетъ мнимый корень а + &?; докажемъ, что' мнимое сопряженное а — 6г будетъ также корнемъ этого ур—нія. * і. .: .
Составивъ произведеніе рг — (а + Ь»)11® (а —ЭДЬ или (# — а)* + ДО, раздѣлимъ Я#) яа (я —а)*-|-ДО, и пусть частное будетъ (}, а возможный оста' токъ Кя + Н'і имѣемъ
/'(я?) = — я)а + ДО] + Шг + К\
Положимъ въ этомъ тождествѣ х == а + &і. Такъ какъ а + по предположенію, есть корень даннаго ур—нія, то Да:) обратится при этой подстановкѣ въ нуль; (я? — а)а4~ДО также обращается въ нуль; слѣд. остается:
Приравнивая нулю дѣйствительную и мнимую части, имѣемъ
Ка+Н' = 0, Ш> = 0.
Но 6, по условію, не есть нуль, слѣд. К=О; а потому п й' —0. Заключаемъ, что остатокъ обращается въ нуль, т.-е. что /(#) дѣлятся на (#—я)*4-ДО, или на [о? — (а 4” &*)] [# — (а — 6»)]; это значитъ, что х — (а — Ьй входитъ множителемъ въ которая, так. обр., при х = а — Ы обращается въ нуль: а — Ы есть также корень ур—нія Да?)=0.
Изъ этой теоремы, по отношенію къ кубичному ур—нію, слѣдуетъ, что оно не можетъ имѣть трехъ мнимыхъ корней; имѣя два мнимыхъ корня, третій корень всегда дѣйствителенъ. Слѣд., кубичное ур. всегда имѣетъ, по крайней мѣрѣ, одинъ дѣйствительный корень.
Кромѣ того, эта теорема облегчаетъ вычисленіе корней куб* ур—нія. Разъ мы нашли одинъ мнимый корень, другой нѣтъ надобности вычислять особо: слѣдуетъ прямо написать мнимое, сопряженное найденному корню.
579. Мы убѣдились, что для всякаю уравненія 3-й и 4-й степени, взятаго въ общемъ видѣ (т.-е. съ буквенными коэффиціентами) можно найти рѣшенія въ алгебраической формѣ, т.-е. выразить корпи посредствомъ радикаловъ. Если же степень уравненія, взятаго въ общемъ видѣ, будетъ выше четвертой, то Норвежскій'ученый Абель доказалъ невозможность алгебраическаго рѣшенія такихъ ур—ній (т*-е. невозможность выразить нхъ корни въ радикалахъ). По въ случаѣ ур—‘НІй съ численными коэффиціентами всегда можно вычислить ихъ дѣйствительные корни съ какою угодно точностью, какова бы ни была степень уравненія.
ГЛАВА XXXIX.
Численные вопросы высшихъ степеней.
580. Когда отвѣтъ на вопросъ, приводящій къ квадратному уравненію, выражается мнимыми корнями, это служитъ признакомъ невозможности задачи. Если же корни дѣйствительны, то могутъ имѣть мѣсто слѣдующіе случаи:
1. Оба корня положительны. Тогда задача допускаетъ два рѣшенія, если только корни неравны; въ случаѣ равныхъ корней вопросъ имѣетъ одно рѣшеніе. Однако же, если одно или оба значенія неизвѣстнаго выходятъ изъ тѣхъ предѣловъ, между которыми, по смыслу вопроса, должно заключаться неизвѣстное, то вопросъ имѣетъ или одно рѣшеніе, или же невозможенъ.
2. Если одно или оба значенія неизвѣстнаго будутъ отрицательны, то всегда можно составить такое уравненіе, котораго корни равны, но противоположны корнямъ даннаго: нужно только въ ур—ніе задачи подставить —х вмѣсто х. Если окажется возможнымъ подобрать задачу, слегка разнящуюся отъ предложенной и отвѣчающую видоизмѣненному ур-нію, этимъ путемъ значеніе отрицательнаго корня и будетъ истолковано.
Эти замѣчанія относятся и къ уравненіямъ второй степени съ нѣсколькими неизвѣстными. Въ поясненіе сказаннаго приводимъ примѣры.
Задача I. Два торговца продали нѣсколько головъ роіатаю скота за 1350 р>; первый на 5 іоловъ больше второю_ Если бы первый продалъ столько головъ^ сколько второй у а второй столько, сколько первый, то яервы# получилъ бы 540 р., а второй 840 р. Сколько головъ продалъ каждый и по какой цѣнѣ?
Пусть будетъ х—число головъ, проданныхъ первымъ; тогда число головъ, проданныхъ вторымъ, будетъ я—5. Первый за х—5 головъ получилъ бы 540 р.; слѣд. за одну голову онъ получалъ по р., а за х головъ вы-ручилъ Р- Второй за х головъ получилъ бы 840 рм слѣд. онъ бралъ за
одну голову — р., а за х — 5 гоаовъ получилъ -----х - р. Слѣд. оба прода-
540й? । 840(2—5) 1 ОЕП
ли скота на----- + -----= 1350 р.
По освобожденіи отъ дробей и по упрощеніи находимъ ур—ніе я2—55я-]~ -|-700 = 0, откуда: х( — 35; х" = 20. Слѣд. а/ —5 = 30; х"—5=15.
Итакъ, задача имѣетъ два рѣшенія: 1-й продалъ 35 головъ по 18 р. *за голову, а второй 30 головъ по 24 рубля за голову (въ самомъ дѣлѣ, 18Х 35—|— 24 X ВО = 630-]“ 720 = 1350); пли же: 1-й продалъ 20 головъ по 36 р., а 2-й 15 по 42 р., что опять составляетъ 1350 р.
Задача II. Отданъ въ банкъ капиталъ и черезъ іодъ получено прибыли #00 р, Капиталъ вмѣстѣ съ процентными деньгами былъ оставленъ въ банкѣ еще нагодъ. Послѣ этою капиталъ съ наросшими на нею процентными деньгами составлялъ #420 р. Какъ великъ былъ первоначальный капиталъ?
Пусть первоначальный капиталъ былъ х р. Черезъ годъ онъ обратился въ і ПЛЛ х 200С0 п ,
х-1- 200 р., слѣд. принесъ процентовъ. Въ концѣ второго года этотъ ка-X
капиталъ, принося
20000 я
%, обратился въ (хг —|—200) 11 —
—) = 2420 р
X I 1
Освободивъ отъ дробей и упростивъ, имѣемъ ур. ж3—2020#-|-40000=0, откуда: я' = 2000 р.; ж*' = 20 р. Такимъ образомъ опять получили два положительныхъ корня; вычисляя проценты, приносимые этими капиталами, находимъ, что первый даетъ 10%, второй 1000%. Такъ какъ въ дѣйствительности банки не даютъ такихъ высокихъ процентовъ, какъ 1000%, то заключаемъ, что корень х" = 20 р. не м. б. допущенъ, и задача имѣетъ одно рѣшеніе: х = 2000 р.
Задача III, Нѣкто купилъ нѣсколько аршинъ сукна за 240 руб.; если бы за ту же сумму онъ получилъ 3-мя аршинами менѣе, то аршинъ обошелся бы 4-мя рублями дороже. Сколько аршинъ сукна куплено?
Пусть куплено было х арш.; цѣна 1 арш. равна, слѣдоват., -тг р. Если
Г
бы за ту же сумму онъ получилъ 3-мя арш. меньше, т.-е. я — 3 аршина, то
240
цѣна аршина была бы —+ 4; а всѣ х— 3 аршина стоили бы опять 240 р.; слѣд* ур—ніе будетъ
Р^+4)(.г-3)=240. .. .(1).
Приведя его къ виду х2 — Зх — 180 = О и рѣшивъ, найдемъ два корня: я'= 15, я" =—12, Положительный корень, какъ не трудно убѣдиться, даетъ . прямой отвѣтъ на задачу, Что касается отрицательнаго корня: — 12, онъ не можетъ представлять отвѣта на данную задачу, ибо неизвѣстное (число куплей' пыхъ аршинъ сукна), по существу своему, положительно* Но мы можемъ попытаться истолковать это,рѣшеніе, т.-е». подыскать задачу, аналогичную дан* ной, отвѣтомъ на которую служила бы абсолютная величина отрицательнаго рѣшенія.
Для этого въ первоначальное ур—ніе (1) вмѣсто х подставимъ (— х); по-/ 240 \
лучимъ — 4'4 (“Ж —3) = 240, или, умноживъ оба множителя 1-й части на (— 1):
— 4-) (я Ц-3) = 240 . . .(2). \ Я/ /
Мы уже знаемъ, что рѣшенія этого ур—нія суть: х* =—15, х" = 4~12Р равныя рѣшеніямъ ур—нія (1), но съ противоположными знаками. Положительное рѣшеніе —[—12 будетъ служить отвѣтомъ на задачу, соотвѣтствующую уравненію (2); задача эта, очевидно, такова: «нѣкто купилъ нѣсколько аршинъ сукна за 240 р.; если бы за ту же сумму онъ получилъ 3-мя аршинами болѣе, то аршинъ обошелся бы 4-мя рублями дешевле* Сколько аршинъ онъ купилъ?» Отвѣтомъ на эту задачу и служитъ число 12 аршинъ*
Задача IV. Нѣкоторое число X есть произведеніе трехъ послѣдовательныхъ нечетныхъ чиселъ; раздѣливъ Я послѣдовательно на каждое изъ этихъ чиселъ и сложивъ частныя, находимъ въ суммѣ 239. Найти X?
Пусть 3 послѣдовательныя искомыя нечетныя числа будутъ 2х — 1, 2x4-1, 2л-|-3; И = (2з — 1)(2х-[-1)(2я-[-3), Ур-ніе задачи будетъ:
(2х-]- 1)(2^ + 3) + (2х- 1)(2я + 3) + (2я— 1)(2х-]-1) = 239, (1),
или, по выполненіи всѣхъ дѣйствій и по упрощеніи: ха 4~ х = 20, откуда: х' = 4, х"= — 5.
Положительное рѣшеніе даетъ для трехъ искомыхъ чиселъ: 7, 9 и 11. Повѣрка: 9 X 11 + ? X 1.1 4~ 7 X 9 дѣйствительно = 239.
Для истолкованія отрицательнаго рѣшенія подставляемъ въ первоначальное ур. (I) — х вмѣсто х, находимъ: (1 — 2х)(3 — 2х) + (— 2л? — 1)(3 — 2#)+ 4- (” 2х — 1)(1 — 2х) = 239, или, перемѣнивъ въ каждомъ членѣ знаки обоихъ множителей, находимъ ур—ніе
(2л? — 1)(2х — 3)4- (2#+ 1)(2х — 3) + (2х+ 1)(2х — 1) = 239,
корни котораго суть: — 4 ц -р5, Взявъ корень =4^5, находимъ, что искомыя числа суть: 2х— 3 = 7; 2х—1=9; 2x4’1 = 11- Такимъ образомъ, рѣшеніе х = 5 даетъ тотъ же отвѣтъ, что и х = 3, требуя только, чтобы
искомыя числа были обозначены формулами 2х—3, 2х—1 и вмѣсто того, чтобы обозначать ихъ знаками 2# — 1, 2#-{- 1 и 2.x—[—3. Но и то и другое обозначенія одинаково возможны, и замѣчательно, что алгебра показываетъ намъ а розіегіогі, что все равно, какое изъ этихъ обозначеній мы примемъ.
Задача V. Мужчины и женщины, аь числя» 33 лицъ, работаютъ на фабрикѣ, причемъ каждый мужчина зарабатываетъ въ день 3-мя рублями больше * нежели каждая женщина; не смотря я а это, еже* дневный заработокъ всѣхъ мужчинъ таковъ же, какъ и заработокъ женщинъ, ѵ составляетъ 60 р* Найти число мужчинъ?
Пусть мужчинъ было х; число женщинъ будетъ 32 — х. Каждый мужчина зарабатываетъ въ день —з каждая женщина равненіе задачи будетъ:
60 60 9 /п
х 32— х~* ‘ ф '
Окончательное ѵр—ніе х* — 92я? 4- 960 = 0 даетъ: #' = 80, аУ'=12; слѣд, 32 — х> = — 48; 32 — я" = 20.
Рѣшеніе я/'=12 для числа мужчинъ, даетъ число женщинъ 20; причемъ ежедневный заработокъ мужчины составляетъ 60: 12 или 5 руб.; заработокъ женщины = 60 : 20 = 3 р. Слѣд. это рѣшеніе удовлетворяетъ всѣмъ условіямъ задачи.
Но рѣшеніе #==80 для числа мужчинъ, будучи больше числа лицъ обоего пола (32), даетъ къ тому же для числа женщинъ отрицательное количество — 48; слѣдов. второе рѣшеніе не соотвѣтствуетъ предложенному вопросу. Для истолкованія этого рѣшенія положимъ 32 — х = у, откуда # = 32— я/, и под-ставимъ эти величины въ ур. (1); найдемъ ур. # У ~ которому удовлетворяетъ у = — 48; подставивъ (—у) вмѣсто у, получаемъ ур—піе
60 .60
32 + у ‘ у
-(2),
изъ котораго у (число женщинъ) = 48, а 32 Ц- у (число мужчинъ) = 80. Эти положительныя рѣшенія отвѣчаютъ на задачу, соотвѣтствующую ур—нію (2); задача эта такова: «мужчины и женщины работаютъ на фабрикѣ, причемъ число мужчинъ 33 больше числа женщинъ; мужчина и женщина зарабатываютъ вмѣстѣ 3 р. въ день; всѣ мужчины зарабатываютъ въ день 60 руб.; столько же и женщины. Найти число женщинъ?* Отвѣтъ: 80 мужчинъ, зарабатывающихъ по 75 к. въ день, и 48.женщинъ, получающихъ по 1 р. 25 к. въ день.
Задача VI. Нѣкто, имѣя капиталъ въ 130000 р., раздѣлилъ ею на двѣ части, которыя помѣстилъ подъ проценты. Первая часть даетъ ему ежегоднаго дохода 3800 руб.; вторая^ принося 1 процентомъ больше, даетъ дохода 3500 р, въ годъ. Каковы обѣ части, и по сколько процентовъ онѣ приносятъ ?
Пусть первая часть приноситъ #%; въ такомъ случаѣ 1 р. прибыли полу-100 ООАП / 280000 і>
чится со — р., а 2800 р. прибыли получится съ —-— р. Разсуждая такимъ
г 250000 , х
же образомъ, найдемъ, что вторая часть капитала равна у руб. А какъ сумма обѣихъ частей равна 120000 рм то имѣемъ ур—ніе
280000 । 250000
х #+ I
120000,
или 12яа — 4 Ія— 28 = 0, откуда: /—4Л я" = —
Положительное рѣшеніе -|-4 даетъ прямой отвѣтъ на вопросъ, и показы-КО/ Л X 1 280000 '7ЛППЛ
ваетъ, что вторая часть приноситъ оу^. Слѣд. Ья часть = —— ~ — 70000 р_;
2-я часть “ 50000 р. Сумма ихъ дѣйствительно составляетъ 120000 р.
/г
Истолкованіе отрицательнаго рѣшенія, —
повело бы къ условіямъ, не-
совмѣстнымъ съ понятіемъ о процентѣ; потому рѣшеніе это должно быть прямо отброшено. Полученіе посторонняго рѣшенія зависитъ отъ того, что ур—ніе, къ которому привела частная задача, общѣе этой послѣдней; оно отвѣчаетъ на всѣ вопросы, которые привели бы къ тому же ур—нію, какъ и разсматриваемый частный вопросъ, и которыхъ безчисленное множество* Поэтому неудивительно, что одно изъ рѣшеній этого ур—нія чуждо частному вопросу.
Задача VII. заставъ Силена спящимъ около бочки, наполненной виномъ, сталъ пить въ продолженіи ~ тою трелюя#, какое Силена ліогь бы выпить всю бочку. Послѣ этого Силенъ проснулся и выпилъ оставшееся вино. Нели бы Вакхъ и Силенъ пили вмѣстѣ, то они выпили бы всю бочку 6-ю часами скорѣе, и на долю Вакха при-2
ш.госъбы только тою, что онъ на самомъ дѣлѣ оставилъ Силену, Во сколько часовъ каждый изъ нихъ можетъ выпить цѣлую бочку?
Означимъ время, въ которое Вакхъ можетъ выпить всю бочку, черезъ З#, а время, въ которое Силенъ можетъ выпить ту же бочку, черезъ 5у. Сначала Вакхъ пьетъ въ продолженіи Зу часовъ, и какъ въ одинъ часъ онъ выпиваетъ бочки, то въ Зу часовъ выпьетъ | бочки. Затѣмъ, легко видѣть, что вмѣ-
стѣ они выпили бы всю бочку въ час* Вакхъ оставилъ Силену 1 — бочки, и слѣд. послѣдній пилъ вино въ продолженіе ^1— |^. 5у часовъ; по-. * г* । Л у\ г (8я — Ъу)у _
этому оба они пили въ течете Зу -М1 — Ч.бу или -—часовъ. Приравнявъ разность временъ, указанную въ условіи, 6 часамъ, получимъ ур—ніе
(8ж — 5у)у 15яу
х Зя + 5у
Выразимъ теперь, что количество вина, выпитаго Вакхомъ, было бы во вто-2
ромъ случаѣ равно того, что онъ на самомъ дѣдѣ оставилъ Силену. Такъ
какъ Вакхъ выпиваетъ въ часъ 5- бочки, то въ 5--. часовъ, въ теченіи > оХ ’ Зж -4- ЭД
— Г>09 —
которыхъ онъ пилъ бы во второмъ случаѣ, онъ выпилъ бы часть бочки, равную 3(3р+5у)* какимъ образомъ второе ур—ніе-будетъ:
% 3(3<г 4- 5у)
2 Л 3\
Освободивъ ур—нія отъ дробей, дадимъ имъ видъ
25.гу3 — 25«/3 -|“ 9 гу — 18х3 — ЗОял/ = О 1О^3 1 Егу — 67;2 = О,
откуда х = 5, 2/ — 2; слѣд. искомыя числа часовъ суть 15 и 10.
ГЛАВА ХЬ
Изслѣдованіе измѣненія нѣкоторыхъ функцій.—Махіта и тіпіта. г
581. Предварительныя свѣдѣнія и опредѣленія. Количество наз. перемѣннымъ, если оно можетъ измѣнять свою величину; перемѣнное наз. яезаяи-с«л(ыл<ь, если его измѣненія произвольны; если же измѣненія перемѣннаго у зависятъ отъ другаго перемѣннаго такъ что каждому значенію х соотвѣтствуетъ одно или нѣсколько совершенно опредѣленныхъ значеній перемѣннаго у, то у наз. зависимымъ перемѣннымъ или функціей перемѣннаго х. Такъ, окружность и площадь круга, измѣняясь съ измѣненіемъ радіуса, суть функціи радіуса, который въ данномъ случаѣ играетъ роль независимаго перемѣннаго; площадь треугольника есть функція основанія и высоты; объемъ прямоугольнаго параллелепипеда есть функція трехъ его измѣреній и т. п. Чтобы обозначить, что у есть функція х, пишутъ: у = /'(х).
Функція непрерывная. Если измѣнять х отъ х=а до = постепенно, такъ чтобы это перемѣнное принимало послѣдовательно всѣ промежуточныя значенія между а и то если при этомъ /*(я) остается дѣйствительною, конечною, а ея приращенія сами могутъ быть сдѣланы какъ угодно малыми,— она наз. функціею непрерывною между а и
Итакъ, чтобы ((х) была непрерывна въ интерваллѣ отъ х = 2 до я = она должна удовлетворять слѣдующимъ условіямъ: 1) не имѣть въ этомъ интерваллѣ мнимыхъ значеній; 2) не обращаться въ +^о;3) когда ^-су даемъ безконечно малое приращеніе, то и соотвѣтствующее приращеніе функціи д. б. безконечно—мало: другими словами, непрерывная функція не должна переходить отъ одного своего значенія къ другому скачками, ве проходя всѣхъ промежуточныхъ значеній. Напр., такая функція не можетъ изъ положительной сдѣлаться отрицательною, не проходя черезъ нуль. Если независимое перемѣнное х непрерывно измѣнять отъ х = а до то сама функція, предполагая, что она въ этомъ интерваллѣ непрерывна, можетъ измѣняться, или постоянно возрастая, или постоянно убывая, или—то возрастая, то убывая.
Махіта и тіпіпіа. Когда функція, сначала возраставшая, начинаетъ уменьшаться, то въ самый моментъ перехода отъ увеличенія къ умепыпепію
— біо —
она принимаетъ значеніе большее сосѣднихъ; это значеніе наз, наибольшимъ значеніемъ или тахітит'оп функціи. Наоборотъ, если функція, сначала уменьшавшійся, начинаетъ йотомъ увеличиваться, то въ самый моментъ перехода отъ уменьшенія къ увеличенію она принимаетъ значеніе, меньшее непосредственно предшествовавшихъ и непосредственно слѣдующихъ; такое значеніе наз. ея наименьшею величиною или жшіткт’омъ.
Пусть у будетъ то значеніе х, содержащееся между а и при которомъ функція принимаетъ значеніе с, и пусть Л будетъ положительное количество, какъ угодное близкое къ нулю. Если эта функція при возрастаніи х отъ у—Л до у возрастала, а затѣмъ при увеличеніи х отъ у до у идетъ убывая, то с и есть шахітиш функціи при я = у. Наоборотъ, если функція уменьшалась при возрастаніи х отъ у —Л до у, затѣмъ увеличивается при возрастаніи х отъ у до у + Л, то с н будетъ тіштипГомъ функціи при х = у Махіта и тіпіта, какъ мы ихъ только что опредѣлили, пе слѣдуетъ смѣшивать съ са-лою большою или съ самою меньшею величиною функціи. Во многихъ вопросахъ независимое перемѣнное не можетъ измѣняться отъ —со до -ф-сс, т.-е. черезъ всю область дѣйствительныхъ чиселъ, по въ своихъ измѣненіяхъ бываетъ ограничено конечными предѣлами, п если въ тотъ моментъ, какъ независимое перемѣнное х достигло своего предѣла, функція получаетъ значеніе большее пли меньшее прежнихъ своихъ значеній, то это самое больпіее или самое меньшее ея значеніе не составляютъ шахішппГа или шіпішшп’а въ выше-опре-дѣленномъ смыслѣ, такъ какъ въ разсматриваемомъ случаѣ пе можетъ быть сравненія этихъ значеній съ непосредственно слѣдующими: послѣднихъ не существуетъ. Такъ функція # дѣйствительна только для х, непревышающихъ. 1; и если измѣнять х отъ до -ф-1, то функція будетъ идти уменьшаясь отъ до О, котораго она достигаетъ ври х = I; здѣсь О есть самое меньшее значеніе функціи, но не есть ийтш въ выше-опредѣленномъ смыслѣ, ибо при х > 1 функція уже становится мнимою, сл. ея значенія не могутъ быть сравниваемы съ предшествующими.
Эти особыя тахіша и тіпіта иногда называются абсоототяылш, въ отличіе отъ наибольшихъ или наименьшихъ значеній функціи по сравненію съ сосѣдними, называемыхъ относительными^.
Въ виду сказаннаго, нѣтъ ничего удивительнаго въ томъ, что одна и та же функція можетъ имѣть нѣсколько относительныхъ піахіта или тіпіта, или въ томъ, что относит. тіпіпшт функціи можетъ быть больше ея ілахітшп’а.
Разрывъ непрерывности. Нѣкоторыя функціи (не цѣлыя относительно х) могутъ для нѣкоторыхъ .значеній перемѣннаго х претерпѣвать разрывъ непрерывности.
Такъ, функція 'з“ обращается въ с© при х = ; въ этомъ случаѣ говорятъ, что она непрерывна при всякомъ значеніи х, кромѣ х — -у; при 3 , ,
# = у* обращаясь въ зс, функція теряетъ свойство непрерывности.
Функція ]/х2— 5x4-6, которую можно представить въ видѣ }/(х—2)(х—3), также не при всякомъ х непрерывна. Въ самомъ дѣлѣ, теорема о знакѣ квадратнаго тринома показываетъ, что триномъ хй — 5х 6 остается положительнымъ прп всякомъ х, не содержащемся между его корнями 2 и 3; но при 2 < х < 3 становится отрицательнымъ, а функція мнимою Слѣд. послѣдняя
611
непрерывна для всякаго заключающагося между -х н -|-2, а также между + 3 и + ос; и теряетъ непрерывность при всякомъ а?, лежащемъ между 2 и 3.
582. Графическое изображеніе измѣненій функціи. Измѣненія функціи можно сдѣлать наглядными, слѣдующимъ пріемомъ.
Пусть данная функція будетъ /‘(я); изображая ее буквою у, получимъ уравненіе у = ((х) . . . (1)
Начертивъ двѣ перпендикулярныя прямыя, пересѣкающіяся въ точкѣ О: и уу\ и принявъ произвольную прямую Ру за единицу, будемъ изображать величины независимаго перемѣннаго х прямыми, наносимыми на оси хх\ вправо отъ точки О, если х положительно, и влѣво, если х отрицательно. Такъ, если х = -р 3, то отложивъ вправо отъ О три раза линію РУ, получимъ прямую ПХ, которая и изобразитъ я; = -]- Зй Взявъ х —— 1, должны отложить линію РУ разъ влѣво отъ точки 0: прямая 0Х3 изобразитъ х =— 1, Разстоянія ОХ, 0Х3, называются абсциссами.
Для всякаго даннаго х можно вычислить величину функціи (т.-е. */), подставивъ вмѣсто я его величину въ ур—ніи (1). Пусть, напр., при я = -|- 3 получится у = Ц-О,7. Возставивъ въ точкѣ X перпендикуляръ къ линіи вверхъ, отложимъ на немъ линію ХМ, равную 0,7 Ру, Линія ХМ и изобразитъ на чертежѣ величину данной функціи, соотвѣтствующую величинѣ 4"^ неза-
висимаго перемѣннаго. Подставивъ въ ур. (1) вмѣсто х другое число, напр*, — 1, получимъ, напр., у = — 3, Возставивъ въ точкѣ Х3 перпендикуляръ къ линіи хх' внизъ, отложимъ на иемъ прямую Х3М3 = ЗРу. Линія Х3М3 изобразитъ величину функціи, соотвѣтствующую значенію — 1 перемѣннаго Перпендикуляры ХМ, К3МЗѴ.. откладываемые вверхъ отъ линіи хх', если у>0, и внизъ, если у < 0, называются ордынаталш.
Давъ достаточно большое число различныхъ значеній #-су, вычисливъ по ур—нію (1) соотвѣтствующія значенія у, наносимъ тѣ и другія указаннымъ образомъ на чертежъ, в соединяемъ всѣ полученныя вершины М. МР... орди-натъ кривою. Измѣненія ординатъ этой кривой и покажутъ, какъ измѣняется функція при измѣненіи перемѣннаго х,—Кривая эта называется, поэтому, кривою функціи.
Абсциссы и ординаты называются координатами точекъ кривой; прямыя хх* и уу’—осями координатъ, первая —осью абсциссъ (или иксовъ), вторая— осью ординатъ (или игрековъ). Точка 0 наз. началомъ координатъ.
Кривая функціи, указывая наглядно измѣненія функціи, имѣетъ еще ту выгоду, что, разъ опа начерчена, она съ перваго взгляда показываетъ тахіта и тіпіта; въ самомъ дѣлѣ, эти значенія, по самому ихъ опредѣленію, суть ничто пвое какъ ординаты самыхъ высшихъ и самыхъ низшихъ точекъ кривой. Такъ, ординаты Х4МѴ Х0М6 суть тяхіта, а ХМ, Х5М5 — пііпіша.
Когда разсматриваемая функція — дробная, то можетъ случиться, что при я = со величина ея ?/ стремится къ конечному значенію Въ такомъ случаѣ построеніе кривой покажетъ (черт. 58), что по мѣрѣ удаленія точки Р влѣво,
Черт. 58.
т.-е. по мѣрѣ приближенія х къ — со, ордината МР будемъ стремиться къ й, и слѣд. точка М болѣе и болѣе будетъ приближаться къ прямой АВ, параллельной оси х'х и отстоящей отъ нея на кривая будетъ имѣть видъ (1) или (2), смотря по тому, будетъ ли функція приближаться къ й уменьшаясь, или же увеличиваясь. Въ такомъ случаѣ говорятъ, что прямая АВ служитъ ассимп-тотою кривой /кривая неограниченно при-
ближается къ прямой АВ, никогда ея не достигая, ибо ордината (или, что то же, величина функціи), обращается въ (I только при # = — со. Такъ какъ при х = -|- со функція получаетъ опять величину гі, какъ и при х = — со, то получится другая вѣтвь кривой, (3) или (4), имѣющая ту же ассимптоту АВ. Въ данномъ случаѣ ассимп-тота параллельна оси х.
Если разсматриваемая функція есть дробь, то можетъ случиться, что знаменатель ея обращается въ нуль при нѣкоторомъ дѣйствительномъ значеніи х1 напр., при х = а. Тогда при х = а^к (гдѣ А какъ угодно мало), т.-е. при я стремящемся къ «, но остающемся всегда < а, дробь стремится къ со, либо къ —со; иначе говоря, по мѣрѣ приближенія абсциссы къ ОР (черт. 59), ордината неограниченно возрастаетъ въ положительномъ, либо въ отрицательномъ направленіи; получается вѣтвь кривой (1),
либо (2). Если, затѣмъ, а? сдѣлается немного больше а, принявъ значеніе а —|—Л, большее а, функція останется безконечно большою, или того же знака, какъ прежде, пли перемѣнивъ знакъ;
но эта величина, сначала безконечно большая, будетъ по абсолютному значенію
становиться все меньше и меньше, по мѣрѣ того какъ # будетъ удаляться отъ «, и получится вѣтвь кривой (3) пли (4).
Прямая РП будетъ ассимптотою кривой, параллельною оси Оу.
Переходимъ къ изученію измѣненія нѣкоторыхъ элементарныхъ функцій.
I. Изслѣдованіе функціи первой степени.
583. Теорема. Функція первой степени.
у =?ах-^Ь
непрерывна на всемъ протяженіи дѣйствительныхъ значеній перемѣннаго х; при увеличеніи х она прогрессивно возрастаетъ ? когда а > 0, /г уменьшается, когда а <0.
1. Во-первыхъ, очевидно, что при всякомъ дѣйствительномъ и конечномъ х функція дѣйствительна и конечна. Затѣмъ, пусть будетъ нѣкоторое опредѣленное значеніе перемѣннаго х; соотвѣтствующее значеніе у пусть будетъ такъ что
Уо = + & •
Дадимъ нѣкоторое приращеніе к, и пусть соотвѣтствующее приращеніе у0 будетъ К; то у0-{-К = а(агв-|-Л)-|-Ь; вычтя изъ новаго состоянія функціи прежнее, найдемъ:
К = [а(хй + к) + Ь] — + Ь) = ак.
Такъ какъ а конечно, то по мѣрѣ приближенія к къ нулю, и произведеніе ак приближается къ нулю; слѣд. ак, т.-е. приращеніе К функціи м. б. сдѣлано какъ угодно мало. Это имѣетъ мѣсто при всякомъ .т0, слѣд. функція непрерывна на всемъ протяженіи дѣйствительныхъ значеній х,
2. Возьмемъ рядъ возрастающихъ значеній
(1)
Если «2>0, то умноженіе на а не измѣнитъ смысла неравенствъ, н получимъ: ах' < а.г” < ах'" < . . . Придавая по Ъ, также не нарушимъ неравенствъ, слѣд.
Если же а < 0, то изъ (1) найдемъ: ах* > ая"> ах’". . . ; а отсюда
ах' + Ъ:>аз” + Ъ>ах'іг+Ъ
Итакъ, когда х возрастаетъ, то функція постоянно возрастаетъ при а>0, и постоянно уменьшается при а<0. .
Примѣръ'!. Функція у = §х — 2 при возрастаніи х возрастаетъ; при х безконечномъ она безконечна; когда увеличиваясь, проходитъ чрезъ зпа-
ченіе у, обращающее функцію въ 0, она изъ отрицательной обращается въ по-ложнтельнѵю:
Примѣръ И. Функція у =— 2я-|“Д при возрастаніи х идетъ убывая; когда х безконечно, абсолютная величина ея безконечна; когда х, увеличиваясь проходитъ чрезъ значеніе обращающее функцію въ 0, она изъ положитель-ной обращается въ отрицательную:
—
Примѣчаніе, Такимъ образомъ, функція не имѣетъ относительныхъ піахіша и шіпіпш, ибо она измѣняется не колеблясь; она имѣетъ абсолютный тіпітит, равный —и абсолижмшй тахітит, равный +^>.
584. Теорема. Линія, изображающая функцію, связанную съ независимымъ перемѣннымъ уравненіемъ первой степени, есть прямая.
Возьмемъ уравненіе у = ах-\-Ь и, положивъ Т = аг, построимъ сперва геометрическое мѣсто точекъ, которыхъ координаты удовлетворяютъ ур—пію Х—ах. Пусть <і, М', М" (черт. 60) будутъ точки искомаго мѣста; проведя ихъ орди-
наты ЦР, М?', М"Р", соединимъ точки 9, М', М" съ 0. Такъ какъ координаты искомаго мѣста должны удовлетворять ур - нію V ~ ах, то
ОР М'Р' — М"Р" ОР М'Р' М"Р"
ОР я** ор ____________ор" и т* Д-т откуда -^р — ^р, 0р„ * *
Изъ этого слѣдуетъ, что треугольники (}0Р, М'0Р\ М"0Р", . . . имѣютъ по равному (прямому) углу, заключенному между пропорціональными сторонами, сл. подобны. Изъ подобія же ихъ слѣдуетъ равенство угловъ (ДОР, М'ОР', М"0Р'\... доказывающее, что линіи 0(), ОМ', ОМ*,... совпадаютъ, а слѣд. точки М',М",... лежатъ на одной и той же прямой, проходящей черезъ начало координатъ. Итакъ, геометрическое мѣсто уравненія У = ах есть прямая 0(}.
Чтобы отъ ординатъ У перейти къ ординатамъ у, соотвѣтствующимъ тѣмъ же значеніямъ <т, достаточно къ первымъ прибавить Ъ (въ ту или другую сторону, см. по знаку й); получится прямая 8Т, либо КП, параллельная первой.
Итакъ, функція а.г-\-Ъ во всякомъ случаѣ представляетъ ординаты прямой.
П. Изслѣдованіе квадратнаго тринома.
585. Теорема. Квадратный триномъ
у ат2-]-
есть функція непрерывная для всѣхъ дѣйствительныхъ значеній х отъ — до 4“^; когда а^>0, функція эта имѣетъ тіпітит, при а<^0 она имѣетъ тагітит; тахітит и тіпітит выражаются формулою
6* - 4а/;
4а ’
а соотвѣтствуюіція значенія х формулою: — ; иаконеп», функція
имѣетъ равныя величины, когда х получаетъ значенія, равноотстоящія отъ (— и наоооротъ.
1. Во-первыхъ, очевидно, что при всякомъ дѣйствительномъ и конечномъ значеніи х триномъ дѣйствителенъ и конеченъ. Давъ перемѣнному гг значенія хь обозначивъ соотвѣтствующія величины черезъ у$ и у^ 4“ К,
находимъ:
к = (Уо + К) — У о = Iя + А)* + Ь (*о++ 0 — (®Ѵ+ + с)
= а№ 4~ (2а#о -|- Ъ)1і — И [2^ 4^ & 4“
Множитель въ скобкахъ, будучи цѣлымъ относительно я0 и Л, конеченъ при всякихъ конечныхъ значеніяхъ и Л, а слѣд. произведеніе этого конечнаго количества на Л можно сдѣлать какъ угодно близкимъ къ нулю, приближая къ нулю приращеніе А; иначе говоря, когда А стремится къ О, то и К стремится къ предѣлу—‘нулю, слѣд. триномъ есть функція непрерывная.
2. Замѣтимъ, что квадратъ какого-либо выраженія измѣняется въ томъ же смыслѣ, какъ и абсолютная величина этого выраженія. Если положительныя числа идутъ возрастая, то и квадраты ихъ идутъ возрастая. Если отрицательныя числа идутъ возрастая, ихъ квадраты уменьшаются. Помня это, дадимъ триному знакомую уже форму:
Г/ і Ц® &2 —4ас~] т
*=аЦ-г+-й) —ігі • - •(1)-
Будемъ измѣнять # отъ —сс до +ос, замѣтивъ въ числѣ этихъ значеній то, при которомъ я обращается въ нуль, именно х — — Напишемъ
рядъ значеній лг, возрастающихъ отъ — сс до — а потомъ отъ — до 4-ес:
Ь_
2л
Придавая къ каждому, воображаемому въ мы не измѣнимъ смысла неравенствъ; слѣд. слѣдующимъ образомъ:
6 этомъ ряду количеству, по
л । Ъ х
измѣненія Н“ 2« будутъ ИДТИ
О-
Возвыіпая значенія воображаемыя здѣсь, въ квадратъ, и замѣчая,
что квадраты отрицательныхъ значеній пойдутъ уменьшаясь, а положительныхъ— • / । Ъ \2
увеличиваясь, получимъ слѣдующій рядъ измѣненій выраженія :
і'х-Ѣ- - 0* * • <Г - ’ - 4-Хк
Замѣтимъ здѣсь
идетъ уменьшаясь до того мо-
мента, когда х достигаетъ критическаго значенія —а потомъ идетъ, без-/ і 6 V
предѣльно увеличиваясь. Такимъ образомъ, выраженіе І^+^І проходитъ че-
„ Л ъ
резъ тіпмпит, равный О, когда х достигаетъ величины —
Придавая къ каждому члену, воображаемому въ послѣднемъ ряду, постоян-Ъ“ ~—~г 4 лс
ное количество — ——, мы не нарушимъ смысла измѣненій, и получимъ і -у х у . I і Ь V Ь2 —4«с
нижеслѣдующій рядъ измѣненій выраженія -----Т^2~:
Ь V б2 — 4лс
’а1 4л‘2
б2 — 4ое
Наконецъ, чтобы отъ этого выраженія перейти къ триному, нужпо ввести множителя «; но здѣсь нужно различать два случая: а>0 и Въ нервомъ случаѣ умноженіе на а не нарушитъ смысла неравенствъ, во второмъ, умноженіе на а измѣнитъ смыслъ всѣхъ неравенствъ. Итакъ, окончательно имѣемъ слѣдующую таблицу измѣненій тринома:
х — •
а.т2 -|- Ъх 4^ с при а > 0 | *
I
ах1 Ъх с при а. <І 0 । — ес
Отсюда непосредственно видно, что:
1) При триномъ ал?34“^х“Ьс идетъ уменьшаясь до того момента,
Ь
когда х достигаетъ величины — а съ этого момента онъ идетъ возрастая неограниченно; слѣд, при а^О триномъ имѣетъ япкгЪшп, равный
Ь2 — 4ас
-----—
когда х получаетъ значеніе
2) При а<СО триномъ идетъ возрастая до того момента,
когда х достигаетъ величины — затѣмъ опъ неограниченно уменьшается; слѣд, при «<^О триномъ имѣетъ тахітит^ равный
б2 —
4а '
котораго достигаетъ при х = —
3, Дадимъ перемѣнному х два значенія, одинаково по абсолютной величинѣ / Ь \ ,
разнящіяся отъ I — ^-1; эти значенія будутъ вида
6 , б
• ” 2« А “ — 2/.
Подставивъ эти значенія х въ формулу (1), найдемъ, что триномъ въ обоихъ . га 4ас\
случаяхъ обращается въ а ---------4^2р т’”е* получаетъ равныя значенія.
Обратно, пусть триномъ получаетъ равныя величины при двухъ значеніяхъ х и я” перемѣннаго х, т-е. пусть
ах4 Ц- с — ітг"2 4“
откуда
- *"*) 4- ь(ж'—= оі
или, раздѣливъ обѣ части на а (я' — ^г"), найдемъ в
у ль У' +- = ():
- . 1 1 а '
пусть х'<\х”; мы можемъ предыдущее равенство • написать въ видѣ
= _ А _ у
2а) 2а '
а это означаетъ, что избытокъ количества х” надъ — Д равенъ избытку —-2а1 • 2а
надъ х\ или, другими словами, что х' и х" равно отстоятъ отъ — ~; если
большее изъ этихъ количествъ равно — ~ -|- Л, то меньшее будетъ — — А?
АІ
586. Примѣчаніе I. Изъ предыдущей теоремы непосредственно заключаемъ, что: * /
Когда а^>0 три номъ два раза проходитъ черезъ нуль^ если его ті-пІтит отрицателенъ > одинъ разъ — когда этотъ тіпітит~Ог и не обращается въ нуль, если тіпітит положителенъ.
Въ самомъ дѣлѣ, трипомъ непрерывенъ п измѣняется въ разсматриваемомъ случаѣ отъ -[-оз до тіпітипГа, а потомъ отъ тінішипГа до проходя чрезъ прежнія значенія; слѣд, онъ можетъ обратиться въ нуль только тогда, когда его тінішпш < 0, и въ такомъ случаѣ два раза пройдетъ черезъ нуль.
Значенія х, обращающія трвномъ въ нуль, даютъ въ атомъ случаѣ полу-сумму равную — ибо они равноотстоятъ отъ этой величины.
Иначе говоря: когда а>0, уравненіе ал2с = 0 имѣетъ дѣйствительные неравные корпи, если ———-<С0, или —4ас>0, а сумма
корней равна — но имѣетъ равные корни, — 4ас = 0, а общая величина ихъ есть — ;
№ — 4ас , о . Л
когда ----у-—>0, или 6*—4ас<0.
//2 —
если ----------г— =0, или
4 а
наконецъ, корни его мнимы.
Все это — знакомые результаты, найденные здѣсь только инымъ путемъ.
Такимъ же образомъ, одного взгляда на таблицу измѣненій тринома достаточно, чтобы убѣдиться, что при а<0 необходимо, чтобы шахітнні былъ положителенъ, для того, чтобы функція- прошла черезъ 0, но тогда она и другой разъ пройдетъ черезъ ту же величину. Этотъ случай изслѣдуется какъ и предыдущій.
Примѣчаніе II. Когда триномъ не можетъ обратиться въ нуль, всѣ его значенія — того же знака, какъ а; тоже самое имѣетъ мѣсто, когда тахііниш или тіпітпш равенъ нулю.
Когда триномъ проходитъ два раза черезъ нуль, знакъ его противоположенъ знаку а для всѣхъ значеній гс, содержащихся между этими двумя частными значеніями ж, но знакъ его одинаковъ съ знакомъ а для всѣхъ остальныхъ значеній а?*
«гг*—Ь.г—[—с при а> О ..()
знакт» коэф. ™ & зн. коэф, -|- а
№—4ас
4а
знакъ коэф.-|-а
а.г2-[-Ь.г-]“С при а < О
; знакъ коэф.+а
знакъ коэф. “ а зн. коэф. -|-а
Такимъ образомъ уже знакомые намъ результаты относительно измѣненія знака тринома ясно вытекаютъ изъ непрерывности измѣненій этой функціи.
Примѣчаніе III Относительный тахітит или тпітит тринома ах* -}- Ьх -|- с есть вмѣстѣ съ тѣмъ и абсолютный.
Пусть напр., а > 0; таблица измѣненій показываетъ, что
б* — 4аг 4а
дѣйствительно меньше всѣхъ другихъ значеній функціи: слѣд. это — тіпітит абсолютный.
Это же непосредственно слѣдуетъ изъ формулы
Въ
имѣетъ
6* —
4а* Г
самомъ дѣлѣ, перемѣнное количество
Ь
будучи
квадратомъ,
наименьшую величину пуль, при а* = —
Слѣд. наименьшая величина скобокъ есть —
б* — 4ас
; умножая па положи-
тельное а, пайдемъ и для у наименьшую величину, которая, слѣд., =
Ь2 — 4ас 4а
587. Графическое представленіе хода измѣненій квадратнаго тринома.
Укажемъ планъ построенія кривыхъ, изображающихъ измѣненія тринома, различая два главныхъ случая: а^>0 и а < О. и въ каждомъ изъ нихъ 3 подраздѣленія: Ь3 — 4ас >0, Ь2 — 4ас = О, Ь* — 4ас < 0.
Пусть «>0 и /? —4ас^>0; въ этомъ случаѣ таблица измѣненій тринома (§ 586) показываетъ, что при х= — ~ онъ имѣетъ отрицательный іпіпі-ліиш =— затѣмъ, при а?, равныхъ корнямъ и а^), обращается
въ нуль; наконецъ, по мѣрѣ: уменьшенія перемѣннаго я отъ х, до — оо и увеличенія отъ#* до —]—оэт триномъ возрастаетъ отъ 0 до 4-*х). При каждыхъ двухъ значеніяхъ равноотстоящихъ отъ — значенія тринома одинаковы по величинѣ н по знаку. Отсюда такое построеніе. Откладываемъ (черт. 61) на оси абсциссъ, вправо или влѣво, смотря но знаку, отрѣзокъ ОА = — Въ точкѣ А проводимъ параллель ВС къ оси уу' и откладываемъ на ней отрѣзокъ < г* б2 — 4ас , / . . лч
АВ=--------— внизъ отъ точки А (т. к. шішшит этотъ О); такимъ
образомъ получаемъ наименьшую ординату, и точка В есть нисшая точка кривой. Вправо и влѣво отъ точки А откладываемъ линіи АН=АНГ=— 0 получа-емъ точки Н и Н', которыми опредѣляются корни ОН и 0Н; тринома; для этихъ значеній я ординаты =0, слѣд. въ точкахъ Н и Н' кривая пересѣкаетъ ось,я>въ. Соединивъ точку В съ точками Н и Н' кривою, продолжаемъ части ВН и ВН' этой кривой вверхъ, располагая обѣ вѣтви симметрично относительно прямой ВС. Въ самомъ дѣлѣ, мы знаемъ (§ 585, 3), что для всякихъ двухъ значеній #5 равноотстоящихъ отъ ОА, значенія у равны, т.-е. что если взять АР=АР\ то перпендикуляры РМ и Р'М' къ оси ха/ въ точкахъ Р и Р', представляющіе ординаты кривой, равны; слѣд. хорда ММ' будетъ параллельна оси я-въ и раздѣ
лится прямою АС пополамъ. Слѣд. линія АС дѣлитъ пополамъ всѣ хорды кривой, ей перпендикулярныя, т.-е. дѣлитъ кривую на двѣ симметричныя части. Поэтому АС наз. осью кривой, точка В вершиною кривой. Самая кривая есть парабола.
Для болѣе точнаго построенія кривой нужно дать я~су большее число значеній и вычислить соотвѣтствующія значенія тринома, нанося ихъ на ордина-тахъ: такимъ образокъ получится большее число точекъ кривой и фигура ея опредѣлится точнѣе. Такимъ образомъ, ходъ измѣненій тринома изображается наглядно и выясняются всѣ частности. Напр., видно, что кривая можетъ пересѣкать ось я-овъ только тогда, когда ішпішппі отрицателенъ, и т. и.
Разъ кривая построена тщательно, т.-е. при помощи достаточнаго числа точекъ, она можетъ служить для болѣе быстраго опредѣленія величинъ функціи (у), соотвѣтствующихъ данной величинѣ перемѣннаго я, и обратно, для опредѣленія значеній дг, соотвѣтствующихъ данному Въ первомъ случаѣ достаточно нанести данный х по оси х*х отъ точки 0, вправо или влѣво, см. по знаку; пусть Р будетъ найденная точка; затѣмъ взять точку М кривой, въ которой перпендикуляръ къ оси х*х^ возставленный въ точкѣ Р, пересѣкаетъ кривую. Длина МР и представитъ абсолютную величину тринома, о знакѣ же судимъ по положенію точки М относительно оси я>овъ.
Для опредѣленія значеній я-са, при которыхъ трипомъ принимаетъ данную величину 7с, наносятъ на ось #-въ, начиная отъ точки 0, въ направленіи, опредѣляемомъ знакомъ 7с, длину 0К = 7с; черезъ точку К проводятъ параллель оси #-въ: пусть она встрѣчаетъ кривую въ точкахъ М и М': абсциссы ОР и ОР' этихъ точекъ и будутъ искомыя значенія х.
Сказаннаго достаточно для построенія кривыхъ во всѣхъ случаяхъ; разъясненія излишни. Поэтому мы нрямо прилагаемъ таблички измѣненій тринома для каждаго случая, а противъ нихъ кривыя, выражающія эти измѣненія.
Значеніе линій указано вслѣдъ за каждымъ чертежомъ.
I случай: а>0.
1. Ъ*—
Черт, 61.
Ь тл _ я™*
0А = -^; АВ=-Ц-^; ОН—.г,; 0Н' = ^.
3. — 4ас<0; и мнимые.
3
588. Примѣръ I. Изслѣдовать'измѣненія тринома ^/ = -х2-^12х-|-18 при измѣненіи х отъ — 'хэ до 4* Представимъ триномъ въ видѣ •
Отсюда, но предыдущему, прямо слѣдуетъ таблица измѣненій:
х — . *<• • -—6* • - <2—4 . • • <С • * •—2 у -Р00 * • •>••• О - • — 6« • .<• • • О
т.-е» данный триномъ уменьшается отъ 4’°* до —6, когда х возрастаетъ отъ —сс до —4; потомъ онъ увеличивается отъ —6 до 4"°^ когда х возрастаетъ отъ — 4 до 4“ Слѣд. трипомъ имѣетъ шінішшп = — 6 при х =— 4; проходитъ дважды чрезъ каждую величину, большую—6, и никогда не дѣлается меньше —6.
€ Графически измѣненія функціи изобразятся измѣненіемъ ординаты параболы, которой ось параллельна оси у, причемъ координаты низшей точки (вершины) суть: х = — 4, у = — 6; кривая два раза пересѣкаетъ ось х, въ точкахъ, коихъ абсциссы суть: ~2 и — 6 (черт. 67).
Примѣръ II. Изслѣдовать измѣненія тринома у =—я2-|- 2х—3 при измѣненіи х отъ *—'хэ до
Представимъ триномъ въ видѣ:
У = -[(^-1)2 + 2].
Имѣемъ таблицу измѣненій
Заключаемъ, что триномъ увеличивается отъ —оа до — 2, когда х возрастаетъ отъ — со до 4-1; затѣмъ онъ уменьшается отъ —2 до —когда х возрастаетъ отъ —1 до 4-00* Слѣдоват. функція имѣетъ пкг. шііпі (—2), соот-
вѣтствующій я = 4“1; слѣд. она не проходитъ черезъ О, но проходитъ дважды чрезъ всякое значеніе, мепыпее — 2.’Парабола, представляющая ходъ измѣненій тринома, вся лежитъ въ области отрицательныхъ игрековъ (черт. 68).
III. Изслѣдованіе биквадратнаго тринома.
589. Теорема. Биквадратный триномъ
у = ах* 4“ Ъх* 4~ с
есть функція непрерывная для всѣхъ дѣйствительныхъ значеній х отъ — до 4~^« Функція эта необходимо имѣетъ тахітит, либо тіпі-тит? равный с; кромѣ того, когда а и Ъ имѣютъ противоположные знаки, она еще имѣетъ либо два тахітит'а, либо два тіцітит'а; если же а и Ь имѣютъ знаки одинаковые, то никакого тах. или тіпіт., кромѣ с, .триномъ не имѣетъ.
1. Очевидно, что при всякомъ дѣйствительномъ и конечномъ значеніи х триномъ дѣйствителенъ и конеченъ. Давъ перемѣнному х нѣкоторое приращеніе
А и вычтя изъ новаго состоянія функціи прежнее, найдемъ соотвѣтствующее приращеніе у (А):
к—а(х^ку+Ь(х+іі)*+с-- ал1—Ьх3—с=А[4ах34*26х+7е(6аа;г4'4а^Л+«Л2Н-Ь)]й
Множитель въ квадратныхъ скобкахъ конеченъ при всякихъ конечныхъ х и А; и слѣд. при безконечно маломъ А, вторая часть м. б. сдѣлана какъ угодно малою; слѣд* триномъ непрерывенъ.
2, Представимъ триномъ въ видѣ
Первый случай: а>0, 6 < О.
Какъ и для квадратнаго тринома, составляемъ таблицу:
Слѣд. ^ + 9^) проходитъ черезъ тішпшш О, когда х проходитъ чрезъ величину — } — затѣмъ тотъ же квадратъ проходитъ чрезъ шахітпт когда х обращается въ 0; уменьшается до тіпітит’а равнаго нулю, когда х увеличивается до 4-а потомъ увеличивается до безконечности.
Прибавляя постоянное количество-----------4л2~’ и Умножая на положитель-
ное количество а, мы не измѣнимъ смысла неравенствъ, и найдемъ:
Итакъ, въ случаѣ: а>0, А<Д биквадратный триномъ имѣетъ два пііпі-шпт’а, равные и одинъ шахІтнпі, равный с. Міпіша триномъ
имѣетъ при х = -I- шахітиш при х = 0.
Для слѣдующихъ случаевъ мы прямо даемъ результаты, которые получаются тѣмъ же пріемомъ.
Второй случай: А^О.
триномъ имѣетъ тіпішшп = с, при х = 0.
— 625 —
Третій случай: а
. О - .
. . с . .
триномъ имѣетъ тахішпш =с? при # = 0.
Четвертый случай: а < О, Ь > О.
X
г 2а
Ъ- — 4яс
— 4ас
4а
ті ж л ч & — 4ас
*' Въ-этомъ случаѣ-триномъ-имѣетъ два-шахншіш-а, равные--------4 а 7
торыхъ онъ достигаетъ при # и одинъ шіпішпт — с, при я = О.
550. Графическое представленіе. 1. Пусть напр. * . я
а > О, Ь < О, Ь*— 4ас > О, с > 0. * * * 7
При этихъ условіяхъ триномъ имѣетъ положительный тахітпшп с и два Ъ“ ________________________________________ 4ас
отрицат. минимальныя значенія, равныя--------Іо-’ тах* с ТРИНОМЪ имѣетъ
при я = О, тіпітпа при # = 4г1/—Д’ Отсюда построеніе: беремъ (черт. 69) Г &С1
ОА
и В'. Ось хх1 пересѣкаетъ кривую въ четырехъ
А кривой, шіпіта—точкамъ В дѣйствительныхъ точкахъ, слѣд. триномъ 4 раза обращается въ нуль, при х попарно равныхъ, но противоположныхъ по знаку. Это совершенно сообразно съ тѣмъ результатомъ, что при данныхъ условіяхъ биквадратное уравненіе + с имѣетъ 4 различныхъ дѣйствительныхъ корня.
Возьмемъ численный примѣръ для разсматриваемаго случая.
Примѣръ. Изслѣдовать измѣненіе связаннаго съ х уравненіемъ 2у = х*— 5, ириг измѣненіи х отъ —со до -[-со.
Въ числѣ критическихъ значеній ^опредѣливъ и корпи тринома .т4—6х2-|-5, которые равные і/о и +1, даемъ у форму:
у=к(®’-з)’-4і
и находимъ слѣдующую таблицу измѣненій у:
—=©••<-----Ѵ5--<-*—ИІ--<--------!••<•• 0 ••<••4-1- < -44/3-’<>-+>/5 -<"
5
1 иішт. шах. тіпілі,
Отсюда заключаемъ, что увеличивается отъ — см до 5 она увеличивается до при
функція уменьшается отъ -ф”00 до —2, когда # — /3, проходя чрезъ 0 при х =— затѣмъ
возрастаніи х до 0, проходя чрезъ нулевое значе-
ніе при х = — 1. Съ этого момента функція проходитъ прежнія значенія, въ обратномъ порядкѣ. На чертежѣ (черт. 70):
0С'=0С=/3;
С'В' = СВ = 2;
0А = |;
ОЕ'=ОЕ= І/б; 01У = 0П—1.
2 . Пусть будетъ: а^>0, Ь^>0.
При этихъ условіяхъ триномъ ах* -|- Ъх* с уменьшается отъ 4"^ Л° а потомъ возрастаетъ отъ с до проходя черезъ шіпітит с при я = 0. Въ нуль онъ можетъ обратиться только два раза, при двухъ равныхъ и противоположныхъ значеніяхъ я, и то лишь въ томъ случаѣ, когда с < О.
Эти измѣненія представлены на чертежѣ 71-омъ, причемъ предполагается с < О.
IV. Изслѣдованіе дроби: у =
591 * Даемъ перемѣнному # нѣкоторое приращеніе Л; для соотвѣтствующаго приращенія Л дроби находимъ:
__ а (я + к) 4- & + б ___ к(аЪ' — агЪ)
а'(х 4- А) + &' а*х + (а'я + &') (а'х Н- й' + а1к)
Отсюда заключаемъ: 1) когда х приближается къ —знаменатель выраженія к приближается къ О, а слѣд. коэффиціентъ при А, т.-е дробь
4> 6" + д'А) пРи^лижается къ поэтому и приращеніе к функціи приближается къ со, т.-е. функція претерпѣваетъ разрывъ непрерывности. При всѣхъ другихъ значеніяхъ по мѣрѣ приближенія к къ 0, и к стремится къ О, т.-е. функція непрерывна. Итакъ, дробь у непрерывна въ тервалловъ:
каждомъ изъ ин-
Ъг
ОТЪ —ДО —^7
Ь'
претерпѣвая разрывъ непрерывности только при х =---------г> общему предѣлу
этихъ интервалловъ.
2) Знакъ выраженія & зависитъ только отъ числителя; въ самомъ дѣлѣ, знаменатель можно представить въ видѣ . а* (^4"^), а это
выраженіе, при достаточно маломъ А, существенно—положительно, ибо знакъ его будетъ зависитъ только отъ перваго члена который (какъ квадратъ)
положителенъ при всякомъ дѣйствительномъ х. Но числитель аЪ' — агЬ, какъ количество постоянное, всегда имѣетъ одинъ и тотъ же знакъ, сл. функція всегда идетъ: или возрастая, или уменьшаясь; т.-е. въ каждомъ изъ интервал-ловъ непрерывности дробь
идетъ постоянно увеличиваясь, если идетъ постоянно уменьшаясь, если имѣетъ постоянную величину, если
— аЪ О; аѴ — аЬ <4 О; аб' — а'Ъ — О,
ибо въ послѣднемъ случаѣ всегда А = О, т.-е. дробь не получаетъ приращеній при измѣненіяхъ х, сохраняя одну и ту же величину.
Итакъ, при изслѣдованіи измѣненій функціи, должны различать три указанные случая; при этомъ, раздѣливъ числ. на знаменателя дроби, получаемъ
аЪ — аЪг
_ а аЪ — аЪг а ,
У а'т Ъ( х • а'
•Кі*
„ а'Ь — аЬг .
Положивъ, для краткости, —— = л,. замѣчаемъ, что знакъ а зависитъ
только отъ числителя, именно: при аЬг—а'Ъ^>0 будё' будетъ 0; дробь можно представить въ видѣ
♦
< а I а
& аг । Ь
і
Соображая все сказанное, прямо находимъ слѣдующіе выводы относительно измѣненій дроби при измѣненіи л? отъ —сѵ до
I. аЪ' — Ьа 2> О.
а
У '.,а*
гдѣ
а'
Ьг
— с
аг
У а*
а а7
до------р функція идетъ постоянно уве-
V Я* ' л,
имѣетъ мѣсто разрывъ пепрерыв-
Тле. при возрастаніи л? отъ — оо а - ।
личиваясь отъ до -]-сс; при ясности: функція изъ Фоз внезапно обращается въ —ес; затѣмъ, при возра-Ь' г а
станіи х отъ —до -[-с©, идетъ постоянно увеличиваясь отъ —со до
Въ одномъ изъ интервалловъ она проходитъ чрезъ О, при'# = —
Измѣненія функціи изобразятся, такимъ образомъ, измѣненіями ординатъ слѣдующей кривой
(гипербола).
На чертежѣ (72):
»"=7
Ь'
ОМ = -а
0Е = —-а
ОС' и ВВ'—двѣ ассимптоты кривой.
У
а а
I
II. а// - Ьа < О.
а аг
Ъ‘г
гдѣ X }> О
7/ а*
ѵг
а
при возрастаніи а? отъ а
Т.-с. .' і непрерывно отъ — до —при
а изъ —сс ВЪ идетъ постоянно уменьшаясь отъ Ц-сс до •’ Въ одномъ изъ внтервалловъ непрерывности она проходитъ чрезъ О, і I ... Ь* V
при а? = — -
Кривая измѣненій (гипербола) такова: . . .
— гѵ -+- сѵ > * ’ • > -г II _ " (Г
// ,
— сс до —-? функція идетъ уменьшаясь
/У
х = — происходитъ разрывъ непрерывности:
Ь*
затѣмъ, при увеличеніи х отъ —
г. 1
Черт. 73.
(Ш
(V
0Е= —-а
СС' и ВВ'— двѣ ассимптоты кривой.
ПК аб' —6а' = О.
а потому при вся-— величинѣ • по-нзмѣненіи х отъ
Черт. 74.
При этомъ и X = О, , а комъ х имѣемъ у = стоянной. Слѣд. при — оо до Ц’Зо, дробь не измѣняетъ своей
величины; ея кривая будетъ прямая СС\ которой ординаты равны ОМ = ^ Задача. Найти прямо условіе пе~ . -обходимое и достаточное для того, л ах +Ь .чтобы арооъ —-г-, о.иіьла постоян-а х 4- о ную величину при всякомъ х,
1-й способъ. Такъ какъ дробь должна имѣть одну и ту же величину при всякомъ х, то, между прочимъ, она должна имѣть постоянную величину, напр. при я = 0 и при я = Но при я = 0, у —при я=1, у~^-^;слѣд.
. а+Ь Ъ а &
должно быть: откуда, по свойству пропорціи, имѣемъ:
ом = ®
с
М
О
і
Это условіе, будучи необходимымъ, вмѣстѣ съ тѣмъ и достаточно; ибо изъ г, аЪ , . .
него: о = — ? и слѣд. дробь обращается въ
Итакъ, условіе необходимое и достаточное для того, чтобы наша дробь имѣла постоянную величину, есть или аЬ' — а'Ъ = 0, что и было найдено
при изслѣдованіи.
2-й способъ. Пусть к будетъ эта постоянная, пока неизвѣстная, величина* Нахожденіе условія, необх. и дост* для того, чтобы сводится къ
нахожденію условія, при которомъ было бы ах Ь = к (агх -|- Ь'), или (а — агк) х + (Ь — Ь’к) = 0 при всякомъ х; а для этого необходимо и достаточно (§ 70), чтобы было: а— а'&=0 и Ь — Ь'&=0, или & = и = откуда — = или аЪ* — а(Ь ~ О* а' Ь'
592. Приложенія,-—«злиъкенія х задачи § 367^ полагая, что шарикъ, помѣщенный внѣ билліарда, можетъ свободно проникать внутрь круга и свободно возвращаться въ исходную точку?
Для х мы имѣемъ формулу
,,_К(Н-а\
х~ 2а~~
Е — величина постоянная, слѣд. х измѣняется въ томъ же смыслѣ какъ дробь Кдд0* Эта дробь даетъ: аЪг — Ьа' =— 2К, а потому заключаемъ, что увеличенію а соотвѣтствуетъ уменьшеніе я-са* Формула даетъ; если я = В, то а = —; если же а = ео, х = — Отсюда заключаемъ, что когда а возрастаетъ отъ своего шіпітшп’а до -рсо, х уменьшается отъ своего тахішпш’а К до тіпітшп'а =—такимъ образомъ сразу находимъ таблицу критическихъ величинъ я:
а
3 ‘ ‘ 2 ‘
в. . Л • • о
В
П Пересѣчь данный шаръ плоскостью такъ, чтобы объемъ одного изъ сегментовъ составлялъ данную дробь К объема цилиндра одной высоты и одною основанія съ сегментомъ. Между какими предѣлами можно задавать число К?
Обозначивъ высоту сегмента буквою я, найдемъ:
х — ЗК ЗаГ^бК
С>31 —
Будемъ измѣнять # отъ О до 2Е. Такъ какъ аЬ' — а*Ь = -ф- 3, то функція К идетъ возрастая; при я = О, К = ~; при х = 2В, Отсюда
таблица:
х О ... Н ... 2В.
К
1
2
2
‘ 3’
Слѣд. для К можно брать всѣ числа отъ до -ф-ес. Каждый разъ задача 2
имѣетъ 1 рѣшеніе. Отношеніе шара къ описанному цилиндру равно результатъ, являющійся деталью изслѣдованія.
Примѣчаніе, Изъ числа дробныхъ функцій элементарному изслѣдованію подлежитъ еще квадратная дробь но изученіе ея раціональнѣе
отнести къ спеціальной статьѣ о шахіша и шіпіта.
V. Примѣры изслѣдованія ирраціональныхъ функцій.
593. Примѣръ I. Я$сля>доштъ функцію у =/я*-}-2,г’—3 при измѣненіи х отъ —до
Триномъ я3-р2я —3 имѣетъ дѣйствительные корни: —3 и —|— 1; слѣд. опъ положителенъ при всѣхъ х, меньшихъ — 3, а также большихъ 1, и отрицателенъ при всѣхъ значеніяхъ заключающихся между — 3 и + 1. Итакъ, функція у дѣйствительна при всѣхъ значеніяхъ лежащихъ внѣ корней тринома, и мнима для всякаго заключающагося между корнями.
Докажемъ, что она непрерывна для всѣхъ х, заключающихся между — оо и-— 3, и между 4“1 в 4“°°- Пусть хг и будутъ два значенія я, лежащихъ внѣ интервалла отъ — 3 до -ф-1 - Имѣемъ:
у' = 4- 2х' — 3
и у' 4- к =,/{х' 4~ Л)3 4" 2 (Х+
отсюда
К = /(?'+&)«4- 2 (а:' + А) — 3 — /я;’14- 2®' — 3;
или, множа и дѣля вторую часть на сумму радикаловъ:
__________^ + 27/^ + 1)
+ 2 +7і) - 3 + ^ + 2^-3’
по мѣрѣ приближенія А къ нулю, числитель стремится къ нулю; знаменатель же, будучи дѣйствительнымъ при х и отличенъ отъ нуля, ибо эти
значенія х отличны отъ —3 и -ф-1. Слѣд* частное К стремится къ нулю вмѣстѣ съ А, а слѣд. функція у непрерывна въ указанныхъ иптерваллахъ ея дѣйствительности.
Сперва изслѣдуемъ измѣненія подрадикальнаго тринома, а отсюда н самой функціи; получаемъ таблицу:
у — мнимый*
Но трудно изобразить измѣненія функціи графически. Для этого замѣтимъ, что триномъ имѣетъ равныя значенія, когда х получаетъ величины,, равноотстоящія отъ — 1; сл. и 2/ имѣетъ это свойство, и потому кривая имѣетъ осью симметріи прямую 22', параллельную оси у и отстоящую , отъ этой оси на ОС = — 1.
Затѣмъ, кривая не имѣетъ точекъ между параллелями къ оси уу\ находящимися • отъ этой оси въ разстояніяхъ: 0А = + 1, ОА' = —3, ибо въ этихъ предѣлахъ у имѣетъ мнимыя значе-
нія; наконецъ, кривая не имѣетъ точекъ, лежащихъ внизу отъ оси ж, ибо у есть положительная величина |/я*-|-2я—3, по заданію.
Примѣръ II. Изслѣдовать функцію у = — ж2 — 2х 4~ 3, когда х
измѣняется отъ —со до 4“^.
Корни тринома —а;2 —2л-)-3 суть —-3 и —рі; изъ закона измѣненій тринома заключаемъ, что онъ имѣетъ положительныя величины только при содержащихся между — 3 ,и -|- I; для всѣхъ значеній я?, лежащихъ внѣ этихъ предѣловъ, триномъ отрицателенъ; слѣд, функція у дѣйствительна, когда х измѣняется внутри корней, и мнима при всѣхъ лежащихъ внѣ корней. Какъ и въ предыдущемъ примѣрѣ докажемъ, что она непрерывна для интервалла отъ — 3 до +1 • Отсюда такая таблица измѣненій:
х —со... — 3 ... <... — 1,.. <С... 4~ 1 ••• 4“^
— х'1— 2х —I-3—О 4~ 4... >4,. —со
274^3 ------—О 4-2... >... О-
у — мнимый. у — мнимый.
е Итакъ, функція возрастаетъ отъ О (при # =—3) до -|-2 (при # = —1), затѣмъ уменьшается до О (при я=-)-1). Слѣд. опа имѣетъ шахішпш =4“^ при х =— 1.
Кривая имѣетъ ось симметріи, параллельную уу1 и проходящую черезъ точку С, причемъ ОС = -—1; на этой оси помѣщается тахітит = 4" 2. Кривая не имѣетъ точекъ внѣ параллелей оси уу', проведенныхъ черезъ точки А и А', такія, что
0А = 1 и ОіѴ=—3; она не имѣетъ точекъ внизу отъ оси яя'. Кривая эта — полуокружность центра С*
а іг. й „ . : 1 *
Примѣръ III. Наслѣдовать функцію у‘= .---------*=пли измѣненіи
, Ѵ^ + 2ж — з ’
х отъ ’—го ’-рсо, * • . . *
Функція непрерывна въ интерваллахъ: отъ — го до —3 и отъ -рі до и претерпѣваетъ разрывъ непрерывности отъ,-—3 до Измѣненія ея обратны измѣненіямъ функціи '|/#24~ 2Ж—3; отсюда таблица: •
Кривая функціи имѣетъ ось симметріи ни'; параллельную'оси уу и опредѣ; ляемую линіей ОВ =—Дч3атѣиъ, она не имѣетъ точекъ, между" пѵ' и параллельными осн уу' и отстоящими отъ этой оси на (ІА = 1 и 0А'₽=* — 3,
Вмѣстѣ съ этимъ, тѣ же прямыя и ось суть три ассимитоты кривой, которая, къ тому же, не имѣетъ точекъ внизу отъ оси я-овъ.
ГЛАВА ХЫ.
Образцы изслѣдованія вопросовъ второй степени.
Задача I.
594. РалЛ&мт» данную прямую АВ еь крайдолга и среднемъ отношеніи, «г.-е найти на ней такую точку С, чмобы большій отрѣзокъ АС былъ среднимъ пропорціональнымъ между всею линіею АВ и меньшимъ ея отрѣзкомъ ВС.
—2
По условію задачи должно быть: АС=АВХСВ, иди, назвавъ данную прямую АВ буквою а, разстояніе АС буквою а?, и слѣд. обозначивъ ВС разностью а — получимъ уравненіе
#2=а(а— #) ... (1) иди а2—О . . . (2).
Изслѣдованіе. Чтобы корень ур—нія (2) представлялъ рѣшеніе задачи въ прямомъ смыслѣ, необходимо, чтобы онъ былъ дѣйствителенъ, положителенъ и былъ <а.
Ур—ніе (2) имѣетъ всегда корпи дѣйствительные, потому что послѣдній членъ (—а2) отрицателенъ; далѣе, корни имѣютъ противоположные знаки, такъ какъ произведеніе ихъ отрицательно (——а2); притомъ, меньшій по абсолютной вели-чинѣ корень положителенъ, ибо сумма корней отрицательна (= — а). Остается убѣдиться, будетъ ли положительный корень меньше а; для этого подставляемъ въ триномъ, образующій первую часть ур—нія (2), вмѣсто а? сперва 0, потомъ а, и замѣчаемъ, что результаты этихъ подстановокъ (—а2 и ч-а2) имѣютъ противоположные знаки. Слѣд. положительный корень меньше а: онъ даетъ точку С, лежащую между А и В и представляющую рѣшеніе задачи въ прямомъ смыслѣ.
Другой корень уравненія отрицателенъ; чтобы найти его значеніе, подставимъ въ ур—ніе (1), первоначальное^ —х вмѣсто я; получимъ ур—ніе
дв=а(а4-а?) . . . (3),
имѣющее корни равные по величинѣ, но противоположные по знаку корнямъ ур—нія (I). Такимъ образомъ, отрицательный корень ур—нія (1), взятый съ противоположнымъ знакомъ, представляетъ прямое рѣшеніе задачи, отвѣчающей ур—нію (3). Послѣднее, какъ не посредственно видно, опредѣляетъ точку С', лежащую на продолженіи линіи ВА вправо отъ А, и также удовлетворяющую вопросу: въ самомъ дѣлѣ, положивъ АС'=э^ имѣемъ ВС'=а-ья, и ур—ніе (3) тождественно съ
АС' = АВХВС'-
Итакъ, отрицательный корень даетъ другое рѣшеніе задачи, а знакъ этого корня показываетъ, что послѣдній долженъ быть нанесенъ на продолженіи линіи АВ, въ сторону отъ А, противоположную первому корню. Алгебраическое рѣшеніе, кромѣ отвѣта на вопросъ въ тѣсномъ смыслѣ заданія, показало намъ, что вопросу, взятому въ болѣе широкомъ смыслѣ, удовлетворяютъ двѣ точки: С и С', причемъ знаки корней указываютъ расположеніе этихъ точекъ относительно А.
Рѣшая ур—ніе (1), находимъ:
Построеніе корней. Взявъ неограниченную прямую и на ней отрѣзокъ АВ=а, возставляемъ къ этой прямой перпендикуляръ въ точкѣ В, откладываемъ на немъ часть В0=^; изъ точки О, какъ изъ центра, радіусомъ ВО
Черт. 78.
описываемъ окружность, и соединивъ А съ центромъ, продолжаемъ прямую АО до пересѣченія съ окружностью въ точкѣ Е; другую точку пересѣченія назовемъ буквою О. Прямыя АО * АЕ представляютъ абсолютныя величины корней х' и х”.
Въ самомъ дѣлѣ, ізъ прямоуг. треуг. АОВ имѣемъ.*
т —2 - / /аѴ
АО = ) ВОч-АВ = р І2/4’п: слѣд. *
ЛІ)-АО-ОВ=у ®г+а2~2 :2’'’
АЕ = АОн-ОВ = ]/«« -Ь ~ = - а-".
Остается нанести АО на АВ влѣво отъ точки А, линію же АЕ на продолженіе АВ вправо отъ А: для этого нужно засѣчь прямую ху двумя дугами круговъ, описанныхъ изъ точки А, какъ изъ центра, радіусами АО и АЕ. Такимъ образомъ получимъ требуемыя точки С и С'.
Задача II.
595. На неограниченной прямой, соединяющей два источника свѣта А и В, найти точку. равноосвѣщенную обоими.
Задача эта впервыѳ появилась въ алгебрѣ Кяерд (1746 г.), и съ тѣхъ поръ вошла въ учебники, какъ одинъ изъ поучительныхъ образцовъ изслѣдованія вопросовъ.
А #С — в
.............
Черт. 79.
Обозначимъ разстояніе АВ буквою с?, разстояніе искомой точки С отъ А буквою ж; тогда ВС будетъ равно <і—х. Далѣе, пусть сила освѣщенія источникомъ А тѣла, находящагося отъ пего на единичномъ разстояніи, будетъ а, а сила освѣщенія источникомъ В на единичномъ разстояніи пусть будетъ р. Изъ физики
— С>36 -
извѣстно» что сила освѣщенія обратно пропорціональна квадрату разстоянія освѣщаемаго тѣла отъ источника. Слѣд*, если сила освѣщенія источникомъ А
на разстояніи 1 есть а, то на разстояніи 2, 3, 4. . * единицъ она будетъ
5Т5 тт, ...» а потому на разстояніи х она будетъ Такимъ же образомъ, 3® 4* я°Л
д
сила освѣщенія точки С источникомъ В будетъ т-г-^—Но, по условію задачи,
—х)*
точка С освѣщена обоими источниками одинаково, слѣд.
или
(4—я-)»’
(а — Р) іг- — 2а * (I * *г -4- ейа — 0 . * •» (2).
Изслѣдованіе. Чтобы задача была возможна, нужно чтобы корни были дѣйствительны, т.-е. реализантъ не былъ бы отрицателенъ* Но рсализантъ —
сЛ/2 — ^2а — аасР Д-
а это есть количество положительное, такъ какъ, по натурѣ задачи, і суть количества существенно-положительныя* Итакъ, корни уравненія всегда дѣйствительны.
Для опредѣленія ихъ знаковъ обращаемся къ произведенію и суммѣ корней; имѣемъ
х*, х” —
хг я" ~
2аг?
^7
гдѣ и ^—количество положительное, въ частности, могущее обратиться и въ нуль. Отсюда возможные случаи' таковы;
1)гі>о, *>?; 2)Й>0, »<₽; 3) гі>0, » = ?; 4) й=0,
и 5) </ = 0, а = ^. ѵ ц
1-й случай: (I > 0, а :
Произведеніе корней положительно: слѣдовательно, знаки ихъ одинаковы; сумма корней также положительна, ‘слѣдовательно, оба корня положительны. Это значить, что въ данномъ случаѣ существуютъ двѣ точки, лежащія вправо отъ А, одинаково освѣщаемыя обоими источниками. Посмотримъ, какъ эти точки, расположены относительно источника В.
Для этого надо сравнить корни съ линіей/2. Подставивъ въ ур—ніе (2) ♦вмѣсто а? букву с?, найдемъ: *
• . • '• /((*) = (а — Й - 2«Р-Ь «й = —
I ’ ’
Результатъ подстановки отрицателенъ, т.-е* имѣетъ знакъ, противоположный знаку коэффиціента при ж3; заключаемъ, что содержится между корнями, слѣдовательно, одинъ изъ нихъ меньше <і, другой больше гі* Итакъ, существуютъ двѣ равноосвѣщаемыя точки: одна, С, находится между А и В; другая, С', вправо отъ В*
Остается узнать, къ которому изъ данныхъ источниковъ первая точка, С, ближе: къ источнику А, или къ источнику В? Подстановка въ первую часть
ур—нія {2) количества - вмѣсто х, даетъ результатъ ;
гіа\ І <>\®
. • • Г\2)=^~^Х-
положительный, т.-е. одного знака съ коэффиціентомъ при ха. Это значить, что находится внѣ корней, и, очевидно, меньше меньшаго корня. Заключаемъ, что точка С находится ближе къ слабѣйшему источнику В, чего и слѣдовало ожидать. Что касается второй равноосвѣщаемой точки, С', то, находясь вправо отъ В, она также лежитъ ближе ігь слабѣйшему источнику, какъ и должно бытъ.
2-й случай: & > 0, а < р.
Произведеніе корней, имѣя въ этомъ случаѣ положительный числитель и отрицательный знаменатель, отрицательно; слѣдовательно, одинъ корень положителенъ, другой отрицателенъ. Сумма корней отрицательна, слѣдовательно абсолютное значеніе отрицательнаго корня больше.
Положительныя корень даетъ точку, лежащую вправо отъ А. Для опредѣленія ея положенія относительно В, замѣчаемъ, что =т.-е. имѣетъ знакъ коэффиціента при а;3; слѣдовательно, й находится внѣ корней, т.-е. положительный корень меньше г/. Онъ даетъ точку, находящуюся между А и В. Къ которому источнику она ближе? Такъ какъ
имѣетъ знакъ )-го коэффиціента, то находится внѣ корней, т.-е. положитель-
* (I
ный корень <2'’ Это значить, что искомая точка С ближе къ источнику А, какъ и должно быть, ибо въ данномъ случаѣ этотъ источникъ слабѣе В.
Что касается отрицательнаго корня, то для истолкованія его обратимся къ ур—нію (Г); подставивъ въ него —я? вмѣсто я, найдемъ ур—ніе
-= -
аЯ (г/ н- я1)2’
которое и получили бы, если бы искали равноосвѣщенную точку влѣво отъ А. Итакъ, отрицательный корень опредѣляетъ точку С", лежащую мгаяо отъ А. Дѣйствительно, такая точка, находясь ближе къ слабѣйшему источнику А, при надлежащемъ разстояніи отъ него, можетъ быть одинаково освѣщена обоими.
слт/чіѵи: (I > 0, а = р.
Въ этомъ случаѣ коэффиціентъ при іг2 обращается въ нуль, и слѣдовательно, одинъ корень уравненія обращается въ безконечность, а другой найдемъ, отбросивъ членъ съ я’2, т.-е. взявъ ур—ніе
— 4- — 0, иди —2г 4- й = О,
откуда
Корень а?’— - означаетъ, что одна изъ искомыхъ точекъ находится какъ разъ въ срединѣ линіи АВ, что и должно быть при равенствѣ освѣщенія обоими источниками.
Для истолкованія безконечнаго корня можно замѣтить/ что при равенствѣ яркости источниковъ всякая точка, взятая на продолженіи линіи АВ въ конечномъ разстояніи отъ источниковъ, будетъ освѣщаться ими неодинаково, но что чѣмъ дальше отодвигать эту точку, тѣмъ разница въ освѣщеніи будетъ становиться все меньше и меньше, но можетъ исчезнуть лишь пцн удаленіи точки въ безконечность. Можно обратиться также къ формулѣ корней. Написавъ ур-ніе въ видѣ
1(1 — яЛ2 _ Р \ я ) а’
имѣемъ
откуда найдемъ
__ <7 Ѵ ' а ______ (і к і
— 'Т* ~ Ѵл — У| ’
. • А
Первый корень при а— ? дастъ первую изъ искомыхъ точекъ: Ж|_
Если въ формулѣ ;г2 взять сначала а> то дастъ точку С7 вправо отъ А; по мѣрѣ приближенія а къ р, и слѣдовательно, знаменателя—къ нулю, х* будетъ болѣе и болѣе возрастать, и точка С' удаляться вправо; наконецъ, когда а сдѣлается равнымъ $, точка С' удалится на безконечно большое разстояніе вправо отъ А. Если бы а было въ началѣ меньше р, то корень далъ бы точку С", лежащую влѣво отъ А; по мѣрѣ приближенія а къ она удалялась бы въ безконечность влѣво отъ А*
4-й случай: —О,
Ур—ніе обращается въ (ч —(1);г2 = 0, откуда х'^х" = 0. Это значитъ, что только одна точка будетъ равно освѣщена: та точка, въ которой находятся оба источника свѣта.
5-й случай: ^ = 0, а —
Уравненіе принимаетъ видъ 0 . #2-|-0 . + 0 = 0; ему удовлетворяетъ всякое значеніе я, такъ что число рѣшеній неограниченно, и задача неопредѣленна. И въ
самомъ дѣлѣ, когда оба источника находятся въ одномъ мѣстѣ и равносильны, то всякая точка соединяющей ихъ прямой будетъ освѣщаться ими одинаково. Въ числѣ ихъ находится и сама точка, гдѣ помѣщены оба источника, и которую опредѣляетъ первый корень х', равный въ этомъ случаѣ нулю.
Примѣчаніе I. Нетрудно построитъ обѣ равноосвѣ-щенныя точки. Возставивъ въ точкѣ А (черт. 80) пер-
пендикуляръ равный /а, а въ точкѣ В два перпендикуляра, одинъ кверху, другой книзу отъ линіи ху, равные і/р, проводимъ прямыя А'В' и А'В", изъ коихъ первая пересѣчетъ линію ху въ точкѣ С', вто-Ѳрая въ С. Это и будутъ искомыя точки; въ самомъ дѣлѣ:
АА' ВВ"
р' АС — ВС ’ ИЛИ х ~а—х’
АА' _ ВВ' |/і_ И _ ✓ ? ас'-вс” или х ~х-а~ а—х
ц 8! Результаты алгебраическаго изслѣдованія
р * * предоставляемъ читателю вывести изъ этого
чертежа.
Примѣчаніе ІЕ Если бы требовалось найти геометрическое мѣсто точекъ плоскости, равноосвѣщенныхъ источниками А и В, то, положивъ, что М (черт. 81) есть одна изъ точекъ искомаго мѣста, мы пашли бы, что
— =-?
-2 —2*
АМ ВМ
или
АМ __ 1/д
ВМ Vх)
Заключаемъ, что искомое мѣсто есть мѣсто такихъ точекъ, отношеніе разстояній которыхъ отъ А и В имѣетъ данную величину. Изъ геометріи извѣстно, что ято есть окружность, описанная на прямой СС' (точки С и С' опредѣляются построеніемъ, указаннымъ въ примѣчаніи І)какъ на діаметрѣ.
Примѣчаніе III» Если бы требовалось опредѣлить лтс?ио точекъ въ яро-странствзь^ равноосвѣщаемыхъ точками А и Вгто достаточно было бы обернуть окружность МСС' около діаметра СС': точки полученной шаровой поверхности и были бы требуемыя.
Наконецъ, если бы требовалось найти точки равноосвѣщенныя источниками А и В, на юъкаторои линіи или на поверхности, расположенныхъ вблизи точекъ А и В, то очевидно, что искомыя точки были бы общими точками данной линіи или поверхности съ вышеуказанною сферою. Въ случаѣ поверхности, этихъ точекъ было бы безконечное множество, но могла бы быть и одна только искомая точка, если бы сфера и поверхность были касательны; могло бы и не быть искомыхъ точекъ, если бы поверхность и сфера не имѣли общихъ точекъ*
Задача III.
596. Манометръ со сжатымъ воздухомъ строю цилиндрической трубки АВОВ; вилквъ гнутая частъ В — ртуть, а вѣтвь 00 находится въ сообщеніи съ паровымъ котломъ паровой машины» Когда уровень ртути стоитъ на одной горизонтальной плоскости АО, давленіе вдеддоа въ манометрѣ равно давленію атмосферы; когда давленіе въ котлѣ увеличивается, поднимается въ
вѣтви ВЕ и на столько же опускается въ ВО* Зноя, что АЕ=?, что давленіе атмосферы = 11, вычг/слмш& высоту х уровня А' надъ А, если давленіе въ котлѣ равно п атмосферамъ»
Рѣшеніе. Ртуть въ трубкѣ ВЕ перестанетъ подниматься и остановится въ А', когда упругость воздуха, сжатаго въ этой вѣтви, увеличенная колонною А'А" ртути, уравновѣситъ давленіе въ котлѣ. Высота А'А" = 2АА'_ 2л?.
Новое давленіе у воздуха, сжатаго въ А'Е, опредѣляется по закону Маріотта, именно: если температура не измѣняется, то давленія, производимыя одною и тою же массою газа, обратно пропорціональны объемамъ, ею занимаемымъ. Въ данномъ слу-
состоитъ изъ дважды согнутой, ЕВ содержи™ъ сухой воздухъ; со-
Чсрт. 82.
чаѣ, объемы, послѣдовательно занимаемые воздухомъ въ манометрѣ, суть цилиндры, имѣющіе одинаковое основаніе, а высоты I и
слѣд., назвавъ сѣченіе трубки буквою <о, имѣемъ:
У ІТ./
-------откуда !/ = НХ 7------------- — Н у I — х
Такъ какъ давленіе въ котлѣ равно нН, то ур. задачи будетъ:
яН = 2я 4- Н X т-
I—х
или, по освобожденіи отъ знаменателя:
2<г2 — (2/ 4-пН)^4-Цп— !)Н=0 * * * (I).
Рѣшивъ его, найдемъ:
21 н- ИІІ А. у\214- ИІІ)2 _ 81 (м — 1) н Л? 1— — -------- ---------------- у
4
пли
Ч-8Ш
И з с л ѣ д о в л и і е. Чтобы тотъ илп другой король удовлетворялъ задачѣ, онъ долженъ быть дѣйствительнымъ, положительнымъ и < К Такъ какъ подъ зна комъ радикала находится существенно-положительное количество, то. оба корня всегда, дѣйствительны* Если «>Ъ то произведеніе корней будетъ положительно; а какъ и сумма ихъ положительна, то оба корня будутъ положительны. Но какъ неизвѣстное должно быть еще <2, то нужно убѣдиться, имѣетъ ли ур—ніе корень, меньшій 2. Подставляя I вмѣсто ш въ первую часть ур—нія (1), найдемъ
Ш или — Ш,
т.-е. результатъ отрицательный; это значитъ, что I заключается между корнями ур—нія (1), и слѣдовательно меньшій, корень <2, а большій >2. Задачѣ отвѣчаетъ меньшій корень, слѣдовательно
22 -н «И - V (пН — 202 -Ь 82 Н
и есть искомый отвѣтъ.
Примѣчаніе 1. Еслп п неограниченно увеличивать, то при я — эо корень принимаетъ неопредѣленный видъ сс—сс; чтобы найти истинное значеніе этой неопредѣленности, нужно числ. и’знам, умножить на 22 нН -ь і/(ЫІ — 22)гч- 82Ш найдемъ
1)Н
При п = оа это выраженіе принимаетъ неопредѣленную форму вида -для раскрытія которой дѣлимъ числ. и знам* на я; такимъ образомъ получимъ
.т'=
- И
«•/
82Н’
а положивъ здѣсь н = со, найдемъ
22П _ 2211 _
Н + П—2Н —
Это значитъ, что по мѣрѣ того какъ давленіе увеличивается, уровень А' ртутной колонны болѣе и болѣе приближается къ вершинѣ *Е трубки ВЕ. к
Примѣчаніе И. Если давленіе въ котлѣ сдѣлается меньше атмосферы, уровень ртути опустился до А"' ниже точки А въ колѣнѣ ЕВ, и поднимается до 0'" въ ВО, причемъ А А'" = 00". Равновѣсіе наступитъ тогда, когда давленіе у воздуха въ манометрѣ будетъ равно давленію пара 4“ колонна ртути 0"0'", равная 2 А А'". Если новое неизвѣстное А А'" назовемъ буквою у опредѣлится изъ пропорціи
2 У п
. ГН=Іі’ откуда у = И.
новое ур—ніе задачи будетъ
пли
пН^Н.у-4------2г,
2г2-|_(2г + яЩя-Н(я — 1)Ы = О. . .(3);
оно отличается отъ (1) только перемѣною & на — я; слѣдов. корни (3) равны по величинѣ и противоположны по знаку корнямъ (1), Такъ какъ здѣсь я<1, то произведеніе корней отрицательно, слѣд. одинъ корень ур—нія 0) положителенъ, другой отрицателенъ; новому вопросу отвѣчаетъ положительный корень
— (2? + Іія) +1/(2? — мН)2 + 8Ш
Сличая гг съ я/ видимъ, что рѣшеніе (2) примѣнимо къ обоимъ случаямъ: и>1 и «<1; достаточно только откладывать отрицательныя значенія, которыя можетъ получать выраженіе (2), внизъ отъ точки Л.
Задача IV.
597. Тяжелое тѣло брошено въ пустотѣ вертикально вверхъ съ начальною скоростью Ѵо; впредпьштъ, въ какое время оно достигнетъ высоты А насй начальною точною?
Въ равномѣрно-замедлительномъ движеніи, какое имѣетъ тяжелое тѣло, поднимающееся вверхъ, пройденное пространство I связано съ временемъ употребленнымъ на его прохожденіе, формулою ч
/='7-1(02. . .(1).
Слѣдовательно, если искомое время назовемъ буквою х} то это неизвѣстное должно удовлетворять ур—нію
Л = ѴвЯ! —Іргг0,
ИЛИ
^ — 27^ + 274 = 0, . Д2).
Изслѣдованіе. Чтобы х, выведенное изъ этого ур—нія, давало отвѣть на вопросъ, нужно, чтобы рѣшеніе было дѣйствительно и положительно. Условіе дѣйствительности корней ур—нія (2) таково;
Ѵв2 — 2#А О, или А С •
Итакъ, различаемъ три случая:
Первый случай: А
V 2 ѵ Г
2/
Корни ур—нія (2) мнимы, слѣд. задача невозможна. Это очевидно й ргіогъ Въ самомъ дѣлѣ, тѣло остановится, когда его уменьшающаяся скорость обратится въ нуль. Но скорость въ концѣ времени і опредѣляется формулою: Ѵ=Ѵ0 — ді; слѣд. она обратится въ нуль, когда время ? — —; пройденное до этого момента
пространство будетъ — Это есть тахітит высоты, до
которой можетъ подняться тѣло при начальной скорости Ѵо.
Ѵп2
Второй случай: Л=2^*
Корни ур—нія (2) въ этомъ случаѣ—дѣйствительные равные, а общая величина \ о
ихъ есть —, что согласно съ вышеуказаннымъ результатомъ.
Т г 2 / ѵ«*
Третіи случай: Л<^’
Въ этомъ случаѣ ур—ніе (2) имѣетъ корни дѣйствительные, неравные и оба положительные (послѣднее потому, что ихъ произведеніе — и сумма —2 — по-<7 9
ложительны).
Чтобы дать себѣ отчетъ въ происхожденіи этихъ двухъ положительныхъ корней, замѣтимъ, что тѣло при движеніи бываетъ дважды въ точкѣ М, отстоящей по вертикалу на Л отъ А; одинъ разъ летя вверхъ, другой разъ, п падая внизъ. Оба положительные корня и даютъ эти времена. Въ Т** самомъ дѣлѣ, эти корни суть
,_ѵ, ^_Ѵ., И7-2рЛ
__ ..... г , х - д
Черт. 83.
Припомнимъ, что сколько времени тѣло употребляетъ на поднятіе отъ М до В, столько же и на паденіе отъ В до М. Пусть это время = Ѳ; слѣд. взявъ случай паденія, имѣемъ: ВМ = ^#Ѳ2 или
— откуда
-У
е==ѵѴ—
9
Затѣмъ, зная, что есть время кульминаціи, находимъ, что меньшій корень, ж', представляетъ разность между временемъ кульминаціи и временемъ, необходимымъ тѣлу на прохожденіе вверхъ разстоянія ВМ, слѣд. — врался до кульминаціи, въ которое тѣло находится отъ точки А на высотѣ 7г; большій корень, а?", представляетъ сумму временъ, необходимыхъ тѣлу на поднятіе вверхъ до высшей точки В и затѣмъ на паденіе внизъ до М, слѣд.—«реля посл/ь кульминаціи, въ которое тѣло находится отъ А на высотѣ /г.
Задача V.
598. Отъ момента, въ который наблюдатель, стоящій у отверстія. колодца, выпустилъ изъ рукъ камень, до момента, въ который услышанъ былъ ударъ камня о воду, прошло і секундъ. Найти глубину колодца, зная; 1) чшо звукъ распространятся равномѣрно со скоростью ѵ; 2) что сся^ь между пространствомъ і, пройденнымъ при свободномъ паденіи, и временемъ н паденія выражается фор*
му лаю I = гдѣ д—ускореніе тяжести.
Рѣшеніе. Пусть искомая глубина колодца будетъ яц данное время 2 составляется изъ двухъ частей:
1) Изъ времени у, которое камень употребляетъ на прохожденіе свободнымъ паденіемъ глубины х колодца, причемъ связь между ж и у выражается формулою
изъ КОТОроЙ
2) изъ времени я, въ которое звукъ проходитъ разстояніе а? равномѣрнымъ движеніемъ со скоростью ѵ, причемъ по закону равномѣрнаго движенія а? — откуда
х я — ~.
ѵ
Приравнивая я-}-# данному времени имѣемъ ур—ніе
. ,(і).
ѵ г г д • ѵ }
Это уравненіе—ирраціональное; для рѣшенія его, изолируемъ радикалы
- И
«7
и возвышаемъ обѣ части въ квадратъ, что даетъ послѣдовательно:
= і2 — или дх2 — 2ѵ (ѵ -+-ді) х 4- дѵ2&=0 . * . (3).
Изслѣдованіе. Ур—ніе (3) не эквивалентно (2)-му, ибо оно есть то же, что ур—ніе
2яг__[ а?\2
9 \ ѵ/
но послѣднее есть результатъ возвышенія въ квадратъ какъ даннаго ур—нія
V 9 V
такъ и ур—нія
_-1/^-5.
Г 9 ѵ
Чтобы корень ур—нія (3) удовлетворялъ данному ур—нію, нужно, чтобы онъ обращалъ разность і — въ количество положительное, т.-е, удовлетворялъ бы неравенству
0. или х < гЛ
Итакъ, чтобы корень ур—нія (3) представлялъ отвѣтъ на данную задачу, нужно, чтобы онъ былъ дѣйствительнымъ, положительнымъ п меньше К
Чтобы корни ур—нія (3) были дѣйствительны, необходимо и достаточно, чтобы было
ѵ2 (у -ь ді)2 — О, пли іР (га -+- 2^г/) 0.
Но каждое изъ количествъ д. г и / положительно, слѣд, условіе дѣйствительности всегда удовлетворено.
Затѣмъ, оба корня положительны, потому что произведеніе ихъ и сумма 2ѵ (ѵ ч-
—--------— положительны. Остается убѣдиться, будетъ ли хотя одинъ пзъ кор-
ней <і#. Для этого въ триномъ, составляющій первую часть ур—нія (3), подставляемъ ѵі вмѣсто ж; получимъ: дѵ-і2— 2ѵ (уч-ді) ѵі-і-дг№, или —2ѵ3#, результатъ отрицательный, т.-е. противоположнаго знака коэффиціенту д при х2 въ триномѣ (3). Это значить, что содержатся между корнями ур—нія (3), и слѣд. меньшій корень <ѵі, и только онъ одинъ даетъ отвѣтъ на задачу. Итакъ
_______
“ (г? Ч- —14?® ч- 2дѵі) 9
Задача VI.
599. Построитъ прямоугольный треугольникъ, зная его периметръ 2р и нлоіцадъ т2.
Рѣшеніе. Обозначимъ искомые катеты буквами я и#, а гипотенузу найдемъ уравненія
ян-#= 2р . , . (1)
= . Д2)
а?# = 2т3. . • (3).
Изъ (1) имѣемъ я-ь# = 2р — возвысивъ обѣ части этого уравненія въ квадратъ и замѣнивъ а^-ь#2 равнымъ этой суммѣ количествомъ & [изъ (2)], получаемъ: я2 ~н 2я# == (2р — я)2; или, замѣчая, что по (3): 2я# = 4ш3, находимъ, раскрывъ (27? — г)2;
Я2 ч- 4>«2 — 4р2 — ^2,
откуда
,-*=!!?. . . (4). р
Подставляя вмѣсто * это значеніе въ ур. (I), имѣемъ:
. р3 4- *п3
® + У = ---— • • (5)-
Изъ ур—ніЙ (3) и (5) видно, что я и # суть корни квадратнаго уравненія ри2 ~ (р2 + т*) и + 2риг* = 0 . , , (6) откуда: _____________
х (____р2 Ч- и»2 ^(р2 + »л3)3 — 8р2т2 .
# I “ 2р
Изслѣдованіе, Чтобы корпи, опредѣляемые вышеданными формулами, представляли отвѣтъ на задачу, они должны быть дѣйствительны, положительны и, каждый, <р.
Формула (4) показываетъ, что г дѣйствительно; оно будетъ положительно, если взять ш<р; но въ такомъ случаѣ # будетъ и меньше р, Итакъ, должно быть
т < р • . • (8).
Чтобы х и у были дѣйствительны, необходимо, чтобы было
(р2 + т2)2 — вр2»!3 $> 0, или (р3 + яг3)3 — (21/2 , рт)2 0, или
(р2 Ц- т2 4- 2Ѵ 2 . р-^ОІР2 + »г2 — 21^2 . р»г) 0,
т.-е. оба множителя 1-й части должны имѣть одинаковый знакъ; но какъ первый множитель положителенъ, то и второй долженъ быть >0; такимъ образомъ, располагая по степенямъ ш, имѣемъ неравенство
т2 — 21х2 . р . ш +р2 0.
Корни этого тринома суть: т'=р(і/2—1) и т"=р(Ѵ2 +1), и какъ триномъ долженъ имѣть знакъ перваго члена, то т должно лежать внѣ корней, т.-е. должно быть
пі — 1) . . . (9) иди »я ^.р(1/2 +1) * . .(10).
Но неравенство (10), будучи не необходимо, протяворѣчитъ необходимому неравенству (8), и потому должно быть отброшено. Тогда останутся два неравенства одинаковаго смысла (8) и (9); но какъ первое изъ нихъ заключается во второмъ, то остается послѣднее, т.-е. «
»і <_р(У2 — 1).
Разъ оно удовлетворено, х и у будутъ дѣйствительны; но въ такомъ случаѣ оня будутъ и положительны, ибо ихъ произведеніе 2т% и сумма -- положительны* Кромѣ того, х и ѵ будутъ и меньше р. Въ самомъ дѣлѣ,
/(р) =рз — рЗ _ гп2р _|_ 2т2р =
слѣдовательно, положительна; это значитъ, что р находится внѣ интервалла кор-
.«2 I ~ Я?2
ур—нія (6), и какъ полусумма этихъ корней, равная -----------
ней
♦
при
X и
меньше р (ибо
«2
условіи т2<р2 имѣемъ •т,'е' т0 расположеніе корней у и числа р на скалѣ дѣйствительныхъ чиселъ таково:
х . • . у * . . р,
т.-е. х и у, каждое, меньше р.
Заключаемъ, что единственное условіе возможности задачи есть
— 1).
Итакъ, числа х, у и я, будучи дѣйствительными, положительными^ меньшими р и удовлетворяя ур—нію (2), служатъ мѣрами сторонъ прямоугольнаго треугольника, который и можетъ быть построенъ.
Неравенство (9) показываетъ, что яакбольшая величина пли тахітит т есть р (/2 — 1); такъ какъ это есть одинъ изъ корней подрадикальнаго тринома, то послѣдній прит=р(І/2 — 1) обратится въ нуль, х и у сдѣлаются равными, а треугольникъ равнобедреннымъ, такъ что находимъ теорему: гоь вело прямоугольныхъ треугольниковъ одинаковаго периметра равнобедренный имѣетъ наибольшую площадь (ибо при наиб. значеніи ш, и »п2 имѣетъ наиб. значеніе).
Черт. 84.
Примѣчаніе. Если бъ мы рѣшили неравенства относительно р, то легко нашли бы подобнымъ же образомъ, что: м.п вто прямоуюльныхъ треугольниковъ* имѣющихъ одинаковую площадь, равнобедренный имѣетъ наименьшій периметръ. Построеніе, Пусть данный периметръ 2р равенъ линіи МХ, а данный квадратъ стороны ш равенъ РС^КЗ. Раздѣливъ линію МХ пополамъ, возставимъ въ точкѣ Т перпендикуляръ ТѴ=ТХ=р, и соединимъ 0 съ X; изъ прямоугольнаго треугольника ХТО имѣемъ: ХЧ’=рѴ/2. Описавъ изъ точки X, какъ изъ центра, дугу радіусомъ =р, получимъ: ПТ'=р( 1/2—1). Изслѣдованіе намъ показало, что для возможности задачи сторона т квадрата гн2 не должна превышать линіи ЪТТ; беремъ для заданнаго квадрата сторону, равную []Ѵ<СГГ'.
Строимъ я по формулѣ (4). Для этого, взявъ прямую БѲ~ 2;^ на половинѣ ея БЕ описываемъ полукругъ, наносимъ въ немъ хорду ЕГ=ш, опускаемъ перпендикуляръ ЕС па БЕ, и соединяемъ точки Б и Е, Изъ прямоугольнаго треугольника БЕЕ имѣемъ: БР"2—БЕ2—ЕЕЗ—р2—т2; съ другой стороны: БР*_ = БЕХБС=рХБС; слѣдовательно _рХОС=р2—ш2, откуда
ос=1*^=^
Р
Замѣчая, что СО—Б6 —БС=2р—я, пзъур—нія (1) видимъ, что СО=ж+#.
Допустивъ, что САВ есть требуемый треугольникъ, имѣемъ:
СА+АВ = аг + у= СО = СА + АО, откуда
ЛВ = АО,
слѣдовательно уголъ 0 треугольника АВ6 равенъ 45°; при этомъ СВ=СБ—я.
Поэтому въ треугольникѣ ВСО извѣстны стороны Си и СО и уголъ О; такъ что дальше продолжаемъ построеніе такъ: продолжаемъ ГС и беремъ СК=СО, соединяемъ точки К и О и опускаемъ перпендикуляръ СП на КО, который раздѣлитъ прямую КО въ точкѣ’ Н пополамъ. Не трудно удостовѣриться, что въ разсматриваемомъ случаѣ СБ>СН; поэтому, описавъ изъ С, какъ изъ центра, дугу радіусомъ СБ, найдемъ, что она пересѣчетъ линію КО въ двухъ точкахъ В и В'. Опустивъ изъ этихъ точекъ перпендикуляры ВА и В'Л' па СО, найдемъ два требуемые треугольника АВС и А'В'С; легко видѣть, что они равны. Въ самомъ дѣлѣ, СО, равно и ЛА' въ точкѣ Т дѣлятся пополамъ; поэтому
АО = АВ — А'С; а также СВ — СВ\
При условіи т=р(Ѵ2—1) легко видѣть, что будетъ СБ=СН, и задача имѣетъ одно рѣшеніе: равнобедренный треугольникъ СШ. Наконецъ, при 1)
будетъ СБ<С11, и задача невозможна.
Задача VII.
600. Зная высоту к усѣченнаго конуса, его объемъ V и радіусъ К одяоіо изъ основаній, вычислить радіусъ х другою основанія.
Рѣшеніе. Объемъ конуса, усѣченнаго параллельно основанію, дается формулою: -гЛ(В2 + Ея+#2), и если*данный объемъ V мы представимъ въ видѣ
конуса той же высоты Л, какъ и искомый, съ радіусомъ а основанія, т.-е. положимъ Ѵ=ігсЛ«2л то прямо получимъ ур—ніе
О
1гЛ(В24-Кж+«г)=ігЛ. а?, или а?Н.т + № — «З —0 . . . (1), о о
откуда
— К±Ѵ'4«‘- ЗК2
— — — —------в
Изслѣдованіе. Если предположить, что искомый усѣченный конусъ состоитъ изъ двухъ конусовъ, сложенныхъ вершинами, т.-е. представляетъ усѣченный конусъ 2-го рода, то нашли бы ур—ніе
ж2 — + № — й2 = 0. . .(2),
отличающееся отъ перваго только перемѣною а? на —ж: слѣдов. отрицательные корни ур—пія (1) служатъ положительными корнями (2), и потому даютъ рѣшенія 2-го рода.
Зная это, обратимся къ изслѣдованію ур—нія (1).
Условіе дѣйствительности корней, какъ легко видѣть, выражается неравенствомъ а2 К2,
4
Знаки корней. Произведеніе корней, равное К2—#2, будетъ >0 при а2<Н2,=0 прм а2—К2 и <0 при л2>1<2.
Сумма корней, равная—К, всегда отрицательна. Такимъ образомъ, критическія значенія а*, въ восходящемъ порядкѣ, сутпі 0, уН2 и К2, л легко составить слѣдующую таблицу знаковъ,
Значенія а2 п 0 н« 4
Реалнзантъ —I—
Произв. корней 1 "
Сумма корней — —
изъ которой тотчасъ выводимъ заключенія:
1) «2<-К2. Реализаптъ отрицателенъ, слѣд. 4
корни ур—нія (1) мнимы, п задача невозможна.
3
2) а2^^К2, (тіпітшп а2). Въ этомъ случаѣ
что даетъ усѣченный конусъ 2-го рода, у котораго радіусъ верхняго основанія вдвое меньше радіуса нижняго основанія. Это значитъ, что изъ всѣхъ усѣченныхъ конусовъ 1-го или 2-го рода, которые можно построить на данномъ основаніи и съ данною высотою, наименьшій объемъ принадлежитъ конусу 2-го рода АВ8В"А" (черт. 86), котораго вершина на-2 ходнтся на = высоты отъ нижняго основанія.
Черт. 86.
3) |кг<«2
К2. Произведеніе корней ур—нія
(1) положительно,
а сумма
ихъ отрицательна (= — К), слѣдов. оба корня отрицательны п даютъ два рѣшенія 2-го рода (2) и (2^, которыхъ основанія расположены по обѣ стороны точки 8 (1).
4) а2 —К2. Ур. (1) приводится къ а# 4"^ = О и имѣетъ корни:
х — 0, х =— К.
Второй корень даетъ усѣченный конусъ 2-го рода (3), имѣющій вершину въ срединѣ высоты; первое рѣшеніе даетъ полный конусъ (3'), который по произволу можно разсматривать или какъ усѣченный 1-го рода, или какъ усѣченный конусъ 2-го рода.
Черт. 87.
5) а2>К2. Произведеніе и сумма корней ур—нія (1) отрицательны; слѣдов* одинъ корень положителенъ, а другой отрицателенъ, причемъ абсолют. знач. послѣдняго больше: первый даетъ усѣченный конусъ 1-го рода, второй—2-го рода, какъ на чѳрт. (1), только радіусъ О'А" длиннѣе О'В'.
Если, теперь, помножить обѣ части предыдущихъ равенствъ и неравенствъ на ІгЛ, чтобы ввести данный объемъ V, то все изслѣдованіе можно резюмиро
вать такъ:
Резюме изслѣдованія.
7 кК2А . . . х' и х" мнимы : 0 рѣшеній.
даетъ : 1 рѣш. 2-го рода.
тіпітит для V.
ѴсікВЯЬ . : я^<0, «"<0 : 2 рѣшенія 2-го рода.
Ѵ>1кК2Л < 4
Ѵ=к-К2Л . : д?'=—К, ®''=0 : 2 рѣшенія 2-го рода.
Ѵ>-кП2Л . : я/<0, : 1 рѣш. 1-го и 1 рѣш. 2-го рода,
о
601. Изслѣдованіе измѣненія объема V. Для объема V мы нашли формулу: "Л (я2 +Кг-|-В2), которую можно написать въ видѣ
Ч4(*+І)!+М
Это есть квадратный триномъ относительно изученіе его измѣненій при измѣненіи х отъ —оо до приведетъ насъ къ вышенайденнымъ результатамъ, но кратчайшимъ путемъ.
Даемъ гг-су сначала значенія отъ О до +^о, и вычисляемъ соотвѣтствующія значенія выраженія въ квадратныхъ скобкахъ; помноживъ каждое изъ этихъ значеній на і гЛ, найдемъ измѣненія объема V. То же самое дѣлаемъ, измѣняя х
отъ 0 до —со. Такимъ образомъ получаемъ двѣ таблицы измѣненій V: для положительныхъ и для отрицательныхъ значеній х.
Итакъ, конусъ перваго рода неограниченно возрастаетъ отъ до без-о
конечности; конусъ второго рода сперва уменьшается отъ до
1 '
потомъ увеличивается до % гЛ2Л, проходя два раза черезъ всѣ величины между о
^гК2Л и а затѣмъ продолжаетъ увеличиваться, проходя разъ черезъ каж^
. 1 * дое значеніе отъ до +ео. о Представимъ эти измѣненія объема кривою. Для этого наносимъ положительныя
С
Черт. 88.
значенія х по оси х вправо отъ начала 0, отрицательныя — влѣво отъ 0. Въ конечной точкѣ каждаго значенія х проводимъ перпендикуляръ къ оси х’х, и откладываемъ на немъ величины функціи V. Соединивъ вершины ординатъ, получимъ параболу, изображающую наглядно измѣненія V. Эта кривая показываетъ:
1) Чтобы найти значеніе V, соотвѣтствующее данному значенію х, нужно нанести х на ось х'х вправо или влѣво отъ точки 0, смотря по знаку а>са, и провести ординату кривой, соотвѣтствующую взятому значенію х,
2) Чтобы найти значеніе ат, соотвѣтствующее данной величинѣ V, нужно пересѣчь кривую параллелью оси х'х, взятою на разстояніи отъ х'х, равномъ значенію V, и построить абсциссы точекъ пересѣченія этой параллели съ кривою.
Такимъ образомъ легко видѣть, что задача не имѣетъ рѣшенія, когда V меньше ибо кривая не имѣетъ точекъ, которыхъ ординаты были бы меньше
что наименьшее значеніе V есть ^К2Л, и что оно соотвѣтствуетъ К 1 1
—тр что V принимаетъ два раза каждое значеніе между и дгКЭД при двухъ различныхъ отрицательныхъ значеніяхъ одномъ, содержащемся между 0 и другомъ—между —и —К: задача имѣетъ 2 рѣшенія 2-го
рода; что, наконецъ, V принимаетъ дважды каждое значеніе большее разъ при я?>0, другой при я< —К: задача имѣетъ 2 рѣшенія —одно 1-го рода, и одяо 2-го рода.
Построеніе. Возьмемъ случай: когда задача имѣетъ два рѣшенія—
усѣченные конусы 1-го и 2-го рода. Верхнія основанія ихъ имѣютъ радіусы, выражаемые формулами:
Взявъ линію 00'—й, проведемъ къ ней въ точкахъ О и 0' перпендикуляры да' и на первомъ отъ точки О отложимъ 0А=0А'=Е, на второмъ отъ точки
Черт. 89.
О' линію а на продолженіи ея линію ВО"— П. Изъ точки О" радіусомъ
0"В описываемъ полукругъ, въ которомъ вписываемъ сторону правильнаго тре-кйз
угольника ВС, и дѣлимъ ее въ точкѣ В пополамъ; линія ВВ — ——. Описавъ на а полукружность, наносимъ въ нее хорду ВЕ=ВВ и соединяемъ точку Е съ О':
очевидно,
Затѣмъ, описавъ изъ точки Е радіусомъ ЕЕ'= ЕЕ
II
полукругъ, получимъ
окончательно:
ОТ = |/ й2 - — §=*"; 0Т'^г/а2 —=
Нанеся линіи О'Г и О'Е' на линію 0'0", получимъ: ОТ —О'Р“я;", Остается соединить I съ А', а Г съ А и повернуть чертежъ около оси 00': вращеніе дастъ искомые конѵсы.
Задача ѴШ.
602. Въ данный полукрул вписать хорду такъ, чтобы сумма ея длины съ разстояніемъ &тъ центра равнялась данной линіи ш.
Рѣшеніе. Пусть будетъ АВ требуемая хорда, ОС ея разстояніе отъ центра. По условію задачи:
АВ ОС — т.
Примемъ за неизвѣстное ОС — яя соединивъ А съ О, изъ^греугольника АСО получимъ: АС = УК2—0й, откуда ур—ніе задачи:
2 УВ2 — х2 + я = т.
Это ур—ніе ирраціональное; для рѣшенія его, изолируемъ корень въ первой части:
2/П2 —я2 —— х . . .(1) и возвышаемъ обѣ части въ квадратъ; приведя члены въ порядокъ, найдемъ уравненіе:
5а?2 — 2?ня + м2 — 4В2 = 0 . . , (2).
Изслѣдованіе, Это ур—ніе не эквивалентно (1)-му, ибо оно получи лось бы и изъ ур—нія: —2УК2 — х2 = т — & . . , (Р), такъ что ур—нію (2) могутъ удовлетворять корни двухъ уравненій: (1) и (V), Поэтому, корни ур—нія (2) только тогда будутъ удовлетворять ур—нію (1), когда они дѣлаютъ разность * т — х положительною, т.-е, когда х < т. Затѣмъ, необходимо, чтобы х было дѣйствительно, положительно и не больше В; при несоблюденіи послѣдняго условія точка С будетъ лежать внѣ окружности и потому не дастъ хорды,
Итакъ, чтобы алгебраическій корень х ур—нія (2) удовлетворялъ предложенной геометрической задачѣ, нужно, чтобы было: х — дѣйствительно, а? > О, х < »», х <
Но если х удовлетворяетъ первымъ тремъ условіямъ, то оно удовлетворяетъ и ур—нію (I), а слѣд. УВ2 —ж2, равняясь дѣйствительному количеству т — ж, также будетъ дѣйствителенъ, а слѣдов, будетъ и д?<К. Такимъ образомъ, предыдущія условія сводятся къ слѣдующимъ тремъ:
я дѣйств,, я>0,
1) Условіе дѣйствительности корней ур—нія (2) выражается неравенствомъ:
т2 __ 5 — 4В2) 0, или, по у проще піи, іи2 — 5К2 0,
или
(т 4- В У5)(нг — В У5) <2 0.
Но первый множитель >0, слѣд. должно быть т— Е/б^О, иди
Отсюда:
I. Когда ж>Еі/5, ур—ніе (2) будетъ имѣть корни мнимые: задача невозможна.
II. Когда т *= В і'б, ж щая величина равна
ур—ніе (2) имѣетъ корни дѣйствительные равные: ихъ обили
КГ5 5 *
Это — величина дѣйствительная, положительная и меньшая т = К15, слѣд. представляетъ рѣшеніе данной задачи; ей соотвѣтствуетъ особое положеніе точки С. Проведя въ точкѣ Б касательную БЕ = 2Е, соединяемъ точки Е и О: прямая ГО будетъ — Е Рб; отрѣзавъ отъ нея пятую часть, ОК, отложимъ ее на радіусѣ ОС: найдемъ точку С и хорда будетъ требуемая.
Замѣтимъ, что величина І<)/5 есть тажітит данной суммы т, ибо задача
невозможна, когда т больше этой величины, но т можетъ достичь этой величины, когда точка С займетъ только что указанное положеніе. Итакъ сумма АВ + ОС достигаетъ тахІ-
тит*& = К15, когда о? — *
о
III. Обратимся теперь къ случаю т < К Ѵ5. Въ этомъ случаѣ корни ур—нія (2) дѣйствительные и неравные; разсмотримъ ихъ знаки и величину.
Знаки корней. Ур. (2)
произведеніе корней, будучи
показываетъ, что Ж* _ 4К2 — -----=---, имѣ-
етъ знакъ разности ж2 —4Е2, которую можно представить въ видѣ (ж+2Е) (т—2К). А какъ ж + 2К всегда >0, то заключаемъ, что произведеніе это положительно, когда т >> 2К, равно 0, когда ж = 2Е, и отрицательно, когда ж < 2К-.
Сумма корней,
2 равная ^ж, о
будетъ всегда положительна.
т В УЪ*
=
Величина корней. Должно быть я<ж. Разсмотримъ, какое положеніе ж занимаетъ относительно корней. Результатъ подстановки т вмѣсто х въ триномъ (2) даетъ, по упрощеніи,
• /г(т) = 4(т^Е2),
и слѣдов. /’(ж) имѣетъ такой знакъ какъ ж2— Е2, или какъ (ж 4~Е) — Е), а
какъ и» + К всегда >0, то знакъ будетъ такой какъ у т — К, слѣдов.
когда ж > Е, то Г(ж) > О, когда ж = К, /*(ж) = 0; когда т < й, ((ж) < О.
Расположимъ теперь найденныя критическія значенія ж, т.-е. числа КѴ5Т 2Е, Е и 0—въ порядкѣ возрастающихъ значеній и помѣстимъ знаки реализанта, произведенія корней, ихъ суммы, а также знаки /(т) и 1-го коэффиціента въ нижеслѣдующую таблицу, въ которой можно прямо читать все, что относится до корней въ любомъ интерваллѣ значеній параметра т.
Скала значеній т 0 К 2К КѴ5
Реализанть 1
Произведеніе корней —•
Сумма корней — —
Дт) —•
Коэф* при я?* +
Разсмотримъ каждый интер вал.ть.
Е т<К. Корни дѣйствительны, ибо реализантъ >0; произведеніе корней отрицат,, слѣдов., знаки корней различны; сумма корней >0, слѣдов. большій по абсол. значенію корень положителенъ. Затѣмъ, знакъ [(т) противоположенъ знаку 1-го коэф., слѣдов. т — между корнями, и имѣетъ мѣсто слѣдующее расположеніе (обозначая меныпій корень х\ большій—я?"):
я?'. . . т . . . х”.
А какъ задачѣ удовлетворяетъ только х положительное и меньшее т, то задача ке илтста рѣшеній, что очевидно, ибо уже АС + ОС, по свойству сторонъ треугольника, больше К, а АВ-|-ОС и подавно.
2. ж = К. Результатъ подстановки числа ш вмѣсто а? обращается при т=К въ нуль, а это значитъ, что К есть корень ур—нія. Задача имѣетъ 1 рѣшеніе, х — К: хорда обращается въ нуль,
3. К<т<2В. Корни дѣйств., против* по знаку, большій по абс. величинѣ кор, положителенъ; и какъ /'(м) имѣетъ знакъ одинаковый съ 1-мъ коэффиціентомъ, то т лежитъ внѣ корней. Чтобы иронизировать мѣсто т относительно * * 1
корней, нужно еще сравнять т съ полусуммою корней, которая яі; очевидно, т > 5 т, слѣдовательно т больше большаго корня, и расположеніе этихъ чиселъ таково хг. . . а?" , . . т,
слѣд. большій корень, будучи >0 и отвѣчаетъ задачѣ, которая такимъ образомъ имѣемъ на этотъ разъ 1 рѣшеніе.
4. т — 2К. Произведеніе корней мѣняетъ знакъ (— на 4"), слѣдовательно обращается въ нуль; слѣдовательно, одинъ корень—нуль, другой удовлетворяетъ 4
УР—нію 5ж — 4К = 0, откуда х ~ - К, и задача имѣетъ два рѣшенія, изъ коихъ о
первое даетъ хорду, сливающуюся съ діаметромъ,
5. 2К < т < К Ѵ5. Произведеніе и сумма корней положительны, слѣд. оба корня положительны; знакъ /’(ш) одинаковъ со знакомъ 1-го коэффиціента, слѣдовательно, т—внѣ корней, и какъ т больше полусуммы корней, то расположеніе хг, х" и т таково
. т,
т.-е. оба положительные корня < т: задача имѣетъ 2 рѣшенія, выражаемыя формулою:
^±Ъ/5К2 _да2
о 5
Случаи т^К/5 и разсмотрѣны выше (см. I и II).
Результаты изслѣдованія, для удобнѣйшаго обозрѣнія ихъ, резюмированы въ видѣ нижеслѣдующей таблицы.
Резюме изслѣдованія.
I. < В /5 :
2В > т > К........................
»и = 2К....а/ = 0; я:" = |е..
О рѣшеній.
1 рѣшеніе.
1 рѣшеніе.
2 рѣшенія.
т > 2К . . . О < х' < пі; 0 < х" < т 2 рѣшенія.
II. т = К |5
" — —=—, даетъ тахшшт для ш: 1 (2 равныхъ) о
III. ?»>Н.У/5. . . .Корни мнимые
рѣшенія.
О рѣшеній
Изслѣдованіе измѣненія функціи у — 2 ѴЁ2 —я? 4-я.
Въ данномъ случаѣ, измѣняя х отъ О до К, легко составить слѣдующую таблицу измѣненій у, которая, вмѣстѣ съ графикой этихъ измѣненій, позволяетъ наглядно су- • дить о томъ, какъ измѣняется разсматриваемая сумма. Вотъ эта таблица съ сопровождающею ее кривою измѣненій:
К Ѵо = /5К2 = /(2йр 4- К2.
ОА-Ц?
О
ОВ^Н ос=й< о
Чертежъ наглядно показываетъ, что когда т измѣняется отъ своего тпахі-*титп’а ВѴб до 2К, задача имѣетъ два рѣшенія; при т меньшихъ 2И, но не • меньшихъ В, она имѣетъ 1 рѣшеніе; при т < К она невозможна.
г
Построеніе. Проведя касательную ЕЕ = К и соединивъ точки В и Г, получимъ линію ВЕ — К /5, Затѣмъ на касательной ВБ откладываемъ отрѣзокъ
1)0 = яі, взявъ его >2П, но <КѴбти проводимъ прямую ОН параллельно ВЕ, Описавъ изъ точки 1) дугу радіусомъ ОЕ до пересѣченія съ прямою іОН въ точкѣ Н, найдемъ:
ОН = Vх 5КЯ — т2;
затѣмъ, беремъ линію ОК —26Н:
ОК = 2
и изъ точки О радіусомъ ОК описываемъ полуокружность, которая пересѣчетъ прямую ВБ въ точкахъ I и Ь; очевидно:
01 = т — 2 іИэЙД — т2>
ВБ = т 2 ЕоК2 — т2.
Остается отъ каждой изъ этихъ прямыхъ отрѣзать пятую часть. Беремъ
ИТ = Е8 — проводимъ 81 и 8Ь , и изъ точки Т прямыя: ТР параллельно 8Ь и ТР' параллельно 81; остается изъ точекъ Р и Р' провести параллели діаметру ВЕ, которыя и дадутъ требуемыя хорды АВ и А'В'.
Задача IX.
603. Построитъ треугольникъ, зная его сторону а, соотвѣтствующую высоту к и радіусъ В описанною круга.
Рѣшеніе. Пусть неизвѣстныя стороны будутъ х и у. По извѣстнымъ теоремамъ геометріи имѣемъ:
оА_-І/(а: + ^ + о) (®+у-«) («+«—у) 1« — (Д — У) ху - ^кл, -у — у 2- 2 2 2
Возвышая обѣ части 2-го ур. въ квадратъ, найдемъ:
4аДО = [(я + у)2 - «2] [а2 — (х — у)2].
Примемъ за вспомогательное неизвѣстное сумму а? + у = $; я и у будутъ корнями уравненія
Х2~зХ + 2ВЛ = 0. . . (1).
Для опредѣленія 8 имѣемъ соотношеніе
4а2*2 = (52 _ Д2) |д2 _ ($2 _ 8ВЛ)], или
я* — 2 (а2 + 4КЛ) 32 + а* + 4а2Л2 4- 8а2КЛ = 0 . . . (2).
Рѣшая это ур—ніе относительно $2, найдемъ, что подрадикальное количество — (4Ю — а2) . 4Л2: оно положительно, если а < 2Н. Если это условіе выполнено, оба значенія з2 дѣйствительны; они и положительны, ибо произведеніе и сумма корней ур—нія (2), разсматриваемаго какъ квадратное, положительны; слѣд. 8, при условіи а < 2К, имѣетъ всегда два положительныя значенія, именно:
8 = /02 + 4ВЛ ±2Л/4№ — о* = Ѵ«2“+2А(2В,“ЕЕ(г), полагая =Ѵ4К2 — а2-
Рѣшая затѣмъ ур—ніе (1), находимъ:
я: = 1 ^а! 4. 2Й(2В * Ѵа2+ 2А(-2ІІ + Й),
У = + 2Л(2К * й) — і Ѵ'ай + 2Л (- 2В, ± гі).
полагая, что я>у, что позволительно; въ этихъ формулахъ нужно брать передъ & или верхніе знаки вмѣстѣ, или нижніе вмѣстѣ (въ силу ур—нія ху = 2КЛ). Такимъ образомъ имѣемъ:
г1 = 1 { Уа2 + 2Л(2В + Ф + Ѵаг4-2Л(— 2К + ф }1
1 ( , ________________ ч ( • • ....(3)
Уі= 9 { Ѵы2 + 2Л(2Н + а) — Ѵ«24-2Л(- 2К + Л) }
аг, = І { »/а2 + 2Л(2В-(і) + /^-|-2Л(-Ж —гі) } |
і ( {' Л...........(4).
У2 = 2 { Ѵа24-2Л(2К —й) — Ѵа2 + 2Л(—2К — гі) 11
Изъ этихъ формулъ вы водимъ слѣдующія заключенія.
Въ системѣ (3) рѣшеній первый корень всегда дѣйствителенъ; чтобы и второй былъ дѣйствителенъ, надо, чтобы было
«2 4- 2Л (— 2В 4- Л) > О,
, п2 откуда
Система (4) рѣшеній будетъ дѣйствительна, если подкоренное количество подъ вторымъ радикаломъ будетъ положительно, т.-е. если «2 —2А (2К + > О, д2
откуда А < Въ этомъ предѣлѣ заключается первый. Умножая оба
члена второй части неравенства на 2К — <7, имѣемъ:
а2(2К-^) . 2В —
2(4К>—“ЛИ 1< 2 ’
или 4<1<—
Итакъ, задача имѣетъ два рѣшенія, если А <11 —
Если «2 — 2А(2К -|- ф < 0, но а2 — 27/(2 К — с?) > 0, откуда
а2 , а2
2(2К —(І) > > 2(2Н + І)’
то система (4) даетъ мнимыя значенія для « и а система (3) дѣйствительныя; заключаемъ, что при условіи
в—^<л<к + ~
задача имѣетъ одно рѣшеніе? выражаемое корнями #| и уѵ
Наконецъ, если к > К то обѣ системы (3) п (4) мнимы и задача невозможна.
Эти результаты легко обнаружить на чертежѣ (черт. 94). Описавъ кругъ
радіусомъ К, проведемъ въ немъ хорду ВС — а и къ ней перпендикулярный діаметръ ММ'; имѣемъ:
слѣдовательно
гі = 20Я
при 7і<О1\Г—СЖ
При к <11—9, т.-е
при Л<ИМ' существуютъ двѣ точки А*, расположенныя въ разстояніи А отъ
К2 —
или А и
ВС, по "ту и по другую сторону отъ ВС и лежащія на данной окружности; слѣд. задачѣ отвѣчаютъ два треугольника: АВС и А'ВС.
Если І< — < к < В + то-есть если
КМ'<А<КМ, одинъ треугольникъ А "ВС отвѣчаетъ вопросу.
Наконецъ, если к >КМ, то невозможно никъ, высота котораго была бы и задача невозможна.
вписать въ окружность
треуголь-
ОК = ѵЧ)В2
= ОК.
а
М
З а дача X.
604. По данной площади ш і/З и периметру 6а шестиугольника, составленною тремя равными равнобедреннымгі треугольниками, построенными па сторонахъ равносторонняго треугольника АСЕ, какъ на основаніяхъ, найти сторону ЛС много правильнаго треугольника.
Рѣшеніе. Замѣтимъ прежде всего, что шестиугольникъ можетъ быть двоякаго вида, смотря во тому, будутъ ли равнобедренные треугольники построены внѣ треугольника А СЕ, пли внутри его: въ первомъ случаѣ будемъ называть шестиугольникъ фигурою перваго рода, во второмъ—ьторого роса.
Пусть (черт* 95) ЛС = 2я; АВ = а; ур-ніе будетъ
т 13 = х213 ± З.г /а2 — я2,
причемъ знакъ -ф- относится къ шестиугольнику 1-го рода, знакъ — къ фигурѣ 2-го рода.
Раздѣливъ обѣ частя на У 3 и изолировавъ радикалъ имѣемъ:
т — х- — ± х Ѵ3(а2 — ж2).
Изслѣдованіе. Для того, чтобы вторая часть была дѣйствительною, необходимо, чтобы существенно положительное количество х содержалось между 0 и а\ затѣмъ, смотря по знаку разности ш — ж2, различаемъ, какой родъ шестиугольника отвѣчаетъ вопросу.
Возвышая обѣ части въ квадратъ, получимъ ур—ніе, отвѣчающее задачѣ въ самомъ общемъ ея смыслѣ:
(ж~ ж2)2 — 3(а2 — х2)ж2,
или, приведя въ порядокъ:
4л4 — (2ш + За2)#2 Д- = О . . , (1)
откуда
х = | (4- і + За2 і V — + За2) . . . (2).
Различаемъ два случая: »і>0пт<0, что возможно, ибо можетъ случиться, что въ шестиугольникѣ 2-го рода площадь каждаго изъ равнобедренныхъ треугольниковъ будетъ больше трети площади равносторонняго треугольника.
і-й случай; т>0. Первое подкоренное, количество >0; чтобы второе было не меньше 0, надо, чтобы было —2т-рЗа2^0, откуда
а2.
Какъ скоро это условіе удовлетворено, значенія ж, выражаемыя формулою (2), дѣйствительны; а какъ абсолютная величина перваго члена въ скобкахъ больше второго, то положительныя значенія ж, которыя только и отвѣчаютъ на вопросъ, будутъ:
* | (Ѵбш Д- За2 — + За2),
#2 = 7 ф- За2 + У— 2т + За2). 4
3 л) 3 *
I. При ія — а2 имѣемъ: и задача имѣетъ одно рѣшеніе; со-*
4Й отвѣтствѵющіп шестиугольникъ—правильный.
3
II. При т <-р2 вопросъ имѣетъ два рѣшенія: существуютъ два шестиуголъ-пика, отвѣчающіе вопросу, и чтобы опредѣлить нхъ родъ, надо знать знаки разностей ш —я’і2 и т — х$* Подстановка ш вмѣсто я2 въ ур—ніе (1) дастъ
/ (т) = 4 т- — (2 ія + За2)ія + т2 = Зт(т — а2).
Отсюда видно, что когда:
т > «2, т
т _ я2,
будетъ /Хт)>0;
л Л™)<0> „ /» = 0.
1) Въ случаѣ т > а2, т находится внѣ интервалла корней, и слѣдоват., или оба корня, я>2 и я22, меньше іи, или оба больше яі. Чтобы знать, тотъ или другой случай имѣетъ мѣсто, сравнимъ т съ полусуммою корней; положивъ 9-удо I 3«2 1
-—о-~— > т, найдемъ т < - а\ что противорѣчигь положенію т > а2. Значитъ ія больше полусуммы корней, и обѣ величины, хр и я22, меньше ія, т.-е. обѣ разности пі — я^ и т —я22 положительны. Заключаемъ, что въ случаѣ
а2 < ія < | а-
оба шестиугольника относятся къ 1-му роду.
2) Когда т < а2, яі находится между корнями:
Я|2 . . . ІИ . . . яа2,
слѣдовательно, яі— яр >0, и корню я1 отвѣчаетъ т — я22 < 0, и корню я2 отвѣчаетъ шистиугольникъ
3) Наконецъ, когда т = «2, будетъ /‘(;я) — О, слѣдоват., = ш — а2.
а2 =
шестиугольникъ 1-го рода; 2-го рода.
т2
одинъ корень Другой корень
а2
-гі то-есть
а * л
Оба ше-
АСЕ.
Я2 = а, стиутольника превращаются въ правильные треугольники: 1-й совпадаетъ съ треугольникомъ АСЕ; второй, сторона котораго о=2яь лаетъ треугольникъ ВВЕ, сторона
котораго вдвое больше стороны треугольника
Итакъ, во всемъ интерваллѣ И шестиугольникъ, соотвѣтствующій корню принадлежитъ къ 1-му роду.
2-й случай: т < 0. Чтобы корни были дѣйствительны, нужно, чтобы бфло
...... 6/2
9 ‘
О, откуда іи
Величина перваго члена скобокъ въ формулѣ (2) будетъ меньше второго члена, и потому положительные корни, отвѣчающіе вопросу, будутъ:
.?,= !( — |/6», + 3«а + у ~2»Г+За2).
х2=1,( + >/6^
Оба соотвѣтствующіе шестиугольника относятся ко второму роду.
Въ частномъ случаѣ: ш—1) имѣемъ
Ели положимъ, что ш приближается къ нулю, оставаясь положительнымъ. 6-къ 1-го рода, соотвѣтствующій а?и имѣетъ видъ чсрт, 97 (1)‘, а 6-къ 2 рода, соотвѣтствующій #2, имѣетъ видъ черт. 97 (2), разнящійся отъ 1-го только расположеніемъ вершинъ относительно правильнаго треугольника АСЕ,
Резюме изслѣдованія.
И* > 7, «2 • • И МНИМЫ . .
з „ «^з
?п=5а2. . . = — •
з
а2<т <;-($♦ #і>0, я3>0 . .
м
О < ж < а2 , я?і > 0» > 0 ♦ •
С/2
— < ж < 0 . . я?! > 0, О .
О рѣшеній.
1 рѣшеніе (перваго рода).
2 рѣшенія (перваго рода).
1‘рѣш. 1-го рода, I рѣш. 2-го р.
₽
2 рѣшеніе (2-го рода).
Задача XI.
605. Шаръ радіуса г дожитъ на плоскости; на той же плоскости поставленъ конусъ, котораго радіусъ основанія равенъ К, а высота 2г, На какомъ разстояніи. х отъ данной плоскости нужно провести параллельную ей плоскость, чтобы объемы, содержащіеся между обѣими плоскостями, были равновелики?— Ллинк)оват* положеніе сѣкуъией плоскости относительно центра шара.
9
— Г»61
Р ѣ ш е н і е. Объемъ сферическаго сегмента, имѣющаго высоту х> выражается формулою і га2(3г— ж). Объемъ усѣченнаго конуса, у котораго радіусы основа-О
ній суть К и у, а высота х, выражается 4ормулою гж(К2-|-#2-Ь^). Кромѣ того, между я: и у имѣемъ соотношеніе у: К — (2 г — ж): 2г, при помощи котораго можно изъ предыдущей формулы исключить у, найдемъ
о
12г2 „бгжЦ-ж2
4г2
Уравненіе задачи, по сокращеніи на будетъ
4г2я2(3г — ж) = К2я*(ж2— 6/г 4-12^),
Рѣшеніе я —О не соотвѣтствуетъ задачѣ, ибо при атомъ значеніи ж оба объема обращаются въ нули; остается квадратное ур—ніе
(К2 + 4г2)ж* — 6г(Е2 + 2г2)ж + 12Н2г2 = 0 . . . (1).
Изслѣдованіе, Чтобы задача была возможна, необходимо, чтобы х было дѣйствительно, положительно и <2г. Условіе дѣйствительности корней выражается неравенствомъ
9г2(Н2 + 2г2)2 — 12К2г2(П2 + 4г2) > 0,
которое, по сокращеніи на положительное количество Зг2 и по упрощеніи, даетъ
— К* — 4№г2 + 12г* > О . . (2).
п К
Положивъ — — т, находимъ, что т2 должно заключаться между корнями г
ур—нія
»»» + 4»»2_ 12 = 0;
и какъ, сверхъ того, д, б. >0, такъ же какъ и т, находимъ, что должно быть
1{<Н2. . .(3).
При соблюденіи этого условія, корни ур—нія (1) дѣйствительны; но они в положительны, такъ какъ ихѵ произведеніе и сумма положительны. Чтобы узнать, какъ расположено количество 2г но отношенію къ корнямъ, подставимъ въ первую часть ур—нія (1) 2г вмѣсто я. Найдемъ въ результатѣ
4г2( К2 + 4г*) — 12г2 (№ + 2г2) + 12К2г2, или (К2 — 2г2)4А
Но въ силу неравенства (3) заключаемъ, что первый множитель этого произведенія отрицателенъ, когда корни неравные; и обращается въ нуль при равныхъ корняхъ.
Этотъ крайній случай означаетъ, что 2г есть величина дѣйствительныхъ равныхъ корней при условіи К = г 1/2 При дѣйствительныхъ же неравныхъ корняхъ, 2г заключается между корнями, сл., большій корень не соотвѣтствуетъ вопросу, меньшій даетъ отвѣтъ на вопросъ: задача имѣетъ 1 рѣшеніе:
3(42 + 2г2) — —4Н2г2- IV) ,.,
ж — г.—----1---—— * Л4).
— 6С2 —
I
Изслѣдованіе положенія сѣкущей плоскости относительно центра шара. Съ этою цѣлью опредѣлимъ знакъ, принимаемый первою частью ур—нія (1) при замѣнѣ а? количествомъ г. Находимъ
г2(7К2^8г2);
слѣд., пока 7Е2<8г2, рѣшеніе (4) меньше г, п потому сѣкущая плоскость и данная лежатъ по одну сторону отъ центра; если 7В2— 8Р- = 0, то %—г: сѣкущая плоскость проходитъ черезъ центръ; наконецъ, когда 7Е2 > 8г2, сѣкущая плоскость проходитъ надъ центромъ.
Резюме изслѣдованія.
1. Е2 < - г2. Одно рѣшеніе; плоскость ниже центра.
гч 8
2. Г№=-г2. Одно рѣшеніе; плоскость проходитъ черезъ центръ.
* $
3. ?г2 < Е2 < 2 г2. Одно рѣшеніе;. плоскость проходитъ выше центра.
4. Е2 = 2г2. Одно рѣшеніе; плоскость касательна.
Е*>2г2. Задача невозможна.
Задача XII.
606. Зная радіусъ Е шара и полную поверхность 2та вписаннаго въ него цилиндра, вычислить радіусъ основанія и высоту цилиндра.
Рѣшеніе. Обозначимъ буквою х радіусъ основанія, а 2у— высоту цилиндра; ур—нія задачи будутъ
,г2+= . .(I) я* + ^ = К2. . .(2)
Изъ перваго имѣемъ: пі* — &
У = ~ъГ' • -(3) . .
а подставляя эту величину у въ ур—ніе (2), имѣемъ
5л?4 — 2(п/2 -н 2Е*)х2 н- = 0 . . . (4) откуда
-ь 2Н2 2Ё2? — 5т* (5)
5
Взявъ со знакомъ 4- корни квадратные изъ второй части ур. (5), получимъ два значенія для -г, а подставивъ ихъ въ формулу (3), найдемъ для каждаго изъ нихъ соотвѣтствующее значеніе у.
Изслѣдованіе. Чтобы значенія х и у, выведенныя изъ ур—ній (3) и (э), давали отвѣтъ на вопросъ, необходимо, чтобы они были дѣйствительны, положительны и меньше Е.
— 6СЗ —
Чтобы значенія #2 были дѣйствительны, должно быть
^2-Ь2Ка)2>5т*,
или
ж2 Ч- 2Нг > яг21Л),
или
(6)г
Когда это условіе удовлетворено, величины & будутъ дѣйствительны; они будутъ и положительны, ибо ихъ сумма и произведеніе положительны. Но чтобы какое-либо изъ значеній х отвѣчало на задачу, необходимо еще, какъ видно изъ ур—нія (3), чтобы оно было меньше ж, для того чтобы соотвѣтствующее значе- • 'ніе у само было положительно. Другихъ условій нѣтъ: ибо какъ скоро дѣйствительныя положительныя значенія х и у удовлетворяютъ ур—ігію {-), въ силу этого уже величины эти меньше В.
Теперь необходимо опредѣлить, сколько значеній я2 содержится между 0 и а для этого подставимъ 0 и т* вмѣсто а? въ первую часть ур—нія (4), какъ квадратнаго относительно я2. Результатъ подстановки нуля—положителенъ; результатъ подстановки ж2 есть 4т2(ж2— II2). Должно прослѣдить измѣненія ж2 отъ
V 5 -4-1
О до В2, и затѣмъ отъ К2 до тахітшп’аж2, равнаго К2. - 9—; так. образомъ,
Ѵ5-+-1 критическія значенія ж2 суть: О, К» и К*. ——
I. ж2 < К2. Въ такомъ случаѣ 4>н2(т2 — В2) < 0; слѣд, одно, и только одно, значеніе содержится между 0 и ж2; друтое > ж2: задача имѣетъ одно рѣшеніе; значеніе <гг его дающее, выражается меньшимъ корнемъ:
ж2 -Ь 21Ѵ — I (т2 4- 2ЕѴ)2 — 5ж*
5
II. ж2 = ІѴ. Результатъ указанной подстановки обращается въ нуль, а это значитъ, что одно изъ значеній я есть ж пли В; соотвѣтствующее значеніе у равно нулю; цилиндръ обращается въ два свои основанія, сливающіяся съ
В2 большимъ кругомъ шара. Что касается другаго рѣшенія, то оно есть: я2 = г , - о
откуда
К Г5 2К
® -- X 1 а V — г.
О
ж1 равно
это-цилиндръ, подобный литру (мѣрѣ жидкостей). Это другое значеніе я получаемъ, замѣчая, что произведеніе двухъ значеній я2, въ силу ур. (4), IV или, въ данномъ случаѣ, — •
III. К2<ж2<В2 - * ~ - Въ этомъ случаѣ 4т2(ж2 — №)> о, и слѣд. или
оба значенія .г2 содержатся между 0 и ж2, или оба больше ж2; по послѣднее предположеніе невозможно, ибо произведеніе обоихъ значеніи я2 т.-е. мень-о
і/гГ і । ше ж4. Заключаемъ, что когда ж2 содержится между В2 и Н2 . задача
всегда имѣетъ два рѣшенія.
1/5^-' 1
IV. ж2 = IV • - о , т,-е. своей наибольшей величинѣ. Оба значенія ,т^ въ
ІП2 2№
этомъ предѣльномъ случаѣ равны —-? или, замѣняя ж* его величиною, □
находимъ: — К3 - —ю“3 отк1да
-‘Уц,-^=йі/Ч-:
у 5 н- 1 >
полная же поверхность цилиндра = 2яНа • —> т.-е. она равновелика боковой поверхности цилиндра, имѣющаго основаніемъ большой кругъ даннаго шара, а высотой сторону правильнаго звѣзднаго десятиугольника, вписаннаго въ этотъ кругъ.
1/5-4-1
V. та>Кя* —для х получаются мнимыя значенія, слѣд., задача не-возможна.
Если, теперь, назовемъ полную поверхность цилиндра буквою 8 и помножимъ на 2п предыдущія неравенства и равенства, можно все изслѣдованіе резюмировать слѣдующимъ образомъ.
Резюме изслѣдованія.
8< 2-Г^ задача имѣетъ 1 рѣшеніе.
8 = 2-К» и 2 рѣшенія.
2Н1«<8< 1) я 2 ’
8 = я 1 рѣшеніе.
8> і:К’(^Ч-о п 0 рѣшеній.
Примѣчаніе. Если въ у р—ніяхъ (1) и (2) перемѣнимъ у на — у, то легко видѣть, что ур—ніе (4) можно истолковать, полагая, что вмѣсто полной поверхности цилиндра дается разность между суммою его основаній и боковою поверхностью. Можно бы было повторить изслѣдованіе предыдущей задачи, называя рѣшеніями второго рода—рѣшенія, отвѣчающія измѣненной задачѣ.
Зада ч-а XIII.
607. Вычислить стороны пря.чоджльнша тред/одьннка, зная его периметръ '2р и сумму 8 гипотенузы и высоты.
Рѣшепі к. Пусть будутъ х и у — искомые катеты, я — гипотенуза, и — соотвѣтствующая высота. Ур—нія задачи будутъ:
# 4- У я — 2р; г + и = 8; = ху = ия.
Изъ перваго имѣемъ: з*Ч-р* ч- 2ху — (2р — *)« = 4р2 — 4рг ч- или, въ силу
третьяго и четвертаго ур—ній: ия = 2ра— 2ря; но н —8 - я, сл.
я(8 — я) = 2р® —2р^, или (2р-н8>Ч-2р* = О . . . (I)
Найдя г, для опредѣленія .т п у получимъ ур—нія
а’ ч-р~ - г и ху = (8 — г) . г,
— 665 —
откуда видно, что х и у суть корни ур—нія
Х« —(2р — ^)Х + (8 — ^ = 0 . . .(2)
Изслѣдованіе. Чтобы корни ур—нія (1) были дѣйствительны, надо чтобы (2р + 8)* — 8р*> 0, откуда
8>2р(Г2- !)•
Пусть это условіе удовлетворено; тогда оба корня ур-нія (I) будутъ и положительны, ибо ихъ произведеніе (2р2) и сумма (2р-1- 8) положительны. Но большій корень долженъ быть отброшенъ; въ самомъ дѣлѣ, высота и есть количество существенно положительное, а изъ ур—нія п —8 — я видно, что для того, чтобы было н>0, необходимо, чтобы было я <8; но большій корень больше полу-5 8
суммы корней, равной ® + — т а само количество рЧ--^ больше 8, ибо для воз-2 2
з
можности треугольника, очевидно, необходимо, чтобы было р>2- Что касается меньшаго корня, то онъ будетъ меньше 8, если результатъ подстановки 8 вмѣсто е въ первую часть ур—нія (1) отрицателенъ, что приводитъ къ неравенству
— 28р-|-2р2<0 или 8>р.
Какъ скоро это условіе удовлетворено, то будетъ удовлетворено и условіе дѣйствительности корней, ибо
।
р>2р()2 —1), или 3>2г2, или 9 >8.
Итакъ, для х получается одно значеніе:
*' =
2р + 8 — Г(2р -Ь 8? - 8р*
-==-—-- ---Д - »
съ условіемъ: р < 8 < 2р.
Условіе дѣйствительности корней ур—нія (2) есть:
(2р — —4(8 — я')У*>0, или 5^ — 4*'(р + 8) + > О,
или, въ силу равенства (1), Р
5я'(2р + 8) — ІОр* — 4^(р + 8) + 4р2 > 0, пли (6р + йг' - 6р* О,
откуда
✓ > Л2
Итакъ, чтобы х и у были дѣйствительны, необходимо, чтобы ^ыло
меньше меньшаго корня ѵр. (1); для этого же необходимо: 1) чтобы результатъ бр2
подстановки $ вмѣсто я въ первую часть ур. (!) былъ >0; и 2) чтобы 6р2 " Р (
при этомъ -- с было < полусуммы корней, т.-е, чтобы было — Ьр о « 6р
Подстановка даетъ:
о
36р< — бр2 (6р + 8) (2р + 8) + 2р2 (6р + 8)2 = 36р* — 248рэ _ 482^ = ‘ = 4р*(9р’- 68р — 82),
этотъ результатъ долженъ быть >0. Замѣтивъ, что „ въ самомъ* дѣлѣ Ьр + 5
I *
< , заключаемъ, что для дѣйствительности х и у должно быть удовлетво-
рено неравенство
- 82 - бйул -Н9/Д > О
вмѣстѣ съ условіемъ р < 8 < 2р.
Отсюда находимъ, что при 8 ^Зр.(Р2— 1) корни «и у будутъ дѣйствительны; а замѣтивъ, что г'<ір и й>р, находимъ, что сумма ж-Р/у, равная 2р—я', и произведеніе хуч равное (8 — ?')*', положительны, слѣд. а? и у положительны.
Итакъ, условія возможности задачи таковы;
*
р<8<2р, 8<Зр(П — 1).
По Зр(Ѵ2— 1)<2р, ибо это неравенство эквивалентно 18 <25; слѣдов., условія, необходимыя и достаточныя для возможности задачи, приводятся къ:
р<8 <Зр(Г2 —1), причемъ задача имѣетъ одно рѣшеніе.
Отсюда, между прочимъ, заключаемъ, что тахітшп 8 = Зр(1/2 — 1); приэтомъ • х — у; слѣд. изъ всѣхъ прямоугольныхъ треугольниковъ одинаковаго периметра равнобедренный имѣетъ наибольшую сумму гипотенузы съ соотвѣтствующею высотою.
Задача XIV.
608. Вписа»» сь данный полукругъ прямоугольникъ, зная сумму р ею основанія и высоты.
Рѣшеніе, Пусть будутъ: К—радіусъ даннаго круга, 2г—основаніе и у— высота искомаго прямоугольника; имѣемъ непосредственно ур—нія:
у + 2х=р. . .(1) я*-Н/г = В3. - . (2).
Рѣшая первое относительно у, имѣемъ:
—2я. . .(3).
Подставляя это выраженіе у въ ур—ніе (2), найдемъ:
□іс2 — 4ря -р ра —К3 = 0 , . . (4) отк у да _______
2р ±2 Ѵ5Ка — р2 ...
* = —-----г------. . До).
Затѣмъ у вычисляется по формулѣ (3).-
Изслѣдованіе. Въ этой задачѣ будемъ разсматривать и отрицательныя значенія х и у. Когда я и у будутъ положительны, будемъ называть рѣшеніе — рѣшеніемъ перваго рода; оно будетъ второго рода, если при а:<0 будетъ у/>0, т.-е. когда дана будетъ разность между высотой и основаніемъ; наконецъ, рѣшеніемъ третьяго рода называемъ то, когда ж>0, а у/ < О, т.-е. когда дана разность между основаніемъ и высотою.
' Условіе дѣйствительности х выражается неравенствомъ
р Н I 5.
Затѣмъ, изъ ур—нія (4) видимъ, что оба значенія х будутъ положительны, пли одно положительно, а другое отрицательно, смотря по тому, будетъ ли р
— А 6 7 —-
больше, или меньше В. Съ другой стороны, изъ формулы (3) заключаемъ, что положительному х будетъ соотвѣтствовать положительный у> когда и от-
рвцательный г/, когда Въ такомъ случаѣ, нужно знать результатъ подста-
новки - вмѣсто х въ первую часть ур—нія (4). Этотъ результатъ — ;
слѣд, надо различать три случая: р<2К, р — 2К, р > 21< (послѣдній случай возможенъ, ибо 2К меньше К 15).
Итакъ, количества, подлежащія разсмотрѣнію, въ порядкѣ возрастающихъ величинъ, таковы: П, 2К, КГ5; мы должны измѣнять рі отъ 0 до К,- отъ К до 2К, и наконецъ отъ 2В до К Ѵ5.
I. р < В. Произведеніе корней ур—нія (4) отрицательно, слѣд. одно значеніе х положительно, другое отрицательно. Отрицательной величинѣ х соотвѣтствуетъ положительное значеніе у\ слѣд. всегда имѣемъ рѣшеніе 2-го рода. Положительное значеніе х больше въ самомъ дѣлѣ, р, будучи меньше К, меньше
х ^ — 41^ р
и 2К, слѣд. количество отрицательно: это значитъ, что заключается
между корнями ур—нія (4), а потому положительный корень долженъ быть Такимъ образомъ, положительному х соотвѣтствуетъ, въ силу ур—пія" (3), отрицательное значеніе у. Слѣд. имѣемъ рѣшеніе 3-го рода. Итакъ, при р< К задача имѣетъ два рѣшенія: одно 2-го рода, другое 3-го рода.
И. р = Въ этомъ случаѣ
«• = 0, = |к.
О о
Первое рѣшеніе можемъ разсматривать, какъ рѣшеніе 1-го или 2-го рода; второе—рѣшеніе 3-го рода. Этотъ случай относится къ первому, но его можно отнести и къ слѣдующему.
__4К-
111. [I <^<2К. Оба корпя ур—нія (4) положительны, но какъ 7—.---------
? 4 отрицательно, одинъ изъ корней меньше, другой больше * Первому соотвѣтствуетъ положительное значеніе у/, второму — отрицательное. Итакъ: одно рѣшеніе относится къ 1-му роду, другое къ 3-му.
IV. ^ = 2К. Оба значенія х положительны, но количество ---------обра-
щается въ нуль, слѣд. одно значеніе х равно пли К, а соотвѣтствующее значеніе у равно нулю. Другое значеніе .тт Ар или “В найдемъ, вычтя изъ суммы корней а для соотвѣтствующаго значенія # находимъ Итакъ, имѣемъ два рѣшенія, изъ коихъ второе будетъ 1-го рода, между тѣмъ какъ первое можно отнести, по произволу, или къ 1-му или къ 3-му роду.
V. 2К < К-1'5. Въ этомъ случаѣ оба значенія х положительны, и оба меньше з* Въ самомъ дѣлѣ, сумма корней, равная меньше р, слѣдов. оба < г р р*— 4К«
корня не могутъ быть больше и какъ количество -— - положительно, они
Л 4
неоиходимо меньше Въ такомъ случаѣ положительнымъ значеніямъ ж.соотвѣтствуютъ и положительные у-кп: имѣемъ два рѣшеніи І-го рода.
VI. р = Егэ. Имѣемъ двойное рѣшеніе 1-го рода.
Нельзя брать _р> ЕѴ5, ибо тогда оба значенія х дѣлаются мнимыми и задача невозможна.
Резюме изслѣдованія.
Измѣненія р.
Число р ѣ ш к и і й:
1-го рода;
р < Е.........\ , . . О
— Е.................... О
Е<_р<2Е.................... 1
р = 2К................. 1
2Е<р<КѴо. 2
р — В 1'5............... 1
р > В Ѵ'5.............. О
2-го рода; 3-го рода. 1 !
1 1
О 1
О I
О о
о о
о о
Задача- XV.
609. .Вычислить ораны >?/>ллауіадьиаіа треугольника, <?мая по ифн.иешръ 2р, если гари толь и^шопмо, что одлглга обьеловь, треуиліькикглиъ
при обращеніи еіо поочередно около каждаго катета, равновелика помри ару радіуса Е.
Рѣшені е: Пусть будутъ а? и у — катеты, я — гипотенуза; непосредственно имѣемъ 3 ур—нія:
я: + у + ^ = 2р; ху (я +$) = 2К3; х2 + ?/* =
Легко исключить изъ этихъ ур—ній я и у; для этого выражаемъ изъ Нго и 2-го # + # и «ту черезъ я; имѣемъ
Отсюда имѣемъ:
а? 7 — -——
2р — Я
4КЭ
= (я -н? — 2^; — (2р - Ф ~ •
Вставляя это выраженіе -г2 + і/2 въ третье ур—ніе системы, находимъ
4К3
** = (2р — *)» —15--,
или
ря2 — Зр*г -]- 2р* — Н3 — 0 .
Итакъ, для опредѣленія хг имѣемъ ур-ніе (Г), квадратное относительно я. въ самомъ дѣлѣ, зная, что сумма найдемъ эти неизвѣстныя изъ ур—нія
Опредѣливъ можемъ вычислить х и ?/; 2Н3 г 4- # — 2р — я, а произведеніе ху = -------------.
лр —-р я
Х»~(2^— г)Х + ^0 . . .(2),
* 2р — #
Изслѣдованіе, Чтобы система опредѣленныхъ такимъ образомъ величинъ х, и я отвѣчала задачѣ, необходимо и достаточно, чтобы эти величины были дѣйствительны и положительны.
Чтобы корни ур—нія (2) были дѣйствительны, необходимо, чтобы
(2р -
_ 8К*
(2р — *)’
а чтобы они были положительны, необходимо, чтобы было
2р — > 0, пли я < 2р,
Пусть это послѣднее условіе удовлетворено; въ такомъ случаѣ, умноживъ обѣ части предыдущаго неравенства на положительное количество 2р—я, найдемъ: (2р— я)1 ^81Р, или, извлекая изъ обѣихъ частей кубичный корень, имѣемъ: 2р — или #^2(р — К); п какъ я должно быть положительно, необхо-
димо, чтобы
ооО(р-к),
а это предполагаетъ, чтобы было р>К. Какъ скоро я меньше или равно 2(р —Щ, оно и подавно будетъ меньше 2р, и условіе я<2р будетъ удовлетворено, Итакъ, число рѣшеній задачи равно числу корней ур—нія (1), удовлетворяющихъ условіямъ
0<*<2(р — Н).
Не трудно убѣдиться, что корни ур—нія (1) всегда дѣйствительны; а какъ предполагается К <р, то они и положительны. Остается изслѣдовать, сколько этихъ корней заключается между 0 и 2 (р — К). Для этого нужно знать величины первой части ур—нія (1) при —О и ^ = 2(р— К), При * — 0, она даетъ 2/л3 — К3 — величину положительную. Подстановка 2 (р — К) вмѣсто я даетъ
- 1ЦК* — 4рК + 2р*), пли — К [И — (2 - V 2)] [К - р (2 + ^2)].
По мы видѣли, что К должно быть <р, слѣд., 3-м множитель <0; 1-й также <0; слѣд. все зависитъ отъ знака 11—р(2 —Ѵ2),
Итакъ, нужно разсмотрѣть три случая:
О < В, <р (2 - ^2); р (2 -/2) < К < р; Н>р.
1. Пусть: 0<К <р(2 —1/2). Въ такомъ случаѣ результатъ подстановки вм. & выраженія 2(р —К) отрицателенъ, а потому одинъ изъ корней ур—пія (1) заключается между 0 и 2(р — К), другой корень больше 2 (р — II). Первый корень даетъ искомое рѣшеніе, второй не соотвѣтствуетъ вопросу: задача имѣетъ 1 рѣшеніе. Это рѣшеніе мы получимъ, взявъ для г меньшій корень ур—нія (1), а для х и у корни ур—нія (2), когда въ немъ у замѣненъ меньшимъ корнемъ ур—нія (1).
И. Когда р(2 — Ѵ2)< К < р, то при # = 2(р —К). триномъ положителенъ, и слѣд, или оба корня ур—нія (1) заключаются между 0 и 2(р—К), или оба больше 2(р —К). Чтобы оба корня содержались между 0 и 2(р—И), нужно, чтобы ихъ полусумма ~р была <2(р —В), т.-е. чтобы Зр<4(р — К), или К<^, условіе, несогласное съ положеніемъ В>р(2 —12). Итакъ, въ данномъ случаѣ оба корня ур—нія (1) больше 2 (р—К), и пи тотъ, ни другой не даютъ рѣшенія.
III. Если Н>р, то уже видѣли, что въ такомъ случаѣ задача невозможна.
Резюме изслѣдованія.
1. К. <^(2 — 12): Задача имѣетъ 1 рѣш.
[#=меньшему корню ур—нія (I)].
2. К — (2 — >2): Задача имѣетъ 1 рѣш.
[дг = 2(р —В), треугольникъ равнобедренный].
3. К >р (2 — I 2): Задача невозможна.
Задача XVI.
610. Въ данный полукругъ діаметра АВ = 211 бммелмь до/ик/ СО, параллелъ-—2 —2 — 2
ную ЛВ, такъ чтобы АС-Ь СЬ-Ь ОВ —иі*, іЭгъ т — данная линія.
Рѣшеніе. Принявъ за неизвѣстное АС = .г, выразимъ СО въ зависимости
отъ К и іг. По СО = 2В-2АЕ и АС = 2ВХАЕ, слѣд. СО = 2В-— Ур—ніе к
будетъ
2х*н- І2К —~ = ш* . . • (1).
Это ур—ніе, выведенное для одного случая, приложимо ко всѣмъ случаямъ. Въ самомъ дѣлѣ, пусть хорда СО приняла положеніе С'Е)\ въ которомъ точки С' и О' лежатъ въ другихъ четвертяхъ: обозначая, какъ и прежде, прямую АС' буквою х, будемъ имѣть’: С'О' = 2ЛЕ' — 2К; а какъ
ЛЕ'Х2Н = АСг то СЪ'=|-2К; ур-ніе у} Е' Е 0 Е Е* В будетъ въ этомъ случаѣ
оно тождественно съ (1). Даемъ ему видъ
аи _ 2КѴ2 + на (4Ні — = о . , . (2).
П з с л ъ д о в л н і е. Для изслѣдованія и рѣшенія итого биквадратнаго уравненія полагаемъ
такъ что ур —ніе будетъ
а,<2 = у . . . (3)
у* — + II* (41<* — ш*) = 0 . . . (4).
Для того, чтобы корень ур—нія (2) служилъ отвѣтомъ на предложенную задачу, необходимо и достаточно, чтобы было
,т дѣйств., *г>0, л*<2К , . . (5).
Но для полученія корней ур—нія (2) нужно рѣшить (4) и найденные корни внести поочередно въ (3); отсюда видно, что а™ будетъ дѣйств., если у будетъ дѣйств. и положительно; поэтому нужно изслѣдовать съ этой точки зрѣнія корни
—нія
Условіе дѣйствительности корней ур. въ ?/.—Оно будетъ II4 — — т*)>0
или /и* ЗВ*.
Знаки корней,—Произведеніе корней = В*(4К*—лі*); оно >0, когда >п*<4В*; равно 0 при ш* = 4В*, и <0 когда > 4К«.
Сумма корней = 2В* и слѣд. всегда положительна.
Величина корней.—а? должно быть < 2К, слѣд. у должно быть < 4В*. Подставляя 4 В* вмѣсто у въ триномъ (4), имѣемъ
/'(4К*) = 16Ш — 2В* . 411* + В* (4К* — ш*) = К* (1211* — ™*).
Отсюда видно, что* если 7в*<12В*, будетъ /’(4І№) >0; при —12К*, /(4В*) = 0; при ш*>12В* будетъ Н4К3)<0<
Такимъ образомъ, критическія значенія т* будутъ:
ЗВ*, 4В*, 12В* и + со,' и легко составить нижеслѣдующую таблицу знаковъ,
Скала значеній ш*. О ЗВ* 4К* 12К*
Знакъ реа.тизанта -— 0 + —
Произведеніе корней — — —
Сумма корней —|—
/’(4К’) 4 1 •» к. —
1-й коэффиціентъ. 1 ~н -Ь
изъ которой заключаемъ:
1. т*<ЗН*. Корни ур—нія (4) мнимые, слѣд. мнимы и корпи (2). Задача невозможна.
2. «і* = ЗВ*. Это значеніе есть тіпітшп (»п2); реализантъ =0, корни ур. (4) дѣйствительные равные, ихъ общая величина = К*; слѣд. ур—ніе (2)имѣетъ два корня равныхъ К, и два корня равныхъ —К. Изъ нихъ задачѣ отвѣчаетъ «г — 4-Н, какъ дѣйстн., положит. и меньшее 2К значеніе а?-са. Искомая фигура— правильны й полу-игестиуг ельникъ.
Слѣдуетъ замѣтить,, что сумма трехъ квадратовъ, равная въ данномъ случаѣ ЗВ*, представляетъ тіпітит, ибо т* вообще больше 311*, но дѣлается = ЗВ* при л'=В. Слѣд. а/жхв трехъ разсматриваемыхъ хордъ имѣетъ
тіпітит — ЗВ2, когда фигура, ими образуемая, есть правильный полушссгпи-уголъникъ.
3. ЗК* < т* < 4К*. Дѣйствительные корни ур. (4) въ этомъ случаѣ положительны, ибо ихъ сумма и произведеніе > 0; слѣд. всѣ 4 корня ур—нія (2) дѣйствительны, и потому оно имѣетъ 2 положительныхъ корня. Далѣе, знакъ /’(4В*) одинаковъ съ знакомъ 1-го коэффиціента, слѣд. 4В*—внѣ корней (^); а какъ полусумма корней — К2, то расположеніе чиселъ таково
у' . . . "... -4Н*,
слѣд. каждый изъ двухъ положительныхъ корней ур - нія (2) меньше 2ІІ, и задача имѣетъ два рѣшенія __
х = рК* + К Ршя - ЗіК
4. ш® = 4№. При переходѣ чрезъ 4В2Э произведеніе корней ур-нія (4) мѣняетъ знакъ, слѣд. при тя = 4Вя оно обращается въ нуль; поэтому одно значеніе у равно нулю, а другое суммѣ корней, т.-е. 2К3; значить, два корня ур—нія (2) равны нулю, а два равны К Г'2, т.-е. задача имѣетъ 2 рѣшенія *
л?' = 0, .г" = + 10'25
первое даетъ діаметръ 2Н» другое — полупериметръ вписаннаго квадрата АНВ.
5. 4Е»<яі« < 12ВЛ Произведеніе дѣйствительныхъ корней (4) отрицательно, слѣд. одно рѣшеніе у меньше, другое больше 0. Первое даетъ два мнимыхъ значенія второе—два дѣйствительныхъ. Такъ какъ сумма корней > 0, то этотъ положительный корень имѣетъ большую абсолютную величину. Нужно сравнить его съ 4ІР; Г(4К3) имѣетъ знакъ 1-го коэффиціента, слѣд. 4Ю — внѣ корней (у). Полусумма корней = расположеніе чиселъ таково
У . . . у" . . . 4№, слѣдовательно ,?/'<4К% и потому. (+)-й корень ур—нія (2) даетъ отвѣтъ на задачу, которая т. о. имѣетъ одно рѣшеніе
X = ]/ В» + К Ѵш^зк».
6. т*^=12Ю. Въ этомъ случаѣ таблица показываетъ, что У(4Ю) = 0, слѣд. положительный корень ур—нія (4) равенъ 411% а слѣд. *
= 2В.
Это—предѣльный случай задачи: контуръ, квадраты сторонъ котораго даютъ въ суммѣ 12К% есть АВАВ.
7. При т3 > 121<% произведеніе корней отрицательно, а сумма положительна, слѣд. одинъ корень ур—нія (4) <0, другой >0, и абсолютная величина положительнаго корня больше; /(4К3) отрицательна, т.-е. имѣетъ знакъ, противоположный 1-му коэффиціенту, слѣд. 4К2 находится между корнями, и расположеніе чиселъ таково: •
у' . . . 4К*. . . у";
значитъ у" >4К% а потому .г>2[{, и задача невозможна. Итакъ: та<г»тит суммы трехъ квадратовъ =12К2.
Резюме изслѣдованія.
т*<ЗВ»: корни мнимые.............. . . ♦ ♦
шя = ЗК2: правильный шестиугольникъ, шіп. (г/*2) .
' т* < 4П*.............................
т* = 4К3: х' = 0, х" = В. I 27.........
Гш3 < 12В2: х1 мнпм.; 0<я" < 211. т* > 4К* ! т* = 12В2: х' мним.; х” = 2К. , I тя > 12К*: х’ мним.; я?">2К.
О рѣшеній
1 рѣшеніе
2 рѣшенія
2 рѣшенія
1 рѣшеніе
1 рѣшеніе О рѣшеній.
611. Изслѣдованіе суммы трехъ квадратовъ .—Для суммы трехъ ква-дратовъ мы нашли (2) выраженіе:
= -ѣ — 2К«а2 + 4К‘],
представляющее биквадратный триномъ, который изслѣдовать мы умѣемъ при измѣненіи Отъ —со до -рсо; слѣд. мы можемъ прослѣдить его измѣненія при измѣненіи х отъ 0 до 2В, какъ требуетъ геометрическій вопросъ, и этимъ путемъ найдемъ въ болѣе сжатой формѣ результаты предыдущаго изслѣдованія. Для этого представимъ ж2 въ видѣ:
т^ѣ^-Н^ + ЗН»].
Отсюда прямо видно, что когда х возрастаетъ отъ 0 до К, (.т4 — К2)2 уменьшается отъ К* до 0, а слѣд. іи* уменьшается отъ 4К2 до ЗК2; при дальнѣйшемъ возрастаніи л? отъ К до 2В, (.г2—В2)2 возрастаетъ отъ 0 до 9К4, и слѣд. ж2 увеличивается оть ЗВ2 до 12В2; иначе говоря, ж2 проходитъ черезъ шіпішигп ЗВ2, когда я—В.
Эти результаты резюмированы въ слѣдующей таблицѣ:
х 0 В К|'2. 2В.
пі* 4В2 ЗВ2 4В2 І2К2.
Величина ж2 измѣняется, уменьшаясь отъ 4В2 до ЗК2, затѣмъ увеличивается до І^В; слѣд. она принимаетъ два раза всякое значеніе, содержащееся между ЗВ2 и 4В2, разъ при яг, содержащемся между 0 и К, другой разъ при *г, лежащемъ между К и ІІИ1; и одинъ разъ всякое значеніе, содержащееся между 4В2 е и 12В2. Это значитъ, что задача невозможна, когда данное ж3 меньше ЗВ2, или больше 12 В2, что опа имѣетъ 1 рѣшеніе, когда ж2 содержится между 12В2 и 4Ка, и имѣемъ 2 рѣшенія, когда ж2 заключается между 4І12 и ЗВ2. Это—результаты предыдущаго изслѣдованія, но представленные въ сжатой формѣ.
Изобразимъ графически измѣненія ж2, представляя величины *г прямыми, откладываемыми на оси О# отъ точки 0, а величины ж2 нанося на перпендикуляры параллельные ОѴ» Такимъ образомъ получимъ кривую ЭЕРО, изображающую измѣненія ж2.
На ней видно, что:
1) Для опредѣленія величины ж2, соотвѣтствующей данному значенію я?, достаточно нанести х на ось ОХ отъ точки 0, и взять ординату кривой, соотвѣтствующую полученной точкѣ.
2) Чтобы найти величину а?, соотвѣтствующую данной величинѣ ж2» достаточно пересѣчь кривую параллелью къ Ол, отстоящею отъ ОХ на ж2, и взятъ абсциссы точекъ пересѣченія кривой съ параллелью.
Черт. 99.
Такимъ образомъ легко видѣть, что задача не имѣетъ рѣшеній, когда ж2 меньше ЗВ2, или больше Г2В-, что получаются двѣ точки встрѣчи, слѣд. и два рѣшенія, когда*ж2 содержится между ЗК2 и 4Н2, и наконецъ—одна точка встрѣчи, или только одно рѣшеніе, когда ж2 содержится между Ш2 и 12В2.
Задача XVII.
612, Дана окружность 0 и къ ней касательная въ точкѣ А. Лрояесяш хорду Ю параллельно этой касательной такъ, чтобы прямоугольникъ МХР(^ нміьль
діагональ М() данной длины т.
Черт. 100.
Рѣшеніе. Примемъ за неизвѣстное разстояніе А8 = я искомой хорды отъ касательной, и замѣтимъ, что это неизвѣстно? можетъ имѣть только величину положительную, не большую 2К.
Изъ прямоугольнаго треугольника Мр.Р -------------2 _*2 ---1 находимъ: М(} = МР 4~ Р^.
Но
--2 ---2
14} = 4М8 = 4 X »Л X 8В = ^(2Е — г); подстановка даетъ
х* 4- 4л7(2Е< — ж) =
Это уравненіе совершенно общее, ибо
—2
выраженіе для Рф остается одинаковымъ, каково бы ви было положеніе хорды МХ. Итакъ, ур—ніе задачи будетъ
За* - 8Ш?-+-тЗ = 0 . . . (1)
Изслѣдованіе. Чтобы корень этого ур—нія давалъ рѣшеніе геометрическаго вопроса, необходимо и достаточно» чтобы онъ былъ дѣйствителенъ, положителенъ и не больше 2Н.
Условіе дѣйствительности корней ур—нія (1) выражается неравенствомъ
161<а — 0, или -------------- — ^0 . . . (2).
,, _4НіЗ
Корни этого неполнаго квадратнаго тринома суть: х——, слѣд., чтобы
удовлетворить неравенству (2), необходимо и достаточно дать т значеніе вну-
три интервалла
4 И РЗ между ——а—
4К ГЗ,
3’ ’
и
но какъ въ данномъ вопросѣ т положительно, то необходимо и достаточно, чтобы г - 4К- ]/3 было т .
о
Знаки корней. Произведеніе и сумма корней ур. (1) положительны, слѣд. корни всегда положительны.
Величина корней. Нужно опредѣлить, какъ расположены корни относительно 2К, а для этого въ первую часть ур. (1) подставитъ 2К вмѣсто я?; найдемъ
Г(2К) = 3 . (2К)з — 8К . 2К -Н иі* = т* —41^ (?н + 2К) (т — 2К), отсюда видно, что Г(2К) >0, если м > 2Н, и Г(2К) <0, если т < 2К. Такимъ образомъ, критическія значенія т суть
О,
2К,
4К 13
и +^>,
и въ изслѣдованіи легко оріентироваться при помощи слѣдующей таблицы знаковъ:
Скала ( значеній ш 0 2К «р О
Знакъ реализ.
Произведеніе корней ”|
Сумма корней
Г(21<) —1—
1-й коэффиц. —|—
Изслѣдуемъ каждый интерваллъ.
1) ш<2К. Оба корня дѣйствительны и положительны; /*(21<) имѣетъ знакъ/ противоположный 1-му коэффиціенту, слѣд. 2К лежитъ между корнями:
0. . .х'. . .211. . .а"
Только меньшій корень хг меньше 2К; слѣд. задача имѣетъ 1 рѣшеніе:
411 — Г16Н» —Зт» х~ 3
2) т 2Е. Такъ какъ при этомъ значеніи т первая часть ур—нія обращается 8Е 2
въ нуль, то2К есть корень ур—нія/другой корень котораго—-- — 2Н — В. Первый корень даетъ прямоугольникъ, сливающійся съ діаметромъ АВ; второй отвѣчаетъ хордѣ, расположенной на~К ниже центра.
о
3) 2І< < т < Оба корня дѣйствительны и положительны; знакъ Д2В.)
одинаковъ съ Пмъ коэффиціентомъ, сл. 2К лежитъ внѣ корней, полусумма кото-4 4
рыхъ =л К; такъ какъ 2К > л В, слѣд. 21< больше большаго корня, и потому «5 о
0. . .а/. . .я?". . .211;
оба корня допустимы, п задача имѣетъ 2 рѣшенія:
, 4К —ИбН’-"»»* 4К + і/161О^»й« ---------з---------’ * =-----------3-------
дающія двѣ точки, равноотстоящія отъ точки I, опредѣляемой отрѣзкомъ АІ=^К. О
4Н13 4
4) т=—з—; уравненіе имѣетъ два равныхъ корня: я'= ;г" = К—ЛІ,
4
а задача—1 рѣшеніе. При этомъ, длина діагонали достигаетъ шахітнт’а ~ — стороны правильнаго вписаннаго въ данный кругъ треугольника.
і
5) яі > невозможна.
' Реализантъ отрицателенъ, сл. корни ур—нія мнимы и задача
4 К Ѵ^З
Примѣчаніе. Въ случаѣ 2П<»н<—~— можно искать, какимъ образомъ па-о
раллели къ касательной расположены относительно центра. Для этого надо со* ставить ДК); найдемъ:
ДН) = — 5№,
количество положительное, когда т цательное для т < КУ5.
пі, 4КѴЗ
жится между 2К и —5,
ІИ'5; равное нулю при ?н = В 15, и отри* Замѣчая, что въ разсматриваемомъ случаѣ еодер-
имѣемъ критическими значеніями т:
Т?1 - 4ВѴ 3 , ІЯ о, —у—
а) 2В <м < іи'5; ДК) отрицательна, сл. К находится между корнями, и потому разсматриваемыя параллели расположены по обѣ стороны центра.
Ь) т = Іи 5; — ()т т.-е- К служитъ корнемъ, іг сл. одна параллель про-
8 5
ходитъ чрезъ центръ. Другой корень = ,.В —сл. другая параллель про-«5 * 3
ходитъ надъ центромъ, въ разстояніи отъ него равномъ -К* О
с) Если Кі'5 < т < 4 то ДК) > 0, п слѣд. Н находится внѣ корней; и
какъ К меньше икъ полусуммы д К, то порядокъ величинъ таковъ:
О. . . И. . .х’
”. . . 2К
т.-е. обѣ параллели проходятъ надъ центромъ, между 0 и В.
Резюме.
1.
о
к
»н < 2К : Д
т = 2Н : 2
по 4ГЗ . К
2В < т <—— О
, . 4ѴЗ.К
(тах.) т ——н—
413 . К
»1 > — Л-
. . 4К-П(№—Зт«
рѣшеніе—меньшій корень, ат = -- —
<3
2
рѣшенія: а/' — 2В.
О
: 2 рѣшенія.
4
2 сливающіяся рѣшенія, ж' = я?” = -й.
: корни мнимые, задача невозможна.
613. Прямое изслѣдованіе длины діагонали.—Ур. (1) даетъ
Вторая часть есть квадратный триномъ, измѣненія котораго мы изучать умЬемъ. Вамъ нужно прослѣдить его измѣненія, когда х возрастаетъ отъ О до
2Й, и затѣмъ взять отъ полученныхъ величинъ ариометпч. квадратный корень. Для изслѣдованія удобнѣе т* написать въ видѣ:
Отсюда видно, что когда я* возрастаетъ отъ нуля до кК,
количество воз-
растаетъ отъ нуля до -В*; затѣмъ, когда а? увеличивается отъ до 2В, и*»
уменьшается до 4КЛ Итакъ, имѣемъ таблицу пзмѣненііі:
Отсюда непосредственно видно, что когда хорда МЯ перемѣщается отъ А до В, длина діагонали мр возрастаетъ до того момента, когда Мй проходитъ 4
черезъ I, для которой АІ = ^К. Затѣмъ длина діагонали уменьшается до 2В, о
когда хорда движется къ В.
Діагональ принимаетъ одинъ разъ всякую длину, содержащуюся между 0 и 2В, когда точка 8 перемѣщается отъ А къ II; напротивъ, она принимаетъ два оо 4К>/3.
раза всякую величину, содержащуюся между 2К и —~: одинъ разъ, когда
точка 8 перемѣщается отъ И къ I, и другой разъ, когда точка 8 пробѣгаетъ отрѣзокъ 1В; эти два положенія хорды симметричны относительно ПС, ибо три-4
номъ ж* беретъ равныя величины при а? = -Е±у. Такимъ образомъ, находимъ о
всѣ результаты прежняго изслѣдованія.
Чтобы графически представить измѣненія т при измѣненіи х отъ 0 до 2 В, откладываемъ х на оси Си, а соотвѣтствующія значенія т на оси О#. Напр., взявъ
ОА=4іі п ав = ас=Лв,
о о
наносимъ па ординатѣ точки А
4НЕЗ
~3~’
АІ) =
па ординатахъ точекъ В и С:
ВЕ = СЕ = 2В.
Такимъ образомъ получимъ дугу ОЕПЕ Черт. ІОЕ
эллипса, ординаты которой и представляютъ
измѣненія діагонали м, соотвѣтствующія измѣненіямъ .г отъ 0 до 2Н.
Задача XVIII.
614. Задача Паппуса. Дана точка А на бнссекпіриссѣ прямого угла составляемаго линіями хх' и уу'; провести черезъ мну точку прямую линію такъ, чтобы отрѣзокъ ея въ обкомъ изъ четырехъ угловъ имѣлъ данную длину р.
Приводимъ эту задачу какъ поучительный образецъ, выясняющій значеніе выбора неизвѣстныхъ. Нерѣдко выборъ неизвѣстныхъ является дѣломъ существенной важности: отъ него зависитъ полученіе ур—ній большей или меньшей сложности. Ііноіі выборъ можетъ повести къ ур-нію биквадратному, иной—къ квадратному, наконецъ—къ полному ур—нію четвертой степени. Какъ скоро взятое неизвѣстное приводитъ къ ур—нію сложному, нужно попытаться взять за неизвѣстное другую величину, чтобы убѣдиться, не приведетъ ли новый выборъ неизвѣстнаго къ менѣе сложному ур-нію.
615. Первый способъ.—Легко видѣть, что если задача имѣетъ рѣшеніе МХ въ углѣ ХОѴ, то будетъ имѣть и другое М'Х' симметричное съ первымъ по отношенію къ О А. Затѣмъ, задача всегда имѣетъ рѣшеніе въ каждомъ изъ угловъ ТОХ' и, ХОѴ'; въ самомъ дѣлѣ, проведя прямую черезъ точки: А и О и поворачивая ее
Черт. 102.
около точки А, въ углѣ ТОХ', затѣмъ въ ХОУ\ видимъ, что ея отрѣзокъ въ каждомъ изъ этихъ угловъ будетъ измѣняться отъ 0 до со.
Итакъ, при всякой величинѣ линіи р задача необходимо имѣетъ 2 рѣшенія— по одному въ каждомъ изъ угловъ УОХ' и ХОУ'; къ этимъ двумъ рѣшеніямъ, въ нѣкоторыхъ случаяхъ, могутъ прибавиться еще два: слѣд. задача можетъ имѣть 4 рѣшенія.
Слѣд., если за неизвѣстное примемъ такую величину, которой значенія, относящіяся къ четыремъ рѣшеніямъ, суть корни одного и того же ур—нія, то получимъ ур. четвертой степени, рѣшеніе котораго въ общемъ видѣ обыкновенно въ рамки начальной алгебры не вводится.
Напр., примемъ за неизвѣстное—разстояніе отъ точки 0 до одной изъ точекъ; М, М', М", М"*; пусть ОМ — о*. Обозначимъ длину равныхъ перпендику-
--2
ляровъ АВ и АС буквою о; треуг. МОХ даетъ: .г2 4-014 =/А но илъ подобія треугольниковъ МОМ и МВА имѣемъ: ОХ :а = .г : (,г— п); отсюда ур—ніе:
1 (іг а/
Освободивъ его отъ знаменателя и развернувъ, убѣдимся, что оно четвертой степени, полное и не возвратное. Въ немъ содержатся всѣ четыре рѣшенія*
Во-первыхъ, очевидно, что для сѣкущей М'Х' получимъ то же самое ур, (1), принявъ ОМ' — ;г. Для сѣкущей АМ"Х", принявъ ОМ" — изъ треугольниковъ ОМ"2І" и АМ"В имѣемъ: Д- 02?" = р2 и — 0№": « — я? : — (а —.т), откуда ОѴ' = га : (л —.г); внося эту величину въ предыдущее ур., получимъ опять ур, --------------------------------------------------------------------------‘4 0), Наконецъ, для сѣкущей АХ'"М"', положивъ 0М'"= —имѣемъ: ;г2-нОХ'"= = рэ и ОУ": а— х: (—а?-|-а) пли ОХ'": а = х : (о? — а), слѣд, снова получаемъ ур, (1), Итакъ, въ ур—ніи (I) содержатся всѣ 4 рѣшенія задачи.
Хотя это ур—ніе и есть полное ур—ніе 4-ой степени, не возвратное, но его можно бы было легко рѣшить, такъ какъ можно бы было показать, что между его корнями существуетъ особое соотношеніе, именно, что ихъ квадраты образуютъ ариѳметическую пропорцію, что даетъ возможность привести вопросъ къ рѣшенію биквадратнаго ур—нія. Но какъ вычисленія были бы длинны и утомительны, то этого метода рекомендовать ^нельзя.
616* Второй способъ. Взявъ за неизвѣстное ВМ (черт. 102), найдемъ ур—ніе («+»)«+ = р* . . . (2),
которое выводится изъ (1) замѣною я? количествомъ # + а; это ур. имѣетъ четыре корня: ВМ, ВМ', — ВМ", — ВМ"\ ибо ур, (1)—общее.
Хотя здѣсь мы опять получили полное биквадратное ур., тѣмъ не менѣе, мы легко можемъ рѣшить его слѣдующимъ искусственнымъ пріемомъ, Ур. (2) можно написать въ видѣ
2дЗ д4 / ді\ / лЗ\
;Г2 4- 2ш: 4- а - ч- а2 — 4-4— = или I а? 4“ 2а2 4- + 2а иг Н----} — р2,
1 1 я 1 х* г \ .г2/ 1 \ ж) г ’
или
отсюда видно, что оно приводится къ рѣшенію двухъ ур—ній
х ч---= у и 4- 2а?/ — р* = О,
X или
—у®ч-л’ = О Іу«4-2лу—р» = 0‘ ' ‘
Итакъ, этотъ искусственный пріемъ даетъ относительно простое рѣшеніе задачи.
Посмотримъ, каково геометрическое значеніе вспомогательнаго неизвѣстнаго у. Проведя перпендикуляръ М(}, на линію А8, параллельную ОХ, и возставивъ къ МХ перпендикуляръ МР, замѣчаемъ, что Р(}. есть третья пропорціональная къ МО и АО — я; слѣд.
А1’ = А(} + (ІР = ж + ^ = у.
«Г
Итакъ, вспомогательное неизвѣстное, соотвѣтствующее рѣшенію МАХ’ есть
АР; точно также, для вспомогат. неизвѣстнаго у, соотвѣтствующаго рѣшенію ХТ'"М"', получили бы (—АР'), возставивъ перпендикуляръ М"'Р' къ ЛМ'".
Ур—ніе въ у системы (3) есть квадратное, слѣд* необходимо, чтобы величины //, относящіяся къ четыремъ возможнымъ рѣшеніямъ задачи, были попарно равны; и въ самомъ дѣлѣ, проведя М'Р, получимъ равные треугольники АМР и АМ'Р, ибо: АМ'= АХ по причинѣ симметричности относительно ОА;-затѣмъ, треугольники ЛСХ и МРу равны, какъ имѣющіе стороны перпендикулярныя и по равной сходственной сторонѣ (АС — МО), слѣд. МР = АМ'; уголъ АРМ — РАМ' ибо ихъ дополненія равны; итакъ, треугольники равны, имѣя по равному углу между порознь равными сторонами*
Отсюда слѣдуетъ, что перпендикуляры, возставленные въ М и М' къ прямымъ МХ, М'№ проходятъ черезъ олну и ту же точку Р линіи Л8, и что тоже самое относится къ перпендикулярамъ, возставленнымъ въ М" и №"' къ М"Х" и М'"Х"\ Этимъ подтверждается вышеприведенное вычисленіе.
Для рѣшенія задачи достаточно знать точки Р и Р', ибо окружности, описанныя на діаметрахъ АР и АР', пересѣкаясь съ прямою XX', дадутъ искомыя точки М, М', М", М'".
Эти точки дало бы намъ рѣшеніе системы (3).
Итакъ, АР и АР' суть абсолютныя величины корней ур—нія
у* + 2ау — р2 — 0 * . * (4)
Изслѣдованіе. Корни этого ур—нія, какъ видно й ргіогі, дѣйствительные, неравные, по знаку противоположные*
I. Чтобы положительный корень у*, который долженъ быть нанесенъ въ направленіи А8, давалъ рѣшеніе задачи, необходимо, чтобы окружность діаметра АР встрѣчала прямую XX'. Но ея радіусъ =у, а разстояніе центра отъ XX' равно а; слѣд* необходимо, чтобы было > 2а; а чтобы это имѣло мѣсто, необходимо и достаточно, чтобы триномъ (4), при подстановкѣ 2а вмѣсто у9 принималъ отрицательное значеніе, т.-е* чтобы было
4а2 + 4а2 —р2 <0,
или р2 —8а2>0*
Корпи тринома р2 — 8«2 суть гЕЗаѴ'З, а какъ р— существенно положительно, то неравенство удовлетворяется при
Первый случай: р < 2а
Въ углѣ ХОТ нѣтъ* рѣшенія.
Второй случай: р = 2аУ2. Положительный корень ур. (4) равенъ въ этомъ случаѣ 2а; сл. окружность діаметра АР касается ОХ, точки М и М' сливаются: задача имѣетъ одно рѣшеніе въ углѣ ХОТ, и это рѣшеніе — перпендикуляръ къ ОЛ* Въ этомъ, слѣд., положеніи отрѣзокъ МХ въ углѣ ХОѴ на прямой, проходящей черезъ А, имѣетъ тіпшгіт величины. Этотъ результатъ легко объяснить геометрически* Пусть МАХ = тіп* и пусть М'Х' какая-либо сѣкущая; очевидно, что Л5Г < АХТ и ЛМ'>ЛМ; а какъ ЛМ — ЛХТ, то ЛМ'>ЛХ', слѣдов. средина
М'Х' линіи М'Х' ниже А, напр., въ К. Соединивъ О съ К, имѣемъ ОК — 7.- ; но
МХ
, и очевидно ОЛ < ОК, сл. 2ОЛ или МХ < 2ОК или М'Х'.
Третій случай: р > 2а ^2. Окружность пересѣчетъ линію ОХ въ двухъ точкахъ, и задача имѣетъ въ углѣ ХОХ два рѣшенія*
И. Во-вторыхъ, чтобы отрицательный корень у", наносимый въ направленіи АР', давалъ рѣшеніе, необходимо и достаточно, чтобы окружность діаметра
(— //') встрѣчала XX', т.-е* чтобы было: — — > а, пли у” < —2а; отсюда слѣдуетъ,
что необходимо и достаточно, чтобы (—2а) содержалось между корнями ур, (4), т.-е. чтобы подстановка количества (—2а і вмѣсто у въ триномъ (4) давала от-рицательныіі результатъ: 4а2— 4я8 — р2 < 0, что всегда удовлетворяется. Слѣд» .задача всегда имѣетъ одно 'рѣшеніе въ углѣ Х'ОѴ, н одно въ углѣ ХОѴ\ что согласно съ выводами предварительнаго изученія задачи.
Резюме.
' р < 2а 12 . . . 2 рѣшенія (ХОѴ', Х'ОѴ). у = 2а 12 , . , 3 рѣшенія.
у > 2а 1^2 . * .4 рѣшенія.
И о с т р о е н і е.—Сдѣлаемъ построеніе для случая четырехъ рѣшеній.
Ур. (4) даетъ: ______
у = У а* у* — а,
— у'= >а2 р2 ч- а.
На параллели къ ОѴ (черт. 102) наносимъ АГ) = р, откуда СР = Га24-?А
Черт. 103. *
Описавъ изъ С какъ изъ центра радіусомъ СИ полуокружность, находимъ на Р1” точки 1’ и которыя п даютъ
АР = У, ЛР;^-/Л
1 Описавъ на АР и АР' полуокружности, получаемъ искомыя точки М, М" и М'", которыми опредѣляются искомыя прямыя: МЛХ, ЛГАУ, АМ"Х" и АУ"М'". Повѣрка—циркулемъ.
617. Третій способъ.—Такъ какъ рѣшенія задачи попарно симметричны относительно О А, то заключаемъ, что точка 0 находится въ равномъ разстояніи отъ двухъ симметричныхъ рѣшеніи. Слѣд. если за неизвѣстное принять разстояніе г точки 0 отъ этихъ двухъ рѣшеніи, то ур. въ г будетъ не выше второй степени.
Итакъ, пусть будетъ ОР = г (черт. 103) радіусъ окружности центра 0, касательной къ рѣшеніямъ въ углѣ ХОѴ; обозначивъ буквами я и $ вспомогательныя неизвѣстныя ОМ и О\\ получимъ три ур—нія:
+ = ! рГ-Лу. . .(1).
•*/ <4* (4
Ь
Остается исключить изъ этихъ ур—ііій х и у, чтобы получить ур. съ главнымъ неизвѣстнымъ г. Для этого второе ур. напишемъ въ видѣ: ху — возвысивъ обѣ его части въ квадратъ: (эд)* = -|-у/*ч-2л7/) и замѣнивъ
и ихъ величинами изъ двухъ другихъ уравненій, получимъ:
р8г3 — а3(р3 -|- 2рг), или — 2д3г — раа = 0 . . . (2).
Чтобы убѣдиться въ общности этого ур—нія, обозначимъ буквою г радіусъ ОР' окружности центра 0, касательной къ рѣшеніямъ въ углахъ ХОУ' и Х'ОѴ. Обозначивъ буквами х и у количества ОМ"', ОХ"\ найдемъ 3 ур—нія:
+ |= рг^гу.
Лг <4- “Г Г»
Второе напишемъ въ видѣ &у~а(х—у), и преобразованіями, подобными вышеприведеннымъ, придемъ къ ур—нію
рг* -и 2а3г — рд3 = 0 . . . (3).
Это ур. отличается отъ (2) перемѣною г на [—г); слѣд. абсолютная величина отрицательнаго корня ур—нія (2) представляетъ радіусъ, дающій рѣшенія въ углахъ ХОУ' н Х'ОУ.
11 з с л ѣ д о в а н і и .—Итакъ, разсмотримъ, при какомъ условія корни ур—нія (2) дадутъ искомыя рѣшенія.
Необходимо и достаточно, чтобы эти корни были дѣйствительны, а ихъ абсолютная величина не превышала ОЛ — а/Г; ибо необходимо, чтобы изъ точки А можно было провести касательную къ окружности, имѣющей радіусомъ абсолютную величину того или другого корня. Но ур. (2) имѣетъ корни дѣйствительные, неравные и противоположные по знаку; сл., что касается положительнаго корня, то если онъ не больше аУ2; то и дастъ искомое рѣшеніе; значитъ, если замѣнить г количествомъ а р'2 въ триномѣ (2), результатъ замѣны не долженъ быть отрицательнымъ, т.-е. должно быть
2ра3 — 2а3/2— ря3 > 0, или р>2а>/2.
Отсюда: 1) если р<2азадача не имѣетъ рѣшеній въ углѣ ХОУ. 2) Если р = 2а |/2Ѵ точка А будетъ находиться на окружности центра 0 и радіуса, равнаго положит. корню; слѣд. будетъ только одна касательная; это рѣшеніе, перпендикуляръ къ О А, есть положеніе прямой МХ, ври которомъ отрѣзокъ въ углѣ ХОУ есть тшітит. 3) Наконецъ, если р > 2а 12, точка А будетъ находиться внѣ окружности; существуютъ двѣ различныя касательныя, выходящія изъ этой точки, и слѣд. два рѣшенія въ углѣ ХОѴ.
Чтобы отрицательному корню г" соотвѣтствовали рѣшенія задачи, необходимо и достаточно, чтобы абсолютная величина (—г") не превышала а/2, т.-е.
г" > - а V 2?
вными словами, необходимо и достаточно, чтобы триномъ (2) не былъ отрицательнымъ при замѣнѣ г количествомъ — оі 2, что лаетъ
2р</2 _р 12 —ря3 > 0, пли рл3 ч- 2л31 2 > 0.
Но /> и а положительны, слѣд. это неравенство всегда вѣрно, т.-е. всегда есть по одному рѣшенію въ каждомъ изъ угловъ ХОѴ и Х'ОѴ.
Построеніе, Уравненіе даетъ
слѣд. нужно построить радіусы:
, , Г а3. „ , а2
г' = 1/ ~ +а3-ь~; — г"= I/ — + а3--------
г \Р/ Г \Р Р
Наносимъ на продолженіи АВ (черт* 103) длину 1Ю=р, проводимъ 00, и въ точкѣ 0 возставляемъ перпендикуляръ ОЕ къ 00; очевидно, что
а3
ЕВ = —, Р
ибо ОВ — а* Слѣд. 0Е = у/ I — 1 -на3; а потому, нанося ЕО— Е(У = ЕВ, имѣемъ: г' —0(4 и —г" = Оф'. Остается провести изъ точки А касательныя къ окружностямъ центра 0, проходящимъ черезъ точки О и ()'.
618- Четвертый способъ,—Можно-принять за вспомогательное неизвѣстное сумму ОМ-рОХ; къ этому выбору приводитъ замѣчаніе, что для двухъ положеній сѣкущей МИ и М'ХТ' величина этого неизвѣстнаго одинакова, ибо треугольники ОМХ, ОМ'Х' равны. Слѣд. для четырехъ положеній сѣкущей получится только два корня; и мы должны придти къ ур—нію второй степени.
Итакъ, пусть
ОМч-ОХ’ — • 0)> затѣмъ: 0М34-0Х3 = р3. . .(2)
Кромѣ того:
* ОМ а ОМ + ОХ ОЫ
ОХ ОХ — а и ОМ а а потому
ОМ X 0Хт = (ОМ ч- ОХ’) . а1 или ОМ . ОХ = . .(3)
Удвоцвъ обѣ части (3) и придавъ ко, (2), найдемъ въ первой части я?3, а ур—ніе будетъ: или
а? — 2аг — р2 = 0 • , . (4) *
Такое же ур—ніе получили бы, взявъ за неизвѣстное ОМ'-нОХ'.
Легко видѣть, что это ур—піе пригодно и для двухъ другихъ положеній сѣкущей, только х тогда будетъ выражать разности ОХ'" — ОМ"' и ОМ" —ОХ".
Какъ скоро х будетъ найдено, останется найти разность отрѣзковъ ОМ—ОХ; для этого удвопваемъ (3) и результатъ вычитаемъ изъ і2л получимъ
ОМ — ОХ’ = У^2 — 2ау; откуда р3 > 2ахг
Найдя я*, вносимъ его величину въ разность ОМ — ОХ, погорая такимъ образомъ и будетъ извѣстна; а какъ извѣстна и сумма отрѣзковъ, то будетъ извѣстенъ и каждый изъ нихъ.
Изслѣдованіе. Нужно, чтобы
Черт, 104.
разность эта была дѣйствительна. При отрицательномъ корнѣ ур—нія (4) это и будетъ безусловно; и въ самомъ дѣлѣ, отрицательны іі корень соотвѣтствуетъ случаю сѣкущей, проведенной или въ углѣ УОХ' или въ ХОУ'.
Итакъ, изслѣдованію подлежитъ толь
ко положительный
быть < слѣд 2а
корень; онъ долженъ р*
должно заключать-
‘ ся внѣ корней (4), а для этого резуль
татъ подстановки этого количества въ триномъ (4) долженъ быть положителенъ:
4а2 2а р ѵ'
или > 0, откуда р > 2а V 2:
условіе, раньше найденное. Отсюда тіо, Р — 2а 12.
Построеніе. Рѣшивъ ур—ніе(4), найдемъ
а*' — а -|- уд» /Я, = — ра* -|-рз4-а.
Пусть 00 = р, то
ВО = 1 а3 4~Р3; нанеся ВО на (Ь, получимъ:
00' = а -Н Уа^-рр& = х\ Слѣд. ОМ — ОХ = 1 р3 — 2ах/ — Ѵр* — 2а . 00Т
Взявъ ВІ = ОВ, на ОС/ описываемъ полуокружность и проводимъ перпендикуляръ IX, тогда ОХ — 1 2ааЛ Слѣд. нанеся 00 на 02:
*
XX = р'022 - ОХ2, 7Х = ѴЯ^2а . ОС' = ОМ — ОХ.
Но ОМ ч ОХ~а?'“ОСі'; сдѣд. если отъ средины (X линіи 00' отложить въ обѣ стороны равныя длины 0'М = 0'М'=у» найдемъ обѣ точки М и М'опредѣляющія искомыя прямыя М АХ и М'АХ'.
Для отриц, корня построенія аналогичны указаннымъ.
619. Пятый способъ. — Можно принять за неизвѣстное разность линій ОМ—ОХ-д?. Для другого положенія сѣкущей, второй корень будетъ ОМ'—ОХ', или ОХ — ОМ; онъ равенъ первому, но противоположенъ по знаку. Также и два остальные корня равны и противоположны по знаку; слѣд. корни попарно равны и противоположны по знаку, а потому этимъ способомъ должны придти къ биквадратному ур—нію.
Имѣемъ:
' ОМ —0Х = я? ОМ34-ОХ2==^...(2) п ОМ X ОХ“а(ОМ + ОХ).. ДЗ); отсюда:
20М X ОХ - 2а(0М + ОХ) и ОМ* + ОХ2 — 20М X ОХ — р* — 2а(0М + 0Х),-*
слѣдовательно
«2 Д’*
я*2 =р* — 2а{ОМ + ОХ), откуда ОМ 4“ 0^ = —*\Г— *
Зная же, что ОМ — ОХ = имѣемъ Т 7
ОМ =
1/^ —.Г2
0Х = <— 4н
*
Внося эти величины въ ур. (2), получимъ
(р2 2а.г — ;г*)2 + (р2 — 2а.т—X*)2 ~ Ѵ>а2р2, или, раскрывъ скобки и приведя въ порядокъ: *
Г* + 2(2а2 —р2>2 + Я/>* — = О-
Чтобы корни ($2) этого ур—нія были дѣйствительны, необходимо, чтобы было: (2а2 — р2)2 — р2 (р2 — 8а2) > 0, или 4а* — 4а2р2 + р1 — р1 + > 0, или 4«* 4-
4п2р2>0, что всегда удовлетворено.
Чтобы оба они были положительны, необходимо, чтобы произведеніе и сумма ихъ были положительны. Произведеніе будетъ положительно при р2>8а2, или при
р > 2а 12.
По при этомъ условіи будетъ р>2а, слѣд. 2а2—р2 будетъ <0, а потому * сумма корней будетъ >05 и оба корня—положительны. Итакъ, единственное условіе возможности задачи будетъ: р > 2а I 2, т,-е. чтобы данная линія была не меньше удвоенной линіи ЛО.
Рѣшивъ уравненіе, найдемъ:
х = р^р2 — 2а2 ±і 2^ Ра2 4* Р2;
выраженіе это легко построить; а имѣя х, нетрудно уже найти ОМ и ОХ.
620. Шестой способъ.— Если за вспомогательное неизвѣстное принять произведеніе отрѣзковъ 0МХ0Х, то какъ для двухъ положеній сѣкущей произведеніе это имѣетъ одну и ту же величину, для четырехъ ея положеній получимъ два значенія для произведенія; поэтому, ур. съ неизвѣстнымъ а?, равнымъ произведенію отрѣзковъ, должно быть квадратнымъ.
Положивъ ОМ X ОХ — .г, имѣемъ еще два ур—пія:
ОМ*4-ОХ2 = р2 и ОМ X ОХ = а (ОМ + ОХ), или х = а (ОМ 4- ОХ).
Возвысивъ послѣднее ур. въ квадратъ, имѣемъ
х2 = «2 (р2 4~ 2я), откуда х2 — 2а2х — а2р2 = 0.
Какъ скоро х найдено, МО и ХО получимъ изъ биквадратнаго ур - нія
X4 — р2Х* + х2 = 0.
Корпи этого ур—нія будутъ дѣйствительны при условіи р1 —4х2>0, или (р2 4- 2,г) (р2 — 2л?) > 0; отсюда видно, что при х > 0, необходимо, чтобы было
Замѣняя х количествомъ^ въ ур. въ х, должны имѣть: —а^2—«2р2>0,
или р3 > 8а2, откуда р>2а)2—условіе извѣстное. должно давать
р2 р2 , .
— т.-е. — должно быть внѣ корней ур—шя въ х, и потому должно
А
, 14
быть + а*р* — а*р* > 0, .что всегда, имѣетъ
условіе есть
р > 2а Ѵ2,
м Ьсто. Итакъ, единственное
Какъ скоро оно удовлетворено, оба значенія & будутъ положительны, а потому всѣ четыре значенія X дѣйствительны.
Впрочемъ, какъ скоро найденъ х, то вмѣсто рѣшенія биквадратнаго ур—нія, дающаго отрѣзки ОМ и ОХ’, стоитъ только замѣтить, что въ треугольникѣ ОМХ
ОМХОХ х
извѣстна гипотенуза р и площадь, равная -------- или
621. Седьмой способъ.—Если за неизвѣстное принять отношеніе отрѣз-
ковъ, то очевидно должно получиться возвратное ур. четвертой степени; ибо для 0Мг ОХ
положенія М'Х*'(черт. 102) сѣкущей второй корень есть или т.-е. онъ обратенъ первому корню; то же самое имѣетъ мѣсто и для двухъ другихъ корней. Для составленія ур—нія стоить только исключить ОМ и 0Хт изъ трехъ уравненій
стоить только исключить ОМ и ОХ изъ трехъ
п
откуда
ОМ
ОХ
. .(1) ОМ34-ОХт* = р3 . . .(2)
ОМ ОМ—а , или ах ч= ОМ — а,
ОХ а
0М = а(^1). . . (3).
Изъ перваго ур—нія имѣемъ ОМ3 ОМ ” 1 ’
отсюда
ОМ3
г
или
РІ
ОМ*
или
я* ’
или
>
или
Положивъ х 4- - _ у, откуда л* 4* ~ = у3 — 2, и раздѣливъ все ур—ніе на я2, находимъ
4" + 2а* (я 4~ - ] 4" — р2 = О, или а2у* 4 2а*у —= О
и
х* — 4” 1 = О*
Изъ ур—нія въ у найдемъ два значенія для у: у’ и —у", который поочС’ ре дно вносимъ въ послѣднее ур—ніе. Но чтобы для і получились величины дѣйствительныя, нужно, чтобы абсолютная величина у была больше 2; и слѣд. замѣна у числами 2 и —2 должна давать отрицательные результаты; т.-е.
4а2 4- 4а2 —р* < 0, или р > 2а 1'2
и
4а2 — 4а2 — р2 < 0, или — р2 < О,
что приводится къ одному условію: > 2а /2, уже извѣстному.
Когда это условіе не выполнено, когда р содержится между 2а/2 и 0, годится только отрицательное значеніе у/, которому отвѣчаютъ два отрицательныя значенія г: сѣкущая проходитъ въ углахъ яЮ/ и
622,— Восьмой способъ—три го но не тричесхій.
Пусть (см. черт. 102) уголъ ОМХ = я. Имѣемъ
АМ =
а
81П X*
АХ= " , СО8 Г
слѣдовательно
откуда
~а__________
8ІІ1 х "г- со§ х
2а (зіп х + сой ж) =р . зіп 2*г,
а по возвышеніи въ квадратъ и по приведеніи въ порядокъ,
р2 зіп2 2.г — 4а2 зіп 2х — 4а2 — 0,
откуда
. 2а2 + /4а* -/4а2/>2 2а
8ІПІГ =------»а“' ' = а-,Л+^)-
Изслѣдованіе. Значенія 8Іп2я, очевидно, дѣйствительны; но они не должны быть больше 1, откуда условіе
2а2 + /4а1 4~ 4а2р2 ^р2, или
ва’р2 <р4, или 4
♦ р 2 12 . а.
623. Въ заключеніе укажемъ рѣшеніе
I. Ищемъ рѣшеніе въ углѣ хОу (черт. 105), и пусть прямая МХ—требуемая, такъ что Ма =р. Вообразимъ, что на МХ, какъ на діаметрѣ, описана окружность, которая, слѣдо-. вательно, пройдетъ чрезъ точку 0; пусть эта окружность пересѣкаетъ продолженіе прямой 0А въ точкѣ I, которая будетъ лежать въ срединѣ полуокружности М1ХТ. Очевидно, все сводится къ нахожденію точки I; въ самомъ дѣлѣ, разъ эта точка найдена,
Р то, описавъ радіусомъ - окружность, проходящую чрезъ точки 0 и 1, мы будемъ имѣть и точки М и X.
Но точку 1 найти легко. Въ с^Момъ дѣлѣ, разность между линіями 10 и ІА извѣстна, ибо она равна 0А. Легко видѣть, что и произведеніе ІОХІА также извѣстно. Дѣйствительно, треугольники при 0 и М въ 45° каждый, подобны,
вопроса чисто геометрическоеЛ
01М и А1М, имѣя общій уголъ I и углы откуда пропорція 01: 1М — 1М : ІА, или
— 2
01 X ІА — 1М ; а какъ точка 1 находится въ срединѣ дуги МІХ, то ІМ есть сто-
—2 «а
ропа вписаннаго квадрата, и потому ІМ — такъ что
& *
0ІХІА=^-и
— Т)"
Зная разность 10 —ІА —аі 2 п произведеніе ЮХІА=~, легко построить
10 и ІА (см* § 472).
Л з с л ѣ д о в а н і е.—Когда точка 1 найдена, остается описать чрезъ точки 1
0 и 1 окружность радіусомъ по чтобы ото было возможно, необходимо, что-бы разстояніе 01 было не больше р. А какъ 01 и (— ІА) суть кори и ур—нія
Р-аѴ'2 .1— ^ = 0,
то, чтобы положительный корень былъ но больше р, необходимо и достаточно, чтобы результатъ подстановки числа р вмѣсто і въ первую часть не былъ отрицательнымъ, т.-е* чтобы было
р« - ра I 2 — > 0, или р > 2п І^.
Заключаемъ, что:
1) если р<2а задача невозможна;
2) если р = 2л вопросу отвѣчаетъ одна окружность, діаметромъ которой служитъ 01 и слѣд., рѣшеніе въ углѣ Х)р одно: перпендикуляръ къ 01 въ точкѣ А (случай пнпітит'а);
Черт. 106.
описать чрезъ точки 0 и I окружность.
3) если р> 2/ѵ] 2, вопросу отвѣчаютъ двѣ окружности, симметричныя относительно 0А: задача имѣетъ 2 рѣшенія въ углѣ ігОу.
П. Будемъ искать рѣшеніе въ углѣ яСу. Пусть это искомое рѣшеніе будетъ прямая АМХ (черт. 106). Вообразивъ опять окружность, описанную на МХ’ какъ на діаметрѣ, найдемъ точку 1 ея встрѣчи съ продолженіемъ О А. Имѣемъ: ІА — ІО — а |'2; затѣмъ, подобные треугольники І0М и ІМА даютъ:
ЮХ1А = ІМ
и вопросъ приводится къ построенію двухъ прямыхъ по ихъ разности и произведенію (§ 472).
И з с л ъ д о в а н і е.—Пусть точка I построена; остается радіусомъ
Чтобы это было возможно, должно быть
10<р.
Нр ІА и (- Ю) суть корни ур—нія
/» — и >2 . і~~ = 0,
и чтобы ТО (отриц. корень съ обратнымъ знакомъ) было не больше уэ, необходимо и достаточно, чтобы результатъ подстановки (—1>) вмѣсто / въ первую
, часть не былъ отрицательнымъ, т.-е- чтобы было
р2 +ра 12 — 5> 0, или р* + 2рд У2 > О»
Такъ какъ это неравенство всегда удовлетворено, то всегда можно радіусомъ описать двѣ различныя окружности чрезъ точки 0 и I; эти окружности и дадутъ рѣшенія въ углахъ хОу' и х’Оу,
Можно, сближая обѣ части способа, найти всѣ 4 рѣшенія однимъ построеніемъ. Построивъ, напр., точку I (черт-106) въ углѣ получимъ точку Іь относящуюся къ двумъ другимъ рѣшеніямъ, нанеся ОІ! = АІ*
Задача XIX.
624. Ба окдужмвстѵ К бедоша стявра, которою уголъ = 45°; требуется въ этомъ секторѣ помѣститъ прямоугольникъ МКР(^ (двѣ вершины котораго находились бы на одномъ радіусѣ, а изъ двухъ остальныхъ одна на другомъ радіусѣ, а другая на дугѣ сектора) шаіга, чтобы діагональ МР гідпьлл доя-ную длину т.
Примемъ за неизвѣстное длину ОР — ж; треугольникъ МОР даетъ
т2 = В* ж* — 2ж , О<5-
По изъ треугольника 0(}М, замѣчая, что М(^ = ОР, имѣемъ: О^ = /К2 —я2. Отсюда
т2 = К2 + я*я? . , .(1)-
Это ур—ніе останется въ томъ же видѣ, пока точка М будетъ находиться на дугѣ ЛС, ибо уголъ РОМ будетъ острый.
Если точка М будетъ находиться на дугѣ СЛ', причемъ прямоугольникъ будетъ, напримѣръ, МЪТ'Р'<4', найдемъ, огіять полагая ОР' = х, ур—ніе
та = К* + я* + 2х ^К2 —ж2 - . . (2)
отличное отъ (1)-
Затѣмъ, безполезно братъ точки на полуокружности А'С'А, потому что, очевидно, найдемъ рѣшенія симметричныя, относительно О, рѣшеніямъ уже полученнымъ.
Итакъ, задача рѣшается двумя ирраціональными уравненіями
—+ —т* . . .(3),
гдѣ я > 0, пли цѣлымъ ур— ніемъ:
4<г2 (К2 — я2) = (^ + II* — т2}2 ♦ . . (3'), или
5^ — 2 (т2 + В2) я* + (т2 — В2)2 = 0 - . . (4),
изъ числа корней котораго надо брать только положительные и наносить пхъ въ направленіи ОЛ.
Нѣкоторой точкѣ Р, для которой ОР есть корень ур. (4), соотвѣтствуютъ двѣ точки окружности, лежащія на одной и той же параллели къ А А', если только РХ = х не больше 11; изъ этихъ двухъ точекъ вопросу отвѣчаетъ та, для которой
і’2 + Е2 — т* > 0, или я2 > ж2 — Н2,
если она находится на дугѣ АС; или та, для которой
ж2 4- Е2 — пг2 < 0, или ж2 < — К2,
если она находится на дугѣ А'С.
Изслѣдованіе. Чтобы корни уравненія (4) отвѣчали на задачу, необходимо и достаточно: 1) чтобы они были дѣйствительны; 2) положительны; 3) меньше Е.
Кромѣ того, а ргіогі видно, что какъ скоро корни будутъ дѣйствительны, они будутъ попарно равны и противоположны по знаку; слѣд. будутъ два положительныхъ корня, и очевидно, что они будутъ меньше К, ибо, удовлетворяя ур—нію (3'), дѣлаютъ разность 4л?2 (Е2— ж2) положительною. Итакъ, остается единственное условіе—условіе*дѣйствительности.
Такъ какъ ур—ніе (4) биквадратное, то для дѣйствительности его корней необходимо, чтобы значенія т2 были дѣйствительны и положительны; но очевидно, что какъ скоро они дѣйствительны, то и положительны, слѣдовательно, необходимо и достаточно, чтобы было
(т2 + Е2)2 — 5(ж2 — Я2)2 > 0, или
[т« -+- — (от« — К8) 1'5] [>н» 4- К» + (іи8 — В.8) Ѵо] > 0,
ИЛИ
[(Ѵб + 1) т» — — 1) К8] [(Ѵ5 — 1) >м8 — (Ѵэ +1) КЯ] < 0.
к
Раздѣляя первый множитель на У5 4-1» а второй на > 5 — 1 и замѣчая, что
даемъ. нер авенств у в идъ:
{та — 1) [^(/54-1)] } <0,
или, по разложеніи на множители первой степени:
[»< + (И5 — !)][>«-ку(Ѵь + !)][*« — (ѵ'б +1)] < 0.
Но первый и третій множители положительны, слѣд. должно быть
[»» — К(Ѵо — 1)][ж — ^(/5 + 1)] <0, откуда видно, что т должно удовлетворять условіямъ;
При этихъ условіяхъ всѣ 4 кбрня ур—нія (4) будутъ дѣйствительны; слѣд. задача будетъ имѣть два рѣшенія въ полуокружности АСА', и два симметричныя имъ рѣшенія въ другой полуокружности.
— 691 —
Остается показать положеніе прямоугольниковъ, отвѣчающихъ задачѣ.
Чтобы оба положительныя значенія х давали прямоугольники съ вершиною М на дугѣ АС, необходимо и достаточно, чтобы для каждаго изъ этихъ значеній было ха > іи — В2; а для этого необходимо и достаточно:
1) Чтобы триномъ, составляющій первую часть (4), былъ положителенъ при замѣнѣ въ немъ а* разностью (т2 — К2);
2) Чтобы полусумма корней не была меньше (?н2 — К2).
Первое изъ этихъ условій даетъ:
о _ Н2)2 — 2 (т2 + К2) (т2 — К2) + (»а2 — П2)2 > 0, или
(ж2 — К2) (т2 - 2В2) > 0 . . . (6).
Второе условіе даетъ
4. н2 - ЗВ2
—?п2 — К2, или ж* -у- - * • (7).
О 4
ЗВ2
Отсюда, такъ какъ —содержится между К2 и 2В2, слѣдуетъ, что: 1) если ?н2<Н2 или оба рѣшенія лежать на лугѣ АО; 2) если К<т<КѴ2,
одно рѣшеніе находится на АС, другое на А'С; 3) если т>В/2, оба рѣшенія на дугѣ А'С.
Итакъ, тахітит т, равный ^(1^5+ 1) (т.-е. сторона правильнаго вписаннаго звѣзднаго десятиугольника), принадлежитъ прямоугольнику, котораго вершина М лежитъ на дугѣ А'С; между тймъ какъ пппппит т, равный I)
(сторона выпуклаго десятиугольника), принадлежитъ прямоугольнику, котораго вершина М находится на дугѣ АС.
Резюме изслѣдованія.
т<^(у5—1), корни мнимые
О рѣшеній.
К
г______
-ііко . . . .
---, пнпітит(т) . , *
10
рѣпъ на дугѣ АС.
9
рѣш. на дугѣ АС.
?и=ІД: % =0, х
9 • м
к
рѣш. на дугѣ АС.
к
| т<ВУ 2............1 рѣш, на АС, 1 р. на А'С,
пі>К ! ............точка С и 1 рѣш. на А'С.
| ??г>1О/2 . ,......1 рѣш. на дугѣ А'С.
В
К
, тах.(тп). 1 рѣш, на дугѣ А'С. о
; корни мнимые
0 рѣшеній.
Задача XX.
625. Дана окружность и одинъ азъ діаметровъ, АВ. ІГь нему проводятъ перпендикуляръ ху въ разстояніи АР = а отъ точки А. Провести чрезъ точку А сѣкущую такъ, чтобы ея ондедоокъ СО даод
прямою ху и второю точкою пересѣченія съ окружностью равнялся данной прямой I.
Составленіе ур—нія. Пусть прямая 37/ находится вправо отъ А, въ разстоянія АР — а отъ точки А; въ этомъ случаѣ а>0. Отрѣзокъ I всегда положителенъ. Искомое разстояніе АЕ = я, Прямоугольный треугольн. АСЕ даетъ
—2
АС = ^н-л(2К — я) . * . (1).
Подобные треугольники АСЕ п АГ)Р даютъ
откуда
АС =
1х а — х
. (2).
Внося въ ур—ніе (1) и сокращая на я, найдемъ
2&г2_ р + 4аВ)#4-2аЖ=0 . . . (3)-
1
Черт, 108.
Для второго чертежа ур. (1) остается безъ измѣненія; ур, (2) беретъ видъ
АР _І — АС х АС
Вторая часть положительна; чтобы и первая была положительна, нужно вмѣсто АР подставить уже не о, но (—а), такъ какъ теперь а<0, и получится опять ур-ніе (3), Итакъ, въ обоихъ случаяхъ имѣемъ одно и то же ур-, въ которомъ нужно принимать о>0, когда отрѣзокъ АР находится вправо отъ А, и «<0, когда онъ располагается отъ этой точки влѣво. *
Изслѣдованіе. Чтобы корень ур—нія (3) давалъ отвѣть на задачу, онъ долженъ быть дѣйствительнымъ, по-
ложительнымъ и < 2К.
Условіе дѣйствительности х. Рѳ-ализантъ долженъ быть 0, т.-е.
р + 4аН)* - 4 . 2Н . 2аШ О, или Д- 8аК 0.
Когда л > 0, это условіе всегда удовлетворено, Когда же а < 0, то знакъ зависитъ отъ вели-
чины Р по сравненію съ — 8аК: если № — ВаК^ корни дѣйствительны; если №<; — 8аК — корни мнимые.
Знаки корней. Корни должны быть положительны. Для сужденія объ
ихъ знакахъ, нужно знать знакъ ихъ произведенія и ихъ суммы. Произведеніе корней слѣд, всегда положительно, и потому дѣйствительные корни имѣютъ одинаковые знаки, л —н4аН
Сумма корней = ——ъ слѣд, знакъ ея зависитъ отъ знака числителя;
очевидно, что при а >0, сумма корней всегда положительна; при а<0, очевидно, всегда будетъ —8аК> —4аК, а какъ дѣйствительность корней требуетъ,
чтобы было Р > — 8аЕ, то и подавно будетъ > — 4аВ, пли Р ч- 4«В > О, слѣд. сумма корней опять >0.
Величина корней. Положительные корни должны быть < 2К; чтобы знать положеніе пхъ относительно 2К, надо знать знакъ /(2К};
Г(2Н) — 2В [(2К — а)* - Р], слѣд. имѣетъ знакъ разности (2В — — Р,
такъ что
/’ (2П) > 0, когда (2Е — «)2 >
/‘(2К) < 0, когда (2В — а)* < ?2. « ч ♦
Критическія значенія?3 суть, слѣдовательно:0, — ВаК, (2К — а)3, 4-со. Пхъ нужно расположить въ восходящемъ порядкѣ, разсматривая два случая: а > О, а < 0* Но въ первомъ случаѣ — будучи отрицательнымъ, не входить въ число значеній положительнаго количества и остаются только значенія: О, (2В-а)*, + сс.
Составляемъ таблицу знаковъ.
Случай а > 0.
Скала значеній № 0 (2В — а)2 + ОС
Реализантъ
Произведеніе корней
Сумма корней —
/(2Н) •> —
1-й коэффиц. —
Разсматриваемъ каждый интерваллъ.
1) Когда Г2 заключается между 0 и (2Е — а2, произведеніе и сумма дѣйствительныхъ корней положительны, слѣд. оба корня положительны. Далѣе: /‘(2В) имѣетъ знакъ 1-го коэффиціента, слѣд. 2В находится внѣ корней, и значитъ либо оба корня меньше 2К, либо оба больше 2К. Чтобы судить объ этомъ, нужно сравнить 2В съ полусуммою корней, которая — Въ разсматриваемомъ
интервалѣ Р < 4Ю — 4лК о2, слѣд., если а < 2ВТ то будетъ и подавно
Р < 4В* — 4аК 4- 4К% пли Р < 8К* — 4аЕ, или Р + 4аЕ 8Е2, откуда
Если же а > 2К, то и подавно
1* Р4-4аК
—+ а>2К, или >2И.
Такимъ образомъ, если а < 2В, полусумма корней меньше 2В, слѣдовательно п оба корня < 2К: задача алгя^ить два рѣшенія.
Если же а>2Е, то полусумма корней больше4 2К, и оба корня больше 2И: задача не имѣетъ рѣшеній.
2) Р = (2к— а)2. Имѣемъ /’(2І<)=0, слѣд. одинъ изъ корней равенъ 2К; этотъ корень даетъ точку В. Произведеніе корней — слѣд. другой корень —этотъ корень долженъ быть <2Е, откуда а2<4К2, и а < 2Е. Для построенія сѣкущей, отвѣчающей этому корню, очевидно, достаточно изъ точки А радіусомъ а нанести хорду АС и продолжить ее до дайной прямой.
3) Р>(2К— а)2. Оба корня опять положительны; но какъ знакъ /'(2К) въ этомъ случаѣ противоположенъ знаку перваго члена, то 2Е заключается между корнями; и расположеніе чиселъ таково
О . * . а'. • . 2К . . * %'**
Заключаемъ, что большій корень (я"), будучи больше 2К, есть корень алгебраическій; меньшій же корень, будучи < 2К, даетъ отвѣтъ на задачу, которая такимъ образомъ имѣетъ 1 рѣшеніе, изображаемое корнемъ
ГМ- 4«Е — I /Г2 -р 8аЕ
Случай а < 0.
Въ этомъ случаѣ, какъ выше указано, корни могутъ быть или дѣйствительные, или мнимые: первое имѣетъ мѣсто при Г2 — 8аЕ, второе при — 8«К. При этомъ (2К—а)2>—8аЕ, ибо это неравенство эквивалентно съ (2Е-на)2>0. Скала критич. значеній Г* въ восходящемъ порядкѣ будетъ, слѣдовательно: 0, — 8аЕ, (2Е—а)2, Ч-с©.
Таблица знаковъ будетъ такова:
Скала значеній Г2 1 0 — 8аЕ (2К — а)2 +50
! Реализантъ —1 —
Произведеніе корней « —|—
Сумма корней —
/(2В) нн —
1-й коэффиц. 1 — 1
Изслѣдуемъ каждый интервалъ.
1) <— 8аЕ: корни мнимые, и невозможна. ► <
2) Р — — 8аЕ: корни дѣйствительные равные, общая величина ихъ
^Рч-.ДаК _ — 4аЕ_
— 4К — 4Н — а:
чтобы можно было допустить такой корень, должно быть
— а < 2Е, или а Э* — 2Е.
3) — 8аЕ < й < (2Н —а)2. Корни дѣйствительны; произведеніе и сумма ихъ положительны; слѣд. оба корня положительны. /’(2К) имѣетъ знакъ одинаковый
съ 1-мъ членомъ, слѣд. 2Е находится внѣ корней. Оба корня тогда будутъ меньше 2Е, когда полусумма пхъ будетъ меньше 2Е. Такимъ образомъ, нужно изслѣдовать, когда удовлетворяется неравенство
41Г-<2Е’
или ему эквивалентное
де<4Е . 2К —4Е > а, или де<4Е(2Е-а).
Когда а > — 2Е, то будетъ 2К — а < 4Е, или, уможивъ обѣ части на положительное количество 2К — «, найдемъ (2К— а)2 < 4К (2Е — а). По условію, Р меньше (2Е—а)2, слѣд. и подавно будетъ <4В(2К — а). Въ этомъ случаѣ полусумма корней положительна и меньше 2К, слѣд. оба корня меньше 2Я, и задача имѣетъ 2 рѣшенія. _ _
Когда а или —8аК^ 4Щ2Е изъ
гои
пли
цателенъ, то первый долженъ быть положителенъ: а + 2Е
_ 4 IV, Ю 41* \ 4 ІА-рі* 41*\ІД. 'Д4 1ѴХ,
4К(2Е— а). Но, по условію, Г1 больше —8аЕ, то и подавно больше — а). Это значитъ, что полусумма корней больше 2К, слѣд, и каждый корней больше 2Е, и задача не имѣетъ рѣшеній.
4) де = (2К — а)2. Въ этомъ случаѣ /’(2Е) = 0, одинъ изъ корней =2К; дру-корень Чтобы онъ удовлетворялъ задачѣ, должно бытьнр'<2Е,
2К -ьіѵ
— 4К2<0, или («Ч-2К)(а — 2Е)<0; такъ какъ второй множитель отри-• > 0, или а > — 2Е.
5) 2* > (2Е — д)2. Оба дѣйствительные корня, произведеніе и сумма которыхъ >0, положительны. Знакъ /’(2Н) противоположенъ знаку 1-го члена, слѣд. 2К заключается между корнями:
0. ,2Е. . .д/'.
Заключаемъ, что задачѣ удовлетворяетъ только меньшій коренъ хг: задача имѣетъ 1 рѣшеніе.
Резюме*
I. а > 0.
ж де -Ь 4аЕ ± I /де + 8ай
рѣшенія: х ——!- —
4К
рѣшеній.
Корни всегда дѣйствительны.
а < 2Е , . .2
а > 2Е . . ‘О
Р = (2Е — а)2...............2 рѣшенія: а?' = и — 2Е.
іа /лп ~I- 4аЕ — / /де —р 8лЕ
де> (2Е — а)2...............1 рѣшеніе: х'= —5—----------—.
4К
И. а < 0.
1) а> — 2Е.
де < — 8аЕ . . - корни мнимые.
де = — 8аК . . . корни равные: о/ — х” = а.
— 8аЕ < де < (2К — а)2...............2 рѣшенія.
де = (2Е —а)2............* . 2 рѣшенія: #" = 2Е.
де > (2Е — а)2 . ...........1 рѣшеніе.
2) а < — 2Н.
де < — 8аК .... корни мнимые.
— 8аЕ < де < (2Н — а)2 * . .0 рѣшеній.
де = (2Е — а)2 ... 1 рѣшеніе: гг — 2К.
де > (2И — а)2. . .1 рѣшеніе.
Задача XXI.
626. Ва каколга ролешляніи отъ центра г)аннто мара провести сѣкущую плоскость, чтобы боковая поверхность конуса 8МХ, описанною окола ?аара по сѣченію, сложенная съ »* разъ взятою поверхностью внѣшняго сегмента МВХ, равнялась данной поверхности (т—число положительное)*
Рѣшеніе, Примемъ за неизвѣстное разстояніе плоскости МХ отъ центра " шара
шара, положивъ 01 = я*, а данный радіусъ назовемъ К.
По условію имѣемъ уравненіе
если лапную поверхность представить въ впдѣ радіуса /г. Нужно вычислить 8Х, XI и В1 въ ціи Ё и я. Прямо имѣемъ
круга фуяк-
Затѣмъ, XI = 1 К2-“А Изъ подобія треугольниковъ 8X1 и ХОІ находимъ:
ХО : 01, откуда 8Х
Подставивъ въ ур—ніе и приведя въ порядокъ, имѣемъ:
Изслѣдованіе. Чтобы значеніе о*, выводимое изъ этого уравненія, давало отвѣтъ на задачу, необходимо и достаточно, чтобы оно было дѣйствительно, положительно и не больше К. Въ самомъ дѣлѣ, приведеніе задачи къ уравненію предполагаетъ, чтобы я было положительно, иначе, значеніе 8Х было бы отрицательно; далѣе будетъ особо указано, какъ можно истолковать отрицательное значеніе ж. Возьмемъ эту задачу какъ примѣръ, на которомъ покажемъ, какъ । ведется изслѣдованіе по плану Жирода. По этому плану, изслѣдованіе разбивается на двѣ части: ищутъ, при какихъ условіяхъ задача имѣетъ одно рѣшеніе, при какихъ —два рѣшенія. Отсюда сами собою вытекаютъ условія, когда она невозможна.
Случай одного рѣшенія. Чтобы задача имѣла одно,, и только одно, рѣшеніе, заключающееся между 0 и К, необходимо и достаточно, чтобы результаты подстановокъ въ /’(г) вмѣсто х—нуля и К имѣли противоположные знаки, т.-е, чтобы /’(О). ЯП) < 0 (см. § 481, сл. 1). Но /,(0) = 1Р> <(Е) = К (4№т-^); искомое условіе будетъ, поэтому
&
т < 4К«’
Случай двухъ рѣшеній. Чтобы задача имѣла два рѣшенія, необходимо и достаточно:
1) Чтобы корни были дѣйствительны,* т,-е. чтобы
— 2шШ)« — 4 (2ж — 1) К* > 0;
рѣшивъ это неравенство относительно т, найдемъ, что ему можно удовлетворить, взявъ либо
А? -4- 2Н2 — 2Ж т< — 2КЗ—
. • О);
либо
А? -+- 2Й» -4- 2ЛК 211»
2) Чтобы корпи были положительны; иначе говоря, чтобы ихъ произведеніе п ихъ сумма были положительны. Условіе положительности произведенія даетъ
»»>!•. -(з), Л
а принимая въ расчетъ это условіе, найдемъ, что сумма корней будетъ положительна, если
*8 /п
' т < 2К* * * *
3) Утобы корни были .меньше К, т.-е. чтобы было заразъ
№
(2т — 1) . /‘(В) > 0, откуда ^>^2- • • (5) п
х’-ь-х" < 2К, откуда т > —. * (6).
Нужно теперь сравнить между собою найденные предѣлы.
Неравенство (4) противорѣчитъ 2-му; и если взять к < К то (3) и (4) также будутъ противорѣчитъ одно другому. Но какъ (3) и (4) неравенства—оба необходимы, то нужно предположить А-’>К; но въ такомъ случаѣ, если написать (I) въ видѣ
да~2(А —Е)К
т " 2№ ’
легко замѣтить, что оно ведетъ за собою (4). Такимъ образомъ имѣемъ одинъ высшій предѣлъ для -ш, выражаемый неравенствомъ (I).
Совмѣстны ли съ нимъ низшіе предѣлы? Эти низшіе предѣлы т суть:
1 да да-ь 2К\
2’ 4К* И 6К» ’
нужно составить разности
й* — 2йК + 2В* 1 _ (й — В)1
1Н» 2— 2П» ’
№ - 2ЙК -н 2В« _ й« __ (к - 2В)*
2ВЗ ’ 4К«— 4К« ’
Й« — 2ЙН -+• 2К» й» -4- 2К2 _ 2 (й — Н) (й — 2К)
2Н2 6К»-- 6К«
Слѣдовательно, чтобы искомая совмѣстность имѣла мѣсто, необходимо взять к > 2В. Но въ такомъ случаѣ будетъ
№ і _ да — 2Е2
4Е* 2“ 4Ш
к* да ч- 2Н-2 __ да — 4№
4К* 6№ — 12В2 >0;
т.-е, изъ низшихъ предѣловъ наивысшимъ будетъ
4К2
Заключаемъ, что задача будетъ имѣть 2 рѣшенія, если будутъ одновременно выполнены условія
к > 2Е,
да да _ 2АК 2Ю
— <Г т <? - — —--
4К2^ 2К*
или
да + (Л - 2К)2
4Е2
Истолкованіе отрицательныхъ значеній х.— Для всякаго отрицательнаго х, большаго (—К), значенія ВІ и М дѣйствительны и положительны, тогда какъ величина 8Х дѣлается дѣйствительною и отрицательною; это значеніе соотвѣтствуетъ, слѣдовательно, соотношенію
или
- . (— 8Х’) . М -ь т . 2гК . ВІ = ~к\ — - . 8Х , Мч-пі . 2гВ . ВІ—АЛ
Слѣдовательно, отрицательное значеніе а? даетъ такое положеніе плоскости сѣченія МХ', при которомъ поверхность сегмента МВХТ безъ боковой поверхности конуса 8МХ’ составляетъ поверхность, равную данной гЛ2.
Задача XXII.
627. Дамы г)#а шара, лежащіе одинъ внѣ другого: О м О'; на ли и де центровъ, между обоими шарами, найти такую точку А, чтобы два конуса, имѣющіе общую вершину въ этой точкѣ и касающіеся къ даннымъ шаримъ, заключали внутри себя два сегмента, сумма поверхностей которыхъ имѣла бы данную величину.
Рѣшеніе. Пусть будутъ г, г' и д—радіусы шаровъ и разстояніе центровъ; х и х'—разстоянія АО и АО'. Зная, что поверхность сферич. сегмента = про-
изведенію окружности большаго круга на высоту сегмента, имѣемъ: пов. сегмента ВСО = 2тт . СО; но СІ) = г —ОС, по свойству же катета имѣемъ: г2=ОСХ®> откуда
4^2 / У® \
ОС = — и 2г.г . СЕ) = 2т: г2 — .
X \ X ]
Сумма поверхностей обоихъ сегментовъ выразится формулой
/ к'® \
За данное можно принять 2г.-а—изобразивъ его формулою 2гт2, и
X X і
замѣнивъ х' равною величиною гі—я?, получимъ уравненіе
= т*
откуда
I
И з с л ъ д о в а н і е. Количество а? будетъ дѣйствительно, если
— г'/?7)3 < .. (гУг-рг'Уг7)3 '
ж2<-——_. (2), или - ——з------------— . . . (3),
л а
а по ур—нію (1) заключаемъ, что оба корня будутъ и положительны.
Но чтобы величина х представляла рѣшеніе даннаго вопроса, нужно еще, чтобы она была >г, но <а—г'. Результаты подстановки количествъ г и с?—г' вмѣсто я въ первую часть ур—нія (1) суть:
г — г3 — т3 — **)] п г' 9 + г3 ~~ г'* — ять* (с/ — г7)];
поэтому главными значеніями будутъ количества
-р г73 —г3 + г3 — г'3
<1— г и — г'
^7*3
Сверхъ того нужно сравнить съ г2 и (гі—г')2 произведеніе корней аэто
б/г® даетъ еще два главныя значенія ж3 именно <іг и 7-5-----
(а — г)2 Положимъ
(г Уг--г'Уг7)2 (гУг 4-г'Ѵ^г7)2 , ^4-г3—/•
гіг2 4“ г8 — г3 1 7
----ІД = /7, 71-= «Г = Л. а — г--------------------------(а —г')3
Во-первыхъ, замѣчаемъ, что неравенство (2) должно отбросить, и слѣд. взять неравенство (3). Въ самомъ дѣлѣ, разности [—а и с —а положительны, ибо
г л____($г'—г^+тУгг7)3 __г' (сіѴг' 4-гУг — гѴг')
4 (СІ — г') У(і (гі — г')
Значитъ, если бы количество »і3 было меньше ау то тѣмъ болѣе оно было бы меньше с и Д и слѣд. произведеніе обоихъ значеній х было бы больше (гі г')3, въ то время какъ результатъ подстановки разности & — г' на мѣсто х въ первую частъ ур—нія (1) былъ бы положителенъ. Обѣ величины а? были бы больше о!—г' и слѣд. должны бы быть отброшены:
Распредѣлимъ теперь въ восходящемъ порядкѣ главныя значенія т3, т.-е. Ь, /’, е, ду Л. Для этого вычислимъ сначала разности: к—ду д — Л /—6; находимъ:
, __г (сІ — г)2 — г'3 . , (^г' — г'3 — г Угг7)3
Л—9 ~ ~а<а—г') ’' а (а—и ’
д — [ _ (г + г') с?2 — (2г3 4- 2г*3 4" Згг') (і 4- (г + 4“ 4- ггг) е
г — г' (г/ — г) (4 — г') *
первыя двѣ разности очевидно положительны; положительна и третья. Въ самомъ дѣлѣ, приравнивая нулю ея числителя и рѣшая получаемое ур. относительно сі, находимъ корни: г 4“ г' и —^4-Ѵ* какъ шаРы лежатъ одинъ внѣ
другого, то (і больше большаго изъ корней г4-*Л и слѣд. числитель дроби, а потому и ^ — /'положительны. Итакъ, доказано, что Ь <(<д <А.
Вычисляя затѣмъ разности с, Ѵб —Ус, получаемъ:
, ѵъ~ у-с^ »:
- г) ]^3
откуда видно, что обѣ разности будутъ положительны, или же обѣ отрицательны, смотря по тому, будетъ ди с? больше пли меньше г' + г^/ -р. Затѣмъ, три ко-/ --------------------------------------------------------г
личества б, с п /* составятъ одно, если будетъ = г'4’г"|Х“г* Отсюда заключаемъ, что когда > г' 4- г количество с будетъ < б, въ противномъ слу-
* /Г
чаѣ будетъ с>>/' Далѣе изслѣдованіе покажетъ, что когда д, < т* 4~ г у/ р-, то достаточно знать, что не фиксируя его мѣста относительно количествъ д и Изъ сказаннаго видно, что слѣдуетъ различать 3 случая, смотря по тому, будетъ ли больше, равно, иди меньше суммы г'4-г"р/~
Распредѣливъ критическія значенія ж2 въ восходящемъ порядкѣ, составляемъ таблицу знаковъ, Такимъ образомъ, найдемъ:
I случай: €? > г' + г . Т/ —
Значенія ж2. 0 а ... с... 6 1 - і г
Реаі ііз антъ. + г_4 -
Произведеніе корной.
Сумма корней. і — І
1 /(г). 1 і «
/(й — г'). + — і 1 г
1-й коэффиціентъ. I ~н н~
Выше было выяснено, что количеству ж2 нельзя давать значеній ни меньшихъ а, ибо въ этомъ интерваллѣ, хотя корни и дѣйствительны, но они оба большіе (і — г', пи между а и б, ибо въ этомъ интерваллѣ корни уравненія мнимы. Итакъ, разсматриваемъ случаи:
У г г* V
1) = Ъ — ---—д------Подставпвъ въ уравненіе это значеніе ж2, най-
СІГ Vп. - х
демъ х = ——--------Это значеніе а? допустимо, если оно будетъ больше г, по
г I г 4» г* Уг
меньше — г'.
Положивъ
вѣрить, что г'
аГ У т /г
— _-----— >г, имѣемъ отсюда гі>г+г'1/ —, и легко про-
ГІг+г'Ѵг' Г г
слѣдовательно, найденный корень > г.
Положивъ —: < с/— г, имѣемъ что и дано.
г| г г' У г' V г
Заключаемъ, что въ данномъ случаѣ задача возможна и имѣетъ 1 рѣшеніе-0X7^ (гѴ^+г'ИР)* гіг'2 н-Г» — Г'З _
2) Ь < < /, пли -------------- < т? < 1_ г*--’ Сумма и произ-
веденіе корней положительны, слѣд., оба корня положительны. Затѣмъ, по знаку Г (г) и /'(гі—г') заключаемъ, что г и сі — г' лежатъ внѣ корней.
Сравненіе г п іі — г' съ полусуммой корней въ данномъ случаѣ неудобно. Чтобы знать, будутъ ли оба корня больше у, замѣчаемъ, что если #'>г и а?">у, то должно быть я/*я">г*, т.-е. нужно сравнить съ г2 произведеніе Й)''® (ГуЗ
корней, равное —р Положивъ — > у2, имѣемъ ж® < гіг, что вѣрно* такъ какъ (іг — к лежитъ въ 5-мъ пнтерваллѣ. Итакъ, оба корня больше у. Чтобы, затѣмъ, провѣрить, будутъ ли оба корня меньше (I — г\ смотримъ, будетъ ли ихъ произ-(ІуЗ с?уЗ
веденіе < — г')2* Положивъ —- < (А — у')2, имѣемъ отсюда т4 > , или
Л / — У )а
что для разсматриваемаго пнтервалла имѣетъ мѣсто.
Заключаемъ, что въ данномъ случаѣ задача имѣетъ 2 рѣшенія.
3) = Л Въ этомъ случаѣ / (^ — г1) = 0, слѣдовательно, одинъ корень
</уЗ
= — г'. Другой корень ~ -~2 у и какъ для даннаго интервалла пі2 больше
гіг3
— г')*'
то другой корень меньше —у': задача опять имѣетъ два рѣшенія.
/7у^ —I— уЗ -— *-'3 (7 У- _1_ — і’З
4) /<т2<я, или ----Т-------<нг2< - ^7 --------- Оба корпя поло-
а — г а —г 1
жителыш, и какъ /‘(<7 —г')<0, то (1 — гг лежитъ между корнями: одинъ корень, слѣдовательно, меньше 4 — г', другой больше — г\ Второй корень отбрасываемъ; а чтобы первый давалъ рѣшеніе, онъ долженъ быть еще > г. Но, находясь въ разсматриваемомъ пнтерваллѣ, т2 меньше Л, а при этомъ условіи оба корня больше г. Задача имѣетъ I рѣшеніе.
5) 7Н2 = 0, Для этого значенія т* имѣемъ /‘(г) = 0, слѣдовательно, одинъ изъ корней = г. А какъ Цй—-г') <0, то & — г1 заключается между корнями, изъ которыхъ одинъ меньше <1 — г*, другой больше (і — г'. Послѣдній не даетъ рѣшенія, а первый отвѣчаетъ на задачу, которая такимъ образомъ имѣетъ 1 рѣшеніе: я = г.
6) т->^. Оба корня положительны; /‘(г) и /'(</ —г') отрицательны, слѣд., г и — у' находится между корнями, такъ что меньшій корень меньше у, а большій корень больше (I—г'; ни тотъ, ни другой не отвѣчаютъ задачѣ, которая въ разсматриваемомъ случаѣ невозможна.
Резюме.
< Ъ . . . Задача невозможна.
4 7 -I 4. (іг г
= . .] рѣшеніе: # = —-----------=
Г I Г + г' Ѵг'
Ь < ш2 < Г . * -2 рѣшенія*
•?и2 = /'. . ,2 рѣшенія*
/<^<#* * - 1 рѣшеніе: меньшій корень. т-_ . .1 рѣшеніе: х — г.
> д . . . Задача невозможна.
II случай:
<1 = г' + г
Въ этомъ случаѣ = Д и /'<<;< А- Интервала а отъ 6 до /' не суще-
ствуетъ; изслѣдованію подлежать два послѣдніе иптервалла предыдущей таблицы.
1) та<Д Такъ какъ / — Ъ, и т2 не можетъ быть <6, то задача невозможна,
2) т3 = Л Какъ и въ предыдущемъ случаѣ, одинъ корень =гі — К Произ-веденіе корней = —; но = с = слѣдовательно, другой корень,
— , '— ; =а — г. Задача имѣетъ два рѣшенія сливающіяся: —
аг3 (а — г)
3) Какъ и въ предыдущемъ случаѣ, задача имѣетъ 1 рѣшеніе.
4) ш2 > д. Задача невозможна.
Итакъ, въ случаѣ д, — г* -н г — задача или невозможна, или имѣетъ 1 рѣ
шеніе.
III случай:
Критическія значенія ?и2 идутъ, возрастая, въ порядкѣ 6, д, А. Но теперь уже с,> Д Пользуемся таблицей 1-го случая, перемѣстивъ с вправо отъ Л
1) ь. Выше мы видѣли, что въ этомъ случаѣ, чтобы задача была возможна, должно быть б? > г’ и- г *|/р * Слѣдов., въ разсматриваемомъ случаѣ опа при ѵі^ — Ъ невозможна.
2) Ь < ж2 < Оба корня положительны. Какъ въ пунктѣ 4-мъ случая 1, чтобы оба корня были >г, должно быть т2<б7г, что и имѣетъ мѣсто. Чтобы оба корня были должно быть т2>с, что въ разсматриваемомъ интерваллѣ
не имѣетъ мѣста, и ола корня —г*: задача невозможна.
3) щз —Д Принтомъ — г') = 0: одинъ корень =4 — г\ Другой корень с??*®
— ± а какъ теперь ш2 < ------то другой корень > — г': и задача
ж2 (а — г) (а — г)2
имѣетъ I рѣшеніе: = — г\
4) /*< тя < д. Въ этомъ случаѣ — г1 находится между^корнями, т.-е. одинъ корень больше —г( и долженъ быть отброшенъ; другой, меньшій г', корень долженъ быть больше г; но, находясь въ разсматриваемомъ интерваллѣ, т® меньше гіг, а при этомъ условія оба корня >г: задача имѣетъ 1 рѣшеніе,
5) Такъ какъ /(г)=0, то одинъ корень =г Такъ какъ &—гг лежитъ между корнями, то другой корень больше гі—г' и не отвѣчаетъ задачѣ, которая, такимъ образомъ, имѣетъ 1 рѣшеніе.
6) ™2><л Задача невозможна по той же причинѣ какъ и въ I случаѣ.
Резюме.
ш* = А . . . .Задача невозможна.
Ь < т№ < /". . . Задача невозможна. п»2 = /’. . .1 рѣшеніе: = г'.
/* < т* < д . . .1 рѣшеніе: меньшій корень.
п^ = д ... 1 рѣшеніе: я? —г.
тпа > д . . * Задача невозможна.
Сумма поверхностей сегментовъ уменьшается съ увеличеніемъ *и4, и увеличивается съ уменьшеніемъ т3: откуда видно, что эта сумма имѣетъ тахігошп, соотвѣтствующій т3=6 въ первомъ случаѣ, и тп2=/’—въ третьемъ.
Задача XXIII.
' 628. 7Л данный таръ радіуса г вписать усѣченный конусъ АВСП, имѣющій данныя: высоту Л и объемъ ^--а^і.
Рѣшеніе. Пусть будутъ т, у, я радіусы ЕВ, АЕ основаній и образующая АВ.
Выражая, что объемъ* тѣла =~-а*Л, имѣемъ ур.
Проведя радіусъ О А. прямыя 01, АП, соот-вѣственно перпендикулярныя къ АВ и ЕВ, и параллелъ ІЬ къ ВЕ, нзъ треугольниковъ АОІ и АНВ имѣемъ:
и
01='
9
(ж — 0)1=^ — Л*. . . (3)
а изъ подобія треугольниковъ ОІЬ и А В11 полу- Черт. 112.
чаемъ
(х ч- ур =
Л* (4г2 —
Л4).
Помноживъ ур. (1) на 4 и вычтя (3), имѣемъ
3(ят -нр)2 = 4^ — +
Приравнивая величины (а?^- ур изъ этого ур. в изъ (4), получаемъ
—4(а2Ч_^)^_ні2/^ = о . . .(5).
Отсюда _________
х - |/а(о2+... .(6).
Изслѣдованіе.
629. Авали зъ. Все дѣло, очевидно, въ вычисленіи Но недостаточно, чтобы величина * была дѣйствительною и положительною; нужно еще, чтобы она была не меньше Л и не больше 2г. Можно разсматривать усѣченные конусы обоего рода, къ которымъ, какъ легко убѣдиться, одинаково прилагаются ур—нія (1) (3) и (4), и слѣд. ур. (5). Значеніе я даетъ усѣченный конусъ 1-го или 2-го рода, смотря потому, меньше ли оно или больше Ѵѣгк, Въ самомъ дѣлѣ, въ трапеціи АВСО произведеніе АВ X АС стороны на діагональ равно 2гЛ, а какъ изъ двухъ линій АВ и АС меньшая есть первая или вторая, смотря потому, 1-го пли 2-го рода усѣчен. конусъ, то сторона г меньше Ѵ2гЛ въ первомъ случаѣ, и больше —во второмъ, Если # = )/2гЛ5 усѣчен. конусъ дѣлается полнымъ.
Зная это, находимъ, во-первыхъ, для дѣйствительности г условіе
«2>Л(г>/3 — к)
(7).
(Можно замѣтить, что когда к равно или больше условіе само собою удо в л створяется -)
Какъ скоро неравенство (7) существуетъ, то, въ силу ур. (5), оба значенія г? дѣйствительны и положительны.
Затѣмъ, для сравненія значеній г2 съ А2, 4г2 и 2гк, подставляемъ поочередно эти три количества въ первую часть ур—нія (5), разсматривая ее какъ триномъ квадратный относительно г2. Находимъ слѣдующіе результаты подстановокъ:
А2(12г2— 4«2— ЗЛ2) для А2 ... (8) 4^(4г2 — 4 «з - А2) 4г2 . . . (9)
8гЛ(2гА— г2 — а*) „ 2гЛ . » ,(10).
Приравнивая нулю каждый изъ этихъ трехъ тельно а2 получаемыя ур—нія, найдемъ слѣдующія
полиномовъ и рѣшая относи-главныя значенія для а2:
| (4 г- - 7(3) = е, к- = а, к[2г — к) = с.
Вторую часть неравенства (7) слѣдуетъ также разсматривать какъ главное значеніе а2; полагаемъ
Такъ какъ произведеніе корней, по ур. (5), не зависитъ отъ а2, то, сравнивая это произведеніе съ количествами Л1, 16г* л 4тШ, новыхъ главныхъ значеній не получимъ.
Теперь слѣдуетъ узнать, въ какомъ порядкѣ идутъ возрастая количества б, с. <2, е> Во-первыхъ, очевидно, что іг что (I < с. Вычислимъ затѣмъ разно-ности А — б, е —с, —с.
Имѣемъ:
<3 —2г)2 ' _(2г — А)(6г — А) , _ (2г - ЗЛ) (2г - Л)
- е —С—- - ; Л-С— -
Двѣ первыя разности всегда положительны; третья же—положительна, равна 1 2г
нулю, или отрицательна, см. пот. будетъ ли к <, пли > Итакъ, видно, о .
2г что смотря по тому, будетъ ли к меньше или больше -гр главныя значенія а4 о распредѣляются такъ: б, е, е; Л, с/, с, е-2г
Когда Л = -~-, с и сі будутъ равны. О
Замѣтимъ еще, что произведеніе обоихъ значеній т.-е. 12А2г2 всегда больше А1 и 4А2г2, слѣд. никогда не можетъ случиться, чтобы два значенія ? были оба меньше к или ) 2гА. Но какъ произведеніе значеній я* меньше или 2г|73
больше 16г*, смотря по тому,будетъ ли А меньше пли больше количества - , это послѣднее количество слѣдуетъ также разсаЗкрпвать какъ главное значеніе количества А.
630. Синтезъ. Изъ предыдущаго анализа видно, что изслѣдованіе распадается на такіе три главные случая:
Первый случай: Л
Измѣненія а*
П2<Ь аа = 6
6 < я* < е
Число рѣшеній 1-го рода. 2-то рода.
О О
О 1
О 2
1 1
1 О
О О
Рѣшеніями 1-го рода названъ усѣченный конусъ 1-го рода, рѣшеніями 2-го рода усѣчен. конусъ 2-го рода. Главныя величины взяты въ порядкѣ: $
г, а2 измѣняемъ съ Ъ до е, проходя черезъ промежуточныя значенія с к 4.
1. а2<д. Обѣ величины # мнимы: задача невозможна.
2. = Для # получаемъ формулу: # = |/2г7а1/3, Эта величина больше 7ц
___ 2г 2г рЗ
и у2гЛ, но меньше 2г, ибо Л а потому меньше и —* Слѣдов., имѣвъ усѣч. конусъ 2-го рода.
3. д<аа<^с. Количество а2 меньше с, е; слѣд. полиномы (8), (9) и (1д)
2г|/3
положительны; я какъ Л меньше — , обѣ величины з меньше 2г и больше 7» и о
]/2гй. Задача имѣетъ два рѣшенія 2-го рода.
Когда аа~с, одна изъ величинъ # равна У2г7ц в ей соотвѣтствуетъ цѣлый конусъ; вторая величина остается меньше 2 г, но больше к и Ѵ%гк; она даетъ усѣч. кон, 2-го рода. Такъ какъ полный конусъ можно разсматривать безразлично какъ усѣч. кон. 1-го пли 2-го рода, то можно сказать, что и въ этомъ случаѣ за* дача имѣетъ два рѣшенія 2-го рода.
4. с < бі. Такъ какъ аа становятся больше с, полиномъ (10) отрицате* оенъ, и одна изъ величинъ # меньше /2гЛ, между тѣмъ какъ другая больше. Но оба эти значенія остаются, какъ и прежде, больше 7ц но меньше 2г: имѣемъ одно рѣшеніе 1-го и одно рѣшеніе 2-го рода.
Когда а2 = гі, одна изъ величинъ я становится равною 2г, другая меньше 2г; но они всегда больше Л, и одна больше 1^2г/ц другая — меньше. Слѣд. опять имѣемъ усѣч, кон» 1-го рода и усѣч» кон. 2-го рода, только этотъ послѣдній имѣетъ образующую = 2г.
5. <і<яа^е Такъ какъ а2>с?, полиномъ (9) отрицателенъ, и одна изъ величинъ я меньше 2г, другая-больше. Значеніе большее 2г, отбрасываемъ, и какъ мепъшее значеніе я меньше /2тЛ, а другое больше, имѣемъ только одно рѣшеніе: усѣч» конусъ 1-го рода.
Когда а2 = ^ получаемъ цилиндръ высоты 7і.
6. а2>е. Задача невозможна. Въ самомъ дѣлѣ, когда аа превосходитъ е» одно изъ значеній г меньше, а другое больше нежели к и 2г. Поэтому, первое должно быть отброшено какъ меньшее 7&, а другое—какъ большее 2г.
2 2
Когда к — з г, заключенія остаются тѣ же, какъ и при к < г» Только оба предѣла с и сі дѣлаются равными» и потому иптервалла между с и <7 въ таблицѣ изслѣдованія не будетъ.
Затѣмъ, безъ новыхъ объясненій^ слѣдуютъ таблицы для двухъ послѣднихъ случаевъ: содержащіяся въ нихъ детали изслѣдованія найдемъ, слѣдуя пути, указанному въ первомъ случаѣ.
Второй случай:
Измѣненія а*
2гѴЗ
3
«а < Ь аа = 5
6 < а3 б?
< аа с
с < а* е
а9 > е
Число 1-го рода.
О О О О 1 О
рѣшеній. 2-го рода.
О
1
2
1 О
О
т - - , 2гУЗ
Третіи случаи: Л> ——
О
Измѣненія аа Число рѣшеній
1-го рода. 2-го рода.
а9 < а О О
а9 = О 1
< л9 < с О 1
с < а2 <1 е 1 О
а9 > е О О
Сдѣлаемъ только слѣдующія замѣчанія:
Когда к = (2 равно 5, и во вторбй таблицѣ нужно только опустить ия-
терваллъ отъ до Ь.
Что касается третьей таблицы, то низшій предѣлъ а9 равенъ сі вмѣсто Ъ, Но 2г/3
ото значитъ, что какъ к больше —— когда а9 меньше сі, то оба значенія & <5
становятся больше 2г.;
Примѣчаніе. Такъ какъ тахішнт па во всѣхъ случаяхъ равенъ е, то заключаемъ, что всѣ усѣченные конусы данной высоты, вписанные въ шаръ, всегда меньше цилиндра той же высоты. Но тіішпшп а* различенъ, смотря по тому, 2гѴ'3
меньше ли к или больше нежели ——; онъ равенъ Ъ въ первомъ случаѣ, и сі— О
2гѴЗ
—о—>
во второмъ. Когда к —
& равно Ь, и оба шіпіша сливаются въ одинъ*
Задача XXIV.
631. На прямой даны три точки А,
В, Л, юишя, что АВ==В0=2а. На отрѣзкѣ АВ найти такую точку С, чтобы перпендикуляръ, возставленный изь нея къ прямой АВ, яердеіыкш окружности, описанныя на АВ и АО какъ на діа~ метрахъ, въ такихъ точкахъ М и X, чтобы СХ + СМ = і, і данная длина,1 Рѣшеніе, Принявъ за неизвѣстное отрѣзокъ АС = #, имѣемъ ур—ніе
Ѵя?(2а — я) + /я?(4а — я?)—? = 0* * .(1)*
Разсматривая I какъ Ѵ&, мы можемъ приложить къ рѣшенію и изслѣдованію этого ур—нія пріемъ, указанный въ § 546* Положивъ
#(2« — #) = Р, ж(4н—дт) — (і, г- = К,
найдемъ резольвентъ ур—нія (1):
&(2а—х)*-ь-э&(4а — #)2-ьР—2#*(2а —#)(4а — — 2Р#(2а——2^#(4а —#)=о,
или
откуда
/'(я;) = 4(а* + 22)#2 — 12аРх -н I* — 0 . . * (2),
6аР ± Ѵ36аЧ< — 4/*(а2 + Р) _ За# =ь # }/8а* — # 4{а2 -н #) “ 2(а* + Р)
Изслѣдованіе* —Корни должны быть дѣйствительны; это будетъ при № 8а2*. Разъ это требованіе удовлетворено, оба корня будутъ положительны. Чтобы они удовлетворяли данной геометрической задачѣ, они должны быть ^2а* Составляя /’(2а), найдемъ
/(2а) = 16а2(^ + #) — 24а2# -ь ?* = (4а2 — г2)2,
результатъ одинаковаго знака съ коэффиціентомъ при я2; слѣдоват., 2а лежитъ внѣ интервалла корней, и чтобы корни были меньше 2а, ихъ полусумма должна быть < 2а, Но неравенство
или З# < 4а2 4- 4#,
всегда удовлетворено. Итакъ, корни резольвента, при условіи I2 8а2, дѣйствительны, положительны и меньше 2а* Но мы знаемъ (см, гл. XXXVI, § 546), что корни резольвента могутъ удовлетворять или данному ур—нію, или одному изъ двухъ сопряженныхъ съ нимъ, а именно:
данному VР + УЦ — ѴК — 0, если будетъ Р — — К < 0 , * . (3) ур—иію УР — Уй + Ѵв = О, „ я Р—(Л-В<0. . .(4)3
„ -/Р + ^ + ѵѢ = 0, „ „ -Р + (г + Н<0. . .(5).
Слѣдовательно, чтобы видѣть, какому изъ этихъ трехъ ур—ній принадлежатъ корни резольвента, нужно опредѣлить, какой знакъ они сообщаютъ триномамъ, находящимся въ первыхъ частфъ неравенствъ (3), (4) и (5), А для этого надо знать, какъ расположены корни резольвента относительно корней выраженій (3), (4) и (5), которыя могутъ быть квадратными либо первой степени относительно г. Такимъ образомъ вопросъ приводитъ къ задачѣ о размѣщеніи корней одного квадратнаго тринома относительно корней другого. Критерій для этого данъ въ § 491 главы XXXII.
I. Уравненіе ѴР + Ѵ — /К = 0.
Ему отвѣчаетъ вопросъ въ прямомъ смыслѣ заданія.
Составимъ выраженіе Р + (^— К* Это будетъ
х(2а — я) + #(4а — х) — или — 2а?2 + ба# —
Если корень х резольвента сдѣлаетъ
— 2#2 4- 6а# — # < О, или 2а2 — 6а# $ > О»
то онъ будетъ корнемъ даннаго ур—нія* Чтобы знать, какъ корни резольвента расположены относительно корней тринома
надо составить Д.
2х2 — 6а#+# . . . (6),
Д = [4#(а2 + — 2#]2 — 24а(а* 4- #) + 24а[— 12а# + ба#] =
= 4# |(2а2 + 22)2 — 36а4] = 4#(8а2 + #) (# — 4а2).
Примѣняя методъ § 491* найдемъ, что:
Если Д>0, т.-е. Р —4а2>0, то корни резольвента и тринома 2я*—бая* не отдѣляютъ другъ друга.
Если Д < 0, т.-е. — 4а2 < 0, то корни одного тринома отдѣляютъ корни
другого.
Наконецъ, при Д —0, или № —4а- = 0, оба тринома имѣютъ общій корень.
Разсмотримъ сначала этотъ послѣдній случай. Когда 22 = 4а2, корни резоль-2
вента суть а, а^ = 2а. Корни тринома (6) суть: ц = а, = 2<ь Въ этомъ случаѣ данная задача имѣетъ два рѣшенія
2
— "г а, Я?2 — 2а,
и легко непосредственно провѣрить, что оба они удовлетворяютъ задачѣ въ прямомъ смыслѣ заданія.
Пусть ?2<4а2. Легко убѣдиться, что аа' (аЪ' — ба') < 0 (см. нотацію § 491), и потому расположеніе корней таково:
< 4 <С <1
т.-е. меньшій корень (а^) резольвента находится внѣ пптервалла корней тринома (6), слѣдовательно сообщаетъ этому триному положительный знакъ, и потому служитъ отвѣтомъ на задачу въ прямомъ смыслѣ заданія. Большій корень резольвента, находясь между корнями трпнома^в), сообщаетъ ему отрицательный знакъ и потому не отвѣчаетъ ур—нію ѴР-рѴХ)— уИ—О.
Когда I* > 4а2, то, какъ легко убѣдиться, будетъ а Р < 0, и слѣдовательно-числа яд, 0*3, располагаются въ порядкѣ
корни резольвента, находясь внѣ корней тринома (6), дѣлаютъ его положительнымъ, и оба корня резольвента отвѣчаютъ задачѣ.
И. Уравненіе /Р— =
Ищется такая точка С, чтобы было СМ — =
Корни резольвента должны удовлетворять условію о?(2а -— я?) — іг(4а — а?) № < 0, или х — •
Р — у _р н < 0, или
Подставляя — вмѣсто о? въ (2), найдемъ
/ 72 \ м
\2а / а2' '
Когда Г1 < 4а2, этотъ результатъ отрицателенъ, слѣдоват. будетъ:
< 2а <Хі’
и слѣдоват., большій корень ур—нія (2) отвѣчаетъ видоизмѣненной задачѣ. '
Когда Р>4а2, результатъ подстановки положителенъ, и — — внѣ корней. Положивъ
2а > 2(а* 4- РѴ
да
найдемъ аа4-/2>3а3, что вѣрно, слѣдоват. оба корня ур—нія (2) меньше— -
видоизм. задача при условіи /2 > 4а2 невозможна.
IIЕ Уравненіе — ѴР + == 0.
Ищется такая точка С, чтобы было СХ — СМ = /.
Условіе — Р + 0 + Е < 0 даетъ 2бгл- + < 0, что при ж > 0 невозможна задача невозможна,—и это видно а ргігогі.
Резюме.
Когда I < 2а, меньшій корень ур—нія (2) даетъ отвѣтъ на предложенную задачу, а большій корень служитъ отвѣтомъ на первое видоизмѣненіе задачи*
Когда Е> 2а, оба корня ур—нія (2) служатъ отвѣтомъ на предложенную задачу.
ГЛАВА ХЬП.
Махіта и тіпіта въ задачахъ.
Махіта и тіпіта простѣвшихъ цѣлыхъ функцій. — Махіта и тіпіта квадратной дроби.—Измѣненія этой функціи. — Махіта и тіпіта функцій нѣсколькихъ пере-мѣнныхъ.
Г Махіта и тіпіта простѣйшихъ цѣлыхъ функцій.
632. Прямой способъ. При опредѣленіи максимальнаго или минимальнаго значенія функціи этимъ способомъ, составляемъ выраженіе функціи и изслѣдуемъ ея измѣненіе, измѣняя независимое перемѣнное въ предѣлахъ, указываемыхъ усло-віями вопроса. Такимъ образомъ мы естественнымъ путемъ находимъ тахішнт или тіпітит функціи вмѣстѣ съ соотвѣтствующимъ значеніемъ независимаго перемѣннаго. Въ этомъ и заключается натуральный, прямой способъ опредѣленія шах. или тіп, функціи.
Этимъ путемъ мы нашли тахітит и тіпітит квадратнаго тринома въ § 585. Здѣсь мы приводимъ примѣры въ поясненіе этого метода.
633. Примѣръ I. Дана окружность діаметра АВ, на которомъ взяты точки: С еа разстояніи отъ А, давноли трети радіуса> и Р въ разстояніи ОР = | раЭг’^са оть центра. Найти на окружности такую точку М, чтобы сумма квадратовъ ея разстояній отъ точки С и отъ перпендикуляра, проведеннаго къ АВ яь точкѣ была тахіта или тіпіта.
За неизвѣстное примемъ разстояніе центра
круга отъ проэкціи Е точки М на діаметръ АВ, I
принимая это неизвѣстное положительнымъ, О______
когда точка Е лежитъ влѣво отъ 0, и отри- р ................/А\
дательнымъ, когда эта точка вправо отъ 0. г :\ \
Такимъ образомъ для точки М изъ тупоуголъ- р [ ; | д
наго А МОС найдемъ: В \ ЕО Е’СП
МС’=М02+0С8+20Сх0Е=В2+ В*+ К . х, \ У
МВ*=(|В- Д3=^В2-^Вх+;г2; Черт. 114.
I о у 3 о
слѣд. МС2 4- МВ2 = В2 + В2 - 2Ис Ц-х2 = (х - К)2 + ? В2.
<7 ѵ
Легко видѣть, что это выраженіе сохраняетъ видъ при всякомъ положеніи точки М на окружности, благодаря условію относительно знака количества х. Итакъ, изслѣдованію подлежитъ выраженіе
у = (Ж~кг+^кв,
представляющее квадратный триномъ, въ которомъ х. нужно измѣнять отъ —-В. до -|-В. Изъ этого выраженія видно, что по мѣрѣ уменьшенія абсолютной величины бинома х— В, и у будетъ идти уменьшаясь, слѣд, достигаетъ шіпІ-іпиш’а при я = В; такимъ образомъ имѣемъ таблицу:
х — В •*•<.. . О * - . <Г . - * -I- В
^5 38 29 р ?
У “<Г К 4 > * * ’ ‘ ‘ ‘ ‘Ти *
29
Слѣд, у имѣетъ тіпітит К3 при дт=-|-Рі. Такимъ образомъ, при дни-женіи точки отъ В къ А по верхней полуокружности, функція у, начиная съ свое-29 - 65
го минимальнаго значенія Ка, увеличивается до тахітит'а -5- К2, кото-У У
раго она достигаетъ, когда точка приходитъ въ А; затѣмъ, при движеніи точки х х 29
по нижней полуокружности, функція уменьшается до
634, Примѣръ II. Зъ крялои круглый конусъ вписанъ цилиндръ; найти, при какихъ размѣрахъ полная поверхность его будетъ тахіта или тіпіта?
Пусть будетъ г — радіусъ основанія конуса, А — его высота. Назовемъ радіусъ основанія ГО цилиндра буквою х, высоту его ІН буквою у. Изъ подобія А-ковъ АЕН и АВІ находимъ связь между х и у, выражаемую пропорціей:
ЕН:ВІ = АН:АІ, или #:г = (Л —у):Л,
Черт. 115,
откуда
Полная поверхность 8 цилиндра выражается формулою: 2п,ВР-|-2п .01.ІН, или 2тг(#3 -ху), или, замѣняя у его величиною:
8 = у[(г-Л)х’ + М . . .(1)
Въ данномъ вопросѣ радіусъ х основанія цилиндра можетъ измѣняться только отъ 0 до г. Припоминая § 585, замѣчаемъ, что смыслъ измѣненій квадратнаго тринома зависитъ отъ знака коэффиціента при я3; слѣд. надо различать 3 случая: г>Л, г~к, г<^к.
I, г > к (конусъ сплюснутый). Въ этомъ случаѣ, представивъ триномъ
(г — -|- Агж
дующую таблицу
въ видѣ (г — Лця -|-измѣненій:
кг
2(г — к) I
, имѣемъ слѣ-
4(г — Л)3~
х
кг у ЛМ 2(г—к)/ 4(г—Л)а
8
Заключаемъ, что когда х возрастаетъ отъ
уменьшается, а затѣмъ увеличивается, когда
—кг , . о
— со до ду функція 8 — Лг
х возрастаетъ отъ 2(7—Л) до
+ со. Но какъ количество
2(г — 7г)
отрицательно, то изъ таблицы видимъ, что
измѣненіямъ х въ области отъ 0 до г отвѣчаетъ возрастаніе функціи 8. Слѣд. когда г > Л, полная поверхность цилиндра увеличивается по мѣрѣ увеличенія радіуса основанія цилиндра. При # = О, и 8 = 0; при я=г, 8 = 2т:г2; такъ что 8 увеличивается отъ 0 до 2кг2; и въ самомъ дѣлѣ, при я = 0, цилиндръ обращается въ прямую АІ; при #==г, боковая поверхность обращается въ 0, полная же поверхность приводится къ суммѣ двухъ круговъ радіуса ВІ=г.
Таблица измѣненій функціи’8 приводится къ слѣдующей части предыдущей таблицы:
х 0 возрастаетъ до г
г> к
- 8 0 возрастаетъ до 2~г\
П. г = к. Триномъ приводится къ кгх, ственно видно, что при возрастаніи я отъ до 2т:г3. Таблица измѣненій та же, что
и 8 = 2тсгл;? откуда неносред-0 до г, 8 увеличивается отъ О
и для
случая I.
Въ обоихъ случаяхъ функція имѣетъ: абсолютный тіпітнш, равный 0, и абсолютный тахшшт = 2т:г2.
Въ обоихъ случаяхъ кривая, изображающая ходъ измѣненій функціи, такова, какъ представляетъ черт. 116, гдѣ на оси О# представлены измѣненія х отъ 0 до г, а измѣненія 8 представлены ординатами кривой. Эта кривая есть часть параболы, отверстіемъ обращенная вверхъ.
III. г < к (конусъ вытянутый). Въ ятомъ случаѣ
Черт. 116.
множитель г — к отрицателенъ, и таблица измѣненій функціи 8 такова:
Такимъ образомъ функція 8 сначала увеличивается до
2(Л — г)1
а потомъ
уменьшается; слѣд. имѣетъ тахіппйп при ^ = 2(^—7)’ ^0ТЯ это коля^ество положительно, но оно можетъ быть или г, или < г; между тѣмъ какъ въ
данномъ вопросѣ х измѣняется только отъ О до г. Посмотримъ, при какой зависимости между г и Л, это значеніе х будетъ Положивъ
кг к ,
П/Т. х * ИЛИ Л/1. \ 1 *
2(л — г)1 2(л — г) *
и умноживъ обѣ части на А— г (большее 0), найдемъ: —2 г, или
Л 2 а
1) Пусть г<Л<2г. Въ этомъ случаѣ я, возрастая отъ О до г, всегда будетъ меньше 2{к — г)' а слѣдовательно, какъ и въ предыдущихъ случаяхъ, полная поверхность цилиндра идетъ увеличиваясь. Изслѣдованіе даетъ таблицу:
а кривая, изображающая эти измѣненія, есть часть параболы, отверстіе которой обращено внизъ (черт. 117).
2) Пусть к — 2г. Полусумма корней вь этомъ случаѣ равна г, триномъ достигаетъ шахітиш’а при х = г\ таблица измѣненій — таже, какъ только что
Черт. 118.
съ тою лишь разницею, что точка
указано; кривая измѣненій — таже, имѣющая абсциссу г, есть вершина параболы (черт. ,118).
3) Пусть, наконецъ, 2(^—или этомъ случаѣ
л л.
растая отъ О до г, проходитъ чрезъ значеніе «т»— а ; слѣд. полная
кривой,
ж, воз-поверх-
ность 8 цилиндра, начиная съ нуля, возрастаетъ, достигаетъ тахіпішп’а при
кг 2(йГ-г)’
затѣмъ, при возрастаніи х до г, идетъ, уменьшаясь.
. п кг ~№г . е
Максимальное значеніе 8, при я = 2(Л^7)’ Равно звачеше й п₽и
х ~ г есть 2кг2. Таблица измѣненій такова:
х
Л>2г
8
* * * 2(Ь — г)
................‘ ’2уГ-г)
Измѣненія эти выражаются дугою параболы, обращенной отверстіемъ внизъ, ѵ№г
причемъ ордината вершины есть На чертежѣ
ов=2',гЬ)і в»-'-
Итакъ: когда Л 2г, полная поверхность 8 цилиндра принимаетъ одинъ, и только одинъ, разъ каждое значеніе, содержащееся между О и 2пга, не дѣлаясь больше 2т^2. Но при к > 2г, 8 при-
2то*2 и
т:г№
2(Л— г)’
нимаетъ однажды всякое значеніе между
О и 2№; дважды всякую величину, содержащуюся между
и не дѣлается больше
гЛаг
2(Л-- Н’
635. Примѣръ ПІ, Чіервзъ данную точку Р внутри окружности О провести двѣ взаимно перпендикулярныя хорды АС и ВВ такъ, чтобы площадь четыреугольника АВ(Л) была тахІта или тіпгта.
Пусть ОР = а и пусть ОЕ = # перемѣнное разстояніе хорды ВВ отъ центра.
V Площадь Д ПАВ = ІОВХАР, А ВСО = |ОВХСР; складывая, найдемъ, что площадь у четыреугольника АВСБ равна ^ВВХАС, или, если перпендикуляръ изъ центра на хорду АС встрѣчаетъ ее въ точкѣ Е, можемъ написать: ь.
у = 2ОРХСЕ; но' ИЕ = уѢ» —
СЕ = /К1 — ОЕ* = /К« — (а’^о^
Черт. 120.
слѣдовательно
у = 2/(К’ — ж’) (В* — аа + ж3).
Но у величина положительная, а потому ея тахітит или тіпітпт будутъ имѣть мѣсто при тѣхъ же обстоятельствахъ, какъ и тахітит или тіпітпт квадрата функціи у:
уа = — 4я* 4- 4а V2 4- 4Е*(Е* — а2).
Вопросъ приведенъ къ изслѣдованію измѣненій биквадратнаго тринома, которому въ этихъ цѣляхъ даемъ видъ:
а а/2
Отсюда видно, что когда х увеличивается отъ нуля до количество у* идетъ возрастая; когда же % продолжаетъ увеличиваться отъ до а,
хорды одинаково наклонены
Черт. 121.
у2 уменьшается; слѣд. количество #а, а слѣд. и ^имѣетъ тахітит, когда обѣ къ діаметру ОР; самый шахішшп у-ка равенъ 2В2 — а*. ‘
Затѣмъ, такъ какъ площадь уменьшается когда аѴ2
х возрастаетъ отъ до а, т.-е. до того момента, когда хорда ВБ становится перпендикулярна къ діаметру ОР, то ясно, что если эта хорда будетъ продолжать вращаться около точки Р, площадь послѣдовательно пройдетъ черезъ всѣ предшествовавшія состоянія, сл, достигнетъ шіпі-тшп’а, когда одна изъ хордъ совпадетъ съ діаметромъ ОР; самый шіпітшп = 2В)/В2— а2. Резюме: когда прямой уголъ совершаетъ полный оборотъ около точки Р, площадь четыреугольника проходитъ дважды чрезъ шахшшш, равный
А'В'С'Л' и дважды чрезъ тіпішшп, равный АВСБ.
636. Непрямой способъ. Сущность этого метода, предложеннаго Симономъ Люилъе^ можно резюмировать такъ: пусть будетъ у нѣкоторая функція перемѣннаго тахітит или тіпішшп которой мы желаемъ найти. Съ этою цѣлью предложимъ себѣ найти, какъ нужно взять ж, чтобы функція имѣла данную величину т, которую на время оставляемъ произвольною; рѣшая эту вспомогательную задачу, мы получимъ ур—ніе въ и если это ур—ніе будетъ такое, которое мы можемъ рѣшить (наприм. квадратное, биквадратное), то опредѣляя условія возможности вопроса, мы п найдемъ предѣлы неопредѣленнаго количества ш; эти предѣлы вообще и будутъ шахітпш или тіштппі т, т.-е. функціи.
Такимъ образомъ здѣсь тахіта и тіпіта опредѣляются не прямо, а кос-яеиио, какъ результаты изслѣдованія условій возможности вопроса. Примѣры этого рода мы имѣли въ главѣ ХЫ. Вотъ еще примѣры примѣненія косвеннаго метода.
637. Вопросъ. Найти тахітит и тіпітит квадратнаго тринома ах2 Ъх с.
Положивъ ах*-\-Ьх-\-с = т, гдѣ т произвольное количество, рѣшаемъ это ур—ніе относительно х; найдемъ
2а
• -О).
Мы ищемъ дѣйствительныя значенія перемѣннаго при которыхъ триномъ получаетъ данное значеніе но чтобы х было дѣйствительно, необходимо, чтобы подрадикальпое количество не было отрицательно; слѣд. триномъ можетъ получать только такія дѣйствительныя значенія т, которыя удовлетворяютъ неравенству
Ьа — 4ас ѣат О, или 4ат > 4ас —- Ь2.
Для опредѣленія отсюда предѣла для ш, придется обѣ части неравенства дѣлить на 4а, причемъ отъ знака а будетъ зависѣть или сохраненіе знака неравенства, или перемѣна его на обратный. Отсюда два случая:
I. а > 0. Въ этомъ случаѣ дѣля на 4а, мы не измѣнимъ смысла неравен-
ства, и получимъ:
4ас—6*
4а
4ас — Ь2 . .
т.-е, т не можетъ быть меньше ——з слѣд. тгпгтит количества т ра~ 4д^ -____
—4а—" Подставляя это значеніе т въ формулу (1), находимъ соотвѣт
ствующее значеніе независимаго перемѣннаго: х =—
II. а<^0. Въ этомъ случаѣ дѣля на 4а, измѣнимъ знакъ неравенства, и получимъ:
4ас — 62
4а ?
О онъ имѣетъ та-4а с — Ъ2
а состон-
6
“----7^*
2а
наибольшее
4дс__Ъ*
т.-е. т должно быть меньше и, въ крайнемъ случаѣ, равно — ; слѣдов.
4ае — № .
—— есть тахгтит тринома. Соотвѣтствующее значеніе х выражается
опять формулою х=— ~ Итакъ
При а^>0 триномъ имѣетъ тіпітит, при а
хітит; тахітит и тіпітит выражаются формулою еѣтствующія значенія независимаго перемѣннаго формулою:
Найденное значеніе представляетъ, такимъ образомъ,
или наименьшее значеніе функціи; но пока не видно, чтобы это были тахшшш или тіпітит относительные. Нужно еще доказать это, т.-е. доказать, что наприм. найденное минимальное значеніе тринома дѣйствительно меньше двухъ смежныхъ съ нимъ значеній функціи. Для этого *мы должны вычислить два значенія тринома, которыя онъ имѣетъ при двухъ значеніяхъ х: одномъ, немного меньшемъ — 2а’ другомъ, немного большемъ — Называя буквою А абсолютную величину нѣкотораго весьма малаго количества, вычислимъ величины тринома при х = —~ — Л и при х = — -]- Л. Приведя триномъ къ виду
а
Ь ? I 1 г ✓
подставляемъ сюда сначала — — л, потомъ — “г Л вмѣсто въ обоихъ
случаяхъ находимъ, что триномъ беретъ видъ
Р = —-4-аЛ2. 4а 1
Замѣчая, что: 1) при а > 0, а№—величина существенно положительная, п 4ас —&2 . 4ас — б2 А
находимъ, что Р > —, т.-е. что дробь - —• меньше двухъ сосѣднихъ
съ нею значеній тринома; дробь эта, слѣдоват., дѣйствительно представляетъ относительный минимумъ функціи; 2) при а < 0, аЛа есть количество суще
ственно отрицательное, а потому въ этомъ случаѣ Р < ———? и слѣд, дробь 4а с — Ь2 .
—— больше двухъ смежныхъ съ нею значеній тринома, т.-е. представляетъ относительный максимумъ функціи.
Результаты эти вполнѣ согласны съ выводами § 585.
638. Примѣръ Е Найти тахітит или тіпітит тринома
“5x4^7.
Положивъ 2#1 — 5х -р 7 = т и рѣшивъ относительно х уравненіе
— 5ж -к 7 '— т = О,
имѣемъ'
5^/25 — 8(7 —т) ж --- *
Для дѣйствительности х необходимо, чтобы было 25 — 8(7 — т)>0, или 31
— 314-8т 5^ О, откуда т>
„ < 31 ... 31
Заключаемъ, что т не должно быть меньше сл. тт> (т) = — ? а со-
отвѣтствующее значеніе =
Для провѣрки беремъ я = гдѣ А безконечно-мало, и при этомъ
(5 /5 \
АІ ~ 5 Ц \ ?
или, по упрощеніи, 4“ 27Л Итакъ, при двухъ значеніяхъ х, смежныхъ съ
триномъ получаетъ величины, большія ибо 2Л2—положительно; слѣдов* 31
д- есть дѣйствительно шшітиш тринома.
639. Примѣръ II. Найти тахітит и тіпітит функціи
' сх* — Ъ(а — х)*.
Приравнявъ это выраженіе т< расположивъ по степенямъ х и собравъ всѣ члены въ первую часть, имѣемъ ур—ніе
(с — Ъ)х* 4“ — (а'2Ь + т) — о»
откуда
— аі — у 'аЭД* -]- (с — Ъ)(а2Ъ + «О
Для дѣйствительности х необходимо, чтобы т удовлетворяло неравенству 4~ (с — 5)(лй5 4~ т) О, или (я — Ъ)т 4- аЧс 0. Рѣшая это неравенство, различаемъ два случая:
I) Если с — Ъ > От то откуда пшитшп = а со-
х • яЪ
отвѣтствующее значеніе х есть д?
аЬ
Ъ— с
л . л2Ьс . / ч аРЪс
О, то т^і)_с откуда тахітит (т) = ^-_ с
аЬ . , именно г--+л:
о — с— 1
Для повѣрки подставляемъ въ данное выраженіе вмѣсто х два. значенія аЪ смежныя съ г-—’ о— с находимъ:
ЧА
\о — с
А+*1*
2
или, по упрощеніе, -р (с — &)Л3. При с — 6>0, членъ (с — Ь)Л2 суще-О' с
аЬ
ственно положителенъ; а это значитъ, что при я смежныхъ съ „ с триномъ
, а2Ъе
больше, нежели послѣднее выраженіе есть, слѣдоват., шіштиш тринома. При с — Ь < О, членъ (е — отрицателенъ; это значитъ, что величины тринома при х смежныхъ съ меньше слѣдов. эта дробь есть тахітит тринома.
640. Примѣръ ПІ. Данъ кругъ радіуса К, углѣ. Провести къ ѳтому кругу касательную
вписанный въ прямомъ такъ, чтобы площадь
отсѣкаемаго ею въ углѣ треугольника АОВ была тіпіта.
Пусть ОА = х, ОВ = у. Площадь Д АОВ = чтобы представить ее въ функціи одного перемѣннаго, выразимъ, что прямая АВ касательна къ кругу С; имѣемъ АВ = ВР + ЕА = ВЕ + АЙ = у — В Ц-4“х — К = #4“У — 2В; съ другой стороны, такъ какъ АВ3 = х2 ~1- у2, связь между х н у будетъ: (#-|~у — 2К)3 = = х2-^-у2. Итакъ, ур—нія задачи суть (называя площадь Д АОВ чрезъ т*):
ху — 2т2, 2В(гг У) = %У + 2ВА
Подставляя во второе ур—ніе вмѣсто ху его величину 2т\ имѣемъ:
Черт. 122/
т* + К2
Е
ху ~ 2т2
и
такимъ образомъ видно, что неизвѣстныя х и у суть корни ур—нія
X’ — ”* + І<2Х 4- 2т9=О,
откуда
„ _ (х 1 т? + К» . / /т? 4- ІѴ\» ~_ да» + К2 ± Ѵ»і‘—6К2п»2+К»
А Ц/ — 2К — г 2В / “т ~ 2К
Для дѣйствительности х и у необходимо, чтобы было
— 6В»т’ + ІІ*>0, или [тг — В»(3+|/8)][т1 — На(3 -}/8)]>О.
Это неравенство будетъ удовлетворено, если количеству т2 дадимъ значенія, лежащія внѣ корней тринома, т.-е.: 1) значенія, содержащіяся между О и К2(3 — 2|/2); 2)значепія, большія К2(3 4“ 2]/2). Махітпт значеній перваго ряда есть Кя(3 — 2|/^); тшіппіт значеній второго ряда равенъ В2(34~2|/2).
Что касается щіпішпт’а, то значенія и ему соотвѣтствующія, суть:
# = У ——= К (2 -р]/2)- Равенство х и у показываетъ, что Д мини-
мальной площади есть равнобедренный прямоугольный Д А'ОВ', котораго гипотенуза есть касательная А'В1 въ конечной точкѣ діаметра-биссектора ОСИ дан-
наго угла.
Что касается тахішшп’а К2(3— 2|Л2), то онъ не можетъ соотвѣтствовать треугольникамъ, образуемымъ касательными, проводимыми къ дугѣ ЕйП, ибо площади этихъ треугольниковъ измѣняются отъ -(-со до 4“ °°т слѣд. не имѣ-
ютъ шахітітГа; съ другой стороны, и самая величина шахітпш’а, К2(3 —2^/2), меньше К3. Онъ соотвѣтствуетъ треугольникамъ, образуемымъ касательными къ дугѣ 1)Н'Е. Въ самомъ дѣлѣ, площади этихъ треугольниковъ измѣняются отъ О до О и слѣд. имѣютъ шахітигп. Обозначивъ: 0А2 = х, 0В3 = у, имѣемъ: АаВа = ЕВа 4“ ВА* = й— х 4~ й — у = 2К — х — */, и ур —нія этой новой
задачи будутъ:
ху = 2 т2, х2 4” = (2П — х — у)\
они не отличаются отъ ур—ній предыдущей задачи, и изслѣдуя подрадикальный триномъ, мы должны были, на ряду съ ішшпшп’омъ первой серіи Д-ковъ, найти и шахіпішп второй серіи.
641, Примѣръ IV. Изъ всѣхъ прямоугольныхъ треугольниковъ одинаковой высоты К (опущенной па гипотенузу) у какою периметръ имѣетъ наименьшую величину?
Пусть будутъ: х и у —катеты, %—гипотенуза и 2р—периметръ (треугольника; ур—иія задачи суть:
х 4- у 4- = 2р,
#24_^2 —
Изъ перваго: #4“^“^— я, или'(ж4”^)2 = затѣмъ, прида-
вая къ третьему удвоенное второе, имѣемъ:
#2 4~ У3 Н- 4~ пли (я 4~ у)* = 4" 2^»
приравнивая оба выраженія (#4~^Л имѣемъ ур—ніе въ я
(2р — #)а = 4” 2Ая,
изъ котораго
Слѣдовательно
х + У = 2Р
-Р3 _ 2р/і + 2р2 __ _
А-|-2р 1і + '2р 1
і+2р’ Л Л+2/
Итакъ, х и у суть корни квадратнаго ур—нія
ѵ і. АіИ . ѵ X —I?2— — о
Х + Х^Л + 2р —
Изъ него
Ѵ—/ДЦ—Р А+р . ./а р+ру х~ 1уІ~р к + %р—тѵ ѴЬ + 2^ Л4-2р
а какъ подрадикальнос выраженіе приводится къ
412
(.р® — А1 — 2кр)
то
X = (А +р ± ѴГ^Г— к* — 2рА).
Чтобы задача была возможна, необходимо, чтобы удовлетворяло неравен ству р^ — -— Л2 О, или
[^ —А(1 4-|/2)] . [р—А(1—}/2)]>О.
Отсюда извѣстнымъ образомъ заключаемъ, что неравенство удовлетворяется двумя серіями значеній а именно: 1) всѣми р <С ^(-1—}/^); 2) всѣми р > Л(1 +/2); слѣд, Л(1 — ѵ"2) есть шахішит р, а А(1 +)/2) тіпітит р.
Что касается тіпітит а, равнаго 7і(1-|-|/2), то отвѣчающія ему значенія х и у суть:
« = „ = й.4+34-Л)/2.
Л(3—21 2) ЗЧ-2Г2
4 Слѣд., «зь (Успда прямоугольныхъ треугольниковъ одинаковой высоты, равнобедренный имѣетъ наименьшій периметръ.
Что касается найденнаго ттіхітит'а, то, будучи отрицательнымъ, онъ не можетъ относиться къ данному геометрическому вопросу. Но замѣчая, что при т> = Л(1—)/2)т количества х и у отрицательны, а я положительно, мы, перемѣнивъ въ ур—яхъ вопроса знаки количества х, у и р, найдемъ уравненія:
х-!Гу~е = 2р, ху = кг, Х*-\~у* = X2.
Этимъ ур —ямъ отвѣчаетъ вопросъ: Изъ всѣхъ прямоугольныхъ треугольниковъ одинаковой высоты Л у какого избы-
о...........________________О’
Черт. 123.
токъ суммы катетовъ надъ гипотенузою будетъ наименьшій? Рѣшивъ этотъ вопросъ, найдемъ, что искомый треугольникъ есть равнобедренный, и что тіпітит половины избытка дается абсолютною величиною отрицагельнаго шахітшп’а
предыдущей задачи.
Примѣчаніе. Если бы требовалось изъ всѣхъ прямоугольныхъ треугольниковъ одинаковаго периметра найти такой, котораго высота, опущенная на гипотенузу, была бы наибольшая; тогда р была бы величина данная и нужно бы было найти А, удовлетворяющія неравенству
А3Н~2у>А—пли [А—— 1)][А+Х^+)/2)]^0.
Отсюда нашли бы, что тахітит (А) =р(]/1>—-1); соотвѣтствующія значенія & и у равны между собою, и общая величина ихъ есть
X у =р =р(2 - 1/2).
Эти результаты легко найти геометрически. Извѣстно, что для построенія прямоугольнаго треугольника по даннымъ: периметру и высотѣ на гипотенузу, откладываютъ на сторонахъ прямого угла ОС = ОЭ = возставляютъ въ точкахъ С и I) перпендикуляры, которыхъ пересѣченіе опредѣляетъ центръ (У круга, внѣ-вписаннаго въ искомомъ А АОВ; изъ точки 0 какъ изъ центра радіусомъ ОК, равнымъ высотѣ, описываютъ другой кругъ. Гипотенуза АВ должна быть касательною къ обоимъ кругамъ 0 и 0'. Слѣд. вообще задача имѣетъ два рѣшенія одинаковыя, ибо тр—-ки ОАВ и ОА'В' равны, такъ какъ ОА = ОВ' и ОА' = ОВ.
возможна, когда обѣ окружности лежатъ одна внѣ другой; для того,
чтобы онѣ были касательны, необходимо чтобы
Задача
Черт. 124.
ОО'=А-]-р, а какъ ОО'=р|/2, то А-Р/>=р^/2, или А=т)(|/2 — 1). Если А будетъ имѣть большую величину, окружности пересѣкутся, и задача станетъ невозможна.
642. Примѣръ V. Задача о пчелиныхъ ячейкахъ. На продолженіи оси 00' правильной шестиугольной призмы возьмемъ точку 8; черезъ эту точку п чрезъ каждую изъ сторонъ правильнаго треугольника АСЕ, полученнаго соединеніемъ чрезъ одну вершинъ верхняго основанія призмы, проведемъ три плоскости, по которымъ отрѣжемі» отъ призмы три тетраэдра ВАСК, ВСЕН и ЕЕАЬ и замѣнимъ ихъ однимъ театраэдромъ 8АСЕ, поставленнымъ надъ призмой* Новый многогранникъ будетъ ограниченъ сверху тремя ромбами 8АКС, 8СЕП, 8ЕАЕ; объемъ его всегда равенъ объему взятой призмы, гдѣ бы ни взять точку 8 на оси, ибо пирамида 8АСЕ составлена изъ трехъ іирамидъ 80АС, 80СЕ и 80ЕА, соотвѣтственно равныхъ тремъ отрѣзаннымъ пирамидамъ; такъ пирамида 80АС — пир. КАВС, ибо они имѣютъ равныя основанія (ДОАС=ДАВС, какъ половины ромба АВСО) и равныя высоты 80 и
КВ (по равенству прямоугольныхъ треугольниковъ 801 и КВІ). Имѣя равные объемы, многогранники имѣютъ, однако, различ-
ныя поверхности, и задача состоитъ вь опредѣленіи точки 8 яіаяь, что-
бы поверхность новаго десятигранника имѣла наименьшую величину.
Пусть АВ=а, ВВ'=ОО'=Ь, ВК=80=а?; въ такомъ случаѣ: АС=<ц/3;
81 = 1/80*4- ОР = 1/ж* 4-^ = 1 }/4а’4-а*; слѣд. 8К = ]/4х* 4~ а»; г ** м
площадь ромба 8АКС, равная полупроизведенію діагоналей АС и 8К, выразится формулою 2а/За2-^ 12д?а; площадь трапеціи СКВ'С'—формулою «(26—#). Слѣдоват., поверхность многогранника, не считая основанія, выражается формулою | « |/За2 Ц- 12-г2 За(26—я), или За | |/3ая 4~ 12#2 —|— 26 — х]. Постоянный множитель За не вліяетъ на условія шах. и шіп., я потому вопросъ приводится къ опредѣленію тіпітит’а скобочнаго выраженія. Положивъ
і /За* 4- 12ж« 4~ 2Ь — х = т
и освободивъ это ур—ніе отъ радикала, найдемъ
8гс2 — 8(т — 26)#4-3а2 — 4(т — 26)* = О, откуда
_ 2И — 26) V 6[2(»» - 26> _ 02]
х_ і
Чтобы я было дѣйствительно, необходимо, чтобы было
2(т — 26)2 — 0, или (ш — 26)* > Ѵг
-О
или
т— 26
Отсюда шіпіт. (т) = 26 -[
Помноживъ на За, найдемъ, что искомая
минимальная поверхность =
Зд2
а соотвѣтствующая величина гг=-а|/"2.
Формула для я показываетъ, что разность двухъ смежныхъ боковыхъ реберъ должна быть = четверти діагонали квадрата, построеннаго на сторонѣ шестиугольника, служащаго основаніемъ призмы.
1/3
Поверхность призмы, пе считая основанія, была бы 6«6 -|- —; слѣд. поверхность многогранника минимальной поверхности меньше на ^ая(|Лз— |/2) поверхности шестиугольной призмы, имѣющей то же основаніе и тотъ же объемъ.
Легко видѣть, что для треугольника КВІ имѣетъ мѣсто пропорція
ВК : ВІ : 1К = 1 : /2 : / 3,
откуда (при помощи тригонометріи) найдемъ, что уголъ ВТК = 3545'52".
Примѣчаніе, Пчелы строятъ ячейки своихъ сотовъ именно въ формѣ такихъ десятигранниковъ съ минимальною поверхностью; шестиугольникъ обра-46
зуетъ входъ въ ячейку; медъ кладется на дно; пчелы строятъ сначала ромбы, затѣмъ боковыя трапеціи. Если вообразить себѣ плоскость, заполненную шестиугольниками и построить на каждомъ изъ нихъ ячейку, то вершины ячеекъ будутъ находиться всѣ въ одной плоскости, параллельной первой. Затѣмъ, если къ такой фигурѣ приложить другую выпуклостями во впадины первой, получимъ совокупность ячеекъ, называемую сотомъ. Улей наполняется сотами, помѣщенными другъ надъ другомъ такъ, чтобы двѣ пчелы могли вмѣстѣ пройти ме&ду двумя послѣдовательными сотами.
Итакъ: 1) наклоненіе трехъ ромбовъ, образующихъ дно, таково, что ячейки при данномъ объемѣ имѣютъ минимальную поверхность; 2) правильный треугольникъ, квадратъ и правильный шестиугольникъ суть единственные правильные многоугольники, которыми можно заполнить плоскость безъ просвѣтовъ, и изъ нихъ шестиугольникъ, при той же площади, имѣетъ наименьшій контуръ. Такимъ образомъ является двоякая экономія на воскъ.—Геометрическое строеніе пчелиныхъ ячеекъ, замѣченное еще Паппусомъ, геометромъ IV* вѣка до Р. X., было изучаемо сначала Филиппомъ Маральди (1712 г.), затѣмъ Реомюромъ, который.и предложилъ вопросъ о минимумѣ Самуилу Кенигу и Маклорену.* Послѣдній впервые далъ точное теоретическое рѣшеніе вопроса. Для угла ромба Кенигъ нашелъ 109*26' вмѣсто 109°28'16'\
643. Примѣръ VI. Зная сумму 2а двухъ параллельныхъ хордъ круга радіуса В, опредѣлить ихъ положеніе такъ^ чтобы разстояніе этихъ хордъ имѣло наибольгиую или наименьшую величину.
Пусть длины параллельныхъ полухордъ будутъ х и прямо имѣемъ, назвавъ разстояніе между ними буквою т*
|/Н*—+ = ж,
гдѣ знакъ (4-) относится къ случаю, когда хорды расположены по обѣ, а (—) по одну сторону центра. Затѣмъ, по условію:
~ а.
Возвышая обѣ части перваго ур—нія въ квадратъ, имѣемъ:
2К« — (х2 4- у») ± 2|/(К* —х2) (П2 — у1) = яі2.
или
(ж3 — + + - 4(В* — #а) (К2 — Л*
Раскрывая и дѣлая приведеніе, имѣемъ:
ж* + (хй + у3)2 — 4ж*К3 + 2т2(х* + у3) =
Изъ второго ур—нія находимъ: х2-[-у2 — а^ — 2ху; слѣд.
ж1 (аз _ + 2ж2(а2 — 2ху) = 4^У г
откуда
_|_ ач)2 _ 4Шчгг
ХУ -- А _±_ «»2Г'
По произведенію и суммѣ х и у можемъ выразить эти количества какъ корни квадратнаго ур—нія
и3 — аи -|-
-Ь а5)а — 4(а* + яі2)
= 0.
Условіе дѣйствительности корней таково:
а3(а3 т2) — (т2 а*)а 4~ 4ш3Е3;> 0, или — т'2 — з3 -|- 4К* )
Такъ какъ по свойству геометрическаго вопроса аа<4Н\ то предыдущее неравенство можно написать такъ:
(|/4Ка ——т)(]/4К2 —«3 + ш)>0 . . . (1)
Когда т>0, изъ неравенства (1) наюдимъ: )/4В3— а2 сл. тахітит (т) = ]/4Еа — а3, а соотвѣтствующія значенія х п у суть я?=*/= Очевидно, этотъ тахітит принадлежитъ функціи }^К3— +Ѵна —у3, ибо другая функ-
а . Л
ція при #=*/ = 9 обращается въ О.
Когда га <2 О, неравенство (1) даетъ: ]/4Кй— а*, откуда тіиітшп (т)
= — }/4К2 — а2. Этотъ тіиітит принадлежитъ функціи: — }/К2—я3 — )/К3— ^2. Опредѣленіе тіпіт. или тах. этой функціи привело бы, послѣ возвышенія въ квадратъ, къ прежнему ур—нію въ и.
Для провѣрки найденнаго шахітнпѴа = |/4ІР —а3, которому соотвѣтствуютъ х=у~^ дамъ количеству безконечно малое приращеніе о, т.-е. полага-емъ# = ^-|-о; въ такомъ случаѣ изъ соотношенія а;-4-^ = а, находимъ: = — 5; вопросъ приводится къ провѣркѣ неравенства
]/к»—(“4-8? + ]/к’ — (5 — 8у < /4Ка — а\
Такъ какъ обѣ части этого неравенства положительны, то возвысивъ въ квадратъ, замѣняемъ эквивалентнымъ ему неравенствомъ
4В3 — а3 + 453;
замѣчая, что 4Ка~а2 положительно, можемъ еще разъ возвысить въ квадратъ, не измѣняя смысла неравенства; н по упрощеніи находимъ; —32К362<4|-32К383, что вѣрно.
644, Третій способъ. Этотъ способъ основанъ на самомъ опредѣленіи та-хітппГа и тіпітшп’а функціи. Пусть данная функція есть квадратный триномъ ах* + с, и пусть она при х = я? достигаетъ шахітиш'а; въ такомъ случаѣ, каковъ бы ни былъ знакъ произвольно-малаго количества Л, должно имѣть мѣсто неравенство
а (я/ 4“к)* + Ь(а/Л) 4” с — (ад/34"йя/с)<О, '
ИЛИ
Ь) <С 0;
такъ какъ к произвольно-мало, то первая часть неравенства имѣетъ знакъ перваго члена; поэтому опа будетъ мѣнять знакъ съ перемѣною знака Л, и слѣд. не будетъ постоянно отрицательною, пока первый членъ будетъ отличенъ отъ нуля; другими словами, неравенство можетъ существовать при измѣненіи знака Ъ только тогда, когда первый членъ будетъ тождественно =0, т.-е. когда 2ах Ь — 0, или х' = — Но при этомъ значеніи л/ неравенство приво-
дится къ аЛ2 < 0, и потому, чтобы оно было возможно, необходимо, чтобы было а<0.
Итакъ, при а <2 0 трипомъ имѣетъ тахітит, когда я'~Самый же — Ъ2 тахітит = 4(7
Подобнымъ же образомъ найдемъ, что триномъ имѣетъ минимумъ при я' = — если Самый тшішшп выражается тою же формулою.
Этотъ способъ, принадлежащій къ числу натуральныхъ, важенъ для насъ въ томъ отношеніи, что даетъ возможность элементарнаго опредѣленія шах. и шіи. въ такихъ случаяхъ, въ какихъ вышеизложенные элементарные методы не примѣнимы. Найдемъ помощію этого способа
645. Махіта и тіпіта кубичной функціи ах3-1- Ь#24-сж-Пусть я и будетъ то значеніе перемѣннаго, при которомъ функція имѣетъ тахітит или тіпітит; въ такомъ случаѣ, назвавши буквою Л произвольно малое приращеніе перемѣннаго будемъ имѣть
а (а? ——|— Ь (д; ——|— е(хг —7і) — (ах* 4" &г2 4“ 4"
гдѣ верхній знакъ неравенства относится къ случаю шахішшп’а, нижній — къ случаю тіиітшп’а; по упрощеніи, найдемъ
(Зал:2+2іх + с)7і+(Зах+Ь)7г2 + «Л3^0 . . .(1). 11
Пока первый членъ, при 7» весьма маломъ, не равенъ нулю, первая часть будетъ мѣнять знакъ вмѣстѣ съ Л, и слѣд. не будетъ постоянно отрицательною, или постоянно положительною, какъ требуетъ неравенство; итакъ, значенія лз, дающія тахітит или тіпітит функціи, должны удовлетворять уравненію
Зах22Ьх + с = 0 . . .(2).
Первое условіе чтобы функція имѣла шах. пли тіп., состоитъ въ томъ,
чтобы корни ур—нія (2) были дѣйствительны, т.-е. чтобы 62 — Зас 0; но равенство 62— Зас = О необходимо исключить, ибо при немъ не м. б. ни шах.,
ни шіи. Въ самомъ дѣлѣ, если Ь2 и равные и общая величина ихъ
Зас = О, корни ур—нія (2) дѣйствительные ‘ — откуда Зах-[-Ъ=0, т.-е. второй
членъ нер. (1) обращается въ нуль, и первая часть этого неравенства обращается въ а№; поэтому разность между максимальнымъ (или минимальнымъ) значеніемъ функціи, если бы таковое существовало, и смежными ея значеніями, выражалось бы количествомъ аА3, мѣняющимъ знакъ вмѣстѣ съ К. Итакъ, первое
условіе, необходимое для того$ чтобы функція имѣла пш. или шіп., есть Ъ2— Зас> 0.
Пусть это условіе удовлетворяется; въ такомъ случаѣ корни ур—нія (2) будутъ дѣйствительные и неравные, и сл* будутъ отличны отъ —т.-е. не-
обходимо будетъ:
За#7 4" Ъ 0, За#" Ь 0.
Пусть #'<#"; тогда
А За
. Ь
ибо —есть полусумма корней*
"Затѣмъ различаемъ два случая*
Первый случай: а>0*—Неравенства (3) въ этомъ случаѣ можно представить въ видѣ:
За#' < — Ъ < За#",
откуда
За#' 4~ Ь < 0 и За#" 4“ И;
слѣд. каковъ бы ни былъ знакъ весьма малаго количества Л, будетъ •>
(За#' 4~ Ь) А® аА3 <С 0 и (За#" &) А3 4- аА3 > 0.
Первое неравенство показываетъ, что приращепія функціи при значеніяхъ #, смежнымъ съ #', отрицательны, а при значеніяхъ #, смежныхъ съ #", положительны, слѣд*: при # = #' функція имѣетъ тахішшп, а при # = х7' она имѣетъ тшіпшш.
Второй случай: а < 0*—Неравенства (3) въ этомъ случаѣ, по умноженіи на положит. количество —За, даютъ:
За#' 4“ Ь О
и За#" —[— Ь 0;
слѣд, каковъ бы ни былъ знакъ А, имѣемъ два неравенства:
(За#' 4- Ь) А® а А® > 0 и (За#" + Ь) А® + аА® < О,
изъ которыхъ выводимъ заключеніе, обратное предыдущему.
Отсюда правило: чтобы найти, тахіта или тіпіта кубичной функціи а#3-|-Ь#а-|-с#4“й-/ приравниваемъ нулю полиномъ За#2-[~2&#-(~с» составляемый умноженіемъ каждаго члена функціи на показателя буквы # въ этомъ членѣ, и уменьшеніемъ этого показателя на 1 *); так. обр, получаемъ уравненіе
За#®4*2Ь#4~с — 0 . . .(1)
Если Ъ2— Зас^О, функція не имѣетъ ни тах,^ ни тІпітит’а; если же 62“Зас>0, меньшему корню ур—нія (1) соотвѣтствуетъ
♦) Изъ этого слѣдуетъ, что послѣднимъ членомъ новаго полинома будетъ с, ибо послѣдній членъ данной функціи* который можно написать въ видѣ с?#®, дастъ, слѣдуя этому закону, 1, или 0. -
тахітит, а большему тіпітпт^ когда а^>0; напротивъ, меньшему корню соотвѣтствуетъ тіпітит, а большему—тахітит, когда а<^0.
646. Примѣръ. Найти тахітит и тіпітит разности объемовъ: конуса, вписаннаго въ данный шаръ и сферическаго сегмента, имѣющаго то же основаніе.
Вопросъ можно понимать двояко, а именно: высота конуса можетъ совпадать или не совпадать съ высотою сегмента. Въ пер-]\[ вомъ предположеніи, означивъ МС буквою х, имѣемъ:
объемъ конуса 8АВ = ~ таг(2В — я)2;
( \ / / объемъ сегмента АВ8 = | я (2В.— я)2(ЗВ— 8С)
\ \ / / = д к (2К — ж)2 (В 4- х).
8
Разность междѵ первымъ и вторыхъ объемомъ вы-Черт. 126. і
ражается формулою: —тгК (2К — я)3. Такъ какъ множитель — 1 кВ, — постояненъ, то измѣненія выраженія зависятъ отъ (2В—д?)2; но это выраженіе есть квадратъ, слѣд. оно имѣетъ тіпітит равный нулю, что имѣетъ мѣсто при х = 2К; а слѣд. выраженіе — ^т:(2К—я)2 К-имѣетъ тахітит при х = 2В, а какъ при этомъ я не можетъ, возрастая, превзойти 2В, то полученный тахітит есть абсолютный.
Во второмъ предположеніи:
объемъ сегмента ЛМВ = 1та2(ЗК— ж),
слѣд. разность между конусомъ и сегментомъ равна діга(2К—я:)2—^тле2(ЗВ—ж) или
^[2®» — 7Яж2 + 4ВЛв]. о
Измѣненія зависятъ отъ перемѣннаго множителя 2я3—7Кга Ц- 4В2#, представляющаго кубичную функцію; значенія ж, дающія этой функціи піахішит и тіпітит, по правилу, суть корни квадратнаго уравненія
3.2я2 — 2 . 7Кг -]- 4В2 == 0, или бя;2 — І4Вгс 4~ = О-
Эти корни суть: #'=^5 я?" = 2Н; а какъ коэффиціентъ при ж2 положи-х , 17-Н.з
телепъ, то меньшему корню соотвѣтствуетъ тахітит разности объемовъ —> а
4
большему ея тіпітит: —«тгВ3, причемъ этотъ тіпітит — абсолютный, о
647. Принципъ Фермата. Знаменитый французскій математикъ Ферматъ, въ одномъ изъ своихъ писемъ къ Паскалю и Робервалю, отъ 23 августа 1636 г. заявляетъ, что изъ всѣхъ своихъ открытій наибольшее значеніе онъ придаетъ методу опредѣленія максимальныхъ и минимальныхъ значеній во всевозможныхъ
Черт. 127.
задачахъ, основанному на принципѣ, который онъ считаетъ фундаментальнымъ. Этотъ принципъ легко понять, разсматривая функцію какъ ординту кривой.
Пусть ордината АВ представляетъ максимальное состояніе разсматриваемой функціи, а абсцисса ОВ = я соотвѣтствующее значеніе перемѣннаго. Принципъ Фермата состоитъ въ томъ, что всегда существуютъ такія два значенія независимаго перемѣннаго—одно я—А, немного меньшее я, другое #-|-А, немного большее которымъ соотвѣтствуютъ два значенія функціи: /(х— А) и /(я-|-А) (или двѣ ординаты А'В' и А"В") равныя между собою. Въ самомъ дѣлѣ, функція, возрастая, и приближаясь къ своему тахіппіш’у АВ, пройдетъ чрезъ свое значеніе / (х — А), безконечно-близкое къ этому тахітит’у АВ; затѣмъ, достигнувъ тахішит’а, она начнетъ убывать и. прежде чѣмъ дойдетъ до нѣкотораго состоянія А'"В"', мень
шаго АВ, должна, по свойству непрерывности, пройти всѣ промежуточныя состоянія, слѣд., между прочимъ, пройдетъ и чрезъ состояніе А"В" или равное А'В' пли / (х— к) и безконечно-близкое къ АВ.
Такое же равенство имѣло бы мѣсто и тогда, если бы АВ изображала тпі-пішит функціи.
Отсюда непосредственно вытекаетъ и самый методъ. Приравниваемъ два значенія функціи, одно, соотвѣтствующее х—А, другое # + А. гдѣ & есть значеніе перемѣннаго, дающее шахіишш или тіпітит функціи, а А и А безконечно-малыя; такимъ образомъ получаемъ уравненіе А) = /($-[- А). Очевидно, что если значенія перемѣннаго х — к и ж-^А. дающія равныя значенія функціи, сближать между собою, т.-е. приближать А и А къ пулю, то оба значенія функціи будутъ приближаться къ піахішнш’у (или шіи.), и въ предѣлѣ, т.-е. при к~к = О, сольются съ шахітипГомъ (или тіп.), а оба значенія перемѣннаго сольются съ тѣмъ значеніемъ, которое соотвѣтствуетъ піахітипГу (или тіп,). Такимъ образомъ, въ предѣлѣ получится ур—ніе вч> я; ір(л:) = О. которому будетъ удовлетворять значеніе перемѣннаго ж, дающее или тахітит или тіпітит. Рѣшивъ это ур—ніе, найдемъ, вообще говоря, нѣсколько значеній для х, напр. х = а, Ь, с, . . . Ничто не указываетъ, чтобы всѣ эти рѣшенія давали ша-хітпт или тіпішпт функціи; слѣд. для каждаго нужна повѣрка. Впрочемъ, если ур—ніе ^(я) = 0 имѣетъ только одно рѣшеніе, и по свойству вопроса можно а ргіогі заключить, что / (#) имѣетъ шах. или тіп., повѣрка будетъ ие необходима.
На практикѣ поступаемъ такъ Выразивъ всѣ неизвѣстныя черезъ одно х и положивъ х — к = х\ х^к = х\ въ ур—ніи /(#г) — /(х”) дѣлаемъ упрощенія, удаляя общія части и сокращая на ж' — въ оставшихся членахъ дѣлаемъ я*— х” равнымъ нулю, послѣ чего и получаемъ ур—ніе ^(л?) = О.
Методъ Фермата есть болѣе общій изъ числа элементарныхъ методовъ опредѣленія максим. и миним. значеній функціи. Въ историческомъ отношеніи онъ важенъ тѣмъ, что послужилъ зародышемъ, изъ котораго позднѣе развилось дифференціальное исчисленіе.
648* Примѣръ I.—.Изъ какой точки гипотенузы даннаго прямоугольнаго треугольника нужно опуститъ перпендикуляры на катеты, чтобы прямоугольникъ, образуемый ими со сторонами прямого угла, м.имаа наибольшую площадь.
Взявъ точку Е на гипотенузѣ и опустивъ изъ нея перпендикуляры ЕВ и ЕЕ на катеты, образуемъ прямоугольникъ ЕВСР; когда точка Е совпадаетъ съ А,
прямоугольникъ превращается въ прямую АС, а его площадь въ нуль; если затѣмъ двигать точку Е отъ А къ В, то площадь прямоугольника сначала будетъ увеличиваться, а потомъ начитаетъ уменьшаться, и когда точка Е совпадаетъ съ В, площадь снова обращается въ нуль. Такимъ образомъ, измѣняясь отъ нуля до нуля, опа необходимо проходитъ чрезъ віахітпт.
Черт. 128, Пусть въ положеніи ЕВСР прямоуголь-
никъ имѣетъ наибольшую площадь ху. По принципу Фермата, всегда существуютъ такіе два безконечно близкіе къ ЭЕГС прямоугольника Э'ЕТС и І>"Е"Р"С? которыхъ площади равны, т.-е*
х^ — х^. Ф . (1)
Чтобы у выразить черезъ я, замѣчаемъ, что для всякаго положенія прямоугольника между его измѣреніями существуетъ соотношеніе (напр, изъ подобія Д-въ ВЕЕ и ВАС), выражающееся пропорціей у : (а — ж) = Ь : а, откуда ^~а^а‘—€ИЛУ этого можно исключить перемѣнное у и
представить (1) въ формѣ
- V (а — = - х** (а —
а ѵ / а к 71
откуда: ах(— х*2 = ах"— х"3, или а(х' — я") = (#'-р &")(&' — х"). Сокративъ на х'—ю", имѣемъ: а=#4*я". Положивъ хг = х"=х, получимъ ур—ніе 2я = а, котораго корень ж = | даетъ искомый шахітпт. Отсюда, изъ вышеприведенной пропорціи, найдемъ: у = Эти результаты показываютъ, что тахітига площади прямоугольника даетъ точка, лежащая въ срединѣ гипотенузы. Самый же шахітпт площади = (половина площади Д-ка).
649. Примѣръ II.—Данъ кругъ и прямая ху. Изъ всѣхъ треугольниковъ, имѣющихъ вершину въ точкѣ данной на этой прямой, а основаніемъ хорду АВ, параллельную этой прямой, найти тотъ, площадь котораго имѣетъ наибольшую величину.
Различаемъ два случая, смотря по тому, пересѣкаетъ данная прямая жу кругъ 0 или нѣтъ.
I. Пусть прямая ху не пересѣкаетъ кругъ 0. Задача имѣетъ шахітпт, потому что если перемѣщать хорду АВ параллельно ху, отъ I)' къ В, она будетъ измѣняться отъ нуля до нуля, а слѣд. такимъ же образомъ будетъ измѣняться и
площадь треугольника; послѣдняя имѣетъ, поэтому, тахітит. Затѣмъ, замѣчаемъ, что если перемѣщать хорду отъ В' къ 8Т, площадь треугольника будетъ увеличиваться, ибо увеличивается высота и основаніе его. Въ другомъ полукругѣ, по мѣрѣ удаленія, хорды отъ центра, она
уменьшается, высота же увеличивается, по- X У Р
этому здѣсь и слѣдуетъ искать тахішиш.
Пусть хорда АВ = 2у, разстояніе ея ОС отъ центра равно радіуъ курга = В, перпендикуляръ Р0 = а. Пусть максимальная площадь соотвѣтствуетъ 0С = я, эта площадь = (а-ря) |/В3— х3.
По принципу Фермата имѣемъ
(а + гс') |/Ва — =
=(а_|_а")|/Вг_ ж"2.
Возвышая въ квадратъ, тотчасъ же освободили бы ур. отъ радикаловъ, но
для опредѣленія х получили бы кубичное ур привести вопросъ къ рѣшенію квадратнаго ур—нія. Даемъ уравненію видъ
Черт, 129.
—ніе. Слѣдующій пріемъ позволяетъ
а (|/В« — х'3 — |/Ка — х"3) = х" |/К» — х"3 — х' )/Е2 — х'3.
Умножая и дѣля первую часть на сумму радикаловъ этой части, а вторую на сумму членовъ второй части, имѣемъ:
я"2 —я/2 _________ — (я"* а/*)
’ у'Щ! _ Х"і ~ х" ѴШ — -н я' —
Раздѣливъ обѣ части на я"3 — я'2 и положивъ затѣмъ хг = х” = получаемъ ур—ніе
а й2---о 2 Г П
—.. =-----, или 2аг -4- ах — К2 = О,
2ѴК2 —
откуда
/Г =--------------- *
Отрицательный корень отбрасываемъ, ибо въ верхнемъ полукругѣ, съ пони-нижепіемъ хорды идетъ постепенное увеличеніе площади Л-ка. Итакъ, х соотвѣтствующій максимальной площади, равенъ
4
Корень этотъ дѣйствительно меньше В, ибо подстановка 0 и К вмѣсто х въ триномъ 2#2-|-а# —К2 даетъ результаты противоположнаго знака: -—К8 и В2-|-аК.
Въ частномъ случаѣ, когда прямая ху касается къ кругу, а = В, и # = Когда точка Р совпадаетъ съ О' (точкою касанія), треугольникъ
О'АВ— равнобедренный и вписанный; площадь его = ^К2)/3. Итакъ; изъвсѣхя. равнобедренныхъ вписанныхъ треугольниковъ правильный имѣетъ наибольшую площадь.
II. Если прямая ху пересѣкаетъ кругъ, то для каждой части круга получается шахітшп. Къ большему сегменту относится разобранный случай; для меньшаго, изъ ур—нія (ж' — а) ]/іР — х'2 = (я" — а) )/К2 — я"2 находимъ:
- Если параллель проходитъ черезъ центръ, то а = 0, и х~~— • к 2
С50. Методъ равныхъ корней. Пусть кривая РАу (черт. 127) изображаетъ ходъ функціи /(.г); давая функціи частное значеніе и рѣшая ур—ніе/(я)—ш=0, мы опредѣляемъ тѣ значенія х, при которыхъ функція получаетъ эту величину т, Съ геометрической точки зрѣнія это приводится къ опредѣленію точекъ встрѣчи кривой съ параллелью, проведенною въ разстояніи т отъ оси я. Когда т мало разнится отъ тахітит’а АВ, мы находимъ для ж двѣ величины ОВ' и ОВ", мало разнящіяся между собою; они дѣлаются равными между собою и ОВ, когда т обращается въ АВ. Итакъ, когда цѣлая въ х функція получаетъ при х = а тахітит уравненіе [(х)—т' = 0 имѣетъ два корня равные а, и слѣд. его первая часть раздѣлится на —а)* Въ самомъ дѣлѣ: если ур. /{&) —т = 0 имѣетъ корни а'и а", то/(а')— т = 0 и /(а") —т=0; первое равенство показываетъ, что [(х)'—т дѣлится на х— а', втрое, что тотъ же полиномъ дѣлится на х — а"; сл. ояъ дѣлится и на (а? — а') (ж — а"), и при а' = а", на (я —а)*. Отсюда правило:
Чтобы найти тахітит цѣлой функціи, дѣлимъ разность / (ж) <— ш на (х— а)2 или на х2— 2а#-р а2, продолжая дѣйствіе до тѣхъ поръ, пока получится остатокъ первой степени, вида что этотъ остатокъ тождественно равенъ нулю при всякомъ х, полагая М = О, К = 0; 2>ѣшивъ оти уравненія, и найдемъ х = а, соотвѣтствующій тахітит'у, и самый этотъ тахітит т.
относится и къ шішшиш’у функціи.
651. Примѣръ. Изъ всѣхъ равнобедренныхъ треугольниковъ, описанныхъ около круга, найти тр—къ наименьшей площади.
Если перемѣщать вершину А по высотѣ АЕ отъ 0 до безконечности, то площадь Д-ка будетъ измѣняться отъ с» до слѣд. имѣетъ шіпітиш. Пусть половина основанія равна х, высота = К-р 2/; чтобы выразить у черезъ х, изъ ДАВЕ, по свойству бпссектриссы, имѣемъ = АВ:я, или у2: Е2 = [(# -|-К)2-{-#а] : а3, откуда найдемъ:
у~ *
Черт. 130. Подставляя это выраженіе въ формулу площади тр—ка, получимъ
л / і тм /К(К2 + ^) , 2Ях3
ДАВС ^(*/-|-К) —К.2 а* — К2’
Вопросъ приводится къ нахожденію тіиіпіипі*а выраженія
а?8 #2ТГ1<2
• Прирав-
нивая это выраженіе получаемъ ур—ніе
а?8 — тх* тВ* — 0.
Раздѣливъ первую часть его на х* — 2ах а2, находимъ въ остаткѣ (За'2—— 2а3-|-а*ж), откуда, слѣдуя правилу, имѣемъ 2 ур—нія
За2 — 2ат — 0, тІР — 2а3 + а2т = 0.
•Изъ перваго находимъ: т= - а; подставляя во второе, получаемъ: х = і^і/ 3; слѣд. т=^В}/3, а минимальная площадь = ЗК2|/3: заключаемъ, что искомый треугольникъ—правильный.
П. Махіта и тіпіта квадратной дроби --24Ч,г“Е“: а д?* 'г- о х і— с
652. Первый методъ. Нужно опредѣлить х ,такъ, чтобы при всякомъ знакѣ безконечно-малаго Л, имѣло мѣсто неравенство
а(а;-р Л)3ч- Ь(я + Л) + с 4- -р с ₽(& + Л)а + + Л) + с' ~ а'х^+~Ъгх^Гсг >
гдѣ знакъ < относится къ случаю тахітшп’а дроби, знакъ >• къ случаю ея тівітпт’а.
Умножая на произведеніе знаменателей, которое положительно, ибо полипомъ
+ разнясь безконечно мало отъ
имѣетъ одинаковый съ нимъ знакъ, находимъ неравенство:
[а(:г ^)2 + “Ь й) + с] [а'#2 4“ Ъ’х с'] —
— [«'(ж ^)2 “Ь 4“ 4" с ] “Н + с) 5* о, которое, будучи упрощено и расположено по возрастающимъ степенямъ при- . водится къ:
Л[(аЬ'—']-|-Л2[(аЬ'—. (1).
Чтобы это выраженіе не перемѣняло знака вмѣстѣ съ А, коэффиціентъ при Л долженъ быть нулемъ; слѣд. значенія ж, которыя могутъ дать дроби максимальное или минимальное значеніе, суть корни уравненія:
(аЬ* — Ъа^х* -ф- 2(ас' — 4~ (&с — ) = 0 . . . (2).
Итакъ первое условіе, чтобы дробь имѣла шахітпт или тіпітит, состоитъ въ томъ, чтобы ур. (2) имѣло корни дѣйствительные, т.-е. чтобы было
(ас' — са')2 — (аУ — Ьа') (Ьс' — сЬ) О . . . (3).
Взявъ равенство, т.*е. полагая, что ур. (2) имѣетъ корни равные, наіо-х г ас/ — са{
дямъ, что общая величина ихъ опредѣляется равенствомъ: х =—
'откуда
х(аЪ* — Ьа') ас? — са' = О;
отсюда слѣдуетъ, что неравенство (1) привело бы къ равенству 0 = 0, каково бы ни было А: въ этомъ случаѣ, слѣдов,, дробь не имѣетъ ни таіішшп’а, ни тіпітшп’а.
Обращаясь къ равенству (ас' — са')2 — (аУ — Ъа‘) (Ъс' — сЫ) = 0, замѣчаемъ, что, какъ доказано въ § 467, оно выражаетъ условіе, необходимое и достаточное для того, чтобы два ур—нія ажа4’Ьх^с=0 и О
4 ас' — са' . . ,
имѣли общій корень, именно: х± = — г слѣд. оба члена дроби дѣлятся ДО щ}
. х егдр В
на х — и, по сокращеніи, дробь приводится къ а эт0 выраженіе не
имѣетъ ни піахіінипГа, ни тшіншпГа (§ 591).
Итакъ, пусть существуетъ неравенство (3), и пусть а/ и х” суть два корня ур—нія (2), причемъ хг<^х*'; сравнивая ихъ съ полусуммою корней, имѣемъ неравенства
асг — еа'
Ьа'
1-й случай: аЪ'—Предыдущія неравенства эквивалентны слѣдующимъ:
(аЪ' — Ъа’)х' ас1 — са' < 0, (аЬ' — Ьа')я" 4~ ас' — са' > 0.
Отсюда выводимъ:
[(аУ — Ъа')х* (ас'— са')]Ѵ < 0, [(аУ — Ъаг)х" -}- (ас' — са')]Л2 > 0.
Первое условіе выражаетъ, что величинѣ х' соотвѣтствуетъ тахітит дроби, а второе, что большему корню яР отвѣчаетъ тіпітит дроби.
2-й случай: аЪ* — Ьа <^0. Умножая на положительное количество
- (аУ - Ьа'), . находимъ
[ (аЪг — Ъа^х' 4~ — са']Аа > 0 и [(аУ — Ъа')х” 4” ас' — са']А2 < 0;
заключенія обратны предыдущимъ.
3-й случай: аЬ'— Ьа' = О. Ур—ніе (2) въ этомъ случаѣ дѣлается 1-й степени, а потому дробь имѣемъ тахітит или тіпітпт, смотря по тому, отрицательно ас' — са' или положительно, ибо неравенство (1) приводится къ А®(аУ — са') 0.
Наконецъ, если бы сверхъ того имѣли ас' — са' = 0, и слѣд. = дробь не имѣла бы ни тахітит'а, ни тшітпт’а: она имѣла бы постоянную величину при всякомъ я, Этотъ анализъ приводитъ къ слѣдующему правилу нахожденія тахітиш'а ц тіштшп’а квадратной дроби:
Составляемъ уравненіе:
(аЬ* —-|- 2(ае' — 4" Ъс' — сѴ ~ 0 . . . (2).
.Если его корни ранные или .мнимые, дробь не имѣетъ ни тахітит'а, ни тіпітит’а; если же корни дѣйствительные и неравные, то меньшему корню соотвѣтствуетъ тахітит, большему тіпітит, если ко-эффиціентъ аЬ' — Ъа* положителенъ; напротивъ* меньшему корню отвѣчаетъ тіпгтит, а большему тахітит, если аЪ* — Ъаг 0; если же аЪ' — Ьаг — 0, дробь имѣетъ тахітит или тіпітит* смотря по тому, будетъ ли ас' — еа' < 0 или > О,
Ба’ — 1
Примѣръ I. Найти тахітит и тіпітит дроби •
Уравненіе, аналогичное (2), въ данномъ случаѣ есть: — 2(Кга 4“ = О,
откуда:
ж' —О, а/'=4. ’ о
Меньшему корню соотвѣтствуетъ абсолютный шіпіппші дроби, равный —со;
25
большему корню—тахітит, равный
Примѣръ II. Найти тахітит и тіпітит дроби
4-1
Уравненіе, дающее значенія х, обращающія дробь въ тахітит и тіпітит, въ данномъ случаѣ есть
— Ъх2 + 2(а — с)ж 4" & = О-
Корни этого ур—нія всегда дѣйствительные и неравные, ибо подрадикальное количество есть сумма двухъ квадратовъ. Такимъ образомъ, если Ь > О, дробь имѣетъ
а 4- с4- Ѵ(а а — с + Г(а — с)2 Ч-Ь2Ф
тахітит = —!——-9---------——> при х = ——\-------------— г і
о
. , аЧ-с — Ѵ(а— с)2-4Б2 а — с — — с)®Ч-&*
и тіттиш ~ ’------------4----~’ при х~ -----------------\
о
Обратно—если Ь < 0.
653. Второй методъ. Приравнявъ дробь произвольному, по опредѣленному количеству т* опредѣлимъ, при какихъ значеніяхъ перемѣннаго х она можетъ имѣть эту величину *п. Искомыя значенія х дастъ ур—ніе
’ = т> вли (« — + (Ь ~ Ь'»»)® + С — С'т = О,
изъ котораго _________________— ф — Ь'т) ~ Ѵф — Ъ'т)* — 4(а — «гт)(с Х________________2(а — а'т) ’
или, расположивъ подрадикальное количество по степенямъ найдемъ:
__Ъ'т — Ь “ 4а/с')л4* + 2(2ае' + + Ь2 — 4ас
Х 2(а~- а'т)
Положивъ
У2 4а'с' = р? 2ас' + 2са' — ЪЪ' = (}, д3 — 4ас = В, дадимъ подрадикальному количеству видъ
Риг*2(}?п-|-К . . . (1).
Для того, чтобы перемѣнное х было дѣйствительно, необходимо, чтобы под* радикальное количество не было отрицательнымъ, т.-е. чтобы было
. .(2).
Итакъ, т можетъ измѣняться только въ предѣлахъ, удовлетворяющихъ этому неравенству; соотвѣтствующія значенія х получатся изъ формулы
__Ъ'т — Ъ - ѵФт2 4- 2(}т4- В (3)
Х 2(а — а'т)
Здѣсь могутъ представиться три слѵчая: — РЕ > О, (і2— РК = О и
<і2—рк<о:
Первый случай: — РК О- Корни тринома (1) будутъ дѣйствительные неравные: пусть меньшій корень будетъ т', большій т”. Извѣстно, что при всякомъ значеніи т, лежащемъ внѣ корней, знакъ тринома (1) одинаковъ съ знакомъ коэффиціента Р; при всѣхъ же значеніяхъ лежащихъ между корнями, знакъ тринома противоположенъ знаку Р. Отсюда необходимость различать два случая:
1. Р>0, т.-е, знаменатель изучаемой дроби имѣетъ дѣйствительные неравные корни. Неравенство (2) будетъ удовлетворено, если количеству ш будемъ давать значенія, лежащія внѣ корней тринома (I); такимъ образомъ дробь т можетъ принимать два ряда значеній: отъ —до м' и отъ яг" до -рсо, и не имѣетъ значеній между т' и яг"; такимъ образомъ ея значенія лежатъ въ областяхъ (1) и (3):
— ео тг т" 4“ со
л (1) (3)
Черт, 131. ; >
См. Зад. III, § 658.
Заключаемъ, что тг есть наибольшее значеніе перваго ряда, а т" — наименьшее значеніе второго ряда, т.-е. тахітит дроби равенъ меньшему корню тринома (1), а тіпітит—большему его корню; и дробь не имѣетъ значеній между корнями тринома. Когда дробь принимаетъ максимальное и минимальное значеніе, подрадикальное количество формулы* (3) обращается въ нуль, и
____ Ъгт — Ъ Х 2 (а — а!ту
подставивъ сюда т* вмѣсто т, найдемъ я, соотвѣтствующій шахіпішп’у дроби, а замѣнивъ т количествомъ т'\ найдемъ х, соотвѣтствующій тіпішипРу.
При этомъ каждое свое значеніе меньшее и каждое значеніе большее т" дробь принимаетъ при двухъ различныхъ значеніяхъ х.
2. Р<0, т.-е. знаменатель дроби имѣетъ корни мнимые. Неравенство (2) будетъ удовлетворено, если количеству т дадимъ значенія, лежащія между корнями тринома (1); такимъ образомъ дробь т можетъ имѣть всѣ значенія въ предѣлахъ: т" т > т\ т.-е. значенія дроби лежатъ въ области (2), и она '
— со т' т" +со
(1) (2) (3)
«------------------------->
Черт. 132,
не имѣетъ дѣйствительныхъ значеній въ областяхъ (1) и (3). Заключаемъ, что менъшій коренъ тринома (1) есть тіпітит дроби* а большій—ея та-хітит. Соотвѣтствующія значенія х вычисляются по прежней формулѣ. Каждое свое значеніе между т* и т" дробь принимаетъ дважды, при двухъ различныхъ значеніяхъ а?; и только значенія т' и т" принимаетъ, каждое, при одномъ опредѣленномъ я-сѣ. См. Зад. I, § 656 и И, § 657.
Примѣры: 1. Найти тахітит и тіпітит дроби
а? —2я? + 21 — 14
Приравнявъ данную дробь произвольному количеству тт рѣшаемъ ур—ніе
й т^21 = *”» или х*— (26т)х Ц-(14т-|-21) = О, откуда __________
х = 1 -|- Зт Ч3 |/9т1 2 — 8т — 20.
Корни подрадикальнаго тринома суть: 2 и —д-‘ Такъ какъ въ данномъ случаѣ Р > 0, то заключаемъ, что тахітит дроби равенъ меньшему корню, а тіпітит—большему; слѣд.
тах. (т) = — у; тіпітит (т) = 2.
Подставивъ въ формулу х вмѣсто т, сперва [ — а потомъ 2, и замѣ-чая, что при этихъ значеніяхъ т подрадикальное количество' обращается въ нуль, находимъ:
10
^(т»х.)— 1 о
---3? ^(тіп.) = 1 4“ 3 .2 = 7.
2. Найти тах. и тіп. дроби
#2 —5^+1 ж - — х -н 1 ’
Приравнявъ дробь количеству т, и рѣшивъ полученное ур. относительно х* имѣемъ
5 — т — V— Зт2 — 2т + 2
Х~ ~~ 2(1 — тр
Корни подрадикальнаго тринома суть: —3 и —|— 2 а какъ Р<^0, то
заключаемъ, что большій корень есть шахітшп дроби, меньшій — ея ттітит; итакъ
тах. (т) == 2 тіпітит (т) = — 3.
О
Вычисливъ соотвѣтствующія значенія х по формулѣ х — находимъ: лах.
№
Второй случай: <і2—РК = 0. Триномъ (1) имѣетъ корни дѣйствительные , <4 г <1?
равные и общая величина ихъ ~ — р-; триномъ принимаетъ видъ Р(ш-грІ 5 а условіе дѣйствительности х—видъ:
Р °-
Заключаемъ, что триномъ всегда имѣетъ знакъ количества Р. Отсюда:
1. Р > 0. При всякомъ ш триномъ (1) остается положительнымъ, а при О
р обращается въ нуль, слѣд. дробь можетъ имѣть какую угодно величину, в слѣд. нѣтъ ни пшітішРа, ни тіштипі’а. Это можно было предвидѣть; въ самомъ дѣлѣ: — РК = (2а<У ^€а/1 — — (Ъ* — 4ас) (Ь'а —► 4а'с');
но въ данномъ случаѣ это выраженіе =0, а мы видѣли (§ 467), что при такомъ условіи триномы а#2-|-Ья + с и а'х* Ъгх -р с? имѣютъ одинъ общій корень, а слѣд. оба члена дроби—общаго множителя; сокративъ его, найдемъ
Отсюда видно, что задача всегда возможна; всегда найдемъ для х одну величину, и только одну, при которой дробь принимаетъ данную величину.
2. Р<0. Въ этомъ случаѣ триномъ (1) будетъ отрицателенъ при всякомъ т, кромѣ т = — слѣд. какую бы величину дробь т пи имѣла, кромѣ ве-личины — р1 остается мнимымъ, и только при т = — р з онъ дѣйствителенъ; слѣд., наворотъ, всякая дѣйствительная величина х должна дѣлать дробь равною иначе говоря, дробь должна имѣть постоянную величину, а сл.
не имѣетъ пи тах., ни шіп.
Можно доказать непосредственно, что когда совмѣстно имѣемъ Р<0 и — РН = О, то дробь имѣетъ постоянную величину. Въ самомъ дѣлѣ:
— РК = а'с'
г 4а'с;—Ъ'2
2агс* 3 Аа'с' •
(ас'
са')а. .
. (4).
По Р или Ьг* — 4а'сг 0, слѣд. 4а'с' — Ь'3 > 0, откуда 4а'с' > 0; слѣд. Ф — РК есть сумма двухъ существенно-положительныхъ количествъ, и потому можетъ быть нулемъ только тогда, когда каждое изъ этпіъ количествъ въ отдѣльности = 0; итакъ, должно быть:
= 0. . .(1) и ас'-са' = 0. . .(2),
пли, замѣнивъ въ (1) е' его величиною, выведенною изъ (2):
| 2Ье • “ 2Уса'= °» или & = &
I а с
( а' сг ’
т.-е. ,
а о с
но мы видѣли (§ 468), что при этихъ условіяхъ дробь имѣетъ постоянную величину, не зависитъ отъ х.
Примѣчаніе. Задача: найти прямо условія, необходимыя и до-_ ч ч е ах^ 4- Ьх + с
статочныя для того, чтобы дробь имѣла постоянную ве-
личину при всякомъ х?
1-й способъ. Оставаясь постоянною при всякомъ дробь должна имѣть одну и ту же величину и для трехъ различныхъ значеній х, напр., для х =—1 и слѣд. должно быть:
с __ а — Ь + с __ + с
ё ~ ~ а' + Ь' + с'’
откуда, по § 309, найдемъ:
е а-\-с Ь а Ь с
ё ат4-Ѵ У’ ИЛИ’ наконеи-ъ’ а'=^Б7=с'*
Эти условія, будучи необходимы, вмѣстѣ съ тѣмъ и достаточны; ибо какъ # скоро они выполнены, то, назвавъ общую величину равныхъ отношеній буквою к, найдемъ. а=а/с, 0 = 0^ с = сгс, и дробь беретъ видъ -* т.-е. = к.
2-й способъ. Пусть постоянная, впрочемъ, неизвѣстная, величина дроби будетъ к. Положить = звачитъ положить, что -{- Ъх с=
= й(а'о!2 Ъгх “Ь с или (а — -р (Ь — Ѵк)х 4” с — с = в, каковъ
бы ни былъ х. Отсюда, по § 72, заключаемъ, что
а — а'к=О Ь — Ь'& = 0, с — с'к=О или А = —
’ 1 1 а о с
Третій случай. (}я— РК<0. Въ этомъ случаѣ корни тринома (1) мнимые, слѣд. триномъ всегда сохраняетъ знакъ коэффиціента 1*. Отсюда:
1. Р > 0. Подрадикальное количество формулы х будетъ при всякомъ т положительно, а слѣдов. х дѣйствителенъ; такимъ образомъ дробь т можетъ имѣть какую угодно величину, п слѣд. не имѣетъ ни піахішшп'а, ни шіпітпт’а.
2. Р <1 0. Подраднкальное количество формулы х будетъ существенно-отрицательно, слѣд. при всякомъ т для х будетъ получаться мнимое значеніе; а слѣд. обратно, какое бы дѣйствительное значеніе мы пи дали перемѣнному дробь т не можетъ получить дѣйствительнаго значенія. Но это заключеніе, оче-
, + Ъх -I- с
видно, нелѣпо, ибо изъ ур—нія т = видно, что дѣйствительному
значенію х соотвѣтствуетъ дѣйствительное же значеніе дроби т. Стало быть, случай совмѣстнаго-существованія условій: Р<0 и (р-—РК< 0 невозможенъ.
Впрочемъ, можно доказать это и прямо; въ самомъ дѣлѣ, изъ формулы (4) видно, что когда Р < О, выраженіе У3 — РК представляетъ сумму двухъ ква-
дратовъ, а такая сумма никогда не можетъ быть отрицательною.
Частные случаи. Когда Р = О, подрадикальное выраженіе формулы х обращается въ 2фп + Н. Чтобы перемѣнное х было дѣйствительно, необходимо,
чтобы К
Если шіи.
Если
только
О, или 2(^п> — К. Отсюда:
), то слѣд. т’ш. (т) = —дробь имѣетъ
и пе имѣетъ шах.
О < О, то т < — Д? откуда піах. (т) = — дробь имѣетъ
только шах., и не имѣетъ шіп.
3) Если 4 = 0, неравенство приводится къ К<> 0; оно всегда удовлетво-, л. і (ас' — са'У* ж „
ряется; ибо въ этомъ случаѣ ол —- —э гдѣ а'с'>0, такъ какъ
Ь'а — 4а'<?'= 0. Слѣд. всякому значенію ш отвѣчаетъ дѣйствительное значеніе я-са: дробь не имѣетъ ни тах., ни тіп.
Изслѣдованіе приводитъ къ слѣдующему результату: Когда корни тринома Рт2 2(^н -{- И лшшіые или дѣйствительные равные > дробь не имѣетъ ни тах., ни тіп.; если же корни этою тринома дѣйствительные неравные, дробь имѣетъ тахітит и тіпітит, выражаемыя корнями тринома; соотвѣтствующія значенія х получаются изъ формулы
Ь — Ьгт 2(а—а'т)’
въ которой т нужно замѣнить корнями тринома.
О результатахъ этого изслѣдованія мы получимъ болѣе ясное понятіе, изслѣдуя измѣненія дроби при измѣненіи х отъ —ео до +<х>.
ПЕ Изслѣдованіе измѣненій дроби При измѣненіи
# X* О X с
X отъ —оо до -р 00.
654. Т е о р е м а.—Квадратная дробь непрерывна при измѣненіи х отъ а до если только въ' промежуткѣ между а и $ не содержится ни одинъ изъ корней знаменателя.
Во-первыхъ, очевидно, что данная дробь дѣйствительна при всякомъ дѣйствительномъ х, и что она конечна, если только значеніе, данное я-су, пе обращаетъ знаменателя въ нуль. Остается доказать, что если есть нѣкоторое значеніе ж, заключающееся между а и то количеству всегда можно дать приращеніе Л, на столько близкое къ пулю, чтобы и приращеніе К дроби уг само было какъ угодно близко къ нулю. Имѣемъ:
__ ах^2 -|- + с _Ь к ^)2 “I" + с + Ъ'хі + с'5 “Г 4- А)2 -|- -|- Л) + <?'’
~ [а(^і+703+&(жі+^0Н^](а%г+6^і+^г)—[а'(^1+/0я+^Х^+?іН’И(аж12+Ьа?|-|-с)
иля, по упрощеніи числителя,
1і {(ай1 — Ьа')^2 т- [(&&' — Ъа’)к + 2(ас'—+ [(ас* — а'с)к + (Ьсг — Б'е)]} + [а'(Яі + А)2 + &'(яі + й) + сКа^® 4- + с') *
По мѣрѣ приближенія Л къ нулю числитель стремятся къ нулю, а знаменатель къ Но не обращаетъ этого тринома въ нуль,
ибо интерваллъ отъ а до содержащій не содержитъ корней знаменателя; слѣд. вмѣстѣ съ Л и К стремится къ нулю; иначе говоря, можно приращенію Л перемѣннаго х дать значеніе настолько близкое къ нулю, чтобы и соотвѣтственъ ное приращеніе К дроби было также какъ угодно близко къ нулю; что и требовалось доказать.
Примѣчаніе. Если я-су дать значеніе обращающее въ нуль знаменателя дроби, то она вообще обратится въ безконечность^ испытывая при этомъ разрывъ непрерывности, перескакивая изъ Ч-ео въ ч-<^, если только корни знаменателя неравные, или если оба члена дроби не имѣютъ общаго множителя я — Если эти исключенія не имѣютъ мѣста, то слѣдуетъ опредѣлить знакъ безконечности, когда х приближается къ*‘я?п возрастая, и затѣмъ переходитъ чрезъ Для этого достаточно опредѣлить знакъ числителя при х=х^ зная знакъ и знаменателя, будемъ знать и знакъ дроби.
655. Прн изученіи измѣненій дроби будемъ держаться слѣдующаго порядка.
1. Опредѣляемъ шахітпт и шінітит, если таковыя имѣются, и соотвѣтственныя значенія х.
2, Приравниваемъ нулю числителя, потомъ знаменателя и рѣшаемъ полученныя ур—нія: корни перваго ур—нія, если они дѣйствительны, дадутъ тѣ значенія при которыхъ дробь обращается въ нуль; второго—тѣ значенія при которыхъ она обращается въ
3. Опредѣляемъ значеніе дроби при х = О.
4. Наконецъ, ищемъ предѣльныя значенія дроби, т.-е. при # = Ч-ео.
Расположивъ значенія х въ порядкѣ ихъ возрастанія, а противъ пихъ соотвѣтствующія величины дроби, составимъ таблицу, ясно показывающую измѣненія дроби по величинѣ и знаку. Для наглядности такую таблицу будемъ сопровождать графическимъ изображеніемъ измѣненій дроби.
Задача I.
дроби пРи непрерывномъ
656. Изслѣдовать измѣненія
возрастаніи х отъ —ео до
Слѣдуя вышеозначенному плану, опредѣляемъ:
1. Махітит и тіпітит дроби.—Приравнивая данную дробь произвольному количеству у, получаемъ ур—ніе
+7 = яли (3 — 4у)ж44~(2 + 10у)ж— (3-|-7у) = 0.
изъ котораго (расположивъ подрадик. колич. по степенямъ у):
_ (1 + 5у) Зу* +19// + 10
3-4у
Приравнявъ подрадик. выраженіе нулю и рѣшивъ ур. Зу* —19у—10 — 0, находимъ: у'= —0,488, у"= 6,821; а какъ въ данномъ случаѣ коэффиціентъ при у2 подъ радикаломъ отрицателенъ, то заключаемъ, что большій коренъ есть шахішпт дроби, меньшій —- ея тіпітит. Итакъ
тах. (у) = 6,821; шіп. (у) =— 0,488.
Соотвѣтствующія значенія ^^уть:
— (1 + 5.6,821) 3 — 4*6,821 ’
1.44а;
ІПІП. ---- ~
(1 + 5. — 0,488) 3-4.-0,488
= 0,291.
Заключаемъ, что дробь можетъ измѣняться только между - 0,488 н -|-6,821 и не имѣетъ значеній, меньшихъ —0,488 и большихъ 6,821. Всякое же значеніе между этими предѣлами она принимаетъ два раза, при двухъ различныхъ значеніяхъ я, потому что для каждаго у, лежащаго между—0,488 и-]-6,821, мы изъ формулы (1) находимъ два различныхъ дѣйствит. значенія х,
2. Нулевыя значенія дроби, соотвѣтствующія конечнымъ значеніямъ х. Алгебраическая дробь обращается въ нуль, когда обращается въ нуль числитель А. знаменатель же В остается отличнымъ отъ нуля; или когда В обращается въ со, причемъ А остается конечнымъ. Но В — выраженіе цѣлое относительно х, сл. оно не можетъ обратиться въ со нрп конечныхъ х\ остается приравнять А нулю. Положивъ Зя2-|-2іе—3 = 0 и рѣшивъ это ур., найдемъ:
х' = —1,387, я" = + 0,721.
3. Безконечныя значенія дроби.—Дробь не обращается въ сс; въ этомъ убѣждаемся, приравнявъ знаменателя нулю, и рѣшивъ ур—ніе 4ха—10#-|-7=0: найдемъ для х мнимыя значенія.
4. Значенія дроби при х = 0.—Положивъ х = 0, найдемъ у = —
5. Предѣльныя значенія дроби.—Положивъ а? —+ находимъ, что у
СКІ принимаетъ пеояред. видъ
для раскрытія котораго дѣлимъ числ. и знам. на
ж2 и затѣмъ полагаемъ я: = Ч-ео, Такимъ образомъ получаемъ, что при # = у = -}
Результаты этого изслѣдованія даютъ слѣдующую таблицу-измѣненій дроби:
Черт. 133.
Кривая измѣненій дроби. Взявъ оси координатъ хя' и уу' и произвольную прямую за 1, наносимъ на оси х-овъ 0Р”= —1*387 и получаемъ точку Р",*Для которой ордината равна О, и въ которой, слѣд., кривая пересѣкаетъ ось отрицательныхъ я-овъ. Отложивъ 0Ц = — 0,428, имѣемъ точку М, въ которой кривая пересѣкаетъ ось отрицательныхъ у-овъ. Нанеся 0Р' = 0,291 и возставивъ въ точкѣ Р' перпендикуляръ къ оси я-овъ, откладываемъ на немъ Р'М'=—0,488 — ординату тіпітит. Нанеся 0І\ = 0,721, получаемъ другую точку Р4, въ которой кривая пересѣкаетъ ось я-овъ. 0Р'"= 1,445 даетъ точку Р'", въ которой, проведя перп. г')Г= 6,821, имѣемъ наибольшую ординату.
3
Наконецъ, отложивъ 01 = и проведя черезъ точку I параллель оси ж-овъ, имѣемъ ассимптоту кривой, къ которой кривая неограниченно приближается, сливаясь съ нею на безконечныхъ рад^тояніяхъ отъ оси у-овъ.
Соединяя построенныя точки непрерывною кривою, получаемъ линію, представленную на черт, 133, Такъ какъ каждую свою величину дробь принимаетъ только два раза, при двухъ различныхъ значеніяхъ ж (напр, у = 3 при я=0Т и х = ОС), то всякая прямая параллельная хх' пересѣкаетъ кривую только въ двухъ точкахъ. Исключеніе составляютъ тах, в-шш.: прямыя, параллельныя оси х и проведенныя отъ нея, одна въ разстояніи —0,488, другая 6,821, встрѣчаютъ кривую, каждая въ одной точкѣ, иначе — касательпы къ кривой» Такимъ обр., кривая не можетъ представлять иныхъ изгибовъ, кромѣ указанныхъ на чертежѣ. Чертежъ наглядно показываетъ, что —0,488 есть наименьшая ордината или тіпітпт дроби, а —|—6,821 —наибольшая, или тахітпт дроби.
Задача П.
657. Изслѣдовать измѣненія дроби ристаніи х отъ —оо о*о -[-со,
яри непрерывномъ 'воз-
1. Махітит и тіпітит дроби,—Приравнявъ дробь у-ку, получаемъ ур.
^+43+5 = вли <2 ~ . ж + 3 — 5^ = О,
откуда * __________
__2у ~ /—у2 + ІЗу — 6.
Корпи подрад. тринома суть: у’ = 0,48 ц у" = 12,52. и какъ коэф, при у* отрицателенъ, то заключаемъ, что
тах. (у) =12,52; ттітпт (у) = 0,48,
Соотвѣтствующія значенія я суть:
_ 2.12,52 _ ^тьх‘“ 2 — І2,52~
_ 2,0,48
2__0,48— 0,63.
Такимъ образомъ дробь можетъ измѣняться только между предѣлами 0,48 и 12,52, принимая каждое свое значеніе между этими предѣлами два раза — при двухъ различныхъ значеніяхъ х.
2. Нулевыя значенія дроби.—Такъ какъ между предѣлами 0,48 и 12,52 не содержится нуль, то дробь ни при какомъ дѣйствительномъ х не обращается въ нуль. Это видно и изъ того, что, приравнивая числителя нулю, получаемъ ур. 2ж24~3 = 0, имѣющее мнимые корни.
3. Безконечныя* значенія дроби.—Дробь не обращается въ со, ибо корни знаменателя мнимые.
3
4. Значенія дроби при х=О,—Положивъ х=О, имѣемъ у = Сл. кри-о
X - I 3
вая пересѣкаетъ ось у на разстояніи отъ начала.
5. Предѣльныя значенія дроби,— Какъ и въ предыдущей задачѣ, найдемъ, что при я^=Ч-со. у=2. Слѣд. кривая неограниченно приближается къ ассимп-тотѣ, параллельной оси х и отстоящей отъ нея на 2.
я’4-1
я® — 4^4-3
при измѣненіи х отъ
658. Изслѣдовать измѣненія дроби — ОЭ (?0
1. Махітит и тіпітит.—Положивъ
—или О—У>8 + 4У ®4-1“Зу = О,
находимъ
„ — 2у — 4- 4у— 1
“V------------------ *
1 —у
Корпи тринома з/2 + 4у — 1 суть: у* — — 4,236; /'= 0,236; а какъ коэффиціентъ при у* положителенъ, то
тах. (у) = — 4,236; шіп. (у) =0,236;
соотвѣтствующія значенія х суть: а?шлх. = Ъ618 Ятіи. =— 0,617.
2. Дробь не обращается въ нуль, ибо числитель существенно положителенъ.
3. Дробь обращается въ го, или претерпѣваетъ разрывъ непрерывности при двухъ значеніяхъ х* обращающихъ знаменателя въ нуль; именно при я/ = 1 и я" = 3. Для опредѣленія знаковъ безконечности, замѣчаемъ, что числитель дроби при всякомъ х положителенъ, сл. нужно изслѣдовать знаки знаменателя. Обозначивъ буквою Л произвольно малое полож. количество, замѣчаемъ, что х = 1 — Л и х = 3 -1- к будутъ находиться внѣ корней знаменателя, и слѣд. при этихъ значеніяхъ х знаменатель положителенъ, а потому и у > 0; затѣмъ, я = 14-А и я = 3 — Л содержатся между корнями знаменателя, а потому знаменатель и вся дробь при этихъ значеніяхъ х отрицательны. Отсюда видно, что если измѣнять х отъ — го непрерывно до то при д;=1 и при #=3 дробь претерпѣваетъ ^разрывъ непрерывности, перескакивая изъ въ — го, ѣъ первомъ случаѣ, т.-е. при я = 1, и изъ —го въ во второмъ, т.-е. при # = 3.
4. При х=0 дробь обращается въ
5. При д? = -+-го она равна !•
Таблица измѣненій дроби.
Значенія X Значенія У Знакъ У
— ГО — 0:,617 1 0,236 (тіп.) -рго +
1+л 1,618 3-Ь — 4,236 (шах.) 1
34-ь 4-ГО 4- го і
।
Кривая измѣненій.
Кривая измѣненій дроби.—Намѣтивъ точки М' и М\ соотвѣтствующія тпах. и тіп. дроби, проводимъ чрезъ нихъ параллели оси л'-овъ: кривая не имѣетъ точекъ между этими параллелями. Затѣмъ наносимъ 0А = 1 и 0В = 3 и черезъ точки Л и В проводимъ параллели оси V, которыя будутъ служить ассимпто-тамп кривой въ мѣстахъ разрыва непрерывности. Такъ какъ при # = У = 1, то параллель оси х на единичномъ отъ пея разстояніи будетъ служить 3-ею ассимптотою. Наконецъ, замѣчая, что для всѣхъ #-овъ, лежащихъ внѣ 1 и 3, дробь >0, и <0 для всѣхъ #-овъ, лежащихъ между 1 и 3, заключаемъ, что точки кривой для х < 1 и для х > 3 находятся въ области положит. ординатъ, точки же кривой для 1 < х < 3 находятся въ области отрицат. ординатъ. Такимъ образ. получаемъ кривую, изображенную на черт. 135.
Задача IV.
дроби
659. Изслѣдовать измѣненія измѣненіи х отъ —со до -|--схл
1. Міттшп и тіпітит.—Положивъ
непрерывномъ
10 = у’ или —(5 — 8у~)х — 4 + 1 Оу = О,
находимъ
__5 — 8?/ ± I7264г/1 — 2401/ 4-57
•
Убѣдившись, что корни подрадикальнаго выраженія мнимые, заключаемъ, что оно всегда будетъ положительно, а потому дробь не имѣетъ ни тах., ни тіп.
2. Приравнивая числителя пулю, найдемъ значенія х, при которыхъ дробь обращается въ 0; эти значенія суть:
я/= — 0,638 и #" = 3,138.
3. Приравнивая знаменателя 0, получимъ значенія при которыхъ дробь обращается въ со; эти значенія суть:
— — 0,824 и х. — 2,424. 4* ' Ж г
Для опредѣленія знаковъ безконечности, даемъ дроби видъ: ' _ 2(х4-0,638..)(*—3,138)
У ~ 5(3! + 0324..) (х — 2,424..)’
Такъ какъ х =:— 0,824 — А лежитъ какъ внѣ корней числителя, такъ и внѣ корней знаменателя, то и числ. и зн. дроби, а потому и самая дробь, положительны; #= — 0,8244“^ находятся внѣ корней числителя и внутри корней знаменателя, слѣд. при этомъ значеніи х числитель > О, а знаменатель <С О» а потому дробь отрицательна. Заключаемъ, что при переходѣ х чрезъ —0,824 дробь претерпѣваетъ разрывъ непрерывности, перескакивая изъ -роэ въ — Подобнымъ же образомъ убѣдимся, что когда я, возрастая, проходитъ чрезъ 4“ 2,424, дробь перескакиваетъ изъ въ —оо.
4* При я = 0 имѣемъ; ^ = |*
2
5* При = + находимъ: у = -
Кривая измѣненій дроби.
Таблица измѣненіи дроби.
Значенія X Значенія. У Знакъ У
—0,82 4—іі 2 ‘ 5 +
—0,824+7» ♦ — 0,638 6 * ? +2,424—А — ОС 6 2 + 5
+2,424+7» + 3,138 к ъ +'со СЛі ю • 0-1 8 1
• Таблица измѣненій дроби показываетъ, что величина дроби постоянно увеличивается, но претерпѣваетъ два, раза разрывъ непрерывности: одинъ разъ при переходѣ х чрезъ -—0,824. другой разъ при переходѣ х чрезъ 2,424: въ томъ и другомъ случаѣ дробь перескакиваетъ изъ въ —со.
2
Кривая измѣненій. Отложивъ на оси у линію ОК — проводимъ че-резъ точку К параллель оси затѣмъ, отложивъ на оси х линіи 0Н =—0,824 и 0В=-р2,424, проводимъ черезъ точки Н и В параллели оси у. Такимъ обр. получаемъ три ассимптоты вѣтвей кривой* Отложивъ на оси ж линіи: 0А =—0,638 и ОС = 3,138, получимъ точки, въ которыхъ кривая пересѣкаетъ ось аювъ. Ось у она пересѣкаетъ въ точкѣ К.
Задача V.
660. Изслѣдовать измѣненія ‘ дроби измѣненіи х отъ —сс до
2х2 — 7я? + 3 ж2 — 7я -рТ2
при непрерывномъ
1. Махітит и тіпітит.—Положивъ
= или (2-у)»»-7(1-1^ + 3(1-430 = О,
находимъ
7(1 - у) ± Ѵ^+Юу + 25
Замѣчая, что ?/3-)-10г/-|-25 = (у-|-5)а и что, слѣд., подрадикальвое выра-женіе всегда положительно, заключаемъ, что дробь не имѣетъ ни шах., ни тіп*
Если у-ку дадимъ какое-либо значеніе, то для х найдемъ два соотвѣтственныхъ значенія; только при у ——5, х принимаетъ одно значеніе = 3, Итакъ, всякую свою величину дробь принимаетъ при двухъ различныхъ значеніяхъ х\ кромѣ величины, равной —5, Значенія соотвѣтствующія данному у, суть:
изъ которыхъ первое не зависитъ отъ у. Эта особенность объясняется тѣмъ, что числ. и знам. дроби имѣютъ* общій корень ж —3 и слѣд* при # = 3 оба члена дроби равны О, а дробь неопредѣленна.
Если сократить дробь на х— 3, она приметъ видъ
2x^1 ----ч
х— 4
1 — 4Т откуда п—у;
всякой величинѣ V соотвѣтствуетъ только одно значеніе х^ слѣд. при возра-станіи х отъ —оэ до 4“^° дробь ---------т проходитъ только одинъ разъ чрезъ
всякое свое значеніе; обращается въ О при ж=п въ х при я = 4; а при а;=-}- со обращается въ 2. Замѣтивъ при этомъ, что при # = 4— Ь, Т=—со, а при ж = І = -рсо, выразимъ ходъ измѣненій сокращенной дроби таблицей:
Черт* 137.
25с2 — 7х + 3 я* —7л+Т2’
Что касается дроби
’то какъ она - принимаетъ какую угодно
величину при я = 3, то чтобъ изобразить вполнѣ ея измѣненія, нужно къ кривой присоединить прямую Ы/, параллельную оси Оу и пересѣкающую ось я-овъ
въ разстояніи 0А = 3 отъ начала координатъ.
Задача VI.
661. Изслѣдовать измѣненія дроби измѣненіи х отъ —со до Ц-со.
Положивъ
ж2 — 8з? +15
З®2 — 24х 45
при непрерывномъ
я2_8*4-15
ЗаЯ-—24Іг-|-45 — У'
или
или
(1 - Зу)^ - 8 (1 - Зу)я +15 (1 - Зу) = О,
(1 - Зу) (х« - 8я+ 15) = О,
находимъ, что ур—ніе удовлетворяется при всякомъ у, когда
равно нулю, т.-е* когда # = 3 и я =5, и, кромѣ того, при всякомъ х, если только у = |- Слѣд. при х = 3 и# = 5, у можетъ имѣть какую угодно величину, и кромѣ того у = ^ при какомъ угодно Это объясняется тѣмъ, что оба члена дроби имѣютъ одинаковые корпи:
_ (х —3)(ж-5) у~ 3(®-3)(я;-5)’
при # = 3 и я=5 величина дроби неопредѣленна; а если сократить дробь на (ж—3)(х — 5), то у дѣлается =д, каковъ и
бы ни былъ х.
Совокупность рѣшеній ур—нія #2—8я-|-15 = у(3я*“24#-|”45), или (#я—8#-415)(Зу—1)=О геометрически изображается двумя параллелями оси у, отстоящими отъ начала на 0А = 3 и 0В = 5, и параллелью оси х> отстоящею отъ начала на 01 = ^ □
662. Задача. На продолженіи стороны Черт. 138.
АВ даннаго прямоугольника АВСВ взятъ та-
кую точку М, чтобы сулла плодадей треугольниковъ АМХ и ВСХ была
тіпіта.
Когда точка М движется по прямой ВМ отъ А внизъ, 1
сумма площадей, вначалѣ равная прямоугольника, начинаетъ уменьшаться: такъ для точки М' треуг* СА8 замѣняется меньшимъ М'АЙ; но когда точка М займетъ положеніе ₽, при которомъ А? = АВ, сумма площадей снова становится равною прямоугольника, сл* при перемѣщеніи точки М отъ А къ Г эта перемѣнная сумма прошла черезъ тіпітит.
Пусть АВ = а, ВС = 5, АМ = #; выраженіе суммы у будетъ:
Черт. 139*
АИ РХ _ Ъ х а а-|-®’
откуда А.Х — .—»
1 а-[~®
ВХ = а-і-х’ и сл^Доват‘
! Ь«2 , Ъ(аЗ + ж»)
У 2(« + ®) ' 2(«4-х)’ или У 2(« + *) ‘
Опредѣляемъ х такъ, чтобы сумма площадей имѣла величину т. Для этого беремъ ур—ніе
Ь(а2 4- я?)
2(а-|-я:) ~тг ПЛИ
Ьх* — 2тпх а(аЬ — 2т) = О,
откуда
ні ~ У'т2 — ай (ай — 2т)
• (1).
Чтобы сумма площадей могла имѣть величину т, необходимо и достаточно, чтобы этой величинѣ т отвѣчало дѣйствительное и положительное значеніе ж. Но х будетъ дѣйств.,.если т2 — аЪ(аЬ — 2т) О,
или т2-}~2айт — а2й2^0 . _ , (2).
А ргіогі видно, что корни тринома (2) дѣйствительные, неравные и противоположнаго знака; слѣд. неравенство (2) будетъ удовлетворено такимъ .положительнымъ т, которое не меньше положительнаго корня тринома; т.-е. необходимо, __чтобы т^ай(|/2— 1). Итакъ, сумма площадей не можетъ быть <^аЬ(}/2— 1); смотримъ, можетъ ли она равняться аЪ()/2~ 1). Когда т достигнетъ этого предѣла, тогда будетъ
х = ^ = а(/2 — 1);
это значеніе х положительно и сл. можетъ быть взято; поэтому тіпіпшт ($) = аЬ(р/2 —1), а соотвѣтствующее значеніе х = а(|/2— 1).
Повѣрка. Полагаемъ х=а(|/2 — 1) ± А, гдѣ А произвольно мало, и подставляемъ это значеніе х въ выраженіе функціи. Найдемъ
(2 — /’2)аѢ ±аЬ(^2 — 1)А
Вопросъ приводится къ провѣркѣ неравенства:
(2-}/2)а’Ь±а6(/2-1)ЛН-^- _
---------- -----------1>аЬ(/2 - 1),
а
которое, по освобожденіи отъ знаменателя и по упрощеніи, приводится къ
что вѣрно.
ІѴ\ Махіта и тіпіта функцій нѣсколькихъ перемѣнныхъ.
663. Произведеніе двухъ перемѣнныхъ множителей, сумма которыхъ постоянна и равна а, возрастаетъ по мѣрѣ тою, какъ абсолютное значеніе разности перемѣнныхъ уменьшается.
Доказательство. Пусть перемѣнные множители будутъ х и у, а ихъ постоянная сумма пусть будетъ а:
х-\-у = а . . . (1)
Взявъ тождества (ж -ру)2 = 4~ У* -ХУ и = —2^,
и вычтя второе изъ перваго, найдемъ (#4“Ю2— (#—=
Замѣнивъ въ силу условія (1), равнымъ количествомъ а, имѣемъ а* — (х — у)2 = 4ху, что можно написать такъ:
Такъ какъ уменьшаемое сохраняетъ постоянную величину, то произведеніе будетъ измѣняться съ измѣненіемъ вычитаемаго, и именно, по мѣрѣ уменьшенія (ж —і/)2, или, что то же, | х— у | , произведеніе ху будетъ увеличиваться. Отсюда слѣдуетъ, что ху достигнетъ тахішшп’а, когда |я — у| достигнетъ ті-пітипГа, и мы находимъ теорему;
Произведеніе двухъ перемѣнныхъ множителей, сумма которыхъ постоянна (и равна а), Эосиші'аетг наибольшей величины, когда абсолютное значеніе ихъ разности достигаетъ своей наименьшей величины; въ частности, если эта разность можетъ обратиться въ 0, т.-е. если х можетъ сдѣлаться = у, то произведеніе будетъ имѣть тахітит, когда множители сдѣлаются равными,
Если имѣетъ мѣсто послѣдній случай, то тахітит будетъ при х = у=^ м х а?
а самый тахітит будетъ
71
Примѣчаніе. Для этого послѣдняго случая можно доказать теорему еще такъ. Пусть одинъ множитель ~х; другой будетъ а — х; произведеніе ихъ выразится формулою у = х(а— х) или —это есть квадратный триномъ, свободный членъ котораго =0. Изслѣдуемъ измѣненіе тринома при - измѣненіи х отъ —-е© до 4”°^* Удобную для такого изслѣдованія форму мы
найдемъ, придавая и вычитая что даетъ:
а
При х = —с© и функція у ——^©. При увеличеніи х отъ —до У
возрастаетъ отъ — с© до -р затѣмъ при увеличеніи х отъ Д° т у
уменьшается отъ до —сс. Получаемъ слѣдующія — таблицу и кривую измѣненій функціи:
Черт. 140.
тт - .
Итакъ, произведеніе сперва возрастаетъ отъ —со до а затѣмъ уменьшается отъ до — со; слѣд. оно не имѣетъ тіпіпшт’а, но имѣетъ тахішшп а2 л , .а а
= -д-’ Соотвѣтствующее значеніе х есть а другого множителя: а — или
2? т.-е. произведеніе получаетъ наибольшую величину, когда оба множителя дѣлаются равными, предполагая, что ихъ можно сдѣлать равными.
Косвенное доказательство. Вмѣсто того, чтобы изслѣдовать измѣненія произведенія я (а — я), соотвѣтствующія измѣненію ж отъ — до можно предложить себѣ вопросъ: при какомъ значеніи х это произведеніе получаетъ данную величину изслѣдовать рѣшеніе, и такимъ образомъ найти, между какими предѣлами величина т произведенія можетъ измѣняться. Такимъ образомъ для опредѣленія х имѣемъ ур—ніе
х(а — х) = ті или х~—ая-|-?п = 0,
откуда
Чтобы х было дѣйствительно, необходимо, чтобы подкоренное количество а*
не было отрицательнымъ, т -е. необходимо, чтобы т С — • Заключаемъ, что произведеніе т можетъ имѣть всѣ величины отъ —со до ; слѣдов. оно не имѣетъ тішшшп а, но имѣетъ тахітиш Но когда »»=-^ радикалъ обра-
щается въ 0, и я = поэтому и другой множитель, какъ равный а—я, обра-&
щается въ сл. произведеніе имѣетъ шахітит, когда множители равны. Но . Д - X
не всегда х можетъ принимать значеніе соотвѣтствующее алгебраическому тла-іи
хітиш’у.
664. Примъ р ы.—1. Произведеніе двухъ множителей, которыхъ сумма = 12, можетъ имѣть всѣ величины отъ —сс до-|-36; тахітит произведенія равенъ 36, а соотвѣтствующіе множители равны, каждый, 6.
П. Произведеніе двухъ множителей, которыхъ сумма равна = — 12, можетъ имѣть всѣ величины отъ — со до -р-36; слѣд. тахітит произведенія равенъ 36, каждый производитель = — 6,
665. Задача I. Изъ всѣхъ прямоугольниковъ, вписанныхъ въ данный треугольникъ, какой имѣетъ наибольшую плогцадъ?
Если основаніе ВЕ прямоугольника передвигать отъ вершины тр—ка до его основанія, то площадь прямоугольника будетъ измѣняться отъ нуля до нуля, и слѣд. проходитъ чрезъ тахітит. Пусть Ь и А будутъ — основаніе и высота даннаго треугольника (черт. 37), х и у— основаніе и высота вписаннаго прямоугольника ОЕЕС. Площадь прямоугольника Изъ подобія треугольниковъ АВС н ОВЕ имѣемъ: откуда У = — ж); слѣдов.
площадь ху выразится произведеніемъ:
Такъ какъ постоянный множитель не вліяетъ на условія ішіт,, то вопросъ приводится къ опредѣленію шах. произведенія х (Ь — ж). Сумма множителей х и Ь — х равна постоянной величинѣ Ь, слѣд. произведеніе имѣетъ ша-хішшщ когда множители равны, т.-е. когда х = Ь — х, откуда х = -; но въ такомъ случаѣ изъ ур—нія у = (Ь — х) найдемъ х — самая же макси-мальная площадь ху равна у, т.-е. половинѣ площади треугольника. Итакъ: наибольшій изъ всѣхъ прямоугольниковъ, какой можно вписать въ треугольникъ, имѣетъ основаніе и высоту вдвое меньшія основанія и высоты треугольника.
Задача II. Изъ всѣхъ конусовъ, описанныхъ около даннаго шара, какой имѣетъ наименьшій объемъ?
Пусть будетъ АВС конусъ, описанный около шара Ой. Если его веріпира А будетъ перемѣщаться по оси ПА отъ М до безконечности, объемъ конуса будетъ измѣняться отъ со до со, и слѣд. пройдетъ чрезъ тіпітпт. Чтобы найти этотъ тіпітит, обозначимъ высоту ОА буквою х, объемъ будетъ:
Ѵ = |г. СП’.ж.
Подобные тр—ки АСП и АОИ даютъ; =
НО А№=х(х — 2П); слѣд. Черт. 141.
„ 1
'=3Л-^=2К-/
Постоянный множитель «тсВ* не измѣняетъ условій тіпітиш’а функціи, а по-
ф2
томѵ V.имѣетъ наин. вел. при тѣхъ же обстоятельствахъ, какъ и -—Но
х__2IX
тіпітит этой функціи соотвѣтствуетъ тахітпю’у обратной: —-2—, которую
1 / 2К\
можно представить въ видѣ: - 1—• —I; наконецъ, мы не измѣнимъ условій тахітшпЪ) введя постоянный множитель 2В. Такимъ образомъ вопросъ приведенъ къ опредѣленію шах. функціи
2К2К\ X \ X )
„ . іі 2К 1 2Е
Замѣчая, что сумма перемѣнныхъ факторовъ — и 1 ~ — равна постоянной величинѣ 1, заключаемъ, что произведеніе достигнетъ наибольшей величины, когда оба фактора сдѣлаются равными, т.-е. когда ~х~1 *-откуда
что по несовмѣстно съ свойствомъ задачи. Итакъ, описанный конусъ имѣетъ наименьшій объемъ, когда высота конуса вдвое больше діаметра; самый же объемъ д
= т.-е. вдвое больше шара.
666. Въ предыдущихъ параграфахъ мы не разъ дѣлали оговорку, что перемѣнныя х и сумма которыхъ постоянна, не всегда могутъ быть сдѣланы равными, по свойству самой задачи; таковы» напр., нѣкоторые вопросы геометріи. Въ такихъ случаяхъ» произведеніе достигаетъ шахішппг а, когда абсолютное значеніе разности перемѣнныхъ достигаетъ шіштшп’а. Вотъ нѣсколько задачъ, иллюстрирующихъ подобные случаи.
г Задача I. Данъ кругъ и хорда АВ; провести
діаметръ такъ чтобы произведеніе отрѣзковъ СМ
-У х. и М, образуемыхъ на немъ хордою, и.ип»до на«-IМ \ большую величину*
\ Сумма отрѣзковъ СМ и МВ, при всякомъ положеніи О I діаметра, постоянна; но эти отрѣзки не могутъ быть / сдѣланы равными; слѣд. ихъ произведеніе достигнетъ / наибольшей величины, когда разность ихъ будетъ наи-меньшая, а это будетъ тогда, когда отрѣзокъ МВ до-л р стнгнетъ своего наименьшаго, а отрѣзокъ СМ своего наи-
Че т 142 большаго значенія, т.-е. когда діаметръ станетъ перпендикуляренъ въ хордѣ. Требуемый діаметръ есть ЕЕ.
Задача II. Найти тахітит произведенія (3 — я3) (7 -|-я’)?
Сумма факторовъ постоянна н равна 10; приравнивая ихъ, получаемъ ур—ніе
3 — х* = 7 -|-яа, или хг3 = —2: равенство невозможное ци при какомъ дѣйствительномъ х* Итакъ, находимъ тіпішшп абсолютной величины ихъ разности: 2я3=[“^- Міпітшп этого бинома, очевидно, есть 4, достигаемый при # = 0; слѣд. тахітит произведенія равенъ 21, при гг = О.
Задача III. Даны: кругъ 0 и внѣ его прямая Ю. Пусть АВС будетъ другая прямая, перпендикулярная къ Й и пересѣкающая кругъ въ точкахъ А и В, а прямую МК—въ точкѣ С. При какомъ положеніи прямой АС произведеніе АВХВС достигаетъ наибольшей величины?
Произведеніе АВХ^С будетъ имѣть шахітшп при тѣхъ же обстоятельствахъ, какъ и половина этого произведенія
* ^Хвс.
Проведя чрезъ центръ параллель РР' къ линіи МИ, пересѣкающую АВ въ Е, АВ
замѣчаемъ, что -у=ЕВ. Такимъ образомъ, вопросъ приводится къ изученію измѣненій произведенія ЕВХВС, котораго множители имѣютъ постоянную сумму, ибо
ВЕ + ВС = ЕС = ОИ = а (пост*)*
Нужно различать два случая:
I. Оу<уН.—Перемѣщая точку В по окружности, замѣчаемъ, что ВЕ всегда остается меньше Оу, а ВС всегда больше УН; слѣд*
ВЕ < ОУ < УН < ВС, а потому ВЕ<СВС. Такимъ образомъ, сомножители ВЕ и ВС никогда не могутъ сдѣлаться равными; заключаемъ, что ихъ произведеніе достигнетъ тахіпіиш’а, когда разность ВС — ВЕ
достигнетъ ттштшп’а; а это будетъ тогда, когда уменьшаемое ВС достигнетъ своего тіпітнш’а уН, а вычитаемое ВЕ — своего пшішит’а оу, т.-е. когда прямая ЕС приметъ положеніе ОН. Итакъ, тахітит произведенія = 2Оу X УН = 2К($— К), если положить Оу = Н и ОН — г?.
II. Оу>уН*—Въ этомъ случаѣ существуетъ два положенія сѣкущей, при которыхъ будетъ КВ = ВС; ибо средина 8 прямой ОН лежитъ въ этомъ случаѣ между О и У, и потому параллель къ МИ чрезъ 8 пересѣчетъ окружность въ двухъ точкахъ Р н и сѣкущія Е1, Е'Р даютъ
ЕЕ = ГІ =ЕТ = ЕГ=^.
Черт. 144.
Такимъ образомъ, произведеніе получаетъ относительный тахітит въ двухъ положеніяхъ сѣкущей; этотг» тахітит
= 2ЕЕХП = 2.5.5=^.
Кромѣ того, въ этомъ случаѣ сѣку
щая ОН даетъ относительный тіпітит. Въ самомъ дѣлѣ, измѣненія произведенія, отвѣчающія измѣненіямъ разности ВС — ВК при перемѣщеніи точки В по дугѣ РУР', видны изъ слѣдующей таблицы:
Когда точка В нахо-
дится въ.......Р .... Г...................У.............Г' .... Р'
Разность ВС—ВК=гі умен. до О увел. до |2К— й[ умен. до О увел. до Л. Произв. 2ВК.ВС...0 увел. до умен. до 2Н(й—К) увел. до ~ умен. до О.
Итакъ, дѣйствительно имѣетъ мѣсто относительный шіпіпіиш = 2К(й—В), когда В находится въ 9.
667. Теорема. Произведеніе нѣсколькихъ положительныхъ множителей^ сумма которыхъ постоянна} и которые никакимъ другимъ условіямъ не подчинены не можетъ бытъ больше произведенія, полученнаго отъ замѣны каждаго изъ этихъ множителей ихъ ариѳметическою срединою.
Эта теорема была нами доказана для случая двухъ перемѣнныхъ множителей, сумма которыхъ сохраняетъ постоянную величину, причемъ не было необходимости налагать условія, чтобы множители были положительны.
Но распространеніе теоремы на опредѣленное число множителей, большее двухъ, требуетъ, чтобы множители могли принимать только положительныя значенія.
Обычное доказательство теоремы, которое приведено было въ 1-мъ изданія нашего курса, не свободно отъ нѣкоторыхъ возраженій, и потому замѣнено было, почти одновременно (въ 1887 г.), строгими доказательствами; одно изъ нихъ дано академикомъ Г. Дарбу (деканомъ парижскаго Факультета Наукъ), другое— профессоромъ Сорбонны Гурза. По строгости и изяществу пріемовъ оба доказательства принадлежатъ къ образцовымъ, оба заслуживаютъ одинаковаго вниманія; приводимъ и то и другое.
Доказательство Дарбу. Пусть дано ш независимыхъ перемѣнныхъ-положительныхъ и имѣющихъ постоянную сумму
ж > О, я>0, ^>0, + * + + = соіі8І_
Покажемъ сначала, что если теорема вѣрна для т множителей, то опа будетъ вѣрна и тогда, когда число множителей будетъ вдвое больше (доказательство отъ т къ 2т). Присоединимъ къ т даннымъ множителямъ еще т положительныхъ множителей: х\ у\ , , . I* и пусть будетъ произведеніе
р = ф , хгу* . . в
состоящее изъ 2т положительныхъ множителей. Пусть будетъ а — ариѳметическая средина этихъ 2т множителей:
2тя = я?4“ у + - • • *
пусть, далѣе, будетъ Ь— ариѳм. средина т первыхъ, Ъг—ариѳм. средина т прибавленныхъ множителей, т.-е.
тЬ = х-\-у-\- - • .
Очевидно, имѣемъ
т(Ь -|- Ь') = 2та, или Ь + 6' = 2а,
а этимъ доказано, что а есть ариѳм. средина Ь и Ь'.
Помня это, замѣчаемъ, что какъ, по допущенію, теорема справедлива для случая т множителей, то
яу. . %‘у\ . Уі'^Ъ'т.
Перемноживъ почленно, имѣемъ
Р < (И')”4.
Но а есть арвом. средина для Ь и Ъ\ и теорема доказана для двухъ множителей' то
ЬЪГ а2, и слѣд., тѣмъ болѣе
Р < а2*:
этимъ доказано, что теорема вѣрна для 2т множителей, если она вѣрна для т. Но она доказана для двухъ множителей, слѣдов. доказана и для 4-хъ; а если такъ, то и для 8-ми, 16-ти и т. д., вообще для случая, когда число множителей есть степень 2.
Теперь уже не трудно распространить ее на какое угодно число множителей. Въ с. д., пусть будетъ Р—произведеніе т положительныхъ множителей (ш—какое угодно), и пусть ихъ ариом. средина = а. Пусть, затѣмъ, д будетъ такое цѣлое число, чтобы было степенью 2-хъ. Присоединяя къ т множителямъ произведенія Р, $ множителей равныхъ а, подучимъ новое произведеніе, Ра*, состоящее изъ множителей, которыхъ<йриѳм. средина опять=а. Такъ какъ число т*]-? множителей этого новаго произведенія есть степень 2, то по доказанному имѣемъ: Ра* откуда, по сокращеніи на положительное число а*, что не измѣнитъ смысла неравенства, найдемъ
Р<аи, что и требовалось доказать.
Это доказательство показываетъ, кромѣ того, что произведеніе Р остается ленъше а*\ пока есть въ немъ множитель отличный отъ а; въ с. д., это имѣетъ мѣсто для двухъ множителей, слѣд. будетъ имѣть мѣсто и для всѣхъ случаевъ.
Итакъ, произведеніе .равно ат только тогда, когда всѣ множители равны. Отсюда теорема:
произведеніе нѣсколькихъ положительныхъ перемѣнныхъ множите-лей, сумма которыхъ постоянна, имѣетъ тахітит, когда всѣ множители равны (если только ихъ можно сдѣлать равными, что бываетъ не всегда).
Доказательство Гурза. Удерживая прежнія обозначенія, замѣчаемъ, что произведеніе Р — ху . . . гі есть функція т — 1 независимыхъ перемѣнныхъ, ибо количествамъ в , . . і можно дать какія угодно положительныя значенія, лишь бы сумма ихъ была меньше та, а затѣмъ #-су даемъ значеніе та — (у + ^- * * Ч“0- Между различными системами значеній, какія можно давать нашимъ перемѣннымъ съ соблюденіемъ сказаннаго условія, есть одна, и только одна, когда всѣ значенія равны, и слѣд. каждое = а. Произведеніе Р1 приметъ тогда значеніе ап|; а соотвѣтствующую систему равныхъ перемѣнныхъ назовемъ
= ’ - • = = а . .(1).
Пусть будетъ взята другая система положительныхъ множителей:
Д'Зі • • • » ^2» ^2 • * • (2),
сумма которыхъ постоянна, и пусть произведеніе ихъ будетъ Р4:
Теорема состоитъ въ томъ, что Ра будетъ необходимо меньше ат.
Между значеніями системы (2) необходимо существуетъ, по крайней мѣрѣ, одинъ множитель большій а, ибо положивъ, что всѣ они не больше а, т.-е. что
то какъ не дано, что всѣ они равны а, т.-е.
мы имѣли бы
я2=а, = -
* О, -—- а
что противно условію. Подобнымъ же образомъ убѣдимся, что въ числѣ значеній системы (2) необходимо хотя одно будетъ <>. Пусть это будутъ значенія
^а = а — й, гдѣ й > О, 0<й<а.
Не трогая другихъ множителей произведенія Ра, замѣнимъ а -|- й чрезъ а, на — к чрезъ а-рЛ — й, получимъ систему
а, а й — й,.
* і ^2т ^2 • • • (2)
въ которой всѣ члены положительны, а сумма не измѣнится, ибо не измѣнилась и сумма измѣненныхъ членовъ системы: какъ прежде, такъ и теперь послѣдняя = 2а Л — А. Новое произведеніе
р3 =а(а-\-к — к) , . .
а предшествующее
Ра — (а Л) (а —
Но
(а + Л) (а — А) = а24~ а(й — й) — йй,
тогда какъ
а(а 4-Й — к) = а24“а(й — й);
слѣд. мы замѣнили положительное произведеніе двухъ факторовъ большимъ произведеніемъ, не измѣняя положительнаго произведенія прочихъ т — 2 факторовъ, а слѣд. произведеніе всѣхъ т факторовъ мы увеличили. Такимъ образомъ Р3 > Ра. Кромѣ того, въ системѣ (3), по крайней мѣрѣ, однимъ факторомъ, равнымъ а, стало больше, нежели въ системѣ (2).
Если всѣ значенія, составляющія систему (3), равны а, то теорема доказана, ибо тогда Рв = а**, между тѣмъ какъ Р2 < а*". Въ противномъ случаѣ опе
рируемъ надъ системою (3) такъ же, какъ мы оперировали надъ (2): составимъ новую систему (4) значеній, положительныхъ и имѣющихъ данную сумму; этой системѣ будетъ соотвѣтствовать значеніе Р4 произведенія, большее Р3, и въ немъ будетъ, по крайней мѣрѣ, однимъ значеніемъ, равнымъ а, больше, чѣмъ въ системѣ (3). Если всѣ значенія системы (4) равны а, то теорема доказана, ибо тогда Р4 будетъ = ат, между тѣмъ какъ Р2<СР3<ат. Если же нѣтъ, то начинаемъ снова ту же операцію, и кончимъ тѣмъ, что получимъ систему (1); а какъ каждый разъ значеніе произведенія увеличивается, то его начальное значеніе Ра навѣрное меньше окончательнаго значенія а™, которое, слѣдов,, и есть искомый шахіппіпі.
668. Задача I. Лякой осжгь треугодьямкога одинаковаго пери-метра имѣетъ наибольшую площадь?
Пусть перемѣнныя стороны будутъ я, у, 2р—постоянный периметръ; по условію, х у + * = -Р'
Площадь 8 треугольника по тремъ сторонамъ выражается формулою
8 = /р(р — — у) (р — я).
Функція 8 имѣетъ тахіпшш при тѣхъ же обстоятельствахъ какъ и ея квадратъ; принтомъ, откинувъ постоянный множитель, мы опять не измѣнимъ условій шахіпіипГа; так. обр. приводимъ вопросъ къ опредѣленію тах. произведенія (р —#)(р—у)(р—Каждый множитель этого произведенія положителенъ, сумма ихъ = Ср — —У)“Н(р —= (я-ру-р*) =2’—вели-
чинѣ постоянной; слѣд. произведеніе достигнетъ тахітпт’а, когда всѣ множители сдѣлаются равными, т.-е. когда р — х ~р~у —р —я, или х = у = я.
2
Слѣд. искомый треугольникъ—правильный. Каждая сторона его = ^Рі а пло-
щадь = “дГ-
669. Задача II. Какой изъ всѣхъ прямоугольныхъ параллелопипедовъ , имѣющихъ одинаковую полную поверхность, имѣетъ наибольшій объемъ?
Пусть я, у и я будутъ перемѣнныя измѣренія этихъ параллелопипедовъ, 8—данная полная поверхность; имѣемъ:
8 = 2ху + 4- 2уг.
Перемѣнный объемъ V = хуя. Его тахітшп будетъ при тѣхъ же условіяхъ, какъ тахітшп его квадрата: И* = (гу) (яя) (уя). Но эти три положительныхъ 8 . , ,
множителя имѣютъ постоянную сумму слѣдов. тахішит имѣетъ мѣсто при ху^=х^ = уя, откуда: х = у = %. Это значитъ, что наибольшій объемъ имѣетъ кубъ; величина максимальнаго объема = х.х.х = х3 —
670. Задача ПІ. Зная, что тх2-1-пу$ргі == д, найти тахітит произведенія хау^^.
Произведеніе я* У^ имѣетъ тахітшп при тѣхъ же обстоятельствахъ * какъ и тпр.х*у^ т.-е. какъ и (тяа)(«у?)(ря'); но сумма факторовъ этого послѣдняго произведенія постоянна (и равна з), слѣд. это произведеніе,
а съ нимъ и предложенное, имѣетъ тахітит, когда множители равны, т.-е. когда тх* = пу$=ряЧ = Такимъ образомъ, максимальное значеніе предложеннаго произведенія =
Напр., найдемъ, что произведеніе ху* при условіи За=4у = 12, имѣетъ 3
тахітит = 3, при х = 2 и у = — Произведеніе при условіи
Зха-{-5і/4'7я8 = 315, имѣетъ тахітит = 35.21.15, при #=]/35, і/ — 21т
671. Примѣчаніе Г Въ теоремѣ (§ 667) было дано, что перемѣнныя х, у, я, . . . подчиняются шолъя# одноліу усжшзд, чтобы сумма пхъ была постоянна; если же эти перемѣнныя будутъ подчинены еще другимъ условіямъ (выражаемымъ равенствами или неравенствами), то мы уже не имѣемъ права замѣнять два множителя а -|- А, а — А, одинъ числомъ а, другой числомъ а-}-к — к, не измѣняя другихъ, ибо новое произведеніе можетъ уже не удовлетворять прочимъ условіямъ, кромѣ относящагося къ суммѣ. Слѣд. приведенное доказательство было бы неприложимо. Вообще, множители не могутъ быть равными, имѣть постоянную сумму и удовлетворять еще другимъ условіямъ; такъ что теорема § 667, вообще, не будетъ имѣть мѣста: тахітит произведенія будетъ вообще меньше той величины произведенія, какую оно имѣетъ при равенствѣ множителей.
Разсмотримъ, наприм., произведеніе трехъ положительныхъ чиселъ х, у. сумма которыхъ постоянна и = 12, слѣд. удовлетворяющихъ условію
12 . . . (1).
Пусть, кромѣ того, числа эти связаны еще условіемъ
а:-|-5у Ц-2г = а . . .(2),
гдѣ а—постоянная величина. Назовемъ перемѣнное произведеніе, удовлетворяющее этимъ двумъ условіямъ, черезъ Р. Разсмотримъ также произведеніе Ч трехъ положительныхъ чиселъ хч у. 0, удовлетворяющихъ только условію (1). Махі-шиш произведеніе У будетъ имѣть при % = у = я = 4; самый же шах. = 64. Что касается перемѣннаго произведенія Р, область его значеній будетъ ограниченнѣе области значеній (): произведеніе Р не можетъ принимать всѣхъ значеній, которыя можетъ имѣть 9; въ самомъ дѣлѣ: для составленія У нужно отыскать всѣ системы положительныхъ рѣшеній, удовлетворяющихъ неопредѣленному ур—нію (1). Для составленія же значеній, которыя можетъ принимать произведеніе Р, нужно изъ всѣхъ сказанныхъ системъ выбрать только тѣ, которыя удовлетворяютъ и ур—нію (2). Отсюда очевидно, что, во-первыхъ, тахітит (Р> не можетъ быть больше шахішипГа (), во-вторыхъ, что только въ исключительномъ случаѣ-тахітит произведенія Р будетъ равенъ пш. (У), вообще же та-хітиш Р будетъ меньше тахітит’а <2.
Сказанный исключительный случай—тотъ, когда ур—ніе (2) удовлетворяется величинами я=?/=^ = 4, что имѣетъ мѣсто при а=4-[-5 Х4-[-2Х4 = 32: въ этомъ случаѣ 64 будетъ находиться въ числѣ значеній, которыя принимаетъ Р, а такъ какъ тах. (Р) не можетъ быть больше шах. ((^), и 64 есть шах. произведенія то тѣмъ болѣе 64 будетъ служить тахітит’омъ и Р.
Обобщая это разсужденіе, заключаемъ, что если факторы произведенія положительны, имѣютъ постоянную сумму и подчинены еще другимъ условіямъ, тахітит произведенія вообще меньше той величины его, какую оно получаетъ, если всѣ множители сдѣлать равными; этой послѣдней величинѣ шахітпш про-изведенія равенъ только въ томъ исключительномъ случаѣ, когда всѣ условія, которымъ факторы подчинены, удовлетворяются, когда сдѣлать эти факторы равными.
Интересный примѣръ на этотъ исключительный случай представляетъ произведеніе %ту*зр, состоящее изъ т множителей равныхъ я, п—равныхъ у, и р множителей равныхъ я, съ условіемъ, что сумма тя-|- пу всѣхъ множителей равна постоянному а.
На основаніи сказаннаго выше, это произведеніе будетъ имѣть тах., когда всѣ множители равны, если только равенство факторовъ будетъ совмѣстно съ остальными условіями, которымъ множители подчинены.
Равенство т множителей я-су дастъ т — 1 соотношеніе; подобно этому имѣемъ еще п—1 и р — 1 условій, что составляетъ усло-
вія; присоединивъ еще равенство суммы всѣхъ множителей количеству а, получимъ —2 соотношенія; присоединяя еще два ур—нія х = у = ял
всего будемъ имѣть ур—ній для опредѣленія столькихъ же коли-
чествъ, а это вообще возможно. Слѣд., въ этомъ случаѣ паибол. всл. произведеніемъ достигается при
х = у =2 =
а
т 4- п +р*
672. Примѣчаніе II. При доказательствѣ теоремы (667) мы предполагали, что всѣ множители положительны* Но теорема, очевидно, имѣетъ мѣсто и въ томъ случаѣ, когда вегь множители отрицательны, если только число ихъ четное. Если же всѣ множители отрицательны и число ихъ нечетное, то произведеніе будетъ шшітиш, когда всѣ множители равны. Въ самомъ дѣлѣ, если, взявъ произведеніе нечетнаго числа положительныхъ множителей, перемѣнимъ у нихъ знаки, то и знакъ произведенія перемѣнится. Но если функція В имѣетъ тахітит М, то функція (—И) имѣетъ тіпітит (—М); потому что, если М есть тах. (11), то И < М для всѣхъ значеній этой функціи, близкихъ къ М; а изъ неравенства Г < М имѣемъ — V > — М, слѣд. — М есть тіпітит функціи (—II).
Наконецъ, если не всѣ множители отрицательны, то произведеніе не имѣло бы шахішипГа, ибо при постоянной суммѣ множителей ихъ абсолютная величина могла бы увеличиваться неопредѣленно; и если число отрицательныхъ множителей четное, произведеніе было бы положительно и могло бы быть какъ угодно велико.
673. Примѣчаніе III. Для двухъ множителей теорема о тах. произведенія была доказана еще Никомахомъ 100 лѣтъ спустя послѣ Р. X.
674. Когда множители, имѣя постоянную сумму, не могутъ быть сдѣланы равными, прямое приложеніе теоремы (667) становится невозможно. Однако же, методъ неопредѣленныхъ коэффиціентовъ даетъ возможность непрямого примѣненія теоремы. Приводимъ въ поясненіи сказаннаго слѣдующую задачу*
Задача. -Ва картонномъ листѣ, стороны котораго
равны а и Ь, требуется вынуть по угламъ такіе равные квадраты
АЕКЬ,..., чтобы, загнувъ всѣ четыре прямоугольника ЕКМК. * .перпендикулярно къ плоскости КМ8Т, составитъ коробку наибольшей вмѣстимости ?
Пусть АР = я, АВ = Ь, АО = а; стороны основанія коробки выразятся формулами а — 2х и 6 — 2а;, высота = а?. Объемъ V коробки (какъ прямоугольнаго параллелопипеда)
V = (а — 2а;) (Ь — 2а;) . х.
Чтобы сдѣлать сумму множителей постоянною, введемъ множитель 4 (введеніе постояннаго множителя 4 не вліяетъ на условія тахішит’а); полупимъ:
4Ѵ = (а — 2л?) (& — 2л?) 4я,
т.-е. произведеніе положительныхъ перемѣнныхъ множителей, которыхъ сумма (а — 2л?) 4~ (Ь — 2а;) + 4а; равна постоянной величинѣ а 110 какъ > а, то ни при какомъ х нельзя сдѣлать а — 2х = Ь—2а;, и теорему (667) въ данномъ случаѣ нельзя примѣнить непосредственно. Чтобы найти тахіінипі произведенія (а — 2а;) (б— 2.г)ж, замѣтимъ, что, не измѣняя условій шах., мы можемъ умножить два изъ этихъ трехъ факторовъ на произвольныя постоянныя количества, напр., первый на а, второй на ?, и искать тахітит произведенія
Ѵі? = (аа — 2хг) (Ь? — 2?а;)а;.
Пользуясь неопредѣленностью постоянныхъ а и ?, можно выбрать ихъ такъ, чтобы •сумма всѣхъ трехъ множителей была постоянна. Представивъ эту сумму въ видѣ
аа + &? — (214-2? —1)я,
находимъ, что она будетъ независима отъ х и слѣдовательно постоянна, когда 2і 4“ 2?—1 = 0. Такимъ образомъ іи? должны удовлетворять неопредѣленному ур—нію, и слѣд. существуетъ безчисленное множество паръ значеній а и дѣлающихъ нашу сумму постоянной. Но изъ этихъ паръ надо выбрать такую пару значеній а и ?, при которой множители были бы равны. Итакъ, для опредѣленія 1, ? и х имѣемъ 3 ур—нія:
214“ 2? — 1 = 0 ... (1) а (а — 2я) — х ... (2) — 2а;) = х . . . (3),
Имѣя 3 ур—нія съ 3 неизвѣстными, мы получимъ опредѣленныя значенія для а, ? но намъ нѣтъ надобности опредѣлять а и ?, а только я; съ этою цѣлью исключаемъ, изъ ур—ній (1), (2) и (3) іи чтобы получить ур—ніе съ однимъ неизвѣстнымъ х. Изъ (2) и (3) имѣемъ
а =
х
а—2а?
подставивъ въ (1) эти значенія а и ?, имѣемъ ур.
2де а—2х
или
12я* — = 0 . . .(4).
Это ур—ніе и даетъ такой я, при которомъ Ѵар, а сл. и V имѣетъ шахіппіт.
Рѣшая это ур., имѣемъ
а 4- Ъ Ѵа2 + Ь2 — аЬ
Я = —!---------------
Оба корня дѣйствительны, ибо аа Ьа — аѣ = а* -р — 2аЬ аЪ = (а — 6)а-|-а& — количеству положительному; они положительны, такъ какъ произведеніе и сумма корней* положительны. Но чтобы корень ур—нія (4) давалъ рѣшеніе задачи, недостаточно, чтобы онъ былъ дѣйствьи положит.; нужно еще, чтобы онъ былъ меньше половины меньшей стороны прямоугольника АВСП. Пусть «а <С Ь; тогда можно взять оба или одинъ корень, смотря по тому, будутъ ли оба они или только одинъ заключаться между 0 и Подстановка въ первую часть
ур—нія (4) вмѣсто х количествъ 0, и даетъ
-]-аЬт а (а—6)т Ъ(Ь— а):
первый результатъ положителенъ, сл. О заключается внѣ корней; второй рез. отрицателенъ (ибо а < &), слѣд. лежитъ между корнями; третій результатъ положителенъ, сл. к — внѣ корней. Такимъ образомъ, называя а/ меньшій ко-Ія
ронь, х" большій, имѣемъ
откуда слѣдуетъ, что большій корень а/', какъ большій не можетъ служить **
отвѣтомъ; меньшій же корень х\ будучи меньше и служитъ отвѣтомъ на
задачу. Итакъ высота коробки наибольшаго объема равна
а + Ъ — 62 — аЬ
6
Когда а = т.-е. картонъ имѣетъ форму квадрата, прямо изъ послѣдней
А Я
формулы находимъ:
Примѣчаніе* Если произведеніе содержитъ п перемѣнныхъ множителей, зависящихъ отъ я, то произвольныхъ постоянныхъ надо брать п — 1; вмѣстѣ съх они составятъ п неизвѣстныхъ. Требованіе, чтобы сумма факторовъ равнялась постоянной, даетъ 1 ур., а сравненіе п множителей дастъ п — 1 ур—ній, всего п ур—ній, т.-е. сколько неизвѣстныхъ; поэтому, метода—общая.
Приложеніе способа неопредѣленныхъ коэффиціентовъ къ вопросамъ о шах. и шіп. принадлежитъ Грилье.
675. Теорема. Если сумма нѣсколькихъ положительныхъ перемѣнныхъ х, у, # постоянна и равна а, то произведеніе хруѴ#г, гдѣ р, г данныя положительныя числал тахітит, когда перемѣнныя
2 -9 полагая
пропорціональны своимъ показателямъ, т.-е. когда — что х, у и я могутъ удовлетворить этимъ условіямъ.
Пусть, во-первыхъ, р, д и г будутъ числа цѣлыя.
Замѣчая, что введеф постоянныхъ множителей не измѣняетъ условій тнт’а, заключаемъ, что данное выраженіе будетъ имѣть тах. при такихъ
тнш’а, заключаемъ, что у, я, какъ и
данное выраженіе будетъ имѣть
шахі-же
или
Произведеніе стоянна л равна
хрі/І2г /х\р Іу\% /яѴ
-и -и- г> или - - -1 5
Рр^г‘ \р \д/ \г/
Р л <1 3 ______________
Р МЯОЖІІТ. 9 множнт.
г мцожнт.
заключаемъ, что произведеніе равными, т.-е. когда
это состоитъ изъ Г множителей, которыхъ сумма по-
х, х । і х х у , у I
Р Р 1 1 Р р <? 1 з 1
Примѣняя сюда теорему § 667.
достигнетъ шахітпнГа, когда множители сдѣлаются
Пользуясь извѣстнымъ = имѣемъ:
СВОЙСТВОМЪ
равныхъ отношеній и помня, что
ра
$а __ га
—.? &-—- —і—
р
X р
V У 5 $ г г
х__у___я
у = -
2
самый же тахітит
Р„9„г I' а \Р^Г
Мы предполагали, что показатели р, г — числа цѣлыя. Но это предположеніе не необходимо, и.теорема остается вѣрна и въ томъ случаѣ, когда показатели будутъ положительныя дроби. Приведя эти дроби къ общему знаменателю, пусть онѣ будутъ
то произведеніе будетъ
г 3= т’
г =-г;
- „г 2 2
У'
а
Очевидно, оно достигнетъ шахішшп’а у*'
одновременно со своей ^-ой степенью: я9***
а это выраженіе, по доказанному, будетъ имѣть шахітпт при
Эти равенства можно написать такъ:
или, наконецъ, такъ:
р Я г*
676. Задача I. Какой изъ всѣхъ конусовъ, вписанныхъ въ данный шаръ, имѣетъ наибольшій объемъ?
Убѣдившись «і ргіогі, что разсматриваемый объемъ имѣетъ тахітит, обозначимъ радіусъ основанія конуса буквою х, разстояніе центра шара отъ этого основанія буквою у, и буквою К радіусъ шара. Имѣемъ
ха + уа = К\ Ѵ=4тсгя(В4-у); О
или, замѣнивъ х* его величиною В2 — у2, найдемъ
V = |тг(Ка - у *) (К + у) = 1 к(В+у)* (К - у).
Отбросивъ постоянный множитель к, и разсматривая произведеніе (В -ру)3* (В—у), замѣчаемъ, что сумма первыхъ степеней множителей, т.-е. (К4-у)4-(^— у} равна постоянной 2К, слѣд. произведеніе имѣетъ шахітшп* когда перемѣнныя п і г» - К+у К—у
К-|~у и К —у пропорціональны своимъ показателямъ, т.-с. ’
К откуда У^з'
677. Задача П. Оиг/сать около даннаго цилиндра конусъ наименьшаго объема.
Если вообразимъ (черт. 115), что вершина А перемѣщается по оси ЛІ, отъ точки Н, то объемъ конуса вначалѣ безконечно-великъ, ибо основаніе его какъ угодно велико, а высота близка къ НІ; по мѣрѣ удаленія точки А въ безконечность, объемъ снова приближается къ безконечности, ибо высота стремится къ безконечности, а основаніе — къ конечной величинѣ основанія цилиндра. Измѣняясь отъ оо до оо, объемъ конуса проходитъ чрезъ шіпітпш.
Пусть Н и К — высота и радіусъ основанія цилиндра, х и у •— высота я радіусъ основанія конуса. Объемъ конуса будетъ V = ^тау1; но у:К=я:(я— Н)г что слѣдуетъ изъ подобія тр—ковъ АВІ и АЕН; слѣд.
- О).
Отбрасывая постоянный множитель тгК\ ищемъ тіпітит выраженія фЦ’щГ , . і . (ж—Н)2
соотвѣтствующій тахітит у выраженія -—которое можно представить въ
видѣ -11— — 1 * Условія шахітит'а этого выраженія не измѣнятся, если по
множимъ его на постоянное количество Н, что даетъ
ИЛ
X \ х)
Сумма первыхъ степеней производителей т и 1 — - есть величина посто-явная 1, слѣд. по теоремѣ § 675, тахітит имѣетъ мѣсто, когда
н 1—н X X
Т~~“Г“
когда # = ЗН.
Итакъ, объемъ конуса достигаетъ тіпітит’а, когда высота конуса дѣлается втрое больше высоты цилиндра* Пооставляя ЗН вмѣсто х въ (1), находимъ, что минимальный объемъ = | тгЕЛН, т.-е. составляетъ | объема цилиндра.
678. Задача Ш. Какой изъ всѣхъ конусовъ, описанныхъ около даннаго полушара, имѣетъ наименьшую боковую поверхность?
Какъ и въ предыдущей задачѣ, сначала & ргіогі убѣждаемся, что разсматриваемая поверхность имѣетъ тіпітит.
Пусть радіусъ шара будетъ К; х, у и 8—высота, радіусъ основанія и бо-
ковая поверхность конуса;
Черт. 146» "
имѣемъ:
8 = гуХАС.
Подобные тр—ни АОС и АОК даютъ:
АС___у___ х
х ~ К — —“К»’
откуда
АСХу____ а? .
п жЯ х% — К*’
" слѣд.
8 « тсК
Вопросъ приводится къ отысканію тшітшп’а ? и слѣд. тахшшт’а я# — В1 2 1 / К2\
обратной функціи —? которой можно дать видъ -11—Возвысивъ въ квадратъ и умноживъ на что не измѣнитъ условій шахітиіп а, приводимъ вопросъ къ нахожденію тахітипГа выраженія
1 В2/, Е2\2
1---= ?
К2
< въ которомъ множители и я слѣд. произведеніе это будетъ
1 — имѣютъ постоянную сумму, равную 1;
имѣть тахітит тогда, когда
откуда я2 = ЗК3, и слѣд. # = К]/3. Заключаемъ, что конусъ минимальной боковой поверхности имѣетъ высоту, равную сторонѣ правильнаго треуг—ка, вписаннаго въ большомъ кругѣ шара; самая же минимальная поверхность = |тсК2|/3*
679. Задача IV. Равнобедренный треугольникъ ЛВС, вписанный въ данный кругъ, вращается около касательной XX, параллельной его осно~ ванію; каковы должны бытъ размѣры треугольника, чтобы объемъ, имъ описанный, имѣлъ наибольшую величину?
Пусть 01 = я, ІА = ?д Объемъ выразится разностью между двойнымъ объемомъ усѣченнаго конуса, описаннаго трапеціей АВЕС, и цилиндромъ, описаннымъ прямоугольникомъ АВЕП, т.-е.
V = [41<2+(К—®)2+2К(іг—*)]—я(В-а>)2.2у;
О
замѣнивъ у его величиною і/К3 — я3 и упро’ стивъ, приведемъ выраженіе къ виду
V = к(2К — х) (К + ж) О
Можемъ искать тахітит квадрата этого выраженія, или, отбрасывая постоянный множитель,—выраженія
(Н4-я)* . (В — я) . (2Н —я)э.
Помноживъ К-|~ # на 2, мы сдѣлаемъ сумму первыхъ степеней этихъ множителей постоянною; но примѣненіе теоремы § 675 поведетъ къ равенствамъ-2(К+іг) К —я? 2К—х
—— = —і— = —2—’ которымъ нельзя удовлетворить никакимъ значе-
ніемъ х. Поэтому обращаемся къ способу неопредѣленныхъ коэффиціентовъ; помноживъ К-4“х и И — я на произвольныя постоянныя а и замѣчаемъ, что сумма а(К+^)+?(Н —а?)+(2Е—я) будетъ постоянна при а — —1 = 0; и тогда тахітит будетъ имѣть мѣсто при условіи
4-а) _ ^(Е — 2Е—а?
3 — 1 “2
Выражая отсюда а и черезъ х, находимъ
_ 3(2Е — х) а— 2(К + а:)’
2К-Д 2(В—х)’
Подстановка этихъ величинъ а и въ ур—ніе а ——1 = 0 даетъ:
3ЯГТ^--Ж=7І-1=О' ™ 3*‘-5В«+В--0.
Легко видѣть, что корни дѣйствительны и оба положительны; но задачѣ можетъ отвѣчать только тотъ изъ нихъ, который < К. Подстановка К въ первую часть ур—нія даетъ результатъ (— К2): заключаемъ, что К находится между корнями, т-е. большій корень больше, а меньшій—меньше В. Откидывая большій корень, соотвѣтствующій знаку 4“ передъ радикаломъ, находимъ:
5К - — 12Н2 К(5 - Iх 13)
6 — 6
680. Теорема. Сумма двухъ перемѣнныхъ, которыхъ произведеніе равно положительному постоянному, имѣетъ тахітит, когда оба слагаемыя отригіателъны, и тййиип, койа они положительны; при чемъ тахітит и тіпітит имѣютъ мѣсто, когда оба количества равны между собою, если только они могутъ бытъ сдѣланы равными. Сумма же двухъ перемѣнныхъ, которыхъ произведеніе равно постоянной отрицательной величинѣ, не имѣетъ ни тахітит'а, ни тіпітит’а.
Прямое доказательство.—Пусть произведеніе =р, а одинъ изъ множителей его = ^; другой множитель будетъ -? а сумма ихъ
Ѵй случай: #<СО. Назвавъ абсолютную величину произведеніяр черезър\ имѣемъ
Будемъ измѣнять х отъ —до 4“^* При х=== — 2/ =— ^4"
“ = — гс>; по мѣрѣ приближенія х къ 0, первый членъ, оставаясь отрица-
го , —г~ ..1--------------~ —-------
тельнымъ, увеличивается до 0, второй членъ (-|ь оставаясь положительнымъ
увеличивается до -|-со; слѣд. и сумма у увеличивается отъ —с© до -4“^« Продолжаемъ увеличивать х отъ 0 до 4-со. При х немного большемъ нуля, первый членъ суммы весьма малъ; второй членъ, будучи равенъ —р\ дѣленному на весьма малую положительную величину, будетъ равенъ отрицательному числу съ весьма большою абсолютною величиною; слѣд. при переходѣ я чрезъ О, функція претерпѣваетъ разрывъ непрерывности, дѣлая скачекъ изъ въ — с©. При дальнѣйшемъ увеличеніи х до -{-со, первый членъ возрастаетъ до второй, оставаясь отрицательнымъ, приближается къ 0: оба члена опять увеличиваются, потому и сумма ихъ возрастаетъ отъ —с© до 4-с©.
Такимъ образомъ при увеличеніи л отъ — со до -|- со, у получаетъ дважды всякое данное значеніе при двухъ значеніяхъ х, дающихъ въ произведеніи р; при двухъ равныхъ и противоположныхъ значеніяхъ х функція принимаетъ два равныя и противоположныя значенія, образуя 2 вѣтви: въ той и другой у идетъ, непрерывно увеличиваясь отъ — со до е©; обѣ вѣтви раздѣлены разрывомъ непрерывности, имѣющимъ мѣсто при я —0. Функція не имѣетъ, слѣд., ни тахішпш’а, ни тіпітит’а.
г
Таблица измѣненій у.
Кривая, измѣненій.
Обѣ вѣтви изображаются ординатами кривыхъ МК и 1*9, имѣющихъ ассимп-тотою ось у; ось # опп пересѣкаютъ въ разстояніяхъ отъ начала, равныхъ +]/? и —Vр'- ибо изъ у = О слѣдуетъ х— — — О, откуда х^—р1 и х^Ч-і/р'-Кривая симметрична относительно точки 0.
2-й случай: Въ этомъ случаѣ
+ • •(!)
Этому равенству послѣдовательно даемъ видъ: »
у = }/ («+1)’=')/х*+ (I)8 — +4р = ]Ар + [х—
Будемъ увеличивать х отъ О до При увеличеніи х отъ О до + }/?,
функція х— т/ по предыдущему, увеличивается отъ —со до О, а слѣдоват. іГ
уменьшается отъ 4~^ до 0. При возрастаніи а? отъ 4~Ѵр до
-4- со, х — - возрастаетъ, а вмѣстѣ съ тѣмъ и квадратъ этой функціи, отъ О 37
до 4’0С- Функція г/, оставаясь положительною, уменьшается сначала отъ -рсо до -р2)/р, а затѣмъ увеличивается отъ 4-2)/р до —Слѣд. ^проходитъ чрезъ тіпітит при # = + ]/?
Изъ (1) непосредственно ясно, что при двухъ значеніяхъ ж, равныхъ по величинѣ, но противоположныхъ по знаку, у имѣетъ величины равныя, отличающіяся только знаками. Слѣд. въ интерваллѣ измѣненій х отъ —со до О, функція возрастаетъ до шахітит’а —2]/\р, при # = а затѣмъ при
увеличеніи х отъ —до О, у уменьшается отъ —2|/р до —со. При переходѣ ж чрезъ О, имѣетъ мѣсто разрывъ непрерывности изъ —со въ Н-сс.
Таблица измѣненій у.
Кривая измѣненій:
Непрямое доказательство.—Обозначивъ данное произведеніе перемѣнныхъ # «
и - буквою р, а сумму ихъ 8, имѣемъ ур—ніе
*+? = 8...(1).
Рѣшая ур—ніе (1) относительно х, имѣемъ:
8 , ^ = у±]/7-А
- $2
Чтобы перемѣнное х было дѣйствительно, необходимо, чтобы было
или 8я 4р. Различаемъ два случая:
I. р < О, Условіе 8* > 4р всегда будетъ удовлетворено, каково бы ни было 8; слѣд. сумма двухъ факторовъ, произведеніе которыхъ равно постоянной отрицательной величинѣ, можетъ имѣть всѣ величины отъ —со до сумма 8 не имѣетъ ни шах., пи шіи,
II. Р>0. Неравенству 8я можно дать видъ
(8 + 2]/^)(8 —2у^)>0;
*
оно будетъ удовлетворено, если оба множителя будутъ имѣть одинаковые знаки; слѣд. должно быть:
ч “ • . ' ;• • 1
1) Или: 8 >2^, откуда: тіп. (8) = 2]/р; причемъ х=Ч = і/р; дру-гой множитель также = - = 1/р. * х г ь
2) Или: 8<;—'2у/р, откуда: тах. (8) =—2]/р; причемъ А V г~
другой множитель—- — — ур.
Итакъ: тіпітит и тахітит суммы имѣютъ мѣсто при равенствѣ слагаемыхъ.
681. Задача I. Изъ всѣхъ прямоугольниковъ одинаковой площади , какой имѣетъ наименьшій периметръ?
Обозначая перемѣнныя измѣренія прямоугольника черезъ х и у, имѣемъ, по условію: лгу = а3, гдѣ а3 постоянно; найти тіпітит периметра 2а? —|— 2у, или тіпітит (ж4“У)- Такъ какъ х можетъ быть сдѣлано равнымъ у, то площадь тогда получжть наименьшій периметръ, когда будетъ х — у = а, т.-е. когда прямоугольникъ обратится въ квадратъ. Самый тіпітит периметра равенъ 4а.
682. Задача П. Даны д$я> параллели и точка А лсежйі/ ними, служащая вершиною прямою угла прямоугольнаго треугольника, котораго другія двѣ вершины лежатъ на каждой изъ параллелей. Какое положеніе нужно датъ треугольнику, чтобы площадь была тіпіта?
Проведенъ общій перпендикуляръ ВЕ къ параллелямъ, и пусть: АП = а, АЕ = і, ЕС = х. Углы ЕАС АВЙ равны по перпендикулярности сторонъ, слѣд. треугольники ЕАСД)АВподобны. н потону д д
”7---
АС:ЕС = АВ:АО, или АС:х=АВ:а. . .(1) / \
Д X
—2 X
Умножая оба предыдущіе члена на АС, имѣемъ АС:я= х. \ АВ.АС:а; слѣд. удвоенная площадь треугольника АВС, или х^
АВ.АС = но АС*= Ь* + х\ откуда: ’ черт,
2 пл. АВС= - (в3 4-я3) = а(-4-хѴ
х\ 1 / \х 1 )
Произведеніе положительныхъ членовъ — и х равно постоянному Ь3, слѣд. X
сумма ~~ "Ь# имѣетъ тіпітит, когда = х, или а:3 = Ь3, откуда & = Ь.
. Но въ такомъ случаѣ ВІ) — а, и задача рѣшается весьма простымъ построеніемъ.
683. Задача III.—Опредѣлитъ наивьподнѣйшее соединеніе элементовъ галъванггческой баттареи при данномъ внѣшнемъ сопротивленіи.
Пусть всѣхъ элементовъ М; электровозбудительная сила каждаго Е, внутреннее сопротивленіе каждаго элемента р, данное внѣшнее сопротивленіе г. Раздѣлимъ элементы на т группу» по п элементовъ въ каждой: М — т . п; въ каждой группѣ соединимъ полюсы параллельно (цинкъ съ цинкомъ, уголь съ углемъ), и полученныя группы соединимъ послѣдовательно; составится бат-тарея какъ бы изъ т большихъ элементовъ. Электровозбудительная сила каж-49
даго изъ нихъ = Е, всей батареи — юіЕ; сопротивленіе каждаго изъ такихъ элементовъ = внутр. сопр. всей баттареи = т Сила тока
т__ шЕ ________ МЕ
1— > і ’ “ М? і
т —-Ч-г —- -4- гп
п 1 п 1
Числитель МЕ этой дроби есть величина постоянная, знаменатель — содержитъ перемѣнное п; дробь будетъ имѣть тахітит, когда знаменатель достиг-нетъ тіпішппГа. Но произведеніе положительныхъ перемѣнныхъ и гп есть величина постоянная (Мрг), слѣд. сумма будетъ имѣть тіпітит, когда
Лір т
= гп. или — р = г,
т.-е. йш тока достигаетъ тахітит'а, когда внутреннее сопротивленіе баттареи равно внѣшнему.
684. Тотъ же вопросъ о минимальномъ значеніи суммы можно рѣшить еще такъ. Можно доказать слѣдующее
Предложеніе. Сумма двухъ положительныхъ перемѣнныхъ, произведеніе которыхъ сохраняетъ постоянную величину, измѣняется въ томъ же смыслѣ, какъ и абсолютное значеніе ихъ разности.
Въ самомъ дѣлѣ, пусть даны два перемѣнныхъ положительныхъ числа х и у, произведеніе которыхъ равно постоянной а2.
ху = а2.
Тождество
(я + ?/)2 = — у)а + 4хУ даетъ
(я -р г/)2 = (х — у)* -|- 4а2.
Отсюда прямо видно, что а слѣд. и ж-|-у измѣняется въ томъ же
смыслѣ какъ (# — у)2 или | х — у | — при увеличеніи я — у увеличивается и и наоборотъ; значитъ, когда | х— у | принимаетъ нанм. значеніе, тогда и х-\-у достигаетъ тіпішипГа. Такимъ образомъ имѣемъ заключеніе:
Если перемѣнныя положительныя слагаемыя, коихъ произведеніе постоянно, не могутъ быть сдѣланы равными, тіпітит изъ суммы будетъ имѣть мѣсто тогда, когда абсолютное значеніе ихъ разности достигнетъ тіпітит'а. Если же они могутъ быть сдѣланы равными, то ихъ сумма будетъ тіпіта, когда они сдѣлаются равными (и равными ихъ геометрической срединѣ).
Такъ, въ задачѣ предыдущаго §, если внутреннее сопротивленіе баттареи не можетъ быть сдѣлано равнымъ внѣшнему, токъ получитъ наибольшею силу, когда внутреннее сопротивленіе будетъ возможно меньше разниться отъ внѣшняго* Вотъ еще примѣръ, иллюстрирующій случаи подобнаго рода.
685. Задача IV. — йлгіьежъ перелмьнный ро.нбъ, описанный около даннаго круга, и вписанный прямоугольникъ, вершины котораю находятся въ точкахъ касанія сторонъ ромба. При какомъ положеніи прямоугольника сумма площадей обоихъ четыреугольниковъ будетъ тіпіта?
Когда точка А будетъ удаляться по линіи 8А отъ точки 8 въ безконечность, площадь ромба будетъ измѣняться отъ безконечности до безконечности; слѣд.
сумма обѣихъ площадей сначала уменьшается, слѣд. проходитъ чрезъ тіпішшп. Затѣмъ, легко доказать, что произведеніе площадей остается постояннымъ; въ самомъ дѣлѣ, обозначая площадь ромба буквою 2, площадь прямоугольника 2', и замѣчая, что 2 = 4ДА0П, 2' = 8ДОРЕ, имѣемъ, 2': 22 = 0РЕ: А(Ю =
= В2:АІ); но 2 = АП.2В, слѣд. 2':22 = = 4К*: 22, откуда 2.2' = 8В1 — величинѣ постоянной. Хотя произведеніе разсматриваемыхъ перемѣнныхъ и постоянно, но какъ мы пе можемъ площади сдѣлать равными (ибо они всегда раздѣлены площадью круга), то для опредѣленія шшіпшпГа 2-|-2' должны искать тіпітит разности 2 — 2' = 4 (РЕу АЕР). Но 0Е<і = 1уХ»Ч = ^Хт = & а АЕР = ^; слѣд.
затѣмъ начинаетъ увеличиваться,
Черт. 151.
Замѣчая, что — К*, имѣемъ отсюда: хІ4~У4 = В<— 2х2у2, слѣд.
Очевидно, это выраженіе имѣетъ тіпітит, когда х*у* имѣетъ тахітит; но сумма равна постоянной В2, слѣд. х*у* имѣетъ тахітит при х = у.
Итакъ, искомый тіпітпт суммы 2-4-2' имѣетъ мѣсто тогда, когда прямоугольникъ обращается въ квадратъ: тогда и ромбъ обращается въ квадратъ, и величина тіп. (2 4^2') = 6К2.
686. Теорема.— Сумма п положительныхъ перемѣнныхъ, которыхъ произведеніе постоянно, имѣетъ тіпітит, когда эти п количествъ равны между собою (полагая, что они могутъ быть сдѣланы равными).
Пусть будутъ х, у, ф . . і, и — п положительныхъ перемѣнныхъ, подчиненныхъ единственнымъ условіямъ:
(1) #>>0, . $>0, м>0; хуя . . . і . и = а*\
гдѣ а — данное положительное число. Ихъ сумма
8 — х 4~ у 4- & "
• • ~НН“и
есть функція п — 1 независимыхъ перемѣнныхъ.
Между системами значеній х, у^ . . .и, удовлетворяющихъ условіямъ (1), 49»
существуетъ одна, и только одна, составленная изъ равныхъ значеній: это —-система
(2) х = у = я = . . . = и — а\
соотвѣтственное значеніе 8 есть па.
Пусть будетъ
а/, у', /, . . . , м',
система значеній, удовлетворяющихъ условіямъ (I), по отличная отъ системы (2). и пусть
Докажемъ, что 8' > па. Въ самомъ дѣлѣ, числа . и, не всѣ
равны между собою, слѣдовательно ихъ ариѳметическая средина больше геометрической средины (§ 339); слѣдовательно
8'
или >а, или Ь ^>па
что и требовалось доказать.
Примѣчаніе,—Эта теорема, вообще, перестанетъ быть вѣрною, если перемѣнныя подчинены инымъ условіямъ, кромѣ неизмѣнности ихъ произведенія. Но если новыя условія дозволяютъ перемѣннымъ я, у, . * * сдѣлаться равными, теорема имѣетъ мѣсто,
687. Задача I.—Изъ всѣхъ треугольниковъ, шиьяодих» одинаковую площадь, какой илтьета наименьшій периметръ?
Обозначивъ стороны черезъ ж, у, я, а постоянную площадь буквою (), имѣемъ
(з-Н-Н) (^+у — •») (« — у+-0 (— »+у +*) — іб<?.
Сумму ж-|-у-(-г можно представить въ видѣ:
3/а?#ж। ж—у+ # і — х + у + -
41 3 "г 1 । І 1 Т~ '
Произведеніе четырехъ членовъ, заключенныхъ въ скобки, равно постоянной слѣд* сумма имѣетъ шіпішиш, когда ея члены равны. Найдемъ, что они равны при х — у=г. Слѣд. минимальный периметръ принадлежитъ правильному треугольнику, а самый шіп. = 2 ^27.
688. 3 а д а ч А- II. —Изъ всѣхъ прямо у гольныхъ,параллелопипедовъ одинаковаго объема какой имѣетъ наименьшую полную поверхность?
Пусть перемѣнныя измѣренія параллелопипедовъ, сохраняющихъ одинаковый объемъ аэ, будутъ ж, у, я; имѣемъ:
хуя = а3.
Ищемъ шіпіт. полной поверхности 8 = 2 (.гу + У^); замѣчая, что ху . хя . уз — х* . у* , #3 = ав, находимъ, что сумма достигнетъ шшітппГа
при ху = хя = уя, или при х — у = # = а, т.-е. когда параллелопипедъ будетъ кубъ; самая минимальная поверхность равна ба3*
дЗ
Повѣрка. Взявъ я = а-|-Л, у = а— /г, и слѣд. # = -5 —д2, найдемъ:
8' = 6а* -I- 2А2 -{- что больше 6а*.
689. Задача III. — Зная, что х*у^ = постя ц, найти тіпітит суммы тх^пу^ ргі,
Изъ условія х*у$0і = # имѣемъ (?пха) (пу^) (да?) = тпрд; слѣдов. мы должны найти тіпітит суммы, зная, что произведеніе ея членовъ постоянно. Искомый тілішит имѣетъ мѣсто при тх* = пу^ = тпрд, а самый тіпітит = 3 тпрд,
Напр.. зная, что ху = 16, найдемъ тіпітит Зж-|-12у, разсуждая такъ: изъ условія ху=16 имѣемъ: (3#)(12у) = 16 . 3 . 12 = (24)*; слѣд. данная сумма имѣетъ тіпітит при Зх= 12у = 24, т.-е, при а? —8 и у = 2; самый тіпітит = 2 . 24, т.-е. 48.
Еще примѣръ. Зная, что ху — а*, найти тіп. #а У*? Изъ ху = а* заключаемъ яэу3 = а8, или #3% ху . у* = а6; произведеніе слагаемыхъ постоянно, слѣд. тіпітит суммы имѣетъ мѣсто при я2 — ху — у3, т.-е. при х = у = а, ибо ху = аа; самый тіпітит = За3.
690. Т е о р е м а. —- -Если произведеніе данныхъ степеней нѣсколькихъ перемѣнныхъ х> у} я имѣетъ постоянную величину: хруѴ=Р, то сумма первыхъ степеней этихъ перемѣнныхъ, «ліьежв тіпі-
тит, коіда числа х, у, # п/?о«ор^іоналъны своимъ показателямъ, т>-е.
х ц в
нои>а- = | = - если только числа эти могутъ имѣть такгя значенія.
Раздѣливъ обѣ части равенства хруѴ = Р на постоянное количество Рр . . **г, найдемъ
что можно представить въ видѣ
х х х у у у г 2 г_______________________________ Р
р ' р ’ , * и д. ' д ’ д г * г ' * ’ г рр . . тг'
р разъ 7 разъ г разъ
Сумма производителей первой части равна ~‘Р~Гд
т.-е. искомая, произведеніе же ихъ — постоянно, § 686, эта сумма будетъ тіпіта при равенствѣ ея
Соотвѣтствующія минимальной суммѣ значенія ур—ній (1) и (2), именно
—рі, слѣд., по теоремѣ частей, т.-е. при
перемѣнныхъ имѣемъ изъ
Самый тіпітит суммы =
р? . * г
691. Задача Г — Зная, что найти тіпітит тха -4-
. ..Л 1
Изъ = $ имѣемъ:
(уь)^ (^)аЬ^ =
слѣдовательно
(тяа)^*(нуЛ)^(р^)«*т — в . - (1).
Такимъ образомъ вопросъ приведенъ къ нахожденію тіпішипГа суммы тЛ;а + пУЬ4"2’А зная, что произведеніе различныхъ степеней ея членовъ постоянно;
по теоремѣ § 690 искомый тіпітит имѣетъ мѣсто при
Ьса
аЪч7
соединяя
тіпітит
Пр и мѣръ.—Зная, что %*у*~а\ найти тіпітит Зх~|-2у.
Изъ х3у8 = а5 имѣемъ: (Зх)3(2у)3 = 9Х^Ха^ слѣд. по теоремѣ § 690 - Зх 2ѵ
заключаемъ, что искомый тшішпш имѣетъ мѣсто при ѵ = у> выражая от* сюда х и вставляя въ условіе, имѣемъ: «у3 = а\ откуда у = а
самый тіпітит есть “
эти два ур—нія съ (1), найдемъ, при какихъ а?, у, я имѣетъ мѣсто данной суммы, и самый шшішнш.
4
Т.-е. - у 1.^
692. Задача ІЕ—Г/айти шпдошт полной поверхности ниши дан-а3 наго объема к-тг-
• ь
Ниша есть тѣло, образуемое вращеніемъ на 180® около оси АС фигуры, состоящей изъ прямоугольника ВВСО, завершающагося квадрантомъ АВО. Пусть радіусъ 0А = х, высота ОС прямоугольника равна у; поверхность ниши
X2
о
В
—I
3
или
О
о3 ~ з । ът3 (Г=.2«Н-з-, слѣд. поверхность ниши -/о * 2а3 — _т: /5
— 2
/2а3Ѵ
1-^- = пост. 20а8, слѣдоват. сумма
Но
2
Черт. 152.
о3 — 2т3 откуда у= ага ;
2а»\ г
За— 6
2а3 я?
2а»
2 дЗ йс
5х2+ ~ч то теор. § 690, будетъ тіпіта, когда — = -у; откуда
Отсюда слѣдуетъ: у = = гг.
693. Задача III.—Найти тіпітит суммы тха-|-^-
Всегда можно найти такія два числа а и чтобы аъ = Ь)* найдя ихъ,
1 / л \ Э
имѣемъ тождество (ла)а = (х^)^ откуда (имг3)* , = . пэ. Такимъ об-
разомъ, вопросъ приведенъ къ нахожденію тіпітшп’а суммы, зная, что произведеніе двухъ степеней ея членовъ — постоянно; по теор. § 690 шіпітшп имѣетъ мѣсто при
откуда
, аІЬ/(п\а /т\ь
самый тініпипп = (а-}-&) , |/ Ш
694. Теоремы § 686 и 690 обратны теоремамъ § 667 и 675. Этотъ результатъ встрѣчается часто, в его можно формулировать такъ:
Теорема. — Если II и V суть функціи нѣсколькихъ перемѣнныхъ х9 у> г, . . . ; если, затѣмъ, при постоянномъ значеніи А функціи Г другая функція V илиьеть тахітит В; если, сверхъ того, В излп>няетея въ томъ же смыслѣ какъ и А, то обратно: II будетъ имѣть тіпітит равный А, когда V будетъ сохранять постоянное значеніе В.
Въ самомъ дѣлѣ, когда В получаетъ значеніе А, то этимъ перемѣнныя х, у, . не опредѣляются, такъ какъ онн должны удовлетворять только одному ур—нію
слѣд. функція V можетъ принимать безчисленное множество различныхъ значеній, въ числѣ которыхъ наибольшее, по условію, есть В; отсюда ясно, что если, наоборотъ, мы дадимъ функціи V постоянное значеніе В, то въ числѣ безчисленнаго множества значеній, которйя можетъ принимать будетъ находиться и А. И легко показать, что II не можетъ получить никакого значенія меньшаго А; въ самомъ дѣлѣ, допустивъ, что II можетъ принять значеніе А' <С А, мы найдемъ, что наибольшее изъ значеній V, совмѣстное съ II = А\ будетъ меньше В, въ силу того условія, что В и А измѣняются въ одномъ смыслѣ. Слѣд. А есть дѣйствительно тшішиш функціи П, когда V сохраняетъ постоянное значеніе В.
Примѣръ. — Пусть
V = х + у + * + V = хугі
по теоремѣ (667), если II сохраняетъ постоянную величину А, то V получаетъ наибольшее значеніе при
— 776 — к
I аѵ а самый этотъ тахітит В = 1^-1 . Но А и В измѣняются въ одномъ смыслѣ ^1 » то наим. изъ значеній, принимаемыхъ П, будетъ А; этого значенія П достигаетъ, слѣд., при
х = у = г = і.
695. Въ заключеніе приведемъ еще нѣсколько примѣровъ тѣхъ аналитическихъ уловокъ, при помощи которыхъ можно элементарно находить шах. и шіи. функцій высшихъ степеней отъ нѣсколькихъ перемѣнныхъ.
I. Найти тіпітит зная, что х -\-у = 2а.
, 1 г 1 а?4-?/ 2а Л . .
Имѣемъ:“ + " =Очевидно, эта дробь будетъ имѣть шіштиш а? 1 у ху ху 1 г |
тогда, когда знаменатель ея достигаетъ тахітипГа; но #-|-у = 2а, слѣд. ху имѣетъ шах, при я = у = а; при этихъ значеніяхъ х п у данное выраженіе и имѣемъ тіпітпт = - а
II. Найти тіпітит ж-ру, зная
я:-]-у будетъ имѣть тіп., когда (а?-1-у)а имѣетъ тіпітпт. Но, по усло-, Ж2+у2 1
вію’ =^’ откда
®4 + Уа + 2^ = (® + # = 52 + 2^ = ^у (5 + 2)*
1
1
Очевидно, это выраженіе имѣетъ тіпітпт, когда ху имѣетъ тіпітит, 1 1 л и 1 1 /
т.-е. когда —, а потому и имѣетъ тах. Но (въ виду того, что сумма этихъ производителей постоянна) имѣетъ тах. при = т.-е.
при ж = у = а^2. При этихъ значеніяхъ х~\-у и имѣетъ тіпітпт, равный 2а/2.
ПІ. Найти тіпітит #а-|-уа-|-я3> зная, что х-\-у -|-0 — За.
Тождественно имѣемъ:
я ь. л Д_<Л—у)ЕЧЧ#—*)2, ЭаЧС* “УЯ+(а>~*)3+(у—
I у 2 *
Отсюда видно, что данное выраженіе имѣетъ тіпітпт тогда, когда имѣетъ тіпітит (д? — у)24~(#—#)2-|-(у— #)3; но эта сумма существенно положительна, слѣд. ея тіиішит есть нуль, и имѣетъ мѣсто при х~ у = #. Потому и данное выраженіе имѣетъ шіп. при х — у = я = а; самый тіпітит =3аа.
IV. Доказать, что если х -|- у = 2а, су лена хт 4~ут имѣетъ тіпітит при х = у = а.
Во-первыхъ, замѣчаемъ, что теорема справедлива для т = 2, ибо х* + У* = + у)’ — -ХУ = 4а* — 2жу,
откуда ясно, что какъ уменьшаемое постоянно, то разность имѣетъ шіп., когда вычитаемое имѣетъ тахітит, т.-е. при х = у.
Затѣмъ, допустивъ, что теорема справедлива для показателя т— 1 и для всѣхъ предыдущихъ, докажемъ, что она справедлива и для показателя т.
Различаемъ два случая: т = 2т' п т ~ 2т” 1.
Положивъ т = 2т\ имѣемъ:
#2т' у2т< _ дт' _ 2гт'і/т?;
по положенію, имѣемъ тіпітит при х = у; съ другой стороны хт'ут'
или имѣемъ тахітпиш при х = у. Слѣд. я2т'Ц-^2т' имѣемъ тіпітит при х~у.
* Положивъ т — 2т” 1, имѣемъ:
Первая часть этой разности имѣетъ тіпітит при х —«/, ибо, по положенію,, оба ея множителя — тіпіта при х = у; вторая часть имѣетъ при х~у тахітит. Слѣд. Ц-у2ш +1 имѣемъ тіііітшп при х = у.
На этомъ основанія заключаемъ такъ: теорема вѣрна для т—2, слѣд.г по доказанному, вѣрна и для ш=3; будучи вѣрна для т — 2 и пг = Зг вѣрна и для т —4 и т, д, Слѣд. она вѣрна для всякаго т.
ОТДЪЛЪ ЧЕТВЕРТЫЙ.
АНАЛИЗЪ СОЕДИНЕНІИ И ЕГО ПРИЛОЖЕНІЯ.
ГЛАВА ХЫІІ.
Размѣщенія, перестановки и сочетанія безъ повтореній я съ повтореніями.
696. Опредѣленія.—Если изъ т данныхъ предметовъ, напр., изъ т буквъ й, о, , г, I взять к буквъ, гдѣ к т, и написать ихъ другъ за
другомъ въ какомъ-нибудь порядкѣ, то получится соединеніе, называемое размѣщеніемъ изъ т буквъ по Ь, или разлоъжк&ль изъ т буквъ к-го порядка. Такимъ образомъ одно размѣщеніе отличается отъ другого или самыми буквами, или только порядкомъ ихъ. Изъ данныхъ т буквъ можно составить нѣсколько размѣщеній й-го порядка; число ихъ обозначаютъ символомъ А™, гдѣ нижній указатель т означаетъ число всѣхъ предметовъ (элементовъ), верхній 7ь—число элементовъ, входящихъ въ каждое размѣщеніе.
Если въ составъ каждаго соединенія мы возьмемъ всѣ данныя буквы, то одно соединеніе будетъ отличаться отъ другого уже не буквами, а только порядкомъ, въ которомъ онѣ написаны. Такія соединенія называются переста- . новками. Число перестановокъ изъ т элементовъ обозначаютъ символомъ Рт. Изъ опредѣленія слѣдуетъ, что РИ1 = АХ-
Если, взявъ т различныхъ буквъ, мы составимъ изъ нихъ соединенія по к буквъ въ каждомъ, такъ, чтобы одно соединеніе отличалось отъ другого по крайней мѣрѣ одною буквою, то получимъ такъ-называемыя сочетанія изъ т буквъ 7>го порядка. Число ихъ обозначаютъ символомъ С™.
Займемся указаніемъ способа составленія и опредѣленія числа соединеній каждаго рода.
Размѣщенія (аггап^етепів).
697. Способъ составленія и опредѣленіе числа размѣщеній.—Пусть будутъ а, Ъ, с, <і, . . , і, 7 данные т элементовъ. Число размѣщеній изъ этихъ т буквъ, по одному элементу въ каждомъ, очевидно, равно числу элементовъ. Слѣд. Ат — т.
Составимъ размѣщенія второго порядка, т.-е, содержащія по два элемента: для этого нужно взять поочередно каждую изъ т буквъ и приписать къ ней оправа каждую изъ остальныхъ т—1 буквъ; такимъ образомъ получимъ таблицу:
| | , Чтобы доказать, что такимъ образомъ получатся
аЬ Іа са . ІА, /а всѣ размѣщенія 2-го порядка, надо доказать, что ни ас /Ьс одно размѣщеніе не было опущено, ни одно не по-
ай С Ь(1 сгі . Іс вторено два раза. И въ самомъ дѣлѣ: 1) возьмемъ
. . , какое-ниб. размѣщеніе, напр., ей; для составленія вер-
тикальныхъ колоннъ мы ставили по-очереди каждую букву па первомъ мѣстѣ; слѣд., въ частности, была ш Ьі « . . . Ік взята и буква с; справа отъ этой буквы ставили каж-
аі Ы сі . . . Іі дую изъ остальныхъ буквъ, слѣд., въ частности, и
букву й; что и дало размѣщеніе ой. Слѣд. ни одно размѣщеніе не было пропущено. 2) Сравнимъ два какія-нибудь размѣщенія таблицы: они будутъ находиться пли въ одной и той же вертикальной колоннѣ, и въ такомъ случаѣ будутъ различаться послѣдними буквами, или же будутъ
содержаться въ двухъ различныхъ вертикальныхъ колоннахъ, — и въ такомъ случаѣ будутъ различаться первыми буквами. Убѣждаемся, что всѣ размѣщенія различны, т.-е. что таблица не содержитъ повтореній. Итакъ, послѣдняя содержитъ всѣ размѣщенія 2-го порядка.
Опредѣлимъ ихъ число. Очевидно, всѣхъ вертикальныхъ колоннъ столько, сколько всѣхъ размѣщеній 1-го порядка, т.-е. сколько всѣхъ буквъ, слѣд. т; въ каждой колоннѣ т—1 размѣщеній; слѣд, всѣхъ двойныхъ размѣщеній т(т — 1). Итакъ, Л« = т(т — 1).
Составимъ тройныя размѣщенія изъ буквъ. Для этого нужно взять поочередно каждое двойное размѣщеніе и приписать къ нему послѣдовательно каждую изъ т — 2 остальныхъ буквъ; такимъ образомъ составимъ таблицу:
Докажемъ, что ни одно тройное размѣщеніе не
аЪс асЪ . . Ьса . , На было пропущено и ни одно пе повторено лишній
аМ ассі . . Ьсй . . иь разъ. И въ самомъ дѣлѣ: 1) возьмемъ какое-ни-
аЬе асе . . Ьсе . . Не будь размѣщеніе Для составленія вертикаль-
4 V * • » * • ныхъ колоннъ мы брали поочередно каждое двой-
* « V № • * « ное размѣщеніе; сл. между прочимъ было взято и И.
• « * 4 А 4 Къ нему приписывали послѣдовательно каждую изъ
аЪі асі . , Ъсі . 4 остальныхъ буквъ, сл, въ частности была припи-
аЫ асі . . Ьсі . . Іік сана и буква А что и даетъ Іі/. Слѣд. таблица
не содержитъ пропусковъ, 2) Сравнимъ два какія-
нибудь размѣщенія таблицы. Или они находятся въ одной вертикальной колоннѣ,
и тогда различаются послѣдними буквами; пли—въ двухъ различныхъ колоннахъ, и въ такомъ случаѣ различаются, по крайней мѣрѣ, порядкомъ двухъ первыхъ буквъ, какъ асі и саі. Заключаемъ, что всѣ размѣщенія таблицы различны. Итакъ, опа содержитъ всѣ размѣщенія 3-го порядка.
Опредѣлимъ ихъ число. Всѣхъ вертикальныхъ колоннъ столько, сколько двойныхъ размѣщеній изъ т буквъ, т.-е. А™ или т(*ю — 1); въ каждой колоннѣ содержится ш — 2 размѣщенія; слѣд, всѣхъ тройныхъ размѣщеній т(т — 1) (т — 2). Итакъ АІ = т (т — 1)(т — 2)\
Разсматривая формулы АІ», А™, А™, замѣчаемъ, что всѣ онѣ составлены по одному и тому же закону: каждая представляетъ произведеніе чиселъ, послѣдовательно уменьшающихся па 1, начиная съ и кончая множителемъ,
равнымъ числу элементовъ, минусъ порядокъ размѣщеній, плюсъ 1; число же множителей равно порядку размѣщеній. Докажемъ общность этого закона, и для этого выведемъ формулу, выражающую зависимость между числами размѣщеній двухъ смежныхъ порядковъ, напр., связь между Ата” и Ат- Вообразимъ, что мы составили всѣ размѣщенія к— 1-го порядка, число которыхъ выражается символомъ А™”1, и желаемъ составить размѣщенія А'-го порядка. Для этого беремъ поочередно каждое размѣщеніе к— 1-го порядка и приписываемъ къ нему поочередно каждую изъ остальныхъ буквъ, число которыхъ — 1), или
т—Такимъ образомъ составимъ столько вертикальныхъ колоннъ, сколько размѣщеній к~ 1-го порядка, а въ каждой колоннѣ т — размѣщеній. Докажемъ, что ни одно размѣщеніе Л?-го порядка не повторено два раза и что ни одно не пропущено. Въ самомъ дѣлѣ: 1) сравнивая два какія-нибудь размѣщенія, найдемъ, что они или находятся въ одной и той же вертикальной колоннѣ, и въ такомъ случаѣ разнятся послѣдними буквами, или же принадле-жатъ двумъ различнымъ колоннамъ, и въ такомъ случаѣ разнятся, по крайней мѣрѣ, порядкомъ к—1 первыхъ буквъ, какъ аЬС'..ік и с»...ЬаЛ. 2) Ни одно размѣщеніе і-го порядка пе будетъ пропущено; въ самомъ дѣлѣ, пусть взято размѣщеніе А-го порядка аЪс...ік. Для составленія этихъ размѣщеній мы брали поочередно каждое размѣщеніе к—1-го порядка, слѣд. въ частности было взято и размѣщеніе аЪс„.і; къ нему приписывали послѣдовательно каждую нзъ остальныхъ буквъ, слѣд. приписали, между прочимъ, и букву А, что и даетъ аЬс...ік. Итакъ, указаннымъ способомъ составлены всѣ размѣщенія А-го пор. нзъ т буквъ.
Для опредѣленія ихъ числа, очевидно, нужно помножить число колоннъ, т.-е. число размѣщеній к — 1-го пор. или Ат”1 на число размѣщеній въ каждой колоннѣ, т.-е. на тп — к -|- 1. Имѣемъ:
Ат = А*й1 • (»'-*-|- 1).
Это и есть формула, связывающая числа А„ и Ат1. Такъ какъ формула эта— общая, то можемъ давать въ ней к всѣ цѣлыя значенія отъ 2 до к. Получимъ:
Ат = Ат (ш — 1)
А?„ = Ат(т-2)
Ат ==: Ат “ 3)
«*•*** ******* Ат=АІГ10» —
Перемноживъ почленно эти равенства, сокративъ въ обѣихъ частяхъ общаго множителя Ат . Ат ♦ . А^-1 и замѣнивъ Ат его значеніемъ т, найдемъ:
Ат = т(ш—1)(т — 2)(т—3) , . , (т — . .(I)
Отсюда
Теорема. Число размѣщеній изъ т буквъ по к равно произведенію к цѣлыхъ чиселъ, уменьшающихся послѣдовательно на 7, изъ которыхъ первое равно т.
698* II р и м ъ р ъ Г. Сколько можно составитъ трехзначныхъ чиселъ изъ нечетныхъ цифръ 1, 3, 5, 7? 9?
Искомое число, очевидно, есть число размѣщеній изъ 5 элементовъ по 3: слѣд. оно равно А$ = 5 X 4 X = 60,
Примѣръ ІЕ Сколько можно бы было составить словъ изъ 20 согласныхъ и 6 гласныхъ > если каждое слово должно заключатъ 3 согласныхъ и 2 гласныхъ, пр и чела послѣднія могутъ занимать только второе и четвертое мѣста?
20 согласныхъ дадутъ размѣщеній по 3 буквы въ каждомъ: Ано; въ каждомъ изъ этихъ размѣщеній 6 гласныхъ, помѣщаемыя по-парно на второмъ и четвертомъ мѣстѣ, могутъ быть размѣщены АІ способами: слѣд* число искомыхъ словъ = АІо X Ае = 20 * 19 . 18 X 6 . 5 ~ 205200.
Перестановки (регтиѣаНопв).
699, Способъ составленія и опредѣленіе числа перестановокъ*—Перестановки различаются отъ размѣщеній только тѣмъ, что берутся всѣ буквы. Изъ этого прямо слѣдуетъ, что для составленія перестановокъ изъ т буквъ падо, изъ этихъ буквъ составить всѣ размѣщенія по 2, изъ нихъ размѣщенія по 3 . д>, пока не дойдемъ до размѣщеній по ш. Отсюда также слѣдуетъ, что для
опредѣленія числа перестановокъ изъ т буквъ нужно только въ формулѣ Ат = т(т — 1)(иі — 2). . . (т— &-|’2)(пг— положить к = т. Такимъ образомъ найдемъ
Рт = А"= 1.2.3. . . (т— 2)(т— 1)т.
Отсюда
Теорема. Число перестановокъ изъ т элементовъ равно произведенію натуральныхъ чиселъ отъ 1 до т.
Можно доказать эту теорему независимо отъ формулы числа размѣщеній. Въ самомъ дѣлѣ, пусть составлены перестановки изъ т—1 буквъ а, Ь, с, <2,..., Л, і, к, и пусть число перестановокъ будетъ ₽т-ь Чтобы составить перестановки изъ т буквъ, беремъ каждую перестановку изъ т — 1 буквъ и вводимъ въ нее ?п-ую букву /, помѣщая послѣдовательно слѣва и справа этой перестановки и во всѣ промежутки между ея буквами. Такимъ образомъ мы составимъ всѣ перестановки изъ т буквъ, безъ повтореній и безъ пропусковъ. Безъ повтореній—потому, что одна перестановка будетъ отличаться отъ другой иля порядкомъ т — 1 первоначально взятыхъ буквъ, или мѣстомъ, которое занимаетъ новая буква /. Безъ пропусковъ. ибо, взявъ перестановку . .4, напр., замѣчаемъ, что она произошла изъ перестановки составленной изъ т— 1
первоначальныхъ элементовъ, въ которую буква I введена на 3-е мѣсто; слѣд. такая перестановка была получена.
Итакъ: указаннымъ способомъ получимъ всѣ перестановки изъ т буквъ. Опредѣлимъ ихъ число. Каждая перестановка изъ т — 1 буквъ даетъ т перестановокъ изъ т буквъ, ибо буква 2 можетъ занять въ первой »г различныхъ мѣстъ; слѣд.
рт = тРт_]:
такова связь между Рт-і и Гт* Формула эта справедлива для всякаго т, будучи совершенно общею: давая въ ней т послѣдовательно всѣ значенія отъ 2 до т, находимъ:
Р2 = Рі .2; Р3 — Р^ * 3; Р4 = Р3 - 4; . . . ; Рт = Рт—1 . Юк
Перемноживъ эти равенства, уничтоживъ общіе множители въ обѣихъ частяхъ, и замѣчая, что Р1 = 1, находимъ:
Рт= 1 . 2 . 3 . 4 . . . (ш- 1) . т . . . (П).
Такое произведеніе т первыхъ натуральныхъ чиселъ часто встрѣчается въ формулахъ анализа: ему дано особое названіе — факторіала т.
700. Примѣръ. Сколькими способами 5 лошадей могутъ быть аа-пряжены въ дилижансъ?
Очевидно, искомое число есть число перестановокъ изъ 5 предметовъ; слѣд. оно равно 1 . 2 . 3 . 4 . 5, или 120.
Примѣчаніе. Помощію перестановокъ въ прежнее время отыскивались анаграммы фразъ и словъ. Такъ, изъ имени Генриха III Валуа, Ненгі <1е Ѵаіоія, выходитъ: Ѵііаіп Негоііе, изъ имени убійцы Генриха ІП, Кгёге Лас^пея Сіё-шені выходитъ: с’еяі ГепГег циі пГа сгёё; нзъ словъ Ботпя Ьевсініа (домъ Лещинскихъ) Яблонскій составилъ слѣдующія фразы: Асісз шсоішпіз, оппіія ея Інсніа, піапе зИпя Іосі, яж соіитпа беі, I ясашіе воіішп; въ послѣдней анаграммѣ было предсказаніе: Станиславъ сдѣлался королемъ польскимъ. Нахожденіе подобныхъ анаграммъ весьма затруднительно, такъ какъ число перестановокъ изъ довольно значительнаго числа буквъ бываетъ чрезвычайно велико; напр. число перестановокъ изъ 12 предметовъ будетъ1.2.3.4.5.6.7.8.9.10.11.12; это число представляетъ, напр., сколькими способами могутъ 12 лицъ размѣститься на 12 мѣстахъ; положивъ, что 1 пересадку они успѣваютъ сдѣлать въ 1 минуту, что въ сутки они употребляютъ на это 12 часовъ п въ годъ 360 дней» найдемъ, что всѣ пересадки могутъ быть‘окончены чрезъ 1848 лѣтъ.
Сочетанія (сотЬіпаізопз).
701. Способъ составленія и опредѣленіе числа сочетаній.—Пусть данот буквъ: а, Ь, с, гі, . . . , Д, і, /: это будутъ сочетанія нзъ буквъ по
одной. Для составленія двойныхъ сочетаній беремъ каждую букву, кромѣ послѣдней, и приписываемъ къ ней послѣдовательно каждую изъ слѣдующихъ за нею. Получимъ таблицу двойныхъ сочетаній:
аЬ, ас, а(1, ...» аЛ, аг, аЕ
Ьс, Ъдч . . . , ЬА» Ь/, Ы
сск . . . . ск„ сі. сі
’ 7 Т г
Чтобы составить тройныя сочетанія, беремъ каждое изъ двойныхъ, кромѣ
I
г*
тѣхъ, которыя содержатъ послѣднюю букву (а?, Ц . . . , й), н приписываемъ послѣдовательно каждую слѣдующую букву; получимъ
аЬс, аЫ, аЬе, . . . , аЪк, аЫ, аЫ ассі, асе, . . . , ас/ц асі, асі
- ♦ . . « и т. д.
Этимъ мы изъ размѣщеній выбрасываемъ такія, которыя отъ имѣющихся уже отличаются только мѣстами буквъ, и сл. получаемъ сочетанія. Но изъ способа составленія сочетаній трудно опредѣлить ихъ число; легче это сдѣлать при по* мощи слѣдующей теоремы.
Теорема. !/нсло 2)азлтг/(енш изъ т буквъ по к равно числу сочетаній изъ т буквъ по к, помноженному на число перестановокъ изъ к буквъ, т.-е. АІ, = С» . Р*.
Вообразимъ, что мы составили таблицу сочетаній изъ т буквъ й-го порядка; число ихъ выражается символомъ С«. Взявъ каждое изъ этихъ сочетаній (содержащее к буквъ), сдѣлаемъ въ немъ всевозможныя перестановки, число которыхъ (изъ одного сочетанія) будетъ Докажемъ, что такимъ образомъ мы составимъ всѣ размѣщенія изъ т по А, безъ пропусковъ и безъ повтореній. Въ самомъ дѣлѣ, если взять изъ составленной таблицы два члена, то: или они происходятъ отъ двухъ разныхъ сочетаній, и въ такомъ случаѣ различаются буквами; или же происходятъ изъ одного и того же сочетанія. — и въ такомъ случаѣ разнятся порядкомъ буквъ. Слѣд. таблица не содержитъ повтореній. Въ ней нѣтъ и пропусковъ. Въ самомъ дѣлѣ, вообразимъ нѣкоторый членъ * группы Ащ, не обращая вниманія на порядокъ буквъ въ немъ; этотъ членъ представляетъ нѣкоторое сочетаніе изъ т буквъ по А, и слѣд., если не обращать вниманія на порядокъ его буквъ, онъ находится въ группѣ СІ»; такъ какъ буквы этого сочетанія были перемѣщены всѣми возможными способами, то я необходимо содержится въ числѣ полученныхъ размѣщеній. Зная это, замѣтимъ,, что одпо сочетаніе порядка к даетъ перестановокъ, слѣд,
—М р ------------------------------------Ъм» * Г&, откуда
рі - Ат _ т<т 2) • • («*—&+!) . ф /ц.ч
рГ 1 , 2.3 . . . А * ’ * \ /
х К
Итакъ, имѣемъ теорему: число сочетаній пзъ т буквъ по к равно произведенію к цѣлыхъ чиселъ, послѣдовательно убывающихъ на 1, первое изъ которыхъ д?ьлеияо.иг/ на произведеніе натуральныхъ чиселъ отъ 1 до к.
Можно доказать эту теорему независимо отъ формулъ числа размѣщеній и числа перестановокъ.
Пусть дано ш буквъ а, Ь, с, Обозначивъ число сочетаній порядка 7с символомъ СІ» и, выразивъ двумя способами число буквъ, содержащихся во всей совокупности этихъ сочетаній, приравняемъ другъ другу результаты счета. Каждое сочетаніе содержитъ к буквъ, а всѣхъ сочетаній СІ»: сл. всѣхъ буквъ въ нихъ будетъ АХСт-.(І).
. Выразимъ это число иначе. Если отбросить букву а, то изъ остальныхъ ^уквъ можно составить СІ^!і сочетаній 7с — 1-го порядка. Если къ каждому приписать букву а, то составятся сочетанія Аг-го порядка съ буквою а; и число ихъ будетъ, слѣдовательно, Итакъ, во всей совокупности сочетаній к-п> порядка число такихъ, въ которыя входитъ буква а, будетъ СІ-ь Подобнымъ же образомъ число сочетаній, въ которыя входитъ буква Б, будетъ С^ьнт-Д. для каждой изъ т буквъ. Слѣдовательно, число всѣхъ буквъ во всѣхъ сочетаніяхъ А-го порядка, будетъ т X Ст”\*-(2).
Приравнивая числа (I) и, (2), имѣемъ
* ________ рі-1 1 л? . Ст —т . С^-1, откуда —
т. к. эта формула общая, то можно написать
р* — а .—гп — а р* —а—1 , ѵт-д д. а—1
Подставляя вмѣсто а числа О, 1, 2, , . . , к — 2, получимъ
г*
ѵт д. ѵт—1
1 — 1 ПІ — 1 —2 і* ; ~ _ ря “
т— 1 д. । ѵт— 2
Л ~2 — П1 — 2 р* “3 т—2 . __2 3
%
2 _ т — к +2„і
т— А-|-2 2 ѵт—і-|-1
Перемножая эти тождества и-сокращая въ обѣихъ мастяхъ общіе множители, найдемъ
і =т(т — 1) . . (»> —й-}-2) і
к(к — 1)(і — 2). . . 2
а какъ Ст-*+і = иг — такъ какъ оно означаетъ число сочетаній изъ іп — Л-|-1 буквъ Но одной въ каждомъ и, слѣд., равно числу этихъ буквъ, то легко видѣть, что
4 _т(т — 1 )(т — 2) (яі ѵт 1 О 5
1.2.3
702. Примѣры.—I. ша 12 лииэ выбираютъ ко.ммиссію
изъ 5 членовъ, для ііазработки нѣкотораго вопроса; сколькими способами эта коммиссія можетъ бытъ составлена?
Такъ какъ одинъ составъ комиссіи долженъ отличаться отъ другого и не содержать всѣхъ тѣхъ же лицъ, то, очевидно, искомое число есть число сочетаній , Л К Л ___ _____ 12* 5 1.10.9.8 < , л о •’ЛП
изъ 12 элементовъ по 5; слѣд. оно = Сіа = —-ѵ- = 11.9,8 = /92.
1 . *. ѵ. 4 .0
II, Сколько различныхъ діагоналей можно провести въ десятиугольникѣ?
Искомое число есть число сочетаній изъ 10 элементовъ по 2, уменьшенное 10-ью (10 стор. мног.), и сл. = Сіо—10 = ^° " — 10 = 35.
703. Число Ст есть необходимо число цѣлое; поэтому изъ формулы (ІИ) прямо получается
Теорема. Произведеніе к послѣдовательныхъ цѣлыхъ чиселъ дѣлится безъ остатка на произведеніе первыхъ к цѣлыхъ чиселъ.
704. Формула (III) можетъ быть представлена въ другомъ видѣ. Помноживъ ея числителя и знаменателя на(т — к)(т— к — 1)(т — к — 2)...3.2.1 или, что то же, на 1.2.3...(т — А), найдемъ
т(т— 1)(ш — 2) . . . (т — & + 1)(т— А)(гп — А — 1) . . ,3.2.1 1.2.3. . . А X 1 • 2 • 3 . . . (т — А)
Прочитавъ числителя въ обратномъ порядкѣ, находимъ, что онъ предста-вляетъ произведеніе натуральныхъ чиселъ отъ 1 до т- слѣд. можно написать:
См 1.2.3...АХ1.2.3,. . (ш —А)’ или еще
Замѣчая, что СІ есть число цѣлое, изъ послѣднихъ формулъ прямо находимъ слѣдующую теорему.
Теорема. Произведеніе ряда натуральныхъ чиселъ отъ 1 до т всегда дѣлится на произведеніе 1.2.3...к> на произведеніе 1.2.3...(т—к) и на произведеніе этихъ двухъ произведеніи, полагая к < т.
705. Свойства сочетаній.—I. Число сочетаній изъ т буквъ по к равно числу сочетаній изъ т буквъ по т — к^ т.-е. С™ = Ст”*-
Въ самомъ дѣлѣ, по формулѣ IV имѣемъ:
л* п Лт“* ___________________________ 1*т
Р*.Рт-* И Рт-ЬРт-(т-і)“" Рт-І . Р/
откуда прямо слѣдуетъ равенство СІ» = Ст”*-
Можно доказать эту теорему еще такъ. Пусть въ урну положено т буквъ. Вынемъ изъ урны какія-нибудь к буквъ. Эти к буквъ образуютъ одно, и только одно, сочетаніе изъ ш буквъ по к. Оставшіяся въ урнѣ т — к буквъ образуютъ своей совокупностью одно, и только одно, сочетаніе изъ этихъ т буквъ по т—А. Такимъ образомъ всякому члену группы Ст соотвѣтствуетъ одинъ, и только одинъ, членъ группы СХ”*, и обратно: слѣд. число членовъ обѣихъ группъ одинаково.
II. Число сочетаній изъ гп буквъ по к равно числу сочетаній изъ т — 1 буквъ по А, слозгсеянолу съ числомъ сочетаній изъ т — 1 буквъ по к—1; Ст = Ст—1 Ст—!•
Въ самомъ дѣлѣ, по формулѣ IV можемъ написать:
* __ 1.2.3. . .(т-1) р*-і_ 1.2.3» . . (т-1)
1.2 » А.1.2 . . » (т—к—1) 0 1.2 . . . (А—1).1.2 . . . (т-к)
Складывая, находимъ:.
п* [. л* „ _ _ 1.2.3 . . . (ш—1) ___/I 1
Ьт-1 ‘ Ът-1 1.2. . ДА—1). 1.2. . . (ш^А—1) ^А •’ім—Ау НО
1 । 1 ____ т ?
А "і” т —к А . (ж—А)
слѣд.
* і _________ 1.2.3. . . (ш — 1).т і
Ст-і “ГС«-і — і72; . .(А^і)ГА X Г?2:. . . (?п—А—1)(т—А) ~ с"'
*. А
Теорема эта можетъ быть доказана иначе. Члены группы СІ» могутъ быть разбиты на двѣ части: пусть первая содержитъ всѣ тѣ сочетанія, въ которыя не входитъ буква а: ихъ число будетъ С™-і. Другая группа будетъ содержатъ сочетанія съ буквою а. Вынеся въ нихъ за скобки букву а, получимъ въ скобкахъ, безъ пропусковъ и безъ повтореній, всѣ члены группы , составленные изъ буквъ 6, с, А, і, I. Итакъ, дѣйствительно, число С™ есть сумма чиселъ Ст—> и Сяі—і*
706. Задача I.’Ла чшшъ сочетаній изъ 12 буквъ а, Ь, с, по 5 сколько такихъ сочетаній, каждое изъ которыхъ содержало бы 3 опредѣленныя буквы, напр. а, Ь, с?
Для рѣшенія вопроса напишемъ подрядъ буквы а, Ь, с; къ этимъ буквамъ нужно послѣдовательно приписывать парныя сочетанія изъ остальныхъ 9 буквъ. Искомое число и будетъ число парныхъ сочетаній изъ 9 буквъ, т.-е. —или 36.
Задача П. Въ числѣ сочетаній изъ т буквъ а, Ь, с,,.. но к, сколько такихъ, которыя не содержатъ ни одной изъ р опредѣленныхъ буквъ
Отдѣливъ эти р буквъ, которыя не должны входить въ составъ требуемыхъ сочетаній, изъ остальныхъ т—р буквъ составимъ сочетанія А-го порядка: ихъ число и будетъ искомое, т.-е.
(т — р)()м—— 1) . . . (>м— р— к -|- 1) — 1Т2~ЗТТТА ‘
З адача III. Въ числѣ сочетаній изъ т буквъ а, Ь, с,... по к, сколько такихъ, которыя содержатъ, по крайней мѣрѣ, одну изъ опредѣленныхъ р буквъ а, Ъ, с,...?
, Очевидно, искомое число есть разность между полнымъ числомъ сочетаній изъ т буквъ по А и числомъ сочетаній, не содержащихъ ни одной изъ ^опредѣленныхъ буквъ, т.-е.
, — 1)(ія — 2) , . . (ш — А 4-1) _ (т— р)(ш — р — 1) . . . — р — АЦ-1)
4 1.2.3. . .А ГЛГ. 3... А
Соединенія съ повтореніями.
707. Размѣщенія СЪ повтореніями—Размѣщенія называютъ подмыли* или съ повтореніями, когда буквы въ размѣщеніяхъ могутъ повторяться нѣсколько 'разъ. . ,
Пусть дано т буквъ: . .9Ъ9і9Ъ Чтобы составить изъ нихъ двойныя
размѣщенія съ повтореніями, нужно къ каждой изъ буквъ приписать послѣдовательно каждую изъ данныхъ буквъ безъ исключенія; такимъ образомъ получимъ двойныя размѣщенія:
съ буквою а въ началѣ: аа,аЪ,ас.........., ак,аі,аІ\
съ буквою Ъ въ началѣ: Ьа9ЪЬ9Ьс ...... Ък9Ы9Ы*9 съ буквою с въ началѣ: ........... сЛ,сі,сі; и т. д.
Способомъ, которымъ пользовались выше, докажемъ и здѣсь, что полученныя размѣщенія всѣ различны и не содержатъ пропусковъ. Легко найти число ихъ. Съ каждою буквою въ началѣ имѣемъ т размѣщеній, и какъ каждая изъ т буквъ поочередно ставится въ началѣ, то всѣхъ размѣщеній будетъ т . т или т*.
Для составленія тройныхъ размѣщеній беремъ одно двойное, напр., аа и приписываемъ къ нему каждый изъ данныхъ элементовъ безъ исключенія; двойное размѣщеніе да дастъ тройныя: * '
ааа9ааЪ,аас,........... аак9ааі9ааІ;
двойное размѣщеніе аЪ дастъ тройныя:
. - . . . , и т. д.
Извѣстнымъ образомъ докажемъ, что, поступая такъ, ни одного тройнаго рази, мы не пропустимъ, и ни одного не повторимъ лишній разъ. Число ихъ опредѣлить легко. Одно двойное размѣщеніе даетъ т тройныхъ; слѣд. гм2 двойныхъ размѣщеній дадутъ тройныхъ.
Вообще, число размѣшеній г-го порядка, обозначаемое символомъ будетъ
Доказать это значить доказать, что если число размѣщеній г—1-го пор. есть то число размѣщеній порядка г есть тг. Въ самомъ дѣлѣ, послѣднія мы получаемъ, приписывая къ каждому размѣщенію г—1-го пор. каждую изъ т буквъ; такимъ обр. одно размѣщеніе г—1-го пор. даетъ ж размѣщеніи порядка г, слѣд. «Г’-і размѣщеній г—1-го пор. дадутъ или тг размѣщеній по-
рядка г.
Примѣры.—I. Сколько можно написать трехзначныхъ чиселъ изъ девяти цифръ 1,-2, . . . , 9?
Очевидно, столько, сколько можно сдѣлать тройныхъ размѣщеній съ повтореніями изъ 9 элементовъ, т.-е. 93 или 729.
II. Сколь кмлш способами могутъ вскрыться 3 игральныя кости (костяные кубики съ нумерованными гранями)?
Очевидно, 63 пли 216 способами.
708. Перестановки съ повтореніями,^Вообразимъ т буквъ, въ числѣ которыхъ буква а повторяется а разъ, Ь —р разъ, о—? разъ и т, дм причемъ а+ІЧ" т+ . . . равно или меньше т.-е. что каждая буква повторяется, или что есть и неповторяющіяся буквы. Группы, получаемыя отъ всевозможныхъ перестановокъ этихъ т буквъ, называются сг яоятрреимши; число ихъ
будемъ обозначать символомъ: ХЯІ.
Обозначимъ на время число ихъ буквою х и опредѣлимъ его. Въ каждой группѣ поставимъ у а буквъ, равныхъ «, значки 1, 2, 3, . . . , а. Переставимъ эти значки всевозможными способами; такъ какъ изъ а элементовъ можно сдѣлать Ра перестановокъ, то получится новая таблица, въ которой будетъ х . Ра группъ. Эта таблица содержитъ всѣ перестановки изъ т буквъ, въ числѣ которыхъ ? буквъ равны 6, 7 буквъ равны с, . . . , а другія различны. Въ самомъ дѣлѣ: 1) каждыя двѣ группы этой таблицы различны, ибо если они получаются изъ одной и той же группы первоначальной таблицы, то разнятся порядкомъ значковъ 1, 2, . . . , з; а если происходятъ отъ двухъ различныхъ группъ, то отличаются порядкомъ буквъ. 2) Какая угодно перестановка изъ ш буквъ, въ которой р буквъ равны б, у равны с, . . . , остальныя же буквы различны, находится въ
этой второй таблицѣ; ибо если въ этой перестановкѣ уничтожить значки 1, 2,. . . , а, то получимъ группу первой таблицы; а, по предположенію, буквы а въ этой группѣ были снабжены индексами 1,2,. . . , а и послѣдніе перемѣщены всевозможными способами.
Затѣмъ, въ каждой группѣ 2-ой таблицы поставимъ у буквы Ъ значки 1, 2, 3, . . . , р и перемѣстимъ эти значки всевозможными способами; получится 3-я таблица, число членовъ которой равно ® . Ра . Р? . Какъ и выше, докажемъ, что эти члены суть различныя перестановки изъ т буквъ, въ числѣ которыхъ у буквъ равны с и т. д.
Продолжая такимъ образомъ, получимъ всѣ перестановки изъ т буквъ числомъ х , Ря . Рр . Рѵ . . . Но когда всѣ равныя буквы замѣнятся неравными, то образуются перестановки изъ ж буквъ, безъ повтореній; число такихъ перестановокъ равно Рт. Итакъ:
р
ж * Рк . Рр . Рт . . . =РзйЭ откуда х— р-—р_—р-----, или
П р и м ъ р ы: I. Сколько можно составитъ пятизначныхъ чиселъ цифрами 3 и 5, шъ которыхъ первая повторяется 2 раза, вторая 3 раза?
1 2 3 4 5
Искомое число, очевидно, есть у——т.-е. 10.
11. Лака велика од.млса иидбръ во всѣхъ перестановкахъ изв цифръ 122334?
р
Число всѣхъ перестановокъ = —^ — 180; въ каждой перестановкѣ сумма Р2. 12
цифръ =: 15, слѣд. во всѣхъ перестановкахъ она= 15X 180 = 2700.
Ш. ІЗъ урнѣ 10 шаровъ: 3 бѣлыхъ, 4 красныхъ, 2 черныхъ и 1 синій. Сколько можетъ бытъ перестановокъ изъ этихъ шаровъ?
р
Число искомыхъ перестановокъ = —о10 г> = 12600.
г3 . Г( . г3
709. Сочетанія съ повтореніями.—Имѣя т данныхъ буквъ а, 5, с,? аа ЬЬ сс - . іі И і, и взявъ букву а, присоединимъ къ ней пооче-
аЬ Ъс ссі . . И редно всѣ буквы, не исключая и буквы а; затѣмъ къ Ъ
ас Ь(і . * присоединимъ послѣдовательно всѣ слѣдующія за ней
* . . буквы и самую букву Ь; къ с— всѣ за ней слѣдующія
. . сі и с, и т. д. Получимъ группы, различающіяся, по край*
Ы сі ней мѣрѣ, однимъ элементомъ и называемыя сонета-
аі Ы ніями изъ т буквъ 2-го порядка съ повтореніями,
аі
Затѣмъ, взявъ каждое сочетаніе 2-го порядка, припишемъ къ нему букву, которою оно оканчивается и каждую изъ слѣдующихъ буквъ; составимъ группы, ааа аЬЪ . , гп Ш Ш разнящіяся, по крайней мѣрѣ, однимъ элемен-
ааЬ аЬс * * ' 01 томъ и образующія сочетанія изъ т элемен-
аас ’ * шяел 5-ю поряда сг> повтореніями, и т. д.
‘ Въ простыхъ сочетаніяхъ порядокъ к былъ
' 1 необходимо <^т; въ случаѣ сочетаній съ по-
втореніями порядокъ ихъ м. б. какой угодно, йаЗ ай? . . . т.-е. & можетъ быть т. ІІапр., изъ двухъ
буквъ а и Ь сочетанія съ повтореніями могутъ быть и 3-го, и 4-го и т. д. порядковъ; такъ полныя сочетанія 3-го пор. изъ двухъ буквъ а и Ъ будутъ: аоа, ааЬ, аЬЬ, ЬЬЬ.
Чтобы опредѣлить число полныхъ сочетаній изъ т буквъ й-го порядка, сосчитаемъ двумя различными способами, сколько разъ какая-нибудь опредѣленная буква, а напр., встрѣчается во всѣхъ этихъ сочетаніяхъ, и приравняемъ одинъ другому результаты счета. Обозначимъ искомое число [сочетаній знакомъ Г* а
буквою х обозначимъ, сколько разъ въ нихъ встрѣчается буква а. Въ каждомъ сочетаніи находится к буквъ; а число сочетаній = Г^, сл. всѣхъ буквъ во всѣхъ сочетаніяхъ будетъ к Г*'; но это же число буквъ равно тх\ слѣд.
ЛР
тх = Ж откуда #=—-•
Вычеркнемъ букву а по одному разу изъ всѣхъ сочетаній, въ которыхъ она встрѣчается. Урѣзанныя такимъ образомъ сочетанія будутъ составлены изъ данныхъ т буквъ, но въ каждомъ будетъ только по Л—1 буквъ; способомъ, не разъ уже указаннымъ, докажемъ, что совокупность этихъ ур'йанныхъ сочетаній представитъ ат полныя сочетанія изъ т буквъ по к—1. Ихъ число, согласно принятой нотаціи, будетъ Г*”1.
Они будутъ содержать и букву а; и чтобы выразить, сколько разъ встрѣчается въ нихъ буква а, нужно только вм. к подставить к — 1 въ вышенайден-к 1 і і ную формулу. Найдемъ —~ .
Такъ какъ буква а изъ сочетаній съ повтореніями изъ т буквъ по к была вычеркнута Г*^1 разъ, то
рй—і I к_____1 __1 гА—і
т ’’ тт ~~ т т
Приравнивая одно другому два выраженія для а?, имѣемъ
к _ т4-А:—1 [,*-! т ~~ т "
откуда
4 1 гі-1
т " & * ’
Подставляя сюда вмѣсто к поочередно 1, к—2, > . ., 2, и замѣчая, что Г* =т, найдемъ
Р*___(т + к — 1) (т + й — 2)’. ♦ . (т 4- 1>і
т“' 1 . 2 ... к
Очевидно, что и слѣдовательно, можно высказать теорему:
Число полныхъ сочетаній изъ ш элементовъ к-го порядка равно числу сочетаній безъ повтореній изъ т -|- к — 1 эле.меитовъ по Л.
‘Можно еще замѣтить, что, какъ по свойству обыкновенныхъ сочетаній, = 10
гі рт—1
Первая формула удобнѣе для случаевъ, когда вторая—въ про-
тивныхъ случаяхъ.
Нижеслѣдующее, иное, доказательство дано профессоромъ Валецкимъ.
Найти число сочетаній съ повтореніями изъ т буквъ а, &, с, . . . , I порядка А. Всякое такое сочетаніе м. б. изображено одночленомъ а* ЬЗ . . . Іх, гдѣ а, , X суть т цѣлыхъ, положительныхъ или равныхъ нулю, чиселъ, которыхъ сумма = к. Всѣхъ сочетаній будетъ столько, сколькими способами можно распредѣлить к единицъ между т числами, нульными или положительными. Чтобы представить одно изъ такихъ распредѣленіи, расположимъ въ рядъ т—1 какихъ-либо знаковъ, напр., 0; затѣмъ напишемъ единицы числа а передъ первымъ 0, единицы ? въ первомъ промежуткѣ и т. д., наконецъ, единицы числа X за послѣднимъ 0; не ставя ничего, если показатель есть нуль. Такимъ образомъ получатся группы въ родѣ: 0.110 • • .01, состоящія изъ й единицъ и т— 1
раздѣлительныхъ знаковъ. Сочетаній столько, сколько группъ этого рода, а число этихъ группъ есть число перестановокъ изъ т^-к—1 буквъ, въ числѣ которыхъ находится к единицъ и т—1 значковъ 0. Такимъ образомъ, обозначая искомое число сочетаній знакомъ получимъ:
г А ______1.2,3. . . 1)_____
т“1 .2,3. . . (до—1) XI • 2 - 3 . . . к ’ ’ '
Эту формулу можно представить въ другомъ видѣ, сокративъ на 1 , 2.3 . . . (до—1); найдемъ
~ __до(т-Н)(™ + 2} . . . (т+& — 1)
1 .2 .3. . . к ' к р
Напр., число тройныхъ сочетаній съ повтор еніями изъ 4 элементовъ будетъ Г 3 — - 5.6 —
1 * — 1 .2,3““^°*
710. Иногда можно упрощать опредѣленіе числа сочетаній съ повтореніями при помощи соотношенія:
г» = ед1... (3).
Въ самомъ дѣлѣ,, на основаніи формулы (1) имѣемъ
г-д. __ 1.2,3. . (до -|- & ’— 1) _] 1.2,3» . ♦ (до Ь — 1)
т ~ 1.2. . . (ів-1) 71 . 2 . . .к И 1 *+і = 1.2. . . (т —1). 1Т2 '7 7 ’ 7 к-
а эти дроби равны.
Напр., Г“= Г* = 21-Ц? = 66.
711. Примѣръ. 11а сколько способовъ могутъ вскрыться 2, 3, , . . шрамныя кости?
Двѣ кости могутъ вскрыться на столько способовъ, сколько существуетъ парныхъ сочетаній съ повтореніями изъ 6 элементовъ, т.-е. на Г| — р~2 = 21 способъ.
™ г 6 .7 * 8 Л
Три кости кости могутъ вскрыться на і 63 = ——0 способовъ и т. д.
ГЛАВА ХЫѴ.
Биномъ Ньютона.
Выводъ формулы бинома Ньютона для цѣлаго положительнаго показателя.—Свойства этой формулы.—Степень полинома.—Ариѳметическій треугольникъ Паскаля,
712. Произведеніе биномовъ (&-]-а) , (я 4~ А) (я 4" г). Пря-
мымъ умноженіемъ находимъ:
1. (я 4" а) “Ь = лА4~ а
х 4~ а-Ь;
2. (а;-|-в)(я:-[-Ь)(ж-]-с) = х*-)-а + ь 4-€
х2 4“ аЪ
-[-ас
-[-Ьс
#4“ аЪб]
3. (яа)(я Ъ)(х -|- с)(ж4” Ф ” д;<4“а
и т. д.
Внимательное разсмотрѣніе этихъ произведеній обнаруживаетъ слѣдующіе законы ихъ состава:
1) Число членовъ каждаго произведенія единицею больше числа перемножаемыхъ биномовъ.
2) Каждое произведеніе расположено по убывающимъ степенямъ общей буквы х биномовъ, причемъ: показатель буквы х въ первомъ членѣ равенъ числу - перемножаемыхъ биномовъ; затѣмъ показатели # идутъ постепенно уменьшаясь па 1, до послѣдняго члена, который пе содержитъ буквы ж, или, что тоже, содержитъ х въ нулевой степени.
3) Коэффиціентъ перваго члена равенъ 1; коэф. 2-го члена равенъ суммѣ вторыхъ членовъ биномовъ, или, что тоже, суммѣ сочетаній перваго порядка изъ вторыхъ членовъ; коэф. третьяго члена равенъ суммѣ двойныхъ сочетаній изъ вторыхъ членовъ; коэф. четвертаго члена — суммѣ тройныхъ сочетаній изъ вторыхъ членовъ, и т. д. Наконецъ, послѣдній членъ равенъ произведенію вторыхъ членовъ всѣхъ биномовъ.
Докажемъ общность этого закона. Для этого, допустивъ, что законъ вѣренъ для ш — 1 бинома, докажемъ, что онъ останется вѣренъ и для произведенія, содержащаго однимъ биномомъ больше, т.-е. для т биномовъ.
Итакъ, пусть будутъ #4”а» ж + #4“^ > • . , #4"^» #4“ А тѣ
т — 1 биномовъ, для которыхъ, по допущенію > вышеуказанный законъ вѣренъ. Обозначимъ символами: — сумму вторыхъ членовъ этихъ биномовъ, 82— сумму двойныхъ сочетаній изъ нихъ, 83 — сумму тройныхъ сочетаній, вообще, 8а—сумму сочетаній А-го порядка, и 8т-і—произведеніе всѣхъ вторыхъ членовъ. По допущенію, произведеніе этихъ т — 1 биномовъ дастъ:
(я 4" а) (#+ь) (х 4~с) • • * 0е Ч~ М Ч* 0 = ^т_1- 4~ ^і^т-2 4~ 8аггт-3 + + 83^-4+. . . 4- * 4- 4- . . . +8^4.
Введя т-го множителя #4“^» найдемъ отсюда:
(х 4- а) (я 4- і) . . . 4^ 0 (х 0 = 4”
4-г
1. Видимъ, что показатель буквы х въ первомъ числѣ равенъ числу т перемножаемыхъ биномовъ, что въ слѣдующихъ членахъ показатели буквы х
идутъ, послѣдовательно уменьшаясь на 1, до послѣдняго члена, гдѣ этотъ по-казатель есть мулъ, т.-е. гдѣ а? не входитъ.
2. Изъ закона показателей прямо слѣдуетъ, что число членовъ произведенія равно #> + 1, т.-е. на единицу больше числа биномовъ.
3. Коэффиціентъ перваго члена есть 1.
Коэф. втораго члена составленъ изъ суммы 8і вторыхъ членовъ первыхъ ш—1 биномовъ, сложенной со вторымъ членомъ, /, т-го бинома; слѣд. онъ равенъ суммѣ вторыхъ членовъ всѣхъ т биномовъ.
Коэф. третьяго члена составляется изъ суммы 83 двойныхъ сочетаній вторыхъ членовъ т—1 первыхъ биномовъ, сложенной съ произведеніемъ 8Х2 суммы вторыхъ членовъ этихъ же т — 1 биномовъ на второй членъ I послѣдняго ш-го бинома; другими словами, этотъ коэф. составленъ изъ суммы такихъ двойныхъ сочетаній т буквъ, въ которыя не входитъ + сумма двойныхъ сочетаній т буквъ, въ которыя входитъ I; а это даетъ полную сумму двойныхъ сочетаній изъ т буквъ.
Коэф. червертаго члена равенъ суммѣ 83 тройныхъ сочетаній изъ вторыхъ членовъ первыхъ т— 1 биномовъ, сложенной съ произведеніемъ 8аІ суммы двойныхъ сочетаній тѣхъ же буквъ на новую букву I введеннаго бинома; другими словами, этотъ коэф. составленъ изъ суммы тройныхъ сочетаній вторыхъ буквъ т биномовъ, сочетаній, не содержащихъ 4~ сумма тройныхъ сочетаній изъ тѣхъ же буквъ, но содержащихъ I; это даетъ полную сумму тройныхъ сочетаній т буквъ.
Вообще, коэф. при или коэф. (Л-|-1)-го члена, составляется изъ суммы 8к сочетаній й-го порядка вторыхъ членовъ первыхъ т — 1 биномовъ, + произведеніе I суммы сочетаній (А?—1)-го порядка изъ тѣхъ же членовъ на второй членъ I новаго бинома; т.-е. этотъ коэф. слагается изъ суммы сочетаній й-го пор. вторыхъ буквъ т биномовъ, сочетаній, не содержащихъ 2, 4“ сумма сочетаній й-го порядка изъ тѣхъ же буквъ, но содержащихъ 2; это даетъ полную сумму к-іъ сочетаній т буквъ.
Наконецъ, такъ какъ 8т-і есть произведеніе вторыхъ членовъ т — 1 первыхъ биномовъ, то 8т-ь I есть произведеніе вторыхъ членовъ т биномовъ.
Итакъ, законъ, допущенный для тп — 1 биномовъ, оказывается вѣрнымъ и для произведенія, содержащаго однимъ биномомъ больше. Но мы непосредственно доказали его для двухъ, трехъ и четырехъ биномовъ, слѣд. онъ вѣренъ и для 5; будучи вѣрнымъ для 5, вѣренъ и для 6 биномовъ, и т. д.; слѣд. онъ вѣренъ для какого угодно числа биномовъ.
713. Формула бинома.—Итакъ, имѣемъ тождество:
(я-|-а)(й;-|-’Ь)(я-|-’С).. .(я 4"*) 0е 4“ О =#т4_віхт~Ч"$і^-2Н_^хт“3_Н ••
. .,(1)
полагая, что число‘биномовъ есть я». При этомъ:
. -Н ;
. 4-й;
. +Ы;
= а4-6 + с . . 8* = аЬ -|- ас -|-8а = аЬс аМ-|- .
8Л — аЬс ,, * 14^ а&с ... 1 |— ...
8ж = аЬсй. ...............Я, (
а какъ всѣхъ слагаемыхъ здѣсь т, то
Для вывода изъ этого тождества формулы бинома, т.-е. (я4"а)т, стоитъ только положить, что во всѣхъ т биномахъ вторые члены равны, т.-е. что а = Ъ = с=.і — Первая часть тождества обратится въ (а?4_а)’"-
Затѣмъ, найдемъ, что:
= а 4- а 4“а +- -4“
81 = та.
8Я = а2 + а3 -[- а3 • сколько двойныхъ сочетаній с _ »и(т—1) „а «а * іо . Л .
* . 4~#а; причемъ слагаемыхъ здѣсь столько, т(т—1) А
изъ т элементовъ, т.-е. —;—слѣдовательно,
88 = а8 . • -гаВ; причемъ а8 повторяется слагаемымъ столько
разъ, сколько есть тройныхъ сочетаній изъ т элементовъ, т.-е. --1;
1 • ш • о
о т (т —1)0» — 2) .
такъ что 8, = —-—--------------- а*.
1 * ш й о
Вообще, 84 = а*а* Н- • • . +«*; причемъ слагаемымъ а* берется столько разъ, сколько есть сочетаній й-го порядка изъ т элементовъ, т.-е.
от>(т —1)(т—2) ... с __»>(>»—1). . (т—* + 1) і
1.2.3...* , ислѣд., &* — 1.2.3...*
Наконецъ, 8„=а . а . а . . . а, гдѣ а повторяется множителемъ т разъ; слѣд., 8т = ат.
Такимъ образомъ, тождество (1) беретъ видъ: (х4-а)’"=Я’»+та^-’+,и^-=^ ~ !> <” ~ <ЛВ-»-|---
| »!(*» —!)(»» — 2) . . . (»» — *+1)„*^,_і । । „т
. . • Н--—-------—-— -------------а х™ * ч— , , . -ч— а ,
Это и есть знаменитая Ньютонова формула бинома; пока она доказана нами для случая возвышенія бинома въ какую угодно степень цѣлаго положительнаго порядка. Вторая часть ея называется разложеніемъ первой.
714. Эйлерово доказательство формулы бинома.—Приводимъ доказательство формулы разложенія (а-]-Ь)т, независимое отъ теоріи соединеній. Оно дано великимъ аналистомъ XVIII вѣка Эйлеромъ. Замѣтимъ, что если въ биномѣ вынести за скобки а, то найдемъ
(а + Ы = [а (1 +|)]т = а” (1 +(1 4-х)“,
положивъ Вопросъ приводится такимъ образомъ къ разложенію
Въ своемъ доказательствѣ Эйлеръ беретъ исходнымъ пунктомъ слѣдующее тождество. Взявъ произведеніе п биномовъ
Л^) = (1+а^)(1+аМ(1 + а^) • . . . .(1),
подставимъ ах вмѣсто найдемъ
Г(ах) = (1 4~ а*х) (1 + «•&)(! 4~а<я) , . . (1 + аня) . (1 ап+1і:);
а помноживъ обѣ части на 14" ах^ имѣемъ
(1 яа?) = (1 -|- ля) (1 4” • • • (14- а”#) • (14^
или
0
* /"(я#) = (1 -|~б/Л+г^) • Л#) (2)
Если перемножить я биномовъ (1), то, очевидно, получится многочленъ, низшій членъ котораго будетъ 1, а высшій будетъ содержать х . Расположивъ его члены по восходящимъ степенямъ х, получимъ * *
. Д#) = 1 + 4- АХ
лХ,. * - (ЗХ
и все дѣло сводится къ нахожденію коэффиціентовъ Ап Ай, . . . , Ап. Для этого въ тождествѣ (2) замѣнимъ Доя) и {(х) ихъ разложеніями, выполнимъ умноженіе и расположимъ члены по восходящимъ степенямъ такимъ образомъ получится тождество
Приравняемъ теперь коэффиціенты при одинаковыхъ степеняхъ я; для коэффиціентовъ при хр найдемъ равенство
А^ + Ак^АДАрч^1, изъ котораго имѣемъ
а*-Н—а?
Полагая здѣсь ^ = 1, 2, 3, . * . ♦ А находимъ
д а* — 1
А« — г- * л
1 а — 1
а«—1 — 1
= Аі -5*=т- •«’
* — 4 а"~® — 1 а
А3 - ^4 ' аЗ -2. 1 ' ' а
• »•***»*♦*.,
Ар—і — Ар«*>-2
а«~р-Н* ар—1 -
А =А , а₽
лр ар— і ар ] •а
Перемножая эти равенства, сокращая обѣ частя на А, . а . д замѣчая, что а* . а’ . а* , . . а₽ = в1+2+а+<--Н> = аІ₽С₽^'1>, наддехъ _ая—1 а»-1 - 1 а»-2 —1 «п-іН-1— 1 і„(»+і)
кр~ б< —1 ' ~в*—1 а8—1 ' ‘ • а,1₽
Обложимъ теперь а = 1; А будетъ представлять въ этомъ случаѣ произ-г о
веденіе р дробей, изъ коитъ каждая обращается въ д. Но, сокращая каждую на а—Іи полагая затѣмъ а= 1, найдемъ иіъ истинныя значенія, а именно
(^)а=1=(“"“,+аП~2+- - +а+1)в=і=”;
Мп-1 — 1 \ _4- ад-ЗЦ-. . . * + 1 \ —1
\ о*—1 /а=і \ а -41 /в=і 2 т
ая-р-|-і — I \ ___/дп-г 4~ а"~Р"1 + • > + Ц ___________п —Р + 1
а? — 1 /а=1 \ (7Р-1 4-6ІР—2 4” • * •+! Р
Слѣдовательно
. __н(н —1)(н —2). . .(и — р + 1)в
— і л. з:. . р
Полагая здѣсь /> = 1, 2Т 3, . . .,п, найдемъ всѣ коэффиціенты Ап Ааг Аэ, . . . , А„ разложенія (3), гдѣ первая часть, /'(я), есть произведеніе (14- а#) (1 -|- а*&) (14- оах) . . . (1 -4 «п^)і обращающееся при а = 1 въ (1 -р а?)” Такимъ образомъ, равенство (3) даетъ
“Т72
П(И—1) .
1 . 2
Если подставить сюда обратно - вмѣсто 4?, то получится выше найденное разложеніе (а-|-Ь)п.
715. Свойства формулы бинома. — Формула бинома [беремъ разложеніе (#“4а)т] обладаетъ слѣдующими замѣчательными свойствами:
I, Члены ея расположены по убывающимъ степенямъ буквы а и [ио воз^ растающимъ буквы а, причемъ показатели буквы х идутъ, послѣдовательно уменьшаясь на 1, начиная отъ т и до нуля (въ послѣднемъ членѣ), а показатели буквы а идутъ, послѣдовательно увеличиваясь на 1, отъ О (въ первомъ членѣ) до т; сумма же показателей при х и а постоянна и равна въ каждомъ членѣ показателю т степени бинома.
II. Число членовъ равно т-|-1, т.-е. единицею больше показателя бинома: это непосредственно видно изъ закона показателей.
ПІ. Коэффиціенты бинома суть:
і ™ т(«і —1) ш(ш — 1)0 — 2)
** *”’ 1.2’ 1.2.3 ’
шО — 1)...О — &4~ І)?
• >т,1,
т.-е. перваго члена равенъ 1, а коэффиціенты членовъ.,
начиная со второго^ суть числа сочетаній изъ т элементовъ порядка, равнаго числу предшествующихъ членовъ.
IV. Обыкновенно (Л-^І)-й членъ, формула котораго есть
ніО — 1) (т — 2)
1.2. ЗТТ
. . О — * 4-1) (А —1)А
акхт~к,
называется обмыли члеяолг разложенія, потому что изъ него можно получить всѣ члены разложенія, начиная со 2-го, полагая 4 равнымъ послѣдовательно 1, 2, 3, 4, . . . , т. Въ самомъ дѣлѣ, полагая
4 = 1, находимъ Тя = уад:т”1, а это есть второй членъ;
А-2, > Т, = а*хт~*9 т.-е. третій членъ;
і-о т ш(т — 1)(т — 2) * „
Л = 3, > Т< =----------<—/ я-------т.-е. четвертый членъ;
к = яг, > елѣдній членъ.
Тт+і =
т — 1) (я* — 2) - . .2 . 1
1,2. . . (т — 1) . т
атх* = ат- а это — по-
Такимъ образомъ для полученія изъ общаго члена—какого угодно члена разложенія нужно только положить 4=числу членовъ, предшествующихъ опредѣляемому.
V. Коэффиціенты членовъ крайнихъ и равноудаленныхъ отъ крайнихъ равны между собою. Въ самомъ дѣлѣ, коэф-ты 1-го и послѣдняго члена равны 1, Затѣмъ, возьмемъ члены: отъ начала и 4+1-й отъ конца. По
свойству III, коэффиціентъ перваго изъ этихъ членовъ равенъ числу сочетаній 4-го порядка изъ т элементовъ, т.-е. СІ». Замѣтивъ, что отъ послѣдняго до к + 1-го члена отъ конца включительно имѣется 44~1 членъ, а всѣхъ членовъ ?п 4*1, заключаемъ что (4+1)-му члену отъ конца предшествуетъ (яъ+1) —(4 + 1) нлн т — членовъ, а потому его коэф., по пунк. III, равенъ Ст~*. Но мы знаемъ, что Ст = СХ-* (§ 705,1).
VI. Если показатель т есть число четное и = 2^?, то число членовъ разложенія будетъ нечетное 2р-{-1, а потому въ срединѣ разложенія будетъ коэффиціентъ не повторяющійся, съ обѣихъ сторонъ котораго коэффиціенты равны и расположены въ обратномъ порядкѣ. Очевидно, въ этомъ случаѣ придется вычислить р + 1 коэффиціентъ.
Если же показатель т есть число нечетное, напр., 2р + 1, то число членовъ будетъ четное и = 2р + 2; коэффиціенты второй половины будутъ тѣже, что и въ первой, но расположены въ обратномъ порядкѣ, а въ срединѣ разложенія находится рядомъ два равныхъ коэффиціента. Вычислить придется половину, (р +1), всѣхъ коэффиціентовъ.
VII. Вычисленіе членовъ разложенія слѣдуетъ вести по слѣдующему пра вилу. Подставивъ въ формулу 4+1-го члена
™ (т —*-Н2)(т —+4-1) * т
— 1 . 2.3 . • . (Л — 1), Л Х ’
к—1 вмѣсто 4, на основаніи п. IV, найдемъ 4-ый членъ
т(т— 1). . .
1.2.3. .
. (А-1)
Раздѣливъ (1) на (2), получимъ
Т »+і т — к + 1. . а
-тг = —к—X?
Т ______Т \/ ^4” 1 V* ® /'9А
откуда Т*+і —> Г*Х & X- • (3)-
Итакъ: гиь к-ъо члена вывести (4 -р 1 )-и члена, надо коэффиціентъ
к-ю помножитъ на показателя т — к 4“1 букеы х ^полса член?ь н раздѣлитъ на число к членовъ, предшествующихъ опредѣляемому; затѣмъ , показателя буквы а увеличитъ на 1, а показателя буквы х уменьшить на 1,
Педхѣри. 1) Разложитъ (я-р®)7-
Число членовъ = 7 -р 1 = 8; поэтому вычисляемъ 4 коэффиціента, а для другой половины разложенія ставимъ тѣ же коэф-ты въ обратномъ порядкѣ. Найдемъ, примѣняя правило ѴП, первые четыре члена: х^-^-Іах* 4“-^--^* 7 6 5
4—а*#1, или л:1-|-7ая:в”)~21а22;и4-35авх|. Все разложеніе будетъ:
(#4~а)7= я7-]- 7а#в-|- 21ааа;3-|- 35а3л:<4- 35а^а4"21а5яа4“7авл;4“о7*
2) Разложитъ (я:4~а)*-
Всѣхъ - членовъ 9; вычисляемъ 5 первыхъ: я8 4“ 8ах7 4“ а*хв 4* 8‘7/а^84--/ или х*+8ая7 + 28а»х* + 56а»а:5+70а‘х‘.
Все разложеніе будетъ
(а;-{-а)’=г64*8ал:'!-|-28а4а:*-|-56а*^’-(-70а,а:‘-{^56авл:*-|-28а,ж,~)-8а7іг-|-а'!.
VIII. ~Коэффиціенты идутъ увеличиваясь до средины разложенія, а затѣмъ уменьшаются.
Соотношеніе (3) пунк. VII показываетъ, что коэффиціентъ &4’1“Г0 члена , , • * пі — к 4-1 п -
получается изъ коэф-та Л-го члена умноженіемъ на дробь --------. Слѣд.,
когда этотъ множитель > 1 /коэффиціентъ будетъ больше й-го; когда
будетъ = 1, оба коэф-та будутъ равны; наконецъ, при --— < 1
предшествующаго. Опредѣленіе,' при какихъ к приводится къ рѣшенію, относительно к.
к
послѣдующій коэф-тъ будетъ множитель -----— будетъ
неравенства
что к > 0, имѣемъ: к
• ’ • (1).
----------> 1, откуда, замѣчая,
Различаемъ два случая: т — число
Первый случай.—Пусть ш число четное и = 2р. Всѣхъ членовъ въ разложеніи будетъ 2р-|-1; одинъ изъ нихъ занимаетъ среднее мѣсто: тотъ, передъ которымъ находится р членовъ и за которымъ слѣдуетъ р членовъ, т.-е. р4“1-й. Подставивъ въ нер. (1) 2р вмѣсто т, найдемъ
четное, т—нечетное.
I
й есть число долое, и оно должно быть меньше это можетъ быть при
й = 0,1,2,3, . . . ,р: т.-е. коэффиціенты возрастаютъ отъ начала до 1*го о
включительно, т.-е. до средняго^ который и будетъ наибольшій. Изъ п. V за* ключаемъ, что дальнѣйшіе коэф-ты будутъ идти уменьшаясь до конца разложенія- Итакъ, въ срединѣ разложенія находится одинъ членъ съ наибольшимъ коэффиціентомъ.
Второй случай.— Пусть ж—число нечетное и = 2^4~1« Число членовъ разложенія будетъ 2р-|-2, такъ что оно распадается на двѣ половины по />“ГІ коэффиціенту въ каждой. Неравенство (1) даетъ
откуда слѣдуетъ, что для полученія возрастающихъ коэффиціентовъ надо давать А значенія 0,1,2, . . . , р; т.-е. коэффиціенты идутъ возрастая въ первой половинѣ строки. Если затѣмъ дадимъ к значеніе ^-{-1, для вычисленія перваго
т м ’ А? —1“ І х 1
коэф-та второй половины разложенія, то множитель------—- обратится въ 1;
слѣд. (р~]-2)-й коэф. = (р + 1)-му (что слѣдуетъ и изъ нун. V).
Итакъ, при т нечетномъ, въ срединѣ разложенія находятся два равные коэффиціента рядомъ, большіе остальныхъ.
IX. Сумма всѣхъ коэффиціентовъ разложенія (#4аГ всегда = 2т. Въ самомъ дѣлѣ, положивъ въ формулѣ бинома я = а = 1, замѣтимъ, что первая часть обратится въ 2"’; а во второй части всѣ степени буквъ а и х обратятся въ 1, такъ что въ этой части останется сумма коэффиціентовъ; именно:
I ж і т(т — 1) і — 1) (т — 2)
Т "1 Г7 2 !" 17 2Тз
+ • • ’ + І.
Примѣчаніе. Замѣтивъ, что коэффиціенты, начиная со второго, суть числа сочетаній изъ т элементовъ порядковъ 1-го, 2-го, . - . , т-го, и перенеся 1 въ первую часть, можемъ предыдущее равенство написать въ видѣ:
__і---рі | р^ г 1 пт 1 ________________________ ѴЛір ѴИ
Это значитъ, что полное число сочетаній изъ ж элементовъ, порядковъ отъ 1-го до «і-го, равно 2"*— 1.
X. Разложеніе (я — а)’л получается изъ (х а) “ подстановкою (—а) вмѣ-
сто а; такимъ образомъ
О - а)™ = [х+(— а)]» = а?" + »»(- а) я—1 + У*™-1) (— а)»®«-»+ X &
. •+(—а)т=хт—та®»-• • •+«’". . .(а). 1 * *
Очевидно, всѣ члены съ четными степенями (— а) дадутъ знакъ -|-, съ нечетными же знакъ —^поэтому знаки разложенія чередуются. Послѣднему члену при т четномъ предшествуетъ (4*)» при ж нечетномъ (—). Общій членъ будетъ
?и(т— 1). .
акхт~*,
гдѣ нужно брать знакъ + при к четномъ, и — при к нечетномъ. Но если замѣтимъ, что —а =— 1.а, откуда (—а)*=(— 1)*.а* и что это произведеніе само собою принимаетъ знакъ (Ц-) при к четномъ и (—) при нечетномъ й, то, очевидно, цѣлесообразнѣе дать общему члену видъ
Ті+і = + (-!)*<
т(т— 1) . . . (ж ^к + 1)
1.2.3. . . й
подъ которымъ онъ самъ ’ собою принимаетъ надлежащій знакъ соотвѣтственно всякому частному значенію й.—Подобно этому и послѣднему члену, цѣлесообразнѣе дать видъ: +(—1)™. ат>
Такъ, общій членъ разложенія (1 — будетъ *
т —/ 1? 9’8‘ • • ПО-АО
Т*+1 ( 1) • 1 ,2. . Л **
XI. Если въ формулѣ (а) положить х = а=\^ то она дастъ п і і ж0м—.1) т(т— 1) (т — 2) <
или, собравъ положительные члены въ одной части, а отриц. въ другой:
. । т(ш — 1) . т(ж — 1) (?н —' 2) (ж — 3) _ , т (іи — 1) (т — 2
Г.“2 1 1 . 2.3.4 Г- • • —т -і 1.2.3
т.-е, сумма коэффиціентовъ нечетныхъ мѣстъ равна суммѣ коэффиціентовъ четныхъ мѣстъ.
Примѣчаніе. Написавъ послѣднее равенство въ видѣ
5
заключаемъ: если изъ т предметовъ составить сочетанія всѣхъ порядковъ отъ _1-Г0 до ж-го включительно, то число сочетаній, въ составъ которыхъ входитъ нечетное число предметовъ, единицею больше числа сочетаній четнаго порядка.
>716. Задача I.—Разложитъ (7а2Ь — ЗаЬ2)5.
Положивъ 7а2Ь = «, За62 = я, имѣемъ:
(и — ѵ)5 = и5 — 5гш* 4- ѵ2а8 — ѵ3а2 4- — іЛ
Подставивъ вмѣсто и и ѵ иіъ величины и выполнивъ всѣ вычисленія, найдемъ:
(7а2Ь—Зой2)5—16807а1065—36015а9Ьв4*30870а8й7— 13230а7Ь*+2835авЬ*
— 243а’&10.
Задача II. Найти седьмой членъ разложенія (а2 -|» Зх5)1Э?
Искомый членъ =С?9 . (Зж’)’ . (а9)іа = 19779228 ®»®а«
Задача III. Найти 15-й членъ разложенія (2 — а3)18.
Искомый членъ = Сі&*(— а2)11 , 2* = Си . 16 . (—а22) = — 21840а31,
< / Задача IV* Найти коэффиціентъ при я18 разложеніи {ах* — Ъх)9?
Данное выр.= [а#4(1— ^^У = а®я:|в(1— и какъ а9д;8е будетъ множителемъ каждаго члена разложенія (і — 1 ? то нужно найти въ этомъ
1 /1 \«
разложеніи коэффиціентъ члена, содержащаго или 1^1 > т.-е. 7-го чл. Такимъ образомъ, искомый коэффиціентъ =а9 * С® . =84а*Ь“.
/ • /1 Xм
/ Задача V. Найти коэффиціентъ при хг въ разложеніи (я—-^1 .
Пусть хг встрѣчается въ 4 + 1~мъ членѣ. Этотъ членъ =
=с*
но въ немъ должно быть хг, слѣд. т — Зй = г, откуда 4 = т Итакъ, о
т—г т—г
искомый коэффиціентъ = (— 1) 3 . Ст 3 , что можно представить въ формѣ
т-г 1.2. . . т
{~ П 3 ' 1.2. . .«=Г. 1.2. . .^ЬГ*
/ .
Задача VI. Найти численно-наибольшій членъ въ разложеніи (ха)*\ &4-1-ый членъ получается изъ і-го умноженіемъ послѣдняго на
п —к + 1 а /я +1 і \ а
т.^_ на —1)._.
Множитель —— 1, очевидно, уменьшается по мѣрѣ возрастанія й; слѣд. . /« + 1 а . 7
и численное значеніе 1^-----4’5 уменьшается при возрастаніи Л, а потому
к 1-ый чл. не всегда будетъ больше й-го. Если п - при нѣкоторомъ к будетъ меньше 1, то &~|-1-й чл. будетъ меньше й-го. Слѣд., чтобы й-й членъ былъ численно большій, необходимо должно быть
п — й-М ® я —(й—1)4-1 а
---— •х<1 и --------------і
т.-е.
Если к будетъ = —— тогда будетъ -—1 • % — 1 и слѣд. будетъ не
* [ X ’ К X
"* а
одинъ наиб. члена, а два, й-ый и А-}-1-ый, которые будутъ равны между собою.
Такъ какъ мы ищемъ наибольшій по численному значенію'членъ, то наше разсужденіе одинаково примѣнимо и къ разложенію (ж — а)*, такъ что въ част
ныхъ примѣрахъ нѣтъ надобности обращать вниманія на знакъ второго члена бинома. Само собою разумѣется, что удобнѣе каждый примѣръ рѣшать независимо отъ общихъ формулъ.
Примѣръ 1-й. Лаштш яаиболъг&ш разложенія (1 -|-4#)б, если 1 3-
7с-ый членъ будетъ наибольшимъ, если будетъ Такъ какъ
и
п, ___8 — & “Н 1 л гг гп _______8 — (к — 1) 1 А т
Т*+1 =----• 4® . Т* и Т* =---------• Т*-1,
то д. б. удовлетворены неравенства
9 — к 4 - 10 — А 4^.
—к~ 'з<1 и
изъ которыхъ найдемъ: -=->«> у Слѣдовательно, наибольшій членъ будетъ шестой. Величина его =
р5 ^Ѵ_Рз МУ _ 57344 ѵв * ^3/ — в ’ \з/ — 243 *
Примѣръ 2-й. Найти наибольшій членъ разложенія (3 — 2а?) если # =
Т*+1 = ^4— . X т4, численно, лр о
И „ 9 —(Л—1)4-1 2х_„,
Т. =---Ч;—г-1— • -я- X Ті-1, численно.
/С — ІО г
Должно быть
10 —й 2 11 — к 2. 1
к ’З^1 И к—1 'З^1*
откуда 5>й>4. Но при й = 4, Т^і = ТЛ; сл. въ данномъ случаѣ два члена, 4-й я 5-й, численно равные, больше остальныхъ. ,
Ихъ общая величина =
Й . (2)8 . 3е = 84 X 8 . 729 = 489888.
717. Приложеніе.—Теоремы Эйлера и Фермата.
I. Теорема Эйлера: если р есть число первоначальное, а т— ка-кое-угодно цѣлое число, то разность тр — т дѣлится на р.
Если р~ число первоначальное, то коэффиціенты разложенія (ж-|-а)р суть цѣлыя числа, содержащія (кромѣ 1-го и послѣдняго членовъ) множителя, р Въ самомъ дѣлѣ, представляя числа сочетаній, коэффиціенты необходимо суть числа цѣлыя; сверхъ того, число р, будучи первымъ, не входитъ въ знаменатели 1.2, 1.2.3, . . . , 1.2 ... (р— 1) коэффиціентовъ.
Такимъ образомъ, имѣемъ право написать
тр = [1(т — 1)]р— 1крат. р-{-(т — 1/, откуда, вычитая по ш, имѣемъ:
тр — т = (т—1)р — (т — 1) —|—кр. р;
и слѣдовательно
тр — т ~ (т — 1)р — (т — 1) кр. р = (т — 2)р —- (га — 2) 4“ кр. р = . . . =1 ? — 1 4~ Кр- Р = кр.
и теорема доказана,
II. Теорема Фермата есть простое слѣдствіе теоремы Эйлера и выражается такъ: если первоначальное число р не дѣлитъ числа т, то оно , дѣлитъ т?-1—1,
Въ самомъ дѣлѣ, найденное равенство тр— га = кр. р можно переписать такъ:
га — 1) = кр.
откуда прямо видно, что если р не дѣлитъ числа га, то, будучи первымъ, оно должно дѣлить другого множителя ^₽-1 — 1.
718. Степень полинома. Практическій пріемъ для разложенія степени полинома заключается въ томъ, что въ выраженіи (а+дЦ-с . . . )от разсматриваютъ Ь-рс-р. . . какъ одну букву, и по формулѣ бинома разлагаютъ [а+(&4-с4-* . Въ разложеніе войдутъ различныя степени (Ь + е 4- . . .); надъ этимъ выраженіемъ оперируютъ такимъ же точно образомъ, разсматривая ) какъ
одну букву; продолжая такимъ образомъ, получаютъ требуемое разложеніе.
Отыщемъ общій членъ разложенія (а + Ь с 4- </ + . . . )ш. Положивъ Ь -г с 4- & ч- * • • = а?, имѣемъ (а 4~ Ь + е + + • • • )т = (« + х)т = + а)т* Обозначивъ этотъ общій членъ буквою X, имѣемъ:
т(га
— 1) . . . (т — г + 1)
1.2.3. . .г
г,
или
ѵ ' 1 . 2.3 . . . га
Х = -— ----------—-------------. (1).
1 . 2 ... г . 1 . 2 ... (га — г) ' 7
Здѣсьа?и—’г=ф+^4-6?...)«-»'= ф4-^)я»—г=(у4-^)т-^ полагая с4-^-р...=у.
Разложеніе (# 4- 6)т~г содержитъ га — г + 1 членовъ; назвавъ общій членъ его, содержащій аг/, буквою V, можемъ этому члену, согласно (1), дать видъ
_____1.2.3. . (т — г)
1.2. . . г' . 1 . 2 . . . (га—г—г')
г—
Подставивъ въ (1) на мѣсто »* общій членъ.У этого выраженія, найдемъ
1.2. . . г.1.2 . , . (га-г)Л.2 . . . <1.2 . . . (га—г-г') '
или, сокративъ коэффиціентъ на 1 . 2 . . . (т—г):
____________1.2.3. . ________
1.2. . .г.1.2. . .г*.1,2. . . (га—г- г')
а'Т^ум-г—. (2).
Выраженіе это представляетъ всѣ тѣ члены искомаго разложенія, которые содержатъ аг и Ъг'. Въ немъ ут-г-н = 4- й 4- е 4- . . . )т-г-гг = ф 4-полагая я = й 4-е , .
Разложеніе О 4- с)т-г—имѣетъ т — г — г' 4-1 членовъ; назвавъ общій его членъ, тотъ, передъ которымъ находится < членовъ, буквою 2, получимъ
1,2.3. . , (ш—г—г')
. г" .1.2.3. . . (га—г-/'—г")
а ГЬ г,^іл г1—г//.
Замѣнивъ во (2) выраженіе ут-г-у* его общимъ членомъ X, имѣемъ
ѵ 1.2...ш.1.2...(ш—г—И * ’ гіі
Х ~ 172...г.1.2...г'.1.2...(ш—г—г').1.2...г".1.2...(»я—г—г'—г") ' аѢ гт~г г и'
а
или, по сокращеніи:
1.2.3 , . . т
Х = 1.2 .. . г.1.2 . . . г7.1.2 . . . г"Л.2 . . . (т—г—г,~г")а’ЪГ'^"гт~т~т)~г" и т. д.
Если бы полиномъ имѣлъ только 4 члена, то былъ бы и если обозначить ш— г— г1—г" буквою то общій членъ разложенія (а4-ь 4-с-+- былъ бы
V =___________________.__1 ‘ *—2—----------------------------агЪг'сг,,(іг"г
1.2. . .г.1.2. . . г' . 1 . 2 . . . г'. 1 . 2 . . . г"’ ’
гдѣ г"' = т — г — г* — т" или г ч- г' 4“ г" + г*” — т*
Условившись произведеніе 1 . 2 . . . к принимать — 1, когда /с = 0, можемъ изъ X получить всѣ члены разложенія (а — Ь ч- с -ь фт, подставляя вмѣсто г, г', г", г"' послѣдовательно всѣ положительныя цѣлыя числа, удовлетворяющія условію г-кг'4-г"4-г"г=ш. в
Для полученія перваго члена, полагаемъ г = т, и слѣд. г' = т" — т"г = 0, вслѣдствіе чего всѣ произведенія 1 . 2 . . . г', 1 . 2 ... г" и 1 . 2 . . . г"' обратятся въ 1; найдемъ
1.2.3... /Н гитла^Л М*
X = —5—а — ------,—і—г атЪ№с№ — ат.
1.2.3. . .т.1.1.1
Желая найти члены, содержащіе ат-*з, нужно положить т — т — 1 и слѣд. г'4-г" 4-г"'= 1. При этомъ получится столько членовъ, сколькими способами • можно удовлетворить уо—нію г'4г"4-г"'—1 цѣлыми положительными числами, со включеніемъ нуля. Очевидно, этому ур—нію удовлетворимъ, полагая поочередно каждое слагаемое=1, и при этомъ каждое изъ остальныхъ двухъ равнымъ 0. Такимъ образомъ
1. При г = т — 1 беремъ г'=1 и г"~г'"=0, что дастъ ѵ 1 . 2 . . . т *
Х = 1.2. . .(т-І).І.і.Т_ ?
2. При г — т — 1 беремъ г"—1 и г'=г"'= о, откуда,
1.2. . . т
. . (т —1) .1.1.1
дт—ІОДДО = ?>гат”1 с;
3. Наконецъ, при г = т —1,’взявъ г"'=1 п г’“г"=0, имѣемъ 1
Х = 1.2. . \(т-І)~ТТТЛ аи'1^1 = тат"1й-
Желая найти члены, содержащіе ат^2, должны въ общемъ членѣ положить г —т— 2, и слѣд. г'4-?'4-г///=2. Послѣднему ур—нію можно удовлетворить 6 способами:
1. г’=2иг',= г’М;
2. -г" = 2 и г’ ~ г'"— 0.
3. г'”=2 и г'=гг"=0.
4. г- — 1, г"— 1 и г"'=0.
5. г' =г/н—\ и г"=0.
6. г" = г"'=1 и ^ = 0.
Такимъ образомъ найдемъ члены:
1.
1.2.3, . . т
1.2.. Г(ш-2) .1 .2.1.1
1 л
.2, . ,т тиОн—1)
Гт-2)-Т7ТГ27І «»-^=^Г2-2а-гЛ
3.
1 • 2 . . . ж ч,л л„ ж(т —1)
^"1.2. . . (т-2) . 1 . 1 . 1 , 2я” — ’і /2 ~
аш-2^
4
»
дт—= — 1)ат—ЭДе.
а»н—— т(ш — 1)а™-ЭД&
Г.
1.2. . * ™
1.2.., (ш—2) .1.1.1
— 1)а™—%С(к
Ариѳметическій треугольникъ Паскаля.
719. Таблицѣ, извѣстной подъ именемъ ариѳметическаго треуголшика Паскаля, даютъ различное расположеніе; мы укажемъ то, которое принято было самимъ Паскалемъ.
»ГхѴИ/И
г+а
г+п
э?+а
35
И Ау,
56
И
Изъ произвольной точки А проводятъ горизонтальную прямую Аж и вертикальную Ау, и на каждой пзъ нихъ, начиная отъ точки *А, откладываютъ равные отрѣзки, обозначенные на фигурѣ нумерами 0, 1, 2, 3, . .. Проведя пзъ точекъ дѣленія прямой Аа? линіи параллельныя Ау, а изъ точекъ дѣленія А// прямыя, параллельныя Аа?, образуютъ ихъ пересѣченіемъ сѣть квадратовъ, которые Паскаль назвалъ клжткали-Прямыя, соединяющія точки дѣленія лішій равноотстоящія отъ точки А, образуютъ съ Аз?
——. _ _ . _ __ . _ _ ♦ ____________ _______
А&
и Ау прямоугольные треугольники; этп линіи’называютъ базами. База, соединяющая на Аа? и Ау точки дѣленія порядка «4-1, считая отъ А, называютъ п-ою базою. Клѣтки, образующія вертикальную полосу, называютъ столбцамъ; клѣтки, образующія горизонтальную полосу, называютъ линіей, Цифры на Ах суть указатели (индексы) столбцовъ
(нулевой, первый, второй,. -); цифры на Ау суть указатели линій. Самую таблицу составляютъ, руководясь слѣдующимъ правиломъ.
Правило построенія таблицы. еь какой уіосіно млижк» С сложеніемъ чиселъ, стоящихъ въ клѣткахъ С'и С", прилежащихъ непосредственно къ С, осЬ/а- другая—слѣва отъ С; т.-е. С — С'+ С\
Таблица чиселъ, такимъ образомъ составленныхъ, и образуетъ ариѳметическій треугольникъ Паскаля. Отсюда прямо слѣдуетъ, что числа, написанныя въ двухъ клѣткахъ, лежащихъ на одной и той же базѣ., въ равныхъ удаленіяхъ отъ ея концовъ, равны между собою.
Фигурныя числа,—Числа, находящіяся въ клѣткахъ линіи съ индексомъ р, называются фигурными числами порядка р. Такъ, фигурныя числа нулевого порядка суть 1,1,1,...; фигурныя числа 1-го порядка суть 1, 2, 3, 4,... ; 2-го порядка: 1, 3, 6, 10, . . . ; и т. д.
ое фигурное число порядка р будемъ обозначать символомъ ; это число написано на линіи подъ нумеромъ р, въ столбцѣ подъ нумеромъ т—1, на базѣ подъ нумеромъ т + р — 1.
По закону составленія треугольника Паскаля имѣемъ соотношеніе
Е₽ = Г’"1 + • • • О)-
Примѣчаніе. Легко видѣть, что Е^ = 1, каково бы ни было т; и = 1, каково бы ни было
Свойства фигурныхъ чиселъ.
720. Теорема, од-ое фигурное число порядка р равно суммѣ т первыхъ фигурныхъ чиселъ порядка р—1.
Складывая соотношенія, указываемыя равенствомъ (1):
П = Р5Г1 + . р^.-! = Р5.-1 + р«—2 . - • ., р?=РГ1 + Р?
и замѣчая, что Б*=1=Е^~1, имѣемъ
Р* =П"1 + Р^\ + - • •• + РГ1 + ЬГ1 • • • (2).
721. Выраженіе фигурнаго числа Е₽ чрезъ т и — Чтобы выразить фигурное число Е* чрезъ т и р, докажемъ слѣдующую ле,шм^ Паскаля.
Два фигурныхъ числа Ь* и стояЩія въ двухъ смежныхъ клѣткахъ одной и той же базы порядка 1, связаны соотношеніемъ
__ р + 1
гр-і-і “ т—1 г ія—1
Это соотношеніе вѣрно для клѣтокъ на базѣ съ индексомъ 1, ибо числа въ двухъ клѣткахъ на этой базѣ суть 1 = Е{ и 1 =Е®. тает> что въ самомъ дѣлѣ Рг°_1 Г,‘— 1'
* Слѣдовательно, теорема будетъ доказана, разъ мы докажемъ, что если свой' ство это имѣетъ мѣсто для базы съ индексомъ до — 2, то оно имѣетъ мѣсто и для базы съ индексомъ до4~Р— 1, Возьмемъ на базѣ индекса до +р — 2 три смежныя клѣтки А', В', С', расположенныя на линіяхъ съ индексами р—1, I
и въ столбцахъ съ индексами до—1, до.—2, до-3, Фигурныя числа, находящіяся въ этихъ клѣткахъ, суть ^—2*
А
По допущенію, имѣемъ
е
Рт-1
—-—- = —? Т?Р до — 1 гт-1
^га-1 ___ р + 1
ѵр-гі ' до — 2
откуда
іи
рт , га—1
га—1
——і—1 до — і
ИЛИ
<
Г*
______
:
Перемножая, найдемъ:
------1
до — 1
•(3).
Но числа и написаны въ смежныхъ клѣткахъ А и В базы индекса до+р — 1; первая прилежитъ къ клѣткамъ А', В1, а вторая къ Вг, С\ Такпмъ образомъ, лемма доказана.
Написавъ соотношеніе (3) въ формѣ
КУ+« 1 + 1
ДО —1—1
га—1—а
и подставляя вмѣсто а числа 0, 1, 2,. , . , до — 2, найдемъ
рр _-іР ~Ь 1 ’рр-'-і
. р*т до —1 *
Г/Ч-2 гм—2
рт+,-1
Перемноживъ почленно ати равенства и замѣтивъ, что Г"+₽ — 1,
имѣемъ
формулу
„ _ (р + 1)(У + 2)-м~ 1.2.3..
. (т + р — 1)
(т — 1)
— 807 —
что можно написать еще такъ:
г
„р »і(т + 1) . . . (»і 4- р —1)
т 1 . 2 . 3 . . . р
полагая р 0,
Изъ этой формулы имѣемъ
Г° =1-
1 т >
1 = - 1?2 — ™ Г* _ + 1) + 2),
« 1 ’ 1.2 ’ т— 1.2.3
722. Приложенія ариѳметическаго треугольника.—Укажемъ важнѣйшія приложенія ариѳметическаго треугольника.
I. Обыкновенныя сочетанія.— Числа^ стоящія на базѣ съ индексомъ пі и въ толбцодъ съ индексами 1, 2, 5, . . , представляютъ числа обыкиовеи-иш'ь сочетаній гт т буква, взятымъ, соотвѣтственно, по одной, по двѣ, по три, и т. д.
Теорема вѣрна для базы съ индексомъ 1; слѣд. она будетъ доказана, разъ мы докажемъ, что если она вѣрна для индекса т — 1, то будетъ вѣрна и для индекса т.
Пусть будутъ двѣ смежныя клѣтки а и Ь, взятыя на базѣ съ индексомъ ш—1, и находящіяся въ столбцахъ съ указателями р и р—I. По допущенію, числа, написанныя въ клѣткахъ а и &, суть С* _х и С^-Д (гдѣ С означаетъ число соче-
таній). Съ друтоф стороны, по закону построенія треугольника Паскаля, число я?, стоящее въ клѣткѣ с, прилежащей и къ а, и къ б, п расположенной на базѣ съ указателемъ т, удовлетворяетъ равенству
а-=СГЛ+С₽ ..
ТН —1 1 яи-^і
Но, по § 705, Щ сумма чиселъ, написанныхъ во второй части
соотношенія, равна С^; слѣд. , и теорема доказана.
Формула для С*.—Клѣтка с, въ которой написано число С^, находится на базѣ индекса т п въ столбцѣ индекса у?, слѣд. на линіи индекса т—Р- Заключаемъ, что
С₽ _ рт-р__т(т — I) . . (ш—р4~1)
т 1 . 2 . . .р
П. Сочетанія съ повтореніями. — Лемма. — Число полныхъ сочетаній изъ т буквъ по р равно числу полныхъ сочетаній изъ т—1 буквъ по р, + число яшмй сочетаній изъ т буквъ по р—7.
Въ самомъ дѣлѣ, полныя сочетанія изъ т буквъ а, Ъ, с, . . . , I по р можно разбить на двѣ группы; на группу сочетаній, содержащихъ опредѣленную букву, а напр,, и на группу, этой буквы не содержащихъ.
Число сочетаній первой группы равно Г^-1, потому что для составленія ихъ нужно сначала составить полныя сочетанія изъ т буквъ по р — 1, а потомъ къ каждому приписать букву а. Число же сочетаній второй группы, очевидно, есть число полныхъ сочетаній изъ т — 1 буквъ 5, с, . . . I взятыхъ по р, или ІТ і. Итакъ
г*=г₽т1 + п’ .. т т 1 т—1
Но совершенно такое же соотношеніе связываетъ-фигур. числа Б*, \ •
сверхъ того, легко видѣть, что и Е^ = Г^; слѣдовательно
Отсюда теорема: т-ое фигурное число порядка р равно числу полныхъ сочетаній изъ т буквъ по р.
Припоминая формулу-для § 721, 5, имѣемъ
р, т(т -+-1) . . .(ти + р—1) т 1.2.3 . . .р
Ш. Суммированіе одинаковыхъ степеней первыхъ п н а т у-ральныхъ чиселъ.-Такъ какъ ЕІ = п. то
7» г
?2 _П(П + 1) _ Яа П
2 2”^ 25
слѣдовательно
?іІ^1=Е?4-Е^+Гг4-• • 1 Гг — р» — п(п + !)(” + 2)
2 Тг2Тгзт । гн гн ф і
откуда
ч и(« + 1)(« + 2) 0 я(п + 1)(2м+1)
Ь, =-----з---------Ь, =-----ё-------
Выраженіе Е^ даетъ величину 8Э; Е^—величину 8(, и т. д.
IV. Вычисленіе кучъ я д е р ъ,—Числа ядеръ въ сдояхъ треугольной кучи
* • * • * и
. і
* « • * « • ♦ * »
равны соотвѣтственно Е*, Г2, • • * , слѣд. если куча состоитъ
• тчЗ и(н —1)(^ Нг 2)
изъ п слоевъ, то число ядеръ равно Г®, т.-е, --—!------
Далѣе (см. § 739) показано будетъ, что число ядеръ квадратной и прямоугольной кучъ зависитъ отъ 82т и какъ 82 можно опредѣлить посредствомъ треугольника Паскаля, то и вопросъ о суммованіи сказанныхъ кучъ рѣшается этимъ треугольникомъ.
Примѣчаніе. Фигурныя числа колонны подъ № 1, т.-е. фигурныя числа 1-го порядка, наз. также яаюдаальяшш.
Фигурныя числа колонны подъ № 2, т.-е. фигурныя числа 2-го порядка, называются треугольными, такъ какъ ихъ числа единицъ можно расположить въ формѣ треугольниковъ (см. выше).
Фигурныя числа, стоящія въ столбцѣ подъ № 3, или фигурныя числа 3-го порядка называются пирамидальными. Числа 4-го порядка наз. тредгодько-тре-уюлъными.
V. Вычисленіе коэффиціентовъ бинома Ньютона.—Если 1, Аі, Ач, . . . суть коэффиціенты членовъ разложенія (х + а)т, то числа
1, 1 А4, А| -р А2, . • ♦
суть коэффиціенты разложенія (х + а)»»+і.
Въ самомъ дѣлѣ, если равенство
(ж 4- я)ж =1 . агт+ Аі . 1 + АяЛ^г*»—2 + . . . + Лтат
помножимъ на то получимъ
(а?+ я)тД-1=1 - &*"+! (1 + + (Аі + 4-. . . +Атот+і.
Так. обр. коэф-ты второго разложенія выводятся изъ коэффиціентовъ перваго по закону составленія ариѳметич. треугольника. Но числа на базѣ индекса 1 суть коэффиціенты (а?+ а)1; слѣд. числа базы индекса 2 суть коэф-ты (а?-ь«)* и вообще, числа базы индекса т суть коэф-ты (яг+а/", расположеннаго по нисходящимъ , степенямъ я?.
Число этой базы, стоящее въ клѣткѣ колонны индекса р> есть С*; слѣдовати общій членъ разложенія (^4-а)т есть р.
723. Примѣчаніе. Теоріей соединеній занимались уже индійскіе математики; въ алгебрѣ Баскары (1114) даны правильныя формулы для опредѣленія числа различныхъ соединеній. Формулы числа размѣщеній и сочетаній позднѣе были вторично найдены Галилеемъ (1564 — 1642). Ариѳметическій треугольникъ былъ извѣстенъ уже китайскимъ математикамъ XI столѣтія, а затѣмъ вновь найденъ былъ Паскалемъ въ ХѴП столѣтіи (1623—1662). Формула бинома дана . Ньютономъ въ 1676 году. Она вырѣзана на гробницѣ Ньютона въ Вестминстерскомъ аббатствѣ.
отдълъ пятый,
ТЕОРІЯ РЯДОВЪ И ЛОГАРИѲМОВЪ.
глава хьѵ.
Прогрессія ариѳметическая.—Общій членъ.—Сумма членовъ.—Вставка среднихъ ариѳметическихъ.—Безконечная прогрессія.—Опредѣленіе суммы одинаковыхъ степеней членовъ ариѳметической прогрессіи.—Приложенія.
724. Опредѣленіе. Ариѳметической прогрессіей наз. ’ рядъ чиселъ, изъ которыхъ каждое получается изъ предыдущаго прибавленіемъ постояннаго, положительнаго или отрицательнаго, количества, называемаго разностью прогрессіи. Очевидно, что когда разность положительна, члены будутъ возрастать, и прогрессія наз. возрастающею; когда разность отрицательна, члены идутъ уменъ-шаясь, и прогрессія наз. убывающею. Слово прогрессія обозначается знакомъ 4-; члены прогрессіи отдѣляются одинъ отъ другого точкою. Такъ:
4-5 . 8 . 11 . 14 . 17 . . . есть прогрессія возрастающая; разность ея = 3.
4-5 «2.— 1.— 4.-7. . . есть прогр. убывающая; разность ея = — 3.
Для полученія разности надо изъ какого-нибудь члена вычесть предшествующій.
Когда число членовъ прогрессіи ограниченное, она наз. конечною; при неограниченномъ числѣ членовъ—безконечною.
. 725. Каждые три смежные члена ариѳм. прогрессіи составляютъ непрерывную ариѳметическую пропорцію. Пусть дана прогрессія въ общемъ видѣ
4-а . Ъ . с . <1. е . . .,а разность ея г.
По опредѣленію прогрессіи: с — Ь = г и Д—с = гу откуда
й — с = с — &:
смежные члены 5, с, й, составляютъ непрерывную ариѳметическую пропорцію.
726. Теорема. Общій членъ. — п-й членъ прогрессіи называется общимъ членомъ. Пусть дана прогрессія
, г . з . і . и . . . (1),
въ которой « есть п-й членъ, а разность = 5. По опредѣленію прогрессіи имѣемъ:
і = с = ЬЦ-5тс? = с-[-5, . . . , = / = и — ^Ц~8.
Складывая эти равенства, находимъ:
Ъ с сі• • • —|* з —I —и = а Ь —|— с —{— в • •(я—1^8^
а отнявъ отъ обѣихъ частей по Ъ -|- с 4“ • • • ~Ь $ 4~ получаемъ: «
\ ы = а-4(п — I)®-
к
Итакъ: общій членъ прогрессіи равенъ первому* сложенному съ разностью помноженною на число предгиествующихъ членовъ.
Примѣры: 1. Найти двадцатый членъ прогрессіи:
4-7 . 3 . — 1 ... . * •
Здѣсь а = 7, і = — 4, п — 20. Слѣд.
«=7 + (20- 1) . (_ 4) = 7 + 19 . (—4) = — 69.
2. Найти величину п-го нечетнаго числа.
Нечетныя числа образуютъ ариѳм. прогрессію, въ которой а=1, -8 = 2; слѣд. я-е нечетное число = 1 -|- (я ~ 1) . 2 — 2п — 1.
3. Пространства, проходимыя свободно-падающимъ тѣломъ въ первую, вторую, . . . секунду, образуютъ ариѳметич. прогр., первый членъ которой — ^д, а разность = д. Наити пространство, пробѣгаемое въ п-ю секунду?
Это пространство = д^(п — 1) <7 — (2п — 1) .
727. Теорема. Во всякай конечной ариѳметической прогрессіи сумма крайнихъ членовъ равна суммѣ двухъ другихъ, равноудаленныхъ отъ крайнихъ.
Пусть имѣемъ прогрессію объ « членахъ:*
. , Ь . с . д' . . . х . . . у . . . к . г . I . и,
разность которой = 8; пусть, кромѣ того, членъ я имѣетъ передъ собою р членовъ, и пусть р членовъ слѣдуютъ за у. По формулѣ общаго члена имѣемъ:
я = а-42) . 8 . . . (1).
Написавъ прогрессію вѵ обратномъ порядкѣ:
замѣчаемъ, что ея разность будетъ (—8); въ ней передъ членомъ-# находится р членовъ, и потому
у = »-\-р . (-8) . . . (2).
Складывая равенства (1) я (2), получаемъ:
#4* у = »+«••
Примѣчаніе. Можно бы было членъ у выразить и изъ начальной прогрессіи, принявъ въ ней у за первый членъ; въ такомъ случаѣ члену « предшествовало бы р членовъ, и потому « = у4~Р®, откуда: у~и—рѢ* выраженіе, одинаковое съ (2).
728- Теорема. Сумма членовъ конечной ариѳметической прогрессіи равна полусуммѣ крайнихъ, помноженной на число членовъ.
Взявъ прогрессію 4-а . &.• с . Л . # , й . й . і . и объ п членахъ и назвавъ ея сумму буквою 8, имѣемъ
8 = а -I- Ь 4“ 4~ & 4~ * • • + & + —Н ~Н • * • (•
Написавъ слагаемыя въ обратномъ порядкѣ, имѣемъ:
8 = « 4“ И- 4~ —Н * * * Н“ 4* 4^ 4~
Складывая (1) съ (2), получаемъ:
28 = (а4-и)4-(Ь4-і)4-(с + Л)4-(^ + Л)+ . . . + . * 4“ Ф ”Ь "Ьс) Ч~ И- ”Ь (и Ч- °0*
Во вторыхъ, третьихъ и т. д. скобкахъ имѣемъ суммы членовъ, равноотстоящихъ отъ крайнихъ; по предыдущей теоремѣ, каждая такая сумма =(а4'мХ слѣд. вторая часть равенства содержитъ слагаемое (&4~^Х повторенное » разъ, а потому
28 — (а 4- и) . п, откуда 8 =---------$----
При мѣчаніе Подставивъ вмѣсто и выраженіе а 4" (п — 1) можемъ этой формулѣ дать видъ
Примѣры: I. сірш/ и пбртмагз матдоальиът чысель. Эти
числа образуютъ прогрессію Н-1 2 . 8 , . . (п — 1) . п, въ которой первый членъ = 1, разность = 1, число членовъ = п; а потому
\ (Т + п) • Л
Ь— 2”
П. Найти сумму первыхъ п нечетныхъ чиселъ.
Выше мы видѣли, что п-ое нечетное число =2»—1; потому вопросъ приводится къ нахожденію суммы членовъ прогрессіи
Н-1.3.5 . . - (2п—1), въ которой первый членъ =1, разность =2, послѣдній членъ = 2»—1, число членовъ = я. Такимъ образомъ
8 = ѵ д-------— = яа.
Итакъ: сумла п первыхъ нечетныхъ чиселъ равна квадрату числа этихъ чиселъ,
Докажемъ, что обратно: если сумма членовъ ариѳметической прогрессіи ^авма квадрату числа этихъ членовъ, каково бы оно ни было, то прогрессія есть рядъ нечётныхъ чиселъ.
Въ самомъ дѣлѣ, каково бы ни было и, должно быть
или, располагая по степенямъ я:
(2 — 8)я* -|" — ^а) п = 0. • »
Такъ какъ полиномъ первой части долженъ быть тождественно равенъ нулю, то должны имѣть:
,2—6 = 0 и 6 — 2а = 0, откуда 5 = 2, 2а = 5; или:
а = 1 И' 5 = 2, т.-е, рядъ будетъ 4~1 .3.5.7...
729. Вставка среднихъ ариѳметическихъ между двумя данными числами.
Между двумя данными числами а и Ь вставить т среднихъ ариѳметическихъ значитъ составить ариѳметическую прогрессію объ т-^2 членахъ, которой а и Ъ были бы крайними членами. Очевидно, вопросъ приводится къ нахожденію разности 8 прогрессіи. Такъ какъ члену Ь предшествуетъ т -|-1 членовъ, то
6 = а^(т-{-1) . 5, откуда
Такимъ образомъ прогрессія будетъ
* „ / । й — а\ I і п Ъ — а\ [ ( „ Ъ — а\ [ , Ъ — а\ ,
-- а • а Ч--. а-4-2--------т а-кЗ-----
• \ 1 т»4-і/ \ 1 »»+1/ \ 1 1
Примѣръ. ЛГежЭу 5 и 32 вставитъ 8 среднихъ ариѳметическихъ.
Разность будетъ или 3. рд^д, имѣемъ прогрессію
4-5 . 8 . 11 . 14 . 17 . 20 . 23 . 26 . 29 . 32.
730. Т в о р е м а.—Тйми въ прогрессіи ~а.Ъ.с.&...г.і.и между каждымъ членомъ и слѣдующимъ вставитъ одинаковое число т среднихъ ариѳметическихъ, то ^анкые члены влсіьсттъ съ вставленными составятъ одну сплошную прогрессію
~а.а.^..Л.Ъ.а!4г...Ѵ.с.ац.
Въ самомъ дѣлѣ, всѣ частныя прогрессіи, такимъ образомъ составленныя 4-а.а.^.М; -Яа'.^.Хс; . . , 4-и,
послѣдовательно имѣютъ разности
б —«а с — Ъ (I — с т + Ѵ ж + 1’ т+1’
и—
по Ъ — а = с — Ъ = сІ — с = • • * =и — I, по опредѣленію прогрессіи, слѣд-всѣ эти отдѣльныя прогрессіи имѣютъ одинаковую разность. А какъ, приэтомъ, послѣдній членъ одной служитъ первымъ членомъ слѣдующей, то совокупность всѣхъ прогрессій составляетъ одну сплошную прогрессію.
731. Т е о р е м а.—.Во всякой безконечной возрастающей ариѳметической прогрессіи члены приближаются къ -|- со, а въ убывающей къ — со.
1. Если буквою и обозначимъ п-й членъ, то требуется доказать, что всегда можно найти такое цѣлое число п, что и будетъ больше всякаго произвольно взятаго количества М. т.-е. что для п всегда можно найти цѣлое значеніе, удовлетворяющее неравенству: —1)>М * * • (О- Въ самомъ дѣлѣ, пере-
неся а во вторую часть и дѣля на положит. число 8, имѣемъ
откуда п
Каково бы ни было М, всегда ° можно выразить цѣлымъ или дроб-нымъ числомъ; найдя цѣлую часть формулы 1 -| ч— и взявъ для п цѣлое число, большее ея, тѣмъ самымъ удовлетворимъ неравенству (1).
Примѣръ. Съ какою мѣста члены прогрессіи Ч-5.8.11 . . . становятся больше 1ОООО?
10000 _5 2
По предыдущему должно быть п > 1 -)--------или п > 3332 слѣд.
члены становятся больше 10000, начиная съ 3333-го*
2. Если прогрессія будетъ убывающая, т.-е. 8<0, то всегда можно найти въ прогрессіи такой членъ и, который былъ бы меньше произвольно взятой величины М, т.-е. всегда можно найти цѣлое число п, удовлетворяющее неравенству а-4“(п — 1)8<М. Въ самомъ дѣдѣ, неравенство даетъ (п — 1)8<М—аг откуда, раздѣливъ на 5 и перемѣнивъ смыслъ неравенства, имѣемъ
М — а
>--5-*
п — 1
а отсюда п
М —а
Взявъ для п цѣлое число, большее 1+?*$ ** удовлетворимъ неравенству.
732. Рѣшеніе нѣкоторыхъ задачъ, относящихся къ ариѳметическимъ прогрессіямъ.
Во всякой ариѳметической прогрессіи фигурируетъ 5 количествъ а, и, 5, я, 5, связанныхъ двумя уравненіями:
« = в-Ня^-1) . і . . .(1) в = . (2)._,
Слѣдовательно, всегда можно найти два изъ этихъ количествъ, когда остальныя три будутъ даны; а потому можно предложить столько различныхъ задачъ, сколько существуетъ сочетаній изъ пяти элементовъ но два, т.-е. С* или 10
задачъ. Эти сочетанія суть: аи, ап, «8, «м, «5, 5м, 5з, п$; а слѣд. задачи таковы:
Данныя. Искомыя.
1. а. г, п 5
9 О* * «т г, п 3
3. а, п г, 8
4. а, и. 2 «, 8
э. 2, п в, и
6. п а, г
і. а, п «, 0
8. и. 3 а, п
9. 5, 8 «, п
10. а, и 3, и.
Изъ числа этихъ задачъ только 8-я и 9-я приводятъ къ квадратному ур—пію, остальныя рѣшаются ур—ми Ьй степени.
733. Задача I. Сколько нужно взятъ членовъ въ ариѳметической прогрессіи, которой І-м членъ есть 16, а разность 8, чтобы сумма-членовъ составила 1840?
Имѣемъ ур—нія
и = 16 Ф (п— 1) .8 и 1840 =(2Ц—
А
Исключая изъ этихъ ур—ній находимъ ур—ніе
ч
(!) 1840= [2 -16 + (п-1) -81» ми „а_{_з„_46о = 0.
Рѣшая это ур—ніе, находимъ корни: п'=20, п” ~ — 23. Заключаема что нужно взять 20 членовъ. Прогрессія будетъ
ѵ 16.24,32.40.48.56.64,72,80.88.96.104.112.120.128.136.144.152.160.168. /
Отрицательный корень. Подставивъ въ ур. (1) — п вмѣсто получимъ:
1840 = і2--И- + или і840=|2-(-16)+Л+^
Ю.п [2.(— 8) + («—]). 8]М или • 1840 = !—1----------—=-»
ур—ніе, положительный корень котораго = 23. Заключаемъ, что, взявъ первымъ членомъ прогрессіи (—8) вмѣсто 16, разность сохранивъ ту же, а число членовъ увеличивъ на 3, получимъ сумму, равную ‘ 1840_ И дѣйствительно, сумма 23 членовъ прогрессіи
4--8 . О . 8 . 16 . 24 ... 168
равна 1840, ибо эта прогрессія сравнительно съ предыдущей имѣетъ три лшп-
I
нихъ члена: —8,0 и + 8, дающимъ въ суммѣ 0, а остальные члены — тѣ же, что и въ предыдущемъ рядѣ.
734* Задача II. Изъ к выѣзжаетъ курьеръ и проѣзжаетъ въ первый день 10 милъ, а въ каждый слѣдующій --ъю мили больше. Спустя 3 дня, другой курьеръ, ѣдущій по тому же пути какъ й первый, выѣзжаетъ изъ юрода В, расположеннаго передъ городомъ А, въ 40 миляхъ отъ послѣдняго. Онъ проѣзжаетъ въ первый день 7 милъ, а въ каждый слѣ-дующій день мили болѣе. Черезъ сколько дней послѣ выѣзда перваго о
оба курьера встрѣтятся? *
Рѣшеніе Штурма. Пусть искомое число дней будетъ х. Путь, пройденный 1-мъ курьеромъ, есть сумма членовъ ариѳм. прогр*, которой крайніе іа іл і я —1 /~Л । я —х (79 + #)я п _
члены суть 10 и 10 -----— з т.-е. [20—]----I или -—з-"' Второй
курьеръ находится въ дорогѣ, до встрѣчи съ первымъ, х — 3 дня, к проѣз-
Гі4 і (я-4).2л х — 3 (17ч-я)(# — 3)
зсаетъ |_14-]----ЙЛИ-----------------------3—‘ —~ миль#
Ур—ніе задачи есть
(1) —3) __40 = 0, или 5хі _ 125а;_|_ 552 = о.
Рѣшивъ ур—ніе, найдемъ: х =5,72 . . . , #"=19,27 . . .
Но, приводя задачу къ ур—нію, мы предполагали, что # — число цѣлое; сл. найденныя рѣшенія не отвѣчаютъ на предложенный вопросъ. Тѣмъ не менѣе, можно показать, что цѣлыя части 5 и 19 корней означаютъ, что были двѣ встрѣчи, первая по истеченіи 5, вторая 19-ти дней*
Во-первыхъ, замѣтимъ, что если буквою а обозначить путь, сдѣланный первымъ курьеромъ, и буквою — путь, пройденный вторымъ, увеличенный на 40 миль, полагая, что первый курьеръ находится въ пути цѣлое число х, а второй—цѣлое число х — 3 дней, то имѣемъ тождественно
(3) 5#2 - 125# + 552 = 24 (? — а).
Это, очевидно, слѣдуетъ изъ того, что ур* (2) было выведено изъ (1) перемѣною знаковъ у всѣхъ членовъ и умноженіемъ ихъ на 24.
Подставимъ теперь въ 1-ую часть ур. (2) вмѣсто х сперва 5, потомъ 6; такъ какъ меньшій корень 5,72 . . . содержится между этими числами, то результатъ первой подстановки будетъ положительный, второй — отрицательный. Но, въ силу тождества (3), разность — а всегда имѣетъ одинаковый знакъ съ триномомъ 5#а—125#4~552; слѣд. въ концѣ пятаго дня а<?, а въ концѣ шестого р < а. Итакъ, первая встрѣча, какъ и было сказано, имѣла мѣсто между пятымъ и шестымъ днемъ. Подобнымъ образомъ докажемъ, что вторая встрѣча имѣла мѣсто черезъ 19 дней. Возможность этой второй встрѣчи легко понять, ибо второй курьеръ, увеличивая свою скорость болѣе перваго, встрѣтитъ его, будучи сначала перегнанъ первымъ. Это подтверждается изслѣдованіемъ, въ концѣ сколькихъ дней оба курьера имѣютъ одинаковую скорость: найдемъ число дней 13, содержащееся между 5 и 19.
Можно, далѣе, опредѣлить дроби, которыя слѣдуетъ придать къ числамъ 5 и 19, для надожденія точнаго времени встрѣчъ, предполагая, что< скорость курьеровъ не измѣняется въ теченіе цѣлаго дня. Опредѣлимъ, напр., время второй встрѣчи.
Чтобы найти промежутокъ, раздѣляющій курьеровъ по истеченіи 19 дней, достаточно, въ силу тождества (3), подставить въ первую часть ур. (2) 19 вмѣсто х и раздѣлить результатъ на 24. Найдемъ знакъ (—) показываетъ, что въ началѣ 19-го дня курьеръ В не догналъ еще курьера А. Но скорости А и В въ теченіе 19-го дня суть 10н 7-|~ —л—> или -у и 17; слѣд., если обозначимъ буквою у искомую часть дня, то для опредѣленія у получимъ 3 * 29
ур—ніе 17^=4 +у У, откуда у = 0,3; слѣд. вторая встрѣча имѣла мѣсто въ концѣ 19х-,3.
735. Задача. III. двухъ ариѳметическихъ прогрессіяхъ
— 2.5.8. 11... и — 3.7.11.15.,.
заключающихъ, каждая, по 100 членовъ, сколько находится общихъ членовъ?
Членъ порядка х въ первой прогрессіи есть 2-|-3(х— 1), или Зх— 1; членъ порядка у во второй равенъ 3 -4 (у — 1), или4у — 1; чтобы эти члены были равны, необходимо, чтобы было Зх=4у. Вопросъ приводятся къ нахожденію цѣлыхъ положительныхъ рѣшеній, меньшихъ 100, удовлетворяющихъ не-1 опредѣленному ур—нію Зя = 4у. Выводя изъ него х, находимъ гг = у-|“ду; слѣд. | должны равняться нѣкоторому цѣлому Л, откуда у = 3&, и слѣд. х=4к. Но какъ х должно быть не болѣе 100, то к можетъ получать только значенія: 1,2, 3,..25. Заключаемъ, что обѣ прогрессіи содержатъ 25 общихъ членовъ.
736. Задача IV. Найта условіе, необходимое и достаточное для того, чтобы три данныя числа А, В, С была членами порядка т, р, $ одной и той же ариѳметической прогрессіи.
Обозначая буквами х и у первый членъ и разность прогрессіи, о которой говорится въ условіи, необходимо и достаточно, чтобы ур—нія
А = я-|-(я»—1)у, в = ®+(^ —1)у, С = аг+(3 —1)У удовлетворялись одними и тѣми же значеніями х и у; другими словами, искомое условіе есть результатъ исключенія х и у изъ этихъ трехъ ур—ній. Имѣемъ
А — В = (т — р)у, В — С = (^ — ц)у,
а исключивъ у, найдемъ
(А—В)(.р—з)=(В — С)(»і—р), или (р—?)А+(з—т)В-)-(яі — р)С=О; это и есть искомое условіе.
737- Задача V-—Найти сумму одинаковыхъ степеней членовъ ариѳметической прогрессіи.
Пусть имѣемъ прогрессію 4~ п . 6 . с . й . & , . . А . І, разность которой=3, а число членовъ ♦»+!> и пусть требуется найти сумму ?н-хъ степеней ея членовъ.— По свойству прогрессіи имѣемъ:
6 а 4 3, е = Ь + . ,1 — & +
Возвышая всѣ ѳти равенства въ т 4* 1-ю степень, по формулѣ бинома Ньютона имѣемъ:
= (а й)*+і — аЛ-Н + (»і + -|~ '-п ат ~13а 4-
(м + 1)т(ш — 1) ГТ2ТЗ
дт—ЗоЗ
С«4-1 = (Ь + 3)«+1 = 6«Н-1 + (т +1) 6тН- Ь"' іг2-+
. (»»+ 1)т(т —1), я *
1.2.0 ’
= (с й)т-Н = с™4-і (т 4- 1) сотй 4~
— с™-132
. (>л 4- 1)т(иг — 1) _ч_ . । . |,
1.2.3
гт+1 = (й 5)«Н-1 = ІЬМ-І + (т +• 1) Л**4 + • т 1 $2 4-
1 » й
(т 4“ 1)*и(т — I)
1.2.3
4-
Складывая эти равенства, замѣчая приэтомъ, что члены ЬМ-і, #*4\ бН-Н,. . . , ЛМ'і общіе обѣимъ частямъ, взаимно уничтожаются, и полагая для краткости
ат 4-Ьм 4-0** 4-. . ^-і-р^-14*. . .4^-і = 8ж-і;
ч в . 4-= 8т_з; . . . ;л4-&4-е4-. . ,4-й=8і,
найдемъ
>+і = дт+! -|- (т 4-1)0.8т + ^±1^' 0« . +
і.2
4- і- —--— ------ йа . 8т-2.4" • ‘ • + (т + 1)* * 31 + ЯбМ-І •*.(])
Выражая отсюда 8т, находимъ:
гж+1 — дж-гі т Ш(»і —1).4 „
8» - (Л>+І)а----2 •8 • Зт-1 —2.3" ’ • 8”-2 -
тіяі — ІХ»»—2). _ п - „
—----2.3.4------«’-З-—з—• • •--81-^+Т*- •
Помощію этой формулы можно найти* 8Ж, если будутъ извѣстны суммы 8™—:, 5т-2,. . ., 8Ѵ Прилагая эту формулу, нужно помнить, что число членовъ второй части равно ?п4-1-
есть сумма членовъ самой прогрессіи и выраженіе ея извѣстно. Зная 81 и полагая »і=2, найдемъ 82. Зная 8і и 82і и полагая іл-^3, найдемъ 8в, и т. д.
— 819 —
Сумма одинаковыхъ степеней натуральнаго ряда, — Положивъ а = 1, 1=1, 1=«4-1, обратимъ нашу прогрессію въ рядъ первыхъ п + 1 натуральныхъ чиселъ: 1 . 2.3 • . . п , (п + ]). Въ этомъ рядѣ будетъ
8т = 1*” + 2т + Зт + • • .+♦**;
і ]л—і _|— 2й*-! Зт 1 —|-
. + п™—Ь
82=1« + 2«+. . 8( = 14-2+3. . • +«.
Формула (2) приметъ видъ
_(«+!)"+!—1 т „ т(т — 1)
т ~ (да + 1) ~2 ' 2.3“
8т—2
т(т — 1)(т - 2) „ „ п
2.3.4 ‘ &1 т + 1
•(3).
1. Положивъ т = 1, и замѣтивъ, что рядъ будетъ имѣть 2 члена, получимъ:
8і = -+ У—- — і . 8. Но 8„=1»+ 2»+3°+ . . . +п«=1-Н + 1 + . . . +1=я; слѣдовательно
о __(« + 1)г— 1 п__(п4-Гр — (М-1} + 1 — 1) _ («+ 1).п .
2 2 ~~ 2 2 2 * * * ^
результатъ, найденный нами въ § 728.
2* Положивъ «< —2, находимъ:
-4- 1 )а — 1 1
82 = ^——— — 8і — - . 80. Подставляя величины, найденныя для 80 и 8Ь О о
получимъ
1 («+1)Я «_(«+!)’—(п4-1)_(п-Н)п_(п+1)[(м+1?-1]
2 3 2 3“ 3 2 — 3 - -
(п + 1)п 4 п(п-|- 1)(п + 2) (« + !)«_2п(м +1)(п+ 2) — Зп(п + 1)_
2 " 3 2“ —— — 8 “
_п(л-Ь1)(2п + 1) _
— - - 6 • • • (В)
Таково выраженіе суммы квадратовъ первыхъ п натуральныхъ чиселъ, извѣстное подъ именемъ формулы Архимеда,
3. Положивъ ш = найдемъ*
8з== ‘ ------Подставляя выраженія, найденныя для
8а, 8і, 5», получимъ:
о _(п4-1)*—1 п(п +1)(2« -|-1) 2я(я-|-1) п_
ьз — 4 4 4“ “ 1 ”
(л-рі)—я(и-}“1)(2л-|-1)—2м(м-]-1) —I—я(2л-]-1)—2м]
— 4 “ = 4 г- —
_ (п+1) [(«+1)® — (2« + 1)(п+1)1 _ (п + і)(п+1)[пН-2я+1- 2я-1 ] _ пКп+1^ _
— 4 ’ 4 ~ 4
= +-«]*= 3... . .(С).
Такимъ образомъ: едлгма кубовъ п первыхъ натуральныхъ чиселъ равна квадрату суммы тѣхъ же чиселъ.
4. Подобнымъ образомъ нашли бы
_ п(п+ 1)(2я + 1)(3п» + Зя - 1)
Ь»- до--------------- • -(П)
и»(« + 1)»(2ия + 2и — 1)
О 5------“ - “12“--------• • • (Ь)
И т. д.
8т
738. Предѣлъ (формула Шлёламіит)»-- Положивъ въ равенствѣ (1) а = 1, 3=1, I = п, имѣемъ:
...ж=1+(™+Ц8.,+ . 8.-. + з__,+... +(и+1)81+„.
Если бы перенесли всѣ члены, исключая второго, въ первую часть, то нашли бы въ ней полиномъ ?п+1-й степени относительно п, такъ что сумма 8т »і*хъ степеней первыхъ п чиселъ есть цѣлая функція т + 1-й степени относительно п, разсматриваемаго какъ перемѣнное* Такимъ образомъ, полиномы 8т—і, 8т—2. . . суть функціи отъ п степени ?н-й, га—1-й, . . * Слѣд., раздѣливъ обѣ части послѣдняго равенства на ят+1, замѣтимъ, что всѣ дроби
8т—1 8«-2 8т—3
пт—!’
обратятся въ нуль при п = со, ибо степень числителя отн. я каждой изъ нихъ ниже степени знаменателя.
Значить, въ предѣлѣ, при и = со, равенство дастъ
8 8 1
1 “ (яг + 1) < /іт —", откуда Ііт ~ — —г;.
Напр., по этой теоремѣ имѣемъ: йш^ = і, и т’ А"
739. Приложеніе I.— Въ настоящее время въ артил-
леріи употребляются ядра двухъ родовъ: сферическія — для гладкихъ орудій, и цилиндро-коническія — для нарѣзныхъ. Тѣ и другія складываютъ въ арсеналахъ въ кучи различныхъ формъ; займемся вычисленіемъ числа ядеръ, заключающихся въ такихъ кучахъ.
1. Опредѣлитъ число ядеръ пирамидальной кучи съ квадратнымъ основаніемъ.— Сферическія ядра въ этого рода кучахъ складываютъ слѣдующимъ образомъ. На землѣ кладутъ ядра рядами, образующими квадратный слои, въ каждой сторонѣ котораго п ядеръ; на немъ помѣщаютъ въ промежуткахъ между ядрами другой квадратный слой, содержащій н — 1 ядеръ въ каждой своей сторонѣ, и т. д. до верхняго слоя, въ которомъ находится одно ядро* Такимъ образомъ число ядеръ въ кучѣ будетъ =
я® (к I)3 (^1 — I3,
т.-е. суммѣ квадратовъ я первыхъ натуральныхъ чиселъ, или, по формулѣ (В):
у _ Я(П ~Ь 1) &П + 1) / х
А —
Усѣченная квадратная пирамида. — Если съ этой кучи снять нѣсколько ядеръ, взявъ сперва верхнее ядро, затѣмъ ядра (4) слѣдующаго слоя и т. д*, то если снято будетъ р слоевъ, получится квадратная усѣченная пирамида, въ основаніи которой я5 ядеръ, а въ верхнемъ слоѣ (р +1)3. Число снятыхъ ядеръ получится изъ (а), гдѣ надо н замѣнить буквою р* Число ядеръ оставшихся
_ я(я 4-1) (2я + 1) — р(р + 1) (2р 4-1) _ (я—р) [2д>Ч-Р (2”+3) 4- (»+1) (2»4~0].
6 6
Положивъ = найдемъ формулу (а).
П. Найти число ядеръ пирамиды съ треугольнымъ основаніемъ. — Основаніемъ кучи служитъ равносторонній Д; въ промежутки его положены ядра, образующія другой равносторонній Д, котораго каждая сторона содержитъ однимъ ядромъ менѣе, и т, д.; наконецъ, верхній слой состоитъ изъ одного ядра.
Пусть нижній слой содержитъ въ каждой сторонѣ п ядеръ; онъ будетъ состоять изъ п рядовъ, изъ которыхъ въ первомъ будетъ 1 ядро, во второмъ 2, въ третьемъ 3 . . . , въ п-мъ п ядеръ. Слѣдоват. число всѣхъ ядеръ нижняго слоя « 14-2 4-3+ . • - +м> или, по формулѣ (А), —, или Полагая
въ этой формулѣ п послѣдовательно равнымъ 1, 2, 3, . . , , п, найдемъ:
, . 1,1’
число ядеръ 1-го слоя =-т + -у 2 2а
“ ш ” 2^2 3 . 32
I» ьз|
* • • *
п
2’ + у»
* п-го
слѣд. число
всѣхъ ядеръ кучи
Ѵ = |(1 + 2 + 3+. . .+»)+|(1’ + 2« + 3»+. . .+«2);
или, по формуламъ (А) и (В):
Ѵ_1 «0 + 1) .1 Ф4- 1)(2н + 1) _п(»Ч-1)(« + 2) /й.
’ ~ 2 ‘ 2 + 2 ’ 6 “ 6 ’ ’ ‘
Утчеинол треугольная куча.—Снявъ р слоевъ сверху, получимъ усѣченную треугольную пирамиду, содержащую въ верхнемъ ребрѣ (р4-1) ядро. По формулѣ (^) найдемъ число ядеръ въ ней
ѵ, _ (и —_р) О» 4-^ (п — 3) + (п + 1) (я 4- 2)]
1 “* 6
ІП. Найти число ядеръ кучи съ прямоугольнымъ основаніемъ.—Пусть меньшая сторона основанія содержитъ п ядеръ, большая п4-р* Замѣтимъ, что число ядеръ въ измѣреніяхъ слоевъ будетъ всегда уменьшаться на 1, при*переходѣ отъ одного слоя къ другому. Слѣд. разность между числами шаровъ въ двухъ сторонахъ каждаго слоя всегда будетъ р. Верхній слой состоитъ изъ одного ряда, имѣющаго р 4-1 ядро.
Число ядеръ нижняго слоя будетъ
«(«+.?) > и я и 4"
Полагая п послѣдовательно равнымъ 1, 2, 3, ядеръ во всѣхъ слояхъ:
, п9 найдемъ числа
Р+^-1
. 2
з»+_?.з
Черт. 153.
4 4 Ь
(и-1)«+/)(»-!)
слѣд. число всѣхъ ядеръ кучи
2 —(Р + 2* + ЗЯ+. . .-(-(я— 1)* + я2) 4- р(1 + 2^3 +
+ (я — 1) + я),
или
«___я(я + 1)(2я + 1) я(п + 1) <«+ 1) (Зр + 2я+ I)
-----------6-------+р ~ 2~~ ----------------6----------
Обыкновенно даютъ число ядеръ сторонъ основанія; пусть формула
приметъ видъ
„ __ я(я + 1) (Зт — « +1)
Л - -б
IV. Куча цилиндро-коническихъ ядеръ.—Въ основаніи кучи находится прямо* угольникъ, въ одной сторонѣ котораго (меньшей) п ядеръ, въ другой Въ виду формы ядеръ, надъ этимъ основаніемъ можно расположить прямоугольный слои съ р ядрами въ одной сторонѣ, (п— 1) въ другой, и т. д. Число 11 ядеръ будетъ:
V =рп +і?(я — 1) + р(я — 2) +
г п . . л(я +1)
+ р ..2,+р . 1 — р .-------
740» Приложеніе И.—Опредѣленіе объема шара я его частей. —Разсмотримъ
шаровой слой, котораго одно основаніе пусть совпадаетъ съ большимъ кругомъ; такой слой мы получимъ, взявъ надугѣ АВ квадранта точку Р, опустивъ пзъ нея перпендикуляръ РР' на радіусъОА и заставивъ фпгугу ОВРР' сдѣлать полный оборотъ около ОА, какъ оси. Раздѣлимъ ОР' = А на произвольное число п равныхъ частей, изъ точекъ дѣленія проведемъ перпендикуляры къ ОА до встрѣчи съ дугою, и на каждомъ изъ нихъ и на отрѣзкахъ построимъ прямоугольники: получимъ рядъ описанныхъ и рядъ вписанныхъ прямоугольниковъ. При обращеніи фигуры около О А, первые образуютъ тѣло, состоящее изъ п цилиндровъ, объемъ а котораго будетъ больше объема слоя; вторые со-л ставятъ тѣло, котораго объемъ меньше слоя.
Для вычисленія объемовъ обоихъ тѣлъ, описаннаго и вписаннаго, обозначимъ радіусъ шара буквою К. Радіусы основаній описанныхъ цилиндровъ будутъ
Радіусы основаній вписанныхъ цилиндровъ будутъ:
Объемъ описаннаго тѣла будетъ:
— мнэт м» - (?п :+• -н- - ті
или, въ виду того, что числомъ слагаемыхъ есть п:
р _ь22-І-3*+ . . .+(п —I)2
ѴѴ =пЮЛ - я .- —— ~ • Л3-
п3
Для объема вписаннаго тѣла такимъ же образомъ найдемъ:
«7 = к В2Л — X
или
Р + 2^ + 3^ + . , + я3
Отсюда находимъ; МГ — до = — . Л®, слѣд. при неограниченномъ увеличеніи п я
разность между обоими объемами м. б. сдѣлана безконечно малою; а потому, на оси. Теоремы I, § 183, заключаемъ, что объемъ слоя есть общій предѣлъ перемѣнныхъ АѴ и до* Итакъ, назвавъ объемъ слоя буквою [}, имѣемъ
Іт - ІІШ { г.ІРЛ — г.
Р + 22 + 32 + . . . + н*
я3
Л3}.
Такъ какъ первый членъ ^Е2Л есть величина постоянная, то задача сво-
—*------‘ __ который, какъ извѣстно
1
равенъ
Итакъ:
и=лкгл-1-лз=глГв«—^1. . ,(і).
О Г- 0-1
При помощи этой формулы можно опредѣлить и объемъ такого слоя, котораго ни одно изъ основаній не есть большой кругъ. Въ самомъ дѣлѣ, если изъ центра опустимъ перпендикуляры к* и к" на основаніи такого слоя, то, полагая л' > Л", можемъ разсматривать данный слой ІГ какъ разность двухъ слоевъ перваго рода; поэтому
О' = к[е* - §*'*]*'— §*"*] к">
что легко привести (введя радіусы основаній и высоту слоя) къ обыкновенной формулѣ объема слоя.
2
Если въ формулѣ (1) положимъ Л=В, найдемъ объемъ полушара (Г*Н3,
а отсюда объемъ цѣлаго шара: яВ3.
Вычтя изъ объема полѵшара объемъ слоя (1), найдемъ объемъ сферическаго 2 1 ”
сегмента: -гИ®— г[Щ —-ЛЭ]Л. * .(2). Отсюда получимъ обыкновенно даваемую въ геометріи формулу объема сегмента, если введемъ его высоту 11=К— к отсюда Л=В-Н, а подставивъ во (2), найдемъ ^ІІ2 ^Е —
Для вычисленія объема шарового сектора, разсматриваемъ его какъ сумму сегмента и конуса; назвавъ высоту сегмента буквою II, находимъ для высоты конуса Е — Н, а для радіуса его основанія КН®— (В—11)®, такъ что объемъ сектора будетъ = я (в—[В®—(В—Н)а](В—Н), или, по упрошеніи, |гВ®Н*
Такимъ образомъ формула (1) рѣшаетъ вполнѣ вопросъ о вычисленіи объемовъ шара и его частей.
ГЛАВА ХЬѴІ.
Прогрессія геометрическая*—Общій членъ.—Вставка среднихъ геометрическихъ.— Сумма членовъ конечной прогрессія.—Леммы о степеняхъ и корняхъ.—Суммированіе безконечныхъ геометрическихъ прогрессій.
741, Опредѣленіе.—ческой прогрессіей наз. рядъ чиселъ, нзъ которыгъ каждое равно предыдущему, умноженному на постоянное количество, называемое знаменателемъ прогрессіи. Когда абсолютная величина членовъ идетъ увеличиваясь, прогрессія называется возрастающею; если же абсолютная величина членовъ идетъ убывая, прогрессія наз. убывающею. Очевидно, въ возрастающей прогрессіи абсолютная величина знаменателя больше 1, въ убывающей она меньше единицы. Для полученія знаменателя прогрессіи надо какой-нибудь членъ раздѣлить на предыдущій. Слово прогрессія обозначается знакомъ -Н-; между членами прогрессіи ставятъ знакъ : . Такъ,
2 : 6 : 18 : 54 ; .
^1-1.1.2.
” 3 • 9 ’ 27 • *
, есть возрастающая прогр. съ знаменателемъ 3;
. есть убывающая прогрессія съ знаменателемъ □*
Общій видъ геометрической прогрессіи будетъ
-Н- а : & : с : й : . . . г : I : и : . , .(1) знаменатель обыкновенно обозначаютъ буквою у.
Каждые три смежные члена прогрессіи составляютъ непрерывную кратную пропорцію. Въ самомъ дѣлѣ, по опредѣленію геометрической прогрессіи: с = Ъ$ и й = су, откуда, раздѣливъ первое равенство на второе, имѣемъ с : й = Ь: с.
742. Теорема. Общій (п-й) членъ.—Пусть въ прогрессіи (1) § 741 членъ « будетъ п-й; по опредѣленію прогрессіи, имѣемъ:
Ь = а#, с = Ьд, й = ед, . . * , і = гу, и — іу.
Перемножая почленно эти (п— 1) равенствъ и сокращая обѣ части на 6 . с . _ . найдемъ
и = а%п~\
т.-е. кодюйый члея» мрвіредеш первому, помноженному на знаменателя прогрессіи въ степени числа предшествующихъ членовъ.
Такъ, найдемъ, что 9-й чл. прогрессіи = 1Х^8, или 6561. Восьмой членъ -н- 3 :
-4- 1 : 3 : 9 : 27 : . , . будетъ
3 о\/ *
-: . . . равенъ 3 X
743. Задача. Найти условіе, при которомъ три данныя числа А, В, С представляютъ члены порядковъ т, п, р одной и той же геометрической прогрессіи?
Обозначивъ первый членъ этой прогрессіи буквою я, а знаменателя буквою у, имѣемъ ур—нія
А = а^т-1і В = яуп~1, С = яур-1.
Три ур—нія вообще не могутъ быть удовлетворены однѣми и тѣми же значеніями х и у; поэтому, чтобы найти искомое условіе, нужно выразить, что существуетъ общее этимъ ур—мъ рѣшеніе, т.-е. исключить х и у. Для исключенія х дѣлимъ почленно первое ур. на второе, а второе на третье:
в У » С у ’
Возвышая первое изъ этитъ ур—ній въ степень п—р, а второе въ степень т— п, имѣемъ:
"I г — м)(«-р) _ ѵ(т-п)(м—р)
В/ У ’ \СУ У ’ откуда
(в) = С ’ ЙЛИ ХС” "=1:
это и есть требуемое условіе.
744. Вставка среднихъ геометрическихъ между двумя данными числами.
Вставитъ т среднихъ геометрическихъ или пропорціональныхъ между двумя данными числами а и Ъ значитъ найти т такихъ чиселъ, которыя между собою и съ данными составляли бы геометрическую прогрессію. Пусть д будетъ неизвѣстный знаменатель этой прогрессіи; послѣднему члену Ъ предшествуетъ т 1 членъ, а потому
Ь = адМ*1,
откуда
д =
Такимъ образомъ искомая прогрессія будетъ
т+уу "Ч-ур «Ч-у&з
}а'йУа^аУ
Примѣръ. Вставить 3 среднихъ геометрич. между 4 и 64. Знаменатель ?= ^16 == 2; искомые средніе члены суть: 4^2, 4X2® и 4>(2\
или 8, 16 и 32.
745. Т в о р е м а.—Если между послѣдовательными членами геометрической прогрессіи вставить одинаковое число среднихъ, то полученныя частныя прогрессіи составятъ одну сплошную прогрессію.
Пусть данная прогрессія будетъ а : Ъ : с : . . . : г : I: и, и пусть между каждыми двумя послѣдовательными членами вставлено т среднихъ геометрическихъ; отдѣльныя прогрессіи -Н- а : а : 3 :............... 1 : Ъ;
4? Ь : а' : ; , . . ; V ; с; . , . 4г I : а(м) : . . - : : и имѣютъ
соотвѣтственно знаменателей
*-Н / Ь т-Н / с т+1/ и
Ѵа’ V I’ ’ ‘ ’ Г 7;
во- = &=- * = гдѣ д—знаменатель данной прогрессіи; слѣд. всѣ
эти прогрессіи имѣютъ общаго знаменателя; и какъ послѣдній членъ одной слу
житъ первымъ членомъ слѣдующей, то всѣ прогрессіи въ совокупности составляютъ одну сплошную прогрессію.
746, Теорема.—Во всякой геолсеифмческой прогрессіи произведеніе крайнихъ членовъ равно произведенію двухъ другихъ, равно удаленныхъ отъ крайнихъ. ‘
Пусть въ прогрессіи а : Ъ : . . . : х : . . . : у : . . . і : и члену я предшествуетъ и за членомъ у слѣдуетъ р членовъ; въ такомъ случаѣ: & = аур . , . (1). Въ прогрессіи, начинающейся членомъ у и кончающейся членомъ и, имѣемъ « = откуда у = -^р* • * (2). Перемноженіе (1) и (2) даетъ = что и т. д.
747. Сумма членовъ конечной геометрической прогрессіи.
Пусть дана прогрессія ~а :Ъ : с :(і : . . . : г : 2: и, содержащая п членовъ, съ знаменателемъ у; сумму членовъ назовемъ 8. По свойству геом. прогр. имѣемъ
Ь = а#, с = Ьу, й = с#, * . , , і = гу, и~іу.
Складывая почленно эти равенства, находимъ:
♦
Первая часть этого равенства есть сумма 8 безъ перваго члена а, т.-е. 8 — а, выраженіе въ скобкахъ есть сумма членовъ безъ послѣдняго, т.-е 8—и; слѣд. равенству можно дать видъ
8 — а = (8 — и) у или 8 — а = 8д — и#: рѣшивъ это ур. относительно 8, найдемъ
8 = «32=«. .
у— 1 4 7
т.-е. чтобы найти сумму членовъ геометрической прогрессіи, нужно: послѣдній членъ умножитъ на знаменателя, «зь произведенія вычесть первый членъ, и раздѣлитъ остатокъ на разность между знаменателемъ и единицей.
Если въ формулѣ (1) замѣнить « его величиною то 8 приметъ видъ
8 _ ... (2)
2 — 1 ѵ 7
Въ этой формѣ справедливость формулы очевидна; въ самомъ дѣлѣ, по закону частнаго отъ дѣленія хт — ат на х— а, имѣемъ
а умноживъ обѣ части на а, найдемъ въ первой части формулу (2), а во второй: а -|- ау -|- . . + адг”-3 + адп~2 -|- ау*^1; но эта сумма есть ничто иное какъ сумма членовъ самой прогрессіи.
Другой пріемъ. Называя сумму членовъ прогрессіи буквою 8, имѣемъ 8=а-|-5-|_с”Н- * . . • (3)
Умноживъ обѣ части этого равенства на & находимъ:
8д = ад-|-’Ьд4~сЗг4~ * • .+ • -(4)
Но, по опредѣленію прогрессіи, с = Ъ$, . * л , і — т$, и= іц; слѣд.
(3) можно написать въ видѣ:
8 = ^-}^+^+. * •+г# + ^ • • • (5)*
Вычитая (5) изъ (4) замѣчаемъ, что всѣ члены уничтожаются, за исключеніемъ члена иу въ (4) и а въ (5); такъ что
8д — 8 = иу — а, или 8 (д — 1) = «д — ат откуда
8=^-Л
Примѣры: I. Найти сумму 6 членовъ прогрессіи, которой первый членъ ~7} а послѣдній 700000?
Знаменатель у опредѣляется изъ ур—нія 700000=7 . дк, откуда д=Ю; слѣд.
’ 3м —1 - 103—1 _ 1000000—1 - 999999 ------
Ь — а * ——- = 7 • = / • —і( • —д— = і 77777.
д—1 10 — 1 10—1 9
П. Найти сумму 10 первыхъ членовъ геометрической прогрессіи, ко* 1 1 П
первый членъ = ^, а знаменатель
/ і \ю
(іп) — 1
8 = и • - , или, помноживъ числителя и знам. на (— 10й):
“ -— 1
10
8 = $-іІтёп = 5' !’ 111 111 Ш=0. 555 555 555 5-& 1 ѴДІѴ Іу —
Безконечныя геометрическія прогрессіи.
748. Изученіе безконечныхъ геометрическихъ прогрессій требуетъ предварительнаго доказательства слѣдующихъ теоремъ о степеняхъ; къ нимъ присоединяемъ и соотвѣтственныя теоремы о корняхъ.
749- Лемма I. Послѣдовательныя цѣлыя положительныя степени положительнаго числа> большаго 1, возрастаютъ съ увеличеніемъ показателя и могутъ быть сдѣланы больше всякой данной величины.
Пусть будетъ а>1; смыслъ неравенства не измѣнится отъ умноженія неравенства на положительное число; такимъ образомъ послѣдовательно найдемъ:
а* > а, а8 а2, а1 а8 и т. д., вообще > ат:
откуда видно, что степени въ самомъ дѣлѣ возрастаютъ съ увеличеніемъ показателя. Но если доказано, что количество идетъ возрастая, то отсюда еще нельзя заключить, что оно можетъ быть сдѣлано какъ угодно большимъ: это еще должно быть доказано. Очевидно, будетъ доказано, что а™ м. б. сдѣлано какъ угодно большимъ, если докажемъ, что для показателя т всегда можно найти такую величину, при которой будетъ ат > К, гдѣ К — заданное количество. Пусть а превышаетъ единицу на а, т.-е. « —1 = а. Такъ какъ а>1, то умноженіе на а поведетъ къ увеличенію, и получится рядъ неравенствъ
а— 1 = а а2 — а > а а3 — а2 > а
• • • •
а”-1 — а™-2 > а ат — ат~1 а,
откуда, складывая, найдемъ
а™ — • ♦ -|-аилв «т — 1 >
откуда
ат > 1 -|- та.
Очевидно отсюда, что а™ будетъ больше К, если будетъ
1 -|- та > К,
откуда
но очевидно, что каково бы ни было а, всегда можно найти для т такое зна-к * К—1
ченіе, которое будетъ больше —-—
Примѣръ. При какомъ значеніи т количество (1,001)™ будетъ больше 1000?
1П00__1
При т > -тпѵѵі-’ т.-е. при т > 999000.
750. Лемма П. Послѣдовательныя цѣлыя положительныя степени числа а, леятаю 1. идутъ уменьшаясь съ увеличеніемъ показателя и могутъ бытъ сдѣланы какъ угодно близкими къ нулю.
Въ самомъ дѣлѣ, изъ неравенства а<1, получаемъ: а8<а2,...,
аш+1<а”1, т.-е. степени становятся тѣмъ меньше, чѣмъ показатель больше. Затѣмъ, число меньшее 1 можно представить въ видѣ .Д—; желая опредѣлить
степень, въ которую нужно возвысить заданнаго числа 3, полагаемъ
, чтобы эта степень была меньше
(І + а)т <0, откуда (1 + а)"
а по предыдущей леммѣ, это неравенство всегда м. б. удовлетворено.
751. Лемма III, ІГорям цѣлаго положительнаго порядка изъ числа большаго 1 уменьшаются съ возрастаніемъ показателя и могутъ быть сдѣланы какъ угодно близкими къ 1, оставаясь, однако же, всегда большими 7, и никогда не дѣлаясь равными ей или меньшими ея.
Пусть а^>1; надо доказать, что
4 э/— 7“ 4/— Ъ/~~ Ь/~~ и»4-1/’^ - т/~
1. уа<^]/а; уа<^уа\ р7а<р; . , , ; уа<^а. г
2. |/а не можетъ быть ни =, ни < Ъ
3, Разность — 1 м. б. сдѣлана < всякой, какъ угодно малой, величины.
Для доказательства первой части теоремы приведемъ корни да"^а и къ общему показателю; найдемъ: уа = ] уат^\ и уа= у а . По первой леммѣ, а^Н-1 атт а слѣд, и тС^^ат+1> или |/а>
Затѣмъ, положивъ р/& = 1 и возвысивъ обѣ части въ ™-ую степень, нашли бы а — 1, что противно условію &^>1. Допустивъ, что р/я<О» нашли бы такимъ же образомъ: л<^1, что опять противорѣчивъ условію. Итакъ, уа > 1.
Докажемъ теперь, что для т всегда можно найти такое значеніе, при которомъ р/а будетъ какъ угодно мало разниться отъ 1. Обозначивъ буквою й очень малое положительное число, будемъ имѣть биномъ 1-|-8, весьма мало разнящійся отъ 1, но все-таки большій ея. Въ леммѣ I мы доказали, что всегда можно найти такое значеніе для при которомъ будетъ (1 й)то К гдѣ К какъ угодно велико; слѣд. какую бы величину ни имѣло а, всегда можно дать т значеніе, при которомъ будетъ (1-5-8)т>а, откуда І^Й^ір/а. Съ другой стороны доказано, что р/а^І, такъ что заключается между двумя количествами 1 и 1Ц-8, разность между которыми 8 м. б, какъ угодно мала; а потому и разность — 1 тѣмъ болѣе м. б. сдѣлана какъ угодно малою.
752. Лемма IV. Корни цѣлаго положительнаго порядка изъ числа меньшаго 1 увеличиваются съ увеличеніемъ показателя, оставаясь всегда <^1, къ которой они могутъ быть сдѣланы какъ угодно близкими.
Для доказательства, что > ра, приведемъ эти корни къ общему показателю; найдемъ: Ноа<1, слѣд. ат>
От-Н ^Л€М а ПОТоМу или т^р/а больше или ра: т.-е.
корни увеличиваются съ увеличеніемъ показателя^ Затѣмъ, допустивъ, что і/а = 1, нашли бы, что а = 1; допустивъ, что ра > 1 нашли бы, что а^>1: тотъ и другой выводъ противорѣчивъ условію а<4- Но, оставаясь всегда <1, Т^а м. б. сдѣланъ какъ угодно близкимъ къ 1. Въ самомъ дѣлѣ, означивъ буквою 8 какъ угодно малое положит. количество, будемъ имѣть: 1 —8<Ч. Поэтому можно выбрать для т такое значеніе, при которомъ, въ силу леммы II, будетъ (1—8)т<а, откуда 1—й^р^а, или 1—рак^Э, какъ бы 8 ни было мало.
753. Теорема. Въ безконечно^возрастаюгцей геометрической прогрессіи абсолютная величина членовъ приближается къ « аь убывающей—къ О.
Будемъ разсматривать абсолютныя величины членовъ прогрессіи, (условившись обозначать абсол. значеніе количества х знакомъ [я?]):
-Н- а : ад* ад* : ; . . . ; адп : . . .
Пусть Щ будетъ > 1* Въ силу леммы I, съ приближеніемъ п къ ос, и приближается къ со, поэтому для п всегда можетъ быть найдено такое значеніе, при которомъ будетъ [вЛ]>[— ’ гдѣ А какъ угодно большое число; а изъ этого неравенства: [а<7п] > [А], т.-е. съ приближеніемъ п къ сс, абсолютная величина членовъ прогрессіи приближается къ
Если, теперь, ц будетъ положительно, то и дп будетъ положительно, слѣд. при а > 0 всѣ члены прогрессіи положительны, а потому величина ихъ приближается къ со; при а<0, они отрицательны и приближаются къ —со.
Пусть, затѣмъ, будетъ [з]<1; на основаніи леммы II, при возрастаніи п до со, [<?м] приближается къ 0, поэтому всегда можно дать п такое значеніе, что будетъ [?”]< гдѣ а какъ угодно мало; а отсюда [а^"] <а, т.-е. [а$я], съ приближеніемъ я къ ю, приближается къ 0.
Если, теперь, то и #”^>0, слѣд.: если а > 0, то члены прогрессіи приближаются къ 0, оставаясь положительными; при < 0 они приближаются къ 0, будучи отрицательны.
754» Теорема. Сумма членовъ возрастающей прогрессіи, при неограниченномъ возрастаніи числа членовъ, приближается къ со, а убы-„ ~ а
вающеи— къ постоянной величинѣ ----------*
1—3
тг ѵ , с Щп —а
Для суммы п членовъ мы имѣемъ формулу о = , которую можно
представить въ видѣ
8 = ^_ * . .(1).
I. —Первый членъ, какъ функція п, измѣняется съ измѣненіемъ числа
членовъ, второй же, не содержа «, есть количество постоянное; измѣненіе суммы зависитъ, поэтому, отъ перваго члена. Мы доказали, что въ возрастающей прогрессіи съ положительнымъ знаменателемъ, величина адл, съ приближеніемъ п къ со, приближается къ 4“ 00 ПРИ ^>0, и къ —со при а<^0; а потому
и первый членъ, знаменатель котораго конеченъ и положителенъ, а вмѣстѣ съ
тѣмъ и 8, приближается къ 4"°^ ПРИ а>0, и къ —со при «<0.
II» Если д < 1, то при я=ео количество ад'\ а сл. и
имѣетъ пре-
ад*
дѣломъ 0, а слѣд. сумма 8 имѣетъ предѣломъ ^<1»
Пт 8 = 1 а ?
1 —з
ЗТр или Итакъ, при
т.-е. предѣлъ суммы членовъ безконечно-убывающей прогрессіи равенъ первому члену, дѣленному на 1 безъ знаменателя прогрессіи*
Это предложеніе можно доказать обратнымъ способомъ, раздѣливъ а на 1—д: частное будетъ имѣть неограниченное число членовъ, ибо одночленъ не дѣлится
безъ остатка на многочленъ, а члены его будутъ слѣдовать закону геометрической прогрессіи. Въ самомъ дѣлѣ:
а + + • * •
+ а9
4~а92 * +«з+
III. Пусть д = 4~1- Взявъ конечную (объ п членахъ) прогрессію, имѣемъ:
„ а(ди —1) ' । , , „ О
Ь = * X положивъ д = +1, найдемъ о =
Для раскрытія неопредѣленности, замѣчаемъ, что
<1Л — 1 = {<1 — 1) (3“-1 + 9”"г + • • --Н+1), слѣд.
а _ «(а— 1) (д»-іЧ-д«-2 + . . .4-9+0. 9-1 '
отсюда видно, что неопредѣленность — кажущаяся и зависитъ отъ присутствія въ числ. и знамен. обіпаго множителя 9—1, обращающагося въ О при 9=1. Сокративъ на 9— 1, и положивъ потомъ 9 = 1, получимъ:
8 = а(1 + 1 + 1+» .
+ 1) = ап*
я разъ,
Этотъ результатъ можно было предвидѣть; въ самомъ дѣлѣ, при 9=1 сумма а -|~ а9 Ч~ 4“ * * ' 4“ а9п-1 обращается въ а 4~ о 4“ а ’ * ’ Ч”
или въ ап.
Если, теперь, положить я = со, то будетъ: 8 = а . со, т.-е. 8“4'х при а^>0, и 8= — со при а <С О.
IV. 9 — отрицательное.—Если въ равенствѣ
а + ая + а^ +
. 4-
_ ацп — а
перемѣнить 9 на — 9, отъ чего только нечетныя степени 9 перемѣнятъ знакъ, то получится выраженіе для суммы прогрессіи съ отрицательнымъ знаменателемъ:
а — ®9 4” а(12 — а98 Ч”
Заключаемъ, что:
1) При 9 большемъ 1
по абсолютной величинѣ,
и при я = со членъ
слѣд. и
2) При 9 < Ъ по абсолютной величинѣ,
и при п = со, будетъ «9П = О,
и слѣд. 8 =
а
Г+1‘
3) При д=1, по абс. вел*, 8 = н сл^* $ Равно или ® (при
четномъ числѣ членовъ) или а (при нечетномъ числѣ членовъ). Въ этомъ случаѣ прогрессія представляетъ рядъ колеблющійся.
755. Рѣшеніе нѣкоторыхъ задачъ, относящихся къ геометрическимъ прогрессіямъ.
Такъ какъ между пятью количествами а, и, п, у, з фигурирующими во всякой геометрич. прогрессіи, существуетъ только 2 различныхъ- соотношенія
и = а?"-1... (1) 8 = . . - (2),
то, какъ скоро даны 3 изъ этихъ количествъ, остальныя опредѣлятся изъ указанныхъ ур—ній. Какъ и въ случаѣ ариѳметической прогрессіи, можно предложить здѣсь 10 задачъ, изъ которыхъ рѣшимъ только 2 слѣдующія:
Задача I. Вычислить а и и по даннымъ зу $ и п.
Исключая и изъ ур—ній (1) и (2), находимъ:
8 = ’ откуда а = 8 X
подставляя эту величину въ ур. (2), получаемъ:
« = 8 • 4
|П—1
Задача II. Вычислитъ 9 и $, зная а, п. Изъ (1) находимъ:
подстановка во (2) даетъ:
♦і-і / и и' I/ — — а
н—1/ н—1/ и у и — а у а «—1/ и—1/—
у и— у а
п—1
Задача Ш.* Найти женератрису данной періодической дроби.
. 1. Пусть чистая періодическая дробь /"=0,3737 . . . : ее можно представить въ видѣ
(_ 37 . 37 , 37 । ' — 100 । 1002 "Г і боз "+* ’ ’ ’
Слѣд. /" есть предѣлъ суммы членовъ безконечно-убывающей геометрической прогрессіи, которой и ®=|^. Потому
37~ 37
100 _ 100 _37 ' , _1_— 99 — 99’
100 100
результатъ, извѣстный изъ ариеметики.
2. Возьмемъ смѣшанную періодическую дробь /= 0,32(745). Ее можно написать въ формѣ
32 । 745 । 745 , 745
: 100 і ІООХ ібОО ' 100X1000* + 100 ХІ6б№
_ 32 | 745 Г! і 1 т э 1
— 100“I" 100хіоооі1^ 1000^10002 ”1” ‘ *
Рядъ въ скобкахъ есть прогр., въ которой а = 1,
а потому
сумма членовъ безконечно-убывающей геометрич. 1
5 — уэдф; рядъ этотъ равенъ, слѣдовательно,
1 _1000
1 — 999*
1000
„32 । 745 _ 32X999 + "45
~ 100 ' 100 X 999 — 1000 X 999
Замѣнивъ въ числителѣ 999 разностью 1000 — 1, находимъ
32000 — 32 + 745 _ 32745 - 32
100 X 999 — 99900 ’
откуда прямо слѣдуетъ извѣстное изъ ариѳметики правило.
Задача ІѴ\ Часовая и минутная стрѣлки показываютъ полденъ. Въ которомъ часу встрѣтятся онѣ снова?
Примемъ за единицу времени часъ, а за 1 длины окружность циферблата. Черезъ часъ минутная стрѣлка возвратится къ цифрѣ XII, а часовая пройдетъ 1 1 р циферблата; слѣд. минѵтная стрѣлка должна пройти эту циферблата, но
въ это время часовая, движущаяся въ 12 разъ медленнѣе минутной, пройдетъ р отъ р циферблата, или его. Слѣд. минутная стрѣлка должна пройти эту послѣднюю долю циферблата, но въ теченіе этого времени часовая пройдетъ еще рз; и т. д. Итакъ, минутная стрѣлка, чтобы догнать часовую, должна отъ полудня пройти путь: іт^Трі + рзт* * ’’ представляющійся подъ видомъ безконечно-убывающей геом. прогрессіи, первый членъ которой = 1, а 1 1 12
знаменатель р- Предѣлъ этой суммы есть ------р или ур Такъ какъ минутная
1 “12
12
стрѣлка единицу пути (циферблатъ) проходитъ въ 1 часъ, то уу этого пути
« і х/ * 12 і г: и? 3
пройдетъ въ 1 ч. X уу = 1 я. 5 м. 27 уу с.
Задача V. Соединяя средины сторонъ квадрата, получаютъ вписанный квадратъ; въ этотъ квадратъ, соединяя средины его сторонъ, вписываютъ новый квадратъ, и т. д. Предполагая, что эта операція продолжается неограниченное число разъ, найти предѣлъ суммы площадей всѣсъ этихъ квадратовъ.
— 834 —
Пусть сторона даннаго квадрата будетъ а; площади послѣдовательныхъ ква-х « а2 а2 а2 р х
дратовъ будутъ: > • • - Сумма иіъ будетъ
Предѣлъ суммы прогрессіи въ скобкахъ =-----г = 2; слѣд. 8 = 2а*.
’~2
Задача VI. Число 195 раздѣлитъ на 3 части, которыя составляли бы геометрическую прогрессію, которой третій членъ былъ бы болъгие перваго на 120.
Пусть первый членъ будетъ х, а знаменатель прогрессіи <?; имѣемъ два ур—нія
195, хд*— х = 120,
которыя можно представить въ видѣ
х(1+^ + ^)=195, а?(з« —1) = 120,
Раздѣливъ первое на второе, исключимъ х, и получимъ квадратное ѵрав-неніе 5д5 — 8д — 21=0, откуда: д' = 3, д = — г Подставляя вмѣсто о въ ур. ж(д8 —1) = 120 сперва 3, потомъ—4’ найдемъ: я! = 15, а/' = 125. Искомыя рѣшенія будутъ:
-Н-15: 45: 135; -Н-125 : — 175 : 245.
ГЛАВА ХЬѴІІ.
О рядахъ вообще; опредѣленія. — Суммированіе конечныхъ рядовъ. — Суммированіе безконечныхъ рядовъ, — О сходимости рядовъ. — Перемноженіе рядовъ.
V
756. Опредѣленія.—Рядомъ называется рядъ количествъ, изъ которыхъ каждое получается изъ предшествующаго по одному и тому же закону. Такъ, ариѳметическая прогрессія есть рядъ, законъ котораго состоитъ въ томъ, что каждое количество составляется изъ предшествующаго приложеніемъ къ нему постояннаго количества. Геометрическая прогрессія есть рядъ, законъ котораго состоитъ въ томъ, что каждый членъ образуется изъ предшествующаго умноженіемъ на постоянное количество.
Количества, составляющія рядъ, называются членами ряда; ихъ обозначаютъ въ общемъ видѣ такъ: и$, , . . , . Членъ, которому предшествуетъ
н —1 членовъ, т.-е. « — ый членъ, ил, называется общила члсяоль ряда. Давая въ алгебраическомъ выраженіи общаго члена «п буквѣ п значенія 1, 2, 3,. . . получимъ послѣдовательно всѣ члены ряда, начиная съ перваго.
Сумму я членовъ ряда обозначаютъ буквою 8М; т.-е.
8Й — «і + на Ыз + - - • + Нн-і +
Рядъ называется конечнымъ, если онъ состоитъ изъ конечнаго числа членовъ; и безконечнымъ, если число членовъ безконечно. Если сумма п членовъ ряда, по мѣрѣ приближенія п къ ео, стремится къ опредѣленному конечному предѣлу 8, то безконечный рядъ называется сдодящ изгоя, а 8 его суммою; если же сумма 8П, по мѣрѣ приближенія п къ оэ, сама приближается къ безконечности, то безконечный рядъ наз. расходящимся; само собою разумѣется, что о суммѣ такого ряда не можетъ быть и рѣчи. Можетъ, наконецъ, случиться, что по мѣрѣ приближенія п къ со, сумма ряда не возрастаетъ до схэ, но и не стремится ни къ какому опредѣленному предѣлу; такіе ряды называютъ иоддагодящмлліся или колеблющимися; ихъ причисляютъ къ расходящимся.
Такъ, мы видѣли, что безконечная геометрическая прогрессія, которой знаменатель есть положительная или отрицательная правильная дробь (—1<д<+1), имѣетъ конечную и опредѣленную сумму такая прогрессія представляетъ, поэтому, примѣръ сходящагося ряда. Если же знаменатель безк. геом. прогрессіи, по абсолютной величинѣ, больше 1, т,-е. если д > 4-1, или д<— 1, то сумма прогрессіи будетъ равна =Ьее, и сл. прогрессія представляетъ въ этомъ случаѣ рядъ расходящійся. При д = + 1> прогрессія также есть рядъ расходящійся. Наконецъ, еслпд =— ], то прогрессія беретъ видъ
-гг а : — а : + а : — а: ...
Сумма ея въ этомъ случаѣ равна или 0, или а, смотря по тому, беремъ ли четное, или нечетное число членовъ; такъ что, по мѣрѣ приближенія я къ ео, сумма членовъ не стремится ни къ какому опредѣленному предѣлу; однимъ словомъ, при д =— 1, прогрессія есть рядъ колеблющійся.
Одинъ изъ важнѣйшихъ вопросовъ, представляющихся въ теоріи рядовъ, относится къ суммированію рядовъ. Суммировать рядъ значитъ найти сумму его членовъ, не вычисляя въ отдѣльности каждаго члена. Для рѣшенія этого’ вопроса не существуетъ общихъ правилъ, и самая задача возможна лишь въ исключительныхъ случаяхъ. Въ предшествующихъ главахъ мы имѣли примѣры суммированія членовъ ариѳметической и геометрической прогрессіи и одинаковыхъ степеней членовъ первой. Приводимъ еще нѣсколько примѣровъ.
757. Суммированіе конечныхъ рядовъ.—Когда рядъ разлагается на прогрессіи, то формулы суммы прогрессій и дадутъ возможность суммировать рядъ.
Примѣръ 1.—Найти сумму п членовъ ряда
6 -р 66 ч- 666 4- 6666 + 66666 4- . . ,
1-й членъ —6X1
2-й я = 6X10 4-6
3-й „ = 6Х Ю2+ 6ХЮ + 6
4-й „ =6Х 103 + 6X102 4-6 X Ю + 6
п-й членъ = 6 х ю”-1 + 6 х Ю"-2 + 6 X ІО"-3 + ... Ч- 6х Ю + 6.
Суммируя вертикальные столбцы, какъ геометрическія прогрессіи, находимъ
„ _ 6(10“ — 1) 6(10"-1 — 1) 6(10"~2 — 1) 6(10-1)
а— 10 — 1 + 10—1 + 10—1 - +•••+ ю —1
= іо1 [Ю“ + 10й-1 + 1О“-2 + ... 4-10] -
(10— іре' (10” 10—Г
Ряды геометрическіе.—Пусть даны числа «, ?, 7, м, . . . Вычтя каждое число изъ слѣдующаго за нимъ, получимъ числа
?—а, 7 — ?, 2 — 7, 5 — о, . . .
называемыя первы.ии разностями данныхъ чиселъ. Обозначая эти разности буквами 7*, . , вычтемъ каждое число изъ слѣдующаго за нимъ; найдемъ
т'-?' 3'-/, .
Числа эти называются вторыми разностями данныхъ чиселъ а, р, 7, . . . Обозначая эти новыя разности буквами 7", е", . . . составимъ третьи разности:
и т. д. Если первыя разности р — а, 7 — р, . - . носжояяяы, то говорятъ, что числа а, р, 7, , . . образуютъ прогрессію перваго порядка: таковы прогрессіи ариѳметическія. Если только вторыя разности дѣлаются постоянными, прогрессія называется—торою порядка. Вообще, прогрессіей т-ю порядка называютъ рядъ чиселъ, которыхъ ш-ыя разности постоянны.
Напр., числа 1, 4, 10, 20, 35, 56, 84 образуютъ прогрессію 3-го порядка, потому что третьи разности постоянны. Въ самомъ дѣлѣ:
Первыя разности суть . . 3, 6, 10, 15, 21, 28;
вторыя разности ............. 3, 4, 5, 6, 7;
третьи разности...................1, 1, 1, 1.
Геометрическимъ рядомъ называютъ рядъ чиселъ, получаемыхъ отъ почлен-наго перемноженія геометрической прогрессіи на прогрессію опредѣленнаго порядка.
Примѣръ 11.—Суммировать п членовъ ряда
8 — 1 + 2а + За» + 4а3 + 5а1 + .. . + ... (1)
Это есть рядъ геометрическій, полученный отъ почленнаго перемноженія геометрической прогрессіи 1, а, а2, а3,. . . на прогрессію 1-го порядка 1, 2, 3, 4,...
Помноживъ обѣ части равенства (1) на а, имѣемъ
а8 == а + 2а» + За3 + 4а4 + 5ад + - - + (п — 1)а*—1 + па1* ... (2)
Вычтя пзъ (2) равенство (1), имѣемъ:
(а — 1) 8 = — [Гн-а + а» + а3 + а! + . . . + + ная,
или
ая — 1 (а — 1) 8 = пап----г 5
4 ' а — I
откуда
. .(3) а —1 (а — 1)’
4- ♦
Приложеніе.—Положивъ а —— 1 въ предложенномъ рядѣ, имѣемъ
5 = 1 — 2 + 3 — 4 + 5— ... п.
Форм фа (3) прямо даетъ
п , (1X1) о — о "Г 4 ’
причемъ верхній знакъ относится къ случаю п нечетнаго, нижній къ случаю п четнаго.
Примѣръ III. сукицровать рядъ (я членовъ):
8 = 1 4-3«4-6«» + 10а’+. . .+^(л + 1)а>‘-’.
Умноживъ обѣ части ва а и вычтя предложенный рядъ, имѣемъ
(а — 1)^ + [I + 2а + 3^ + 4аз+. . . + иа*-1] . . . (1)
Положивъ 8' = 1 яа* аЛ — 1
1 а^Т”"(а —1)3
-Ь 2а + За* + 4а3 + _. . + на**1, до предыдущему имѣемъ
• Замѣнивъ въ (1) 8' ого величиною, находимъ
(«^ 1)8 —-5(п+ 1)ап —
паи , ап — 1 а^І (а — 1)2’
откуда
я (н-|-1)а’‘ 2ид” 2 (о* — 1) 2 (а — 1) 2(« — 1)2+2(а — 1)»'
Приложеніе.—Положивъ а — — 1, получимъ
8 = 1 -3 + 6— 10+ 15 —
и формула суммы даетъ для этого ряда
± я (я +1)
Изъ приведенныхъ примѣровъ видно, что всегда можно найти сумму даннаго числа членовъ геометрическаго ряда порядка т, полагая, что знаменатель геометрической прогрессіи есть аг.
Если всѣ члены положительны, достаточно вычесть сумму 8 этого ряда изъ произведенія аг. 8; остатокъ (аг—1)8 будетъ содержать новый геометрическій рядъ 8' порядка т — 1. Вычтя эту сумму 8' изъ произведенія аг8'? получимъ остатокъ (аг—1)8', который будетъ содержать новый геометрическій рядъ 8" порядка ж — 2- Продолжаютъ такимъ образомъ до тѣхъ поръ, пока дойдутъ до геом. ряда, котораго разности постоянны, т.-е. до геометрической прогрессіи въ собственномъ смыслѣ, сумма которой извѣстна. Это дастъ возможность опредѣлить сумму 8" ряда перваго порядка, а слѣд. сумму 8' втораго порядка и, наконецъ, 8.
Приводимъ еще примѣры суммированія нѣкоторыхъ рядовъ.
Примѣръ IV,—п членовъ ряда Лейбница
1-4- 1 -4- —4- I 1 -
1.2 ^2.3 3.4^ ‘ ' ^я(и4-1)
Замѣтивъ, что п-ыгі членъ м. б. представленъ въ видѣ
1 1 1
-1 ---------?
«(« + !) я п + 1
полагаемъ въ этомъ равенствѣ я = 1, 2, 3, - -., я; такимъ образомъ всѣ члены разложимъ на разности, и дадимъ ряду видъ:
Замѣчая, что второй членъ каждой разности уничтожается съ первымъ членомъ слѣдующей, найдемъ, что останутся только крайніе члены; а потому
Примѣръ V, — Няй/ни ср.кч# п членовъ ряда. 11 1 Р
1.2.3^~ 2.3.4 3.4.5 ' я(я + 1)(» + 2)
Попытаемся разложить общій членъ на 2 члена, употребляя для этого способъ неопредѣленныхъ коэффиціентовъ; для этого полагаемъ тождество
_____1______А В я(я 4- 1)(к -ф- 2) п(л 4- ]) (Л 4-” 1) (п + 2)’
въ которомъ А и В не зависятъ отъ п. Освободивъ отъ знаменателя, получаемъ тождество 1 = (п 4- 2) А 4“ «В, или
(А + В)п4-(2Л — 1) = 0, откуда: А = І и В= —Слѣд.
1______1 1 1 _____________1______
м(я + 1)(я ф 2) 2 * л(п -41) 2 ' (п 4 1) (и + 2)
Полагая здѣсь послѣдовательно й— 1, 2, 3,..-, п9 представимъ каждый членъ въ формѣ разности и дадимъ ряду видъ:
5 = 1П______V , 1 г-_____Ы -и 4-1 Г—!________________1 ~І
24.2 2.3-І^2І2.3 3.4-1' г2Ія(п+1) (я + 1) (л + 2) _| ’
откуда, какъ к предыдущемъ примѣрѣ, имѣемъ:
Ч_1П 1 ' 1 2І2 (М + 1) (Л + 2)Т
Примѣръ VI.—п членовъ 1 1 1 1 22—1+з2_1+42^-1*І Н (М 4 ] )2 —Г 1'
Общій членъ -——-т—т = -—= 1 Г“--------------кі Полагая послѣдова-
(Н4-1)2—-1 п<я4-2) 2 1-л №4-23
1 о о 1 Г1 1“І
тельно в&ь2г3,... , і», дадимъ первому члену видъ к I т — з р второму видъ 1*1 0-1
1 П 1П 1 Г1 11 „ ,
5 I о—л ’ тРетьѳму видъ _ — = р и т. д. Сумма ряда будетъ
-ЧР + ’-П-и -и 1 4-4 Р+ѴЧ + 1 і 1 П-“2ЦТ + 2+ 3+ '' ' +Г=і + йОЗ + 4+5+ " ’ +5Г+1+п+2Л
П 1 1
Члены, начиная съ 5, до взаимно уничтожаются; такъ что
Примѣръ VIТ.—Дака ариѳметическая профессія съ радостью г:
-4 аЛ.с.<і . чЛ.Л.І.
т г 1 । 1 । 1 , 1,1 ѵ 1 п
Л<шти сумму 4т—Ь —э + • • • тт + т ІІли ?
аЪ 1 Ъс 1 с<і 1 кк * кГ аЪ
Имѣемъ
1 _ 6 — а_г
а ? аЬ аЬ
1__1 _с —Ъ___г
5 с Ъс Ъс
1 __ 1 = I — к = _г_ к I ~ кі ~ кі
п 1 1 ѵ 1
Складывая эти равенства, находимъ: - — у — гХ откуда
ѴІ=1Г1_11.
аЪ гчі I -1
Эта формула даетъ простое средство суммированія ряда примѣра IV; стоить только положить а = 1, г = 1, I = п +1, и тотчасъ находимъ
2. Найти сумму Имѣемъ: ^Ъс<і+---+ШІ И1И’ к°Р°че’2аЬс? 1 Ъс — Ьа 2 г аЪ Ъс а&с ~~ аЪс 1 1 _ сй — Ъс 2г Ъс С(і~~ Ъс~& ~ Ъсй • 1 1 И — 7іІ- 2г кк кі ~ ]і№1 ~ Ый
откуда
Складывая, найдемъ: — 2гХ-=—,
аЪ кі аЪс
ѵ 1 1 /1 П
аЬс 2г И)
По этой формулѣ легко суммировать рядъ примѣра V; положивъ я=1, 6=2, к = и + 1, I = п -у 2, тотчасъ имѣемъ:
1 Г1 1
2 І2 (п + 1) (и + 2)
Такимъ же образомъ получимъ
ѵ 1 _ 1 Г 1 _ 1 "|
" аЪаі ~~ Зг Іабс ЛЫ-Г ” Д
3. Можно вывести аналогичныя формулы для суммы произведеній послѣдовательныхъ членовъ ариѳметической прогрессіи-
Называя а0 членъ, предшествующій л, и — слѣдующіе за Іг имѣемъ:
Ь — й^=2г, откуда умножая на й: ай—л#й“2гд
с — а = 2г, „ „ я Ъ: Ъс — = 2гЬ
(1 — Ъ = 2г, „ „ в с: Ы — Ъс “ 2гс
Іо к = 2г, „ п „ к йд. кі — 2/1»
Сложеніе даетъ: ябга = 2г8| откуда
с _И0— Ь2г
Такъ, взявъ рядъ натуральныхъ чиселъ: 1 + 2 + 3+ ... + и, и положивъ о0 — 0, а = 1, I — я, 70 = п. + 1 ,• г — 1, получимъ
я (я + 1) — 1 • 0 я(я +1)
2.1 ~ 2
Такимъ же образомъ:
с — а0=Зг; по умноженіи на аЬ: аЬс—аоаЬ=^ЗгаЪ сі — а =3г, „ „ „ Ъс*. Ъссі — аЬс = Згбс
!0—7і=Зг; „ » ~ кі: кІЦ—ккі — ЗгУ.
Сложивъ, получимъ: Іод —
ЗГ
Такъ, чтобъ суммировать
8 = 1.2 +2.3 + 3++ . . .+«(« + !),
полагаемъ а0 — 0, п = 1, Ь~2, А*_ я, Г=я + 1, 70_ я + 2, г=1, и находимъ
п(п + 1)(»Ч-2).
Такимъ же образомъ найдемъ: ~<фс— .
' » хЛ
» а отсюда
8 = 1.2.3 + 2.3.4 + 3.4.5 +
> / , іѵ / । лч я (я + I) (я + 2) (« + 3)
• +« (я + I) (н +2) = 1 м 4Т- '
758. Суммированіе безконечныхъ рядовъ.—Если удастся сумму я первыхъ членовъ безконечнаго ряда представить въ видѣ функціи отъ я, то вопросъ о суммированіи ряда будетъ приведенъ къ вопросу о нахожденіи предѣла сказанной функціи при я = сс.
Такъ, если взять безконечный рядъ
I 1 ! . I
1 .2'2 . 3 + 3 .4- Нф + 1)
то, какъ указало въ примѣрѣ IV, сумма п первыхъ его членовъ равна 1 — —। * положивъ здѣсь я = сс, находимъ въ результатѣ 1. Заключаемъ, что предѣлъ суммы членовъ даннаго ряда есть конечная величина 1. Отсюда видно, что данный рядъ есть сходящійся.
Но такой методъ суммированія безконечныхъ рядовъ примѣнимъ лишь въ рѣдкихъ случаяхъ; высшій анализъ показываетъ, что обыкновенно легче дать формулу суммы для всего безконечнаго ряда, чѣмъ для его первыхъ я членовъ. Ііо какъ скоро данъ безконечный рядъ и поставленъ вопросъ о его суммированіи, то предварительно долженъ быть разрѣшенъ вопросъ о томъ, существуетъ ли искомая сумма, чтобы не пришлось потратить время п трудъ на опредѣленіе такой величины, которая не м. б. опредѣлена: иначе говоря, нужно предварительно изслѣдовать — сходящійся данный рядъ, илп расходящійся.
759. Условіе сходимости.—Для шоіо, чжобы ^?ядъ былъ сходящимся, необходимо, чтобы члены «о, начиная съ нѣкотораго мѣста/ болѣе или менѣе уда.іен-паю отъ начала ряда, стремились къ нулю.
Въ самомъ дѣлѣ, если рядъ и( 4- и* 4- Мз + . . - 4- ип 4- ин+і 4-. . . есть сходящійся, то онъ имѣетъ конечную сумму 8. Въ такомъ случаѣ, назвавъ черезъ 8п—і и 8П суммы первыхъ я — 1 и п членовъ, замѣчаемъ, что по мѣрѣ приближенія п къ обѣ суммы стремятся къ предѣлу 8, т.-е.
Ііт 8П = 8, Ііт 8н-и = 8, откуда, вычитая, находимъ: ІІт 8Ц— ІІт8«-і=-0; или, какъ разность предѣловъ равна предѣлу разности перемѣнныхъ, то Ііт (8Й— 8»-і) — 0; но 8М—8н—і = и„, слѣд. въ сходящемся рядѣ
Ііт («„) = 0.
Иначе: если въ ряду положительныхъ членовъ члены, хотя и уменьшаются, но не стремятся къ нулю, такой рядъ никогда не можетъ быть сходящимся* Въ самомъ дѣлѣ, если всѣ члены будутъ больше нѣкоторой конечной величины г, то
Пі 4- 4- * . . >г + е + г + е + . . .
Вторая часть, содержа безконечное число конечныхъ слагаемыхъ, безконечно велика; тѣмъ болѣе, свойство это принадлежитъ лѣвой части, которая больше правой; слѣд. рядъ 4- **2 + + • * расходится.
Итакъ, мое условіе сходимости ряда состоитъ въ томъ, чтобы члены его неограниченно уменьшались, приближаясь къ нулю* Но одного этого условія, по крайней мѣрѣ, для рядовъ съ положительными членами, еще недостаточно. Въ самомъ дѣлѣ, есть такіе ряды, члены которыхъ хотя и приближаются къ нулю, но сумма ряда не имѣетъ конечной величины. Это можно видѣть изъ слѣдующихъ примѣровъ.
1. Члены ряда — 4—= + —+• • * 4—- + • - стремятся къ нулю, иоо > 1 Ѵ2 ѴЗ Гп
при п = сс, 1іт«п = )іт ] = -^ = 0. Не смотря на это, данный рядъ—рас-
Vх»/ 1^»
холящійся; въ самомъ дѣлѣ, назвавъ сумму п членовъ его черезъ 8П, имѣемъ
—
Си )п
1 п
т.-е. 8л>н.—, или 8Н > Ги, откуда, при п — сс, имѣемъ Ііт 8Й е^: зна-I п
читъ, рядъ — расходящійся.
2, Для другого примѣра возьмемъ такъ называемый гармоническій рядъ, члены котораго суть обратныя величины чиселъ натуральнаго ряда.
1 . 1 .
п п 4 1
Члены его стремятся къ нулю, ибо Ііт - | = — = 0; и однако, это — рядъ \П/ СХ-1
расходящійся. Въ самомъ дѣлѣ, если взять п членовъ за я-мъ, то сумма 1 । 1 . , 1 * 1 к х 1
—|—г4----г-л + • * + больше т—, взятой п разъ, т.-е. больше Слѣд. если
п 4-1 п 4- 2 2» 2я’ 1 2
сгруппировать члены ряда такъ:
то видно, что эта сумма больше
/ 1 г I И
\п 4-1 «4-2^” 2и/
по послѣдняя сумма — ес, слѣд- и гармопич. рядъ — безспорно расходящійся.
Итакъ, одного приближенія членовъ къ нулю недостаточно для сходимости ряда. Отсюда—необходимость указанія признаковъ, по которымъ можно бы было отличатъ сходящіеся ряды отъ расходящихся. Укажемъ простѣйшіе изъ этихъ признаковъ, различая случаи: 1) рядовъ, члены которыхъ имѣютъ одинаковый знакъ: 2) рядовъ, у которыхъ знаки членовъ мѣняются.
Признаки сходимости знакопостоянныхъ рядовъ.
760. Теорема О’А л ампера,— I. Если въ ряду положительныхъ членовъ
«2, «3, • ’ > Чі» Ин+Ъ М«+2» ’ ‘ -
- - «я+1
сь возрастаніемъ п членъ нп приближается къ нулю, а отношеніе —— къ пре-а, меньшему 1, то рядъ будетъ сходящійся.
Въ самомъ дѣлѣ, представимъ себѣ правильную дробь которая заключалась бы между іи 1 (а <л < 1)- По условію, отношеніе Цп4~1 приближается къ та* кому предѣлу а, которыя меньше <?; но это возможно не иначе, какъ только тог-
да, когда съ нѣкотораго мѣста ряда отношеніе —— сдѣлается и будетъ оста-
ваться Значитъ, съ этого мѣста будутъ справедливы неравенства
Ян : 2
Ни ]-1
« н-гЗ
• * •
Умножая обѣ части каждаго неравенства на положительнаго знаменателя, мы этимъ не измѣнимъ смысла неравенствъ и найдемъ
*
«« 4-2 < Я . Нм4і; Ни-ЬЗ < • «М-І-2І «Н-4 < V • «»-гЗі * •
замѣняя во второмъ неравенствѣ ««д-2 большею величиною до»+ь въ третьемъ н«-|-з большимъ количествомъ * «н-ь ... мы не нарушимъ смысла неравенствъ, и найдемъ
«п-Н* < з . «о4-і; ««4-3 < Ч2 . н«4-< < -
Сложивъ эти неравенства и прибавивъ къ обѣимъ частямъ имѣемъ
«п-Н + ««4-2 + + «я н+ • • • < «н-гі (1 Ч- Я + + 23 + • • * )•
Первая часть есть сумма ряда, слѣдующая за н-мъ членомъ и называемая осжатколА ряда; обозначимъ ее чрезъ гн; безконечный рядъ въ скобкахъ есть сумма членовъ безконечно-убывающей геометрич, прогрессіи (ибо с/ < 1), равная конечной величинѣ : такимъ образомъ получаемъ
г Цп+1-
Сумма 8 даннаго ряда состоитъ изъ 8Н + гя, гдѣ и 8Н есть конечная величина, какъ сумма конечнаго числа конечныхъ слагаемыхъ. Значитъ
8 < 8„ +
ИпЛІ
1 — 9
т.-е. сумма даннаго ряда метшіе конечной положительной велтггпны, а потому сама есть величина конечная, а данный рядъ — сходящійся.
II. Если въ ряду положительныхъ членовъ отношеніе сэ возросшаяіезсъ
п, приближается къ предѣлу а> 1, то рядъ есть расходящійся.
Въ самомъ дѣлѣ, вообразимъ между а и 1 нѣкоторую неправильную дробь д, т.-е» Од>1. По условію, отношеніе ц”^"1 приближается къ такому предѣлу «, который больше д; но чтобы это было возможно, необходимо, чтобы съ нѣкотораго мѣста ряда сказанное отношеніе сдѣлалось и оставалось больше ц. Съ этого мѣста, слѣд., возникнутъ отношенія, большія д, а потому будутъ имѣть мѣсто неравенства
ІЫ-2. «п4 4 .
----> д; ------> >,д, - - *
мп-н ’ и«+2
Изъ нихъ имѣемъ
Мп-нг > д . «н-рі; а отсюда
«п^2 > д . «»+і;
Нп ]-з > д ын-5-й;
шн-з> д2 *
«Кр > д , Ійі 1 з; * . *
««-и > д3 - «п-рі;...
Складывая п придавая къ обѣимъ частямъ Мп-рі, имѣемъ
+ «п-н2 + + ... > шн-і (1 + д + д2 + д3 +. •)
Обозначивъ сумму первыхъ п членовъ ряда чрезъ 8Я, и придавъ къ обѣимъ частямъ это количество, получимъ
8П -}- «п-рі + шц-2 +
>8„ + ««+і(і + 9 4-<г4+...).
Первая часть представляетъ сумму всего ряда; затѣмъ, д> I, и слѣд. 1+д+ + д2 + • • - — со; неравенство означаетъ, такимъ образомъ, что данный рядъ — расходящійся.
Примѣняя эту теорему, должно: составить отношеніе общаго члена къ предыдущему и найти предѣлъ этого отношенія при п = оо. Если окажется, что этотъ
предѣлъ < 1, заключаемъ, что данный рядъ есть сходящійся; если продѣлъ
при я = со будетъ > 1, рядъ будетъ расходящійся. Если же окажется, что
1ІШ
= 1, наши теоремы ничего пе рѣшаютъ относительно сходимости
ряда, ибо нервъ доказательства — въ томъ, что съ опредѣленнаго мѣста отношеніе Ян-рі;ип должно оставаться меньше или больше 1; это предположеніе уже не находитъ себѣ мѣста, когда сказанное отношеніе имѣетъ предѣломъ самую 1, и потому въ послѣднемъ случаѣ рядъ м. б, какъ сходящимся, такъ и расходящимся, Вопросъ рѣшается въ этомъ случаѣ другими признаками.
Во всякомъ случаѣ, если отношеніе стремится къ 1, оставаясь съ нѣ-котораго мѣста ряда постоянно больше 1-цы, то рядъ будетъ радездЫщі-иея. Въ самомъ дѣлѣ, члены ряда начнутъ, наконецъ, постоянно возрастать, и общій членъ не будетъ имѣть предѣломъ нуль.
761. Примѣры. I. І&сліъдввать въ отношеніи сходимости рядъ
еі» которомъ предполагается х > 0. Имѣемъ
_ хп
“""1.2.3 . . . п’
__ а»4-1______.
«»+’ —2.3... «(»+!)’
X
п ; но при всякомъ конечномъ а? дробь обращается въ 0 при "п = со. Заключаемъ, что рядъ сходится при всякомъ опредѣленномъ конечномъ х. Но не лишнее —прямо удостовѣриться въ сходимости ряда, ибо
съ перваго взгляда можетъ показаться, что при нѣсколько значительной величинѣ х, напр., при л: —10, рядъ —какъ будто бы расходящійся, ибо имѣемъ: 1+10+ 500
+ 50 + -Х-+ ... Но хотя вначалѣ члены ряда идутъ возрастая, все-таки поз-
днѣе наступитъ сходимость, какъ въ этомъ можно убѣдиться слѣдующимъ разсмотрѣніемъ. Въ § 340 мы имѣли:
я* < / я
1 , 2.3 . . . А* Ѵ'А’
Произвольное цѣлое положительное число А* выберемъ такъ, чтобы ГА- > г, или А- >яа, и разложимъ рядъ на двѣ части:
ЗГ 1
1 + Т + ГГг-^' *' 'Ъ .2.3.. ,<ь—і)
я* а:Ж
+ I . 2 . . . к + 1 . 2 . . . [к 4- 1) "Г 1 . 2 . . . (*. + 2)+ *
Первая часть есть конечный рядъ и имѣетъ конечную сумму; вторая часть меньше
х \1 ( х । / ж Ѵ"*~а ГѴ ѵ А\/
т.-е. меньше суммы геометрпч. прогрессіи, представляющей восходящія степени правильной дроби Слѣд. данный рядъ съ мѣста А* > я* сходится сильнѣе сходящейся геометрической прогрессіи, а слѣд. есть безспорно сходящійся рядъ.
II. Въ рядѣ
1 + 1 .я + 1 . 2 . я*+ I . 2.3 . а?+1 .2.3.4. . .
имѣемъ — (п + 1)з. Предѣлъ этого произведенія, при и безконеченъ при всякомъ значеніи х, отличномъ отъ нуля; если же #=0, рядъ не существуетъ (ибо приводится къ 1), Слѣд. если рядъ существуетъ, то окъ всегда — расходящійся.
ІП. Въ рядѣ
± + ± + ±+.. +±+_Л—и... /1 Г 2 13 I п Гм + І
Ь’Аламберовой теоремою вопросъ о сходимости ряда ие рѣшается; но если замѣ-тіімъ, что члены даннаго ряда соотвѣтственно больше (начиная со 2-го) членовъ гармоническаго ряда, завѣдомо расходящагося, то расходимость даннаго ряда становится внѣ всякаго сомнѣнія.
IV* Въ рядѣ
* і №• и 1
гдѣ х > 0, ——- : — = ? а= х.--г; слѣд. предѣлъ этого отношенія при
«+1 л « +1 _ , 1 1 1
— 845 —
п — эа, равенъ я. Заключаемъ, что при .т>1 рядъ — расходящійся, при я<1 — сходящійся; при % = I — сомнѣніе. Но, замѣтивъ, что въ послѣднемъ случаѣ рядъ обращается въ гармоническій, заключаемъ, что и при я—1 онъ расходящійся,
762. Въ послѣднихъ двухъ примѣрахъ для рѣшенія вопроса о сходимости въ сомнительномъ случаѣ приходилось прибѣгать къ сравненію даннаго ряда съ другимъ, сходимость или расходимость котораго уже извѣстна.
При сравненіи двухъ рядовъ, въ которыхъ члены положительны, можно пользоваться слѣдующею теоремою.
Пусть всѣ члены ряда
«і + мз + ні4* *
положительны и идутъ, постепенно уменьшаясь; въ такомъ случаѣ, очевидно, имѣемъ соотношенія
2іц —
4и4 < 2н3 + 2м4
< 2ы3 + 2?*в -|- 2а7 + 2ы8
2ив 4~ 2м10 4~ 2мц + < . .4-
и т. д.
Складывая, имѣемъ
4~ 4- 4м4 4“ ^8 4“ 4~ ’ • • 4" «з 4~ «з4~ «і4^ ’ ’ •) — «і - ’ (1)"
Если первоначальный рядъ 4~ 4- * * • сходится, то сумма его конечна, а слѣд. правая часть (1) есть также величина конечная; слѣдм лѣвая и подавно конечна, а потому производный рядъ и14-2«2-т-4и44“ - - - сходится, если сходится первоначальный.
Раздѣливъ (1) на 2 и придавъ къ обѣимъ частямъ дадимъ неравенству (1) видъ:
«т 4- «2 Н- пэ “Ь * * * ^ ^ «і4“ 2 "I" 2*4 4" 4" &«з + *,.).
Если производный рядъ расходится, то, какъ члены его положительны, сумма его будетъ = ес; тѣмъ болѣе будетъ безконечна сумма первонач. ряда, т.-е/если производный рядъ—'расходящійся, то и начальный таковъ же,
Далѣе, очевидно, имѣютъ мѣсто неравенства
«! = «!
2н2 > «-2 4~ «з
4н< > і*4 -р 4" «і
> «8 + «9 4- «ю 4“ ’ - *Ч“ «ів
и т. д.
откуда сложеніемъ находимъ:
4- + 4п4 + &*8 4- • - • > «1 + «2 + «3 4“ «1 4- < - •
Пзъ этого неравенства заключаемъ: 1) если начальный рядъ расходится, то тѣмъ болѣе расходится производный, и 2) если производныя сходится, то сходится и начальный.
Результатомъ соединенія этихъ четырехъ предложеній является:
Теорема Коши. Два безконечные ряда
+ «я 4“ «з +* • - и «і +- 2н2 + 4«| + бия +> . . сходятся или расходятся одновременно^
Такимъ образомъ о сходимости или расходимости начальнаго ряда можно судить по сходимости или расходимости производнаго,
763. Однимъ нзъ замѣчательныхъ приложеній этой теоремы является изслѣдованіе сходимости ряда
Въ данномъ
его, при я — рядъ будетъ:
/ н \* / 1 'А
случаѣ, отношеніе и«4і : — -?) — -----И ; предѣлъ
'” +1 1 + 1 \ и/ есть 1: сомнѣніе относительно сходимости ряда. Производный
П1 4. + 8и8 + . . . = 1 + 2*-* + 41-л + 81-* + 4~. . .
= 1 _|_ 91-* + (21-*)* + (21 -*)3 4-. . .
Но это есть геометрическая прогрессія съ знаменателемъ 21-*: для сходи-21 мости ея необходимо, чтобы знаменатель былъ <1, т.-е. чтобы 2*—* или —<1,
т.-е.& > 1; во всѣхъ друг. случаяхъ прогрессія расходится. По теоремѣ Коши, и данный рядъ будетъ сходящимся при и расходящимся прп &СК Отсюда,
напр., прямо видно, что изъ четырехъ рядовъ:
I 1'1 11Т + 21 2 + 31 3
(4)
два первые — сходящіеся, послѣдніе два — расходящіеся, между тѣмъ какъ для всѣхъ Ііт і — 1.
Сомнѣніе, оставляемое теоремою д’Аламбера, можно иногда разрѣшать при помощи слѣдующей теоремы*
764. Теорема Дюгамеля. Рядъ 8 = и14“«24'из+" • -4“ 4-Ыл+і 4~- • * члены котораго постепенно уменьшаются, будетъ сходящійся, если рядъ 3' = + г2 + • * • 4'<*н4" - • • сходящійся, и, начиная съ нѣкотораго члена, отно-
шеніе
Наоборотъ, первый рядъ будетъ расходящійся,
если второй расходится, и
отношеніе ——
Въ самомъ дѣлѣ, если рядъ 8' сходится, то изъ неравенства
и«4-і .
находимъ
отсюда
Ні»4-і < і'н4і
Н«4-2
VI —♦ Ѵп
и
Слѣдовательно
я >4-2 ип-н 14
Ѵп+2 V «4-1 V.,/
и >4-3 и н-з-2
Д я—1~3 Д'
и«4і 4~ н»*42 4* •
• •< (Гя+14“ г’«4-2 4- Ѵн4-з 4“ • • •).
а это значитъ, что остатокъ Кн перваго ряда меньше произведеніи остатка 1Ѵ„ второго на Если рядъ 8' сходящійся, то К'„ стремится къ нулю, а потому изъ послѣдняго неравенства заключаемъ, что и Кп стремится къ нулю, и что слѣд. рядъ 8 — сходящійся.
П п4-1 і’ н-М
Если рядъ.8' расходящійся, то условіе ——>—7- поведетъ къ неравеи-ствамъ, отличающимся отъ вышепаписапныхъ смысломъ; такимъ образомъ, найдемъ, что КП>К'М —• .Но если 8' — рядъ расходящійся, то остатокъ В/„ не стремится къ нулю, а потому и Нп не стремится къ нулю; слѣд. 8 есть строка расходящаяся. Напр., для ряда
11.31.3.5
2 ‘ 2.4 ‘2.4.6
1.3.5.. /(2п —1)
2.4.6. . . 2п
найдемъ, что
2п-Н_
~2п + 2~~ 2’
п
и слѣд. при п—жэ даетъ 1, Но сравни-
вая этотъ рядъ съ гармоническимъ, завѣдомо расходящимся, для котораго отно-. я-М 2п -к 1. п +1
шеніе соотвѣтствующихъ членовъ есть м-^р"2» нах°Дпмъ: 9>| 9 > а ио'
тому заключаемъ, что взятый рядъ — расходящійся.
Ряды знакоперемѣнные.
765. Теорема. Коіда знаки членовъ чередуются (+» —, +, —, . . . ), жо рядъ будетъ сходящійся, если съ нѣкотораю мѣста члены его неопредѣленно уменьшаются, приближаясь къ нулю, ж.-е. если —О при п — со.
Въ самомъ дѣлѣ, пусть съ опредѣленнаго мѣста п=&, каждый членъ больше слѣдующаго за нимъ, т.-е.
и* > «*4-і > > и*_і_з . ..
н кромѣ того 1ітип = 0. Обозначимъ буквами К2, К3, . .. величины:
К1 =
К3 = м* —(м*и —«*»)
^3 = «4 — («ІЦ — «*+,) “ («І+З— м* "«)•
Замѣчая, что всѣ разности въ скобкахъ положительны, имѣемъ Кі>Кз>В5>К7 . . .(1)
Съ другой стороны, положивъ
ка = («* — «Ж>
К» — («* — «Ж> + («Ж — «ж)
К6 = («4 — + (м*4 2 — «ж) + («Ж ~ МЖ)
имѣемъ:
• 1^2 < Вц... (2)
Наконецъ, для неопредѣленно возрастающаго т
1
Ііт (Взт—1 — Кзт) = Ііт и*+гт-1 =0 ... (3)
Итакъ, если съ мѣста к (съ котораго члени идутъ убывая) брать суммы нечетнаго числа членовъ, и суммы четнаго числа членовъ, то изъ (3) прямо слѣдуетъ, что эти суммы, ІЬщ-і и Кгт, приближаются къ нѣкоторому общему предѣлу К; причемъ суммы К2т^і приближаются къ нему, постепенно уменьшаясь, суммы В2т постепенно увеличиваясь. Затѣмъ, общій ихъ предѣлъ В, во-первыхъ, положителенъ, какъ непосредственно ясно изъ неравенствъ (2), а во-вторыхъ, будучи, въ силу неравенства (3), меньше каждой изъ величинъ Е^, Кз, В$, . . ., онъ представляетъ опредѣленную конечную величину. Вслѣдствіе ур—нія В = 15тВ-2яі-і== = Ііт 1<2т:
В — ик — и* 2
а слѣд. при данныхъ условіяхъ рядъ ик — икгі + . . . сходящійся, а потому сходится и первоначальный рядъ
м0— «і + «і— «з + . . . + (—и*-1 «А-і + (—1)* (ик - иь+і + Ш4-2 — + •*•),
и теорема доказана.
Такъ, напр., рядъ у —^ + 3— 4‘ Г ’ ’ схоляи^|“ся» а сУмма его содержится между слѣдующими, болѣе и болѣе сближающимися числами
и т. д.
766. Теорема. Для сходимости ряда, въ которомъ знаки членовъ измѣняются по какому угодно закону, достаточно, чтобы рядъ оставался сходящимся по перемѣни всѣхъ знаковъ на -(-•
Въ самомъ дѣлѣ, абсолютная величина суммы втораго ряда, очевидно, больше, нежели перваго, такъ какъ во второмъ всѣ члены положительны, а въ данномъ нѣкоторые изъ этихъ членовъ отрицательны. Но, по условію, сумма второго ряда конечна, слѣд. и сумма даннаго конечна, т.-е. данный рядъ — сходящійся,
Слѣд. о сходимости даннаго ряда можно судить, примѣняя къ производному^ ряду вышенайденные признаки сходимости для рядовъ съ положительными членами.
767. Условная и безусловная сходимость. Нерѣдко приходится встрѣчаться съ такого рода мнѣніемъ, что предложеніе, имѣющее силу для всякаго конечнаго числа величинъ, должно оставаться вѣрнымъ и въ томъ случаѣ, когда число величинъ дѣлается безконечнымъ. Первый, доказательно убѣдившій въ несостоятельности такого принципа, былъ Лежекъ-Дирикле (въ 1837 г.). Онъ показалъ, что предложеніе о неизмѣняемости суммы отъ перемѣны мѣстъ слагаемыхъ, вообще, невѣрно для безконечнаго числа слагаемыхъ. Примѣръ его былъ слѣдующій. Возьмемъ рядъ
1 1.1 1,1 1 , т
°“"Т 2 + 3 4'5 6+ ’ * ’
и сгруппируемъ его члены по четыре:
гдѣ общая группа есть н-ая. Такимъ образомъ сумма г равна суммѣ значеній.
принимаемыхъ я-ою группою, если въ ней давать п всѣ цѣлыя значенія отъ I до -х>, т.-е.
1_______1 1 1
4п—3 4я—2 "і- 1 4п
Затѣмъ, въ суммѣ (1) переставимъ члены такъ, чтобы за двумя положительными слѣдовалъ отрицательный; получимъ рядъ
и сгруппируемъ его члены по три:
гдѣ общая группа есть я-ая. Сумму а можно сокращенно представить въ видѣ
________________1 ! \4и— 3 4п— 1 2я
Наконецъ, сгруппировавъ члены ряда (1) по два, не измѣняя ихъ порядка, получимъ
Д 1\ /1 П, ./ 1 1\ ,
’ \1 2^“Цз 4.Н Ц2м— 1 2«Р
гдѣ общая группа есть я-ая. Эту сумму можно представить въ видѣ
1 1 \
3 7 \2п— 1 2н/ ~
Вычитаніе даетъ-
1 11 1 \ 1 / 1 іу
4»—3 4п—2"’4я— 1 4я/ 2 \2я—1 2я/
Если въ этомъ тождествѣ положить послѣдовательно я—1,2, 3. . .я, сложить результаты и перейти къ предѣлу п — со, то получится
у/ 1 1 _1\ у/ 1 1 , 1 1\
7 \4п— 3 ”^4н— 1 2я/ 7НП"3 4я— 2 '4»-1 4н/ —
і і у /
1 3
или з — ; = откуда т.-е. сдолсы а и з
Отсюда вытекаетъ необходимость различать два рода сходящихся рядовъ: ряды у словно-сходящіеся, когда сумма ихъ зависитъ отъ порядка членовъ, и бе-зусловяо-сходящіеся, если сумма остается всегда одинаковою, какъ ни переставлять члены. А отсюда задача объ опредѣленіи признаковъ безусловной сходимости.
Пусть будетъ О,, сумма нѣкотораго я-членнаго ряда:
ип=«0-І’«1 - * • +#н-і •(!)
и пустъ предѣлъ при п = со будетъ опредѣленная конечная величина II, слѣд.
V — и® + 4“ Щ 4“ 4- * > (2)
т.-е. имѣется рядъ сходящійся. Узнать, будетъ ли новый безконечный рядъ ѵв 4-4- я* 4- ѵз + * * (3)
отличающійся отъ перваго только перестановкою членовъ, имѣть ту же сумму V? Возьмемъ въ новомъ ряду р первыхъ членовъ и положимъ
‘ у04-+ и2 + .. . 4- ѵр-і ... (4)
Можно взять р настолько большимъ, чтобы всѣ п членовъ суммы СЛ содержались въ суммѣ Ѵр. Кромѣ того, пусть въ Ѵр будетъ еще р— п членовъ, совокупность которыхъ
и* + 4" и* + * • *
будетъ имѣть индексы д, г, 8, ♦ . . большіе я — 1. Поэтому
\ р ІІП === Мд 4* 4~ 4~ • • *
а слѣд., при неограниченномъ возрастаніи п и р
Ііш Ѵр — П = Ііт («д 4- «г 4-^4- • • • )•
Чтобы рядъ й) 4-4-#2 4- • • имѣлъ сумму О, должно быть: Ііт Ѵр = ІІ, а слѣд. должно быть
Ііт («д + иг 4- Щ 4- * - *) = 0. . . (5)
Это и есть признакъ безусловной сходимости ряда (2).
Можно найти другую форму такимъ путемъ. Если рядъ (2) съ опредѣленнаго мѣста содержитъ только положительные члены, то можно я взять настолько большимъ, чтобы въ ур—НІИ
V — ПЛ = 4- Ип4-1 + ш4-2 + . . .
справа находящіеся члены всѣ были положительны: сумма иЛ 4- «п-+-і +. . . есть такъ называемый остатокъ ряда и имѣетъ предѣломъ нуль, ибо при п—сс лѣвая часть обращается въ II — Ііт т.-е. въ нуль.
Далѣе, что касается суммы + мг Д- . . . , число членовъ которой = р — и, а
каждый индексъ >я —1, то какъ всѣ члены положительны, имѣемъ
0 < 4- 4“ • * • < 4- и» |-і 4- ««4-2 4- • •
слѣд. прід я п приближающихся къ со:
Ііт (ид + и,. 4- гсв4- . . . ) = 0;
слѣд. при взятомъ предположеніи рядъ сходится безусловно.
Когда первоначальный рядъ содержитъ члены, частію положительные, частію отрицательные, и нѣтъ такого мѣста, начиная съ котораго шли бы члены одинаковаго знака, къ такому ряду приведенныя заключенія неприложимы, и сходимость въ этомъ случаѣ возможна только условная.
Но въ частномъ предположеніи, что рядъ остается сходящимся, если вмѣсто его членовъ взять ихъ абсолютныя значенія, можно далѣе вести изслѣдованіе. Означая абсолютныя величины членовъ скобками, пусть рядъ
[?/о] 4“ М 4-1^14“ - • •
будетъ сходящійся. По предыдущему
Ііт {[«,] + [мг],+ [и8] + . . . } = О,
— 851
т.-е, абсолютное значеніе суммы «9-|-иг+ - • * м, б. сдѣлано какъ угодно малымъ. Отсюда же прямо слѣдуетъ, что и9 + «т * * * также имѣетъ предѣломъ нуль, а слѣд. рядъ безусловно сходится. Отсюда
768. Т еорема ШеЙбнера.—7>декоядоным оголится безусловно, если
сохраняетъ сходимость и тогда, когда во» членыеіо золггьчи.нг игъ абсолютными значеніями.
Этимъ объясняется, почему рядъ д—^”>3—• • оказался лишь условно сходящимся; въ самомъ дѣлѣ, рядъ изъ абсолютныхъ значеній его членовъ—расходящійся.
769. Перемноженіе рядовъ.—Теорема.—Ійми имѣемъ два сходящіеся ряда
Ст = «1 + па + и3+ . * ,
V — + #2 4“ г3 + • *
знакопостоянные, «.«« лнакотеерелюнные, я о в» посдлдм&ч» случаѣ такіе, что оба, или, по крайней мѣрѣ, одинъ, напр. Б, остается сходящимся послѣ замѣны — на -|-; то доказать, что произведеніе БѴ выражается безкояечяылп рядомъ
—Н Івд 4" ... —3— - , .
члены котораго составляются по слѣдующему закопу:
н- и^д
й’3 = н- і^г’2 -|- ^Зѵ1
вообще н?п = іц#п-ы/аѵп_1-ь . . . -ЬНя^!
т.*е* что п-ый членъ произведенія равенъ суммѣ произведеній первыхъ п членовъ ряда Б на первые п членов» ряда V, взятыя?» въ обратномъ порядкѣ.
Доказать, что БV выражается безконечнымъ рядомъ + и\ 4- . . . значитъ доказать, что БѴ есть предѣлъ, къ которому приближается сумма п членовъ:
АѴП = и\ + гга + ю3 + . . . +
при неограниченномъ возрастаніи п. Для этого составимъ разность между суммою и произведеніемъ двухъ суммъ
ОР = «1ч-ия+. . и Ѵ(г = ѵ1Ч-і?2+. . -+^,
гдѣ ^4-д=п, причемъ: если я четное, то _р=5= -у, а при п нечетномъ р~
* ш
п Ч-1
9 — - * Всѣ члены произведенія БрѴ? содержатся въ суммѣ \ѴЛ, ибо въ про-
изведеніи Б^Ѵд индексы при и и ѵ не больше р и д. Вынеся въ ХѴЯ за скобки «і, «2, . • . мн, можемъ эту сумму представитъ въ видѣ
ил = «|(»1 + Я, + •. 4-», + ®Н-1 + • ••+».) + «з(»і + ѵ, + . .. + г, 4- ... 4- ₽м-і)
«» + ч«-|іиВѵвв*в*в« + »Фйа
+ «₽(»і +1’» 4- - • • 4- ѵѵ + гн-1)
4- нрч-і^’! 4- ѵг -ь ... 4- юа) -ь ... 4- «„гр
Составивъ произведеніе Ир Ѵд и вынеся также,за скобки и(, . . имѣемъ:
V. = «((і?! 4- ѵ, 4-... ч-1?4) 4-ч- ѵг 4- ... 4- і’в) ч-...
... 4- 4- »а 4- . . . ѵв).
Вычтя это произведеніе изъ М’и, находимъ:
Чі “ , -Ь Ѵ,<) + +
+ +^2 + • * . ^) + Ир4-2(^'1 + і’л-Ь
- + Гп-1) +
• + Ѵ$—1) +
+ вд.
Прп увеличеніи я до безконечности, неограниченно возрастаютъ н р и 9. Такъ какъ рядъ V сходящійся, то его общій членъ г?+і и суммы ^^14~' - •-Н’н, + . . . 4-гл—і,. . * стремятся къ нулю; а суммы первыхъ членовъ: Гі+ гв4-• **+«)»••*» гі будутъ конечны* Подставивъ вмѣсто первыхъ суммъ положительную безконечно малую величину а, большую кажюй изъ нихъ, а вторыя суммы замѣнивъ положительною величиною А, также большею каждой изъ нихъ, найдемъ, что вторая часть послѣдняго равенства будетъ меньше
’Оі + «»-+-----------1- Чр) + А(н/>4-і + . - . + и„).
Но рядъ С сходящійся и, по условію, не теряетъ сходимости и послѣ за-мѣны его членовъ ихъ абсолютными значеніями, то сумма иі + и2 + , * . будучи меньше суммы абсолютныхъ значеній своихъ членовъ, будетъ меньше нѣкотораго конечнаго положительнаго количества В, а остатокъ этого ряда і^і . .. сдѣлается менѣе нѣкоторой положит. безконечно малой Итакъ, при достаточно большомъ п будетъ
АѴ „ — С^А в < В* А^, т.-ѳ. наша разность м. б. сдѣлана какъ угодно малою; а потому въ предѣлѣ, при п = со, Ііт (АѴН — 0, или АА’ = С’Ѵ.
ГЛАВА ХЬѴІІІ.
Распространеніе формулы бинома Ньютона для всякаго дѣйствительнаго показателя.—Остатокъ биноміальнаго ряда —Приложенія.
770, Формула возвышенія бинома въ степень, доказанная для показателя цѣлаго положительнаго, можетъ быть распространена на какой угодно показатель. Замѣтивъ, что + достаточно разсматривать только при неравныхъ а и б, потому что при а = Ъ эта степень приводится къ одночлену 2"'аж, преобразуемъ ее вынесеніемъ а за скобки въ биномѣ а Ъ\ какъ показано въ § 714, найдемъ: (а 4- = лв,(1 4- х)’”, полагая | ~ я. Вопросъ приводится такимъ об-
разомъ къ разложенію (1 4~ я?)ш.
Когда показатель т—число цѣлое и положительное, мы имѣли прп всякомъ л? конечный рядъ
(1 +ж)-= 1 + ~2) *> + •..
т(т — 1) . . . (щ — & + 1)
1 . 2.3 . . . А’
. 4- □?*%
содержащій т 4- 1 членовъ. Коэффиціенты при степеняхъ а? представляли числа сочетаній изъ т элементовъ по 1, по 2, . . . , по А-, . . . . Условившись обозначать эти числа буквою т съ индексами 1, 2, 3, . . . , т.-е.
т . »»(« —1) , ч пфп—1)(ш —2) , ч ж
Т= ( " ; Г: 2" ; I 9 з ~ ' = (™)з» вообще
— 1) . . . (т —А‘4-1) , . пч
-----П2.3..Л----------’ = • -(1)
можемъ короче написать разложеніе въ формѣ:
(1 л-)1" = ] 4- (т)1Я! + (т)*/? + (м*)^ + • • • + (»»Ѵ* + . . . 4- (т)тх?а . . . (2).
Спрашивается: если ш не есть цѣлое положительное число, то можно ли представить въ видѣ ряда, расположеннаго но восходящимъ степенямъ
буквы ху съ коэффиціентами закона, выражаемаго формулою (1)?
Здѣсь прежде всего замѣчаемъ, что коэффиціентъ
при ж цѣломъ положительномъ можетъ обратиться въ нуль, вслѣдствіе чего рядъ (2) будетъ законченный. По если ж—число отрицательное или дробное, то число членовъ ряда будетъ безконечно. Дѣйствительно, при ж отрицательномъ множители ж, ж — 1, т — 2, -, . числителя выраженія будутъ идти увеличиваясь по абсолютной величинѣ, и потому ни одинъ коэффиціентъ ряда не можетъ сдѣлаться нулемъ. Когда ш— дробь, то и всѣ множители ж—I, т—2, , .. будутъ дроби, и не могутъ обратиться въ нуль: рядъ биноміальныхъ коэффиціентовъ будетъ безконеченъ. Слѣд., если только возможно разложеніе въ рядъ закона (2) бинома (1 -Ьа;)”1, гдѣ ш не есть цѣлое положительное число, то такой рядъ долженъ быть безконечный. Это замѣчаніе заставляетъ формулировать нашу за-дачу окончательно такъ: безконечный рядъ, расположенный по восходящимъ степенямъ буквы «г, съ коэффиціентами закона (1), при ш не цѣломъ и положительномъ, т.-е. рядъ
1 4- 4 + ж^я3 + . . . + + • • * (ЗУ
можетъ ли представлять разложеніе степени бинома (1 4 ®)‘"? Хтя рѣшенія вопроса нужно найти сумму этого ряда; если окажется, что эта сумма = (14*)т> вопросъ будетъ рѣшенъ въ утвердительномъ смыслѣ; если окажется, что сумма не равна (1 въ отрицательномъ смыслѣ. По о суммированіи безконечнаго
ряда рѣчь можетъ быть только тогда, когда мы напередъ знаемъ, что это рядъ сходящійся; поэтому прежде всего необходимо опредѣлить, при какихъ условіяхъ рядъ (3) будетъ сходящимся. По изъ предыдущаго мы знаемъ, что (3) будетъ безусловно сходящимся рядомъ, если сходится рядъ, составленный изъ абсолютныхъ значеній его членовъ. Итакъ, нужно взять предѣлъ отношенія жп-і-ьгЖ: при п = Имѣемъ:
.. ж — п _. Г . т+1 1
' тнхп } = Іип —г-— • х = Ііт < — т -4-—г- # } •
г I п +1 I ' и 4 1 4
При л = со, при всѣхъ конечныхъ значеніяхъ ш и я, второй членъ обращается въ нуль, и слѣд.
Ііт {Жи4і,г»+і : = — &.
Заключаемъ, что рядъ будетъ сходящимся, когда абсолютная величина —х будетъ < 1, т.-е. когда — 1 <4-1> или, короче, когда 1; если же абсо-
лютная величина количества (—а?) будетъ >1, рядъ — расходящійся. При = 1 —сомнѣніе; рѣшенія вопроса въ этомъ случаѣ мы касаться не будемъ,
въ виду его сложности. Итакъ, полагая — 1 <4 <41, найдемъ сумму ряда (3). Обозначивъ эту сумму чрезъ 8/п, гдѣ значекъ т показываетъ, что эта сумма зависитъ отъ ж, имѣемъ
— 1 ж "4— 4" —|- . * «
Перемѣнивъ ж на другое дѣйствительное количество получимъ: 8Р= 1+Л®+^4-рзЖ»+. . .
Такъ какъ оба эти ряда сходятся безусловно при я? < 1, то можно приложить къ нимъ теорему о перемноженіи рядовъ; найдемъ:
8>и • 8р=1+(»»і+1»і)®Н*и2-ь-’«іРі+Рг)а;*-г
+0«вн-»»м-У>і+»и,і-»л+ . . .
. . •+>»і₽я-і+»<іРп-1+і’л)а!’,Н_ • • 0).
Докажемъ, что коэффиціенты его составлены изъ ж4-р по такому же закону, какъ коэффиціенты рядовъ 8,п и 8р составлены изъ мі и р. Во-первыхъ, такъ какъ = ш и = то + Затѣмъ:
»і2+т1Л+Т’г- ~[-Т2—773"~--------------ІТ2----+-----1~2---“
_ш(т+р— 1) +р('п+ р—1)__ (т4“Р)(т+.Р—1)
_ і ; 2 • — і,2 1
а это есть ничто иное какъ (ж + ^)й.
Чтобы доказать, что
-ь ?ИП₽1Р1 + ЖН_2Р2 + - • + + ГЛ1 Рн~1 = (т + р)л • • (?)
допустимъ, что равенство (5) вѣрно, и докажемъ, что слѣдующій коэффиціентъ есть («і 4“Р)*Ч-ь Но этотъ слѣдующій коэффиціентъ есть
тп+і + тпРі + ж^р^ + . .. + ж^Рн-і + Ш;рЛ +р„+1
Чтобы онъ былъ равенъ (ж4-р)«4-Ъ нужно, чтобы онъ представлялъ произведеніе предыдущаго коэффиціента, по*допущенію, равнаго (ж4-д?)п, на •
Составляемъ это произведеніе:
(^п+^л-іРі+^л-іР2+ - - + и^Рн-г + ^ЧРд-1 і— • • (6)
п 1
тт л- Ж »— Я
Члены этого произведенія имѣютъ видъ пцр^ . —> а это выраже-
Я —Н 1
ніе можно представить въ формѣ
ж — А ™лРм-Л - —ГТ
ж — к
но д т і “ ?нл+і » это равенство можно представить въ видѣ
а на основаніи этого равенства имѣемъ
Рп-ъ (р + к — п)= р„_*+1(я - к + 1).
Слѣд.
ж 4- р — п п — к +1 . к 4-1
• й + 1 =»»*РЯ_*+1 - „-р, +
Полагая здѣсь послѣдовательно 7* = 0, 1, 2, 3, . . . , щ получимъ всѣ члены произведенія (6):
1
Ач-і + ”'1Р» • ІГЦГГ •
н I
ТПг + ™іРл-1 *
П — 1
я 4“ 1
+ >"зРн-2
3
« + 1
+
п — 2
+ *П«-2Рз *
п — 1
п
™Н-1^
+ *
Суммируя по діагоналямъ, имѣемъ:
+ тзр^і + . . . -Ь тй_іР2 + жир! + шп+1;
а это есть не что иное, какъ (т 4- .
Итакъ, допустивъ, что коэффиціентъ при яЛ есть (т+^)п, мы доказали, что слѣдующій коэффиціентъ есть (т + р)^. Но непосредственнымъ вычисленіемъ мы убѣдились, что третій коэффиціентъ = (т 4-р)2; слм по доказанному, четвер-тый —(ж4-^)з» пятый (т 4~Р)і и т. д. Такимъ образомъ, ур—ніе (4) принимаетъ видъ
= 1+(т + р)^ 4- (т + р)^ 4- (т 4- * • • + (™ + '”+ - • -
то-есть
(т-Нр)(ж4-р—1) г3 , (ш+р)(т4-р—1 2)
1.2.3
Вторая часть представляетъ рядъ, составленный по тому же закону, какъ ряды 8т и 8^, съ тою разницею, что вмѣсто т или р находится т 4- р; сл. рядъ этотъ мы можемъ обозначить тѣмъ же знакомъ 8, но съ указателемъ т 4-.Р* Слѣд.
— ^т4-р • • * СО-
ж
Положивъ ж — р, имѣемъ:
ИЛИ [8т]® —-
Помноживъ обѣ части на 8т и примѣнивъ къ произведенію 8Ягп . 8т формулу (7), имѣемъ
[8т]8 = 8Ш.
Продолжая такимъ же образомъ, получимъ для какого угодно цѣлаго числа к:
Ы=зкт.
ь
Если теперь т есть положительная дробь = -, гдѣ ц и г—цѣлыя положительныя числа, то мы можемъ произвольное цѣлое к взять равнымъ знаменателю г, и получимъ
Г8 ? ”Г ~ 8«*
Такъ какъ д есть цѣлое положительное число, то 8? представляетъ, какъ извѣстно, конечный рядъ, сумма котораго равна (1 4“ слѣд.
— 856 -
извлекая изъ обѣихъ частей корень порядка г, имѣемъ
этимъ и доказано, что (1 + а?)** разлагается въ безконечный рядъ того же закона, какъ и при цѣломъ показателѣ.
Если въ равенствѣ (7) положимъ, что есть число отрицательное, цѣлое или дробное, и что = — ш, то равенство это дастъ
* 5_,й = 8?н_т = 8д.
Но 80 = 1: слѣд. и 8,ГІ . 8_щ = 1, откуда
' - 8 — — •
-- С
т
Здѣсь — т > О, а для этого случая доказано, что 8_гп = (1 -|- сл.
= (Г+=
этимъ формула бинома доказана для отрицательнаго показателя.
Итакъ, мы доказали справедливость формулы для всякаго соизмѣримаго показателя* Чтобы распространить это ур. на несоизмѣримое т *), пусть будетъ н— соизмѣримое число, безконечно къ нему близкое, и а безконечно-малая" разность ш— Формула (7) даетъ:
8т = ^4-* — . 8^
Но и — число соизмѣримое, слѣд. 8И — (1 + затѣмъ, формула (3) даетъ
83 — 1 -(-32-Г8 + ^3^4“ • •
= 1+«{ . }
Рядъ въ скобкахъ — сходящійся, потому что отношеніе каждаго члена къ предыдущему въ предѣлѣ даетъ — лт, что по абсолютной величинѣ < 1; слѣд* сумма этого ряда есть нѣкоторая конечная величина А; а потому
87=1 + аА, и 8Ш = (1 + (1 + &А).
По мѣрѣ приближенія р къ т, а приближается къ О, слѣд. 1 4~а^“~къ Ь а вторая часть къ (1 4- а какъ эта часть всегда — 8Ш, то
8ЙІ-(І+Г.
Итакъ, при всякомъ дѣйствительномъ т: ’
(1 + х)"= 1 + х» + т(т= 2) ^ + . .
причемъ, когда іи — цѣлое положительное число, х можетъ быть какою угодно дѣйствительною величиною; если же т не есть цѣлое полозшт* число, то должно быть — I < а? < 1 *
*) Опредѣленіе степени съ несоизмѣримымъ показателемъ см. далѣе, § 775.
Примѣчаніе 1. Идея вышеизложеннаго доказательства общности формулы бинома Ньютона принадлежитъ Эйлеру; а усовершенствованное доказательство— Коши.
Примѣчаніе 2. Теорем а.—Одна и таже функція разлагается въ сходящійся рядъ, расположенный по цѣлымъ положительнымъ степенямъ перемѣннаго, единственнымъ способомъ^ Въ самомъ дѣлѣ, пусть, если возможно, будутъ два различныя разложенія одной и той же функціи.
^ + «^4-^4-... 4-а„я”4- .. * и б0-нМ + М*4- • • • +^"4- • * *
сходящіяся то и другое при всѣхъ значеніяхъ я, меньшихъ X, по абс. значенію. Такъ какъ, по усл., оба-эти разложенія должны имѣть равные предѣлы для всякаго х < X, то для этихъ значеній перемѣннаго должно бытъ
К &о) + (^1 —— 4“ * - * 4“ + • • • -—
гдѣ — разность остатковъ рядовъ, которая, какъ и эти остатки, д. б* безконечно малою при п — ?с, при всякомъ а*<Х. Какъ бы велико ни было значеніе, взятое для н, всегда можно взять я настолько малымъ, чтобы совокупность членовъ («і — бДгч- . .. 4-(<Ъ«—5,,)^“ была какъ угодно мала, а отсюда слѣдуетъ, что «0 — равно разности двухъ безк. малыхъ. Слѣд., какъ </0—не зависитъ ни отъ п, ни отъ аг, то оно строго равно нулю (на основаніи очевидной истины: постоянное, о которомъ можно доказать, что оно менѣе всякой данной величины, есть нуль; короче: постоянная безконечно-малая есть не что иное какъ нуль). Такимъ образомъ а0 = б0 и равенство приводится къ
-г[(оі — Ьі) + (“2 “ + . . . + («,, — Ь„)а;'‘-1] = г„;
но чтобы первая часть была безконечно мала при всякомъ х < X, необходимо, чтобы скобки были безконечно малы, откуда, по предыдущему, заключаемъ, что «і — &! — 0, т.-е. «! = &(- Продолжая такимъ образомъ, убѣдимся что всѣ коэффиціенты равны каждый каждому.
3.— Эту теорему (служащую основаніемъ способа неопредѣлен. коэф-въ для безконечныхъ строкъ) можно примѣнять къ разложенію функцій въ безконечные степенные ряды, но только въ такомъ случаѣ, когда напередъ м. б. доказано, что функція способна разлагаться въ сходящійся степенной рядъ: въ противномъ случаѣ способъ этотъ можетъ привести къ невѣрнымъ результатамъ, такъ какъ въ немъ не обращается вниманія на остатокъ ряда. Кромѣ того, по этому способу трудно бываетъ найти общую формулу для членовъ ряда. Въ виду этого, какъ для бинома, такъ и для другихъ функцій у насъ указаны другіе, болѣе строгіе, пріемы разложенія въ ряды.
771. Остатокъ биноміальнаго ряда,—Разложимъ биноміальный рядъ на двѣ части, изъ которыхъ первая пусть содержитъ первые к членовъ, а вторая, которую мы назовемъ осяншкома и обозначимъ чрезъ 14, остальные члены.
Итакъ, положимъ:
(I 4- я)ш = 1 + жр? 4- 4- 4- ... 4- 4- . (1)
гдѣ остатокъ КА будетъ
14 — ж^ 4. -+- 4~
здѣсь
щ(ш — 1). . . (ж — 14- 1)
М* — ІЛГЗ. . .к ’
__ш(-т — 1) . , * (ш— А*4-1){ш — А)____
М'*+1 — 1.2.3 . . . к.(к.+ I) “ ' Т+Т;
>н(т — 1)
н'*+2 ’ Г“2
. . (т —к). (т — к - 1) (т—к). (т - к-Л)
. . (1-ЬIX* + 2) ~ т“' (*+1)(*+2) 1
И т. д.
Вынеся во всѣхъ членахъ за скобки тк а?, получимъ:
ж— & Он — й)(я» — к— 1)
(2)
Различаемъ слѣдующіе случаи.
1-й случай: т—цѣлое положительное число.—Понятно, что въ этомъ случаѣ к<т, рядъ будетъ конечный объ (т-+-1) членахъ, и если:
1. а?>0, то сумма въ скобкахъ (2) будетъ больше нуля» Съ другой стороны, если во множителяхъ числителей коэффиціентовъ отбросимъ вычитаемыя, а во множителяхъ знаменателей вторые члены, то всѣ коэффиціенты увеличатся, и рядъ въ скобкахъ будетъ меньше
т.-е. конечной геометрической прогрессіи, которой знаменатель =-^та послѣд-/ж ѴН~Л
ніи членъ ; потому сумма ея
к ) тх
Такимъ образомъ остатокъ Кь заключаясь между 0 и
1 ~ГГ/
„ тх
равенъ произведенію послѣдняго выраженія на нѣкоторую положительную правильную дробь р; т.-е.
(I) Н* =? ----------------> гдѣ 0 < р < 1.
1 — Т
2. #<0. Нѣкоторые члены будутъ положительные, другіе отрицательные; и если условимся абсолютную величину количества з обозначать знакомъ [$], то сумма въ скобкахъ (2) будетъ содержаться между
Ч’Ч—1+Ш+ • •} и +Ѵ+Ы+Ы +•••)>
такъ что легко заключить, что въ этомъ случаѣ
(II) П*=р .
т.-е. р есть положит. или отрпцат. правильная дробь.
Формулы (I) и (II) можно соединить въ одну, одинаковаго вида съ послѣдней, замѣтивъ только, что при х > 0 должно быть и р > 0.
» м.
Въ частномъ случаѣ, когда есть правильная дробь, будетъ и
произведеніе этой правильной дроби на дробь р < 1 дастъ также правильную дробь; назвавъ послѣднюю буквою р', получимъ для этого случая болѣе простую формулу:
= гдѣ- !<,'<+!.
И здѣсь также при # > О будетъ р' > О,
2-й случай: т — дробное положительное число.— Биноміальный рядъ будетъ ' безконечный и сходящійся при — тоже самое относится и къ ря-
ду (2). Возьмемъ произвольное цѣлое положительное число к > ш, и разсмотримъ опять два случая—положительнаго и отрнцат. а?, именно: х = + х = — Е.
Въ первомъ случаѣ рядъ (2) будетъ и
к~т , , (Ь — т)(к — «+ 1)
і+І-'-і- (к + 1Кй + 2) ” ' '
во второмъ:
, , (к —тЦЬ->т4-1) .. .
1 + Т+Т ’; + =(к+і)№ + 2) • '(4)
Такъ какъ факторы
к^т к — т + 1 к — т2
& + 1 * А;+ 2 ’ “Кр” * ’ 1
суть положительныя правильныя дроби, Е также < 1, то въ обоихъ рядахъ каждый членъ больше слѣдующаго; отсюда легко заключить, что сумма ряда (3) заклю-. _ к — т .
чается между 1 и 1 — । 5 и потому положительна; также непосредственно
видно, что и сумма (4) положительна* Затѣмъ, очевидно, что сумма перваго ме-, . 1
нѣе суммы второго, а эта послѣдняя меньше 1 + ; + ? + ^+ • —=—
Вообразивъ между $ и 1 еще правильную дробь (:<з<1), имѣемъ
1 1 .
1—^1 —г’
сумма каждаго изъ рядовъ (3) и (4) содержится между 0 и ; поэтому ту и другую можно представить подъ общимъ видомъ । _ е» гдѣ р положител. прав. дробь. Итакъ для остатка имѣемъ формулу
(іѵ) кі=е^^,
въ которой: [я] <е<1, &>ж, 0<р <1, и [а*] означаетъ абсолютную величину#.
3-й случай: т — отрицательное число; пусть т = — X. Рядъ (2) при х > О будетъ
1 _Щ : + Ц.+Ш1+1+Л:а- (5)
к + I (I- + 1)(Л + 2) ' •
а при #<0:
1 хШ : + № + Х)(1- + Х + 1) (кн-1)(*г-н2) -14
Въ
виду того, что
? при неограниченномъ возрастаніи А приближается
ч
А; X 1 -н у-
къ предѣлу < ибо Ііт 5 = 1іт----------— - ?
і— Ак Ч- I . 1
14"Т
выбрать настолько большое значеніе, чтобы
и какъ $ < 1, то можно для к
кч- ).
Лч-1
гдѣ г прав. дробь, лежащая между и 1. Въ самомъ дѣлѣ, предыдущее нера-
венство даетъ
а это требованіе всегда м. б. выполнено. Какъ скоро для к выбрано такого рода значеніе, то тѣмъ въ большей мѣрѣ справедливы будутъ неравенства
или
слѣдовательно
Еч-1 + 1 ,
А; —н2
*+1
і
(Ь + к)(А:+кН-1) (к + к)(* + к + 1)(Х-+1 + 2) а а
(й-Ы^ + 2) ”"<'Е (і + іМі.+2)(к + 3)
Суммы рядовъ (5) и (6) будутъ, слѣд., положительны и менѣе
1 4- г -ьг2 + гз_|_ .
и потому могутъ быть представлены подъ общимъ видомъ и для остатка имѣемъ выраженіе
гдѣ И<з<1,
Это изслѣдованіе можно резюмировать такъ:
Если т.не есть цѣлое положительное число и я2< 1, то отаток» Ньютонова ряда выражается общею формулою
н Р^, * 1 — Е
гдѣ
И 0 <С 2 <С 1 т
причелп слѣдуетъ браты к^>т, если т положительно, отрицательно.
, — г
и А; > 1—т
772. Пгимѣ р ы.—Примѣняя формулу бинома, найдемъ:
з
„ , я* , 1 • З.я* 1 .3.5.я*. 1.3.5.7. ж» 1
3. {а-—г) — а 1(ІТ2«2Ч'2.4.а‘^2’.4.“б.а* + 2.4-6.8.а»'і",3 п т. п*
773. Приложенія формулы бинома Ньютона.—Укажемъ нѣкоторыя приложенія формулы бинома.
I. Извлеченіе корней.—Пусть требуется извлечь корень порядка г изъ цѣлаго числа X. Разобьемъ X на двѣ части такъ, чтобы первая аг представляла точную г-овую степень и была бы возможно больше по сравненію съ другою частью б, которую въ этихъ видахъ можно брать и отрицательною. Всегда можно взять аг > Ь. Получимъ:
Г/аг Ь — 1 / аг 1 4—- = а 1 4—- = «(1 -I- д-)г полагая -ж = я. г у \ 1 аЧ \ 1 аг х ' * (Г
Примѣняя формулу бинома, найдемъ
(г —1)(2г;—1)/т\з_
1.2.3 \г)
Напр*
У129 = У125ч-4 =5 (1 4-А\’ = ѵ ѵ \ 1 12а/
Г 1 4 2 I 4 \г 2 . 5 і 4 \з
— ° 11 +3 * 125 3.6\125/ +3.6.9\125/
— «о -+- «і — «і Н- «з — м| • •
«оЧ-Н^бЧ-
16
3. 100
5,0533333333
2 4 _ 32
—6'125 ’ ’<1 — 3 . 1000
«3 = 0,0005688889 (—)
5,0527644444
"=5 • А •'•“ТТ0ІІ-
о,0э2і74оэом
и‘ • м» = “» = 0,0000002158 (-)
12 І_5 4.11X10 5,0527743422
и т. д
Вслѣдствіе чередованія знаковъ искомый корень всегда заключается между двумя смежными значеніями.
П. Рѣшеніе уравненія аэ$ ч-Ъх-\-с = 0; когда коэффиціентъ а весьма малъ. Взявъ формулу корней, можемъ ей дать видъ
я = — А — — 4ас— —
2а 2а
_______ і
Ь , 1 „ Д ,/. 4ае\ Ь . Ь / 4йс\а 2^±2^У Ь (і-^-; = _25±Ц1--ЬГ) •
Когда корни уравненія дѣйствительные неравные, мы имѣемъ: б2 * — 4ас>0, 4ае
откуда < 1; но при а весьма маломъ дробь эта будетъ, весьма мала и полу-
чится бы стро-сходящійся рядъ; а именно
А /1 ч- /1 _ 1 __1 V /4ае\Д
2а V “Ц б* Г8 ^2") 16 ( & )
— 862 —
ПІ. Раскрытіе неопредѣленностей.—Приводимъ примѣры. а?п — ат ' 0 *
1. Дробь —$—теі гдѣ т и к какія угодно числа, обращается въ 7- при х = а. Полагаемъ х = а 4- А и разлагаемъ числителя и знаменателя по восходящимъ степенямъ 7г; затѣмъ полагаемъ Л = 0; так. обр. находимъ:
дт— к
А —1) № а 1.2 а2
А —1) к2 а 1.2 ’ а2
Всѣ члены числителя и
А Л
знаменателя содержатъ множителя сокративъ на -
и положивъ А = 0 (чтобы имѣть величину дроби при а? = «), находимъ, что всѣ члены числителя и знаменателя, кромѣ первыхъ, исчезаютъ, и получается-г- а*-*.
* О
обращается въ -д- при х = а. Положивъ
2. Дробь
^Х2 — х — а + 7г, даемъ ей видъ
1 Л
а
сдѣлавъ приведеніе и раздѣливъ числит. и знам. на ѴЛ, имѣемъ
/А 2а
что при к = 0 обращается въ
IV. Элементарный методъ Жоффруа для вывода рядовъ, служащихъ къ вы-численію п.
1. Взявъ окружность радіуса В= 1, проведемъ къ точкѣ Е касательную, затѣмъ на окружности возьмемъ нѣкоторую дугу АВ и проведемъ радіусы ОА. ОВ, продолженіе которыхъ пусть встрѣчаетъ касательную въ точкахъ С и 1). Сравнимъ хорду АВ съ дугою АВ. Опустивъ изъ центра перпендикуляръ 01 на АВ, возьмемъ отношеніе площадей треугольниковъ ОАВ и ОСІ), имѣющихъ общій уголъ:
‘ ДОАВ —ОАХОВ _ АВХ01 , АВ _ 1
ДОСИ- ОС х 00 - СВ х ОЁ’ "ли какъ ’ СВ “ ОС х ов х оГ
Замѣнивъ 01 единицей и 00 линіей ОС, мы уменьшимъ вторую часть, и потому Съ Другой стороны щ<0])2' • (2)- Доказатель-
1 I ство неравенства (2) сводится къ доказательству, что пли
гй < ттгѵ или тгп < но, проведя АМ параллельно СП (пусть V есть
точка пересѣченія АМ съ ОТ, а точка М съ ОВ), имѣемъ: = а какъ-1 -01
ОА = 1, и ОМ < ОѴ < 01, то этимъ неравенство (2) доказано. Итакъ
ОС> (И)
^^ав_е си
002^00^002' ‘
Если положимъ, что АВ стремится къ нулю, то и СО будетъ приближаться 4В 1
къ нулю, и въ предѣлѣ: Ііт ~ ибо ОС и 00 сливаются въ предѣлѣ.
Если на касательной возьмемъ часть ЕР —I и соединимъ Р съ 0, то дута ЕН = ^* Для вычисленія этой дуги раздѣлимъ ЕР на п равныхъ частей и точки дѣленія Г, О, С соединимъ съ центромъ. Эти прямыя дадутъ на окружности вершины неправильной ломаной, которой периметръ будетъ приближаться къ по мѣрѣ увеличенія п. Пусть будетъ АВ одна изъ сторонъ этой ломаной: соот’
ЕР 1
вѣтствующій элементъ СП касательной =-— = -• По доказанному, мы имѣемъ
ЦП<61№; ГДѣ 0138 = 1 +ЕГ)2-
Пусть р будетъ число дѣленій отъ Е до П: сл. ЕЕ>=р Д, СЕ) — и
ЛВ<1.—Ц,, пли АВ<-Т1—„• П . . Р2 П2+р2
Итакъ, периметръ Р вписанной ломаной меньше суммы дробей вида гдѣ р нужно измѣнять отъ 0 до я—1. Слѣд.
п
Я4 +р2Э
Г1 1 1 I 1 4_ 1 I 1 ‘ 1
Ь«_|~п2 + 1','«2+22 + и’+32_1_’ ’ ’+и’ + (я —Т)2.]' ' ’
Въ предѣлѣ, при я = ес, Р сливается съ дугою ЕИ, слѣд.
т=1іткй+-йягі+йчт2+* • •+й2+(п-і)і]' • ’<5>‘
Съ другой стороны, мы нашли, что
Ж >№ гй 0С.= Ч-ЕС5=1+»±1>*, откуда
АВ>н2-4-(р+Г)«’
Взявъ сумму этихъ неравенствъ отъ 73 = 0 до ^з = я — 1, найдемъ
р>"[Лт +
И2_|_2>+ •
И 1
Сближая неравенства (4) и (6), найдемъ два значенія для Р—одно по избытку, 1 “1 1
другое по недостатку. Эти два значенія разнятся на и 2 — слѣдов.
— 864 —
оба они стремятся къ ~ Взявъ п достаточно большимъ, можно' вычислить - съ 4
желаемою точностью.
Формула (5) послужитъ намъ для разложенія ~
въ скобкахъ общій членъ
или (я2 + Ц
въ сходящійся рядъ. Взявъ разложимъ его по формулѣ
бинома:
—*—= (Я» + »»)-1= 1 +^-•
Я24"Р2 ' п- я*^я* я8 я10
Полагая послѣдовательно р = 0, 1, 2, 3,. . >, я — 1, найдемъ:
1 1
п* ~~ я2
1 _ 3*_3*
я2 -рЗ2 ~ п* я4 ’ и8 я8
і = 2. _— г>* । (* — Р* _ О* — 1У , я2 4- («— I)2 п* я1 ‘ я* я8 "г
Складывая по вертикальнымъ столбцамъ, умножая на я, и обозначая суммы вторыхъ, четвертыхъ, . . . степеней я— 1 первыхъ цѣлыхъ чиселъ знаками 8ІТ 8і, . - . , находимъ:
^=ит/1-^ + ^-^ + ^
4 I я8 я8 я7 яа
п г $2 1
Но Ііт ;5, я3 3
г 84 1 тт
Ііт ^ == -» и т. д. Потому
одинъ изъ рядовъ, которые даетъ интегральное исчисленіе.
2. Взявъ четверть круга ОАВ, положимъ, что радіусъ 0В=^1. Раздѣлимъ радіусъ ОВ на п равныхъ частей и изъ точекъ дѣленія проведемъ параллели другому радіусу ОА. Такимъ обр. дуга АВ = у будетъ раздѣлена на я неравныхъ частей; хорды, какъ СГ>, стягивающія эти дуги, образуютъ вписанную ломаную длины Р, предѣломъ которой прп я = сч>, будетъ служить Пусть ЕЕ будетъ дѣленіе радіуса ОВ, соотвѣтствующее дугѣ СО. Проведя 01 перпендикулярно къ хордѣ СИ, Ш перпендикулярно къ ОА, и СО перпендикуляръ на ЬЕ, найдемъ изъ подобныхъ треугольниковъ СЕЮ и ОІН, что Но СО = ЕЕ, слѣд.
СЬ* ѵі
г ЕЕ г ОН ЕО • .. .. ЕЕ .
ІПП 7Ѵга= ШП7ѴГ—-Ѵ-; а ПОТОМУ ІШ1 СІ) = Ііт СІ) 01 1 ьп
Далѣе; ЕЕ = — = ЕО — Ѵ'ОО» - ОЕ» 1/1 -Я Л г П*
сло дѣленій отъ 0 до К Отсюда
если у означаетъ чіь
ііт СО —-------------1;—= = Ііт
Ііт п 1/1 — — . Г
1 -----------* |/ я2 —
Но периметръ Р есть сумма элементовъ, такихъ какъ СО, слѣд.
п—1
о СО =
Ѵя« —1
* |/н* — (я — 1)«
а какъ = Ііт Р, то
К . гі I 1 I 1 г I і 1 1-І
зт-— Ііт I —I— -— ~Н* * ’ ’Ч“ ~ 1 -
2 1_п — 22 у'пі — рі Еи8 —(я—I)»
Взявъ общій членъ, имѣемъ 1 13 13 5
Ея» —р»
(н« —Р«) 2 = и-14- тр2п-з + р‘»-5 4- ] 2 3 Р®»»-7 4-
1 3 13 5
р8 । 2'2 у? 2’2’2 р8 я» ‘ 1 . 2 ’ я» + 1 . 2 . 3 ’ я»
Полагая у> = 0, 1, 2, 3,. . . , п — 1, имѣемъ отсюда:
»
1=1
п п
1 13 13 5
1 _1 2 1 2212221,
>я» — 1 ~ «+1 ’ н,-Ь1 • 2 ‘ я’ + 1 . 2.3 ‘ я» +
1 13 13 5
1 1 2 2? 2 * 2 21 2 2 2 2е
|/ __22”я Т ’ п3 1 . 2 ’ п5^1 . 2 * 3 ’ л7 ’
1 13 1 3 5
_____1______- 1 ~ О2 । * 2 . («-О1, 2'2'2 (н — !)•
—(н— ])2 я~*"1 п* П5 •’і . 2.3 ’ я’
Суммируя, найдемъ въ предѣлѣ
1 1 3 5
к Г, . 1 % .2’2 8И 2’2'2 8, . 1
2 - Ііт1 { . 2 . ^4-і /2 з - я7+ • • • ]’
ѵ 82
или, подставляя Ііт —, окончательно я«* *
।
П _ 1 11.3 1 , 1 . 3.5 1 , 1 . 3.5.7 1
2 * + 2 ' З4' 2.4 ’ 5+2.4.6’ 7~^2.4.6.8 ’ 9+ ’ ’
другой рядъ, предлагаемый въ курсахъ интеграловъ.
ГЛ А В А ХЫХ.
Изслѣдованіе свойствъ показательной функціи,— Общія свойства логариѳмовъ.—Системы логариѳмовъ.—Условія соизмѣримости логариѳмовъ.—Приложеніе къ десятичнымъ логариѳмамъ.
Изслѣдованіе свойствъ показательной функціи.
774. Опредѣленіе. Функція а35, гдѣ а количество постоянное, а перемѣнное, называется показательной функціей, Изслѣдованіе свойствъ этой функціи служитъ основаніемъ теоріи логариѳмовъ.
Докажемъ, что если то функція непрерывна на всемъ протяженіи дѣйствительныхъ значеній ж, соизмѣримыхъ или несоизмѣримыхъ, положительныхъ или отрицательныхъ. Изслѣдованіе это подраздѣляемъ на двѣ части: а^> 1 я а<С 1.
775. Теорема. Если а >- 1, функція ах возрастаетъ непрерывно отъ 0 йо сс, когда х возрастаетъ непрерывно отъ — до оі.
I. Во-первыхъ, пусть х измѣняется отъ —до получая соизмѣримыя значенія. .
1) Если эти значенія будутъ цѣлыя и положительныя, то ьъ .'еммѣ I, § 749, уже доказано, что если т я/ то' и а™ > ан.
2) Пусть # получаетъ соизмѣримыя дробныя значенія и р, п пусть Отсюда: > а'8, и такъ какъ это — чпсла цѣлыя, то по предыдѵ-
г г щему: Извлекая изъ обѣихъ частей корень порядка мы не на-
рушимъ смысла неравенства, а потому или что и
требовалось доказать.
3) Дадимъ показателю х отрицательныя значенія, цѣлыя или дробныя; пусть — — п, гдѣ т и п положительны. Изъ неравенства имѣемъ: т < п; а
слѣд. ам<^ап; раздѣливъ обѣ части на положит, количество аш . находимъ:
или а~п<а~“"-
(.V I*
то же заключеніе.
П. Наконецъ, даемъ я-су несоихюь/щ.чыя значенія, и прежде всего опредѣлимъ, что слѣдуетъ разумѣть подъ степенью съ несоизмѣримымъ показате-
лемъ; напр., что означаетъ а ?
Возьмемъ рядъ приближеній къ уа, по иедостатку и по избытку, точныхъ 1111
до То’ іоб’ 1000’ ’ ‘ ’ 10й ’ ПОЛУЧИИЪ два Ряда »
1,7 1,73 1,732 ,
1,8 1,74 1,733 ’Х1,
общимъ предѣломъ которыхъ,
по опредѣленію, служитъ }/з^.
Затѣмъ» напишемъ два ряда степеней а съ этими показателями:
ді«"32
дЬЭ а1,74 дІЛЗЗ
а10" . . . (1)
* 4- *
а іо* . . . (2).
Такъ какъ эти показатели соизмѣримы, то, по вышедоказанному, степени (1) идутъ возрастая; но существуетъ безчисленное множество состояній величины, какихъ эти количества не могутъ достигнуть и превзойти: таковы, напр., со* отвѣтствующія имъ числа ряда (2). Необходимо заключить, что числа (1) стре^ мятся къ нѣкоторому предѣлу I. Подобнымъ же образомъ убѣждаемся, что числа ряда (2) стремятся, уменьшаясь, къ нѣкоторому предѣлу ь - Легко видѣть, что оба эти предѣла равны, ибо разпость
« 4" 1 а а «іо*
стремится къ нулю, когда п приближается къ безконечности. Дѣйствительно/эта разность =
Оіой( аі№Г _ 1) = а™\іауа — 1),
но мы доказали, что предѣломъ для служитъ 1; слѣд. разсматриваемая а
разность имѣетъ предѣломъ нуль, ибо множитель аІ0* конеченъ (онъ, напр., меньше а*).
Этотъ общій предѣлъ рядовъ (1) и (2) и представляютъ, по опредѣленію, въ видѣ о/3. Итакъ:
Степень съ несоизмѣримымъ показателемъ т отъ положительнаго числа а есть предѣлъ, къ которому стремятся степени этого числа, коихъ показатель стремится къ т, увеличиваясь или уменьшаясь.
Докажемъ теперь, что большему несоизмѣримому показателю (при а>1) соотвѣтствуетъ п большая степень; напр.
ѵз Ѵ2
а
Въ самомъ дѣлѣ, если и 1
до руя по недостатку, то:
суть приближенія къ \/2 н точныя
— а + 1 10” ь “ іо»
Слѣд., по предыдущему:
а потому и предѣлы» которые не равны,* не равны въ томъ же порядкѣ, ибо этотъ порядокъ не измѣняется, когда п неограниченно возрастаетъ,
III. Измѣненія функціи а* непрерывны на всемъ протяженіи измѣненій х.
Дадимъ конечному нѣкоторое приращеніе к, и докажемъ, что если это приращеніе будетъ неограниченно приближаться къ нулю, то и приращеніе Л функціи у0 будетъ также неограниченно приближаться къ нулю. Въ самомъ дѣлѣ:
у0 = а*°, сл.
к = ах<*’к — а*® = а** (ак — 1).
ах» — величина конечная; остается доказать, что Л можно взять настолько близкимъ къ нулю, что а1' будетъ какъ угодно близко къ 1, т.-е. что ак стремится къ предѣлу 1.
Пусть 1і >0; всегда можно найти такое цѣлое положительное число а, чтобы
ибо л есть частное, точное до 1, отъ раздѣленія 1 : А, и это частное будетъ неограниченно возрастать по мѣрѣ того, какъ Л будетъ приближаться къ нулю. Изъ предыдущаго неравенства выводимъ
откуда, по вышедоказанному:
Но крайнія количества — то же, что и а эти корни, въ силу леммы Ш §751, имѣютъ общимъ предѣломъ единицу, когда а неограниченно возрастаетъ; а слѣд. и то теор. § 186, имѣетъ тотъ же предѣлъ, т.-е. 1, когда Л стремится къ нулю. Заключаемъ, что въ формулѣ для к второй множитель стремится къ 0, а сл. и і приближается къ тому же предѣлу, по мѣрѣ приближенія к къ нулю.
IV, Когда х приближается къ соѵ то и ах стремится къ 'V
Это предложеніе было уже доказано въ леммѣ I, § 749, для показателя цѣлаго. Пусть теперь показатель т есть число дробное или несоизмѣримое; это число будетъ заключаться между двумя послѣдовательными цѣлыми числами р и рЦ- 1, такъ что
ар<ат<а?±\
Но, по упомянутой леммѣ, ар и стремятся къ со, когда р приближается къ ос, слѣд. и ат стремится къ со, когда т неограниченно возрастаетъ.
Итакъ: при а>1, есть функція непрерывная, возрастающая отъ
О до -|-со, когда х возрастаетъ отъ —со до -|-оэ.
Этотъ результатъ можно представить въ формѣ слѣдующей таблицы:
Изображая измѣненія у ординатами кривой, найдемъ крн-» вую, которой Оя' служитъ ас-симптотою, а ординаты растутъ неограниченно* 9та кривая пересѣкаетъ осъ у въ такой точкѣ А, для которой 0А= 1. Соотвѣтственно абсциссѣ 0В= 1 имѣемъ ординату
у^ВС = а*
Черт. 153*
776. Т е о р е м а. Если О а <1 1, то яри измѣненіи
<т отъ —сх Йо -|-сс, функція а* непрерывно уменьшается отъ до О.
Въ самомъ дѣлѣ, когда л<^1, то можно положить а = ~ь гдѣ а' > 1; (1 |
=^тг Если будемъ здѣсь увеличивать х отъ — зо до
то, по предыдущей теоремѣ, а'г будетъ увеличиваться отъ О до а слѣд* будетъ уменьшаться отъ до —, т*-е. отъ ос до 0. Что и здѣсь измѣне-нія функціи а* непрерывны — это непосредственно вытекаетъ изъ предыдущаго Таблица измѣненій будетъ слѣдующая:
Таблица В.
Этн измѣненія наглядно изображены измѣненіями ординатъ кривой, для которой положительное направленіе О.т оси абсциссъ служитъ ассииптотою*
Чертт 154*
Л огариемы,
777. Опредѣленіе,—Имѣя ур—ніе у=а* можно предложить себѣ три вопроса:
1. По даннымъ: основанію а и показателю х вычислить степень а* или у. • Дѣйствіе это называется возвышеніемъ въ степень.
2. По даннымъ: степени у и ея показателю х найти основаніе а. Дѣйствіе это есть извлеченіе корня и выражается злакоположеніемъ: а = )/у.
3. По даннымъ: степени или числу у и основанію а найти показателя я. Показатель х называется логариѳмомъ числа у при основаніи а. Итакъ: логатшѳлолса даннаго числа называется показателъ степени, въ которую нужно возвыситъ основаніе, чтобы получитъ данное число.
Слово логариѳмъ обозначается знакомъ 1о^; такимъ образомъ, чтобы показать, что х есть логариѳмъ числа у при основаніи а, пишутъ: х = 1о^а у, Напр. 1о^8 = 3, потому что 23 = 8; 1о^^ = — 2, ибо 2~2 = ^ = 1ит. о.
778. Выборъ основанія.—Главное значеніе логариѳмовъ заключается въ томъ, что опи служатъ могущественнымъ средствомъ для облегченія вычисленій. Но чтобы они могли служить для этой цѣли, необходимо имѣть для всѣхъ положительныхъ чиселъ дѣйствительные логариѳмы. Этому требованію удовлетворяетъ не всякое основаніе. И прежде всего легко видѣть, что отрицательнаго числа нельзя братъ за основаніе логариѳмовъ, ибо при такомъ основаніи не для всѣхъ положительныхъ чиселъ получатся дѣйствительные логариѳмы. Такъ, ур—нію (—2)® =8 нельзя удовлетворить никакимъ дѣйствительнымъ значеніемъ х.
Затѣмъ, 0 не можетъ быть принятъ за основаніе логариѳмовъ, потому что вторая часть ур—нія 0® = у при положительномъ х всегда даетъ нуль; при я = 0, О"1 О
у = О® = От т.-е. представляетъ неопредѣленность; а при отри-
цательномъ значеніи х, положивъ х = — т, получаемъ у=0-т = ~=і=сю. Такимъ образомъ, различныя степени пуля не воспроизводятъ всевозможныхъ положительныхъ чиселъ.
Обращаясь къ положительнымъ числамъ, замѣчаемъ, что единица не можетъ быть принята за основаніе логариѳмовъ, потому что различныя степени единицы равны 1.
Взявъ за основаніе число, большее или меньшее 1, и возвышая его во всевозможныя дѣйствительныя степени отъ —сю до мы, какъ видно изъ таблицъ А и В, §§ 775 и 776, получимъ всевозможныя положительныя числа отъ О до сю, такъ что въ этихъ случаяхъ всякое положительное число имѣетъ дѣйствительный логариѳмъ. Итакъ: за основаніе логариѳмовъ только и можно братъ положительныя числа, большія или меньшія 7.
779. Свойства логариѳмовъ при основаніи большемъ 1.—1. Всякое положительное число имѣетъ дѣйствительный логариѳмъ, и только одинъ. Ври изслѣдованіи функціи у = ах (см. таблицу А) мы видѣли, что если измѣнять .г отъ —сю до У непрерывно возрастаетъ отъ 0 до-рсю. Возьмемъ
въ этой строкѣ значеній у-ка какое-нпб. число у'; функція у (или а®), будучи непрерывна и измѣняясь чрезъ всю область положительныхъ чиселъ, пройдетъ, по крайней мѣрѣ, разъ п чрезъ значеніе у', прп нѣкоторомъ значеніи х1 пере
мѣннаго х; но функція эта постоянно возрастаетъ, и потому только одинъ разъ пройдетъ чрезъ это значеніе у’. Это наглядно обнаруживаетъ и кривая у = а* (черт. 153); въ самомъ дѣлѣ, пусть / = 0М; проведя параллель МР оси Ох, замѣчаемъ, что она встрѣтитъ кривую только въ одной точкѣ; логариѳмъ числа у будетъ абсцисса Оу точки встрѣчи Р.
Итакъ: всякое положительное число имѣетъ дѣйствительный логариѳмъ, и только одинъ. Высшая алгебра показываетъ, что кромѣ одного дѣйствительнаго логариѳма всякое положительное число имѣетъ безчисленное множество мнимыхъ логариѳмовъ.
2. Отрицательныя числа не имѣютъ дѣйствительныхъ логариѳмовъ. Дѣйствительно, на всемъ протяженіи строки чиселъ (таблица А) въ ней находятся одни положительныя числа.
3. Логариѳмы чиселъ, большихъ 7, положительны; въ самомъ дѣлѣ, числамъ отъ 1 до -|--ос строки у соотвѣтствуютъ* въ строкѣ х числа отъ О ДО +<».
4. Логариѳмы чиселъ, меньшихъ 1, отрицательны; и въ самомъ дѣлѣ, числамъ отъ О до 1 таблицы А соотвѣтствуютъ въ строкѣ логариѳмовъ значенія отъ —х до О.
5, Логариѳмъ нуля равенъ —с\<
6. Логариѳмъ единицы равенъ нулю.
7. Логариѳмъ основанія равенъ единицѣ.
8. Логариѳмъ -1- оэ равенъ -|-сс.
780. Свойства логариѳмовъ при основаніи меньшемъ 1.. Подобно предыдущему, изученіе таблицы В прямо даетъ слѣдующіе результаты:
1, Всякое положительное число имѣетъ дѣйствительный логариѳмъ, и только одинъ.
2. Логариѳмы чгісель, большихъ 7, отрицательны, а чиселъ меньшихъ единицы — положительны.
3. .Тоодшѳлю основанія равенъ единицѣ.
4. Логариѳмъ единицы равенъ нулю.
5. нуля равенъ
6. Лоіорг/ѳ.нь 4"!^ —ес.
7. Отрицательныя числа не имѣютъ дѣйствительныхъ логариѳмовъ.
781. Теоремы, на которыхъ основано употребленіе логариѳмовъ въ вычисленіяхъ.
Е Логариѳмъ произведенія равенъ суммѣ логариѳмовъ производителей.— Пусть имѣемъ числа К, У, У\ имѣющія логариѳмами: х, х\ а? при одномъ и томъ же основаніи а.
Зависимость между числами и ихъ логариѳмами выражается уравненіями
К = а*. . %(і) У = ^'. . . (2) К" = а"'. . . (3).
Перемноживъ ихъ, получаемъ уравненіе
ХУА" = ах+*'-Н"
изъ котораго видно, что яя'я" есть логариѳмъ числа КО": і8(тт'9=я4-я'+^';
но изъ данныхъ ур—ній имѣемъ: ж = ]^К, я/= ]<*№, =!{;№'; подстановка
въ предыдущее ур—ніе даетъ, такимъ образомъ:
1? (КХ'Г) = 1^ + ів И' + 1? Х'\ и теорема доказана.
II. Логариѳмъ частнаго равенъ логариѳму дѣлимаго безъ логариѳма дѣлителя.— Раздѣливъ ур—ніе (1) на (2), имѣемъ:
откуда, по опредѣленію логариѳма:
I* = х — х —1<? X — I* №. I г 1 *» &
Если К=1, то К = О, и предыдущее равенство даетъ:
т.-е. дроби, имѣющей числителемъ 1, равенъ отрицательному
логариѳму знаменателя.
III. Лоищиѳмъ степени съ какимъ угодно показателемъ равенъ произведенію показателя на логариѳмъ возвышаемаго числа.—Возвысивъ обѣ части ур—нія (1) въ степень т, имѣемъ
Г = (а*р = откуда (ІГ) = іш; = т. ]? К,
и теорема доказана.
ІГ. Логариѳмъ корня равенъ логариѳму подкореннаго числа, раздѣленному на показателя корня.—Извлекая изъ обѣихъ частей ур—нія (1) корень порядка р, имѣемъ:
^/Х = ^/а^ =а/\ откуда (}/К)=
Эти теоремы даютъ возможность значительно облегчать выполненіе болѣе трудныхъ ариѳметическихъ дѣйствій. Для этого должны быть построены таблицы, содержащія логариѳмы чиселъ. Имѣя такія таблицы, и зная, что логариѳмъ произведенія равенъ суммѣ логариѳмовъ производителей, мы можемъ умноженіе чиселъ свести на простѣйшее дѣйствіе — сложеніе ихъ логариѳмовъ: такимъ образомъ мы опредѣлимъ 1о^ произведенія, а для отысканія самаго произведенія останется взять изъ таблицъ число, соотвѣтствующее найденному логариѳму. Дѣленіе чиселъ, при помощи теоремы И, сводится къ простѣйшему дѣйствію — вычитанія логариѳмовъ; возвышеніе въ степень, при помощи теор. ІИ, приводится къ умноженію, а извлеченіе корня, по теор. IV*, къ дѣленію. Однимъ словомъ, при помощи логариѳмовъ, дѣйствія высшаго порядка надъ числами приводятся къ дѣйствіямъ низшаго порядка надъ ихъ логариѳмами.
782. Теорема. Если числа составляютъ прогрессію геометрическую, то ихъ логариѳмы составятъ прогрессію ариѳметическую.
Пусть имѣемъ геометрическую прогрессію
~ а : ад : ад2: ад*: : адн.
Взявъ логариѳмъ каждаго члена, имѣемъ:
1?а; 1?а + 21§9; І8«4-3; 1$а-}-п1§д:
*
а это есть рядъ, составляющій ариѳметическую прогрессію съ разностью, равною
Свойство это было взято Неперомъ за исходный пунктъ въ теоріи логариѳмовъ.
783. Если надъ данными количествами, входящими въ составъ выраженія, подлежащаго вычисленію, указаны только дѣйствія дѣленія, умноженія, возведенія въ степень и извлеченія корня, то такое выраженіе м. б. вычислено съ помощію логариѳмовъ. Пусть напр.
««х г'с8
6»х У&Р
Примѣняя теоремы о логариѳмѣ дроби и т. д., послѣдовательно получаемъ:
I? х = 18 [а* X — 1? [Ь8 х *]
= 1?а»1? ^7»— (186»•
= 6І8в4-|і8С— 2І8& — | (318^4-518/).
Такимъ образомъ будетъ извѣстенъ; а по опредѣлится и соотвѣтствующее число, какъ скоро будутъ даны численныя значенія а, Ь, с, Л и /. I Дѣйствіе, имѣющее цѣлью составленіе выраженія для логариѳма по данному Выраженію для числа, называется логариѳмированіемъ.
Обратно, но данному выраженію логариѳма можно составить выраженіе для соотвѣтствующаго числа, пользуясь тѣми же теоремами. Пусть, напр., дано
18 х = | [18 (а 4- Ъ) 4-18 (а - Ь) + 1е (а8 4~ Ь8)] — § I? < 1 -4- а’).
Послѣдовательно имѣемъ:
І8« = |18(а4-Ь)(а —Ь)(а84-Ь’)-|18(1+«8)
= ? 18 [(а4 — Ь4) (а4 4- Ь4)] — 118 (1 4~ а4)
-118 («‘ - Ь‘) - і 18 (і 4- «*) = і? — 1? ГП7®8 ч о
Изъ равенства логариѳмовъ заключаемъ о равенствѣ соотвѣтствующихъ чи-
селъ; такимъ образомъ, находимъ
х =
^14-а2
784. Перемѣна основанія.—Пусть извѣстны логариѳмы чиселъ при нѣкоторомъ данномъ основаніи а, и предложимъ себѣ вычислить логариѳмы тѣхъ же чиселъ, взявъ другое основаніе Ь. Рѣшеніе этого вопроса основывается на слѣдующей теоремѣ:
Теорема.— Отношеніе логариѳмовъ двухъ чиселъ X и № не зависитъ отъ основанія, т.-е, это отношеніе остается одинаково, каково бы ни было основаніе.
Въ самомъ дѣлѣ, пусть логариѳмы числа И при основаніяхъ а и Ь будутъ а н |і; а логариѳмы числа Х'при тѣхъ же основаніяхъ пусть будутъ а' и Но опредѣленію, имѣемъ
Отсюда:
Х = а’ = ^, Х' = а’' = Ь\
а = Ъ* =
и слѣдовательно,
- = Ѵ пли а яг
или, наконецъ
и теорема доказана.—Если положить здѣсьХ'=Ь, то будетъ 1^ЬХГ = 1$ь6 = 1, и пропорція дастъ:
л=о? ою х Л • • - (о
т.-е. построена таблица логариѳмовъ при основаніи а, то изъ нея легко вывести логариѳмы по другому основанію Ь: стоитъ только старые логариѳмы помножить на дробь равную единицѣ, дѣленной на I# нояаю основанія, взятый по старому. Этотъ постоянный множитель называется модулемъ перехода отъ старой системы къ новой.
Изобрѣтатель логариѳмовъ, Ііеперъ, взялъ за основаніе построенной имъ системы несоизмѣримое число, равное приблизительно 2,718281828459045. . . Это число обыкновенно обозначаютъ буквою е; а самые логариѳмы называютъ
неперовыми, или натуральными, или іняер&мкческилш; они имѣютъ важ-. пое значеніе въ высшемъ анализѣ. Но для практическихъ вычисленій они не удобны; поэтому уже самъ Неперъ посовѣтовалъ своему современнику Бриггу вычислить новые логариѳмы, принявъ за основаніе число 10* Этими послѣдними логариѳмами и пользуются обыкновенно для практическихъ вычисленій, и называютъ обыкновенными, или десятичными логариѳмами.
Примѣчаніе, Если въ равенствѣ (1) положимъ Х = а, то, какъ будетъ ІігаХ = 1, найдемъ соотношеніе
часто употребляемое въ вычисленіяхъ.
785. Условія соизмѣримости логариѳмовъ.—Замѣтивъ, что всякое число можно представить въ видѣ произведенія степеней его первоначальныхъ множителей, опредѣлимъ условія, при которыхъ логариѳмъ даннаго числа И будетъ соизмѣримымъ числомъ, ограничиваясь разсмотрѣніемъ случая, когда основаніе цѣлое положительное число.
1- Требуется опредѣлить условія, при которыхъ цѣлое число И имѣетъ со-измѣримый логариѳмъ —, т.-е. при какихъ условіяхъ возможно равенство
Х’ = ан, или, по возвышеніи обѣихъ частей въ п-ую степень, равенство
Х” = а"\ . . (1).
Пусть основаніе а разлагается на первоначальные множители а, у соотвѣтственно въ степеняхъ г, і, такъ что а = аг р'у*; равенство (1) будетъ
X” =
Такъ какъ вторая часть его дѣлится на а, и у, то и первая должна дѣлиться на тѣ же числа, иначе вышло бы, что дробь равна цѣлому. Сверхъ того К не можетъ содержать другихъ первоначальныхъ множителей, кромѣ а, и у, по той же причинѣ. Слѣд. должно положить К = сГ* Р'1 уЧ Ур. (2) при
метъ видъ:
Ъяя, уПІі ___ д1пг
Чтобы зто равенство было возможно, необходимо, чтобы было яг, = »»•; пз1 тз; пі. =а тпі, откуда — - — = 4; заключаемъ: чтобы цѣлое число
Г1 ч
X при цѣломъ основаніи а имѣло соизмѣримый логариѳмъ, необходимо, чтобы а и X состояли изъ одинаковыхъ первоначальныхъ множителей, и чтобы показатели этихъ множителей были пропорціональны между собою.
2. Пусть дана неправильная дробь гдѣ с > с?. Пусть логариѳмъ (въ данномъ случаѣ—положительный) будетъ = соизмѣримой дроби имѣемъ:
т
ТГ~ С с*
а* =7;’ ИЛИ а =
Но я-ая степень несократимой дроби есть также дробь несократимая, и слѣд. не можетъ равняться цѣлому числу а*”: допущеніе невозможно, а потому заключаемъ: при цѣломъ основаніи неправильная дробь не можетъ имѣть соизмѣримаго логариѳма.
3. Пусть, наконецъ, данное число есть дробь правильная гдѣ, слѣдовательно, При а>1 логариѳмы правильныхъ дробей отрицательны; пусть этотъ отрицательный логариѳмъ есть —Въ такомъ случаѣ
т
- ~ с т ая
« ‘(і’ 0ТКУДа “ = ^‘
Такъ какъ л* — число цѣлое, то предыдущее равенство возможно только при сп—1, или с=1; но въ такомъ случаѣ имѣемъ:
ат = Г,
а такое равенство возможно только тогда, когда <1 и а состоятъ изъ одинаковыхъ первоначальныхъ множителей и показатели зтихъ множителей пропорціональны. Итакъ:
При цѣломъ основаніи логариѳмы правильныхъ дробей несоизмѣримы, за исключеніемъ такихъ дробей, у которыхъ числитель = 19 а знаменатель состоитъ изъ тѣхъ же первоначальныхъ множителей какъ и основаніе, а показатели этихъ множителей пропорціональны.
786. Приложеніе. Приложимъ эти изысканія къ случаю обыкновенныхъ или бригговыхъ логариѳмовъ. Здѣсь основаніе равно 10=2X5. Слѣд., по доказанному, изъ всѣхъ цѣлыхъ чиселъ только тѣ имѣютъ соизмѣримые логариѳмы, которыя состоятъ изъ тѣхъ же первоначальныхъ множителей, какъ и основаніе, въ данномъ случаѣ, изъ 2 п 5, т.-е. числа вида 2\ 5\ Притомъ, г и 5 должны быть пропорціональны показателямъ основанія, т.-е. должно быть: г: 1=$:1, или г = $. Такимъ образомъ, цѣлое число, имѣющее при основаніи = 10 соизмѣримый логариѳмъ; имѣетъ видъ 2Г. 5Г= (2.5)г= 10\ т.-е. представляетъ точную степень 10-ти.
Затѣмъ, неправильныя дроби имѣютъ логариѳмы несоизмѣримые; а изъ правильныхъ дробей только тѣ имѣютъ соизмѣримые логариѳмы, у которыхъ числитель = 1, а знаменатель есть точная степень 10, т.-е. дроби ^5 1
100СУ * ‘ '
Вычисленіе логариѳмовъ.—Ряды для показательной функціи н логариѳмическіе.
787. Опредѣленіе предѣла
.—Разсмотримъ сначала
и
О)
пусть, во-первыхъ, « проходитъ область натуральныхъ чиселъ 1, 2, 3, 4, . до безконечности. Формула бинома для цѣлаго положительнаго п даетъ:
Отсюда, во-первыхъ, видно, что каково бы ни было число п>1, всегда / 1 \п
11 4-- ) >2. Во-вторыхъ, что по мѣрѣ того какъ п растетъ, каждый членъ разложенія замѣняется членомъ того же порядка, численно большимъ, и въ то же
/ IV1
время число членовъ увеличивается; слѣд., 1 4-- постоянно увеличивается вмѣстѣ съ п-
- - 877 —
Если въ каждомъ членѣ разложенія (А) откинуть дроби, стоящія въ скоб-/12 3 \
кахъ • I, то каждый членъ разложенія увеличится, и слѣд*,
1
Е2.3 . . . п
Тѣмъ болѣе вѣрно будетъ неравенство
I
Отсюда видно, что при я = ео будетъ
Ііт
/ [ѴП / 11
(1+-) ]<пт(1+і+1+
и какъ Ііт 2 — 1 = 3, то заключаемъ, что
3
каково бы ни было цѣлое положительное число н.
(1 \
1 -И -1 постоянно возрастаетъ съ увеличеніемъ
п, но всегда остается между 2 и 3; слѣд*, стремится къ нѣкоторому предѣлу, лежащему между 2 и 3. Этотъ Ііт обыкновенно обозначаютъ буквою е. Итакъ, при цѣломъ положительномъ ш, приближающемся къ счх
ііт[(і+у,,’]=е-
Если и не есть цѣлое число, но положительно, то всегда можно дать два цѣлыя положительныя послѣдовательныя числа т и т +1, между которыми лежитъ тогда очевидна справедливость неравенствъ
Возвышая первый биномъ въ ш-ую, второй въ степень третій въ степень /н +1, не нарушимъ смысла неравенствъ, а потому
Умноживъ и раздѣливъ первое на 1 + ^рр жители, находимъ
а третье разложивъ на мно-
Переходя къ предѣлу, увеличиваемъ ш до сс, тогда и ш и ш + 1 будутъ приближаться къ с©. По теоремѣ о предѣлѣ частнаго, имѣемъ
ибо, по доказанному,для т цѣлаго: Ііт Г1 н--
затѣмъ, 1ігпИі + 11 |1 + —— е.1— е.
(1Ѵ1*
1 +— заключается между двумя перемѣнными, имѣю-
щими общій предѣлъ с. слѣд. и
(1 Vй
1 + — = г,
1 іа) т
и въ томъ случаѣ, когда положительное число приближающееся къ оо, не есть цѣлое.
Если — число отрицательное, то можно положить ш = —(? + !)> гдѣ р — положительное, неограниченно возрастающее цѣлое или дробное число. Имѣемъ:
Первый множитель приближается къ предѣлу е, второй къ 1, сл.
Такимъ образомъ, послѣднее равенство имѣетъ мѣсто при всякомъ неогранн-ченно-возрастающемъ дѣйствительномъ ш.
1
Нерѣдко этому равенству даютъ другой видъ, подставляя — = 5; имѣемъ:
Ііт [ (1 + ?)«] = е,
гдѣ & означаетъ количество, приближающееся къ нулю.
Теперь легко уже опредѣлить предѣлъ общаго выраженія
(2 \Ч> / 1 \ <0
1 + ^-1 =/1 ,
<о/ ш I
\ 2/
гдѣ я — нѣкоторое дѣйствительное количество.
Дробь “ вмѣстѣ съ со стремится къ сс, и потому, положивъ — = откуда я #
ю ~ имѣемъ
Но предѣлъ степени (я) перемѣннаго равенъ той же степени предѣла этого перемѣннаго, такъ что послѣднее выраженіе, въ предѣлѣ, даетъ г. Итакъ
1іт К1 + 3“‘] =е=--®.
788. Разложеніе е* въ рядъ.—Послѣднее уравненіе показываетъ, что г есть предѣлъ, къ которому стремится (1 -) при неограниченномъ увеличеніи т. Для
нахожденія этого предѣла нужно тѣмъ положить =
по формулѣ бинома и за-
Ь79 —
По формулѣ (III) § 771,, полагая т цѣлымъ и положительнымъ и Л*>яы*, имѣемъ:
, т(т — I) _ ( , т(ж — 1) * . [пі — (й— 2>І . . ,
(1 +«)-"= I + ,»х 4- *»+...+ -5—і^з - ;1 ----!«*-* +
. іп(т -1) . . . [ш — (Аг— 1)| А я**
+ 1.2.3 . . . Г" ~ * Г1 _ ’
гдѣ р означаетъ положительную правильную дробь. Чтобы по зтоіі формулѣ на-/ 2 Vй
писать разложеніе для , нужно, очевидно, положить о* = — и к > г.
Найдемъ
Мы ищемъ предѣлъ (1 +—) при —сс; для итого увеличиваемъ неограниченно ш, не измѣняя произвольнаго цѣлаго числа А;. Если перемѣнныя равны, то равны и предѣлы ихъ, а потому приравниваемъ предѣлы обѣихъ частей ра-тт х х , н к 1 2 Л — і
венства. Предѣлъ лѣвой части есть г, а въ правой дроби —» —> • • * » —
имѣютъ общимъ предѣломъ нуль; слѣд.
। . г । । ______________-I__________
11.2+І.2.3”1" ' “ “г 1.2.3 ... (!•— 1)^1.2.3 . . * 1—|У|’(и) прячемъ к > 0 < е < 1.
Такимъ образомъ, мы получили конечную строку для г, — съ остаточнымъ членомъ; но изъ нея уже легко вывести безконечный рядъ для с3. Для этого переносимъ остаточный членъ въ первую часть:
й=____?_ в* , I I г* I . I **-1 ,пп
। + + 1.2' 1.2.3^ ^1.2...(Ь—1)
и увеличиваемъ А-, означающее число членовъ второй части, до безконечности. Выше мы доказали, что Ііт Г,——0* слѣд. предыдущее равенство обращается въ безконечный рядъ
^3
^=1+г+г_+ж+...(ІѴ)
гдѣ 2 какая угодно конечная величина.
789. Рядъ для е; опредѣленіе числовой величины е; несоизмѣримость числа е.
Если, въ частности, положимъ #~1, то ряды (II) и (IV) дадутъ:
е=1 + 1+Г2 + Т^З+ЁОл +‘ ' ‘+1.2.3...(Д-^Л)+1.2.8...(»-1)’гН (Ѵ)
е = 1 1 13Г?2?зЕ2Тзл"I"' •№)
Съ этими рядами связаны существенныя замѣчанія. Во-первыхъ, что касается формулы (V), то она служитъ для численнаго опредѣленія е, причемъ точность можетъ быть доведена до какой угодно степени выборомъ достаточно большого значенія для к. Такъ, при Д=11 найдемъ.
1
1.2.3
Ч4^7ЯЧТП = 2*718^18011» 0.4.0.Ѵ.І .о.У.11)
1 Р
причемъ остатокъ = —— 0,0000000276?; слѣд. если дадимъ?его нап-меньшее значеніе 0, а затѣмъ наибольшее его значеніе 1, то найдемъ
2,7182818011 < й < 2,7182818287;
откуда, взявъ е = 2,7182818, будемъ имѣть его величину точно до 7-го десятичнаго знака включительно. Это число было принято Неперомъ за основаніе предложенной имъ системы логариѳмовъ, по Причинѣ, которая вскорѣ будетъ указана.
Съ помощію формулы (VI) рѣшается вопросъ о томъ, есть ли е число соизмѣримое или несоизмѣримое. Сумма ряда VI, начиная съ третьяго члена, т.-е.
1
9
гпз+-
менѣе суммы ряда
слѣд. сумма (VII) есть правильная дробь. Допустимъ, что эта дробь соизмѣрима р
и = -, т.-е.
1 _1 2±2.
_ Р а
гдѣ р и </ >др цѣлыя положительныя числа. Умноживъ обѣ части на 2.3.4 ... г/, получимъ
3.4.5 .. • 7 + 4.5.6 .../? + 5.6 . . . д + . . . +1
9 + 1 ' (9+!)('/ +(9 + 1)(9 + 2)(Н-3)
= р-2.3.4 . . . (д— 1).
Сумма членовъ до —. есть сумма цѣлыхъ положительныхъ чиселъ, дающая 7 + 1
нѣкоторое цѣлое положительное число М; вторая часть также есть цѣлое поло-
жительное число, которое назовемъ X; сл.
М -I -----1_____-— ---+ .
^9+1 Ч9+1)(9 + 2Г
і. I 1 1,1.1,
Но сумма —г— + -— ~ - И--меньше —т-т +, . . + - - •
9 + 1 (7 + 1) (9+2) 9+1 (9+1)2 (9+ІГ
1 Л 1 X 1
= : ^1—=~> а какъ 9 > 1> то разсматриваемая сумма меньше 1.
Такимъ образомъ, цѣлое число М, сложенное съ правильною дробью, должно давать цѣлое число \т; но это невозможно, а потому сумма ряда (VI) не можетъ равняться никакой соизмѣримой дроби, а сл. и е есть число несоизмѣримое.
Приведенное доказательство несоизмѣримости числа е принадлежитъ Стпен-вил.ію.
— 881
790. Разложеніе а*. Мы нашли разложеніе показательной функціи съ основаніемъ е; пусть основаніе будетъ какое угодно число а. Положивъ & = а*, и взявъ отъ обѣихъ частей логариѳмъ по какому угодно основанію, получимъ
я 1»е = 5г.1*«, откуда
X 1®" (I
Подставивъ въ формулу (IV) ах вмѣсто е% и *? вмѣсто я, найдемъ 1 й
аг.І^а 18*
Основаніе, по которому взяты логариѳмы, здѣсь совершенно произвольно; взявъ е за основаніе, и замѣтивъ, что въ такомъ случаѣ ]^с=1, найдемъ (условившись обозначать Неперовы логариѳмы характеристикою 2):
»-=1 + Л+^ + ^!>’ + ... (IX)
Взявъ за основаніе «, найдемъ рядъ
Послѣдній выводъ имѣетъ то значеніе, что даетъ возможность находить число по данному логариѳму; въ самомъ дѣлѣ, изъ ур—нія = у имѣемъ а* = 1§ау; слѣд.
Въ случаѣ а — е имѣемъ:
У = 1 + Іу + ^2 + ] 9 з + ’ * *
Отсюда и видно, что логариѳмическая система съ основаніемъ с есть простѣйшая, а потому наиболѣе естественная; вслѣдствіе этого она и названа натуральною.
791. Логариѳмическіе ряды. Исходнымъ пунктомъ послужитъ
при О = 0.
Пусть 0 означаетъ число, приближающееся къ нулю; тогда будетъ имѣть предѣломъ 1, а разность — 1 нуль; поэтому можно положить 1 = с, гдѣ $ исчезаетъ вмѣстѣ съ 0. Написавъ это ур—ніе въ видѣ
и* = 1 о, заключаемъ, что 0 = 1^« (1 + &)•
Раздѣливъ обѣ части ур—нія л* — 1=2 на О, найдемъ выраженіе, предѣлъ котораго ищемъ, именно
Переходя къ предѣлу, полагаемъ 0 = 0; вмѣстѣ съ этимъ и 2 — 0; въ первой 1 0
части получимъ неопредѣленность а послѣднее выраженіе раскроетъ истинное значеніе этой неопредѣленности; именно получимъ
• (I)
— 882 — і
Это равенство можно представить въ болѣе удобной формѣ» принявъ за основаніе логариѳмовъ число с. Логариѳмируя обѣ части равенства а = по основанію а, находимъ
I
1 — /аЛп,,е, или . = ?«,
Подстановка въ (1) дастъ
Положивъ о = 1 4-^} имѣемъ
уп і’ \ г (1+я-р — 1 I (I 4гс) = 11П1 І--7-,
й
откуда видна возможность примѣненія биноміальнаго ряда для разложенія ?(14а'1-При разложеніи (1 4^)г будемъ разумѣть подъ 5 нѣкоторую положительную правильную дробь; слѣд. х должны подчинить условію — 1<#<+Е Примѣняя формулу (Ѵ) остатка биноміальнаго ряда, т.-е. взявъ
А>о, [т]<:<1, 0 <(;<!,
Перенеся 1 въ первую часть и раздѣливъ ур—ніе на &, получимъ
Переходя къ предѣлу, т.-е. полагая 2=0, и замѣчая, что равенство перемѣнныхъ ведетъ за собою равенство ихъ предѣловъ, причемъ предѣлъ первой части
I (1 4 получаемъ:
і . 1 1 „ 1 . , . (— П*—г (_і)Д—і
2(1 4 Я?) = ~;Г2-|--жЭ — -Т1 4-|____ІРк-14--------2-----#
Это — рядъ коночный; для полученія безконечнаго ряда переносимъ остатокъ въ первую часть:
ч 2(1 + х)--------= -------И Г—і"8*-1’
и заставляемъ произвольное цѣлое А, означающее число членовъ, возрастать до безконечности» 'Гакъ какъ я есть правильная дробь (положвт. или отрицат.), то Ііт = о, такъ что въ предѣлѣ первая часть обратится въ 2(1 +&), а вторая дастъ безконечный рядъ; находимъ разложеніе
2(1 +□') = х — г*+ • * • (2)
— 1 < я* < 4* 1*
Рядъ этотъ виервЫе встрѣчается у Меркатора (1686). Если въ формулѣ (2) вмѣсто х подставимъ —а?, то получимъ:
2(1 — іг) = —х — 1 .г*— | я-»4 . (3)
м О 4
'Гакъ какъ въ рядахъ (2) и (3) х есть правильная дробь, то они могутъ служить только для вычисленія логариѳмовъ чиселъ, меньшихъ 2^ Чтобы получить ряды для вычисленія логариѳмовъ какихъ угодно чиселъ, притомъ ряды съ сильнѣйшею сходимостью, вычтемъ формулу (3) изъ (2); получимъ
рядъ, сходящійся при — 1 < Л* < + 1.
Положивъ
= откуда -«=”5
получимъ изъ ур. (4) слѣдующее*:
(5)
имѣющее мѣсто при всякомъ положительномъ г, ибо въ такомъ случаѣ г всегда будетъ правильною дробью. При небольшомъ г формула (5) всего удобнѣе: такъ напр. прп ^ = 2 получимъ:
?2—2[—-4- - 4- —Н______Т
Н.3^3.3^5.3*^ -!
Если рядъ, заключенный въ скобки, прервать на членѣ гдѣ ш нѣкоторое нечетное число, то остатокъ
1 ! 1 (т + 2),3»<+^(?Л4*4).3"*ѵ4 + (т4 6).3«±«^
будетъ меньше
1 1 1
(пі 4- 2) .3м г2 ’ 1 _ X ” 8 (пі + 2) * 3"' ' Зз
Такимъ образомъ, если ; будетъ неизвѣстная правильная положительная дробь, то
Послѣдовательнымъ нахожденіемъ степеней получимъ, что остатокъ
ѵіч = 0.000000001, слѣд., положивъ пі ~ 15, получимъ величину Г2 вѣрно до 8 4.17. о15 десятичныхъ знаковъ, именно: /2 = 0,69314718.
Если извѣстенъ /а, то найдемъ /(« + &) на основаніи замѣчанія, что
? (а 4 Ь) = I [а (1 4 +* (1 + ” )»
причемъ послѣдній I можно разложить по формулѣ (2), если только абсолютная величина Ъ меньше сі; найдемъ
7/ . М 7 * Ъ I/6\з , 1/6ѵ»
17 а 2Ѵ 1 Зѵа/
рядъ СХОДЯЩІЙСЯ при
Такимъ образомъ можно, напр., найти ІЗ, положивъ а = 2, 6 = 1 и воспользовавшись уже вычисленною величиною 12,
Болѣе удобная формула для вычисленія 2(а + 6) получается изъ замѣіГаніяг
что
?(а + Ь) =г«4-г(1 +^) «2а +?
разложивъ послѣдній I по формулѣ (4), получимъ
{6 1 / 6 1 / 6 ѵ
) +Н^-!Т-к) +
2а + 6 3 ^2а + 6/ ‘ о ^2а + Ъ'
}.. .(6)
рядъ сходящійся при всѣхъ положительныхъ значеніяхъ а и 6, потому что тогда будетъ правильною дробью. Положивъ а = 2, 6 = 1, получимъ
Прервавъ рядъ на ш-ой степени, можемъ опредѣлить остатокъ вышеуказаннымъ способомъ, и найдемъ, что онъ меньше
При ш = 9 остатокъ будетъ такъ малъ, что не повліяетъ на 8-ое десятичное-мѣсто; это дастъ: 13 = 1,09861229, и т. д.
Вычисленіе обыкновенныхъ логариѳмовъ. Модуль.—Построивъ указаннымъ путемъ таблицы натуральныхъ логариѳмовъ, можно изъ нихъ безъ труда вывести логариѳмы по какой угодно системѣ; для этого надо натуральные логариѳмы по-1
множить на модуль, равный, какъ извѣстно,его обозначаютъ чрезъ Мй. Для обыкновенныхъ логариѳмовъ а—10; 110 = /2-нІ5 = 2,33258509; слѣдовательно ^іо=у|0 —0,43429448. На это число и нужно множить натуральные логариѳмы для вычисленія обыкновенныхъ.
792. Теорема, на которой основано употребленіе табличекъ пропорцій-налъныіп частей.
Изъ формулы (6) предыдущаго § имѣемъ
Для полученія логариѳма по другой системѣ, нанр. по десятичной, надо этотъ логариѳмъ помножить на модуль умножая обѣ части на М|0, получимъ
и-ш >81. ( а ------|
2а
Удержавъ здѣсь только первый членъ —-& х "а
2(і\оа т'бУ ПОЛУ’ШМЪ приблизительную формулу
\ / г і 6.МІ0 68.М1в
(а + 6) —а =------------ —
а а (2а -ЬI
и обративъ его дѣленіемъ нъ
При 6 1 и а 10000 второй членъ меньше 0,0000(ХХ)0()2, а потому можно
имъ пренебречь; отъ этого получимъ:
. к М I 6»М(Л '? (я + ») —18 « =—- •
Подставилъ въ эту формулу вмѣсто Ь другое число 6'<1, будемъ имѣть
ІВ(а + 6'> —=
Раздѣливъ это равенство на предыдущее, имѣемъ пропорціи» (а + 60 — а________________________________?/
I" (а + 6) — ’
€лѣд. разности леждр лош/ліѳмал» пропорціональны разностямъ между числами, если только разности чиселъ не превышаютъ I, а числа не менѣе 10000, ибо только при этихъ условіяхъ и могла быть установлена послѣдняя пропорція.
ГЛАВА ЪІ.
О десятичныхъ логариѳмахъ ,*-Ч Г хъ отличительныя свойства.—Расположеніе п употребленіе таблицъ.—Вычисленія прп помощи логариѳмовъ.
Отличительныя свойства десятичныхъ логариѳмовъ.
793. Въ этихъ логариѳмахъ число X связано съ своимъ логариѳмомъ л? понизите льннымъ уравненіемъ 1О’С = Х. Такъ какъ здѣсь основаніе больше единицы, то логариѳмы чиселъ, большихъ 1, положительны, логариѳмы же чиселъ, меньшихъ 1, отрицательны; затѣмъ, логариѳмъ основанія равенъ 1, а 1^1=0.
794. Логариѳмы чиселъ, большихъ 1. Возвышая 10 въ цѣлыя положительныя степени, имѣемъ:
10«=1; Ю,=10; 10*=100; 10э= 1 000; 10*=10000; . . . ; 10”=10".
Отсюда, замѣчая, что показатели основанія 10 суть логариѳмы вторыхъ частей, имѣемъ:
1? 1=0; 1^10=1; 18 100=2; 18 1000=3; 1* 10000=4; . . . ; 1" 10н=п.
Заключаемъ, что чис.ш, состоящаго изъ 1 съ нулями, т.-е.
точной степени 10* равенъ числу нулей при единицѣ. Эти точныя степени 10 суть единственныя числа, большія 1, которыхъ логариѳмы сомзлоъ-2>ылш; всѣ остальныя числа большія 1 (цѣлыя и неправильныя дроби), какъ мы уже знаемъ, имѣютъ логариѳмы несоизмѣримые* которые вычислить можно только приблизительно. Ихъ обыкновенно выражаютъ десятичными дробями.
Пусть, напр., имѣемъ число 452,48. Число это больше 100, но меньше 1000, слѣд. его логариѳмъ содержится между І8 100 и 1$ 1000, т.-е. между 2 и 3, л потому равенъ 2 несоизмѣримая прав. дробь. Цѣлое число 2 называется
характеристикою^ дробь — лаяягаесою. Пзъ предыдущаго примѣра заключаемъ, что характеристика лоіариема числа большаго 7, равна числу цифръ безъ 1 «га цѣлой части даннаго числа.
Докажемъ, что это правило для опредѣленія характеристики логариѳма даннаго числа — общее. Пусть число А содержитъ въ своей цѣлой части п цифръ; въ такомъ случаѣ
10м-1 < А < 10",
ибо ІО11-1 и 10“ суть наименьшія числа о п и цифрахъ.
Отсюда
»—!.< 1& А < п,
такъ какъ большему числу соотвѣтствуетъ и большій логариѳмъ; итакъ, цѣлая часть І^А равна »— 1, т.-е. числу цифръ безъ единицы въ цѣлой части числа.
795. Логариѳмы чиселъ, меньшихъ 1. Возвышая 10 въ цѣлыя отрицательныя степени, находимъ:
-1 .— _1_. іп-2— 1 • 1 Л-3 —, *. . . •
10’ 100’ 1000’
10”" = -- -10"
Отсюда:
^)0 1; І^іоо- 1000 3; ’ * ' ’ ^10”
Слѣд. логариѳмъ дроби, которой числитель = 1, а знаменатель есть точная степень 10, соизмѣримъ и равенъ отрицательному числу нулей знаменателя. Всѣ остальныя числа, меньшія 1, какъ доказано, имѣютъ логариѳмы несоизмѣримые и отрицательные.
Эти отрицательные логариѳмы представляютъ въ видѣ бинома, котораго цѣ-'лый членъ отрицателенъ, а дробный положителенъ. Пусть, напр., данъ отрицательный логариѳмъ
— 3,4827129.
Разбивъ его па два члена: —3—0,4827129, вычтемъ и придадимъ 1: дадимъ логариѳму видъ:
— 4Н- (1 — 0,4827129), или - 4 + 0,5172871.
Очевидно, разность между 1 и десятичною дробью получимъ, вычтя всѣ десятичныя цифры изъ 9, исключая послѣднюю значащую цифру справа, которую вычитаемъ изъ 10. Преобразованный ' биномъ условились писать въ видѣ 4,5172871, помѣщая знакъ (—) надъ цѣлою частью, къ которой онъ относится; цѣлая часть называется отрицательною характеристикою.
Итакъ, во всѣхъ случаяхъ мантисса есть положительная десятичная часть логариѳма, а характеристика всегда цѣлое число, положительное, либо отрицательное, смотря по тому, больше данное число единицы, или меньше ея.
Примѣчаніе. Разность между 1 и дробью 0,4827129 называется й’опод-.неніемъ этой дроби до 1. Вообще дополненіемъ числа до 1, 2, 3 . . . , 10 называется разность между 1, 2, 3, . . . , 10 и даннымъ числомъ. Чтобы
получить дополненіе логариѳма, надо послѣднюю цифру мантиссы вычесть изъ 10, а остальныя ея цифры изъ 9. Употребленіе дополненій даетъ возможность избѣгать вычитанія логариѳмовъ, замѣняя это дѣйствіе приданіемъ ихъ дополненій; это особенно выгодно въ тѣхъ случаяхъ, когда приходится дѣлать нѣсколько вычитаній.
Отрицательная характеристика логариѳма положительнаго числа, .меньшаго 7, содержитъ столько отрицательныхъ единицъ, сколько находится. нулей слѣва отъ первой значу щей цифры числа, включая сюда и 0 цѣлыхъ.
Въ самомъ дѣлѣ, пусть будетъ число А, имѣющее слѣва отъ первой значу-щей цифры п нулей, имѣемъ:
10“ < Л < іо-і
ибо значущія цифры числа начинаются съ десятичнаго знака порядка я. Отсюда
— п А < — (и — 1)
ибо большему числу принадлежитъ и большій логариѳмъ.
Заключаемъ, что 1а?А равенъ (—п), или этому числу, увеличенному положительною правильною дробью, ибо этотъ логариѳмъ меньше иначе
говоря,
А = — п А*, гдѣ 0 < к < 1;
слѣд. (—я), по опредѣленію, и есть отрицательная характеристика кгА. Такъ, логариѳмы чиселъ 0,529 и 0,00743 имѣютъ отрицательныя характеристики: — 1 и — 3.
796. Если число увеличимъ въ 10, 100, 1000, . . . 7 вообще въ 10? разъ, то характеристика логариѳма его увеличивается на 1, на 2, . . . , вообще, на р единицъ, мантисса же останется безъ перемѣны.
Въ самомъ дѣлѣ, пусть
т, 0 < ш < 1,
1і,г А — к
гдѣ к — характеристика, положительная или отрицательная, а т — мантисса логариѳма А. Имѣемъ
I? (А X 10^) = А = к + т +Р = (й +^)
но р — число цѣлое, слѣд. и есть цѣлое, положительное или отрица-
тельное, число; и какъ 0<^т<Ч, то (А 4-^) есть характеристика. а >н — мантисса логариѳма числа ЛХ^Р- Итакъ, мантисса осталась безъ перемѣны, а характеристика увеличилась р единицами.
797. Если число уменьшимъ въ 10, 100, 1000, . . . , яоо&це, въ 10? разъ, то характеристика логариѳма уменьшится на 1, на 2, на 3, . . . , вообще, на р единицъ, мантисса же останется безъ перемѣны.
/ \ '
Въ самомъ дѣлѣ, 1^г | = І& А — 1 Ор = к -|- т — р = (к — р) + т,
т.-е. характеристика уменьшилась р единицами.
Отсюда слѣдуетъ, что обѣ части логариѳма, характеристики и мантисса, суть функціи, рѣзко отличающіяся между собою. Мантисса зависитъ отъ абсолютнаго значенія цифръ и отъ порядка, въ которомъ онѣ слѣдуютъ одна за другою; характеристика же зависитъ только отъ положенія запятой, т.-е. отъ относительнаго значенія цифръ. Отъ перемѣщенія запятой мантисса не измѣняется: измѣняется только характеристика.
Расположеніе и употребленіе таблицъ логариѳмовъ.
798, Разсмотримъ употребленіе таблицъ логариѳмовъ Бремикера. Эти таблицы содержатъ логариѳмы цѣлыхъ чиселъ отъ 1 до 100009, вычисленные съ семью десятичными знаками; такимъ образомъ изъ этихъ таблицъ можно прямо брать логариѳмы чиселъ одно-, дву-, . . . , пятизначныхъ.
799. Расположеніе таблицъ.—Страницы отъ второй до пятой включительно содержатъ логариѳмы чиселъ отъ 1 до 1000, причемъ въ таблицахъ (какъ и далѣе) помѣщены только мантиссы, такъ какъ характеристику легко опредѣлить по числу цифръ числа. Колонны кодъ литерою X содержатъ числа, противъ которыхъ подъ знакомъ Ій: находятся мантиссы соотвѣтствующихъ логариѳмовъ. Съ шестой до 185 страницы расположеніе таблицъ таково: въ колоннѣ подъ литерою X находятся первыя четыре цифры чиселъ, пятыя же цифры помѣщены въ первой горизонтальной строкѣ: О, 1, 2, . . . , 9; мантиссы же расположены такимъ образомъ: такъ какъ первыя три цифры мантиссы одинаковы для нѣсколькихъ послѣдовательныхъ логариѳмовъ чиселъ, то онѣ написаны одинъ разъ для всѣхъ этихъ чиселъ, противъ наименьшаго числа колонны X. къ которой онѣ принадлежатъ, и въ вертикальной колоннѣ подъ цифрою 0. Послѣдніе четыре знака мантиссы помѣщены противъ четырехъ первыхъ цифръ числа и въ вертикальной колоннѣ, имѣющей въ заголовкѣ пятую цифру числа. Сверхъ того, всѣ страницы, начиная съ 6-й, содержатъ таблички подъ литерами Р . Р: это — таблички пропорціональныхъ частей, употребленіе которыхъ будетъ указано въ своемъ мѣстѣ.
800. Употребленіе таблицъ. Помощію таблицъ рѣшаются два вопроса: 1) о нахожденіи логариѳма даннаго числа и 2) о нахожденіи числа, соотвѣтствующаго данному логариѳму.
Первый вопросъ.
«
Нахожденіе логариѳма цѣлаго числа.
801. Первый случай: данное число находится въ таблицахъ. — Пусть требуется найти і? 36459. На стр. 58 находимъ первыя три цифры мантиссы: 561; послѣднія же четыре цифры ея помѣщены въ горизонтальной строкѣ противъ числа 3645 и въ вертикальной колоннѣ подъ цифрою 9, именно: 8048; характеристика же логариѳма, по § 794, равна 4, слѣд. 1^36459=4,5618048.
Пусть еще требуется найти 1$ 48868; первыя три цифры мантиссы (стр. 83) суть 688; для послѣднихъ четырехъ, на пересѣченіи горизонт. строки противъ числа 4886 съ вертик. колонною подъ цифрою 8, находимъ 0246; черта надъ
первою изъ этихъ цифръ показываетъ, что предшествующая цифра (8) мантиссы должна быть увеличена на 1, Такимъ образомъ имѣемъ: Ііт 48868 = = 4,6890246.
Когда за пятью значущими цифрами числа слѣдуютъ нули. напр. 48868000, то, замѣчая, что это число больше 48868 въ 1000 разъ, на основаніи § 796, заключаемъ, что его логариѳмъ 'больше логариѳма 48868 на 3 единицы, такъ что кг 48*68000 = 7,6890246.
802. Второй случай: дюнное число не содержится въ таблицахъ. Пусть требуется пайти числа, содержащаго болѣе пяти цифръ, напр. числа 4159*2687. Такъ какъ логариѳма этого числа нѣтъ въ таблицахъ, то отдѣляемъ отъ правой руки къ лѣвой столько десятичныхъ цифръ, чтобы слѣва отъ запятой получилось пятизначное число; такимъ образомъ имѣемъ 41592.657. Это число, будучи въ 1000 разъ меньше даннаго, имѣетъ логариѳмъ съ тою же мантиссою, какъ и заданное число* Находимъ мантиссу логариѳма числа 41592.687. Число это заключается между 41592 и 41593, откуда изъ таблицъ имѣемъ, что логариѳмъ его содержится между
1^41592 = 4,6190098 и 1* 41593 = 4,6190202.
Разность между числами 41592 и 41593 равна 1, а между соотвѣтствующими логариѳмами — составляетъ 0,0000104. Отсюда видно, что если къ ближайшему меньшему числу придадимъ 1, то къ соотвѣтствующему логариѳму слѣдуетъ придать 0,0000104. Но намъ нужно ближайшее м. ч. увеличить не на цѣлую единицу, а на 0,687; спрашивается: на сколько соотвѣтственно этому придется увеличить ближ. меньш. логар. 4,6190098? Для рѣшенія вопроса замѣчаемъ, что по § 792: если разности между числами не превышаютъ 1 (что у насъ и есть), то разности между логариѳмами соотвѣтствующихъ чиселъ, большихъ 10000, пропорціональны разностямъ между числами. Основываясь на этомъ и называя искомую разность между 1^41592,687 п к 41592 буквою л?. имѣемъ пропорцію
,г : 0,0000104 = 0,687 : 1, откуда х = 0,0000104 \ 0,687.
Умноженіе этихъ дробей дѣлается сокращенно при помощи слѣдующей таблички пропорціональныхъ частей (стр. 69):
1 о чМ 3 4 о 6 7
10.4 104 20.8 31.2
41.6 52.0
62.4 72.8
8,83.2
9 93.6
Въ ней помѣщены сокращенно, для сбереженія мѣста, произведенія 104 десятимилліонныхъ на 0,1; 0,2; . . , 0,9; причемъ точками въ этихъ произведеніяхъ отдѣлены десятимилліонныя доли отъ стомилліонныхъ долей. Такимъ образомъ эта табличка ностав-влена вмѣсто слѣдующей:
0,1 0,2 0,3 0.4 0,5 0.6 0,7 0,8 43,9
О, 0000 104 0,00000104 0,00000208 0,00000312 0,00000416 0,00000520 0.00000624 0,00000728 0ДОХХ1832 0,000(Ю936
При помощи ея можно прямо выписать частныя произведенія дроби 0,0000104 на 0,6, затѣмъ на 0,08 и наконецъ на 0,007. Первое изъ этихъ произведеній прямо беремъ изъ таблички, отдѣливъ стомилліонныя доли точкою, что даетъ 0,0000062.4. Уменьшивъ произведеніе 0,0000104 на 0,8, т -е. 0,00000832 въ 10 разъ, имѣемъ произведеніе табличной разности на 0,08 или 0,0000008.32. Наконецъ, уменьшивъ произведеніе табл. разн. на 0,7 во сто разъ.
имѣемъ произведеніе ея на 0,007, именно 0,9000000.728. Сложивъ эти частныя произведенія, имѣемъ
0,0000104 X 0,687 = 0,0000071.448.
Это-то произведеніе и нужно придать къ логариѳму блнж. мен. числа, для полученія 1^41592,687; имѣемъ
1$г 41592,628 = 4,6190169.448.
Цифры 448, слѣдующія за десятимилліонными, откидываемъ, такъ какъ табличныя мантиссы имѣютъ только 7 десятнчн. знаковъ; принтомъ, если первая изъ отбрасываемыхъ цифръ произведенія меньше 5, какъ въ нашемъ случаѣ, то послѣднюю сохраненную цифру произведенія оставляемъ безъ перемѣны; въ противномъ случаѣ, послѣднюю сохраненную цифру произведенія увеличиваютъ на 1« Такимъ образомъ:
1? 41592,687 = 4,6190169.
Такъ какъ данное число въ 1000 разъ больше 41592,687, то, оставивъ мантиссу найденнаго логариѳма безъ перемѣны, увеличиваемъ характеристику на 3 единицы; такимъ образомъ:
1& 41592687 = 7,6190169.
На практикѣ вычисленіе располагаютъ такъ:
41592 = 4,6190098
пропорц. часть для ...... 0,6 . . . 62,4
> » »............0,08 . . . 8,32
з » »............ 0,007 . . . 0,728
К' 41592,687 = 4,6190169,448.
Наконецъ
1$ 41592687 = 7,6190169.
803. Примѣчаніе, Пусть требуется найти числа, содержащаго болѣе 8 цифръ, напр. 72546892548. Характеристика логариѳма равна 10, а мантисса та же, что у логариѳма дроби 72546,892548. Опредѣляемъ мантиссу вышеизложеннымъ способомъ:
72546 = 10,8606135
0,8 .... . 48.0
9 . . . . 5.40
2 . . . . 0.12
5 . . . . 0.030
4 . . . 0.0024
8 . . . 0.00048
1^ 72546892'548^10,8606189. ’
Изъ этого примѣра видно, что уже 8-я цифра даннаго числа увеличиваетъ мантиссу только па 0,12, а потому не оказываетъ вліянія на 7-ю десятичную
цифру мантиссы; поэтому, при отыскиваніи числа, содержащаго болѣе 8 цифръ, употребляютъ только первыя 8 цифръ, остальныя же, какъ не вліяющія на семизначную мантиссу, замѣняютъ нулями, или просто не пользуются ими при опредѣленіи поправки* Въ самомъ дѣлѣ, наибольшая табличная разность = 0.0000435, а потому девятая цифра числа, даже если она имѣетъ наиб. величину, т.-е. = 9, измѣнитъ мантиссу только на 0,0000435 X ^<9009 = 0,00000003915. т.-е.
1
менѣе чѣмъ на единицы 7-го десятичнаго мѣста; п это — въ самомъ неблагопріятномъ случаѣ, когда и табл. рази, и девятая цифра числа имѣютъ наибольшія величины.
Изъ сказаннаго выводимъ правило: если число имѣетъ болѣе 5 цифръ, то, отдѣливъ слѣва запятою 5 цифръ, подыскиваютъ логаринли полученнаго пятизначнаго числа и придаютъ къ нему произведеніе табличной разности на три первые десятичные знака, составленное вышеуказаннымъ способомъ.
Опредѣленіе логариѳма дроби.
804. Сначала разсмотримъ нахожденіе логариѳмовъ десятичныхъ дробей. Пусть требуется найти Ьг 347,84762. Замѣтивъ, что характеристика искомаго логариѳма —2, а мантисса та же, что и у логариѳма числа 34784,762, имѣемъ:
1? 34784 =2,5413795
0,7 87.5
0,06 7.5
0,002 0.25
Откуда 1ц 347,84762 = 2,5413890.
Для второго примѣра пусть требуется найти логариѳмъ десятичной дроби, меньшей 1, напр. Ііг 0,0076806. Имѣемъ:
I? 0,0076806 = I? = 176806 — 1г 10000000 1 чД_Л_Лі-Л»^Л.я
= 4,8853951 — 7.
Вычитая 7 изъ 4, чтобы мантиссу оставить положительною, получимъ отрицательную характеристику — 3, такъ что
Іа 0,0076806 = 3,8853951;
знакъ минусъ ставится надъ характеристикою для указанія, что только характеристика отрицательна.
Отсюда правило: для нахожденія логариѳма десятичной дроби менъ-илей 1* беремъ мантиссу логариѳма числителя дроби* а въ характеристикѣ ставить столько отрицательныхъ единицъ, сколько въ лѣвой части дроби «годится нулей* включая сюда и 9 цѣлыхъ.
805. Пусть требуется найти Іи обыкновенной дроби, напр. =• Ииѣемъ:
І!Гп = 1г8- 1? 11 = 0,9030900 — 1,0413927 = —0,1383027;
чтобы сдѣлать мантиссу положительною, поступаемъ по указаніямъ § 795 и находимъ: 1,8616973.
Тотъ же результатъ получимъ, обращая въ десятичную дробь и ограничиваясь восемью цифрами въ числителѣ; находимъ 0,72727272. Слѣд.
І?Д- = 1? 0,72727272 = 1,8616957
для 0,2 11.8
0,07 4.13
0,002___________0.118
1?^ =1,8616973.
Второй вопросъ.
Нахожденіе числа, соотвѣтствующаго данному логариѳму.
806. Первый случай: мантисса даннаго логариѳма находится въ пю-блицахъ. Пусть 1? .г = 3,7592749; найти .г? Находимъ прежде всего число 759, образуемое первыми тремя цифрами мантиссы: оно находится въ колоннѣ 0 на стр. 100; опускаясь въ этой же колоннѣ, доходимъ до числа 2144 — ближайшаго, меньшаго по сравненію съ 2749: наконецъ, въ горизонтальной строкѣ, начинающейся съ 2144, находимъ число 2749 въ колоннѣ подъ цифрою 8. Такъ какъ 2749 находится въ горнзонт. строкѣ противъ числа <5744, то выписываемъ это число и приписавъ къ нему справа цифру 8, получаемъ 57448, а какъ характеристика даннаго логариѳма равна 3, то въ цѣлой части искомаго числа должно быть четыре цифры; а потому х = 5744,8.
807. Второй случай: йаяяая .мантисса не содсдосмтсл въ таблицахъ. Пусть = 4592786; найти х? Замѣнивъ характеристику 3 четырьмя, замѣ-
чаемъ. что логариѳмъ 4,4592786 содержится между логариѳмами
4.4592869, которому соотвѣтствуетъ число 28793.
* я
4.4592718, > > > 28792.
Разность этихъ логариѳмовъ =0,0000151, а разность соотвѣтствующихъ чиселъ = 1. Заключаемъ, что если ближайшую меньшую мантиссу увеличить на 0,0000151, то бл. м. ч. 28792 надо увеличить на 1; но мантисса логариѳма 4,4592786 превышаетъ меньшую мантиссу только на 0,0000068; спрашивается, на какое число у, соотвѣтственно этому, искомое число х превышаетъ 28792? Зная теорему, что разности между числами пропорціональны разностямъ между логариѳмами, если первыя не превышаютъ 1, какъ и есть въ данномъ случаѣ, заключаемъ, что у во столько разъ меньше 1, во сколько 0,0000068' меньше 0,0000151. откуда пропорція
у: 1 = 0,0000068:0,0000151, или по умноженіи обоихъ членовъ второго отношенія на 10000000:
у: 1—68; 151, откуда ^ = 68:151*
-Іто частное вычисляемъ съ 2 десятичными знаками, такъ какъ остальные будутъ невѣрны; а для вычисленія пользуемся табличкой пропорціональныхъ частей для числа 151 (стр. 43), въ которой числа 15Д, 30.2, • • * , 135*9 суть произведенія изъ 151 на 0,1, 0,2, . . . , 0.9. Намъ нужно найти, на сколько слѣдуетъ помножить 151 для полученія 68? Табличка показываетъ, что, умноживъ 151 на 0,4, находимъ 60,4 — число ближ. меньше къ 68: нтакъг въ частномъ имѣемъ, во-первыхъ, 0,4; вычтя произведеніе 60,4 изъ дѣлимаго, находимъ остатокъ 7,6. Наша табличка показываетъ далѣе, что, умноживъ 151 на 0,5, находимъ 75,5; а слѣд., умноживъ 151 на 0,05, найдемъ произведеніе 7,55 — ближ. м. къ остатку 7,6. Итакъ, въ частномъ имѣемъ еще 5 сотыхъ долей. Окончательно # = 0,45. Прибавивъ эту дробь къ 28792, имѣемъ 28792,45 — число, соотвѣтствующее логариѳму 4,4592786; а уменьшивъ это число въ 10 разъ, найдемъ число, соотвѣтствующее данному логариѳму. Итакъ ж = 2879/245.
На практикѣ вычисленіе располагается такъ:
1 я =3,4592786 для 28792 . . . 2718
68
4 . . . 60.4
тг 5 . , . 7*55
2879,245
Еще примѣръ. Укажемъ нахожденіе числа, соотвѣтствующаго логариѳму съ отрицательною характеристикою (къ этому виду всегда слѣдуетъ приводить отрицательный логариѳмъ, такъ какъ въ таблицахъ нѣтъ отрицательныхъ мантиссъ). Пусть І^ # = 2,4832107, найти Придавая 6 къ данному І8, чтобы сдѣлать характеристику равную 4, и вычитая 6, имѣемъ
18 х = 4,4832107 — 6 — 4,4832107 — 1" 1000000*
Находимъ число, соотвѣтствующее логариѳму — 4.4832107.
1<гу = 4,4832107
30423 020
87
6 85,8
19
1 1,43
у = 30423,61
Итакъ: = I? 30423,61 - 1^ ІОООООО = =1д 0,03042361Г
откуда х~ 0,03042361.
Отсюда правило: для нахожденія числа7 лоіа-
ривму съ отрицательною характеристикою, опредѣляемъ чис.ю, соотвѣтствующее положительной мантиссѣ, приписываемъ съ лѣвой стороны ею столько нулей, сколько единицъ въ характеристикѣ, и первый слѣва нуль отдѣляемъ запятою»
Дѣйствія надъ логариѳмами съ отрицательною характеристикою.
808. Сложеніе. — Сложеніе мантиссъ, какъ чиселъ положительныхъ, не представляетъ никакпхъ затрудненій; что касается характеристикъ, то пхъ соединяютъ по правилу приведенія подобныхъ членовъ. Напр.:
3,2173980
7,8239172
2,3758630
- 24-1,4171782, или 1,4171782.
809. Вычитаніе. — Пусть требуется сдѣлать вычитаніе:
5,4567895
2,6356789
4,8211106
Прибавляя къ мантиссѣ уменьшаемаго 1, а къ характеристикѣ—1, ио вычитаніи мантиссъ находимъ 0,8211106’ затѣмъ, вычтя нзъ — 6 характеристику^- 2 вычитаемаго, находимъ въ остаткѣ — 4; полный остатокъ = 4,8211106.
810. Умноженіе.— Пусть требуется 2,4367894X5. Имѣемъ:
(— 2 4-0,4367894) X 5 = — 104-2,1839470 = 8,1839470.
811. Дѣленіе. — Пусть требуется раздѣлить 6,2466724 на 2. Имѣемъ: (— 6 4“0,2466724): 2 = — 3 4-0,1233362 = 3,1233362.
Если бы тотъ же логариѳмъ требовалось раздѣлить на 5, то, чтобы характеристика дѣлилась на-цѣло на 5, слѣдуетъ къ ней придать —4, а потому къ мантиссѣ надо придать -р 4; такимъ образомъ имѣемъ:
0,2466724 : 5 = (— 10 4» 4,2466724): 5 = — 2 4» 0,8493345 =1,8493345.
Когда встрѣчается случай дѣленія логариѳмовъ съ отрицательными характеристиками, слѣдуетъ мантиссы пхъ дѣлать отрицательными. Напр., при раздѣленіи 2,3142890:1,3156782 замѣчаемъ, что дѣлимое —— 1,6857110, а потому частное приводится къ—1,6857110 : 1,3156782. 1
812. Употреленіе дополненій.—Когда въ выраженіи содержится нѣсколько вычитаемыхъ логариѳмовъ, удобнѣе замѣнять ихъ дополненіями, такъ какъ принтомъ оба дѣйствія — сложенія и вычитанія логариѳмовъ приводятся къ одному
дѣйствію — сложенія ихъ. Такъ, употребляя дополненія до 10. замѣняемъ выраженіе
І^а — 7; -[-Ігс — Іяс? — Іее
равнымъ ему выраженіемъ
1? а + (10 — 1? Ъ) 4-1? с -{- (10 — I? Л) + (10 — 1? е) — 30 илп
1?а4-^01?і4_І&с4~Со1?й4_*-'°1?в — 30?
причемъ Со есть сокращеніе слова сотріетепіпіп— дополненіе.
813. Примѣры вычисленій съ логариѳмами.—I. Вычислитъ х =Логариѳмируя, имѣемъ: г=т: — 1^173 = 0,4971499— 2,2380461, или, замѣ-
- нивъ вычитаемый 1? его дополненіемъ до 3:
Ііга- = 0,4971499 4- (3 — 2,2380461) — 3 = 0,4971499-40,7619539 — 3=
= 2,2591038.
Отсюда х = 0,0181595.
ІЕ Вычислитъ ж—оооаіія' Логариѳмируя и употребляя дополненіе логариѳма знаменателя до 1. послѣдовательно имѣемъ:
Ія х = 0,4971499 — 3,7551123 = 0,4971499 4~ (1 — 3,7551123) - 1 = = 0,4971499 -}- 2,2448877 = 2,7420376.
Отсюда х = 552,125.
0.0084321 X 1/
III. Вычислитъ х=-------—--------.
1/8,37 ,
1* ж = I* 0,00843214~ (1? 2 -р доп. І§ 15 — 2)4* доп. I* 8,37— I
1{Г 0,0084321 = 3,9259357 ]? 2 = 0,3010300 доп. 15 = 0,8239087 — 2
Г,1249387
но раздѣленіи на 3:
Т.7083129 1^8,37 = 0,9227255 5^8,37 = 0,4613627
доп. 8,37 = 0,5386373 — 1. •
Вычисленіе х.
3,9259357
2/083129 1,5386373
Ія х = Т, 1728859 х = 0,00148897.
1V. Вычислитьх=
/ ^15,92 X Г/О.О162 ' 0,00526 X (196)»
1? 15,92= 1,2019431 11^15,92 = 0,1717062 І8 0,0182 = 2,2600714 ^1? 0,0182 = Г,42ОО238 доп. 1^0,00526 = 2,2790143 1^196 = 2,2922561 ]г196» = 11,4612805
0,1717062
1,4200238
2,2790143
12,5387195 1$х= 10^4094638:2 = 5,2047319 ,г = 0,00001602256.
ГЛАВА ЫІ.
Приложенія логариѳмовъ.—Рѣшеніе показательныхъ н логариѳмическихъ уравненіи.— Финансовыя операціи: сложные проценты, срочные вклады, срочныя уплаты и т. д.
Рѣшеніе показательныхъ и логариѳмическихъ уравненій.
814. уравненіями называются такія, въ которыхъ неиз-
вѣстныя входятъ своими логариѳмами, а показательными уравненіями называютъ такія, въ которыхъ неизвѣстныя входятъ показателями. Элементарная алгебра даетъ средства рѣшать такія ур—нія только въ случаяхъ, когда въ ур—ніе неизвѣстное входитъ исключительно только своими логариѳмами, или исключительно въ показателяхъ, и не можетъ рѣшать ур —ній смѣшаннаго типа. Напр. ур—нія
х -|- 31^ # = 5, Зл = 12.
неразрѣшимы средствами элементарной алгебры.
При рѣшеніи этого рода ур—ній нерѣдко приходится пользоваться тѣмъ принципомъ, что всякое положительное число имѣетъ лишь одинъ, вполнѣ опредѣленный, логариѳмъ, и обратно* Это обыкновенно выражаютъ, говоря: „Если два числа равны, то и логариѳмы ихъ равны; и обратно, если два логариѳма равны, то и соотвѣтственныя имъ числа равный
815. Рѣшеніе уравненія «* = &.—а есть положительное число, отличное отъ 1. Если Ь^О, ур — ніе не имѣетъ рѣшеній. Итакъ, полагаемъ Ь > 0. Взявъ логариѳмы отъ обѣихъ частей: = находимъ отсюда
II р и м ъ р ъ* Рѣшить уравненіе 0,06971* = 0,00856.
Логариѳмируя, находимъ
лЛ? 0,06971 =]? 0,00856,
откуда
0,00856 = 3,9324738 18 0,06971 — 2^8432951 ’
или» замѣчая, что 3,9324738 — — 3 4” 0,9324738 = — 2,0675262 и такимъ же образомъ 2,8432951 = —1,1567049, имѣемъ
х = 2,0675262:1,1567049.
Выполнивъ дѣленіе, находимъ х = 1,787, съ точн. до 0,001.
Подобнымъ же образомъ рѣшаемъ ур—ніе а = с, гдѣ а, Ъ и с — три положительныя числа, а числа а и б, кромѣ того, отличны отъ 1. Положивъ = имѣемъ: а^ = с, откуда, по предыдущему,
. .(1).
Найдя у, изъ ур—нія &* = у находимъ
_ ,и _ * і 1^ — 1§г> ‘
Такъ какъ приходилось брать у, то, очевидно, должно быть у > 0, сл». какъ видно изъ (1), логариѳмы чиселъ с и а должны быть одинаковаго знака, а сл. числа а и с должны быть или оба < 1, или оба > 1, что можно выразить такъ:
(а—1) (с—1)>0 . . .(2).
Заключаемъ, что если а, Ь, с суть три положительныя числа, отличныя отъ 1, если» сверхъ того, удовлетворяется неравенство (2), то наше ур—ніе имѣетъ одно, и только одно, рѣшеніе; во всѣхъ остальныхъ случаяхъ оно не имѣетъ, рѣшеній.
® т
с —*
Пусть еще требуется рѣшить ур—ніе а =
т
Положивъ с* = у, Ъу — г, имѣемъ ур—ніе &* = <!*'
Взявъ логариѳмы, найденъ
х 1е с = 1^ у, у 1^ Ь — я а = — Іег й,
откуда
Отрицательныя числа не имѣютъ дѣйствит. логариѳмовъ, сл. всѣ числа, отъ которыхъ берутся логариѳмы, д. б.' > 0; т.-е. во-первыхъ, числа а, 5, с, й д. 6. >0; во-вторыхъ, д. 6.
ж 1§й п 1&б
Различаемъ два случая: полож. число *5< 1, я Ь> 1.
Когда Ъ< 1, то 1? Ь < О, и нер. (I) даетъ
или. раздѣляя на
18
18 а*
или
имѣемъ:
п ' І^а
когда
т 1" а п
когда
то
то
п <8
Если Ь>1, то и нер. (1) даетъ
1Л’“ .^>0, Ія. І8Я/
или
ш п
откуда либо
а
п
либо
п 18
Итакъ, отн.
ш . * Щ а
— д. б. одного знака съ и смотря но тому, будетъ ли-Н 18 и
X - МІ * . ІС Я Ъ
абсолютное значеніе — меньше или больше абсолютнаго значенія о должно
*
быть <Г или “> 1.
816. Рѣшеніе уравненія аі2г4“с— О. — Положивъ а?—у (1). имѣемъ • • • (2).
Квадратное ур. (2) даетъ у, а для всякаго значенія у находимъ изъ (1) соотвѣтственное значеніе х. Но для х получится дѣйствительное значеніе только тогда, когда у будетъ дѣйствительно и положительно. Отсюда, при а > 0, данное ур. будетъ имѣть два дѣйствительныхъ корня только тогда, когда удо-’ влетворяются условія:
5* — 4ас 0, ас 2> 0. аЪ О
Пусть эти положительныя значенія у (^гь у^ и Остается рѣшить два показательныхъ ур—нія: ах = #і и = откуда
1 ^5
Примѣръ. Рѣшитъ уравненіе 5^ -|“ ~^г =
Освободивъ отъ знаменателя, имѣемъ
?Я8
*
52,-н _ 626 X 5* 125 = 0:
положивъ 5я=у, даемъ ур—нію видъ 5уа-626у-]“ 1^5=0, откуда у'=125,
у"—-- Такимъ образомъ получимъ два ѵр—нія: 5* =125, откуда х' = 3, я О "
5Ж — откуда я" = — 1.
817. Рѣшитъ
уравненіе
(2 - ая _ 1^(1 -х) “
Такъ какъ отрицательныя числа не имѣютъ дѣйствительныхъ лагориомовъ, то необходимо, чтобы было 2—#*>0 и 1—х^О, или х</2и или. наконецъ, х 1.
Домни это, рѣшаемъ ур.: 1^(2—а?) = 31^(1 — х) = 1^ (1 — «)*, откуда 2 — х3 = (1 — х)3. или Зх3 — Зх — 1=0.
Корни этого ур—нія дѣйствительны, одинъ <0, другой >0. Первый, какъ меньшій 1, отвѣчаетъ задачѣ; чтобы и второй отвѣчалъ, необходимо, чтобы онъ былъ с 1. Подстановка 1 въ первую часть ур—нія даетъ результатъ — 1, т.-е. со знакомъ, противоположнымъ 1-му коэффиціенту, сл. -рі содержится между корнями: хг . . . -р 1 . . . х", т.-е. положительный корень >1. и потому долженъ быть отброшенъ. Итакъ
121 -3 с — 6
есть единственное рѣшеніе даннаго уравненія.
818. Рѣшеніе системы: = ш и ах-р^У = с-
Первое ур—ніе можетъ быть представлено въ видѣ 1$ху = т, откуда ху = 10** . . . (1); такимъ образомъ вопросъ приводится къ рѣшенію системы: ху=10?" и = Исключеніе у даетъ ур—ніе ах2—ех4-ЬХЮт=0.
Рѣшивъ это ур—ніе. найдемъ значенія соотвѣтствующія каждой величинѣ х^ с — ах изъ уравненія у — , ‘ ' о
Примѣръ I. Рѣшить систему:
Іе: х-(-!{* у = 3 . . .(1), 5х3— Зі/3= 11300 . . . (2).
Первое уравненіе можно представить въ видѣ ху = 1000, или
ху=1000. . .(3).
Исключеніе у изъ (2) и (3) даетъ, по упрощеніи, уравненіе
х4 — 2260ха — 600000 = 0, .
• »»
имѣющее два мнимыхъ корня в два дѣйствительныхъ; дѣйствительный положительный корень й
х = |/ 1130-1- }/1Т30»-|-600000,
или х—50, и сл. у = 20.
Примѣръ 11. Рѣшить систему.
2 1{г у — \%х = 0.1249387; Іі; 321^ я:-(-у 1,7323939.
57*
21^г/ — 1§х = І8—; 0,1249387 =1^1,333.. .==1^; слѣд. первое ур. при-3? м
приводится къ^“|* откуда я = |у2. Съ другой стороны
-|-у = Цг Зхс2*/; 1,7323939 = 1^ 54; сл. второе ур* приводится къ 3#®у=54.
Исключая х, находимъ ур. у5 = 32, откуда у = 2; и наконецъ х = 3.
ФИНАНСОВЫЯ ОПЕРАЦІИ.
Сложные проценты.
I. Сложные проценты для цѣлаго числа лѣтъ.
819. Опредѣленіе.—Говорятъ, что капиталъ помѣщенъ на сложные проценты, когда въ концѣ каждаго года процентныя деньги прибавляются въ капиталу, или, какъ говорятъ, капитализируются, и наращеніе процентными деньгами въ теченіе слѣдующихъ лѣтъ идетъ не только на капиталъ, но и на причисляемыя къ нему процентныя деньги.
820. Основной вопросъ.—Вычислить^ во чиго обратится капиталъ а руб», отданный на сложные проценты по р со ста, въ і лѣтъ.
100 руб. приносятъ въ годъ р руб. прибыли; слѣд.
1 руб. принесетъ въ
это время р., а потому 1 р. къ концу перваго года или, обозначая ^д буквою г, въ 1 Ц- г (сумма 1 -р г
обратится въ 1 +
Гоо’
наз. юдоеылсь оборо-
томъ рубля), а слѣд. а руб. въ концѣ года составятъ сумму а(1 Ц-г), Каждый рубль этой суммы въ концѣ второго года обратится опять въ 14*Л а слѣд. вся сумма а(1-|~г) обратится къ этому сроку въ а(1 —|—г)(1 -|-г), или а(1 Къ концу 3-го года каждый рубль этой новой суммы обратится въ 14~г» а потому вся сумма въ «(1 -|-г)2(1 4-г) или въ а(1 -(- г)а и т. д. По аналогіи заключаемъ, что въ концѣ ^-го года составится сумма а(14“г)*; называя эту сумму буквою А, имѣемъ ур—ніе
А = а(1+гЛ . . (1).
821. Формула (1) содержитъ четыре количества: а, А, і и ^(заключается въ г); сл. когда*три изъ нихъ будутъ даны, то можно опредѣлить четвертое. Отсюда четыре задачи.
822. Основная задача.’— Опредѣленіе А по даннымъ а, р и I прямо рѣшается ур—мъ (1); логариѳмируя его, имѣемъ
1?А = І8а + * . 16(1 + 0 - . .(2).
Примѣръ: а = 20000, р = 4,5 и #=Ю.
4.5 а = 4,3010300
г — 166 — Ю(1 4-г) = 0,1911629
0,045. іе^ А = 4,4921929
А = 31059, 38 руб.
823. Какой капиталъ а нужно помѣститъ на сложные проценты по р со ста* чтобы въ концѣ I лѣтъ составилась сумма А?
Ур—ніе (2), рѣшенное относительно 1§«, даетъ ♦
а = А-|-доп. І1е(1+г). . .(3).
П р н мѣръ. А = 40324, / — 21, р = 4.
1? (1+г) = 0,0170333
* 1?(1 + г)= 0,3576993
1§ А = 4,6055630 дои. /. (1 + г)= 1,6423007
1^ а = 4,2478643 а = 17695,56.
824. На сколько лѣтъ нужно помѣстить капиталъ ак чтобы, при сложныхъ процентахъ по р со ста, составилась сумма А? Прибыль на 1 руб, равна г.
Рѣшая ур. (2) относительно і, имѣемъ
Примѣръ. А = 40324; « = 17695,56; р = 4.
4,6055636 — 4,2478643 _ 0,3576993 __
0,0170333 — 0,0170333 “
825. При какихъ процентахъ капиталъ а дастъ, по истеченіи I лѣтъ, сумму А?
Рѣшая ур. (2) относительно 1§(1 ++ имѣемъ'
І5(1+,) = Ч±=^.
Найдя отсюда 1 + г, легко опредѣлить и р.
Примѣръ. « = 21319, А = 42327, « = 15.
1& А = 4,6266237
1е а = 4,3287668
= ?,297?-- = 0,0198571 1э ’
14-г =1,04678.
Отсюда г или—0 = 0,04678, а слѣд. р~ 4,678 или приблизительно въ цѣлыхъ копейкахъ, р ~ 4 руб. 68 кон.
II* Время помѣщенія капитала—дробное.
826. Обыкновенно время, въ теченіе котораго капиталъ находится подъ процентами, слагается изъ цѣлаго числа лѣтъ и нѣкоторой доли года, которую условимся обозначать буквою /• цѣлое же число лѣтъ, попрсжнему. обозначимъ буквою Л Если, напр., доля года равна 3 мѣсяцамъ 25 днямъ, то
/._ЗХ30 + 25_ 23
360 — 72*
принимая каждый мѣсяцъ въ 30 дней.
827. Основной вопросъ. Какая сумма А составится, если капиталъ а, отданный на сложные °/0 по р, находится въ оборотѣ I лѣтъ и долю /' года?
По истеченіи і лѣтъ капиталъ а обратится въ а(1-|-г)'. Каждый рубль этой суммы, получая въ годъ приращеніе Л въ теченіе доли года дастъ приращеніе /г; полное же приращеніе суммы а(14~г/ будетъ а(1-рг)*-Л*. Такимъ образомъ къ концу $4-/* лѣтъ составится сумма <414-ГУ“Н1(1”ЬГ)<./Н или
А = а(1+г)'(1+М • - .(И
Примѣръ. « = 41524,75, р = 5, і — 1 и /'= 10 мѣс.
1 +/г = 14-1^X0.05 12 а = 4.6183070
= 1+-б5 і 1^(1+г) =0,1483251
= 1,0416667 18(1 +/»•) = 0,0177288
ІЕ А = 4,7843609
А ~ 60863,05 руб.
828. Какой капиталъ,' помѣщенный на сложные по 5 со 100, дастъ въ 18 лѣтъ и 3 мѣсяца сумму 48734^05 руб?
Логариѳмируя ур. (1) и опредѣляя 1§«, имѣемъ
а — 1? А доп. 11? (1 + г) + доп. (1 +/>) • • . (2)
1,05 = 0,0211893 ' 1§ А = 4.6878325
181§ 1,05 = 0,3814074 доп. Л&(1 + г) = 1,6185926
/г = 2^ = 0,0125 доп. 1§ (14- /г) = 1/1946050
14- /г =1,0125 • 1§ а = 4,3010301
а = 20000 руб.
829. Какое время сумма а должна находиться подъ сложными °/0У ‘читая по р со ста, чтобы образовать капиталъ А?
Нужно опредѣлить і и Д Рѣшая ур. (2) относительно і, имѣемъ:
— 903
Пусть частное дѣленія, указаннаго въ первомъ членѣ, будетъ а остатокъ К; имѣемъ:
х а і__11__+ М
Ч +18(1 + П 18(1 + 0 • * ’<3)
Первая часть ур—нія есть число цѣлое, слѣд, и вторая должна быть цѣлымъ числомъ. Но Ч есть цѣлое число, слѣд. и разность дробей должна быть цѣлою. В, какъ остатокъ, меньше дѣлителя (1 -1- г), слѣд. первая дробь
меньше 1. Затѣмъ. слѣд. /г<+, откуда 1 4" /г < 1 4- г, а потому и
1?(1 4~/гХІ8(1такъ что и вторая дробь меньше 1- Но разность двухъ правильныхъ дробей только тогда м. б. цѣлою, когда она равна нулю, откуда: К = (1 -4/г), и ур—ніе (3) даетъ —Такимъ образомъ, для опредѣленія времени имѣемъ два ур—нія
Г = . .(4) и 1В(1+/г) = К . . .(5),
показывающія, что для нахожденія цѣлаго числа лѣтъ надо взять цѣлую часть частнаго отъ раздѣленія 1?А — на 1&(1 4~ГХ а для опредѣленія доли года—приравнять (1 4“/г) остатку указаннаго дѣленія и рѣшить полученное
ур. относительно /.
Переходя въ ур—ніи (о) отъ логариѳма къ числу, найдемъ: 1 4" і т — 1 откуда / = - „ ♦
Примѣръ 1. А = 48734,04; а = 20000; г = 0,05. 1ц А = 4 0878324 а = 4,3010300
І^А — 1? а = 0,3868024
А - Іе: а__0,3868024 _ . . 0,Ш53950
’1,05 “ 0,0211893 — “Г 0.0211893 1^(1[ 4“/О = 0,0053950
1 4-/г= 1,0125
0,0125 0.05
= 0,25.
Итакъ, /=18г. и / = 4 года.
Примѣръ II. Населеніе страны возрастаетъ ежегодно на нѣкоторую долю а своей величины, какую оно имѣетъ въ началѣ года. По истеченіи какого времени оно будетъ находиться въ данномъ отношеніи к къ первоначальной своей величинѣ?
Пусть первоначальное населеніе равно а; населеніе въ концѣ I лѣтъ и доли / года пусть будетъ Л. Имѣемъ: А = а(1 4-а)'(1 4“М); «о, по условію, А = &а; слѣд.
* = (1 + аУ(1+/а).
Иусть, напр., требуется узнать, черезъ сколько времени удвоится населеніе, возрастая на 5%*?
Въ данномъ вопросѣ к = 2, і = 0,05; ур—ніе будетъ
- 904 —
Чаетвое, подлежащее вычисленію, будетъ
1§ 2 __ 0,3010300____. , . 0,0043798
18 1,05 — 0,0211893 “ 14 "г" 0,0211893’
18 (1 + 0,05/) = 0,0043798 14-0,05/= 1,010136
хи.
. 0,010136 Д,0136 365X 1,0136
-0ДГ = “5“ “-----------5-----= 74 ДН-
Итакъ, населеніе удвоится черезъ 14 лѣтъ и 74 дня.
830. На какіе проценты нужно помѣститъ капиталъ а, чтобы въ лѣтъ онъ обратился въ А?
Вопросъ приводится къ рѣшенію относительно г ур—нія
А = а( 1 -|-гУ(1
по раскрытіи (1 -1- г)\ получимъ ур—ніе і -1- 1-й степени въ г; сл, не можетъ быть рѣчи о рѣшеніи его въ этомъ общемъ случаѣ обыкновенными пріемами; но оно м. б. рѣшено яо способу послѣдовательныхъ приближеній.
Взявъ логариѳмы отъ обѣихъ частей ур—нія, выводимъ
+ . .(1) I V
Откинувъ второй членъ (обыкновенно г содержится между 0,03 и 0,06, а Г<1» такъ что 1+Л близко къ 1, а *п--1 весьма малое число), най-
демъ первое приближеніе числа г, по избытку, изъ ур—нія
І^(14-уі) = І8А і '*“• • -(2)
гдѣ 1\>Г.
Затѣмъ полагаемъ
І?(И:Г,)=!ЬЦ^_!Е<!+Лй. . ,(3)
второй членъ 2-й части больше второго члена 2-й части ур—нія(1), и потому г8 нѣсколько меньше г. Итакъ, и г* суть два приближенія къ г, первое по избытку, второе по недостатку. Взявъ то или другое вмѣсто г, сдѣлаемъ ошибку меньшую — га. Взявъ для у ариѳметич. средину сдѣлаемъ ошибку, меньшую даже ^-3—• Въ самомъ дѣлѣ, пусть
+ га = г —і3,
гдѣ и а2 положительны; отсюда
н
«? г- — .--•-’Ч -л. ; ,
*’ а
— 905 —
« в
Взявъ Г1~^Г2 за г, сдѣлаемъ ошибку, равную -1-~; но абсолютная вели-оі — а? 4 + аз гі — г2
чина 9 " <С " 2 * й сд’ < 2
Если приближеніе г2 недостаточно, опредѣляемъ два новыя приближ. значенія, г3 и г4, по формуламъ
І8(1 + г.) = 'ед;|8°_18<І +Д,і. . ,(4)
іг(і+,,І = ЬЦі1^_*А±Щ. .
Изъ того, что Г3<Л очевидно, что вторая часть (4) больше второй части (1), но она меньше второй части (2); слѣд, Слѣд. г3 есть новое
избыточное приближеніе числа г, и менѣе ошибочное, чѣмъ
Затѣмъ, такъ какъ г3^>г, то вторая часть (5) меньше второй части (1), слѣд. га<г; а какъ то вторая часть (5) больше второй части (3);
слѣд. У|> ГГ
Отсюда видно, что г1 есть приближеніе по недостатку, менѣе ошибочное чѣмъ слѣд. причемъ промежутокъ отъ г3 до Гд меньше про-
межутка отъ г3 до га.
Такимъ образомъ, имѣемъ рядъ значеній для г:
Г3' г4, • • •
поперемѣнно приближенныхъ по избытку (прибл. четнаго пор.) и по недостатку (прибл. нечетн. пор.), причемъ ихъ точность идетъ возрастая.
Остается доказать, что числа г3, . . . , г2р, . имѣютъ об-
щимъ предѣломъ г. Для этого достаточно доказать, что абсол. велич. разности между г* и г, при неограниченномъ возрастаніи к, стремится къ нулю. Имѣемъ
|?(1 + »•) =
1в А—18 а_18 (1 + /г)
і і
1г(1 + »Ѵн) =
І^А — 1е<*____1§(1 +/*•»),
і і
откуда
Но
18 (1 + г*,+і) - І8 (1 + г)=(1 + ^)-18(1+/г»).
въ самомъ дѣлѣ, приводя къ общему знаменателю, который положителенъ, и сравнивая числителей: І^/гг2Р-{-гір-±/г и 1+/гг2р“ГгН~/г2р^ или /(г—г*р) и г — г2р, замѣчая, что /<1 и г — г2г>0, имѣемъ /(г — *>р) <Л — **2я что и требовалось доказать. Итакъ
18 (1 + г,,,- ) -18 (1 + И < 'е'' +-' ~ '"а + Ч
— 906 — . «
а слѣд., обозначая буквами
ЗЦ, Яд. . . > &2р, ^2рН~ 1» * -
абсолютныя значенія разностей между
1? (!+») и 18(1+»',), 1?(1Н-г3),... имѣемъ:
Перемножая эти неравенства, получаемъ
Но I—число цѣлое, 2р—число положительное, возрастающее неограниченно, слѣд. и & возрастаетъ неограниченно, а потому можно взять 2р настолько большимъ, чтобы а2р+і было какъ угодно близко къ нулю: слѣд. разность
-Нѵн) — ^(1 Н~г) «
стремится къ нулю, а слѣд. къ г: это и нужно было доказать.
831. Примѣръ. На какіе проценты (сложные) помѣченъ былъ капиталъ 7300 рублу если въ концѣ 6 лѣтъ 8 мѣсяцѣ 10 дней онъ обратился въ 10448 руб. 10 кои. (проценты капитализируются въ концѣ каждагб года)?
Примѣняя указанный методъ, имѣемъ
10448,1 — I" 7300 ІВ(1 + 36Г) -
6 6
или 1? (1 г) = 0,02595240-}- 0,25938375 — ^,36 + 2ог) •
Первое приближеніе для г получимъ, откинувъ два послѣдніе члена:
.18 (1 + М = 0.02595240. откуда
гі = 040615791. причемъ
Второе приближеніе вычисляемъ изъ ур—нія
І?(1+»-а)= 0,28533615 — ІВ(36 + 2-?^,
откуда, замѣчая, что 364-25г. = 37,53947. и ^~25г^ = 0,26241435, имѣемъ:
1?(І-Ь г,) = 0,02292180.
слѣд.
г4 = 0,05419706. причемъ >,<г.
І?(1 4-г) —
Третье приближеніе находимъ изъ ур—нія
1? (1 +»'.) = 0,28533615 —
* I д / т К э
замѣчая, что 36 4~ 25г2 = 37,354926, и 2^Гг 1 = 0,26205796. находимъ:
1^(1 4. г3) =0.02327819, откуда
гя = 0,0550625. причемъ г3>г.
Четвертое приближеніе.
1« (1 _[_ г ) = 0,28533615 — 18-(—+-^4
гдѣ 3<> + 25гч = 37,376756, и = 0,26213321; слѣд.
1§ (1 + г,) = 0,02320294, откуда і
^=0,0548797, причемъ ^<4'.
Разность ^ — >1=0,0001828, слѣдов. каждое изъ приближеній г3 и га представляютъ г съ ошибкою, меньшею 0,0002. Итакъ
Гз + Г‘= 0,0549711 4^
представляетъ г съ ошибкою, меньшею 0.0001: отсюда, умножая на 100, на-ходимъ проценты: />=5,49711. съ ошибкою, меньшею 0,01 р. Слѣд. приблизительно беремъ р = 5,497.
Примѣчаніе. Обыкновенно же на практикѣ, для вычисленія времени и процентовъ берутъ формулу, выведенную для цѣлаго числа лѣтъ: д=а(14-*‘)\ подставляя въ нее вмѣсто 2 данное дробное число лѣтъ. Примѣняя эту формулу къ данпой задачѣ, имѣемъ
— 1_е 7300 _ 36 X 0,15571442
25 ~ 241
36 « •»
= 0,02326024; отсюда
1 4~ г~ 1.0550189, и г = 0,0550189; наконецъ
/> = 5.50189,
1^10448,1
6
результатъ, мало разнящійся отъ прежде найденнаго.
Срочные вклады.
832. Основной вопросъ. — Въ теченіе і лѣтъ вносятся въ банкъ въ началѣ каждаго года послѣдовательно капиталы бг3, . . ,,
Какая сумма накопится къ концу срока} если считать сложные про*-центы по />%?
Первый срочный вкладъ, а находясь подъ процентами лѣтъ, обратится къ концу этого срока въ ^(іЦ-г)1, или, полагая для краткости 1+г = д, въ
Второй вкладъ, находясь въ банкѣ і — 1 лѣтъ, обратится къ концу срока въ
Третій взносъ къ концу того же срока обратится въ <М*-2 и т. д.
Послѣдній вкладъ, находясь подъ процентами 1 годъ, даетъ
Сложивъ эти суммы, получимъ накопившійся капиталъ
а=м(+м(-1+м'_2+- • •+«»?. • . (О
Когда вклады различны, формула (1) не допускаетъ упрощеній; если же ежегодные взносы равны, то, обозначивъ каждый изъ нихъ буквою а и вынеся за скобки общій множитель а#, найдемъ:
А = (д**1 -|- + **-)- 9 +1).
Выраженіе въ скобкахъ представляетъ сумму членовъ геометрич. прогрессіи первый членъ которой =1, а знаменатель 2; по формулѣ суммы имѣемъ
А = ад — • (2)
д— 1 х
Примѣчаніе. Если бы сумма а была вносима въ концѣ каждаго года, то первый вкладъ находился бы въ банкѣ і—1 лѣтъ, второй і — 2;.**? послѣдній 0 лѣтъ, и получили бы
А' = 1•4^а#_Ь а
или
833* Ур, (2) содержитъ 4 количества; А, а, р и и позволяетъ найти одно изъ нихъ, когда остальныя три будутъ даны* Отсюда 4 задачи:
1* Для опредѣленія А непосредственно служитъ ур. (2).
2. Опредѣляя а, имѣемъ
_ А (7 —1).
3. Для нахожденія освобождая ур* (2) отъ знаменателя, имѣемъ:
Л (3 — 1) = 1), откуда г/ = 1
ур—ніе показательное,
4. Опредѣленіе р приводится къ нахожденію д* Изъ послѣдняго ур—нія прямо находимъ
«//+1 — (А 4” °) + А = О,
ур—ніе *4’1“й степени относительно ц.
Численный примѣръ, а = 2000, і — 20, р = 5; найти А?
А = 2000 1,05- - - = 42000(1,05” — 1).
Такъ какъ разности 1^05*®-варительно вычисляемъ
Вспомогат. вычисл.
У = 1,05*® 1? у = 201* 1,05 = 0,4237860 26532 7700
9 160:16
147.6
7 12.4
1 нельзя найти непосредственно, то пред-
I ; Вычисленіе А.
і
1? 42000 = 4,6232493
1? (1,05*°—1) = 0.2183510
1 1? д = 4,8416003
А = 69438,5.
у — 1 = 1,653297
834. Приводимъ еще нѣсколько упражненій на срочные вклады.
1. Какой капиталъ накопится чрезъ п лѣтъ, если, въ концѣ каждаго полугодія вноситъ по ? руб,, или по концѣ каждой четверти годау или по въ концѣ каждаго мѣсяца?
Внося ^р. въ концѣ каждаго полугодія, составимъ капиталъ
если “ означаетъ прибыль на 1 р. въ полугодіе.
Внося | въ концѣ каждой четверти года, составимъ капиталъ
Т
гдѣ означаетъ прибыль на 1 р. въ четверть года.
Наконецъ, вклады въ концѣ каждаго мѣсяца дадутъ
Примѣчаніе. Принимая ~
за полугодичные, трехмѣсячные и мѣ-
сячныс проценты, получаемъ въ концѣ года прибыль, нѣсколько большую г. Чтобы годичные проценты составляли въ точности г, надо вести вычисленіе такъ. Пусть процентныя деньги капитализируются по истеченіи доли года; чтобы 1 руб. въ концѣ года обратился въ 1 4*г» надо, чтобы проценты были
ибо, прибавляя 1 къ и возвышая результатъ въ степень к, имѣемъ: (1 + гг/ = (/!"+ г)‘=14-г.
Такимъ образомъ, въ вышеприведенныхъ задачахъ получимъ
П + і
— 1 ’
результаты, весьма мало разнящіеся отъ прежнихъ.
II. Какой капиталъ составится въ концѣ п лѣтъу если въ концѣ каждаго года вноситъ суммы > измѣняющіяся въ ариѳметической прогрессіи?
Пусть а есть первый вкладъ; а 6, а Ц- 26. дующіе. Искомый капиталъ X будетъ
а4~(я—1)6 слѣ-
X = а (1 + г)’*-* + (а + ѣ) (1 4- г)”~24- -
• -|-а + (я — 1)6;
г
полагая Гі =3» имѣемъ 14’**
(1 + г)“ ! + (а + &) а» + (а + 26) 3’ Н--------------Н« + («
1)6ИЯ|-
Выраженіе въ скобкахъ можно представить въ видѣ
«(а+<?2 Ч-----ь 2")+ь [?’ Ч- 2з» ч-Н (« - I) Л,
, | 4 । „ в'*-1 --Л
гдѣ ? + ? — • •Ч’З =---------------положивъ
> 1 ц — і
8 = Ч" 2?* Ч" 3?* Ч-' * "Ч- (й — О 9я, имѣемъ
8д= 2»Ч~ 25*4— -+(м—' 2)я“Ч“(и—откуда
—з) = чаЧ-ч’Ч-9*Ч—
Ч~ — (м — 1)9"+*, или
<? і Оп-г2 — л2
8(1 — д.) — - , —«5Я+1, откуда
— 1) > «г/п 1 (7-П®
Подстановка въ формулу X и замѣна у дробью даетъ
ПІ. Какой капиталъ накопится чрезъ п лѣтъ, если въ концѣ каждаго года вноситъ суммы, измѣняющіяся въ геометрической прогрессіи?
Пусть будутъ а, ак, ак*.......послѣдовательные взносы.
Къ концу срока они обратятся въ
ай»-ів
Л . к
Сумма членовъ этой прогрессіи, знаменатель которой = будетъ ѵ (1 + г)п— &•"
IV. Цѣнностью въ настоящее время долга А, подлежащаго уплатѣ черезъ п лѣтъ* называется сумма, коягоэдю «^жко бы было тотчасъ положить въ банкъ на сложные 9/йл чтобы спустя п лѣтъ получитъ А руб.
Слѣд., если цѣнность въ настоящее вр. суммы А назовемъ Аь то А^І-рг^^А. откуда
V. Учетъ при сложныхъ процентахъ. Учетомъ наз. разность между номинальною величиною долга и его дѣйствительною величиною; поэтому, формула учета будетъ
Положивъ для краткости = д, предыдущія формулы представимъ въ сокращенномъ видѣ
е=А(1—2м).
VI. Задача. Нѣкто долженъ уплатитъ суммы А, А\ Аг'э... соотвѣтственно черезъ /, Г*.... лгътъ: черезъ сколько лѣтъ онъ вполнѣ
можетъ погасить долгъ единовременнымъ взносомъ В рублей?
гала В і в
Пусть х — будетъ искомое число лѣтъ; цѣнность въ настоящее время капи-д. б. равна суммѣ цѣнностей въ настоящее время капиталовъ А. А', потому ур—ніе задачи будетъ:
В
н ч-
Ѵаетнмй случай. Если имѣются только два платежа, и притомъ В = 2А. предыдущее ур. приводится къ
чМ(9‘ + А
м
Легко видѣть, что г/сколгое ярелія всегда короче средняго изъ эпохъ обѣихъ уплатъ. Въ самомъ дѣлѣ, положивъ и вынеся мнѵжителя
найдемъ
По количество, сложенное съ своею обратною величиною, даетъ всегда сумму, большую 2; слѣд. а какъ 2 <С1) то необходимо
Примѣръ. Уплатѣ подлежатъ: 12500 р. чрезъ 7 лѣтъ и 12500 р. чрезъ 43 года. Чрезъ сколько лѣтъ можно погаситъ долгъ однимъ взносомъ въ 25000 р.9 полагая сложные % по 4,5 со ста?
Вопросъ рѣшается ур—мъ
1 Г — /" 1 Ѵд-/ 1 V* иіО45^ V,045/ “1”\І»045/ ’
при помощи логариѳмовъ находимъ
(т4^Г = 0-7348283
\1,04э/ ’
(- 0,1506605
\ 1,04а / 1
\ |Г |Г
2 . (т~еГ = 0,8854888 \1,О45/ ’
_ ІЕ 0,4427444 Т,6461531 _ 3538569
~ 1 "“М806837- 191163
в 1,045
* = 18 лѣтъ 6 мѣс.
Срочныя уплаты.
835. Опредѣленіе. Срочною уплатою называется постоянная сумма, которую слѣдуетъ вносить въ концѣ каждаго года для погагиенія долга вмѣстѣ съ сго сложными процентами.
836. Основной вопросъ.— Занятъ въ банкѣ капиталъ а по р °/о въ іодъ (считая сложные и/0) на і лѣтъ. Какую сумму х нужно вносить въ концѣ каждаго года, чтобы долгъ былъ погашенъ?
Долгъ а въ концѣ 1-го года обращается въ ау; по внесеніи же срочной уплаты х онъ обращается въ ау — гг: таковъ долгъ въ началѣ 2-го года.
’Въ теченіе года эта сумма обращается въ (ау—х)у или въ ау*—ху; по уплатѣ же въ концѣ 2-го года х руб., долгъ въ началѣ 3-го года будетъ «5я — ху — X.
Такимъ же образомъ въ началѣ 4-го года долгъ будетъ ау*—ху*—ху — х, и т. д.
По аналогіи съ этими формулами заключаемъ, что по истеченіи і лѣтъ долгъ банку будетъ
ау1 — ху*~г— ху*—2— • *—ху — х . . . (А)
По условію, черезъ і лѣтъ долгъ д. 6. погашенъ; отсюда ур.
ау* — ху*-1 — ху*-2— - • - — ху — # = О, или
ау* — х(у*~1 -|- • • • Н"3“|“1) = О,
или, наконецъ:
аІ* — ж'^Ег = ° •••(!)
Другой способъ вывода. Если бы должникъ ничего не вносилъ ранѣе окончанія срока, то въ концѣ і-го года онъ долженъ бы былъ внести
Но въ концѣ 1-го года онъ вноситъ х руб.; если бы онъ удержалъ эту сумму и помѣстилъ ее на сложные то въ —1 лѣтъ, оставшихся до срока, ♦та сумма обратилась бы въ хд^х. Слѣд., 1-я уплата этого величиною и должна войти при окончательномъ расчетѣ. Такимъ же образомъ:
2-ая срочная уплата, при окончат. расчетѣ, эквивалентна рублямъ;
3-ья > > > > » » ху*~8 »
4-ая > > .> » » » 4 »
Предпослѣдняя уплата равновелика суммѣ..................ху, »
вносимой въ концѣ ^-го года.
Наконецъ, послѣдняя, > » ............х *
членамъ х
Всѣ эти суммы, образуя геом. прогр. въ I членовъ съ первымъ , - X — 1]
и съ знаменателемъ 2, даютъ вмѣстѣ у- » каковая сумма и должна погашать долгъ а</; откуда ур—ніе
ад1
1| ~ <?-1 '
По прежнему имѣемъ 4 задачи.
837. Опредѣленіе срочной уплаты.—Рѣшая ур. (1) отн. х, имѣемъ
___а^'Ч — 1)
Х~ ^-1 ‘
Частный случай. Если срокъ займа неограниченно великъ, то, положивъ $ = оз и замѣтивъ, что при ? > 1 и / = оо, обращается въ находимъ: х = — * Для раскрытія неопредѣленности дѣлимъ числителя и знамен. на д ;
находимъ
Ііт
гдѣ г= ^-
= а($ — 1) = аг, 1=^
Легко истолковать этотъ результатъ, замѣтивъ, что аг или есть формула простыхъ годовыхъ процентовъ долга а. Итакъ, предѣлъ срочной уплаты при неогранич. срокѣ займа равенъ простымъ годовымъ процентамъ занятаго капитала, — результатъ, который не трудно было предвидѣть заранѣе. Въ самомъ дѣлѣ, очевидно, что срокъ займа м. б. безконечно великъ только тогда, когда срочная уплата погашаетъ одни простые проценты, оставляя капиталъ безъ измѣненія. На такихъ условіяхъ въ большинствѣ случаевъ дѣлаются государственные займы; государство ограничивается уплатою, въ опредѣленные сроки, простыхъ процентовъ своего долга, такъ что срочныя уплаты, вносимыя государствомъ, не могутъ служить къ погашенію долга, которое достигается другими средствами, когда это дозволяетъ финансовое положеніе страны. Сказанная уплата называется, поэтому, непрерывною рентою.
Заемъ, совершаемый государствомъ на такиіъ условіяхъ, называется консолидированнымъ долгомъ.
Обыкновенно же срочная уплата бываетъ больше непрерывной ренты, и разность между ними выражается такъ:
аг х — аг — .-----
<Г — 1
Этотъ избытокъ срочной уплаты надъ непрерывною рентою, которую слѣдовало бы уплачивать въ случаѣ неограниченнаго срока займа, и составляетъ фондъ погагиенія,
838. Опредѣленіе займа. Изъ ур—ія (1) прямо имѣемъ
х(^ — 1)
839. Опредѣленіе процентовъ приводится къ опредѣленію Освобождая ур. (1) отъ знаменателя и приводя въ порядокъ члены, находимъ ур—ніе
— (а 4~ х)#* 4- х = О,
I 1-й степени относительно вообще, оно неразрѣшимо обычными пріемами элементарной алгебры. Но можно найти численную величину % помощію методическихъ попытокъ (значительно облегчаемыхъ таблицами сложныхъ %)* Раздѣливъ уравненіе (1) на можно представить его въ видѣ
Замѣняя г послѣдовательно числами 0,03, 0,04, 0,05, 0,06 . . . т.-е. наиболѣе употребительными процентами, смотримъ на результатъ подстановокъ. Если этотъ результатъ будетъ 0, г въ точности равно взятому числу; вообще же первая часть ур—нія будетъ отлична отъ нуля. Численная величина и знакъ этой разницы укажутъ степень точности испытуемаго числа и смыслъ приближенія.
1. Смысла полученнаго приближенія. Если дать г значеніе, большее настоящаго, первая часть ур—нія будетъ положительна; для г слишкомъ малаго, она будетъ отрицательна. Для доказательства беремъ выраженіе (А):
а$*—+ * • 'Ч-#),
въ которомъ первый членъ есть долгъ съ процентами, а выраженіе въ скобкахъ есть сумма, необходимая для покрытія долга. Если за прибыль на 1 р. взять число К, большее истинной величины г, то данная уплата будетъ недостаточна для погашенія долга: въ самомъ дѣлѣ, таблицы, вычисленныя при помощи формулы § 838, показываютъ, что при а и і постоянныхъ, х возрастаетъ вмѣстѣ СЪ Г; слѣд.
а(1Ч-К)<>д;(14-Ку-14-я;(14-Ку-гЧ------------р*
или а(1 4-В)‘> я • ,
Если же вм. г взять меньшую величину К', то данная уплата будетъ слишкомъ велика для покрытія долга; слѣд. будетъ
К <л[1 —(1-І-К'у]'
2. Выборъ перваго приближенія,—Если і весьма велико (больше 30), —1 - будетъ мало; пренебрегая этимъ членомъ, найдемъ для г приближенную (14-г) по избытку величину
а
Но это приближеніе весьма грубо, когда і содержится между 15 и 30, а если оно не дастъ полезнаго указанія.
X I
Вмѣсто того, чтобы пренебрегать въ ур—ніи уплатъ членомъ - • за-мѣнимъ знаменателя (1 + ?)1 биномъ 1 + *г, меньшимъ (1+ + получимъ
1 1
(14-г/ 1 +
И слѣд. . а? а? 1 х 1
а а 1 + ?г а I
Слѣд. приближеніе по недостатку для г будетъ
3. Приближеніе точное до 0,01. Сначала испытываемъ г'; затѣмъ подставляемъ
га= г'4-0,01; г3 = г +0,02; г4 = г'+ 0,03;
и первое изъ этикъ чиселъ, которое сдѣлаетъ первую часть ур—нія (2) положительною, и будетъ значеніемъ г, точнымъ до 0,01 по избытку; а предыдущее будетъ точно до 0,01 по недостатку. Такимъ образомъ найдемъ два значенія для г: г2 и г3, напр., приближенныя въ противоположномъ смыслѣ съ точностью до 0,01.
4. Слѣдующія приближенія, получаемыя интерполированіемъ. Пусть е* есть величина первой части ур—нія (2) для г = г^ е3 ея величина для г = г3; можно принять, съ малою погрѣшностью, что въ интервалѣ г3 — г* измѣненія первой части пропорціональны приращеніямъ г.
Пусть будетъ у — поправка для говоримъ: когда г измѣняется отъ до **3, первая часть измѣняется отъ до е3; на сколько г должно измѣниться начиная отъ чтобы разница уменьшилась отъ е2 до 0? Это сводится къ пропорціи
еа + <?з 001
«2 У ’ изъ которой
* 0,01 х
и = 1---<- *•
’ «і + «3 ’
— 916 —
въ у достаточно ограничиться цифрою тысячныхъ; приближеніе # «тда будетъ по недостатку. Вычисляемъ разницы первой части для
г — г?+у и г = г2-|-у + 0>001,
и если послѣднее значеніе положительно,
гі-тУ И >2 4-У-|-0,00!
будутъ два приближенія — одно по недостатку, другое по избытку, точныя ♦ до 0,001*
Выходя отъ этихъ двухъ результатовъ, получимъ такимъ же путемъ цифру десятитысячныхъ, и т. д.
Численный примѣръ. Вычислить проценты, если а= 10000, х= 1202,41 р.ѵ і=10.
Прежде всего находимъ:
- = 0,12024; — у = 0,0202 (по недостатку),
*
Испытаніе 0,03.
(1,03)-’° = 0,744074; 1 — (1,03)-10= 0,255926;
255926 = 0,0307728.
Уклоненіе = — 0,0007728, слѣд. 0,03 есть приближеніе яо недостатку.
Испытаніе 0,04.
(1,04)_ 10 = 0,6755642; 1 - (1,04)-10 = 0,3244358;
-X 0.3244358 = 0,0390105;
уклоненіе = -(-0,0009895: слѣд. 0,04 — приближеніе по избытку.
Интерполированіе пропорціональными частями.
Сумма абсолютныхъ значеній уклоненій =
у =0,01
0,00077280,0009895 = 0,0017623,
0,0007728 п пп.
0.00Г7623 = °’°04’
и новое приближеніе есть 0,034.
Испытаніе 0,034*
(1,034)-10 = 0,715805; 1 — (1,034)“10 = 0,284195;
5Х0'284195 = 0,0341719!
уклоненіе = — 0.0001719, елѣд. 0,034 — приближеніе по недостатку.
Это уклоненіе составляетъ приблизительно четверть перваго: потому увеличиваемъ проценты на 0,001 и испытываемъ 0,035.
Испытаніе 0.035.
ІІ.О35)-10 = 0.708919; 1 — (1,035)"™ = 0,291081:
х
а
X 0.291081 =0,0349999;
уклоненіе равно нулю; сл. 0,035 есть точная прибыль на 1 рубль. Такимъ образомъ р = 3,5.
840. Опредѣленіе времени. -Изъ ур. (1) имѣемъ:
д* = --х— аг
откуда, взявъ логариѳмы обѣихъ частей: V
Изслѣдованіе. Неизвѣстное і должно быть числомъ дѣйствительныя ъ положительнымъ и цѣлымъ.
Но формула времени содержитъ (я — аг). который повсегда можетъ быть взятъ, такъ какъ отрицат. число не имѣетъ дѣйствительнаго логариѳма. Отсюда необходимость различать три случая:
1. х < аг; —ат) будетъ мнимый, и задача невозможна. Это легко видѣть а ргіогі. Въ саномъ дѣлѣ, аг — представляетъ простые % долга, и какъ срочная уплата меньше зтихъ проц. денегъ, то ея недостаточно даже для уплаты процентовъ, такъ что долгъ съ теченіемъ времени будетъ увеличиваться.
2. # = аг. Въ атомъ случаѣ ж — аг = 0, кр(^ — аг) =—счэт и 2 = ^. Это означаетъ опять, что долгъ не можетъ быть погашенъ. Въ самомъ дѣлѣ, а ргіогі видно, что.когда сроч. упл. х равна простымъ процента, деньгамъ, то она будетъ погашать только эти деньги, и долгъ всегда будетъ оставаться одинаковымъ. Это н есть непрерывная рента, о которой было говорено выше.
* 3. я>-аг: обыкновенный случай возможности задачи, такъ какъ срочная уплата, будучи больше годовыхъ процентовъ на капиталъ, будетъ погашать не только эти послѣдніе, но и часть капитала; такъ что черезъ нѣсколько лѣтъ долгъ будетъ погашенъ.
Самая формула даетъ положительное значеніе для Я; но еще нужно, чтобы это значеніе было и цѣлое. Но если для $ получается число дробное, то это означаетъ, что данною срочною уплатою долгъ не м. б. погашенъ, и что по истеченіи времени, равнаго цѣлой части остается часть долга, меньшая срочной уплаты. Пусть цѣлая часть і будетъ Т; замѣтивъ, что долгъ выражается первою частью уравненія (1), заключаемъ, что по истеченіи Т лѣтъ остатокъ долга будетъ
в т ж(дТ _ ])
Н=а9т —
Примѣръ. Во сколько лѣтъ уплачивая ежегодно по 600000,
можно погасить долгъ въ 5000000 р., если платится по 5^/^?
аг = 250000 р. 1ц х — 5,7781513
х — аг = 350000 р. (а; — аг) = 5,5440680 0,2340833 0,2340833 _ ..
0,021.19 _ 11’ • ' •
Такъ какъ для і получилось число дробное, то вычисляемъ остатокъ К долга.
1,05“ == 1,710339 1д 5.10е = 6,6989700
1,05“ — 1 = 0,710339 1^1,05“ = 0,2330822
1? 1,05“ = 0,2330822 6^)320522
адт = 8552700
1? 6.10» =5.7781513 18 0,710339 = 1,8514658 доп. 18 0,05 = 1_,3010300 6,9306471
= 8524072
9 — 1
К = 8552700 — 8524072 = 28628 р.
841. Займы посредствомъ облигацій,—Большія промышленныя общества, напр, желѣзнодорожныя компаніи и т. п,, дѣлаютъ займы, пуская въ обращеніе іаціич приносящія опредѣленный годовой или полугодовой процентъ; облигаціи погашаются, по извѣстной цѣнѣ, при помощи тиражей, въ теченіе извѣстнаго числа лѣтъ.
Ежегодно компанія отчисляетъ изъ барышей предпріятія опредѣленную сумму для уплаты процентовъ и для погашенія возможно большаго числа облигацій.
Пусть число выпущенныхъ облигацій будетъ Ьг; номинальная цѣна каждой, т.-е. цѣна, по которой облигація д. б. выкуплена, пусть будетъ V; пусть погашеніе продолжается п лѣтъ; наконецъ, прибыль на 1 рубль вь 1 годъ пусть будетъ г.
Такимъ образомъ весь подлежащій погашенію заемъ = МѴ, а по истеченіи п лѣтъ этотъ долгъ обратится въ ИѴ (1 -р г)71,
Если отчисляемая ежегодно на погашеніе долга сумма будетъ а, то цѣнность этихъ уплатъ къ концу срока будетъ
*
а(14-г)»-і + а(14-г)»-2+. . .-^а = я-|(-±гГ-)-~И.
Такъ какъ эта сумма должна погашать накопившійся къ концу я лѣтъ долгъ, то
?К1.±П,,~11 = XV (1 + г)4,
откуда и находимъ, какова должна быть ежегодная уплата а, погашающая долгъ;
найдемъ
Часть этой суммы а идетъ на уплату процентовъ на непогашенныя облигаціи, а другая часть на выкупъ возможно-большаго числа облигацій.
При выпускѣ облигацій компанія составляетъ предварительно такъ наз, таблицу погашенія займа, т.-е* таблицу ежегодныхъ уплатъ, а, чтобы заранѣе знать, сколько облигацій должно быть ежегодно погашено,
II г и м ъ у ъ. Компанія выпускаетъ 600,000 облигацій, по 500 р. каждая, дающихъ ежегодно 5°/^ прибыли, Выкупъ долженъ бытъ оконченъ въ 92 года. Какова д, б, срочная уплата, погашающая долгъ^ и по сколько облигацій каждый годъ д. б. погашено?
Вычисляя а, найдемъ
а = 9,635,083 р.
Составимъ теперь таблицу погашенія.
1’й годъ. Въ концѣ 1-го года общество должно уплатить по 15 р, прибыли
на каждую облигацію, всего 9.000.000 р. На погашеніе остается 9,635.083—
9.000.000 = 635*083 р.
Этою суммою можно
635.083 . х
погасить ™—=1.2/0 обли-500
гаціи, и останется 83 р., которые прибавляютъ къ слѣдующей срочной уплатѣ.
2-й годъ. Осталось 600.000 — 1.270 = 598.730 облигацій. На нихъ нужно уплатить процентовъ 598.730)^ 15 == 8*980.950 р. Срочная уплата, съ остаткомъ въ 83 р,, составитъ 9.635.166 р. Вычитая отсюда проценты на облигаціи, найдемъ, что па погашеніе облигацій останется 9.635.166 — 8.980.950 = 654,216 р., что дозволяетъ погасить
<і5™~ = 1-308 «ХА/
облигацій.
съ остаткомъ въ 216 р,. которые присоединяютъ къ третьей уплатѣ.
Продолжая такимъ обр., найдемъ, что въ концѣ 3-го года будетъ погашено 1.347 обл. и останется 469 р.; что въ концѣ 4-го тода погасится 1.388 обл.: въ копцѣ 5-го—1.432 обл., въ концѣ 6-го—1.475, въ концѣ 7-го—1.519, къ концѣ 8-го—1.564, въ концѣ 9-го—1.610, въ концѣ 10-го—1.660 ит.д. Ежегодныя срочныя уплаты, вообще, какъ видимъ, изъ года въ годъ измѣняются.
842. Пожизненныя ренты. Такъ называются срочныя уплаты, выплачиваемыя ежегодно вкладчику, въ теченіе всей его жизни, банкиромъ пли заемщикомъ. Капиталъ, отданный вкладчикомъ, д. б. таковъ, чтобы, при сложныхъ процентахъ, онъ могъ дать сумму, равную суммѣ всѣхъ выплатъ, которыя банкиръ обязуется выдавать вкладчику въ концѣ каждаго года, въ продолженіе всей его жизни.
Пусть извѣстны лѣта вкладчика, внесенный имъ банкиру капиталъ и норма процентовъ: пользуясь яшолмиллш смертности, можно опредѣлить вѣ^юатное число лѣтъ, которое осталось прожить вкладчику.
Такимъ образомъ задача о пожизненныхъ рентахъ есть ничто иное, какъ частный случай задачи о срочныхъ уплатахъ.
Страхованіе жизни, пожизненныя ренты, сбе2)егапіелъныя кассы, — все это основано на вѣроятной продолжительности человѣческой жизни я па быстротѣ наростанія капитала, помѣщеннаго на сложные проценты.
843. Задача. Нѣкто для покупки своей женѣ ежегодной пенсіи въ Ъ руб., платитъ ежегодно во вдовью кассу а руб. По истеченіи п лѣтъ умираетъ вкладчикъ, а т лѣтъ спустя — его жена. Сколько пріобрѣла или потеряла касса, если проценты считались тою и другою стороною по р въ годъ?
Пусть плата тою и другою стороною совершается въ началѣ каждаго года, а заключеніе счетовъ—по истеченіи лѣтъ: въ такомъ случаѣ 1-й взносъ
приноситъ проценты п-{-т лѣтъ, и слѣд. достигаетъ величины а#п+от; второй — годомъ меньше и достигаетъ величины ац" ”1~1 и т. д. Послѣдній вкладъ находится подъ % яз-|-1 годъ, и цѣнность его =адт~~\ Такимъ же образомъ, цѣнность первой пенсіи Ь черезъ т лѣтъ равна Ьдм, послѣдней = Ьд. Прибыль (положит. или отрпц.) кассы будетъ
и*-1-]- . . , • * * “г^)
или Д<?НЖ(^ —1) —&у(дот- 1)
V —1
Примѣръ. Если а = 50 р., 6 = 200 р*, ш = 8, п = 20 и /> = 4 р., то касса имѣетъ прибыль = 202 р.
844. Задача. ѵ составили общество. Какой капиталъ А каждое
изъ нихъ должно датъ банкиру, чтобы получатъ отъ нею пожизненную ренту, равную а рублямъ?
Расчетъ ведется такъ: ѵ лицъ, по истеченіи 1 года, составятъ товарищество изъ ѵ' лицъ; банкиръ долженъ имъ выдать аѵ’ руб. Въ концѣ 2-го года оставшимся въ живыхъ онъ долженъ выплатить аѵ" и т. д.
Но ренты а, которыя банкиръ долженъ выплатить ѵ', г/', ѵ" . . . оставшимся въ живыхъ вкладчикамъ, обращаются въ концѣ 1-го, 2-го, 3-го . . . годовъ въ
“(1+0, а(!+»•)«, а(14-г)’, . ..
V* вкладчиковъ, которые въ концѣ 1-го года должны получить ренты по а руб. каждый, должны бы были внести р. въ началѣ 1-го года; ѵ” вкладчиковъ, которые въ концѣ 2-го года должны получить ио а руб., должны бы были въ началѣ 1-го года внести руб., и т. д. Такъ что ѵ
вкладчиковъ должны бы были внести въ началѣ 1-го года сумму
Такимъ образомъ капиталъ А, внесенный каждымъ, равенъ
или. положивъ
1
Если принять гипотетическій законъ Моавра, что, начиная съ извѣстнаго возраста число смертей составляетъ величину постоянную, то, назвавъ это число для каждаго года буквою й, можно предыдущей формулѣ дать видъ
А = ^[(ѵ —(/) + (» —2Л)7+(»-ЗЙ)д4+. — и<7)в—Ч, *
гдѣ я — число лѣтъ періода. ,
Послѣднюю формулу можно написать въ видѣ
А • -Н?"-1)—(1+2?+32І-Г4?’" ’ ’ •+№’>,
или. замѣчая, что
1+2д + 3^+- • =
въ видѣ:
л = «г!'-і-?Г'-4-
1 I I - ѵ Ь (I “ д)2 1 — д Л
845. Историческое примѣчаніе. — Еще въ 1544 г. Михаилъ Стпифелъ далъ, въ нѣкоторомъ родѣ, теорію логариѳмовъ; однако же изъ своего открытія онъ не сдѣлалъ примѣненія къ упрощенію вычисленій. Позднѣе, лордъ Джонъ Неперъі шотландскій баронъ, примѣнилъ теорію логариѳмовъ къ практикѣ вычисленій. опубликовавъ свое открытіе въ 1614 г. въ сочиненіи Мігііісі Іо^а-гііЬтогипі санопіз (Іевсгірііо. Но онъ принялъ для своихъ логариѳмовъ основаніе (е = 2,71828 . . ). неудобное для вычисленій надъ числами десятичной
системы нумераціи. Его другъ Бриггъ (1556—1630), оксфордскій профессоръ, устранилъ зтотъ недостатокъ, взявъ за основаніе системы логариѳмовъ число 10. но указанію самого Непера. Теорія логариѳмовъ въ той формѣ, какъ она изложена у насъ, дана Эйлеромъ въ 1748 г.
1
ОТДЪЛЪ ШЕСТОЙ.
НЕПРЕРЫВНЫЯ ДРОБИ И ПХЪ ПРИЛОЖЕНІЯ.
ГЛАВА 1Л1І.
Непрерывныя дроби.
Опредѣленіе.—Происхожденіе непрерывныхъ дробей.—Свойства приближеній.—Пері-
одическія непрерывныя дроби.—Приложенія.
846, Непрерывною дробью наз. выраженіе, состоящее нзъ цѣлаго числа (которое, въ частности, м. б. нулемъ), сложеннаго съ дробью, у которой знаменатель есть опять цѣлое съ дробью, н т. д.; однимъ словомъ, выраженіе вида
Элементарная алгебра изучаетъ частный видъ такихъ дробей, а именно случай, когда числители Ь, <7,... равны 4-1, а знаменатели с, е,... суть цѣлыя положительныя числа; слѣд., элементарная алгебра имѣетъ дѣло съ дробями вида
Количества ап а2, наз. неполными частными; а№ называютъ к-мъ неполнымъ частнымъ; полнымъ же частнымъ на этой ступени называютъ г і л й 1 1 1
<**+-—ггтг Дроби * • • называютъ члеяолш, или зеенья-
.ни непрерывной дроби. Если число членовъ непрерывной дроби ограниченно, дробь наз. конечною; при неограниченномъ числѣ членовъ она наз. безконечною.
Сокращенно непрерывную дробь пишутъ въ видѣ:
«і I <*», «я» • • I или | а,; «41 аа .
дѣ — цѣлое число.
847. Происхожденіе непрерывныхъ дробей.—Этого рода дроби совершенно натурально являются въ анализѣ. Въ самомъ дѣлѣ, вообразимъ нѣкоторое коли-
чество х, соизмѣримое или несоизмѣримое; оно необходимо содержится между двумя послѣдовательными цѣлыми числами: и «іН-1. Слѣд. можно положить
если *!>!. Изъ равенства (1) выводимъ
1
1 X — «I
Количество также содержится между двумя послѣдовательными цѣ-лыми числами а, и а^-}-1, гдѣ а* но меньшей мѣрѣ равно 1, что ясно изъ (1). Такимъ образомъ можно написать
гдѣ Продолжая такимъ образомъ, имѣемъ для опредѣленія х формулу
х =аг
Это — непрерывная дробь въ вышеуказанномъ тѣсномъ и обычномъ смыслѣ слова; аа, а3, . . . — числа цѣлыя и положительныя; изъ нихъ одно только а1 м. 6. нулемъ, когда
848. Теорема. Всякая конечная непрерывная дробь представляетъ нѣкоторое соизмѣримое число.
Пусть
отсюда
= а
Перенося
а2 въ лѣвую часть
равенства, находимъ
х — ах
аз
Продолжая такимъ же образомъ, будемъ получать въ лѣвой части всегда частное двухъ линейныхъ относительно х выраженій. Наконецъ, получимъ
— У24 —
откуда
а — і'а„
количество соизмѣримое (во равное ни О, ни ?<, ибо х содержится между а4 И 01 + 1).
849. Теорема обратна я.—Всякое соизмѣримое число можетъ бытъ представлено подъ видомъ конечной непрерывной дроби.
• л
Пусть данное соизмѣримое число будетъ гдѣ а и Ъ — цѣлыя, первыя между собою, числа; и пусть, во-первыхъ, будетъ Совершая дѣленіе,
указываемое дробью, получаемъ въ частномъ д1 и въ остаткѣ такъ что
совепшая дѣленіе — (пусть частное = ^, остатокъ га) находимъ гі
Продолжая такимъ же образомъ далѣе, самымъ ходомъ дѣйствія мы вынуждены выполнять надъ а и Ь такія же дѣйствія, какія пришлось бы совершать надъ зтимп числами при нахожденіи ихъ о. п. д.; и какъ а и числа первыя между собою, то необходимо дойдемъ до остатка гп= 1. Такимъ образомъ дѣйствіе закончится и получится конечная непрерывная дробь
Если а < Ь и дробь — правильная, то, раздѣливъ оба ея числа на а,
находимъ
а 1
I —ь.
гдѣ ~ развертывается, по предыдущему, въ конечную непрерывную дробь.
850. Теорема.—Развертываніе соизмѣримаго числа въ непрерывную
дробь возможно единственнымъ способомъ.
Пусть предложенное число будетъ я, и пусть, по обращеніи въ непрерывную дробь вышеуказаннымъ способомъ, оно даетъ результатъ
3» • • - I • • • (1)}
Допустимъ, что какимъ либо инымъ способомъ оказалось возможнымъ найтм для х другое разложеніе въ непрерывную дробь
аЭ’ • • ’ 5 Яр I **•(-)
Докажемъ, что оба результата тождественны. Равенство (I) доказываетъ, что х содержится между двумя послѣдовательными цѣлыми числами ах и : равенство (2) доказываетъ, что х заключается между'"двумя послѣдовательными цѣлыми числами Сближая эти два заключенія, видимъ, что <^=04.
Затѣмъ равенства (1) и (2) можно представить такъ:
Х ------- I ‘ ‘ Н — Л1 I 2э • * • % I
» г
Разсуждая какъ выше указано, выводимъ, что —
Такимъ же образомъ найдемъ/ что а3 = а3 и т. д.
851. Приближенія или подходящія дроби. — Соединеніе нѣсколькихъ членовъ непрерывной дроби
дг — | &3, а4, . . . .
со включеніемъ всегда цѣлой части, т.-е. выраженія
*
представляющія величину непрер. дроби х приближенно, называются приближеніями или дробями, Займемся изученіемъ свойствъ этихъ
величинъ.
852. I. Законъ составленія приближеніи,—Первое приближеніе получимъ, сохранивъ только цѣлую часть и отбросивъ дробную часть непрерывной дроби: такимъ образомъ первое приближеніе = ~
Второе приближеніе найдемъ, придавъ къ а, дробь — и откинувъ все ѳсталь-, । 1 Лі Д-О *4* 1
ное: второе приолиженге будетъ поэтому: а1 —• или ~д-
Третье приближеніе получается изъ второго прибавленіемъ къ его знаменателю звена ”; поэтому 3-е приближеніе будетъ
ах
1
«3
Замѣчаемъ, что числитель этого приближенія получается умноженіемъ числи-теля + 1 предшествующаго приближенія на неполное частное а3 составляемаго, п приданіемъ къ произведенію числителя аг предпредыдущаго приближенія. Точно такъ же знаменатель 3-го приближенія подучается умноженіемъ знаменателя предшествующаго прибл. па неполное частное составляемаго, и при
давленіемъ къ этому произведенію знаменателя предыдущаго приближенія. До-кажемъ, что законъ этотъ имѣетъ мѣсто для составленія приближенія какого угодно порядка. Пусть будутъ
Рр_2 1Ѵі ІѴч
Чр—2 Ор“1 Чр Чр-Н
четыре рядомъ стоящія приближенія; ар — неполное частное, соотвѣтствующее приближенію и — соотвѣтствующее приближенію Допустивъ, что законъ, замѣченный нами на третьемъ приближеніи, справедливъ для приближенія докажемъ, что онъ будетъ имѣть мѣсто и для приближенія
По допущенію, имѣемъ:
Пр Рр—1 Н" Р р—2 в 4 /і \
Чр Ор—і 4~ Чр^2
Для образованія слѣдующаго приближенія замѣняемъ въ (1) ар биномомъ
—; находимъ
(Рр—1 йр “Ь Рр—2)Ор~-1 Рр—1
(Чр—1 Лр + Чр— 2)#р-Н 'Р Чр— 1
Рр Др4-1 Ч~ Рр—1 Чр ор-В + Чр”і*
Доказано, что если законъ справедливъ для какого-либо приближенія, то онъ справедливъ и для слѣдующаго приближенія. Непосредственнымъ составленіемъ приближеній мы убѣдились въ справедливости закона для третьяго приближенія, слѣд., по доказанному, онъ вѣренъ и для четвертаго; будучи вѣренъ для четвертаго приближенія, онъ вѣренъ и для пятаго, и т. д.; общность закона такимъ образомъ доказана. Итакъ: составленія приближенія
какою угодно порядка* нужно умножитъ оба члена предшествующаго приближенія на неполное частное составляемаго, и къ произведеніямъ прибавить соотвѣтственно члены приближенія* стоящаго двумя ѵо-рядками ниже.
Примѣръ. — Пусть имѣемъ непрерывную дробь
а = 0 | 36, 7, 1, 1, 1, 4, 2 | .
і , . О 1 . .
1-е приближеніе = у; второе = ^; для составленія слѣдующихъ поступаемъ такъ: дѣлаютъ столько графъ,
1 36 253 289
1 1
15 23 542 831
4
107
3866
2
237
8563
сколько слѣдуетъ составить приближеній, причемъ въ первыхъ двухъ графахъ помѣщаютъ 1-е и 2-е приближенія, а въ заголовкахъ слѣдующихъ графъ—неполыя частныя 3-го, 4-го, . . . приближеній. Для составленія какого-либо приближенія остается, слѣдуя правилу, помножить числит. и знам. предыдущаго приближенія на цифру, стоящую въ заголовкѣ составляемой дробя, и къ произведеніямъ прибавить соотвѣтственно числителя и знаменателя приблия^енія. твумя порядками ниже составляемаго. Такамъ образомъ, для третьяго приближенія находимъ к?+0 7 . , 7.1 + 1 8
38.7 + 1’ ИЛИ 253’ ДЛЯ 4"Г0'253.1 + 36’ КЛИ 289’ И Т* Д*
Примѣчаніе. — Если данная непрерывная дробь не имѣетъ цѣлой части, то за первое приближеніе берутъ у
853. II. Приближенія четнаго порядка—большеа нечетнаго—меньше величины непрерывной дроби.
Пусть дана непрерывная дробь
Первое приближеніе очевидно, меньше х на —Ц-1 ...
Второе приближеніе а. 4- — больше х; ибо знаменатель «. дроби 4- меньше 1 1 (1^ * *
1 . > 1
г...» сдѣд. дробь т
I ”2
Третье приближеніе а1 —
, 1 лсеяъше я; такъ какъ дробь
опять
* * «3
I х 1 х 1
придаваемая здѣсь къ знаменателю а* дроби —, больше —
; а по*
I 1 л х 1
тому знаменатель ------больше настоящаго, а дробь —-г- менѣе
3 аа + ~
аТ«з
настоя-
.между
! | I . ді і. А» ,
4- —
854. Слѣдствіе. — непрерывной дроби содержатися
каждыми двумя смежными приближеніями.
Въ самомъ дѣлѣ, всѣ приближенія четнаго порядка—больше, а нечетнаго— меньше величины непрерывной дроби; а какъ изъ двухъ смежныхъ приближеній одно—четнаго, а другое—нечетнаго пор., то очевидно, что величина непрерывной дроби заключается между ними, *
855. ПІ. Разность между двумя смежными приближеніями всегда равна +1, раздѣленной на произведеніе ихъ знаменателей.
р і_2 р _। Р
Пусть будутъ ТРИ €межныя приближенія, и ар— неполное
частное, соотвѣтствующее послѣднему.
По закону составленіе приближеній
Рр Рр—І&р-рРр—2
Чр ^р—1 + Чр—2
Вычтя первое изъ втораго, имѣемъ
Рр-1 Рр-2 Рр~1 <ІР—2 — рр— 2 1
1 . Оір—2 С^р—1 —2
Вычтя второе изъ третьяго:
Р;)__ Рр-1 __Р^~] Ор + Рр-2 _ Рр-1 _Рр-2 *^р-1 — Рр-1 <ір~2_
Ор Чр—і Чу—і ар ~Ь О.р— 2 Чр~і (С}р^і ар Ч- Чр—2) Ор—і
_ — (Рр-1 (Зр-2 — Рр-2 Ор-~1) ,9ѵ
“ Ор-іОр "
Сравнивая обѣ разности, замѣчаемъ, что знаменатель каждой изъ нихъ есть произведеніе знаменателей соотвѣтствующихъ приближеній; числители же игъ равны по абсолютной величинѣ, но противоположны по знаку. Изъ равенства абсолютныхъ величинъ числителей всѣхъ разностей слѣдуетъ, что для ихъ опредѣленія можно взять два какія угодно смежныя приближенія. Такъ, вычитая изъ второго первое, находимъ
а* г/* 1 сц___________ г 1
а2 1 — ' оа’
отсюда заключаемъ, что абс. велич. числителей всѣхъ разностей равна 1; знакъ же, очевидно, будетъ (-[-), когда изъ приближенія четнаго порядка вычитаемъ приближеніе порядка нечетнаго (ибо первое больше второго), и (—) въ противномъ случаѣ. Такимъ образомъ
Ор Ор-і Ѵр-і О/
. 856. IV. Предѣлъ разности между непрерывною дробью и однимъ изъ приближеніи,
Такъ какъ величина непрерывной дроби заключается между двумя смежными приближеніями, напр., и тА2—, то, очевидно, разность между величиною # этой дроби и однимъ, изъ этихъ приближеній, по абсолютной величинѣ, меньше ф ОД? такъ что’ юнвъ вмѣсто истинной величины непрерывной дроби приближеніе можемъ быть увѣрены, что ошибка, которую мы пріютомъ дѣлаемъ. 'Р .
меньше единицы, раздѣленной на произведеніе знаменателей взятаго приближенія и непосредственно за нимъ слѣдующаго.
Примѣръ. “ Непрерывная дробь '
.г = О | 2, 11, 2, 1, 10 |
- г • О
имѣетъ приближенія: т’
—, Я , I >
2 23 48 71 758
Взявъ вмѣсто истинной величины непр. дроби, наприм., ея третье прибли-1 I
женіе, дѣлаемъ погрѣшность, меньшую нмй*
р
Если бы мы пожелали имѣть предѣлъ погрѣшности приближенія не вы-Чр числяя знаменателя слѣдующаго приближенія, то достаточно взять въ сообра-1 1 . і
женіе, что п п , т > п—Т ГДѢ такъ-что наименьшая ве-
О#» Чр-і ЧР(Ч₽ вг’-і -г Чр-О»
личина количества Ор-н равна Чр + Ур-і, чаще же—больше этой суммы. Такимъ 11 р
образомъ дробь д- /х ~г~п—а слѣдов. ошибка приближенія
Чр (Чр ~г Чр—ч ЧР Чр-г1 Чр
1 1 * .
меньшая и подавно меньше -Ро^у таковъ второй, болѣе гру-
бый, предѣлъ погрѣшности приближенія тЛ
Если бы въ знаменателѣ дроби 51,4 ОТКИНУЛЛ слагаемое ЧР-і,
р р 1 і
то этимъ уменьшили бы знаменателя; слѣд. _[_ Ор_>)* Заключаемъ,
I Р Р
что и дробь 5-2 можетъ также служить предѣломъ погрѣшности приближе-Чв
. Рр 1ПЯ
р
Итакъ, для опредѣленія погрѣшности приближенія служатъ неравенства чР
«іЛОрОя+і1
Примѣняя второй предѣлъ къ приближенію имѣемъ:
11 1
23 23(23+2) ’
1 или 5/о
Формула для третьяго предѣла даетъ 11 1 1
Х 23 <23=’ Т-‘е* 529'
857. V. Всякое приближеніе есть дробь несократимая. Въ самомъ дѣлѣ, пусть числ. и знам. приближенія имѣютъ общаго множителя &, от-личнаго отъ 1, такъ что Рр_і = 7сг, оР_1 = Лг\ Если есть слѣдующее при-
х • чР •
б.іижеше, то
—о,-!Ор’ 0ТКУда рЛр-» рр-іЧр—±е
Подставляя сюда вмѣсто Рр-і и соотвѣтственно кг ц кг\ находимъ: — ^гЧр = ±1, и слѣд. г'Р^ — + І, т.-е. что разность двухъ цѣ-
лыхъ чиселъ равна правильной дроби: результатъ невозможный; сл. невозможно и предположеніе, что Р^-і и ЧР_і имѣютъ общаго множителя.
858. VI. Всякое приближеніе ближе подходитъ къ величинѣ непре-рывной дроби, нежели ему предшествующее, Пусть —-? и
будутъ три, рядомъ стоящія, приближенія непрерывной дроби
X Л { ’ Ч ^П— 1ч " I
п ан ;_і — неполное частное послѣдняго изъ нихъ. Имѣемъ
Ри~рі _РЛ “I- Р«—1
’ <ія+1 Оп СЬі-Н + Уп-1
Если въ это выраженіе вмѣсто »л -і подставимъ полное частное
то получимъ точную величину дроби х. Обозначивъ (1) буквою у и замѣтивъ, что у>1, ибо наименьшая величина ам_|_і ест-ь 1, найдемъ, что
Чл?/ + Фи-1
Намъ нужно доказать, что разность между х и приближеніемъ п<> ѵ Р абсол. велич., больше разности между х и слѣдующимъ приближеніемъ “•
'Составимъ эти разности:
П — Рм~1 — Рп#+Р*-1 _ Р»~1 = (Р*Чн-1 — Ри-1й,і)# } <2п—і Чн#4~Чп—і і і(Чн$ + <2>і—і)
а какъ . — Р*-іЧп = ± Ъ
__ Рп-І __ У _ д
Чп—і Чн—і(Чл+Ч«—О
9\ _ Ря _ Р^ + Рн-І _ Ру _ Рп-і Чи — Ря <2*і-і _ — 1 ___<
чЛ—ч^+Чп-і о» шн<м Чи(<ин-ч«~і) *:
Отсюда выводимъ абсолютную величину отношенія Л1: именно
: <2«—ь
Такъ какъ у^>1, а (}п > (}„і (по закону составленія приближеній), то У<іп>Чл-і, а потому и Д1>Д1, что к требовалось доказать.
859. Слѣдствіе.—Приближенія четнаго порядка всѣ больше непр. дроби х, а нечетнаго—всѣ меньше ея. Но каждое послѣдующее прибл. подходитъ къ величинѣ непр. дроби ближе предыдущаго, то 1-е, 3-е, 5-е, . . . т.-е. приближенія нечетнаго порядка, хотя всегда остаются меньше х, но приближаясь болѣе и болѣе къ х, представляютъ рядъ возрастающихъ чиселъ. Приближенія четнаго порядка (2-е, 4-е, 6-е, . . . ), оставаясь больше х и приближаясь болѣе и болѣе къ х, составляютъ рядъ убывающихъ чиселъ. Общимъ же предѣломъ тѣхъ и другихъ служитъ сама непр. дробь.
860. VII. Всякое приближеніе подходитъ къ величинѣ непрерывной дроби ближе всякой иной несократимой дроби съ меньшими членами. р
Пусть 7^ будетъ одно изъ приближеній непрерывной дроби х: надо доказать, Чн
что не существуетъ никакой иной несократимой дроби, которая, имѣя меньшіе Р Р
члены, чѣмъ подходила бы къ х ближе, нежели 77-Чн Чя
Въ самомъ дѣлѣ, допустимъ, что существуетъ несократимая дробь д, выра-г Р
жаюіцая величину х точнѣе, кчѣмъ 7А, и вмѣстѣ съ тѣмъ имѣющая члены менъ-шіе, чѣмъ взятое приближеніе; и посмотримъ, къ чему поведетъ это допущеніе. Во-первыхъ, ясно, что дробь д не м. б, ни однимъ изъ приближеній пред-р
шествующихъ дроби 77, ибо послѣдняя, по доказанному, ближе лежитъ къ х. п А -
чѣмъ всѣ предыдущія приближенія, а д, по допущенію, лежитъ къ х еще
Р А
ближе, чѣмъ Затѣмъ, д'не можетъ быть ни однимъ изъ приближеній. ”р /
слѣдующихъ за ибо эти приближенія, хотя и лежатъ ближе къ х какъ и ’ Чп * \
А \ Р
дробь ді, чѣмъ о®, но выражаются большими членами, нежели эта послѣдняя
дробь (по закону составленія приближеній), между тѣмъ какъ члены дроби д * Р А
по условію, меньше членовъ дроби Итакъ, убѣждаемся, что д не м. б. ни однимъ изъ приближеній.
Р * Р«—і
Пусть, далѣе, -тА есть приближеніе четнаго порядка, и Л—------емѵ пред-
чп ч»»—1
шествующее; очевидно
с. .
р„-1
Фп—1
о
₽п
пространство для ѵт-о
Такъ какъ всякое приближеніе выражаетъ величину непрерывной дроби точнѣе предшествующаго, то — х < х — 41,0 на чертежѣ указано тѣмъ,
что промежутокъ СЕ (Е мѣсто непрер. дроби х) больше ЕВ.
А р
Пусть р выражаетъ величину х точнѣе, нежели а потому и подавно точнѣе, нежели цп_х; слѣд. дробь д должна лежать гдѣ-нибудь или въ про-Р Р і
межуткѣ между х ц —2, или въ промежуткѣ между х и т-і"—, а слѣд. не-_ Мбп ’ Чп-1
. Р„ Рп-1
премѣнно—между 77 и , такъ что Чд ЧЛ—1
РЛ Рп—1 А Рп—'1 Рл Ч«—1 — Рп—I Афн—1 — ВРп—1
о;~>в--о^і’ или - —>—во^і—’
иля
I > А.9»-1 - ВР.-19 откуда в > (АЧп_і _ ВРя_і)
Выраженіе въ скобкахъ есть число цѣлое, неравное нулю: цѣлое — потому, что А, В и Рп-і—числа цѣлыя; неравное нулю—потому, что изъ допущенія АЦп-1 — ВРп_і — 0 вышло бы: п — чего, по доказанному, быть
Л Ц,н—1’
не можетъ. Такимъ образомъ, наименьшая величина скобокъ равна 1, а потому В>9„ - 1, или В>уп, т.-е. чтобы дробь выражала величину непрерывной р
дроби точнѣе приближенія надо, чтобы знаменатель этой дроби былъ больше знаменателя разсматриваемаго приближенія.
V а Р„^1 ря
Если д заключается между и тг, т.-е ливъ 1 на каждую изъ этихъ дробей,
Р„ Р—1 X
Щ>в>о^Т' т0’ Радѣ' найдемъ р;<а<р^» откуда
1 л
р”’ 1 л
1 А(^п—1 — ВРп-і
или р- > -----------7--------
1 п
откуда А > — ВРп-і); а
какъ шіиіпшт скобокъ равенъ 1, то А > РЛ . 1 или А > Р»; это значитъ, что для выполненія вышесказаннаго требованія и числитель дроби 4 долженъ быть больше числителя приближенія
Такимъ образомъ доказано, что не существуетъ такой дроби, которая, имѣя простѣйшій видъ, чѣмъ нѣкоторое приближеніе, выражала бы величину непрерывной дроби точнѣе этого приближенія.
Примѣчаніе.—Теперь становятся понятны выгоды, представляемыя обращеніемъ чиселъ въ непрерывныя дроби. Пусть, напр., рѣшеніе нѣкотораго вопроса привело къ несократимой дроби у, члены которой выражены большими числами, затрудняющими употребленіе этого результата въ приложеніяхъ. Тогда мы обращаемъ дробь у въ непрерывную и составляемъ подходящія дроби. Выбравъ одну изъ послѣднихъ и замѣнивъ ею дробь у, мы теперь увѣрены, что не существуетъ никакой иной дроби, которая имѣя меньшіе члены, нежели взятая подходящая, выражала бы величину дроби у точнѣе.
Р — і Р
861. ѴШ.— Если тЛ-А н ситъ два послѣдовательныя прибли-р і р
женія къ непрерывной дроби х, то будетъ больше, либо меньше
Ѵьн—1
Ри—1 Рп
смотря по тому, будетъ ли -— больше или меньше чѣмъ
Пусть г будетъ полное частное, соотвѣтствующее приближенію пеи0"
Р Р Рп—1.
средственно слѣдующему за тА Въ такомъ случаѣ ж = о\ц-О—і’
слѣдовательно
-”= оГ-і9.,о!,+<Діі -Ч.-Л.ОР.+Р.-.)11
= Ря-1 <Ь-і)(Р„-і - Ря <и»).
<ік-і 4- ч«—о*
Множитель я*Рп(іп — Рй-іЗн-і положителенъ, такъ какъ „>У^і и а отсюда прямо слѣдуетъ, что
смотря по тому, будетъ ли Рп-^« — Р*9п~і > О, или <0; т.-тому, будетъ ли Л—>, или <тг*
Чп-1 Чп
смотря по
Слѣдствіе.—Изъ этого доказательства слѣдуетъ, что разности
Р„-10л - Рп^-І, Р„_1Р„ — * «
имѣютъ одинаковый знакъ.
Періодическія непрерывныя дроби.
862. Опредѣленіе.—Пусть дана непрерывная дробь
•® = I «1, »«, «3, . . а„, I . . . (1).
Положивъ, что число п неполныхъ частныхъ неограниченно возрастаетъ, разсмотримъ ряды (А) и (В)
(А) IX IX IX. . .
1 } Оз Оз
(В)
Рг Р. Р.
Чг Ч< Ов
изъ которыхъ въ первомъ содержатся подходящія дроби нечетнаго, во второмъ— четнаго порядка. Рядъ (А) содержитъ дроби, возрастающія, но всегда меньшія р
а потому члены этого ряда имѣютъ нѣкоторый предѣлъ Л Члены ряда (В),
, рі
унывая, но оставаясь всегда больше дЧ также стремятся, въ силу этого, къ Р
нѣкоторому предѣлу Г. Легко доказать, что /*=/*. Въ самомъ дѣлѣ, пусть 77
есть нѣкоторый членъ ряда (А); — представляетъ въ такомъ случаѣ со-
отвѣтствующій членъ ряда (В); но
причемъ Чи и Чп-|ч идутъ неограниченно возрастая, такъ что 5-5— стремятся
къ нулю, по мѣрѣ того какъ п приближается къ со. Такимъ образомъ, оба предѣла / и Г равны между собою. Этотъ-то общій предѣлъ рядовъ (А) и (В) и разсматриваютъ какъ величину безконечной непрерывной дроби.
Этотъ предѣлъ есть число несоизмѣримое* Въ самомъ дѣлѣ, предположивъ, что оно соизмѣримо, мы при обращеніи его въ непрерывную дробь, получили бы конечную непрерывную дробь.
863. Періодическая непрерывная дробь.—Когда въ безконечной непрерывной дроби, значеніе которой теперь вполнѣ опредѣлено, неполныя частныя воспроизводятся въ одномъ и томъ же неизмѣнномъ порядкѣ, дробь называютъ періодическою. Различаютъ два рода непрерывныхъ періодическихъ дробей: 1) простую періодическую дробь
1 ^21 йзг м ’ •* * • ' - - * • I
въ которой р первыхъ неполныхъ частныхъ повторяются въ одномъ и томъ же порядкѣ; 2) сл/ъшаяяую яе/моЭнч^схую фо#ъ
3? I 31 , ЗЦу . « . , СЕд» ч ^2, » . « ч ... |
въ которой періодической части предшествуетъ часть неперіодическая.
864. Теорема Лагранжа. Всякій дѣйствительный ирраціональный корень квадратнаго уравненія съ соизмѣримыми коэффиціентами разлагается въ непрерывную періодическую дробь. ►
1-й случай. Корни имѣютъ противоположные знаки.
Пусть уравненіе, имѣющее такіе корни, освобождено отъ дробей и приведено къ виду
Ах*4-2Вх — С = 0. . .(1).
А, В и С суть цѣлыя числа, а А и С — положительны. Если бы коэффиціентъ В не былъ четнымъ числомъ, то, перемѣнивъ я на 2Х, могли бы разсматривать ур. въ X. Ва-|-АС не есть точный квадратъ, ибо въ противномъ случаѣ ур. имѣло бы корни соизмѣримые, которые разлагались бы въ конечную непрерывную дробь.
Разложеніе положительнаго корня.—Полагая, что вышеуказанныя условія относительно.коэффиціентовъ имѣютъ мѣсто въ ур—ніи (1), разложимъ въ непрерывную дробь его положительный корень
— В + ѴВ2ННАС
х содержится между двумя послѣдовательными цѣлыми числами ац и а, 1, такъ что
гдѣ > 1. Уравненіе (1) беретъ видъ
или
Ак+іУ+2в(а1 + ^)-С = О
\ ^1/ \ х1/
— С, =0 . . .(4)
причемъ
АХ = С — 2В04 — Аа^ ]
Вг = — Аіх— В / (5).
Сі = А )
Ур—ніе (4) даетъ мѣсто слѣдующимъ замѣчаніямъ:
( Коэффиціенты Ап В1? Сх—числа цѣлыя;
(6) \ Числа А; и Сх положительны.
I + А/; = В* + АС . . . (7).
Формулы (5) непосредственно показываютъ, что Ар Ви С! суть числа цѣлыя и что С\ — положительно. Остается показать, что Аі положительно и что равенство (7) вѣрно.
Во-первыхъ, Аі>0. Въ самомъ дѣлѣ, положительный корень ур—нія (1), заключаясь между зц и а, —|- 1, заключается также между а, и Отсюда очевидно, что триномъ (!) отрицателенъ при # = и потому
Аа^+гВОі -С<0
ИЛИ А! > О.
Во-вторыхъ, формулы (5) даютъ
В1і + Мі = (В + Азц)* + А (С - 2Ва4 — Аз0,
*
или, по приведеніи: В^-]- А^ =В* + АС; и слѣд., корни ур—нія (4) также ирраціональны.
Изъ этихъ замѣчаній и вытекаетъ теорема Лагранжа.
Въ самомъ дѣлѣ, изъ ур—нія въ хі можно вывести ур—ніе въ точно такъ, какъ изъ ур—нія (1) выведено (4). Продолжая такимъ образомъ, составимъ нижеслѣдующій рядъ уравненій
Ах2 * 4-2Вл- — С =0
(8) I мг 4- звЛ - с, = о
I А + 2ВЛ - С„ = о причемъ
X = 2і ; Л?і = 23 —; • • • ; #н—1 = ;
*Ч **!»
И ”
^л-1»
(ВМ)4 + АЯСП = В‘2 + АС.
Изъ послѣднихъ двухъ равенствъ имѣемъ соотношеніе
(ВнГ4-АнА_і = Л. - -(9)
означая буквою к цѣлое положительное число В*-1-АС. Такъ какъ Ан, Ам_х и В„ суть цѣлыя положительныя числа и сумма (В*)2 + А*!^ равна опре-
дѣленному цѣлому А, то Ап, Ап_( и В„, удовлетворяющія неопредѣленному ур—нію (9), могутъ быть взяты только въ конечное числѣ значеній: въ самомъ дѣлѣ, изъ этого ур—нія непосредственно ясно, что должно быть: Вп<7*. Ап < А, < к. Число комбинацій изъ этихъ чиселъ, взятыхъ въ порядкѣ Ап, Вн, Ап_,, необходимо, конечно. А потому, составляя таблицу (8), непремѣнно найдемъ въ ней ур—ніе А<а;/ + 2Віх< — 1^ = 0, тождественное съ уравненіемъ — ранѣе полученнымъ*
Отсюда неизбѣжно слѣдуетъ, что вычисленія приведутъ къ повторенію, въ найденномъ разъ порядкѣ, однихъ и тѣхъ же неполныхъ частныхъ, и для х получится непрерывная періодическая дробь*
Разложеніе отрицательная корня. — Измѣнивъ въ предложенномъ ур—ніи х на — х, получимъ ур—ніе
А#* — 2Ю; — 0 = 0.
Разложивъ въ непрерывную дробь, указаннымъ пріемомъ, .положительный корень этого ур—нія и перемѣнивъ знакъ въ полученномъ результатѣ, найдемъ разложеніе отрицательнаго корня.
2-й случай. — Оба корня положительны. — Пусть будетъ а — большій корень, и пусть онъ содержится между двумя послѣдовательными цѣлыми числами а и а-(-1. Пусть, затѣмъ, другой корень, 3» не содержится въ этомъ интерваллѣ. Положивъ & = ^ + Х, найдемъ ур—ніе въ X, имѣющее два дѣйствительныхъ корня X' и X"; корни же а и вычислимъ по формуламъ
2 = а
гдѣ, слѣд., X' есть положит. количество, меньшее 1; напротивъ, X" — отрицательно. Такимъ образомъ, X' и X" можно разложить въ непрерывныя дроби вышеуказаннымъ пріемомъ.
Въ томъ случаѣ, когда оба корня а и содержатся между двумя послѣдовательными цѣлыми числами а и а 4-1, числа X' н X" — оба положительны и < 1 - Въ этомъ случаѣ дѣлаемъ подстановку
Ур—ніе въ у имѣетъ оба корня положительные и большіе 1. Если большій корень этого уравненія содержится между двумя послѣдовательными цѣлыми числами Ь и Ь-рІ; а другой корень < Л, то имѣемъ разсмотрѣнный уже случай. Въ противномъ случаѣ полагаемъ
У = Н
и т. д. Непремѣнно дойдемъ до такого ур—нія. котораго большій корень содержится между двумя послѣдовательными цѣлыми числами, а другой не заключается въ этихъ предѣлахъ. Это объясняется тѣмъ, что разность между корнями і и р есть количество конечное, между тѣмъ какъ разность двухъ послѣдовательныхъ подходящихъ дробей стремится къ нулю, когда число неполныхъ частныхъ неограниченно возрастаетъ. Слѣд. невозможно, чтобы оба корня а и разлагаемые въ непрерывныя дроби по формуламъ
имѣли, неопредѣленно, одни и тѣ же неполныя частныя.
3-й случай.— Оба корня отрицательны.— Этотъ случай непосредственно сводится къ предыдущему замѣною х на (—х).
865. Примѣръ I.—Развернуть въ непрерывныя дроби корни уравненія Зх2 — 2я— 2 = 0,
Корни этого уравненія противоположны по знаку. Положительный корень
1 +Ѵ7
3
2 < <3; 3<1-)-]/7<4, слѣд. 1 < х < и потому а1 = 1, и
3 ‘
Отсюда ' Р /7 — 2 3
Находимъ, что содержится между 4 и 5; слѣд.
4: и х. — 2 -4-1/7 ~ 4 •
* ’ 1 1 Г I іГа
Отсюда
1 ,/= о 1 2 + Г7
✓ ѵ = Ѵ *—2» и х* = ~^------------=—4г - •
Продолжая такимъ образомъ, найдемъ
^8 11 ***3 9 *
Слѣд., начиная съ четвертаго, неполныя частныя будутъ періодически повторяться; періодъ будетъ 1, 4, 1, 1; и .
с
1
_ і
Г. Л 7
(Г
Отрицательный корень,
1
онъ выражается смѣшанною періодическою дробью, и въ неперіодической части ея — только одно неполное частное, равное 0; періодъ же =1, 1, 4. 1, т-е. равенъ обращенному періоду положительнаго корня.
Примѣръ II. — Развернуть въ непрерывную дробь корни уравненія 2х» —6л-{-1 =0.
< Оба корня положительны и суть ,
х' содержится между 2 и 3; слѣд. ах = 2, и
34-1'7 „ . 1 14-1'7
х — --= 2 + —; откуда Хі = —-д —>
что приводитъ къ предыдущему примѣру; слѣд.
ж'=|2; ІТІГІД, ГѴѵІ.. • • I
Такъ какъ х" < 1, то = 0; затѣмъ
3 = у = 3 4-/7; затѣмъ
2 4-1'7
• ' «,=э. Уі=~
_і __1 + Ѵ7 .
— 1* Уа ’ о
_ 1 _ 1 + 1'7
1 ’ У» з
что снова приводитъ къ предыдущему примѣру; слѣд,
я"=іо; 5, і, і, 17Т17Т ЛТХТХ- . - і
Это еще можно написать такъ:
= I 0; 5,1, ГТХі ГТ.Т1,: • • I-
866. Теорема (обратная Л а гр а и же вой). — Всякая непрерывная періодическая дробь представляетъ корень квадратнаго уравненія съ соизмѣримыми коэффиціентами.
Разсмотримъ два случая.
I. Случай чистой періодической непрерывной дроби. — Пусть дана чистая періодическая дробь
/- 1 ’Ч
у = I «п а* - * • а»; «г • • - аЛ; • I •
Назовемъ ур и Ур-м конечныя непрерывныя дроби, полученныя, если взять р ир+1 періодовъ; имѣемъ
Если р приближать къ ос, то уР и Ур-р стремятся къ у; слѣд.
у = I аг . . . а„, у | . и- потому
„ = ^ + Рл-ЗІ ’ 7 УЧ« + Ч..-Г
Р—і Р« < ,
если — и о1 суть два приближенія п—1-го и м-го порядка къ конечной непрерывной дроби, образуемой періодомъ. Изъ послѣдняго ур. имѣемъ <иг+(<и-рй)у-р„-і=о- • -<і). -«
Отсюда видимъ, что чистая періодическая дробь у есть положительный корень квадратнаго ур—нія, коэффиціенты котораго суть числа цѣлыя, а знаки корней противоположны.
II. Данная дробь смѣшанная, — Пусть дана смѣшанная періодическая дробь
я = | а2 , . . а5; ап ая . . . аи; . . . | .
Если положить
I оп в, . . . ая, Яц а, . . . ап, . . . | = у, то
х= I 01, х» . . . Ог у I , откуда . .
х— . . . р)
гдѣ и суть приближенія порядковъ ц — 1 и д къ конечной непрерывной дроби | а1т аа . . . , образуемой неперіодическою частью.
Съ другой стороны, у есть корень ур—нія (1). Если исключить у изъ (1) и (2), то получится квадратное ур. въ (я) съ соизмѣримыми коэффиціентами.
867, Примѣчаніе. — Естественно изслѣдовать, что представляетъ отрицательный корень ур—нія (1), положительный корень котораго равенъ чистой періодической дроби
I - • • ан» «і, а3 • - ан; . . . | .
Для этого докажемъ лемму: ,
Если | ап ай . . . а I еть конечная непрерывная дробь, въ ко-р Р
торую развертывается число большее 1; то р равно непрерывной дроби | ая, ая-4 . . . а2, а2 | , которая получится, если неполныя частныя данной Написать въ обратномъ порядкѣ; а есть пред-Чп—і р послѣдняя подходящая дробь къ непрерывной .> - - •
Нужно доказать равенства:
Отсюда легко вывести требуемыя равенства.
Еслибы было ^<4, тогда было бы = 0, и первое равенство, содержа* 1 Р
щее дробь —, не имѣло бы мѣста. Въ этомъ случаѣ тт замѣняютъ обратною дробью, которая > 1.
Пользуясь этою леммою, можно показать, что абсолютное значеніе отрицательнаго корня уравненія ’ ♦ е
Ч,^ + (Чя-і-рл)у -Ря->=0 -0)
равно обратному значенію чистой періодической дроби, которая получится, если написать въ обратномъ порядкѣ звенья періода данной періодической дроби.
Сгруппировавъ вмѣстѣ члены съ одинаковымъ указателемъ, можно ур. (1) написать въ видѣ
(<Іиу—р„) у = р..-і—Я,._р
' отсюда
__Рн-1 — уфи—1
У~ ЗиУ-Р« ’
и это ур—ніе .удовлетворяется. если у замѣнить отрицательнымъ корнемъ у1 ур—нія (1).
Положивъ у = — даемъ этому равенству видъ
Р^ + Ом ' ‘ ‘ Н
Такъ какъ теперь положительный корень ур—нія (1) представленъ простою періодическою дробью, то первое неполное частное а1 уже не равно нулю, ибо во всякой непрерывной дроби всѣ неполныя частныя, слѣдующія за первымъ, отличны отъ нуля.
При этихъ условіяхъ можно примѣнить нашу лемму, и это даетъ
р^4 = | . а2аі I ,
А Д—1
а уЯ— будетъ предпослѣднею подходящею дробью къ этой непрерывной дроби; слѣдовательно х * —. ---- ---------
& == 1 • • • Л1» ДЛ“1 • * • ’ I »
и теорема доказана.
Примѣръ. Пусть дана чистая дробь
х = | а; а, а, . . . | .
Непосредственно имѣемъ
х = а 4- или — аж — 1=0,
• х1 7
откуда
4 а + Ѵ«а + 4
• 7? ‘-------
число несоизмѣримое, ибо я —дробь безконечная.
Отсюда, между прочимъ, ченмъш 4-лл, «е можетъ
Отрицательный корень
равенъ непрерывной дроби -
слѣдуетъ, что квадратъ цѣлаго числа, увели-бытъ игочнъміѣ квадратомъ.
а — / а2 4
Приложенія.
868. Превращеніе обыкновенныхъ и десятичныхъ дробей въ непрерывныя.
Когда числитель и знаменатель обыкновенной дроби выражены въ большихъ числахъ, удобнѣе, для болѣе яснаго сужденія о ея величинѣ, обративъ ее въ непрерывную, составить приближенія. Пріемъ для обращенія прос/ой дроби въ непрерывную, указанъ въ § 849.
Примѣръ. Обратитъ дробь вг непрерывную.
Дѣлимъ числ. на знам., знаменателя на 1-й остатокъ, 1-й остатокъ на 2-й и т. д.; дѣйствія эти располагаемъ такъ
3 1 15 10 5 ** а 1 3
76895 19527 18314 1213 119 23 3’ 4 3 1
18314 1213 119 23 4 3 0
Неполныя частныя помѣщены въ верхней графѣ. Имѣемъ
76895
І9527
1
і / Г
юн-і
3
Подходящія дроби суть:
3 4 63 1! Г 1б’
634 3233 16799 20032 76895
161* 8 2* 4266 ’ 5087'’ 19527’
Взявъ, напр., за истинную величину данной дроби приближеніе нашли бы, л 1 1 что погрѣшность меньше пли и т. д.
Приводимъ примѣръ на превращеніе десятичныхъ дробей въ непрерывныя.
При м о ъ.—Найти пішближенія числа г.
Оно содержится между двумя дробями
__ 3141592653
А— ]0В
„ 3141592654
и В =--------10Г—
Развертывая ихъ въ непрерывныя лаженіямъ неполныя частныя суть: 3,
дроби, находимъ, что общія обоимъ раз-7, 15, 1, 292, 1, 1, 1; такъ что
- = | 3; 7, 15, 1, 292, 1, 1, 1 . . . | .
Отсюда имѣемъ слѣдующія подходящія дроби къ
3 22 333 355 103993
Г 7; 106’ 113; 33102 *
Таковы простѣйшія значенія т:; изъ нихъ второе приписываютъ третье1—Риварду * четвертое—Лфіаму Мецію.
869, Обращеніе несоизмѣримаго квадратнаго корня въ непрерывную дробь.
Очевидно, что несоизмѣримый квадратный корень нельзя превратить въ конечную непрерывную дробь; ибо каждая такая дробь приводится въ обыкновенную дробь, члены которой соизмѣримы. Слѣдовательно, несоизмѣримый квадратный корень превратимъ только въ безконечную непрерывную дробь. Докажемъ, что такая дробь необходимо будетъ періодическою непрерывною дробью.
Пусть Ь будетъ положительное цѣлое число, которое не есть точный квадратъ; и пусть будетъ наибольшее цѣлое число, содержащееся въ |/ Очевидно
Ѵк=а1+(}/к-й1)=ва^=аі+-и-.• .(і)
г А 4~ У К ~гд1
»1
Такъ какъ }/К — есть положительное число меньшее 1, то изъ (1) слѣ У'К + л, «
л ѵетъ, что ——- 1 > 1. гі
Пусть наибольшее цѣлое, содержащееся въ —-—, будетъ то <
У К+яі т 1 - (Ь1П - Д1) _ м ~ - а^- =
-О1-І Г| — °1 -I- +(Ѵ1 _«,)]
=ь. ч—=д—-1Тт± гі .
гдѣ
Здѣсь снова
И ’
І
- аа«
п
^-^>1; и если Ьа будетъ наибольшее цѣлое, содержа* г2
щееся въ
, ТО
— (Ьу2— йд)
Кт — (&2 — &>)*
'!•
л ь И-*»*
гдѣ а3 = Ѵа —а2 И Г3 = —
Можно вести вычисленіе такимъ способомъ какъ угодно далеко; такъ что вообще • •
п
гн-1
я
Ы —а *
* Слѣдовательно
гдѣ «„ = ^1^-1—а„^ И ги
* л—1
Выше было показано, что эта непрерывная дробь безконечна. Докажемъ теперь, что это будетъ яеркх>ичеекдя непрерывная дробь.
Для этого, во-перкыіъ. докажемъ, что всѣ количества ап а2, а3, . . . ; гп га* гл • - • цѣлыя иоложжтедьныя числа.
Будемъ называть V Л5 ~—5—-Ч --------5 . яашылсѵ часткы-мм.
Г1 г2
' Р Р* Р" г~
Пусть будутъ ф’ фг, три послѣдовательныя приближенія къ уК, изъ р."
коиіъ о;; пусть будетъ приближеніе, соотвѣтствующее неполному частному Ь„.
Полное частное на этой стадіи процесса обращенія будетъ -
Р" 5 р' । р
Извѣстно, что 0^, = и если свда
вмѣсто Ъп подставить
то найдемъ рЛЙ- Итакъ
Iй РХГ + а» Р' + г» Р
<і'ѴХ + «н(1' + гя(гИ
Освобождая отъ знаменателя и приравнивая раціональную часть раціональной, а ирраціональную ирраціональной, находимъ
апР'4-г„Р = Я(Г, ай(Г + ^ = Р', откуда
ап (IV - Р'ф) = РР' - г* (Р<Г - Р^) = ОД'* - рг
Такъ какъ Р(/— Р'9= + ^ то отсюда, во-первыхъ, очевидно, что ап и суть числа цѣлыя; а какъ, по § 861, Р<}' — Р'О, РР' —09'Х и ” Р'’ имѣютъ одинаковый знакъ, то ясно, что ап и гп положительны.
Теперь легко показать, что неполныя и полныя частныя повторяются. Мы видѣли, что X ~ &па, а какъ и гп_{ положительны, то заключаемъ,
что ая*<И, откуда аЛ<[/К, и потому не можетъ быть больше аѵ Отсюда слѣдуетъ, что не можетъ имѣть иныхъ значеній, кромѣ 1, 2, 3, . . . , аг Итакъ, число различныхъ значеній ап не можетъ превосходить аѵ
Затѣмъ, а^і = гп6п — апт т.-е. = ап + , н слѣд. гЛ&№ пе мо-
жетъ быть больше 2а^ а какъ Ьп есть положительное цѣлое, то не можетъ быть больше 2аѵ Итакъ, гп не можетъ имѣть иныхъ значеній, кромѣ 1, 2, 3, , , . , 2ап т.-е. число различныхъ значеній гп не можетъ бытъ больше 2а,.
Такимъ образомъ, полное частное 1 пе можетъ имѣть болѣе 2^ .
*Л
различныхъ значеній, т.-е. никоторое полное частное, а яотолу и осп» по-слѣдующгя, должны повториться.
Такъ какъ Ьл есть наибольшее цѣлое, заключающееся въ * то не-гп
полныя частныя также должны повторяться^ и число ихъ въ каждомъ циклѣ не можетъ быть больше 2а12.
Заключаемъ, что всякій несоизмѣримый квадратный корень развертывается въ періодическую непрерывную дробь.
870. Примѣръ I.— Развернуть ^/13 въ непрерывную дробь.
Вычисляя I/ 13 съ точностью до 1, находимъ, что онъ содержится между 3 и 4, такъ что
|/13=3-|-і5 гдѣ у > 1.
Для нахожденія у пользуемся этимч, ур—мъ*, изъ него
= ___— ___/13 + 3 _г'Тз + з
пз-з (Из^з)(Из + з)“ 4
Но 3 < у 13 < 4; откуда 6 у/1 д _з < 7, 'слѣд. содержится
6 7.,
между ? и 4, т.-е. больше 1, но <;г, такъ что
_/І8 + 3 1
У — 4 ==1 + у’ гдѣ У!>1.
Уі
Отсюда 1
ѵ = _А_===4(/Тз-ні)_/ТЗ + 1
• /13 — 1 ]2 — з *
Замѣчая, что 3<ХР 13<^4, имѣемъ отсюда 4<<}/ІЗ-|-1 <С5, слѣд,,
/ГЗ +1 4 5
—3— содержится между % и т.-е. > 1, но <2; потому
Продолжая такимъ образомъ, имѣемъ
/13= 3 4-1 гдѣ 1==/Тз —3 </ іУ
/13 —2 3
1 У»
1 гдѣ — = У2
/ > і і 1 л, 1 /13 — 1
7 Уъ= 1 Н---1 гдѣ — —---т—
,,.=«+1^1=^-..
Отсюда заключаемъ, что ув=у, такъ что начиная съ зтого мѣста будутъ повторяться прежнія неполныя частныя, и потому
14-ит. д.
»
Для повѣрки результата, обратимъ найденную періодическую дробь въ ирраціональность, изъ которой опа возникла* Перенеся 3 въ первую часть, имѣемъ і • л
1
есть періодическая дробь съ пятичленнымъ періодомъ; къ знаменателю
Это
пятаго члена прикладывается снова вся періодическая дробь х —3; такъ что
Обращаемъ вторую часть этого ур—нія въ обыкновенную дробь.
і । 1 18 + 5* „ 11+3*
+ К+3*\= ІИ7НаК0НеЦЪ Х~ = 18+^’ \ 7 + 2я ]
Это ур—ніе приводится къ квадратному я2 =13, откуда положит. корень х = |/13.
Примѣръ II.— Разложитъ |/а24“1 непрерывную дробь, полагая, что а — цѣлое положительное число, \
Л I
Пусть # = у'а*-|-1; такъ какъ & содержится между а и «4-1, то можемъ положить х —аД-г- а слѣд. 1/а*4- 1 =:« 4“ откуда ----
________________хі г ' 1 1 Уа2-}-1— а = а 4- 4“ 1 -
Замѣчаемъ, что содержится между 2а и 2а 4~ 1, такъ что = 2а 4—’
«4* /а24-*1=2а4”^-, откуда = ---• Отсюда видно, что
у а2 +1 —а
х^ = х^ а потому
|/а«-}-1= | а; 2а, 2а, 2а, . . , | .
Полагая здѣсь послѣдовательно а=1; 2; 3; . . . найдемъ
Примѣръ ІП. — Развернуть въ непрерывную дробь у а* — 2а. иЬь а—-щыае положительное число.
Пусть #=|/а2-|-2а; х содержится между а и а-|-1; слѣд.. х=а-4^
откуда я, =------х—— ; затѣмъ, т. = 1 -ртг, откуда = а — )/а* — 2а.
Число х* содержится между 2а и 2а 4~Ъ положивъ = 2анайдемъ х3 = х^ такимъ образомъ
х = | а; 1, 2а, 1, 2а, . .
Напр., положивъ а=1, найдемъ
1/3= | 1; 1, 2, I. 2
Примѣръ IV. — Развернуть еторнн ур—нія х* — 5& — 3 = О въ непрерывныя дроби.
„ , 5 д: Ѵ37 . , 5 и- > §7
Имѣемъ х ~ —2~—; взявъ большій корень, находимъ х = —ъ— =
- Ѵ37 — 5 , , 6
= о-
9
*
1
4
Затѣмъ: —
и т. д. Получаемъ неполныя частныя 5. 11 61 72 2; п; Уз и т- Д*
О ~ 0 4" —* = 0; т?
1 Ѵ37 + 5 ' 1
871. Вычисленіе логариѳмовъ.
Примѣръ. — Найти 1а 200?
Вопросъ приводится къ рѣшенію ур—нія 10х =200.
Полагая х послѣдовательно = 1, 2, 3, находимъ для 10х величины 10, 100, 1000, . . , Такъ какъ 200 содержится между двумя послѣдними числами, то х заключается между 2 и 3; слѣд. можно
положить
-- • л’і
причемъ я^Ж Подставляя это выраженіе вмѣсто я въ начальное ур—ніе, 2_|_і 2. 1
находимъ 10 «і =200, или 10210^ =200, или 10г» = 2; а отсюда, по возвышеніи въ степень
Полагая = 2, 3, .4, я . находимъ для 2\ величины 4, 8, 16 * . . Такъ какъ 10 содержится между 8 и 16, то находится между 3 и 4, такъ что
<г1 —3^ — ? • • * (3)
гдѣ ^>1- Подставляя это значеніе въ ур—ніе (2):
2^х« = 10, иля 23 . 2х» = 10 или 2х* == “?
отсюда, по возвышеніи въ степень
*
(^•=2. . . (4)
/10\
Полагая послѣдовательно равнымъ 2, 3, 4 . • * находимъ для 1-^-1 100 1000 10000
числа ^5 512 ’ ’доЭб • * -
Число 2 содержится между послѣдними двумя дробями; слѣд. а* заключается между 3 и 4, а потому
гдѣ > 1. По подстановкѣ въ (4), получимъ
откуда
34*1 1
10 V а* /10 \ _ 1024
8/ ,“2’ ІШІ \8 "“1000
/1О24\^_1О .
УіООО^ ~ 8 ' * ’
Подставляя вмѣсто числа 2, 3, .. . . , найдемъ, что 9<Ул*3<уіО, такъ что можно положить
= 9гдѣ х, > 1.
Сближая результаты (1). (3) . . . , имѣемъ
х = | 2: 3, 3, 9 . . . | .
Г
Первыя четыре приближенія къ х будутъ;
2
7 23 214
3’ ІО’ 93 ’
ИЗЪ
которыхъ
послѣднее
точно до д^д
Впрочемъ этотъ методъ вычисленія логариѳмовъ непрактиченъ, такъ какъ требуетъ кропотливыхъ вычисленій; потому-то для вычисленія логариѳмовъ п употребляютъ болѣе совершенный методъ безконечныхъ рядовъ.
872» Рѣшеніе неопредѣленнаго ур—нія Н/ = с въ цѣлыхъ числахъ.
Примѣръ. Рѣшитъ ур—ніе 8я -|- IЗу = 159.
' 8
' ♦- Развернувъ отношеніе коэффиціентовъ въ непрерывную дробь, находимъ
А— I о- 1 І 1 I 2 I
13 Ѵт 1 ’ 1» 11 I
отктда подходящія дроби:
оіі2за
м 1’ І’ 2’ з’ 5* 13"
мі 8
“ Взявъ разность двухъ послѣднихъ и замѣтивъ, что есть приближеніе четнаго порядка, по § 855 имѣемъ
।
' П-5- + ізУ5.»'кУ®8Х5+13Х(-3)=+1.
к
Умноживъ обѣ части на 4-159, находимъ
8 . (5 . 159)4-13 . (—3X159) = 159. *
Сравнивая это тождество съ даннымъ ур—мъ, замѣчаемъ, что послѣднее сдѣлается тождествомъ, если положить
х = 5 X 159 = 795; у = — ЗХ 159 = — 477.
Такова одна пара цѣлыхъ рѣшеній; всѣ прочія цѣлыя рѣшенія содержатся въ формулахъ
х = 795 4 13* и у = — 477 — 81.
।
Неудобство этого метода заключается въ томъ, что обыкновенно формулы для х и у ч получаются недостаточно простыя.
Обобщимъ этотъ пріемъ. Если подъ а и Ъ разумѣть абсолютныя значенія коэффиціентовъ, то, измѣнивъ; если это окажется нужнымъ, знаки неизвѣстныхъ х и у, можно всегда дать ур—нію видъ ах — Ъу=с.
Р _
Если тс-— будетъ предпослѣдняя подходящая дробь къ непрерывной, въ ко-Чм-1
а • торую развертывается & то
откуда, умноживъ обѣ части на с . (—1)'\ найдемъ
і’. ;
Сравненіе съ даннымъ ур—мъ покажетъ, что данное ур—ніе обратится въ тождество, если положить ’
такова одна пара цѣлыхъ рѣшеній даннаго ур—нія. ' $'*
♦ ф
• . ъ-А • ѵ
873. Историческое примѣчаніе. Изобрѣтеніе непрерывныхъ дробей приписываютъ лорду Бруннеру (1655); онъ напалъ на это открытіе, пытаясь преобразовать безконечныя выраженія, данныя Валлисомъ для площади круга. Затѣмъ, Гюйгенсъ указалъ примѣненіе непрерывныхъ дробей къ приблизительной замѣнѣ сложныхъ отношеніи простѣйшими. Настоящая теорія непрерывныхъ дробей дана была Эилсроліг и усовершенствована Латрамже.ш, .Га#сеолъ и другими.
ГЛАВА ЕІѴ.
Неопредѣленный анализъ второй степени.
874. Начнемъ разсмотрѣніемъ простѣйшихъ случаевъ рѣшенія въ положительныхъ цѣлыхъ числахъ уравненія вторбй степени съ двумя неизвѣстными
а#* + Ъху + си* 4- + / = 0
гдѣ а, 6, с, . , . суть числа цѣлыя.
I. е = 0. Въ ур—ніи недостаетъ члена съ квадратомъ одного изъ неизвѣстныхъ; пусть, напр., е = 0. Выражая х черезъ у, найдемъ
х = —
или, совершая дѣленіе:
, а(^_ _ а . ай е 62 6 '
Х ~ ~Ь & + Ъу + сГ~ ’
а умноживъ обѣ части на 62, получимъ
, , , , а&—
Ъ*х — — (іоу 4- оа — ое---——4-----
Чтобы для ЬѴ имѣть число цѣлое, биномъ й# + гі долженъ дѣлить на цѣло Находимъ всѣхъ множителей числа а№ — Ме + 63/’ и приравниваемъ Ъу + гі, поочередно, каждому изъ нихъ. Если получится такимъ образомъ для# число цѣлое и если соотвѣтствующее значеніе х будетъ также числомъ цѣлымъ, то цѣль будетъ достигнута. Такъ какъ число множителей—ограниченное, то число цѣлыхъ рѣшеній необходимо будетъ ограниченное.
Въ частномъ случаѣ, если числитель а<і* — Ые + б9/* обращается въ нуль, ур—ніе приметъ видъ
(№х + аЬу — ай 4" М (Ь# 4“ Ф — 0.
Приравнивая нулю того или другого множителя. найдемъ: либо опредѣленное значеніе для у, при произвольномъ я:, когда й дѣлится на Ь; либо неограниченное число цѣлыхъ значеній для у и а?, когда можетъ быть рѣшено въ цѣлыхъ числахъ неопредѣленное ур—ніе Ых 4- аЪу — ай +&е — 0.
Оба эти рода рѣшеній могутъ случиться и одновременно, какъ, наприм. въ ур—ніи,
2#2 + Зач/— 9#— 6а;+10 = 0,
котораго коэффиціенты удовлетворяютъ соотношенію ай2 — Ые + /63 — 0, и которое поэтому можно представить подъ видомъ
(2у + За? —5) (# — 2) = 0,
Приравнивая нулю перваго множителя, получимъ рѣшенія: у = 1-^3/, я = 1 — 2г. Приравнявъ нуль второго множителя, найдемъ: # = 2, не содержащееся между предыдущими рѣшеніями, причемъ а? остается совершенно произвольнымъ.
И, с —0 и а —0: въ ур—ніи недостаетъ членовъ съ квадратами обоихъ но извѣстныхъ; заключенія остаются тѣ-же, а дробный членъ принимаетъ видъ
И — Ъ& + *
Если числитель этой дроби обращается въ нуль, что можетъ пмѣть мѣсто только при соотношеніи
Ь[— сіе = 0,
такъ какъ (ибо ур—ніе было бы въ такомъ случаѣ только 1-й ст.), ур—нію можно дать видъ
№ху 4~ 1)еУ + Ь( — 0 или (Ьу -р с?) (бж + е) = 0.
Это ур—ніе или вовсе не имѣетъ цѣлыхъ рѣшеній; или оно можетъ быть удовлетворено опредѣленнымъ значеніемъ одного неизвѣстнаго при произвольной величинѣ другого; или, наконецъ, когда и е и сі дѣлятся на б, которое-ри-будь одно изъ неизвѣстныхъ остается совершенно произвольнымъ, а другое получаетъ опредѣленное значеніе.
Найдя цѣлыя рѣшенія, остается выбрать изъ нихъ положительныя.
875. При мъры.—I. Рѣшить въ положительныхъ цѣлыхъ числахъ ур—міе.
2ху — 12а? — оу = 11.
Это есть ур—ніе первой степени относительно у. Выражая у чрезъ г, находимъ:
—12^+11
& ” 2х— 5 1
и исключая цѣлое, имѣемъ:
у = 2х — 1 + 9 1 2а? — 5
Чтобы у было числомъ цѣлымъ, необходимо должно быть числомъ цѣлымъ; мы найдемъ это цѣлое, приравнивая 2ж — 5 дѣлителямъ б тп, которые суть: ±1, ±2, ±3, ±6. Такимъ образомъ получаемъ ур—нія
2я— 5 = ±1, 2г— 5 = ^2, 2# — 5 = =ЬЗ, 2т — 5 = ^6.
Изъ нихъ второе и четвертое не допускаютъ цѣлыхъ рѣшеній, а первое и третье даютъ для х значенія 3, 2, 4, 1. Вычисляя соотвѣтствующія значенія у, находимъ рѣшенія:
г = ?/ —11; а? = 2, ?/ = — 3; я = 4, # = = Ж ——1, .
изъ коихъ оставляемъ только положительныя рѣшенія, и такимъ образомъ находимъ двѣ пары:
х = 3, у = 11; я = 4, у — 9.
П. Рѵыиший положительныхъ цѣлыхъ числахъ ур—ніе.
Рѣшая относительно у, имѣемъ:
_ — Зд;» +2ЛУ+35, 7 а?— 5
Исключая цѣлое число, для чего обѣ части множимъ на 7, находимъ:
Умножая обѣ части на 7, и снова исключая цѣлое имѣемъ:
ІО I П1 <1 1710
49у + 2ІЯ7 + 1 = ~--- *
1 га? — о
Приравнивая, какъ и въ предыдущемъ примѣрѣ, 7 г —5 множителямъ числа 1710, найдемъ, что единстванішя положительныя цѣлыя рѣшенія суть:
*г 2, у — 3; г — 1, у —- 1
ПІ. Въ ур—ній За? 4* Засу — 4у = 14, выражая у черезъ я;, имѣемъ:
„14-3ж_ 10 .
У~ Зх — 4— +3ж — 4’
затѣмъ За?—4 —±1, ±2, ±5, ±10,
откуда ж=х2, у = 4; <т=3, у = 1-
876. Покажемъ теперь! какъ рѣшается въ положительныхъ цѣлыхъ числахъ общее ур—ніе второй степени съ 2 неизвѣстными, которому для удобства дадимъ видъ:
а?/* + 2Ло?у + Ьх* + 2дя + 2/у 4*с = 0-
Рѣшая его какъ квадратное относительно у, найдемъ:
ау + ^ + Г“ — аЪ)& + 2 (Л/ — ау)г Ч- (У'2 — ас). . .(1).
Чтобы у и х могли имѣть положительныя цѣлыя значенія, подрадикальное выраженіе, которое для краткости представимъ въ видѣ 7x^4- 2д#+ должно быть точнымъ квадратомъ; пустъ
ря? + + г =
Рѣшая это ур—ніе какъ квадратное въ х, имѣемъ
<7 — ± ^2 — _рг 4-
подобно предыдущему, подрадикальное количество должно быть точнымъ квадратомъ; пусть оно =/3, такъ что
& — = д2 — рт.
Если это ур—піе не можетъ быть рѣшено въ цѣлыхъ положительныхъ числахъ, то и данное ур—ніе не можетъ имѣть положительныхъ цѣлыхъ рѣшенііЕ
Если а, Л, всѣ положительны, то ясно, что число рѣшеній будетъ ограниченное; въ самомъ дѣлѣ, при достаточно большихъ численныхъ значеніяхъ х и у знакъ первой части ур—нія зависитъ отъ знака трехчлена ау2 4- 21іху-\-Ъз^ слѣд., первая часть при большихъ положительныхъ цѣлыхъ значеніяхъ х и у не можетъ быть нулемъ.
Также, если /г2 — аЪ въ (1) отрицательно, число рѣшеній будетъ ограниченное
с
— 953 —
Примѣръ. Рмшшь фмы.та ноложшпе.гьиьт чжлаяь уу--ніе. х* — 4ху + бу2 — 2г — 2Оу = 29.
Рѣшая это ур—ніе какъ квадратное относительно имѣемъ
х = 2у + 1 ± ѴЗО + 24у — 2/.
Написавъ подрадикальное количество въ видѣ 102—2 (у — 6)3, замѣчаемъ, что (у— 6)2 не можетъ быть больше 51. Попытками убѣждаемся, что подрадикальное количество дѣлается точнымъ квадратомъ, когда будетъ (у— 6)2=1,или 49. Отсюда находимъ, что положительныя цѣлыя значенія у суть: 5, 7 и 13. Когда у = 5, будетъ а? = 21, или 1; когда у = 7, тогда х — 25, или 5: когда у = 13, будетъ # = 29, или 25.
877. Уравненіе ах* 21іху + Ъу* + Н“ -{у -^с — к можетъ быть рѣшено въ положительныхъ цѣлыхъ числахъ, если лѣвая часть его можетъ быть разложена на два раціональныхъ линейныхъ множителя. Напр., пусть требуется рѣшить ур—ніе
— 13#у Ч~ бу2 = 16.
Первая часть разлагается въ произведеніе (З# — 2у)(2#— Зу); и какъ# и у должны быть числами цѣлыми, то оба множителя—числа цѣлыя, изъ которыхъ одно должно равняться одному изъ множителей 16-ти, а другое—другому. Та* кимъ образомъ, вопросъ приводится къ рѣшенію 5 системъ совмѣстныхъ ур—ній.
Зх —2у= + ]6, Зл? — 2у = л+і 8, З# — 2у=± 4, З# — 2у = ^ 2, З# — 2у = л± 1,
2х — Зу = 1;
2#-Зу = г?г 2;
2#— Зу = 2к 4;
—Зу=і^ 8;
2# — Зу = 16;
Отсюда находимъ, что 5з? должно равняться
±:(48 —2), ^(24-4), - (12 - 8), ^(6-16), +(3- 32), и слѣдовательно, единственныя цѣлыя значенія х суть 4 и 2, а соотвѣтствующія значенія у суть 2 и 4.
878. Мы нашли, что рѣшеніе общаго ур—нія можно привести въ зависимость отъ рѣшенія ур—нія вида Ху2 = ± а, гдѣ X и а положительныя цѣлыя числа.
Уравненіе #2-)-Хуа =— а, очевидно, не имѣетъ дѣйствительныхъ рѣшеній, такъ какъ сумма положительныхъ чиселъ не можетъ равняться отри на тельному. Уравненіе #2-(-А‘у2 = а имѣетъ опредѣленное число рѣшеній, которыя можно найти попытками. Остается разсмотрѣть ур—нія вида х*—
879. Теорема. Уравненіе я? — Хуа = 1 .ігожет быяіъ л
положи/нельмы#^ числияъ.
/— Р Р* Р*1
Обратимъ УАТ въ непрерывную дробь; пусть І7" бУдГгь ТРИ послѣдовательныя подходящія дроби, и пусть полное частное, соотвѣтствующее дроби
РХ I о
"Цр будетъ -4 — » Изъ теорія непрерывныхъ дробей (§ 869) извѣстно, что
Я
>п(Р9'—р'д)=Ка'2—р'2 . - . (іх •
УК *4- д
Но въ концѣ періода гп = 1. Въ самомъ дѣдѣ, пусть----;5 будетъ полное
7’я
УА-Н?! частное, непосредственно предшествующее второму полному частному —-—, гі
н
когда оно повторяется, то ------7—и
* м
полныя частныя; слѣд.
*
будутъ два послѣдовательныя
і/
но К — Н|» = Г|, слѣд., гм = 1. Итакъ, — М” +2*1 —У? — гдѣ есть предпослѣднее приближеніе нѣкотораго періода.
Если число частныхъ въ періодѣ — четное, то есть четное приближеніе;
такъ что р’([ — рд'=1. Въ такомъ
слѣд., оно больше І'Х, и потому больше случаѣ, рг* — Хтд'2 = 1, и слѣд.
х = рг,
даютъ рѣшеніе ур-нія —К#»=Е
Такъ какъ Я есть предпослѣднее приближеніе какого угодно періода, то число рѣшеній неограниченно.
Если число частныхъ въ періодѣ—нечетное, то предпослѣднее приближеніе въ первомъ періодѣ есть приближеніе нечетное; но предпослѣднее приближеніе во второмъ періодѣ есть приближеніе четкое. Слѣд., цѣлыя рѣшенія полу-р#
пАплгал ~гдѣ ^7 есть предпослѣдннее приближеніе во вто-. , періодахъ. Заключаемъ, что число рѣшеній—не-
чатся, полагая #=У, # = д', ромъ, четвертомъ, шестомъ, . ограниченно *
880. Рѣшеніе въ цѣлыхъ
Если число частныхъ въ
«оложи?ме.іь«ы<Го числахъ ур—мія я* — ?^=— ].
періодѣ—нечетное, и если —г есть нечетное пред-
послѣднее приближеніе въ какомъ-либо-періодѣ, то я слѣд., р'ч—рд'=—1.
Въ этомъ случаѣ у4 — Мд'2 = —1, и цѣлое рѣшеніе ур—нія — \ѵ2— — 1 наѣдемъ, положивъ х =^', # = д', гдѣ есть предпослѣднее приближеніе въ первомъ, третьемъ, пятомъ,... періодахъ.
881. Примѣръ. Ььяпмь въ цѣлыхъ положительныхъ числахъ уравненіе
Имѣемъ: ѴіЗ = | 3; I, I, 1, 1, 6; . . . | .
Число частныхъ въ періодѣ—нечетное, предпослѣднее приближеніе въ пер-18
вомъ періодѣ — “; слѣд., х = 18, # = 5 представляетъ одно нзъ рѣшенія ур—нія о
649
Предпослѣднее приближеніе во второмъ періодѣ ~ слѣдоват. ас = 649, #=180 даетъ еще пару рѣшеній ур—нія іе3 —13#* = —1.
Составляя послѣдовательныя приближенія періодовъ, можно такимъ путемъ получить сколько угодно цѣлыхъ рѣшеній предложенныхъ ур—ній.
882. Коикі имѣется одна пара цпглыаъ рѣшеній ур—нія
а? — М#2 = ік 1.иожяо сколько угодно такихъ рѣшеній слѣдующимъ
способомъ.
Пусть будетъ я = а, # = ^, одна пара цѣлыхъ положительныхъ рѣшеніи ур—нія и? — = въ такомъ случаѣ при всякомъ цѣломъ положительномъ
« будетъ (а* — = 1 * Слѣдовательно, я* — = (а2 — или
Положивъ х-ьу Г X — (і н- я — у і'Х = (а — ? і'Х)",
находимъ отсюда
„ _(а + ^Х)\+^“Н^Л
ж —~
(* + ? ІхХ)п
2і/х
Значенія х и у, представляемыя этими выраженіями, суть цѣлыя положи* тельныя числа; полагая въ нихъ п^О, 1, 2, 3,..., получимъ сколько угодно цѣлыхъ положительныхъ рѣшеній. Такъ:
и —О, х— 1
= а* -Ь 3X4^
6Х42^ н- №^1
;= а* Ч-10X4^4-5X2^
= а6 4- 15X4^ 4-15№^< + №?°,
У = 0
~2і?
= 3^ -4- Х-із
= 4*9 -ь 4Х’^з
= 5<х*?4-10Х42^4-Х«р
= 615?-Ь 20Х43?3-4-6Х>Ф* и т. д*
Подобно этому, если а? = а, = ? есть одна пара цѣлыхъ положительныхъ рѣшеній ур—нія а?2— X?/2 = —1, и если ?г—нечетное положительное число, то
& - Ху2 = _ х^)н
откуда найдемъ тѣ же формулы х и у, что н вышенай денныя, но п нужно полагать = только 1, 3, 5, . . .
883. Положивъ я ===О”, у = аг„ мы приведемъ уравненіе я- — Х’уЗ=±а2 къ виду с* — Хт* = ± ], рѣшать которое умѣемъ.
884. Мы видѣли, что
— Хд'2 = — гп(р$' — р'%) = = гЛ.
Отсюда видно, что если а есть знаменатель нѣкотораго полнаго частнаго, встрѣчающагося при обращеніи )/Хт въ непрерывную дробь, и если есть приближеніе, какъ разъ предшествующее этому полному частному, то одно изъ уравненій а?—удовлетворяется значеніями х—р\ у = ц'*
Нечетныя приближенія вегѣ меньше Ѵ'Х, четныя — всѣ больше ) Хт: значитъ, если есть четное приближеніе, то ® у = д' есть рѣшеніе уравненія рг
я* — Ху* — 4-д; если же есть нечетное приближеніе, то х—р\ у = есть рѣшеніе ур—нія я? — Ху2 — — а.
Такимъ путемъ мы можемъ найти рѣшенія одного изъ ур—ній Х$в = ^а
только въ томъ случаѣ, когда а есть одинъ изъ знаменателей, встрѣчающихся при обращеніи у'Х въ непрерывную дробь. Такъ, обращая въ непрерывную дробь I 7, найдемъ:
)/7=|2; 1, 1, 1,4, . . . |;
Полныя частныя
+ 2 /7 + 1
3 ’ 2 ’
/7 ч-2
~ 1
и т. д., имѣютъ знаменателями числа 3, 2. 3, I.
Послѣдователь]! и я приближенія суть:
2 3 5 8 37 45 82 127 Г Г 2’ з’ 14* 17* 31* 48**
и если взять циклъ уравненіи
#2—=—3, ш2 — 7у* = 2, яР—7у2=— 3, ж2 —7у2=],
то найдемъ, что они удовлетворяются значеніями
а? = 2,
3, 5, 8, 37, 45, 82,
1, 2, 3, 14, 17, 31,
127, . < .
48, . . .
Иногда можно найти пару положительныхъ цѣлыхъ рѣшеній уравненія х2 — = ±а, когда « не есть одинъ изъ вышеуказанныхъ знаменателей, пу-
темъ попытокъ >
Такъ, легко убѣдиться, что ур—ніе я?—7^ = 53 удовлетворяется, если положить я^9, у=2. Имѣя одну пару цѣлыхъ рѣшеній, можемъ найти сколько угодно такихъ рѣшеній, а
885. До сихъ поръ мы предполагали, что К не есть точный квадратъ: когда X будетъ точнымъ квадратомъ, ур—ніе будетъ х2 — пЪр = а, и рѣшается легко.
Пусть а = 5.е, гдѣ 5 я с суть цѣлыя положительныя числа и 6>с; ур—ніе можно написать такъ:
(я?+пу) (х—му)=Ь. с.
Положивъ х-\-пу=Ь, х—пу=с, рѣшаемъ эту систему.
Если найденныя прпэтомъ значенія х и у будутъ цѣлыя, то найдемъ одну пару рѣшеній; приписывая Ъ и с всѣ допустимыя значенія, найдемъ другія.
Примѣръ. Найти дна цѣлыя положительныя числа, если разность ихъ квадратовъ равна 60?
Назвавъ искомыя числа буквами х и у, имѣемъ ур—ніе х2 — у2 = 60, или (® + у)(® — 0 = 6О.
60 разлагается на слѣдующія пары сомножителей:
1X60, 2X30, 3X^0, 4X15, 5X12, 6ХЮ-
Искомыя значенія получатся изъ ур—ній
х4-у=30, х—у — 2;
#-ьу = 10, я- у=6.
Эти значенія суть: 16 и 14; 8 и 2.
Остальныя системы дадутъ дробныя значенія для х и у.
КОНЕЦЪ.