В.Е.Захаров, С.В.Манаков, С.П.Новиков, Л.П.Питаевский
ТЕОРИЯ СОЛИТОНОВ: МЕТОД ОБРАТНОЙ ЗАДАЧИ
Книга представляет собой первое в мировой литературе систематическое
изложение чрезвычайно популярного метода обратной задачи рассеяния, включая
все необходимые математические сведения. До сих пор с методами теории
солитонов возможно было познакомиться лишь по журнальным статьям и
сборникам обзоров, не содержащим систематического изложения основ.
Содержание
Предисловие 5
Введение. Слабая нелинейность и дисперсия 9
Глава I. Метод обратной задачи рассеяния 20
§ 1. Сведения из теории рассеяния. Обратная задача квантовой теории 21
рассеяния
§ 2. Схема интегрирования уравнения КдФ методом обратной задачи 33
рассеяния
§ 3. Безотражательные потенциалы и JV-солитонные решения 37
§ 4. Уравнение КдФ как гамильтонова система 44
§ 5. Полиномиальные интегралы движения 48
§ 6. Полная интегрируемость уравнения КдФ. Высшие уравнения КдФ 51
§ 7. Дифференциально-разностные системы 60
§ 8. Нелинейное уравнение Шредингера и уравнение sin-Gordon 74
§ 9. Обратная задача рассеяния для системы двух дифференциальных 78
уравнений
§ 10. Нелинейное уравнение Шредингера 85
§ 11. Уравнение sin-Gordon 98
Глава II. Периодические решения уравнения КдФ 112
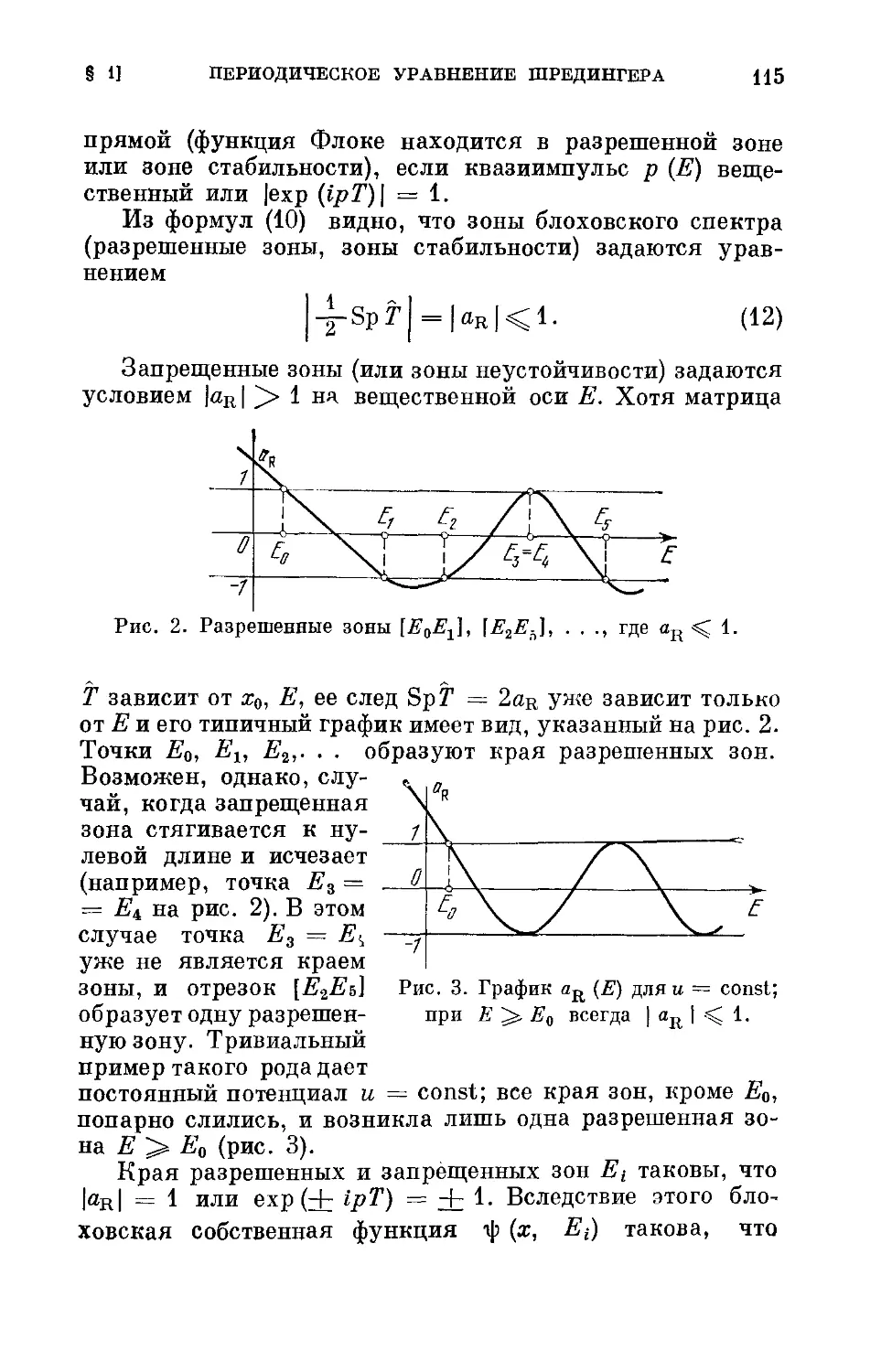
§ 1. Уравнение Шредингера с периодическим потенциалом. Периодический 112
аналог уравнений Гарднера — Грина — Крускала — Миуры
§ 2. Стационарная задача для высших КдФ. Метод отыскания точных 120
решений КдФ
§ 3. Стационарные решения высших КдФ и потенциалы уравнения 127
Шредингера с конечным числом зон. Римановы поверхности
§ 4. Аналитические свойства блоховской собственной функции 132
конечнозонного потенциала на римановой поверхности
§ 5. Некоторые приложения 138
§ 6. Сведения из теории римановых поверхностей. Циклы на римановой 147
поверхности
§ 7. Дифференциалы на римановых поверхностях. Абелевы (голоморфные) 158
дифференциалы и дифференциалы с полюсами
§ 8. Елоховская собственная функция и квазиимпульс. Связанные с ними 168
дифференциалы на римановой поверхности, их временная динамика
§ 9. Точные формулы для конечнозонных потенциалов и решений КдФ 178
§ 10. Некоторые частные решения КдФ 181

Глава III. Дальнейшее развитие методов построения интегрируемых 187
систем и их решений
§ 1. Регулярная задача Римана 187
§ 2. Задача Римана с нулями 190
§ 3. Обратная задача рассеяния для матричной системы первого порядка 197
§ 4. Задача и-волн 209
§ 5. Солитонные решения 216
§ 6. Системы, интегрируемые при помощи задачи Римана 222
§ 7. Релятивистски-инвариантные системы — киральные поля 227
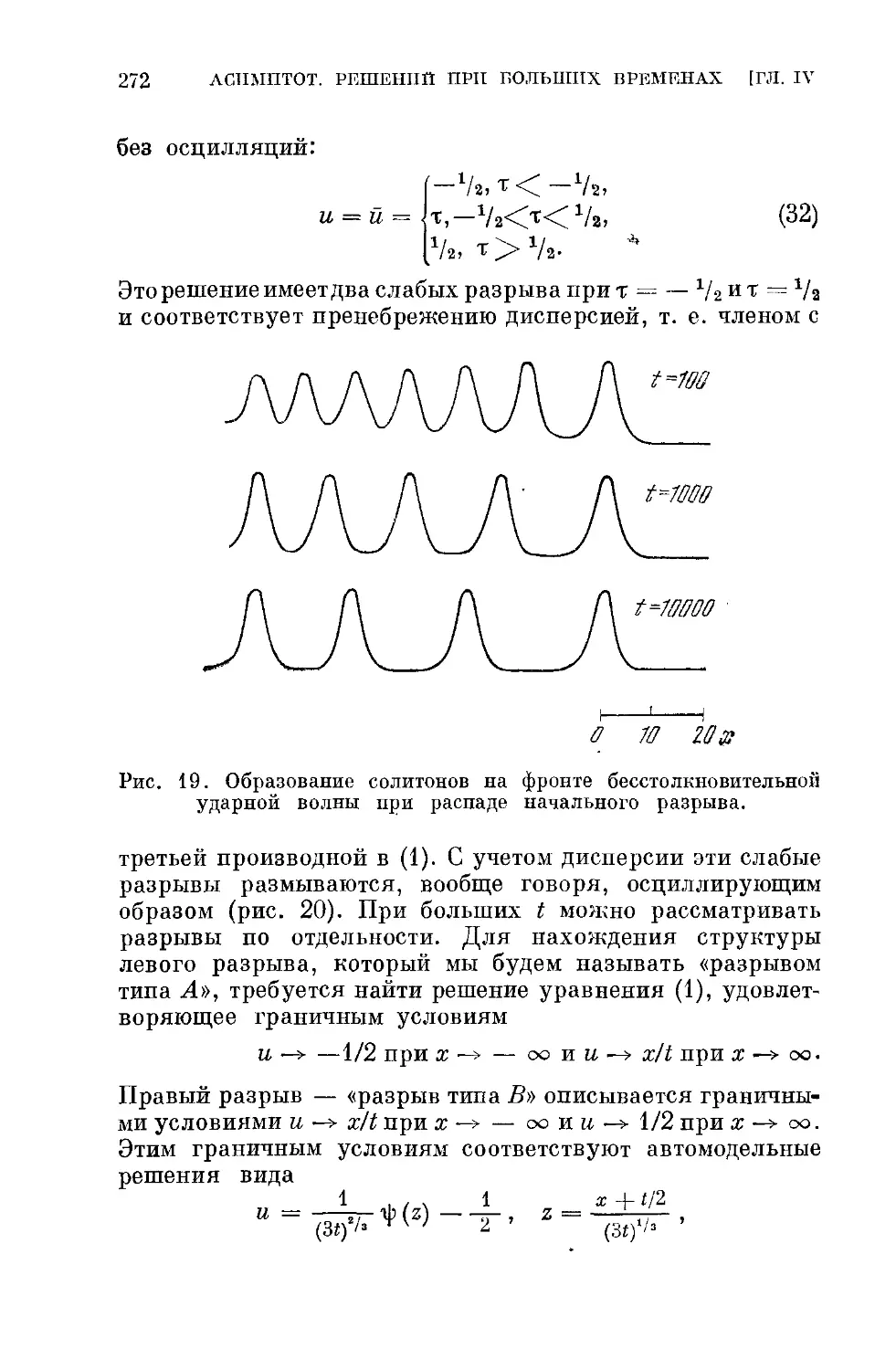
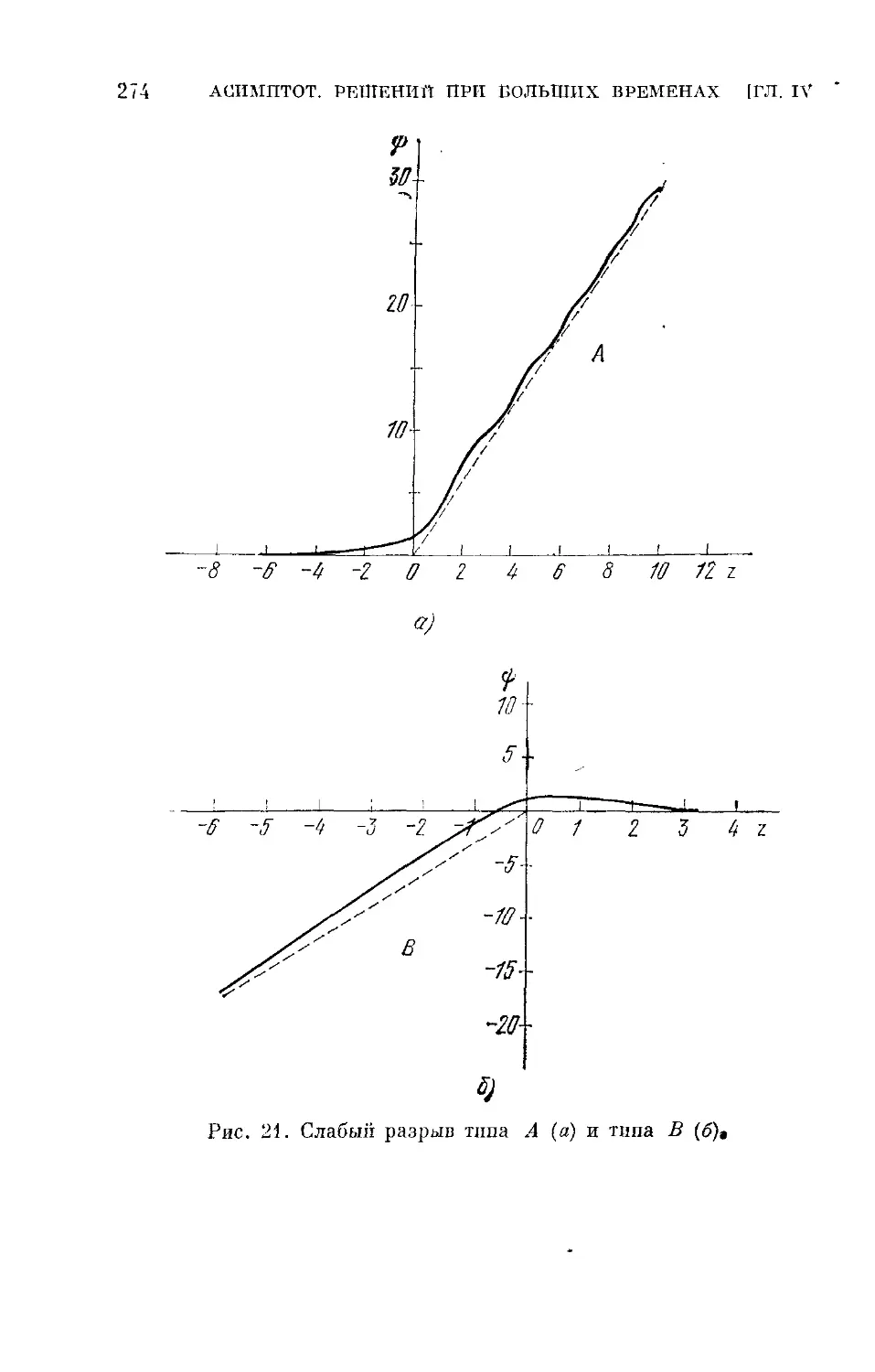
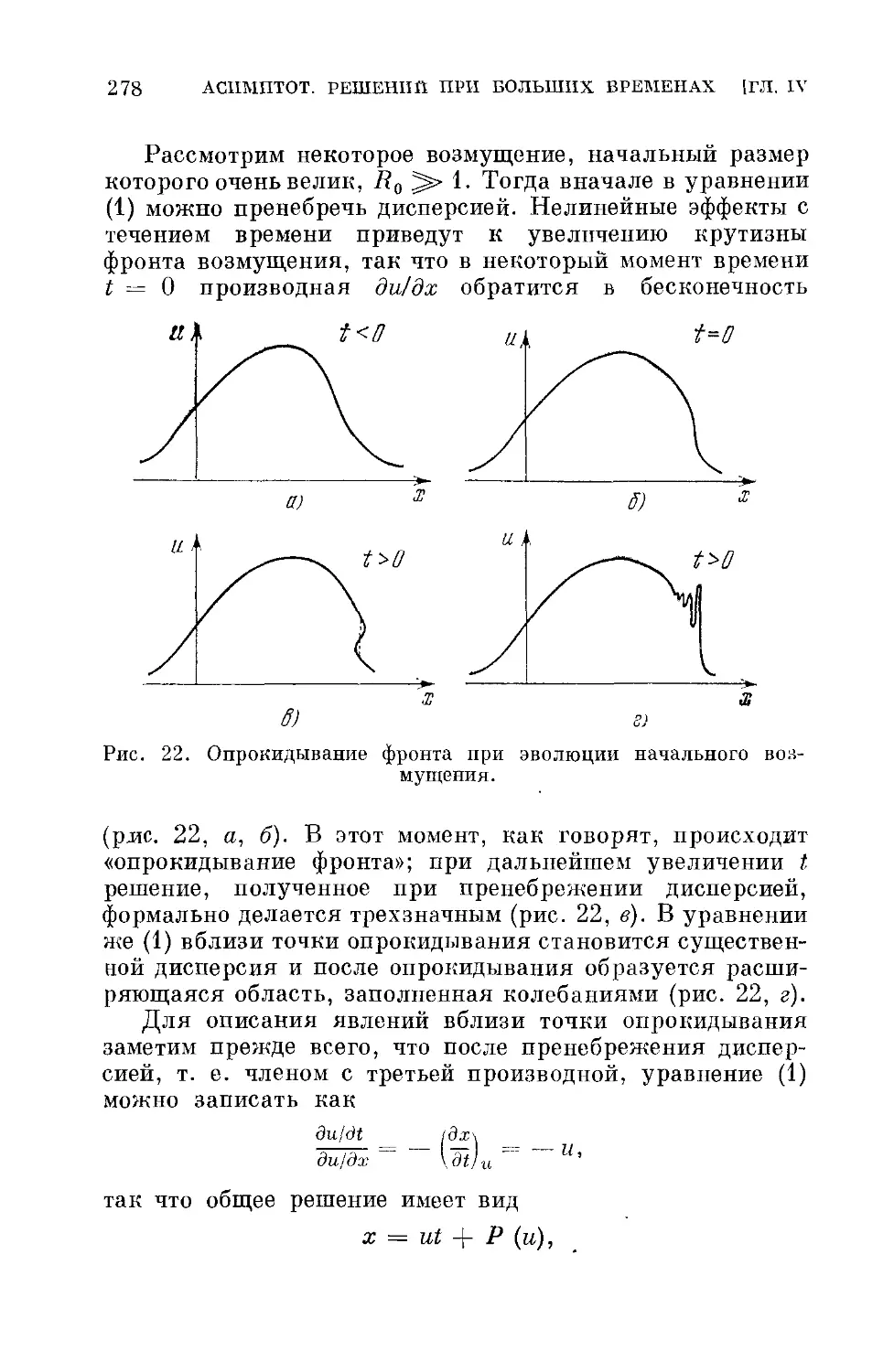
Глава IV. Асимптотики решений при больших временах 245
§ 1. Интегральные соотношения. Нелинейная дифракция Фраунгофера 247
§ 2. Явные формулы для асимптотик (нелинейное уравнение Шредингера) 251
§ 3. Явные формулы для асимптотик (уравнение Кортевега — де Фриза) 257
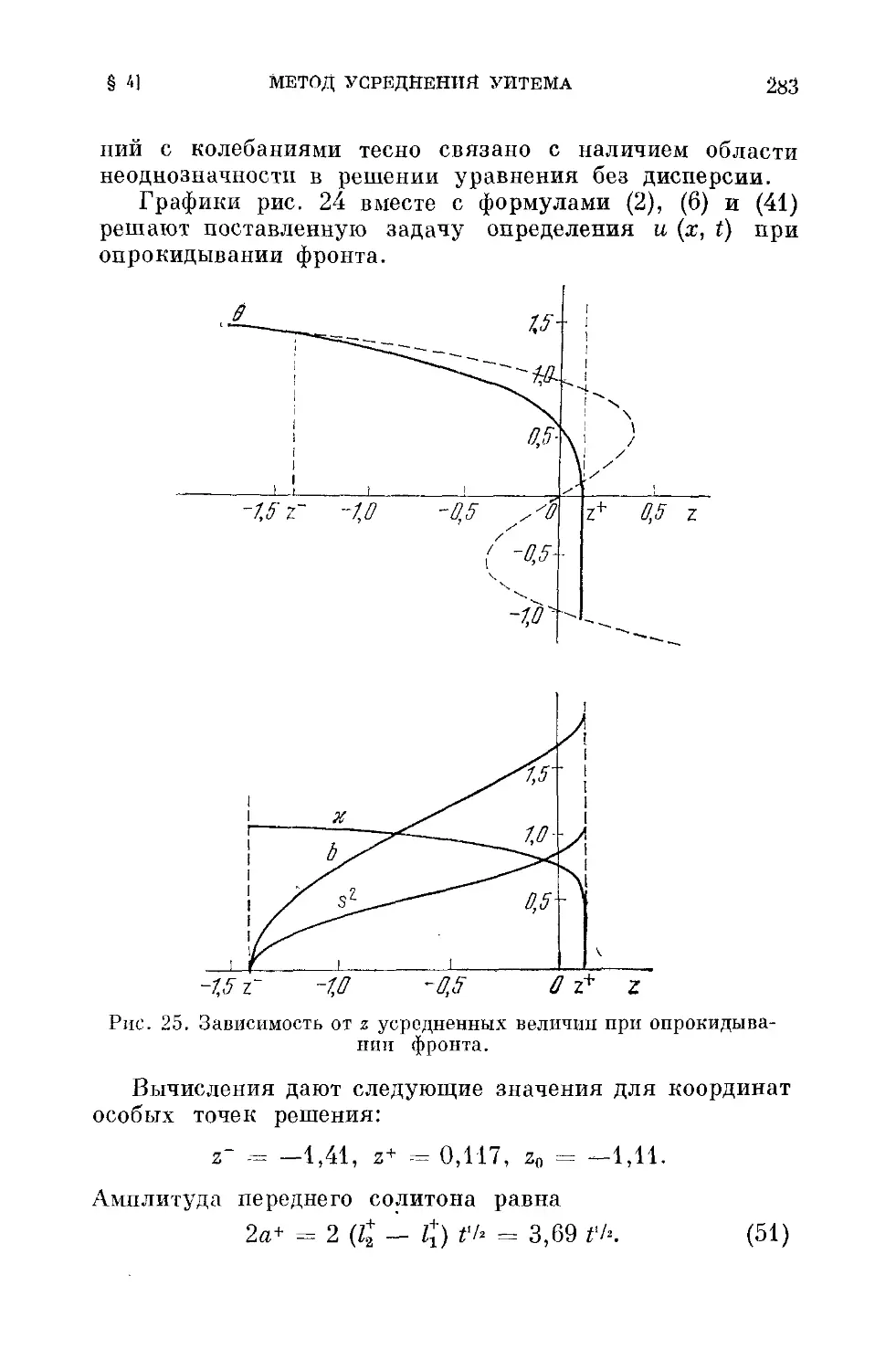
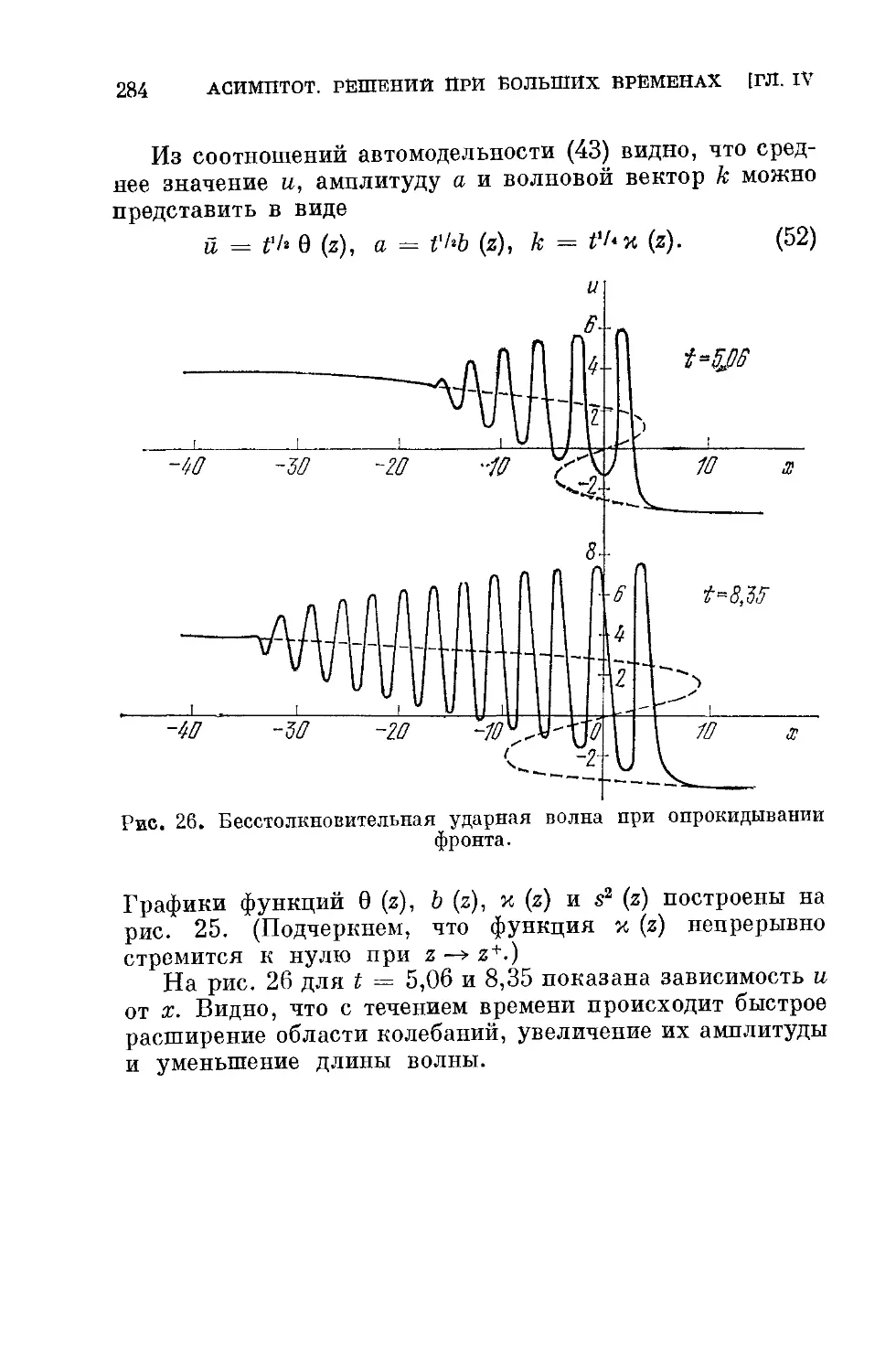
§ 4. Метод усреднения Уитема 261
Приложение. Теория уравнения Кадомцева — Петвиашвили (двумерного 285
КдФ). Некоторые дискретные системы
§ 1. Некоторые интегрируемые двумерные системы 285
§ 2. Законы сохранения 289
§ 3. Метод одевания 291
§ 4. Солитоноподобные решения уравнения КП 294
§ 5. Точные решения, зависящие от функциональных параметров 298
§ 6. Метод римановых поверхностей. Конечнозонные решения ранга 1 300
§ 7. Рациональные решения уравнения КП. Дискретные системы частиц на 304
прямой
§ 8. Метод голоморфных векторных расслоений над ри-мановыми 307
поверхностями. Функциональные параметры в точных решениях
§ 9. Некоторые замечания о периодической цепочке То да 315
Литература 317

ПРЕДИСЛОВИЕ
В течение последних 15—20 лет в различных областях
физики большое количество исследований было посвящено
изучению нелипейных волновых процессов. Это относит-
ся в первую очередь (кроме классических задач гидро-
динамики) к различным вопросам теории плазмы и не-
линейной оптики. В процессе развития теории нелиней-
ных волн выявились простейшие «модельные» нелиней-
ные волновые уравнения, которые обладают, в некотором
смысле, свойством универсальности, т. е. могут встречаться
в задачах самой разной физической природы подобно
классическому линейному уравнению Даламбера. К чи-
слу таких уравнений относятся, например, известное
уравнение Кортсвега — де Фриза (КдФ), нелинейное
уравнение Шредингера, уравнение sin-Gordon. Эти урав-
нения — по крайней мере, в одномерном случае — об-
ладают замечательным математическим свойством. В них
имеется скрытая алгебраическая симметрия, приводящая
к «интегрируемости» с помощью так называемого метода
обратной задачи для вспомогательного линейного опе-
ратора. Изложению этого математического метода и его
обобщений посвящена, в основном, данная книга, глав-
ной целью которой является элементарное, по мере
возможности, изложение этого метода вместе со всеми
необходимыми сведениями из теории рассеяния, римано-
вых поверхностей, гамильтоновых систем и т. д. Особую
главу книги представляют асимптотические задачи о по-
ведении решений на больших временах. Здесь в некоторых

6 ПРЕДИСЛОВИЕ
случаях существенные качественные результаты могут
быть получены с помощью методов, не связанных с тео-
рией рассеяния (см. § 4 гл. IV) и аналогичных классиче-
скому «методу усреднения» Боголюбова и др.
Для иллюстрации тезиса об «универсальности» уравне-
ний КдФ и нелинейного уравнения Шредингера мы при-
ведем во Введении их вывод в некоторых физических за-
дачах.
Метод обратной задачи рассеяния ведет свое начало
с работы Гарднера, Грина, Крускала и Миуры [3]. В на-
стоящее время литература по методу обратной задачи
содержит сотни статей, обозрение которых представляет
значительные трудности. Мы цитируем в тексте книги
только список обзорных статей и сборников, посвящен-
ных развитию нового метода [1—26]. Авторы сочли нуж-
ным приложить к литературе список основных работ, на
которых основывается научный материал книги: это статьи
[27—40] по материалу главы I, [41—51] по главе II,
[52—59, 63] по главе III и [60—62] по главе IV.
Дадим краткий исторический обзор теории солитонов,
предшествовавшей знаменитой работе [3].
Солитонное решение — для длинных волн на поверхно-
сти жидкости — было впервые получено Буссинеском
в 1872 г. Уравнение Кортевега — де Фриза (КдФ) было
выведено его авторами в 1895 г. — тогда же были полу-
чены периодические (кноидальные) волны, выражающиеся
через эллиптические функции. В последующие годы
происходило постепенное уточнение этих результатов,
закончившееся строгим доказательством существования
солитона на поверхности жидкости конечной глубины,
предъявленным Лаврентьевым и Фридрихсом; историю
этого периода можно найти в прекрасной книге Стоке-
ра [14].
Интерес к солитонам возобновляется в связи с ис-
следованиями по физике плазмы. В 1958 г. Сагдеев [13J

ПРЕДИСЛОВИЕ 7
показал, что в плазме могут распространяться солитоны,
вполне аналогичные солитонам на поверхности жидкости;
Гарднер и Морикава [4] установили прямую аналогию
между уравнениями, описывающими плазму в сильном
магнитном поле, и уравнениями мелкой воды. С этого
времени уравнение Кортевега — де Фриза приобретает
общефизический характер и вскоре устанавливается воз-
можность его применения к разнообразным волновым
задачам (см. монографию Уитема [15а]). Параллельно
прогресс в области нелинейной оптики (см. монографии
Ахманова и Хохлова [1] и Бломбергена [2]) привел к
рассмотрению задачи о трехволновом параметрическом
взаимодействии и позднее к нелинейному уравнению
Шредингера (см. обзор Кадомцева и Карпмана [8]).
Открытию метода обратной задачи предшествовала рабо-
та по численному моделированию уравнения Кортевега —
де Фриза. Еще в 1954 г. Ферми, Паста и Улам (см. 16]),
изучая на ЭВМ поведение цепочки нелинейных осциллято-
ров, обнаружили аномально медленную стохастизацию
этой динамической системы. В 1964 г. Крускал и Забуский
(см. в [3]) обнаружили путем численного моделирования,
что солитоны в КдФ сталкиваются упруго. Этот резуль-
тат дал толчок к новым аналитическим исследованиям.
Вскоре были открыты бесконечные серии законов сохра-
нения и, наконец, в 1967 г. это развитие увенчалось
открытием метода обратной задачи рассеяния [3].
Дальнейшее развитие этого метода началось с работ,
в которых был вскрыт алгебраический механизм, лежащий
в основе процедуры работы [3] (П. Лаке, 1968), и построена
теория уравнения КдФ как гамильтоновой системы
(С. S. Гарднер, В. Е. Захаров, Л. Д. Фаддеев, 1971).
Уже в начале 70-х годов стали обнаруживаться другие
важные нелинейные уравнения, интегрируемые методом
обратной задачи, в частности, нелинейное уравнение
Шредингера, уравнение sin-Gordon и др. Процедура

8 ПРЕДИСЛОВИЕ
нахождения периодических решений, потребовавшая глу-
бокого использования гамильтонова формализма и при-
влечения методов алгебраической геометрии, была найдена
только в 1974—75 гг. даже для уравнения КдФ. Об-
зор этого периода можно найти в [6]. Развитие самых
последних лет происходило в следующих направлениях:
1) выявление новых физически важных систем, интег-
рируемых методом обратной задачи или его обобщениями»
2) развитие методов теории рассеяния и алгебраической
геометрии для нахождения решений; 3) построение и изу-
чение квантовых релятивистски-инвариантных моделей,
в которых сохраняется точная интегрируемость.
По мнению авторов, накопленная информация о точных
решениях пока -еще слабо используется для расчета
конкретных физических эффектов. Мы надеемся, что
данная йнига, по которой можно овладеть всей необ-
ходимой техникой, будет способствовать расширению
приложений этого метода, который, без сомнения, пред-
ставляет собой одно из самых красивых открытий мате-
матической физики XX века.
Авторы

Вь'в е д е н и е
СЛАБАЯ НЕЛИНЕЙНОСТЬ И ДИСПЕРСИЯ
Как известно, широкий класс волновых процессов
в самых различных однородных средах описывается вол-
новым уравнением вида
¦?-¦*?¦ («
описывающим распространение незатухающих волн с по-
стоянной скоростью ц0. При выводе этого уравнения
используются три основных обстоятельства. Во-первых,
отсутствие диссипации. Оно выражается инвариантно-
стью A) относительно обращения времени, т. е. замены
t -у —t. Во-вторых, амплитуда колебаний должна быть
достаточно мала. При этом нелинейные по колеблющейся
величине я]) члены малы и ими можно пренебречь. Нако-
нец, в рассматриваемом диапазоне длин волн должна
отсутствовать дисперсия, т. е. зависимость скорости
распространения от частоты и длины волны. Обычно
(и мы будем иметь в виду вначале именно этот случай)
это соответствует пределу сколь угодно больших длин
волн.
Подчеркнем еще раз универсальность уравнения A),
вид которого не зависит от конкретных свойств среды;
эти свойства отражаются только на величине скорости
и0. Если отказаться от пренебрежения диссипацией, не-
линейностью и дисперсией, эта общность, разумеется,
исчезнет. Каждая среда будет описываться своей особой
системой уравнений. Замечательно, однако, что если не
пренебрегать полностью указанными эффектами, но счи-
тать их малыми, то снова можно получить уравнение, вид
которого один и тот же для широкого класса явлений.

10 ВВЕДЕНИЕ
У равнение Кортевега — де Фриза. Прежде всего, воз-
никает вопрос, имеет ли смысл учитывать эти малые по-
правки, т. е. имеются ли случаи, когда эти малые поправ-
ки приводят к новым качественным эффектам. В против-
ном случае они, разумеется, были бы совершенно неинте-
ресны. Легко понять, однако, что если процесс происхо-
дит достаточно длительное время, то все указанные
эффекты могут существенно изменить решение. Действи-
тельно, даже малая диссипация энергии приведет за до-
статочно большое время к затуханию волны. Дисперсия
приводит к расплыванию волнового пакета, что также
за достаточно большое время может исказить решение до
неузнаваемости. Что касается нелинейных эффектов, то
они приводят к «укручению фронтов» в решении — эф-
фекту также вовсе не малому.
Наша цель сейчас состоит в получении приближенного
уравнения, которое будет правильно описывать эти
«большие эффекты малых поправок». При этом мы огра-
ничимся консервативными системами, тем самым по-преж-
нему полностью пренебрегая диссипацией.
Решение уравнения A) имеет вид суммы двух волн,
бегущих в противоположных направлениях:
ф = ^ (х - uot) + q2 (х + uot). B)
Легко убедиться в том, что и при учете малой нелинейно-
сти и дисперсии можно рассматривать волны, бегущие
в разных направлениях, независимо. Физическая причина
этого состоит в том, что такие волны слишком быстро
движутся друг относительно друга, так что «накопление
поправок» не успевает происходить. Уже это замечание
позволяет существенно упростить задачу. Каждая из
бегущих волн в B) удовлетворяет уравнению первого
порядка, в частности, волна, бегущая в положительном
направлении оси х, уравнению
а* 4-7/ ** О (Ч\
Нам, таким образом, нужно искать поправки именно
к этому уравнению.
Проще всего определить поправку, связанную с дис-
персией. Пусть точный закон дисперсии линейных волн

ВВЕДЕНИЕ Л
в нашей среде имеет вид
со = ки (к). D)
При к -> 0 скорость и должна стремиться к и0. В общем
случае и (к) — аналитическая функция к, разложимая
по степеням к. Легко понять, что в отсутствие диссипации
это разложение происходит по степеням к2. Действительно,
закон дисперсии D) получается из некоторой системы
линейных дифференциальных уравнений с вещественными
коэффициентами. Поэтому результат решения этой систе-
мы можно представить в виде зависимости ?со от ik с веще-
ственными коэффициентами. Чтобы со в D) была вещест-
венной (что выражает отсутствие диссипации), необ-
ходимо, чтобы разложение и шло по четным степеням ik.
С учетом сказанного при малых к зависимость со (к)
можно записать, учитывая только первую поправку:
со = иок - (ЗА3. E)
Сразу ясно, что для того чтобы получить правильный
закон дисперсии E), нужно добавить к C) член с третьей
производной:
Перейдем теперь к нелинейности. Это удобнее всего
сделать, если учесть, что в консервативных системах,
которые мы здесь рассматриваем, всегда имеются точные
законы сохранения некоторых величин. (Фактически
речь может идти о законе сохранения числа частиц.)
Запишем один из таких законов сохранения в виде
? + ?-"• о
(Поскольку в линейном приближении все колеблющиеся
величины удовлетворяют одному и тому же волновому
уравнению, всегда можно считать, что уравнение A) было
написано именно для возмущения сохраняющейся вели-
чины я|з.) Задача вывода состоит в том, чтобы приближенно
выразить поток / через г|з. Из сравнения G) и F) видно, что
в линейном по т)з приближении / = uoty + C d2ty/dx2.
В следующем приближении появится квадратичный по

12 ВВЕДЕНИЕ
op член:
где а — постоянная. В результате получаем искомое урав-
нение, учитывающее первые неисчезающие поправки:
Произведем теперь замену переменных
Уравнение тогда сведется к стандартному виду уравнения
Кортевега — де Фриза:
*L + .gn +T,_gL = O. (8a)
, Во избежание недоразумений заметим, что изложенные
соображения охватывают наиболее общие случаи, когда
нет специальных причин для особых зависимостей диспер-
сионных и нелинейных членов. Можно, однако, предста-
вить себе случай, когда в силу соображений симметрии
в разложении / по i|i могут быть только нечетные члены.
Тогда в (8) появится нелинейность вида ц2дц/дх. Могут
быть и более сложные неаналитические зависимости
/ (i|i). Изложенная схема вывода уравнения Кортевега —
де Фриза оказывается весьма удобной при фактических
вычислениях, поскольку позволяет независимо определять
коэффициенты аир.
Проиллюстрируем эту процедуру на нескольких при-
мерах. Определим прежде всего коэффициент а в гидро-
динамике среды с политропическим уравнением состоя-
ния р = Сру. (Для адиабатического движения идеального
газа с постоянной теплоемкостью значение у равно отно-
шению теплоемкостей cp/cv.) В качестве величины я|) вы-
берем изменение плотности р' (р = р0 + р', где р0 — не-
возмущенная плотность). Уравнению G) будет тогда со-
ответствовать уравнение непрерывности
др д (рг>) п .р.

ВВЕДЕНИЕ lg
которое следует дополнить уравнением Эйлера
i!L_L — — = L_?A. (Ю)
dt 2 дх р дх ^ '
С точностью до членов второго порядка связь р с р' мож-
но записать как р — р0 = и\ [a -J- -^—р'2) i гДе ио =
= (dp/dp)'!' — «невозмущенная» скорость волны. Систему
уравнений (9), A0) можно поэтому, с точностью до чле-
нов второго порядка, представить в виде
dp'
dt
dv
dt
_l_ n
T" Po
1 On
dv
dx
dx
д (р'х)
dx
Or,''
- 2) dp'2
! dx
1
A1)
dx
Исключим теперь из этих уравнений v, для чего продиф-
ференцируем первое уравнение по if и выразим dvldt из
второго уравнения. Получаем
Id d \ I d , d
"" ~ ~d7dT + T"Po a^2 ¦+" 2 "
Теперь в левой части A2) можно с должной точностью
сделать замену -~т — ио-^~ — — 2м0 -*- , а в правой части
положить -кг ^ ио-я— и v~—u'. (Последнее приближен-
ное равенство следует из предыдущего и любого из урав-
нений A1).) Опуская знак д/дх в левой и правой частях
уравнения, получаем значение а
«=^и0. A3)
Применим полученные результаты к важному случаю
ионно-акустических волн в бесстолкновительнои плазме
при условии Te^>Tt. В этом случае можно пользоваться
для ионов гидродинамическим уравнением, пренебрегая
тепловым разбросом их скоростей:
~W + V dx ~ M dx
(M — масса иона).

14 ВВЕДЕНИЕ
Электроны же можно считать распределенными по
Больцману:
пе = ZnoeetflTe
(п0 — равновесная плотность ионов), так что уравнение
Пуассона для потенциала ср имеет вид
Дф = -4ле (Znt - Zn0ee<t/To). A5)
Для определения коэффициента а пренебрежем диспер-
сией, что эквивалентно пренебрежению второй производ-
ной в уравнении A5). Тогда вместо A5) получается усло-
вие квазинейтральности
еф , п
Я~= In— .
Те "о
Подставляя ец> из этого соотношения в A4), получаем
dt + дх м
Это, однако, просто уравнение гидродинамики, причем
скорость звука и0 = yZTe/M, а показатель политропы
7 = 1- Поэтому для этого случая
„ /
п~ Мщ~ У М
Для определения коэффициента |3 линеаризуем уравнение
A4), считая, что все величины ~ <?*(fr*-«>0:
— icoi; = — ikZe<p/M,
и используя уравнение Пуассона
и уравнение непрерывности
—ianii 4- iknov = 0.
Приравнивая нулю определитель системы, находим закон
дисперсии

введение 15
где D = У rre/(inZn0e2) — дебаевский радиус экраниро-
вания электронов в плазме. Таким образом, мы опреде-
лили и второй коэффициент в уравнении (8) для этого
случая:
р == 42D2 ]fZTjM. A8)
Классическим примером применения уравнения Кор-
тевега — де Фриза является проблема распространения
волн на мелкой воде. (Именно для этой проблемы Корте-
вег и де Фриз вывели уравнение в 1895 г.) Имея в виду
прежде всего получить коэффициент а, выпишем урав-
нения для случая предельно длинных волн (к -*¦ 0).
Пусть h — колеблющаяся толщина слоя жидкости. Тог-
да, считая жидкость несжимаемой и учитывая, что в тон-
ком слое жидкость течет практически вдоль поверхности,
запишем уравнение непрерывности в виде
Уравнение же для скорости имеет вид
jL. + y^L^-g^L , B0)
поскольку изменение потенциальной энергии жидкости
при изменении h есть dU = gp dh.
Система уравнений A9), B0), однако, опять формально
совпадает с системой уравнений гидродинамики, если
считать, что h есть плотность, а давление равно gh?/2.
Тогда
Щ Уф; 7 = 2, B1)
так что в уравнении для Ы
Для определения коэффициента |3 нужно решить ли-
неаризованную задачу о колебаниях с конечной длиной
волны в слое толщиной h0. Закон дисперсии для этого
случая (см. [14]) имеет вид
со- /gMA - V, (**„)"]•
Таким образом, в этом случае
B2)

16 ВВЕДЕНИЕ
Нелинейное уравнение Шредингера. Нелинейные члены
в уравнении распространения волн, рассмотренные в пре-
дыдущем разделе, имеют, в общем, тот же характер, что
и нелинейности в уравнениях гидродинамики. Эти члены
выражаются через значения колеблющейся величины
в тот же момент времени и ее производные. Можно ска-
зать, что они носят «локальный» характер. Если в началь-
ный момент возмущение носило гармонический во времени
характер, то нелинейности этого типа вызовут быстрое
появление высших гармоник и исказят начальный профиль.
Существуют, однако, нелинейности и другого типа.
Рассмотрим, например, электронные плазменные коле-
бания. (Количественно этот пример будет рассмотрен
далее. Здесь нас интересует только общий характер явле-
ний.) Эти колебания происходят с электронной плазмен-
ной частотой со0 = ]^4ппее2/т. Ионы, благодаря своей
большой массе, принимать участие в колебаниях практи-
чески не будут. Поскольку, однако, в силу квазипейтраль-
ности плотность ионов должна быть равна плотности элек-
тронов, последняя не может иметь переменной составля-
ющей с частотой порядка соо. Это, тем не менее, не мешает
изменению плотности плазмы за счет средней но времени
силы, действующей на плазму в поле. Такое, в первом при-
ближении не зависящее от времени возмущение будет
определяться средним по времени значением зависящих
от поля величин. В слабых полях, мало отличающихся от
гармонических, это означает зависимость закона диспер-
сии от | i|i0 I2! гДе ^о здесь означает комплексную амплиту-
ду поля ty =tyo exp [i (кх — at)]. Нелинейности такого
рода легко возникают при нагреве среды, поскольку тем-
пература при условии со ^> v (v — эффективное число
соударений) не может успеть за колебаниями поля, а
определяется его средним значением.
Нетрудно получить уравнение, учитывающее слабые
нелинейные поправки такого рода для полей, мало отли-
чающихся от гармонических. Пусть поле имеет вид
¦ф = olv^»*-40-'), B3)
где ty0 медленно меняется в пространстве и во времени.
Тогда в спектральном разложении ноля будут лишь вол-
новые векторы, близкие к к0. Поэтому правую часть дис-
персионного уравнения со = со (к) можно разложить по

ВВЕДЕНИЕ 17
Степеням к — к0:
со = со (Ао) + щ (к - Ао) + р (А - *0)а. B4)
Этому закону дисперсии соответствует линейное уравне-
ние
-|1 = щц + щ (-1-^- - fro) 1> + Р D--^- - А-оJ г|>. B5)
Если подставить в B5) поле в виде B3), то для г|з0 полу-
чится уравнение вида
дх
Нам осталось учесть нелинейность. Согласно сказанному,
она сводится к зависимости закона дисперсии от | г|H |.
В первом приближении можно учитывать только зависи-
мость со (к,,) и взять только поправку порядка | i|H |2:
со (к0) = соо + « I ^ I2-
Комбинируя эти уравнения, получаем
-р^ + нфоГ*.- B6)
В пренебрежении правой частью это уравнение описывает
распространение волнового пакета с групповой скоростью
"о = (-5г) • Правая часть учитывает дисперсионные и
\ ok /fc=J:0
нелинейные поправки.
Интересно отметить, что уравнение B6) встречается и
в совсем другом классе физических задач. Оно описывает
поведение неидеального бозе-газа со слабым взаимодей-
ствием между частицами. В этой задаче уравнению B6)
удовлетворяет так называемая волновая функция кон-
денсата, так что оно имеет буквальный смысл уравнения
Шредингера [17]. Разумеется, в этом случае вывод урав-
нения не содержит какого-либо усреднения по быстрым
колебаниям и требует только разреженности газа.
Определим постоянные в уравнении B6) для уже упо-
минавшегося случая ленгмюровских плазменных волн,
в которых нелинейность создается при вытеснении плаз-
мы электрическим полем.

18] ВВЕДЕНИЕ
Как известно, закон дисперсии ленгмюровских волн
при малых к имеет вид
со = соо + % (kDf B7)
(kD < 1).
Поэтому в нашем случае со (к0) = «0
О 3/2
р2
Для определения а необходимо найти изменение плот-
ности плазмы под влиянием поля волны. На электроны
в поле действует сила, равная
где
Распределение электронов в этом поле имеет вид
гее = zre0 ехр I ^
где ф — потенциал электростатического поля, возникаю-
щего из-за возмущения плазмы силой /. Действием же пере-
менного поля на ионы вообще можно пренебречь, так что
распределение ионов имеет вид
щ = noe-Zet<>/T ~ п0 A — Zecp/T).
Учтем теперь, что плазма квазинейтральна:
пе = Znt. ,
Исключая из этих трех уравнений ф, легко получаемв
что
s 2, е2
Поскольку 6соо/<»о — 11фпе1пе, окончательно находим
а — —
Z-И 8mco* '
Мы же будем останавливаться на важном в этом примере
вопросе о возможности пренебрежения эффектами нагрева
плазмы, решение которого требует большей конкретиза-
ции условий эксперимента.

ВВЕДЕНИЕ 1 g
Полезно сделать также замечание об уравнении
sin-Gordon
дхду
= smu.
Это уравнение появилось впервые в XIX веке в задачах
геометрии. Именно, если задана метрика постоянной от-
рицательной кривизны на поверхности, то так называемое
«уравнение вложения» этой метрики в евклидово трехмер-
ное пространство (вытекающее из соотношений Гаусса —
Петерсона — Кодацци между метрикой и второй квадра-
тичной формой) в наиболее естественных переменных
точно сводится к уравнению sin-Gordon. Классиками гео-
метрии были обнаружены (на геометрическом языке)
так называемые «беклунд-преобразования» для этого
уравнения — т. е. подстановки, которые позволяют из
более простых решений строить более сложные. В насто-
ящее время известно, что наличие беклунд-преобразова-
ний всегда или почти всегда указывает на интегрируемость
методом обратной задачи и наоборот.
Как известно, к уравнению sin-Gordon сводятся неко-
торые задачи теории сверхпроводимости, а также «теория
«-поля» — кирального поля единичных (трехкомпонент-
ных) векторов в двумерном пространстве, используемая
как в задачах геометрии, так и в моделях ферромагне-
тизма.

Глава I
МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ
В классической форме метод обратной задачи рассе-
яния весьма удобен при решении задачи Коши для нели-
нейных эволюционных уравнений. Можно даже сказать,
что он идеально приспособлен для этого. В быстроубыва-
ющем случае, когда задача Коши решается в классе до-
статочно быстро убывающих на бесконечности функций,
эффективность метода обратной задачи та же, что и ме-
тода Фурье при интегрировании линейных уравнений
в частных производных с постоянными коэффициентами.
В последнем случае преобразование Фурье превращает
уравнение в частных производных в бесконечную совокуп-
ность обыкновенных линейных дифференциальных урав-
нений. При этом, если коэффициенты уравнения не
зависят от координат, эти уравнения для фурье-гармоник
независимы и тривиально интегрируются. Аналогичная
ситуация имеет место и в методе обратной задачи. Роль
преобразования Фурье в этом методе играет отображение
коэффициентных функций некоторого линейного диффе-
ренциального оператора в совокупность «данных рассе-
яния». Так, уравнение Кортевега — де Фриза (КдФ)
интегрируется с помощью перехода от потенциала одно-
мерного уравнения Шредингера
к коэффициенту отражения г (к) на этом потенциале;
при эволюции потенциала в силу КдФ зависимость коэф-
фициента отражения от времени оказывается тривиаль-
ной:
г (к, t)=r (к, 0) e-*ik'K

s 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ 21
Таким образом, задача интегрирования КдФ приводит
к задаче о восстановлении потенциала и (х) по данному
коэффициенту отражения — обратной задаче квантовой
теории рассеяния.
В этой главе мы будем изучать нелинейные уравнения,
интегрируемые с помощью перехода к данным рассеяния
для линейпых уравнений второго порядка. Наиболее ин-
тересные среди таких эволюционных уравнений — это
КдФ, нелинейное уравнение Шредингера и уравнение
sin-Gordon. Кроме этих уравнений в § 7 мы рассмотрим
некоторые дискретные системы — конечно-разностный ана-
лог КдФ и систему уравнений, известную как «цепоч-
ка Тоды». Качественная структура решений этих, на
первый взгляд не имеющих ничего общего, систем в значи-
тельной мере одинакова. Много общего имеют и соответ-
ствующие спектральные задачи. Все это связано с тем, что
эти системы интегрируются с помощью уравнений второго
порядка (или их дискретных аналогов); именно по этой
причине они и объединены в рамках одной главы.
Мы начинаем изложение метода обратной задачи рас-
сеяния с теории уравнения КдФ, следуя как историче-
скому развитию, так и (прежде всего) педагогическим
соображениям—многие факты из спектральной теории
оператора Штурма — Лиувилля на прямой хорошо извест-
ны читателю-физику из курса квантовой механики.
§ 1. Сведения из теории рассеяния.
Обратная задача квантовой теории рассеяния
Рассмотрим одномерный оператор Шредингера (опе-
ратор Штурма — Лиувилля) L = —cP/dx2 -f- и (х) на всей
прямой — оо <С х < оо. Вещественный потенциал и (х)
будем считать достаточно гладким и обращающимся
в нуль при |х | -> оо.
Задачу на собственные значения
будем рассматривать в классе ограниченных па всей оси
функций ар (х). Кроме дискретного спектра, собственные
функции которого квадратично интегрируемы, имеется
двукратно вырожденный непрерывный спектр с ненорми-

22 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
руемыми собственными функциями. Непрерывный спектр
заполняет вещественную полуось X 1> 0; собственные зна-
чения дискретного спектра оператора L отрицательны.
Из стандартных учебников квантовой механики известно,
что число их может быть бесконечным — собственные
значения могут накапливаться в окрестности X = 0. Это
имеет место для медленно спадающих при | х | -> оо
потенциалов, например, кулоновского и (х) = —а/х или
же потенциала и (х) = а/х2. Потенциалы с бесконечным
числом связанных состояний мы будем исключать, нала-
гая на и (х) ограничение
o. A)
Перейдем к описанию задачи рассеяния. При этом нам
вместо энергии X будет удобнее пользоваться импульсом к
(X = к2). Уравнение на собственные функции запишем
в виде
Непрерывному спектру теперь отвечают вещественные к,
дискретному же спектру соответствуют точки мнимой
оси к = ixn, п = 1, 2, . . ., N, кп ^> 0.
При каждом вещественном к Ф 0 множество решений
уравнения B) образует двумерное линейное пространство
Gii. Фиксируем в Gk два базиса. Первый из них состоит
из решений ijii^ (x, к) уравнения B), определяемых асимпто-
тическим условием на + °° по х:
"Фх (х, к) = e'ikx + о A),
г|;2(*, ^ = е** + о A), х-^ + оо;
второй базис ф1]2 (х, к) задается аналогичными условиями
на —оо:
ф1(а:, к) = e~ikx + о A),
ф2 (а:, к) = eikx + о A), х -* - оо.
Ввиду вещественности потенциала имеем
<Pi (х, к) = ф2 (х, к), -фх (х, к) = Ц2 (х, к). C)

§ 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ 23
Кроме того, очевидно, что
<Pi (ж, к) = ф2 (х, —к), ^ (х, к) = г|з2 (ж, —/с). D)
Векторы любого из базисов представляют собой линейную
комбинацию векторов другого:
<Pi (х, к) = S Г« (А?) фг (х, fr), г = 1, 2.
г=1, г
Определенную таким образом матрицу 71 (/с) мы будем на-
зывать матрицей перехода. Ввиду C) Т имеет вид
[а (к) Ъ (к)\
У W - \Ъ{к) а (к)} •
В дальнейшем индекс 1 у функций <рх и \J)X мы будем
опускать. Таким образом,
ф {х, к) = а (к) г|з (ж, к) + b (к) $ (х, к). E)
Определитель Вронского W(fu /2) = fi-J^ /2"^~ ЛК)бой
пары решений /х, /2 уравнения B) не зависит от х. Очевид-
но, W (<р, <р) = W (г|), if) = 2ik. Это соотношение вместе
с формулой E) означает, что
\а(к) р- \Ь(к) |» = 1, F)
т. е. матрица перехода унимодулярна: det 71 (/с) == 1.
Легко видеть, что величины а'1 (к) и b (к) а (А;)
представляют собой соответственно коэффициенты про-
хождения и отражения для волны, падающей на потен-
циал и (х) справа. В самом деле, асимптотика собственной
функции ф (х, к) а (к) имеет при х -у + °° вид
?% = в +111^ + 0A),
а (к) 'а (к) ' v ''
т. е. представляет собой суперпозицию падающей (e~it!x)
и отраженной (ba~1eikx) волн. На другом конце прямой х
а (к) а (к) +0^'
т. е. имеем прошедшую волну. Иными словами, t (к) =
= а~г (к) представляет собой амплитуду рассеяния впе-
ред, а г (к) = b (к) а'1 (к) — назад. Из F) следует при
этом, что рассеяние унитарно:
| * (к) |» + | г (к) |2 = 1.

2A МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
В учебниках квантовой механики подробно изучаются
аналитические свойства амплитуды рассеяния вперед.
Известно, что t (к) является аналитической функцией
энергии к на физическом листе римановой поверхности
У к (Im У к ^> 0), за исключением точек дискретного спек-
тра к = кп, в которых амплитуда имеет простые полюсы.
Кроме того, амплитуда рассеяния вперед не обращается
в нуль на физическом листе. Для функции а (к) все это,
очевидно, означает, что а (к) аналитична в верхней полу-
плоскости к и имеет простые нули в точках кп = Ып,
Хп= — кп. Ясно также, что а (к) ->- 1 при | к | ->¦ оо,
Im к ;> 0. Ввиду принципиальной важности и опреде-
ленной универсальности этих аналитических свойств
диагональных элементов матрицы перехода (аналогичные
утверждения имеют место в теории рассеяния для других
дифференциальных операторов), мы приведем ниже дока-
зательства этих фактов.
Матрица перехода Т (к) доставляет нам исчерпываю-
щую информацию о непрерывном спектре оператора Шре-
дингера. Фактически же вся информация о Т (к) содер-
жится в коэффициенте отражения
г (к) = Ь (к)/а (к)
(который ввиду C), D) достаточно задать на полуоси
к ^> 0, поскольку г (—к) = г (к)). Действительно, из F)
находим
| а (к) Р = A - | г (к) IT1,
т. е. модуль г (к) однозначно определяет \ а (к) |. Зная же
нули аналитической в верхней полуплоскости функции
а (к), мы можем однозначно определить аргумент послед-
ней по ее модулю. Для этого рассмотрим функцию аг (к):
N k '
71=1
Эта функция по-прежнему аналитична при Im к ^> 0,
но уже не имеет там нулей, так что In ax (к) аналитичен
в верхней полуплоскости и обращается в нуль при | к \ ->
-»- с». При этом на вещественной оси | ах (к) | = [ а (к) |.
Дисперсионное соотношение для функции In аг (к) =

§ 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ 25
= In | аг (к) | + i arg ax (к) дает arg аг (к):
ln\a(k')\dk'
arg а± (к) = У
—оо
Таким образом,
/г\ 1 V* 1 к~Ып If In I а (к') I ,,, ,о.
argatt =— ) In , , . —— \ ' ,dk. (8)
n=i — х
Эта простая формула будет весьма полезна в дальнейшем.
Итак, а (к) восстанавливается по модулю коэффициен-
та отражения. Функция же Ъ (к) есть просто г (к) а (к).
Опишем теперь соответствующие характеристики дис-
кретного спектра оператора Шредингера, естественным
образом примыкающие к характеристикам рассеяния.
Собственные функции, соответствующие собственному
значению %п = —и^, удовлетворяют уравнению
Дискретный спектр оператора Шредингера, как извест-
но, простой, так что все решения этого уравнения получа-
ются из какого-либо одного умножением последнего на
константу. На бесконечности собственные функции имеют
асимптотики
иж, х -» + оо.
Фиксируем собственную функцию фA1> (х) ее асимптотикой
на — оо по ж: j
ф(п) (а;) = eV + о (еКпх). (9)
При этом при х ->- + оо функции
ф(«) (х) = й„е-и«х + о (е~ипх),
очевидно, вещественны, так что вещественны и величины
Ъп. Занумеруем собственные значения Хп обычным образом,
в порядкр возрастания Х„ (т. е. убывания хп):
кг < Я2 < . . . < XN < 0.
При этом Хг представляет 'чобой энергию основного со-

26 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
стояния, а ф^) — волновую функцию этого состояния;
фв) не имеет нулей, а ф(п> ровно п — 1 раз проходит
через нуль. Поэтому
ьп= | ьп |(-1)"-ч (Ю)
Положительные величины | Ъп | составляют дополнитель-
ные к собственным значениям характеристики дискрет-
ного спектра. Эти характеристики вместе с коэффициен-
том г (к) и набором собственных значений А,ц, Я2, . . ., "к-н
полностью определяют спектр задачи B). Совокупность
s = (г (к), х„, | Ъп |, п = 1, . . ., N) называется данными
рассеяния. Отображение и (х) —>- s потенциалов и (х)
в данные рассеяния однозначно обратимо. Процедура
восстановления и (х) по s составляет предмет обратной
задачи теории рассеяния.
При изучении обратной задачи фундаментальную роль
играют аналитические свойства введенных выше специ-
альных решений уравнения Шредингера. Оказывается,
именно, что при любом х функция ф (х, к) exp \ikx) ана-
литична в верхней полуплоскости к и имеет там асимпто-
тику
Ф (х, к) exp (ikx) = 1+0 {ilk), \ к \ -> с», 1щ к > О,
а решение г|) (х, к) аналитично в нижней полуплоскости к
и также имеет асимптотику
¦ф (х, к) exp (ikx) = 1 + О A/к), \ к \ ->- оо, Im к < 0.
Для того чтобы убедиться в этом, перейдем от уравне-
ния B) к эквивалентному интегральному уравнению для
Ф (х, к), используя для этого функцию Грина G (х, х', к)
оператора —cP/dx2 + к2:
ф (х, к) — e~ikx — \ G(x, х, к) и{х')<р(х', k)dx.
—оо
Имея в виду асимптотику ф (х, к) на — оо по х, найдем
нужную нам функцию Грина:
( sin к (х — х') ^ ,
G(x,x',k)~\ к ' *->*'
I 0, ж<ж'.
Таким образом, %+ (х, к) = ц> (х, к) ег1сх удовлетворяет

§ 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ ^7
уравнению
Х+ (х,к) = 1 + \ ш и(х)Х+ (х, к)dx. A1)
—оо
При выходе в верхнюю полуплоскость А1 экспонента в ядре
уравнения A1) остается ограниченной (более того — зату-
хающей). Интегрирование ведется по области х' < х.
По этой причине %+ (х, к) допускает аналитическое про-
должение в область Im к ^> 0. Совершенно аналогично,
записывая уравнение на функцию %- (х, к) — ф (х, к) e~ilix,
видим, что %_ (х, к) аналитически продолжима в нижнюю
полуплоскость к; при | к | ->- оо имеем
оо
Отметим, наконец, что функция т|) (ж, А) аналитична в верх-
ней полуплоскости к, что следует непосредственно из ана-
литичности ty (x, к) внизу.
Функция а (к) может быть выражена через аналитиче-
ские в верхней полуплоскости функции <р (х, к), т|) (х, к).
Вычисляя вронскианы W (ф, "ф) и W (ij), ф) и используя
E), находим
а (к) = BJA;)-1 1^х (*, к) ф (х, к) - ^ (ж, A) q^ (ж, А)],
6 (А) = Bга:)-1 [фх (ж, А) г|> (ж, А) - Ф (х, к) Цх (х, к)].
A3)
Из первой из этих формул следует, что а (к) аналитична
в верхней полуплоскости А: и имеет асимптотику
а (А) = 1 + О (Щ, |А|->оо, ImA>0.
Точки верхней полуплоскости, в которых а (к) обра-
щается в нуль, соответствуют дискретному спектру опера-
тора L. Действительно, равенство нулю вронскиана функ-
ций ф (х, Ао), ty (х, Ао) (а (к0) = 0) означает линейную

28 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ (ГЛ. I
зависимость последних:
ф (х, к0) = с$ (х, к0).
Из этого соотношения следует, что <р (х, к0) экспоненциаль-
но убывает как при х —>¦ —оо (что является непосредст-
венным следствием определения ср), так и на +оо по i
(поскольку ij) (х, к) = eii!X, x -у +оо). Таким образом,
Ф (х, к0) является собственной функцией дискретного
спектра L, а к\ — собственным значением L. Из самосо-
пряженности вытекает, что к\ вещественно, т. е. все нули
а (к) лежат на мнимой оси. Пусть, далее, Я,„ = — xl —
собственное значение L. Функция ф (х, ixn) имеет ту же
асимптотику при х —>- — оо, что и определенная выше соб-
ственная функция ф<п> (х), поэтому ф(п) (х) = ф (х, ixn).
На +оо по х ф<") (х) = Ьпе~У'пХ + о (е~к™х), т. е. *)
Ф (ж, ixn) = bn^ (х, —Ып) = bnty {x, —Ып). A4)
Таким образом, a (ixn) = 0 и между нулями а (к),
расположенными в верхней полуплоскости к, и собствен-
ными значениями L имеется взаимпо-однозначное соот-
ветствие.
Нули а (к) простые. Для того чтобы убедиться в этом,
продифференцируем уравнение Ьц> (х, к) = к2ц> (х, к) по
к в точке к = ixn:
(L + xl) ф' (х, ixn) — 2ixn(p (x, ixn).
Умножим это соотношение на ф (х, ixn) и проинтегрируем
полученное равенство по всем х. Дважды перебрасывая
дифференцирование в интеграле
ф (х, ixn) (L + xl) ф' (х, ixn) dx
и учитывая, что главный член в асимптотике ф' (х, ixn)
на -f- оо по х имеет вид a' (ixn) е1*1" (поскольку a (ixn) = 0),
получим
оо
^ Ф2 (х, ixn) dx = ia' (ixn) bn, A5)
*) На мнимой оси функции ф (х, к) и хр (х, к), очевидно, вещест-
венны.

§ 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ 29
т. е. a' (ixn) =ф 0. Из этой формулы следует также, что
величина ia' (гх„) вещественна и имеет тот же знак, что
и Ьп.
Вместе с A5) отметим еще формулу для скалярного
произведения собственных функций непрерывного спектра:
ос
\ ? (х, к) ср (.г, к') dx =
—-ос
= 2я | а (к) |2 б (к — к') + 2па (к) Ъ (к) б (к + к').
Теперь мы готовы заняться выводом уравнений обрат-
ной задачи рассеяния.
Умножим формулу E) на е'кх а~г (к) и, вспоминая оп-
ределение функций %+ (х, к), напишем
Х+аУ = Х- % к) + г (к) х_ (х, к) в***. AG)
Левая часть A6) аналитична в верхней полуплоскости к,
за исключением точек мнимой оси к = Ып, п = 1, ...
. . ., N, в которых %+ (х, к)а~х (к) имеет простые полюсы.
Функция Х- (х> Щ аналитична при Im к ^ 0. Рассмотрим
функцию
Ф(х,к) = \ ... Т n (I/
I Х-(^. fc)> 1шА-<0;
Ф (ж, /с) имеет простые полюсы в верхней полуплоскости
и скачок на вещественной оси, равный, как видно из A6),
г (к)х_ (х, к)еШх. Во всех остальных точках комплексной
плоскости функция Ф (х, к) аналитична и на бесконеч-
ности имеет предельным значением единицу. Очевидно,
что функция Ф (х, к) может быть представлена в виде
2jii
где введено обозначение Тп(х) для вычета функции Ф (х, к)
в точке к = Ып. Выражение A8) является непосредст-

МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ.
венным следствием формулы Коши
в которой контур интегрирования 7 выбран, как показа-
но на рис. 1. Величину Гп (х) можно связать со значением
Рис. 1. Контур интегрирования у.
Ф (х, к) в точке нижней полуплоскости к = —Ып (т. е.
с ~%- (х> —ип)). В самом деле, используя A4), видим, что
<р (х, Ып) е~Лп* Ъ^ (х, — Ып) г~Кп*
Г« ~ а' (Ы)
Определяя /_ (х, —Ып) с помощью A8), находим
N
a'(iy.n)
й ) к' + Ып |
A9)

§ 1] СВЕДЕНИЯ ИЗ ТЕОРИИ РАССЕЯНИЯ 31
Устремим теперь к в формуле A8) к вещественной оси сни-
зу; так как согласно определению A7) Ф (х, к — Ю) =
= Х- {х, к), то •
*Гх dk'
к-Ып + Y^i 3 , ft'-A +
Г» Г /№') J;'
Выражение типа \ —,—, .- cttf следует понимать, как
— х>
всегда, как +яг/(&)-{- У ^ dk', где символ У означает
интеграл в смысле главного значения. Соотношения A9),
B0) представляют собой замкнутую систему линейных
уравнений на функцию /_ (х, к) и набор Г„ (х), п = 1, . . .
. . ., N, т. е. на собственные функции оператора L, и
являются одним из вариантов записи уравнений обратной
задачи. Остается выразить потенциал и (х) через решения
системы A9), B0). Проще всего это сделать, сравнив асимп-
тотическое разложение /_ (х, к) по степеням 1/к, следую-
щее из B0), с формулой A2):
N ~
г« W - 4-
Уравнения A9), B0) однозначно разрешимы. В качестве
собственных значений хп можно выбирать произвольные
положительные числа %1 > х2 ^> . . . >• х„ > 0, от вели-
чин с„ = (—l)"^, n = 1, . . ., N, также требуется лишь
положительность. Коэффициентом г (к) может являться
любая комплексная функция, удовлетворяющая следую-
щим условиям:
1. г (^к) = г (к);
2. \г(к) | <
Щ
4. Преобразование Фурье коэффициента Ъ (к), пост-
роенного по г (к),
В{х)= \ b(k)eiKxdk

32 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
должно удовлетворять условию
В частности, можно рассматривать потенциалы, для кото-
рых г (к) = О при всех к. Такие потенциалы называются
безотражательными и полностью определяются характе-
ристиками дискретного спектра.
Мы написали уравнение обратной задачи в форме си-
стемы сингулярных интегральных уравнений. Для опера-
тора Шредингера (Штурма — Лиувилля) более известной
формой уравнений обратной задачи является так называе-
мое уравнение Гельфанда — Левитана — Марченко. Для
того чтобы получить это уравнение, заметим, что преобра-
зование Фурье аналитической в нижней полуплоскости
к функции Х- (х, к) обрывается, т. е. /_ всегда представи-
ма в виде
X. (х,к) = 1 + j А (х, y)er"tvdy.
о
Для г|) (х, к) это означает, что существует такая функция
К (х, у), что
я|) (х, к) = е-ых + ([ К (х, у) е-«у dy. B2)
X
Очевидно, что К (х, у) = А (х, у — х). Из формулы B2)
следует, что существует линейный оператор, преобразую-
щий решение уравнения Шредингера с нулевым потен-
циалом (е~гкх) в решение этого уравнения с потенциалом
и (х). Функция К (х, у) называется ядром оператора пре-
образования. Поскольку я|) (х, —к) = \р {х, к), Im к = 0,
то К (х, у) вещественно.
Умножим равенство E) на el]tlJ/a (к) и проинтегриру-
ем по всем вещественным к:
а (к)
= J dk еаУ [г|з [<г, к) — e~i):x +r (к) ijj (x, к)}. B3)

§ 2] СХЕМА ИНТЕГРИРОВАНИЯ УРАВНЕНИЯ КдФ 33
Вычислим интеграл в левой части этой формулы. Подын-
тегральная функция имеет в верхней полуплоскости лишь
конечное число простых полюсов и убывает при | к \ —>-
—>- оо. Поэтому интеграл представляется в виде
N -у. у
. (х, м) е п
п=Х
Используя A4) и представление B2) при к = ixn, n =
= 1, . . ., N, получаем выражение для рассматриваемого
интеграла:
v~< be71 с х~ч о е п
2яг > "",.. ч h 2яА К (х, z) У п ,r . dz.
n=l ж n=l
Подставляя далее B2) в правую часть равенства B3) и
вводя обозначение
П=1
находим окончательно:
Я (я, у) + F(x + у) + J K(x, z)F(z + y)dz = O B5)
уравнение Гельфанда— Левитана — Марченко.
Из B2) следует асимптотическое разложение %_ (х, к):
Сравнивая это выражение с A2), приходим к выражению
для потенциала и (х) через ядро оператора преобразова-
ния:
и(х) = -2±К{х,!с). B6)
§ 2. Схема интегрирования уравнения КдФ
методом обратной задачи рассеяния
Возникновение метода обратной задачи рассеяния свя-
зано с замечательным наблюдением Гарднера, Грина,
Крускала и Миуры (ГГКМ).

34 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
Рассмотрим уравнение Шредингера
с убывающим на бесконечности потенциалом и (х). Для
определенности под / будем понимать какое-нибудь спе-
циальное решение задачи A), например, задаваемое асимп-
тотикой / (х, к) = е~гкх 4- о A), х -»- — с», т. е. опреде-
ленное в § 1 решение <р (х, к). Если потенциал в уравнении
A) зависит от дополнительного параметра t (времени),
то ф (х, к) также приобретает зависимость от t. Функ-
циями t становятся и данные рассеяния; асимптотика
Ф (х, к) на -\-оо по х выглядит так:
Ф (х, к) = а (к, f)e-ikx + Ъ (к, t)eikx + о A). B)
В случае произвольной зависимости и (х, t) от t найти
зависимость данных рассеяния от времени, очевидно, не-
возможно. Однако, если и (х, t) меняется во времени как
решение КдФ
иг — <оиих -f иХХгХ — О,
то а (к, t) и Ъ (к, t) подчиняются уравнениям ГГКМ
а (к) = О, Ь (к, t) = Ык*Ъ (к, *)(!!!), C)
а зависимость ф (х, к) от t дается уравнением
ф (х, к) = —А(р (х, к) + 4гА3ф (х, к), D)
где оператор А есть
Верно и обратное утверждение: если данные рассеяния
меняются во времени как решения ГГКМ, то потенциал
и (х, t) (однозначно ими определяемый) удовлетворяет
КдФ. Простейший способ 'убедиться в справедливости
сделанных утверждений — это заметить, что КдФ тож-
дественно уравнению для операторов L = —cP/dx2 -f- и
и А, задаваемому выражением E):
L = [L, А]. F)
Действительно, L есть оператор умножения на функцию
Uf, а коммутатор [L, А), как показывают простые вычис-

§ 2] СХЕМА ИНТЕГРИРОВАНИЯ УРАВНЕНИЯ КдФ 35
ления, также является оператором умножения на 6иих —
— Uxxxi так что F) совпадает с КдФ.
Представление.эволюционных уравнений в форме F)
называется представлением Лакса. тривиальным следст-
вием этого представления является независимость собст-
венных чисел оператора L от времени, поскольку, ввиду
антисимметричности А в L2 (R), оператор L (t) унитарно
эквивалентен L @). Таким образом, собственные значе-
ния L суть интегралы КдФ. Рассмотрим теперь уравне-
ние A) и продифференцируем его по времени:
Используя выражение F) для L, находим
(L - **)(/ + Af) = 0,
т. е. / -f- Af является собственной функцией L с тем же
собственным значением, что и /. Обозначим эту функцию
через f:
f f f O. G)
Выше мы фиксировали / ее асимптотикой на — <х> по х:
/ = ф (х, к). Это однозначно определяет решение /: асимп-
тотика / при х —>¦ —со не зависит от времени и имеет вид
e~iltx, значит, / + Af v 4?&3<riftx, т. е.
Ж» оо
f = 4iA3e-ifc3C -f о A), х -»- —оо,
или f = Aik3^ (x, к). Таким образом, уравнение G) в точ-
ности совпадает с D). Уравнения же ГГКМ являются не-
медленным следствием D) и определения данных рассея-
ния B). Устремляя в D) х ->- -f-oo и полагая и (х) — 0,
находим
ae-ihx ^_ iexkX = I 4 J!L + 4i/c3l (ae~il!X -f beikx),
т. е. уравнения (З).
Столь же просто решается задача об эволюции во вре-
мени данных рассеяния в дискретном спектре х„ (t), Ъп (t),
п = 1, . . ., N. Как уже выяснилось, собственные значе-
ния Хп = —и? от времени не зависят, поскольку L (t) эк-
вивалентно L @). Этот же результат извлекается и непо-
средственно из уравнения а (к) = 0: Ып представляют со-

Зб МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
бой нули не зависящей от времени аналитической функции
а (к), т. е. у,п = 0. Зависимость же bn (t) находится из урав-
нения D), поскольку Ъп по определению является коэффи-
циентом в асимптотическом разложении ц> (х, Ып)\
ф (х, Ып) = bn (tyynx -f о (е~'^х), х -+ +оо.
Подставляя эту асимптотику в D) при к = ixn, находим
К = 8xlbn. (8)
Итак, эволюция данных рассеяния во времени имеет вид
s (t) = {г (ft, 0) е*^>, хп, Ьпеак"', п = 1, . . . , А'}. (9)
Фактически мы проинтегрировали КдФ путем (неяв-
ной) замены переменных и (х) —>¦ s. В новых переменных
уравнения движения s = F (s) превратились в совокуп-
ность тривиально интегрируемых обыкновенных диффе-
ренциальных уравнений. Обращение замены s (t) —>¦ и (х, t)
дает решение КдФ. Таким образом, схема решения за-
дачи Коши для КдФ выглядит так:
I it in
и (х, 0) —> s @) -* s (t) -^ и (х, t).
Первый этап в этой схеме состоит в вычислении данных
рассеяния s @) по начальному условию и (х, t) |j=0 =
= и (х, 0) с помощью решения уравнений на соб-
ственные функции оператора Шредингера с потенциалом
и (х, 0). Второй этап заключается в решении задачи Коши
в терминах данных рассеяния. Эта задача оказывается
тривиальной: ее общее решение дается формулами (9).
Наконец, на последнем этапе нашей схемы необходимо ука-
зать потенциал и (х, t) в операторе Шредингера, имею-
щий s (t) в качестве данных рассеяния, т. е. решить обрат-
ную задачу рассеяния — найти, например, решение урав-
нения A.25).
Все этапы схемы связаны с изучением линейных за-
дач. Несмотря на то, что общее аналитическое решение
как прямой, так и обратной задачи рассеяния отсутству-
ет, последовательное применение метода позволяет иссле-
довать решения КдФ с той же степенью подробности, что
и решения линейного уравнения в частных производных.
Мы сможем предъявить, во-первых, множество весьма

§ 3] БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ И СОЛИТОНЫ 37
замечательных точных решений КдФ. Это iV-солитонные
решения в быстроубывающем случае (и —>- 0 при | х | —>-
-> оо) и аналоги этих решений в периодической задаче.
Во-вторых, мы опишем явными формулами асимптотику
общего решения и (х, t), t -> оо задачи Коши непосредст-
венно в терминах начальных данных — т. е. сделаем все,
что можно сделать в линейных задачах.
§ 3. Безотражательные потенциалы
и 2V -солитонные решения
Существует замечательный класс потенциалов, для ко-
торых как прямая, так и обратная задачи рассеяния реша-
ются точно. Это безотражательные потенциалы, для кото-
рых коэффициент отражения г (к) тождественно равен
нулю при всех к. С этим классом потенциалов связано
семейство точных решений уравнения КдФ — так назы-
ваемые Л^-солитонные решения. Эти решения описывают
процесс столкновения солитонов. Замечательной особен-
ностью уравнения КдФ является отсутствие неупругих
эффектов при столкновениях солитонов — после столк-
новения возникают те же солитоны, что и до столкнове-
ния. Именно этот факт, установленный впервые с помощью
численных экспериментов на ЭВМ, и вызвал повышенный
интерес к этому уравнению.
Рассмотрим данные рассеяния вида s = (г (к) = 0, хп,
Ъп, п = 1, . . ., N). Поскольку 6 (к) = 0, то | а (к) | = 1
и а (к) однозначно определяется своими нулями:
Пк — va
_
к + Ы '
п=1 «
По этой причине мы можем считать известными величины
—тг- , =а'(гхп).При этом ia' (?xn) вещественны и имеют
тот же знак, что и удовлетворяющие условиям A.10) ве-
личины Ъп (см. формулу A.15)). Таким образом, ядро F (х)
A.24) уравнения Гельфанда — Левитана имеет вид
п=1

38 МЕТОД ОБРАТНОЙ ЗАДАЛИ РАССЕЯНИЯ [ГЛ. t
Уравнение A.25)
при этом легко решается, поскольку является уравнени-
ем с вырожденным ядром. Решение К (х, у) необходимо
искать в виде
К(х,у)= 3 Кп(х)е-хпУ. B)
Выполняя интегрирование, получаем систему линейных
алгебраических уравнений на функции Кп (х)
= -p>-V n = l,2,...,N. C)
Обозначим через А (х) квадратную матрицу N X N с эле-
ментами
Согласно известной формуле линейной алгебры, решение
системы C) есть
к м
~ det Л (х) '
где через 4<п)(а:) обозначена матрица, получающаяся из
матрицы А заменой и-го столбца в последней на столбец
Поскольку потенциал и (х) определяется функцией
К (х, х), подсчитаем ее с помощью формулы B):
N
К (х, х) = (det A)'1 S det А(П) (х) е~"п*-
п=1
Вспоминая известное правило дифференцирования опреде-
лителя, заметим, что числитель в этом выражении пред-

§ 3] БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ И СОЛИТОНЫ 39
ставляет собой производную det.4, так что К(х,х) =
= -з— lndet A(x). Это замечание позволяет записать выра-
жение для потенциала и (х) A.26) в компактной форме:
и{х)=- 2-^- In del A (х). E)
Эта формула дает полное описание всего семейства безот-
ражательных потенциалов. Поскольку свойство безотра-
жательности сохраняется во времени при динамике КдФ
(если г (к, 0) = 0, то г (к, t) = г {к, 0)ешч = 0), уравне-
ние E) определяет набор точных решений КдФ. Времен-
ная динамика безотражательных потенциалов получается
простой заменой в определении D) матрицы А
Простейший нетривиальный безотражательный потен-
циал имеет один-единственный дискретный уровень —и2)
А (х) = 1 -f- -s-—^ и решение и (х, t) есть
U (X, t) = Г5 ; т-г; , (Ь)
v ' ' ch2 К (х — 4х2« — ф) у '
где введено обозначение
<p = _LlnJL = _Linfc. G)
т 2-л 2-х, 2к s '
Решение F) представляет собой солитон уравнения КдФ.
Таким образом, солитон — это безотражательный потен-
циал, в котором имеется одно связанное состояние. Энер-
гия этого состояния — и2 определяет как амплитуду, так
и скорость v солитона: v = 4и2. Величина <р представляет
собой координату центра солитона при t = 0 — эту вели-
чину мы будем далее, для краткости, именовать фазой
солитона.
В !общем/'случае решение E) зависит от 2N параметров
кх, . . ., hn, $i @), . . ., Piv @). Имея в распоряжении яв-
ную формулу E) для решения, можно убедиться, что оно
описывает процесс столкновения N солитонов со скорос-
тями Vn = 4х? (и соответствующими амплитудами), ины-
ми словами — асимптотика решения E) при t -*¦ —оо

40 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
представляет собой суперпозицию солитонных решений F):
u(z,t)-+'2iun(x — i;nt), t-^ — oo, (8)
n=l
где ип (х, t) — решение F) с х = хп. Однако извлечение
этого утверждения непосредственно из формулы E) свя-
зано с весьма длинными вычислениями. Мы поступим ина-
че: покажем, что данные рассеяния для потенциала (8)
(при соответствующем выборе фаз солитонов срп G)), отне-
сенные к моменту t = 0, совпадают с набором (х;, bt),
определяющим решение E). В силу взаимной однознач-
ной связи потенциала и данных рассеяния этого вполне
достаточно. Фиксируем некоторое большое по модулю
отрицательное число Т: 21 <С 0, | Т\ !§> 1, и рассматри-
ваем функцию и (х, Т), построенную по формуле (8) в
качестве потенциала в операторе Шредингера. Если мо-
дуль Т достаточно велик, то вне зависимости от выбора
фаз фп отдельных солитонов, составляющих и (х, Т),
потенциал представляет собой последовательность соли-
тонных потенциальных ям; координата n-й ямы хп =
= vnT -f- фп, так что расстояние между соседними ямами
хп — ?„_! ~ (vn — 1>п_г) Т много больше их размеров
~х-1. Такой потенциал, очевидно, с точностью до экспо-
ненциально малых по | Т | членов является безотражатепь-
ным: | г (к) | = О (е-^1Г1) при всех к. Поэтому мы вправе
забыть про непрерывный спектр оператора Шредингера.
Рассмотрим поведение решения ср (х, ixn). Его асимпто-
тика при х -*- —оо есть еух. Если бы мы имели один-един-
ственный солитон (данные рассеяния х0, Ьо) с координатой
х0, то при «прохождении» через солитон, т. е. в области
х ^> хй, асимптотика ф (х, Ы) имела бы вид а (х, хо)еКХ,
а (и, и0) = (х — хо)/(х -f- x0), т. е. представляла бы собой
растущую с х экспоненту, за исключением случая х =
= х0, когда растущая экспонента сменяется затухающей
и ф (х, гх0) = boe~K^, x -> с».
Вернемся теперь к потенциалу и (х, Т) и разобьем ось
х на области
ii (. i) ^ (^ 2)
• • •, In = (xn-i,
В области ?i функция ф (x, i%) имеет вид еКх. При про-
хождении через первый солитон, т. е. в |8 вид ф (х, гх)

§ Я] БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ II СОЛИТОНЬТ /, {
сохраняется; ф приобретает лишь множитель а (х, хх)
(если х Ф Xj); ф (х, ix) = а (х, щ)еКх. Теперь перед нами
второй солитон и та же самая задача, т. е. в Е3 ф (х, ix)
есть а (х, хх)-а (х, х2)-еух, если х =^ х1; х2. Продолжая
этот процесс до конца, найдем, что если х не совпадает ни
с каким из xit то при х ->¦ +оо (т. е. в ?)у.ц) асимптотика
Ф (я, /х) есть
Л'
ф (ж, Ы) = П «(и, хп) е*ж.
Таким образом, в потенциале и (х, Т) не может быть свя-
занных состояний с энергиями, отличными от —Хп (опять-
таки с экспоненциальной по | Т \ точностью).
Пусть теперь х = щ, 1 <^ к ^ N. Поступая как и вы-
ше, найдем, что в области ^ функция ф (х, ix^) имеет вид
Ф (х, i%k) = [[ а (хц, хп) ev"kX. Однако для к-то солитона е""*х
представляет собой асимптотику собственной функции
слева от него, так что в ?t+i растущая экспонента сменя-
ется убывающей:
»—1
Ф (х, ix,) = bw (Т) П а (х,, пп) e'V, xee Ь+1, (9)
где b^ (T) связано с координатой &-го солитона форму-
лой
хк
-4~ In bm (T) = Ах\Т + щ A0)
(см. F), G)). Продолжить решение (9) за (к — 1)-й соли-
тон мы уже не можем, ввиду некорректности такой задачи;
вместо этого изучим поведение решения, имеющего асим-
птотику e~x**i х -> +оо, т. е. решения г|) (х, —1щ). Как
и для функции ф (х, ix), мы можем заметить, что при про-
хождении справа налево через п-ш солитон ty{x, —ix) при-
обретает всего лишь множитель а (х, х„). Таким образом,
в области |я+1
N
yp(x,-ixk)^ П a(xk,%n)e-**x. A1)

42 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. t
Сравнивая A1) и (9), находим, что
ф {х, 1щ) = 6(fr) (Г) П a («t, *n) П а (Щ, *«) я|> {ос, — Ьек).
n=l п=Л+1 (\')\
Таким образом, —х*, к = 1, 2, . . ., N, суть собствен-
ные значения оператора Шредингера с потенциалом и (х,
Т). Рассмотрим теперь и (х, Т), Т -> —с» в качестве на-
чального условия для уравнения Кдф, т. е. рассмотрим
задачу о столкновении солитонов со скоростями vn = Ах„
и фазами ф„, п = 1, . . ., N. Данные рассеяния для тако-
го начального условия мы сосчитали: г (к) = 0, собствен-
ные значения —x\i а соответствующие нормировочные
( 1 ( 2
щ рр
множители ф (х, ix^-ty'1 (х, —ixn) даются формулами A2),
A0). Эти данные относятся к моменту времени t = Т.
Отнесем их теперь к моменту t = 0. Тем самым мы ука-
жем, какое именно из семейства решений D), E) отвечает
задаче столкновения данных при t ->-—с» солитонов.
Достаточно, очевидно, подсчитать Ьк @):
М0)=^АП^ П ^^. A3)
Эта формула задает взаимно-однозначное соответствие
между ф? и Ьк @), удовлетворяющими условию A.10)
(_i)»-i6n > о.
Итак, любое из решений E) описывает столкновение
N солитонов. Эти решения называются iV-солитонными.
Каков результат столкновения, т. е. какова асимптотика
./V-солитонного решения при t ->• +<х>?
Совершенно очевидно, что в результате столкновения
мы снова получим набор солитонов с теми же самыми ско-
ростями (и амплитудами), что и до столкновения. Это сле-
дует из того, что скорости равны vn = Axn и из инвариант-
ности КдФ относительно замены t -> — t, x —»- —х. Мо-
гут измениться, таким образом, лишь фазы солитонов
фп. Это изменение проще всего найти, воспользовавшись
указанной инвариантностью и формулой A3). При замене
х -»- —х изменится порядок расположения солитонов на
оси х; поэтому для того, чтобы связать фазы ц>1 образую-

§ 3] БЕЗОТРАЖАТЕЛЬНЫЕ ПОТЕНЦИАЛЫ И СОЛИТОНЫ 43
щихся при t -*¦ +00 солитонов с Ък @), достаточно поме-
нять местами символы Ц в A3):
ьк @) = rrt fi -?9г П ^г ¦ <14)
п=ш х* + хп п=1 Ч хп
Снабдим фазы солитонов на — оо по времени значком «ми-
нус». Формулы A3), A4) дают
N )с_1
1 1 2
* „ЭЕ+1
A5)
(Напомним, что солитоны занумерованы в порядке убы-
вания их скоростей, так что самый быстрый солитон име-
ет первый номер, номер самого медленного— N.)
Рассмотрим подробнее столкновение двух солитонов.
В этом случае
- 1 ,
— Ш-, = — In
+ - — 1 .
ь — ш2 = ш
т. е. быстрый солитон получает в результате столкновения
дополнительный сдвиг вперед на величину Ац>х = <Pi —
— %, а медленный — назад. Наиболее интенсивно взаи-
модействуют солитоны с близкими скоростями. Если
Дх = хг — х2 <^ х, то
Дф1=— hi 4х- A6)
и неограниченно возрастает при Ах -> 0. Логарифмиче-
скую зависимость сдвигов солитонов от расстояния меж-
ду уровнями при Ах/х <^ 1 нетрудно понять. Из анализа
явной формулы E) двухсолитонного решения (которая
хотя и весьма громоздка, но все же обозрима) можно уви-
деть, что при малой разности скоростей солитонов каче-
ственная картина решения такова. Решение и (х, t) в лю-
бой момент времени имеет два ярко выраженных миниму-
ма, причем расстояние между ними много больше
их характерных размеров. При достаточно больших по мо-
дулю отрицательных t каждый из этих минимумов дви-
жется с постоянной скоростью, и быстрый солитон приб-
лижается к медленному. По мере его приближения ампли-
туда быстрого минимума уменьшается, а медленного —

44 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
увеличивается. Соответственно скорость первого умень-
шается, а второго — возрастает. В момент максимального
сближения минимумов амплитуды их совпадают. Даль-
нейшее развитие событий происходит в том же направле-
нии: амплитуда первоначально меньшего минимума про-
должает монотонно возрастать, асимптотически прибли-
жаясь к начальной амплитуде быстрого солитона. Быстрый
же солитон превращается в медленный, после чего соли-
тоны, обменявшись скоростями и амплитудами, расходят-
ся. При этом, очевидно, сдвиг быстрого солитона по по-
рядку величины равен минимальному расстоянию, на
которое солитоны сближаются. Это расстояние легко оце-
нить. В момент максимального сближения амплитуды ми-
нимумов потенциала и (х, t) одинаковы. Если бы второго
минимума не было, в потенциальной яме первого был бы
один дискретный уровень с энергией —х2 и наоборот. Из-за
наличия двух минимумов этот уровень расщепляется на
величину Ах ~ е~"/Л (интеграл перекрытия), где I — рас-
стояние между минимумами. Отсюда, поскольку Ах нам
известно, I In —г— , что приводит к формуле A6).
В заключение отметим замечательное следствие фор-
мулы A5): полный сдвиг фазы солитона равен сумме сдви-
гов фаз при рассеянии его на всех остальных солитонах по
отдельности, т. е. многочастичные .з^ф_екты в ТУ-солитон-
ном решении полностью отсутствуют.
§ 4. Уравнение КдФ как^ гамнльтонова система
В отличие от других уравнений, изучаемых в этой кни-
ге, факт гамильтоновости уравнения КдФ не является
вполне очевидным и требует определенных пояснений.
Прежде всего напомним общее определение гамиль-
тоновой системы. Гамильтонова структура в четномер-
ном фазовом пространстве М размерности п задается скоб-
кой Пуассона. Скобка Пуассона {/, g} сопоставляет каж-
дой паре функций /, g на М, /, g: M ->¦ R третью функцию
h = {/> #}> ^: М -у R. Если |1; ?2, . . ., \п — координаты
точки \ ЕЕ М, то операция {,} по определению имеет вид

§ 4] УРАВНЕНИЕ КдФ КАК ГАМИЛЬТОНОВА СИСТЕМА 45
где со — невырожденная матрица п X п. Скобка Пуассо-
на обязана обладать свойством антисимметричности
{/. g) = ~{g, /}• B)
Это означает, что матрица сог?с (|) кососимметрична:
to* (|) = -to** (|). C)
Кроме того, скобка Пуассона должна удовлетворять тож-
деству Якоби
{{/- g}h} + {{h, f}g} + {{g, h}f) = 0, D)
которое эквивалентно некоторой системе уравнений на
со (t), которые совпадают с первой парой уравнении
Максвелла для обратной к со матрице W: W^ = (со),^,
WiKl + Wliik + Wu,i = V. Da)
В математической литературе определяют дифференци-
альную форму, т. е. выражение W = Wu $? Д dlk, где
dc,1 Д d^k = —d%k Д dg. Уравнение Dа) называется «зам-
кнутостью» формы W.
Скобка Пуассона превращает линейное пространство
функций на фазовом пространстве в алгебру Ли. Выбрав
какую-либо функцию h (I) и назвав ее функцией Гамиль-
тона, мы можем определить зависящее от параметра t
отображение этой алгебры на себя / (?) —> / (?, t), f (|, 0) =
= / (I) с помощью дифференциального уравнения
4 = {/, h}. E)
В частности, выбрав/ в виде /(^, ?) = Дб(|; — \i{t)),no-
лучим для |; (t) уравнения
3^
dt
— уравнения Гамильтона.
Всякая кососимметричная невырожденная матрица
со с помощью линейного преобразования в фазовом прост-

46 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
ранстве может быть приведена к блочному виду
л/ 0 .
О J О .
(U=|O°J.-...oj
\о о . о /
Обозначая соответствующие координаты в М посредством
b2t-i = A-i ?г<с = ?ь к — 1, . . ., ге/2, получим из F)
уравнения
т. е. уравнения Гамильтона в привычном виде. Пары пе-
ременных рк и дк являются канонически сопряженными.
В этих переменных скобка Пуассона записывается в виде
LJl df dg
Переходя теперь непосредственно к уравнению КдФ,
заметим, что оно может быть переписано в виде
Щ — -Я- (Зм2 — ихх) = -д— — , G)
' дх х хх/ дх Ьи (х) ' у '
где функционал Н есть
Н [в] = J (-^L + «3) Лг. (8)
а символ ЫЬи означает вариационную производную. За-
а ьн
писывая далее -т, «, , . как
" дх Ьи (х)
го
V
\
6 (х — х ) - ¦ dx ,
убеждаемся, что уравнение G) имеет вид F). При этом под
координатами функции и (точки в фазовом пространстве)
следует понимать совокупность ее значений в точках пря-
мой х, так что х ш х' играют роль индексов в формуле F);
со (х, х') = —б' (х — х), т. е. со очевидным образом ко-
сосимметрична и на функциях, убывающих при | х \ ->

§ 4] УРАВНЕНИЕ КдФ КАК ГАМИЛЬТОНОВА СИСТЕМА 47
—>- оо, невырождена ввиду обратимости оператора dldx
на таких функциях. Поскольку, далее, со не зависит от
точки и в фазовом пространстве, то скобка Пуассона
оо
{S, R] = \ , . -тг- , , dx (9)
1 ' J Sii(i) дх ои(х) v '
—оо
удовлетворяет тождеству Якоби C).
Итак, уравнение КдФ является гамильтоновым. Функ-
цией Гамильтона является функционал Н (8), фазовое
пространство состоит из достаточно гладких, убывающих
на бесконечности функций и (х), а гамильтонова структу-
ра задается скобкой (9), т. е. кососимметричным в L2 (R)
оператором dldx.
В заключение этого параграфа отметим, что всякое урав-
д 6Н
нение вида щ — -^—г— с трансляционно инвариантным
гамильтонианом Н имеет по крайней мере три интеграла
движения. Первый из них очевиден — это функция Га-
мильтона Н. Другой интеграл связан со структурой скоб-
ки Пуассона (9), т. е. с наличием в ней оператора -^
оо
это \ u(x)dx. Наконец, сохранение третьего интегра-
—ее
ла, играющего роль импульса, связано с трансляцион-
ной инвариантностью гамильтониана Н. Именно, если
Н [и (х+ а)] — Я [и (х) ] =0 для любой функции и (х),
то, разлагая при а —у 0 функционал Н [и (х + я)] по а,
получаем
-т г— dx = 0.
ои дх
—-оо
оо
Замечая, что и{х) = — -^^ Р= \ u2dx, находим
—оо
{Р, Щ = 0,
т. е. Р = 0 (см. E)).

48 Метод обратной задали рассеяний [гл. 1
§ 5. Полиномиальные интегралы движения
Уравнение КдФ имеет бесконечный набор интегралов
движения. Это, в силу уравнений ГГКМ, функция а (к),
О < к <С оо, которая при каждом к представляет собой
однозначно определенный функционал от и. Однако эти
функционалы определены неявным образом (с помощью
решений уравнения Шредингера). В этом параграфе мы
построим по а (к) интегралы движения вида
Оо
In = J Pn {U, Ux, Uxx, ..., «<.')) UX,
— 00
где Р — полиномы по функции и (х) и ее производным. Ин-
тегралы такого типа называются локальными полиноми-
альными.
Решение уравнения Шредингера <р (х, к) при достаточ-
но больших | к | можно представить в виде
ср
, к) = exp f— ikx -f \ % (х', к) Ах' .
—со
Если Im к ^> 0, то при х -> оо <р (х, к)егкх = а (к). По-
этому
lna(A;)= J %{х, к) Ах. A)
—ОО
Поскольку а (к) не зависит от времени при изменении по-
тенциала и (х) в силу КдФ, то выражения j % {х, к) dx
при всех к представляют собой интегралы движения.
Поскольку, далее, ф (х, к) есть решение уравнения Шре-
дингера, функция % (х, к) удовлетворяет уравнению типа
Рикатти
Хх + X2 - и - 2ik% = 0 B)
и допускает асимптотическое разложение
Подставляя это разложение в уравнение B), получаем

ПОЛИНОМИАЛЬНЫЕ ИНТЕГРАЛЫ ДВИЖЕНИЯ
пг
Xn+i (х) = -^ %п {х) + Yj X* (*) Хп-ь (*)» и = 1, 2, . . . ,
рекуррентные соотношения для %п (х):
п—г
D)
Xi {х)= -и (х).
Несколько первых коэффициентов %п (х) имеют вид
Ъ = — "*> Хз = —"хх + ,
Х4= — мххх + 2— и2,
Мы видим, что %2 (х) и %i (x) являются полными произ-
водными. Это свойство справедливо для всех %2п (х). Дей-
ствительно, полагая к в уравнении B) вещественным, пред-
ставим х (х, к) в виде суммы действительной и мнимой
частей: % = %r + i%i- Отделяя, далее, мнимую часть в
B), находим
dv
-Ж + 2*kXi - 2^R = 0,
откуда xR = 2~"^ln^i ~ ^' т- е- Хк W является пол-
ной производной; коэффициенты же %ш (х) представляют
собой, очевидно, коэффициенты асимптотического разло-
жения Xr (x).
Обозначим
J х2п+1 И dx, п = 0, 1, 2, . .. E)
—оо
Ввиду A), C), /„ являются интегралами движения урав-
нения КдФ. Приведем явный вид первых четырех:
/_! = — I и (х) dx, 2I0 = J и2 (х) dx,
— С» GO
ОО
2/х=- j (в^ + 2«в)Лс, F)
—оо
оо
2/2= j (^х _ Ъи2ихх + 5м4) dr.

50 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ (ГЛ. I
Первые три из /„ имеют, как было указано в предыдущем
параграфе, простую интерпретацию и одинаковое для всех
д 67/ „ г
уравнении вида ut = -тг- -г- происхождение. Сохранение 1^
связано со структурой скобки Пуассона, отвечающей урав-
нениям типа КдФ; сохранение /0 является следствием
трансляционной инвариантности КдФ, т. е. /0 играет
роль импульса, а —11 представляет собой функцию Га-
мильтона уравнения КдФ и имеет смысл энергии. Высшие
/„, п ;> 2, не допускают простой интерпретации.
Мы получили рекуррентные формулы D), позволяю-
щие строить полиномиальные интегралы движения 1п
в терминах и (х). Выразим теперь 1п непосредственно че-
рез а (к). С этой целью воспользуемся формулой A.8),
которую перепишем в виде
N . оо
'~IV" " '' In Ia (fc/) I dk'. G)
к' — к — iO \ '
Для бесконечно гладких потенциалов и (х) (а только для
таких и (х) и имеют смысл все 1п, п < оо) коэффициент
отражения г (к) убывает при | Л; | —^- оо быстрее любой
степени 1/| к |. Поэтому, вычисляя коэффициенты асимп-
тотического разложения In а (к) по степеням ilk, мы мо-
жем забыть про наличие в знаменателе интеграла в G)
символа Ю. Поскольку, далее, | а (—к) \ = \ а (к) \, ко-
эффициенты при четных степенях ilk в таком разложении
равны нулю. Таким образом,
3=0 1=1 О
(8)
Сравнивая теперь соотношения A), C), (8) и E), получаем
Оо
(-if1 -i- J k2j
-if1 -i- J k2j In | a (it) | dk. (9)
о

§ 6] ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ КдФ. ВЫСШИЕ КдФ 51
В частности, гамильтониан Н = —1Х, есть
JV оо
Н=~Щ-^\ + ^\кЧп\а{к)\йк. A0)
г=1 о
Любопытно отметить, что вклад в энергию от переменных
непрерывного спектра положителен (так как \ а (к) | ^>
^> 1), а дискретного — отрицателен.
§ 6. Полная интегрируемость уравнения КдФ.
Высшие уравнения КдФ
Выше мы установили серию замечательных и совершен-
но удивительных фактов, касающихся КдФ. Оказалось,
во-первых, что имеется замена переменных, состоящая в
переходе от потенциала оператора Шредипгера к дан-
ным рассеяния для последнего — такая, что в новых пе-
ременных КдФ, т. е. нелинейное уравнение в частных про-
изводных, распадается в бесконечный набор тривиально
интегрируемых обыкновенных дифференциальных ургв-
нений — уравнений ГГКМ. Далее нам удалось сконст-
руировать счетную совокупность локальных полиноми-
альных интегралов КдФ, смысл которых пока что совер-
шенно неясен, за исключением, правда, трех интегралов,
один из которых — гамильтониан уравнения КдФ.
Все эти факты получают естественную интерпретацию
при рассмотрении КдФ как гамильтоновой системы.
Именно, оказывается, что КдФ представляет собой пол
ностью интегрируемую гамильтонову систему; замена
и (х) —>- «данные рассеяния» является преобразованием
в фазовом пространстве к переменным типа действие —
угол, а каждый полином 1}[и], представляющий собой
интеграл КдФ, определяет, в свою очередь, вполне ин-
тегрируемую гамильтонову систему, задаваемую нели-
нейным уравнением в частных производных
дх Ьи (х) v '
Уравнения вида A) с / > 3 называются высшими уравне-
ниями КдФ; они интегрируются с помощью той же замены
переменных и имеют те же интегралы движения, что и
КЯФ.

52 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
Следует заметить, что до появления метода обратной
задачи рассеяния нетривиальных примеров интегрируе-
мых систем с большим числом степеней свободы известно
не было. Существовавшие примеры сводились к линей-
ным задачам.
Для «линейного уравнения КдФ»
д 6ffL
' XXX а_ S-.
с гамильтонианом
Нт. = 4- \ uldx
переменные действие — угол получаются фурье-преобра-
зованием и (х). Вводя комплексную функцию с (р) (р ^> 0)
оо
с (р) = -Д= { и (х) e-ip* dx
— оо
и используя выражение для скобки Пуассона D.9), лег-
ко видеть, что
{с (р), с (р')} = ib(p- р'), {с (р), с (р')} = 0,
т. е. с (р) и с (р) — канонически сопряженные перемен-
ные. Выражая через с (р) гамильтониан HL, получаем
со
Hl= <\>P3c{p)c(p)dp.
0
со
При этом полный импульс системы Р = ~- \ к2 dx есть
о
Уравнения движения в новых переменных имеют вид
с (Р) = {с (р), Нг) или
с (р) = ip3c (р), т. е. с (р, t) = c (p, 0) е^'г.
Переменные с (р), с (р) являются классическими анадо,-

6] ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ КдФ. ВЫСШИЕ КдФ 53
гами квантовомеханических операторов рождения и унич-
тожения; переменные типа действия 7V (р) представляют
собой числа заполнения состояний с импульсом р
N(p) = c(p)c (p).
Сопряженной к 7V (р) канонической переменной является
фаза с (р), Ф (р) = arg с (р), так что
{N (р), Ф (р')} = -б (р - р%
{N (р), N (р')} = {Ф (р), Ф (р')} = 0.
В переменных действие — угол гамильтониан зависит
только от половины полного набора переменных — он
является функцией действий
так что уравнения движения гласят
N (Р) = 0, Ф (р) = ps.
Перейдем теперь к непосредственной задаче этого пара-
графа — введению переменных действие — угол для КдФ.
Прежде всего укажем канонические переменные в терми-
нах данных рассеяния. Для этого необходимо вычислить
скобки Пуассона D.9) от всевозможных пар последних.
Рассмотрим, например, {а (к), Ъ (&')}
и [х) ох ои \х)
— оо
оо
1 Г / Ьа д 6Ъ db д 6а \ 1 ,г>ч
~~ 2 J \ 6и дх ди ди дх 6и ) ' * '
— оо
да (к) 66 (/с)
Для вычисления т—т-у, , , ¦ воспользуемся представле-
нием A.13):
бфBЛ к) д - &$(у,к) д ,,
бм (-к) 2г

54 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
Функция G [х, у, к) = . ' удовлетворяет, очевидно,
уравнению
— ^_^^_ 1 77 I4l\ /т ^^ "L^ii- Л (Т 1l\ CT\ 111 1?\ (Li\
~"~" п к | М» 14 1 ^-Г ^^ П/ KJT \s V"** ~-^ Ц I \у \ч 1 it)f \ ¦*/
получающемуся в результате «дифференцирования» урав-
нения Шредингера по и (х). При этом, поскольку ф (х, к)
определена асимптотикой при у -> — оо, решение
G (х, у, к) уравнения D) фиксируется дополнительным
условием
G (х, у, к) = 0 при у <. х.
Как решение уравнения D) G (х, у, к) является непрерыв-
ной функцией у при всех у; однако dGldy имеет разрыв в
точке у = х. Граничное значение 8G (х, у, кIду справа от
этой'точки легко находится из D):
/г IA (^Л
ду
У-+Х+0
Используем теперь то обстоятельство, что правая часть
выражения C) не зависит от у. Положим у = х -\- е,
е >» 0, е -> 0. Так как значение функции i|) (у, к), опреде-
ленной асимптотикой при х-*- + оо, очевидным образом
не зависит от значений потенциала в точках, лежащих
левее у, то бгр (у, кIЬи (х) = 0 (у > х) и формула C)
приобретает вид
6а (к) 1 — . 7 \ / т \ /?\
-Щ^)= гйг№ А) Ф (*.*)¦ F)
Совершенно аналогично находим
Подставляя найденные выражения в B), приходим к за-
даче вычисления интеграла
{a (fc),b (*')>-
оо
5 , к)-^$(х, к')ц>{х, к') —
- ф (х, к') ф (х, к') 4z у (х, к) ф (я, к)] dx. (8)

§ 6) ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ КдФ. ВЫСШИЕ Кдф 55
Подынтегральная функция в (8) является, на самом деле,
полной производной. Действительно, пусть flt gu /2, g2 —
произвольные пары решений уравнения Шредингера с
ft2, равными к\, к\ соответственно, т. е.
d2gh2
Тогда, как нетрудно убедиться,
A. f ' - d
-Т7 [(Л/г* — hhx) {gigix — gigix)\- (9)
k\-k\
Полагая fx = ty(z, k), /2 = \f> (x, k'), g1 = ф (х, к), g2 =
= <p (re, А;'), находим из (8), (9)
{a (ft), b (A;')} = -^ lim Го (А) о (/с') <r2ir* - Ь (к) Ъ {к') en-ik* -
- СТ «(к) Ъ (к') - 1±^г а (к') Ъ (к) е*<«'>*] -
- -^ lim Г — о (ft) а (к') е-™'* + Ъ(к)Ь {к') е-*** —
- jb? a (ft) Ь (ft') - ^ a (ft') b (ft) «-««**»')*] . A0)
При этом мы воспользовались тем обстоятельством, что
при х -> + оо
•ф (ж, ft) -> e-*te, ф (ж, ft) -> a (ft)e-ifC3C + 6 (ft)ei?C3C,
а при х-*- — оо
Ф (х, ft) -> e-J**, i|) (ж, ft) -> a (ft)e-tt5C — 6 (ft)e*4
Теперь необходимо выяснить, в каком смысле следует
понимать фигурирующие в A0) пределы. Для этого за-
метим, что при вычислении скобок Пуассона функциона-
лов от и (ж) величины типа {a (ft), b (ft')} всегда интегри-
руются по ft, ft' с некоторыми гладкими функциями ft, ft'.
Поскольку {a (ft), b (ft')} содержит сингулярные знамена-
тели, договоримся понимать такие интегралы в смысле
главного значения. Используя теперь известное в теории

56 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [Ы. t
обобщенных функций соотношение
eihx
lim P—— = nib (к),
где символ Р означает главную часть, получаем из (9)
{а (к), Ъ(к')} = -i-"ff^ff ~ -W* WЪ (*)б^ - *')•
Аналогичным образом считаются скобки Пуассона ос-
тальных пар элементов данных рассеяния. Вычислив их,
нетрудно убедиться, что величины
удовлетворяют каноническим перестановочным соотно-
шениям
{п (А), п (к')} = {Ф (к), ф (к')} = О,
{ф (А), п (к')} = в (А — А').
В общем случае данные рассеяния содержат также ха-
рактеристики дискретного спектра. Для вычисления ско-
бок Пуассона, содержащих эти характеристики, необхо-
димо найти вариационные производные бх^/бц (х),
bbjbu (x). Выражение для первой из этих производных
следует из известной формулы теории возмущений:
сю . оо
l = J Ьи (х) Д {x)dx Г J fn (x) dxT1,
ОО —СХЗ
где /„ (х) — собственная функция оператора Шредингера
с собственным значением — х*. Выбирая в качестве /п
функцию ф (х, Ып) и используя выражение A.15) для нор-
мы этой функции, находим
-^у = - ф2 (х, Ып) [ia (Ып) Ъп\~\ A2)
Для вычисления bbjbu (x) воспользуемся следующим
стандартным приемом. «Обрежем» потенциал и (х) на не-
котором конечном интервале, т. е. рассмотрим потенциал,
обращающийся в нуль вне этого интервала. Для обрезан-
ного потенциала все решения ф (х, к), ij) (x, к) могут быть

§ 6] ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ КдФ. ВЫСШИЕ Кдф 57
аналитически продолжены с вещественной оси в любую
точку комплексной плоскости к. (Это следует из теоремы
об аналитической зависимости решений уравнений от
параметра.) Поэтому для финитных потенциалов
Ъп = Ъ
и вариационная производная от Ьп находится из формулы
G), в которой следует положить к = ixn. Вычисляя скоб-
ки Пуассона, содержащие хп, Ъп (возникающие интегралы
без труда вычисляются с помощью формулы (9)), находим,
что переменные
Nt^n], Фг = 2 1Пт^ (Z-1, 2,,..,Л0 A3)
также имеют канонические перестановочные соотношения
{Nh Фр} - - &ir, {Nlt Ni>} = {Ф,ФГ} = О
и, кроме того, коммутируют с переменными непрерыв-
ного спектра п (к), ц> (к).
Совокупность канонических переменных п (к), <р (к),
TV;, Ф;, 1 = 1, . . .,N, является, очевидно, полной, пос-
кольку данные рассеяния однозначно ими определяются:
1-е 2k J X
/г (/с')
A4)
Мы выполнили первую часть нашей программы — в
фазовом пространстве, состоящем из функций и (х) со
скобкой Пуассона D.9), мы ввели канонические коорди-
наты п (к), ф (к), Ni, Фг. Мы можем, далее, используя
формулы предыдущего параграфа, указать явный вид
полиномиальных функционалов /,- [и] в этих координа-
тах. Формула E.9) выглядит так:
N~

58 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
Поскольку все п (к), Ni коммутируют между собой, то
и скобки Пуассона функционалов Ij [и] равны нулю:
{Ij, Iy) = О A6)
для любых / и /'. Это значит, что
6и дх 6u
Подынтегральное выражение в A7) представляет собой
некоторый полином по и (х) и ее производным. Равенство
нулю интеграла от этого полинома при произвольном виде
функции и (х) означает, что -г—^—5— является полной
производной:
Ы} д Ыу _ д
Ы дх 6и ~ дх Г]>3''
где Fj,y — также полином по и (х) и ее производным.
Этот факт позволяет утверждать, что построенные с по-
мощью рекуррентных соотношений предыдущего параг-
рафа функционалы Ij коммутируют между собой и в
случае, до сих пор не рассматривавшемся, когда и (х)
является периодической функцией х. В частности, это
означает, что КдФ и в периодическом случае имеет счет-
ный набор интегралов движения:
Вернемся, однако, к случаю убывания и (х) на беско-
нечности. Рассмотрим функционал Н вида
м
3=1
Мы можем объявить Н функцией Гамильтона, т. е. рас-
смотреть уравнение в частных производных вида
*-¦?•?¦• <19>
Любое такое уравнение будет полностью интегрируемым,
так как во введенных здесь канонических переменных Я
является функцией только от п (к), Ni и не зависит от

g 6] ПОЛНАЯ ИНТЕГРИРУЕМОСТЬ КдФ. ВЫСП1ЙЕ КдФ 59
угловых переменных <р (к), Ф;. В частности, полностью
интегрируемым является и КдФ, гамильтониан которого
E.10) в новых переменных имеет вид
ос
н = - Т" Ц| n^' + 8 S кЧ № dk-
Т
Уравнения движения
п = 0, ф = 8к3, Ni = 0, Ф, = -
в точности воспроизводят уравнения ГГКМ B.3), B.8)
и тривиально интегрируются:
п (к, t) = n (к, 0), ф (к, t) = <р (к, 0) + 8кН,
TVi (о = Ni @), ф, (о = фг @) - mNiht.
Таким же образом обстоит дело и с произвольным «выс-
шим» КдФ A9) с гамильтонианом A8). Все эти уравнения
сохраняют собственные значения оператора Шредингера
и имеют в качестве интегралов движения^функцию а (к)
и полиномиальные интегралы 13 [и]. Зависимость же уг-
ловых переменных от времени дается формулами
При этом из A5), A8) видно, что дН/дп представляет со-
бой полином по нечетным степеням к:
Таким образом, зависимость коэффициента отражения от
времени при эволюции потенциала и (х) в силу высшего
КдФ A9) имеет вид
г (п, t) = r (к, 0)e"W. B1)
Рассмотрим теперь дифференциальный оператор Ат
степени 2т -f- 1 с коэффициентами, зависящими от и (х) и
ее производных, такой, что, во-первых, он при и = 0
равен —-P[j-r-| и, во-вторых, удовлетворяет условию
~ и
где F — оператор умножения на функцию. Такой опера-

60 Метод обратной задачи рассеяния [гл. i
тор Ат очевидно, существует; длящего коэффициентов
нетрудно получить рекуррентные формулы, позволяющие
выражать эти коэффициенты через и (х). Очевидно, далее,
что уравнение
ut = F(u, ux,. . ., 42т+1)), B2)
тождественно представимое в форме Лакса
— = [L, Am],
будет в точности совпадать с уравнением A9), поскольку
эволюция данных рассеяния в силу B2), по построению,
имеет вид B1). Таким образом, всякое высшее КдФ имеет
лаксовское представление. Этим фактом мы воспользуем-
ся при изучении периодических решений КдФ.
§ 7. Дифференциально-разностные системы
*й Метод обратной задачи рассеяния может быть исполь-
зован и для изучения систем обыкновенных дифферен-
циальных уравнений. Рассмотрим, например, систему
dc
-^- = с„ (сп+1 — cn_x), — оо<гс<оо, сп(*)>0. A)
Эта система возникает, в частности, при изучении тонкой
структуры спектров ленгмюровских колебаний в плазме.
По этой причине мы будем иногда называть систему A)
«ленгмюдр_в?кпй папочкой». Уравнения A) записываются
в лаксовской форме L = [L, А] с помощью пары беско-
нечных квадратных матриц L и А с элементами
i-'nm == Сп On, m+l ~г СщОп+i, m> (/')
«пш = ~2~ L^n Cn-^On, m+г СтСт_д.Оп.+2, т'' \ )
где 6пт — символ Кронекера: 6пт = 0, если и =^ т и
бпт =±= 1 при п = т. Непосредственно вычисляя коммута-
тор LA — AL, убеждаемся, что он совпадает с dL/dt,
вычисленной согласно A).
Другим примером интегрируемой дифференциально-
разностной системы является система уравнений, описы-
вающая динамику одномерной цепочки частиц с экспонен-

§ 7] ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ
циальным взаимодействием ближайших соседей:
D)
где хп (t) можно донимать как координату n-го атома в
решетке. Система D) называеся цепочкой Тоды, впервые
в 1970 г. рассмотревшего решетку такого типа и обнару-
жившего точное решение уравнений D) — солитон, описы-
вающее движение дислокации в решетке. Уравнения D)
тождественно переписываются в виде
сп = сп (vn — iv-i), vn = сп+1 — сп, E)
где vn = хп, сп = ехр (хп — хп-г), сп > 0.
Система E) интегрируется с помощью следующей
L — А -пары:
пт == ^п On, in+l "г Cm On+i т "г ^rfinmi \P)
Апт = Va (Cn'Sn, m+l — Cm'&n+li m). G)
Заметим, что оператор F) отличается от оператора B)
лишь на диагональную матрицу.
Уравнение A) представляет собой разностный аналог
уравнения КдФ и в континуальном пределе переходит в
последнее. Для того чтобы убедиться в этом, рассмотрим
функцию с (х, t), — оо < х < оо, удовлетворяющую урав-
нению A):
с (х) = с (х)[с (х + б) — с (х — б)].
Будем считать 0 <С б<^ 1, а с (х) предполагать достаточ-
ное число раз дифференцируемой по х. Положим далее
с (ж) = 1 — ЬН (х),
где v (х) удовлетворяет уравнению
v = v (х + б) — v (х — б) — 62v (x)[v (х + б) —
~v (х — б)].
Разложим правую часть этого уравнения в ряд по б с
точностью до членов б3:
v =
Член 26vx устраняется галилеевским преобразованием

62 МЕТОД ОБРАТНОЙ ЗАДАЛИ РАССЕЯНИЯ [ГЛ. 1
t' ¦=. t, z' — х — 2б?; в штрихованных переменных урав-
нение приобретет вид
dt i дхл дх
Полагая, наконец, о- ? = т, получаем
дх дх» ' "" дх
Устремляя теперь б к нулю, получаем уравнение КдФ.
Аналогичный предельный переход может быть осуще-
ствлен и в терминах L —• ^4-пары. Для этого рассмотрим
эквивалентные представлению Лакса уравнения
со с©
+ ]T Aty = 0, — oo < n <oo,
(8)
где операторы Lh А определены формулами B), C). Запи-
сывая (8) в виде
A — б2 v (x))l!\ty (х — б) +
+ A — б2г; (х + d))Vn|> (х + б) — 2$ (х) = (X — 2Щх)
и разлагая это соотношение по б, получим
б2 (Цхх - v (х)) = (К - 2) ф (х) + О (б3).
Обозначим X — 2 = —6zk2. При этом
фжя - г? (ж)ф = -А:2ф + О (б).
Проводя аналогичную процедуру для второго из урав-
нений (8) с учетом использованных выше замен х->х',
t -> ? -> х, найдем, что
где оператор Л в точности совпадает с B.5). В этом смысле
континуальным пределом L — Л-пары B), C) является
соответствующая пара операторов для КдФ, а оператор
B) представляет собой конечноразностный аналог опера-
тора Штурма — Лиувилля — Шредингера. Отметим, на-
конец, что континуальным пределом системы D) является
уравнение нелинейной струны
д*и . дЧ 3% J" ,
~W ~ С ~д& +~дх^ "Г" Э» и >

§ 7] ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ Q
также интегрируемое с помощью метода обратной зада-
чи [6].
Перейдем к изучению задачи Коши для систем A),
D). В случае бесконечных цепочек естественными гранич-
ными условиями являются с„ -> 1, | п | -> оо для ленг-
мюровской цепочки A) и cn-> I, vn-+ О, | п | -> оо для
цепочки Тоды D). В последнем случае с„= 1 эквивалент-
но хп — ?„_! = 0. Если хп — смещение n-й частицы о т
положения равновесия хп = 0, то принятое условие оз-
начает, что на бесконечности решетка получается, вообще
говоря, сдвигом из покоящейся решетки хп = 0. Решая
задачу Коши для исследуемых уравнений по схеме метода
обратной задачи (!Ц2), мы должны прежде всего изучить
прямую и обратную задачи рассеяния для соответствую-
щих операторов L. Эти задачи естественным образом фор-
мулируются и имеют очень много общего с теорией рас-
сеяния для оператора Шредингера.
Уравнение на собственные функции оператора L F)
имеет вид
/^^n-l + /w^n+l + IVtn==4>n. — оо<п<оо; (9)
tpn мы будем считать комплексными числами. Собственные
функции оператора L, ассоциированного с ленгмюровской
цепочкой, удовлетворяют (9) при vn = 0. Мы будем счи-
тать, что коэффициенты задачи A9) удовлетворяют ус-
ловиям
Первое из этих условий, в терминах цепочки Тоды, озна-
чает, что сдвиги решетки на бесконечности по п конечны,
второе означает, очевидно, конечность импульса. (При-
веденные выражения являются, очевидно, интегралами
движения системы E).)
Задача (9) имеет вырожденный непрерывный спектр,
заполняющий отрезок — 2 ^ X ^ 2; кроме того, она
имеет, вообще говоря, дискретный спектр. Собственные
значения дискретного спектра по модулю больше двух,
соответствующие собственные функции я])п квадратично
суммируемы. Собственные функции непрерывного спектра
tyn (X) ограничены при всех п. Если X принадлежит не~

64 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
прерывному спектру, то асимптотика я])п при п -> ± оо
имеет вид
я|>п = Clzn + ciZ~n + о A), |z| = l, k^z + z-1.
Введем специальные решения задачи (9) я])п (z) и фп (z),
определенные асимптотиками
tn (Z) = Z" + О A), П-ХХЭ,
фп (z) = z~n + о A), n -»- — оо.
Функции фп (z), iJ3n (z) при любом п аналитичны внутри
единичного круга комплексной плоскости z. Вторая пара
решений (9) %г (z), ф„ (z), определенная асимптотиками
^п (z) = z-n + о A), и-* + оо,-
ф„ (z) = zn + о A), п -> — оо,
аналитична вне этого круга *). На единичной окружно-
сти, очевидно,
•Фп (z) = г^п (z), фп (z) = фп (z), | Z | = 1.
Продолжая эти соотношения в комплексную плоскость,
получим
^n ^z^= ^п (т)= фп {у
В плоскости z (к = z + z") непрерывный спектр задачи
(9) представляет собой единичную окружность. При
| z | = 1 решения я])„ (z) и oj),, (z) линейно независимы.
Поскольку, далее, число линейно независимых решений
уравнения (9) не больше двух, то всякое решение (9)
должно быть линейной комбинацией ij> (z) и я]) (z). В част-
ности,
Ф„ (z) = о (z) fn (z) + р (z) Фп (z), |z| = l. A2)
Для любых двух решений я])'1.2) уравнения (9) с одним и
*) Заметим, что как решения вещественного уравнения с асимп-
тотиками, даваемыми вещественными функциями z введенные
функции удовлетворяют соотношениям фп (z) = фп (г), tyn (z) =;
= г|)„ (I) и т. д,

§ 7] ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ 65
тем же к выражение
W (тр
не зависит от номера п. В нашей теории форма Наиграет
роль вронскиана; в частности, если W (г|5A), я])B)) = О,
то решения фО и я])B> линейно зависимы. В описанном
выше континуальном пределе W непосредственно пере-
ходит в определитель Вронского. Вычисляя вронски-
ан W(<p(z), ip (z)):
П—>ос
W (ф, т|>) = a (z) W (-ф, 1(з) = а (z) (z - z),
находим
а(,),- ^CPWJW) , A4a)
Эта формула показывает, что a (z) аналитична при | z | <
< 1. Вычисляя аналогичным образом W (ф, ф), найдем,
что
| a (z) |" - | р (z) |« = 1, | z | = 1. A46)
Точки вещественной оси zn, 0< | zn | <^ I, n = 1, 2, ...
...,7V, в которых а (zn) = 0, взаимно-однозначно соот-
ветствуют собственным значениям дискретного спектра
оператора L: Хп = zn + z^1, Im zn = 0. В этих точках
Фп Ы = Ькф„ (zfr), Im bk = 0, A5)
т. о. фп (zft) — собственные функции.
Совокупность
s = (r (z), zn, Ь„, га = 1, 2, . . ., iV),
где /• (z) = p (z)a (z), | z | = 1, по аналогии с теорией
оператора Шредингера назовем данными рассеяния для
оператора L. Оператор L B) является частным случаем
F). Полагая в (9) vn = 0, легко видеть, что при этом
Фп (—z) = (-1)" Ф„ (z), г|}„ (—z) = (-1)" r|)n (z) для всякого
п, так что для оператора L B)
a (-z) = a (z), p (-z) = р (z), | z | = 1.
Поэтому в терминах данных рассеяния выделение опера-
тора B) состоит в том, что г (—z) = г (z), | z | = 1. Точки
zn при этом образуют множество, симметричное относи-
тельно z = 0; в симметричных точках нормировочные
множители Ьк совпадают.

66 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. Г
Эволюция данных рассеяния вь времени в силу дина-
мики системы E) определяется из уравнения
9Ф„ (z) 1
в котором правая часть выбрана так, чтобы асимптотика
фп (z) при п —>- — оо не зависела от времени; оператор А
задается матрицей G). Подставляя в это уравнение вы-
ражения A2), A5), найдем
r(z, t)=r(z, 0) exp l(z - z) *],
bn (t) = bn @) exp l(Zn - zl1) t]. {Щ
При этом, разумеется, собственные значения (zn) от вре-
мени не зависят.
Аналогичным образом находится зависимость от вре-
мени данных рассеяния, если коэффицинты оператора B)
удовлетворяют уравнениям A):
г (z, t)=r (z, 0) exp t(z2 - z) t],
bn (t) = bn @) exp [D - z;2) t].
.« .-24 „ A7)
Переходя к обратной задаче рассеяния, введем обозна-
чения
со
I \ ТТ -Чгп I \
Ф„(г) =2Г" 11 сн Вп(г),
ОО
&,(*) = *-" П c^'uiz), A8)
ос
Ввиду (И), по-прежнему имеем
An \z) — An \z )¦ \Ly)
Функции 0n (z) и х„ (z), аналитичные соответственно
внутри и вне единичного круга, удовлетворяют уравне-
нию
(такому же уравнению удовлетворяет и %п). При z ->¦ 0 из

§ 7] ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ (j?
B0) следует
en_l(o)
Сп - еп@) '
%„ (z) при | z | ->- со имеет асимптотическое разложение
Подставляя это разложение в B0), находим
vп = Хп — Xn-i-
Перепишем теперь соотношение A2) в терминах A8):
^ + z™r(z)Xn(z), N| = l. B3)
Повторяя соответствующие рассуждения § 1, введем в рас-
смотрение кусочно-аналитическую функцию Фп (z):
Эта функция имеет простые полюсы в точках единичного
круга zlt z2, . . ., zn, в которых a (z) обращается в нуль.
Вычет Фп (z) в точке z^ согласно A5), A8), A9) равен
На единичной окружности скачок функции Фп (z) есть,
как видно из B3),
z2nr (z) зс (*).
Наконец, при | z | -> со функция Фп (z) -> 1.
Эти характеристики однозначно определяют Фп (z):
Фп(«)-1-
Е1 |г|1
B4)
Интегрирование в B4) по единичной окружности ведется
в положительном направлении (против часовой стрелки).
Формула B4) позволяет написать замкнутую систему

88 МКТОД ОБРАТНОЙ ЗАДАЧИ РАССКЯНИЯ [ГЛ. Г
уравнений на функцию. %„ (z), | z | = 1 и величины
Xn (zic1), которые мы для краткости обозначим через Г„ •
Устремляя точку z к единичной окружности снаружи,
получим из B4)
/?=1
Полагая, далее, в B4) z = z^1, получим N уравнений
на If\ к = 1, 2 ЛГ,
i' (г ^ (zT1 -! ) 2 m
^ т> ^ к т' | z | _ j " "л1
B6)
Величины cn, vn определяются через решения системы
B5), B6) формулами B1), B2), в которых следует поло-
жить
N
а (О) /_iZ"' °та \Zm> п 2яГ \ Z r\zl%n\z) zi
771=1
B7)
т=1
Нетрудно проверить, что при указанных выше ограниче-
ниях на данные рассеяния, выделяющих оператор L B),
функция XnW автоматически обращается в нуль, что га-
рантирует vn = 0.
Как и для оператора Шредингера, уравнения обратной
задачи B5), B6) легко решаются, когда коэффициент г (z)
есть тождественный нуль. В этом случае сп, vn определя-
ются исключительно характеристиками дискретного спект-
ра. При р (z) = 0 на окружности | z | = 1
как это следует из A46). В этом случае a (z) однозначно
определяется своими нулями zt, i — 1,2, .. .,7V, и усло-
вием a @) > 0. Последнее условие не имеет отношения

§ 71 ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ 6§
к ситуации р (z) = 0 и является общим. Оно является
следствием формулы
по
а@)= ГЬ;'/2>0,
— со
вытекающей непосредственно из A4а) и A8). При E = О
Z — Z.
a (z) = sign (IIzj) П ¦
zz.— 1
Знаки нормировочных множителей bt должны удовлет-
ворять условиям, вытекающим из формулы
со
Зфп(ч> = -^а'B,)&г, B8)
следующей из тех же соображений, что и формула A.15).
В остальном bt могут выбираться произвольно.
Рассмотрим простейшую ситуацию, когда a (z) внутри
единичного круга имеет единственный нуль в точке z =
= z1 = x. В этом случае система алгебраических уравне-
ний B6) состоит из единственного уравнения па Г„ = Гн:
где через с обозначена величина
Ъ
с => —
а' (х) (х-1 — ж) '
которая, ввиду B8), положительна. Вычисляя с помощью
B7) 9П @), ХпЧ, находим
Xn — {x x> i + CT2n
Введем обозначение
В силу A6), п0 является линейной функцией времени:
п0 (t) = щ @) - (in -У (х'1 - х) t.

70 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
Используя B1), найдем смещения частиц решетки хп (t):
хп (t) = — InOn(O) + const =
Таким образом, решение B9) представляет собой движу-
щуюся с постоянной скоростью деформацию решетки,
причем форма деформации не меняется во времени. Та-
кое решение мы будем называть солитопом. Скорость
солитона зависит от положения нуля a (z),
(х-*- — х),
причем v положительно, если х < О, и отрицательно,
если х > 0. (Напомним, что | х | < 1.) Легко видеть, что
\v |>1.
В общем случае, когда a (z) имеет N нулей, а г (z) = 0,
система уравнений обратной задачи B5), B6) сводится,
как и в односолитониой ситуации, к системе N линейных
алгебраических уравнений на величины Г„ , /? = 1,2, . . .
. . . , N, и всегда может быть решена. Как и для КдФ,
соответствующее решение уравнений D) является 7V-co-
литонным, т. е. описывает процесс столкновения солито-
нов. Рассмотрение этой задачи может быть проведено точ-
но так же, как и в теории КдФ; такими же оказываются
и результаты. Скорости солитопов до и после столкнове-
ния одинаковы, изменения испытывают лишь фазы (п0 @))
солитонов, причем «многочастичные» эффекты в столкнове-
ниях солитонов отсутствуют.
Столь же просто находится солитон ленгмюровской
цепочки A). В этом случае, ввиду четности, a (z) имеет
четное число нулей внутри единичного круга, причем
если a (zt) — 0, то и а (—z{) = 0. В простейшем случае
(г (z) = 0) a (z) имеет два нуля, zx = х > 0, z2 = — х.
Обозначим
ввиду B8) с > 0. Полагая Г?° = Г^2) = Гп и решая
уравнение B6), находим

§ 7J
ДИФФЕРЕНЦИАЛЬНа-РАЗНОСТНЫЕ СИСТЕМЫ
71
Формулы B7), B1) дают решение системы A) сп (t). При.
этом следует вспомнить, что ввиду A7)
с (t) = с @) ехр [(х2 - x~z) t],
X-x C0)
Таким образом, C0) представляет собой солитон, движу-
щийся со скоростью
v = —(In аг2)-1^-2 — х2).
Очевидно, что для любого х скорость v (х) < — 1. IIpi
х -*¦ 1 решение C0), как и следовало ожидать, превраща-
ется в солитон КдФ. Многосолитониые решения ленгыю-
ровской цепочки ведут себя так же, как и TV-солитонные
решения КдФ.
В заключение этого параграфа докажем полную ин-
тегрируемость периодической цепочки Тоды. Такую це-
почку можно представлять как систему N частиц на ок-
ружности, соединенных «пружинками». Для бесконечной
системы уравнений E) выделение такой системы эквива-
лентно наложению периодических условий
Z'n+iV = Vn, Cn+N = Сп.
Задачу на собственные значения (9) также будем рассмат-
ривать в классе периодических функций, полагая ij>n+jv =
= ijjn. При этом бесконечная матрица F) редуцируется
до симметричной матрицы N X N, имеющей 7V независи-
мых собственных значений. Эта матрица имеет вид
v3
N-i vN-i VCN
~i о о yi^ vN
а ее собственные значения A,;, i =1, 2, . . ., TV, удовлет-
воряют характеристическому уравнению
det \\L — U\\= 0,
где / — единичная матрица.

72 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
Покажем, что все собственные значения kt находятся
в инволюции, т. е. скобка Пуассона любой пары kt, Xj
равна нулю (собственные значения L коммутируют между
собой). Система D) гамильтонова. Ее гамильтониан есть
п
a vn, xn — канонически сопряженные переменные. В этих
переменных скобка Пуассона имеет обычный вид:
—
х dvn dvn дхп ¦
п
В переменных сп, vn {S, Т} переписывается следующим
образом:
dS дТ ЛЁ дт
Вычислим теперь производные dkifdcn, dX/dvn. Для этого
воспользуемся известной формулой теории возмущений,
определяющей изменение собственных чисел оператора
при малом изменении последнего:
вЛ,=-<1> I 6X | oj)>.
Здесь г]з — нормированный на единицу собственный век-
тор L. Имеем
6Я,; I
где я|) (/) — собственная функция L с Я = kj.
Заметим теперь, что для любых двух собственных функ-
ций оператора L справедливо следующее, непосредствен-
но вытекающее из (9) соотношение:
(h ~ h) 4>nG) 1>n@ =
= Wn (г|> (/), ф @) - Wn+l (ф (/), Ф @).
р,е W дается формулой^ A3).

§ 7] ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ СИСТЕМЫ 73
Используя приведенные выражения, нетрудно убедить-
ся, что
N
l @, r|) (;)) - PFn № @,
-Ц- V
I^ A @. 1> (/)) - Wi A> @.
Это выражение при наложении периодических граничных
условий обращается в нуль, т. е.
{Xh lj} = 0.
Собственные значения Xt являются, в силу представления
Лакса, интегралами движения. Таким образом, мы по-
казали, что гамильтонова система D) с 7V степенями сво-
боды имеет N независимых, коммутирующих между собой
интегралов движения. В силу известной теоремы Лиу-
вилля (см., например, [20]) это означает полную интегри-
руемость рассматриваемой системы.
Заметим еще, что гамильтониан цепочки Тоды выра-
жается через след квадрата матрицы L:
N
п=1
Согласно той же теореме Лиувилля, величины Яг- могут
быть выбраны в качестве канонических действий системы
D). Последняя же формула демонстрирует гамильтониан
в этих переменных. Обратим теперь внимание на следую-
щее обстоятельство: тот факт, что все собственные значе-
ния L коммутируют, никак не связан с конкретным ви-
дом системы D). Поэтому мы можем утверждать, что пол-
ностью интегрируемой является любая система вида
. дН . дН
Х V
Vn — ~~
Г
где гамильтониан Н — произвольная функция от инва-
риантов матрицы L; последние можно выбрать в виде
/„ (х, v) = Sp Ln, так что Н = f (/1( /2, . . ., In) и
/п, п = 1, . . ., N, являются каноническими действиями.

74 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ 1ГЛ. I
§ 8. Нелинейное уравнение Шредингера
п уравнение sin-Gordon
Развитая в первых параграфах этой главы теория
уравнения КдФ опиралась на представление Лакса
L = [L, А] уравнения КдФ. Сейчас мы укажем другое
коммутационное представление этого уравнения, отправ-
ляясь от которого мы увидим возможности обобщения
надлежащим образом модифицированной теории на другие
эволюционные уравнения.1
При интегрировании КдФ фундаментальную роль иг-
рало обыкновенное дифференциальное уравнение второго
порядка — уравнение Шредингера
fee == И> = —кЦ. A)
Было отмечено, что если потенциал в этом уравнении
меняется во времени согласно КдФ, то i?> удовлетворяет
еще одному линейному уравнению, а именно
+ Зи^-Цз. B)
Эти два дифференциальных уравнения на "ф являются,
вообще говоря, переопределенными. Условие совместно-
сти этих уравнений при всех кг является условием на по-
тенциал и (х, t) и есть не что иное, как требование, чтобы
и (х, t) удовлетворяло КдФ
щ — 6иих + иххх = 0. C)
Для того чтобы убедиться в том, что C) представляет со-
бой условие совместности A) и B), удобно поступить сле-
дующим образом. Перейдем от уравнения второго поряд-
ка A) к системе двух уравнений первого порядка, вводя
новую неизвестную функцию г|515 так что
% = гЛгф -J- г^. D)
Тогда из A) имеем
¦ф1х = — гАг-фх + иф. E)
Система D), E) очевидно тождественна A). С помощью
D), E) можно исключить все производные по х из уравне-
ния B), в результате чего получим
F)

§ 8] НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ШРЕДИНГЕРА 75
Из этого уравнения, используя D) и E), можно получить
аналогичное уравнение для г^:
+ Bм2 - ихх) 1]) + М>х. G)
Формируя из гЬ и ib, столбец (, ) = <р, системы уравнений
D), E) и F), G) можно записать в компактной форме
Фх = U (X) Ф, (8)
Ф» = У(Ц Ф (9)
с помощью матриц U и V, зависящих от параметра X:
Матрицы С/, F зависят от х, t через посредство функции
и (х, t).
Система уравнений (8), (9) на вектор ф является пере-
определенной. Дифференцируя (8) по t, (9) по ж и прирав-
нивая ответы, получим условие совместности (8), (9):
Матрицы U и V зависят от произвольного комплексного
параметра X (в рассматриваемом случае U, V — полиномы
по А.). Поэтому левая часть A1) также представляет собой
полином по X. Поскольку A1) должны выполняться при
всех X, коэффициенты этого полинома должны быть равны
нулю. Подставляя A0) в A1), находим, что указанная
структура A0) матриц U и V обеспечивает обращение в
нуль всех коэффициентов этого полинома, за исключе-
нием свободного члена, и левая часть A1) имеет вид
О 0\
Требование равенства нулю этой матрицы означает, что
и (х, ^удовлетворяет КдФ. Таким образом, (И) представ-

76 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. 1
ляет собой новое коммутационное представление КдФ,
которое играет большую роль в теории периодических
решений — см. § 3 гл. II, где U — Q, V = А.
Коммутационное представление A1) КдФ подсказы-
вает путь обобщения теории КдФ на другие эволюционные
уравнения: интегрируемое уравнение должно представ-
ляться условием совместности уравнений (8), (9) с матри-
цами U и V, зависящими рациональным образом от спек-
трального параметра К и содержащими в качестве коэф-
фициентов решения рассматриваемого уравнения. Изу-
чение возникающей при этом конструкции в случае произ-
вольной матричной размерности U, V и общей зависимо-
сти U от X мы отложим до гл. III. Здесь же мы ограни-
чимся случаем, когда U, V являются матрицами 2x2
и U — линейная функция X. Этот случай, как видно из
A0), представляет собой естественное (и минимальное)
обобщение КдФ и требует лишь пезначительной модифи-
кации теории. Будем считать, что U (x, t\ к) имеет вид
где q. r — вообще говоря, комплекснозначные функции
х, t. Матрицы же V (Я) будем подбирать из условия, чтобы
A1) сводилось к некоторым уравнениям в частных произ-
водных для д, г. Уже такое минимальное обобщение ока-
зывается весьма содержательным.
Выбирая V в виде
A3)
убеждаемся, что A1) эквивалентно системе уравнений
irt + rxx + 2qr2 = 0,
iQt — Яхх — 2rq2 = 0.
Полагая г — q или т = —д, получаем
irt + rxx + 2 | г I2 г = 0 (г = q), A4а)
irt + rxx - 2 | г |2 г = 0 (г = ~д). A46)
Уравнения A4) будем называть нелинейными уравне-
ниями Шредингера.

8] НЕЛИНЕЙНЫЕ УРАВНЕНИЙ ШРЕДИНГЕРА 77
Выбрав в качестве V матрицу
A5)
получим уравнения
qt + qxxx + 6rqqx = О,
Будем считать q и г вещественными. Частным случаем
A6) с г = —1 является уравнение КдФ. Полагая же г = q
или г = —q, получаем
rt + rxxx + 6r2rx = О (/• = ?), A7а)
rt + rxxx - 6г2гж = 0 (г = -д) A76)
— так называемые модифицированные КдФ (МКдФ)
или КдФ с кубической нелинейностью. Если q = —1 +
+ ост-, то
Гг + ГГХх — &ГГХ + 6(Х77"Г = 0.
Таким образом, это уравнение также попадает под дей-
ствие метода обратной задачи.
Положим теперь г = q == ux/2 и рассмотрим матрицу
Т/_ ^ (cosu — j sin u\ ..n,
4iX \? sin u — cos и J * '
Для и получим из A1)
wx; = sin u (r = q = uJ2) A9a)
— уравнение sin-Gordon.
Полагая же г = —g = —wx/2 и
Tr 1 i ch и — ? sh и
iik \— i sh и — ch и
находим
uxt = sh и A96)
— уравнение sh-Gordon.
Все перечисленные уравнения связаны с задачей (8), в
которой матрица U(k) имеет вид A2). Поэтому нашей бли-

78 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. 1
жайшей задачей является изучение связанных с системой
уравнений (8) прямой и обратной задач рассеяния и вы-
числение зависимости от времени соответствующим обра-
зом определенных данных рассеяния. Все это мы сделаем
в следующем параграфе.
§ 9. Обратная задача рассеяния для системы
двух дифференциальных уравнений
Рассмотрим систему двух дифференциальных уравне-
ний на комплексные функции W a
iq{x)
+ ir (x)
От комплексных функций г (х), q (x) потребуем, чтобы
J | г (ж) | da: < ос, J |g(a:)|da-<oo. B)
— ОО —'СО
При каждом вещественном X система A) имеет два ли-
нейно независимых решения. Как и при изучении обрат-
ной задачи для оператора Шредингера (§ 1), мы рассмот-
рим в пространстве решений два базиса. Один из них будет
состоять из пары функций, определенных асимптотиками
при х —>- + со, другой — при х —у — оо.
Итак, пусть %(х, X), i|j2 (x, X) — решения A), опреде-
ляемые с помощью асимптотического условия
решения же (рг(х, X), (р2(х, X) определяются асимптотиками
ф1 (¦*, Л) = [ Q
/ °
ф2 (х, Л) = I ^^
векторы %, •фз образуют базис, так что
фг (Ж, Я,) = 2 ^fci (^) "Фй (^i ^)- C)

g 9J
OBPATHAft ЗАДАЧА РАССЕЯНИЯ ДЛЯ СИСТЕМЫ
79
Определенную таким^образом матрицу Т(Х) снова будем
называть матрицей перехода; Т(Х), очевидно, унимоду-
лярна:
det Т (X) = 1, D)
поскольку определитель Вронского
А2
любой пары решений %х, %2 уравнения A) с одним и тем
же X не зависит от х.
Вычисляя W (ф1( ф2)> W (фг. ^i)- находим
Тц(Ц = W Ых, X), %(х, X)),
Тп(Ь) = W (щ(х, X), %(х, X)).
Так же, как и в § 1, мы можем показать, что решения
tyx(x, X) и ф2(?, X) допускают аналитическое продолже-
ние в верхнюю полуплоскость X, а ^2(х, X), фх(х, X) анали-
тичны в нижней полуплоскости X. При этом
Q
(х, X)
, Я,)
| Х\
Ф2 (х, X) е
Im X ^> 0;
1тЯ,<0.
Из E) теперь следует, что Тп(Х) аналитична в нижней
полуплоскости, а Т22(Х) — в верхней полуплоскости, при-
чем эти функции при | X | -> оо стремятся к единице.
При комплексных значениях X уравнения A) могут,
вообще говоря, иметь решения, убывающие (при выпол-
нении B) — экспоненциально) как при ж—>-оо, так
и при х-*- — оо. Такие значения спектрального параметра
X мы будем называть точками дискретного спектра. Если
ImA, ^> 0, то, как легко видеть, дискретный спектр совпа-
дает со множеством нулей функции Т22(Х), точки же дис-
кретного спектра, лежащие в нижней полуплоскости X,
совпадают с нулями Тп(Х). В точках дискретного спектра
Фх(х, Хп) = сА(х, Хп) (Ти(Хп) = 0, 1тлп< 0);
Ф,(*, Хп) = M>i(*> К) (Тм(Хп) = 0, 1т Хп > 0).

83 МЕТОД ОБРАТНОЙ ПАДАЧЙ РАССЕЯНИЯ [ГЛ. 1
Не ограничивая общности, будем считать нули Тп и T2i
простыми.
Установив аналитические свойства решений и описав
дискретный спектр, мы могли бы немедленно получить
систему уравнений обратной задачи совершенно аналогич-
но тому, как это было сделано в § 1 или в § 7, сведя обрат-
ную задачу к задаче сопряжения аналитических функций.
Именно так мы несколько ниже и поступим, ограничив-
шись однако специальными случаями связи г (х) и q (x):
г = q или г = —q, представляющими особый интерес.
Если положить в системе A)
г = q, ¦ (а)
то в решениях уравнений A) возникает инволюция. Имен-
но, если гЬ = ( . — решение A) с вещественным X, то
столбец
также является решением A) с тем же самым X. Наличие
инволюции позволяет, очевидно, зная какое-либо одно
решение, найти другое решение, линейно не зависимое
от первого. При редукции (а)
При этом из C) следует, что
ЗД) = Т22(Х), Т12(Х) = -Т21(Х) AтХ = 0),
т. е. матрица Т имеет вид
а (К) Ь(Х)
Ввиду D)
!«(*) I2+ I*W|2 = I. Ga)
Если же в системе A)
г (х) = -q (x), (б)

91 ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ ДЛЯ СИСТЕМЫ 81
/ Ф \
то вместе с гр = \ решением A) является и столбец
uFС1)
В этом случае i|J(a;, X) = tyi(x, X), (р^х, X) = Ф2(#, X),
матрица Г (X) выглядит так:
/г (Я,) Ь (Х)\
так что
I « (^) I 2 — \Ь(Х) |2 = 1. G6)
Обозначим теперь ф (х, X) = ф2(аг, ^), "ф (а;, ^) =
= ^(х, X). При любой из редукций (а), (б) имеем из C)
Ф (х, X) = а (X) Ц, (х, X) + Ъ(Х)$ (х,\),
так что
а(Х) =W (ф (х, X), 1(з (х, X)). (8)
Функции ф (х, Я), г|; (х, X), а (X) аналитичны в верхней
полуплоскости X. В пулях а (X)
Ф (х, Хп) = fen^ (x, Хп), п = 1, 2, ..., N. (9)
Заметим, однако, что при редукции (б) задача A) является
самосопряженной; поэтому в этом случае дискретный
спектр отсутствует.
Переходя к обратной задаче, рассмотрим функцию
Ф {х, X) =
Ввиду (8), (9) Ф (х, X) имеет представление в виде
1 ?
где через г (X) обозначен «коэффициент отражения»
г (X) = Ь (%Iа (X), —оо <),<», Поступая так же, как

82 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
и в §§ 1, 7, извлекаем из представления A0) замкнутую
систему уравнений на ij) (х, к), —оо << X < оо, и ij> (x, Хп),
п = 1 ... N:
n=l
, 1
m=l
Вместе с определением операции инволюции (а) или (б)
уравнения A1), A2) представляют собой полную систему
уравнений обратной задачи.
Вычисляя, далее, коэффициенты асимптотического раз-
ложения функции ij) (х, К) е** по степеням 1А из уравне-
ний A), найдем, что
- Ч И/2
X '
Определяя те же самые величины из A0), приходим к фор-
мулам
N ь
q (х) = — 2 V ,,? oj)A) {x, %n) eiXnx +
П=1
г (х) q(x')dx' = - 2* ?у^
4"

§ 9] ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ ДЛЯ СИСТЕМЫ 83
выражающим «потенциал» q (х) непосредственно через
решения уравнений A1), A2).
В случае уравнения sin-Gordon потенциал в уравне-
нии A) кроме условия (а) удовлетворяет еще одному допол-
нительному условию — он является вещественным:
q{x) = q (х) = г (х). A4)
При этом, как легко видеть, возникает связь между ре-
шениями системы A) с противоположными знаками X.
Именно, если о|) = ( | — решение A) с X = X , то
есть решение A) с % = —X'. Вместе с инволюцией Fа)
последнее обстоятельство означает, что
(х, X) = - Ф<« (х, -1),
-I),
-I),
op) (а-Д) = — i|)<2) (.г, — X).
При этом из (8) видно, что
а (X) = о (—I), Ь (Я,) = —"Ь (-Х). A5)
Первая из формул A5) означает, в частности, что нули
а (X) расположены симметрично относительно мнимой оси;
при Re X = 0 а (X) вещественно. Вторая же из формул
A5) имеет смысл, строго говоря, лишь на вещественной
оси, где она дает
г(-Х) = -г(Х). A6)
Однако, если q (х), г (х) — финитные функции, решения
<р (х, X), г|з (х, X) являются целыми функциями X и Ъ (X)
может быть определено во всей комплексной плоскости.
При этом, если Хп является нулем а (X), то нормировочный
множитель Ьп, определенный формулой (9), есть
Ъп = Ъ (Хп).
Таким образом, A5) означает, что если Хп лежит на мни-

8i МЕТОД ОБРАТНОЙ ЗАДАЧИ ГАССЕЯНИЯ [ГЛ. I
мой оси, то Re Ъп — 0. Если же кп = —Х~т, то из A5) сле-
дует, что Ъп — —Ъп.
Уравнения обратной задачи показывают, что потен-
циал в уравнении A) однозначно определяется совокуп-
ностью
s = (кп, Ьп, п = 1, . . ., Л', Im кп > 0;
г (к), —оо < А,< оо),
которую назовем данными рассеяния для уравнений A).
Отображение q (х) ->- s в силу A1), A2) однозначно обра-
тимо.
Найдем зависимость данных рассеяния от времени, если
q (x) удовлетворяет какому-либо из перечисленных в пре-
дыдущем параграфе уравнений. Заметим прежде всего,
что при приведенные выше матрицы V (X) определены
с точностью до матрицы, пропорциональной единичной.
Эту добавку к V (X) мы каждый раз будем выбирать таким
образом, чтобы асимптотика ср (х,Х) при х —>¦ — оо не за-
висела от времени (напомним, что зависимость ср от t дается
уравнением (8.9)). Для нелинейного уравнения Шредин-
гера (8.14) это условие означает, что к матрице V(k) (8.13)
следует добавить 2iX2; устремляя затем х к +°°, подстав-
ляя вместо ср (х, X) ее асимптотическое выражение, сле-
дующее из (8), и полагая г, q = 0, находим из (8.9)
а (к) = 0, b (X) = Ш2Ь {X),
т. е.
а (X, t) = а (к, 0), Ъ (X, t) = Ъ (к, 0) exp (AiXH). A7)
Собственные значения Хп, являясь нулями не зависящей
от времени функции а (X), также не зависят от времени. За-
висимость же от t множителей Ъп может быть найдена либо
путем продолжения A7) в комплексную плоскость, либо
же непосредственно из (8.9), (9):
bn (t) = Ъп @) exp Diftt). A8)
Отметим, что зависимость данных рассеяния от времени
для уравнений (8.14а), (8.146) одна и та же. При этом, разу-
меется, следует помнить, что операция инволюции для этих
задач устроена по-разному; это обстоятельство, в част-
ности, приводит к тому, что для уравнения (8.146) г (к),-

§ 10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА 85
ввиду G6), по модулю не превосходит единицы:
\г(Х) |<1.
Кроме того, данные рассеяния для (8.146) не содержат ха-
рактеристик дискретного спектра, ввиду отсутствия по-
следнего при редукции F). Все сказанное, очевидно, от-
носится в равной степени ко всем эволюционным уравне-
ниям предыдущего параграфа, номер которых содержит
букву б.
Совершенно аналогично находится зависимость дан-
ных рассеяния от времени для уравнений МКдФ (8.17):
а (X, t) = а (X, 0), Ъ (X, t) = Ъ (X, 0) exp (-8iX4),
Хп = 0, bn(t) = Ь„@) ехр (~8iXit). A9)
Для уравнения sin-Gordon (8.19а) естественным гра-
ничным условием при | х | —>- оо является
и (х) -> 0 (mod 2я).
Поэтому эволюция данных рассеяния в силу (8.19а) имеет
вид
а (X, t) = a (X, 0), b (X, t) = b (X, 0) ехр (—A-t),
1 B0)-
Этими же формулами дается зависимость данных рассея-
ния от времени и для уравнения (8.196). При этом, есте-
ственно, следует полагать и —у- 0 при | х \ —у оо.
§ 10. Нелинейное уравнение Щредингера
В этом параграфе мы подробно изучим решения нели-
нейного уравнения Шредингера (8.14а)
irt + rxx + 2 (г|2г = 0 A)
с быстроубывающими начальными условиями
\r(x,0)\dx<oo.
Прежде всего опишем семейство точных решений A) —
Л^-солитонные решения. Как и в теории КдФ, им отве-

86 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
чают «безотражательные потенциалы», для которых г (к) —
= 0 при всех %. Обращение в нуль коэффициента отраже-
ния означает, что
| а (X) |2 = 1 (Im A, = 0)
и аналитическая в верхней полуплоскости к функция
а (К) полностью определяется своими нулями Ях ... ку
(Im lt >0):
п=\
При этом система уравнений обратной задачи (9.11), (9.12)
превращается в систему линейных алгебраических урав-
нений на функции о|) (х, Хп):
$ (х, %п) eil"x =
где через сп обозначены величины сп — bja' (kn). При-
меняя к уравнениям B) операцию эволюции и учитывая,
что о|) = —1|), найдем
(^УЩ^Ц-^. C)
Подставляя, далее, B) в C), получим замкнутую систему
уравнений на г|з {х, Хп); обозначая г|з (а;, кп)ег>"пХ = %п {х),
получим
+ 1
m=l
При этом уравнения для компонент векторов %п (х) незави-
симы. Как видно из (9.13), Хп'2> (я) определяют у (х)>

10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ П1РЕДИЯГЕРА 87
N
X%){z), E)
i
q(x)=-2%cnx%\x). F)
Решая систему D) и подставляя %я2) в E), найдем, исполь-
зуя рассуждения, аналогичные приведенным в § 3, что
\r(x)\' = ~lndel(l+IA), G)
где квадратная N X N матрица А (х) имеет вид
-2гХпХ
Апт- У , . (8)
Зависимость решения G) от времени следует из формулы
(9.18), согласно которой ст в (8) следует заменить на
cm(t) = ст@) ехр (Ши).
Простейшим представителем указанного класса решений
уравнения A) является солитон. Полагая N = 1 и вводя
обозначения
Rebi-fc, Im^-t], xo = —lnj^ @)|, (9)
получим из G)
г(х ^!]!
Находя же XnJ (ж) и подставляя в F), найдем непосред-
ственно г {х)
v ' ' ch 2т) (я — х0 + 4^) v '
Здесь
Фо - arg ^@). A1)
Таким образом, r\ = Im^ определяет амплитуду (и ши-
рину) солитона, а ? = Re А,х — его скорость v = —4g.
В общем случае, если среди величин Re А^, п =1,..., N,
нет совпадающих, решение G), (8) асимптотически

88
Метод обратной задачи рассеяния]
(гл. i
при t -> ±°о представляет собой сумму N солитонов A0)
с амплитудами r\t = Im %t и скоростями i>j = —4ReX;. Эти
параметры солитонов одни и те же как при t -*~ — сю, так
и при t -*¦ + 00. Как и в теории КдФ, изменение испыты-
вают лишь фазы солитонов xOi, фО{. При подсчете изме-
нения последних можно буквально следовать процедуре
§ 3. Если занумеровать солитоны в порядке возрастания
их скоростей, полагая
ReX2 > ... > ReXN,
Дср0 ==
то разности AxOi = xoi (+«?) — xQi (—oo),
= ф<н (+°°) — Фог (—°°) даются формулами
N ... i-l
Axni =
In
n=i+l
2V
In
n=i
АфОг = 2
n=i+l
¦ - к
-2
n=l
Эти формулы можно интерпретировать, приняв, что
солитоны попарно сталкиваются (причем каждый солитон
сталкивается с каждым). При каждом парном столкнове-
нии более быстрый солитоп дополнительно сдвигается впе-
ред на величину
-In
^m~^p
а более медленный сдвигается назад на величину
Полный сдвиг солитона равен алгебраической сумме его
сдвигов при парных столкновениях, так что эффект много-
частичных столкновений полностью отсутствует. Ана-
логично обстоит дело и с фазами фОг.
Скорость расхождения пары солитонов пропорцио-
нальна разности значений их параметров |{ = Re %t.
При совпадающих \t солитоны не расходятся, а образуют
связанное состояние. Рассмотрим связанное состояние
N солитонов, положив для простоты \j = 0. Тогда ст (t) =
= ст@) ехр (—4irfint). Непосредственно из общих формул

§ 10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРЛ уд
G), (8) видно, что связанное состояние представляет собой
условно периодическое решение уравнения A), характери-
зующееся в общем случае N частотами con = 4if^. Факти-
чески в ответ G) входят всевозможные разности частот, по-
этому связанное состояние из двух солитонов характери-
зуется всего одной частотой 4 (г\\ — т||) и представляет
собой периодическое решение уравнения A). Следует,
однако, подчеркнуть, что связанного состояния в бук-
вальном смысле здесь нет: энергия описанного образова-
ния в точности равна сумме энергий отдельных солитонов
(см. ниже), т. е. энергия связи равна нулю. Это состояние
является неустойчивым, поскольку практически любое
малое возмущение в начальном условии г (х, 0) приводит
к распаду связанного состояния на отдельные солитоны,
скорости которых пропорциональны возмущению и, во-
обще говоря, различны.
Рассмотрим теперь в рамках уравнения A) «большое»
рачальное условие, при котором число собственных зна-
нений системы (9.1)
велико. Кроме того, будем полагать начальную функцию
меняющейся плавно, так что rjr <^ к. Применительно к
нелинейному уравнению Шредингера это означает, что
рассматривается начальное условие, при котором нелиней-
ный член много больше линейного члена гхх. При этих
условиях к уравнению A) применима «нелинейная геомет-
рическая оптика», позволяющая найти решение г (х, t)
методом характеристик. При этом, однако, оказывается,
что гладкое решение существует только до конечных t —
решение разрушается из-за образования фокусов или ка-
устик, после чего приближение геометрической оптики
становится неприемлемым.
С нашей точки зрения случай большого начального ус-
ловия — это случай, когда к системе A2) можно приме-
нить квазиклассическое приближение. Выражая я[з<2> че-
рез a|)W с помощью первого из уравнений A2) и подстав-
ляя во второе, получим в пренебрежении гх(х, 0):
- ч>? - I г (х, 0) | у« = я* f i\ A3)

90 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ (ГЛ. I
т. е. уравнение Шредингера. В квазиклассическом прибли-
жении коэффициент отражения оказывается 'экспонен-
циально малым для всех не слишком малых X2. Поэтому
эволюцию решения с квазиклассическим начальным усло-
вием можно с экспоненциальной точностью моделировать
неким ./V-солитонным решением. Для нахождения пара-
метров входящих в него солитонов, отметим, что с ука-
занной точностью собственные значения A2) ввиду A3)
лежат на мнимой оси: %\ < 0; Хп = ir\n. При этом г\п да-
ются правилом квантования Бора:
=* 2тт (п
Фактически %п расположены не строго на мнимой оси, а
имеют малые действительные добавки, которые обеспечи-
вают расхождение отдельных солитонов. Простая оценка
дает характерное отношение действительной части к мни-
мой: ?/т] ~ TV-1/2, где N — общее число уровней,
n—— f \rir\\fjr ал)
— в квазиклассическом пределе большая величина.
Рассмотрим теперь противоположную ситуацию и по-
ставим вопрос: какому условию должен удовлетворять
потенциал задачи A2) для того, чтобы последняя вообще
не имела дискретного спектра? Ответ формулируется до-
вольно просто: для этого достаточно выполнения нера-
венства
ос
J \r(x)\dx<hi{2+ /3)~ 1,32. A5)
Таким образом, если начальное условие г (х, 0) для урав-
нения A) удовлетворяет A5), то решение г (х, t) не будет
содержать ни одного солитона.
Для того чтобы убедиться в сделанном утверждении,
рассмотрим решения cpfl> (х, X), ц>№ (х, X) задачи A2) с асим-
птотикой фA> —>- 0, срB> -> охр (—iXx), х —>- —оо. Как сле-
дует из (9.8), % = срB> exj) (iXx) ->- а (X) при х->¦ + оо.

Й ю] Нелинейное уравнение шредингерл
Функция х (#» ^) удовлетворяет уравнению
X X'
% {х,1) = 1 — ^ r (*') f exp BiK (х' ~ Х'У Х
Xf(x")i(x",l)dx"dx'. A6)
Из A6) следует, что при Im A, ^ 0
| X (*, *) |< 1 + J | г (*') | J | г (х") 11 Х (х", Я) | dx"dx. A7)
Итерируя полученное неравенство, найдем
Уравнение A6) означает также, что
ж х'
X1 Iv 9Л \ \ <~ \ \ г 1т'\ I \ I г (т"\ I I л/ i'i" \ \ I /7т" /7т'
^х, л; — -1 | % J |' \х ) | J I' \х )\ | х (,•<- > Aj | аа. а.г .
— оо ¦ —лэ
Подставляя в правую часть этого неравенства A7), полу-
чим
х
\yi(x, X) — 11<^ch \ \г (х') |dx — 1.
— оо
Таким образом, при Irn % ]> О
оо
U(X)-l|<ch \ \r{x)\dx-l. A8)
—оо
Если теперь
оо
ch \ | г (ж) | da; — 1 <^ 1,
—оо
то из A8) следует | а (А.) | ^> 0, т. е. задача не имеет ди-
скретного спектра. Предыдущее же неравенство экви-
валентно A5), что и требовалось проверить.

Ei2 Метод обратной задачи рассеяния ггл. г
Изучим теперь вопрос о структуре интегралов движе-
ния нелинейного уравнения Шредингера. Как и рассмат-
ривавшиеся ранее уравнения, интегрируемые методом об-
ратной задачи, уравнение A) имеет бесконечное число од-
нозначных первых интегралов. Этими интегралами, как
видно из (9.17), являются функционалы а (X) [г, г] при лю-
бом X. Из этой совокупности мы выделим счетный набор
локальных полиномиальных по г, ? интегралов движения
уравнения A). Как и для уравнения КдФ, мы получим их
из разложения In а (X) по степеням 1/Х:
A9)
B&)n
Поскольку а (X) не зависит от времени для всех указанных
в § 8 уравнений, функционалы сп [г, q] будут интегралами
движения уравнения sin-Gordon и МКдФ. Поэтому мы "вы-
числим сп [г, q] в общем случае системы (9.1):
Так как а (X) = lira фB) (х, X) eilx, где ф<х 2> — решение
этой системы с асимптотикой ф<*> -> 0, ф'2> ->- e~iXx при
X -+¦ — ОО, ПОЛОЖИМ ф<2> (х, X) = е-'^-»Ф(ж,'О и, ИСКЛГО-
чая фA), получим для Ф (х, X):
= г<7 + Ф| + г -^г-75- • B0)
При этом
оо
In a (X) = Ф (оо, X) = ^ Фх (х, X) их.
Подставляя, далее, разложение
ФУ =
в B0), получим рекуррентную систему для ф„ (х):
фя+1 = г-г- —=- + \; фП1фя2, ) п = 1, 2,...,

§ 10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА 93
причем фх(.г) = г (х) q (х). Искомые функционалы с„ [г, q]
даются интегралами
Приведем явный вид первых четырех сп:
ОС
cj = j rqd.c, c2 =
oo
сз = 3 (rg«x-l-r2<f)da;>
— oo
OO
ci:= \ (''Яхххх + г -^ rg2 + 2r2ggx] dx.
Интегралы движения нелинейного уравнения Шредингера
A) получаются из сп lr, q], если в последних положить
= \ |7-[2d.x, с2 = ^ rrxdx,
-о» -'со B2)
j
Первые три из сп[г, г\ имеют простой физический смысл:
сх имеет смысл «числа частиц», с2 — с точностью до множи-
теля совпадает с полным импульсом поля, а —с3 представ-
ляет собой гамильтониан уравнения A). Сохранение с2
связано с трансляционной инвариантностью нелинейного
уравнения Шредингера, с3 — с инвариантностью относи-
тельно сдвигов во времени; сх сохраняется, поскольку
уравнение A) инвариантно по отношению к преобразова-
ниям вида г ->- reia, r -> fe~ia.
Уравнение A) является гамильтоновой системой. Фа-
зовое пространство состоит из пар функций (г (х), г (#)),
скобка Пуассона имеет вид
{о, 1} — — i \ ах
1 ' J
br{x) 8f(x) 6f(x) Ьг{х)

94 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ (ГЛ. 1
так что A) записывается следующим образом:
где Н = — с3. При этом при дифференцировании функции
гиг следует считать независимыми.
Как гамильтонова система нелинейное уравнение Шре-
дингера является полностью интегрируемым. Переменные
действие —угол просто выражаются через данные рассе-
яния. Соответствующие вычисления мало чем отличаются
от приведенных в § 6, поэтому детали выкладок мы опу-
скаем.
Прежде всего необходимо найти производные от эле-
ментов матрицы перехода по г (х), г (х). Это нетрудно
сделать, воспользовавшись представлением (9.8) для а (к):
а (к) = W (г|> (х, к), Ф (х, к)),
и аналогичным выражением для Ь (к):
Ь (к) = W (ф (х, к), 1|з (.г, к)).
Вычисляя теперь вариационные производные
бф (у, к)/8г (х), бф (у, к)/8г (х) и т. д., находим, что
6а {к)
дг (х) ' \ ' / т I ч
6г(х)
дг (х)
Теперь можно найти скобки Пуассона между элементами
матрицы перехода. Так, например,
оо
{а (к), Ь (%')} = — t J dx [^'D (х, к) ФA) (х, к) фИ (х, А,') X
X фB) (х, к') - о|)(а) (х, к) Ф(«) (ж, Я) фО> (х, X') $A) (х, к')\.
Как и в § 6, подынтегральное выражение является полной
производной, поскольку имеет место непосредственно про-

§ 10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА <M
веряемое соотношение
Ф(" (х, X) o|)<i) (х, X) Ф<*> (х, X') $B) {х, X') -^
- г|;B) (ж, А,) ср<2> (х, X) ф« (х, %') о|)а) (а;, Я,') =
= 2НХ-%>) -Ш lW <Ч ^ ^ *Р (^- ^')) W (о|) (х, X), $ (х, X'))].
Выражая, далее, асимптотики ф и о|) через данные рассе-
яния, приходим к формуле
{а(X), Ъ{X')} = а^Щ ~^-а{Х)Ь(X) б(X - X').
Вычисляя таким образом скобки между всевозможными
парами элементов матрицы перехода, нетрудно найти, что
переменные
являются канонически сопряженными. Так же можно
найти, что дискретному спектру отвечает дополнительный
набор канонически сопряженных переменных
Nk = 2Xlt, Ф* = 1пу-, к = 1,2 N. B6)
Эти переменные комплексные.
Восстанавливая далее In а (X) по п (X), Nk, находим, что
B7)
В частности, функция Гамильтона нелинейного уравне-
ния Шредингера представляется в виде
B8)
т. е. уравнение A) является полностью интегрируемым.
Вместе с нелинейным уравнением Шредингера полностью
интегрируемым будет любое уравнение вида B4), гамиль-
тониан которого является функцией только сп [г, г]. Взяв,

96 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
например, в качестве //"функционал <?4[г, г], получим урав-
нение _. .. ...
! in + rsxx + 6 | г I2 rx = О
— комплежщыд_вариант МКдФ. Собственно МКдФ (8.17а)
представляется в виде '
_ д J^-L
Г( ~ ~дх ~W '
где Н = —с3/2 при г = q, и также является полностью
интегрируемым. Последнее утверждение требует специаль-
ного доказательства, чего мы, однако, делать не будем.
Отметим еще, также без доказательства, что полностью ин-
тегрируемой является любая система вида
, _ Ш_ . _ _ Ш_ „„
'" ~ dg ' q ~ 6г \ '
с гамильтонианом Н, функционально порожденным ин-
тегралами cn[r, q]. Например, система уравнений (8.16)
получается из B9) при Н = cA[r, q].
Вернемся, однако, к уравнению A). Вместо набора
комплексных переменных B6) весьма удобно ввести уд-
военный набор вещественных канонических переменных.
Положим
Nk = i {Nk - Nk), Us = (Фь - Os)/2i,
"k = - (Nk + Nk), vk = - (Фк + Ф,)/2,'
так что Nit ^> 0.
Пары переменных Nk, цк и vk, vk являются канониче-
ски сопряженными. Интегралы движения в новых пере-
менных выглядят следующим образом:
«число частиц»
^ C0)
к
импульс
Р =¦= ic2 = i С rrx dx = V VX~ — 2 14 n (%) dl, C1)

§ 10] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА 97
энергия
Введенная таким образом переменная vk = —4 Re Afc
есть не что иное, как скорость к-то солитона. Из C1) при
этом видно, что Nii/2 следует интерпретировать как мас-
су солитона; слагаемое iV"fty|/4 представляет собой кине-
тическую энергию солитона, а —iV|/12 — его энергию
покоя. Из C1), C2) видно также, что (п (Х)/2) dX следует
интерпретировать как массу частиц, движущихся в ин-
тервале скоростей (—4Х, —АХ + dX). Как будет показано
в гл. IV, эти высказывания можно понимать буквально,
если речь идет об асимптотиках решений уравнения A)
при t —*- -f- оо.
В заключение этого параграфа рассмотрим нелинейное
уравнение Шредингера при другом знаке нелинейного
числа, т. е. уравнение (8.146):
irt + гхх - 2\ф = 0. C3)
С этим уравнением связана редукция q = — г в задаче
(9.1). Как уже отмечалось, в этом случае |а(Х)|>1
в верхней полуплоскости % и, следовательно, C3) не имеет
(при |г|->-0, |ж|->-оо) солитонных решений. Нелинейное
уравнение Шредингера в форме C3) также является пол-
ностью интегрируемым. Функцией Гамильтона является
интеграл с3 [г, q\\ = -г', в канонических переменных
п (Я) = -L In | а (X) |а, ф (X) = arg Ъ (X)
гамильтониан имеет вид
Н=
При этом
ДГ= —Cl=
Р = — ie2 =

У8 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
§ 11. Уравнение sin-Gordon
Этот параграф посвящается изучению уравнения
д2и
Непосредственно в такой форме это уравнение возникает
как уравнение вложения плоскости Лобачевского в трех-
мерное евклидово пространство. В переменных | =
= х -\- t, г — t — х оно приобретает вид
и также имеет разнообразные физические приложения.
Уравнение sin-Gordon в форме B) интересно также и тем,
что служит нетривиальной моделью теории поля.
Уравнение A) интегрируется с помощью системы диф-
ференциальных уравнений (8.12), в которой следует по-"
ложить г = q = uJ2:
C)
Результаты предыдущих параграфов позволяют не-
медленно указать семейство TV-солитонных решений урав-
нения A). В самом деле, для безотражательных потенциа-
\лов система уравнений на собственные функции задачи
C) имеет вид A0.4)
в которой, однако, следует учесть факт вещественности
потенциала. Последняя, как мы знаем, приводит к огра-
ничениям на расположение нулей а {%); именно, эти нули
расположены симметрично относительно мнимой оси,
у, е, вместе с точкой % множеству нулей принадлежит и точ-

g и] Уравнение sIn-gorDon 99
ка —%. Кроме того, ввиду (9.15) фигурирующие в урав-
нениях D) величины сп = bja (X) в симметрично рас-
положенных нулях комплексно сопряжены друг другу.
Потенциал же определяется по решениям D) по формуле
A0.6):
Имея в виду указанные ограничения, уравнение D) для
(n можно переписать в виде
к, m
Вводя матрицу
е
F)
и обозначая через о|), еЛх столбцы ty^\ щ ,. . ., tyx и
eiXlX, eiXiX ,. . ., el%NX, представим систему Eа) в виде
A — У2) ^ = егхх.
Таким образом,
A — v) -ф = A + y)-V^,
A + у) -ф = A — у) е*Ч
откуда
^ = 4" 1A + ^Г1 + A - v)-1] е**.
Теперь нетрудно видеть, что правая часть формулы E)
представляет собой логарифмическую производную и
/ \ 2 1 det A + v)
и (х) = In , . . ; .
v > i det A —v)
Вместо матрицы v удобнее использовать подобную ей
матрицу
vnm(x, t) = "V ' exp [2i%mx —г?-А, G)
где мы уже учли зависимость cn(t) согласно (9.20). Та-
ким образом, ./V-солитонные решения уравнения A) дают-

100 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
ся формулой
и (z,t) = - 4- In ddeett((i1+!j? = - 4arg det A + v). (8)
Рассмотрим простейшие из них.
1 Пусть а (X) имеет единственный нуль, расположенный
на мнимой оси в точке Хх = iX; при этом величина с @)
обязана быть вещественной. Тогда
и (х, t) = 4е arctgexp[— 2Х (х — х0) — t/2X] =
= 4arctgexp [— е BА (х — х0) + t/2X)] (mod 2л), (9)
/Г1. 1 , с @)
где е = sign с (U), xo=-^j-m ——- .
Решение (9) с г = —1 мы будем называть солитоном,
а с е = 1 — антисолитоном уравнения A). Наиболее ес-
тественно эти решения выглядят в переменных | = t -\- х,
х = t — х:
A0)
где v = DЯ,Я - 1)/DЯ2 + 1), |0 = A + v) x0. Решение A0)
представляет собой солитон (антисолитон) уравнения B),
движущийся со скоростью v. Эти решения имеют нену-
левой «топологический заряд» Q
—оо
являющийся, очевидно, первым интегралом уравнения B).
На решениях A0)
Для солитона Q — 1, для антисолитона Q = — 1.
Другим элементарным образованием является решение
G), (8), когда а (X) имеет пару симметричных относитель-
но мнимой оси нулей, Х± = Re X -\- i Im X = X, Х2 =
= —Re X + i Im X. При этом сг = с2 = с и выражения
G),' (8) приводят к ответу
Г ReX
Sln v i ¦> 12 t — 2 Re %x — ф0
a (x, t) = 4arctg [-^^ L ¦ ^-
(H)

§ И] УРАВНЕНИЕ SIN-GORDON Ю1
или, в терминах уравнения B),
Im А,
и (I, т) = 4arctg
Re к | [Im I ( \ — vt — ^
СГ1
где
А I к I2 — 1 1 , Г Re Я, с
, A2)
7
с "I
2>„ J '
•У: j Л j —р 1 ilr 1Ш J
фо = arg -^- , гр0 = I г фо> 1о = С1 + и) хо-
Эти решения мы будем называть двойными (или пульси-
рующими) солитонами. Их можно интерпретировать, во
всяком случае при достаточно малых значениях Re Я/Im Я,,
как связанное состояние солитона и антисолитона. При
|Я,| = Vj,л1, е. при v = 0, решение A2) является периоди-
ческой функцией времени т. Посмотрим, как выглядит
A2) в моменты времени т0, когда sin [2Re Я (т0 — о|H)] =1.
Очевидно, при этом -^— и (%, т) |T=to = 0. Пусть, далее,
Re А,<^1. Тогда при |||>>1п-|^^ функция в(^, г0) = 0;
области же |g|<^ln ^ функция и{1, то)~2я.
1 / 1 \
При | — Inп-^-или l~ — ln-g-^- имеем из A2)
пе л \ ие л/ ч '
и (^, т0) = 4arctg ехр (—^ -f- In R . J (соответственно
и (^, т0) = 4arctg ехр (? -f- In „ . П . Таким образом,
при т = т0 выражение A2) представляет собой су-
перпозицию неподвижных солитона и антисолитона, раз-
несенных на расстояние порядка I m т;—г~, что и позво-
ляет говорить о двойном солитоне, как о связанном со-
стоянии. Его топологический заряд равен нулю.
Перейдем теперь к рассмотрению столкновений соли-
тонов. Простейшим (и совершенно нетривиальным) из
решений такого рода является решение, получающееся
из A2) предельным переходом Re Я, ->- 0. При v = 0
имеем из A2)

102 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ (ГЛ. 1
Это решение описывает взаимодействие солитона и анти"
солитона, имеющих на бесконечности нулевую скорость.
Общее двухсолитонное решение получается из формул
G), (8), когда а (%) имеет два нуля на мнимой оси в точках
iXlt iX2 (A-ii К > 0):
= 4 arctfif
6
A3)
где vt — DЯ? — l)/DAi + 1). Непосредственный анализ
этого выражения показывает, что A3) описывает при
т -> + оо пару невзаимодействующих солитонов, движу-
щихся со скоростями vx и 1>2- Действительно, полагая,
например, i>2 ^> vx, рассмотрим асимптотику A3) на пря-
мой | = Vx%--\- |', т-> — оо, как функцию |':
-Е',т)—>4 arctg Г-^- ехр /- -7Л=
В зависимости от знака сх это выражение описывает соли-
тон или антисолитон с координатой центра
Рассматривая, далее, асимптотику A3) на той же прямой
при т ->¦ + °° > находим
т. е. имеем солитон с тем же топологическим зарядом, что
и на — оо по т; его координата есть

§ 11] УРАВНЕНИЕ SIN-GORDON ЮЗ
Таким образом, при столкновении со вторым солитоном
первый испытывает сдвиг на величину
Д^о К 1 — ^In (X>1_W2<0-
Совершенно аналогично для второго (быстрого) солитона
Мы видим, что быстрый соЯитон дополнительно сдвигает-
ся вперед, а медленный — назад. При этом рассеяние со-
литонов совершенно не зависит от их зарядов. Наиболее
просто полученные результаты выглядят в системе центра
инерции солитонов, где v2 = v = — ь\. В этой систе-
ме отсчета
Так же, как для других систем, рассмотренных в этой гла-
ве, можно показать, что при многосолитонном столкнове-
нии полный сдвиг каждого солитона равен сумме сдвигов
при столкновениях со всеми остальными по-отдельности,
т. е. многочастичные эффекты отсутствуют.
Развитые выше методы позволяют эффективно иссле-
довать уравнение A). В частности, задача Коши для A)
сводится к решению прямой и обратной задач рассеяния
для системы C). Однако для уравнения B) приведенная
схема дает лишь некоторую параметризацию всей сово-
купности решений, но не позволяет решать задачу Коши.
Для решения последней использованную схему необхо-
димо переформулировать непосредственно в переменных
6, т.
Уравнение A) представляется как условие совместно-
сти системы
1 /cos и — i sin u\ .,
т' iii% \i sin и — cos и ) •'

104 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
В переменных ?, т эта система приобретает вид
о
1 /cos и — i sin и\
j
1 /cos и — i sin и\
~"8iX\ismu -cosuj'4''
1*=--Ио -l)*—Г U-ut 'о
cosit -isinu
-cos»
Условием совместности системы A4), A5) является, оче-
видно, уравнение B). Теперь мы можем действовать по
стандартной схеме метода обратной задачи: определить
данные рассеяния для уравнения A4), найти зависимость
последних от времени с^помощью A5) и, наконец, иссле-
довать вопрос о восстановлении и (?, т) по данным рас-
сеяния, т. е. решить обратную задачу рассеяния для
уравнения A4). Однако, как мы сейчас увидим, нет ни-
какой необходимости детально исследовать уравнение A4),
поскольку имеется тождественное соответствие решений
задач C) и A4). Рассмотрим, например, решение Ф = ( )
системы A4), A5), определенное асимптотикой при | ->
—>- — оо:
Фа>->0,
Как решение A4) Ф имеет асимптотику на + оо по ? вида
Определенные таким образом функции А (к), В (Я) дают
нам данные рассеяния для A4) в непрерывном спектре.

I 11] УРАВНЕНИЕ SIN-GORDON
При этом из A5) имеем
дА (к, т) п дВ{Х,Х) U 1\в
—Тс— = 0' дх =
Эти формулы определяют эволюцию данных рассеяния во
времени. Решение Ф как функция \ и т, Ф (X, ?, т), одно-
значно определено во всей плоскости \, т. Совершенно
очевидно, что Ф (X; х + t, t — х) как функция х удовлет-
воряет системе C) с потенциалом и (х, t), являющимся
решением B). Спрашивается, какую асимптотику имеет
Ф (X; х + t, t — х) при х-*- — оо, t = const? Для ответа
на этот вопрос заметим, что всякое решение уравнения
B), отвечающее достаточно гладким убывающим при
|?|->-оо начальным условиям и (?, т)|?=0 = и (|),
и% (?, т)|т=0 = w (g), заключено при т-^- + оо внутри
светового конуса |т|^> |||. Это утверждение достаточно
очевидно. По этой причине при продолжении асимптотики
Ф (к; |, т) из области ?->¦ — оо, х — const в область
| = — т, |->- — со (т. е. ?->- — оо, t = const) мы по-
стоянно находимся в области, где и (?, т) = 0. Таким об-
разом, при ж~> = оо
и совпадает с введенным выше решением <р (х, X) системы
C). Точно так же обстоит дело и при ?,-+-\-оо,х-*--}-оо:
решение A4) ^ (X; ?, т), определенное асимптотикой
[]
|->4-°° I получается из решения г|з (X, х, t) системы C) про-
стой заменой переменных. Итак, имеет место следующее ут-
верждение. Пусть и (I) =u (|, 0), w (g)=их (|, 0)—начальные
условия для уравнения B), А (X), В (Я) — данные рас-
сеяния задачи A4), отвечающие этим значениям и, их.
Пусть далее и (?, т) — решение B) с указанными началь-
ными условиями; и (х, 0) = и (х, — х) — начальное ус-
ловие для уравнения A), а а (X), Ъ (X) — данные рассея-
ния системы C), отвечающие этому начальному условию.
Тогда, если и (?), и; (?) — достаточно гладкие и хорошо
убывающие при |?| ~> оо функции а (X) == А (X), Ъ (X) =
= В (Я), соответствующие характеристики дискретных
спектров задач A4) и C) также совпадают. Уравнения
обратной задачи получаются из уравнений (9.11), (9.12)

106 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
тривиальной заменой переменных:
W
тг=1
R (V) ф (V, 5) ехр Г-у- (v -
В этих уравнениях г|з = ( -т ], суммирование ведется
по всем нулям Л (К), лежащим в верхней полуплоскости,
R(X)=B (Х)/А (к), сп = В {Хп)/А' (Хп). Под ф (Я, 6)
следует понимать решение уравнений A4) с асимптотикой
4,B) _^ о, ^,A)^ехр[-|-(Х-^^, Б-»-+ оо. Данные рас-
сеяния удовлетворяют, ввиду (9.15), известным ограни-
чениям:
R (X) = - Я (- Я,); A8)
вместе с Хп собственным значением является —Яп; соот-
ветствующие с„ комплексно сопряжены. Если sin и и
ut как функции | бесконечно дифференцируемы и у бы-
вают при ||| ->• оо вместе со всеми своими производными,
то коэффициент отражения R (X) при А, -> сх> убывает бы-
стрее любой степени 1/Я. Этот факт справедлив как для
системы C) с потенциалом общего положения, так и для
системы A4). Однако для системы A4) при указанных ус-
ловиях R (Я) убывает быстрее любой степени Я и при

11] УРАВНЕНИЕ SIN-GORDON 107
Я. ->- 0. В этом легко убедиться, совершив в A4) замену
(и . и \
COS -7Г- I Sin -s- \
и и W
i sin-5- cos -5- /
и замечая, что ij/ удовлетворяет уравнению
'1 i
Н—о- е 2 взв 1E > (^U)
где
(О 1\ /1 0\
/0 1\
01=ll о)'
Из A9), B0) видно также, что при Я -> П
г sin
г{з (A,, g) ехр -4р (Х — -jt-)
Сравнивая это выражение с A6), находим
,cos
B1)
Формула B1) позволяет восстановить потенциал по реше-
ниям уравнений обратной задачи A6), A7).
Уравнение B) записывается в стандартной лагранже-
вой форме
дх дих ди
где
и является, очевидно, гамильтоновым. Его гамильтониан

108 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
есть
<22>
где и; = ЬЬ/Ьих — канонически сопряженная к и (|) пе-
ременная. Постоянная у играет роль константы взаимо-
действия. Гамильтонова система имеет вид
ди 6ff дш 6Н O'W
~дтГ=7ыГ' ~дх~ = ЫГ ' \ '
Укажем канонические переменные в терминах данных
рассеяния, которые, как и в рассмотренных выше приме-
рах, окажутся переменными действие — угол для системы
B2), B3). Вариационные производные от данных рассея-
ния можно, как всегда, вычислять, исходя из формул
a(k) = W (Ц> (Я,), Ф (Я,)), b(k) = -W$ (Я), Ф (Я)). B4)
При этом, поскольку задача A4) содержит щ, удобно перей-
ти к функциям ф' = ехр ( 1~ 0i) Ф> 'Ф' = ехР ( т~
являющимся решением уравнения
iux , iX
ff +
= [—— ffi + ^exp [- — ел] ax exp (-j-
^- i—Oij\ Ф- B5)
и
Так как det ехр u —стИ = 1, выражения для а (X) и 6 (Я)
через штрихованные переменные совпадают с B4).
Применяя, далее, стандартные рассуждения и возвра-
щаясь от ср', т|/ к ф, i|5, находим
7
B6)
(X.) i Г / iX
&Г 2" L С~2

§ И] УРАВНЕНИЕ SIN-GORDON Ю9
4- №-Щ **+**>+
Вычислим теперь скобки Пуассона:
{о(Я,), b(a,)}_YJd^__ 5^ ^ gjj-j. B7)
Здесь мы учли, что 8/bw = у б/бит. Путем прямых, но
несколько утомительных вычислений можно убедиться,
что подынтегральное выражение в B7) является полной
производной. Именно,
оа (А) о» (А ) оа (К) ос (Л. )
J__d_(lk
¦ +к'
би Ьи% бит Ьи
1 d П% — %' к + к' 7 \
~ 16 d?,\ Х+К' ^ к-к' г'1) '
где
2i (i|i (Я), ф (Я); iji (Я'), Ф (Я')) =
— 1]J (Я) ^2i (Я)) (ф1 (Я) ц>1 (Я) — ф2 (Я) с
Аналогичные формулы имеются и для других скобок:
бд (X) ба (V) _ &а(к) 6а (V) _
би б"- бмг би
и т. д. Производя интегрирование в B7), находим
-А- {а (X), 6 (X')} = 4" .йПГ^Г (в W Ь (Я') -
- ^ о (X) Ь (V) б (X - V) + -^ а (к) Ъ {%') б (% + %'), B8)
{а (Я), а {%')} = 0 и т. д.
Используя эти выражения и свойства симметрии
о (А) = а (— Я), Ъ (Я) = — Ь (— Я), нетрудно проверить,

110 МЕТОД ОБРАТНОЙ ЗАДАЧИ РАССЕЯНИЯ [ГЛ. I
что переменные
являются канонически сопряженными. Продолжая фор-
мулы B8) в комплексную плоскость
{а (X), Ъ (К')} = -?- (*±? - !*=?) а (X) Ъ (V)
и учитывая, что изменение положения ЬХп нуля а (X) свя-
зано с вариацией 6а соотношением ЬХп = , , 6а,
а (V
находим
где Ъп = Ъ (Хп). Таким образом, каноническими пере-
менными дискретной части спектра являются
Q
рп = \пХп, qn= — — 1пЬ„, Re?un>0, Im^n>0.
Эти переменные комплексны, если Re Xn Ф 0. Удобно пе-
рейти к вещественным переменным
Vn = \n\Xn\, qn~ 5-ln|6n| (ReXn = 0), B9)
C0)
16 Л, 7. /П ^ Л^Я\
Щ = -zr argAb -фл- = arg6fc U<argAk<-^-.
Набор переменных B9) относится к солитонам (антисоли-
тонам). Следует отметить, что рп, qn B9) не определяют
полностью эту часть спектра, поскольку они не чувстви-
тельны к заряду солитона, определяемому, как мы знаем,
знаком Ъп. Эти характеристики, имеющие не динамичес-
кое, а топологическое происхождение, должны быть до-
бавлены к B9). Переменные же C0) полностью описывают
двойные солитоны.
Выразим теперь гамильтониан через новые перемен-
ные. Это нетрудно сделать, заметив, что непосредственно
из A4) следует, что первые члены разложения In а (Я)
на бесконечности по Л и в окрестности точки X = 0 имеют,

§ 11] УРАВНЕНИЕ SIN-GORDON Ш
соответственно, вид
+ 0 (¦?-), Х-><~,
In о (Я.) = -f- ^ [ ("s + "tJ + A - cos ц)] <% + О (X2), Я,-¦О.
Восстанавливая далее In а (К) по переменным Р%, рп, на-
ходим
Импульс поля записывается в новых переменных в виде
C2)
В терминах частиц, связанных с нашей динамической
системой, эти формулы имеют простую интерпретацию.
При фиксированном К переменные Р%, Ф% образуют пару
канонических переменных типа «число частиц — фаза», так
что Р% можно, интерпретировать как плотность частиц,
A/4Я — Я) Р% — как импульс, а A/4Я + К) Р% — как со-
ответствующую энергию. Таким образом, первые члены
в первых частях формул C1), C2) представляют собой
вклад в энергию и импульс от частиц с единичной массой.
Вторые слагаемые, отвечающие вкладам солитонов, пред-
ставляют собой вклад от частиц с массой 8/у, т. е. масса
солитона есть 8/у. Наконец, последние слагаемые в C1),
C2) отвечают двойным солитонам. Их масса меняется
в интервале от 0 до 16/у, в зависимости от их «амплитуды».

Глава II
ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ
Как уже отмечалось во Введении, периодические по х
решения типа стационарной простой волны и (х — ct)
(их еще называют «кноидальными волнами») были открыты
в XIX в. в теории мелкой воды. Позднее, в 50-х годах
XX в. волны этого типа были обнаружены также в теории
плазмы. Численный эксперимент, проводившийся в 60-х
годах для решения уравнения Кдф с периодическими по х
начальными условиями, указывал на квазипериодичес-
кую по времени динамику. Кроме того, периодическая
задача обладает бесконечным числом законов сохранения
(см. § 5 гл. I). Все это указывает на полную интегрируе-
мость задачи Коши с периодическими граничными усло-
виями. Однако, по причинам математического характера,
периодическая задача для КдФ оказалась более трудной,
чем в быстроубывающем случае. В частности, долгое время
не было известно ни одного точного периодического по х
решения, кроме кноидальной волны. Не удавалось также
применить аналог метода обратной задачи рассеяния. Ре-
.дпение периодической задачи, найденное в 1974 г. (см.
обзор [6]), потребовало существенного развития теории
одномерного уравнения Шредингера с периодическим по-
тенциалом и использования ряда нетрадиционных для
физики математических средств.
§ 1. Уравнение Шредингера
с периодическим потенциалом.
Периодический аналог уравнений
Гарднера — Грина — Крускала — Миуры
В этом параграфе мы изложим необходимые для нас
элементарные сведения из теории уравнения Шредингера
и выведем периодический аналог уравнений ГГКМ для

§ 1] ПЕРИОДИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРЛ ЦЗ
Динамики в силу КдФ коэффициентов прохождения и от-
ражения (см. A.2.3)), из которого будут отчасти видны
трудности периодической задачи сравнительно с быстро-
убывающей.
Пусть, как и ранее, L = — cP/dx2 + и (х) есть одно-
мерный оператор Шредингера, и потенциал и имеет пе-
риод Т: и (х + Т) = и (х). Представление Лакса A.2.6)
для временной динамики уравнения КдФ сохраняет свое
значение и в периодическом случае:
L = [A, L],
если Ut = Quux — иххх, где потенциал и (х, t) зависит
от времени t как от параметра. Рассмотрим задачу на соб-
ственные значения для оператора L
Z4 = Щ. A)
Для удобства выберем базис решений уравнения A),
нормированный в точке х0 одним из двух способов:
Lq>+ = Ец>+, Ф± (аь) = 1, <р'± (*„) = ±ik, к2 = Е; B')
Ьс = Ее, Ls = Es, с (х0) = 1, с' (х0) = О,
{2"]
s (х0) = 0, *' (хо) = 1.
Базисы B') и B") мы будем обозначать соответственно че-
рез <р± (х, х0, Е) и с (х, х0, Е), s (х, х0, Е). Как обычно,
рассматривается оператор трансляции на период, комму-
тирующий с оператором Шредингера L (потенциал и
имеет период Т):
Т: г|> (х) -»- ф (х + Т), TL = LT. C)
В математической литературе оператор трансляции Т
называют часто «оператором монодромии». В любом из
базисов решений уравнения A) оператор Т запишется
как матрица второго порядка:
Гф+ = аф+ + Ьф_, Тц_ = сф+ + йф_,
Тс = апс + ai2s, Ts = a2ic + a^s.
При вещественных к, где к2 = Е, мы имеем
Ф_ = ф+, с = 5, d~a, Г

114 Периодические решения уравнения КдФ [гл. и
Для базиса B) при вещественных Е матрица Т = (а^)
будет вещественна (потенциал п предполагается всегда
вещественным). Как известно, детерминант Вронского
любой пары решений является константой. Отсюда сле-
дует
det Т = а11а22 — а12а21 = ad — be = 1. F)
При вещественных к, в силу E), получаем
И2 - \Ъ? = 1. G)
Матрица Т зависит, вообще говоря, от начальной точки х0
и от Е (или от к), f =Т (х0, Е).
Важной величиной в теории уравнения Шредингера
с периодическим потенциалом является след матрицы
трансляции
Sp f = ou + сс22 = а + d. (8)
При вещественных к мы имеем d = а и поэтому
Spr = o-fd = fl + a = 2aR, a = ац + i«i- (9)
Собственные числа матрицы t мы будем всегда обозна-
чать через ехр (+ ipT), где Т — период; число р = р(Е)
называется «квазиимпульсом». Так как det T = 1, соб-
ственные числа выражаются через след Sp Г и имеют вид
ехр (+ ipT) = aR ± Vai-i,
A°)
2 cos (pT) = Sp T = 2aR = ац + а22.
Строго говоря, эти формулы написаны при вещественном
к, но мы всегда будем величину х/г Sp Т = V2 (йц + а22)
обозначать через aR даже при комплексных Е.
Напомним, что собственная функция ajj-j. (я) называет-
ся блоховской (или функцией Флоке), если она является
собственным вектором также коммутирующего с L опе-
ратора трансляции Т:
= ехр (
Как говорят, блоховская собственная функция а|)± (ж, ^)
принадлежит блоховскому спектру оператора L на

§ 1]
ПЕРИОДИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
115
прямой (функция Флоке находится в разрешенной зоне
или зоне стабильности), если квазиимпульс р (Е) веще-
ственный или |ехр (ipT)\ = 1.
Из формул A0) видно, что зоны блоховского спектра
(разрешенные зоны, зоны стабильности) задаются урав-
нением
-g-Spr| = |oR|<l. A2)
Запрещенные зоны (или зоны неустойчивости) задаются
условием \aR | ^> 1 на вещественной оси Е. Хотя матрица
N
7
и
-1
F \ '
8 NL
Ег /
Рис. 2. Разрешенные зоны [ЕаЕг], \E2Eh], . . ., где aR < 1.
Т зависит от х0, Е, ее след Sp?1 = 2aB уже зависит только
от Е и его типичный график имеет вид, указанный на рис. 2.
Точки Ео, Еи Е2,- . ¦ образуют края разрешенных зон.
Возможен, однако, слу-
чай, когда запрещенная
зона стягивается к ну-
левой длине и исчезает
(например, точка Ег =
= Z?4 на рис. 2). В этом
случае точка Е3 = Е^
уже не является краем
зоны, и отрезок [Е2Еь]
образует одну разрешен-
ную зону. Тривиальный
пример такого рода дает
постоянный потенциал и = const; все края зон, кроме Ео,
попарно слились, и возникла лишь одна разрешенная зо-
на Е !> Ео (рис. 3).
Края разрешенных и запрещенных зон Е{ таковы, что
\aR\ = 1 или ехр (+ ipT) = ± 1. Вследствие этого бло-
Ховская собственная функция i|) (x, Е() такова, что
\
7
0
-7
"R
\
N
/\
Е
Рис. 3. График aR (E) для и = const;
при Е ^ Ео всегда | aR I < 1.

116 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Щ — + 'Ф ПРИ Е = Et. Это означает, что функция i|)
при Е = Ei является периодической с периодом Т или
периодом 2Г. Сама матрица Т при Е = Ег имеет совпадаю-
щие собственные числа exp (ipT) = ехр (— ipT), где
рТ = О, я.
В невырожденном случае матрица Т при Е = Et при-
водится к жордановой клетке: она имеет два совпадающих
собственных значения, но лишь один собственный вектор.
В этом случае Ъ (х0, Et) ^=0ияЕ=+ 1. В невырожден-
ном случае уровень Е-г действительно является концом
зоны.
Если матрица Т диагональна при Е = Et или Т =
~ ~ @ 1 )' где b (х°' Ей s °' т0 такой Уровень Ег дву-
кратно вырожден и не является концом разрешенной зоны.
Мы не доказываем эти элементарные факты, хорошо извест-
ные из любого учебника по теории линейных уравнений
с периодическими коэффициентами или из учебников по
теории твердого тела [18].
Заметим, что матрица Т (х0, Е) является периодичес-
ким аналогом квантовомеханической матрицы перехода,
для быстроубывающих потенциалов и (х) использованная
в § 1 гл. I. Действительно: пусть Т—>оо, хо-> — оо,
х0 + Т —»- + оо , а потенциал и (х) стремится к быстро-
убывающему при Г—>-оо. Тогда базис (ср+, <р_) в точках
х0 и х0 + Т стремится к базисам, имеющим асимптотику
двух экспонент ехр (+ ikx) при х—> + оо. Поэтому мат-
рица Т перехода от х0 к х0 + Т при Т -> оо перейдет
в матрицу рассеяния, использованную в гл. I для решения
КдФ на быстроубывающих по х функциях. Для быстро-
убывающих решений КдФ и (х, t) мы получили в § 2 гл. I
уравнение Гарднера — Грина — Крускала — Миуры (ГГКМ)
а = О, Ъ = 8ik3b.
Выведем сейчас периодический аналог этого уравнения
дли матрицы Т (х0, t, E), если периодический по х потен-
циал и (х, t) меняется со временем в силу КдФ или любого
из высших КдФ. Рассмотрим уравнение Лакса
L = [L, А\
для динамики в силу любого из высших КдФ. Здесь

§ i] ПЕРИОДИЧЕСКОЕ УРАВНЕНИЕ ШРЕДИНГЕРА Ц7
П
4=S ci^-n-i — оператор порядка 2га + 1, коэффициенты
i=o
которого зависят от и, и, и",. . . Для исходного Кдф
оператор А = Ах имеет вид A.2.5). Рассмотрим любой из
базисов B') или B") решений уравнения A). В базисе
B') по аналогии с A.2.4) имеем
Ф+ = — Ф+ + p+ + цФ_,
Ф_ = — Ац>_ + 7ф+ -\- бф_. '
При вещественных к (к2 = Е) имеем у — ]Г, б = Я и
К + б = 0, так как ф_ = ф+ и 4 — вещественный опе-
ратор. Действительно, из уравнений L = [L, А] и Ьф+ =
Е имеем равенство
(LE) L + (L- E) Ф± =
= {LA - AL) Ф± + {Ь - Е)ф± = - (L - Я) D<р± + ф±),
которое эквивалентно уравнениям A3).
Рассмотрим теперь матрицу Л (х0, Е)
Периодический аналог ГГКМ пишется следующим об-
разом:
^- = [Л, 7'] = Л7' —ГЛ. A5)
Матрица Л (х0, Е), входящая в это уравнение, опреде-
ляется из уравнения A3) подстановкой х = х0, где
ф+ = ф_ = (ф+) = (ф_) = 0 при х = х0. По определе-
нию базиса ф+, ф_ мы получаем
= к + ц, (Лф_)ж=Жо =7 + 6,
A6)
Так как коэффициенты дифференциального оператора А
выражены через и, и, и",. . ., то формулы A6) дают вы-
ражение матрицы Л через и (х0), и (х0), и" (х0),. . . Ана-
логичные вычисления можно проделать и в базисе B")
для определения матрицы Л, которая будет полиномиаль-

118 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
но зависеть также от Е (в базисе B') матрица кЛ полино-
миально зависит от к).
Для вывода уравнения A5) мы воспользуемся тем же
уравнением A3) в точке х0 + Т, применяя оператор
трансляции Т. Обозначим пару (ф+, ф_) через ф, и Ау =
= (Ац>+, А(р_), ф = (ф+, ф_). В матричной записи мы имеем
Т (ф) = f Ац> + ГЛф,
(ТФ)- = А (ГФ) + Л (ГФ), A7)
так как для базиса Тц> также справедливо уравнение A3).
Коэффициенты оператора А выражаются через и, и, и",...
с постоянными коэффициентами. Поэтому получаем
ТАц> = А Ту,
= 4?- ф + Гф = ^- ф + ТАц + 7'Лф, A8)
Последнее равенство равносильно уравнению A5). Если
потенциал и (х) быстроубывающий, то х0 = — оо, х0 +
+ 71=+°о, 7 = 00, ц^-0, и' ->- 0,. . ., ц<п) ->¦ О
при z -к + оо. Поэтому матрица Л для быстроубыва-
ющих потенциалов окажется постоянной. Вследствие
этого ГГКМ A5) будет сразу проинтегрировано. На-
пример, для основного уравнения КдФ мы имеем (ба-
зис B')):
л I d? о / d , d \ . ( X и
dxs \ dx dx I \[i 1
% = ik'i (- ~- + u2 - 4i&4 j , A9)
W2 *?Z-'
если и (х0) = и (хо) = . . . = м<") (ж0) = 0, то Л =
и уравнение A5) сведется к виду A.2.3):
о = 0, Ь =
Именно эта ситуация реализуется в случае быстроубываю-
щих потенциалов. В периодическом случае мы получили
общее уравнение A5), где матрица Л зависит сложнымоб-

§ 1] ПЕРИОДИЧЕСКОЕ УРАВНЕНИЕ ШРЕДЙНГЕРА Ц9
разом от и (х0), и (х0),... Это уравнение уже не интегри-
руется — во всяком случае, столь просто. В базисе B")
матрица Л всегда полиномиальна по Е. Для КдФ она
имеет вид
След матрицы Т является интегралом уравнения A5).
Действительно, этот факт вытекает из того, что правая
часть A5) имеет вид коммутатора. Так как 72 Sp f = aR
определяет блоховский спектр оператора L, то весь этот
спектр сохраняется (т. е. сохраняются все края зон Et).
Этот набор интегралов, однако, эквивалентен уже ранее
найденным законам сохранения Крускала (см. § 5 гл. I),
так как набор концов зон полностью определяет функцию
ur (Е), где Ei определяются из уравнения а^ = 1, ес-
ли все кратности равны единице.
Дело в том, что целая функция а.%, (Е) комплексной
переменной Е имеет порядок V2, т. е. оценивается по мо-
дулю \а%, (Е)\ <; const-exp (a]/?). Такие функции пол-
ностью определяются набором значений aft = 1 с указа-
нием кратности с помощью разложения в бесконечное
произведение.
Таким образом, прямой аналог процедуры ГГКМ не
дает серьезных результатов в периодической задаче, хотя
периодический аналог уравнения ГГКМ A5) будет поле-
зен в ряде случаев.
Выведем еще одно полезное уравнение для матрицы Т-
Так как матрица Т зависит от параметра х0 и при изме-
нении х0 ее собственные числа не меняются, то можно на-
писать
T^-lQ.fh B0)
Здесь матрица Q зависит от и (хо), и' (х0),. . ., Е. В бази-
сах B') и B") для матрицы Q несложно получаются фор-
мулы
- ,о„. „ [ / 0 Е — и
базисB): Q (
базисB'): Q - ik (J_J) - -*L (J ij),

120 Периодические решения уравнения КдФ tra. п
§ 2. Стационарная задача для высших КдФ.
Метод- отыскания точных решений КдФ
Как было указано в предыдущем параграфе, периоди-
ческий аналог уравнения ГГКМ A.15) не дает серьезных
результатов для интегрирования периодической задачи,
в отличие от быстроубывающей. При отыскании точных
решений КдФ мы воспользуемся другим методом. В гл. I
вводились так называемые «высшие уравнения КдФ»,
также интегрируемые методом обратной задачи рассея-
ния для оператора Шредингера L (см. A.6.1)). Все эти
уравнения имеют вид
t
3=0
где /n_j — интегралы (законы сохранения) Крускала
уравнения КдФ, указанные в § 5 гл. I. Все эти уравнения
представляют собой гамильтоновы системы с бесконечным
числом степеней свободы, коммутирующие друг с другом,
согласно § 6 гл. I. Эти уравнения также допускают пред-
ставление Лакса
L = [L, А], B)
п
где L = —-г-%-\-и(х), А = Ап-\-\ An-jCj, с-, —
31
константы.
3=1
31
Наша программа построения точных решений КдФ
такова: найдем все стационарные решения любого из выс-
ших КдФ
Возьмем любое из найденных решений уравнения C)
в виде начального условия для исходного КдФ. Исполь-
зуем то, что при сдвиге по времени в силу КдФ из началь-
ной" функции будет с течением времени в любой момент
получаться снова функция этого же типа: решение урав-
нения C) с теми же константами clt. . ., сп, cn+i. Для
реализации этой программы необходимо полностью ре-
шить стационарное уравнение C) и найти зависимость
этих функций и (х) от времени t в силу КдФ.

§ 2] СТАЦИОНАРНАЯ ЗАДАЧА ДЛЯ ВЫСШИХ КдФ 121
Говоря языком динамических систем, любое из высших
КдФ определяет нам однопараметрическую группу пре-
образований пространства всех функций и (х), причем
все эти группы попарно коммутируют. Поэтому совокуп-
ность (множество) стационарных точек (решений) любого
из высших КдФ инвариантна относительно всех осталь-
ных высших КдФ — в частности, исходного КдФ.
В виде простейшего примера рассмотрим случай п = 1.
Уравнение C) здесь имеет вид
где
/о = \ '\- dx, 1г = ^ [—¦ + и3) dx.
Таким образом, уравнение D) приобретает вид
Решение этого уравнения есть эллиптическая функция
Вейерштрасса
X — ?0 = \— F)
Само КдФ имеет вид
й = Ыи'-и"' =
Функция и (х — ct) является решением уравнения КдФ,
если с = с1# Мы получаем обычную кноидальную волну.
Более сложным является случай п = 2. Уравнение
C) будет иметь четвертый порядок. Его элементарное ин-
тегрирование весьма затруднительно.
В дальнейшем выяснится, что все быстроубывающие
многосолитонные решения КдФ и (х, t) удовлетворяют од-
ному из уравнений C) по х. Оказывается, почти все решения
уравнения C) периодичны или квазипериодичны по х.
Поэтому соответствующие решения КдФ являются перио-
дическим и квазипериодическим аналогом многосолитон-
ных решений (см. далее § 10 этой главы). Все уравнения
C) имеют рид вариационных производных
-?--=0; G)

122 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
здесь / = 1п + cjn-t + . . . + сп10 + сп+11^, где /_4 =
= J и dx. Отсюда с учетом невырожденности лагранжиа-
нов /„ извлекается гамильтоновость уравнений C) по х
р\ = дН/dqu q\ = — dHldpu i = 1,. . ., п,
где
s=0 '
и гамильтониан Н имеет вид
причем dHldx = u' Ы1Ьи.
Построим интегралы уравнения G) по ж. Согласно ин-
волютивности интегралов Крускала для КдФ, установ-
ленной в § 6 гл. I, мы имеем
или
то
, если
/ = j
и,
Pi
(Р
Ii
(и..
п 4
}
t
= о,
и,. .
ClPn-
б/
6и
г -f
* = 0, 1
ц^^) dx,
¦ . . . ~f~ (
6/. с
ы
т *
dx
., п
и) dx
-1,
= j
dx,
A0)
где Ti (и, и'',. . ., и*2"-1') — некоторый многочлен от и,
И', В*,. . ., UB«-1>.
Из соотношения A0) и уравнения G) мы видим, что
Tt — интеграл уравнения G). Итак, мы имеем набор ин-
тегралов То, Ти. . ., Тп-х уравнения G). Так как
* , dT0 61 d Ыо , Ы
г -
2 ' dx Ъи dx Ьи Ьи
то Го = Н (р, q) согласно обычному определению энер-
гии.
Оказывается, все интегралы Н = То, Тг,. . ., Тп^
инволютивны и независимы; гамильтонова система G)
вполне интегрируема; «почти» все решения окажут-
ся периодическими и квазипериодическими функциями
(возможно, с полюсами). Однако инволютивность этих

§ i\ Стационарная задача для высших кдФ 123
интегралов трудно проверить прямым вычислением. Ее
удобно непосредственно извлечь из коммутативности всех
высших КдФ, рассматриваемых как однопараметрические
группы преобразований пространства функций и (х).
Рассмотрим высшее КдФ с номером i, имеющее вид
6li\
-т—) , как группу преобразовании множества стацио-
нарных решений уравнения A). Стационарные решения
уравнения A) параметризуются набором констант си. . .
. . ., cn+i и начальной точкой при х = х0, т. е. набором
фазовых координат (plt. . ., рп, qu. . ., qn), указанных
в (8). Зависимость этих решений от х определяется далее
из гамильтоновой системы с гамильтонианом (9).
Тем самым высшее КдФ с номером i, рассматриваемое
на множестве стационарных точек уравнения A), изобра-
жается как динамическая система в пространстве (р1г. . .
. . ., рп, qx, . . , qn). При разных номерах i эти системы,
по определению, коммутируют как группы преобразова-
ний. Мы проверим, что полученная конечномерная систе-
ма с номером i является гамильтоновой с теми же кано-
ническими переменными р, q и гамильтонианом Tt. Это,
очевидно, достаточно для инволютивности интегралов Tt.
Кроме того, отсюда вытекает другой важный вывод:
само исходное КдФ в координатах р, q запишется как
гамильтонова система с гамильтонианом Н1 = Тг.
Согласно формулам (8), (9), гамильтониан Н имеет
вид
п п—1
Н = 2 рги<П— Q = 2 Pi?i+i + Vnin— Q (<7i, ...,qn, q'n) =
i=l i=l
n—l
= 21 Pi?l+1 + Ф (?1. • • • . ffn. Pn), A1)
где рп = dQldq'n согласно (8). Отсюда вытекают, в част-
ности, простые соотношения:
= °> 1<п< s<n-
Легко непосредственно проверить общее тождество:
дН Ы

124 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Поэтому лишь первое из гамильтоновых уравнений с га-
мильтонианом// (р, q) эквивалентно уравнению 81/би = 0.
Все же остальные гамильтоновы уравнения, кроме этого,
можно рассматривать как соотношения, позволяющие
выразить и, и', . . ., м'2'1) через фазовые переменные
ри . . ., рп, glt . . ., д„. Тождество A3) в силу A0) имеет
вид
1 = (_ „ifJ
dx \ d(Jl ri) { dx
j-, ' - * ^ dp>'
Тождество A3) верно для любой функции и (х), поэтому
в тождестве A4) можно считать, что р[ — любое число.
Отсюда имеем
dx cw о Pi '
Рассмотрим теперь поток и — (81г/8и)' в фазовом про-
странстве (р, q). Производные вдоль этого потока будем
обозначать точкой. Производные по г в силу гамильто-
ниана Н будем обозначать штрихом. Из A5) следует ра-
венство q\ = — dTJdp-y, так как и = qx. Если уравнение
qj = —dTjdpj (j = 1, . . ., к) уже выведено, то для / =
= к + 1 имеем
</fr+i = м(^ = (м^*)' = Oft = з ^— • A6)
Скобку Пуассона в пространстве (р, q) мы обозначим че-
рез [, ]. Из уравнения A6) и тождества Якоби получим
to, [#, 7\]]. A7)
Кроме того, имеют место равенства
[qk, Н] = - -Щ- = ъ

§ 2] СТАЦИОНАРНАЯ ЗАДАЧА ДЛЯ ВЫСШИХ Кдф 125
Так как Ть — интеграл гамильтоновой системы G), то
[Tt, H] = 0. Поэтому для qk+i получаем
Тем самым половина гамильтоновых уравнений выведена.
Выведем вторую половину уравнений, начиная с индекса
п до единицы.
Так как (?„)¦' = (qn)', то имеем
дн V / от. у
Из формулы A1) извлекаются равенства
дП дФ
? pndgj OPj
РП-Ы. A8)
Далее, мы получаем из тождества Якоби и вида Н (р, q)
(сп)' = - [я, -^-] = - [Н, [Tit Рп\] -
= [Тг, [qn, Щ] + [qn, [H, Ti]] = - [тг, -Ц-] =
== — > -з—з 5—^ 1 з—- • A9)
^j op одj opj Qp*> од
з n
Сопоставляя A9) и A8), находим уравнение
дТ.
Рп
до '
1 П.
Выведем теперь уравнение Гамильтона для p'j для всех
/< п; используем равенство (fij)' = (pj)'- Если для но-
мера / гамильтоновость уравнения для pj уже установлена,

12б ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЯ. It
мы получаем
(Д;)' = [Н, -^i-j = [Н, [р.и Т{]) = - [Pi, [Ть Н]] +
= y.
ат
dpndq} dqn dqfp^ dq^ '
jb qiq Щ j^ ^7
Так как из вида гамильтониана Н (см. A1)) следует равен-
ство
dw/dqjdp;^ 1,
получаем окончательно
Дм = dTi/dqj-x.
Тем самым мы установили, что поток (высшее КдФ й =
= (Ыг/Ьи)') является гамильтоновой системой в пере-
менных р, q с гамильтонианом Tt. При этом все скобки
Пуассона [Гг, Ts] равны нулю, поскольку соответствую-
щие потоки коммутируют. Отсюда уже следует, что ста-
ционарное уравнение G) является вполне интегрируемой
(по Лиувиллю) системой.
Заметим, что при выводе гамильтоновости потока
й = (Ыг/ЬиУ в переменных р, q (т. е. на множестве стационар-
ных точек другого потока) мы опирались лишь на тожде-
ство A0), означающее равенство нулю скобок Пуассона:
{/, 11) — 0. Поэтому фактически мы вывели общее ут-
верждение о сохранении гамильтоновости при такой опе-
рации ограничения потока. Это утверждение неочевидно
a priori ввиду отсутствия какой-либо прямой связи между
скобками Пуассона в функциональном пространстве
и (х) и скобками Пуассона в конечномерном пространстве
(р, q) для уравнения типа Эйлера — Лагранжа 81/8и = 0.
Тем не менее, утверждение о сохранении гамильтоново-
сти при описанной выше операции ограничения потока
оказывается чрезвычайно общим. Итак, мы установили
факт инволютивности интегралов Н = То, Тх,. . ., Tn-i
стационарного уравнения G) для высших КдФ. Первым
нетривиальным случаем является случай п — 2. Урав-

§ 3] ПОТЕНЦИАЛЫ С КОНЕЧНЫМ ЧИСЛОМ ЗОН 127
нение C) приобретает вид
Заменой и -> и + const можно добиться того, что сг = 0.
Прямое вычисление по формулам A0), A.5.6), C) дает
нам формулы для интегралов (р, q -> p, q):
То = Н = pjjj, + F (glt ?,),
Го+Г! = pi + 2wp!p2 + B? - с) pl+D (qu q2),
U = qu <7 = <Ь = |^г , Pi = ?'• Pa = —u, B2)
r, o2 5 „ 5 . с» о ,
F= —-^ n-qu2 — -7Ги4 + -|-ы2 + сзЫ,
Lj Li О ^
Напомним, что ^ (р, q) есть гамильтониан временной ди-
намики в силу КдФ в этих переменных. Гамильтонова
система B1) с двумя степенями свободы зависит от двух
констант с2, с3 (сх = 0) и является вполне интегрируемой
в смысле Лиувилля. Известен алгоритм введения угловых
переменных на поверхности То = const, Тг = const; од-
нако этот алгоритм технически неудобен, и мы не будем
его использовать. Интегрирование этих уравнений будет
завершено позднее (в § 8 гл. II) из других соображений.
§ 3. Стационарные решения высших КдФ
и потенциалы уравнения Шредингера
с конечным числом зон. Римановы поверхности
Периодические потенциалы и (х) одномерного уравне-
ния Шредингера, удовлетворяющие стационарным высшим
КдФ B.3), обладают замечательным спектральным свой-
ством: в их блоховском спектре имеется лишь конечное
число запрещенных зон. Вывод этого факта будет приве-
ден ниже в данном параграфе. Свойство конечнозонности
лежит в основе отыскания точных решений КдФ, а также
аналитического вида самих конечнозонных потенциалов
и их собственных функций. Давно известно, что эллипти-
ческая функция Вейерштрасса и = 2!Р (х) является перио-
дическим потенциалом (уравнение Ламе) с одной конечной
запрещенной зоной,. Этот факт указан, например, в [26]

128 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
(см. т. 3). Там же указано, что высшие потенциалы Ламе
ип (х) = п (п + 1) $> (х) при всех целых п имеют ровно
п конечных запрещенных зон в блоховском спектре. Дру-
гих конечнозонных потенциалов до теории уравнения КдФ
известно не было. Обратим внимание на то, что для эллип-
тической функции Вейерштрасса и (х) = 2$ -f- const
функция и(х — ct) при определенном с является кнои-
дальной волной уравнения КдФ и удовлетворяет ста-
ционарному уравнению B.3) при п = 1. Это совпадение
оказывается не случайным: мы покажем, что все периоди-
ческие и квазипериодические решения стационарных выс-
ших КдФ B.3) являются конечнозонными потенциалами,
а быстроубывающие решения тех же уравнений — без-
отражательными потенциалами.
Предположим, что потенциал является периодическим
с периодом Т, как в § 1. Воспользуемся уравнениями A.15)
и A.20) для матрицы трансляции Т (х0, t, E), где матрица
Т зависит от t в силу какого-либо из высших КдФ B.1).
Уравнения A.15) и A.20) должны быть совместны:
д
~дТ
Из требования совместности вытекает
' дТ \ _ _д__ ldf_ \
дх0 I ~~ дхй \ dt ) '
A)
Из тождества Якоби
[<?,[Л, ?)] + [Т, [Q, А]] + [Л, [f, Q]} = 0
получаем
Матрицы Л, Q, [Л, Q] имеют нулевой след и зависят по-
линомиально от Е, и (х0), и' (х0),. . . Отсюда следует
окончательное уравнение, которое несколько иначе было
выведено в § 8 гл. I,— см. A.8.11), где Q ~ U, V =^ Л:
^-4-[А.О-0 C)

§ 3] ПОТЕНЦИАЛЫ С КОНЕЧНЫМ ЧИСЛОМ ЗОН 129
или
[4--л. ?¦-<?]-<>•
Матрица Q указана формулами A.21). Вычисление ма-
трицы Л через коэффициенты оператора А указано в фор-
мулах A.16) для базиса A.2'). Уравнение C) дает новое
весьма полезное коммутационное представление уравне-
ния КдФ и его высших аналогов, отличающееся от
представления Лакса L = [L, А]. В базисе A.2") обе
матрицы Л, Q полиномиально зависят от параметра Е, а
также от и (х0),. . ., и^ (х0). Удобство этого представ-
ления, например, видно из следующего. Рассмотрим
стационарное уравнение B.3) для любого из высших
КдФ. Тогда мы имеем
и = О, Л = Q = Т = О, L = [L, А] = 0. D)
Сопоставляя уравнения D) и C), получаем
-з?-[Л,С1; E)
это дает нам представление типа Лакса для стационарных
высших КдФ B.3), через замену х0 на х. Из представления
E) мы сразу получаем интегралы уравнения B.3), со-
ставленные из коэффициентов характеристического много-
члена матрицы Л:
det A-1 - Л) = Р (I, Е) = Я2 - (Sp Л) Я + det Л. F)
Однако, Sp Л = 0. Поэтому
det A-1 - Л) = А,2 + det Л = А,2 + R (Е), G)
Для высшего КдФ с номером п сам детерминант —
—det Л = R (Е) является полиномом от Е степени 2и +
+ 1 с постоянным старшим членом и коэффициента-
ми, полиномиально зависящими от и (х0), и' (х0),. . .
. . . , и(»"-«(а:0):
R (Е) = Е*^ + п1Е2п + . . . + а2п Е + а2п+1. (8)
Можно показать, что первые п + 1 коэффициентов
%,. . ., ап+1 фактически выражаются лишь через констан-

130 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
ты сг,. . ., сп+1, входящие в уравнение B.3); нетривиаль-
ными интегралами являются Qj = an+i+j, / = 1,. . ., п.
Набор интегралов Qlt. . ., Qn для системы B.3) с п сте-
пенями свободы эквивалентен набору интегралов То,. . .
. . ., Гп_!, указанных в § 2 (см. B.10)). (На самом деле
эти наборы даже совпадают.) Для базиса A.2') решений
ф = (ф+, ф_) мы из формул A.13) получим
?ф — Е<р = 0, А<р — Лф = 0. (9)
Поэтому, в частности, в полиноме Р (Я, Е) = det (X-1 —
— Л) можно вместо Е подставить оператор L и вместо к —
оператор А. После этого получится соотношение между
операторами L и А, если [L, А] = 0:
Р (A, L) = Л2 + R (L) = 0. A0)
Здесь R (Е) — полином степени 2п + 1 с постоянными
коэффициентами. Соотношение A0) вытекает из формул
(9), поскольку оператор Р (A, L) ф == 0 при всех Е, в си-
лу (9).
Применим периодический аналог уравнения ГГКМ
л.
A.15), учитывая, что Т = 0:
[А, Л = 0. (И)
Напомним, что блоховская собственная функция
ilxj. (x, E) определялась как собственный вектор матрицы
трансляции (см. A.11)):
Так как матрицы Т м А коммутируют (см. A1)), то бло-
ховская собственная функция a|)± (x, E) является собствен-
ным вектором также и для матрицы Л:
A2)
Вспомним теперь, что матрица Л (Е) полиномиально за-
висит от ? в базисе A.2"). В линейной алгебре известен
такой простой факт: если матрица Л полиномиально за-
висит от параметра Е, то ее собственные векторы и соб-
ственные значения (как функции от Е) будут многознач-
ными мероморфными функциями от Е, причем риманова
поверхность этих многозначных функций Я (Е) опреде-

§ 3] ПОТЕНЦИАЛЫ С КОНЕЧНЫМ ЧИСЛОМ ЗОН Ш
ляется из уравнения
О = Р (к, Е) = det (Я-1 - Л (Е)) = 0. A3)
В нашем случае матрица Л имеет порядок два и Sp Л = 0.
Отсюда мы имеем
Х± (Е) = ц± (Е) = ± УЩЩ- A4)
Формула A4) дает нам двулистную риманову поверхность,
ветвящуюся в точках Ео,. . ., Е2п:
R (Е}) = det Л (Ej) = 0, / = 0,. . ., In. A5)
Таким образом, блоховская собственная функция
¦ф-j. (х, Е) оказывается мероморфной функцией комплексной
переменной Е, определенной на двулистной римановой по-
верхности У R (Е) с точками ветвления в нулях Ео,
/?!,. . ., Е2п. Покажем, что эти точки ветвления Ej яв-
ляются точно концами зон блоховского спектра. Действи-
тельно, функция i|Xj- (х, E) согласно A.11) определялась
как собственный вектор операторов L и Т и зоны спектра
совпадали с отрезками вещественности квазиимпульса
р (Е). Концы зон согласно § 1 определялись как точки
Ej, где рТ = 0, п, ехр (+ ipT) == + 1 и матрица Т жор-
данова, т. е. имеет лишь один собственный вектор при дву-
кратно вырожденном собственном числе. Таким образом,
над каждым значением энергии Е (вещественным и комп-
лексным) мы имеем ровно две функции г[з± (х, Е) кроме
концов зон Ej, где эти функции сливаются в одну. Мы
видим, что блоховская собственная функция ty± (x, E)
для любого периодического потенциала определена фак-
тически на римановой поверхности, причем точками вет-
вления являются концы зон. Однако, у типичного потен-
циала число зон бесконечно, и тем самым число точек
ветвления бесконечно. В нашем случае, если потенциал-
удовлетворяет стационарному уравнению B.3), число
точек ветвления и тем самым число зон конечно и равно
п. Разрешенные зоны располагаются так:
(¦So^i)' (^2-#з)»' • •> (E2n-zEzn-i), (Е2п °°)
(рис. 4). Для того чтобы г|)± [х, Е) имела наименьшее чис-
ло нулей и полюсов, ее удобно нормировать следующим

132 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
образом:
г|>±(*, Е) = 1, х^ха
для всех Е.
Нормированную так собственную функцию мы обозна-
чим через г|5± (х, xQ, E). Очевидно, при вещественных
р (Е) — т. е. в разрешенных зонах — мы имеем г|->_ == гр+.
—#?
Рис. 4. Разрешенные зоны (заштрихованы).
Для гладкого вещественного потенциала нули и полю-
сы функции г|)_|- (х, х0, Е), располагаются по одному в за-
прещенных зонах или на их границах. Более детально
аналитические свойства функции г|з± (х, х0, Е) на римано-
вой поверхности мы выясним в следующем параграфе.
§ 4. Аналитические свойства блоховской
собственной функции конечнозонного потенциала
на римановой поверхности
Риманову поверхность двузначной функции }Aft (E)
мы обозначим буквой Г, а точки этой поверхности буква-
ми Р, Q,. . ., которые изображаются точкой ^-плоскости
и знаком листа: Р = (Е, ±), кроме точек ветвления Ео,
Еи. . ., Е2п, где (Ej, +) и (Ej,— ) изображают одну и ту
же точку римановой поверхности. Операция «забывания
знака» Р = (Е, ±) ->- Е может рассматриваться как
проекция римановой поверхности Г на ^-плоскость или
как числовая (комплексная) функция точки римановой
поверхности Е (Р). Поскольку риманова поверхность Г
определяется спектром оператора L (набором концов зон
Ej, являющихся точками ветвления), то мы часто будем
саму риманову поверхность Г называть «спектром» опе-
ратора L. Блоховская собственная функция г[;± (х, х0, Е),
нормированная условием C.16), может рассматривать-
ся как однозначная функция -ф = -ф (х, х0, Р) точки
Р = (Е, ±) на римановой поверхности, зависящая от
параметров х, х0.

§ 41 АНАЛИТИЧЕСКИЕ СВОЙСТВА ЕЛОХОВСКОЙ ФУНКЦИЙ 133
Введем функцию i%± = d In ty±/dx = % — ik (см. A.5.2)).
Согласно определению имеем формулу
¦ф-t- (х, х0, Е) = exp \ i
причем х± пе зависит от х0. Функция х± также является
однозначной функцией на римановой поверхности Г.
Из определения вытекает уравнение Риккати для %+ и
формула для квазиимпульса:
iy'± — jjr? — ¦• с
1
= Т
Изменим далее обозначения из § 5 главы I Xr —* Хь
Xi — к —>%л. Мы получаем:
Х± = Xr + »Xi. Xi = - — (ln Xr)'- C)
Поэтому, в частности, имеем
зс„+Г
Сопоставляя C) с A), получаем выражения для о|з±:
ж0, Е)=у ^ (^°'Д) ехр {+ i ^ Xr <Ц • E)
Отсюда следует
Произведение i|)+i|>_ по самому определению уже является
однозначной функцией на ^-плоскости (напомним, что
¦ф+г|)_ = |г|5±|а в разрешенных зонах, где а|э+ = ij5_). В ба-
зисе A.2") функция ур± (х, х0, Е) имеет вид
о|з± (х, х0, Е) = с(х, х0, Е) + i а± (х0, Е) s(x, х0, Е) G)
в силу нормировки C.16).

134 ггерйоди*1ескйе решений уравнения КдФ [Гл. п
Оказывается, коэффициент <х± совпадает с х± (х0, Е):
а± («01 Е) = х± (х0, Е). (8)
Дадим вывод формулы (8). При х = х0 мы имеем
i|4 (х0, х0, Е) = гос± (л:0, Е),
Поэтому —? (In i|)±)i=Ko = х± (ж0, ?) = а± (х0, Е). Так
как с (х, х0, Е) ж s (х, х0, Е) являются однозначными це-
лыми функциями комплексной переменной Е, то полюсы
я|з± (х, х0, Е) на римановой поверхности Г и их кратности
точно совпадают с полюсами х± (х0, Е) и тем самым за-
висят лишь от х0.
Для гладких вещественных потенциалов и(х) из этого
факта вместе с формулой F) вытекает важный вывод: если
полюс блоховской функции г[з+ (х, х0, Е) находится в точ-
ке (Е, +) поверхности Г, то в точке (Е, —) полюса нет
(за исключением точек ветвления (Ej, +) = (Ej, — )).
Действительно, из формулы G) следует, что полюсы г|)±
те же, что и полюсы х± с учетом кратностей. Если o|3± имеет
полюсы одновременно в точках (Е/ +) и (Е, —) кратностей
т+ и т_, то произведение i|)+ajj_ будет иметь в точке Е
комплексной плоскости полюс кратности т+ + т_,
т. е. большей. Это противоречит формуле F), из которой
следует, что произведение 1[з+г|)_ имеет те же полюсы, что
и %± (х0, Е) вместе с кратностями.
Позднее мы покажем, что все полюсы функции
г|)+(.г, х0, Е) просты и находятся в точках Pj = (yj (x0), ±),
/ = 1,. . ., п, по одному в каждой запрещенной зоне ко-
нечной длины или в их границах Ej.
Выведем формулу для %± (х0, Е) через коэффициенты
матрицы трансляции Т (х0, Е). Так как a|3± = с + i%± (xo)s
в силу (8) и fty± = е±*Ргг|э±, Тс = оспс + a12s, Ts =
== а21с -f- a22 s, мы из определения собственного вектора
для Т через коэффициенты atj получим
= f (С + i%+s) = ИцС + U12 S (
= e^T (c
или

§ 4] АНАЛИТИЧЕСКИЕ СВОЙСТВА ЕЛОХОВСКОЙ ФУНКЦИИ 135
где 2aR = Sp 7* = ап -f- а22. При вещественных Е все
atj вещественны. В разрешенных зонах по Е имеем а^ <^
<1 и поэтому величина %± = %r + ixi> где
%R@,E) a ,
021
Xl (xo, ?)=- 4- (ь zR)-=4- —^ •
При вещественных /с (к2 = ?) имеем а21 = (сц + &i) &-
Аналитические свойства целых функций 1 — Or (E) и
а21 (х0, Е) комплексной переменной Е таковы: функция
1 — «r (Е) имеет простые нули в концах зон Ео,. . .
. . ., Е2п, если потенциал и-зонный, и двукратные нули
в остальных точках Еу (у^> 2п, а\ = 1); все эти точки веще-
ственны и Т (х0, Еу) = + L . J. В тех же точках Еу функ-
ция а21 (х0, Е) имеет нули. Функция /в, = V 1 — a\Ja.2l
двузначна и имеет асимптотику %ъ ~ ± к при ? -> оо,
как следует из уравнения Риккати B) и уже указывалась
в § 5 гл. I. Напомним, что функция 1 — or (E), как указы-
валось в § 1 данной главы, имеет порядок роста V2 при
Е -> оо (т. е. оценивается |1 — а\\ < Сеа1/?). Тем самым
1 — aft определяется полностью как бесконечное произ-
ведение своими нулями:
In
1 - а\ (Е) = const П (l - -§-) П fl - Л'- (И)
Рассмотрим функцию / (Е), определяемую равенством
Из аналитических свойств функций 1 — afj (^) и а21
следует, что корень в знаменателе извлекается (все нули
Еу двукратные) и нули знаменателя сокращаются с ну-
лями числителя. Поэтому функция / (Е) — целая на
реей ?-цдоскости,

136 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Так как XR / Iе) = V& (Е) и /д (Е)
оо , то / (Е)
/, ()
Вывод: / (Е) есть полином степени и (га — число зон)
п
U A3)
Окончательно имеем следующие формулы для %r и %i:
у (х Е) УЩЩ
П (?-у» (*))
^ A4)
Xi — ~2~ U11 Xr) — 2
П (Е - Y,f
Согласно формуле F) получаем
П(Е-ук(х))
A5)
П (?-
Вронскиан W (ф15 ф2) = Ф1Ф2 — ФхФг любой пары ре-
шений уравнения Lq> = ?ф не зависит от х. Из формулы
(8) мы получаем в разрешенных зонах
W (о|>+, Ю = 2iXR (^0, ?) = 2?
l 1й — ук (ха))
A6)
W(c, s) = — W*(«, с) = — 1.
Формулы A6) определяют аналитическое продолжение
на все Е величины %r (x, E) как комплексно-аналитичес-
кую функцию от Е. Это определение может применяться
и для комплексных потенциалов и (х), где для х± =
= — i (In a|)±)' с учетом C) получим
v (r f\ ~w {^ ^-] l ( w'
Х± (Хо, Е) = ^г ~
Такая величина х± удовлетворяет уравнению Риккати B).

§ 4] АНАЛИТИЧЕСКИЕ СВОЙСТВА ЕЛОХОВСКОЙ ФУНКЦИИ 137
Как известно, для гладкого вещественного периодичес-
кого потенциала и (х) функция г[з+ (х, xQ, E) обязана иметь
нуль в каждой запрещенной зоне конечной длины. Отсюда
следует, поскольку мы имеем ровно п нулей ук(х) и п
зон согласно формуле A5), что в каждой запрещенной зоне
имеется ровно один нуль ук (х) и ровно один полюс
Ук(х0). Более точно, как указывалось выше, полюс у}; (х0)
может лежать лишь на одном листе римановой поверхно-
сти Г — либо в точке Р+ = (ук, +), либо в точке Р- =
= (ук, —), если эти точки различны (т. е. кроме ветвле-
ний). Если же ук (х0) = Е} совпадает с точкой ветвления
(Ej, +) = (Ej, —), то произведение i[)+i[>- имеет двукрат-
ный полюс на римановой поверхности Г (заметим, что
г[з+ = я|э_ при Е = Ej). Локальная координата на Г около
этой точки связана с координатой на ^-плоскости корне-
вым преобразованием — поэтому на ^-плоскости двукрат-
ности полюса нет.
Итак, мы приходим к следующим выводам (и (х) —
гладкий вещественный периодический потенциал):
1. Блоховская функция г|)± (х, х0, Е) мероморфна на
римановой поверхности Г и имеет асимптотику \р± ~
~ exp {± iYЕ {х — х0)} при Е —>- оо.
2. Функция г[з± имеет ровно п нулей yt (x) и п полю-
сов Y; (#(,) по одному в запрещенных зонах или на их гра-
ницах.
3. На поверхности Г нули и полюсы (у:, ±) все про-
стые; нуль или полюс могут лежать лишь в одной из двух
точек (ук, +) и (ук, —).
4. Нули г[з+ (х, х0, Е) являются функциями лишь от х;
эти точки поверхности Рк = (у^ (х), ± ) зависят от х
точно так же, как полюсы Qk = (у^ (х0), ±) зависят от
х0: Рк (х) = Qk {х0) при х = х0, поскольку г|з± {х0, х0,
Е) = 1.
5. Функция Xr = 27 СФ''Ф- ~ ¦Ф1'Ф+) выражается на
поверхности Г через набор нулей по формуле A4). Сопо-
ставим формулу A4) с уравнением Риккати и асимптотиче-
ским разложением при Е —>- оо (к2 = Е) (см. (I. 5.3)):
П>0
A8)

138 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Отсюда мы получим выражение коэффициентов %п (х)
через набор нулей уц (х), где %„ вычислены через и, и',
и",. . . согласно § 5 гл. I. В частности, получаем
() Sv*()+ iih
A9)
4- C«- - и") - ? УкУ1 - ^-2,ад + -§-(?
§ 5. Некоторые приложения
I. Выведем уравнение по х для нулей и полюсов
(х, х0, Е). Рассмотрим величину ;
Щ
Х± {*о, Е) = *=i , A)
П (Е - ук (*0))
где полюсы х+ расположены в одной (и только в одной)
из точек (ук (х0), +) или (ук (х0), —) на римановой по-
верхности Г над точкой 7ft (^o) B ^-плоскости. Пусть по-
люс находится в точке Qk = (уи (х0), + ). Условие от-
сутствия полюса в точке G^, —) равносильно обращению
в нуль при Е = ул (х0) числителя формулы A), поскольку
знаменатель имеет нуль:
Y» Ы)] |в=^(ЖоГ B)
Уравнение B) можно разрешить относительно у'ц. Сделав
замену х0 —>- х, получим
Vft-7;)- C)
При этом, согласно D.19), потенциал имеет вид
и(х) = -2St*(*) + S^.
Пример 1. Пусть п = 1. Тогда имеем одно урав-
нение
Y"W D)

§ 5] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 139
при
u(x)=-2y1(x)+%Ej. D)
3—0
Мы еще раз получаем однозонный потенциал Ламе.
Пример 2. Пусть п = 2. В этом случае имеем два
уравнения
Как легко видеть, отсюда получаем
V - R (Yi) У -ВЫ Y2~^
При этом всегда у2 — 7i ^> 0> так как уг и у2 лежат в раз-
личных запрещенных зонах по Е, разделенных разрешен-
ной зоной:
Ео < Е1 < 7i < Е2 < Е3 < 72 < Et,
Ег < Е2, Е3 < Ei.
Уравнение E), очевидно, можно проинтегрировать, после
чего получим потенциал и (х) = —2 (yt + 7г) + S ^j-
Введем две вещественные периодические функции Fx (т)
и F2 W» Для которых имеем соответственно:
т-
у — л
Очевидно, функции Рг и F2 определены в областях
Ег < Fi < ^2, (8)
так как график полинома R {Е) имеет вид, указанный на
рис. 5.

140
ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ
[ГЛ. II
Из уравнения E) получаем
и (т (х)) = - 2 (Л (- т) + F2 (т + т0)) + .2 Eh
4
3=0
x — x0 = \ -5- (у2
(9)
Эти формулы дают, вообще говоря, двухзонные квази-
периодические потенциалы, если задать набор краев зон
Ej произвольно. Выбор
Ct'ff
Рис. 5. График полинома П (Е).
начальных точек т0, х0
однозначно определяет-
Е, ся формулами G), (9)
вместе с определением
гиперэллиптических
функций Fx и F2- Заме-
тим кстати, что в комп-
лексной области две
функции Fx и F2 по су-
ществу представляют собой одну функцию. Используя фор-
мулы D.19), легко непосредственно проверить, что урав-
нение E) совпадает со стационарным высшим уравнением
КдФ при п = 2, где 7i и 7г — координаты на поверхности
уровня двух интегралов B.22). Поэтому сам потенциал
и (х) удовлетворяет уравнению B.3) при п = 2. Полное
интегрирование уравнения C) для всех п ^> 2 и удобную
аналитическую формулу
для потенциала и (х) мы
получим позднее, в § 9 этой
главы.
Решения уравнения E)
являются квазипериоди-
ческими функциями с дву-
мя, вообще говоря, рацио-
нально-независимыми периодами 7\, Т2, полностью опреде-
ляемыми римановой поверхностью Г (см. § 9). Геометричес-
ки уравнение E) можно представить себе так: точки
римановой поверхности, лежащие над запрещенными зо-
нами, образуют циклы аг, а2 (здесь п — 2) (рис. 6); нули
Ли Рг функции ip± (х, х0, Е) лежат по одному на циклах
ах и «3, как показано на рисунке, и меняют свое положение
Рлс.
нами
0. Над запрещенными зо-
«висят» циклы а-ъ на 'ри-
мановой поверхности.

§ 5] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 141
при изменении х. Топологически циклы аг и а2 являются
окружностями, а «фазовая точка» (Р1: Р2) = (у1; ±, у2, ±)
лежит на двумерном торе. Уравнение E) описывает дина-
мику «фазовой точки» (Рг, Р2) по этому тору.
Общее уравнение C) аналогичным образом описывает
движение фазовой точки (Рг, . . ., Рп) = (уи ±, у2, ± , . . .
• • •> Тп> ±) по га-мерному тору, где каждая из точек
Pj = (yj, ±) лежит на цикле aj на поверхности Г над за-
прещенной зоной с номером /.
Замена переменных, вводящая «угловые» координаты
ф/с на этом торе, такие, что (pi = const, будет указана
позднее (см. § 8). Для этой цели придется ввести ряд фак-
тов из теории римановых поверхностей (см. §§ 6, 7).
II. Укажем сопоставление нашего языка с традицион-
ным языком спектральной теории операторов. Параметры
Yi, . . ., уп имеют интерпретацию на языке дополнитель-
ного спектра задачи типа Штурма — Лиувилля для опе-
ратора L = — cP/dx2 + и, традиционного в теории «об-
ратных задач». Собственная функция \р± (х, х0, Е) обра-
щается в нуль при Е = уи на одном из листов поверхно-
сти Г. Пусть этот лист со знаком плюс. Тогда г[\ (х, х0,
ук (х)) = 0. Кроме того, я|з+ ->¦ 0 при х -»- + °о (если нуль
лежит на листе «минус», то я|э_ (х, х0, Yt (ж)) = 0 и г|з_ -> 0
при х ->- — оо). Рассмотрим %р+ (х + т, х0, уц {х)) и опера-
тор Ьх = — cPldx2 + и (т + х). Мы имеем
Lx i[>+ {х + х, х0, у,,- (х)) = ук (х) г[з+ (х + т, х0, у,- (х)),
причем
i[j+ = 0 при т = 0; i|)f -> 0 при т ->- -f оо.
Следовательно, функция г|з+ (х + т, х0, Ук (^)) является
собственной функцией дискретного спектра оператора Ьх,
отвечающей уровню Е = ук (х) на полупрямой т> Ос ну-
левым граничным значением при т = 0 (здесь х — па-
раметр). Это дает спектральную интерпретацию точки
Ри = (ук, +)• Если бы нуль лежал в точке Рк = (ук,—)
на поверхности Г, то аналогичный оператор Lx имел бы
точку дискретного спектра на полупрямой т <С 0, так
как г|з_ (х + т, х0, ук (х)) ->- 0 при т ->- — оо. Согласно
формулам D.19), набор нулей функции г[э+ (х, х0, Е)
определяет однозначно потенциал и (х) вместе с исход-
ным блоховским спектром, задающим риманову поверх-

142 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
ность Г. Указанная здесь спектральная интерпретация
нулей (ук (х), ±) не единственна. При тех же условиях
функция г|э± (х + т, х0, ук (х)) имеет нули при всех т =
= пТ, где Т — период потенциала, поскольку a|)+ (x -f-
+ х + Т) = е^т% (х + т) и о|5+ (х + т,' х0, у* (х)) = О
при т = 0. Поэтому уровень Е = ук (х) для оператора Ьт
является точкой спектра задачи Штурма — Лиувилля
с нулевыми граничными условиями на отрезке @, Т).
Однако такая интерпретация не указывает никакой ин-
формации о листе ± на поверхности Г, где лежит нуль
функции я|з± (х, х0, Е).
III. Выведем общие формулы для вариационных про-
изводных квазиимпульса р (Е) по потенциалу и (х) при
фиксированном периоде и установим как следствие тот
факт, что всякий конечнозонный потенциал удовлетворяет
одному из уравнений B.3) — стационарному высшему
КдФ.
Согласно D.2), D.4) для квазиимпульса мы имеем
+ pf= J X±dx= J Xndx. A0)
Жо Жо
В силу уравнения Риккати D.2), квазиимпульс р (Е)
фактически зависит лишь от и — Е. Для вариационной
производной мы выведем формулу
J_
Ы{х) 2Xr ¦
Заметим следующее: так как р = р {и —• Е}, то из A1)
получим
dp
дЁ
Жо+Г
1 (* dx
Т 1 2у
1
т
г
J
п
11 (
1
й1 - Yft (»))
Рассмотрим оператор Шредингера Lt = —
+ ut (х). Пусть уи у2 — решения уравнений Ьгуг = Еуи
где i = 1,2. Для вронскиана W (уи у2) = угу'2 — у'хуг
имеем
-^- = (иг - Щ) У1у2. A3)
Оба потенциала wx, ц2 мы считаем периодическими с пе-

§ 5] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 143
риодом Т. Рассмотрим блоховские функции г|>± {х, х0, Е)
для обоих этих операторов Lt в разрешенной зоне и по-
ложим
Интегрируя тождество A3) от х0 до х0 -f- Т, получим
зсо+Г
W \х^+т -<¦ W |х=ЙСо = J (Ul - и,)
Ха
Так как г|з± = с* + i%± (xo)s^ в силу D.8) для обоих
потенциалов ut {x) в базисе A.2"), мы найдем из определе-
ния i|5± (ж, ж0, ?):
Ко+Г
Це^-^-1)(^)Ы-^2)Ы)= J (их-щ)^ЩЫх.
Хс
A4)
В разрешенных зонах мы имеем х+ = — 5L-
Пусть теперь цх — щ == би (ж) мало. Оставляя в ра-
венстве A4) линейные члены, получаем
зсо+Г
-(вр)Г(х + х)*= S *и|ф±|вАс. A5)
Так как
в силу формулы A5) находим
ж„+Г
¦> 1 (' Ьи (ж) dx
Тем самым выведены формулы A1) и A2).
Мы знаем вид xr Для конечнозонных потенциалов (см.
D.14)). Разложим теперь обе части равенства A1) по 1/]/Е
при Е —>~ оо. Получим (к2 — /?)
in -'/г
*)

144 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Хс+Г
где 2/„_2 = -=г \ %2n+1dx есть полиномиальный интеграл
Крускала и гамильтониан высшего КдФ. Правая часть
равенства A6) имеет вид
2VE ^ Е &
причем все bt для i ]> 1 линейно (с постоянными коэф-
фициентами) выражаются через набор из п элементарных
симметрических функций от уъ. . ., уп. Отсюда следует
линейное соотношение вида
п
Ъп+1 + 2 ск+1Ъп„к = 0, A7)
fc=o
где съ. . ., сп+1 — константы и Ьо = 1. Однако, из ра-
венства A6) следует
bk = ±2^±, k = 0,...,n. A8)
Сопоставляя соотношения A7) и A8), получаем вывод:
любой /г-зонный периодический потенциал удовлетворяет
одному из стационарных уравнений B.3) для высших КдФ
1 Г
где cft = + ск и /-J = ~y \ и dx.
IV. Выведем уравнения для временной динамики ну-
лей и полюсов блоховской собственной функции в силу
КдФ и высших КдФ.
Рассмотрим любое из высших КдФ B.1) и его пред-
ставление Лакса B.2). Напомним уравнение A.13) для
базиса собственных функций A.2') или A.2") оператора L:
ф = — Лф + Лф,
где матрица Л указана в A.16). Выведем общую формулу
XR = (Яхн)', B0)
где X = Я21 в базисе A.2") и Я, = -г- (Я,х -}-• [ii) в базисе A.2')

§ 5] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ 145
при вещественных к (к2 = Е). Напомним, что Л = (Xtj)
в базисе A.2") и Л = ( ?-) в базисе A.2') при веществен-
ных к, согласно A.13). Отметим, что формула A9) представ-
ляет собой полезное уточнение законов сохранения для
КдФ и высших КдФ, так как согласно § 5 гл. I мы имели
О
и полиномиальные законы сохранения Iq получались из ве-
личины -=- \ %Rdx асимптотическим разложением по l/jAZ?
при Е ->¦ оо. Напомним кстати, что согласно D.4) величи-
г
1 Г
на -=- \ %я<1х есть точно квазиимпульс р (Е) + тп. Для
о
вывода формулы B0) мы воспользуемся уравнением для
матрицы трансляции Т по параметру х0 A.20). Из уравне-
ний C.3), A.20) в базисе A.2') вытекают общие тождества:
Ц70
( )
d*
Воспользуемся теперь периодическим аналогом урав-
нений ГГКМ A.15) для динамики матрицы Т в силу любого
из высших КдФ, а также выражением величины %r (х0, Е)
через коэффициенты матрицы трансляции ?Vo> ^)>
указанным в D.10). Произведем вычисления в базисе
A.2'). Так как %R = У 1 — a^ ai\, где aR = 0 в силу
любого из высших КдФ, нам необходимо вычислить а21
или (ai — Ъ\Iк в базисе A.2"). Подставив выражение для
временных производных из A.15) и воспользовавшись
B1), мы приходим к требуемой формуле B0), заменив х0
на х.
Применим теперь общую формулу B0) к динамике
конечнозонного потенциала и (х); величина %r, со-
гласно D.12), имеет вид %R = ]/R (Е) Р^ (х, Е), где

146 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
п
Рп = Д (Е — Ytt{x))- Из формулы B0) получаем (при всех Е):
Рп=К'Рп-ХР'п. B2)
Пусть теперь Е = ук. Тогда Рп = 0. Из этого следует
Р ; к = 1, 2,. . ., п. B3)
Для величины (Pn)E=Vfc мы уже получили ранее формулу
B), откуда вместе с B2) имеем
У1ГЫ, B4)
П {Е — Е}) и Я, = ^12в базисе A.2"). Как и для
3=0
уравнений C), мы можем разрешить уравнение B) отно-
сительно величин Yfc и получить окончательно
у, = 2* (*,) E=Vfc /Щ П (V* - Y;)- B5)
В частности, для динамики в силу обычного КдФ мы имеем
формулу A.19) для матрицы Л, где
К = к12 = -I" 0* + ^Ч) = - 2 (" + 2?). B6)
Есл!'число зон п = 1, то мы из формул B5) обычным об-
разом получим снова кноидальную волну и (х — ct)
Кортевега — де Фриза. Первым нетривиальным случаем
является п = 2. Уравнения B5) для п = 2 имеют вид
V- R (Yi) Ti - Y2
У — Л (Та) Та — Ti
Рассмотрим потенциал и такой, что ]^Е} = 0. Введем па-
раметр w по формуле
dt. B8)
Ух — Та У '

§ 6] СВЕДЕНИЯ ИЗ ТЕОРИИ РИМАНОВЫХ ПОВЕРХНОСТЕЙ 147
Уравнения B7) приобретут вид
Ф _ъп. B9)
V-R(yi) V-ЯЫ
Уравнения B9) очевидным образом интегрируются. Опус-
кая вычисления, приведем ответ для динамики и (х, t)
в виде (9)
и(х, t) = - 2 [Л (- т (х - х0 (*)) + F2 (т0 (^ +
+ т (х - *„))], C0)
где 3 #; = 0.
Для параметров t0 (t), x0 (t) получим
T0(t) = 4t, ?0 = 4Ft (to(t)). C1)
Формулы C0) полностью описывают временную динамику
двухзонных потенциалов в силу КдФ.
§ 6. Сведения из теории римановых поверхностей.
Циклы на римановой поверхности
Как известно из теории функций комплексного пере-
менного, риманова поверхность определяется как график
многозначной функции на комплексной плоскости неза-
висимой переменной Е. Удалив из ^-плоскости некото-
рое количество отрезков (прямых или кривых и, воз-
можно, уходящих одним концом в оо), именуемых
«разрезами», обычно получают область iJ-плоскости,
над которой график многозначной функции распадается
на куски, не связанные друг с другом непрерывным
путем. Каждый из таких кусков есть график однозначной
функции и одна из «ветвей» многозначной функции.
Этот стандартный для математического анализа язык
неудобен для наших целей. Мы вводим риманову поверх-
ность Г следующим образом: пусть задана комплексно-
аналитическая функция F (у, Е) двух комплексных пере-
менных у, Е; риманова поверхность Г («комплексная кри-
вая») задается как совокупность решений уравнения
F(y, E) = 0. A)
Уравнение A) определяет многозначную функцию у =
= у (Е) и поверхность Г является римановой поверхно-
стью ^этой многозначной функции. Наглядно можно себе

148 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
представлять, что многозначная функция у (Е) получается
из поверхности Г проектированием ее на Е- и на г/-плоско-
сти. Если Р — некоторая точка поверхности Г, заданная
координатами у0, Ео, то по определению у0 = у (Ео).
Проекция поверхности Г на ^-плоскость может не быть
взаимно однозначной: может быть несколько точек Pi =
= (ylt Ео), имеющих общую координату Ео. Тогда все
yi являются значениями многозначной функции у (Ео) =
= {;/;}. Это и есть источник многозначности функции
У(Е).
Точка Р = (у0, Ео) поверхности Г A) называется неосо-
бой, если комплексный градиент не равен нулю:
&U B>
Рассмотрим два случая.
1. Если -~— =7^0, то около точки Ео можно определить
однозначную ветвь у (Е) такую, что у (Ео) = у0. В этом
случае точки поверхности Г около (у0, Ео) имеют вид
Г = (у (Е), Е). C)
Говорят, что параметр Е в малой области около Ео яв-
ляется локальной координатой на поверхности Г.
2. Если -jr=r Ф 0, то около точки у0 можно определить
однозначную ветвь обратной функции Е (у) такую, что
Е (г/0) = Ео. В этом случае точки поверхности Г около
(уо, Ео) имеют вид
Г = (У, Е (у)). D)
Во втором случае говорят, что параметр у является ло-
кальной координатой около точки (у0, Ео) = Р. Около
точек, где dFldy ^0и dFldE Ф 0, локальной координатой
являются как у, так и К, поэтому можно делать замены
У^Е.
Особые точки римановой поверхности Г определяются
условием Vc F = 0.
Точки ветвления многозначной функции у (Е), опре-
деленной поверхностью Г в (у, ^-плоскости, находятся из
условия
dFldy = 0. E)

§ 6] СВЕДЕНИЯ ИЗ ТЕОРИИ РИМАНОВЫХ ПОВЕРХНОСТЕЙ 149
Вместе с уравнением поверхности Г, два условия A),
E) на точки ветвления в (у, ^-пространстве дают дискрет-
ное множество точек Ро, Рг,. . ., Pn поверхности Г. Про-
екции Ео, Ег, Е%,. . ., En этих точек на ^-плоскость дают
точки ветвления функции у (Е). Ввиду дискретности мно-
жества точек ветвления, оно не разделяет поверхность Г
и ^-плоскость на части. Над оставшейся частью ^-плоско-
сти листы (значения функции у (Е)) варьируются непре-
рывно при изменении Е, не сливаясь друг с другом, хотя
и могут меняться местами после обхода по замкнутому
контуру.
Наиболее содержательной является теория алгебраи-
ческих римановых поверхностей Г. Мы будем считать, что
функция F (у, Е), определяющая поверхность Г с помощью
уравнения A), является полиномом от двух переменных
у, Е степени т
F (у, Е) = 2 аиу*& = О F)
для ? > 0, / > 0, г -{- / <^ т. Это и есть общая алгебраи-
ческая риманова поверхность Г. Ее уравнение можно за-
писать в виде
ут + а, (Е)у^ + . . . + ат (Е) = F = 0, G)
где все аг (Е) являются рациональными функциями (от-
ношениями многочленов от Е). В этом случае функция
у (Е) имеет т значений, кроме точек ветвления dFjdy = О,
где корни многочлена F кратные.
Простейший класс римановых поверхностей, который
и будет нужен нам в теории уравнения КдФ и уравнения
Шредингера с конечнозонным периодическим потенциа-
лом,— это так называемые гиперэллиптические римановы
поверхности Г, задаваемые уравнением
F (у, Е) = у2 + R (Е) = 0, (8)
где R (Е) — полином от Е с постоянными коэффициентами
(в теории уравнений КдФ и Шредингера важен случай
полиномов Ft (E) нечетной степени).
Если степень полинома R (Е) равна 1 или 2, то такую
поверхность называют «рациональной» или рода 0 (топо-
логия сферы).
Если степень полинома R (Е) равна 3 или 4, то по-
верхность Г называют эллиптической или рода 1 (тополо-

150
ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ
[ГЛ. II
гия тора). Мы будем рассматривать неособые римановы
поверхности Г, для которых VcF Ф 0 всюду, где F = 0.
Для гиперэллиптической поверхности (8) условие не-
особости означает следующее:
F = y2 + B (Е), VCF = Bу, R' (Е)) ф 0. (9)
1. Если у Ф 0, то 4GF Ф 0 и локальной координатой
около таких точек Р = (у0, Е) поверхности Г является Е.
2. Если у = 0, то в силу (9) неособость точек Р =
= @, Ej) поверхности Г равносильна неразрешимости
пары уравнений
R (Ej) = 0, Л' (Ej) = 0 A0)
или отсутствию кратных корней полинома R (Е). Если
у = 0, то локальной координатой около такой точки
@, Ej) поверхности Г является у и Л {Ej) = 0. Эти точ-
ки являются точками ветвления функции у = У—R (Е),
причем поверхность Г имеет ровно два листа.
at S)
Рис. 7. Поверхности: а) рода g = 1,
2 4
2/2= Д (Я - ?a); б) рода * - 2, у« = Д (В - Ва).
а=о а=о
Пусть, для удобства, все корни Ej полинома R (Е) ве-
щественны и различны (неособая поверхность Г):
Е0<Е1<. . .<Ет, A1)
если полином/? (Е) имеет степень т + 1. Разберем топо-
логию такой поверхности Г. Удалим из ^-плоскости от-
резки (Е0Ех), (Ег Е2),. . . Рассмотрим два случая (рис. 7
а 8).

6]
СВЕДЕНИЯ ИЗ ТЕОРИИ РИМАНОВЫХ ПОВЕРХНОСТЕЙ 151
Случай 1. Степень т + 1 полинома нечетна. Уда-
лим отрезки (Е0Е^),. . ., (Ет-ъЕт-.$, (Ет оо) из Е-плос-
кости (как говорят, делаем разрезы). Оставшаяся часть
поверхности Г распадается на два куска Dx и D2 с оди-
наковыми границами («берегами» разрезов). После склей-
ки этих двух кусков вдоль краев выкинутых отрезков
Рис. 8. Поверхности: а) рода g = 1,
з 5
У'= П (Е~ЕаУ> б) Р°Да ё = 2> У*= П (Е~Еа).
а=о
получится поверхность рода g = т/2 (сфера с g «ручками»).
Строго говоря, из этой поверхности выкинута одна точ •
ка — бесконечно удаленная — так как мы рассматривали
пока риманову поверхность Г над конечной частью
^-плоскости.
Случай 2. Степень т + 1 полинома R (Е) четна.
Удаляем отрезки (EqE-^),. . ., (ЕтЕт+1); оо не является
точкой ветвления. Все остальное полностью аналогично
случаю, изображенному на рис. 8 для g = 1, 2 (g = т/2).
Точка оо, как и в случае 1, удалена из Г, но эта точ-
ка расширенной ^-плоскости уже не является точкой
ветвления. Фактически на каждом листе ?)х и D2 есть своя
бесконечно удаленная точка ooj и точка оо2, которая уда-
лена из Г, пока мы рассматриваем риманову поверхность
лишь над конечной частью ^-плоскости.
В теории одномерного уравнения Шредингера с бес-
конечнозонным периодическим потенциалом блоховская
функция мероморфна на неалгебраической римановой по-
верхности Г, где у2 = g (Е) (см. §§ 1, 3 данной главы),

152
ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ
[ГЛ. II
если все нули g (Е) простыв. Топологически эта риманова
поверхность изображена на рис. 9. Как видно, точка оо
на этой поверхности для трансцендентной функции
g (Е) = 1 — Ян. с бесконечным числом простых нулей уже
является точкой скопления циклов а;, размеры которых
Рис. 9. Поверхность бесконечного рода, у2 = У g (Е), где g (Е) —
трансцендентная функция. Размеры запрещенных зон уменьшаются
при п —» оо.
уменьшаются при / -> оо (эти циклы получены из запре-
щенных зон на ^-плоскости).
Алгебраические римановы поверхности F) обладают
«бесконечно удаленными» точками, присоединение кото-
рых делает поверхность Г, как говорят, «замкнутой»
(компактной, не имеющей границы, т. е. имеющей конеч-
ное число ручек). Гиперэллиптические примеры уже ука-
зывались на рис. 7 и 8. Введем формальную процедуру
определения бесконено удаленных точек поверхности Г,
задаваемой уравнением F)
Рассмотрим «проективные координаты» (и, v, w) та-
кие, что у = ulw при Е = vlw. Будем считать, что вектор
(и, v, w) Ф 0 и что пропорциональные (с комплексным X)
векторы определяют одну и ту же точку:
(и, v, w) — (ки, kv, kw), кф 0. A2)
Если ги ф 0, то выбором к = \/ги всегда можно в классе
эквивалентных векторов (u, v, w) найти вектор вида
(у, Е, 1), где у = ulw, Е = vlw. Точки, где w = 0, мы
назовем «бесконечно удаленными».

§ 6] СВЕДЕНИЯ ИЗ ТЕОРИИ РИМАНОВЫХ ПОВЕРХНОСТЕЙ 153
Уравнение F) приобретает вид
О = Ф = wmF (-?- , -?-) *= Yj ациУют-'-\ A3)
При этом полином Ф (и, v, w) уже однородный степени т:
Ф (Хи, Xv, %w) = ХтФ (и, v, w). A4)
Конечные решения уравнения Ф = 0 (т. е. w ф 0) сов-
падают с поверхностью Г после перехода к переменным у, Е.
Кроме этого имеется конечное число бесконечно удаленных
точек, задаваемых парой уравнений
ф = О, w = 0. A5)
Напомним, что векторы (и, v, w) и (Хи, Xv, Xw) определяют
одну и ту же точку.
Полная риманова поверхность Г вместе с бесконечно
удаленными точками задается в проективных координа-
тах уравнением Ф = 0. Локальная координата около бес-
конечно удаленной точки w = 0 на поверхности Г выби-
рается так: если точка Р = (и0, v0, 0) бесконечно удален-
ная и и0 Ф 0, то следует перейти в окрестности этой точки
к координатам
и уравнение ф (и, v, w) = 0 привести к виду Ф {и, v, w) =
= ит F (у, Е) = 0 (и Ф 0). Далее, если точка Р неособая
(т. е. Vc F Ф 0), то локальная координата около нее вы-
бирается, как и ранее, но в переменных у, Е.
Для гиперэллиптических поверхностей Г мы имеем два
случая.
Случай 1. у2 = R (Е), где степень R (Е) нечетна.
Здесь имеется одна бесконечно удаленная точка Р — оо,
являющаяся^точкой ветвления. Локальная координата
около этой точки на поверхности Г есть z = 1 /}/~Е. Раз-
ложение по переменной z — разложение в ряд Тейлора
no'z около точки Р = оо для функций на поверхности Г.
Например, проекция поверхности Г на ^-плоскость мо-
жет считаться числовой функцией Е (Q) для точек*Q на
поверхности Г со следующими свойствами: 1) функция Е
имеет полюс второго порядка'в точке Р = оо; 2) функция

154 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ (ГЛ. II
Е (Q) имеет нулевой градиент во всех точках ветвления
на поверхности Г.
Случай 2. г/2 = R (Е), где R (Е) — полином чет-
ной степени. Здесь имеется две бесконечно удаленные точ-
ки Рг = оо1? Р2 = оо2, так как бесконечность не является
точкой ветвления и попадает на оба листа поверхности
Г. Величина z = НЕ может быть принята за локальную
координату около обеих точек Р1 = оо1; Р2 = оо2. Проек-
ция на ^-плоскость есть числовая функция Е (Q) для то-
чек Q на поверхности Г; эта функция имеет два простых
полюса в точках Рг и Р2 и нулевой градиент во всех точ-
ках ветвления.
Перейдем теперь к циклам на римановых поверхно-
стях. Конечно, замкнутая направленная кривая у (глад-
кая с ненулевой касательной или кусочно-гладкая с ко-
нечным числом изломов), будет считаться циклом на по-
верхности Г. Циклом будет считаться также формальная
сумма замкнутых направленных кривых у} (возможно, пе-
ресекающихся друг с другом):
цикл у = Yi + Y2 + • • • + Ук, (Щ
где у./ — замкнутые направленные кривые.
Циклом —y называется сумма тех же кривых с про-
тивоположными направлениями. Итак, мы описали цик-
лы. Нам нужно четко сказать, какие циклы мы будем счи-
тать эквивалентными друг другу и какие — эквивалент-
ными нулю. Введем отношение эквивалентности, называе-
мое в топологии «гомологичностью циклов», более сильное,
чем «гомотопность» двух замкнутых кривых, которые мож-
но непрерывно деформировать друг в друга по поверхности
Г. Сформулируем некоторые правила.
1. Если два цикла у и у гомотопны друг другу (т. е.
переводятся друг в друга непрерывной деформацией в Г),
то они, конечно, гомологичны.
2. Более того, разрешается разделять замкнутую на-
правленную кривую на замкнутые части и переставлять
их порядок прохождения (рис. 10)
Y ~ Yi + Y2 » Y2 + Yi.
Y ~ Yi + Y2 + Ys ~ Yi + Ys + Y2 — • • •>
где значок ~ означает эквивалентность (гомодогичность).

§ 6.) СВЕДЕНИЯ ИЗ ТЕОРИИ РИМАНОВЫХ ПОВЕРХНОСТЕЙ 155
3. Цикл, состоящий из набора несамопересекающихся
направленных кривых у = у1 + . . . + Ун и не пересе-
кающихся попарно, гомологичен нулю, если этот набор
кривых ограничивает
кусок поверхности Г,
причем кривые уу вхо- j ji г
дят в границу куска с ; 2
правильными ориента- У^Уг* Уг*1 Уг+Уг
циями (рис. 11). Если
сумма циклов у, 4- у, ?ж. 10- Гомологичность циклов -
(i i г-! более грубое понятие, чем гомотоп-
эквивалентна нулю, то FJ ность.
Yi ~ — уг- Если у^^О»
то Yi + Y ~ Yi и т. д.
Применяя правила 1, 2, 3, мы получим из цикла все ему
эквивалентные (гомологичные).
Классы эквивалентных циклов образуют «группу од-
номерных гомологии», обозначаемую в топологии через
#i (Г).
В группе одномерных гомологии Нх (Г) поверхности Г
имеется еще одна важная операция (кроме сложения и вы-
читания циклов), именуемая «пересечением циклов». Мы
Рис. 11. Примеры гомологичное™ циклов.
будем предполагать, что на поверхности Г определено по-
нятие «правого» и «левого» базисов (поверхность ориенти-
руется); это всегда верно для римановых поверхностей,
ввиду их комплексности (все используемые замены коор-
динат комплексно-аналитичны и имеют тем самым положи-
тельный якобиан).
Индекс пересечения Yi ° Ъ ДВУХ замкнутых направлен-
ных кривых Yi и Y2 определяется так:
1. Предполагается, что кривые Yi и 7г пересекаются
в конечном числе точек под ненулевыми углами на по-

156 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
верхности Г. Обозначим точки пересечения через Ра,
а = 1,. . ., q. В каждой точке Ра имеем два вектора ^i
и 7г- Положим
sign Ра = 1, если репер (уи у2) правый в точке Ра,
sign Ра = — 1, если репер (yi, у2) левый в точке Ра.
Индекс пересечения равен
q
Yi°Y2 = ^j sign Ра = — Ya°Yi-
a=i
2. Если пара кривых yi> Y2 пересекается не так, как
требуется в пункте 1, то надо продеформировать у2, при-
ведя пересечение пары Yn Y2 к условиям пункта 1 и затем
взять пересечение. Это и будет индекс пересечения.
3. По определению, индекс пересечения аддитивен по
обоим аргументам, кососимметричен и имеет целочислен-
ные значения
(Yi + Yx) ° Ъ = Yi ° Y2 + Yi » Y«, ., _.
Yi ° T2 = ~ Y2 ° Yi-
4. Индекс пересечения корректно определен на клас-
сах гомологичных циклов (цикл, гомологичный нулю,
имеет нулевые индексы пересечения с любым другим цик-
лом).
Каноническим базисом циклов на замкнутой поверх-
ности рода п называется набор циклов аъ. . ., ап,
Ъъ. . ., Ьп, где все аи bt независимы и матрица индексов
пересечения устроена так (рис. 12):
biobj = 0, aiobj — di]. A9)
Вычислим нужные нам в дальнейшем канонические ба-
зисы циклов на гиперэллиптических римановых поверх-
ностях у2 = R (Е) для обоих случаев — четной и нечет-
ной степени R (Е).
Случай 1. Степень В (Е) нечетна. Точки ветвле-
ния имеют вид Ео ¦< Ех < . . . < Еш ¦< оо. На поверх-
ности Г имеются два набора циклов:
а) Циклы аи лежащие над запрещенными зонами
(ЕхЕг), . . ., (Evi-iEzi), (Ezn-iEzn) поверхности Г, яь. . .
. . ., ап.

§ 6] СВЕДЕНИЯ ИЗ ТЕОРИИ РЙМАНОВЫХ ПОВЕРХНОСТЕЙ 157
б) Циклы Cj над всеми разрешенными зонами на по-
верхности Г (всего п + 1 штук), (Е0Ег), . . ., (Е2п оо),
с0, . . ., сп. Удаляя циклы с0, . . ., сп из поверхности Г,
Рис. 12. Индекс пересечения циклов. Канонический базис циклов
на поверхности.
мы разбивали ее на две части (делались разрезы). Отсюда
имеем
с0 + сг + . . . + сп « 0. B0)
Из рис. 7 для п = 1,2 легко видна матрица пересечений:
= ...=а„осп = 1. B1)
Все остальные пересечения равны нулю. Для рода g = 1
канонический базис образуют циклы а1; Ьх = с1г ах°Ъх =
= 1. Заметим, что канонический базис аг, —с0 совпадает
с предыдущим, так как с0 -\- сх^ 0. Для любого рода
п ^> 1 канонический базис выглядит так:
аи. . ., ап, Ьи. . ., Ьп, B2)
где
Ъ\= — с0, Ь2= — С\ — Со,
п—1
Ьз = — с2 — сх — с0,
3=0
Из формул B1) вытекает соотношение
atoaj = bt°bj = 0 (a^bj = 8г
B3)
Случай 2. Степень R (Е) четна. Точки ветвления
имеют вид Ео <; Ех < . . . < ?2n+i- Полностью аналогич-

158 ПЕРИОДИЧЕСКИЕ РЕШЕНИИ УРАВНЕНИЯ/ КдФ [ГЛ. IT
но нечетному случаю (точки оо заменяется на Е2п+1)
здесь вводятся циклы а1? . . . , ап, с0,. . ., сп, удовлет-
воряющие соотношениям B0), B1) (см. рис. 8). Поэтому
канонический базис циклов запишется в виде B2).
Существование канонического базиса at, bt есть след-
ствие замкнутости и ориентируемости римановой поверх-
ности. Не на всех двумерных поверхностях (многообра-
зиях) это так. Например, если из плоскости выколоть лю-
бое число точек, то нетривиальные циклы будут (число
независимых циклов равно числу выколотых точек), но
индекс пересечения тождественно равен нулю. На замк-
нутых ориентируемых поверхностях матрица пересечений
базисных циклов имеет детерминант ± 1 и кососимметрич-
на — поэтому и существует канонический базис B3).
§ 7. Дифференциалы на римановых поверхностях.
Абелевы (голоморфные) дифференциалы
и дифференциалы с полюсами
Напомним, что в области плоскости с координатами
х, у дифференциалом (или дифференциальной формой сте-
пени 1) называется выражение
Q = P(x, у) dx + Q (x, у) dy, A)
где пара (Р, Q) ведет себя как компоненты градиента
функции при заменах координат (тензора первого ранга
с одним нижним индексом):
х = х(х\ у'), у = у(х', у'), B)
Q = Pdx + Qdy = P'dx + Q'dy' =
Когда речь идет о произвольной двумерной поверхности
(двумерном многообразии), то дифференциал ?2 должен
быть определен на всей поверхности и записывается в лю-
бой локальной системе координат ха, уа в виде A), где
Q = Padxa -f- Qadya', в области действия двух локальных
систем координат ха, ja и г», у$ одни координаты выра-
жаются через другие:
ха = ха {х$, ур),
Уа = Уа (Яр, У?)-

§ 7] ДИФФЕРЕНЦИАЛЫ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 159
Две разные записи одного и того же дифференциала Q
в координатах ха, уа и х?, у? должны переходить друг
в друга по формулам B) в общей области действия этих
координатных систем.
По существу дифференциалы (или дифференциальные
формы первой степени) представляют собой дифферен-
циальную форму записи тензоров первого ранга с одним
нижним индексом. (Точно так же дифференциальные ф{ор-
мы любой степени к О = У\ at с1хг'/\ . . . A dx f на
гК...<г,{
любом тг-мерном многообразии представляют собой просто
форму записи кососимметрич-
ных тензоров ранга к со
всеми нижними индексами.
Эти формы можно интегриро-
вать по любым ^-мерным по-
верхностям, расположенным
в многообразии, абсолютно
инвариантным образом —ре- 1С- 13- Интеграл от 1-формы
зультат не зависит от метри- Q п0 и>'тп У на "^ерхностн.
ки и от координат на поверх-
ности и в многообразии.)
Дифференциал Q на римановой поверхности можно оче-
видным образом интегрировать по любому (направленно-
му) пути у между точками Р и (? этой поверхности (рис. 13).
Дифференциал Q называют замкнутым, если выполне-
но тождество (в любой системе локальных координат)
дР 8Q ш
~df— Эх ' К '
и точным, если на поверхности имеется всюду определен-
ная гладкая однозначная числовая функция /, такая, что
в любой системе координат компоненты дифференциала
являются компонентами градиента этой функции (точный
дифференциал всегда замкнут).
Свойства дифференциалов:
1. Интеграл точного дифференциала по любому циклу
на поверхности равен нулю.
2. Интеграл от замкнутого дифференциала по циклу,
эквивалентному (гомологичному) нулю, тождественно ра-
вен нулю.

160 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
3. Если известны все интегралы от замкнутого
ференциала по циклам на поверхности, то он определяется
однозначно с точностью до прибавления любого точного
дифференциала. Все определения интересующих нас дву-
мерных многообразий — римановых поверхностей —
производятся с помощью комплексно-аналитических функ-
ций. Все локальные координаты, которые мы вводили
в § 6, на римановых поверхностях таковы, что переход
от одних к другим осуществляется конформным преобра-
зованием.
В этом случае удобно вводить, как обычно, комплекс-
ные координаты
z = х + iy, z = х — iy
и дифференциалы
dz = dx -f- idy, dz =; dx — idy. E)
Если формально ввести операторы
±±(±-i±
dz 2 I dx dy
d~z 2 I dx i" dy
то дифференциал функции будет иметь вид
df=-^-dz + ^L-dz. G)
Любой дифференциал Q вида A) может быть записан в
виде
Й = Р dx + Qdy = Adz + Bdz. (8)
Условие замкнутости D) приобретет вид
дР _ 3Q дЛ __ дВ
dx g~z dz
(9)
Условия комплексной аналитичности функции / (z)
(уравнения Коши — Римана), как известно, имеют вид
Д-=о
или
df = -%-**¦

§ 7] ДИФФЕРЕНЦИАЛЫ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 161
Рассмотрим любой замкнутый дифференциал вида
Q = A dz, (И)
где условие замкнутости (9) имеет вид
dA/dz = 0.
Поэтому коэффициент А замкнутого дифференциала вида
A1) комплексно-аналитичен и наоборот. Такие дифферен-
циалы мы далее будем называть голоморфными.
Полюсом дифференциала вида A1) называется, есте-
ственно, полюс коэффициента А; все эти понятия инвари-
антны относительно голоморфных (аналитических) замен
z = z (w), z = х + iy, w = х' + iy', A2)
dz/dw = 0,
и поэтому имеют смысл на римановых поверхностях, изу-
чавшихся в § 6 и задававшихся комплексно-аналитичес-
ким уравнением вида F.6).
Важнейшими дифференциалами на алгебраических ри-
мановых поверхностях вида F.6), к которым присоеди-
нены также и бесконечно удаленные точки (см. § 6), яв-
ляются так называемые абелевы или всюду голоморфные
дифференциалы (именуемые иногда дифференциалами
первого рода) на римановой поверхности Г, не имеющие
полюсов нигде на этой поверхности, а также и в бесконеч-
но удаленных точках из Г.
Кроме того, для нас будут важны также голоморфные
дифференциалы на Г, имеющие ровно один полюс (второго
рода) на поверхности Г. Если Р — точка поверхности Г,
в которой дифференциал Q имеет единственный полюс,
и z = х -f- iy — локальная координата около точки Р
на поверхности Г, то мы имеем при z, близких к нулю:
где / (z) аналитична в точке z = 0. Оказывается, для та-
ких дифференциалов ; (однополюсных) слагаемое a^/z
всегда равно нулю (на замкнутой поверхности Г). Число
а_х называется вычетом дифференциала Q в полюсе Р.
Вычет не зависит от выбора локальной координаты z.

162 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Более общий факт состоит в следующем: если голоморф-
ный дифференциал Q имеет ровно к полюсов Рг, . . .
. . ., Рк на замкнутой поверхности Г и а!1^, . . ., aiV —
его вычеты в полюсах Ри . . ., Р^, то их сумма есть нуль:
5У? = 0. A4)
<z=l
Для нас также будут важны дифференциалы QPQ («ди-
польные»), имеющие ровно два полюса первого порядка на
Г в точках Р и Q с вычетами соответственно 1 и —1 (диф-
ференциалы третьего рода).
Известны следующие утверждения:
1) на римановой поверхности Г (алгебраической) всег-
да имеется базис Qx,. . ., Qn абелевых дифференциалов
(первого рода), число которых п равно роду поверхности.
Любой всюду голоморфный (абелев) дифференциал Q
есть линейная комбинация базисных с постоянными комп-
лексными коэффициентами:
2) Любой замкнутый (не обязательно голоморфный)
дифференциал Q, всюду определенный и гладкий на по-
верхности Г, представляется в виде суммы точного диф-
ференциала и некоторой линейной комбинации базисных
абелевых дифференциалов Q1). . ., Qn и их комплексно
сопряженных Ql7. . ., Qn. Размерность линейного про-
странства замкнутых дифференциалов (с пренебрежением
точными) равна 2п, где п — род (число ручек).
Рассмотрим теперь важнейшие для нас примеры ги-
перэллиптических римановых поверхностей.
Для поверхности рода п = 0, задаваемой уравнением
г/2 + R (Е) = 0, где R (Е) = Е — Ео или R (Е) =
= (Е — Ео) (Е — ZJj), абелевых дифференциалов вообще
нет, так как их число равно роду. Рассмотрим общий слу-
чай полиномов R (Е). Любой голоморфный дифференциал
на поверхности Г (имеющий, возможно, полюсы) можно
написать в конечной части ^-плоскости в виде (корни по-
линома R (Е) некратны)
о Р(Е) dE , „
п = ~щу ТШЩ тРивиальныи'

g 7] ДИФФЕРЕНЦИАЛЫ НА ШШАНОВЫХ ПОВЕРХНОСТЯХ 1GH
где Q и Р — полиномы; тривиальная часть имеет вид
Рг (Е) dE/Q1 (E) (Pj и Q1 — полиномы от Е). Исследуем
полюсы дифференциала О, без тривиальной части. Они
могут быть следующих видов: а) в нулях Q (Е), б) в точ-
ках ветвления Еа, где R (Еа) = О, в) в бесконечно уда-
ленной точке Е = оо. Случай в) мы рассмотрим позднее.
а) В любой точке, где Е ^ Еа, полюс О может быть
лишь в нулях Q (Е).
б) Если мы находимся в точке ветвления поверхности
Г, где Е = Еа и у = 0, то согласно § 6 должны выбрать
у за локальную координату около этой точки. Совершив
замену Е (у), мы получим
о = dE (у) Р{Е(ц))
у " Q(E(y)) ¦
Так как R (Е) ~ (Е — Еа) const около точки Еа, то имеем
d(E-Ea) P(E-Ea)
У Q(E — En) '
причем Е — Еа ~ const -f- у1 около Еа. Окончательно
получаем
A7)
<2(.v2)
Таким образом, дифференциал Q имеет полюс в точке
у = 0, Е = Еа римановой поверхности Г только в том
случае, если полином Q (Е) имеет нуль в точке Е = Еа.
Если мы хотим найти абелевы дифференциалы без полюсов,
мы должны искать их в виде
fi = P(,gll/? , A8)
где Р (Е) — полином. Дифференциалы вида A8) не имеют
полюсов на поверхности Г над конечной частью .Е-плос-
кости.
Рассмотрим теперь два случая.
Случай 1. Степень полинома R (Е) нечетна,
1т
tl(lL)— ll \tL —И<а), La^t,a.

164 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ trft. И
Как указывалось в § 6, имеется одна бесконечно уда-
ленная точка Е = оо на поверхности Г и локальной коор-
динатой около этой точки является параметр z = \lYЕ-
Если дифференциал Q имеет вид A8), где Р (Е) = а0 +
+ . . . + апЕп и ап Ф 0, то после замены Е (z) около точ-
ки z = 0 мы получим (Е = z~2)
a*Vm+1 l/ П A - Eaz*)
а=о
или окончательно, при малых z:
q = _ 2z2m-2"-2 dz (fln + / (z)), B0)
где ап Ф 0 я f (z) аналитична и обращается в нуль в точ-
ке z = 0.
Итак, мы можем сделать следующие выводы:
1. Дифференциал Q вида A8) не имеет полюсов нигде
(в том числе в точке Е = оо), если степень полинома
Р (Е) равна 0, 1,. . ., т — 1. Здесь т — род поверхности
Г. Мы имеем базис абелевых дифференциалов вида
E%Jf- , i = 0, ...,m-\. B1)
) v
2. Если степень полинома Л (Е) равна т + &, то диф-
ференциал Q вида A8) имеет единственный полюс в точке
z = 0 на Г (второго рода), причем кратность полюса рав-
на 2к + 2 для к = 0, 1, 2,. . . Разложение в ряд Лорана
в этом полюсе, вытекающее из A9), содержит лишь четные
степени г~2к~%,. . ., z~2\. . ., z~2:
(z) аналитична при z = 0.
2m+l
Случай 2. Степень полинома R(E) = П (^ — Еа)
а=о
о
четна и корни различны Еа Ф Е$, у2 + R {Щ = 0. В ко-
нечной части ^-плоскости все рассуждения полностью
аналогичны, и полюсов здесь не имеют дифференциалы

, § 7] ДИФФЕРЕНЦИАЛЫ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 165
вида
Q = А11Ж B3)
Yr(E) ' v" '
где Р (Е) = апЕн + . . . + а0, ап Ф 0.
Согласно § 6, имеются две бесконечно удаленные точки
на Г, локальной координатой в которых может быть при-
нята (в обеих) z = ME. Около точек Р+, Р_ в координате
z дифференциал Q приобретет вид
Q « =F z-"^ (an + Ф (z)), B4)
где ф (z) аналитична около z = 0 и ф @) = 0. Дифферен-
циал Q является абелевым (не имеет полюсов), если
т — п — 1 > 0. Согласно § 6, род поверхности Г равен
т. Мы получаем ровно т независимых абелевых диффе-
ренциалов вида B3)
Qi = TT§T' i-°.--'m-1- <25>
Если п = т и ап = 1, то дифференциал О имеет два по-
люса первого порядка в точках Р+, Р_с вычетами ±1.
Здесь, как и в § 6, Р+ и Р_ — две бесконечно удаленные
точки. В качестве первой иллюстрации мы посмотрим,
какие виды дифференциалов мы фактически уже встре-
чали в § 5 в различных формулах, связанных с конечнозон-
ными потенциалами оператора Шредингера и их динами-
кой в силу уравнения КдФ и его высших аналогов.
1. Поверхности рода I, г/2 + R3 (E) — 0. Здесь
Ra (Е) = (Е- Ео) (Е - Ег) (Е - Е2), все Ео, Elt E2
вещественны и E0<i Ех<1 Е2. Если и (х) — однозонный
потенциал Ламе и Ео, Ег, Ег — концы зон, то блоховская
собственная функция i|)-j- (х, х0, Е) фактически мероморф-
на на этой поверхности Г (см. § 5). Мы имеем один абелев
дифференциал
Интеграл от этого дифференциала по пути на Г как функ-
ция концевой точки есть многозначная функция на Е-
плоскости
Q
х = [ Qt. B6)

166 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. 11
Выберем точки Ро, Q на цикле аг (см. § 6) на поверхности
Г над запрещенной зоной — отрезком [Ех, Е2] ^-плоско-
сти. Тогда обратная функция к B6) будет вещественной пе-
риодической функцией Q (х). Согласно E.4), имеем фор-
мулу для потенциала и (х — х0)
2
и(х~хо) = -2Q{x)+ 21 Еа.
а—о
Функция, обратная к B6), является двоякопериодической
функцией комплексного аргумента х. Она называется
эллиптической функцией Вейерштрасса (обозначается че-
рез № (х)). Изменение и (х) в силу КдФ имеет вид
и (х, t) = и(х — ct),
и (х, 0) = и (х), с = 2Х/2 ( >
2. Поверхность рода II, уг + i?5 (Е) = 0, Яъ =
= Ц(Е-Еа), ?0<?i<..-<?40. Для двухзон-
ных потенциалов и (х) функция \\>± (х, х0, Е) мероморф-
на на Г (см. § 5). Здесь имеется два абелевых дифферен-
циала
dE o EdE
_ - ,  = г
При вычислении аналитического вида двухзонного по-
тенциала мы опять вводили обратные функции Ft (т),
F2 (т) (см. E.7) - E.9)),
Q Q
т = С Q,, т = \" Qi,
Ei Ез
где Q берется в первой или второй запрещенной зоне (на
циклах а2 или а2 из Г). При вычислении временной дина-
мики и (х, t) двухзонного потенциала в силу КдФ в фор-
мулах E.29) появлялся дифференциал Q2. Вспомним те-
перь, что на римановой поверхности имеется каноничес-
кий базис циклов %,. . ., ап, Ьи. . ., Ъп с индексами пере-
сечения F.19). Набор абелевых дифференциалов й1}. . .
. . ., Qn связан с базисом циклов следующими нетри-
виальными соотношениями (Римана):

§ 7] ДИФФЕРЕНЦИАЛЫ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 167
1. Матрица интегралов по циклам ак невырождена:
Поэтому можно выбрать новый базис дифференциалов
j2=—1. B8)
2. В базисе Q} матрица bq; интегралов по циклам b,L
обладает свойством симметрии bqk — bkq и ее веществен-
ная часть Re b,lf! — Re bkq отрицательно определена,
Если риманова поверхность гиперэллиптична и все
точки ветвления вещественны, то матрица ^-периодов
Ъц вещественна, симметрична и отрицательно определе-
на. Рассмотрим простейшую 9-фуикцию (Римана):
B9)
Из свойства Re bkq вытекает, что ряд B9) быстро сходится
и определяет целую аналитическую функцию 9 комплекс-
ных переменных %,. . ., цп. Если род поверхности g = 1,
то Э-функция Римана сведется к обычной 9-функции
Якоби одной комплексной переменной
Ьт? + п
6 (л) = ^ exp i—
где т — это все целые числа.
Из определения 9-функции Римана вытекает
. ., Г1„) — 9 (л,,. . .,цк, ..., цп),
C0)
=-= exp {—6^/2 — %} 9 (%,. . ., r|n).
Тождества C0) показывают, что Э-функция Римана свя-
зана с так называемой решеткой Якоби из 2га векторов
В «-мерном комплексном линейном пространстве Сп, Эти

168 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
векторы имеют вид ех,. . ., еп, elt . . ., еп,
е, = @,. . ., О, 2я/, 0,. . ., 0),
C1)
ец = (Ьщ,. . ., Ькп).
Любой вектор решетки Якоби имеет вид ^mqeq + itiqeQ,
где mq, nq — целые числа. По существу, решетка C1)
задается матрицей периодов абелевых дифференциалов
на римановой поверхности Г по базисным циклам ah
Ъг при нормировке B8). В случае рода g = 1 мы обычным
образом имеем решетку на комплексной плоскости. В об-
щем случае g !> 1 фактор-группа С™, по решетке представ-
ляет собой 2ге-мерный комплексный тор, называемый
в математической литературе «многообразием Якоби ри-
мановой поверхности Г».
§ 8. Блоховская собственная функция
и квазиимпульс. Связанные с ними дифференциалы
на римановой поверхности,
их временная динамика
Рассмотрим периодический конечнозонный потенциал
и (х) оператора Шредингера L = — d2/dx2 + и, его бло-
ховскую собственную функцию ty+ (х, х0, Е), определен-
ную в § 1, и квазиимпульс р (Е), !Гф± = exp (± ipT) г|э±,
Т — оператор трансляции на период. Мы уже выяснили
в § 4 аналитические свойства функции ty+ на римановой
поверхности Г вида
чп
y2 + R (Е) = 0, R (Е) = П (Е - Еа), Еа - концы зон.
а=0
Рассмотрим дифференциал следующего вида на рима-
новой поверхности Г:
Оказывается, дифференциал W имеет лишь нули и полюсы
на поверхности Г, включая бесконечно удаленную точку.
Это вытекает из следующих свойств функции i|xj-:

§ 8] елоховская собствен, функция й квайнймпульс 169
1. Если z = \l\f~E — локальная координата около
бесконечно удаленной точки на Г, то около z = О диффе-
ренциал W имеет вид
W = i (х - х0) dz A/z2 + Ф (z)),
где функция ф (z) аналитична при z = 0. Это свойство сле-
дует из асимптотики
¦ф± ~ exp [± iY"E (х — ж0)]
при Е ~> оо.
2. Дифференциал Й7 в конечной части ^-плоскости на
Г имеет ровно п полюсов первого порядка с вычетами +1
в нулях i|Xf. и ровно п полюсов первого порядка с выче-
тами — 1 в полюсах ty+. Напомним, что нули и полюсы
функции г|)± (х, х0, Е), согласно § 4, лежат в точках
Q] ~ (Vi (х)' ±) и Р] ~ (Ту (^о). ±) соответственно по
одному над запрещенной зоной [?/-1 E2j\ на поверхно-
сти Г или, как мы указывали, на цикле a,j.
3. В силу определения A) дифференциала W на рима-
новой поверхности Г, экспонента от его интеграла по
пути дает однозначную функцию
где Q — (Е, ±) — точка поверхности Г, Qo — начальная
точка и интеграл берется по любому пути на Г, соединяю-
щему эти точки. Из однозначности функции г|5± {х, х0, Е)
на Г следует важный вывод: все интегралы от W по цик-
лам на Г являются целыми кратными 2яг:
W = 2aimj, j>W = 2nmj? C)
b
где rrij vl tij — целые числа.
Оказывается, свойства 1—3 для функции гр± (х, х0, Е)
на любой замкнутой римановой поверхности Г одно-
значно определяют функцию г^; мы будем называть такую
функцию tjj-i- «функцией Бейкера — Ахиезера» на рима-
новой поверхности Г. При этом набор нулей Qj однозначно
определится ниже через набор полюсов Р}. Здесь Р — точ-
ка поверхности Г (в нашем случае Р = (Е, ±)) и х, х0 —
параметры. Проекция поверхности Г на ^-плоскость, как

170 ПЕГИбДПЧЕСКПЁ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. It
уже указывалось в § 4, можно считать числовой функцией
/ (Р), где / (Я, ±) = Е по определению.
Для потенциала и (х) в § 4 уже указывалась формула
D.19), откуда следует
и (х) = - 2 ? Tj (a) + 2S Яа = - 2 2/@j И) + 2 ?«-
i=l а=о j а=о
D)
Мы уже ввели в § 6 канонический базис циклов на по-
верхности Г (а;-, 67) и в § 7 — нормированный базис абеле-
вых дифференциалов Qj (см. G.28)), где
2ш6д, § Qf = ЬЛ' = b"r E)
Введем теперь нормированные дифференциалы II и III ро-
да. Рассмотрим некоторые виды дифференциалов, которые
нам понадобятся на гиперэллиптической поверхности Г,
задаваемой уравнением
гп
у"- -|- В2п+1 (Е) = 0, В2п+1 (Е) = П (Е - Еа);
все Еа вещественны (концы зон спектра), Ео < Е1<^
< . . . < Е2п.
а) Дифференциалы II рода со^-, имеющие полюс лишь
в бесконечно удаленной точке с локальной координатой
z = 1/|/~Я. Около этой точки потребуем, чтобы выпол-
нялось равенство
F)
где ф (z) аналитична при z = 0 и к = 0, 1, 2,. . ., и, кро-
ме того, чтобы дифференциал ш^ был нормирован условием
|со,= О. G)
Условия F) и G) полностью определяют (ofc. Как указы-
валось в § 7,
АЕ ! 1 , _ „ , „., .
(8)

§ 8] БЛОХОВСКАЯ СОБСТВЕН. ФУНКЦИЯ II КВАЗИИМПУЛЬС 171
где коэффициенты aq определяются из условий F), G).
Нас особо будут интересовать дифференциалы соо и щ.
б) Дифференциалы III рода QPiQi, имеющие два полю-
са первого порядка в точках Pj, Qj, где Pj, Qs — нуль
и полюс блоховской функции г|)+ (х, х0, Е) над запрещен-
ной зоной [E2j^1E2]) на поверхности Г. Мы требуем, чтобы
вычет дифференциала QPJQ> был равен +1 в точке Pj
и —1 в точке Qj. Нормировка такова:
pj°; = O, q = l,...,n. (9)
Из указанных выше свойств дифференциала W — dE In i|)±
вытекает представление
где Q — абелев дифференциал
Q = jj к}й}, (И)
и
Q
ijIi | о' ¦у ft \ O"VT1 \ \ Т/1/
Qo
где Q = (?, ±), Qo — некоторая начальная точка на Г.
Представление A0) для W вытекает из того, что раз-
ность W — i {х — х0) (d0 — 2 QPjQi уже не имеет полюсов
на поверхности Г и является тем самым абелевым диффе-
ренциалом.
Коэффициенты к] в формуле A1) могут быть определе-
ны из условия однозначностия|)±, откуда вытекает, что все
а-периоды от W — целые кратные 2ni. Из условий нор-
мировки (9), G) для ю0 и QPJQJ имеем
aj ai ai
где rrij — целые числа. Из нормировки E) для Qq полу-
чаем
2ninij = 2ni 2j kqbjq «= 2nikj. A3)

172 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Отсюда следует, что все kj — целые числа, kj — nij.
Используем теперь условие целочисленности ^-периодов
дифференциала W:
i (х - *0) J ш0 + S | QP«°« + 2 «г, $
9=1
Пусть t/j = усоо — периоды дифференциала со0.
ь;
В теории абеловых дифференциалов имеется важное
соотношение: если aj, bj — канонический базис, QPQ —
дипольный дифференциал III рода с вычетами +1, —1
в точках Р, Q, соответственно в полюсах Р и Q первого
порядка на поверхности Г и если qp Ор<3 = 0 для всех / =
= 1,. . ., п, то можно провести путь уизРв Q, так что
верна формула
j Jj A5)
(интеграл сярава берется вдоль пути у) при нормировке E).
Применяя общее соотношение A5) к формуле A4)
для ^-периодов, получаем
9 9=1 ,/
где ^иР, — нули и полюсы г|5± на Г, интегралы берутся
по некоторому пути на Г, соединяющему точки Pj и Qj.
Напомним, что мы ввели решетку в n-мерном комплексном
пространстве из векторов ег, . . ., еп, е'ъ . . ., ей, где
е? = 2я^6«, е? -= ф ii} = baj = bia.

§ 8] ЕЛОХОВСКАЯ СОБСТВЕН. ФУНКЦИЯ И КВАЗИИМПУЛЬС 173
Соотношение A6) можно переписать в виде
B nieQ + 2 miei — ч* — хо) иK •= 2 з ^ (*7)
Вектор U имеет компоненты IP = ф ш0.
Если мы изменим пути yq справа между точками Pq и
Qq на любой цикл yq~> yq -f 2^а/с + Pqkh, где Я„л-,
/с
Иф — любые целые числа, то весь вектор изменится на
некоторый вектор решетки (е, е'). Заметим, что слева
стоит вектор i (х — х0) U плюс некоторый вектор решетки.
Введем вектор А с компонентами, равными
п Qq
Aj(Qlt ...,Qn, Pi, ..., Pn) =- 2 J Qj- A8)
4=1 ^q
Пренебрегая векторами решетки в формуле A7), мы имеем
где значок = означает равенство с точностью до любого
вектора решетки.
Напомним, что нули и полюсы г|) на Г имели вид
Q) = (V; (*). ±). ^ = (yj (xo), ±)-
Для этого набора уг,. . ., уп с учетом знаков ± (их по-
ложений на Г) мы имели ранее дифференциальное уравне-
ние E.3) по х и уравнение E.25) по времени t в силу КдФ,
причем потенциал выражался формулой D.19).
Рассмотрим замену переменных, именуемую отобра-
жением Абеля, от набора точек Qq = (yq (x), +) на поверх-
ности Г к набору параметров А1, где
A* {Q(X),P(XO)) =%$$;. B0)
«р<1
Точки PQ (х0) здесь фиксированы, и набор параметров А'
определяется с точностью до добавления любого вектора
решетки. В силу формулы A7) замена Абеля B0) линеа-

174 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
ризует уравнения E.3) для ух,. . ., уп, так как А1 (х) =
= i (х — х0) U' и вектор U постоянен.
Фактически параметры Абеля Aj представляют собой
«углы» Aj = ifj, которые можно ввести для вполне ин-
тегрируемой гамильтоновой системы B.3) согласно из-
вестной теореме Лиувилля. Можно ввести также и кано-
нически сопряженные переменные «действия».
Замена Абеля B0) обратима. Можно выразить, наобо-
рот, точки Qj = (у,-, ±) через параметры А' и тем самым
потенциал и = — 2^у7- + ^i?a будет функцией от пара-
метров А'. Это задача «обращения абелевых интегралов»,
которая, как известно, решается через многомерные 0-
функции, связанные с решеткой G.31) из 2п векторов в п-
мерном комплексном пространстве. Удобное выражение
для потенциала и (х) через 0-функцию Риманн, определен-
ную в § 7, будет дано позднее (в § 9).
Временная динамика конечнозонного потенциала
и (х) в силу КдФ (а также всех высших уравнений КдФ)
линеаризуется при переходе от набора точек Qj —
= (yj, ±) к набору параметров А1 с помощью замены
A8). Для проверки этого факта надо обратить внима-
ние на следующее: блоховская собственная функция
г|)± (х, х0, Е) имеет асимптотику exp {± i (х — х0) У Е) при
Е ->¦ оо. Если же потенциал меняется в силу КдФ и
и -*¦ и (х, t), то асимптотика функции г|) при Е -> оо бу-
дет иметь вид
г|)± (х, х0, t) — exp {± i (x — х0) к ± гЩ, B0')
где к = У~Е.
Асимптотика B0') вытекает из представления Лаксд
dLldl = [L, А], B1)
указанного в § 1 для КдФ , где оператор третьего порядка
А имеет вид A.2.5). При Е ~+ оо потенциал и несущест-
вен. Полагали = 0, мы из B1) немедленно получаем B0)
при Е —>- оо. Для высших КдФ все аналогично, но опе-
ратор А = Aq + c^q-i + • • • + cqA0 имеет порядок
2q -Ь i' Рассуждая, как и выше, мы из B1) получим

§ 8| ЕЛОХОВСКАЯ СОПСТПЕН. ФУНКЦИЯ II КГ.АЗИПМПУЛЬС 17t>
для я|) (. (х, х0, Е) асимптотику
я|)± (х, х0, Е) ~ ехр (г [(х — х0) к +
+ (k2q+l + с1к-ч~х + . . . + с„к) Й} B2)
при Е -v оо.
Из асимптотики B2) мы получим, как и ранее,
4 (<?!,. . ., Qn, Plt. . ., Рп) -^i {х- х0) U + Vt,
B3)
где знак ^ означает равенство с точностью до вектора
решетки G.31). Для вектора F = Vq + CiFa_i + . . . +
+ c4F0 имеем формулу (Fo = f/)
B4)
Дифференциалы II рода ш9 (см. (8)) имеют нулевые а-пе-
риоды: ф сод = 0, единственный полюс в точке оо на Г
с лорановским разложением
где z = 1/(/Е, ф (z) аналитична при z = 0. Точки ^ =
= Gу> ±) уже зависят от х и t. Формула B4) следует из
асимптотики B2) точно так же, как и для зависимости от
х. Формулы B3) и B4) для производных по г и по t от
параметров А1 можно получить и непосредственно, не
используя асимптотики собственной функции xp_j_ при
Е~+оо. Для этого надо вычислить замену переменных
A8) для Aj в уравнениях E.3) и E.25) по х и по t и убедить-
ся, что замена A8) их линеаризует. Мы не будем проводить
здесь это вычисление. Динамике в силу КдФ в параметрах
Aj отвечает вектор F1; где сг = 1, с0 = 0, с,- = 0, / ^> 1.
Так как параметры А' фактически являются угловыми
координатами на тг-мерном вещественном торе для глад-
ких вещественных и (х, t), то из формулы B3) следует
квазипериодичность динамики по t для решений и (х, t).
В формуле B3) угловой характер этих вещественных па-
раметров А' следует из того, что они определены с точно-
стью до добавления любого вектора n-мерной решетки,

176 ПЕРИОДИЧЕСКИЕ РЕШЕНИЙ УРАВНЕНИЙ КдФ [?П. V
порожденной в вещественном re-мерном пространстве
векторами е'ъ. . ., е'п (см. G.31)).
Обратим внимание на весьма любопытное аналитиче-
ское свойство решений и(х, t) и вообще конечнозонных по-
тенциалов и (х). Все они квазипериодичны также по мни-
мым осям, если считать х и t комплексными. Это свойство
вытекает также из формулы B3), так как мы имеем дело
фактически с решеткой из 2п векторов в /г-мерном комп-
лексном пространстве. Оно является естественным обоб-
щением на все n-зонные потенциалы двоякопериодичности
эллиптической функции Вейерштрасса в комплексной
области С, которая была однозонным потенциалом и кно-
идальной волной для КдФ.
Обратимся теперь к квазиимпульсу р (Е), определен-
ному в § 1 равенством
где Т — период потенциала. Как мы уже знаем, квази-
импульс р (Е) определен с точностью до прибавления це-
лых кратных я, коэффициенты его разложения по z ==
= 1/]/~Е при ?-> оо в точности совпадают с полиномиаль-
ными интегралами /„ уравнения КдФ и всех его высших
аналогов, введенными в гл. I,
iP B5)
а сами высшие КдФ имеют вид
д <
и —
дх Ьи (х)
Для р {Е) мы имели формулу
т т
Р(Е)= jH
о о
_ 1 с VWjEjdx
ц
к
Воспользуемся теперь видом дифференциала W =

§ 8] ЕЛОХОВСКАЯ СОБСТВЕН. ФУНКЦИЯ II КВАЗИИМПУЛЬС" 177
В силу A0) мы имеем
W =i{w~ х0) щ + Jj Qpj<*>«i<*> + ?kj&j, B6)
j
где Pj = G;, +), Q} = (y} (x), ±). Если все Qj (ж) перио-
дичны no jc периодом j (а это так для периодических по
х потенциалов и (х)), то оператор трансляции Т: х —>-
-> х + Г действует на W следующим образом:
Т : VV-> W + iTcoo 4- 2 Ь$;, B7)
где Xj — целые числа. Меняя непрерывно х от х0 до х0 + ^
и учитывая установленную выше целочисленность чисел
kj, получаем для Х}- = 0
Т: W ^ W + гГсо0. B8)
Так как г|Х)- = exp {\ W}, то можно записать
^dE = a0. B9)
Теперь мы можем сделать следующий вывод: квази-
импульс р представляет собой интеграл по пути на по-
верхности Г от дифференциала II рода м0, нормирован-
ного условиями F), G). Набор ^-периодов U' — Ф о>п опре-
деляет производные по х от параметров А1 (см. B3)). Из
формулы B9) для р (Е) мы видим, что в случае д-зонного
потенциала квазиимпульс р (Е) представляется в виде
интеграла от выражения вида Рп (Е) dE/YR (Е). Ранее
этот факт был получен иначе из формулы D.4). Мы видим,
что Рп (Е) — полином степени п со старшим членом еди-
ница, определяемый условиями нормировки (нулевые а-
периоды). Так как 6-периоды этого дифференциала не
равны нулю, для определения однозначной ветви функции
р (Е) следует сделать разрезы в ^-плоскости вдоль всех
запрещенных зон конечной и бесконечной длины (их ров-
но п + 1):
(- оо, Ео), (Elt E2), . . ., (Е2п^Е2п).
Поверхность Г распадается на два куска над этой плоско-
стью с разрезами. На каждом куске функция р (Е) уже

178 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. 11
будет определена однозначно, так как обходы вокруг раз-
резов являются циклами cij и а-периоды равны нулю для
AеР = ?о0. Можно выбрать «физический лист», где значе-
ния функции р (Е) лежат в верхней полуплоскости
Im p :> 0. Мы не будем здесь заниматься более детально
аналитическими свойствами этого и обратного отображе-
ния Е (р).
§ 9. Точные формулы
для конечнозонных потенциалов и решений КдФ
Пусть, как и выше, и (х) — д-зонный потенциал опе-
ратора Шредингера L = — cP/dx2 + и (х); гиперэллип-
тическая риманова поверхность Г (у2 + R (Е) = 0) оп-
ределена спектром Ео, Ех,...; (у}-,+)—нули и полюсы бло-
ховской собственной функции гр± (х, х0, Е) на Г. Для по-
тенциала мы имеем выражение D.19)
п 2п
и (х) = - 2 ^ Ъ (х) + S Еа.
3=1 а=0
Было получено также соотношение (8.16)
„ (Vj(.x), ±)
i(x-Xo)Uqm2i J Q,-
;=i (vy-(xo), ±>
Для случая п = 2 уравнение E.3) динамики параметров
Yii Тг по х точно совпадает с уравнением (по времени)
для случая Ковалевской в найденных ею перемен-
ных в теории тяжелого волчка (см. книгу [22]). Фор-
мула D.19) выражает потенциал и (х) через простей-
шую симметрическую функцию 2j7i от набора из п то-
чек (yx, ±), . . ., {уп, +) на поверхности Г рода п.
В силу замены Абеля (8.20), все симметрические функции'
вида 2jYu" • • • ' Via от набора из п точек поверхности
Г определены как мероморфные функции п комплексных
переменных, 2д-периодические относительно решетки
G.31). В стандартной литературе по 0-функциям (см.
Kratzer A. Lehrbuch der Thetafunktionen.— Leipzig: Te-
ubner, 1903) указывается выражение таких симметри-
ческих функций через 0-функции, используемое в [22],
откуда следует формула для потенциала и (х). Однако

ТОЧНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЙ КдФ
179
для первого симметржческого полинома можно сущест-
венно улучшить вид формулы. Оказывается возмож-
ным получить простое выражение через 0-функцию Ри-
мана
и (х) = —
К) + С(Т),
A)
где значение констант С (Г) и Kq будет дано ниже.
Опишем основное аналитическое свойство 0-функции
Римана, которое используется при выводе формулы A).
Рассмотрим многозначную функцию одной комплексной
переменной
01
0,
B)
где
п V,0)
'IV
q=l oo
Функция / (Е) является однозначной в области о~, полу-
ченной из поверхности Г разрезанием всех циклов а,-,
(рис. 14). При этом функция
/ (Е) имеет ровно п нулей на
а; оказывается, эти нули точно
совпадают с набором точек
[<>>! (х), . . ., уп (х)], дающих
решение проблемы Якоби об
обращении абелевых интегра-
лов (см. [21]). Указанный в [21]
алгоритм решения проблемы
Якоби требует интегрирования
выражения Е din f (E) по гра-
нице ст. Отсюда получается система алгебраических урав-
нений
Рис. 14. Разрез по циклам
^ 6j превращает тор
(род g = 1) в квадрат.
-res
C)
Сопоставляя C) с D.19), получаем формулу для потен-
циала
и (х) = 2 res {E din f{E)}+ С (Г), D)
El

180 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
где
С(Г)= 2 Ясс-2 ЗфяФг
а=0 3=1 aq
Для вывода основной формулы A) необходимо вычислить
вычет в точке Е = оо, где локальной координатой на по-
верхности Г является z = \/\/Е. Мы имеем, по опреде-
лению,
Еа1п}(Ь)= > —Zs-*—^ ^p-az^ —2г5 > ?2ft-д—,
a /i
E)
p
где %= J Й,,., P = (?¦, +). Пусть
&k = (c,^"-1 + . . . + c?) dE U(E- Eay/;
как указано в § 7. При Е -у оо имеем
Отсюда для Е din f получим
dz = — 2 dz V (~ + . . . ) Ц^- , G)
" ~* Zb^J \ / I Л"
где r],f = J Qfc + (,z- — х0) Uk + gfr, Р = (Е, +). Так как
оо
функция д In Q/dr\k регулярна на ст в окрестности точки
z = 0 (или Е = оо), мы находим
a a in о i\
-я—з— сд- =
'/f /Z—У
= 4 У Ct с) -Z—-q— In 0. (8)
U з l 3

§ 10] НЕКОТОРЫЕ ЧАСТНЫЕ РЕШЕНИЯ КдФ 181
В окрестности точки z = О (Е = оо) мы имеем
со~^-, Qk 2e\dz. (9)
Далее, сопоставляя тождество (см. [24])
U4 = — 2ягсл A0)
с формулой (8), мы окончательно получаем
a q~
где
р
!fr + (ж — ^C/fc + gfc- A2)
Сравнивая формулу A1) с результатом § 8, мы получим
окончательную общую формулу для конечнозонных реше-
ний КдФ
и (a; t) = — 2 ~ In В ((х — х0) ?/ + Vt + Z) + С1 (Г). A3)
§ 10. Некоторые частные решения КдФ
1. Многосолитонные решения. Среди построенных ко-
нечнозонных решений и (х, t) уравнения КдФ имеются
как предельный случай известные (см. § 3 гл. I) многосоли-
тонные решения, убывающие при | х |—»- + оо. Дело
в том, что безотражательные потенциалы уравнения Шре-
дингера могут быть получены как пределы периодических
(и квазипериодических) потенциалов ит (х) с периодом Т
при Г —>- оо, где число зон не меняется. При Т ~-> оо раз-
решенные зоны конечного размера стягиваются к изоли-
рованным точкам дискретного спектра, а край бесконечной
разрешенной зоны сходится к нулю.
На языке римановых поверхностей Г происходит сле-
дующее (поверхность Тт имеет вид у1 =П(# — Еа(Т))):
а
при Г-^-оопары точек ветвления [Е0(Т), Е1 (Т)],
1Е2(Т),Е3 (ТI, . . ., [?г„-г (Т), Е9№.г (Т)\ сближаются и

182 ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ УРАВНЕНИЯ КдФ [ГЛ. II
Еъп {Т) —> 0. Кроме того, при Т —*¦ оо риманова поверхность
вырождается в рациональную {у2 = Е) = Тх и предель-
ное положение пар таково:
E%i (оо) = E2i+1 (оо) = — х-.
Само уравнение римановой поверхности приобретает вид
п
У" = Е П (Е + х?J.
1=0
Уравнения E.3) и E.25) для набора нулей уъ . . ., уп при-
обретут вид
^^
;-. 11 (yj — ™.i) V y;-
". ^'j W q=X
Эти уравнения легко решаются и приводят к формулам
(§ 3 гл. I) для многосолитонных решений. Можно непосред-
ственно проследить вырождение при Т —>- оо в формулах
(9.13) через 9-функцию Римана: при Т —*- оо мы из форму-
лы (9.13) получим в точности выражение A.3.5) для много-
солитонных решений через вторую логарифмическую про-
изводную от детерминанта А.
На языке стационарной задачи B.3) для высших КдФ
можно сказать, что эти решения представляют собой наи-
более вырожденный тип сепаратрис.
Отыскание многосолитонных решений, конечно, мож-
но излагать без всяких методов a posteriori, так как эти ре-.
шения являются рациональными выражениями от экспо-
нент (в таком виде их можно искать).
2. Солитоны на фоне конечнозонных потенциалов. Воз-
можна ситуация, когда риманова поверхность Гг при
Т —*¦ оо вырождается лишь частично: часть пар [Е21 (Т),
E2i+1 (Т)] при Т ->- оо сближается к изолированным точ-
кам —и? для i = г0, • ¦ ., г*,-, где k <c.n — 1. Соответствую-
щие потенциалы ит (х) при Т ->¦ оо вырождаются в потен-
циал их (х), который имеет конечнозонную асимптотику

§ 10] НЕКОТОРЫЕ ЧАСТНЫЕ РЕШЕНИЯ КдФ 183
при х —>- + оо. Точно это означает, что имеется два конеч-
нозонных потенциала и+ (х) и и_ (х) с числом зон
q =-- п — к, такие, что
«<*> {х) — и+ (х) -*¦ 0 (х -*¦ + оо),
их (х) — м_ (х) -> 0 (х ->¦ —оо).
Оба потенциала и+ (х) имеют общий спектр — риманову
поверхность Г вида
i/= П (Е-Еа). B)
Однако потенциалы ц± (х) различны. Если ^
...,Р(п-к — набор нулей блоховской функции потенциа-
ла и+ (х), где Pj = (yj (x), +), то набор нулей
Р\~\ . . ., Р(п-ь потенциала и^ (х) будет иметь вид
Р^ = (yj, —). Лишь в случае четных потенциалов
и+ (х) = и+ (—х) мы будем иметь и+= и_. Для этого не-
обходимо и достаточно, чтобы yj для всех / = 1, . . ., п — к
лежало в концах точек ветвления.
Такие потенциалы и^ (х) порождают решения и (х, t)
уравнения КдФ, называемые «многосолитонными решения-
ми на фоне конечнозонных»; сами эти потенциалы называ-
ются «безотражательными потенциалами на фоне конечно-
зонных». Эти потенциалы являются сепаратрисными реше-
ниями стационарной задачи для высших КдФ.
Уравнения E.3), E.25) приобретут вид
П (Y, - Еа)I'2 ¦ П (Ya - Ea),
g fc a^2ls, 2i,
% \ ( П
X
П (yq-Ea). C)
«=2i.
В случае одной зоны п — к = 1 эллиптические формулы
см. Кузнецов Е. А., Михайлов А. В. — ЖЭТФ, 1974,
т. 67, вып. 11.

184 ПЕРИОДИЧЕСКИЕ РЕШЕНИЙ УРАВНЕНИЯ КдФ [ГЛ. П
3. Решение в эллиптических функциях. Кроме вырож-
денных типов решений, указанных выше в пунктах 1, 2,
имеются некоторые невырожденные решения уравнения КдФ
и конечнозонные потенциалы, записываемые через эллипти-
ческие функции. Напомним, что простейшее решение
типа простой (кноидальной) волны и (х — ct) имеет вид
эллиптической функции Вейерштрасса
и (х- ct) ~-=2{®{х — ct) - с/6,
Функция $> (х) комплексной переменной х является, как
известно, двоякопериодической с действительным перио-
дом Т и мнимым периодом Т', где
Т = ЪШЪ Г = 2ni/U1. E)
Общий конечнозонный потенциал и (х) с римановой по-
верхностью Г fу2 — \\{Е — Еа)) и соответствующей мат-
а
рицей Римана
BKi8kq, bk(l)
имеет набор действительных периодов
г-1 = s ьки}, b%s = &i F)
i
и мнимых периодов
Тд = 2ni/Uq. F')
Поэтому потенциал и (х) такого вида является квазиперио-
дической функцией комплексной переменной х. Для пе-
риодичности потенциала на действительной оси х необхо-
димо и достаточно выполнение п — 1 целочисленных со-
отношений
SbA=C Л-1,...,в-1. G)
9=1
Однако из соотношений G) еще не вытекает никаких соотно-
шений на мнимые периоды Tq. Поэтому потенциал и (х)
будет квазипериодической функцией комплексной пере-
менной х. Для того чтобы потенциал был двоякопериоди-
ческим и тем самым выражался через эллиптические функ-

§ 10] НЕКОТОРЫЕ ЧАСТНЫЕ РЕШЕНИЯ КдФ 185
ции, необходимо и достаточно выполнение еще п—1 соот-
ношений на мнимые периоды
= 0, к= 1, ...,и-1. (8)
9=1
Совокупность всех n-зонных потенциалов образует Зге +
+ 1-мерное семейство Bп + 1 точек ветвления или краев
зон и ге параметров при заданном спектре). Учитывая
тривиальное преобразование и —>- и + const и 2га — 2
соотношений на действительные и мнимые периоды G), (8),
мы видим, что эллиптические потенциалы должны образо-
вывать не более, чем (ге + 2)-мерное семейство с точностью
до прибавления константы.
Соотношения G), (8) на группу периодов определяются
только поверхностью Г. Поэтому из эллиптического
n-зонного потенциала при движении во времени в силу
любого из высших КдФ будет снова получаться эллипти-
ческий потенциал. Мы знаем следующие re-зонные эллип-
тические потенциалы Ламе — Айнса:
(9)
Спектр этого семейства потенциалов зависит от двух пара-
метров (кроме прибавления константы). Итак, мы получим
(ге + 2)-мерное семейство эллиптических n-зонных потен-
циалов из потенциалов Ламе — Айнса, решая задачу
Коши для всевозможных высших КдФ. Мы не знаем, су-
ществуют ли другие семейства эллиптических потенциалов.
Рассмотрим теперь случай п = 2. Спектр потенциала
и (х) = 6$> (х) имеет вид
Ео = Зеи Ех = -C^)'/., Е% = Зе2,
Е; -- Cft)'/., Ел - Зе3, 4е? - gie, - g3 - О,
i - 1, 2, 3. A0)
Решим задачу Коши для уравнения КдФ с начальным ус-
ловием и (х, 0) = 61? (х). Все эллиптические потенциалы
этого семейства будут иметь вид (см. [6])
и (х — х0, t) + const, A1)
где и (ж, 0) = 61? {х).

186 ЦиШОДНЧИСКИЕ РЕШЫШЯ УРАВНЕНИЯ КдФ [ГЛ. II
Мы знаем заранее, что решение КдФ будет эллипти-
ческой функцией — как следствие ранее полученных ре-
зультатов. Используя этот факт и начальное условие, эле-
ментарным вычислением получим
и (л; 0= S 2F(x — ai(t)), A2)
где
сс2 — а3 = -тр i?-~'{— о' (ut — а3)
-f Iga —
Найденное здесь точное решение ураинения КдФ представ-
ляет собой сумму трех простых волн, движущихся без из-
менения формы, но с весьма сложно скоррелированными
фазами a, (t). По-видимому, это простейшее с аналитиче-
ской точки зрения невырожденное двухзониое решение
КдФ.

Глава III
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МЕТОДОВ
ПОСТРОЕНИЯ ИНТЕГРИРУЕМЫХ СИСТЕМ
И ИХ РЕШЕНИИ
Классический метод обратной задачи, изложенной
в гл. I, позволяет решать уравнение с убывающими при
х -> +оо коэффициентами, поскольку при решении суще-
ствепно используется асимптотическая область веществен-
ной оси, необходимая для построения теории рассеяния.
В настоящей главе мы переформулируем метод обратной
задачи так, что он позволит нам строить некоторые реше-
ния интегрируемых уравнений локально, в окрестности
каждой точки х, t. Эта переформулировка окажется чрез-
вычайно полезной и позволит наметить общий подход
к построению как систем уравнений, интегрирование ко-
торых возможно, так и их точных решений.
§ 1. Регулярная задача Римана
Центральную роль в новой формулировке метода игра-
ет одна из классических задач теории функций комплекс-
ного переменного, известная как задача Римана. Она фор-
мулируется следующим образом. Пусть на плоскости
комплексного переменного к задан замкнутый контур Г,
возможно, проходящий через бесконечно удаленную точку,
и пусть на нем задана матричная (порядка N) функция
G (к). Требуется построить матричную функцию а^ (к),
аналитичную внутри контура, и матричную функцию
я|52 (к), аналитичную вне контура, причем я^ ия|52 на контуре
удовлетворяют условию
1>1 (Я) Ч>2 (к) = G(k). A)

Ш ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ (ГЛ. П1
Очевидно, что решение задачи Римана не единственно.
Так, еслн г|эх, г|з2— некое такое решение, a g — произволь-
ная невырожденная матричная функция, не зависящая
от X, то пара матричных функций i^g1, g'1 ijj2 снова есть
решение задачи Римана с той же функцией G (К).
Чтобы избавиться от этой неоднозначности, необходи-
мо нормировать задачу Римана, задав значение одной из
функций -фх, яр2 в некоторой точке из области аналитично-
сти. Разным выборам этой точки и функции отвечают раз-
ные нормировки задачи Римана. В большинстве случаев
мы будем рассматривать нормировку на единичную ма-
трицу в бесконечно удаленной точке. Такую нормировку
мы будем называть канонической.
Предположим, что функции г^ и т|J в областях своей
аналитичности нигде не вырождаются, т. е. det "фх Ф О,
det i|j2 =}= 0. В этом случае задача Римана называется регу-
лярной. Решение регулярной задачи Римана с данной нор-
мировкой является единственным. Действительно, пусть
^\ "Фг4 и ^i2\ i|42) — Два решения регулярной задачи.
Тогда на контуре имеем
Рассмотрим функцию % (X) = frj)?2) (Я)]"^ (X) =
= "Ф22) (^) ["Фа1* (А-)!- Эта функция аналитически продол-
жается с контура Г на всю комплексную плоскость и, сле-
довательно, по теореме Лиувилля является постоянной.
После фиксации нормировки это означает, что X = 1.
Решение регулярной задачи Римана сводится к реше-
нию определенной системы сингулярных интегральных
уравнений на контуре Г. Пусть задача Римана нормирова-
на в точке к0, находящейся, например, вне контура Г,
и пусть
¦фа (h) = g-
Будем искать решения задачи Римана в виде
Ч1!1^) = h + \ ?_\ dl внутри контура B)
г
¦фа (Ц = h + \ -^-Ц-dg вне контура.

§ 11 РЕГУЛЯРНАЯ ЗАДАЧА РНМЛЙА 189
Тогда из условия нормировки имеем
г
На контуре по формулам Сохоцкого — Племеля имеем
г
Подставляя C) и D) в A), получим для ср сингулярное ин-
тегральное уравнение (X 6= Г)
l^-O, E)
где Т = (G + 1) (G — 1) 1, решение которого и дает реше-
ние регулярной задачи Римана. В наиболее простом слу-
чае, когда контур представляет собой вещественную ось
и нормировка является канонической (h — g = 1), урав-
нение E) приобретает вид
оо
1 Г Г Ф (Н 1
—-\ л , Л "S Ч- 1 + Ф Ш Т (к) = 0. F)
Если N = 1 и -фх и 1|з2 являются числовыми функциями
(скалярный случай), регулярная задача Римана допускает
явное решение. Логарифмируя соотношение A), имеем
In ф2 — In 1рг1 = In G. G)
Поскольку по предположению регулярности функции я|5х
и я|з2 не имеют нулей в областях аналитичности, их лога-
рифмы также являются аналитическими функциями, до-
пускающими представление в виде интеграла Коши.
Уравнение G) удовлетворяется, если положить
(8)

190 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Таким образом,
(9)
Формулы (9) дают представление об условиях разрешили)
сти регулярной задачи Римана. Видно, что достаточным
условием разрешимости является сходимость интегралов
(8), в частности отсутствие полюсов и нулей у функции
G (к) (нулевой индекс задачи Римана). В матричном слу-
чае условия разрешимости задачи Римана являются более
сложными, и требование ограниченности и невырожден-
ности матричной функции G (К) может оказаться недоста-
точным. Как показано в [25], достаточным является, на-
пример, требование Re G ^> О, т. е. требование положи-
тельности вещественной части матрицы G (X) при всех
значениях X на контуре Г. Ниже мы будем всюду, если не
оговорено противное, предполагать, что регулярная за-
дача Римана разрешима. Как мы уже знаем, в этом случае
после наложения нормировки она разрешима однозначно.
§ 2. Задача Римана с нулями
Будем говорить, что матричная функция ф (Я) имеет
нуль в точке X = Xq, если в этой точке ее определитель
равен нулю (det "ф (Хо) = 0). Очевидно, в этой точке
обратная матрица имеет особенность — полюс конечного
порядка. Будем называть нуль X = Хо простым, если этот
полюс имеет порядок единицу, т. е. если в окрестности
А, ~ %0
Сама функция г|з в окрестности X = Хо имеет разложение
•ф (Я) = В + D (X - Хо) + . . . B)
Очевидно,
АВ = ВА = 0, C)
AD + СВ = ВС + DA = 1.

§ 2] ЗАДАЧА РИМАНА С НУЛЯМИ 19 1
В скалярном случае числовых функций -ф очевидным об-
разом В = О, и точка % = Яо является нулем функции
"Ф (Я) в обычном смысле.
Мы начнем изучение задачи Римана с нулями с рассмо-
трения именно этого случая. Калибровку задачи Римана
будем предполагать канонической. Пусть функция 1|)ь
аналитичная внутри контура Г, имеет там п простых ну-
лей къ . . ., кп, и функция а|52, аналитичная вне контура,
имеет в этой области также п простых нулей Цг, . . ., цп
и пусть ни один из нулей Х;, ц,г не лежит на контуре Г.
Рассмотрим вспомогательные функции
п
ъ= П т-х^1- D)
K~K
E)
которые также являются аналитичными, но нулей уже не
имеют. Очевидно, чтог^г (оо) = г|;2 (оо) = 1 и на контуре Г,
где определены обе функции а|зь ¦фг^А = "ФЖ = G.
Таким образом, задача об определении функций а^, а[з2
является регулярной задачей Римана и дается формула-
ми A.9). Этот пример показывает, что при наличии нулей
единственность задачи Римана нарушается — кроме функ-
ции G, контура Г и нормировки, необходимо еще задавать
расположение нулей. Заметим, что задача с нулями и
единичной калибровкой на бесконечности разрешима, если
только число нулей вне и внутри контура одинаково.
В отличие от регулярной задачи Римана, задача Ри-
мана с нулями имеет смысл, даже если функция G на
контуре тождественно равна единице. В этом случае
¦ф2 = 1/ф1; нули функции ij;2 являются полюсами функции
ajjj и решение задачи Римана сводится к построению меро-
морфной аналитической функции по ее нулям и полюсам..
В общем случае решение задачи может быть разбито на две
части — построение рациональной аналитической функ-
ции с заданными особенностями и решение регулярной
задачи Римана.
Перейдем теперь к матричному случаю. В матричном
случае уже нетривиальной является задача о построении

192 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИИ [ГЛ. III
рациональной функции по нулям и полюсам. Начнем с
простейшего случая функции, имеющей один нуль и
один полюс.
Пусть даны функции -фл и "Фг такие, что -ф^ = 1,
о^ (оо) — я|;2 (оо) = 1, причем функция ¦\р1 имеет един-
ственный нуль в точке к = к0, а функция я|J -• единствен-
ный нуль в точке К = ц0. Требуется найти в общем виде
функции -фи i|)a.
Заметим, что пули г^>t совпадают с полюсами я|з2, а нули
я|52 — с полюсами я|51. Поэтому функции i^j и я|52 имеют
всего по одному полюсу и их разложение на простейшие
дроби имеет вид
Из o|5ii|32 = 1 следует
A
Разлагая произведение на простые дроби, получим
Л AlA* — п и | ^И2 _ п
Ао — Цо Ао — |Д,0
Откуда следует, что А.2 = —Ах и
где Р2 = Р.
Матрицы Аъ А2 можно рассматривать как матрицы
линейных операторов в комплексном TV-мерном простран-
стве CN. Очевидно, Р является матрицей некоторого про-
екционного оператора. Этот оператор моншо задавать про-
извольно — он и характеризует ту степень произвола,
с которой восстанавливаются матричные функции •^1 и я|52
по положению их нулей. Явные выражения для я^ и я|J
имеют вид
,1, _ А ^') ~" И-о р ,|, л, ^о ~ У-о р (Н\
Ti — 1 г 7.— 1у Y2 — -I H 5 5—Г' V)
л — ^0 л — л-о
При этом
= 1 - Р = 5Х.
В дальнейшем нам будет удобно использовать язык
линейной алгебры в пространстве CN. Пусть в этом про-

§ 21 ЗАДАЧА РИМАНА О НУЛЯМИ 193
странстве задан некоторый линейный оператор U. Обозна-
чим через ker U ядро оператора U, т. е. совокупность тех
векторов из CN, которые оператор U переводит в нуль,
а через Im U — образ оператора U, т. е. результат при-
менения оператора U ко всему пространству CN. Очевидно,
ker U и Im U суть линейные подпространства в CN, а их
прямая сумма составляет все пространство CN. Последний
факт мы обозначим таким образом:
ker U e Im U = CN.
Вернемся к операторам А и В. Легко проверить, что из C)
следует
ker A = Im В и ker В = Im A.
Подпространства ker U и Im U являются нетривиальными
только для вырожденных операторов, в невырожденном
случае det U Ф 0, ker V = 0, Im U = CN.
Вырожденный оператор U, вообще говоря, не характе-
ризуется однозначно подпространствами ker U и Im U.
Исключение представляет проекционный оператор Р2 = Р,
который на подпространстве Im P действует тривиально
как единичный. Поэтому проекционный оператор пол-
ностью определяется своим образом и ядром. Заметим
еще, что оператор 1 — Р также является проекционным,
причем
ker A - Р) = Im P, Im A - Р) = ker P.
Итак, проекционный оператор Р в формулах G) мы можем
построить по подпространствам
N = 1т^1 (Ао), М = ker а|52 (ц.о)
(в данном случае % (kQ) = о|э2 (jJ-o))-
Теперь ясно, как построить функции % и я|J при нали-
чии у каждой из них п нулей. Зададим п проекционных
операторов Рх, . . ., Рп и построим произведения

194 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Рассмотрим фь ф2 в точках К = Кк, К = ^:
5, = ф, (^) = «7* A - Р») 7Ь
Вк = ф2 Ы = V? A - Pk) ??\ (9)
где
A0)
v ^ \l i. _„.. . ' Hi • ¦
— невырожденные матрицы.
Пусть Nok = Im A - i\), Mos = ker A - Pt). Из
(9) следует, что
Nk = Im фг (A,fc) = f/^jVofc, Mft = ker ф2 ([ift) = UkM01(.
A1)
Очевидно, подпространства Noit и AfOft не имеют нетри-
виального пересечения и их прямая сумма составляет все
линейное пространство CN. Из A1) следует, что это же
справедливо для подпространств Nk и Мк.
Для последующего важную роль будет играть задача
построения матриц о^ и г|J по заданным Nk, Mk. Итак,
пусть на комплексной плоскости "к задано два набора то-
чек Къ . . ., %п и [хь . . ., jj,n, а также два набора подпро-
странств Nk и Мк, причем Л',, © Мк = CN и Nk и Мк
не пересекаются. Требуется построить пару функций
я|зь я|52 таких, что тфх (А,) г|;2 (X) = 1, Im i^1 (кк) = Nk и
ker "ф2 (|Л*) = Affe. Приведем два способа решения этой
задачи.
Первый из них есть способ рекуррентного построе-
ния проекционных операторов Рк. Положим Im Рх =
= ker A — Pi) = Nlf ker P1 = Im A - P,) = Mt. Да-
лее, пусть к — 1 первых проекционных операторов уже
построены. Тем самым мы знаем невырожденную матри-
цу Uk. Теперь подпространства, определяющие к-ж про-
ектор Pi, могут быть найдены из формул A1): ker Ph ~
= MitU^1, Im Pk = NhUl'1. Окончательно функции ^>1
и ^2 даются формулами (8). Второй способ основан на

§ 2] ЗАДАЧА РИМАНА С НУЛЯМИ 195
разложении функций я^, o|52 на простые дроби. Положим
Отсюда очевидно, что Im Ак = Мк. Введем в подпростран-
стве Mi- базис m\(i ¦= 1, . . ., q};). Тогда оператор Ак
может быть представлен в виде
где XI — некоторые неизвестные векторы. Введем также
базис в подпространстве Nh] пусть он состоит из векторов
щ (i = 1, . . ., Рк), рк + qh - N,
и дополним его векторами п\ (i = 1, . . ., qk) до базиса
во всем пространстве CN¦
Введем в CN каким-нибудь образом скалярное произ-
ведение (например, просто определив ху ~^хауа) и по-
требуем, чтобы векторы п{ были ортогональными в смысле
этого произведения векторам п\:
п\п{ = 0.
Из условий Nk = Im я|зх (кк) имеем
Рк
№W = S in\)a(Yl)?. A 3)
i=l
Отсюда следует набор соотношений
2 D)а[я|I (Xi.)]ep =0, / = 1, . . . , д,. A4)
Подставляя A2) и A3) в A4), получим систему линейных
уравнений на векторы Х{
Находя из A5) X3q, мы полностью определяем функцию \\>i
Аналогичным образом можно найти функцию -фа-

196 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Вернемся к задаче Римана с нулями. Мы сформулируем
ее следующим образом. Пусть на комплексной плоско-
сти Я задан контур Г и два набора точек: къ . . ., кп внутри
контура, и \х,ъ . . ., \хп вне контура. Кроме того, на кон-
туре определена матричная функция G (Я) и заданы два
набора подпространств Nk и Мк, причем iVf,- @ Мм = CN.
Требуется найти аналитические внутри и вне контура
функции -фа (Я), я|J (Я), фг (°°) = 1, такие, что на контуре
^i (^) Ч>2 Ф) ~ G С0> и> кроме того,
Iin ijji (Яг) = Nt, кегг|з2 (цг) = Mt.
Для решения этой задачи вначале одним из двух пред-
ложенных выше способов построим рациональную функ-
цию г|з0 (Я) такую, что
Im -фо {кд = Nu ker ^ (ц,) = Ми
и представим гр!, -ф2 в виде
Очевидно, гр! и я|52 являются аналитическими и неособыми
матричными функциями внутри и вне контура соответ-
ственно. На контуре Г
0^2 = G == фо1 Сфо-
Задача об определении я^, -фз свелась к регулярной ма-
тричной задаче Римана. Можно и непосредственно свести
задачу Римана с нулями к решению системы алгебраиче-
ских и интегральных уравнений. Для этого представим
функции я]5х, гра1 в виде
1>1 = 1 -
к-Ъ ' 2т J Я-S '
A6)
л i V1 fr 1 (" Ф (С) rf^
/ i /»— u,. ' 2яг ,1 Я — E,
где Я внутри Г в верхней формуле и Я вне Г в нижней.
Как мы знаем, Im A}i = Ml;, следовательно, Ак может
быть представлена в виде A3). Повторяя предыдущие
рассуждения для точек Я = Я,с, получим систему

§ 3] ОБРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ 197
линейных алгебраических уравнений на Х{
V V ("*'"Ф уз п
Л/Т^г «=
а э=1
Далее, подставляя A6) в соотношение
получим интегральное уравнение вида
Г? Ф<Е>^
A8)
где Т =A—G)l(l-\-G) — преобразование Кэли матрицы G.
Уравнения A7), A8) образуют полную систему уравнений,
решающих матричную задачу Римана с нулями.
§ 3. Обратная задача рассеяния
для матричной системы первого порядка
Покажем, каким образом задача Римана может быть
использована для решения обратных задач рассеяния
в более общей ситуации, чем разобранная в гл. I. Рассмо-
трим спектральную задачу
—щх = (Л + ?/)ф. A)
Здесь / — заданная постоянная диагональная матрица
TV-го порядка, U — зависящая от х матрица с нулевыми
диагональными элементами. Выразим этот факт, записав
матрицу U в виде
U = [/, Q], B)
C)
Пусть матрица / вещественна и невырождена и среди ее
собственных чисел нет одинаковых. Тогда /
L «nJ

198 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
(обозначается / = diag а{). Упорядочим числа аг в поряд-
ке убывания:
o-i > <h > . . . > о».
Решением уравнения A) являются векторы из N эле-
ментов ф*. Полные наборы решений образуют фундамен-
тальные матрицы решений ф^. Здесь первый индекс —
векторный, второй обозначает номер решения, det <p Ф 0.
Если ф — матрица решений, то q>R (где R = R (X),
det R Ф 0) — тоже матрица решений. Здесь Л (X) — про-
извольная невырожденная матричная функция X. В даль-
нейшем удобно рассматривать A) как матричное дифферен-
циальное уравнение. Наряду с A) полезно рассмотреть
родственные матричные уравнения
iyx = Ф (Л, + V), D)
— ?а|5ж = (Л + ?/)я|5 — Ал|з-Л E)
$ U) — Я/ф. F)
Очевидно, для любых двух решений уравнений A), D)
имеет место соотношение
^ G)
В частности, уравнению D) удовлетворяет обратная ма-
трица ф = ф. Уравнениям E), F) удовлетворяют ма-
трицы
¦ф = фе*Лж, ijj = e~iJXxq>. (8)
Имеет место соотношение
^ (х, X) -ф (х, X) = e~iJKx G (l)eiJKx. (9)
В этих формулах G (X) — некоторая произвольная невы-
рожденная матричная функция X.
Рассмотрим два набора решений уравнения A) <р±,
определяемые асимптотиками
X ->- + СХ).
Каждый из этих наборов является фундаментальным,
поэтому найдется матрица S (X), такая что
Ф- (х, X) = Ф+ (х, X)S (X). (И)

3]
ОПРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ
199
Воспользуемся известным тождеством
- i — lndet ф = Sp (Л + U) = Sp /Я =
из которого следует
det ф+ = det ф~,
и
det S (I) = 1.
A2)
Обратная задача рассеяния для системы A) состоит в вос-
становлении матричной функции U (х) по заданной ма-
тричной функции S (X), а также в выяснении требований,
которые нужно наложить на S (к), чтобы такое восстанов-
ление было возможно. Последнее не тривиально, посколь-
ку матрица S (к) содержит больше элементов, чем матрица
U (х) (диагональные элементы U (х) равны нулю).
Рассмотрим задачу о факторизации матрицы S (К),
т. е. представим ее в форме
S+ = SS~, A3)
где S+, S~ — треугольные матрицы вида
0
0
0
0
^22
^32
0
0
^33
0
0 ...
0 ...
A4)
Элементы матриц S+, S могут быть определены решением
некоторых систем линейных уравнений, следующих из
A3). Наиболее простое уравнение связывает S+ и S~:
Snn=SnnSnn- A5)
Далее имеем
Для величин S;v_i, jv-i и ^Ъ, n-i возникают два уравнения
5jV—1, W—1 = Sn—1? лг—i<5.v—1, JV—1 'r 5jv_i, nSn, Лт—1
О = «Sjv—1, N$N—1, N—l + $JV, iV^iV, JV—1-
,,r>\

200 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Остальные уравнения получаются аналогично. Как видно
уже из A5) и A6), задача факторизации не вполне одно-
значна — именно, можно произвольным образом задавать
диагональные элементы одной из матриц S±. Неодно-
значность можно убрать, потребовав, чтобы элементы
матриц 5* целым образом без деления выражались через
элементы матрицы S. Тогда
Snn = «SW,
Sn—1, JV—i = $N—1, JV—l^JVJV — Sn—i, nSn, N—l-
Вообще,
где A/j — к-й нижний главный минор матрицы S. При
этом легко показать по индукции, что
5й = Л^-*, До = 1- A8)
Остальные элементы матриц S± также составлены из ми-
норов матрицы S. Умножая соотношение A1) справа
на iS~, введем новую матрицу х+:
Х+ = ф+5+ = ф-?-. A9)
Из A9) следует, что решение %+ имеет при х -> +оо
«треугольные» асимптотики
Xtk ~> Aw-fr+i (Ц eiXa«x, х->-\-сх>, B0)
Xift —*¦ 0, i<^k при х—> — оо.
Из однозначной разрешимости задачи факторизации сле-
дует, что х+ полностью определяется этими асимптоти-
ками; при этом автоматически
Х& -> Дя-fc (Я) еаа"х, a -> - оо.
При построении обратных задач, рассмотренных в гл. I,
основную роль играл факт аналитичности функций Йоста,
определенных асимптотиками типа A0). В нашем случае
функции ф± (х,Х), вообще говоря, не допускают никакого
аналитического продолжения с вещественной оси X. За-
мечательно, однако, что уравнение A) все же имеет ана-
литическое в верхней полуплоскости X решение, и этим

§ 3] ОБРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ 201
решением оказывается введенная по формулам A9) ма-
трица %+ (х, К).
Вместо матрицы %+ удобно рассматривать решение
системы E)
¦ф+ __ y+g-ijhx_
Оно имеет те же асимптотики, что и % (см. B0)), за исклю-
чением диагональных элементов, для которых
¦фи- ->- Ajv-ft+i (ty при х ->- +оо,
¦фм ->- Ajv-fc (X) при х -> — оо.
Покажем, что матрица г^ удовлетворяет интегральному
уравнению
X
tf* = i J 2 Ui3 (*') ^ (*', ^) «* ^-"^^'W, i <к,
—оо ;
-фкя: = A^-ft+i (Я,) - i J S Ut} (х, X) rptk (ж', X) <&', B1)
X j
оо
^ = - i J S ^ (х') ф^ (*', ?.) eiX <-i-°fc)(«-^')da.'t t > кш
X 3
Действительно, прямым дифференцированием формул B1)
легко убедиться, что решение системы B1) удовлетворяет
уравнению E). С другой стороны, устремляя х к +оо,
легко проверить с учетом C) выполнение асимптотик B0).
Произведем теперь «обрезание» U (х), т. е. положим,
что вне некоторого большого интервала (—L,L) функция
U (х) = 0. Матричные функции <р± (х, К) являются теперь
решениями задачи Коши
<р?(*Д)=а«еЧ*|*=±ь B2)
и, следовательно, целыми функциями К. Соотношение
A1) можно переписать в виде
S (I) = Ф~ (х, Ь)(<р+ (х, X))-1. B3)
Обратная к ф+ матрица есть решение уравнения D) с на-
чальным условием
и тоже является целой функцией X. Следовательно, S (к) —

202 ПОСТРОЕН. ИНТЕГРИР СИСТЕМ II ИХ РЕШЕНИЙ ГГЛ. III
целая функция X; при выбранном нами способе фактори-
зации матрицы iS^ (и с ними %+) также оказываются це-
лыми функциями параметра К.
После обрезания уравнение B1) примет вид
X
Га- = i $ 2 UV (.т') tf* (х\ Я) ел
$
—L
L
г|4 = A^_s+1 (A,) - i j 2 # « («') *l& (*'. Я.) da;', B4)
ж j
<» = - i 12
X j
При вещественных "к уравнение B1) получается из B4)
предельным переходом L-*- сх>. При комплексном Л воз-
можность такого предельного перехода не очевидна,
поскольку интегралы в B4) могут оказаться при L —>¦ оо
расходящимися. Вспоминая, что числа аг упорядочены
(at ^> aj, если j ^> i), убеждаемся, что такой предельный
переход возможен в верхней полуплоскости К, если только
выполнено условие C), и, вообще говоря, невозможен
в нижней полуплоскости. Это означает, что функция
ч|з»)с (х, к) допускает аналитическое продолжение в верх-
нюю полуплоскость X.
Пусть Im К ^> 0, |Я| -> оо. Из B4) имеем
а|4 = A^_ft+16rt + О (Ш). B5)
Устремляя х к +оо и пользуясь асимптотиками B0),
заключаем, что при \К\ —>¦ оо
Аь - Д^ = О
Отсюда, поскольку До = 1, имеем
д; = 1 + О (Ш). B6)
С учетом B6) имеем из B4)
или
U = lim M/, i|)+]. B8)

§ 3] ОБРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ 203
Формула B8) показывает, что для определения U доста-
точно найти асимптотику функции я|)+ при Я -*- оо. Наряду
с факторизацией A3) можно рассмотреть факторизацию
R- = SR+, B9)
где R~, R+ — треугольные матрицы вида A4). Фактори-
зация является однозначной, если, как и раньше, пред-
положить, что элементы матриц R± (к) целым образом
зависят от Su (к). При этом Rkk = &t (ty, Rkk = &t-i {%),
где Ак (К) — верхние главные миноры матрицы S (К):
До = 1-
Определим решение системы A)
X" = Ф-Л+ = ф+Д-. C0)
Повторяя приведенные выше рассуждения, можно дока-
зать, что %~ (х, К), а также г|э-= %~e~iXJx и миноры Ак (Я)
допускают аналитическое продолжение в нижнюю полу-
плоскость и имеют такие асимптотики:
%s->Sifc +0A А),
А; -> 1 + О {11%), C1)
|А,1-> оо, Im ^< 0.
Обратимся теперь к уравнению D). Определим его решения
ф± асимптотиками
Введем матрицу iS' условием
ф- = 5ф+.
Очевидно, ф± = (ф±)~х, S = S'1. Поскольку det 5 = 1,
элементы матрицы S целым образом выражаются через
элементы матрицы S.
Рассмотрим две целые факторизации матрицы S:
S* = SS, Л-=Я+5(. C2)
Здесь
S+ = (Sy1 A", S- = (S-)'1 А-;
J?+ = (д+)-1 Д+, Я' = (й-) А+-

204 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
где
N—1
А" = det 5" = det S+ = Д А?,
!Й C3)
A+ = det R~ = det Л+ = П At
Определим два набора решений уравнения D):
х- = /?+ф- = л-ф+,
а также соответствующие решения уравнения F):
ifi = eiXJx %±.
Очевидно, функции %+ аналитичны в верхней, а %~ —
в нижней полуплоскости параметра К и, как и %^, имеют
единичную асимптотику на бесконечности.
Для произведений матриц "ф, г|з в согласии с формулами
(9) имеем
ijj+T|3- = eiJXx Gi (к)е~Шх,
Здесь
Gt (К) =
Формулы C6) дают способ решения обратной задачи
рассеяния для A). Нужно по $ (к) найти одну из матриц
'-'i, г (^) — это сводится к решению конечного числа линей-
ных алгебраических уравнений, затем решить при каж-
дом х одну из задач Римана C5). Контуром Г в обоих
случаях является вещественная ось, нормировка задачи
Римана в обоих случаях каноническая — единичная при
Я, = оо.
Пусть N = 2. Тогда
(К) = 5+ (Я,)Л~ (Я,). ( '
о Г<?ц S121 ее С С
О = „ „ , ОЦО22 2^21 =
L 2J
22J

§ 3] ОБРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ 205
Произведя факторизацию, получим
L о
1 J' - Ui s»j'
R+ = Г^и sni R__ г i o
L о l J' n ~ l-sn su
г _Г 1
L— Л21
Анализируя формулы C7), можно сделать важный вывод.
Именно, матрицы Gu G2, входящие в задачу Римана,
содержат только два элемента матрицы 5, 512 и S21,—
столько же, сколько ненулевых элементов в матрице U.
Поэтому задача восстановления матрицы S по матрице
G1 или G2 является нетривиальной. При ее решении не-
обходимо использовать свойства аналитичности диаго-
нальных элементов S. В данном случае элемент Su ана-
литичен в нижней, a S22 — в верхней полуплоскости.
Так же обстоит дело и в общем случае. Матрицы Glt 2
содержат по N (N — 1) независимых элементов, и при
восстановлении по ним матрицы S необходимо использо-
вать аналитичность ее главных миноров — нижних в
верхней полуплоскости и верхних в нижней. Условие ана-
литичности главных миноров и единичности детерминанта
вместе с условием разрешимости задачи Римана является
полным набором достаточных условий, определяющих
матрицу S. Доказательство этого факта выходит за рамки
настоящей книги.
Обе задачи Римана эквивалентны, поэтому мы в даль-
нейшем будем говорить только об одной из них, например
о задаче, связанной с матрицей G2 (Я). Эта задача не обя-
зательно является регулярной. Миноры А^ (Я), At (к)
могут иметь в областях их аналитичности конечное число
нулей. Покажем, что с этими нулями связаны нули за-
дачи Римана.
Пусть потенциал U (х) «обрезан» вне интервала (—L, L)
и минор Ajv-j+i имеет пуль в точке X = Хо. Тогда в этой
точке треугольные матрицы 5± вырождены, причем

206 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
S\k = 0и «Sit-!, k-v Вырожденной является и матрица %+,
ранг ее равен N — 1. Существует, следовательно, един-
ственный вектор с, для которого %+с = 0. Пользуясь
формулами A9) и сокращая на невырожденные матрицы
Ф+, <р~, получим
S+с = 0, S~c = 0. C8)
Из треугольности матриц S+ и S~ легко получить, что
вектор с имеет всего две ненулевые компоненты c^-i и
Cjc. Таким образом, при X — %о
Ъс-г = const- xt- C9)
Устремим теперь L к оо. Формула C9) при этом со-
хранится, что и доказывает тот факт, что К = Ко есть
нуль задачи Римана в верхней полуплоскости. Поскольку
матрицы <S"+ и S~ состоят из алгебраических дополнений
к матрицам S+, S~, они тоже вырождены — вместе с ними
в точке X = Ко вырождена матрица }J+. Ранг ее по-преж-
нему равен 7V — 1, однако линейную зависимость между
ее компонентами в общем виде вычислить не удается,
так как все диагональные элементы матриц 3+ и 3~,
кроме одного, равны нулю. Аналогичным образом устанав-
ливается, что нули миноров Aj являются нулями задачи
Римана в нижней полуплоскости. Формула C9) показы-
вает, что простые нули одного из главных миноров —
весьма частные случаи нулей задачи Римана. В общем
случае простого нуля задачи Римана матрица г[5+ (и со-
ответственно х+) может быть сколь угодно сильно выро-
ждена — иметь произвольный ранг; даже при ранге
N — 1 зависимость между ее столбцами может иметь
более общий вид. Чтобы осуществить эти варианты, не-
обходимо обращение в одной точке Ко в нуль нескольких
главных миноров. Так, для того чтобы цепочка C9) содер-
жала в правой части р элементов
%
необходимо одновременное обращение в нуль р главных
миноров
AjV-»+1, • • ч А
В дальнейшем нас будет интересовать только случай,
рассмотренный в § 2, когда задача Римана имеет одина-

§ 3] ОБРАТНАЯ ЗАДАЧА ДЛЯ МАТРИЧНОЙ СИСТЕМЫ 207
новое количество нулей в верхней и нижней полуплос-
костях:
det5c+Mn=0, detx"|^n = O,
1шя,„>о, inan<o,
причем степени вырождений матриц %+ \\=% и % |л.=ц сов-
падают. Поскольку коэффициенты линейных связей между
столбцами матриц %+ и строками матриц % очевидным об-
разом не зависят от х, можно ввести два подпространства
№п - Im x~ \%=„ , М°п = ker x+ \%=к,
dx dx ) n vjy n
Для решения задачи Римана с нулями нам нужны под-
пространства
Nn = Im гр~ (\in)i Mn = ker г|з+ (^п). D1)
Очевидно,
Nn = ег ^п*№п, Мп — ё~г пЖМ°. D2)
Задание матрицы S (X) (точнее, матрицы G (X), чисел \ап,
Хп и подпространств 7V° и Мп) и представляет собой набор
данных рассеяния, по которым восстанавливается по-
тенциал при помощи решения задачи Римана с нулями.
Вклад нулей А* напоминает вклад дискретного спект-
ра в рассмотренных в гл. I примерах обратной задачи
рассеяния.
При положительной матрице / задача A) не может
иметь собственных значений в обычном смысле, поскольку
на одном из концов оси х все элементы матрицы eiJ%x
экспоненциально растут при любом X. Тем не менее нули
задачи Римана представляют собой — в некотором обоб-
щенном смысле — собственные значения спектральной
задачи. Пусть в точке X = Хо, Im Хо ^> О
Алг-м-i (^о) = 0, Длг-*: ф 0.
Рассмотрим к-ш столбец матрицы %+. С учетом C8) в
его асимптотике при х -> -j-oo присутствуют экспоненты
еЛоа**, i < к. В асимптотике же при х -> —с» присутствуют
экспоненты е1 *м, i > к. Поэтому вектор %кег%фх, где

208 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
пи < b <C fflfc_i, является экспоненциально убывающим
при х-н^+оо. Это рассуждение позволяет нам сформу-
лировать понятие обобщенного собственного числа спек-
тральной задачи A) — точка Яо называется обобщенным
собственным числом, а вектор г|зг — обобщенной собствен-
ной функцией, если существует такое вещественное Ь, что
¦ф. e-ttob* -+ о при х ->¦ +оо. D3)
Очевидно, что если число b существует, то ах^> b ^> ajv;
при этом оно может попасть в один из интервалов между
числами ак. Пусть а^ < b < a;^. Из анализа асимптотик
компонент вектора о|зг легко убедиться, что условие D3)
выполняется для всех чисел внутри этого интервала.
Поэтому можно классифицировать обобщенные собствен-
ные числа по интервалу между числами at, к которому
принадлежит Ъ. Таким образом, возникает N — 1 тип
обобщенных собственных значений. Эти собственные зна-
чения могут лежать в любой полуплоскости. В верхней
полуплоскости они совпадают с нулями нижних главных
миноров, а в нижней — с нулями верхних главных ми-
норов матрицы S. В рассматриваемом нами случае число
обобщенных собственных значений в верхней и нижней
полуплоскостях одинаково. Простому нулю задачи Рима-
на в общем положении соответствует совпадение в точке
X = Хо обобщенных собственных значений всех типов.
Спектральная задача A) обычно используется в пред-
положении, что потенциал U удовлетворяет некоторым
дополнительным "хловиям. Пусть В = В+ = В~х — диа-
гональная матрица, состоящая из чисел +1, и пусть по-
тенциал Q удовлетворяет соотношению
Q* = —BQB. D3')
(Здесь знак * обозначает эрмитово сопряжение.)
Очевидно,
U* = BUB.
Из уравнения A) легко получить следующее соотношение:
Сравнивая D4) с D) и пользуясь совпадением асимптотик,

§ 4J ЗАДАЧА N ВОЛН 209
получим
ф-1 = Вц*В, ф± = Ву±*В, D5)
откуда вытекает равенство
Is = S-1 = bs*b.
В частности, при В = 1 матрица S унитарна. Для тре-
угольных факторов имеем
Отсюда для матрицы G имеем
G* = BGB. D6)
Основные аналитические функции г|з±, г|з± подчиняются
инволюциям
ф± (Я,) = ВМр* (Х)В. D7)
Из D7) следует, что точки вырождения матриц, аналити-
ческих в верхней и нижней полуплоскостях — нули за-
дачи Римана — сопряжены друг другу:
[in = Хп-
Из D7) также следует, что подпространства Мп и Nn ор-
тогональны с метрикой, определяемой матрицей В:
(Nn, BMn) = 0, D8)
а проектор Р является .S-эрмитовым:
Р* = ВРВ. D9)
Таким образом, при выполнении условия D3) доста-
точно задавать расположение нулей и вырождение матриц
гM+ в верхней полуплоскости.
§ 4. Задача Ж волн
Спектральная задача C.1) применяется для решения
важной системы дифференциальных уравнений, имеющей
приложение в нелинейной оптике. Рассмотрим наряду
с C.1) уравнение
-1Ъ = (IX + у)ф. A)

210 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Здесь / = diag bi есть заданная диагональная веществен-
ная матрица, причем [/,/] = 0. Дифференцируя C.1)
по t, A) по х и приравнивая вторые производные тождест-
венно по К, получим систему уравнений
U,V] = U,U], B)
Ut-Vx + i[U,V]=0. C)
Уравнение B) может быть разрешено относительно U,V:
V = [I, Q], U = [J, Q). Тогда из C) имеем
U,Qt\ - U, QJ + i [[/, Q), t/, Q]] = 0. D)
Система D) и является упоминавшейся интегрируемой
системой. Если матрицы /, / невырождены, она, как легко
убедиться, допускает представление Лакса. Соответствую-
щая L — Л-пара состоит из операторов
')•
E)
Система D) имеет физический смысл, если предположить,
что потенциал удовлетворяет соотношению C.43'). Легко
проверить, что это соотношение не ротиворечит уравне-
нию D). Наложение условия C 43') вдвое уменьшает
число неизвестных функций в уравнении D). Такое умень-
шение числа неизвестных функций путем наложения сов-
местных с уравнением дополнительных условий мы будем
называть редукциями. Проблема перечисления релгукций,
совместимых с данным уравнением, является однойиз
самых важных в теории интегрируемых систем.
Перейдем теперь к описанию систем, возникающих
после редукции C.43') в уравнении D). В простейшем
случае Б = 1 в этой системе удобно ввести переменные
для верхней половины матрицы Q:
Q№- J^
У аг - ак
В этих переменных система D) окажется гамильтоновой
системой
dw№ дюп дНы
V1[) (')

§ 4] ЗАДАЧА N ВОЛН 211
Здесь
•*-$=?< <8>
a /Tint — гамильтониан взаимодействия
# int *= 21 eiftJ {wilcwrju>H + ЩкЩ;Щ}), (9)
где
«A ~ агЬ/
Система G) нетривиальна начиная с N = 3. В этом
случае, вводя обозначения
Ul =
получим
ди-, , ди, , _
-яг + vi irr = гем2м3,
дщ , ^ дщ ,л_ ,_ ,^q.
at
дщ
V3
dt
Для скоростей (8) имеем
v2 — v3
а а - (И>
Из A0), A1) видно, что переменные иъ и2 входят в урав-
нения симметрично, тогда как переменная и3 выделена.
Причина этого становится понятной после физической
интерпретации системы A0). Эта система описывает вза-
имодействие трех волновых пакетов с комплексными
огибающими иъ и2, и3 в среде с квадратичной нелинейно-
стью, при котором происходит распад волны и3 («накачка»)
на волны их и и3 и обратный процесс их слияния
u3^Ul + щ. A2)
Величины t>i представляют собой групповые скорости
волновых пакетов. Соотношение A1) показывает, что
на них наложено некоторое ограничение — в системе

212 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. Ш
отсчета, где накачка покоится, скорости волн их и и2
противоположны по направлению.
При N ^> 3 система G) описывает взаимодействие
N (N — 1)/2 волн различных типов. Гамильтониан взаи-
модействия (9) состоит из членов типа (wuv + uvw),
соответствующих элементарным процессам w *-* и + v, од-
нако он содержит далеко не все такие процессы. Так,
в случае /V = 4 разрешены следующие процессы:
иы <-> и12 -f- м24,
U24 <-> Ы2з -f- U-34,
u13 <-> ы12 ~г им.
Все эти процессы могут быть изображены на диаграмме
Видно, что все волны разбиваются на три типа: простые
волны (un,ui3,u3i), составные из двух (и13 и ии) и состав-
ная из трех (м14). Составные из двух могут распадаться
на две простые; составная из трех — на составную из
двух и простую.
Аналогичная ситуация имеет место и в общем случае.
В системе имеется N — 1 типов простых волн с амплиту-
дами Mfc,fc+i; N — 2 типов составных из двух (wfciJl-+2) и т. д.
вплоть до единственной волны uxn, составной из всех 7V — 1
простых волн. Все процессы идут по схеме
ит *^ ирг + и,,д, где р < г < q.
В случае /V = 3 групповые скорости взаимодействующих
волн находились в общем положении, подчиняясь только
неравенству A1). Начиная с N = 4 на значение скоростей
и константы взаимодействия егд накладываются алгебра-
ические условия, число которых быстро растет с номером N.
Пусть теперь В Ф 1. Обозначим В = diag гь где
rt = +1. В этом случае переменные w^ уже не будут ка-

§ 4] ЗАДАЧА N ВОЛН 213
ионическими переменными, вместо них нужно ввести но-
вые переменные
Фи- = гггкю1к = г ¦ A3)
У ai - ч
Заметим, что и в исходных переменных uift = (а, — a^Q^
система D) формально гамильтонова:
dt "lK дх " Ьиы
_
A4)
dt u дх 6uik '
где
хотя гамильтониан и является комплексным. Веществен-
ный гамильтониан возникает при подставновке A3) в
A5) и учете того обстоятельства, что
Рассмотрим различные варианты систем, возникающих
в простейшем случае W = 3. Пусть В = diag (—1,1,1).
В этом случае система D) приводится к виду
дщ . дщ
~дГ + ^~дГ
дщ , ди»
(i 6)
.-— -|- t7o
где
Ф12 == ^12' U1 == Ф23
U3 = Ф13 =
Система A6) отличается от A0) только тем, что накачкой
является волтта и,. С учетом неравенства A1) это различие
существенное: в системе отсчета, где накачка покоится,
волны м2 и и3 движутся теперь в одном направлении.

214 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ 1ГЛ. Ш
Аналогичная система (с заменой и1 <-> и2) возникает, если
В = diag A,1,-1).
Пусть теперь В = diag A,—1,1). В этом случае воз-
никает система
дщ . ди, . _ _ дщ ди2 . _ _
A7)
It + Vl ~дТ~ = lBU^U^ д
дщ дщ
Здесь щ = ф12 = — w12, м2 = ф23 = —w23, г*з = Ф13 =
= и13. Система A7) описывает «взрывную неустойчивость»—
взаимодействие трех волн, при котором они взаимно
усиливают друг друга. Все три волны в A7) равноправны.
При N ^> 3 и возникают системы, являющиеся комбина-
циями систем всех описанных видов.
Большой интерес представляет вопрос о дальнейших
редукциях системы D). Естественной редукцией является
переход к чисто вещественным уравнениям Q = iQ. По-
лагая Ut = iwt, получим из A0)
ди)л , dw-i
dw., dw.2
~W + Vi ~&Г"
dw3 , dw3
+ v
Уравнения A8) известны в нелинейной оптике как урав-
нения «точного резонанса» при параметрическом взаимо-
действии волновых пакетов. Дополнительная редукция
накладывает новые ограничения на данные рассеяния.
Совершая в уравнении C.1) комплексное сопряжение,
убеждаемся, что теперь
Ф(Ь) = Ф(-Д). A9)
Отсюда следует, что нули задачи Римана расположены
симметрично относительно мнимой оси и делятся на про-
стые — лежащие на мнимой оси — и двойные (это явле-
ние уже встречалось в теории уравнения sin-Gordon
(гл. I)). Для матрицы S получим также
¦S {-X) = S^l). B0)

§ 4]
ЗАДАЧА N ВОЛН
215
Аналогичное соотношение имеет место для всех треуголь-
ных матриц и для матрицы G.
Другие нетривиальные редукции возможны, если на
матрицы / и / наложены специальные ограничения.
Пусть, например, N = 3 и / = diag (а,0,—а), / =
= diag (ЬъЬг,—bij — две диагональные матрицы. Тогда
г>12 = у23 и в предположении эрмитовости и оказывается
возможна редукция системы A0), т. е. их = иг. При этом
возникает система уравнений
dui i „
ди3
at
¦ v3
дх
ди3
B1)
известная в нелинейной оптике и описывающая генера-
цию второй гармоники в нелинейной среде.
Пусть теперь iV = 4, / = diag (a1,a2,—а2,—ах), / =
= diag (ЬЪЬ2,—62,—bi). Тогда возможна новая редукция
Q = —CQtTC-\ B2)
где С — антидиагональная матрица одного из двух видов
0 ... 1"
С= ! 1 , B3)
1 О
О 1"
С= _! 1 , B4)
•1 0_
ltr означает транспонированную матрицу. Если редукция
B2) производится одновременно с редукцией C.43'), то
между ними должно выполняться условие согласования
С ВС = ±В.
Среди систем, возникающих в результате таких редук-
ций, наиболее интересна система, получающаяся, если
взять С из B4) и положить 6 = 1. При этом
= Wla, W3i = —Wn,
B5)
Я
int ;

216 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
а уравнения имеют вид
dwu дгоц
dt dx
dwls dw13
B6)
дш12 . dw12
dt dx
dww , ч< dw23
dl
Здесь
6 = e123 = 6124 =
f 6., o_.
23 ^2 2' 14 X t*"l>
Из B7) следует, что скорость v^ не могут быть выбраны
произвольными. Между ними имеется соотношение
(^12 ^14) (^13 — ?*2з) ~Ь (^13 — ^14) {Vl2 1^1з) == О-
Система B6) описывает взаимодействие в нелинейной
среде четных волн по схеме
+щ3,
Такая ситуация может встретиться при «модифицирован-
ной распадной неустойчивости» — распаде волны го13 на
волны w12: w23 при наличии «холостой» антистоксовой вол-
ны м>14.
§ 5. Солитонные решения
Опишем теперь процедуру интегрирования системы
D.4). Заметим, что уравнение C.1) и уравнение D.1)
играют в интегрировании этой системы совершенно равно-
правные роли. Поэтому должны иметь место формулы
типа C.35), C.42), отличающиеся от них лишь заменами
х -> t, I -*- J. Таким образом, мы приходим к выводу,

§ 5] СОЛИТОННЫЕ РЕШЕНИЯ 217
что каждому решению системы D.4) соответствует набор
не зависящих от х и t «данных рассеяния» — матрицы
G (X), нулей Хп, \in и подпространств Мп, Nn. Для его по-
строения необходимо решить при всех х я t задачу Римана
<р~ (x,t,X) а|з+ (x,t,%) = ei(-Jx+It^G (А,)е"* <•**+"> я. A)
с фиксированными нулями Хп, \in, в которых заданы под-
пространства
Мп = e-i(Jx+It)KnMl
B)
и воспользоваться формулой C.28). Если на системе D.4)
определены некоторые редукции, то данные рассеяния
должны быть подчинены соответствующим ограничениям.
Необходимо подчеркнуть, что из доказанной нами теоремы
об аналитичности функций ф±, if± следует, что мы можем
получить любое решение системы D.4), для которого
[ \u\dx < оо. Способ определения данных рассеяния
зависит от тех граничных условий, которые наложены на
D.4). Так, если для D.4) задана задача Копта, то данные
рассеяния извлекаются из изучения асимптотики функ-
ций ф± (х,Х) при х —*- +оо и из обобщенных собственных
функций задачи C.1) при t = 0. Аналогичным образом,
если задана задача Коши по х, то данные рассеяния сле-
дует извлекать из спектральной задачи D.1). Если задана
более сложная краевая задача, то необходимо пользоваться
обоими уравнениями C.1) и D.1).
В общем случае для построения U по данным рассея-
ния необходимо решать систему сингулярных интеграль-
ных уравнений. Замечательно, однако, что отдельные
наборы точных решений системы D.4) можно получить
в явном виде, решая только алгебраические уравнения.
Речь идет о случае, когда S = G = 1. Соответствующие
решения мы будем называть солитонными решениями.
Мы ограничимся анализом простейшего класса соли-
тонных решений, когда функции \|з±, \j5± имеют по одному
полюсу Хо, [i0. Будем предполагать, что выполнена одна
из редукций C.43'), поэтому [хо=Яо. Из формул B.16) имеем
гЬ+= 1— я°-^° р. C)

218 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ II ИХ РЕШЕНИЙ [ГЛ. III
Для потенциала U получаем из C.28)
U = (X0~ X0)[J,P] = 2ir\[J,P], D)
где к0 = Е + щ. При наличии редукции C.34') проектор
Р полностью определяется одним из своих подпространств
М или N. Напомним, что
М = «?-(¦**+")*.. Мо = кег г|5+|х=Хо = Im P.
В § 3 мы видели, что в случае, если нуль задачи Римана
является простым,— на обобщенном собственном числе
спектральной задачи C.1),— то подпространство Мо имеет
размерность единицу. Соответствующий проектор Р легко
построить. Пусть М натянуто на вектор с компонентами
1Щ = g-^+V'4^, E)
где а{ — заданный постоянный комплексный вектор. Проек-
тор Р проектирует все пространство CN в М, следовательно,
Ptj = niiJlj, F)
где rij — некоторый неизвестный вектор.
Из условия Р2 = Р имеем
г
Из условия Р* = ВРВ (В = diag rt) находим
Окончательно имеем
r
Для потенциала U теперь получаем
m,.m;
|2
к
т -т-
ц,, = гЛа,-а,-) I . (8)
Формула (8) даст явный вид однополюсного солитонного
решения с одномерным проектором. Для модуля этого

§ 5] СОЛИТОННЫЕ РЕШЕНИЯ 219
решения имеем
| _ 2tl (а» — Qj) / «г ' I ai I exP Kai + aj) 1* + ^i + й>> Ч<]
' ^г|аРехр[2(«г +
(9)
Формула (9) позволяет выяснить условие существования
солитонных решений различных типов. Пусть В = I,
Г}; = 1. Тогда знаменатель в (9) не может обращаться
в нуль при конечных х, а при х-++ °° |м,-7-| экспоненци-
ально убывает. Поэтому солитонное решение существует
при любом виде вектора а^. Пусть вектор а^ содержит
всего две ненулевые компоненты at и а,-, тогда потенциал
имеет только дна ненулевых элемента utj и ил = Тщ-
При этом
Щ) = Ч (аг — ai) X
ехр {II [{аг + а-) хУ + F. -!- &.) f^ -j- arg (о. - а;)]}
Х сЪ{1\[(а-а)х + (Ь-Ь^ + х]} ' A }
где х0 = — In —
Решение A0) будем называть солитоном волны utj.
Пусть нуль X = Хо есть обобщенное собственное значение
типа к. Тогда вектор а^ содержит две ненулевые компо-
ненты ak_i, ак. В потенциале U будут отличны от нуля
лишь компоненты uk_lih, ufc>A_i, и мы приходим к следую-
щему выводу: обобщенные собственные значения задачи
C.1) соответствуют солитонам простых нераспадающих-
ся волн в системе D.4). Чтобы получить солитон состав-
ной волны uitt+v, p^> 1, необходимо обращение в нуль
в точке X = Хо подряд расположенных р главных мино-
ров матрицы 5. Матрица % должна иметь при X = Хо ранг
N — 1, а ее нулевой собственный вектор а — две нену-
левые компоненты а, и аг -f- p.
Пусть N = 3. Исследуем асимптотику решения (8)
при t —к + оо, если все компоненты вектора а отличны
от нуля.
Легко проверить, что ненулевая асимптотика возни-
кает только на характеристиках х = Рд2 -f- с, где vti: —
скорость одного из солитонов (солитона волны и hi), и на
этой характеристике при t —>¦ + °° могут быть отличны

220 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ II ИХ РЕШЕНИЙ [ГЛ. III
от нуля только элементы и^, щь соответствующие этому
солитону. Проследим за компонентой и13, соответствующей
составному солитону (солитону накачки). Обозначим
(аг — as)x + (&! — b3)t = z.
Пусть выполнены соотношения
h~ba>bl-bi_^
а2 — аЗ а1 — а2
Тогда, как легко убедиться, при t ->¦ оо элемент и13 стре-
мится к нулю экспоненциальным образом, а при ?-н> оо
— к солитону накачки с положением центра '
A2)
Проследим теперь за компонентами ип и м23. При ?->¦ — оо
они экспоненциально стремятся к нулю. При t —>¦ + оо
они стремятся к соответствующим солитонам простых волн
с положением центров
A3)
Таким образом, решение (8) описывает распад состав-
ного солитона на два простых. Положение центров «про-
дуктов распада» логарифмически зависит от величины а2.
При а2 ""*" 0 продукты распада находятся в бесконечно-
сти, т. е. распад происходит за бесконечное время. Ана-
лиз солитонного решения с двумерным проектором, ког-
да ранг матрицы X |^=0 равен двум и подпространство М
характеризуется двумя векторами, показывает, что оно
описывает обратный процесс слияния простых солитонов
в солитон накачки. При выполнении неравенства, обрат-
ного неравенству A1), решение с одномерным проектором
описывает слияние, а с двумерным — распад составного
солитона.
При#> 3 ситуация значительно сложнее — солитон-
ные значения с единственным полюсом X = Яо описывают
все возможные процессы распада и взаимопревращения
простых и составных солитонов разной сложности, соот-
ветствующих разным элементам матрицы иц.
1
1
1
In
cu
а..
аз

§ 51 СОЛИТОННЫЕ РЕШЕНИЯ 221
Все явления такого рода мы будем называть нетри-
виальным взаимодействием солитонов в отличие от три-
виального взаимодействия — рассеяния. Нетривиальное
взаимодействие возможно только для солитонов, значения
спектрального параметра X для которых совпадают.
Двухполюсные решения задачи Римана описывают уже
столкновения двух групп солитонов, нетривиально взаимо-
действующих внутри каждой группы.
Случай, когда В ф- 1, мы рассмотрим только на при-
мере N = 3. Пусть В = diag (—1, 1, 1). Очевидно, в этом
случае решения (8), (9) не имеют особенности, только если
аг = 0. Таким образом, в этом случае может существо-
вать только один вид солитонов — солитоны простой вол-
ны м23. Солитоны другой простой волны и12 и составные
солитоны и13 отсутствуют, и имеется только один тип
обобщенных собственных значений. Аналогичная ситуа-
ция имеет место, если В = diag A, 1,-1). Итак, в системе
D.16) отсутствует нетривиальное взаимодействие солито-
нов.
Очень интересная ситуация имеет место, если В =
= diag A, —1,1). В этом случае также может неопреде-
ленно долго существовать только один тип солитонов —
и13. Однако, в течение конечного времени может сущест-
вовать и общее решение (8). Рассмотрим с точностью до
множителя знаменатель выражения (9)
Д = 1 _ | pt р e-e.x-w + | р2 |Ve**-™, A4)
где
8j = аг — а2, б2 = ах — а3, 62> 6j> 0,
Yi = bi — b2, ?2 = &i — b3.
Выражение А не имеет нуля, если
Ш^^-у^). A5)
Неравенству A5) можно удовлетворить при любом t, по-
ложив рх достаточно малым. Однако, если Yi/Sj ф у2/82,
это неравенство нарушится при достаточно большом по-
ложительном или отрицательном t = t0. Если неравен-
ство нарушается при положительном t0, соответствующее
решение описывает процесс взрывной неустойчивости с
образованием в конечный момент времени особенности в

222 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
некоторой точке х0. Если t0 <;0, то решение описывает
обратный процесс «рассасывания» существовавшей в на-
чальный момент времени особенности.
§ 6. Системы, интегрируемые
при помощи задачи Римана
Как мы видели на примере задачи п волн, для построе-
ния частных солитонных решений пет необходимости
производить полное исследование спектральной задачи
и соответствующей задачи Римана. Такое исследование, по
необходимости включающее доказательство теоремы о
существовании аналитических решений, может оказаться
достаточно трудной проблемой. Поэтому мы изложим пря-
мой метод вычисления интегрируемых при помощи задач
Римана систем и их солитонных решений. Ключевую роль
в этом методе имеют формулы, обобщающие полученные
нами для случая п волн формулы E.1), E.2). Рассмот-
ренные ниже интегрируемые системы есть условия совме-
стности уравнений типа C.1), D.1), в которых, однако,
имеется более общая зависимость от спектрального пара-
метра К.
Рассмотрим переопределенную систему дифференци-
альных уравнений
фх = ?/ф, ф( == Уц>. A)
Здесь U vi V — комплексные (N X ./У)-матрицы, рацио-
нальным образом зависящие от комплексного параметра
X. Условие совместности этих уравнений имеет вид
Ut-Vs + [U, V) = 0. B)
Если число полюсов функции U (с учетом их кратности)
равно Ni, а функции V — равно iV2, то функции U и V
имеют Ni + N2 + 2 независимых матричных функцио-
нальных параметров. Условие A) накладывает на них
Л^ + N2 + 1 уравнений. Эта система уравнений и явля-
ется рассматриваемой нами интегрируемой системой.
(Для случая КдФ Q = V, U = А, и обе матрицы явля-
ются полиномами от к — см. (II.1.16), (II.1.21).) Если U
и V имеют простые полюсы
Л*=1 А1—1

§ 6] ИНТЕГРИРОВАНИЕ ПРИ ПОМОЩИ ЗАДАЧИ РИМАНА 223
то получаем
UQt - Пх + [Uo, Vo] = 0, D)
Vnx + [Vn, Тп] = 0, E)
где
Nz T. N,
R I/ 4 V m Т TI I ^ U
6n-am
В C) — E) ап = ап (х) шЪп = Ъп (t) — заданные функции
х и t.
Неопределенность системы B) объясняется ее «калиб-
ровочной инвариантностью». Пусть U, V — некоторое ее
решение, ср — соответствующее решение системы A).
Рассмотрим функции
U = gUg'1 + gxg-1; V - gVg-^ + gtg~\ F)
где g — произвольная невырожденная матрица. Легко
проверить, что U и V снова удовлетворяют уравнению B).
Соответствующее решение системы A) есть ср = gcp. Пре-
образование U, V^>-U, V мы будем называть калибро-
вочным. Применительно к системе D), E) имеем
Uo = gUog-1 + ekg-1, Fo = gVog-1 + gtg~\ G)
Vn = gUng'\ К = gVng~\ (8)
Система B) может быть доопределена наложением на
U, V дополнительного условия. Например, можно поло-
жить Uo = 0, при этом с точностью до калибровки можно
считать Vo = 0. Решение уравнений, доопределенных
при помощи любого другого условия, отличаются от
этого случая лишь преобразованием с некоторой матри-
цей g. Все такие уравнения мы будем называть калибро-
вочно-эквивалентными. Заметим еще, что уравнения име-
ют естественные тривиальные решения U = А (х, X),
V — В (t, X), [А (х, К), В (t, X)] = 0. Соответствующее ре-
шение уравнения A) обозначим через со. В рассмотренном
ранее случае уравнений U = J'K + [/, Q\, V ----- IX +
-\-\I, Q] решение есть со = e»MJ*+JO.

224 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ II ИХ РЕШЕНИЙ [ГЛ. III
Покажем теперь, как имея одно решение системы A),
B), — например, А, В, ш, строить новые ее решения, за-
висящие от функционального параметра.
Пусть Г — замкнутый или уходящий в бесконечность
контур на плоскости комплексной переменной Я. Рассмот-
рим при всех х ж t регулярную задачу Римана
oh (x, t, Ща (х, t, X) = фо (х, t, K)G (ЩоЧх, t, X). (9)
Здесь фо — некоторое решение системы A) (для простоты
можно считать ф0 — ш). Может оказаться, что контур Г
проходит через полюсы функций U, V. В этих полюсах
мы должны положить G — 1. Это позволит нам диффе-
ренцировать (9) по х п t. После дифференцирования по х
получим
Определим матричную функцию U формулой
U = -4Г1 Ьрьс - А^) = (i()te + яМЖ1- (И)
Из формулы A1) следует, что U продолжается с контура
Г на всю комплексную плоскость и является там рацио-
нальной функцией, полюсы которой совпадают с полюса-
ми А. Из A1) следует
\!pix = Щг — я|52Л. A2)
Аналогично, дифференцируя по I, определим функцию
V = -я^1 (о|I4 - В^) = (i|>ai + ^ВЦГ,1. A3)
Полюсы функции V совпадают с полюсами В. Полагая
i|>i = ыф!1; 'Фг = Фг1»'1! убеждаемся, что фъ ф2 удовлет-
A) Т б
|i ф Ф Ф фъ ф2
воряют уравнениям A). Таким образом, эти уравнения
совместны, и функции U, V удовлетворяют системе B).
До сих пор нормировка задачи Римана была произволь-
ной. Рассмотрим новое решение задачи Римана, отличаю-
щееся от прежнего нормировкой ц>1 = tyig'1, яр2 = gtyz,
где g — произвольная матричная функция х и t. Легко
проверить, что функции U и V испытывают калибровочное
преобразование F). В связи с этим возникает естественный
способ доопределения системы B), состоящий в выборе
определенной нормировки задачи Римана. Особую роль
играет единичная нормировка в одном из полюсов функ-

§ 6] ИНТЕГРИРОВАНИЕ ПРИ ПОМОЩИ ЗАДАЧИ РИМАНЛ 225
ций U, V. Так, в задаче п волн матрицы U, V имели един-
ственный полюс при Я = оо, и задача Римана была нор-
мирована в бесконечности на единичную матрицу. В при-
мере E) нормировка задачи Римана была той же: я^ (оо) =
= 1, но в этом случае точка Я = оо не совпадала ни с од-
ним из полюсов U и V.
Изложенную процедуру построения решений системы
B) можно называть «одеванием» «затравочных» решений
А, В при помощи задачи Римана с контуром 1 и функцией
G (Я). Приведем на примере системы D), E), когда U и V
имеют лишь простые полюсы, явные формулы, осуществ-
ляющие «одевание»:
Uо = — go1 gox,
У о = -g? got, A4)
Un = gnAngn\ Vn = gnBng~\
Здесь g0 =^i (оо), а матрицы gn и gn представляют со-
бой значения в точках Я = ап и X = Ъп функций тр^1 или
г|;2 в зависимости от того, вне или внутри контура рас-
положена данная точка. Напомним, что если ап или Ьп
лежат на контуре, то в этой точке G = 1 и г^1 = г|?2. Фор-
мулы A4) показывают, что при «одевании» инварианты
матриц Un и Vn сохраняются.
В A4) предполагалось, что gn Ф 1, %пФ 1, т. е. что
задача Римана не нормирована на единицу ни в одном из
полюсов. Если ^j \\=а =1, то Un = Ап, но меняется
формула для Uo. Именно, пусть \\)г си 1 -\- (к — ап) Q,
тогда, очевидно, Uo = [An, Q] в полном соответствии с
C.2). Заметим еще, что вся изложенная процедура триви-
альным образом переносится на случай, когда одна из
переменных х, t или обе они являются комплексными.
Очевидно, что изложенная выше процедура интегрирова-
ния является локальной по х и t — при подходящем вы-
боре Г и G можно добиться, чтобы решение U (х,* ^/нап-
ример, экспоненциально росло при х -> + сю.
Для построения солитонных решений необходимо рас-
сматривать задачу Римана с нулями. Как и прежде, мы
задаем не зависящие от х и t наборы нулей кп и цп и в каж-
дом из них подпросч ранства
7V7l = Im ip! Ij^jl, Mn = ker ipa \x=u. A5)

226 ПОСТРОЕН. ИНТЕГРШ». СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. Ill
При этом в формулах A1), A3), определяющих U и V,
вообще говоря, появляются дополнительные полюсы в
точках кп, \in. Необходимо потребовать, чтобы вычеты в
этих полюсах были равны нулю. Определим дифферен-
циальные операторы
= дх - A |,=v D?> = дх~А v
DM = dt-B k=v Dp = dt~B\ K^n-
Из (И), A3) следует
CnD™Fn = О, CnD^Fn = О,
Здесь Сп — вычеты я];, Fn — значения *фх в точках
Я = Хп, сп — вычеты т^г1, Рп — значения тр2 в точках
Из формул A6) следует, что подпространства Мп ин-
вариантны относительно действия операторов Dx , D\ ,
а подпространства Nn инвариантны относительно дейст-
вия А?', Мп)- Ясно, что подпространства
Мп (х, t) = <i> (x, t, ц„) М%\
Nn (x, t) = со (х, t, К) Nf
обладают свойством инвариантности тогда и только тогда,
когда М^ и N\? не зависят от х и t. Формулы A7) обоб-
щают формулы C.42).
Если G = 1, можно строить солитонные решения об-
щей системы B) по той же схеме, что и для задачи и-волн.
Остановимся еще на проблеме редукций в системе A).
Разумеется, возможность той или иной редукции в силь-
ной степени зависит от расположения полюсов U, V и
от вида «затравочного» решения А, В. Тем не менее,
можно сделать ряд общих замечаний. Ясно, например,
что U и V в системе A) можно сузить с алгебры всех
комплексных матриц па любую ее подалгебру, допускаю-
щую умножение на комплексные числа. Если все полюсы
матриц U и V лежат на вещественной оси, то можно счи-
тать U и V принадлежащими любой подалгебре, напри-
мер — антиэрмитовыми матрицами. В общем случае

§ 7] КИРАЛЬНЫБ ПОЛЯ 227
можно считать
U* = CUC, С2 = 1, С+ = С,
[АС] = [ВС] = 0.
Вытекающие из редукции следствия на задачу Римана
устанавливаются так, же, как это было сделано в § 3.
Заметим еще, что система B) в качестве простого част-
ного случая содержит все интегрируемые системы, допус-
кающие представление Лакса в виде L — Л-дары. Именно,
ото системы, для которых функция U, входящая в первое
из уравнений A), имеет единственный простой полюс, а
функция V — полюс произвольного порядка. Не огра-
ничивая общности, можно считать, что этот полюс нахо-
дится в точке К = оо, при этом V становится полиномом
по X.
Следующим по уровню сложности является случай,
когда U имеет единственный простой полюс, а располо-
жение полюсов V произвольно. В этом случае система B)
также допускает L — Л-пару, но оператор Л является уже
интегральным, и его вычисление нетривиально; что же
касается оператора L, то он только калибровочным пре-
образованием отличается от оператора, возникающего из
C.1). Поскольку для применения метода достаточно пост-
роения теории прямой и обратной задач рассеяния для
одного из операторов L и Л, теория таких систем лишь
несущественными деталями (другой временной динами-
кой и другой нормировкой задачи Римана) отличается от
теории, изложенной в §§ 3 — 5, и легко может быть по-
строена с той же полнотой.
§ 7. Релятивистски-инвариантные системы —
киралыше поля
Замечательно, что среди уравнений (fi.2) имеются об-
ширные классы уравнений, описывающих релятивистски-
инвариантные двумерные модели классической теории
поля. Простейшим примером таких моделей является
разобранное в гл. I уравнение sin-Gordon. Рассмотрим
вместо уравнений F.1) уравнения
Щ = Uq, Щ\ = Fi]> A)

228 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ II ИХ РЕШЕНИЙ [ГЛ. III
и их условие совместности
[/„- Vl = i[U, V]. B)
Здесь | = V2 (г + а;), т] = V2 (i — х) — «конусные» пере-
менные в пространстве-времени, a U, V, как и прежде,—
рациональные функции к с полюсами ап, Ьп.
Обсудим вопрос о релятивистской инвариантности
рассматриваемых систем. Система B) очевидным образом
становится инвариантной относительно специальной груп-
пы Лоренца, если считать, чго U, V преобразуются при
преобразованиях Лоренца как компоненты вектора. Дей-
ствительно, при преобразовании с параметром у имеем
1 -> у\, х\ -> у\\, и Для инвариантности достаточно поло-
жить U-*-у^16Г, V-^-yV. При отражении координаты
х происходит замена Н <-» л. Поэтому для инвариантности
относительно полной группы Лоренца достаточно потре-
бовать существования дискретной инволюции, включаю-
щей дробно-линейное преобразование плоскости X, при
котором происходит переход U -> V, V -> U.
Рассмотрим пример системы, инвариантной относи-
тельно полной группы Лоренца:
71=1 П-=1
Тогда
iVnl = [Ф„, Vn], Штл = [Qn, Un], D)
Фп =
П
Причем a, + a7- ^= 0 при любых г, /.
He представляет труда выписать систему типа D) и в
тОхМ случае, когда полюсы могут быть кратными и допус-
каются нули знаменателей у Фп и fin.
Заметим еще, что матрицу г|з в A) можно считать эле-
ментом некоторой группы матриц G. Тогда U и V окажут-
ся элементами соответствующей алгебры Ли; очевидно,
что уравнение B) не выводит за пределы этой алгебры.
Мы будем изучать простейший случай системы D), когда
матрицы U я V имеют по одному простому полюсу, по-
ложение которого не зависит от х и t. He ограничивая

§ 7) КИРАЛЬНЫЕ ПОЛЯ 229
общности, можно положить
Система уравнений D) имеет вид
um~ vo%~ nu0, ig = o, F)
= 0, Gа)
- 0. G6)
Представляют интерес различные калибровки системы
F), G). Полагая Uo = Vo = 0, придем к системе урав-
нений
2 2
Здесь А = Оъ В = —Уг.
Уравнения (8) — условия совместности системы урав-
нений
— л ь i — в
Другая калибровка состоит в диагонализации мат-
рицы Uv Положим в E) U1 = A0(^). Тогда уравнение
Gа) может быть явно разрешено. Положим Uo=—AQ/2-{-
+ С, T = V1 = 2(V0~ S), (X - 1IA + 1) = z; здесь
S — некоторая диагональная матрица.
Тогда система A) примет вид
а уравнение (E)
I (Сц ~ Съ) = У, \А0, TJ - IS, С].
Полагая С = Сх + Сц, где С\\ — диагональная матрица,
заметим, что
Св„-5| = 0, т. е. Сц =Rb S = Rn.

230 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЯ [ГЛ. III
Окончательно система F) — (8) примет вид
A0)
*ГЕ = -[Cj_+ Rb Г].
Система уравнений A0) (U — Т^-система) в частном слу-
чае сводится к уравнению sin-Gordon.
Уравнения (8) связаны с одной из классических мо-
делей теории поля, имеющей геометрический смысл, —
^главным киральным полем. Пусть в каждой точке плос-
кости (?;, г)) задан g (?,, г\) — элемент группы Ли G и пусть
G реализована как подгруппа группы комплексных мат-
риц. Рассмотрим плотность лагранжиана
Выражение A1) замечательно тем, что является двусто-
ронпе инвариантной формой на G. Действительно, произ-
ведем левый сдвиг при помощи постоянной матрицы
h €E G {g-^hg) и, совершая в A1) циклическую перес-
тановку, убедимся в инвариантности L. Очевидна также
инвариантность лагранжиана L относительно правых
сдвигов g —>- gh. Лагранжиану L соответствуют уравнения
движения
л
Уравнения A2) называются уравнениями главного ки-
рального поля на группе G. Им можно придать другую
форму. Введем поля А и В, принадлежащие алгебре Ли
группы G:
А = iglg-\ В = ig^g-K A3)
Очевидно, имеет место соотношение
Л„ - Я6 = i [А, В]. A4)
Из A2) следует также легко проверяемое соотношение
Аъ+Въ = 0. A5)
Система уравнений A4), A5) очевидным образом эквива-
лентна системе (8). Величины А и В можно интерпрети-

§ 7] КИРАЛЫШЕ ПОЛЯ 2Л1
ровать как токи, порожденные симметрией лагранжиана
относительно сдвигов на группе, а уравнение A5) — как
закон сохранения этих токов.
В переменных A3) лагранжиан A1) имеет вид
L = -2-SVAB, A6)
а уравнение A5) является соответствующим уравнением
Лаграгока с учетом связи A4).
Разрешим явно уравнение A5). Получим
А = Ф|, В = — Ф„,
тогда уравнение A4) примет вид
Оно может быть получено из лагранжиана
L = -i-SpOjO,, + 4-^р(Ф [Ф6, Ф„1). A8)
Уравнение (8) в эрмитовых матрицах второго порядка
при дополнительных условиях
Sp A = Sp В = О, Sp A2 = Sp В2 = 1
описывает движение в четырехмерном пространстве-вре-
мени релятивистской струны, помещенной в однородное
безмассовое скалярное поле.
Вообще из (8) следует
SVA = 0, SpB = 0 A9)
при произвольной степени п. Из (8) следует также, что
нормальная жорданова форма Ао матрицы А не зависит
от г), а Во — нормальная форма матрицы В — не зависит
от \. Таким образом, Ао = Ао (?), Во = Вог(т)). Представ-
ляя А и В в виде
убеждаемся, что матрицы/], /2 определены с точностью до
умножения справа на произвольные матрицы /i, fl, ком-
мутирующие соответственно с Ао, Во.

232 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ II ИХ РЕШЕНИЙ [ГЛ. III
Пусть G = SU (N). Тогда матрицы А и В — эрмитовы,
причем Sp А = Sp В = 0, при этом Ао и Во — диаго-
нальные матрицы, а матрицы /х и /2 могут быть выбраны
элементами группы SU (Лг). Если при этом собственные
значения матриц А и В различны, то матрицы/15 /2 оказы-
ваются определенными с точностью до умножения на
произвольную диагональную унитарную матрицу. Таким
образом, матрицы /х и /2 можно считать определенными на
многообразии М, возникающем при факторизации группы
SLJ (Лг) по подгруппе И диагональных матриц, т. е. на
«пространстве флагов» SU (N)lH. При фиксированных А„,
Вп па этом же пространстве определены и матрицы А и В.
Если среди собственных чисел А, В имеются совпадаю-
щие, соответствующее многообразие М — «вырожденное
пространство флагов» — будет иметь меньшую размер-
ность.
Перейдем в системе A7) от конусных переменных %, Г|
к физическим переменным х0 = t = г] + %, хх = х —
= г) — | и вычислим тензор энергии — импульса
в результате получим
J00 и у-!! = _1_ Sp (ф2 + ф2} = 1 gp (ф2
B0)
Г и = Tw = Sp Ф(ФЯ = Sp {Ф\ - Ф|).
Отсюда следует выражение для гамильтониана системы
Я = J Г°Ш' =-- 4" $ Sp (Ф? + Ф«) da; =
;a;. B1)
Из B1) видно, что гамильтониан системы A7) — величи-
на, не зависящая от вида А и В. При вычитании
постоянной части гамильтониан обращается в нуль.
Аналогичный результат — равенство нулю гамильто-
ниана — можно получить и непосредственно для системы
A2) и систем A4), A5).

§ 71 КИРАЛЬНЫЕ ПОЛЯ 233
Чтобы избежать трудностей, связанных с нулевым
гамильтонианом, например, трудности с правильным
определением энергии, нужно разрешить связи A9), фик-
сируя матрицы А и В и вводя координаты на многообразии
Мо. При этом возникает новая трудность — показать, что
полученные уравнения являются лагранжевыми, т. е.
следуют из некоторого принципа наименьшего действия.
Покажем, как эта трудность преодолевается, если G =
= SU2. Положим для простоты
4-БрЛ2 =-Lsp5a= 1 B2)
и разложим А и В по матрицам Паули
А = оА, В = аВ,
Векторы А и В имеют единичную длину. Введем обозна-
чение cos а =АВ и вычислим производные А^ и />'t
Al = [А, агВ + а2[А В]],
Вп = [В, ЬХА + Ь2 [А В}},
где аъ а2, Ьъ Ъ2 — числовые функции. Вычисляя
д д
—¦(АВ), -тг-(АВ), найдем
а2 = ag/sin a, b2 = а^/sin а. B4)
Введем еще
аг = f//sin а, Ьг = Wsin a, ^25)
U = A^B^/am a, V = A^B^/sin a.
Дифференцируя a, U, V и используя B3) — B5), полу-
чим следующую систему уравнений:
аЪп -|- sin a + UV/sin a = 0, B6)
иц = a^Wsin a, B7)
V% = a^U/sin a. B8)
Из B7), B8) следует
^- +flE Fctg^- =0,

234 ПОСТРОЕН. ИНТЕГРЙР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
так что
Величины
к-
а, C
1
= U ctg ¦
а
~2~
. Рл
удовлетворяют
iTi ' si
+ sin a
1
па
¦КРЕ
sin -
= -Fctg-^-.
уравнениям
+ афц)-0,
а
B9)
C0)
Уравнения B9), C0) являются уравнениями Лагранжа
для лагранжиана
Компоненты тензора энергии — импульса имеют при этом
вид
Т™ = 4- д^а <9'la + 4- 1ё2 "Г" ^Р 5'1Р + cos a — 1, C2)
Вектор энергии — импульса для полей а и E может быть
выражен и в терминах исходных полей А и В:
C4)
4 [1 — (ЛВJ]
В рассмотренном нами случае
II О']
В более общем случае Ло = а (?)а3, Во = b (ц)о3. Одна-
ко, полагая
^ '' 5; ~ 15;л ^' ё;> C6)
(л. D»

§ 7]
КИРАЛЬНЫЕ ПОЛЯ
235
где ц = J Ъ (т|) dr\, § — Ja (g) <2g, придем в переменных
Я, 5, f), | к рассмотренному выше случаю. Заметим, что
замена переменных C6) является взаимно-однозначной,
только если функции а (?) и Ъ (г\) не имеют нулей.
Покажем, что предложенная выше процедура разреше-
ния связей обобщается на случай группы SU (N) и явля-
ется в сущности переходом от исходной системы (8) к си-
стеме A0). Действительно, при выводе системы A0) уже
проделано частичное интегрирование — введение произ-
вольной диагональной матрицы R. Сведем систему A0)
к одному уравнению второго порядка. Для этого заметим,
что матрица Г может быть представлена в виде
Г =
= /i/f ¦
Матрица ф унитарна и принадлежит «пространству фла-
Ров» SU {N)/H. Из уравнений A0) следует
Во] = 0
или
где W — некоторая коммутирующая с В диагональная
матрица, элементы которой W^ = бд- Wt.
Величины Wi могут быть найдены из условия равен-
ства нулю диагональных элементов матрицы Сх.
Заметим, что матрица ф определена с точностью до
). При
умножения на диагональную матрицу eiL(Lik =
таком преобразовании происходит замена
Полагая в случае группы SU B)
C7)
Ф
COS
cos
= 0, C8)
придем для а и р к системе B9), C0).
В общем случае, полагая Ь% =—W, R == 0, можно
добиться
W = 0.
C9)

236 ПОСТГОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Соответствующая система
Зт,(ФбФ*) + 4" 1Ф^Ф*' 4>] = 0 D0)
при Во = Ао для случая группы SU C) может быть при-
ведена к лагранжеву виду. Заметим еще, что система D0)
хотя и задана на группе ортогональных матриц, отнюдь
не совпадает с главным киральным полем на ортогональ-
ной группе. Действительно, вещественное пространство
флагов группы SU (N) состоит из всей группы ортогональ-
ных матриц, тогда как пространство флагов ортогональной
группы имеет очевидным образом меньшую размерность.
В частности уравнение D0) на группе SO B) есть уравне-
ние sin-Gordon, тогда как главное киральное поле на
группе SO B) в силу ее коммутативности описывается ли-
нейными уравнениями.
Построенные нами системы представляют уравнения
для очень большого числа взаимодействующих полей.
Общая система D) в случае «полюсов на SU (N) содержит
nN (N — 1)/2 комплексных полей и лишь при нескольких
первых значениях этого числа можно надеяться, что она
будет применима в теории поля. Поэтому очень большую
роль приобретает проблема уменьшения числа взаимо-
действующих полей — проблема редукции. Редукции для
главных киральных полей замечательны тем, что имеют
ясный геометрический смысл. Рассмотрим главное ки-
ральное поле на группе G (в дальнейшем будем предпола-
гать G = SU (N) или SO (N)) и допустим, что оно удовлет-
воряет дополнительному условию
g2 = I- D1)
Покажем, что это условие совместимо с уравнениями глав-
ного кирального поля, которые имеют вид
(/ @ 00 Л_ 0 00 \ {A^\
Продифференцируем D1) по | и г). Получим
gl-ng + ggfn + g\gn + gngl = °- D3)
Подставим D2) в D3) и воспользуемся следующими из
D1) соотношениями g%g = —ggb gng = —ggn. При этом
мы убедимся в тождественном выполнении D1), что и до-

§ 7] КИРАЛЬНЫБ ПОЛЯ 237
называет совместимость уравнения D2) и условия D1).
Замечательно, что условие D1) имеет геометрический
смысл. Представим g в виде
g = i-2P, D4)'
тогда из D1) следует Р2 -— Р, т. е. Р является оператором
проектирования, действующим в пространстве присоеди-
ненного представления группы G. Условие C1) выделяет
в группе G как в римановом пространстве некоторое под-
пространство G. Подпространство G не является связным.
Каждый проекционный оператор /\ характеризуется раз-
мерностью к своего образа — пространства, в которое он
проектирует. Очевидно, что в процессе эволюции число к
не может меняться, поэтому можно считать g = 1 — 2/V
Пусть размерность пространства присоединенного пред-
ставления группы g есть N. Элемент g группы G предста-
вим также в виде g = —1 + 2Р, где Р' = 1 — Р — до-
полнительный к Р проектор. Поэтому, не ограничивая
общности, можно считать, что к ^ [iV/2]. Таким образом,
уравнение D3) представляет собой набор уравнений
[Род, Р};\ = О, /?==1,2,..., [N12] D5)
(знак [а] обозначает целую часть числа а). Соответствую-
щие выражения для действия имеют вид
D6)
Каждое из уравнений D5) представляет собой кираль-
ное поле, заданное на пространстве проекторов размер-
ности к. Это пространство в вещественном случае называ-
ется вещественным грассмановым многообразием Г$, jp
в комплексном случае — комплексным грассмановым мно-
гообразием Tn,ic- Грассмановы многообразия являются
однородными пространствами групп SO (N) и SU (TV)
и представляют собой результат факторизации этих групп
по подгруппам меньшей размерности:
гк SO (N) гс SU (N) ,,ъ
lN>'!- О (к) SO (N — к) ' iN.k~ U{k)SU(N-k) ' ( >
Грассмановы многообразия представляют собой множест-
ва плоскостей данной размерности к в вещественном или

238 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ 1ГЛ. Ill
комплексном пространстве размерности TV, группы SO (N)
или SU (N) действуют на них как группы поворотов.
В частном случае к = 1 грассмановы многообразия назы-
ваются проективными (вещественными или комплексными)
пространствами размерности N и обозначаются J\PN
и CPN. В этом случае проектор Рх может быть записан
в виде
N
(Pi)ih. = щпк, 21 пгщ = (и п) = 1. D8)
г=1
Подставляя D8) в действие D6), получим
j + 2 (пщ)(ппц)Ы1 с1ц. D9)
Соответствующее уравнение движения в вещественном
случае есть
«In + (щп^п = 0, E0)
в комплексном случае —
— (тъщ) пц — (ппц) щ + 2 (ппц) (пщ) п = 0. E1)
В соотношениях D8) в вещественном случае вектор п
определен с точностью до знака, т. е. киральному полю
на вещественном проективном пространстве соответству-
ют только те решения уравнения E0), при которых вектор
п совершает движение лишь в одной полусфере SN~1.
Уравнение E0) имеет смысл и при снятии этого ограниче-
ния. В этом случае оно есть уравнение п-поая на сфере
SN~1. Локальное совпадение уравнений кирального поля
на RP14'1 и на сфере SN~X объясняется тем, что проектив-
ное пространство R/5^ есть результат факторизации сфе-
ры по дискретной группе Z2-
Вещественная и комплексная сферы также являются
однородными пространствами групп SO (N) и SU (JV) и
представляют собой результат факторизации этих групп
по подгруппам SO (N — 1) и SU (N — 1). Сферы являются
примером более общих однородных подпространств —
многообразий Штифеля а^, s и о^ к. Эти многообразия
представляют собой множества ортонормировапных репе-
ров из к векторов в вещественном или комплексном прост-

§ 7] КИРАЛЬНЫЕ ПОЛЯ 239
ранстве
о
r _
SO (N — k) ' N, к SU (N — к) "
На многообразиях Штифеля естественно возникают ки-
ральные поля, которые можно интерпретировать как си-
стемы из к ортогональных и-полей. Действия и уравнения
этих полей имеют вид
к
S
Заметим, что в комплексном случае даже при к = 1 (комп-
лексное гс-поле) мы получаем уравнение, отличное от E1).
Это объясняется тем обстоятельством, что CPN отличается
от комплексной BN -f- 1)-мерной сферы факторизацией
по непрерывной группе U A).
Киральные поля как на грассмановых, так и на штифе-
левых многоообразиях являются естественными моделя-
ми теории поля, имеющими геометрический смысл. Выше
мы показали, что уравнения для киральных полей на
грассмановых многообразиях являются редукцией глав-
ных киральных полей. Ниже, пользуясь этим фактом, мы
покажем интегрируемость полей на грассмановых много-
образиях. Для киральных полей на многообразиях Шти-
феля кроме сводящегося к грассмапову случаю веществен-
ной сферы факт редукции и интегрируемость пока не дока-
заны. Тем не менее, можно высказать гипотезу, что ре-
дукция и интегрируемость имеют место. Эту гипотезу
можно высказать в более общем виде. Представляется ве-
роятным, что интегрируемы киральные поля на всех одно-
родных пространствах групп SO (N) и SU (JV) и что все
соответствующие уравнения могут быть получены в ре
зультате редукции уравнений для главных киральных по-
лей. Представляется вероятным также, что таким образом
исчерпываются все редукции уравнений главных кираль-
ных полей.

240 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Метод обратной задачи к главному киральному полю
проведем по схеме, изложенной в § 6. При этом следует
иметь в виду, что поскольку уравнения главного кираль-
ного поля допускают интегральную L — Л-пару (матри-
цы U и V имеют по одному простому полюсу), теория глав-
ного кирального поля вполне аналогична теории задачи
п волн. Опишем кратко солитонные решения главных ки-
ральных полей на группе SU (N).
Солитонное решение с одним полюсом по % в точке
X = к0 имеет в терминах матрицы g вид
^ок=о, E2)
я,„
где -фо (А., ?, л) — решение «затравочных» уравнений A)
при U = Ло, F = 50:
•фо (К I, Ц) = ехр \jA-f \ А (%) d%' — -~-j ^ Во (ц
— со —оо
E3)
Проекционный оператор Р строится по подпространствам
М = а|з0 \%=%№ь, N = -ф0 \%jjyQ,
М = Im Р, N = ker P
и является эрмитовым (Р* = Р), так что пространства М
и iV, а также Af0 и ^о являются ортогональными дополне-
ниями друг к другу. Поэтому достаточно задавать одно
из подпространств — например Мо. Пусть это подпрост-
ранство натянуто на векторы of (р = 1, . . ., г); г —
размерность пространства Мо. Пусть Ао = diag at (|),
Во = diag bt (ц). Тогда для векторов mf, составляющих
базис в М, имеем
S Ь S } E4)
В наиболее простом случае, когда т] = 1,
т„тй
Р " р
2j I my I"

§ 7] КИРАЛЬНЫБ ПОЛЯ 241
В случае группы SU B) солитонное решение зависит от
двух комплексных параметров (Яо = Яо + 'Яо, с2/С]) и
представляет собой солитон в собственном смысле, т. е.
уединенную волну, при постоянных Ао, Bo имеющую по-
стоянную скорость
_ (W — h) | 1 + Хо |2 — (at — a.) | 1 — Х„ [д
(&! — b2) | 1 -\- Xo |2 -\- («i — a2) | 1 — Ха |2
По формулам C4), C5) можно вычислить энергию и им-
пульс солитона и получить выражение для его массы:
4Хп (а, — а2) (&1 — 62)
м Г, ТТ7, • (М>
Матрица PtJ для солитона имеет вид
1 I e" e-iS"
^ ' ' E6)
2сЪу \ ei8 е-
где
у = Я'оСХо (x — vt — ,х0), Яо = -s— In ~- ,
I-7-; E7)
г, _ ai~Q2 _¦_ _ 6i — h
U0 I Л . , -I 12 ~Г
¦о г -1 г 1^о — Ч I ло т~
При (ax — a2)(^i — Ь2) ^> О солитон является обычной
частицей, при (ax — а2)(Ъ1 — b2) <0 — тахионом. В слу-
чае группы SU (N), если N ^> 2, имеется нетривиальное
взаимодействие солитонов. Пусть TV = 3, тогда, как и в
задаче о трех волнах, солитонное решение характеризу-
ется, кроме числа Яо, целым вектором (съ с2, с3). Если од-
на из компонент этого вектора равна нулю, мы получаем
простое солитонное решение— в этом случае есть, очевид-
но, три типа солитонов. Два из этих солитонов при сг = 0
и с3 = 0 являются простыми солитонами, третий при с2 =
= 0 — составным.
Как следует из формулы для маасы E5), в случае
нормальных солитонов квадрат массы составного солито-
на больше суммы квадратов масс простых солитонов:

242
ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ
[ГЛ. III
при
3)(bL — Ь3)
>¦ а2 ^> аз>
— b2) + (а2 — а3)F2 — b3)
- Таким образом, возмо-
жен распад составного солитона на два простых. Соли-
тонное решение в случае общего положения (все ct =^= 0)
действительно описывает такой распад. Из анализа об-
щего решения E.8), E.9) легко можно получить, что при
t —> — оо
12 '
0, Р,
23 '
1
0,
13
при t -> -f-
Ла|->
'IS
Ри-+
2chrk0 <xj2x —
о,
^•oai2
< + ln
г + ln
)
tl)
(Величины а"д вычислены по формуле E7) путем замены
индексов 1, 2 на i и j. ) Таким образом, числа с2/с1 и с3/с1
характеризуют конечные координаты продуктов распада.
Уравнения B) обратимы относительно изменения знака
времени, поэтому существует обратный процесс слияния
простых солитонов в составной. Эти процессы находятся
в солитонном решении, в котором образ дополнительного
проектора 1 — Р есть одномерное подпространство.
Рассмотрим теперь процедуру интегрирования полей,
возникающих в результате редукции. Мы ограничимся
рассмотренным в § 3 случаем редукции g2 = 1 в главном
киральном поле на группе SU (N), приводящим к кираль-
ным полям на комплексных грассмановых многообразиях.
Для проведения интегрирования необходимо выяснить,
как отражается редукция на данной задаче Римана, т. е.
какие ограничения на матрицы Ао, Во, G (к), на распо-
ложение нулей функций tyu i|J и на структуру подпрост-
ранств Ni, Mt из нее следуют. Заметим прежде всего,
4ToJ из формул A3) и условия g2 = 1 следуют соотно-
шения
Ag + gA = 0, Bg + gB = 0, E8)

§ 7] КИРАЛЬНЫЕ ПОЛЯ 243
а также, с учетом g = 1 — 2Р, соотношения
А = -2i IP, Ръ], В = -2i [P, Рц1 E9)
Из соотношений E.8) и основных формул A) следует, что
можно выбрать фундаментальную матрицу решений ф,
удовлетворяющую условиям
Ф AА) = *<Р (Л), ^ = Ф @). F0)
Иначе говоря, нули функций у1 расположены симметрич-
но в смысле инверсии от единичной окружности и делятся
на простые нули (при | X \ = 1) и двойные. В теории урав-
нения sin-Gordon этот факт давно известен (см. гл. I).
Соответственно возникнут простые и двойные солитонные
решения. Поскольку формула
Фо AА) = ^оФо(Я), F1)
где go = ty @), имеет место и для заданного исходного
решения системы A) (решений задачи Римана), для функ-
ций oj?!, г|J выполняются инволюции
(к) g,
откуда следует
G (VI) - goG (I) g0, (G3)
Go AA) = Go (k).
Вторая формула F3) представляет собой условие на «оде-
вающую» матрицу Go (Я).
Из формул E7) следуют соотношения
РА+АР = А, Р0А0 + А0Р0 = Ао, F4)
РВ + ВР = В, Р0В0 + В0Р0 = Во
(здесь Ро — «затравочный» проектор g1 = 1 — 2Р0), а
из F2) следуют формулы для «одевания» затравочного
проектора Ро
Поэтому для полного решения задачи необходимо уста-
новить вид Ро и Ао. Из формул F4), вспоминая, что Ао,
Во диагональньт, имеем
Рои,- (at -\ «I.) ----- б;/,«/,, (C5)
Рт (bt + Ъ}!) = 8lhbH.

244 ПОСТРОЕН. ИНТЕГРИР. СИСТЕМ И ИХ РЕШЕНИЙ [ГЛ. III
Расположим квадраты чисел at в порядке убывания. Диа-
гональ матрицы А2 разобьется на отрезки с равными квад-
ратами собственных чисел. Расположим внутри каждого
из этих отрезков отрицательные собственные числа за по-
ложительными. Из F5) следует, что матрица Ро имеет
блочно-диагональный вид, причем в каждом блоке мат-
рица Ро сводится к матрице Р* вида
= R*R* = !> F6)
где Rk — унитарная матрица.
Из формул F4) легко установить, что матрица Во, ком-
мутирующая с Ао, должна при описанном выше упорядо-
чении чисел а( также распадаться на согласованные со
структурой Ао диагональные матрицы. Окончательно
Ar-й блок матриц Ло и Во характеризуется функциями
% (?), Ьк (г|). Подставляя F6) в E7), получим выражение
для матриц Rh-
Rh- = Rl exp (i J a, d|' + i J b}: (n) di\'}. F7)
Здесь Rl — произвольная постоянная унитарная матри-
ца. Общая размерность образа проектора Ро определяет-
ся суммарным рангом матриц Л?.
Формулы F6), F7) решают вопрос о структуре асимп-
тотических состояний киральных полей на грассмановых
многообразиях. Дальнейшая схема построения решений
этих полей не отличается от изложенной в §§ 4, 6. Заметим
еще, что в простейшем случае кирального поля на комп-
лексном проективном пространстве матрицы Ао и Во мо-
гут содержать всего один нетривиальный блок, так что
асимптотические состояния здесь характеризуются одной
парой функций а, Ъ. Из результатов § 6 следует, что в
этом случае нетривиальное взаимодействие солитонов
отсутствует. Всю изложенную теорию можно перенести и
на киральные поля на вещественных грассмановых мно-
гообразиях и на га-поля на вещественных сферах. Заметим
еще, что из всего предыдущего с очевидностью следует
отсутствие нетривиального взаимодействия солитонов в
га-полях на сферах при любой их размерности.

Глава IV
АСИМПТОТИКИ РЕШЕНИЙ
ПРИ БОЛЬШИХ ВРЕМЕНАХ
Развитый в предыдущих главах формализм обратной
задачи позволил нам описать обширные классы точных ре-
шений интегрируемых уравнений. В быстроубывающем
случае это были iV-солитонные решения, распадающиеся
при больших временах в суперпозицию односолитонных
решений. Целью настоящей главы является описание
асимптотического поведения решений при t-^-oo, отве-
чающих в достаточной степени произвольным начальным
условиям. Использование метода обратной задачи позво-
лит нам исследовать временные асимптотики решений с той
же степенью подробности, что и в линейных системах, т. е.
позволит получить явные формулы для асимптотики в тер-
минах начальных данных, относящихся к моменту вре-
мени t = 0. Едва ли будет преувеличением сказать, что
именно асимптотические формулы наиболее ярко демон-
стрируют эффективность метода обратной задачи.
Обсудим прежде всего, что нам хотелось бы получить
в качестве конечного результата. Для этого рассмотрим
ситуацию, имеющуюся в линейных задачах. В подходя-
щих переменных решение всякого консервативного ли-
нейного уравнения представляется интегралом Фурье
f(x,t) =
где со (к) — закон дисперсии волны, a g (к) — фурье-об-
раз начального условия

24G АСИМПТОТ. РЕШЕНИЙ Ш'П БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Если рассматриваемая система диспергирующая, т. е.
для почти всех к со" (А-) =f= 0, то решение / (х, t) при t -> оо
сосредоточено в области x/t =- v = О A). Действительно,
полагая х — vL и вычисляя интеграл по методу стационар-
ной фазы, получаем
/ (х, t) = const-Г'/^ (к (г'))охр {i [к (v) - со (к (и))Щ,
где к (v) — корень уравнения со' (к) --- v (для простоты
считаем, что этот корень единственный). Эта формула
вместе с выражением для g (к) через начальные данные
полностью (и явно) решает задачу об асимптотике.
К формулам такого типа мы и будем стремиться.
Следует отметить, что структура асимптотических ре-
шений нелинейных диспергирующих систем определяет-
ся и без привлечения метода обратной задачи. Имей мы
дело с неодномернътми уравнениями, мы ожидали бы, что
асимптотика при t -> со будет иметь чисто линейный ха-
рактер (разумеется, если в асимптотике нет солитонов).
В одномерных задачах вид асимптотики несколько услож-
няется Tirt-за медленного убывания амплитуды решения.
Действительно, если амплитуда решения убывает как
?~'/2 (как во всякой линейной задаче), то нелинейный
сдвиг частоты волны, как правило, квадратичен по амп-
литуде и пропорционален t~1%, это должно приводить к
появлению добавки к фазе, пропорциональной In t. По-
этому, например, для нелинейного уравнения Шрединге-
ра
1Ь + t« ± 2 I г|> |2 я|> = О
асимптотика должна иметь вид
!}> (x,t) = t-4.f (-L-) exp \i ? ± 2 | / (jfj ]" hi t j + о (l-'i.)
(справедливость этого предположения проверяется пря-
мой подстановкой). Наша задача состоит, следовательно,
в определении связи комплекснозначной функции / (?)
с начальным условием \р (х, t) |(==0. Несколько неожидан-
ным обстоятельством оказывается, что определение моду-
ля и аргумента этой функции — задачи разного уровня
сложности. Первая из них решается в § 1 этой главы; ре-
шению второй посвящен § 2. Полученные в § 1 результа-
ты применяются к задаче о дифракции Фраунгофера в не-

§ 1] НЕЛИНЕЙНАЯ ДИФРАКЦИЯ ФРАУНГОФЕРл 247
линейной среде. На протяжении этих параграфов мы ра-
ботаем, в основном, в бессолитонном секторе фазового
пространства. Учет солитонов в асимптотике не представ-
ляет особой сложности, и мы не останавливаемся специ-
ально на этой задаче.
§ 1. Интегральные соотношения.
Нелинейная дифракция Фраунгофера
Рассмотрим нелинейное уравнение Шредингера
irt + rxx + 2 | г | 2 г = 0. A)
В бессолитонной ситуации уравнения обратной задачи
A.9.11) упрощаются до вида
B)
При этом г (к, t) — г (к, 0)е1Уь2(. Рассмотрим решение
уравнений B) при t—.>- оо. Функции i|>li2 являются реше-
ниями задачи на собственные значения A.9.1)
с асимптотикой г]^ = eihx, а|з2 ¦= 0 при а;-> со. При боль-
ших t мы ожидаем, что г (х, t) будет всюду близко к нулю.
По этой причине г|I( »|J должны мало отличаться от экспо-
нент. Поэтому будем искать решение системы B) в виде
г|>г - Л (к, х, t)e"*,
г|>2 = 5 (А,, ж, г)е-^-*^!',
где 4 ий — медленно меняющиеся по сравнению с пока-
зателями экспонент функции х, t. Подставляя A) в B),

248 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
получаем
Vx+4iV2(
E)
Положив теперь х = vt ж воспользовавшись извест-
ным соотношением теории обобщенных функций
Х'-Х + Ю = ( О, Ф' (Я)> О,
находим из первого уравнения E)
В (Я) =.-= г (Х)А (Я)9 (—у/4 - Я), @)
где
о,
Обозначим, далее, /¦ (ЯH (—у/4 — Я) = R (Я, у). С учетом
F) второе из уравнений E) переписывается в виде
л (л, у) _ 1 + -^
Заметим теперь, что решение этого уравнения на самом
деле нам хорошо известно. Действительно, при v = —оо
функция R (X, v) = г (к) = Ъ (к)/а (Я), а А (Я, v) = а (Я);
учитывая аналитичность а (Я) в верхней полуплоскости и
соотношение | а (Я) | 2 + I Ъ (Я) |2 = 1, мы очевидным об-
разом удовлетворяем G). Следовательно, решением G)
является аналитическая в верхней полуплоскости функ-
ция А (Я), не имеющая там нулей (напомним, что мы рас-
сматриваем бессолитонный случай) и стремящаяся к еди-
нице на бесконечности; модуль А (Я) при вещественных А.
есть, очевидно,
I а (Я) I, Я < - у/4,
Такая структура | А (Я) | позволяет переписать подынтег-
ральное выражение в формуле G) в следующем виде:

§ 1] НЕЛИНЕЙНАЯ ДИФРАКЦИЯ ФРАУНГОФЕРА 249
[А (X') — А (Х')](Х' — X + Ю). Перечисленные свойства
функции А (X) позволяют немедленно восстановить ее:
\А (X) | нам известен, а аргумент дается дисперсионным
соотношением
—И/4
Формулы D), F), (8) и (9) определяют г^ (X) и x|j2 (X).
Найденное решение справедливо при всех v = x/t, за иск-
лючением узкой (~t~4*) области вблизи v = —АХ. Вторая
из формул A.9.13) (первой по понятной причине мы не
имеем права пользоваться) дает нам интеграл
R(X)\*I{X)dX.
vt
Интеграл в правой части этого равенства определяется
вычетом функции А (X) на бесконечности; окончательно
имеем
A0)
Формула A0) дает нам физическую интерпретацию вве-
денных в § 10 гл. I переменных действие — угол для не-
линейного уравнения Шредингера. Именно, переменные
типа действия п (X) (см. A.10.25)) для непрерывного спект-
ра представляют собой «числа заполнения» асимптотиче-
ских состояний. Кроме того, A0) означает, что при боль-
ших t
Формулы A0), A1) имеют любопытное физическое при-
ложение. Уравнение A), приведенное к виду
описывает поведение стационарной электромагнитной вол-
ны в нелинейной среде. Предполагается, что показатель

250 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ IV
преломления в зависимости от поля ведет себя как п =
= щ + бинл | Е |2 (кубическая нелинейность). Величи-
на Е в A2) имеет смысл комплексной огибающей электри-
ческого поля, волновой вектор к направлен вдоль оси z,
а второй член в левой части A2) учитывает дифракцион-
ную расходимость волны. Рассмотрим теперь задачу о
дифракции Фраунгофера в нелинейной среде, т. е. зада-
чу о дифракции волны па экране со щелями, за которым
расположена нелинейная среда. Пусть экран расположен
в плоскости z -= 0; поле волны в плоскости экрана будем
считать заданным и постоянным, и пусть, для простоты,
в экране имеется всего одна щель ширины I. Начальное
условие для уравнения A2) имеет в таком случае вид
Г 0,
U
Полагая г — I: |/ Ьпип12щЕ, t = z/'lk имеем уравне-
ние A) для г (х, /). Данные рассеяния а (А), Ъ (А) для на-
чального условия вида A3) легко вычисляются; так,
| г0
| а (X) р V- + | r0 p cos2 %l '
где
к?6п
X (Л) = (Л + г0 | )'-, | г0 | g^
Так как t — z/2k, то A0) дает нам, по сути дела, интеграль-
ную интенсивность дифрагированного излучения на уг-
лы, большие чем arctg (v/2k). Поскольку, далее, уравнение
A2) применимо только для рассмотрения дифракции на
малые углы, то, полагая 8 <^ 1, получаем простое выра-
жение для интенсивности излучения, дифрагированного
в интервале углов от 9 до 8 -f- dQ:
dl (9) = — hi , . * ., dQ,
v ' яи \a(— fee/2) |2
где x =- k28nim/n0. Таким образом, при дифракции на ще-
ли
? = ±]п
гН) п-л №°-/4 ; \ го\ со& \1 {кЧУ>/4 \ |г„Р)'^1 "
Эта формула справедлива, пока в начальном условии A3)
не содержится солитонов, т. е. до тех пор, пока а (к) не

§ 2] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕЛИНГВРА 251
имеет нулей в верхней полуплоскости. Первый нуль у
а (X) появляется, когда интегральная интенсивность вол-
ны, падающей на щель, / = | Ео |2 I становится равной
я2 п0
^кр = ~2Тбга № ' таким образом, формула A4) справедлива
НЛ
при / </кр.
Явные выражения для распределения интенсивности
по направлениям могут быть получены и для задачи о ди-
фракции на экране с произвольной системой параллель-
ных щелей, поскольку матрица рассеяния на потенциале,
являющемся суперпозицией финитных потенциалов с не-
перекрывающимися носителями, равна произведению мат-
риц рассеяния на каждом из потенциалов по отдельности.
§ 2. Явные формулы для асимптотик
(нелинейное уравнение Щредингера)
В предыдущем параграфе нам удалось получить явное
выражение для амплитуды г (х, t) при t —> °о в терминах
начальных данных, не делая фактически никаких пред-
положений о виде решения. Мы выяснили, что г (х, t)
на любой прямой х = vt убывает как t~1^, отсюда следу-
ет, что асимптотика г (х, t) имеет описанный во введении
осцилляторный характер. В этом параграфе мы сначала
предположим, что г (х, t) имеет именно такую структуру,
затем мы вычислим матрицу рассеяния на потенциалах
такого типа в явном виде; обращение полученных таким
образом выражений позволит нам найти потенциал, от-
вечающий быстроосциллирующему по А. коэффициенту
отражения (поскольку г {X, t) = г (Я, 0)<?4Л2(, то при
больших t функция г (X) действительно быстро осцилли-
рует). В конечном итоге мы сможем предъявить явную
формулу для асимптотики г (х, t) и оправдать тем самым
исходное предположение.
Перепишем систему уравнений A.3) в виде
i ig- + Ae-&u2 = 0, i i?- -|- ЛЛ, = 0, A)
где мы ввели обозначения
г = Ае№ (Im А = 0, А > 0), Ф = Ф + 2%х,
vi ~ ^\е~Лх, v2 = ty2eiXx.
Предположим, что модуль и аргумент г (х, t) удовлетво-

252 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ TV
ряют следующим условиям:
0,
¦?. In А
In Фх
2
B)
и интеграл \ -=—dx сходится в окрестности обеих беско-
нечностей. Условия B) означают, что на основе системы
A.3) функция г (х, t) может быть в окрестности любой
точки представлена как экспонента с постоянной амплиту-
дой и линейно меняющейся частотой. При каждом К выде-
лим резонансную область — окрестность точки ха (к),
определенной условием
Ф* Ы = Фх (х0) + 2% = 0.
Поскольку Фхх ^> 0, это уравнение при каждом X имеет
не более одного решения. В ^резонансной области систе-
ма A) упрощается до вида
<3)
i -gi- + А (х0) exp [i (ф0 + iflj j у, = О,
где Фо = Ф (ж0), /0 = Фжж (ж0), г/ = х — ж0.
Вдали от точки х0 система A) также существенно упро-
щается. Именно, в области, где
Ф* > Фхх, D)
для v1 и v2 получаем
|i4-^- + 42i!,=0, — iUK ^p- + A2v-2 = 0. E)
Область, в которой выполнено условие D), будем называть
асимптотической. В этой области v± и v2 легко находятся
из E). Общий вид решения в резонансной области так-
же нетрудно указать. Для этого введем переменную
z = уФ'Хх (#о) и исключим из системы C) величину vx.
Для v2 получим
где

§ 2] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРа 953
Общее решение уравнения F) выражается через функции
параболического цилиндра (см. [26], т. 2):
L=\ + с2О_1+Ц y=\ I . (8)
Функция vx (у) находится при этом из второго уравнения
C). Таким образом, решение в резонансной области опре-
деляется двумя произвольными константами сг и с2.
При выполнении условий B) резонансная и асимптоти-
ческая области перекрываются. В области перекрытия
решения уравнений E) и F) должны быть сшиты, после
чего мы получаем решение задачи A) на всей оси х. В част-
ности, для решения
опр „ / 0 \
I (х, X) = о); (а; X) -> -Лх , х -> + зо
получаем, учитывая граничные условия на — оо по х:
ос
1г (х, X) = 0, |2 (х, X) = exp [i {-?-dx\. (9)
В области перекрытия формулы (9) дают
.г = \(х - ^0)Фд.хЫ]-;а2ехр (- i [ 1пФхА_?1 dx) . A0)
Асимптотики же интересующих нас функций параболиче-
ского цилиндра имеют вид (z —>• + оо)
e U* z**-i + О (z-2),
Подставляя эти формулы в vx и v2 и сшивая полученные

2 5-4 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
выражения с A0), находим
Таким образом, мы нашли | (ж, Я) в резонансной обла-
сти. Сшивая далее аналогичным образом решение урав-
нений E) в области перекрытия х < х0 с уже найденным
решением, мы определяем решение в асимптотической
области слева от резонансной точки. Устремляя затем х
к —оо и учитывая, что
а (X) = |а (х, А)е'Ч
Ъ (Я) = —Zi {x, k)e~iXx, х ->¦ —оо,
получим матрицу рассеяния
а(Х) = охр Г- яа2 + i J 4^-^:1, A2)
—оо
A3)
где
оо X
L1=[lnQ)x^--^~dx, L2= \ ЩФх\4--^Aх. A4)
J x dx Фхх ' J x I dx Фхх v ;
X —со
В формулах A2)—A4) следует положить х0 = х0 (к), най-
денное из уравнения Фж (х0) = —2Х. Итак, мы явно ре-
шили прямую задачу рассеяния для класса потенциалов,
удовлетворяющих условиям B).
Нетрудно проверить, что полученная матрица рассея-
ния обладает необходимыми свойствами. Во-первых, вос-
пользовавшись формулой
I Г /;а2\ |2 _ я
1 v '' a2 sh яа2

§ 2] НЕЛИНЕЙНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА 255
убеждаемся, что | а (к) |2 + | Ъ (к) |2 = 1. Заметим, во-
вторых, что показатель экспоненты в формуле A2) можно
переписать в виде
означающем, что In а (я) аналитически продолжается
с вещественной оси в нижнюю полуплоскость к; это в свою
очередь значит, что а (к) аналитична в области Im Х>0
и не имеет там нулей. Как мы знаем, эти утверждения
относительно матрицы рассеяния справедливы в общем
случае; здесь же мы установили их для потенциалов,
удовлетворяющих условиям B), прямым вычислением
а (к), Ъ(к).
fG той же точностью, имея в распоряжении формулы
A2)—A4), мы можем решить и обратную задачу рассея-
ния — восстановить А (х), Ф (х) по заданным а (X), Ъ (к).
Для этого заметим, что
есть заданная функция спектрального параметра %. Обо-
значим arg Ъ (К) = 8 (Я) и заметим, что интегралы Lx и
L2 выражаются только через а (к):
к
Положим
0 (Я,) = 0 (к) + Lx (к) — L2 (к) + я/4 + arg Г (га2).
Из A3) следует соотношение
9 (X) = -2кх - Ф (х) - a2 In Фхх, Фх = -2к. A5)
Рассмотрим сначала случай, когда членом a2 In Фхх в A5)
можно пренебречь. Тогда Ф (х) находится преобразова-
нием Лежандра

256
АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Вычисляя a2 In Фхх как поправку, заметим, что
(Т) д эф 9 эх
Ф 2
поэтому A5) можно переписать в виде
Ф{х)= — 2%х—
=—-L|i. A6)
В силу свойств преобразования Лежандра условие
Фхх ^> 0 влечет за собой дхк ^> 0 и наоборот; условия B)
могут быть переписаны в виде
d
dx
A7)
Интегрируя A7), находим, что за исключением окрестно-
сти нуля член a2 (к) In 8u мал по сравнению с 9, что и
оправдывает предыдущее рассмотрение. Теперь вспомним,
что г (к, t) = г (к, 0) ехр (ШН), т. е. 0 (к, t) = 00 (к) +
+ 4A,2i. Очевидно, что при t —>- оо условия A7) оказыва-
ются выполненными независимо от вида а (к), 00 (к). Это
обстоятельство и позволяет найти асимптотику начальной
задачи для нелинейного уравнения Шредингера.
Имеем при t -> оо
х = —
хх (к), xL (к) = g- "af" >
т. е. Фхд. = 1/2^, а2 (>.) = а2 (—ж/4?). Таким образом,
имеем окончательно
(х, 0 =
Ф (х, t) =
2яг
In
2 (- -?-J In
A8)
A9)
Формулы A8), A9) полностью определяют главный член
асимптотики г (х, t) = Ае1ф. (Формула A8) уже была
нами получена в предыдущем параграфе.)
В заключение этого параграфа скажем несколько слов
о характере использованного приближения. Условие B)
АХХ<^.АФ% эквивалентно для уравнения A.1) переходу
к приближению «нелинейной геометрической оптики».

§ 3] УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА 257
или к уравнениям одномерной газовой динамики с отри-
цательным давлением. Условие отсутствия солитонов
в этой терминологии означает выбор начальных условий,
при которых эффекты отрицательного давления принци-
пиально не сказываются. Величина Аг соответствует
плотности газа, Ф — гидродинамическому потенциалу,
Фх — скорости. Условие Фжх ^> 0 означает, что имеет
место разлет газа с монотонным профилем скорости,
асимптотическому режиму соответствует автомодельный
режим разлета.
§ 3. Явные формулы для асимптотик
(уравнение Кортевега — де Фриза)
Займемся теперь исследованием асимптотического по-
ведения решений уравнения КдФ
ut — 0>иих + иххх = 0.
Как было установлено в гл. I, решение уравнения
с асимптотикой oj) = ell!x, х —>- оо имеет на —оо по х асимп-
тотику
¦ф = а (k)eikx + Ъ (k)(riikHe-ikx. B)
При этом ij) (к) удовлетворяет уравнению
(/О *«» = 1 -
представляющему собой уравнение обратной задачи рас-
сеяния.
При' достаточно больших t и (х, t) всюду мало (мы
снова рассматриваем бессолитонную ситуацию) и решение
уравнения A) локально будет мало отличаться от суммы
экспонент. Будем поэтому, как и в § 1, искать г|з (к, х, t) —
решение уравнения C) в виде
г|) (к, х, t) =\A&* + Be~il!x-Sim, D)
где А и В — медленные по сравнению с показателями

258 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ ]ГЛ. IV
экспонент функции х, t. Подставим теперь D) в C):
А + В exp Bikx -f SikH) =
, 1 f Ь(к') B(k')dk'
X -X Г
а (//) /г' — к -\- Ш
1 I' Ь (/t-') , 1 (/¦:') охр №к'х ¦ ¦ - Sik'H) й1, ,Г
2т ) ~ЦРУ к' - к +Ти ' ^
Устремим теперь 6 к со, полагая ж = vt, v < 0 и исполь-
зуя описанный в § 1 прием. Получим из D) два соотноше-
ния:
B(i<>-^A(kH(s'-k% F)
где введено обозначение
v = -12 ?2, т. е. ж = -12s2 *• (8)
Так же, как и в § 1, находим решение уравнений F), G):
^ \
Решение (9), A0) справедливо при |2, не слишком близких
к к2, т. е. в области, которая выше была названа асимпто-
тической.
Обсудим поведение А, В в окрестности к ~ \. Поло-
жим
1-к = к, А<?, '&>(). (И)

§ 3] УРАВНЕНИЕ КОРТЕВЕГА —ДЕ ФРИЗА 259
Из (9), A0) получаем
Л ^ A2)
+^s
1
В (I, к) = 8(Х)Ь(А:)Я,~«Г1 Varga(fc)-i<I>(t); A3)
где введено обозначение
ф (А-) = — ]п | 2A | In | a (/;) | -f
t
In | k' — к | -^- In | a (A') | dA'. A4)
Итак, как и в § 1, мы определили решение задачи A)
почти всюду, фактически но делая никаких предположе-
ний о поведении потенциала и (х, t). Для определения же
i|5 (А;) в резонансной области необходимо такие предполо-
жения сделать. Используя мотивировку, изложенную во
Введении, будем искать асимптотическое решение урав-
нения КдФ в «квазилинейном» виде
и (х, t) = - ^ (ф (I) e-iio5'4toE) + к. с), A5)
где |2 = — x/12t (см. (8)). Единственное отличие A5)
от асимптотического решения «линейного уравнения
КдФ» Uf -\- иххх = 0 заключается в появлении в A5)
множителя tia{^> = eia(?>ln', связанного, как мы знаем,
с медленным убыванием нелинейной поправки к ча-
стоте.
Подставим потенциал и (х, t) в форме A5) в уравнение
A) и перейдем в последнем от переменной х к |, связанной
с х посредством F). В переменных \ A) перепишется в виде
+ ф= (Ф (I) /V?' + к. с.) г|> = 0. A6)
Решение A6) в асимптотической области мы уже знаем,
так что нас интересует поведение aj) лишь в непосредствен-
ной окрестности | ~ к, т. е., по терминологии предыду-

260 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
щего параграфа, в резонансной области. Подставляя D)
в A6) и предполагая, что в интересующей нас области А
и В являются функциями (| — k)t'l*, получим, отбрасывая
малые члены и обозначая Я = ? — к, систему уравнений
7 Л Л
— -_ 1_ ф (ftj pa[K)g-2iiKtK Jj _. (J(
_ A7)
-i-.-j,- + Ф (ft)f-to.№)eM»^ Л = о.
Вводя обозначения
у = (АШ)Ч'к, в(А) = ]/-^-Ф (А) «**(*), A8)
перепишем A7) в виде
A9)
Решения системы A9), как мы уже знаем, выражаются
через функции параболического цилиндра. Исключая
из A9) В, получаем уравнение для А
d2A , . dA . г, /nrv\
W + Ly^T~vA^0' B0)
а исключая А, находим уравнение для В
d?B . dB r» n
Здесь v = | 9 (к) |2.
Решения уравнений B0), B1) имеют вид
B1)
B2)
Константы cli2 и df^ однозначно определяются из сшивки

§ 4] МЕТОД УСРЕДНЕНИЯ УИТЕМА 261
B2) с выражениями A2), A3):
„ /t JIV
Г A — iv) j-
Cl= /2S e
3tV . V
C2 = r t1 ~ iv) e" ~ D8^f)i T g№(*) | a
JtV .V
di = O, d2 = Г (\±_tv) g *"D8A;«)~*T6(A:)x
X exp [i arg а (/с) — 1Ф (k)].
Сшивка определяет и значение v (к) = | 0 (&) |2:
B3)
Итак, мы нашли о|) (х, t, к) в резонансной области. Фаза
6 (к), определяющая как а (к), так и фазу ф (к), находится
из подстановки А и В B2) в любое из уравнений A9).
Это дает
в (к) = - 4-_ FA + 'v) D8W)-- b(fe),; x
X exp[iarga(/c)
Легко проверить, что это выражение удовлетворяет B3).
Итак, в формуле A5), определяющей асимптотику
и (х, t), следует положить
Г ^ -
X ехр [ — t arg a (g) + 2гФ (|) + я j/4],
где v (^) определено выражением B3), а Ф (!) дается A4).
Тем самым полностью определен главный член асимпто-
тики и (х, t).
§ 4. Метод усреднения Уитема
До сих пор мы рассматривали решения уравнения
Кортевега — де Фриза, соответствующие задачам, в ко-
торых возмущение в начальный момент времени достаточ-

262 АСИМПТОТ. РЕШЕНИЯ: ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
но быстро убывает с увеличением х:
и -> 0, | х | ->- оо.
Мы определили, в частности, число и амплитуды солито-
нов, на которые в пределе t ~*-<х> распадается такое «ло-
кальное» начальное возмущение.
Существуют, однако, и задачи другого типа. Весьма
интересным, например, является вопрос о том, что соот-
ветствует в бесстолкновительном случае ударной волне
обычной гидродинамики. Как было показано Сагдеевым
[13а], такая бесстолкновительная ударная волна имеет
осциллирующий характер. Решенные до сих пор задачи
не могут, однако, дать количественный ответ на этот
вопрос. Действительно, заранее ясно, что асимптотически
при t —v оо всякое локальное возмущение разойдется
в стороны подобно тому, как оно затухло бы в обычной
гидродинамике из-за вязкости. Среднее по периоду коле-
баний значение и в локальном возмущении с течением
времени стремится к нулю. Для того чтобы исследовать
структуру «ударного фронта» с помощью КдФ, необходи-
мо рассмотреть задачи, в которых возмущение при всех t
поддерживается соответствующими граничными условиями
при | х | —v оо. Иными словами, такие задачи, в которых
в обычной гидродинамике существует ударная волна не
убывающей с течением времени интенсивности.
Мы изложим здесь решение двух из этих проблем [5].
Во-первых, рассмотрим задачу, в которой в начальный
момент величина и испытывает в точке х = 0 конечный
скачок. В гидродинамике в этом случае образовалась бы
ударная волна постоянной интенсивности. Во-вторых, мы
рассмотрим ситуацию вблизи точки «опрокидывания»
профиля простой волны. (Точная постановка этой задачи
будет сформулирована ниже.) В гидродинамике за этой
точкой образуется ударная волна, интенсивность которой
возрастает с течением времени.
Качественно картина решения имеет одинаковый ха-
рактер в обоих случаях. При любому ^> 1 имеется конеч-
ная область в пространстве, занимаемая колебаниями.
Справа и слева от нее решение является гладким. Удар-
ного фронта определенной ширины не образуется. Возни-
кающая область колебаний автомодельно расширяется
со временем. Она ограничена слабыми разрывами, причем

§ 4] МЕТОД УСРЕДНЕНИЯ УИТЕЫА 263
слабый разрыв на переднем фронте такой бесстолкнови-
тельной ударной волны носит сингулярный характер *).
Мы будем строить решение при больших t, когда длина
осциллирующей области много больше характерной дли-
ны волны осцилляции. В этом случае естественно восполь-
зоваться весьма эффективным квазиклассическим методом
Уитема [15]. В пределе t -> оо полученное таким образом
решение будет асимптотически точным.
В целях упрощения формул в этом параграфе мы не-
сколько изменим обозначения, использовавшиеся в пре-
дыдущих разделах. Уравнение Кортевега — де Фриза
мы будем теперь записывать как
ди ди д3и __ п . ..
dt дх дх3 v '
т. е. устраним множитель 6, что всегда можно сделать
тривиальным масштабным преобразованием.
Стационарное бегущее решение уравнения A) мы будем
выражать теперь не через эллиптическую функцию Вейер-
штрасса I?,] а через связанную с ней эллиптическую функ-
цию Якоби dn (у, s). Это решение будет иметь тогда вид
и (.г, t) = -J-dn* [(„У" V - Vt),s] + у, B)
где s — модуль функции Якоби, 0 ^ s < 1. Параметры а,
s и у являются произвольными постоянными, причем а
определяет амплитуду колебаний:
СкороСТЬ V волны равна
V=2a^-+y. C)
Согласно свойствам эллиптических функций, волновой
вектор волны, связанный с длиной волны Я обычным соот-
ношением к = 2л/Я, есть
*-те-(¦?¦)""¦ D>
Среднее же по периоду значение колеблющейся величи-
*) Надо иметь в виду, что наличие сингулярности есть след-
ствие используемого здесь приближенного метода: в точном реше-
нии КдФ сингулярностеи нет. '

264 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
ны и, как легко проверить, есть
а = у + 2аЕ (s) E)
где КжЕ — полные эллиптические интегралы соответствен-
но первого и второго рода.
Рассмотрим теперь слегка нестационарные (квазиста-
ционарные) волны. Они описываются по-прежнему фор-
мулой B). Параметры a, s и у (а следовательно, и V, к
и и), однако, являются теперь медленно меняющимися
функциями х ш t. Подставляя B) в A) и усредняя по пе-
риоду колебаний, можно получить уравнения для усред-
ненных величин. Такие уравнения были выведены Уите-
мом [15]. Их удобно записать, введя три новых функции,
связанные с a, s и у соотношениями
У = г, + Г1~ г3. F)
гз — П
При этом
rs>r2>r1. G)
Уравнения для га имеют вид
?^=0' «=1.2-3. (8)
(В этой формуле и везде ниже отсутствует суммирование
по а!)
Три «групповые скорости» va равны
„ - >-1 + г2 + га 2 K(s)
Vl 3 Г ^а ~ Г1> K{s)-E (») '
р2 g _ ^а - ц; Е {s) _ A _ j2) A. (s) ,
„ r,+r2+r3 2 A -««) A" (g) q
» = + -fa ri) ^ (У)
Заметим также, что скорость V, а также максимальное
и минимальное значения величины и волны выражаются
через га следующим образом:
V = 4" (П + Г2 + гз),
"max = ^з + Ъ — ГХ, Mmin = Г3 + Гх — Г2.

§ '»] МЕТОД УСРЕДНЕНИЯ УИТБМА 265
Уравнение Кортевега — де Фриза A) инвариантно от-
носительно преобразований
и = Си, х^^, t-*^, A0)
где С — произвольная постоянная и
x^x + Ct, u~>-u + C. (И)
Усредненные же уравнения (8) инвариантны еще и отно-
сительно преобразования
х~+Сх, t~+Ct. A2)
Отметим, что такой инвариантностью обладают и уравне-
ния обычной гидродинамики невязкой жидкости.
Выпишем для справок приближенные формулы для
функций К (s) и Е (s) при s -> 0 и s ^- 1:
1 . 16
64" т-
A3)
Как отмечалось выше, параметр г2 моя№т меняться от
ri Д° гз- Поэтому естественно считать, что область, заня-
тая осцилляциями, ограничена с одной стороны точкой
х~ (t), в которой г2 = гг. В этой точке обращаются в нуль
амплитуда а и параметр s. С другой стороны область осцил-
ляции ограничена точкой х+ (t), в которой г2 = г3, так что
s = 1 и согласно D) волновой вектор к обращается в нуль.
В обеих рассмотренных нами задачах х+ >¦ аг, поэтому
мы будем называть точку с а = 0, s = 0 задним фронтом,
а с s = 1 — передним. Это соответствует обычной карти-
не, когда солитоны большей амплитуды движутся с боль-
шей скоростью *).
*) В работе [156] предполагалось существование сильных раз-
рывов в решении усредненных уравнений (8), аналогичных удар-
ным волнам в обычной гидродинамике. Наш анализ показывает, что
в действительности таких разрывов не возникает — по крайней
мере в задачах рассматриваемого типа.

2G6 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Распад начального разрыва. При распаде малого раз-
рыва в гидродинамике образуются две волны — волна
сжатия и волна разрежения,— движущиеся в противо-
положных направлениях со скоростями, близкими к ско-
рости звука (рис. 15). Эти волны расходятся очень быстро.
Рис. 15. Образование волны сжатия и волны разрежения при рас-
паде начального разрыва.
Поэтому их дальнейшую эволюцию можно рассматривать
по отдельности с помощью КдФ. При этом можно считать,
что в начальный момент величина и испытывает конечный
скачок:
Для волны сжатия w ^> и+; для волны разрежения,
напротив, и~ < и+.
Рассмотрим вначале волну сжатия. Заметим, что
в обычной вязкой гидродинамике такая волна описывается
уравнением Бюргерса. Она представляет собой слабую
ударную волну со стационарным фронтом. Таким образом,
рассматриваемая здесь волна сжатия в дисперсионной
гидродинамике соответствует ударной волне в обычной
вязкой гидродинамике."
Заметим, что с помощью преобразований A1), A2) на-
чальные условия для волны сжатия всегда можно при-
вести к виду
1,
При небольших значениях t нелинейный член в урав-
нении A) несуществен и им можно пренебречь. Решение

§ 4] МЕТОД УСРЕДНЕНИЯ УПТЕМА 267
линеаризованного КдФ имеет вид
u(x,t)=
где Ф (z) — функция Эйри:
ос
Ф (z) = -L [ cos (-^-+kz) dk.
о
Подставляя сюда начальное распределение u0{x) в виде
A4), находим
со
[ (?>(z)dz. A6)
u(x,t) =
У я
ж/(з() /з
Эта функция представлена на рис. 16. Первый макси-
мум расположен в точке z = x/CtI/is = —2,45, его высота
^тах = 1,28; первый минимум — в точке z = —4,19;
"шп = 0,81; второй максимум и минимум UmLc = 1Д6,
wmin = 0,86 в точках z = —5,58 и —6,89. Асимптотиче-
п скири больших отрицатель-
ных значениях
n{x,t) =
_^г,а 7 2
afcf)
Видно, что вблизи разрыва ~ '> 0 j
возникают осцилляции. Их .//Г//;-'
амплитуда растет при приб- Рис 16 Линейная стадия рас-
лижении к разрыву. Область, Пада начального разрыва,
занятая осцилляциями, авто-
модельно растягивается со
временем. При этом роль дисперсионных эффектов ослаб-
ляется и все более существенной становится роль нели-
нейности. Сопоставляя дисперсионный и нелинейный
члены в уравнении A), находим условие применимости
линейного решения A6) в виде

268 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Отсюда ясно, что при больших t ^> 1 определяющее влия-
ние на структуру волны всегда оказывает нелинейность.
При больших t ^> 1 будем искать асимптотическое ре-
шение уравнения A) в виде квазистационарной волны B),
F). Тогда для усредненных уравнений (9) начальное усло-
вие A4) нужно наложить на и, а амплитуду а следует счи-
тать нулем при t = 0. Важно, что в силу инвариантно-
сти A2) решение уравнений (9) при начальных условиях
A4) должно носить автомодельный характер, т. е. зави-
сеть только от отношения
т = xlt. A7)
Таким образом, можно считать, что
Га = Га (Т). A8)
Граничные условия в переменных т, согласно описанной
выше общей картине, должны иметь следующий вид.
На «переднем фронте» области колебаний при некотором
х = т+ должно выполняться равенство
s{x+) = 1,
rs (т+) = г2 (т+) = г+. A9)
В силу нее непрерывности величины и (т) должно быть
п (т+) = 0. B0)
Далее, при т ^> т+ просто га = 0. На заднем фронте при
некотором т = х~ амплитуда а = 0, так что
Г2 (Т") = ГХ (Х~) =Г~,
й(т-) = 1. B1)
При т <С %~ а = 0, п = 1.
Подставляя A8) в (8), получаем
B2)
Легко сообразить, что осмысленное решение получится,
лишь если приравнять нулю выражение в круглых скоб-
ках в одном из уравнений B2), а в двух других считать
ra = const. Очевидно, что граничные условия A9) и B0)
можно выполнить, только если г2 зависит от т. Поэтому

§ 4] МЕТОД УСРЕДНЕНИЯ УЙТЕМА 269
интересующее нас решение имеет вид
v2 (т) = т, B3)
r3 = const, rx = const.
Заметим прежде всего, что при а —> 0, учитывая, что
a/s2 = rs — гг, из E) получим
п = гя. B4)
Тогда согласно B1)
га = 1.
На переднем же фронте при s -v 1 имеем
м = г1; B5)
так что
гх = О, s2 = г2.
В результате
а = Д F = A + s2)/3, y = -A - А B6)
а формула B3) переписывается в виде
1 -г S2 2 S2 A _ S2) /С (s) x
3 E (s) — (i — s*) К (s) t
B7)
Формулы B6), B7) вместе с B) полностью решают постав-
ленную задачу. Подчеркнем, что сама величина и (х, t)
определяется формулой B) и зависит, разумеется, не толь-
ко от отношения xlt (только от xlt зависят медленные ве-
личины Га).
Исследуем специально поведение решения вблизи пе-
реднего и заднего фронтов.
На заднем фронте, при а -> 0, используя формулы A3),
легко находим
+ — s- = т
или
тГ = —1, о = ^ж-д-т' ^8)
(Т = т- + т' = -1 + т'),
так что амплитуда обращается в нуль по линейному за-
кону при стремлении т к х~.
На переднем фронте, при s-*• 1, вместо B8) получаем
2 1 — Sa 16

270
АСИМПТОТ. РЕШЕНИИ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Отсюда находим
Закон обращения 1 —- s2 в нуль имеет вид
9\ 1
- S-) In
16
= 3 | т
B9)
где т = т+ + т", т" ¦< 0, или с логарифмической точ-
ностью
! „а.. 3|т'|
' 1пA/|т"|)
Из D) видно, что при s —>- 1 волновой вектор к обраща-
ется в нуль по закону
h~ я \ 3 ) In A/| х" |) ' { }
Наконец, среднее значение а ведет себя при s -»¦ 1 как
^^^ 1-
и =
m (l/l
C1)
Функция п (т) имеет при
т = т+ бесконечную произ-
водную и испытывает в
этой точкеслабый разрыв—
разрыв производной duldx.
Важно, что этот разрыв
движется со сверхзвуковой
скоростью (так как х+ =
= 2/3, а скорости звука
соответствует т = 0). Мы
будем называть его сингу-
лярным разрывом *).
Ha 1? построены
графики величин и, а = s2
и волнового вектора А; сог-
ласно формулам B6), B7).
На рис. 18 представлены значения неусредненной вели-
чины и (х, t) при t = 50, 100. Видно, что область занятия
осцилляциями быстро увеличивается со временем. На пе-
реднем фронте волны постепенно выделяются солитоны,
*) См. сноску на стр. 263.
-0,5
Рис. 17. Зависимость от т = xlt
усредненных величин при рас-
паде начального разрыва.

МЕТОД УСРЕДНЕНИЯ УИТЕМА
271
расстояние между ними логарифмически растет со вре-
менем (см. C0)). Это видно из рис. 19, где показан перед-
ний фронт волны при t = 100, 1000 и 10 000 *).
В заключение заметим, что переход от единичного
скачка A4) к скачку с произвольным и~ согласно A0)
j _
-100 -80 -60 ~
60
-z
-WO SO -ffO -40 -20 О 20 40 ffO 80s
Рис. 18. Бесстолкновительная ударная волна при распаде пачаль-
ного разрыва.
достигается умножением в полученном решении значений
и на и~ и одновременным делением значений х па и'?_2
и значений t на u'fj_. Значения т при этом умножаются на
и~. Например, для скачка св"=2 графики на рис. 18
соответствуют теперь t = 17,7 и 35,4.
Остановимся теперь кратко на эволюции волны разре-
жения, т. е. разрыва другого знака, с и" <^ и+ (не умаляя
общности, можно положить и~ — —1/2, и+ = 1/2). Ясно,
что решением вида B7) описать такой скачок нельзя, так
как г2 ^> гг и из B4), B5) сразу следует, что и' ^> и+.
Уравнения (8) имеют тогда, однако, тривиальное решение
*) При вычислении по формулам B) и B7) на переднем фронте,
т. е. при т = т*, и = 2, однако форма первого горба искажена, его
передняя половина «срезана». Более детальное исследование пока-
зывает, что на переднем фронте колебания имеют форму солитонов.
Поэтому на графиках передний горб достроен как солитон с ампли-
тудой 2а = 2. Отмеченное обстоятельство связано с недостаточной
точностью формулы B7): асимптотический характер теории не по-
зволяет установить точную фазу волны при не слишком больших
значениях t. Поэтому вся картина, представленная на рис. 18 и 19,
может сдвинуться на расстояние порядка ширины солитона. (То
же относится и к рис. 26, см. стр. 284.)

272
АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
без осцилляции:
C2)
Это решение имеет два слабых разрыва при т = — V2и т = х/г
и соответствует пренебрежению дисперсией, т. е. членом с
t-100
О 10 lOff
Рис. 19. Образование солитонов на фронте бесстолкновительной
ударной волны при распаде начального разрыва.
третьей производной в A). С учетом дисперсии эти слабые
разрывы размываются, вообще говоря, осциллирующим
образом (рис. 20). При больших t можно рассматривать
разрывы по отдельности. Для нахождения структуры
левого разрыва, который мы будем называть «разрывом
типа А», требуется найти решение уравнения A), удовлет-
воряющее граничным условиям
и —5* —1/2 при х —> — оо и и —> x/t при х —> оо.
Правый разрыв — «разрыв типа В» описывается граничны-
ми условиями и —> x/t при х —> — оо и и —s- 1/2 при х —^ оо.
Этим граничным условиям соответствуют автомодельные
решения вида
1 .,/_ч 1 _ x+t/2
и =
Ct)'
h

§ 4] МЕТОД УСРЕДНЕНИЯ УИТЕМЛ 273
для разрыва типа А, причем o|v—»• 0 при z —>• — оо и -ф —у
—> 3z при z —> оо. Для разрыва типа 5
1 , . . . 1 x — t/2
и = ,, -ф (z) 4- -п-, z = п~>
C0/з W 2 C0/з
причем -ф —> 3z при z —> — оо и ijj -> 0 при z -^ оо. Функ-
ция "ф (z) удовлетворяет обыкновенному дифференциаль-
ному уравнению *)
V (z) Ь (г|) - z) 1])' - 2ф = 0. C3)
Отметим то нетривиальное обстоятельство, что, несмотря
и
0,5-
-0,5
J~0,5\
0,5
Рис. 20. Структура волны разрен;ения.
на слабость разрыва, для его структуры существенны и
нелинейные члены в уравнениях A) или C3).
Решение уравнения C3) при выписанных граничных
условиях производилось численно. Структура разрыва
типа А показана на рис. 21, а; типа В — на рис. 21, б.
Отметим, что в первом случае она носит осциллирующий,
а во втором — монотонный характер. Осциллирующий
член в разрыве типа А при больших z убывает по закону
-^ cos [Bz)V3/3].
(Асимптотическое значение "ф = 3z показано на рис. 21
штриховой линией.) Заметим, что ширина разрыва оказы-
вается порядка t1/'. Поскольку, однако, вся картина
«волны разрежения» расширяется согласно C2) пропор-
*) Автомодельные решения уравнения A) используемого здесь
вида рассматривались и ранее, однако, без связи с задачей о слабом
разрыве, а потому при других граничных условиях.

2D АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
p
10
10-
-z о z ь e 8 w iz z
Рис. 21. Слабый разрыв типа А (а) и типа В (б)«

§ 4] МЕТОД УСРЕДНЕНИЯ УПТЕЫА 275
ционально t, относительная ширина разрыва уменьшается
с течением времени.
Укажем, что в обычной — диссипативной — гидроди-
намике структуру слабого разрыва в вязкой жидкости
можно найти аналитически. В этом случае задача сводится
к построению некоторого решения уравнения Бюргерса
определенного автомодельного вида.
Таким образом, в случае волны разрежения картина
решения в дисперсионной гидродинамике, в общем, подоб-
на решению в обычной гидродинамике. С другой стороны,
в случае волны сжатия дисперсионная гидродинамика
приводит к существенно новым явлениям. Вместо сильного
разрыва со стационарным фронтом здесь возникает автомо-
дельно расплывающаяся область осцилляции. Иначе гово-
ря, благодаря генерации колебаний фронт бездиссипатив-
ной ударной волны быстро расплывается.
Возникновение осцилляции вблизи точки опрокидывания
фронта. Рассмотрев возникновение бесстолкновительной
ударной волны в сравнительно простом случае начального
разрыва плотности, мы перейдем теперь к решению более
трудной задачи — исследованию явлений вблизи точки
«опрокидывания фронта».
Как известно, в гидродинамике идеальной жидкости
нелинейные эффекты приводят к укручению фронта
распространяющихся в среде возмущений. Это приводит к
тому, что в некоторый момент времени возникает точка, в
которой производная, скажем, от плотности по координате
обращается в бесконечность — фронт «опрокидывается».
В обычной гидродинамике после опрокидывания возни-
кает ударная волна. В дисперсионной гидродинамике
вблизи точки опрокидывания становится существенной
дисперсия, а после опрокидывания возникает область,
заполненная колебаниями. Если рассматривать достаточно
большое время, прошедшее с момента опрокидывания, так
что число колебаний уже велико, то для описания процесса
можно воспользоваться усредненными уравнениями (8).
Эти уравнения справедливы внутри области, заполненной
колебаниями. Возникает поэтому вопрос о граничных усло-
виях, которым должны удовлетворять функции га на гра-
ницах этой области. Мы уже говорили, что на переднем
фронте области колебаний должно выполняться равенство
г2 = г3, а на заднем г2 = гх. Такие точки, однако, как мы

276 АСИМПТОТ. РЕШЕНИЙ ПРН БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
увидим, являются особыми для решений системы (8) и
для эффективного использования этих граничных условий
необходимо выяснить вид решения вблизи этих точек. .
Рассмотрим сначала передний фронт. Пусть г2 = га ~
= r+ (t) в некоторой точке х — х+ (t). Используя выраже-
ния (9), легко проверить, что при г2 = га совпадают также
скорости v2 и v3: v2 = v3 = v+ = (гг -f- 2г+)/3. Из урав-
нений (8) следует тогда, что
dx+/dt = v+ = D + 2r+)/2. C4)
Положим
г2 = г+ •-}- ог2, г3 = т -\- ог3, х = х+ -\- х ,
где бг2, бгх и х" — малые вблизи переднего фронта величи-
ны. Легко проверить перебором всех возможных случаев,
что вблизи фронта
| 8г2 — 8г3 | ;> | бг2 -]- 8г3 |, | гх — г\ \ {г\ = гг {х+, t)),
так что наиболее быстро меняющейся величиной является
параметр s. Уравнение для 6>2 имеет вид
N ' \дх' It \ at /x=x+
и аналогично для бг3. Используя разложение эллиптиче-
ских интегралов при s -> 1, находим для групповых скоро-
стей
где s'2 = 1 — s2 и L = In [16/A — s2)].
Вычитая теперь уравнение для 6>2 из уравнения для
бг3, получаем уравнение
_а_ .. _ 2 з
дх" ^ ' r+ _ r+ \ dt /x=x+ ,л „>.\1„ 16
1—S3
Решение этого уравнения определяет закон обращения s в
единицу и, следовательно, длины волны колебаний в
бесконечность вблизи переднего фронта области осцилля-

§ 4] МЕТОД УСРЕДНЕНИЯ УИТЕМА 277
ций
Из C5) следует, что при х" -> 0 волновой вектор к обраща-
ется в нуль пропорционально (In | x" | )-1, как и в рас-
смотренном выше особом случае распада начального раз-
рыва. Легко проверить, что среднее значение п стремится
при х" —> О к своему предельному значению также по зако-
ну (In | х' | )~1. Поэтому на переднем фронте п (х) ив
общем случае имеет особенность с бесконечной производ-
ной.
Вполне аналогичные вычисления можно произвести для
заднего фронта. И здесь, отмечая значения всех величин на
заднем фронте при х = х~ знаком «—», имеем
__ о O/tC /Q?i\
1 ~ 2 ' 1 ~~ 2 ~~ 1 3 ' dt ~~ ^ '
Параметр s снова является наиболее быстро меняющейся
величиной и закон его обращения в нуль определяется
формулой
Чг
, х = х — х". C7)
дг~
Из этой формулы видно, в частности, что амплитуда коле-
баний а обращается в общем случае в нуль по корневому
закону а со Y\ х' I- (В этом пункте имеется отличие от
специального случая распада начального разрыва. Напом-
ним, что там амплитуда обращалась в нуль линейно.)
Среднее же значение и стремится к предельному значению
линейно.
Выражения C4) и C6) должны использоваться в каче-
стве естественных граничных условий к уравнениям (8) в
задачах, где колебания занимают ограниченную область
пространства.
Мы можем вернуться теперь к исследованию осцилля-
ционной структуры, возникающей в дисперсионной гидро-
динамике после «опрокидывания фронта» некоторого воз-
мущения.

278
АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Рассмотрим некоторое возмущение, начальный размер
которого очень велик, Ro ^> 1. Тогда вначале в уравнении
A) можно пренебречь дисперсией. Нелинейные эффекты с
течением времени приведут к увеличению крутизны
фронта возмущения, так что в некоторый момент времени
t = О производная ди/дх обратится в бесконечность
Рис. 22. Опрокидывание фронта при эволюции начального воя-
мущения.
(рлс. 22, а, б). В этот момент, как говорят, происходит
«опрокидывание фронта»; при дальнейшем увеличении t
решение, полученное при пренебрежении дисперсией,
формально делается трехзначным (рис. 22, в). В уравнении
же A) вблизи точки опрокидывания становится существен-
ной дисперсия и после опрокидывания образуется расши-
ряющаяся область, заполненная колебаниями (рис. 22, г).
Для описания явлений вблизи точки опрокидывания
заметим прежде всего, что после пренебрежения диспер-
сией, т. е. членом с третьей производной, уравнение A)
можно записать как
dujdt
ди/дх
\di)
так что общее решение имеет вид
х = ut + Р (и),

§ 4]
МЕТОД УСРЕДНЕНИЯ УИТЕМА
279
где Р (и) — произвольная функция. В момент опрокидыва-
ния, когда точка, в которой
(—) = 0, C8)
\ouJt '
впервые появляется, в этой точке должно быть еще
(pi) = 0, C9)
причем выбором начала отсчета t, x и и всегда можно до-
Fiic. 23. Начальная автомодельная стадия опрокидывания фронта.
биться того, что в этой точке t = х = и = 0. Разлагая
Р (и) но и и учитывая C8), C9), находим, что
Р (и) ж — (ш3,
причем с помощью преобразования A0) всегда можно
сделать ц равным единице *).
Окончательно решение вблизи точки опрокидывания
(и незадолго до момента опрокидывания) описывается
формулой
х = ut — иъ. D0)
Оно показано на рис. 23. При i ^> 0 решение делается не-
однозначным (штриховая кривая). В действительности при
*) Чтобы вернуться к случаю |х =/= 1, достаточно в окончатель-
ном результате умножить значения и на |х~2'7, значения х на fil/('
и значения t на ц3/7. Значения z при этом умножаются на \С^2.

280 АСИМПТОТ. РЕШЕНИИ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
t ^> 0 возникают колебания. Мы опять предположим, что
они занимают конечную область пространства. В этой
области решение описывается уравнениями (8). Вне этой
области по-прежнему справедливо D0), так что и имеет
там вид
и = fh Э (z), z = x/f\ D1)
где 0 определяется уравнением
z = е - е3. D2)
Чтобы сшить решения (8) и D2) на границе области
колебаний, нужно положить *)
га = Ша {х/Щ = th la (Z). D3)
Таким образом, в этом случае область, занимаемая колеба-
ниями, расширяется со f/*, а амплитуда колебаний воз-
растает при заданном z как г1/». Подставляя D3) в (8),
получаем для 1а систему трех обыкновенных дифференци-
альных уравнений
dla 1„
-г2- = о а , D4)
где Wa, = vjfi'„ так что wa выражаются через 1а теми же
формулами (9), которыми выражаются va через га. Систему
уравнений D4), разумеется, нельзя решить в квадратурах.
Используя полученные выше формулы C4) и C5), легко,
однако, выяснить поведение решения вблизи переднего и
заднего фронтов.
Пусть, например, переднему фронту соответствует
значение z = z+. Из условия dx+fdt = v+ следует тогда, что
z+ = 4 It + 4 И D5)
С другой стороны, при z = z+ условие непрерывности с
учетом формулы B5) дает
z+ = ? [1 - AЩ D6)
При этом надлежит выбирать значения t[ <] 0, так как
решение должно сшиваться с той ветвью функции 0 (z),
*) В общем случае уравнения (8) имеют автомодельные решения
вида ra = tyla (x/t1+y) с произвольным показателем у.

§ 4]
МЕТОД УСРЕДНЕНИЯ УИТЕМА
281
которая уходит на ъ = -j- оо (рис. 24). При z = z+ имеем
*¦?
2 г
так что из формулы C4) прямо следует поведение решения
вблизи переднего фронта:
16
1
z" = z-z+<0, Z+>0. D7)
Разумеется, свойства переднего фронта в рассматриваемом
1,5 \
/, ^-'0,5'
Рис. 24. Зависимость от z = ж//'2 параметров Уитема при опроки-
дывании фронта.
частном случае оказываются теми же, что и в общем случае,
о чем было сказано выше.
Аналогично, вблизи заднего фронта имеем из условия
движения фронта со скоростью vt = v ,= v~:
4 ,_ 2 ,-
z _ _
D8)
Из условия непрерывности решения следует, что
г- = ? [1 - (?)'], ^ < 0. D9)

282 АСИМПТОТ. РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Наконец, вид решения вблизи заднего фронта следует
сразу из C6)
9 I l~z' \Чг
s2 = "_' 1 _' , z = г - 2" > 0. E0)
1 1
Решение уравнений D4) для определения значений 1а
во всей области колебаний производилось численно. Ре-
зультаты представлены на рис. 24. Мы видим, что при всех
значениях z параметры 13 ^> 0, 1г <С 0. Параметр же 12
меняет знак в некоторой точке z0. Эта точка является осо-
бой. Действительно, из уравнения для 1г видно, что эта
величина может обращаться в нуль только там, где обраща-
ется в нуль знаменатель 3z — 2ыл>. Легко показать, одна-
ко, что особенность в точке z0 относительно слабая. В ней
непрерывны не только величины 1а, но и их первые произ-
водные. Тем не менее, наличие такой особенности сущест-
венно: только благодаря ей оказывается возможным
удовлетворить граничным условиям. Дело в том, что на
решение наложены четыре граничных условия D5), D6)
и D8), D9). Между тем общее решение системы D4) содер-
жит только три произвольные постоянные. Недостающая
постоянная добавляется благодаря наличию особой точки
Zq. Чтобы понять, как это происходит, будем строить
решение с двух сторон — из неизвестных заранее точек z~
и z+. После удовлетворения условий D5), D6) и D8), D9)
в нашем распоряжении останутся две произвольные по-
стоянные, в качестве которых можно выбрать, например,
значения 13 и l\. Распорядимся одной из них так, чтобы
обращение 12 в нуль с двух сторон происходило в одной и
той же точке z0. Вторую же постоянную подберем так,
чтобы при z = z0 была непрерывна величина 13. Тогда
непрерывность 1г будет обеспечена автоматически благода-
ря тому, что
3z0 = 2iA>2 при z = z0.
Решение фактически строилось именно таким способом.
Следует отметить любопытное сходство между графиком
la (z) и формальным трехзначным решением уравнения D2).
(График трехзначной функции В (я) показан на рис. 24
штриховой линией.) Таким образом, существование реше-

МЕТОД УСРЕДНЕНИЯ УИТЕМА
283
ний с колебаниями тесно связано с наличием области
неоднозначности в решении уравнения без дисперсии.
Графики рис. 24 вместе с формулами B), F) и D1)
решают поставленную задачу определения и (х, t) при
опрокидывании фронта.
15- \
-1,5
-1,0
-05
( -0,5-
V
\
\
\
/
z+ 0,5 г
-1,5 г
Рис. 25. Зависимость от z усредненных величин при опрокидыва-
нии фронта.
Вычисления дают следующие значения для координат
особых точек решения:
Z" -¦= —1,41, z+ = 0,117, z0 = —1,11.
Амплитуда переднего солитона равна
2а+ = 2 (it — l\) tl* = 3,69 VIк
E1)

284
АСИМПТОТ. РЕШЕНИЯ ПРИ БОЛЬШИХ ВРЕМЕНАХ [ГЛ. IV
Из соотношений автомодельности D3) видно, что сред-
нее значение и, амплитуду а и волновой вектор к можно
представить в виде
й = f/« в (а), а = *'/.Ь (z), /с = f/'x (z). E2)
1 1
-40 -30
——л
]
-10
д Л
с
у,.-
4.
^-
i-5JlB
А
Рис. 26. Бесстолкновительная ударная волна при опрокидывании
фронта.
Графики функций 0 (z), Ь (z), x (z) и s2 (z) построены на
рис. 25. (Подчеркнем, что функция х (г) непрерывно
стремится к нулю при z -* z+.)
На рис. 26 для t = 5,06 и 8,35 показана зависимость и
от х. Видно, что с течением времени происходит быстрое
расширение области колебаний, увеличение их амплитуды
и уменьшение длины волны.

Приложение
ТЕОРИЯ УРАВНЕНИЯ
КАДОМЦЕВА - ПЕТВИАШВИЛИ
(ДВУМЕРНОГО КдФ).
НЕКОТОРЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ
§ 1. Некоторые интегрируемые двумерные системы
Предыдущая теория касалась интегрирования уравне-
ний, содержащих неизвестные функции двух переменных.
Исследования последних лет показали, что техника обрат-
ной задачи рассеяния может быть перенесена иногда и на
случай большего числа переменных.
До сих пор в представлении Лакса
17 = tL' 41 W
фигурировали дифференциальные операторы L. А от
единственной переменной х. При этом по заданному опера-
тору L удавалось в любом порядке по д/дх найти соответ-
ствующий класс операторов А, порождающий интегрируе-
мую систему уравнений. Ситуация резко меняется, если
оператор L содержит производные по нескольким пере-
менным; правильное обобщение теории на этот случай
нетривиально и обсуждается в работах [1—3]. Пусть
например
Прямым вычислением легко проверить, что уравнение A)
порождает теперь уравнение на и, только если оператор А
есть оператор первого порядка с постоянными коэффициен-
тами; при этом уравнение на и является тривиальным.
Настоящая ситуация типична, если L содержит произвол-

286 ПРИЛОЖЕНИЕ
ные по двум или более переменным. Однако, из нее есть
исключения. Пусть
L = а— —• М B)
ду '
где М — обыкновенный, дифференциальный по х оператор.
Тогда соотношение A) переписывается в симметричном виде
и становится соотношением на обычные дифференциальные
операторы.
Рассмотрим несколько примеров.
1. Пусть
Тх
тогда условие C) приводит к системе (см. [4, 5])
Л = ~ 4 h — 6U Тх ~
x = uv, E)
ut — &uux — uxxx — 3a2wv = 0,
эквивалентной уравнению
_ (ut — QUUx — uxxx) = За2и„у. F)
Уравнение F) представляет собой обобщение уравнения
КдФ на двумерный случай и известно как уравнение КП
(Кадомцева — Петвиашвили или двумерное КдФ). Оно
имеет ту же степень универсальности, что и уравнение
КдФ.
Чтобы убедиться в этом, рассмотрим закон дисперсии
для среды со слабой зависимостью скорости звука от вол-
нового числа
со2 = fc2 + efc4, e/<;2< 1. G)
Пусть среда двумерна к = (кх, ку); причем ку <^; кх. Тогда
можно положить
со2 - kl = (со - кх) (со + кх) = гк* + kl
Переходя в движущуюся систему отсчета (полагая со —

§ i] ИНТЕГРИРУЕМЫЕ ДВУМЕРНЫЕ СИСТЕМЫ 287
= кх + &, & <§^ кх), получим приближенно
Ак &к к
т. е. соотношение, с точностью до простой замены перемен-
ных совпадающее с фурье-преобразованием линейной
части уравнения F), где е = — (За2).
Свойства решений уравнения КП существенно зависят
от знака а2. Не ограничивая общности, можно считать, что
а2 = + 1. При а = 1 (мы будем называть этот случай
устойчивым), //-оператором является оператор теплопро-
водности
В неустойчивом случае — при а = i — L-оператором яв-
ляется нестационарный оператор Шредингера
L= fiL-f-^i + u. (9)
ду ' дх2 ' ч '
2. Пусть МиА — матричные операторы первого поряд-
ка [6, 7]:
дх
д
А = bg- + W.
дх
Здесь а, Ь, V, W — квадратные матрицы третьего порядка.
Пусть матрицы а и Ъ вещественны и диагональны:
а = diag {ахафй), b -= diag (bxb2bz),
а матрицы V и W подчиняются соотношению
[a, W] = [Ь, V]. (И)
b. — b-
Положим v-ti = iutj у | at — aj |, iva = _ v^, где.
U;j — эрмитова матрица с нулевой диагональю., имеющая
вид
О щ Uj
Щ О «а ) .
п, п8 О

288 приложение :
Тогда условия C) приводят к системе уравнений
ult + i%ulx + v\uly = iqu^Ua,
u2t -f vx2u2x -f и(щу = iqu^s, A2)
u3t -f- УдЫ3х + У
Здесь
o^&a •— a2bt + a^ — a-ib3 -+- a2b:i —• a3b2
У{ах — a2) (ai — a3) (a2 — a3)
vx = 61дз — Mi y ^1—&з
1
a
a3 ' 1 at — o3
Ь3аг „ _ &2 — b.i
, t/-' •— (A
2 2
Система уравнений A2) является обобщением на случай
двух пространственных переменных рассмотренной в
гл. III системы трех волн (см. § 4 гл. III.).
3. Пусть
м = _П + 1 018 ГО 1П
[о zjd* [±\|> oj
A3)
Здесь
(fi = <xtyy -\- (I — 2ft — 1) if>x,
ф2 = ^P (аФу 4" {I — 2a) ij)x)-
Условия (З) дают теперь систему уравнений
гф( 4" -Dity 4" Щ1 = ^> и = rt — r2,
D2u = q= 2 D, | ф | 2, A4)
где Z?x, Z?2 — дифференциальные операторы
Dx — a2 -3-j 4- 2 (i — a) a -тг—5 j- (^2 — 2!a — a) j-j- ,

§ 2] ЗАКОНЫ СОХРАНЕНИЯ 289
Квадратичные формы коэффициентов операторов D1, D2
всегда имеют различную сигнатуру. В частности, при
I = а = -V2
Л — 2 _^_ , ! 52 г) _ 2 д2 Id2
1 ~" а а?/2 + Т dl2 ' и2 — а ду2 4 да-2 •
Удобно ввести обозначение и = + 2 | г|) | 2 4- v\ ПРИ этом
система A4) приобретает вид
i/[Pi + — ¦Фхж + а2^»!/ + 2 | я|) |2 я|5 4- vty = О,
При а = i система A5) описывает квазимонохроматические
волновые пакеты на поверхности жидкости небольшой
глубины (система Дэви — Стюардсона \8]).
Другим замечательным случаем является случай вы-
рождения квадратичной формы оператора D±. Пусть а = О,
тогда система сводится к виду
ал ду ' v" ' ; дх '
д д . , д
rf I /
о^ ог/ дх
Система A6) может иметь приложения в физике плазмы.
Очевидно, системы A2), A4) являются двумерным
обобщением нелинейного уравнения Шредингера и сводят-
ся к нему, если д/ду = с д/дх.
§ 2. Законы сохранения
Спектральная задача для оператора A.2) заменой
х
-ф —>ea'ty приводится к решению уравнения
|? A)

290 ПРИЛОЖЕНИЕ
В силу представления Лакса A.3) с ним совместно уравне-
ние
-f- - А*. B)
Непосредственно из системы A), B) можно построить бес-
конечную серию законов сохранения соответствующего
нелинейного уравнения. Поясним это на примере уравне-
ния Кадомцева — Петвиашвили. В этом случае линейные
уравнения имеют вид
Ы% + tyxx + Щ = 0,
Ь + 4 %хх + вЩх + 3 (их + aw) ф = 0.
Будем искать решение этих уравнений в виде
¦ф = exp (ikx + — у -f- ШЧ + X) .
Тогда на функцию X возникают два уравнения
LTJ_x 4~ —(X I 3X X 4-Х3}
Z (_ О О
+ ux -f awj , E)
2 = — 2ik.
Устремим z к ею и разложим Х в асимптотический ряд по
n=0
Члены асимптотического ряда могут быть вычислены
независимым образом из каждого из уравнений E). Срав-
нение этих рядов для Хх, Х2 дает, как легко проверить,
уравнения A.5). Непосредственным их интегрированием

§ 3j МЕТОД ОДЕВАНИЯ 291
получаем соотношения
wdx-
Пусть и —> О при \ у | —> оо. Интегрируя соотношение G),
получим формально
JL^dxdy^O. (8)
Однако, как легко видеть из F), интеграл в (8) конечен,
только если
I udx = O. (9)
В этом случае (8) выражает собой факт существования
первого интеграла уравнений A.5). Последующие интегра-
лы возникают из сравнения выражений для Х„ при четных
п. Полагая п -— 2, 4, получим интегралы
O, A0)
Интегралы A0) имеют смысл импульса и энергии среды,
описываемой уравнением Кадомцева — Нетвиашвили.
Второй из них — интеграл энергии. При w = 0 эти интег-
ралы движения перейдут в обычные интегралы уравнения
КдФ (см. § 5 гл. I).
§ 3. Метод одевания
Решение задачи Коши для уравнений типа A.3) требует
постановки и решения прямой и обратной задач рассеяния
для оператора L — а. д/ду — М (в случае уравнения КП —
для уравнения Шредингера). Однако, для построения
широких классов частных решений можно использовать
метод, который мы назовем «методом одевания» [5]. Рас-
смотрим на прямой —оо <^ х <^ оо интегральный оператор

292 ПРИЛОЖЕНИЕ
F, зависящий от t, у:
FW(x) -I F(x,z,l,y)W (z)dz, A)
и предположим, что он допускает треугольную факториза-
цию, т. е. представление в виде
1 -|- f = A + кт1 A + к-). B)
Здесь К+, К~ — вольтерровы операторы
z,t,y)W(z)dz. C)
Пусть, далее, задан дифференциальный оператор Lo =
= а д/ду — Мо, где
= т0
+ 1Щ
Эх Эх
Коэффициенты mt оператора Мо — функции, вообще гово-
ря, х, у, t.
Пусть оператор F коммутирует с Lo:
FL0 - LaF = 0. D)
Применяя соотношение D) к произвольной функции Т (х)
и интегрируя п раз по частям, убедимся, что ядро опера-
тора F удовлетворяет соотношению
^t E)
В соотношении E) Мо — оператор, сопряженный к М,
причем
M0F = (т0 -^- -f .. . +тп) F (x, z, у, t),
+ [ дХ д j F)
FM+0 = (_ 1)» -?_ *7n0 + . . . + Fmn.
dzn
Из D) следует, что преобразование пространства функции
W (х) при помощи оператора 1 + F оставляет оператор Lo
инвариантным:
A + F)-1 Lo A+F)= Lo.

§ з] метод одевания 293
Рассмотрим преобразование Lo при помощи операторов
1 + К+ и 1^ + К~, где К+, К" — «треугольные факторы»
оператора F, задаваемые формулой B),
Lo —> L = A -J- Л'+) Lo A + R+Ylk= (I + R~) Lo A + К')'1. G)
Из G) следует, что L — дифференциальный оператор (ибо
он вольтерров одновременно в обе стороны) и имеет вид
L = а -з М.
ду
Здесь
где иъ . . ., ип — функции от х, t, у, выражающиеся че-
рез ядро оператора К+ (или К~). Формулы для них могут
быть получены из уравнения
L A + К-) = A + К-) Lo, (8)
следующего из G). Приведем, в предположении постоянст-
ва т0, mi, формулы для м^ щ:
"l = Ыо, lol +
+ — [т0, 111 + Kilo + [mu go]. (9)
Здесь
h (х, У, П = (-^ 1-)* К (х, z, у, t) |x=2. A0)
Оператор L можно назвать «одеванием» оператора Lo
при помощи интегрального оператора F. Пусть оператор
F коммутирует еще с оператором d/dt — Ао, где Ао —
дифференциальный по х оператор. Тогда)
§ = о (И)
и операторы 1 + К± осуществляют одевание оператора

294 ПРИЛОЖЕНИЕ
д/dt — Ао, приводя его к оператору 31 dt — А, где диффе-
ренциальный по х оператор А связан с Ао формулами
типа F). Пусть операторы Lo = а д/ду — М 0 и d/dt — Aa
связаны соотношением Лакса A.3). Тогда существует класс
функций Wo, для которого совместна система уравнений
L0W0 = О,
8
0
Применяя к х?0 соотношение (8) и соответствующее соотно-
шение для оператора 31 dt — А, получим
т = A + к-) ?0.
Из A3) следует, что операторы Мм А удовлетворяют соот-
ношению Лакса A.3), а их коэффициенты — рассматривае-
мой нелинейной системе уравнений, которой, конечно,
удовлетворяют и коэффициенты операторов Мо, Ао. Таким
образом, метод одевания позволяет «размножить» решения,
строя по известным решениям обширные классы новых.
Для конкретного проведения одевания нужно знать
ядро оператора К+. Умножая B) слева на 1 + К+ и пола-
гая z <^ х, придем к интегральному уравнению, обобщаю-
щему уравнение Гельфанда — Левитана — Марченко:
К+ + F + j K+ (х, s, у, t) F(s,z, у, t) ds = 0. A4)
§ 4. Солитоноподобные решения уравнения КП
Использование метода одевания позволяет решить ряд
задач, прежде всего — задачу о солитонных решениях,
впервые численно найденных в [9], и их устойчивости. Мы
ограничимся рассмотрением уравнения КП.
Будем производить одевание следующего тривиального
решения, следуя работе [10]:
щ = 0, w0 = 0.

§ 4] СОЛИТОНОПОДОБНЫЕ РЕШЕНИЯ УРАВНЕНИЯ КП 295
Рассмотрим сначала случай а = 1. Тогда ядро F под-
чиняется уравнениям
8F , дЧ' _ d*F __ 0
0
Выбирая решение этих уравнений в виде
F = 2 с„ B/, 0 ехр (рпж + gnz),
1
где
сп {у, t) = сп @) ехр \{ql -pl)y-A (pi + ql) t]
и Pni Чю сп Ф) ^>0, и решая уравнение для ядра К~ (= К)
K + F+ J K(x,z',y,t)F(z',z,y,t)dz' =0, B)
мы найдем решение уравнения Кадомцева — Петвиашви-
ли по формуле
и (х, у^)=-2~К (х, х, у, t). C)
Поскольку ядро уравнения B) является вырожденным, его
решение находится без труда и имеет вид (ср. § 3 гл. I)
К (ж, z, у, t) |г=х = q~ lndet A,
где матрица А представляет собой квадратную матрицу
N X N с элементами
<4„т = бпт + сп (y,t)
т
Таким образом, решение и {х, г/, t) есть
u(x,y,t)^2~
E)
Формулы D), E) описывают взаимодействие N одно-
мерных солитонов. В частности, полагая N = 1, имеем

296 ПРИЛОЖЕНИЕ
СОЛИТОН
{p + qf ^
u— 2 cn
F)
превращающийся при р = q в хорошо знакомый солитон
уравнения КдФ. При р Ф q со литой движется под некото-
рым углом к оси х. Ясно, что в общем случае решение D),
E) описывает пересечение таких «косых» солитонов и не
убывает в направлениях х/у — рп — дп, п = 1,. . .,7V, при
х, z/-> оо. Представляет интерес вопрос о существовании
солитонов, убывающих во всех направлениях и динамика
их взаимодействия. Оказывается, что такие солитоны
уравнения КП существуют только при а2 < 0. Мы полу-
чим явные выражения для них путем специального вы-
рождения решения D), E), предварительно заметив, что
изменение знака а в уравнении КП эквивалентно продол-
жению решений с вещественных' у на чисто мнимые, т. е.
замене в формулах а2 -»- — а2, у -> iy.
Переходя к вырождению решения D), E), удобно
обозначить рп + дп = %п, рп — qn = vn, cn @) =
= — ап%п. Перепишем, далее, матрицу А D) в виде
( Х"Х" х+ V"V" х)впт, G)
где
X ехр {%п [х - vny - (Зу'г + х**)]> • (8)
Поскольку преобразование G) от А к В является преоб-
разованием подобия, получим det A = det В и вместо E)
З2
и (х, у, t) = 2 -5-g In det В.
Теперь перейдем к пределу хп-> 0, полагая
an = i- 1пкп + О (и2).
В результате получим для определителя В:
det В = П (- ип) det 5 + О (х

§ 4] СОЛИТОНОПОДОБНЫЕ РЕШЕНИЯ УРАВНЕНИЯ КП 297
где матрица Я имеет вид (после замены у ->- iy)
Впт = б„т (^ — ™пУ — In — 3\lt) + A — бпт) .
v
(9)
(Последний член в правой части следует считать равным
нулю при п = т.) Очевидно, что
u(x,y,t) = 2-|^-lndet? + O(x).
Полагая теперь к = О, получим
u(x,y,t) =2-^-lndet Б. A0)
При некотором выборе v и ? можно добиться как веществен-
ности, так и регулярности при вещественных значениях ар-
гументов. Так, при N = 2 и при v2 = — vb ?2 = 1Х
получим из (9)
det В = 4 (Vl + Vi)-2 + |s - ivtf - Ei - 3v^ | \ (li)
Это выражение строго положительно, т. е. определяемая
формулой A0) функция и (х, у, t) вещественна и ограни-
чена. При х2 -j- у2 -*¦ оо решение w оо (х2 + у2), т. е.
убывает по всем направлениям в плоскости х, у. Это ре-
шение представляет собой двумерный солитон, движущий-
ся со скоростью v = (vx, vy):
ох = 3 | vj. | 2, oy = — 6 Im vv
В общем случае решение (9), A0) вещественно и не-
сингулярно, если ./V = 2К, а константы vn и \п удовлет-
воряют соотношениям
= —Vn, |к+п=1„, П = 1,. . .,«", A2)
причем среди набора комплексных чисел vl5. . .,vK нет
совпадающих. Эти условия гарантируют положительную
определенность матрицы В. Доказательство этого вполне
элементарного алгебраического факта мы опускаем.
Построенное решение (9), A0), A2) описывает столкно-
вение К двумерных солитонов, т. е. при t -> ± °о решение
есть сумма решений A0), A1). Рассматривая асимптотику

298 ПРИЛОЖЕНИЕ
решения при t ->- + оо как функцию х0, у0, где
X = Хд + VKX 't, У = у0 + Щ 't,
легко видеть, что соответствующие величины ?* совпа-
дают: |? = ^п = |п. Фазовые сдвиги солитонов, всегда
имеющиеся и хорошо известные в одномерных задачах,
при столкновении двумерных солитонов тождественно рав-
ны нулю [10]. Замечательный факт состоит в том, что дина-
мика полюсов рациональных решений уравнения КП опи-
сывается известной системой Мозера — Калоджеро (см.
ниже § 7).
§ 5. Точные решения, зависящие
от функциональных параметров
Применение метода одевания к двумерным уравнениям
позволяет получить, кроме солитонных решений, набор
точных решений, содержащих произвольные функции
одной переменной [5]. В качестве примера рассмотрим
уравнение КП с а2-< 0 и перепишем систему D.1), за-
менив d/ду на i д/ду:
, dF , d*F дЧ' п
Выберем решение этой системы в виде
F (х, у, z,t) = ff (x, у, t) ф (z, у, t) B)
с функцией ф, удовлетворяющей уравнениям
Тем самым функция ф (х, у, t) определяется произвольным
начальным условием ф (х, 0, 0). Мы получаем из ф ре-
шение уравнения D.2) (ядро F B) снова вырождено):
'. у.
K(x,z,y,t)- Ф(^ У.«
—эо
При этом единственным ограничением' на выбор решения

§ 5] ФУНКЦИОНАЛЬНЫЕ ПАРАМЕТРЫ 299
системы C) является, как видно из D), достаточно быст-
рое убывание <р (ж, у, t) при х -> — <х> (именно, <р е
G ^2 (-°°i s) Для любого s <. оо). Этому'условию удов-
летворяет, например, любая функция вида
ffi14 (k = h + ik2) E)
с произвольной интегрируемой функцией двух перемен-
ных с (къ к2), если область интегрирования D целиком
лежит в нижней полуплоскости к; функция с (къ к2) оп-
ределяется через ф неоднозначно. Соответствующее реше-
ние уравнения КП дается, согласно D.3), формулой
X
и (х, у, t) = 2 J^- (I + J | Ф (z, У, t) |2 dz). F)
—no
Решение E), F) можно рассматривать как обобщение
односолитонного решения D.6). Односолитонному реше-
нию соответствует выбор с (къ к2) в виде двумерной
б-функции:
с (къ к2) ¦= сЬ (кг — аг) б (/с2 + я2)> ^2 ^> 0.
Нетрудно обобщить также TV-солитонное решение D.4),
D.5). Для этого достаточно выбрать ядро Fb форме
F=2i^(x,y, 1)уг{г, у, t), G)
где фг — функции вида E) с соответствующими сг (кг, к2).
Решение уравнения КП есть
и (ж, у, t) = 2~lndetA, (8)
X
Апт = Кт+ } <Рп (Z, У, t) фт (г, у, t) dz. (9)
—со
Вещественность и (х, у, t) обеспечивается самосопряжен-
ностью матрицы А (9).
Полагая
к
а (g) gzx+mj-n't dl, (Ю)
о
нетрудно видеть, что и (ж, у, t), даваемое формулой F)

300 ПРИЛОЖЕНИЕ
при t-*~— oo, представляет собой обычный солитон. Од-
нако, внимательный анализ выражений A0), F) показы-
вает, что в асимптотике t —*¦ -f- oo солитон отсутствует
(если а (?) не имеет 6-образных сингулярностей). Таким
образом, решение, соответствующее A0), описывает ан-
нигиляцию солитона. Это решение служит прекрасной
иллюстрацией известного факта неустойчивости плоских
солитонов уравнения КП при а? < 0 (см. [11]). Ниже бу-
дет обсужден еще один класс решений, зависящих от
произвольных функций (см. ниже § 8), полученный дру-
гим методом.
§ 6. Метод римановых поверхностей.
Конечнозонные решения ранга 1
Довольно широкий класс решений уравнения КП по-
лучается как обобщение теории конечнозонных периоди-
ческих и квазипериодических' потенциалов уравнения
Шредингера и решений КдФ,' 'развитой в гл. II. Мы
начнем с понятия «скалярной функции Бейкера — Ахие-
зера» гр по алгебраической римановой поверхности Г рода
g ;> 1, на которой отмечена точка Ро (часто называемая
«бесконечностью»). Зададим локальную координату z =
= к~х около точки Ро, где1 z = 0. Рассмотрим функцию
гр (х, у, t, Р), зависящую от точки Р поверхности Г и
параметров х, у, t, с такими* свойствами: функция гр ме-
роморфна при P"V= Ро'Г^> имеет g полюсов первого по-
рядка уи. . . ,yg на Г, положение которых зависит от
х, у, t; г|) имеет асимптотику при к —у оо (или Р —*- Ро)
вида1
1)з = ехр <кх + о„ {к) у + К (к) Ц A + 3 It (x, у, t) к-% A)
где сс„ (А,), рт (к) — многочлены степеней п, т. Такая
функция г|>, по аналогии с блоховской функцией гр из § 6
гл. II, единственна и может быть с использованием клас-
сической теории 9-функций записана точной формулой
(см. обзор [12], Приложение 3 и работу [13]). Использование
функции гр для нахождения решений уравнений вида A.3)
основывается на следующем Гфакте [14].ч При указанных
аналитических свойствах функция гр аннулируется двумя

§ 6] МЕТОД РИМАНОВЫХ ПОВЕРХНОСТЕЙ 301
скалярными линейными операторами, не зависящими от Р:
(-^-Лф-О, D—Л)ф-О, B)
где М и А — дифференциальные операторы по х порядков
п и т соответственно с коэффициентами, зависящими толь-
ко от х, у, t и не зависящими от Р.
Из B) для всех Р следует, что выполнены A.3)
При п = 2, т = 3 мы приходим, согласно A.4) —г A.6),
к уравнению КП A.5), где связь 1]з с потенциалом и (х,
у, t) имеет вид, такой же, как и в § 6 гл. И:
u(x,y,t)--2^1{x,y,t), D)
где |х (х, у, t) — коэффициент разложения в формуле A).
Для и (х, у, t) имеет место формула, обобщающая форму-
лу (II.9.13) (коэффициенты выбраны согласно (8.10)):j
и (х, у, t) = - 2 ~ In 0 (Ux + Vy + Wt + Uo) + const. E)
Для рода g = 1 эти решения вырождаются. При g = 2
решение E) является «кноидальной волной» вида
и (х — at, у — Ы). Если Г — гиперэллиптическая рима-
нова поверхность любого рода g^>l иР0 = оо — точка
ветвления, то V = 0. Мы получаем решения КдФ, описан-
ные в гл. II. Если риманова поверхность Г имеет вид
w3 + ф1 (Е) w + cp2(E) = 0 F)
и точка Ро = оо, то W = aU + bV. Преобразование
и' = и + 2р, w' = w — 2cot -f- const,
x' =x + lay + 3 (a2 + P)*,
y' =y + 3at, t' = t
сохраняет уравнения КП при нормировке (8.10) ниже
и сводит кноидальные волны КП к решениям КП, не
зависящим от t. На решениях E) это преобразование
эквивалентно замене локальной координаты z = к~г.
Предельным переходом из решений E) можно * по-
лучить решения, являющиеся рациональными функциями

302 ПРИЛОЖЕНИЕ
и (х, у, t). Этот класс решений уже обсуждался выше в
§ 4; он представляет особый интерес, и мы обсудим его в
следующем параграфе. Рациональные решения получают-
ся вырождением из решений в эллиптических функциях
вида
Щ ¦ :f и {х, у, t) = 2 S Ъ (х - хх {у, t)), G)
:¦-•; г=1
обобщающих решение (II.10.13) при п = 3и кноидальную
волну при п = 1. Детальные вычисления в этом случае
не проводились.
Возвращаясь к функции Бейкера — Ахиезера if), мож-
но отметить одно обстоятельство. Рассмотрим случай,
когда многочлен <%п (к) в формуле A) является главной
частью [/] разложения по к — z некоторой алгебраиче-
ской функции / (Р) на поверхности Г с единственным
полюсом в точке Ро (z = 0). Тогда функция ф может быть
найдена в виде
г]) (х, у, t, Р) = ехр {/ (Р) у} г]H (х, t, P). (8)
Уравнение B) по у приобретет вид
Вследствие этого коэффициенты операторов М, А не будут
зависеть от переменной у, так как они выразятся через ipa.
Тем самым уравнение C) сведется к уравнению Лакса.
Если, кроме того, полином р*т (к) также является глав-
ной частью аналогичной алгебраической функции g (P),
то оба уравнения B) будут иметь вид
^ /^, ^- = ^ = ^ A0)
или
Ш, А] = 0. A1)
Мы получаем вывод: риманова поверхность Г с отмечен-
ной точкой Ро и парой алгебраических функций /, g,
имеющих единственный полюс в точке Ро порядков т, п,
порождает пару коммутирующих операторов М, А. Ко-
эффициентьГэтих операторов М, А могут быть выражены
через 0-функцию' (см. [13]). Сама по"себе задача классифи-
кации коммутирующих пар М, А была поставлена"^и от-
части решена еще в 20-х годах, хотя и недостаточно эф-

g 6] МЕТОД РИМАНОВЫХ ПОВЕРХНОСТЕЙ 303
фективно (см. [15—17]). Перефразируя на современный
язык эти старые результаты, их можно представить так:
а) указанная конструкция всегда дает кольца коммути-
рующих операторов, базис которых М, А зависит от ко-
нечного числа параметров; б) обратно: если порядки т
и п операторов М, А взаимно просты, то коммутирующие
операторы М, А получаются приведенной выше кон-
струкцией. В работах [13, 14] найдены явные формулы
для коэффициентов и установлено, что так построенные
операторы М, А «общего положения» являются периоди-
ческими и квазипериодическими функциями от х. При
этом уравнения коммутативности оказываются вполне
интегрируемыми гамильтоновыми системами по х на ко-
эффициенты (см. обзор [18]). Описанным способом можно
построить, конечно, много примеров коммутирующих
операторов М, А также и не взаимно простого порядка,
где оба числа тип делятся на I. Однако, еще в 20-х го-
дах отмечалось, что эта конструкция не может дать пол-
ной классификации. Коммутирующие операторы Л?, А
имеют всегда общую собственную функцию:
А/гр = tap, Aty = Щ\ A2)
При этом X и [I связаны уравнением, определяющим неко-
торую риманову поверхность:
F (X, ii) = 0 «-> F (М, А) = 0. A3)
Если собственная функция гр = гр (х, к, \i) является одно-
кратной в каждой точке римановой поверхности, то она
совпадает с функцией Бейкера — Ахиезера, построенной
выше, при
гр (х, X, ц) = гр (х, 0, 0, Р), A4)
где Р — точка поверхности Г.
Важным специфическим свойством данной конструк-
ции является то, что общая собственная функция гр одно-
кратна. Вообще говоря, она может оказаться ^-кратной
для всех точек Р поверхности Г. Число I называется «ран-
гом» коммутирующей пары М, А. Можно показать, что
число I обязано быть делителем обоих порядков т, п.
Если т и п взаимно просты, то обязательно 1 = 1.
Если т и п не взаимно просты, то возможно I ^> 1. Для
случая I ^> 1 исследование существенно более сложно
(см. [19—21]). Результат зависит от функциональных

304 ПРИЛОЖЕНИЕ
параметров и не сводится к 8-функциям. Техника построе-
ния коммутирующих операторов ранга I имеет прило-
жения к задаче о построении решений уравнения КП, ко-
торые будут называться «конечнозонными ранга I». В ка-
честве примера укажем простейшую невырожденную пару
коммутирующих операторов ранга I = 2. Эти операторы
имеют порядки 4 и 6:
М = L, = Ь\ + Сх(®(с + а) + $>(с + Ъ)) ± +
+ $>{с + а)-®(с + Ъ), A5)
где а = const, b = const, 1A = b\ + D, L2 = д2/дх2 +
+ u, (x), D —¦ оператор третьего порядка, который мы не
выписываем. Произвольная функция с (х) связана с
и (х) формулами (8.21), где у = t = 0 (см. ниже). Опера-
торы L4 = М и Ьв = А связаны алгебраическим соотно-
шением рода g = 1
А2 = UP + g,M + g3) A6)
откуда без труда находится оператор D.
Коммутирующие операторы ранга 2, указанные фор-
мулой A5), заимствованы из работы [21].
Напомним, что простейшие нетривиальные известные
еще в 20-х годах коммутирующие пары ранга 1 имели
порядки 2, 3. Они указаны в связи с классической «кнои-
дальной волной» для КдФ в § 1 гл. II, где L2 = д^/дх2 +
+ 2!? (х) — оператор Ламе.
§ 7. Рациональные решения уравнения КГГ.
Дискретные системы частиц на прямой
Как уже говорилось выше, уравнение КП обладает
рациональными «слабо локализованными» решениями
и (х, у, t), не имеющими особенностей при всех веществен-
ных х, у, t и убывающими как (х2 + у2)'1 при х2 + у2 —>¦
-> оо (см. § 4). Простейшим решением такого вида являет-
ся «двумерный солитон» D.11), обнаруженный впервые
лишь в 1976 г. в результате численного счета [9].
Более общие рациональные решения даются формулой
D.10). Оказывается, общее рациональное решение урав-
нения КП, убывающее при | х \ -> оо,— возможно, с по-
люсами при вещественных х, у, t, также описывается фор-

§ 7] РАЦИОНАЛЬНЫЕ РЕШЕНИЯ УРАВНЕНИЯ КП 305
мулой D.10). Другая форма записи решений D.10) та-
кова:
1 Х;(у,1)]-', A)
и(х, у, 1)='—2
3=1
где положения полюсов Xj являются функциями от у, t.
Не предполагая этого заранее, можно показать, что реше-
ния вида A) будут рациональны по всем переменным х,
у, t. Решения A) обладают некоторыми замечательными
свойствами.
Рассмотрим систему частиц на прямой с координатами
Pi, X{ и гамильтонианом взаимодействия
(«система Мозера»). Напомним результаты работы [22].
Время обозначим через х. Определим две матрицы
li} = рД; + i}
L = Aц), А х x
1 ] - C)
2 A-М у 25jt
*ФЗ
Гамильтонова система B) представляется в виде
U = IL, А]. D)
В частности, мы имеем
Sp L = 0, Sp U = Н == F2, Sp L1 = Ft (x, p). E)
Интегралы F (x, p) инволютивны, и система B) вполне ин-
тегрируема. В силу инволютивности интегралов Н = F'i
и F3, соответствующие гамильтоновы системы коммути-
руют как группы преобразований фазового пространства
(х, р). Интересную связь с уравнением КП открыл Кри-
чевер [23]. Мы будем рассматривать двупараметрические
траектории потоков с гамильтонианами R' = F% и F3
на фазовом пространстве (хъ . . ., хп, ръ. . -,рп)
dxi dl'\ dPi dF-i
дх2 др. ' дх2 дх.

30G ПРИЛОЖЕНИЕ
Тем самым определены функции xt (xu т2), pt (r1, т2).
Произведем сопоставления
^1-+У, т2 ^ t. G)
Важное утверждение (теорема Кричевера). Решения
п
КП вида D.10) получаются как и = —2 ^[х —
г=1
— xi (У, t)]~2, где полюсы xt двигаются по y=t1 в силу сис-
темы B) с гамильтонианомН = F2vl по t = тх в силу сис-
темы с гамильтонианом F3. Это — все рациональные
по х решения, убывающие при | х \ -> оо. Сформулиро-
ванное утверждение является итогом целой серии исследо-
ваний. Еще в 1974 г. были найдены простейшие невырож-
денные двухзоыные решения КдФ, сводящиеся к эллипти-
ческим функциям и имеющие вид суммы трех кноидальных
волн с нелинейно связанными фазами [24]
и (х, t) = 21? (х - a {t)) + 2W (х — Ъ (t)) -f- 2W (х - с (t)).
Вид а, Ь, с дан в § 10 гл. II (см. формулы (II.10.13)). Эти
решения могут быть вырождены в рациональные по х,
так как функция Вейерштрасса 1? (х) вырождается в х~2.
Далее, в [25] была открыта глубокая связь рациональных
решений КдФ с системой частиц на прямой B) и найдены
все рациональные решения, убывающие при | х | -> оо.
Все эти решения являются вырождением конечнозон-
ных и имеют вид
п
«(*,*) =-?,2 [я-я,-@1-*, ^=-^2^. (8)
Связь с системой частиц такова: функция и (х, t) вида
(8) тогда и только тогда удовлетворяет КдФ, когда а) 2п =
= d(d+ 1); б) набор [хг (t0), . . ., xn(t0),Pl (t0), . . .,рп (t0)]
является фазовой точкой (х, р), стационарной для гамиль-
тониана B), т. е. grad H = 0; в) по переменной t величины
Xj (t) являются решением гамильтоновой системы с гамиль-
тонианом F3 (x, р).
Несколько позднее такие же результаты были получе-
ны в [26], где связь дискретных динамических систем с дви-
жением полюсов решений и (х, t) была перенесена на урав-
нение Бюргерса — Хопфа и сам вопрос о такой связи об-
суждался в более общем аспекте. Наконец, в обзоре [18]

§ 8] МЕТОД ГОЛОМОРФНЫХ ВЕКТОРНЫХ РАССЛОЕНИЙ 307
(см. Заключительные замечания) сформулирована упо-
мянутая выше теорема о решениях КП вида A), даю-
щая естественное завершение начинаний работ [25, 26].
Действительно, если решение и (х, у; t) уравнения КП
вида A) не зависит от у, то оно сводится к решению КдФ.
В силу теоремы Кричевера это равносильно тому, что фа-
зовая точка (х, р) должна быть стационарной для гамиль-
тониана B). Однако это бывает лишь при выполнении ра-
венства 2п = d (d + 1)- Таким образом, для решений,
не зависящих от у, теорема Кричевера сводится к резуль-
татам работ [25, 26]. Построение рациональных решений
(8) является естественным вырождением излагавшейся
выше процедуры построения решений уравнения КП с
помощью функции Бейкера—Ахиезера. Риманова поверх-
ность Г является в данном случае рациональной (сферой
Римана) с координатой к, точка Ро = оо. Функция
Бейкера — Ахиезера ищется в виде
N
где uj рациональны по к. В этом случае функция
и (х, у, t), найденнаяпо функции^ в соответствии с общими
формулами F.4), имеет вид (8). Эта функция удовлетво-
ряет уравнению КП, если ty аннулируется скалярными ли-
нейными операторами F.2). Вычисление показывает, что
функция ij) аннулируется оператором д/ду —• М тогда и
только тогда, когда матрицы C) удовлетворяют уравне-
нию D). Тем самым набор полюсов Xj зависит от у в силу
B). Функция i|) аннулируется оператором d/dt — А тогда
и только тогда, когда полюсы xj no t двигаются в силу
гамильтоновой системы с гамильтонианом F3 E).
§ 8. Метод голоморфных векторных расслоений
над римановыми поверхностями.
Функциональные параметры в точных решениях
Уравнение КП обладает широким классом точных реше-
ний, зависящих от некоторого количества произвольных
функций одной переменной х. Один такой класс, получен-
ный из «метода одевания», описан в § 5. Мы опишем здесь

308 ПРИЛОЖЕНИЕ
еще один метод получения точных решении, содержащих
произвольные функции одной переменной х, который яв-
ляется дальнейшим развитием описанного в § 6 метода
римановых поверхностей.
Рассмотрим риманову поверхность Г рода g> 1 с от-
меченной точкой Ро и локальной координатой z = к'1
около Ро, как и в § 6 (см. выше). Нашей целью является
построение векторного аналога ¦ф-функции Бейкера —
Ахиезера ij; = tyq ix-> У, *i P), 1 = !>• • -Л, описанной в
§ 6. Зададим (I X /)-матрицу ф0 (х, у, t, к) с такими свой-
ствами:
а) Ai = -jr^-tyo1— Ai(x, у, t, к) — полиномы по /с,
dAi dAi
~дх- 1x7 ~ f '' ?!' Xl = х> хг = У, %ъ — t, A)
б) ¦фо («о, У о, to, к) = 1.
Зададим набор точек уъ. . ., y;q поверхности Г и на-
бор (I — 1)-векторов
«1 = («1, а). а2 = (а2,д),. • -,alg = (algiq).
Будем строить вектор-функцию \|j (x, у, t, P), имеющую
полюсы первого порядка в точках уъ. . ., yig, не зави-
сящие от х, у, t. Обозначим через ф* (х, у, t) вычеты ком-
поненты tyq (x, у, t, P) в полюсе у]. Потребуем, чтобы при
данном / все I вычетов ср' (х, у, t) были пропорциональны
одному из них — вычету ц>] с постоянным коэффициентом
CLjq, не зависящим от х, у, t:
Ф^ (х, у, t) = ajqylj (x, у, t). B)
При Р -> Ро (или .к ->- оо) потребуем, чтобы вектор
t|) (x, у, t, P) имел асимптотику
* (ж, У, t, Р) - (|о + 51 6i (ж, 2/, 0 ^j) ipo, C)
где |0 = A, 0, 0,. . .) и |7- (х, у, t) — векторы. Такая век-
тор-функция г|> (х, у, t, P) определяется однозначно указан-
ными аналитическими свойствами. Ее построение сводит-
ся к системе сингулярных интегральных уравненийДсм.
[19, 20]). Следуя [20], для построения решений уравнения
КП матрицы A t = ip0Xi t^1 подбираются так:

§ 8) МЕТОД ГОЛОМОРФНЫХ ВЕКТОРНЫХ РАССЛОЕНИЙ 309
Случай 1 = 1. Этот случай рассматривался выше,
где полагалось Щ
А1 = к, А2 = к\ А3 = к3.^ D)
Более общим является вид —
Случай 7 = 2. При 1 = 2 зададим матрицы А;-.
л , , - /01 1\ . /0 0\ /О 1\
А2 = гр^о1 = @ J = к2, Л = ibo^o1 = и3 + (р 0) ft + g,'
E)
где ^ — матрица, не зависящая от к. Из условий совмест-
ности мы найдем, что щ = ип (х, t) не зависит от у и
удовлетворяет уравнению КдФ (при некоторых соотно-
шениях на р ид):
Это дает возможность построить г|H для 1 = 2.
Случай Z^3. Зададим матрицу А\ вида
/0 0 ... О ОЧ /° 1 ° • • • °\
. / \ I 0 0 1 . . . 0\
К+ I , «= ,
VwoKi • • • и^0/ \ft" о'о::: о/
где р ж q — матрицы, не зависящие от к.
Положим q = 0 при Z = 3. Из условия A) мы найдем
и0,. . .,м;_2. При Z = 3 эти условия сведутся к тому, что
обе функции it0, ut не зависят от <, а пара щ, щ удов-
летворяет уравнению Буссинеска (т. е. КП, не завися-

310 ПРИЛОЖЕНИЕ
щего от t) по х, у при некоторых соотношениях на р и q:
Т I 2
' —-ти1 ° °
0, р= [ «о-4 Т- ° I- (8)
"ож — ~з~ uixx "о — ~з~ ~з
Отсюда извлекается вид матриц -ф0 для I = 3. В простей-
ших примерах (которые отнюдь не будут тривиальными)
можно положить для всех I ^> 2:
А1 = к, А2 = х2, А3 = х3. (9)
Если матрицы Ль Л2, А3 выбраны в виде D) — G), то вся
вектор-функция t|) (x, у, t, P) аннулируется скалярными
линейными операторами, которые имеют вид
Поэтому в силу A0) пара (u, w) удовлетворяет уравнению
КП, масштабным преобразованием сводящемуся к A.4).
Таким образом, мы получаем способ построения точных
решений КП, определяемых следующими наборами:
а) поверхностью Г с отмеченной точкой Ро = оо и ло-
кальным! параметром z = к'1 около Ро;
б) набором точек уъ. . .,y{g поверхности Г и набором
(I — 1)-векторов аъ. . .,a;g;
в) матрицами Аъ А2, А3, определяемыми некоторым
числом произвольных функций от х, зависимость которых
от у, t определяется уравнениями совместности A).
I Рассмотрим снова случай 1 = 1. Все решения КП, по-
лученные из вида D) матриц Аи сведутся к тем, которые
уже рассматривались при постоянных At = к1, с помощью
преобразования
и' = \i(t) + u(x— -f-vOO, у, )
. ^ ^
, -ГГ, 41* da. dv

§ 8] МЕТОД ГОЛОМОРФНЫХ ВЕКТОРНЫХ РАССЛОЕНИЙ 311
Преобразование A1) обладает тем свойством, что оно пере-
водит решение КП в решение КП для любых функций
и, w. Отсюда вытекает, в частности, что для осмыслен-
ной (математически корректной) постановки задачи Коши
необходимо, чтобы функции и, w были ограничены при
всех у.
Более интересен случай I = 2. При I = 2 набор Аг
определяется одним решением и0 (х, t) уравнения КдФ
F).
При I = 3 набор Ai определяется одним решением
v (х, у) уравнения Буссинеска — т. е. уравнения КП,
не зависящего от t,— по переменным х, у, их = vx, 2uQ —
— ulx = vv.
Если даже все функции щ тождественно равны нулю,
то получаемые решения уравнения КП будут существен-
но зависеть от всех трех переменных х, у, t.
Рассмотрим первоначально вырожденный случай, где
Г имеет особенности типа «двойных точек», Ах = к, Аг ~
= к2, А3 — к3, и0 == 0. Вектор г|> (х, у, t, k) имеет вид
A2)
здесь |0 = A, 0,. . .,0) и а} = (ajlt. . .,ая) — векторы.
Задан также набор (I — 1)-векторов аь. . ,,aig. Для реше-
ний и (х, у, t) из A0) следует формула
N
A3)
В «двойных» точках хп -~ хг2 мы требуем выполнения
равенства
г|з (х, у, t, xrl) = ф (х, у, t, иГ2), г = 1, 2,. . .,g. A4)
Условия на вычеты приобретут вид
i i
2=1 t

312 ПРИЛОЖЕНИЕ
Линейные уравнения A4), A5) однозначно определяют^,
если матрица г]H (х, у, t, к) задана. В простейшем случае
I = 2 (At = х1) можно взять г^0 в виде
-A1'1 sin в, cos9 )'
где Э = kll* {х + Щ.
В случае g = i, 1 = 2 можно подобрать парамет-
ры %rj, у, а так, что возникнут периодические по х, у, t
решения и (х, у, t), не имеющие особенностей в полу-
плоскостях \ у \^> у0 при всех значениях х, t. По-види-
мому, при g = 1, 1 = 1 все построения решения имеют
особенности при вещественных х, t. Подробный анализ
для g ^> 1 не проводился. Этот анализ может привести к
определенным трудностям вычислительного характера, но
вся задача решается в элементарных функциях.
Гораздо трудней случай, когда риманова поверхность Г
не имеет особенностей. Вычисление векторного аналога
функции Бейкера — Ахиезера сводится по схеме работы
[19] к системам сингулярных интегральных уравнений на
окружности и не может, по-видимому, быть упрощено.
В связи с этим в работе [20] был предложен дру-
гой метод вычисления решения и (х, у, t) уравнения
КП, обобщающий уравнения, полученные в §§ 4, 5 гл.
II для полюсов у1г. . .,yg блоховской функции г|з.
Обратим внимание на то, что в определение векторного
аналога функции Бейкера — Ахиезера *ф выше, как и для
блоховской собственной функции оператора Шредингера
¦ф в §§ 4, 5 гл. II, входила «точка нормировки» (х0, у0, t0),
варьируя которую можно получить зависимость величин
у\,. . .,yig w. (I — 1)-векторов о^,. . .,ctig от параметров
хо> У01 К- Эта зависимость определяется обыкновенными
дифференциальными уравнениями, где в правые части
входят у, а, а также сама величина и (х, у, t). В простей-
шем нетривиальном случае g = 1, I = 2 эти уравнения
имеют вид (локальный параметр z —¦ простейший)
Ъх = (— 1){ (аа — aj)-1, ylv = 1,
aix = a] + и (х, у, t) + (- 1)'Ф (Yl, v,), A7)
aiy = v (x, y, t).
Здесь i = 1, 2, at = au, a2 = a21, величины ж0, г/0, tQ

§ 8] МЕТОД ГОЛОМОРФНЫХ ВЕКТОРНЫХ РАССЛОЕНИЙ 313
заменены на х, у, t, 2vx = uv,
ф = Б (?. - Ti) + I (- Уг) - 6 (- Ti). A8)
где—I' (z) = W (z), (I?'J = 4f3 + g2if 4- g3, № (z) — эл-
липтическая функция" Вейерштрасса (см. [27]). Можно
полностью забыть «происхождение» системы A7): функция
и (х, у, t) удовлетворяет уравнению КП в силу системы
A7). Введем обозначение, используя A7):
У1 = У + с (x,t), у2 = у — с (х, t) 4 с0,
w (х, у, z) = аг + а2, z (x, t) = аг — а2, A9)
и (х, у, t) = — а\ — а\ 4- Ф (ж, t).
В новых обозначениях получим
сх = z, zx = wz — 2Ф (у, с),
iyi2 я2 -1
^ __ __ J__ . l 2(т) (х fl с = (z со") / 20^
Заметим, что величина Q = Фс 4" Ф2 не зависит от у в
силу теорем сложения [27]. Ир этих уравнений, подстав-
ляя в уравнение для wx выражение w через zx, получим
4ф (х, t) = A 4- 3cL) Сх + 4<) — 2сжхх с,
8и (х, у, t) = (с», - 1) с? + 8Фсхх +
4- 4с2 (Фе - Ф2) - 2craxc-i, B1)
8с, = Зс^1 A - cL) - 4(?сж + 2сжхх.
Величина Q (с, с0) = Фс + Ф2 не зависит от у. Любое
решение B1) порождает решение уравнения КП и (х, у, t).
Периодическая по х гладкая функция с (х, t) порождает
периодическое по у, квазипериодическое по х решение
и (х, у, t), не имеющее особенностей, если z -ф- 0 и сх =
= z Ф 0. Решения B1) вида с (х -\- at) порождают
«солитоны» вида и (х + at, у). Для нахождения этих
«солитонов» мы должны Грешить уравнение ct = асх.
Уравнения B1) в этом случае можно исследовать. Возь-
мем с за независимую переменную вместо х и сделаем под-
становку z = h~2 (с). Из уравнений B1) получим
h" _ h _ _ ZWQuc)
B2)

314
ПРИЛОЖЕНИЕ
причем Q (с) — периодическая функция. График Wo (h)
имеет вид представленный на рис. 27 для й^Ои рис. 28
для а ^> 0.
Качественным анализом можно получить следующие
выводы а) начиная с некоторого «порога»^ ч> о0 ^> 0 урав-
а>0
Рис. 27. Нелинейная часть
потенциала W для скоростей
а < 0.
Pro, 28. Нелинейная часть
потенциала W для скоростей
а>0.
нение B2) всегда имеет всюду ненулевое периодическое
решение; поэтому возникает «солитон» или «кноидальная
волна» и (х + at, у), неособая и периодическая по х, у, t;
б) для а <; 0 уравнение B2) имеет всюду ненулевое пе-
риодическое решение, если (и только если) точка X = 0
лежит ниже первой точки спектра периодического потен-
циала Q, т. е. уравнение h" = Qh имеет всюду ненулевое
решение. Именно в этом случае возникает решение
и (х + at, у) уравнения КП без особенностей.
Решение КП получаем из B2), находя с (х), где сх =
== /г2 (с), и затем пользуясь формулой B1). Преобразова-
нием, указанным на стр. 301 (внизу), мы получим реше-
ние u{x-\-axt, у-\-Ы)с любым направлением. Любопытно
отметить, что возникшая в процессе решения уравнений
A7) величина с (х, t) удовлетворяет нелинейному уравне-
нию B1) типа КдФ. Мы знаем, что это уравнение должно
быть «скрыто изоморфно» обычному КдФ: функциональ-
ный параметр ц0 (х, t), входивший в первоначальную кон-
струкцию решений (в матрицу \|j0), удовлетворял обычному
уравнению КдФ, как отмечалось выше. Однако, этот изо-
морфизм пока не удается проследить.

§ 9] ЗАМЕЧАНИЯ О ПЕРИОДИЧЕСКОЙ ЦЕПОЧКЕ ТОДА 315
§ 9. Некоторые замечания
о периодической цепочке Тода
Цепочка Тода, изучавшаяся в § 7 гл. I, представляет
собой набор частиц одинаковой массы т = 1, которые рас-
положены на прямой в точках с координатами п + хп
(п — целое число). Гамильтониан цепочки Тода имеет вид
II (х, Р) = ? 4- Pl + ? ехр (*„ -
п
Цепочка Тода допускает представление типа Лакса (см.
[28, 29]), где L — разностный аналог оператора Шре-
дингера. Спектральная задача для оператора L имеет вид
Щ (п, Е) = Е$ (п, Е) = vn$ (n, E) +
(п + 1, Е). B)
В периодическом случае мы имеем
ф -— у* тч Л> л л PYT* { V т \' C-W
•^п '— "п ^п+Л, t-n+JY — <*п — сл.р \^п ' •bn-i) I \OJ
зоны спектра определяются так же, как в § 1 гл. II. Мно-
гими авторами указывалось, что периодическая цепочка
Тода исследуется полностью аналогично теории конечно-
зонных решений уравнения КдФ (см., например, обзор
[6]). Это утверждение относится также ко многим другим
системам — нелинейному уравнению Шредингера, sin-
Gordon и др. Вместе с тем полезно обратить внимание на
одно обстоятельство, отличающее дискретную систему ти-
па цепочки Тода от непрерывных систем типа КдФ, не-
линейного уравнения Шредингера, sin-Gordon и др. Как
неоднократно отмечалось в гл. II, одним из интересных
свойств теории конечнозонных решений уравнения КдФ
является практическая невозможность выделить эффек-
тивно периодические по х решения с заданным периодом Т
среди квазипериодических. Набор границ зон Ео,. . .,Е2п
n-зонного оператора Шредингера L формирует гиперэл-
липтическую риманову поверхность
У2 = П (Е — Еа).
а=о
Для разностного оператора L выделение периодиче-
ского случая с целым периодом N производится абсолют-

316 ПРИЛОЖЕНИЕ
но эффективно. Класс римановых поверхностей, отвечаю-
щий цепочке Тода,— с целым периодом N таков:
ц + fi-1 = 2PN (E), D)
где Pn (E) — полином степени N. Такую риманову поверх-
ность можно задать через края зон Еа оператора L:
w* = П (Е - Еа) = [Рп (Е) + 1] [PN (E) - 1]; E)
a=i
здесь 2PN (E)—след матрицы монодромии (сопоставьте фор-
мулы D) и E) с формулами B.1.10), где Pn—^ur). Учиты-
вая некоторую неаккуратность формул для цепочки Тода
в обзоре [6] (см. § 1 гл. III), укажем формулы, следуя [30J:
tv+w^ -
-ЫЩп-\)и + tV + W+)], G)
In cn (t) = In [0 (nil + tV + W-)/B [nU + tV + W+)] -
- in e i((n -i)u + tv+ w-)/e ((л - i) и +
+ tV + W+)],
где U, V, W — некоторые векторы, которые легко вы-
числяются точно так же, как ивтеорииКдФ.
Это утверждение относится также и к общим разност-
ным операторам на прямой (см. [30, 31]). Конечно, в пол-
ной аналогии с непрерывным случаем можно рассматри-
вать также и общий квазипериодический случай.
Замечание. Для справок укажем также кра-
сивый результат работы Flaschka H., Mclaughlin D.W.—
Progr. Theor. Phys., 1976, v. 53, относящийся как к ко-
нечнозонной теории КдФ, так и к периодической цепоч-
ке Тода: переменные «действия», сопряженные к «углам»
на торах, меняющимся от 0 до 2я, имеют вид площадей
под графиком функций | яд | — 1 в пределах запрещен-
ных зон.

ЛИТЕРАТУРА
К главам I—IV
1. Ахманов С. А., Хохлов Р. В. Проблемы нелинейной оптики
М.: ВИНИТИ, 1964.
2. Бломберген Н. Нелинейная оптика.— М.: Мир, 1966.
3. Gardner С. S., Green J. M., Kruskal M. D., Miura R. М —
Phys. I\ev. Lett., 1967, v. 19, p. 1095.
4. Gardner C. S., Morikawa G. K.— Courant Inst. of Math. Sc.
Rep., 1960, N 40, p. 9082.
5. Гуревич А. В., Питаевский Л. П.— ЖЭТФ, 1973, т. 65, с. 590.
6. Дубровин Б. А., Матвеев В. Б., Новиков С. П.— УМН, 1976,
т. 31, вып. 1, с. 55.
NJ 7. Захаров В. Е.— В кн.: Кунин И. А. Теория упругих сред
с микроструктурой.— М.: Наука, 1975.... ^ | '.
8. Кадомцев Б. Б., Карпман В. И.— УФН, 1971, т. 103, с. 193.
9. Карпман В. И. Нелинейные волны в диспергирующих средах.—
М.: Наука, 1973.
10. Кричевер И. М.— УМН, 1977, т. 32, вып. 6, с. 183.
11. Miura R. M. (editor) Lecture Notes in Mathem.— Springer,
1976, v. 515.
12. Scott A. C, Chu F. Y. F., Mclaughlin D. W.— Proc. IEEE,
1973, v. 61, p. 1443.
13a. Сагдеев P. 3. В сб.: Вопросы теории плазмы.— М.: Атомиздат,
1964, вып. 5.
136. Сагдеев Р. 3. В сб. Физика плазмы и проблема управляемых
термоядерных реакций.— М.: Изд-во АН СССР, 1958, т. 4,
с. 384.
14. Стокер Дж. Волны на воде.— М.: ИЛ, 1959.
15а. Withem G. В.— Proc. Roy. Soc, 1965, v. A 283, p. 238.
156. Уизем Дж. Линейные и нелинейные волны.— М.: Мир, 1977.
16. Ферми Э. Научные труды, ч. П.— М.: Наука, 1972.
17. Ландау Л. Д., Лифшиц Е. М. Квантовая механика.— М.:
Наука, 1963.
18. Займан Дж. Принципы теории твердого тела.— М.: Мир, 1974.
19. Айне 9. Обыкновенные дифференциальные уравнения.—
Харьков: Гостехиздат Украины, 1939.
20. Арнольд В. И. Математические методы классической механики.—•
М.: Наука, 1974.
21. Зверович 9. И.— УМН, 1971, т. 26, вып. 1, с. ИЗ.
22. Голубев В. В. Лекции по интегрированию уравнений движения
тяжелого твердого тела около неподвижной точки.— М.:
Гостехиздат, 1953.

B18 ЛИТЕРАТУРА
23. Спрингер Дж. Введение в теорию римановых поверхностей.—
М.: ИЛ, 1960.
24. Чеботарев Н. Г. Теория алгебраических функций.— М.: Гос-
техиздат, 1948.
25. Calogero F. (editor). Nonlinear evolution equations solvable by
the spectral transform (Collection of papers).— London: Pitman,
1978.
26. Бейтман Э. Г., ЭрдейиА. Высшие трансцендентные функции.—
М., Наука, 1967, т. 2, 3.
27. Фаддеев Л. Д.— УМН, 1959, т. 14, с. 57.
28. Kay I., Moses H. Е.~ Nuovo Cimento, 1955, v. 2, p. 917;
Kay /., Moses H. E.— Nuovo Cimento, 1956, v. 3, p. 66.
29. Gardner C, et al.— Phys. Rev. Lett., 1967, v. 19, p. 1095.
30. Lax P. В.— Commun. Pure Appl. Math., 1968, v. 21, p. 467.
31. Захаров В. Е.— ЖЭТФ, 1971, т. 60, с. 993 C).
32. Gardner С— J. Math. Phys., 1971, v. 12, p. 1548.
33. Захаров В. Е., Фаддеев Л. Д.— Функц. анализ, 1971, т. 5, вып. 4,
с. 18.
34. Flaschka Н.— Phys. Rev., 1974, v. B9, p. 1924.
Flaschka Я.—Progr. Thoor. Phys., 1974, v. 51, p. 703.
35. Манаков С. В.— ЖЭТФ, 1974, т. 67, с. 543.
36. Захаров В. Е., Шабаш А. В.— ЖЭТФ, 1971, т. 61, с. 118,
37. Ablowitz И., et al.— Phys. Rev. Lett., 1973, p. 1262.
38. Гахтаджян Л. А.— ЖЭТФ, 1974, т. 66, с. 476.
39. Захаров В. Е., Манаков С. В.— ТМФ, 1974, т. 19, с. 332.
40. Тахтаджян Л. А., Фаддеев Л. Д.— ТМФ, 1974, т. 21, с. 160.
41. Новиков С. П.— Функц. анализ, 1974, т. 8, вьш. 3, с. 54.
42. Дубровин Б. А., Новиков С. П.— ЖЭТФ, 1974, т. 67, вып. 12,
с. 2131.
43. Марченко В. А., Островский И. В.— Матем. сборник, 1974,
т. 95, вып. 3, с. 331.
44. Lax P. D.— Lect. in Appl. Math., 1974, v. 15, p. 85.
45. Дубровин Б. А.,— Функц. анализ, 9, вып. 3, с. 41, 1975.
46. Итс А. Р., Матвеев В. В.— ТМФ, 1975, т. 23, вьш. 1, с. 51.
47. Lax P. D.— Comm. Pure and Appl. Math, 1975, v. 38, № 1, p.
141.
48. Mckean H., Van Moerbeke P.— Inventiones Mathem., 1975,
v. 30, p. 217.
49. Гелъфанд И. М., Дикий П. А.— УМН, 1975, т. 30, вып. 5.
50. Богоявленский О. И., Новиков С. П.— Функц. анализ, 1976,
т. 10, вып. 1, с. 1095.
51. Дубровин Б. А. я др.— УМН, 1976, т. 31, вып. 1, с. 55.
52. Захаров В. Е., Манаков С. В.— Письма в ЖЭТФ, 1973, т. 18,
с. 413.
53. Захаров В. Е., Манаков С. ?.— ЖЭТФ, 1975, т. 69, с. 1654.
54. Каир D.— Studies Appl. Math., 1976, v. 55, p. 9.
55. Шабат А. В.— Функц. анализ, т. 9, вып. 3, с. 75, 1975.
56. Захаров В. Е., Шабат А. Б.— Функц. анализ, 1979 (в печати).
57. Захаров В. Е., Михайлов А. В.— Письма в ЖЭТФ, 1978, т. 27,
с. 47.
58. Захаров В. Е., Михайлов А. В.— ЖЭТФ, 1978, т. 74, с. 1953.
59. Будагов А. С, Тахтаджян Л. А.— ДАН СССР, 1977, т. 235,
с. 805.

ЛИТЕРАТУРА 319
60. Манаков С. В.— ЖЭТФ, 1973, т. 65, с. 1392.
61. Захаров В. Е., Манаков С. В.— ЖЭТФ, 1976, т. 71, с. 203.
62. Гуревич А. В., Питаевский Л. if.— ЖЭТФ, 1973, т. 65, с. 590.
63. Pohlmeyer К.— Com. Math. Phys., 1976, у. 46, p. 207.
К приложению
1. Манаков С. В.— УМН, 1976, т. 31, вып. 5, с. 245.
2. Дубровин Б. А., Кригевер И. М., Новиков С. П.— ДАН АН
СССР, 1976, т. 229, вып. 1, с. 15.
3. Захаров В. Е., Шабат А. Б.— Функц. анализ, 1979.
4. ДрюмаВ. С— Письма в ЖЭТФ, 1973, т. 19, вып. 12, с. 219.
л 5. ЗахаровВ. Е., Шабат А. Б.— Функц. анализ, 1974, т. 8, вып. 3, <0
с. 43.
• 6. Захаров В. Е., Манаков С. В.— Письма в ЖЭТФ, 1973, т. 18,
с. 413.
• 7. Захаров В. Е.— ДАН СССР, 1976, т. 229, с. 1314.
8. Davey A., Stewartson К.— Ргос. R. Soc. Lond., 1974, v. A338,
p. 101.
9. Петвиашвили В. И.— Физика плазмы, 1976, т. 2, вып. 3 с. 650.
10. Bordag L. A., Its A. R., Matveev V. В., Manakov S. V., Zatiha-
rov V. Е.— Phys. Lett., 1979, v. 63A, № 3, p. 205.
11. Кадомцев Б. Б., Петвиашвили В. if.—ДАН СССР, 1970,
т. 192, вып. 4, с. 753.
12. Дубровин Б. А., Матвеев В. Б., Новиков С. П.— УМН, 1976,
т. 31, вып. 1, с. 55.
13. Кричевер И. М.~ Функц. анализ, 1977, т. 11, вып. 2, с. 15.
14. Кричевер И. М.— ДАН СССР, 1976, т. 227, вып. 2, с. 291.
15. Burchnall J. L., Chaundy Т. W.— Proc. Royal Soc. London,
1922, v. 21, p. 420.
16. Burchnall J. L., Chaundy T. W.— Proc. Royal Soc. London,
1928, Ser. A, v. 118, p. 557.
17. Baker H. E.— Proc. Royal Soc. London, 1928, Ser. A, v. 118,
p. 573.
18. Кричевер И. М.— УМН, 1977, т. 32, вып. 6, с. 183.
19. Кричевер И. М.— Функц. анализ, 1978, т. 12, вып. 3, с. 20.
20. Кричевер И. М., Новиков С. П.— Функц. анализ, 1978, т. 12,
вьш. 4, с. 41.
21. Кричевер И. М., Новиков С. П.— ДАН СССР, 1979, т. 247, с. 33.
22. Moser /.— Adv. Math., 1975, v. 16, p. 354.
23. Кричевер И. М,— Функц. анализ, 1978, т. 12, вып. 1, с. 76.
24. Дубровин, Б. А., Новиков С. П.— ЖЭТФ, 1974, т. 67, вып. 12,
с. 2131.
25. Airault H., Mckean H. P., Moser /.— Comm. Pure Appl. Math.,
1977, v. 30, № 1, p. 95.
26. Choodnovsky D. V., Choodnovsky G. V.— Nuovo Cimento, 1977, v.
40B, p. 39.
27. Бейтман Э. Г., Эрдейи А. Высшие трансцендентные функции.—
М.: Наука, 1967, т. 3.
28. Flaschka Н'.— Progr. Theor. Phys., 1974, v. 51, p. 703.
29. Манаков С. В.— ЖЭТФ, 1974, т. 67, вып. 2, с. 543.
30. Кричевер И. М.— УМН, 1978, т. 33, вып. 4.
31. MumfordD., VanMoerbekeP.— Acta Mathem., 1979, v. 61, p.225.

ОГЛАВЛЕНИЕ
Предисловие 5
Введение.. Слабая нелинейность и дисперсия 9
Глава I. Метод обратной задачи рассеяния 20
§ 1. Сведения из теории рассеяния. Обратная задача кван-
товой теории рассеяния 21
§ 2. Схема интегрирования уравнения КдФ методом об-
ратной задачи рассеяпия 33
§ 3. Безотражательные потенциалы и iV-солитонные решения 37
§ 4. Уравнение КдФ как гамильтопова система 44
§ 5. Полиномиальпые интегралы движения 48
§ 6. Полная интегрируемость уравнения КдФ. Высшие
уравнения КдФ 51
§ 7. Дифференциально-разностные системы 60
§ 8. Нелинейное уравнение Шредингера и уравнение sin-
Gordon 74
§ 9. Обратная задача рассеяния для системы двух диф-
ференциальных уравнений 78
§ 10. Нелинейное уравнение Шредингера 85
§ 11. Уравнение sin-Gordon 98
Глава II. Периодические решения уравнения КдФ ... 112
§ 1. Уравнение Шредингера с периодическим потенциалом.
Периодический аналог уравнений Гарднера — Гри-
на — Крускала — Миуры 112
§ 2. Стационарная задача для высших КдФ. Метод оты-
скания точных решений КдФ 120
§ 3. Стационарные решения высших КдФ и потенциалы
уравнения Шредингера с конечным числом зон. Ри-
мановы поверхности 127
§ 4. Аналитические свойства блоховской собственной фун-
кции конечнозонного потенциала на римановой по-
верхности 132
§ 5. Некоторые приложения 138
§ 6. Сведения из теории римановых поверхпостей. Циклы
на римаповой поверхности 147
§ 7. Дифференциалы на римановых поверхностях. Абелевы
(голоморфные) дифференциалы и дифференциалы с
полюсами 158

ОГЛАВЛЕНИЕ
§ 8. Елоховская собственная функция и квазиимпульс.
Связанные с ними дифференциалы на римановой по-
верхности, пх временная динамика 168
§ 9. Точные формулы для конечнозонных потенциалов
и решений КдФ 178
§ 10. Некоторые частные решения КдФ 181
Глава III. Дальнейшее развитие методов построения
интегрируемых систем и их решений 187
§ 1. Регулярная задача Римана 187
§ 2. Задача Римана с нулями 190
§ 3. Обратная задача рассеяния для матричной системы
первого порядка 197
§ 4. Задача и-волн 209
§ 5. Солитонные решения 216
§ 6. Системы, интегрируемые при помощи задачи Римана 222
§ 7. Релятмвистски-иннариантныосистемы—киральные поля 227
Глава IV. Асимптотики решений при больших временах ?45
§ 1. Интегральные соотношения. Нелинейная дифракция
Фраунгофера 247
§ 2. Явные формулы для асимптотик (нелинейное урав-
нение Шредиыгера) 251
§ 3. Явные формулы для асимптотик (уравнение Корте-
вега — де Фриза) 257
§ 4. Метод усреднения Уитема 261
Приложение. Теория уравнения Кадомцева — Пет-
виашвили (двумерного КдФ). Некоторые дискретпые
системы 285
§ 1. Некоторые интегрируемые двумерные системы . . . 285
§ 2. Законы сохранения 289
§ 3. Метод одевания ^91
§ 4. Солитоноподобныо решения уравнения КП 294
§ 5. Точные решения, зависящие от функциональных па-
раметров 298
§ 6. Метод римановых поверхностей. Конечнозонные ре-
шения ранга 1 300
§ 7. Рациональные решения уравнения КП. Дискретные
системы частиц па прямой 304
§ 8. Метод голоморфных векторных расслоений над ри-
мановыми поверхностями. Функциональные параметры
в точных решениях 307
§ 9. Некоторые замечания о периодической цепочке Тода 315
Литература , * 317