Автор: Танаев В.С. Сотсков Ю.Н. Струсевич В.А.
Теги: исследование операций математика информатика
ISBN: 5-02-013984-Х
Год: 1989
Текст
Экономико-
математическая
БИБЛИОТЕКА
В.С. ТАНАЕВ, Ю.Н. СОТСКОВ, В.А. СТРУСЕВИЧ
ТЕОРИЯ
РАСПИСАНИЙ
МНОГОСТАДИЙНЫЕ
СИСТЕМЫ
МОСКВА ’’НАУКА”
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1989
ББК 22.18
Т18
УЖ 519.8
Танаев В.С., С о т с к о в Ю.Н, Струсевич В.А. Теория рас-
писаний. Многостадийные системы. — М.: Наука. Гл. ред. физ.-мат.
лит., 1989. - 328 с. - (Экон.-мат.б-ка). - ISBN 5-02-013984-Х.
Рассматриваются вопросы построешя оптимальных расписаний для детер-
минированных обслуживающих систем с одинаковыми, различными и нефик-
сированными маршрутами прохождения приборов. Значительное внимание
уделяется вопросам полиномиальной сводимости задач теории расписаний
и оценкам сложности алгоритмов их решения. Развивается теоретико-графо-
вый подход к анализу детерминироваьных обслуживающих систем.
Для специалистов в области прикладной математики и информатики,
студентов и преподавателей математ«ческих специальностей вузов, а также
специалистов в области экономики, занимающихся вопросами календарного
планирования и применяющих в своей работе математические методы.
Табл. 30. Ил. 67. Библиогр. 839 назв.
Рецензент доктор фи зико-математических наук В. К. Леонтьев
Научное издание
Танаев Вячеслав Сергеевич
Сотсков Юрий Назарович
Струсевич Виталий Александрозич
ТЕОРИЯ РАСПИСАНИЙ
Многостадийные системы
Серия ’’Экономико-математическая библиотека”
Заведующий редакцией Е.Ю. Ходан
Редактор А.Д. Вайнштейн
Художественный редактор Т.Н Колъченко
Технические редакторы: С.В. Геворкян, С.Н. Баронина
Корректоры: Т.С. Родионова, ?.В. Обод, ТА. Печко
Набор осуществлен в издательстве
на наборно-печатающих автоматах
ИБ № 32302
Сдано в набор 10.05.88. Подписано к печати 31.08.88.Т—15862
Формат 60X90 /16. Бумага пргчая
Гарнитура Пресс-Роман. Печать см^сетная
Усл.печл. 20,5.Усл.кр.отт. 2 0,5- Уч.-изд.л. 25,24
Тираж 3000 экз. Тип. зак. 234цена 5 р. 40 к.
Ордена Трудового Красного Зжамени
издательство ’’Наука”
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Четвертая типография издательства ”Наука”
630077 г. Новосибирск-77, ул. Станиславского, 25
1602110000-009
Т---------------29-89
053 (02)-89
ISBN 5-02-013984-Х
© Издательство ’’Наука”.
Главная редакция
физико-математической литературы,
1989
ОГЛАВЛЕНИЕ
Предисловие............................................................. 4
Введение................................................................ 5
Г л а в а 1. Одинаковые маршруты........................................ 26
§ 1. Общее время обслуживания. Два прибора..................... 27
§ 2. Общее время обслуживания. Три и более приборов............ 35
§ 3. Общее время обслуживания требований без задержек.......... 43
§4 . Максимальное временнбе смещение........................... 56
§5 . Суммарное время обслуживания.............................. 60
§ 6. Упорядоченные матрицы длительностей....................... 66
§7 . Доминантные матрицы длительностей......................... 79
§ 8. Приближенные алгоритмы.................................... 93
§9 . Библиографическая справка................................ 101
Г л а в а 2. Различные маршруты....................................... 110
§ 1. Оптимальное обслуживание двух требований................. 111
§2. Максимальное временнбе смещение........................... 121
§ 3. Общее время обслуживания. Одинаковые длительности........ 127
§4. Общее время обслуживания. Различные длительности.......... 137
§5. Общее время обслуживания требований без задержек.......... 146
§6. Библиографическая справка................................. 152
Г л а в а 3. Нефиксированные маршруты................................. 157
§ 1. Общее время обслуживания. Два прибора.................... 158
§ 2. Общее время обслуживания. Три и более приборов........... 179
§3. Общее время обслуживания. Прерывания...................... 187
§4. Общее время обслуживания. Упорядоченность................. 200
§5. Директивные сроки......................................... 213
§6. Суммарное время обслуживания. Одинаковые длительности... 224
§7. Суммарное время обслуживания. Различные длительности.... 233
§8. Библиографическая справка................................. 242
Г л а в а 4. Задачи на смешанных графах............................... 248
§ 1. Сетевое представление обслуживающих систем............... 249
§ 2. Смешанные графы.......................................... 258
§3. Последовательный анализ вариантов......................... 266
§ 4. Оптимизация обслуживающей системы........................ 277
§5. Устойчивость оптимальных расписаний....................... 282
§6. Библиографическая справка................................. 289
Список литературы..................................................... 296
1* 3
ПРЕДИСЛОВИЕ
Предлагаемая вниманию читателя книга является естественным продол-
жением и дополнением опубликованных в издательстве ’’Наука” книг
В.С. Танаева, В.В. Шкурбы ”Введение в теорию расписаний” (1975 г.)
и В.С. Танаева, В.С. Гордона, Я.М. Шафранского ”Теория расписаний.
Одностадийные системы” (1984 г.). В ней приводится систематизированное
изложение современного состояния исследований многостадийных детер-
минированных обслуживающих систем.
Заметное в последнее время возрастание интереса к вопросам построе-
ния оптимальных расписаний для различных обслуживающих систем
обусловлено существенным повышением уровня автоматизации всех
видов человеческой деятельности, в том числе и управления этой
деятельностью. Качество функционирования современного производства
во многом определяется решениями, принимаемыми на этапах кален-
дарного планирования и оперативного управления. Наряду с улучше-
нием качества плановых решений все более жесткими становятся требова-
ния к сокращению сроков их выработки, повышению оперативности и
гибкости управления.
В книге рассматриваются детерминированные обслуживающие системы
как с фиксированными (одинаковыми и различными), так и с нефикси-
рованными маршрутами про хождения приборов. Все главы книги, а подчас
и параграфы, относительно независимы. Используемые обозначения и тер-
минология соответствуют упомянугым выше книгам. Каждая глава соп-
ровождается библиографической справкой и иллюстрируется многочис-
ленными примерами.
При подготовке книги к издании» были учтены замечания и пожелания
участников семинара по теории управления в дискретных системах Инсти-
тута технической кибернетики АН БССР. Соответствующие курсы лекций
читались авторами в Белорусском государственном университете им.
В.И. Ленина. Ряд замечаний по рукописи сделали С.А. Бородич, В.С. Гордон,
М.Я. Ковалев, АВ. Тузиков и Я.М. Шафранский. Большую помощь в оформле-
нии рукописи оказали Р.А. Бенарадская, С.Н. Воронкова и С.И. Крючкова.
Авторы признательны П.С. Краснощекову, В.С. Михалевичу, Н.Н. Моисе-
еву, Г.С. Поспелову и Д.А. Супрунэнко за постоянное внимание к работе.
В.С, Танаев, Ю.Н, Со тс ко в, В.А. Струсевич
4
ВВЕДЕНИЕ
Многие практические ситуации приводят к необходимости изучения
многостадийных обслуживающих систем, т.е. таких систем, в которых
процесс обслуживания каждого требования состоит из нескольких последо-
вательных стадий, на каждой из которых это требование обслуживается
тем или иным прибором, либо, в более общем случае, той или иной сово-
купностью приборов. Так,изготовление детали обычно включает несколько
последовательных операций, каждая из которых выполняется на некотором
из имеющихся в цехе станков. Преподаватель последовательно про-
водит занятия с несколькими вполне определенными группами сту-
дентов. Процесс подготовки книги к изданию включает такие ста-
дии, как написание рукописи, рецензирование, редактирование, набор
и т.д.
В любом случае имеется конечное множество 7V = { 1, 2, ...,и} требова-
ний (деталей, преподавателей, книг и т.п.) и конечное множество
Л ={1,2,... ,М} приборов (станков, групп студентов, авторов, редакто-
ров, наборщиков и т.п.). Процесс обслуживания требования i£N включает
г, стадий. При этом каждому требованиюiENn каждой стадии q, 1 < q <
О/, его обслуживания сопоставляется некоторое множество приборов
Л'ц С Л . В зависимости от типа обслуживающей системы требование i
на стадии q либо может быть обслужено любым из приборов L Е Л lq
(но не более чем одним одновременно), либо должно одновременно обслу-
живаться всеми приборами из множества Л q. Обычно предполагается,
что каждый прибор одновременно может обслуживать не более одного
требования.
Если rt = г1 >2, Л q = Л q, i= 1,. - • >п, Л qu^ Л lqv= Ф, 1 <qu Ф
Qv > то обслуживающая система называется системой поточного типа.
В этой системе множество приборов разбито на г1 попарно непересекающих-
ся групп, обычно пронумерованных числами 1, 2,.. . ,г'. Каждое требова-
ние i€N сначала обслуживается приборами 1-й группы, затем 2-й и т.д.
пока оно не будет обслужено приборами г '-й группы.
Наиболее изученной системой поточного типа является система, в кото-
рой г’~Ми, следовательно, | Л q I = 1, q = 1,... ,М. В этой системе каж-
дое требование i&Nсначала обслуживается прибором 1, затем прибором 2
и т.д., пока оно не будет обслужено прибором М. Такая система получила
название системы с последовательными приборами и одинаковым поряд-
5
ком (маршрутом) их прохождения всеми требованиями. В зарубежной
литературе она известна под названием flow shop.
В системе поточного типа с последовательно-параллельным характером
обслуживания предполагается, что хотя бы при одном q, 1 <q<M, величи-
на \Jtq |>2 и все приборы в каждом из множеств Л q одинаковы,
либо отличаются друг от друга только производительностью. В этой систе-
ме каждое требование /ЕТУна стадии q может обслуживаться одним при-
бором множества Jtqf но не более чем одним одновременно.
Среди систем с различными порядками (маршрутами) прохождения
приборов требованиями наиболее изученными являются системы с после-
довательными приборами. В этих системах для каждого требования i Е N
задается своя, специфическая для этого требования последовательность
Ll = (L\ Llri) его обслуживания приборами. Требование i сначала
обслуживается прибором L\, затем прибором Ll2 и т.д., пока оно не будет
обслужено прибором 11г.. Последовательности обслуживания могут быть
различными для разных требований и могут содержать повторения при-
боров. В зарубежной литературе такие системы получили название,
job shop.
Определенный интерес представляют системы с последовательными
приборами и нефиксированным порядком их прохождения для всех или
некоторых требований. В наиболее изученной системе такого рода (извест-
ной под названием open shop) каждое требование i Е. N должно быть обслу-
жено всеми М приборами при условии, что каждый прибор одновременно
не может обслуживать более одного требования, а каждое требование
одновременно не может обслуживаться более чем одним прибором.
В любом случае, если требование i на стадии должно или может быть
обслужено прибором L = L'q, то предполагается заданной длительность
1ц>0 его обслуживания этим прибором. Запись = 0 означает, что
требование i на стадии q должно быть обслужено прибором L = Llq, но
длительностью этого обслуживания можно пренебречь. Зачастую запись
tiL = 0 употребляют и в том случае, когда необходимо отметить, что по
условию задачи требование i на стадии q прибором L не обслуживается.
Наряду с величинами tiL могут быть заданы также момент dj>0 поступ-
ления требования i в систему, директивный срок Р/>0, к которому
необходимо или желательно завершить обслуживание требования i , и
некоторые другие величины, обусловленные особенностями рассматри-
ваемой задачи. В теории расписаний все эти величины предполагаются
детерминированными.
Весьма распространенными являются ситуации, в которых накладывают-
ся некоторые ограничения на возможную последовательность обслужива-
ния требований. Ситуации такого рода обычно описываются заданием на
множестве N требований некоторого отношения строгого порядка. В тео-
рии многостадийных обслуживающих систем запись i-+j может интерпре-
тироваться двояко: 1) обслуживание требования/ может начаться только
после завершения обслуживания требования i всеми обслуживающими
его приборами либо 2) обслуживание требования / каждым обслуживаю-
щим его прибором L может начаться только после завершения обслужи-
вания требования i этим прибором (при условии, что требование i обслу-
живается прибором L).
6
В процессе обслуживания требования прибором могут допускаться
прерывания. Если допускаются прерывания обслуживания требования i
прибором L, то это означает, что прибор L может обслуживать требование
i ”по частям”. При этом обычно предполагается, что число ’’частей” конеч-
но, суммарная длительность обслуживания всех ’’частей” равна tiL и преры-
вания не сопряжены с дополнительными затратами. Процесс обслуживания
требования i прибором L без прерываний удовлетворяет следующему
условию. Если обслуживание требования i прибором L начинается в
момент времени то оно протекает непрерывно и завершается в момент
времени 7iL = t°iL + tiL.
Определенный практический интерес представляют ситуации, в которых
необходимо соблюдать одно из двух дополнительных условий: каждый
прибор должен обслуживать требования непрерывно одно за другим либо
каждое требование должно обслуживаться непрерывно одним прибором
за другим. В первом случае не допускаются простои обслуживающих
приборов, во втором - задержки в обслуживании требований.
Процесс функционирования обслуживающей системы может быть
описан путем задания расписания (календарного плана, временндго графи-
ка и тл.), т.е. некоторой совокупности указаний относительно того, какие
именно требования какими именно приборами обслуживаются в каждый
момент времени. Обычно предполагается, что каждое требование не может
одновременно обслуживаться двумя и более приборами и каждый прибор
не может одновременно обслуживать более одного требования. При этих
предположениях расписание можно рассматривать как совокупность
{ $1(0, $2(0> • • • кусочно-постоянных непрерывных слева функций,
каждая из которых задана на интервале 0 <г<°°и принимает значения
0,1,.. ., п. Если sL(t') = i =#0, то в момент времени t' прибор L^J6 обслу-
живает требование /Е/V. Если sL(t') = 0, то в момент времени t' прибор L
простаивает.
Иногда вместо функций sL(t), ,описывающих функционирова-
ние каждого прибора, используют аналогичные функции i G N, описы-
вающие процесс обслуживания каждого требования 0, если в
момент времени г'требование i не обслуживается, и ^(г') = £, если в
момент времени г' требование i обслуживается прибором L).
При задании расписания должны соблюдаться все условия и ограничения,
вытекающие из постановки рассматриваемой задачи, т.е. расписание должно
7
быть допустимым. Следует отметить, что построение допустимого расписа-
ния и даже выяснение того факта, существует ли оно вообще, является
зачастую далеко не тривиальной задачей.
На рис. В.1 приведен график расписания sf(0, iGN, обслуживания
требований N = {1, 2, 3, 4} приборами = { 1, 2, 3} при различных марш-
рутах обслуживания требований. Здесь все длительности обслуживания
равны единице, L1 = (1, 2),Z* 1 2 = (3,2), L3 = (2, 1, 2, 3),Z4 = (2, 3, 1);
di = 1, d2 = d$ = 0, d4 = 2j ~ Z?4 = 5, D2 ~ 2, = 6.
Прибор 1 во временном интервале (1,2] обслуживает требование 1, в
интервале (2,3] - требование 3, в интервале (4,5] - требование 4. При-
бор 2 в интервале (0,5] обслуживает без простоев требования в порядке
3, 2, 4, 1 и снова 3. Прибор 3 в интервале (0,1 ] обслуживает требование 2,
в интервале (3,4] — требование 4, в интервале (5,6] — требование 3.
Нетрудно убедиться в том, что это расписание является допустимым.
На рис. В.2 приведены графики sL(fy LEjU, описывающие функциони-
рование каждого прибора. Над графиками — соответствующие значения//.
Если существует несколько допустимых расписаний, то естественным
является стремление построить наилучшее из них. В связи с этим возникает
весьма сложный и многоплановый вопрос оценки качества расписания. В те-
ории расписаний наибольшее распространение получил следующий способ
оценки. Каждое (допустимое) расписание s однозначно определяет вектор
t(s) = (11 (s), , ^и(5)) моментов завершения обслуживания требова-
ний. Задается некоторая действительная неубывающая по каждой из пере-
менных функция F(x) = F(Xi ,х2,. . . и качество расписания s оцени-
х = t(s). Из двух расписаний лучшим
считается то, которому соответству-
ет меньшее значение F(x). Расписа-
ние, которому соответствует наи-
меньшее значение F(x) (среди всех
допустимых расписаний), называ-
ется оптимальным.
В частности, при построении оп-
тимального по быстродействию рас-
писания F(x) = max {xf-}. В этом
1 < i < п
случае F(7(s)) = Fmax(s), где
fmax(s)= max {?,(s)J.
1 < i < n
При построении расписания с наи-
меньшим суммарным временем об-
п _ п _
служивания F(x) = S xf. В этом случае F(t (s)) = S tj(s). При построении
i=i , 1=1
расписания с наименьшим временным смещением моментов завершения
обслуживания требований i относительно директивных сроков Dt функция
F(x) = max { х, - D(}. В этом случае F(F(s)) = Lmax (s), где Amax(s) =
1 < i < п
= max - D-}.
1 < i < n
вается значением этой
при
s(t)
4
2
3
2
3
2
2
2
7
О 1 2 3 4 5 6 t
Рис. В2
8
В большинстве рассматриваемых в этой книге ситуаций оптимальное
расписание может быть найдено в результате перебора конечного множества
возможных вариантов. Основное затруднение состоит в том, что число
таких вариантов обычно оказывается исключительно большим и растет,
по меньшей мере, экспоненциально с ростом размерности задачи.
Среди задач теории расписаний можно выделить полиномиально разре-
шимые и АР-трудные. Для каждой полиномиально разрешимой задачи
известен по крайней мере один эффективный алгоритм ее решения, т.е.
алгоритм, трудоемкость которого (число выполняемых элементарных опе-
раций, время решения) ограничена сверху некоторым полиномом от длины
записи исходной информации задачи, закодированной в бинарном алфавите.
Для NP-трудных задач такие алгоритмы неизвестны и, по всей видимости,
не существуют. Во всяком случае, если бы существовал полиномиальный
алгоритм решения какой-либо одной АР-трудной задачи, то существовали
бы полиномиальные алгоритмы для очень многих задач, которые тради-
ционно считаются труднорешаемыми.
С вопросами оценки сложности алгоритмов и теорией полиномиальной
сводимости дискретных задач можно ознакомиться по монографиям
[88, 215, 238, 256, 350, 352, 651, 754] или статьям [133, 158, 174, 190,
480, 532, 616, 621, 652, 657, 659, 736, 765, 793]. В данной книге исполь-
зуется общепринятая техника доказательства NP-трудности экстремальных
задач. Пусть требуется отыскать в конечном множестве S допустимых
расписаний расписание s*, которому соответствует наименьшее значение
F(t(s)). Сформулируем соответствующую задачу_распознавания: существу-
ет ли во множестве S такое расписание s°, что F(t (5°)) <у для заданного
числа у? Очевидно, указанное расписание s° существует тогда и только
тогда, когда F(t (s*)) <у. Таким образом, экстремальная задача не легче,
чем соответствующая ей задача распознавания, и из TVP-трудности задачи
распознавания следует ЛР-трудность исходной экстремальной задачи. Для
доказательства АР-трудности задачи распознавания достаточно осуществить
полиномиальное сведение к ней некоторой (заведомо АР-т рудной) задачи.
Формулировки используемых в каждой главе эталонных задач приводятся
во введениях к этим главам.
Среди АР-трудных задач можно выделить задачи, для которых сущест-
вуют псевдополиномиальные алгоритмы решения, т.е. алгоритмы, слож-
ность которых ограничена сверху некоторым полиномом от длины записи
исходной информации задачи, закодированной в унарном алфавите (нату-
ральное число к в этом алфавите представляется последовательностью к
единиц). Остальные АР-трудные задачи относятся к классу NP-трудных
в сильном смысле. Если эталонная задача является ^VP-трудной в сильном
смысле, то нет необходимости строить полиномиальное ее сведение к
рассматриваемой задаче распознавания. Достаточно построить псевдополи-
номиальное сведение и тем самым убедиться в АР-трудности (в сильном
смысле) исходной задачи.
В этой книге описывается современное состояние исследований много-
стадийных обслуживающих систем.
В гл. 1 рассматриваются системы с последовательными приборами и оди-
наковым порядком их прохождения. В § 1 этой главы установлены неко-
торые свойства расписаний (без прерываний) и описаны полиномиальные
9
алгоритмы решения задачи построения оптимального по быстродействию
расписания для двух приборов и некоторых ее обобщений. NP- трудность
задачи минимизации общего времени обслуживания (как при запрещении,
так и при разрешении прерываний) для трех и более приборов установлена
в § 2. В § 3 рассматривается задача построения оптимального по быстро-
действию расписания без задержек в обслуживании каждого требования.
В § 4 и 5 содержатся доказательства WP-трудности задач построения
расписаний, которым соответствует минимальное временное смещение и
суммарное время обслуживания соответственно. В § 6 и 7 приведены
условия, выполнение которых позволяет строить оптимальное расписание
за полиномиальное число действий. В § 8 основное внимание уделяется
приемам построения алгоритмов с априорными оценками качества
решения.
В гл. 2 рассматриваются системы с различными маршрутами обслужива-
ния требований. В § 1 этой главы описываются эффективные алгоритмы
построения оптимальных расписаний (с прерываниями и без прерываний)
обслуживания двух требований при произвольной неубывающей целевой
функции. В § 2 рассматривается задача минимизации максимального вре-
менного смещения при обслуживании (без прерываний) двумя приборами
требований с одинаковыми длительностями обслуживания. В § 3 устанав-
ливается NP-трудность некоторых частных случаев задачи построения
оптимальных по быстродействию расписаний обслуживания (без прерыва-
ний) требований с одинаковыми длительностями обслуживания.
В § 4 рассматривается задача построения оптимального по быстродействию
расписания при произвольных длительностях обслуживания. В § 5 устанав-
ливается NP-трудность задачи построения оптимального по быстродейст-
вию расписания без задержек в процессе обслуживания каждого тре-
бования.
Гл. 3 посвящена задачам теории расписаний для систем с нефиксирован-
ными маршрутами обслуживания требований. В § 1 этой главы приведены
полиномиальные алгоритмы решения задачи построения оптимального по
быстродействию расписания для двух приборов и ее обобщения.
NP-трудность задачи минимизации общего времени обслуживания (без
прерываний) для трех и более приборов установлена в § 2. Там же описано
несколько частных случаев, когда решение указанной задачи можно найти
за полиномиальное число операций. В § 3 приведены полиномиальные ал-
горитмы построения оптимального по быстродействию расписания с преры-
ваниями. В § 4 исследуется ситуация, когда на множестве требований
задано отношение строгого порядка. Различные аспекты решения задачи
построения расписания с минимаксным временным смещением рассмотре-
ны в § 5. В § 6 приведены полиномиальные алгоритмы построения
расписаний, которым соответствуют наименьшие значения суммарного и
суммарного взвешенного времени обслуживания, если длительности обслу-
живания одинаковы. В § 7 установлена NP- трудность задачи минимизации
суммарного времени обслуживания в случае произвольных длительностей.
В гл. 4 рассматриваются сетевые формы представления обслуживающих
систем с использованием смешанных графов. В § 1 описываются алгорит-
мы построения допустимых относительно заданного графа расписаний.
В § 2 исследуются некоторые полезные в дальнейшем свойства смешан-
10
ных графов. В § 3 рассматриваются основанные на идеях последователь-
ного анализа вариантов алгоритмы построения оптимальных и близких
К ним расписаний. В § 4 рассматривается задача оптимального выбора
необходимого количества приборов, распределения заданного множества
требований по выбранным приборам и составления расписания их обслу-
живания. Устойчивость оптимальных расписаний исследуется в § 5.
Каждая глава сопровождается библиографической справкой. Дополни-
тельную информацию о результатах, полученных в области теории расписа-
ний и некоторых смежных областях, заинтересованный читатель может
найти в монографиях [1, 23, 77, 123, 147, 153,157, 189, 211, 212, 215, 231,
241-243, 247, 251, 269, 280, 286-288, 350-352, 385, 402-404, 446, 504,
528, 651, 754] и обзорах [45, 49, 50, 61, 76, 80, 98, 233, 263, 337, 345, 365,
430, 432, 501,502, 514, 535, 546, 548, 568-570, 605, 622, 635, 636, 643, 646,
654-656,755,784].
Для облегчения поиска информации о конкретно интересующих читателя
задачах ниже приводятся таблицы, содержащие краткие сведения о боль-
шинстве рассматриваемых в книге задач.
В табл. В.1 приведены полиномиально разрешимые задачи, в табл. В.2 —
NP-трудные задачи, а в табл. В.З — 7VP-трудные задачи, для которых извест-
ны полиномиальные приближенные алгоритмы решения.
В первых шести графах каждой таблицы приводятся описания задач
с использованием определенной символики. В последней графе даются
ссылки на соответствующие разделы книги.
В первой графе указывается тип обслуживающей системы. Системы
с нефиксированными маршрутами обслуживания требований обозначены
буквой О, системы с различными фиксированными маршрутами — бук-
вой /, системы с одинаковыми маршрутами - буквой F.
Во второй графе указывается число обслуживающих приборов.
В третьей графе приводятся значения двух параметров — ’’длительности
операций” и ’’моменты поступления”. Под операцией подразумевается
процесс обслуживания требования отдельным прибором. При произволь-
ных длительностях операций первый параметр принимает значение tiL, при
целочисленных - [tiL ], при одинаковых - tiL =1, при двух возможных
значениях t х и 12 — tiL € { 11, t2 } .
Параметр ’’моменты поступления” принимает значение , если требова-
ния поступают в очередь га обслуживание неодновременно. Если требова-
ния поступают только в целочисленные моменты времени, то используется
символ [dt ]. Если оба этих символа отсутствуют, то предполагается, что
d( = 0 для всех i G N.
В четвертой графе приводятся значения параметров ’’прерывания”,
’’порядок”, ’’ресурсы” и некоторых других параметров, определяющих
условия обслуживания требований.
Параметр ’’прерывания” может принимать значения Рг и [Рг ] в зависи-
мости от того, разрешены ли прерывания в процессе обслуживания требова-
ния прибором в произвольные или только целочисленные моменты време-
ни. Символ (Рг) означает, что процесс обслуживания каждого требования
любым прибором может быть прерван, а потом возобновлен, но между
моментами прерывания и возобновления требование не может
11
Таблица В.1
Тип системы Число Приборов Длительности операций; моменты поступления Условия обслуживания Дополнитель- ные условия Критерий Оценка сложности Раздел книги
F 2 fiL *max 1 n log n гл. 1, п. 1.3 (♦)
F 2 tiL я *max n tog n гл. 1.П.1.3, 9.1
F 2 fiL я 8п>0, 6/2>0, *max n log л гл. 1, п. 9.1
тп >0> тО>0>
J7 >0,
F 2 tiL я 0, *max n tog n гл. 1, п. 9.1
ТИ > 0, т^2 > 0,
^♦>0,
F 2 fiL Go = SP, я Gnax n tog n гл. 1, п. 9.2
F 2 *iL я, без задержек *max n log n гл. 1, п. 3.5
F 2 tiL без простоев ^max л tog л гл. 1,п. 1.2, 9.3 (♦)
F 2 tiL = i RsW *max n togn гл. 1, п. 9.4 (♦)
F 2 tiL = 1 Rs (1), без *max n tog n га. 1, п. 9.4
задержек
F 2 tiL*l /Щ1),Я* = 1, *max n гл. 1, п. 9.4
рЛе(0,1}
F 2 tiL Я 41 >tn, iGN pl n tog n гл. 1, ц. 6.2,3)
F 3 fiL я tn < min On, r/3}, ?max n log n гл. 1, п. 9.9
ietf
F 3 tiL я til <42 <ti3,i^N *max n1 гл. 1, п. 9.9
F 3 tiL я til >ti2>ti3,i&N ^max n1 гл. 1, п. 9.9
F М tiL я, без за- II tiL II - упорядо- Gnax n log n гл. 1, п. 6.3,5)
держек чена до строкам,
iEN,
1 = 1...M- 1
F M tiL я, без за- II ^iL И - упорядо- *max и log и гл. 1,п. 6.3,5)
держек чена по строкам, L~2,...,M
F M tiL я, без за- держек II tiL И “ упорядо- чена по строкам, и log и гл. 1, п. 6.4
F M tiL я, без за- держек 1 — упо- рядочена по строкам *max n*M гл. 1, п. 6.3,3)
F M tiL я II t^ И “ упорядо- чена, i^N, L = 2,... ,М ^max ntogn гл. 1, п. 6.1,2)
F M tiL я II tjL || - упорядо- чена, tiM > t^, Ze N, = 1,...,M- 1 ^max n log и гл. 1, п. 6.1,2)
F M tiL я II t^ II - упорядо- чена 27, и log и гл. 1, п. 6.2,2)
F M tiL я II t^ II - доми- нантная *max nM гл. 1, п. 7.1
F M tiL я • II tiL II - (7.6) *max nM + п log п гл. 1, п. 7.2,2)
F M tiL я II t^ II - (7.8) Gnax nM + п log п гл. 1, п. 7.2, 3)
F M tiL я II tiL II - (7.11) *max пМ + иа гл. 1, п. 7.3
F M tiL я II t^ II - доми- нантная пМ + п* гл. 1, п. 7.5
F M *iL я, без за- держек II tiL II - доми- нантная Gnax пМ гл. 1, п. 7.7
Таблица В.1 (продолжение)
Тип системы Число приборов Длительности операций; мо- менты по- ступления Условия обслуживания Дополнитель- ные условия Критерий Оценка сложности Раздел книги
F М {iL я, без за- II tn || - (7.19) ^шах nM + и log и гл. 1, п. 7.8,1)
держек
F М fiL я, без за- II tfL || - (7.20) ^шах пМ + и log и гл. 1, п. 7.8,2)
держек
F М fiL я, без за- II t^ II - доми- S Witi пМ + п2 гл. 1, п. 7.9
держек нантная
J 2 tiL-I ^max r(N) log п гл. 2, § 2
J 2 tiL-i [/>,] ^max r(N) гл. 2, § 2
J 2 tiL = l<di ^max r(N) log n гл. 2, п. 3.2
J 2 tiL-Vi] Gnax r(N) гл. 2, п. 3.2
J 2 tiL ri 2 ^max m log m гл. 2, п. 4.2
J 2 tiL без простоев ^max m log m гл. 2, п. 4.3
J М tiL и = 2 F r2log r гл. 2, п. 1.8-1.12
J М tiL Рг п = 2 F r3 гл. 2, п. 1-3-1.6, 1.12
J м tiL и = 2,гг-<М F AflogAf гл. 2, п. 1.12
J м tiL Рг п = 2, г/ <М F M2 гл. 2, п. 1.12
О 2 tiL ^max n гл. 3, п. 1.2 (*)
О 2 tiL-1 ^max n3 гл. 3, п. 8.4
О 2 tn = ai+^>(t'p [«•] - неубы- ^max n log n гл. 3, п. 8.4
ti2 — + вающая функция
О 2 fiL Рг, G = С и Г Gnax n гл. 3, п. 4.3
О 2 fiL G0=C Gnax n log n гл. 3. п. 4.6
О 2 tiL Pr, Go = C ?тах п2 гл. 3. и. 4.6
О 2 tiL Pr, Gq = ^тах п2 гл. 3. п. 4.7
= C1 v C2 и . .
... и Cp и г
О 2 tiL Рг ^-тах п log п гл. 3. п. 5.4
о 2 tiL Рг Я, < D2 < . . . ^-тах п гл. 3. п. 5.4
. . . <
о 2 tiL Рг на одном ^тах п3 гл. 3. п. 8.5
приборе
о М tiL G = C *тах пМ гл. 3, п. 4.1 (*)
о м fiL> di Pr, G = С и г *тах ЛП гл. 3, п. 4.2
0 м tiL доминирующий ^тах пМ гл. 3, п. 2.2
прибор, п>М
о м tiL два доминирую- ^тах пМ гл. 3, п. 2.3
щих прибора,
п>М
о м tiL Г*(Л) > (№ + *тах п2ЛГ гл. 3, п. 2.5
+ 2М- 1)Г*
о м fiL r*(7V)> *тах п2^3 гл. 3, п. 8.2
>(16Af°logM° +
+ 5M0)f‘, М" = 2к,
2к-1 <М<2к
о м tiL Г‘(Л)> ^тах пМ3 + пМ2 log пгл. 3, п. 8.2
> (8M°log№ +
+ 5Af°)r*,Af° =2к,
2к~1 <М<2к
и» о м kit! [*] ^тах Я log2 (п+М) гл. 3, п. 3.2, 8.3
Таблица В.1 (окончание)
Тип системы Число приборов Длительности операций; мо- менты по- ступления Условия обслуживания Дополнитель- ные условия Критерий Оценка сложности Раздел книги
О М I'aJ [/>] ^max (и + M)2 X X log(n + Af) гл. 3, п. 3.2, 8.3
О М [Qd UH rmax (n + M)/flog Г* гл. 3, п. 3.2, 8.3
О м *iL Pr Gnax H2 гл. 3, п. 3.4, 8.3
О м ‘iL Pr *max H(mm{H,M2} + + M log ri) гл. 3, п. 3.4, 8.3
0 м tiL Pr *max H + + min{Af4, n4, H2} гл. 3, п. 3.4, 8.3
0 м tiL Pr параллельные приборы на каждой стадии Gnax ЛП гл. 3, п. 3.6
О м tiL, di Pr r i < Di ЛП гл. 3, п. 5.1
О м tiL.diG G{0,d} Pr 0 <d <D ti < Df n3 + M3 гл. 3, п. 5.2, 2)
О м fiL Pr DiG{D', D"}, 0 < ft’ < ft" n3 +M3 гл. 3, п. 5.2, 3)
В. С. Танаев
Тип системы Число приборов Длительности операций, моменты поступления Условия обслуживания Дополнительные условия Критерий — — < Раздел книги
F 2 G = CU Г, я ^max гл. 1, п. 9.2
F 2 tiL Go, * ^max гл. 1, п. 9.2
F 2 fiL Rs(Y),Rk=\, ^max гл. 1, п. 9.4
pfte{0,1}
F 2 tiL>0 без задержек ^max гл. 1, п. 3.3
F 2 tiL я, 0 < £ < л - 1 ^max гл. 1, п. 9.5.
F 2 *iL я, без задержек гл. 1, п. 5.2
F 2 fiL=l G = Cu г гл. 1, п. 9.8
F 2 tiL ^max гл. 1, п. 4.1
F 2 tiL Рг ^max гл. 1, п. 4.1
F 2 tiL я, без задержек ^max гл, 1, п. 4.2
F 2 tiL > 0 без задержек Di = D, i&N ^max гл. 1, п. 4.2
F 2 tiL я sr; пт. 1, п. 5.1
F 3 tiL Рг s?; гл. 1, п. 9.8
F 3 tiL = l ^max гл. 1, п. 9.4
F 3 tiL *max гл. 1, п. 2.1
1 F 3 tiL без простоев ^max гл. 1, п. 2.1, 9.3
F 3 tiL Рг Gnax пт. 1, п. 2.3
F 3 tiL Рг r- = 2, i^N ^max гл. 1, п. 2.4 (*)
F 3 tiL Рг, без простоев ^max гл. 1, п. 2.3, 9.3
F 3 tiL я, без задержек ^max гл. 1, п. 3.7
F м tiLG{0, 1} Gnax гл. 1, п. 9.8
F м Рг *max гл. 1, п. 9.8
co
Тип системы Число приборов Длительности операций, моменты поступления Условия обслуживания
F M fa,e{0,1} без задержек
F М ttL ^{01}
F М 1} Pr
F М fa е {0,1} без задержек
J 2 tiL = 1 G = Cj и С2 и ...
... и Ср и г
J 2 tiL G {1, 2}
J 2 *iL
J 2 tiL
J 2 fiL Рг
J 2 tiL Рг
J 2 tiL без задержек
J 2 tiL = 1 без задержек
J 2 fa = i G = С, и С2 и ...
... и Ср и Г
J 2 fas{1.2}
J 3 t.iL = 1
J 3 tiL = 1
О 2 tiL без задержек
Таблица В.2 (окончание)
Дополнительные условия Критерий Раздел книги
*тах di. 1, n. 9.8
гл. 1, п. 9.8
SFf гл. 1, п. 9.8
s?,. гл. 1, п. 9.8
Gnax гл. 2, п. 3.5
^max гл. 2, п. 3.6
ri = 3, rz = 1, ^max гл. 2, п. 4.6 (*)
i = 2,... , п
г. = 2(п-Г), гГ 2, ^max гл. 2, п. 4.7
i = 2,.. ., и
7*1 = г2 = 3, г/= 2, Gnax гл. 2, п. 4.5 (♦)
i = 3,..., п
г2 = Ги/3“1,г.= 2, ^max гл. 2, п. 6.4
i = 2, ... , п
г^г ^max гл. 2, п. 5.1-5.4
Gnax гл. 2, п. 5.5 (*)
^max гл. 2, п. 3.7
^max гл. 2, п. 3.7
^max гл. 2, п. 3.7
^max гл. 2, п. 3.4
^max гл. 3, п. 1.5
О О О С) О О С) О О О С) ОООО ООО
2 to. Pr, без задержек
2 tiL G = Cu г
2 tiL Pr, G = Cj и C2 u
... и Cp и г
2 tiL Go = С и г
2 tiL
2 tiL Рг
2 t/L зависит от
маршрута
2 G1 = в/ + *>(ф
Г,-2 =М*(ф
2 liL
2 tiL
2 liL Рг
2 fiL
2 tiL Рг
3 tiL {Рг}
3 tiL Рг
3 tiL
4 tiL
М tiLe{0, 1}
М ri£e{0,1} Рг
М tiL e{0,1} без задержек
Gi»»t nt 3, п_ЗЛ0(*)
^max гл. 3. IL 4.1
*max гл. 3, n. 4.5
^max гл. 3, n. 4.6
^=7>0 Gnax гл. 3, n. 8.4
1-=7>0 ^max гл. 3, n. 8.4
^max гл. 3, n. 8.4 (*)
Kp(t} - кусочно- *max гл. 3, n. 8.4
постоянная не-
убывающая функция ^max гл. 3, n. 5.6
Df-D, i<=N S sign (max {tf - - D, 0}) гл. 3, n. 5.7
Dt = D, ieN S sign(max{tf- - D, 0}) pi. 3, n. 5.7
гл. 3, n. 7.1, 7.2
S tp t i < Dj гл. 3, n. 8.7
^max гл. 3, n. 3.9 (*)
гл. 3, n. 7.3
^max гл. 3, n. 2.1 (*)
rz-< 2 ^max гл. 3, n. 8.1 (*)
St; гл. 3, n. 6.4
sg- гл. 3, n. 6.4
гл. 3, n. 6.4
3
Тип системы Число прибо- ров Длительности операций, мо- менты по- ступления Условия обслужива- ния Дополнитель- ные условия
F 2 tiL, di я
F 2 tjL,dt я
F 2 tiL я, 0<b <п - 1
F 2 tiL я
F 3 tiL я
F 3 tiL я
F 4 tiL я
F 4 fiL
F 4 tiL Рг
F М *iL я
F М fiL
F м tiL Рг
F м fiL
F м tiL
F м tiL Рг
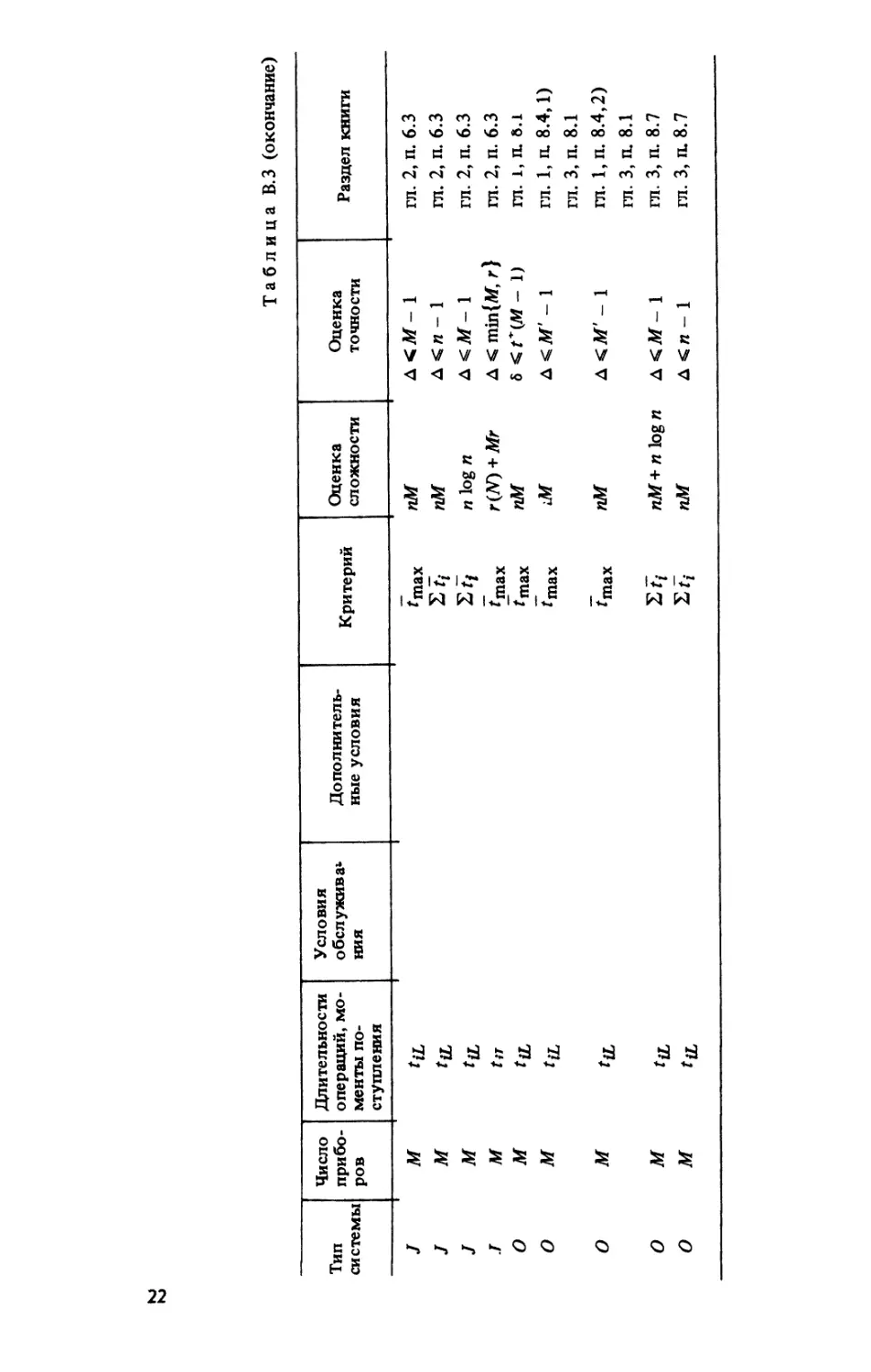
Таблица В.З
Критерий Оценка СЛОЖНОСТИ Оценка ТОЧНОСТИ Раздел книги
^шах n log n А<1 гл. 1, п. 9.12
^шах n3log n A <2/3 гл. 1, п. 9.12
^шах n log и А <Ы(Ь+ 1) гл. 1, п. 9.12
^шах и log и (^max(s°) — гл. 1, п. 9.12
— ^тах(у*)):
• C£max(s*) +
+ max{Dj fe
еАГ})< 1
Gnax n 6 <4r* гл. 1, п. 9.11
^тах n log n 5 <3f* гл. 1, п. 9.11
Gnax n2 6 <9Г* гл. 1, п. 9.11
Gnax n2 6 <9f* гл. 1, п. 9.11
Gnax n2 6 <9r* гл. 1, п. 9.11
Gnax n2M3 6 <M(M- 1)Г * гл. 1, п. 8.2
Gnax n2M3 6 <M(M-l)f * гл. 1, п. 8.2
^max n2M3 6 <M(M- 1)Г * гл. 1, а 8.2
^max nM Д <M- 1 гл. 1, п. 8.3,1)
Gnax nM log и Д <M'- 1 гл. 1, п. 8.4,1)
Gnax nM tog n Д<М'-1 гл. 1, п. 8.4,1)
F M tn Я nM+abfn А<М'- 1 гя. 1, к. 8.4,2)
F M *IL Gnax пМ + п tog п А <М' - 1 гл. 1,п. 8.4,2)
F M tiL Pr ^max пМ + п tog п А <М' - 1 гп. 1, п. 8.4,2)
F M fiL я, без задержек Gnax пМ + п tog п А <М- 1 гл. 1, п. 8.4, 2)
F M tiL GQ = SP, я *max пМ +п tog п А <М' - 1 гл. 1, п. 8.4, 2)
F F F M M M fiL tiL tiL #, без простоев * ^max SFf sr. nMlog п пМ пМ + л tog л (*тах($°) ~ ~ *тах<5*)) : : (Gnax<s*) + л М-1 + S S < f=l L=2 А < П - 1 А<М- 1 гл. 1,п. 9.12 гл. 1,п. 8.3,2) гл. 1, п. 8.5
J J 3 M liL tiL ri < 3 *max hnax л2 л2М2Р S < 6Г* 6 <г(М*Г» + + r-2)f* гл. 2, п. 6.3 гл. 2, п. 6.3
J M tiL идентичные приборы Г щах на каждой стадии ЛРл2г2 + + (гл + + M)310g/72 6 < (г3№ + + rs - 1г + + 2)Г* гл. 2, п. 6.3
J M tiL £* = (1,2,..., JW) Гтах /»1,... л £У = (М,М- 1,..., 1), п2М2 6 < (2М3 - - (М+ 3)/2)Г* гл. 2, п. 6.3
j= k + 1,... ,n
Тип системы Число прибо- ров Длительности операций, мо- менты по- ступления Условия обслуживав НИЯ Дополнитель- ные условия
J М fiL
J М tiL
J М tiL
Т м tn
О м tiL
О м fiL
о M tlL
о м tiL
о М tiL
Таблица В.З (окончание)
Критерий Оценка СЛОЖНОСТИ Оценка ТОЧНОСТИ Раздел книги
^шах пМ Д <М- 1 гл. 2, п. 6.3
пМ Д < п - 1 гл. 2, п. 6.3
п log п Д <М- 1 гл. 2, п. 6.3
{шах r(N) + Mr Д < min{М, г} гл. 2, п. 6.3
^тах пМ 6 - 1) гл. 1, П. 6.1
^тах lM Д<М'- 1 гл. 1, п. 8.4,1)
гл. 3, п. 8.1
*тах пМ Д <М' - 1 гл. 1, п. 8.4,2)
гл. 3, п. 8.1
sf; пМ+ п log п Д <М- 1 гл. 3, п. 8.7
пМ Д < п - 1 гл. 3, п. 8.7
обслуживаться другими приборами. Если не указано ни одно из этих значе-
ний, то прерывания запрещены.
Если на множестве N требований задано отношение -> строгого порядка
и запись i ->/ (z, / G N, i Ф j) означает, что должно выполняться нера-
венство min{r?L | £€JO> тах{Г/£ | £ ^Л}, то граф редукции такого
отношения обозначается символом G. Если же запись i -> / (z, j Е TV,
i Ф j) означает, что должно выполняться неравенство t^L > tj L для каж-
дого £ Е Л, то для обозначения графа редукции употребляется символ Go.
В тех случаях, когда требуется уточнить структуру графа G (или Go),
могут использоваться следующие обозначения:
G =SP - если граф редукции представляет собой последовательно-парал-
лельный граф;
G = С - если граф редукции - цепь, иными словами, если множество N
линейно упорядочено;
G = Ci U С2 U ... U Ср U Г — если каждая компонента связности графа
редукции представляет собой цепь Q (и число цепей равно р > 1) либо
одновершинный граф.
Эти же обозначения могут употребляться и для графа Go. Если для графа
G или Go не указано ни одно из перечисленных обозначений, то граф редук-
ции отношения -* является произвольным бесконтурным. В случае, когда
не указаны ни символ G, ни символ Go, множество N требований не упо-
рядочено.
Параметр ’’ресурсы” принимает значение Rs(q), когда имеются ограниче-
ния на используемые при обслуживании требований ресурсы (отличные от
обслуживающих приборов) и число видов ресурсов равно q. Через Rk и pik
обозначается соответственно запас ресурса вида к и его потребление при
обслуживании требования i в любой момент времени.
Запись ’’без задержек” означает, что каждое требование обслуживается
без задержек: начавшись в момент времени Г?, обслуживание требова-
ния i завершается в момент времени = t ? + S tiL.
L E Л
Запись ’’без простоев” означает, что каждый прибор £ Е Л , начиная с
некоторого момента времени , функционирует без простоев до момента
времени tL = + S tiL.
J i(= N
Если для систем с одинаковыми маршрутами указан символ л, то опти-
мальное расписание ищется среди расписаний, при которых все приборы
обслуживают требования в одной и той же последовательности.
Запись 0 < b < п - 1 также употребляется для систем с одинаковыми
маршрутами и означает, что в любой момент времени число требований,
обслуживание которых предыдущим прибором закончилось, а последую-
щим прибором не началось, не может превосходить значения Ь.
В пятой графе приводятся различные ограничения на число требований л,
число стадий обслуживания требования i Е N, маршруты L1 обслужива-
ния требований i EN и некоторые другие условия.
Запись [Dj ] означает, что все директивные сроки целочисленные, а
запись Di=D — что все они одинаковые.
23
В тех случаях, когда необходимо указать вид матрицы длительностей
обслуживания, приводится либо номер соотношения из главы 1, которому
должны удовлетворять элементы этой матрицы, либо наименование типа
матрицы в соответствии с терминологией, принятой в § 6 и 7 гл. 1. Наличие
в системе одного или нескольких доминирующих приборов указывается
явно (определение доминирующего пэибора приводится в § 2 гл. 3).
Для систем с одинаковыми маршрутами при М = 2 могут быть заданы
длительности > 0 и TiL > 0 пуско-наладочных и пере наладочных работ,
выполняемых для прибора L перед обслуживанием и после обслуживания
требования i прибором L £{1,2} ссответственно. Могут также быть зада-
ны величины f* >0, 7?/>0и|-1^0 такие, что при любом расписании
должны выполняться неравенства ti2 ~ >
Большинство приведенных в таблицах задач состоит в минимизации
функции F(r(s)), вид которой указан в шестой графе с использованием
принятых обозначений.
В седьмой графе табл. В.1 приводггся асимптотические оценки сложнос-
ти (с точностью до постоянного мгожителя) алгоритмов решения задач.
Запись ЛП в этой графе означает, что рассматриваемая задача сводится к
задаче линейного программирования. Задачи, в которых разрешение
прерываний не приводит к уменьшению целевого функционала, отмечены
в этой таблице знаком (*).
В табл. В.2 знаком (*) отмечены ТУР-трудные задачи, для которых
псевдо полиномиальные алгоритмы н? известны, а TVP-трудность в сильном
смысле не установлена. Остальные задачи являются тУР-трудными в
сильном смысле.
В табл. В.З приводятся сведения о полиномиальных приближенных ал-
горитмах: в графе 7 - асимптотические оценки сложности алгоритмов,
а в графе 8 — оценки точности получаемых решений. Как правило, в ка-
честве оценки точности получаемого решения $° используется оценка
его относительной погрешности Д z (F(f(s0)) — /F(t(s*)) или
абсолютной погрешности 6 = F(Z(s*)) - F(r(s*)), где s* — оптимальное
расписание.
В таблицах наряду с уже вве^нными обозначениями используются
следующие: г = max{ rt | iE.N } , г(Л) = S rh t* = max{tiL \ IG.N, L = Z?,
i£N
- M~
2
^=l,...,rf}, M*-
, г*(7У)=тах{ S tiL\LejC}, H - \{tiL >
i£N
> 0 | Z £/У, Через m обозначено наибольшее число требова-
ний из множества N с одинаковый маршрутом обслуживания, а через
Га Я — наименьшее целое число, которое не меньше а.
В табл. В.1, В.З и далее в книге ice логарифмы берутся по основанию 2.
В табл. В.1, как правило, не приводятся специальные случаи рассматри-
ваемых задач, если для них не известны более простые алгоритмы решения.
Под специальным случаем задачи А юнимается такая задача В, что множест-
во всех наборов входных данных задачи А содержит в качестве подмно-
жества все наборы входных данных задачи В.
В табл.В.2 приведены в основном ’’минимальные” ТУР-трудные задачи,
т.е. задачи, специальные случаи которых являются либо полиномиально
разрешимыми, либо для них не установлена принадлежность множеству
тУР-трудных. Очевидно, если задача имеет тУР-трудные специальные случаи,
то и сама она является NP-трудной. Так, все результаты относительно
ТУР-трудности задач с одинаковыми маршрутами обслуживания требований
справедливы и для задач с различными маршрутами. Часть задач не включе-
на в табл. В.1 и В.2, поскольку их полиномиальная разрешимость или
NP-трудность следует из приведенных в таблицах результатов для задач
с другими критериями оптимальности. Сравнительная сложность решения
задач с различными критериями оптимальности рассматривается в [350,
569, 646].
В табл. В.2 не приведены также задачи, которые являются ЛР-трудными
в случае одного или нескольких параллельных (одинаковых) приборов,
иными словами, для одностадийных систем обслуживания. Эти задачи, как
и результаты по трудоемкости алгоритмов их точного и приближенного
решения, представлены в соответствующих таблицах [350].
ГЛАВА I
ОДИНАКОВЫЕ МАРШРУТЫ
Множество N = { 1, 2,..., и} требований обслуживается в системе,
состоящей из М последовательных приборов. Требование i G N поступает
в систему в момент времени df > 0. Для всех требований множества N
маршруты обслуживания (порядки прохождения приборов) одинаковы и
определяются последовательностью приборов 1, 2, ...,7И. Длительности
tiL 0 обслуживания каждого требования i G.N каждым прибором Z, 1 <
предполагаются заданными. Одновременное обслуживание любого
требования несколькими приборами не допускается. Каждый прибор об-
служивает не более одного требования одновременно. Такие обслуживаю-
щие системы в этой главе называются системами поточного типа (с после-
довательными приборами и одинаковым порядком их прохождения).
Для доказательства ТУР-трудности задач теории расписаний в данной
главе используются следующие эталонные задачи.
Задача о разбиении. Дано множество ТУ0 = { 1, 2,. .., и0}, каж-
дому элементу i которого сопоставлено натуральное число в/, и S в/ =
= 2Е. Существует ли разбиение множества ТУ0 на два подмножества Аг? и
ТУ 2 таких, что S е,- = S е,- = F?
Задача о 3-разбиении. Дано множество ТУ0 ={1,2,..., Зи0 } и
натуральное число Е. Каждому элементу i Е ТУ0 сопоставлено натуральное
число в/ такое, что Е/4 < е/ < Е/2 и S = nQE. Существует ли такое
lG №
разбиение множества ТУ0 на и0 трехэлементных подмножеств ТУ у, что
S е^Е, /=1,...,и0?
iZzNj
Задача о трехмерном паросочетании. Даны три попар-
но непересекающихся множества Х2 и Х3 натуральных чисел, I | =
= | Х2 | = | Х3 | = л0, и множество Е QXt X Х2 X Х3 упорядоченных троек
элементов этих множеств. Существует ли такое подмножество Е9 Q Е,
называемое трехмерным паросочетанием, что | Е9 | = п0 и любые две трой-
ки, вошедшие в Е9, не совпадают ни по одной компоненте?
Задача о гамильтоновом цикле. Дан неориентированный
граф G = (К, U) без петель. Существует ли в графе G гамильтонов цикл?
Задача о 3-разбиении TVP-полна в сильном смысле [531]. Остальные пере-
численные задачи являются ТУР-полными [133].
26
§ 1. Общее время обслуживания. Два прибора
В этом параграфе устанавливаются некоторые свойства оптимальных
по быстродействию расписаний обслуживания п требований в системе с М
последовательными приборами и одинаковым порядком их прохождения
для всех требований. Особое внимание уделяется рассмотрению ситуации,
когда ЛГ = 2.
1. 1. В обслуживающую систему, состоящую из М последовательных при-
боров, в момент времени d = 0 поступает множество N = {1, 2,..,,п} тре-
бований. Каждое требование сначала обслуживается прибором 1, затем при-
бором 2 и т.д., пока оно не будет обслужено прибором М. Длительности
0 обслуживания каждого требования i Е N каждым прибором L,L =
1, . .. ,ЛГ, предполагаются заданными. Если процесс обслуживания требо-
вания i прибором L начинается в момент времени t{QL, то он протекает не-
прерывно и завершается в момент времени tiL = + tiL. Каждый прибор
одновременно может обслуживать не более одного требования, а каждое
требование одновременно может обслуживаться не более чем одним
прибором.
В рассматриваемом случае расписание s обслуживания требований одно-
значно определяется заданием матрицы || tfL || моментов начала или матри-
цы II tiL || моментов завершения обслуживания требований приборами.
При этом момент завершения обслуживания всех требований всеми прибо-
рами равен
^max(s) = max{7/L I i&N, L - 1,... ,М}.
Задача состоит в построении расписания $*, которому соответствует
наименьшее значение ^max(s)- Это расписание будем называть оптималь-
ным (по быстродействию) расписанием.
Если при некотором расписании s прибор 1 обслуживает требования в по-
следовательности л 1 = (i 1, i2,. . . , iп), а некоторый прибор L, 2 <£ <ЛГ, —
в последовательности = (/ь то имеют место следующие
очевидные неравенства:
11 1 ikl ik_ j 1 ]\ L 1 ’
для всех к = 2,. .. , п.
Если x = 0, то 7rnax(s) - общее Время обслуживания требований.
При построении расписания s* можно ограничиться рассмотрением класса 5
расписаний, при которых все приведенные нестрогие неравенства выпол-
няются как равенства. Каждое расписание s Е S, очевидно, однозначно оп-
ределяется заданием последовательностей (перестановок) ttl обслужива-
ния требований каждым прибором L, L = 1,. .. ,М. В дальнейшем рассмат-
ривается именно этот класс расписаний.
1. 2. Рассмотрим некоторые свойства оптимальных (по быстродействию)
расписаний.
1) Покажем, что расписание s* можно искать в классе расписаний, при
которых приборы 1 и 2 обслуживают требования в одной и той же после-
довательности.
27
Пусть s G S. Предположим, что при этом расписании прибор 1 обслужи-
вает требования в последовательности = (G, , /л), а прибор 2 —
в последовательности я2 = (/i = h, h =h,-,ip=ip, Jp+i = *r+i>--Jp+q =
= fr,. q>\, r>p>0.
Для расписания s справедливы соотношения
г+ i _
rfr+12(S) = max{fc^/«fc1’ Г/р2(«)}>
?°r2(s) = max {k^tiki, % + q_i2(s>} =% + q_12(s)>
_ _ r + 1
fy + 12(s)^ ^r+1l(s) = fikl-
Рассмотрим расписание s’ G S, отгичающееся от расписания s только тем,
что прибор 1 обслуживает требования в последовательности = (i i,.. .
• • • > G — 1 > G + 1 , *r , *r + 2 » • • • > *n ) •
Для расписания s' справедливы ссотношения
г— 1 _
tir +12(s') = max {fc2i tikl +'f,+ ,b %2(s')}>
r?2(s') = max { J* tikl, ^p+<?_12(s')} .
Так как Tjp2(s) = i}p2(s'), To z*r+i2<» > tfr+i2(s')- Отсюда следует,
что tip+q-iiW и, следовательно, ^r2(s) > 0°r2(s').
Повторяя описанныерассуждени! не более чем О(п2) раз, приходим к
расписанию s, при котором оба пэибора 1 и 2 обслуживают требования
в одной и той же последовательности, причем выполняется соотношение
^2(«)>^г(Д »6У.Тем самым 7n,ax(s) < ТщахО)-
2) Покажем, что расписание s* можно искать в классе расписаний, при
которых приборы М — 1 и М обслуживают требования в одной и той же
поел едовательности.
Пусть s G S. Предположим, что при этом расписании прибор М обслу-
живает требования в последовательности тгм = (JiJi*- • • , Jr-1 JrJr+1,
/r+2,••• , in) у a прибор M — 1 — в последовательности Км-х = (G = Л,
г 2 = /г> • • •, ip =jp, ip+i =ir+i>- > ip+q -ir,- • • ,in},q> l,r >p> o.
Для расписания s справедливы ссотношения
0) = max < йг _ ! M (Д hr, М-1 (s) } .
+! M 0) = maX < M (S), Tjr +11 M_ ! (S) } = TirM (S).
Рассмотрим расписание s' G 5, отличающееся от расписания s только тем,
что прибор М обслуживает требоважя в последовательности тг'м = j29.
• • • ,/л— 1 >/г +1 ,/г,/г+ 2 , • • • ,/ п) •
28
Для расписания s' справедливы соотношения
^ + 1М(«') = таХ<^-1мО')> ^r + I,M-l(S'» =
= max{^r lM(s), Zyr+1,M_i(s')} ,
= max{^r+1M(s'),
Поскольку 7jr+i,M-i^) <*/nM-i(s)>To r°r+1M(s') <max { Tjr_1M(s),
> = ?/rw(s) • ТогДа
< max { r?rM (s) + tir+! M, (s) } + tjrM =
= ?/гм(5)+ Чг+1М + tirM ~ {ir+iM^'
Таким образом,
max { TlrM (s'), Tir+j M (s')} = 7)rM (s') <
< ^г+,м(«) = max { 7tr ¥lM(s), TjrM(s)} .
Повторяя описанные рассуждения не более чем 0(п2) раз, приходим к
расписанию Г, при котором оба прибора М — 1_и М обслуживают требования
в одной и той же последовательности, причем fmaxCD ^max (s) •
3) Из п. 1) и 2) непосредственно следует, что при М<3 оптимальное по
быстродействию расписание 5* можно искать среди расписаний, при кото-
рых все приборы обслуживают требования в одной и той же последова-
тельности.
Покажем, что при Л/ > 3 это, вообще говоря, не имеет места.
Действительно, рассмотрим задачу построения оптимального по быстро-
действию расписания обслуживания двух требований четырьмя последо-
вательными приборами. Длительности обслуживания приведены в табл. 1.1.
Если все приборы обслуживают требования в одной и той же последова-
тельности (1, 2) или (2, 1), то общее время обслуживания равно 14 едини-
цам времени. Если приборы 1 и 2 обслуживают требования в последователь-
ности (2, 1), а приборы 3 и 4 - в последовательности (1,2), то получаем
расписание, при котором общее время обслуживания равно 12 единицам
времени (рис. 1.1).
29
4) При любом расписании s Е S прибор 1 функционирует без простоев,
начиная с момента времени d = 0. Покажем, что расписание s может быть
преобразовано в некоторое новое расписание s (не обязательно из класса
5), при котором ^тах(^) = zmax(5) и приборы 1 и М функционируют без
_ п
простоев, начиная с моментов времени 0 и fmax(s) — S tiM соответ-
i - 1
ственно.
Действительно, пусть s 6 5 и пэибор М при этом расписании обслужи-
вает требования в последовательюсти тгм = (/i, /2, •. ., iм )• Положим
прибор!
прибор 3
прибор 2
прибор 1
0 1 5 6 7 1112
Рис. 1.1
= '/£(*) для всех/ =1,.. „п, L = 1,.. . ,М- 1; = rmax(s),
tjkMib = GnaxO) - 2 tjlM, fc = 1,.. . ,n - 1. Поскольку Z°M($) >
> f/kAfO)> k = 1...n> и = Gnax(s) ~ T0 * - искомое
расписание.
5) Рассмотрим часто встречающуюся ситуацию, которая отличается от
описанной в п. 1.1 тем, что заранее оговорено, что все приборы обслужи-
вают требования множества Nb одюй й той же последовательности.
Пусть 7Г = (i i, i2,.. ., iп) — некоторая перестановка элементов множест-
ва N= { 1,2,.. ., п}. Рассмотрим расписание s € S, при котором все прибо-
ры обслуживают требования в последовательности л.
Для этого расписания справ едп1вы соотношения
^1=0’ ^i=^>-ii’ & = 2, ...,и;
= L = 2,...,M;
Г/кл=тах{^_1£, l'i/(L_1}, k = 2,...,n, L = 2,...,M.
Нетрудно убедиться, что в згом случае общее время обслуживания
равно
^тах С^) =
11 М2 п
= max {2 tf , + S f/k2 + - -+ 2
1 < ux < u2 < ... < им _ i < n fc=l k = ul
(1.1)
где u2,..., uM- i - целые чиста.
30
1.3. Перейдем к более подробному рассмотрению случая, когда М = 2,
Пусть система состоит из двух приборов А и В, длительности обслужи-
вания требования i G N приборами А и В равны соответственно и .
Как уже отмечалось, в рассматриваемом случае расписание s* можно
искать в классе расписаний, при которых оба прибора функционируют без
простоев и обслуживают требования в одной и той же последовательности.
Пусть тг = (fl, i2,. . . , in) - произвольная перестановка элементов мно-
жества N- { 1,2,. .., п } .
Поскольку требования обоими приборами обслуживаются в одной и
той же последовательности, то для расписания s 6 5, определяемого пос-
ледовательностью л, из (1.1) следует, что
4ах(’г)= max { 2 at + 2 bt }.
ug/v /с = i л = и
Преобразуя расписание s в расписание s в соответствии с п. 1.2, 4), полу-
чаем
^пах(’г) = ^.в(«) + 2 Z>( = max { 2 at - 2 b( } + 2 bt.
i= 1 uGA' k= 1 Л k= 1 K i=l
Таким образом, задача построения оптимального (по быстродействию)
расписания сводится к нахождению перестановки я*, которой соответ-
ствует наименьшее значение шах { Дм(л) | u G N}, где
Ди(я)= 2 aik - 2 bj u&N.
к = 1 к = 1
Введем в рассмотрение перестановку л1, отличающуюся от л транспози-
цией элементов i г и i г +1, т.е. л' = (z i, i2,..., ir_ i, ir + 1, ir> ir+2> • • • > in) •
Найдем достаточные условия, при которых
max{ Ды(л)| и G7V} < max{ Ды(л')| и GN}. (1.2)
Очевидно, Дм(л) = Ды(лг) при всех иб { 1,2, .. ., г - 1,г + 2, .. . ,и }.
Следовательно, для выполнимости неравенства (1.2) достаточно, чтобы
тах{ Дг(л), Дг + 1(л)} <max{ Дг(л'), Дг+1(л')} .
Последнее неравенство равносильно неравенству
тах{Д/г,Д/г+а,>+1 -bir} <max{a/r+1>4+aj>+i-bir+l),
которое в свою очередь равносильно неравенству
тт{а,гЛг + 1} <min{e,r+p6/r }. (1.3)
Таким образом, из неравенства (1.3) следует неравенство (1.2).
Пусть iJ,kGN. Легко показать, что в случае, когда имеют место нера-
венства
min {ah bj} < min {^,6/ }, min{az-, bk} < min {a*., bj} ,
выполняется также неравенство
minCminfa^d/} .
31
Отсюда следует, что если неравенство (1.3) выполняется для всех г =
= 1, ... . , п — 1, то тт = (i 1, 1*2, • * •, in) является искомой оптимальной пе-
рестановкой.
Таким образом, для поароения оптимальной перестановки достаточно
разбить множество N на дза (не обязательно непустых) подмножества
- { i I cii <bf} и N2 ={ i ai> bj ) и сначала обслужить требования мно-
жества N\ в порядке неубывания значений aif а затем - требования мно-
жества N2 в порядке невозрастания значений bj.
Для построения оптимальной перестановки можно также сопоставить
каждому требованию i вес
w(z) = (W - min { aiy bi} ) sgn(af - &z),
где IV - достаточно большое число (И/ > max{ min {ai9 bt} | z G TV}), и упо-
рядочить требования в порядке неубывания весов.
В любом случае трудоемкость построения оптимальной перестановки
не превосходит О(п log и) операций.
1.4. Рассмотрим некоторое обобщения ситуации, описанной в предыду-
щем пункте.
Пусть по-прежнему имеется два прибора А и В. Каждое требование
i G7V={l,2,...,z?} обслуживается начиная с прибора А, известны дли-
тельности at > 0 и bj > 0 обслуживания требования i приборами Л и В со-
ответственно. Если требование i начинает обслуживаться прибором А в мо-
мент времени , то момент времени начала его обслуживания прибором
В > tiA + где %i - данное число. Если < а/, то требование / мо-
жет одновременно обслуживаться обоими приборами. Будем предполагать
также заданными наименьшие промежутки времени 5^ > 0 и Ьвк > 0 меж-
жу возможными моментами начала обслуживания требований i и к прибо-
рами А и В соответственно пэи условии, что требование i начинает обслужи-
ваться первым. Если Ъ^к <аь то требования i и к могут обслуживаться
прибором А одновременно. Аналогично, если Ьвк < , то эти требова-
ния могут одновременно обслуживаться прибором В. Пусть riA > 0 и
г,*# > 0 — заданные моменты времени, раньше которых не может быть на-
чато обслуживание требовашя i приборами А и В соответственно.
Если положить li = = at,Ьвк = bj,TiA = т{в = 0, i,к GN, то получим
ситуацию^)писанную в предыдущем пункте.
Через Гтах(эт, я') обознашм наименьший момент времени, к которому
можно завершить обслуживание всех требований обоими приборами при
условии, что прибор А обслуживает требования в последовательности тт =
= G i, *2 > • • • > * и) > а прибор# — в последовательности я' = (/ь/2,.. . ,/„).
По условию обслуживание требования i { прибором Л может быть начато
в момент времени А = TilA, требования i2 — в момент времени Г® А =
= max { Ti2 А , А + 6^ } i т.д., требования in - в момент времени t®nA =
= тах{7/пЛ>г?1Л +Sf_ ,Г?п_1Л +5;ni/n}_
Самый ранний момент нашла обслуживания требования/( прибором Дра-
вен г/,в ~ тах( г/1 в. ^/,л *&,}> требования / 2 - Т/2 в = max { 2 s, '/, а +
+ $/, ’ О9, в + 5л/, > « т.д, требования /„ - = max{ rinB,
t? в + i > Т/ я + s® • , Т/ п + Зв . J
hJn J hfn" ln—\B Q]n—Un*'
32
Наконец, гтах(я, я') = max{ tikA, tikB | к G.N}, где tikA = tikA + aik,
TikB = t^kB+bik, k£N.
_ 1) Сформулируем достаточные условия, при которых леравенство
Гтах(я» я) < ^тах(я> я ) выполняется для любых перестановок я и я'.
Не нарушая общности рассуждений, будем считать, что я = (1, 2,..., и)
иг’= (/1,72, • • • ,/„)•
Если для любых требований i ,k,r Е 7V выполнился неравенства
5+ «1, ткА - riA < (1.4)
то для всех i GAT справедливо
= + ^/+i •
Если для любых требований i,k,r Е Довыполняются неравенства
т(в-т1А<^, (1.5)
то для всехkENсправедливо
к-1
УкВ=гмк{%А 5/В///+11г=1,. • ,Н.
Если наряду с (1.4) и (1.5) для любой пары требований i ,к G Wewnon-
няются неравенства
а,- -b( < bi -ak<S?k, (1.6)
то имеет место соотношение
_ ir~1 n-i
^тах(’г,’г') = ^тах{т1Л + +£/r + z?r &fih+l +bin} . (1.7)
Покажем, ЧТО ДЛЯ ТОГО чтобы ^тахС^ < ^maxG^ *') ПРИ любых я и
я', достаточно, чтобы наряду с неравенствами (1.4) — (1.6) выполнялись
соотношения
bfk=bit ii-ik<^k . (1.8)
для любой пары требований i,kEN.
По-прежнему полагаем я = (1, 2,.. ., п) и пусть я1 = (/i,... , jp_1,
ip,---,jp+u.....in), где h = 1, 1=1......p- 1, jp*p, jp+u = P, u> 1.
Рассмотрим перестановку n' = (1,2....p- l,p,jp,... ,/p+u_i,/p+u+i>--'
_ Покажем, что при сделанных предположениях имеет место неравенство
^тах(я, Я ) < ^rnaxGr? Я )•
Действительно, в силу (1.8) выражение (1.7) может быть записано в виде
_ ir~1 п
Гшах(я,я') = тах { т1А + S 5fz+i+^+s */, >
Z= 1 1 1= г 1
При ЭТОМ
_ /г-1 п
Гтах(’г,’т') = тах{ max { т1А + S 5п+1+& +S Ь,-,),
1<г<р-1 1=1 ' r 1=г 1
р+и+1<г<п
3. В.С. Танаев
33
Пл + 2 61 i+i + + S bjp max {Т1Л + S 5//+J +
/= 1 ' l = p 1 p<r<p+u-l i=i '
+ 2+i 6^/ + 1 +^> + Л bfl
/= p + 1 l = r
Для того чтобы доказать соотношение *тах(я, ^тах(я> я'), доста-
точно показать, что
?1А + 2 & 1,1+1 + £р + 2 Ьц )• (1.9)
I = 1 ’ I = р
Имеем
_ /р-1 п
ЛпахСЛ, Я ) > Т1У1 + ^2^ ^^/ + 1 + fyp + 2
Из (1.8) следует, что
,р-1 А
%р ^1,1 + 1 +^ip
1= р и
и неравенство (1.9) выполняется.
2) Опишем способ построения оптимального расписания в предположе-
нии, что выполняются соотношения (1.4) — (1.6), (1.8) и = 8^ > о для
всех!,к &N.
Как показано выше, достаточно рассматривать такие расписания, при
которых оба прибора обслуживают требования в одной и той же последо-
вательности. Пусть тг = 0*1, ;*2, • • • , и) “ некоторая перестановка элемен-
тов множества N = { 1,2, ..., п } . Тогда
*maxG0= шах{т1Л + 2 8f + 2 Ь, } . (1.10)
«ед' 1 к = 1 * “fc=uK
Пусть известно, что в оптимальной перестановке на первом месте стоит
требование v. Тогда задача сводится к нахождению перестановки я* =
= 05, z з > • • Jn) из множества всех перестановок вида irv = (i2, z 3 , • • •, in)
элементов множества TV \ { и) , которой соответствует наименьшее значение
7(irv) = max { S + 2 bf } =
2<u<n k=2 k u k=u K
= max { S (6^ -bf )f - И +bt } - 2 b{
2<и<п к = 2 k K U u U к = 2 k
Полагая aik = - bik и Piu = %iu - + biu, приходим к задаче ми-
нимизации функционала
/(я0) = max { 2 а,- + ft }
2<и«п к = 2
на множестве перестановок вида nv = (12^3^ • п) элементов множества
7V\{17} .
34
Пусть ir'v = (i2, Jr-iJr + iJrJr+i^ • • • Jn)-Имеем
u r-1
f(ir'v) = max{ max { S a, +ft }, S a/fc + a, + ft ,
2 < u<r-l, к = 2 к = 2
г +2 < и < п
г + 1
к = 2 К Г
Для того чтобы/(яи) </(Яр), достаточно, чтобы
max { air + fty, aif +air + l + Pir+
<max{a/r + 1 + ftr + 1 ,a/r + a,r + 1 + ftrL
Это неравенство равносильно неравенству
min{a<r+ftr, ftr + 1> <min{a,r+1 + ftr + 1,fty},
для выполнимости которого достаточно, чтобы
(И/ - min { а,у + ft,, fty } ) sign (a<r) <
< (V - min { a,r+j + fty+,, ftr+j > ) sign (a,у+j),
где W — достаточно большое число (W> max{ min {a, + ft, ft } | i &N}).
Таким образом, для нахождения оптимальной перестановки я* доста-
точно
а) каждому требованию i G N сопоставить вес w(z) = (И/ — min{ £/,
- bj + bt } ) sign {bj -bf);
б) построить n перестановок вида (у, я£), где v G N, а требования мно-
жества JV\ {у } упорядочены по неубыванию их весов;
в) среди построенных перестановок вида (у^_Яу) выбрать ту, которой
соответствует наименьшее значение величины *тах(я)> определяемой со-
отношением (1.10).
Трудоемкость нахождения я*, очевидно, не превосходит O(nlogn)
операций.
§ 2. Общее время обслуживания.
Три и более приборов
В этом параграфе показано, что задача построения оптимального по
быстродействию расписания при М > 3 является АР-трудной независимо
от того, допускаются прерывания в процессе обслуживания требований
или нет.
2.1. Пусть множество N = { 1,2,..., и } требований поступает в момент
времени d = 0 в систему поточного типа, состоящую из трех последователь-
ных приборов. Покажем, что задача построения оптимального {по быстро-
действию) расписания является NP-трудной в сильном смысле, если в про-
цессе обслуживания не допускаются прерывания и все tiL>Q, iEN,
L =1,2,3.
Сформулируем соответствующую задачу распознавания: определить,
существует ли такое расписание s°,при котором tтах(^°)<.У для заданно-
го числа у.
3
35
Покажем, что к этой задаче сводится задача о 3-разбиении (см. вводную
часть этой главы).
Положим п = 4и0 + 1, -V = { 1, 2,... , п}. Требования множества N
разобьем на две группы: ^-требования, обозначаемые Ub i = 1,..., Зл0»
и К-требования, обозначаемые Ру, j = 0,..., п0. Положим
tup. = ~ 1, *=1,...,3ио;
= ^к02=£’, *коз = 2#-3;
ty. 1 = 2Е — 3, ty^2 — Е, ^Vj3 = 2# — 3, / = 1,..., «о — 1;
%О»=2£,-3> %,2=£> %Э=1>
Покажем, что в построенной задаче расписание sQ, при котором
tmax (s°) У ~ (2^о + 1)# + 2, существует тогда и только тогда, когда имеет
решение задача о 3-разбиении.
1) Пусть задача о 3-разбиении имеет решение и ЛГ?, j = 1,..., п0, —
найденные трехэлементные подмножества элементов Множества 7V0. Через
irj(U) обозначим произвольную перестановку ^/-требований с номерами
из множества N?, j = 1,... , nQ.
Расписание s° можно посгроить, например, следующим образом. Все три
прибора обслуживают требования множества N в одной и той же последо-
вательности (Ко, Я1(Ю, flzGO, • • •, ^л0 - 1, яи0(Ю, ^л0) и функцио-
нируют без простоев: прибор 1 — во временном интервале (0, 2п0Е + 1],
прибор 2 — в интервале (1, (2и0 + 1)# + 1] и прибор 3 - в интервале
(£ + 1,(2ио +1) #+2].
2) Пусть существует расписание s°. Будем полагать, что в задаче о
3-разбиении Е > 8, так как в противном случае задача о 3-разбиении либо
не имеет смысла (при Е Е { 1, 2, 4}), либо проверка существования ее
решения не вызывает затруднений (при#G { 3, 5, 6, 7, 8}).
Учитывая результаты п.1.2 § 1 этой главы, можно считать, что при распи-
сании s° все три прибора обслуживают требования множества N в одной
и той же последовательности 7г°, а приборы 1 и 3 функционируют без
простоев.
а) Покажем, что в последовательности л° первым должно обслужи-
ваться требование Ко.
Очевидно, прибор 1 функционирует в интервале (0, 2п0Е +1]. Кроме
того, тш{г*3 | i EN } < # -F 1, так как в противном случае t max(s°) >У-
Тогда в последовательности л° ни одно из требований Vi9 V2,... ,
не может обслуживаться первым, поскольку обслуживание этого требо-
вания прибором 3 начиналось бы в момент времени ЗЕ — 3 > Е + 1 (при
#>8).
Предположим, что первым в последовательности л° обслуживается не-
которое ^/-требование. Пусть Яц — множество номеров ^/-требований,
обслуживаемых прибором 1 непрерывно одно за другим в интервале
(О, 1 > 1. Поскольку прибор 2 начинает функционировать
не раньше чем в момент времени 1, он должен функционировать без просто-
ев в интервале (1,у - 1].
36
Если вслед за требованиями этого множества прибор 1 обслуживает
Требование Ко, то для того чтобы приборы 2 и 3 функционировали без
Простоев, должны выполняться неравенства
1+ 2 et > \Ry\ +1, F+1+ |Яа| >1+ 2 ez + Е.
i^Ru i^Ru
Эти неравенства, однако, не могут одновременно иметь места приЕ> 8.
Если после требований множества { Ut \ i ЕЯц} прибор 1 обслуживает
одно из требований К2,..., КЛо, то для того чтобы приборы 2 и 3
функционировали без простоев, должны выполняться неравенства
1+ 2 ei>\Ru\+2E-3, £+1 + |Яа|>1 + 2 et+E.
i е Ry i G Ry
Эти неравенства также одновременно не могут иметь места при Е > 8.
Таким образом, первым в последовательности тг° обслуживается тре-
бование Ио.
При этом t^v о = Е + 1 и fmax(s°) = У- Поскольку t^v 2 > 1, S ti2 =
0 0 /GN
•> у - 2 и min{ ti3 | i E N } = 1, то прибор 2 функционирует без простоев
В интервале (1,у — 1].
б) Покажем, что в последовательности я0 последним должно обслужи-
ваться требование К„о.
Очевидно, ни одно из требований Vi9 К2,... , _ i не может обслу-
живаться последним, поскольку тах{г/21/е^) = у— 1 и ty.3 =
« 2£ - 3 > 1, / = 1,. .., и0 — 1.
Пусть Vq9 1 < q < п09 - последнее из V-требований в последователь-
ности я0. Пусть Ry — множество номеров ^/-требований, обслуживаемых
после требования Vq. Для того чтобы прибор 2 функционировал без про-
стоев, должно выполняться неравенство < /^2, или» что то же»
2и0 Е - | Ry | + 1 < 2nQE + 1 - 2 ez.
i^Ru
Последнее неравенство означает, что 17?^! > 2 ez. Получаем проти-
воречие. iERu
Поскольку требования У19 И2,..., К„о _ х не отличаются друг от друга
по длительностям обслуживания, то они могут обслуживаться в произволь-
ном порядке. Для удобства дальнейших рассуждений будем предполагать,
что в последовательности я0 эти требования обслуживаются в порядке
возрастания их номеров.
в) Пусть Rj — множество номеров {/-требований, расположенных в по-
следовательности я0 между требованиями VJ _1 и Vj9 j = 1,..., п0. По-
кажем, что |7?у | G { 2, 3,4}, j = 1,..., л0-
Рассмотрим пару требований Ко и . Так как все приборы функцио-
нируют без простоев в соответствующих интервалах, то имеют место соот-
ношения
* Ио 1 + I I = 1»
2 е-4 2 > FFo1 +|/?t I +2F-3,
i £= R}
j з +1I = з > 2.
Поскольку t уо 2 = t уо ! + Е И t у ° 3 = t уо i + ЗЕ - 3, т° t Г1 2 = t уо j +
+ 2Е + 2 eh Таким образом, должно выполняться равенство
ICRt
2 e; = F-3+ |. (2.1)
Нетрудно проверить, что при | Л i | = 1 равенство (2.1) не имеет места,
если Е > 8. Если |ЯХ | > 4, то 2 е{ > I/?! |F/4 и при Е > 8 значение
iGflj
|7?1|Е’/4>Е’-3 + |Л1|, т.е. равенство (2.1) не имеет места.
Таким образом, | G { 2, 3, 4}, причем в силу (2.1) ^к12 = ^и11
и з = 2-
Рассуждая аналогичным образом, можно показать, что для всех j = 2,...
. .. , п0 значения | Rj | G { 2, 3, 4 } и
2 et = F-3+ |Я7|, (2.2)
i^Rj
причем 4/2 = lVji и t°Vj3 = ~tv.2.
г) Покажем, что задача о 3-разбиении имеет решение.
Если \Rj 1 = 3, / = 1,...,л0,то в силу (2.1), (2.2), полагая N? = Rj,
получаем решение задачи о 3-разбиении.
Пусть число множеств Rj таких, что \Rj | = 3, равно к <п0. Тогда най-
дется ровно (п0 - к)/2 множеств Rj таких, что |Л; | = 2, и столько же
множеств Rj таких, что | Rj | = 4.
Рассмотрим произвольное множество Rj с |Я/| = 2. Пусть Rj = { , i2}.
Тогда в силу (2.1), (2.2) имеем = Е — 1. Если Е - четное число,
то et и должны быть не больше чем Е/2 — 1‘. Но тогда их сумма не пре-
восходит Е - 2, что невозможно. Таким образом, Е - нечетное число, при-
чем = (Е — 1)/2, так как только в этом случае = Е — 1.
Рассмотрим произвольное множество Rj, |/fy| = 4. Пусть Rj =
4
= { Pi, Р2,Рз, Л»}-Из (2.1), (2.2) следует, что 2 ер = Е + 1. Как уже
/=1 1
_ 4
отмечалось, Е - нечетное число. Если Е = l(mod4), то 2 ер > 4(Е + 3)/4 >
1=1 1
> Е + 1, что невозможно. Следовательно, Е = 3(mod4), причем epi =
4
= (Е + 1)/4,1 = 1, 2, 3, 4 (поскольку только в этом случае 2 epi = Е + 1 ).
Каждую пару множеств вида { it, i2} и { plt р2, Рз> Рл } преобразуем
в пару множеств { , рх, р2 } и { i2, р3, р4} . Очевидно, + ер^ + ер^ =
= + ер^ + ер* = Е. Построенные множества вместе с теми из множеств Rj,
для которых |Я,| = 3, образуют решение задачи о 3-разбиении. Таким
образом, за О(п0) операций построено сведение задачи о 3-разбиении к рас-
сматриваемой задаче распознавания, и следовательно, задача построения
оптимального (по быстродействию) расписания обслуживания требований
в системе, состоящей из трех и более приборов, является АТ’-трудной
в сильном смысле.
33
2.2. Введем понятие расписания с прерываниями процесса обслужива-
ния и установим основные свойства таких расписаний.
В систему, содержащую М последовательных приборов, в момент време-
ни d = 0 поступает множество 7V = { 1, 2,..., п} требований. Известны
длительности tiL > 0 обслуживания требования i G N прибором Z, L =
11 1,... , М. Каждое требование обслуживается прибором 1, после заверше-
ния этого обслуживания - прибором 2 и т.д. до тех пор, пока оно не будет
обслужено прибором М. По-прежнему предполагается, что каждый прибор
одновременно обслуживает не более одного требования, а каждое требо-
вание одновременно обслуживается не более чем одним прибором.
В процессе обслуживания требований допускаются прерывания: каждое
требование i может обслуживаться каждым прибором L в несколько
’’приемов” при сохранении условия, что суммарная длительность такого
обслуживания равна tiL. Процесс обслуживания требования i прибором L
может быть прерван в любой момент времени и затем возобновлен. Число
прерываний может быть произвольным, но конечным. После каждого
прерывания прибор L может облуживать любое требование, в то время
как требование i не может обслуживаться прибором L + 1 до тех
пор, пока полностью не завершится процесс его обслуживания при-
бором Z.
Если tiL - момент (полного) завершения обслуживания требования i
прибором L при некотором расписании (с прерываниями) s, то, как и преж-
де, полагаем fmax(s) = max{ tiL | i £N,L = 1,... ,7И}. Расписание s*, мини-
мизирующее значение Jmax(s), будем называть оптимальным по быстро-
действию.
Сформулируем и докажем некоторые свойства оптимальных (по
быстродействию) расписаний с прерываниями.
1) Покажем, что оптимальное расписание s* можно искать в классе
расписаний, при которых число прерываний не превосходит Мп(п - 1).
Пусть s - произвольное расписание, и при этом расписании прибор Q,
1 < Q < М, во временном интервале (г, г'] обслуживает требования
Ч, h, • Требование it обслуживается прибором Q в интервале
I = 1,... ,k, где т < < 7i < < Т2 < ... < t*k < 7k < т',
причем обслуживание каждого из требований i19 i2,..., ik не завершает-
ся в интервале (г, т'].
Пусть прибор Q во временных интервалах (Г, г] и (г', г'] обслуживает
требование i G7V.
Нетрудно видеть, что расписание s можно преобразовать в расписание s ,
которое отличается от s только тем, что прибор Q обслуживает требова-
ние i во временном интервале (Г, т + Д], а требование ц — во временном
интервале (Zj° + Д, 11 + Д], I = 1,... , к, Д = t* — т'. При этом, очевидно,
^max(5 )“^maxW*
Повторяя этот процесс исключения прерываний, приходим к расписа-
нию s, при котором между моментами прерывания и последующего
возобновления процесса обслуживания каждого требования каждым при-
бором завершается обслуживание какого-либо требования этим прибором,
39
т.е. процесс обслуживания каждого требования каждым прибором преры-
вается не более п - 1 раз, причем tmax (?) = tmax (s) •
2) Покажем, что оптимальное расписание s* можно искать в классе
таких расписаний, при которых приборы 1 и М обслуживают требования
без прерываний.
Действительно, пусть при некотором расписании s прибор 1 во времен-
ном интервале (г, г*] обслуживает (возможно, с прерыванием и не пол-
ностью) последовательность требований R, в которой не все требования,
вообще говоря, различны, а во временных интервалах (t, г] и (г', ^'] -
некоторое требование i E.N.
Нетрудно видеть, что расписание s можно преобразовать в расписание s',
которое отличается от s только тем, что последовательность требований R
обслуживается прибором 1 во временном интервале (t, t + г' - г], а тре-
бование i - в интервале (Г + т - г, /']. При этом t max(s') = ^max(s) •
Повторяя этот процесс исключения прерываний, приходим к расписа-
нию Т, при котором все требования обслуживаются прибором 1 без пре-
рываний, и Fmax (s ) = Fmax (з).
Исключение прерываний в обслуживании требований прибором М можно
осуществить аналогичным образом.
Действительно, если при некотором расписании s прибор М обслужива-
ет последовательность требований R в интервале (г, г'], а некоторое требо-
вание i G N — в интервалах (Г, г] и (тг, /г], то можно преобразовать это
расписание в расписание s', огличающееся от s только тем, что требование i
обслуживается прибором М в интервале (t, t* - т’ + т], а последова-
тельность требований R - в интервале (t' - т’ + г, t'], причем
^maxO )“^max($)*
Доказанное свойство означает, что при М = 2 оптимальное (по быстро-
действию) расписание с прерываниями можно искать в классе расписаний
без прерываний.
2.3. Покажем, что и в том случае, когда в обслуживании каждого требо-
вания каждым прибором допускаются прерывания, задача построения
оптимального (по быстродействию) расписания s* при М > 3 является
NP-трудной в сильном смысле.
Сформулируем соответствующую задачу распознавания: определить,
существует ли такое расписание s° обслуживания (с прерываниями) мно-
жества N ={ 1, 2, ..., л } требований М приборами, при котором
^max(s°) < У для заданного числа у.
Покажем, что при М = 3 к этой задаче сводится задача о 3-разбиении.
Положим п = 4и0 + 2,ЛГ = { 1,2,..., п}. Множество N требований разобьем
на две группы: (/-требования, обозначаемые U^i- 1,..., Зи0, и К-требо-
вания, обозначаемые Vj, j = 0,..., nQ + 1. Положим
Q/ji = Q/f-3 = /uf-2 = 0, < = 1,..., Зл0;
Ч 1 = fvt 2 = 0, 3 = Е, гУП"! = Е, tVrt' 2 = 2Е, fr„o 3 = 0;
Ч»=0’ tVi2~2E, tVi3 = E, tVn^li=E, ^„o + 12 = ^o + 13 = O;
4'i =tVj3=^> fr/-2 = 2-E’, j = 2,... ,n0 — 1.
40
Покажем, что в построенной задаче расписание s° (с прерываниями),
При котором Гтах($°) <7 ~ 2h0F, существует тогда и только тогда, когда
имеет решение задача о 3-разбиении.
1) Пусть задача о 3-разбиении имеет решение и JV?, / = 1,..., и0 —
найденные подмножества множества NQ. Пусть itj(U) — произвольная пере-
становка (/-требований с номерами из множества N? 9 j,...
Расписание s°, при котором Tmax(s°) = У и все требования обслужива-
ются без прерываний, существует и может быть построено следующим
образом. Все три прибора функционируют без простоев во временном ин-
тервале (0, у ], причем прибор 1 обслуживает требования в последователь-
мости (тг! (U), К2, тг2 ([/), F3, ..., к„в _ 1, ff„o _ 1 (U), F„o, я„о (U), F„o +1 ).
прибор 2 — в последовательности (Р\, V2,..., Vn ) и прибор 3 — в после-
довательности (К0) Trt(t7), 7t, n2(U), V2,..., Vn<>-2,
Ч(Ю).
2) Пусть существует расписание s°. Покажем, что имеет решение зада-
ча о 3-разбиении. Как уже отмечалось, не нарушая общности рассуждений,
можно считать, что приборы 1 и 3 обслуживают все требования без пре-
рываний. Так как суммарная длительность обслуживания всех требований
каждым прибором равна у, то при расписании s° все три прибора функцио-
нируют без простоев во временном интервале (0,7].
Рассмотрим временной интервал (О, 2Е}. Поскольку прибор 3 функ-
ционирует без простоев и обслуживает требования без прерываний, то
требование Ко должно обслуживаться этим прибором в интервале (О, F].
Поскольку требование Ki — единственное требование, которое может
обслуживаться прибором 2, начиная с момента времени 0, то при расписа-
нии s° имеем tQv 2 = 0 и t г 2 > 2F.
Пусть суммарная длительность обслуживания (/-требований прибором 1
в интервале (О, 2Е} меньше Е. Тогда имеем простой в функционировании
прибора 3, поскольку эти (/-требования будут обслужены прибором 3
раньше момента времени 2Е, в то время как t у 3 > t v 2 > 2Е.
Пусть суммарная длительность обслуживания (/-требований прибором 1
в интервале (О, 2Е} больше Е. Тогда в интервале (Q, 2Е] прибор 1 не за-
вершит обслуживание ни одного из К-требований и, следовательно, при-
бор 2 в интервале (2F, 4F] будет простаивать, что невозможно.
Следовательно, прибор 1 в интервале (О, 2Е} обслуживает некоторые
(/-требования в течение Е единиц времени. Если при этом обслуживание
хотя бы одного из этих требований прибором 1 завершается в момент
времени 2/Г, то это требование не может быть обслужено прибором 3
в интервале (О, 2Е], т.е. возникает простой прибора 3, что невоз-
можно.
Итак, прибор 1 обслуживает (/-требования в интервале (О, Е1], а в интер-
вале (F, 2Е} он обслуживает одно из К-требований. Этим требованием
не может быть ни , ни К„о + х, так как в противном случае возникает
простой прибора 3 либо прибора 2 соответственно. Не нарушая общности
рассуждений, можно считать, что прибор 1 обслуживает в интервале (/Г, 2Е}
требование V2.
41
Таким образом, прибор 1 обслуживает в интервале (О, /Г] некоторые
(/-требования (их будет ровно три), а в интервале (Е, 2Е} — требова-
ние И2; прибор 2 обслуживает требование Vr без прерываний в интер-
вале (О, 22?] (так как появление прерываний в процессе обслуживания
этого требования привело бы к возникновению простоя прибора 2); нако-
нец, прибор 3 обслуживает в интервале (0, £] требование Ко, а в интер-
вале (/?, 2Е} — те (/-требования, которые были обслужены прибором 1
в интервале (0,2?].
Рассуждая аналогичным образом, приходим к заключению, что при рас-
писании s° прибор 1 в интервале (2 (/ - 1)F, (2/ - 1) £] обслуживает
три (/-требования, а в интервале ((2/ — 1)£, 2jE} — требование К/ + 1;
прибор 2 в интервале (2(/ - 1)Е, 2]Е\ обслуживает без прерываний требо-
вание Ру; прибор 3 в интервале (2(/ - 1)2?, (2/ - 1)2?] обслуживает требо-
вание Ру-!, а в интервале ((2/ — 1)2?, 2/Е] — те из (/-требований, которые
обслужены прибором 1 в интервале (2(/ — 1)2?, (2/ - 1)2?], / = 2,..., и0.
Обозначая через N? множество номеров (/-требований, обслуживаемых
прибором 1 во временном интервале (2(/ - 1)2?, (2/ - 1)2?], получаем
решение задачи о 3-разбиении. Таким образом, за О(п0) операций построе-
но сведение задачи о 3-разбиении к рассматриваемой задаче.
2.4. В заключение этого параграфа покажем, что задача построения
оптимального (по быстродействию) расписания при М = 3 остается NP-
трудной, если каждое требование множества N = {1,2,..., п} обслужи-
вается только двумя из трех имеющихся приборов.
Сформулируем соответствующую задачу распознавания: определить,
существует ли расписание s° (с прерываниями), при котором /тахО°)^.У
для заданного числа у.
Покажем, что к этой задаче сводится задача о разбиении (см. ввод-
ную часть этой главы).
Положим п = п0 + 2, N = { 1, 2,... , п }; ttl = ti3 = eb ti2 = 0, i G NQ;
Ц+1,1 " ^n0+l,2 “ 22?,/„q+1 3-O’, (n0+2,1 " 0, 6i0 + 2,2 = 22?, tn^+2t3=E.
Покажем, что задача о разбиении имеет решение тогда и только тогда,
когда в построенной задаче существует расписание s°, при котором
Ъпах(з°')<у = 4Е.
1) Пусть задача о разбиении имеет решение и/У?, TV? - найденные под-
множества. Тогда расписание s° существует и может быть построено сле-
дующим образом. Прибор 1 во временном интервале (0, 32?] обслуживает
требования множества 7V\{«0 + 2} непрерывно одно за другим в после-
довательности (тг^о, «о + 1, nNo), где тг^о, Яууо - произвольные перестанов-
ки элементов множеств /V? и 7V? соответственно. Прибор 2 во временном
интервале (0, 42?] обслуживает требования nQ + 1 и nQ + 2 в последователь-
ности («о + 2, nQ + 1) непрерывно одно за другим. Прибор 3 во временном
интервале (Е, 42?] обслуживает требования множества N\{n0 + 1} в
последовательности (л^, nQ + 2, л^) непрерывно одно за другим.
2) Пусть существует расписание s°. Если Г„о+2>2 = 4£, то7„о+2>3 > 4Е
И (max (s°) > У- Таким образом, /Ло+1,2 = 42?, следовательно, +14 < 2Е.
Кроме того, /ие+2,2^22? и /J}o+2>3 > 22?.
42
। Предположим, что задача о разбиении не имеет решения. Пусть R С
С {1, 2, .. ., nQ} - множество требований, обслуживание которых прибо-
ром 1 начато и закончено в интервале (О, 2Е}. Так как требование nQ + 1
должно быть обслужено прибором 1 в этом интервале и задача о разбиении
Ш) имеет решения, то S < Е. Но тогда S ti3 > 2Е и так как
if=R if=N\R
Обслуживание каждого из требований множества N\ R прибором 3 не мо-
жет быть начато ранее момента времени 2Е, то fmax(s0) > 4£, что невоз-
можно. Это означает, что задача о разбиении должна иметь решение.
Таким образом, за O(nQ) операций построено сведение задачи о разбие-
нии к рассматриваемой задаче распознавания.
§ 3. Общее время обслуживания требований без задержек
В этом параграфе рассматривается задача построения оптимального по
быстродействию расписания без задержек в процессе обслуживания каж-
дого требования.
3.1. В систему поточного типа, состоящую из Мприборов, в момент вре-
мени d = 0 поступает множество 7V={1, 2,...,«} требований. Длитель-
ности tiL > 0 обслуживания каждого требования i Е ТУкаждым прибором
L, L = 1,..., М, предполагаются заданными. Каждое требование i обслу-
живается без задержек, т.е. для любых двух приборов и L2,LX < L2,
таких, что tл х > 0, tiL 2 > 0 и либо L 2 = L j + 1, либо tiL = 0, £ =
~ Lx + 1,.. ., Z 2 - 1, должно выполняться соотношение t ?L = tiL , при-
чем процесс обслуживания каждого требования каждым прибором про-
текает без прерываний. Другими словами, если требование i начнет обслу-
живаться в момент времени , то процесс обслуживания этого требова-
ния завершается в момент времени = tf + S tiL.
3.2. В теории расписаний нулевые длительности обслуживания имеют
две различные интерпретации. При первой из них запись - 0 содержа-
тельно означает, что требование i прибором L не обслуживается. При вто-
рой интерпретации запись tiL = 0 содержательно означает, что требование i
прибором L обслуживается, но длительность обслуживания настолько мала,
что ею можно пренебречь и считать, что tiL = t .
В зависимости от принятой интерпретации нулевых длительностей об-
служивания могут быть построены различные оптимальные расписания с
различными значениями оптимизируемого функционала.
Рассмотрим, например, задачу построения оптимального (по быстро-
действию) расписания обслуживания без задержек четырех требований
тремя приборами. Длительности обслуживания tiL приведены в табл. 3.1.
Таблица 3.1
1 1 6 3 3 4 1 3
2 2 0 4 4 2 3 1
43
Если запись tiL = 0 понимать таким образом, что требование 2 прибо-
ром 2 не обслуживается, то оптимальным является расписание $*, изобра-
женное на рис. 3,1, а. Если же считать, что требование 2 прибором 2 обслу-
живается, но длительность этого обслуживания мала и ею можно пренеб-
речь, то оптимальным будет расписание sj, изображенное на рис. 3.2,6.
Отметим, что fmax(s‘)= 15 < 7max(s?) = 17.
3.3. Пусть запись t(L = 0 означает, что требование i G 7V = { 1,2,..., и}
прибором L, 1 < L < М9 не обслуживается. Покажем, что в этом случае
задача построения оптимального (по быстродействию) расписания обслу-
живания без задержек является NP-трудной в сильном смысле при 2.
Сформулируем соответствующую задачу распознавания: определить,
существует ли расписание s°, при котором Onax(s°) ^7 Для заданного
числа у.
Покажем, что к этой задаче при М = 2 сводится задача о 3-разбиении
(см. вводную часть этой главы).
Положим п = 4и0 + 2, N = { 1, 2,..., п}9 множество N требований
разобьем на две группы: ^-требования, обозначаемые Ui9 i = 1,..., Зи0,
и F-требования, обозначаемые F), / = 0,..., nQ + 1. Положим
О/,. 1=0, tUi2=ei, f = 1,..., Зи0>
*vQ 1 = °, tvQ 2 = 2£,
ty. j = 2Е, ty. 2 = Et j = 1, . . . , Hq + 1.
Покажем, что в построенной задаче расписание s°, при котором
Zmax fa0) У ~ Ръ + 3)Я, существует тогда и только тогда, когда имеет
решение задача о 3-разбиении.
прибор 3 -
прибор 2 -!
0 1 3 5 7 9 10 11 131916
44
Пусть задача о 3-разбиении имеет решение и Л^°, j = 1,...., nQ, - най-
денные трехэлементные подмножества элементов множества 7V0. Через 7Т;-
Обозначим произвольную перестановку (/-требований с номерами из мно-
жества N?. Расписание s° существует и может быть построено следующим
образом. Прибор 1 обслуживает требование Vj во временном интервале
(2 (/ - 1)2?, 2/Е], j = 1,... , nQ + 1. Прибор 2 в интервале (0,2Е] обслу-
живает требование Ко, в интервале ((2и0 + 2)1?, (2и0 + 3)2?] - требова-
ние + 1 и в каждом из интервалов (2/2?, 2(/ + 1)1?] - последователь-
ность требований (К,, тгу) непрерывно одно за другим, j = 1,..., п0.
Пусть существует расписание s°. Поскольку 2 ti2 - у, то прибор 2
при расписании s° функционирует без простоев во временном интервале
(О,.у] и (max (s°) = у. Так как прибор 1 обслуживает только требования Ку,
I = 1,..., nQ + 1, то этот прибор при расписании s° функционирует без
простоев во временном интервале (0, .у - 2?]. Требования Vj не отличаются
друг от друга по длительностям обслуживания, поэтому можно считать,
что эти требования обслуживаются прибором 1 в порядке возрастания их
номеров. Поскольку при расписании s° требования Vj обслуживаются
без задержек, то прибор 2 обслуживает требование Vj в интервале (2/1?,
(2/ + 1)1?], j = 1,..., nQ + 1. При этом требование Vo обслуживается
прибором 2 в интервале (О, 2Е] (поскольку это единственный не занятый
подынтервал длины 2Е интервала (0,.у]).Требования (/,- должны обслужи-
ваться прибором 2 в интервалах ((2/ + 1)1?, 2(/ + 1)2?], / = 1,..., п0.
Обозначая через N? множество номеров (/-требований, обслуживаемых
прибором 2 в интервале ((2/ + 1)1?, 2(/ + 1)1?], / = 1,...»«о > получаем
решение задачи о 3-разбиении.
3.4. Здесь и далее в этом параграфе запись tiL = 0 понимается таким
образом, что требование i прибором L обслуживается, но длительность
этого обслуживания мала и ею можно пренебречь.
Установим некоторые свойства расписаний обслуживания требований
без задержек.
1) Покажем, что если все tiL > 0, i G TV, L - 1,..., М, то при любом
расписании обслуживания без задержек все приборы обслуживают требо-
вания множества N в одной и той же последовательности.
Действительно, если бы прибор L + 1 обслуживал требования в некото-
рой последовательности л' = (...,/, i,...), а прибор L - в последова-
тельности то имело бы место соотношение
t°L +1 > hL + ‘/L + tiL+l>‘tL> ЧТО НеВОЗМОЖНО.
Если tiL > 0, i G N, L = 1,..., М, то нетрудно видеть, что при ука-
занной интерпретации записи tiL = 0 оптимальное расписание также можно
искать в классе расписаний, при которых все приборы обслуживают требо-
вания в одной и той же последовательности.
2) Пусть tiL > 0 и все приборы обслуживают требования в одной и той
же последовательности тг = (z*i, i2,... , in) • Поскольку все требования
должны обслуживаться без задержек, то минимальное общее время обслу-
живания
_ _ м
(maxGO = hnM “ + S tinL' ,
L — 1
45
Положим t =0 (так как при >0 общее время обслуживания
только увеличится). Выберем произвольное к, 2 < к < п. Очевидно,
1 + t’k-l 1;
е-i q
f/*l + tlkL ** fik-l 1 + L’ Q=2’ -
Xj — i Li “ i
Другими словами,
Q 2-1
1 i max { Z tjk — Z l) • (3.1)
* z = i K 1 l=i K
В качестве наиболее раннего момента времени t выберем такой мо-
мент времени, при котором в (3.1) имеет место равенство.
Таким образом, приходим к рекуррентному соотношению
'Ь=0,
Q 2-1
11 ~ max { *1к iL~ Л = 2,...,И,
* 1<Q<M L = ] k~1 L=l k
из которого следует, что
tQ
% *
п — 1 Q
= Z max { Z
fc = l 1<Q<M L=1
2-i
r?i
Li — 1
и следовательно,
____ n—i 2 2—1 м
^max W " 2 max { Z t- r — Z L } + Z ti L. (3.2)
k = l L = l k L=l k+1 £ = 1 n
Таким образом, задача построения оптимального (по быстродействию)
расписания обслуживания без задержек сводится к задаче нахождения
перестановки я* которой соответствует наименьшее значение функционала
(3.2).
3) Задача минимизации ?тах(я) очевидным образом сводится к задаче
о коммивояжере с п + 1 городами, пронумерованными целыми числами от
0 до и, и матрицей расстояний I cpq II, где срр = + 00 и cpq > 0, р = 0,..., п,
q = 0,...., п, р Ф q. Пусть яс = (0, ц, z2,. .., in) - некоторая переста-
новка номеров городов. Задача о коммивояжере заключается в поиске
перестановки я$, минимизирующей величину
п— 1
Qtto) = ^oi1 C/Jtz4+i +сл°’ (3-3)
м Q
Если положить сОр = 0, c9q = S tpL, сра = max { S toL -
L=1 1<Q<M L^l
2-1
- S tQL}, p= 1,... ,n, q= 1,...,w, p^q, то получаем функционал
L=1
(3.2).
46
Тем самым, если Яо = (0, f J, i2,... , i„) — решение задачи о комми-
вояжере, то перестановка я* = (/*, ?2, - • • , in) определяет оптимальное
расписание.
В обшем случае задача о коммивояжере является NP-трудной в сильном
смысле. Тем не менее при некоторых предположениях относительно вида
матрицы II cpq II эта задача может быть решена за полиномиальное число
операций. Один из таких разрешимых случаев задачи о коммивояжере
используется ниже для нахождения перестановки я* при М = 2.
3.5. Пусть каждое требование множества N= { 1,2,..., п } должно быть
обслужено без задержек в системе поточного типа, состоящей из двух при-
боров. Опишем алгоритм построения оптимального (по быстродействию)
расписания из класса расписаний, при которых оба прибора обслуживают
требования в одной и той же последовательности.
Обслуживающие приборы обозначим через А и В, а длительности обслу-
живания требования i EN приборами А и В — через д,- и соответствен-
но. Каждое требование обслуживается сначала прибором Л, затем прибо-
ром В. Если оба прибора обслуживают требования в некоторой последова-
тельности я = (z’i, i2i • • ., 1Л), то наименьшее возможное значение общего
времени обслуживания
_ л — 1
GnaxOO =ftS max{ai/t,aik + blk-a(k+i}-hain + bin.
Это соотношение можно переписать в виде
4 ах (тг) = max { bik - aik+,, 0 } + ^а1к+ bin. (3.4)
Очевидно, для построения оптимального расписания достаточно найти
перестановку я* элементов множества N, которой соответствует наимень-
шее значение
п — 1
g(*) = к = j maX { bik ~ а‘к+1 ’ 0 > + bin • (3-5)
Если положить сОр = 0, ср0 = bp, cpq = max { bp - aq, 0), p= 1.n,
q = 1,.. ., n, p q, то задача минимизации функционала (3.5) сводится
к задаче о коммивояжере с п + 1 городами, пронумерованными целыми
числами от 0 до и, и матрицей расстояний II cpq II (см. п. 3.4,3)). При этом
если Яо = (0, i*, i2,.. ., z„) - решение задачи о коммивояжере, то я* =
= On 1г.....in) •
Положим Оо = 0о = 0, а,- = ai9 = bi9 i G N. Введем в рассмотрение
функции и(х) = 0 и v(x) = 1. Тогда
cpq
f u(x)dx,
*₽
0p
f v(x)dx,
<kq< 0P-
(3.6)
ая ’
47
Опишем полиномиальный алгоритм решения задачи о коммивояжере
в предположении, что расстояния cpq между городами вычисляются по
формуле (3.6), где и(х) ии(х) — произвольные интегрируемые функции,
удовлетворяющие условию и(х) + и(х) > 0, a aq и 0р, 0 < р, q < п, -
произвольные неотрицательные числа.
Перенумеруем города целыми числами от 1 до m = п + 1 таким образом,
чтобы 0! < 02 < ... < 0W. Отыщем перестановку <р = (r<, r2t... , rm)
такую, что arj < аГ2 < ... < Обозначим = min{0z, ar/}, =
= max{0f, ar/}, i = 1,..., m. Положим c* (f) = f (u(x) + u(x))dx,
если < 7l + 1, и c^ (1) =0 в противном случае.
Построим неориентированный граф на m вершинах, пронумерован-
ных целыми числами от 1 до т, в котором вершина i смежна с верши-
ной / тогда и только тогда, когда i = Гу, /, j = 1,..., т. Если граф
связен, то перестановка <р является решением рассматриваемой задачи
о коммивояжере (относительно новой нумерации городов). В противном
случае построим граф G^, заменив каждую компоненту связности гра-
фа Gy новой вершиной. Если вершины i и i + 1 принадлежали разным
компонентам связности графа G^, то вершины графа G^, соответствую-
щие данным компонентам, соединим ребром Rit приписав ему вес с^ (/),
i = 1,..., т — 1. Полученный в результате (мульти) граф по-прежнему
будем обозначать через G^. Отыщем в графе G^ остовное дерево с наимень-
шей суммой весов ребер (минимальное остовное дерево).
Ребра, вошедшие в остовное дерево, разобьем на две группы. К пер-
вой группе отнесем такие ребра Rj, что аГ/ < 0/, а ко второй - все ос-
тальные.
Пусть число ребер в первой группе равно Z > 1. Положим равным
наибольшему значению i такому, что ребро Rj принадлежит этой группе.
Рассматривая оставшиеся ребра первой группы, аналогичным образом
найдем значение /2 и т.д., пока не будет найдено значение ц.
Пусть число ребер во второй группе равно h> 1. Положим //+1 рав-
ным наименьшему значению i такому, что ребро Rj принадлежит этой
группе. Рассматривая оставшиеся ребра второй группы, аналогичным об-
разом найдем //+2 ит.д., пока не будет найдено значение jl+h.
Рассмотрим перестановку (1, 2,..., т). Поменяем местами элементы
h и h + 1. В полученной перестановке поменяем местами элементы /2 и
/2 + 1 и тд. до тех пор, пока не поменяются местами элементы jJ+h и
jl+h + 1. В результирующей перестановке элемент i заменим на rit i =
= 1,..., т, в соответствии с перестановкой Обозначим полученную пе-
рестановку через тг = (i’i, 1’2,..., iw). Построим перестановку тг* =
- (1,/*,72, • • • ,/п),полагая 7* = il9 j* = i.* ,fc = 2,... ,п. Возвращаясь
к исходной нумерации городов, получаем искомую перестановку ttq — ре-
шение задачи о коммивояжере.
Наиболее трудоемким этапом нахождения ttJ является нахождение
минимального остовного дерева в графе G^. Известно, что эта задача мо-
жет быть решена не более чем за O(elog и) операций, где е и v - число вер-
шин и ребер графа, в котором ищется остовное дерево.. Поскольку для
48
Таблица 3.2
i 1 2 3 4 5
at 1 12 4 5
hi 4 3 4 1 1
Таблица 3.3
i ai Pi ri
1 0 0 1 1
2 5 1 4 0
3 4 1 5 1
4 1 3 6 1
5 1 4 3 0
6 2 4 2 —
графа G[p значения е<лир<л+1,то решение задачи о коммивояжере
в рассматриваемом случае может быть получено за О (и log и) операций.
Таким образом, оптимальное по быстродействию расписание без задер-
жек при М =2 может быть построено за О (п log п) операций.
3.6. Пример. Две бригады А и В должны выполнить монтаж пяти
единиц оборудования. Бригада А заливает фундаменты, а бригада В сразу
после подготовки очередного фундамента размещает соответствующую
единицу оборудования. Длительность подготовки фундамента под z-ую
единицу оборудования обозначим через ai9 а длительность размещения
этой единицы на подготовленном фундаменте - через bi9 i = 1, 2, 3, 4, 5.
Значения и bi приведены в табл. 3.2.
Необходимо таким образом организовать работу бригад, чтобы все
единицы оборудования были установлены как можно раньше.
Если бригады рассматривать как приборы, а единицы оборудования -
как требования, то получим ситуацию, описанную в п. 3.5.
Положим а0 =0О =0, az =ai9 ~bi9 i = 1,2,3,4,5; и(х) = 0, и(х) =
= 1. Следуя алгоритму, произведем перенумерацию, найдем перестановку
у = (г 1,r2 ,г3 ,г4,г5,г6) И вычислим значения с^ (z) (см. табл. 3.3).
Рис. 3.2
4. В.С. Танаев 49
Построим графы Gy и Gy (рис. 3.2,а, б). Минимальное остовное дерево
графа Gy приведено на рис. 3.2, в и содержит два ребра — Rt и Rs. Эти реб-
ра принадлежат второй группе.
Меняя местами в перестановке (1, 2, 3, 4, 5, 6) элементы 1 и 2, а в по-
лученной перестановке - элементы 5 и 6, получаем перестановку
(2,1,3,4,6,5). Если в этой перестановке элемент, равный /, заменить на эле-
мент, равный i = 1,... , 6, приходим к перестановке я = (4,1,5,6,2,3).
приборе - > ! | | 1 А
прибор А —I I I I I 11 —И ’
1 | | 1 1 I । I 1 I I I 1 1-1__
012 4 89 131415 t
Рис. 3.3
Построим перестановку я* = (1,4,6,3,5,2). Возвращаясь к исходной нуме-
рации, получаем перестановку яо = (0,2,3,4,1,5). Следовательно, при опти-
мальном расписании оба прибора обслуживают требования в последователь-
ности (2, 3, 4, 1, 5) (рис. 3.3).
3.7. Покажем, что задача построения оптимального (по быстродействию)
расписания обслуживания без задержек является NP-трудной в сильном
смысле, если число приборов 3.
По-прежнему предполагается, что запись tiL = 0 означает, что требова-
ние i прибором L обслуживается, но длительностью этого обслуживания
можно пренебречь. Оптимальное расписание ищется в классе расписаний,
при которых требования обслуживаются всеми приборами в одной и той
же последовательности.
Доказательство проведем в несколько этапов.
1) Покажем, что задача нахождения гамильтонова контура минимальной
длины в ориентированном графе является NP-трудной в сильном смысле,
если длины его дуг принимают значения 0 или 1.
Сформулируем соответствующую задачу распознавания. Задан (ориен-
тированный) граф G = (К, U), длины дуг которого равны 0 или 1. Требу-
ется определить, существует ли в графе гамильтонов контур, длина кото-
рого не превосходит заданного числа у.
Покажем, что к этой задаче сводится задача о трехмерном паросочета-
нии (см. вводную часть этой главы).
Пронумеруем тройки из множества Епроизвольным образом: е2,.. .
..., в| Е|. Положим № = { 1, 2,..., | Е\} и зададим на 7V0 произвольную
циклическую подстановку Напомним, что подстановкой называется
взаимно однозначное отображение конечного множества на себя. Подста-
новка называется циклической, если при повторении ее достаточное число
раз каждый из элементов может быть отображен в любой другой элемент.
Пусть ег = (хг1, хг2, ху3), г G №. Для каждого элемента х Е Хр, р =
= 1, 2, 3, положим Nx = { г G №| хгр = х} и зададим на Nx произволь-
ную циклическую подстановку <рх. Отметим, что все множества Nx, х Е
Е Хр, р= 1,2, 3, не пусты.
50
I;, Построим граф G = (И, U) следующим образом. Каждой тройке еГ9
j £ №, поставим в соответствие множество УГ9 состоящее из восьми вер-
шин. Эти вершины будем обозначать через [г,/], / = 1,. . ., 8. Положим
V * U Vr . Множество U дуг графа G определим как объединение всех
rGtf0
Перечисленных ниже множеств:
Я„={([г,8], [<р(г),1])|геЛГ<>};
Ям,х = {([г,2р],[1рх(г),2р + 1])| rCN*}, хеХр, р=1,2,3;
Fr = { ([г, 2q - 1], [г, 2q])| q = 1,2,3,4} U
U {([г,2р + 1], [г,2р])|р= 1,2,3} U
U {([r,2p- 1], [г, 8])| р= 1,2,3}, г&№.
Положим длину каждой дуги ([г, 1 ], [г, 2]), г € №, равной единице,
а длины всех остальных дуг равными нулю.
По построению множество вершин графа G состоит из 8|/Г| вершин
вида [г, /], г Е. NQ9 j = 1,..., 8. Вершины вида [г, 2q\, г G #°, q =
• 1, 2, 3, 4, назовем четными (полустепень исхода каждой из этих вершин
равна единице). Вершины вида [г, 2q — 1], г G. NQ, q = 1, 2, 3,4 назовем
нечетными (полустепень захода каждой из этих вершин равна единице).
На рис. 3.4 изображен подграф Gr графа G, порожденный множеством
вершин Vr, а также изображены вершины, смежные с вершинами множест-
ва Кг (нечетные вершины для наглядности заштрихованы). Множество U
дуг графа содержит дуги двух типов. Во-первых, U содержит все дуги
множеств и //^х, х Е Хр, р = 1, 2, 3. Эти дуги будем называть //-ду-
гами. Каждая из них исходит из четной вершины некоторого множества
V , и заходит в одну из нечетных вершин некоторого другого множества
V „ (на рис. 3.4 //-дуги изображены сплошными линиями). Остальные
дуги множества U (т.е. все дуги множеств Fr9 г G. 7V0) будем называть
/’-дугами. Каждая из этих дуг исходит из нечетной вершины некоторого
множества Vr и заходит в некоторую четную вершину этого же множества
(на рис. 3.4 F-дуги изображены пунктирными линиями.)
Нетрудно проверить, что для каждого х G Хр, р = 1, 2, 3, F-дугй вида
([г, 2р + 1], [г, 2р\), г € Nx, и все //-дуги множества Н^х образуют кон-
Рис. 3.4
4
51
тур Кх. В этом контуре F- и Я-дуги чередуются, и он проходит только через
вершины [г, 2р + 1] и [г, 2р], принадлежащие всем таким множествам ,
что элемент х встречается в р-ой компоненте соответствующей тройки ег.
Заметим также, что F-дуги вида ([г, 1], [г, 8]), г G Я0, и все Я-дуги из
множества Я^ образуют контур К. В этом контуре F- иЯ-дуги чередуются,
и он проходит только лерез вершины [г, 1] и [г, 8], г G №.
Выделим в графе G один или несколько контуров так, чтобы каждая
вершина графа принадлежала ровно одному контуру. При движении по
этим контурам для каждого из множеств Vr, г Е Я0, возможен один из
следующих способов обхода его вершин. Обход, схематически представлен-
ный на рис. 3.5, а, назовем нулевым. При этом обходе проходятся только
дуги контуров К и KXrpf р = 1, 2, 3. Суммарная длина дуг, инцидентных
вершинам множества Vri в этом случае равна нулю. Три других способа
обхода представлены на рис. 3.5, б, в, г. Обходы такого вида назовем
д-при соединенными, 1 < д < 3. При каждом из этих обходов суммарная
длина дуг, инцидентных вершинам множества Vr, равна единице. Название
обхода отражает тот факт, что между ’’посещениями” вершины [г, 1 ] и
вершины [z, 8] к дугам контура К ’’присоединяются” дуги контуров
KXrpf р=19...,р, 1< д< 3.
Покажем, что в построенном графе G гамильтонов контур, длина ко-
торого не превосходит у = nOf существует тогда и только тогда, когда
имеет решение задача о трехмерном паросочетании.
а) Пусть существует паросочетание Е9 С Е, | Е' | = и0 и N9 = { г Е
Е Я°| G Е'}. Рассмотрим Зи0 + 1 контуров-Л', Кх, х Е Хр, р = 1,2,3.
Рис. 3.5
52
|(Иитидно, каждая вершина множества V принадлежит равно одному из
{указанных контуров. В данном наборе контуров содержатся все Я-дуги
К обходы каждого множества вершин Vr являются нулевыми (см.
JH<C. 3.5,а).
Для каждой тройки er G Ef заменим нулевой обход вершин множества
И, на 3-присоединенный. Так как Е' — трехмерное паросочетание, то для
Осуществления такой замены необходимо из каждого контура КХгр,
I < р < 3, удалить ровно одну F-дугу ([г, 2р + 1], [г, 2р]) и присоеди-
нить пути, образовавшиеся из контуров ^хг2^хг3 в результате та-
кого удаления, к дугам контура К с удаленными F-дугами ([г, 1], [г, 8]),
Г € N'. Получаем гамильтонов контур, в котором ровно nQ дуг имеют
длину, равную единице.
б) Пусть в графе G существует гамильтонов контур, длина которого
не превосходит у = nQ. Следовательно, при движении по этому контуру
обходы вершин по крайней мере |Я°| - у множеств Vr должны быть
нулевыми, а обходы вершин не более у множеств Vr должны быть р -при-
соединенными, 1 < 3.
Покажем, что для любого из Зи0 элементов xG Хр, р = 1,2,3, найдется
по крайней мере одно множество Vr, rEN*, обход вершин которого
не является нулевым. Предположим противное. Пусть для некоторого
k G Xpt р = 1, 2, 3, обходы вершин всех множеств Vr, r€NQ-, являются
нулевыми. Всякий гамильтонов контур обязательно содержит все Я-дуги,
и в данном случае он должен содержать также все F-дуги вида ([г, 2р + 1],
(С 2р]), г G Я|. Однако эти F-дуги вместе с Я-дугами множества Н^х
образуют контур К$х, что невозможно.
Следовательно, имеется ровно и0 множеств Vr,r G Я0, обходы вершин
которых являются р-присоединенными. Тройки ег, соответствующие этим
множествам Vr, образуют паросочетание. Действительно, если две какие-
либо тройки ег> и ег" имеют общую р-ю компоненту, то найдется элемент
хЕХр такой, что обходы вершин всех множеств Kr, г G TV0, являются нуле-
выми, что невозможно.
Поскольку задача о трехмерном паросочетании ЯР-полна, а реализация
ее сведения к рассматриваемой задаче требует полиномиального (относи-
тельно |F|) числа операций, то задача нахождения гамильтонова контура
наименьшей длины в графе, длины дуг которого равны 0 или 1, является
ЯР-трудной в сильном смысле. _ _ _
2) Рассмотрим полный (ориентированный) граф G = ( V,U) без пе-
тель, вершины которого пронумерованы числам! эт 1 до т = | V |. Каждой
вершине v G V сопоставлена тройка действительных неотрицательных
чисел (аи, Ду, уу). Длину дуги (u, w), и, w G V, v =# w, положим равной
~ шах {0, Ду, Уу } . (3.7)
Покажем, что задача построения гамильтонова контура минимальной
длины в графе G является NP-трудной в сильном смысле.
Сформулируем соответствующую задачу распознавания: определить,
существует ли в графе G гамильтонов контур, длина которого не превос-
ходит заданного числа у.
53
Покажем, что к этой задаче вводится задача о существовании гамильто-
нова контура, длина которого ie превосходит заданного числа у, в графе
G = (К, U), введенном в рассморение в п. 1).
Построим граф G, исходя № графа G, следующим образом. Положим
К = К = { [г, j ] | г G №, j = 1,... , 8 } . Пронумеруем вершины графа G
числами от 1 до т = | К|. Наряду с обозначением вида [г,/] для вершин
графа G будем употреблять их юмера и, w и т.п.
Для любой вершины [г, /] G И положим
{(т +/ + 8(г — 1))у, если/ нечетно;
(/ + 8(г — 1))у, еслх/ четно.
Кроме того, положим а[ ,8] = 0(r, i ] > a[r,/] ~ 0[г»7-1 ]’^ Е {2,4,6},
и a[rj j =Ди,/ G { 1, 3, 5, 7 } , где дуга (у, [г,/]) является Я-дугой в графе G.
Наконец, положим 7[м1= 1 ЬД[Г>2],7[Г,/е {3,5,7}
и 7[r,/j = Pw.,7 {2, 4, 6, 8} , ще дуга ( [г,/], w) является Я-дугой в гра-
фе G. _
Покажем, что в графе G, длины дуг которого вычислены по формуле
(3.7), гамильтонов контур, длша которого не превосходит у = у, сущест-
вует тогда и только тогда, когд1 в графе G существует гамильтонов контур,
длина которого не превосходит^.
а) Пусть в G существует искомый гамильтонов контур. Нетрудно прове-
рить^что длины дуг графа G совпадают с длинами соответствующих дуг гра-
фа G, Следовательно, в графе G также существует гамильтонов контур,
длина которого не превосходиту. _
б) Пусть в графе G сущеспует гамильтонов контур К, длина которого
не превосходит у. Покажем, что в этом случае ни одна из дуг множества
U\U не принадлежит контуру F.
Покажем, что контур К содержит множество всехЯ-дуг графа G. Напом-
ним, что каждая из этих дуг исходит из четной вершины и заходит в нечет-
ную. Заметим также, что контор К не содержит дуг вида (u, w), исходящих
из четной вершины и заходяцих в четную, так как в этом случае aw >
>1Ъ+У-
Для каждой Я-дуги (u, w) имеем cvw = 0, так как = |3V, по
построению. Множество Я-дуг вида (и, w) упорядочим по возрастанию зна-
чений Ру = aw или, что то же саиое, по возрастанию (в лексикографическом
смысле) их начальных вершин вида [г, 2q\, 1 <4. Пусть (у , wr) — пер-
вая (относительно указанного порядка) Я-дуга, aw — произвольная нечет-
ная вершина. Так как aw — (fy > 2у при w Ф w' 9 то контур К должен со-
держать дугу (и', w'). Рассматривая Я-дуги последовательно одну за другой
(относительно указанного порщка)^ убеждаемся, что все они принадлежат
контуру К. Следовательно, копур К не содержит дуг, исходящих из нечет-
ной вершины и заходящих в нечетную.
Покажем, что в контуре К цуга, исходящая из нечетной вершины [г, j ]
и заходящая в четную вершшу [г',/'], является F-дугой. Действительно,
если вершина [г, /] лексикографически предшествует вершине [г', /'],
то j при условии, что г =r,j' G{ j + 1,8} и j - Д[г j j>
>у в противном случае. Кроме того, 7^ уjf j с единственным исклю-
чением 7( г, 1 ] = 1 + Р[г,2 ] •
54 г
EiciiH [r', j'] лексикографически предшествует [г,/], то = fyr'j'p
Фили г' = г, f -j — 1, и ур у । - Др/ ;']> J7 в противном случае. Кроме того,
*1ЛЛ
Таким образом, в графе G длина любой дуги, не принадлежащей графу
(/, больше, чему.
Тем самым за О(\ К|2) операций построено сведение задачи о гамиль-
IOhobom контуре в графе G к задаче о гамильтоновом контуре в графе G.
3) Рассмотрим полный ориентированный граф GQ = (Ко, Uo), вершины
которого пронумерованы числами от 0 до т = | Ко I — L Каждой вершине
и G Ко сопоставлена тройка действительных неотрицательных чисел
(о^, Ди, уу), причем «о = До = То = Покажем, что задача построения га-
мильтонова контура наименьшей длины в графе GQ является NP-трудной
в сильном смысле, если веса дуг вычислены по формуле (3.7).
Сформулируем соответствующую задачу распознавания: определить,
существует ли в графе GQ гамильтонов контур, длина которого не пре-
восходит заданного числа у0.
Покажем, что к этой задаче сводится задача о существовании гамильто-
нова контура, длина которого не больше заданного числа у, в графе G,
введенном в рассмотрение в п. 2).
Положим Ко = {0} U_K, ао = До = То = 0; av = av, Ду = Ду, tL = Tv,
и G К. Выберем в графе G произвольную Я-дугу вида (у, w) и положим
у'- = = 0. Вычислим длины дуг по формуле (3.7). Покажем, что в графе
Go гамильтонов контур Ко, длина которого не более у0 у, существует
тогда и только тогда, когда в графе G существует контур К, длина которо-
го не больше у. _
Действительно, пусть существует такой контур К. Заменим дугу (ТУ, w) G
G К парой дуг^й, 0) и (0, w). Получим контур Х0‘, длина которого равна
длине контура К.
Пусть существует контур Ко. Поскольку длины всех дуг, заходящих в
вершину 0 (кроме дуги (й,0))и исходящих из этой вершины (кроме дуги
(0, w)), больше у, то дуги (у, 0) и (0, vv) принадлежат контуру KQ. Сле-
довательно, дуга (у, w) этому контуру не принадлежит. Заменяя дуги
(и, 0) и (0, vv) дугой ( и, w), получаем контур К.
4) Покажем наконец, что задача построения оптимального по быстродей-
ствию расписания обслуживания без задержек множества N= {1,2,..., п }
требований в системе поточного типа из трех приборов эквивалентна задаче
построения гамильтонова контура минимальной длины в графе Gq (при
т=п).
Действительно, из формулы (3.2) приА/ = 3 следует, что
_ п-1
GnaxW- 1 ГЛ ах { j , tt* i ~ *
3 n
+ - tik+ ! 1 - rik+12 } + S UnL = 1 + . 2( r/2 +
n — 1
+ 2 max{0,r/fc+11- rIfc2, r/fc3 - r/fc+12 } +tin3.
k - 1
55
Если положить Ло = До = То “ 0»at = ti\>0i =/#2>Т/ = Г/3,z то за-
дача нахождения перестановкв я*, минимизирующей значение ^тах(я),
эквивалентна задаче нахождения гамильтонова коштура Kq минимальной
длины в графе Go, длины дуг которого вычислены шо формуле (3.7).
Поскольку задача построена контура ^является/VP-трудной в сильном
смысле и ее сведение к рассмприваемой задаче реализовано за (?(| Ко|)
операций, то задача построения оптимального расписания в данном случае
также является ЛТ’-трудной в сильном смысле.
§ 4. Максимальное временное смещение
В систему поточного типа, состоящую изМ прибюров, в момент времени
d = 0 поступает множество N = { 1, 2,. .., и} требований. Длительности
tiL 0 обслуживания требования i G TV прибором! L, L = 1,. .., М, пред-
полагаются заданными. Для какдого требования i •€ TV задан директивный
срок Di9 к которому желательно завершить обслуживание требования i
всеми приборами. В этом параграфе рассматривается задача построения
расписания s*, при котором значение максимального временного смещения
£max(s) = max{f/(s) - Dj\i G TV} является ^наименьшим. Показано,
что эта задача является TVP-трудной в сильном смьксле приА/> 2 независи-
мо от того, допускаются прерывания в процессе обслуживания или нет.
Задача минимизации максимального временного смещения оказывается
/VP-трудной в сильном смысле при ТИ> 2 и в том (случае, когда все требо-
вания обслуживаются без задеркек.
4.1. Покажем, что задача построения расписания s* (как в случае, когда
допускаются прерывания, так и в случае, когда шрерывания запрещены)
является NP-труд ной в сильном смысле приМ> 2.
Сформулируем соответствующую задачу распюзнавания: определить,
существует ли расписание $°,при котором £maxi($°) для заданного
числа у.
Покажем, что при М = 2 к этой задаче сводится задача о 3-разбиении
(см. вводную часть этой главы).
Положим п = 4и0 + 1, TV = {1,2,..., и } . Множество требований разобь-
ем на две группы: ^/-требования, обозначаемые £//,, i = 1,. .., Зи0, и ^-тре-
бования, обозначаемые Ру J = 1,. .. , п0 + 1. Положили
/= еь 2 = 2в/, Dy. = (Зи0 + 2)Е, i = 1,... , Зи0;
tVji ~2£, tу.2 = Е, Dv. - 3fi, j = 1,. .., и0;
ги„о + 11 = 2£'. ^„о + 12 =о, 0г„о + 1 =(3ио +2)jE.
Покажем, что при .у = 0 в построенной задаче расшисание $° (как с преры-
ваниями, так и без прерываний существует тогдаа и только тогда, когда
имеет решение задача о 3-разбиении.
Пусть задача о 3-разбиении шеет решение и ZVy, / = 1,. . . , и0, — найден-
ные трехэлементные подмножества элементов множества TV0. Тогда рас-
писание $° существует и может быть построено, навпример, следующим об-
разом. Все требования обслужтваются без прерываний прибором 1 во вре-
менном интервале (0, (Зио +2iF] и прибором 2 взо временном интервале
(2Е, (Зпо + 2)£]. Оба прибор в указанных интеервалах функционируют
56
Вез простоев и обслуживают требования в одной и той же последователь-
ности (Ki, Я1, К2, я2,. . ., К„о, я„о, К„о + 1), где я, - произвольная после-
довательность {/-требований с номерами из множества^,/ = 1, . . . , п0.
Пусть существует расписание 5°. Поскольку tyxi + tv^2 = ЗЕ = Dyt,
то при расписании 5° требование Ki обслуживается без прерываний прибо-
ром 1 в интервале (О, 2Е\ и прибором 2 в интервале (2#, 3#]. Поскольку
суммарная длительность обслуживания остальных требований прибором 1
равна Зп0Е, а прибором 2 — (Зи0 + 1) Е, то при расписании s° оба прибора
функционируют без простоев в интервалах (О, (Зи0 + 2) Е ] и (2Е, (Зи0 +
t 2) #] соответственно.
Рассмотрим временной интервал (ЗЕ, 6Е ]. В этом интервале прибор 2
должен обслужить требование К2. При этом прибор 2 не может начать об-
служивание ни одного из оставшихся К-требований. Действительно, пусть
V* - некоторое К-требование, отличное от V\ и К2. Даже если ty i = 2# и
t у i = ty'! = 4Е, то tQv>2 > 6Е. Следовательно, в интервале (ЗЕ, 6#] при-
бор 2 должен обслуживать некоторые {/-требования в течение 2Е единиц
времени. Перед обслуживанием прибором 2 эти требования должны быть
обслужены прибором 1 в течение Е единиц времени. _
Очевидно, при расписании $° значение tv i < ЗЕ, иначе ty^2 > Ву2 •
Предположим, что t у i = ЗЕ - С, где Е > С> 6. Тогда прибор 1 в интервале
(2Е, ЗЕ - С] обслуживает некоторые {/-требования в течение# - С единиц
времени. Так как t*y2 2 > t у2 j, то прибор 2 должен обслуживать эти С/-тре-
бования в интервале (ЗЕ, ?уз2] по крайней мере в течение 2Е - С единиц
времени. Это означает, что при расписании s° прибор 1 в интервале (2Е,
5#] обслуживает три {/-требования, суммарная длительность обслужи-
вания которых равна#, а также требование К2, причем t у1 = 5#. Если пре-
рывания запрещены, то требование И2 обслуживается в интервале (3#, 5#],
а ^/-требования — в интервале (2#, 3#]. Прибор 2 обслуживает требование
К2 без прерываний в интервале (5#, 6#], а также обслуживает (возможно,
с прерываниями, если они разрешены) в интервале (3#, 5#] те три {/-тре-
бования, обслуживание которых прибором 1 завершено.
Рассуждая аналогичным образом, убеждаемся, что при расписании 5°
прибор 2 в каждом из временных интервалов (3/#, (3/ + 2) #], 1 </ <и0,
обслуживает по три {/-требования в течение 2# единиц времени. Обозначая
через N® множество номеров {/-требований, обслуживаемых прибором 2
в интервале (3/#, (3/ + 2) # ], / = 1,. . . , п0, получаем решение задачи о
3-разбиении.
Таким образом, за О(п0) операций реализовано сведение задачи о 3-раз-
биении к рассматриваемой задаче распознавания.
4.2. Пусть расписание $♦, минимизирующее значение #max(s), ищется
в классе расписаний без задержек.
Если среди tiL имеются нули и запись tiL =0 означает, что требование
i прибором L не обслуживается, то задача построения расписания s*,
очевидно, является NP-трудной в сильном смысле при М > 2, даже если
все Dt = D. Этот вывод непосредственно следует из результатов п. 3.3 этой
главы.
Пусть запись tiL = 0 понимается таким образом, что требование i при-
бором L обслуживается, но длительностью этого обслуживания можно
пренебречь. Напомним, что в этом случае оптимальное расписание $♦ есте-
57
ственно исють в классе расписаний, при которых все приборы обслужива-
ют требования в одной и той же последовательности..
Если Dj ~D,i Е N, то задача построения расписания $ ♦ является ^-труд-
ной в сильюм смысле при М > 3 (см. п. 3.7.) Прэи М = 2 расписание 5*
может бытьпостроено 3aO(wlogM) операций (см. п. 3.5).
Покажем что задача построения s* является NP-трэудной в сильном смыс-
ле, если М =2 и не все одинаковы.
Предварительно установим справедливость следующего вспомогательно-
го утвержретия.
Пусть G = (К, U) — неориентированный граф, сощержащий гамильтонов
цикл. Покакем, что ориентированный граф G = (JK, U), полученный из G
путем заметы каждого ребра парой противоположн<о направленных дуг, со-
держит эйлфов контур, | К| последних дуг которого образуют гамильто-
нов контур Напомним, что эйлеровым контуром называется замкнутый
остовный мфшрут, в котором каждая дуга графа шстречается ровно один
раз. Для суцествования такого контура необходимо и достаточно, чтобы
граф был (слабо) связен и у каждой его вершины шолустепень захода была
равна полус епени исхода.
По построению граф G содержит эйлеров контур). Кроме того, если граф
G содержит гамильтонов цикл С, то граф G содержшт по крайней мере два
гамильтонош контура Сг и С2, соответствующих различным ориентациям
ребер циклг С. Если из графа G удалить дуги конпура С2, то полученный
при этом гр1ф G' содержит эйлеров контурEf, так нсак полустепени исхода
и захода какдой вершины в графе G ровно на ещиницу меньше соответ-
ствующих згачений в графе G и, следовательно, раины между собой. Если
контур Е' дшолнить контуром C2i то получим исжомый эйлеров контур
графа G.
Перейдем к рассмотрению задачи построения расписания 5*. Сформули-
руем соответствующую задачу распознавания: определить, существует ли
расписание ?, при котором L maX (s° ) для заданшого числа у.
Покажем что к этой задаче сводится задача о гамильтоновом цикле
(см. вводную часть этой главы). Будем считать, чтго | К| = п0 и вершины
графа G пронумерованы числами от 0 до и0 — 1, Степень вершины и обоз-
начим через i(y), v = 0,. .. , п0 - 1. Напомним, что S d(y) = 2 j U |.
v е v
Положим^ = 4 11/|, 7V = { 1,2, . . . , и } . Каждому ребру [и, w] Е U поста-
вим в соответствие два требования Uvw и Uwv. Этш требования будем на-
зывать £7-тр;бованиями. Каждой вершине v Е V поставим в соответствие
d(y) требований Ки;-, j = 1,.. . ,d(y). Эти требования! будем называть И-тре-
бованиями. 1оложим
= v fuvw2 = 2по - [и, w] е и,
= и’ = 2«о - и, К w] G и,
tvvji = 2п> - 'ги/2 = V, v е к i = 1,..., d(v);
£>1 =2иоС1&1-«о), D2 =4ис|£/|.
Директивой срок Dr назначим всем К-требованшям, кроме требований
Vvd(v), v =0> • • •, по “1- Всем остальным требовааниям назначим дирек-
тивный срок#2.
58
Покажем, что при у = 0 в построенной задаче расписание $° существует
! Тогда и только тогда, когда в графе G существует гамильтонов цикл.
1) Пусть в графе G существует гамильтонов цикл. Построим граф G =
* (К, U), заменив каждое ребро графаG парой противоположно направлен-
ных дуг. Как было показано выше в графе G существует эйлеров контур,
последних дуг которого образуют гамильтонов контур.
Совершим обход указанного эйлерова контура, начиная с вершины 0.
В результате может быть выписана чередующаяся последовательность
дуг и вершин графа G, начинающаяся с дуги, исходящей из вершины 0, и
заканчивающаяся вершиной 0. Каждой дуге (u, w) из этой последователь-
ности поставим в соответствие требование Uvw. Каждой вершине v, встре-
тившейся в этой последовательности ;-й по порядку раз, сопоставим тре-
бование Ку/ ,/ = 1,..., d(y). В результате получаем чередующуюся после-
довательность U- и К-требований. Обозначим эту последовательность че-
рез я.
Будем считать, что оба прибора обслуживают требования в последова-
тельности я и функционируют без простоев во временно'м интервале (0,Z>2 ] •
Последовательность я можно разбить на 2| U\ подпоследовательностей— пар
вида (Ку/, Uvw) в случае прибора 1 и вида (UVWf в случае прибора 2.
Для обслуживания каждой такой пары требований соответствующим прибо-
ром необходимо 2и0 единиц времени. Из всех К-требований в последних
и0 парах указанного вида содержатся только требования Vva(v) > v = 0, •. •
..., л о ” 1- Следовательно, оставшиеся К-требования будут обслужены до
момента времени D2 — 2п% = Dx. Таким образом, построенное расписание
является искомым расписанием s°.
2) Пусть существует расписание я0. Определим суммарную длительность
обслуживания всех требований каждым прибором. Для прибора 1 имеем
по ~ 1 d(u)
2 + S ~г</и,и1+ 2 2 =
[и, м>]€=С7 [ и, w ] GE С/ V = О / = 1
"о"1 "о”1
= S vd (у) + L (2и0 - d(y) = 4и0 | U | = D2.
v = О v = О
Аналогично для прибора 2
S ~tUvw2 + S ~ {uwv2 +
"о -1
v = О
d(v)
S t у .о =
f = 1 Vv>2
n0-i n0-l
= S (2nQ-v)d(y) + S и<7(и) = 4и0 I tf|=P2.
v - 0 v = 0
Следовательно, при расписании s° оба прибора функционируют без
простоев в интервале (0, D2 ].
Пусть при расписании s° требования обслуживаются обоими приборами
в последовательности я0. Нетрудно видеть, что я0 является чередующейся
последовательностью U- и К-требований. Сопоставим требованию Uvw дугу
(и, w), а требованию Ку/ — вершину v графа G. В результате получаем че-
редующуюся последовательность дуг и вершин графа G. Поскольку s°
является расписанием без задержек и оба прибора функционируют без
простоев, то указанная последовательность определяет некоторый обход
59
эйлерова контура в графе G. Тас как при расписании s° значения tyvj.2
,/ = 1, . .., d(y) - 1, v G Г, то «о последних дуг этого контура обра-
зуют гамильтонов контур. Следовательно, граф G имеет гамильтонов цикл.
Поскольку число требования, а также длительности их обслуживания
и директивные сроки полиномтально зависят от | V | = и0 и задача о га-
мильтоновом цикле является 7VP-полной, то задача построения расписания
$*в рассматриваемом случае MF-трудна в сильном смысле.
§ 5. Суммарное время обслуживания
В многостадийную систему поточного типа, состоящую из М > 2 прибо-
ров, в момент времени d = 0 поступает множество М = {1, 2,..., п } требова-
ний. Заданы длительности tiL > 0 обслуживания каждого требования i EN
каждым прибором L, L = 1,..., М. Прерывания процесса обслуживания
каждого требования каждым прибором не допускаются. Рассмотрим задачу
построения расписания $*, при котором суммарное время обслуживания
S fy(s) минимально. Здесь,как и прежде, fy(s) — момент завершения
i G N
обслуживания требования i при расписании $.
5.1. Покажем, что эта задач! является NP-трудной в сильном смысле
при М> 2.
Сформулируем соответствукщую задачу распознавания: определить, су-
ществует ли расписание $°, при котором S f/(s°) для заданного
ZG N
числа у.
Покажем, что к этой задаче при М = 2 сводится задача о 3-разбиении
(см. вводную часть этой главы) Положим
и = 3 nQE +1, v = и + 3 nQEnQu + Ho(wo — 1) и (£ + 1 )/2,
г =v-u, f=uv+E+l, х = 2(и0 + 2)/+ и,
п = и0 + 1 + и + N = {1,2,..., п}.
Множество N требований разобьем на три группы: F-требования, обозна-
чаемые Fj, j. = 0, ..., п$, X-требования, обозначаемые Xt, I = 1, ..., и,
а также ^/-требования, среди которых будем различать К-требования, обо-
значаемые Vjk, j = 1, ..., и0, 1 = 1, ..., и — 3, и W-требования, обозначае-
мые Wi9 i. = 1,..., 3 nQ.
Доказательство приведем для случая, когда запись tiL = 0 означает, что
требование i прибором L не обслуживается.
Положим
= о, tFt>2 = 1;
tFji - f, = 1; / = 1.........n0;
tx/i = 0, (xt2 = x, I = 1,..., v;
60
tVjki = °> 7 = 1, ...,u - 3;
^Krl = 0» 7^/2 = v + ei> i ~ l,...,3n0.
Положим также у = F + X + £/, где
ло
F = S (// + 1) = п0 + 1 +no(«o + l)//2,
7 = o
X =• S (n0/+ 1 +Zx) = и(л0/+ 1) + u(u+ l)x/2,
/ =? i
_ Ло ~ 1 M
U = S S (kv + jf+ 1) + 3 nQE = nou(nQu + l)u/2 +r.
j = О к = 1
Покажем, что в построенной задаче расписание $°, при котором
S />($°) < у, существует тогда и только тогда, когда имеет решение
i е N
задача о 3-разбиении.
1) Пусть задача о 3-разбиении имеет решение и Nf = {а71, <*/£><*/3},
j = 1, n0, — найденные трехэлементные подмножества элементов множе-
ства NQ. Построим расписание, при котором прибор 1 обслуживает F-тре-
бования в последовательности (Flt F2i ...» Fna), функционируя без про-
стоев в интервале (0, nQf]. Прибор 2 функционирует без простоев в интер-
вале (0, nQvu + 3 nQE + их] и обслуживает требования множества N в по-
следовательности (Fo, К11я К12, ..., И/Л1з, К21,
У22, У2.и-з, W*2i, И/а2з, Wa23,F.2, ..., F„09X19X2) ...,Xv). При по-
строенном расписании
^Fj = if + 1, i = 0, ...,n0;
= «о/ + 1 + Zx, I = 1,v;
= (7 - 1)/+ 1 +^v, /= 1, ...,л0, k = 1, ...,u - 3;
%! = (7- 1)/+1 +(w-2)u + ea/1, 7 = l,...,«o;
Tw«j2 = (7 - 1)/+ 1 +(w-l)u + ea/1 +ea/2, 7 = l,...,«0;
= (Z- 0/+ 1 +uv + E, /=l,...,n0.
«/3
61
Имеем
Л0 _ _ V _ _
S tF. = F, S tXl = X,
j = о i = i
n0 w-3 _ n0 _ no _ n0 _
S S tVjk + s tw + S tw + s tw =
j = 1 к = 1 7 = 1 71 7 = 1 72 i = 1 73
n0 w-3 n0
= S S ((/ — 1)/+ 1 + kv) + S 3((/-l)/44)+(u-2)u+(u-l)u+uu +
i = i к = i j = i
*0
+ S (3 + 2 eaj2 + £<*/3) <
7 = 1
n0 и n0
< S S ((/- 1)/+ 1 +fcv) + 3 s (ea + e + ea) =
/=1 k=l /=1
n0-l и _
= S S (if + 1 + kv) + 3nQE = U.
j = 0 к = 1
Следовательно, построенное расписание является искомым расписа-
нием s°.
2) Пусть существует расписание s°. Не нарушая общности, можно счи-
тать, что при этом расписании прибор 1 обслуживает требование F, во вре-
менном интервале ((/ - 1)/, j/], 7 = 1, л0, а прибор 2 обслуживает
F-требования таким образом, что tF.2 < 7 = 0, •••> «о ~ 1-
Поскольку ^-требования не обслуживаются прибором 1 и имеют одинако-
вые длительности обслуживания прибором 2, то можно считать, что при
расписании s° имеет место tXl2 <txt + 12> f = 1,и — 1.
а) Покажем, что при расписании 5° значение tXl2 > nQf +1, I = 1,..., v.
Предположим, что найдется требование Xj9 такое, что tx^,2 < nQf + 1.
Так как х > nQf +1, то Л9 = 1. При этом к моменту времени tx^2 все
F-требования будут обслужены прибором 1.
Очевидно, суммарное время обслуживания А"-требований будет не мень-
ше чем X9 =х + S (п0/+ 1 + /*) = X - nof - \.
I = 2
Так как tx 2 < nQf + 1, то, по крайней мере, tF„ 2 > tx 2 > х, поэтому
суммарное время обслуживания F-требований можно ограничить снизу
величиной
"° ” 1 „
F9 = S (jf + 1) + х > F + («о + 2)/ + v.
/ = о
62
Оценим снизу суммарное время обслуживания U-требований. Предполо-
жим, что длительность обслуживания каждого из них (включая ^-требова-
ния) прибором 2 равна v и они обслуживаются прибором 2 непрерывно
одно за другим в интервале (0, nouv ]. В качестве нижней оценки получим
«п0 _
величину U9 = S qv = U— г. Таким образом, суммарное время обслу-
ч = 1
живания всех требований множества N не меньше чем F9 + X9 + U9 >
>у + (п0 + 2)/ + v - nQf - 1 >у, что невозможно.
б) Итак, tx 2 nof + 1- Покажем, что при расписании 5° значение
2 = nof + 1- Предположим от противного, что txt 2 = nof + Суммар-
ное время обслуживания ^-требований при этом не меньше чем
X" = S («о/ + 2 + lx) = X + и.
I = 1
Тогда суммарное время обслуживания всех требований множества N не
меньше чем F + X99 + U9 =у + и — г >у, что невозможно.
в) Покажем, что прибор 2, функционируя без простоев в интервале
(О, nof + 1 ], обслуживает все F- и U-требования.
Действительно, в указанном интервале прибор 2 не обслуживает других
требований (так как 2 = nof + О - Кроме того, суммарная длительность
обслуживания F- и {/-требований равна длине интервала. Если предполо-
жить, что прибор 2 простаивает во временном интервале (0, nQf + 1], то
найдется требование V (из числа F- и U-требований), обслуживание кото-
рого прибором 2 начнется после момента времени tX1 2 = nof + 1 + х.
Так как tV2 < ^2, то в последовательности, в которой требования об-
служиваются прибором 2, требования Х^ и V можно поменять местами и
суммарное время обслуживания при этом не увеличится. Но при построен-
ном расписании $ г > «о/ + 1, что невозможно.
г) Обозначим через Uj множество всех (/-требований, обслуживаемых
прибором 2 во временном интервале (0, tQp. 2]. Покажем, что при расписа-
нии 5° значение | Uj | = /и, / = 0,..., п0.
Пусть найдется такое q, 1 <q <п0, что | U q | < qu. Даже если множест-
во Uq содержит все ^-требования, то суммарная длительность обслужива-
ния требований этого множества и требований Fi9 F2i Fq-\ не больше
чем q + (qu - 1)и + nQE < qf < t*Fq2- Следовательно, прибор 2 простаи-
вает в интервале (0, ^^2], что невозможно.
Пусть найдется такое q, 0 <q <п0, что | Uq | >qu. Даже если множест-
во Uq не содержит ни одного Истребования, то суммарная длительность
обслуживания требований этого множества и требований Flf F2, ..., Fq_x
не меньше q + (qu + 1)и =qf + v - qE. Тогда суммарное время обслужива-
63
ния F-требэваний будет не меньше чем
’о
F" = 2 (//+ 1) + и - = F + и - qE.
iо
Суммарное время обслуживания всех требований множества N окажется
не меньше юм F " + U9 = у + v — qE - г > у, что невозможно.
д) Обозначим через U? множество всех U-требований, обслуживаемых
прибором 2 во временном интервале ( tp. _12, ^2] • Из доказанного вы-
ше следует, что при расписании $° значения | U® | = и, j. =1, ..., и0-
Покажем, по tp.2 = //, / = 0,..., nQ .
Пусть ьайдется такое q, 0 < q < л0 > что ^Fq2 > qf. Так как txt 2 =
= nQf + 1 > tp 2 , то q < nQ. Поскольку Uo = ф, то q Ф 0.
Суммарюе время обслуживания требований множества £/°+ х не мень-
и
ше S (qf + 2 + ки). С другой стороны, суммарное время обслуживания
к = 1
требований каждого из множеств U?, j. = 1, ..., nQ, j. Ф q + 1, не меньше
и
чем S (г/ + 1 + ки). Поэтому суммарное время обслуживания всех
к = 1
U-требований ограничено снизу величиной
nt- 1 и _
U" = S S (if + 1 + ки) = и + 1.
/ = О к = 1
Тем самим, суммарное время обслуживания всех требований множест-
ва N не метьше чем F+X + U" «у + 1, что невозможно.
е) Покахем, что имеет решение задача о 3-разбиении.
Поскольку число U-требований, обслуживаемых в каждом из интерва-
лов (tp._ 2,^2], равно и и длина каждого из этих интервалов равна
uv + F, тов каждом из них должно обслуживаться ровно и - 3 К-требова-
ний и ровю три Истребования, суммарная длительность обслуживания
которых ргвна 3v + Е. Обозначая через множество номеров ^-требо-
ваний, попавших во множество (/;°, j. = 1,..., и0, получаем решение задачи
о 3-разбиенш.
Тем самим за О(п^Е) операций реализовано сведение задачи о 3-разбие-
нии к рассматриваемой задаче распознавания.
Нетрудно видеть, что приведенное доказательство может быть использо-
вано и в тон случае, когда запись tiL = 0 означает, что требование i прибо-
ром L обслуживается, но длительностью его обслуживания можно пре-
небречь. Дгя этого достаточно считать, что при расписании $° значение
tn = /д =0 для всех требований i, являющихся U- или ^-требованиями и
ПОЛОЖИТЬ tp t = tp* 2 =0.
64
5.2. В заключение этого параграфа рассмотрим задачу построения распи-
сания 5* без задержек в обслуживании требований, которому соответ-
ствует наименьшее значение S (s ).
i е N
Если среди tiL имеются нули и запись tiL = 0 понимается таким обра-
зом, что требование i прибором L не обслуживается, то задача построения'
s* является NP-трудной в сильном смысле при > 2. Это непосредственно
следует из доказательства, приведенного в предыдущем пункте.
Пусть запись tiL = 0 означает, что требование i обслуживается, но дли-
тельностью этого обслуживания можно пренебречь. Напомним, что в этом
случае расписание естественно искать в классе расписаний, при которых все
приборы обслуживают требования в одной и той же последовательности.
Покажем, что и в этом случае задача построения расписания s* является
NP-трудной при Af > 2.
Сформулируем соответствующую задачу распознавания: определить,
существует ли расписание s° обслуживания требований множества
N = {1, 2, п} без задержек, при котором S tj(s) ^у для заданного
ZG N
числа у.
Покажем, что к этой задаче при М- 2 сводится задача о гамильтоновом
цикле (см. п. 4.2) в неориентированном графе G = (К, U), где | V | = п0 и
вершины пронумерованы четными числами от 0 до 2 nQ — 2. Степень верши-
ны v Е V обозначим через d(v ), и = 0, 2,..., 2 п0 - 2.
Множество N требований построим следующим образом. Каждому ребру
[u, w] G U поставим в соответствие два требования Uv w и Uwv . Каждой
вершине v Е V поставим в соответствие d(v) требований Ки7,
j = 1, ..., d(y ). Введем в рассмотрение также требования Fpkt р.Е {1,2},
к = 1, ..., п20.
Положим
Ч»' = V‘ = 8«0-W, [v,W] G U-
fuwvi = w- ^„(,2 = 8n0 - i>, [u,w]Gt/;
t vvtj ~ 8 fl° ~ v + i {Vvji = v' ° e К / = i,, «о;
= °’ = 16л0 + 1>
tp2ki ~ 16и0 + 1; *F2fc2 =0, к =
У1 = 16 | U | (2 | U | + l)n0 - S +
ver
= 2 «§(4 | U\n0 + l) + (16n0 + 1)wq(«o + О-
5. В.С. Танаев
65
При помощи рассуждений, аналогичных проведенным в п. 4.2, мож-
но показать, что в построенной задаче расписание s°, при котором
S tt(s) < yi + У2, существует тогда и только тогда, когда в графе G
N
существует гамильтонов цикл.
§ 6. Упорядоченные матрицы длительностей
В систему поточного типа, состоящую из М последовательных приборов,
в момент времени d = 0 поступает множество N = {1,2, ..., п } требований.
Длительность обслуживания требования i Е N прибором L, 1 < L < М,
равна tiL > 0. Запись tiL = 0 означает, что требование i прибором L обслу-
живается, но длительностью этого обслуживания можно пренебречь.
Прерывания в процессе обслуживания каждого требования каждым прибо-
ром не допускаются. Оптимальное расписание ищется в классе расписаний,
при которых каждый прибор обслуживает требования в одной и той же
последовательности. В п. 6.1, 6.2 рассматриваются задачи построения опти-
мальных последовательностей я* обслуживания требований, которым соот-
ветствуют наименьшие значения общего fmaxCO или суммарного
S tt (я) времени обслуживания. В п. 6.3, 6.4 эти же задачи решаются
JG N
в предположении, что задержки в обслуживании каждого требования не
допускаются. Предполагается, что матрица || tiL || обладает определенными
свойствами.
Будем говорить, что матрица || tiL || упорядочена по строкам, если для
любой пары требований i и к справедливо либо tiL > tkL для всех
L = 1, ..., М, либо tiL <tkL для всех L = 1,..., М.
Аналогично будем говорить, что матрица || tiL || упорядочена по столб-
цам, если для любой пары приборов Q и Н справедливо либо tiH> ttQ для
всех i Е N, либо tiH <ttQ для всех i Е N.
Если матрица || tiL || одновременно упорядочена по строкам и по столб-
цам, то будем называть ее упорядоченной.
Так, например, матрица
10 12 15 7
2 8 14 6
13 7 5
упорядочена по строкам, в то время как матрица
10 12 15 11
2 8 14 6
15 7 3
66
является упорядоченной и по строкам, и по столбцам, (т.е. является упоря-
доченной) .
6.1. Рассмотрим задачу построения оптимального по быстродействию
расписания в предположении, что матрица || tiL || длительностей обслужи-
вания является упорядоченной.
Напомним (см. п. 1.2 § 1 этой главы), что если требования обслужи-
ваются каждым прибором в последовательности я = (f ь ,..., in), то
их и2 п
'max 00 = .max { S ttkl+ s rZfc2 + ...+ 2 ttkM}.
1 <u2 < k=l k = ul
(6.1)
1) Поскольку матрица || || является упорядоченной, то существуют
прибор R такой, что tiR = max {tiL | L = 1,..., М} для всех i G TV, и требо-
вание г Е N такое, что trL = max{^L | i G N} для всех L = 1, ..., ТИ.
Пусть в перестановке я = (fn z2, ..., in) значение iq = г и максимум
в (6.1) достигается при L = 1, ..., М — 1. Ясно, что
... < vм-1 <Покажем, что существуют такие значения v i, v2,...» v,
что ил-! < q <vR.
Предположим, что q < Пусть Q — такой прибор, что vq_y <
< q < v q . Положим
Л ”i ”2-1 Я
^rnax CO ~ 2 fyfci + • • • + 2 q _ i + S t}. q +
* = 1 к = vq_2 к = ug_i
K-l
*iqL
VR
+ ^kR
k~q
VR +1 "
+ 2 ^fc,/? + l+...+ ^kM'
к = vR к = vM -1
+ 2
L = 2 + 1
Имеем
л _ R - i VR
^maxCO" ^maxM ~ 2 tj т + 2 hkR ~
L = Q q k = q K
VQ ”2+1 VR
~ ( 2 *‘к<2 + . 2 '<fc,e+i + -- + 2 0кя)-
к = q к = Vq к = vr_ i
Поскольку
равенства
в силу упорядоченности матрицы || tiL || справедливы не-
”2~х
2 tikR > 2 ti Q +
k=q К k=q
”Я - 1 - 1
. -. + 2 tik R _ i +
* = ”Я -2
”2+i”1
. 2 + • • •
= VQ
VR
s
= VR _ 1
R - 1 R - 1
S Л* r Z/ t- r
L = Q q L = Q 1,VlL’
to tmaxttf) > ЛпахСя). Из (6.1) следует, что Гтвх(я) >/тах(я). Таким
образом, ?тах (я) = ?тах (я).
5* 67
Полагая vL = q, L = Q9 , , . , I - 1, и не изменяя остальных значений
vL, получаем vR _ i < q.
Рассуждая аналогичным образ>м, можно показать, что существуют
такие значения , vM~ 9 что vR > q (и неравенство ид-i ^q
не нарушается).
2) Пусть R = 1, т.е. тах{Г/£ |Z = 1,. . . , М } = tix для всех i G N. По-
кажем, что в этом случае оптималная последовательность it* обслужива-
ния требований может быть построена за О(п log п) операций.
Доказательство проведем в несюлько этапов.
а) Пусть при обслуживании ребований в последовательности я =
= (fl, i2, . . . , in) максимум 1 (6.1) достигается при uL = vL, L =
= 1,... 9М — 1. Покажем, что существуют такие значения Vi, v2,..., vM- х,
что max{tikL\k = vit... fn} = tivL9 L = \9...9M.
Предположим, что max{7/fcL |/ = . . , n}=tipL, P> - Пусть
Я, 2 < H < M, - такой прибор, чт* j > р. Положим
л р -1 77-1 »н п
rmaxW = 2 tiki + S tt I + S ti H + ... + S tiM.
k = 1 K L = 1 P k = p K k = vM_t K
Имеем
_ p - 1 77—1 UT7
^maxOO" ^maxW “ H hpL + k^ p^kH ~~
Vi v2
- ( S tikl + 2 tj 2 + • • + 2 ^кн>)-
Jt = 1 fc = Uj fc = U77-1
Поскольку в силу упорядоченюсти матрицы || tn II и сделанных пред-
положений справедливы неравенств
р-1 Л”1 ”2-
2 г > 2 tiki + S ц 2 + • • •
к ~ 1 К к = 1 К к = \_
р - 1 77 — 1 77—1
• • + ^кН * ЪрЬ** 2 ti т9
k = vH_r К L = 1 Р L = 1 VL
то ?maxG0 > imaxGO- С другой стороны, Гтах(я) > ?тах(я). Следова-
тельно, /тах(л) = ?тах(я).
Полагая vL = р, L = 1, . . . , / — 1, и не изменяя остальных значений
vL , получаем искомые значения I?! v2,..., vM_ х.
б) Пусть максимум в (6.1) достигается при uL = vl,9 L = 1,... 9М — 1,
где Vi = v2 = . . . = vq-i 2.Покажем,
что существует такое Q9 что тах{^^ | L = Q,..., М} = tiQ9 i E.N.
Предположим, что max{f/L |L = Q, . . . , М} = tiHf i G N9 H > Q. По
условию
2-i VQ
^тах(я) = S i + S ti L + S q + ...
к = 1 K L = 2 k = vxK
VH n
. . . + S hkH + • • • + 2 tikM.
fc = UH-1 fc=VM-l
68
Положим
Л ”1 77—1 VH п
6nax(X) = S + S l + S tikH + • • • + 2
fc=l K L = 2 v* k = vx K * = ”М-1
Имеем
a _ H - 1 VH
^maxOO “ ^maxW "~ £ ? q ^vi L + tikH ~
»Q VQ+1 VH
- ( tikQ + s ^fc,e+i+... + S ^fc77 )•
к = Uj к = vq к = vh- i
77- 1 77—1
Из доказанного выше следует, что S £ > S h L-
L = Q V' L = Q VL
Кроме того, из условия упорядоченности матрицы || tiL || и сделанного
предположения следует, что
у 77 VQ - 1 VQ +! - 1 VH
S *ikH 2 tt Q + S tik,Q+\ + • • • + • *1кН*
к = vx к = Uj = = и77-1
Таким образом, ?тах(л) > ^тах(л)- С другой стороны, 7тах(*0
> ?тах(я). Следовательно, £тах(я) = ^тах(я)- Полагая vL = и>, L =
= 0, . . . , Я — 1, и не изменяя остальных значений vL, получаем искомые
значения i>i, v2,. .., vM- t.
Рассуждая аналогичным образом, можно показать, что существуют такие
значения иь и2, . . . , при которых из неравенства u^-i < vq,
2 < Q < М - 1, следует, что tiQ = max{r/L | L = Q,... , М}.
в) Пусть для перестановки я = (il9 i2, . . . , ip, ip + j, . . . , in) значения
hpL > hp+iL для всех! = 1, . . . 9M. Покажем, что 7тах(я) <Fmax(^),
где я' = (71,/2,... ,«р-ь *р+ь *р, ip + 2,- -Jn)-
Предположим, что для последовательности я максимум в выраже-
нии (6.1) достигается при«£ = vL, L = 1,.. . ,Af- 1. _
Если все vLi L = 1, . . . , М - 1, отличны от р ир + 1,то ^тах(^)^
^maxW*
Пусть все V£,L = l,...,Af — 1, отличны от р, но существуют такие Q
и Н, 1 <0<Я<7И-1, что vL=p + 1, L-Q,... ,Н - 1. Тогда
_ ui р+1 н
^maxGO ~ tik\ + ... + 2 t^kQ + ^’р + \L +
*= 1 К ^ = vn-l L = Q + l Р+ 1
и77 п
+ 2 tt н + ... + 2 ttkM-
к = р + 2 К fc = vM_1
Очевидно,
_ ui р+1 н
tmax(.‘n ) > 2} tt I + ... + S tt Q + S ti L +
к = 1 K k = VQ_i L = Q+1 p
VH n
+ 2 tikff + • • • + s tikM.
k=p+2 K k=vM_i
69
Следовательно,
_ f _ н н
^maxC^ )“ max GO ipL ~~ 2 + \L‘
£ = 2 + 1 L = Q+ 1 р
Так как по условию tipL > L для всех! = 1,... ,М, то Гтах(*) >
^maxGO-
Пусть все vLi L = 1,.. . , М - 1 отличны от р + 1, но существуют такие
Q и Я, 1 < Q < Я <М - 1, что vL zp,L = 0, . . . , Я - 1. Из приведенных
выше рассуждений следует, что tp = max{f/£ |! = 0, . . . , М}, i G Я.
Имеем
_ ui ’
^maxGO = Е tiki + . . . + tikQ +
к = 1 к =vq_ 1
Н- 1 иН п
+ ti L + S tf н + . . + S tiM.
L- 2+1 Р к = р К к = им -1
Очевидно,
_ ”1 +1
^шах(я ) S tiki + ... + S tikQ +
t = 1 К kF VQ-i
H - 1 »H п
+ h т + tikH + •• • + S ~ ^р + \Н>
L=2+l Р к = р К k=vM-l Р
Следовательно,
^тахСг0— ^maxGO ^р + \ Q ~~^р+1н
Аналогичным образом можно убедиться в справедливости неравенства
^тахС7^) > ^тах(^) и в случае, ктда среди vL, L = 1, . . . , М, содержат-
ся значения р и р + 1.
Таким образом, если шах{^£ = 1, . . . , М} = tiv для всех i Е Я,
то искомая оптимальная последсзательность я* может быть построена
за O(rtlogH) операций посредствм упорядочения требований по невоз-
растанию значений tt t.
Аналогичным образом можно пказать, что если R-М, т.е. max{rZ£| L =
= 1......М} = tiM для всех i ЕЯ, то требования следует обслуживать в
порядке неубывания значений tiM.
3) Пусть max{f/£ |! = 1,= tiR, 2 <7? - 1 для всех i еЯ.
Не нарушая общности, будем с«тать, что требования пронумерованы
по неубыванию значений tiR. Пкажем, что оптимальная перестановка
я* принадлежит классу так называемых пирамидальных перестановок,
т.е. перестановок вида (/i,..., jq> jq+ i,... ,/л), где/i < - <Jq-u
iq=n> iq + i> • • • > in (при этом £ исключаются случаи q = 1 и q-п).
Пусть Я1 С я и Ядг' — некотрая перестановка элементов множест-
ва Я1. Обозначим через tQH^njj) момент завершения обслуживания
требований множества N* в систме поточного типа, состоящей из при-
боров 0, 0 Н, 1 < 0 < I при условии, что процесс обслужи-
вания начинается в момент времен d = 0 и каждый из указанных приборов
обслуживает требования в последоательности я^\
70
Любую перестановку я элементов множества N можно представить в
виде (яЛГ1, п, 7Гуу2), где П N2 = Ф, U N2 = 7V\{ п}. Введем в рас-
смотрение пирамидальную перестановку я1 вида (я^ , п, я^2).
Покажем, что 7тах(я/) 7тах(я). Из доказанного в п. а) следует, что
GnaxOO = hR^N^* tRM(l<N2) ~ tnR,
^тах(^ ) = ^lR(jrNl ) + ^RM(?rN2 ) “ ^nR •
Как показано в п. 2), 71Л(я^) <T1R(nNi) и Тям(тг^) <TRM(rrN*),
Это означает, что для любой перестановки я найдется такая пирамидаль-
ная перестановка я', для которой ^тах(я') < *тах(я)-
6.2. Покажем, что перестановка п* элементов множества N которой
соответствует наименьшее значение S /7(я), может быть построена
N
за O(wlogw) операций в предположении, что матрица II tiL || длительно-
стей обслуживания либо упорядочена, либо М = 2u Г(1 > tl2 для всех
i G N,
1) Если требования обслуживаются в последовательности я = (fi, G,...
. . . , in), то, как и прежде, через ^н(я) будем обозначать момент завер-
шения обслуживания требования ik прибором Н.
Покажем, что перестановке я* = (/ь/2,... ,/„) соответствует наимень-
шее значение S t{ (я), если существует такой прибор Н, 1 что
f G N
_ _ М
Ькм(**) = + L^f/+itikL' к=\',...,п, (6.2)
и для любой перестановки я = (zb i2,. .. ,in) справедливо неравенство
S (6*3)
к = 1 К к = 1
_ _ м
Действительно, из (6.1) следует, что > Ъкн(л) + S **kL9
к = 1,..., п, и тем самым
п _ п _ п М
S ^я(я) + S S tt L =
к= 1 к-\К к = 1 L = H+1
п _ п М
= 2 + S S tiL.
к = 1 I = 1 L = Н+ 1
С другой стороны, из (6.2) следует, что
» _ п _ п м
s %м(я») = S + ? 2 =
К — к к — 1 К— к Ь-'Н+к
п _ п М
= 2 ?/ля(я*)+ S S tiL.
к= 1 К 1 L = Н + 1
71
Учитывая неравенство (6.3), приводим к заключению, что
S Г,(я*) < S tt (я).
i = 1 i = 1
2) Пусть матрица || tiL || являе'ся упорядоченной и требования прону-
мерованы таким образом, что tiL + ltL, i = 1,. . . , п — 1, 1 <Af.
Покажем, что я* = (1, 2, . . . , п) является искомой оптимальной последо-
вательностью обслуживания требов1ний.
Пусть я = (ц, z2, . . . , in) - произвольная перестановка элементов
множества N и Я, 1 - таюй прибор, что max{^L |£ = l,...,Af} =
= tiR для всех i G N.
Как показано в п. 6.1 б) для вех к, 1 < л, справедливо соотноше-
ние tkR(Tr*) < и, следовательно, выполняется соотношение (6.3)
(при Я = Я).
В силу упорядоченности матриц! II tiL || из п. 6.1 а) следует, что
_ _ м
*км(л») = tkRfir-) + S kL, fc
L = R + 1
т.е. имеет место соотношение (6.2 (при Я = R). Таким образом, переста-
новка я* = (1,2,. . . , п) является искомой. Для ее построения достаточно
упорядочить требования по неубыванию длительностей обслуживания
любым прибором, т.е. выполнить н« более чем О(п log л) операций.
3) Пусть М = 2 и tix > t{2 дл^всех i G Я, т.е. матрица || tiL || являет-
ся упорядоченной по столбцам. Понумеруем требования таким образом,
что t{1 < t{ + 1д, i = 1, . . . , п— 1. Покажем, что перестановка я* =
= (1,2,.. ., п) является искомой.
Как известно, перестановка я* оответствует наименьшее значение сум-
марного времени обслуживания сех требований прибором 1, т.е. имеет
место соотношение (6.3) (при Я = ).
Поскольку tk +11 > tki > tk2 к = 1,.. ., п — 1, то
^2^*)= 2 hl + hc2>
1 = 1
т.е. имеет место соотношение (6.2) (при Я = 1).
Следовательно, перестановке я*= (1,2,,.., п) соответствует наимень-
п _
шее значение S (я), и она мскет быть построена в результате выпол-
i = 1
нения не более чем О(п log п) оперций.
6.3. Рассмогрим задачу пострения оптимального по быстродействию
расписания обслуживания множесва N = {1,2,. .. , л } требований в систе-
ме поточного типа, состоящей из Л приборов. Предполагается, что задерж-
ки в обслуживании каждого требования запрещены, матрица || tiL || упоря-
дочена по строкам и требования понумерованы таким образом, что tiL <
i,£> * = h • • - 1, 1 < £ < М.
Как показано в п. 3.4, 3) § 3 эой главы, последовательность я* обслу-
живания требований, которой оответствует оптимальное расписание,
может быть найдена в результае решения задачи о коммивояжере с
72
п + 1 городами и матрицей расстояний || cpq ||, где
м
^Ор ~~ ^рО ~~ j ^Р 1 ’
Q 2-1
Cpq = max{ S tpL - S tqL | Q = 1,... ,M}, p,qeN, p^q.
рч l= i l = i
1) Покажем, что в рассматриваемом случае
Clk - cik > Сц - Сц, (6.4)
где п > j > к > \9 п > I > i >
Для пары требований (р, q), р = 1,.. ., л, q = 1,. .., nt p^q, обозначим
Q 2-1
ypq(H) = max{ S tpL - S tqL | Q = 1,... ,H}, H=19...9M,
L = 1 L = 1
Очевидно, cpq = ypq(M).
Покажем, что для всех L9 1 справедливо U(L) > V(L)f где
U(L) = 7z*(L) - y.k(L), V(L) = 7//(L) - yif(L).
Воспользуемся методом математической индукции. При L = 1 имеем
Я(1) = К(1) = ttl - tilt Предположим, что U(L) > V(L) для всех£,
1 <£ <Я-1 <М- 1. Покажем, что Я(Я) > И(Я).
Имеем
U(H) = U(H- 1) + max{0, ttH - tkH_ t} - max{0, tiH - tk H_ ,},
К(Я) = V(H - 1) + max{0, ttH - tf H_ t} - max{0, tiH - t) H_,
а) Пусть tlfi <tk,H-\. В силу упорядоченности матрицы || tiL || по
строкам имеем tlH < < tk,H-i < Следовательно, U(H) —
- V(H) = U(H- 1) - V(H- 1) >’ 0.
б) Пусть tlff > tkH_ 1 и ttH < tkH_ 1. В этом случае tiH < tf> H_ t.
Если to U(H)- V(H) = U(H- 1) - V(H - 1) + tlH -
~ tk,H-l 0-
Если tIH > to U(H) - V{H) = U(H- 1)- V{H- + -
~ tk,H- 1 О-
в) Пусть tin> tkff_l И tlH > tk H-l.
Если ^tj'ff-i, а следовательно, и ttfI <tj tHto U(H) -V(H) =
= U(H- 1)-И(Я- 1) +tiff-tiH > 0.
Если ttH > thff и ttff < to U{H) - V(H) = U(H - 1) -
- ~ О + г/,я-1 ~ t/H 0-
Если же tiff < tj>ff_1 и tiff > tj'ff-i, to U(H) - V(H) = U{H - 1) -
- V(H- 1) >0.
Таким образом, неравенство (6.4) выполняется.
2) Покажем, что в рассматриваемом случае оптимальная перестановка
л* принадлежит классу пирамидальных перестановок (см. п. 6.1, 3)).
Рассмотрим произвольную перестановку тг = (/n i2.......ip-i, ip,
ip + i, • ,iq-i, iq,.--,ir - n,..., in), где max{/ZjtL |fc=l,...,r-l} =
= tiqL и max{fffct \ = tlpL , L = 1,. . . , M. Пока-
73
жем, что fmsxw) > rmsx(n'), где я' = (Ц........'p-i,ip + i. • • . iq-i,
ip, iq, • • • , ir '• • • • > in)- Учитывая результаты п. 3.4, 3) § 3 этой главы,
нетрудно убедиься, что
~ ^шах(я,““ ^шахОО =
^Cip-lip + ipip + 1 ~ Cip-lip+ 1^ ~ ^Ciq- lip + Cipiq Ciq- 1Z<P ’’
Покажем, чт Д > 0.
Действительо, если iq_\ > ip_\, то, прибавляя и вычитая значение
Ciq-lip+V Имем
~ ((%- й ” Ciq— 1*р) ” (Cip-lip + 1 ” Ciq- lzp + 1^ +
+ ((Ciq-liq ~Cipiq)~ (%-1'p + l ~Cipip+l^-
Поскольку ij_i > ip_i и ip > ip+l, а также f4-i < ip и iq > ip+1,
то в силу (6.4) юлучаем Д > 0.
Если iq-i < ip-i, то, прибавляя и вычитая значение cip^^ имеем
+ ((Cip— iiq ^ipi^ ~ (C*p- lip + 1 ~ Cipip^\))’
Так как zQ_ < ip_1 и iq > а также ip-i < ipniq> ip+ ь то в силу
(6.4) получаемД > 0.
Следователь©, существует оптимальная перестановка, в которой тре-
бования, предгествующие л, упорядочены по неубыванию значений
(для любого L 1 CJW). Аналогично можно показать, что существует
оптимальная поестановка, в которой требования, следующие за п, упоря-
дочены по неворастанию значений tiL (для любого L, 1 < L < М).
3) Покажем что перестановка л* (из класса пирамидальных переста-
новок) , котора соответствует наименьшее значение ^тах(я), может быть
построена за On2Nf) операций.
Рассмотрим юрестановку вида я = ( . . . ,p,q,... ) ,р G A, G А,р =# tj.
Из результатов п. 3.4, 2) следует, что величина cpq содержательно озна-
чает разность ьежду моментами начала обслуживания требования р и тре-
бования q приором 1, если каждый прибор обслуживает требования в
последовательности я.
Введем в расмотрение величину bpq, где
м м
ЬРЧ = СРЧ 4 ? t ~ J tpL, p & N, q e N, p q. (6.5)
Величина Ьр содержательно означает разность между моментами завер-
шения обслуживания требования р и требования q прибором М, если каж-
дый прибор обауживает требования в последовательности я.
Обозначим чрез fp(q) наименьшее значение общего времени обслужи-
вания (без задржек) требований множества {р, р + 1,... , п } при условии,
что обслуживаме этих требований начинается в момент времени d = 0 и
74
требование q(q > р) обслуживается последним. При этом не нарушая общ-
ности можно считать, что требование р обслуживается первым.
Обозначим через fp(q) наименьшее значение общего времени обслужи-
вания (без задержек) требований множества {р, р + 1,.. ., п} при условии,
что обслуживание этих требований начинается в момент времени d = 0 и
требование q (q> р) обслуживается первым. При этом не нарушая общно-
сти можно считать, что требование р обслуживается последним.
Нетрудно видеть, что имеют место рекуррентные соотношения
/р1 (Р + 1) = min{/p2+i(q)+Cp4 | q > р + 1},
fp(Q)~fp+i(.Q) + cp,p+i< q = P + 2,...,n,
fp(P + О = minffp^i^ + Spq | q > p + 1},
= /p2+i(Q) + 5p+i,p> q = p+ 2 ... ,n, p = n— 2, n— 3, ...1,
с начальными условиями
м
= сп-1,п + 2
L = 1
М
= сп,п-1 + tnL.
L = 1
Используя приведенные соотношения, можно построить 2п — 2 пира-
мидальных перестановок. В качестве я* следует выбирать ту из них, кото-
рой соответствует min {//(р), Л2(Р) IР = 2,..., и}.
Вычисление значений cpq и bpq, р = 1, .. . , п, q = 1,... , п, р ^q, требу-
ет выполнения не более чем О(п2М) операций, для последующего выбора
перестановки я* требуется не более О(п2) операций.
4) Пример. Четыре группы экскурсантов желают осмотреть выстав-
ку, экспонаты которой размещены в пяти последовательно осматривае-
мых залах. Пусть tiL означает длительность осмотра f-й группой экспози-
ции зала£, i = 1,2,3,4, L = 1,2, 3,4, 5. Матрица || tiL || имеет вид
1 6 3 4 3
4 8 3 5 5
5 8 4 6 7*
6 8 6 7 7
Будем считать, что единица времени равна пяти минутам.
Матрица || tiL || упорядочена по строкам, что можно объяснить различием
в численном составе групп и индивидуальными интересами. Требуется
таким образом организовать просмотр выставки, чтобы в любой момент
времени в каждом зале находилось не более одной группы; все экскурсан-
ты каждой группы одновременно находились в одном и том же зале;
переход каждой группы из зала в зал осуществлялся непосредственно
после завершения осмотра экспозиции предыдущего зала; все четыре
группы экскурсантов осмотрели всю выставку как можно быстрее.
Имеем ситуацию, рассматриваемую в данном пункте. Для построения
оптимального расписания воспользуемся алгоритмом из п. 3).
75
(1,2,3,4) (2,3,4,1) (1,3,4,2) (3,4,2,1)
f?(3)=51
(2,4(3)^
f](3)=54
(1,2,4,3)
f^(4)=5O
-f?(4)=53
(4,3,2,1)
Рис. 6.1
Матрица || ca || имеет вид
3 2 1
12 - 7 6
17 10 - 17 ’
21 14 И -
а матрица || Ьр || - вид
12 16 19
3 - 12 15
3 5 - 11 •
3 5 7 —
Процесс даьнейших вычислений удобно изобразить в виде графа
(рис. 6.1). В саждой вершине графа указана вычисляемая величина и
ее значение. 1иже вершины записана соответствующая последователь-
ность требовамй (групп). Направления дуг указывают порядок вы-
числения.
На последнее шаге алгоритма (р = 1) получено шесть пирамидальных
перестановок, (ерестановка (3, 4, 2, 1) определяет оптимальное расписа-
ние. Моменты времени, в которые группа покидает зал L (и переходит в
зал £ + 1), i = 1, 2, 3, 4, L = 1, 2, 3, 4, при условии, что группы осматри-
вают выставкув последовательности (3, 4, 2, 1), приведены в табл. 6.1.
5) Пустьмарица II tiL II упорядочена по строкам и tiM> tiL, L = 1,...
..., М - 1, i £N. Покажем, что в этом случае я* = (1,2,.. ., п).
Таблица 6.1
L i 1 2 3 4 5
3 5 13 17 23 30
4 13 21 27 34 41
2 25 33 36 41 46
1 34 40 42 46 49
76
Пусть величины bpq удовлетворяют (6.5). Нетрудно видеть, что для
любой перестановки я = (ix, i2,..., in)-
_ п — 1 М
^maxGO” 2 ^ijcik + l + fyb’
к= 1 КК 1 L= 1 1
Положим
&РЯ ~ ^РЯ ~ ^ЯМ ~
М-l М
= max { S tqL - S tpLi 0}, р EN, q ^N,p ^q.
KQ^M-1 L=Q L = Q + 1
Очевидно, 8'pq = 0 приp>q. Имеем
_ n —1 n Ml
ЛпахОО ” * j + S t^ + S t^
n- 1
Положим б'(я0) = 2 5J z , где я0 = (0,я) = (z0 = 0, z’i,z2,..
* = о 1
м-i
5'o‘> = l?1 tfkL-
Пусть я — пирамидальная перестановка и ir = п. Выберем ip, iq G N
такие, что 1 <r, г <q <и и iq > iр> iq+i. Покажем, что 5'(я0) ^5'(яо) ,
где Яо = (z*o,. • •, Zp_ j , Zp + j ,..., zr,..Zq, Zp, Zq + j ,..., zn).
Имеем
S'(7ri) - б'(тг0) = 6'tp_lip++ Slqip* b'tp{(l + l-8,ip_ Jip - 8'ipip+1 -S'lqlq+l.
Очевидно, /р_1 < ip < ip+1, &'tqip= 6'fplq+t = 6'iqiq+1 = 0.
Покажем, что 8}p_ 1<p+1 > 6}p_{ip + 5^ptp+J.
M-l M
Пусть p = 1 и 8j { = S tiL - S tf L >0 (в случае 8} { =0,
1 2 L L =0*1 1 12
M-l M-l
очевидно, имеем 6-o i2 = S ti2 L > S L = 5-o ).
L — 1 h — 1
Имеем
M-l м-i м
i +5J i = Z tt L+ S h l - S tt L =
01 12 L=1 1 L = Q L = Q + 1 1
Q M-l M-l
= 2 ti L - ti M + S S
L = 1 1 1 L = 22 L= 1 2 02
Пусть p > 1. Предположим, что
5«р'р +1 ' М-1 м ' tip + iL ~ S ^i„L > 0, L = H Р 1 L = H + 1 Р
M-l М = *1р1~ L = Q р L = 2 + 1 Р
и Q >H (в остальных случаях доказательство аналогичное).
77
Имеем
М-1 м М-1
Ч-1'Р +5'р'Р + 1 = L?Q t(PL ~ L = 0+1 ttp~1L * L^Htip*1L ~
М М-1
Е tipL= ( Е h.
W + 1 Р L=H ‘
Q
S h ,l~
-.н+х 1P-1L
е-1 , Q
~ L =H+ltipL ~ ЧрМ SiP-lip^ +L = H + 1 ^Р- 1L ~ Ч-1'P+l •
Таким образом, перестановке itq = (0, 1,2,..,, л) соответствует наи-
меньшее значение 6г(я0). Следовательно, перестановка я* = (1, 2,..., я)
является искомой. Она может быть построена 3aO(nlogn) операций путем
упорядочения требований по неубыванию значений tiL, i G TV, 1 < M.
Если матрица II tiL II упорядочена по строкам и > tiLii £N,L = 2,...
...,M, то рассуждая аналогичным образом, можно показать, что оптималь-
ной является перестановка я* = (п, п — 1,. .. , 1).
6.4. В заключение этого параграфа покажем, что перестановка элементов
п _
множества N, которой соответствует наименьшее значение S (я),
i = 1
может быть построена за О (n log л) операций. Предполагается, что задерж-
ки в обслуживании каждого требования запрещены и матрица llf/L II упо-
рядочена по строкам. Пронумеруем требования по неубыванию значений
tiL ,i G TV, 1 <£ <ТИ. Покажем, что перестановка я* = (1,2, ... , п) являет-
ся искомой.
Пусть я = (i!, 1’2,..., in) — произвольная перестановка элементов
множества TV = { 1,2,... , п } . Из п. 3.4. § 3 этой главы следует, что
_ л-1 п м
S г,(я)= S (n-k)ci t + S S tiL.
i^N 1 к к 1 i = 1 L = 1
1) Пусть tiM = max{rZL |Zt = 1,..., ТИ}, i G TV. Из n. 6.3,5) следует,
что для любой последовательности я = (ii, z2,..., in) справедливо
< TikM(y). Таким образом,
S 7}(я«)= S s tikM(n)= S z-(ir)
i^N к = 1 к = I i<=N
или, что то же, самое,
П-1 И—1
s («-*)<jt,fc + i < S (n-k)ct i
к = 1 1 К K±1
2) Пусть tiR = max {tjL | L = 1,.. . ,M} JEN, 1 <1? <ТИ. Очевидно,
r Q Q-i
cpq= max { S tpL - S =
l= i l= i
Q 2-1
= max { S tpL - S tqL}, q>p.
1<Q<R l = i l = i
78
Рассмотрим задачу нахождения последовательности обслуживания
требований, которой соответствует наименьшее значение S (я). Не-
грудно видеть, что искомой последовательности соответствует наимень-
п- 1
luce значение S (п - к) cikik + f, где
Q <2-1
Сра ~ Шах { tpL S tqL' •
1 L = 1 L = 1
Как показано выше, имеет место соотношение
п- 1 и- 1
S (п -к)с'к,к+1< S (и -k)c'ikik
к = 1 к = 1 1
Поскольку <?fcfc + 1 =c*jfc+i HCpu > c'pq, P>q, то
п - 1 п — 1
S (и-£)<*,*+1< S (« -k^ikik+i-
к= 1 к= 1 КК 1
Таким образом,-Перестановке я* = 0,2,..., и) соответствует наимень-
шее значение S tt (if). Она может быть построена за О(п log п) операций
i е N
путем упорядочения требований по неубыванию значений tiL, i G N,
1 CM.
§ 7. Доминантные матрицы длительностей
В систему поточного типа, состоящую изМ последовательных приборов,
в момент времени d = 0 поступает множество N= {1,2,..., п} требова-
ний. Длительность обслуживания требования i G ТУприбором/., 1 <£ СМ,
равна tiL > 0. Запись tiL = 0означает, что требованиеi прибором/, обслу-
живается, но длительностью этого обслуживания можно пренебречь. Преры-
вания в процессе обслуживания каждого требования каждым прибором
не допускаются. Оптимальное расписание ищется в классе расписаний, при
которых каждый прибор обслуживает требования в одной и той же после-
довательности.
В п. 7.1—7.4 рассматриваются задачи построения оптимальных последова-
тельностей я* обслуживания требований, которым соответствуют наимень-
шие значения общего гтах(я) или суммарного взвешенного S wtti (я)
i е N
времени обслуживания. В п. 7,5—7.7 эти же задачи решаются в предположе-
нии, что задержки в обслуживании каждого требования не допускаются.
Предполагается, что матрица II tiL II обладает определенными свойствами.
Матрицу II tiL II длительностей обслуживания будем называть доминант-
ной (Q-доминантной), если для некоторого Q, 1 < (2 СМ, имеет место
соотношение
Q Q-l R R+1
min { S tiL — S S tjL — S tjL } > 0,
L=H + 1 L = H L = Q L-Q + X
где/7= 1,..., (2 — 1 = e,...,M-l (Q*M)\ iJEN, i*j.
79
Так, наприме», матрица
16 4 10 1
7 5 8 4
3 7 6 2
является З-домнантной.
7.1. Рассмотр1м задачу построения последовательности я* обслуживания
требовании, коброй соответствует оптимальное по быстродействию распи-
сание. Предполаается, что матрица И tiL II является доминантной.
Для заданные последовательностей U = (ub и2,..., им_^) целых
чисел таких, чтс1 <и2 <... ^им-1 и перестановки я = (il9
in) элемента множества TV положим
я) = 2 + 2 tik2 + • • •+ 2 (7.1)
к = 1 к - иг к - иу_ j
Напомним, чв
'maxW = max (f(U,K)). (7.2)
1 __1 < л
1) Покажем, (то
_ М-1 п
^тах(я) = tj £ + 2 (7-3)
L =1 к = 1
для всех перестновок я = (z i, i2,. . ., in) тогда и только тогда, когда мат-
рица II tiL II является7И-доминантной.
а) Действительно, если для всех перестановок я выполняется соотноше-
ние (7.3), то дщ любой последовательности U = (иг, и2,. .. , Мм- 1) целых
чисел таких, что1 <w2 <. .. i справедливо
M-l i
L = 1 1 к 1 к
В частности, ля всех Я, 1 <Ж7И — 1, имеем
м-i i н м-i п
2 ^/l + '*1км^ 2 L + 2 ti L + 2rf M,
L = 1 к 1K L = 1 L = H к = 2
откуда следует, то
В силу произольности перестановки я заключаем, что матрица \\tlL II
является 7И-домшантной.
б) Пусть марица II tiL II является 41-доминантной. Покажем, что для
любой последовательности U = (Ui, и2,..., Um-i) целых чисел таких,
что 1 < и2 j и любой перестановки я = (z!, i2,. . ., in)
справедливо
м- п
S tiiL+ S tikM. (ТА)
L= 1 ' к= 1 K
80
Положим р = им_ 1,R = minuL=p} и
4 =
1,
R> 1
R = 1
Определим
р-1
F(p, q, R, п)= S
к = q
Af-l n
?ikR + tipL +
L - R к — p
Так как матрица II tiL II является M-доминантной, то, в частности,
м-i м
2 hkL< 2 =Р, Р - 1, • • • + 1.
L = R L = R+1 К 1
Тогда
F( р, q, R, я) <
М-1
liqL
S
L = R
п
+ 2 Ькм,
к = q
и следовательно,
М1 U2
S tj J + S ti2+---
к - 1 к - и.
M-l
tik,R-l* 2 ti
K L = R q
n
+ 2 tikM.
к = q
Q
s
к = UR-2
Положим uR -uR +i = .. , = um-i = q, а остальные uL оставим без изме-
нения. Повторяя описанные выше рассуждения конечное число раз, полу-
чаем неравенство (7.4).
Таким образом, если матрица II tiL II является 7И-доминантной, то опти-
мальной является любая перестановка вида (/,...), где
м - 1 м-1
2 tn - min { S tiL 1 i = 1, ..., n } .
l = i l = i
Элемент j E TV может быть найден за О(пМ) операций.
Рассуждая аналогичным образом, можно показать, что
п м
^maxGO “ 2 + 2 tj l
k= 1 L = 2 n
для всех перестановок я = (z i, i2,..., i n ) тогда и только тогда, когда мат-
рица II tiL II является 1-доминантной.
В этом случае оптимальной является любая перестановка вида где
м м
S tjL = min { S tiL | i = 1,. .., n}.
L = 2 L = 2
Элемент j EN может быть найден за О(пМ) операций.
2) Покажем, что при некотором Q, 2<Q < М - 1,
_ Q-1 п м
^тахС^) “ 2 tj £ + S tikQ + 2 tj l (7.5)
L = 1 1 к = 1 K L = 2+1
6. В.С. Танаев
81
для всех перестановок я = (iit i2, * • . , /л) тогда и только тогда, когда
матрица II tiL II является б-доминанпой.
Пусть ?ля(я) означает общее время обслуживания требований множест-
ва N системой поточного типа, состоящей из приборов R, R + 1, . . . , Я,
при условии, что каждый прибор обслуживает требования в последователь-
ности я и процесс обслуживания начинается в момент времени d = 0.
Очевидно, соотношение (7.5) имеет место для всех я тогда и только тог-
да, когда для всех я
_ Q —1 п , п м
= S ti с + S tikQ; tQM(n) = S tikQ + S tinL-
L = 1 к - 1 к =1 L = Q + 1
Как следует из п. 1), это эквиватентно утверждению, что матрица II tiL II
является 0-доминантной.
В рассматриваемом случае оптимальной является любая перестановка
вида (/1,... ,/л), где
Q -1 м
= min { S tn, + S I *= 1, • • •,и, i^k} .
L = 1 l = 2 + i
Нахождение элементов /ь /2 можно осуществить за О(пМ) опе-
раций.
7,2. Заменим исходную систему, состоящую из М приборов, двухстадий-
ной системой лоточного типа, состсящей из приборов Л и В. Каждое требо-
вание i G N оэслуживается прибором А в течение ц единиц времени, за-
тем прибором В в течение bt единш, времени, где
м-i м
at ~ 2 tlL, = S tiL, iEN.
L - i l = 2
В этом пункте приводятся некоторые условия, накладываемые на матри-
цу II tiL 'I достаточные для того, чтобы в исходной и во вновь построенной
системах оптимальное (по быстродействию) расписание определялось
одной и той же перестановкой я*.
1) Пусть я * = ( / i, / 2,..., /„ ) - оптимальная последовательность обслу-
живания требсваний в построенно! системе. Покажем, что я* является оп-
тимальной последовательностью и сля исходной системы, если
_ Р — 1 М п
^тахОг ) ~ тах { 2 + 2 tj т + 2 Чкм} •
1 < р < л fc = 1 L = 1 Р к=р + 1
Обозначим через £тах(я) общее время обслуживания требований мно-
жества N в системе, состоящей из приборов А и В, при условии, что каж-
дый прибор обслуживает требования в последовательности я = (z i, Z 2, • • •
.. . , i п ). Нетрудно видеть, что
л р — 1 М п М — 1 п
*maxW= ^ах + fipL + 2 t j м } + 2 S tiL.
L = I р к = p + 1 K L - 2 i = 1
82
Тогда
_ а Af-i « л М-1 п
^maxOO ^maxW- 2 S ^тах(^ )— S S tj^ -
L = 2 i = 1 L = 2 i = 1
“^max(ff )•
2) Предположим, что при некотором Q, 1 <Q <М - 1, матрица II tiL II
удовлетворяет условию
н н+ 1 м м-\
min { S tiL - S tjL, S tiL - S tjL} > 0, (7.6)
L = 1 L = 2 L - R + 1 L = R
(2=A1); Я = 2+1,...,М-1
i^j.
Условие (7.6) допускает интерпретацию в терминах доминантных мат-
риц. Действительно, сопоставим матрице II tiL II пару матриц 7\ и ^со-
стоящих соответственно из Q первых и М — Q последних столбцов матрицы
II tiL II. В матрице Т2 сохраним нумерацию столбцов, принятую в матрице
llflLll. Условие (7.6) означает, во-первых, что матрица Т\ либо является
1-доминантной, либо состоит из одного столбца с номером Q = 1, а во-
вторых, что матрица Т2 либо является М-доминантной, либо состоит из од-
ного столбца с номером М = Q + 1.
Так, например, матрица
10 5 6 7
8 9 4 10
И 7 7 12
удовлетворяет условию (7.6) при Q = 3, а матрица
10 3 4 16
8 7 15 8
11 1 7 20
удовлетворяет этому условию при 2 = 2 (здесь вертикальная черта разде-
ляет матрицы Ti и Т2 ).
Пусть U = (mj , и2, , им_ i) - последовательность целых чисел таких,
что 1 <м2 <. . . <м^-1 UQ ~Р ^uQ+i • ^uM-i <п. Покажем,
что в случае, когда справедливо соотношение (7.6), неравенство
р-i м п
имеет место для всех перестановок тг = (q, /2, , in) •
Доказательство проведем для 2 <Q - 2 (в случае 0=1 или Q = М-1
доказательство аналогичное).
Из результатов п. 7.1 и из (7.6) следует, что
р-i П U\ U2 р
? tfkl + ? + ZU2 + •••*
к - 1 к - 1 к к - 1 к - их к -uq_\
М п м2 + 1 п
+ . , *'кМ ? *‘к’ С + 1 + • • • + Ji tjkM
L - Q + 1 к ~ р + 1 к - р к = им— 1
6
83
Складывая эти неравенства, получаем требуемое соотношение.
3) Покажем, что для любой перестановки я = (zb z2,.. . , in)
^maxGO шах { S + S hpL + (7*7)
1 < p < n fc = 1 K £ =1 P k = p + 1 K
если существует такое a G [0,1 ], что
2-i Q H H~*
a( S tiL - S tjL) + (1 - a) ( S tjL - S tiL) > 0,
£ = 1 £ - 2 L - Q + 1 L - Q
Q = 2,..., M, H=Q+19...9 K. (7.8)
Предположим, что для некоторой перестановки я значение 7тах(я) <
</(17, я), причем не все uL в посдедовательности U = (uj, и2,..., uM-i)
равны между собой, L = 1, . . . , М - 1. Положим р = Ui, Q = max{L | L =
= 1,... ,Af, uL _i =р }, q =UQ,H-max {Z| L = Q9. ,, ,M,uL = q} .
По условию
p - 1 Q-l q-l H
S 7/1 + S ti T + S tkQ + S ti T >
fc = 1 K £ = 1 P k = p к L = Q q
P ~ 1 H q q - 1 H
>max{ S ti j + S tt L - S tikIf, S t( t + S t, L}.
k=l L=1 p k=p+l K fc=Ife L=l 4
Другими словами, имеет место система неравенств
g-1 Н- I Н q-1
S + s tiQL > 2 tipL + S tikH,
k = p + 1 * L = Q q L=2 + 1 P k = p + 1 K
Q <?-l f-1 Q-l
tipL + tiKQ > S tiki + S Ь L,
L = 2 P k = p + l k = p + l K L = 1 4
которая равносильна системе первенств
q Н-\ q-l Ч
2 tfkL S
fc = p + l£ = 2 k = p L =Q + 1
(7.9)
q - 1 Q q Q-l
S S tikL > s s
k = p L = 2 k = p + 1 L= 1
^kL •
С другой стороны, из (7.8) следует, что
Q - 1 Q
tik — \L )'
L = 1 L = 2 K 1
H Н - 1
+ (1—ot)( S tik_xL - S ^£)>0,
L = Q + 1 K 1 Q K
k = p + 1, . . . 9 q.
84
Суммируя эти неравенства, получаем соотношение
<7 2-1 <7-1 Q
а( 2 S tt L - S S ti L) +
к = p + 1 L = 1 K к = p L = 2
q — \ H q H-l
+ (l-a)(S S tikL - S S ^L)>0,
fc = p L = 0 + 1 K к = p + 1 L = Q K
которое противоречит системе неравенств (7.9).
Положим Uq =uq+i = ... = ин = P, если
p-1 H q q-\ H
S ti+ S ti L + S tikH > S I + s ti L,
Jt = 1 L = 1 p к = p + 1 k = \ L = 1 4
и Ui = u2 = . . . = Uq-x = q - в противном случае; остальные uL оставим
без изменения. Повторяя описанные выше рассуждения конечное число раз,
получаем соотношение (7.7).
Например, матрица
10 7 12 1411
6 9 6 21
12 8 15 23II
удовлетворяет (7.8) при a Е [1/2, 2/3]. Для любой перестановки требова-
ний имеет место равенство (7.7), причем для перестановки (1, 3, 2) мак-
симум в (7.7) достигается при р = 2, а для всех остальных перестановок —
при р = 1.
Таким образом, условия, приведенные в п. 2) и 3), являются достаточ-
ными для выполнения соотношения (7.7) при всех перестановках я. Сле-
довательно, согласно п. 1) оптимальная перестановка я* может быть найде-
на при помощи алгоритма из п. 1.3. § 1 этой главы. Трудоемкость ее по-
строения не превосходит О(пМ + п log п) операций.
73. Предположим, что при некотором Q, 1 — 1, матрица II tiL II
удовлетворяет условию
Q 2-1 R R + 1
min{ S tiL — S tjL, S tiL - S tjL} > 0,
L = H+ 1 L=H L = Q + 1 L = 2 + 2
(7.10)
H = l,...,e-I (G^l); Л = С+1,...,7И-1 (G¥=Af-l);
Условие (7.10) так же, как и условие (7.6), допускает интерпретацию
в терминах доминантных матриц. Пусть матрицы Л и Т2 те же, что и в
п. 7.2 б). Условие (7.10) означает, во-первых, что матрица 7\ либо являет-
ся С-доминантной, либо состоит из одного столбца с номером Q = 1, а
во-вторых, что матрица Т2 либо является (Q + 1)-доминантной, либо со-
стоит из одного столбца с номером М = Q + 1.
85
Оказывается, что при некотором Q, 1 <Q — 1,
Q-1 и
7тах(тг) = 2 ti L + max { S ti Q +
L=1 1 l<u<n fc = 1 *
n M
+ + ^пЬ
k = u L = Q + 2
(7.П)
для всех перестановок я = (fn Z2, . . . , Z„) тогда и только тогда, когда
справедливо условие (7.10).
Ограничимся доказательством достаточности этого утверждения. Будем
счйтать, что 2 < Q - 2 (в случае Q = 1 или Q = М - 1 доказательство
аналогичное). Выберем произвольную перестановку я и рассмотрим такую
последовательность U = (Ui, и2, . .., ^м-1) целых чисел, что 1 ^их ^и2 <
Из (7.10) и п. 7.1 следует, что
U2 UQ
2 J*fci + 2 r,-fe2 + ••• + 2 tfkQ <
k - 1 t = Uj A - uq_ j
n
s
k=им-I
2-1 UQ
2 ti l + 2 tikQ,
L = 1 1 k = 1
"2+1 "2+2
2 fik, C+i + 2 r»fc, <2+2 + • • • +
k = UQ k = и 2+1
n M
C 2 fik, <2+1 + f 2 + tit.
Складывая эти неравенства, получаем
2-1 UQ п
tL + j:tlkQ+i:
т = i 1 k - 1 k = и
M
В силу произвольности последовательности U заключаем, что имеет
место соотношение (7.11).
Оптимальная перестановка монет быть построена следующим образом.
Найдем перестановку я', которой соответствует наименьшее общее время
обслуживания требований множества N системой поточного типа, состоя-
щей из двух приборов Q и Q + 1,в предположении, что процесс обслужи-
вания начинается в момент времен! d = 0.
Если Q = 1 (Q = М — J), то, 1спользуя (7.11), вычислим наименьшее
общее время обслуживания требований при условии, что требование /,/ =
= 1, . . . , п обслуживается последним (соответственно первым), а осталь-
ные требования обслуживаются в последовательности, задаваемой переста-
новкой я1. В качестве искомой следует выбрать ту из рассмотренных п пере-
становок, которой соответствует таименьшее значение ^тахОО- Трудоем-
кость построения я* не превосходи 0(пМ + п2) операций.
Если 2 < Q - 2, то рассмэтрим п(п - 1) /2 последовательностей,
в которых требование i обслуживается первым, требование / — послед-
ним, а остальные требования - согласно перестановке it1, i = 1, . . . , п,
j = 1, . .. ,п, i Ф] .В качестве искомой выбирается перестановка с наимень-
86
шим значением ^maxW- Трудоемкость ее построения не превосходит
0{пМ + л3) операций.
7.4. П ример. Рассмотрим задачу построения оптимального по быстро-
действию расписания обслуживания четырех требований в системе поточ-
ного типа из пяти приборов. Предполагается, что обслуживание начинает-
ся в момент времени d = 0, все приборы обслуживают требования в одной
и той же последовательности, а матрица II tiL II имеет вид
1 6 6 3 1
5 7 4 10 2
6 5 9 2 3
2 8 7 8 1
Нетрудно проверить, что эта матрица удовлетворяет условию (7.10) при
Q = 3. Для нахождения перестановки я*, определяющей оптимальное рас-
писание, воспользуемся подходом, описанным в п. 7.3.
При помощи алгоритма из п. 1.3 § 1 этой главы отыщем перестановку
я1, которой соответствует наименьшее общее время обслуживания четырех
требований в системе, состоящей из приборов 3 и 4. Имеем я1 = (2,4, 1,3).
Результаты последующих вычислений приведены в табл. 7.1.
Таблица 7.1
7Г ^maxOO j 7Г *тах(я)
(1,4, 3, 2) 58 (2,4, 1,3) 49
(2, 4, 3, 1) 49 (3,4, 1, 2) 69
(1,2, 4, 3) 48 (2, 1,3,4) 59
(3, 2, 4, 1) 58 (4, 1,3,2) 65
(1, 2, 3, 4) 56 (3,2, 1,4) 63
(4, 2, 3,1) 50 (4, 2, 1, 3) 50
В качестве я* выбирается перестановка (1, 2, 4, 3), ^тах(я*) = 48.
7.5. Рассмотрим задачу нахождения перестановки я*, которой соот-
ветствует наименьшее значение суммарного взвешенного времени
п
S л (я) обслуживания.
к = 1 к
Покажем, что при некотором Q, 1 < Q < Л/,
п п 2-1 л м
2 = 2 2 f»>b+ 2 + 2 (712)
к = I К К к = 1 К L= I 1 j = I 1 L = Q + 1 *
для всех перестановок я = (/j, z2, ... , in) тогда и только тогда, когда
матрица \\tiL II длительностей обслуживания является Q-доминантной.
Действительно, соотношение (7.12) имеет место для всех перестановок я
тогда и только тогда, когда для всех я
2-1 к м
^к^^ "" tijQ + — 1, . . . , М.
К L — I 1 / = 1 7 L = 2 + 1
87
Как следуетиз п. 7.1, последнее утверждение эквивалентно тому, что
матрица II tiL II вляетея 0-доминантной.
Оптимальная перестановка тг* может быть построена следующим обра-
зом. Найдем поестановку я', которой соответствует наименьшее значение
л к
S wik S tjQ. Для этого достаточно упорядочить требования по не-
к = 1 / = 1
возрастанию зняений WtfttQ, i G N.
Если Q = 1, о я* = я'. Если Q > 1, то я* содержится среди п перестано-
вок, в которыхэлемент /, j = 1, . . ., и, стоит на первом месте, а остальные
элементы упордочены согласно перестановке я'. Используя (7.12), для
каждой из них южно вычислить значение суммарного взвешенного време-
ни обслуживани и выбрать наилучшую перестановку я*. Трудоемкость ее
построения не иевосходит О(пМ + и2) операций.
7.6. П р и ive р. Рассмотрим задачу построения расписания обслужива-
ния четырех трбований в системе поточного типа из пяти приборов, при
котором суммрное взвешенное время обслуживания S (я) ми-
i е N
нимально. Предполагается, что обслуживание начинается в момент времени
d = 0;, все приоры обслуживают требования в одной и той же последова-
тельности; Wi --w2 = 2, w3 = 5, vv4 = 4, а матрица II tiL II имеет вид
1 6 6 37
5 7 4 62
6 5 9 45
2 8 7 3 5
Нетрудно прверить, что эта матрица является 3-доминантной.
Для нахождния перестановки я*, определяющей искомое оптимальное
расписание, воаользуемся подходом, описанным в п. 7.5.
Упорядочимгребования по невозрастанию значений i = 1,2, 3, 4.
Получим пересановку я' = (4, 3, 2, 1). Результаты последующих вычисле-
ний приведены! табл. 7.2.
Таблица 7.2
тг S Wftf(7r) i(=N тт S Wftf(7T) if=N
(4, 3, 2, 1) 443 (2, 4, 3, 1) 473
(3, 4, 2, 1) 457 (1. 4, 3, 2) 430
В качестве 7i‘ выбирается перестановка (1,4, 3, 2).
7.7. Рассмотим задачу построения перестановки я*, которой соответст-
вует наименыее значение общего времени обслуживания fmaxW при
условии, что здержки в обслуживании каждого требования запрещены.
88
1) Как следует из соотношения (3.2) § 3 этой главы, для любой переста-
новки я = (z‘i, z2, in)
n - 1 Q 2-1 n
4ax(’T)= 2 max < 2 tikL - S hk+iL^ 2 tinL
k = 1 1 L = 1 L = 1 k = 1
n - 1 Q 2-1
= S max {max { 2 tikL - S
k = 1 2<Q<M L =2 L = 1
п — 1 М
+ S tikl + S tinL (7.13)
к = 1 L = 1
Пусть tk{n) означает момент завершения обслуживания (возможно,
с задержками) двух требований ik и z\ + 1 в рассматриваемой системе при
условии, что каждый прибор сначала обслуживает требование ik, а затем
требование г\ + 1, и обслуживание требования ik прибором 1 начинается
в момент времени d = 0, к = 1,..., п — 1.
Очевидно,
Q м
tk(n)= max { S tikL + S Z4+1Z,K
1 <Q<M L - \ L = Q
Преобразуя последнее соотношение, имеем
Q 2- i
ГЛ(7г) = max {max { S L - S rik+iL>°B +
2<Q<M L = 2 L = 1
M
+ + 2 ‘ik + iL’ к = 1,...,и- 1. (7.14)
L = 1
Соотношение (7.13) можно переписать в виде
п — 1 п — 1 М
7тах(я) = s г» - s S tikL. (7.15)
/с = 1 к = 2 L = 1
2) Покажем, что при некотором Q, 1
Q - 1 п М
^maxGO ~ L + 2 ^ikQ + (7-16)
L = 1 к = 1 L = Q + 1
для всех перестановок к тогда и только тогда, когда матрица || tiL || дли-
тельностей обслуживания является Q-доминантной.
Вначале докажем необходимость. Пусть при некотором Q, 1 < Q < М,
соотношение (7.16) справедливо для всех я. Используя метод математиче-
ской индукции, покажем, что для всех Л,1<£<л — 1,и всех я
Q М
tk(7() = S + 2 tik+iL-
L = 1 L = Q
(7.17)
89
Пусть т>(я) означает сумму элементов строки матрицы || tiL ||,вхо-
Q
дящих в (7.15) Из (7.15) следует, что Ti (я) = S tikL и, следовательно,
L
tk (я) удовлетворяет (7.17) при к = 1.
Пусть (7.17) справедливо для всех к, £ = 1,...,р—1,1<р<и-1.
Покажем, что эо соотношение справедливо и при к=р.
Предположи!, что
н м
= S '/,£ * 2
L = 1 L = Н И
Тогда
нм м
ТР<5) = 2 h L + tipL - 2 ti L.
L = } L = Q L = 1
С другой стор<ны, в силу (7.16) тр(я) = hpQ. Следовательно, H = Q и
(7.17) выполнится для всех к = 1, ..., п - 1.
Последнее утверждение в свою очередь означает, что матрица || tiL ||
является доминантной (см. п. 7.1).
Для доказательства достаточности заметим, что из п. 7.1 следует, что
для всех я имеет место соотношение (7.17). Подставляя его в (7.15),
получаем требу мое соотношение (7.16).
Оптимальна; перестановка я* может быть построена за О(пМ) операций
так же, как и вя. 7.1.
7.8. Заменим исходную систему, состоящую из М приборов, двухстадий-
ной системой d точно го типа, состоящей из приборов Л и В. Каждое требо-
вание i € N бел уживается прибором А в течение а{ единиц времени,
затем (без задожки) прибором В в течение единиц времени, где
м -1 м
di — S bi — S tn,, i £ N.
L=1 L-2
Пусть ?тахя) означает общее время обслуживания требований множе-
ства N в пострюнной системе. Как следует из п. 3.5 § 3 этой главы,
г- 1 М М-1
finaxOO = S max { S tlkL - S ^/k+1z,,0} +
1 L = 2 L = 1
M n Mr 1
+ tini + s S tikL.
L = 2 к = 1 L = 1
Если для люой перестановки я в исходной системе
-1 м м-1
^maxW = max tikL “ + 0^ +
1= 1 L = 2 L = 1
п - 1 М
+ S tikl+ S tinL, (7.18)
к = 1 L = 1
90
то оптимальные по быстродействию расписания в исходной и вновь по-
строенной задачах определяются одной и той же перестановкой я*.
В этом пункте приводятся достаточные условия выполнимости (7.18)
для всех л.
1) Пусть для любых двух требований i и /, i G N, j G N, i Ф j , най-
дется такое Q , 1 < Q — 1, что
H H+l
min { S tiL - S tjL,
L = 1 L =2
H H+\
min { S tjL - S tiLi
L = 1 L = 2
M M — 1
S til, - tjL} 0
L = Я + l L = R
M M — 1
L = R + 1 L = R
(7.19)
я=1,...,е-1 (e^i),+ i (e^Af-i).
Покажем, что в этом случае для всех л выполняется соотношение (7.18).
Заметим, что если (7.19) выполняется при одном и том же Q для всех
пар требований, получаем условие (7.6).
Из результатов п. 7.2, 2) следует, что для всех л и к имеет место
соотношение
м м
t (л) — max{f/fci + X 2
L = 1 L = 1
которое можно переписать в виде
м м-1 м
ГЛ(тг) = тах { S tikL - S ^k+iL,0} + tikl + S hk+1L.
L = 2 L = 1 L = 1
Подставляя это соотношение в (7.15), получаем
л-1 м м-1
^maxW “ max { S ti^L ~ +
к = 1 L = 2 L = 1
п — I п М п — 1 М
+ tikl +2 S hkL - S 2 4kL =
fc = 1 к = 2 L = 1 к = 2 L = 1
n — 1 M M — 1 n — 1 M
= S max { S tikL- S + 2 tiki + S hnL-
к = 1 L = 2 L = 1 к = 1 L = 1
3) Пусть для любой пары требований i и j, i. G N, j G N, i =£j, най-
дется такое a =a(f, j ) G [0, 1], что
Q-1 Q м
a ( 2 tjL - S tiL) + (1 — a)( S tiL -
L = 1 L=2 L = Q + 1
M- 1
- S tjL) >0, Q = 2,...,Л/- 1. (7.20)
l = Q
91
Покажем, что в этом случае для всех л выполняется соотношение (7.18).
Пусть i и j - произвольная пара требований, для которых при некото-
ром «G [0, 1] справедливо (7.20).
Тогда для всех Q, 2 < С <7И — 1, выполняется неравенство
Q 2-1 М
S tiL - S tjL < (1 -а)( S tiL - s ?/l)-
L -2 L = 1 L = 2 M M — 1 Если при ЭТОМ S tiL > S tjL,TQ L =2 L = 1 L = 1
Q 2-1 M M- 1
max {max { S - S = s tiL - S t/L
2<Q<M L =2 L = 1 В противном случае 2 2-1 L=2 L = 1
max {пцх { S tiL - S Z/L,0}} 2 < Q < M L =2 L = 1 M M- 1 = max { S tiL - S . L=2 L=1 = 0 =
Следовательно, для любой перестановки л = (и, it, in) имеют место
соотношения
Q 2-1
max {max { S tikL - 2 G>+1l,0}} =
2 < 0 < Af L = 2 L = 1
M M- 1
= max { S fikL - s tik+iL,®}>
L =2 L = 1
Сравнивая эти соотношения с (7.13), убеждаемся, что для всех л спра-
ведливо (7.18).
Таким образом, если матрица || tiL || длительностей обслуживания удов-
летворяет условиям (7.19) или (7.20) для всех пар требований i и j,
i, j G N, i & j , то оптимальная перестановка л* может быть построена при
помощи алгоритма из п. 3.5 § 3 этой главы. Трудоемкость ее построения
не превосходит 0(пМ + п log п) операций.
7.9. В заключение этого параграфа рассмотрим задачу построения пере-
становки л*, которой соответствует наименьшее значение суммарного
п _
взвешенного времени S ^^^^(л) обслуживания требований. Предпола-
к = 1
гаётся, что каждое требование обслуживается без задержек.
Покажем, что при некотором Q, соотношение
п _ п Q- 1 к М
S ™*к^ г/>2 + 2 Чкь) (7.21)
к = 1 к = 1 L = 1 /=1 £ = 2 + 1
92
имеет место для всех перестановок л = (Ji, i2 ,..., in) тогда и только тогда,
когда матрица || tiL || является Q-доминантной.
Соотношение (7.21), очевидно, имеет место для всех перестановок л
тогда и только тогда, когда для всех л
_ 51 к м
t= S f^ £ + S S ttkLi к = 1, ..., п.
L = 1 / = 1 L = Q + 1
Как следует из п. 7.7, последнее утверждение эквивалентно тому, что
матрица || tiL || является 0-доминантной.
Оптимальная перестановка может быть построена за О(п log п) опера-
ций при Q = 1 и О(пМ + п2) операций при Q > 1 таким же образом, как
и в п. 7.5.
§ 8. Приближенные алгоритмы
В этом параграфе описываются некоторые эффективные приближенные
алгоритмы решения задач теории расписаний для систем поточного типа,
гарантирующие построение расписания, имеющего ограниченную абсолют-
ную или относительную погрешность.
8.1. Пусть дана некоторая задача теории расписаний, заключающаяся в ми-
нимизации целевого функционала F(s), и s* — оптимальное расписание.
Предположим, что имеется алгоритм Ф, который по любому набору вход-
ных данных задачи отыскивает некоторое допустимое расписание s°. Каче-
ство расписания 5° будем оценивать величиной абсолютной | F(sQ) — F(s*) |
или относительной & = \F(sQ) -F(s*)\/| F(s*)| погрешности. Будем го-
ворить, что алгоритм Ф имеет априорную оценку точности, если для любого
набора входных данных задачи известна (может быть вычислена за полино-
миальное число операций) такая величина К, что либо | F(s0) —F(s*) |
либо ДСК. Ниже рассматриваются именно такие алгоритмы.
В п. 8.2 доказано утверждение, на основании которого построен алго-
ритм приближенного решения задачи минимизации общего времени обслу-
живания требований в системе поточного типа. Алгоритм отыскивает
расписание, имеющее ограниченную абсолютную погрешность. В последую-
щих пунктах описываются алгоритмы приближенного решения различных
задач теории расписаний для систем поточного типа, которые отыскивают
расписания, имеющие ограниченную относительную погрешность Д.
8.2. В систему поточного типа, состоящую из М > 2 приборов, в момент
времени d = 0 поступает множество N = {1, 2, ..., п } требований. Дли-
тельности tiL обслуживания каждого требования каждым прибором L,
L = 1, ..., М, предполагаются заданными. Обозначим max{r^L | i G ДГ,
L = 1,..., М} через t* и max { S tiL | L = 1,..., М}- через /*(А)«
г е N
В этом пункте будем предполагать, что L tiL = t*(N) для всех L,
i е N
L = 1, ..., М. В противном случае исходные длительности обслуживания
можно было бы соответствующим образом ’’удлинить”, не увеличивая при
этом значение Г*. Если s — произвольное расписание для задачи с изменен-
ными длительностями, то в качестве расписания для задачи с исход-
93
ними длительнстйми может быть выбрано расписание s, при котором
Ниже показао, что не более чем за О(п2М3) операций может быть по-
строено такоерсписание s°, что ^max(s°)—Gnax(s*)^^(X~ l)f*.
1) Докажем ледующее вспомогательное утверждение.
Пусть дано можество V, состоящее из г векторов v с m действитель-
ными компонетами. Предполагается, что || v || < 1 для всех v G V и
S v = 0. В ячестве нормы || v || вектора и может быть выбрана любая
v g v
норма, наприме максимум из модулей его компонент.
Покажем, чэ можно так пронумеровать векторы и из К, что V =
I
= {и1, v2, ..., f} и max || S vk || <т, причем трудоемкость такой
1 <1 <г к = 1
нумерации непрвосходит O(r2m3) операций.
Если г < га,го указанное утверждение тривиально. В дальнейшем пред-
полагается, что > га.
Найдем таки множества К/ С И и такие числа Ху (и), v Е Ру, j =
= га, ..., г, что С + 1 С ... С Vr = V, | Ру | = у и справедливы соот-
ношения
0 < Ху(и) < 1, v Е Ку, j = га, ... , г,
S Ху (и) j - га, / = га, ... , г,
v G Vj
S Ху (и) 0, / = га, ... , г.
vG Vj
Положим Vr = V и Хг (и) = (г — га)/г для всех v Е Vr .
Пусть найдем множества Vr, Kr ,..., Ку +1 и соответствующие числа
Хг (и), Xr_iV), ..., Ху + 1(и), где j > m. Опишем способ нахождения
множества Ку ]чисел Ху (и), и Е Vj .
Рассмотрим истему линейных соотношений с переменными д (и ):
0<д(и)<1, uGK/+1; (8.1)
S д(и)=/-тп;
(8.2)
S д(о> = 0. (8.3)
us r/+i
Многограннк, описываемый системой соотношений (8.1) — (8.3),
непуст, посколку, например,
А /
Kv)=---------v&Vj+l, (8.4)
J - AZ+ 1
является решемем системы (8.1) — (8.3).
94
Для любой вершины указанного многогранника по крайней мере / +1
соотношение из (8.1) —(8.3) должно выполняться как точное равенство.
Поскольку число равенств (8.2), (8.3) равно т + 1, то каждая вершина
многогранника среди своих / + 1 координат имеет по крайней мере j — т
координат д(и) Е {0, 1} . Если предположить, что у некоторой вершины
все координаты строго положительны, то среди этих координат имеется
не менее j — т единиц, что противоречит соотношению (8.2). Таким об-
разом, среди точек многогранника, описываемого соотношениями
(8.1) - (8.3), имеется точка (например, любая из его вершин), у которой
по крайней мере одна из координат равна нулю.
Пусть д° (и), v G Vj + i, - координаты такой точки, и0 G Е/+1 и
д° (и0) =0. Положим Vj = К/ +1 \ {и0 }, X/ (и) =д° (и), v G Vj.
Этот процесс продолжается до тех пор, пока не будут найдены множест-
во Vm и числа v Е Vm. Сопоставим вектору Vj \ K/-i номер /,
т.е. положим у7 = Vj \Vj-X, j =т + 1, ..., г. Остальные векторы пронуме-
руем числами 1,2,..., т в произвольном порядке.
Покажем, что полученная нумерация векторов v множества V является
искомой.
При 1 < / < т, очевидно,
i i
|| S vk || < S || vk || < I < т.
к = 1 к = 1
Если I > т, то
i i
|| S ^ || = II 2 vk - 2 Х/(у)у || =
к = 1 к = 1
= II S v - S Xz(y) v || <
и £ Г/ vfzVj
< S (1 -х/(у))||у|| < I - (I-т) = т.
U& Vj
Нетрудно видеть, что наиболее трудоемким этапом описанного метода ну-
мерации векторов v множества V является получение на каждой итерации
/, j = г - 1, г - 2,..., т, решения д°(и), v Е ^+1, системы (8.1) - (8.3) тако-
го, что для некоторого vQ Е К/ + 1 значение д°(и°) = 0. Опишем один из воз-
можных подходов к нахождению д°(и), vEVj+i.
Если среди значений д(и), vE ^+1, вычисляемых по формуле (8.4), со-
держится хотя бы один нуль, то можно положить д°(и) = д(и), v Е Vj+ j.
Если все д(у) > 0, vE Vj+1) то в силу (8.2) из множества Ру+1 можно выде-
лить т + 2 вектора и таких, что 0 < д(и) < 1. Обозначим множество выде-
ленных векторов через W и найдем нетривиальное решение р(и), v Е W,
95
следующей однородной системы из т + 1 линейных уравнений с т + 2
неизвестными p(v ), v G W-.
S p(v) = О,
v e и'
S p(v)v = 0.
v e w
Решение p(v ), v G И', может быть получено за О(т3) операций. Найдем
максимальное значение т° параметра т, при котором выполняются неравен-
ства 0 < д(и) + тр(и) < 1, v G И'.
Положим p(v ) =0, v G Vj+ 1 \ И', и д(и) = д (и) + т°р(и), v GK/ + 1.
Нетрудно убедиться, что р (и), v G К/ +1 является решением системы
(8.1) - (8.3) и среди д (и), v G +1, дробных величин меньше, чем сре-
ди д(и), v G К/+1.
Если среди Д (и), v G У) +1, содержится хотя бы один нуль, то можно
положить д° (и) = д (и), v G К/+1. В противном случае д(у) можно
выбрать в качестве д(и) и повторить описанный процесс. В результа-
те не более чем через j — т шагов будет получено искомое решение
д°(и), v G Г/+1.
Тем самым, общее число операций на всех г — т итерациях процесса
нумерации векторов v множества V не превосходит О (г 2 т3).
Отметим, что в случае, когда || v || < С, v G V, при найденной нумерации
векторов v множества V имеет место соотношение
i
шах || S vk || < Ст.
1 < / < г к = 1
2) Описанный выше процесс нумерации векторов может быть использо-
ван для приближенного решения задачи построения оптимального по
быстродействию расписания обслуживания требований множества N-
= {1,2,...,л}в системе поточного типа из М приборов.
Введем в рассмотрение множество К, состоящее из п векторов v вида
(hi - tn - ti3. • • . - tiM) Так как Z tiL = L = 1, . . .
i&N
.. . , M, to S v = 0, и если в качестве нормы II v II вектора v выбрать
ие v
максимум и. модулей его компонент, то II у II < t *, v G V.
Нумеруя векторы v множества V в соответствии с алгоритмом, описан-
ным в п. 1), получаем V = {v1, и2,. .. , vn} . Перенумеруем, если это необ-
ходимо, требования множества Nтаким образом, чтобы vl = (fa -
^2 ~ Ьз» • • • , ~
Из утверждения, доказанного в п. а), следует, что
к к
— (М — 1)Г*<2 tiL - S
i=l i= 1
<(7И-1)Г*, к А=1,...,Л/-1.
96
Расписание s° построим следующим образом. Все приборы обслуживают
требования в одной и той же последовательности (1,2,. . . , и), причем
r^L=(£- 1)Л/г*,^=^_1Л+£_1>£, / = 2,...,и,£=1,...,Л£
Покажем, что при этом ни одно требование не обслуживается двумя
и более приборами одновременно, т.е. tk^ < tk l+ 1Д = Ъ • . ., л, £ = 1,.. .
Действительно,
к— 1 к
t°k L+i-^L = (LMt* + S r/>z,+ 1)-((L-l)^‘+ ZtiL) =
’ 1 = 1 1=1
fc-1
=m* + 2 (^L+1 -tiL)-tkL>Mt* -(M- i)r*- e =o.
i = 1
Очевидно, Fmax(^*)>^*(^)- С ДРУГОЙ стороны, 7тах(*°) = Лм + t*(N) =
= M(M — l)r* + Следовательно, ^max($0)-^max0*) <M(M— l)r*.
Трудоемкость алгоритма построения расписания s° определяется трудо-
емкостью нумерации векторов множества К и не превосходит О(п2М3)
операций.
Отметим, что при расписании s° все приборы обслуживают требования
в одной и той же последовательности. Расписание s° может быть выбрано
в качестве приближенного решения и в том случае, когда разные приборы
могут обслуживать требования в различных последовательностях, а также
в том случае, когда допускаются прерывания. Оценка абсолютной погреш-
ности при этом не изменится.
8.3. В систему поточного типа, состоящую из М >2 приборов, в момент
времени d = 0 поступает множество N = {1, 2,... , п} требований. Заданы
длительности £L>0 обслуживания каждого требования каждым
прибором £, 1 <£ <Л£ Введем в рассмотрение класс S расписаний таких,
что для всех sGSbo временном интервале (0, *max(s)] в любой момент
времени функционирует по крайней мере один прибор. Установим неко-
торые свойства расписаний из класса S.
_ 1) Рассмотрим задачу минимизации общего времени обслуживания
гтах($)- Пусть s* - оптимальное расписание. Очевидно, s*ES. Покажем,
что_ для любого расписания sGS имеет место неравенство Д = (^тах(5) ~
~ ^max(s*))/^max(s*) — 1-
_ ( п | 1 п М
Действительно Zmax(5*)^ max] 2 tiL | £ = 1,.. . , М\> — 2 2 tiL.
li-l п М i- I L - I
С другой стороны, очевидно, ?maxG) 2 2 tiL. Отсюда
i = i L = !
?max(s)/Fmax(s°) < М, Т.е. Д < М - 1.
Покажем, что полученная оценка достижима.
Положим п = М, tiL = W, i - 1,. . . , М, i = £; tiL = eh i = 1,.. . , M, L =
= 1,. .., My i # £. Здесь W > ej, > el + ! > 0, i = 1 ,. .. , M — 1. При опти-
мальном расписании $*каждый прибор обслуживает требования в последова-
м
тельности (и, п — 1,. . ., 2, 1) и Zmax(s *) = + W + (М — 1) ei. В качестве
/ = 2
расписания 5 выберем расписание, при котором каждый прибор обслуживает
требования в последовательности (1, 2,...,«), т.е. в порядке невозрастания
7. В.С. Танаев 97
м _ м-1
значений S tiL. Имеем rmax(s) = MW + S е.. Устремляя ez, i = 1, ...
L= i i= i
..., M, к нулю, получаем Д -> М— 1.
2) Рассмотрим задачу минимизации суммарного времени обслуживания
S Fz(s). Пусть s* - оптимальное расписание. Очевидно, s* ES. Покажем,
1=1 п _
что для любого расписания имеет место неравенство Д = ( S rz(s)-
п п _ i = 1
- S7,(s‘))/ 2 <п -1.
1=1 '”1 n _ " м
Действительно, S 2 S tlL. С другой стороны, при распи-
/= 1 t= 1L= 1
_ п М п _
сании s 6 S значения rz(s) < S S tiLi i = 1,..., п, т.е. S rz(s) <
/=1L = 1 f=l
<л S S tiL. Отсюда S Tj(s)l S ^($*)<л, т.е. Д <л - 1.
i = IL = 1 i=l i=l
Покажем, что полученная оценка достижима.
ПоложимМ - 2, ZZ1 = е,i = 1,... , л; tx2 = W, ti2 = 6,z = 2, . . . , п. Здесь
О < 6 < е< W/п2. При оптимальном расписании s* оба прибора обслужи-
вают требования в последовательности (2, 3, ... , л, 1). При этом
S ti(s *) *= (е + 6) + (2е + 6) + . .. + ((и — 1) е + 6) + (л е + IV) = л (и + 1) е/2 +
i = 1
+ (л — 1) 5 + W. В качестве расписания s выберем расписание, при котором
оба прибора обслуживают требования в последовательности (1,2, . . . , л).
Отметим, что это расписание будет оптимальным по быстродействию и
может быть получено при помощи алгоритма из п. 1.3 § 1 этой главы.
Имеем = W + е + (z - 1) 6, т.е. S = п (IV + е) + (л - 1) п6/2.
Устремляя е и 6 к нулю, получаем Д~>л - 1.
8.4. Опишем алгоритмы построения такого расписания s° ES, при кото-
ром Д = (?max(s°) - Fmax(s*))/Fmax(s*) </и - 1, где/n =ГЛ//2Ъ и запись
Га] означает наименьшее целое число, не меньшее а.
1) Пусть процесс обслуживания каждого требования iEN каждым
прибором L, l<L<Af, протекает без прерываний и последовательности,
в которых приборы обслуживают требования, могут быть различными для
разных приборов.
Если число приборов М нечетно, то множество приборов дополним
фиктивным прибором М + 1, положив tit м + 1 = 0, z ЕN. Разобьем множест-
во приборов на m пар вида (2L — 1,2L), L = 1,... , ш. Каждую пару прибо-
ров указанного вида будем интерпретировать как двухстадийную систему
поточного типа, в которую в момент времени d = 0 поступает множество
требований W = { 1,2,..., л } .
Согласно алгоритму из п. 1.3 § 1 этой главы найдем последовательность
которой соответствует оптимальное по быстродействию расписание
обслуживания требований множества N в системе поточного типа, состоя-
щей из приборов 2L — 1 и 2£, L = 1,. .., т, с общим временем обслужи-
вания, равным l)- Искомое расписание $° определим как расписание
98
из класса S, при котором приборы 2L — 1 и 2L обслуживают требования
И последовательности , L = 1,... 3 т. Трудоемкость построения s° не
превосходит 6>(wJHlog п) операций.
Оценим величину относительной погрешности Д построенного расписа-
ния $°. Очевидно, 7inax(s*) > тах{/(я£,) | L = 1, ..., т}. С другой сто-
га
роны, fmax(j0) £ ? /Оъ) < т тах{/(яь) | L = 1, . . ., т}. Тогда
KnaxO°)/Fmax(S*)<"’> Т.е. Д<7П-1.
Покажем, что полученная оценка достижима. Положим М = 3, tir = 6,
tt2 = Ьз = 0, i = 1,. .., п - 1; tn 1 = tn2 = е, tn 3 = (п - 1) IV. Здесь W > е >
> 6 > 0. При оптимальном расписании 5* приборы 1 и 2 обслуживают
требования в одной и той же последовательности (п, 1, 2, . . . , п — 1), а
прибор 3 обслуживает требование и, причем T°3(s*) = 2e. Следовательно,
Fmax(s*) = 2е+ (и — 1) IV. Для построения расписания s° дополним мно-
жество приборов прибором 4, положив Т/4 =0,z = 1, ... , п. Убеждаемся,
что при расписании s° приборы 1 и 2 обслуживают требования в последо-
вательности (1, 2. . . . , п), которую можно найти, используя алгоритм
из п. 1.3. § 1 этой главы. С другой стороны, прибор 3 обслуживает требова-
ние п, причем Ги3(5°) = е + 6 + (п — 1) IV. Отсюда Fmax(s°) = е + 6 + 2(п — 1)IV.
Устремляя е и 6 к нулю, имеем Гтах0°)Лтах(5*) 2 =ГЗ/2*1, т.е.
Д -> 1.
Отметим, что расписание s° может быть выбрано в качестве приближен-
ного решения рассматриваемой задачи и в том случае, когда допускаются
прерывания процесса обслуживания. Оценка относительной погрешности
при этом не увеличится.
2) Пусть процесс обслуживания каждого требования iEN каждым
прибором Z, 1 протекает без прерываний, но в отличие от п. а)
все приборы должны обслуживать требования в одной и той же последо-
вательности.
Заменим исходную систему двухстадийной системой поточного типа,
состоящей из двух приборов А и В. Каждое требование i множества N
m
обслуживается сначала прибором Л в течение а^ = S tiL единиц времени,
м 1
затем прибором В в течение bj = S tiL единиц времени. Используя
L - m + 1
алгоритм из п. 1.3 § 1 этой главы, отыщем последовательность я0, которой
соответствует оптимальное (по быстродействию) расписание обслуживания
требований множества N в построенной двухстадийной системе при усло-
вии, что обслуживание требований начинается в момент времени d = 0.
Искомое расписание s° определим как расписание из класса S, при кото-
ром приборы 1,2,...,... ,М исходной системы обслуживают требования
в одной и той же последовательности я0. Трудоемкость построения s°,
очевидно, не превосходит О (пМ + п log п) операций.
Оценим величину относительной погрешности Д построенного расписа-
ния. Общее время обслуживания при расписании s° и при оптимальном
расписании s* (которое определяется последовательностью я*) обозначим
соответственно через FmaxOr°) и ^тах(я*).
7* 99
Пусть Q и Н, 1 ^т< Н ^М, - такие приборы, что S =
( 1 ( i^N
= max] S tiL I L = 1,..., ml и S tiH = max] S I L = m + 1, . . .
Ugw J । gw new
... , M|. Через /£н(я°) обозначим общее время обслуживания требований
множества N в системе поточного типа, состоящей из двух приборов Qu Н,
в предположении, что, во-первых, длительности обслуживания требований
приборами Q и Я равны соответственно исходным длительностям и tiH,
iEN, во-вторых, обслуживание начинается в момент времени d = 0 и, в
третьих, оба прибора Q и Н обслуживают требования в одной и той же
последовательности я0.
Очевидно, другой стороны,7тах(я°)<mfQH(it0).
Отсюда ^тах(я°У*тах(я*) < те. Д < т - 1.
Покажем, что полученная оценка достижима. Рассмотрим М требований
г, положив tiL = е, i Ф L, и tiL = W, i = L, i = 1,... , M, L = 1,.. . , M. Пусть
Nj — множество требований, состоящее из k > 1 экземпляров требования i
м
указанного вида, i = 1,..., М. Положим N = U Нетрудно убедиться,
i = 1
что я* = (ялтм,яЛгм_1>... и следовательно, Гтах(я*) = kW +
+ (М- 1)(к + 1)е. С другой стороны, я0 = (itNm +1,itNm + 2, . . . , я^,
Ядг,, Ядг,, - • •, nNm) и, следовательно, 7тах(я°) = mkW + (М - I + кт) е.
Устремляя е к нулю, имеем ^maxC71"0)/^maxC71*)т.е. Д -> т — 1.
Аналогичный подход может быть использован для приближенного
решения задачи построения оптимального по быстродействию расписания
без задержек в процессе обслуживания каждого требования. В этом случае
в качестве расписания s° выбирается расписание из класса S, при котором
все приборы обслуживают требования в одной и той же последовательности
я0. Эта последовательность отыскивается по алгоритму из п. 3.5 § 3 этой гла-
вы. Трудоемкость построения и в этом случае не превосходит О(пМ +
+ п log л) операций, а относительная погрешность Д — 1.
8.5. Рассмотрим задачу минимизации суммарного времени обслужива-
ния требований. Опишем алгоритм построения расписания s° Е 5, при
котором Д = ( Siy(s0)- S 7}(s*))/ S
i = 1 i = 1 i- 1
Пусть я0 — перестановка требований, упорядоченных по неубыванию
м
значений S Расписание s° определим как расписание из класса S,
L = 1
при котором все приборы обслуживают требования в одной и той же после-
довательности я0.
Оценим величину относительной погрешности Д построенного расписа-
ли м
ния. Не нарушая общности, будем предполагать, что S tiL < S t2L <
l = i l = i
M Z м
S г„£,т.е.я°= (1,2,..., и). Тогда F.(s°) < S S tkL, i =
Ь=1 fc=1L=1
100
п _ п i М
• 1,...,м, и следовательно, 2 fi(s0)< 2 2 2 tk£. Пусть я* =
1=1 /= 1 к- 1L = 1
• (G, /а,. .., in) ~ перестановка, определяющая оптимальное расписание s*.
j м j м
Тогда ь. (s*)>( 2 2 tikL)lM>( 2 2 tkL)!M. Таким образом,
7 \ = i£=i к fc=l£=l
2 F/(s*)>( 2 2 2 tkL)lM. Следовательно, 2 Ff(s0)/ 2 7j(s*) < М
/«1 i = Ifc = 1 £ = 1 i= i /= i
и Д <M- 1.
Покажем, что полученная оценка достижима. Положим M=2,tV=
« {1, 2,..., 2п } ; tir = W, = 5, z = 1,... , м; = е, ti2 = W,i= п + 1, . . .
. . . , 2п. Здесь 0 < 5 < е < W/n2. Очевидно, я0 = (1, 2,..., 2п). Тогда при
расписании s° имеем
^•(5°) = /^+ 5, i = 1,. . . , м,
F/(s°) = iW + е, i = п + 1,... , 2 м,
2" _ 2п
поэтому 2 ^(5°) = s iW + nb+ne.
/=1 1=1
Нетрудно проверить, что в качестве s* можно выбрать расписание, при
котором оба прибора обслуживают требования, например, в последователь-
ности я * = (п + 1,1, п + 2, 2,.. ., 2п, п). При этом
7j(s*) = zW + S + ze, i= 1,. .. , м,
7i(s*) = (z - п) И/ + (i - п) 6, i = п + 1,. .., 2м.
Поэтому 2 7I(s*) = 2 2 zTV + 2 2/е + м5.
i=i i=i i=i
Устремляя е и 5 к нулю, имеем 2 tj(s°) / 2 f/(s*)
i£N i£N
-> 2м (2м + 1) W/2n (м + 1) W, т.е. Д -> 1 при м -> °°.
§ 9. Библиографическая справка
Системы поточного типа принадлежат к числу наиболее известных много-
стадийных систем, изучаемых в рамках теории расписаний.
Далее предполагается (если не оговорено противное), что требования
поступают в очередь на обслуживание в момент времени d = 0, длительности
обслуживания tiL > 0 и t* = max {tiL | i E.N.L = 1,... ,М}. Все требования
обслуживаются без прерываний и все приборы обслуживают требования
в одной и той же последовательности.
9.1. Задача минимизации общего времени облуживания известна в ли-
тературе как (м ХМ)-задача Веллмана — Джонсона. Свойства расписаний
для этой задачи (см. п. 1.2) приведены в [147]. В.Ф. Золотухин [110]
предложил подход, позволяющий исключить из рассмотрения заведомо
не оптимальные расписания из числа тех, при которых не все приборы
обслуживают требования в одной и той же последовательности. Большинст-
во авторов рассматривают ситуацию, описанную в п. 1.2,5). В этом случае
задача состоит в нахождении перестановки, доставляющей минимум функ-
101
ционалу (1.1), который впервые, по-видимому, встречается в явном виде
в работе Г. Яшке [609]. Задача максимизации функционала (1.1) на мно-
жестве веек перестановок требований рассматривалась Н.А. Лепешинс-
ким [188] и В. Шварцем [806]. Разнообразные свойства перестановок,
которым соответствует оптимальное (по быстродействию) расписание,
•установлены О.И. Мельниковым [200].
Алгоритм решения задачи при М = 2 (см. п. 1.3) предложен С. Джон-
соном [612] и Р. Веллманом [25, 464, 465]. Этот алгоритм можно ис-
пользовать я в том случае, когда задано число Д > 0 такое, что t®2 > Д,
i G А, [149]. Н.А. Лепешинский [187] исследовал вопрос о том, в каких
пределах можно изменять значения длительностей обслуживания, чтобы
перестановка, генерируемая алгоритмом из п. 1.3, оставалась неизменной.
Условия, прл которых любая перестановка является оптимальной, установ-
лены О.И. Мельниковым [204]. Методы нахождения всех оптимальных
перестановок предложены в [118, 201,722, 806].
Обобщение задачи минимизации fmax(s) приТИ = 2, описанное в п. 1.4,
рассмотрено С.А. Баркан [20]. Известны и другие обобщения этой задачи.
Пусть заданы длительности biL >0, riL 0 пуско-наладочных и перенала-
дочных работ, выполняемых для прибора L перед обслуживанием и после
обслуживания требования i G N этим прибором, L = 1, 2. Предполагаются
также заданными величины 0, тц >0, ^>0 такие, что при любом распи-
сании значения t^i2 - ti2 - tix > т?/, Г?2 - tix > i EN. Задачи
построения оптимальных расписаний рассматривались в [48, 178, 179]
(учитывались только значения £z), в [690] ($, = 1?/), в [671,795, 796, 799]
«/), в [613, 630, 691] ^), в [838] (6П, 5/2.), в [703] fe, тц, тп),
В [675] (М/Л).в [619] (6П)8ЙЛ/=/?,).в [789,790] (8{1,8п,т(1,тп),
в [445] («нЛд.Тп.Тй.ГО.в [178-180] (Wn, Wn.Mf).
Как правило, для каждой из указанных задач перестановка, опреде-
ляющая оптимальное расписание, может быть построена за О (л log л) опе-
раций. Как показал В.С. Танаев [336], многие из этих задач сводятся к за-
и
даче минимизации функционала max { S ailr + ft | и = 1,... , п} на мно-
* = 1 к и
жестве всех перестановок вида я = , i2, ..., /л). Если не все приборы
обслуживают требования в одной и той же последовательности, то эти за-
дачи могут оказаться АР-трудными [180]. Обобщения указанных ситуаций
на случайМ> 2 обсуждаются в [705, 790, 809].
Некоторые другие задачи построения расписаний для системы поточного
типа при М = 2 рассматривались в [441, 495]. Случай, когда на каждой из
двух стадий имеются параллельные приборы, исследуется в [56,363, 689].
9.2. Если М = 2, на множестве N требований задано отношение строгого
порядка -> в запись i -> / означает, что при любом допустимом расписании
Г/2 < , к ] то задача минимизации £тах (я) является АР-трудной,
даже если отношением -> связаны ровно два требования [657].
Пусть М = 2, на множестве А требований задано отношение строгого
порядка запись i -> / означает, что при любом допустимом расписании
tiL = Ъ 2, и G - граф редукции этого отношения.
Задача построения оптимального по быстродействию расписания в случае,
102
р Когда каждая компонента связности графа G есть либо цепь, либо одновер-
шинный граф, рассмотрена Т. Курису [632]. Случай древовидного графа G
1 исследовался Я.М. Шафранским [392, 393], Е.В. Левнером и М.Ш. Леви-
ным [176]; случай последовательно-параллельного графа G - В.С. Гордо-
ном и Я.М. Шафранским [81-83], М.Ш. Левиным [175], К. Монмой и
Дж. Сиднеем [697, 701, 774]. Я. Секигучи [770] разработал алгоритм
решения более общей задачи в предположении, что G - последовательно-
параллельный граф. Трудоемкость построения оптимального расписания
для всех указанных задач не превышает O(Hlogn). Оптимизируемые функ-
ционалы в задаче Веллмана — Джонсона при М = 2 и некоторых ее обобще-
ниях являются приоритето-порождающими в смысле [392, 699]. Систе-
матическое изложение результатов, касающихся минимизации приоритето-
порождающих функционалов на упорядоченных множествах содержится
в монографии В.С. Танаева, В.С. Гордона и Я.М. Шафранского [350].
Если G - произвольный бесконтурный граф, то задача минимизации
Fjnax (я) при М = 2 является TVP-трудной [698]. В этом случае для ее реше-
ния, а также для минимизации пооизвольного приоритето-порождающего
функционала разработаны разнообразные методы направленного перебора
вариантов [44, 394, 395, 593, 637, 699, 775]. Частные случаи задачи мини-
мизации общего времени обслуживания при М = 2, 3 и заданном на N отно-
шении порядка рассмотрены в [382, 634, 697].
Определенный интерес представляет ситуация, когда оба прибора обслу-
живают требования в последовательности, которая содержит одну или
несколько заранее заданных подпоследовательностей. Задача минимизации
jmax (я) и некоторые ее обобщения в указанном случае рассматривались
в [445, 620, 668, 670, 672, 673]. Как правило, трудоемкость построения
оптимального расписания во всех рассматриваемых случаях не превос-
ходит (9 (и log и) операций.
9.3. По-видимому, первый результат, из которого следует TVP-трудность
задачи построения оптимального по быстродействию расписания при7И> 3,
получен Э.М. Лившицем и В.И. Рублинецким [190]. Другие доказательства
этого факта можно найти в [480, 552, 657, 765]. Доказательство ^-труд-
ности в сильном смысле, приведенное в п.2.1, использует замечание
В.Г. Тимковского [354] относительно работы М. Гэри, Д. Джонсона и Р. Се-
ти [533]. Основу пп. 2.2 — 2.4 составили результаты Т. Гонсалеса и С. Сах-
ни [552].
О.И. Мельников [203] исследовал устойчивость оптимальных расписа-
ний, а также рассмотрел случай, когда все длительности обслуживания
равны нулю либо единице, и операции нулевой длительности не выполня-
ются [202].
Определенный интерес представляет задача минимизации Fmax(s) при
дополнительном условии, что каждый прибор должен функционировать
без промежуточных простоев [14, 43]. Если М = 2, то соблюдение этого
условия не приводит к увеличению общего времени обслуживания (см.
п. 1.2). Если М > 3, то задача построения оптимального расписания явля-
ется ДСР-трудной в сильном смысле независимо от того, допускаются
прерывания или нет (см. § 2, а также [317,419]).
103
9.4. Во многих публикациях исследуется задача минимизации fmax(s)
при запрещении задержек в процессе обслуживания требований. Принци-
пиальный характер различий той или иной интерпретации нулевых длитель-
ностей обслуживания подчеркивается в [596, 730, 764]. Результат, при-
веденный в п. 3.3, получен С. Сахни и Ю. Чо [764]. Утверждение из п. 3.4,1)
доказано В. Шварцем [807], уточнившим доказательство Дж. Гупты [586].
Функционал (3.2) и связь его минимизации с задачей о коммивояжере
изучены Я. Пилером [738], Н.А. Лепешинским [185, 186] и другими авто-
рами [94, 557, 662, 749, 750, 823, 824, 837]. Ю. Грабовский и М. Шиш-
ло [567, 792] свели к задаче о коммивояжере несколько более общую
задачу. В [424, 839] показано, что задача минимизации функционала (3.2)
сводится также к задаче нахождения гамильтоновой цепи максимальной
длины в ориентированном графе специального вида. Задача минимизации
общего времени обслуживания (без задержек), когда на каждой стадии
имеется несколько параллельных идентичных приборов, рассмотрена
М. Сальвадором [766].
Полиномиальный алгоритм решения задачи о коммивояжере с матрицей
расстояний вида (3.6) разработан П. Гилмором и Р. Гомори [543, 544].
Трудоемкость алгоритма в том виде, в котором он опубликован в [544],
составляет О(п2) операций [542]. Однако, как отмечено в [734], трудо-
емкость алгоритма может быть уменьшена до O(wlogH) за счет применения
на одном из его шагов быстродействующего алгоритма нахождения мини-
мального остовного дерева (см., например, [238]). Описание алгоритма
в п. 3.5 проведено с учетом этого замечания. Несколько отличается от него
алгоритм из [545], также имеющий трудоемкость O(nlogH). Последняя
работа содержит строгое обоснование алгоритма в более современном из-
ложении, чем в [544], а также достаточно подробный обзор других эффек-
тивно разрешимых классов задачи о коммивояжере. Отметим также, что
Р. Чадрасекаран [489] построил полиномиальный алгоритм проверки
выполнимости условий (3.6) для произвольной матрицы.
Я. Ленстра, А. Ринной Кан и П. Бруккер [657] (см. также [651, 754])
установили АР-трудность задачи построения оптимального расписания
без задержек для переменного числа приборов. X. Пападимитриу и П. Ка-
нелакис [734] доказали аналогичный результат для М > 4. Доказательст-
во из п. 3.7 принадлежит X. Рёку [757] (см. также [656]). В [758] пока-
зано, что задача остается АР-трудной в сильном смысле при М = 3, если
допускается либо ti2 =# t^3 либо tix =# , iEN.
Если в любой момент времени для обслуживания каждого требования
каждым прибором необходимо использовать один вид ресурса, запас
которого и потребление каждым требованием в любой момент времени
известны, то задача построения оптимального по быстродействию распи-
сания (без задержек) при М = 2 и tix = ti2 = 1, z G А, может быть решена
за О(пlogzz) операций с использованием алгоритма из п. 3.5 [758]. При
этом общее время обслуживания не уменьшится, если задержки будут
разрешены (независимо от того, допускаются прерывания или нет) [758].
При М > 3 эта задача становится АР-трудной в сильном смысле [758].
Если же в каждый момент времени запас ресурса равен единице, а его
потребление каждым требованием равно нулю или единице, то при М = 2
104
Ндача построения оптимального по быстродействию расписания (без
| Прерываний, задержки разрешены) может быть решена не более чем
1М О(п) операций, если = r/2 = 1, f G 7V, и является АР-трудной в силь-
ном смысле в противном случае [470,471].
9.5. Следует отметить, что условие запрещения задержек, вообще говоря,
не эквивалентно условию отсутствия промежуточных емкостей складиро-
вания между соседними приборами. В последнем случае требование i, i GA,
не обязательно обслуживается без задержек, а может ’’пролеживать” на
Приборе L, 1 < L — 1, после завершения его обслуживания этим при-
бором в ожидании освобождения очередного прибора, причем во время
пролеживания требования i прибор L не может обслуживать никакого
другого требования. Если все приборы обслуживают требования в одной
и той же последовательности, то задача минимизации fmax(s) допускает
естественную сетевую интерпретацию, предложенную Е.В. Левнером [177].
Нижние и верхние оценки общего времени обслуживания для этой задачи
получены В.А. Струсевичем [316]. При М = 2 условия запрещения задер-
жек и отсутствия промежуточных емкостей складирования эквивалентны
[177, 749]. Случай М = 3 при отсутствии емкостей только между прибора-
ми 2 и 3 рассмотрен в [46].
Определенный интерес представляет ситуация, когда между соседними
приборами существуют емкости складирования ограниченной вмести-
мости Ь, 0 < b < и - 1 (случай b > п - 1 равносилен ’’обычному” харак-
теру обслуживания). Задача построения оптимального по быстродействию
расписания является АР-трудной при М > 2 и любом Ь, 0 < b < п - 1 [734].
Для ее решения при М = 2 С. Датта и А. Кэннингхам [510] предложили ал-
горитм, основанный на идеях динамического программирования, а С. Ред-
ди [748] - алгоритм трудоемкости О(и2е + 1), где с = и- 2- £>0.
9.6. В [93, 290, 409] рассматривается ситуация, когда для каждого тре-
бования порядок прохождения приборов задается последовательностью
1, 2,... , М, повторенной определенное количество раз. В.Г. Тимковский
[354, 356] исследовал сложность задачи построения расписаний для таких
систем и предложил приближенные алгоритмы ее решения. В. Лев и
А. Адири [660] исследовали сложность построения расписаний для систем,
в которых маршрут обслуживания каждого требования определяется
последовательностью 1, 2,... , М - 1, М, М — 1,..., 2, 1.
Ряд публикаций посвящены исследованию систем с операторами пере-
носа. Вопросы совмещения примитивных циклических процессов рассмат-
ривались Д.А. Супруненко, Р.И. Тышкевич, В.С. Айзенштатом и А.С. Ме-
тельским [4, 5, 207—209, 328, 330]. Процессы с ограниченным и неогра-
ниченным числом операторов переноса изучены А.Ш. Блохом, В.С. Та-
наевым и И.В. Романовским [27, 257, 335, 351]. (См. также [85, 86, 167,
168, 227,283].)
9.7. АР-трудность задачи минимизации максимального временного сме-
щения установлена Я. Ленстрой, А. Ринной Каном и П. Бруккером [657]
для случаяМ > 2 при запрещении прерываний.
В основу п. 4.1 положена работа Ю. Чо и С. Сахни [493]. Результаты,
изложенные в п. 4.2, получены X. Реком [758]. Более подробные сведения
об эйлеровых циклах и контурах содержатся в монографиях [111, 232,
105
377]. Если в любой момент врмени для обслуживания каждого требова-
ния каждым прибором необхщимо использовать один вид ресурса, то
задача минимизации Lmax(s) является TVP-трудной в сильном смысле
при 7И > 2 как в случае, когдг разрешаются прерывания, так и в случае,
когда они запрещены, а также при запрещении задержек [758]. Отметим,
что ЛСР-трудность указанных за,ач означает также TVP-трудность соответст-
вующих задач минимизации общего времени обслуживания неодновремен-
но поступающих в систему требшаний.
9.8. Доказательство, привединое в п. 5.1, получено М. Гэри, Д. Джон-
соном и Р. Сети [533]. Деталное доказательство утверждения из п. 5.2
можно найти в [758]. Если >азрешены прерывания, то, как указано
в [635], задача минимизации сммарного времени обслуживания являет-
ся АР-трудной в сильном смысл при 7И > 3 (доказательство не опублико-
вано) .
Если все tiL G { 0, 1 } и залсь tiL = 0 означает, что требование i прибо-
п _
ром L не обслуживается, то задча минимизации S tj(s) является NP-
i= 1
трудной при переменном числе приборов независимо от того, допускают-
ся ли прерывания и запрещены и задержки [550]. Аналогичный результат
справедлив и для минимизации ощего времени обслуживания.
Анализ сложности задачи мИимизации суммарного взвешенного вре-
мени обслуживания упорядоченого множества требований при М = 2
и = tl2 = 1, i проведен в f>53].
9.9. Упорядоченные матриц! длительностей обслуживания введены
в рассмотрение М. Смитом, С. [анвалкаром и Р. Дудеком [776]. Резуль-
таты, приведенные в п. 6.1, сорржатся в работах [776, 777] (см. также
[778]). Эффективные алгоритмы решения некоторых других задач тео-
рии расписаний с упорядочеными матрицами можно найти в [618,
729].
Ситуации, описанные в п. 6.2,2) ип.6.2, 3), рассмотрены соответственно
С. Панвалкаром, А. Ханом [77] и О.И. Мельниковым, Я.М. Шафранс-
ким [205]. Результат из п. 6.2, 1)получен В. Шварцем [810].
Тот факт, что перестановка которой соответствует оптимальное по
быстродействию расписание (60 задержек) в случае упорядоченной по
строкам матрицы длительности обслуживания, принадлежит классу пира-
мидальных перестановок (см. пб.З, 1), 2)), установили Р. Арора и С. Ра-
на [427]. В их работе приведи алгоритм построения оптимальной пере-
становки, имеющий трудоемкое О(п3М). Менее трудоемкий алгоритм,
описанный в п. 6.3, 3), предложи С Аксатером [440]. Результаты, изло-
женные в п. 6.3, 4) и п. 6.4, редставляют собой некоторое обобщение
работ С. Панвалкара и С. Вуллам [731, 732].
Задачу построения оптималдого по быстродействию расписания с
упорядоченной по столбцам мгрицей длительностей обслуживания рас-
смотрели Ф. Чин и Л. Цай [492] В этом случае полиномиальные алгоритмы
нахождения оптимальной перестновки удается построить лишь при неко-
торых дополнительных предположениях. Случай М = 3 исследовался рядом
авторов [24,69, 90, 228,236,237,13,485]. Отметим алгоритм трудоемкости
O(HlogH) для случая ti2 < min {и, ti3}, i EN, предложенный Н.И. Глебо-
вым [69], а также Ф. Б урн см и Дж. Рукером [485]. Дж. Ачугбью и
106
ф. Чин [413] предложили алгоритм трудоемкости О (и7) для случая
ttl h2 ^3, * либо tit > ti2 > ti3, i G7V. Попытка построения алго-
ритма меньшей трудоемкости предпринята в [228]. В [229] предложен
полиномиальный алгоритм построения оптимального по быстродействию
расписания без задержек, если М = 3 и tir > max{/j2, ti3}, i G TV, либо
ti3 > max{ tix ,ti2} , i ^N.
9.10. Основу § 7 составили результаты, получейные В.А. Струсевичем
[313-316, 318]. Для минимизации функционала (7.11) в [179, 325] пред-
ложены менее трудоемкие алгоритмы, чем приведенные в п. 7.3. Резуль-
таты, приведенные в § 7, являются обобщением ранее известных резуль-
татов, формулируемых в терминах последовательно доминирующих прибо-
ров (понятие доминирующих приборов рассматривается в § 2 гл. 3).
Вопросы такого рода рассматривались в [41,69, 170, 178, 179, 322,414,419,
428, 483, 484, 511, 583, 586, 609, 613, 796, 799, 800, 802, 803, 805, 808].
А. Смите и К. Бейкер [781] провели вычислительный эксперимент с целью
выяснения того, насколько часто выполняются те или иные условия, га-
рантирующие существование полиномиальных алгоритмов построения
оптимального по быстродействию расписания при М = 3. Некоторые другие
условия существования полиномиальных алгоритмов можно найти в [321,
700,710].
9.11. Утверждение о том, что векторы и множества V, удовлетворяющие
условиям из п. 8.2, 1), можно пронумеровать таким образом, что V =
= { и1, и2,... ,vr} и
i
max {|| S vk || | Z= 1,... ,r } < c(m),
к = i
известно в отечественной литературе как лемма Штейница. Идея об исполь-
зовании этого утверждения для приближенного решения задачи построения
оптимального по быстродействию расписания высказана И.С. Беловым
и Я.Н. Столиным [26], а также С.В. Севастьяновым [271, 272].
Сначала в работах [26, 73, 121, 272, 273] (см. также [215]) были пред-
ложены экспоненциальные по трудоемкости алгоритмы нахождения ука-
занной нумерации векторов множества V и соответственно построения
расписания s° с ограниченной абсолютной погрешностью 6 = Zmax(s°) -
~ Zmax(s*)- Значение 5 при этом также оказывалось довольно большим.
И. Барани [460] предложил алгоритм построения расписаний s° с 5 <
< (37И—1)(7И—l)Z*/2 не более чем за О(п2М3+пМ4) операций. С.В.Се-
вастьянов [275], а также И. Барани и Т. Фиала [461], опираясь на резуль-
тат, доказанный в [87], разработали алгоритмы построения s°, для кото-
рого 6 < М(М — l)f*. Трудоемкость алгоритма из [461] составляет
О(п2М3) операций (см. п. 8.2). Как утверждается в работе [275], трудо-
емкость описанного в ней алгоритма не превышает О(п2М2), если на одном
из его этапов применять алгоритм из [274].
Для конкретных значений М известны алгоритмы с меньшей оценкой
величины 5. Так для случая М = 3 известны алгоритмы трудоемкости
O(nlogH) и О(и), гарантирующие построение расписания s° с 5 < 3Z* и
5 < 4Г* соответственно [96, 227]. Для М = 4 в [276] предложен алгоритм
107
трудоемкости#(и2) построения расписания s° с 5 < 9Z*. Более трудоем-
кие и (или) ленее точные алгоритмы предложены в [96] (для М = 4)
и в [89, 311, >19] (для М = 3). В [18, 276] обсуждается возможность ис-
пользования днного подхода для приближенного решения других задач
теории расписний (см. также § 6 гл. 2 и § 2 гл. 3). Следует отметить
также работ) [462], где дана несколько иная интерпретация леммы
Штейница.
9.12. Осное/ пп. 8.3 — 8.6 составили результаты Т. Гонсалеса и С. Сах-
ни [552], а тагже X. Река и Г. Шмидта [759].
К. Потс [73] рассмотрел задачу построения оптимального по быстро-
действию распсания s* при М = 2 и неодновременном поступлении требо-
ваний. Им проложены три алгоритма трудоемкости #(nlogw) построения
расписания s° для которого относительная погрешность А = (штах($°) ~
- *max(s*))/Gax(s*) < L и алгоритм трудоемкости О(п3logп) построения
расписания с 2/3.
М.Я. Ковал в [138] разработал е-приближенный алгоритм трудоемкости
#((и/е)2™ ~ Минимизации fmax(s) ДЛЯ двухстадийной системы, на каж-
дой стадии каорой имеется по т параллельных (идентичных) пар при-
боров.
В [734] расмотрена задача минимизации 7max(s) при условии, что
М = 2 и межу приборами имеется емкость ограниченной вместимости
Ь, 0 < b < п -1. Предложен алгоритм трудоемкости #(wlogw) построения
расписания s° Д < b/(b + 1). _
В.А. Струсвич [317] рассмотрел задачу минимизации fmax(s) при
условии, что се приборы функционируют без промежуточных простоев.
Описан алгор1гм трудоемкости #(nfl/logw) постооения расписания s°,
_ _ и м — 1
при котором (max 0°)-ЛпахО‘))/(Лпах 0‘) + S S 1/(М-1).
1=1 L = 2
О.И. Мельнков и Я.М. Шафранский [206] рассмотрели задачу построе-
ния оптимальрго по быстродействию расписания при условии, что М = 2
и = Я/i 0'2 = ai2 + <p(f) - монотонно воз-
растающая фикция. Предложен полиномиальный алгоритм решения
с апостериори# оценкой абсолютной погрешности. Сведения о некоторых
других приблженных алгоритмах минимизации £max(s) с априорными
и апостериорыми оценками погрешности приведены в [1, 84,
356 ] . Асимпотическое поведение расписаний для этой и некоторых
других задач исследовано В.М. Португалом [248—250] (см. также
[386]). В [*80] показано, что если при расписании s° требования
упорядочены то неубыванию директивных сроков и М = 2, то
(^max(s°) " ^laxO ))/(^max(s ) + ГПаХ {Dj | Z ^N} ) С 1.
9.13. Большинство задач теории расписаний относится к классу NP-
трудных (по ценкам, сделанным в [755], их доля составляет около 80 %
от общего чипа задач). Для решения таких задач разработан ряд алго-
ритмов, основнных на общих идеях метода последовательного конструи-
рования, аналза и отсеивания вариантов. Многие из этих алгоритмов
специально раработаны для систем поточного типа. Их обзор приведен
в § 6 гл. 4.
108
В ряде публикаций предлагается сводить задачи построения оптималь-
ных расписаний к решению задач (целочисленного) линейного и нелиней-
ного программирования [58, 152, 224, 312, 433, 459, 541, 677] и теории
игр [459]. Как правило, размерность возникающих при этом задач на-
столько велика, что получить точное решение за приемлемое время весь-
ма затруднительно. Для нахождения приближенного решения в [224, 541]
предлагается отказываться от условия целочисленности переменных с по-
следующим округлением полученного решения.
Использование метода динамического программирования для построе-
ния оптимальных расписаний оказывается оправданным лишь при малых
значениях Л/ (М < 3) [25, 57, 95,411, 510, 513].
Для нахождения приближенного решения рассматриваемых в этой главе
задач разработано большое количество эвристических алгоритмов. Для
задачи минимизации общего времени обслуживания предлагаемые алго-
ритмы, как правило, состоят в назначении каждому требованию специаль-
ным образом вычисляемого приоритета и последующего упорядочения
требований согласно этим приоритетам. При другом подходе в результате
многократного применения алгоритма из п. 1.3 строится несколько пере-
становок требований, из которых выбирается наилучшая. Эвристические
процедуры, основанные на этих подходах, описаны в [134,230,233,241,312,
415, 486, 496, 579, 581, 584, 589, 712, 718, 719, 721, 735, 788, 811]. Об-
зоры, содержащие результаты обширных вычислительных экспериментов,
опубликованы в [415, 496, 663, 735]. Ряд других эвристических процедур
предложен в [28,197,255, 279,534,628,629,664,763].
А.И. Бабушкин и И.С. Белов [19] разработали алгоритм трудоемкости
О (л7) построения наилучшей перестановки требований для Л/ = 3 из числа
тех, которые могут быть получены в результате комбинирования двух
произвольных правил назначения приоритетов. В этой же работе указаны
два таких правила, комбинируя которые, за О(п3) операций можно по-
строить расписание s° с абсолютной погрешностью 5 < 4Г*. Обсуждаются
также обобщения этого подхода на случай произвольного М.
Эвристические процедуры минимизации суммарного и взвешенного сум-
марного времени обслуживания описаны в [695] и в [674,694] соот-
ветственно.
За исключением работы [473] в литературе не рассматриваются методы,
специально предназначенные для решения задачи минимизации общего
времени обслуживания при запрещении задержек. Это объясняется тем,
что указанная задача сводится к задаче о коммивояжере, которой посвяще-
на весьма обширная библиография [605, 810].
Декомпозиционный подход к решению задачи минимизации fmax(s)
обсуждается в [429, 588, 772]. В последней работе излагаются общие
принципы построения декомпозиционных алгоритмов и их связь с мето-
дом ветвей и границ. В.Н. Владимиров и С.В. Егоров [55] предложили
декомпозиционный метод решения существенно более общей задачи.
Разнообразные вероятностные методы построения расписаний для систем
поточного типа предложены в [9, 40, 75, 135, 331-334, 375, 597, 720].
Задачи со случайными длительностями обслуживания рассматривались
в [42, 504, 631,676, 723, 739, 740, 744, 835].
109
ГЛАВА 2
РАЗЛИЧНЫЕ МАРШРУТЫ
Множество N = {1, 2,... ,п} требований обслуживается в системе, со-
стоящей- из М приборов. Требование i & N поступает в систему в момент
времени dj > 0. Обслуживание этого требования включает последова-
тельных стадий. На стадии q, 1 требование i обслуживается прибо-
ром Lq € Л = {1, 2,...,7И}. Приборы Lq, 1 < q < rh не обязательно
различны. Маршруты прохождения приборов Lf = L2,--,Lr.)
предполагаются заданными для всех требований i Е ТУи могут быть раз-
личными для разных требований. Каждый прибор обслуживает требования
последовательно, причем не более одного требования в каждый момент
времени.
Процесс обслуживания требования отдельным прибором на некоторой
конкретной стадии обычно называется операцией. В этой терминологии
процесс обслуживания требования i состоит в последовательном выполне-
нии операций. Каждая операция характеризуется упорядоченной тройкой
чисел (f, L, q), i Е N, L , 1 Длительности tiLq > 0 выпол-
нения всех операций предполагаются заданными.
В зависимости от постановки задачи прерывания в выполнении каждой
операции могут либо допускаться, либо не допускаться. Если прерывания
запрещены, то расписание обслуживания требований однозначно определя-
ется моментами начала rfLq или завершения t{Lq выполнения всех опера-
ций. В этом случае tiLq = t*Lq + tiLq.
Момент начала (завершения) обслуживания требования £в системе при
расписании s будем обозначать через ^°(s) (соответственно fy(s)). Очевид-
но, что
iL .1
И г.
ri 1
независимо от того, допускаются
прерывания или нет.
При доказательстве NP-трудности задач теории расписаний в данной
главе используются следующие эталонные задачи.
Задача о разбиении. Дано множество 7V°= {1,2,..., и0 }, каж-
дому элементу i которого сопоставлено число eh и S = 2Е, где в/ и
f(=2V°
Е - натуральные числа. Пусть NZ. С TV0, тогда обозначим Ек = S в/.
i*Nk
110
Требуется определить, существует ли разбиение множества № на два под-
множества N® иЛ^ таких, что Ех -Е2.
Задача о 3-разбиении. Даны множество 2V0 = {1,2,... , Зи0 }
и натуральное число Е. Каждому элементу i G ЛГ° сопоставлено натураль-
ное число такое, что Е\Ь < < F/2 и S et = nQE. Существует ли такое
ДГ°
разбиение множества № на nQ трехэлементных подмножеств что
S е^Е, , и0?
lew,?
Задача о трехмерном п а р о со ч е т а н и и. Пусть задано
конечное множество N 0 = {1,2,.. ., и0} XNq XjV° - множество
упорядоченных троек элементов из №. Существует ли такое подмножество
Е* QE, называемое трехмерным паросочетанием, что | Е* | = nQ и две любые
тройки, вошедшие в Ef, не совпадают ни по одной компоненте?
Задача о разбиении и задача о трехмерном паросочетании являются
NP -полными [133], задача о 3-разбиении NP -полна в сильном смыс-
ле [531].
§ 1. Оптимальное обслуживание двух требований
В систему, состоящую из М приборов, в момент времени d = 0 поступают
два требования, т.е. N = { 1, 2 }. Известны маршруты L* = (L!, L2 ,..., L г^)
обслуживания требований i G N и длительности выполнения всех операций.
Качество расписания s характеризуется .значением заданной неубываю-
щей по каждому из аргументов действительно^ функции t2) при tx =
= G(s) и t2 = Z2(s). Расписание s* считается оптимальным, если ему соот-
ветствует наименьшее значение указанной функции.
Поскольку F(ti, t2) — неубывающая функция, то при поиске расписа-
ния s* можно ограничиться рассмотрением класса S расписаний s, при
которых в каждый момент времени из интервала (0, max{/i(s), Z2(s))]
обслуживается хотя бы одно требование.
1.1. Опишем широко используемую в этом параграфе форму графи-
ческого представления расписаний.
и V
Пусть Хи = S w= 1, . . . ,Г1, yv= S 1, . • ,Г2, *0
/=1 7 /=1 7
Уо = 0. Введем в рассмотрение прямоугольную систему координат на плос-
кости. Изобразим в этой системе прямоугольник W с вершинами (0, 0),
(X, 0), (0, У), (X, Y), где X =xr , Y ~Уг2 • Под длиной отрезка, соединяю-
щего точки (х, у)и(х',;/)из W, будем понимать величину р((х, y),(x't J1)) =
= max {| х* — x |, I у' - ^ |}, а под длиной ломаной линии - величину, рав-
ную сумме длин составляющих ее отрезков.
Расписание s будем представлять в виде некоторой непрерывной ло-
маной линии (траектории) о в прямоугольнике W, соединяющей вершины
(0, 0) и (X Y). Пусть точка (х, у) G о, xM_j <х <хм, 1 yv_r <
< jy, 1 г2, и Z = pCT((O, 0), (х, у))— длина траектории о от точки
(0, 0) до точки (х, у).
111
Это означает, что при расписании s к моменту времени t за-
вершено выполнение операций (1, L\, 1), (1, L2, 2), . . . , (1, L„ _j, и - 1)
и (2, L1,1), (2, L2, 2),... , (2, r, v - 1), а на выполнение операций
(1,£„,и) и (2, £у, и) затрачено х -хм_! и у -yv_1 единиц времени соот-
ветственно.
По условию задачи составляющими траектории о могут быть отрезки
следующих трех видов: горизонтальные (обслуживается требование 1),
вертикальные (обслуживается требование 2) и наклонные под углом 45°
к оси абсцисс (одновременно обслуживаются оба требования).
Через Wuv будем обозначать прямоугольник с вершинами (хм_ j, yv_ j),
(xw, уи_х), (xM_i, yv), (xM, yv). Выделим все прямоугольники W uv c
L\ = L2v. Эти прямоугольники и их внутренние точки будем называть
особыми.
Поскольку каждый прибор в любой момент времени может обслу-
живать не более одного требования, то наклонные отрезки траектории о
не могут содержать особых точек. Если прерывания при выполнении
любой операции запрещены, то траектория о вообще не может содержать
указанных точек. В этом случае она может проходить только вне особых
прямоугольников и по их границам.
1.2, П р и м е р. На стендовом полигоне необходимо провести испытания
двух новых изделий. Для каждого изделия (требования) известен порядок
(маршрут) прохождения испытательных стендов (приборов). На полигоне
имеется по одному испытательному стенду А, В, СnD. Порядки и длитель-
ности испытаний на стендах первого и второго изделий заданы соответ-
ственно в табл. 1.1 и табл. 1.2.
Прямоугольник W для этого примера изображен на рис. 1.1. Значения
xUi и- 1, 2, 3, 4, 5, и значенияv = 1,2,3,4,5,6,отложены соответственно
на оси абсцисс и оси ординат. Особые прямоугольники заштрихованы.
На этом же рисунке изображены траектории и о2> ДЛЯ расписаний
и s2, представленных на рис. 1.2, а и б соответственно. При расписании
в процессе выполнения операций нет прерываний. Поэтому траектория
Таблица 1.1
Порядок испытаний А В С D А
Длительности 2 2 8 3 6
испытаний
Таблица 1.2
Порядок А В А С А С
испытаний
Длительности 1 3 2 4 4 2
испытаний
112
Рис. 1.1
01 34 5 6 76 14 16 1613202122 25 27 2330 t
Рис. 1.2
проходит либо вне, либо по границам заштрихованных прямоугольников.
При расписании $2 допускаются прерывания. В частности, при выполнении
операции (2, С, 4) имеют место прерывания в моменты времени =
= р„г ((0,0), (4,7)) = 8 и t2 = рО1 ((0,0), (10,9)) = 16.
Моменты завершения обслуживания требований при расписании $1 и
расписании s2 принимают следующие значения:
[1(s1) = pai((0,0),(21,10)) = 23,
[2(S1) = pfft((0,0),(21,16)) = 29,
F1(s2) = P<Xj((0,0),(21,16)) = 30,
Ms2) = paj((0,0),(20,16)) = 29.
8. B.C. Танаев 113
1.3. Рассморим задачу нахождения оптимального расписания s* при
условии, что прерывания в процессе выполнения каждой операции допус-
каются в любо'1 момент времени. Как уже отмечалось, расписание s* содер-
жится в классе^ расписаний, каждое из которых может быть представлено
некоторой травсторией о в прямоугольнике IV. При этом наклонные отрез-
ки траектории т не содержат особых точек.
Покажем, что задача нахождения расписания s* (траектории а*) сводит-
ся к задаче носождения путей наименьшей длины в некотором ориенти-
рованном граф G = (Q, R), где Q — множество вершин (некоторых точек
из прямоуголыика IP), R — множество дуг.
Опишем алоритм последовательного конструирования графа G. Сопо-
ставим вершшам (xu,yv_x) и (хи_\,Уи) каждого особого прямоуголь-
ника Wuv пар.метры auv и соответственно. Эти параметры будут
принимать знаюния 1 или 0 в зависимости от того, включена или не
включена сооветствующая вершина прямоугольника во множество вер-
шин конструируемого графа G.
На первом лаге полагаем 2° = {(хо,Уо), (X У)}, х Ф> auv =Puv = О
для всех особмх прямоугольников Wuv.
Если прямсугольник И/j j является особым, то полагаем Q1 = (2° U
Щ(*о,Ух), (•ьУо)},^1 = {((Хо^о), ((х0> Ух)), ((*о, Уо), (*х, Уо))}
и «ц = 0ц = 1. В противном случае выполним следующую про-
цедуру.
Из точки (jo, уо) проводим наклонную (под углом 45° к оси абсцисс)
прямую да те; пор, пока не встретится особая точка либо не будет достиг-
нута граница грямоугольника W. Пусть указанная особая точка принадле-
жит прямоупльнику Wuu и (х, у ) - ближайшая к началу коорди-
нат точка пресечения наклонной прямой с границей прямоуголь-
ника Wuu.
EcHHX=xt_i и у = Уи_1, то полагаем Q1 = Qq U {(х, у), (хи_ь у„),
=К° и{((-*о,Уо),(^«-1,Уо-1)),((*и-1,Уи-1),С*и,Уи-1)),
(С*и-1,Уи-1)(*и-1,Уи))} и auv = 0uv=l. Если x#=xu_j иу=у1)_1) то
полагаем Q1 -Q° U {(х,у), (х, yv), (xu,yv_ J}, Rl =R° и{((х0,Уо),(х,у)),
((x,y),(x,y„))((x,y),(xu,yv_i))} и аи1, = 1. Если x = xu_j и у Ov-ьто
полагаем Q' -Q° {(х,у),(хи,у),(хи-1,У»}}, =/?° U{((хо,Уо),(х,у)),
((*. У), (xu,y), ((x, y), (xu_ j ,y„))} и 0UV = 1.
Пусть доспгнута граница прямоугольника И7 и (х, у) — точка пересе-
чения наклонюй прямой с этой границей, тогда полагаем Q1 = Q° U {(х, у)}
и R1 =R°UK(xo,yo),(x,y)),((x,y),(X У))}.
Для выпошения /-го шага алгоритма выбираем во множестве Q1 1 от-
личную от (Д У) вершину (х\ у’), из которой не исходит ни одной дуги
множества R”1. Если такая вершина существует, то к точке (х1, у'),
множеству в;ршин Ql~x и множеству дуг Rl~x применим процедуру,
аналогичную гой, которая применялась к точке (х0, у о), множеству вер-
шин Q0 и мюжеству дуг R 0. При этом если у = yv_ j и auv = 1, т.е. верши-
на (xu, yv_^e 0!~х, то полагаем Ql =Ql~1 U {(х, у), (х, уи)}. Аналогич-
но, если х и 0ми = 1, то полагаем Q1 = Ql~x U {(х, у), (хи, у)}.
114
Рис. 1.3
Если (X У) — единственная вершина из множества Q1 1 с нулевой по-
лустепенью исхода, то искомый граф G = (Q, А) построен: Q = Ql~x и
R=R1~1.
1.4. В условиях описанного в п. 1.2 примера граф G представлен
на рис. 1.3.
1.5. Обозначим через о((7) множество всех траекторий — путей в графе G
из вершины (xQ, у о) в вершину (X У). По построению каждая траектория
о С o(G) представляет некоторое расписание s Е S. Это расписание будем
обозначать через s(a). Аналогично, если s Е S и о — соответствующая ему
траектория в прямоугольнике И7,то эту траекторию будем обозначать че-
рез o(s).
Покажем, что существует оптимальное расписание s* = s(а*), где а* Е
Е o(G). Доказательство проведем по индукции относительно числа h осо-
бых прямоугольников, которые встретились в процессе построения
графа G.
При h = 0 множество o(G) состоит из единственной траектории вида о =
= ((*о, Уо)> (*, У), (X У)), где либо х = X, либо у = У, либо о-
= ((х0, уо), (X У)) • Поскольку для любого расписания s ES выполняются
соотношения ti(s)>X = ^(stp)), t2(s)> Y = t2(s(p)) и функция Fi(ti,t2)
неубывающая, то s(a) = s*.
Предположим, что утверждение справедливо при всех h ^ho, и докажем
его справедливость при h = ho + 1. Пусть на шаге 1 описанного алгоритма
первая особая точка, которую встретит наклонная прямая, проведенная
из точки (х0, уо), принадлежит прямоугольнику Wuv. Предположим для
определенности, что max {хи_ j, yv_ х} = yv_х (рис. 1.4).
Через И7 j обозначим прямоугольник с вершинами (xu,yv_t), (X, yv_t),
(хи, У), (X У), а через W2 — прямоугольник с вершинами (Уу_Р yv),
(X, yv), (yv_t, Y), (X, У). Пусть t2) = F(tt + xu, t2 + xu) и
^2 (6 > h) = F(tx + уv,t2 + yv). Рассмотрим две новые задачи: задачу 1 поис-
8
115
ка расписаниях! при х0 = Уо “ Л>-ь W и функции F(tx, t2) =
= F1(t1, t2) и ядачу 2 поиска расписания s2 при х0 =yv_ \,Уо = yv, И/ = И/2
и функции F(tу t2} = F2(tlft2).
По индуктивному предположению существуют расписания sf = s(o*) и
s2 = s (и2 ), дл j которых и * ё u(Gi), и2 G o(G2 ) и графы Gi = (Qi, Л х) и
G2 = (Q2,R2) юстроены по описанному в п. 1.3 алгоритму для задачи 1 и 2
соответственно
Обозначим <5 =(0,0),(yv_b>’v_i),(xM,^u_1)),a3t' = ((0,0), (yv_ 1, yv_ i),
(Л>-1>Уи)) и Р кажем, что хотя бы одно из расписаний s(a{, о*) или
s(o2,°2 ) являлся оптимальным для исходной задачи.
Предположи, что существует расписание s Е S, для которого выполня-
ется неравенсво
F(h(s) J2(s) = С< min {F(Ti(s(u[, of )),
^(s(oi,aj )),F(Fi(s(ct2,ct2‘)), (1-0
Траектория o(s) должна пересечь один из следующих отрезков:
а) ((хи,Уи-1)(Хл,-1)), б) ((дси,^и_1 ),(*„,/„)), в) (Ои-ь уЖ.Л,))
или г) ((yv_ 1 ,у„), (yv_ 1, У) ).
Рассмотрим например, случай, когда траектория o(s) имеет общую
точку (хи9 У) с отрезком ((xU9yv_.\), (xU9yv)) . Обозначим часть траекто-
рии o(s) от течки (0, 0) до точки (хи, у') через а от точки (хи, у') до
точки (X У)-через о". Положим4 Оо =(о{ ,(хи,^'))иоо =((*w> Уи-i )> a”)-
Поскольку прямоугольник Wuv особый, то рст*((0, 0), (хи, у')) >
> рст*((0, 0),(хи, У)) ив силу монотонности функции F(t19 t2) выпол-
няется неравенство
F(ti(s(of0, о")), 72(s(ai, о"))) <F(ti(s(o))9T2(s(o))) = С.
Отсюда и и: соотношения (1.1) получаем
F,(7i(s(ao), t2(s(oi'))) = F(ti(s(oi, ~t2(s(o^ о"))) < C<
<F(h(*(<h »*)), h(«(стI, a* ))) = F, (Fj («(af )), F2(s(at))),
что противорегит оптимальности расписания s(o*) для задачи 1.
116
Если траектория s(o) пересекает отрезок а), то получаем аналогичное
соотношение, которое противоречит предположению об оптимальности
расписания s(of) для задачи 1. Если же траектория s(o) пересекает отре-
зок в) или г), то получаем противоречие с предположением об оптималь-
ности расписания $(02) для задачи 2.
Следовательно, не существует расписания s Е S, для которого выполня-
ется соотношение (1.1). Поскольку Q = Qx U {(0, 0), , yv_i) } и
R =Ri U/?2 U {((0 0)
(yv-i ’/«))}» то (ai ’ °* ) е S(Q и (°2 > °2 ) е 5(G) > что завершает доказа-
тельство утверждения.
1.6. Каждая траектория о Е o(G) имеет вид о =((0, 0),..., (х, у), (X, У)),
где а) х = X, у < У, либо б) х < X, у = У, либо в) х < X, у < У. Обозначим
длину траектории пот точки (0, 0) до точки (х, у) через t. В зависимости
от вида траектории моменты завершения обслуживания требований при
расписании $ = s(o) вычисляются по формулам
a)F,(s) = £ Г2(х) = Г+У-^;
б) tt(s) = t + X - х, t2(s) = t;
В) 71 (S) =72(s) = t+ pa((x, у), (X, У)) = pa ((0,0), (X, У)).
Поскольку t2) - неубывающая функция, то при поиске оптималь-
ной траектории о* среди всех траекторий с фиксированной точкой (х, у)
следует выбирать траекторию с наименьшим значением t.
Таким образом, задача нахождения траектории о* сводится к
1) построению графа G = (Q, К), выделению всех его вершин вида
(Ху)и(х, У);
2) нахождению путей наименьшей длины из вершины (0, 0) в каждую
из выделенных вершин, вычислению значений ^(s) и t2{s) по приведенным
выше формулам; _ _
3) вычислению значений функции F(ti9 t2) при = ^(s) и t2 = t2(s) и
выбору пути, которому соответствует наименьшее из этих значений.
1.7. Возвращаясь к примеру из п. 1.2, рассмотрим задачу построения
оптимального расписания $* (при разрешении прерываний операций), если
F(t\, Г2) = 30Z1 +tl.
Граф G для этого примера представлен на рис. 1.3. В результате поиска
кратчайших путей из вершины (0, 0) в вершины (8, 16), (9, 16), (11, 16),
(14, 16), (15, 16), (18, 16), (21, 10) и вычисления соответствующих зна-
чений функции F(G, t2) получаем о*= ((0, 0), (2, 0), (3, 1), (4, 1), (9, 6),
(9J0), (15, 16), (21, 16)), ^(s*) = 19 + (21 - 15) = 25, T2(s*) = 19,
F(Fi(s*), F2(s*)) = 30-25 + 192 = 1111. Здесь s* =s(o*).
1.8. Перейдем к рассмотрению задачи нахождения оптимального распи-
сания $*, когда прерывания в процессе выполнения каждой операции запре-
щены. В этом случае расписание однозначно определяется моментами нача-
ла tfLq или завершения tiLq выполнения операций, причем tiLq =
= + *iLq •
Как и в предыдущем случае, расписание $* содержится в классе S
расписаний, каждое из которых $ может быть представлено траекторией
117
a(s) в прямотольнике W. Существенное отличие от рассмотренной в
пп. 1.3—1.7 задчи состоит в том, что траектория a(s) может проходить
только вне особых прямоугольников и по их границам. _
Опишем алоритм последовательного конструирования графа G =
= (Q, А), в котором существует путь, определяющий оптимальное распи-
сание s*.
Сопоставим вершинам (xu, yv_x) и (xu_19yv) каждого особого прямо-
угольника Wux параметр ?ии, который будет принимать значение 1 или О
в зависимости >т того, включены или нет указанные вершины прямоуголь-
ника во множетво вершин конструируемого графа G.
На первом гаге полагаем Q0 = {(х0 > У о), (X У)}, А0 = ф и у^ = 0 для
всех особых прмо угольников Wuv. _
Если прямотольник IV11 является особым, то полагаем yi i = 1, Q1 =
= Q° U и R1 = {((х0,у0),(х0,уг)), ((х0,у0), (х1гу0У)}.
В противном сучае выполняем следующую процедуру.
Из точки (Х), у о) прово дим наклонную (под углом 45° к оси абсцисс)
прямую до те: пор, пока не встретится особая точка или не будет
достигнута граица прямоугольника W. Если указанная особая точка при-
надлежит прям> угольнику то полагаем Q1 = Q° U {(xu_1} yv),
(хи, yv_t)}, р = R° ^{((xf>,y0),(xu_1,yv)),((x0,y0),(xu,yv-i))} И
^UV ~ 1 •
Если достииута граница прямоугольника IV и (х, у) - точка пересе-
чения наклоним прямой с этой границей, то полагаем 01 =0° U {(х, у)} и
R1 = R° U {((ЛьЗ'о)), (х, jz)),((х,у), (X, У))} .
Для выполвния Z-ro шага алгоритма во множестве Ql~x выбираем от-
личную от (X,Y) вершину (х\ у'), из которой не исходит ни одной дуги
множества R1'1. Если такая вершина существует, то к точке (х\ yf),
множеству веипин Ql~l и множеству дуг Rl~x применим процедуру,
аналогичную вй, которая применялась к точке (х0, yQ), множеству вер-
шин Qq и множеству дугR°. При этом если yuv = 1, то полагаем Ql =Ql~i,
если же 7^ =(, то полагаем Ql = Ql~* U {(xu_ityv), (x^tyv_{)}.
Если (X, Y - единственная вершина из множества Ql~* с нулевой по-
лустепенью иаода, то искомый граф G = (Q, R) построен: Q = Ql~x и
A=F~1.
1.9. П р и ive р. На рис. 1.5 изображен граф G для примера, описанного
в п. 1.2. _
1.10. В отлние от графа G не каждый путь в графе G из вершины (0,0)
в вершину (X У) является траекторией. В качестве составляющих он мо-
жет содержат! наклонные отрезки с углом наклона к оси абсцисс, отлич-
ным от 45°.
Нетрудно пжазать, что каждый такой отрезок ((х^,, yv>), (хи, yv)),
и < и, vf < v, можно заменить единственной ломаной линией, соеди-
няющей те же точки (x^,, у ,) и (хи, yv), имеющей длину, равную длине
исходного от]езка, и состоящей из двух отрезков, первый из которых
118
((хм>, yv>), (х, у)) имеет угол наклона 45° к оси абсцисс, а второй
((х, у), (хи, yv)) является вертикальным (х = хм) или горизонтальным
(y=yv)-
Тем самым каждому пути о в графе G сопоставляется единственная
траектория о в прямоугольнике И7, проходящая через вершины этого
пути и имеющая ту же длину. По построению графа G траектория о не со-
держит особых точек и, следовательно, представляет некоторое расписание
$(п) G S. Поскольку все вертикальные (горизонтальные) отрезки траекто-
рии о имеют вид ((х, у), (хм, yv)), где х = хи (соответственно у = yv),
то при расписании s(a) прерывания в процессе выполнения операций не до-
пускаются. Обозначим это расписание через s(а).
Как и в случае задачи с прерываниями операций, можно показать, что
существует оптимальное расписание s* = s(o*), где а* - некоторый путь
в графе G.
Доказательство этого утверждения аналогично приведенному в п. 1.5.
Отметим только, что для рассматриваемой задачи траектория п($) должна
иметь общую точку с отрезком ((xu, yv_i), (X Уи-i)) или отрезком
((xu-i> Уу)> (xu-i> У)) Для любого особого прямоугольника
Как и в п. 1.6, можно показать, что в рассматриваемом случае задача
нахождения расписания s* также сводится к задаче нахождения кратчай-
ших путей в графе G = (Q, R) из вершины (0,0) в каждую вершину
(х, у) Е Q, для которой х = X или у = У.
1.11. Пример. В результате поиска кратчайших путей в графе G (см.
рис. 1.5) из вершины (0,0) в вершины (4,16), (14,16), (17,16), (21,10)
и вычисления соответствующих значений целевой функции F(t19 t2) =
= 30Г1 + t2 получаем искомый путь а* = ((0,0), (0,1), (2,4), (4,10),
(12,14), (14,16), (21,16)), которому соответствует траектория а* = ((0,0),
(0,1), (2,3), (2,4), (4,6), (4,10), (8,14), (12,14), (14,16), (21,16)). Зна-
119
чения t,(s') = 27, t2(s‘) = 20, f2(s*)) = 30-27 + 202 = 1210.
Здесь s* = s(a *).
1.12. Оценим сложность описанных алгоритмов построения оптималь-
ных расписаний обслуживания двух требований М приборами.
Обозначим через Qw множество вершин графа G = (0, R), являю-
щихся вершинами особых прямоугольников IVMU. Поскольку число всех
особых прямоугольников равно гхг2у то | | не превосходит О (г2}, где
г= тах{гь г2}.
Множество вершин особых прямоугольников IVMU, для которых
min {и, и} = к, к< г, обозначим через
В графе G существует не более одного пути из каждой вершины (х, у)
множества Q А в вершину (X, У), не содержащего вершин множест-
ва Qw> отличных от (х, у) и (X У). Этот путь содержит не более чем
О (г — к) вершин множества Q\Qw. Поскольку |Q^| не превосходит
О (г — к), то все указанные пути содержат не более О {(г - к}2) вершин
множества Q \ . Следовательно, | Q \ Qw | не превосходит
<?( £ (г -fc)2)= О(г3).
к = 1
Поскольку число | Q\ вершин графа G не превосходит О (г3 ), число | R |
дуг не превосходит 2| QI и граф не содержит контуров, то для выделения
кратчайших путей из вершины (0,0) во все остальные вершины достаточно
выполнить О (г3) элементарных действий.
Очевидно, что для построения графа G требуется не более О (г3) дей-
ствий.
Таким образом, оптимальное расписание (с прерываниями) может быть
построено в результате выполнения О (г3) действий.
В случае, когда прерывания в процессе обслуживания требований запре-
щены, указанная оценка может быть уменьшена до О (г2 log г).
Действительно, вершины графа G = (Q,R) являются вершинами особых
прямоугольников Wuv (за возможным исключением вершин (0,0) и
(X У)). Следовательно, число | Q\ вершин и число | R | дуг графа G не пре-
восходит О (г2). _
Опишем процедуру построения графа G, трудоемкость которой не пре-
восходит О (г2 log г).
Пронумеруем особые прямоугольники Wuv в лексикографическом по-
рядке пар индексов (и, и). Если с — наибольший из полученных номеров,
то номер с + 1 присвоим области W* - {(х, j>)|x > 0, > У}, а номер
с + 2-области IV" = {(х,у)\х>Х, У}.
Через Q обозначим множество вершин вида (xu, yv~i) и (хм_ь yv)
всех особых прямоугольников Wuv. Положим (2 = [2 U {(0, У), (X У)} •
За О (г2 log г) элементарных действий упорядочим вершины (х, у) из мно-
жества Q в порядке неубывания величины Л(х, у) = х - у.
Все наименьшие номера особых прямоугольников, с которыми могут
встретиться (в процессе построения графа G) наклонные прямые, прохо-
дящие через вершины множества Q, можно определить в результате после-
довательного просмотра вершин множества Q в порядке неубывания ве-
личины h(x, у). Для этого будем использовать список X упорядоченных
по возрастанию номеров особых прямоугольников и областей W' и IV",
120
с которыми пересекается наклонная прямая, проходящая через рассмат-
риваемую вершину из множества £2. Перед просмотром первой вершины
множества £2 список X полагаем пустым.
При просмотре очередной вершины (х, у) G £2 включаем в список X
номер прямоугольника если х = хи__г и у = yv, и исключаем номер
этого прямоугольника, если х = хи и у = yv __i. Кроме того, если х = 0 и
у - У, то в список X включаем номер с + 1, а если х = X и у = Y, то включа-
ем номер с + 2 и исключаем из списка X номер с + 1.
За б? (log г) элементарных действий в упорядоченном списке X можно
найти наименьший номер с*, который больше номера прямоугольника Wuv.
Номер с* соответствует первому особому прямоугольнику (или областям
W', И'"), с которым ’’встретится” наклонная прямая, направленная из вер-
шины (х, у). _
Таким образом, для построения графа G достаточно выполнить
О (г2 log г) элементарных действий.
Отметим, что в случае, когда каждое требование обслуживается каж-
дым прибором не более одного раза (т.е. rt < Af, пРи /1 ^/2,
i G {1, 2}), оптимальное расписание может быть построено в результате
выполнения не более чем О(М2) действий при разрешении прерываний и
О(М\ъ%М) действий, если прерывания запрещены. Этот результат непо-
средственно следует из приведенных выше рассуждений с учетом того фак-
та, что число особых прямоугольников Wuv в данном случае не превосхо-
дит М.
§ 2. Максимальное временное смещение
В этом параграфе рассматривается задача минимизации максимального
временного смещения при обслуживании двумя приборами требований с
одинаковыми длительностями всех операций. В качестве вспомогательной
используется задача построения расписания, при котором все требования
обслуживаются не позднее заданных директивных сроков.
2.1. В систему, состоящую из двух приборов А и В, в момент времени
d = 0 поступает множество N = {1, 2,..., и} требований. Маршрут L* об-
служивания требования i G N представляет собой чередующуюся последо-
вательность приборов (L{ , L\,. . ., L,), в которой Zg G {А, В}, q =
... ,rh и L‘q =ALlq+i, q = 1,... ,rt - 1.
Длительности всех операций предполагаются одинаковыми (не нарушая
общности, дх можно считать единичными). Прерывания в процессе выпол-
нения каждой операции запрещены. Известны директивные сроки D( об-
служивания требований i6N.
Необходимо построить расписание s *, которому соответствует наимень-
шее значение функционала
imax (s) = rnax{7j-(s) -Djii G N},
где tj(s) — момент завершения обслуживания требования i прибором Llr,
при расписании s, a 7z(s)-D/ - временное смещение в обслуживании
требования /.Расписание s* будем называть оптимальным.
При решении поставленной задачи можно ограничиться рассмотрением
класса $ расписаний $, при которых каждая операция начинается (изавер-
121
шается) в целочисленные моменты времени и в каждый момент времени t,
О < t < rmax (s), выполняется хотя бы одна операция. Здесь, как и раньше,
4ах (5) = max{F/(s)| i G TV}. В этом параграфе операции будем обозначать
через (г, q) (требование i G У на стадии q, 1 < q < ri9 обслуживается
прибором L G {А, В}, однозначно определяемым значениями z, q и!*).
Символ 7 будем употреблять для обозначения простоя прибора.
Присвоим временным интервалам единичной длины, начиная с момента
п
времени d = 0, номера 1, 2,. .., R, где R = S rt. Интервал с номером t
z=i
имеет вид (t - 1, t ].
Очевидно, что для любого расписания s G S выполняется неравенство
£max(s) Я. Для задания расписания s достаточно указать две последо-
вательности вида а = («х, а2, • • •, «#) и /3 = (01,02, • • •, Pr) > где at =
= (z, q) (0t = (z, q)), если операция (z, q) выполняется во временном
интервале с номером t и Lq = А (соответственно Llq -В}. Если в ука-
занном временном интервале прибор А (прибор В) простаивает, то at = у
(соответственно = 7). Поскольку общее число операций равно А, то
суммарное число символов у в последовательностях а и 0 равно R.
2.2. Опишем алгоритм построения оптимального расписания.
Каждой операции (z, q} сопоставим вес
«(’>«) = Di - rt + q. (2.1)
Содержательно u(z, q) означает самый поздний срок (возможно, отрица-
тельный) завершения выполнения операции (г, q), при котором не нару-
шится директивный срок Dt обслуживания требования z, если операции
(z, q + 1), (z, q + 2),. .., (z, rf) будут выполняться непрерывно одна за
другой (начиная с момента времени u(z, q)).
Сформируем список X = ((/1э 44), (z2, q2),...» (iR, qR)) всех опе-
раций (z, q), q = 1,..., rz, z G N, упорядочив их по неубыванию весов
y(z, q). Заметим, что по определению величины u(z, q) порядок следова-
ния операций в списке X не противоречит порядку следования операций
при обслуживании каждого требования z EN.
Построим расписание, соответствующее списку X. На каждом шаге ал-
горитма для очередной операции (z, q) из списка X будем находить вре-
менной интервал ее выполнения. При этом будем использовать следующие
параметры: для каждого требования i е N параметр t(i) будет обозна-
чать номер единичного интервала, в течение которого выполняется опе-
рация (z, q - 1); параметр Т(£) будет обозначать наименьший но-
мер единичного интервала, в течение которого прибор L = L*q простаи-
вает.
Первоначально полагаем Т(А) = Т(В) =1, at =7 для всех t = 1,...
..., R и t(i) = 0 для всех z G N, На первом шаге алгоритма в списке X вы-
бираем первую по порядку следования операцию (zx, qr). Очевидно,
qi = 1.Если£х1 =Л,тоах = 7 заменяем на ах = (zx, 1) и полагаем Г(Л) =2
и t (z\) = 1. Если L\' = В, то =7 заменяем на 0Х = (zx, 1) и полагаем
Т(В) = 2 и t (z 1) = 1.
122
Пусть после выполнения т - 1, 2 < т < R, шагов построены некоторые
последовательности а и Р. На /и-ом шаге в_ списке X выбираем очередную
операцию (im,qm) и вычисляем значение t по формуле
7 = max{r(im) + l, Т(£^)}. (2.2)
Пусть для определенности = Л, тогда полагаем £(zm) = t и а- =
= (zm, Остальные компоненты последовательностей а и Р оставляем
без изменения. Если t = Г(4), то просматриваем подпоследовательность
ау+2,..., R, начиная с компоненты до первой по порядку
следования компоненты а = 7, и полагаем Т (А) = t'.
Обозначим последовательности а и Р, полученные в результате выпол-
нения R шагов описанного алгоритма, через а = (cq, а2> •»•, <*r) и Р =
= (P1,P2,---,PR)-
2.3. Покажем, что последовательности а и Р определяют некоторое
расписание из множества S.
Очевидно, каждая операция (z, q), q = 1,..., rz, i G TV, встречается в
указанных последовательностях не более одного раза. Покажем, что каж-
дая операция встречается точно один раз в соответствующей последова-
тельности 5 или р.
Для этого достаточно показать, что если на шаге m алгоритма t(im) +
+ 1 > то при L1^ = А компонента ar(/m) + I = 7, а при = В
компонента Pt(/ ) +1 = 7- Для определенности рассмотрим случай = А
и докажем вначале следующее вспомогательное утверждение.
Если в процессе выполнения алгоритма на шагет компонента a t после-
довательности а равна у, то из равенства (*k+\ = (i, q) при t и q>\
следует равенство Pk = (i,q - 1) •
Для доказательства справедливости этого утверждения воспользуемся
методом математической индукции относительно числа к.
Утверждение справедливо при к = t. Действительно, если af+1 = (z, q)
и Pt Ф (z, q - 1), то выполнение операции (z, q) должно быть назначено
раньше интервала времени с номером t + 1 (например, в интервале с но-
мером t, поскольку Qf=7).
Предположим, что утверждение имеет место для всех к < £°, и пусть
aJt°+i = ВыбеРем максимальное значение Л, для которого t
< к° и ah = 7. По индуктивному предположению Рк_г и ак - последо-
вательные операции по обслуживанию одного и того же требования для
каждого kt h + 1 < к < кР - 1.
Предположим, что # (i,q - 1). Тогда для каждого к G { Л, h + 1,. ..
.. ., kQ - 1} компонента Рк Ф (z, q), q е { 1, 2,..., г,}, поскольку Рк и
а*+1 являются операциями по обслуживанию одного и того же требо-
вания при h < к < кР — 1 (рис. 2.1).
Следовательно, выполнение операции (z*, q) должно быть назначено в
интервале времени с номером h или раньше. Это противоречит предполо-
123
жению о том, по £fco+1 = (Z, <?), и завершает доказательство вспомога-
тельного утверждения. .
Вернемся к доказательству равенства at ) +1 = 7 ПРИ £= .
Предположил, что У- неравенства t(im) + 1 > Т(А)
следует, что qn >1. Непосредственно по определению параметров Т(А)
и t(im) получам «г(л) = 7 и 0t(im) = Vm, 4m - О- ТогДа в СИЛУ Д°ка'
занного утверждения и + 1 являются операциями по обслу-
живанию одною и того же требования im, т.е. что
противоречит гредположению о том, что на шаге т из списка X выбира-
ется операция (т, qm).
прибо^В
Zz i2
прибо/А
Рис. 2.1
Следователью, каждая операция (/,#), q = 1,..., гь i G N, точно
один раз встречается в соответствующей последовательности а или 0.
По построению порядок следования операций в последовательностях
а и (3 не противоречит маршруту (L{, Ll2,..,, обслуживания требо-
вания i G TV. При этом если для некоторого t£ {1,2,1} значе-
ние ak = Pt = у,то at+1 =0t+1 =7.
Таким обраюм, последовательности а и 0 определяют некоторое рас-
писание s из множества S. Это расписание обычно называется списочным
или Х-расписанъем.
2.4. Покажеи, что расписание s является искомым оптимальным рас-
писанием.
Для этого дфстаточно доказать, что из условия существования расписа-
ния, при которм все требования обслуживаются в заданные директивные
сроки, следует что и Х-расписание s является допустимым относительно
тех же директтвных сроков. Действительно, если s* - оптимальное рас-
писание, Г = Lnax(s*) и = £Х + Г, i= 1,. . . , и, то s* является допус-
тимым расписанием относительно модифицированных директивных сро-
ков D- (т.е. ф*) < D'it i = 1,... , п) и хотя бы при одном i G {1,2,...
... ,п} . Если i = 1,. . . ,и, то £max(s ) < Z*, т.е.
s — оптимальнее расписание.
Покажем, что для существования допустимого (относительно дирек-
тивных сроков) расписания необходимо и достаточно, чтобы было до-
пустимым \-ратисание, соответствующее списку X = ((z^, ^), (z2, <72), • •
’ 0’к» <7/+1), 7=1...R - 1.
Достаточное ^ утверждения очевидна. Докажем необходимость.
124
Предположим, что при расписании s' существует хотя бы одно запаз-
дывающее требование. Тогда из соотношения (2.1) следует, что найдет-
ся номер t, 1< t < R, единичного временного интервала, для которого
t > y(5f) или t > v(0t). Среди всех таких значений t выберем минималь-
ное значение Z0. Для определенности пусть Г° > у(af0).
Докажем справедливость следующих соотношений:
at ¥= 7, u(2f) < f(5fo) при t = 2,.. ., - 1,
ufSj) < u(afo) при cq Ф y.
Если afo = (i, 1), to at Фу при 1 - 1 и из неравенства вида
v(St) > v(ato) следует, что при расписании Г операция at<* выполняет-
ся раньше операции at, т.е. f° < t. ~
Пусть afo = (z, q) и q > 1. Тогда (z, q - 1) = где h < tQ - 1.
Из определения v(i, q) и равенства h = t° - 1 следовало бы соотношение
и(0Л) = 17(0,0) — 1 < г° - 1 = Л, что противоречит минимальности вы-
бранного значения tQ.
Отсюда следует, что at Ф у и u(af) < и(а,о) при h + 1 — 1,
так как в противном случае операция а, о выполнялась бы во временном
интервале, номер которого меньше .
Кроме того, должно выполняться и неравенство у(аЛ)< и(2Л+1 ).
В противном случае операция оЛ + х выполнялась бы во временном интер-
вале, номер которого меньше h + 1, поскольку ah + г и - операции по
обслуживанию разных требований.
Таким образом, при Л = 1 соотношения (2.3) выполняются.
Пусть h > 1 и ah = (z', q'). Если q' = 1, то, как «уже было показано выше,
at Ф у и v (at) < и (2Л) при t = 1,. . . , h - 1,и соотношения (2.3) имеют
место.
Пусть q > 1, Если (z', q - 1) = 0р, где р < h ~ 1, то, повторяя при-
веденные выше рассуждения, получаем at Ф у и v(at) < и (аЛ) при
t = р, . . . , h — 1. Если (i*, q' — 1) = ь т0 найдем наименьший номер
р' такого временного интервала, что j3t и о,+ 1 - операции по обслужива-
нию требования i' при t = р', . . . , h - 1. Тогда v(at) =Cv(Sh) при t =
= р\ . . . , h — 1. Поскольку Q/J+ х является операцией по обслуживанию
требования, отличного от z', то v(ah) <v(ah+1). Следовательно, при
q* > 1 выполняются неравенства и (at) < v (ah +1) при t = p\ . .. , h.
Если p1 = 1, то соотношения (2.3) имеют место. В противном случае
описанные рассуждения можно повторить.
Поскольку число R временных интервалов конечно, то за конечное
число шагов приходим к заключению о справедливости соотношений (2.3).
Покажем, что из этих соотношений следует существование хотя бы од-
ного запаздывающего требования при любом расписании s Е S.
Пусть Qj = 7, тогда неравенства v(at) < у(а,о) < справедливы
при t = 1, . . . , t°. Следовательно, для того чтобы при расписании s не
было запаздывающих требований, необходимо, чтобы при этом расписа-
нии операции о2, . . . , at° (единичной длительности каждая) выпол-
нялись прибором А в течение интервала времени (0, tQ — 1], что невоз-
можно.
125
Пусть Si = у, тогда все операции вида (/, 1), i G TV, должны выполнять-
ся прибором В. Поскольку v (ar) < t° при t = 2,.. . , tQ, то для того чтобы
не было запаздывающих требований, необходимо операции а2, <*3,... , аго
выполнить прибором А в течение интервала времени (1 ,t° — 1], что также
невозможно.
Итак, из предположения о том, что при расписании Г существует хотя
бы одно запаздывающее требование, следует, что и любое другое расписа-
ние 5 G S не может быть допустимым относительно заданных директивных
сроков. Утверждение доказано.
Таким образом, Х-расписанию Г, построенному согласно алгоритму из
п. 2.2, соответствует наименьшее значение £max(s), s £ S. В частности,
если существует допустимое относительно директивных сроков расписа-
ние, то Г является одним из таких расписаний.
2.5. Оценим временную сложность описанного в п. 2.2 алгоритма по-
строения оптимального расписания. _
Трудоемкость построения последовательностей а и /3 по известному
списку X определяется, по существу, трудоемкостью нахождения значе-
ний tf. Поскольку при поиске этих значений на всех шагах алгоритма
ни одна из компонент последовательностей а и /3 не просматривается
более одного раза, то последовательности а и 0 строятся за O(R) эле-
ментарных действий.
Список X можно сформировать за O(R log R) элементарных действий
или, учитывая, что v (f, q + 1) = v (i, q) + 1, q = 1, . . . , rz- - 1, i G N, -
за O(R log ri) действий.
Если все Df, i = 1, . . . , n, — целые числа, то список X можно сформиро-
вать за О(R) действий.
Действительно, обозначим через I нижнюю оценку значения Zmax(s*).
В качестве / может быть выбрано, например, значение max{rz- - Z)z-1 i G TV}.
Через Nr обозначим множество всех требований i Е. N, для которых
R -D, < I.
Для всех i G N\Nf и 1 <rz имеет место соотношение -/ <
<21? — I. Поскольку v(i, q) - целые числа, то для упорядочения по не-
убыванию всех чисел v (i, q), i G 7V\jV', 1 < q < rz-, достаточно O(R)
действий.
Нетрудно видеть, что при любом расписании 5 G S для всех i G N' вы-
полняются соотношения ti(s) —Dt <1? — Di </</*. Поэтому для каждо-
го i G Nf и 1 < q можно положить u(Z, q) = W + q, где И7 - достаточ-
но большое число, например, W > 2R — /, и упорядочить по неубыванию
все числа v(i, q), 1 < q < rz, i G N1, за O(R) действий.
Таблица 2.1
i l‘ 1 Я/
1 8 10
2 (A,B,A,B,A,B,A,B,A,B) 10 18
3 (А, В, A, B, A,B} 6 10
4 (В, А, В, A, В) 5 20
5 (В, А, В, А, В, А, В, А, В) 9 20
126
Таким образом, для построения оптимального расписания достаточно
выполнить O(R log п) действий, а при условии целочисленности директив-
ных сроков - О (R) действий.
2.6. Пример. Группа ’’летающих” лыжников Nпроводит тренировку
по прыжкам с трамплина. В распоряжении спортсменов имеется подъемник
на одного человека (прибор А) и трамплин (прибор В), Время подъема
на трамплин равно единице и равно времени, отведенному на прыжок
с трамплина. Для каждого лыжника i G N задан директивный срок Di9
к которому желательно закончить тренировку.
прибор В
приборА
I
1
б 1 3 1 3 121325242524545
0 1 2 3 4 5 6 7 3 9 1О 11 12 13 14 15 16 17 1в 19 20
Рис. 2.2
t
В задаче требуется составить такое расписание s * тренировки спортсме-
нов, при котором принимает наименьшее значение величина £max(s) =
= max{f/(s) — Dj\i G N} (tj(s) — Di — временное смещение момента
tt(s) завершения тренировки спортсмена i G N относительно заданного
директивного срока Z)z). Исходные данные задачи приведены в табл. 2.1.
По формуле (2.1) вычисляем значения весов v(i, q), 1 z' =
= 1, 2, 3, 4, 5, и упорядочиваем все операции по неубыванию полученных
значений: Х = ((1,1), (1,2), (1,3), (3,1), (1,4), (3,2), (1,5), (3,3), (1,6),
(3,4), (1,7), (2,1), (3,5), (1,8), (2,2), (3,6), (2,3), (2,4), (5,1), (2,5),
(5,2), (2,6), (5,3), (2,7), (5,4), (2,8), (4,1), (5,5), (2,9), (4,2), (5,6),
(2,10), (4,3), (5,7), (4,4), (5,8), (4,5), (5,9)).
Применяя описанный в п. 2.2 алгоритм, получаем Х-расписание s, пред-
ставленное на рис. 2.2.
Х-расписание является оптимальным. Поскольку значение целевого
функционала £max(^) = max{8-10, 16-18, 9-10, 19—20, 20-20} = 0,
то расписание Г является допустимым относительно заданных директив-
ных сроков.
§ 3. Общее время обслуживания. Одинаковые длительности
В данном параграфе рассматривается задача построения оптимальных
по быстродействию расписаний (без прерываний) обслуживания требова-
ний с одинаковыми длительностями всех операций.
В системе, состоящей из М приборов, обслуживается множество требо-
ваний N = { 1, 2, . . . , п}. Для каждого требования i G N задан момент
времени d{ > 0 его поступления в систему и маршрут обслуживания
L* = . . . , где G Л ={1, 2, . . . . , М}, q = 1,. . . , rit
и Lg Ф + r, q = 1,. . . , - 1. Для каждой операции (z, L, q) по обслу-
127
живаним требования i Е N прибором L = Lq на стадии q известна дли-
тельность ее выполнения tiLq > 0. Почти всюду в этом параграфе длитель-
ности выполнения операций предполагаются одинаковыми (без потери
общносаи в таких случаях их можно считать единичными). Прерывания
в процессе выполнения каядой операции не допускаются. На множестве
требований может быть задано отношение -> строгого порядка: если
i -> / (i,j G TV), то должно выполняться неравенство > tj(s), где
t^(s) (соответственно — момент начала (завершения) обслужи-
вания требования / (требования i) при расписании s.
Необходимо построить расписание s *, при котором общее время обслу-
живания требований ^max(s" - max{(s) | i6N } является минимальным.
Расписание s * принято назывггь оптимальным по быстродействию.
3.1. Покажем, что пострсение оптимального по быстродействию рас-
писания при произвольных значениях di > 0 сводится к построению рас-
писания с наименьшим значением максимального временного смещения
npudi = О, i = 1,.. . ,п.
Рассмэтрим две задачи псстроения расписания обслуживания требова-
ний TV = {1, 2, . . . , п } с наименьшим значением величины Zmax (5) =
= max{??(s) - jDJ iEN},
В первой из этих задач ice требования поступают в систему одновре-
менно (d\ = 0, i = 1, . . . , г), известен маршрут L* = (£\ ... , Z*f)
обслуживания каждого требования i G TV и директивный срок D\. На
множестзе TV может быть задано отношение строгого порядка
Во второй задаче требоваше i G TV поступает в систему в момент вре-
мени d" = D — маршру: ...,L\) обслуживания требо-
вания i € TV является обратном маршруту L* и директивный срок =D,
где D = max{Z)y | i G TV}, На множестве TV задано отношение строгого поряд-
ка =», обратного порядку -> (т.е. i => / тогда и только тогда, когда j
Длительности t\Lq операшй (z, L, q) первой задачи и длительности
q операций (i,L, q) второ! задачи связаны соотношениями
lLq<* iLri_q^ri-q + b ’
Эти задачи будем называть сопряженными.
Пусть s' — расписание д;и первой задачи, при котором максимальное
временное смещение принимает наименьшее значение £max(sz) = V.
Обозначим через Г совоьупность М кусочно-постоянных функций
{Fi(0, ^(0, • • • > таких, что sL (f) = L ЕЛ, если t
не являегся точкой разрыва функции s'L (Z). В точках t разрыва функции
(Г) положим (Г) = ~sL[t + е) для достаточно малых е > 0. Таким
образом, в отличие от s'L (t) функция s~L (t) непрерывна справа, а не слева.
Для каждого L полагав s'[ (t) = (D + Lr — t) при t G (0, £+ L']
и (r) = 0 ПРИ t > D + L', io лучим допустимое расписание s" для второй
задачи.
Нетрудно видеть, что Z,malc(s") = max{rz(s") - D” | i EN} = 11 и s" -
оптимальное расписание для второй задачи. Поскольку D" = D, i G TV,
то расписание s' является штимальным и по быстродействию, причем
GnaxO ) “ + D.
128
Следовательно, для решения задачи построения оптимального по быстро-
действию расписания при произвольных значениях dt достаточно
решить сопряженную ей задачу построения расписания с наименьшим
значением bmax(s) при = О, D\ = D — dit D- max{di\i G TV}, i =
= 1,... , n.
Поскольку приведенные рассуждения обратимы, то имеет место и об-
ратное сведение задачи построения расписания с наименьшим значением
максимального временного смещения при d { = 0, i G TV, к задаче построе-
ния оптимального по быстродействию расписания при произвольных зна-
чениях di > 0.
3.2. Рассмотрим задачу построения оптимального по быстродействию
расписания обслуживания п требований двумя приборами А и В. Требова-
ние i Е N поступает в момент времени d j > 0. Длительности выполнения
всех операций равны единице.
Как показано в предыдущем параграфе, сопряженная данной задача
построения расписания с наименьшим значением £max(s) ПРИ - 0,
Dj = D - dif D = max{d/1 i G TV}, i = 1,. . . , n, относится к классу полино-
миально разрешимых.
Таким образом, задача построения оптимального по быстродействию
расписания при М = 2 и t i = 1,4 = 1,.. . 9 rhi = 1, ... , л, также поли-
номиально разрешима, и для ее решения можно воспользоваться алгорит-
мом, описанным в п. 2.2. Напомним, что трудоемкость этого алгоритма
не превосходит <?(/?logn), а при условии целочисленности значений
п
dit f G TV, - величину O(R), где R = S rt.
i
3.3. Пример. Группа парашютистов проводит тренировку по прыж-
кам с вышки. В их распоряжении имеется лифт на одного человека (при-
бор А) и парашют для прыжков с вышки (прибор В). Время подъема на
вышку и время прыжка с вышки равны между собой. Для каждого па-
рашютиста известны момент времени dt готовности к началу тренировки
и число Г//2 прыжков, которые нужно совершить.
Требуется построить оптимальное по быстродействию расписание тре-
нировки парашютистов при исходных данных, приведенных в табл. 3.1.
Исходные данные для сопряженной задачи приведены в табл. 3.2
В соответствии с алгоритмом, описанным в п. 2.2, сформулируем список
X операций (i, q), q = 1,... , rt, i = 1,2, 3,4, упорядочив их по неубыванию
весов и(/, q) = Dt - + q: X = ((1,1), (4,1), (1,2), (4,2), (1,3), (4,3),
Таблица 3.1
1 ‘ 1 L1 ri di
1 (А, В, А, В, А, В) 6 7
2 {А, В, А, В} 4 0
3 (А, В) 2 3
4 (А, В, А, В, А, В, А, В) 8 5
9. В.С. Танаев
129
Таблица 3.2
Li п di
1 (В, А, В, А, В, А) 6 0
2 (В, А, В, А) 4 7
3 (В, А) 2 4
4 (В, А, В, А, В, А, В, 4) 8 2
(1,4), (4,4), (1,5), (4,5), (1,6), (4,6), (4,7), (4,8), (3,1), (2,1), (3,2),
(2,2), (2,3), (2,4)). Х-расписание s, представленное на рис. 3.1, является
оптимальным расписанием для сопряженной задачи и Lmax(з) = 7.
Расписание s' однозначно определяет оптимальное по быстродействию
расписание $* для исходной задачи, которое представлено на рис. 3.2.
Значение fmax(s*) =^max(s~) + max{Df | i = 1, 2, 3, 4 }= 7 + 7 = 14.
прибор В
приборА
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 t
Рис. 3.1
2
4
приборе
приборА
। । । ! ।
i i i I |
2 4 3 4 1 4 1 4 1
—4— I—.............
3! -Я
1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
t
Рис. 3.2
3.4. Покажем, что при М - 3,di = 0, z G N, и единичных длительностях
всех операций задача построения оптимального по быстродействию рас-
писания является NP-трудной в сильном смысле.
Сформулируем соответствующую задачу распознавания.
В обслуживающую систему, состоящую из трех приборов А, В и С, в
момент времени d = 0 поступает множество требований N = {1,2,. . . ,п}.
Для каждого требования i G TV задан маршрут обслуживания L1. Длитель-
ность выполнения каждой операции равна единице. Необходимо опре-
делить, существует ли расписание s° (без прерываний операций) такое,
что fmax (s°) <у для заданного значения у.
Построим псевдополиномиальное сведение задачи о 3-разбиении (см.
вводную часть данной главы) к сформулированной задаче распознава-
ния.
Положим п = Зи0 + 2, у = п^(2Е + 9), Ll = (А, С, [А, В]е\ С),
i = 1, . . . , Зи0, Ln~~l = ([В, С, В, А, В, А, [В, С\Е, А, В, A]"0), Ln =
130
п п-1 п п-1 п п-1 пп-1п п п-1 п п-1
п п-1 п
приборе । । ।
п-1 п п^пп-1п\п-1 п-1 п-1 \nn-1n n-1nn4nnln\nJ п-1
прибор В I I I I I II М ••• М II I ..................
\n-1nn-1 п п п\пАпп-1
прибор А - J-4—Ы Н Н • • • M-l-4-
0 3 6
xn-1nrtl п п
2Е+6
т+3 т+б
t
Рис. 3.3
= ( [С, В, С, В, А, В, [С, А]Е, В, А, Я] л°). Здесь и далее [ • ]h - последо-
вательность, состоящая из h повторений стоящего в скобках выражения.
Например, [А, 5]2 = А, В, А, В.
Заметим, что число операций по обслуживанию как требования п — 1,
так и требования п равно у. Следовательно, можно считать, что при
расписании s° операция (и - q) и операция (п, Lq, q) выполня-
ются во временном интервале (q - 1, tj], т.е. = tnLqq = <7 ~ 1-
На рис. 3.3 представлен фрагмент расписания обслуживания требований
п — 1 и п. Отметим, что это расписание является периодическим, т.е. график
расписания состоит из п0 одинаковых частей. На рис. 3.3 первая такая
часть отделена сплошной вертикальной чертой, а период расписания обозна-
чен через т и равен 2Z? + 9.
Как нетрудно заметить, для обслуживания требований i = 1, .. . , Зи0
остается последовательность непрерывно следующих один за другим вре-
менных интервалов, начинающаяся в момент t = 0 и заканчивающаяся в
момент t = у. Используя принятые обозначения, эту последовательность
можно записать в виде ([ [Л]3, [С]3, [А, В]Е, [С]3]"о ).
Покажем, что требования i = 1, . . . , Зи0 могут быть обслужены в соот-
ветствии с указанной последовательностью (и, следовательно, существу-
ет расписание, при котором общее время обслуживания требований рав-
но у) тогда и только тогда, когда задача о 3-разбиении имеет решение.
Предположим, что задача о 3-разбиении имеет решение, т.е. существу-
ет разбиение множества 7V0 на nQ подмножеств TV?, TV®, • • • > ^л0 таких,
что S = Е при j = 1, . . . , п0. Тогда, обслуживая каждое требова-
i е Nf
ние i G Nf от начала до конца в течение интервала времени (т(/ — 1), т/],
j = 1,.. . , и0, получаем расписание s°, при котором ах (s0) = у.
Предположим, что существует расписание s°, при котором /max(s°)
и докажем по индукции относительно /, что при расписании во времен-
ном интервале (т( j — 1), т/], 1 </ <и0, обслуживаются (причем пол-
ностью) ровно три требования из множества {1,2,..., Зи0 }.
Очевидно, что такие требования будут представлять собой трехэле-
ментное подмножество N°, для которого S в/ = Е.
i G 7V?
9
131
Рассмотрим случай j = 1. Если при расписании $° обслуживание неко-
торого требования z‘, 1 < i < Зи0, начинается во временном интервале
(О, т], то последовательность операций по его обслуживанию, выполне-
ние которых заканчивается в этом же интервале, можно отнести к одному
из следующих четырех типов:
1) (Я);
2) (Л, С, [Л, 2?]h ), 0 < h < ez;
3) (Л, С, (Л,В]\Л), 0 < h < е^
4) (Л, С, [Л,В]ЧС).
Через пк обозначим число требований z, 1 <z <3ио, обслуживание ко-
торых начинается в интервале (0, т] и указанные последовательности
операций относятся к типу к, к = 1,. .. , п. Через тк обозначим суммарное
число операций по обслуживанию этих требований прибором В во времен-
ном интервале (0, т].
Нетрудно видеть, что суммарное число операций (единичной длитель-
ности), которые необходимо выполнить каждому из приборов, равно
Следовательно, при любом расписании с общим временем обслуживания
требований, равным у, каждый из приборов Л, В и С во временном ин-
тервале (0, иот] не простаивает. Соответственно получаем следующие
уравнения относительно пк итк:
пх +п2 +т2 + 2п3 + т3 + и4 + т4 = Е + 3, (3.1)
+ т3 + т4 = Е, (3.2)
п2 + л3 + 2и4 = 6. (3.3)
Вычитая уравнение (3.1) из суммы уравнений (3.2) и (3.3), получаем
- и3 + и4 = 3. Отсюда следует, что и4 > 3, а из уравнения (3.3) получаем
и4 < 3. Следовательно, и4 = 3. Из уравнения (3.3) получаем п2 = п3 = 0.
Тогда по определению т2 = т3 = 0. Из уравнения (3.2) получаем nz4 = Е,
а из уравнения (3.1) - пх = 0.
Таким образом, при расписании $° в интервале (0, т] обслуживают-
ся (причем от начала до конца) точно три требования из множества
{1,2, . . . , Зи0). Эти требования, очевидно, составляют искомое трех-
элементное подмножество N°, для которого S ez- = Е.
Пусть при расписании s° в каждом интервале (т( / - 1), ту] для всех
7 < /о и начинается и заканчивается обслуживание требований множест-
ва 7V° TV0, 17V° | = 3. Тогда, повторяя рассуждения, аналогичные при-
веденным для интервала времени (0, т], можно показать, что при любом
расписании с общим временем обслуживания требований, равным у, в ин-
тервале (т( j - 1), т/о ] должно начинаться и заканчиваться обслуживание
точно трех ранее не обслуженных требований из множества №.
Таким образом, расписание s°, при котором ^тах($0) = У, однозначно
определяет требуемое разбиение множества 7V0 на трех элементные подмно-
жества.
Нетрудно видеть, что для реализации описанного сведения достаточно
выполнить О(п0Е) элементарных действий. Поскольку задача о 3-разбие-
132
нии NP-полна в сильном смысле, то задача построения оптимального по
быстродействию расписания обслуживания тремя приборами п одновре-
менно поступающих требований с единичными длительностями всех опера-
ций является NP-трудной в сильном смысле.
3.5. Покажем, что если на множестве требований N задано отношение
строгого порядка, то задача построения оптимального по быстродействию
расписания является NP-трудной в сильном смысле при М = 2 и dt = О,
i = 1, . . . , п. Этот результат справедлив даже в том случае, когда каждая
компонента связности графа редукции заданного отношения строгого
порядка является цепью.
Сформулируем соответствующую задачу распознавания.
В обслуживающую систему, состоящую из двух приборов Л и В, в мо-
мент времени d = 0 поступает множество требований N = {1,2, .. . 9п}.
На множестве N задано отношение -> строгого порядка. Каждая компо-
нента связности графа редукции отношения -> является цепью. Длитель-
ность выполнения каждой операции равна единице. Требуется определить,
существует ли расписание s° обслуживания требований множества7Vтакое,
что ^щах (5°) для заданного значения у.
Построим псевдо пол ин омиальное сведение задачи о 3-разбиении к сфор-
мулированной задаче распознавания.
Зи0 + 1
Положим п = 4л0^, У = 2,nQEt N = S Nk, где ={1,2,. . . , 2eJ ,
k =1
k - 1 k - 1 k
Nk = {2 S + 1,2 S et + 2, . . . , 2 S k = 2,. .. , Зи0, иN 3n +1 =
i = i i = i i = i 0
= {2n0F + 1,2л0Е + 2,... , 4nQE},
На множестве требований N зададим отношение -> строгого порядка,
полагая i -*/, тогда и только тогда, когда i G Nk, j Е Nk, 1 < к <3ио + 1,
и i < /. Каждая компонента связности графа редукции этого отношения,
очевидно, является цепью.
Пусть процесс обслуживания каждого требования i Е N состоит в выпол-
нении единственной операции. Для требований из множества положим
L1 = (В) при I = 1,. . . , ех и L1 = (А) при I = ех + 1,. . . , 2в1. Для каждого
к, 2 < к < Зи0, положим
к- 1
2 S er- + I
L 1 = (В) при I = 1,...,ек,
к- 1
2 S + I
L 1 = (А) при I = ек + 1,.. ., 2ек.
Для требований из множества N3n +1 положим ("о+ О+ 1 =
= z2E(n0 + /) + 2 = = £2E(n0 + /5+E = ^2E(m0 + Z)+E+ 1 =
= £2Е(м0+/) + Е+2 = = L2E(nQ+l+ 1) = П() _ у
Поскольку множество N3n^ + j является линейно упорядоченным и
число его элементов равно 2nQE = у, то при любом расписании с общим
временем обслуживания требований, равным у, требования множества
N3n + j должны обслуживаться непрерывно одно за другим начиная с
момента времени t = 0.
133
На рис. 3.4 представлен фрагмент расписания обслуживания требова-
ний множества N3n0+ь при кстором общее время обслуживания требо-
ваний равно у. Это расписание язляется периодическим с периодом т = 2Е.
Таким образом, обслуживание требований множества TV\7V3Wo+1 при
любом расписании с общим временем обслуживания требований, рав-
ным у, мохет быть осуществлено только в тех единичных интервалах,
которые определяются последовательностью ( [ [B]F, [Л]Е] .
приборе
приборА
е+Е + 7 у+Е+2 y+ZE
»! I • • • I—|
У'Е | У^2Е+7 у+2Е +2
* I * * *
।
• —I 1---1---1— • • • —L 1-----1— • г « --
Е 2Е t
Рис. 3.4
Покажем, что расписание s° существует тогда и только тогда, когда
имеет решение задача о 3-разбиении,
Пусть существует разбиение множества № на п0 трехэлементных под-
множеств N*, N2,. ,. таких, что S et =Е при / = 1,.. . ,п0. Тогда,
0 I G nJ
обслуживая множество требований U в интервале (т( / - 1), rj],
k g nJ
j = 1,.. . ,nQib соответствии с отношением получаем расписание с общим
временем обслуживания требований, равным у.
Пусть существует расписание s°, при котором Zmax(s°) = У- Посколь-
ку суммарная длительность обслуживания всех требований прибором А
(прибором £) равная, то при расписании s° как прибор Л, так и прибор В
в интервале {0, лот] не простаивают.
По условию обслуживание каждого требования i G Nk, к Е № =
= {1,2,... Зл0}, Для которогс L1 ~ (В), должно предшествовать обслу-
живанию каждого требования / 6 TV*, для которого Li = (А). Во множест-
ве NA = { i 11 E Nki Ll = (А)} содержится столько же элементов, сколько
и во множестве Nk = { Z \i G Nk, Ll - (В)}. Для того чтобы прибор А
не простаивал в интервале (Е, 2Е], необходимо и достаточно, чтобы мно-
жество всех требований, которые обслуживаются прибором А в указан-
ию
ном интервале, можно было представить в виде U Nk где kt G TV0,
i = i
I = 1, . . . , w, причем в интервале (О, Е] прибором В обслуживались бы
m
все требования множества U ТУ^ и только они. При этом из неравенств
Е/4 < ек < Е/2, к = 1,. . ., Зи0, следует, что m = 3.
Таким обэазом, получаем подмножество TV0 = {&,, к2, к3} множест-
ва TV0, для кэторого Z С: = X | Na | = Е.
zG/Vj zG/V° 1
134
Повторяя аналогичные рассуждения, можно показать, что при расписа-
нии $° в каждом интервале (т(Л - 1), т/i], h = 2, ... , nQ, обслуживаются
все требования трех множеств вида Nk, к G №, и только они. В результате
получаем разбиение множества № на трехэлементные подмножества
/V?, ^2, • • • , такие, что S et = Е, 1 < j < nQ.
0 i е n °
Для реализации этого сведения задачи о 3-разбиении к сформулирован-
ной задаче распознавания достаточно выполнить О(п0Е) элементарных
действий.
Таким образом, задача построения оптимального по быстродействию
расписания обслуживания двумя приборами частично упорядоченного
множества одновременно поступающих в систему требований с операция-
ми одинаковой длительности является NP-трудной в сильном смысле.
3.6. Если длительности выполнения операций принимают значения из
множества {1,2} то задача построения оптимального по быстродействию
расписания обслуживания п одновременно поступающих в систему требо-
ваний является NP-трудной в сильном смысле при М=2.
Сформулируем соответствующую задачу распознавания.
В обслуживающую систему, состоящую из двух приборов Л и В, в
момент времени d = 0 поступает множество требований N = {1,2, ... ,п}.
Предполагается, что длительности выполнения операций tiLq 6 {1, 2}.
Необходимо определить, существует ли расписание s° обслуживания тре-
бований множества N такое, что Fmax(s°) <у для заданного значения у.
Построим псевдополиномиальное сведение задачи о 3-разбиении к сфор-
мулированной задаче распознавания.
Положим п = Зи0 + 1, у = 2и0(2Е + 9), L' = (2Л, В, [2Л, 2B]ei,A, 2В\
i = 1, . . . , Зи0, = (\2В, Л, 2В, Л, 2В, Л, [2В, 2А]Е, В, 2Л, В, 2Л, В,
~ 2А или
t i выполнения операции (z, /А, q) равна
= В, ТО t.Ti = 1.
2А]п°). Здесь используются следующие обозначения: если Lq
Lq = 2В, то длительность
двум; если Llq = А или Llq
прибор В
прибор А
Поскольку число операций по обслуживанию требования п равно у,
то при любом расписании с общим временем обслуживания требований,
равным у, эти операции должны выполняться непрерывно одна за другой,
начиная с момента t = 0.
На рис. 3.5 представлен график обслуживания требования во временном
интервале (0, т], где т = 2 (2Е + 9) — период расписания.
135
Таким образом, обслуживание требований множества NQ = {1, 2, . . .
. .., Зи0 } ПРИ любом расписанш с общим временем обслуживания требова-
ний, равным у, может быть осуществлено только в тех временных интер-
валах, которые определяются последовательностью ([2А, В, 2А, В, 2А,
В, [2А, 2В\Е, А, 2В, А, 2В, А, 2В]п*).
Покажем, что расписание $° при котором = у, существует
тогда и только тогда, когда имеет решение задача о Зразбиении,
Предположим, что существует разбиение множества 7V0 на и0 трех-
элементных подмножеств N°, Л?, • • • , Nn таких, что S et = Е при
0 / е nJ
j = 1, . . . , п0- Тогда, обслуживая полностью каждое требование i Е Nj
в интервале (т(/ - 1), tj] , / = 1,. . . , и0, получаем расписание с общим
временем обслуживания требований, равным у. _
Предположим, что существуем расписание s°, при котором ^mex(s0) =у.
Покажем, что при этом расписании точно три требования из множества
№ полностью обслуживаются в штервале (0, т].
Поскольку суммарная длительность всех операций, выполняемых при-
зл0
бором А (прибором В), равна9и0 +2 S е{ + nc(9 + 2Е) = у, то при
i = 1
любом расписании с общим временем обслуживания требований, рав-
ным у, как прибор А, так и првбор В не простаивают во временном интер-
вале (0, иот].
Для того чтобы приборов ин-ервале (0, 9] не простаивал, необходимо и
достаточно, чтобы в этом интервале начиналось обслуживание точно трех
требований из множества №. Аналогично, для того чтобы прибор Л в ин-
тервале (4Е + 9, 4Е + 18] не прэстаивал, необходимо и достаточно, чтобы
в этом интервале заканчивалось обслуживание тсчно трех требований
из множества JV0. Очевидно, vro это те же требования, обслуживание
которых начинается в интервале (0, 9]. Эти три требования и составля-
ют подмножество TV? 5 , длл которого S q = Е.
Далее индукцией по / можно показать, что при расписании s° обслужи-
вание точно трех требований из множества JV°\TV? шчинается и завершает-
ся в интервале [ т( / - 1), rj], 1 < / < и0. В результате получим разбиение
множества № на трехэлементные подмножества №{,N%, .... ,Nn такие,
что S в/ = Е, 1 < / < п0.
i<= nJ
Нетрудно видеть, что для реализации описанного сведения задачи о
3-разбиении к сформулированнсй задаче распознаваяия достаточно выпол-
нить O(nQE) элементарных действий.
Следовательно, задача построения оптимального по быстродействию рас-
писания. обслуживания двумя пр1борами п одновременно поступающих тре-
бований со значениями длительностей операций из множества {1,2} являет-
ся NP-трудной в сильном смысле
3.7. Изложенные в п. 3.4—3.6 результаты, очевидно, справедливы и в
случае неодинаковых значений В силу эквивалентности сопряженных
задач (см. п.3.2) задача построения расписания, которому соответствует
наименьшее значение максимального временного смещения
136
при заданных директивных сроках Dh является NP-трудной в сильном
смысле в следующих случаях '.
a) М=3, = tiLq = 1, L = L'q, q= 1......rb i= 1,. .. ,и;
б) 7И = 2, Jf = 0, tiLq=l, L=L'q, q-\,...,rb z EW= {1,2,..., и},
на множестве N задано отношение -* строгого порядка (достаточно, чтобы
все компоненты связности графа редукции этого отношения были цепями);
в) М=2, di = 0, tiLq G {1,2}, L- Llq, q = 1,... ,rit i = 1,... ,n.
§ 4. Общее время обслуживания. Различные длительности
Рассматривается задача построения оптимального по быстродействию
расписания обслуживания п требований двумя приборами. В отличие от пре-
дыдущего параграфа длительности выполнения операций представляют со-
бой произвольные действительные числа и могут допускаться прерывания
в процессе выполнения операций.
4.1. В обслуживающую систему, состоящую из двух приборов А и В, в
момент времени d = 0 поступает множество N = {1,2,. .., и } требований.
Маршрут L* обслуживания требования i £ N представляет собой чередую-
щуюся последовательность приборов (L\, , Ь1Г.), lJq £ {А, В},
q = 1,.. ., Г/, где Llq Ф Llq+i, q = 1,.. ., - 1. Известны длительности
tiLq > 0 выполнения всех операций (z, L, q), i £ N, L = L'q £ {A, B},
<7 = 1...
Необходимо построить расписание 5*, при^котором общее время обслу-
живания всех требований fmax(s) = max {t{(s) |z £ N} принимает наи-
меньшее значение.
4.2. Опишем эффективный алгоритм построения оптимального по
быстродействию расписания (без прерываний) обслуживания п требований
двумя приборами при Г/ <2, z = 1,..., и.
В .этом случае множество требований N можно разбить на четыре попар-
но непересекающихся (необязательно непустых) подмножества: N-NAB U
^NBA Здесь NAB(NBA) ~ множество требований z £ N, обслу-
живаемых приборами А и В в последовательности L* = (А, В) (соответ-
ственно L1 = (В, А)). Если L1 = (А ), то z G NA . Аналогично, если L1 = (В),
то z £ NB .
Поскольку при < 2 требование z £ N обслуживается каждым прибо-
ром L £ {А, В } не более одного раза, то на протяжении этого пункта
во всех обозначениях будем опускать номер стадии q, полагая (z, L,q) =
— (z, L) , tn, q — tn,, tiL q “ ^iL » til q ~ tiL •
Напомним, что в § 1 гл. 1 описан алгоритм трудоемкости O(nlogH)
построения оптимального по быстродействию расписания обслуживания
двумя приборами п требований с одинаковыми маршрутами обслуживания.
В случае, когда N = NAB, оптимальным по быстродействию будет рас-
писание, при котором требования множества N обслуживаются обоими
приборами в одной и той же последовательности л = (z\, z2, .. ., in) удов-
летворяющей условию
min {tilA,til+]B} <min{fy+14, tilB} (4.1)
137
для всех Z = 1,. .., и - 1. В частности, каждому требованию i G N можно
приписать ве:
a>(z)= [W- min {tiA, tiB }] sign(7M - tiB)
и упорядочиь требования в порядке неубывания их весов. Здесь W — дос-
таточно больное число (W > max min {tiA, tiB } ).
i < i < n
Аналогичю при N = NBA наименьшее значение величины дости-
гается для ^списания s, при котором требования множества N обслужи-
ваются прибсрами А и В в одной и той же последовательности тт = (z i, i2,...
..., in) удовлетворяющей условию
min л) <min{f,z+lfi,(4.2)
для всех I = 1..., п — 1.
Если NAB~ Ф или NBA - ф и хотя бы одно из множеств требований 7УЛ
или NB непуто, то все требования множества NA <JNB можно отнести ко
множеству или ко множеству NBa, полагая tiB = 0 при i G NA и tiA =
= 0 при i е VB. В результате получим множество требований с одинако-
выми маршрутами обслуживания.
Таким обрзом, построение оптимального по быстродействию расписа-
ния обслужшания требований множества N двумя приборами не вызывает
особых затруднений, если NAB = ф или NBA = ф.
Пусть Nab^ Ф hNba • Каждое расписание s для рассматриваемой за-
дачи однозна’но определяет некоторые последовательности я = (> i > >2 > • • •
z.., inA) и я = (/ь/э,. .. , ]пв ) обслуживания требований множества N
прибором А 1 прибором В соответственно. Здесь пА = | N\NB | и пв =
= 1МЛ^1- ,
Обозначимся - NAB и 7Vв а ~ ^ва Нетрудно видеть, что
при расписаши s имеют место следующие соотношения. Если G N'ab,
то *^а > 0,1 противном случае t^iA > tixB.Ecr\^ir £NBAyot^B > О,
в противномаучае tf^B > всех = 2, ..., пА значение rfkA >
> Ч*_1Л> ест ik GN'ab, и t?kA > max{Fik_ 1A, ~tikB}_, если ik e NBA.
Аналогично для всех k = 2,..., пв значение если/* €
€ N в a , и t °jkB > max {tjk _ x , T, k A } , если jk € NA B.
Кроме тоге, поскольку прерывания в процессе выполнения операций
не допускают<3,то 7}fcj4 = tfkA + tikA для всех k = 1,..., пА и TjkB = rfkB +
+ tjkB для все>£ = 1,..., пв.
Очевидно, 1то существует бесконечное множество наборов значений
t^kA ~ 1, • >пА и rfkB ~ 1, • • >пв> удовлетворяющих перечисленным
соотношениям и каждый из таких наборов определяет некоторое расписа-
ние s. Если п’И расписании s набор значений tfkA и t®kB удовлетворяет
этим соотношениями как равенствам, то общее время обслуживания требо-
ваний max{Ff|^4, Tin^B} достигает наименьшего (при фиксированных
я и я*) значения, которое будем обозначать через г (я, я;).
Пусть в поаедовательности я = (z’i, z2, ..., inA) требование z*/ G NBA
и требование z+i в NAB, 1 < Z < nA. Покажем, что г(я, я') <£(я, я'),
где я = (z’i, z2, • • Ji- i U’z+n 6, Z/+2, • • • ,*Лл).
138
Если требования множества N обслуживаются в последовательности
я прибором Лив последовательности я* прибором В, то моменты начала и
окончания выполнения операции (i,L) будем обозначать через и f/L
соответственно.
Нетрудно видеть, что т°;+1л = Тца ~ + а значения мо-
ментов начала выполнения остальных операций сохраняются неизмен-
ными:
TikA =t°ikA> 1 <k<nA,k^l, k*l + l,
TikB = t^kB’
Поскольку Tfl+1A < 7(l+iA < t^l+lB и TflA > t°ilA > TilB, то значения
Tik, 1 ^пл, и значения , 1 определяют некоторое расписа-
ние s' (без прерываний) и7тах($') <7 (я, я').
Аналогично можно показать, что если в последовательности тт' = (/я,
/2,..., 7* пв) 71 G Nab u h+i G N'ba, to в результате обслуживания требо-
ваний множества N прибором В в последовательности тт' = (j19 /2,.. .
... , 7/-1,7/4-1,7/, 7/4-2» • .. JnB) общее время обслуживания требова-
ний при соответствующем расписании может только уменьшиться по сравне-
нию со значением 7тах(5), т.е. t(ir, я') < 7(я, я').
Таким образом, достаточно рассматривать только такие последователь-
ности я и л' обслуживания требований, при которых прибор А сначала об-
служивает требования множества Nab , а затем — требования множества
NBA, а прибор В сначала обслуживает требования множества А, затем -
требования множества NAB. При этом, поскольку Nab ^Nba =ф, требо-
вания множества N'ab можно обслуживать прибором Л непрерывно одно
за другим начиная с момента t = 0, а требования множества N'ba аналогич-
ным образом можно обслуживать прибором В.
Покажем, что общее время обслуживания всех требований не увеличит-
ся, если потребовать, чтобы прибор А (прибор В) непрерывно обслу-
живал требования множества NB А (множества NAB) начиная с некоторого
момента времени dA (я, тт') (соответственноdB (я, я')) .
Пусть требования множества NBA обслуживаются прибором Л в после-
довательности (ik, ik+i,... , i nA),k = | N'ab | + 1, причем t°k+lA =hkA>
t i k+2 A ~ л»• ’ * ’ i A ~ ^0 — i и ^i+iA ~ где h > 0 и I > k.
Положим T°ipA = + h viTipA = TipA + h для всех p = k./.
Поскольку T°ikA = t°ikA +h> TlkB +h> TikB и т^А = t°ipA + h>
> max {TtpiA,TipB} + h > max {rip_lA, 7ipB} для всех p = k + 1....
..., Z, то требования ik, i,. .. , можно начинать обслуживать прибо-
ром Л в моменты времени ?1кА, т^к+хА,... , соответственно. При
этом значение и, следовательно, общее время обслуживания требо-
ваний не изменятся.
Применяя описанное преобразованйе конечное число раз, получим
искомые значения t®pA , р = 1,... , пА.
139
Очевидно, 04(я, я ) > S tkA, dB (я, тт') > L tkB к общее
f k^N’pA
время обслужшания требований г(я, я ) = шах{б?л(я, я ) + S tkA,
nab
dB(n,i<') + 2 tkB}.
k^IBA
Таким обраом, решение исходной задачи сводится к построению опти-
мальных по бьстродействию расписаний для двух однотипных задач с оди-
наковыми марпрутами обслуживания требований. В первой необходимо
определить порядок обслуживания требований множества N9 = NAB U
U {и+ 1 } , полгая £л + 1 = (Л, B),tn+i А = О, tn+r в = S tkB ntiB =
к^^ВА
= 0, если i EiN^2lbq второй — требований множестваN" =N9ba U { и + 2 },
полагая £л+2 = (В, A), tn+2 в~®’*п+2 А~ S *кА HtjA=Q9ecJinjeNB.
WAB
В соответствш с алгоритмом, описанным в § 1 главы 1, получаем сле-
дующий резуллат. Общее время обслуживания требований множества N
достигает наиленыиего значения для расписания, при котором прибор А
обслуживает цебования в последовательности NAB, NA, NBA, а прибор
В-в последовательности NBA, NB, NAB. При этом требования множества
NAb (множества NBA ) обслуживаются прибором А и прибором В в одной и
той же последовательности, удовлетворяющей условию (4.1) (условию
(4.2)), а требсвания множеств NA и NB обслуживаются в произвольном
порядке.
Следователыо, оптимальное расписание может быть построено в резуль-
тате выполнены не более чем d(wlogAw) элементарных действий, где m =
= тах{ЦУлв|,|№л |}.
4.3. Покажем, что без увеличения общего времени обслуживания тре-
бований оптимальное (по быстродействию) расписание s* можно преобра-
зовать в расписание, при котором каждый прибор функционирует без
простоев, т.е. обслуживает требования непрерывно одно за другим.
Действителью, как показано в предыдущем пункте, требования мно-
жества N*ab (мюжества NBA) обслуживаются прибором А (приборомВ)
непрерывно одю за другим начиная с момента t = 0, а требования мно-
жества Nba (мюжества NAB) обслуживаются прибором А (прибором В)
непрерывно одю за другим начиная с момента </л(я, я') (с момента
dB(i<, *'))•
Если dA(it, я) = S tkA + h,h> 0, то dB(ir,it ) = S tkB >
keN’AB- kGN’BA
> dA(n, it') и ьожно увеличить моменты начала обслуживания требований
множества NAB прибором А на величину h без изменения общего времени
обслуживания требований. Аналогично, если dB(n, я') = S tkB + h,
k^NfBA
h > 0, то dA (я,я') = S tkA > (я, я') и без изменения общего вре-
k^NAB
мени обслуживания требований можно увеличить на величину h моменты
начала обслужшания требований множества NBA прибором В. В обоих слу-
чаях каждый прибор будет обслуживать требования непрерывно одно за
другим: один прибор — начиная с момента t = 0, а другой - начиная с мо-
мента t -h.
140
Таблица 4.1
nAB nba "А "в
к 12 3 4 5 6 7 8 9 10 11
fkA 3 2 11 2 4 3 1 2
*кВ 2 12 1 4 8 9 — — 2 1
4.4. Пример. При подготовке радиопередачи требуется прослушать
и записать на магнитную ленту п музыкальных произведений. Для этого
можно использовать аппаратуру воспроизведения А и аппаратуру звукоза-
писи В. Музыкальные произведения NAB необходимо вначале прослушать
на аппаратуре А, а затем дополнить комментариями на аппаратуре В. Музы-
кальные произведения NBA необходимо записать на аппаратуре В, а затем
прослушать на аппаратуре А. Музыкальные произведения NA достаточно
только прослушать, a NB — только записать.
Необходимо составить оптимальное по быстродействию расписание
подготовки радиопередачи. Исходные данные задачи приведены в табл. 4.1.
Упорядочим требования множества NAB так, чтобы полученная после-
довательность 71ав удовлетворяла условию (4.1): tiab = (3, 4, 1,2). Тре-
бования множества NB А упорядочим так, чтобы полученная последователь-
ность тгВА удовлетворяла условию (4.2) : тгвл = (6, 7, 5).
Таким образом, при расписании 5* музыкальные произведения прослу-
шиваются на аппаратуре А в порядке л = (3,4, 1, 2, 8, 9, 6, 7, 5) и записы-
ваются на аппаратуре В в порядке л' = (6,7,5, 10, 11,3,4, 1,2).
На рис. 4.1 представлено расписание, соответствующее последователь-
ностям лил'.
Для того чтобы аппаратура работала непрерывно, достаточно увеличить
моменты времени начала воспроизведения музыкальных произведений на
аппаратуре Л, как показано на рис. 4.2.
приборВ —..........♦'
к л34 1 2 6 9
прибор A "I I 4—4-4—4-
_1. I I I L-J. 1111
О 7 10
7 б 10 11 3 4 1 2
I I II II II
। * !
i । 1
6 7 I 5 । '
----1 Ь- I I—I '
i Н :
L_L1_ 1 llllll |
21 2324 30 t
Рис. 4.1
6
приборВ -
прибор А -
О
3 4
HI-+
।
I
л9
I
I
1-.J .11111
314| 1 /|
/7 14 21 2324 30
б . 7
4
t
Рис. 4.2
141
4.5. Покажем, что задача поспоения оптимального по быстродействию
расписания обслуживания множетва N одновременно поступающих требо-
ваний двумя приборами являетсяNP-трудной в случае, когда значения г{ =
= 3 хотя бы для двух требований в N.
Рассмотрим вначале случай, согда в процессе выполнения операций
допускаются прерывания. Сформируем соответствующую задачу распоз-
навания.
В обслуживающую систему, согоящую из приборов А и В, в момент вре-
мени d = 0 поступает множество /= {1, 2,. .. , и } требований. Для каждо-
го требования i G N задан маршрт обслуживания £*, причем число стадий
обслуживания < 3. Для кажда операции (z ,L,q),i G N,L G { A, В },
1 <6? < rf, известна длительносъ tiLq > 0 ее выполнения прибором L =
= Llq.Длительности выполнения аераций представляют собой целые числа.
Необходимо определить, существ ет ли расписание 5° (возможно, с преры-
ваниями в процессе выполнения спераций) обслуживания требований мно-
жества N такое, что Гтах(5°) яя заданного числа .у.
Построим полиномиальное свдение задачи о разбиении (см. вводную
часть данной главы) к сформулирезанной задаче распознавания.
Положим п = п0 + 2, у = 10F, / = (В, A),tiBl = tiA2 =Cj для всех тре-
бований i = 1,. . . ,и0;
Ln*1 = (А, В, A), tn + i А1 - tn^ B2 ~ 61 + 1,43 =
£"+2 = (В, Л, В), tn+2f А 2 = tn+ вз = Е, tn+2 Bi = 6Е.
Покажем, что для построенног задачи расписание s° существует тогда
и только тогда, когда существует разбиение множества NQ на подмножест-
ва и N2, для которых Ei = Е2.
Если указанное разбиение мносества NQ существует, то существует и
расписание с общим временем облуживания требований, равным^. Одно
такое расписание (без прерывани в процессе выполнения операций) при-
ведено на рис. 4.3.
п+1 п+2 п+2
прибОрВ — I ' I ' — » !'
п+1 п+1 \п+2 |А=л/;
прибор А--» । — - | < |
i i ill
ii til
li iii
___i___i_________________________i_i___i_>.
О E 2E 6E 9E 1OE t
Рис. 4.3
Если задача о разбиении не имет решения, то общее время обслужива-
ния требований при любом распиании (в том числе и с прерываниями в
процессе выполнения операций) бс!ьше.у.
Действительно, предположим, чо существует расписание s°, при кото-
ром Fmax(s°) <*у. Поскольку сухарная длительность всех операций, вы-
полняемых как прибором А, так i прибором В, равна 10F - у, то при рас-
писании s° приборы Л и В во врменном интервале (О, 10F] не простаи-
вают.
142
Обозначим через множество требований i G;V, 1 <z <и0, которые
при расписании м° обслуживаются (возможно, частично) прибором А в
интервале (О, 2Е]. Кроме операций вида (z ,Л, 2),z GTVi, прибор Л в ука-
занном интервале может выполнять только операцию (п + 1, Л, 1). Сле-
довательно,
2 tiA2 “ *п + 1 ,а 1
Поскольку L1 = (В, Л) для всех i = 1,. .., и0, т0 множество N° может
содержать только такие требования i, для которых операции (z, В, 1) вы-
полняются полностью во временном интервале (О, 2Е]. Таким образом,
имеет место соотношение
(4.3)
Заметим, что при любом расписании с общим временем обслуживания
требований, равным^, выполнение операции (и + 1, В, 2) должно быть за-
вершено не позднее момента времени t = 4£, а выполнение операции
(п + 2, В, 1) — не позднее момента времени t = 8/Г. Следовательно, для об-
служивания требований из множества 7V0 = {1,2,..., и0} прибором В
может быть использовано не более чем SE - 6Е - Е = Е единиц времени во
временном интервале (О, SE] (и тем более в интервале (О, 2Е]).
Так как CjV°,to S Г/В1<2?и, учитывая (4.3), получаем
i G
S = S в/ = E, что противоречит предположению о том, что
i е N*
задача о разбиении не имеет решения.
Нетрудно видеть, что для реализации описанного сведения требуется не
более д(и0) элементарных действий.
Таким образом, задача построения оптимального по быстродействию
расписания (с прерываниями) является TVP-трудной в случае, когда хотя
бы для двух требований множества N значения = 3, а для остальных тре-
бований г{ = 2.
4.6. Если прерывания в процессе выполнения каждой операции запреще-
ны, то задача построения оптимального по быстродействию расписания,
оказывается NP-трудной уже в случае, когда для одного требования из N
значение г{ =3,а для остальных требований = 1.
Построим полиномиальное сведение задачи о разбиении к соответствую-
щей задаче распознавания.
Положим п - п^ + l,j = 2£’+l,£l = (Л), tiA! = ez- для требований z =
= 1,. . . ,zz0J Ln = (В, Л, В), tnBi tnA2 = 1-
Покажем, что для этой задачи расписание м° (без прерываний в процессе
выполнения операций), при котором 7max(s°) =Z существует тогда и толь-
ко тогда, когда существует разбиение множества № = { 1, 2,. .. , nQ ) на
подмножества NQi и N%, для которых S = S = Е.
i^№2
Если указанное разбиение множества NQ существует, то существует
и расписанием °, для которого Fmax(s°) =у (рис. 4.4).
Если задача о разбиении не имеет решения, то докажем от противного,
что общее время обслуживания требований при любом расписании без
прерываний в процессе выполнения операций должно быть больше у.
143
Предположим, что существует расписание s° (без прерываний), для
которого 7max(s°)<.>'.
Поскольку суммарная длительность операций по обслуживанию требо-
вания п равна у, то при любом расписании (без прерываний) с общим вре-
менем обслуживания требований, равным у, операция (и, В, 2) единичной
длины должна выполняться во временно'м интервале (Е, Е + 1].
Так как процесс обслуживания каждого требования /О0 состоит из
единственной операции, L' = (В), то при расписании s° нет прерываний в
приборе
приборА
Рис. 4.4
процессе обслуживания требований i €tf°. Обозначим через TV? подмно-
жество требований из 7V0, которые обслуживаются во временном интерва-
ле (0,Е].
Поскольку суммарная длительность всех операций, выполняемых при-
бором В, равна у, то при любом расписании с общим временем обслужи-
вания требований, равным у, этот прибор в интервале (0, .у] не простаи-
вает. Получаем S е,- = Е, что противоречит предположению о том, что
1’6
задача о разбиении не имеет решения.
Для реализации описанного сведения требуется О («о) элементарных
действий.
4.7. В п. 3.6 предыдущего параграфа показано, что при М = 2, dt = О,
z G N, tiLq G {1,2} задача построения оптимального по быстродействию
расписания (без прерываний) является NP-труда ой в сильном смысле.
Покажем, что аналогичный результат имеет место и в случае, когда
М = 2, d{ = 0, i G N, tiLq - целые числа и разрешены прерывания. Сфор-
мулируем соответствующую задачу распознавания.
В обслуживающую систему, состоящую из двух приборов Л и В, в мо-
мент времени d = 0 поступает множество требований N = {1, 2,..., п} .
Для каждого требования i G N заданы маршрут обслуживания L1 =
= (Z, 1, Z, а». •., Llr.) и целочисленные длительности tiLq выполнения
всех операций (z, L, q), L = Llq, q = 1, .. . , ry. Необходимо определить,
существует ли расписание х°(возможно, с прерываниями в процессе выпол-
нения операций) обслуживания требований множества N такое, что
6пах(5°)^^ Для заданного числам
Построим полиномиальное сведение задачи о 3-разбиении (см. ввод-
ную часть данной главы) к сформулированной задаче распознавания.
Положим п = Зи0 + 1,У ~ 2nQE, L1 = (А, В), tiA i = цдя всех
требований i = 1,. .., Зи0; Ln = ([2?, А] л°), tnL nq = Е для всех q = 1,...
..., 2и0’ Напомним, что [ • ]л означает последовательность, состоящую из
h повторений стоящего в скобках выражения.
144
Покажем, что расписание 5°, при котором tmax(s°) = У и возможны пре-
рывания в процессе выполнения операций, существует тогда и только
тогда, когда имеет решение задача о 3-разбиении,
Пусть существует разбиение множества NQ = {1, 2,... Зиог} на nQ
трехэлементных подмножеств ЛГ?, Л^,... , таких, что е{ =Е
при j = 1, . .. , nQ. Тогда существует и расписание с общим временем обслу-
живания требований, равным у = 2nQE, Одно такое расписание (без пре-
рываний) приведено на рис. 4,5.
Пусть существует расписание s°, при котором 7max(s°) = у. Так как
суммарная длительность выполнения всех операций прибором А (прибо-
ром/?) равна
Зп0
S в/ +nQE= 2nQE = y,
! = 1
то при расписании 5° как прибор А, так и прибор В во временном интерва-
ле (0, 2ио/Г] не простаивает. Поскольку
гп
2 ^£л<7= 2п0Е = у,
Q = 1
то при расписании s° операции по обслуживанию требования п должны
выполняться непрерывно одна за другой начиная с момента времени t = О,
как показано на рис. 4.5. Из равенства tiA х = z = 1, • •, Зи0> сле-
дует, что для того, чтобы при расписании с общим временем обслужива-
ния требований, равным у, не было простоев прибора В в интервале (Е,
2Е], необходимо и достаточно, чтобы в интервале (О,/Г] были полностью
выполнены операции вида (ii,A, 1), (il + 1, А, 1),..., (z’/, Л, 1), где/\ G
6Лг0Д = 1,...,/, и только они, а в интервале (Е, 2Е] были полностью
выполнены операции (z’i, В, 2), (z’i + \,В, 2),..., (z’z, В, 2). В силу нера-
венств F/4 < et < Е/2, i = 1, . . . , Зи0, получаем / = 3.
п
1--------!----------1
I I n |
прибор В
приборА
О E 2E 3E 4E
n
••• 4——I——j
... ,1. j
। । ।
। । ।
। । ।
'z(n0-1)E (2п0-1)Е 2n0E t
Рис. 4.5
Таким образом, выделено трехэлементное подмножествоN\ ={ /1,12,1’3}
множества TV0, для которого
S в,- = S 2 = Е.
Далее индукцией по / можно показать, что при расписании 5° в интервале
(2Е(j — 1), 2Е/], 1 < / <и0, начинается и завершается обслуживание точ-
но трех требований из множества N °. В результате получим разбиение мно-
10. В.С. Танаев 145
жества № на тэехэлементные подмножества TV?, N%, • . ., N„ такие, что
S е, -Е, 1 < п0.
i(=N?
Реализация отисанного сведения требует выполнения O(nQ) элементар-
ных действий. Это сведение является как полиномиальным, так и псевдо-
полиномиальным. Следовательно, задача построения оптимального по
быстро действии расписания (как с прерываниями, так и без них) обслужи-
вания двумя приборами п одновременно поступающих требований являет-
ся NP-трудной з сильном смысле даже в том случае, когда для одного из
требований множества N значение г{ не превосходит 2 (и — 1), а для каждо-
го из остальных требований г{ = 2.
4.8. Поскольку задача с одинаковыми маршрутами L* обслуживания
всех требования i Е N является частным случаем рассматриваемой в этом
параграфе задач!, то все результаты относительно ^-трудности задач, при-
веденные в главе 1 справедливы и для соответствующих аналогов при раз-
личных маршрутах L1 обслуживания требований i Е N.
В частности, задача построения оптимального по быстродействию рас-
писания (как с прерываниями, так и без прерываний) обслуживания тре-
бований i Е N, поступающих в моменты времени >0 в обслуживаю-
щую систему, состоящую из М приборов, NP-трудна в следующих случаях:
а) М=3, di-0, г, <2, f=l,.. . ,п\
б)М=2, dtE {d,d'), г{<2, 1,. .. ,n,
и NP-трудна в сильном смысле в случае
в)М=2, rf<2, z= 1,. . .,п.
§ 5. Общее время обслуживания требований без задержек
В этом параграфе рассматривается задача построения оптимального по
быстро действию расписания без задержек в процессе обслуживания каждо-
го требования.
5.1. В систему, состоящую из двух приборов, в момент времени d = О
поступает множество N = {1, 2,...,«} требований. Маршрут L* обслужи-
вания требования i Е N представляет собой чередующуюся последователь-
ность приборов (£i, ...,£*), в которой Lq Е(А, В}, q = 1,.. . ,г/}
Lq + q = 1,..., — 1. Длительности tiLq выполнения всех опера-
ций (z, L, q) предполагаются заданными. Каждое требование должно об-
служиваться непрерывно и без задержек, т.е. оптимальное по быстродейст-
вию расписание s* ищется в классе расписаний s, при которых Л0,/ =
/ь qq
ri
, a г ? = 2, •.. ,rf, и tt(s) = f®(s) + 2 t i i&N.
/Lq-bQ-l < Q = 1 tbqq
Как показано в § 3 гл. 1, если = 2, i Е N, все iJ одинаковы и все
tiLq > О, то расписание s* может быть построено за О(п log п) элементар-
ных действий. Если же при этих условиях допускаются нулевые длитель-
ности выполнения операций, то задача построения расписания 5* является
TVP-трудной в сильном смысле.
146
Таким образом, если rt < 2, z ENt все tiLq>§n допускаются различные
маршруты прохождения приборов - L* Е {(Л, В), (В, Л), (Л), (В)}, то
задача построения расписания s* является NP-трудной в сильном смысле,
поскольку NP-трудным в сильном смысле является ее частный случай
при L* €{(Л, В), (Л), (В)}.
Покажем, что если L* Е {(Л, В), (В, Л) } и tiLq> 0, то задача построе-
ния расписания s* также NP-трудна в сильном смысле. Доказательство про-
ведем в три этапа.
5.2. Введем в рассмотрение так называемую задачу о четырех-
элементных суммах. Имеется четыре множества U={ui9 и^...,ир}9
V = {и1} и2,... ,ир}, W = { w2, ..., wp} и X = {хь х2,. .. ,хр}, эле-
ментами каждого из которых являются натуральные необязательно различ-
1 р
ные числа, и пусть Q = — S (и/ + и/ + + х/) - натуральное число. Тре-
р z = i
буется определить, существует ли разбиение множества С/U К U W UX на
четырехэлементные подмножества 1 < тп < р, такие, что в каждое
подмножество Rm входит по одному элементу из каждого множества U, V,
W и X, причем их сумма равна Q.
Покажем, что эта задача является NP-трудной в сильном смысле. Рас-
смотрим известную задачу о трехмерном паросочетании (см. вводную
часть данной главы).
Число упорядоченных троек в Е, m-я компонента которых равна i Е TV0,
обозначим через дт(г), 1 <3. Можно считать, что все gw(z‘) > 1,так
как в противном случае Е не содержит требуемого паросочетания. Пусть
й = и0 + 1иЯ=1 + Й + Й2 + h3. Для каждой тройки (/,/, k) G Е, компоненты
которой необязательно попарно различны, положим U(i, j, к) = Н —
- (z + jh + kh2) и определим множество U как совокупность всех U(i9 f, к).
Для каждого z ETV0 положим
K(z, l) = z + 3/z4, V(i, l) = i + 5h4, 2</<pi(0,
W(z, l) = z7z + 3/z4, W(i, l) = ih+2h4, 2</</z2(z),
X(z,l) = z7z2 +3/z4, X(i,l) = ih2 +2h4, 2^l^p3(i)9
и определим множество V как совокупность всех K(f, 1) и V(if Z), мно-
жество W - как совокупность всех W (i, 1) и W (i, I) и множество X -
как совокупность всех X(i, 1) и X(i, I).
Заметим, что S pm(j) = \ Е\, 1 < т < 3, и поэтому | U\ = | К] =
= | W I = |Х | = | Е |. Очевидно, Q = Н + 9/z4. Максимальный элемент в по-
строенных множествах ограничен полиномом четвертой степени, зависящим
от Л < |Е|. Число элементарных действий, необходимое для построения
этих множеств, не превосходит 0(h41 Е |).
Пусть множество троек Е содержит требуемое паросочетание Е9. Тогда
имеет решение и построенная задача о четырехэлементных суммах, причем
подмножества Rm, 1 < т < | Е |, могут быть найдены следующим образом.
Если тройка (z, /, к) Е Е9, то одно из искомых множеств Rm состоит из эле-
ментов U(i, j, к), K(z, 1), W (i, 1), X(z, 1). Если же тройка (z,/, к) не вошла
в паросочетание Е9, то можно сформировать множество Rm, состоящее из
10* 147
элементов U(i, j, к), V(i, ZJ, W(j, Z2), X(k, Z3), где 2 C lx Cp^z), 2 C
</2<Д2(/),2<73<Дз(^).
Пусть имеет решение построенная задача о четырехэлементных суммах
и Rtn - одно из найденных подмножеств, 1 С т С | Е |. Покажем, что в
этом случае имеет решение и задача о трехмерном паросочетании.
Предварительно докажем, что если подмножество Rm содержит элемент
U(i, j, к), то оно содержит также элементы K(z, , W (/, Z2) и Х(к, 13). Рас-
смотрим величину Q = Н + 9Zi4 как число, представленное в системе счисле-
ния по основаниюh. ’’Вклад” величины7/=1+Zi + Zi2+Zi3b значение Q соот-
ветствует цифрам четырех младших разрядов, в то время как величина 9Zi4
определяет цифру более старшего разряда в записи числа Q в системе счис-
ления по основанию h = nQ + 1. Для того чтобы цифра старшего разряда
оказалась равной 9, необходимо, чтобы либо Ц = Z2 = l3 = 1, либо 2 CZj С
<М1(0, 2CZ2Cp2(/), 2CZ3CM3(*).
Таким образом, среди подмножеств Rm, 1 Cm C | E|,имеется ровного
таких, что Rm = { U(iJ9k), R(i, 1), И/ (z, l),X(z, 1)} для некоторой тройки
(z, /, к) G E.
Очевидно, множество таких троек образует искомое трехмерное паро-
сочетание Е' из nQ троек.
5.3. Введем в рассмотрение задачу распознавания, которую в дальней-
шем будем называть задачей о равных парах. Имеется четыре
множества U= {ць и2ир}, V = {и1? и2,..., vp}, И/ = {wj, w2,..., wp} и
X = {xi, x2,... ,xp}, каждое из которых состоит из натуральных необяза-
тельно различных чисел. Требуется определить, существует ли разбиение
множества UUV UW иу на четырехэлементные подмножества Rm, 1 С
С т С р, такие, что в каждое из них входит по одному элементу из каждого
множества U, V, W иХи для каждого Rm = {uli,v1^,w1^, Хц } имеет место
равенство + и?2 =wz
Покажем, что к этой задаче полиномиально сводится задача о четырех-
элементных суммах. Пусть U9 = { и J, и2, ..., и'р}, Vf= {v\, v2,... ,vp},
W' = {wj, w2, . .. , w'p} и X' ={x'i, x2,. . . ,Xp} - множества, определяю-
, 1 P ! ,
щие задачу о четырехэлементных суммах, и Q = — S + wf + xf).
p i = i
Для каждого i, 1 Cz Ср, положим u{ = Q* + 2uJ, = Qf + 2u'., =
= 20'-2wp xf = 2£?'-2xz.
Предположим, что задача о четырехэлементных суммах имеет решение
и R 9т, 1 Ст Ср, - найденные подмножества. Тогда имеет решение и задача
о равных парах, причем искомые подмножества Rm, 1 Cm Ср, могут быть
построены, например, следующим образом. Пусть R'm ={u,li1 vrt , , x\j .
Положим Rm = {uZi, Vi2 ,Wi3 ,Хц} . Так как и'ц + -Q' - Wi3 - x^, то
= v% +х/д.
Пусть имеет решение задача о равных парах и Rm, 1 Cm Ср, - найден-
ные подмножества. Если Rm = {«Z1, , w/3, Х/4}, то можно положить
’ у/2 5 ’ Поскольку +i>j2 = wz3 +xz4> то> очевидно,
< +и/2 +Ч +ч =°-
148
Для реализации этого сведения достаточно выполнить О(р) элементар-
ных действий, и следовательно, задача о равных парах является NP-трудной
в сильном смысле.
5.4. Рассмотрим задачу распознавания, соответствующую задаче построе-
ния оптимального по быстродействию расписания s* без задержек в процес-
се обслуживания требований при условии, что допускаются только два
возможных маршрута (Л, В) и (В, А) обслуживания требований прибо-
рами. Необходимо определить, существует ли расписание s° обслуживания
(без задержек) множества требований N такое, что rmax($°) Су для за-
данного числа у.
Покажем, что к этой задаче полиномиально сводится задача о равных
парах. Без потери общности в задаче о равных парах можно предполагать,
р р р р
что S ut + 2 U|= S wf-+ S X/, так как в противном случае эта задача
z=i z=i /= 1 /=1
не имеет решения.
р
Положим п = 4р, у =2р + 3pz +4 S + иД где z = 8 max и,, wj, x/}.
Введем в рассмотрение следующие четыре множества требований: мно-
жество Nu = {1,2,... ,р}, полагая L1 = (А, В), tiA i = 1 и tiB2 = для
каждого требования i ; множество Ny = {р + 1,р + 2, ...,2р}, пола-
гая L1 = (В, Л), tiBX = + 3z и tiA 2 = 1 для каждого z G/VK; множество
Nw = { 2р + 1,2р + 2,. .. , Зр}, полагая Ll = (А, В), tiA i = 4wf + z и tiB2 = 1
для каждого i G Nw , и множество Nx = { Зр + 1, Зр + 2,.. ., 4р}, полагая
L* = (В, A), tiB\ = 1 и tiA2 ~ + 2z для каждого i^Nx •
Покажем, что для построенной задачи расписание s°, при котором
4пах0°) Сум нет задержек в процессе обслуживания требований множест-
ва N= Ny UNy UNW существует тогда и только тогда, когда имеет
решение задача о равных парах. Заметим, что поскольку величина у равна
полусумме длительностей выполнения всех операций по обслуживанию
требований множества N приборами А и В, то при любом расписании с
общим временем обслуживания требований, равным у, ни один из прибо-
ров Л и В не простаивает во временном интервале (0, у], а расписания с
общим временем обслуживания требований, меньшим у, не существует.
Пусть задача о равных парах имеет решение и Rm, 1 С/л Ср, - найден-
ные подмножества множества U U V U W U X. Расписание s° может быть
построено следующим образом. Если = {и^ 9v^9 wz3>xz4}> то во вре-
менном интервале (0, т], где т = 4(и^ + vZa) + 3z + 2, прибор А обслу-
живает требования в последовательности 1\,3р + Z4, 2р + l3,p + Z2, а при-
бор В-в последовательности 3p + Z4,Z1,p + Z2,2p + Zs (рис. 5.1).
Вслед за указанными требованиями аналогично обслуживаются требо-
вания, определяемые подмножеством В2 , и т.д. _
Пусть существует расписание s° (без задержек), при котором fmax(s°)
Су. Предположим, что при расписании s° прибором А первым обслужива-
ется требование z, а прибором В — требование /. Требование z должно при-
надлежать множеству N у или множеству N , так как в противном случае
149
приборВ
приборА
t
приборВ
приборА
Рис. 5.2
прибор А будет простаивать, пока требование из множества Nv будет
обслуживаться прибором В. Аналогично / Е Nv U Nx.
Покажем, что если i Е Nw , то хотя бы один из приборов будет простои*
ваты Действительно, если / Е NVi то простаивает прибор Д, поскольку не-
равенство tiA! < tjg! выполняется для требования i Е Nw и каждого тре-
бования / Е Му и при расписании s° требования обслуживаются без задерж-
ки (рис. 5.2,а). Если же j Е Nx, то простаивает прибор В, поскольку
tjB 1 = 1 < Ча 1 ПРИ i е , J е Nx и требования обслуживаются без
задержки (рис. 5.2, б).
Таким образом, i Е Ny. Отсюда следует, что при расписании 5° имеем
/ Е NXi так как в противном случае прибор В будет простаивать в интерва-
ле (0, 1].
По определению величины z получаем, что tjA2 — Чв2 > 1 для всех
i Е Ny и всех j Е Nx, Следовательно, после выполнения операции (z, В, 2)
прибором В должно обслуживаться требование к из множества Nv (в про-
тивном случае либо прибор В будет простаивать, либо требование к будет
обслуживаться с задержками).
На рис. 5.3 представлено расписание обслуживания без задержек требо-
ваний z, j и к, принадлежащих множеству Ny, Nx и Nv соответственно.
По определению величины z получаем, что tiB2 + ЧсВ1 ~ Ча2 > 1 для
всех i Е N х, j Е N х нкЕ Nv , и для того, чтобы исключить простои прибо-
150
ров и задержки в обслуживании требований, необходимо, чтобы после вы-
полнения операции (/, А, 2) прибором А обслуживалось требование I из
множества Nw и, кроме того, выполнялось равенство tiB2 + *кВ1 =
~ tjA2 + tlAl-
Таким образом, элементы U/, vki Wj и множеств U, V, W иХ соот-
ветственно образуют подмножество Rlf для которого + vk = Wy + xz.
Рассуждая аналогичным образом, нетрудно построить и остальные под-
множества Rm, 2 <т <р, составляющие решение задачи о равных парах.
Реализация описанного сведения требует выполнения О(р) элементар-
ных действий.
Таким образом, задача построения оптимального по быстродействию
расписания без задержек в процессе обслуживания требований является
NP-трудной в сильном смысле даже в том случае, когда система состоит
из двух приборов А и В и допускаются два возможных маршрута (А, В)
и {В, А) обслуживания требований,
5.5. Покажем, что при единичных длительностях всех операций задача
построения оптимального по быстродействию расписания без задержек
в процессе обслуживания каждого требования является NP-трудной.
Сформулируем соответствующую задачу распознавания.
прибор В - ь—I-----1—1---h—< • • • —1----•—I---»—|
приборА —<-----1—<----1—1----h- • • • —»—•-----h—I
___I__I___I__I__I___L_ . . . -J____I__I__I___I_>.
0 12 3 4 5 6 2Е-Ч 2E~3 2E~2 2E~12E t
Рис. 5.4
В обслуживающую систему, состоящую из двух приборов А нВ, в мо-
мент времени d = 0 поступает множество N= {1,2,..., п } требований. Дли-
тельность tiLq= 1 для всех i G N,L = Llq,q = 1,... ,rit Необходимо опре-
делить, существует ли расписание s° без задержек в процессе обслуживания
требований N такое, что fmax(s°)^.P Для заданного числа у.
Построим полиномиальное сведение задачи о разбиении (см. вводную
часть данной главы) к сформулированной задаче распознавания.
151
Положим п = п0, у = 2Е + 1, L1 = ([Л, В]**), tiLi q = 1, i € N} q =
= l,...,2ez. Q
Нетрудно показать, что для построенной задачи расписание s° существует
тогда и только тогда, когда существует разбиение множества 7V0 на под-
множества N? nN2, ДДя которыхEi =Ег.
Действительно, если указанное разбиение множества NQ существует,
то при расписании, приведенном на рис. 5.4, 2max(s°) = У и все требования
обслуживаются без задержек (обслуживание требований множества N\
изображено тонкой линией, а требований множества N% — жирной).
Если же указанного разбиения множества № не существует, то очевид-
но, что при любом расписании s обслуживания требований N приборами
А и В либо выполняется неравенство 4nax(s) > у, либо хотя бы одно из
требований не обслуживается непрерывно (без задержек).
Поскольку для реализации описанного сведения достаточно выполнить
O(nQ) элементарных действий, то задача построения расписания s° являет-
ся NP -трудной.
§ 6. Библиографическая справка
Системы с различными маршрутами обслуживания требований наиболее
широко распространены на практике. Как отмечали В. Дудек, М. Смит
и С. Панвалкар [507, 724], в 57% из 300 обследованных промышлен-
ных компаний США маршруты обслуживания требований были раз-
личными.
6.1. Графический подход к построению оптимального по быстродейст-
вию расписания обслуживания двух требований М приборами предложен
С.Акерсом и Дж.Фридманом [422, 423]. Основанные на этом подходе
полиномиальные алгоритмы решения данной задачи в случае, когда преры-
вания запрещены, предложены В.Шварцем [794], В.В.Сервахом [281],
Н.И.Глебовым [67], В. Хардгрэйвом и Г.Немхаузером [592]. Алгоритм
с наилучшей оценкой трудоемкости <?(со log со) описан В.В.Сервахом [281]
(здесь со — число особых прямоугольников в графическом представлении
задачи). В [67] предложен полиномиальный алгоритм решения указанной
задачи при разрешении прерываний. Оценки общего времени обслуживания
двух требований М приборами получены В.Э.Хенкиным [381], Н.И.Глебо-
вым и В. А .Перепелицей [68,70].
Описанные в § 1 полиномиальные алгоритмы решения задачи оптималь-
ного обслуживания двух требований М приборами при произвольной
неубывающей целевой функции предложены Ю.Н.Сотсковым [302]. Вопро-
сы программной реализации этих алгоритмов рассматривались А.В .Тузи-
ковым [360].
Попытки обобщения графического подхода на случай М > 2 предприни-
мались в [281, 688, 794, 813, 822]. В.В.Сервахом [281] предложен псевдо-
полиномиальный алгоритм трудоемкости О(МТ log М) для построения оп-
тимального по быстродействию расписания обслуживания трех требований
М приборами при условии, что число выполняемых каждым прибором
операций ограничено, длительности всех операций целые числа и их сумма
равна Т.
152
6.2. В.Г.Тимковский [355], НЛифитц и И.Адири [595] предложили по-
линомиальные алгоритмы построения оптимального по быстродействию
расписания обслуживания двумя приборами п одновременно поступающих
требований с единичными длительностями операций. Трудоемкость этих
алгоритмов — О (Я), где R — общее число выполняемых операций. При неод-
новременном поступлении требований оптимальное по быстродействию
расписание может быть построено за O(R log/?) действий [481, 595]. Для
решения сопряженной задачи минимизации максимального временного
смещения П.Бруккер [482] предложил алгоритм трудоемкости 6>(Я)при
условии целочисленности директивных сроков.
Приведенное в пп.4.1-4.4 обобщение алгоритма СДжонсона [612]
получено Дж.Джексоном [608].
6.3. Описанный в § 8 гл. 1 подход к построению полиномиальных ал-
горитмов с априорными оценками абсолютной или относительной пог-
решности получаемого решения можно использовать и для систем с раз-
личными маршрутами обслуживания требований.
С.В.Севастьяновым [278] предложен алгоритм трудоемкости О(р2М2г2)
построения расписания s°, при котором 6<г(ЛГ2г2 + г — 2)Г*, где 6 =
= Лпах(«°)-Gnax(s*)> г = max {г, | i&N } и t* = max {tiLq | i E.N, L=L^,
= 1,..., Г/ }. Для случая, когда каждая операция может выполняться
любым прибором из заранее выделенного множества приборов, в [278]
предложен алгоритм трудоемкости O(M2n2r2 + (rn + Af)3logm) построе-
ния расписания s°, при котором 6<(г37И3 +г2 -2г + 2)Г*.
Для случая Л/ = г=3 А.И.Бабушкин, А.И.Башта и И.С.Белов [17]
предложили алгоритм трудоемкости О(п2) с оценкой 6 < 3(3>/2 + 5)Г*,
а С.В.Севастьянов [277] — алгоритм той же трудоемкости с оценкой 6 <6Z*.
Для обслуживающих систем, в которых часть требований обслужива-
ется приборами в порядке 1,2, ...,7И, а остальные требования — в по-
рядке М,М — 1,..., 1, С.В.Севастьянов [276] предложил алгоритм тру-
доемкости О(п2М2) построения расписания s°, при котором 6 < (2Л/2 —
- (М + 3)/2)f*. Эта же задача рассматривалась в [16], предложенный
алгоритм имеет худшие оценки.
Т.Гонсалес и С.Сахни [552] показали, что для любого расписания s°,
при котором в любой момент времени из интервала (0, fmax(s°)]
функционирует хотя бы один прибор, справедливы оценки
п _ п __ _ _
S l,-(s°)/S tt(s*)<n и tmax(s°)/tmax(s*)<M, причем эти оценки
i=l i=l
достижимы при малых значениях М. В этой же работе предложен алго-
ритм трудоемкости O(nlogn) построения расписания s°, при котором
п __ п _
S tjfs0)/ S /,($*) В.Г.Тимковским [353] описан алгоритм трудо-
i=l 1 = 1
емкости O(R +Мг) построения расписания s°, при котором
^max(5°)Amax(5 ) niin {М, г},
6.4. Доказательству АР-трудности различных частных случаев задачи
построения оптимального по быстродействию расписания обслуживания
(без прерываний) п одновременно поступающих требований М прибора-
ми посвящен ряд публикаций.
153
Приведенное в п. 3.4 доказательство /VP-трудности в сильном смысле
этой задачи при М = 3 и tiLq = 1 предложено Я.Ленстрой и А.Ринной Ка-
ком [652]. Ранее Я.Ленстра, А.Ринной Кан и П.Бруккер [657] доказали
ее NP-трудность при целочисленных tiLq. В [652] установлена /VP-труд-
ность в сильном смысле указанной задачи при М = 2 и tiLq G { 1,2 } (см.
п. 3.6). В.Г.Тимковским [354] и Ю.Н.Сотсковым (см. п. 3.5) доказана ее
^-трудность в сильном смысле при М = 2, tiLq = 1 и заданном отноше-
нии строгого порядка, граф редукции которого состоит из цепей.
Я. Ленстра, А. Ринной Кан и П. Бруккер [657] установили/VP-трудность
задачи в случае, когда М = 2, хотя бы одно г,- = 3, а остальные г/ = 1 (см.
to. 4.6). М. Гэри, Д. Джонсон и Р. Сети [533] доказали /VP-трудность в силь-
ном смысле задачи в случае, когда М = 2, хотя бы одно = 2(п — 1), а осталь-
ные гг = 2 (см. п. 4.7). Т. Гонсалес и С. Сахни [552] показали, что при
разрешении прерываний в процессе выполнения операций задача оказывает-
ся /VP-трудной в случае, когда М = 2, rt = 3 для двух требований и г, - 2
для остальных требований (см. п. 4.5), и /VP-трудной в сильном смысле
в случае, когда М = 2, г, = и/3 для одного требования и rt = 2 для остальных
требований.
С. Сахни и Ю. Чо [764] доказали /VP-трудность в сильном смысле задачи
построения оптимального по быстродействию расписания обслуживания
без задержек п одновременно поступающих требований двумя приборами
(см. § 5). В.Г. Тимковский [354] установил, что /VP-трудной является
задача построения оптимального по быстродействию расписания обслужи-
вания без задержек п одновременно поступающих требований двумя прибо-
рами, когда длительности выполнения операций одинаковы.
Поскольку система с одинаковыми маршрутами обслуживания требова-
ний — частный случай рассматриваемой, то все результаты о /VP-трудности
задачи, приведенные в гл. 1, справедливы и для систем с различными
маршрутами обслуживания требований.
После подготовки рукописи книги к изданию Ю.Н. Сотсковым была
доказана /VP-трудность задач оптимального по быстродействию обслужи-
вания (с прерываниями или без прерываний операций) трех требований с
фиксированными (одинаковыми или различными) маршрутами прохож-
дения приборов. Аналогичные результаты установлены и для задач мини-
мизации суммарного времени обслуживания трех требований.
6.5. Для решения /VP-трудных задач построения оптимальных расписаний
разработан ряд методов последовательного анализа вариантов, целочислен-
ного линейного программирования, различные эвристические процедуры.
Целочисленные линейные модели описаны Е. Балашем [449], Е. Боума-
ном [475], X. Вагнером [826], X. Гринбергом [571], Дж. Данцигом [497],
М. Фишером [522], А.Л. Лурье [194, 195], А. Манном [678], С. Ланзенау-
ром и Р. Химесом [641], Дж. Чарлтоном и С. Детом [491], Ю.А. Заком,
[106], В.С. Солдатовым [289] и другими авторами. Систематическое
исследование применимости методов линейного программирования для
решения задач теории расписаний проведено Ю.В. Глебским и В.Н. Шевчен-
ко [71, 72, 397, 398]. Этим же вопросам посвящены работы [91,117, 642].
Возможности использования теории двойственности при решении задач
календарного планирования анализировались М. Фишером [522], В.К. Де-
154
миным и А.С. Чеботаревым [91], А.И. Кук сой и Ю.П. Лаптиным [159 — 161],
А.Л. Ильницким [113, 114] и другими.
Достаточно полное изложение теории двойственности применительно
к задачам построения оптимальных расписаний содержится в монографии
В.С. Михалевича и А.И. Куксы [215]. Изучение релаксированных задач,
возникающих в результате замены нескольких ограничений линейной
модели их линейной комбинацией, проведено М. Фишером, Б. Лагевегом,
Я. Ленстрой, А. Ринной Каном [524].
Э. Андерсон [425], И.Н. Зимин и Ю.П. Иванилов [108] рассматривали
возможности сведения некоторых задач теории расписаний к задачам
оптимального управления.
Попытки применить декомпозиционный подход к решению задач боль-
шой размерности предприняты в [126, 429, 794,822].
6.6. Методы построения различных классов расписаний рассматривались
Дж. Геллером и Г. Логеманом [598], Б. Гиффлером и Дж. Томпсоном
[540], Л. Шрейджем [768, 769], Л.П. Матюшковым и В.С. Танаевым [199],
С.А. Канцедалом и О.Н. Малых [127, 129, 131], Ю.Н. Сотсковыми В.С. Та-
наевым [296, 297, 307 , 308] и другими авторами. Исследование влияния
правил предпочтения (приоритетов) на качество получаемых расписаний
проведено в работах [30, 99, 199, 247,251,537].
Различные по сложности правила предпочтения предложены Э.Г. Иоффе
[117], П.К. Выгнаном и Б.И. Кузиным [59], Н. Стейнхофом [786],
В.В. Шафранским [388, 390], Дж. Джексоном [92], Н.Б. Мироносецким
[260] и другими авторами. Вопросам выбора правил предпочтения, опти-
мальной их композиции и настройки посвящены работы В.В. Шкурбы [399],
Г. Фишера и Г. Томпсона [373] ,У. Максвелла и М. Мехры [682], Т.П. Подча-
совой [246], М.Х. Ангуладзе [7], Л.В. Кочнева [154], А.И. Семенова и
В.М. Португала [251, 280], А-Б. Ароновича [9], А. Тизена [817]. См. также
[131,146,192,199,222, 284,292,293,437,438,782, 783].
Методы локальной оптимизации расписаний использовались в работах
Л.И. Фейгина [370], С. Петерсона [737], Дж. Кинга и А. Спачиса [622, 782],
С.А. Канцедала и О.Н. Малых [130].
Методы случайного поиска рассматривали Б. Гиффлер, Д Томпсон и
В. Ван-Нессе [66], Дж. Геллер и Г. Логеман [598], С.А. Канцедал и
О.Н. Малых [127, 130, 131], В.В. Шкурба [400], П. Рандолф, Г. Суинсони
С. Эллингсен [746,747], Г. Фишер и Г.Томпсон [373], С. Элмаграби [517],
Н.Б. Мироносецкий [211] и другие. В [66, 145, 537] проведен сравнитель-
ный экспериментальный анализ разнообразных правил предпочтения.
В обзоре Дж. Блекстона, Д. Филлипса и С. Хогга [467] рассмотрено
34 правила предпочтения. Авторы отмечают, что ни одно из этих пра-
вил не лучше остальных, однако можно выделить несколько правил,
которые в совокупности дают хорошие результаты. В обзоре С. Пан-
валкара и В. Искандера [725] проведен анализ 113 правил предпоч-
тения.
6.7. Систематическое исследование правил предпочтения проводится
и в рамках изучения стохастических обслуживающих систем, в которых
те или иные параметры (длительности операций, моменты поступления
требований в систему, маршруты обслуживания требований и т.п.) являют-
ся случайными величинами с заданными или неизвестными законами
155
распределения. В работах [104, 105, 368, 369, 417, 498, 512, 515, 516,553,
599 , 600, 607, 614, 658, 693, 702 , 756, 827 , 836] используются методы
статистического моделирования таких систем. В работах [546, 591, 825,
610] отмечаются преимущества расписаний, составленных в интерактивном
режиме. Аналитические методы исследования предложены в [8, 164—166,
206, 218, 367—369, 501, 607, 693, 771]. Системы с нечеткими длительностя-
ми операций рассматривались в [371]. Обзоры работ по указанному
направлению приведены в [501,504, 535, 546, 725].
6.8. С. Гойал [558], С. Редди и С. Рамамурти [751], А. Хартвиг и
Дж. Терно [594] предложили сведения задачи построения оптимального
по быстродействию расписания обслуживания без задержек п требований М
приборами к задаче о коммивояжере. Постановки некоторых задач теории
расписаний в терминах задачи о коммивояжере и различных ее обобщений
рассматривались, например, в [27, 259, 260, 335]. Метод ветвей и границ
для решения задачи о коммивояжере впервые предложили Д. Литл, К. Мур-
ти, Д. Суини и К. Кэрел [191]. В [611] приведен список работ, посвящен-
ных различным аспектам задачи о коммивояжере, который насчитывает
около 600 наименований.
Одна из наиболее популярных тестовых задач построения оптимального
по быстродействию расписания (п = 10, М = 10) описана в [373]. Лучшие
из известных для нее расписаний получены методом ветвей и границ [524,
686]. Краткие сведения о публикациях, посвященных методам последова-
тельного анализа вариантов, приведены в § 6 гл. 4.
ГЛАВА 3
НЕФИКСИРОВАННЫЕ МАРШРУТЫ
Множество N = {1, 2,... ,и} требований обслуживается в системе,
состоящей из М последовательных приборов. Требование iGN поступает
в систему в момент времени Для всех требований множества N
маршрут обслуживания (порядок прохождения приборов) заранее не задан
и может быть различным для разных требований. Длительности tiL > О
обслуживания каждого требования iGN каждым прибором L, 1 < Я </И,
предполагаются заданными. Запись tiL = 0 означает, что требование i
прибором L не обслуживается. В любой момент времени каждое требова-
ние обслуживается не более чем одним прибором и каждый прибор обслу-
живает не более одного требования. Такие обслуживающие системы назы-
ваются системами с нефиксированными маршрутами.
Для доказательства /VP-трудности задач построения оптимальных распи-
саний в данной главе используются следующие эталонные задачи.
Задача о разбиении. Дано множество /V0 ={1,2, • • • > и0 } ,
каждому элементу i которого сопоставлено натуральное число et и
S et = 2Е. Существует ли разбиение множества № на два подмножества
Ni и№ таких, что 2 е, = S et = Я?
zETV® ^G^20
Задача о 3-разбиении. Дано множество № = {1, 2, . .. , Зи0}
и натуральное число Е. Каждому элементу i G/V0 сопоставлено натуральное
число Ci такое, что Е/4 < et < Е/2 и S et = п^Е. Существует ли разбиение
множества А0 на и0 трех элементных подмножеств № таких, что S ez =
7 i е nJ
= Е, j = 1,...,и0?
Задача о 3-р цскраске 4-регул ярно го графа. Дан неориен-
тированный граф G = (X U) без петель, степень каждой вершины которого
равна четырем. Можно ли раскрасить вершины графа G в три цвета таким
образом, что никакие две смежные вершины не окрашиваются в один цвет?
Задача о разбиении /VP-полна [133], задача о 3-разбиении /VP-полна
в сильном смысле [531]. /VP-полнота о 3-раскраске 4-регулярного графа
доказана в [550].
В этой главе используются следующие обозначения. Пусть (ai, а2, . . .
.. . , аг) - вектор с действительными компонентами и Я' С Я = { 1, 2, ...
157
...,г} , тогда a(R’) = S af. Аналогично, если IIaif II — матрица размерно-
iER'
сти rX q и Q' CQ = {1,2, ...,#}, то
а;(Л')= S aif, и а,(0')= S alf, 1 < i < г.
ieR j&Q'
Если л — некоторая перестановка элементов конечного множества X, то
через {л} будем обозначать множество X, т.е. {л} = X.
§ 1. Общее время обслуживания. Два прибора
В этом параграфе рассматривается задача построения оптимального по
быстродействию расписания обслуживания п требований М приборами
в предположении, что все требования поступают в очередь на обслуживание
в момент времени d = 0, каждое требование может обслуживаться прибора-
ми в произвольном порядке, прерывания процесса обслуживания каждого
требования каждым прибором запрещены. Обсуждаются также некоторые
обобщения указанной ситуации. Особое внимание уделено случаю,когда
М=2.
1.1. Имеется множество N = {1, 2, . . . , и} требований и множество
Л = {1,2,..., М} обслуживающих приборов. Известны длительности
> 0 обслуживания каждого требования i GN каждым прибором L G Л
Если tiL >0, то требование i должно быть обслужено прибором L. Если
= 0, то требование i прибором L не обслуживается. Порядок прохожде-
ния приборов заранее не задан и может быть различным для разных требо-
ваний. Каждый прибор может обслуживать требования в произвольной
последовательности, но одновременно не более одного требования. Каждое
требование одновременно обслуживается не более чем одним прибором.
Процесс обслуживания каждого требования iGN каждым прибором L GЛ
предполагается непрерывным, т.е. если обслуживание требования i прибо-
ром L начинается в момент времени то оно протекает без прерываний
и завершается в момент tiL = t*iL + tiL.
В рассматриваемом случае расписание $ однозначно определяется зада-
нием матрицы II ifL II моментов начала или матрицы II7^ II моментов завер-
шения обслуживания требований приборами. Общее время обслуживания
при этом равно Fmax0) = max{7/£ I i'G N, LGJtC } . Необходимо построить
расписание s, при котором величина fmax(s) минимальна. Это расписание
будем называть оптимальным (по быстродействию) и обозначать через s *.
Отметим, что задача построения оптимального расписания обладает
определенной симметрией: приборы и требования можно поменять ролями
без изменения существа задачи.
Нетрудно видеть, что для любого расписания $ общее время обслужи-
вания
TmaxO) тах { тах )> тах • (1-0
i (= N
Ниже показано, что при М = 2 (или, что то же самое, при п = 2) для
построения оптимального расписания требуется не более О(п) (соответст-
венно О(М)) операций. Описан полиномиальный алгоритм построения
оптимального расписания в случае, когда часть требований имеет фиксиро-
158
ванные маршруты обслуживания и М = 2. В заключение параграфа доказана
NP-трудность задачи построения оптимального расписания, если М > 2
и все требования обслуживаются без задержек.
1.2. Покажем, что при М= 2 оптимальное по быстродействию расписание
может быть построено в результате выполнения не более чем О(п) опе-
раций.
Пусть система содержит два прибора А пВ и известны длительности
и bi обслуживания требования i£N= {1,2,... ,п} приборами А и В
соответственно.
В этом случае из (1.1) следует, что для любого расписания справедливо
соотношение
^maxG)> max{a(N),b(N), max + (1.2)
где a(N)= S ah b(N) = S bh
i<=N i€N
Покажем, что существует такое расписание s*, что в соотношении (1.2)
при s = s* имеет место равенство, и опишем способ его построения. Расписа-
ние s* будем искать в классе таких расписаний, что для каждого прибора
имеется не более двух временных интервалов, в каждом из которых этот
прибор функционирует без простоев, обслуживая требованйя непрерывно
одно за другим. Расписания этого класса однозначно определяются зада-
нием двух наборов вида ;я2 ^о’^ь), где L — наименование прибора,
Го - момент начала непрерывного обслуживания требований множества
{тт!} в последовательности 7^, - длительность простоя прибора L
после завершения обслуживания требований множества {я^ и до начала
непрерывного обслуживания требований множества {я2} в последователь-
ности я2.
Множество Nтребований разобьем на два подмножества ={/ G TV | я, <
<bj} и N2 sW\7Vi. Предположим, что Ф ф и N2 ± ф. Среди требований
множества выберем такое требование к, что bk > max {яг-1 f , а
среди требований множества N2 выберем требование г, для которого
ar > max { | i G N2} .
Рассмотрим пару наборов (рис. 1.1, а)
(А;(к, itN t\ 0;^л); ц 3>
(В;(к, ak,wB),
где лдг' — произвольная перестановка элементов множества N' С N, а в
качестве wA и выбраны любые неотрицательные числа, удовлетворяю-
щие условию
a(N)-ak+wA=b(N)-br + wB. (1.4)
Нетрудно проверить, что эта пара наборов определяет расписание, по-
скольку требования обслуживаются обоими приборами в одной и той же
последовательности, причем к моменту начала обслуживания каждого тре-
бования прибором В оно уже обслужено прибором А.
Опишем процесс преобразования этого расписания в искомое оптималь-
ное расписание.
1) Предположим, что a(N) - ак > b(N) - br. Тогда из (1.4) следует,
что wA < .
159
' ' Wg ^\r г
приборВ - Н- I------------1-----1-------Н
А /УДА wA ^z\r г
прибор А —I------1--------Н | |
г к NAk НАп
приборВ - Н-----1 !—I—--------I
к Л>\А лДг г
приборА | -Ч----------------1—1
приборВ
приборА
О д t
л к /vjk В2\г г
приборВ — --4---------......I I
/ИДА Nz\r г к
приборА-----1—-—4---------1 I
О е t
М * Л7\А/^\гг
приборВ ..... — I I I I
/ИДА/1£\~ г к
приборА - I t ! I ...........—!
О
t
Рис. 1.1
Введем в рассмотрение пару наборов
(А; (к, irNi\ky, (irNt\r, г); 0; 0); 5>
(В; (г, к, irNi\ky, max (a(N)-b(N), 0}; 0).
а) Если имеет место неравенство
max{ a(TV) — b(TV), 0} + Ьг < a(N)-ar,
to (1.5) определяет расписание с общим временем обслуживания, равным
max {a(N), b(N)} (см. рис. 1.1, б, в).
б) Пусть выполняется неравенство
max {a(N) — b(N)9 0} + br > a(N)-ar. (1.6)
При этом, очевидно, в некоторый момент времени требование г обслу-
живается обоими приборами одновременно, т.е. (1.5) не определяет рас-
писания.
Заменим (1.5) парой наборов
(Л; (к, ^ЛкУ (1rNiy, ry ar + br - a(Ny 0); (1 ?)
(В; (г.к.^^у пыЛг- 0; 0).
Если a(N) < b(N), то неравенство (1.6) равносильно неравенству
ar + br > a (N) и (1.7) определяет расписание с общим временем обслужи-
вания, равным max {ar +br,b (TV)} (см. рис. 1.1, г).
Пусть a (TV) > b(N). Тогда неравенство (1.6) равносильно неравенству
ar + br > b (TV).
Если ar + br > a (TV), то (1.7) определяет расписание с общим временем
обслуживания, равным ar + Ьг (см. рис. 1.1, г).
Еслиаг +br < a (TV), то нетрудно убедиться, что пара наборов
(Л; (fc, vNSky г). о; 0);
(В; (г, к, irNt\ky nN^r,a(N) - ar -br\ 0)
определяет расписание с общим временем обслуживания, равным a (TV)
(см. рис. 1.1,6).
2) Предположим, что а (TV) - ак < b (TV) - br . Тогда из (1.4) следует,
что wA
Введем в рассмотрение пару наборов
(Л; 1ткЛк-, (л^\г, г, к)- °; °);
(1.6)
(В; (к, ^ЛкУ (ял?Лг, г); 0; 0).
Если ак + bk <a(TV), то (1.8) определяет расписание с общим временем
обслуживания, равным max {a (TV), b (TV)} (см. рис. 1.1, е).
Если ак + bk > a (TV), то пара наборов (1.8) не определяет расписания,
поскольку в некоторый момент времени требование к одновременно об-
служивается двумя приборами.
11. В.С. Танаев
161
Заменим (1.8) парой наборов
(л-> ('»,v ' + °);
°;0)-
Нетрудно убедиться, что эта пара наборов определяет расписание с об-
щим временем обслуживания, равным max{ajt + bjt, b(N)} (см. рис. 1.1,ж).
Таким образом, во всех рассмотренных случаях может быть построено
расписание s* такое, что в соотношении (1.2) при s = s* имеет место знак
равенства.
Можно показать, что и в случаях, когда = ф илиТУ2 = Ф , также может
быть построено расписание s *, обладающее указанным свойством.
Если Ni = ф, то искомое оптимальное расписание определяется парой
наборов вида
(Л; к ; г; max{ar + br - a(N), 0}; 0);
(В; г; ir„ v ; max {min {a(N) - b(N), a(N)-ar- br}, 0}; 0).
jv2 \r
Если N2 = Ф, — то парой наборов вида
(A; it . ; к-, max{afc + bk - a(N), 0}; 0);
IV J
Если Nx ф и N2 ± ф , то из приведенных выше рассуждений следует,
что искомое оптимальное расписание определяется наборами
(A,(k, irNi\k)-, (*N2\r> И; max {ar + br - a(N), 0} ; 0);
(В; (г, к, nN^k)-, nNi\r', max {min { a(N) - b(N), a(N) -ar- br}, 0); 0),
если a(N) — ak> b(N) - br, и
И; ^,\fc; r’k^ тах{а* + bk - a(N), 0}; 0);
(*« r>> °; °)’
если a(N) - ak < b(N) - br.
Отметим, что формирование множеств Nx и (или) N2, выбор требова-
ний к G и (или) г G N2, вычисление a(N) и b(N) требуют выполнения
не более чем О(п) элементарных операций. Трудоемкость последующего
построения искомой пары наборов не зависит от и.
Таким-образом, при М = 2 оптимальное по быстродействию расписание
может быть построено в результате выполнения не более чем О(п) опера-
ций. В силу симметрии задачи описанный алгоритм может быть использо-
ван и в случае, когда М>2,но п = 2.
1.3. П р и м е р. Имеются две разные книги А и В и шесть читателей,
желающих прочесть эти книги. Длительности а{ и bj (количество дней,
затрачиваемых читателем на прочтение каждой из книг А и В) приведены
в табл. 1.1.
Предполагается, что каждый читатель может одновременно читать толь-
ко одну книгу и, раз начав ее читать, читает непрерывно до тех пор, пока не
162
Таблица 1.1
i 1 2 3 4 5 6
а/ 2 6 2 3 3 6
4 3 1 5 4 4
процтет всю книгу. Каждая книга в каждый момент времени может на-
ходиться не более чем у одного читателя. Необходимо, чтобы все читатели
прочли все книги в кратчайший срок.
В рассматриваемом случае N = {1, 2, 3, 4, 5, 6 }, 7V\ ={1,4, 5 } , N2 =
= {2, 3, 6}, к G {1, 4, 5}, г G {2, 6}, для определенности положим к = 4,
г =2. Имеем a (TV) =22,b(7V) =21, a(N)-ak = \9>b(N)-br = 18.
Соответствующая пара наборов, определяющих одно из искомых опти-
мальных расписаний s *, имеет вид
(А; (4,1,5); (3,6,2); 0; 0);
(В; (2,4, 1,5); (3,6); 1; 0).
Расписание $ * представлено на рис. 1.2.
приборВ
приборА
Рис. 1.2
1.4. Рассмотрим следующее обобщение ситуации, описанной в п. 1.2.
В обслуживающую систему, состоящую из двух приборов А и В, в мо-
мент времени d = 0 поступает множество N = {1, 2, . . . , п} требований.
Длительность обслуживания требования i G N прибором А равна at > 0
единицам времени и прибором В равна > 0 единицам времени. Запись
Ui = 0 или bi = 0 означает, что требование не обслуживается прибором А
или В соответственно.
Множество N требований состоит из трех попарно непересекающихся
подмножеств NАВ, Nba и No. Требования множества N обслуживают-
ся сначала прибором Л, затем прибором В (маршрут обслуживания (А, 2?));
маршрутом обслуживания требований множества Nba является (В, Л);
требования множества No могут обслуживаться в соответствии с любым
из маршрутов (Л, В) или (В, Л), причем маршруты заранее не заданы и
могут быть различными для разных требований. Ко множеству No отне-
сены также все требования, для которых либо ц = 0, либо = 0.
В любой момент времени каждый прибор обслуживает не более одного
требования и каждое требование обслуживается не более чем одним прибо-
11* 163
ром. Прерывания процесса обслуживания каждого требования каждым
прибором запрещены.
Необходимо построить оптимальное (по быстродействию) расписание s *
обслуживания требований множества N. Если N = No, имеем ситуацию,
рассмотренную в п. 1.2, если N = N АВ (или N = NBA) ~ ситуацию, рас-
смотренную в п. L3 гл. 1, и если No = ф - ситуацию, рассмотренную в
п. 4.2 гл. 2.
Ниже описан алгоритм построения расписания s* в случае, когда все
три подмножества NAb> Nba и No могут быть не пустыми. Трудо-
емкость построения s* не превосходит О(п + nlogn) операций, где п =
= тах{|#лв| , |7УВЛ|} •
Введем некоторые обозначения. Для множества RQN положим Ra =
= {i G /?| Qj <bi} nRb ={z G A | bi < at} . Через тт(/?) обозначим произ-
вольную перестановку элементов множества/?.
Оптимальное расписание s* будем искать в классе расписаний, которые
однозначно определяются парой наборов вида (L; ; Н2 , . . . , HPL ),
pL > 1, £ G {А, В}. Элемент этого набора имеет вид Hj = [г£° (/), тт7 (TV7) ],
где /О (/) — момент времени, начиная с которого прибор L, функциони-
руя без простоев, обслуживает без прерываний требования множества
Nj QNb последовательности яу (TV7).
Если в системе обслуживаются только требования множества N^,
то оптимальное (по быстродействию) расписание будем обозначать через
s*AB. Напомним способ построения такого расписания (см. п. 1.3 гл. 1).
Требования множества №АВ упорядочим по неубыванию значений ец,
вслед за ними упорядочим требования множества NbAB по невозрастанию
значений Ь, . Полученную последовательность обозначим через (N) =
= (i i, i2, . .., iq), q = INАВ I . Расписание определяется парой наборов
(Л; [О, ^(/V4B)] );
(В; [t°B, <p(Nab]>,
и и — 1
где ri = max {at , max { S ati - S bt. | и = 2, . . . , n}}. Трудоем-
1 7=1 1 7=1 1
кость построения расписания не превосходит O((/log q) операций.
Если в системе обслуживаются только требования множества No, то
можно описать несколько способов построения расписаний, которые, во-
обще говоря, не являются оптимальными, но могут быть преобразова-
ны в оптимальные в соответствии с п. 1.2.
Действительно, если Nao Ф ф , выберем требование к G Nao такое, что
bk > ati i G NaOi иначе положим {к} = ф . Аналогично, если N° Ф ф,
выберем требование rG N& такое, что ar > bi9 i G N&, иначе положим
{г} = ф. Построим последовательности ф(1Уо) = (к, ir(Nao\ {к}),
{r })>r) и ^'(^o) = {г}),я(^о\{ft}),*). Для произ-
вольного требования т G No через ф(1Уо\ {ти } ) будем обозначать после-
довательность требований множества No\ {т}, расположенных в том же
порядке, что и в последовательности ф (No ).
164
Если имеет место неравенство a(No\ {к}) <b(No\ {г}), то можно
построить расписание s к обслуживания требований множества No, кото-
рое определяется парой наборов
(Л; [О, ^о)]);
(В; [ак,
и расписание которое определяется парой наборов
(Л; [*(2VO) - a(No\{k}\ t'(No)]y,
(В-, [о,
Нетрудно проверить, что lkA (sk) = t%B (sk) и Г1А (sk) < t?B (sk), а так-
же что?кВ(Гк) =rk4(sk) и^в(Гк) e N0\{k}. Расписания sk
и Sk представлены на рис. 1.3 а и 1.3 б соответственно.
Если имеет место неравенство a(No\{k}) > b(No\{r}), то можно
построить расписание sr обслуживания требований множества No , кото-
приборе - |-----1 * | J—I
I
о t
к, W; W/ *
приборе —..... I ... | I
л д \r .N^}\h t
приборА - I——I———'4 —4—1
О
приборе
приборА
^o\^l t г )
^о\^} ^o\{r} t г ! в
прибор В
приборА
О
t
Рис. 1.3
165
рое определяется парой наборов
(Л; [О, ЖО)]);
(В; [a(No)-b(No\{r}),
и расписание sr, которое определяется парой наборов
(Л; [Ьг, М)П
(В; [0,
Нетрудно проверить, что TrA (sr) = и Г/лОг) z* G
G 7Vo\{r}. Аналогично 1Гв (Гг) = t*A 07) и7/в(?г)
£ No\ {r) • Расписания sr и представлены на рис. 1.3, в и 1.3, г соответ-
ственно.
Трудоемкость построения каждого из расписаний skf sr, sk и sr не
превосходит О(| No | ) операций.
1) Оценим величину fmax(s) общего времени обслуживания требова-
ний множества N = NAB U NBA U No при произвольном расписании s.
Пусть sAB и SBA ~ оптимальные расписания обслуживания только тре-
бований множества NAB и только требований множества NBA соответст-
венно, а ^гпах(5лв) и ^тах(5вл) “ соответствующие этим расписаниям
значения общего времени обслуживания.
Очевидно, имеет место соотношение rmax (s) > 7\ = max{7, Fmax
*тах($вл)}> гДе 7 = max{a(7V), b(N)}. Кроме того, если ат + Ьт =
= max{ai + bf|iGNo) > 7\ , то 7max(s) > ат + bm, m^No.
Покажем, что расписаниям (без прерываний), при котором fmax(s) =
= ат + Ът > Т} не существует.
Действительно, при таком расписании в любой момент времени во
временном интервале (0, 7тах0)1 требование т должно обслуживаться
одним из приборов. Следовательно, за время обслуживания требования т
прибором А (или В) все остальные требования должны быть обслужены
прибором В (соответственно прибором А). При этом, однако, нарушится
маршрут обслуживания всех требований одного из множеств NAB или NB А,
что недопустимо. _
Оценим величину rmax (м), если ат + Ьт > Т\ . Рассмотрим класс распи-
саний, при которых требованию т назначается маршрут обслуживания
(А, В). Построим расписание Sj из этого класса, определяемое парой на-
боров
(A;[O,(it(NAB),m, n(NbABUNba U7Vo\{w}))]);
(В- [a(N°AB U {m}) - b(NaASUNBA UNo\{m}),
Wab unba я(А^в))]).
Тогда ^max(sl) = am + + + b(NAB) .
Это расписание будет оптимальным в рассматриваемом классе, по-
скольку
а) ни одно из требований множества NAB не может быть обслужено
обоими приборами в интервале обслуживания требования т\
166
б) значение a(NAB) + b(NAB) < Д(^дв) + b(NAB) для любого разбие-
ния множества NAB на подмножества NAB и NAB‘9
в) обслуживание требований множества NBA U No\{m} вне интервала
обслуживания требования т не уменьшит общего времени обслуживания.
Рассуждая аналогичным образом, можно показать, что в классе расписа-
ний, при которых требованию т назначается_маршрут обслуживания (В, А),
оптимальным будет расписание s2 такое, что rmax(s2) = ат + bm + a(NBA) +
Таким образом, для любого расписания s (без прерываний) имеем
^тах(5) тах{Т, ^тах(5лв)> ^тах(5вл)’
max {a, + 6,|iG2V0} + min{a(A%) + b(NbAB),a(NaBA) + b(NbBA)}} .
2) Опишем процесс построения расписания s, при котором в (1.9)
имеет место знак равенства. Это расписание, очевидно, и является искомым
оптимальным расписанием s*.
Рассмотрим следующие пары наборов, каждая из которых при опре-
деленных условиях задает расписание s*.
I. (А; [О, ^А в), k(Nba U ЛГО))]);
(В; [0, тг (NBA UNO)] -,
[max.{b(NBA UNo),
^max (5лв) ~ b(NAB)}> ^(^Лв)1);
II. (Л; [0,(я(ЛГдв)>я^вл),Ф'(ЛГО))]);
(в- [о, (v(Nba), *(Nab))]);
III. (A- [0,(4>(No\{k}), it(NAB), n(NBA), Л)]);
(B; [0, (n(NBA), k, 4>(No\{k}), *(NabM );
IV. (A; [0, (я(ЛГлв), *(Xba ), WN0\{r}, r)l);
(В;[0,(я^вл),Пя(^лв))];
V. (A; [0, (я^л в), и 7Vo\{/n}))]; { w}), m]);
(B; [0, (n(NBA ), m, ir(NAB No\{m}))]);
VI. (A; [0, (v(Nab), n(NbA U 7V0\{/n}))];
[тах{л(А^лв U NbBA UN^m}),
b(NbBAV {nz})}, (m, *(NaBA))]y,
(B, [0, (n(NbA),m, n(NaBA), v(Nab UN0\{m}))]);
VII. (A; [0, (m, n(NAB))]; [max {a(NAB U{m}),
b(NBA и^О\{^})},я^вл UWo\pn})]);
(B; [0, (*(Nba), Tt(No\{m}), m, n(NAB))]);
167
VIII. (А; [0,(я(^4в), я(ЛГо),7г(^вл))]);
(5; [0, (я(Ло), *(Nba ), V(Naв))] );
IX. (А; [О, (я(ЛГ“ в), т, ANbAB), n(NBA U No\{m}))]);
(5; [О,(я(ЛГвл UAro\{m}),ff(A^B))J; [max{e(^B U{m}),
b(NBA VKaAB UNo\{m})},(m, *(ХЬАВ))]У,
X. (A; [0, (ir(NAB U No\{m}), m, AN ba ))]);
(5; [0,(m, n(NBA),n(NAB Utfo)\{m}))]);
XI. (A; [0, (ir(No), tt(Nab), AN ba ))]);
(Я; [0, (ANba), ANO), ANab»} )•
Алгоритм построения расписания s* заключается в проверке выполне-
ния ряда неравенств и выборе одной из перечисленных пар наборов. Поря-
док проверки выполнения неравенств указан на рис. 1.4. Цифры в круглых
скобках слева от неравенства означают номер неравенства, на который
далее в тексте имеются ссылки. Римские цифры в кружках означают номер
пары наборов.
Мод Nar
приборе ~ | ° kJ-------—-------1
прибор А -----«А3 I |
О t
прибор В
прибор А
О
Рис. 1.5
169
Если неравенство a(NAB) > b(NBA) не имеет места, то можно поменять
местами наименования приборов, построить расписание м*, воспользовав-
шись описанной выше схемой, и затем восстановить исходные наименова-
ния. При каждом таком переименовании приборов меняются ролями
длительности обслуживания at и bi9 требования к и г, множества каждой
пары NAB и Nba, N£b и Nba , Nab и Nba , N& и Nq, а также расписания
каждой пары млв и мвл, sk и мг, и sr.
3) Покажем, что описанный алгоритм действительно приводит к построе-
нию оптимального расписания.
а) Пусть выполняются неравенства (1.10) и (1.11). Покажем, что опти-
мальное расписание м * определяется парой наборов I.
Действительно, в силу (1.11) имеем тах{^в(м*)|/ е ^вл и NO) =
= b(NBA U No) <a(NAB) = тт{Г°л (s*)|i G NBA U Nq}. Если
'maxOJs) > b(N) (рис. 1.5,a, 6), TO tfL(s*) = rfL(s*AB), tiL(s*) = tiL{s*AB),
i e L e (Л, В}. Если же b(N) > (рис. 1.5, в, г), to
tjB <s‘) - Ъа («*)_> г?в(5лв) - Ъа (sab) > ' e naв - Кроме того,
^maxO ) — mexfr, ^max($4b)^ '
б) Пусть выполняются неравенства (1.10), (1.12)-(1.14). Покажем,
что оптимальное расписание з * определяется парой наборов II.
Действительно, в силу (1.10) max{ffB (s*)| i G NBA} = b(NBA) <
< a(NAB) = minfr^ (s*)|i Е^л}. Вейлу (1.12) имеем тах{7/л (s*)| i E
^nab} =^nab)< b(NBA U No) = min{^B (s*)|z £NAB}. Из неравен-
ства (1.14) следует,что tkA (s*) - tkB (s*) -a(N\{k}) -b(NBA U No) >
> 0 = t°kA Ok) -~tkB Ok) и, тем самым, tQiA (s*) - tiB (s*) > t^A (sj -
- tiB (s^) >0, i G No\{k}, Кроме того, fmax(s*) = Расписанием*
изображено на рис. 1A
в) Пусть выполняются неравенства (1.10). (1.12), (1.13), (1.15) и
(1.16). Покажем, что в этом случае оптимальное расписание м* опреде-
ляется парой наборов III.
О t
„р1Л.рВ ,
Ч/ W' л 1
О t
Рис. 1.6
170
В силу (1.10) имеем max{fZB (s*)|i & NBA} = b(NBA) ^а(^лв)
<a(.NAB u ЛГо\Ш) = min{t’j (s’)l i G NBA}. Далее, в силу (1.15)
max{7M(s’)|f G Nab} = a(NAB U No\{k}) < b(NBA U No) =
= (s*)| i G NAB}. Из неравенства (1.16) следует, что f^O*) =
= a(N\{k}) > b(NBA U {£}) = ~tkB(s*). Поскольку b(NBA) > 0, to
t°iB (s‘) - Ъа (s‘) > tfB (sk) - Ъа (sk) > °> » e No\{k}. Кроме того,
rmax (5 *) = Г. Расписание s * изображено на рис. 1.7.
г) Пусть выполняются неравенства (1.10), (1.12), (1.17) и (1.18).
Покажем, что оптимальное расписание s* определяется парой наборов II.
В силу (1.10) имеем max{f/B ($*)I i G NBA) = b(NBA) < a(NAB ) =
= min{r?4 (s*)| i £Nba}> b силу (1-12) имеем тах{7/л (s*)l1 =
= a(NAB) < b(NBAU No) = mmO?B0*)U e Nab} . Из неравенства
(1.18) следует, что7гВ (s‘) = b(NBA U {r}) < a(NAB U NBA) =t^A (s‘)
прибор В
прибор A
"ba к N0\{k} NM
—-------------------------7—
7 J
No\(k} 1 Nab A
A
nba No\{^l Nab
приборе .................... Я ..1
/ /
o t
Рис. 1.7
прибор В
прибор A
О
t
о NBA К r , NfX/r) MAe
приоорв ----------—-------—”-4------ 1
прибор А —------1-----------И-;;. , . I
nab nba r N0\fr/
о t
Рис. 1.8
171
и, тем самым, t®A ($*) - tiB ($*) > t*iA (sr) - tiB (sr) > 0, i G No\{r}.
Кроме того, rmax (s *) = T. Расписание s * изображено на рис. 1.8.
д) Пусть выполняются неравенства (1.10), (1.12), (1.17), (1.19) и
(1.20). Покажем, что в этом случае оптимальное расписание $* опреде-
ляется парой наборов IV.
Вейлу (1.10) имеем тах{Г/в (s*)| f ^NBA) < тш(г?л (s*)| i £NBA}.
Далее, в силу (1.19) max{FM (s*)| i G NAB} = a(NAB) <a(NAB U
U Nba) < b(NBA U {r}) = (s*)| i G NAB}. Из неравенства
(1.20) следует, что trB(s*) ~b(NBA^ {г}) < a(N\ {г}) = t°A ($*). Если
a(N) > b(N) (рис. 1.9, а), то = t°iB (sr) -»м(’г) > 0,
i& No\{r}. Если a(N) < b(N) (рис. 1.9, б), то -7iA(s*) >
>*?в(«г)-7/л0г) > 0, i&No\{r}. Кроме того, 7max(s‘) = T.
e) Положим m = к, если имеют место неравенства (1.13) и (1.15), и
т = г, если имеют место неравенства (1.17) и (1.19). Пусть выполняются
неравенства (1.10), (1.12), (1.21) и (1.22). Покажем, что оптимальное
расписание s * определяется парой наборов V.
В силу (1.10) имеем max{FfB (s*)| i в NBA} = b(NBA) <a(NAB) =
= min{^ (s*)| i G NBA}. Далее, в силу (1.21) имеем max{FM (s*)I i G
G Nab U No\{m}} = a(N\{m})< b(NBA U {m}) = (s*)| i G
G NAb u {m}}.Кроме того, по построению tmB ($*) = t^mA ($*). He-
приборВ
приборА
приборВ
приборА
приборВ
приборА
^ВА , r t ^АВ ,
—|-------1
^АВ ^ВА Г |
о
»ВА Г
К *
^АВ МВА г
6
ч
Рис. 1.9
..*
\ / j_________
nab nba * N^/ny т
Рис. 1.10
172
равенство (1,22) означает, что fmax(s*) = ft (N). Расписание s * изображе-
но на рис. 1.10.
ж) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23)-
(1.25). Покажем, что оптимальное расписание s* определяется парой набо-
ров VI.
В силу (1.10) имеем max{r/B (s*)| z G NBA) = b(NQA) <a(NAB) =
= min{^ (s*)| i G N%a} . В силу (1.21) имеем max{FM (s*)| i G NAB U
u 7VO\{m}} <a(NAB U NBA u Afo\{m}) <a(N\{m}) < b(NBA U
U {zn}) = min{r®B (s*)| i G NAB U No\{m}}. Если b(N%A U {m}) >
> <i{nab u nba u No\{m}) (рис. 1.11,a, 6), to t°mA (s’) = 7mB(s‘) ив
силу (1.25) имеем min{r®4(s*)|i G nba^ = ^(^ba u + am
> b(NBA U {m}) = max(z/B (s’)| i GNgAl. Если же b(N^A U {/n}) <
< “(Nab u nbA U No\{m}) (рис. 1.11, в, г), to t°mA (s’) >7mB(s‘)
и в силу (1.25) имеем min{r®4 (s*)| i G NBA) = a(N\NgA) = am +
+ a(NAB U N*a U No\{m}) > am + b(NBA U (m))>b(NBA U {m}) =
npub op В
прибор A
NBA . m ^BA. ^Ad .
\ / I
\ / I
-----1---------------------—г
*ab NbBA N0\(m} m N°A
приборВ
прибор A
^BAt N%a Nab
^AB ^BA No\im} m ^BA
приборВ
приборА
NBA I m iNBA t NAB k^o\{m)
\ \ / \
\ \ /
--------4—5—1---------------------^4—....
^ab ^ba N0\(m} m NqA
приборВ
приборА
Nba m *ba Nab . *о\М ,
* * ’*
\ t \ / v t
"ab Ца''
0
6
0
Рис. 1.11
173
= max{rfB (s*)| i G NBA}. Кроме того, fmax(s*) ~ max{T, am + bm +
+ a(NgA) + b(NgA)}.
з) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23), (1.24),
(1.26) и (1.27). Покажем, что в этом случае оптимальное расписание s*
определяется парой наборов VII.
В силу (1.26) имеем ^в(5*) = b(NBA U No\{m}) > b(NBA) >
>b(NaBA) > am = Gnx(s*). в силу (1.27) имеем max {TiA (s*)\i^NAB} =
= a(NAB U {m})<b(NBA UNO) = min {t*iB (s*)| i G NAB } . Если a(NAB U
U {m }) > b(NBA UNo\W) (рис. 1.12a, б), to min {rfA (s*)| z’G NBA U
UA£>\{w}} > max {TiB (s*)| i ^NBAUNo\{m}} . Если жеа(;Улв U {/л}) <
< b(NBA UNO\ { m}) (рис. 1Л2, в) to min fru(s*)UGNB4 U7VO\ {m} } =
= b(NBA UNO\ {m } ) = max {tiB (s*) | i G NBA VNO\ {m} } . Отметим, что в
последнем случае ТтВ (s ♦) > max {TiA (s *) | z G NBA U7VO\ {m } }, посколь-
ку, вычитая неравенство (1.10) из неравенства (1.21), имеем a(NBA U
<JNO\ { тп}) < bm. При расписании $* значение fmax(s*) = Т.
и) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23), (1.24),
(1.26) и (1.28). Покажем, что в этом случае оптимальное расписание 5*
определяется парой наборов VIII.
Действительно, вычитая из неравенства (1.28) неравенство b(NBA) >
> ат, которое следует из (1.26), получаем b (No) < a (NA в). Это означает,
что max {~tiB ($•)( i е No} - b(Ng) < a(NAB) = min {t°iA (s*)| i eNo}.
Далее, в силу (1.12) имеем max {FM(s*)| i G NAB } = a(NAB) <b(NBA U
, a nba Ai^m) m ,nab,
прибор В - ....I ——... ^4 | a
\ '
4. —1
0 t
x a Nba m , nab
приборе -------""4”.......... I
прибор A ---f11 "' ---ih"?"1 > . z . I
r r m Nab Nba No\fm}
0 t
A 6
c o NbA > . m tNABt
приборе " л- •Л................. } I
/ z I I
прибор A ....’Г-" . Г k I . , t
m nab Mba
0 t
Рис. 1.12
174
прибор В
приборА
N0 , NBA #ав
----4/—\------
^АВ ^О ^ВА
а
Рис. 1.13
и No) = min {t°B (s*)| i E NAB} . Из неравенства (1.28) также следует,
что max {TiB ($*)I i G NBA) = b(NoVNBA) < a(NAB U (m }) <a(NAB U
^No) = min {tQiA (s*) I i E NBA } . Кроме того, /max(s*) = T. Расписание s*
изображено на рис. 1.13.
к) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23),
(1.29) и (1.30). Покажем, что оптимальное расписание $♦ определяется па-
рой наборов IX.
Действительно, складывая неравенства (1.10) и (1.23), получаем нера-
венство a(Nab U {т}) >b(N\ {т }), которое означает, что min
i Nba и No\ {т}) = a(NAB и {т}) >b(N\{m}) =max {TiB (s*)| i E
G Nba UNo\{m }}. Поскольку b(NBA) > a(NaBA) + b(NBA), to b(NBA) >
> “WaAB) nmin{J>B(s*)|f E NaAB} ~b(NBA UNO\ {m}) > b(NBA) >
> a(NAB^ = max (tiA (s*)| i E NaAB} .Если a(NaAB U {m }) > b(NBA U
UjV^B UNo\ M) (рис. 1.14, a, 6), TO tmA(s*) = t°mB(s*) = min {t?A(s*) |
i e Nab ) • В силу (1.30) это означает, что min {t°B (s*) | i G NAB ) =
= *bm > tQmB(s*) + a(NbAB) =m^{TiA(s^)\ieNbAB} . Если же
a(NaAB U {m }) < b(NBA UNaAB VNo\{m }) (рис. 1.14, в, г), то TmA ($♦)<
< ^в(5*)> и следовательно, в силу (1.30) значение max {tiA (s♦) | i E
e NABi <TmB(s*) = min{r?B(s*)|z ^NbAB}. Кроме того, 7max(s*) =
- max { Tt am + bm + a(NAB) + b(NAB)} .
л) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23), (1.29),
(1.31) и (1.32). Покажем, что в этом случае оптимальное расписание s*
определяется парой наборов X.
В силу ^1.31) имеем tQmA ($♦) = a(NAB V No\{m}) > a{NAB) >
> Ьт = tmB(s*). В силу (1.21) max {tiA (s*)| i £NAB VNO\ {m }} =
= a(NAB UNo\{m}) <a(N\{m}) <b(NBA U {m}) = min{r?B (s*)| i E
e Nab VNo\{m}} . Из неравенства (1.32) следует, что max {tiB (s*)| i E
175
приборВ-------J I------к I Л----------------1
/ \!
приборА - ' Г--------------H—г - К I .......И
^АВ т ^АВ Ц>УтГ ^ВА
О t
приборВ
приборА
приборВ
приборА
приборВ
приборА
^ВА ^о\Н ^АВ . . » NAB
7 1 ‘\ ’
/______________Чч| / । I
^АВ т NAB /fa
^ва , Но\(т) N%B т N%B
—----......" *..........I
/________r
^AB m ^40 ^оУ™] NBA
^BA J^^M^AB , m . NAB
A A ......У* '1
/ X zZ
iee^
m ^AB fyhfrrf NBA
о
Рис. 1.14
г m . NBA t ^ab ,^o\fm) , a
приборВ - " R-----—------...........I------------1
приборА -------4----------------------------------1
^AB ^o\(m} 777 Мда
0 t
K n t ^BA , *AB , "оУт/ ,
приборВ----------------------------4--------4
\ / X
1 4 1
о t
Рис. 1.15
&Nba} jb(NBA U {m})<a(NAB VNO) = min (t°iA (s*)| iGNBA} . Kpo-
ме того, rmax(s*) = T. Расписание s* изображено на рис. 1.15.
м) Пусть выполняются неравенства (1.10), (1.12), (1.21), (1.23),
(1.29), (1.31) и (1.33). Покажем, что в этом случае расписание s* опреде-
ляется парой наборов XI.
Вычитая из неравенства (1.33) неравенство a(NAB) > bm, которое сле-
дует из (1.31), получаем a(No) > b(NBA). Это означает, что max {7}a(s*) I
i G No } = a(No) < b(NBA) = min {t*B (s*)| i £NO}. В силу неравенства
(1.32) min{r?B(5*)|f ^NAB} = b(NBA UNO) > b(NBA U {m}) >
> aQ^AB Uj4?)' = max{ tiA (s*)| i G NAB } . Из неравенства (1.10) еле-
дует, что min {rfA (s*)| i G NBA} = a(No^)NAB) > a(NAB) > b(NBA) =
= max {tiB (s»)| i G NBA} . Кроме того, 7max(s*) = T. Расписание s♦ изоб-
ражено на рис. 1.16.
Расписание s*, определенное парой наборов I, может быть построено в
результате выполнения не более чем О(п + Н°81^лв I) операций.
Расписание s*t определяемое любой из пар наборов II - XI, может быть
построено не более чем за О(п) операций. Следовательно, трудоемкость
построения расписания s* не превосходит О(п + и log и) операций, где
п = тах{|2Улв |, \NBA |} .
1.5. В заключение покажем, что задача построения оптимального (по
быстродействию) расписания 5* является NP-трудной в сильном смысле
при М >2, если потребовать, чтобы каждое требование обслуживалось без
задержек.
Будем говорить, что процесс обслуживания требования i EN= {1,2,...
..., п } в системе, состоящей из множества {1,2,. .. ,7И } приборов,
протекает без задержек, если этот процесс начинается в момент времени
и завершается в момент времени tj = ^ + t(J£).По-прежнему предпола-
гается, что процесс обслуживания каждого требования каждым прибором
протекает без прерываний.
Рассмотрим задачу распознавания, соответствующую задаче построения
оптимального (по быстродействию) расписания без задержек в процессе
прибор В
приборА
NBA t No ^АВ ,
---------Т'Т—-------3-----1
/ /
/ /
No nab Nqa
а
я о NBA . No Nab t
приборе------------тк- ' ------i-----—-----------1
/ 7
приборА --------' ----------------------1
No Nab Nba
О t
12. B.C. Танаев
177
Рис. 1.16
обслуживания требований в случае, когда система состоит из двух прибо-
ров А и В. Требуется определить, существует ли расписание s° обслужива-
ния (без задержек) множества N требований такое, что7тах(х°) < у для
заданного числа у. Длительности обслуживания требования i Е N прибора-
ми А и В соответственно равны и .
Покажем, что к этой задаче сводится задача о равных парах, 7VP-труд-
ность которой (в сильном смысле) была доказана в п. 5.3 § 5 гл. 2. Напом-
ним формулировку этой задачи. Имеется четыре множества U = { , и2,...
. Up}, V = {l>i, Vl, . . . , Vp}, W= {witWz, . . . ,Wp} И X = {*!, x2t...
..., xp}, каждое из которых состоит из натуральных необязательно попар-
но различных чисел. Требуется определить, существует ли разбиение мно-
жества t/UKUR/UXHa четырехэлементные подмножества Rm, 1 <т^р,
такие, что в каждое из них входит по одному элементу из каждого мно-
жества U, V, И/ и X и для каждого Rm = {w/x, U/2, , x^} имеет место
равенство + vl2 = W/ +
Положим п = 4р, N = {1,2,...,m},Z=8 max {ut, vf, ы{,х{ } . Мно-
1 < i < p
жество N требований разобьем на четыре группы: ^/-требования, обозначае-
мые Uit 1 К-требования, обозначаемые Vif 1 <z И/-требова-
ния, обозначаемые , 1 <z Х-требования, обозначаемые Xf, 1 <z <
Ср. Положим
aut = 1, ^i/z = 4wb /= 1,. . . ,р;
av. = 1, bVi = + 3Z, i = 1, . . .,p;
ац,. = 4wj +Z, bw. = 1, i = 1,. . ., p;
axi = ^xi^2Z> bXi=l, i=l,...,p.
Покажем, что в построенной задаче расписание s° такое, что 7max(s°) <
р
^у = 2р + 3pZ + 4 S (Uj + Vi), существует тогда и только тогда, когда
имеет место решение задача о равных парах. Заметим, что величина у рав-
на полусумме длительностей обслуживания всех требований множества N
обоими приборами. При задании значения у учитывается тот факт, что
р Р
S (wz + v^ = S (Wi + Xi), ибо в противном случае задача о равных па-
i=i i = 1
pax, очевидно, не имеет решения.
Пусть задача о равных парах имеет решение и Rm, 1 <т <р, - найден-
ные подмножества. Расписание s° может быть построено следующим обра-
зом. Пусть/?! = {и^ , Vi2, W/3 ,Xi4) . Тогда начиная с момента времени J = О
прибор Л обслуживает требования , Хц, JV/3, Р/2 в указанной последо-
вательности, а* прибор В обслуживает эти же требования в последователь-
ности Xf4, , Vi2, Wi3, причем в интервале (0, 4wZi + 4п/г + 3Z +2] оба
прибора А и В функционируют без простоев. Вслед за указанными требо-
ваниями аналогичным образом обслуживаются требования, определяемые
подмножеством R2 ит.д.
Пусть существует расписание s°. Поскольку a(N) = b(N) = у, то при
расписании s° оба прибора А и В функционируют без простоев. Предполо-
178
жим, что для требования j EN выполняется t®A = 0, и это требование яв-
ляется либо Истребованием, либо Х-требованием, В этом случае нельзя
указать такое требование к Е N, к Ф j, что tkB = 0 и требование к обслужи-
вается без задержек. Отсюда следует, что требование/ являетсялибо £7-тре-
бованием, либо К-требованием. Для определенности предположим, что тре-
бование / является {/-требованием (случай, когда требование / является
К-требованием, аналогичен рассматриваемому). Поскольку требование /
является {/-требованием, то = tjB = 1 и требование такое, что tkB = О,
может быть либо Истребованием, либо Х-требованием (так как в этом слу-
чае tkB = 1 и требование к может обслуживаться без задержек). Пусть / —
требование, которое обслуживается прибором В после завершения обслу-
живания требования /. Очевидно, требование I не может быть ни £/-требо-
ванием, ни Истребованием, ни Х-требованием, так как в этом случае ttB <
< ТкА и требование / не может обслуживаться без задержек. Следователь-
но, требование / должно быть К-требованием. Для того чтобы прибор А
функционировал без простоев, необходимо, чтобы требование q, обслужи-
ваемое прибором А вслед за требованием к, было либо И/-требованием, либо
Х-требованием, но не одного вида с требованием к. При этом должно вы-
полняться условие ак + aq =bj + Ьь так как в противном случае требование
q не может быть обслужено без задержек. Элементы множеств U, К, И/иХ,
определяющие длительность обслуживания требований/, 7, к nq, образуют
подмножество Ri в решении задачи о равных парах. Рассуждая аналогич-
ным образом, нетрудно построить остальные подмножестваRт, т-2, ...,р.
Тем самым за О(р) операций реализовано сведение задачи о равных па-
рах к рассматриваемой задаче распознавания.
§ 2. Общее время обслуживания. Три и более приборов
Рассматривается задача построения оптимального по быстродействию
расписания s* обслуживания множества N = {1, 2, . . . , п / требований в
системе с нефиксированными маршрутами, состоящей из множества
Л = {1, 2, . . . , М / приборов. Длительности tiL > 0 обслуживания каждо-
го требования i G N каждым прибором L ^Л предполагаются заданными.
Все требования поступают в систему в момент времени d = 0. Прерывания
процесса обслуживания каждого требования каждым прибором запрещены.
Напомним, что при любом расписании s значение
*max(s) > max { max max tL(N)} . (2.1)
i e iv l e м
В этом параграфе показано, что задача построения оптимального рас-
писания у* является NP-трудной при Af > 3. Приводятся алгоритмы по-
строения s *, трудоемкость которых не превосходит 0{пМ) операций,
при наличии в системе так называемых доминирующих приборов. Описан
алгоритм трудоемкости О(и2М3) операций построения s*, если
max tL (N) > (М2 + 2М — 1)г*, где Г* = max{^-£ | i G N,L G Л}.
L ем
2.1. Покажем, что приМ> 3 задача построения оптимального по быстро-
действию расписания является NP-трудной. Этой задаче соответствует сле-
дующая задача распознавания ', определить, существует ли такое расписа-
ние s° обслуживания требований множества N, что Fmax(s°) для за-
данного числа у.
12* 179
Покажем, что при М = 3 к этой задаче сводится задача о разбиении (см.
вводную часть этой главы).
Положим п = п0 + 1, tiL =ebi = 1,... ,и0; tnL = L = 1,2,3, у = ЗЕ.
Покажем, что в построенной задаче расписание s° существует тогда и толь-
ко тогда, когда имеет решение задача о разбиении.
Если существует указанное разбиение множества /V0 на подмножества
Ni и #2, то искомое расписание $° можно построить, например, следую-
щим образом. Каждый прибор должен обслуживать требования непрерыв-
но одно за другим, начиная с момента времени d = 0; первый прибор обслу-
живает требования в последовательности (п, л>?), второй - в после-
довательности (ядго, п, Идт»), третий - в последовательности (ttn^, п).
Пусть существует расписание s°. Поскольку tL (N) = ЗЕ, L = 1,2, 3, то в
силу (2.1) fmax(s°) = 3£ и каждый прибор во временном интервале
(0, ЗЕ*] функционирует без простоев. Так как tn(Jt) = ЗЕ, то в любой
момент времени t Е (0, 37?] требование п обслуживается одним из при-
боров. Следовательно, найдется прибор L, 1 <£ <3, такой, что требова-
ние п обслуживается во временном интервале (Е, 2Е\, а требования мно-
жества/V0 -в интервалах (0,7?] и (2Е, 3£]. Обозначая через ТУ? иТУ£ мно-
жества требований, обслуживаемых в интервалах (0, F] и (2Е, 3F] соот-
ветственно, получаем решение задачи о разбиении.
Реализация сведения задачи о разбиении к задаче о существовании рас-
писания $° требует выполнения не более О(и0) операций.
Таким образом, задача построения оптимального по быстродействию
расписания в случае, когда М> 3, является NP-трудной.
2.2. Рассмотрим систему, содержащую > 3 приборов, среди которых
имеется один доминирующий прибор, и покажем, что оптимальное по
быстродействию расписание обслуживания п требований (п> М) в этой
системе может быть построено в результате выполнения не более чем
0(пМ) элементарных операций.
Будем говорить, что прибор Q доминирует прибор Н, Q,H , Q^H,
если ttQ > tfff для всех i, j Е N, i Ф j.
Аналогично требование i доминирует требование /, N, i Ф j, если
Uq tfH для всех Q^H.
Прибор (требование) назовем доминирующим, если он (оно) доминиру-
ет все остальные приборы (требования).
Не нарушая общности, будем считать, что доминирующим является
прибор 1.
Введем в рассмотрение матрицу || \Li || размерности М X п, каждая
строка которой представляет собой некоторую перестановку элементов
множества N. Если XLi = к, то содержательно это означает, что прибор
L обслуживает требование к f-м по порядку.
Зададим матрицу || \Li ||, полагая
= i, i = 1,..., п\
= = i = 2,... ,п, L = 2,... ,М.
Эта матрица представляет собой латинский прямоугольник, построенный
на множестве N. Напомним, что латинским прямоугольником (квадратом),
построенным на конечном множестве S, называется прямоугольная (квад-
180
ратная) матрица, каждая строка которой представляет собой некоторую
перестановку элементов множества 5 и каждый элемент 5 встречается
не более одного раза (ровно один раз) в каждом столбце матрицы.
Положим
1 = G 1 > = h-1,1 + / = 2,.. ., л;
~t\LiL = hi, Z = 2,
Нетрудно убедиться, что построенная матрица || II определяет расписа-
ние с общим временем обслуживания, равным
t\(N) = max{ max max
l еле i e n
Из (2.1) следует, что это расписание является оптимальным. Трудоем-
кость построения каждой из матриц || X L11| и || tiL || не превосходит
О(пМ) операций.
В силу симметрии рассматриваемой задачи можно заключить (см. п.1.1
§ 1 этой главы), что построение оптимального по быстродействию расписа-
ния в случае, когда одно из обслуживаемых требований является домини-
рующим и п также может быть осуществлено за О(пМ) элементар-
ных операций.
Условие л > М при наличии доминирующего прибора (или, что то же,
условие п < М при наличии доминирующего требования) является су-
щественным. Если это условие не выполняется, то задача построения опти-
мального расписания является NP-трудной (Ъ п. 2.1 при сведении задачи
о разбиении к задаче построения оптимального расписания приМ= 3 требо-
вание п = nQ + 1 является доминирующим).
2.3. Пусть система, содержащая М приборов, обслуживает п требований
(л > М) и среди приборов имеются два прибора, доминирующие все осталь-
ные приборы, но не друг друга. Покажем, что и в этом случае построение
оптимального по быстродействию расписания требует выполнения не
более О (пМ) операций.
Не нарушая общности, можно считать, что указанными приборами яв-
ляются приборы с номерами 1 и 2. Приборы, отличные от приборов 1 и 2,
назовем недоминирующими.
При помощи алгоритма, описанного в п. 1.2 § 1 этой главы, найдем опти-
мальное по быстродействию расписание обслуживания всех требований
приборами 1 и 2. Для удобства дальнейших рассуждений будем полагать,
что в построенном расписании последовательности обслуживания требова-
ний приборами 1 и 2 определяются соотношениями
X11 = 1, Xlz- — i, Х21 =: w, ,i— 1 > /=2,...,л (2.2)
(в противном случае требования можно соответствующим образом пере-
нумеровать) .
В силу соотношения (1.2) § 1 этой главы общее время обслуживания
требований приборами 1 и 2 равно max{ti(TV), 12(Af)+ tn2}.
1) Предположим, что
tni +tn2 > тах{Г1(ЛГ), Г2(ЛЭ)- (2.3)
Тогда общее время обслуживания в исходной задаче будет не меньше
tn(Jl),
181
Пусть первые две строки матрицы || XLi || заполнены в соответствии
с (2.2). Положим
~ 1 ,п- 1 > ~ ^L- 1 j- i > £ = 2,. .. ,М, i = 2,. . ., п - 1.
Из алгоритма, описанного в п. 1.2 § 1 этой главы, следует, что
Гц = /„1 +
hi = 1.1 + hi. i = 2,
tn2 ~ 612, ?12 = ?n2+?12;
62 = 6-1,2 + 6’2, i=2,...,n.
Положим
t\LiL = 61, L = 2,...,M, i=l,...,n—1.
Проведенные построения означают, что за время обслуживания требова-
ния п прибором 2 все остальные требования будут заведомо обслужены
всеми остальными приборами. Затем, во время обслуживания требова-
ния п прибором 1, все остальные требования обслуживаются прибором 2,
а недоминирующие приборы простаивают.
Положим
\Ln = п, L = 3,..., М;
tn з = tn 1 + з ’
^nL ~ tn,L - 1 + tnL-> L = 4,.. ., М.
В результате получаем расписание с общим временем обслуживания,
равным tn(Jt).
2) Пусть неравенство (2.3) не имеет места. Как и выше, полагаем, что
первые две строки матрицы II XLi || заполнены согласно (2.2). Осталь-
ные строки этой матрицы заполним таким образом, чтобы строка L имела
вид (п - L + 2,п - L + 3, . . . , и, 1,2, ... ,п - L + 1),£=3,...,М. От-
метим, что построенная матрица || t1| представляет собой латинский
прямоугольник, построенный на множестве N.
Моменты ti ], ti2i i - 1, . . . , и, завершения обслуживания требований
приборами 1 и 2 могут быть найдены из расписания, построенного по ал-
горитму, описанному в п. 1.2 § 1 этой главы. Положим
xLiL = ^*1 ’ L = 3,... ,М, i = 1,..., £ - 2,
\LiL = *7-1,2, А = 3, ...,7И, /=£,..., и.
Первое из этих соотношений означает, что каждое требование с номером
/, / = 2,. . . , п - 1, перед его обслуживанием прибором 1 будет обслужено
недоминирующими приборами в порядке возрастания номеров от Lj =
= п - j + 2 (Lj < М) до М. Из второго соотношения следует, что каждое требо-
вание с номером к, к = 1, . . . , п — 2, после завершения его обслуживания
прибором 2 будет обслужено недоминирующими приборами в порядке
возрастания номеров от 3 до Lk = п -к + 1(£Л< М). Таким образом,
построено расписание обслуживания всех требований множества N\{n}.
182
Для требования п положим tn3 = tn2 + tn3 и tnL = tn L_v + tn L_r,
L = 4, ...,M
Если t X(N) > To построенная матрица || tiL || определяет рас-
писание с общим временем обслуживания, равным max{fi(#), •
В противном случае положим tnl = tnM + tnX. В результате получаем
расписание с общим временем обслуживания, равным max^GV), (7V)} .
Таким образом, в любом случае построено оптимальное_ расписание
s*. Трудоемкость построения каждой из матриц || XLj || и || tiL || не пре-
восходит О(пМ) операций.
В силу симметрии рассматриваемой задачи можно заключить, что по-
строение оптимального по быстродействию расписания в случае, когда
п < М и среди требований имеются два требования, доминирующие все
остальные требования, но не друг друга, также может быть осуществлено
за О(пМ) операций.
Указанные соотношения между п и М являются существенными. Если
эти соотношения не выполняются, то соответствующая задача оказыва-
ется NP-трудной.
Действительно, рассмотрим задачу о разбиении. Положим и = п0 + 2,
М = ti3 - 0, tix = ti2 - eh i = 1, . . . , n0; + jj - tn^^x 2 = ^0 + 2,i =
= ^„o + 2,2 ~ E', Gi0 + i,3 = Gi0 + 2,3 = 2£. Заметим, что требования л0 + 1
и По + 2 доминируют остальные требования, но не друг друга, причем
п > М.
Нетрудно показать, что задача о разбиении имеет решение тогда и только
тогда, когда при указанных и, М и tiL существует расписание $° такое, что
2.4. П р и м е р. Построим оптимальное по быстродействию расписание
обслуживания пяти требований четырьмя приборами. Длительности
приведены в табл. 2.1.
Нетрудно убедиться, что приборы 1 и 2 доминируют остальные приборы,
но не друг друга.
Поскольку неравенство (2.3) не выполняется (^51+^52 = 43, = 45,
t2(N) ” 63), то матрицы || XLi || и || Где, II стр°им так, как это описано
в п.2.3, 2).
Используя алгоритм п.1.2 § 1 этой главы, строим оптимальное расписа-
ние обслуживания всех требований двумя приборами 1 и 2. Таким распи-
Таблица 2.1
1 2 3 4
1 7 12 1 3
2 7 8 5 2
3 10 6 4 7
4 8 7 3 3
5 13 30 5 2
183
Таблица 2.2
i L 1 2 i L 1 2
1 7 42 4 32 63
2 14 50 5 45 30
3 24 56
санием является, в частности, расписание, определяемое моментами t iLi
L = 1,2, завершения обслуживания требований, приведенными в табл. 2.2.
В рассматриваемом случае исходная нумерация требований такова, что
выполняется (2.2) и матрица || XLi || имеет вид
1 2 3 4 5
5 12 3 4
4 5 12 3
3 4 5 1 2
Учитывая, что fi (/V) = 45 < Г5 (Jfc) = 50, получаем матрицу
7 42 50 56
14 50 56 63
lira II = 24 56 63 7
32 63 7 14
50 30 35 37
определяющую оптимальное расписание $*. Общее время обслуживания
равно 7m ах (s‘ ) = ^ 0V) = 63.
2.5. Опишем алгоритм трудоемкости О(п2М3) операций построения
оптимального (по быстродействию) расписания s* в предположении, что
r*(7V) = max tL (N) > (М2 +27И-1)г*,гдеГ*=тах{^|,
L GM
Далее везде будем предполагать tL(N) = t*(N), L = 1,..., М. В против-
ном случае исходные длительности обслуживания tiL можно было бы соот-
ветствующим образом ’’удлинить”, не увеличивая значения г*.
Введем в рассмотрение множество V, состоящее из п векторов v вида
(til ~ tt2, ti2 - ti3, ••• > Чм-1 - tiM - til), t e К. Очевидно,
S v = 0, и если в качестве нормы ||и|| вектора v выбрать максимум мо-
ие v
дуля его компонент, то || v || < t *, v G V.
Нумеруя векторы v множества V согласно алгоритму, описанному
в п.8.2 § 8 гл. 1, получаем V = {и1, и2,..., и"}. Перенумеруем (если
это необходимо) требования множества N так, чтобы vl = (tix - ti2,
ti2 ~ • • • > ~ *iM> *iM ~ tn)-
Из утверждения, доказанного в п.8.2 § 8 гл. 1, следует неравенство
~МГ < StiL- S tlrL+l<Mt*,
1 = 1 /=1 ’ (2.4)
k= 1,..., n,
184
а также неравенство
-Mt'< VtiM- fc=l......n. (2.5)
Z=1 Z = 1
Расписание s* построим следующим образом. Все приборы функциони-
руют во временном интервале (О, Г* (7V)] без простоев и обслуживают
требования непрерывно одно за другим. Первый прибор обслуживает тре-
бования в последовательности 1, 2,. .., п; прибор L, 2 <£ — в после-
довательности iL + 1, iL + 2,..., п, 1,2,..., iL.
Опишем процедуру выбора требований i2, i3,..., in.
В качестве i2 выберем наибольшее значение j, для которого
S ti2>(M + 1)г‘.
t = i + i
п
Положим Г12 = 2 ^2-
i = i, + 1
Пусть выбраны требования i2, i3,... , Iq _ j и вычислены моменты
времени Г? г = S tiL , L = 2,..., Q - 1, 2 < Q <М.
В качестве iQ выберем наибольшее значение j, для которого
Q - 1 + •
п
Положим S tfQ.
i= iQ + i *
Этот процесс продолжается до тех пор, пока не будет выбрано требо-
п
вание и вычислено значение = S tiM.
Реализуемость описанной процедуры выбора требований /2, *з, • • • > *м
можно обосновать следующим образом.
Нетрудно видеть, что ti2< (М + 2)Г*, так как противоположное нера-
венство противоречило бы правилу выбора требования i2. Так как
(М + 2)f* < (М2 + 2М — l)f* = Г* (TV) для всех М > 2, то требование i2
действительно может быть выбрано.
Далее, из аналогичных рассуждений следует, что t\L-t^Ll<
< (М + 2)z*, L = 2,... , М. Отсюда получаем < (L — 1)(М + 2)Г*. Так
как даже при L = М имеем (М — + 2)Г* = (М2 + М — 2)г* <
< (М2 + 2М — 1)г* для всех М > 0, то все требования iL, Z = 2,...,7И могут
быть выбраны. Кроме того,
+ (2.6)
так как t<(М — 1)(7И + 2)Г*.
Покажем, что при обслуживании требований в указанных последователь-
ностях каждый прибор может функционировать без простоев во времен-
185
ном интервале (0, t* (/V)]. Для этого достаточно показать, что ни одно из
требований не будет обслуживаться несколькими приборами одновре-
менно.
Пусть / G7V - произвольное требование. Обозначим через Q такое макси-
мальное значение Z, 1 < L <М, ддя которого t\L + S tiL < Это
означает, что требование / обслуживается приборами L, L = 2,..., 0,
после момента времени tQiL, а приборами L,L = Q + 1,... ,М (если
Q<M) — до момента времени t^L.
Чтобы требование j одновременно не обслуживалось несколькими
приборами, должны выполняться неравенства
l-i, £ = 2,...,М, £#=е+1; (2.7)
0*^; (2.8)
Q*M. (2.9)
Пусть L<Q. Тогда
_ 7-1 7-1
“ О» L - 1 “ 1L + —( 1, £ — 1 + _ 1 + tj, L — 1 ) •
i=l i=l
Поскольку по построению - г® , > (М + 1)?* и в силу (2.4)
/1 / -1 _
,Л tiL ~ Z/b - '/,£ -1 >(Л/ + O'* ~Mt* - '/.Л -1 =
= - t),L -1 0-
Аналогично, при Q + 2 < L имеем
7 -1 i - i
r/L-r/,L-l= tiL - 2 ti L_i-tj L-l-
Нетрудно убедиться, что
’s 1 = tiL>
t = iL + i i = i
i-i 1-1
S flL = 11, Д - I - t*{N) + S t(< L _ j.
i ~ ‘L - 1 + 1 ' = 1
Тогда _ j
z/l-z/.l-i=z?l-'i,l-i+ UL~ ,2=1Z'^-i
1 = 1
Таким образом, неравенство (2.7) выполняется.
/ - i
Нетрудно проверить, что tjQ = t^ + S ttQ и
i = i
/ /-1
tj, Q + 1 ” ti, Q + 1 = J 1 Q+ | - t*(N) + S tft Q + 1 + tj, Q + j ,
।r = iQ + 1 + 1 1=1
186
поскольку, кроме того, t°Q - 4(2+1 > - (М + 2)г*, то с учетом (2.4)
имеем
- Ь, Q +1 > - (М + 2)'* - Mt* + (Ю ~ 2 +1 > (^2 - 4)Л
т.е. при М >2 неравенство (2.8) также выполняется.
Нетрудно проверить, что
i - 1 i - i
fJM ~ 2 fiM = ~ t*(№) + S tiM-
i=iM + l i= 1
В силу (2.5)
i - i / - i
S ifM 2 + Mt*.
1=1 i=l
Кроме того, из (2.6) следует, что
t\M-t*(N)^Mt*<-t*.
Таким образом,
/ - 1 j - 1
'/м < S ttl + t\M - t'(N) +Mt* < S - Г = _ t.9
i = 1 i = 1 1
откуда вытекает неравенство (2.9).
Нетрудно видеть, что оптимальное расписание s* может быть построено
в результате выполнения не более чем О(п2М3) операций, поскольку
наиболее трудоемким этапом при его построении является этап перенуме-
рации требований множества N (нумерации векторов v множества V (см.
§8 гл. 1)).
§ 3. Общее время обслуживания. Прерывания
В этом параграфе рассматривается задача построения оптимального по
быстродействию расписания функционирования систем с нефиксирован-
ными маршрутами при условии, что в процессе обслуживания каждого
требования каждым прибором допускаются прерывания.
3.1. В систему, содержащую М последовательных приборов, в момент
времени d = 0 поступает множество N = {1, 2, . . . , п} требований. Извест-
ны длительности tiL > 0 обслуживания каждого требования i Е N каж-
дым прибором L Е 2, . . . , М}. Порядок прохождения приборов
каждым требованием может быть произвольным и необязательно одина-
ковым для разных требований. По-прежнему предполагается, что каждый
прибор одновременно обслуживает не более одного требования, а каждое
требование одновременно обслуживается не более чем одним прибором.
В процессе обслуживания требований допускаются прерывания, каждое
требование i может обслуживаться каждым прибором L в несколько
’’приемов” при сохранении условия, что суммарная длительность этого об-
служивания равна tiL (если tiL >0). Процесс обслуживания требования i
прибором L может быть прерван в любой момент времени. После прерыва-
ния прибор L может обслуживать любое другое требование, а требование
187
i — обслуживаться любым другим прибором. Процесс обслуживания тре-
бования i прибором L может быть возобновлен в любой момент времени.
Число прерываний может быть произвольным, но конечным.
Если tiL — момент (полного) завершения обслуживания требования i
прибором L при некотором расписании s и7тах(х) = тах{ tiL | i G /V,
7 GUK), то, как и прежде (см. (1.1)),
^max(s) > Г, Т= max {max tjijl), max tL(N)} . (3.1)
few
Как следует из результатов, приведенных в § 1 этой главы, при М = 2
существует расписание s* без прерываний, при котором Fmax(s*) = Т,
и это расписание может быть построено за О (и) операций.
Ниже описываются полиномиальные алгоритмы построения расписания
s* (с прерываниями), при котором ^тах(5*) = Т Для произвольного /И.
В силу (3.1) это расписание является оптимальным по быстродействию.
В п. 3.6 рассматриваемая ситуация обобщается на случай, когда каждый
прибор L представляет собой систему, содержащую несколько параллель-
ных (необязательно идентичных) приборов.
Задача, рассматриваемая в п. 3.8, отличается от той, которая была опи-
сана в п. 1.4 этой главы, только тем, что в процессе обслуживания каждого
требования каждым прибором допускаются прерывания.
В заключение параграфа устанавливается /VP-трудность задачи построе-
ния оптимального по быстродействию расписания в случае, когда после
прерывания процесса обслуживания требования i любым прибором L
это требование не может обслуживаться другими приборами. Устанавли-
вается также /VP-трудность построения оптимального расписания (с пре-
рываниями) , когда в процессе обслуживания каждого требования запреще-
ны задержки.
3.2. Пусть все tiL - целые числа. Покажем, что существует расписание $*
такое, что fmax (s*) = Т и прерывания процесса обслуживания имеют место
только в целочисленные моменты времени.
Построим двудольный неориентированный мультиграф Г = ; U),
где N = {1, 2, . . . , л } и ={ 1, 2, . . . , М} - множества вершин, U - мно-
жество ребер, каждые две вершины i G N и L GJK соединены tiL ребра-
ми (если tiL > 0).
Под реберной раскраской мультиграфа будем понимать, как обычно,
такое сопоставление цветов (чисел 1, 2, ... ) ребрам, при котором ника-
кие два ребра, инцидентные одной и той же вершине, не окрашены в одина-
ковый цвет (им не приписано одно и то же число).
Известно, что минимальное число цветов, необходимых для раскраски
ребер двудольного графа (мультиграфа), равно максимальной степени
вершины. Поскольку по построению максимальная степень вершины муль-
тиграфа Г равна 7, то он может быть раскрашен в Т цветов (т.е. его ребрам
могут быть сопоставлены числа 1,2,..., Т).
Интерпретируя цвета - числа 1, 2, . . . , Т — как номера временных
интервалов (0, 1], (1, 2], . . . , (Г — 1, Г], а окраску ребра (/, L) G U
в цвет т — как обслуживание требования i прибором L во временном
интервале (т — 1, т], приходим к заключению, что искомое расписание s*
188
существует, и для его построения достаточно решить задачу раскраски
мультиграфа Г в Тцветов.
Построенное таким образом расписание s * может оказаться неприемле-
мым из-за неоправданно большого числа прерываний. Для построения опти-
мального расписания с меньшим числом прерываний может быть исполь-
зован следующий подход.
Введем понятие обобщенной реберной раскраски мультиграфа. Эта рас-
краска отличается от обычной только тем, что, во-первых, ребра, инци-
дентные одной и той же паре вершин, могут окрашиваться в одинаковый
цвет и, во-вторых, если в цвет т окрашено кт ребер вида , L1), то ребра
вида (i2, L2) Gi & i2, Li L2) либо не окрашиваются в цвет т, либо
окрашиваются ровно кт из них. Число кт будем называть кратностью
цвета т. При кт < 1 получаем обычную реберную раскраску мультиграфа.
Обобщенная реберная раскраска мультиграфа Г называется оптималь-
ной, если сумма кратностей кт всех использованных при раскраске цветов т
равна Т. Известно, что такая раскраска может быть получена в результате
выполнения О((п + М)г log f*) операций, где t* = max{tiL | i e N,L Gjt},
r - число ненулевых tiLi iEN,L ЕЛ. При этом число используемых
цветов не превышает О (г log t*).
Если известна оптимальная обобщенная раскраска ребер мультиграфа Г,
то соответствующее оптимальное (по быстродействию) расписанием* может
быть построено следующим образом. Пронумеруем использованные при
раскраске цвета числами 1, 2, . . . , Л (очевидно, 7\ <Т). Пусть кт, т =
= 1, 2, . . . , Г1, - соответствующие кратности цветов. Разобем интервал
планирования (О, Т] на Л подынтервалов (0, fcj, (кх, кг + к2\, . . .
г, -1 тх
..., ( S kr, S кг ] и пронумеруем их числами 1,2,.. ., Л. Если хотя
7=1 7=1
бы одно из ребер вида (i, L) окрашено в цвет т, 1 <т (а следователь-
но, в цвет т окрашено ровно кт ребер вида (/,£)), то во временном интер-
вале с номером т требование i непрерывно обслуживается прибором L.
Для уменьшения числа прерываний естественно стремиться к нахожде-
нию оптимальной обобщенной раскраски в наименьшее число цветов Л.
3.3. Пример. Имеется четыре источника и три приемника информа-
ции. Длительности tiL передачи информации от источника f, i = 1, 2, 3, 4,
приемнику Z,, L Е {/, II, III} приведены в табл. 3.1.
Если tiL - 0, то от источника i приемнику £ информация не передается.
Предполагается, что передача информации от каждого источника каждо-
му приемнику может производиться по частям, причем возобновление пе-
редачи осуществляется с прерванного места.
Таблица 3.1
L I П III
1 4 3 2
2 3 5 0
3 0 1 3
4 3 0 4
189
Требуется передать информацию от всех источни-
ков всем приемникам как можно скорее.
Для решения этой задачи используем подход, из-
ложенный в п. 3.2 Положим N = {1, 2, 3, 4}
II, III} и построим двудольный мультиграф Г =
= {N, Л; U}, соединяя вершину i &N с вершиной
tiL ребрами, если tiL > 0, и не соединяя их
в противном случае. Полученный при этом мульти-
граф Г изображен на рис. 3.1; числа, приписанные
ребрам, означают их кратность. Максимальную сте-
пень в мультиграфе Г имеет вершина I, и значит
Рис. 3.1 Т= 10.
Найдем оптимальную обобщенную реберную раскраску мультиграфа Г.
Одна из таких раскрасок приведена в табл. 3.2.
Таблица 3.2
ребро 1 2 3 4 S
(U) 4
(1, П) 3
(1,Ш) 1 1
(2,1) 3
(2, II) 4 1
(3, II) 1
(3, III) 3
(4,1) 1 1 1
(4, III) 4
В этой таблице указаны кратности цветов и ребра, окрашенные в соот-
ветствующий цвет.
Соответствующее расписание представлено на рис. 3.2.
3.4. Пусть tiL - произвольные неотрицательные^ числа. Покажем, что и
в этом случае существует расписание s * такое, что rmax (s *) = Т, и укажем
способ его построения.
Построим матрицу А = Иярд11 размерности (и+Л/) X (п+М) вида
|| II tj^ II Dn
А =11-------------,
II &м В
где II tiL II - матрица размерности п X М длительностей обслуживания тре-
бований, Dn и Dm - диагональные матрицы размерностей п X п и М X М
соответственно, В - матрица размерности М X п такие, что
п + М п+М
2 apq = Т, р= 1,..., S ар„ = Т, ?=1,..., п+М.
q = l 1
Напомним, что в диагональной матрице все элементы, за возможным
исключением элементов, стоящих на главной диагонали, равны нулю. В
190
качестве матрицы В может быть выбрана, например, матрица, транспони-
рованная к II tiL II.
Построенная таким образом матрица А кратна дважды стохастической
матрице (т.е. суммы ее элементов, расположенных в каждой строке и каж-
дом столбце, равны) и, следовательно, допускает разложение вида
Л=Л^1б*П*> (3.2)
где I < (п + М - I)2 + 1, S 6fc = Т, Sk>O,Jt = l.Z, а ПЛ = II0* II -
k = 1
перестановочные матрицы (матрицы размерности (п + М) X (и + М) с
элементами 0 и 1, в каждой строке и каждом столбце которых содержится
ровно одна единица).
Если найдено разложение (3.2), то соответствующее оптимальное (по
быстродействию) расписание 5* может быть построено следующим обра-
зом. Разобьем интервал планирования (О, Т] на I подынтервалов (О, SJ,
I -1 I
(6i, 61 + 62 ], . . . , ( 2 S б*. ], пронумеровав их числами от 1
к = 1 к = 1
до I. Если при некотором к, 1 < к <Z, элемент 0pq =1,1 1
то будем считать, что требование i = р непрерывно обслуживается прибо-
ром L = q во временном интервале с номером к. Нетрудно видеть, что
при этом выполняются все требования, предъявляемые к расписанию, и
^шах (5 ) “
Отметим, что если все tiL - целые числа, то в разложении (3.2) все
8к - целые числа и прерывания в расписании s * имеют место только в цело-
численные моменты времени.
Для нахождения разложения (3.2) можно воспользоваться следующим
очевидным приемом. Выделим в матрице А множество R (А) ее ненулевых
элементов таким образом, чтобы в каждой строке и каждом столбце на-
ходился ровно один элемент этого множества. Поскольку матрица А кратна
дважды стохастической матрице, то множество R (А) существует.
Пусть 6 - наименьший из элементов множества R(Л), а П = ll0pQll -
перестановочная матрица, у которой 0P(f = 1 тогда и только тогда, когда
apqE R (Л). Положим Si = 6 и Щ = П. Уменьшим в матрице Л все ее эле-
менты apq G R (Л) на величину S, Обозначим полученную в результате мат-
191
рицу через А. Эта матрица по-хрежнему кратна дважды стохастической мат-
рице. Проводя относительно гее те же рассуждения, получаем второй член
62П2 разложения (3.2) и т.д. Поскольку на каждом шаге хотя бы один из
ненулевых элементов матрица А обращается в нуль, то через конечное
число шагов (порядка О(пМ)) будет получена нулевая матрица и процесс
нахождения разложения (3.2) 5удет завершен.
Существуют различные спссобы выделения множества R (Л) по задан-
ной матрице А. Так, множество R (Л) может быть выделено в результате
решения задачи о назначения? (на узкие места) со стоимостной матрицей
Л либо в результате решения едачи о максимальном паросочетании в соот-
ветствующем двудольном граре и т.п. В любом случае для выделения мно-
жества R (Л) достаточно полхномиально ограниченного (относительно п
и М) числа операций.
3.5. В условиях примера пЗ.З в качестве матрицы Л можно выбрать,
например, матрицу
Одним из возможных разлокений вида (3.2) этой матрицы является раз-
ложение
Л = 2 - Щ + 3 • П2 + 2 • Пз+1 • П4 + 1 • П5 + 1 • П6,
где
^11 ~ 02 2 “ 03 3 “ 047 “054”065 ““076 “h
д2 — д2 — д2 д2 _д2 — л2 — д2 — i
"12 “ "21 “ "36 “ "43 “"54 “ "65 “ "77 “ 1,
013 = 022 ~ 036 = 041 = 054 ~ 065 = 077 = h
01 1 = 025 = 032 = 043 =054 = 066 = 077 = 1,
014 = 022 = 033 = 041 = 055 = 066 = 077 ”
0?1 = 0^5 = 036 = 047 =054 = 062 = 073 = 1,
остальные 0pq = 0, 1<р<7,
Расписание, соответствующее этому разложению, приведено на рис. 3.3.
3.6. Рассмотренная ситуашя допускает естественное обобщение. Пусть
имеются множество N = {1 2, . . . , п } требований и множество М -
= { 1, 2, . . ., М } обслуживакщих приборов. Процесс обслуживания каждо-
го требования включает т стадий. Порядок прохождения стадий заранее
не фиксирован и может бытьразличным для разных требований. На стадии
/, 1 </ для обслуживашя требования i,i G TV, могут использоваться
приборы множества^, QМ Если L и требование i на стадии/ об-
192
служивается только прибором L, то длительность его обслуживания долж-
на равняться tijL > 0. Величины tijL предполагается заданными. В процес-
се обслуживания допускаются прерывания. Беги суммарная длительность
обслуживания требования i на стадии / прибором L равна F//L <
< tijL> то для обслуживания требования i используется хотя бы один из
приборов множества отличный от L. При этом должно выполняться
соотношение S 7цL It цL = 1.
L е Яц
По-прежнему, предполагается, что одновременно каждый прибор L G М
обслуживает не более одного требования i G N и каждое требование обслу-
живается не более, чем одним прибором.
Если положить m=MJ - L, {£}, ttjL = tiL, то получим обслужи-
вающую систему, описанную в п. 3.1.Если положить т = 1, Jlix ~Л, tiiL ~
= tiL, то получаем одностадийную систему с М параллельными приборами.
Для построения оптимального (по быстродействию) расписания в рас-
сматриваемом случае можно воспользоваться следующим подходом.
Суммарные длительности обслуживания требований > 0 в интер-
вале планирования (0, То], где То - достаточно большое число, должны
удовлетворять следующим ограничениям:
S = 1, i = 1,..., п, j' - 1,. .., <п, (3.3)
L t^L
S S tijL < TQ, ЬЕЛ, (3.4)
i e N j = 1
S S tijL < To, i£N. (3.5)
j - 1 L $=. *№> ij
Обозначим через решение задачи лиаейного программирования,
состоящей в минимизации величины То при указанных ограничениях.
m ~
Положим t*L = S i = 1, • • • » п, L = 1, . . . , М. Интерпретируя
/ - 1
величину th как длительность обслуживания требования i G N прибором
L G М в системе с М приборами и нефиксированным порядком их прохож-
13. В.С. Танаев 193
дения, приходим к рассмотренной выше ситуации (см. п. 3.1). Используя
один из описанных в пп. 3.2 и 3.4 методов, получаем искомое оптимальное
расписание 5 *.
Для нахождения величин (решение задачи линейного программиро-
вания) и последующего построения расписания 5* (с прерываниями) для
системы с нефиксированным порядком прохождения приборов требуется
не более полиномиального (относительно п, т и М) числа операций.
Трудоемкость построения оптимального расписания может быть сущест-
венно уменьшена при некоторых дополнительных предположениях отно-
сительно обслуживающей системы.
Пусть, например, множество Л приборов разбито на т, т < М, непус-
тых попарно неперескающихся подмножеств Л], j = 1, . . . , т ъЛц =Л],
i EN. Все приборы каждого множества Л] предполагаются идентичными,
т.е. tЦБ = 1ц,Ь ЕЛ].
Поскольку каждый прибор L используется только на одной из стадий,
то можно положить rtjL = и записать соотношения (3.3)-(3.5) в виде
2 Ъь = *ib 1 *, • • •, J = 1, • • • > т> (36)
L е л/у
2 Ъь < ЬЕЛЬ j* 1,..., т, (3.7)
i g N
S S ~tiL < Го, 1 = 1,..., п. (3.8)
j - 1 LG Jhl j
Суммируя неравенства (3.7) по всем L ЕЛ] при фиксированном, д
1 </ < т, и учитывая (3.6), приходим к заключению, что наименьшее
значение То при указанных ограничениях равно
т 1
То* 3 max { max S tih max ----------- S ty } .
i G N 1 1 < j < m \Л]\ i G N
Чтобы найти значения t *L, можно поступить следующим образом. Для
каждого /, 1 построим оптимальное (по быстродействию) распи-
сание sy обслуживания множества N требований параллельными идентичны-
ми приборами множества^, разрешая прерывание процесса обслуживания
любого требования i Е N любым прибором L ЕЛ]. Как известно, построе-
ние такого расписания требует не более чем О(п) операций, причем общее
время обслуживания требований при расписании s * равно max { max t{],
1 i G N
1 >
---- S tn /. В качестве t*L выберем суммарное время обслужива-
\Л] I I G N
ния требования i прибором L ЕЛ] при расписании Sy*. Поскольку каждый
прибор L принадлежит только одному из множеств Л], 1 можно
положить t*L = t*L.
3.7. В качестве примера рассмотрим задачу построения оптималь-
ного по быстродействию расписания двухстадийного обслуживания четы-
рех требований тремя приборами А, В и С. На стадии I используются при-
194
Таблица 3.3
боры А и В, на стадии II — прибор С, Приборы А и В идентичны. Порядок
прохождения стадий произвольный. Допускаются прерывания. Длитель-
ности обслуживания требований на каждой стадии приведены в табл. 3.3.
В рассматриваемом случае значение Т£ = 9.
Оптимальное по быстродействию расписание обслуживания требований
параллельными идентичными приборами А и В приведено на рис. 3.4.
Значения t*iL, i = 1,2, 3,4, Z G {А, В, С } приведены в табл. 3.4.
Используя любой из алгоритмов, описанных в пп. 3.2 и 3.4, построим
оптимальное (по быстродействию) расписание обслуживания четырех
приборе
приборА
требований в системе с тремя приборами Л, В и С, нефиксированным
порядком их прохождения и длительностями обслуживания, приведенны-
ми в табл. 3.4. Это расписание (рис. 3.5) и является искомым оптимальным
расписанием.
3.8. Рассмотрим следующую задачу построения оптимального по быстро-
действию расписания.
В систему, состоящую из двух приборов А и В, в момент времени d = О
поступает множество N - {1,2,..., и } требований. Длительность обслу-
живания требования i G N прибором А равна > О единицам времени
13
195
и прибором В равна bj > 0 единицам времени. Запись а, = 0 или = 0 озна-
чает, что требование не обслуживается приборами Л или Л соответственно.
Множество N состоит из трех попарно непересекающихся подмножеств
NAB, Nba и No требований. Требования множества NAB обслуживаются
сначала прибором Л, затем прибором В (маршрут обслуживания (Л, В));
маршрутом обслуживания требований множества NBA является (В, Л);
требования множества No могут обслуживаться в соответствии с любым
из маршрутов (Л, В) или (В, Л), причем маршруты заранее не заданы
и могут быть различными для разных требований. Ко множеству No отне-
сены также все требования, для которых либо = 0, либо = 0.
В любой момент времени каждый прибор обслуживает не более одного
требования и каждое требование обслуживается не более чем одним при-
бором. Разрешены прерывания процесса обслуживания любого требо-
вания любым прибором.
Требуется построить оптимальное (по быстродействию) расписание 5*
обслуживания требований множества N.
Отметим, что в случае запрещения прерываний имеем ситуацию, рас-
смотренную в п. 1.4 этой главы. Далее в этом пункте обозначения и по-
нятия, введенные в п. 1.4, употребляются без специальной оговорки.
В рассматриваемом случае для любого расписания 5 (с прерываниями)
справедливо очевидное неравенство
^maxO)rnax{a(7V), b(N\ tmax(sAB), (3.9)
'тах(*вл)> тах{а{ + Ь( |i€jV0}}.
Это означает, что пары наборов I-V, перечисленные в п. 1.4, определяют
оптимальное расписание s* с прерываниями в тех же случаях, что и без
прерываний.
Рассмотрим пару наборов
(Л; [0, т]; [а’т, (n(NAB), ir(NBA U No \ {m }))]; [f0, m]);
(В; [0,7г(ЛЬл)]; [max{a^, b(NBA)}, m];
[r°, n(NAB UNo\{m})]),
где dm = am - b(NAB UN0\{m}) и t° = max {a'm + a(N\{m}), a'm + bm,
b(NBA U {ro})}.
Покажем, что эта пара наборов определяет оптимальное расписание $*
(с прерываниями) в случае, когда выполняются неравенства (1.10), (1.12),
(1.21) и (1.23) (см. рис. 1.4 в п. 1.4 этой главы).
Действительно, если Г10 = ат + Ьт, то ат > b(NBA) и bm >a(N\{m})\
v№x{iiB($*) Iiе Nba } = b(NBA) < ат <min{t^A ($*)|iGNBA } и
max{FM(s*)|z <£Nab U No\{m}} = am + a(N\{m}) < am + bm =
= min{r?B(s*)|z € Nab U No\{m }} Требование m обслуживается прибо-
ром В во временном интервале (ат) ат + Ьт\ и прибором А в интервалах
(0, (&т + Ьт > + Ьт ] • Кроме того, tmах (s ) — йт + Ът. Расписа-
ние s* изображено на рис. 3.6, а.
Если Г° = b(NBA U {т}), то b(NBA) >ат. В силу (1.10) и (1.23) имеем
minU?^*) | i G Nba} = am + a(NAB) > a(NAB) > b(NBA) =
196
приборВ
приборА
О
t
приборВ
приборА
/ \
т nab ^ва
о
приборВ
приборА
nba к ! т__________________
\ I \ । ! в
Ч , , \_* [
~ 1 NAB 1 NBa ’ *о\/т? "> 1
>
о----------------------------------t
приборВ
приборА
"вА ™^/|^|
/ \ \ I I
----V---------------!....4 \.... j
rn "ав nba No\!mf
О
Рис. 3.6
= max{F/B(s*) | i Е NBA} . Далее, шах{г/л($*) | i G NAB U No\{m} } =
= am + a(N\{m}) < tQ = min{f?B(s*) | i E NAB U No\{m}}. Требова-
ние m обслуживается прибором В во временном интервале (b(NBAX
b(NBA и { >и})] и прибором А в интервалах (0, ат} и (b(NBA U { ш}),
b(N)]. Кроме того, ^тах($*) = b(N). Расписание $* изображено на
рис. 3.6 б.
Если tQ = ат + а(У\{ти}), то в силу (1.10) и (1.23) имеем
min{r^(s‘)|z е Nba} = а'т + > a(NAB) > b(NBA) =
= max{r/B(s*) | i € NBA} . Далее, тах{г,л (s*) | i G NAB U No\{m }}= t° =
= min{r®B(s*) | i E NAB U No\{m }}. Требование m обслуживается прибо-
ром В во временном интервале (max{aj„, b(NBA)}, Г°] и прибором А
в интервалах (0, ат\ и (r°, a(/V)]. Кроме того, fmax(s*) = a(N). Распи-
сание s* изображено на рис. 3.6, в, г.
Трудоемкость построения этого расписания не превосходит O(ri) опе-
раций.
197
Если не имеет места неравенство (1.10), то, как и в п. 1.4 § 1, можно
поменять ролями приборы.
Учитывая трудоемкость построения расписаний, которые определяются
парами наборов I—V, заключаем, что в рассматриваемом случае оптималь-
ное расписание 5* (с прерываниями) может быть построено не более чем
за О(п + и log#) операций, где п = max {\Nab I, I NBA I}-
Отметим также, что в случаях, когда NAB = ф или NBA = ф, разрешение
прерываний не уменьшает общего времени обслуживания.
3.9. Рассмотрим задачу построения оптимального (по быстродействию)
расписания обслуживания множества N требований М приборами при
следующем дополнительном ограничении на процесс обслуживания: если
начат процесс обслуживания требования прибором, то это требование
не может обслуживаться никаким другим прибором до завершения его
обслуживания (возможно, с прерываниями) данным прибором.
Покажем, что рассматриваемая задача является NP-трудной при М = 3.
Этой задаче соответствует следующая задача распознавания', определить,
существует ли такое расписание 5° обслуживания требований множества 7V,
1110 ^тах(5°) У ДЛЯ заданного числа у. Покажем, что к ней сводится
задача о разбиении (см. вводную часть этой главы).
Положим п = п0 + 3; ti{ = ti2 = eh ti3 = 0, /G/V°; tn^ + il=3E,
6i0 + l,2 ” Gi0 + l,3 ” 3E\ Gi0 + 2,1 ” ^n0+2,2 = 4/Г, ^n0+2,3 ~
tnQ + 3,1 =0Ло+з,2 = 0» ги0 + 3,3 = 2E. Покажем, что в построенной задаче
расписание s° такое, что rmax(s°) У ~ существует тогда и только
тогда, когда имеет решение задача о разбиении.
Если существует указанное разбиение множества /V0 на подмножества
NihN2, то искомое расписание s° можно построить, например, сле-
дующим образом. Каждый прибор, начиная с момента времени d = 0, об-
служивает требования без прерываний процесса обслуживания и непре-
рывно одно за другим; прибор 1 обслуживает требования в последова-
тельности (и0 + 1, , nQ + 2), прибор 2 — в последовательности
(tfjvo, п0 + 2, я^о), прибор 3 - в последовательности (п0 + 2, п0 + 3,
По + 1).
Пусть существует расписание s°. Поскольку ГПо + j (JhC) = tn^+2 М0 = У>
то в силу (3.1) значение ^maxO0) = 6F, причем требования и0 + 1ии0 + 2
в любой момент времени t G (0, 6F] обслуживаются одним из приборов.
Отсюда следует, что в процессе обслуживания этих требований любым
прибором не может быть прерываний. Поскольку tr(N) = t2(N) =
= t3(N} = 6F, N = {1, 2,. . . , и0 + 3 }, то во временном интервале (0, 6F]
каждый прибор функционирует без простоев.
Предположим, что при расписании s° значение /^0+2,2 = 0- Тогда тре-
бование п0 + 1 не может обслуживаться прибором 1 либо прибором 3
во временном интервале (ЗЕ, 6F], что говорит о невозможности сделан-
ного предположения. Аналогично убеждаемся в невозможности предпо-
ложения, что +2,2 ~ Следовательно, требование п0 + 2 обслуживает-
ся прибором 2 во временном интервале (Е, 5Е] и требования множест-
ва А0 обслуживаются этим прибором в интервалах (0, Ё] и (5Е, 6Е].
198
Предположим, что яри расписании $° обслуживание хотя бы одного
из требований множества jV° прибором 2 начато, но не закончено
в интервале (О, Е]. Тогда во временном интервале (Е, 5Е] имеет место
простой прибора 1, в то время как при расписании s° все приборы функ-
ционируют без простоев. Отсюда следует, что все требования множества 7V0,
обслуживание которых прибором 2 начато в интервале (О, Е], должны
быть полностью обслужены этим прибором в указанном интервале, причем
суммарная длительность обслуживания этих требований должна быть
равна Е. Обозначая через jV? подмножество всех требований множества jV°,
обслуживаемых прибором 2 в интервале (О, Е], и полагая TVj =7V°\7V?,
получаем решение задачи о разбиении.
Тем самым за О(по) операций реализовано сведение задачи о разбиении
к рассматриваемой задаче распознавания.
3.10. В заключение этого параграфа рассмотрим задачу построения оп-
тимального (по быстродействию) расписания s* обслуживания множества
N = {1,2,..., п} в системе, состоящей из М приборов, в предположении,
что в процессе обслуживания каждого требования не допускаются задерж-
ки. Покажем, что эта задача остается NP-трудной при М > 2, даже если
разрешены прерывания процесса обслуживания каждого требования каж-
дым прибором.
Сформулируем соответствующую задачу распознавания-, определить,
существует ли расписание $° (с прерываниями), при котором процесс
обслуживания каждого требования протекает без задержек и fmax(s°)
для заданного числами.
Покажем, что к этой задаче при М = 2 сводится задача о разбиении.
Положим п = и0 + 2, N- {1, 2,. .., п }. Пусть
rfl=0, hi = еь i^NQ\
+1,1 ~ tn0 + 2, i ~
?nQ +1,2 ~ Q +2,2 "" Е-
Покажем, что в построенной задаче расписание $°, при котором
^тах(5°) У ~ 4Е, существует тогда и только тогда, когда имеет реше-
ние задача о разбиении.
Пусть задача о разбиении имеет решение и , N$ — найденные подмно-
жества множества 7V0. Тогда расписание s° существует и может быть построе-
но, например, следующим образом. Оба прибора функционируют в интерва-
ле (0, 4Е] без простоев, процесс обслуживания каждого требования множест-
ва N протекает без прерываний. Прибор 1 обслуживает требования в последо-
вательности (и0 + 1, и0 + 2), а прибор 2 — в последовательности
(Яуо,«о + 2, «о + 1, ТГдго).
Пусть существует расписание 5°. Так как t^N) = t2(/V) = 4Е, то
rmax(s°) - У и при расписании $° оба прибора функционируют без просто-
ев в интервале (0, 4Е]. Поскольку прибор 1 обслуживает только требо-
вания п0 + 1 и nQ + 2 и эти требования не различаются по длительностям
обслуживания, будем считать, что при расписании s° значение + j t = 0
(доказательство в случае, когда + 2, i =0, аналогичное).
199
Так как требование nQ + 1 должно обслуживаться без задержек, то про-
цесс его обслуживания протекает в интервале (О, ЗЕ]. Поскольку при-
бор 1 функционирует без простоев и tn* + 1} х = 2£, то в интервале (0, 3£]
прибор 1 обслуживает требование и0 + 2 в течение ровно Е единиц времени.
Далее, поскольку tn° + 1,2 = ^п0 + 2,2 = требование nQ + 2 может обслу-
живаться прибором 2 в течение Е' ^Е единиц времени в интервале (О, ЗЕ].
Покажем, что Е' = Е. Действительно, в противном случае в интервале
(ЗЕ, 4£] прибор 1 обслуживает только требование и0 + 2 и это же требо-
вание в этом же интервале должно обслуживаться в течение Е - Ег > О
единиц времени прибором 2.
Таким образом, прибор 2 в интервале (О, ЗЕ] обслуживает требования
и0 + 1 и и0 + 2 в течение Е единиц времени каждое. Следовательно, требо-
вания множества № должны обслуживаться прибором 2 в течение Е еди-
ниц времени в интервале (О, ЗЕ] ив течение Е единиц времени в интервале
(ЗЁ, 4Е]. Это означает, что задача о разбиении имеет решение.
Тем самым за O(nQ) операций реализовано сведение задачи о разбиении
к рассматриваемой задаче распознавания.
§ 4. Общее время обслуживания. Упорядоченность
В этом параграфе рассматривается задача построения оптимального
по быстродействию расписания обслуживания требований в системе с не-
фиксированными маршрутами в предположении, что на множестве требо-
ваний задано отношение строгого порядка, регламентирующее (в том
или ином смысле) возможную последовательность их обслуживания.
4.1. Пусть на множестве N = { 1, 2,..., и } требований задано отноше-
ние -> строгого порядка и G - граф редукции этого отношения. Запись
i -> / (’’/предшествует /”),/, / G N, содержательно означает, что обслужи-
вание требования / любым прибором L Е Л = { 1,2,... ,М} не может
быть начато, пока не завершится процесс обслуживания требования i всеми
приборами.
Если G - цепь (т.е. N — линейно упорядоченное множество), то по-
строение оптимального расписания (как с прерываниями, так и без пре-
рываний) не вызывает особых затруднений: первое по порядку требование
должно быть обслужено всеми приборами (в произвольной последова-
тельности) , после завершения его обслуживания должно быть начато обслу-
живание второго по порядку требования и т.д.
Покажем, что если все компоненты связности графа G - одновершин-
ные графы, за исключением одной, являющейся цепью, то задача построе-
ния оптимального расписания (без прерываний) является NP-трудной
в сильном смысле при ЛГ > 2.
Этой задаче соответствует следующая задача распознавания: определить,
существует ли такое расписание s°, при котором общее время обслужи-
вания ^тах(5°)^.У ДЛЯ заданного числа у.
Покажем, что при М = 2 к этой задаче сводится задача о 3-разбиении
(см. вводную часть этой главы).
Положим п = 5п0, N = {1, 2,... , п }. Множество N требований обслу-
живается двумя приборами А и В, длительности обслуживания требова-
200
ния i 6 N приборами А и В обозначим через at и Z>f- соответственно. Положим
а^Ь^е^ iENQ;
= E.bf-Q, i=3n0 + 1, Зл0 +3,... , 5л0 - 1;
af = 0, bi = E, / = Зл0+2, Зи0 + 4,..., 5и0-
Зададим на множестве N отношение полагая, что i непосредственно
предшествует /, z, / G N, тогда и только тогда, когда j = i + 1, i = 3nQ + 1,...
..., SnQ - 1.
Покажем, что в построенной задаче расписание $°, при котором
^тахО°) У = 2.nQE, существует тогда и только тогда, когда имеет реше-
ние задача о 3-разбиении'
Если существует указанное разбиение множества NQ на подмножества
TV?, 1 < j < nQi то искомое расписание $° можно построить, например,
следующим образом. Каждый прибор, начиная с момента времени d = О,
обслуживает требования непрерывно одно за другим; прибор Л обслужи-
вает требования в последовательности (Зл0 + 1, Зи0 + 3, я
2V 1 /V 2
..., Зл0 + 2/ — 1, я., о,, 5и0 — 1, ), а прибор В — в последова-
27 / & па
тельности (я „о, Зи0 + 2, я,г0, Зл0 + 4, . .., я^о, Зи0 + 2/,.. ., я „о , 5л0).
/V 1 2 Ду Д по
Пусть существует расписание s°. Поскольку a(N) = b(N) = у, то
fmax(5°) = У> причем оба прибора во временной интервале (0,у] функцио-
нируют без простоев.
Так как множество JV\№ требований линейно упорядочено, то
^5л0,В>
ио
+2/ -1
ио
+ 2 Ь3п +2/ = 2п0Е = у.
/ = 1
Отсюда следует, что tn^B = 2nQE и tQSn^ в = (2и0 - 1)£. Далее,
_ «о и0 -1
^5и0 - 1,Л ^03ио+2/-1 + ^Зп0 + 2/ = (2^0 — 1)#
и
?5п0 - 1,А ^5и0,В~ (2л?о ~ !)£•
Эти неравенства означают, что t5n^ = (2и0 - 1)£ и _ 1Л =
= (2и0 - 2)£.
Рассуждая аналогичным образом, убеждаемся, что требование
Зл0 + 2/ — 1 обслуживается прибором А во временном интервале
((2/ - 2)£, (2/ - 1)£], 1 < j < п0, а требование Зи0 + 2/ обслуживается
прибором В во временном интервале ((2/ - 1)£, 2jE], 1 < / < nQ. Тре-
бования множества NQ должны обслуживаться прибором А во времен-
ных интервалах (F, 2Е], (ЗЕ, 4£],..., ((2л0 — 1)£, 2п0Е], а прибо-
ром В - во временных интервалах (0, £], (2Е, 3F],.. . , ((2и0 — 2)£,
(2и0 - 1)^] • Поскольку Е/4 < < Е/2, i Е №, и каждый из приборов
А и В функционирует без простоев, то в каждом из указанных интерва-
лов должно обслуживаться ровно три требования множества №, суммар-
201
ная длительность обслуживания которых равна Е. Обозначая через N?
множество требований, обслуживаемых прибором А во временном интер-
вале ((2/ - 2)£, (2/ - 1)£], 1 </ < nQi получаем решение задачи о 3-раз-
биении.
Тем самым за O(nQ) операций реализовано сведение задачи о 3-разбие-
нии к рассматриваемой задаче распознавания.
4.2. Пусть все компоненты связности графа G — одновершинные графы,
за исключением одной, являющейся цепью. Требование i Е N поступает
в систему в момент времени > 0. Покажем, что оптимальное (по быстро-
действию) расписание с прерываниями может быть построено за полино-
миальное число операций.
Пусть Nq С N — непустое множество требований, соответствующих
изолированным вершинам графа G, Множество требований, соответству-
ющих вершинам компоненты—цепи графа G, обозначим через N^. По усло-
вию Nt U Nq = N.
Пусть IJVi | = к. Пронумеруем требования таким образом, чтобы Nx =
= {1,2,... ,ki,N0 = { к+ 1,Л + 2,... ,п}.
Вычислим наиболее ранние моменты начала и завершения обслужива-
ния требований множества Nt. Имеем
Г? =</i, G = ti + S
L <М
t? = max{d/, G-i), t{ = t? + 2 f=2,...,fc.
l ел
Построим последовательность 5i, 52,..., +1 — монотонно воз-
растающую последовательность попарно различных значений tf, tb i ENi,
ndb iENq. Обозначим Ду = 6/ +1 - 5y, 7 = 1,... ,p.
Решим задачу линейного программирования
r->min,
S x{r iEN, j=\,...9p\
L ел
S xL <Af, LE Ji, j=l,...,p;
t eN
yiL<t, i&N0, L&Jl;
p
2 xiL +?iL = 1 e7V0, L E JI ;
/=1
S xt = tiL, iENi, LE Л \
/ = i
Г>0, >0, 7=1,...,p, LEjl, iEN\
yiL>Q, i^Nq, LE JL\
x\L = если +1 ’ z e ;
xiL = 0,*если<//> 5y, iENq, LE Jt .
Пусть ? — найденное наименьшее значение t и xJiL , yiL - значения пере-
менных, при которых t = t,
202
Величину xJiL будем интерпретировать как суммарную длительность
обслуживания требования i G N прибором L G Л во временном интерва-
ле (5/, 6/ + 1]. Аналогично величину yiL будем понимать как суммарную
длительность обслуживания требования i EN0 прибором Z Е Л во времен-
ном интервале (Ьр + 1,Ьр + 1 + t ].
Для построения расписания s* достаточно при помощи одного из алго-
ритмов, приведенных в п.3.2, 3.4 § 3 этой главы, построить оптимальное
(по быстродействию) расписание обслуживания требований множества N
в каждом из интервалов (5у, 5 /-ц ], / = 1,.. ., р, считая длительность
обслуживания требования i Е N прибором L Е Л в интервале (5,-, 5/ + 1]
равной xJiL. Если ? > 0, то следует также построить оптимальное расписа-
ние обслуживания требований множестваNQ в интервале (5р + j, 5р + j + ,
считая длительность обслуживания требования i Е Nq прибором L Е Л в
этом интервале равной yiL.
Поскольку сформулированная задача линейного программирования
может быть решена за полиномиальное число операций, трудоемкость
алгоритмов из п.3.2 или 3.4 также полиномиальна и число решаемых ими
подзадач не превосходит р + 1 < Зп, то задача построения s* в рассматри-
ваемом случае имеет полиномиальную трудоемкость.
4.3. Рассмотрим ситуацию, отличающуюся от описанной в предыдущем
пункте только тем, что М = 2 и все = 0, i EN. Покажем, что оптимальное
по быстродействию расписание (с прерываниями) в этом случае может
быть построено за О(п) операций.
Обслуживающие приборы по-прежнему будем< обозначать через А и В,
а длительности обслуживания требования i Е N этими приборами — через
а,- и соответственно.
Пусть Nq С N — непустое множество требований, соответствующих изо-
лированным вершинам графа G. Компоненту-цепь графа G обозначим
через G\, а множество требований, соответствующих ее вершинам, — че-
рез Ni. По условию Nq U Nt = N.
Положим
Т= max{a(/V),b(N), S (оу+ />.), шах {а/ + fy}}.
j e re No
Очевидно, для любого расписания 5 (с прерываниями) справедливо
соотношение fmax(s) > Т. Построим расписание s*, при котором
^max(s) = Г. Расписание s*, очевидно, будет искомым оптимальным рас-
писанием.
Пусть |7V\ | = к. Пронумеруем требования таким образом, что Nx =
= {1,2, ...,&} и Nq = { £ + 1, £ + 2,..., л }. Требование г будем об-
служивать (без прерываний) прибором А во временном интервале
г — 1 г — 1
( S (aj + fy), S (а; + fy) + ar ] и прибором В во временном интервале
/=1 /=1
г — 1 г
( S (aj + fy) + ar, S (aj + fy) ] , r = 1,..., k.
203
Предположим, что построено расписание sq _ х обслуживания требова-
ний 1, 2,..., 4 - 1, к < q < и, при котором tp = max Ff- < Т.
1 < i < q - 1
Построим расписание обслуживания требования q.
Если Г > tp + aq + bq, то требование q будем обслуживать (без пре-
рываний) прибором А во временно'м интервале (Fp, Тр + aq\, а прибо-
ром В - в интервале (t р +aq, tp+aq+bq].
Если Т < tp + aq + bq,iQ требование q не может быть полностью обслу-
жено в интервале (tp, Г]. Вычислим значение
я _ _
t = min {Г-max { S bj-tp, 0), tp+aq}.
i
Требование a будем обслуживать прибором А в течение aq - t + tp
единиц времени в тех подынтервалах интервала (0, fp], в течение которых
прибор А простаивает, а также в течение t - tp единиц времени (если
t > tp) в интервале (tp, f]. Такое обслуживание возможно, поскольку
суммарная длительность простоя прибора А в интервале (0, равна
_ Я -1 Я
tp - S at и выполняется неравенство 2 a; < t, равносильное нера-
/ = 1 / = 1
я -1
венству aq - t + tp < tp - S я7.
/= i
Требование q будем обслуживать прибором В в течение max{/>g - Г+1, 0}
единиц времени в тех подынтервалах интервала (0, tp}, в течение кото-
рых прибор В простаивает, а также в течение Т - t единиц времени (если
t < Т) в интервале (t, Г]. Такое обслуживание возможно, поскольку
суммарная длительность простоя прибора В в интервале (0, tp\ равна
_ Я -1 Я _
tp - S bj и выполняется неравенство S bj < tp + Т - t, равно-
/ = 1 i = i
я -1
сильное неравеьству bq - Т + t < tp - S bj.
/= i
Выполняя описанные построения для каждого требования q, q =
= к + 1,..., п. придем к расписанию 5* = , при котором ^max(s*) = Т.
Таблица 4.1
i 1 2 3 4 5
ai bi 3 3 2 14 2 13 6
204
Можно показать, что при использовании специальной структуры данных
(стека) для хранения интервалов простоя каждого прибора расписание $*
будет построено за О(п) операций.
4.4. Пример. Две ремонтно-строительные бригады А и В разного
профиля должны произвести ремонт пяти объектов; продолжительность
ремонта объекта i бригадами А и В обозначим через at и fy соответственно.
Значения а{ и fy приведены в табл. 4.1.
7 2 3
•----->•-----э*
4 5
• •
Рис. 4.1
Порядок, в котором бригады ведут работы на данном объекте, не имеет
значения. На каждом объекте должна работать вся бригада, т.е. одновремен-
ная работа одной и той же бригады на различных объектах не допускается.
Две бригады не могут одновременно работать на одном и том же объекте.
Работы, проводимые бригадой на любом объекте, могут быть прерваны,
а затем возобновлены.
Первые три объекта находятся на различных этажах одного и того же
здания. Ремонтные работы на каждом из этих объектов, кроме первого,
могут начаться лишь после того, как будет полностью отремонтирован
предыдущий объект. Другими словами, на множестве объектов задано
отношение строгого порядка, граф редукции которого изображен
на рис 4.1.
Требуется построить такое расписание выполнения ремонтных ра-
бот, при котором все объекты были бы отремонтированы как можно
раньше.
Воспользуемся алгоритмом из п. 4.3. В данном случае = { 1, 2, 3},
7V0 = {4,5},Г=шах{12,15, 13, 10} =15.
Расписание ремонта объектов множества изображено на рис. 4.2, а.
Построим расписание выполнения ремонта объекта 4. Поскольку tp =
= t3 = 13, то tz + + b4 > Т. Вычислим t = min{15 — max{9-13,0},13 + 1}
Расписание ремонта объектов {1, 2, 3, 4} представлено на рис. 4.2, б.
Искомое расписание ремонта всех пяти объектов изображено на
рис. 4.2, в.
4.5. Пусть каждая компонента связности графа G является цепью. По-
кажем, что в этом случае задача построения оптимального по быстродейст-
вию расписания (с прерываниями) является NP-трудной в сильном смысле
приМ > 2.
Этой задаче соответствует следующая задача распознавания: опреде-
лить, существует ли такое расписание 5° обслуживания требований мно-
жества JV, что rmex ($°) для заданного числа у. Покажем, что к послед-
ней задаче в случае М = 2 сводится задача о 3-разбиении.
Пусть п = 7и0 и N = {1,2,. . . , и0}• Каждое требованиеi Е Nобслужи-
вается двумя приборами А и В, длительности обслуживания равны at и
205
л
бригада В
бригада А
1 2 3
0 2 5 8 10 1213
а
бригада В
бригадаА
0 2 б 8 10 12131413
Ъ{ соответственно. Положим
aj ~ bj = Е, / = 1,.. ., п0,
ап0+к — ^л0 + к “ ек> к — !>•••> Зи0,
л4и0+к ~~ ^к’ Ь$п0 + к ~ “ !>•••> ЗЛо.
На множестве N зададим отношение строгого порядка, полагая, что
it непосредственно предшествует i2 i2 £ Ю тогда и только тогда,
когда ii = ]\ i2 = j + 1, j = 1,. . . , n0 - 1, либо Ц = n0 + к, h = 4и0 + Л,
к = 1,... , Зи0.
Покажем, что в построенной задаче расписание 5°, при котором
^max(s°) = 2nQE, существует тогда и только тогда, когда имеет реше-
ние задача о 3-разбиении.
Пусть задача о 3-разбиении имеет решение и N® = {a/i, &j2) «/3}, / =
= 1, . . . , nQi — найденные трехэлементные подмножества. Тогда искомое
расписание s° можно построить следующим образом. Каждый прибор
начиная с момента времени d = 0 обслуживает требования множества
N непрерывно одно за другим, причем прибор А обслуживает требования
в последовательности 1, 4и0 + «и, 4и0 + «12, 4и0 + «13, 2, 4и0 + й2ь
4и0 + «22, 4и0 +<*2 3,3,.. . , По, 4ло + «По 1, 4и0 + «и02, 4и0 + «и0 з, а
прибор В — в последовательности и0 + «11, Ио + «12, Ио + а i з, 1, Ио + <*2 i,
По + «22, По +«23,2, . . . ,И0 - 1,Ио +«и0 1, "о + <*n0 2, "о +% 3,^0-
Пусть расписание s° существует. Покажем, что задача о 3-разбиении
имеет решение.
206
Так как a(N) = b(N) = у, то ^max(s°) =У и при расписании 5° оба
прибора в интервале (0, у] функционируют без простоев. Кроме того,
«о
поскольку S (я/+ £/) = >\ то при расписании sQ для каждого требова-
ния /, 1 < j < и0, справедливы*соотношения = 2(j — 1)£ и tf -2jE.
Рассмотрим временной интервал (О, 2Е), в котором оба прибора обслу-
живают требование 1. Кроме того, в этом интервале прибор В в течение
Е единиц времени обслуживает требования вида и0 + к, 1 < к < Зи0, а
прибор А также в течение Е единиц времени обслуживает те требования
вида 4 и0 + к, 1 < к < Зи0, которым предшествуют (относительно задан-
ного на Nпорядка) требования, уже обслуженные прибором В,
Прибор В в интервале (О, 2Е) не может полностью обслужить более
трех требований вида и0 + к, так как ек > Е/4, к 1,. . . , 3 и0. Если сум-
марная длительность обслуживания прибором В тех требований, которые
полностью обслужены в интервале (О, 2Е\ этим прибором, меньше Е, то
в интервале (О, 2Е) прибор А будет простаивать, что невозможно. Отсюда
следует, что при расписании $° не существует требований, обслуживание
которых прибором В начато, но не закончено в интервале (О, 2Е).
Рассуждая аналогичным образом, нетрудно показать, что в каждом
временном интервале (2(/ - 1)£, 2jE\, 1 </<и0, каждый прибор Л и
В обслуживает кроме требования / еще три требования, суммарная дли-
тельность обслуживания которых равна Е. Это означает, что задача о 3-раз-
биении имеет решение.
Тем самым за O(nQ) операций реализовано сведение задачи о 3-разбие-
нии к рассматриваемой задаче распознавания.
4.6. Пусть на множестве N = {1,2,... , и } требований задано отноше-
ние строгого порядка и G — граф редукции этого отношения. В отличие
от предыдущих пунктов здесь и далее в этом параграфе запись i -> /
(’7 предшествует /”) будем интерпретировать следующим образом: об-
служивание требования / любым прибором L - {1,2,... , 7И} не
может быть начато, пока не завершится процесс обслуживания требова-
ния i этим прибором.
Если G - цепь, то задача построения оптимального расписания (как
с прерываниями, так и без прерываний) эквивалентна задаче построения
оптимального расписания обслуживания неупорядоченного множества тре-
бований в системе поточного типа. Чтобы убедиться в этом, достаточно
поменять ролями приборы и требования. Последняя задача рассматрива-
лась в § 1 гл. 2, откуда, в частности, следует, что исходная задача при
М = 2 может быть решена за O(wlogn) операций (если не допускаются
прерывания) и за О (п2 ) операций (если прерывания допускаются).
Покажем, что если все компоненты связности графа G - одновершин-
ные графы, за исключением одной, являющейся цепью, то задача построе-
ния оптимального расписания (без прерываний) является NP-трудной
в сильном смысле при М> 2.
Этой задаче соответствует следующая задача распознавания ', определить,
существует ли такое расписание s° обслуживания требований множества
N, что fmax(s°) Для заданного числа у. Покажем, что к последней
задаче в случаеМ = 2 сводится задача о 3-разбиении.
207
Положим п = 7nQ + 1 и N = {1,2,.. . ,п}. Обслуживающие приборы
обозначим через А и В, а длительность обслуживания требования i G N
этими приборами - через а* и bt соответственно. Пусть
С= [£/2],
Л/ = bi = eit i € Nq;
a3n0 + i = &зл0 + 1 ” E - C\
a3n9 + j = E - C, b3no+i = Eno +C, i = 4k - 2, к = 1,.. . ,zz0;
Лзл0 +1 + 1 = ^зл0 + i + i - E — C, i = 4k — 2, к = 1,..., и0;
*зи0 + i + 2 = Eno + E — C, b3n^ + {+ 2 - Cf i — 4k — 2, к — 1,...,Mq,
Лзи0 + i + з = С ^зл0 + i + з = En§ + E — C, i - 4k — 2, к - 1,...,n— 1;
ain 0 + i = Et bqn^ + i = Eno + E — C.
Зададим на множестве N отношение -+, полагая, что z непосредственно
предшествует / тогда и только тогда, когда j = i +1, i = Зи0 + 1, • • •, 7п0.
Покажем, что в построенной задаче расписание 5°, при котором
^max(s°) = (2ио + Зл0 + - С, существует тогда и только тогда,
когда имеет решение задача о 3-разбиении.
Пусть задача о 3-разбиении имеет решение и , 1 < / < и0, - найден-
ные трехэлементные подмножества. Тогда расписание 5° может быть по-
строено следующим образом (рис. 43). Каждый из приборов А и В обслу-
живает требование непрерывно одно за другим начиная с момента времени
d = 0. Прибор А обслуживает требование множества 7V\7V° в порядке воз-
растания их номеров; между требованиями с номерами Зл0 + 4(/ - 1) + 3
и Зи0 + 4/ обслуживаются требования множества Л^°, 1 </ <и0- Прибор В
обслуживает требования множества 7V\7V° в порядке возрастания их
номеров; между требованиями с номерами Зи0 + 4/ + 1 и Зи0 + 4/ + 2
ЗП(?13п0+2 Зп0+4 Зп0+б N? Зп0+6 Зп0+8 Зп0+9 N° 7п0~2 7п0~1 7п0+1 N„Q
приборВ Н-------ИЙ--------->—I-------ЬЙ---------1—I • • • J—I--------ЙН---------1—I
Зп^З Зп^7 7Hq
Зп0+2 3n0+3 N° Зп0+4 Зп0+б Зп0+7 Зп0+8 3nQ+W 7п0-2 7п0~1 7п0 7п0+1
приборА Ч-------1—I--------НЧ--------1—I--------h-Й ••• НЧ-----------1—I--------Ы
Зп^5 Зп^рд 2Пд 3
Рис. 4.3
обслуживаются требования множества N?, 1 < j < nQ - 1; требования
множества обслуживаются вслед за требованием 7и0 + 1. Требования
каждого из множеств N? могут обслуживаться каждым прибором в произ-
вольной последовательности.
Пусть существует расписание s°. Поскольку a(N) = b(N) = у, то
^шах(5°) = У и при расписании s° оба прибора функционируют без
простоев.
208
Обозначим через NАВ множество требований из TV\TV°, которые при
расписании s° обслуживаются сначала прибором Л, затем прибором В.
В аналогичном смысле будем употреблять обозначение NB А.
Если предположить, что требование 7и0 + 1 принадлежит NABi то полу-
чим расписание, для которого общее время обслуживания оказывается
не меньше чем
7и0+ 1
s ai + b7„ + ! = у + Е- С.
i = Зи0 + 2 °
Следовательно, требование 7и0 + 1 принадлежит NBA. Требование
7л0 также принадлежит NBA, поскольку в противном случае общее вре-
мя обслуживания ограничено снизу числом
7и0+ 1
S Cli + bqn + ЬПп + х > у,
i= 3n0 + 2 0 0
С другой стороны, требования 7и0 — 1 и 7и0 - 2 должны принадлежать
множеству Nab. Действительно, если 7и0 — 1 G NBA, то общее время
обслуживания оказывается не меньше чем
7и0- 1 7n0+ 1
S bj + S = у + Е.
3nQ + 1 I = 7л0 - 1
Если же 7и0 — 2 G NBA, то общее время обслуживания оказывается
не меньше чем
7л0 — 2 7n0 + 1
X bj + S at = у + Е.
i = 3n0 + 1 i = 7и0 — 2
Рассуждая аналогичным образом, нетрудно убедиться, что NAB =
= {Зи0 + L Зи0 + 4(/ - 1) + 2, Зи0 + 4(/ - 1) + 3 |/ = 1, . . . , nQ}, а
NBA = (Зи0 + 4/, Зи0 + 4/ + 1 | / = 1,. . . , и0}. При этом требования мно-
жества /V0 должны обслуживаться прибором А во временных интервалах
(£(и0 + 1) + E{j - 1) (2и0 + 3), £(и0/ + 2) + E(J - 1)(2и0 + 3)],
< j < и0, а прибором В - во временных интервалах (£/(2n0 + 3) — С,
Ej(2nQ +3) + Е - С], 1 </ < и0. Поскольку оба прибора функционируют
без простоев, длина каждого интервала равна Е и выполняются неравенст-
ва £/4 < е{ < Е/2, i G TV0, то в каждом из указанных интервалов должно
обслуживаться ровно три требования множества TV0, суммарная длитель-
ность обслуживания которых равна Е. Обозначая через множество
требований, обслуживаемых прибором А во временном интервале
(E(nQ + 1) +£(/- 1) (2и0 +3),Е(и0 + 2) + E(j - 1) (2и0 + 3)], 1 </ <
< п0, получаем решение задачи о 3-разбиении.
Тем самым за O(nQ) операций реализовано сведение задачи о 3-разбие-
нии к рассматриваемой задаче распознавания.
4.7. Пусть каждая компонента связности графа G является либо цепью,
либо одновершинным графом. Покажем, что при М - 2 оптимальное рас-
писание s* (с прерываниями) может быть построено не более чем за О(п2)
операций.
Обслуживающие приборы по-прежнему будем обозначать через А и В,
а длительности обслуживания требования i G TV этими приборами через
а,- и bi соответственно.
14. В.С. Танаев ^0?
Компоненту-цепь графа G обозначим через Gb а множество требований,
соответствующих ее вершинам, — через Nh I = 1,. . . 9ptp> 1. ПустьNo -
множество (возможно, пустое) требований, соответствующих изолиро-
ванным вершинам графа G. _
Каждому множеству Nt, 1 <7 сопоставим новое требование I (от-
личное от требований множества JV), полагая cty = a(Nt) и by = b(N{).
При помощи алгоритма из п. 1.2 § 1 этой главы построим расписание
обслуживания (без прерываний) множества {1, 2, . . . , р } U No неза-
висимых требований. Если при этом
/max(si) - max{a(7V), b(N)9 max{af- + bt | i €У0Н,
то расписание 5i может быть преобразовано в расписание 5 ♦ путем замены
каждого из требований I на линейно упорядоченное подмножество требо-
ваний Nj9 обслуживаемых соответствующим прибором непрерывно одно
за другим. При этом, очевидно, rmex(s*) = ^max(si)-
Если 7max (st) = а- + b- = max{a- + by 11 = 1,. . . ,р}, то при помощи
алгоритма из § 1 гл. 2 построим расписание (с прерываниями) обслужива-
ния линейно упорядоченного подмножества требований^. Обозначим это
расписание через s2.
Пусть wA и юв означают суммарную длительность простоя прибора А и
прибора В во временной интервале (0, ^тахС^з)] ПРИ расписании s2.
Заметим, что в указанном интервале оба прибора одновременно не простаи-
вают. Очевидно, TmiX(s2) = а- + wA = b- + wg.
Введем в рассмотрение новое (отличное от ранее рассмотренных) требо-
вание z, полагая az = a(N\Nq) ,bz = b(N\Nq).
Поскольку ^max(5i)> max{a(7V), 5(7V)}, to az < b— и bz < a-.
Если az <vv4 и то требованиеz будем обслуживать (с прерыва-
ниями) в интервалах простоя прибора А и прибора В в течение az и bz
единиц времени соответственно. Полученное при этом расписание обозна-
чим s3.
Пусть не выполняется хотя бы одно из неравенств az < и bz < .
Предположим, что a(N) > b(N) (в противном случае можно провести
аналогичные рассуждения). Отсюда следует, что az > wA.
Требование z будем обслуживать (с прерываниями) прибором А в те-
чение az единиц времени в интервале (0, tf(/V)] и прибором В в течение
min{5z, wB} единиц времени в интервале (0, fmax(s2)]- Обслуживание
будем проводить только в тех подынтервалах указанных интервалов, в
которых соответствующий прибор не обслуживает требований из множест-
ва^.
Если при этом > bz, то получаем расписание 5 3 обслуживания тре-
бований множества Nq U { z }. _
Если wB < bz, то в интервале (^тах (Ъ),Л0О] длины az — wA при-
бор В простаивает. Так как wA = b— + wB - а- и a(N) > b(N), то
аг - wA > bz - wB.
Пусть 5i, 62, . . . , Ь2г — возрастающая последовательность моментов
времени такая, что при расписании s2 в каждом интервале (62/ - i, ^2/],
210
1 < j < г, оба прибора функционируют одновременно, причем
S (62/ - - а- -
/ = 1 4
Поскольку bz найдутся такой интервал (62к-1» &2к\, 1
и такой момент времени £ (&2к-1, ^2к\ , 410
52Л. - tQ + S (62/ - 62/_ j) = bz - wB.
/= i
Все требования, обслуживаемые прибором В при расписании s2 в интер-
валах (7°, 62fc], (b2k+ 1, 62А- + 2], ’ • • , (§2г -1» &2г], будем обслуживать
этим прибором в той же последовательности в интервале (Гтах($2),
fmax(s2) + bz - wB]. При этом не исключено, что обслуживание одного
из требований множества Nq прервется в момент времени Г° и возобно-
вится в момент времени Гтах ($2) •
В интервалах (70, Ь2к\9 (62к+1, &2к+2], • • • , (52г-ь §2г] будем
обслуживать прибором В требование z. Полученное расписание обслужи-
вания требований множества Nq U {z} обозначим через $3.
Таким образом, в любом случае будет построено расписание $3 обслужи-
вания требований множества Nq U {z}. Это расписание может быть пре-
образовано в расписание 5* путем замены требования z на требования
множеств TV/, I = 0.....р, q, с сохранением линейного порядка на
указанных множествах (если I > 0) .
Очевидно,
Gnax(s*) ~ ^тах(5з) = ГПах{ ^тах(52)>
и расписание 5 * является оптимальным.
Наиболее трудоемкой процедурой описанного алгоритма является
построение расписания s2, требующее 0(1 Nq Р) операций. Тем самым,
расписание s* может быть построено в результате выполнения не более
чем О(п2) операций.
4.8. Пример. Несколько изменим условия примера из п.4.4. Число
ремонтируемых объектов увеличим до восьми. Величины а, и fy приведе-
ны в табл. 4.2.
Каждая бригада может ремонтировать объект 6 только после того,
как она отремонтировала объект 5. Аналогично каждая бригада может
ремонтировать объекты 2, 3 и 4 только после того, как она отремонти-
ровала объект с меньшим номером. Другими словами, на множестве
Таблица 4.2
i 1 2 3 4 5 6 7 8
Qi 2 3 5 4 2 2 2 1
fy 1 3 2 2 5 4 1 3
14
211
объектов задано отношение строгого порядка (в смысле п. 4.6), граф
редукции которого изображен на рис. 4.4,
Требуется таким образом организовать ремонт объектов, чтобы все
они были отремонтированы как можно раньше.
Воспользуемся алгоритмом из п.7. В данном случае NQ = {7, 8}, =
= {1,2,3,41, jV2 = {5, 6}.
12 3 4
•----X------X-----х
5 6 7 6
•-----• •
Рис. 4.4
Введем в рассмотрение два новых ’’объекта” 1 и 2, для которых по-
ложим a- =a(Ni)= 14, b- = b(Nx) = 8, a- = a(N2) = 4, b- = b(N2) = 9.
Так как выполняется соотношение а у + Ь- = 22 = max{fl(7V), 6(jV),
max{az + bt | i G jV0}, max{az + bt 11 = 1, 2 11, то построим по алгорит-
му n. 1.3 - 1.6 § 1 гл. 2 расписание s2 ремонта объектов 1, 2, 3 и 4
(рис. 4.5,а). _
Получим fmax(s2)= 16 < max{fl(2V), b(N)} =21.
5 1
бригадаВ
6 3 6 7 8 2 4
г
бригадаА
2
3 । 5 । з ।
! 6 । 7 в
4
0 2 3 5 6 8 1О 1213 16 18 2021
t
Рис. 4.5
212
Введем новый ’’объект” z, для которого положим az = a(TV\TVj) = 7,
bz^b(N\Nx) = \3.
При расписании s2 в интервале (0, 16] имеем wA = 2 и wB = 8, т.е.
az > wa- ’’Объект” z должен ремонтироваться бригадой А в интервале
(О, 21] так, как изображено на рис. 4.5, б. На этом же рисунке изображе-
но, как ’’объект” z мог бы ремонтироваться бригадой В в течение
min { bz, = 8 единиц времени.
Бригада В должна ремонтировать ’’объект” z еще в течение пяти еди-
ниц времени.
Выберем интервалы (5,8] и (10, 12]; их суммарная длина равна 5, и
при расписании s2 (см. рис. 4.5, а) в этих интервалах обе бригады ремон-
тируют объекты множества . Объекты, ранее ремонтируемые бригадой
В в выбранных интервалах, будут теперь ремонтироваться этой бригадой
в интервале (16, 21], а в освободившихся интервалах бригада В будет
ремонтировать ’’объект” z. Расписание ремонта объектов 1, 2, 3 и 3, а
также ’’объекта” z изображено на рис. 4,5, в.
Чтобы получить искомое расписание, достаточно в построенном распи-
сании заменить ’’объект” z на объекты 5, 6, 7 и 8 (в указанной после-
довательности). Полученное в результате расписание s* изображено на
рис. 4.5, г.
§ 5. Директивные сроки
Рассмотрим систему с М последовательными приборами и нефиксиро-
ванным порядком их прохождения, на вход которой в момент времени
di > 0 поступает требование i Е N = { 1, 2, ..., п}. Для каждого требова-
ния i задан директивный срок Di, к которому необходимо или, во всяком
случае, желательно завершить обслуживание этого требования. В этом пара-
графе описываются эффективные методы построения расписаний, при кото-
рых все требования обслуживаются в заданные директивные сроки
(если такие расписания существуют), а также расписаний с минимаксным
временным смещением. Предполагается, что в процессе обслуживания тре-
бований допускаются прерывания. Если прерывания запрещены, то задача
минимизации максимального временного смещения оказывается NP-труд-
ной в сильном смысле при М > 2, dt = 0, i G N, Показано также, что
задача построения расписания, минимизирующего число запаздывающих
требований, NP-трудна при ТИ > 2, d{ = 0, Di = D, i G TV, независимо от
того, допускаются прерывания или нет.
5.1. Пусть требование i G N поступает в очередь на обслуживание
в момент времени > 0, длительность его обслуживания прибором
L G Л = { 1, 2, ..., М} равна tiL > 0, директивный срок — Z); > 0.
Порядок прохождения приборов каждым требованием не фиксирован,
допускаются прерывания в процессе обслуживания.
Опишем один из возможных подходов, который позволяет построить
расписание 5°, при котором все требования обслуживаются в заданные ди-
рективные сроки (т.е. ti(sQ) <D{), либо убедиться в невозможности
построения такого расписания.
Пусть Ьк, 1<&<р+1<2и,- упорядоченная по возрастанию последо-
вательность попарно различных значений dt и Di, i G N. Временные интер-
213
валы (5i, 52], (52, 53], (5р, 5р+1] пронумеруем числами от 1 до р и
положим Дк =^ + 1 - 5*, 1<£<р.
Рассмотрим систему линейных соотношений
V 2 xiL L (ЕМ <дк, к = i€N-, (5.1)
v к 2 xiL ' iEN к = 1,...,р, L &Л; (5.2)
£ * 2 xiL = к = 1 = 4L, itN, L &Л. (5.3)
к Здесь xtL означает суммарную длительность обслуживания требования
i G N прибором L во временном интервале (5fc, 5jt + i ] • Величины
неотрицательные, если сЦ < 5^ и Л/ > 5jt + i, и равны нулю в противном
случае.
При указанной интерпретации величин соотношения (5.1) и (5.2)
соответственно означают, что суммарная длительность обслуживания требо-
вания i в N всеми приборами в интервале (5fc, 5fc + 1] и суммарная дли-
тельность функционирования прибора L GМъ этом интервале не превосхо-
дят длины интервала Д^. Соотношение (5.3) означает, что все требования
будут полност!Ю обслужены.
Очевидно, если система (5.1) —(5.3) несовместна, то расписания s° не
существует. Если же система совместна и xiL, i G N, L G<^, к = 1,..., p, -
ее решение, тс расписание 5° существует и может быть построено, напри-
мер, следующем образом.
Для каждого к, 1 < к < р, используя один из методов, описанных
в п. 3.2 или п.3.4 § 3 этой главы, построим оптимальное по быстродейст-
вию расписание обслуживания (с прерываниями) множества N требований
множеством приборов во временном интервале (5к, + 1 ], считая вели-
~~к
чины xiL длительностями обслуживания требования i G N прибором
L G М в указанном интервале.
Поскольку*р < 2 п и алгоритмы из § 3 этой главы имеют полиномиаль-
ную (относительно п и М) трудоемкость, а решение системы (5.1) —(5.3)
также может быть найдено за полиномиальное число операций, то в резуль-
тате выполнения полиномиального числа операций можно построить
расписание s° при котором все требования обслуживаются в заданные ди-
рективные срски, либо убедиться в невозможности его построения.
5.2. Рассмотрим некоторые частные случаи.
1) Пусть = 0, Df = D, i. G N. В этом случае можно воспользоваться
одним из описанных в § 3 этой главы методов построения оптимального
по быстродействию расписания s* обслуживания (с прерываниями) требо-
ваний множества N. Расписание s* является искомым, если fmax(5*)
214
В противном случае не существует расписания, при котором все требования
обслуживаются в заданные директивные сроки.
2) Пусть dt =0, iEN1 С N; dj = d, i G N” =N\TV'; Dt = D, i G N;
0 < d < D. Построим сеть G, множество вершин которой состоит из мно-
жества V={vt | i ElN9} вершин, соответствующих требованиям множест-
ва N9, множества W ={wL | L G JZ) вершин, соответствующих приборам,
а также содержит источник и сток. Источник соединен дугой с каждой вер-
шиной Vf G И, величина допустимого потока по этой дуге ограничена снизу
величиной max (ОИ) — d, 0} и сверху - величиной D — d}.
Каждая вершина G W соединена дугой со стоком, величина допустимо-
го потока по этой дуге ограничена снизу величиной max{rL (N9) - d, 0} и
сверху — величиной min{rL(7VF), D — d — tL{N99)}. Каждая вершина
Vf, i G N9, соединена с каждой вершиной wLf L GM, дугой пропускной
способности tiL .
Покажем, что расписание $° существует тогда и только тогда, когда
в сети G существует допустимый поток.
Пусть допустимый поток существует и fiL — значение потока по дуге
(иь wL), i LEM.
Для требования i G N99 суммарные длительности его обслуживания
прибором L во временных интервалах (df D] и (0, J] соответственно рав-
ны tiL и 0. Величины fiL и tiL — fiL будем интерпретировать как сум-
марные длительности обслуживания требования i G N9 прибором L в ин-
тервалах (d, D] и (0, d} соответственно. Тогда величина потока по дуге
из источника в любую вершину vif i G N9, означает суммарную длитель-
ность обслуживания требования i всеми приборами во временном интерва-
ле (d, Z)]. Из допустимости потока следует, что каждое требование i ^.N9
обслуживается всеми приборами в интервале (d, D] не более D — d единиц
времени и в интервале (0, d] — не более d единиц времени. С другой сторо-
ны, величину потока по дуге из вершины , L E.JH, в сток можно интер-
претировать как суммарное время обслуживания требований множества
N9 прибором L во временном интервале (J, D]. Из допустимости потока
следует, что каждый прибор L во временном интервале (0, J] обслуживает
требования множества N9 не более d единиц времени, а во временном
интервале (d, /Э] - требования множества N не более D — d единиц
времени.
Таким образом, если в сети G существует допустимый поток, то могут
быть найдены суммарные длительности обслуживания каждого требования
каждым прибором в каждом из временных интервалов (0, cZ] и (d, D] и
для построения расписания $° с fmax(5°) можно использовать подход,
описанный в предыдущем пункте.
Нетрудно убедиться, что если в сети G допустимого потока нет, то распи-
сание $° не может быть построено.
Отметим, что для построения допустимого потока в сети G требуется
выполнить не более О(п3 + М3) операций.
215
3) Пусть d/ = 0, i&N- Di = Dr, iEN'c N; D^D", i&N" = N \ N',
0 <£>*< D". Полагая D = D' и d = D* — D", приходим к ситуации, рас-
смотренной в п. 2).
5.3. Перейдем к рассмотрению задачи построения расписания s*, которо-
му соответствует наименьшее значение максимального временного смеще-
ния Lmax(s) =max{rf(s) - Dt | i G N}.
Нетрудно убедиться, что величина Lmax(s*) равна наименьшему значе-
нию X* параметра X такого, что каждое требование i Е N может быть об-
служено не позднее момента времени Dt + X. Обозначим множество таких
расписаний через 5(Х). Для нахождения X* воспользуемся методом
дихотомии.
Положим X = — max{Z>r- - - dt | i G N} и X = max{Z>z | i GN} +
+ max{max rz(^), max tL (TV)}; Д = X + X. Очевидно, 5(X) = ф и
if= N LEM
5(X)#=0.
Вычислим X = ( X + X )/2. Используя подход, описанный в п. 5.1, прове-
ряем выполнимость условия 5(Х) Ф ф. Если 5(Х) = ф, то полагаем
X = X, в противном случае полагаем X = X, и переходим к следующей итера-
ции. Процесс продолжается до тех пор, пока не выполнится равенство
X = X. Это значение X и является искомым X*.
На каждой из О (log Д) итераций алгоритма нахождения X* требуется
проверять выполнимость условия S ( X) Ф ф. Так как алгоритм из п. 5.1
имеет полиномиальную трудоемкость, то нахождение значения X* и по-
строение соответствующего расписания потребует выполнения не более чем
полиномиального числа операций.
5.4. В некоторых частных случаях объем вычислений, необходимых для
нахождения значения X* и построения соответствующего расписания s*,
может быть существенно уменьшен. Рассмотрим, например, задачу миними-
зации максимального временного смещения Lm2LX(s) при М = 2 и
dt = 0, / Е N.
Пусть в момент времени d = 0 в систему, состоящую из двух приборов
А и В, поступает множество /V = { 1, 2, ..., п} требований, а{ и Ь{ — дли-
тельности обслуживания требования i Е N приборами А и В соответствен-
но. Заданы директивные сроки D{ > 0, требования пронумерованы таким
образом,что Dy <D2 <...<Dn.
1) Установим необходимые и достаточные условия существования распи-
сания, при котором все требования обслуживаются в заданные директив-
ные сроки.
Пусть Nj ={1,2,...,/}, 1 </ < и; 7V0 = Ф,
a(N,) = S ait b(Nj) = S b{, a(N0) = b(N0) = 0.
i G Nj i G Nj
216
Выберем некоторое требование j G N и предположим, что существует
расписание обслуживания требований множества 7V/-1, при котором для
всех требований этого множества не нарушаются директивные сроки.
Рассмотрим временной интервал (0, Dj ]. Суммарную длину всех его
подынтервалов, в течение которых простаивает только прибор А, только
прибор В или оба прибора А и В, обозначим соответственно через
Ху , У j И Zj .
Поскольку обслуживание каждого требования множества 7V/-1 завер-
шается не позднее соответствующего директивного срока, то имеют место
соотношения
xi + zi = Di ~
у,- + г, = Dj - (5'4)
Для того чтобы обслуживание требования / завершилось не позднее ди-
рективного срока Dj , необходимо и достаточно, чтобы выполнялась систе-
ма неравенств
Ху + Zj > dj,
У] + zi > bh (5-5)
xi + У/ + zi > ai + bi-
Подставляя (5.4) в (5.5), получаем равносильную систему неравенств
а(Л» < Dj,
b{Nj) < Dj, (5.6)
a(Nj) + b(Nj) < 2 Dj - Zj.
Вычислим наименьшие возможные (в смысле существования расписания
без запаздывающих требований) значения Zy, / G N. При / = 1, очевидно,
Zi = Z>i. При / = q, q > 1, значение zq будет не меньше чем Dq — Dq_i.
Кроме того, длительность одновременного простоя обоих приборов в ин-
тервале (0, в худшем случае* будет равна maxfz^»! - aq-i -
— 0}. Следовательно, получаем рекуррентное соотношение
Zi =£>ь Zy=£)y- £>у_! + max {0, Zy_i -ау_! . (5.7)
Таким образом, для существования расписания, при котором все требо-
вания обслуживаются в заданные директивные сроки, необходимо и доста-
точно, чтобы система неравенств (5.6) была совместна для каждого j,
1 </ < п, и значений Zj , вычисленных по формулам (5.7). Проверку вы-
полнимости этого условия можно осуществить за О(п) операций.
2) Как уже отмечалось в п. 5.3, минимальное значение £max(s) равно
минимальному значению X* параметра X такого, что каждое требование
i6 N может быть обслужено не позже директивного срока /Э, + X.
217
В рассматриваемом случае может быть предложен специальный метод
нахождения величины X* (отличный от метода дихотомии).
Нетрудно получить соответствующее рекуррентное соотношение для Zj,
подставив в (5.7) Dj + X вместо Dj. Для дальнейших рассуждений удобно,
однако, чтобы параметр X не фигурировал в рекуррентном соотношении.
Покажем, что
Zj = max{ Dj + X - a(Nj_l) - z\}, 1 </ < n, (5.8)
где
z{ = — oo z’j^Dj - Dj_ t + max{ 0, z'j-i - af_ i - bj_x} , j = 2,n.
(5.9)
Воспользуемся методом математической индукции. При j = 1 соотноше-
ние (5.8), очевидно, выполняется. Пусть (5.8) справедливо при всех /,
меньших некоторого q Е N. Из (5.7) следует, что
zq=Dq - Dq-i + max{0,zQ_1 - aq_x - bq_x} .
Заменяя в этом соотношении zq_ t согласно (5.8), получаем
zq = Dq - Dq_i + max {0, max{(Z><?_1 + X)-
- a{Nq-2> - b(Nq_2Y zq-\} -aq_1 -Z)g_1} =
= Dq -Dq-i + maxfo,^.! + X -^(Mz-i) - £(М?-1),
Zq — 1 ~ aq-\ ~ bq_i} .
Из (5.9) при / = q следует, что zq = Dq - Dq_x + max {Dq_x + X -
- a(7VQ-i) - b^Nq-i), Zq - (Dq -Dq-i)} , откуда непосредственно
следует соотношение (5.8) при / =q.
Подставляя в (5.6) Dj + X вместо Dj и учитывая (5.8), получаем систе-
му неравенств
a(Nj) < Dj + X,
b(Nj) < Dj + X, (5.10)
aj + bj C Dj + X,
a(Nj) + b(Nj) < 2(Dj + X) - z).
Наименьшее значение параметра X, при котором система (5.10) совмест-
на для каждого / Е 2V, равно
a(Nj\ b(Nj), af + | (a(Nf) + b(Nj)+z
(5.И)
Значение X* может быть найдено за О(п) операций путем вычисления
значений z),/ Е TV, и последующего использования формулы (5.11).
3) Опишем способ построения расписания, минимизирующего величи-
ну Z/max(5)> или, что то же> расписания, при котором директивные сроки
Di -Di + X* не нарушаются ни для одного требования.
218
;•)} -л,}
X* = max J max
/е n I
Рассмотрим интервал (0, £>*]. Поскольку at + </)*, положим t\B =
= О, -bt = Тогда в интервале (0, Z>2] перед обслуживанием
требования j = 2 оба прибора одновременно простаивают в подынтервале
(£>2 ~ z2 > D2] и только в этом подынтервале. Кроме того, имеется подын-
тервал (Z>2 - и2 - y2i D2 — 22], в котором простаивает только прибор В.
Пусть построено расписание обслуживания требований множества Nj_!,
7 > 1, при котором ни одно из требований i не запаздывает относительно
директивного срока /)*, i Е TV7- Это расписание построено таким обра-
зом, что в интервале (О, DJ] оба прибора простаивают одновременно
только в подынтервале (Dj* — Zj,DJ},Dj -Zj <Z>7- и один из подын-
тервалов, в которых простаивает только прибор В, имеет Вид (г, D* — z7].
Требование / будем обслуживать таким образом, чтобы ~tj в
интервале (0, D* + i] после обслуживания требования / перед обслужи-
ванием требования / + 1 оба прибора одновременно простаивали толь-
ко в подынтервале (Z>7* + 1 — Zj +1, D;* + 1]; нашелся бы интервал вида
(Г, D* + j - Zj +! ], в течение которого прибор В простаивал.
Возможны следующие ситуации.
а) Пусть а7- + bj < Zj. Тогда требование / может быть полностью об-
служено в интервале (DJ - Zj, D*]. Положим tfB = DJ - zj ,t~jB = tJB +
+ bj - > tj Д - tjA + •
б) Пусть aj + bj > Zj. Максимально возможная длительность обслу-
живания требования j прибором А в интервале (DJ - Zj , D * ] равна aj =
= min {aj, Zj, Zj - (bj - yj)}, где— суммарная длительность простоя
прибора В в интервале (О, DJ] после завершения обслуживания требо-
ваний множества jV7 _ i.
I) Пусть afj = aj . Тогда требование / может быть обслужено без пре-
рываний прибором А, причем tjA-DJ. Требование / может обслуживать-
ся прибором В в интервале (/Э* — z7 , D* - aj ], а также в течение aj + bj — Zj
единиц времени в интервалах, где простаивает только прибор В. Дейст-
вительно, так как a? = а;9 то aj<Zj - (bj - yj) ,т.е.а; + bj - Zj<yj.
II) Пусть a'j = Zj. Тогда требование j может обслуживаться прибором
А в интервале (DJ - Zj, Dj ], а также в течение aj - z7 единиц времени
в интервалах, где простаивает только прибор А. Прибор В может об-
служивать требование / в интервалах, где он простаивает. Так как aj =
= Zj, то bj < yj и такое обслуживание может быть осуществлено.
III) Пусть a'j =Zj - (bj —yj). Это означает, что bj > yj. Поэтому требо-
вание / может обслуживаться во всех интервалах, где простаивает прибор В,
а также в течение bj — yj единиц времени в интервале (DJ - z7-, DJ — а\\.
Требование j может обслуживаться прибором А в течение а] единиц вре-
мени в интервале (DJ -a'j.Dj], а также (поскольку aj ^a'j), в течение
aj - a'j единиц времени в интервалах, где простаивает прибор Л.
Нетрудно проверить, что построенное таким образом расписание об-
служивания требований множества Nj удовлетворяет всем указанным
выше условиям.
219
Таблица 5.1
/ 1 2 3 4 5
ai 2 4 1 3 4
bi 3 3 2 3 6
Di 6 9 13 15 16
Таблица 5.2
i 1 2 3 4 5
a(Nj) 2 6 7 10 14
b(Nf) 3 6 8 11 17
z'i — oo 3 4 3 1
Можно показать, что трудоемкость описанного процесса последователь-
ного построения расписания s* не превосходит О(п) операций, если для
хранения подынтервалов простоя каждого из приборов использовать спе-
циальную структуру данных (так называемый стек).
5.5. Пример. Построим расписание 5* обслуживания п = 5 требований
двумя приборами А и В9 которому соответствует наименьшее значение
^тах(5)- Длительности обслуживания и директивные сроки приведены
в табл. 5.1. Каждое требование может обслуживаться, начиная с момента
d = 0. Допускаются прерывания.
Вычислим частичные суммы a(Nj), b{Nj) и найдем значения z’j по
формуле (5.9). Результаты вычислений приведены в табл. 5.2.
Значение X*, вычисленное по формуле (5.11), равно единице. Положим
£>* = Dj + 1.
Построим расписание, при котором не нарушаются директивные сро-
ки DJ, Для /=1 расписание изображено на рис. 5.1, а.
При /=2 имеем z2 = 10 — 5 = 5, у2 = 2. Выполняется неравенство
а2 + Ь2 = 4 + 3 > z2 = 5. Вычислим а2 = min {4, 5, 5 - (3 - 2)) = 4. Тре-
бование 7=2 обслуживается так, как представлено на рис. 5.16.
При /=3 имеем z3 = 4 и а3 + Z>3 = 1 + 2 < z3 = 4. Расписание обслу-
живания требований {1,2,3} изображено на рис. 5.1,в.
При / = 4 имеем z4 = 3, у4 = 5. Так как а4 + Ь4 = 3 + 3 > z4 = 3, вычис-
лим а4 = min {3, 3, 3 - (3 - 5)} = 3. Расписание обслуживания требова-
ний {1,2, 3,4} представлено на рис. 5.1, г.
При / = 5 имеем zs = 1, у$ = 5; так как а$ + Ь$ = 4 + 6 >zs = 5, вычис-
лим а 5 = min {4, 1, 1 - (6-5)} = 0. Искомое расписание изображено на
рис. 5.1,6.
5.6. Задача построения расписания s*, минимизирующего максимальное
временное смещение существенно усложняется, если прерыва-
ния процесса обслуживания каждого требования каждым прибором запре-
щены. Покажем, что эта задача является NP-трудной в сильном смысле при
M>2udf =0,/ e/V.
220
прибор В
приборА
приборВ | 2 | Н^Ч б
I / I 2 i lj
приборА - 1—4 к- I НН
-1--1 I- I 1 lllllllli I х
О б 6 67 10 121314 16 t
27/ 27/ 27/ 27/
прибор В
приборА
I 1 2 I U’ 4
Ь—4 I-1-----1 Н------1
l I l l I I I I
Ll..i I.J... I i .L.l^
О 3 5 67 6 10 121314 1617 t
27/ 27/ 27/ 27/27/
приборВ — | 2 I- I * I J l*| J I
приборА ->-д ।1 |д!—т—UU4 k 11
। । 11 । । 11 ii
11111111111111111 а
0 1 3 5 67 8 10 121314 1617 t
п/ 27/ 27/ 27/27/
Рис. 5.1
Рассмотрим соответствующую задачу распознавания при М = 2: опреде-
лить, существует ли расписание 5° обслуживания (без прерываний) мно-
жества N требований двумя приборами А и В такое, что Lmax (5°) для
любого заданного числа у
Покажем, что к этой задаче сводится задача о 3-разбиении (см. вводную
часть этой главы).
221
Пусть (ц и bj — длительности обслуживания требования приборами
А и В соответственно, — директивные сроки. Положим
п - 4и0, 7V={1, 2,. .. , п}\
di =0, bf = eb Di= 3n0E, iEN°;
a3n0+i = ^3n0+i ~ 22Г, ^зп0+1 =2ZT;
^3n0 +/ ” 3^, ^з«0 +j ^3nQ + j ~ (?j — E, j - 2,no.
Покажем, что в построенной задаче расписание $° такое, чтоЛтах ($°) <
= 0, существует тогда и только тогда, когда имеет решение задача о
3-разбиении.
Пусть задача о 3-разбиении имеет решение и Nf, / = 1, .. . , и0, - найден-
ные подмножества. Тогда искомое расписание $° существует и может быть
построено следующим образом. Каждый из приборов А и В обслуживает
требования непрерывно одно за другим начиная с момента времени d = 0.
Прибор А обслуживает требования Зи0 + 2, Зи0 + 3, . . . , 4и0 в указанной
последовательности, а прибор В обслуживает все требования множества N
в последовательности Зи0 + 1, я\го, Зи0 + 2, я.г0, . • • , 4и0 — 1, л
77 з 7Vn0-l
4«о,я „ .
"о Л
Пусть существует расписание s , при котором все требования обслужи-
ваются в заданные директивные сроки Dj, it N. Поскольку &зи0 + х =
= ^зи0+х> ази0+2 + ^Зи0+2 = ^зи0+2> то ПРИ расписании 5° значения
^Зло + 1,в = 0, ?зи0+2,л = 0, '°Ло+2,в = hna+2,A- Требование Зи0 + 3
не может обслуживаться сначала прибором В, затем прибором А, так как в
этом случае ^зл0+з,в > D3n„+2 и 1зп„ +з >Dзп0 +3-Поэтому для требова-
ния Зл0 + 3 справедливы соотношения Гз„о +3)j4 = ^п0+2,л> гзл0+з,в =
= ^зп9+з,л- Рассуждая аналогичным образом, приходим к заключению,
что прибор Л обслуживает требования Зи0 + 2, Зи0 + 3,... , 4и0 непрерывно
одно за другим, а требование Зи0 + / обслуживается прибором В во вре-
менном интервале (3(/ -Д)2Г, (3/ - 1)£], 1 </ ^п0. Тогда требования
множества № должны обслуживаться прибором В во временных интерва-
лах ((3/ - 1)£, 3/7Г], 1 </ <и0. Так как£/4< < Е/2 и длина каждого
из указанных интервалов равна Е, то в каждом из них обслуживается ров-
но три требования множества №. Обозначая через множество требова-
ний, обслуживаемых прибором В во временном интервале ((3/ - l)E,3jE],
/ = 1,... , nQ, получаем решение задачи о 3-разбиении.
Тем самым за O(nQ) операций реализовано сведение задачи о 3-разбие-
нии к рассматриваемой задаче распознавания.
5.7. Рассмотрим задачу построения расписания, минимизирующего чис-
ло требований, запаздывающих относительно директивных сроков. Пока-
жем, что задача построения такого расписания (как с прерываниями, так
и без прерываний) NP-трудна, даже если имеется только два обслуживаю-
щих прибора, все требования поступают в систему одновременно и имеют
общий директивный срок.
Доказательство проведем в несколько этапов.
1) Введем в рассмотрение задачу распознавания, которую в дальнейшем
будем называть задачей о разбиении с ограничениями. Эта
222
задача заключается в следующем. Имеется множество 7V°= {1, 2,. .., 2и0},
каждому элементу i которого сопоставлено (рациональное) число eh при-
чем е (TV0) = 2Е, 0 < еi < 2E!nQi i = 1,.. ., 2и0- Требуется определить,
можно ли разбить множество № на два подмножества и N2, каждое
из которых содержит ровно nQ элементов и е (М°) = е (М°) = Е-
Докажем, что эта задача NP-трудна. Для этого покажем, что к ней сво-
дится следующая задача распознавания. Имеется множество № = {1,2,...
...,п0}, каждому элементу которого сопоставлено натуральное число
Еt,причем E(NQ) -2Е. Требуется определить, можно ли разбить множест-
во NQ на два таких подмножества № и TV2, каждое из которых содержит
ровно nQ/2 элементов, что Е(№) = E(N2) Сформулированная задача
NP-полна и представляет собой известную задачу о разбиении (см. вводную
часть этой главы) в несколько суженной постановке.
Для доказательства сводимости положим:
nQ = п о, ei = ei i = 1,. . . , и0;
2й0 - 1 _
Cj = — ----- Е, / = По + 1,. .. , 2и0;
По
Нетрудно проверить, что 0 < в/ < 2Е/п0, * = 1,. .., 2и0.
Покажем, что построенная задача имеет решение тогда и только тогда,
когда множество № можно разбить на два подмножества и N2 с ука-
занными свойствами. _
Пусть существует требуемое разбиение множества N 0 на подмножества
М° и N2°. Тогда имеет решение задача о разбиении с ограничениями, причем
N0! =N°1 и{йо + 1,й о + 2,. ’. , Зпо /2), TV2° = NQ2 и{Зй0/2 + 1, 3 nQ/2 + 2,...
.. • , 2n0}.
Пусть теперь подмножества и N2 — решение задачи о разбиении с ог-
раничениями. Тогда каждое из них содержит ровно й0/2 элементов, боль-
ших nQ-
Действительно, пусть, например, подмножество № содержит й0/2+1
элементов, больших п0. Тогда
Л 2по — 1 -/ По \ 2ио + ЗиО“2 _
e(N?)>—------ е(-^~ +11=------------ Е
По \ 2 / 2и0
Z_-Ox . 2й0--1 -/По \ _ 2по-5по+2 _
е(Л<§)< —---- Е( — - 1 +2Е= --------2-- Е + 2Е.
Hq \ 2 / 2п о
Следовательно, e(7Vi°) - e(TV2°) > (2 - 2/п0) Ё > 0.
Таким образом, в каждом из подмножеств № и N2 содержится ровно
По 12 элементов, больших лг0, и ровно й0/2 элементов, не меньших й0.
Полагая
7V? = {/€Л<10 | 7V?={zG7V2° | 1
получаем требуемое разбиение множества №.
223
Тем самым за 0(nQ) операций реализовано сведение задачи о разбиении
(в суженной постановке) к задаче о разбиении с ограничениями.
2) Рассмотрим следующую задачу распознавания, соответствующую за-
даче построения расписания, минимизирующего число запаздывающих
требований.
Имеется два прибора А и В и множество N- {1,2,.. , и} требований.
Длительности обслуживания требования i G N приборами А и В соответ-
ственно равны а, и Ь^. Задан директивный срок D, общий для всех требо-
ваний. Необходимо определить, существует ли такое расписание s °, при ко-
тором число запаздывающих требований не больше заданного числа у.
Покажем, что эта задача является NP-трудной независимо от того, разре-
шены прерывания или нет. Для этого покажем, что к ней сводится задача
о разбиении с ограничениями.
Положим и = 2«o, Д/ - eif Ь{ = 2ElnQ - eh i = 1,. .. , п\ D-Е. Покажем,
что в построенной задаче расписание 5 °, при котором число запаздывающих
требований не больше у = п0, существует тогда и только тогда, когда имеет
решение задача о разбиении с ограничениями.
Пусть задача о разбиении с ограничениями имеет решение, и -
найденные подмножества. Поскольку е (М°) = D, то а(М°) = Ди b(Ni) =
= и0 • 2D/h0 -D-D. Следовательно, множество требований Л\° может быть
полностью обслужено во временном интервале (О, D], причем в этом ин-
тервале оба прибора не обслуживают требований множества TV2°.
Расписание обслуживания множества требований Л\° может быть построе-
но в соответствии с алгоритмом из п. 1.2 § 1 гл. 3 (если прерывания запре-
щены) или в соответствии с одним из алгоритгиов в § 3 той же главы
(если прерывания разрешены). Множество требований TV2° может обслужи-
ваться во временном интервале (Д +°°) произвольным образом.
В результате получаем расписание 5 0, при котором число запаздываю-
щих требований равно | TV2° | = и0 = У-
Пусть существует расписание s°, при котором число запаздывающих
требований не превосходит у. Пусть R - множество всех незапаздываюших
требований. Тогда a(R) <Д b (R) ^D. Заметим, что I R | > п0. Если при
этом I R | > п0, to b (R) = 2D I R | /n0 - a(R) > (2 I R I -n0) E/n0 >D.
Поэтому | Я | =п0. Далее, если a(R)<D, то b (R) = 2D - a(R ) > D.
Следовательно, a(R) = b (R) =D. Полагая N® =R и TV2° = 7V\ R, получаем
решение задачи о разбиении с ограничениями.
Тем самым за O(nQ) операций реализовано сведение задачи о разбиении
с ограничениями к рассматриваемой задаче распознавания.
§ 6. Суммарное время обслуживания. Одинаковые длительности
В систему с М приборами в момент времени d = 0 поступает множество
N = {1,2,. .. , п } требований. Порядок прохождения приборов нефик-
сирован и может быть различным для разных требований. Предполагается,
что длительности tiL обслуживания требований приборами одинаковы.
Не нарушая общности рассуждений, их можно считать равными единице.
В этом параграфе описываются эффективные алгоритмы построения рас-
224
писаний без прерываний, минимизирующих (взвешенную) сумму момен-
тов завершения обслуживания требований, при условии, что все tiL « 1,
i = 1,..., п, L = 1,... ,М. Если некоторые tiL = 0, то задача минимизации
суммарного времени обслуживания оказывается ЛТ-т рудной.
6.1. Рассмотрим задачу построения расписания s* без прерываний, мини-
мизирующего суммарное время обслуживания требований мно-
жества N системой, состоящей из М приборов. Предполагается, что каждое
требование должно быть обслужено каждым прибором, причем все дли-
тельности обслуживания tiL = 1.
Пусть дано произвольное расписание s и требования пронумерованы
по неубыванию значений rf($), i G7V. Положим
N„= N, р= 1......п, 7(Np,s)= S F,(s).
Произвольному расписанию s для исходной задачи соответствует рас-
писание Г обслуживания требований множества N = {1, 2,..., и } в сис-
теме, состоящей из М параллельных идентичных приборов, при условии,
что длительность обслуживания каждого требования равна М и в процессе
обслуживания каждого требования допускаются прерывания. Отметим,
что rf(s) = ?,•($), z€7V.
Расписание, которому соответствует минимальное значение суммарно-
го времени обслуживания в системе с параллельными приборами, можно,
как известно, искать в классе расписаний, при которых процесс обслу-
живания каждого требования протекает без прерываний.
Пусть п = кМ + г, к> 0, 0 < г <М, к иг — целые числа. В качестве оп-
тимального расписания для построенной задачи с параллельными прибо-
рами может быть выбрано, например, расписание, при котором г приборов
функционируют без простоев во временном интервале (0, (к + 1)М] и
обслуживают (без прерываний) по к + 1 требований каждый, а остальные
М - г приборов функционируют без простоев в интервале (0, кМ] и обслу-
живают (без прерываний) по к требований каждый. Суммарное время
обслуживания при таком расписании равно (к + \}Мг + М2к(к + 1)/2.
Таким образом, при любом расписании s для исходной задачи имеет
место соотношение
+г, *)>(£ + 1)Мг+М2к(к + 1)/2. (6.1)
Укажем несколько способов построения расписания s*, при котором
в (6.1) имеет место знак равенства.
Поскольку в процессе обслуживания не допускается прерываний, то ис-
комое расписание s* однозначно определяется матрицей || tiL (s*)|| момен-
тов завершения обслуживания каждого требования каждым прибором.
Введем в рассмотрение матрицу Л = ||X£Q||, где \Lq = z, если прибор L
обслуживает требование q-ъш по порядку.
1) Пусть п = кМ. Матрицу Л построим следующим образом. Пусть Л/ -
матрица размерности М X М, представляющая собой латинский квадрат,
построенный на множестве {(/ - 1)М + 1, (/— l)Af + 2,..., jM},
1 </ < к (см. § 2 этой главы).
15. В.С. Танаев 225
Будем интерпретировать матрицу Лу как подматрицу матрицы Л, содер-
жащую ее столбцы с номерами (/ - 1)М + 1, (/ — 1)7И + 2,.. ., jM. Поло-
жимГХ£<г>ь(5?) = ^,«= 1, • • • >«> Ъ = 1,... ,М.
При расписании s*, определяемом матрицей || tiL (s* )||, ровно М требо-
ваний будут обслужены к каждому моменту времени ;7И, 1 к, поэто-
му t (Nn, si ) = М2к(к + 1)/2, т.е. расписание sf оптимально.
Отметим, что в рассматриваемом случае расписание si является также
оптимальным по быстродействию. Кроме того, t (Np, sj ) < t(Np, s) для
всех p, 1 < и, и любого расписания s.
2) Пусть п = кМ + г, к > 0, 0 < г <М. Дополним множество требований
М - г фиктивными требованиями п + 1, и + 2,... ,п+М - г, длительность
обслуживания каждого из которых любым прибором положим равной
единице. Матрицу Л = || \Lq || размерности М X (к + 1)Л/ разобьем на к + 1
подматриц Лу, содержащих столбцы матрицы с номерами (/ - 1)М + 1,
(/— l)Af + 2,...,/7И,
а) Пусть каждая из подматриц Лу представляет собой латинский квад-
рат, построенный на множестве {(/ - 1)М + 1, (/ - 1)М + 2,..., jM},
1 < /< к + 1.
Положим t\Lq>L(s2 ) = <7, <7 = £ = 1,..., 7И, XLq < п.
При расписании s£ , определяемом матрицей || tiL ($1 )||, ровно М требо-
ваний обслуживаются к каждому моменту времени jM, 1 < j < к. и г тре-
бований - к моменту времени (к + 1)М. Поэтому
_ к
2 jM2 + (£ + 1)гМ = М2(к+1)кЦ +(к+1)гМ,
т.е. расписание Si оптимально.
Нетрудно проверить, что t(Np, sj) < t(Np, s) для всех р, 1 < р < л,
и любого расписания $.
Отметим, что расписания sj и sj остаются оптимальными и в случае,
когда каждое требование должно обслуживаться без задержек.
б) Пусть > 1 и каждая из подматриц Лу представляет собой латинский
квадрат, построенный на множестве {(/ — l)Af + 1, (/ — 1)М + 2,..., jM},
1 < j < к - 1. Пусть подматрица Ак представляет собой латинский квад-
рат, построенный на множестве {(& — 1)М + 1, (к - Г)М + 2, ...
1)М + г, кМ + г + 1, кМ + г + 2,..., (к + 1)7И}, а подматрица
Лк + 1 - латинский квадрат, построенный на множестве {(к - 1)7И + г + 1,
(к - 1)М + г + 2,... ,кМ + г}.
Если в некоторой строке £, 1 < L < М, матрицы Л расположен элемент,
равный кМ + г + j, 1 < j < М - г, заменим его на элемент, расположенный
в той же строке и в столбце с номером кМ + г + j. После того как подмат-
рица Ак не будет содержать элементы, большие чем кМ + г, исключим из
рассмотрения столбцы матрицы Л, номера которых превышают кМ + г.
Полученная при этом матрица Л имеет размерность М X (кМ + г) и пред-
ставляет собой латинский прямоугольник, построенный на множестве N.
Положим t\Lq,L(s3 ) = 1, - - - >п> L = 1,... ,М.
226
Таблица 6.1
i L 1 2 3 4 5 6 7 8
1 1 2 3 4 5 6 7 8
2 23156489
3 31264597
При расписании $з , определяемом матрицей || tiL (s% )||, ровно М требо-
ваний обслуживаются к каждому моменту времени /Л/, 1 < j < к — 1,
г требований - к моменту времени кМ и М требований - к моменту вре-
мени кМ + г. Поэтому
_ к - 1
2 ;7И2+Шг + 7И(Ш + г) =
/= 1
= М2к(к + l)/2 + (fc + \)Мг,
т.е. расписание оптимально.
Отметим, что это расписание будет также оптимальным по быстродейст-
вию, так как max{($з) |i EN} = кМ + г = п. Построение матриц Л и
II (s* ) II в каждом из рассмотренных выше случаев требует выполнения
не более чем О(пМ) операций.
6.2. Пример. Восемь одновременно пришедших в поликлинику па-
циентов должны пройти медицинский осмотр, побывав на приеме у трех
врачей различной специализации. Время пребывания пациента у каждого
из врачей равно 10 минутам. Требуется таким образом организовать про-
хождение медосмотра, чтобы суммарное время, затраченное всеми пациен-
тами, было минимальным.
В качестве единицы измерения времени выберем 10 минут и придем к
ситуации, рассмотренной в п. 6.1. Здесь и = 8, М= 3, к = 2, г = 2.
Построим оптимальное расписание вида из п. 6.1.
Добавим фиктивного ’’пациента”, присвоив ему номер 9. Остальных
пациентов пронумеруем числами от 1 до 8.
Положим
1 2 3 4 5 6
3 1 2 6 4 5
2 3 1 5 6 4
7 8 9
9 7 8
8 9 7
Моменты завершения обслуживания пациентов приведены в табл. 6.1.
Соответствующее расписание изображено на рис. 6.1 а.
Построим также расписание вида $з из п. 6.1.
В качестве исходной выберем матрицу
1 2 3
3 2 1
2 3 1
4 5 9 6 7
9 4 5 8 6
5 9 4 7 8
8
7
6
15
227
Преобразованная матрица выглядит следующим образом:
Моменты завершения обслуживания пациентов приведены в табл. 6.2.
Соответствующее расписание представлено на рис. 6.1 б.
Суммарная длительность обслуживания при обоих построенных распи-
саниях равна 45 единицам времени (450 минут). Последнее расписание
оптимально по быстродействию.
63. Рассмотренная в предыдущих пунктах ситуация допускает естест-
венное обобщение. Каждому требованию i G N сопоставим вес wz- > 0 и
укажем способ построения расписания 5* (без прерываний), при котором
величина S W/f/O) была бы минимальна. По-прежнему предполагается,
i е N
что все tiL - 1, i = 1,... , п, L= 1,... ,М.
Пронумеруем требования таким образом, что > w2 > ... >
Очевидно, для любой последовательности хх, хг,. .., хп неотрицатель-
п
ных чисел линейная форма S wpfy достигает наименьшего значения
Таблица 6.2
i L 1 2 3 4 5 6 7 8
1 1 2 3 4 5 7 8 6
2 23156847
3 31264578
228
на множестве всех перестановок вида (ц, j2>. . ., jn) при ^Х/2 < . . .
. . . < ху- . Следовательно, расписание $* следует искать в классе S рас-
писаний 5 таких, что последовательность /4($), ^2(х), • • •, tn(s) моментов
завершения обслуживания требований является неубывающей.
Покажем, что в качестве расписания s* может быть выбрано либо распи-
сание sj, если п = кМ, либо s2, если :г = кМ + г, 0 <г <М, где расписания
sj и s2 построены так, как описано в п. 6.1. При этом, очевидно, 5* £ 5.
Из п. 6.1 следует, что для произвольного расписания s G5 и указанного
расписания справедливы соотношения
р _ р _
S /,($*)< S р=1,...,п. (6.2)
1=1 i=1
п _ п _
Покажем, что S wzfz(s*) < S wzZz(s). Действительно, положим =
i = 1 i = 1
= wn, ур - wp - wp + р = п - - 2, . . . , 2, 1. Заметим, что все> О
п
и справедливо соотношение wz = S ур, i = 1,. . . , п.
р= 1
Учитывая (6.2), имеем
п п __ и
S wi'ti(s*)= S Z ур =
i=1 1 = 1 р = i
п Р _ п Р - п -
= S Ур s ti(s*) < S Ур S z,(x) < S wVi(s).
p = i р| = 1 p = i / = 1 < = 1
Таким образом, для построения оптимального расписания $* достаточно
пронумеровать требования по невозрастанию весов wz, положить s* = ,
если п = кМ, или s* = s2 , если п = кМ + г, к > 0, 0 < г <М, Трудоемкость
построения 5* не превосходит 6?(nlogw + пМ) операций.
6.4. Покажем, что в случае, когда некоторые tiL = 0, а остальные tiL = 1,
задача построения расписания, минимизирующего суммарное время обслу-
живания, является NP-трудной. Напомним, что запись tiL = 0 означает,
что требование i е N = {1,2,...,и} прибором L Е Jt = {1,2,..., М}
не обслуживается.
Рассмотрим соответствующую задачу распознавания: определить, су-
ществует ли расписание 5° (как с прерываниями, так и без прерываний)
такое, что Z fz(s°) У заданного у. Покажем, что к ней сводится
i G Лг
задача о 3-раскраске 4-регулярного графа (см. вводную часть данной главы).
Положим п = 95|Х| + 5 \U\, N = {1, 2,..., п}, М = 25\Х | + 5 | U\,
Ж ={1,2,. . . , М}. Как известно, число ребер произвольного графа равно
полусумме степеней его вершин. Так как граф G 4-регулярный, заключаем,
что |С/| = 2|Х|,т.е.и = ЗМ.
Множество Л приборов разобьем на два подмножества (U)
нЛ(Х). Первое подмножество содержит 5| С7| приборов, соответст-
вующих ребрам uk G U графа G и обозначаемых U^k), 1 < I < 5,
1 < к < | U\ . Второе подмножество состоит из 25 |Х| приборов, соответст-
229
вующих вершинам xf- G X графа G и обозначаемых Xiq(j\ 1< Z<5,
К<7<5, 1</< |Х|.
Множество N требований разобьем на три подмножества
N(U\N(X}.
Множество 7V(W) требований состоит из 25 | X | требований, обозна-
чаемых wlq (/), 1 < Z < 5, 1<<?<5, 1< j < |Х|. Если в графе G вер-
шине Xj инцидентны ребра ик^ , ик* , икз, ик*, то требование wlq(j),
1 < Z <5, 1 <# < 5, обслуживается четырьмя приборами Ui(ki), Ul(k2)i
Ui (к3\ Ul(к4) из множества (U), а также прибором Xlq (j) и не обслу-
живается всеми другими приборами.
Множество N(U) требований состоит из 5 |t/| требований, соответству-
ющих ребрам ик графа G и обозначаемых ир(к), 1 < р <5, 1 < к < | U|.
Требование ир(к} обслуживается только пятью приборами вида Ui(k)9
1< I <5.
Множество N(X} требований состоит из 701X | требований, соответст-
вующих вершинам х, графа G и обозначаемых х/р (/), 1< I <5,
1 < р <14, 1 < j < |Х|. Требование х/р(/) обслуживается пятью при-
борами Xiq{j\ 1 < q < 5.
Таким образом, каждое требование множества N должно быть обслу-
жено ровно пятью приборами. Длительности обслуживания положим рав-
ными единице.
Покажем, что задача о 3-раскраске 4-регулярного графа имеет решение
тогда и только тогда, когда в построенной задаче существует расписание s°
такое, что S t (s° ) < 1 On.
i e N
1) Пусть граф G 3-раскрашиваем и X1,X2,X3 - найденные подмно-
жества вершин. Разобьем множество требований N на три непересекающих-
ся подмножества N19 N2 и N3 следующим образом. Для каждого г,
1< г < 3, положим Wr = {w/Q(/)|Z= 1,2,3,4,5,(?= 1,2,3,4,5, xf GXj.
Пусть Ur - множество, состоящее из всех требований вида up(k\ 1 < р < 5,
таких, что ребро ик не инцидентно вершине из Хг. Определим также
И = bZp(/)|/= 1,2,3,4,5, р=1,2,3,4, XyEXj U
U {x/p(/)|Z= 1,2,3,4,5, Р = 5,6,7,8,9, х^Х^},
V2 = {x/p(/)|Z= 1,2, 3,4, 5, р = 5,6,7, 8, 9, XyGXj} U
U {x/p(/)|Z= 1,2,3,4,5, р= 1,2, 3,4, xfeX2} U
U {x/p(/)|Z=l,2,3,4,5, p= 10,11, 12, 13,14, xyGX3} ,
Из = {x/p(/)|/= 1,2,3,4,5, p= 10,11, 12, 13,14, XyG^U^} U
U { xZp(/) | Z= 1,2, 3, 4, 5, p=l,2,3,4, х^Х3}.
Положим Nr = Wr U Ur U Vr, r = 1, 2, 3. Покажем, что обслуживание
всех требований каждого из подмножеств Nl9 N2 и N3 может быть
осуществлено за 5 единиц времени. Доказательство проведем для подмно-
жества TVi (для других подмножеств доказательство аналогичное).
Зафиксируем некоторый прибор Uj (к) G Л (U). По построению,
он может обслуживать только требования из множеств N(U) и N(W).
Если ребро ик инцидентно некоторой вершине xz G Xit то требования
w/g(f), 1 < q < 5, принадлежат множеству СА^ и должны обслуживать-
ся прибором Ui(k). С другой стороны, если uk = (xz, х;), то требования
230
wlq(j\ 1 < / < 5, 1 < ? < 5, не принадлежат множеству W19 так как вер-
шина Xj не принадлежит Х{. Так как ребро ик инцидентно вершине х^Хх,
то требования ир(к), 1 < р < 5, не принадлежат множеству Ui9 а значит,
и множеству Nx.
Пусть ребро ик не инцидентно ни одной вершине из Хг. Тогда при-
бор Ui(k) не обслуживает ни одного требования множества С другой
стороны, этот прибор будет обслуживать требования ир(к), р = 1,2, 3,4, 5.
Зафиксируем некоторый прибор Xtq{j) Е Л (X). По построению, этот
прибор может обслуживать только требования из множеств N(X) и .
Предположим, что Ху Е Хг. Тогда требование wZQ(/) принадлежит
и обслуживается прибором Xlq (/). Кроме того, прибор Xlq (/) обслуживает
требования xZp(/), 1 < р < 14. Однако по построению требования xZp(/),
р = 1, 2, 3, 4, принадлежат множеству Хх, а оставшиеся требования это-
му множеству не принадлежат.
Если Xj $Х19 то прибор XJq(j) не обслуживает ни одного требования
из множества Кроме того, требования xZp(/), рб {1, 2, 3, 4, 10, 11,
12, 13, 14} не принадлежат множеству . Таким образом, из требований
множества прибор Xiq(f) обслуживает только требования xZp(/),
5< р <9.
Итак, каждый прибор обслуживает ровно пять требований каждого
из подмножеств Nx, N2 и 7V3. Поскольку суммарная длительность обслу-
живания каждого требования также равна 5, можно сделать вывод, что
|7Уг|=7И,г= 1,2,3.
Используя методы, описанные в § 3 этой главы, можно построить
расписание 5° обслуживания требований множества Nr в интервале
(5 (г — 1), 5г]. При этом обслуживание каждого требования множества ^
завершится в момент времени 5 г, откуда следует, что расписание 5° явля-
ется искомым.
2) Покажем, что из существования расписания s° такого, что
S ti(sQ) < 1 On, следует, что граф G 3-раскрашиваем.
i е N
Рассмотрим произвольное расписание s и предположим, что требования
пронумерованы таким образом, что ti(s) < t2(s) < . .. < tn(s)-
Пусть tM(s) = 5. Тогда rz(s) = 5, 1 < i <М, и в интервале (0, 5] обслу-
живаются только требования с номерами, не превосходящими М. Это
означает, что tM +1 (s) > 10. Аналогично можно доказать, что t2M +
> 15, если tM + l (s) = 10.
а) Покажем, что для каждого г, 1 < г < 3, справедливо следующее
соотношение:
гМ
S ti(s) > SrM. (6.3)
i = (г- 1)М + 1
Зафиксируем некоторое г, 1 < г < 3. Если f(r-i)M+i(5) 5г, то
(6.3), очевидно, имеет место. Пусть t(r< 5г. Исключим из рас-
смотрения требования с номерами, большими гТИ (если г < 3). В интер-
вале (t\r _i)M+ i 0), 5г] может быть обслужено не более М - 1 требо-
ваний, поэтому суммарная длительность простоя всех приборов в этом
231
интервале отлична от нуля. Так как суммарная длительность обслужива-
ния каждого требования равна 5 и в интервале (0, 5 г] имеются простои,
то Tr M(s) > 5г. Следовательно, найдется такое требование т < гМ, что
^(r — 1)М+10) t (г — 1) М + (5) < 5 Г, tm + 1 (5) > 5г.
Пусть Дг — суммарная длительность простоя всех приборов в интервале
т _
(О, 5г]. Очевидно, Дг > S (5z* - Zz($)). С другой стороны,
i = (г - 1)М+ 1
требования т + 1,.. ., гМ могут быть обслужены в интервале (5г, 5г + Дг],
гм _
откуда следует, что S (Zz(s) — 5г) > Дг. Из полученных соотноше-
i = т + 1
ний непосредственно следует соотношение (6.3). _
’ б) Покажем, что для расписания s соотношение S t{(s) < 10/7 (или,
_ ZG N
что то же самое, S ti(s) < ЗОЛ/) справедливо тогда и только тогда,
_ i е N
когда trM = 5r, 1 < г < 3.
Достаточность этого утверждения очевидна. Докажем необходимость.
Так как (6.3) выполняется для любого расписания и любого г, 1 <г < 3,
то S > 30М Покажем, что trM(s) = 5r, 1 < г < 3, если
/_е N
S rI(s)=30M.
i G N n __ n _
Пусть TM(s) > 5. Тогда S rz(s) > 5Af и в силу (6.3) S r/(s)>30Af,
i = 1 i = 1
что невозможно. Итак, tM(s) = 5. В этом случае, как было показано выше,
fM+ 1 (s) > Ю- Следовательно, ?2Л/(Х) 10. Предположим, что t2M(s) >
п _ _
> 10. Тогда в силу (6.3) S t^s) > 30М. Поэтому (s) = Ю- Рас-
i = 1 _
суждая аналогичным образом, убеждаемся, что ^зл/($) = 15. _
Таким образом, при расписании s°, для которого S (s°) < 10и,
i е N
к каждому моменту времени 5, 10, 15 завершается обслуживание ровно
М требований. Пусть Сг — множество требований, обслуживание которых
завершается в момент времени 5r, 1 <г < 3. Так как | Cr | = М, то требо-
вания этого множества и только они обслуживаются в интервале
(5 (г — 1), 5г], причем в этом интервале ни один прибор не простаивает.
в) Пусть некоторое требование WZ Q (Л) из множества Л^И7) принад-
лежит множеству Сг. Покажем, что Wiiq(j i) G Cr,q = 1, 2, 3,4, 5.
Предположим противное: существует требование Wi q2(h) Сг,
1 < q2 < 5. В этом случае прибор Х/^Д/i) обслуживает требование
wz (/j) в интервале (5(г - 1), 5г], а прибор Xi Q2 (/i) не обслужи-
вает требование ^itq2{j\} в этом интервале. Кроме того, приборы
^Z1^(/i)> Q ~ 1, 2, 3, 4, 5, должны обслуживать требования из множест-
ва N(X), принадлежащие Сг. Таких требований может быть не более че-
тырех, поскольку прибор Xt q уже обслуживает одно требование.
Но тогда прибор Xi q2(Ji) в интервале (5(г - 1), 5г] обслуживает не
более четырех требований, что невозможно.
232
г) Если существуют такие w/Qi(z) G Сг и w/Qj(/) G Сг, то ребро
ик ~ (xi^ Действительно, если бы граф содержал указанное ребро,
то прибор Ui(k} должен был бы обслуживать не менее 10 требований во
временном интервале, длина которого равна 5.
Положим Xr = {xi G X | (z ) G Cr}, 1 < r < 3. Очевидно, Xlt X2
и X3 задают 3-раскраску множества вершин графа G.
Поскольку задача о 3-раскраске 4-регулярного графа МР-полна и реали-
зация ее сведения к рассматриваемой задаче распознавания требует вы-
полнения полиномиального (относительно | X |) числа операций, то за-
дача построения расписания, минимизирующего суммарное время обслу-
живания, в случае, когда все tiL G {0, 1}, является NP-трудной.
§ 7. Суммарное время обслуживания. Различные длительности
В систему с нефиксированными маршрутами, содержащую М приборов,
в момент времени d = 0 поступает множество 7V= {1, 2, ...,л} требова-
ний. Известны длительности обслуживания tiL > 0 каждого требования
i G Nкаждым прибором А, 1 Запись tiL - 0 означает, что требо-
вание i не обслуживается прибором L. Необходимо построить расписание,
минимизирующее суммарное время обслуживания требований 2 tf.
i е N
В этом параграфе показано, что рассматриваемая задача является NP-труд-
ной в сильном смысле при М > 2 (если прерывания в процессе обслужи-
вания запрещены) и приМ> 3 (если прерывания допускаются).
7.1. Пусть в процессе обслуживания каждого требования каждым при-
бором запрещены прерывания. Покажем, что задача построения расписа-
ния, которому соответствует наименьшее значение суммарного времени
обслуживания 2 является NP-трудной в сильном смысле.
i(E N
Сформулируем соответствующую задачу распознавания при М = 2:
имеется два прибора А и В и необходимо определить, существует ли такое
расписание s° (без прерываний), при котором 2 Г/(5°) для любо-
i е N
го заданного числа у. Покажем, что к ней сводится задача о 3-разбиении
(см. вводную часть этой главы).
Положим
и = Зп^Е + Зи0 + 1, g = 3nQE + Зи0 + 6,
v = п0(Е + l)g, f = uv + g + E,
r= 3n0E + n0ug+n0(n0 - l)u(g + E)/2,
h = r + 1 + (n0 + l)g, x = 2(n0 + h)f,
n = n0 + 1 + 2h +nQu, N ={1,2,...,/?}.
Множество N требований разобьем на 4 группы: F-требования, обозна-
чаемые Fj, j = 0, . . . , л0; ^-требования, обозначаемые Xt, I = 1, . . . , h*9
У-требования, обозначаемые У/, I = 1, . . . , h; [/-требования, среди ко-
торых будем различать К-требования, обозначаемые Vjki / = 1, . . . , и0,
к = 1, . . . , и — 3, и Истребования, обозначаемые И^, i = 1, . . . , Зи0.
Длительность обслуживания требования i G N приборами А и В обозна-
233
чим соответственно через at и Z>z-. Положим
aFo = °’ ЬР. =
aFj = f, bFj = g, / = 1,... ,и0;
aXt = = *> bxi ~ aYl ~ 0, I = 1,.. . ,h\
aVfk = 0, bVjk = v, j=l,...,n0, к = 1,. .. ,u - 3;
aw. ~ 0, bw. = u + e6 i = 1,..., Зи0.
Обозначим
_ "о _ h
F= S (g + lf), x= s (nof+lx),
j = о i = i
_ Й _ nQ "1 u
У = S (nof + g + /x), U = 3n0E + S S (g + kf + fv),
i = i / = о fc = i
у = F + Y+ Y+ U.
Покажем, что в построенной задаче расписание s° такое, что
S Fz(s°) < у, существует тогда и только тогда, когда имеет решение
/е N
задача о 3-разбиении.
7.2. Пусть задача о 3-разбиении имеет решение и Л7?, • • • , №0 ~
найденные подмножества множества №. Каждое подмножество /V)0,
1 < / < nQ, состоит из трех элементов а у i, «у г > а/з множества №.
Расписание $° можно построить следующим образом. Положим
fF0 = - g, tF.A = jf 1F. = tFjB = jf + g, j = i,... ,n0;
fXi = fXiA = nQf+lx, tYl - tYlB = «0 f+ lx + g, 1= 1, ... ,h.
Пусть, кроме того, в интервале (g + (/ — 1)/,//] прибор j? обслужи-
вает требования V^, Ку2, . . . , KyjW_3, ^а/1, Ва/3 в указанной
последовательности, / = 1,.. . ,и0-
Нетрудно проверить, что суммарное время обслуживания всех F-, X-
и У-требований равно F + X + У. Вычислим суммарное время обслужива-
ния всех tZ-требований. По построению имеем'
nQ и ~ з зп0 п0 и - з
tvik + ~ (g + (/- 1)/+^1>) +
j = 1 к = 1 7 i = 1 j = 1 к = 1
«о по
+ S (g + (/-l)/+(w-2)у + еа ) + s (g + (/-l)/ +
/ = 1 7 /= 1
«о
+ (и - l)w + ee/1 +eaf2) + S J (g + ti- l)f+4v + eaji +ea.2 +ea/3) =
"o • и no
= S S (g + (/~ l)f+kv) + S (3ea. +2eaj2+ea. ) <
j = 1 к = 1 / = 1 71 72 7‘5
Mo - 1 u _
< S S (g + if + kv) + 3nQE =• U.
О к= 1
234
Таким образом, при построенном расписании s° суммарное время обслу-
живания всех требований множества/V не превосходит у. _
7.3. Пусть существует расписание s°, при котором S ^($°) < у.
i G W
Покажем, что в этом случае имеет решение задача о 3-разбиении.
Не нарушая общности, можно считать, что F-требования и У-требова-
ния обслуживаются прибором Л, а У-требования - прибором В в такой
последовательности, что
fFQA = fFQA = °, , / = h • • • Ло,
fX[A tXi+ , ^YtB < iB, I = 1, • • Л-
1) Покажем, что при расписании s° выполняются соотношения tQx А >
- 1
> nQf и tYl В > "of + X
Предположим, что /у л nof и существует требование У/, 1 </
о 1
для которого t y tB < + S- В этом случае I = 1, поскольку bY. - х>
‘ — q *
> Ио/+ g и, следовательно, > п0 f + g, даже если tYfB = 0.
Суммарное время обслуживания У-требований можно ограничить снизу
величиной
h _
Y = х + S (n0 f + g + lx) = Y - n0 f - x.
I = 2
Если предположить, что все [/-требования обслуживаются в интервале
(0, и0 / + ^], то суммарное время обслуживания этих требований можно
М
ограничить снизу величиной Ux = S jv = U-r.
i = 1
Оценка [/j вычислена в предположении, что ^длительность обслужива-
ния каждого [/-требования, включая ^-требования, равна и, и эти требова-
ния обслуживаются прибором В непрерывно одно за другим начиная с
момента времени 0.
Сделаем предположение, что найдется по крайней мере одно F-требова-
ние, например Fn , для которого tF в >х +g. Суммарное время обслу-
"о-1 .
живания F-требований можно ограничить снизу величиной Fi = S if +
_ / = 1
+ х + g = F- nof- nQg + x.
Тогда суммарное время обслуживания всех требований множества N
не меньше величины Fi + X + У + Ux = у + х - 2и0 /- (и0 + l)g - г, кото-
торая больше у, что невозможно.
С другой стороны, если предположить, что все F-требования обслужи-
ваются прибором В в интервале (0, п0 f + g], то суммарное время об-
служивания F-требований может быть ограничено снизу величиной
F2 = S //=F-(n0 + l)g.
/= i
Тогда суммарное время обслуживания [/-требований будет не меньше
«0м-1 _
чем [/2= S /и + и+ х= [/ - г — nouv + и + х, поскольку по крайней
/= 1
235
мере одно из (/-требований будет обслужено не ранее момента времени
х + V.
Суммарное время обслуживания всех требований множества N будет
в этом случае не меньше чем F2 + X + Y + U2 = y+ x + v- r- nQuv -
- «о/ - (и о + 2)£,что невозможно.
Таким образом, при расписании $° соотношения tQx А > nQf и tQY B <
< Ио / + g одновременно не могут иметь места.
Проводя аналогичные рассуждения, можно показать, что при расписа-
нии $° одновременно не могут иметь места следующие пары соотноше-
НИЙ: < nof » t°Y,B > "of + g, f°¥, л < «о/ и 41В <
2) Покажем, что при расписании $° выполняются соотношения t®x А =
= "о/ = Ио/ + ^.
Предположим, что t°x А > и0/, например t°x А - nof + 1. Тогда суммар-
ное время обслуживания всех Х-требований окажется не меньше чем X + h.
Если в качестве нижней оценки суммарного времени обслуживания F-тре-
бований взять величину F2, (/-требований - величину Ui9 У-требований -
величину У, ю суммарное время обслуживания множества N требований
будет не меньше чем у + (h - г - (nQ + l)g) - у + 1, что невозможно.
Аналогичным образом доказывается недопустимость соотношения
/у, в > nOf + g-
Итак, /у А - nof и t°Y в = nof + g. Отсюда, очевидно, следует, что
tF.A = //, / = 1, • . . , л0. Кроме того, в интервале (0, nQf + g] прибор В
не простаивает и обслуживает все F-требования и (/-требования. Если бы
прибор В простаивал, то обслуживание этим прибором по крайней мере
одного из (/-требований или F-требований началось бы не ранее момента
времени t у в = nof + £ + х> что привело бы к тому, что суммарное время
обслуживания всех требований превысило бы допустимое значение.
3) Покажем, что расписание s° без увеличения суммарного времени
обслуживания может быть преобразовано в расписание s такое, что
tp.A , J - 0,.. . ,nQ. Число выполняемых при этом операций ограни-
чено полиномом от п. _
Пусть р, 0 - наименьший индекс, для которого tFpA >tQp
Докажем существование такого К-требований (обозначаемого через К*),
что pf + g < 7V*B < pf + g + v.
Если в интервале (pf - v - Е/2, (р + 1)/] прибор В обслуживает
некоторое F-требование, то им окажется требование Ff, где i < р. Тогда,
не увеличивая суммарного времени обслуживания, можно поменять места-
ми требование Fz и непосредственно предшествующее ему требование в
последовательности, в которой эти требования обслуживаются прибором В.
Описанное преобразование будем повторять до тех пор, пока не придем
к расписанию, при котором tF.B < pf — v - Е/2. При этом прибор в ин-
тервале (pf — v - Е/2, (р + 1)/] обслуживает только (/-требования.
Длина интервала такова, что даже если все И7-требования обслуживают-
ся прибором В в этом интервале, то в нем может быть обслужено еще не
менее четырех И-требований.
236
Поскольку длительность обслуживания каждого И-требования меньше
длительности обслуживания любого И7-требования, можно считать, что в
последовательности, в которой прибор В обслуживает требования в ин-
тервале (pf ~v - Е/2, (р + 1)/], И-требования предшествуют И7-требо-
ваниям.
Пусть V9 — первое из указанных И-требований, для которого имеет
место соотношение tV'B > pf- Из предыдущих рассуждений вытекает,
что такое требование существует и следующее за ним требование будет
также И-требованием. Очевидно, tyfB < pf + v + g. Если при этом
> pf + 8, т0 положим И* = V9. В противном случае в качестве И*
выберем требование, следующее за требованием V9, Нетрудно проверить,
что обслуживание требования И* завершается в интервале (р/ + g,
р/ + g + у].
Используя требование И*, осуществим дальнейшее преобразование
расписания. Уменьшим на величину g время начала обслуживания прибо-
ром В всех требований, следующих за требованием Fp до требования V*
включительно. Положим *ррв = Поскольку tFpB > pf + g,TO полу-
чаем 7FpA < tFpB.
При указанном преобразовании может возникнуть конфликтная ситуа-
ция, когда некоторое требование Fy, 1 < j < р, должно обслуживаться
прибором В в интервале ((/ - 1)/,//]. В этом случае в последовательно-
сти, в которой требования обслуживаются прибором В, выделим требова-
ние, непосредственно следующее за Fj. Это требование является И-тре-
бованием, в чем нетрудно убедиться, проводя такие же рассуждения, как и
при доказательстве существования И*. Поменяем местами требование
Fj с выделенным требованием. __
В любом случае получаем расписание s1, при котором tF.A < ^р.в,
j = 0, . . . , р. К расписанию s1 могут быть применены те же преобразова-
ния и т.д., пока не будет получено расписание s, при котором tF^A <
< / = 0, . . . , и0. Нетрудно убедиться, что число выполняемых при
этом элементарных операций полиномиально зависит от числа F- и {/-тре-
бований.
Покажем, что при переходе от одного расписания к другому суммар-
ное время обслуживания требований не увеличивается. Для этого, очевид-
но, достаточно рассмотреть расписания s° и s1.
Поскольку при исходном расписании 5° имеем tF.B > jf, можно счи-
/ 7
тать, что в каждом временном интервале (jf, ( / + после
выполнения описанных преобразований прибор В обслуживает только
одно F-требование, а именно требование Fj. Кроме того, в каждом из
эгих интервалов прибор В обслуживает не менее чем (/ - g)/(u + F/2)
(/-требований (поскольку длительность обслуживания этим прибором
любого (/-требования не превосходит v + F/2).
Из соотношений v = Но(Е + l)g > nQEg > nQEu > uEj2 -3Ej2 следует,
что E > uE/2 - v -E/2. Отсюда uv + E > uv + uE/2 - v - E/2 = (u - 1) X
X (u + E/2).
Так как uv + E - f - g, приходим к заключению, что число {/-требова-
ний, обслуживаемых в каждом интервале (jf, (j + 1)/], 0</ при-
237
бором В, больше чем и - 1. Другими словами, в интервале (0, (р + 1)/]
на каждое обслуженное прибором В F-требование приходится не менее
и (/-требований.
Пусть п — число требований, для которых время начала обслуживания
прибором В было уменьшено в процессе преобразования исходного рас-
писания. Тогда среди них окажется не менее L.n/u J F-требований. Для
требования Fp при исходном расписании выполнялось соотношение
tFpB < поэтому tpp~ fFpA = Pf- После преобразования расписа-
ния имеем tFpA < tFpB и fFp = ^FpB ^pf + v + S по построению. Таким
образом, момент завершения обслуживания требования Fp увеличился
не более чем на v + g единиц времени.
При ликвидации конфликтных ситуаций момент завершения обслу-
живания каждого из требований Fh 0 < i ^р, мог увеличиться на v еди-
ниц времени.
Таким образом, чтобы показать, что проведенные преобразования не
увеличили суммарное время обслуживания требований, достаточно убедить-
ся в справедливости неравенства
ng > v+g+Ln/uJv.
Очевидно, и > и. Положим п =ки + z, где к> 1 иг,0 <z < и, — целые
числа. Интересующее нас неравенство равносильно неравенству (ки + z)g>
> v + g + kv. В результате деления обеих частей этого неравенства на g и
выполнения очевидных преобразований получаем
ки + z > (fc + l)n0(F + 1) + 1.
Учитывая, что и = 3nQE + Зи0 + 1, получаем
3nQkE + 3nQk + k + z > покЕ + пок + п0Е + и0 + 1.
Последнее неравенство, очевидно, имеет место и равносильно исходному.
4) Покажем, что расписание s без увеличения суммарного времени
обслуживания требований может быть преобразовано в расписание Г такое,
что tFjB - tFjA < v + F/2,/ = 0, . . . , nQ. Число выполняемых при этом
операций ограничено полиномом от п.
Если при расписании s выполнено tQFpB — tppA v + £7 2 для некото-
рого р, 0 <и0, то в последовательности, в которой требования обслу-
живаются прибором В, выделим требование, непосредственно предшествую-
щее требованию Fp. Это требование является (/-требованием, так как во
временном интервале (pf, (р + 1)/] прибор В не обслуживает других
F-требований, кроме требования Fp. Поменяем местами требование Fp
и выделенное (/-требование. Суммарное время обслуживания не увели-
чится, и поскольку длительность обслуживания любого (/-требования
прибором В меньше чем v + F/2, то требование Fp по-прежнему будет
единственным F-требованием, обслуживаемым прибором В в интервале
(р/, (р+1)/].
Приводя указанные преобразования необходимое число раз, получаем
искомое расписание Г. Нетрудно убедиться, что число выполняемых при
этом операций зависит полиномиально от числа F- и (/-требований.
238
5) Покажем, что при расписании Г в каждом временном интервале
(tpjB, *Fy + хв], / = 0, . .. , и0 - 1, прибор В обслуживает не более и + 1
и не менее и — 1 [/-требований. _
Предположим, что существует интервал {tppB, tFp + хв], О ^по — 1,
в котором число [/-требований, обслуживаемых прибором В, равно и — 2.
Длина указанного интервала будет не меньше чем f — v - Е/2, что дости-
гается при tFрВ = pf + v + Е/2 и tpp + {B = (р + 1)/. Даже если в этом
интервале прибор В будет обслуживать все И7-требования, то суммарная
длительность их обслуживания окажется равной (и — 2) v + п0Е. Так как
f — v - Е/2 = uv + Ef2 — u+gng + u+ Е/2 > nQE, то в рассматриваемом
интервале приборВ будет простаивать, что невозможно.
Предположим, что существует интервал (tppBi tFp+lB]> 0 < и0,
в котором число [/-требований, обслуживаемых прибором В, равно и + 2.
Длина указанного интервала будет не больше чем f + v — g + Е/2, что дости-
гается при tFpB = pf + g и = (р + 1)/ + v + Е/2. Даже если в
указанном интервале прибор В обслуживает только И-требования, то
суммарная длительность их обслуживания окажется равной (и + 2)и.
Поскольку v > Е/2, то (и + 2) и > (и + 1)и + Е/2 > f — g + v + Е/2. Это
означает, что и + 2 [/-требований не могут быть полностью обслужены в
указанном интервале. f
6) Покажем, что при расписании Г в каждом временном интервале
{tpjBi tFj+ хв] 5 0 / wo - 1. прибор В обслуживает ровно и [/-требо-
ваний.
Предположим, что найдется требование Fp, 0 < р < п0) такое, что в
интервале (0, 1ррв] число [/-требований, обслуживаемых прибором В,
меньше чем ри. Если учесть, что в указанном интервале приборВ обслужи-
вает также требования Fy, 0 </ - 1, то суммарная длительность обслу-
живания прибором В всех требований, предшествующих Fp, окажется
не больше чем pg + {ри - 1)и + и0Е. Эта величина, однако, меньше pf,
т.е. в интервале (0, t°FpB] приборВ простаивает, что невозможно.
Число [/-требований, обслуживаемых прибором В в интервале
{tFjB* t0Fj + jb] > 0 < j < п0 - 1, обозначим через Су. Предположим, что
существуют такие рнц, 0 < р < # < и0 - 1, что ср = cq = и + 1, в то время
как су = и, j = р + 1, . . . , q_ — 1. Тогда число [/-требований, обслуживаемых
прибором В в интервале (JFpB, tpqB], равно (q + 1 — p)u + 2. Суммар-
ная длительность обслуживания прибором В всех требований в интервале
(tFpB, fFqb] будет не меньше чем ((q + 1 - р)и + 2)v + (q + 1 - p)g,
что больше максимально возможной длины указанного интервала (рав-
ной (q + 1 - p)f+ v + Е/2).
Таким образом, в последовательности cOt cit . . . , сп i либо все
с,- = и, либо эта последовательность содержит по крайней мере одну под-
последовательность вида ср = и + ], су = и, 0 <р </ < q < п0 - 1, cq = и -1.
Покажем, что второй случай не может иметь места. Пусть последова-
тельность с0, С], . . . , сПо _ j содержит ровно одну подпоследовательность
239
указанного вида. Тогда каждое требование Fy, р < j < q, не может быть
обслужено прибором В ранее момента времени pf + ( / - p)g + ((/ - р)и +
+ 1)и = jf + v - (j-p)E.
Положим Rj = v — (j - р)Е, j в {р + 1, р + 2, . . . , q} и Rj = 0, j G
е{0, 1,. . . ,p,q+ \,q + 2,. . . ,и0Ь
Суммарное времз обслуживания F-требований и ^/-требований можно
ограничить снизу соответственно величинами
«о "о-1 cj
F3 = (g + if+Rf> И U3 = 2 2 (g + //+^y+Fz).
j = о j = о к = i
Имеем
F3-F = S (g + if+ v-(j-p)E) - S (g + //) =
I = p + 1 / = p + 1
q- 1
= u-(^-p)£’+ S (u-(/-₽)£),
/ = p + 1
Q-l
где 2 (u-(/-p)E) = 0 при q = p + 1.
/ = p + i
Аналогично
~ "o'1 ci
u3 - U= — 3n0E + 2(2 (g + //+^y+E7) -
/ = о fc = i
и M + 1
- 2 (g+if+ kv)) = -3hqE + ( 2 (g + kv + pf) -
к = 1 к = 1
и я - i и
- 2 (g + ь + р/)) + 2 2 Rj +
к 1 / = p + 1 Л = 1
u.- 1 u
+ ( 2 (g + kv + qf+Rq) - 2 (g + kv + qf)) =
к = 1 к = 1
q - 1
= -3n0E- (q -p)(g + uE) - S u(j — p)E,
t I = p + 1
q- i
где 2 u(j - p)E = 0 при q = p + 1.
/ = P + i
Поскольку v - (q - p)E > (q - p) (g + uE) + 3nQE и v - (/ - p)E >
> u(j - p)E, p < j < q, то получаем соотношение f/3 + F3 > £/ + F. Если
суммарное время обслуживания X- и У-1ребований ограничить снизу ве-
личинами X и Y соответственно, то суммарное время обслуживания всех
требований множества А будет больше чем у, что невозможно.
7) Покажем, что при расписании s значение = у/, j = 0, . . . ,г/0-
Предположим, что найдется требование Fp, 0 Для которого
>р/. Положим для определенности 1?рв ~Pf + Ь
Тогда суммарное время обслуживания F-требований можно ограни-
чить снизу величиной F +1.
240
Нижнюю оценку суммарного времени обслуживания [/-требований
вычислим в предположении, что длительность обслуживания каждого
И7-требования прибором В равна v. Если бы при расписании s' значение
~ if, f = 0, . . . , п0, то суммарное время обслуживания [/-требова-
ний было бы не меньше чем U - Зп0Е. Поскольку t^FpB =pf + 1, то указан-
ная нижняя оценка равна U + и - 3nQE.
Выбирая в качестве нижних оценок_суммарного времени обслужива-
ния X- и У-требований величины X и Y соответственно и учитывая, что
и + 1 > 3nQE, приходим к заключению, что суммарное время обслужи-
вания всех требований больше^, что невозможно.
8) Таким образом, при расписании Означение t*p.B = //,/ = 0,. . . ,и0,
/ /
в каждом временном интервале ((/ - 1)/ + g, jf], 1 </ прибор В
не простаивает и число обслуживаемых им [/-требований равно и.
Следовательно, в каждом из указанных интервалов прибор В обслужи-
вает ровно три И/-требования, сумма длительностей обслуживания кото-
рых равна 3v + Е. Тем самым получаем решение задачи о 3-разбиении.
Таким образом, за 0(ПоЕ) операций реализовано сведение задачи о
3-разбиении к рассматриваемой задаче распознавания.
7.4. Покажем, что задача построения расписания s* которому соответ-
ствует наименьшее значение суммарного времени обслуживания
S G(s), является NP-трудной в сильном смысле при М > 3, если в
N
процессе обслуживания каждого требования каждым прибором до-
пускаются прерывания.
Сформулируем соответствующую задачу распознавания, определить,
существует ли расписание $° (с прерываниями), при котором
S G0°) У Для заданного числа у. Покажем, что при М = 3 к этой
i е N
задаче сводится задача о 3-разбиении.
Положим N = /V0 = {1, 2, . . . , Зи0}, ttl = eh ti2 = t{3 = (Е - ez)/2,
i - 1,... , Зи0.
Очевидно, tix + ti2 + G’3= E.
Покажем, что в построенной задаче расписание $°, при котором
S G(s°) = 3/Гио(Ио + 1)/2, существует тогда и только тогда, ког-
ie n
да имеет решение задачи о 3-разбиении.
1) Пусть задача о 3-разбиении имеет решение и Ni,N2, . . . , ~
найденные трехэлементные подмножества множества №. Тогда для любо-
го /, 1 < j < nOt справедливо S tiL = £, L = 1, 2, 3.
i е nJ
Расписание $° существует и может быть построено следующим обра-
зом. Пусть во временном интервале ((/ — 1 )£’,/£’] обслуживаются толь-
ко требования множества Д/° и требования этого множества не обслужи-
ваются вне указанного интервала.
При помощи одного из алгоритмов, описанных в § 3 гл.З, можно по-
строить расписание обслуживания множества требований Д^° во временном
интервале ((/ — 1)Я, jE], j = 1, . . . , nQ. Так как при этом t{ = jE для
16. В.С. Танаев
241
всех i Е N?, j = 1,. . . , nQ, to S tt = у. Следовательно, получаем иско-
' z g N
мое расписание s°.
2) Пусть существует расписание s°.
а) Покажем, что S ^0°) = ^.
i G N
Рассмотрим задачу построения расписания s' обслуживания Зи0 требо-
ваний тремя параллельными идентичными приборами, которому соот-
ветствует минимальное значение суммарного времени обслуживания.
Пусть длительность обслуживания каждого требования равна Е. Не-
трудно видеть, что S = у и S Ff(s') < S /7(5°) (см.
i g n i &jv i & n _
§ 6 этой главы). Так как по условию S rf(s°) то S ~У-
IEN N
б) Предположим, что при расписании $° требования множества Л"прону-
мерованы таким образом, что tx < ^зп0 • Выберем произволь-
ное /, 1 < / < и0> и покажем, что 73/_2 + ^з/-1+ ^з/ 3/Е.
Обозначим t3j _ 2 = и и t3j _ i — 13j- _ 2 = t>, 73y — t 3/- _ t = w; пусть
v' и и/ соответственно означают суммарную длительность обслуживания
требований 3/ — 1 и 3/ во временном интервале (0, и].
Так как t3f _ 1Д + t3j _ 1>2 + t3i _ 1>3 = Е и t3j i + t3j>2 + t3f 3 = Е, то
v + v'>Env + w+w'>E. Кроме того, так какЛ/= 3 и Г3у _ 2 > Г3у _ 3,
то Зи > 3(/- 1)Е + Е + и1 + w'.
Поскольку Z3/_2 + hl-1 + hl= 3w + 2v + w, имеем
hl-2 + hi-i +hi > 3w + 2E- i/-w' >
> 3(/ — l)E + 3E + i/ + w'-(i/ + w') = 3jE.
в) Покажем, что задача о 3-разбиении имеет решение. Так как /3/ _ 2 +
+ t3f _ 1 + t3j > 3jE, / = 1, . . . , л0, то из существования такого что
hf-2 + hj'-
+ t3i> > ^j’E, следует, что S Zz(s°)>y.
i G 2V°
Следовательно, ?3/-2 + *3/- 1 + гз/ = 3/F, j = 1,... ,п0.
Отсюда получаем, что при расписании х° в каждом интервале (3(/ - 1)Е,
З/Е], / = , и0, обслуживается ровно три требования, суммарная дли-
тельность обслуживания которых прибором 1 равна Е. Обозначая через
N? множество требований, обслуживаемых в интервале (3(/ — 1)Е, З/Е],
7 = 1,... , Мо> получаем решение задачи о 3-разбиении.
Тем самым за O(nQ) операций реализовано сведение задачи о 3-раз-
биении к рассматриваемой задаче распознавания.
§ 8. Библиографическая справка
Системы с нефиксированными маршрутами изучаются сравнительно
недавно. Принято считать, что первой работой, посвященной этому классу
систем, является статья Т. Гонсалеса и С. Сахни [551]. Однако уже в моно-
графии Р. Веллмана [25, с. 115] приводится формулировка задачи миними-
зации общего времени обслуживания для двухстадийной системы с нефик-
242
сированными маршрутами. Кроме того, в работе Д. де Верра [829] факти-
чески описан алгоритм построения оптимального по быстродействию
расписания с прерываниями, основанный на раскраске ребер двудольного
мультиграфа. Насколько известно авторам, задачи построения расписаний
для систем с нефиксированными маршрутами до сих пор не нашли отраже-
ния в монографической литературе. Не было также обзорных статей, спе-
циально посвященных этим задачам, хотя некоторые вопросы затрагива-
лись в обзорах [569, 635, 646, 655]. Ниже предполагается (если не огово-
рено противное), что множество N = {1, 2, . . . , и} требований поступа-
ет в систему, состоящую из М > 1 приборов, в момент времени d = 0.
Значения tiL > 0. Оптимальным называется оптимальное по быстро-
действию расписание; оно обозначается 5*. Используются обозначения
t* = max{/ZL | i e N, L = 1,. . . ,M}, = max{ S tiL \ L= 1, . . . ,M}
i G N
nr - число отличных от нуля tiL .
8.1. Алгоритм построения расписания 5*при М = 2 (см. п. 1.2) предложен
Т. Гонсалесом и С. Сахни [551] (см. также [569, 646]). Результаты, при-
веденные в п. 1.4, получены В.А. Струсевичем. Случай, когда NAB = ф или
NBA ~ рассмотрели Т. Масуда, X. Ишии и Т. Нишида [681]. WP-труд-
ность (в сильном смысле) задачи построения расписания s* без задержек
в обслуживании требований при М > 2 установлена С. Сахни и Ю. Чо [764].
TVP-трудность задачи построения оптимального расписания (без прерыва-
ний) при М > 3 доказана в [551] (см. также [323]). В [551] показано,
что эта задача остается NP-трудной, если М > 4 и каждое требование обслу-
живается не более чем двумя приборами. Отметим, что в [569,646] указа-
но, что при переменном числе приборов задала является NP-трудной в
сильном смысле.
В [461] показано, что если прерывания запрещены, то при любом
расписании 5 значение Jmax(s) t*(N) + (М-1) г*. Из результатов,
полученных в [759], следует, что, применяя приемы, описанные в п. 8.4
§ 8 гл. 1, можно построить алгоритмы трудоемкости О(пМ) опе-
раций, позволяющие находить такое расписание s°, для которого
Gnax(5°)Amax(5* ) [М/2] .
Попытка оценить устойчивость оптимальных расписаний без преры-
ваний предпринята С.И. Василенко [51].
8.2. Описанные в пп. 2.2 и 2.3 эффективные алгоритмы минимизации
общего времени обслуживания при наличии в системе одного или двух
доминирующих приборов и запрещении прерываний предложены
В.А. Струсевичем [322, 323]. Алгоритм трудоемкости О(и2М3) решения
этой задачи в предположении, что Z*(7V) > (М2 + 2М - l)f* (см. п. 2.5),
разработали И. Барани и Т. Фиала [461]. В этой же работе указано, что
для решения задачи требуется не более 0(пМ3 + нА/2 log и) операций, если
t*(N) > (8m\ogm + 5zn)Z* где т = 2к, 2k~l < М < 2*. Отметим, что
в [520] предложен алгоритм трудоемкости О(и2М3), если r*(7V) >
> (16т log ди + 5я?)Г*.
8.3. Подход к решению задачи построения расписания s* (с прерыва-
ниями) в случае целочисленных длительностей обслуживания, основанный
на раскраске ребер двудольного мультиграфа (см. п. 3.2), предложили
Д. де Верра [829, 830] и А.С. Асратян [12, 13]. В.Г. Визинг [53] показал,
16
243
что минимальное число цветов, необходимых для раскраски ребер дву-
дольного мультиграфа, равно максимальной степени вершины. К числу
наиболее эффективных алгоритмов нахождения оптимальной реберной
раскраски двудольного (мульти)графа G - (V, £), где V и Е - множест-
ва вершин и (мульти)ребер (мульти)графа G, принадлежат алгоритмы,
разработанные Г. Габоу и О. Каривом [529] и имеющие трудоемкости
О( | Е | log2 I И |) и О( | К2 | log I V |). Они позволяют строить оптимальное
расписание для рассматриваемой задачи за О (г log2(и + 7И)) и О((п + М)2 X
X log (и + М)) операций соответственно. Заметим, однако, что число пре-
рываний при этом может оказаться неоправданно большим.
Алгоритм нахождения оптимальной обобщенной раскраски ребер дву-
дольного мультиграфа G = (И, Е), требующий выполнения не более
О( I V | R log К} операций, где R - число смежных пар вершин в G, а
К — наибольшее число ребер, инцидентных одной и той же паре вершин,
также предложен в [529]. Используя этот алгоритм, можно построить
оптимальное расписание за О((п + М)г log t*) операций.
Обзоры других результатов, касающихся реберной раскраски (муль-
ти) графов, приведены в [521,627].
Подход к решению задачи построения расписания s * (с прерываниями),
основанный на нахождении разложения (3.2) (см. п. 3.4), предложен в
[551, 644] (см. также [569]). Утверждение о существовании разложе-
ния (3.2) известно в комбинаторном анализе как теорема Биркгофа (см.,
например, [198, 270]). Обзоры результатов по этой проблематике при-
ведены в [225, 226]. Обобщения теоремы Биркгофа и их приложения к
решению задач теории расписаний рассмотрены Д. де Верра [832 - 834].
Указанный подход использован Т. Гонсалесом и С. Сахни [551] для
разработки двух алгоритмов построения расписания s*, трудоемкость
которых не превосходит О (г2) и O(r(min{r, М2} + Mlogn)). Осно-
ванный на этом же подходе алгоритм из [549] имеет трудоемкость
О (г + min{M4, л4, г2}).
Отметим, что задача построения оптимального расписания (с преры-
ваниями) имеет не только самостоятельное значение, ио и находит при-
менение при решении других задач теории расписаний, в частности при
построении оптимального по быстродействию расписания (с прерывания-
ми) для одностадийной системы, состоящей из параллельных приборов
различной производительности [643,644, 833] (см. также [350]).
Задача построения расписания 5 * в случае, когда на каждой стадии имеет-
ся несколько параллельных приборов (см. п. 3.6), рассмотрена в [648].
Для решения системы линейных соотношений (3.3)-(3.5) можно ис-
пользовать предложенный Л.Г. Хачияном [380] (см. также [238]) ал-
горитм, имеющий полиномиальную трудоемкость. Алгоритм построения
оптимального по быстродействию расписания (с прерываниями) для одно-
стадийной системы с параллельными идентичными приборами, имеющий
трудоемкость О(п) и использующийся в п. 3.6, описан Р. Мак-Нотоном
[687] (см. также [350]). Результаты п. 3.8 получены В.А. <грусевичем.
АР-трудность задачи из п. 3,9 доказана в [493].
АР-трудность задачи построения оптимального расписания (с пре-
рываниями) без задержек в обслуживании требований (см. и. 3.10) уста-
новлена В.А. Струсевичем и Е.Р. Брошиной.
244
Следует отметить, что в терминах построения оптимальных расписа-
ний для системы с нефиксированными маршрутами могут быть сформу-
лированы многие задачи, возникающие при организации спутниковой
связи. Так, например, в [116, 120, 606] фактически рассматривается за-
дача построения оптимального расписания с прерываниями; в [661] описан
полиномиальный алгоритм построения оптимального расписания, при ко-
тором процесс обслуживания каждого требования прерывается и возоб-
новляется ровно один раз. Другие результаты, полученные в этом направле-
нии, можно найти в [455,472, 554 — 556, 752].
8.4. Задачи построения оптимальных расписаний обслуживания упоря-
доченных множеств требований рассматривались С.А. Бородичем,
В.А. Струсевичем и А.В. Тузиковым. Результат, приведенный в п. 4.1,
получен в [38] (см. также [319, 320]). Алгоритм из п. 4.3 предложен
в [38].
7VP-трудность (в сильном смысле) задач из пп. 4.5 и 4.6 доказана в [37]
и [320] соответственно. Алгоритм из п. 4.7 получен в [37]. Обзор резуль-
татов по этому направлению содержится в [36].
В обзоре Я. Блажевича, Я. Ленстры и А. Ринной Кана [470], посвящен-
ном задачам теории расписаний с ограниченными ресурсами, отмечается,
что для построения оптимального расписания (без прерываний) в случае,
когда имеется произвольное число видов ресурсов, необходимых для
обслуживания каждого требования, достаточно О(п3) операций, если
М - 2 и tix = ti2 = 1, i G N. (См. также [471].)
C.A. Бородич [34] рассмотрел ситуацию, когда транспортировка каждо-
го требования i от прибора к прибору осуществляется операторами пере-
носа и требует т, > 0 единиц времени. Показано, что независимо от того,
допускаются или нет прерывания в процессе обслуживания требований,
а также от того, ограничено или нег число операторов переноса, задача
построения оптимального расписания является NP-трудной при М > 2,
даже если все тг= т > 0, i = 1, . . . , п. В некоторых случаях удается за
полиномиальное число операций построить либо оптимальное расписа-
ние, либо расписание, имеющее ограниченную абсолютную погрешность
(см. также [38]).
И. Адири и Н. Амит [418] рассмотрели задачу построения расписания
s* (без прерываний) в предположении, что длительности обслуживания
каждого требования зависят от выбираемого маршрута обслуживания.
Установлено, что эта задача является NP-трудной приТИ > 2; описаны не-
которые эффективно разрешимые случаи.
С.А. Бородич [35] рассмотрел ситуацию, когда М = 2 и длительности
обслуживания являются функциями моментов начала обслуживания требо-
ваний, г.е. когда tn = <- <p(r?), ti2 = bt + <^(r?), i = 1, . . . , n, где -
неотрицательная неубывающая функция. Показано, что в случае, когда
прерывания допускаются только в целочисленные моменты времени,
оптимальное расписание может быть построено в результате выполнения
O(HlogH) операций. Если же прерывания допускаются в произвольные
моменты времени, то за О(п log и) операций может быть построено такое
расписание $°, что jmax(s’°) " GnaxM € для любого е > 0. (Здесь
5* - оптимальное расписание в случае, когда ^(Г) = 0.) Если прерыва-
245
ния не допускаются, то задача является NP-трудной, даже если функ-
ция у является кусочно-постоянной.
8.5. Задача из п. 5.1 рассмотрена Ю. Чо и С. Сахни [493]. Для решения
системы (5.1) —(5.3) можно использовать метод, предложенный Л.Г. Ха-
чияном [380].
Сведение задачи из п. 5.2, 2) к задаче о существовании допустимого
потока также проведено в [493]. Основные понятия и терминологию,
относящиеся к теории потоков в сетях, читатель может найти в [3, 156,
238, 374, 547]. В частности, в этих работах описан метод, позволяющий
свести задачу о существовании допустимого потока к задаче нахождения
максимального потока в специальным образом построенной сети. Для
нахождения максимального потока А.В. Карзановым [132] (см. также
[3, 238, 815]) предложен алгоритм, трудоемкость которого пропорцио-
нальна кубу числа вершин сети. Этот метод и позволяет найти допустимый
поток в сети G за О(п3 + М3) операций.
Задача минимизации максимального временного смещения в случае
М = 2 рассматривалась Е. Лоулером, Я. Ленстрой и А. Ринной Каном [645].
Если допускаются прерывания, то для решения этой задачи достаточно вы-
полнить О(п log и) операций (или О(п) операций, если требования упоря-
дочены по неубыванию директивных сроков (см. п. 5.4)). Если же пре-
рывания .не допускаются, то задача является АР-трудной в сильном смысле
(см. п. 5.6). Отметим, что доказательство этого факта, приведенное в
[645], содержит неточности. Соответствующие исправления сделаны в
[647]. С.А. Бородич [33] рассмотрел ситуацию, когда на одном приборе
прерывания допускаются, а на другом-нет. Предложен алгоритм трудоем-
кости О (и3). АР-трудность задачи минимизации числа запаздывающих
требований приМ> 2 (см. п. 5.7) доказана С.А. Бородичем [32].
8.6. Задачи минимизации суммарного и взвешенного суммарного време-
ни обслуживания требований единичной длительности рассмотрены
В.А. Струсевичем [324]. Тот факт, что решение задачи минимизации
суммарного времени обслуживания для одностадийной системы с парал- ;
лельными идентичными приборами можно искать в классе расписаний |
без прерываний, установлен Р. Мак-Нотоном [687], а в случае мини-
мизации произвольной е-квазивогнутой неубывающей функции -
В.С. Танаевым [341] (см. также [350]). Задача минимизации линейной
п
формы S на различных подмножествах множества всех пере-
i = 1
становок элементов конечного множества рассматривалась многими ав-
торами (см., например, [198, 210, 266 — 268, 326, 327, 329, 350, 351,378,
780]).
Результат, приведенный в п. 6.4, получен Т. Гонсалесом [550]. Как
отмечено в этой работе, сложность задачи не изменится, если расписание
искать в классе расписаний без задержек в обслуживании требований.
8.7. Дж. Ачугбью и Ф. Чин [412] показали, что задача минимизации
суммарного времени обслуживания при М > 2 является АР-трудной в
сильном смысле, если прерывания запрещены (см. пп. 7.1,7.2).
Отметим, что используемый при этом подход является развитием
метода доказательства аналогичного результата для системы поточного
246
типа [533]. В [412] показано также, что при любом расписании s, при ко-
тором в любой момент времени t G (0, Zmax(s)] функционирует
п _ п —
хотя бы один арибор, имеет место соотношение S (s)/ S Z/(s*) <
i = 1 i = 1
< и, причем эта оценка достижима. Там же предложен алгоритм трудо-
емкости О(пМ + «log и) построения такого расписания $°, что
п _ п _
S ti (s0)/ S ti ($*) <Af. Эта оценка также достижима.
i = 1 i = 1
К. Лиу и. Р. Булфин [665] доказали, что указанная задача при М > 3
является ТУР-трудной в сильном смысле, если допускаются прерывания
(см. п. 7.3). Если потребовать, чтобы процесс обслуживания требова-
ния i завершался не позже заранее заданного момента времени Diy i =
= 1, . . . , задача оказывается TVP-трудной в сильном смысле и при
М=2.
Задачи со случайными длительностями обслуживания требований рас-
сматривались в [504,741].
ГЛАВА 4
ЗАДАЧИ НА СМЕШАННЫХ ГРАФАХ
Все рассмотренные ранее ситуации допускают естественную интерпрета-
цию в терминах сетевого планирования с ограниченными ресурсами. Для
этого достаточно ввести понятие операции как некоторого протекающего
во времени процесса, имеющего определенную длительность и требующего
определенных ресурсов. Каждые две операции могут быть зависимыми
или независимыми в том смысле, что календарное время выполнения
одной из них оказывает или не оказывает влияния на календарное время
выполнения другой. Каждый прибор можно рассматривать как нескладируе-
мый неделимый ресурс, ограничивающий возможности одновременного
выполнения двух или более операций по обслуживанию требований.
Характерные особенности рассматриваемых в этой книге обслуживаю-
щих систем позволяют при поиске оптимальных расписаний их функциони-
рования использовать специфические сетевые модели в виде смешанных
(дизъюнктивных) графов.
Для доказательства ЛТ-полноты рассматриваемой в § 2 задачи распоз-
навания используется следующая задача о выполнимости.
Пусть X = {хь х2, . . -, хт } - множество булевых переменных, прини-
мающих значение 1 (истина) или 0 (ложь). Дизъюнкцией над % называется
множество литералов, т.е. переменных xt из множества X или их отрица-
ний Xi (Х{ = 1 тогда и только тогда, когда =0). Предполагается, что все
переменные в дизъюнкции различны. Дизъюнкция выполнена при некото-
ром наборе значений переменных тогда и только тогда, когда при этом
наборе хотя бы один из ее литералов принимает значение 1. Множество
дизъюнкций £2 = {^i, £22, - . . , £2^ } называется выполнимым в том и
только том случае, когда найдется некоторый набор значений переменных,
при котором выполнена каждая дизъюнкция £lk,k = 1, . . . , go.
Задача о выполнимости состоит в следующем. Даны мно-
жество переменных X и множество £2 дизъюнкций над X. Выполнимо ли
множество дизъюнкций £2?
Если каждая дизъюнкция из £2 содержит к литералов, получаем з а-
дачу о ^-выполнимости. Эта задача TVP-полна при к > 3 [158],
а при к < 3 решается за О (во) элементарных действий [518].
248
§ 1. Сетевое представление обслуживающих систем
В этом параграфе приводятся алгоритмы построения расписаний, допус-
тимых относительно взвешенных смешанных графов. Под смешанным
графом понимается конечный (мульти) граф, содержащий дуги и (неори-
ентированные) ребра.
1.1. Пусть дано конечное множество операций Q - {1,2, Под
операцией в теории расписаний обычно понимается процесс обслуживания
отдельного требования отдельным прибором при некотором конкретном
обращении к этому прибору или в более общем случае — процесс одно-
временного обслуживания нескольких требований несколькими при-
борами.
Каждой операции i в Q сопоставляется положительное действительное
число tt - длительность ее выполнения. Момент начала (окончания) опе-
рации i G Q обозначим через tf (соответственно tf). Предполагается, что
каждая операция i Е Q выполняется без прерываний и > 0. Значение
7/ равно Г/+ tj.
Расписание выполнения операций однозначно определяется заданием
моментов начала (или окончания) всех операций. Качество расписания ха-
рактеризуется значением заданной неубывающей по каждому из аргумен-
тов действительной функции F (xY, х2,. . . , xq) при X/ = 7/, i = 1,... ,q.
Расписание считается оптимальным, если ену соответствует наименьшее
значение указанной функции.
Типичные для задач теории расписаний ограничения на порядок выпол-
нения операций, возможности их одновременного выполнения и т.п. могут
быть описаны посредством задания на множестве операций специфичес-
ких бинарных отношений.
В дальнейшем разность t*- - будем обозначать через Д/у. Если по усло-
вию задачи операция i должна предшествовать операции j, то должно выпол-
няться неравенство Д/у > Г/. В ряде случаев приходится принимать во внима-
ние временные затраты, связанные с переналадкой приборов, транспортиров-
кой требований и т.п. Если при переходе отоперации i к операции/ эти затра-
ты равны Tjj >0, то должно выполняться неравенство Д/у > Г/ + т/у. Если раз-
решено частичное или полное совмещение во времени операций i и / , то
должно выполняться неравенство вида Д/у > 6/у, где Ьц — заданное число,
<Г/.
Естественным обобщением этих ситуаций является условие Д/у > Д/у,
где а/у - заданное действительное (возможно, отрицательное) число.
Иногда это условие удобно записывать в виде Д/у (- °°, а^).
Отметим, что если задано несколько неравенств вида Д/у > ац (для од-
них и тех же операций i и/), то достаточно оставить наиболее сильное из
них (исключив из рассмотрения остальные). Поскольку Д/у = tf — -
= - (Г/ - Гу) = - Ду/, то неравенства Дц > ац и > а^ совместны тог-
да и только тогда, когда ац + ац <0.
Если операции i и / могут выполняться в любой последовательности
одним и тем же прибором и этот прибор одновременно может выполнять
не более одной операции, то должно выполняться либо неравенство Д/у >
> //, либо неравенство Ду/ > Гу. Если при переходе от одной операции к
другой требуется переналадка прибора, то должно выполняться одно из
249
неравенств Д/;- > tt + тр или Д7/ > tj + тц, где тц и г, z -соответствующие
длительности переналадок прибора.
В общем случае можно потребовать, чтобы выполнялось хотя бы одно из
неравенств Д/7 > или Д/7 > ар, гдеа/7 иа/7 - заданные действительные
(возможно, отрицательные) числа. Это условие может быть записано в виде
Д/7 £ (-ар, ар). Оно является существенным, если ар + ар > 0.
Отметим, что если для одной и той же пары операций i и / задано нес-
колько условий вида Д7/- (—ар, ар), то можно найти объединение всех
интервалов вида (-а7/, а/7). В результате будет получена некоторая сово-
купность, вообще говоря, новых интервалов, для каждого из которых
следует записать соответствующее условие. Совокупность этих условий, оче-
видно, эквивалентна исходным. В частности, если всеац и ар неотрицатель-
ны, то будет получено единственное условие вида кц ф (—а*ц, а'ц)-
Аналогично можно поступить и в том случае, когда наряду с условиями
вида Д/7 £ (-ар,ар) заданы условия вида Д/7 (-<», aif) и Д/7 (-ар, ©°)
(последнее условие эквивалентно Д71- (~°°, ар)).
Множество операций с заданными на нем бинарными отношениями
указанного вида удобно представить взвешенным смешанным (мульти)
графом G = (Q, Uf V). Здесь Q — множество вершин (операций); U — мно-
жество дуг, каждой из которых (/,/) приписан вес#/,; V — множество
ребер, каждому из которых [/,/] сопоставлена пара весов ар и ар . Дуга
(/, /) определяет условие Д/;- > ар или, что то же самое, условие Д17
(-°°, ар). Ребро [/,/] определяет условие: либо Д7/- > ар, либо A/z- >
> ар (иначе говоря, Д/7 (-ар, ар)) .
Из приведенных выше рассуждений следует, что граф G не содержит
петель, его подграф (Q, И) может содержать кратные ребра, в то время
как подграф (Q, U) не содержит кратных дуг.
1.2. Примеры, а) Пусть заданы условия Д7/ ф (-°°, 3), Д/7 (7, 10),
Д/7 (9, 15), Д/7 (18, 22), Д/7 (21,°°).Объединением перечисленных
интервалов является совокупность {(—°°, 3), (7, 15), (18, °°)} . Описан-
ная ситуация представлена на рис. 1.1,а. Вес ар- указан над ребром [/,/],
авеса7,- — под ним.
б) На рис. 1.1, б заданы следующие условия: Д/7 (-6, -4), Д/7 $
$ (-2,3),Д^(7,10),Д0^(13,оо).
в) Условия До £ (-°°,-7), Д„£ (-8,-1), До ? (-2,2), Д,7е (1,8),
Д/7- (5, °°) противоречивы, поскольку объединением указанных интерва-
лов является (—°0,00).
1.3. Как уже отмечалось, расписание выполнения операций множества Q
однозначно определяется заданием моментов > 0 их начала (либо мо-
ментов tf > 0 их завершения).
250
Допустимое относительно графа G = (Q, U, V) расписание должно
удовлетворять следующим условиям:
а) Г/-Г/> а,/для всех (/,/)€(/;
б) > akj либо г9 - Гу > akt для всех [i ,j]k £ И, где индекс к
отражает возможное наличие в графе G кратных ребер.
Если дано некоторое (допустимое) расписание, то для каждого ребра
[/,/]* G V известно, какое именно из двух указанных в условии б) нера-
венств имеет место. Если справедливо первое неравенство, то заменим реб-
ро [/,/ дугой (i,j)k, приписав ей вес ак,. В противном случае заменим
ребро [/,/]* дугой (/, z)\ приписав ей вес ац. Удалим все кратные дуги
вида (i,j) за исключением одной, имеющей наибольший вес.
Обозначим через P(G) множество всех ориентированных графов, по-
рождаемых смешанным графом G = (Q, U, V) в результате замены каж-
дого ребра [/,/]* Е V дугой (/,/)* с весома^ или дугой (/, i)k свесом
afj и последующего удаления всех кратных дуг за исключением дуг наи-
большего веса для каждого набора дуг вида (z,/).
Каждое (допустимое относительно G) расписание однозначно опреде-
ляет некоторый граф из множества P(G). Обратное, вообще говоря, не вер-
но. Покажем, что для существования расписания, допустимого относитель-
но некоторого графа (Q, U') из P(G), необходимо и достаточно, чтобы
этот граф не содержал контуров положительного веса. Под весом контура
или пути будем понимать, как обычно, сумму весов дуг, входящих в этот
контур или путь.
Действительно, если в графе (0, U’) содержится контур (z1? i2), (z*2,
z3), . . . , 07-i, z\), 0‘r, z’i) веса v, то должны выполняться соотношения
^а‘к'к+1, ~ ^r>airii.
Просуммировав эти соотношения, получаем v <0.
Пусть граф (Q, Uf) не содержит контуров положительного веса. Для
каждой упорядоченной пары вершин i и/ выделим все пути из вершины i
в вершину j и выберем среди них путь наибольшего веса. Этот вес обозна-
чим Vjj. Если в графе (Q, U') не существует пути из i в/, то положим =
= -°°. Поскольку в графе (Q, U'} не содержится контуров положительного
веса, то значения uz/- < «> для всех пар вершин i ,j Q.
Для каждой вершины i положим Г9 = max {0, u,z} . Значения Г9,
1 <j<q
i = 1, . . . , q, очевидно, удовлетворяют условиям tf — Г9 > а^ для каждой
дуги (z,/) G U1 и тем самым определяют искомое расписание.
Нетрудно видеть, что в этом случае графу (Q, U’) соответствует беско-
нечно много (допустимых) расписаний. Построенное выше расписание
принято называть активным, оно однозначно определено для каждого гра-
фа (Q, U'), не содержащего контуров положительного веса. Поскольку
при активном расписании выполнение операций начинается в наиболее ран-
ние сроки, то оно является наилучшим среди всех допустимых относитель-
но графа (Q, и') расписаний.
Таким образом, существует взаимно однозначное соответствие между
множеством всех активных расписаний, допустимых относительно графа G,
и множеством P(G) всех графов из множества P(G), которые не содержат
контуров положительного веса. При поиске оптимального расписания дос-
251
таточно выделить из множества ориентированных графов, порождаемых
смешанным графом G, все графы, не содержащие контуров положительно-
го веса, построить для каждого из этих графов активное расписание и выб-
рать среди них наилучшее (относительно заданного критерия оптималь-
ности) .
1.4. Пусть дан граф G = (0, U, V), у которого ф, V = ф и > 0 для
всех дуг (/,/) G U.
Этот граф принято называть временной моделью, а его графическое
изображение - сетевым графиком.
Поскольку все > Одо в графе G могут содержаться контуры только
положительного веса. Следовательно, для существования расписания, до-
пустимого относительно графа G, необходимо и достаточно, чтобы он не
содержал контуров.
Покажем, что в рассматриваемом случае активное расписание (допусти-
мое относительно бесконтурного графа С) может быть построено в резуль-
тате выполнения не более чем O(q2) элементарных действий.
За один просмотр списка дуг графа G сформируем списки A (i) =
= { j | (/,/) Е U} потомков и списки B(i) = {/ | (/, z) Е U} предшествен-
ников каждой вершины i Е Q. Распределим вершины графа G по рангам.
Для этого каждой вершине i Е Q сопоставим признак , равный числу
вершин из множества B(i), ранг которых еще не определен. Вначале поло-
жим = | В (Г) | для всех i = 1,. . . , q.
К нулевому рангу отнесем вершины i, для которых gj = 0 (если gj Ф О
для всех z = 1,. . . , б?,тов графе£ содержится контур). Для каждой верши-
ны i нулевого ранга уменьшим на единицу значение gj, если /G Л(/). В
результате значение gj для некоторых вершин j Е Q станет равным нулю
(в противном случае в графе G содержится контур). Все такие вершины j
отнесем к первому рангу и уменьшим на единицу значения gk для всех
k Е А (/). Процесс продолжается до тех пор, пока все вершины множества
Q не будут распределены по рангам.
Для всех вершин i нулевого ранга положим Г/ = 0. Вычисление значений
tf для остальных вершин j Е. Q выполним последовательно в порядке не-
убывания рангов вершин по формуле
Г? = max {t® +а„} .
ieB(j)
Нетрудно видеть, что полученные значения tf,i = 1, . . . , q, определяют
искомое расписание, и трудоемкость описанного алгоритма не превышает
б?(| U|) для связного графа G, О(| U\ + q) для несвязного графа или, в
общем случае, О (q2).
1.5. Пусть дан граф G = (Q, U, И), у которого U Ф ф, V Ф ф и веса всех
дуг и ребер положительны.
Как уже отмечалось, в этом случае совокупность нескольких условий
вида Д/у (-<*//, ^ij) эквивалентна единственному условию того же вида,
и следовательно, граф G = (Q, U, V) не содержит кратных ребер. Пара ус-
ловий Д/7 <£. (-°°, а^) и Д/у ft а'ц) эквивалентна условию Д/у
ф (-<*>, max{£/y j'y }), а пара условий Д/7 (-о©, а^) и Д7/ (-°°, а^) -
условию Д/у ф (--°°, °°). Таким образом, если (z,/) Е U, то (/, i) ф Un
[/,/] t V.
252
Поскольку веса дуг множества U положительны, то для существования
расписания, допустимого относительно графа G, необходимо, чтобы под-
граф (Q, U) графа G не содержал контуров. Покажем, что это условие
является и достаточным.
Пусть граф (Q, U) не содержит контуров. Для построения бесконтурно-
го графа, принадлежащего множеству P(G), воспользуемся следующим
преобразованием графа G.
Пусть G1 — смешанный граф, у которого / > 0 вершин отмечено и су-
ществует неотмеченная вершина / , в которую не заходит ни одной дуги,
исходящей из неотмеченной вершины. Отметим вершину i, и в случае, если
в графе G1 есть ребра, инцидентные этой вершине, заменим их исходящими
из нее дугами. Полученный в результате граф обозначим через 6^/ + 1.
Нетрудно убедиться, что бесконтурный граф множества P(G) может
быть получен из исходного графа G° - G ъ результате конечного числа ука-
занных преобразований. Если для каждого графа G1 рассматривать все воз-
можные варианты выбора вершины /, то получим множество P(G) всех
бесконтурных ориентированных графов, порождаемых смешанным гра-
фом G в результате замены каждого ребра [z, j ] G V дугой (/,/) свесом
а^ или дугой (/, z) с весом .
Трудоемкость описанного алгоритма, очевидно, не превосходит б)(| U\ +
+ I У I + q) следовательно, общая трудоемкость построения активного
расписания (допустимого относительно графа G) не превосходит O(q2).
Для того чтобы получить все активные расписания выполнения операций
множества Q, требуется не более чем 0{q21 P(G) |) элементарных дейст-
вий. Алгоритмы вычисления и оценки величины | P(G) | рассматриваются в
следующем параграфе.
1.6. Пример. Рассмотрим задачу построения оптимального расписа-
ния обслуживания требований множества N - {1,2} приборами А, В, С и
D. В табл. 1.1 и 1.2 § 1 гл. 2 заданы маршруты А1 = (А, В, С, D, А) и L2 =
= (А, В, А, С, А, С) прохождения приборов при обслуживании первого и
второго требования соответственно и указаны длительности выполнения
всех операций.
Пусть Qi = {1,2,...,5} и Q2 = { 6, 7,. . . , 11} - множества операций
по обслуживанию первого и второго требований соответственно.Операция 1
состоит в обслуживании требования 1 прибором А, операция 2 — в обслужи-
вании требования 1 прибором В и т.д., операция 11 состоит в обслуживании
требования 2 прибором С. Введем в рассмотрение фиктивную операцию
12 - завершение обслуживания обоих требований.
На рис. 1.2, а представлен смешанный граф G = (Q, U, К). Множество
операций Q = Qi U Q2 U {12 } . Множество дуг ^определяет последователь-
ности выполнения операций (маршруты Z1 и L2 обслуживания требова-
ний) . Множество ребер V задает невозможность одновременного обслужи-
вания двух требований одним и тем же прибором. Каждой дуге (/, / ) G I/
приписан вес равный длительности Г,- выполнения операции i G Q.
Каждому ребру [?,/] G V сопоставлена пара весов а^ = и а^ = tj (веса
ребер на рисунке не указаны).
На рис. 1.2, б представлен один из графов множества P(G). Используя
алгоритм, описанный в п. 1.4 этого параграфа,, построим активное распи-
сание, допустимое относительно этого графа. Построенное расписание яв-
253
Рис. 1.2
ляется оптимальным для целевой функции F(xlf х2,.. ., х12) = 30х5 +
+ х] j (см. § 1, гл. 2).
1.7. Пусть дан граф G = (Q, U, К), у которого ЦФ ф, V = ф и не для всех
дуг (/,/) £ t/весаа^ положительны.
Этот граф обычно называют обобщенной временной моделью, а его гра-
фическое изображение — обобщенным сетевым графиком.
Если граф G не содержит контуров, то для построения активного распи-
сания (допустимого относительно графа 67) можно воспользоваться алго-
ритмом трудоемкости O(q2}, описанным в п. 1.4 этого параграфа. Если
граф G содержит контуры, то можно воспользоваться описанным ниже ал-
горитмом (трудоемкости <7(д3)), который позволяет построить допусти-
мое активное расписание либо убедиться в невозможности его построения
(из-за наличия в графе G контуров положительного веса).
Как показано в п. 1.3, если в графе G нет контуров положительного
веса, то искомое (активное) расписание определяется значениями г? =
= max {0, Vji}, где, как и прежде, сц — максимальный вес пути из вер-
1
шины / в вершину/ графа G (значение равно — *», если не существует
пути из j в i).
ДУГУ С , /) будем называть базисной, если ее вес равен . Для вычис-
ления значений для всех упорядоченных пар вершин i и / из множества
Q будем последовательно добавлять в граф G базисные дуги.
Рассмотрим квадратную матрицу порядка q с элементами
40,=
afy, если
О, если /=/,
— если i^j.
Последовательно для каждого индекса I = 1, 2, . . . , q вычислим значения
элементов матрицы На И* II, используя соотношение
[z] , U-1 ] [/-И [Z-1K
atj = max{af/- , ац + az/ }.
254
(1.1)
Каждая матрица ||а/;. ||, 1 < I < q, однозначно определяет граф
(Qf (Н 1) следующим образом: если ’ > — ©о, то дуга (z,/) свесом
[z 1 rr[l 1 /• ч тт[11
принадлежит множеству U , в противном случае (z,y) £ с/
.. 1 ..
Очевидно, что трудоемкость построения всех матриц || • ||,
1</ не превосходит О (q3).
г. 1 Л , .1 1<И
Покажем, что если аИ = 0 для всех i = 1,q, то значение = uf/-
[<И
при i и а у > — ©о. Рассмотрим произвольную пару вершин i,j &Q,
[ q 1
для которой >— ©о. Если дуга (i,j) в графе G является базисной,
[/ ]
то согласно (1.1) для всех I - 1, ..., q.
Пусть д = (z = z’i, z2, ..., zr_i, ir = j) — максимальный по весу путь
из вершины z в вершину / в графе G, г >2 и z\ = min{z2, ..., ir-i} .
Очевидно, что все дуги пути д являются базисными, и их вес в графе G и
[/ ]
в графах (С, U ), I = 1, один и тот же.
При вычислении значения aik_iik^i по формуле (1.1) имеют место
соотношения
Ufc-1] Ufc-1] Ufc-1] _
а*к-1*к+1 ^aik-lik + aikik+l +
Следовательно, в графе (Q, U ) содержится дуга (jk-i, z\ + 1) веса
+ j = + aikik + i> которая является базисной (в противном
случае путь д не был бы максимальным по весу).
Рассмотрим путь, полученный из д в результате замены пары дуг
(z\-i, ik) и (z’fc, z‘fc + 1) дугой (ffc-i, z\ + 1). Этот путь также имеет
вес Vjf, но состоит из меньшего числа дуг по сравнению с путем д.
Повторяя эти рассуждения конечное число раз, получим путь веса
из вершины z в вершину /, состоящий из единственной (базисной) дуги,
I я ]
И С1ц - Vfi .
° ° 1Z ]
Если при некоторых I < q и i £ Q значение аИ > 0, то в графе
U 1
(Q, U ), а следовательно, и в графе G содержится контур положитель-
ного веса, проходящий через вершину z.
1.8. Использование неположительных весов дуг и ребер позволяет естест-
венным образом описывать многие типичные для задач теории расписаний
ситуации. В частности, можно задавать директивные сроки обслуживания
255
требований, ограничения на суммарную длительность выполнения операций,
необходимость обслуживания требований без задержек или без простоев
приборов и т.п. Рассмотрим несколько примеров.
На рис. 1.3,а представлено требование, которое необходимо обслужить
в течение интервала длительности t. Иными словами, общее время выполне-
ния множества операций {1, 2, 3} по обслуживанию этого требования
не должно быть больше t. Если Z = G +12 + ?з,то требование будет обслу-
живаться непрерывно без задержек при любом (допустимом) расписании.
Выполнение операций, представленных на рис. 1.3,6, должно быть начато
одновременно.
На рис. 1.3, в задан момент dk поступления и директивный срок Dk об-
служивания требования к. Операции по обслуживанию требования к обо-
значены 1, 2, 3 и 4. Фиктивная операция 0 означает начало обслуживания
всех требований, значение = 0.
На рис. 1.3,г представлена ситуация, в которой прибор не должен про-
стаивать при выполнении операций множества {1,2,3}. Предполагается, что
значения ац = и ац = tj для каждого ребра [/,/]£ {[1,2], [1,3], [2,3]}
и значение t + t2 +13.
1.9. Пусть дан граф G = (Q, U, V), у которого U = ф и ау — произволь-
ные числа.
В этом случае построение расписания, допустимого относительно гра-
фа G, не вызывает особых затруднений.
Действительно, если V = ф, то положим = 0 для всех i G Q. Пусть
V Ф ф. Используя алгоритм, описанный в п. 1.5, построим бесконтурный
граф (Q, U9) G ?(G), где | U9 | = | V | (нетрудно видеть, что этот алго-
ритм можно применять и в случае, когда граф G содержит кратные ребра).
Для построения активного расписания, допустимого относительно графа
(С, U9} и графа G, воспользуемся алгоритмом, описанным в п. 1.4.
Общая трудоемкость построения этого расписания не превосходит
О(| И| +?).
256
1.10. Перейдем к рассмотрению общего случая. Пусть дан граф G =
= (Q, U, V), у которого 1/Ф ф, V Фф иац — произвольные числа.
Поскольку задача проверки существования расписания, допустимого
относительно графа G, сводится к задаче проверки существования во мно-
жестве Р (G) графа без контуров положительного веса, то для существова-
ния указанного расписания достаточно, чтобы граф (Q, U) не содержал
контуров, и необходимо, чтобы этот граф не содержал контуров положи-
тельного веса.
Покажем, что при наличии в графе (Q, U) контуров неположительного
веса задача проверки существования допустимого расписания является
NP-трудной в сильном смысле даже в том случае, когда все веса положи-
тельны за исключением одного, приписанного некоторой дуге графа G.
В § 2 гл. 1 доказана NP-трудность в сильном смысле следующей задачи
распознавания. В обслуживающую систему, состоящую из трех прибо-
ров А, В и С, в момент времени d поступают требования множества
N = {1, 2, ..., п}. Каждое требование k Е N обслуживается приборами в од-
ной и той же последовательности (Л, В, С). Необходимо определить, суще-
ствует ли расписание $° (без прерываний) обслуживания требований мно-
жества N такое, что общее время обслуживания требований ^max(s°) не
превосходит заданного положительного числа у. Можно считать, что d > 0,
хотя доказательство NP-трудности в сильном смысле этой задачи приве-
дено для d = 0.
Введем в рассмотрение смешанный граф (0, £/°, К), представленный
на рис. 1.4. Здесь Q — множество операций по обслуживанию требований
приборами. Операциям по обслуживанию требования к Е N приборами
Рис. 1.4
А, В и С присвоены номера 3 к — 2, Зк — 1 и 3 & соответственно. Фиктив-
ные операции 0 и 3 п + 1 означают начало и окончание обслуживания требо-
ваний N. Множество дуг £7° задает маршрут прохождения приборов при
обслуживании каждого требования, а множество ребер V указывает на не-
возможность одновременного выполнения двух и более операций одним
прибором. Каждой дуге (z, / ) G Uприписан вес ац = , а каждому ребру
[i, / ] G V - пара весов а^ = Zz и = tj .
17. В.С. Танаев
257
Очевидно, что для построения графа (Q, UQ, К) требуется не более
О(п2) элементарных действий.
Через G = (Q, U, V) обозначим граф, полученный из графа (Q, UQ, К)
в результате добавления дуги (3 п + 1, 0) с отрицательным весом
^Зп + 1,0 ~ ~У-
Нетрудно видеть, что расписание $° существует тогда и только тогда,
когда множество P(G) содержит граф без контуров положительного веса.
Следовательно, задача проверки существования допустимого относительно
графа G расписания является NP-трудной в сильном смысле.
§ 2. Смешанные графы
В данном параграфе исследуются свойства смешанных графов, которые
можно использовать для построения допустимых относительно этих графов
расписаний.
2.1. Пусть G = (Q, U, К) — конечный смешанный граф без петель и
кратных дуг. Заменим в G каждое ребро [z, j ]к Е V парой дуг (z,/ и
(/, z)k. Индекс к отражает возможность наличия в графе G кратных ребер
вида [z, / ]. Полученный ориентированный граф обозначим через G, а мно-
жество всех его контуров — через Н.
Каждый из контуров множества Н в общем случае содержит дуги двух
видов: собственно дуги множества U и дуги (z,/)\ которым в смешан-
ном графе G соответствует ребро [i,j Е КВ последнем случае будем
говорить, что контур содержит ребро [z, / ]k независимо от того, содержит
ли этот контур дугу (/,/ )к или дугу (/, i)k.
Обозначим через P(G, Н) множество всех ориентированных графов, по-
рождаемых смешанным графом G в результате замены каждого ребра
[z,/ ]к Е V одной из дуг (i,j}k или (/, z)fc и не содержащих ни одного
контура из заданного множества Н С Н. Мощность множества P(Gf Н)
обозначим через p(G, Н). Очевидно, что p(G, ф) = |P(G) | = 2’ v । и
p(G9H) =|P(G)| .
Покажем, что задача проверки неравенства p(G,H} > 0 является
NP-полной даже в том случае, когда в графе G нет кратных ребер и каж-
дый контур множества Н содержит не более трех ребер и не более трех дуг.
Для этого построим полиномиальное сведение к ней задачи о 3 - в ы -
полнимости (см. вводную часть данной главы).
Будем использовать следующее обозначение. Пусть у Е {0, 1}, тогда
[ х при у = 0,
xv = <
I х при у = 1.
Рассмотрим множество дизъюнкций Я = {Я1? ..., Я^}, содержа-
vk vk vk
щих по три литерала каждая: £lk = {xk^1 j xk*2, xk^3} , где ykjE[Q9 1},
xklEX, IE {1,2,3}, fc=l,...,co.
258
Построим смешанный граф (Q, UQ, V) следующим образом. Каждой
переменной х^Х поставим в соответствие пару вершин , х} и ребро
[х®,х{]. Каждой дизъюнкции £1к, &=1,...,со, сопоставим три дуги:
1-Рж. Vj, Vk
(xk2 (xk2 2> Xk3*) и (xk3 3’ Xk1i)-
В построенном графе нет петель и кратных ребер. Через G- (Q, U, К)
обозначим граф, полученный из (Q, £7°, К) в результате отождествления
кратных дуг. Каждой дизъюнкции £1к, к - 1,. .., со, соответствует замк-
нутый путь
vk 1-
Рк^&к^ xkl
vk2 '-Ч
Хк2\ *к2
vk
Х^3
Поскольку в все переменные различны, то - простой замкну-
тый путь, т.е. контур.
Положим Я = {дь д2,. .. ,Mcj} и рассмотрим задачу проверки нера-
венства p(G, Н)>0. Трудоемкость построения графа G и множества
контуров Я, очевидно, ограничена полиномом от т и со.
Покажем, что если множество дизъюнкций Q выполнимо, то
p(G, Н)> 0. Пусть существует набор значений переменных Х/=Л/, G
G{0, 1}, Z= 1,... ,m, при котором выполнены все дизъюнкции £1к, к =
= 1,. .., со. Иными словами, для каждого к = 1,. . . , со существует ин-
и к
деке ZG {1,2,3} такой, что хк^=1 при xkj = akr
По набору значений переменных ах, а2,... ,ат построим ориентиро-
ванный граф (Q, U')^P(G, ф), положив Uf = U U {(Xpx/)|az = 1} U
U {(х/, xz°) | di = 0} . Граф (£>,£/') не содержит контура рк, к = 1,...,со,
. , г.
поскольку множество и не содержит дуги (хк ‘ хк ). Следователь-
но, (Q, U’)€P(G, Я).
Покажем, что при p(G, Н)> 0 множество дизъюнкций Q выполнимо.
Если существует граф (Q, U")G.P(G, Я), то для любого контура рк^Н
1-»к vk
во множестве U" найдется дуга (хк г, хк г) такая, что дуга
z vkr l~vk.
(*kr , *kr )^д*.
Для каждого к = 1,. . . , со положим xkr = vkr. Остальным переменным
присвоим произвольные значения из множества {0, 1). Тогда по опреде-
vk
лению xkrr = 1 и каждая дизъюнкция к = 1,. .. , со, выполнена.
Таким образом, задача о 3-выполнимости полиномиально сводится к
задаче проверки неравенства р((7, Я)>0, и следовательно, последняя яв-
ляется АТ5-трудной задачей. Отметим, что задача проверки неравенства
p(G, Н)> 0 остается сложной и в том случае, когда мощность множест-
ва Я сравнительно невелика (например, когда значение |Я| не пре-
восходит 0(g), где q = | Q |).
Для доказательства NP-полноты задачи проверки неравенства p(G, Н) >
> 0 покажем, что она полиномиально сводится к задаче о выполни-
мости. Пусть G = (Q, U, И) - произвольный смешанный граф без петель
и кратных дуг и Я = {д1?д2,. .. , дл}.
17*
259
Скг
I V I
Пронумеруем элементы множества V. V= U [z,/]z. Соответственно
/я i
ориентациям ребра [z, /] z припишем тот же индекс Z: (z, /)z и (/, z)z.
Каждому ребру [z, /] z сопоставим булеву переменную xz, которая
принимает значение!, если ребро [z, /]z, i<ij, заменяется дугой (JJ)i,
и значение 0, если это ребро заменяется дугой (/, z)z. Таким образом,
каждый граф (Q, U') £P(G, ф) однозначно определяет некоторый набор
значений переменных xz = bh l~ 1,. . . , | V |, и наоборот.
Если контур рк из множества Н содержит ребра с номерами кг, к2,...
то он определяет набор значений переменных хк - ск , г -
= 1....6, где г г
1, если Й/)гг6д*, i<j,
О, если (/,
Очевидно, что граф (Q, £/')не содержит контура цк тогда и только
тогда, когда bi^ckr хотя бы для одного индекса 1-кг. Следовательно,
для того чтобы P(G, Н)Ф ф, необходимо и достаточно, чтобы было вы-
полнимым множество дизъюнкций £2 = {£7 t, 12 2 , • • . ,12/J, где 12 w =
f }~ск, х~ск2
= {**, > хкг .......xks > - m =
Отметим, что в формулировке задачи проверки неравенства р((7, Н) >
> 0 в виде задачи о выполнимости длина записи входных данных за-
висит только от | V | и h и не зависит от | U | и q. Для построения гра-
фов из множества P(G, Н) можно использовать известные алгоритмы
решения задачи о выполнимости. В частности, если в каждом контуре
рк, к= 1,. . . ,/z, содержится не более двух ребер, то алгоритм решения
задачи о 2-выполнимости позволяет построить граф (Q, U') Е P(G, Н)
или установить, что P(G, Н)- ф, за 0(h) элементарных действий.
2.2. Для построения всех графов множества P(G, Н) можно восполь-
зоваться следующей процедурой последовательного ориентирования ре-
бер смешанного графа G.
Пусть д1 - один из контуров множества Н, содержащий наименьшее
число ребер множества V, a [z, /]к - содержащееся в контуре д1 ребро
(для определенности контур д1 содержит дугу (/,/)*), которое принад-
лежит наибольшему числу контуров множества Н по сравнению с дру-
гими ребрами данного контура. Если контур д1 не содержит ребер мно-
жества И, отличных от ребра [z, j]k9 то заменим в G ребро [z, j]k ду-
гой (J,i)k. Полученный в результате граф обозначим через G2. В про-
тивном случае наряду с G2 построим граф G3, заменив в G ребро
[z, j]k дугой (z, j)k. Таким образом, получим граф G2 и, возможно,
граф G3, отличающиеся от графа G тем, что одно из его ребер замене-
но дугой. Построим множество контуров Н2 Q Н графа G2 и множест-
во контуров H3Qh графа G3, удалив из множества Н все контуры,
содержащие дугу (z, j)k, и все контуры, содержащие дугу (/, i)k, соот-
ветственно. (Напомним, что G1 обозначает граф, полученный из G1 ~
260
~(Q,Ul, И1) в результате замены каждого ребра [z, /]/сЕИ/ парой дуг
(О’)* и (/, i)k.)
Пусть построены граф G1 и множество контуров HlQH. Если Н1 =
= ф, то переходим к рассмотрению следующего по порядку графа.
Если Н1^ф, то среди элементов множества Н1 выделим контур, со-
держащий наименьшее число ребер множества V (без учета ребер, кото-
рые уже заменены дугами). Если таких контуров несколько, то выбе-
рем любой из них. Пусть [a, Z>]с — ребро выбранного контура, которое
принадлежит наибольшему числу контуров множества Н1 по сравнению
с другими ребрами, содержащимися в выбранном контуре. Относитель-
но графа G1, ребра [а, Ь]с и множества Н1 проведем рассуждения, ана-
логичные тем, что проводились относительно графа G, ребра [z, /]к и
множества Н.
Нетрудно заметить, что в каждом построенном графе не содержится
контура из множества Н, в котором все ребра заменены дугами.
Процесс заканчивается, когда каждому полученному графу Gm =
~(Q, Um, Vm) соответствует пустое множество контуров Нт, Смешан-
ный граф Gm определяет множество, состоящее из 2ll/W1 искомых ^ори-
ентированных графов, каждый из которых получается из графа Gm в
результате замены всех ребер множества Vm дугами, ориентированны-
ми произвольным образом. Поскольку на каждом шаге реализуются все
возможные альтернативы, то получаем все графы множества P(G, И).
2.3. При вычислении значения p(G,H) можно использовать следующее
обобщение описанной процедуры ориентирования ребер множества V,
Пусть д1 - один из контуров множества Н с наименьшим числом ре-
бер. В смешанном графе G заменим дугой каждое ребро [z, /] \ принад-
лежащее контуру д1. Если д1 содержит ребер, то в результате полу-
чим 2и» различных графов: Gx = (Q, Uh ИД /= 1, 2,. . . , 2U1. Пусть кон-
тур р1 содержится в графе G Число графов множества Р(С,ф), со-
держащих контур р1, равно 2 2и» . Для каждого I = 1,2,.. ., 2^ — Ь
отметим граф Gj и определим подмножество Hi контуров множества Я,
которые содержатся в графе G}.
Таким образом, на первом шаге алгоритма рассмотрен исходный граф
G, отмечены графы Glf G2,.
и отобран граф G
На вто-
1
”1
ром шаге аналогично из графа Gx выбирается контур р2 ЕН, содержа-
щий наименьшее число v2 ребер графа Gl9 и каждое ребро этого конту-
ра заменяется дугой. В результате граф G^ оказывается рассмотренным,
некоторые графы , G^Vi + v2 х ~ отмеченными, а граф
G v + v , содержащий контур д2, — отобранным. Очевидно, число всех
2 1^ + 1
графов множества P(Gf ф), содержащих контур р2, равно 2 2U* .
Таким образом, после выполнения т шагов получаем равенство
р((7, Я) = 2|Г| - S [2IK/I - pdG^H,)],
1 = 1 zfa
i
где W/ = S vj и Л — множество индексов отмеченных, но не рассмотрен-
/=1
ных до ди-го шага включительно графов.
Поскольку процедуру замены дугами ребер, содержащихся в конту-
ре р1^Н, требуется выполнить не более чем для П (2Vk — 1)рассмот-
Jt=i
Л l-l Vjc
ренных графов, то справедлива оценка O(S Vj П (2 — 1)) трудоем-
1=1 к=1
vk*Q
кости описанного алгоритма вычисления p(G,H). При выполнении ус-
ловия vk < 1 для всех к = 1,...»h — 1 получаем оценку 0(h).
2.4. При сравнительно небольшой мощности множества контуров Я =
= { gi, р2, • • • , Дл) более эффективным является следующий алгоритм
вычисления значения p(G,H).
Обозначим через 0(7) число графов множества P(G, ф), содержащих
контур и в общем случае через в(12, 12, • • ,lm) ~ число графов
множества Р(О,ф), каждый из которых содержит контуры Д/ ,...
... , pim из множества Н. Контуры ра и рь будем называть совмести-
мыми, если не существует ребра [/, /]к G V такого, что дуга (/, j)k при-
надлежит одному из этих контуров, а дуга (/, /^-второму.
Очевидно, что для того чтобы 0(71,/г,.. •,/ш)О, необходимо и
достаточно, чтобы контуры Щ ,Pi ,. • •, Pim были попарно совмести-
мыми.
Составление всех множеств попарно совместимых контуров можно вы-
полнить следующим образом. Пусть составлены все множества попар-
но совместимых контуров мощности m — 1: {р к, р к,..., р к }, к =
lm—l
1с 1с к
= 1,. . . , и. Для определенности можно считать, что 7* < 12 < . . . < lm _ ь
к- 1,. . . , и.
Для того чтобы составить все множества попарно совместимых кон-
туров мощности ш, достаточно рассмотреть пары совместимых множеств
вида{д.л, дл......g.fc , Ц.к } и {д к, ц к,.. .,д к , 1к.р },где
*1 Ч lm — 2 1 *i *2 — 2 lm — 1
ZW_1 Если контуры р.к и p p совместимы, то и контуры
'm-l 'm — 1
с индексами lt , 12 ,.. . ,lm_2 ,lm _ i ,lPm_ 1 попарно совместимы. Состав-
ление списка пар совместимых контуров осуществляется непосредствен-
ной проверкой условия совместимости.
Используя известный в комбинаторном анализе принцип включения и
исключения, получаем
р(С;Я)=2,Г| -2 0(я) + 2 0(я, Ь)-Ъ®(а, Ь, е) + ... ,
где суммирование проводится соответственно по всем контурам ра, по
всем парам совместимых контуров ра и рь, по всем тройкам попарно
совместимых контуров ра, рь и рс и т.д.
Пусть w — максимальное число попарно совместимых контуров мно-
жества И, a V(lx, 12,... ,lm) — число различных ребер, каждое из
262
которых содержится хотя бы в одном из попарно совместимых конту-
ров nit, ,..., , где /1 < /2 <... < 1т. Тогда, очевидно,
...'">>
и, следовательно,
w
p(G, Я)=2|Г| + S (-1У” S 2^1-^,/,.....................im)
т = 1 01 > 11’— > )
Легко показать, что оценка трудоемкости описанного алгоритма вы-
числения значения p(Gf Н) равна О (v 2w + 1), где v — максимальное чис-
ло ребер, содержащихся в одном контуре из множества Н. Сравнивая
ее с оценкой, приведенной для алгоритма из п.2.3, можно предложить
следующую комбинацию алгоритмов. Вначале, используя алгоритм из
п.2.3, подсчитать графы из множества P(G, ф) без контуров из множест-
ва Н со сравнительно небольшим числом ребер, а затем, используя ал-
горитм из данного пункта, вычислить p(Gj9Hi) при сравнительно неболь-
ших значениях \Ht\.
2.5. Очевидно, P(G,H) представляет собой множество P(G) всех бес-
контурных графов, порождаемых смешанным графом G в результате за-
мены каждого ребра множества V дугой. В этом случае наряду с
p(G, Н) будем использовать обозначение p(G).
Отметим, что в любом графе (Q, U')EP(G) все кратные ребра [z, j]kG.
GK графа G имеют одну и ту же ориентацию: либо либо
(/, i)k EU' для всех к. Таким образом, при изучении множества P(G)
ограничимся рассмотрением смешанных графов G, которые не содер-
жат кратных ребер и удовлетворяют следующему условию: если (i,/) G
GG, то (/, i)fiU и [ij] V.
Пусть G' = (Q, U') и G" = (Q, U") — различные графы из множества
P(G). Обозначим через e(G’, G") число ребер [/,/]€ V таких, что (/,/) G
G U', а (/, Z)GG". Пусть E(G'f G") — наименьшая из абсолютных вели-
чин разностей рангов вершин i и /, вычисленных для всех указанных
пар вершин itj^Q относительно графа G'.
Покажем, что если Gf EP(G), G" E/P(G) и e(Gf, G") = m, то существу-
ет такая последовательность графов G' = GQ, Gl9. . ., Gm = G" из мно-
жества P(G), что e(Gi_lt Gi)= 1 и E(Gi_19 Gj) = E(Gj_lt Gn)t 1=
Пусть граф G' содержит дугу (a, b), граф G" - дугу (b,a), граф Gx
получен из графа G' в результате замены дуги (а, Ь) дугой (Ь, а), при-
чем E(G', Gx) = E(G't G"). Для доказательства утверждения достаточно
показать, что Gi GP(G). Допустим от противного, что существует кон-
тур в графе Gi, а следовательно, не содержащий дуги (а, Ь) путь из
вершины а в вершину b в графе G'. Поскольку абсолютные величины
разности рангов вершин, инцидентных каждой дуге этого пути, меньше
E(G',G"), то в графе G" существует тот же путь из вершины а в верши-
ну Ъ, и следовательно, G" не принадлежит P(G). Получаем противо-
речие.
Если G', G" GP(G) и и=ф, то существует последовательность графов
G' = GQf Gi ,... ,Gr = G" из множества P(G), такая, что e(Gj_i, Gz) =
= E(G/_1,GZ)= 1, 1= 1,.. . ,r.
263
При доказательстве этого утверждения достаточно рассмотреть слу-
чай, когда e(G'f G") = 1. Пусть графы G’ и G” отличаются ориентацией
ребра [а,Ь], причем граф G' содержит дугу (а, />), а граф G" - дугу
(д, а). Возможны два случая: либо граф G’ содержит вершину с ФЬ, по-
лустепень исхода которой равна нулю, либо он не содержит такой вершины.
В первом случае предположим, что утверждение имеет место при чис-
ле вершин, равном q > 3, и докажем его справедливость при числе
вершин, равном q + 1. При 7 = 2 утверждение очевидно.
Удалим из графов G' и G" вершину с и все инцидентные ей дуги.
Полученные подграфы обозначим соответственно через G* и (7".По
предположению существует последовательность бесконтурных графов Gf =
= Go, Gt,... , Gr = G" таких, что e(Gz_ i, Gz) = E(GZ_ x, Gz) = 1,1 = 1,... , r.
Присоединив вершину с вместе с инцидентными ей дугами к каждому
графу Gb 1=0,... ,г, получим искомую последовательность.
Во втором случае единственной вершиной в графе G', полустепень
исхода которой равна нулю, является вершина Ь. Выберем в G' верши-
ну d, для которой (d, b)^U' и R(b) — R(d) = 1, где R(k) - ранг верши-
ны к в графе G'. Будем рассматривать нетривиальный случай^ когда
R(b) -R(a)> 1 и, следовательно, dJ^a. Обозначим через G' и G" гра-
фы, отличающиеся соответственно от G' и G" только ориентацией реб-
ра \b,d]. Нетрудно видеть, что графы G' и G" не содержат контуров,
отличаются ориентацией ребра [а, Ь] и содержат вершину d Ф Ъ, полусте-
пень исхода которой равна нулю. Следовательно, к этим графам приме-
нима доказанная часть утверждения. Аналогичное Л заключение может
быть сделано относительно бесконтурных графов G" и G". Действитель-
но, они отличаются ориентацией ребра [£, J], и поскольку в них не су-
ществует пути, соединяющего вершины а и d, то эти графы содержат
вершину ei^d, полустепень исхода которой равна нулю. Утверждение
доказано.
2.6. Исследуем влияние на величину p(G) некоторых преобразований
смешанного графа G.
Пусть [z, /] — некоторое ребро, возможно, [z, И Через fjG обозна-
чим граф, полученный из G в результате отождествления вершин i и
/ с последующим отождествлением всех кратных ребер, всех кратных
дуг, удалением всех петель и всех ребер [а, £], для которых в получен-
ном графе есть дуга, инцидентная вершинам а и Ь. Нетрудно обобщить
эту процедуру на множество И7 ребер. Через WG обозначим граф, по-
лученный из G в результате последовательного применения описанной
процедуры отождествления пар вершин i и / для каждого ребра [z,/] Е
Е W. Если W= ф, то будем полагать WG = G.
Вершины i и ’/ графа G будем называть несмежными, если они не
инцидентны одному и тому же ребру или дуге. Несмежные вершины i и
/ будем называть сравнимыми, если в графе (Q, U) существует путь,
содержащий эти вершины.
Покажем, что если i и j - несмежные вершины графа G, то
P(G) = p(Q, U, ru[/,/])-H,yG). (2.1)
264
Доказательство этого утверждения проведем по индукции относитель-
но числа ребер графа G.
Пусть У=ф. Если в графе (Q, U) имеется контур, то p(G) =
- p(Q, U, [4/] ) = p(ijG) = 0. Пусть граф (0, U) не содержит контуров.
Если вершины i и / сравнимы в G, то p(G) = p(Q, Ut [/,/])= 1 и p(/yG) =
= 0, в противном случае p(G) = p(ijG) = 1 и p(Q, U, [/,/])= 2.
Итак, для И=ф равенство (2.1) выполняется. Предположим, что
утверждение имеет место при | У | = т, и докажем его при | У | = т + 1.
Выберем произвольное ребро [а, £] G У. Очевидно, что
р(2, У У U [г, /]) = p(Q, U U (a, b), V U [i, /] \[а, Ь] ) +
+ p(Q,UU(b, а), У U [i, j]\[a, Z>]).
По предположению
р(0, U U (a, b\ У U [i, у] \ [a, b] )= p(Qf U U (а, Ъ\ И\[а, />)]) +
+ р(//«2 UU(a,b), К\[а, 6]))
И
Р(0, UU(b, а\ KU [z, j]\[a, b]) = p(Q, UU(b, а), И\[О]) +
+ p(jf(Q.UU(b, а). К\[а, £>]))•
Наконец, p(G) = p(0, UV(a, b\ И\[a, b]) + p(Q, U\J(b,a), И\р, b]) и
P(o^) = p(v(a (л, b), К\[а, b])) +p(f/(2, UU (b, а), Г\[а, b])).
Утверждение доказано. | к' I
Пусть элементы множества У'Q У пронумерованы: У'= U [/,/]/•
/= 1
Применяя равенство (2.1) конечное число раз, можно получить следующее
соотношение'. jt_1
p(G) = р(& У И\ У') + S Р(z,«2, И\ U [а, Ь] ,)).
ЮДек' /=1
Это равенство позволяет свести вычисление значений p(G) при | Q | = к
к вычислению значения p(Q, U) и значений p(G) при | Q | = к — 1.
Аналогично, если И' £ У и граф (0, U') ациклический, то p(G) =
= 2р(и/(£?, Е\И')), где суммирование проводится по всем WQ У,для
которых в графе (Q, И7) нет цепи, соединяющей смежные вершины гра-
фа (Q, U, У\У').
2.7. В заключение отметим, что если i и j - несмежные вершины
графа G, то
2p(G) > р(& У, У U [i, /]) > р(0 > р(0, UU (/, /), У) > 0.
Сформулируем условия, при которых в этом соотношении имеет место
знак равенства.
Если i и j — несмежные вершины графа G и p(G)^Q, то следующие
утверждения эквивалентны:
а)р(2,^, ИО [/,/]) = р(С;);
б) р(,^)=У
в) i и j - сравнимые вершины графа G.
Действительно, условия а) и в) эквивалентны согласно равенству
(2.1). Поскольку граф {Q. U) не содержит контуров, для б) необходи-
мо и достаточно, чтобы выполнялось условие в).
265
Нетрудно убедиться в справедливости и следующих утверждений.
Если i и j - несмежные и несравнимые вершины графа G, то
P<Q, U, ИU [z,/]) = 2p(G) и p(G) = p(ifG).
Если i и j - несмежные вершины графа Gue графе G не существу-
ет пути из j в i, то p(Q, UU (z,/), y) = p(G) и p(Q, UU (j, z), V)= p(ijG).
Если i и j — несмежные вершины графа G и p(G)¥:0, то следующие
утверждения эквивалентны’.
a)p(fll/U(f,/),K) = O;
б) р(2, UU(j, г), И) = Р(С7) + Р(170;
в) в графе (Qf U) существует путь из вершины j в вершину i.
Приведенные утверждения могут быть использованы при разработке
методов вычисления значения р((7).
§ 3. Последовательный анализ вариантов
В этом параграфе рассматриваются основанные на идеях последова-
тельного анализа вариантов точные и приближенные алгоритмы построе-
ния допустимого относительно взвешенного смешанного графа G =
= (2, U, И) расписания, которое является оптимальным (т.е. заданная
неубывающая по каждому из аргументов действительная функция
Г(хьх2,... ,xQ) принимает минимальное значение при X/, равном
моменту ti завершения выполнения операции z, i= 1, . . . ,q, при этом
расписании).
Как показано в § 1 данной главы, оптимальное расписание можно ис-
кать в классе активных расписаний. Для этого достаточно из множества
P(G) ориентированных графов, порождаемых смешанным графом G, вы-
делить множество P(G) графов, ^не содержащих контуров положительно-
го веса. Каждый граф (Q, U')G.P(G) однозначно определяет активное
расписание, допустимое относительно графа G (и наоборот). Для по-
строения этого расписания достаточно определить наиболее ранний срок
ti = ij(Q, U') завершения выполнения каждой операции i£Q относи-
тельно графа (Q, U').
3.1. Для организации целенаправленного перебора графов множества
P(G) будем использовать процедуру последовательного разбиения
множества P(G} на подмножества. При этом множествоP(G) сначала раз-
бивается на подмножества P(Gr), P(G2),. .. ,P(Gh), где Gk, k =
графы, получаемые из графа G в результате замены одного или не-
скольких его ребер дугами. Затем одно из множеств P(Gk), скажем P(Gi),
в свою очередь разбивается на подмножества P(Gh+1), P(Gh+2), ...,P(Gh + p).
В результате получаем разбиение исходного множества P(G) на подмно-
жества Р^),.. .,P(Gi-i), P(Gi+i), ,P(Gh+p) ит.д.
Этот процесс удобно представлять ’’растущим” выходящим деревом
где Zm — множество вершин, a Wm — множество дуг. Каж-
дой вершине дерева сопоставлен некоторый граф Gk = (Q, Uk, Vk), где
UQUk и Vk С V. В дальнейшем вершину дерева будем отождествлять с
сопоставленным ей графом. Корнем дерева является граф Gq = G.
266
Остальные вершины (графы) нумеруются последовательно по мере их
получения. Множество Zm = {Go, G15 . . . , Gm} . Корень Go дерева соеди-
няется исходящими дугами с вершинами Gx, G2,. . . , Gh, вершина Gj —
с вершинами Gh+i, Gh+2, • • • > Gh+p и т.д. ~
Обозначим множество висячих вершин дерева (Zw, через Zm.
Это множество определяет текущее разбиение множества P(G) на под-
множества.
Введем в рассмотрение функцию
/(Gfc) =
г min {F(ti (ft U'), U')) \{Q,U')e P(Gk)}, если P(Gk) * Ф,
I oo? еслиР(С*)= 0-
Очевидно, если Vk- ф и граф (Q, Uk) не содержит контуров положи-
тельного веса, то f(Gk) = F(ti(Q, Uk),. . . ,tq(Q, Uk)).
Через fo(Gk) и fQ(Gk) будем обозначать соответственно оценки снизу
и сверху значения f(Gk). Число rm = min{fQ(Gk) \ Gk ЕZm} будем назы-
вать (текущим) рекордом, а граф (Q, Um)G.P(Gk), для которого rm =
- ЯС, Um ) и Gfc G - рекордным.
Отношение строгого порядка заданное на множестве Zm, называет-
ся отношением доминирования, если из соотношения Gk-+Gj следует,
что /(G^^fiGj) и в дереве (Zw, Wm) нет пути из Gk в Gb
Вершину Gi^Zm будем называть конечной, если выполняется хотя бы
одно из условий:
а)Ш=№;
6)/o(Cz)>rw;
в) существует граф Gk^Zm такой, что Gk-+Gj.
Множество всех конечных вершин дерева (Zw, Wm) будем обозначать
через Zm.
При выполнении условия а) получаем точное значение f(Gj). Из ус-
ловия б) следует соотношение f(Q, U'} для любого графа
(Q, U'}^P(Gi). При выполнении условия в) существует граф (Q,U',y)^
EP(Gk) такой, что f(Q, Следовательно, если выполняется
условие б) или в), то при поиске оптимального расписания граф Gt
можно исключить из рассмотрения.
3.2. Опишем одну из типичных схем поиска оптимального расписа-
ния - схему ветвей и границ. л
1) Полагаем m = 0, Gq = G и строим рекордный граф (Q, Um)^P(Go).
Если P(Go)=0, то выполняем шаг 10. В противном случае полагаем
Zm=Zm={GQ}, zw=0, rm=fQ(Go)=f(Q,Um) и выполняем
шаг 2).
2) Из множества Zm\Zm выбираем граф Gj = (Q, Ui, Vf) и выполняем
шаг 3). Если Zm\Zm=ф, то выполняем шаг 10).
3) Вычисляем оценку fQ(Gi) значения функции f(Gi). Если /0(67) =
= /°(G/), то выполняем шаг 8), в противном случае — шаг 4).
267
4) Если справедливо соотношение
(3.1)
то выполняем шаг 9) , в противном случае — шаг 5) .
5) Если существует граф GkE.Zm, для которого выполняется соот-
ношение Gk~+Gi, то включаем Gi во множество Zm и выполняем
шаг 2). В противном случае выполняем шаг 6).
6) Строим разбиение множестваP(fii) на р > 2 подмножеств P(G'nj + 1),...
. . . , P(fim+p). Полагаем Zm+p - Zm и {Gm + !>•••, &m+p } > ^m+p ~ m
{ (fib ^m + 1) ’ • • • ’ fil > Gm+p) } , Zm+p ~ Zm U {Gm + i, . . . , Gm+p} \ {Gj t .
Выполняем шаг 7).
7) Вычисляем оценки /° (Gm +!), . . . ,/° (Gm+p) и выбираем среди них
наименьшую fQ(Gh}. Выполняем шаг 8), полагая I и т равными h и т + р
соответственно.
8) Если rm > fQ(Gi), то полагаем рекорд rm = fQ{Gi) и строим новый
рекордный граф (Q, Um) Е Pfii), для которого /°(G'/) = f(Q, Um). В
любом случае выполняем шаг 9).
9) Во множество конечных вершин Zni включаем все вершины Gk из
множества Zm, для которых /0 ?т, и выполняем шаг 2).
10) Если т = 0, то не существует расписания, допустимого относительно
графа G. Если т > 0, то оптимальным является расписание, при котором
G = G (2» Um), i = 1, . . . , б/. Оптимальное значение целевой функции рав-
но рекорду гт.
Полученный на последнем шаге граф (Zw, обозначим через
(Z, W), а множество Zm - черезZ.
При практической реализации этой схемы описанные шаги и после-
довательность их выполнения могут меняться в зависимости от особен-
ностей решаемой задачи.
33. Перейдем к более детальному описанию основных фрагменов пред-
лагаемой схемы.
Для проверки условия Pfi) Ф ф и построения рекордного графа
(2, Um) G Pfi) можно использовать алгоритмы, описанные в § 1 и § 2
этой главы. Напомним, что если граф (2, U) содержит контур положитель-
ного веса, то Pfi) = ф . Если же граф (Q, U) содержит контуры и все они
неположительного веса, то задача проверки условия Pfi) Ф ф является
TVP-трудной в сильном смысле.
Опишем алгоритм построения активного расписания, допустимого от-
носительно заданного графа G = (2, U, И).
а) Вычисляем наиболее ранний срок U) начала выполнения каж-
дой операции i G Q. Если при этом в графе (2, U) будет обнаружен
контур положительного веса, то Pfi) = ф. В противном случае выпол-
няем п. б).
б) Во множестве V выбираем конфликтное ребро, т.е. такое ребро
[ij ] k Е И, для которого выполняется соотношение
-akti < tf(Q, U) -t?(Q,U)< ak, (3.2)
268
и выполняем п.в). Если в графе (Q, U, И) нет конфликтных ребер, то
искомые времена начала выполнения операций (2, U),l = 1,. . . , q.
в) Вычисляем наиболее ранние сроки (Q, U U (z, /)*), I = 1,... л,
и выполняем п. б), заменяя граф (2, U, V) графом (2, U U (z, j)k,
V\ [*,/]*)• Если в графе (2, U U (z,/)*) содержится контур положитель-
ного веса, то вычисляем наиболее ранние сроки (2, UU (Л 0*)» / = 1,... л,
и выполняем п. б), заменяя граф (2, К) графом (2, U U (/, i)k,
И\ [*> /1 *) • Если в графе (2» U U (/, i)k) содержится контур положитель-
ного веса, то допустимого относительно графа G расписания не существует.
Через V обозначим множество всех конфликтных ребер графаG = (2, U, И).
Очевидно, что при И = ф для каждого ребра [/,/]к Е V выполняется одно
из соотношений г ° (2, U) - (Q,U) > ак- или г ° (2, U) - tf (2, U) > akj .
Для каждой дуги (z,/) Е U имеет место соотношение (Q, U) -
- (2, U) > ац. Следовательно, значения = tj (Q, G), I = 1, . . . , q,
определяют допустимое относительно графа G расписание и f (G) =
=/(2, и,лФ).
Если V ф , то для улучшения качества получаемого расписания целе-
сообразно при выборе очередного ребра [/,/]* G И использовать те или
иные правила предпочтения (приоритеты) в зависимости от вида целевой
функции. А
3.4. Если граф (2, U) не содержит контуров, тоР(С) ф и для построе-
ния активного расписания, допустимого относительно графа G, можно
воспользоваться следующим алгоритмом, трудоемкость которого не
не превосходит O(q2 + | V | ) элементарных действий.
а) Полагаем р = 0, 2° = Ф, (2, ^°, К0) = (2, У) и вычисляем наи-
более ранние сроки (2, UQ) начала всех операций i Е Q. Очевидно, иско-
мые времена начала выполнения операций tf > tf (2, U°), i = 1, . . . , q-
б) В графе (2, Gp) выбираем одну из вершин /, для которой не сущест-
вует дуги (z, /) в Up при z Е 2\ Qp- Определяем момент начала выполне-
ния операции j в искомом расписании, полагая = tj (Q, Up). Вершину j
включаем во множество упорядоченных вершин: 2р+1 = 2Р и{/}.
в) Заменяем в графе (2, Up9 Vp) все ребра, инцидентные вершине /, на
исходящие из нее дуги. Полученный граф обозначаем через (2, t/p + 1, Ир+1).
г) Используя вычисленные значения r?,z Е2р+1,и (2, Up), i Е
Е 2\ 2p+1, определяем наиболее ранние сроки (2, Up+1), i Е 2\ 2p+1 •
д) Если Ир+1 = ф, то полагаем 11 (2, Up+i) для всех z в Q\ Qp + i.
В противном случае переходим к п. б), заменяя граф (2, Up, Vp) графом
(2, 1, Ир+1), а множество Qp — множеством Qp+1.
Применяя эту процедуру к исходному графу G не более чем q раз,
получаем значения Г®, z в 2, определяющие некоторое активное рас-
писание.
При выборе очередной вершины j в п. б) обычно используют соответ-
ствующие правила предпочтения.
269
3.5. Если на шаге 2) приведенной выше схемы ветвей и границ \Zm\ Zm | >
> 2, то необходимо выбрать очередной граф из множества Zm\ Zm
возможных кандидатов.
Пусть на множестве Z задана некоторая действительная функция
Gk G Z. Будем говорить, что используется стратегия, основанная на функ-
ции \ls(Gk), если выбирается граф Gi G Zm\Zm, для которого \Ij(Gj) =
= min{0(Gfc) \GkeZm\Zm}.
Стратегию, основанную на функции ф (<7Л), называют
поиском в ширину, если значение функции ^(Gk) равно рангу R(Gk)
вершины Gk в графе (Zw, Wm);
поиском в глубину, если ^(Gk) = —R(Gky
поиском по наилучшей оценке снизу, если ф(С7Л) = /o(Gjt);
поиском по наилучшей оценке сверху, если ^(Gk) =fQ(Gk).
Эффективность той или иной стратегии определяется тем, насколько
полно функция \}j(Gk) отражает специфику решаемой задачи.
3.6. При выборе алгоритма вычисления оценок fo(Gi) на шаге 3) необ-
ходимо учитывать два противоречивых обстоятельства. С одной стороны,
уточнение оценок позволяет обычно сократить процесс ветвления. С другой
стороны, уточнение оценок сопряжено с увеличением объема вычислений,
что может компенсировать выигрыш от сокращения процесса ветвления.
Пусть (Gk, Gj) е Wm. Поскольку P(Gt) Q P(Gk), то f(Gk)
и значение /0 ) можно положить равным/0 (Gjt) • Поэтому в дальнейшем
будем предполагать, что для любой дуги (Gk, Gj ) G Wm имеет место
соотношение
(3.3)
При получении оценок снизу обычно используется прием релаксации,
т.е. замены исходной задачи белее простой задачей путем исключения из
рассмотрения некоторых ограничений.
Поскольку F(xb Хг, ...» не убывает по каждому из аргументов,
то релаксированную задачу можно получить, например, в результате удале-
ния из графа Gi = (Q, Ut, Vj ) всех или части ребер.
Если удалены все ребра графа Gj, то получаем релаксированную задачу,
состоящую в определении ранних сроков t? (Q, Uj) начала выполне-
ния операций i G Q относительно графа (0, Fz), и полагаем /о (С?/) =
Пусть некоторый порожденный подграф ((У, С/, И') графа Gj являет-
ся полным (в качестве О' Q Q обычно выбирается множество операций,
выполняемых одним и тем же прибором). Удаляя из графа 6’/ все ребра
за исключением ребер множества К', получаем релаксированную задачу
построения допустимого относительно графа (Q, Uj, I7') расписания,
при котором минимально значение заданной целевой функции.
Например, если все а^ = Г/ и требуется минимизировать общее время
выполнения операций, т.е. F(хъ х2, . . . , xQ) = max {jq | i G Q} , то ука-
занная релаксированная задаче по существу представляет собой задачу
минимизации максимального временного смещения при обслуживании
270
одним прибором частично упорядоченного множества требований Q* 9
для каждого из которых задан момент = t®(Q, Ui) поступления в си-
стему, длительность обслуживания и директивный срок Df = v(Q, Ut) +
+ ti - Vi (2, Ц), где Vi (Q, Ui) -максимальный вес пути в графе (Q, Ui)
с началом в вершине i и v (Q, = max {(Q, Ui) | i G Q} .
3.7. Рассмотрим некоторые способы разбиения множества P(Gj} на
подмножества на шаге 6) описанной в п. 3.2. схемы при различных пред-
положениях относительно графа G.
Пусть Г/ - множество конфликтных ребер графа (7Z = (2, t/z, Kz).
Как уже отмечалось, если V = ф, то f(Gf) = f(Q, Ui9 ф) и вершина Gt яв-
ляется конечной.
Если Vt ф, то разбиение множества P(Gt) определяется выбором неко-
торого конкретного подмножества Vt Q Kz. В результате замены каждо-
го ребра [/, j]k G Vi дугой (ij)k или дугой (/, i)k получаем р = 2|К/|
различных графов + . . . , Gm+p, причем P(Gi) = P(Gm + l) U. . .
• • • ^Р(Рт+р)‘ Как правило, в качестве Vt выбирают множество сравни-
тельно небольшой мощности (обычно | Vt | = 1).
Рассмотрим несколько правил предпочтения при выборе множества Vt
на примере задачи минимизации общего времени выполнения операций,
сформулированной в п. 3.6. Для каждого ребра [/,/] G Vt вычислим ве-
личину hij = rz (g, Ui) + а^ + Vj(Q, Ut) - v(Q, Ui). Поскольку ребро
[/, j ] конфликтное и вес abc = tb для каждой дуги (Z>, с) G Uh то в графе
(g, Ui) не существует пути из вершины / в вершину i. Следовательно, в
графе (g, Ui U (/,/)) найдется путь веса v (2, Ui) + hij •
Таким образом, при выборе ребер [/, /] G V} для включения во мно-
жество Vi можно использовать одну из следующих величин: hij + hjt ,
min {hij, hjt} и max {hij, hjt} , отдавая предпочтение тем ребрам, для
которых соответствующая величина больше. Использование приорите-
тов при выборе множества Vt позволяет на ранних итерациях метода рас-
смотреть /’наиболее существенные” из конфликтных ребер, после чего
остальные ребра уже не будут конфликтными.
3.8. Если в графе G - (Q, U, V) все веса а^ > 0, то каждый граф из
P(G) не содержит контуров. В этом случае обычно используют процедуру
разбиения множества P{G} на подмножества, основанную на последова-
тельном выборе вершин графа G.
Пусть я = (Zi, i2, . . . , ic) - некоторая перестановка элементов (не
обязательно всех) из множества 2- Обозначим через G (я) граф, получен-
ный из G следующим образом. Выбираем в G вершину i i и заменяем все
инцидентные ей ребра исходящими из нее дугами. В полученном графе
выбираем вершину i2 и заменяем все инцидентные ей ребра исходящими
из нее дугами и т.д., пока не будет рассмотрена вершина ic. Очевидно,
если для каждого h = 1, . . . , с вершина ih имеет нулевую полустепень
захода в подграфе графа (7(z!, z2,. . . , zZ1 - j), порожденном множеством
вершин Q\{iiJ2t. . . Jh-i}, то граф G(tt) не содержит контуров (пред-
полагается, что G (ф ) = G ).
271
Соответствующую процедур; можно описать следующим образом.
Полагаем <2о=0, Go = (Q, Ug, Ko) = G. Пусть Qo = -
множество всех вершин с нулеюй полустепенью захода в графе (Q, UQ).
Для каждой вершины i'k G Qo полагаем Qk={ik}, ^к ~ Ок) и строим
граф Gk ~G(nk). Получаем разбиение множества Р(<70) на подмножества
P(G1),. . . ,P(GqQ). Очевидно, что при любом активном расписании,
допустимом относительно графаGk, имеет место равенство 7^ = 0.
Пусть Gi = (Q, Uh Vi) = G(tt ) — граф, который рассматривается на
очередной итерации, kz - некоторая перестановка элементов множества
Qi CQ и Qi = {/i ,/2,.. . ,jqi} - множество всех вершин с нулевой полу-
степенью захода в подграфе граоа (Q, Ц), порожденном множеством вер-
шин Q\Qi. Для каждой вершшы jk^Qt строим граф Gm+k = G(itm+k)
и полагаем Qm+k - Qi U{/\} , ще лт+£ = (я/»7\)и т — число ранее пост-
роенных графов. Очевидно, Р Gz) =P(Gw + 1) U. . . 'JP(Gw+q/) и tfk =
= tJk(QtUi) при любом активюм расписании, допустимом относительно
графа Gm+k,
Если Qi - Q, то Vi -ф и вершина Gt является конечной. При таком
способе разбиения множества /(G) максимальный ранг вершин дерева
(Z, W), очевидно, не превосходив q.
3.9. Описанная в предыдущей пункте процедура разбиения множества
P(G) на подмножества может быть дополнена отсеиванием некоторых
из этих подмножеств. Ограничился рассмотрением случая, когда в графе
G = (Q, U, V ) веса
Расписание называется комшктным, если любую из операций нельзя
начать раньше, чем при этом расшсании, при условии, что остальные опера-
ции начнутся не позже. Ясно, чю любое компактное расписание является
активным (но не наоборот) и в классе компактных расписаний содержится
хотя бы одно оптимальное.
Пусть на очередной итеращп рассматривается граф Gz = (Q, l/h Кz) =
= G(kz). Из множества Qt выберем вершину /в, для которой t ja {Q, ut) =
= min {iik (Q, Ui) | jk e Qt) . Обозначим Qt ={ja} U {jk I jk e Qb [jk,
ja} e Иг)и для каждой вершины/k G Qt построим граф G{Ttt,jk). Получен-
ные графы обозначим через Gm+2> • •, Gm+p, где р= I I и m -
число ранее построенных графов р
Если Qi — собственное подмюжество Qh то, возможно, U P(Gm+k) Ф
A 1 /
¥=P((7Z). Покажем, что активное расписание s, допустимое относительно
А Р А
графа (Q, U') G P(Gt) \ U P(lm+k)i не является компактным.
к = 1
Пусть (С, U') = G (irh iiJ2, .. . , я)5 гДе iv G Q\ Qi, v = 1, .. . , co,
и через л обозначена некоторая перестановка элементов множества
272
Q\Qi\{iiJi, • • • ,ja} . Если не существует ни одного ребра [/„ Ja] G
G Vt при некотором v Е {1,2, . . ., со}, то граф (Q,U') есть G(7iiJai
р л
/1, • • • ,я) и принадлежит множеству U P(Gm+ky
fc=i
В противном случае, если найдется вершина G О1 такая, что 1 < b <
и не существует ребра [z6, zc] G Vb, 1 - 1, то граф (Q, U') есть
G(iTh ib, ii,. . - , ib-i> ib+i, - - 1‘а>л) и принадлежит множеству
p a
U P(Gm+k). Если же такой вершины не существует, то для каждого реб-
к= 1
pa \ivJa\^Vb 1 в графе (Q, U') существует путь, который за-
канчивается в вершине iv и проходит через некоторую вершину z'jG Qh
Следовательно, вес этого пути не меньше tid(Q, Ui), причем
Поскольку и
О Дб’^") <^(2’t7') при (Q, U") =G(7TiJaJiJ2, - < - то рас-
писание s не является компактным.
3.10. Рассмотрим некоторые оценки сложности метода ветвей и границ.
Напомним, что через (Z, И7) обозначено дерево (Zm, И7^), полученное на
последней итерации метода, т.е. когда Zm -Zm. Положим Z-Zm -Zm.
Введем в рассмотрение дерево (Z', И7'), полученное из (Z, И7) в резуль-
тате последовательного ветвления (на шаге 6)) каждой вершины Gx из
множества Z до тех пор, пока не будут сориентированы все ребра графа
Gz. Таким образом, дерево (Z, И7) является порожденным подграфом
дерева (Z', И7' ), и в качестве показателя сложности метода ветвей и границ
можно использовать мощность I Z \ Z | множества вершин, которые были
подвергнуты ветвлению при реализации этого метода.
Вершину Gx GZ'будем называть минимальной тогда и только тогда,
когда соотношение Gk^Gt не выполняется ни для какой вершины Gk G
G Z'. Множество всех минимальных вершин обозначим через Z. Пусть
Z = {G*GZ'| /0(Gfc) </(Go) ^/°(^)} • Нетрудно показать, что мно-
жество Z п ZC Z \ Z.
Действительно, если граф Gt G Z A Z выбран на шаге 2) описанной в
п. 3.2 схемы ветвей и границ, то после шага 3) будет выполнен шаг 4),
поскольку fq(Gi) ^f°(Gi), после шага 4) - шаг 5), поскольку/0 (Gz) <
<f(GQ) <rm, а после шага 5) - шаг 6), поскольку Gz G Z. Таким обра-
зом, если Gz G Z, то Gz Z.
Покажем, что граф Gi принадлежит множеству Z. Рассмотрим путь
Go, Gdi . . . ,G[ в графе (Z', И7'). Из соотношения (3.3) получаем/0 (Go)
</о (Gd) <. . . (Gz). Следовательно, все вершины этого пути принадле-
жат множеству Z, а поскольку Go G Z, то эти вершины принадлежат и
множеству Z. _ Л )
Таким образом, справедливо соотношение | Z \Z | > | Z П Z I.
18 В.С. Танаев 273
3.11. Предположим, что используется стратегия, основанная на функции
^(Ph)yGh G 2Г. Будем говорить, что отношение доминирования -> согласо-
вано с функщей ф(рь)9 Gh ^Z*, если из условия Gk^Gi следует нера-
венство ф (Gc) < Ф(рг) для любого предшественника Gc вершины Gk в
графе (Z', И'). Отношение -> согласовано с оценками fo(Gh), Gh £Z',
если из Gk следует /0 (Gk) (Gf). Отношение -> согласовано с гра-
фом (Z', W' , если из Gk -+Gf следует, что для любого потомка G, вер-
шины Gi найдется потомок Gkf вершины Gk такой, что Gk' -*Gi • .
Покажем, ito если отношение доминирования согласовано с Ф(Рь)>
fQ(Gh)u(Zf W'),toZ\ZCZ.
Пусть для 1екоторой итерации на шаге 2) описанной в п. 3.2 схемы выб-
ран граф Gi 6 Zm\ Z m и существует граф Gk Е Z' такой, что Gk -+Gf. По
определению иношения -> в дереве (Zm, Wm) не существует пути из Gk в
Поскольку отношение -> согласовано с функцией ^(Gk), Gk G Z', то
либо Gk G Zn, либо в графе (Z, W) найдется предшественник Gc вершины
Gky который принадлежит множеству Z т. Если Gk G Zm, то на шаге 5)
граф Gi будет включен в множество Z т. Если Gk Zmi то имеет место
одна из следующих возможностей.
а) Граф включен в множество конечных вершин Zw', 0<т' <ту
в силу равенства /0 (^с) =/° (£<?)• Тогда выполняются соотношения гт <
<гт> Поскольку отношение -* согласовано с /0(671),
Gh G Z' , то (Pk) ^f(Pi)- Получаем соотношение /0 (Gz) > гт, из ко-
торого следует, что на шаге 4) вершина 6/ должна быть включена в мно-
жество Z т.
б) Граф Gc включен в множество Z в силу выполнения неравенства
/о <Ре) гт Аналогично случаю а) получаем rm <rm> (Gc) <
</0 (рк) ^fc(Pi)- Следовательно, Gt Е Z т.
в) Граф включен в множество Z т» на шаге 5), т.е. существует граф
Ga G Zm' таюй, что Ga -*GC. Поскольку отношение -> согласовано с (Z',
1/ ), то найдется потомок Gar вершины Ga такой, что Ga' ~+Gk. Из транзи-
тивности отнешения -> получаем Ga’ ^Gt.
Если Ga> eZy то Gaf £Zmy так как отношение -*согласовано с функ-
цией Фрь). Следовательно, граф Gj должен быть включен во множество
Z т на шаге 5).
Пусть G^ Z, т.е. некоторый предшественник Gb вершины Gaf содер-
жится во мюжестве Z т. Тогда повторяем приведенные рассуждения,
заменяя графя Gk и Gc на графы Ga> и Gb соответственно.
Поскольку отношение доминирования является отношением строгого
порядка и мюжество Z'конечно, то, повторяя эти рассуждения конечное
число раз, приходим к заключению, что граф Gt должен быть включен во
множество Z п.
Следовате1ьно, Z \ Z С Z.
274
Пусть Z = {GkE Z' I fe(Gk) = f° (Gk)}, тогда, очевидно, IZ\Z|<
<1 Z\Z|.
Если отношение доминирования на множестве Z' не задано, то, полагая
Z = Z', получаем оценки | Z A Z' [ <| Z\Z | <| Z*\Z | .
3.12. Пример. Рассмотрим задачу построения оптимального по
быстродействию расписания обслуживания множества требований N=
= {1, 2,..., п} приборами А и В при условии, что каждое требование
сначала обслуживается прибором А, затем прибором В (см. § 1 гл. 1).
Покажем, как можно за О(п2) элементарных действий решить эту зада-
чу по описанной схеме ветвей и границ.
На рис. 3.1, а приведен граф G = (Q, U, V ) для п = 4. Операция по обслу-
живанию требования i G TV прибором А имеет тот же номер i, а операция
по обслуживанию этого требования прибором В имеет номер i + п. Фик-
тивная операция 2и+ 1 =9 обозначает завершение обслуживания всех тре-
бований. Каждой дуге (i,j)EU приписан вес ац, равный длительности
tt операции i EQ, Каждому ребру [f,/] е V сопоставлена пара весов
ац = ti и aji = tj (веса ребер на рисунке не указаны).
Для организации процесса ветвления будем использовать процедуру,
описанную в п. 3.8, причем одновременно с упорядочением операции i бу-
дем упорядочивать и операцию i + п (поскольку в § 1 гл. 1 показано,
что существует оптимальное по быстродействию расписание, при котором
требования множества N обслуживаются прибором А в той же последо-
вательности, что и прибором В), Из условия (1.3) гл. 1 следует, что отно-
шение доминирования можно задать следующим образом: Gk-*Gi тогда
и только тогда, когда выполняются условия:
а) ранги вершин Gk и Gt в дереве (Z, W) равны;
б) Gk = G(tt, i, п+ i) и Gi = G(tiJ,n + j),i
в) либо min {ti, tn+j} < min {tj, tn+i} , либо min {ti, tn+j} = min{tj,
tn+i} ni <j.
Очевидно, что среди вершин одного и того же ранга дерева (Z, W) су-
ществует единственная минимальная вершина. Следовательно, если отно-
шение -> согласовано с функцией ^(G^), то выполняется неравенство
I Z\Z| <и-1, и в вычислении оценок f0 (Gk) и /0 (Gk), Gk G Z, нет
необходимости.
На рис. 3.1,6 приведено дерево (Z, W), полученное при решении этой
задачи для графа G, представленного на рис. 3.1, а. Если граф (7/ получен
из Gk в результате упорядочения требования i Е N, то дуге (Gk, Gt) Е W
приписан параметр i.
На рис. 3.1, в представлен граф G9EP(G), Допустимое относительно
этого графа активное расписание является оптимальным по быстро-
действию.
3.13. Отметим, что если процесс вычислений будет прекращен, когда
Zm\Z m ^ф, то нет гарантии, что наилучшее из полученных расписаний
(допустимое относительно рекордного графа) является оптимальным.
В этом случае можно вычислить (апостериорные) погрешности наилуч-
шего из полученных к данному шагу (рекордного) расписания.
18
275
б
б
Рис. 3.1
Пусть fm = min {/о (Gk) | Gk G Zm\Z m}. Очевидно, абсолютная пог-
решность рекордного расписания не превосходит значения rm-fmi а
относительная погрешность - значения (rm - fm)Ifm.
Существенно более эффективными являются приближенные методы,
в которых вычислительный процесс с самого начала ориентирован на полу-
чение расписаний с заданной (априорной} абсолютной или относительной
погрешностью.
Так, для получения расписания с абсолютной погрешностью е вместо
соотношения (3.1) на шаге 4) описанной в п. 3.2 схемы достаточно использо-
вать более слабое условие rm ^f0 (Gf) + е. Аналогично для получения
расписания с относительной погрешностью е° вместо (3.1) достаточно
использовать соотношение rm (Pi) + е°/о (Pi )• Использование ука-
занных соотношений, как правило, обеспечивает значительное сокраще-
ние процесса ветвления.
Эффективность метода ветвей и границ существенно зависит от того,
насколько полно учитывается специфика решаемой задачи, а также полу-
чаемая в процессе решения задачи информация. Определенное распростра-
нение получили так называемые гибридные алгоритмы, в которых на раз-
ных итерациях используются различные алгоритмы вычисления оценок
/o(Gjt) и fQ(Gk)t различные функции ^(Gk), различные способы ветвле-
ния и т.д. В результате удается лучше приспособить вычислительный про-
цесс к особенностям рассматриваемого на данной итерации графа Gk и пост-
роенного дерева (Zm, И^).
276
§ 4. Оптимизация обслуживающей системы
В данном параграфе рассматривается задача оп шмального выбора
необходимого количества приборов, распределения заданного множества
операций по выбранным приборам и составления расписания их выпол-
нения.
4.1. Рассмотрим следующую обслуживающую систему. Множество Л =
= {1,2,.. . ,М} приборов разбито на пг попарно непересекающихся непу-
стых подмножеств Лх, Л г,.. . , Л m . Каждое множество Лк состоит из
Мк одинаковых приборов. Множество Q = {1, 2,... ,4} операций также
разбито на m попарно непересекающихся непустых подмножеств 0i,02, • ♦ •
.. . , Qm. Для выполнения операций i 6 Qk может быть использован любой
из приборов множества Лк. Каждая операция i€-Q выполняется без
прерываний.
Известны длительности выполнения операций, длительности пуско-нала-
дочных, не ре наладочных и транспортных работ. На множестве операций
может быть задано отношение строгого порядка, регламентирующее воз-
можную последовательность их выполнения. Могут быть указаны возмож-
ности совмещения процессов выпблнения операций во времени и т.п.
Предполагается, что все условия и ограничения представимы в виде обоб-
щенной временной модели (Q, U) (см. § 1 этой главы).
В задаче требуется:
1) определить число гк, гк ^Мк, к = 1,.. ., т, приборов множества Лк,
используемых в процессе выполнения операций;
2) распределить операции множества Qk, к = 1,...,ти, по этим приборам
(т.е. разбить множество Qk на гк попарно непересекающихся непустых
подмножеств Qk, Q2k,. . . , Qkk);
3) построить расписание выполнения операций (т.е. для каждой опера-
ции zG Q указать момент ее начала > 0 или окончания F,). При
этом значение заданной неубывающей по каждому из аргументов
функции Ф (Г 1, t2t ... , tq\ г j, г 2, . . . , г т) должно быть мини-
мальным.
4.2. Введем в рассмотрение взвешенный смешанный граф G = (Q, U, К),
где (0, U) — указанная выше обобщенная временная модель, а ребро [/, /]
принадлежит V тогда и только тогда, когда операции i и / принадлежат
одному и тому же множеству Qki 1 < к < тп.
Если операции i и / принадлежат множеству Qk и назначены на один
и тот же прибор множества Лк, то в зависимости от порядка их выполне-
ния должно иметь место одно из соотношений /Р - г? > aq или
rz° - tf > ац, где Д/у и а/7 - заданные неотрицательные действительные
числа (веса, приписанные ребру [Z, /]).
Если операции i и / принадлежат множеству Qk и назначены на разные
приборы множества Лк, то не требуется выполнения указанных соот-
ношений.
В первом случае ребро [?, /] G V заменяется дугой (z, /) веса а^ или
дугой (/, f) веса д/7. Во втором случае это ребро удаляется. Удаление реб-
ра [/, /] интерпретируется как назначение операций i и / на разные прибо-
ры множества Лк.
277
4.3. Если Мк = 1, к = 1,. .. , т, то очевидно, что rk = 1 и Qk = Qk, т.е.
все операции множества Qk выполняются одним и тем же прибором. Такая
задача рассматривалась в предыдущих параграфах этой главы.
Для ее решения достаточно построить множество P(G) ориентирован-
ных графов и выбрать из него гра£ (Q, U*)9 для которого значение функ-
ции Ф(Г1(С, U')9 t2(Q9 ... , fQ(2, U'\9 1, 1,.. ., 1) минимально. Вели-
чина tj(Q, U*) означает наиболее ранний срок завершения операции i G Q
относительно графа (2, U'). Напомним, что графы множества P(G) не со-
держат контуров положительного веса и получаются из графа G в резуль-
тате замены каждого ребра [/, /] € V дугой (/, /) весаа^- или дугой (/, г)
веса ац и последующего удаления всех кратных дуг за исключением дуг
наибольшего веса.
4.4. Пусть хотя бы для одного к9\ < к <т9 значение Мк > 1.
Зададим число гк < Мк используемых приборов множества J6k9 и рас-
гк
пределим операции множества Qk по гк приборам: Qk = U Qlk9 где Qlk9
i = i
I = 1, . .., rk, — непустые попарно непересекающиеся подмножества мно-
жества Qk9 1 < к < т. В результате из смешанного графа G получим сме-
шанный граф G' = (2, U, Й'), V' С К, в котором [z, /] G V' тогда и только
тогда, когда операции г и / принадлежат одному и тому же множеству
Qk9 1 < I < rk9 1 <:к<т.
Каждый (ориентированный) граф из множества P(G') однозначно опре-
деляет активное расписание, допустимое относительно графа G',u наобо-
рот. Наилучшее среди допустимнх относительно графа G' расписание
определяет граф (2, U') G P(G')9 для которого минимально значение
функции Ф(?1 (Q, U’), 12(Q9 7'), .. .9lq(Q9Ut)\ r19 r2i .. . , rm).
Очевидно, что для решения задачи достаточно:
а) построить все смешанные гргфы G1, G2, ... , GK, соответствующие
различным наборам чисел гк <Мк9 к = 1,.. . 9ш9 используемых приборов
и различным распределениям операций по приборам;
б) построить множество ориентированных графов P(GV) для каждого
смешанного графа Gvt v = 1,. .., X;
в) выбрать из множества R(G) = U P(GV) граф (Q, (7'), которому
V = 1
соответствует наименьшее значение целевой функции.
4.5. Для сокращения трудоемкости решения задачи целесообразно сов-
местить процессы распределения операций по приборам с упорядочением
операций, назначенных на один и тог же прибор.
Выбирая последовательно ребра графа G и применяя к каждому из них
(для определенности к ребру [z, ;]) °ДН0 из трех возможных преобразо-
ваний (удаление ребра, замену его дугой (г, /) веса а^ либо дугой (/, z)
веса ац), получаем последовательность а = (oti, а2, • • • , «|У|) преобразо-
ваний графа G. Здесь az указывает, какое именно ребро выбрано на /-ом
шаге и какое из преобразований к нему применено.
Ориентированный граф, полученный из графа G в результате последо-
вательности преобразований а и последующего удаления всех кратных
278
дуг за исключением дуг наибольшего веса, обозначим через G[a] =
= (2,
Последовательность а преобразований графа G будем называть допусти-
мой, если G[а] ЕЯ((7).
Нетрудно видеть, что G[a] Е R(G) тогда и только тогда, когда он не со-
держит контуров положительного веса, для каждого k = 1,..., m число
гк [а] компонент связности порожденного подграфа (Qki £/*[<*]) графа
(С, U[a]\U) не превосходит Мк и эти компоненты связности являются
полными ориентированными графами (каждая пара вершин такого графа
соединена дугой).
Каждый граф G[а] из множества R(G) однозначно определяет число
z>[a] приборов множества 1 < к < т, единственное (с точностью
до нумерации приборов) распределение операций множества Qk по rk [а]
приборам, 1 < к < т, и единственное активное расписание выполнения
операций соответствующими приборами. При этом расписании tt =
= h (Q, £/[a]), i Е G- Таким образом, задача сводится к поиску допустимой
последовательности а* преобразований графа G, при которой будет получе-
но минимальное значение целевой функции.
4.6. При конструктивном подходе к поиску а* желательно располагать
условиями, при которых заданная частичная последовательность а =
= (ai> , az), / < I К|, может быть достроена до полной допустимой
последовательности а = (а', а/ + 1,. .. , а । v |).
Сопоставим последовательности а и числу к, 1 < к < т, вспомогатель-
ный граф //*.[</] = (Qk [a'], Vk [a']). Этот граф строится следующим об-
разом. Если представляет собой удаление ребра [/,/], ij G Qki из графа G,
то граф Нк [«! ] получается из графа Нк = (Qk, Ф) в результате добавления
ребра [z, /]. Если представляет собой замену ребра [z, /] одной из дуг
(z, /) или (/, z), то граф Нк [aj получается из графа Нк в результате отож-
дествления вершин z и / в одну вершину. Если - преобразование ребра
[Л/], iJ^Qc- k^c,mHk[ai\ = Hk.
Пусть построен граф Нк [a"], а" = (cq , a2, ... , ap _ j), p^l\ &p пред-
ставляет собой преобразование ребра [z,/], i,j G Qk, в графе G; а и b - вер-
шины графа Hk [a"], в которые отождествлены соответственно вершины z и /
либо а = z и (или) b = /. Если ар - удаление ребра [z, /], то граф
Нк[(а", ар)] получается из графа Нк[а"] в результате добавления ребра
[а, &]. Аналогично, если ар - замена ребра [z, /] одной из дуг (z, /) или
(/, z), то граф Нк [(а", ар)] получается из графа Нк [а"] в результате
отождествления вершин а и Ь. Если ар — преобразование ребра [z,/],
к^с, то Як[(а",ар)] = Нк[а"].
Нетрудно видеть, что если а — допустимая последовательность преоб-
разований графа G, то графы [or], к = 1, . . . , т, являются полными,
не содержат петель и число | Qk [а] | их вершин не превосходитМк.
Обозначим через x(#fc[°d) хроматическое число графа т.е.
наименьшее число цветов, которые можно приписать вершинам этого гра-
фа так, что никакие две смежные вершины не получат одинакового цвета.
Пусть граф G[a'] = (Q, U[a ], V[a ]) получен в результате последователь-
279
носги а преобразований графа G и последующего удаления всех кратных
дуг за исключением дуг наибольшего веса. Покажем, что для того чтобы
R (G[а' ]) =£ ф, необходимо, чтобы
а) граф (Q, U[a ]) не содержал контуров положительного веса}
б) для каждого k= 1,... ,т граф Нк [а' ] не содержал петель;
в) выполнялись соотношения X(Hk[ot]) ^Мк, к - 1,... fm.
Действительно, для всех к = 1,. .. , тп имеем | Qk [а] | > Х(Нк [<*']), и если
граф Я*-[а'] содержит петлю, то и граф Нк[а] содержит петлю. Если граф
(Q, Ща']) содержит контур положительного веса, то этот же контур со-
держится и в графе (Q, £/[а]).
Напомним, что ребро [z, /] € V называется конфликтным, если для него
выполняется соотношение (3.2) (см. п.3.3 этой главы). Очевидно, что
для того чтобы R(G[a ]) 0, достаточно, чтобы выполнялись перечислен-
ные выше условия и граф G [а' ] не содержал конфликтных ребер.
4.7. Для сокращения перебора графов множества R(G} можно вос-
пользоваться методом ветвей и границ.
Пусть [z, /] - некоторое конфликтное ребро графа G. Через а}, а?
и а? обозначим соответственно удаление из графа G ребра [z, /], замену
этого ребра дугой (г, /) веса а^ и дугой (/, z) весаау/. На первой итерации
получаем разбиение множества R(G) на подмножества /?(<7[а/]),
Я (б [а?]) и Я (б [а? ]). Затем одно из полученных множеств R (G [а? ]),
1 < h < 3, в свою очередь, разбивается на подмножества вида
A(G[(ail, аз)], Л (б[(а?, «!]) и R(G[(а*, а23)], где aj, а* и а2 - соответст-
вующие преобразования некоторого конфликтного ребра [а, графа
б[о^],ит.д.
Пусть на очередной итерации рассматривается граф б [а'] = (Q, б [а'],
Ф']).
Если для графа (7[а ] не выполняется хотя бы одно из условий а), б)
или в) предыдущего пункта, то этот граф исключается из дальнейшего
рассмотрения, поскольку R (G [а1 ]) = 0.
Если же указанные условия выполняются и граф б [а'] содержит хотя бы
одно конфликтное ребро, то можно вычислить оценку снизу значения
целевой функции. Для этого можно воспользоваться соотношением
^>(7l(Q,U[a]),... ,7q(Q,U[a]y, | <2i [«] I.I Qml<* Л) >
> Ф(7, (Q, U[a']), ...,7q(Q, Ща'|); Х(Я, [«']).х{Нт [а'])). (4.1)
Справедливость этого соотношения для любой допустимой последова-
тельности а = (а', а/ + 1, . .. , «|к|) следует из неравенств tj(Q, б[а]) >
> 7,- (<2, t/[a' ]), i = \, ... ,q, | I > X(H [a']), k = 1.m, и неубыва-
ния целевой функции по каждому из аргументов.
Если условия а), б) ив) выполняются для графа б [а'] и в нем нет
конфликтных ребер, то не вызывает затруднений построение последова-
тельности а, для которой соотношение (4.1) выполняется как равенство.
280
Для этого достаточно заменить все ребра [/, /] множества И[а'] дугами
(/, /) так, чтобы выполнялись соотношения t^Q, {/[а']) < /у(2, Ща1 ])•
4.8. Пример. В гибкой производственной системе, состоящей из стан-
ков с ЧПУ (приборов) трех типов (т = 3), необходимо обработать три
детали (обслужить три требования). Множества станков = {1,2,3},
Л2 = {4,5} и = {6}. Обработка первой детали состоит в последо-
вательном выполнении множества операций {1,2, 3}, второй - множества
операций { 4, 5 } и третьей — множества операций { 6, 7, 8}.
Множества операций Qx = {1,4, 6},2з = {2,5,8} и Q3 = {3,7}.
Фиктивная операция 9 означает завершение обработки всех деталей. Зада-
ны длительности выполнения операций: = 3, t2 = 2, Z3 = = 7, r5 = 5,
= 10, tq = 8, Zg = 1, tg ~ 0.
Целевая функция Ф(Г1? 12, ... , Z9; >4, r2, r3) = 79 + rx + 4r2 + 3r3.
Она отражает стремление минимизировать общее время обработки деталей
с учетом длительности пуско-наладочных работ для каждого из исполь-
зуемых станков.
На рис. 4.1, а представлен смешанный граф G = (Q, U, V) для данной
обслуживающей системы. Вес дуги (z, /) € U равен zz. Каждому ребру
[/, /] G V сопоставлена пара весов = Zz и zzyi- = tj. Веса ребер на рисунке
не указаны.
Для решения задачи воспользуемся методом ветвей и границ, схема
которого описана в предыдущем параграфе.
Пусть на очередной итерации рассматривается граф С/ = (2, Ц, Kz).
В качестве ребра, определяющего разбиение множества R (Gt) на подмно-
жества, из множества конфликтных ребер графа Gj выбирается ребро [/,/ |,
281
для которого величина min { hif, Л/7}(см. п. 3.7 этой главы) принимает
наибольшее значение.
Для оценки целевой функции используется соотношение (4.1). В ка-
честве стратегии метода используется поиск по наилучшей оценке (см.
п. 3.4 предыдущего параграфа).
На рис. 4.1,в представлено дерево (Z, И7), полученное при решении дан-
ной задачи. Граф 67О = G, Каждой дуге (Gk, Gj) из множества W приписано
либо ребро [Z, /], либо дуга (z, /) или (/, z), в зависимости от того, полу-
чен ли граф Gj из графа Gk в результате удаления ребра [z, /] либо замены
этого ребра дугой (z, /) или (/, z). Каждому графу Gt Е Z при / Ф 7 при-
писана оценка целевой функции. Графу G7 приписан символ 00, поскольку
Х(Н3 [а']) >М3 и, следовательно, R(G2 ) = ф. Здесь G [а'] = (77.
Граф б711} представленный на рис. 4.1,6, не содержит конфликтных
ребер и определяет решение задачи: г2 = 2, r2 = r3 = 1, Q} = {1,4},
<21 = (6), Qi = {2, 5, 8}, Qi = {3,7), = О, = 3, = 5, = 3, = 10,
= 0, t, = 12, tg = 20, tg =21. Оптимальное значение целевой функции
равно 21 + 2 + 4 + 3 = 30.
§ 5. Устойчивость оптимальных расписаний
В заключение рассмотрим некоторые вопросы, связанные с устойчиво-
стью оптимальных по быстродействию расписаний относительно длительно-
стей выполняемых операций.
5.1. Пусть G = (Q, U, И) - конечный смешанный граф без петель, крат-
ных дуг и кратных ребер, Q = {1, 2, ..., q} — множество вершин (операций),
U — множество дуг и V — непустое множество ребер. Каждой дуге
(z, j) Е U сопоставлен вес ац , равный длительности tj > 0 операции
z Е Q. Каждому ребру [/,/] в V приписана пара неотрицательных весов
= ti и аЦ = tj .
Как показано в § 1 этой главы, существует взаимно однозначное соот-
ветствие между множеством всех активных расписаний, допустимых отно-
сительно графа G, и множеством Р(G) ={6'1, G2,..., Gp} всех бесконтурных
графов, порождаемых смешанным графом G в результате замены каждого
ребра [z, /] Е V одной из дуг (z,/) веса ац или (/, z) веса ац. Будем
предполагать, что граф (Q, U) не содержит контуров, поскольку в против-
ном случае P(G) = ф. Графу Gk = (Q, UЕ P(G) соответствует активное
расписание sk, при котором момент t® (sk) начала операции z Е Q равен
наиболее раннему сроку начала операции z относительно этого графа.
Положим t = (Г i, t2, —, tq). Через I* (p) обозначим вес пути р в графе
Gk EP(G), а через {р} — множество вершин (операций), через которые про-
ходит путь р, без последней вершины этого пути. Путь р будем называть
доминирующим, если в графе Gk не существует пути р, для которого
{р} С {и}. Путь наибольшего веса в графе принято называть критическим.
Пусть Н и Нк — множества всех доминирующих путей графов (Q, U) и
Gk Е P(G) соответственно. Очевидно, Н С Нк для всех к = 1, ..., р и хо-
тя бы один критический путь в графе Gk является доминирующим.
Оптимальное по быстродействию расписание sh определяется графом
282
G P(G) с наименьшим весом критического пути:
max /г(д) = min max l* (у). (5.1)
м e Hh i<k<pv<EHk
5.2. Обозначим через S(t) множество всех номеров h графов Gh G P(G)
с наименьшим весом критического пути. Если h G 5 (г) , то граф Gh будем
называть оптимальным. Исследуем вопрос о том, насколько можно изме-
нять длительности операций t (независимо одна от другой), чтобы граф
Gh, h G S (t), оставался оптимальным.
Пусть Rq - множество неотрицательных действительных ^/-мерных век-
торов с чебышевской метрикой и r(t, t') = max ] tj — t\ | - расстояние от
вектора t до вектора t* = (t\, t2,..., tq). Замкнутый шар 0y(t) радиуса у
с центром в t будем называть шаром устойчивости графа Gh, h G S(t),
если для любого вектора t* G 07(r) A Rq выполняется h G S(t').
Наибольшее значение радиуса у шаров устойчивости 0y(t) графа Gh будем
называть радиусом устойчивости графа Gh и обозначать через уЛ (г).
5.3. Покажем, что для того чтобы yh(t) = необходимо и достаточно,
чтобы для любого пути р G Hh \ Н и любого графа Gk G P(G) существо-
вал путь р G Нк такой, что {р} С {р}.
Пусть yh (t) = 00, а путь р' G Hh \ Н и граф G к» G Р (G) таковы, чю ни
для какою пути р G Н /(1 соотношение {д}С { р } не выполняется.
Выберем число е, для которого 0 < е< max /у, и положим ts =
= ('ь t’2, где
( е, если i G {р’} ,
'' I
I 0, если i {р } .
Для любого пути р G Н kt имеет место равенство 1Т (р) =е| {р} О {р }|.
Поскольку включение {р'} С {р} не выполняется, то /г (р) < /г’(д').
Следовательно,
max lT (р)< I* (р')= max Zf (д)
v е И к ’ р Hh
и h $ Получили противоречие: уh(t) < max < 00.
Докажем достаточность утверждения. Для любого сколь угодно большо-
го е > 0 возьмем произвольный вектор G 0€(t) GiRq. Пусть
max = 1г\ц0).
n e nh
283
Если д0 - Н, то при любом к - 1, ..., р
lf (д0) < max /г (р).
Если До £ Hh \ Н, то по условию утверждения для любого к = 1, ..., р
существует путь р0 е Нк такой, что {д0} С {р0} и, следовательно,
/г’(д0) < < max /' О).
V е нк
Таким образом, в обоих случаях h G S (tf).
Как следствие доказанного утверждения получаем оценку: если
7л(0 < “>> то 7,,(т) < max tt.
iS Q
5.4. Пусть Т/7(0 < <». Выведем формулу для вычисления радиуса
устойчивости.
Поскольку шар устойчивости 07(f) графа Gh является замкнутым, то
yh(t) = h $
Учитывая (5.1), получаем
уЛ(г) = inf {r(t, t') | /' G Rq, max /'(д) > min max lf (p)} .
д G ///, к Ф h v E. Ик
Определим ближайший к t вектор tr G Rq, для которого
max l* (д) > max I* (v). (5.2)
g e нк v g nk
Отметим, что множество Hh в неравенстве (5.2) можно заменить
на Н h \ Нк
Не1рудно видеть, что для выполнения неравенства
/''(д) > /''(р) (5.3)
в качестве t1 достаточно взять век гор t' (г ), полученный из / в результате
уменьшения длительностей операций из множества { р } \ { д } и увеличения
длительностей операций из множества { д} \ { р) на величину
г>г /'(^) ~ /Г(Д)
I {М} и {и} I - I {ц} П {р} I
Очевидно, что для любого ^-мерного вектора tr, для которого
< , выполняется соотношение I1 (д) < /г (р).
При уменьшении компонент вектора t некоторые из них могут стать
отрицательными, т.е. возможно tf (г ) Rq.
284
Пусть = 0 и , tin > • “ неубывающая последователь-
ность длительностей операций множества {и} \ {д } Вычислим величину
Л(р)-/Г(д)- S tavli
а - О
rVn = птах------------------------------------ (5.4)
1{д} ^{^}|-|{д}П {р}\-р
и через Д* обозначим то значение /3, при котором правая часть равенства
(5.4) достигает наибольшего значения.
Очевидно, неравенство (5.3) будет выполняться, если в качестве t1
взять вектор t(r ) G Rq, полученный из t в результате увеличения компо-
нент tif i G {д} \ {р}, на величину г >г„п , уменьшения на ту же величи-
f fl + 1 fl +2 Г 1 2
ну компонент I, ..., t^ } и замены компонент ,...
/3*
.... } нулями. Очевидно, для любого вектора t' G Rq, для которого
г(?, г') <rV(l, справедливо соотношение lf (д) < 1Т (р).
Таким образом, для любого вектора t1 G Rq из условия (5.3) следует
неравенство г (t, t') из условия (5.2) следует неравенство
r(t, t') > max min
v<E.Hk
и,наконец, из условия
max (д) > min max ll (p)
де Hh к h v e нк
следует неравенство
r(t, tr) > min max min
к Ф h v e Hk ii£Hh\Hk
В результате получаем оценку снизу радиуса устойчивости yk(f).
Отметим, что знаменатель в соотношении (5.4) может быть равен нулю
только при условии {д}С {р}. Поскольку yk(t) < ©о, то в силу п. 5.3
существуют граф Gkt G Р (G) и путь д' G Hh \ Н такие, что для любого
пути р G Нkt множество { р) не содержит множества {д '} . Следовательно,
величина г = min max min конечна.
к * h v е нк це Hh\ нк
Покажем, что для любого сколь угодно малою числа е > 0 существует
вектор te G 0Г +е(0 GiRq такой, что h S (te).
Пусть г = max и вектор tQ получен из t в результате увеличе-
v е нкь
ния компонент ti9 i G {д0}, на величину г и замены компонент tj ,
7 {д°} , на max {0, — г} .
285
Согласно приведенным рассуждениям h G S (7°),£° £5 0°), Л (д°) =
= max (д) и для любого пути v G Нк* множество {р} не содержит
Hh
множества {д0}.
Через te обозначим вектор, полученный из г° в результат увеличе-
ния на е длительностей операций {д0}. Нетрудно видеть, что для любого
е > 0 имеет место неравенство
(д°) > max I* (р)
у е нк<*
и, следовательно, h Ф S(te).
Таким образом, радиус устойчивости может быть вычислен по следую-
щей формуле:
^(0=
а = 0
= min max min max ———— --------——— ---------
к ф h v е нк Hh\Hk о < /з < 1{д}и{р}I - 1{д}П(р} I - /3
(5.5)
5.5 Пример. На гибком автоматизированном участке, в состав
которого входят станок А и станок В, необходимо обработать две
детали. Первая деталь вначале обрабатывается на станке А (операция
2), а затем на станке В (операция 3). Вторая деталь вначале обрабаты-
вается на станке В (операция 5), а затем на станке Л (операция 6).
На рис. 5.1 представлен смешанный граф G = (Q, Uy V) для рассматри-
ваемой обслуживающей системы. Операции 1 и 4 означают поступление
на участок первой и второй детали соответственно. Фиктивная операция
7 означает завершение обработки обеих деталей. Вес дуги (/, /) G U
равен длительности tt операции /. Каждому ребру [Z, j ] G V соответствует
пара весов ац = и = tj. Веса ребер на рисунке не указаны. Вектор
длительностей операций t = (40, 50, 40, 30, 70, 60, 0).
Требуется построить оптимальное по быстродействию расписание sh об-
работки двух деталей и определить радиус устойчивости оптимального
графа Gh.
Очевидно, P(G) = {Gj, G2, <73}, где Gx = (0, U U {(2, 6), (5,3)}),G2 =
= (0, t/U {(2,6), (3,5)}), G3 = (0, t/U {(5,3), (6,2)}). Построим мно-
жества доминирующих путей Дг, Дз, AU) , #2 = {Дг, Ms) , #з =
= {д15д6}, гдеМ1 = (1,2, 3, 7), д2 =(4,5,6, 7), д3 = (1,2, 6, 7), д4 = (4, 5, 3,
286
7), Ms =(1 > 2, 3, 5, 6, 7), д6 = (4, 5, 6, 2, 3, 7), и вычислим их веса: /Г(Д1) =
= 130, Zf(p2) = 160, /f(M3) = 150, /'(д4) = 140, /г(д5) = 260 и /,(р6) = 250.
Таким образом, оптимальными являются граф Gi и расписание $1 :
Г?(М = = 0, r$(Si) = 40, ^(s,)=100, = 30, ^(Sl) = 100,
^7^,) = 160. По формуле (5.5) получаем 7j (г) = 25.
5.6. Через обозначим множество всех доминирующих критических
путей графа Gh G Р (G).
Нетрудно убедиться в том, что существует число е > 0 такое, что ни
один путь из множества Hh\H*h не станет критическим, если вектор t за-
менить вектором t* G 0€ (z).
Действительно, в качестве е достаточно взять любое положительное
число, которое меньше
tf - /Чи
eh = min -----------------,
vehM 2mh
где tf = max /*(д) и mh = max I{д} I.
д G Hh Д G
5.7. Покажем, что для того чтобы выполнялось неравенство 7^(z) > 0,
h G S(z), необходимо и достаточно, чтобы для любого пути р 6 Н^Ни
любого kE S(t) существовал путь v Е Нк такой, что ( р}с {v}.
Пусть 7Л (z) = е > 0, а путь д' G H*h и граф Gk>, kf G 5(z), таковы, что
ни для какого пути v G Нк> не выполняется включение {р} С{р}.
Через z' обозначим вектор, полученный из t в результате увеличения
длительностей операций i G {д'} на величину е° = тт{еЛ,е^', е }. Очевид-
но, г' G 0eo(Z) п Rq и согласно п. 5.6
max I* (р) = max (р) = I* (р) +
v<EHk' v(EHk'
+ е°1{д}П{р}| = /'(д') + е°1{д)П{р}|.
Поскольку включение {д'}С {р} не выполняется, то I {д'} П { р } I <
< 1{м } I max /'(р) </'(д') и, следовательно, Л S(z'). Получили
* Нк’
противоречие с предположением о том, что 7Л(г) = е > е°.
I * ~ I
Докажем достаточность утверждения. Пусть 0 < е < min \eh, 2m I ’
где / = min l* и m= max mk.
к £ S(t) K к к < p
Для любого вектора z'G 0e(z) A Rq согласно n. 5.6 имеет место ра-
венство max lf (д) = max lf (д). Поскольку для любого пути д G
м е Hh р g Hhf
&Нь\Ни любого к G S(t) существует путь р G Нк такой, что {д}С{р} , то
max (д) < max lf (р).
д G // и G Н к
Следовательно,
max lf (д) < max Л (р).
д е и е нк
287
Поскольку e < (/ - /^)/2га, то из условия к ^S(t) следует, что к
S(t') . Таким образом, h Е S(t') и уЛ (г) > е > 0.
Из доказанного утверждения получаем следствие: если S(t) = {h } ,
т°Ул(О > 0- Аналогично, если Л £S(t) иН£ ^/7, тоуЛ(г) > 0.
5.8. П р и м е р ы. На рис. 5.2, а представлен смешанный граф G для
описанной в п. 5.5 обслуживающей системы, когда вектор длительностей
операций t = (60, 50, 40, 0, 40, 20, 0). Нетрудно видеть, что S(t)= {1,3}
и согласно утверждению из п. 5.7 ?! (г) > 0 и у3 (t) = 0. Точное значение
(г) = 10 можно получить по формуле (5.5).
Рис. 5.2
На рис. 5.2Д представлен смешанный граф G с вектором длительностей
операций t = (50, 40, 70, 60, 0) при условии одновременного поступления
двух деталей в обслуживающую систему. В этом случае оптимальными яв-
ляются граф G! = (Q, U U {(1, 4), (3, 2)}) и расписание (st) =
= ^з(51) =0>^2(si) =^4 0i) =70, £5(51) = 130. Согласно утверждению
из п. 5.3 получаем У1 (О = °°.
5.9. Наряду с шаром и радиусом устойчивости фиксированного опти-
мального графа определенный интерес представляют аналогичные понятия
относительно всего множества оптимальных графов.
Открытый шар 0y(t) радиуса у с центром в t будем называть шаром
устойчивости t, если для любого t' Е A Rq имеет место включе-
ние S(t') S(t)- Верхнюю грань радиуса у шаров устойчивости t будем
называть радиусом устойчивости t и обозначать через у (Г).
Из данного определения следует, что у (г) = «> для любого вектора
t Е Rq = {t Е Rq I S(t) = { 1 , 2, ..., p}} . Множество Rq не пусто, поскольку
заведомо содержит нулевой ^-мерный вектор 0. Следовательно, для любого
t Е выполняется оценка
У (0 < г (г, 0) =шах {Г/1 i Е Q }.
Таким образом, для того чтобы y(t) = 00, необходимо и достаточно,
чтобы t Е Rq.
Покажем, что для любого t Е Rq значение y(t) > 0. Пусть t€Rq \ R°q.
Выберем число е, для которого 0 < е < (/ - /0/2га, h Е S(t). Очевидно,
что для любого t' Е 0е(Г) П Rq выполняется включение S(f) S(t).
Следовательно, у (f) > е > 0.
Так как е можно выбрать сколь угодно близким к величине (/ - Z Д )/2га,
то справедлива оценка
7 - l‘h) I 2m.
288
Поскольку шар устойчивости t является открытым, то у(7) =
= min{r (7, г') | t' GRq,k $S(t) ,к GS(t')} и в силу (5.1) для вычисления
у (t) достаточно решить следующую задачу нелинейного программирования:
max |х/ — rj -*min, (5.6)
1 < i < q
min max /х(д)> min max Iх (v), /с
1<Л<р k$S(t) vEHk
Xj>0, i = l,...,q, (5.8)
Очевидно, еслих*= (x*,x2*, . . . ,x^) - решение задачи (5.6)-(5.8), то
y(t) =r (Г,х*).
5.10. Множество всех векторов t G Rq, для которых h G будем
называть областью устойчивости графа Gh и обозначать через Th. Учитывая
(5.1), получаем
Th={tGRq\ max min max I* (и)}. (5.9)
I д e Hh\H к * h v e нк
Покажем, что множества Th,h = 1,... , p, обладают следующими
свойствами:
1) Th - замкнутый конус, содержащий вектор 0;
р
2)Rq = U Th\
h =1
л Р
3)Я$=П Th.
h = l
Действительно, из условия t G Th следует, что \t G Th для всех 0.
Согласно соотношению (5.9) конус Th является замкнутым.
Справедливость свойства 2) следует из того, что для любого вектора
t G Rq множество 5(0 не пусто, поскольку по предположению (см. п. 5.1)
граф {Q ,U) не содержит контуров.
Справедливость свойства 3) следует непосредственно из определений
множеств R £ и Th .
Отметим, что все полученные в этом параграфе результаты (за исключе-
нием верхних оценок радиуса устойчивости) легко переносятся на случай,
когда изменяются только длительности некоторого подмножества Q' мно-
жества операций Q. Для этого достаточно в приведенных утверждениях
вместо множеств {д}и {v} рассматривать множества {ц } П Q' и{р} C\Q*
соответственно.
§ 6. Библиографическая справка
Модели обслуживающих систем в виде смешанных графов G = (2, U, V)
предложены В.В. Шкурбой [401], Л.П. Матюшковым и В.С. Танаевым
[199] и исследовались в работах [125, 126, 128, 129, 291, 294, 296, 298,
303, 304, 307-309, 342, 352]. Случай U = ф рассматривался в [47, 119].
В зарубежной литературе вместо смешанного графа G используется
так называемый дизъюнктивный граф (Q, U U W), в котором каждому
ребру [z, /] G V соответствует пара симметричных дуг (z, /)О и
(/, z) G W. Термин ’’дизъюнктивный граф” непосредственно связан с опе-
рацией выбора одной из двух возможных дуг из каждой такой пары.
Й19. В.С. Танаев 289
Модели обслуживающих систем в виде дизъюнктивных графов предло-
жены Б. Руа и Б. Суссманом [762] и развиты Е. Балашем [449—451],
И. Набешимой [706-708], С. Ашауром и Р. Паркером [437, 438], Дж. Чарл-
тоном и С. Детом [490, 491], Ю. Грабовским [559—561], Б. Лагевегом,
Я. Ленстрой и А. Ринной Каном [637, 638, 651, 754]. Эти вопросы рас-
сматривались и в работах [420, 434, 436, 477, 487, 488, 509, 525, 526,
538, 565, 603, 713, 715, 745, 760, 783, 791, 812].
6.1. Представление обслуживающих систем в виде смешанных мульти-
графов (см. § 1 этой главы) предложено Ю.Н. Сотсковым и В.С. Та-
наевым. При построении расписания, допустимого относительно графа
(2, U) (см. п. 1.7), используется алгоритм Р. Флойда [527] и С. Уоршел-
ла [828], а в случае бесконтурного графа (Q, U) (см. п. 1.4) - алгоритм
Е. Дейкстры [506].
Условия существования расписания, допустимого относительно смешан-
ного графа, описаны в [291, 517, 791]. Ю.Н. Сотсковым доказана NP-
трудность задачи проверки существования расписания, допустимого отно-
сительно графа G (см. п. 1.10).
В [2, 234, 261] рассматривались возможности использования обобщен-
ных временных моделей для описания типичных для календарного плани-
рования ситуаций.
6.2. В основу § 4 положены работы Ю.Н. Сотскова [294, 303, 304].
Условия допустимости последовательности преобразований смешанного
графа описаны в [303, 304].
Другие формы сетевого представления обслуживающих систем с после-
довательными и параллельными приборами предложены Е. Балашем [452]
и Ю. Грабовским [561]. См. также [538, 696].
6.3. Методы построения активных расписаний (в [147] такие расписа-
ния называются квазикомпактными) предложены Б. Гиффлером [65,
539], В. Гере [537], Л.П. Матюшковым и В.С. Танаевым [199], Ю.Н. Сот-
сковым и В.С. Танаевым [295-297, 307, 308], С.А. Канцедалом и О.Н. Ма-
лых [127,129,131].
В работе [540] показано, что множество компактных (а следовательно,
и активных) расписаний содержит хотя бы одно оптимальное при любой
целевой функции, не убывающей относительно моментов завершения
обслуживания требований. Множества незадерживающих [147] и структур-
но уплотненных расписаний [131] могут не содержать оптимального рас-
писания.
6.4. Описанные в § 2 алгоритмы построения множества P(G, Н) и нахож-
дения его мощности (см. пп. 2.2-2.4) предложены Ю.Н. Сотсковым и
В.С. Танаевым [295, 297, 299, 307, 308]. Задача построения множества
P(G) (см. п. 2.5) рассматривалась Н.В. Ламбиным и В.С. Танаевым [163],
а при U = ф - Р. Стенли [785]. Случай полного смешанного графа G иссле-
довался В.С. Танаевым [339], С.С. Кислицыным [136], К. Окамурой и
X. Ямашиной [717], Т. Кобаяши [624] и другими авторами. Влияние
локальных преобразований графа G на величину p(G) (см. п. 2.6, 2.7)
исследовалось в [308].
Доказательство АР-полноты задачи проверки выполнимости неравенст-
ва |Р(<7, Н)\ > 0 (см. п. 2.1) проведено Ю.Н. Сотсковым [299]. Е. Аркин
и X. Пападимитриу [426] доказали /VP-трудность в сильном смысле зада-
290
чи проверки существования в G контура отрицательного веса и задачи
нахождения пути наименьшего веса в смешанном графе, не содержащем
контуров отрицательного веса. В [733] установлена /VP-трудность в силь-
ном смысле так называемой задачи о китайском почтальоне на смешан-
ном графе. При U = ф или V = ф перечисленные в этом абзаце задачи поли-
номиально разрешимы [654, 638].
Задача раскраски вершин смешанного графа исследовалась Г.М. Ле-
виным, Ю.Н. Сотсковым и В.С. Танаевым [171, 172, 309]. Хроматический
многочлен смешанного графа описан в [309]. Вопросы программной реали-
зации алгоритмов раскраски вершин смешанного графа рассматрива-
лись в [137].
6.5. Для решения TVP-трудных задач разработано большое количество
разнообразных методов направленного перебора вариантов, которые широ-
ко используются и в теории расписаний.
Общий формализм методов оптимизации, основанных на идее последо-
вательного конструирования, анализа и отсеивания вариантов, разработан
В.С. Михалевичем, Ю.М. Ермольевым, В.В. Шкурбой, Н.З. Шором и др.
[213—217]. Детальное описание метода динамического программирова-
ния содержится в монографии Р. Веллмана [25]. Значительное развитие
конструктивный подход получил в работах Н.Н. Моисеева и его учени-
ков [219—223]. Ряд общих схем решения задач дискретной оптимизации
предложен в работах Ю.И. Журавлева [100—102], В.П. Черенина [383],
В.Р. Хачатурова [379], В.А. Емеличева и В.И. Комлика [115], И.В. Сергиен-
ко [282], Ю.Ю. Финкельштейна [372], Г.М. Левина и В.С. Танаева [173,340].
Формализации и теоретическому обоснованию метода ветвей и границ
посвящены работы И.В. Романовского [258], А. Лэнд и А. Дойг [640],
Т. Ибараки [601-603], X. Кисэ [623], В. Коглера и К. Стайглица [625],
Л. Миттена [692], В. Руа [761], Д. Танга и К. Вонга [814], К. Бейкера
[549], А. Джеффриона и Р. Марстена [536], Ю.С. Афонина [15] и ряд
других. Обширную библиографию по этим вопросам содержат обзорные
работы А.А. Корбута, И.Х. Сигала и Ю.Ю. Финкельштейна [148], Е. Бала-
ша и М. Гиньяр [454], Е. Лоулера и Д. Вуда [649]. (См. также [605].)
Описанные в п. 3.10, 3.11 оценки сложности метода ветвей и границ
предложены Т. Ибараки [602].
6.6. Значительное количество работ посвящено использованию метода
ветвей и границ при построении оптимальных по быстродействию расписа-
ний. Различные схемы организации процесса ветвления (разбиения мно-
жества допустимых расписаний на подмножества) рассматривались Е. Ба-
лашем [450], Г. Бруксом и С. Уайтом [478], Л. Немети [714], Ю.Н. Сот-
сковым [291], И. Набешимой [706, 707], С. Ашауром и С. Хиремасом
[435], Дж. Чарлтоном и С. Детом [491], М. Флорианом, П. Трепангом
и Г. Мак-Махоном [526].
В работах [54, 126, 193, 199, 291-293, 300, 420, 426, 436, 450, 490,
559-561, 706-708. 713, 783, 791] оптимальное расписание ищется в клас-
се активных расписаний, а в работах [125, 477, 478, 525, 526, 686, 714] -
в классе компактных расписаний. _
Для вычисления оценки снизу величины ^тахО*) обычно решается
та или иная релаксированная задача. П. Братли, М. Флориан и П. Робайар
[477] предложили использовать для этой цели задачу минимизации мак-
'/2 19* 291
симального временного смещения обслуживания частично упорядоченного
множества N требований одним прибором, если для каждого требования
i G N задан момент dj его поступления и директивный срок Dj. Эта задача
является /VP-трудной в сильном смысле [657]. Обзор методов ее
решения приведен в [637, 686]. Б. Лагевег, Я. Ленстра и А. Ринной
Кан [638] показали, что почти все известные в литературе оценки снизу
величины fmax(s*) могут быть получены в результате решения указанной
задачи или ее частных случаев. Так, в работах [291, 434—437, 491, 768]
значения dj = Dj = 0 для всех i G7V; в работах [291, 436, 478, 526] значе-
ния Dj = 0, i G /V; в [767] значения dj = 0, i G TV; в работах [291,300, 434,
436, 437, 490, 491, 571, 706, 714, 768, 791] предполагалось, что прибор
может обслуживать все требования множества N одновременно, а в рабо-
тах [291,477, 686] - что множество требований W неупорядочено. Послед-
няя из перечисленных релаксированных задач является /VP-трудной
в сильном смысле [351, 657], для остальных известны полиномиальные
алгоритмы решения [351, 603, 686]. В [291] для получения оценок ве-
личины Гтах0*) предложено использовать методы оптимизации функций
на перестановках. Эти методы развиты в работах [210, 264-268, 326,
329,343].
При некоторых дополнительных ограничениях удается получить более
точные оценки величины ГтахО*)- В работах [426, 477, 686] существенно
использовалось предположение о целочисленности длительностей опе-
раций. В [376, 429, 434, 435, 437, 438, 478] предполагалось, что каждое
требование обслуживается каждым прибором точно один раз.
6.7. Разнообразные варианты метода ветвей и границ разработаны для
решения задачи минимизации общего времени обслуживания требований
в случае одинаковых маршрутов, т.е. для систем поточного типа. Как
правило, рассматривается ситуация, когда множество требований посту-
пает в систему одновременно и все приборы обслуживают требования
в одной и той же последовательности. В этом случае расписание однозначно
определяется перестановкой требований. Принципиальная схема ветвей
и границ для решения экстремальных задач на множестве перестановок
предложена В. Коглером и К. Стайглицем [143, 625]. Большинство авто-
ров рассматривают правило ветвления, согласно которому на основании
некоторой перестановки а, { о } С /V, строятся все перестановки вида
(о, z), i £ 7V\{o}. Нижние оценки величины ^тах(я), гДе я = (о, . . .) для
заданной перестановки о, { а } С А\ предложены в [11,361,362, 384, 421,
431, 439, 466, 479, 574, 576, 580, 604, 667, 685, 704, 709] (см. также [45,
352, 446, 651, 754]). Вопросы вычисления глобальных нижних оценок
({о} =0) рассматривались в [10, 457, 458]. Б. Лагевег, Я. Ленстра, А. Рин-
ной Кан [639, 651, 754] и В. Шварц [805] описали два различных подхода
к генерированию нижних оценок общего времени обслуживания требо-
ваний, позволяющих получать большинство ранее известных и некоторые
новые нижние оценки. Метод ветвей и границ, основанный на ином пра-
виле ветвления, предложен К. Потсом [742] (см. также [772]).
В целях сокращения обьема вычислений метода ветвей и границ в ряде
работ используются те или иные отношения доминирования, которые
задаются условиями, достаточными для того, чтобы требование i GA^ пред-
292
шествовало в оптимальной перестановке требованию к G N, к #= i. Выявле-
нию такого рода условий посвящены работы [448, 508, 578, 585, 684, 778,
779, 797, 798, 801]. Отметим, что условия из [448, 508, 778] не корректны
(контрпримеры приведены в [685, 617, 797] соответственно). Кроме того,
установлено, что остальные условия, по существу, эквивалентны [651,
754, 798,801], и если они выполняются для некоторой пары требований
i Е N и к G N, i ф к, то справедливы соотношения < tiL либо tit
> tiM, L = 2, . . . , M. К. Бейкер [448] и Дж. Гупта [582] провели анализ
вероятности выполнения указанных соотношений. В [590, 804] предприня-
ты попытки задания отношений доминирования, когда указанные соот-
ношения не имеют места и значение М = 3.
Другие методы сокращения объема вычислений метода ветвей и гра-
ниц исследуются в [11,444, 563, 726].
К числу методов решения данной задачи, использующих идеи последо-
вательного анализа вариантов, следует отнести и метод лексикографичес-
кого поиска, предложенный Дж. Гуптой [573] и получивший развитие
в [494,587].
Сведения о результатах наиболее крупных вычислительных эксперимен-
тов с различными схемами ветвей и границ приведены в [430,447,639,742].
Там же содержатся некоторые рекомендации по выбору правил ветвления
и вычисления оценок.
6.8. Для решения задач с критериями оптимальности, отличными от ми-
нимизации /тах ($), в случае одинаковых маршрутов обслуживания требо-
ваний предложены разнообразные схемы ветвей и границ. Задача миними-
зации Lmax (5) рассматривалась У. Таусендом [818] , если <7/ = 0, i G N, а
также Ю. Грабовским [562], если d > 0, i Е N (см. также [564, 566]) . За-
дача минимизации линейных и экспоненциальных функций штрафа рассмат-
ривалась в [819], а задача минимизации максимального штрафа произволь-
ного вида - в [820, 821] (см. также [416]). Различные схемы ветвей и
границ для минимизации суммарного времени обслуживания требований
предложены в [143, 443, 604, 626] для случая М - 2, в [456, 711] - для
произвольного числа приборов М и в [503] - для произвольного М при
условии обслуживания требований без задержек. К. Калра, С. Бенсел и
П. Багга [615] предложили метод ветвей и границ Д1я решения задачи ми-
нимизации суммарного взвешенного времени обслуживания L ссу при
i G Д'
условии, что все Т] <Dt . В [143, 626, 711] обсуждаются возможности ис-
пользования методов ветвей и границ в качестве е-приближенного алгорит-
ма. Отношения доминирования для задачи минимизации суммарного време-
ни обслуживания описаны в [582].
6.9. Методы типа ветвей и границ применялись и для оптимального об-
служивания требований в системах с различными маршрутами. Так, в
[104, 105, 478, 716] рассматривалась задача минимизации суммарного за-
паздывания при обслуживании требований, в [522] — задача минимизации
суммарного штрафа за обслуживание требований, в [150, 538] - задача
минимизации стоимости использования приборов, в [818] - задача мини-
мизации максимального запаздывания при обслуживании требований, в
[572] — задача минимизации обшей стоимости переналадок приборов. См
также [22, 29, 107, 155, 244, 252, 298, 396, 398, 410, 517, 666, 679, 786].
293
Задачи построения оптимальных расписаний при произвольных неубы-
вающих по каждому из аргументов целевых функциях рассматривались
И. Набешимой [706—708] и Ю.Н. Сотсковым [294, 302-304].
Б. Суссманом [791], Ю.Н. Сотсковым [298], Дж. Чарлтоном и С. Детом
[490] рассматривалась задача построения оптимального по быстродействию
расписания, допустимого относительно смешанного графа G = (0, U, И),
где ((Л (7) - обобщенная временная модель.
6.10. Использованию метода ветвей и границ для получения приближен-
ных решений задач теории расписаний посвящены работы [245, 293, 706,
708]. Полиномиальные 6-приближенные алгоритмы предложены в [139—
141, 181,523].
В [298] предложен метод минимизации максимального штрафа за обслу-
живание требований, существенно использующий алгоритм выделения кон-
туров смешанного графа (см. [254]) и алгоритм проверки выполнимости
конъюктивной нормальной формы (см. [107, 500, 518]). Использование
линейного от числа дизъюнкций алгоритма решения задачи 2-выполнимости
из [518] и алгоритма из [307] позволяет выделить некоторые полиноми-
ально разрешимые случаи указанной задачи теории расписаний [301, 306].
L. Балашем [453] исследовался многогранник расписаний, допустимых
относительно смешанного графа.
В.Б. Алюшкевичем и Ю.Н. Сотсковым [6, 305] рассматривались вопросы
устойчивости множества оптимальных по быстродействию расписаний, до-
пустимых относительно смешанного графа. При этом использовался подход,
предложенный В.К. Леонтьевым и Э.Н. Гордеевым [78, 79, 182, 183]. Необ-
ходимые и достаточные условия, при выполнении которых радиус устойчи-
вости оптимального графа равен нулю (см. п. 5.7 гл. 4) и бесконечности
(п. 5.3), получены Ю.Н. Сотсковым. Формула для вычисления радиуса
устойчивости оптимального графа (п. 5.4) получена В.Б. Алюшкевичем и
Ю.Н. Сотсковым. Исследование области устойчивости оптимального графа
(п. 5.10) и радиуса устойчивости множества оптимальных графов (п. 5.9)
проведено Ю.Н. Сотсковым.
Вопросы устойчивости оптимальных расписаний при критериях оптималь-
ности. отличных от Гтах, также рассматривались в работах В.Б Алюшкеви-
ча и Ю.Н.Сотскова.
6.11. Ситуации, в которых для выполнения отдельной операции требу-
ется несколько приборов, рассматривались А.И. Куксой, Ю.П. Лаптиным,
Б.Е. Поляченко [159-162], Я. Блажевичем [468,469] и другими авторами
[150,245,499,505,530, 531,611,650, 666,696,707, 708,786, 787]. Обзоры
результатов по решению таких задач содержатся в монографии В.С. Михале-
вича и А.И. Куксы [215], а также в работах М. Гонсалеса [548], Я.Блаже-
вича, Я. Ленстры и А. Ринной Кана [470].
Ряд других обобщений задач теории расписаний рассматривался в рабо-
тах [29, 74, 80, 122, 124, 151, 206, 218, 239, 253, 337, 338, 344, 364, 366,
389, 391, 396, 398, 407, 408, 410, 463, 476, 575, 577]. Многокритериальные
задачи теории расписаний исследовались в [31, 109, 140, 193, 357-
359, 474].
6.12. Много публикаций посвящено прикладным аспектам теории распи-
саний, в частности рассмотрению вопросов календарного планирования
крупномасштабных проектов [63, 64, 240], химического производства
294
[60, 124, 405, 406], строительного производства [112, 115, 261, 292], вы-
числительных центров [22, 23, 76, 77, 104, 105, 262, 548], гибких производ-
ственных систем [103, 142, 196, 235, 243, 244, 353, 385, 387]. См. также [1,
21, 52, 142, 211, 212, 231, 241, 242, 269, 280, 287,288,346,404,575,577,
724,773,831].
Описания программных реализаций методов решения отдельных задач
теории расписаний приведены в [31, 142, 144, 169, 285, 310, 387].
В [635, 636] сообщается о программе, позволяющей вести обработку и на-
копление результатов по исследованию сложности задач теории расписаний.
В [348, 349] описан пакет программ РУПОР для решения широкого
круга задач построения оптимальных расписаний обслуживания требований
в одностадийных и многостадийных системах. Функциональные модули па-
кета написаны на алгоритмическом языке ФОРТРАН-IV, управляющая
часть — на ассемблере. Пакет программ может эксплуатироваться в ин-
терактивном режиме, имеет развитые информационно-справочные и
обучающие средства.
СПИСОК ЛИТЕРАТУРЫ
1. Автоматизированное проектирование и производство в машиностроении / Под
ред Ю.М Соломенцева и В.Г. Митрофанова. - М.. Машиностроение, 1986. -
256 с.
2. Адельсон-Вельский ГМ О некоторых вопросах сетевого планирования // Иссле-
дования по дискрет, мат - М. Наука, 1973. - С. 105 - 134.
3. Адельсон-Вельс кий Г.М., Диниц Е.А., Карзанов А.В. Потоковые алгоритмы. -
М . Наука, 1 975. -- 120 с.
4. Айзенштат В.С. Совмещение примитивных циклических процессов // Докл.
АН БССР.- 1963 -Т.',№3. С 148 151.
5 .Айзенштат В.С. Многоопераюрные циклические процессы // Докл. АН БССР.
1963. Т. 7, №4. С. 224 -227.
б. Алюшкевич ВБ., Сотсков Ю.Н. Исследование устойчивости оптимальных по
быстродействию расписаний Препринт/ИТК АН БССР. - Минск, 1987. -
№ 9. - 20 с.
7. Ангуладзе М.Х. Об использовании метода статистического поиска с применени-
ем правил предпочтения в задачах составления расписаний // Сообщ. All ГССР. -
1972. - Т. 65, № 2. - С. 417-420
8 Андронов А.М, Хижняк А.П. Математические методы планирования и управле-
ния производственно-хозяйственной деятельное!ью предприятий гражданской
авиации - М.: Транспор!, 1977. - 215 с.
9 Аронович А Б. О выборе оптимальных комбинаций локальных правил календар-
ного планирования // Экон, и маг. методы. - 1970. - Т. 6, № 4. - С. 548-557.
10 Артамонов И.М Алгоритмы определения последовательности обработки деталей,
имеющих одинаковый технологический маршрут // Мат. исследования. - Ки-
шинев, 1979. - Вып. 5 2. - С. 3-8.
11. Артамонов И.М. Об одном алгоритме решения задачи Беллмана - Джонсона //
Модели и алгоритмы решения задач планирования и управления. - Киши-
нев, 1982. - С. 3 10.
12. Асратян А С. О существовании реберной раскраски специального вида в двудоль-
ном графе // Сб. по мат. кибернетике. - М.: ВЦ АН СССР, 1977. - Вып. 2. -
С. 45-57.
]3. Асратян А.С О построении реберной раскраски специального вида в двудольном
1рафе и ее применении в задачах теории расписаний // Вестник МГУ. Сер. XV,
выч мат. и киберн. - 1978. - № 1 - С 74-81.
14. Афанасьев В.А., Карелин В.В. Определение возможного минимума продолжитель-
ности выполнения комплекса работ // Кибернетика. - 1974. - № 1. С. 89 - 90.
15. Афонин Ю.С. Блочный метод ветвей и границ // Автомат, и телемех. - 1986.
№8. С. 98-108
16. Бабушкин А.И., Башта А.Л., Белов И.С Построение календарного плана для за-
дачи встречных маршрутов // Кибернетика. - 1977. - № 4. - С. 130 135.
17. Бабушкин А.И., Башта АЛ., Белов И.С Построение календарных планов для
многомаршрутной задачи трех станков // Автомат, и телемех. - 1976 - № 7.
С 154- 158.
296
18. Бабушкин А.И., Башта АЛ., Белов И.С., Душин Б.И. Минимизация цикла рабо-
ты поточной линии // Автомат, и телемех. - 1975. - № 6. - С. 161-167.
19. Бабушкин А.И., Белов И.С. Оптимальные комбинации приоритетных правил
составления расписаний // Автомат, и телемех. - 1986. - № 5. - С. 82-90.
20. Баркан СА. Об общей модели двухстадийного производства // Изв. АН БССР.
Сер. физ.-техн. наук. - 1969. - № 2. - С. 42-47.
2\. Баркан СА., Танаев В.С. О построении расписаний учебных занятий // Изв.
АН БССР. Сер.физ.-мат.наук. - 1970. - № 1. - С. 76-82.
22. Барский А.Б. Две задачи оптимизации использования неоднородных вычислитель-
ных систем // Изв. АН СССР. Техн, кибернетика. - 1971. - № 4. - С. 119-125.
23. Барский А.Б. Планирование параллельных вычислительных процессов. - М.:
Машиностроение, 1980. - 192 с.
24. Белецкий С.А., Данильченко А.М., Панишев А.В. Перестановочный прием в зада-
че трех станков // Кибернетика. - 1985. - № 2. - С. 106-109.
25. Беллман Р. Динамическое программирование. - М.: ИЛ, 1960. - 400 с.
26. Белов И.С., Сталин Я.Н. Алгоритм в одномаршрутной задаче календарного пла-
нирования // Математическая экономика и функциональный анализ. - М.: Наука,
1974. - С. 248-257.
27. Блох А.Ш., Танаев В.С. Многооператорные процессы // Изв. АН БССР. Сер. физ.-
мат. наук. - 1966 - № 2. - С. 5-11.
2Ъ. Болун И.Ф. К задаче упорядочения работ в многофазных системах обслужива-
ния // Модели и алгоритмы АСУ. - Кишинев, 1986. - С. 29-58.
29. Большаков В.А., Уздемир А П., Шмелев В.В. Задачи планирования дискретного
(штучного) производства и численные методы их решения. III // Автомат,
и телемех. - 1976. - № 1. - С. 146-156.
3Q. Бондаренко О А. Эвристические подходы к решению задач календарного плани-
рования // Автоматиз. системы vnp. предприятиями. Труды семинара. - 1968. -
Вып. 1. - С. 47-65.
31. Борзенко В.И., Зрахтенгерц Э.А., Шершанов В.М. Аппроксимационная много-
критериальная диспетчеризация в вычислительных системах // Автомат, и теле-
мех. - 1986. - № 9. - С. 152-162.
32. Бородич СА. О трудноразрешим ости задач минимизации числа запаздывающих
работ в двухстадийной системе обслуживания с нефиксированными маршрута-
ми // Сложность и методы решения задач оптимизации. - Минск: ИТК АН БССР,
1984. - С. 4-8.
33. Бородич СА. Об одной задаче минимизации максимального временного сме-
щения в двухстадийной системе обслуживания с нефиксированными маршру-
тами // Изв. АН БССР. Сер. физ.-мат. наук. - 1985. - № 5. - С. 109.
34. Бородич СА. К вопросу сложное!и построения оптимальных по быстродействию
расписаний для одного класса обслуживающих систем с операторами переноса //
Изв. АН БССР. Сер. физ.-мат. наук. - 1986. - № 4. - С. 116- 117.
35. Бородич С А. О параметрической задаче для двухстадийной обслуживающей
системы с нефиксированными маршрутами // Применение маг. методов и вы-
числ. техники при решении народно-хозяйственных задач: Тез. докл. респ. науч.-
техн. ^овещ. - Минск, 1986. - С. 14-15.
36. Бородич С.А., Струсевич В.А. Обслуживание упорядоченного множества требо-
ваний ь системе с нефиксированными маршрутами, - Препринт/Ин-т математи-
ки АН БССР. - Минск, 1986. - № 7 (243) . - 24 с.
37. Бородич СА., Струсевич В А. Расписания обслуживания частично упорядоченно-
го множества требований для одного класса детерминированных систем // Изв.
АН БССР. Сер. физ.-мат. наук. - 1986. - № 3. - С. 19 -22.
3%. Бородич С А., Тузиков А.В. О сложности построения оптимальных по быстро-
действию расписаний для некоторых двухстадийных систем обслуживания с не-
фиксированными маршрутами // Методы, алгоритмы и программы решения
экстремальных задач. - Минск: ИТК АН БССР, 19Ь5. - С. 76-85.
39. Бродский И.Л. Оптимальная реакция на единичное возмущение расписания //
Экон, и матем. методы. - 1976, № 6. - С. 1206-1210.
40. Букина В.Н., Беккер Р. О решении задачи Джонсона в пространстве перестано-
вок // Исследование операций и АСУ. - Киев: КГУ, 1977. - Вып. 10. - С. 116-122.
20. В.С. Танаев
297
41. Бурдюк В.Я, О задаче т станков (т >2) // Кибернетика. - 1969. - № 3. - С. 74-76.
42. Бурдюк В.Я. Стохастическая задача двух станков // Кибернетика. - 1969. -
№5. - С. 110-114.
43. Бурдюк В.Я. О выборе последовательности загрузки станков // Экон, и мат.
методы. - 1970. - Т. 6, № 1. - С. 112-116.
44. Бурдюк В.Я., Рева В.Н. Об одном методе оптимизации функционала от переста-
новок при наличии ограничений // Кибернетика. - 1980. - № 1. - С. 99-103.
45. Бурдюк В.Я., Шкурба В.В. Теория расписаний. Задачи и методы решений. 1. //
Кибернетика. - 1971. - № 1. - С. 89-102.
46. Бурдюк ТА. Оптимальное упорядочение работ для станков равной производи-
тельности // Изв. АН СССР. Техн, кибернетика. - 1972. - № 1. - С. 32-36.
47. Бурков В.Н. Распределение ресурсов как задача оптимального быстродействия //
Автомат, и телемех. - 1966. - Т. 27, вып. 7. - С. 119-129.
4%. Бурков В.Н., Ланда В.Д., Ловецкий С.Е., Тейман А.И., Чернышев В.Н. Сетевые
модели и задачи управления. - М.: Сов. радио. - 1967. - 144 с.
49. Бурков В.Н, Ловецкий CJE. Методы решения экстремальных комбинаторных
задач (обзор) // Изв. АН СССР. Техн, кибернетика. - 1968. - № 4. - С. 82-93.
50. Бурков В.Н., Ловецкий С.Е. Методы решения экстремальных задач комбина-
торного типа (обзор) // Автомат, и телемех. - 1968. - № И. - С. 68-93.
51. Василенко С.И. Об одной задаче теории расписаний // ЖВМ и МФ. - 1983. -
Т. 23, №3.-С. 713-718.
52. Васильев ГА. Алгоритм нахождения допустимого решения в задачах календар-
ного планирования горных работ // Вопросы кибернетики. Ташкент: АН УзССР,
1978. - Вып. 100. - С. 13-21.
53. Визинг В.Г. Хроматический класс мультиграфа // Кибернетика. - 1965. - № 3. -
С. 29-39.
54. Вишняков В.А., Герман О.В. Планирование мультипрограммной работы в парал-
лельных вычислительных системах // Изв. АН СССР. Техн, кибернетика. - 1984. -
№1.-С. 206-213.
55. Владимиров В.Н., Егоров С.В. Декомпозиционный метод решения задачи Вел-
лмана - Джонсона с возмущениями // Изв. АН СССР. Техн, кибернетика. -
1982.-№ 2.-С. 86-91.
56. Власюк В А. Задачи оптимального расписания при параллельно-последовательном
соединении машин // Изв. АН СССР. Техн, кибернетика. - 1966. - № 4. -
С. 67-80.
57. Власюк В А. Оптимальное расписание обработки на трех последовательных ма-
шинах // Изв. АН СССР. Техн, кибернетика. - 1967. - № 4. - С. 79-84.
58. Волошин В.В. Об одной задаче производственного планирования // Труды Ле-
нингр. политехи, ин-та им. М.И. Калинина. - 1967. - Вып. 291. - С. 43-46.
59. Выгнан П.К., Кудин Б.И. Алгоритм построения календарного графика работы
оборудования на участках с разнонаправленными маршрутами обработки //
Применение мат. в экон. - Л.: ЛГУ, 1969. - С. 68-78.
60. Ганеев В.В., Соболев О.С., Софиев А.Э., Шлепаков ПА. Задача расчета оптималь-
ного плана-графика производства полиэтилена // Оперативное планирование
и управление производством. - М.: Энергоатомиздат, 1985. - С. 23-27.
(А. Гимади Э.Х., Глебов НИ., ПерепелицаВ.А. Исследования по теории расписаний //
Управляемые системы. - 1974. - Вып. 12. - С. 3-10.
Ь2. Гимади Э.Х., Глебов Н.И., Перепелица В А. Алгоритмы с оценками для задач
дискретной оптимизации // Проблемы кибернетики. - Вып. 31. - М.: Наука,
1975. - С. 35-42.
63. Гимади Э.Х., Пузынина Н.М. Задача календарного планирования крупномасштаб-
ного проекта в условиях ограниченных ресурсов: опыт построения мате-
матического обеспечения // Управляемые системы. - 1983. - Вып. 23. -
С. 24-32.
64. Гимади Э.Х., Пузынина Н.М., Севастьянов С.В. О некоторых экстремальных за-
дачах реализации крупных проектов типа БАМ // Экон, и мат. методы. - 1979. -
Т. 15, вып. 5. - С. 1017-1020.
65. Гиффлер Б. Алгебры календарного планирования и их применение при форму-
лировании моделей общих систем // Календарное планирование. - М.: Прогресс,
1966. - С. 62-83.
298
66. Гиффлер Б,, Томпсон Д., Ван-Нессе В. Опыт вычислений с применением линей-
ного алгоритма и алгоритма Монте-Карло для решения задач календарного плани-
рования на производстве // Календарное планирование. - М.: Прогресс, 1966. -
С. 42-61.
67. Глебов НМ. Алгоритм составления расписания для двух работ//Управляемые
системы. - 1968. - Вып. 1. - С. 14-20.
68. Глебов НМ. О верхней оценке длины оптимального расписания для двух работ //
Пробл. кибернетики. - М.: Наука, 1968. - Вып. 20. - С. 225-229.
69. Глебов НМ. Некоторые случаи сводимости m-станочной задачи Джонсона к задаче
с двумя станками// Управляемые системы. - 1978. - Вып. 17. - С. 46-51.
70. Глебов НМ., Перепелица В.А. О нижней и верхней оценках для одной задачи
теории расписаний // Исслед. по кибернетике. - М.: Сов. радио, 1970. - С. 11-17.
71. Глебский Ю.В., Шевченко ВМ. О составлении оптимального плана работ // Научн.
труды Моск, инж.-экон. ин-та. - 1964.- Вып. 21. - С. 318-324.
72. Глебский Ю.В., Шевченко В.Н. О составлении оптимального расписания работы
на п станках // Труды по вопр. пр имен. ЭВМ в нар. хозяйстве. - Горький. -
1964. - С. 31-34.
73. Голенко ДМ., Гофман Э.Ф., Тарнопольский Ю.Я., Столин Я.Н. Асимптотические
точные оценки для одномаршрутных задач теории расписаний // Численные мето-
ды нелинейного программирования: Материалы I Всесоюзн. семинара. - Киев,
1976. - С. 180-186.
74. Голенко ДМ., Тарнопольский Ю.Я. Оптимизация календарных планов методами
направленного поиска // Кибернетика, - 1970. - №6. - С. 138-144.
75. Голенко Д.И., Фишбейн С.М. Некоторые методы решения одномаршрутных задач
календарного планирования // Труды Ленингр. инж.-экон. ин-та им. П. Тольят-
ти. - 1972. - Вып. 94. - С. 51-66.
76. Головкин БА. Классификация методов диспетчеризации работы многопроцессор-
ных и многомашинных вычислительных систем // УС и М. - 1982. - № 3. -
С. 3-11.
77. Головкин БА. Расчет характеристик и планирование параллельных вычислитель-
ных процессов. - М.: Радио и связь, 1983. - 272 с.
78. Гордеев Э.Н., Леонтьев В.К. Устойчивость в задачах на узкие места // ЖВМ и
МФ. - 1980. - Т. 20, №4. - С. 1071-1075.
79. Гордеев Э.Н., Леонтьев В.К. Траекторные параметрические задачи // ЖВМ и
МФ. - 1984. - Т. 24, № 1. - С. 37-46.
80. Гордон В.С., Танаев В.С. О минимаксных задачах теории расписаний с одним при-
бором // Изв. АН БССР. Сер. физ.-мат. наук. - 1983. - № 3. - С. 3-9.
81. Гордон В.С., Шафранский Я.М. Об одном классе задач теории расписаний с частич-
но упорядоченными требованиями // IV Всесоюзн. конф, по проблемам теорети-
ческой кибернетики: Тез. докл. - Новосибирск, 1977. - С. 101-103.
82. Гордон В.С., Шафранский Я.М. Оптимальное упорядочение при последовательно-
параллельных ограничениях предшествования // Докл. АН БССР.- 1978. - Т- 22,
№3, - С. 244-247.
83. Гордон В.С., Шафранский Я.М. Об оптимальном упорядочении при последователь-
но-параллельных ограничениях предшествования // Изв. АН БССР. Сер. физ.-мат.
наук. - 1978.- №5. - С. 135.
84. Гофман Э.Ф., Кеслер С.Ш. Алгоритмизация решения задач календарного планиро-
вания // Труды Ленингр. инж.-экон. ин-та. им. П. Тольятти. - 1976. - Вып. 120. -
С. 12-33.
85. Григер В.А. О точном алгоритме составления оптимального расписания много-
операторной поточной линии // Вопросы радиоэлектроники. Сер. ЭВТ. - 1983. —
Вып. 12. - С. 58-63.
86. Григер В.А., Нуриев Н.К., Гинзбург М.М. Построение расписаний для много-
процессных автооператорных поточных линий гальванического производства //
Вопросы радиоэлектроники. Сер. ЭВТ. - 1985. - Вып. 12.- С. 59-64.
87. Гринберг В.С., Севастьянов С.В. О величине константы Штейница // Функцион.
анализ и его прил. - 1980. - Т. 14, № 2. - С. 56-57.
88. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. -
М.:Мир, 1982. - 416 с.
2.0
299
89. Данильченко А.М., Левченко С.Н., Панишев А.В. Приближенный алгоритм решения
задачи трех станков // Автомат, и телемех. - 1985. - № 7. - С. 133-139.
90. Данильченко А.М., Панишев А.В. О частных случаях задачи трех станков // Изв.
АН СССР. Техн, кибернетика. - 1986. - № 4. - С. 197.
91. Демин В.К., Чеботарев А.С. Оптимальное обслуживание детерминированного
потока требований. I, П // Изв. АН СССР. Техн, кибернетика. - 1976. - № 4. -
С. 193-199; 1976. - № 5. - С. 65-70.
92. Джексон Д.Р. Очереди с динамическим правилом приоритета // Календарное
планирование. - М.: Прогресс, 1966. - С. 357-377.
93. Доцатов В.В., Тогер А.В. О некоторых обобщениях одномаршрутной задачи
календарного планирования // Машинная обработка информации. - Киев, 1970. -
Вып. 29. - С. 92-98.
94. Драхлин Е.Х., Якимов Р.М. Об одном методе определения оптимальной последо-
вательности непрерывного процесса обработки // Науч, труды. - Пермь: Перм.
политехи, ин-т, 1966. - Вып. 21. - С. 55-59.
95. Драхлин Е.Х., Якимов Р.М. Анализ свойств оптимального варианта последова-
тельности обработки изделий // Науч, труды. - Пермь: Перм. политехи, ин-т,
1966. - Вып. 21. - С. 59-61.
96. Душин Б.И. Замечание к алгоритму в одномаршрутной задаче Джонсона // Кибер-
нетика. - 1980. - № 2. - С. 129-131.
97. Емеличев В.А., Комлик В.И. Метод построения последовательности планов для
решения задач дискретной оптимизации. - М.: Наука, 1981. - 207 с.
98. Емеличев В.А., Супруненко Д.А., Танаев В.С. О работах белорусских математиков
в области дискретной оптимизации // Изв. АН ССР. Техн, кибернетика. - 1982. -
№6. - С. 25-45.
99. ЕфетоваК.Ф., Подчасова Т.П., Португал В.М., Тринчук Б.Е. Планирование произ-
водства в условиях АСУ: Справочник. - Киев: Техшка, 1984. - 135 с.
100. Журавлев Ю.Н. Оценки сложности алгоритмов построения минимальных дизъюнк-
тивных нормальных форм для функций алгебры логики // Дискретный анализ. -
Новосибирск, 1964. - Вып. 3. - С. 41-77.
101. Журавлев Ю.Н. Оценка сложности локальных алгоритмов для некоторых экстре-
мальных задач на конечных множествах // ДАН СССР. - 1964. - Т. 158, № 5. -
С. 1018-1021.
102. Журавлев Ю.И. Локальные алгоритмы вычисления информации. I, II // Киберне-
тика. - 1965. - № 1. - С. 12-19; 1966. - № 2. - С. 1-11.
1О3. 2Л^гаев С.Н., Соколицын А.С, Распределение производственной программы по
плановым периодам на участках, оснащенных станками с ЧПУ // Резервы повыше-
ния экономической эффективности машиностроительного производства. -
Саратов: СПИ, 1982. - С. 84-87.
104. Зайченко Ю.П., Вишталь Д.М., Клитовченко О.А. Организации планирования работ
на ВЦКП с учетом всех стадий технологического процесса // Вестник Киевского
политехи, ин-та. Техн, кибернетика. - 1980. - Вып. 4. - С. 72-78.
105. Зайченко Ю.П., Клитовченко О.А. Исследование эвристических алгоритмов плани-
рования работы ВЦ при многостадийном обслуживании // Вестник Киевского
политехи, ин^га. Техн, кибернетика. - 1982. - Вып. 6. - С. 29-83.
106. Зак Ю.А. Некоторые свойства задач теории расписаний // Автомат, и телемех. -
1978.-№1. - С. 123-132.
107. Закревский А.Д. Алгоритмы синтеза дискретных автоматов. - М.: Наука, 1971. -
С. 213-268.
108. Зимин И.Н., Иванилов Ю.П. Решение задач сетевого планирования сведением их
к задачам оптимального управления // ЖВМ и МФ. - 1971. - Т. 11, № 3. -
С. 632-641.
109. Зиндер Я.А., Шкурба В.В. Эффективные итеративные алгоритмы теории расписа-
ний // Кибернетика. - 1985,- № 1. - С. 72-75.
110. Золотухин В.Ф. Об исключении заведомо неоптимальных решений задачи Велл-
мана - Джонсона //Изв. АН СССР. Техн.кибернетика.- 1979. - № 1. - С. 44-51.
111. Зыков АЛ. Теория конечных графов. - Новосибирск: Наука, 1969. - 544 с.
112. Ильницкий А.Л. Об одном подходе к решению задачи календарного планирова-
ния в строительстве // Исследование операций и АСУ. - Киев: КГУ, 1976. -
Вып. 8. - С. 25-31.
300
113. Ильницкий АЛ Двойственность в целочисленном программировании при реше-
нии задач календарного планирования // Исследование операций и АСУ. - Киев:
КГУ, 1978. - Вып. 11. - С. 75-81.
114. Ильницкий АЛ. Оценка целевой функции одной дискретной задачи теории распи-
саний // Исследование операций и АСУ. - Киев: КГУ, 1979. - Вып. 13. - С. 54-58.
115. Ильницкий А.Л. Универсальность и условия существования решений одного
класса задач теории расписаний // Исследование операций и АСУ. — Киев: КГУ,
1980. - Вып. 15. - С. 38-46.
116. Инукаи Т. Замечания к статье ’’Анализ коммутационной матрицы для системы
ПБ/МДВУ” // ТИИЭР. - 1978. - Т. 66, № 12. - С. 94-95.
117. Иоффе Э.Г. Об одном алгоритме расчета календарных расписаний для произ-
водственного участка // Экон, и мат. методы. - 1971. - Т. 7, № 6. - С. 876-882.
118. Иоффе Э.Г. Алгоритм для определения всех оптимальных расписаний в двух-
операционной задаче Джонсона // Автомат, и телемех. - 1973. - № 7. - С. 95-101.
119. Ириков В.А. Некоторые задачи упорядочения // Изв. АН СССР. Техн, кибер-
нетика. - 1970. - № 4. - С. 38-42.
120. Яго Я., Урано Е„ Муратани Т., Ямагути М. Анализ коммутационной матрицы
для системы ПБ/МДВУ // ТИИЭР. - 1977. - Т. 65, № 3. - С. 152-162.
121. Кадец М.И. Об одном свойстве векторных ломаных в «-мерном пространстве //
УМН..- 1953. - Т. 8, № 1. - С. 139-143.
122. Казанцев Э.Н. Математическая модель графика выпуска изделий, удовлетворяю-
щего требованию комплектации сборки // Изв. АН БССР. Сер. физ.-мат. наук. -
1968.- № 1. -С. 54-60.
123. Календарное планирование/Сост. Мут Д>к. Ф., Томпсон Дж.Л. - М.: Прогресс,
1966.-466 с.
124. Калюжный Б.И, Солдатов В.С. Модель диспетчеризации дискретных производст-
венных процессов // Изв. АН СССР. Техн, кибернетика. - 1976. - № 6. - С. 21-26.
125. Канцедал СА. Алгоритм сокращения поиска решений в задаче теории расписаний
сетевой структуры // Автомат, и телемех. - 1982. - № 4. - С. 72-77.
126. Канцедал С.А. Декомпозиционный подход к решению задач теории расписаний
большой размерности // Автомат, и телемех. - 1983. - № 10. - С. 144-151.
127. Канцедал СА.., Малых О.Н. О построении допустимых планов в общей задаче
календарного планирования // Автомат, системы управл. и приборы авто-
мат. - Харьков: Вища школа, 1978. - Вып. 45. - С. 81-86.
128. Канцедал С.А., Малых О.Н. Математические модели календарного планирования
производства и их использование. Сообщение. I, II // Автомат, системы управл. и
приборы автомат. - Харьков: Вища школа, 1978. - Вып, 47. - С. 29—35;
С. 36-41.
129. Канцедал С А., Малых О.Н. Классы расписаний и алгоритмы их построения //
Автомат, системы управл. и приборы автомат. - Харьков: Вища школа, 1979. -
Вып. 51. - С. 69-75.
130. Канцедал СА., Малых О.Н. Случайный поиск в задачах теории расписаний //
Автомат, системы управл. и приборы автомат. - Харьков: Вища школа, 1979. -
Вып. 51. - С. 75-81.
131. Канцедал СА., Малых О.Н. О классах расписаний // Кибернетика. - 1981.-№6.-
С. 66-74.
132. Карзанов А.В. Нахождение максимального потока в сети методом предпотоков //
ДАН СССР. - 1974. - Т. 215, № 1. - С. 49-52.
133. Карп Р.М. Сводимость комбинаторных проблем // Кибернет. сб. Новая серия. -
М.: Мир, 1975. - Вып. 12. - С. 16-38.
134. Катаев В.А. Оптимальная очередь обработки деталей на произвольном количест-
ве станков (теория расписаний) // Науч, труды НИИ управляющих машин и сис-
тем. - Пермь. - 1967. - Вып. 1. - С. 57-68.
135. Киладзе Ю.В., Кварацхелия О.И. Модель локальной оптимизации для одномарш-
рутной задачи календарного планирования // Труды Тбилисского гос. ун-та. -
1980. - Вып. 212. - С. 178-191.
136. Кислицын С.С. Конечные частично упорядоченные множества и соответствующие
им множества перестановок // Мат. заметки. - 1968. - Т. 4, вып. 5.-
С. 511-518.
301
137. Климова Л.И., Сотсков Ю.Н. Раскраска вершин смешанного графа // Алгоритмы
и программы решения задач оптимизации. - Минск: ИТК АН БССР, 1983. -
С. 90-95.
138. Ковалев М.Я. Эффективный е-приближенный алгоритм для задачи максимизации
быстродействия в двухстадийной системе из параллельных приборов // Изв.
АН БССР. Сер. физ.-мат. наук. - 1985. - № 3. - С. 118.
139. Ковалев М.Я. Приближенное решение задачи минимизации суммарного запазды-
вания требований // Изв. АН БССР. Сер. физ.-мат. наук. - 1985. - № 5. - С. ПО.
140. Ковалев М.Я., Тузиков А.В. Построение е-аппроксимации множества Парето
некоторых двухкритериальных задач // Мат. вопросы автоматизации проектиро-
вания и испытаний. - Минск: ИТК АН БССР, 1986. - С. 126-130.
141. Ковалев М.Я., Шафранский Я.М. Построение е-приближенных алгоритмов опти-
мизации функций на последовательно конструируемых множествах // ЖВМ и
МФ. - 1986. - № 7. - С. 1006-1018.
142. Коган Я.А., Лищинский Л.Ю., Парадизов Н.В. Модели обслуживания станков в
гибких производственных системах // Автомат, и телемех. -1986. - № 6. -
С. 147-155.
143. Коглер В., Штиглиц К. Перечислительные и итеративные алгоритмы // Теория
расписаний и вычислительные машины. - М.: Наука, 1984. - С. 249-317.
144. Козлик ГА., Карась В.М., Кириллов ИА. Пакет прикладных программ для
решения основной задачи теории расписаний // УС и М. - 1979. - № 2. - С. 40-43.
145. Конвей Р., Джонсон Б., Максвелл У. Экспериментальные исследования распреде-
ления работ в соответствии с фиксированными правилами очередности их вы-
полнения // Применение статистических методов в производстве. - М. - 1963. -
С. 212-232.
146. Конвей Р.У., Максвелл У.Л. Календарное планирование в условиях сети очередей
с дисциплиной по кратчайшей операции // Календарное планирование. - М.: Прог-
ресс, 1966. - С. 321-347.
147. Конвей Р.В., Максвелл В.Л., Миллер Л.В. Теория расписаний. - М.: Наука, 1975. -
360 е.
148. Корбут А.А., Сигал И.Х., Финкельштейн Ю.Ю.' Метод ветвей и границ // Math.
Operationsforsch. Statist., Ser. Optimization. - 1977* - V. 8, № 2. - P. 253-280.
149. Корбут AA., Финкельштейн Ю.Ю. Дискретное программирование. - M.: Наука,
1969. - 368 с.
150. Корнилова Л.Е. Оптимальное распределение ресурса в сетевом планировании
методом оптимального потока // Кибернетика. - 1970. - № 6. - С. 145-148.
151. Косарев Н.Г., Уздемир А.П. Динамическая задача планирования научных исследо-
ваний и разработок и метод ее решения // Автомат, и телемех. - 1977. - № 1. -
С. 62-73.
152. Косолап А.И. Применение нелинейного программирования к задачам теории
расписаний // Численные методы нелинейного программирования: Материалы
I Всесоюзн. семинара. - Киев, 1976. - С. 145-149.
153. Костевич Л.С., Лапко А А. Теория игр. Исследование операций. - Минск: Вы-
шэйшая школа, 1982. - 232 с.
154. Ксчнев Л.В. Оптимизация системы приоритета в задачах расписания // Киберне-
тика и ВУЗ. - Томск: Томск, гос. ун-т, 1970. - Вып. 3. - С. 114-122.
\55. Крейнин М.И., Никонов В.А., Савицкая Т.Н. О решении одной задачи загрузки
оборудования // Вычисл. методы и мат. обеспечение ЭВМ. - Казань, 1979. -
С. 76-83.
156. Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1978. -
432 с.
157. Кузин Б.И., Дуболазов ВА. Организация и оперативно-календарное планирование
машиностроительного производства в АСУП. - Л.: ЛГУ, 1978. - 238 с.
158. Кук СА. Сложность процедур вывода теорем // Кибернет. сб. Новая серия.
М.: Мир, 1975. - Вып. 12. - С. 5-15.
159. Кукса А.И. К использованию теории двойственности для решения сетевых задач
теории расписаний // ЖВМ и МФ. - 1982. - Т. 22, № 5. - С. 1074-1079.
160. Кукса А.И., Лаптин Ю.П. Динамическое программирование в сетевой задаче
теории расписаний // Кибернетика. - 1978. - № 1. - С. 111-113.
302
161. Кукса А.И., Лаптин ЮЛ. Использование динамического программирования при
двойственном подходе к решению задачи календарного планирования // Изв.
АН СССР. Техн, кибернетика. - 1981. - № 4. - С. 79-85.
162. Кукса АЛ., Поляченко Б.Е. Алгоритм ветвей и границ для решения двух сетевых
задач календарного планирования // Кибернетика. - 1984. - № 1. - С. 73-76.
163. Ламбин Н.В., Танаев В.С. О бесконтурной ориентации смешанных графов //
Докл. АН БССР. - 1970. - Т. 14, № 9. - С. 780-781.
164. Лапко А.А. Об оптимизации приоритетных систем обслуживания // Изв. АН БССР.
Сер. физ.-мат. наук. - 1977. - № 2. - С. 117-120.
165. Лапко А.А. Обслуживание детерминированных потоков требований в заданные
сроки // Изв. АН БССР. Сер. физ-мат. наук. - 1980. - № 5. - С. 130.
166. Лапко А.А., Поварич М.П. Диспетчеризация потоков требований с переменными
параметрами в приоритетных системах массового обслуживания // Теория и
методы оптимизации в проектировании. - Минск: ИТК АН БССР, 1978. -
Вып 1. - С. 98-104.
167. Латыпов И.Ш. Об алгоритме управления одним классом технологических линий //
Исследование операций и аналитическое проектирование в технике. - Казань,
1979. - С. 47-51.
168. Латыпов И.Ш. О сложности одной задачи теории расписаний // Системы программ-
ного обеспечения решения задач оптимального планирования: Тез. докл. IX Все-
союзн. симпозиума. - М., 1986. - С. 88-89.
169. Лебедева Т.Т., Михалевич В.С., Рощин В.А., Сергиенко И.В., Стукало А.С, Тру-
бин В.А., Шор Н.З. Структура, состав и назначение пакета программ ДИСПРО
для решения задач дискретной оптимизации // Изв. АН СССР. Техн, киберне-
тика. - 1983. - № 1. - С. 193-196.
170. Левин В.И. К задаче трех станков // Изв. АН СССР. Техн, кибернетика. - 1982. -
№ 1. - С. 76-85.
171. Левин Г.М. К оценке хроматических характеристик смешанного графа // Изв.
АН БССР. Сер. физ.-мат. наук. - 1980. - № 2. - С. 37-41.
172. Левин Г.М., Сотсков Ю.Н., Танаев В.С. О раскраске вершин смешанного графа //
Методы и программы решения оптимизационных задач на графах и сетях, ч. 1:
Тез. докл. III Всесоюзн. со вещ. - Новосибирск, 1982. - С. 87-90.
173. Левин 1 .М., Танаев В.С. Декомпозиционные методы оптимизации проектных
решений. - Минск: Наука и техника, 1978. - 240 с.
174. Левин Л.А. Универсальные задачи перебора // Проблемы передачи информа-
ции. - 1973. -Т. 9, №3. - С. 115-116.
175. Левин М.Ш. Об эффективном решении некоторых задач теории расписаний на
сетях // Кибернетика. - 1980. - № 1. - С. 131-135.
176. Левин М.Ш., Левнер Е.В. Об эффективном решении задач Беллмана - Джонсона
на сети, имеющей вид дерева // Автомат, и телемех. - 1978. - № 10. - С. 110-116.
177. Левнер Е.В. Оптимальное планирование обработки объектов на ряде машин //
Автомат, и телемех. - 1969. - № 17. - С. 94-100.
178. Левнер Е.В. Сетевой подход к задачам теории расписаний // Исследования по
дискрета, мат. - М.: Наука, 1973. - С. 135-150.
179. Левнер Е.В. Сетевой подход к задачам теории расписаний // Современные пробле-
мы теории управления. - М.: ИПУ. - 1973 - С. 43-54.
180. Левнер Е.В. Теория расписаний в экономических системах (некоторые математи-
ческие вопросы). - Препринт /ЦЭМИ АН СССР. - М.» 1977. - 54 с.
181. Левнер Е.В., Генс Г.В. Анализ вычислительной сложности приближенных алгорит-
мов для некоторых дискретных оптимизационных задач // Мат. методы решения
экон, задач. - 1980. - № 9. - С. 97-106.
1^2. Леонтьев В.К. Устойчивость задачи коммивояжера // ЖВМ и МФ. - 1975. -
Т. 15, №5. - С. 1298-1309.
183. Леонтьев В.К. Устойчивость в комбинаторных задачах выбора // ДАН СССР. -
1976. -Т. 228, № 1. - С. 23-25.
184. Леонтьев В.К. Дискретные экстремальные задачи // Итоги науки и техники.
Теория вероятностей. Математическая статистика. Теоретическая кибернетика. -
1979. -Т. 16. - С. 39-101.
185. Лепешинский Н.А. К вопросу упорядочения обработки деталей // Изв. АН БССР.
Сер. физ.-мат. наук. - 1966. - № 2. - С.31-35.
303
186. Лепешинский НА. Об одной задаче теории расписаний // Изв. АН БССР. Сер.
физ.-мат. наук. - 1966. - № 3. - С. 90-96.
187. Лепешинский НА. О классификации 2 X п задач Джонсона - Веллмана // Изв.
АН БССР. Сер. физ.-мат. наук. - 1967. - № 1. - С. 18-21.
№>. Лепешинский НА. Одна задача теории расписаний и максимум суммы линейных
форм на множестве подстановок // Изв. АН БССР. Сер. физ.-мат. наук. - 1967. -
№3. - С. 51-54.
189. Лескин А А. Алгебраические модели гибких производственных систем. - Л.:
Наука, 1986. - 153 с.
190. Лившиц Э.М., Рублинецкий В.И. О сравнительной сложности некоторых задач
дискретной оптимизации // Вычислит, мат. и вычислит, техн. - 1972. - Вып. 3. -
С. 78-85.
191. Литл Дж., Мурти К., Суини Д., Кэрел К. Алгоритм для решения задачи о комми-
вояжере // Экон, и мат. методы. - 1965. - Т. 4, вып. 1. - С. 94-107.
192. Ломинадзе Н.Н О некоторых возможностях построения и использования эври-
стических правил предпочтения // Труды Проблемной лаб. автомат, и вычислит,
техн. Техн, кибернетика. - Груз, политехи, ин-т, 1974. - № 4. - С. 43-46.
193. Ломинадзе Н.Н. О решении задачи упорядочения и составления расписаний при
нескольких показателях качества // Труды Проблемной лаб. автомат, и вычислит,
техн. Техн, кибернетика. - Груз, политехи, ин-т, 1974. - № 4. - С. 37-42.
194. Лурье АЛ. О некоторых задачах календарного планирования // Пробл. киберне-
тики. - М.: Наука, 1962. - Вып. 7. - С. 201-208.
195. Лурье АЛ. О математических методах решения задач на оптимум при планирова-
нии социалистического хозяйства. - М.: Наука, 1964. - 323 с.
196. Макаров ИМ., Рахманкулов В.З., Назаретов В.М., Блинов С А., Михайлов А.М.,
Манько С.В., Ахрем АА. Робототехника и гибкие автоматизированные производ-
ства. Управление робототехническими системами и гибкими ав-томатизи ров эн-
ными производствами. - М.: Высшая школа, 1986. - 160 с.
197. Марков ЛА., Первозванский А А. Правило узких мест в задаче Джонсона // Ки-
бернетика. — 1974. - № 5. - С. 142-144.
198. Маршалл А., Олкин И. Неравенства: Теория мажоризации и ее приложения. - М.:
Мир, 1983.-576 с.
199. Матюшков Л.П., Танаев В.С. Программные генераторы допустимых расписаний.
I, II//Вычислит. техн, в машиностроении. - Минск: НТК АН БССР, 1967. -
С. 35-48; 1968. - С.12-28.
200. Мельников О.И. К задаче Беллмана-Джонсона // Изв. АН БССР. Сер. физ.-мат.
наук. - 1975. - № 4. - С. 43-47.
201. Мельников О.И. Свойства оптимальных расписаний задачи Веллмана-Джонсона
для двух станков //Изв. АН БССР. Сер. физ.-мат. наук. - 1976. - № 3. - С. 19-25.
202. Мельников О.И. Решение некоторых задач Беллмана-Джонсона с (0,1)-матри-
цами // Изв. АН БССР. Сер. физ.-мат. наук. - 1976. - № 4. - С. 11-16.
203. Мельников О.И. Устойчивость оптимального расписания задачи Веллмана-Джон-
сона // Изв. АН БССР. Сер. физ.-мат. наук. - 1976. - № 6. - С. 99-101.
204. Мельников О.И. О 2 X w-задаче Беллмана-Джонсона, для которой все расписания
оптимальны // Изв. АН БССР. Сер. физ.-мат. наук. - 1984. - № 2. - С. 31-33.
205. Мельников О.И., Шафранский ЯМ. Минимизация средней длительности обслужи-
вания в детерминированных системах с двумя приборами // Изв. АН БССР. Сер.
физ.-мат. наук. - 1971. - № 3. - С. 124.
206. Мельников О.И., Шафранский ЯМ. Параметрическая задача теории расписаний //
Кибернетика. - 1979. - № 3. - С. 53-5 7.
207. Метельский А.С. О некоторых периодических процессах // Докл. АН БССР. -
1963. - Т. 7, № 9. - С. 584-587.
208. Метельский А.С. К системе периодических процессов // Докл. АН БССР. - 1963. -
Т. 7, №11. —С. 724-728.
209. Метельский А.С. Периодические процессы // Докл. АН БССР. - 1965. - Т. 9,
№12.-С. 788-790.
210. Метельский Н.Н. Об экстремальных значениях линейной формы на некоторых
множествах подстановок // Изв. АН БССР. Сер. физ.-мат. наук. - 1972. - №5. -
С. 5-10.
304
211. Мироносецкий НЛ. Экономико-математические методы календарного планирова-
ния. - Новосибирск : Наука, 1974.- 140 с.
212. Мироносецкий Н.Б., Андерсон А.Р. Управление подготовкой производства. -
Новосибирск: Наука, 1976. - 160 с.
213. Михалевич В.С. Последовательные алгоритмы оптимизации и их применение.
I, II // Кибернетика. - 1965. -№ 1. - С. 45-56; 1965. -№ 2. - С. 85-89.
214. Михалевич В.С., Волкович ВЛ., Волошин А.Ф., Поздняков Ю.М. Алгоритмы
последовательного анализа и отсеивания вариантов в задачах дискретной оптими-
зации II Кибернетика. - 1980. - № 3. - С. 76-85.
215. Михалевич В.С., Кукса А.И. Методы последовательной оптимизации в дискретных
сетевых задачах оптимального распределения ресурсов. - М.: Наука, 1983, -
217 с.
216. Михалевич В.С., Шкурба В.В. Последовательные схемы оптимизации в задачах
упорядочения выполнения работ // Кибернетика. - 1966. - № 2. - С. 34-40.
217. Михалевич В.С., Шор Н.З. Численное решение многовариантных задач по методу
последовательного анализа вариантов // Науч.-метод, материалы экон.-мат. семи-
нара. - М.: ВЦ АН СССР. - 1962. - Вып. 1, - С. 15-42.
218. Мищенко А.В., Сушков Б.Г. Задача оптимального распределения ресурсов на
сетевой модели при линейных ограничениях на время выполнения работ // ЖВМ
и МФ. - 1980. - Т. 20, № 5. - С. 1324-1328.
219. Моисеев Н.П. Численные методы оптимального управления. - М.: ВЦ МГУ, 1968.
220. Моисеев Н.Н. Численные методы в теории оптимальных систем. - М.: Наука,
1971.-424 с.
221. Моисеев Н.Н. Элементы теории оптимальных систем, - М.: Наука, 1975. - 526 с.
222. Моисеев Н.Н. Математика ставит эксперимент. - М.: Наука, 1979. - 223 с.
223. Моисеев Н.Н., Иванилов ЮЛ., Столяров ЕМ. Методы оптимизации, - М.: Наука,
1978. - 351 с.
224. Муравьев В.И., Романовский ИЛ. Использование метода переменного базиса для
решения непрерывного аналога задачи Джонсона // Исследование операций и
статист, моделирование. - Л., 1974. - Вып. 2. - С. 27-37.
225. Носов В А., Сачков В.Н., Тараканов В.Е. Комбинаторный анализ. Матричные
проблемы, теория выбора // Итога науки и техники. Теория вероятностей. Мате-
матическая статистика. Теоретическая кибернетика. - 1981. - Т. 18. - С. 53-93.
226. Носов В А., Сачков В.Н., Тараканов В.Е. Комбинаторный анализ (неотрицатель-
ные матрицы, алгоритмические проблемы) // Итоги науки и техники. Теория
вероятностей. Математическая статистика. Теоретическая кибернетика. - 1983. -
Т. 21.-С. 120-178.
227. Нуриев Н.К., Гудин Н.В., Кайдриков РА., Журавлев Б.Л. Организация оптималь-
ной работы автооператорных гальванических линий // Казань: Казанский хими-
ко-технолог. ин-т им. С.М. Кирова, 1986. - 80 с.
228. Оганесян ГА. Некоторые свойства и решение частных случаев задачи теории
расписаний // Вопросы совершенствования планирования и управления. - Душан-
бе: НИИЭМП Госплана ТаджССР, 1978. - Вып. 14. - С. 133-145.
229. Оганесян ГА. Эффективный алгоритм решения частного случая задачи ком-
мивояжера // Экономико-математическое моделирование в системах управления.-
Душанбе: НИИЭМП Госплана ТаджССР., 1980. - Вып. 16. - С. 123-125.
230. Озерной ВМ., Рябов ЛИ. Эвристический метод оптимизации последовательности
выполнения операций // Автомат, и телемех. - 1967. - № 12. - С. 169-172.
231. Организация, планирование и управление предприятием электронной промышлен-
ности / Под ред. П.М. Стукалова. - М.: Высшая школа, 1980. - 351 с.
232. Оре О. Теория графов. - М.: Наука, 1980. - 336 с.
233. Осколкова С.Е., Осколков И.О. Применение некоторых эвристических методов
к решению задач календарного планирования (обзор) // Автомат, и телемех. -
1968. —№ 2. - С. 177-184.
234. Основные положения по разработке и применению систем сетевого планирования
и управления. - М.: Экономика, 1974. - 216 с.
235. Офицеров Д.В., Свирин ЮЛ. Метод решения задачи оперативно-календарного
планирования автоматизированного производства//Изв. АН БССР. Сер. физ.-техн.
наук. - 1985. - № 3. - С. 78-83.
305
236. Панишев А.В. Метод дихотомии в задаче трех станков // Изв. АН СССР. Техн,
кибернетика. - 1986. - № 4. - С. 181-186.
237. Панишев А.В., Данильченко AM. Вычисление границ в задаче трех станков // Ав-
томат. системы управл. и приборы автомат. - Харьков: Вища школа, 1984. -
Вып. 69. - С. 62-66.
238. Пападимитриу X., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и слож-
ность. - М.: Мир, 1985. - 510 с.
239. Перепелица В А. Об одной задаче теории расписаний // Кибернетика. - 1966. -
№5.-С. 75-78.
240. Перепелица В А., Севастьянов СВ. Об одной задаче теории расписаний на сети //
Управляемые системы. - Новосибирск, 1976. - Вып. 15. - С. 48-67.
241. Петров В А. Планирование поточно-группового производства. - Л.: Машино-
строение, 1966. - 192 с.
242. Петров ВА. Групповое производство и автоматизированное оперативное управ-
ление. - Л.: Машиностроение, 1975. - 312 с.
243. Петров В А., Масленников А.Н., Осипов ЛА. Планирование гибких производ-
ственных систем. - Л.: Машиностроение, 1985. - 182 с.
244. Пилипенко В А., Канарский В.Ф., Воловин Л.Н. Система краткосрочного плани-
рования работы механообрабатывающего участка в условиях АСУ // УС и М. -
1986. — №3. -С. 108-110.
245. Плещинский Л.С. е -подход к оптимизации сетевой модели // Экон, и мат. мето-
ды. - 1976. - Т. 12, № 6. - С. 1212-1215.
246. Подчасова Т.П. Об оценках и выборе правил предпочтения в задачах календарного
планирования // Автомат, системы упр. предприятиями: Тр. семинара. - 1968. -
Вып. 1. - С. 5-46.
247. Подчасова TJT., Порту гал ВМ., Татаров В А., Шкурба В.В. Эвристические методы
календарного планирования. - Киев: Техшка, 1980. - 140 с.
248. Португал ВМ. Исследование асимптотического поведения задачи Джонсона // Ки-
бернетика. - 1971. - № 1. - С. 105-107.
249. Португал ВМ. Асимптотическое поведение решений некоторых задач теории
расписаний // Кибернетика. — 1976. — № 2. - С. 132-134.
250. Португал ВМ. Асимптотическое поведение решений задач теории расписаний
по различным критериям // Кибернетика. - 1976. - № 5. - С. 97-99.
251. Португал В.М., Семенов А.И. Модели планирования на предприятии. - М.: Наука,
1978.- 270 с.
252. Потшебовски Г. Приближенные алгоритмы решения общей задачи теории распи-
саний // Прикл. пробл. больших систем управления. - София, 1980. - С. 115-124.
2531 Рев«ук И.Н. Условия осуществимости полного обслуживания в системе с М при-
борами, имеющими окна доступности // Изв. АН БССР. Сер. физ.-мат. наук. -
1977.-№4. -С. 123.
254. Ревчук Т.Н., Сотсков Ю.Н. Выделение контуров смешанного графа // Методы
и программы решения экстремальных задач. - Минск: ИТК АН БССР, 1981. -
С. 46-52.
255. Резниченко В.Н. Решение одной задачи теории расписаний эвристическим мето-
дом // Алгоритмизация производственных процессов: Тр. семинара. - Киев,
1968. - Вып. 1. - С. 91-110.
256. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практи-
ка. — М.: Мир, 1980. — 476 с.
257. Романовский И.В. Асимптотика рекуррентных соотношений динамического про-
граммирования и оптимальное стационарное управление // ДАН СССР. - 1964. -
Т. 157, №6.-С. 1303-1306.
258. Романовский И.В. Численные методы дискретного программирования // Тр.
4-й зимней школы по мат. программированию и смежн. вопр. - М., 1972. -
Вып. 5.-С. 76-128.
259. Рубинов А.Р. Теоремы о магистралях в обобщенной задаче коммивояжера и их
применение к задачам раскроя и теории расписаний // ДАН СССР. - 1981. -
Т. 259, №3.-С. 542-546.
260. Рубинов А.Р. О сводимости обобщенной задачи коммивояжера к задаче комми-
вояжера меньшей размерности // ДАН СССР. - 1982. - Т. 264, № 5. - С. 1087-
1090.
306
261. Рыбальский В.И. Кибернетика в строительстве. - Киев: Будшельник, 1975. -
232 с.
262. Рысцов И.К. О понятии расписаний для многопроцессорных систем // Развитие
теории многопроцессорных систем. - Киев, 1984. - С. 63-68.
263. Сальвадор М. Календарное планирование и упорядочение работ // Исследование
операций. - М.: Мир, 1981. — Т. 2. - С. 232-263.
264. Санникова А.К. Об оптимизации функций на перестановках с ограничением на
группирование элементов // Изв. АН БССР. Сер. физ.-мат. наук. - 1982. - № 1. -
С. 116-117.
265. Санникова А.К., Танаев В.С. Об одном классе экстремальных задач на переста-
новках // Докл. АН БССР. - 1979. - Т. 23, № 9. - С. 784-786.
266. Сарванов В.И. Приближенное решение задачи минимизации линейной формы
на множестве циклических подстановок // Изв. АН БССР. Сер. физ.-мат. наук. -
1977.-№ 6.-С. 5-10.
267. Сарванов В.И. К оптимизации на подстановках // Изв. АН БССР. Сер. физ.-мат.
наук. - 1979. - № 4. - С. 9-11.
268. Сарванов В.И. О сложности минимизации линейной формы на множестве цикли-
ческих подстановок // ДАН СССР. - 1980. - Т. 253, № 3. - С. 533-535.
269. Сафроненко В А. Математическое и электронное моделирование задачи опти-
мального календарного планирования. - Минск: Наука и техника, 1972. -
182 с.
270. Сачков В.Н. Комбинаторные методы дискретной математики. - М.: Наука, 1977. -
320 с.
271. Севастьянов С.В. Об асимптотическом подходе к некоторым задачам теории
расписаний // ШВсесоюзн. конф, по проблемам теорет. кибернетики: Тез. докл. -
Новосибирск, 1974. - С. 67-69.
272. Севастьянов С.В. Об асимптотическом подходе к некоторым задачам теории
расписаний // Управляемые системы. - 1975. - Вып. 14. - С. 40-51.
273. Севастьянов С.В. О приближенном решении некоторых задач теории расписаний //
Дискретный анализ. - 1978. - Вып. 32. - С. 66-75.
274. Севастьянов С.В. О приближенном решении задачи календарного распределения //
Управляемые системы. - 1980. - Вып. 20. - С. 49-63.
275. Севастьянов С.В. Приближенные алгоритмы в задачах Джонсона и суммирования
векторов // Управляемые системы. - 1980. - Вып. 20. - С. 64-73.
276. Севастьянов С.В. Некоторые обобщения задачи Джонсона // Управляемые систе-
мы.-1981. - Вып. 21. - С. 45-61.
277. Севастьянов С.В. Алгоритмы с оценками для задач Джонсона и Акерса - Фридма-
на в случае трех станков // Управляемые системы. - 1982. - Вып. 22. - С. 51-57.
278. Севастьянов С.В. Эффективное построение расписаний, близких к оптимальным,
для случаев произвольных и альтернативных маршрутов деталей // ДАН СССР. -
1984. -Т. 276, №1. - С. 46-49.
279. Семенов И.Г. Алгоритм упорядочения работ в конвейерной системе по критерию
минимума времени прохождения работ и неизменном порядке их выполнения
на всех машинах // Автоматизация управления промышленными объектами. -
Киев, 1980.-С. 85-98.
280. Семенов А.И., Португал В.М. Задачи теории расписаний в календарном планирова-
нии мелкосерийного производства. - М.: Наука, 1972. - 183 с.
281. Сервах В.В. О задаче Акерса - Фридмана // Управляемые системы. - 1983. -
Вып. 23. - С. 70-81.
282. Сергиенко И.В. Математические модели и методы решения задач дискретной
оптимизации. — Киев: Наукова думка, 1985. - 384 с.
283. Скворцов В.В., Нуриев Н.К. Постановка и подходы к решению много экстремаль-
ной задачи оптимизации работы поточной линии в изменяющихся условиях //
Теория оптимальных решений. - Вильнюс, 1978. - Вып. 5. - С. 55-59.
284. Скрыдлов Н.В., Шафранский В.В. Применение правил приоритета для составления
расписания работ при ограничениях на ресурсы // Работы по техн, кибернетике. -
М.: ВЦ АН СССР, 1967. - Вып. 1. - С. 67-79.
285. Смирнов А.Н. Математическая модель объемного календарного планирования
технологически зависимых операций // Автомат и телемех. - 1985. - № 10. -
С. 108-115.
307
286. Смоляр Л.И. Теория расписаний и управление. - М.: Знание, 1977. - 64 с.
287. Смоляр Л.И, Модели оперативного планирования в дискретном производстве. -
М.: Наука, 1978. - 320 с.
288. Смоляр Л.И. Оперативно-календарное планирование (Модели и методы). - М.:
Экономика, 1979. — 136 с.
289. Солдатов В.С. Оптимальное решение задач теории расписаний; работы допускают
прерывания // Тр. XXII Научной конф. Моск, физ.-техн. ин-та. - Долгопрудный:
МФТИ, 1976. - С. 125-128.
290. Солих Р. Задача календарного планирования для циклически повторяющегося
производства // ЖВМ и МФ. - 1973. - Т. 13, № 2. - С. 326-342.
291. Сотсков Ю.Н. Оптимальное расписание множества работ, заданного смешанным
графом // Изв. АН БССР. Сер. физ.-мат. наук. - 1977. - № 4. - С. 133.
292. Сотсков Ю.Н. Сетевое планирование и управление в строительстве с использова-
нием смешанных графов // Системный подход в управлении строительством. -
Минск: ИС и А Госстроя БССР, 1977. - С. 109-114.
293. Сотсков Ю.Н. Составление расписаний на смешанных графах е -методом // Авто-
матизированное проектирование технических систем и.процессов. - Минск:
ИТК АН БССР, 1979. - С. 49-53.
294. Сотсков Ю.Н. Задача теории расписаний на смешанных графах // Теория и методы
автоматизации проектирования. - Минск: ИТК АН БССР, 1980. - С. 19-22.
295. Сотсков Ю.Н. Определение числа орграфов, порождаемых смешанным графом //
Алгоритмы и программы решения задач оптимизации. - Минск: ИТК АН БССР,
1980.-С. 36-39.
296. Сотсков Ю.Н. Перечисление расписаний, заданных смешанным графом // Изв.
АН БССР. Сер. физ.-мат. наук. - 1980. - № 5. - С. 132-133.
297. Сотсков Ю.Н. Построение орграфов, порождаемых смешанным графом // Алго-
ритмы и программы решения задач оптимизации. - Минск: ИТК АН БССР, 1980. -
С. 40-44.
298. Сотсков Ю.Н. Расписания на смешанных графах с ограниченным максимальным
штрафом // Изв. АН БССР. Сер. физ.-мат. наук. - 1980. - № 2. - С. 37-41.
299. Сотсков Ю.Н. Об ориентировании ребер смешанного графа // Изв. АН БССР.
Сер. физ.-мат. наук. -1981.-№5.-С. 22-24.
300. Сотсков Ю.Н. Составление оптимального по быстродействию расписания выполне-
ния взаимосвязанных работ последовательными приборами // Методы и програм-
мы решения экстремальных задач. - Минск: ИТК АН БССР, 1981. - С. 28-34.
301. Сотсков Ю.Н. О методе решения общей задачи теории расписаний // I Всесоюзн.
совещание по статист, и дискр. анализу нечисловой информ., экспертным оценкам
и дискр. оптимизации: Тез. докл.: - М., 1981. - С. 218-219.
302. Сотсков Ю.Н. Оптимальное обслуживание двух требований при регулярном кри-
терии // Автоматизация процессов проектирования. - Минск: ИТК АН БССР,
1985. - С. 86-95..
303. Сотсков Ю.Н. Сетевые модели в теории расписаний // Оптимизация, принятие
решений, микропроцессорные системы. - София: ИТКР БАН, 1985. - С. 157-162.
304. Сотсков Ю.Н. Сетевой подход к решению задач теории расписаний // Методы,
алгоритмы и программы решения экстремальных задач. - Минск: ИТК АН БССР,
1985. - С. 52-62.
305. Сотсков Ю.Н., Алюшкевич В.Б. Устойчивость оптимальной ориентации ребер сме-
шанного графа// Докл. АН БССР. - 1988. - Т. 32, №4. - С. 108-111.
306. Сотсков Ю.Н., Барановская С.М. Минимизация максимального штрафа за обслу-
живание требований последовательными приборами // Сложность и методы
решения задач оптимизации. - Минск: ИТК АН БССР, 1984. - С. 37-47.
307. Сотсков Ю.Н., Танаев В.С. О перечислении ориентированных бесконтурных гра-
фов, порождаемых смешанным графом // Изв. АН БССР. Сер. физ.-мат. наук. -
1974.-№2.-С. 16-21.
308. Сотсков Ю.Н., Танаев В.С. Об одном подходе к перечислению ориентированных
бесконтурных графов, порождаемых смешанным графом // Изв. АН БССР. Сер.
физ.-мат. наук. - 1976. - № 5. - С. 99-102.
309. Сотсков Ю.Н., Танаев В.С. Хроматический многочлен смешанного графа // Изв.
АН БССР. Сер. физ.-мат. наук. — 1976. - № 6. - С. 20-23.
308
310. Сотсков Ю.Н,, Черняк ЖА. Определение параметров сетевого графика // Алго-
ритмы и программы решения экстремальных задач и смежные вопросы. - Минск:
ИТК АН БССР, 1982. - С 42-53.
311. Столин Я.Н. Решение одномаршрутной задачи Джонсона для трех машин с по-
грешностью 4 max tjj // Численные методы нелинейного программирования:
Тез. II Всесоюзн. семинара. - Харьков, 1976. - С. 287-289.
312. Стори А.Е., Вагнер Х.М. Опыт применения целочисленного программирования
при расчете календарного плана для предприятий единичного и мелкосерийного
производства // Календарное планирование. - М.: Прогресс, 1966. - С. 241-256.
313. Струсевич В А. Некоторое эффективно разрешимые классы задачи Веллмана-
Джонсона // Математические методы и их приложения в больших экономических
и технических системах Тез. докл. Всесоюзн. школы-семинара. - М., 1980. —
С. 177-180.
314. Струсевич В А. К задаче Веллмана - Джонсона // Докл. АН БССР. - 1981. - Т. 25,
№6. - С. 518-521.
315. Струсевич В А, Задачи конвейерного типа с регулярными матрицами. - Минск,
1981. - 39 с. - Деп. в ВИНИТИ 4.08.81., № 3857-81.
316. Струсевич В А. Эффективно разрешимые классы задачи Веллмана - Джонсона
и ее модификаций. - Минск, 1981. - 43 с. - Деп. в ВИНИТИ 4.08.81, № 3858-81.
317. Струсевич В А. О возможности приближенного решения одной задачи теории рас-
писаний // I Всесоюзн. со вещ. по статист1, и дискр. анализу нечисловой информа-
ции, экспертным оценкам и дискр. оптимизации: Тез. докл. - М., 1981. - С. 222-
223.
318. Струсевич В А. Класс регулярных задач Веллмана - Джонсона // Изв. АН БССР.
Сер. физ. -мат. наук. - 1)82. - № 1. - С. 28 -33.
319. Струсевич В А, Об одной задаче теории расписаний с древовидными ограничения-
ми предшествования // Методы и программы решения оптимизационных задач
на графах и сетях, ч. 1.: Тез. докл. III Всесоюзн. совещ. - Новосибирск, 1984. -
С. 221-223.
320. Струсевич В А. Сложность решения некоторых задач теории расписаний с задан-
ными отношениями предшествования // Сложность и методы решения задач опти-
мизации. - Минск: ИТК АН БССР, 1984. - С. 9-20.
321. Струсевич В А, Задача трех станков: достаточное условие сводимости в выпуклой
форме // Вести. БГУ им. В.И. Ленина. Сер. 1, физ., мат., мех.- 1985. - № 1. -
С. 36-39.
322. Струсевич В А. Доминирующие приборы в детерминированных системах // При-
менение матем. методов и вычисл. техники при решении народнохозяйственных
задач: Тез. докл. респ. научн. -техн, совещ. - Минск, 1986.-С. 151-152.
323. Струсевич В А, О возможности построения оптимальных по быстродействию рас-
писаний для многостадийной системы с нефиксированными маршрутами прохож-
дения стадий // Изв. АН БССР. Сер. физ. -мат. наук. - 1986. - №6. - С. 43-48.
324. Струсевич В А. Минимизация суммарного времени обслуживания для системы с
нефиксированными маршрутами // Вести. БГУ им. ВЛ. Ленина. Сер. 1,физ., мат.,
мех. - 1988. - № 1. - С 44-46.
325. Струсевич В А., Довнрр Ю.С. Модифицированный алгоритм решения одного клас-
са задач Беллмана - Дхонсона // ЭВМ - учебному процессу, науке и технике. -
Минск: Вышэйшая школа, 198*5. - С. 58-62.
326. Супруненко ДА, О значениях линейной формы на множестве подстановок // Ки-
бернетика. - 1968. - №2. - С. 59-63.
327. Супруненко ДА., Айзенштат В.С., Лепешинский НА. Экстремальные значения
функций на множествах подстановок // I Всесоюзн. конф, по исслед. операций:
Тез. докл. - Минск, 19'т7. - С. 61-64.
328. Супруненко ДА,, Айзенштат В.С., Метельский А,С, Многоэтапный процесс прев-
ращения // Докл. АН БССР. - 1962. - Т. 6, № 9. - С. 541-544.
329. Супруненко ДА., Метельский Н.Н. Задача о назначениях и минимизация суммы
линейных форм на симметрической группе // Кибернетика. - 1973. - № 3. -
С. 64-68.
330. Супруненко ДА., Тышкевич Р.И. Динамические отображения и один класс детер-
минированных машин // Кибернетика. - 1965. - № 2. - С. 9-17.
309
331. Сытник В.Ф. О математической структуре задачи календарного планирования //
Исследования операций и АСУ. - Киев: КГУ, 1975. - Вып. 5. - С. 14-23.
332. Сытник В.Ф. Некоторые результаты исследования задачи Джонсона // Исследова-
ние операций и АСУ. - Киев: КГУ, 1976. - Вып. 8. - С. 17-25.
333. Сытник В.Ф., Кузьменко Л.И. Некоторые модификации алгоритма решения ка-
лендарной задачи по методу Монте-Карло // Исследование операций и АСУ. -
Киев: КГУ, 1975. - Вып. 6.- С. 45-51.
334. Сытник В.Ф., Кузьменко Л.И. Симультативная модель календарного планирова-
ния и ее реализация на ЭВМ // Исследование операций и АСУ. - Киев: КГУ, 1976.-
Вып. 7. - С. 39-48.
335. Танаев В.С. К задаче составления расписания работы поточной линии с одним ав-
тооператором // Инж. -физ. ж. - 1964. - Т. 7, № 3. - С. 111-114.
336. Танаев В.С. Об одной задаче теории расписаний // Изв. АН БССР. Сер. физ. -мат.
наук. - 1964. - № 4. - С. 128-131.
337. Танаев В.С. Теория расписаний. - М.: Знание. - 1988. - 40 с.
338. Танаев В.С. Некоторые оптимизируемые функции одностадийного производст-
ва// Докл. АН БССР. - 1965. - Т. 9,№ 1. - 11-14.
339. Танаев В.С. О числе перестановок п частично упорядоченных элементов // Докл.
АН БССР. - 1967. - Т. 11, № 3. - С. 208.
340. Танаев В.С. Метод решения задач дискретного программирования // Экон, и мат.
методы. - 1968. - Т. 4, вып. 5. - С. 776-782.
341. Танаев В.С. Прерывания в детерминированных системах обслуживания с парал-
лельными идентичными приборами // Изв. АН БССР. Сер. физ. -мат. наук. -
1973.-№ 6.-С. 44-48.
342. Танаев В.С. Смешанные (дизъюнктивные) графы в теории расписаний // Большие
системы информации и управления. - София: ИТКР БАН, 1975. - С. 181.
343. Танаев В.С. Об оптимизации функций, рекуррентно заданных на множествах пе-
рестановок // Изв. АН БССР. Сер. физ. -мат. наук. - 1977. - № 3. - С. 27 -30.
344. Танаев В.С. Об оптимальном разбиении конечного множества на подмножест-
ва // Докл. АН БССР. - 1979. - Т. 23, № 1. -С. 26 -28.
345. Танаев В.С. Современное состояние и основные тенденции развития теории рас-
писаний // Оптимизация, принятие решений, микропроцессорные системы. -
София: ИТКР БАН, 1985. - С. 148-151.
346. Танаев В.С. Некоторые вопросы оптимизации проектных решений в САПР //
Автоматизация процессов проектирования. - Минск: ИТК АН БССР, 1985. -
С. 73-85.
347. Танаев В.С. Декомпозиция и агрегирование в задачах математического прог-
раммирования. - Минск: Наука и техника, 1987. -184 с.
348. Танаев В.С., Гордон В.С., Сотсков Ю.Н., Янова О.В., Шафранский ЯМ., Горох О.В.,
Барановская СМ. Пакет программ решения задач оптимального упорядочения
(ППП РУПОР). - Минск: ИТК АН БССР, 1986. - 66 с.
349. Танаев В.С., Гордон В.С., Сотсков Ю.Н., Янова О.В., Шафранский Я.М., Горох О.В.,
Барановская С.М. Пакет программ решения задач оптимального упорядочения
(ППП РУПОР). Описание программ. - Минск: ИТК АН БССР, 1987. - 86 с.
350. Танаев В.С., Гордон В.С., Шафранский Я.М. Теория расписаний. Одностадий-
ные системы. - М: Наука, 1984. - 381 с.
351. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. - М.: Наука, 1975. -
256 с.
352. Теория расписаний и вычислительные машины // Под ред. Э.Г. Коффмана. -
М.: Наука, 1984. - 336 с.
353. Тимковский В.Г. Приближенный полиномиальный алгоритм для общей задачи
теории расписаний // Мат. методы оптимизации и их приложения в больших
экон, и техн, системах: Тез. докл. Всесоюзн. школы-семинара. - М.: 1980. -
С. 181-184.
354. Тимковский В.Г. К сложности составления расписания произвольной системы //
Изв. АН СССР. Техн, кибернетика. - 1985. - № 3. - С. 102-109.
355. Тимковский В.Г Полиномиальное решение задачи Ленстры - Ринноя Кана о со-
ставлении расписания работ на двух машинах // Кибернетика. - 1985. - № 2. -
С. 109-111.
310
356. Тимковский В.Г. Приближенное решение задачи составления расписания цикличе-
ской системы // Экон, и мат. методы. - 1986. - Т. 22, № 1. - С. 171-174.
357. Тузиков А.В. Минимизация максимального штрафа и решение некоторых двух-
критериальных задач теории расписаний // Докл. АН БССР. - 1983. - Т. 27,
№ 10. - С 907-910.
358. Тузиков А.В. О двухкритериальной задаче теории расписаний с учетом изменения
длительностей обслуживания //ЖВМ и МФ. - 1984. - № 10. - С. 1585 — 1590.
359. Тузиков А.В. О двухкритериальных задачах теории расписаний // Оптимизация,
• принятие решений, микропроцессорные системы. - София: ИТКР БАН, 1985. -
С. 163-168.
360. Тузиков А.В. Оптимальное обслуживание двух требований в системе с ограничен-
ными ресурсами // Методы, алгоритмы и программы решения экстремальных
задач. - Минск: ИТК АН БССР, 1985. - С. 43-51.
361. Тютюкин В.К, Нахождение оптимальных планов в многооперационных процессах
обработки изделий методом "ветвей и границ" // Применение математики в эко-
номике. - Л., 1970. - Вып. 6. - С. 29-45.
362. Тютюкин В.К. Об оптимизации календарной длительности обработки изделий при
одинаковой последовательности запуска на всех станках // Оптимальное планиро-
вание. - 1970. - Вып. 16. - С. 89-97.
363. Тютюкин В.К. Оптимальное двухоперационное расписание при параллельно-пос-
ледовательном движении производства // Применение математики в экономи-
ке. -Л., 1976. - Вып. 11. - С. 60-69.
364. Уздемир А.П. Задачи планирования дискретного (штучного) производства и чис-
ленные методы их решения I, II // Автомат, и телемех. - 1975. -- № 9. - 115-122;
1975. -№ 10. - С. 90-104.
365. Уздемир АЛ., Большаков В.А. Система планирования дискретного производст-
ва. - М.: ВНИИСИ. - 1983. - 32 с.
366. Уздемир А.П., Шмелев В.В. Целочисленные динамические задачи экономического
планирования с сетевыми ограничениями. I, II// Автомат, и телемех. - 1978. -
№7. - С. 106-115; 1978. - № 9. - С. 110-120.
367. Фейгин Л.И. Управление и прогнозирование в задачах теории расписаний при не-
полной информации // ДАН СССР. - 1971. - Т. 200, №6. - С. 1298-1301.
368. Фейгин Л.И. Общая задача теории расписаний при неполной информации // Авто-
мат. и телемех. - 1972. - № 3. - С. 110-116.
369. Фейгин Л.И. Векторная оптимизация в задачах теории расписаний при не-
полной информации // Изв. АН СССР. Техн, кибернетика. - 1976. - № 5. -
С. 3-9.
370. Фейгин Л.И. Статистическая оценка оптимизации в общей задаче теории расписа-
ния // Изв. АН СССР. Техн, кибернетика. - 1982. - № 2. - С. 221-223.
371. Фейгин Л.И. Задачи теории расписаний при нечетких длительностях операций //
ДАН СССР. - 1983. - Т. 272, №4. - С. 812-815.
372. Финкельштейн Ю.Ю. Приближенные методы и прикладные задачи дискретного
программирования. - М.: Наука, 1976. - 264 с.
373. Фишер Г., Томпсон Г.Л. Комбинации локальных правил календарного планирова-
ния применительно к самонастраивающимся на вероятностной основе програм-
мам для ЭВМ // Календарное планирование. - М.: Прогресс, 1966. - С. 260-290.
374. Форд Л., Фалкерсон Д. Потоки в сетях. - М.: Мир, 1966. - 276 с.
375. Франчук В.И. Некоторые алгоритмы решения задач календарного планирования //
Мат. методы решения экон, задач. - 1974. - Вып. 5. - С. 109-113.
376. Халафян А.А. Разномаршрутная задача теории расписаний // Ученые - науке и на-
родному хозяйству. - Краснодар,. 1983, - С. 276-280.
377. Харари Ф. Теория графов. - М.: Мир, 1973. - 300 с.
378. Харди Г.Г., Литтлвуд Дж.Е., Полиа Г. Неравенства. - М.: ИЛ, 1948. - 456 с.
379. Хачатуров В.Р. Аппроксимационно-комбинаторный метод и некоторые его при-
ложения //ЖВМ и МФ. - 1974. -Т. 14, №6. - С. 1464-1487.
38О. Хач«ян Л.Г. Полиномиальный алгоритм в линейном программировании // ДАН
СССР. - 1979. -Т. 244, №5. - С. 1093-1096.
381. Хенк-цн В.Э. Об одном вопросе теории расписаний (2 X Мзадача упорядочения) //
Кибернетика. - 1966. - № 6. - С. 67-71.
311
382. Чеботарь К.С. Об одной задаче оптимизации на множестве перестановок // Изв.
АН МССР. Сер. физ. -мат. наук. - 1984. - № 1. - С. 51-53.
383. Черенин В.П. Решение некоторых комбинаторных задач оптимального планирова-
ния методом последовательных расчетов//Науч.-метод, материалы экон.-мат. семи-
нара лаб. экон -мат. методов АН СССР. - М.: ВЦ АН СССР. - 1962. - Вып. 2.-44 с.
384. Чернова Г.В. Задача определения последовательности обработки деталей, имею-
щих одинаковые технологические маршруты // Применение математики в эконо-
мике. - Л.. 1967. - Вып. 4. - С. 66-81.
385. Чудаков А.Д., Фалевич Б.Я. Автоматизированное оперативно-календарное плани-
рование. - М.: Машиностроение, 1986. - 224 с.
386. Шапиро А .Д. Применение некоторых алгоритмов теории расписаний в календар-
ном планировании индивидуального и мелкосерийного производства // Автомати-
зированные системы управления промышленными предприятиями. - Киев,
1975. -С. 21-34.
387. Шаров В.Г., Фалевич Б.Я., Зафранская ЛА. Алгоритмы моделирования пакетной
передачи партий деталей на последующую обработку в задаче оперативно-кален-
дарного планирования // УС и М. - 1986. - № 5. - С. 123-125.
388. Шафранский В.В. Применение правил приоритета для оптимизации использования
ограниченных ресурсов // Изв. АН СССР. Техн, кибернетика. - 1968. - № 5. -
С. 62-74.
389. Шафранский ВЛ. Алгоритм расчета сетей по заданным правилам приоритета //
Программный метод управления. - М.: ВЦ АН СССР. - 1971. - Вып. 1. - С. 59-
94.
390. Шафранский ВЛ. Минимизация времени выполнения программы работ при задан-
ных ограничениях на ресурсы // Программный метод управления. - М.: ВЦ
АН СССР, 1973. - Вып. 2. - С. 63-99.
391. Шафранский ВЛ. Математические модели и методы планирования развития от-
раслей промышленности. - М.: Наука, 1984. - 224 с.
392. Шафранский Я.М. Оптимизация детерминированных систем обслуживания с дре-
вовидным частичным порядком // Изв. АН БССР. Сер. физ. -мат. наук. - 1978. -
№2. - С. 119.
393. Шафранский Я.М. Об оптимальном упорядочении в детерминированных системах
с древовидным частичным порядком // Изв. АН БССР. Сер. физ. - мат. наук. -
1978. - № 2. - с. 120.
394. Шафранский Я.М. О задаче минимизации на множестве перестановок частично
упорядоченных элементов. I, II // Изв. АН БССР. Сер. физ.-мат. наук. - 1980. -
№5.-С. 132; 1982. - № 1. - С. 113.
395. Шафранский Я.М. Об алгоритме отыскания минимума приоритето-порождающих
функций на специальных множествах перестановок. I, II // Изв. АН БССР. Сер.
физ. -мат. наук. - 1982. - № 3. - С. 38-42; 1983. - № 1. - С. 15-20.
396. Шахбазян К£., Лебединская Н.Б. Минимизация суммарного штрафа в задаче
параллельного упорядочения независимых работ // ДАН СССР.-1977. - Т. 237,
№4. - С. 790-792.
397. Шевченко В.Н. Задача оптимального календарного планирования с ограничени-
ем на число рабочих // Изв. вузов. Радиофизика. - 1965. - Т. 8, № 3. — С. 635-
637.
398. Шевченко В.Н. Задача о равномерном распределении простоев (несколько смен) //
Экон, и мат. методы. - 1967. - Т. 3,вып. 4. - С. 619-623.
Шкурба ВЛ. Вычислительные схемы решения задач теории расписаний // Кибер-
нетика. - 1965. - № 3. - С. 72-76.
400. Шкурба В.В. Применение метода статистических испытаний в задачах календарно-
го планирования // Мат. методы в организации и экономике производства. - М.:
1966. - С. 209-223.
WL. Шкурба ВЛ. О задачах упорядочения // Кибернетика. - 1967. - № 2. - С. 63-65.
402. Шкурба ВЛ. Задача трех станков. - М.: Наука, 1976. - 96 с.
403. Шкурба ВЛ.» Белецкий СА.» ЕфетоваК.Ф. Планирование и управление в автома-
тизированном производстве. - Киев: Наукова думка, 1984. - 224 с.
ММ. Шкурба В.В.,Подчасова Т.П.,Пшичук А.Н.» Тур Л.П. Задачи календарного плани-
рования и методы их решения. - Киев Наукова думка, 1966. - 155 с.
312
405. Шлепаков ПЛ., Зиглина А.Л. Алгоритмы и программы оперативно-календарного
планирования производств нефтепереработки // Оперативное планирование и уп-
равление производством. - М.: Энергоатомиздат, 1985. - С. 27-31.
406. Шлепаков ПЛ., Зиглина АЛ., Соболев О.С. Пакет программ для календарного
планирования производства // Механизация и автоматиз. производства. - 1984. -
№ 12. - С. 27-30.
407. Шмелев В.В. Метод составления расписания обработки одинаковых партий изде-
лий // Автомат, и телемех. - 1973. - № 7. - С. 124-127.
408. Шмелев ВЛ. Динамическая задача межцехового планирования // Моделирование и
управление в развивающихся системах. - М.: Наука, 1978. - С. 120-125.
409. Шурайц Ю.М. Минимизация времени ожидания комплексов работ при двух этап-
ном обслуживании // Автомат, и телемех. - 1977. - № 12. - С. 138-144.
410. Щербак А.Ф., Левин ГЛ., Волчек Б Л. Об одном классе задач оптимального вре-
менного распределения работ // Экон, и мат. методы. - 1974. - Т. 10, вып. 5. -
С. 947-956.
411. Якимов Р.М. Об одном функциональном уравнении, описывающем оптимальную
последовательность обработки изделий // Науч, труды. - Пермь: Перм.политехи,
ин-т., 1960. - Вып. 21. - С. 62-71.
4 12. Achugbue J.O., Chin F.Y. Scheduling the open shop to minimize mean flow time//
SIAM J. Comput. - 1982. -V.il, №4. -P. 709-720.
413. Achugbue J.O., Chin F. Y. Complexity and solutions of some three-stage flow shop
scheduling problems // Math. Oper. Res. - 1982. - V. 7, №4. - P. 532-543.
414. Achuthan N.R. A special case of the (M|m|F|Fmax) problem// Opsearch. - 1977. - V.14,
№2.-P. 71-87.
415. Achuthan N.R., Ghosh D.T. A note on heuristic rules for the («iSlFlFmax) problem//
Opsearch. - 1980. - V. 17, №1. - P. 50-56.
416. Achuthan N.R., Grabowski J., Sidney J.B. Optimal flow-shop scheduling with earliness
and tardiness penalties // Opsearch. - 1981. - V. 18. - P. 117- 138.
417. Adam N.R., Surkis J. Priority update intervals and anomalies in dynamic ratio type
job shop scheduling rules// Manag. Sci. - 1980. - V. 26, № 12. - P. 1227-1237.
418. Adiri I., Amit N. Route-depended open-shop scheduling// HE Trans. - 1983. -V. 15,
№3.- P. 231-234.
419. Adiri I., Pohoryles D. Flowshop/no-idle or no-wait scheduling to minimize the sum of
completion times// Nav. Res. Log. Quart. - 1978. - V.29, № 3. — P. 495-504.
420. Adrabinski A., Grabowski J. An algorithm for solving the machine sequencing problem//
Zastosow. Matem. - 1977. -V. 15, №4. -P. 536-540.
42\.Aggarwal S.C. An example of Ignall and Schrage // Oper. Res. - 1973. - V. 21, № 3, -
P. 862.
422. Akers S.B. A graphical approach to production scheduling problems// Oper. Res. -
1956. - V. 4, № 2. - P. 244-245.
423. Akers S.B., Friedman J. Anon-numerical approach to production scheduling problems//
Oper. Res. - 1955. - V. 3. - P. 429-442.
424. Albrycht J., Matloka M. On certain strict methods for solving sequential problems//
Funct. et Approximatio. Comment. Math. - 1980. - V. 9. - P. 49-53.
425. Anderson E.J. Anew continuous model for job-shop scheduling//In t. J. Sy st. Sci z-1981.-
V. 12, №12. - P. 1469-1475.
426. Arkin E.M., Papadimitriou C.H. On negative cycles in mixed graphs//Oper. Res. Lett.-
1985.- V. 4, №3. - P. 113-116.
427. Arora R.K., Rana S.P. Scheduling in a semi-ordered flow-shop without intermediate
queues// AI1E Trans. - 1980. - V. 12, № 3. - P. 263-272.
428. Arthanari T.S., Mukhopadhyay A.C. A note on a paper by W. Szwarc// Nav. Res. Log.
Quart - 1971. - V. 18, № 1. - P. 135- 138.
429. Ashour S. A decomposition approach for the machine scheduling problem// Int. J. Prod.
Res. - 1967. - V. 6,№2. - P. 109-122.
430. Ashour S. An experimental investigation and comparative evaluation of flow-shop sche-
duling techniques // Oper. Res. - 1970. - V. 18, №3. - P. 541-549.
43l. Ashour S. A branch-and-bound algorithm for flow shop scheduling problems// AIIE
Trans. - 1970. - V. 2, №2. - P. 172-176.
432. Ashour S. Sequencing theory// Leet. Notes Econ. Math. Syst. - 1972. - V. 69. -133 p.
21. В.С. Танаев
313
433. Ashour S., Char A.R. Computational experience on zero-one programming approach to
various combinatorial problems// J. Oper. Res. Soc. Japan. - 1970. - V. 13, № 2. -
P. 78-108.
434. Ashour S., Chin K. -Y.t Moore T.E. An optimal schedule time of a job shop-like dis-
junctive graph// Networks. - 1973. - V. 3. - P. 333-349.
435. Л$йоиг S., Hiremath S.R. A branch-and-bound approach to the job-shop scheduling
problem// Int. J. Prod. Res. - 1973. - V. 11, № 1. - P. 47-58.
436. 4sAour S., Moore T.E., Chin K.-Y. An implicit enumeration algorithm for nonpreemp-
tive shop scheduling problem// AIIE Trans. - 1974. - V. 6, № 1. - P. 62-72.
437. Ashour S., Parker R.G. An out-of-kilter approach for machine sequencing problems//
Leet. Notes Econ. Math. Syst. - 1973. - V. 86. - P. 206-223.
438. Ashour S., Parker R.G. A precedence graph algorithm for the shop scheduling problem//
Oper. Res. Quart. - 1971. - V. 22, № 2. - P. 165-175.
439. ЛхЛоиг S., Quraishi N. Investigation of various bounding procedures for production
scheduling problems// Int. J. Prod. Res. - 1969. - V. 7, № 3. - P. 249-252.
440. Axsater S. On scheduling in a semi-ordered flow shop without intermediate queues//
AIIE Trans. - 1982. - V. 14, №2. - P. 128-130.
441. Bagga P.C. Two machine scheduling problem// Logist. Rev. - 1967. - V. 3,№1.-
P. 27-37. .
442. Bagga P.C., ChakravartiN.K. Optimal rw-stage production schedule//CORS J.- 1968.-
V. 6, №2. - P. 71-78.
443. Bagga P.C., ChakravartiN.K. Minimizing waiting cost over two stage production sche-
dule// Z. angew. Math. Meeh. - 1969. - V. 49, №5. - P. 299-301.
444. Bagga P.C., Kalra K.P. Node elimination in three-machine flowshop scheduling prob-
lem// Indian J, Pure Appl. Math. - 1982. - V. 13, №8, - P. 871-878.
445. Bagga P.C, Khurana K. Transportation of job-blocks with separated setup times and
removal times//Cahiers C.E.R.O. - 1984.-V. 26, №3-4. - P. 195-200.
446. BakerK.R. Introduction to sequencing and scheduling. - New York: Wiley, 1974. - 305 p.
447. Baker K.R. A comparative study of flow-shop algorithms// Oper. Res. - 1975. - V. 23,
№1. - P. 62-73.
44%. Baker K.R. An elimination method for the flow-shop problem//Oper.Res.- 1975.-
V. 23, №1. - P. 159-162.
449. Balas E. Discrete programming by the filter method// Oper. Res. - 1967 - V., 15,
№5. -P. 915-957.
450. Balas E. Machine-sequencing via disjunctive graphs: an implicit enumeration algorithm//
Oper. Res. - 1969. - V. 17, №6.- P. 941-957.
451. Balas E. Machine sequencing: disjunctive graphs and degree-constrained subgraphs//
Nav. Res. Log. Quart. - 1970. - V. 17, № 1. - P. 1-9.
452. Balas E. Project scheduling with resource constraints// Applications of Mathem. Pro-
gramming. - London: English University Press, 1971. - P. 187-200.
453. Balas E. On the facial structure of scheduling polyhedra// Math. Progr. Study.-1985.-
V. 24.- P. 179-218.
454. Balas E., Guignard M. Report of the session on branch and bound/implicitenumeration//
Ann. Discr. Math. - 1979. - V. 5. - P. 185-191.
455. Balas E., Landweer P.R. Traffic assignment in communication satellites// Oper. Res. Lett. -
1983. - V. 2, №4. - P. 141-147.
4S6. Bansal S.P. Minimizing the sum of completion times of n jobs over m machines in a
flowshop. - A branch and bound approach// AIIE Trans. - 1977. - V. 9,№ 3. - P. 306 -
315.
4S1. Bansal S.P. On lower bounds in permutation flowshop problems// Int. J.Prod. Res.-
1979. - V. 17, №4.- P. 411-418.
458. Bansal S.P., Kuan D Global lower bound in the How-shop problem// Opsearch. -
1976. -V. 13, № 2.- P. 115-118.
459. Baran-Jarosz B. Metoda rozwiazywania pewnego zagadnienia sekweneyjnego// Prz.
statyst. - 1973. - T. 20, №2. - S. 181-192.
460. Barany I. A vector-sum theorem and its application to improving flow shop guarantees//
Math. Oper. Res. - 1981. - V. 6,№3. - P. 445-452.
461. Barany I., Fiala T. Tdbbge'pes iitemeresi problemak kozel optimalis megoldasa//Szigma.-
1982. - V 15, № 3. - P. 177-191.
314
462. Barany I., Grinberg V.S. A vector-sum theorem in two-dimensional space// Period. Math.
Hung. - 1985. - V. 16,№2. - P. 135-138.
463. Barker J.R., McMahon G.B. Scheduling in general job shop//Manag. Sci. - 1985. - V. 31,
№5. -P. 594-598.
464. Bellman R. Mathematical aspects of scheduling theory// J. SIAM. - 1956. - V.4,№3. -
P. 168-205.
465. Bellman R., Gross O. Some combinatorial problems arising in the theory of multistage
processes//J. SIAM. - 1954. - V. 2, № 3. - P. 175-183.
466. Bestwick P.F., Hastings N.AJ. A new bound for machine scheduling//Oper. Res. Quart-
1976. - V. 27, №2ii. - P. 479-487.
467. Blackstone J.N., Phillips D.T., Hogg C.L. A state-of-the-art survey of dispatching rules
for manufacturing job shop operations// Int. J. Prod. Res. - 1982. - V. 20, №1. -
P. 27-45.
46%. Blazewicz J. Deadline scheduling of tasks - a survey//Found. Control Engin.- 1977.-
V. 1,№4. - P. 203-216.
469. Blazewicz J. Solving the resource constrained deadline scheduling via reduction to the
network flow problem// Eur. J. Oper. Res. - 1981.-V. 6.-P. 75-79.
470. Blazewicz J., Lenstra J.K., Rinnooy Kan A.H.G. Scheduling subject to resource
constraints: classification and complexity// Discr. Appl. Math. - 1983. - V. 5. —
P. 11-24.
471. Blazewicz J., Weglarz J. Zlozonosc obliczeniowa problemow szeregowania zadan na
maszynach z ograniczeniami zasobowymi// Archiv. Automat. Telemech. - 1984. - T. 29,
№1-2. —S. 3-33.
472. Bongiovanni G., Coopersmith D., Wong C.K. An optimal time slot assignment algorithm
for an SS/TDMA system with variable number of transponders// IEEE Trans. Com-
mun. - 1981. - V. COM-29, № 5. - P. 721-726.
473. Bonney M.C., Gundry S.W. Solutions to the constrained flowshop sequencing problem//
Oper. Res. Quart. - 1976. - V. 27, №41. - P. 869-883.
474. Borowits I., Ein-dor P. Two issues in the evaluation of job shop schedules//OMEGA.-
1976. - V. 4, №3. - P. 313-320.
475. Bowman E.H. The schedule-sequencing problem// Oper. Res. - 1959. - V. 7,№5.-
P. 621-624.
476. Bozoki G., Richard J.-P. A branch-and-bound algorithm for the continuos-process job-
shop scheduling problem// АПЕ Trans. - 1970. - V. 11, № 3. - P. 246-252.
477. Bratley P., Florian M., Robillard P. On sequencing with earliest starts and due dates with
application to computing bounds for the (nIm|G |Fmax) problem//Nav. Res. Log. Quart-
1973. - V. 20. - P. 57-67.
478. Brooks G.H., White C.R. An algorithm for finding optimal or near optimal solutions to
the production scheduling problem// J. Indust. Engrg. - 1965. - V. 16. - P. 34-40.
479. Brown A.P.G., Lomnicki Z.A. Some applications of the “branch-and-bound” algoiithm
to the machine scheduling problem// Oper. Res. Quart. - 1966. - V. 17, №2. - P. 173-
186.
4%Q. Brucker P. ЛТ-complete operation research problems and approximation algorithms//
Z. Oper. Res. - 1979. - Bd. 23. № 3. - S. 73-94.
481. Brucker P. Minimizing maximum lateness in a two-machine unit-time job shop// Comput-
ing. - 1981. - V. 27. - P. 367-370.
482. Brucker P. A linear time algorithm to minimize maximum lateness for the two-machine
unit-time, job-shop, scheduling problem// Leet. Notes Control Inform. Sci.-1982.-
V. 38. - P. 566-571.
483. 5ur»s F, Rooker J. A special case of 3 X л flow shop problem// Nav. Res. Log.Quart-
1975. - V. 22, №4. - P. 811-817.
484. Burns F., Rooker J. Johnson’s three-machines flow-shop conjecture//Oper. Res. - 1976.-
V. 24, №3.-P. 578-580.
485. Burns F., Rook er J. Three-stage flow-shop with recessive second stage//Oper. Res. -
1978. - V. 26, № 1, - P. 207-208.
486. Campbell H.G., Dudek R.A., Smith M.L. A heuristic algoritm for the n job, m machine
sequencing problem// Manag. Sci. - 1970. - V. 16, № 10. - P. B630-B637.
487. Carlier J. Disjonctions dans ordonnan cements// RAI RO. Rech. Oper. - 1975. - V. 2,
№ 1-2 - P. 83-100.
21
315
488. Carlier J. Ordonnancements a conuained disjonctives// RAIRO. Rech. Oper.- 1978.-
V. 12, №4. - P. 333-351.
489. Chadrasekaran R. Recognition of the Gilmore - Gomory travelling salesman problem//
Discr. Appl. Math. - 1986. - V. 14, № 3. - P. 231-238.
490. Charlton J.M., Death C.C. A generalized machine scheduling algorithm// Oper. Res.
Quart. - 1970. - V. 21, № 1. - P. 127-134.
491. Charlton J.M., Death C.C. A method of solution for general machine scheduling prob-
lems// Oper. Res. - 1970. - V. 18, № 4. - P. 689-707.
492. Chin F.Y., Tsai L.-L. On /-maximal and/-minimal flow-shop schedules// J. Assoc.
Comput. Mach. - 1981. - V. 28, № 3. - P. 462-476.
493. Cho Y.t Sahni S. Preemptive scheduling of independent jobs with release and due times
on open, flow and job shops// Oper. Res. - 1981. - V. 29, № 3. - P. 511 -522.
494. Ciobanu G. A general algorithm for solving flow shop scheduling// Econ. comput.
econ. cybern. stud. res. - 1975. - № 3. - P. 207-212.
495. Corwin B.D., Esogbue A.D. Two machine flow shop scheduling problems with sequence
dependence setup times: a dynamic programming approach// Nav. Res. Log. Quart. -
1974. - V. 21, № 3. - P. 515-524.
496. Dannenbring D.G. An evaluation of flow shop sequencing heuristics// Manag. Sci. -
1977. - V. 23, № 11. - P. 1174-1182.
491. Dantzig G.B. A machine-job scheduling model// Manag. Sci. - 1960. - V. 6, №2. -
P. 191-196.
498. Ztas D.t Dowsland W.B. A model to examine the effect of loading conditions on the
scheduling rules in job shop environment// Int. J. Prod. Res. - 1981. - V. 19, №5. -
P. 577-587.
499. Dew's E.W., Heidorn G.E. An algorithm for optimal projects scheduling under multi-
ple resource constraints// Manag. Sci. - 1971. - V. 17, №12. - P. 803-816
500. Davis M., Putnam H. A computing procedure for quantification theory// J. Assoc.
Comput Mach. - 1960. - P. 201-215.
501. Dey J.E., Hottenstein M.P. Review of sequencing research// Nav. Res. Log. Quart. -
1970.-V. 17,№1.-P. 11-39.
502. Dekel E., Sahni S. Parallel scheduling algorithms// Oper. Res. - 1983. - V. 31, № 1. -
P. 24-49.
503. Deman J.M., van, Baker K.R. Minimizing mean flow time in the flow shop with no inter-
mediate queues// AIIE Trans. - 1974. - V. 6, № 1. - P. 28-34.
504. Deterministic and stochastic scheduling/ Eds Dempster M.A.IL, Lenstra J.K., Rinnooy
Kan A.H.G. - Reidel: Dordecht. - 1982. - 419 p.
505. Dewess G. Die Methode der markierten Verschiebung - ein neues Verfahren zur Opti-
mierung ressonrcenbeschrankter Netzplanablanfe/Math. Operationsforsch. Statist. Ser.
Optimization. - 1983.-V. 14, № 2. - P. 217-235.
506. Dijkstra E.W. A note on two problems in connection with graphs// Numer. Math. -
1959. - № 1. - P. 269.
507. Dudek R.A., Smith M.L., Panwalkar S.S. Use of a case study in sequencing/ scheduling
research// OMEGA. - 1974. - V. 2. - P. 25 3-261.
50%. Dudek R.A., Teuton 4LF. Development of M-stage desicion rule for the scheduling n
jobs through m machines// Oper. Res. - 1964. - V. 12, № 3. - P. 471-497.
509. Durand A. Une methode optimale de traitement des contraintes disjonctives dans les
problems d’ordonnancement// Revue Franc. Inform Rech. Oper. - 1967. - № 3. -
P. 49-61.
510. Dutta S.K., Cunningham A.A. Sequencing two-machine flow-shops with finite interme-
diate storage// Manag. Sci. - 1975. - V. 21, №9. - P. 989 -996.
511. Eilon S., Chowdhury LG. Conditions for optimal scheduling for the three-machine prob-
lem// J. Inst. Math. Appl. - 1976. - V. 17, № 1. - P. 1-4.
512. Eilon S, Chowdhury LG. Due dates in job shop scheduling//Int. J. Prod. Res. - 1976. -
V. 14, №2. - P. 223-237.
513. Ellman D., Towsend W. A dynamic programming approach to the three-machine schedu-
ling// J. Inst. Math. Appl. - 1974. - V. 13, №2. - P. 161-167.
514. Elmaghraby S.E. The machine sequencing problem - review and extensions// Nav. Res.
Log. Quart. - 1968. - V. 15, №2. - P. 205-232.
515. Elvers D.A. The sensivity of the relative effectiveness of job shop dispatching rules with
respect to various arrival distribution// AIIE Trans. - 1974. - V. 6, № 1. - P. 41-49.
316
516. Elvers D.A., Taube L.R. Deterministic/stochastic assumptions in job shops// Eur. J. Oper.
Res. - 1983. - V. 14, № 1. - P. 89-94.
517. Erschler J., Roubellat F., VernhesJ.P. Finding some essential characteristics of the feas-
ible solutions of a scheduling problem// Oper. Res. - 1976. - V. 24. № 4. - P. 774-
783.
518. Even S'., Itai A., Shamir A, On the complexity of timetable and multicommodity flow
problems// SIAM J; Comput. - 1976. - V. 5. - P. 691-703.
519. Fiala T. Kbzelito algorithmus a harom gep problemara// Alkalmazott. mat. lapok. -
1977. - V. 3, № 3. - P. 389-398.
520. Fiala T. An algorithm for the open-shop problem// Math. Oper. Res. - 1983. - V. 8,
NM.-P. 100-109.
521. Fiorini S. A bibliographic survey of edge-colorings// !. Graph. Theor. - 1978.- V. 2. -
P. 93-106.
522. Fisher M.L. Optimal solution of scheduling problems using Lagrange multipliers, part 1 //
Oper. Res. - 1973. - V. 21, №5. - P. 1114-1127.
523. Fisher M.L. Worst-case analysis of heuristic algorithms// Manag. Sci. - 1980. - V. 26,
№1. - P. 1-17.
524. Fisher M.L., Lageweg В J., Lenstra J.K., Rinnooy Kan A.H.G. Surrogate duality relaxa-
tion for job shop scheduling//Discr. Appl. Math. - 1983. - V. 5. - P. 65-75.
525. Florian M., Tilquin C., Tilquin G. An implicit enumeration algorithm for complex sche-
duling problems//Int. J. Prod. Res. - 1975. - V. 13, № 1. - P. 25-40.
526. Florian M., Trepant P., McMahon G. An implicit enumeration algorithm for the machine
sequencing problem//Manag. Sci. (B). - 1971. - V. 17, № 12. - P. 782-792.
527. Floyd R.W. Algorithm 97, shortest path//Comm. ACM. - 1962. - №5. - P. 345.
528. French S. Sequencing and Scheduling: an introduction to the mathematics of the
job-shop. - Horwood: Chichester, 1982. - 245 p.
529. Gabon H.N., Kariv O. Algorithms for edge coloring bipartite graphs and multigraphs//
SIAM J. Comput. - 1982.-V. 11,№1.-P. 117-129.
530. Garey M.R., Graham R.L., Johnson D.S., Yao A.C.-C. Resource constrained schedu-
ling as generalized bin packing//!. Combin. Theory (A). — 1976. - V. 21, №3. - P. 257-
298.
531. Garey M.R., Johnson D.S. Complexity results for multiprocessor scheduling under re-
source constraints//SIAM J. Comput. - 1975. - V. 4, №4. - P. 397-411.
532. Gtorey M.R., Johnson D.S. ’’Strong” ^-completeness results: motivation, examples
and implications//!. Assoc. Comput. Mach. - 1978. - V. 25, № 3. - P. 499-508.
533. Garey M.R. Johnson D.S., Sethi R. The complexity of flow-shop and jobshop schedu-
ling//Math. Oper. Res. - 1976.-V. 1,№2.—P. 117-129.
534. Gelders L.F., Sambandam N. Four simple heuristics for scheduling a flow-shop//Int.
!. Prod. Res. - 1978. - V. 16, № 3. - P. 221-231.
535. Gelders L.F., Wassenhove L.N.V. Production planning: a review//Eur. !. Oper. Res. -
1981. - №7.-P. 101-110.
536. Geoffrion A.M., Marsten R.E. Integer programming algorithm: a framework and state-
of-the art survey//Manag. Sci. - 1972. - V. 18, № 9. - P. 465-491.
537. Gere W.S. Heuristics in job shop scheduling//Manag. Sci. - 1966.- V. 13, №3.- P. 167-
190.
538. Gorenstein S. An algorithm for project (job) sequencing with resource constraints//Oper.
Res. - 1972. - V. 20, №4. - P. 835-850.
539. Giffler B. Schedule algebra: a progress report//Nav. Res. Log. Quart. - 1968. - V. 15,
№2.-P. 255-280.
540. Giffler B., Thompson G.L. Algorithms for solving production-scheduling problems//
Oper. Res. - 1960. - V. 8, №4. - P. 487-503.
541. Giglio R., Wagner H. Approximate solutions to the three-machine scheduling prob-
lem//Oper. Res. - 1964. - V. 12. № 2. - P. 305-324.
542. Gilmore P.C. A solvable case of the traveling salesman problem//Canad. Math. Bull. -
1966. - V. 9, № 6. - P. 743-744.
543. Gilmore P.C., Gomory R.E. A solvable case of the traveling salesman problem//Proc.
Nat. Acad. Sci. USA. - 1964. - V. 51, № 2. - P. 178-181.
544. Gilmore P.C., Gomory R.E. Sequencing a one-state variable machine: a solvable case
of the traveling salesman problem // Oper.Res.- 1964. - V. 12, №5. - P. 655-
679.
317
545. Gilmore P.C., Lawler E.L., Shmoys D.B. Well-solved special cases//The traveling sales-
man problem. A guided tour of combinatorial optimization. - Chichester: Wiley, 1985.
546. Godin V.B. Interactive scheduling: historical survey and state of the art//AIIE Trans. -
1978. - V. 10, № 3. - P. 331-337.
547. GondranM., Minoux M. Graphs and algorithms. - Chichester: Wiley, 1984. - 650 p.
548. Gonzalez MJ. Deterministic processor scheduling//Сотри ting Surveys. - 1977. -
V. 9, №3.-P. 173-204.
549. Gonzalez T. A note on open shop preemptive schedules//IEEE Trans. Сотриt. -
1979. - V. 28, № 10. - P. 782-786.
550. Gonzalez T. Unit execution time shop problems//Math. Oper. Res. - 1982. - V. 7,
№ l.-P. 57-66.
551. Gonzalez T., Sahni S. Open shop scheduling to minimize finish time// J. Assoc. Comput.
Mach. - 1976. - V. 23, № 4. - P. 665-679.
552. Gonzalez T., Sahni S. Flowshop and jobshop schedules: complexity and approxima-
tion//Oper. Res. - 1978. - V. 26, № 1, - P. 36-52.
553. Goodwin J.C., Elvers D.A., Goodwin J.S. Overtime usage in a job shop environment//
OMEGA. - 1978. - V. 6, № 6. - P. 494-500.
554. Gopal I.S., Bongiovanni G., Bonuccelli M.A., Tang D.T., Wong C.K. An optimal switch-
ing algorithm for multibeam satellite systems with variable band with beams//IEEE
Trans. Commun. - 1982. - V. COM-30, № 11. - P. 2475-2481.
555. Gopal I.S., Bonuccelli MA., Wong C.K. Scheduling in multibeam satellites interfering
zones//IEEE Trans. Commun. - 1983. -V. COM-31, № 8. - P. 941-951.
556. Gopal I.S., Wong C.K. Minimizing the number of switchings in a SS/TDMA system//
IEEE Trans. Commun. - 1985. - V. COM-33, № 6. - P. 497-501.
557. Goyal S.K. A note on a paper: On the flow-shop sequencing problem with no wait in
process//Oper. Res. Quart. - 1973. - V. 24, № 1, - P. 130-133.
558. Goyal S.K. Job-shop sequencing problem with no wait in process//Int. J. Prod. Res. -
1975. - V. 13, № 2. - P. 197-206.
559. Grabowski J. A new formulation and solution of the sequencing problem: mathemati-
cal model//Zastosow. Matem. - 1976.- T. 15, №4. - S. 325-343.
560. Grabowski J. A new formulation and solution oT the sequencing problem: algorithm//
Zastosow. Matem. - 1976. - T. 15, № 4. - S. 463-474.
561. Grabowski J. Formulation and solution of the sequencing problem with parallel ma-
chines//Zastosov. Matem. - 1978. - T. 16, № 2. - S. 215-292.
562. Grabowski J. On two-machine scheduling with release and due dates to minimize maxi-
mum lateness//Opsearch. - 1980. - V. 17, №4.-P. 133-154.
563. Grabowski J. A new algorithm of solving the flow-shop problem//Operations research
in progress. Theory and decision library. - Dordrecht-Boston-London, 1982. - V. 32. -
P. 57-75.
564. Grabowski J, A note on an algorithm for solving the n|2l F, r{ > 0 IL max problem//
Opsearch. - 1983. - V. 20, № 2. - P. 107-112.
565. Grabowski J., Janiak A. On job-shop scheduling with resources constraints//Leet.Notes
Contr. Inf. Sci. - 1984. - V. 59. - P. 193-200.
566. Grabowski J., Skubalska E., Smutnicki C. On flow shop scheduling with release and
due dates to minimize maximum lateness//J. Oper. Res. Soc. - 1983. - V. 34, № 7. -
P. 615-620.
567 .Grabowski J., Syslo M.M. On a machine sequencing problem (I)//Zastosow Matem.-
1973. - T. 13, № 3. - S. 339-345.
568. Graham R.L. The combinational mathematics of scheduling//Scientific American. -
1978.-V. 238.-P. 124-132.
569. Graham R.L., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and appro-
ximation in deterministic sequencing and scheduling: a survey//Ann. Discrete Math. -
1979.-V. 5. - P. 287-326.
570. Graves S.C. A review of production scheduling.//Oper. Res. - 1981. - V. 29, № 4. -
P. 646-675.
571. Greenberg H.H. A branch-and-bound solution to the general scheduling problem//
. Oper. Res. - 1968. - V. 16, № 2. - P. 353-361.
572. Gupta S.K. n jobs and m machines, job-shop problems with sequence-dependent set-
up times// Int. J. Prod. Res. - 1982. - V. 20, № 5. - P. 643-656.
318
573. Gupta J.N.D. A general algorithm for the n\M flow-shop scheduling problem//Int.
J. Prod. Res. - 1969. - V. 7, № 3. - P. 241-247.
574. Gupta J.N.D. M-stage flow-shop scheduling by branch and bound//Opsearch. - 1970. -
V. 7,№ 1. — P. 37-43.
575. Gupta J.N.D. Economic aspects of production scheduling systems//}. Oper. Res. Soc.
Japan. - 1971. - V. 13. - P. 169-193.
576. Gupta J.N.D. M-st&gz scheduling problem - a critical appraisal//Int. J. Prod. Res.
1971. - V. 9, № 2. - P. 267-281.
577. Gupta J.N.D. The generalized n job, m machine scheduling problem//Opsearch. -
1971.-V. 8.-P. 173-185.
578. Gupta J.N.D. An improved combinatorial algorithm for the flow-shop scheduling prob-
lem//Oper. Res. - 1971. -V. 19, №7. -P. 1753-1759.
579. Gupta J.N.D. A functional heuristic algorithm for the flowshop scheduling problem//
Oper. Res. Quart. - 1971. - V. 22, № 1. - P. 39-47.
580. Gupta J.N.D. Optimal scheduling in a multistage flowshop// AIIE Trans. - 1972. - V. 4,
№ 3. - P. 238-243.
581. Gupta J.N.D. Heuristic algorithm for multistage flowshop scheduling problem//AIIE
Trans. - 1972. - V. 4,№ 1. - P. 11-18.
582. Gupta J.N.D. Analysis of combinatorial approach to flowshop scheduling problems//
Oper. Res. Quart. - 1975. - V. 26, № 2ii. - P. 431-440.
583. Gupta J.N.D. Optimal schedules for special structures flow shops//Nav. Res. Log.
Quart. - 1975. - V. 22, №2. - P. 255-269.
584. Gupta J.N.D. A heuristic algorithm for the How shop scheduling problem// Rev. Franc.
Automat., Inform., Rech. Oper. - 1976. - V. 10, № 6. - P. 63-73.
585. Gupta J.N.D. Errata//Oper. Res. - 1976. - V. 24, № 4. - P. 796.
586. Gupta J.N.D. Optimal flowshop schedules with no intermediate storage space//Nav.
Res. Log. Quart. - 1976. - V. 23, № 2. - P. 235-243.
587. Gupta J.N.D. An improved lexicographic search algorithm for the flowshop scheduling
problem//Comput. Oper. Res - 1979. - V. 6,№ 2. - P. 117-120.
588. Gupta J.N.D., Maykut A.R. Flow-shop scheduling by heuristic decomposition//Int. J.
Prod. Res. - 1973.-V. 11, №2. - P. 102-105.
589. Gupta J.N.D., Maykut A.R. Heuristic algorithms for scheduling n jobs in a flowshop//
J. Oper. Res. Soc. Japan. - 1973. - V. 16,№3.-P. 131-150.
590. Gupta J.N.D., Reddi S.S. Improved dominance condition for the three-machine flow-
shop scheduling problem//Oper. Res. - 1978. - V. 26, № 1. - P. 200-203.
591. Haider S.W., Moodie C.L., Buck J.R. An ivestigation of the advantages of using a man-
computer interactive scheduling methodology for job shops//Int. J. Prod. Res. -
1981. - V. 19, № 4. - P. 381-392.
592. Hardgrave W.W., Nemhauser G. A geometric model and graphical algorithm for a sequenc-
ing problem//Oper. Res. - 1963. - V. 11, № 6. - P. 889-900.
593. Hariri A.M.A., Potts C.N. Algorithms for two-machine flow-shop sequencing with pre-
cedence constraints//Europ. J. Oper. Res. - 1984. - V. 17, № 2. - P. 238-248.
594. Hartwig A., Terno J. Transformation von Reihenfolgeproblemen auf Rundreiseprob-
leme// Drezden: Technische Universitat Dresden, 1978. - 12 p.
SVS.Hefetz N., Adiri I. An efficient optimal algorithm for the two-machines, unit-time,
job-shop, schedule-length, problem//Math. Oper. Res. - 1982. - V. 7, № 3. - P. 354-
360.
596. Hefetz N., Adiri I. A note on the influence of missing operations in scheduling prob-
lems//Nav. Res. Log. Quart. - 1982. - V. 29, № 3. - P. 535-539.
597. Heller J. Some numerical experiments for M\J flow shop and its decision theoreti-
cal aspects//Oper. Res. - 1960. - V. 8, №2.
598. Heller J., Logemann G. An algorithm for construction and evaluation of feasible schedu-
ling//Manag. Sci. - 1962,- V. 8, №2. - P. 168-183.
599. Hershaner J.C., Evert R.J. Search and simulation of a job shop sequencing rule //Manag.
Sci. - 1975. - V. 21, № 7. - P. 833-843.
600. Holloway CA., Nelson R.T. Job shop scheduling with due dates and overtime capabi-
lity//Manag. Sci. - 1974. - V. 21, № 1.- P. 68-78.
601. Ibaraki T. Computational efficiency of approximate branch and bound algorithms//
Math. Oper. Res. - 1976. - V. 1. - P. 287-298.
319
6Q2. Ibaraki T. On the computational efficiency of branch-and-bound algorithms//J. Oper.
Res. Soc. Japan. - 1977, - V. 20. - P. 16-35
6Q3. Ibaraki T. Branch-and-bound procedure and state - space representation of combina-
torial optimization problems//Inform, and Contr. - 1978. - V. 36, № 1. - P. 1-27.
604. Ignall E., Schrage L. Application of the branch and bound technique to some flow-
shop scheduling problems//Oper. Res. - 1965. - V. 13, № 3. - P. 400-412.
605. Integer programming and related areas. A classified bibliography//Leet. Notes Econ.
Math. Syst. - 1976. - V. 128; 1978. - V. 160; 1982. - V. 197.
60 6.Inukai T. An efficient SS/TDMA time slot assignment algorithm//IEEE Trans. Com-
muns. - 1979. - V. COM-27, № 10. - P. 1449-1455.
607. Jackson J.R„ Job shop-like queueing systems//Manag. Sci. - 1963. - № 10. - P. 131 —
142.
608. Jackson J.R. An extension of Johnson’s results on job lot scheduling//Nav. Res. Log.
Quart. - 1956. - V. 3, № 3. - P. 201-203.
609. Jaeschke G. Das Reihenfolgeproblem fiir Erzeugnisse mit gleichem Ablaufplan//Elekt-
ron. Rechenanlag. - 1964. - Jg. 6, № 3. - S. 137-144.
610. Jam S.K., Scott K.L., Vasold EG. Orderbook balancing using a combination of LP
and heuristic techniques//Interfaces. - 1978. - V. 9, № 1. - P. 55-67.
611. Janiak A., Grabowski J. Job-shop problem with resource constraints//Large Scale
Syst.: Theory and Appl. Proc. IFAC/IFORS Symp.- Oxford, 1984. - P. 475-480.
612. Johnson S.M. Optimal two and three stage production schedules with set up times
included//Nav. Res. Log. Quart. - 1954. - V. 1, № 1. - P. 61-68. (Имеются пере-
воды: Джонсон C«M. Оптимальные двух- и трехоперационные календарные планы
производства с учетом подготовительно-заключительного времени//Календарное
планирование. - М. Прогресс, 1966. - С» 33—41; Джонсон СМ. Оптимальное рас-
писание для двух- и трехступенчатых процессов с учетом времени наладки// Ки-
берн. сб. - М-: Мир, 1965. - Вып. 1. - С. 78-86).
613. Johnson S.M. Discussion: sequencing п jobs on two machines with arbitrary time lags//
Manag. Sci. - 1959. - V. 5, № 3. - P. 299-303.
614. Jones C.H. An economic evaluation of job shop dispatching rules//Manag. Sci. -1973. -
V. 20, №3.-P. 293-301.
615. Kalra K.R., Bansal S.P., Bagga P.C. Minimization of weighted sum of completion times
with due dates in permutation flowshop problems//!. Comb. Inform. Syst. Sci. -
1979. - V. 4,№ 2. - P. 169-177.
616. Karp R.M. On the computational complexity of combinatorial problems//Networks. -
1975.-V. 5, № l.-P. 45-68.
6\l. Karuch W. A counterexample to a proposed algorithm for optimal sequencing of jobs//
Oper. Res. - 1965. - V. 13, № 2. - P. 323-325.
618. Khurana K., Bagga P.C. Ordered flowshop problem with setup considerations//Cahiers
C.E.R.O. - 1984. - V. 26, № 1-2. - P. 65-76.
619. Khurana K., Bagga P.C. Minimizing the makespan in a 2-machine flowshop with time lags
and setup conditions//Z. Oper. Res. Ser. A. - 1984. - V. 28, №2.-P. 163-174.
620. Khurana K., Bagga P.C. Scheduling of job-block with dead line in nX 2 flow shop prob-
lem with separated set-up times//Ind. J. Pure Appl. Math. - 1985. -V. 16, № 3. -
P. 213-224.
621. King J. P. Scheduling and the problem of computational complexity//OMEGA. - 1979. -
V. 7, № 3. - P. 233-240.
622. King J. R., Spachis A.S. Scheduling: bibliography and review//lnt. J. Physical Distribu-
tion and Materials Manag.- 1980. - V. 10, № 3. - P. 100-132.
623. Kise H. Scheduling and branch-and-bound method//Syst. and Contr. - 1973. - V. 17,
№ 5.-P. 275-281.
624. Kobayashi T. A method for counting the number of feasible subsets of a partially orde-
red finite set//J. Oper. Res. Soc. Japan. - 1966. - V. 8, № 4. - P. 155-171.
625. Kohler W.H., Steiglitz K. Characterization and theoretical comparison of branch-and-
bound algorithms for permutational problems//!. Assoc. Comput. Mach. - 1974. -
V.21,№ 1. - P. 140-156.
626. Kohler W.H., Steiglitz K. Exact, approximate and guaranteed accuracy algorithms forthe
flow shop problems12\F\F //J. Assoc.Comput. Mach. - 1975.- V.22, № 1.- P..J0b-
114.
320
627. Krarup J., Werra D., de. Chromatic optimization: limitations, objectives, uses, refe-
iences//Eur. J. Oper. Res. - 1982. - V. 11, № l.-P. 1-19.
628. Х>оле M. Heuristic programming applied to scheduling models//Proc. 5th Annu. Prin-
ceton Conf. Inform. Sci. and Syst. - Princeton, 1971. - P. 193-196.
629. Krone M.J., Steiglitz K. Heuristic programming solution of a flow shop-scheduling prob-
lem//Oper. Res. - 1974. - V. 22, № 3. - P. 629-637.
63$. Kurisu T. Flow shop sequencing problem with time lags//Technol. Repts Osaka Univ. -
1973. - № 22. - P. 303-314.
631. Kurisu T. Two-machine sequencing problem with exponential processing times//Tech.
Repts. Osaka Univ. - 1973. -№ 23. - P. 1-8.
632. Kurisu T. Two-machine scheduling under required precedence among jobs//J. Oper.
Res. Soc. Japan. - 1976. - V. 19, № l.-P. 1-13.
633. Kurisu T. Two-machine scheduling under arbitrary precedence constraints// J. Oper.
Res. Soc. Japan. - 1977. - V. 20, № 2. - P. 113-131.
634. Kurisu T. Three-machine scheduling problem with precedence constraints//!. Oper. Res.
Soc. Japan. - 1977. - V. 20, № 3. - P. 231-242.
635. Lageweg B.J., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Computer aided comp-
lexity classification of deterministic scheduling problems // Preprint/Mathematische
Centrum. - Amsterdam, 1981. - Afdeling mathematishe Besliskunde BW 138/81. -
20 p.
636. Lageweg В J., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Computer aided comp-
lexity classification of combinatorial problems//Comm. ACM. - 1982. - V. 25, №-l 1. -
P. 817-822.
637. Lageweg B.J., Lenstra J.K., Rinnooy Kan A.H.G. Minimizing maximum lateness on one
machine: computational experience and some -applications//Statist. Neerlandia. -
1976.-V. 30.-P. 25-41.
638. Lageweg B.J., Lenstra J.K., Rinnooy Kan A.H.G. Job-shop scheduling by implicit
enumeration//Manag. Sci. - 1977. - V. 24, № 4. - P. 441-450.
639. Lageweg B.J., Lenstra J.K., Rinnooy Kan A.H.G. A general bounding scheme for the
permutation flow-shop problem//Oner. Res. - 1978. - V. 26, № 1. - P. 53-62.
640. Land A.H., Doig A.G. An automatic method of solving discrete programming prob-
lems//Econometrica. - 1960. - V. 28, № 3. - P. 497-520.
641. Lanzenauer C.H., Himes R.S. A linear programming solution to the general sequencing
problem//CQRSJ. - 1970. - V. 8, № 2.-- P. 129-134.
642. Lasdon L.S.. Terjung R.S. An efficient algorithm for multi-item scheduling//Oper.
Res. - 1971. - V. 19, № 4. - P. 946-969.
643. Lawler E.L. Recent results in the theory of machine scheduling//Math. Progr. State
Art: 11th Int. Symp. - Bonn, 1982. - P. 202-234.
644. Lawler E.L., Labetoulle J. On preemptive scheduling on unrelated parallel proces-
sors by linear programming//!. Assoc. Comput. Mach.- 1978. - V. 25, № 4. - P. 617-
619.
645. Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Minimizing maximum lateness in a two-
machine open shop//Math.Oper. Res. - 1981. - V. 6,№ 1. - P. 153-158.
646. Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Recent developments in deterministic
sequencing and scheduling: a survey//Deterministic and Stochastic scheduling. - Reidel:
Dordrecht, 1982. - P. 35-73.
647. Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Erratum//Math. Oper. Res. - 1982. -
V. 7. - P. 635.
648. Lawler E.L., Luby M.G., Vazirani V. V. Scheduling open shops with parallel machines//
Oper Res. Letters. - 1982. - V. 1. - P. 161-164.
649. Lawler E.L., Wood D.E. Branch-and-bound methods: a survey//Oper. Res. - 19o6. -
V. 14, №4.- P. 699-719.
650. Lefeman L.J. Some graphtheoretical problems of network analysis under resource con-
straints//Oper. Res. Verfahren - 1979. - V. 30. - P. 194-205.
651. Lenstra J.K. Sequencing by enumerative methods. - Amsterdam: Math. Center Tracts
69, 1977. -- 202 p.
652. Lenstra J.K., Rinnooy Kan A.H.G. Computational complexity of discrete optimization
problems//Ann. Disc. Math. - 1979. - V. 4. - P. 121-140.
653. Lenstra J.K., Rinnooy Kan A.H.G. Complexity results for scheduling chains on a single
machine//Eur. J. Oper. Res. - 1980. - V. 4, № 4. - P. 270-275.
321
654. Lenstra J.K., Rinnooy Kan A.H.G. Complexity of vehicle routing and scheduling prob-
lems//Networks. - 1981. -V. 11. -P. 221-227.
655. Lenstra J.K., Rinnooy Kan A.H.G. Scheduling theory since 1981: an annotated biblio-
graphy: Preprint/Mathematische Centrum. - Amsterdam, 1983. - Afdeling mathe-
matische Behskunde BW 188/83.
656. Lenstra J.K., Rinnooy Kan A.H.G. New directions in scheduling theory//Oper. Res.
Lett. - 1984. - V. 2, № 6. - P. 255-259.
657. Lenstra J.K., Rinnooy Kan A.H.G., Brucker P. Complexity of machine scheduling prob-
lems//Ann. Discr. Math. - 1977. - V. 1. - P. 343-362.
658. Lenstra J.K., Rinnooy Kan A.H.G., Stougie L. A framework for the probabilistic ana-
lysis of hierarchical planning system//Preprint: Mathematische Centrum. - Amsterdam,
1983. - Af de lung mathematische Beliskunde BW 180/83. - 20 p.
659. Lenstra J.K., Rinnooy Kan A.H.G., Van Emde Boas P. An appraisal of computational
complexity for operations researchers // Eur. J. Oper. Res. - 1982. - № 11. - P. 201 -210.
660. Lev V., Adiri I. 7-shop scheduling // Eur. J. Oper. Res. - 1984. - V. 18, № 1. - P.51-56.
661. Lewandowski J.L., Liu J.W.S., Liu C.L. SS/TDMA time slot assignment with restricted
switching modes//IEEE Trans. Commun. - 1983. - V. COM-31, № 1. - P. 149-154.
662. Liesegang G., Ruger M. Letter//Oper. Res. Quart. - 1972. - V. 23, № 4. - P. 591.
663. Liesegang G., Schirmer A. Heuristische Verfahren zur Maschinenbelegungs plannung bei
Reihenfertigung//Z. Oper. Res. - 1975. - B. 19. - S. 195-211.
664. Littger K. W. A new approach for the optimum solution of the Mby J production schedu-
ling problem// Int. J. Prod. Res. - 1976. - V. 14, № 1. - P. 77-83.
665. Liu C.Y., Bulfinn R.L. On the complexity of preemptive open-shop scheduling prob-
lems//Oper. Res. Lett. - 1986. - V. 4, № 2. - P. 71-74.
666. Lofts N.R Multiple allocation of resources in a network - an optimal scheduling algo-
rithm//lNFOR. - 1974. - V. 12,№ 1. - P. 25-38.
667. Lomnicki Z.A. A “branch-and-bound” algorithm for the exact solution of three-machine
scheduling problem//Oper. Res. Quart. - 1965. - V. 16. - P. 89-100.
66%. Maggu P.L., Das G. Equivalent jobs for job-blocks in job scheduling//Opsearch. -
1977. - V. 14, № 3. - P. 277-281.
669. Maggu P.L., Das G. Short note on the paper: “Equivalent jobs for job blocks in job
sequencing” // Pure Appl. Math. Sci. - 1979. - V. 9, № 1-2. - P. 53-54.
670. Maggu P.L., Das G. On idle/waiting time operator OjW having application to solution
of some sequencing/scheduling problem//Pure Appl. Math. Sci. - 1980. - V. 11,
№ 1-2. - P. 71-78.
671. Maggu P.L., Das D. On 2 X n sequencing problem with transportation time of jobs// Pure
Appl. Math. Sci. - 1980. - V. 12, № 1-2. - P. 1-6.
672 Maggu P.L., Das G., Kumar R. On equivalent-job for job-blocks in 2X n sequencing prob-
hem with transportation-times//. J. Oper. Res. Soc. Japan. - 1981. - V. 24, № 2. -
P 136-146.
673. Maggu P.L., Das G., Singh M., Singhal M.L. On 3Xn sequencing problem involving
equivalent-job for a job-block with transportation-times of jobs//Math. Operations-
forsch. Statist. Ser. Optimization. - 1981.-V. 12,№2.-P. 271-279.
614. Maggu P.L., Singhal M.L., Mohammad N. On “TV-job, 2-machine” How-shop scheduling
with minimization of weighted mean flow-time of jobs//Pure Appl. Math.Sci. - 1982. -
V. 16, № 1-2. - P. 77-83.
615. Maggu P.L., Singhal M.L., Mohammad N., Yadav SK. On TV-job, 2-machine flow-shop
scheduling problem with arbitrary time lags and transportation times of jobs//J. Oper.
Res. Soc. Japan. - 1982. - V. 25, № 3.- P. 219-227.
676. Makino T. On a scheduling problem//J. Oper. Res. Soc. Japan. - 1965. - V. 8, № 1. -
P. 32-44.
677. Malicka-Wasowska J. Model sekwencyjny z ciagla praca maszyn//Prz. statyst. - 1974. -
T. 21, № 2. - S. 211-219.
61%. Manne Л.5. On the job shop scheduling problem//Oper. Res. - 1960. - V. 8. - P. 219-
223.
679. Mason T.A., Moodie C.L. A branch and bound algorithm for minimizing cost in project
scheduling//Manag. Sci. (B). - 1971.-V. 18, №4. - P. 158-173.
680. Masuda T., Ishii H„ Nishida T. Some bounds on approximation algorithms for
fl|w|Z|Lmax and fl|2|F|Zinax scheduling problem//!. Oper. Res. Soc. Japan. -
1983. - V. 26, № 3. - P. 212-224.
322
681. Masuda T., Ishii H., Nishida T. The mixed shop scheduling problem//Discr. Appl.
Math. - 1985.-V. 11, №2. - P. 175-186.
682. Maxwell W., Mehra M. Multiple-factor rules for sequencing with assembly constraints//
Nav. Res. Log. Quart. - 1968. - V. 15, № 2. - P. 241-254.
683. McMahon G.B. Optimal production schedules for flow shops//CORS J. - 1969. — V. 7,
№2. - P. 141-151.
684. McMahon G.B. Note on optimal production schedules//CORS J. - 1969. - V. 7,
№2.-P. 154-155, 156.
685. McMahon G.B., Burton P.G. Flow-shop scheduling with the branch-and-bound method//
Oper. Res. - 1967. - V. 15, № 3. - P. 473-481.
686. McMahon G.B. , Florian M. On scheduling with ready times and due dates to minimize
maximum lateness//Oper. Res. - 1975. - V. 23.- P. 475-482.
687. McNaughton R. Scheduling with deadlines and loss functions//Manag. Sci. - 1959. -
V. 6,№ l.-P. 1-12.
Mensch G. Generalization of Akers ’’two-dimensional job-shop scheduling model” to
n dimensions//SIAM J. Appl. Math. - 1970. - V. 18, №2. - P. 462-466.
689. Mittal B.S., Bugga P.C. Flow shop scheduling with parallel machine s//Cahiers C.E.R.O. -
1979. -V. 21.-P. 87-91.
69$. Mitten L.G. Sequencing n-jobs in two machines with arbitrary time lags//Manag. Sci. -
1959. -V. 5, №3.- P. 293-298.
69 Mitten L.G. A scheduling problem: an analytical solution based on two machine, n jobs
arbitrary start and stop lags and common sequence//!. Industr. Eng. - 1959. - V. 10,
№2. - P. 131-135.
692. Mitten L.G. Branch-and-bound methods: general formulation and properties//Oper.
Res. - 1970. - V. 18, № 1. - P. 24-34.
693. Miyazaki S. Combined scheduling system for reducing job tardiness in a job shop//Int.
J. Prod. Res. - 1981. - V. 19, № 2. - P. 201-211.
694. Miyazaki S., Nishiyama N. Analysis for minimizing weighted mean flow-time in flow-
shop scheduling // J. Oper. Res. Soc. Japan. - 1980. - V. 23, №2. - P. 118-
132.
695. Miyazaki S., Nishiyama N., Hashimoto F. An adjacent pairwise approach to the mean
flow-time scheduling problem//!. Oper. Res. Soc. Japan. - 1978. - V. 21, № 2. -
P. 287-319.
696. Mohring R.H., Radermacher F.J. Scheduling problems with resource duration//Con-
trib. Prob. Theory, Natur. Resour., Econ. Indices and Relat. Top. -Konigstein. -
1984. -P. 423-452.
697. Monma CI.The two machine maximum flow-time problem with series-parallel prece-
dence constraints: an algorithm and extensions//Oper. Res. - 1979. - V. 27, № 4. -
P. 792-797.
698. Monma C.L. Sequencing to minimize the maximum job cost//Oper. Res. - 1980.- V. 28,
№4.-P. 942-951.
699. Monma C.L. Sequencing with general precedence constraints//Discr. Appl. Math. -
1981. - V. 3,№ 2. - P. 137-150.
700. Monma Cl., Rinnooy Kan A IL G. К concise survey oi the efficiently solvable special cases
of the permutation flow-shop problem//RAIRO Rech. oper. - 1983. - V. 17, № 2. -
P. 105-119.
701. Monma C.L., Sidney J. B. Sequencing with series-parallel precedence constraints//Math.
Oper. Res. - 1979. - V. 4,№ 3.- P. 215-224.
702. Muhlemann A.P., Lockett A.G., Fam C.-K. Job-shop scheduling heuristics and fre-
quency of scheduling//Int. J. Prod. Res. - 1982. - V. 20, № 2. - P. 227-241.
703. Nabeshima I. Sequencing on two machines with start lag and stop lag//J. Oper. Res.
Soc. Japan. - 1963.- V. 5, № 3. - P. 97-101.
704. Nabeshima I. On the bound of makespans and its application in M-machine schedu-
ling problem // J. Oper. Res. Soc. Japan. - 1967. - V. 9, №3-4. - P. 98-
136.
705. Nabeshima I. Some extensions of the M-machine scheduling problem//!. Oper. Res.
Soc. lapan. - 1967. -V. 10, № 1-2. - P. 1-17.
706. Nabeshima I. General scheduling algorithms with applications to parallel scheduling
and multiprogramming scheduling//!. Oper. Res. Soc. Japan. - 1971. -V. 14, № 2.-
P. 72-99.
323
707. Nabeshima I. Algorithms for multiprojects scheduling with resource constraints and
related parallel scheduling// Дэнки цусин дайгаку гакухо. Repts. Univ. Electro-
Comm. - 1972. - V. 23, № 1. - P. 29-50.
708. Nabeshima I. A backtrack programming algorithm and reliable heuristics programms
for general scheduling problem//Дэнки цусин дайгаку гакухо. Repts. Univ. Electro-
Comm.- 1973.- V. 24, № l.-P. 23-36.
709. Nabeshima I. The order of n items processed on m machines. Ill//J. Oper. Res. Soc.
Japan. - 1973. - V. 16,№ 3. - P. 163-185.
710*Nabeshima I. Notes on analytical results in flow shop scheduling I, II, Ш, IV//Дэнки
цусин дайгаку гакухо. Repts Univ. Electro-Comm. - 1977. - V. 27, № 2. - P. 245-
252; 1977. - V. 27, № 2. - P. 253-257; 1977. - V. 28, № 1. - P. 35-44; 1977. -
V. 28., № 1. - P. 57-65.
711. Nabeshima I., Maruyama Sh. On nXm mean completion time flow-shop problem: ana-
lytical results, extended branch-and-bound algorithm and computational experience//
Дэнки цусин дайгаку гакухо. Repts Univ. Electro-Comm. - 1977. - V. 28, № 2. -
P. 219-226.
712. Nawaz M., Enscore E.E., Ham I. A heuristic algorithm for the ^-machine, n-job flow-
shop sequencing problem.//OMEGA. - 1983. - V.l 1, № 1. - P. 91-95.
713. Neidereichhols J. Minimaximale wege in disjunkten grophen//Oper. Res. Verfahren. -
1972.-V. 14. - P. 336-346.
714. Nemeti L. Das Reihenfolgeproblem in der Fertigungsprogrammierung und Lenear-
planung mit Logischen Bedingungen//Mathematica (RPR). - 1964. - V. 6, № 1. -
P. 87-99.
'IXS.Nghiem P.T. Les problemes d’ordonnancement avec contraintes disjonctives//Les
problemes d’ordonnancement. - Dunod, 1964. - P. 136-151.
716. Nicholson T.A.J., Pullen R.D. A permutation procedure for job-shop scheduling//
Comput. J. - 1968. - V. 11,№ 1. - P. 48-56.
717. Okamura K., Yamashina H. Establishment of linear sequences//Mem. Fac. Engng. Kyoto
Univ. - 1969. - V. 31, № 3. - P. 307-331.
718. Page E.S. An approach to the scheduling of jobs on machines//!. Royal Statist. Soc.
Ser. B. - 1961. - V. 23, № 2. - P. 484-492.
719. Page E.S. On the scheduling jobs by computer//Comput. J. - 1962. - V. 5, №3. -
P. 214-220.
720. Page E.S. On Monte-Carlo methods in congestion problems: I. Searching for optimum
discrete situations//Oper. Res. - 1965. - V. 13, № 2. - P. 291-299.
721. Palmer D.S. Sequencing jobs through a multi-stage process in the minimum total time. -
A quick method of obtaining a near optimum//Oper. Res. Quart. - 1965. -V. 16,
№ 1. - P. 101-107.
722. Pandit S N.N., Subrahmanyam Y. V. Enumeration of all optimal job sequences//Op-
search. - 1975. - V. 12, № 1-2. - P. 35-39.
723. Panwalkar S.S., Charles O. Analysis of the left tail for the makespan distribution in
flow-shop problems//Opsearch. - 1981. - V. 18. - P. 215-220.
724. Panwalkar S.S., Dudek R.A., Smith M.L. Sequencing research and the industrial schedu-
ling problem//Leet. Notes Econ. and Math. Sy st. - 1973. - V. 86. - P. 29-38.
725. Panwalkar S.S., Iskander IP. A survey of scheduling rules//Oper. Res. - 1977. - V. 25. -
P. 45-61.
726. Panwalkar S.S, Khan A.W. An improved branch and bound procedure for n X m flow
shop problcm//Nav. Res. Log. Quart. - 1975. - V. 22, № 4. - P. 787-789.
727. Panwalkar S.S., Khan A.W. An ordered flow-shop sequencing problem with mean com-
pletion time criterion//Int. J. Prod. Res. - 1976. — V. 14, № 5. - P. 631-635.
728. Panwalkar S S., Khan A.W. A convex property of a ordered flow shop sequencing
problem//Nav. Res. Log. Quart. - 1977. - V. 24. № 1. - P. 159- 162.
729. Panwalkar S.S., Khan A.W. An ordered flow shop sequencing problem with TWK due
dates and total tardiness criterion//J. Inst. Math. Appl. - 1979. - V. 23, №3. - P. 367-
372.
730. Panwalkar S.S., Smith M.L., Woollam C.R. Counterexamples to optimal permutation
schedules for certain How shop problems//Nav. Res. Log. Quart. - 1981. - V. 28,
№ 2. - P. 339-346.
* Опубликовано более 20 частей этой работы.
324
731. Panwalkar S.S., Woollam C.R. Flow shop scheduling problem with no in-process waiting:
a special case//J. Oper. Res. Soc. - 1979. - V. 30, № 7. - P. 661-664.
732. Panwalkar S.S. Woollam C.R. Ordered flow shop problem with no in-process waiting:
further results//!. Oper. Res. Soc. - 1980. - V. 31, № 11. - P. 1039-1043.
733. Papadimitriou C.H. On the complexity of edge traversing//J. Assoc. Comput. Mach. -
1976.- №23.- P. 544-554.
734. Papadimitriou C.H., Kanellakis P.C. Flow-shop scheduling with limited temporary sto-
rage//J. Assoc. Comput.Mach.- 1980.-V. 27, №3. - P. 533-549.
735. Park Y.B., Pegden C.D., EnscoreE.E. A survey and evaluation of static flowshop schedu-
ling heuristics//Int. J. Prod. Res. - 1984.- V. 22, № 1.- P. 127-141.
736. Parker L.G., Rardin R.G. An overview of complexity theory in discrete optimizations:
part I. Concepts; part П. Results and implications//IIE Trans. - 1982. - V. 14, № 1. -
P. 3-10.
737. Peterson C.C. Solving sequencing problems through reordering operations// AIIE Trans. -
1973.-№ 5.-P. 68-73.
73%. Piehler J. Ein Beitrag zum Reihenfolgeproblem//Unternehmensforsch. - 1960. - Bd. 4,
№ 3. - S. 138-142.
739. Pinedo M. A note on the two machine job shop with exponential processing times//Nav.
Res. Log. Quart. - 1981. - V . 28, № 4.
740. Pinedo M. Minimizing the expected makespan in stochastic How shops//Oper. Res. -
1982. - V. 30. - P. 148-162.
741. Pfm?do M. A note on the flow time and the number of tardy jobs in stochastic open
shops//Eur. J. Oper. Res. - 1984.- V. 18, № 1. - P. 81-85.
742. Potts C.N. An adaptive branching rule for the permutation flow-shop problem//Eur.
J. Oper. Res. - 1980. - V. 5, № 1. - P 19-25.
743. Potts C.N. Analysis of heuristics for two-machine flow-shop sequencing subject to re-
lease dates//Math.Oper. Res. - 1985. - V. 10, № 4. - P. 576-584.
744. Prasad V.R. иХ2 flow-shop sequencing problem with random processing times//Op-
search. - 1981. - V. 18. - P. 1-14.
745. Raimond J.F. Minimaximal paths in disjunctive graphs by direct search//IBM J. Res.
Developm. - 1969. - V. 13. - P. 391 - 399.
746. Randolph P.H Job shop scheduling - a case study//OMEGA. - 1976. - V. 4, № 4 -
P. 463-477.
747. Randolph P.H., Swinson G., Ellingsen C. Stopping rules for sequencing problems//
Oper. Res. - 1973. - V. 21. - P. 1309-1315.
TMb.Reddi S.S. Sequencing with finite intermediate storage//Manag. Sci. - 1976. - V. 23,
№ 2. - P. 216-217.
IW.Reddi S.S., Ramamoorthy C.V. On the flow shop sequencing problems with no wait
in process//Oper. Res. Quart. - 1972. - V. 23, № 3. - P. 323-331.
ISQ.Reddi S.S., Ramamoorthy C.V., Reply to Dr. GoyaPs comments//Oper. Res. Quart. -
1973. - V. 24, № 1. - P. 133-134.
"ISX.Reddi S.S., Ramamoorthy C.V. A scheduling problem//Oper. Res. Quart. - 1973. -
V. 24. - P. 441-446.
752. Rendle F. On the complexity of decomposing matrices arising in satellite commu-
nications// Oper. Res. Lett. - 1985. - V. 4, № 6. - P. 5- 8.
753. Richter K. The robot sequencing problem: polynomial algorithm and complexity//
Optimization. - 1985. - V.J6, № 4. - P. 597-605.
754. Rinnooy Kan A.H.G. Machine scheduling problems: classification, complexity and
computation. - Hague: Martinus Nijhoff, 1976.- 180 p.
755. Rinnooy Kan A.H.G., Magazine MJ. Report of the session on scheduling//Ann. Discr.
Math. - 1979. - V.5. - P. 423-426.
756. Rochette R., Sadowski R. A statistical comparison of the performance of simple dis-
patching rules for particular set of job shops//Int. J. Prod. Res. - 1976. - V. 14, № 1. -
P. 63-75.
757. Rock H. The three-machine no-wait flow-shop problem is VP-complete//J. Assoc.
Comput. Mach. - 1984. - V. 31, № 2. - P. 336-345.
758. Rock H. Some new results in flow-shop scheduling//Z.Oper. Res. - 1984. - V. 28,
№ 1. - P. 1-16.
759. Rock H., Schmidt G. Machine aggregation heuristics in shop-scheduling//VII Symp.
Oper. Res., Nochsch. St. Gallen: Proc. Sekt 1-3. - Konigstein /Ts., 1983. -P. 303—314.
325
760. Roy В. Prise en compte des contraintes disjonctives dans la methode du chemin critique//
Revue Franc. Inform. Rech. Oper. - 1966. - № 38. - P. 68-84.
761. /toy B. Procedure d’exploration par .separation et evaluation//Revue Franc. Inform.
Rech. Oper. - 1969. - V. 3,№ 1 - P. 61-90.
762. Roy B., Sussmann B. Les problemes d’ordonnancement avec contraintes disjonctives//
SEMA, Note DS. - Montrouge, 1964. - № 9.
763. Ruiz J.P., Lara R.A. Soble la implementacion en computadora pequenos de un metodo
combinado de sequenciacion//Investig. Operat. - 1977. - № 21-22. - P. 137-145.
764. Sahni S., Cho Y. Complexity of scheduling shops with no wait in process//Math. Oper.
Res. - 1979. - V. 4, № 4. - P. 448-457.
765. Sahni S., Horowitz E. Combinatorial problems: reducibility and approximation//Oper.
Res. - 1978.-V. 26, №5.- P. 718-759.
766. Salvador M.S. A solution to a special class of flow shop scheduling problems//Leet
Notes. Econ. Math. Syst. - 1973. - V. 86. - P. 83-91.
767. Schrage L. A bound based on the equivalence of min-max-completion time and min-
max-lateness scheduling objectives // Report 7042. - Chicago. University of Chicago,
1970.
7№. Schrage L. Solving resource-constrained network problems by implicit enumeration,
nonpreemptive case//Oper. Res. - 1970. - V. 18, № 2. - P. 263-278.
769. Schrage L. Solving resource-constrained network problem by implicit enumeration,
preemptive case//Oper. Res. - 1972. - V 20. - P. 668-677.
770. Sekiguchi Y. Optimal scheduling in a G7’-type flow-shop under series-parallel prece-
dence constraints///. Oper. Res. Soc. Japan - 1983. - V. 26, № 3. - P. 226-251.
771. Shanthikumar J,G., Buzacott J.A. The time spent in a dynamic job shop//Eur. J. Oper.
Res. - 1984. - V. 17. - P. 215-226.
772. Shanthikumar J.G., Wu Y.-B. Decomposition approaches in permutation scheduling
problems with application to the Af-machine flow-shop scheduling problems//Eur. J.
Oper. Res. - 1985. - V. 19. - P. 125-141.
773. Shapiro R.D. Scheduling couple tasks//Nav. Res. Log. Quart. - 1980. - V. 27, № 3. -
P. 489-498.
774. Sidney J.B. The two-machine maximum flow time problem with series-parallel prece-
dence relation//Oper. Res. - 1979. - V. 27, № 4. - P. 782-791.
775. Sidney J.B. A decomposition algorithm for sequencing with general precedence con-
straints//Math. Oper. Res. - 1981 - V. 6, № 2. - P. 19t>- 204.
776. Smith M.L., Panwalkar S.S., Dudek R.A. Flowshop sequencing problem with ordered
processing time matrices//Manag. Sci. - 1975. - V. 21, № 5. - P. 544 -549
777. Smith M.L., Panwalkar S.S., Dudek R.A. Flow shop sequencing problem with ordered
precessing time matiices: a general case//Nav. Res Log. Quart. - 1976. - V. 23, № 3 -
P. 481-486.
778. Smith R.D , Dudek R.A. A general algorithm for solution of the я-job Af-machine sche-
duling problem of the flow shop//Oper. Res. - 1967. - V. 15, № 1. - P. 71-82
779. Smith R.D., Dudek R.A. Errata//Oper. Res. - 1969. - V. 17, № 4. - P. 756.
780. Smith W.E. Various optimizers for single state production//Nav. Res. Log Quart. -
1956.-V. 3,№ 1-2. -P. 59-66.
781. Smits A.J.M., Baker K.R. An experimental investigation of the occurence of special
cases in the three-machine flowshop problem//Int. J. Prod. Res. - 1981. - V. 19,
№ 6. - P. 737-741.
782. Spachis A.S., King J.R. Job-shop scheduling heuristics with local neighbourhood search//
Int. J. Prod. Res. - 1979. - V. 17, № 6. - P. 507-526.
783. Spencer D.L., Dudek R.A. The dependent shop sequencing algorithm. A general algo-
rithm for solving flow shop, job shop and dependent shop sequencing problems//Int.
J.Prod. Res. - 1973.-V. 11, №4. - P. 325 -339
784. Spinner A.H. Sequencing theory - development to date//Nav. Res. Log. Quart -
1968. - V. 15, № 2. - P. 319-330.
7%5. Stanley R.P Acyclic orientations of graphs//Discr. Math. - 1973. - V. 5, № 2. -
P. 171-178.
786. Stcinhoff H.W. Two receiu developments in scheduling applications//Leet. Notes Econ.
Math. Syst. - 1973.- V. 86. - P. 92-108.
787. Stinson J.P., Davis E. W., Khuriawala B.M. Multiple resource-constrained scheduling
using branch and bound//AIIE Trans. - 1978. - V. 10, № 3. - P. 252-259.
326
tfth A. W. A heuristic programming procedure for sequencin
. Prod. Res. - 1982. - V. 20, № 6. - P. 753-764.
788. Stinson ju
flowshoji// nil. J. nvu. ГЧ.С». — 1704. — V . z,v, 41- U. — Г . / J /мт.
789. Sule £>jk; (Sequencing n jobs on two machines with setup, processing and remdi
separatea//Nav. Res. Log. Quart. - 1982. - V. 29, № 3. - P. 517-519.
790. Sule D.R.t Huang K. Y. Sequencing on two and three machines with setup processing ЦП 4
removal times separated//Int. J. Prod. Res. - 1983. - V. 21, № 5. - P. 723-732. 1 I
19\. Sussmann B. Scheduling problems with interval disjunctions//Z. Oper. Res. (A) .*) ।
1972.-V. 16,№5.-P. 165-178. J I
792. Syslo M. On some machine sequencing problems (II)//Zastosow matem. - 1974. Л.|
T. 14, № 1.-S. 93-97.
193. Syslo M. О zlozonosci obliczeniowej problemow kombinatoryki i teorii grafow//Roci, । •
Polsk. towarzystwa matem. Ser. 3. Matematyka stosowana. - 1980. - T. 16. - S. 53** .
98.
794. Szwarc W. Solution of the Akers - Friedman scheduling problem//Oper. Res. - 1960. —
V. 8, № 6. - P. 782-788.
195. Szwarc W. О pewnym zagadnieniu kolejnosci II//Prz. statyst. - 1963.- T. 10, № 1. -
S. 139-154.
796. Szwarc W. On some sequencing problems//Nav. Res. Log. Quart. - 1968. - V. 15,
№ 2. - P. 123-155.
797. Szwarc W. Elimination methods in the mXn sequencing problem// Nav. Res. Log.
Quart. - 1971. - V. 18, № 3. - P. 295-305.
798. Szwarc W. Optimal elimination methods in the mXn flow-shop scheduling problem//
Oper. Res. - 1973. - V. 21, № 6. - P. 1250-1259.
799. Szwarc W. Mathematical aspects of the 3Xn job-shop sequencing problem//Nav. Res.
Log. Quart. - 1974.-V 21, № 1. - P. 145-153.
800. Szwarc W. A note on mathematical aspects of the ЗХи job-shop sequencing problem//
Nav. Res. Log. Quart. - 1974. - V. 21, № 4. - P. 725-726.
801. Szwarc W. Remarks//Oper. Res. - 1975. - V. 23, №5. - P. 1043.
802. Szwarc W. Optimal two-machine ordering in the ЗХл flow-shop problem//Oper. Res. -
1977. - V. 25, № ]. - P. 70-77.
803. Szwarc W. Special cases of the flow-shop problem//Nav. Res. Log. Quart. - 1977. -
V. 24, № 3. - P. 483-492.
804. Szwarc W. Dominance conditions for the three machine flow-shop problem//Oper.
Res. - 1978. - V. 26, № 1. - P. 203-206.
805. Szwarc W. Permutation flow-shop theory revisited//Nav. Res. Log. Quart. - 1978. -
V. 25, № 3. - P. 557-570.
806. Szwarc W. Extreme solution of the two-machine flow-shop problcm//Nav. Res. Log.
Quart.- 1981.-V.28,№ l.-P. 103-114.
807. Szwarc W. A note on the flow-shop problem without interruptions in job processing//
Nav. Res. Log. Quart., - 1981. - V. 28, № 4. - P. 665-669.
808. Szwarc W. Precedence relations of the flow-shop problem//Oper. Res. - 1981. - V. 29,
№2.- P. 400-411.
809. Szwarc W. Flow-shop problems with time lags//Manag. Sci. - 1983. - V 29, № 4. -
P. 477-491.
810. Szwarc IP. The How-shop problem with mean completion time criterion// HE Trans.-
1983.-V. 15, №2. -P. 172-176.
811. Szwarc W.f Hutchinson G.K. Johnson’s approximate method for the 3Xn job shop prob-
lem//Nav. Res. Log. Quart. - 1977. - V. 24, № 1. - P. 153-157.
812. Tabourier Y. Problemes d’ordonnanccment a contraintes purement disjonctives//Revue
Franc. Inform. Rech. Oper. - 1969. - V. 5, № 3. - P. 5 1-66.
813. Takagi M. Graphical solution of 2-job ^-machine sequencing problem//Дэн ки сикэнсё
ихо. Bull. Elektrotechn. Lab. - 1961. - V. 25, № 8. - P. 575-584.
814. Tang D.T., Wong C.K. A modified branch-and-bound strategy//Inf. Process. Lett. -
1973. - V. 2,№3.-P. 65-69.
815. Tarjan R.E. Algorithms for maximum network flow//Math. Progj. Study. - 1986. -
V. 26.- P. 1-11.
816. The traveling salesman problem. A guided tour of combinatorial optimization. - Chi-
chester: Wiley, 1985. -465 p.
817. Thesen A. Heuristic scheduling of activities under resource and precedence restric-
tions//Manag. Sci. - 1976. - V. 23, № 4. - P. 412-422.
327
818. Tow send W. Sequencing n jobs on m machines to minimize maximum tardiness: a!
branch-and-bound solution//Manag. Sci. - 1977. - V. 23. - P. 1016-1019. *
819. Towsend W. A branch-and-bound method for sequencing problem with linear and
exponential penalty functions//Oper. Res. Quart - 1977. - V. 28 , № lii. - P. 191 —
200.
820. Towsend W. Minimizing the maximum penalty in the two-machine flow-shop//Manag.
Sci. - 1977. - V. 24, № 2. - P. 230-234.
821. Towsend W. Minimizing the maximum penatly in the /л-machine sequencing problem// \
Oper. Res. Quart. - 1977. - V. 28, № 3 ii. - P. 727-734. ,
822. Turksen I.B., Shankar R. Some extensions of Akers-Friedman production scheduling ?
problem//Leet. Notes Econ. Math. Syst. - 1973. - V. 86. - P. 426-431. ‘
823. Ullrich M. Konstruktion optimaler Reihenfolgen bei spezielen Reihenfolgeproblemen//
Math. Operationsforsch. Statist. - 1976. - Bd. 7, № 3. - S. 361-370. 1
824. Ullrich M. Zusammenhang zwischen dem Rundreiseproblem und einem Reihenfolge-
problem der Machinenbelegungsplanung//Math. Operationsforsch. Statist. - 1976. - ;
Bd. 7, №6.- S. 843-846.
825. Viviers F. A. decision support system for job shop schcduling//Eur J. Oper. Res. -
1983.-V. 14.-P. 95-103.
826. Wagner H.M. An integer linear programming model for machine scheduling//Nav. Res.
Log. Quart. - 1959. - V. 6.- P. 131.
827. Wang М.-F, Rosenshine M. Sched <liug for a combination of made-to-stock and made-
to-order jobs in a job shop//Int. J. Prod. Res. - 1983. - V. 21, № 5. - P. 607-616.
828. Warshall S. A theorem on boolean matrices//]. Assoc. Comput. Mach. - 1962. - V. 9,
№ 1. - P. 11-12.
829. Werra D., de. On some combinatorial problems arising in scheduling//CORS J.- 1970. -
V.8,№ 3.- P. 165-175.
830. Werra D., de. Balanced scheduling//INFOR. Canad. J. Oper. Res. Inf. Proc. - 1971. -
V. 9, № 3. - P. 230-237.
831. Werra D., de. Scheduling in sports//Ann. Discr. Math. - 1981. - V. 11.- P. 381-395.
832. Werra D., de. Preemptive scheduling, linear programming and network flows//SIAM J.
Alg. Discr. Meth. - 1984. - V. 5, № 1. - P. 11-20.
833. Werra D., de. A decomposing property of polyhedra//Math. Progr. - 1984. - V. 30,
№2.- P. 261-266.
834. Werra D., de. Variations on the integral decomposition property//Math. Progr. Study. -
1986.- V. 26.- P. 197-198.
835. Wie S.-H., Pinedo M. On minimizing the expected makespan and flow time in stochastic
flow shops with blocking//Math. Oper. Res. - 1986. - V. 11, № 2. - P. 336-342.
836. Wilbrecht J.I., Prescott W.B. The influence of setup time on job shop performance//
Manag. Sci. - 1969. - V. 16, № 4. - P. 274-280.
837. Wismer D.A. Solution of the flowshop-sequencing problem with no intermediate queues//
Oper. Res. - 1972. -V. 20, № 3. - P. 689-697.
838. Yoshida T., Hitomi K. Optimal two-stage production scheduling with setup times se-
parated//AIIE Trans. - 1979.-V. 11, № 2. - P. 261-263.
839. Zorychta K. Optymalizacja dynamiezna na zbiorze permutacji//Rocz. Polsk. towarzys-
twa matem. Ser 3. Matematyka stosowana. - 1977. - T. 9. - S. 25-33.
j
7
7
7