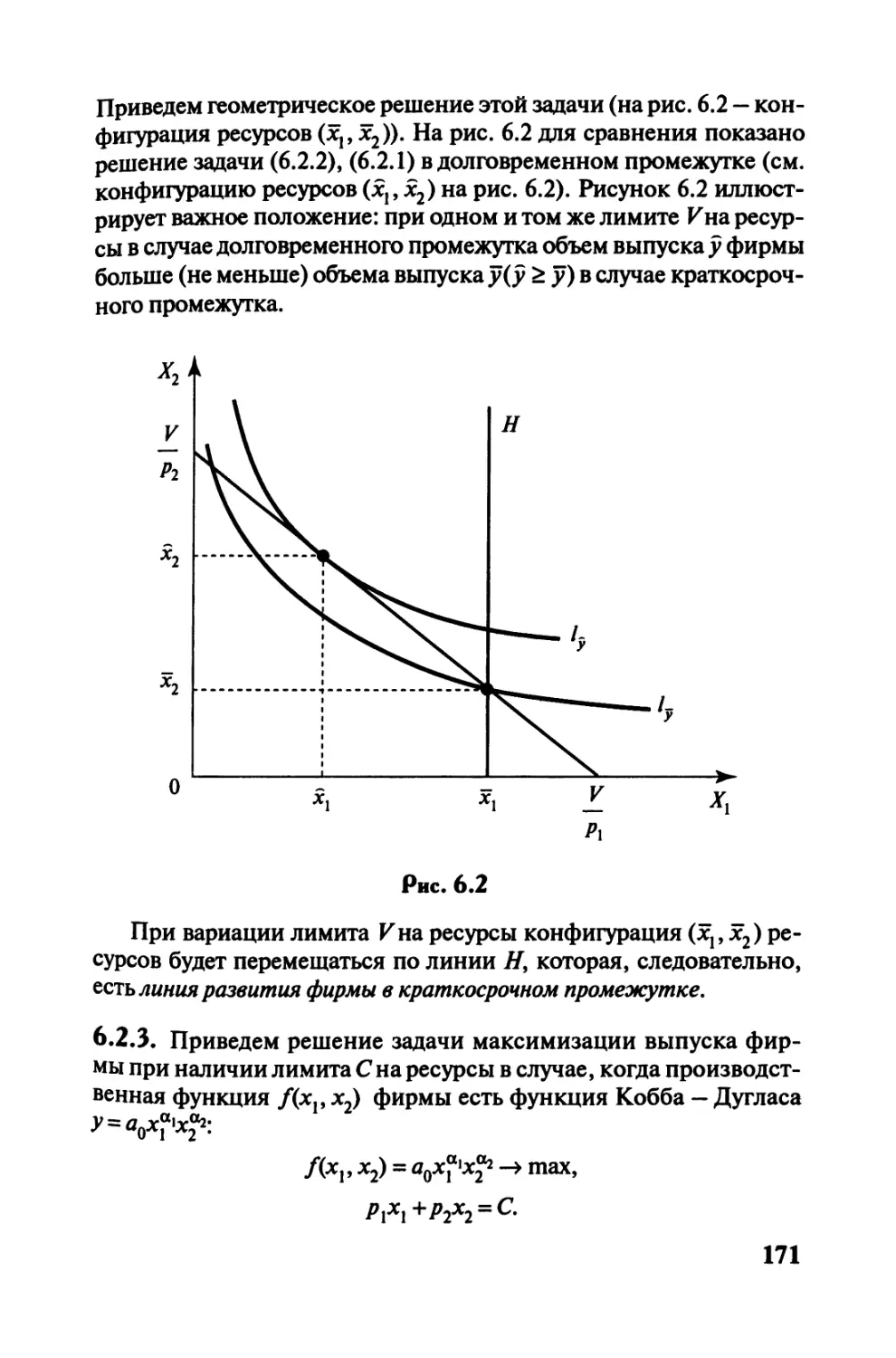
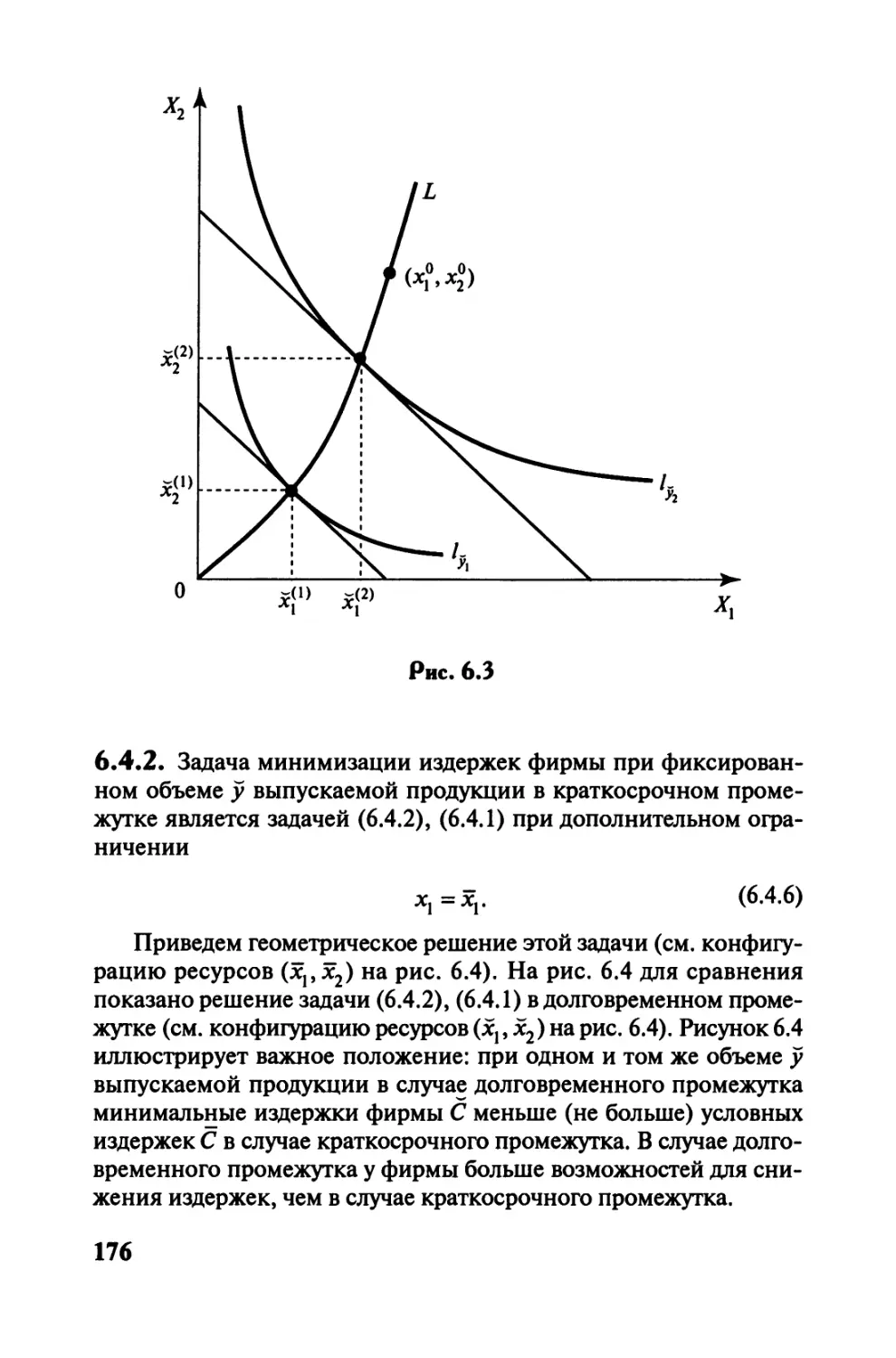
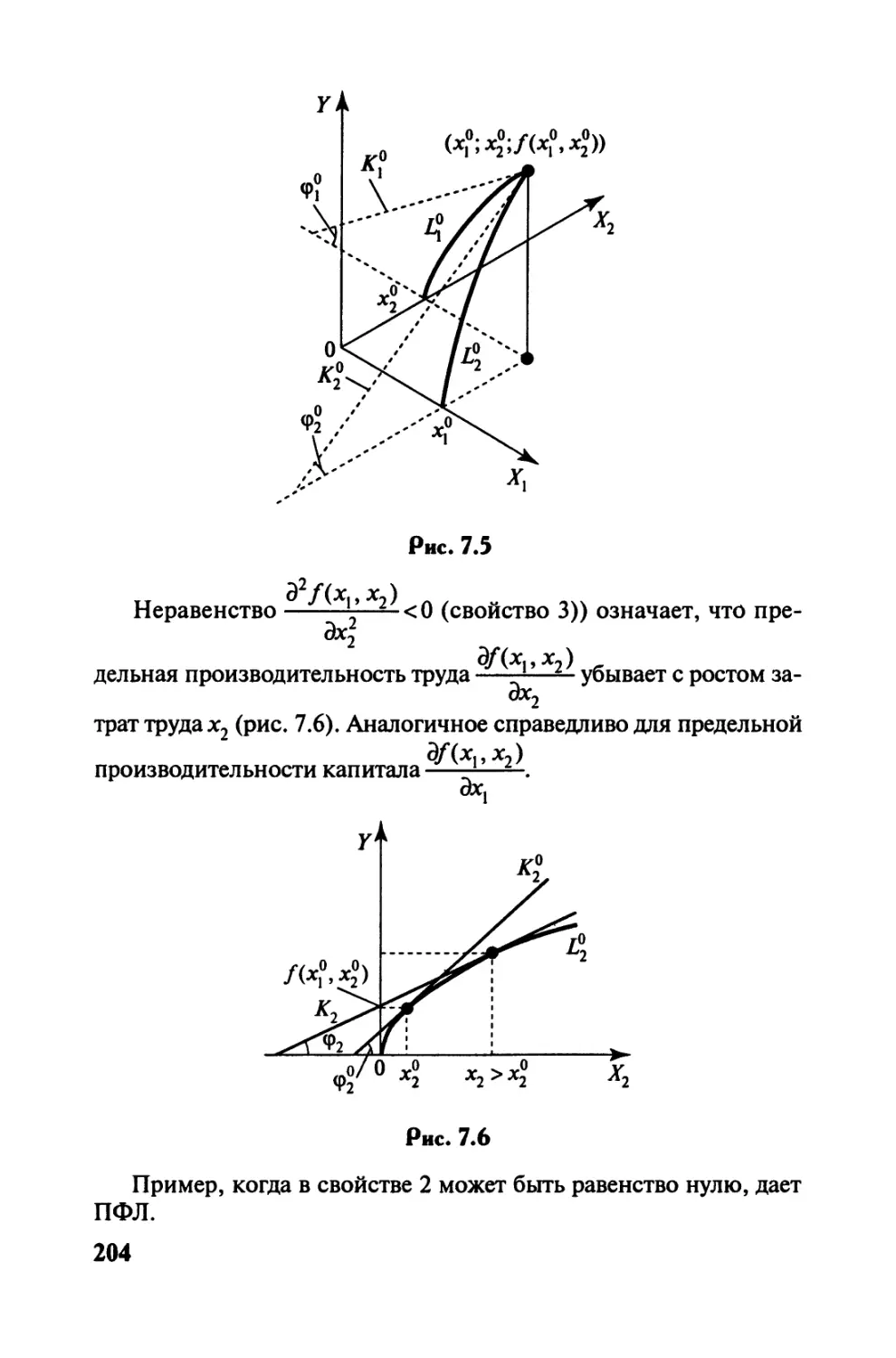
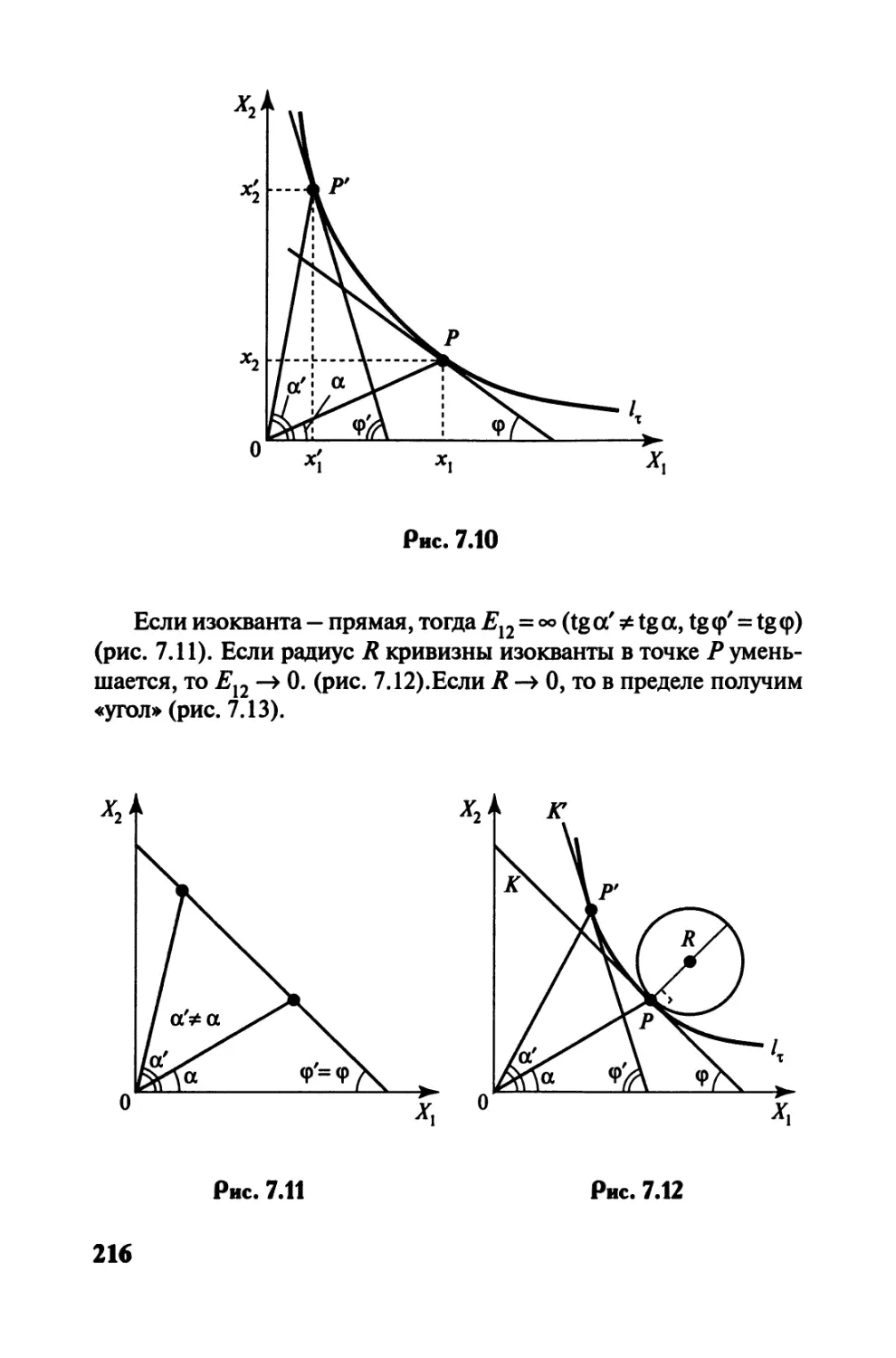
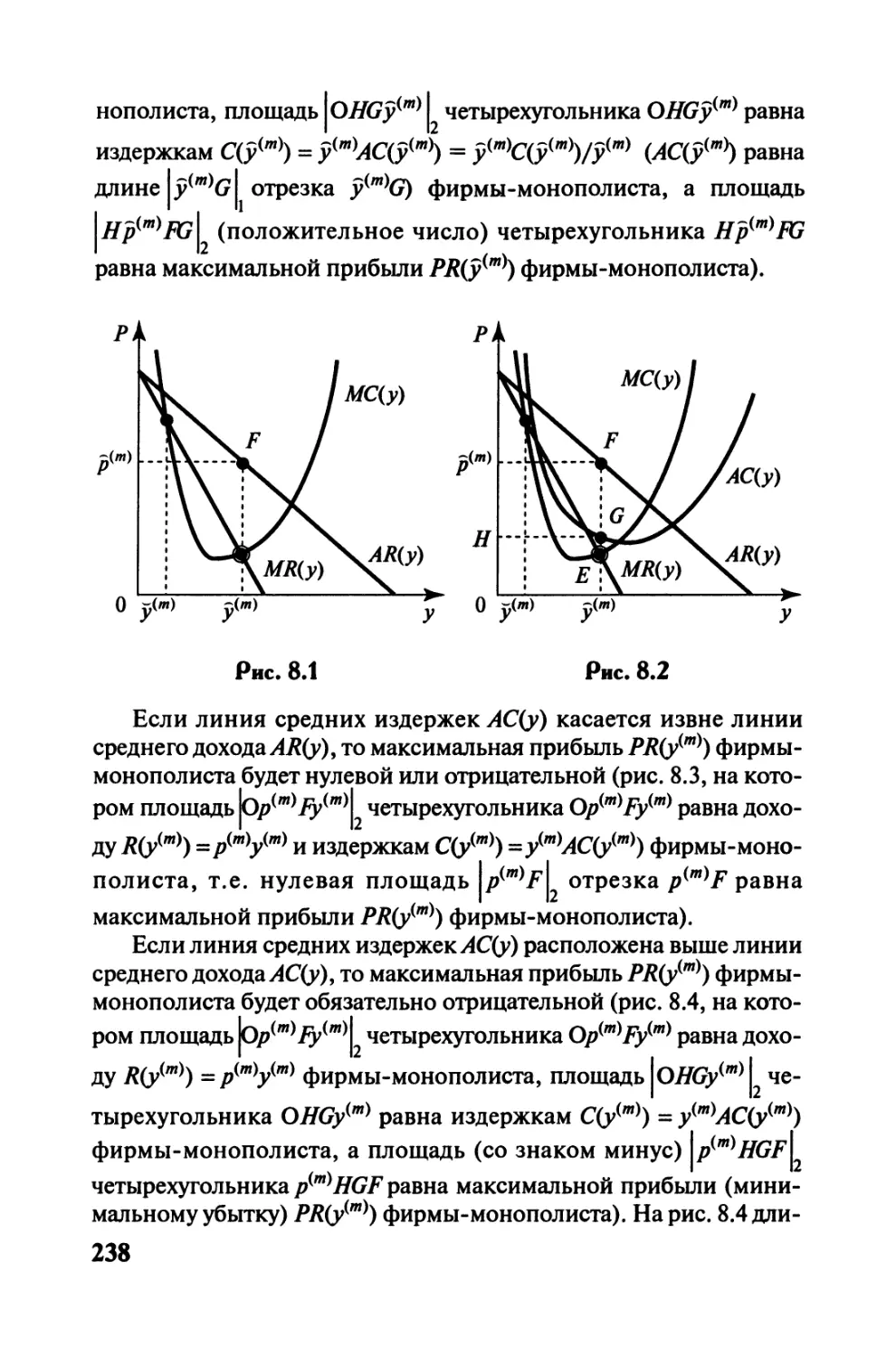
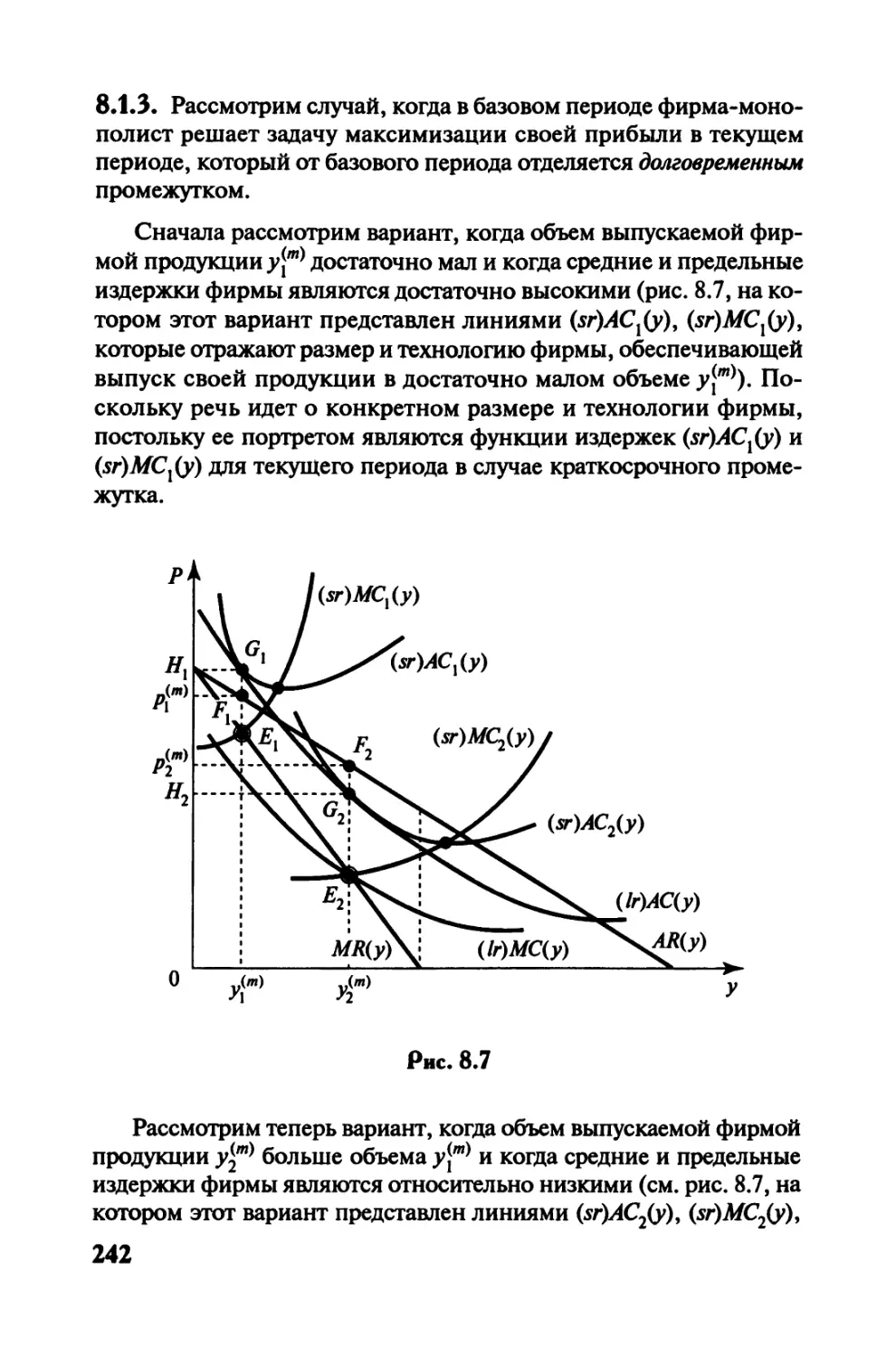
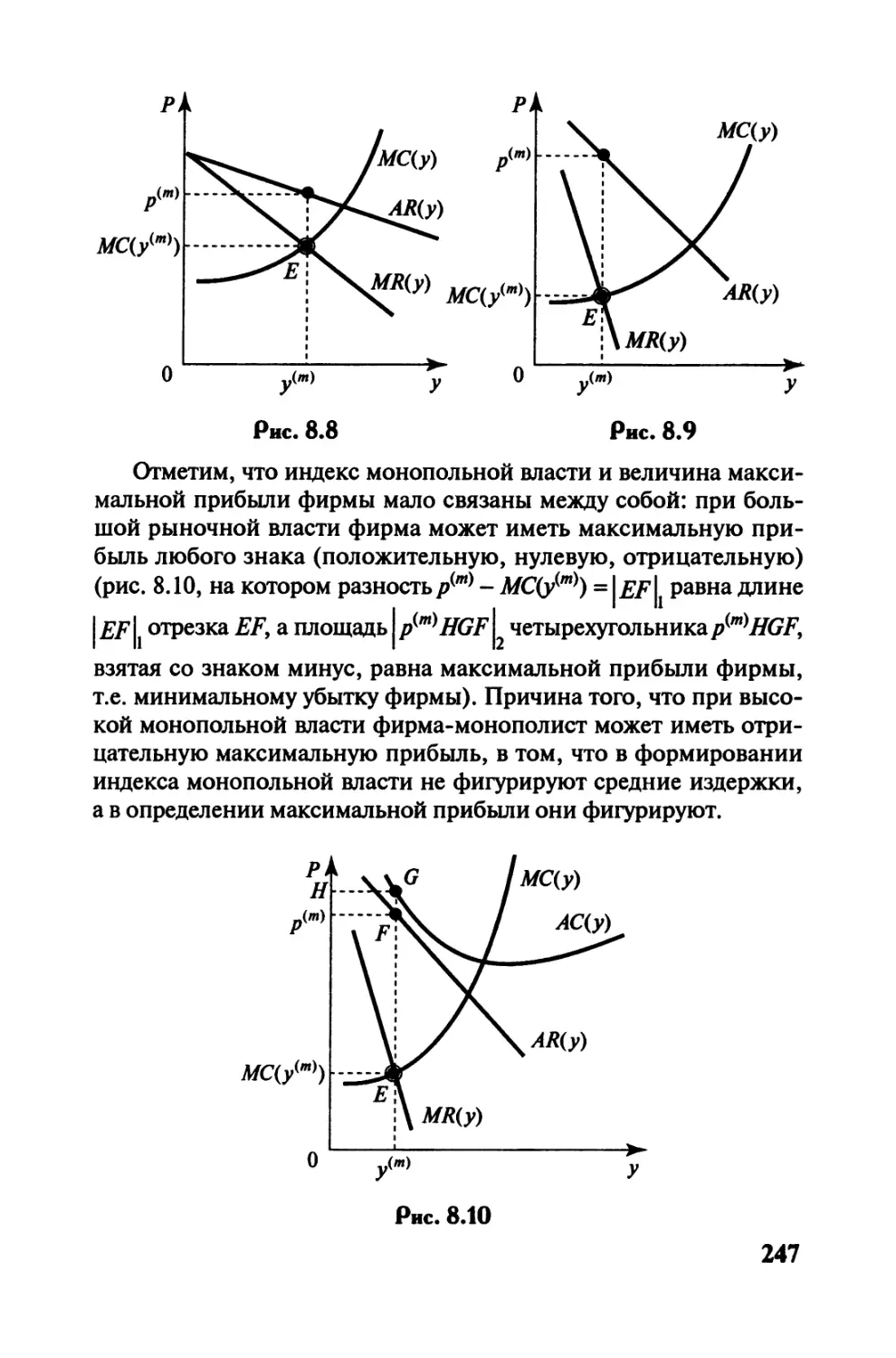
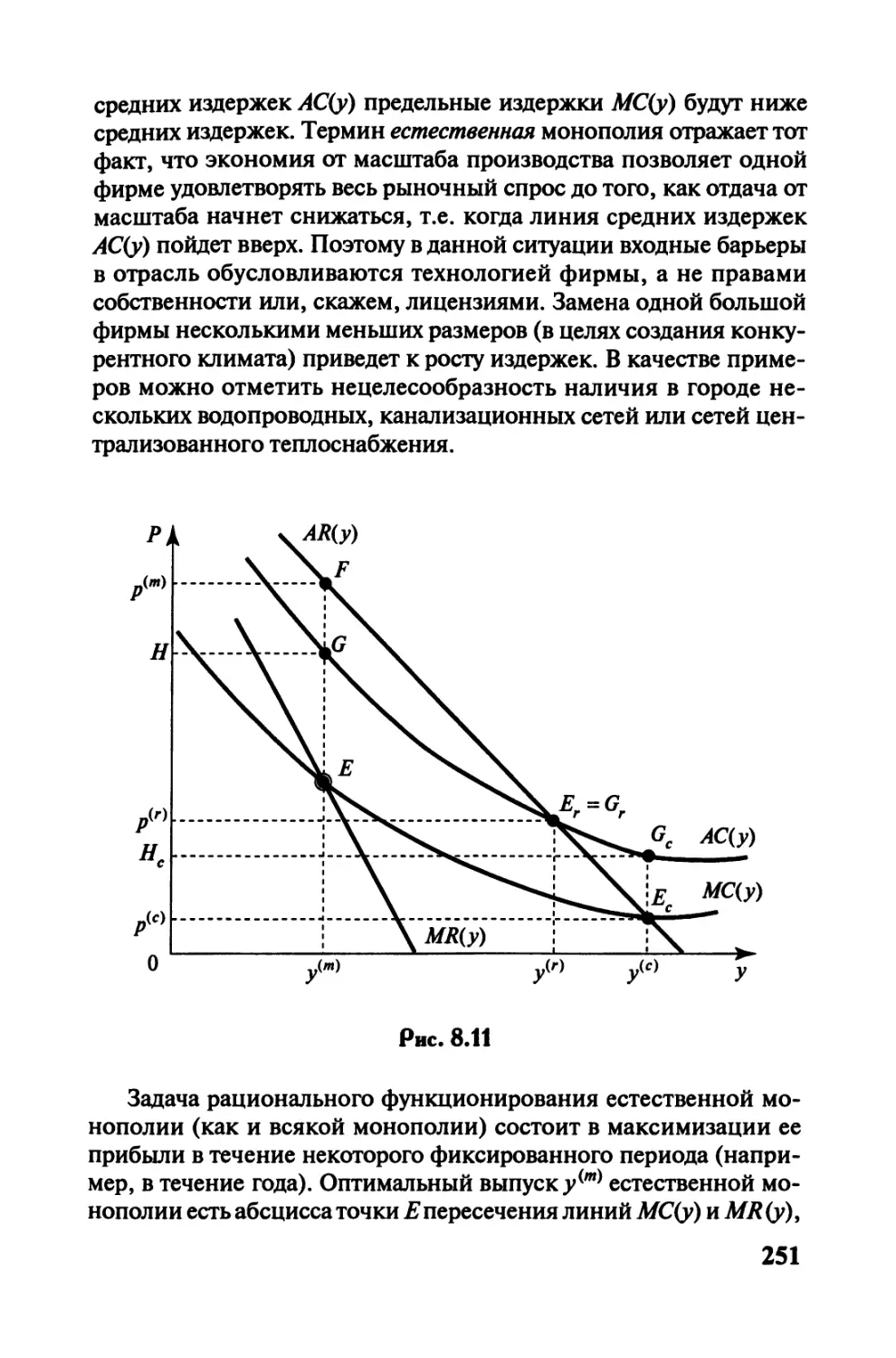
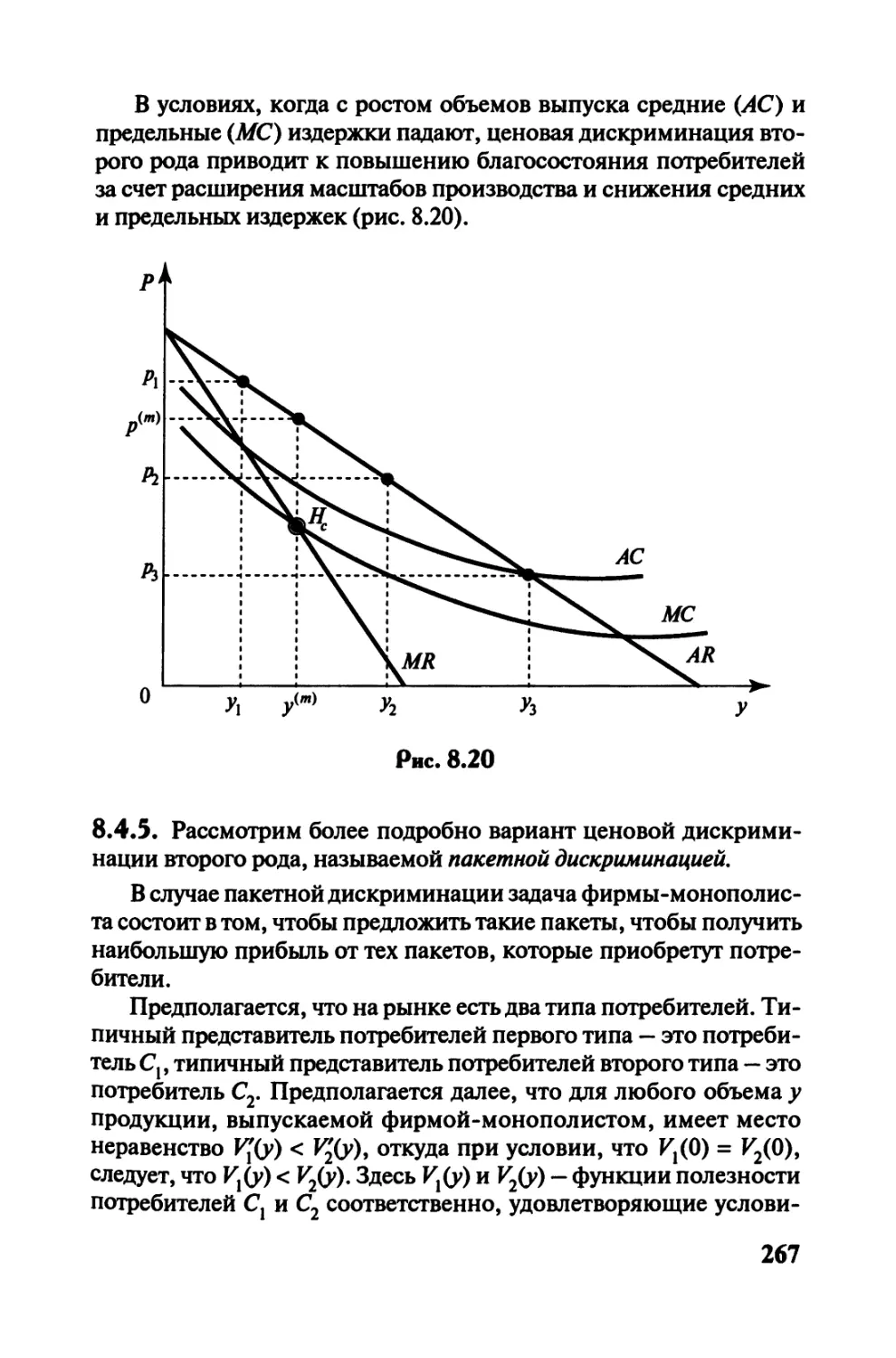
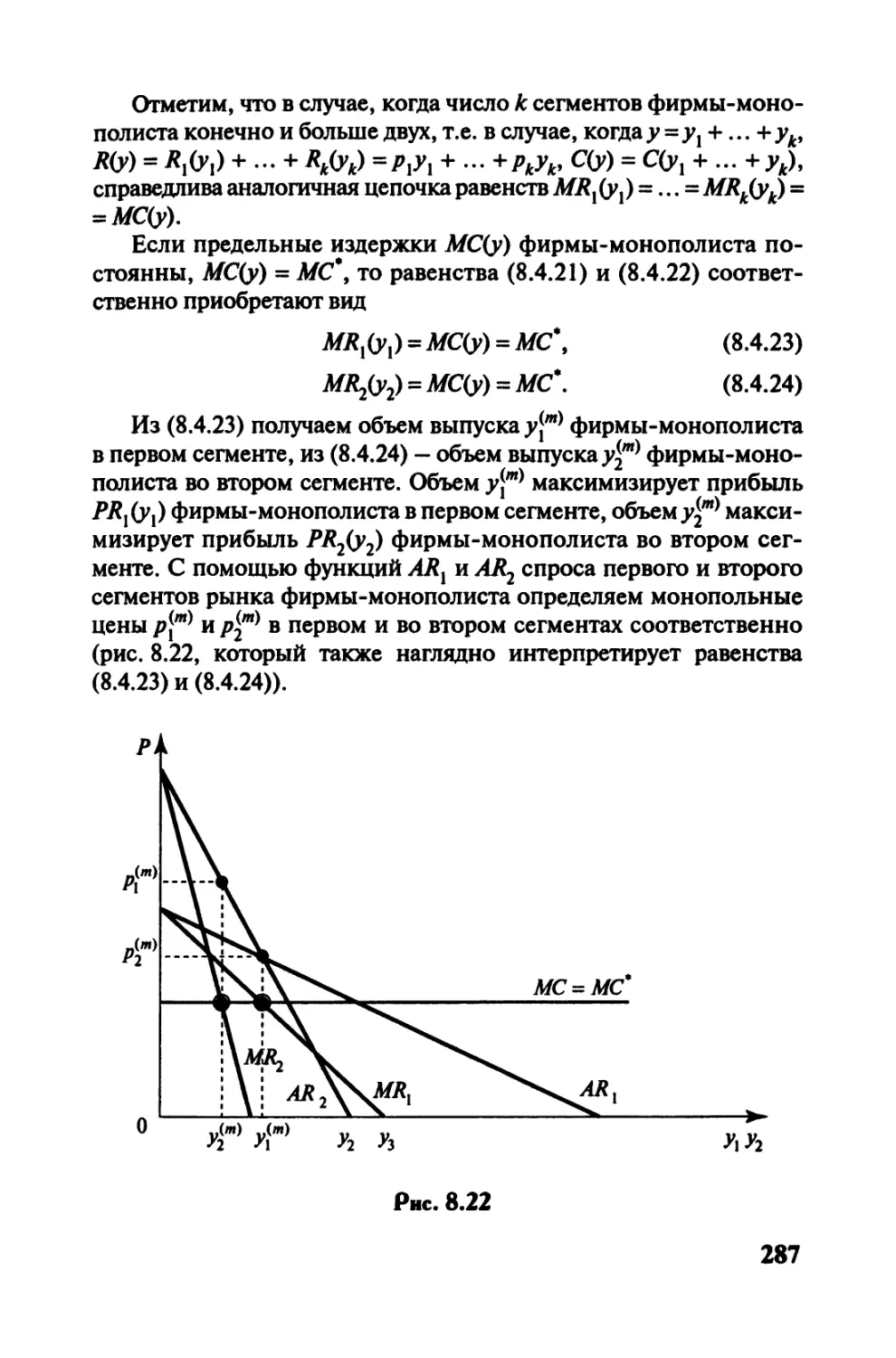
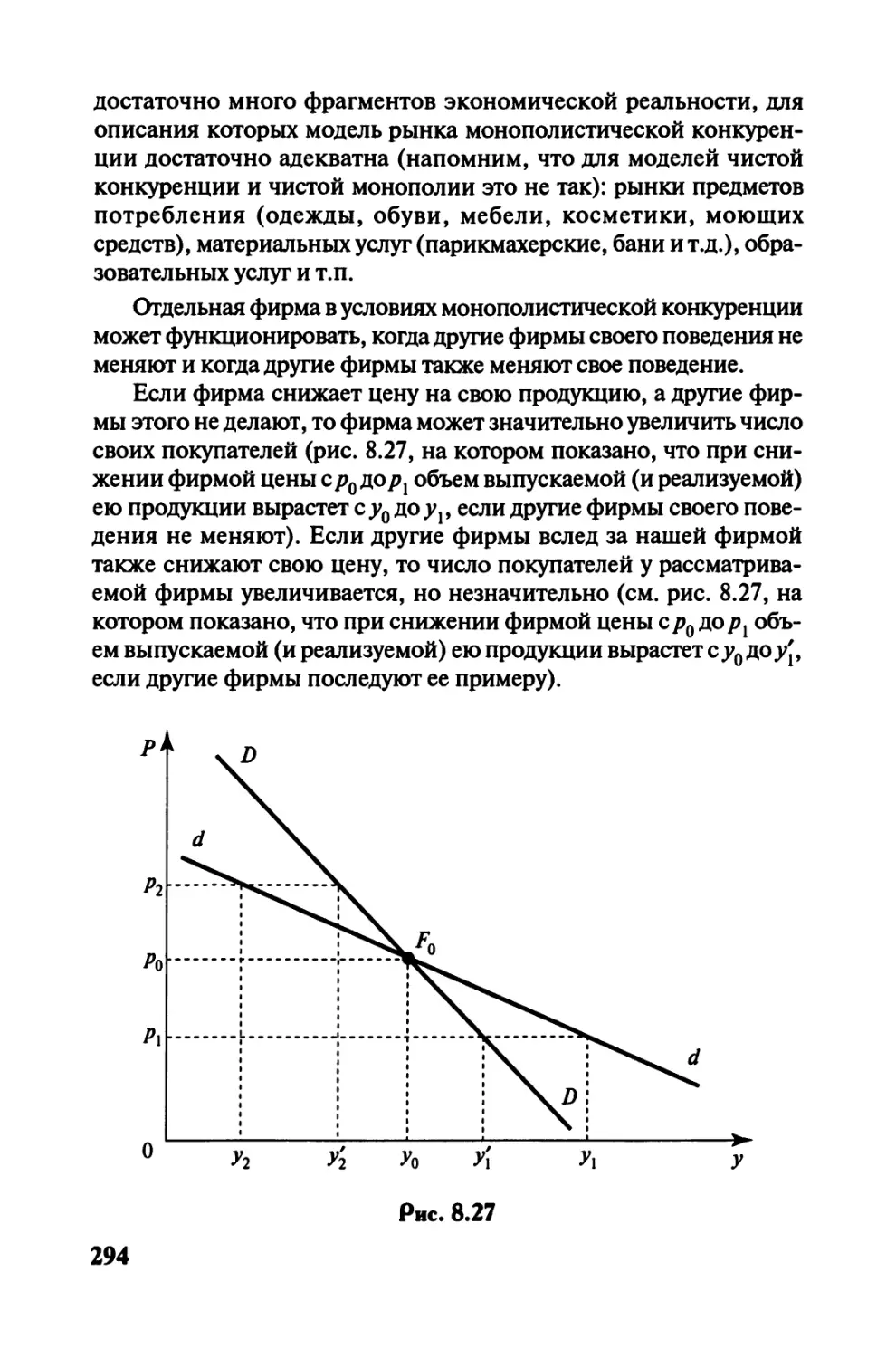
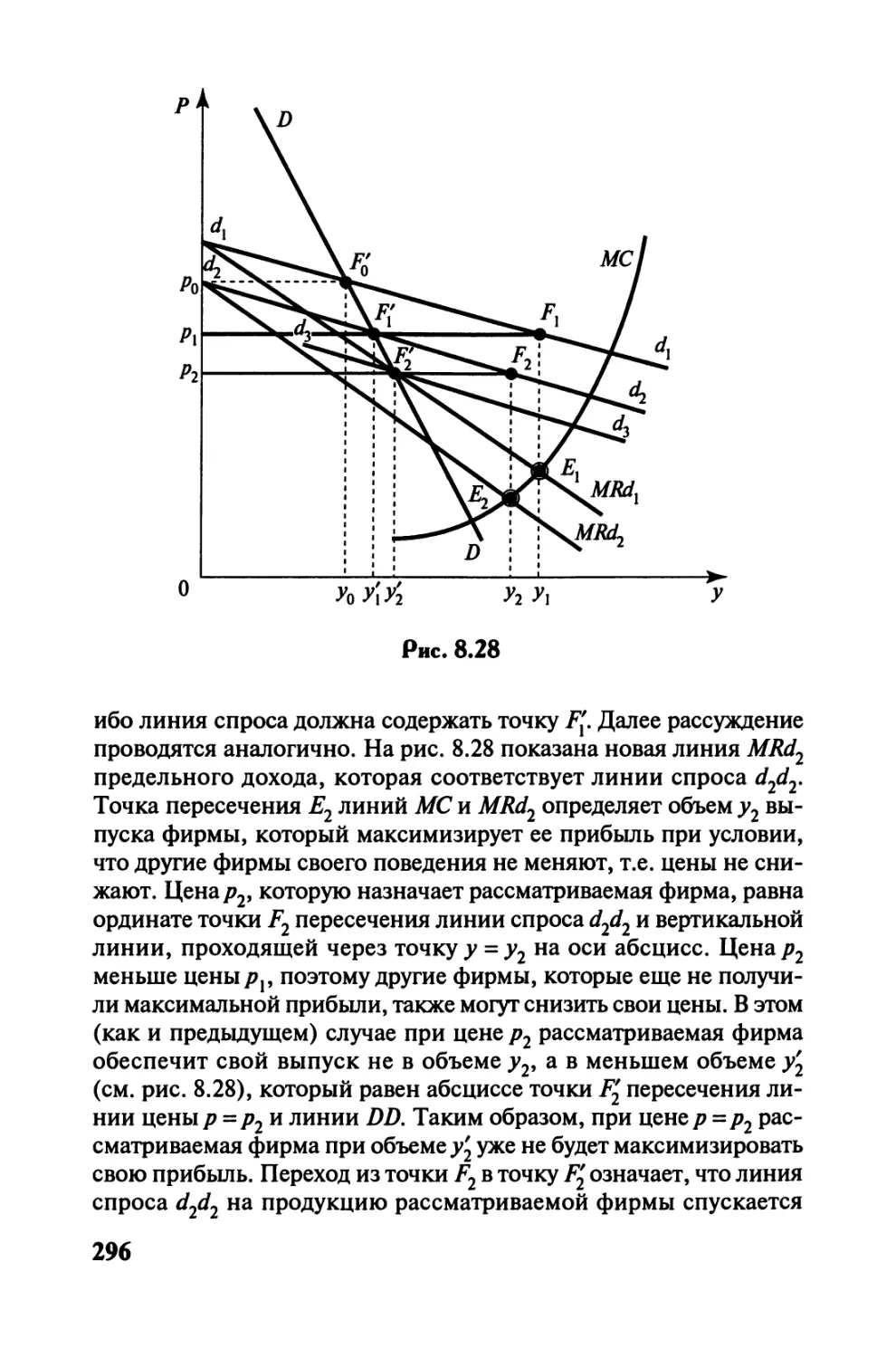
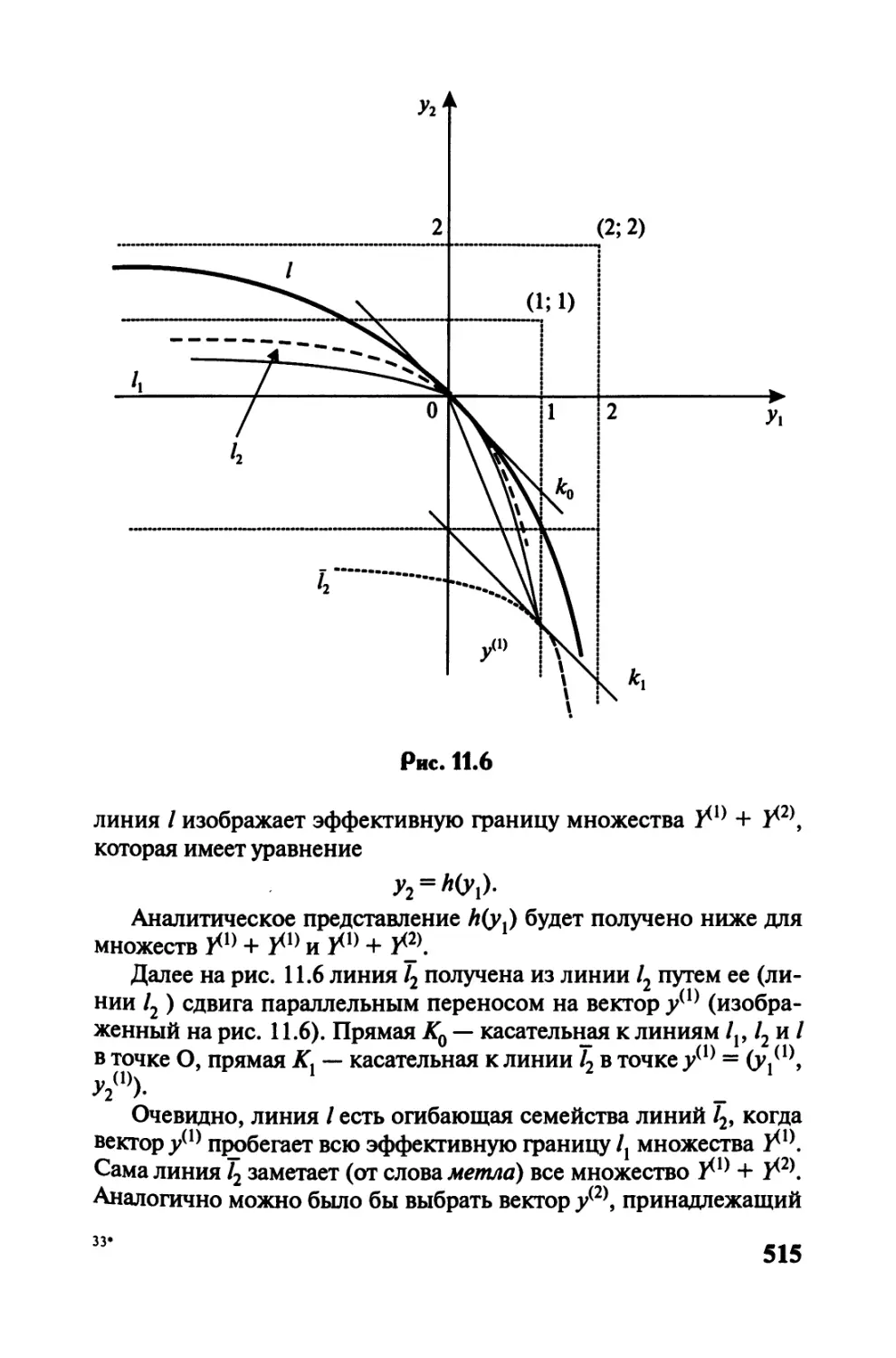
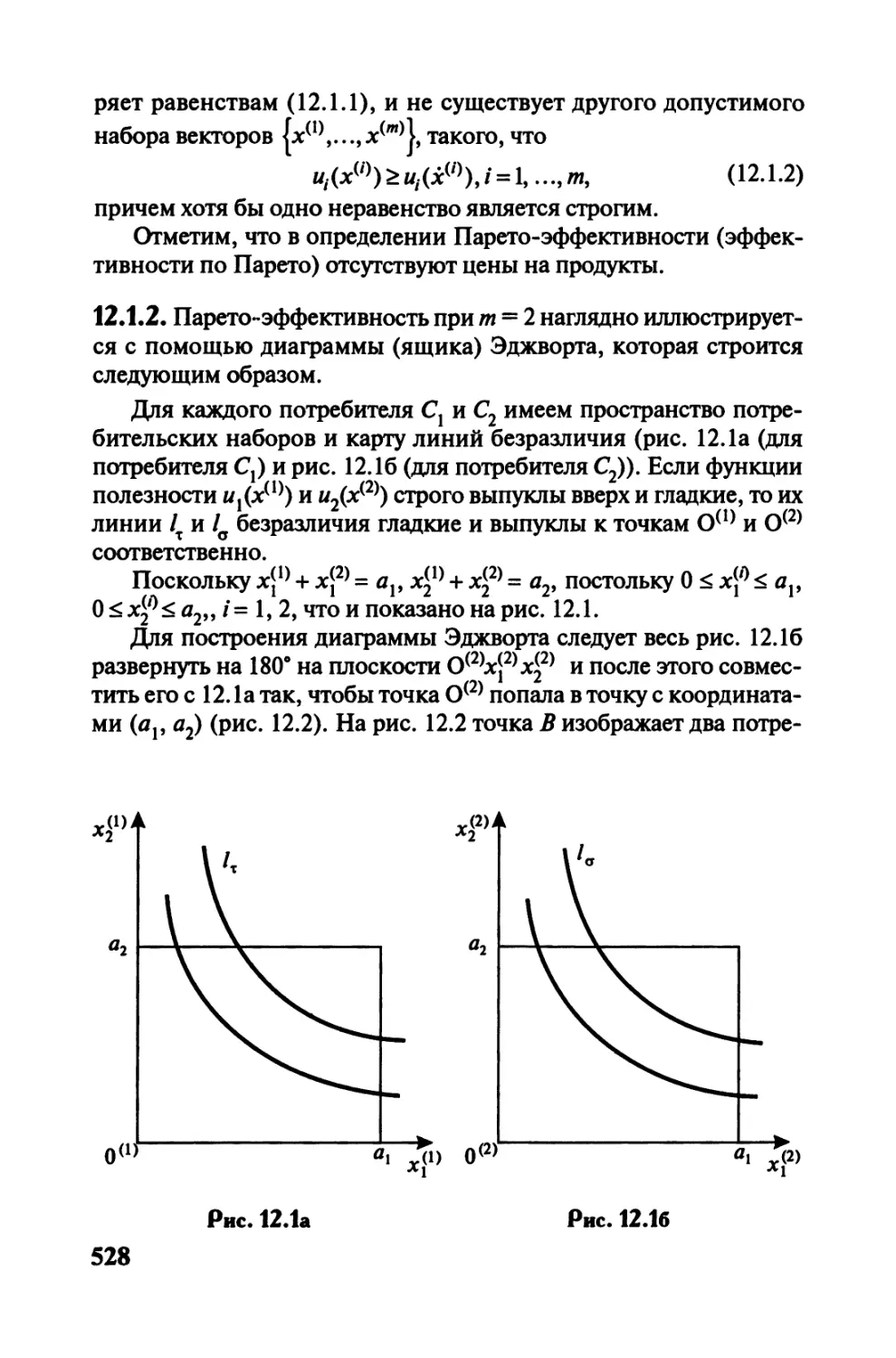
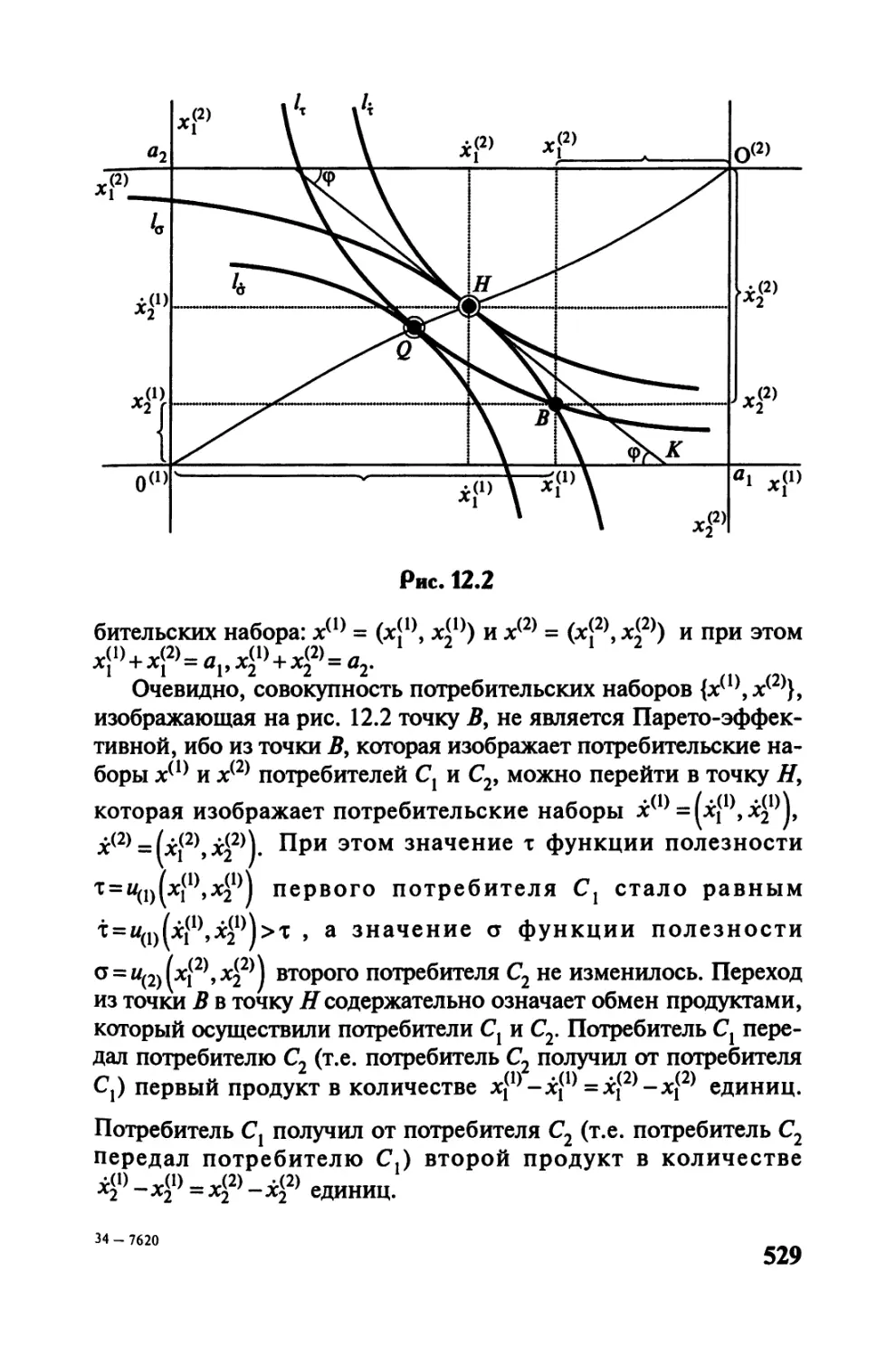
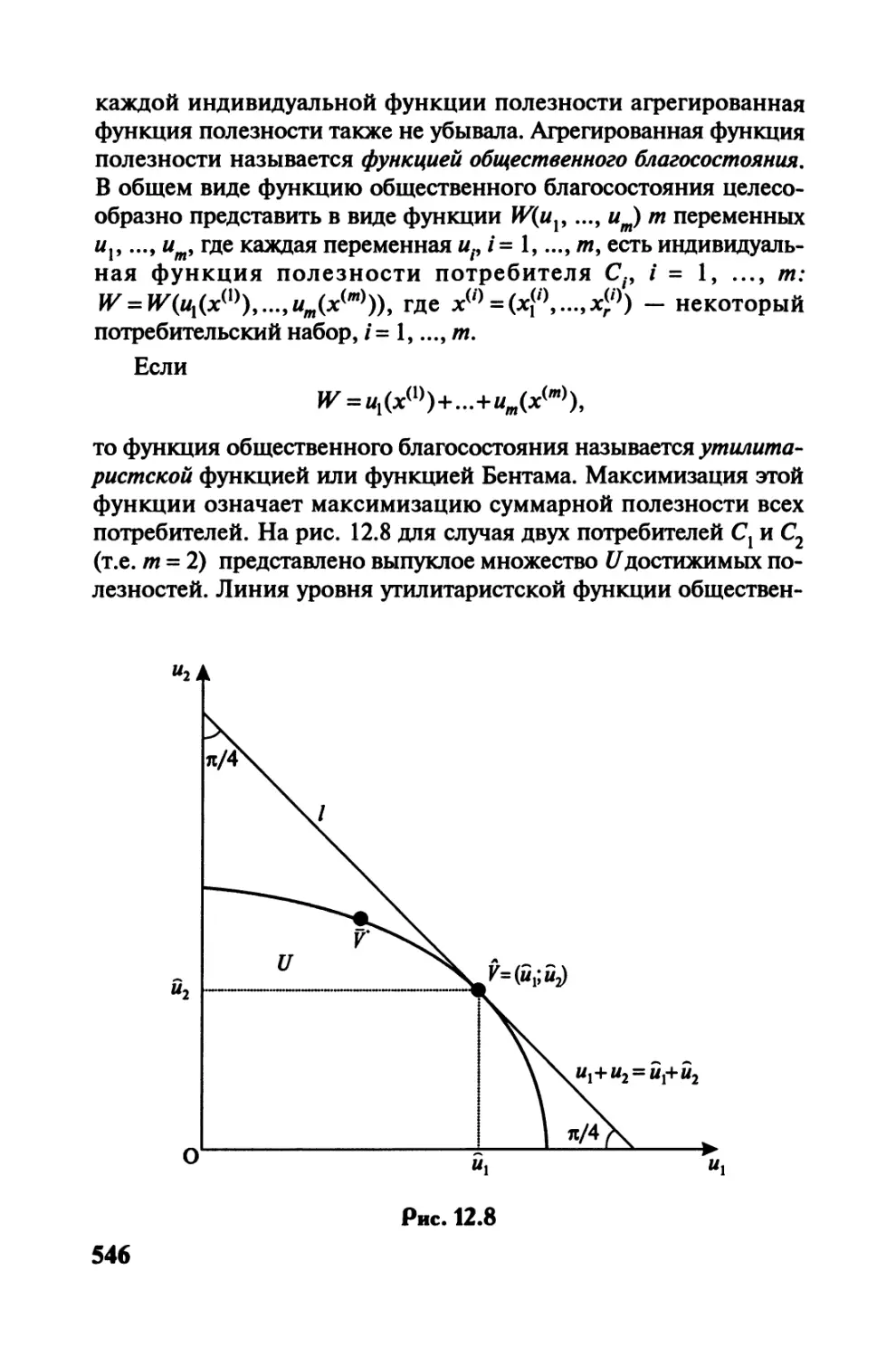
Автор: Черемных Ю.Н.
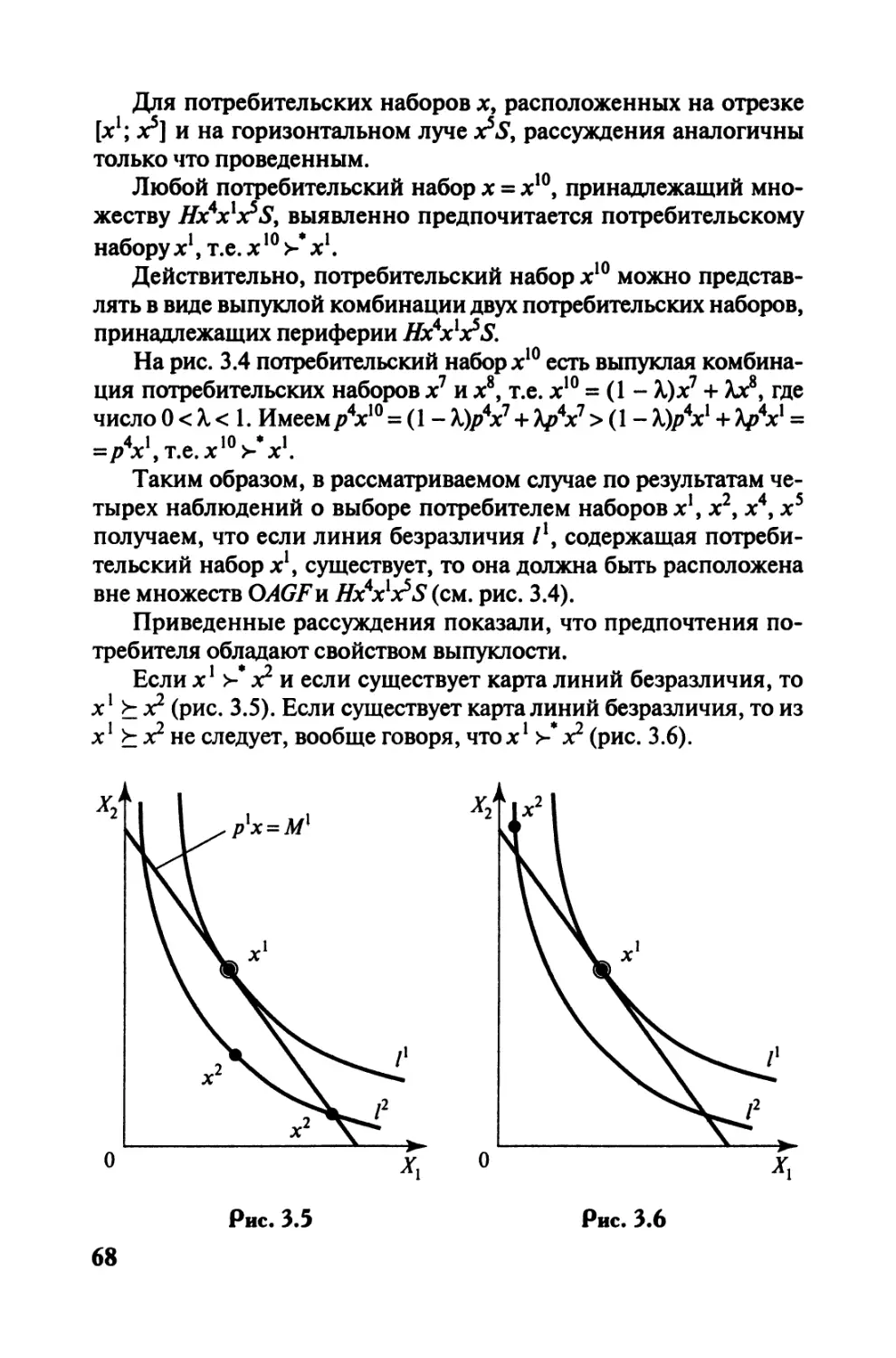
Теги: экономические науки в целом политическая экономия рынок: суть и структура экономика микроэкономика мгу учебник по экономике экономикс инфра-м
ISBN: 978-5-16-002041-9
Год: 2008
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М.В. ЛОМОНОСОВА
ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ
Ю.Н. Черемных
МИКРОЭКОНОМИКА
ПРОДВИНУТЫЙ УРОВЕНЬ
УЧЕБНИК
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М.В. ЛОМОНОСОВА
ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ
Ю.Н. Черемных
МИКРОЭКОНОМИКА
Продвинутый уровень
Учебник
Рекомендовано
Учебно-методическим объединением по классическому
университетскому образованию в качестве учебника
для студентов высших учебных заведений,
обучающихся по экономическим специальностям
МОСКВА
ИНФРА-М
2008
УДК 330(075.8)
ББК 65.012.2я73
400
Черемных Ю.Н. Микроэкономика. Продвинутый уровень:
Учебник. - М.: ИНФРА-М, 2008. - 844 с. - (Учебники эконо-
мического факультета МГУ им. М.В. Ломоносова).
ISBN 978-5-16-002041-9
Учебник включает темы курса «Микроэкономика. Продвинутый уро-
вень», для анализа которых используется разнообразный математичес-
кий аппарат. Главы учебника заканчиваются учебно-методическими ма-
териалами, включающими вопросы, упражнения и задачи для самоконт-
роля, а также вопросы и задачи, которые могут служить ориентирами при
составлении преподавателями контрольных работ.
Для студентов бакалавриата, магистратуры и аспирантов экономичес-
ких факультетов университетов и экономических вузов.
Подготовлено при содействии НФПК — Национального фонда подго-
товки кадров в рамках Программы «Совершенствование преподавания
социально-экономических дисциплин в вузах» Инновационного проекта
развития образования.
ББК65.012.2я73
ISBN 978-5-16-002041-9
© Экономический факультет МГУ
им. М.В. Ломоносова, 2008
© Оформление ИНФРА-М, 2008
250-летию
Московского Государственного
Университета им. М.В. Ломоносова
посвящается
Уважаемый читатель!
Настоящий учебник выходит в рамках серии «Учебники эко-
номического факультета МГУ им. М.В. Ломоносова», венчающей
многолетние усилия коллектива факультета по обновлению со-
держания и структуры университетского экономического обра-
зования.
Переход страны к рынку потребовал пересмотра профессии
экономиста, освоения и применения невостребованных ранее зна-
ний, известных, может быть, лишь ограниченному кругу кри-
тиков «буржуазной» экономической мысли.
Для обогащения содержания экономического образования
путем включения в него новых экономических дисциплин и об-
новления ряда традиционных нужно было переобучить препода-
вателей и решить проблему учебников. Первые попытки включения
в учебные планы новых дисциплин показали невозможность этого
в рамках одной ступени, поэтому, обновляя содержание, пришлось
попутно решать проблему перевода обучения на двухступенчатую
систему.
Истекшие 10 с небольшим лет — это годы освоения техно-
логии двухступенчатого образования «бакалавр—магистр», которое
факультет осуществляет без параллельной подготовки специали-
стов. Присоединение страны к Болонскому процессу сделало этот
переход необратимым.
Все эти годы велась переподготовка преподавательского кор-
пуса: благодаря программам международного сотрудничества
около 160 преподавателей факультета в среднем не меньше двух
раз стажировались в лучших зарубежных университетах.
Что касается учебников, то первые годы приходилось исполь-
зовать лучшие зарубежные учебники, многие из которых были
переведены преподавателями на русский язык. Сейчас пришло
время готовить качественные отечественные учебники. Препо-
давательский корпус имеет возможность создавать оригинальные
Учебники и учебные пособия, подготовленные с учетом опыта
преподавания и дифференцированные по уровню подготовки
3
слушателей (учебники для программ бакалавров и учебники для
программ магистров).
Решению этой задачи способствовало и участие факультета
в Инновационном проекте Министерства образования РФ, фи-
нансируемом Всемирным банком. Непосредственным исполни-
телем проекта стал Национальный фонд подготовки кадров.
Благодаря этому проекту факультет в течение трех лет осу-
ществил свой проект «Совершенствование высшего экономичес-
кого образования в МГУ», в результате чего преподаватели эко-
номического факультета подготовили 74 учебника и учебных по-
собий по основным дисциплинам, формирующим профессии
экономистов и менеджеров.
Мы считаем, что данные учебники в полной мере отражают
наиболее важные достижения университетской экономической
мысли, необходимые для полноценной подготовки экономистов
и управленцев высшего звена.
Сейчас на экономическом факультете МГУ обучается более
3000 студентов, факультет располагает самой большой в стране
магистратурой по экономике, наибольшим числом аспирантов
по экономическим специальностям. Образовательное «поле» на-
считывает более 300 общих дисциплин и специальных курсов.
Часть общих курсов представлена в данной серии учебников.
Коллектив факультета с благодарностью примет замечания и
предложения относительно улучшения предложенной серии учеб-
ников.
В.П. Колесов
декан экономического факультета
МГУ им. М.В. Ломоносова
профессор, доктор экономических наук
СОДЕРЖАНИЕ
Предисловие.............................................15
Введение ...............................................17
Глава 1 Теория поведения потребителя
на рынке................................................21
1.1. Решение задачи максимизации функции полезности
при бюджетном ограничении методом Лагранжа.
Локальное рыночное равновесие потребителя.
Функции спроса по Маршаллу (по Вальрасу),
косвенная функция полезности и их свойства...21
1.2. Предельная полезность по доходу и предельная
полезность по цене продукта (тождество Роя).
Значение этих выражений для решения
теоретических и прикладных задач
потребительского поведения на рынке.................28
1.3. Решение задачи минимизации расхода потребителя
при фиксированном уровне полезности методом
Лагранжа. Функции спроса по Хиксу (функции
компенсированного спроса), функция расходов
и их свойства.......................................32
1.4. Предельный расход по полезности и предельный
расход по цене продукта (лемма Шепарда).
Значение этих выражений для решения
теоретических и прикладных задач
потребительского выбора.............................35
1.5. Взаимосвязь между решением задач максимизации
функции полезности и минимизации расходов.
Вывод уравнений Слуцкого. Уравнения Слуцкого
в эластичностях..............................38
5
1.6. Оценка изменения благосостояния потребителя.
Эквивалентная и компенсирующая вариации
дохода.............................................42
1.7. Об использовании результатов социологических
обследований для оценки параметров функций
полезности социальных групп........................45
Глава 2 Теория отношения
предпочтения-безразличия................................51
2.1. Понятие отношений предпочтения, безразличия
и отношения предпочтения-безразличия...............51
2.2. Свойства и предположения отношения
предпочтения-безразличия...........................52
2.3. Взаимосвязь между отношением предпочтения-
безразличия и функцией полезности..................55
2.4. Лексикографическое упорядочение как пример
отношения предпочтения-безразличия,
для которого нельзя построить функцию
полезности.........................................57
Глава 3 Основы теории выявленных
предпочтений................................62
3.1. Предпосылки теории выявленных предпочтений...62
3.2. Связь теории выявленных предпочтений
с теорией линий (поверхностей) безразличия..65
3.3. Слабая и сильная аксиомы выявленных
предпочтений................................69
3.4. Связь между теорией выявленных предпочтений
и индексами цен.............................80
Глава 4 Учет свойств продуктов
при моделировании потребительского
поведения (теория технологии
потребления)................................88
6
4.1. Продукты и их свойства. Предпосылки
о квантифицируемости, аддитивности
и однородности свойств........................88
4.2. Пространство продуктов и их свойств. Свойства
продуктов как объект потребительского выбора..90
4.3. Неявные цены свойств и уравнения для их
определения...................................92
4.4. Оценка рыночной перспективы нового продукта...97
Глава 5 Выбор в условиях риска
и неопределенности...........................101
5.1. Понятия риска и неопределенности.............101
5.2. Общие принципы классификации рисков..........106
5.3. Предпринимательские риски....................109
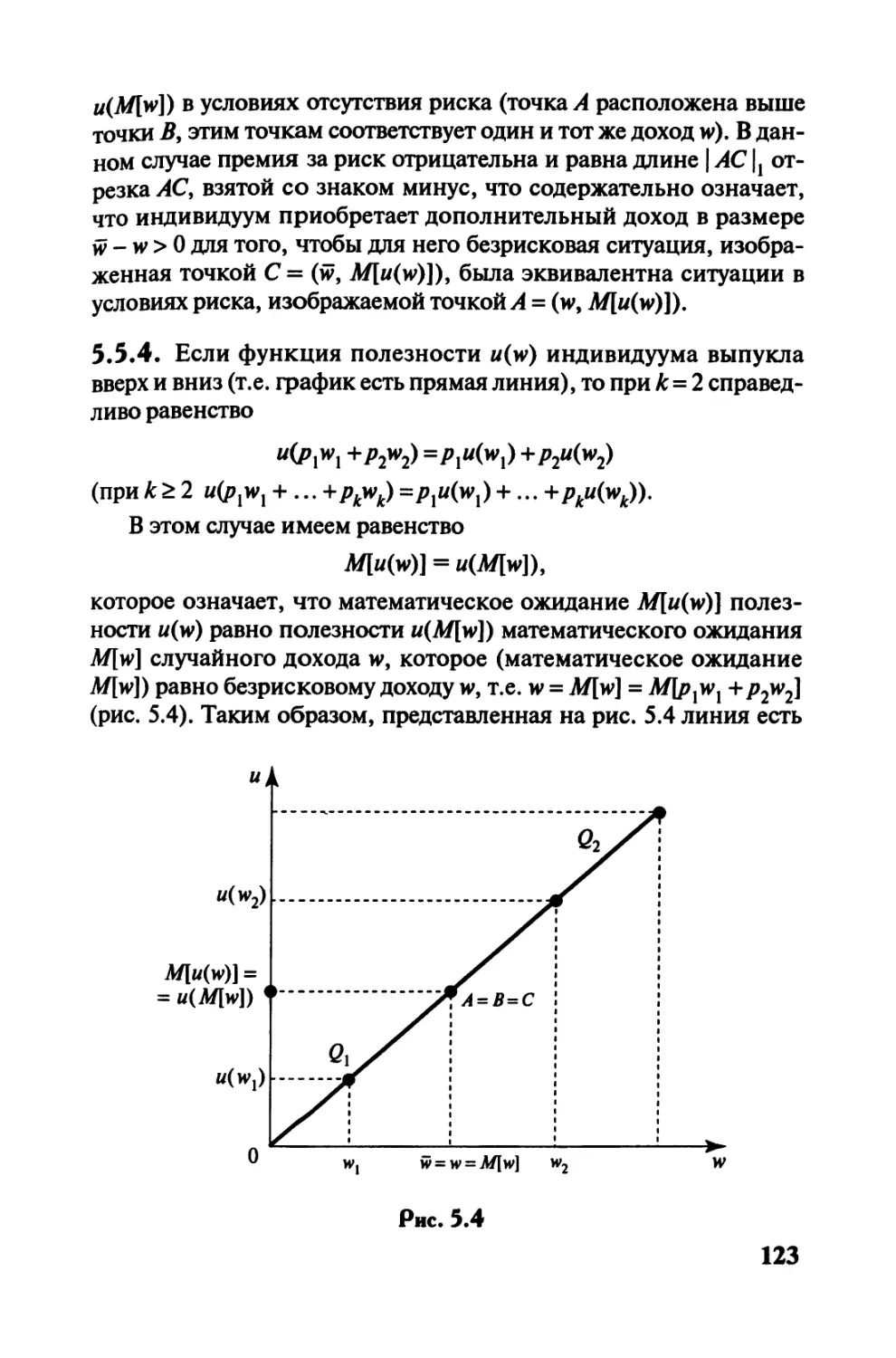
5.4. Элементы теории полезности Дж. фон Неймана
и О. Моргенштерна............................114
5.5. Отношение к риску. Количественные оценки
риска........................................119
5.6. Шкалы уровней риска..........................130
5.7. Методы предупреждения и снижения риска.......132
5.8. Спрос на рисковые активы. Задача оптимизации
инвестиционного портфеля.....................138
5.9. Принятие решений в условиях неопределенности.142
Глава 6 Теория фирмы, функционирующей
в условиях чистой конкуренции..............159
6.1. Задача максимизации прибыли фирмы
в долговременном и краткосрочном промежутках.
Локальное рыночное равновесие фирмы.
Функции спроса на ресурсы со стороны фирмы
и функция предложения фирмы. Аргументы
«за» и «против» максимизации прибыли. Понятие
«разумной прибыли»............................159
7
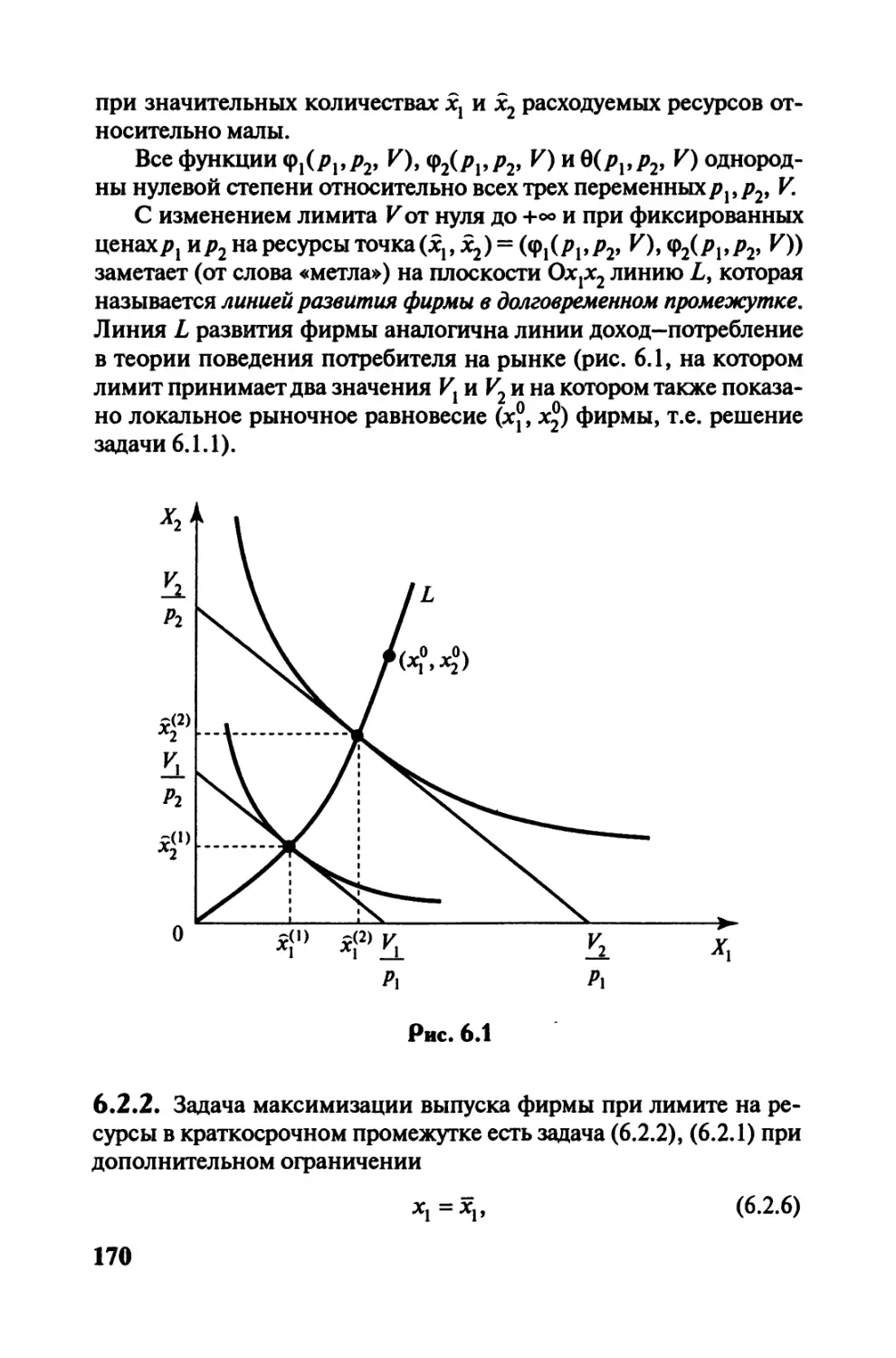
6.2. Задача максимизации выпуска фирмы при лимите
на используемые ею ресурсы в долговременном
и краткосрочном промежутках. Функции условного
спроса по Маршаллу (по Вальрасу) на ресурсы
со стороны фирмы и функция условного выпуска
фирмы............................................168
6.3. Предельный условный выпуск по лимиту
и предельный условный выпуск по цене ресурса
(тождество Роя)..................................173
6.4. Задача минимизации издержек фирмы
при фиксированном выпуске фирмы
в долговременном и краткосрочном промежутках.
Функции условного спроса по Хиксу на ресурсы
со стороны фирмы и функция условных издержек
фирмы............................................174
6.5. Предельные условные издержки по объему
выпуска и предельные условные издержки по цене
ресурса (лемма Шепарда)..........................180
6.6. Альтернативы максимизации прибыли фирмы
и многообразие целей фирмы.......................181
Глава 7 Производственные функции
и научно-технологический прогресс.....................199
7.1. Производственные функции, используемые
в экономическом анализе и прогнозировании,
и их свойства....................................199
7.2. Эластичность замены одного ресурса другим,
ее логарифмическое представление и геометрическая
интерпретация. Вывод ПФ с постоянной
эластичностью замены ресурсов....................212
7.3. ПФ с постоянной эластичностью замены ресурсов
и ее связь с ПФ Кобба—Дугласа, линейной
и ПФ Леонтьева....................................221
7.4. Учет в ПФ НТП в экзогенной и эндогенной
формах............................................223
8
Глава 8 Рыночные взаимодействия в случае
несовершенной конкуренции...................236
8.1. Максимизация прибыли монополии
в краткосрочном и долговременном промежутках,
монопольная цена и монопольный выпуск.......236
8.2. Монопольная власть и ее источники, индекс
монопольной власти..........................245
8.3. Естественные монополии и их регулирование...250
8.4. Монополистическая ценовая дискриминация
первого, второго и третьего рода............254
8.5. Максимизация прибыли в краткосрочном
и долговременном промежутках для фирмы,
функционирующей в условиях монополистической
конкуренции.................................293
8.6. Учет расходов на рекламу в задаче максимизации
прибыли фирмы в условиях монополистической
конкуренции........................................299
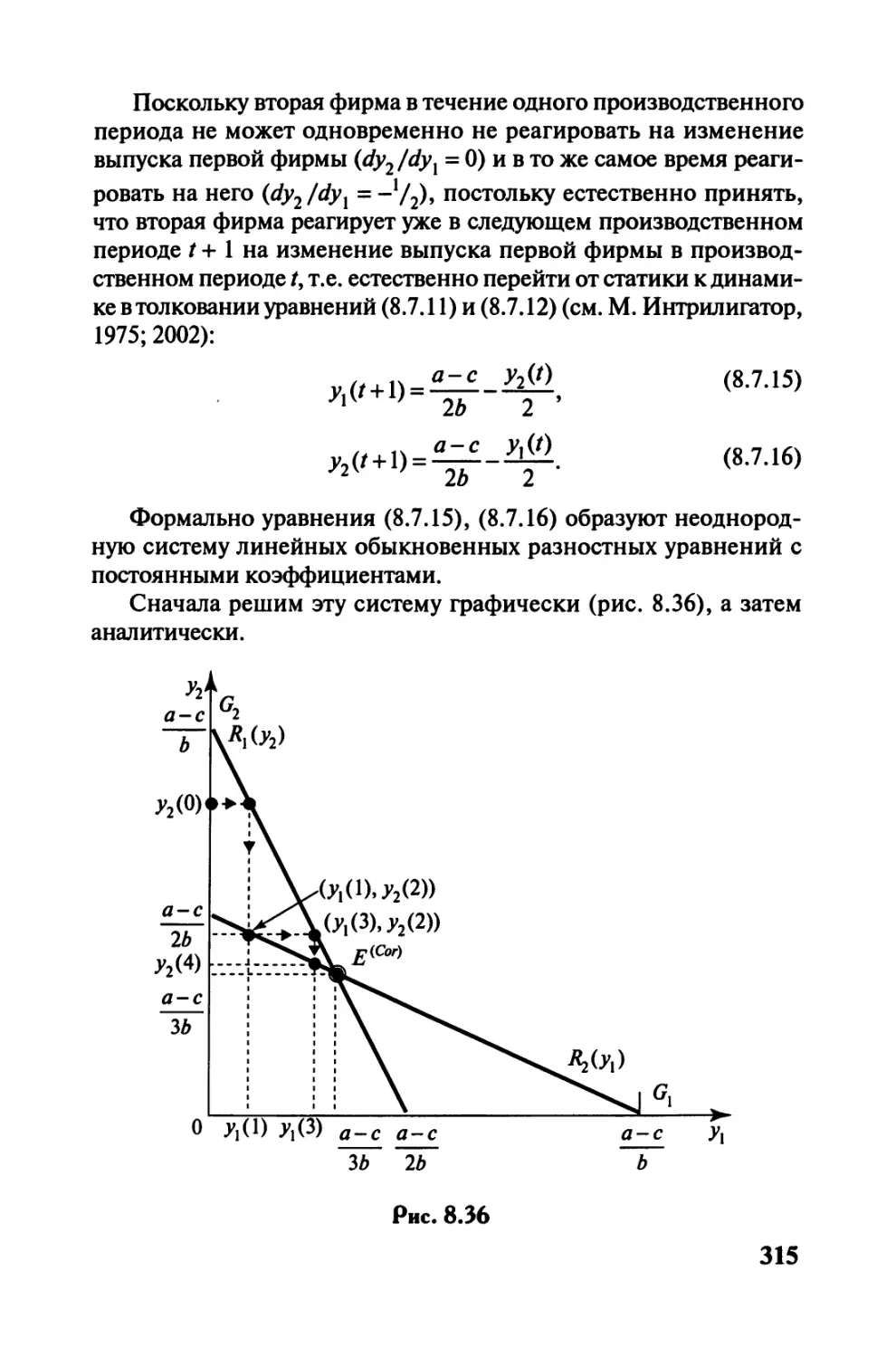
8.7. Модели дуополии и олигополии Курно.........302
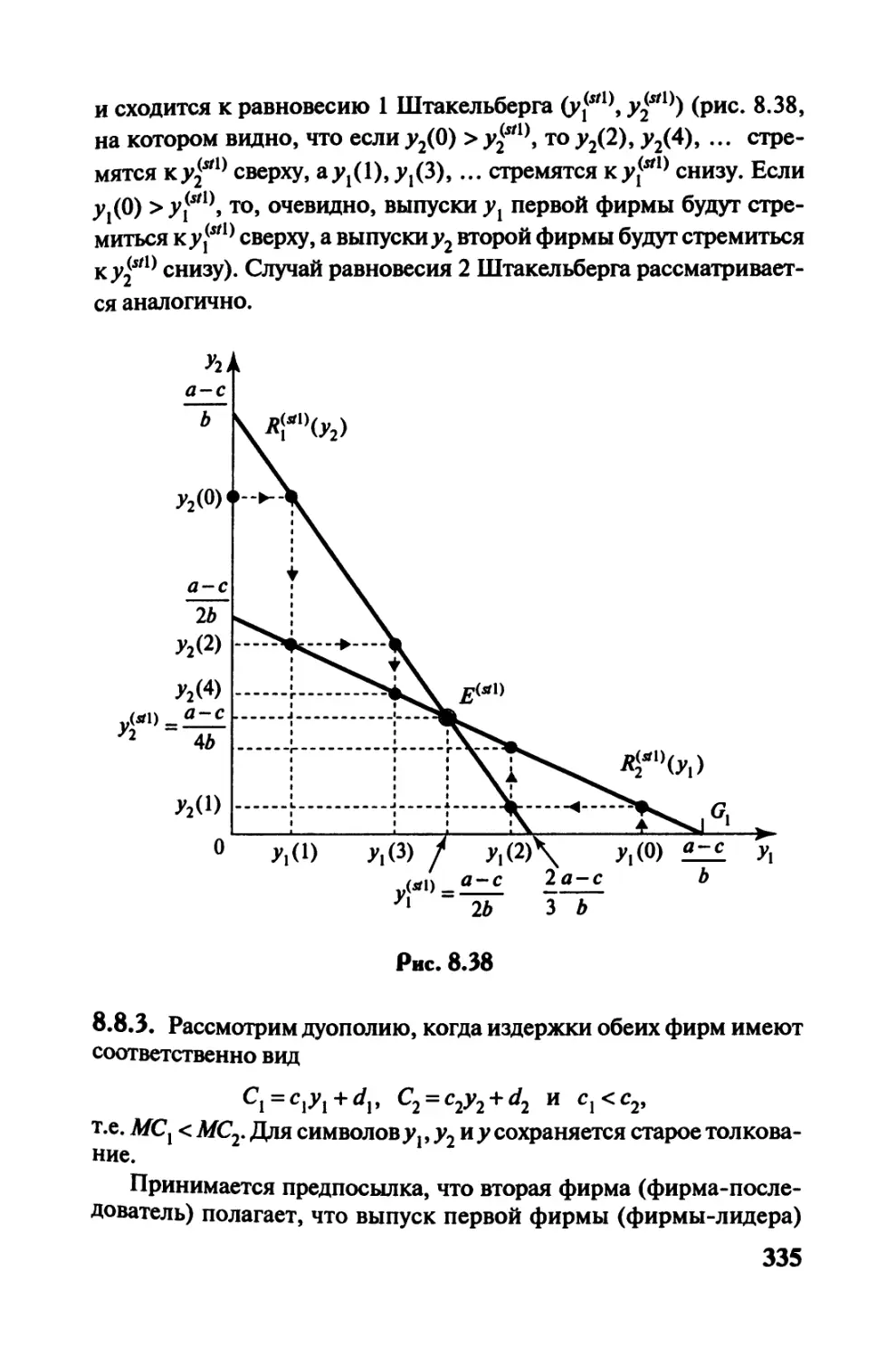
8.8. Модели дуополии и олигополии Штакельберга..325
8.9. Модели сговора в дуополии и олигополии......342
8.10. Модели дуополии и олигополии Бертрана......347
Глава 9 Основы теории
некооперативных игр.........................370
9.1. Некоторые понятия теории игр и их краткая
характеристика..............................370
9.2. Статические игры с полной информацией
в нормальной форме. Биматричные игры........372
9.3. Равновесие в статических играх с полной
информацией.................................375
9.4. Смешанное расширение биматричных игр........386
9
9.5. Биматричные игры с матрицами второго порядка.393
9.6. Парето-эффективность в статических играх
с полной информацией........................403
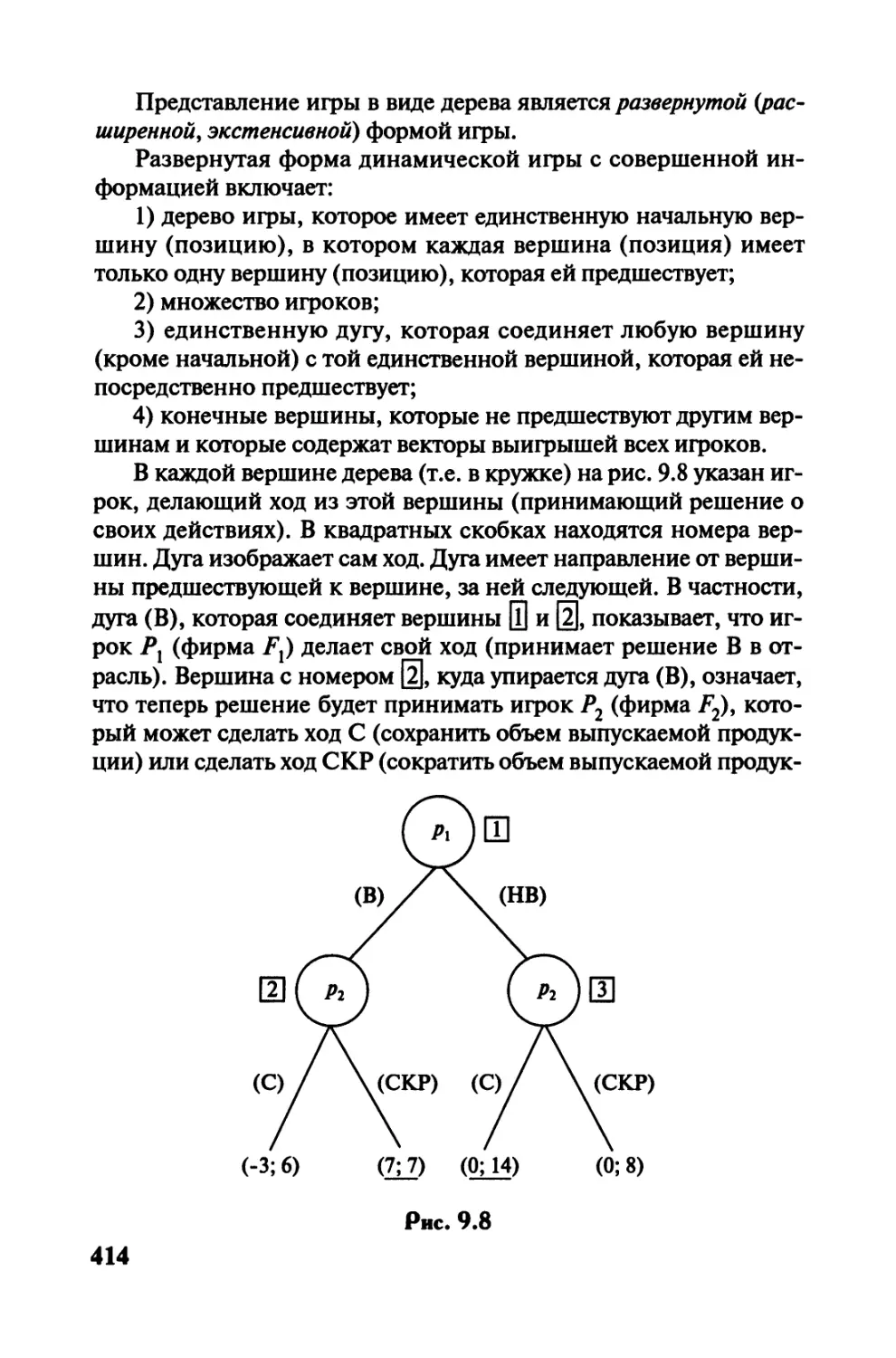
9.7. Динамические игры с совершенной
и несовершенной информацией.................412
9.8. Статические игры с неполной информацией......433
9.9. О динамических играх с полной и неполной
информацией.................................446
Глава 10 Теория рыночной конкуренции.................460
10.1. Толкование понятия рыночной конкуренции......460
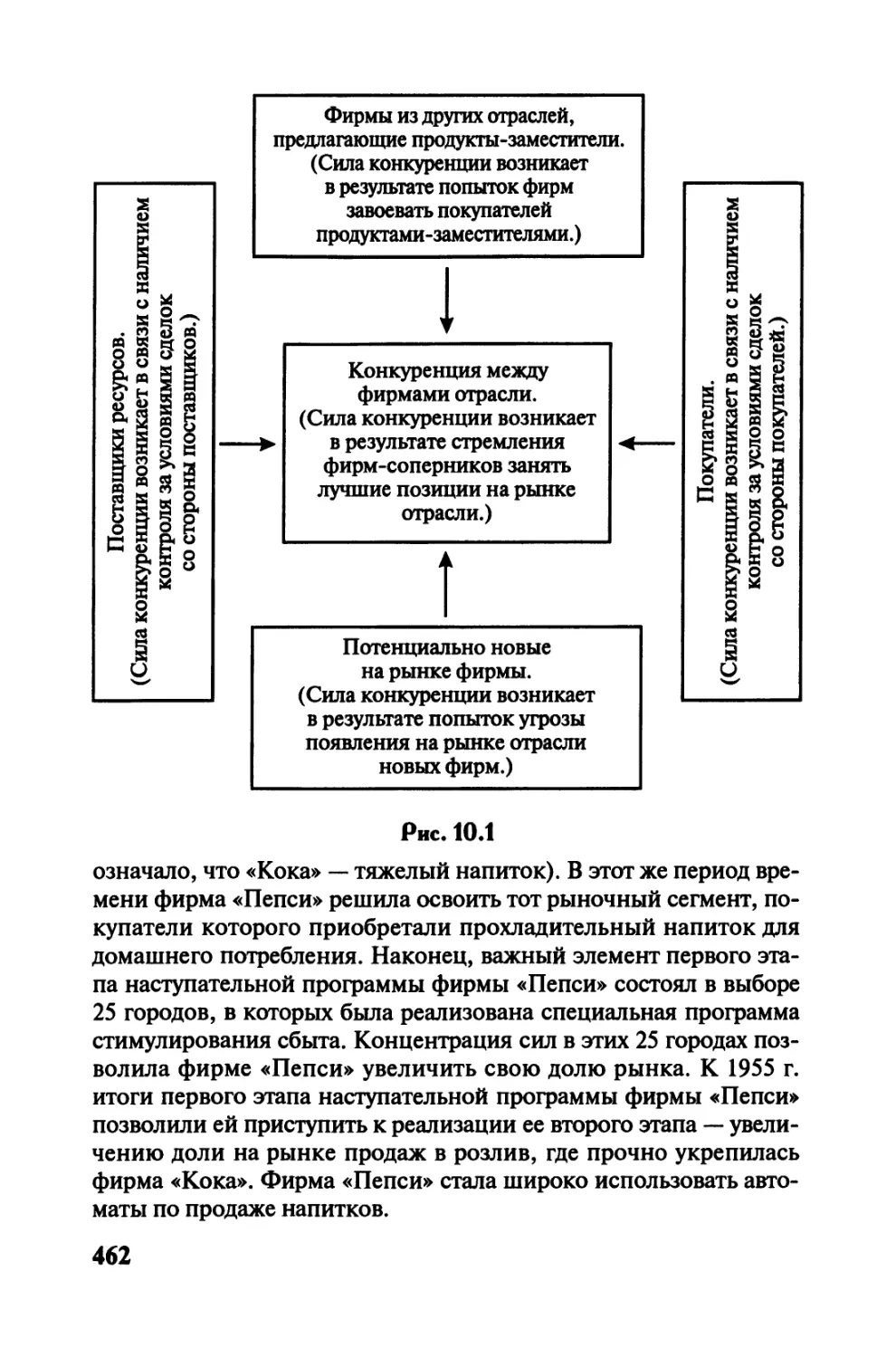
10.2. Модель пяти сил конкуренции..................461
10.3. Конкурентное преимущество. Стратегии,
используемые фирмами для получения
конкурентного преимущества..................471
10.4. Риски стратегий, используемых фирмами
для получения конкурентного преимущества....476
10.5. Достижение конкурентного преимущества
на основе стратегий лидерства по низким
издержкам, дифференциации и рыночной ниши...477
10.6. О становлении и потере конкурентного
преимущества................................481
10.7. Конкурентное преимущество на глобальных
рынках......................................482
10.8. Стратегические намерения фирм, «заповедники»
прибыли, перекрестное финансирование........487
Глава 11 Моделирование статического
экономического равновесия...................494
11.1. Сфера производства модели Эрроу—Дебре.
Функция рыночного предложения и ее свойства.494
10
11.2. Сфера потребления модели Эрроу—Дебре.
Функция рыночного спроса и ее свойства......496
11.3. Определение статического экономического
равновесия модели Эрроу — Дебре
и формулировка теоремы о его существовании..498
11.4. Примеры модели Эрроу — Дебре и цен
равновесия..................................500
11.5. Критические замечания по МЭД и ее обобщения.521
Глава 12 Экономическая теория
благосостояния..............................527
12.1. Парето-эффективность и статическое
экономическое равновесие в экономике обмена.
Первая и вторая теоремы экономики
благосостояния..............................527
12.2. Парето-эффективность и статическое
экономическое равновесие в экономике обмена.
Первая и вторая теоремы экономики
благосостояния (общий случай)...............543
12.3. Функции общественного благосостояния........545
12.4. Теорема о демократических групповых
рыночных решениях и ее значение для теории
общественного выбора...............................553
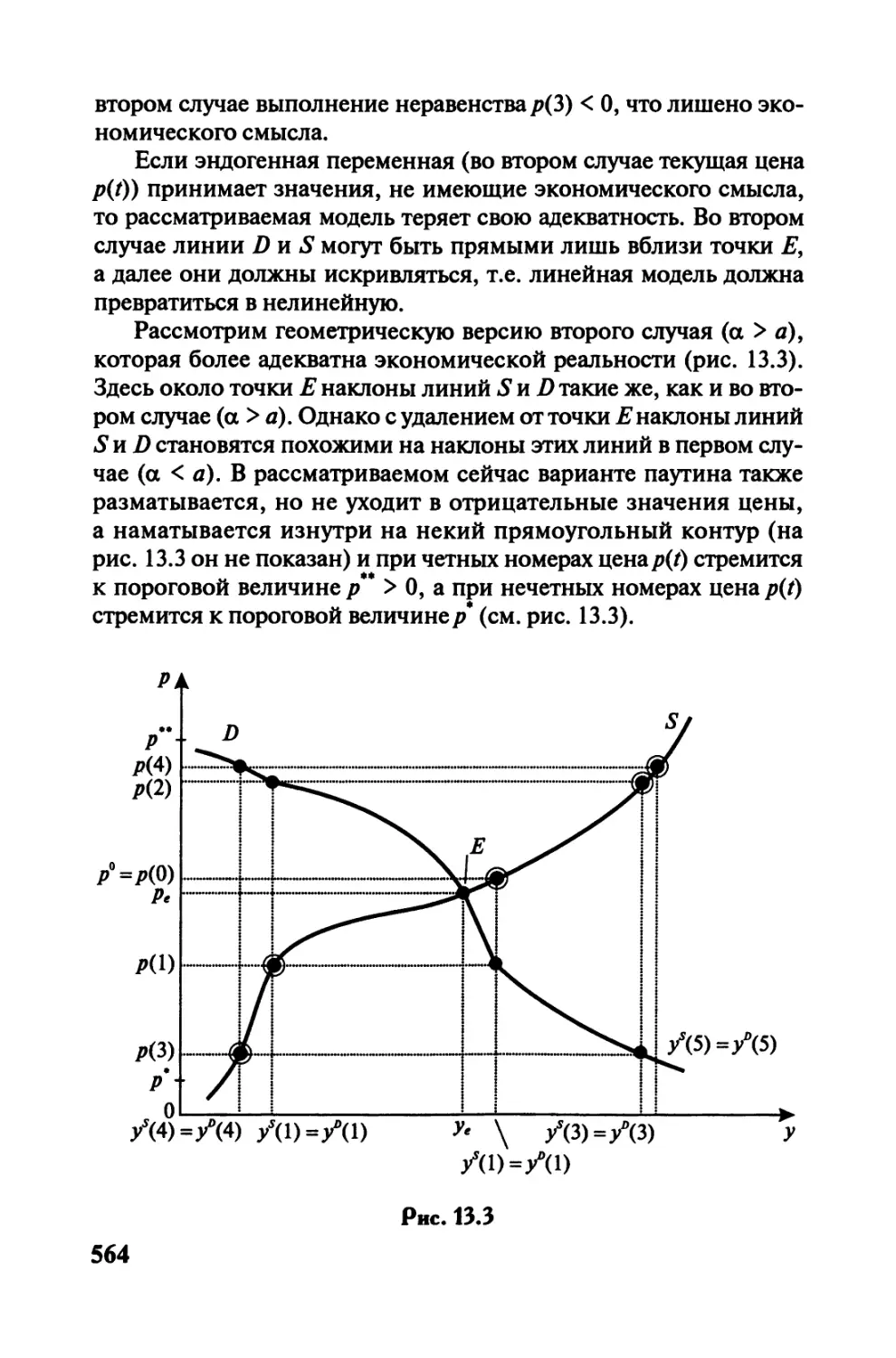
Глава 13 Моделирование динамики цен...................561
13.1. Простейшая однопродуктовая модель
экономической динамики (паутинообразная
модель) и ее обобщения............................561
13.2. Избыточный спрос и моделирование
динамики цен с использованием аппарата
теории обыкновенных дифференциальных
уравнений.........................................568
11
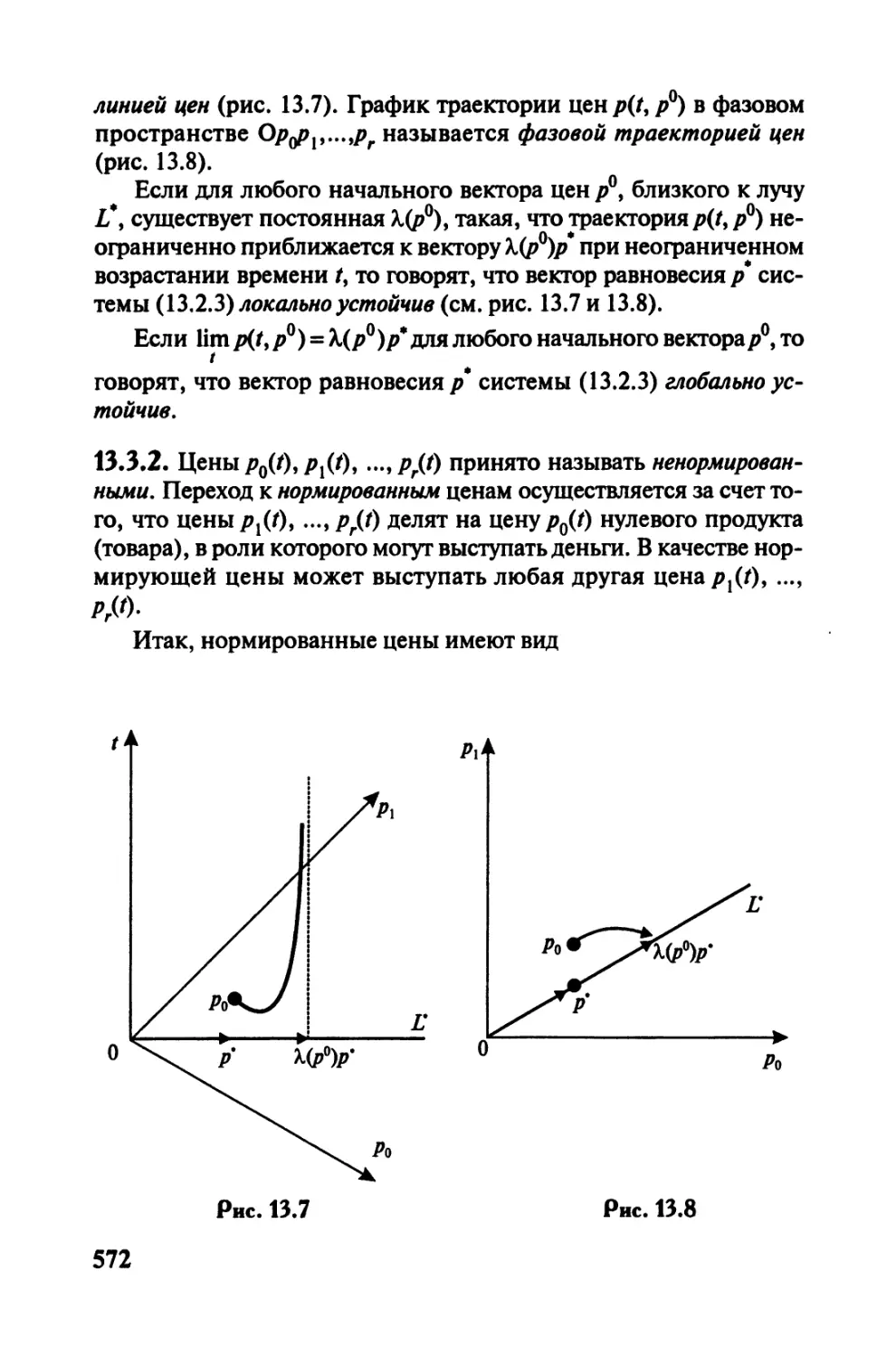
13.3. Динамика цен в случае, когда они не нормированы,
и в случае, когда они нормированы.................570
13.4. Достаточные условия локальной
устойчивости цен равновесия.......................574
13.5. Достаточные условия глобальной
устойчивости цен равновесия.......................577
13.6. Критические замечания по модели
динамики цен................................... 578
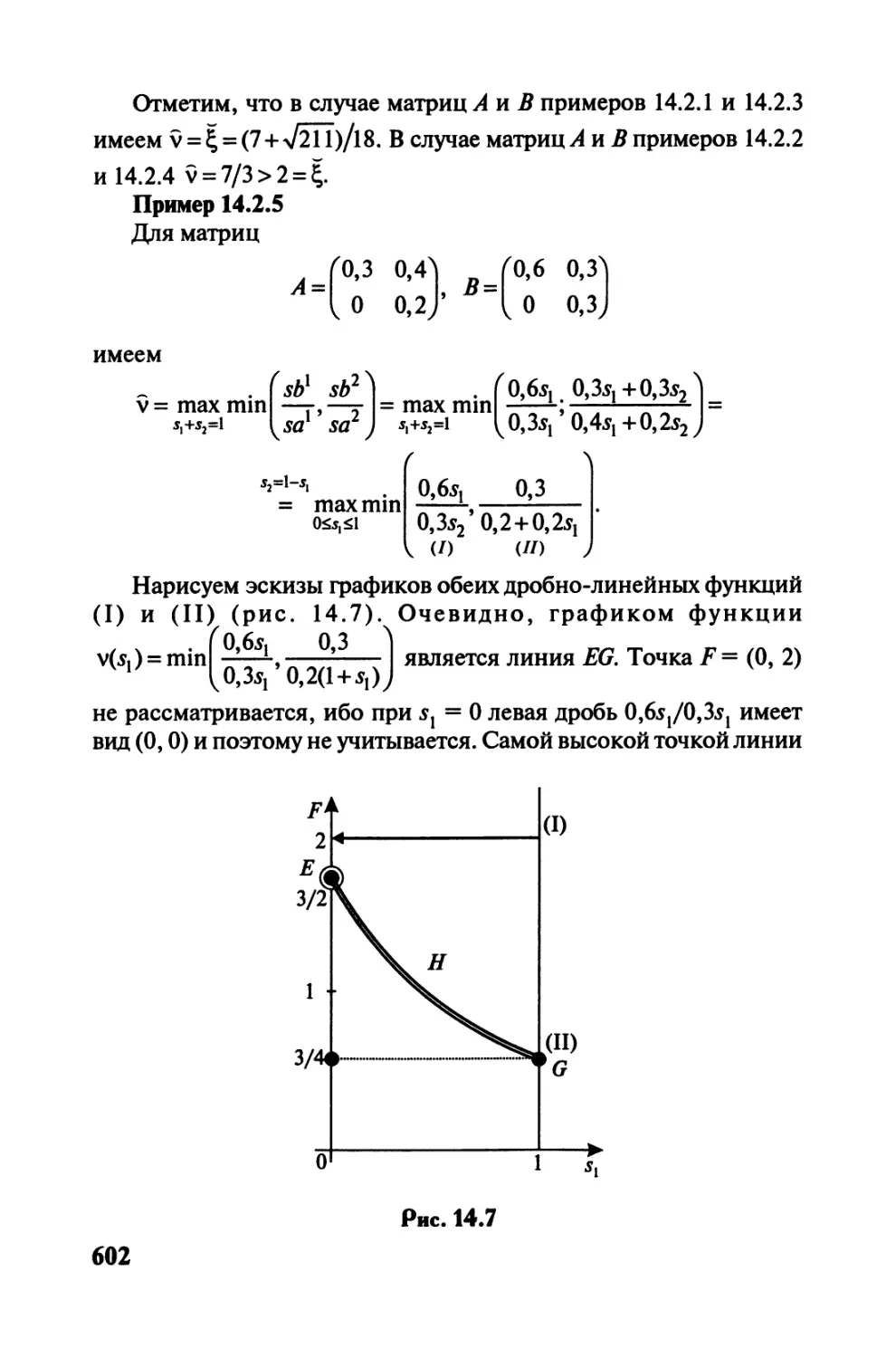
Глава 14 Моделирование динамического
равновесия........................................... 584
14.1. Динамическая модель в матричной форме
и оптимизация ее траекторий.......................584
14.2. Стационарные траектории динамической модели
в матричной форме и их основные
характеристики....................................590
14.3. Динамическое равновесие динамической модели
в матричной форме.................................604
14.4. Взаимосвязь между оптимальными траекториями
и траекториями равновесия динамической модели
в матричной форме................................611
Глава 15 Внешние эффекты............................625
15.1. Отрицательные внешние эффекты...............625
15.2. Положительные внешние эффекты...............631
15.3. Модель для определения стандарта на вредные
выбросы и платы за вредные выбросы...............633
15.4. Рынок прав на вредные выбросы...............643
12
Глава 16 Общественные блага.............................648
16.1. Характеристики общественных благ...............648
16.2. Частное и общее равновесие в модели экономики
с общественными благами.........................650
16.3. Равновесие Линдаля.............................658
16.4. О налоге Кларка................................660
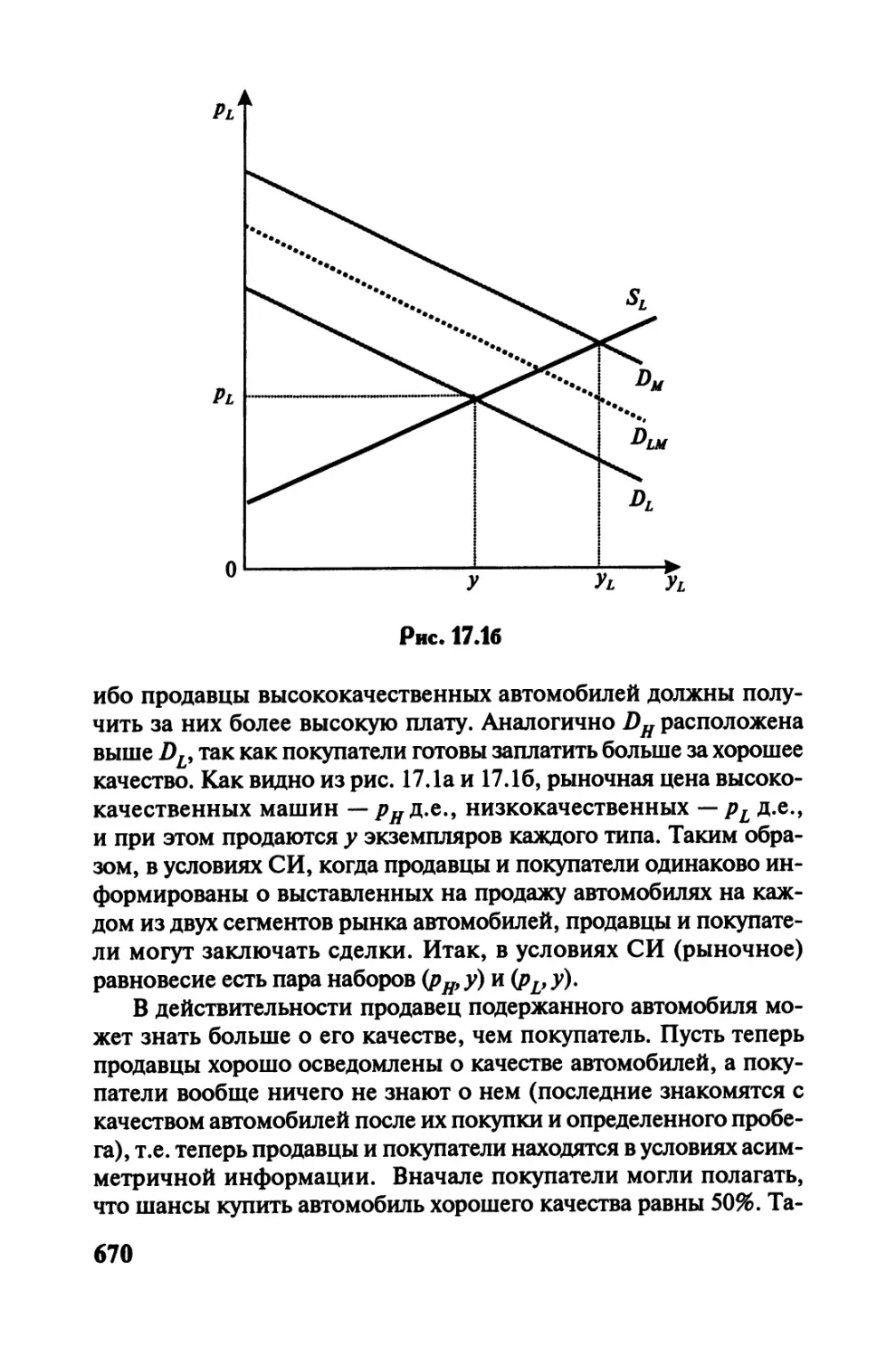
Глава 17 Асимметричная информация.......................667
17.1. Неблагоприятный отбор на рынке товаров и услуг.667
17.2. Моральный риск.................................675
17.3. Модели сигналов и фильтрации...................689
17.4. О модели «принципал — агент»...................711
17.5. О теории эффективной заработной платы..........715
Глава 18 Специальные микроэкономические
проблемы........................................725
18.1. Влияние современных форм научно-технологического
прогресса (телекоммуникационных систем
и компьютеризации) на микроэкономические
процессы...................................... 725
18.2. Рынок интернет-магазинов и его проблемы
в российской экономике........................ 732
18.3. Глобализация и микроэкономические проблемы..737
18.4. Технологический монополизм
и микроэкономические проблемы...................744
18.5. Экономический национализм
и микроэкономические проблемы...................747
18.6. Об экономической безопасности фирмы.............750
18.7. О теневой экономике и некоторых
микроэкономических проблемах....................756
13
Приложение
Основные математические понятия
и результаты, используемые в курсе
«Микроэкономика.
Продвинутый уровень»......................762
П 1. Множества и отображения...................762
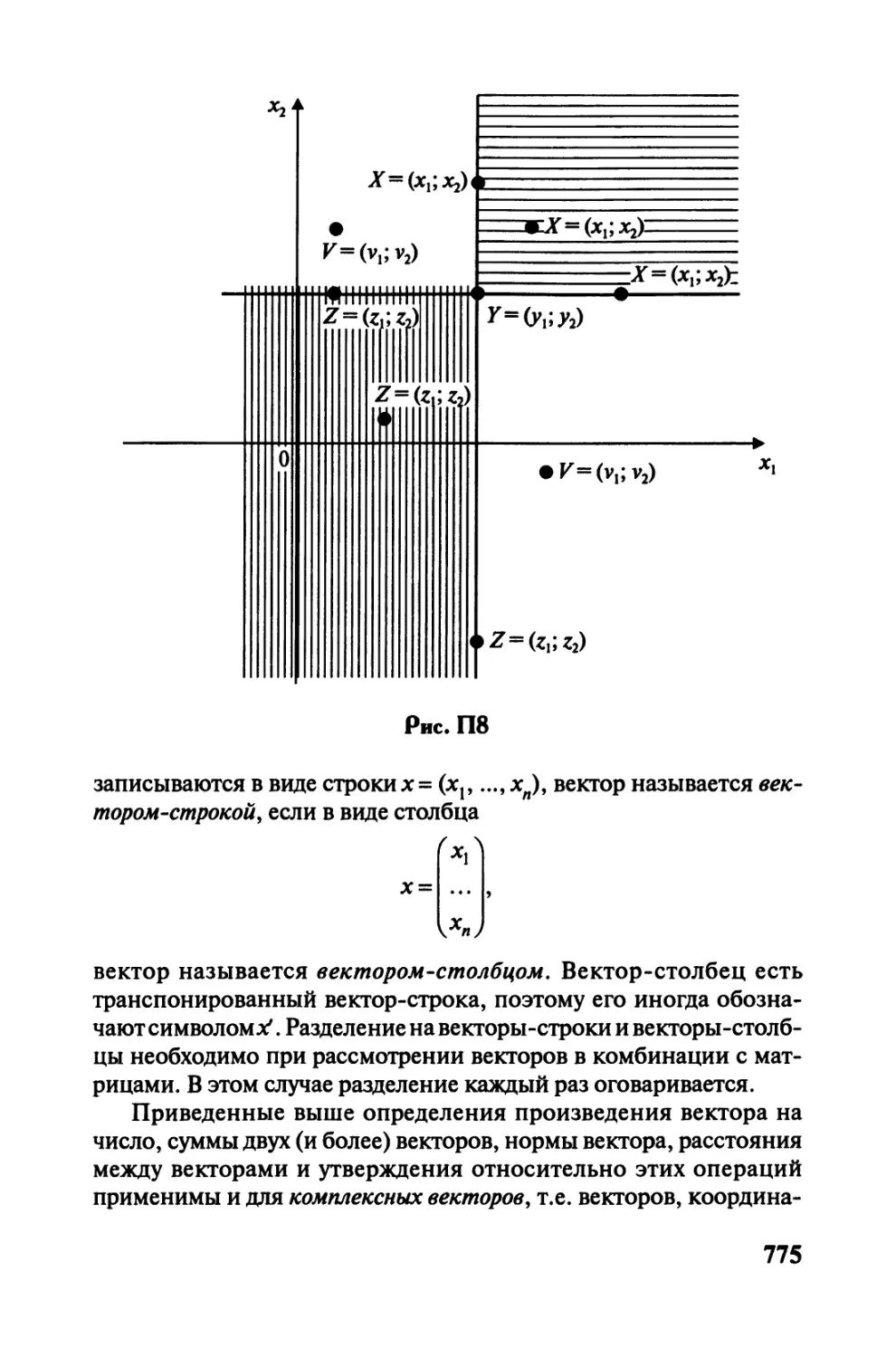
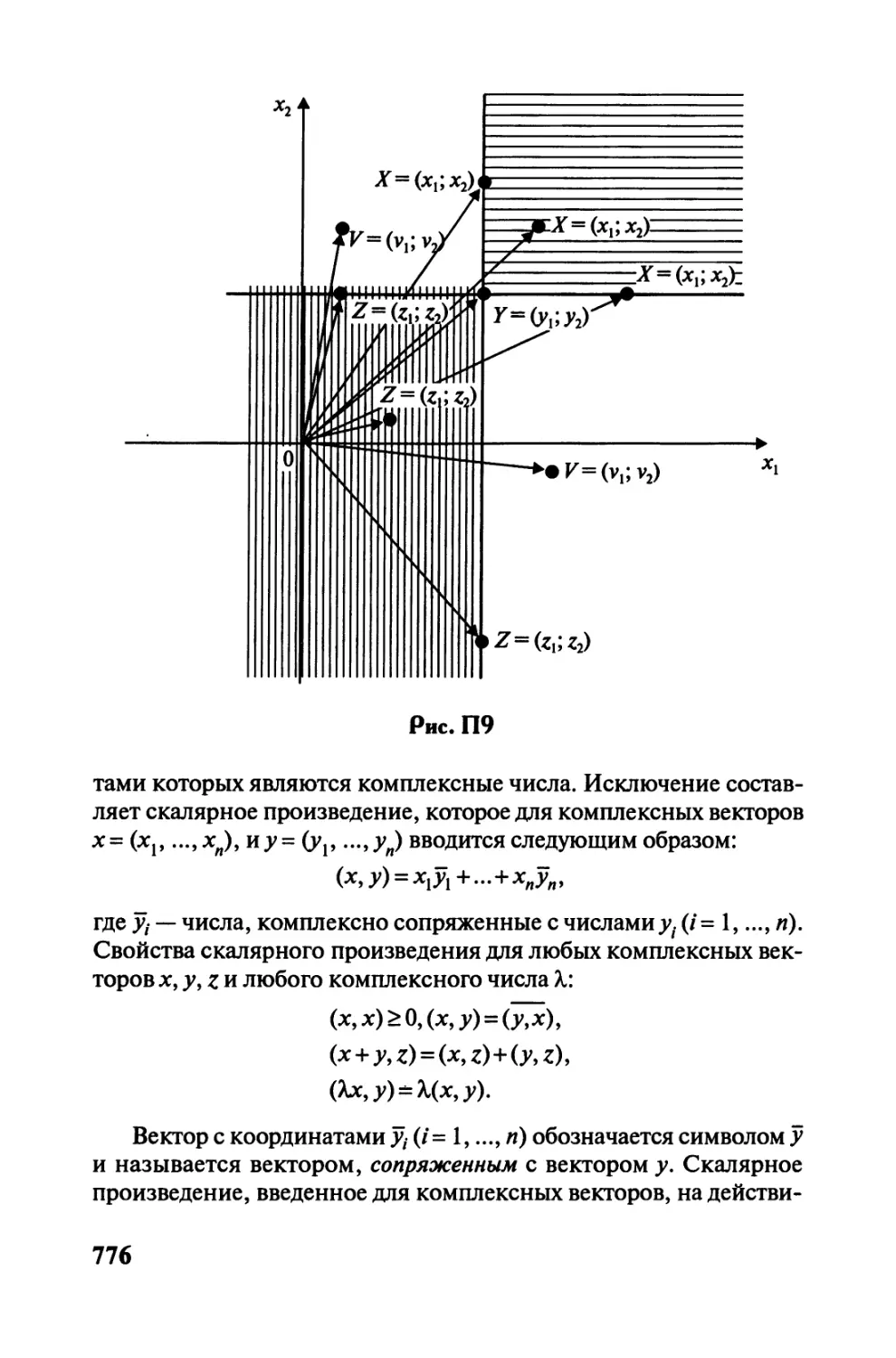
П 2. Векторы и множества векторов..............769
П 3. Матрицы и операции над матрицами..........784
П 4. Определитель матрицы и его свойства.......788
П 5. Основные результаты теории квадратных матриц.790
П 6. Основные результаты теории экстремума
функций одной и нескольких переменных.....798
П 7. Теоремы об огибающей......................805
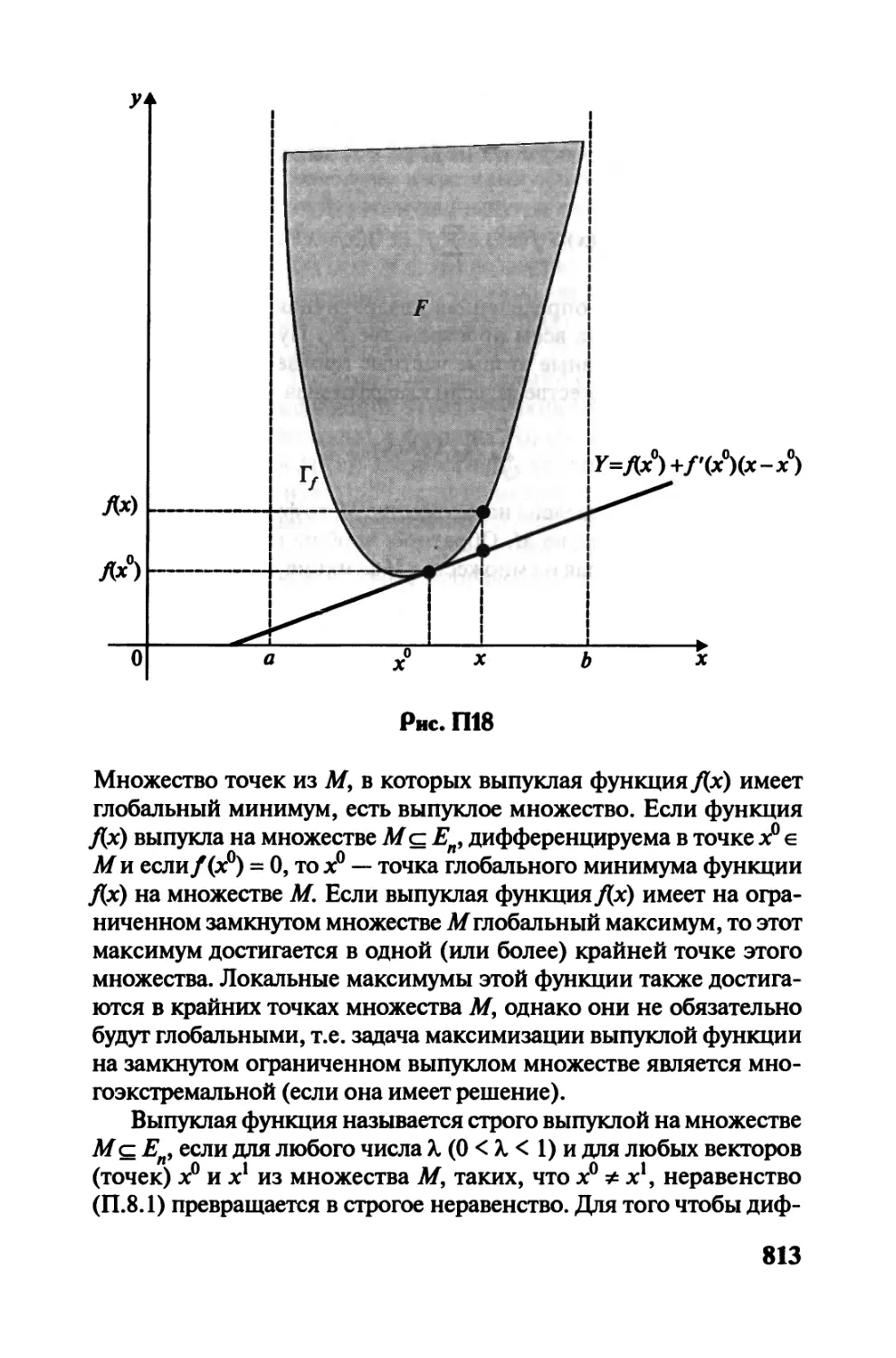
П 8. Функции выпуклые, вогнутые, квазивогнутые,
псевдовогнутые.......................... 810
П 9. Дифференциальные уравнения и системы
дифференциальных уравнений................817
П 10. Задача оптимального управления и принцип
максимума Л.С. Понтрягина.................825
Список литературы................................. 828
ПРЕДИСЛОВИЕ
Настоящий учебник «Микроэкономика. Продвинутый уро-
вень» подготовлен на базе курса «Микроэкономика — 3», который
автор читал более 10 лет студентам 1-го курса Школы магистров
экономического факультета МГУ. При подготовке курса «Микро-
экономика — 3» и учебника «Микроэкономика. Продвинутый
уровень» автор использовал опыт преподавания курса «Экономи-
ко-математическое моделирование», который (под разными на-
званиями) он читал более 20 лет студентам отделения «Планиро-
вание и экономическая кибернетика», а позже студентам отделе-
ния «Математическая экономика» экономического факультета
МГУ, опыт преподавания западными авторами курса микроэко-
номики продвинутого уровня, который был аккумулирован в объ-
емных томах с разными названиями — от микроэкономики до
микроэкономической теории, результаты и методические при-
емы, локализованные в многочисленных позициях списков лите-
ратуры к главам настоящего учебника.
Некоторые разделы (в частности, версии теорем об огибающих
в теории потребления и производства) продвинутого курса по мик-
роэкономике читались автором в курсе «Микроэкономика — 2»
студентам Школы бакалавров экономического факультета МГУ.
Эти разделы, естественно, были включены в настоящий учебник
«Микроэкономика. Продвинутый уровень».
Автор выражает искреннюю и глубокую благодарность:
Национальному фонду подготовки кадров (НФПК) за предо-
ставленную возможность для подготовки настоящего учебника
«Микроэкономика. Продвинутый уровень»;
профессору В.П. Колесову — руководителю-координатору
Проекта НФПК «Обновление университетского экономического
образования» и доценту В.Х. Эченике — заместителю руководите-
ля-координатора Проекта НФПК «Обновление университетского
экономического образования» за постоянное внимание и помощь
в преодолении принципиальных проблем, которые возникали в
процессе подготовки учебника, и поддержку его автора; рецен-
зенту НФПК за положительную оценку в целом учебника «Мик-
роэкономика. Продвинутый уровень» и за глубокие критические
замечания и корректно сформулированные рекомендации, учет
15
которых позволил, по мнению автора, значительно поднять уро-
вень подачи материала учебника для его читателей;
коллегам по кафедре «Математические методы анализа эко-
номики» экономического факультета МГУ профессору М.В. Гра-
чевой и доценту В.А. Чахоян за постоянную поддержку и понима-
ние необходимости преодоления неизбежных организационных и
профессиональных проблем;
сотрудникам группы реализации Проекта НФПК «Обновле-
ние университетского экономического образования»: менеджерам
Проекта М.Е. Ульяновой, Е.Ю. Архиповой и секретарю Проекта
О.Г. Корягиной за постоянное внимание и помощь в преодоле-
нии текущих проблем, которые возникали в процессе подготовки
учебника;
директору издательства «ТЕИС» экономического факультета
МГУ Т.А. Фомичевой за неоценимую помощь при решении тех-
нических проблем при подготовке материала настоящего учебни-
ка к печати;
Р.С. Хромченко, И.А. Алешковскому, М.Г. Башковой, С. Ива-
нову, И.В. Сметаниной, Р.Д. Соломатиной, А.В. Федорец за боль-
шой труд по компьютерному набору рукописного материала учеб-
ника и его верстке;
О. Степановой, М. Ковалевой, И. Левиной, Н. Овчиннико-
вой, Е. Голентовской, Б. Яценко — бывшим студентам экономи-
ческого факультета МГУ за возможность использовать превосход-
но сделанные ими записи лекций автора по курсам «Микроэконо-
мика — 2» и «Микроэкономика — 3»;
А. Андрияшину, Е. Авилову, А. Бланк, А Бондареву, М. Додло-
вой, Е. Ефремовой, О. Колобаевой, К. Лядской, А. Окатенко,
А. Пановой, А. Панферову, А. Салимову, А. Тимошенкову, М. Ху-
далову, А. Шишкину — бывшим студентам факультета экономики
Государственного университета — Высшей школы экономики за
возможность использовать подготовленные ими материалы до-
кладов, которые ими были сделаны в рамках курса лекций «Со-
временные микроэкономические проблемы»;
З.А. Басыровой — редактору Издательского Дома «ИНФРА-М»
за ценные замечания, учет которых позволил существенно улуч-
шить подачу материала читателям настоящей книги, и Л.С. Кули-
ковой — корректору Издательского Дома «ИНФРА-М».
ВВЕДЕНИЕ
Во многих странах Запада и в России принято преподавать
микроэкономику в виде комплекса трех учебных дисциплин:
«Микроэкономика. Вводный уровень» (аналог: «Микроэкономи-
ка — 1»), «Микроэкономика. Промежуточный уровень» (аналог:
«Микроэкономика — 2»), «Микроэкономика. Продвинутый уро-
вень» (аналог: «Микроэкономика — 3).
На каждом уровне (кроме вводного) расширяется и углубляет-
ся поле содержательных областей предыдущего уровня, повыша-
ется интенсивность подачи материала, привлекается более слож-
ный математический инструментарий. В связи с этим имеют мес-
то пересечения теоретических положений и практических
приложений, хотя повышение интенсивности подачи материала
может достаточно сильно деформировать тот или иной раздел
микроэкономики так, что он станет мало похожим на себя в курсе
предыдущего уровня.
Курсы микроэкономики вводного и промежуточного уровней
являются фундаментальными составляющими системы экономи-
ческих курсов для студентов-экономистов бакалавриата. В этих
курсах часто даются только принципиальные ответы на вопросы
экономической теории и хозяйственной практики и не всегда
принципы доводятся до их реализации. Например, задача макси-
мизации прибыли фирмы является теоретической моделью широ-
кого класса задач рационального поведения реальной фирмы на
рынке. Теория чистой конкуренции аналогична теории идеально-
го газа в физике, благодаря которой реальные газы изучаются не
столько сами по себе, а скорее с точки зрения того, насколько они
похожи на идеальный газ. В микроэкономике различные рыноч-
ные структуры также часто рассматриваются с точки зрения сте-
пени их сходства или различия с чистой конкуренцией, а не сами
по себе.
На курсы микроэкономики вводного и промежуточного
уровней опираются такие более специальные дисциплины, как
«Теория фирмы», «Теория отраслевых рынков», которые в свое
время постепенно отпочковывались от дисциплины «Микроэко-
номика».
2 - 7620
17
Курсы микроэкономики вводного и промежуточного уровней
читаются раньше, чем теория игр и дифференциальные уравне-
ния, которые используются для описания и анализа многих мик-
роэкономических проблем.
Курс микроэкономики продвинутого уровня также является
фундаментальной составляющей системы экономических курсов
для студентов-экономистов магистратуры. В отличие от курсов
микроэкономики вводного и промежуточного уровней курс мик-
роэкономики продвинутого уровня читается после ряда более
специальных экономических курсов («Теория фирмы», «Теория
отраслевых рынков»), а также после теории игр и дифференци-
альных уравнений, читаемых в бакалавриате.
Отмеченные обстоятельства являются причиной необходимос-
ти корректировки содержательной проблематики курса микроэко-
номики продвинутого уровня за счет ее расширения и более широ-
кого и глубокого привлечения математического инструментария.
Особенность курса «Микроэкономика. Продвинутый уро-
вень» заключается прежде всего в достаточно высоком научном
уровне подачи материала, наличии проблемных содержательных
областей и привлечении серьезного математического аппарата —
естественно, там, где он необходим.
В частности, интенсивность подачи материала теории потреб-
ления и теории производства повышается благодаря их расшире-
нию за счет использования версий теорем об огибающей, которые
представляют собой выражения частных производных по парамет-
рам оптимальных значений экстремальных задач рационального
поведения потребителя и фирмы в условиях чистой конкуренции.
В теории производственных функций на основании решения диф-
ференциального уравнения демонстрируется появление произ-
водственной функции с постоянной эластичностью замены ресур-
сов — одной из важных производственных функций для теорети-
ческих построений и практических приложений и одной из тех
производственных функций, которые были получены в результате
теоретических построений, а не с помощью эмпирического «на-
щупывания», как это было, например, с производственной функ-
цией Кобба — Дугласа. В теории экономического равновесия ин-
тенсивность подачи материала повышается за счет подробного
описания производственной сферы и сферы потребления модели
статического равновесия Эрроу — Дебре и за счет модели динами-
ческого равновесия.
18
Проблемные содержательные области в настоящем учебнике
локализованы в главе 18 «Специальные микроэкономические
проблемы».
Применяемый в учебнике математический аппарат отличает-
ся значительным разнообразием. Помимо результатов математи-
ческого анализа (классические методы оптимизации, элементы
теории устойчивости по Ляпунову решений систем дифференци-
альных уравнений), активно используются некоторые результаты
выпуклого анализа, матричной алгебры, относящиеся к квадрат-
ным матрицам с неотрицательными элементами вне главной диа-
гонали, теории биматричных игр, теории оптимального управле-
ния.
Подчеркнем, что первостепенной проблематикой в курсе
микроэкономики продвинутого уровня является содержательная
теоретическая (в основном) и прикладная проблематика. Матема-
тический аппарат (который может использоваться на достаточно
высоком уровне) играет роль вспомогательного инструментария,
предназначенного обслуживать «основное производство», т.е. со-
держательную проблематику. В связи с этим обстоятельством
курс микроэкономики продвинутого уровня отличается от мик-
роэкономического раздела курса математической экономики,
в котором математические методы (наряду с содержательными
задачами) представляют предмет самостоятельного исследова-
ния.
Под влиянием многих факторов (прежде всего такого, как на-
учно-технологический прогресс) содержательные области микро-
экономики активно меняются во времени, стимулируя корректи-
ровку и частичное элиминирование используемых и появление
новых модельных построений. Так, в задачах долговременного и
среднесрочного перспективного или ретроспективного анализа
(в отличие от статических задач) понятие потребительского набо-
ра может оказаться малосодержательным в связи с быстрым об-
новлением потребительских характеристик продуктов, с интен-
сивным уходом с рынков одних продуктов и появлением других.
Достаточно упомянуть персональные компьютеры, мобильные
средства связи, потребительские характеристики которых актив-
но растут параллельно со снижением их рыночных цен.
Аналогичным является положение с пониманием конфигура-
ции ресурсов, характер поведения которых может сильно менять-
ся во времени в связи с повышением, например, их производи-
2*
19
тельности. В частности, много проблем возникает с описанием и
анализом дистанционной формы организации труда, когда не ра-
ботник перемещается в пространстве для соединения со своим
рабочим местом, а рабочее место, например автоматизированное
рабочее место на базе персонального компьютера, перемещается
по месту жительства работника. Косвенным эффектом такого
преобразования взаимосвязи между работником и его рабочим
местом является, в частности, уменьшение нагрузки на обще-
ственный транспорт или на личный транспорт.
Востребованность математических методов и средств, исполь-
зуемых для решения микроэкономических задач, также меняется
во времени. После Второй мировой войны для решения приклад-
ных и теоретических задач активно использовалось линейное и
выпуклое программирование. В настоящее время, особенно в об-
ласти теоретических исследований, доля линейного программи-
рования уменьшается, зато доля теории игр увеличивается.
Благодаря интенсивному развитию вычислительной техники
резко возросла доля инструментальных методов эффективного
решения экономических задач, что, в свою очередь, привело к
повышению доли вычислимых микроэкономических моделей в
общей массе всех математических моделей микроэкономики.
Глава 1
ТЕОРИЯ ПОВЕДЕНИЯ
ПОТРЕБИТЕЛЯ НА РЫНКЕ
1.1. Решение задачи максимизации функции
полезности при бюджетном ограничении методом
Лагранжа. Локальное рыночное равновесие
потребителя. Функции спроса по Маршаллу
(по Вальрасу), косвенная функция полезности
и их свойства
1.1.1. Теория потребления изучает поведение потребителя на
рынке. Потребитель характеризуется функцией полезности и до-
ходом, который он готов потратить на приобретение продуктов,
а рынок — потребительскими наборами и ценами (ценой на еди-
ницу каждого продукта). Все величины имеют одну и ту же вре-
менною «привязку». Они постоянны в течение некоторого фикси-
рованного периода времени (само время предполагается дискрет-
ным).
Потребитель ведет себя рационально, если он максимизирует
функцию полезности при бюджетном ограничении. Поведение
потребителя может быть описано в вербальной форме: максимиза-
ция полезности, если хватит содержимого кошелька; в виде зада-
чи на условный максимум (Задача I) в аналитической форме:
£/(хр х2)-> (max),
р1х]+р2х2 = М-
(1.1.1)
(1.1.2)
и в геометрической форме (рис. 1.1).
21
Отметим, что здесь и далее под максимумом понимается гло-
бальный максимум, если нет специальной оговорки.
Рассмотрим линии безразличия (например, линии /т, /%), ко-
торые имеют общие точки с бюджетной прямой. Двигаясь по ли-
ниям безразличия на «северо-восток» до упора, выбираем линию
безразличия /?, которая имеет с бюджетной прямой точку касания
(хр х2). Это означает, что потребитель выбирает потребительский
набор (, х2), который называется локальным рыночным равновесием
потребителя (ЛРРП). При этом его функция полезности U(xv х2)
достигает своего условного максимума т = U. Рисунок 1.1 демон-
стрирует, что U(xx, х2) = т > т, = U (х|, х2), где (хр х2) — любая точ-
ка бюджетной прямой ptxt + р2х2 = М, отличная от точки (хр х2).
Картина взаимного расположения линий безразличия и бюджет-
ной прямой на рис. 1.1 типична для задач экономической теории.
Представленные на рис. 1.1 линии безразличия являются строго
выпуклыми к точке О. В частности, если линия безразличия
строго выпукла, то точка х = (хр х2) ее касания с бюджетной пря-
мой является единственной. Если линия безразличия выпукла,
но не строго выпукла к точке О, точка х касания может быть не
единственной.
22
1.1.2. Потребитель достиг определенного уровня полезности
U{хх, х2) = и. Как выйти на этот уровень полезности с наименьши-
ми расходами? (Вербальная форма задачи минимизации расхода
при фиксированном уровне полезности.) Аналитическая форма за-
дачи минимизации расхода потребителя при фиксированном уров-
не полезности имеет вид задачи на условный минимум (Задача II):
р1х1+р2х2 = Л/->(тш), (1.1.3)
U(Xl,x2)-U. (1.1.4)
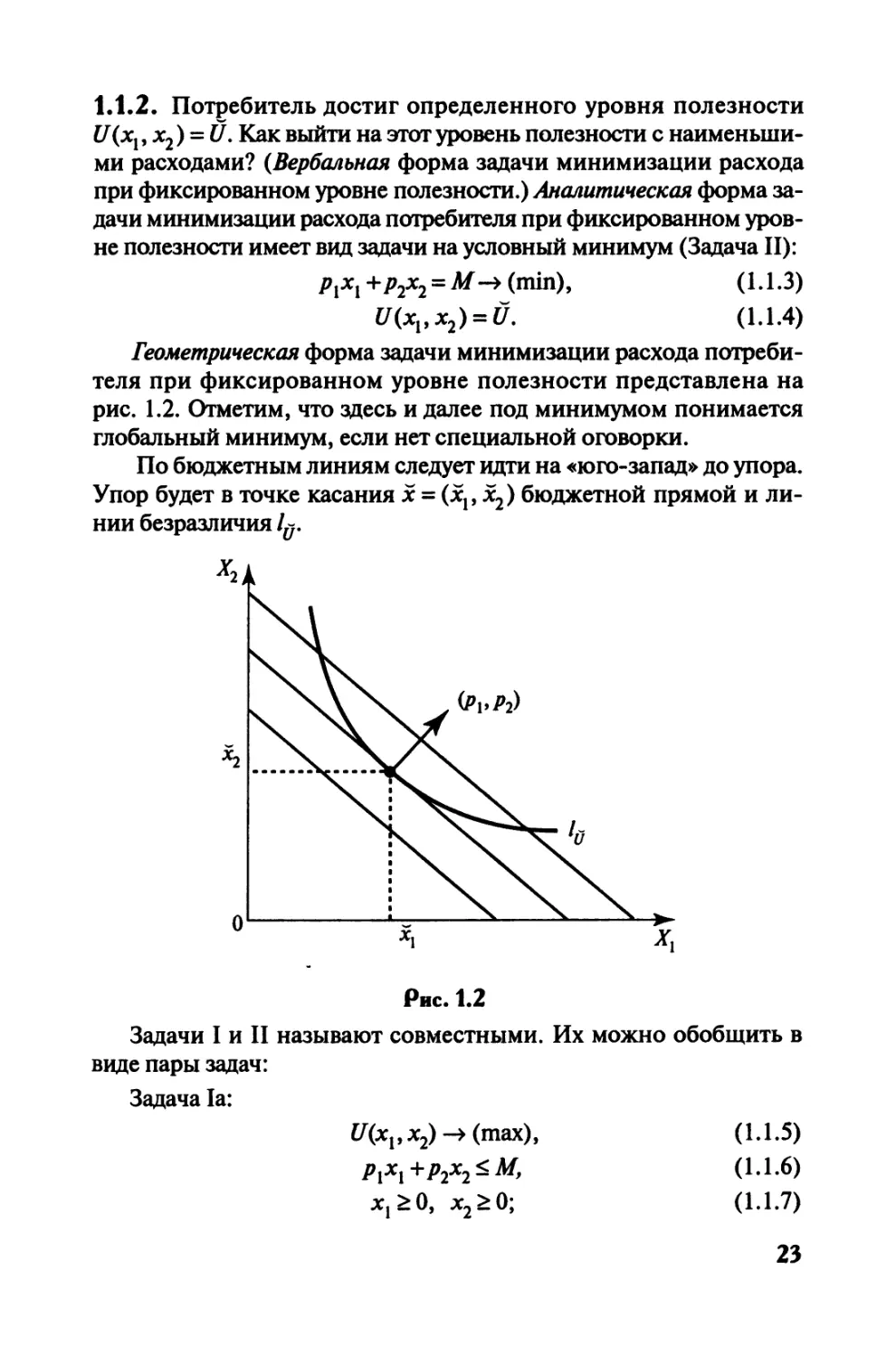
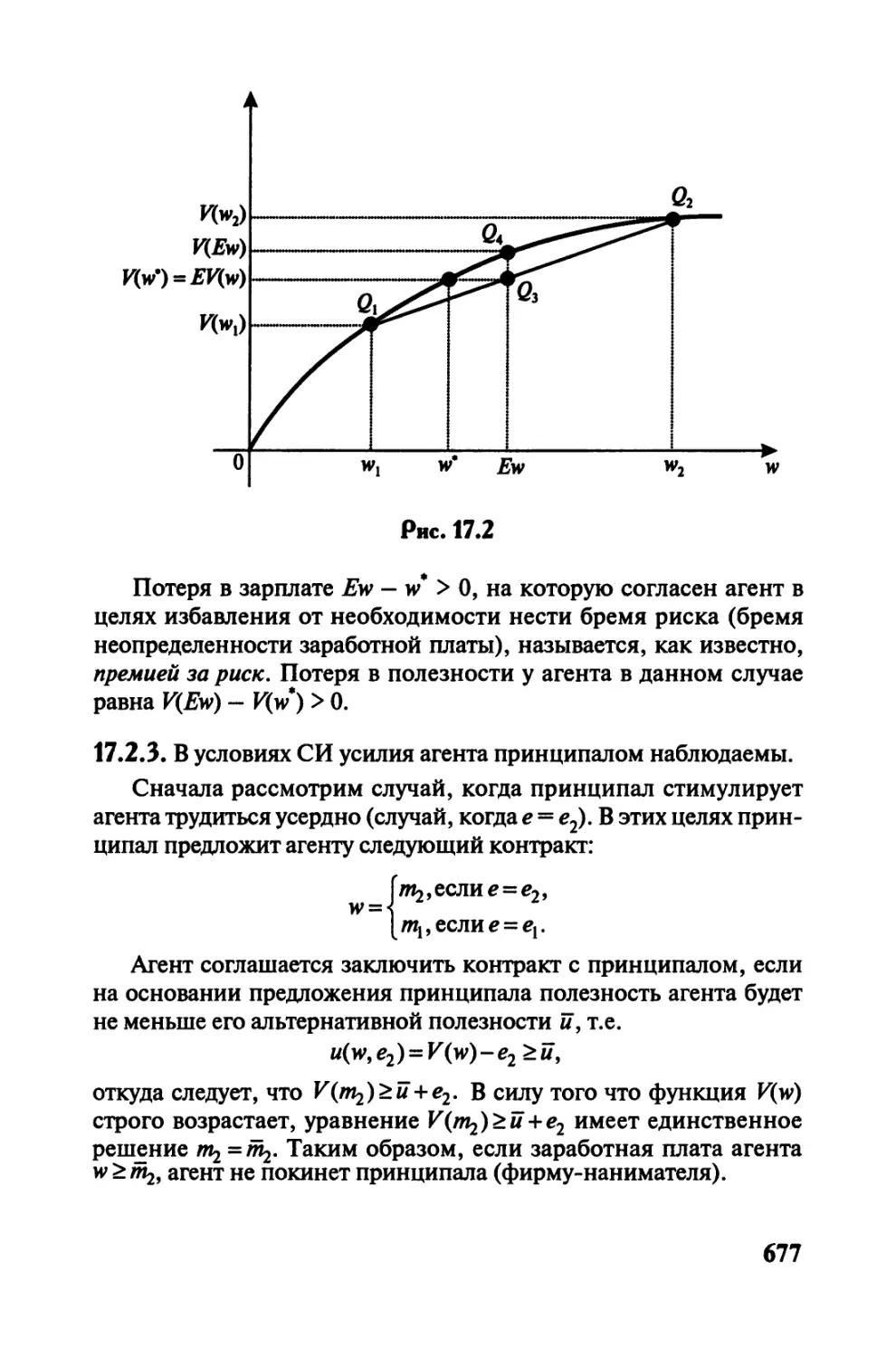
Геометрическая форма задачи минимизации расхода потреби-
теля при фиксированном уровне полезности представлена на
рис. 1.2. Отметим, что здесь и далее под минимумом понимается
глобальный минимум, если нет специальной оговорки.
По бюджетным линиям следует идти на «юго-запад» до упора.
Упор будет в точке касания х = (хр х2) бюджетной прямой и ли-
нии безразличия 1у.
Рис. 1.2
Задачи I и II называют совместными. Их можно обобщить в
виде пары задач:
Задача 1а:
£7(хрх2) —> (max), (1.1.5)
plXl+p2x2^M, (1.1.6)
х(>0, х2>0; (1.1.7)
23
Задача Па:
^ixi+ ?2Х2 = (min),
U(xx,x2) > U,
(1.1.8)
(1.1.9)
(1.1.10)
Формально Задачи 1а и Па — это задачи математического про-
граммирования. Задачи I и II, как уже отмечалось, — задачи на
условный экстремум.
Задачи I и la, II и Па разные, но ответы у них одинаковые (если
1.1.3. Для задачи (1.1.1), (1.1.2) на условный экстремум функция
Лагранжа имеет следующий вид:
£(хр х2, X) = U(xx,х2) +‘к(М-рххх -р2х2).
Выпишем условия первого порядка локального экстремума
функции (1.1.1) при наличии ограничения (1.1.2):
dL(x{, х2, X) _ Э£(Х], х2, X) Э£(х(, х2, X)
" ’ ~ ~ ’ ЭХ
= 0, т.е.
dxj
(1.1.11)
Эх2
dXj 1
дх2 1
М-р}х{ -p2x2 = Q.
Получили систему (1.1.11) из трех уравнений стремя неизвест-
ными х,,х2, X. Решение системы (1.1.11) называется критической
точкой функции Лагранжа
(хрх2, X)
Критическая точка (хрх2, X) называется длинной точкой.
Критическая точка без последней координаты X, т.е. (хр х2), на-
зывается короткой точкой. Точки локального условного экстре-
мума задачи (1.1.1), (1.1.2) следует искать только среди коротких
точек (Хр х2), в которых локальный условный экстремум может
быть, а может его и не быть. В связи с тем что функция полез-
(1.1.12)
24
ности — это функция, которая обладает рядом специальных
свойств:
Э£(хр^)>
< Ц ’ Эх2
;() ,0
Эх2 ’ Эх2
у системы (1.1.11) существует обязательно единственное решение
(Xj, х2, X), т.е. существует только одна критическая точка функции
Лагранжа, а следовательно, только одна короткая точка (хр х2),
и эта точка — не только точка локального, а также глобального
максимума функции (1.1.1) при наличии ограничения (1.1.2). Это
можно доказать с помощью условий второго порядка локального
экстремума функции (1.1.1) при наличии ограничения (1.1.2) и с
использованием условия строгой выпуклости вверх функции
(1.1.1).
Функции
* 1 = Ох{рх,р2, М) (1.1.13)
* 2 = D2<PvP-i> М) (1.1.14)
называются функциями спроса по Маршаллу {по Вальрасу) на пер-
вый и второй продукты со стороны потребителя. Очевидно, что
X=D3{px,p2,M).
Функция U{xx, х2)= U[Dx(pvp2, М), D2(px,p2, M)]=v(px,p2, М)
называется косвенной (неявной) функцией полезности параметров
р(, р2, М; выражение v(px, р2, М) есть максимум функции полез-
ности.
Функции спроса D.{px, р2, М), i = 1,2 однородны нулевой сте-
пени по всем переменным, т.е. для любого числа у > О
Di{pvp2, М) = D/y-Pp ур2, y-M)=xt, i= 1, 2.
Для доказательства перепишем задачу (1.1.1), (1.1.2) следующим
образом:
tZ(xpx2) —> (шах), (1.1.1)
У Р1хх,у р2х2 = у-М, (1.1.15)
0<уе £р
25
Задачи (1.1.1), (1.1.2) и (1.1.1), (1.1.15) одинаковы и имеют одно и то
жерешениеЦ, х2). Задача (1.1.1), (1.1.2) имеет ответ(1.1.13), (1.1.14),
а задача (1.1.1), (1.1.15) имеет ответ X] = Dx(y-px, у-р2, у-М),
x2 = D2(ypx,yp2,y-M)M.
Следовательно,
YP2’ У‘ Ю = №i> Pi' W, (1.1.16)
D2(y pv y p2, y-M) = D2(pvp2, At), (1.1.17)
т.е. функции спроса (xp x2) однородны нулевой степени по всем
переменным/>,, р2, М.
1.1.4. Свойства косвенной функции полезности v(ppp2, М)
1. Косвенная функция полезности v(px,p2, М) является одно-
родной функцией нулевой степени по всем переменнымрх,р2, М:
v(y-Px, 1Р2> У' Ю = U[Dx(y pv у р2, у-М), D2(y pv у р2, у-М)] =
= U[Dx(pvp2, М), D2(pvp2, M)] = v(px,p2, М).
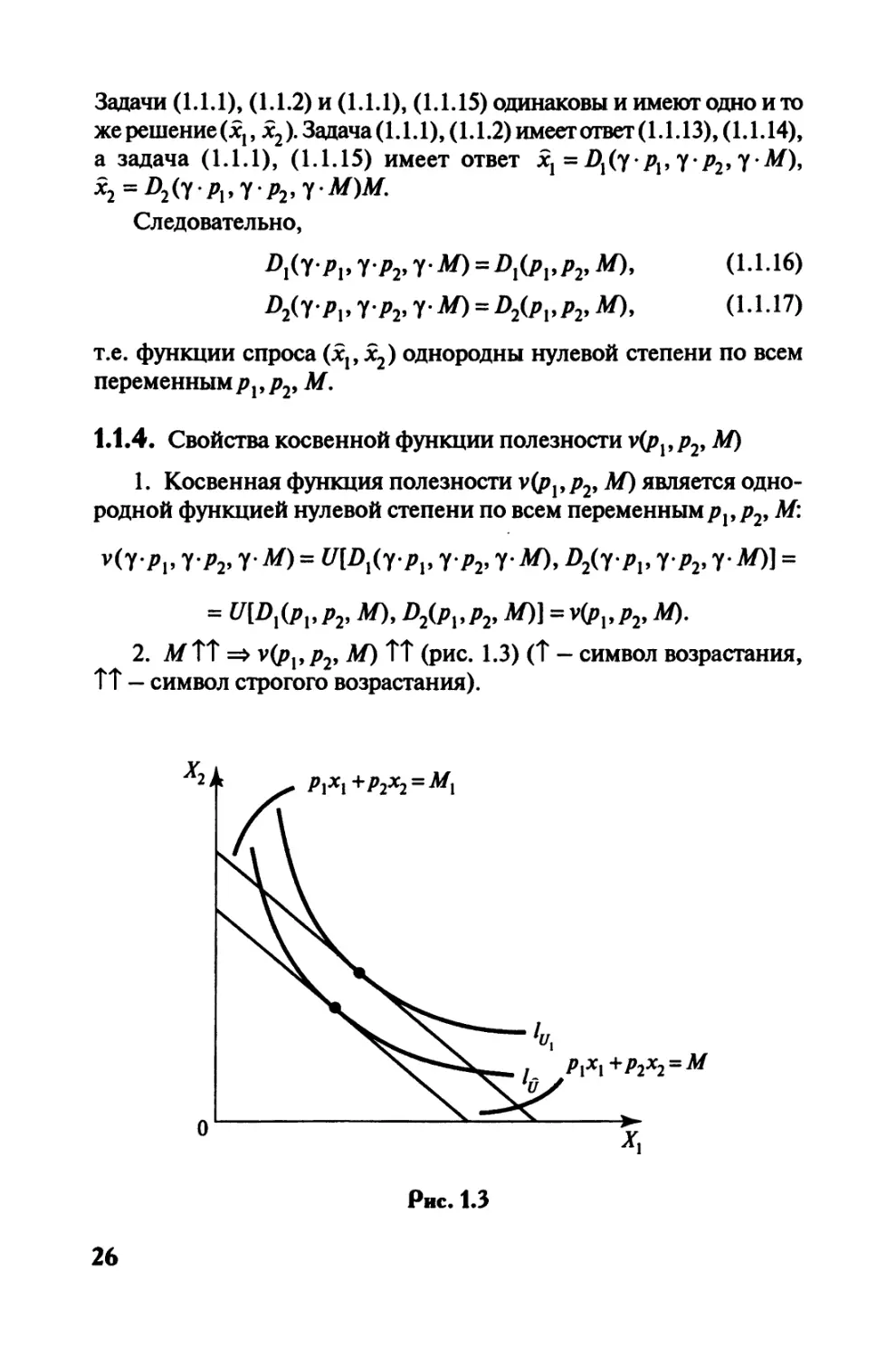
2. М ТТ => v(P\,P2, М) ТГ (рис. 1.3) (Т — символ возрастания,
П — символ строгого возрастания).
26
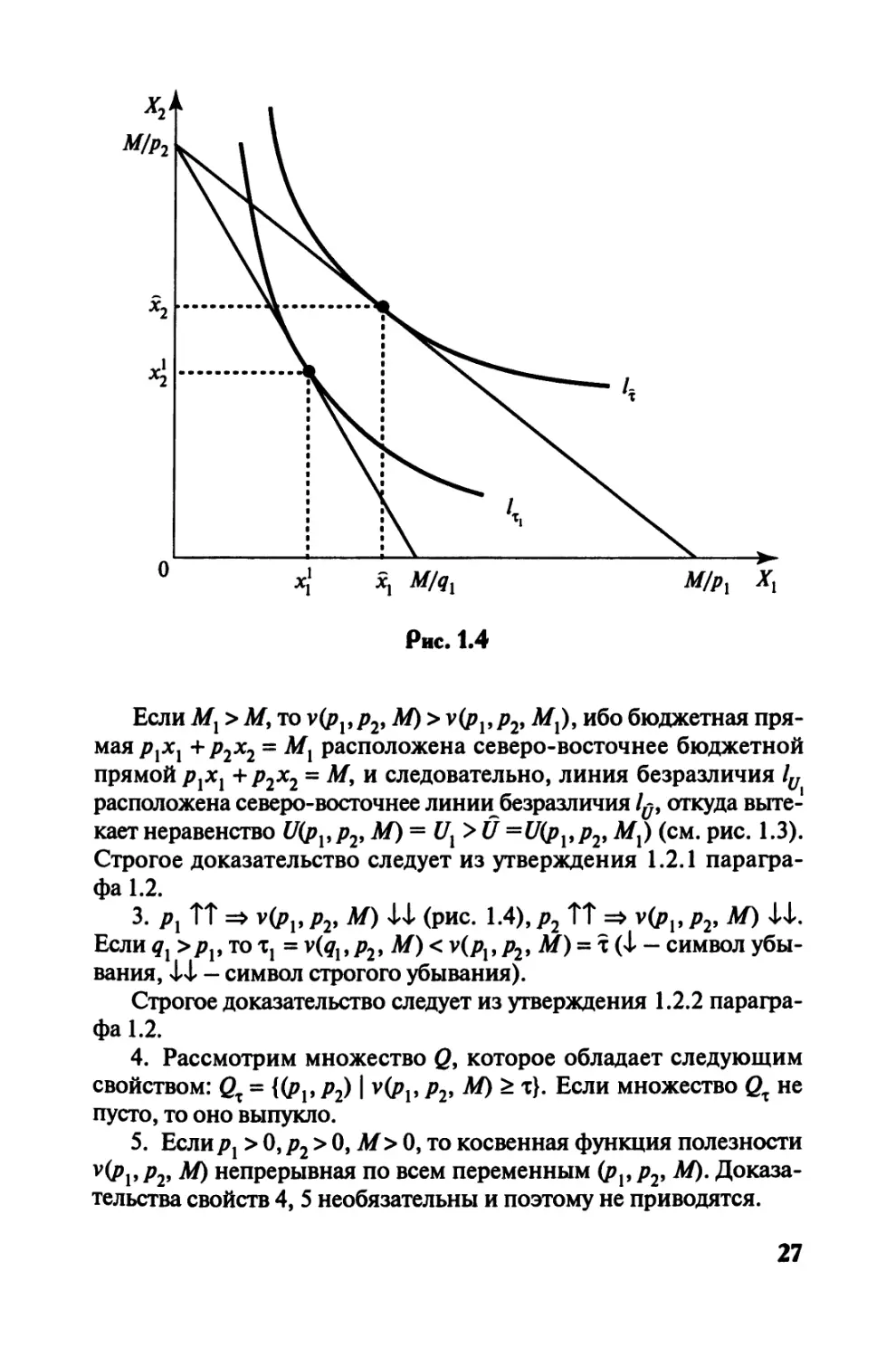
Рис. 1.4
Если Мх > М, то v(ppp2, М) > v(px,p2, Мх), ибо бюджетная пря-
мая рххх + р2х2 = Мх расположена северо-восточнее бюджетной
прямой рххх + р2х2 = М, и следовательно, линия безразличия 1и
расположена северо-восточнее линии безразличия Iq, откуда выте-
кает неравенство U(px,p2, M) = UX>U =U(px,p2, MJ (см. рис. 1.3).
Строгое доказательство следует из утверждения 1.2.1 парагра-
фа 1.2.
3. рх ТТ => v(px, р2, М) J-J- (рис. 1.4), р2 ТТ => у(рр р2, М) 4-i.
Если qx >рх, то Tj = v(qx, р2, М) < v(px,p2, М) = т (J- — символ убы-
вания, J-X — символ строгого убывания).
Строгое доказательство следует из утверждения 1.2.2 парагра-
фа 1.2.
4. Рассмотрим множество Q, которое обладает следующим
свойством: Qx = {(рр р2) | v(px, р2, М) > т}. Если множество Qx не
пусто, то оно выпукло.
5. Если рх > 0, р2 > О, М> 0, то косвенная функция полезности
v(₽p Р2, -^0 непрерывная по всем переменным (рх, р2, М). Доказа-
тельства свойств 4, 5 необязательны и поэтому не приводятся.
27
1.1.5. Все построение этого и остальных параграфов главы 1 ес-
тественным образом переносится на случай произвольного п > 2.
В частности, Задачи I' и 1Г имеют следующие формулировки:
Задача Г:
CZ(XpX2,.... хп) (max),
= М;
Задача II':
Р j +... +Рнхп = (min),
tf(xpx2, ...,х„) = т.
Функции спроса по Маршаллу (Вальрасу) имеют вид
Xj = Д(А, .М), ...,хп = Dn(Pl, ...,рп, М).
1.2. Предельная полезность по доходу
и предельная полезность по цене продукта
(тождество Роя). Значение этих выражений
для решения теоретических и прикладных задач
потребительского поведения на рынке
1.2.1. Утверждение 1.2.1 (о предельной полезности по доходу)
Предельная полезность по доходу равна множителю X Лаг-
ранжа:
Эу(РрР2,Я) - (1.2.1)
ЭМ
Доказательство утверждения 1.2.1
Пусть (xj, х2, X) — решение задачи Лагранжа, т.е.
(1.2.2)
dXj
Э(/(ХрХ2) -
---rz—- = Л-р2. (1.2.3)
dx2
Равенство
М=р} Dx(pvpv М) +р2 • D2(pvp2, М) (1.2.4)
является тождеством поpit р2, М, поэтому
,_dM _ Ы\(рх,р2, М) dD2(pvp2,M) (12 5)
дМ +Р2' дМ
28
Имеем
ду(рг,р2, М) dU[P[(pl,p2, М), Р2(рх,р2, М)}
ЭМ дМ
ЭЦ(Х},Х2) Щ(Р],р2,М) । ЭЩх,,Х2) дР2(р{,р2,М) (1,2,2),(1.2.3)
' ъм ах2 эм *
_£_ ЫЦрх,р2,М) - ЭД2(/>,,р2,М) _ (1,2,5) у ЭМ _ у
"Р| ай Р1 эм--------------------------------”
Утверждение 1.2.1 доказано.
Отметим, что v(pl,p2,M) = U(xl,x2) = тах£/(хр х2) при нали-
чии ограниченияр1х] + р2х2 = М, тогда на основании (1.2.1) имеем
Этах£/(хр х2) _ -
дМ ~ ’
т.е. производная глобального максимума функции полезности по
параметру М равна X.
Утверждение 1.2.1 позволяет оценить новый max t/(xpx2) функ-
ции полезности, который получается при относительно малом
AM изменении дохода (при этом новую задачу на условный мак-
симум
t/(X],X2)->max,
Р]Х( + Р2х2 = М+ДМ
решать не следует):
г dU(pvp2,M) v(pvp2,M + AM)-v{pvp2,M)
х=—hr—я—---------------------пт---------’ откУда
дМ AM
v(p{,Рг>М + ДМ) = v(px, р2, М) + X • ДМ, т.е.
max С/(х.,х2)= max Щх.,х2)+Х-ДМ,
р|лс1+р2х2=Л/+ДЛ/ pixi+p2x2=M
что важно с теоретической и практической точек зрения.
Если функция полезности Z7(xp х2) выпукла вверх, то множи-
тель Лагранжа X скорее мал (является «моськой»), чем велик
(т.е. не «слон»). В связи с этим последнее приближенное равен-
ство означает, что для заметного увеличения уровня полезности
следует значительно увеличить объем расхода потребителя.
29
Косвенная функция полезности v(px,р2, М) по определению есть
max U(xx при наличии ограничения/»^] +р2х2=М, т.е. косвенная
функция полезности — это функция параметров рх,р2, М Задачи I
на условный экстремум (см. в параграфе 1.1 Задачу (1.1.1) —
(1.1.2)). Утверждение 1.2.1 — это утверждение о том, что частная
производная условного максимума v(px, р2, М) целевой функции
С/(Х], х2) по параметру М равна X.
В приведенных ниже утверждениях 1.2.2 (утверждениях 1.4.1,
1.4.2) также фигурируют частные производные условного макси-
мума функции U(xx, х2) (условного минимума функции/>]Х] + р2х2)
по параметрам рх, р2, М (по параметрам рх, р2, U).
Теоремы о частных производных экстремальных значений
целевых функций различных экстремальных задач по параметрам
этих задач называются теоремами об огибающей. Приведенное
здесь утверждение 1.2.1 и приводимые далее утверждения 1.2.2,
1.4.1 и 1.4.2 представляют собой частные версии теорем об огиба-
ющей в случае, когда специальное ограничение или целевая функ-
ция являются линейными по переменным экстремальной задачи.
1.2.2. Утверждение 1.2.2 (тождество Роя)
(= (126)
Эр,
<Эу(/»1,/»2,М) = __ Эу(/>,,/>2, МЙ (1 2 7)
k Э/», ' дМ J
Мерой изменения значения косвенной функции полезности в
связи с изменением цены ^.является произведение (-х. • X), i = 1,2.
Доказательство утверждения 1.2.2
Пусть (X], х2, X) — решение задачи Лагранжа, т.е.
ЭС/(Х],х2) - Э<7(Х],х2) *
ЭХ] Эх2 -Х/’2-
Из тождества (1.2.4) следует, что
дрх дрх
аналогично
(,.2.9)
Эр2 Э/>2 Э/>2
30
Имеем
Эг(р,,р2,М) dU[Dx(Pl,p2, М), P2(Pl,р2,М)}
Ърх Ърх
_dU(xx,x2) ЭРх(рх,р2,М) [ ЭЩхрх2) ЭР2(рх,р2,М) _ (Ш)>(Ш)
3btj дрх дх2 дрх
дРх(рх,р2,М) дР2(рх,р2,М)
* Рг Sp,
Аналогично
=-!kD1(p1,p2,M)=-kxl.
=%• рх-
dv(px,p2,M) -
Эр2 ”
Отметим, чтоX = (см. (1-2.1)).
дм
Утверждение 1.2.2 доказано.
Поскольку v(px ,р2, М) = U(xx,x2)- max U (х, ,x2 )при наличии ог-
,, dmaxCA(x,,x,) - _
раниченияр.х. + р2х2 = М, постольку имеем-------—!—— = -X • хр
о/»!
т.е. производная глобального максимума функции полезности по
параметру рх равна -X • х,.
Утверждение 1.2.2 позволяет оценить новый max U[xx, х2)
функции полезности, который получается при относительно ма-
лом Др] изменении цены р( (при этом новую задачу на условный
максимум
(7(хр х2) -> max,
(р,+Др1)х1+р2х2 = Л/
решать не следует):
- ? Эу(РрР2,Л/) v(Pi + Аррр2, Л/)-v(p,,р2,М)
’ ЭА “ Др,
откуда
v(p, + ДРр р2, М) « v(pp р2, М) - X, • X • ДРр т.е.
max Щх.,х,)« max t/(x., х,)-х.Х-Др.,
(Pl+APjJXj+PjJCjsM ^JC]+ftX2=M
что важно с теоретической и практической точек зрения.
31
1.2.3. Утверждения 1.2.1 и 1.2.2 при п > 2 имеют вид
dv(/>P -,Р„,М)
дМ
= Х,
dv(Pl, -;Рп,М)
dpi
= -X] X,
Эу(Р}, ...,рп,М)
п
1.3. Решение задачи минимизации расхода
потребителя при фиксированном уровне полезности
методом Лагранжа. Функции спроса по Хиксу
(функции компенсированного спроса),
функция расходов и их свойства
1.3.1. Решим задачу (1.1.3), (1.1.4) (см. параграф 1.1) методом
Лагранжа:
Функция Лагранжа задачи (1.1.3), (1.1.4) имеет вид
£(х,, х2, X) = + р2х2 + k(U -U(xi,x2)). (1.3.1)
Выписываем условия первого порядка для функции Лагранжа
Z>(X], х2, X).
,,-Х^^О, (1.3.2)
1 (Ц
—— = 0, (1.3.3)
йх2
U-U(xi,x2) = 0. (1.3.4)
Получим систему трех уравнений (1.3.2), (1.3.3), (1.3.4) стремя
неизвестными х2, X. Решение системы (1.3.2), (1.3.3), (1.3.4)
(ХрХ2,Х) называется критической точкой функции Лагранжа
(1.3.1). Критическая точка (хр х2, X) называется длинной точкой.
Критическая точка без последней координаты X, т.е. х = (хр х2),
называется короткой точкой.
32
Если U = U(xx, х2) — функция полезности, то система (1.3.2),
(1.3.3), (1.3.4) имеет единственное решение (ХрХ^Х) и точка
(Хр х2) есть точка глобального минимума задачи (1.1.3), (1.1.4)
(см. параграф 1.1). Имеем ситуацию, аналогичную задаче (1.1.1),
(1.1.2) (см. параграф 1.1).
Функции
xx=Hx(px,p2tU)t (1.3.5)
^=Я2(РрР2,Щ (1-3.6)
называются функциями спроса по Хиксу (функциями компенсирован-
ного спроса) на первый и второй продукты со стороны потребите-
ля. Очевидно, А. = Я3(рр р2, U).
Функции спроса = Нх(рх,р2, U), х2 = Н2(рх, р2, U) по Хиксу
подставляем в целевую функцию М = т(рх, р2, U) = рххх + р2х2 =
= рхНх(рх,р2, U)+р2Н2(рх,р2, U)и получим функцию т(рх,р2, U),
которая называется функцией расходов. Она зависит от P\>P2,U и
явно не зависит от потребительского набора.
Функция спроса Hf(px, р2, U), i = 1, 2 однородна нулевой сте-
пени по переменным рх и р2, т.е. для любого числа у > О
ЗД а» у р2, U) = H.(px,p2, U), i = 1, 2.
Для доказательства перепишем задачу (1.1.3), (1.1.4) (см. па-
раграф 1.1) следующим образом (число у> 0):
y-pxxx + y-p2x2 = y-M-*min, (1.3.7)
U(xx,x2) = U. (1.3.8)
Задачи (1.3.7), (1.3.8) и (1.1.3), (1.1.4) (см. параграф 1.1) одина-
ковые и имеют одно и то же решение (х(, х2). Задача (1.1.3), (1.1.4)
(см параграф 1.1) имеет ответ (L3.5), (1.3.6). Задача (1.3.7), (1.3.8)
имеет ответ Xj = Нх(урх, ур2, U),x2 = Н2(урх, ур2, U).
Следовательно,
Нх(урх,ур2,й) = Нх(рх,р2,й), (1.3.9)
н2(урх,ур2,й)=н2(рх,р2,й). (1.3.Ю)
т.е. функции спроса (хр х2) однородны нулевой степени по пере-
меннымр|Ир2. '
3 - 7620
33
1.3.2. Свойства функции расходов
1. Функция расходов т(рх, р2, U) однородна первой степени
по переменным рх и р2.
Имеем
HY A’ Y /’i’ и> = VPrHx(ypx, ТР2’ U)+y p2 H2(y px, у р2, U) =
= У-[РгНх(рх,р2, U) + p2 H2(px,p2, U)] = y m(px,p2, U).
2. Если U ??=> т(рх, р2, U) ТТ,
рх
р2 ??=>m(Pi,p2, tZ)?t.
Доказательства следуют из утверждений 1.4.1 и 1.4.2 парагра-
фа 1.4.
3. Функция расходов выпуклая вверх по переменным рх и р2
(рис. 1.5):
т [(1 - X) р° + X • р1)] £ (1 - Х)/и(р°) + X • т(р1) для любого числа
О < X £ 1 и любых векторовр° £ О,/»1 £ б.
34
4. рх > 0, р2 > О, U > О — функция спроса по Хиксу и функция
расходов непрерывны.
Доказательство свойства 4 является необязательным и поэто-
му не приводится.
Докажем свойство 3.
Число X удовлетворяет неравенствам 0 < X < 1, векторы р° > О,
рх > 0. Имеем р2, U) = pfxx + р2х2 = min(p°x, + р2х2) при ус-
ловии, чтоб/ (хр х2, U) - U.Аналогично «(р*, р\, U) = pjx{ + р2х2 =
= min(p1'x1 +р\х2) при условии, что U(xx,x2, U) = U. Положим
р=(1-А,)-р°+Х-р,^р1 +К-р},р2 =(1-к)-р2 +Х-р2]. Имеем
М(рх,р2, U) = + р2х2 = minCpjXj + р2х2) при условии, что
U(xx,x2, U) = U.
Имеем следующую цепочку равенств и неравенств:
т(рх,р2, й)-р х = рххх + р2х2 = ((1-Х)-р1° + Х-р11)х1 +
+(1 - X) • р2 + X • р2 )х2 = (1 - А-ХаЧ + P°x2)+к(р}хх + рх2х2) =
= (1 - Х)р°х + X • рхх (1 - Х)р°х° + X • рххх =
= (1-Х)т(р°,р°, ^)+X m(p11,p*, U),
откуда следует, что функция расходов т(р[,р2, U) выпукла вверх
по переменным р{ и р2.
Свойство 3 доказано.
При л > 2 функции спроса по Хиксу имеют вид
х, =Я,(р, U), ...,х„ = Н„(Р, ...,Р„, U).
1.4. Предельный расход по полезности
и предельный расход по цене продукта
(лемма Шепарда). Значение этих выражений
для решения теоретических и прикладных задач
потребительского выбора
1.4.1. Утверждение 1.4.1 (о предельном расходе по полезности)
Предельный расход по полезности равен множителю Лагранжа:
дт(рх,р2,(1.4Л)
дй
3.
35
Доказательство утверждения 1.4.1
Пусть (Хр х2, X) — решение задачи (1.1.3), (1.1.4) на условный
экстремум, тогда имеем тождества по хр х2, X:
а=ХЭЩ5|,^), (1.4.2)
dXj
= (1.4.3)
Равенство 2
17 = а[Я1(А,р2, й),Н2(рх,р2, й)] (1.4.4)
является тождеством по рх, р2, U, поэтому
1 = ^ЭЩхрЗ^) дНх t ЭСА^р^) ЭЯ2 (1 4 5)
дй ах, ’ дй дх2 ' дй’
Имеем
dm{p^p2,U) = Л(^ Ц, р2 гй) + р2Н2(рх, р2 ,U)) =
_ p2,U) dH2(pv р2,й) _ (1,4,2), (1,4,3)
Л ’ ди Р1' дй
- рЩхрх2) дНх(рх,р2,й) t ЭЩхрХ2) ЭЯ2(А>р2>У)\
\ ах, ' дй дх2 ' дй }
=-^цх.
Утверждение 1.4.1 доказано.
Отметим, что т(рх,р2, й) = рххх + р2х2 = min _(дх, + р2х2),
UlXj.^U
dmin(ax. +р,х,) -
тогда на основании (1.4.1) имеем---—i-i- = Л, т.е. произ-
водная глобального минимального расхода по полезности й равна
множителю Лагранжа X.
Утверждение 1.4.1 позволяет оценить новый min^^j + р2х2)
расхода, который получается при относительно малом лй изме-
нении уровня полезности (при этом новую задачу на условный
минимум
PjXj +р2х2 -»(min),
и(*х,х2)=й
решать не следует):
36
- Э/и(р1,р2, U) т(рх,р2, U + &U)-m(px,p2, U)
К = ' ,
ъи ди
откуда вытекает, что
m(ppp2, U + Дй)~ т(рх,р2, U) + X• Д(7, т.е.
"Йил,/**» + ^2*2)s т mi" ,7<A*i + Pixi)+* * A&>
U(xA t х2)=(/-^ЛС/ и(х^,Х2)=и
что важно с теоретической и прикладной точек зрения.
Если функция полезности U(xx, х2) выпукла вверх, то множи-
тель Лагранжа X скорее велик (является «слоном») чем мал (т.е. не
«моська»). В связи с этим последнее приближенное равенство со-
держательно означает, что при увеличении уровня полезности,
скажем, на одну единицу, потребителю требуется значительно
увеличить расход.
(1.4.6)
(1.4.7)
1.4.2. Утверждение 1.4.2 (лемма Шепарда)
Э/и(РрР2, U) _
За Хр
Э/й(ррр2, й) _
Зр2 Хг
Доказательство утверждения 1.4.2
Из (1.4.4) следует, что
q _ 3^ _ 3(7(5^, х2) ЪНХ + Э€А(х|, х2) ЪН2 (14 8)
Эр, Эх. Эр, Эх, Эр,
Имеем
3z»(PpP2, й)+р2-н2(рх,р2, й)]=
ЬНх(рх,р2,й) t дН2(рх, р2, й) _ (1.4.2),(1.4.3) ч
+Р1 •
=я<» » ЭЯ, эа(х„х;) анЛ
1 ’’ 3’ Эх, Эр, ЭХ} Эр2 J
Равенство (1.4.7) получается аналогично.
Утверждение 1.4.2 доказано.
Э/>]
= Я1(Рр/’2> ^)+А
37
Утверждение 1.4.2 позволяет оценить новый min^jX] + р2х2)
расхода, который при относительно малом Др( изменении ценыр,
(при этом новую задачу на условный минимум
(р, + Apj)*! +р2х2 -> (min),
U(xvx^ = U
решать не следует) имеет вид
- ... Э/и(р,,р2, U) т(рх +Лрх,р2, U)-m(pvp2, U)
*' 3pj Apj
откуда следует, что
м(РЬ+Дд,р2, U)~m(pvp2, й)+хх^рх, т.е.
min _[(pI+Ap1)x.+p2x2]® min Др.х. +р2х2]+х.Лр.,
U(xt,x2)=U ,
что важно с теоретической и практической точек зрения.
Утверждения 1.4.1 и 1.4.2. при п > 2 имеют вид
Эот(рр ...,р„, к
дй
дт(рх, ...,рп, U)_ _ Эт(рр ...,ри, U)_ _
ЭА =Х1’"’ Эрл
1.5. Взаимосвязь между решением задач
максимизации функции полезности и минимизации
расходов. Вывод уравнений Слуцкого.
Уравнения Слуцкого в эластичностях
1.5.1
Задача максимизации функции полезности имеет вид: Задача минимизации расходов:
U(xv х2) -» (шах), (1.5.1) Pi*! +р2х2 = М—> (min), (1.5.3)
р1х1+р2х2 = Л/. (1.5.2) Вектор (Хр х2) — ее максимальное решение, Х!=Д(ррР2,Л/), х2 = Р2(ррР2,Л/), U = I/(XpX2) = v(ppP2, М). (рис. 1.6) 17=1/(ХрХ2). (1.5.4) Вектор (X], х2) — ее минимальное решение, х1 = Я1(ррр2, 17), Х2 = Я2(РрР2, Я), m(pt,p2, С/) = р1х1 + р2х2.
38
Положим в (1.5.2) М = л|(рр р2, U), тогда, очевидно,
Р,(Рр?2, «О’р/’р U)) = Я,(ррР2, U), (1.5.5)
ЯгО’р/Ъ’ т<РуР2> = Н2<Р\’Р2’ &>> О-5-6)
и=й.
Использовав теорему о частных производных сложной функ-
ции, получим
ЭЯ,(ррр2, Я) _ ЭРДррР2, /и(ррр2, Я)) ।
*> . (1.5.7)
dPt(pvp2,m(px,p2, U)) дт(рх,р2, U)
дМ dpj
Подставив в (1.5.7) *Р1’ = Н (р р., U) (лемма Ше-
. dPj J
парда — см. параграф 1.4), получим уравнение (точнее, первую
версию уравнений) Слуцкого:
^L=^.+ n
dPj dPj j ЪМ'
(в общем случае i,J=1,..., л).
(1.5.8)
39
В уравнении (1.5.8) вместо Н. фигурирует D., ибо они равны
(см. (1.5.5), (1.5.6)).
По лемме Шепарда (см. параграф 1.4)
Э/»(/>|, Р2, U) _ fj (р , р > jjY i,j = \, 2 (в общем случае/, j = 1, ..., л),
Эр,.
откуда следует, что
d2m(pi,p2,U) dHj(tpi,p2,U)
dpjdpi dpj
В связи с тем, что
Э2от(р, ,p2,U) д2т(р1 ,p2,U)
др^ dp^pj
имеем
^i_+D _ dHi _ &т(р\, P2’ d2/n(p!,p2,U) =
dpj J dM др}. dpjdp. dp^
dH, dD. dD,
= —J- =—-+D.—J-, т.е.
Эр; dp. ' dM
dD, n dD. dD. dD,
dpj J dM dp/ ' dM’ (1-5.9)
/,./ = 1,2 (в общем случае/, J=1, ...,л).
Выражение (1.5.9) — это вторая версия уравнений Слуцкого.
с , », д2т(р.,р2, U)
1.5.2. Матрица из вторых частных производных-------- 12-----
называется матрицей Слуцкого. °PjoPi
Из математического анализа известно, что для выпуклости
(вверх) функции m(pitp2, U) расходов необходимо и достаточно,
чтобы матрица Слуцкого была неположительно определенной.
Это эквивалентно тому, что квадратичная форма, соответствую-
щая матрице Слуцкого, была неположительно определенной. Пос-
кольку функция m(pt,p2,U) расходов выпукла вверх по перемен-
ным рх и р2 (см. параграф 1.3), постольку матрица Слуцкого непо-
40
ложительно определена, откуда следует, что все элементы ее
главной диагонали неположительны:
^U.P2.g>s0(<0)| , = 1>2>
Эр;
или
ЭЯ.
—— < 0 (<0), i = 1, 2 (в общем случае i = 1, ..., л),
Эр.
т.е. с точки зрения функций спроса по Хиксу все продукты обык-
новенные и продуктов Гиффена у этих функций не бывает.
1.5.3. Уравнение Слуцкого
др. dpj дМ
после деления на умножения на р. перепишется так:
Pj_ <Щ = Ъ_ D щ
Di dpj Н( дрj Di J дМ'
Преобразовав последнее слагаемое
dDi = M dD, PjDj
DiJ'dM~Di'dM‘ M ’
получим следующее уравнение:
pj = ЭЦ PjDj (1.5.10)
Di dp. Hi dp. Di дМ M ’
где — перекрестная эластичность Ej{D^ спроса (по Мар-
Dt °Pj шаллу) на f-й продукт по цене р^. у-го продукта (если
i = j, получаем обычную эластичность спроса (по
Маршаллу) на /-Й продукт по цене р(.);
—Ё • —- — перекрестная эластичность Ej (Н) спроса (по Хиксу)
°pj на /-Й продукт по цене Pj у-го продукта (если i =j,
получаем обычную эластичность спроса (по Хиксу)
на z'-й продукт по ценер);
М 3D,
^ "дМ ~ эластичность спроса по доходу;
PiDi
— доля р, дохода A/потребителя, который он тратит на
приобретение у-го продукта.
41
Таким образом, получено уравнение (точнее уравнения)
Слуцкого в эластичностях:
£//),) = £/^)-£Л/(Р,) р/, /,/-1,2 (1.5.11)
(в общем случае i, J = 1,..., л)
1.6. Оценка изменения благосостояния
потребителя. Эквивалентная и компенсирующая
вариации дохода
1.6.1. Уравнение бюджетной плоскости + р2х2 +... + рпхп=Мх
можно переписать так: р{хх + у = Мх, где у=р2х2 +... + pjcn — коли-
чество композитного продукта (товара). Первый продукт приоб-
ретается в количестве х1 по цене р,.
При цене р1 на первый продукт потребитель выбирает набор
х(|) = (х^, у(|)), т.е. потребитель тратит на приобретение первого
продуктар,х^ руб. иу(1) руб. на приобретение остальных продук-
тов. х(1) — точка касания линии безразличия и бюджетной
прямой I (р,х( +y = Afj) (рис. 1.7).
42
Если цена р} на первый продукт выросла и стала равной
(?1 > Р])> бюджетная прямая I перейдет в бюджетную прямую II.
В этом случае потребитель выберет набор х<2) = (х*2), у(2)), который
изображается точкой касания х<2) линии безразличия и бюд-
жетной прямой II (qlx} +у=М[). Очевидно, < Uw, т.е. уровень
полезности потребителя (удовлетворение потребительских
амбиций) снизится до уровня (А2).
Определим величину АМр на которую следует увеличить но-
минальный доход Мх потребителя, чтобы потребитель вернулся
на прежний уровень U^, т.е. прежний реальный доход по Хиксу.
Для этого следует переместить бюджетную прямую II парал-
лельно самой себе на «северо-восток» так, чтобы она перешла в
положение III. Бюджетная прямая III (д1х1 +у=Мх+ДМ\, ДМ, > О,
если цена р, растет) касается линии безразличия в точке х(3) =
= (*j3\ У2)) и параллельна бюджетной прямой II.
Величина ДА/, и есть компенсирующая вариация дохода (СИ),
ибо она показывает, на какую величину следует изменить (увели-
чить) номинальный доход Mv чтобы компенсировать потерю ре-
ального дохода потребителя в связи с повышением цены р{ на
первый продукт.
Критерием того, что потребителю вернули его реальный доход,
является то, что потребитель вернулся на прежний уровень С(1)
полезности (уровень удовлетворения потребительских амбиций).
В связи с повышением цены р, на первый продукт переход из
точки х(1) ввточку х<3) отражает простой эффект (эффект замены —
ЭЗ), вызванный изменением только одного параметра (ценыр,) и
сохранением неизменным другого параметра (реального дохода
потребителя). Переход из точки х(3) в точку х(2) отражает простой
эффект (эффект дохода — ЭД), вызванный изменением только од-
ного параметра (дохода, который изменяется с величины Мх + ДМ,
до величины Л/,) и сохранением неизменным другого параметра
(цены р,). Переход из точки х(1) в точку х(2) отражает сложный
(составной) эффект (общий эффект — ОЭ), вызванный измене-
нием двух параметров (цены р, и реального дохода потребителя),
т.е. имеем для первого продукта (прямые) эффекты — общий (ОЭ),
замены (ЭЗ) и дохода (ЭД):
ОЭ = ЭЗ + ЭД,
где ОЭ =х® -х^; ЭЗ =х*3)-х^; ЭД -х® -х^3) (см. рис. 1.7).
43
Для другого продукта (в данном случае композитного) имеем
(перекрестные) эффекты - общий (ОЭ'), замены (ЭЗ') и дохода
(ЭД'):
ОЭ' = ЭЗ' + ЭД',
где ОЭ'=у(2)-у(1); ЭЗ'=У3)-/,); ЭД'=/2)-у(3) (см. рис. 1.7).
Формула ОЭ = ЭЗ + ЭД наглядно интерпретирует уравнение
Слуцкого
ЭД ЭЯ! D дРх
Эр, Эр, 1дМ'
(ОЭ) (ЭЗ) (ЭД)
Формула ОЭ' = ЭЗ' + ЭД' наглядно интерпретирует уравнение
Слуцкого
ЭЯ ЭЯ, Л ЭЯ
дрх Эр, ЪМ
(Q&) (ЭЗ') (ЭД')
Напомним (см. рис. 1.7), что еслих{2) <х^3), то первый продукт
является нормальным; если xj2) > х*3), то первый продукт — про-
дукт низкого качества; если xj2) < х^\ то первый продукт обыкно-
венный; еслих® >х{*\ то первый продукт — продукт Гиффена.
1.6.2. При повышении ценыр( снижается реальный доход потре-
бителя. Определим величину ДА/р на которую снизится номи-
нальный доход потребителя так, чтобы при неизменной цене р,
потребитель остался на новом уровне С/(2) полезности (t/<2) < t/(1)).
Для этого следует переместить бюджетную прямую I на «юго-
запад» так, чтобы она перешла в положение IV. Бюджетная пря-
мая IV (PjX, + у = Мх + ДА/р ДА/[ < 0, если цена рх растет) касается
линии безразличия в точке х(4) = (х*4), у(4)) и параллельна бюд-
жетной прямой I.
Величина — эквивалентная вариация дохода (EV), ибо она
показывает, на какую величину следует изменить (уменьшить)
номинальный доход Мх, чтобы потребитель остался на новом
уровне С/(2) полезности без повышения ценыр,.
44
1.7. Об использовании результатов
социологических обследований
для оценки параметров функций полезности
социальных групп
В теории потребления один потребитель взаимодействует с
рынком потребительских товаров. Потребитель оставляет на
рынке свой доход в обмен на потребительский набор, который
он выбирает. Выбираемый потребительский набор максимизи-
рует функцию полезности. Если она есть, то задача выбора пред-
ставляет собой достаточно простую задачу на условный макси-
мум с линейным ограничением в вйде равенства. Оценивать
параметры полезности реального индивидуума практически не-
возможно.
Однако под потребителем не обязательно следует понимать
конкретного индивидуума. Под потребителем можно понимать
домашнее хозяйство и даже отдельную социальную группу (на-
пример, молодежь региона, пенсионеры региона, жители городов
и поселков региона, сельские жители региона и т.п. В роли регио-
на может выступать целая страна). Оценка параметров функций
полезности отдельных социальных групп позволяет использовать
эти функции в конкретных расчетах по оценке потребительского
поведения этих групп.
Для оценки параметров функций полезности социальных
групп можно использовать оценки сдвигов предпочтений этих
групп. Для оценки сдвигов предпочтений можно использовать
результаты социологических обследований представителей соци-
альных групп на основании специально подготовленных анкет.
После обработки на ПЭВМ результатов социологических обсле-
дований появляются данные о сдвигах групповых предпочтений.
Оценки сдвигов групповых предпочтений позволяют провести
операцию интегрирования этих сдвигов и получить явное выра-
жение функции полезности социальной группы.
Таким образом, обработанные данные результатов социологи-
ческих обследований могут быть использованы при формирова-
нии модельной информации. Следовательно, экономические за-
дачи можно решать с использованием не только математических
методов, но и методов прикладной социологии.
45
Вопросы для самоконтроля к главе 1
1. Как формулируется задача максимизации функции полезности по-
требителя при бюджетном ограничении (приведите три постановки)
и ее обобщение в форме задачи математического программирования?
2. Как формулируется задача минимизации расхода потребителя при
фиксированном уровне полезности (приведите три постановки) и ее
обобщение в форме задачи математического программирования?
3. Что представляют собой метод Лагранжа решения задачи максими-
зации функции полезности потребителя при бюджетном ограниче-
нии, локальное рыночное равновесие потребителя (ЛРРП) и его
геометрическая характеристика?
4. Что такое функция спроса по Маршаллу на продукт со стороны по-
требителя и косвенная функция полезности? Сформулируйте свой-
ства этих функций.
5. Чему равна предельная полезность по доходу?
6. Чему равна предельная полезность по цене продукта (тождество
Роя)?
7. Что представляет собой метод Лагранжа решения задачи минимиза-
ции расхода потребителя при фиксированном уровне полезности?
Что такое геометрическая интерпретация этого решения?
8. Что такое функция спроса по Хиксу на продукт со стороны потреби-
теля и его функция расходов? Сформулируйте свойства этих функ-
ций.
9. Чему равен предельный расход по полезности?
10. Чему равен предельный расход по цене продукта (лемма Шепарда)?
11. Как выглядит первая версия уравнений Слуцкого? Приведите вывод
первой версии уравнений Слуцкого.
12. Что представляет собой наглядная геометрическая интерпретация
первой версии уравнений Слуцкого?
13. Что такое матрица Слуцкого и вторая версия уравнений Слуцкого?
14. Как выписываются уравнения Слуцкого в эластичностях?
15. Что такое эквивалентная вариация дохода и ее геометрическая ин-
терпретация?
16. Что такое компенсирующая вариация дохода и ее геометрическая
интерпретация?
Задачи и упражнения для самоконтроля к главе 1
1. Функция полезности потребителя имеет вид U(xy, х2) = х}/4 • х2/4. Це-
ны продуктов соответственно равны рх = 8, р2 = 2, доход потребителя
Л/=64:
а) найдите методом Лагранжа локальное рыночное равновесие по-
требителя (ЛРРП): (Xj, х2) и множитель Лагранжа X;
46
б) постройте точку (хр х2) на плоскости Ох}х2;
в) напишите уравнение и постройте (используя не менее трех то-
чек) линию безразличия, содержащую точку (Xj, х2);
г) напишите уравнение и постройте данную бюджетную прямую;
д) найдите и постройте grad U (Xj, х2), выходящий из точки (х,, х2);
е) постройте вектор цен (ррр2), выходящий из точки (хрх2);
ж) дайте геометрическую интерпретацию множителю Лагранжа 1.
2. Функция полезности потребителя имеет вид U(xx, х2) = х^2 • х^2. Це-
ны продуктов соответственно равны рх = 4, р2 = 1. Уровень полезнос-
ти U = 8:
а) найдите методом Лагранжа потребительский набор (х,, х2), кото-
рый минимизирует функцию расходов потребителя, а также
множитель Лагранжа 1;
б) постройте на плоскости OxjX2 точку (Xj, х2);
в) напишите уравнение и постройте, использовав не менее трех то-
чек, линию безразличия потребителя, содержащую точку (хр х2);
г) напишите уравнение и постройте линию минимального расхода;
д) найдите и постройте grad U (х}, х2), выходящий из точки (Xj, х2);
е) постройте вектор цен (рх, р2), выходящий из точки (Xj, х2);
ж) дайте геометрическую интерпретацию множителю Лагранжа X.
3. Функция полезности потребителя имеет вид U(xx, х2) = х[/3 • х2/4. Най-
дите эластичность по рх максимума функции полезности U при за-
данном бюджетном ограниченииPjXj + р2х2 = М.
4. Функция полезности потребителя имеет вид U(xp х2) = х2/3 • х2/4. Це-
ны на продукты соответственно равны рх и р2, доход потребителя ра-
вен М:
а) найдите функции спроса (по Маршаллу) на первый и второй
продукты;
б) выпишите косвенную функцию полезности.
5. Функция полезности потребителя имеет вид U(xp х2) = xj/4 • х^/3. Це-
ны на продукты соответственно равны рх и р2, уровень полезности
потребителя равен U:
а) найдите функции спроса (по Хиксу) на первый и второй про-
дукты.
б) выпишите функцию расходов.
6. Косвенная функция полезности v(pp р2, М) имеет вид v(pp р2, М) =
Л/,3/15
= —1/5—2/з. Выпишите функцию x{D2(pvp2. М) спроса на второй
A Pi
продукт.
47
7. Функция полезности потребителя имеет вид U(xv х2) = Xj • х2. Цены
на единицы первого и второго продукта соответственно равны рх = 2,
р2 = 4, доход равен М = 24. Цена на первый продукт повысилась и
стала равной qx = 8. Найдите эквивалентную вариацию дохода.
8.
dm(pt,p2,M)
bPi
— предельный расход по ценер. /-го продукта (/ = 1,2):
а) равен множителю Лагранжа задачи минимизации расхода при
фиксированном уровне U полезности;
б) пропорционален предельному расходу по полезности;
в) равен предельному расходу по полезности;
г) равен величине х. = х^рх,p2,U) спроса по Хиксу на /-й продукт;
д) ответы а)—г) не верны.
9. Функция расходов т(рр р2, U) как функция цен рх ир2 на продукты и
фиксированного уровня U полезности:
а) однородна нулевой степени относительно вектора цен р = (рх, р2);
б) однородна первой степени относительно вектора цен р = (рх, р2);
в) однородна нулевой степени относительно всех переменных
г) не имеет однозначной характеристики относительно вектора цен
p=(pvp2>-
10.
Эу(Р|,р2>1И)
Эр,
- предельная полезность по цене р. /-го продукта
(/=1,2):
а) равна значению х. функции спроса по Маршаллу на /-й продукт;
б) пропорциональна значению xz;
в) равна значению х. функции спроса по Хиксу на /-й продукт;
г) пропорциональна значению х. функции спроса по Хиксу на /-й
продукт;
д) ответы а)—г) не верны.
11. Косвенная функция полезности v(ppp2,
а) однородна нулевой степени относительно вектора цен р = (рр р2)
на продукты (при фиксированном доходе М)\
б) однородна первой степени относительно вектора цен р = (рр р2)
на продукты (при фиксированном доходе М);
в) однородна нулевой степени по всем переменнымрх,р2, М\
г) однородна первой степени по всем переменнымрх,р2, М;
д) ответы а)-г) не верны.
48
Вопросы, тесты и задачи для контрольных работ к главе 1
1. Укажите неверный ответ.
ЭтСд, U)
Предельный расход по полезности --:
dU
а) равен множителю Лагранжа задачи максимизации полезности
при бюджетном ограничении;
б) равен множителю Лагранжа задачи минимизации расхода при
фиксированном уровне полезности.
2. Функция спроса по Хиксу Xj = х1(ррр2, Юна первый продукт:
а) однородна нулевой степени относительно всех переменных
PVPVO-,
б) однородна первой степени относительно всех переменных
Pi,PvU\
в) однородна нулевой степени относительно вектора цен р = (рх, р2)
на продукты;
г) однородна нулевой степени относительно вектора цен р = (Pj, р2)
на продукты;
д) не допускает однозначной характеристики относительно своих
переменных.
3.
Предельная полезность по доходу
Ъу{рх,р2,М)
дМ
а) равна отношению величины х. спроса по Маршаллу на /-й про-
дукт к предельной полезности по цене р. /-го продукта;
б) пропорциональна отношению величины х, спроса по Маршаллу
на /-й продукт к предельной полезности по цене pi /-го продукта;
в) равна отношению предельной полезности по цене pt i-тъ про-
дукта к величине х{ спроса по Маршаллу на /-й продукт;
г) пропорциональна отношению предельной полезности по цене
р. /-го продукта к величине х. спроса по Маршаллу на /-й про-
дукт;
д) ответы а)—г) не верны.
4. Функция Xj = Xj(pj, р2, М) спроса по Маршаллу на первый продукт:
а) однородна нулевой степени относительно вектора цен р = (pj, р2)
на продукты (при фиксированном доходе М);
б) однородна нулевой степени по всем переменным рр р2, И;
в) однородна первой степени относительно вектора цен р = (рр р2)
на продукты (при фиксированном доходе М)\
г) однородна первой степени по всем переменным;
д) ответы а)-г) не верны.
4 - 7620
49
5. Функция полезности потребителя имеет вид U(x{i х2) =х^/3-х|/4. Най-
дите эластичность по максимума функции полезности U при за-
данном бюджетном ограничении р{х{ + р2х2 = М.
6. Функция полезности потребителя имеет вид U(xv х2) = xj/4 • х2/5. Це-
ны на продукты соответственно рх и р2, доход потребителя равен М:
а) выпишите функции спроса (по Маршаллу) на первый и второй
продукты;
б) выпишите косвенную функцию полезности.
7. Функция полезности потребителя имеет вид U(xv х2) = х^/3 • х2/4. Це-
ны на продукты соответственно равны р{ и р2, уровень полезности
потребителя равен U:
а) выпишите функции спроса (по Хиксу) на первый и второй про-
дукты;
б) выпишите функцию расходов.
Л/11/12
8. Косвенная функция полезности имеет вид v( д, р2, М) = ———
Рх -Рх
Выпишите функцию спроса Xj = х2(ррр2, М) по Маршаллу на пер-
вый продукт.
9. Функция полезности потребителя имеет вид U(x{, х2) = х}/2 • х2/2. Це-
ны на единицы первого и второго продуктов соответственно равны
Pj = 9, р2 = 4, доход равен М = 12. Цена на первый продукт повысилась
и стала равной qx = 16. Найдите компенсирующую вариацию дохода.
10. Постройте пример функции/(хр х2) такой, что ее линия уровня каса-
ется в единственной точке х = (хр х2) бюджетной прямой р{хх + р2х2 =
= Ми эта точка не является точкой условного локального экстремума
функции/(хр х2) при наличии ограничения р}х{ + р2х2 = М. (Этот
пример нетипичен для микроэкономики.)
11. Постройте пример функции f(x{, х2) такой, что ее линия уровня каса-
ется в единственной точке х = (хрх2) прямой и эта точка не является
точкой условного локального экстремума функции р{х{ + р2х2 = М
при наличии ограничения /(хрх2) = /. (Этот пример нетипичен для
микроэкономики.)
Глава 2
ТЕОРИЯ ОТНОШЕНИЯ
ПРЕДПОЧТЕНИЯ-БЕЗРАЗЛИЧИЯ
2.1. Понятие отношений
предпочтения, безразличия и отношения
предпочтения-безразличия
2.1.1. Если потребитель предпочитает потребительский набор
х1 = (х}, потребительскому набору х°=(xj*, ...,х°) (т.е. из двух
разных предлагаемых потребителю наборов х1 и х° он обязатель-
но выберет набор х1), то говорят, что на потребительских набо-
рах х1 и х° задано отношение (сильного) предпочтения, что записы-
вается символически так: х1 > х°.
Очевидно, отношение предпочтения не обладает свойством
рефлексивности: х > х.
Если из двух потребительских наборов х1 и х° потребителю все
равно, какой набор выбирать, то говорят, что на потребительских
наборах х1 и х° задано отношение безразличия, что записывается
так:х* ~х°.
Очевидно, отношение безразличия ость отношение эквивалент-
ности, т.е. бинарное отношение, обладающее свойствами рефлек-
сивности (х - х), симметричности (х1 - х° => х° ~ х1) и транзитив-
ности (х° — х1, х1 -х2 =>х° -х2).
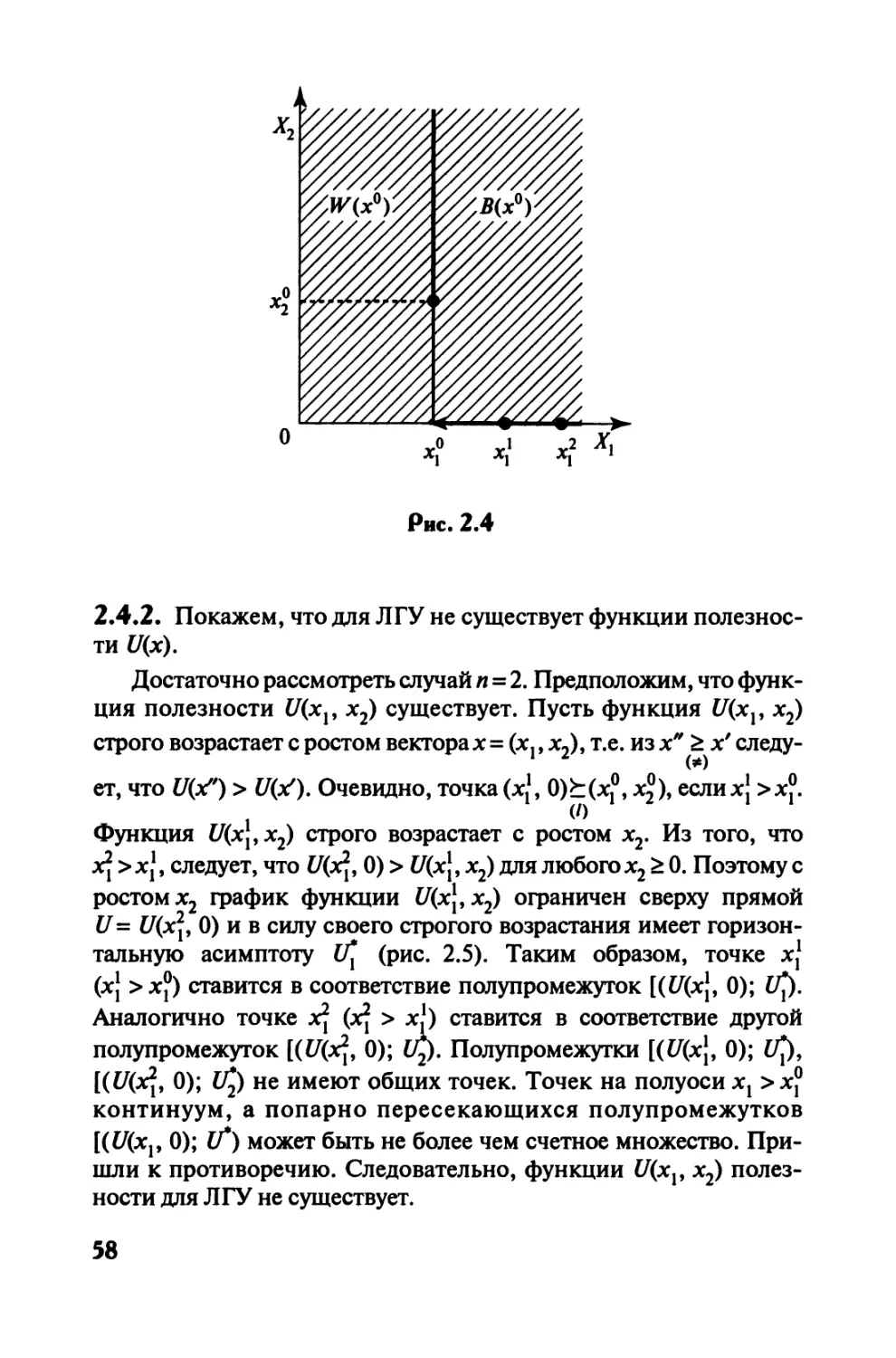
2.1.2. Если потребительский набор х1 предпочитается или без-
различен для потребительского набора х°, то говорят, что на по-
требительских наборах х1 и х° задано отношение предпочтения-без-
различия, что символически записывается так: (х1 £ х°).
4*
51
Отношение предпочтения-безразличия есть отношение порядка,
т.е. такое бинарное отношение, которое обладает свойствами реф-
лексивности (х £ х), антисимметричности (х1 > х°, х° > х1 => х* - х°),
транзитивности (х2 > х1, х1 > х° => х2 >: х°).
Функция полезности задает отношение предпочтения-безраз-
личия следующим образом: 1/(х1) £ (/(х0) <=>х* х°. Более конкрет-
но: U(xl) — U(x°) «х1 ~х°, £7(х’) > U(x°)^x{ >-х°.
Карта линий безразличия индуцирует класс функций полез-
ности, замкнутый относительно монотонного преобразования.
Карта линий безразличия задает отношение предпочтения-без-
различия следующим образом: если потребительский набор х*
принадлежит поверхности (линии при п = 2) безразличия /*, рас-
положенной строго «северо-восточнее» поверхности (линии) без-
различия Z °, которой принадлежит потребительский набор х°, то
естественно, чтох1 >- х°. Если потребительские наборых1 их0 при-
надлежат одной поверхности (линии) безразличия, то х1 ~ х°.
Ниже (см. параграф 2.4) будет показано, что есть пример отно-
шения предпочтения-безразличия, для которого нельзя постро-
ить функцию полезности (карту линий безразличия), которая бы
индуцировала это отношение предпочтения-безразличия.
Таким образом, теория отношения предпочтения-безразли-
чия есть третья теория (после двух теорий—теории количествен-
ной полезности и теории порядковой полезности) предпочтения
потребителя, и эта теория представляет собой более общую кон-
струкцию по сравнению с теориями количественной полезности
и теории порядковой полезности.
2.2. Свойства и предположения отношения
предпочтения-безразличия
2.2.1. В параграфе 2.1 уже отмечалось, что отношения предпоч-
тения-безразличия обладают свойствами:
1) рефлексивности',
2) антисимметричности",
3) транзитивности.
Отношение предпочтения-безразличия обладает еще рядом
свойств. Следующие свойства — это:
52
4) полнота (для любой пары х1 и х° потребительских наборов
справедливо одно из двух отношений х1 > х°, х° > х1 или оба вмес-
те (последнее означает, чтох* ~х°)).
Свойство полноты означает, что множество всех потребитель-
ских наборов х = (хр ..., хп), таких, что х, > 0,..., хп > 0, является
вполне упорядоченным множеством по отношению предпочте-
ния-безразличия > (напомним, что по отношению >, которое для
«-мерных векторов понимается покоординатно, множество по-
требительских наборов является только частично упорядоченным
множеством).
2.2.2. Прежде чем переходить к другим свойствам отношения
предпочтения-безразличия >, определим три понятия.
Множество -5(х°) всех потребительских наборов х (х, > 0, ...,
хп > 0), предпочитаемых или безразличных набору х°, называется
хорошим множеством для наборах0, т.е.
Л(х°) = {х | х > х0}.
Множество И^х0) всех потребительских наборов х, которым
набор х° предпочитается или безразличен, называется плохим
множеством для набора х°, т.е.
Иг(х0) = {х|х0>х}.
Множество /(х°) всех потребительских наборов х, безраз-
личных набору х°, называется множеством безразличия для на-
бора х°, т.е.
£(х°) = /(х°) = {х|х~х0}.
Неравенство xt > х° для «-мерных векторов х1 и х° понимается
покоординатно(х| Sx°, ...,х* >х°), неравенствох1 > х°означает,
что справедливо неравенство х1 > х° и хотя бы для одной коорди-
наты /0 справедливо строгое неравенство х^ > х°;
5) ненасыщаемость (из х1 > х° следует, что х1 >- х°, рис. 2.1).
(*)
Обратное (х1 >х° =>х’ >х°), очевидно, не имеет места (см. рис. 2.1,
на котором х1 >- х°, однако неверно, что х1 £ х°, ибо для них
X]1 < х°, х] > х%). На рис. 2.2 представлен фрагмент карты линий
безразличия. Здесьх2 >-х* >-х0, однако х1 > х2 и х1 > х°. Рисунок 2.2
(*) (*)
показывает, что свойство ненасыщаемости справедливо не всег-
53
да, поэтому далее предполагается, что свойство ненасыщаемости
имеет место, и случаи, аналогичные представленному на рис. 2.2,
не рассматриваются.
2.2.3. Далее все рассуждения проводятся при условии, что спра-
ведливы свойства:
6) непрерывности множеств безразличия /(х°) (что эквивалент-
но предположению о замкнутости множеств 2?(х°) и lK(x0) или от-
крытости множеств Д°(х°) = {х | х >-х0}, Ифс0) = {х | х° >-х});
7) строгой выпуклости (для любого потребительского набо-
ра х° множество И(х°) строго выпукло);
8) гладкости функции полезности, если функция полезности
включается в рассмотрение.
Отметим, что отношения предпочтения, безразличия и предпоч-
тения-безразличия были определены исходя из наглядных экономи-
ческих соображений (см. параграф 2.1). Тогда свойства 1)—5) выво-
дятся из этих определений. Свойства 6)—7), по существу, являются
дополнительными предположениями. Можно эту наивную схему
обернуть, превратить ее в аксиоматическое определение отношения
предпочтения-безразличия следующим образом: бинарное отноше-
ние на множестве потребительских наборов называется отношением
предпочтения-безразличия, если для него имеют место аксио-
мы 1)—8). Отметим, что при таком подходе свойства 1)—8) берутся в
качестве (исходных) аксиом — (исходных) предположений.
54
2.3. Взаимосвязь между отношением
предпочтения-безразличия и функцией полезности
2.3.1. В параграфе 2.1 отмечалось, что функция полезности инду-
цирует отношение предпочтения-безразличия. Покажем, что от-
ношение предпочтения-безразличия, для которого выполнены
свойства 1)—6) (см. параграф 2.2), определяет однозначно функ-
цию полезности U(x{,..., хп). В этом построении одним из основ-
ных является свойство 6) о непрерывности и свойство 5) о нена-
сыщаемости. Подробное построение проведем для случая п = 2.
Построим множество /(х°) безразличия потребительского на-
борах0 (рис. 2.3).
Согласно свойству 6) множество /(х°) непрерывно (т.е. не имеет
«дыр»), поэтому его обязательно пересечет в точке х° = (х°, х°)
(х° = х° = £°) прямая, которая выходит из точки О под углом л/4
(45°). Положим Щх°) = U(x°) = £, т.е. частное значение С/(х°) функ-
ции полезности С/(х) на потребительском наборе х° определяется
так: если ~ х° (вектор е = (1,1)), то £7(х°) = £.
2.3.2. Покажем, что определенная в разделе 2.3.1 функция U(x)
есть функция полезности, т.е. докажем, что она непрерывна и
U(xx) £ СА(х°) <=>х‘ > х°. (2.3.1)
55
Сначала докажем, что из х1 >г х° следует U(xx) > U(x°).
Пусть х* >2 х° и х1 - ^1е, х° ~ ^°е. По свойству транзитивности из
-х1, х1 > х° следует, что %'е х°; по свойству транзитивности из
Е,1е £ х° и х° - £°е следует, что Vе > £°е, т.е. (ибо е = (1,1)),
откуда вытекает на основании определения функции Щх), что
t/(x‘) > 17(х°).
Докажем, что из U(xx) > 1/(х°) следует х1 £ х°.
Пусть х° > х1. Тогда по свойству транзитивности из х° >- х1 и
х° - ^°е следует, что >- х1. Аналогично по свойству транзитив-
ности из > х1 и х1 ~ следует, что ^°е >- ^'е, т.е. £/(х°) = > J;1 =
= U(xx), а это противоречит условию, что U(xx) > U(x°). Следова-
тельно, х1 х°.
Для доказательства непрерывности функции Щх) используем
понятие отделимых множеств. Два множества М{ и М2 отделимы,
если ни одна точка одного из множеств не является граничной
точкой другого множества. Очевидно, множества В°(х°) и И/0(х°)
отделимы.
Для непрерывности функции Щх) (Xj >0,...,хл >0) необходи-
мо и достаточно, чтобы для каждой пары Uv U2 подмножеств зна-
чений функции Щх) имела место отделимость их полных прооб-
разов A/j = {х | Щх) € 17]} и М2 = {х | Щх) е U2} в случае отделимости
самих множеств Ц и U2.
Пусть х° — потребительский набор и 1/(х°) — частное значе-
ние функции полезности. Пусть Ul = [U, U(х0)) и U2 = (U(х°), 17],
где числа U < £7(х°) и 17(х°) < U произвольны и достаточно близ-
ки к числу 17(х°). Множества Щ и U2 отделимы. Множество
Л/] = {х|£7(х)е £11}£И/О(х°)и1И2 = {х|17(х)€ U2}^B°(x°).Множест-
ва В°(х°) и ^(х0) расположены по разные стороны от множества
безразличия 7(х°), поэтому они отделимы. Значит, отделимы мно-
жества Мх и М2. Поскольку потребительский набор х° был выбран
произвольно, непрерывность функции 17(х) доказана.
В случае произвольного п > 2 функция 17(х) определяется чуть
сложнее, а доказательства связки (2.3.1) и непрерывности функ-
ции 17(х) почти дословно повторяют только что приведенные до-
казательства.
56
Непрерывность функции полезности можно доказать, не ис-
пользуя свойство 5) о ненасыщаемости, с использованием неэле-
ментарных математических средств (результат Ж. Дебре 50-х го-
дов XX в.).
2.4. Лексикографическое
упорядочение как пример отношения
предпочтения-безразличия, для которого
нельзя построить функцию полезности
2.4.1. Лексикографическое упорядочение (ЛГУ) «-мерных век-
торов аналогично упорядочению студентов (школьников) в груп-
пе по алфавиту: Александров, Афанасьев, Белоусов, Блинов, Ва-
сильев, Власов и т.д.
Если х{ > х°, то вектор х1 = (х{, х^, ..., х\) лексикографически
предпочитается векторух° = (х°, х2, ..., х°), что символически за-
писывается так: х11 х°.
(/)
Если х! =х? и xi > х?, то х1 х° и т.д.
(/)
ЛГУ обладает свойствами рефлексивности, антисимметрич-
ности, транзитивности, полноты, ненасыщаемости. Однако ЛГУ
не удовлетворяет предположению 6) о непрерывности. Для этого
покажем (достаточно рассмотреть случай п = 2), что множества
В(х°) и И^х0) не являются замкнутыми.
На рис. 2.4 хорошее множество В(х°) есть подмножество пер-
вой четверти (Xj > 0, х2 > 0) координатной плоскости OxjX2, со-
держаще® вертикальный луч с началом в точке х0 = (х°, х2), мно-
жество точек оси Oxj таких, что Xj > х°, и полуплоскость х( > х°
(см. рис. 2.4). Точки (х°, х2), 0 <х2 <х2 не принадлежат множеству
5(х°), т.е. множество 5(х°) не является замкнутым. На рис 2.4
плохое множество Ифс0) есть подмножество первой четверти
(х, > 0, х2 > 0) координатной плоскости Ох(х2, содержащее отрезок
{(ХрХ2) |0<х2<х2}, множество точек оси Ох( таких, что0<х, <х®,
и полосу {(хр х2) 10 <Xj <х°, х2 > 0} т.е. множество W(x°) не являет-
ся замкнутым.
57
Рис. 2.4
2.4.2. Покажем, что для ЛГУ не существует функции полезнос-
ти U(x).
Достаточно рассмотреть случай п=2. Предположим, что функ-
ция полезности U(xv х2) существует. Пусть функция U(xp х2)
строго возрастает с ростом вектора х = (х., х,), т.е. из х* > х' следу-
(*)
ет, что t/(x") > U(x'). Очевидно, точка(х.1, 0)>(х.°, х2), еслих! >х?.
(О
Функция t/(x[,x2) строго возрастает с ростом х2. Из того, что
xj > х{, следует, что £/(х^, 0) > U(x\, х2) для любого х2 > 0. Поэтому с
ростом х2 график функции С/(х},х2) ограничен сверху прямой
U = £7(Хр 0) и в силу своего строгого возрастания имеет горизон-
тальную асимптоту U\ (рис. 2.5). Таким образом, точке xj
(х} >х°) ставится в соответствие полупромежуток [(£/(х{, 0); ity.
Аналогично точке xj (х^ > х!) ставится в соответствие другой
полупромежуток [(Щх^, 0); Сф. Полупромежутки [(С/(х{, 0); бф,
[(U(x?v 0); U2) не имеют общих точек. Точек на полуоси xt >х°
континуум, а попарно пересекающихся полупромежутков
[(1А(хр 0); U*) может быть не более чем счетное множество. При-
шли к противоречию. Следовательно, функции U(xv х2) полез-
ности для ЛГУ не существует.
58
рис. 2.5
Вопросы для самоконтроля к главе 2
Что представляет собой отношение предпочтения-безразличия, за-
даваемое функцией полезности?
Что представляет собой огношение предпочтения-безразличия, за-
даваемое картой поверхностей (линий) безразличия?
Что такое отношение эквивалентности, отношение порядка?
Как формулируются свойства отношения предпочтения-безразли-
чия (рефлексивность, антисимметричность, транзитивность, полно-
та, ненасыщаемость, гладкость, непрерывность, выпуклость)?
Как формулируются определения «хорошего», «плохого» множеств,
множества безразличия в пространстве потребительских наборов?
Что такое лексикографическое упорядочение (ЛГУ)? Показать, что
ЛГУ - пример отношения предпочтения-безразличия. Что представля-
ют собой множества безразличия, хорошие и плохие множества ЛГУ?
Как строится функция полезности для отношения предпочтения-
безразличия, обладающего свойством непрерывности?
В каком отношении находятся понятия ЛГУ и функции полезности?
Задачи и упражнения для самоконтроля к главе 2
Докажите, что отношение безразличия есть отношение эквивалент-
ности.
Докажите, что отношение предпочтения-безразличия есть отноше-
ние порядка.
59
3. Приведите аналитический пример функции полезности, для кото-
рой не выполнено свойство ненасыщаемости.
4. Приведите аналитический пример функции полезности, для кото-
рой существует хорошее множество, не являющееся строго выпук-
лым.
Вопросы, тесты и задачи для контрольных работ к главе 2
1. Теории количественной полезности (ТКП), порядковой полезности
(ТПП), отношения предпочтения-безразличия (ТОПБ) по уровню
общности (в порядке возрастания) следует расположить следующим
образом:
а) ТОПБ, ТКП, ТПП;
б) ТОПБ, ТПП, ТКП;
в) ТКП, ТОПБ, ТПП;
г) ТКП, ТПП, ТОПБ;
д) ТПП, ТКП, ТОПБ.
2. Отношение предпочтения обладает свойством:
а) рефлексивности;
б) антисимметричности;
в) транзитивности;
г) ненасыщаемости;
д) полноты.
3. Отношение безразличия обладает свойством:
а) полноты;
б) ненасыщаемости;
в) антисимметричности;
г) рефлексивности;
д) ответы а)-б) не верны.
4. Множество безразличия:
а) представляет собой собственное подмножество границы хоро-
шего множества;
б) содержит в качестве собственного подмножества границу хоро-
шего множества;
в) представляет собой общую границу хорошего и плохого мно-
жеств;
г) представляет собой собственное подмножество границы плохого
множества;
д) ответы а)-г) не верны.
5. Множество безразличия ЛГУ (п = 2) представляет собой:
а) линию на плоскости OxjX2;
б) точку на плоскости OxjX2;
60
в) двумерное множество на плоскости Oxtx2;
г) не существует понятия множества безразличия для ЛГУ;
д) ответы а)—г) не верны.
6. Для ЛГУ выпишите уравнение функции спроса на первый продукт
(л = 2) или докажите, что такой функции не существует.
7. Докажите, что в предположении о непрерывности множества безраз-
личия при (л = 2) прямая х2 = к • х, обязательно пересечет множество
безразличия (0 < к < «>).
Глава 3
ОСНОВЫ ТЕОРИИ
ВЫЯВЛЕННЫХ ПРЕДПОЧТЕНИЙ
3.1. Предпосылки теории
выявленных предпочтений
3.1.1. В связи с тем что не вполне ясны экономические основы
понятия полезности и функции полезности, в экономической те-
ории неоднократно предпринимались попытки уточнить эти по-
нятия именно с экономической точки зрения. Так, после теории
количественной полезности, в которой основным понятием явля-
ется функция полезности, была предложена теория порядковой
полезности, в которой, по существу, основное понятие — это кар-
та поверхностей (линий) безразличия, на основании которой
функция полезности восстанавливается с точностью до монотон-
ного преобразования. Эти две теории обобщает теория отноше-
ния предпочтения-безразличия, в которой был построен пример
лексикографического упорядочения, для которого не существует
функции полезности.
В этих трех теориях существенным является то обстоятель-
ство, что отношение предпочтения задается независимо от рыноч-
ной ситуации, т.е. независимо от рыночных цен рх,..., рп на про-
дукты и от дохода М, с которым потребитель выходит на рынок.
В теории выявленных предпочтений отношение предпочте-
ния уже связано с рыночными ценамирх,...,рп на продукты и за-
висит от них.
Теория выявленных предпочтений опирается на следующие
предпосылки.
1. Потребитель, приобретая на рынке потребительский набор
х1 = (х{,..., х„), обязательно тратит весь свой доход, т.е. plxl = М1
62
(пара, состоящая из вектора цен р1 = (р},р1) и дохода М1, как
уже отмечалось выше, называется рыночной ситуацией).
2. Выбор потребителя является единственным, т.е. х1 =
= (х{,..., х1) — единственный потребительский набор такой, что
р’х1 = М* (предпосылка о строгой выпуклости предпочтений по-
требителя).
3. Если выбран потребительский набор х1, то он определяет
единственным образом (с точностью до положительного множи-
теля) рыночную ситуацию, т.е. х1 => (у- р1, у • М[) так, что у • р*х’ =
=у- М1.
Предпосылка 2 может быть ослаблена (это ослабление далее
специально оговаривается), что означает возможность использо-
вания нестрого выпуклых предпочтений потребителя.
3.1.2. Говорят, что потребительский набор х1 = (х[,..., х1п) прямо
выявленно (т.е. явно) предпочитается потребительскому набору
х2 = (х2,..., х2), если р’х1 >р'х2, где р’х1 = Мх и (р1, Л/1) — некоторая
(вполне определенная) рыночная ситуация. Символиках1 х-’х2.
Содержательно прямое выявленное предпочтение набора х*
набору х2 означает, что из двух потребительских наборов х1 и х2
потребитель выбрал именно набор х1, а набор х2 не выбрал,
т.е. потребитель выбирает самый дорогой потребительский на-
бор х1, а среди самых дорогих единственный (рис. 3.1, на котором
потребительский набор х1 обязательно расположен на северо-вос-
точной границе АВ бюджетного множества ОАВ, которое соот-
ветствует рыночной ситуациир1, Л/1, а потребительские наборы х2,
которым прямо выявленно предпочитается потребительский на-
бор х1, могут располагаться на северо-восточной границе АВ бюд-
жетного множества ОАВ или внутри него).
Обратим внимание на то, что прямое выявленное предпочте-
ние х1 х-’х2 означает, что потребительские наборых* их2 сопостав-
ляются в ценахр1 рыночной ситуации (р1, Мх), соответствующей
набору х1, и что сопоставляются только доступные потребителю
наборы х1 их2. Если один из двух потребительских наборов потре-
бителю недоступен, то он может быть как более, так и менее пред-
почтительным потребителю, чем доступный потребительский
набор. В связи с возможностью неоднозначного ответа такие па-
ры потребительских наборов не сопоставляются. Далее отноше-
63
ние прямого выявленного предпочтения обобщается на совокуп-
ности, содержащие более двух потребительских наборов.
В случае трех потребительских наборов х1, х2, х3 (рис. 3.2)
пусть потребительский набор х1 расположен на северо-восточной
границе АВ бюджетного множества ОАВ, соответствующего ры-
ночной ситуации р1, Л/1; потребительский набор х2 принадлежит
бюджетному множеству ОАВ, а потребительский набор х3 принад-
лежит бюджетному множеству ODF, соответствующему рыночной
ситуации р2, М2 = р2*2.
Очевидно,
р'х’^р’х2, р2з?>р2£, т.е. }
х'^-’х2, х2>*х3.
Если потребительский набор х3 принадлежит бюджетному
множеству ОАВ, то х1 >* х3 (т.е. потребительский набор х1 прямо
выявленно предпочитается потребительскому набору х3), если же
потребительский набор х3 не принадлежит бюджетному множест-
ву ОАВ, то, строго говоря, нельзя писать, чтох1 х3. Следователь-
но, отношение прямого выявленного предпочтения не обладает
свойством транзитивности.
64
3.1.3. Говорят, что потребительский набор х1 косвенно выявлен-
ие предпочитается потребительскому набору х3, если р*х* >р'х2,
р2х2 > р2х3 и если потребительский набор х3 не принадлежит
бюджетному множеству, соответствующему рыночной ситуации
(pi,Mi=pixi).
Однако приведенное разделение выявленного предпочтения
потребительского набора х* потребительскому набору х3 на пря-
мое и косвенное не вполне конструктивно, ибо часто бывает не
ясно, принадлежит потребительский набор х3 бюджетному мно-
жеству, соответствующему рыночной ситуации (pl, Мх = р1х1), или
не принадлежит. В некоторых случаях приходится специально
оговаривать, о каком конкретно выявленном предпочтении идет
речь (прямом или косвенном).
В дальнейшем вне зависимости от того, принадлежит потреби-
тельский набор х3 бюджетному множеству, соответствующему ры-
ночной ситуации (р1, Л/1 = р’х1), или не принадлежит, использует-
ся терминология: потребительский набор х1 выявленно предпо-
читается потребительскому набору х3, если рххх > р'х2, р2х2 > р2х3.
Символика: х1 >-* х3.
В случае цепочки х1, х2,..., хк, содержащей четыре и более по-
требительских наборов, будем говорить о выявленном предпочте-
нии потребительского набора х1 потребительскому набору хк и
использовать символику х1 >-* хк.
В случае двух потребительских наборовх1 их2 во фразе «потре-
бительский набор х1 прямо выявленно предпочитается потреби-
тельскому набору х2» слово «прямо» также будет опускаться.
3.2. Связь теории выявленных предпочтений
с теорией линий (поверхностей) безразличия
3.2.1. В теории выявленных предпочтений нет функции полез-
ности и нет линий (поверхностей) безразличия. Однако по ре-
зультатам наблюдений за поведением потребителя на рынке мож-
но дать качественную оценку характеру поведения линий (поверх-
ностей) безразличия потребителя. Под результатом наблюдения
за поведением потребителя на рынке понимается пара, состоящая
из вектора цен р и потребительского набора х, который был вы-
бран потребителем при этом векторе цен.
Если при векторе цен р* потребитель выбрал набор х1, а при
векторе цен р2 потребитель выбрал набор х2, то можно построить
5 - 7620
65
объединение QAGF бюджетных множеств Q1 (ОАВ) и Q2 (ODF),
соответствующих рыночным ситуациям (р1, Л/1 = р*х*) и (р2, М2 =
= р2х2) (рис. 3.3). Поскольку р’х1 > р1х (здесь х «пробегает» мно-
жество Q1) и р2х2 > р2х (здесь х «пробегает» множество Q2), по-
стольку х1 х2, х2 >-* х3 и, следовательно, х1 х для всех х из объ-
единения ОЛСГбюджетных множеств Q1 и Q2.
Рис. 3.3
При любом векторе цен р для потребительского набора х из
угла х* NR справедливо неравенстворх > рх1, т.е. для любого потре-
бительского набора х из угла х’ЛГЯ справедливо отношение х х1.
Из сказанного следует, что если линия безразличия содер-
жащая потребительский набор х1, существует, то она должна быть
расположена во множествах AxlNn FGxxR, т.е. вне множеств ОЛ(2Г
и х1 NR (см. рис. 3.3). Если бы линия безразличия /' имела общую
точку, скажем z, со множеством ОЛ<7Г, отличную от точки ^с1, то
это бы противоречило отношению х* >-* Z, ибо на линии безразли-
чия не могут находиться точки, одна из которых предпочитается
другой. Аналогичные рассуждения следует провести для точки у
множества xlNR.
3.2.2. Если при изменении цен число наблюдений о выборе по-
требителя растет, то можно сузить множество, которому принад-
66
лежит линия безразличия /’ индивидуума, содержащая потреби-
тельский набор х1.
Пусть при векторе цен р4 потребитель выбрал набор х4 и пусть
бюджетная прямая L4, имеющая уравнение р4х = р4х4, содержит
потребительский набор х1 (рис. 3.4). Тогда очевидно, что р4х4 =
=р4х1 и, следовательно, х4 >-* х1.
Рис. 3.4
Пусть при векторе цен р5 потребитель выбрал набор х5 и пусть
бюджетная прямая L5, имеющая уравнение р5х = р5х5, содержит
потребительский набор х1 (см. рис. 3.4). Тогда очевидно, чтор5х5 =
=Р5х* их^’х1.
Любой потребительский набор х, принадлежащий периферии
Hx4xlx5S (см. рис. 3.4), выявленно предпочитается потребитель-
скому набору х1.
Действительно, если потребительский набор х = х6 располо-
жен на вертикальном луче х4Н, то очевидно, что р4х > р4х4 = р4хх,
откуда вытекает, что х=х6 х1. Если потребительский набор х=х7
находится на отрезке [х*;х4] между точками х1 их4, тох= (1 -1)х’ +
+ , где число 0 < X < 1. В этом случае р4х = (1 - К)/»4*1 + "кр4х4 =
= (1 - Х)р4х* + \р4хх =р4х1, откуда следует, чтох=х7>*х1.
5*
67
Для потребительских наборов х, расположенных на отрезке
[х1; х5] и на горизонтальном луче x?S, рассуждения аналогичны
только что проведенным.
Любой потребительский набор х = х10, принадлежащий мно-
жеству Hxxxxx‘S, выявленно предпочитается потребительскому
набору х1, т.е. х10 >»* х1.
Действительно, потребительский набор х10 можно представ-
лять в виде выпуклой комбинации двух потребительских наборов,
принадлежащих периферии Hx4xx^S.
На рис. 3.4 потребительский набор х10 есть выпуклая комбина-
ция потребительских наборов х7 и х8, т.е. х10 = (1 - А)х7 + Ах8, где
число 0 < 1 < 1. Имеем р4х10 = (1 - typ^x1+Ар4х7 > (1 - Х)рАхх + Ар4х* =
=/>4х’,т.е. х’^’х1.
Таким образом, в рассматриваемом случае по результатам че-
тырех наблюдений о выборе потребителем наборов х1, х2, х4, х5
получаем, что если линия безразличия Iх, содержащая потреби-
тельский набор х1, существует, то она должна быть расположена
вне множеств ОАGFи Hx^x’S (см. рис. 3.4).
Приведенные рассуждения показали, что предпочтения по-
требителя обладают свойством выпуклости.
Если х* х2 и если существует карта линий безразличия, то
х1 £ х2 (рис. 3.5). Если существует карта линий безразличия, то из
х1 > х2 не следует, вообще говоря, чтох1 >-* х2 (рис. 3.6).
68
3.3. Слабая и сильная аксиомы выявленных
предпочтений
3.3.1. Слабая аксиома выявленных предпочтений (СлАВП) форму-
лируется так: если х1 >* х2 и х1 * х2, то неверно, что х2 х1.
Другими словами, если р*х* >р’х2, то р2х? <р2хх (pte = М2,
p2t М2 — рыночная ситуация, соответствующая потребительскому
набору х2, если он был бы выбран). Неравенстворххх > р’х2 (в ко-
тором единица в качестве индекса фигурирует 3 раза и левая часть
рххх больше или равна правойр’х2) означает, что потребителю до-
ступны оба потребительских наборах1 и х2 и из этих наборов по-
требитель выбирает набор х1. Неравенствор2£ < р2хх означает, что
при ценахр2 потребитель выбрал набор х2, а набор х1 потребителю
недоступен.
Если СлАВП имеет место, то отношение выявленного предпоч-
тения не обладает свойством симметричности: если х1 х2, то не-
верно, чтох2 >* х1. Если СлАВП не имеет места, т.е. если существу-
ют одновременно два отношения: х1 >-* х2 и х2 >-* х1, то отношение
выявленного предпочтения обладает свойством симметричности.
Рисунок 3.7 иллюстрирует выполнение СлАВП, рис. 3.8 — си-
туацию, когда СлАВП не имеет места.
69
На рис. 3.7 рххх = /Их2, т.е. х* >* х2, но М3 > М2, где М3 = р2хх,
М2 = р2^2, т.е. р2э? < р2хх\ таким образом, СлАВП имеет место. На
рис. 3.8 рххх = рхх?, т.е. х1 >* х2, но М3 < М2, где М3 = р2хх, М2 = р2х2,
т.е. р2х? >р2хх,э? >* х1; таким образом, СлАВП не имеет места.
3.3.2. Если существует функция полезности U(xv х2), то потре-
бительский набор х* = (х}; х|) — точка касания бюджетной прямой
рхх = Мх (Мх = рххх) и линии безразличия Iх, содержащей точку х1
(рис. 3.9, на котором представлена ситуация, когда СлАВП имеет
место). Линия безразличия /2, содержащая точку х2 = (х^; х2), каса-
ется бюджетной прямой р2х=М2 (М2 = р2^2). Линия безразличия I2
расположена «юго-западнее» линии безразличия /*, что, естест-
венно, согласуется с тем, чтох* х2.
На рис. 3.10, на котором представлена ситуация, когда СлАВП
не имеет места, ситуация иная. Здесь, так же как и на рис. 3.9, ли-
ния безразличия Iх касается бюджетной прямойрхх=Мх в точке х1,
а линия безразличия I2 касается бюджетной прямой р2х = М2 в
точке х2. Взаимное расположение линий безразличия I2 и Iх сви-
детельствует о том, что они должны пересечься, а это принципи-
ально невозможно, если, конечно, речь идет о линиях безразли-
чия Iх и I2 одной и той же функции полезности. Если же линия
безразличия Iх является линией, соответствующей одной функ-
70
ции полезности, а линия безразличия I2 является линией, соот-
ветствующей другой функции полезности, то пересечение таких
линий вполне возможно. Следовательно, в случае невыполне-
ния СлАВП единая (для двух наборов х1 и х2) функция полезнос-
ти существовать не может. Остается принять, что переход потре-
бителя от набора х’ к набору х2 продиктован изменением его
функции полезности. Таким образом, невыполнение СлАВП
свидетельствует либо о смене предпочтений потребителя (что
выражается формально в изменении его функции полезности),
либо в отрицании того факта, что на рынке потребитель ведет
себя рационально.
Таким образом, СлАВП является вполне естественной с со-
держательной экономической точки зрения.
3.3.3. Результаты наблюдений за поведением потребителя на
рынке позволяют получить ответ на вопрос, соответствует поведе-
ние потребителя на рынке СлАВП или не соответствует. Так,
/-е наблюдение за поведением потребителя на рынке фиксирует
вектор ценр' = (p\,pty и выбранный потребителем наборх' = (х{, Xj).
Результаты, скажем, к наблюдений можно представить в виде
табл. 3.1.
Таблица 3.1
Номер наблюдения Цены Выбираемые потребительские наборы
Pi Рг *1 Хг
1 Р\ Р\ х>
i Р‘\ Pi X*! yj
к А Р2 А •*2
Положим Оу== р'х7, i,j=l,..., к, т.е. —расход
потребителя, если он по ценам У = (У,Х) приобретает набор
Элементы а&.табл. 3.2 образуют квадратную матрицу Л.
71
х1 ••• х1 Таблица 3.2
••• X7 ••• хк
р1 °П - % ••• - Ък
р‘ - аи ... ау - aik
PJ ар - ал - а~ - ajk
рк ак\ aki - % " акк
Элементы /-й строки, i = 1,..., к, матрицы А показывают расхо-
ды потребителя, которые он имел бы, если бы по ценам р' = (р\, р2)
приобретал последовательно все потребительские наборы
х1 = (х},хр, ...,хк = (хк,хк), кроме наборах' = (х\,х2), который был
реально выбран потребителем по ценамр'=(p'ltp2). Таким образом,
элементы главной диагонали показывают реальные расходы по-
требителя, который приобретал наборых1 = (х[,хр, ...,хк=(хк,хк)
соответственно по ценам р1 = (р[, р2), ...,рк = (рк, рк)- Остальные
(внедиагональные) элементы показывают гипотетические расходы
потребителя, которые он бы имел, приобретая по ценамр' = (р\,р2)
другие наборы x'=(xil,xl2), отличные от выбранного им набора
х' = (х1], х^), т.е. i Фj.
Если аи=рjх'] + р‘2х‘2 >//] х{ + р2х^2 = ау, j =1, ...,к, j * /, то это
означает, что наборх7 = (х{, xp, j = 1,..., к, j* i, доступен потреби-
телю, когда он приобретал набор х' = (х'р хр, и набор х' = (х', хр
выявление предпочитается потребительскому набору xi = (х7, л7),
У= 1, ...,к, j*i.
Пометим такой элемент ау (а.. < а(7), например, звездочкой и
назовем его меченым.
Если аи=р\х\ +р2х'2<р'1х[ +р'2х12 = ау, j= 1, к, j* i,ro это
означает, что набор х7 = (х{, xty, j = 1,..., к, J * i недоступен потре-
бителю, когда он приобретал набор х' = (х'р хр. Поэтому в данном
случае ничего нельзя сказать о выявленном предпочтении одного
потребительского набора другому (речь идет о наборах х' и х7 и
ценах У = (р'рРр).
72
Используя матрицу А, можно проверить, есть ли нарушения
СлАВП, когда рассматриваются пары потребительских наборов,
или таких нарушений нет.
Если в матрице А мечеными являются ее элементы а., и а.., / # j,
то это означает, что для потребительских наборов х‘ и х7 СлАВП не
выполняется.
Действительно, поскольку элемент а у матрицы А меченый,
постольку аи > а у, т.е. р'х1 > р'х1 и, следовательно, х' х7. Посколь-
ку элемент матрицы А меченый, постольку a- > aJp т.е. р/х/ > /г'х'
и, следовательно, х7 >-* х'. Одновременное наличие выявленных
предпочтений х‘ х^и х7 >* х‘ означает, что для потребительских
наборов х‘ и х7 СлАВП не выполняется.
3.3.4. Пример 3.3.1
Результаты трех наблюдений за поведением потребителя на
рынке представлены в табл. 3.3 (все числа условные).
Таблица 3.3
Номер наблюдения Цены Выбираемые потребительские наборы
Р\ Рг Х1 х2
1 1 1 2 3
2 3 1 3 1
3 1 2 1 3
В рассматриваемом примере
а1|=р1х1=1-2+1-3=5,а12 = р1х2=1-3+1-1=4,а13 = р1х3=1-1+1-3=4,
а21=р2х|=3-2+1-3=9, а22=р2х2 = 3-3+11=10, а23=р2х3=31+1-3=6,
a3i =р3х1 =1-2+2-3=8, о32 = р3х2 =1-3+21=5, а33=р3х3=11+2-3=7
и матрица А имеет вид
Ч °12 ' 5 4* 4’Л
А = Й21 °22 а23 = 9* 10 6’
<°31 °32 °33> 8 к 5* 7 7
73
Имеем
°н = .Р1*1 >Р1*2 = ai2=*xl >*х2,
а22 = р2х? > р2х1 = а21 => х2 >-* х1,
а22 = р2х? > р2х3 = а23 => х2 >-* х3,
а33 = р3х3 > р3х? = а32=эх3 >-* х2.
Таким образом, в рассматриваемом примере СлАВП не вы-
полняется на двух парах потребительских наборов: на паре х1 и х2,
а также на паре х2 и х3. Отсюда следует, что результаты наблюде-
ний за выбором потребителя наборов х1 и х2 на рынке не отражают
его поведения с устойчивыми предпочтениями, т.е. поведения,
когда потребитель выбирает из того, что может себе позволить.
Аналогичный вывод справедлив и для пары наборов х2 и х3.
На рис. 3.11 представлена геометрическая интерпретация ре-
зультатов трех наблюдений примера 3.3.1: построены потребитель-
ские наборы х^л^.х3 в виде точек х1 = (2, 3),х2 = (3,1)их3 = (1, 3),
а также бюджетные прямыер*х=Л/1(х1 +х2=5),р2х=М2(3х{ +х2 = 10)
и р3х = A/3(Xj + 2х2 = 7).
74
Рисунок 3.11 показывает, что рххх > рхх*, т.е. х1 >-* х2,
ир2х2 > Р2х1, т.е. х2 >-’ х1. Рисунок 3.11 геометрически подтвержда-
ет полученный ранее аналитический факт (ап > а12, а22 > а21), что
для наборовх1 их2 СлАВП не выполняется.
Аналогично рис. 3.11 геометрически подтверждает получен-
ный ранее аналитический факт (а22 > а23, а33 > а32), что для набо-
ров х2 и х3 СлАВП не выполняется.
3.3.5. Сильная аксиома выявленных предпочтений (СиАВП) фор-
мулируется так: если х1 >’х2, х2 / ..., х*-1 их1 гх*, то
неверно, что хк х1.
Другими словами, еслирххх >р'х1, р2х2 >р2£,..., /Л-1х*_| >рк~х^,
то />*х* < ркхх. СиАВП включает СлАВП (при к # 2).
Рисунок 3.11 иллюстрирует выполнение СиАВП (при к = 3),
рис. 3.12 — ситуацию, когда СиАВП (при к = 3) не имеет места.
На рис. 3.11 имеемрххх > рхх2, р2^2 > р2х3 и р3х3 = М3 <МЗХ = р3хх.
На рис. 3.12 имеем рххх = рхх2, р2х? = р2х3 и р3х3 = М3 > Мзх = р3хх.
Как уже отмечалось в примере 3.3.1, на рис. 3.11 видно, что для
двух пар потребительских наборов х1, х2 и х2, х3 не имеет места
СлАВП. На рис. 3.12 видно, что р1х1 < р2хх и р3х3 > р3^1, т.е. для
пары потребительских наборов х1, х2 имеет место СлАВП, а для
пары потребительских наборов х2 и х3 СлАВП места не имеет.
Рис. 3.12
75
Рисунок 3.13 иллюстрирует выполнение СиАВП и выполне-
ние СлАВП для двух пар потребительских наборов: х'.х2 их2,?.
Имеем рххх = р'х2, р2х* = р*х* и р3х3 = М3 < Мзх = р3хх, т.е. для по-
требительских наборов х1, х2, х3 СиАВП выполняется.
Далее имеемрххх = р2х* ир2х* <р2хх, т.е. СлАВП для пары потре-
бительских наборов х1 и х2 выполняется. Имеем также р2х* = р2х? и
р3х3 < р3х2, т.е. для пары потребительских наборов х2 и х3 СлАВП
выполняется.
Рисунок 3.14 иллюстрирует выполнение СлАВП для двух пар
потребительских наборов — х1, х2 и х2, х3 и невыполнение СиАВП
для потребительских наборов х1, х2, х3. Имеем рххх = р1^,
р2х2 > р2х3 и р3х3 > р’х1 = Л/31, т.е. СиАВП для потребительских
наборов х1, х2, х3 места не имеет. Далее р’х1 = р'х2 и р2х2 < р2хх,
т.е. для пары потребительских наборов х1, х2 СлАВП выполня-
ется. Для потребительских наборов х2 и х3 имеем р2х2 > р2х3 и
р3х3 < р3^, т.е . для них СлАВП выполняется.
Рисунок 3.15 иллюстрирует невыполнение СиАВП для потре-
бительских наборов х1, х2, х3 и невыполнение СлАВП для обеих
пар потребительских наборов: х1, х2 и х2, х3. Имеем р'х1 = р’х2,
р2^2 = р2х?, р3х2 >р3хх, р2х2 >р2хх,р3з? >р3х?.
76
Пример, приведенный на рис. 3.11, показывает, что формаль-
но СиАВП имеет место для полного набора векторов х1, х2, х3, од-
нако для поднаборов х1, х2 и х2, х3 она не имеет места. Если СиАВП
не имеет места хотя бы для одного упорядоченного поднабора
полного набора векторов х1, х2, ..., х\ считается, что СиАВП не
имеет места и для полного набора векторов.
77
3.3.6. Поясним на примере, как с помощью матрицы А, кото-
рая построена по результатам наблюдений, определить, выпол-
няется СиАВП для всей совокупности наблюдений или не вы-
полняется.
Пример 3.3.2
Пусть матрица Л имеет вид
"зо
А = 31
10*
20* 40(,)>
25 10*
20 15
В связи с тем что ах (= р'хх = 30 > 20 =/>1х2 = о12, х1 >-* х2. Поэтому
элемент 20, расположенный в первой строке и втором столбце,
является меченым, что показано символом *. Проводя аналогич-
ные рассуждения, получаем, что мечеными являются также эле-
менты 10 (вторая строка и третий столбец) и 10 (третья строка и
первый столбец).
В примере 3.3.1 и до сих пор в этом примере 3.3.2 метились
только те элементы матрицы А, которые были не больше элемен-
тов соответствующих строк, расположенных на главной диагона-
ли матрицы А, что содержательно означало, что речь шла о пря-
мых выявленных предпочтениях. Меченые элементы 20 (первая
строка, второй столбец матрицы А) и 10 (вторая строка и третий
столбец) означают, что первый набор х1 косвенно выявленно
предпочитается набору х3, поэтому теперь следует пометить звез-
дочкой (в скобках) элемент 40 (первая строка и третий столбец).
Далее сопоставляются между собой любые меченые элементы,
причем не важно, есть у звездочек скобки или их нет.
В рассматриваемом примере х1 >' х2 (20’), х2 х3 (10*),
т.е. х1 >* х3 (40*), а также х3 >* х1 (10*).
Если бы для потребительских наборов х1, х2, х3 была выполне-
на СиАВП, то мы должны были иметь отношения х1 >-* х2, х2 >-* х3
и отрицание отношения х3 >-* х1. Однако, как только что мы виде-
ли, отношение х3 >* х1 в рассматриваемом примере выполняется,
а это означает, что результаты наблюдений за поведением потре-
бителя на рынке несовместимы с основными положениями эко-
номической теории, т.е. мы здесь должны получить вывод, анало-
гичный выводу примера 3.3.1.
78
На основе построенной матрицы А прямые выявленные
предпочтения одних потребительских наборов другим вычленя-
ются непосредственно, т.е. непосредственно метятся звездочка-
ми элементы матрицы А. Вычленение косвенных выявленных
предпочтений опирается на вычленение цепочек разной длины,
что совсем не просто, если анализируются результаты большого
числа наблюдений, т.е. если порядок матрицы А является доста-
точно большим. На этот счет существуют компьютерные про-
граммы, которые вычленяют цепочки, описывающие косвенные
выявленные предпочтения на основе прямых выявленных пред-
почтений.
Если наблюдения за поведением потребителя на рынке осу-
ществлялись на продолжительном временнбм промежутке, то,
скорее всего, СиАВП не будет выполняться, ибо потребитель мо-
жет перейти на другую шкалу предпочтений.
В связи с тем что цепочку, состоящую из к звеньев прямых
выявленных предпочтений
х1 /х2,?/?, ...,хк~1 >* хк,
можно заменить на цепочку, состоящую из одного звена косвен-
ных выявленных предпочтений
X1 >* хк,
СиАВП можно перефразировать так: если х1 >-* хк (прямо или кос-
венно), то неверно, что хк >* х1.
3.3.7. Отметим, что до этого момента явно или неявно использо-
валась предпосылка о строгой выпуклости предпочтений потре-
бителя, что означает в случае наличия линий безразличия их стро-
гую выпуклость к точке О и, следовательно, касание бюджетной
прямой только в одной точке.
Если отказаться от предпосылки о строгой выпуклости пред-
почтений потребителя, оставив предпосылку о выпуклости пред-
почтений потребителя, то от СиАВП можно перейти к обобщенной
аксиоме выявленных предпочтений (ОбАВП), которая формулиру-
ется так: еслих1 >-*хк (прямо или косвенно) их1*хк, то неверно,
чтох^’х1.
Отношение х* >-* х* рассматривается при предпосылке о вы-
пуклости предпочтений потребителя, а отношение х* >-* х1 — при
предпосылке о строгой выпуклости предпочтений потребителя.
79
Имеет место теорема Эфриата.
Теорема Эфриата
Для того чтобы данные о потребительском поведении индивиду-
ума соответствовали ОбАВП, необходимо и достаточно, чтобы в
основе потребительского поведения лежали рациональные предпоч-
тения.
Приведем формулировку ослабленной версии теоремы Эф-
риата:
Пусть потребительские предпочтения индивидуума строго
выпуклы, тогда для того, чтобы данные о потребительском пове-
дении индивидуума соответствовали СиАВП, необходимо, чтобы
в основе потребительского поведения лежали рациональные
предпочтения.
Доказательства этих двух теорем достаточно сложны и поэто-
му являются необязательными.
Обратная задача теории потребительского спроса и теоремы
Эфриата подробно представлены в главе 5 монографии В.К. Гор-
бунова (2004).
3.4. Связь между теорией
выявленных предпочтений и индексами цен
3.4.1. Для анализа динамики благосостояния используются ин-
дексы цен и дохода, а также индексы объемов. В теории индексов
принято сопоставлять величины двух периодов: текущего и базо-
вого (базисного). Величины, привязанные к базовому периоду,
имеют индекс 0 (или Ь), величины, привязанные к текущему пе-
риоду, — индекс 1 (или /). Базовый и текущий периоды могут
быть, а могут не быть соседними. Обычно в качестве периода бе-
рут один год.
Вектор х = (Xj,..., хл) представляет собой потребительский на-
бор (потребительскую корзину), вектор р = (рр ...,рл) — это вектор
цен. Далее элементы теории индексов описываются для случая
п = 2. Общий случай п > 2 по существу не отличается от случая п = 2.
Индекс (номинального) дохода определяется так:
^х’+^х*
хо. оо’
Р\ *1 +
80
Он показывает, во сколько раз вырос (если I> 1) или снизился
(если /< 1) номинальный доход потребителя в текущем периоде
по сравнению с базовым периодом. Индекс номинального дохода
сам по себе не может служить показателем динамики реального
благосостояния потребителя, ибо номинальный доход может вы-
расти за счет, например, роста цен.
В индексе цен
= р\хх+р\х2
Р _0v . О
Р\ Х1 + &2Х2
цены меняются от базового периода к текущему периоду, а потре-
бительский набор х— (хр х2) остается неизменным.
Если потребительский набор берется в базовом периоде,
т.е. х° = (х°; х°), то имеем индекс цен Ласпейреса
n’r°4- n*r0
r(£) Р\ХХ +Р2Х2 .
Р ЛМ . „0 0 ’
Р1*1 + Р2Х2
если потребительский набор берется в текущем периоде,
т.е. х1 = (х{; х2), то имеем индекс цен Пааше
т(Р}=р\Х\+р\Х\
Р PlXi+P2Xl2
Индекс цен Ласпейреса показывает, во сколько раз выросла
стоимость р[ х® +р2х° = р'х0 потребительского набора х° базового
периода в текущих ценах относительно стоимости р°х° этого же
потребительского набора х° в базовых ценах р°. Индекс цен Пааше
показывает, во сколько раз выросла стоимость р}х{ + р2х2 = р1х1
потребительского набора х1 текущего периода в текущих ценах
относительно стоимости р°х* этого потребительского набора х1 в
базовых ценах р°. Индексы цен Ласпейреса и Пааше сами по себе
не могут служить показателями динамики реального благосостоя-
ния, ибо они не привязаны к динамике дохода потребителя. Ин-
дексы цен Ласпейреса и Пааше характеризуют динамику цен.
Однако оба индекса цен не дают верного представления об изме-
нении цен, ибо не учитывают влияния этого изменения на струк-
туру потребления. Например, если р[ > р°, то х{ < х°, и наоборот,
если р{ < р°, то х{ > х°. Поэтому индекс цена Ласпейреса I^L\ в ко-
тором в качестве весов фигурируют координаты (х°, х°) потреби-
тельского наборах0, дает преувеличенное представление об изме-
6 - 7620
81
нении цен (от р° = (р®, р°2) к р{ = (р[, р2)) в случае их роста и пре-
уменьшенное — в случае их снижения. Индекс цен Пааше 1^,
в котором в качестве весов фигурируют координаты (х{, х2) потре-
бительского набора х1, дает преуменьшенное представление об
изменении цен в случае их роста и преувеличенное — в случае их
снижения.
В индексе уровня жизни (индексе объемов)
у ^Р1Х1+Р2Х1
объемы х( и х2 меняются от базового периода к текущему периоду,
а цены р{ и р2 остаются неизменными.
Если используются ценыр° = (р^,р2) базового периода, то име-
ем индекс уровня жизни (индекс объемов) Ласпейреса
тШ ^Рй\х\+Р2Х\.
х 0 0 0 0’
Pi *1 + PtX2
если используются ценыр' = (р\,р\) текущего периода, имеем ин-
декс уровня жизни (индекс объемов) Пааше
r(P^PlXtl+P2X2
Х пМхпМ'
Р]Х1 + р2Х2
Индексы уровня жизни (индексы объемов) Ласпейреса и Па-
аше являются индексами реального дохода потребителя, ибо в
этих индексах цены неизменные.
3.4.2. Используем теорию выявленных предпочтений и тео-
рию индексов для оценки динамики благосостояния потреби-
теля при переходе от базового периода к текущему. Если < 1,
то р®х{ + р^х\ < р^х®+р2х2, что °значает> чт° х° >"* х*> т.е. потреби-
тельский набор х° базового периода выявленно предпочитается
потребительскому набору х1 текущего периода, откуда следует,
что в базовом периоде благосостояние потребителя лучше, чем в
текущем периоде.
Таким образом, неравенство < 1 означает, что при перехо-
де от базового периода к текущему благосостояние потребителя
снизилось.
Если > 1, тоР|Х} + р2х\ >р®х®+р2х2. Это означает, что в ба-
зовом периоде текущий потребительский набор х1 = (х[, х12) потре-
бителю недоступен. В теории выявленных предпочтений сопо-
82
ставляются только доступные потребителю пары наборов. Если
среди пары наборов есть недоступный потребителю набор, то эти
наборы не сопоставляются, ибо недоступный потребителю набор
может быть для потребителя более или менее предпочтительным,
чем доступный потребительский набор.
Следовательно, неравенство > 1 не дает однозначного от-
вета о росте или снижении благосостояния при переходе от базо-
вого периода к текущему.
Если/^> 1,то
р\Х\+р\Х\^р\Х*+р\^2.
Это означает, что х* >-* х°, т.е. потребительский набор х1 теку-
щего периода выявленно предпочитается потребительскому на-
бору х° базового периода, откуда следует, что в текущем периоде
благосостояние потребителя лучше, чем в базовом периоде.
Таким образом, неравенство > 1 означает, что при перехо-
де от базового периода к текущему благосостояние потребителя
выросло.
Если< 1, тор[х} +р12Х12<р1{Х°1 +/>2х2-
Этот случай аналогичен случаю > 1. Здесь нет однозначно-
го ответа о росте или снижении благосостояния потребителя при
переходе от базового периода к текущему периоду.
3.4.3. Сопоставим между собой индексы (номинального) дохода
и индексы цен Ласдейреса и Пааше.
^Xi' + ^xj р/хр + ^хв
Если 1> ТО _0 О . 0 0 - 0 0 . 0 0 *
Р АХ1 + Р2Х2 "1Х1 +Р2х2
После сокращения на общий знаменатель получаем, что
х{ +Рзх2 ^р\+ />|*2- ®Т0Т случий У*е разобран выше (см. 1^ >1).
Здесь мы имеем х1 >-* х°, т.е. при переходе от базового периода к
текущему благосостояние потребителя выросло.
Случай 1< 1^ сводится к случаю < 1, так что здесь нет од-
нозначного ответа о росте или снижении благосостояния потре-
бителя при переходе от базового периода к текущему.
Случаи 1< 1^ и /> № вполне аналогичны случаям < 1 и
1{х ' > 1. В случае /< благосостояние потребителя в базовом
периоде лучше, чем в текущем периоде. В случае /> нет одно-
значного ответа о росте или снижении благосостояния при пере-
ходе от базового периода к текущему.
6»
83
На практике индексы цен и дохода формируются для страны в
целом или для отдельных регионов, поэтому в качестве потреби-
теля должен фигурировать средний потребитель страны или отде-
льного региона. Потребительский набор среднего потребителя
есть потребительская корзина всего населения страны или отде-
льного региона, поделенная на численность населения страны
или отдельного региона.
Вопросы для самоконтроля к главе 3
1. Сформулируйте основные предпосылки теории выявленных пред-
почтений.
2. Сформулируйте определение выявленного предпочтения (прямого и
косвенного).
3. В чем отличие теории выявленных предпочтений от трех других тео-
рий потребительского предпочтения (теории количественной полез-
ности, теории порядковой полезности, теории отношения предпоч-
тения-безразличия)?
4. Что следует понимать под результатом наблюдения за поведением
потребителя на рынке?
5. Что представляет собой качественная характеристика линии безраз-
личия с точки зрения теории выявленных предпочтений?
6. Приведите формулировку слабой аксиомы выявленных предпочтений
(СлАВП) и ее экономическую и геометрическую интерпретации.
7. Опишите ситуацию, когда СлАВП не имеет места, а также экономи-
ческую и геометрическую интерпретации этой ситуации.
8. В чем суть проверки поведения потребителя на рынке на соответ-
ствие СлАВП?
9. Приведите формулировку сильной аксиомы выявленных предпочте-
ний (СиАВП) и ее экономическую и геометрическую интерпретации.
10. Опишите ситуацию, когда СиАВП не имеет места, а также экономи-
ческую и геометрическую интерпретации.
11. В чем суть проверки поведения потребителя на рынке на соответ-
ствие СиАВП?
12. Приведите вторую формулировку сильной аксиомы выявленных
предпочтений.
13. Приведите формулировку обобщенной аксиомы выявленных пред-
почтений.
14. Приведите формулировку теоремы Эфриата и формулировку ее ос-
лабленной версии.
15. Выпишите выражение индекса дохода и дайте ему экономическое
толкование.
16. Выпишите выражение индекса цен Ласпейреса и дайте ему экономи-
ческое толкование.
84
17. Выпишите выражение индекса цен Пааше и дайте ему экономичес-
кое толкование.
18. Выпишите выражение индекса объемов Ласпейреса и дайте ему эко-
номическое толкование.
19. Выпишите выражение индекса уровня жизни (индекса объемов Па-
аше) и дайте ему экономическое толкование.
20. Опишите связь теории индексов цен, уровня жизни (объемов) и тео-
рии выявленных предпочтений.
21. Опишите связь теории индексов цен и дохода и теории выявленных
предпочтений.
Задачи и упражнения для самоконтроля к главе 3
1. Приведите геометрический пример ситуации (п = 2), когда цена на
первый продукт растет (р* >/>}, = р^) и имеет место СлАВП.
2. Приведите геометрический пример ситуации (п = 2), когда цены
на первый продукт растут (р\ > р* > р[, р^ = р\ = р\) и имеет место
СиАВП.
3. Результаты трех наблюдений за поведением потребителя на рынке
представлены в табл. 3.4 (все числа условные):
Таблица 3.4
Номер наблюдения Цены Выбираемые потребительские наборы
Р\ Рг *1
1 2 2 3 4
2 4 1 4 2
3 1 3 2 4
а) постройте матрицу Л;
б) проверьте выполнение СлАВП на двух парах потребительских
наборов х1 их2, а такжех2 их3;
в) проверьте выполнение СиАВП на полном наборе х1, х2, х3;
г) дайте геометрическую интерпретацию результатам трех наблю-
дений;
д) сопоставьте результаты аналитической и геометрической прове-
рок выполнения СлАВП и СиАВП.
4. Постройте три потребительских набора х1, х2 и х3, такие, что СлАВП
для наборов х1, х2 не имеет места, СлАВП для наборов х2, х3 имеет
место, СиАВП для всей совокупности потребительских наборов
х1, х2, х3 имеет место (не имеет места).
85
5. Потребитель расходует весь свой доход на приобретение трех про-
дуктов: (7р (72, Gy В таблице содержатся данные о ценах и объемах
потребления каждого продукта в периодах 1, 2, 3.
Период Объемы продуктов Цены
Х1 Х2 хз Р\ Рг Рз
1 5 6 7 10 25 30
2 6 5 6 20 50 70
3 6 5 7 30 80 90
Оцените изменения благосостояния потребителя:
а) в период 2 по сравнению с периодом 1;
б) в период 3 по сравнению с периодом 2;
в) в период 3 по сравнению с периодом 1.
Ответы обоснуйте. 1
6. Функция полезности потребителя имеет вид U(x{, х2)=(xt - 2)1/3 • х2 /з,
где Xj и х2 — количества потребляемых продуктов. В базовом периоде
потребитель, располагающий доходом = 32 денежных единицы,
приобрел х2 = 10 при Pt = 1. В текущем периоде номинальный доход
вырос до Мх = 94 денежных единицы, х21 = х2 = 10, = 2. Вычислите
индекс цен Ласпейреса.
Вопросы, тесты и задачи для контрольных работ к главе 3
1. Приведите геометрический пример ситуации (п = 2), когда цена на
первый продукт растет (р* >р}, р2 = р2) и СлАВП не имеет места.
2. Приведите геометрический пример ситуации (п = 2), когда цены на
первый продукт растут (р3 > р] > р}, р2 = р2 = р2) и СлАВП не имеет
места.
3. Потребитель расходует весь свой доход на приобретение трех про-
дуктов: <7р (72, Gy В таблице содержатся данные о ценах и объемах
потребления каждого продукта в периодах 1, 2, 3.
Период Объемы продуктов Цены
*1 Х2 *3 Pi Рз Рз
1 5 6 7 12 5 15
2 6 7 8 28 15 40
3 8 9 6 25 12 35
86
Оцените изменения благосостояния потребителя:
а) в период 2 по сравнению с периодом 1;
б) в период 3 по сравнению с периодом 2;
в) в период 3 по сравнению с периодом 1.
Ответы обоснуйте. 1 2
4. Функция полезности потребителя имеет вид U(xv х2)=-4) /з • х2 /з,
где и х2 - количества потребляемых продуктов. В базовом периоде
потребитель, располагающий доходом = 64 денежных единицы,
приобрел х2 = 20 при р® = 1. В текущем периоде номинальный доход
вырос до М1 = 136 денежных единиц, х} = 2, х2 = 22. Вычислите ин-
декс объемов Пааше.
Глава 4
УЧЕТ СВОЙСТВ ПРОДУКТОВ
ПРИ МОДЕЛИРОВАНИИ
ПОТРЕБИТЕЛЬСКОГО ПОВЕДЕНИЯ
(ТЕОРИЯ ТЕХНОЛОГИИ
ПОТРЕБЛЕНИЯ)
4.1. Продукты и их свойства.
Предпосылки о квантифицируемости,
аддитивности и однородности свойств
4.1.1. Потребитель выбирает потребительский набор х°=(х°,..., х°)
для удовлетворения своих потребительских амбиций. Однако час-
то потребителя интересуют не столько сами продукты (товары),
сколько их свойства (их характеристики), носителями которых
являются эти товары. Например, потребитель приобретает теле-
визор не столько для мебели (хотя и не без этого), сколько для
того, чтобы с его помощью получать видео- и аудиоинформацию.
Здесь телевизор — это продукт (товар), а информация и мебель —
его свойства (его характеристики).
Покупая билет на самолет, потребитель арендует это транс-
портное средство (наряду с другими пассажирами) для того, что-
бы преодолеть определенное расстояние. Здесь самолет — продукт
(товар), а преодоление расстояния между городами — свойство
(характеристика) данного (и других) транспортного средства.
Свойства (характеристики) продуктов (товаров) более консер-
вативны во времени, чем сами продукты (товары). Информацию в
разные эпохи передавали с использованием костров, голубей, ра-
88
диоприемников, телевизоров. Перемещение в пространстве осу-
ществлялось с помощью лошадей, автомобилей, самолетов и т.п.
Таким образом, естественно рассматривать не только потре-
бительские наборы, но и наборы их свойств (характеристик). Для
того чтобы рассматривать наборы свойств, необходимо эти свой-
ства квантифицировать, т.е выявлять. Если свойство (характерис-
тика) не выявляется, оно (она) для моделирования не существует.
Таким образом, свойства (характеристики) предметов должны
удовлетворять следующим предпосылкам.
1. Свойства (характеристики) квантифицируются, т.е. они вы-
явлены и могут быть описаны не только качественно, но и коли-
чественно. Например, в одной единице продукта содержится ап
единиц свойства А р а21 единиц свойства Л2,..., ат1 свойства Лт.
2. Имеет место однородность: если одна единица продукта б?,
содержит atj единиц свойства Ар то х. единицы продукта G. содер-
жат а...х. единиц свойства Аг
3. Имеет место аддитивность: если х. единиц продукта б?. со-
держат а.уХ. единиц свойства А., а хк единиц продукта Gk содержат
a.ikxk единиц свойства Ар то х(. единиц продукта G. и хк единиц про-
дукта Gk содержат и..^х. + а.1кхк единиц свойства Аг
4.1.2. На основании приведенных предпосылок получаем модель
технологии потребления
°1 = аих1+ +а1Л> И-1-1)
Wl++Vn’
где х = (хр ..., хя) — потребительский набор, a — количество
свойства At в потребительском наборе х; ... ат — количество
свойства Ат в потребительском наборе х. По экономическому
смыслу все коэффициенты > 0, все Xj > 0, все a.j > 0, i = 1,..., т,
J= 1, ..., п. На основании предпосылок 2 и 3 модель технологии
потребления является линейной.
Аналогом модели технологии потребления является извест-
ная задача о диете, в которой речь идет о потребительском наборе
х = (хр ..., хл) из продуктов (7р ..., Gn, которые содержат т пита-
тельных веществ Ар ..., Ат. Требуется найти такую диету, которая
обеспечивала бы нормы ор ..., ат питательных веществ А{,..., Ат
и которая была бы самой дешевой:
89
YjXj + ...+у^ -> (min),
«11х1 + - + «1Л2:ор
«ж1Х1 + -+«жЛ^аж>
Xj>0, ...,хл>0,
где у —цены одной единицы продукта (?., j =1,п;
а.у — количество питательного вещества Л;. в одной единице
продуктаGj, i = 1,
В задаче о диете питательные вещества являются аналогами
свойств в модели технологии потребления.
4.2. Пространство продуктов и их свойств.
Свойства продуктов как объект
потребительского выбора
4.2.1. Пространство продуктов (потребительских наборов) — это
неотрицательный ортант £л+ = {(х(,..., хя) | Xj £ 0,..., хп > 0} «-мер-
ного пространства Еп. Пространство свойств — это неотрицатель-
ный ортант Е* = {(ар ат) | а{ > 0, ат > 0} m-мерного про-
странства Ет.
Выражения (4.1.1)—(4.1 .т) переводят неотрицательный ортант
Ея в конус С, расположенный в неотрицательном ортанте Е*. На-
пример, ось Ох, = {(Xj,..., хл) | х( > 0, х2 =...=хп = 0} переходит в луч
OLj = {(ар ..., а ) | а, = анхр ..., ат = amlxpX] > 0} неотрицатель-
ного ортанта Е±, а ось Охл = {(хр ..., хл) | xt =...=хл_, = 0, хл > 0} —
в луч OL = {(в., ...,«)!«.= а, х...а= ах. х„ £ 0}. Точка
В{ = (М/р{, 0,..., 0) бюджетной плоскостир{х{ + ... + рпхп = Мпе-
реходит в точку С] = (ап М/рх, ..., ат1 М/р^) луча О£р ..., точка
Вп = (М/рп, 0,.... 0) переходит в точку Qn = (а[пМ/рп,..., аппМ/рп)
луча О£л. Поскольку модель технологии потребления (4.1.1)—
(4.1 .т) с математической точки зрения есть линейное отображе-
ние неотрицательного ортанта Ея в неотрицательный ортант,
постольку образом бюджетной плоскости р{х{ + ... +рпхп = М
(Xj > 0,..., хл > 0) является выпуклая комбинация точек 5р ..., Вп
в неотрицательном ортанте Е*. Проиллюстрируем переход из
пространства продуктов в пространство свойств на примере 4.2.1.
90
Пример 4.2.1
Цена рх одной единицы продукта Gx равна рх = 4, ценар2 = 3,
цена р3 = 7, доход потребителя равен М = 12. В одной единице
продукта Gx имеется 0,4 единицы свойства Ах и 0,3 единицы
свойства А2, т.е. ап = 0,4; а21 = 0,3; в одной единице продукта G2
имеется 0,6 единицы свойства Ах и 0,8 единицы свойства А2,
т.е. а12=0,6; =0,8; в одной единице продукта (73 имеется 0,7 еди-
ницы свойства Ах и 0,7 единицы свойства А2, т.е. а13 = = 0,7.
Координаты точек Вх, В2, В3 в пространстве продуктов соот-
ветственно равны Вх = (М/рх; 0; 0) = (3; 0; 0), В2 = (0; М/р2, 0) =
= (0; 4; 0), В3 = (0; 0; М/р-^ = (0; 0; 12/7) (рис. 4.1, на котором бюд-
жетная плоскость 4х( + Зх2 + 7х3 = 12 изображается треугольни-
ком ВХВ2В-^.
Модель технологии потребления (4.1.1)—(4.1.т) в этом приме-
ре имеет вид (п = 3, т = 2)
ах = 0,4х( + 0,6х2 + 0,7х3,
а2 = 0,3xt + 0,8х2 + 0,7х3.
Образом точки Вх = (3; 0; 0) является точка Qx = (аххМ/рх,
®2i-^/P|) = (0,4-3; 0,3 • 3) = (1,2; 0,9), образом точки В2 = (0; 4; 0) —
точка Q2 = (ах2М/р2, а22М/р2) = (0,6 • 4; 0,8 • 4) = (2,4; 3,2), образом
точки В3 = (0; 0; 12/7) является точка Q3 = (а13М/р3, а23М/р3) =
91
= (0,7 • n/7; 0,7 • 12/7) =(1,2; 1,2) (рис. 4.2, на котором также показа-
ны лучи О£р OZ2, QLy которые являются образами в простран-
стве свойств осей Охр Ох2, Ох3 пространства продуктов). Образом
бюджетной плоскости ВХВ2В3 в пространстве продуктов является
треугольник Q{Q2Q3 в пространстве свойств.
Образом бюджетного множества 4xj + Зх2+7х3 < 12, х( > 0, х2 > 0,
х3 > 0 (множества ОВХВ2В3 - см. рис. 4.1) в пространстве продук-
тов является выпуклая оболочка точек О, Ср Qv Q3 (см. рис. 4.2).
4.2.2. По аналогии с задачей рационального поведения потреби-
теля на рынке
Щхх, ..., хи) -> max (4.2.1)
при наличии ограничения
р1х1 + ...+рпхп<М, (4.2.2)
х, >0, ...,хй>0 (4.2.3)
ставится задача выбора оптимальной комбинации свойств
(а..., ат) в следующей постановке:
W(a j,..., om) -> max (4.2.4)
при наличии ограничений (4.1.1)—(4.1./и), а также ограничений
(4.2.2) и (4.2.3). Задача выбора оптимальной комбинации свойств
сводится к следующей задаче рационального поведения потреби-
теля на рынке (4.2.1)—(4.2.3), в которой
U{xx,...,xl)= (4 2 5)
= lF(a11x1 + ...+fl1„x„ + ...+amlx1 + ...+V„). ’ >
Решив задачу (4.2.1)—(4.2.3), в которой целевая функция
С7(хр...,хл) имеет представление (4.2.5), получим набор х =
= (х, ...,£„), который выбирает потребитель, и по формулам
(4.1.1)—(4.1.т) найдем оптимальную комбинацию Ц, ...,ат)
свойств.
4.3. Неявные цены свойств и уравнения
для их определения
4.3.1. Каждый продукт <7р ..., Gn имеет свою цену рр ..., рп.
У свойств А}, ...,Ат цен нет. Можно поставить вопрос об опреде-
лении неявных цен vp ..., vm свойств, которые были бы аналогич-
ны ценамр{, ...,рт.
92
Неявные цены vp vm свойств Ах, ..., Ат можно определить,
используя следующие соображения.
Если а = (о,, .... ат), набор свойств потребительского набора
х=(хр ..., хл), то естественным должно быть равенство
vi°i + ••• +V. = М=рххх + ... +рихп, (4.3.1)
т.е. общая «стоимость» набора свойств а = (ар ..., ат) в неявных
ценах Ур .... vm должна равняться общей стоимости потребитель-
ского наборах=(хр ...,хл)вценахрр ...,рп, т.е. числу М.
Одна единица первого продукта (7, имеет представление в виде
вектора (ап, ...» ат1), координаты которого равны количествам
свойств (Лр ..., Лт), содержащимся в этой единице продукта (7Г
Поскольку единица продукта покупается ради приобретения ко-
личеств составляющих ее свойств, то естественным должно быть
равенство
/’i = vian + -+vAr (4.3.2)
Аналогично выписываются равенства
P2 = v1a12 + ... + vmam2,
^ = ViaU+-+Vm«m«- <4-3-3)
Система уравнений (4.3.1), (4.3.2), (4.3.3) для определения не-
явных цен Vp ..., vm свойств Ар ..., Ат выписывается как двой-
ственная (сопряженная) система к системе уравнений
vi *1=anx1+...+aI„x„,
Vm em=«mlXl+- + amn^>
М = рххх+...+рпхп
аналогично тому, как выписывается двойственная (сопряженная)
задача к задаче линейного программирования.
Вообще говоря, для системы (4.3.2), (4.3.3) линейных алгебра-
ических уравнений возможны три варианта ее разрешимости: су-
ществование единственного решения, существование бесконеч-
ного множества решений, полное отсутствие решений. С эконо-
мической точки зрения представляет интерес первый вариант, из
которого следует наличие единственной системы неявных цен
свойств. В случае выполнения третьего варианта система неявных
93
цен свойств не существует. Этот вариант возможен, если цены
,..., рп на продукты не соответствуют распределению свойств по
продуктам.
4.3.2. Рассмотрим ряд примеров.
Пример 4.3.1
Модель технологии потребления имеет вид
V] а( =0,3Xj +О,3х2, (4.3.4)
v2 о2=0,4х1+0,4х2, (4.3.5)
цены на продукты (7, и G2 соответственно равны рх = 12, р2 = 24,
доход потребителя равен М = 720. В рассматриваемом примере
система уравнений (4.3.2), (4.3.3) имеет вид
0,3Vj + 0,4у2 = 12,
0,3Vj + 0,4v2 = 24.
Ее несовместность очевидна.
Отображение (4.3.4), (4.3.5) переводит бюджетную прямую
В}В2 пространства продуктов (рис. 4.3) в отрезок С]С2 пространс-
тва свойств (рис. 4.4):
В отличие от ценр(, ...,рл на продукты^,..., Gn, которые всег-
да положительны, неявные цены vp..., vm свойств Л р ..., Ат могут
быть и отрицательными. Отрицательная цена ^.свойства А(свиде-
тельствует о том, что свойство является нежелательным для по-
требителя (например, наличие никотина в сигарете).
Таким образом, неявные цены свойств (если они существуют)
выступают в качестве индикаторов полезности свойств.
94
Пример 4.3.2
Модель технологии потребления имеет вид
Vj =0,4Х| + 0,6х2, (4.3.6)
v2 а2 = О,3х1 +0,5х2, (4.3.7)
цены на продукты (7, и G2 соответственно равнырх -4,р2 — 3, до-
ход потребителя равен М = 12. В рассматриваемом примере систе-
ма уравнений (4.3.2), (4.3.3) для определения неявных цен vp v2
свойств А (и Л2 имеет вид
0,4v1 + 0,3v2 = 4,
0,6Vj + 0,5v2 = 3.
Непосредственно проверяется, что единственное решение
v° = (v®; v2) этой системы имеет вид v° = (55; -60).
Отображение переводит бюджетную прямую В{В2 пространства
продуктов (рис. 4.5) в отрезок QXQ2 пространства свойств (рис. 4.6).
Рис. 4.5
Рис. 4.6
При п = 2 и т = 2 в примере 4.3.3 проиллюстрируем еще одну
характеристику неявных цен признаков.
Пример 4.3.3
Продукты <г( и G2 имеют цены рх = 3, р2 = 4, доход М= 12, мо-
дель технологии потребления имеет вид
у, =0,Зх1 +0,5х2, (4.3.8)
v2 = 0,5xj+0,2х2. (4.3.9)
95
В рассматриваемом примере система уравнений (4.3.2), (4.3.3)
имеет вид
0,3V] + 0,5v2 = 3,
0,5v( + 0,2v2 = 4.
Непосредственно проверяется, что единственное решение
v° = (v°; v2) этой системы имеет вид v0 = (140/19;
Отображение переводит бюджетную прямую В{В2 пространства
продуктов (рис. 4.7) в отрезок Q{Q2 пространства свойств (рис. 4.8):
Очевидно,
М
tg(p = 7 = ^ = ~
4 М р2
Pi
Имеем
2-0,6 1,4 14 у,0
“1,5-1,2“ 0,3 ” 3 v0'
V.
Формула tgy = —*- имеет место в общем случае, если неявные
V2
цены (у”; v2) свойств существует. В частности, в примере 4.3.2
2-0,9 1,1 55 г.0
tgV~ 2,4-1,2" 1,2"-60-у0’
96
Равенство tgy = -*r свидетельствует о том, что неявные цены
V2
действительно похожи на рыночные цены продуктов (товаров).
4.4. Оценка рыночной перспективы
нового продукта
4.4.1. Неявные цены свойств (если они существуют) могут ис-
пользоваться для оценки рыночной перспективы нового продук-
та. Проиллюстрируем это использование для случая п = т = 2.
Пусть модель технологии потребления имеет вид
а2 = °21Х1 "*
Цены продуктов и G2 соответственно равны рх и р2,доход
потребителя равен М. Пусть появляется продукт G3, в одной еди-
нице которого содержится свойство Ах в количестве а13 единиц,
а свойство А2 — в количестве единиц. Рыночная цена единицы
продукта G3 предполагается равной р3.
Требуется оценить рыночную перспективу продукта G3.
С появлением продукта G3 модель технологии потребления
приобретает вид
v, д,=апх1+а12х2+а13х3,
v2 а2= «21 + а22х2 + <х23х3,
а бюджетное ограничение М=рххх + р2х2 преобразуется в выраже-
ние М=рххх + р2х2 + р3х3.
С появлением нового продукта (73 новые свойства не появля-
ются. Для определения неявных цен свойств выписываем систему
линейных алгебраических уравнений
^ан + у2а21=р,,
v1a12 + v2a22=P2.
v1a13 + v2a23=p3.
Если система из первых двух уравнений имеет решение v° =
= (Vj; v2), то полагаемр3 = v°a13 + v2a23- Еслир3 >р3, то продукт G3
не имеет рыночной перспективы, ибо его цена р3 слишком высо-
ка. Если р3 < р3, то продукт (73 имеет рыночную перспективу.
’ - 7620
97
Таким образом, неявные цены свойств позволяют оценить
пороговую величину р3 цены продукта Gy
4.4.2. Пример 4.4.1
Пусть новый продукт <73 имеет цену р3 = 7 и в одной единице
продукта G3 содержится а13 = 0,8 единицы свойства А{ и Oj3 = 0,6
единицы свойства А2. Оценим рыночную перспективу продук-
та Gy
В примере 4.3.2 были найдены неявные цены = 55; v° = “60
свойств А । и Аг Найдем пороговую величину
р3° = a13v,° + a23v2° = 0,8 • 55 - 0,6 • 60 = 44 - 36 = 8 > 7 = р3,
из последней цепочки следует, что продукт G3 имеет рыночную
перспективу. Если бы р3 = 9, то тогда продукт G3 не имел бы ры-
ночной перспективы.
Вопросы для самоконтроля к главе 4
1. Как формулируются предпосылки модели технологии потребления?
2. Представьте модель технологии потребления в аналитической фор-
ме. Дайте геометрическую интерпретацию пространства продуктов и
пространства свойств.
3. В чем сходство и различие модели технологии потребления и задачи
о диете?
4. Как взаимосвязываются продукты, их свойства и фактор времени?
5. Что такое неявная цена свойства (продукта)? Как определяются но-
вые цены свойств продуктов?
6. В чем сходство и различие рыночных цен на продукты (товары) и
неявных цен признаков?
7. Как выразить доход потребителя, используя неявные цены свойств?
8. Как используются неявные цены для оценки рыночной перспективы
новых продуктов?
9. Какими полезными качествами обладают неявные цены свойств?
Задачи и упражнения для самоконтроля к главе 4
1. Цена Pi одной единицы продукта G{ равна />,=10, цена р2 одной еди-
ницы продукта G3 равна р2 =15. Доход потребителя равен М = 300.
В одной единице продукта G{ содержится 0,4 единицы свойства Л, и
0,3 единицы свойства Л2 (т.е. ан = 0,4; = 0,3). В одной единице
продукта G2 содержится 0,2 единицы свойства Л, и 0,6 единицы
свойства Л2 (т.е. а12 = 0,2; = 0,6):
98
а) выпишите модель технологии потребления;
б) постройте в пространстве продуктов бюджетную прямую
10xj + 15х2 = 300 и ее образ в пространстве свойств. Постройте
в пространстве свойств образ бюджетного множества 10xj + 15х2 <
< 300, Xj > 0, х2 > 0;
в) найдите неявные цены V® и v2 свойств A } и Л2;
г) найдите tgcp в пространстве продуктов и tgy в пространстве
свойств (см. рис. 4.7 и рис. 4.8);
д) оцените рыночную перспективу продукта G3, если а13 = 0,5;
«23 = 0,4; ир3 = 13 (р3 = 12).
Приведите пример модели технологии потребления (п = 2; т = 2),
в которой свойства не имеют неявных цен. Дайте геометрическую
интерпретацию образа бюджетной прямой в пространстве свойств.
Приведите примеры модели технологии потребления (п = 2; т = 2;
п = 3; т = 2), в которых неявные цены свойств не являются одно-
значными. Дайте геометрическую интерпретацию образа бюджет-
ного множества в пространстве свойств.
Вопросы, тесты и задачи для контрольных работ к главе 4
Модель технологии потребления позволяет определить (выберите
один вариант):
а) величины свойств, содержащихся в заданном потребительском
наборе;
б) потребительский набор, который содержит заданную конфигу-
рацию свойств;
в) неявные цены свойств, если известны рыночные цены товаров;
г) ответы а)—в) не верны.
Неявные цены свойств:
а) существуют и определяются единственным образом по рыноч-
ным ценам продуктов;
б) существуют и определяются не единственным образом по задан-
ным ценам продуктов;
в) не существуют при заданных ценах продуктов;
г) возможен только один из трех вышеперечисленных вариантов.
Неявные цены свойств всегда позволяют (укажите неверный ответ):
а) определить рыночные цены продуктов (товаров);
б) оценить уровень полезности свойства для потребителя;
в) определить пороговый уровень цены нового продукта;
г) их использовать в качестве анализа рыночных цен продуктов
(товаров) на воображаемом рынке свойств продуктов.
99
4. Ценар{ одной единицы продукта G{ равнар{ = 12, ценар2 одной еди-
ницы продукта G3 равна р2 = 16. Доход потребителя равен М= 480.
В одной единице продукта G{ содержится 0,5 единицы свойства А{ и
0,2 единицы свойства А2 (т.е. ап = 0,5; = 0,2). В одной единице
продукта G2 содержится 0,4 единицы свойства At и 0,3 единицы
свойства А2 (т.е. а12 = 0,4; = 0,3):
а) выпишите модель технологии потребления;
б) постройте в пространстве продуктов бюджетную прямую
12Xj + 16х2 = 480 и ее образ в пространстве свойств. Постройте в
пространстве свойств образ бюджетного множества 12х, + 16х2 <
<480,х1>0,х2>0;
в) найдите неявные цены V® и v2 свойств А1 и Л2;
г) найдите tgcp в пространстве продуктов и tgy в пространстве
свойств (см. рис. 4.7 и рис. 4.8). Сопоставьте тангенсы с рыноч-
ными ценами продуктов (товаров) и с неявными ценами свойств;
д) при а13 = 0,4; = 0,6 ир3 = 15 постройте в пространстве продук-
тов бюджетную плоскость 12х} + 16х2 + 15х3 = 480 и ее образ в
пространстве свойств. Постройте в пространстве свойств образ
бюджетного множества 12х3 + 16х2 + 15х3 = 480 < 480, > 0, х2 > 0,
х3>0;
е) найдите пороговое значение р3 цены нового продукта G3 и оце-
ните рыночную перспективу этого продукта, используя данные
пункта д).
Глава 5
ВЫБОР В УСЛОВИЯХ РИСКА
И НЕОПРЕДЕЛЕННОСТИ
5.1. Понятия риска и неопределенности
5.1.1. Экономический субъект (индивидуум), принимая то или
иное решение, не всегда может одинаково оценить его послед-
ствия. Например, приобретая акции некоторой фирмы, индиви-
дуум рассчитывает на получение дивидендов в определенном
объеме, исходя из картины текущей экономической конъюнкту-
ры. Однако в будущем конъюнктура может измениться далеко не
в лучшую сторону для фирмы, которая вынуждена будет перейти
на выплату дивидендов в гораздо меньшем объеме. Не исключен
вариант и банкротства фирмы в будущем.
Список примеров, когда экономические субъекты (индивиду-
умы) должны принимать решения в условиях неопределенности,
можно продолжать до бесконечности.
Понятие неопределенности является неоднозначным. Приня-
то говорить собственно о неопределенности, если множество вари-
антов возможных исходов (последствий) принимаемого решения
известно, но ни одному из этих вариантов нельзя приписать ка-
кую-либо вероятность его появления или хотя бы оценить ее. Ес-
ли варианты возможных исходов (последствий) характеризуются
вероятностями их появления, то говорят о ситуации риска.
Здесь приведен один из ранних и простейших вариантов тол-
кования связанных между собой понятий риска и неопределен-
ности, на который далее опирается излагаемый материал. Другие,
более продвинутые варианты толкования понятий неопределен-
ности и риска широко представлены в специальной литературе и
в этой книге не рассматриваются.
101
Индивидуум (субъект), который выбирает из нескольких аль-
тернатив, может опираться на объективные вероятности послед-
ствий принимаемого решения. Объективные вероятности могут
основываться, например, на проведенных статистических иссле-
дованиях.
Вероятности могут быть субъективными. Возможна ситуация,
когда при подготовке и принятии решения индивидууму прихо-
дится учитывать как объективные, так и субъективные вероятнос-
ти. В дальнейшем под термином «риск» понимается в основном
экономический риск.
Наиболее важные решения, принимаемые индивидуумом в
условиях риска, связаны не столько с покупкой тех или иных
потребительских благ (хотя покупка потребительских благ быва-
ет связана с риском, например покупка автомобилей, дорогой
бытовой техники, недвижимости), сколько с разумными финан-
совыми операциями (страхование, покупка и продажа ценных
бумаг, выбор пенсионного фонда, выбор валюты для сбережения
денег и т.п.). Поэтому в дальнейшем уровень и полезности по-
требителя будет увязан с его доходом w, который является слу-
чайной величиной, т.е. функция и = u(w) полезности потреби-
теля будет функцией только его дохода, а не потребительского
набора, как это обычно принято в теории потребления. Вопросы
дисконтирования уровня полезности во времени рассматривать-
ся не будут.
Экономический риск представляет собой опасность возник-
новения неожиданных потерь ожидаемой прибыли или дохода в
связи со случайным изменением экономической конъюнктуры.
Риск возникает, когда экономическая деятельность осуществля-
ется в ситуации неопределенности из-за информационного дефи-
цита, и по этой причине достижение ожидаемого результата не
гарантируется.
Природа риска может быть объективной, субъективной и
субъективно-объективной.
Субъективная природа риска проявляется в том, что риск мо-
жет быть связан с использованием субъективных вероятных оценок
выбираемых альтернатив, а также с тем, что разные индивидуумы
по-разному относятся к риску. Есть рискофобы (индивидуумы,
которые относятся к риску отрицательно, и таких индивидуумов,
в том числе среди предпринимателей, большинство), рискофилы
(индивидуумы, которые относятся к риску положительно, т.е. лю-
102
бят рисковать) и рисконейтралы (индивидуумы, которые относятся
к риску безразлично).
Объективная природа риска проявляется в том, что объектив-
но существует вероятностная сущность многих природных, соци-
альных, технологических явлений, многовариантность матери-
альных и нематериальных отношений между индивидуумами.
Ситуация риска часто существует объективно, независимо от то-
го, учитывают ее при принятии решений или не учитывают.
Субъективно-объективная природа риска проявляется в том,
что ситуация риска может возникать в результате функциониро-
вания процессов субъективного и объективного характера, соче-
тание которых может быть как управляемым, так и неуправля-
емым. В качестве примера ситуации субъективно-объективной
природы риска можно указать ситуацию использования авиаци-
онной техники в условиях джунглей, когда к традиционным объ-
ективным факторам риска добавляются субъективные, которые
проявляются в том, что крысы могут прогрызть изоляцию прово-
дов, а у пилотов замедляется реакция на те или иные штатные и
нештатные ситуации во время взлета или посадки самолета.
5.1.2. В качестве основных причин неопределенности и риска
можно отметить следующие.
1. Стихийные бедствия (землетрясения, ураганы, бури, на-
воднения), а также некоторые природные явления (грозы, град,
поздние и ранние заморозки, засуха) могут оказать серьезное от-
рицательное влияние на результаты предпринимательской или
иной деятельности, стать источником неожиданных издержек.
2. Элементы случайности имеют место, когда в условиях, ко-
торые мало отличаются друг от друга, одни и те же процессы про-
текают неодинаково. Из-за этого бывает невозможно однозначно
предвидеть появление предполагаемого результата.
Например, невозможно точно предсказать, сколько человек
купит билеты на премьеру нового кинофильма. Отмеченное об-
стоятельство может оказать существенное влияние на принятие
решения о выборе того или иного кинотеатра для демонстрации
этого фильма.
Не всегда предсказуемое влияние на результаты предприни-
мательской деятельности оказывают аварии (пожары, взрывы,
ядовитые выбросы), выход из строя оборудования, несчастные
случаи на производстве и т.п.
103
Перечисленные случайные события, к сожалению, вполне
возможны, несмотря на высокие реальные достижения по их пре-
дупреждению.
3. Столкновения противоречивых интересов проявляются на
широком поле деятельности индивидуумов: от локальных и гло-
бальных войн до элементарного выяснения отношений между
индивидуумами. В результате объявления войны предпринима-
тель может столкнуться с запретом на совершение сделок или
экспроприацией активов либо доходов за рубежом.
В конкурентной борьбе могут появиться (проявиться) элемен-
ты недобросовестной конкуренции, когда используются такие
недозволенные средства, как подкуп должностных лиц, дискре-
дитация конкурента, организация процедуры банкротства конку-
рента.
В инновационном процессе его разные участники могут зани-
мать различные и даже противоположные позиции. Обычно по-
зицию инициативы занимают разработчики, позицию содей-
ствия — проектировщики, позицию бездействия — пользователи.
В связи с неизбежной перестройкой технологических процессов,
требуемой инновациями, возникают новые организационно-тех-
нологические проблемы.
Таким образом, наличие противоборствующих сторон в обще-
ственно-экономическом развитии страны вносит в социально-
экономическую жизнь элементы неопределенности.
4. Вероятностный характер научно-технологического про-
гресса (НТП) является очередной причиной появления неопреде-
ленности и риска. Заранее трудно, а то и невозможно предсказать
с большой точностью появление того или иного открытия, зара-
нее определить конкретные его последствия. Вложения в НТП
всегда характеризовались как крайне рискованные. Это с одной
стороны. С другой стороны, без этих вложений не были бы реали-
зованы такие достижения НТП, как телекоммуникационные сис-
темы, вычислительные системы и т.п.
5. Неполнота, недостаточность информации о том или ином
явлении или процессе — следующая причина возникновения неоп-
ределенности и риска.
Наличие достаточно полной и правильной информации необ-
ходимо для подготовки и принятия решения. Такая информация
предполагает осведомленность о наличии и величине спроса на
товары и услуги, на капитал, о финансовой устойчивости и плате-
104
жеспособности будущих партнеров, конкурентов, клиентов,
о ценах, курсах, тарифах, о характеристиках оборудования и но-
вой техники и т.п. На практике такая информация бывает разно-
плановой, подготовленной по не вполне ясным методикам.
Информация может быть искаженной, сфальсифицирован-
ной (например, фирма «Майкрософт» в ранний период ее функ-
ционирования).
Известны случаи, когда фирмы-лидеры делали объявления о
перспективных, но достаточно дорогостоящих проектах, а фирмы-
последователи в рамках подражательного поведения вкладывали в
эти проекты большие средства, после чего фирмы-лидеры объяв-
ляли об ошибочности этих проектов, что приводило к существен-
ному ухудшению положения конкурентов или их разорению.
Таким образом, чем ниже качество информации (независимо
от источника ее поступления), необходимой для принятия реше-
ний, тем выше риск появления отрицательных последствий тако-
го решения.
Список причин неопределенности и риска можно дополнить
такими позициями.
6. Ограниченность ресурсов, необходимых для принятия и
реализации решений.
7. Невозможность однозначного понимания объекта, относи-
тельно которого должно быть принято решение.
8. Относительная ограниченность сознательной деятельности
индивидуумов, наличие существенных различий в социально-
психологических установках, стереотипах поведения.
9. Частичное или полное функционирование фирмы в рамках
теневого сектора, что приводит к расширению поля ее факторов
риска.
10. Необходимость использования новых средств и методов
для решения производственных задач при смене модели хозяй-
ствования.
11. Наличие несбалансированности основных компонентов
хозяйственного механизма: планирования (стратегического), це-
нообразования, материально-технического снабжения, денежно-
кредитных отношений.
В экономической теории риска анализируются ситуации, свя-
занные с риском, исследуются вопросы количественного измере-
ния риска, формулируются принципы принятия решений в усло-
виях риска. С математической точки зрения многие задачи эконо-
105
мической теории риска сводятся к описанию правил сравнения
случайных величин будущих благ (в частности, дохода). При срав-
нении вероятности распределений необходимо одновременно
учитывать как средние значения случайной величины (понима-
емые в разных смыслах), так и характеристики разброса (диспер-
сии, среднеквадратичные отклонения и др.) значений случайных
величин относительно средних значений.
5.2. Общие принципы классификации рисков
5.2.1. В экономической литературе нет общепринятой системы
классификации рисков и, в частности, хозяйственных рисков.
Рассматриваемая ниже классификация рисков охватывает следу-
ющие важные элементы: время возникновения рисков, основные
факторы возникновения рисков, характер учета рисков, характер
последствий, сфера возникновения рисков.
По времени возникновения риски распределяются на ретро-
спективные, текущие и перспективные. Результаты анализа рет-
роспективных рисков могут помочь в более точном прогнозиро-
вании текущих и перспективных рисков.
По основным факторам возникновения риски подразделяются
на политические и экономические (коммерческие).
Политические риски — риски, появление которых обусловле-
но теми или иными политическими решениями, оказывающими
существенное влияние на экономическую деятельность (повыше-
ние пошлин и понижение квот на ввозимые продукты (товары),
например актуальное для автопрома современной России значи-
тельное повышение пошлин на ввозимые подержанные иномар-
ки, начало военных действий в отдельных регионах страны (Чеч-
ня, Югославия, Ирак) и т.п.).
Экономические риски — риски, появление которых обуслов-
лено неблагоприятными изменениями в мировой, национальной
или региональной экономиках, в деятельности фирм. В частнос-
ти, имеются в виду резкие колебания мировых цен на нефть и
другие изменения в конъюнктуре рынков товаров, ресурсов, цен-
ных бумаг, несбалансированная ликвидность, когда нет возмож-
ности своевременно выполнить платежные обязательства.
Политические и экономические риски на практике могут
быть трудноразличимыми. Например, резкие колебания мировых
106
цен на нефть могут быть отнесены к факторам политических и
экономических рисков.
По характеру учета риски делятся на связанные с деятельнос-
тью экономического субъекта (в частности, фирмы). К факторам
внешних рисков, естественно, относятся факторы политические,
глобальные и макроэкономические, демографические, социаль-
ные и т.п.
К внутренним относятся риски, появление которых обуслов-
лено деятельностью самого экономического субъекта (фирмы).
На уровень внутренних рисков оказывают влияние уровень уп-
равления экономическим субъектом, его экономический потен-
циал, уровень специализации, техника безопасности.
У\о характеру последствий риски подразделяются на чистые и
спекулятивные.
Чистые риски (простые, статические риски) характеризуют-
ся тем, что их появление означает потери для хозяйственной де-
ятельности. Причинами чистых рисков могут быть стихийные
бедствия, войны, несчастные случаи, преступные действия
и т.п.
Спекулятивные риски (коммерческие, динамические риски)
характеризуются тем, что их проявление означает не только поте-
ри для хозяйственной деятельности, но и дополнительную при-
быль к ожидаемому результату. Причинами спекулятивных рис-
ков могут быть изменения валютных курсов, налогового законо-
дательства и т.п.
5.2.2. Сфера возникновения рисков — это важный элемент класси-
фикации рисков, в основу которого положены сферы экономи-
ческой деятельности.
Экономическая деятельность охватывает производственную,
коммерческую, финансовую, посредническую деятельность и
страхование.
В производственной деятельности используются факторы
производства (капитал, труд, материалы) и фирмой производится
готовая продукция в виде товаров, услуг, информации для прода-
жи на рынке товаров и услуг.
В коммерческой деятельности продаются потребителям гото-
вые товары и услуги, приобретенные у других лиц. Прибыль ком-
мерческой фирмы образуется за счет разницы в ценах продажи и
приобретения.
107
В финансовой деятельности в качестве предмета купли-про-
дажи предпринимателя выступают деньги и ценные бумаги, про-
даваемые покупателям или предоставляемые ему в кредит.
В посреднической деятельности предприниматель (фирма) не
производит и не продает товар, а выступает в роли связующего
звена в процессе товарного обмена и в товарно-денежных опера-
циях. За оказание посреднической услуги, которая заключается в
сведении заинтересованных в сделке сторон, предприниматель
(фирма) получает доход.
Суть страхования в том, что предприниматель (фирма), ко-
торый называется страховщиком, за определенную сумму, на-
зываемую страховым взносом, гарантирует потребителю, назы-
ваемому страхователем, компенсацию возможной потери (пол-
ной или частичной) имущества, ценностей, жизни в результате
наличия определенных обстоятельств, т.е. в результате наступ-
ления так называемого страхового случая. В связи с тем что
вероятность наступления страхового случая относительно ма-
ла, оставшаяся часть страховых взносов образует доход стра-
ховщика.
В связи с только что описанными сферами экономической
деятельности выделяют следующие риски: производственный,
коммерческий, финансовый, посреднический и страхования.
Производственный риск связан с невыполнением фирмой
своих обязательств по производству товаров и услуг, с нерацио-
нальным использованием новых технологий, основного и оборот-
ного производственного капитала, рабочего времени. Причины
вышеназванных проблем: снижение объемов производства, на-
пример в связи с ростом издержек, низкой дисциплиной поста-
вок, ростом налоговых отчислений.
Коммерческий риск связан с проблемами, возникающими в
процессе реализации товаров и услуг, произведенных или закуп-
ленных фирмой (предпринимателем). Причинами возникнове-
ния таких проблем являются снижение объема реализации в связи
с изменением рыночной конъюнктуры, повышение закупочных
цен на товары, потери в процессе обращения, повышение издер-
жек обращения и т.п.
Финансовый риск связан с возможностью невыполнения
фирмой своих финансовых обязательств. К причинам невыпол-
нения фирмой своих финансовых обязательств относятся: изме-
нение курса национальной валюты и обесценение вследствие
108
этого инвестиционного портфеля фирмы, введение военного по-
ложения, возникновение беспорядков и т.п.
Посреднический риск связан с возможностью невыполнения
фирмой посреднической услуги, в результате чего посредничес-
кая фирма может нести большие потери в связи с неполучением
дохода за успешную посредническую услугу. Причины посредни-
ческого риска связаны прежде всего с изменением экономичес-
кой конъюнктуры, когда для одного или сразу для двух сделка
может оказаться невыгодной.
Риск страхования — риск наступления страхового случая, ког-
да страховщик обязан выплатить страхователю всю (или часть)
страховой суммы. Результатом этого риска являются убытки, вы-
званные недостаточно квалифицированной страховой деятель-
ностью как на этапе, предшествующем заключению договора
страхования, так и на последующих этапах — перестрахование,
формирование страховых резервов. Основными причинами риска
страхования являются: ошибочно определенные страховые взно-
сы и страховые суммы, войны, стихийные бедствия, беспорядки,
которые не были учтены при заключении страхового договора.
5.3. Предпринимательские риски
5.3.1. Структура предпринимательских рисков представлена
на рис. 5.1.
Страновые риски связаны с участием предпринимателей
(фирм) во внешнеэкономической деятельности. На эти риски
влияет политико-экономическая стабильность стран — импорте-
ров и экспортеров. Причинами странового риска могут быть неэф-
фективность государственной и экономической политики, осо-
бенности государственного и регионального законодательства,
региональные проблемы, поляризация различных социальных
групп. На функционирование фирм оказывают влияние (в разной
степени) глобальные экономические процессы, торговое и валют-
ное регулирование, квотирование, лицензирование, таможенные
пошлины и т.п.
Одним из наиболее авторитетных показателей уровня страно-
вого риска является индекс БЕРИ, регулярно публикуемый гер-
манской фирмой «БЕРИ» и определяемый группой численностью
около 100 экспертов с помощью различных методов экспертных
109
Рис. 5.1
оценок 4 раза в год. В состав анализируемых экспертами частных
показателей входят:
1) эффективность национальной экономики, определяемая
на основе прогнозируемого среднегодового изменения валового
национального продукта (ВНП) страны;
2) уровень политического риска;
3) уровень задолженности, рассчитываемой по данным Ми-
рового банка реконструкции и развития с учетом размера задол-
женности, качества обслуживания задолженности, объема экс-
порта, баланса внешнеторгового оборота;
4) доступность банковских кредитов;
5) доступность краткосрочного финансирования;
6) доступность долгосрочного ссудного капитала;
7) вероятность возникновения форс-мажорных обстоятельств;
8) уровень кредитоспособности страны;
9) сумма невыполненных обязательств по выплате внешнего
долга.
110
Результаты проведенного анализа уровня странового риска
представляются в виде базы данных, характеризующих оценку
степени риска инвестирования и надежности деловых связей раз-
личных стран, представленной в виде ранжированного перечня
стран с интегральными балльными и частными оценками риска.
Валютные риски связаны с колебанием валютных курсов. Ве-
личина валютного риска зависит от потери покупательной спо-
собности валюты и поэтому находится в прямой зависимости от
продолжительности временндго промежутка между моментом за-
ключения сделки и моментом платежа. Экспортеры страны несут
убытки, если они заключали контракты до падения курса нацио-
нальной валюты, ибо после падения курса национальной валюты
за одну единицу свободно конвертируемой валюты экспортер по-
лучает больше единиц национальной валюты, чем до ее падения.
С импортерами страны обратная ситуация. Импортеры несут
убытки, если они заключали контракты до повышения курса на-
циональной валюты, ибо до повышения курса национальной ва-
люты за одну единицу свободно конвертируемой валюты импор-
тер должен заплатить больше единиц национальной валюты, чем
после ее повышения.
Системные риски связаны с тем, в какой сфере функциони-
рует фирма: в сфере белого (прозрачного) бизнеса, в сфере серо-
го (теневого) бизнеса или в сфере черного (криминального)
бизнеса.
Если фирма функционирует в сфере белого бизнеса, ее сис-
темный риск равен нулю, однако из-за высокого уровня налого-
вого бремени функционирование фирмы становится весьма рис-
кованным предприятием. Если фирма функционирует в сфере
серого бизнеса, то она имеет системный риск, величина которого
равна вероятности того, что ее теневая деятельность может быть
обнаружена. Но зато фирма при этом может получить значитель-
ные «налоговые льготы», ибо она уклоняется от уплаты части на-
логов. Если фирма функционирует в сфере черного бизнеса, то ее
положение аналогично фирме, функционирующей в сфере серого
бизнеса. Отличие лишь в том, что в последнем случае резко воз-
растает системный риск и, возможно, фирма будет иметь еще бо-
лее значительные «налоговые льготы».
Риск форс-мажорных обстоятельств — это риск, связанный со
стихийными бедствиями (наводнение, землетрясение, изверже-
ние вулканов, ураганы), социально-экономическими потрясени-
111
ями, вызванными революциями, забастовками, которые препят-
ствуют нормальному функционированию фирм.
В случае форс-мажорных обстоятельств стороны, заключив-
шие сделку до этих обстоятельств, освобождаются от взаимных
обязательств по такой сделке согласно статье 79 Конвенции ООН
о договорах купли-продажи.
Возмещение потерь, вызванных форс-мажорными обстоя-
тельствами, осуществляют специализированные страховые ком-
пании.
5.3.2. В отличие от внешних рисков, которые не зависят от само-
го предпринимателя (фирмы), внутренние риски в значительной
степени зависят от ошибочных решений, принимаемых предпри-
нимателями (руководителями фирм) вследствие их некомпетент-
ности или иных, зависящих от предпринимателей обстоятельств
(в качестве примера можно указать привлечение на ответствен-
ные должности родственников или знакомых, которые могут на
своих рабочих местах пренебрегать интересами фирм, где они ра-
ботают).
Отметим ряд конкретных причин внутренних рисков фирм:
несоответствие уровня профессиональной подготовки руководя-
щего состава фирмы требованиям рабочего места, которое прояв-
ляется в принятии ошибочных решений по рациональному рас-
пределению ресурсов, по проведению маркетинговой политики,
по регулированию финансовых и информационных потоков фир-
мы, по своевременному адаптированию фирмы к переменам в
окружающей рыночной среде.
Рассмотрим более подробно внутренние риски фирмы.
Организационный риск обусловлен недостатками в организа-
ции работы фирмы. К причинам организационного риска фирмы
относятся:
1) низкий уровень организации:
1.1) ошибки планирования и проектирования;
1.2) недостаток координации работ;
1.3) слабое регулирование;
1.4) нерациональное распределение ограниченных ресурсов;
2) недостатки в организации маркетинговой деятельности:
2.1) неправильный выбор выпускаемой продукции, а это при-
водит к тому, что продукция не пользуется спросом;
2.2) неправильный выбор рынка сбыта;
112
2.3) неверное определение емкости рынка;
2.4) неправильная ценовая политика;
3) неустойчивое финансовое положение.
Ресурсный риск имеет следующие причины:
1) отсутствие необходимых резервов по ресурсам в случае из-
менения рыночной ситуации;
2) дефицит рабочей силы и материалов;
3) срывы поставок;
4) нехватка выпускаемой фирмой продукции.
Портфельный риск состоит в том, что фирма имеет потери по
отдельным типам ценных бумаг, а также по всей категории ссуд.
Если у предпринимателя (фирмы) имеются свободные денеж-
ные средства, он на эти средства может приобрести различные
ценные бумаги, совокупность которых называется портфелем
ценных бумаг, или инвестиционным портфелем.
Задача оптимизации инвестиционного портфеля анализиру-
ется в параграфе 5.8. Решение этой задачи снижает портфельный
риск фирмы до оптимальной величины.
Кредитный риск представляет собой риск невозврата долга,
т.е. риск неуплаты заемщиком кредитору основного долга и/или
процентов по нему в сроки, установленные кредитным догово-
ром.
Причинами кредитного риска являются: недобросовестность
заемщика с его попытками намеренного банкротства или другими
попытками уклонения от выполнения обязательств по выплате
долга, а также с опасностью невольного банкротства из-за того,
что расчеты заемщика на получение необходимого дохода не оп-
равдались.
Причинами невольного банкротства могут быть:
1) спад производства и/или спроса на продукцию определен-
ного вида;
2) невыполнение договорных отношений;
3) форс-мажорные обстоятельства.
Кредитный риск зависит от вида предоставляемого кредита,
и кредиты различаются:
1) по срокам — кратко-, средне- и долгосрочные;
2) видам обеспечения — обеспеченные, необеспеченные;
3) виду дебитора — промышленные и персональные;
4) направлению использования — промышленные, инвести-
ционные, на формирование оборотного капитала, сезонные, на
« - 7620
113
устранение временных трудностей, на операции с ценными бума-
гами и др.;
5) размеру — мелкие, средние и крупные.
Инновационный риск связан с финансированием и использо-
ванием научно-технологического прогресса (НТП). Затраты и
результаты НТП растянуты во времени, но их можно предвидеть.
Мировой опыт свидетельствует, что доля получения предпо-
лагаемых результатов на стадии фундаментальных исследований
не превышает 10%. Доля прикладных научных разработок состав-
ляет 80%. В наиболее развитых странах допускается, что при жест-
ком отборе, в ходе которого отвергается 80—90% предложений, из
оставшихся проектов, получивших финансирование из иннова-
ционных фондов, 15—30% может закончиться неудачей. .
Создатели новых технологий и новых видов техники могут
двигаться по первому пути медленно и осторожно, с минималь-
ным риском, частично модернизируя действующие технологию и
конструкции. С современной точки зрения такой путь беспер-
спективен, ибо вгоняет экономику в неэффективные расходы.
Создатели новых технологий и новых видов техники могут
идти по второму пути, с большим риском, ориентируясь на миро-
вой рынок. Второй путь ведет к созданию принципиально новых
технологий.
Вследствие неизбежности инновационного риска на Западе
приняты практика безвозмездных пожертвований научно-иссле-
довательским организациям, значительные налоговые льготы и
предоставление государственной помощи венчурным фирмам,
которые с большим риском занимаются практическим освоением
новых технологий.
5.4. Элементы теории полезности
Дж. фон Неймана и О. Моргенштерна
5.4.1. Рассмотрим ряд положений теории полезности Неймана-
Моргенштерна. Одним из основных понятий этой теории являет-
ся лотерея, которая определена ниже.
Пусть имеется два множества символов: множество хр ..., хк
и множестворр ...,рк. Символы хр ..., хк могут интерпретиро-
ваться как некоторые исходы, например выигрыши (доходы) не-
которого индивидуума (потребителя) или потребительские набо-
114
ры, которые может получить (выиграть) индивидуум. Символы
pv ...,рк интерпретируются как вероятности, так что рх> 0, ...,рк>0
ир! + ...+^=1.
Лотерея L представляет собой вектор (точнее, кортеж), такой,
что
L = (px,xx, р2,х2; рк,хк),
или
Z = (xI,...,xjfc; р,.рк),
гдеР] — вероятность наступления исходахр ...,рк — вероятность
наступления исхода хк. Символы хр ..., хк, рх, ...,рк называются
параметрами лотереи L.
Далее для определенности используется термин «потреби-
тельский набор», а не термин «исход».
В частности, символ
(1,хр 0,х2; ...; 0,xJt) = (l,x1)
представляет собой лотерею, в которой индивидуум получает (вы-
игрывает) набор Xj с вероятностью единица, т.е. получает набор Xj
наверняка, а символ
(Pj.Xjj (1-р),х2)
означает лотерею, в которой индивидуум получает набор Xj с веро-
ятностью р, а наборх2 — с вероятностью (1 -р), где 0 <р < 1.
Предполагается, что у индивидуума на множестве возможных
лотерей есть отношение > предпочтения-безразличия, которое
удовлетворяет следующим аксиомам:
1) аксиома полноты—для любых двух лотерей £, и L2 индиви-
дуум может указать, какое одно из следующих трех отношений
выполняется: Lx >- L2 (символ Lx >- L2 означает, что лотерея
предпочитается лотерее L2 и лотереи Lx и L2 не эквивалентны,
т.е. не находятся в отношении безразличия), L2 > Lx (лотерея L2
предпочитается лотерее Z, и лотереи L2 и Lx не эквивалентны),
Lx ~ L2 (лотереи Lx и L2 эквивалентны, т.е. находятся в отношении
безразличия. Лотереи Lx и L2 находятся по определению в отно-
шении безразличия, если им соответствует одинаковое распреде-
ление вероятностей);
2) аксиома рефлексивности — для любой лотереи L £ L\
3) аксиома транзитивности — для любых лотерей Lx, L2, L3
справедлива импликация: если Lx >- L2, L2 >- L3, то Lx >- L3;
8-
115
4) аксиома монотонности — для любых двух наборов х, и х2,
таких, чтоХ] >-х2, имеет место отношение предпочтения
(р{, ; (1 - Р')> х2) >• (рх, х,; (1 - р), х2)
тогда и только тогда, когда р' > р. Это содержательно означает, что
индивидуум предпочитает с большей вероятностью получить
предпочитаемый набор хр В частности, Xj >- (р, хр (1 - р), х2) для
всех вероятностейр, 0 <р < 1, т.е. наборхр который индивидуум
получает наверняка, предпочитается им любой лотерее, содержа-
щей набор xt и набор х2, который является для индивидуума менее
предпочитаемым;
5) аксиома непрерывности—для любых трех наборов хр х2, х3,
таких, что хх>-х2>- х3, существует вероятность р, 0 <р < 1, для ко-
торой
(р,хр (1 —р),х3) ~х2,
что содержательно интерпретируется так: индивидуум не делает
различий между лотереей (р, хр (1 -р), х3), содержащей наиболее
предпочтительный набор xt и наименее предпочтительный на-
бор х3, и определенностью получения набора х2, занимающего
промежуточное положение между наборами х, и х2;
6) аксиома о независимости не связанных между собой аль-
тернатив — для любых двух наборов х, и х2, таких, что х, ~ х2, и
любого третьего набора х3 справедливо следующее отношение
безразличия:
(р, х,; (1 -р), х3) ~ (р, х2; (1 -р), х3)
для любых р, 0 <р < 1, что содержательно интерпретируется так:
присутствие третьего набора х3 не нарушает отношение безразли-
чия.
Прежде чем формулировать последнюю (седьмую) аксиому,
дадим определение сложной лотереи.
Пусть имеется т (шт.) лотерей
А=<Р/р*р Pivxv ->
Сложная лотерея — это такая лотерея
L = (qx,Lx\ q2,L2\ ...;
в которой в качестве исходов (наборов) выступают лотереи
£р ..., Zm, в качестве qv ..., qm выступают вероятности, где
q. - 1,..., т — вероятность получения индивидуумом лотереи Zz,
?z>0,z=l, ...,m, qx +... + qm=A',
116
7) аксиома о приведении сложных лотерей — сложная лотерея L
может быть приведена к лотерее с соответствующими вероятнос-
тями гр ...,гк, г^О,гк>0,+... +rk= 1,
£~Г = (ГрХр r2,x2; ...; rk,xk),
ri=9iPn + -+9mPmi,
rk~ 9\P\k +ЯтРтк-
Теория полезности Неймана—Моргенштерна исследует пред-
почтения на множестве лотерей, удовлетворяющих приведенным
выше аксиомам.
5.4.2. Согласно основной теореме теории полезности Нейма-
на-Моргенштерна (при соблюдении всех приведенных аксиом)
существует функция полезности, определенная на всех лотереях,
которая является однозначной с точностью до монотонного стро-
го возрастающего линейного преобразования.
В связи с тем что набор х=(1, х) есть лотерея, функция полез-
ность определена на всех наборах и
U(x) > U(y) <=> х > у.
В общем виде имеем
^(ррХр р2,х2; ...; pk,xk)=plU(xl) + ...+pkU(xk),
т.е. полезность лотереи L = (pl,xi‘ рк,хк) есть математическое
ожидание полезности (т.е. ожидаемая полезность), равное взве-
шенной сумме полезностей и(хх),..., U(xk) наборов хр ...,хк, где в
качестве весов выступают вероятности...,рк получения инди-
видуумом этих наборов.
Функция U(x) полезности Неймана-Моргенштерна опреде-
ляется однозначно с точностью до монотонного строго возраста-
ющего линейного преобразования, т.е. функция aU(x) + Ь, а > 0 —
также функция полезности Неймана—Моргенштерна. Напомним,
что классическая функция полезности определяется однозначно с
точностью до монотонного строго возрастающего (линейного,
а также нелинейного) преобразования.
Функцию U(x) полезности Неймана—Моргенштерна можно
построить, выбрав произвольным образом числовые значения для
Двух уровней полезности. Полезности других наборов оценивают-
ся соответствующим взвешиванием вероятностями. Продемон-
117
стрируем это. Пусть, например, х( >- х2 и пусть числа U(x}) и U(x2)
таковые, что Ufy) > U(x2) и в остальном произвольны. Для пост-
роения значения U(x3) функции полезности для любого другого
набора х3 взвесим значения полезностей ЦХ]) и U(x2) наборов х, и
х2 с помощью вероятностей. Если, например, имеет место цепоч-
ка Xj >- х2 >- х3, то по аксиоме 5 непрерывности существует вероят-
ность р, такая, что
(p,Xj;(l-p),x2)~x3,
поэтому
U(X3) = U(p, Хр (1 -р), Х2) =pU(xl) + (1 -P)U(X2),
ибо, во-первых, значения функции полезности на лотереях, кото-
рые находятся в отношении безразличия, являются равными и,
во-вторых, полезность лотереи есть математическое ожидание ее
полезности.
Если х3 >- х( (>- х2), то по аксиоме 5 непрерывности существует
вероятность р, такая, что
*1 ~(Р,х3; (1-р),х2),
откуда
U(Xi)=pU(x3)^(l-p)U(x2)9
или
и(х3) = -и(хх)-^^-и(х2).
Р Р
Таким образом, выбрав два произвольных числа U(x}) и CZ(x2),
мы получим значения U(x) функции полезности Неймана—Мор-
генштерна для любых наборов х.
На базе основной теоремы теории полезности Неймана—Мор-
генштерна (теоремы об ожидаемой полезности) формируется пра-
вило рационального поведения индивидуума в процессе принятия
решения в условиях риска, суть которого (правила) в следующем.
Пусть индивидуум, принимающий решение, должен выбрать
одну из т (шт.) стратегий sv где исходом стратегии s.явля-
ется лотерея
1/=ФЛ,Х1; Р/2»х2; ..., pik,xk), i=\,2,...,m.
В связи с тем что полезность лотереи L. оценивается вели-
чиной
U(L)=pilU(x.l) + ...+pikU(xik),
118
индивидуум, принимающий решение на основании максимиза-
ции полезности, выберет стратегию, которая обеспечивает макси-
мальное значение ожидаемой полезности
max С/ (Lt) = max(pnU (ха)+...+p^U (xft)).
5, S,
Если, например, m = 3,a£=2, то искомый максимум равен
тах£/(Д.)=
si
=тах(рн(/(xn )+pi2U (x,2), p2lU (x21 )+p22U(x22), p3lU (x31 )+p32U (x32)),
где каждая (из трех) сумма, стоящая в круглых скобках, есть эле-
мент главной диагонали произведения матриц
't/Ц,) Z7(x12)V .
tzu2l) f/c22) Г11 М
^,) Р(х,2)^! Ы
5.5. Отношение к риску.
Количественные оценки риска
5.5.1. Для описания поведения индивидуума в условиях риска и
отношения индивидуума к риску используются понятия ожида-
емого дохода и ожидаемой полезности индивидуума.
Пусть индивидуум имеет функцию полезности u(w), где w—ве-
личина дохода, a u(w) — уровень полезности индивидуума, если
его доход равен и». Пусть р^ — вероятность реализации варианта
u(w{) (в этом варианте доход величиной имеет для индивидуума
уровень полезности «(м^)), р2 — вероятность реализации варианта
w(w2), ...,рк — вероятность реализации варианта «(w*) (pt +... +рк = 1,
Pj > 0,..., рк > 0), тогда выражение
=pJ«(w1) + ... +pku(y/J (5.5.1)
представляет собой ожидаемую полезность (среднюю полезность)
рассмотренных вариантов. Выписанная сумма представляет со-
бой функцию ожидаемой полезности, или функцию полезности
Неймана—Моргенштерна (см. раздел 5.4.2). Здесь и далее М —
119
символ математического ожидания случайной величины u(w),
имеющей следующее распределение вероятностейрх, ...,рк.
u(yv{) ... u(wk)
Pi |-I Рк
Величина w = р^ + ... + pkwk представляет собой ожидаемый
доход, т.е. математическое ожидание величины w, имеющей рас-
пределение вероятностей/>р ...,рк.
wi ••• wk
Pi I- Рк'
Таким образом, ожидаемая полезность есть математическое
ожидание A/[w(w)] (случайной) полезности u(w), а ожидаемый до-
ход есть математическое ожидание случайного дохода w.
5.5.2. Рассмотрим функцию полезности ХИ = а + bu(w), где а и
Ь > 0 — скалярные параметры. На основании свойства линейности
математического ожидания имеем M[v(w)] = а + Z>A/[w(>p)] , т.е. обе
функции полезности u(w) и v(w) представляют одно и то же отно-
шение предпочтения в условиях риска.
Если функция полезности u(w) выпукла вверх, то при к = 2
справедливо неравенство
m(P|W, +p2w2) ZppiwJ +p2u(w2) (5.5.2)
(при к > 2 имеем и(рхWj +... + pkwk) >pptwj +...+ Pku(wk)).
Левая часть неравенства (5.5.2), очевидно, равна
«(Р^! +P2w2) = «(W”]), (5.5.3)
где ЛЯ»*’] — математическое ожидание дохода w = р^, + p2w2:
A/[w] = M\p{wx +p2w2].
Правая часть равенства (5.5.2) есть математическое ожидание
A/[«(w)] =Р]И(м’1) +p2u(w2) полезности u(w).
Используя равенства (5.5.1), (5.5.3), перепишем неравен-
ство (5.5.2) следующим образом:
M«(w)] < w(A/[w]). (5.5.4)
Неравенство (5.5.4) показывает, что математическое ожида-
ние A/[w(w)] (случайной) полезности u(w) дохода w = рхWj + p2w2
(т.е. полезности в условиях риска) не больше полезности w(M[w])
математического ожидания A/[w] случайного дохода, которое (ма-
тематическое ожидание A/[w]) равно безрисковому доходу w,
т.е. м' = Л/[и’] = Af|PiM’i +P2W21 (рис. 5.2).
120
На рис. 5.2 точка В = (w, н(Л/[и’]) = (Af[w], w(A/M) изображает
полезность безрискового дохода w, равного математическому
ожиданию w = AffPjWj + />2w2] случайного дохода p{w{ + Pjw2, точ-
ка А = (w, ЛДн(и')]) изображает ожидаемую полезность (т.е. полез-
ность в условиях риска), если вероятность дохода w, индивидуума
равна pv вероятность дохода w2 индивидуума равна р2, а ожида-
емый доход p1w1 + p2w2 также равен w.
Таким образом, в условиях риска ожидаемая полезность
A/[w(w)] индивидуума строго меньше полезности «(ЛДи»]) индиви-
дуума в условиях отсутствия риска. Откуда следует, что представ-
ленная на рис. 5.2 линия есть график функции полезности инди-
видуума, не склонного к риску (т.е. рискофоба).
На рис. 5.2 также видно, что в условиях отсутствия риска по-
лезность и, равная ожидаемой полезности, т.е. и = A7[tz(w)], дости-
гается при доходе w, равном w = w. Содержательно это означает,
что индивидуум готов потерять часть своего дохода в размере
w - w > 0 для того, чтобы безрисковая ситуация, изображаемая
точкой С = (w, Af[«(w)]), была эквивалентна ситуации в условиях
риска, изображаемой точкой А = (w, Af[«(w)]). Отметим, что в обо-
их случаях полезность одна и та же и равна A/[«(w)]. Разность w - w
(равную длине | СА |, отрезка СА) принято называть премией за
риск. В случае индивидуума, который не склонен к риску, премия
за риск положительна.
121
Если график Г функции полезности больше похож на прямую
(т.е. радиус ее кривизны относительно велик), то премия за риск
будет меньше. Если же график Г функции полезности имеет силь-
ное искривление (радиус кривизны относительно мал), то премия
за риск будет больше при той же разности «(Af[w]) - Jl/[«(w)]. Та-
ким образом, степень искривления трафика функции полезности
характеризует степень неприятия риска индивидуумом.
5.5.3. Если функция полезности u(w) выпукла вниз, то при к = 2
справедливо неравенство
w(Pi*i +/>2w2) <^1и(и’1) +p2«(w2)
(при к > 2 u(pxw} +... +pkwk) £рхи(кх) +... +pku(wk)).
По аналогии с предыдущим случаем имеем неравенство
Л/[и(мО] > w(A/[w]),
которое означает, что математическое ожидание ЛДи(м')] полезнос-
ти u(w) не меньше полезности «(Лфф математического ожидания
Л/[и'] случайного дохода w, которое (математическое ожидание
Af[w]) равно безрисковому доходу w, т.е. w = М[w] = M\pxwx + p2w2]
(рис. 5.3), т.е. представленная на рис. 5.3 линия есть график функ-
ции полезности индивидуума, который склонен к риску (т.е. рис-
кофила). В этом случае в условиях риска уровень ожидаемой
полезности 3/[«(w)] индивидуума строго выше уровня полезности
122
ы(Л/1и/]) в условиях отсутствия риска (точка А расположена выше
точки В, этим точкам соответствует один и тот же доход w). В дан-
ном случае премия за риск отрицательна и равна длине | AC |j от-
резка АС, взятой со знаком минус, что содержательно означает,
что индивидуум приобретает дополнительный доход в размере
й? - w > 0 для того, чтобы для него безрисковая ситуация, изобра-
женная точкой С = (w, Af[w(w)]), была эквивалентна ситуации в
условиях риска, изображаемой точкой А = (w, A/[«(w)]).
5.5.4. Если функция полезности u(w) индивидуума выпукла
вверх и вниз (т.е. график есть прямая линия), то при к=2 справед-
ливо равенство
«(PjW, +p2w2) =pxu(yvx) +p2u(w2)
(при к > 2 u(pxwx +... +pkwk) =pxu(wx) +... +pku(wk)).
В этом случае имеем равенство
= w(3/[w]),
которое означает, что математическое ожидание JH[«(w)] полез-
ности u(w) равно полезности m(3/[w]) математического ожидания
Л/fw] случайного дохода w, которое (математическое ожидание
A/[w]) равно безрисковому доходу w, т.е. w = Af[w] = M\pxwx + p2w2]
(рис. 5.4). Таким образом, представленная на рис. 5.4 линия есть
123
график функции полезности индивидуума, нейтрального к риску
(т.е. рисконейтрала). В этом случае, очевидно, премия за риск
w-w = 0.
Для индивидуума, который не склонен к риску (т.е. является
рискофобом), функция полезности u(w) от его дохода выпукла
вверх (см. рис. 5.2). Для такой функции u(w) ее производные
u'(w) > 0 и u"(w) < 0. Это означает, что предельная полезность i/(w)
дохода w индивидуума убывает с ростом такого дохода. Интуитив-
но ясно, что чем график функции u(w) полезности больше похож
на отрезок прямой, тем меньше степень неприятия риска со сто-
роны индивидуума. Наоборот, чем сильнее искривлен график
функции полезности, тем выше степень неприятия индивидуума
к риску. Степень искривления графика функции определяет вто-
рая производная этой функции.
5.5.5. Для построения показателя степени неприятия риска со
стороны индивидуума используются меры Эрроу—Пратта, кото-
рые определяются так.
Абсолютная и относительная меры Эрроу—Пратта для функ-
ции полезности u(w) имеют вид
APa(w) =—АР(м’) = h’AP(w) =
и (w) r a u (w)
В связи с тем, что v'(w) = bu'(w), v"(w) = bu"(w) (y(w) = a + Z>«(w)),
абсолютная и относительная меры Эрроу—Пратта одни и те же
для целого класса функций полезности v(w) = a + bu(w), поэтому
эти меры выражают свойства предпочтений индивидуума, а не
только описывающих их функций полезности.
Если считать, что уровень полезности u(w) измеряется в юти-
лях (ю), а доход — в денежных единицах (д.е.), то размерность пер-
вой производной u'(w) имеет вид ю/д.е., размерность второй про-
изводной u"(w) имеет вид ю/(д.е.)2, поэтому абсолютная мера Эр-
роу-Пратта имеет размерность вида 1/д.е., а относительная мера
Эрроу—Пратта — безразмерная величина.
Имеем
лв/ \ «"(w) («'(w))' w du’
и (w) и (w) и dw
где — эластичность предельной полезности u'(w) по доходу w.
124
Если индивидуум склонен к риску, то и"(м>) > 0, и если
u'(w) > 0, то
AP.(w) = -^^^Q, APr(w) = -w^^-<Q. (5.5.5)
° и (w) r u (w)
Точнее, если u"(w) > 0 и u'(w) > 0, то справедливы неравен-
ства (5.5.5).
Если u"(w) < 0 (означает, что индивидуум не склонен к риску)
и если u'(w) > 0, то
APa(w)>0, APr(w)*0.
Если u"(w) = 0, это эквивалентно тому, что индивидуум ней-
трален к риску, и если u'(w) > 0, то
APa(w) = 0, APr(w)-Q.
Меры APa(w) и AP^w) обладают следующими свойствами.
1. Пусть мера APg(w) растет с ростом w, тогда с ростом w без-
рисковый эквивалент случайного выигрыша убывает, и наоборот.
2. Пусть мера APa(w) возрастает с ростом w, тогда с ростом w
спрос на рисковый актив убывает (т.е. рисковый актив — товар
низкого качества).
Пусть мера APg(w) убывает с ростом w, тогда с ростом w спрос
на рисковый продукт возрастает (т.е. рисковый актив-товар нор-
мальный).
3. Пусть APg(w) убывает, a APr(w) возрастает, тогда эластич-
ность спроса на рисковый актив по доходу меньше единицы,
т.е. рисковый актив — продукт первой необходимости. Пусть APr(w)
убывает, тогда эластичность больше единицы (т.е. рисковый ак-
тив — предмет роскоши).
Для описания функций полезности u(w), для которых абсо-
лютная и относительная меры ЛРд(^) и APr(w) постоянны, следует
решить обыкновенные дифференциальные уравнения
ЛРа(*) = а, ЛРг(^) = р,
где а и Р — постоянные положительные параметры.
Эти уравнения путем понижения их порядка сводятся к урав-
нениям с разделяющимися переменными, которые легко интег-
рируются.
Общее решение дифференциального уравнения
u"(w)
—77“V = a
w(w)
имеет вид u(w) = -Cle~aw+С2 (проверяется непосредственно). При
фиксированных постоянных (Ц > 0) и С2 функция u(w) строго
125
возрастает и выпукла вверх. Это означает, что индивидуум с функ-
цией полезности «(w) не склонен к риску.
Общее решение дифференциального уравнения
«"(w)
-И'-" =В
«(*)
имеет вид
и(и,) = СТ^ф+С1
w](w) = ClnC1w (Р = 1)
(проверяется непосредственно).
При фиксированных положительных постоянных Си функ-
ции u(w) и w,(w) строго возрастают и выпуклы вверх, что означает,
что индивидуумы с функциями полезности u(w) и K|(w) не склон-
ны к риску.
5.5.6. Пример.
Пусть функция полезности индивидуума имеет вид
где н» — доход индивидуума;
и — уровень полезности индивидуума, которого он достига-
ет, приобретая потребительский набор на сумму, равную
его доходу н».
Для этой функции абсолютная и условная меры Эрроу—Прат-
та имеют вид (проверяется непосредственно)
.D, \ u"(w) 1-а . u"(w) ,
APe(w) =—77Т =------> AP(w) = -w——- = 1-а.
и (w) w u(w)
При 0 < а < 1 имеем случай, когда индивидуум не склонен к
риску. Очевидно, при этом APa(w) > 0, APr(w) > 0. Чем меньше а
(т.е. чем ближе степень а к нулю), тем больше индивидуум не
склонен к риску.
Рассматриваемый случай степенной функции полезности на-
глядно демонстрирует зависимость между отрицательным отно-
шением к риску и относительной мерой Эрроу—Пратта: чем боль-
126
ше индивидуум не склонен к риску, тем ближе к единице относи-
тельная мера Эрроу-Пратта.
В частности, при а = 1/2 меры Эрроу—Пратта соответствен-
но равны APa(w) = 0,5/w, APr(w) = 0,5, а при а = 1/6 они равны
APa(w) = 5/6 w, APr(w) = 5/6.
При а > 1 имеем случай, когда индивидуум склонен к риску,
при а = 1 он к риску нейтрален. При а > 1 APa(w) < 0, APr(w) < 0,
при а = 1 APa(w) = 0, APr(w) = 0.
Пусть а = 1/2, а = 10, b = 60, w1 = 10, w2 = 50, р{ =р2 = 0,5.
Тогда при безрисковом уровне дохода w, = 10 (w2 = 50) уровень
полезности индивидуума равен
( Ю Y/2 Л 50 Y/2
«I = u(Wl) = Ю — = 4,08 = «(w2) = 10 g = 9,13).
\ OU / I OU J
Равенство p{ = p2 = 0,5 эквивалентно тому, что индивидуум с
равными вероятностями выбирает доход w( = 10 или доход w2 = 50,
откуда вытекает, что математическое ожидание дохода индивиду-
ума равно Л/fw] = piwi + p2w2 = 0,5 • 10 + 0,5 • 50 = 30.
Полезность математического ожидания дохода A/[w] = 30 равна
«] = u(Af[w]) = 10
= 7,07,
а ожидаемая полезность индивидуума (математическое ожидание
полезности) равна
Л/[и/| = p^wj + p2u(w2) = 0,5«( + О,5«2 = 30.
Определим безрисковый уровень w дохода, при котором по-
лезность равна ожидаемой полезности Af[w], из следующего урав-
нения:
/ _ \1/2
I W I
I OU 1
откуда получаем, что
» = 6оМ = 26,18.
I 10 I
Премия за риск в рассматриваемом случае равна
Af[w]-w = 30-26,18 = 3,82.
т.е. безрисковый доход w = 26,18 дает индивидууму полезность,
равную ожидаемой полезности Л/[«] = Pj«(Wj) + p2w(w2) = 6,61 ин-
127
дивидуума при его случайном доходе с математическим ожидани-
ем A/[w] = PjWj + p2w2 = 30. Другими словами, премия за риск равна
той части дохода индивидуума, от которой он должен отказаться
для того, чтобы ситуация определенности для него была эквива-
лентна ситуации неопределенности: М\и] = u(w) (рис. 5.5), на ко-
тором представлен случай, когда а = 1/2. Линия OAtAsA3A2C есть
график функции полезности u(w) = 10(w/60)1/2, точки Л, = (wp Uj),
А2 = (w2, и2), А3 = (Л/М, mA/Iw])) = (30; 7,07), А4 = (Af[w], ЛДи]) =
= (30; 6,61), А5 = (w, ЛДи]) = (26,18; 6,61). Длина отрезка Л5Л4, взя-
тая со знаком плюс, равна премии за риск - w = 30 - 28,18 =
Пусть теперь а = 1/6, а остальные величины a, b, wv w2, pv р2
такие же, как в случае, когда а = х/г В рассматриваемом варианте
имеем
Г1оУ/6 Г5оУ/б
u1=«(W1) = 10^ =7,42 «2 = u(w2) = 10^ = 9,7,
I OU / I OU )
= PjWj + p2w2 = 0,5 • 10 + 0,5 • 50 = 30,
ГзоУ/6
m = «(JH[w]) = 10= 8,9,
128
A/[w] = + p2«(w2) = 0,5«j + 0,5и2 = 8,56,
w = 60p77^1 a60p^| =23,59,
I 10 J I 10 J
Mw]-w = 30-23,59 = 6,41.
Мы видим, что во втором случае (а = */6), в котором уровень
(степень) неприятия риска индивидуумом значительно выше, чем
в первом случае (а = */2), премия за риск также значительно боль-
ше, чем в первом случае (рис. 5.6, на котором линии ОА1А5А3А2Си
ОВХВ5В3В2С суть графики функций полезности «(w) = 10(w/60)1/2 и
w(w) = 10(w/60)1/6 соответственно). Длины отрезков Л5Л4 и В5В4,
взятые со знаком плюс, равны соответственно премиям за риск в
первом случае (а = */2) и во втором случае (а = */6) I ^5Я41 = 3,82 и
| Д5Д41 = 6,41).
9 - 7620
129
5.Ь. Шкалы уровней риска
5.6.1. К настоящему времени еще не появились конкретные ре-
комендации по определению того, насколько «приемлем» тот или
иной уровень риска в той или иной конкретной ситуации. В ка-
честве ориентира для выработки таких рекомендаций могут быть
использованы шкалы уровней риска, позволяющие классифици-
ровать поведение лиц, которые идут на хозяйственный риск. В ли-
тературе отсутствует единый подход к формулировке и критериям
оценки шкал риска.
Приведем ряд шкал уровня риска, которые содержатся в учеб-
ном пособии В.М. Гранатурова (1999; 2002). Начнем с эмпиричес-
кой шкалы уровня риска (табл. 5.1).
Таблица 5.1
Эмпирическая шкала уровней риска
№ п/п Величина (уровень) риска (вероятность нежелательного результата принятого решения) Градация риска
1 0,0-0,1 Минимальный риск
2 0,1-0,3 Малый риск
3 0,3-0,4 Средний риск
4 0,4-0,6 Высокий риск
5 0,6-0,8 Максимальный риск
6 0,8-1,0 Критический риск
Первые три градации вероятностей нежелательного результа-
та принятого решения относятся к «нормальному», «разумному»
риску, при котором можно принимать обычные хозяйственные
(предпринимательские) решения. Принятие хозяйственного ре-
шения с большим уровнем риска зависит от склонности к риску
лица, принимающего решение (ЛПР).
Рассмотрим еще одну шкалу, в которой величина (уровень) рис-
ка определяется на основании коэффициента вариации V= <з/М(х),
130
где М(х) — математическое ожидание случайной величины, а а —
ее квадратичное отклонение (о2 — дисперсия случайной величи-
ны) (табл. 5.2).
Таблица 5.2
Шкала уровней риска
№ п/п Величина (уровень) риска (вероятность нежелательного результата принятого решения) Градация риска
1 До 0,1 Слабый риск
2 От 0,1 до 0,25 Умеренный риск
3 Свыше 0,25 Высокий риск
Для оценки коэффициента вариации, определяющего риск
банкротства, существуют разные точки зрения. Одни авторы счи-
тают, что оптимальным является коэффициент вариации, рав-
ный 0,3, а коэффициент вариации 0,7 и выше соответствует уров-
ню риска, который ведет к банкротству. Промежуток от 0,3 до 0,7
представляет собой зону повышенного риска. Принятие решения
о реализации рискового мероприятия в зоне повышенного риска
(от 0,3 до 0,7) определяется величиной возможного выигрыша в
случае, если рисковое событие не произойдет, и склонностью к
риску ЛПР.
5.6.2. Безотносительно к величине (уровню) риска существуют
относительные характеристики шкал риска по величине ожида-
емых потерь. Эти шкалы можно рекомендовать для оценки при-
емлемости рискового решения. Опишем одну из таких шкал.
1. Промежуток (зона) приемлемого (минимального) риска
характеризуется уровнем потерь, которые не превышают величи-
ну чистой прибыли фирмы.
2. Промежуток допустимого (повышенного) риска характе-
ризуется уровнем потерь, которые не превышают величину рас-
четной прибыли фирмы.
3. Промежуток критического риска характеризуется тем, что в
этом промежутке возможны потери, объем которых превышает
величину расчетной прибыли, но не превышает величины ожида-
емого дохода.
9*
131
4. Промежуток катастрофического (недопустимого) риска
характеризуется тем, что в его границах ожидаемые потери могут
быть больше ожидаемых доходов и достичь величины, равной
всему имущественному состоянию предпринимателя (фирмы).
К катастрофическому риску следует отнести (вне зависимости от
величины денежного и имущественного ущерба) такой риск, ко-
торый связан с возникновением непосредственной опасности для
жизни или экономических катастроф.
5.7. Методы предупреждения и снижения риска
5.7.1. В этом параграфе рассматриваются универсальные методы
предупреждения и снижения риска. Эти методы имеют широкую
область эффективного применения. Методы предупреждения и
снижения риска в специфических условиях описаны и проанали-
зированы в специальной литературе, посвященной проблемам
риска.
К универсальным методам предупреждения риска принято
относить методы:
1) страхования;
2) резервирования средств;
3) диверсификации;
4) лимитирования;
5) повышения уровня достоверности информации.
Страхование — один из наиболее распространенных методов
предупреждения и снижения рисков. Страхование — это соглаше-
ние между страховой компанией, называемой страховщиком,
и страхователем (т.е. индивидуумом или фирмой). Согласно это-
му соглашению страхователь выплачивает страховщику страхо-
вую премию, а страховщик обязуется возместить страхователю
убытки (полностью или частично, в зависимости от договорен-
ности) в случае наступления так называемого страхового случая.
Например, индивидуум (страхователь), приобретая недвижи-
мость, может иметь убытки, в частности в связи со стихийным
бедствием. Вероятность р того, что индивидуум будет иметь убы-
ток, равный сумме а руб., может иметь субъективную и объектив-
ную оценки. Математическое ожидание возможных потерь инди-
видуума, очевидно, равно р • а руб. Если индивидуум приобретает
страховой полис, уплачивая страховщику страховую премию в
132
размере р • а руб., то в случае наступления страхового случая
страховщик возмещает индивидууму сумму не вр • а руб., а в раз-
мере а руб.
Сущность страхования состоит в том, что страхователь за оп-
ределенную плату, равную страховой премии, передает риск (от-
ветственность за негативные последствия принятого решения)
страховщику, т.е. страховая премия есть премия за риск индиви-
дуума, не склонного к риску (см. параграф 5.5).
Существуют три вида страхования: личное страхование, иму-
щественное страхование и страхование ответственности.
В имущественном страховании объектом страховых соглаше-
ний выступают движимое и недвижимое имущество, а также иму-
щественные интересы. Часто имущество страхуется на случай
повреждения или его утраты в результате стихийных бедствий,
несчастных случаев и т.п. Имущественные интересы страхуются
на случай недополучения прибыли или доходов (т.е. упущенной
выгоды), неплатежа по счетам продавца продукции, простоя обо-
рудования, изменения валютных курсов.
Специфической формой страхования имущественных интере-
сов является хеджирование, которое представляет собой систему
мер, позволяющих исключить или ограничить риски финансовых
операций в связи с неблагоприятным изменением валютных кур-
сов, цен на товары, процентных ставок и т.п. в будущем. Такими
мерами являются форвардные операции, опционы и др. В част-
ности, хеджирование с помощью опционов предусматривает пра-
во (но не обязанность) страхователя за определенную плату (опци-
онную премию) купить заранее оговоренное количество валюты
по фиксированному курсу в определенный момент (в случае евро-
пейского опциона) и в течение фиксированного временнбго про-
межутка (в случае американского опциона). Опционная премия
представляет собой аналог страхового взноса.
Хеджирование является, по сути, передачей риска одним лицом
другому лицу, однако в отличие от других традиционных договоров
страхования хеджирование не всегда предусматривает выплату
страхователем страховых взносов, т.е. страховой премии. Напри-
мер, в случае форвардных операций, предусматривающих куплю-
продажу валюты в заранее согласованный день (в будущем) по
фиксированному курсу, страхователь не несет никаких предвари-
тельных затрат. В качестве страхователя здесь выступает спекулянт,
который принимает на себя риск, рассчитывая получить прибыль.
133
Страхование ответственности — это такой вид страхования,
в котором объектом выступает ответственность страховщика пе-
ред третьими лицами за причиненный им ущерб вследствие ка-
кого-либо действия или бездействия страхователя (непогашение
кредитов, нанесение ущерба окружающей среде и т.п).
Страхование риска имеет две разновидности: сострахование и
перестрахование. Форма сострахования используется тогда, когда
страховщик может выплатить только часть страховой суммы в
страховом случае. Поэтому страхователь в случае наступления
страхового случая должен получить оставшуюся часть страховой
суммы у другого (других) страховщика(ов), с которым (с которы-
ми) страхователь заключает отдельный договор, возможно на
других условиях. Форма перестрахования свободна от недостат-
ков сострахования, ибо в случае перестрахования страхователь
делегирует (за определенную сумму) весь свой риск страховщику,
который в случае необходимости уже от своего имени обращается
к другому страховщику (страховщикам) с предложением о переда-
че ему части уже своего риска за определенную плату.
5.7.2. В случае резервирования средств как метода предупрежде-
ния и снижения отрицательных последствий наступления риско-
вых событий предприниматель (фирма) создает специальные
фонды возмещения убытков за счет части собственного оборот-
ного капитала. Резервирование средств целесообразно, если издер-
жки резервирования меньше величины страховых взносов (стра-
ховых премий) в случае страхования. В связи с тем что резервные
(т.е. страховые) фонды создаются на самом хозяйствующем субъ-
екте, резервирование средств на покрытие убытков называют са-
мострахованием.
Резервные фонды могут создаваться в натуральной или денеж-
ной форме. Например, субъекты сельскохозяйственного произ-
водства для предотвращения или возмещения потерь, вызываемых
неблагоприятными природными условиями, создают натуральные
резервные фонды (например, семенной фонд). В промышленном
производстве, торговле создаются резервные запасы сырья, мате-
риалов на случай срыва поставок. Резервные денежные фонды со-
здаются на случай непредвиденных расходов, которые могут по-
явиться в связи с изменением тарифов, цен, оплатой исков и т.п.
В процессе оценки эффективности, выбора и обоснования ва-
риантов снижения риска путем резервирования средств необходи-
134
мо определить оптимальный объем этих резервируемых средств,
т.е. оптимальный размер запасов. Для определения оптимальных
размеров запасов в различных конкретных ситуациях построено
большое число специальных экономико-математических моделей,
совокупность которых составляет теорию управления запасами.
В связи с тем что задачи теории управления запасами могут
быть сложными, используют на практике различные упрощенные
критерии для определения требуемого размера резервных (стра-
ховых) фондов. За рубежом одни фирмы формируют страховые
фонды в размере 1—5% от объема продаж, другие — 3—5% от годо-
вого фонда выплат акционерам. В Российской Федерации фир-
мам разрешено создавать свои страховые фонды за счет издержек
в размере не более 1% реализованной продукции (товаров, услуг).
Источником возмещения потерь при наступлении рискового слу-
чая служит прибыль.
5.7.3. В системе методов предупреждения и снижения риска
важную роль играет диверсификация. Она представляет собой про-
цесс распределения инвестируемых средств между различными
объектами вложения, которые непосредственно не связаны меж-
ду собой.
Диверсификация — эффективный метод снижения рисков в
процессе управления портфелем ценных бумаг (см. параграф 5.8).
Помимо этой важной области диверсификация широко применя-
ется в промышленном производстве, торговле и в других областях
предпринимательской деятельности. В частности, для снижения
риска потерь, связанных с падением спроса на определенный вид
продукции, фирма должна осваивать выпуск других видов про-
дукции.
В страховом бизнесе диверсификация имеет форму расшире-
ния страхового поля, которое уменьшает вероятность одновре-
менного наступления ряда страховых событий. В то же время
страхование урожая, строений только на небольшом простран-
стве в случае стихийного бедствия может привести к необходи-
мости одновременной выплаты значительных сумм.
Приведем примеры диверсификации в целях снижения бан-
ковских рисков:
1) при сохранении общего объема кредитования целесообраз-
но предоставлять кредиты относительно мелкими суммами воз-
можно большему числу клиентов;
135
2) образование валютных резервов в разной валюте в целях
уменьшения потерь в случае падения курса одной из валют;
3) привлечение депозитных вкладов, ценных бумаг более
мелкими суммами от большего числа вкладчиков и т.п.
Диверсификация акций, клиентов, услуг эффективна в случае
независимости объектов вложения капитала друг от друга. В слу-
чае зависимости диверсификация неэффективна. Если, скажем,
средства вложены в автопром, прокат тонких листов и в произ-
водство шин, т.е. формально достаточно диверсифицированы, то,
по сути, такая диверсификация неэффективна, ибо эти произ-
водства зависят друг от друга.
Наиболее эффективна диверсификация в случае, когда выби-
раемые производства таковы, что спрос на их продукцию меняет-
ся в противоположных направлениях, т.е. корреляция между по-
казателями этих производств отрицательна.
Диверсификация не может уменьшить систематический риск,
который обусловлен общей экономической конъюнктурой и свя-
зан с войнами, инфляцией, глобальными изменениями налогооб-
ложения, изменениями денежной политики.
5.7.4. Лимитирование представляет собой установление ниж-
них и верхних пределов в целях уменьшения риска. В частности,
ограничение размеров кредитов, выдаваемых одному заемщику,
позволяет уменьшить потери банка в случае невозврата кредита
и процентов по кредиту. Превышение этой суммы может по-
влечь за собой отказ от страхования или использования пере-
страхования.
Приведем еще ряд примеров лимитирования. Применяются
ограничения по срокам (заемных средств, инвестиций), по струк-
туре (доле отдельных затрат в общем объеме, доле каждого вида
ценных бумаг в общей стоимости портфеля), по уровню отдачи
(установление нижнего уровня доходности проекта) и т.п.
5.7.5. Повышение уровня достоверности информации представляет
собой важный метод предупреждения и снижения риска. Если
индивидууму (потребителю, предпринимателю) информация бо-
лее доступна, он может сделать лучший прогноз и уменьшить
риск. Информация — это ценный товар, за который индивидуумы
готовы платить и достаточно хорошо. Ценность полной информа-
ции равна разности между ожидаемой ценностью выбора при на-
136
личии полной информации и ожидаемой ценностью, когда ин-
формация неполная. Заплатив эту разность, можно получить
значение ожидаемой ценности выбора при наличии полной ин-
формации и уменьшить риск.
Проведенный анализ методов предупреждения и снижения
рисков показал, что любое мероприятие, направленное на пре-
дупреждение и снижение риска, имеет свою цену.
При страховании имущества или ответственности такой це-
ной является величина страховой премии (страховых взносов).
При страховании посредством распределения риска за счет парт-
неров и инвесторов платой фирмы за снижение риска является
отказ от части ее доходов в пользу других участников проекта, ко-
торые приняли на себя ответственность за часть риска.
При хеджировании с помощью опционов платой за снижение
риска является опционная премия (которая аналогична страховой
премии).
При резервировании платой за снижение риска являются из-
держки по созданию резервных фондов, а также уменьшению
оборачиваемости оборотного производственного капитала, воз-
можное ухудшение использования основного производственного
капитала, что приводит к снижению прибыли фирмы.
Уменьшение риска путем диверсификации приводит к сниже-
нию ожидаемой отдачи (дивидендов, доходов, прибыли), ибо
расширение области вложения средств, как правило, сопряжено с
привлечением менее доходных областей вложения средств.
При лимитировании в качестве платы за снижение риска вы-
ступает снижение отдачи как следствие принятых дополнитель-
ных ограничений и исключения из рассмотрения возможных
привлекательных вариантов.
На основании сказанного следует сравнивать получаемые ре-
зультаты с целью и степенью их достижения и делать выводы об
экономической целесообразности использования в каждом кон-
кретном случае конкретных методов предупреждения и снижения
риска.
В конкретных прикладных случаях целесообразно комплекс-
но использовать различные методы предупреждения и снижения
риска, комбинируя которые следует стремиться к оптимальному
сочетанию уровня достигаемого снижения риска и необходимых
Для этого затрат.
137
5.8. Спрос на рисковые активы.
Задача оптимизации инвестиционного портфеля
5.8.1. Актив — источник, обеспечивающий денежные поступле-
ния его владельцу. В частном жилом доме квартиры могут быть
сданы в аренду, обеспечивая рентный доход его владельцу. Если
индивидуум имеет срочный счет в банке, то банк ему выплачивает
проценты (обычно ежегодно или ежемесячно), которые вновь
поступают на тот же счет.
Рисковый актив дает денежные поступления, которые частич-
но зависят от случая, т.е. предстоящие поступления неопределен-
ны. Примером рискового актива является акция «Дженерал мо-
торе» (ДМ), ибо владелец акции не знает, поднимется или упадет
ее курс со временем, даже не может быть уверен, что ДМ будет
продолжать выплачивать тот же дивиденд за акцию. Даже долго-
срочные государственные облигации США (которые подлежат
погашению через 10 или 20 лет) имеют элемент риска. Маловеро-
ятно, что федеральное правительство станет банкротом, но темпы
инфляции могут неожиданно вырасти и обесценить выплаты по
процентам и погашению номинала в реальном выражении и тем
самым снизить стоимость облигаций.
Безрисковый (свободный от риска) актив обеспечивает денеж-
ные поступления в заранее установленном размере. Например,
казначейские векселя США (краткосрочные государственные об-
лигации США) погашаются через несколько месяцев, поэтому
они являются почти безрисковыми активами.
Доходность актива — отношение общего объема денежных по-
ступлений от актива к его цене. Если, скажем, цена дома, квартиры
которого сдаются в аренду, выросла за год с 10 млн до 11 млн д. е.,
в течение года дом обеспечил чистый рентный доход в размере
0,5 млн д. е. Тогда (11 - 10) + 0,5 = 1,5 и 1,5/10 = 0,15 = 15% - до-
ходность актива.
Реальная доходность актива (с поправкой на инфляцию) равна
номинальной доходности актива минус темп инфляции.
Ожидаемая доходность — это математическое ожидание его
доходности, т.е. доходность, которую актив принес в среднем.
Ожидаемая доходность близка к средней действительной доход-
ности на длительном временнбм промежутке.
138
Различные активы имеют разные ожидаемые доходности. На-
пример, табл. 5.3 показывает, что ожидаемая реальная доходность
по казначейским векселям США была ниже 1%, в то время как
доходность типичной акции на Нью-Йоркской фондовой бирже
составляла почти 9%. Однако типичная акция в отличие от казна-
чейского векселя США является более рисковым активом. Вели-
чина риска, измеряемого в показателях среднего квадратичного
отклонения реальной доходности, равна 21,2 для обычной акции,
8,5% — для долгосрочных корпоративных облигаций и 3,4% — для
казначейских билетов США. В табл. 5.3 наблюдается следующая
закономерность: чем выше доход от инвестиций, тем больше свя-
занный с этим риск. Следовательно, не склонный к риску вклад-
чик должен соизмерить ожидаемую доходность с величиной рис-
ка. Таким образом, спрос на активы зависит не только от их ожи-
даемой доходности, но и от риска.
Таблица 5.3
Инвестиции — риск и прибыль в США (1926—1991)
Ценные бумаги Ожидаемая реальная доходность (%) Величина риска (среднее отклонение) (%)
Обычные акции 8,3 21,2
Долгосрочные промышленные облигации 0,9 8,5
Казначейские векселя 0,15 3,4
5.8.2. Предположим, что индивидуум (далее — инвестор) вкла-
дывает свои сбережения в активы двух видов: в казначейские век-
селя, которые почти не сопряжены с риском, и в акции, которые
являются рисковым активом. Инвестор должен определиться с
тем, какую часть своих сбережений ему следует вложить в казна-
чейские билеты, а какую часть — в акции.
Пусть Rf— свободная от риска доходность (скажем, от казна-
чейских векселей), Rm — ожидаемая доходность от акций, куплен-
139
ных на фондовой бирже, гт — реальная доходность (она связана с
риском).
Ожидаемая (Rm) и реальная (rffl) доходности связаны между
собой так: Rm = где символом М обозначено математичес-
кое ожидание реальной доходности, которая является случайной
величиной. Отметим, что Л/[Лу] = Rp ибо R? — детерминирован-
ная, а не случайная величина.
У рисковых активов ожидаемая доходность выше, чем у без-
рисковых, т.е. Rm > Rp Если бы это было не так, то рискофобы при-
обретали только казначейские билеты, а акции не покупали бы.
Пусть b — доля средств инвестора, размещенных на фондовой
бирже, (1 - Ь) — доля средств инвестора, используемая для покуп-
ки казначейских векселей.
Ожидаемая доходность (математическое ожидание доходнос-
ти) Rp всего набора ценных бумаг равна средневзвешенным значе-
ниям ожидаемых доходностей (математических ожиданий доход-
ностей) двух активов
-*)*/, (5.8.1)
ибо математическое ожидание M\bRm + (1 - b)Rf] суммы двух слу-
чайных величин bRm + (1 - b)Rj равно сумме их математических
ожиданий:
M[bRm + (1 - b)Rf} = M[brm] + М [(1 - b)R,] =
= ЬМ[гт} + (1 - b)M[Rf] = bRm + (\- b)Rp
Риск от такого набора (портфеля) ценных бумаг ((1 - Ь), Ь) опреде-
ляется с помощью дисперсии (квадратичного отклонения) общей
доходности Rp всего набора ценных бумаг.
Пусть с2т — дисперсия (ат — среднее квадратичное отклоне-
ние) доходности от вклада в фондовую биржу.
Дисперсия а2 доходности набора (портфеля) ценных бумаг по
определению дисперсии
c2p = M[brm + (l-b)Rf-Rp]2 =
= M[bRm + (1 - b)Rf - M(brm + (1 - b)Rf)]2,
откуда следует, что
(5.8.1)
<з2р = M\brm + (\-b)Rf-bRm-{\-b)Rf]2 ^M[b{rm-Rm)]2 ^b2c2m,
т.е.
<з=Ь<з . (5.8.2)
pm ' z
140
Имеем
(5.8.1) (5.8.2) (R~Rf)
Л, = bK, + (l-b)K, = R,-HX.R,-Rf) = йг + -^.^-ар,
откуда вытекает, что ожидаемая доходность Rp имеет вид
Выражение (5.8.3) с содержательной точки зрения описывает
взаимосвязь между риском (с^) и ожидаемым доходом (математи-
ческим ожиданием доходности) Rp, с формальной точки зрения
уравнение (5.8.3) — это уравнение бюджетной прямой L в плос-
кости ар и Rp. Здесь Rp Rm, ст — параметры, а
Л — Rf
—-----f— (5.8.4)
т
угловой коэффициент прямой (5.8.3) (рис. 5.7).
Рис. 5.7
141
С содержательной точки зрения дробь (5.8.4) есть цена риска,
а
ибо ее обратная величина ——показывает, насколько возрас-
m /
тет риск инвестора, если он намерен получить дополнительную
единицу ожидаемой доходности
(/L-/L)
R=Rf+—--------£-<у„.
р / о р
т
Линия безразличия инвестора показывает сочетание размеров
риска и ожидаемой доходности, она идет с юго-запада на северо-
восток, ибо рост размера риска следует компенсировать повыше-
нием ожидаемой доходности (рост ожидаемой доходности озна-
чает рост риска).
Фрагмент карт линий безразличия инвестора А содержит три
линии безразличия № и 1(А) (т. < тп < т,). Линия № касается
Ч Х0 х2 1 и * Ч»
бюджетной прямой L в точке с координатами (ст, л ), что содер-
жательно означает, что ожидаемая доходность инвестора А рав-
на Л°, а риск равен о®, откуда Ь=о°/от. Следовательно, оптималь-
ный инвестиционный портфель инвестора А имеет вид (1 - о°/от,
<Рр/<з„)- Точка касания линии безразличия 1<Р инвестора В с бюд-
жетной прямой имеет координаты (о*, R*p). Поскольку о* < о®, то
инвестор А более склонен к риску, инвестор В менее склонен к
риску.
5.9. Принятие решений
в условиях неопределенности
5.9.1. В условиях неопределенности вероятности результатов
принятых решений неизвестны или не имеют оценок. В условиях
риска вероятности результатов принятых решений известны или
для них могут быть получены оценки.
Для постановки и решения задачи оптимизации принима-
емых решений используем табл. 5.4, называемую таблицей эффек-
тивностей.
В табл. 5.4 представлено конечное число (л) ситуаций и конеч-
ное число (от) принимаемых решений. Если решение Bi принима-
ется в ситуации Aj, то результат (эффективность) этого решения
характеризуется показателем а~, / = 1,..., от, у = 1,..., л.
142
Таблица 5.4
Таблица эффективностей
Ситуации
А1 Л AJ Ап
°п °12 аи ат
м В2 Й21 fl22 аУ а2п
1 ... ... ... ... ...
§ НН В, ап аа аи ain
... ... ... ... ...
Вт ат\ ат2 а . т/ атп
В ситуации Aj,j = 1,..п, наиболее эффективным является ре-
шение Вк, тогда > а у, i - 1,т. Если в ситуации Aj,j= 1,п,
принимается решение Вр i- 1,..., т, такое, что ay<akj, то потери hy,
которые появляются в связи с принятием этого решения Вр оче-
видно, равны hy = ац - а у.
Теперь можно построить новую таблицу потерь (табл. 5.5),
в которой вместо показателей эффективности а/у. помещаются по-
тери hy.
Таблица 5.5
Таблица потерь
Ситуации
Ai А2 ... AJ ... An
Решения в1 ^12 hv hm
в2 Л21 Л22 hy ^2л
... ... ... ... ...
Bi л/1 hv ... hin
... ... ... ... ... ...
Вт hm\ ... hna ... ntn
143
Если ситуация^! появляется с вероятностьюситуация^ —
с вероятностьюpv ..., ситуация Ап — с вероятностью^, то реше-
ние принимается в условиях риска. В этом случае средние потери
первого варианта Bt принимаемых решений равны
R^h^ + .-. + h^,
второго варианта В2 равны
^1 =Лпр1 +... +hlnpn,...»
варианта равны
Лт = АЛ + -+^
Предпочтение отдается тому решению Bg, для которого средние
потери минимальны.
Средние потери R. решения Вр i = 1,..., т, естественно интер-
претировать в качестве средневзвешенного показателя риска реше-
ния Вр тогда решение Bg с минимальным средневзвешенным рис-
ком должно предпочитаться остальным решениям В., i = 1,..., т,
i *g. Решение, предпочитаемое остальным решениям, называется
оптимальным.
5.9.2. Если вероятности появления ситуаций неизвестны или
для них невозможно получить какие-либо удовлетворительные
оценки, приходится принимать решение в условиях неопределен-
ности.
Классическими критериями принятия решения в условиях
неопределенности являются:
1) принцип недостаточного обоснования Лапласа;
2) максиминный критерий Вальда;
3) минимаксный критерий Сэвиджа;
4) критерий обобщенного максимина (пессимизма — опти-
мизма) Гурвица.
Принцип недостаточного обоснования Лапласа применяется,
если можно предположить, что все ситуации равновероятны.
В этом случае выбирается то решение Bg, у которого средневзве-
шенный показатель риска минимален, т.е.
A, = min {Яр ...,Ят},
1
при условии, что р. =... = р„ = —.
п
Выбираемое решение называется оптимальным по принципу
недостаточного обоснования Лапласа.
144
Максиминный критерий Вальда используется, когда показатель
эффективности в любой ситуации должен быть не меньше, чем
наибольший показатель эффективности из возможных наихуд-
ших показателей. Формально максиминный критерий Вальда
имеет вид
max min а,,,
т.е. следует в каждой строке табл. 5.4 выбрать минимальный эле-
мент atj, а потом из этих минимумов выбрать максимальный эле-
мент. Пусть это будет элемент а/ОуО, тогда решение B.Q должно
предпочитаться всем остальным решениям.
Решение В10, предпочитаемое остальным решениям, называ-
ется оптимальным по максиминному критерию Вальда.
Максиминный критерий Вальда ориентирует ЛПР на слиш-
ком осторожную стратегию поведения, поэтому этот критерий
используется, когда необходимо обеспечить успех при любых воз-
можных условиях.
Минимаксный критерий Сэвиджа используется, когда требует-
ся при любых условиях избежать большого риска.
Формально минимаксный критерий Сэвиджа имеет вид
min max Л,,,
т.е. следует в каждой строке табл. 5.5 выбрать максимальный эле-
мент h.., а потом из этих максимумов выбрать минимальный эле-
мент А/0у.0. Тогда решение B.Q должно предпочитаться всем осталь-
ным решениям.
Решение В.о, предпочитаемое остальным решениям, называ-
ется оптимальным по минимаксному критерию Сэвиджа.
Этот критерий также ориентирует ЛПР на слишком осторож-
ную стратегию поведения, только в отличие от критерия Вальда
получения гарантированной эффективности критерий Сэвиджа
минимизирует возможные потери. Это особенно важно, если
конкуренты уже успели реализовать все свои преимущества.
Критерий обобщенного максимина (пессимизма — оптимизма)
Гурвица используется, если требуется выбирать что-то промежу-
точное между двумя крайними стратегиями — стратегией, рассчи-
танной на получение худшего, и стратегией, рассчитанной на по-
лучение лучшего.
Ю- 7620
145
Формально критерий обобщенного максимина Гурвица имеет
вид
max Н,,
где Н, = \ min а„ + (1-Х) max а,,, где скалярный множитель
' 15/2» * ISjin »
1 е [0,1] фиксирован.
Пусть max Н, = Н,а, тогда решение В1Л должно предпочитать-
1Шт 1 'и "
ся всем остальным решениям. Решение В.о, предпочитаемое ос-
тальным решениям, называется оптимальным по критерию обоб-
щенного максимина Гурвица.
Если скалярный множитель X изменить, то может появиться
новое оптимальное решение.
При X = 1 критерий обобщенного максимина совпадает с кри-
терием максимина Вальда. При X = 0 мы имеем максимаксный
критерий
max max а„,
ориентированный на максимальную эффективность, которая,
как правило, сопряжена с большим риском. Значения параметра X
между 0 и 1 являются промежуточными между осторожностью
(X = 0) и большим риском (X = 1) и выбираются в зависимости от
конкретной ситуации и склонности к риску ЛПР.
Приведенные здесь классические методы решения задачи в ус-
ловиях неопределенности не исчерпывают всех существующих ме-
тодов, рассмотрение которых выходит за рамки данного учебника.
5.9.3. Пример
Пусть таблица эффективностей имеет следующий вид (табл. 5.6).
Таблица 5.6
Ситуации
А л2 А
Решения 4 0,3 0,4 0,6
0,7 0,25 0,45
0,4 0,9 0,15
0,85 0,2 . 0,5
146
Здесь каждый показатель эффективности представляет собой
относительную величину, например, удельную прибыль, удель-
ный доход, т.е. прибыль, доход на единицу выпускаемой продук-
ции.
Таблица потерь, построенная на основе таблицы эффектив-
ностей (см. табл. 5.6), имеет, очевидно, вид
Таблица 5.7
Ситуации
4 л2 Аз
Решения Л 0,55 0,5 0
0,15 0,65 0,15
0,45 0 0,45
0 0,7 0,1
Пусть вероятностир,, р2, р3 появления ситуаций А{, А2, А3 со-
ответственно равны р, = 0,3; р2 = 0,6; р3 = 0,1.
Тогда
R{ = 0,55 • 0,3 + 0,5 • 0,6 + 0 • 0,1 = 0,465,
R2 = 0,15 0,3 + 0,65 0,6 + 0,15 0,1 = 0,45,
Я3 = 0,45 0,3+ 0 0,6+ 0,45 0,1 = 0,18,
Л4 = 0-0,3+ 0,7 0,6+ 0,1 0,1 =0,43.
Поскольку средние потери R3 минимальны, постольку решение В3
является наименее рискованным.
Используя принцип недостаточного обоснования Лапласа,
положим р{ -р2 =р3 = */3 = 0,33.
Тогда
Rx = (0,55 + 0,5 + 0) • 0,33 = 0,35,
R2 = (0,15 + 0,65 + 0,15) • 0,33 = 0,31,
R3 = (0,45 + 0 + 0,45) • 0,33 = 0,3,
R4 = (0 + 0,7 + 0,1) • 0,33 = 0,26.
Поскольку средние потери R{ минимальны, постольку следует в
качестве оптимального выбрать решение Bv
10*
147
Используя максиминный критерий Вальда, будем иметь для
табл. 5.6 (эффективностей)
4 4 4
*1 0,3 о,4 0,6 о,з
в2 0,7 0,25 0,45 0,25
*3 0,4 0,9 0,15 0,15
*4 0,85 0,2 0,5 0,2
0,3
(в правом крайнем столбце выписаны минимальные элементы
всех строк, самый нижний элемент крайнего правого столбца есть
максимальный среди всех элементов правого столбца), т.е.
max min аи - 0,3,
1S/S41S/S3 9
откуда следует, что в качестве оптимального следует выбрать ре-
шение Вг
Используя минимаксный критерий Сэвиджа, будем иметь для
табл. 5.7 потерь
4 4 4
4 0,55 0,5 0 0,55
4 0,15 0,65 0,15 0,65
4 0,45 0 0,45 0,45
0 0,7 0,1 0,7
0,45
(в правом крайнем столбце выписаны максимальные элементы
всех строк, самый нижний элемент крайнего правого столбца есть
минимальный элемент среди всех элементов правого столбца), т.е.
min max h,, = 0,45,
1S/S41S/S3 9
откуда следует, что в качестве оптимального следует выбрать ре-
шение By
148
Используя критерий обобщенного максимума Гурвица, будем
иметь при X = 1 случай максиминного критерия Вальда с опти-
мальным решением Вг
При X=0,67 имеем для табл. 5.6 эффективностей
0,3 + 0,33 0,6 = 0,42 •
0,25 0,7 0,4
0,67 0,15 0,9 0,4
0,2 0,85 0,41
0,42
Здесь в левом столбце расположены минимальные элементы
всех строк табл. 5.6, во втором столбце — максимальные элементы
всех строк, третий столбец есть выпуклая комбинация первых
двух столбцов. Самый нижний элемент последнего столбца — это
максимальный элемент последнего столбца. Следовательно, при
X=0,67 Вх — оптимальное решение.
При X = 0,33 имеем для табл. 5.6 эффективностей
0,3 + 0,67 0,6 = 0,5
0,25 0,7 0,55
0,33 0,15 0,9 0,52
0,2 0,85 0,64
0,64
т.е. при X=0,33 Б4 — оптимальное решение.
При X=0 имеем для табл. 5.6 эффективностей
0,6
0,7
0,9 ,
0,85
0,9
т.е. при X = 0 В3 — оптимальное решение.
149
В рассматриваемом примере в условиях риска (р, = 0,3; Р2 = 0,6;
р3 = 0,1) наименее рискованным является решение В3.
Оптимальным решением по критерию Лапласа является ре-
шение Вг
Оптимальным решением по критерию Вальда является реше-
ние В{.
Оптимальным решением по критерию Сэвиджа является ре-
шение Ву
Оптимальным решением по критерию Гурвица при X = 1 явля-
ется решение В[9 при X = 0,67 — решение Вр при X = 0,33 — реше-
ние В4, при X = 0 — решение Ву
Таким образом, из всех четырех решений Вр В2, Ву В4 в рас-
смотренном примере решения В{ и В3 являются самыми осторож-
ными, а максимальным (т.е. самым рисковым) опять получилось
решение Ву
Вопросы для самоконтроля к главе 5
1. Что представляют собой понятия неопределенности и риска? В чем
сходство и различие этих понятий?
2. В чем проявляется объективная природа риска?
3. В чем проявляется субъективно-объективная природа риска?
4. Какие основные причины неопределенности и риска?
5. Чем занимается экономическая теории риска?
6. Какие важные элементы охватывает классификация рисков?
7. Что такое производственный риск? Назовите причины возникнове-
ния производственного риска.
8. Что такое коммерческий риск? Перечислите причины возникнове-
ния коммерческого риска.
9. Что такое финансовый риск? Раскройте причины возникновения
финансового риска.
10. Что такое посреднический риск? Назовите причины возникновения
посреднического риска.
11. Что такое риск страхования? Перечислите причины возникновения
риска страхования.
12. Что представляет собой структура предпринимательских рисков?
13. Что представляют собой внешние риски?
14. Что такое страновой риск?
15. Что такое валютный риск?
16. Что такое системный риск?
17. Что такое налоговый риск?
18. Что такое риск форс-мажорных обстоятельств?
150
19. Что представляют собой внутренние риски?
20. Что такое организационный риск?
21. Что такое портфельный риск?
22. Что такое кредитный риск?
23. Что такое инновационный риск?
24. Что такое ожидаемый доход?
25. Что такое ожидаемая полезность?
26. Как связаны между собой математическое ожидание (случайной)
полезности и полезность математического ожидания (случайного)
дохода, равного безрисковому доходу, если индивидуум рискофоб?
Приведите графическую иллюстрацию.
27. Как связаны между собой математическое ожидание (случайной)
полезности и полезность математического ожидания (случайного)
дохода, равного безрисковому доходу, если индивидуум рискофил?
Приведите графическую иллюстрацию.
28. Как связаны между собой математическое ожидание (случайной)
полезности и полезность математического ожидания (случайного)
дохода, равного безрисковому доходу, если индивидуум рисконей-
трал? Приведите геометрическую интерпретацию.
29. Что такое премия за риск? Чему равна премия за риск, если индиви-
дуум рискофоб? рискофил? рисконейтрал? Дайте геометрическую
интерпретацию для всех трех случаев.
30. Как определяется абсолютная мера Эрроу — Пратта? Какую она име-
ет размерность?
31. Как определяется относительная мера Эрроу — Пратта? Какую она
имеет размерность? Как она связана с эластичностью предельной
полезности по доходу?
32. Каковы свойства абсолютной и относительной мер Эрроу — Пратта?
33. Для каких функций полезности абсолютная мера Эрроу — Пратта
постоянна?
34. Для каких функций полезности относительная мера Эрроу — Пратта
постоянна?
35. Что представляет собой шкала уровней риска? Приведите практи-
ческие значения шкал уровней риска.
36. Каковы универсальные методы предупреждения и снижения риска?
37. В чем суть страхования как метода предупреждения и снижения
риска?
38. Что такое хеджирование?
39. В чем суть резервирования средств как метода предупреждения и
снижения риска?
40. В чем суть диверсификации как метода предупреждения и снижения
риска?
41. В чем суть лимитирования как метода предупреждения и снижения
риска?
151
42. В чем суть повышения уровня достоверности информации как мето-
да предупреждения и снижения риска?
43. Что представляет собой таблица решений по снижению риска? При-
ведите практическое значение таблицы решений.
44. Что представляют собой актив, рисковый актив, безрисковый ак-
тив?
45. Что представляют собой доходность актива, реальная доходность
актива, ожидаемая доходность актива?
46. Что представляет собой ожидаемая доходность инвестиционного
портфеля?
47. Что представляет собой содержательная интерпретация углового ко-
эффициента бюджетной прямой?
48. Как объяснить, что линии безразличия функции полезности инвес-
тора имеют положительный наклон?
49. Как строятся таблицы эффективностей и таблицы потерь?
50. Как с помощью таблицы потерь выявляется оптимальное решение в
условиях риска?
51. Как формулируется принцип недостаточного обоснования Лапласа?
52. Какое решение называется оптимальным по принципу недостаточ-
ного обоснования Лапласа?
53. Как формулируется максиминный критерий Вальда?
54. Какое решение называется оптимальным по максиминному крите-
рию Вальда?
55. Как формулируется минимаксный критерий Сэвиджа?
56. Какое решение называется оптимальным по минимаксному крите-
рию Сэвиджа?
57. Как формулируется критерий обобщенного максимина Гурвица?
58. Какое решение является оптимальным по критерию обобщенного
максимина Гурвица?
Задачи и упражнения для самоконтроля к главе 5
1. В лотерею можно ничего не выиграть с вероятностью рх = 0,5, выиг-
рать 10 руб. с вероятностью р2 = 0,3, выиграть 50 руб. с вероятностью
р3 = 0,07, выиграть 100 руб. с вероятностьюр4 = 0,03:
а) найдите математическое ожидание участника лотереи;
б) найдите дисперсию всех исходов лотереи, а также среднее квад-
ратичное отклонение и вариацию;
в) сколько готов заплатить рисконейтрал, чтобы принять участие в
лотерее?
г) сколько готов заплатить рискофоб, чтобы принять участие в ло-
терее?
152
2. Вложение в бизнес имеет три возможных исхода: получение прибы-
ли 1000 д.е. с вероятностью рх = 0,2, получение прибыли 500 д.е.
с вероятностьюр2 = 0,5, получение убытка — 200 д.е. с вероятностью
р3 = 0,3:
а) найдите математическое ожидание этого неопределенного вло-
жения в бизнес;
б) найдите дисперсию всех возможных исходов, а также среднее
квадратичное отклонение и вариацию.
3. Фермер может оказаться в одной из двух ситуаций: дождливое лето,
засушливое лето. Вероятность дождливого лета равна р{ = 0,4, веро-
ятность засушливого лета равна 0,6. У фермера два варианта реше-
ний — вносить удобрения, не вносить удобрения. Сведем все эти
данные в платежную таблицу, содержащую информацию о возмож-
ных доходах (в д.е.) фермера:
Ситуации
Дождливое лето Засушливое лето
Решения Не удобрять 100 д.е. 10д.е.
Удобрять 60 д.е. 30д.е.
Вероятности 0,4 0,6
а) какое решение примет рискофоб, рисконейтрал, рискофил?
б) дайте геометрическую интерпретацию всех трех случаев.
4. Функция полезности индивидуума имеет вид и = wa, где w — доход
индивидуума, а параметр 0 < а < 1 (все расчеты проводить при = */3
иа2 = '/7):
а) является ли индивидуум рискофобом, рисконейтралом или рис-
кофилом? Ответ обоснуйте. Дайте геометрическую интерпрета-
цию;
б) доход индивидуума равен 20 д.е. Индивидууму предлагают новые
условия, в которых с вероятностями 0,5 его доход может вырасти
на 10 д.е., но может и упасть на 15 д.е. Примет ли индивидуум
новые условия?
в) определите абсолютную и относительную меры Эрроу — Пратта
для данной функции полезности;
г) выполните пункты а), б), в) и г) при а3 = 2 и а4 = 6.
5. Приведите в графической и аналитической формах пример функции
полезности и = u(w) индивидуума (w - его доход), который при низ-
ком доходе является рискофилом, а при высоком доходе — рискофо-
бом.
153
6. Таблица эффективностей имеет вид:
Ситуации
А А
j *1 0,5 0,6 0,6 0,7
В2 0,4 0,3 0,5 0,15
Вз 0,7 0,8 0,2 0,3
В. 0,9 0,2 0,3 0,1
а) постройте таблицу потерь;
б) найдите оптимальное решение в условиях риска, если вероят-
ность появления ситуации Ах равна рх = 0,1, ситуации Аг - 0,3,
ситуации А3 — 0,4, ситуации А4 — 0,2;
в) найдите решение, оптимальное по принципу недостаточного
обоснования Лапласа;
г) найдите решение, оптимальное по максиминному критерию
Вальда;
д) найдите решение, оптимальное по минимаксному критерию Сэ-
виджа;
е) найдите решение, оптимальное по критерию обобщенного мак-
симина Гурвица (рассмотрите Х=1, А, = 0,8, Х = 0,6, Х = 0,4, А =
0,2, Х = 0).
Вопросы и тесты для контрольных работ к главе 5
1. Риск —это:
а) возможность опасности;
б) действие на удачу;
в) вероятность возникновения убытков;
г) ответы а)—в) не верны;
д) ответы а)—в) верны.
2. Основные причины неопределенности:
а) случайность;
б) столкновение противоречивых интересов;
в) вероятностный характер НТП;
г) все ответы а)—в) верны;
д) ни один из ответов а), б), в) не является верным.
3. Основные причины неопределенности и риска:
а) ограниченность ресурсов при принятии решения;
б) невозможность выйти на такой уровень познания объекта, кото-
рый был бы достаточным для принятия верного решения;
154
в) относительная ограниченность сознательной деятельности
ЛПР;
г) все ответы а)—в) верны;
д) все ответы а)—в) не верны.
4. По времени возникновения риски распределяются на:
а) внешние;
б) текущие;
в) политические;
г) чистые;
д) внутренние.
5. По характеру учета риски делятся на:
а) перспективные;
б) политические;
в) коммерческие;
г) внутренние;
д) ретроспективные.
6. К внешним предпринимательским рискам необходимо отнести сле-
дующий риск:
а) организационный;
б) системный;
в) кредитный;
г) ресурсный;
д) инновационный.
7. К внутренним предпринимательским рискам необходимо отнести
следующий риск:
а) валютный;
б) налоговый;
в) системный;
г) кредитный;
д) все ответы а)-г) не верны.
8. Для рискофоба:
а) ожидаемая полезность строго больше полезности в условиях от-
сутствия риска;
б) ожидаемая полезность равна полезности в условиях отсутствия
риска;
в) ожидаемая полезность строго меньше полезности в условиях от-
сутствия риска;
г) нет однозначного ответа о взаимосвязи между ожидаемой полез-
ностью и полезностью в условиях отсутствия риска;
д) все ответы а)-г) не верны.
9. Для рискофоба премия за риск:
а) положительна;
б) отрицательна;
в) равна нулю;
155
г) нет однозначного ответа;
д) все ответы а)—г) не верны.
10. В случае перестрахования:
а) страхователь перекладывает риск за определенную плату одно-
временно на двух (и более) страховщиков;
б) страховщик перекладывает часть своего риска за определенную
плату на другого страховщика;
в) страховщик заключает со страхователем договор на часть общей
суммы страхового договора;
г) перестрахование — теоретическое понятие, которое не имеет
аналогов в практике страхования.
д) все ответы а)—г) не верны.
11. Диверсификация в целях снижения банковских рисков представляет
собой:
а) уменьшение кредитуемых вкладчикам сумм;
б) расширение числа клиентов при сохранении или уменьшении
общей суммы, выделяемой для их кредитования;
в) образование резервов в разных валютах;
г) привлечение депозитных вкладов более мелкими суммами от
большего числа вкладчиков;
д) все ответы а)-г) верны.
12. Применяемый принцип недостаточного обоснования Лапласа —
это:
а) частный вариант выбора оптимального решения в условиях
риска;
б) обобщение максиминного критерия Вальда;
в) обобщение минимаксного критерия Сэвиджа;
г) обобщение критерия Гурвица;
д) все ответы а)-г) не верны.
13. Оптимальное по критерию Вальда решение:
а) минимизирует возможные потери;
б) обеспечивает успех при любых возможных условиях;
в) может быть получено при условии наличия равновероятных си-
туаций;
г) совпадает с максимальным решением Гурвица;
д) все ответы а)-г) верны.
14. Оптимальное по критерию Сэвиджа решение:
а) минимизирует возможные потери;
б) обеспечивает успех при любых возможных условиях;
в) может быть получено только при условии наличия равновероят-
ных ситуаций;
г) совпадает с максиминным решением Вальда;
д) все ответы неверны.
156
Задачи для контрольных работ к глава 5
1. В лотерею можно ничего не выиграть с вероятностью = 0,7, выиг-
рать 10 руб. с вероятностью р2 = 0,2, выиграть 50 руб. с вероятностью
р3 = 0,08, выиграть 100 руб. с вероятностью р4 = 0,02:
а) найдите математическое ожидание участника лотереи;
б) найдите дисперсию всех исходов лотереи, а также квадратичное
отклонение и вариацию;
в) найдите премию за риск для участника лотереи, если участник
рискофоб, рисконейтрал, рискофил.
2. Вложение в бизнес имеет три возможных исхода: получение прибы-
ли 2000 д.е. с вероятностью р} = 0,1, получение прибыли 800 д.е.
с вероятностью р2 = 0,4, получение убытка 300 д.е. с вероятностью
Р3 = 0,5:
а) найдите математическое ожидание этого неопределенного вло-
жения в бизнес;
б) найдите дисперсию всех возможных исходов, а также среднее
квадратичное отклонение и вариацию.
3. Ближайшее для студента лето может оказаться дождливым или за-
сушливым. Вероятность дождливого лета равна р, = 0,3, вероятность
сухого лета - 0,7. У студента два варианта решений - подрядиться на
работу или отдохнуть. Сведем все эти данные в платежную таблицу,
содержащую информацию о возможных доходах (в д.е.) студента:
Ситуации
Дождливое лето Засушливое лето
Решения Работать 1000 1500
Отдыхать -500 -800
Вероятности 0,3 0,7
а) какое решение примет рискофоб, рисконейтрал, рискофил?
б) дайте геометрическую интерпретацию всех трех случаев.
4. Таблица эффективностей имеет следующий вид:
Ситуации
А А2 Аз А4
Решения в, 0,9 0,5 0,4 0,3
0,4 0,2 0,7 0,5
В> 0,5 0,8 0,5 0,2
в< 0,3 0,6 0,3 0,6
157
а) постройте таблицу потерь;
б) найдите оптимальное решение в условиях риска, если вероят-
ность появления ситуации А{ равна = 0,4, ситуации Л2 — 0,3,
ситуации А3 — 0,1, ситуации А4 - 0,2;
в) найдите решение, оптимальное по принципу недостаточного
обоснования Лапласа;
г) найдите решение, оптимальное по максиминному критерию
Вальда;
д) найдите решение, оптимальное по минимаксному критерию Сэ-
виджа;
е) найдите решение, оптимальное по критерию обобщенного мак-
симина Гурвица (рассмотрите Х=1, Х = 0,75, Х = 0,5, Х = 0,25,
Х = 0).
5. Функция полезности индивидуума имеет вид и = где w - доход
индивидуума, а параметр 0 < a < 1 (все расчеты проводите при = [/4
иа2 = 1/9):
а) доход индивидуума равен 40 ед. Индивидууму предлагают новые
условия, в которых равновероятно его доход может вырасти на 30
д.е., но может и упасть на 20 д.е. Примет ли индивидуум новые
условия?
б) определите, сколько будет стоить страховка индивидуума, при-
обретаемая в целях элиминирования неопределенности, связан-
ной с новыми условиями;
в) выполните пункты а) и б) при а3 = 3 и а4 = 7.
6. Приведите в графической и аналитической формах пример функции
полезности и = u(w) индивидуума (w — его доход), который при низ-
ком доходе является рискофобом, а при высоком доходе - рискофи-
лом.
Глава 6
ТЕОРИЯ ФИРМЫ,
ФУНКЦИОНИРУЮЩЕЙ
В УСЛОВИЯХ чистой
КОНКУРЕНЦИИ
6.1. Задача максимизации прибыли фирмы
в долговременном и краткосрочном промежутках.
Локальное рыночное равновесие фирмы.
Функции спроса на ресурсы со стороны фирмы
и функция предложения фирмы.
Аргументы «за» и «против» максимизации прибыли.
Понятие «разумной прибыли»
6.1.1. Согласно теории микроэкономики и соображениям мно-
гих практиков задача максимизации прибыли является основной
целью функционирования фирмы в условиях конкуренции. Это
положение кажется бесспорным, если рассматривать фирму как
исходный элемент (атом) системы производства.
Суть проблемы максимизации прибыли фирмы усложняется,
если фирму рассматривать самостоятельно в качестве сложной
системы.
Приведем ряд аргументов «за» и «против» максимизации при-
были фирмы. Ряд аргументов наиболее убедителен «в случае ато-
ма», другой ряд — «в случае сложной системы».
Сначала аргументы «за»:
* мотив прибыли — самая универсальная и устойчивая сила, на-
правляющая деловое поведение фирмы, в связи с тем, что
159
влияние других целей фирмы на ее поведение относительно
невелико, ибо их учет не способствует лучшему объяснению и
прогнозированию поведения фирмы, но значительно услож-
няет анализ;
• конкуренция заставляет фирмы преследовать цель максими-
зации прибыли, ибо если фирма в конкурентной борьбе имеет
шанс заработать хоть какую-то прибыль, то она должна стре-
миться ее максимизировать;
• допущение о максимизации прибыли фирмы позволяет точно
предсказать ее поведение, ибо экономисты успешно применя-
ли это допущение в качестве основы для прогнозирования
поведения во времени цен и объемов производства фирм;
• допущение о максимизации прибыли фирмы полезно для об-
щего понимания и объяснения ее поведения.
Приведем аргументы «против»:
• цель максимизации прибыли фирмы бессмысленна в качестве
основы для принятия решений о поведении фирмы, ибо в ус-
ловиях неопределенности невозможно установить, какое из
направлений деятельности фирмы приведет к максимизации
прибыли. Лучшее решение в одной ситуации не обязательно
будет таковым в другой;
• отделение управления от собственности дает менеджерам сво-
боду преследовать другие, отличные от максимизации прибы-
ли цели;
• существует много примеров того, что практическая деятель-
ность фирмы не связана с максимизацией ее прибыли;
• фирма находит выгодным для себя избегать получения макси-
мально возможной прибыли, ибо максимальная прибыль мо-
жет привлечь новых конкурентов, спровоцировать антитрес-
товские акции, требования профсоюза повысить заработную
плату;
• максимизация прибыли — дело трудное, малореалистичное и
даже аморальное, ибо может спровоцировать бизнесменов на
торгашеские уловки (понижение зарплаты, повышение цен,
снижение качества производимого продукта, давление на по-
ставщиков, чтобы они снизили цены). Мотив максимизации
прибыли может быть решающим для повышения уровня де-
градации окружающей среды за счет роста общественных из-
держек в связи с сокращением затрат на охрану окружающей
среды и борьбу с загрязнениями.
160
Если фирму рассматривать как сложную систему, основны-
ми элементами которой являются собственники (акционеры),
менеджеры (управляющие) и наемная рабочая сила, то сразу в
поле зрения появляются по меньшей мере три целевые функции:
максимизация прибыли (целевая функция собственников, кото-
рые получают дивиденды из прибыли), долговременный устой-
чивый рост (целевая функция менеджеров) и максимизация
заработной платы (целевая функция наемных работников).
К числу системных целевых элементов следует отнести также
минимизацию степени риска, с учетом которого прибыль фир-
мы может оказаться недостаточной для ее дальнейшего разви-
тия. Таким образом, речь идет о векторной целевой функции
оптимального функционирования фирмы в условиях конкурен-
ции. Векторная целевая функция путем свертки ее координат с
определенными весами может быть превращена в скалярную
целевую функцию.
Если фирма имеет сильный профсоюз, то это обстоятельство
должно быть отражено в повышении относительного веса той ко-
ординаты векторной целевой функции, которая показывает уро-
вень заработной платы наемных работников. Если на фирме
сформировался крепкий и влиятельный корпус менеджеров, от-
носительно больший вес получает та координата векторной целе-
вой функции, которая характеризует темп долговременного ус-
тойчивого роста фирмы. Если на фирме большим влиянием поль-
зуется совет директоров (совет акционеров) (заметим, что для
конкретной реальной фирмы это может и не иметь места), то от-
носительно больший вес получает та координата векторной целе-
вой функции, которая равна собственно прибыли фирмы.
В связи со сказанным актуальным становится понятие «разум-
ной» прибыли, которое разными руководителями высшего звена
управления фирмы толкуется совершенно по-разному:
* «разумная» прибыль позволяет фирме выполнять свои обяза-
тельства перед акционерами и приобретать средства, необхо-
димые для производства в будущем товаров, услуг и создания
рабочих мест;
* прибыль «разумная», если она позволяет фирме выживать;
* «разумная» прибыль фирмы должна несколько превышать
уровень, необходимый для привлечения инвесторов в другие
аналогичные фирмы, которые характеризуются той же степе-
нью риска;
11 - 7620
161
• в связи с тем что «высокая» (по сравнению с неким средним
уровнем) прибыль с учетом риска может оказаться недоста-
точной для дальнейшего развития фирмы, такие описатель-
ные ярлыки, как «справедливая прибыль», «разумная при-
быль», имеют мало смысла.
Для анализа и прогнозирования поведения фирмы, функцио-
нирующей в условиях конкуренции, одних качественных рассуж-
дений недостаточно, ибо необходимо получение конкретных ве-
личин, характеризующих рациональное поведение фирмы.
Далее будут рассмотрены и проанализированы три классичес-
кие модели оптимального функционирования фирмы, в которых
четко разграничиваются экзогенные и эндогенные переменные,
отражающие рыночную ситуацию и характеризующие оптималь-
ное состояние фирмы. Развитие этих моделей путем перехода к
векторной оптимизации и путем учета рисков и неопределеннос-
ти в этой книге не рассматривается.
6.1.2. Задача максимизации прибыли фирмы и две ее версии (за-
дача максимизации выпуска при лимите на ресурсы и задача ми-
нимизации издержек при фиксированном объеме выпускаемой
продукции) будут рассмотрены в случаях долговременного и крат-
косрочного промежутков.
В случае долговременного промежутка задача максимизации
прибыли имеет вид (в случае двух ресурсов — капитала и труда)
PR(xp х2) =p0-f(xp х2) -р2х2 -> (max), (6.1.1)
где f(xx, х2) — производственная функция (ПФ) фирмы;
р0 — цена выпускаемой фирмой продукции (например,
валенок);
рх ир2 — цена на капитал и труд;
Xj — количество капитала;
х2 — количество труда.
Данными (экзогенными) величинами являются ценыр0, рх,р2,
искомыми (эндогенными) величинами — количествах] их2 капи-
тала и труда. Все величины р0, рх, р2, х, и х2, а также производ-
ственная функция/(Х], х2) привязаны к текущему периоду (атому
времени) / (номер / в модели явно не показывается). Число перио-
дов между базовым (нулевым) периодом и текущим периодом та-
кое, что они составляют долговременный промежуток, в течение
162
которого фирма может свободно распоряжаться как капиталом,
так и трудом.
Таким образом, если в базовом периоде фирме известны цены
р0, рх, Р2 текущего периода, то, решив задачу (6.1.1), фирма будет
знать, какое количество капитала х® и какое количество труда х°
фирма должна приобрести в текущем периоде, чтобы в этом пери-
оде максимизировать свою прибыль.
Особо отметим, что необходимый расчет фирма производит
заранее, чтобы в течение долговременного промежутка подгото-
вить к функционированию требуемое количество капитала х°х и
требуемое количество труда х2. Фиксированные цены р0, рх, р2
означают, что фирма на эти цены влиять не может, т.е. принима-
ется важная предпосылка, что фирма является конкурентной,
т.е. на рынке готовой продукции (например, валенок) и на рынке
ресурсов фирма функционирует в условиях чистой конкуренции.
6.1.3. Для решения задачи (6.1.1) следует выписать условия пер-
вого порядка, т.е. систему двух уравнений с двумя переменными
dPR d/(xpx2)
57='’»-^-'’'=0’
dPR Э/(хрХ2)
Ч— = Ро——Рг=0
дх2 Эх2 (6.1.2)
и решить эту систему.
Решение (х®, х2) системы (6.1.2) является глобальным максиму-
мом прибыли РЛ(Х], х2), ибо производственная функция/(хр х2)
обладает рядом специфических свойств (в частности, ее изокван-
ты, как правило, суть линии строго выпуклые к точке О = (0,0)).
Решение (х°, х2) системы (6.1.2) называется локальным ры-
ночным равновесием фирмы. Термин «локальный» означает, что
на рынке готовой продукции (например, валенок) и на рынках
ресурсов (капитала и труда) функционирует одна (а не несколько)
фирма. В связи с тем что решение (х°, х2) зависит от экзогенных
переменныхр0, рх, р2, получаются две функции спроса со стороны
фирмы на рынке ресурсов: функция спроса х° = gx(p0, рх, р2) на
капитал и функция спроса на труд х2 = g2(p0, РХ,Р2)-
Функция у° = Л(р0, рх, р2) = /(хр х2) есть функция предложения
фирмой своей продукции на рынке продукции.
п»
163
Хорошо известно, что все три функции х^ = g^ip^, pv р2),
х2 = g2(p0, pv Р2), / = А(р0,РрР2) однородны нулевой степени по
Эйлеру. Это означает, что при изменении масштаба цен значения
хр х°, у° не меняются.
6.1.4. В случае краткосрочного промежутка задача максимиза-
ции прибыли имеет вид (6.1.1) с дополнительным условием
х1=х„ (6.1.3)
т.е. в математическом отношении это задача на абсолютный мак-
симум одной переменной
РЯ(х,, х2) = pof(x}, х2) - PjX, - р2х2.
Здесь фиксированное количество х{ капитала означает, что в тече-
ние краткосрочного промежутка между базовым и текущим пери-
одами фирма не имеет возможности скорректировать количество
X] капитала.
Здесь и далее вместо условия вида (6.1.3) может фигурировать бо-
лее общее условие g(xp х2) < 0.
6.1.5. Приведем решение задачи (глобальной) максимизации
прибыли фирмы в случае, когда ПФ/(хр х2) фирмы есть ПФ Коб-
ба — Дугласа.
/(хр х2) = аох“1 х“2 (а, > 0, а2 > 0, оц + а2 < 1).
В рассматриваемом случае имеем
РЛ = poaoxf ‘х2 2 — Р|Х| — р2х2.
Условия первого порядка имеют вид
ЭРЛ а,-1 а, л
“ А)°оа1Х1 Х2 ~ Р\~ 0’
ЭРЛ <Х. ОЦ—1 л
~ РоаОа2Х1 Х2 ~ Р2~ 0-
После деления первого уравнения на второе и сокращений
Ло°Ь«1Х| ‘ х22 _ Р\ Х2 _ ^2 А
р0о0а2х“‘х“2-1 ” Р2’ *1~а|Р2
получим выражение для х2
Х2Лхр
а,р2
164
Подставив его в первое из двух уравнений, будем иметь
Гг ^2-А = о>
\al?2 J
откуда после ряда элементарных преобразований выражения
Р\
(\аг
а2^1 I
cq+aj-l
*1
получим
х°
Л1
Объединяя первое и последнее звенья цепочки
1 , а2 '~а2
д.0 — д.0 _ а2^1 /д _ xl-o^-oij | а2 |,-а1_<х2 | <Х| j1-**!-**!
2 ctjPj 1 00 (pj Ц)
будем иметь
$
Точка (х°, х°) — критическая точка прибыли РЛ(хр х2), ибо
обращает в нуль частные производные прибыли.
Выше отмечалось, что в экономических задачах весьма часто
критическая точка является точкой не только локального, но и
глобального максимума.
Проверим в рассматриваемом случае выполнение условий
второго порядка:
= A)°oai (“1" 1)*Г* ~2х?2 < О,
ах«
165
Э PR / i\ ai а?~2
2 “ ^ОаОа2 (а2 “ Х2 ’
дх2
Э2 PR 01,-1 а -1
^- = Р0ДЬа1а2Х11 Х22 ’
&PR&PR d2PR =
дх2 дх2 дх{дх2
= (Po^b)2 «l0^ <«1 -1><а2 -1Ц2а,'2Х22“2“2 -(Poflo)2a2a2Xl2<Ct'’1>X2(a24> =
= (р0о0)2х12(“,-1)Х2(<Х2"1)(а1(а1 - 1)а2(а2 -1)-а2а2) =
= (Ро^>Ч^’1)^в,Ч)((<х1 -«iX«2 -а2)-а2а2) =
= (р0а0)2х12(“1-1)х2<а2-1)(а2а2 -а^ -а2а2 +aja2-а2а2) =
= (р0^)2х2(в|",)^(а1’,)(а,а2 -aia2(a, +а2)) =
= (р0<%)2х12(в''1)^(в»‘1)(1-а1 -а^а^ >0-
Поскольку
Э^М)
Зх2
Э2Р/?(х®; х2°) Э2РЛ(х.°; х®) d2PR(x°;x®) Л
Эх2 Sxj HXj&Cj
на основании условий второго порядка критическая точка (х®, х®)
есть точка локального максимума функции РЛ(хр х2).
Поскольку функция у = о^х®' х£2 (<Xj 0, a2 > 0; 0 < af + a2 < 1)
выпукла вверх для всех xt £ 0, х2 £ 0, постольку локальный макси-
мум является глобальным.
Таким образом, при конфигурации ресурсов (х®, х®) фирма
будет иметь максимальную прибыль:
166
PR0 = (x2°)“2 - prf - p2x°2 =
1
= (/’oflo)(flb/’o)1'“1’<X2
_5_
l-a,-a2
•OWoA’*2 :
-MW-0'1-0'2
_5_
l-aj-a2
_5_
l-ctj-aj
1
167
Задача (глобальной) максимизации прибыли фирмы в случае
ПФ Кобба — Дугласа (cq + otj < 1, otj > 0, а2 > 0)) решена.
Если cq > 0, aj > 0, а, + Oj = 1, прибыль PR(xx, х2) имеет вид
Р/? = OqPqXi 'Xj 1 — Р\Х^ — Р2%2'
Если, например, х2 = кхх, то
Р/? = 1 (ArXj) 1 — — р2кхх =
= *^i— (Pi + Рг^”^1 = («оМ 1 — Р]— Р2^)^р
Отсюда вытекает, что если в последнем звене круглая скобка
равна нулю, то максимальная PR = 0. Если круглая скобка поло-
жительна, то максимальная PR -> +°° при Xj -> +°°. Если круглая
скобка отрицательна, то максимальная PR = 0. При а( > 0, > 0 и
а( + а2 > 1 и при х2 = kxxPR-+ +°о при хх -> +°°. То есть в случае
а( + а2 > 1 и х2=кхх задача максимизации PR либо имеет тривиаль-
ное решение х°=х2 = 0 и PR0 = 0, либо решения не имеет.
6.2. Задача максимизации выпуска фирмы
при лимите на используемые ею ресурсы
в долговременном и краткосрочном промежутках.
Функции условного спроса по Маршаллу
(по Вальрасу) на ресурсы со стороны фирмы
и функция условного выпуска фирмы
6.2.1. Задача максимизации выпуска фирмы при лимите на ре-
сурсы — первая версия задачи максимизации прибыли фирмы.
Второй версией задачи максимизации прибыли фирмы является
задача минимизации издержек при фиксированном объеме вы-
пускаемой продукции, которая анализируется в параграфе 6.4.
Если фирма имеет лимит на ресурсы, равный К, т.е.
рххх+р2х2=У, (6.2.1)
то задача (6.1.1) максимизации прибыли фирмы в долговремен-
ном промежутке приобретает вид PR = pQf(xx, х2) - V—> шах, что
эквивалентно задаче
/(хр х2) -> max (6.2.2)
при наличии ограничения (6.2.1) на условный экстремум.
168
Хорошо известно, что задачу (6.2.2), (6.2.1) следует решать ме-
тодом Лагранжа: составить функцию Лагранжа
£(хр х2,1) =f(xx, х2) + Х(И-р,х1 -р2х2) (6.2.3)
и решить систему трех уравнений с тремя неизвестными хр х2,X:
Э£(хр х2, %) _ Э/(хр х2) _
— — U,
Эх( Эх(
Э£(Хр х2, X) _ Э/(Хр х2) _
— лр2 “
Эх2 Эх2
Э£(Х|, х2, X)
-------------= V - Р\ Х1 - Р1Х2 = °’
(6.2.4)
которые представляют собой условия первого порядка.
В связи с тем что ПФ/(хр х2) обладает рядом специфических
свойств, одним из которых является строгая выпуклость изоквант
к точке О, короткая точка (х,, х2) есть точка глобального максиму-
ма целевой функции (6.2.2) при наличии ограничения (6.2.1).
Напомним, что длинная точка (хр х2, X) является единственным
решением системы (6.2.4).
В связи с тем что формальная задача (6.2.2), (6.2.1) максимиза-
ции выпуска фирмы при лимите на ресурсы не отличается от зада-
чи максимизации функции полезности потребителя при бюджет-
ном ограничении (см. параграф 1.1), мы воспользуемся формаль-
ными результатами параграфа 1.1.
ФункцииХ] =<р1(Рр/>2> Ю, *2 = ф2(Рр/’2> И называются функ-
циями условного спроса по Маршаллу (по Вальрасу) на ресурсы
со стороны фирмы на рынках ресурсов (капитала и труда). Функ-
ция^ = /(х1,х2)=/(Ф1(Рр/’2’ П,ф2(РрР2» к)) = 6(/’рР2’ И) назы‘
вается функцией условного предложения фирмы на рынке про-
дукции (например, на рынке валенок), X = ф3(рр р2, V).
Подставив длинную точку (хр х2, X) в первые два уравнения
системы (6.2.4), получим равенство
grad/(xp х2) = Х- (рх,р2), (6.2.5)
откуда следует, что множитель Лагранжа X, как правило, получа-
ется достаточно малым, ибо цены р{ ир2 на ресурсы относительно
велики, а предельные производительности ресурсов
д/(х,,х2) Э/(хрх2)
ЭХ| ’ Эх2
169
при значительных количествах х, и х2 расходуемых ресурсов от-
носительно малы.
Все функции и 0(/’р/,2’ однород-
ны нулевой степени относительно всех трех переменныхр{, р2, V.
С изменением лимита V от нуля до +°° и при фиксированных
ueHax/ijHpj на ресурсы точка(х1,х2) = (<р1(^1,/>2, И),ф2(рр/>2, И))
заметает (от слова «метла») на плоскости Ох,х2 линию L, которая
называется линией развития фирмы в долговременном промежутке.
Линия L развития фирмы аналогична линии доход—потребление
в теории поведения потребителя на рынке (рис. 6.1, на котором
лимит принимает два значения Vx и V2 и на котором также показа-
но локальное рыночное равновесие (х°, х2) фирмы, т.е. решение
задачи 6.1.1).
6.2.2. Задача максимизации выпуска фирмы при лимите на ре-
сурсы в краткосрочном промежутке есть задача (6.2.2), (6.2.1) при
дополнительном ограничении
х,=Хр (6.2.6)
170
Приведем геометрическое решение этой задачи (на рис. 6.2 — кон-
фигурация ресурсов (хр х2)). На рис. 6.2 для сравнения показано
решение задачи (6.2.2), (6.2.1) в долговременном промежутке (см.
конфигурацию ресурсов (хр х2) на рис. 6.2). Рисунок 6.2 иллюст-
рирует важное положение: при одном и том же лимите Ина ресур-
сы в случае долговременного промежутка объем выпуска у фирмы
больше (не меньше) объема выпуска у (у > у) в случае краткосроч-
ного промежутка.
Рис. 6.2
При вариации лимита V на ресурсы конфигурация (хр х2) ре-
сурсов будет перемещаться по линии Н, которая, следовательно,
есть линия развития фирмы в краткосрочном промежутке.
6.2.3. Приведем решение задачи максимизации выпуска фир-
мы при наличии лимита С на ресурсы в случае, когда производст-
венная функция /(хр х2) фирмы есть функция Кобба — Дугласа
У^а^х^хр:
/(Хр х2) = аох“'х^ -> max,
/>1Х1+р2х2 = С.
171
Здесь рх и р2 — рыночные цены на ресурсы. Искомыми пере-
менными являются объемы xt и х2 первого и второго ресурсов.
Составим функцию Лагранжа
L = аох“'х^ + ЦС-р^ -р2х2)
и выпишем для нее условия первого порядка
— = aoajX| * х2 2 - = О, —— = х“2 1 - \р2 = О,
dXj aXj
3L г .
— = с-р1х,-р2х2=о,
откуда получаем равенство дробей
°bai*i1 х2* _ А
^а2Х1а|х“2-1 Р2
После элементарных преобразований имеем
х2 a2Pj а2д
Xi а,р2 ахр2
Подставив выражение для х2 в ограничение С=рххх + р2х2, по-
лучим
С - рххх - р2 хх = 0, или =(а]+а2)Р|Х],
а1А
откуда
а.С
X = Ч>!О1,Р2, С) = -—-
(а,+а2)Р]
(функция условного спроса (по Маршаллу) на первый ресурс со
стороны фирмы на рынке).
Для х2 имеем
- = ^-х =а2Р' “|С а2С
2 а,р2 1 а]Р2 (o^+appj (ах+а2)р2'
х2 = ----—— = <Р2 (РР Р2 > О
(ах+а2)р2
(функция условного спроса (по Маршаллу) на второй ресурс со
стороны фирмы на рынке).
172
Имеем
Дх, ,х2) = а0(х1)а-(х2)а2
( а.С V1 ( а,С V2
Q I __1 I I * I
° Ца1 + а2 )а J ца1+ а2 )?2 J
OjLp Г (Xjp
Р\) W (а1+а2)“,+аг
= 0(А’/,2’С)
ИЛИ
Г а1 | 1 [ а2 ]
e(A>p2>c) = flo т- “Г
к ”1 7 \Р1)
Са1+О2
(aj+a2)O|+°2
(функция условного предложения выпуска фирмы на рынке).
6.3. Предельный условный выпуск по лимиту
и предельный условный выпуск по цене ресурса
(тождество Роя)
6.3.1. Предельный условный выпуск по лимиту равен множите-
лю Лагранжа А
Э6(р,, р2, И) _ г (6.3.1)
ЭК
Предельный условный выпуск по цене р. ресурса вида i (Z = 1,2)
равен -х;А, т.е.
эе(/>1,р2,и)= , = 1 2 (632)
Эр,-
Формально эти результаты ничем не отличаются соответственно от
предельной полезности по доходу и предельной полезности по це-
не р. продукта Gj (/ = 1,2) в теории потребления (см. параграф 1.2).
6.3.2. Выражения (6.3.1) и (6.3.2) принято называть утверждени-
ями (теоремами) о маргинальных значениях. Эти выражения поз-
воляют проводить анализ чувствительности условного выпуска
относительно изменения лимита на ресурсы и цен на ресурсы.
Формула (6.3.1) показывает, что при росте на ДК(относитель-
но малых) единиц лимита на ресурсы условное предложение фир-
мы 0(ррр2, V) увеличится приблизительно на А ДИединиц. Учиты-
173
вая достаточную малость множителя Лагранжа X, получили важ-
ный качественный результат, основанный на использовании
формулы (6.3.1):
Аналогично формула (6.3.2) показывает, что при росте на Др,
(относительно малых) единиц цены р. на ресурс вида i (i = 1, 2)
условное предложение фирмы 0(ррр2, И) уменьшается приблизи-
тельно на ХД/>. единиц. Учитывая достаточную малость множите-
ля Лагранжа X, получим важный качественный результат, осно-
ванный на использовании формулы (6.3.2):
ео^+др,,/^, V)=e(pvp2, n-X x^.
Для цены р2 на второй ресурс получим аналогичное выражение:
е(ррр2+др2, У)=е(рх,р2, п-х2 х.
6.4. Задача минимизации издержек фирмы
при фиксированном выпуске фирмы в долговременном
и краткосрочном промежутках. Функции условного
спроса по Хиксу на ресурсы со стороны фирмы
и функция условных издержек фирмы
6.4.1. Вторая версия задачи максимизации прибыли фирмы есть
задача минимизации издержек при фиксированном объеме у вы-
пускаемой фирмой продукции.
Если фирма имеет фиксированный выпуск у = /(хр х2), т.е.
y=f(.xvx2), (6.4.1)
то задача (6.1.1) максимизации прибыли фирмы в долговремен-
ном промежутке приобретает вид PR=роу - р{х{ - р2х2 —> max, что
эквивалентно задаче
+ р2х2 —> min (6.4.2)
при наличии ограничения (6.4.1) на условный экстремум. Для ре-
шения задачи (6.4.2) и (6.4.1) составим функцию Лагранжа
£(хр х2, у) =plx[ +р2х2 + Х(ух2)) (6.4.3)
174
и затем выпишем условия первого порядка
Э£(Хр х2, X) _ Э/(хр х2) _
як
Э£(х.,х,,Х) .сУХХцХ,) Л
—1Р-22_' = ^_Х ’ ?' = 0, (6.4.4)
ОХ^ cfA*
Э£(хрх2,Х) _
----“------= У - /(*,, х2) = 0.
иЛ»
Аналогично системе (6.2.4) система (6.4.4), в которой фигури-
рует ПФ со своей спецификой, имеет единственное решение
(Хр х2, X) (длинная точка). Короткая точка (хр х2) есть точка гло-
бального минимума задачи (6.4.2), (6.4.1), которая формально
ничем не отличается от задачи минимизации расхода при фикси-
рованном уровне полезности (см. параграф 1.3).
Функции х, = Yj(Pp р2,у), х2 = Рг* У) называются функ-
циями условного спроса по Хиксу на ресурсы со стороны фирмы
на рынках ресурсов (капитала и труда), X = у3(/>1, р2, У)-
Функция С = рххх + р2х2 = р2, у) + Р2У2(Р1> Р2»У> =
= С(рх,р2,у) называется функцией условных издержек фирмы.
Подставив длинную точку (хр х2, X) в первые два уравнения
системы (6.4.4), получим равенство
(Pi,P2) = ^gradf(xl,x2), (6.4.5)
откуда следует, что множитель Лагранжа X, как правило, получа-
ется достаточно большим, ибо цены рх и р2 на ресурсы относи-
тельно велики, а предельные производительности ресурсов отно-
сительно малы.
Функции х|/,(р,,р2, у), Y2(A’^2’ У) однородны нулевой степе-
ни по переменным рх ир2, а функция С(рх, р2, у) однородна пер-
вой степени по переменным рх и р2.
С изменением объема у от нуля до +<» и при фиксирован-
ных ценах рх и р2 на ресурсы конфигурация ресурсов (хр х2) =
= (Vi(P],P2’ ?)»¥2^1» ^2» У?) заметает на плоскости Оххх2 линию
развития фирмы L (см. параграф 6.2, рис. 6.1 и рис. 6.3). На рис. 6.3
фиксированный выпуск у принимает два значения — ух и у2
(у2 > У]). На рис. 6.3 также показано локальное рыночное равнове-
сие (хр х2) (см. параграф 6.1).
175
6.4.2. Задача минимизации издержек фирмы при фиксирован-
ном объеме у выпускаемой продукции в краткосрочном проме-
жутке является задачей (6.4.2), (6.4.1) при дополнительном огра-
ничении
(6.4.6)
Приведем геометрическое решение этой задачи (см. конфигу-
рацию ресурсов (хрх2) на рис. 6.4). На рис. 6.4 для сравнения
показано решение задачи (6.4.2), (6.4.1) в долговременном проме-
жутке (см. конфигурацию ресурсов (х,, х2) на рис. 6.4). Рисунок 6.4
иллюстрирует важное положение: при одном и том же объеме у
выпускаемой продукции в случае долговременного промежутка
минимальные издержки фирмы С меньше (не больше) условных
издержек С в случае краткосрочного промежутка. В случае долго-
временного промежутка у фирмы больше возможностей для сни-
жения издержек, чем в случае краткосрочного промежутка.
176
При вариации объема j, выпускаемой фирмой продукции кон-
фигурация (хр х2) ресурсов будет перемещаться по прямой Н, ко-
торая, следовательно, есть линия развития фирмы в краткосроч-
ном промежутке.
6.4.3. Приведем решение задачи минимизации издержек фирмы
при фиксированном объеме у выпускаемой продукции в случае,
когда ПФ/(хр х2) фирмы есть функция Кобба—Дугласа:
PjXj +р2х2 = С (min),
у = а0х“'х“2,
гдерхир2 — рыночные цены на ресурсы. Искомыми переменными
являются объемы х) и х2 первого и второго ресурсов.
Составим функцию Лагранжа
L = рххх + р2х2 + ц(у - f(xx, х2)).
Имеем условия первого порядка
^ = р1-цаоа1х1а--1х2^=О,
ОХу
^P1-^2x^xa2^=Q,
3“ = У-/(ХрХ2) = 0,
12-7620
177
откуда получаем равенство дробей
Р\ _ МД0а|Л'| 1 х2 2
А 'Х2 2
После элементарных преобразований получим
Р1 = «1*2
A a2Xj ’
или х, = х..
aiA
Подставив выражение для х2 в ограничение у = /(хр х2), по-
лучим
.aiA
/ \«J / \«2
ИЛИ Z = x«.^ А р. ,
°0 lal) kA)
откуда
1 а2 а2
У Vl+a2 ((*1 V1+OC2 ( Р2 Vi+Ct2
aoJ <PlJ la2 7
= Xj = »fx(px,p2,y)
(функция условного спроса (по Хиксу) на первый ресурс со сторо-
ны фирмы на рынке).
Объединяя первое и последнее звенья цепочки
1 «2 «2
- агА - _ агА | У |а'*аг | а! |а1 +аг | Pl |а1+а2
2 ад2 1 ад Ia )
-А—Г V А—
у ai+«2 [ а2р, Il а2Р! |«| +«2
aoJ («аддад;
1 а,
jfjai+a2 (а2Рх У|+а2
ао> laiA J
X—1—z x-^z х-^1-
У |“|+“2 [ а2 |«1+«2 ( Рх |а1+а2
aoJ IaJ laJ
=v2(a>a>^)>
получим
x2 = V2(A»A«^) =
x—!—/ X-51-/ Ч-55-
У |“l+“2 I a2 |«l+«2 | Px |al+a2
°oj IaJ laJ
(функция условного спроса (по Хиксу) на второй ресурс со сторо-
ны фирмы на рынке).
178
Имеем
12-
179
1
_____ a, a2
/ / У lai+a2 ( P\ Vi+a2 ( P, 1ai+aJ
= (04+02) — pl- -2.
) la l) la2 )
т.е.
al <X2
Д^а1+а2 ( /И«|+«1
a J W
(функция условных издержек фирмы при фиксированном объеме у
выпускаемой продукции).
6.5. Предельные условные издержки
по объему выпуска и предельные условные издержки
по цене ресурса (лемма Шепарда)
6.5.1. Предельные условные издержки по объему выпуска равны
множителю Лагранжа
эс(рРр2,у)
дУ (6.5.1)
Предельные условные издержки по цене р(. ресурса вида i (i = 1,2)
равны х., т.е.
дС(/>рР2,у) _
др< ' (6.5.2)
Формально эти равенства ничем не отличаются соответствен-
но от предельного расхода по полезности и предельного расхода
по цене р(. продукта G. (/ = 1, 2) в теории потребления (см. пара-
граф 1.4).
6.5.2. Выражения, называемые утверждениями о маргинальных
значениях, позволяют проводить анализ чувствительности услов-
ных издержек относительно изменения выпуска у фирмы и цен на
ресурсы.
Формула (6.5.1) показывает, что при достаточно малом увели-
чении (уменьшении) выпуска на величину Ду условные издержки
растут (падают) приблизительно на величину X-Ду. Напомним,
180
что множитель Лагранжа А может быть достаточно большим, так
что условные издержки фирмы могут измениться на весьма зна-
чительную величину. Из формулы (6.5.1) следует приближенное
равенство при относительно малой величине Ду:
C(pv р2,у + &y) = C(pv р2,У) + Ъ-Ьу.
Аналогично формула (6.5.2) показывает, что при росте цены pt
/-го ресурса на относительно малую величину Др. (/ = 1, 2) услов-
ные издержки увеличиваются приблизительно на величину хг
В связи с тем что множитель Лагранжа А может быть достаточно
большим, условные издержки фирмы могут измениться на весьма
значительную величину. Из формулы (6.5.2) следуют приближен-
ные равенства при относительно малых величинах Apt и Др2
С(Р] + Д^, р2, у) = С(Р], р2, у) + %] Д Р],
C(pj, р2 + Др2, у) = С(р(, р2, у) + х2 Д р2.
6.6. Альтернативы максимизации прибыли фирмы
и многообразие целей фирмы
6.6.1. Этот параграф продолжает и развивает ряд положений па-
раграфа 6.1.
Неудовлетворенность максимизацией прибыли как един-
ственным фактором, управляющим решениями, принимаемыми
на рынке, вызвала к жизни несколько альтернативных критериев
«наилучших» действий.
Одной из широко дискутируемых альтернатив максимизации
прибыли является положение о том, что фирмы стремятся к «удов-
летворительной», а не «максимальной» прибыли. Другими слова-
ми, фирмы скорее жертвуют прибылями, нежели максимизируют
их. Суть заключается в том, что принимающие решения руководи-
тели довольствуются выполнимыми или удовлетворительными ре-
шениями и действиями и не берут на себя хлопоты по вычислению
самых лучших вариантов деятельности.
Вкратце: сторонники концепции стремления получить удов-
летворение рассматривают предприятия как стремящиеся зара-
ботать в будущем по крайней мере не меньше, а может быть и
181
больше нынешней прибыли. Принятие решений, связанных с
прибылью, они связывают с опорой менеджеров на прошлый
опыт, правила принятия решений и информацию, позволя-
ющую выбрать ту из известных альтернатив, от которой ожидается
удовлетворительная прибыль. Утверждается, что обычно руко-
водители не стремятся тщательно изучать каждую возможность в
поиске самой прибыльной альтернативы, так как процесс поис-
ка максимизирующей альтернативы может оказаться дороже,
чем он того стоит, и отнять слишком много времени с учетом
рыночной неопределенности, неточной информации относи-
тельно спроса, издержек, реакции конкурентов и будущих эко-
номических условий.
Существует еще одно логическое обоснование стремления
получить удовлетворительную прибыль. Современная теория
корпорации рассматривает руководителей высшего звена как по-
печителей организации, несущих ответственность не только пе-
ред акционерами, но и перед сотрудниками, покупателями, кре-
диторами, поставщиками, общественностью, государством и об-
ществом в целом. Руководитель корпорации должен искусно
балансировать между заинтересованностью акционеров в высо-
ких прибылях, требованиями сотрудников более высоких зарплат
и большей экономической безопасности, стремлением покупате-
лей получить качественные товары по низким ценам, желанием
розничных продавцов получать приличную прибыль, склоннос-
тью поставщиков к стабильным условиям поставок и требования-
ми общественности к чистоте окружающей среды — и все это в
конструктивных и общественно приемлемых рамках. Согласно
теоретикам удовлетворительной прибыли, эти соображения за-
ставляют руководителей занимать такую позицию, с которой они
могут разрешать организационные конфликты и на которой воз-
можно повышать благосостояние всех групп, заинтересованных в
том, как организация делает свой бизнес.
Более того, многие управленцы среднего и высшего звеньев
занимают ключевые для принятия решений и выработки полити-
ки позиции. Многие из них заинтересованы в увеличении бюдже-
та собственных отделов, в более высоких зарплатах и пенсиях;
в увеличении численности сотрудников, занятых выполнением их
проектов, уютных кабинетах, собственной значительности, влас-
ти и полномочиях принятия важных решений; большей финансо-
вой ликвидности, технологическом превосходстве и т.д. В целях
182
удовлетворения таких интересов могут формироваться коалиции,
что приводит к отказу предприятия от курса максимизации при-
были.
Вследствие этого крупные корпорации имеют много центров
власти различных уровней, над которыми «парит» высшее руко-
водство (топ-менеджеры). Согласно теоретикам удовлетворитель-
ной прибыли, результатом этого является принижение целей и
решений корпорации до уровня политиканства, компромиссов и
уступок. В такой среде невозможна забота о максимизации де-
нежного благосостояния акционеров, так как преследование цели
извлечения прибыли ограничивается требованием удовлетворить,
по крайней мере минимально, конкурирующие вожделения. Ни
один центр силы, за исключением акционеров, не имеет органи-
зационной поддержки, необходимой для достижения общей цели
и, следовательно, для ее достижения в максимальной степени.
В результате этого поведение, характеризующееся стремлением
получить удовлетворение, становится скорее правилом, нежели
исключением, и является примером стандарта деятельности, на-
правленной на получение «удовлетворительной прибыли», взима-
ние «справедливых цен», завоевание «удовлетворительной доли
рынка» — деятельности, растущей «в приемлемой степени».
6.6.2. Второй часто упоминающейся альтернативой максимиза-
ции прибыли является ограниченная максимизация выручки.
Согласно этой альтернативе, когда прибыль достигает прием-
лемого уровня, некоторые фирмы склонны ставить во главу угла
объем выручки, а не прибыль. Они делают это якобы потому, что
рост выручки является важным показателем деятельности фирмы.
Выручка от продаж отражает положительное отношение покупа-
телей к продукции фирмы, конкурентную позицию фирмы на
рынке и ее рост, а все эти показатели свидетельствуют о жизне-
способности фирмы. Если объем продаж падает, то любое пре-
имущество, которым обладает фирма, подрывается, а ее конку-
рентоспособность ослабевает. Кроме того, в повышении объема
продаж заинтересованы руководители фирмы, поскольку есть
много свидетельств тому, что их заработная плата имеет более
тесную связь с масштабом операций фирмы, чем с ее прибыль-
ностью.
Тем не менее максимизация выручки не означает, что из виду
упускается прибыль. Для удовлетворения акционеров и получе-
183
ния новых инвестиций прибыль должна быть довольно высокой.
То есть, стараясь максимизировать выручку, руководители могут
действовать лишь в ограниченных рамках, в степени, которая не
позволяет прибыли упасть настолько низко, что фирма окажется
без средств для роста и расширения рынков сбыта.
6.6.3. Многие фирмы преследуют цели, связанные с увеличени-
ем объемов продаж и долей рынка. Ясно, что большая доля рынка
есть ценный актив, в частности потому, что она отражает способ-
ность фирмы эффективно конкурировать, извлекать выгоду от
масштаба производства и быть признанным лидером рынка. Од-
нако завоевание большей доли рынка совсем не обязательно спо-
собствует повышению прибыльности и не означает более крепких
экономических позиций. По этой причине доля рынка, по всей
вероятности, не является действительно принципиальной целью
фирмы. На деле агрессивная борьба за долю рынка посредством
урезания цен и завоевания потребителей «любой ценой» может
создать опасность для прибыльности. Успешное завоевание боль-
шой доли рынка может привести к доминированию на рынке, что
приведет к принятию антитрестовских мер.
Некоторые экономисты считают, что фирмам, как большин-
ству других организаций и индивидуумов, присущ инстинкт вы-
живания. Стремление выжить есть мотив более фундаментальный,
нежели прибыль. То есть утверждается, что цель выживания до-
минирует над другими целями, особенно в стрессовых ситуациях.
Важность выживания в долговременном промежутке очевид-
на. Но как цель выживание не помогает объяснить и предсказать
поведение фирмы. Путей выживания всегда много, и выбор одно-
го из них зависит от тех или иных факторов. И если уж выживание
в ближней перспективе обеспечено, то на управленческие реше-
ния наверняка будут влиять другие цели. Основное значение цели
выживания состоит в том, что она является предпосылкой для до-
стижения других целей. Ее отношение к объяснению поведения
ограничено только теми случаями, когда фирма попадает в такую
тяжелую ситуацию, что все ее усилия должны быть направлены на
то, чтобы пережить плохие времена.
6.6.4. В последние годы много говорится и пишется о необходи-
мости «социально ответственного» поведения фирм, особенно
крупных корпораций. Социальная ответственность означает мно-
184
гое: представительство в управленческой структуре корпорации и
ее властно распоряжающемся руководстве групп с различными
интересами; соответствие деятельности всей фирмы изменя-
ющимся потребностям общества; сбалансированность интересов
акционеров с интересами общества в целом; построение полити-
ки и практической деятельности фирмы таким образом, чтобы
увеличивать общественное достояние; стремление фирм лечить
социальные болезни общества одновременно со своей основной
деятельностью.
В сущности, возложение на фирмы социальной ответственнос-
ти направлено на формирование некой корпоративной совести.
Лежащая в основе цели социальной ответственности филосо-
фия говорит о том, что интересы акционеров в долговременном
промежутке лучше всего удовлетворяет политика фирм, вносящая
вклад в построение такого рода общества, в котором фирмы могут
прибыльно развиваться. То есть преследование цели извлечения
прибыли и преследование социальных целей полагаются взаимо-
усиливающими процессами. Прибыли могут быть получены по-
средством выполнения функций, которые влекут за собой боль-
шие или малые социальные выгоды. В то же время социальные
цели могут быть эффективнее и быстрее достигнуты, если фирмы
могут получать прибыль за общественно позитивную деятель-
ность и наказание за деятельность общественно негативную.
Достижение целей социальной ответственности может снизить
уровень прибыли фирмы. Фирма, которая в области снижения
вредных выбросов в атмосферу делает больше того, что требуется
законом, возможно, делает это за счет своей прибыли. Фирма, ко-
торая содержит неэффективное производство ради сохранения
рабочих мест в районе, возможно, поступает так за счет прибыли.
Весьма вероятно, что усилия фирмы демонстрировать социальную
ответственность приводят к использованию ею привлекательных
методов управления. Но социальная ответственность ни в коей
мере не означает, что прибыльность отходит на второй план. Адек-
ватная прибыль является предпосылкой организационной способ-
ности и финансовой возможности фирмы решать социальные за-
дачи.
Призывы к фирмам быть социально ответственными встреча-
ют глухое сопротивление со стороны некоторых руководителей и
общественных групп. Возможно, справедливо высказывание, что
«бизнес бизнеса есть бизнес». Утверждается, что руководители
185
корпораций не готовы решать социальные задачи и не могут пре-
небрегать интересами акционеров. Дело в том, что во многих си-
туациях ответ на вопрос о соответствии общественным интересам
дается по отношению к индивидуальным ценностям, а не по от-
ношению к ясному подходу: «это лучше всего соответствует инте-
ресам всех». Однако появляется все больше фирм, которые при-
стально следят за влиянием корпоративной политики и стратегии
на общество, и они определенно озабочены тем, чтобы избежать
обвинений в «бесчувственности» и «отсутствии гражданской по-
зиции».
6.6.5. Сегодняшние достоинства фирмы могут обесцениться зав-
тра, когда изменятся вкусы потребителей, появятся новые това-
ры, усилится конкуренция со стороны отечественных производи-
телей и импортеров и вырастет сила поставщиков и потребителей.
Компания, которая не развивается и не занимается инновацион-
ной деятельностью, может в конце концов обнаружить, что она
производит никому не нужную продукцию. Немногие фирмы
предпочитают «плыть по течению» — в мире бизнеса хуже сохра-
нения статус-кво может быть только ведущая к закату ловушка
стагнации.
Существуют несколько причин, по которым фирмы выбирают
цели роста и диверсификации. Первое: рост — хорошая защита от
несчастий. Рост посредством расширения рынков ставит фирму в
более прочное, более безопасное положение на рынке по сравне-
нию с конкурентами, поставщиками и покупателями. В той сте-
пени, в которой фирма может догнать или опередить конкурен-
тов, она имеет ббльшую свободу маневра и большее влияние на
принятие важных отраслевых решений. Рост путем диверсифика-
ции, расширения номенклатуры продукции освобождает фирмы
от чрезмерной зависимости от узкого круга продуктов и услуг.
Если один из продуктов начинает приносить убытки, фирма мо-
жет не только продолжать существовать, но и набирать силу в
других сферах деятельности.
Второе: рост в долговременном промежутке (например, рост
объема продаж, повышение объема производства, увеличение
прибыли) почти повсеместно признается лучшим измерителем
делового успеха. Тема роста и диверсификации проходит красной
нитью через годовые отчеты процветающих компаний и постоян-
но акцентируется на страницах журналов, посвященных пробле-
186
мам финансов бизнеса. Инвесторы и аналитики оценивают пред-
приятие не только по текущим прибылям, но и по потенциалу
роста. Почти всегда упор делается не на абсолютный объем про-
даж и прибылей, а на величину их роста. Следовательно, фирмы
имеют мотив повышения степени роста, они почти всегда стре-
мятся проникнуть на живой рынок, а когда они на него попадают,
то, за редким исключением, не желают занимать иного места,
кроме первого.
Наконец, рост и диверсификация представляют собой эффек-
тивные средства преследования других корпоративных целей.
Они могут быть совместимы с получением повышенных прибы-
лей, увеличением продаж, защитой и укреплением конкурентных
позиций фирмы, выплатой высоких дивидендов акционерам, по-
вышением курса акций, созданием здорового корпоративного
имиджа и т.д. Рост и диверсификация фирмы, как показывает ус-
тойчивая тенденция, дополняют и поддерживают ее деятельность
по достижению других целей. Уже одно это делает их приоритет-
ными.
6.6.6. Из предыдущих рассуждений ясно, что у фирм может быть
множество целей и извлечение прибыли — лишь одна из них. За-
явления руководителей и стратегические планы фирм подтверж-
дают, что фирмы обычно одновременно преследуют несколько
целей, что ведет к конфликтам и компромиссам.
Например, перед фирмой существует выбор из следующих
вариантов.
* Упор на краткосрочные или долгосрочные прибыли.
• Увеличение маржи прибыли или увеличение доли рынка.
• Расширение деятельности на данных рынках или выход на
новые рынки,.
• Диверсификация на основе родственной или чужеродной
продукции.
* Конкуренция в среде низкого уровня риска или на высокорис-
ковых рынках.
* Преследование целей извлечения прибыли или неприбыль-
ных целей.
• Поиск возможностей быстрого развития в новых сферах рын-
ка или удовлетворенность улучшением текущих операций.
Современная теория реальной фирмы принимает в расчет
многообразные цели. Она расширяет модель максимизации при-
187
были и признает ценность других направлений деятельности фир-
мы, в том числе многообразие целей, преследуемых в рамках
максимизации полезности. Например, помимо прибыли, она мо-
жет преследовать цели увеличения доли рынка и роста. Когда од-
на цель фирмы начинает конфликтовать с другой целью, что мо-
жет легко произойти при наличии многих целей, руководитель
фирмы ищет компромисс между целями и выбирает лучшую ком-
бинацию прибыли, выручки и роста. Лицо, принимающее реше-
ния, обычно имеет некоторую свободу действий, и малые фирмы
отличаются от больших в образе действий по ранжированию це-
лей и поиску компромисса. В разное время фирмы приходят к
разным компромиссам. Выбор может быть очень жестким. На-
пример, фирма, чья прибыль падает, может поддаться соблазну
ликвидировать расходы на НИОКР, рекламу и стимулирование
сбыта; прекратить инвестиции в новые виды деятельности, зда-
ния и оборудование или новые продукты, т.е. в то, отчего зависят
долгосрочные прибыли и рост. Имеются данные, свидетельству-
ющие об обратном соотношении между прибылью и маржей при-
были, с одной стороны, и ростом и долей рынка — с другой. Ком-
промиссы между иными целями могут быть достаточно серьезны-
ми. В итоге многообразие целей в совокупности с изменяющейся
динамикой рынка затрудняет прогнозирование поведения фирм.
При наличии нескольких целей ключевые руководители ищут
компромисс и баланс между конфликтующими целями. Разумно
ожидать, что если руководители имеют свободу выбора из не-
скольких альтернатив, то они выберут наиболее благоприятную
для себя альтернативу. Фактически, даже если хозяева корпора-
ции (акционеры) признают только цель максимизации прибыли,
отделение владения от управления в крупных корпорациях предо-
ставляет руководителям возможность преследовать личные цели,
отличающиеся от целей хозяев, посредством чего формируется
многоцелевая среда.
Например, исполнительный директор корпорации, в которой
владение (собственность) отделено от управления, может доби-
ваться славы ведущего производителя в отрасли, удовлетворять
личное тщеславие, испытывать гордость от того, что он стоит во
главе крупной империи бизнеса; добиваться профессионального
признания в кругу себе подобных, стремиться занимать роскош-
ные апартаменты и добиваться для себя большого размера мате-
риальной компенсации. Все это может отвлечь его от цели чистой
188
максимизации прибыли в интересах акционеров. Стремление ру-
ководителей к спокойной, легкой жизни, бдлынему свободному
времени также не способствует максимизации прибыли, посколь-
ку руководители с «нормальными» предпочтениями не будут от-
давать всю свою энергию максимизации прибыли. Таким же об-
разом стремление создать устойчивый интерес к техническим
трюкам и продемонстрировать профессиональное превосходство
может привести действия руководителей к конфликту с макси-
мально возможной прибылью. Стремление, вопреки прибыли,
к достижению технологического превосходства и передовых по-
зиций в разработке продукции, как утверждается, характерно для
руководителей с научным или техническим образованием и для
отраслей высоких технологий. Поскольку техническое мастерство
дает возможность техническим специалистам удовлетворять
собственный интерес, а также повышать квалификацию с целью
продвижения, получения более высокой заработной платы и по-
иска работы, оно хорошо подходит тем сотрудникам фирмы (ин-
женерам, техническим специалистам, исследователям), которые
занимаются удержанием фирмы на передовых позициях науки и
техники, а также обеспечивают производство передовой продук-
ции.
Общее правило состоит в том, что если руководители фирмы
имеют свободу преследовать свои собственные цели, то можно
ожидать, что они будут их преследовать и наличие многоцелевой
среды весьма вероятно. Вопрос в том, будут ли руководители кор-
пораций преследовать свои личные цели в долговременном про-
межутке, когда они вступят в противоречие с долгосрочными ин-
тересами владельцев фирмы. Это сложный вопрос, и ответ на него
включает решение проблемы принципала—агента. Он включает
также тонкую посылку относительно рынка управленцев и не
столь тонкую — относительно контроля рынка над фирмами. Пе-
реходим к обсуждению этой важной проблемы.
6.6.7. Принимающие решения ответственные лица (принципа-
лы) зачастую полагают полезным нанять агентов, обладающих
соответствующими квалификациями, способностями и инфор-
мацией, которые могут быть использованы на благо ответствен-
ного лица. Проблема между принципалом и агентом возникает,
когда последний обладает большей информацией и знаниями и
использует их к собственной выгоде за счет принципала. Спор-
189
тивная «звезда» (принципал) нанимает агента для заключения
контракта с профессиональной спортивной командой. Если за-
ключенный агентом контракт приносит максимальную пользу не
спортсмену, а агенту (скажем, агент получает от спортивной ко-
манды гонорар), то это пример проблемы между принципалом и
агентом.
Конфликты между принципалом и агентом могут возникнуть
по самым разным поводам; и для крупных корпораций, в которых
владение отделено от управления, такие конфликты являются
обычным делом. Акционеры корпорации выступают в качестве
принципалов, а высокопоставленные исполнительные руководи-
тели (топ-менеджеры) — в качестве агентов. Обычно агенты более
информированы о положении дел и перспективах фирмы, чем
акционеры. Информационная асимметрия позволяет агентам
преследовать личные цели, в результате чего стоимость фирмы
падает, а принципалы попадают в положение, худшее, чем то,
в котором бы они находились, если бы агенты действовали ис-
ключительно в их интересах. Несмотря на то, что деятельность
высших исполнительных руководителей контролируется советом
директоров корпорации, последний не способен выявить истин-
ную подоплеку всех действий первых. Совет директоров не обла-
дает всей полнотой информации, и у большинства его членов есть
другие обязанности.
Для того чтобы избежать необходимости мониторинга за пове-
дением руководителей (топ-менеджеров), совет директоров может
выплачивать им специальное вознаграждение за деятельность в
соответствии со сформулированными советом целями фирмы. Та-
кое вознаграждение может, например, принимать форму участия в
прибылях или получения пакета акций и способствовать обогаще-
нию руководителей. Но руководители смогут получить доступ к
материальным благам тогда и только тогда, когда прибыль корпо-
рации высока и достигаются другие необходимые показатели. Та-
кие вознаграждения способствуют предотвращению конфликтов
между принципалами и агентами. Однако советы директоров дале-
ко не всегда способны ликвидировать проблему принципала-
агента и направить исполнительных руководителей на достижение
целей фактических владельцев фирмы. Основная причина этого в
том, что в крупных корпорациях, в которых владение отделено от
управления, советы директоров могут рассматриваться в качестве
агентов акционеров и проблема принципала—агента может воз-
190
никнуть между советом директоров и акционерами. Советы дирек-
торов могут находиться в зависимости от исполнительных руково-
дителей (топ-менеджеров) корпораций, поскольку они подчас
выдвигают кандидатуры в совет и предлагают их на суд акционе-
ров. То есть действия советов директоров крупных корпораций,
большинство акций которых принадлежит сторонним инвесто-
рам, не обязательно ликвидируют проблему принципала—агента.
Следствием названной проблемы является снижение прибы-
лей, повышение издержек и отклонение от целей, совпадающих с
интересами акционеров. Существо дела заключается в том, что
руководители могут извлекать собственную выгоду за счет акцио-
неров. Это снижает прибыль по сравнению с той, которая могла
бы быть достигнута, если бы не существовало проблемы между
принципалами и агентами.
6.6.8. Хотя между принципалами и агентами возникают конф-
ликты, они не всегда столь серьезны, как об этом можно подумать
на основании предыдущего раздела 6.6.7. Существуют ограничи-
вающие факторы, которые в крупных фирмах снижают остроту
проблемы принципала-агента и поощряют руководителей (топ-
менеджеров) действовать в интересах владельцев. Эти факторы
относятся к рыночной конкуренции.
Жесткая конкуренция заставляет фирму действовать в на-
правлении извлечения прибыли. Прибыль увеличивает стоимость
фирмы, повышает курс ее акций и благосостояние акционеров.
Чем жестче конкуренция на рынке, на котором действует фирма,
тем выше уровень ее дисциплины и выше вероятность ее вовлече-
ния в деятельность по максимизации прибыли. На рынках с наи-
высшей конкуренцией проблема принципала—агента отодвига-
ется далеко на задний план, так как выживание фирмы обусловле-
но максимизацией прибыли. На таких рынках выживают самые
приспособленные, среди которых трудно найти фирмы, погряз-
шие в конфликтах между руководителями и фактическими вла-
дельцами.
Рынок трудовых ресурсов хорошо развит, и если руководитель
заботится о собственном благе, то он старается сохранить свою
рыночную конкурентоспособность. При высоком спросе на хоро-
шо зарекомендовавших себя с точки зрения увеличения прибыли
исполнительных руководителей дисциплина рынка заставит по-
следних проводить политику повышения прибылей, максимиза-
191
ции курса акций и повышения благосостояния акционеров. То
есть рынок управленческих ресурсов снижает внутрифирменные
конфликты между принципалами и агентами. Когда же конфлик-
ты приводят к падению уровня руководства и понижению курса
акций, тогда возникает вероятность смены контроля над фирмой.
Это главный способ избавления фирмы от негодных руководите-
лей. Ясно, что у руководителей есть возможность избежать такой
ситуации, управляя корпорацией так, как того желают акционе-
ры, и делая это наиболее эффективно.
6.6.9. Лишь немногие экономические концепции могут срав-
ниться с концепцией прибыли по числу сбивающих с толку опре-
делений. Мало того, что существуют бухгалтерская прибыль, нор-
мальная прибыль и экономическая прибыль, так каждая из них
может еще и по-разному измеряться в зависимости от принятой
бухгалтерской практики или от того, измеряется ли прибыль в
долларах или как степень дохода на вложенный капитал. В основе
бухгалтерской прибыли лежат доходы фирмы, и она определяется
как превышение доходов над расходами прошлого периода после
уплаты налогов. Нормальная прибыль есть прибыль (или доход на
вложенный капитал), минимально достаточная для удержания
фирмы на плаву в долговременном промежутке. Экономисты рас-
ценивают нормальную прибыль как часть совокупных издержек.
Экономическая прибыль есть доход сверх минимальной прибы-
ли. Фирмы стремятся к извлечению именно экономической при-
были, и именно эта прибыль определяет их поведение.
Прибыль (как нормальная, так и экономическая) есть резуль-
тирующая различных факторов влияния, включая деловую хват-
ку, успешное выполнение предпринимательской функции, пре-
доставление покупателям качественных услуг, умелое обращение
с неопределенностью, быстрое реагирование на возникающий на
рынке дисбаланс, получение конкурентных преимуществ, техно-
логическое превосходство, разработку и производство инноваци-
онной продукции.
Взгляды экономистов на максимизацию прибыли со време-
нем изменились. Вот уже несколько лет существуют разногласия
относительно того, действуют ли фирмы, особенно крупные кор-
порации, так, как если бы они стремились максимизировать при-
быль. Ныне широко признается, что фирмы не обязательно стре-
мятся максимизировать прибыль; и внимание экономистов со-
192
средоточено на том, чтобы теория фирмы рассматривала и другие
цели и задачи. Современная теория фирмы выявляет причины, по
которым фирма стремится к извлечению максимальной прибыли,
условия, в которых фирма стремится к извлечению максималь-
ной прибыли, а также условия, при которых фирма преследует и
другие цели. Полагают, что к достижению других целей, помимо
цели максимизации прибыли, фирму подталкивают распылен-
ные между многочисленными акционерами права собственнос-
ти, неопределенность, проблема принципала—агента и изоляция
от жесткой конкуренции. Наиболее известными альтернативами
максимизации прибыли являются, как уже говорилось в разде-
лах 6.6.1—6.6.3, стремление получить удовлетворение, максими-
зация выручки и рост посредством диверсификации. Менее важ-
ные цели и (или) цели, вытекающие из основных, включают
увеличение доли рынка, выживание в долговременном плане,
удовлетворительный уровень прибылей, увеличение размера ди-
видендов, финансовую ликвидность, технологическое лидерство,
приобретение хорошего имиджа, социально ответственное пове-
дение, занятие сильной конкурентной позиции и достижение
личных целей руководителей высшего звена (власть, престиж,
чувство самоудовлетворения, профессиональное признание и
высокие премии). Эффективным средством одновременного до-
стижения многих из этих целей является стратегия агрессивного
роста и диверсификации.
Несомненно, что благодаря уже просто многочисленным от-
тенкам поведения и серьезным ограничениям, накладываемым на
принимаемые решения, не существует единственной цели, кото-
рая охватывала бы все аспекты делового поведения. Более того,
разнообразие целей и мотивов является естественным результа-
том рыночной экономики, состоящей из самых мелких, индиви-
дуальных фирм и гигантских многономенклатурных корпораций.
Весьма маловероятно, что все фирмы будут с той же интенсивнос-
тью и приоритетностью преследовать одинаковые цели, посколь-
ку фирмы различаются по занимаемой на рынке позиции, фор-
мам собственности и контроля, величине конкуренции, неопре-
деленности, технологическим возможностям, прибыльности,
потенциалу прибыльности, личностным качествам владельцев и
руководителей.
Но несмотря на это, мотив прибыли глубоко внедрен в созна-
ние и фольклор современного бизнеса. И совершенно справедли-
13 - 7620
193
во. Высококонкурентные рынки продуктов и ресурсов, существо-
вание рынков управленческих ресурсов и контроля над корпора-
циями дисциплинируют поведение управленцев и фирм и
заставляют их настойчиво преследовать цель извлечения прибы-
ли. Вследствие этого императив извлечения прибыли является
распространенным и сильным. Конечно же прибыль стоит во гла-
ве иерархии целей большинства фирм; и если бы пришлось на-
звать только одну цель, характеризующую деловое поведение, то
выбор пал бы на максимизацию прибыли в долговременном про-
межутке.
Вопросы для самоконтроля к главе 6
1. Какие целевые функции имеет фирма в условиях конкуренции?
2. Какие аргументы приводятся за максимизацию прибыли?
3. Какие аргументы приводятся против максимизации прибыли?
4. Что понимается под «разумной» прибылью?
5. Существует ли в реальности «разумная» прибыль?
6. В чем состоит различие между временном периодом и временном
промежутком?
7. Какие характерные черты имеет долговременный промежуток?
8. Какие характерные черты имеет краткосрочный промежуток?
9. Что такое локальное рыночное равновесие фирмы, функциониру-
ющей в долговременном промежутке?
10. Что такое локальное рыночное равновесие фирмы, функциониру-
ющей в краткосрочном промежутке?
11. Какими формальными свойствами обладает локальное рыночное
равновесие фирмы, функционирующей в долговременном проме-
жутке?
12. Что такое первая версия задачи максимизации прибыли фирмы?
13. Как определяются функции условного спроса по Маршаллу (по Валь-
расу) со стороны фирмы на ресурсы?
14. Какими формальными свойствами обладают функции условного
спроса по Маршаллу?
15. Как определяется функция условного предложения фирмы на рынке
готовой продукции?
16. Какими формальными свойствами обладает функция условного
предложения фирмы?
17. В чем состоит теоретическое значение утверждений о маргинальных
значениях функции условного предложения фирмы?
18. В чем состоит практическое значение утверждений о маргинальных
значениях функции условного предложения фирмы?
194
19. Что такое вторая версия задачи максимизации прибыли фирмы?
20. Как определяются функции условного спроса по Хиксу со стороны
фирмы на ресурсы?
21. Какими формальными свойствами обладают функции условного
спроса по Хиксу?
22. Как определяется функция условных (минимальных) издержек
фирмы?
23. Какими формальными свойствами обладает функция условных (ми-
нимальных) издержек?
24. В чем состоит теоретическое утверждение о маргинальных значениях
функции условных (минимальных) издержек фирмы?
25. В чем состоит практическое утверждение о маргинальных значениях
функции условных (минимальных) издержек фирмы?
26. Каковы альтернативы максимизации прибыли фирмы?
Задачи и упражнения для самоконтроля к главе 6
1. ПФ конкурентной фирмы имеет вид/(Х1, х2) • х1/4 (х, - количест-
во капитала, х2 - количество труда). Цены на выпускаемую фирмой
продукцию и на ресурсы соответственно равны р0, рх,рт Найдите:
а) локальное рыночное равновесие фирмы (хр х2);
б) доход Л° = р°/(Хр х2), издержки С° = р,х® + р2х2 и максимальную
прибыль РЛ° = - С°.
2. Конкурентная фирма производит единственный продукт, реализу-
емый на рынке по цене р0. Цены капитала и труда соответственно
равны рх и рт ПФ фирмы имеет вид у=х1/3 • х1/2 (Xj — количество ка-
питала, х2 — количество труда). Определите эластичность функции
спроса на труда по ценам р0, рх, р2.
3. ПФ конкурентной фирмы имеет вид/Ц, х2) =х}/4 • х2/2 (Xj - количест-
во капитала, х2 - количество труда). Цены капитала и труда соот-
ветственно равнырх = 4 ир2 = 5. Лимит на ресурсы равен К= 120:
а) определите конфигурацию ресурсов (хр х2), максимизирующую
выпуск фирмы при лимите на ресурсы;
б) определите объем максимального выпуска f (Xj, х2);
в) напишите уравнение изокванты, содержащей точку (х}, х2);
г) постройте точку (Xj, х2). Постройте по трем точкам (одна из кото-
рых есть точка (Xj, х2)) изокосту;
д) постройте по трем точкам (одна из которых есть точка (хр х2))
изокванту.
4. ПФ конкурентной фирмы имеет видДХ], х2) = х}/4 • х|/4 (х, - количест-
во капитала, х2 - количество труда). Фиксированный выпуск фирмы
у = 4. Цены на капитал и труд соответственно равны рх = 16, р2 = 4:
13*
195
а) определите конфигурацию ресурсов (хр х2), минимизирующую
издержки фирмы при фиксированном объеме у = 4 выпускаемой
фирмой продукции;
б) определите минимальные издержки фирмы с = РЛ + р2х2->
в) напишите уравнение изокосты С = рххх + р2х29
г) постройте точку (х,, х2). Постройте изокосту по трем точкам (од-
на из которых есть точка (хр х2));
д) постройте изокванту по трем точкам (одна из которых есть точ-
ка(хрх2)).
Вопросы, тесты и задачи для контрольных работ к главе 6
1. Координаты рыночного равновесия (хр х2) конкурентной фирмы
есть однородные функции:
а) первой степени по всем переменным р0, рХ9 р29
б) нулевой степени по всем переменным р0, рх, р2;
в) первой степени по переменным pv р2 при фиксированной пере-
менной р0;
г) нулевой степени по переменным рх, р2 при фиксированной пере-
менной р0;
д) среди всех ответов а)-г) нет ни одного верного.
2. Координаты конфигурации ресурсов (х}, х2), максимизирующей вы-
пуск фирмы при лимите Кна ресурсы, есть однородные функции:
а) первой степени по ценам pvp2 при фиксированном лимите;
б) нулевой степени по ценам рх и р2 при фиксированном лимите;
в) первой степени по всем переменным рр р2, К;
г) нулевой степени по всем переменным рх, р29 К;
д) для полного ответа условий недостаточно.
3. Координаты конфигурации ресурсов (хр х2), минимизирующей из-
держки фирмы при фиксированном объеме у выпускаемой фирмой
продукции, есть однородные функции:
а) нулевой степени по всем переменнымр{9р29 у;
б) первой степени по всем переменным рх, р2, у;
в) нулевой степени по переменнымрХ9р2;
г) первой степени по переменнымрх,р29
д) среди всех ответов а)-г) нет ни одного верного.
(t\h( п п
4. Предельный выпуск ----— по ценер. /-го ресурса (/=1,2):
I J
а) противоположен по знаку множителю X Лагранжа;
б) равен значению х. функции условного спроса по Маршаллу на
/-й ресурс;
196
в) пропорционален значению xt функции условного спроса по Хик-
су на /-й ресурс;
г) равен значению х. функции условного спроса по Хиксу на /-й
ресурс;
д) среди всех ответов а)-г) нет ни одного верного.
5.
Предельные издержки
по цене р{ /-го ресурса (/ = 1,2):
I )
а) пропорциональны (с коэффициентом пропорциональности, не
равном единице) значению х, функции условного спроса по Хик-
су на /-й ресурс;
б) равны значению х. функции условного спроса по Хиксу на /-й
ресурс;
в) пропорциональны значению х. функции условного спроса по
Маршаллу на /-й ресурс;
г) равны значению х. функции условного спроса по Маршаллу на
/-й ресурс;
д) среди всех ответов а)-г) нет ни одного верного.
6. Конкурентная фирма производит единственный продукт, реализу-
емый на рынке по цене р0. Цены капитала и труда соответственно рав-
ны рх и р2. Производственная функция фирмы имеет вид у=х}/4 • х^/3
(Xj — количество капитала, х2 — количество труда). Определите элас-
тичность функция спроса на капитал по ценам р0, рр р2.
7. Производственная функция конкурентной фирмы имеет вид/(х,, х2) =
= х1/4 • Х23 Ц - количество капитала, х2 - количество труда). Цены
капитала и труда соответственно равны р{ = 1 и р2 = 4. Лимит на ре-
сурсы равен И= 11:
а) определите конфигурацию ресурсов (хр х2), максимизирующую
выпуск фирмы при лимите на ресурсы;
б) определите объем максимального выпуска f , х2);
в) напишите уравнение изокванты, содержащей точку Ц, х2);
г) постройте точку (Xj, х2). Затем постройте по трем точкам (одна из
которых есть точка (хр х2)) изокосту;
д) постройте по трем точкам (одна из которых есть точка (хр х2))
изокванту.
8. Производственная функция конкурентной фирмы имеет вид/О^, х2) =
=х1/3 ‘ х2/4 “ количество капитала, х2 — количество труда). Фикси-
рованный выпуск фирмы у = 6912. Цены на капитал и труд соответ-
ственно равны Pj = 4, р2 = 1:
а) определите конфигурацию ресурсов (хр х2), минимизирующую
издержки фирмы при фиксированном объеме у = 4 выпускаемой
фирмой продукции;
197
б) определите минимальные издержки фирмы С = рххх + р2х2;
в) напишите уравнение изокосты С = рххх + р2х2;
г) постройте точку (х,, х2). Постройте по трем точкам (одна из кото-
рых есть точка , х2)) изокосту;
д) постройте изокванту по трем точкам (одна из которых есть точ-
ка(хрх2)).
Глава 7
ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ
И НАУЧНО-ТЕХНОЛОГИЧЕСКИЙ
ПРОГРЕСС
7.1. Производственные функции,
используемые в экономическом анализе
и прогнозировании, и их свойства
7.1.1. Понятие производственной функции (ПФ) хорошо из-
вестно из курса «Микроэкономика. Промежуточный уровень»:
ПФ у = /(хр ..., хя) — это функция, независимые переменные
(хр хя) которой принимают значения объемов затрачиваемых
или используемых ресурсов (число п переменных равно числу ре-
сурсов), а значение у функции равно объему выпускаемой про-
дукции. Вектор (Хр ..., хл) называется конфигурацией ресурсов.
ПФ зависит от параметров (одного или нескольких).
ПФ, используемые для описания функционирования фирмы
или отрасли, называются микроэкономическими. ПФ, использу-
емые для описания функционирования региона или националь-
ной экономики, называются макроэкономическими.
Результаты теории ПФ используются и для микро-, и для мак-
роэкономических ПФ. Элементы теории ПФ рассмотрим в ос-
новном для случая п = 2 по следующим двум причинам:
1) при л = 2 многие построения допускают наглядную геомет-
рическую интерпретацию;
2) принципиальные результаты при л > 2 ничем не отличаются
от результатов при л = 2. При л = 2 Xj = К, х2 = L (К — количество
199
(основного) капитала, L — количество труда). ПФ определена при
х^О, ...,хл>0(Х1>0, х2>0).
7.1.2. Рассмотрим примеры ПФ (при п = 2).
1. ПФ Кобба—Дугласа (ПФКД): У = л0 • х^'хр.
2. Линейная ПФ (ЛПФ): y=bQ + blxl + b2x2 и ПФ с линейными
изоквантами (ПФЛИ): у = (b0 + /^х, + b2x2)h.
3. ПФ Леонтьева (ПФЛ) (ПФ затраты — выпуск — ПФЗВ):
y=min (CjXp с2х2).
4. Классическая ПФ с постоянной эластичностью замены ре-
сурсов (ПФ ПЭЗР): у = а0 • (aix^a + a2x^a)~h/a.
В этих примерах постоянные а0, а{, а2, b0, bvb2, h, а, с{, с2 иг-
рают роль параметров, которые являются обычно положительны-
ми величинами.
Примеры ПФ (при п > 2):
Г. ПФКД:
у = аох“1-...-хяа».
2'. ЛПФ:
y=i0+Mi + -+V.
и ПФ с плоскими изоквантами (ПФПИ):
y = (b0 + blxl + ... + bnxn)h.
3'. ПФЛ (ПФЗВ):
y=min(c1x1; ...;с„хл).
4'. Классическая ПФ с постоянной эластичностью замены ре-
сурсов:
y = a0(aix^a+... + anx^)-l,/a.
В этих примерах величины а0, ар..., ал, bQ, Ь{,..., bn, h, ср..., сл, а,
ар..., ап играют роль параметров, которые обычно положительны.
ПФКД — пример ПФ, задаваемой в мультипликативной форме,
ЛПФ — пример ПФ, задаваемой в аддитивной форме. Переход от
мультипликативной формы к аддитивной осуществляется с помо-
щью операции логарифмирования: In у = In а0 + ajn х{ + a2ln х2.
Полагая In у = w, In xt = vp In x2 = v2, получим ПФ в аддитивной
форме: w = lna0 + + a2v2. Переход от аддитивной формы к
мультипликативной осуществляется с помощью операции по-
тенцирования: полагая b0 = In а0, xt = In vp х2 = In v2, у = In w, по-
лучим In w = In aQ + Z>]ln Vj + Z>2ln v2, откуда следует, что w = a0v*iv2J,
т.е. ПФ в мультипликативной форме.
Фрагменты карт изоквант ПФ 1—4 приведены на рис. 7.1—7.4.
200
Рис. 7.1. Фрагмент карты Рис. 7.2. Фрагмент карты
изоквант ПФКД изоквант ПФЛ
Рис. 7.3 Фрагмент карты изоквант
ПД с линейными изоквантами
Рис. 7.4. Фрагмент карты
изоквант ПФ ПЭЗР
Рисунки 7.1 и 7.4 наглядно демонстрируют, что ПФ ПЭЗР бо-
лее адекватна реальности, чем ПФКД, ибо не бывает ситуации,
когда капитал есть и практически нет работников или много ра-
ботников и практически нет капитала. То есть ПФКД можно рас-
сматривать только в конечной части первой четверти плоскос-
ти ОХ]Х2. В случае ПФ ПЭЗР для выпуска продукции в объеме,
скажем, т0 каждый ресурс требуется в количестве не менее чем х°
(первый ресурс) и х° (второй ресурс), что естественно с содержа-
тельной экономической точки зрения.
201
7.1.3. Напомним свойства ПФ (при п=2) (для конкретной ПФ не
обязаны выполняться все свойства):
1) /(0, 0) = 0 (нет ресурсов, значит, нет выпускаемой продук-
ции);
/(0,х2)=/Ц,0) = 0;
2) X > X (Х * х) =Ф f(xx, Х2 ) > f(xx, *2 ) (свойство монотонности).
nPHx=(x1,x2)>0^ii>>0(SO),^i2>0(>0),
оХ| 0^2
т.е. если затраты одного ресурса увеличиваются, а затраты другого
ресурса остаются неизменными, то объем выпускаемой продук-
ции растет (точнее, не убывает);
3) при х=(хх, х2) > 0 f(x\>x2} <о (<о) <о (<0),
12 Эх2
т.е. имеет место падение эффективности производства с ростом
объема затрат одного из ресурсов и сохранением затрат другого
ресурса неизменными;
4) существует число р > 0, такое, что для любого числа у> 0 и
любого вектора х = (Xj, х2) > 0 справедливо равенство
/(у-хх; ух2) = ур • f(xx, х2) — свойство однородности ПФ.
Свойства ПФ (при п > 2):
1')/(0,..., 0) = 0,/(0,х2, ...,хл) = ... =/(хр ...,хл_р0) = 0;
2') х £ х (х * х) => /(х) > /(х) (более детально /(хр ..., хл) >
>/(Хр ...,х )), прих>0 >о (>0), д/(хр •♦•>**) >q
1 л Эх ох„
(>0); 1
У) „ри^О^'-^-Ао^О). .... <0 (S0);
дхх Эх2
4') существует число р > 0, такое, что для любого вектора х > О
справедливо равенство/(ухр ..., ухл) = ур/(хр ..., хл) — свойство
однородности ПФ.
7.1.4. Проверим выполнение свойств 1—4 для ПФ 1—4.
Для ПФКД свойства 1, 2, 4 выполняются, а свойство 3
выполняется, если cq < 1, ocj < 1 и число р = cq + о^: /(ухр ух2) =
= e0(yx,)“i (ух2)“2=y“i+a2aox“ix^2 = y“i+<)t2/(Xp х2).
Для ЛПФ при 60 * 0 свойства 1 и 4 не выполняются, при
bQ = 0 свойства 1 /(0, 0) = 0 и 4 выполняются, свойство 2 выпол-
202
няется при bx > 0 и Ь2 > О, вторые частные производные равны
нулю.
Для ПФЛ свойство 1) выполняется. Для свойств 2) и 3) имеем
С, df(x.,x-,) d2f(x.,x^) л . С,
при хх>-^х2 —=----------------И ~ = 0’ ПРИ 0<Х1<^Х2
С] оХ| dxt С|
Э/(х,,х2) л d2f(x.,x2) пд С. df(x,,x2)
ах, ’ах,2 2 С2 1 ах2
= Э2/(х, х2) = ^ при Q< д/(х,,х2)>0> а7(х^,х2)=0
Зх2 С2 дх2 Зх2
Свойство 4 выполняется.
Для ПФ ПЭЗР при а > 0 и h > 0/(0,0),/(0, х2),/(х,, 0) равны 0,
при 0 > а > -1 /(0, 0) = 0, /(0, х2) # 0, f(xv 0) * 0. При h > 0
df(x.,x^) Л df(x.,x~) Л „ _
----!—— > 0 и —-1—— > 0, т.е. свойство 2) выполнено. При h < 1
Эх, дх2
, . Э2/(х,х2) л Э2/(х,х2) л
иа+1 >0------•— 2 <Ои------L—1L<о,приh> 1 иа+1 >0вторые
ax? ах2
/ х *1 f Л|(Л —1) 1
(чистые) частные производные отрицательны, если—> ——----
х2 ^(a+l)^
х2 ( <^(й-1)У/а „
и — > —------ , т.е. свойство 3) выполняется. Свойство 4) вы-
х, ^a,(a+l)J
полняется при р = й.
7.1.5. Рассмотрим геометрическую и экономическую интерпре-
тации свойств ПФ.
Если увеличиваем количество капитала на единицу, то объем
а/
производства вырастет на :
йх,
а/(х,,х2) /(х,+Дх,,х2)-/(х,,х2)^ д*
Эх, Дх, ’ 1
Проведем вертикальные плоскости через точки (х°, х2,/(х°, х2)),
(х°, 0), (0, х2). Они пересекают график ПФ у = f(xt, х2) по плоским
линиям и L2 (рис. 7.5). Далее проводим касательные Кх и К2
к линиям Lx и L2 в точке (х°, х2,/(х°, х2)).
м о а/(х°х°) л 0 д/(х°,х®) п. „
Имеем tg(p] = 1 1 >0, tg(p2 = 1 2 > 0 (свойство 2).
ЭХ| дх2
203
Рис. 7.5
f(x х )
Неравенство-------'* 2 <0 (свойство 3)) означает, что пре-
dxi
д/(х.,х7)
дельная производительность труда —-1—убывает с ростом за-
Эх2
трат труда х2 (рис. 7.6). Аналогичное справедливо для предельной
Пример, когда в свойстве 2 может быть равенство нулю, дает
ПФЛ.
204
При у> 1 рост масштаба производства (увеличение затрат капи-
тала и труда в ураз) увеличивает объем выпуска в раз (при р > 0).
Если при этом р > 1, то растет эффективность производства
(случай возрастающей эффективности с ростом масштаба произ-
водства). Если, например, р = 2 и у= 3, то свойство 4) означает, что
при росте объема капитала и труда в 3 раза объем выпуска растет
в у₽ = 9 раз.
Если р = 1, то/(у-Хр у-х2) = у-/(хр х2) (случай постоянной эф-
фективности с ростом масштаба производства). Если, например,
у= 3, то свойство 4) означает, что при росте объема капитала и
труда в 3 раза объем выпуска растет также в у₽ = 3 раза.
Если р < 1, то имеем убывающую эффективность с ростом мас-
штаба производства. Если, Например, р = 1/2 и у= 3, то свойство 4)
означает, что при росте объема капитала и труда в 3 раза объем
выпуска растет в ур = 7з = 1,7 раза.
7.1.6. Приведем понятийный аппарат теории ПФ (и = 2).
При х, > 0, х2 > 0 дробь Xj/ х2 называется капиталовооружен-
f (х , X )
ностью труда, дробь -——-— средней производительностью ка-
f (х X )
питала, дробь -——-— средней производительностью труда.
х2
Средние производительности капитала и труда — это относи-
тельные величины (первого порядка), ибо они равны отношени-
ям абсолютных величин (количества выпуска на количество соот-
ветствующего ресурса). Предельные производительности капита-
f (х , х ) У*(х х )
ла и труда -—и -—— также относительные величины.
Xj Х2
Э/*(х х ) / Эх
Дробь ———-——- = Е. (/(х., х,)) называется (частной)
/(Xj,X2)/Xj
эластичностью выпуска по первому ресурсу (капиталу), дробь
<У(х., х,)/Эх, „ ,
----!—*----- = EAf(x., х,)) называется (частной) эластичнос-
/(Xj,x2)/x2
тью выпуска по второму ресурсу (труду). Эти эластичности назы-
ваются точечными (предельными).
Точечные (предельные) частные эластичности — это относи-
тельные величины (второго порядка), ибо они равны отношениям
относительных величин (первого порядка). Сумма E(f(xv х2)) =
=£] (/(Xj, х2))+E2(f(x{, х2)) называется эластичностью производства.
205
Имеем
^(/(xpx2)) =
/(xpx2)-/(xpx2) /(XpX2)-/(xpx2)
Х|-Х| /(хрх2)
5221.100%
*1 Xj
Обе дроби после знака = (приближенного равенства) называются
конечной (процентной) частной эластичностью выпуска по перво-
му ресурсу, т.е. справедливо приближенное равенство
Точечная (предельная) эластичность (по первому ресурсу) =
= Конечная (процентная) эластичность (по первому ресурсу).
Конечная (процентная) эластичность выпуска по первому ре-
сурсу (капиталу) показывает, на сколько процентов изменится
выпуск, если объем затрачиваемого первого ресурса (капитала)
изменится на 1%. Аналогично поясняется (частная) эластичность
выпуска по второму ресурсу (труду) £2(/(Хр х2)).
Если нет особой оговорки, то под термином «частная эластич-
ность» следует понимать точечную (предельную) эластичность.
Частные эластичности для ПФКД имеют вид
’>Х22)- 1 -^^Xj1 -X/ -ССр
«Ох1 'х2
Е{ (аох“*, х“2) = а2 (обычно ар а2 < 1).
Частные эластичности для ПФ ПЭЗР имеют вид
-A-i)
А I —а ~~<х
-77Х1аоКХ1 + а2х2
^(/Ц,х2)) = -е----------i------------±
ao(°lXl_<X + fl2X2a) “
OjXj-” + О)Х2 “
^2(/(ХрХ2)) = —ЧХ2~а
v 1’ z'' —а . —а
OjXj -hOjXj
206
Эластичность производства
х2)) = Е{ + Е2 для ПФКД и для ПФ ПЭЗР имеет соот-
ветственно вид Е=(Xj + а2, Е=h.
Напомним важное понятие предельной нормы технологичес-
кой замены одного ресурса другим.
Если точка х2 расположена левее точки х’, то дробь RTSn =
х2-х*
= —|—р — это норма технологической замены первого ресурса
*f-*i
вторым (рис. 7.7), ибо количество х, первого ресурса уменьшает-
ся, а количество х2 второго ресурса растет.
Если точка х2 расположена правее точки х1, то дробь RTS,. =
2 1
х2-х‘
= —f — это норма технологической замены второго ресурса
х, -х,
первым (см. рис. 7.7), ибо количество х{ первого ресурса растет,
а количество х2 второго ресурса уменьшается.
RTS., -> = MRTS
ы ах{
dx (
RTS2X ------= MRTS,..
21 dx. 21
207
«Идем» к точке х1 с разных сторон, а получаем один и тот же
результат--i——, который следует интерпретировать по-разно-
dx{
му (как предельную норму технологической замены первого ре-
сурса вторым MRTS 12, если к точке х1 идем слева, и как предель-
ную норму технологической замены второго ресурса первым
MRTS2V если к точке х1 идем справа. Поскольку по выражению
abc2(x*)
----г—нельзя определить, как оно было получено, постольку
ах1
подойдем к определению предельной нормы технологической за-
мены одного ресурса другим чисто формально:
MRTSl2=-^il
dxl
Снизу находится тот ресурс, который заменяют, сверху нахо-
дится тот ресурс, который заменяет, т.е. MRTSl2 — это предельная
норма технологической замены первого ресурса вторым, a MRTS2i =
<&i(x2)
=---!—-— это предельная норма технологической замены вто-
ах2
рого ресурса первым.
(х2-х2) <&2(Xj) х2-х2
Имеем lim-----*---f- =-----—— = —%—f-.
х1~х1 Х1-Х1
Уравнение/(хр х2)=т описывает изокванту — линию постоян-
ного объема выпускаемой продукции. Это уравнение задает неяв-
ную функцию х2 = x2(x,). По теореме о неявной функции
ЭДХр^)
ЭХ|
Д^2Ц)______________
dx} df(xi,x2)>
дх2
т.е.
ЭДхрХ^
3lX|
ч = MRTS.j.
Э/(хрх2) 12
Таким образом, получили, что предельная норма технологи-
ческой замены первого ресурса вторым есть отношение предель-
208
ной производительности первого ресурса к предельной произво-
дительности второго ресурса. Имеем MRTSl2 = tg у (рис. 7.8). Если
угол у, мал, тогда его тангенс tg также мал. Это означает, что для
замены одной единицы капитала (A=Xj) в конфигурации ресурсов
х1 = (х*, х2) требуется мало единиц труда (L = х2). Если угол у2 ве-
лик, то tg у2 также велик, что означает, что для замены одной еди-
ницы капитала (А'=х1) в конфигурации ресурсов х2=(х2, х2) требу-
ется много единиц труда (L=х2).
Рис. 7.8
В точке (xj*, х2) локального рыночного равновесия фирмы (ЛРРФ),
т.е. в точке (х° х2), максимизирующей прибыль PR(xv х2) =
=PQf(xvx^-pxxl- р2х2 фирмы, имеем (рис. 7.9):
ЭДх®,^)
р° ~tr=p-
ЭЛ^.х")
р°~=/>2-
(р0 — цена единицы выпускаемой продукции, р, — цена единицы ка-
ЭЛХ!0,*?)
Эх, р.
питала, р2 — цена единицы труда), а тогда MRTSi2 =-Q -Q- = —
а/* (Х|, х2) Р2
дх2
14-7620
209
Таким образом, в точке ЛРРФ MRTSX2 =—, что является важ-
ным результатом. ^2
Рис. 7.9
Если рх относительно велика, а р2 относительно мала, то
MRTSX2 велика. Это означает, что в ЛРРФ (х° х®) координата х2
относительно велика, а координатах®относительно мала, что оче-
видно с содержательной точки зрения: дорогой ресурс фирма
приобретает в относительно скромном объеме, а дешевый — в от-
носительно большом объеме. На изокванте 10(У°-/(х®, х®)) ЛРРФ
(х®, х®) изображается точкой с большим количеством труда х® и
относительно малым количеством капитала х®. Случай, когда це-
на р, относительно мала, а цена р2 относительно велика, аналоги-
чен только что рассматриваемому. Здесь уже координата х? отно-
сительно мала, а координатах” — относительно велика.
Если параметры рассматриваемых ПФ и сами ПФ не зависят
от времени t, то такие ПФ называются статическими. Объемы
ресурсов и объем выпуска могут зависеть от времени /, т.е. могут
иметь представление в виде временных рядов х((0), Xj(l),..., Х](7);
х2(0),х2(1),...,х2(7); у(0),у(1), ...,у(7); ХО =/Ц(0, х2(/)). Здесь
время дискретное, t — номер года, /=0,1,..., Т; /=0 — базовый год
временного промежутка, охватывающего годы 1,2,..., Т. ПФ, ис-
пользуемые для решения прикладных задач, имеют, как правило,
дискретное время. ПФ для решения теоретических задач могут
иметь как дискретное, так и непрерывное время.
210
ПФ называется динамической, если: 1) время t фигурирует в
качестве самостоятельной переменной величины (как бы само-
стоятельного ресурса — фактора производства), влияющей на
объем выпускаемой продукции; 2) параметры ПФ и она сама за-
висят от времени: y(t) =f(t, xx(t), x2(t)).
Простейший пример динамической ПФ дает ПФ вида y(f) =
= euf(xx(t), x2(t)), где число X характеризует темп прироста (если
X > 0) или темп падения (если X < 0) выпуска под влиянием факто-
ра времени, который учитывает всю совокупность факторов (на-
учно-технологический прогресс (НТП), сезонные колебания,
природные факторы и т.д.), которые отличны от труда и капитала.
Из всей совокупности факторов, отличных от труда и капитала,
одним из самых значимых является фактор НТП. Вопросы учета
НТП в ПФ рассматриваются в параграфе 7.4 этой главы.
7.1.7. Приведенные понятия естественным образом переносятся
на случай п > 2.
Дробь -—р *“* ” , /=!,...,«, называется средней производи-
. Х‘ Э/Ц......хп)
тельностью i-tq ресурса, частная производная -------Ч----
i = 1,..., п, называется предельной производительностью /-го ресур-
_ <У(х,, ...,х„) //(х., ...,х„)
са, дробь ----Ц-----— /----1----— = Ei(f(xl, ...,х )) называ-
дх( / Xj
ется частной эластичностью выпуска по /-му ресурсу, сумма
£(/(хр ..., х„)) = Ex(f(xx,..., х„)) + ... + En(J(xx,..., хя)) называет-
ся эластичностью производства.
Предельная норма технологической замены /-го ресурсау-м
(при сохранении неизменным объема выпускаемой продукции и
объемов хк остальных ресурсов k*i,k*j) определяются так:
Эх,
MRTS„=-J-
J Эх,
По теореме о неявной функции имеем
MRTSy =
Э/(хр ...,xn)!dxj
Э/(Хр ...,хя)/Эху'
14*
211
В точке x° = (х®,...,хя) локального рыночного равновесия фирмы
(ЛРРФ) имеем
У(х®, ...,хя°) Э/(х,°, ...,х„°)
Ро-----------= Рр -^0-^----------= Р„
(р0 — цена выпускаемой фирмой продукции, р. — цена f-го ресур-
са), а тогда
MKTS = jfot ftfa = Л
' ....P,
7.2. Эластичность замены одного ресурса другим,
ее логарифмическое представление и геометрическая
интерпретация. Вывод ПФ с постоянной
эластичностью замены ресурсов
7.2.1. Приведем важное понятие эластичности замены одного
ресурса другим.
Эластичность переменной х по переменной у имеет вид
Еух =
у dx
х dy‘
Если в приведенном выражении Еух положить чисто формально
»
Х2
y~MRTSn
Э/(Х|,Х2)/аХ!
Э/Ц,х2)/ах2
и добавить знак минус, то получим эластичность замены первого
ресурса вторым (ЭЗ ПРВ):
(х
MRTSn (х2)
х, dMRTSn'
х2
212
Заменив в выражении Е12 предельную норму технологической за-
мены первого ресурса вторым MRTSn на отношение предельных
производительностей, получим
Э/(х,,х2)/Эх2
xi
*2
\Х2/
Э/Ц, х2)/дхх
дДхх,х2)/дх2
(уц.лр/ах,^ /э/(х|,х2)/ах1
^д/(Х], Х2 )/Эх2 )/ df (х,, Х2 )/дх2
dln^
_________Х2______
f д/(хр х2)/дхх У
^эдхрх^/эх., J
Получили представление ЭЗ ПРВ в форме логарифмической
х,
производной капиталовооруженности труда — по предельной
Х2
норме технологической замены MRTSn первого ресурса вторым.
Если в последнем выражении под знаком обоих логарифмов
поменять местами числитель и знаменатель, то, очевидно, «шес-
тиэтажная» дробь не изменится, поэтому получим, что
£12 £г1’
Э/(ХрХ2)/ЭХ]
т.е. получим эластичность замены второго ресурса первым.
Таким образом, Ех2 = Е2Х (т.е. «эластичности все равно, кто
кого заменяет»). Поэтому естественно далее использовать термин
эластичность замены одного ресурса другим (ЭЗ ОРД).
213
7.2.2. Найдем эластичность замены одного ресурса другим для
некоторых основных ПФ.
h
ДляПФПЭЗРу = о^(а1х1_а + а2л^“) “ имеем
( h\ 1
э/(х„хг)/ах, + ° ‘.(-“К-'
3/(x„x2)/&r2 f лА _о -А-! fl,!,--1’
1-аГ° а'*1 +а2х2 ) а/_а)х2
Ji *1
d In—
I *1 1
En=-------Mtr =
din-3-рИ
a2\X2 )
Для ПФ КД у = а0х“‘х“2 имеем
У(хр х2)/дхх aoaxxxl~lxf2
df , х2 )/дх2 а0а2хх' хр'1
1
1+а
ai А
а2 х.
d| In— I din—
*12 =----1Мг = ^- = 1.
dlnl^l din—
^а2 Xj) х2
Для ПФ с линейными изоквантами у = (b0 + 6)х1 + b2x^h имеем
Э/(х„х2)/ах| h(bQ+bxxx+b2x2)h~x-Ьх Ьх
df(xx, х2)/Эх2 h(bQ+bxxx +/’2х2)л-1 Ь2 Ь2 ’
dlln—I din—
£12" Га)" 0 "
din -Ч
Для ПФЛ (ПФЗВ) у = minCCjXp С2х2) имеем £12 = 0.
214
7.2.3. Рассмотрим геометрическую интерпретацию эластичнос-
ти замены одного ресурса другим.
Поменяв в числителе выражения £12 местами xt и х2 (в резуль-
тате чего перед дробью исчезнет знак «минус») и использовав фор-
„ . Э/(хрх2)/аХ] dx2
мулу производной неявной функции ——!£ у--- =--------будем
Э/(ХрХ2)/ах2 dxx
иметь следующую цепочку равенств:
Э/(хр х2)/5х,
_ Э/(ХрХ2)/Эх2
Е{2~ X
*1
*2
4—]
1*2 J
/ ЭДХрХ;)/^
[э/(ХрХ2)/Эх2
УЦ, х2)/Эх;
д/(х1гх2)/дх2
*2
*1
Я —
l*J
/ ЭДхрХдУах,
^э/(хрх2)/ах2
tg<p tgq'-tgq
tgq tg<p'-tg<p’
где
= tg<p;
P
-2- =tgq; — =tgq; --г2- =tgq> (рис.7.10).
X| p X] p' OX| p'
215
Если изокванта — прямая, тогда Еп = 00 (tg а' # tg а, tg ср' = tg ф)
(рис. 7.11). Если радиус R кривизны изокванты в точке Р умень-
шается, то Е12 —> 0. (рис. 7.12).Если R -» 0, то в пределе получим
«угол» (рис. 7.13).
Рис. 7.11 Рис. 7.12
216
Рис. 7.13
7.2.4. Приводимый ниже вывод ПФ с постоянной эластичнос-
тью замены ресурсов следует статье К.В. Аршакуни (2001).
Если эластичность замены одного ресурса другим постоянна
(£12=о), то получаем дифференциальное уравнение второго порядка
с частными производными (в уравнении фигурируют частные
Э/(хрх2) Э/(хрх2)
производные —-1—— и —-1—— и дифференциал от логарифма
dXj дх2
их отношения):
,. f ^1
rfln —
\Х2/
УЦ>Хг)/ЭХ|
Э/(хрх2)/Эх2
откуда следует, что
rfln— = rfln
о х2
э/(Х|,х2)/ах|
э/(хрх2)/ах2
(7.2.1)
Дальше можно рассуждать так. Уравнение/(хр х2) = т опреде-
ляет неявную функцию х2 = Л(хр т) (или xt = g(x2, т)), графиком
которой является изокванта. Полагая в (7.2.1) в последнем выра-
217
жении х2 = Л(Хр т), проинтегрируем его левую и правую части как
функции одной переменной:
1
ln| — I =1пС.
1*2,1
где С, 0 — произвольная постоянная. Освободившись от лога-
рифмов в (7.2.2), получим
ЭЛХрХр/Зх,!
Э/(Хр х2)/3х2 J’
(7.2.2)
*2
Э/(ХрХ2)/
/ЗХ]
Э/Ц,х2)/
/^*2,
откуда следует, что
“ <У(*р*2) с
xi Чх2 - -и-
(7.2.3)
Эх2 ~*"2 сЦ
Формально (7.2.3) — это дифференциальное уравнение в част-
ных производных первого порядка. При а * 1 будем искать решение
( .-1 >-11
/(х1,х2)уравнения(7.2.3)ввиде/(х,,х2)=1:'(и)=Г С2х, О+С3х2 ° .
Выпишем частные производные первого порядка этой функ-
ции:
Э/(хрх2)
Эх,
Э/(х,,х2)
дх2
1-1
'2*1 а‘г1'Зл2
1-1
’ у а
'2Л1
>— о-1
(7.2.4)
(7.2.5)
1
i
i
и
и
1 ° ° х °
~ 2*1 «
а
W 1 —
—сл«.
о 3 2
Подставив (7.2.4) и (7.2.5) в (7.2.3), получим
1
1— >-11 -1
O=C3x1° F(; C2Xj °+С3х2 " °
3Л1
о
1-1
-С{С2х2°-F' C2Xj °+С3х2 а
2Л! ’Г'-Зл2
о ** ’
218
откуда следует, что
F' С,х, а+С,х, ° —— (х.х,) °(С,-С|С,)=0, еслиС,=С.С,,
U Л* 1 «Л X 1 л» «J 1 X «Э 1
и
с
Г 1— 1—
т.е. функция /(X],x2)=F С2х, °+С3х2 а
при С3 = С(С2 есть ре-
шение уравнения (7.2.3) и, следовательно, уравнения (7.2.1).
( 1 1 \
1— 1—
Является ли функция j\xvx2)=F С2х{ а+С3х2 ° общим ре-
шением уравнения (7.2.1), мы анализировать не будем.
Если положить ——- = В; -В = -—1,т.е. — = 1-3 |а = —— |,
о н о а *4 1-р/
то функция/(хр х2) перепишется так:
/(x1,x2) = F(C2xf + C3x2P). (7.2.6)
Если 0<<у<1,тоР=-аиа>0.В этом случае решение f(x{, х2)
имеет вид
/(х1,х2) = Г(С2х1“ + С3х2“). (7.2.7)
Полагая F(w) = aQu h/a, получим (классическую) ПФ ПЭЗР в
виде
/(хр х2) = а0(а}х~а + а2х2аГ1,/а. (7.2.8)
В качестве функции F(u) можно взять любую функцию, такую,
что /’'(и) < 0.
Если о > 1, то 1 > Р > 0. В этом случае решение /(хр х2) имеет
вид (7.2.6). Полагая F(u) = а0«А/^, получим (классическую) ПФ
ПЭЗР в виде
/(Хр х2) = Og^xf + fl^xf )А/Р.
(7.2.9)
Таким образом, функции (7.2.6) и (7.2.7) представляют собой
более общие ПФ, чем (классические) ПФ с постоянной эластич-
ностью замены ресурсов вида (7.2.8) и (7.2.9).
В качестве функции F(u) можно взять любую функцию, такую,
что F\u) > 0.
Функции (7.2.8) и (7.2.9) однородны степени А.
219
При о = 1 будем искать решение /(хр х2) уравнение (7.2.3) в
виде /(%] , х2) = F(u) = F(aox“' х“2 )•
Выпишем частные производные первого порядка и этой функ-
ции:
Э/(?,Хг) = (7.2.10)
У(*1» х2^ _ „а, а,х <Х) а2-1 /7 7 ...
— /'„ВД Х2 '^0^‘2Х1 Х2 ' (/.2.11)
Подставив (7.2.10) и (7.2.11) в (7.2.3) (при о= 1), получим
xi'Fu(aoxi'x22 На^^'х"2-1 - С'Х-^а^'хр )aQalx^i~ixp = 0,
откуда следует, что
a0Fu<a0X\'Х22)'Ц*2Г’ХГ‘Х22 (“2 "С1“1 > = °’
если о^-Ца^О, т.е. С]=02/0], т.е. функция /(хр х2) = Г(аох“'х“2)
при С1 = а2/ах есть решение уравнения (7.2.3) (при с = 1) и, следо-
вательно, уравнения (7.2.1).
Не будем анализировать, является ли функция /(хрх2) =
= /’(аох“'х“2 ) общим решением уравнения (7.2.1).
Если F(u) = Uили F(u) = Uy (число у > 1), то функция f(xt, х2) =
= J’(aox“lx2 2) есть (классическая) ПФ КД.
В качестве функции F(u) можно взять любую функцию, такую,
что F'(u) > 0.
Таким образом, /(хрх2) =/7(<^х“,х22) представляет собой
ПФ, более общую, чем (классическая) ПФ Кобба—Дугласа.
При п > 2 понятие эластичности замены /-го ресурсаj-м ресур-
сом (при фиксированном объеме выпуска и объемах хк остальных
ресурсов k*i,k*j) можно определить так:
где х = (хр ..., хл), MRTSg =
Э/(х)/Эх;
Э/(х)/Эх. ‘
220
13. ПФ с постоянной эластичностью
замены ресурсов и ее связь с ПФ Кобба—Дугласа,
линейной и ПФ Леонтьева
7.3.1. Покажем, что ПФКД, ПФЛ и ЛПФ — это асимптотические
версии ПФ ПЭЗР:
1) при а -»О ПФ ПЭЗР -> ПФКД;
2) при а -» +<*» ПФ ПЭЗР -»ПФЛ;
3) при а -» -1 ПФ ПЭЗР -»ПФЛИ (это тривиально).
7.3.2. Докажем сначала пункт 3.
Имеем при а = -1 /(хр х2) = а^(а}х} + д2х2)А. При h = 1 получим
частную версию ЛПФ у = Ьххх + Ь2х2, при Л # 1 получаем ПФЛИ
y = a0(alxl+a2x2)h.
Докажем пункт 1).
Перепишем ПФ ПЭЗР в развернутом виде:
h
f(xx, х2) = а^х^ + а2х~а) « =
(7.3.1)
Если Д] +а2> 1, h > 0, то при а—> О
°1+а2
—> (Д| + д2)“ = 00 => у = 0.
Если а( + а2 < 1, h > 0, то при а -> 0
—> 0 => у = оо.
221
Если aj+a2 = l,TO
откуда вытекает, что
— а гЛ (») (»»)
+О2х-) « =-^ = V1^‘> =
1 — 1
UJ
(♦) Используем здесь, что at + а2 = 1.
(**) Полагаем = ахЛ, а2 = h - axh.
133. Докажем пункт 2).
Еслих2 >х, (Oj > 0), то (см. (7.3.1))
откуда вытекает при х2>х{(ах> 0)
lim д0(а1х1"“+а2х2“) “ =^^7-=aox1A=^min(x1A;x^').
1->+оо ( \П
—
W
222
Аналогично при х2 < xt (at > 0)
h
lim a(i(aix^a¥a2x2a) “ = ^oxA = aomin(xA;x2).
(X—^+°°
При*! =x2 (cm. (7.3.1))
h Ji Ji
a0(alx;a+a2X2a) <x=a0(a1+a2) “(x““) “=——--x*.
(ai+a2)a
При flj + a2 = 1 имеем
h
lim (^(а^х^0,+a2x2a) « =aox^ = aomin(x^;x2).
Таким образом,
h
lim a^^x^+a2x2a) « = flomin(x1A; x2 )•
При h = 1 получаем ПФЛ у = a0 min(x,, x2).
7.4. Учет в ПФ НТП
в экзогенной и эндогенной формах
7.4.1. В экономико-математическом моделировании под НТП
понимают совокупность всех факторов, которые обеспечивают
выпуск без увеличения количества используемого труда и капита-
ла. В этой совокупности факторов собственно НТП играет, ко-
нечно, первостепенную роль.
Простейшим способом учета НТП в ПФ f(x{(t), х2(0) является
ее умножение на экспоненциальный множитель е^: y(t) =
= А^хД/), х2(0). Темп прироста (Хо > 0) и темп прироста с обрат-
ным знаком (Хд < 0) выпуска/(х^О, х2(0) обусловлены НТП. Па-
раметр Хо задается извне (т.е. экзогенно), например оценивается
статистически. Отсюда и термин «экзогенная форма НТП». Эта
форма позволяет оценить вклад НТП в экономическое развитие
моделируемой системы (фирмы, отрасли, региона, национальной
экономики). Однако экзогенная форма не объясняет мотивацию
НТП и воздействия региона, национальной экономики на эконо-
223
мическое развитие. Для этого следует использовать эндогенную
(внутреннюю) форму учета НТП в ПФ.
В литературе было предложено достаточно много подходов к
описанию воздействия НТП на объем выпускаемой продукции.
Остановимся на одном из самых простых и самых конструктив-
ных походов. Этот подход основан на автономном экзогенном
учете НТП, суть которого в том, что динамическая ПФ представ-
ляется в одном из следующих видов (фигурирующая ниже функ-
ция у(0 > 1 и представляет собой индекс НТП, она строго возрас-
тает во времени):
у(0 = 'И0У(х1(0,^2</))
(продуктоувеличивающий НТП, нейтральный по Хиксу),
(капиталосберегающий НТП, нейтральный по Солоу),
ЯО =f(xl(t), у(0*2(0)
(трудосберегающий НТП, нейтральный по Харроду),
ЯО =/(Vj(O^j(r), у2(/)х>(0)
(случай капитале- и трудосберегающего НТП). Анализ различ-
ных способов учета в ПФ НТП широко представлен в учебной и
монографической литературе (см., например, А.В. Лотов (1984),
Г.Б. Клейнер (1986), О.Б. Голиченко (1999)).
-7.4.2. Как уже отмечалось выше, простейшим и наиболее часто
применяемым способом учета НТП является использование в ка-
честве функции у(0 экспоненты eV, т.е. \|/(?) = eV.
Этот вариант выбора содержит важную предпосылку о строгой
монотонности экономического роста и априори исключает нали-
чие колебаний во времени объемов выпускаемой продукции, что,
конечно, противоречит экономической реальности, которая час-
то демонстрирует наличие колебаний и отсутствие строгой моно-
тонности.
Модель, учитывающая колебания во времени факторов произ-
водства, отличных от труда и капитала, более адекватна экономичес-
кой реальности. Она представляет собой динамическую ПФ вида
y(t) = f<xt (t), х2 (/))eV^1sin(Wr+e) ,
предложенную А.К. Смирновой (2001), которая также разработа-
ла метод оценки параметров этой динамической ПФ.
224
Параметр Х^, описывает тенденцию роста и падения выпуска в
зависимости от знака параметра Хц. Параметр X, измеряет ампли-
туду циклических колебаний объемов выпускаемой продукции.
Значение параметра Х( равно максимальному отклонению (вверх
и вниз) выпуска от тренда ехо'. Параметр со описывает фазовую
частоту циклических колебаний объемов выпускаемой продук-
ции. Период Т циклических колебаний объемов выпускаемой
продукции дается формулой Т = 2л/со. Наконец, параметр 0 опре-
деляет величину еМ"9 отклонения от тренда в начальный момент
времени t = 0.
Содержательными областями приведенных ПФ и динамичес-
ких моделей, в которых будут фигурировать ПФ, могут быть как
макро-, так и микроэкономические объекты.
7.4.3. Начиная со второй половины XX в. наряду с трудом и ка-
питалом все возрастающую роль среди факторов экономического
роста стали играть аккумулирование человеческого капитала,
продукция сектора НИОКР, а также экологический фактор. От-
сюда вытекает, что все эти три фактора (аккумулирование челове-
ческого капитала, продукцию сектора НИОКР и экологический
фактор) следует выделять особо и рассматривать их наряду с тру-
дом и капиталом. Далее речь пойдет о первых двух из трех назван-
ных факторах, которые дополняют труд и капитал.
Рассмотрим одну из первых двухсекторных моделей (назовем
ее Модель 1), в которой в явном виде представлен не только про-
изводственный сектор, но и сектор НИОКР (см.: А.В. Лотов (1984,
с. 255-256)).
Производственный сектор рассматриваемой динамической
модели (с непрерывным временем) описывается ПФ
y(/) = V(^(x1(/),x2(0),
где y(f) — объем выпускаемой продукции (например, ВНП стра-
ны или выпуск большой фирмы, которая сама финан-
сирует НИОКР);
\|/(Z) — индекс НТП, который увеличивает выпуск;
х,(/) — количество капитала;
х2(0 — количество труда.
Сектор НИОКР описывается дифференциальным уравнением
У(0 =/2(У(0, Ф(0),
где ф(/) — объем вложений в НИОКР.
15- 7620
225
Полное описание модели имеет следующий вид:
у(0=у(/У(^(0,х2(0), V(0=/2(V(0,l(0), 7(0=-Si(0y(0,
Ф(/))=52(0у(0, х1(0=/(0-§(Пх1(0, ^(0 = ^(0х1(0,
^(0) = ^°, х2=х2, \|/(0)=у°,
где 5j(r)—доля выпуска у(Г), которая инвестируется в производ-
ственный сектор;
s2(t)— доля выпуска y(t), которая инвестируется в сектор
НИОКР;
£(0 — норма выбытия основного производственного капитала;
£(/) — темп прироста рабочей силы.
Очевидно, $,(/) > 0, s2(t) > 0, s}(t) +s2(t) < 1.
Представленную модель можно дополнить целевым функцио-
налом
т
(г) - s2 (Г))Я0]Л(тах)
о
и получить задачу оптимального управления с параметрами уп-
равления st(0 и s2(t).
Целевой функционал в случае, когда содержательная область
модели рассматривается на макроэкономическом уровне, т.е. мо-
делируется, например динамика национальной экономики, сле-
дует толковать как дисконтированный суммарный эффект от
текущего потребления населения. Если целевой функционал
имеет вид
т
J е-8' [(1 - 5] (Г) - s2 (0)у(0]Л(тах),
о
он интерпретируется как дисконтированный суммарный объем
потребления населения.
Если содержательная область модели рассматривается на мик-
роэкономическом уровне, т.е. моделируется экономика (круп-
ной) фирмы, то последний целевой функционал можно интер-
претировать как дисконтированный суммарный доход трудового
коллектива фирмы — естественно, за вычетом инвестиций в про-
изводственный сектор и в сектор НИОКР.
226
7.4.4. Рассмотрим другую модель (Модель 2), также состоящую
из двух секторов: производственного и НИОКР (см.: Е.В. Анти-
пов (2002)). Символы, которые не комментируются в Модели 2,
взяты из Модели 1.
Производственный сектор Модели 2 описывается ПФ
у(0=Л(ф(Г))/(х](0,х2(0),
где ф(0 — объем инвестиций в сектор НИОКР;
Л(ф(0) — мультипликатор, описывающий эффективность ин-
вестиций в НИОКР.
Выражение для инвестиций в производственный сектор имеет
вид
Xj(0=«i(0y(0-^(0xj(0,
где 5,(0 — доля выпуска у(0> которая инвестируется в производ-
ственный сектор;
£(/) — норма выбытия основного производственного капи-
тала.
Сектор НИОКР Модели 2 описывается так:
ф(0 =s2(t)y(t).
Выпишем остальные условия Модели 2:
^(0=g(x2(0), х](0)=х“, ф(О)=ф°, х2(0)=х°
Положим Xj(T’) = хр где Xj — заданный объем основного произ-
водственного капитала, который должен быть достигнут за крат-
чайшее время Т, т.е. Дггйп), и мы получили Модель 2 в форме за-
дачи на быстродействие.
По экономическому смыслу st(t) > 0, s2(t) > 0, Sj(O + s2(t) < 1.
В работе Е.В. Антипова (2002) задача оптимального управле-
ния на быстродействие была решена с помощью принципа макси-
мума Л.С. Понтрягина при следующих предположениях о ПФ
/(х/О, х2(0) и мультипликаторе Л(ф(0):
/(хр х2) =/(О(х1)/(2)(х2), /(ухр ух2) = у/(Хр х2),
к=х}/х2,
z = y/x =f(^x2V =/pL,l =/(Л, 1) = Й(Л),
/Х2 1*2 )
h\k) > 0, h"(k) < 0, А(0) = 0, lim h'(k)= ~, lim h'(k) = 0,
Л—>0 Л—
15*
227
А(0) = 1, ton Л(ф) = о», Л'(ф) > 0 при ф > О, А'(О) = О,
ф->оо
1ш1Л'(ф) = °о, ПтЛ'(ф)=О,
ф—>д ф—>©©
Л"(ф) > О при ф < а, Л"(ф) < О при ф > а.
Здесь а > О - некоторое число (пороговая величина инвести-
ций в НИОКР, которую следует оценить для каждого конкретно-
го случая специально).
Графиком мультипликатора Л(ф) является s-образная линия,
поэтому этот мультипликатор и был назван s-образным. По мне-
нию Е.В. Антипова (2002), s-образный мультипликатор более
адекватен реальности, чем классический мультипликатор, кото-
рый удовлетворяет условиям: Л'(ф) > 0, Л"(ф) < 0, Л(0) = 1,
ton Л(ф)=°°, ton Л'(ф) = 0, ton Л'(ф)=
ф—>оо ф—>оо ф—>0
Неоклассический мультипликатор мал, если объем ф инвести-
ций в НИОКР также мал. Для качественного изменения техноло-
гического уровня (национальной экономики или большой фир-
мы) требуется достаточно высокий объем инвестиций в НИОКР.
5-образный мультипликатор описывает резкий скачок инвес-
тиций в НИОКР вблизи порогового значения а инвестиций в
НИОКР, что более адекватно реальности, ибо если национальная
экономика (или крупная фирма) еще не достигла порогового
уровня (а) инвестиций в НИОКР, отдача этих инвестиций будет
относительно мала. Если национальная экономика (или крупная
фирма) перешла пороговый уровень (а) инвестиций в НИОКР,
отдача от этих инвестиций будет относительно велика.
7.4.5. Трехсекгорная модель (Модель 3), предложенная А.Н. Мои-
сеевым (2004), включает секторы производственный, НИОКР и
образования. Модель 3 была преобразована А.Н. Моисеевым (2002)
в двухсекторную модель НТП с закупкой технологии. Модель 3
обобщает трехсекторную модель Бакси (Bucci А. (2001)), двухсек-
торные модели Муллигано—Ребелло, П. Ромера, Узавы—Лукаса и
классическую односекторную модель Солоу—Свена.
Модель 3 может использоваться для описания как макро-, так
и микроэкономических содержательных областей.
Производственный сектор Модели 3 описывается следующим
выражением:
у(0 = YW/jCd - аДО^а), х2(0), (7.4.1)
228
где y(t) — выпуск модели (в макроэкономическом случае у(Г) мо-
жет равняться ВНП, в микроэкономическом случае y(f)
равен выпуску (большой) фирмы);
у(0 — индекс НТП, который увеличивает эффективность ис-
пользования капитала и труда;
Xj(/) — количество капитала;
x2(t) — количество труда;
eq (0 — доля (физического) капитала, которая направляется в
сектор НИОКР (0 < a, <S l),/i(xp х2) - ПФ.
Сектор НИОКР Модели 3 описывается следующим выраже-
нием:
W) =f2(k(t), a2(t)m(t), а//)*//)) - bk(t)k(t), (7.4.2)
где k(t) — прирост знаний (новые технологии);
£(/)-уровень (запас) знаний;
т(0—человеческий капитал (число квалифицированных
работников, умноженное на качество (квалифика-
цию) среднего работника);
а2(/)—доля человеческого капитала, которая направляется в
сектор НИОКР (0 < < 1);
5Л(0—норма выбытия знаний (т.е. используются только ак-
туальные, востребованные знания);
f2(k, т, X])—функция, которая показывает, как запас знаний, че-
ловеческий капитал и основной производственный
капитал определяют новые технологии.
Сектор образования Модели 3 описывается следующим выра-
жением:
«(/) =/3(*(0, а3(0«(/)) - (7.4.3)
где а3(/)—доля человеческого капитала, направляемая в сек-
тор образования (0 < а3 < 1), + а3(/) £ 1;
5ОТ(/)—норма выбытия человеческого капитала (уход на
пенсию, потеря работоспособности, смерть и т.п.);
/3(Л(0, т(0)— функция, которая показывает, как запас знаний и
человеческий капитал определяют прирост челове-
ческого капитала.
В секторе образования рост числа квалифицированных работ-
ников моделируется эндогенно, а рост числа неквалифицирован-
ных работников моделируется экзогенно в классической форме в
видех^г)=лх2(0, где л > 0 — темп прироста числа неквалифициро-
ванных работников. Отметим также, что фундаментальные иссле-
229
дования, которые ведутся в секторе образования, относятся к
сектору НИОКР..
Модель индекса НТП в Модели 3 описывается следующим вы-
ражением:
Ш =№& + 5Л(0*(0,«(/) + 8m(/>(/)) - 8vv(0, (7.4.4)
где 8^(/) — норма выбытия (в силу устаревания) технологий из
производства. Зависимость прироста у(/) индекса НТП от при-
роста знаний (новых технологий) k(t) и от прироста человеческого
капитала m(t) содержательно означает, что новые знания (новые
технологии), полученные в секторе НИОКР, поступают в произ-
водственный сектор, лишь будучи обеспеченными соответству-
ющими количеством и уровнем квалификации работников.
Модель основного производственного капитала в Модели 3
имеет вид
х1(0=Х0у(0-8(0х1(/), (7.4.5)
где s(t) (0 < s(f) < 1) — норма накопления, которая показывает ту
долю выпуска, которая инвестируется в основной производ-
ственный капитал, а 8(0 (0 < 8(0 < 1) — норма выбытия основно-
го производственного капитала производственного сектора Мо-
дели 3.
Наличие трех секторов (производственного, НИОКР и обра-
зования) является естественным для национальной экономики
развитой страны. Для крупной фирмы наличие этих трех секторов
также вполне естественно. В качестве примера крупной фирмы
можно привести автомобилестроительную фирму. По оценкам
экспертов последних лет XX в., необходимым условием позитив-
ной долговременной рыночной перспективы автомобилестрои-
тельных фирм является объем их ежегодного выпуска, равный
примерно 2,5—3 млн автомобилей.
При таком объеме выпуска фирма имеет возможность полно-
ценно финансировать и обновлять не только основное произ-
водство, но и секторы НИОКР и образовательный и за счет этого
получать конкурентные преимущества, снижая издержки на вос-
требованные рынком автомобили (в свое время в течение 20 лет
после окончания Второй мировой войны фирма «Фольксваген»
не корректировала модель знаменитого «жука», что позволило ей
довести его рыночную цену до величины, практически равной
цене мотоцикла), а также дифференцируя продукцию (за счет,
например, «наворотов» в электронной начинке автомобилей).
230
Перепишем Модель 3 в виде нелинейной системы обыкновен-
ных дифференциальных уравнений первого порядка:
х,(0 + 8(|)х,(0=XOW/d - а/Ох/0, х2(0), (7.4.6)
V(') + 3¥(OV(O =/4(*(0 + 8А(0*(0, m(t) + 6да(0«(0), (7.4.7)
k(t) + 6А(0*(/) =f2(k(t), а^ХО, а/Ох/О) (7.4.8)
m(t) + 8да(0т(0 =/3(W), а3((Х0), (7.4.9)
х2(О = лх2(О. (7.4.10)
При заданных долях и нормах а, (0, a2(t), а3((), s(t),
8v(0. 8(0 и заданных начальных значениях х,(0) = х°, х2(0) = х2,
у(0) = ц/0, Л(0) = Л°, т(0) = т° Модель 3 приобретает вид задачи
Коши для системы (7.4.6)—(7.4.10), у которой при достаточно
гладких функциях f{,f2,f3, /4 существует единственное решение
(х,(Г), х2(0, у(0, k(t), Гладкость функций/,, f2,fyf4 имеет
место на основании содержательных соображений.
Все доли и нормы а, (Г), а2(/), s(t), F>k(f), Зу(/), 8(0
(или их часть) могут быть параметрами управления, и тогда Мо-
дель 3 приобретает вид задачи оптимального управления, в качест-
ве целевого функционала которой может фигурировать, напри-
мер, дисконтированный суммарный доход трудового коллектива
(крупной) фирмы (в случае, если содержательная область Моде-
ли 3 рассматривается на микроэкономическом уровне) и дискон-
тированный суммарный объем потребления населения (в случае,
если содержательная область Модели 3 рассматривается на мак-
роэкономическом уровне).
Функции /р/2,/3, f4 могут быть выбранными так, чтобы они
имели, например, мультипликативную форму (которую имеет
ПФ Кобба—Дугласа):
Z1 ((1 - аДДОхДГ), Х2(/)) = (7 4 11)
= d,((l - a,(0)Xj(0, х2(0)₽|х^((),
/2(*(0. а/^ХО. = (14 12)
= /i2(A:(Z)1f|(a2(ZX0)Y:!(a,(0x,(0)T3,
/#(», а3((Х0) = Zi3( W'(a3((X/))4 (7.4.13)
/4(*(0 + \(t)k(t), m(t) + 6ж(ГХ0) = ,7 4 14)
А#(О + 8/ОЛ(О)0|ХО + 8и(/ХОЛ,
231
где bv b2, b3, b4, pp P2 (0 < pj < 1, 0 < p2 < 1), Yp y2, y3 (0 < y, < 1,
0<y2< 1, 0<y3< l),T|pT|2 (0 < rij < 1,0 <T|2 < 1), 0p 02 (O^e^l,
0 < 02 < 1) — постоянные параметры, оценки которых получают-
ся методом наименьших квадратов.
Задачу Коши или задачу оптимального управления, которые
представляют собой версии Модели 3, при наличии оценок по-
стоянных параметров можно решать с помощью ЭВМ и содержа-
тельно анализировать полученные решения.
7.4.6. Задачу Коши и задачу оптимального управления на основе
системы (7.4.6)—(7.4.10) можно исследовать качественно, выяв-
ляя характерные свойства их решений без явного знания этих ре-
шений. В частности, большой интерес представляют траектории
постоянного пропорционального роста, т.е. такие траектории,
у которых постоянные темпы прироста^ (/)/%,(/)=пх, v(0/Y(0=
k(t)/k(t) = пк, = пт, х^(/)Д2(/) = п, среди которых темп при-
роста (неквалифицированной) рабочей силы определяется экзо-
генно, а остальные темпы прироста пх , п^, пк, пт определяются
эндогенно из уравнений (7.4.6)—(7.4.16), правые части которых
имеют мультипликативную форму (7.4.11)—(7.4.14). Эндогенно
определяемый темп прироста конечного выпуска у (/) может быть
выше, чем экзогенно заданный темп прироста (неквалифициро-
ванной) рабочей силы, а может равняться ему или быть ниже.
Первый из названных трех случаев отражает ситуацию темпа при-
роста, источником которого является истинно эндогенный НТП.
Работы, посвященные оценкам параметров двух- и трехсек-
торных моделей, практически отсутствуют в связи с тем, что, во-
первых, вычислимые версии этих моделей были предложены
сравнительно недавно и, во-вторых, серьезную проблему пред-
ставляет наличие (точнее, отсутствие) данных, необходимых для
формирования модельной информации, например, с помощью
использования регрессионного анализа.
Анализируя разнообразные данные, характеризующие состоя-
ние национальной экономики Соединенных Штатов Америки с
1980 по 1997 г., А.Н. Моисеев (2004) с помощью метода наимень-
ших квадратов оценил параметры Модели 3 и построил оптималь-
ную траекторию и траекторию постоянного пропорционального
роста для национальной экономики США, темп прироста кото-
рых превосходит аналогичный реальный показатель. А.Н. Моисе-
ев выявил резервы более высоких расчетных (по сравнению с ре-
232
альными) темпов прироста. Полученные А.Н. Моисеевым (2004)
результаты интересны также тем, что продемонстрировали полез-
ность Модели 3 как средства для оценки потенциала экономичес-
кого роста национальной экономики США.
На микроэкономическом уровне для проведения прикладных
или экспериментальных расчетов версии Модели 3 (а также трех-
секторная модель Бакси и многие двухсекторные модели) не ис-
пользовались.
Вопросы для самоконтроля к главе 7
1. Что такое производственная функция? Что представляют собой ее
структурные элементы?
2. Как формулируются основные свойства ПФКД?
3. Как формулируются основные свойства ЛПФ и ПФЛИ?
4. Как формулируются основные свойства ПФЛ?
5. Как формулируются основные свойства ПФ ПЭЗР?
6. Как геометрически интерпретируются предельные производитель-
ности капитала и труда?
7. Как геометрически интерпретируются средние производительности
капитала и труда?
8. Что такое возрастающая эффективность с ростом масштабов произ-
водства? Приведите примеры и дайте обоснование.
9. Что такое постоянная эффективность с ростом масштабов произ-
водства? Приведите примеры и дайте обоснование.
10. Что такое убывающая эффективность с ростом масштабов произ-
водства? Приведите примеры и дайте обоснование.
11. Как определяется точечная (предельная) эластичность выпуска по
первому (второму) ресурсу? Выпишите точечные (предельные) част-
ные эластичности выпуска по первому (второму) ресурсу для ПФКД,
ЛПФ, ПФ ПЭЗР.
12. Как определяется конечная (процентная) частная эластичность по
первому (второму) ресурсу?
13. Как определяется эластичность производства? Выписать эластич-
ность производства для ПФКД и ПФ ПЭЗР.
14. Что такое норма технологической замены одного ресурса другим и
предельная норма технологической замены одного ресурса другим?
15. Как связаны между собой предельные производительности ресурсов
и предельная норма замены одного ресурса другим? Как выглядит
предельная норма замены одного ресурса другим в точке ЛРРФ?
16. Как определяются статическая и динамическая ПФ? Приведите при-
мер простейшей динамической ПФ.
233
17. Как определяется эластичность замены одного ресурса другим в слу-
чае п = 2?
18. Как геометрически интерпретируется эластичность замены одного
ресурса другим?
19. Как выводится ПФ с постоянной эластичностью замены одного ре-
сурса другим?
20. Что представляют собой асимптотические версии ПФ ПЭЗР?
21. Как в ПФ формально учитывается продуктоувеличивающий НТП,
нейтральный по Хиксу?
22. Как в ПФ формально учитывается капиталосберегающий НТП, ней-
тральный по Солоу?
23. Как в ПФ формально учитывается трудосберегающий НТП, ней-
тральный по Харроду?
24. Как выглядит динамическая ПФ, которая учитывает колебания во
времени факторов производства, отличных от труда и капитала?
25. Что представляет собой Модель 1, охватывающая производственный
сектор и сектор НИОКР? Дайте содержательную интерпретацию
модели на макро- и микроэкономическом уровнях.
26. Что представляет собой Модель 2, охватывающая производственный
сектор и сектор НИОКР?
27. Что такое ^-образный мультипликатор и в чем его отличие от класси-
ческого мультипликатора?
28. Что представляет собой Модель 3, охватывающая секторы произ-
водственный, НИОКР и образования?
29. Что собою представляет Модель 3 в виде задачи Коши для системы
обыкновенных дифференциальных уравнений первого порядка?
Задачи и упражнения для самоконтроля к главе 7
1. Выпишите уравнение изокванты ПФКД, значение которой рав-
но у0.
2. Выпишите уравнение изокванты ПФЛ, значение которой равно у0.
3. Выпишите уравнение изокванты ПФ ПЭЗР, значение которой рав-
но у0.
4. Выпишите уравнение асимптот изокванты ПФ ПЭЗР, значение ко-
торой равно у0.
5. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ с линейной эластич-
ностью замены ресурсов, которая имеет вид
В выражении для эластичности замены одного ресурса другим ис-
пользуйте капиталовооруженность труда Xj/x2.
234
6. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ с линейной эластич-
ностью замены ресурсов, которая имеет вид
у = а0(1 -е’си1/*2)х2.
7. Выпишите решение Модели 1 с использованием принципа максиму-
ма Понтрягина.
Вопросы для контрольных работ к главе 7
1. Чему равна предельная норма замены одного ресурса другим для
ПФКД?
2. Чему равна предельная норма замены одного ресурса другим для
ПФЛИ?
3. Чему равна предельная норма замены одного ресурса другим для
ПФ ПЭЗР?
4. Как выводится ПФ с постоянной эластичностью замены одного ре-
сурса другим, равной единице (п = 2)?
5. Как определяется эластичность замены одного ресурса другим в слу-
чае п > 2?
Задачи и упражнения для контрольных работ к главе 7
1. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ, которая имеет вид
2. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ, которая имеет вид
Л Л
у = а0(о1х1-а + (1-а1)х-а) + (1-^)^) а.
3. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ, которая имеет вид
2 2
у = аххх + а2х2 + a3XjX2 + д4хр + а5х2.
4. Найдите предельную норму замены одного ресурса другим и элас-
тичность замены одного ресурса другим для ПФ Солоу, которую
также называют ПФ Хилхорста:
1
У = + (1 - О, )^2 °2) “3.
5. Выпишите решение Модели 2 с использованием принципа максиму-
ма Понтрягина.
Глава 8
РЫНОЧНЫЕ ВЗАИМОДЕЙСТВИЯ
В СЛУЧАЕ НЕСОВЕРШЕННОЙ
КОНКУРЕНЦИИ
8.1. Максимизация прибыли монополии
в краткосрочном и долговременном промежутках,
монопольная цена и монопольный выпуск
8.1.1. В условиях функционирования чистой монополии фирма
одна, поэтому линия рыночного спроса AR(y) есть линия спроса
на продукцию этой фирмы. Таким образом, в модели чистой мо-
нополии линия спроса АЛ (у) характеризует рынок, а линии издер-
жек (предельных МС(у) и средних АС(у)) — технологию и размеры
фирмы.
В рассматриваемой ситуации прибыль фирмы PR(y) традици-
онно представлена в виде разности дохода (выручки) R(y) фирмы
и ее издержек С(у) (здесь у — объем выпускаемой фирмой продук-
ции: PR(y) = R(y) - С(у)). Для определения объема у(д,) выпуска
фирмы, который (глобально) максимизирует ее прибыль PR (у)
(т.е. для определения монопольного выпуска у(т)), следует исполь-
зовать условия первого и второго порядков. Из условия первого
порядка (необходимого условия максимума прибыли)
dPR(y)
dy
(8.1.1)
определяется объем y(m). С помощью знака второй производной
d2PR[y(m})
dy2
(8.1.2)
236
проверяется, действительно ли объем максимизирует при-
быль PR (у). Если
«<0 (8.1.3)
dy2
(условие второго порядка), то объем у(т) максимизирует прибыль
PR(y) (т.е. неравенство (8.1.3) — достаточное условие максимума
PR(yM) — обычно не только локального, но и глобального — при-
были PR(y)); если вторая производная (8.1.2) равна нулю, требует-
ся дополнительное исследование. Если у(/в) — монопольный вы-
пуск, то =AR (у</и)) — монопольная цена.
Подставив в уравнение (8.1.1) его решение у =у<~т\ получим
ay dy ay
откуда следует хорошо известное равенство
MR(y(m}) = MC(y(m\
Расписав подробно левую часть неравенства (8.1.3), получим
d2R(y(m}) d2C{y(m})
dy2 dy2
что эквивалентно неравенству
dMR{y{m)) dMC{y(m})
dy dy
откуда следует, что если в точке у(т) (такой, что MR(y(m)) =
= Л/С(у(т>)) угол наклона линии Л/С(у(т)) строго больше, чем угол
наклона линии MR(y(m\ то в точке у(т) прибыль PR(y) достигает
своего максимума (на рис. 8.1 в точке у(т) прибыль PR(y) мини-
мальна, а в точке у(т) прибыль максимальна, т.е. у(т) — монополь-
ный выпуск, а р(т) — монопольная цена). Для определения вели-
чины максимальной прибыли Р/?(у(т)) требуется линия средних
издержек АС(у).
Если линия средних издержек АС(у) имеет точки, которые рас-
положены ниже линии среднего дохода AR(y), то максимальная
прибыль PR(yM) фирмы-монополиста будет скорее положитель-
ным числом (рис. 8.2, на котором площадь четырех-
угольника Op^Fy^ равна доходу R(yM) = р<">у<"> фирмы-мо-
237
нополиста, площадь |0Ж7у(т) четырехугольника OHGy^ равна
издержкам С(у<т>) = у^т\АС(у^) = у(т)С(у(т))/у(т) (АС(у(т)) равна
длине |у('я)(?|] отрезка у(т)(7) фирмы-монополиста, а площадь
|Яр(ж)Я;|^ (положительное число) четырехугольника Hp(m}FG
равна максимальной прибыли Р7?(у<т)) фирмы-монополиста).
Если линия средних издержек АС{у) касается извне линии
среднего дохода AR(y), то максимальная прибыль РЛ(у(и,)) фирмы-
монополиста будет нулевой или отрицательной (рис. 8.3, на кото-
ром площадь |Ор(и’) /т<т)|2 четырехугольника равна дохо-
ду R(y(m)) = и издержкам С(у(ш)) =^АС(у(т}) фирмы-моно-
полиста, т.е. нулевая площадь |р(,я)/’|2 отрезка p(m^F равна
максимальной прибыли РЛ(у(ш)) фирмы-монополиста).
Если линия средних издержек АС(у) расположена выше линии
среднего дохода АС(у), то максимальная прибыль Р/?(у(л,)) фирмы-
монополиста будет обязательно отрицательной (рис. 8.4, на кото-
ром площадь |0р(ш)Л/т)|2 четырехугольника Op(m)Fy^ равна дохо-
ду Я(у(т)) = р(т}у(т} фирмы-монополиста, площадь |о/К?у<ж) |2 че-
тырехугольника OHGy(nf> равна издержкам С(у(л,)) = у(пе>АС(у^)
фирмы-монополиста, а площадь (со знаком минус)
четырехугольника p(m^HGF равна максимальной прибыли (мини-
мальному убытку) PR(y(m)) фирмы-монополиста). На рис. 8.4 дли-
238
на | y(m)G ( отрезка y^G равна AC(y(m)) и, следовательно, площадь
|oMz/m) четырехугольника OHGy(ne> равна издержкам C(y(m)) =
В рассмотренных трех примерах линии среднего AR(y) и пре-
дельного MR(y) доходов были неизменными, что свидетельствует о
неизменности рыночной конъюнктуры, а технология фирмы-мо-
нополиста менялась, причем в сторону роста средних издержек.
8.1.2. В рассмотренных в разделе 8.1.1 трех примерах время явно
не фигурировало.
Предположим, что время дискретно и «атомом» времени явля-
ется производственный период (для краткости — период), которо-
му в экономической реальности может соответствовать, например,
один год (или, скажем, один месяц). Фирма-монополист решает
задачу максимизации прибыли в течение периода, т.е. в задаче
максимизации прибыли фирмы (см., например, рис. 8.2) величи-
ны средних и предельных издержек, объем выпускаемой фир-
мой продукции и цена «привязаны» к одному периоду. То же
самое справедливо для среднего и предельного дохода. Упорядо-
ченная совокупность производственных периодов называется
временном промежутком. Временной промежуток — это упорядо-
ченная совокупность между базовым периодом и текущим перио-
дом. Если в течение этого промежутка фирма-монополист не име-
ет возможности изменить свои постоянные издержки, то проме-
239
жуток называется краткосрочным, если имеет возможность
изменить свои постоянные издержки, т.е. все издержки становятся
переменными, то промежуток называется долговременным.
Сначала рассмотрим случай, когда в базовом периоде фирма-
монополист решает задачу максимизации своей прибыли в теку-
щем периоде, который от базового периода отделяется кратко-
срочным промежутком.
Если у фирмы-монополиста прибыль положительная или ну-
левая, фирма с рынка не уйдет. Возникает вопрос, обязательно ли
она уйдет с рынка в случае отрицательной прибыли.
Максимальная прибыль фирмы-монополиста Р7?(у(т)) =
=_ С(у<т)) (< 0) в случае краткосрочного промежутка имеет
следующее детальное представление (С(у(т))) = ИС(у(т)) + JC(y(CT)):
отрез-
', и поэто-
PR(y(m}) = р(т}/т}-y(m}AVC(y(m}) -y(m}AFC(y(m}) (<0).
На рис. 8.5 площадь |Op^Fy^ прямоугольника
равна доходу /?(у(ст)) фирмы-монополиста. Площадь | ONKy(m)|2
прямоугольника QNKy№ равна переменным издержкам КС(/т)) =
= у<т)АРС(у(т)) фирмы-монополиста, ибо длина
каУ"^равна АУС(у(т>), адлина Оу(т) отрезка равнау(т)
му KC(y(m)) = |оАгЛ'у(т) |2 = |оу(т) j =y(m)AFC(y(m)). Площадь
прямоугольника NHGK равна постоянным издержкам
FC(y(m)) = у<т)ЛЛС(у(т)) фирмы-монополиста, ибо длина отрезка
1^1, = |y<m)G j i = АС(у(т)) - AVC(y(m)) = AFC(y(m\ а пло-
щадь \NHGK 2 = |Oy(m) f -IxgIj = у(т) AFC(y(m)) = £С(у(л,)). В рас-
сматриваемом случае дохода у(тУт) =|оУж)/У'*) |2 фирмы хватит,
чтобы компенсировать полностью переменные издержки и час-
тично постоянные издержки, ибо прямоугольник Op^Fy^ пол-
ностью покрывает четырехугольник ОЛАу(ж), площадь которого
равна |07VA>(m) |2 = |Oy(m)[ •|y(m)fji =yMAVC(y(m}) = VC(yM) - пе-
ременным издержкам, и частично четырехугольник NHGK, пло-
щадь которого равна постоянным издержкам FC(y(m^). Поэтому в
рассматриваемом варианте, когда р(ж) > ЛКС(/т)), в случае крат-
косрочного промежутка фирма-монополист с рынка не уйдет.
240
На рис. 8.6p(m) < Л KC(/m)) и доход a фирмы-монополис-
та не хватит, чтобы компенсировать даже переменные издержки
КС(у(т), ибо /'">/'"> = | < |0ЛАГу(т) |2 = VC(yM). В этом
случае (т.е. когда р(от) < А ИС(у(т>)) фирма-монополист должна уйти
с рынка в случае краткосрочного промежутка. Случай p(m) <AVC(yM)
означает либо низкий уровень рыночного спроса, либо высокие
средние переменные издержки.
•6-7620
241
8.1.3. Рассмотрим случай, когда в базовом периоде фирма-моно-
полист решает задачу максимизации своей прибыли в текущем
периоде, который от базового периода отделяется долговременным
промежутком.
Сначала рассмотрим вариант, когда объем выпускаемой фир-
мой продукции у\т) достаточно мал и когда средние и предельные
издержки фирмы являются достаточно высокими (рис. 8.7, на ко-
тором этот вариант представлен линиями (sr)JC|(y), (sr)MCx(y),
которые отражают размер и технологию фирмы, обеспечивающей
выпуск своей продукции в достаточно малом объеме у{ж)). По-
скольку речь идет о конкретном размере и технологии фирмы,
постольку ее портретом являются функции издержек (sr)ACx(y) и
(sr)MCx(y) для текущего периода в случае краткосрочного проме-
жутка.
Рассмотрим теперь вариант, когда объем выпускаемой фирмой
продукции у(2т) больше объема у^ и когда средние и предельные
издержки фирмы являются относительно низкими (см. рис. 8.7, на
котором этот вариант представлен линиями (sr)AC2(y), (sr)MC2(y),
242
которые описывают размер и технологию фирмы, обеспечива-
ющей выпуск своей продукции в объеме у£\ который больше
объема Здесь, как и в предыдущем варианте, речь идет о кон-
кретных размере и технологии фирмы, поэтому ее портретом яв-
ляются ее функции (линии) издержек (sr)AC2(y) и (sr)MC2(y) для
текущего периода в случае краткосрочного промежутка.
Если в базовом периоде размер и технология фирмы характе-
ризуются линиями (зг)АС\(у) и (зг)М(\(у), то в случае краткосроч-
ного промежутка в текущем периоде фирма максимизирует свою
прибыль по первому варианту и имеет объем выпускаемой про-
дукции, равныйу^\ и ценур^ (см. рис. 8.7).
Если в базовом периоде размер и технология фирмы характе-
ризуются линиями (sf)AC2(y) и (sr)MC2(y), то в случае краткосроч-
ного промежутка в текущем периоде фирма максимизирует свою
прибыль по второму варианту и имеет объем выпускаемой про-
дукции, равный у^\ и цену (см. рис. 8.7).
Если в базовом периоде размер и технология фирмы характе-
ризуются линиями (sryAC^ty) и (зг)МСх(у), а в текущем периоде —
линиями (зг)АС2(у) и (зг)МС2(у), то требуется долговременный
промежуток для того, чтобы фирма могла от первого варианта с
(5г)ЛС|(у) и (sr)MCY(y) перейти ко второму варианту с (sr)AC2(y) и
(sr)MC2(y).
Поскольку фирма-монополист может в базовом периоде точ-
но не знать, какой конкретно вариант функционирования ей сле-
дует выбрать в текущем периоде, фирме необходимо рассмотреть
все возможные варианты (sr)AC(y) и построить линию (1г)АС(у)
в виде огибающей семейства всех линий (sr)AC(y) (на рис. 8.7 по-
казаны два представителя (sr)ACt(y) и (sr)AC2(y) семейства всех ли-
ний (sr)AC(y) и огибающая (1г)АС(у) этого семейства). На рис. 8.7
также представлена линия (!г)МС(у), которая из линии (1г)АС(у)
получается естественным образом: (Jr)MC(y) = (у(1г)АС(у)Уу =
= (1г)АС(у)+у((1г)АС(у)Уу.
Задача выбора фирмой «оптимального» варианта функциони-
рования в текущем периоде в случае долговременного промежут-
ка решается так. При этом предполагается, что в текущем периоде
известна линия спроса AR на продукцию фирмы-монополиста и,
следовательно, линия предельного дохода MR. Отыскивается оги-
бающая (1г)АС(у) семейства линий (sr)AC(y) и функция (линия)
(!г)МС(у). Строятся эти линии (см. рис. 8.7). Отыскивается точ-
16*
243
ка Е2 пересечения линий MR(y) и (1г)МС(у), т.е. решается уравне-
ние MR(y) = (lr)MC(y), которое в рассматриваемом на рис. 8.7
случае дает у = С помощью функции (линии) AR(y) находим
р = р%"\ Линии (sr)MC2(y) и (sr)AC2(y) «оптимального» варианта
функционирования фирмы в текущем периоде выбираются сле-
дующим образом. Из семейства всех линий (sr)MC(y) выбирается
та, которая проходит через точку Ет Поскольку линии (sr)AC(y) и
(sr)MC(y) образуют пары, постольку после выбора линии (sr)MC2(y)
однозначно выбирается линия (sr)AC2(y) (она должна касаться ли-
нии (1г)АС(у)). Выбор функции (линии) (sr)AC2(y) можно осущест-
влять непосредственно из однопараметрического семейства функ-
ций (линий)
(5Г)АС2(у)=(5Г)С2(у) =- j (sr)MC2(y)dy +—D
у у£> У
Уг
(здесь D — произвольная постоянная). Из однопараметрического
семейства линий в качестве (sr)AC2(y) выбирается та, которая ка-
сается линии (1г)АС(у).
На рис. 8.7 площадь |2 прямоугольника
взятая со знаком минус, равна максимальной прибыли, т.е. ми-
нимальному убытку фирмы в первом варианте (srjACfo) и
(зг)МС}(у).
На рис. 8.7 площадь |//2/^m).F2G2|2 прямоугольника H2p^F2G2
равна максимальной прибыли фирмы во втором варианте с
(sr)AC2(y)H(sr)MC2(y).
Рисунок 8.7 иллюстрирует ситуацию развития фирмы-моно-
полиста в целях повышения эффективности ее функционирова-
ния (фирма из убыточной за счет наращивания производства и
снижения издержек становится прибыльной). Приведенный при-
мер показывает, что в случае долговременного промежутка фирма-
монополист может иметь положительную прибыль в отличие от
конкурентной фирмы, которая в случае долговременного проме-
жутка может иметь только нулевую прибыль. Если линия (1г)АС(у)
располагается строго выше линии AR(y) среднего дохода, то, оче-
видно, фирма-монополист будет иметь отрицательную прибыль и
поэтому обязательно покинет данный рынок.
244
8.2. Монопольная власть и ее источники,
индекс монопольной власти
8.2.1. Функция (линия) спроса на продукцию фирмы-монопо-
листа есть функция рыночного спроса. Согласно закону спроса эта
функция убывает с ростом объема у выпуска фирмы-монополис-
та. Отсюда следует, что, варьируя объем выпускаемой продукции,
фирма-монополист может корректировать цену предлагаемого ею
продукта. Когда фирма путем варьирования объема выпускаемой
ею продукции корректирует цену предлагаемого ею продукта, го-
ворят, что фирма обладает монопольной (или рыночной) властью.
Монопольная власть характеризуется индексом монопольной
власти, предложенным Лернером:
р-МС
Р ~ Ed
£ =
(8.2.1)
т.е. индекс монопольной власти есть обратная величина (со зна-
ком минус) эластичности спроса на продукцию фирмы-монопо-
листа по цене.
Для вывода формулы (8.2.1) выпишем представление дохода R
фирмы-монополиста
R(y) =р(у)у-
Предельный доход MR(y) имеет вид
MR(y) = ^^y + p(y),
откуда следует, что
MR(y) = Ху)( -y-r +1 Г PW
I dy P(y) J
P_dy_
У dp
= Ху)| 1+4-1
I Ed)
т.е.
p(y)-MR(y) = -^,
Ed
или
p(y)-MR(y) 1
Р(У) Ed'
245
В точке у(т) максимизации прибыли фирмы-монополиста
MR(yM) = Л/С(у(т)), поэтому имеем
р(у^)-МС(у(т}) _ 1
Р<У(т}) " Ed(y™)
Левая часть последнего равенства и есть индекс Лернера по
определению.
Формула (8.2.1) может быть выписана не только для фирмы-
монополиста, но и для любой фирмы, имеющей убывающую
(но не горизонтальную!) функцию (линию) спроса AR(y). Следу-
ет здесь специально отметить, что в индексе Лернера для фирмы,
которая не является чистым монополистом, фигурирует эластич-
ность спроса по цене на продукцию, производимую фирмой, а не
эластичность рыночного спроса.
Если эластичность спроса на продукцию фирмы Ed--o° (слу-
чай чистой конкуренции), то р = МС, и следовательно, индекс
Лернера равен нулю. Верно и обратное. Если L = 0, то р = МС и
Если эластичность спроса на продукцию фирмы Ed приближа-
ется к числу, равному 1, то, очевидно, индекс Лернера L —> 1.
Поскольку в случае линейной функции спроса пара (у(т\р(т)) при-
надлежит эластичному (верхнему) участку линии спроса, т.е. участ-
ку, где \Ed | > 1, постольку в случае линейной функции спроса ин-
декс Лернера не может быть больше единицы.
Чем больше (по модулю) эластичность Ed спроса по цене
(т.е. чем ближе линия спроса на продукцию фирмы к совершенно
эластичной линии спроса), тем ближе к нулю индекс Лернера,
т.е. монопольная власть фирмы мала (рис. 8.8). Если, например,
эластичность спроса по цене равна £у=-10, то индекс Лернера при-
нимает значение равное £ = 0,1, что означает, что р(т) - Л/С(у(л’)) =
= 0,lp</n), т.е. к предельным издержкам Л/С(у(т)) добавляется всего
10% от цены р(т\
Чем ближе к -1 эластичность спроса на продукцию фирмы по
цене, тем ближе к единице индекс Лернера, т.е. монопольная власть
фирмы велика (рис. 8.9). Если эластичность спроса по цене равна
£^=-1,5, то индекс Лернера принимает значение, равное L = 2/3 =
= 0,67, что означает, чтор(т) - МС()№) = 0,67/><т), т.е. ценовая до-
бавка к предельным издержкам равна 67% от цены р(т).
246
Рис. 8.8
Рис. 8.9
Отметим, что индекс монопольной власти и величина макси-
мальной прибыли фирмы мало связаны между собой: при боль-
шой рыночной власти фирма может иметь максимальную при-
быль любого знака (положительную, нулевую, отрицательную)
(рис. 8.10, на котором разность - Л/С(у(ш)) =| £7^ равна длине
| EF [ отрезка EF, а площадь | p^HGF четырехугольника p^HGF,
взятая со знаком минус, равна максимальной прибыли фирмы,
т.е. минимальному убытку фирмы). Причина того, что при высо-
кой монопольной власти фирма-монополист может иметь отри-
цательную максимальную прибыль, в том, что в формировании
индекса монопольной власти не фигурируют средние издержки,
а в определении максимальной прибыли они фигурируют.
Рис. 8.10
247
Формула (8.2.1) может быть переписана так:
МС
Ed (8.2.2)
Если фирма (не обязательно монополист) может оценить
эластичность спроса на свою продукцию и свои предельные издер-
жки, то формула (8.2.2) позволяет получить оценку цены на про-
изводимую фирмой продукцию, т.е. формула (8.2.2) дает простое
правило ценообразования для такой фирмы.
Если МС = АС, то индекс Лернера будет выглядеть так:
р(т} - АС(у(т})
L = —----—-• Умножив числитель и знаменатель на у1 ,
р™
будем иметь
l р^у^-у^АС(у(т}) _ PR(y(m)) (8 2.з)
pWyW JfyM ’
т.е. индекс Лернера становится равным отношению максималь-
ной прибыли фирмы-монополиста к ее доходу, т.е. норме прибыли.
Получается, что чем выше норма прибыли фирмы, тем выше ее
монопольная власть. Если в правой части формулы (8.2.3) числи-
тель и знаменатель поделим нау(т), то получим следующую дробь:
L = — , ;—, которая означает, что индекс Лернера равен
р™
также отношению средней прибыли к цене р(т).
8.2.2. Источниками монопольной власти являются: эластичность
рыночного спроса, число фирм на рынке и такое важное обстоятель-
ство, как взаимодействие фирм. Эти источники представляют ин-
терес, когда на рынке действуют несколько фирм, а не одна, как
это имеет место в случае чистой монополии. Поэтому сейчас мы
ограничимся краткими замечаниями, а более подробный анализ
проведем позже, когда будем рассматривать монополистическую
конкуренцию и олигополию.
Первым источником монопольной власти является эластичность
рыночного спроса. Если речь идет о фирме-монополисте, то ры-
ночный и индивидуальный спрос в этом случае совпадают и индекс
монопольной власти определяется на основании эластичности ры-
ночного спроса. Если фирма не является фирмой-монополистом,
248
то эластичность спроса Ed на ее продукт больше (точнее, не меньше)
по модулю эластичности Edm рыночного спроса | Ed | > | Edm |, откуда
следует, что
т.е. эластичность рыночного спроса позволяет получить оценку
сверху для индекса монопольной власти (8.2.1) отдельной фирмы.
В связи с тем что в случае краткосрочного промежутка спрос
часто бывает неэластичным по цене, а в случае долговременного
промежутка спрос является более эластичным по цене, моно-
польная власть в случае краткосрочного промежутка может быть
большой, а в случае долговременного промежутка — значительно
меньшей.
Вторым источником монопольной власти является число
фирм на рынке. Говоря точнее, число фирм на рынке и соотноше-
ние между объемами выпусков этих фирм, т.е. концентрация фирм
на рынке. Последние десятилетия одним из популярных индексов
концентрации является индекс Хиршмана—Херфиндаля
который определяется так:
ЯЯ/=$2 + ...+$2, (8.2.4)
где п — число фирм на рассматриваемом рынке; sj-yj/(y{ +... +уя),
i = 1, ..., п — рыночная доля z-й фирм: у. — объем ее выпуска,
ау1 + ... + уп — суммарный объем выпусков всех фирм, которые
действуют на рассматриваемом рынке. В приведенном представ-
лении максимальное значение индекса HHI равно единице. Это
возможно только в случае фирмы-монополиста, которая одна
представлена на рынке. Здесь я = 1 и J, = у,/У] = 1.
Если, например, п = 2 и = s2 = 0,5, то НН1= 0,52 + 0,52 = 0,5.
При п = 3, Sj = s2 = 0,4, s3 = 0,2 имеем HHI = 0,42 + 0,42 + 0,22 =
= 0,16 + 0,16 + 0,04 = 0,36.
Если = s2 =... = sn = —, т.е. доли рынка у всех п фирм одина-
ковы, то п
и с ростом числа фирм на рассматриваемом рынке, т.е. при п —><»,
индекс НШ-ь 0.
249
Индекс Хиршмана—Херфиндаля (НШ) используется и в та-
ком виде:
НШ = (j2 + ...+S2)-10 000,
где выражение s( • 100, i = 1,..., п — рыночная доля /-й фирмы в
процентах. В этом случае максимальное значение HHI равно
10 000, а минимальное значение может быть сколь угодно малым,
если число фирм неограниченно растет.
Индекс НШ используется правительственными органами в
качестве основного ориентира для принятия решений в антимо-
нопольной (антитрестовской ) политике. С 1982 г. HHI в США
стал основным ориентиром при оценке разного рода слияний
различных фирм на предмет допустимости таких слияний. Если
НШ < 1000, то рынок оценивается как неконцентрированный
(«достаточно многочисленный») и слияние фирм, как правило,
допускается без каких-либо ограничений. Если 1000 < НН1< 1800,
то рынок оценивается как «умеренно концентрированный», од-
нако при НН1> 1400 рынок оценивается «как угрожающе немно-
гочисленный». Это обстоятельство может служить поводом для
дополнительной проверки допустимости слияния со стороны Де-
партамента юстиции США. При НШ> 1800 рынок оценивается
как высококонцентрированный (или «немногочисленный»).
В этом последнем случае если в результате слияния НШувеличи-
вается более чем на 100 пунктов, то оно не разрешается. Если рост
НШ находится в пределах 51—100 пунктов, то существует основа-
ние для дополнительного анализа слияния на предмет его допус-
тимости или недопустимости.
Взаимосвязь между индексом Лернера и НШ будет проанали-
зирована в параграфе 8.7, посвященном дуополии и олигополии.
Третьим источником монопольной власти является взаимо-
действие фирм на рынке, которое также будет проанализировано
в параграфе 8.7. Здесь в качестве предварительного положения
отметим, что в случае агрессивной конкуренции фирм на рынке
монопольная власть уменьшается, а в случае сотрудничества
фирм монопольная власть увеличивается.
8.3. Естественные монополии и их регулирование
8.3.1. Фирма является естественной монополией, если убывание
ее средних и предельных издержек наблюдается на всем проме-
жутке ее объемов производства (рис. 8.11). В связи с убыванием
250
средних издержек АС(у) предельные издержки МС(у) будут ниже
средних издержек. Термин естественная монополия отражает тот
факт, что экономия от масштаба производства позволяет одной
фирме удовлетворять весь рыночный спрос до того, как отдача от
масштаба начнет снижаться, т.е. когда линия средних издержек
АС(у) пойдет вверх. Поэтому в данной ситуации входные барьеры
в отрасль обусловливаются технологией фирмы, а не правами
собственности или, скажем, лицензиями. Замена одной большой
фирмы несколькими меньших размеров (в целях создания конку-
рентного климата) приведет к росту издержек. В качестве приме-
ров можно отметить нецелесообразность наличия в городе не-
скольких водопроводных, канализационных сетей или сетей цен-
трализованного теплоснабжения.
Рис. 8.11
Задача рационального функционирования естественной мо-
нополии (как и всякой монополии) состоит в максимизации ее
прибыли в течение некоторого фиксированного периода (напри-
мер, в течение года). Оптимальный выпуск у<т) естественной мо-
нополии есть абсцисса точки Е пересечения линий МС(у) и MR (у),
251
цена одной р(т} единицы продукции естественной монополии
есть ордината р(т) точки F, максимальная прибыль PR^ естест-
венной монополии равна площади |/ф('")Ял|2 прямоугольника
Hp(m)FG (см. рис. 8.11). В связи с высокими средними издержками
АС(ум) и относительно небольшим выпуском у(т) максимальная
прибыль PR^m) естественной монополии (даже при наличии высо-
кой монопольной цены р(т)) относительно невелика.
Если естественная монополия выпускает продукцию, востре-
бованную обществом, то ее относительно малый выпуск у(/и> (при
относительно высокой цене/>(т)), который максимизирует ее при-
быль PR(m) и является для монополии наилучшим решением, мо-
жет оказаться неприемлемым для общества. Отсюда вытекает не-
обходимость регулирования функционирования естественной
монополии. Для этого следует рассмотреть возможные варианты
регулирования.
8.3.2. Регулирующий орган может установить за единицу про-
дукции естественной монополии цену р(с), которая аналогична
цене, появляющейся в условиях чистой конкуренции, ибо р(с)
(см. рис. 8.11) — ордината точки Ес пересечения линий МС(у) и
AR(y). Установление цены р(с) на уровне МС(у) называют также
предельным ценообразованием. В связи с тем что цена р(с) анало-
гична цене в условиях чистой конкуренции, данное решение о
регулировании функционирования естественной монополии на-
зывается первым наилучшим решением. Однако это решение (отно-
сительно высокий выпуск у(е) и относительно низкая цена р(с),
которая является таковой из-за низких предельных издержек
МС(у)) наилучшим является для общества, но не для естественной
монополии, ибо при таких цене р® и выпуске она будет иметь
отрицательную прибыль PR^ (равную площади |р(е)Яс(?с£с |2 пря-
моугольника p^HcGcEc, взятую со знаком минус, — см. рис. 8.11)
в случае как краткосрочного, так и долговременного промежутка
и поэтому уйдет с рынка. Чтобы этого не произошло, естествен-
ной монополии следует предоставить дотацию в размере, по
крайней мере необходимом для компенсации отрицательной
прибыли. Однако практическое решение о размере дотации мо-
жет оказаться достаточно сложным в связи трудностями получе-
ния оценок высоких постоянных издержек и возможной неэф-
фективности технологии и управления естественной монопо-
252
лии. Тем не менее в ряде социально значимых случаев государство
(а чаще муниципальная власть), являясь владельцем естествен-
ной монополии или сдавая ее в аренду, предоставляют ей дота-
ции, обеспечивая тем самым ее приемлемое функционирование.
В качестве примеров можно отметить наземный городской
транспорт, подземный городской транспорт, которые нормаль-
но функционируют благодаря тому, что получают значительные
дотации.
8.3.3. Компромиссным решением для регулирования естествен-
ной монополии можно считать установление цены р(г) за единицу
продукции естественной монополии (см. рис. 8.11). Такое реше-
ние принято называть вторым наилучшим решением. Здесь цена
равна ординате точки Er (= G) пересечения линий АС(у) и AR(y),
а прибыль PRV* естественной монополии равна нулю (см. рис. 8.11,
на котором доход Д(г) и издержки С(г) равны площади | Ор^Егу^
прямоугольника Qp(r)£ry(r). При нулевой прибыли естественная
монополия может функционировать как в краткосрочном, так и в
долговременном промежутке.
Более детально проблемы регулирования естественных моно-
полий анализируются в дисциплине «Экономика отраслевых
рынков».
В заключение кратко рассмотрим еще один вариант регулиро-
вания естественной монополии. Поскольку на рынке монополии
(не обязательно естественной) нет конкуренции (она там невоз-
можна в принципе или обременительна из-за высоких издержек),
конкуренция может иметь место в борьбе за рынок. Регулиру-
ющий орган может провести аукцион и по его результатам пере-
дать рынок той фирме, которая обязуется вносить в бюджет, ска-
жем, наибольшую сумму. Конкуренцию за рынок принято назы-
вать конкуренцией по Демзетцу, который ее впервые описал.
Фирма, победившая на аукционе, скорее всего, обеспечит выпуск
продукции в объеме у(т) по цене р(т\ однако часть (возможно,
значительную) своей максимальной прибыли PRM фирма будет
перечислять в бюджет в качестве оплаты за право обслуживать
рынок. Относительно малый объем /т) выпуска фирмы является
одним из недостатков такого способа регулирования естествен-
ной монополии.
253
8.4. Монополистическая ценовая дискриминация
первого, второго и третьего рода
8.4.1. Фирма-монополист проводит ценовую дискриминацию пер-
вого рода, если цена каждой своей единицы продукции фирма ус-
танавливает на уровне цены рыночного спроса именно на эту
единицу. Продукция фирмы может иметь форму продукта или
услуги.
Сначала проанализируем ценовую дискриминацию первого
рода на вербальном уровне, а затем на более детальном уровне с
использованием формальных построений.
При отсутствии ценовой дискриминации фирма определя-
ет свой выпуск у (и свою монопольную цену р(ш)) как реше-
ние уравнения MR(y) = МС(у). В случае когда предельные из-
держки постоянные МС= С (рис. 8.12), максимальная прибыль
фирмы-монополиста равна PR^ = (р№ - МС)у(т) = |, где
|Яр(т)Г£|2 — площадь прямоугольника Hp^FE. (см. рис. 8.12).
Максимальная прибыль PR^ фирмы-монополиста может
у(») у(.т)
быть рассчитана по формуле = J MPR(y)dy = J MR(y)dy-
0 о
254
- J MC(y)dy, где символом MPR(y) обозначена предельная
о
прибыль.
В этом случае максимальная прибыль PRM равна площади
|ЯС£|2 треугольника HQE, которая, естественно, равна площади
прямоугольника Hp^FE.
При проведении ценовой дискриминации первого рода в
случае постоянных предельных издержек при реализации одной
у-й единицы продукции фирма-монополист получает прибыль,
приближенно равную площади полоски КВВХКХ, ибо цена этой
У-й единицы продукции равна ординате точки В. Следовательно,
при реализации у(т} единиц своей продукции, когда каждая еди-
ница продукции реализуется по цене ее рыночного спроса, фир-
ма-монополист получает прибыль, равную площади |Я0ЛЕ|2 че-
тырехугольника HQEF, которая больше площади | ffp(m)FE^ четы-
рехугольника Hp(m)FE (площади |#<2F£|2 треугольника HQE).
Фирма-монополист может продолжить (после объема реали-
зацию каждой своей единицы продукции по цене этой единицы
вплоть до объема у(с) и получить дополнительную прибыль, рав-
ную площади | EFN |2 треугольника EFN.
Таким образом, при проведении ценовой дискриминации
первого рода фирма-монополист получает дополнительную при-
быль, равную сумме площадей | P(m)QF |2 и | EFN |2 двух треугольни-
ков p(ni}QF и EFN.
В рассмотренном случае потребительский излишек равен пло-
щади |Я0Я|2 треугольника HQN. В случае отсутствия ценовой
дискриминации прибыль фирмы-монополиста, равная площади
прямоугольника Hp(m)FE, составляет часть потреби-
тельского излишка. При использовании ценовой дискриминации
первого рода фирма-монополист получает весь потребительский
излишек |Я0Я|2, равный ее максимальной прибыли. Таким обра-
зом, используя ценовую дискриминацию первого рода, фирма-
монополист понижает уровень общественного благосостояния.
Решение задачи максимизации прибыли фирмы-монополиста в
условиях ценовой дискриминации первого рода Парето-эффек-
тивно, ибо не существует способа увеличить прибыль фирмы-мо-
255
нополиста и повышать благосостояние потребителей: прибыль
фирмы-монополиста максимальна, а излишек потребителей не-
льзя увеличить, не уменьшая прибыль фирмы-монополиста.
Предпосылка о том, что предельные издержки МСпостоянны,
означает, что издержки Сесть линейная функция выпуска фирмы.
Эта предпосылка справедлива во многих ситуациях экономичес-
кой реальности.
Более сложным является вопрос о принятой предпосылке, что
фирма-монополист знает (или умеет оценивать) координаты то-
чек линии спроса на свою продукцию. Как правило, эта предпо-
сылка далека от реальности. Однако можно отметить ряд ситуа-
ций, в которых данная предпосылка может быть использована.
Например, успешно практикующий врач обычно хорошо знает
своих пациентов и поэтому может дифференцировать размер
своего гонорара, исходя из их материального положения.
Другой пример реального использования предпосылки о зна-
нии линии спроса дает практика дифференцированной оплаты за
учебу, принятая в ряде отечественных и зарубежных вузов: успеш-
но успевающие студенты платят за учебу меньше (или вообще от
нее освобождаются), не вполне успевающие — платят больше.
В общем случае, когда предельные издержки МС не являются
постоянными, в случае отсутствия ценовой дискриминации пер-
вого рода максимальная прибыль PR(m^ фирмы-монополиста
у(т) у(т) у(т)
J MPR(y)dy = J MR(y)dy- J MC(y)dy
О 0 0
(рис. 8.13) равна площади |JVC£|2 криволинейного треугольни-
ка NQE. В случае наличия ценовой дискриминации первого рода
максимальная прибыль фирмы-монополиста
у(С) у(С)
J MPR(y)dy = J AR(y)dy- J MC(y)dy
0 0 0
равна площади | NQG |2 криволинейного треугольника NQG, кото-
рая больше площади | М?£|2 криволинейного треугольника NQE.
То есть при проведении ценовой дискриминации первого рода
фирма-монополист улучшает свое положение за счет увеличения
максимальной прибыли. Переход от MR(y) к AR(y) связан с тем,
что в случае ценовой дискриминации первого рода цена каждой
256
единицы продукции фирмы устанавливается на уровне цены ры-
ночного спроса именно этой единицы, т.е. линия MR(y) перехо-
дит в AR(y), как это имеет место в случае чистой конкуренции
(когда AR = MR).
8.4.2. Переходим к более детальному анализу ценовой дискри-
минации первого рода. Применяя ценовую дискриминацию пер-
вого рода, фирма-монополист, по существу, с каждым потребите-
лем работает индивидуально и может назначать разные цены в
зависимости от того, кому и какое количество выпускаемой про-
дукции она продает.
В рамках ценовой дискриминации первого рода рассматрива-
ется имеющая преимущественно теоретическое значение идеаль-
ная (совершенная) ценовая дискриминация, при которой фирма-мо-
нополист выбирает оптимальную для себя схему ценообразования
в условиях, когда: 1) она знает функцию спроса каждого потреби-
теля; 2) она может отличать потребителей; 3) невозможен арбит-
раж, т.е. перепродажа продукта одним потребителем другому.
Пусть предпочтения каждого потребителя Ср i= 1, ..., к, опи-
сываются квазилинейной функцией полезности и.(у., z) = ^(yJ+Z/,
где у( — количество продукции, выпускаемой фирмой-монопо-
листом, которое приобретает на рынке потребитель Ср a интер-
претируется как количество денег, которое расходует потреби-
17-7620
257
тель на приобретение других продуктов. Каждый потребитель Ср
i = 1,к, обладает фиксированным доходом в размере w(. Далее
функция V.(y) также называется функцией полезности.
Функция ^(у,) определена при у, > 0, имеет конечную положи-
тельную производную Vj'vi отрицательную вторую производную
И"(у,) при у, > 0. Функция издержек С(у) фирмы-монополиста вы-
пукла вниз, имеет положительную конечную производную С'(у)
при у > 0 (здесь у — объем выпускаемой фирмой-монополистом
продукции). Символом tp Г> 0, обозначим денежную сумму, кото-
рую платит потребитель С. фирме-монополисту за приобретаемое
им (потребителем) количество у; выпускаемой фирмой-монопо-
листом продукции. Пара (ур называется контрактом между
фирмой-монополистом и потребителем С., i = 1,..., к.
Пусть функция i=l,...,k, полезности нормирована так,
что ¥.(0) = 0 и что ее частные значения имеют денежную размер-
ность.
Неравенство
¥.(y^t.,i=l,...,k
называется условием участия потребителя С( в рыночной ситуа-
ции, которое содержательно означает, что уровень ^(у.) полез-
ности потребителя С, после приобретения им продукта в объеме у;
должен быть не меньше денежной суммы tp потраченной потре-
бителем С, на приобретение продукта в объеме у.. Неравенство
¥(у.) < t. означает, что потребителю С, выгоднее уйти с рынка.
Очевидно, фирма-монополист заинтересована в максимиза-
ции функции
PR = tl + ... + tk-C(yl + ...+yk),
которая равна ее прибыли (разности выручки + ... + tk и издер-
жек С(У| +... +УЛ)) при выполнении условия участия каждого по-
требителя С;., / = 1, ..., к, т.е. фирма-монополист решает задачу
максимизации
PR=t} + ... + /Jt-c(y1 + ...+ук) (max)
при наличии ограничений (условий участия)
¥(у)Ыр1=1,...,к.
Это содержательно означает, что фирма-монополист имеет
дело только с потребителями, которые участвуют в рыночной си-
туации.
258
Если в точке (ур t*), i = 1,..., к, максимального решения хотя
бы одно ограничение является строгим неравенством У(ую) /да,
то существует положительное число Ео, такое, что У(у*ю) /да + Еда-
Это означает, что существует допустимое решение (у*р /j),
(Уд, /^ + е0),..., (ук, tk) задачи максимизации, на котором значение
целевой функции
/; +... + /да + е0 +... + tk-с(у\ +... +y‘t)
строго больше максимального значения
/]+...+/>...+/;-с(у;+...п4)
этой целевой функции.
Полученное противоречие означает, что допущение о нали-
чии хотя бы одного строгого неравенства ^(у*0) > /^ является оши-
бочным.
Следовательно, в точке (у*., I*), i= 1,..., к, оптимума приведен-
ной задачи максимизации ограничения в виде неравенств превра-
щаются в равенства
^) = /’, /=1, ...,£.
Поэтому задача максимизации прибыли фирмы-монополиста
может быть переписана в эквивалентной ей форме
РЛ(у1,...,ук) =
= J'lO'i) + • • • + W - С(у, + ... + ук) (max), (8.4.1)
которая разрешима, например, при постоянных предельных издер-
жкахи при ^'(у() -> 0, при у.->+<», /= 1,..., к.
Оптимальное решение (у‘, t.),i= 1,.... к, задачи максимизации
(8.4.1) называется идеальным (совершенным), ибо рассматривается
идеальная (совершенная) ценовая дискриминация.
Предположим, что задача максимизации (8.4.1) имеет внут-
реннее решение у* > О, /= 1,..., к. Предположение выполняется в
случае, если, например, предельные издержки С'(у{ + ... +ук) по-
стоянны. Тогда внутреннее решение удовлетворяет условиям пер-
вого порядка
ТО-Пу1 + -+У*) = 0, 1=1,..., к, (8.4.2)
откуда следуют равенства
К,(У1) = ...К<Ук)-С(у\ + ...+ук),
которые показывают, что предельная полезность V! (у.) каждого
потребителя С., i= 1,..., к, равна предельным издержкам фирмы-
17»
259
монополиста, т.е. ситуация с производством продукта такая же,
как и в случае совершенной конкуренции.
Если при любом у > 0 ^'(у) > Ц'(у), ‘ *J> Т°У* > Ур
Оптимальная плата t* потребителя С(. за количество у* приоб-
ретаемого им продукта, выпускаемого фирмой-монополистом,
очевидно, равна
У,
t* = ^/(/) = J Р/СОЛ» / = 1,...»к-
о
Пара (у*, /*), 1= 1,..., т, называется оптимальным контрактом
между фирмой-монополистом и потребителем Сг
Положим PR* = Pjfy*) +... + Vk(yk) - С(у\ +... +у*).
На рис. 8.14 дана геометрическая интерпретация отыскания
фирмой-монополистом «идеальной» пары (у*, t*). Для этого фир-
ме-монополисту следует найти точку у*, в которой линии K;(yz) и
С(у.+У-j) имеют параллельные касательные Кх и К2. Здесь
Уч=У1 + -+У,_1+Ум + ...+Ук-
На основании условия второго порядка (которое здесь не при-
водится) расстояние по вертикали между точками касания будет
больше, чем расстояние по вертикали между любыми другими
точками на линиях Kty.) и С(у.+у_.) в пределах точек А и В
(см. рис. 8.14).
260
Пример 8.4.1. Этот пример иллюстрирует случай идеальной
ценовой дискриминации. Функция полезности потребителя С.
имеет вид ut(yp zt) = К/у,) + zP ^(у,) = Jy^, /= 1,...» к, С(у) = Су =
= С(у, +... +ук) (С—скалярный параметр).
В этом случае уравнение (8.4.2) имеет вид
/
т.е.
откуда
* 1 л Г* 1
И^=^=2С-
8.4.3. Фирма-монополист может предложить каждому потреби-
телю С;, i = 1, ..., к, некоторую схему оплаты приобретаемого по-
требителем количества у; продукта, т.е. схему ценообразования
(тариф), в виде размера tf(y() денежной оплаты потребителя С.
фирме-монополисту как функцию количества у, приобретаемого
им у фирмы-монополиста продукта.
При выбранной фирмой-монополистом схеме ценообразова-
ния /Ду.) потребитель С., i = 1.к, если он не уходит с рынка,
решает задачу максимизации своей функции полезности и.(у., z)
при бюджетном ограничении /(.(у.) + z(. < аг, / = 1,..., к.
То есть
и,(УР Z,) = ВД + Zi (max),
W + =
Условия первого порядка для функции Лагранжа L(y., z) =
= Щу) + Z/ + А.(<0/ - tj(y) - z,) имеют вид
^=к/(у/)-и;(у/)=о, ^=i-x=o,
Эу,- Эг,-
откуда следует равенство
W-W=o,
которое есть условие первого порядка для максимизируемой функ-
ции
w-w-
261
Следовательно, задачу максимизации потребителем С, своей
функции полезности и.(ур z) можно представить в эквивалентной
форме
W -ф) (max). (8.4.3)
Если при оптимальном решении у(°этой задачи V$) -t$) < О,
то это означает, что не выполнено условие участия и потребителю
Ct выгоднее уйти с рынка. Отметим, что прибыль монополиста
будет одна и та же как в случае, если потребитель Ц. уйдет с рынка,
так и в случае, если он останется на рынке и приобретет нулевой
объем у. с нулевой оплатой |Д) = 0.
Линейная схема ценообразования (линейный тариф) имеет вид
tj(y() = Ру, (цена Р — единая для всех потребителей). Нелинейная
схема ценообразования (нелинейный тариф) имеет вид /Д) =А +Руt
(параметры Ри А — единые для всех потребителей). Вообще, нели-
нейной схемой ценообразования называется любая схема, отлич-
ная от линейной схемы. Рассмотрим схемы ценообразования, ко-
торые позволяют реализовать оптимальный контракт (у’, /*) меж-
ду потребителем С;, i = 1,..., к, и фирмой-монополистом.
В схеме 1 («не хочешь — не бери») функция tfy) имеет вид
'А)=
t*, ecnuyt £ у*,
-к», еслиу(. > у*.
Очевидно, в этом случае оптимальным решением задачи
У(у) - t/y) = КД) -1* (max) будет объем у*, ибо при 0 у. < у*
ИД)-^<0, а при у.=у‘ КД)-/‘ = 0 (рис. 8.15).
262
В схеме 2 (двухкомпонентный тариф) функция /(у,) имеет вид
/.(у.) = А + Ру.. Двухкомпонентный тариф можно интерпретиро-
вать как описание практики двойной оплаты, используемой,
например, в парках культуры и отдыха: отдельная плата А с по-
требителя Ц, /= 1,..., к, за вход и отдельная плата за каждый ат-
тракцион. В случае схемы 2 задача максимизации для потреби-
теля Ct, i = 1,..., к, имеет вид
ТО -Pyt-A (max). (8.4.3.1)
Выпишем для этой задачи условие первого порядка V.'(y^ -
-Р=0.
Пустьу*— решение этого уравнения. Тогда объем у*удовлетво-
ряет равенству PC'(у*) = Р, т.е. параметр А не влияет на оптималь-
ный выбор у* потребителя Сг Отметим, что на основании равен-
ства Р = V! (у*) функцию V! (yz) следует интерпретировать как об-
ратную функцию спроса потребителя С;, i = 1,..., к, на продукцию,
выпускаемую фирмой-монополистом. Положим А = Kz(y‘) - Ру..
При схеме 2 потребитель С., /=1, ...,к, выберет объем у*
(рис. 8.16).
Схема 2 (двухкомпонентный тариф) подсказывает, что в об-
щем случае нелинейная схема ценообразования Л = t.(y) в услови-
ях идеальной ценовой дискриминации должна быть такой, чтобы
график функции tt = t.(yt) был расположен строго выше графика
Функции полезности И-(У,) потребителя Ср i = 1, ..., к, при у. * у*
263
и чтобы графики функций /^/Ду.) и касались в точке у.
(на рис 8.17 касательные Кх и К2 параллельны). Эти два требова-
ния означают, что функция РДу) - /Ду) в точке у’ имеет сильный
локальный максимум (рис. 8.18). Это содержательно означает,
что, во-первых, потребитель С;, i = 1,..., к, вообще не будет опла-
чивать покупку, объем у которой не равен объему у* (ибо размер
оплаты /Ду) этой покупки строго больше значения Vj(y) его функ-
ции полезности) и, во-вторых, при у,* У* РДу) - /Ду) < 0» т.е. не
выполнено условие его участия в рыночной ситуации.
Рассмотренная идеальная ценовая дискриминация эффектив-
на как политика ценообразования при выполнении ряда доста-
точно жестких предпосылок, которые были перечислены выше и
которые не обязательно могут выполняться в реальных условиях.
Тем не менее концепция идеальной ценовой дискриминации по-
264
лезна в качестве крайней точки зрения, в частности как ориентир
для понимания возможных вариантов политики ценообразования
в целях их использования в теоретических построениях и на прак-
тике.
8.4.4. Переходим к анализу ценовой дискриминации второго рода,
суть которой в том, что фирма-монополист назначает разные це-
ны за различные объемы выпускаемой ею продукции. Фирма не
может (не умеет) различать потребителей.
В экономической реальности ценовая дискриминация второ-
го рода часто принимает форму разного рода скидок.
Например, чем больше объем поставки, тем больше скидка к
цене продаж. Сезонный железнодорожный билет значительно
дешевле суммы разовых билетов. Аналогичная ситуация имеет
место с единым проездным билетом, цена которого меньше сум-
мы цен всех разовых билетов.
При ценовой дискриминации второго рода фирма-монопо-
лист предлагает всем потребителям единую систему ценообразо-
вания и объемов своей продукции. Потребитель сам выбирает
элемент (элементы) этой системы, т.е. сочетание (у{, t) объема у.
продукции и размера оплаты tp которое называется пакетом.
Рассмотрим сначала (как и в случае ценовой дискриминации
первого рода) ситуацию на вербальном уровне. Пусть предельные
издержки МС фирмы-монополиста постоянны, т.е. МС = АС=С.
Тогда задача максимизации прибыли фирмы-монополиста
имеет решение y<m), которое получается из уравнения MR(y) = С
(рис. 8.19). Цена р(т) определяется с помощью функции спроса
= AR(y(m\ В рассматриваемом варианте максимальная при-
быль фирмы-монополиста равна
PR(m} = (p(m) - МС)у(т} = |^(т)/Е|2,
где — площадь прямоугольника Hp(nC>FE (см. рис. 8.19).
Фирма-монополист может, например, назначить три цены: рх, р2, ру
По ценерх фирма реализует свою продукцию в объеме у £ух, по це-
не/^ фирма реализует свою продукцию вобъемеу-ур гдеу, <у<у2,
по цене р3 фирма реализует свою продукцию в объеме у - (у, + у2),
гдеу2 <у <у3. При такой структуре цен фирма-монополист на рын-
ке может реализовать свою продукцию в объеме у3, который мо-
жет быть значительно больше объемау(т^ (см. рис. 8.19). При реа-
265
лизации продукции в объеме у3 фирма-монополист получит при-
быль, равную сумме площадей +|£’](г1.ЗД2|2 +|£’2б!27^£3|2
четырехугольников Hp{F{E{, ElGlF2E2, E2G2F3E3, которая может
быть значительно больше максимальной прибыли фирмы PR^
в условиях отсутствия ценовой дискриминации второго рода. На-
помним, что эта максимальная прибыль PRM равна площади
|/ф(т)/’£|2 прямоугольника Hp^FE.
Замечание 8.4.1
Отметим, что приведенный выше пример, иллюстрирующий
суть ценовой дискриминации второго рода в случае постоянных
предельных издержек МС=С, аналогичен примеру, иллюстриру-
ющему суть ценовой дискриминации первого рода в случае посто-
янных предельных издержек МС-С. В случае ценовой дискрими-
нации первого рода каждая единица выпускаемой фирмой про-
дукции имеет свою цену, равную цене спроса, т.е. в случае МС= С
ценовая дискриминация первого рода представляет собой, по су-
ществу, асимптотический непрерывный вариант дискретной по
сути ценовой дискриминации второго рода.
266
В условиях, когда с ростом объемов выпуска средние (АС) и
предельные (МС) издержки падают, ценовая дискриминация вто-
рого рода приводит к повышению благосостояния потребителей
за счет расширения масштабов производства и снижения средних
и предельных издержек (рис. 8.20).
8.4.5. Рассмотрим более подробно вариант ценовой дискрими-
нации второго рода, называемой пакетной дискриминацией.
В случае пакетной дискриминации задача фирмы-монополис-
та состоит в том, чтобы предложить такие пакеты, чтобы получить
наибольшую прибыль от тех пакетов, которые приобретут потре-
бители.
Предполагается, что на рынке есть два типа потребителей. Ти-
пичный представитель потребителей первого типа — это потреби-
тель С{, типичный представитель потребителей второго типа — это
потребитель С2. Предполагается далее, что для любого объема у
продукции, выпускаемой фирмой-монополистом, имеет место
неравенство V[(y) < V^(y), откуда при условии, что КДО) = К2(0),
следует, что V}(y) < К2(у). Здесь К,(у) и V2(y) — функции полезности
потребителей С\ и С2 соответственно, удовлетворяющие услови-
267
ям, приведенным в случае ценовой дискриминации первого рода.
Неравенство И, (у) < И2(у) содержательно означает, что уровень
потребительских амбиций у потребителя С2 выше, чем у потреби-
теля Ср
Далее ограничимся случаем двух пакетов (ур /j) и (у2, ф, кото-
рый принципиально не отличается от общего случая конечного
числа пакетов. Добавим ограничение — условие участия каждого
потребителя в рыночной ситуации, которое означает, что ни один
потребитель не уйдет с рынка:
И2(у2)-^0.
Предполагается далее (в отличие от случая идеальной (совер-
шенной) ценовой дискриминации), что фирма-монополист не
может определить тип потребителя.
Пусть пакеты (ур фи (у2, ф максимизируют прибыль фир-
мы-монополиста при выполнении условий участия для потреби-
телей С] и С2. Тогда, как и в случае идеальной (совершенной) це-
новой дискриминации, условия участия выполняются как ра-
венства
НОф-4=о, и2(у‘2)-4=о.
Имеем (на основании неравенства V\ (у*,) < И2(у*))
и (на основании неравенства Kj(y2) < И2(у2))
Vx(y\)-t\<V2(y\)~ 4 = 0.
Выписанные равенства и неравенства содержательно означают,
что, во-первых, для потребителя С2 «чужой» пакет (ур ф лучше,
чем «свой» пакет (у2, t*2), ибо K2(yj) -> И,(у*) - Г* = 0 = И2(у2) -12
(разность значения функции полезности К2(у‘) потребителя С2 и
оплаты Г, им этого объема у^ больше разности значения функции
полезности К2(у2) потребителя С2 и оплаты t2 им этого объема у2),
и, во-вторых, для потребителя С( «свой» пакет (у*, ф лучше, чем
«чужой» пакет(у2, ф, ибо Ух(у2)-t*2< И2(у2)-t2 = 0 = Ух(у\)-ф
Таким образом, если фирма-монополист не может определить
тип потребителя, она теряет потребителя С2 (ибо ему выгоднее
стать потребителем Ср с более высоким уровнем потребительских
амбиций, т.е. «качество» потребителей снижается. Снижение «ка-
чества» потребителей на рынке фирмы-монополиста снижает ее
прибыль, что, конечно, фирме-монополисту не нравится. Поэто-
268
му фирма-монополист заинтересована на рынке иметь дело толь-
ко с теми потребителями, которые будут приобретать «свои» паке-
ты и не будут приобретать «чужие» пакеты, ибо это им будет не-
выгодно. Фирма-монополист может использовать механизм
фильтрации, который формально описывается двумя условиями
самовыявления, т.е. неравенством
д ля потребителя и неравенством
К2(у2)-/2>
для потребителя С2.
Первое из этих неравенств yt(yt) - S Kt(y2) -t2 по существу
означает, что при переходе потребителя от «своего» контракта
(ур /,) к «чужому» контракту (у2, t2) снижается (точнее, не повы-
шается) разность между значением его функции полезности на
приобретаемом им объеме продукта (выпускаемого фирмой-мо-
нополистом) и оплатой этого объема. Аналогично толкуется вто-
рое неравенство И2(у2) -12 > K2(yt) - tv
Доказательство того, что прибыль фирмы-монополиста сни-
жается, если потребитель С2 превращается в потребителя Ср при-
ведено ниже для случая постоянных предельных издержек фир-
мы-монополиста.
Переходим к формальному решению задачи максимизации
прибыли фирмы-монополиста PR, которая имеет дело с кх > О
одинаковыми потребителями С, первого типа и с к2 > 0 одинако-
выми потребителями С2 второго типа:
PR = kjx + k2t2 - C(kltl + k2t2) (max) (8.4.4)
при условиях
(8.4.5)
W>/2 (8.4.6)
(условия участия) и
V^-t^y^)-^, (8.4.7)
И2(у2)-Г2^ЗД)-Г, (8.4.8)
(условия самовыявления).
В точке максимума (Ур/2;/р ?2) задачи (8.4.4)—(8.4.8) есть
по крайней мере одно из каждой пары специальных ограниче-
ний (8.4.5)—(8.4.6) и (8.4.7)—(8.4.8), которое выполняется как
равенство.
269
Если оба ограничения (8.4.5) и (8.4.6) в точке максимума вы-
полняются как строгие неравенства, то тогда можно увеличить
значение переменных t] и t2 на достаточно малые величины так,
чтобы ограничения (8.4.5) — (8.4.6) сохранились как строгие нера-
венства и при этом максимальное значение целевой функции
(8.4.4) увеличилось за счет роста переменных и t2. Описанное
возмущение значений и t2 можно осуществить независимо от
того, чем являются в точке максимума ограничения (8.4.7)—
(8.4.8) — строгими неравенствами или равенствами.
Следовательно, по крайней мере одно из ограничений (8.4.5)—
(8.4.6) в точке максимума должно быть равенством.
Пусть в точке максимума ограничение (8.4.6) выполняется как
равенство V2(y2) = t2. Подставив это равенство в (8.4.8), будем
иметь ij > К2(у,) > ^(pj). Последнее звено цепочки добавлено на
основании того, что уровень потребительских амбиций у потре-
бителя С2 выше, чем у потребителя Cv Сопоставляя первое и тре-
тье звенья последней цепочки, получаем, что для потребителя С\
не выполнено условие участия.
Таким образом, обязательно V2(y2) > t2, и на основании выше-
изложенного = Г г
Если оба ограничения (8.4.7) и (8.4.8) выполнятся в точке мак-
симума как строгие неравенства, то, увеличив только значение t2
на достаточно малую величину, мы сохраним как строгие нера-
венства ограничения (8.4.6)—(8.4.8) и в то же время увеличим мак-
симальное значение целевой функции (8.4.4).
Поэтому по крайней мере одно из ограничений (8.4.7), (8.4.8)
в точке максимума выполняется как равенство.
Пусть ограничение (8.4.7) в точке максимума (у,; у2, /2) це-
левой функции (8.4.4) выполняется как равенство
(8.4.9)
а ограничение (8.4.8) выполняется как строгое неравенство
Г2(у2)-/2>И2(у1)-;1. Л (8.4.10)
На основании доказанного выше равенства = t{ из (8.4.9)
получаем равенство t2 = Vt(y2).
Таким образом, при выполнении равенства (8.4.9) имеем
= Kjtpj) и t2 = Vt(y2), поэтому максимум
^/1 + ^2*2 ~ + ^2^)
целевой функции (8.4.4) можно переписать так:
И (у,) + к2 Vt(y2) - C(klyl + к2у2).
270
Отсюда вытекает, что задача максимизации (8.4.4)—(8.4.8) эк-
вивалентна задаче макисимизации
к\ К1<У1) + УМ ~ С<^\У\+V2) <тах)-
На основании того, что функции И^) и И,(у2) выпуклы вверх,
условия первого порядка
^-(^ri(y1)+^(y2))-C(Vi+V2)) = 0>
^-(kxvx{yx)-vk2vx{y2))-c{kxyx + V2))=°
ЧУ2
являются необходимыми и достаточными условиями того, что
решение (ур у2) СУ] > 0, у2 > 0) есть точка глобального максимума
целевой функции кх^(У]) + ^2K((y2) - С(кхух + £2у2).
Перепишем частные производные поу] иу2 в развернутом ви-
де и подставим в условия первого порядка значение у, и у2:
к\ = к\с'(к\ А +
Л2^<У2) = к2С'(к\У\ + к2У2>-
Отсюда вытекает равенство V{(yx) - Р^(у2), которое при ух *у2
невозможно, ибо по экономическому смыслу И*(у) строго убывает
с ростом у. Ниже показано, 4royj <у2.
Таким образом, допустив, что ограничение (8.4.8) в точке мак-
симума (ур у2; 7р /2) целевой функции (8.4.4) выполняется как
строгое неравенство, мы пришли к противоречию, поэтому оста-
ется принять, что ограничение (8.4.8) выполняется как равенство
И2(у2)-/2= ^(yp-Zp
В комбинации с доказанным ранее равенством ^(у^ = 1Х оно
дает представление для оплаты ?2:
/2=^)-^,)+^,) =
= V2(y^-(y2(yx}-Vx(yx}. (8.4.11)
На основании последнего равенства в целевой функции (8.4.4)
можно переменные и /2 заменить соответственно на выражения
HO'i) и К2(у2) - И2(У]) + И (у) и переписать целевую функцию так:
РЛ(Ур у2) = кх Vx(yx) + к2(У2(у2) - У2(ух) + ^(у,)) -
- С(кхух + к2у2) (max). (8.4.12)
Задача максимизации (8.4.12) эквивалентна задаче максими-
зации (8.4.4)—(8.4.8).
271
Если функции кх И, (у,), £2(И2(у2) - И2(у,) + ^(у,)), -С(к1у1 +
+ к2у2) выпуклые вверх, условия первого порядка
^/1(у|) + Л2(И2(у2)-И2(у1) + К1(у1))-С(Л1У1+^2)] = 0.
^^(У1)+^(И2(у2)-И2(у1)+^(у,))-С(Л1у1+*2У2)] = 0
являются необходимыми и достаточными условиями того, что
решение (у,; у2) (у ( > 0, у2 > 0) этой системы есть точка глобального
максимума PR = PR(yx; у2) целевой функции (8.4.12).
Перепишем частные производные в развернутом виде и под-
ставим в условие первого порядка значения^ иу2:
(*! + Л2)^(у,) - к2 ^(у,) = Л.С^.у, + к2у2), (8.4.13)
Г2(у2)^С\кхух + к2у2). (8.4.14)
Из равенства (8.4.13) следует, что
Л,У{(у,) = kxC'(ktyt + к2у2) + к2(^(ух) - Vfij),
откуда вытекает на основании неравенства (У2(ух) - У[(ух)) > 0,
что
У[(у1)>С'(кху1 + к2у2). (8.4.15)
Попутно отметим, что из неравенства У^у^ > FJ(y,) и соотно-
шений (8.4.14), (8.4.15) следует цепочка неравенств У2(ух) > У[(Ух) >
> lj(y2), откуда на основании того, что предельная полезность
^'(у) убывает, вытекает, чтоу( <у2.
Таким образом, в рассматриваемом варианте пакетной дис-
криминации ценовой дискриминации второго рода система опти-
мальных контрактов (ур /,), (у2, t2) фирмы-монополиста с потре-
бителями С{ и С2 соответственно обладает следующими свойства-
ми:
И(У1) = ^^2)>?2.
В случае постоянных предельных издержек (С'(х) = С — ска-
лярная постоянная) имеем (на основании (8.4.14) и (8.4.15))
^(у2)=с,Р7(у1)>с.
272
Напомним, что в случае идеальной ценовой дискриминации
(и в случае чистой конкуренции) система оптимальных контрак-
тов (у*, zj) и (у2, t2) в случае постоянных издержек обладала свой-
ствами:
и2(/2)=>;,
У,1(у\)=с, Щу2)=с.
8.4.6. Сопоставим между собой обе системы оптимальных конт-
рактов: систему (ур f j), (у2, /2) и систему (у*р ф, (у2, /2).
Для потребителя С2 имеем 1^(у2) = С и У^(у2) = С, т.е. потреби-
тель С2 получит одно и то же количество продукцииу2 =у2. Однако
размер платежа i2 за это количество продукцию у потребителя С2
меньше, чем в случае идеальной дискриминации, ибо t2 = К2(у2) > /2,
И2(у2) = /2(у2=у2).
Рассмотрим геометрическую интерпретацию этого положе-
ния. Размер платы t2 потребителя С2 в условиях идеальной цено-
вой дискриминации равен
У1
J V'(y)dy = К2(у2) - К2(0) = К2(у2) = г;,
о
что геометрически (в случае постоянных предельных издержек
С(у) (С'(у) = С, где С — скалярная постоянная)) интерпретируется
как площадь |аиРиуи5иеит|ит|2 множеств а, Р, у, 5, е, т| и т
(т]=П1^П2)(Рис. 821).
Размер оплаты i2 потребителя С2 равен (на основании (8.4.11)
и равенства К2(у2) = И2(у2) = /2)
G = к2#2) - (^1) - = 4" (^1) - И(У1))«
где (И2(0) = Kj(O) = 0), разность
»S6;1)-K1(y1)=
о
равна площади |у|2 криволинейного четырехугольника у
(см. рис. 8.21). Следовательно, в условиях пакетной дискримина-
ции потребитель С2 платит на величину | у |2 меньше, чем в услови-
ях идеальной ценовой дискриминации.
18-7620
273
Из неравенства У[(Уу) > С и равенства ^(у*) = С следует, что
у* > ур т.е. в случае идеальной ценовой дискриминации потреби-
тель С] получает больше, чем в случае пакетной дискриминации.
Равенство Pj'CPj) = означает, что потребитель С( оплачивает ко-
личество У] в объеме в случае пакетной дискриминации.
Равенство
й
(И1(0) = 0)/, = Г1(у1)= jv'(y)dy = |aup|2
о
означает, что в случае пакетной дискриминации оплата потреби-
теля С{ равна его потребительскому излишку |a и р|2. Равенство
Я
f] = Ki^i) = J = |a и р о ео |2
о
означает, что в случае идеальной ценовой дискриминации оп-
лата потребителя С( равна его потребительскому излишку
|a оР ueui)! |2
Таким образом, при переходе фирмы-монополиста от идеаль-
ной ценовой дискриминации к пакетной оплата потребителя С,
осталась равной его потребительскому излишку, т.е. потребитель
С( ничего не выиграл и не проиграл, хотя объем приобретаемой
им продукции и размер оплаты за нее уменьшились (У| < У*, =
= (aup^lauPueurij|2=ф. Потребитель С2 выиграл, ибо за
274
одинаковый объем приобретаемой им продукции (у2 = у2) он за-
платил меньше (i2 = t*2-1у|2), т.е. получил выигрыш, равный пло-
щади! у |2.
Проигрыш (отрицательная величина) фирмы-монополиста
оказался равным величине -к{ |е|2 - к21у|2, ибо
PR-PR*=PR(yl,y2)-PR(yl; у2)=[*/1 +*?2+M2>J“
. . . . (Ъ=У'2) а . А .
— [^"1^1 +^2“ *"^2^2^ = ~ )+^>2^2 — ~-И )) =
л
I» О
=Ч(|е^П1|2-|П1|2)-^(|аороу|2-|аор|2)=-Л1|е|2-^|у|2.
Чистые потери общественного благосостояния (отрицатель-
ная величина) равны сумме выигрышей всех потребителей С{ и
всех потребителей С2 и проигрыша монополиста, т.е.
-/)£=^|у|2-А:1|е|2-Л2|у|2=-Л1|е|2.
Из равенства (8.4.13) следует, что
k^yJ-C'tk^ +к2у2)) = МВД)- Ш)),
откуда получаем в случае постоянных предельных издержек
С'(кхух + к2У2У = С следующее равенство:
ед)-ед> = кх
Vx\yx)-C к2’
которое геометрически интерпретируется так: длина отрезка вер-
тикальной прямой у, =ур расположенного между линиями V^(y) и
Vx(y) (см. рис. 8.21), относится к длине отрезка вертикальной пря-
мой между линией V[(y) и линией постоянных предельных издер-
жек как кх к к2.
В модели пакетной дискриминации в отличие от модели иде-
альной (совершенной) ценовой дискриминации предполагается,
что фирма-монополист не может определить тип потребителя. Бы-
ло показано, что для потребителя С2 «чужой» пакет (у*р ф лучше,
275
18’
чем «свой» пакет (у*2, t*2); для потребителя Сх «свой» пакет (у,, ф
лучше, чем «чужой» пакет. Поэтому потребителю С2 выгоднее
стать потребителем Ср что содержательно означает, что более «ка-
чественный» покупатель С2 уходит с рынка, чтобы прийти на ры-
нок менее «качественным» покупателем Сх.
Докажем, что с уходом с рынка относительно более качествен-
ного потребителя С2 и заменой его относительно менее качествен-
ным потребителем Сх прибыль фирмы-монополиста понижается.
Доказательство проводится для случая постоянных предельных
издержек.
Выше была выписана максимальная прибыль PR* фирмы-мо-
нополиста в случае идеальной (совершенной) ценовой дискрими-
нации.
Имеем
(/;=^(л))
PR* = kxt*x + k2t*2 - С(кху*х + к2у*2) =
(С =с)
= Wy^+k^ty^-c^y*-ск2у2 =
= кх (Vx (у* )-су*) + к2 (И, (у*2) - су*2).
Если потребитель С2 поведет себя как потребитель Сх, он выбе-
рет контракт (ур ф, то максимальная прибыль фирмы-монопо-
листа получится равной
. .
PR = kxtx+k2tx-C(kxtx+k2tx)
= ki (yf) - cy*i) + k2 (/) - cy* )•
Сопоставим между собой слагаемые k2(V2(y*^ - cy*J и
Имеем (см. рис. 8.21)
И2(у2)-<у2 = J>7(y)rfy-cy* = j(V2(y)-c+c)dy-cy2 =
О о
Уг У2 Уг
= J О-У) - c)dy +jcdy- су* = J (И2'(у) - c)dy = |р о у о е о б|2.
о оо
276
Имеем (см. рис. 8.21)
я е X X
= j(yi<y)-c)dy+ jcdy-су* =
ООО
X
= J(Kl'(y)-c)rfy = |pue|2.
О
Очевидно, |риуиео§|2 >|рие|2, откуда вытекает, что
т.е. PR* > PR**.
Пример 8.4.2. иллюстрирует случай пакетной дискриминации.
Пусть функции полезности потребителя Cz, i = 1, 2, имеет вид
Ц(у., zz) = Vjiy) + zr Для потребителей Ц и С2 их функции полез-
ности соответственно равны Vl(yl) = Jy^, V2(y2) = 2^j^; функция
издержек фирмы-монополиста имеет вид С(у) = С-у. Число потре-
бителей типа С, равно kv число потребителей типа С2 равно к2.
Тогда функция прибыли фирмы-монополиста имеет вид
(см. (8.4.12))
0^2 ~2Jyi+4>\У)-+ кгУ2) <тах)-
Выпишем для этой функции условия первого порядка (т.е. част-
ные производные поу] иу2 приравняем нулю):
к. к? „ кэ
—т=-----г= -Ckt= 0, —i= = Ct2.
Пусть к} > к2, тогда
- (к\~к2^ - 1
=К*(^) = ^С’’ ?2 =К2^2)-К2^1) + К1<Л) = ^^
Если кх = 2к2, то
. 1 а 1 ; 1 ; 7
У' 16С2’ У2 С2’ 1 4С 2 4С
277
Максимальная прибыль PR = PR(yx, y2) фирмы-монополиста
в случае применения ею пакетной дискриминации равна (следует
ч Л ( ^2 Л 1 \
выполнить прямой счет при у{ = —1—* и у( = —у)
2
PR = +к2 (2^/Jj - - Сук^ - С2к2у2 = х * .
*TVz/V|
Выигрыш (положительная величина) потребителя С2 при пе-
реходе от идеальной ценовой дискриминации к пакетной равен
4-4=>- и>=27л -Д’ = Д =
выигрыш (положительная величина) потребителей С2 равен
Л2 (/2 - i2) = к2 (К2 (у,) - К, (^)) = Х 2Скх 2
Проигрыш (отрицательная величина) фирмы-монополиста при
переходе от идеальной ценовой дискриминации к пакетной равен
РР-РР‘=-Л1(Г;(у1)-^(у1))-Л2(И2(у1)-^(у1))-Л1С(у1-у;) =
_ к2(к2-2кх)
АСк^
ибо кх > к2 по предположению.
Максимальная прибыль PR* фирмы-монополиста в условиях
идеальной ценовой дискриминации равна
PR* = PR — ~2^i) _ (^i _ ^2(^2 ~2^i)
4ОЦ 4ОЦ 4Скх
Чистые потери общественного благосостояния (отрицатель-
ная величина) при переходе от идеальной к пакетной дискрими-
( . 1 "I
нации равны! У] ~^2"1
пт , <* п» nn* 2ЛА-2Л,2 Л2-2^Л к*
-DL = kj(tj-t2)+PR-PR = 1 2 —L+ ? —1 ? = -•-*--•
22 2 4Ck} 4Ckx 4ОЦ
При (Л(/Л2) —> О
5>1^4^ = У1*’ ~DL^°-
278
ЗАЛ. Переходим к рассмотрению варианта дискриминации вто-
рого рода, который называется двухкомпонентным тарифом, т.е. к
случаю, когда размер оплаты Ry) потребителем продукции фирмы-
монополиста в объеме, равному единиц, равен сумме 1(у) =А+ру,
где А > 0 — фиксированный размер оплаты за право приобретения
любого положительного количества у продукции и ру — размер
оплаты, пропорциональной количеству у приобретаемой продук-
ции по цене р за одну единицу продукции. Таким образом, двух-
компонентный тариф Ry) — это такая функция, что
t(y)JA + Py, у>0
ш [0, у = 0
Напомним, что параметры Аир называются характеристика-
ми двухкомпонентного тарифа. Фирма-монополист заинтересо-
вана в определении характеристик оптимального двухкомпонент-
ного тарифа.
Известно, что оптимальная величина спроса потребителя С.,
определяется из условия первого порядка У'(у) = р, тог-
да функция РС'(у) = р представляет собой обратную функцию спро-
са потребителя Срi = 1,..., к.
Далее, как и раньше, рассматривается случай двух типов по-
требителей, Cj и С2, число потребителей С{ равно число потре-
бителей С2 равно к2. Для любого у > 0 V[(y) < V2(y) и И, (у) < К2(у)
функции К,(у) и V2(y) полезности гладкие, выпуклые вверх, функ-
ция С(у) издержек гладкая и выпуклая вниз.
Обозначим символом Dx(p) = yt функцию спроса потреби-
теля С(, символом D2(p) = у2 — функцию спроса потребителя С2,
тогда функция совокупного спроса на продукцию, выпускаемую
фирмой-монополистом, имеет вид
Z>i(p) = kxDx(p) + k2D2(p).
Условия участия потребителей и С2, очевидно, имеют вид
К,(Р,(р)) - A-pD^fp) > 0, У2Щр)) - A-pD2(p) > 0.
Далее предполагается, что каждый из потребителей С, и С2 при-
обретает положительное количество продукции, т.е. у, = D{(p) > 0,
у2 = D2(p) > 0, т.е. имеет место случай внутреннего решения.
Задача максимизации прибыли PR фирмы-монополиста при
условии участия обоих потребителей Ct и С2 имеет вид
PR(yx, у2) = к^А +РУ') + к2(А +ру2) - С(к\У} + ку2) (max)
V^J-A-py^O, V2(y2)-A-py2*0.
279
Напомним, что А +рух = А + ру2 = /2(у2).
В точке (рр р2) максимума прибыли PR(yx, р2) по крайней мере
одно из условий участия должно выполняться как равенство.
В противном случае фирма-монополист сможет увеличить свою
прибыль, увеличив параметр А.
Покажем, что в точке (р,, р2) максимума прибыли фирмы-мо-
нополиста
^](Pi)-^-ppi = O.
Пусть это не так, т.е.
Vx(yx)-A-pyx>Q и И>(р2)-Л-/>р2 = 0.
Потребитель С2 выбрал продукцию в количестве у2, а не в ко-
личестве ух, поэтому
v2(yx) - А-ру х< V2(y2) - А-ру2 (= 0).
Приведенную цепочку можно проложить влево на основании
неравенства И2(у) > Vx(y), т.е.
^(у,) - А - рух < Г2(р2) - А - ру2 = 0,
откуда следует, что для потребителя Сх не выполнено условие
участия. На основании полученного противоречия следует напи-
сать, что
И2(р2)-Л-др2>0 и Ух(ух)-А-рух = 0.
Тогда естественно, что при фиксированной цене р фирме-мо-
нополисту выгодно выбрать значение параметра А(р) так, чтобы
A(p) = ^x(Dx(p))-pDx(p).
Тогда выражение
РР(У}, У2) = */10'1) + *2/г0'2> ~ + *2>9 =
= кх(А +рух) + к2(А +ру2) - С(кхух + кр2)
для прибыли фирмы-монополиста в качестве функции цены р
следует переписать так:
PR(p) = кх(А(р) +pDx(p)) + к2(А(р) +pD2(p)) -
-C(kxDx(p) + k2D2(p)) =
= кх Vx(Dx(p)) + к2[ Vx(Dx(p)) -pDx(p)] + k2pD2(p)
- C(kxDx(p) + k2D2(p)) = (8.4.16)
= (fc, + k2)(Vx(J)x(p)) - kxpDx(p) - k2pDx(p) +
kxpDx(p) + k2pD2(p) - C(kxDx(p) + k2D2(p)) =
= (kx + k^V^ip) -pDx(p)) +pD(p) - C(D(p)) =
= (kx + k2)(Vx(Dx(p)-pDx(p)) + = (kx + k2)A(p) + PR0(p),
280
где выражение Р/?0(р) = pD(p) - C(D(p)) есть прибыль фирмы-мо-
нополиста, которая не применяет ценовую дискриминацию.
Имеем
+ Л2)[(К1'(Р1(р))-р)/)1'(р)-Л1(р)] + ^^ =
= -(^i + )/>! (р) + —
где последнее равенство имеет место на основании того, что
К[(Л(р)) = р\ это последнее равенство (точнее, тождество по р)
справедливо, ибо ^'(у,) = р есть обратная функция спроса потре-
бителя С(.
Обозначим символом р решение задачи максимизации при-
были PR(p) фирмы-монополиста (см. (8.4.16))
PR(p) (max).
Если р > 0, то необходимо выполнение неравенства (случай
краевого экстремума)
dp i l i jp
Если p > 0, то необходимо выполнение равенства (случай
внутреннего экстремума)
^> = -(МВД®+^ = о,
dp 1 z 1 ф
откуда вытекает, что
^^р^ =^ki+k2 > А > °’
ибо выше было принято, что оба потребителя Сг и С2 обязательно
приобретают продукцию фирмы-монополиста.
„ dPRJp) п
Из неравенства —-— > 0 следует, что в точке р = р функция
</р
PRq(p) строго возрастает, поэтомур0 — точка ее максимума—долж-
на быть строго больше, чем р, т.е. р <р°.
В связи с тем что функция D(p) спроса убывает, wsp<pQ следу-
ет, что 2)(р) > Z)(p0), т.е. при использовании двухкомпонентного
тарифа фирма-монополист выпускает продукции больше, чем в
случае отсутствия ценовой дискриминации.
281
Перепишем первое и последнее звенья цепочки (8.4.16) при
р = р «р =р°, полагая Pi(Z>,(p) -pDx(p)) = А(р):
PR = PR(p) = (Л, + k2)A(p) + PR^p),
PR0 = PR(p0) = (kx + k2) A(p°) + PR^p0).
В обоих случаях справедливы неравенства PR(p) > PR^p) и
PR(p°) > PR0(p°), откуда следует, что при любом выборе цены из
двух вариантов р и р° максимальная прибыль PR = PR(p) фирмы-
монополиста в условиях двухкомпонентного тарифа строго боль-
ше максимальной прибыли PR0 = PR(p°) при линейном (т.е. без
ценовой дискриминации) ценообразовании.
Таким образом,
рад=рл>р^(Ро).
Принимая во внимание выражения (при р > 0)
D(p) = kxDx(p) + k2D2(p),
= (Л, + к2 Щ (р), = D(p) + (Р - C'(D(p))D'(p)),
dp z dp
получаем
kxDx(p) + k2D2(p) + (р - C'(D(p))D'(p)) = kxDx(p) + k2Dx(p),
откуда вытекает равенство
к2Щр) - Dx(p)) + [?- C\D{p))]D'(p) = 0, (8.4.17)
в котором левое слагаемое D2(p) - Dx(p) положительно, поэтому
правое слагаемое отрицательно.
В связи с тем что функция спроса D(p) с ростом р строго
убывает, имеем неравенство 1У(р) < 0, откуда следует, что
р - С(Р(р)) > 0, т.е.
p>C(D(p)). (8.4.18)
Прежде чем комментировать неравенство (8.4.18), докажем, что
D2(p) > Dx(p)(cm. выше). Имеем у, =ух(р) = Dx(p), у2=у2(р)=D2(p),
откуда для обратных функций спроса вытекает, что ^'(7 () = Р -
= > > ^((у) РАЯ любого у > 0). В связи с тем
что предельная полезность Vx(y) (строго) убывает, из неравенства
*7(У1) > ^(Я2) следует, что у2 > ух, т.е. D2(p) > Dx(p).
282
Возвращаемся к неравенству (8.4.18), которое показывает, что
цена р выпускаемой фирмой-монополистом продукции строго
выше предельных издержек C'(D(p)), поэтому фирма-монополист
производит меньший объем продукции у = к1у1 + к2у2, чем объем
продукции у оптимальный с общественной точки зрения, кото-
рый должен удовлетворять условию D(C'(D(y)))=у.
Пример 8.4.3 (продолжение примера 8.4.2)
Пример иллюстрирует двухкомпонентный тариф и пакетную
ценовую дискриминацию. Пусть, как и в предыдущем примере,
функции полезности потребителей С\ и С2 соответственно имеют
вид Ul(yl,zl)= +zlnu2(y2,z2) = ъ/ъ + г2’ функция издержек
линейна С(у) = Су. Обратные функции спроса потребителей Ci и
С2 имеют вид
^'(у,) = -4= = Р, У{(у2) = -4= = р,
2У/У1 \1У2
откуда получаем представление функций спроса потребителей Cj
иС2
= Щр) = -L, у2 = D2(p) = 4» (8.4.19)
4/ р*
а тогда
к +4£
D(p) = kj\ (р)+k2D2(p) = -J—
4/
„ к +4к,
и D'(p) = - 1 3 2. (8.4.20)
2р
Подставив (выражения (8.4.19) и (8.4.20) при р-ръ (8.4.17),
получим
-(р-С)
к\ +4A^
2(Р)3
= 0,
откуда следует, что
2(^+4^)
2кх + 5Л2
С>С.
283
Параметр А=А(р) равен
^(?) = ^1(2>1(Р))-РД(?) = ^.
4р
В случае фирмы-монополиста, которая не использует цено-
вую дискриминацию, условие первого порядка задачи максими-
зации прибыли
РЛ0(р)=рВД-С2)(р)
имеет вид
D(p) + (p-C)D'(p) = 0,
откуда получаем (используя уравнение 8.4.20)
Л.+4Л, z „Л.+4Л, Л
-ТТ^"(/”С)“Тз =0’
4р 2р3
которое имеет решение р° = 2С> р. Неравенство 2С> р проверяет-
ся непосредственно.
Максимальная прибыль PR? фирмы-монополиста, которая не
использует ценовую дискриминацию, равна
PR0 = PR°(p°) = (р0 - C)D(p0) = C-L—L = -L^i
Максимальная прибыль PR фирмы-монополиста, который
использует двухкомпонентный тариф, равна (см. (8.4.16))
PR = PR(p) = ^(Atpy + pD^ + k^Aipy + pD^p))-
-С(кгЦ(р)-к2О2(р)) =
.fl -11,(1 - 1 1 Л *1 кг 1
V4/’ 4(р)2; \4р (р)2) \4(р)2 (р) )
_ р(2к} + 5к2) - С(кх + 2к2) _ (2^ + 5Л2 )2
4(р)2 ” 16(Л, +4к2)С'
Непосредственно проверяется, что
(Ik^Sk^
4ОЦ 16(^+4^2)C
= PR = PR(p) > = PR* = PR(p*\
1OC
284
где PR — максимальная прибыль фирмы-монополиста в случае
применения ею пакетной дискриминации (см. пример 8.4.2).
Чистые потери общественного благосостояния (отрицатель-
ная величина) при переходе фирмы-монополиста от идеальной
ценовой дискриминации к двухкомпонентному тарифу равны
Л,
-DL = jDtf) + 2*2 7Z)2(p) - CD(p) -
- кх 7Д(С) - 2k^D2(C) + CD(C) =
=, pz+2. d;_cV^_
W)2 W 4(p)2
П~ 2/, Г*~|ГАГ1+4^_ ~9k2
V4C2 2Vc2 4C2 16C(kt+4k2)'
Можно показать, что и в общем случае имеет место нера-
венство
PR = PR(p)> PR(p) = 'PR,
т.е. максимальная прибыль фирмы-монополиста, которая исполь-
зует пакетную дискриминацию, строго больше максимальной при-
были фирмы-монополиста в случае двухкомпонентного тарифа.
8.4.8. При использовании фирмой-монополистом ценовой дис-
криминации третьего рода потребители продукции фирмы разде-
ляются на два (или более) рыночных сегмента. На каждом сегмен-
те существует своя линия спроса, своя монопольная цена и свой
монопольный объем продаж. Рыночные сегменты выбираются
монополистом так, чтобы потребитель, который приобрел про-
дукцию по более низкой цене на одном сегменте, не мог бы ее
реализовать по более высокой цене, но меньше той, которая име-
ет место на другом сегменте.
Так, например, авиакомпания, которая является монополис-
том на определенном направлении пассажирских авиаперевозок,
может сравнительно дешево и заранее продавать авиабилеты пен-
сионерам (по предъявлении пенсионного удостоверения) и ту-
ристам (по предъявлении турпутевок) и назначать достаточно
высокую цену на авиабилеты деловым людям (которые часто при-
обретают билеты по принципу «продайте прямо сейчас и как мож-
но быстрее»). Все авиабилеты именные и поэтому не могут быть
реализованы, что называется, «с рук».
285
Другие примеры ценовой дискриминации третьего рода: цены
на билеты в кинотеатры, театры, в городском транспорте для сту-
дентов, пенсионеров, военнослужащих, сотрудников отдельных
министерств; гостиничные тарифы для граждан России и ино-
странных граждан, плата за обучение в вузах России для россиян
и иностранных граждан и т.п.
Случай, когда фирма-монополист не использует ценовую дис-
криминацию, был проанализирован в параграфе 8.1. Переходим к
анализу случая, когда фирма-монополист реализует свою продук-
цию в двух сегментах. Случай любого конечного числа к сегмен-
тов анализируется аналогично и поэтому здесь подробно не рас-
сматривается.
В каждом сегменте рынка фирмы-монополиста имеет место
своя линия спроса. Фирма-монополист в каждом сегменте выби-
рает объем продажу^ иу^т) (соответственно монопольные цены
/?|т) и р^т)) так, чтобы общая прибыль PR фирмы была наиболь-
шей.
Для общей прибыли PR монополии имеем следующее пред-
ставление:
PR = R-C,
где R(y) = Rl(yl) + R2(y2) = + py2 (у = у, + у2) - доход фирмы-
монополиста, который равен сумме дохода Rv = plyl фирмы в пер-
вом сегменте и дохода R2 = ру2 во втором сегменте. Издержки С(у)
фирмы-монополиста равны С(у) = С(у, +у2).
Для максимизации прибыли фирмы-монополиста, которая
использует ценовую дискриминацию (третьего рода), выпишем
условия первого порядка:
3PRJR дС _dR ЭС(у) ду =d(Rl(yl)+R2(y2))
ЭУ1 Эу, Эу] Эу Эу, dy{
= MRl(yl)-MC(y), (8.4.21)
dPR^dR dC dR дС(у) dy _d(Rl(yl)+R2(y2))
Эу2 Эу2 ду2 Эу2 Эу Эу2 dy2
= MR2(y2)-MC(y). (8.4.22)
Напомним, что dRl(yi)/dyl = MR^), dR2(y2)/dy2 = MR2(y2),
dC(y)/dy = MC(y). Из (8.4.21) и (8.4.22) следует
MRftJ = МС(у) = MR2(y2).
286
Отметим, что в случае, когда число к сегментов фирмы-моно-
полиста конечно и больше двух, т.е. в случае, когда у=ух +... + ук,
R(y) - + ••• + =/>1?! + ... +РкУк, С(у) = С(ух + ... +ук),
справедлива аналогичная цепочка равенств MRx(yx) -... = MRk(y^=
= МС(у).
Если предельные издержки МС(у) фирмы-монополиста по-
стоянны, МС(у) = МС*, то равенства (8.4.21) и (8.4.22) соответ-
ственно приобретают вид
MRx(yx) = МС(у) = МС*, (8.4.23)
MRJy^MCly^MC*. (8.4.24)
Из (8.4.23) получаем объем выпуска фирмы-монополиста
в первом сегменте, из (8.4.24) — объем выпуска у^ фирмы-моно-
полиста во втором сегменте. Объем у^ максимизирует прибыль
PRx(y^ фирмы-монополиста в первом сегменте, объем у^ макси-
мизирует прибыль PR2(yJ фирмы-монополиста во втором сег-
менте. С помощью функций ARX и спроса первого и второго
сегментов рынка фирмы-монополиста определяем монопольные
цены и в первом и во втором сегментах соответственно
(рис. 8.22, который также наглядно интерпретирует равенства
(8.4.23) и (8.4.24)).
Рис. 8.22
287
Полагая в известном равенстве AfR(y) = p 1 + — сначала
\ А/)
У = Р - р{т\ а затем у = у^т\ р = р2т\ получим для первого и
второго сегментов представления для предельного дохода:
МЩ (у<м)) = р<т) 11 + -J- L (8.4.25)
к Ed\)
(8.4.26)
(8.4.27)
м^у^р^ 1+4-
\ Edl)
(Edl и Ел — эластичности спроса по ценам и р^ первого и
второго сегментов на продукцию фирмы-монополиста). Поделив
равенство (8.4.25) на равенство (8.4.26) и принимая во внимание
равенство MR{(y^m)) = Л/Я2(у|'”)) (см. равенства 8.4.23) и (8.4.24)),
получим важное соотношение для цен р\т} ир2т^
4*1. 1 + 1/£д
1 + 1/V
которое показывает, что более высокая цена фирмой-монополистом
назначается в том сегменте рынка, в котором спрос менее эластичен
(см. рис. 8.22, на котором линия спроса AR- менее эластична, чем
линия спросаЯЛр и, следовательно, ценар2 выше цены р^).
Рассмотрим случай, когда предельные издержки МС(у) не яв-
ляются постоянными, т.е. случай, когда в цепочках (8.4.23) и
(8.4.24) последние звенья МС* отсутствуют. Здесь уже необходимо
определить, чему должны быть равны предельные издержки и,
следовательно, общий объем у=у(т) выпуска фирмы-монополис-
та, максимизирующий ее прибыль.
Для того чтобы определить этот объем, следует для прибыли
dPR
PR(y) = R(y) - С(у) выписать условие первого порядка 0 = —— =
^dy^ ~ МЖУ) ~ МС(у) (отметим, что MR(y) = ^ =
dy dyy dy dy2 dy 11 2
откуда получаем требуемый общий объем у =у(т) выпуска фи ты-
монополиста (MR(y) = МС(у)). Для определения объема у = j
строго говоря, условие первого порядка следует дополнить услови >м
288
второго порядка или проанализировать ситуацию с переменой зна-
ка у предельной прибыли MPR(y) = MR(y) - МС(у) в точке у =у(т\
Для определения объема у^ выпуска фирмы-монополиста,
который максимизирует прибыль фирмы-монополиста в первом
сегменте, следует относительно решить уравнение
MRx(y{) = MC(y).
Аналогично в случае второго сегмента следует относительно у2
решить уравнение
Л/А2(у2) = Л/С(у).
Таким образом, в случае переменных предельных издержек
МС(у) следует в правых частях (8.4.23) и (8.4.24) вместо МС* поста-
вить МС(у).
С помощью функций спроса AR{ и первого и второго сег-
ментов определяем монопольные цены и р^ в первом и во
втором сегментах соответственно (рис. 8.23, на котором ломаная
BGNесть сумма по горизонтали линий MRX и Л/А2, точка Е пересе-
чения линий МС(у) и MR(y) (ломаной BGN), объем у = + у2т),
точки Ех и Е2 есть точки пересечения горизонтальной линии МС(у)
(т.е. линии EF) с линиями MRX и Л//?2 соответственно).
19 - 7620
289
Отметим, что и — абсциссы точек £j и Е2 соответствен-
но, а не точек Е} и Е2, в которых линия МС(у) пересекает линии
MRl и MRr
Как и в случае МС(у) = МС*, используя равенства (8.4.25) и
(8.4.26), получаем соотношение (8.4.27) для ценир^т\
Приведем пример, когда монополия при высоких предельных
издержках МС не использует ценовую дискриминацию, хотя в
принципе могла бы это сделать (рис. 8.24, на котором линии MR}
и МС не имеют общих точек, т.е. монополии невыгодно продавать
свою продукцию в первом сегменте по низкой цене).
Рис. 8.24
Замечание 8.4.2
Прежде чем переходить к примеру, иллюстрирующему ситуа-
цию с использованием фирмой-монополистом ценовой дискри-
минации третьего рода, отметим, что не существует четкой грани-
цы между понятиями ценовой дискриминации второго и третьего
рода, как не существует четкой границы между понятиями цено-
вой дискриминации первого и второго рода (см. приведенное
выше замечание 8.4.1).
Само понятие ценовой дискриминации на сегодняшний день
является недостаточно разработанным, на что обращают внима-
ние отдельные авторы (см., например, В.М. Гальперин, С.М. Иг-
натьев, В.И. Моргунов (1997). Микроэкономика. Т. 2. С. 112).
290
Рассмотрим иллюстративный пример.
Фирма-монополист имеет два сегмента рынка, в каждом из ко-
торых функция, обратная функции спроса, имеет вид AR{ = 18 - у,
иЛ/?2 = 24-2у2 (сами функции спроса имеют вид yf = 18-p и
у2 = 12 -р/2, предельные издержки МС постоянные и равны МС= 8).
Решим задачу максимизации прибыли фирмы-монополиста в
условиях ценовой дискриминации третьего рода и в случае от-
сутствия ценовой дискриминации третьего рода.
1. Сначала решим задачу максимизации прибыли фирмы в
первом сегменте рынка. Поскольку ARX = 18 - ур постольку =
= 18у, -у?, откуда MR. =^-=18-2у..
Из уравнения MRt = МС следует, что 18 - 2yt = 8, т.е. у{т) = 5,
р™ = 18 - y<m) = 18 - 5 = 13 и PR™ = (р™ - МС) у™ = (13 - 8) • 5 =
= 5 • 5 = 25 = |2 ^Нр^РД |2 — площадь прямоугольника
Hp^Ffii (рис. 8.25).
Рис. 8.25
19*
291
2. Решим задачу максимизации прибыли монополии во втором
сегменте рынка. Поскольку AR2 = 24 - 2у2, постольку MR^ = 24 - 4у2.
Из уравнения Л/Л2 = МС следует, что 24 - 1у2 = 8, т.е. у^ = 4,
/><т) = 24-2-4= 16 и PP<M) = (p<m)-JHQy<m) = (16-8)-4 = 8-4 =
= |Я/><т)Р2£212 (см. рис. 8.25).
3. Суммарная максимальная прибыль РР^ фирмы-монопо-
листа равна РР<т) = PR(^ + PR^ = 25 + 32 = 57.
4. Найдем максимальную прибыль фирмы-монополиста в слу-
чае отсутствия ценовой дискриминации третьего рода. Для этого
сначала построим линию AR (линию QGN, G = (3; 18)) среднего до-
хода фирмы-монополиста путем суммирования по горизонтали
линий ARX и AR2 (рис. 8.26). Аналитически линия AR описывается
следующими уравнениями, разрешенными относительно/»:
У=12—у (18</»<24), у=30-|р (0<р<18),
и относительно у:
2
р = 24-2у (0<у£3), р=20-|у (3</><30).
292
Линия MR (QF.F-V) описывается следующими уравнениями,
4
разрешенными относительно у: р = 24 - 4у (0 < у < 3), р=20-—у
(3<у£15). Точки Q, Fp F2 и V имеют координаты £?= (0; 24),
Fx = (3; 12), F2 = (3; 16), И= (15; 0). При 0 <у < Зр > 12, поэтому при
0 <у < 3 линии MR и МС- 8 не пересекаются, при 3 <у < 30 име-
ем MC=MR, т.е. 8=20—jу, откуда у(|я) = 9, а р(от) = 20—|у(т) =
=20-~9=14, следовательно, точка £= (9; 8), точка F- (9; 14).
Осталось найти PF^m) = (р(т) - МС))№ = (14 - 8) -9 = 6-9 = 54 =
=|Яр(т)Г£|2(см. рис. 8.26).
Отметим, чтоу}от) +у*'") = 5+4 = 9=у(л,), р(^= 13< 14=р(и,)< 16 =
=р^ и +PR^ = 25 + 32 = 57 > 54=Р1&"\ т.е. сумма площадей
|Hp\m}F{E{ |2 и ^Hp^F2E212 прямоугольников Hp\m)FlEi и Hp^m)F2E2
(см. рис. 8.25) больше площади |£5>(m)F£|2 прямоугольника
Hp^FE. (см. рис. 8.26). В рассматриваемом примере фирме-мо-
нополисту выгодно проводить ценовую дискриминацию третьего
рода, ибо суммарная максимальная прибыль PR(^ + PR^ фирмы
строго больше максимальной прибыли PRM фирмы при отсут-
ствии ценовой дискриминации третьего рода.
8.5. Максимизация прибыли в краткосрочном
и долговременном промежутках для фирмы,
функционирующей в условиях монополистической
конкуренции
8.5.1. Характеристики модели рынка монополистической конку-
ренции подробно анализируются во вводном и промежуточных
курсах микроэкономики. На рынке монополистической конку-
ренции много продавцов и покупателей (но не так много, как в
случае чистой конкуренции), достаточно свободный вход на ры-
нок и уход с него, имеет место совершенная информированность
покупателей и продавцов и, что весьма существенно, продукция
фирм дифференцирована (однако все продукты мало отличаются
Друг от друга по качеству (являются близкими субститутами)),
а также активно используется ценовая конкуренция. Существует
293
достаточно много фрагментов экономической реальности, для
описания которых модель рынка монополистической конкурен-
ции достаточно адекватна (напомним, что для моделей чистой
конкуренции и чистой монополии это не так): рынки предметов
потребления (одежды, обуви, мебели, косметики, моющих
средств), материальных услуг (парикмахерские, бани и т.д.), обра-
зовательных услуг и т.п.
Отдельная фирма в условиях монополистической конкуренции
может функционировать, когда другие фирмы своего поведения не
меняют и когда другие фирмы также меняют свое поведение.
Если фирма снижает цену на свою продукцию, а другие фир-
мы этого не делают, то фирма может значительно увеличить число
своих покупателей (рис. 8.27, на котором показано, что при сни-
жении фирмой цены ср0 до/>] объем выпускаемой (и реализуемой)
ею продукции вырастет с у0 до у j, если другие фирмы своего пове-
дения не меняют). Если другие фирмы вслед за нашей фирмой
также снижают свою цену, то число покупателей у рассматрива-
емой фирмы увеличивается, но незначительно (см. рис. 8.27, на
котором показано, что при снижении фирмой цены с р0 до объ-
ем выпускаемой (и реализуемой) ею продукции вырастет с у0 до у,,
если другие фирмы последуют ее примеру).
294
Если фирма повысит цену с р0 до р2, то реакция на это потре-
бителей также будет неоднозначной и будет зависеть от поведе-
ния других фирм. Если другие фирмы повышать свои цены не
будут, фирма потеряет много покупателей (у2 значительно мень-
ше у0); если другие фирмы также повысят свои цены, то фирма
потеряет немного своих покупателей (у2 меньше у0, но больше у2)
(см. рис. 8.27).
Отсюда следует важный содержательный вывод. Фирма, функ-
ционирующая в условиях монополистической конкуренции,
имеет две линии спроса на свою продукцию: линию dd (более
эластичную, т.е. более пологую) и линию DD (менее эластичную,
т.е. менее пологую) (см. рис. 8.27).
Отметим, что линии dd и DD пересекаются в точке Fo с коорди-
натами у0 (объем текущего выпуска) и р0 (значение текущей цены
фирмы, функционирующей в условиях монополистической кон-
куренции (см. рис. 8.27)).
8.5.2. Рассмотрим задачу максимизации прибыли фирмы, функ-
ционирующей в условиях монополистической конкуренции в
случае краткосрочного промежутка.
При текущей ценер0 фирма предлагает на рынке свою продук-
цию в объеме у0, который не максимизирует прибыль (рис. 8.28,
на котором изображены точка F^ пересечения линий dxdx и DD,
линия предельного дохода MRdx, соответствующая линии dxdx
спроса на продукцию фирмы, а также линия предельных издер-
жек фирмы). Точка пересечения линий МС и MRdx Ех определяет
объем выпуска фирмы ух, который максимизирует ее прибыль
при условии, что другие фирмы не меняют своего поведения.
При этом условии ценарх есть ордината точки Fx пересечения ли-
нии dxdx и вертикальной линииу=уР Новая ценарх ниже ценыр0,
т.е. ради максимизации своей прибыли фирма снижает цену с р0
дорг Если другие фирмы еще не максимизируют свои прибыли,
они также захотят снизить свои цены. В таком случае при цене рх
рассматриваемая фирма обеспечит свой выпуск не в объеме ур
а в меньшем объеме у р который равен абсциссе точки /[пересече-
ния линии цены р = рх и линии DD. Следовательно, при цене рх
рассматриваемая фирма при объеме выпуска у, уже свою прибыль
не максимизирует.
Переход из точки Fx в точку F[ означает, что линия спроса dxdx на
продукцию рассматриваемой фирмы переходит в положение d2d2,
295
ибо линия спроса должна содержать точку F'. Далее рассуждение
проводятся аналогично. На рис. 8.28 показана новая линия MRd2
предельного дохода, которая соответствует линии спроса d2d2.
Точка пересечения Е2 линий МС и MRd2 определяет объем у2 вы-
пуска фирмы, который максимизирует ее прибыль при условии,
что другие фирмы своего поведения не меняют, т.е. цены не сни-
жают. Цена р2, которую назначает рассматриваемая фирма, равна
ординате точки F2 пересечения линии спроса d2d2 и вертикальной
линии, проходящей через точку у = у2 на оси абсцисс. Цена р2
меньше ценырх, поэтому другие фирмы, которые еще не получи-
ли максимальной прибыли, также могут снизить свои цены. В этом
(как и предыдущем) случае при цене р2 рассматриваемая фирма
обеспечит свой выпуск не в объеме у2, а в меньшем объеме у2
(см. рис. 8.28), который равен абсциссе точки F2 пересечения ли-
нии цены р =р2 и линии DD. Таким образом, при цене р =р2 рас-
сматриваемая фирма при объеме у2 уже не будет максимизировать
свою прибыль. Переход из точки F2 в точку F2 означает, что линия
спроса d2d2 на продукцию рассматриваемой фирмы спускается
296
ниже в положение J3</3, линия спроса должна проходить через
точку Fj (см. рис. 8.28) и т.д. Мы видим, что точки ур у2 и т.д. дви-
жутся по оси Оу справа налево, а точки ур движутся по оси
слева направо. Процесс сходится к точке у (рис. 8.29), которая
есть абсцисса точек Е* (точки пересечения линий МС и MRd*) и F*
(точки пересечения линий DD и d*d*). Линия d*d* — предельная
для линий dxdx, d2d2 (см. рис. 8.28) и т.д. В рассматриваемом слу-
чае F'* = X, и поэтому у фирмы нет заинтересованности изменить
цену р*.
Рис. 8.29
Максимальная прибыль рассматриваемой фирмы в случае р=р*
иу = у может быть положительной, нулевой и отрицательной в
зависимости от того, где проходит линия АС(у) средних издержек.
Если АС(у') > р*, то PR(y*) < 0, если АС(у*) = р*, то PR(y*) = 0, если
АС(у) <р‘, то PR(y*) > 0.
8.5.3. Рассмотрим задачу максимизации прибыли фирмы, функ-
ционирующей в условиях монополистической конкуренции в
случае долговременного промежутка.
В связи с тем что барьеры на вход отрасли, функционирующей
в условиях монополистической конкуренции, практически от-
сутствуют, максимальная прибыль PR(y*) средней фирмы в случае
долговременного промежутка должна равняться нулю. В случае
297
положительной прибыли в долговременном промежутке в отрасль
будут приходить новые фирмы, что приведет к последующему
снижению цен на продукты и снижению максимальной прибы-
ли средней фирмы, пока она не станет равной нулю.
Факт нулевой максимальной прибыли средней (типичной)
фирмы, функционирующей в условиях монополистической кон-
куренции в течение долговременного промежутка, проиллюстри-
руем на рис. 8.30.
Линия (1г)АС средней фирмы представляет собой огибающую
линий ее краткосрочных средних издержек (sr)AC (на рис. 8.30
показаны линии (sr)AC} и (sr)AC2). Объем у* выпуска средней
фирмы есть абсцисса точки Е пересечения линий MRd и (1г)МС
(см. также параграф 8.1). Этот объем у* фирма выпускает в теку-
щем периоде, в котором она выбрала (технологический) вариант с
линиями (srjAC^ и (sr)MC{, причем линия (sr)MCl пересекает ли-
нию (1г)МС и линию MRd в точке Е, линия (srjAC^ касается линии
(1г)АС в точке F, абсцисса которой равна./, а ордината — р*. В этом
случае доход фирмы в текущем периоде и ее издержки равны друг
другу и площади |о/Ту* прямоугольника Op*Fy*.
298
8.6. Учет расходов на рекламу в задаче
максимизации прибыли фирмы в условиях
монополистической конкуренции
8.6.1. Реклама может быть эффективным средством стимулиро-
вания спроса на продукцию фирмы, которая функционирует в
условиях монополистической конкуренции, ибо реклама являет-
ся одним из источников информации о результатах стратегичес-
кого поведения фирмы по снижению издержек или/и повышению
уровня дифференциации ее продукции.
Сначала кратко рассмотрим проблему учета расходов на рек-
ламу в аналитической форме.
Объем затрат фирмы в течение периода времени на рекламу
обозначим символом а, тогда издержки С фирмы есть функция
двух переменных С(у; а): переменной у, которая равна объему
продукции, выпускаемой фирмой в течение периода, и перемен-
ной а.
Прибыль, которую получит фирма в этот период времени,
имеет вид
PR(y‘, а)=ру- С(у; а).
Функция спроса на продукцию фирмы и обратная к ней в
рассматриваемом случае имеют вид у = D(p, а) ир = Н(у, а). Заме-
нив в выражении для прибыли PR(y, а) цену р на ее представле-
ние Н(у, а), получим
’ PR(y, а) = уН(у, а) - С(у, а). (8.6.1)
Выпишем условия первого порядка максимизации прибыли
фирмы:
(8.6.2)
ду ду ду
dPR(y, а) = дН(у,а) _ дС(у, а) = Q (8 6 3)
да да да
Пусть вектор (у0; а0) есть решение системы (8.6.2)—(8.6.3).
Если для этого вектора выполнены условия второго порядка,
то при объеме выпуска у° и расходах на рекламу о0 фирма в рас-
сматриваемом периоде получит максимальную прибыль
= PR(y°-, а°) =у°Н(у°', а°) - С(у°; а0).
299
В учебнике трех авторов (см.: В.М. Гальперин, С.М. Игнатьев,
В.И. Моргунов (1997). Т. 2. С. 269—274) анализируется задача мак-
симизации прибыли фирмы не только с учетом расходов на рекла-
му, но и с учетом показателя g качества продукции.
8.6.2. Проанализируем влияние расходов на рекламу с помощью
наглядных геометрических построений (рис. 8.31).
На рис. 8.31 линия (1г)АС} есть линия долговременных сред-
них издержек фирмы, которая не имеет расходов на рекламу.
Точка — минимальная точка линии (/г)ЛСг Точка Ех — точка
пересечения линий MR{, (sr)MCt и (lr)MCv Ее абсцисса у, — объем
выпускаемой фирмой продукции, который вместе с ценой рх (ор-
300
динатой точки Fx, абсцисса которой естьу^ максимизирует при-
быль фирмы в течение периода в случае долговременного проме-
жутка. Максимальная прибыль равна площади |2 прямо-
угольника HxpxFxGv На рис. 8.31 линия (1г)АС2 есть линия
долговременных средних издержек фирмы, которая имеет расходы
на рекламу, повышающие средние издержки фирмы, что иллюст-
рируется высоким расположением линии (1г)АС2 по сравнению с
линией (1г)АСх. Точка Q2 — минимальная точка линии (1г)АС2. Рас-
положение линии спроса AR2 выше и правее линии спроса
означает, что после рекламной кампании спрос на продукцию
фирмы значительно вырос (см. рис. 8.31). В точке Е2 пересекают-
ся линии MR2, (sr)MC2, (lr)MC2, откуда следует, что абсцисса у2
точки Е2 есть объем выпускаемой фирмой продукции, который
вместе с ценой р2 (ординатой точки F2, абсцисса которой есть у2)
максимизирует прибыль фирмы в течение периода долговремен-
ного промежутка в том случае, когда фирма имеет расходы на рек-
ламу. Максимальная прибыль во втором случае равна площади
Я2/>2/^<72|2 прямоугольника H^2F2G2, которая больше площади
HxpxFxGx |2 прямоугольника, равной максимальной прибыли фир-
мы в случае отсутствия расходов на рекламу (важного средства сти-
мулирования спроса). В этом примере расходы на рекламу позво-
лили фирме снизить цену на свою продукцию (срх до р2) и повысить
свою прибыль (с величины |НхрхFXGX |2 до величины |#2p2.F2(7212).
Рисунок 8.32 аналогичен рис. 8.31 и иллюстрирует ситуацию,
когда при стимулировании спроса путем рекламной кампании
фирма повышает цену (р2 > рх) и снижает свою прибыль в течение
периода времени в случае долговременного промежутка. Площадь
|2 прямоугольника HxpxFxGx, которая равна прибыли
фирмы в случае отсутствия у нее расходов на рекламу, больше
площади |H2p2F2G212 прямоугольника H2p2F2G2, которая равна
прибыли фирмы в случае наличия у нее расходов на рекламу.
Рассмотренные примеры показали, что не существует одно-
значного ответа на вопрос, как влияют меры фирмы по стимули-
рованию спроса в форме расходов на рекламу на ее прибыль, цену
выпускаемой ею продукции. Не существует однозначного ответа
и на вопрос о влиянии расходов на рекламу на выпуск фирмы,
который максимизирует ее прибыль.
301
8.7. Модели дуополии и олигополии Курно
8.7.1. Олигополия — это важная рыночная структура. Ей принад-
лежат отрасли, которые функционируют на гребне научно-техни-
ческого прогресса (аэрокосмическая отрасль, отрасль, производя-
щая оборудование для телекоммуникационных и компьютерных
систем, автопром и т.п.), отрасли топливно-энергетического комп-
лекса, черной и цветной металлургии. Исследованию и, в частнос-
ти, математическому моделированию дуополии и олигополии по-
священа обширная литература, ряд позиций которой представлен
в списке литературы к главе 8. Краткий аналитический обзор клас-
сических результатов и их обобщений содержится в конце парагра-
фа 20 учебного пособия АА Васина, В.В. Морозова (2005).
Сначала проанализируем количественную дуополию, т.е. ры-
нок однородного продукта, на котором функционируют две фир-
мы. Каждая фирма принимает решение об объеме (количестве)
только своего выпуска, который бы максимизировал ее прибыль
302
в течение определенного (производственного) периода (напри-
мер, в течение одного года). Естественно, что при этом фирма
должна не только ориентироваться на свои издержки и условия
спроса, но и учитывать поведение другой фирмы.
Выбор формы учета поведения другой (конкурирующей) фир-
мы должен базироваться на определенных предпосылках (допуще-
ниях). Сначала будет рассмотрена простейшая предпосылка о том,
что первая (вторая) фирма, принимая решение об объеме у, (у2)
своего выпуска, максимизирующего ее прибыль в фиксирован-
ном производственном периоде, полагает, что конкурирующая с
ней вторая (первая) фирма имеет в данном периоде фиксирован-
ный выпуск у2 (У[), т.е. не изменяет своего выпуска в этом перио-
де, даже если первая (вторая) фирма изменит свой выпуск. Содер-
жательным оправданием этой простейшей предпосылки является
основанное на фактах экономической реальности соображение о
том, что первая (вторая) фирма уверена, что вторая (первая) фир-
ма не успеет в течение производственного периода отреагировать
на изменение объема выпуска первой (второй) фирмы, даже если
бы попыталась это сделать. Далее мы увидим, что простейшая
предпосылка не означает, что модель, построенная на ее основе и
называемая моделью дуополии Курно, также будет простейшей.
Переходим к формальному описанию и анализу модели Курно.
На рынке в течение производственного периода функциони-
руют две фирмы. Их функции издержек являются линейными
функциями, т.е. имеют вид
С] = су|+</р C2 = cy2 + d2,
где с = МС, = МС2, d, = ЛС(, d2 = FC2, у, — объем выпуска первой
фирмы; у2 — объем выпуска второй фирмы; у = у, + у2 — суммар-
ный выпуск обеих фирм (т.е. отраслевой выпуск); МС, и МС2 —
предельные издержки фирм; FC, и FC2 — постоянные издержки
обеих фирм.
Функция, обратная к функции рыночного спроса, предпола-
гается линейной и имеет вид
р = а-Ь(у,+у2),
где а и Ь — положительные параметры. Тогда доход (выручка) у
первой фирмы равна R, = ру,, а у второй R2 = ру2. Для прибыли
каждой фирмы получаем следующие выражения:
P/?,(y„ у2) = Л, - С, = (а - by, - by2)y, -су,- d,, (8.7.1)
РЛ2(у„у2) = R2-C2 = (a-by, -by2)y2-су2-d2. (8.7.2)
303
Из приведенных формул следует, что прибыль каждой фирмы
зависит не только от объема ее собственного выпуска, но и от объ-
ема выпуска другой (конкурирующей с ней) фирмы.
Далее все построения будут выполнены только для первой
фирмы. Ряд результатов для второй фирмы выписывается по ана-
логии.
В соответствии с принятой предпосылкой (первая фирма по-
лагает, что выпуск второй фирмы в рассматриваемом периоде не
меняется, т.е. у2 = у2 и, следовательно, dy2 /dy{ = dy2 /dyl = 0) при-
быль первой фирмы имеет вид
PRi = (а- с)у, - by* - byxy2 - dv (8.7.3)
Аналогично если вторая фирма полагает, что выпуск первой
фирмы в рассматриваемом периоде не меняется, т.е. У] = (и, та-
ким образом, dyx /dy2 = dyx /dy2 = 0), то прибыль второй фирмы
имеет вид
РЛ2 = (а - с)у2 - by* - byxy2 - d2.
Для решения задачи максимизации прибыли PRX следует сна-
чала использовать условие первого порядка
Ту-1 - (а - с) - 2Ьух - Ьу2 = 0
(выписанное с учетом равенства dy2/dyx = 0), откуда следует, что
, . а-с у2
Отметим, что 0 < у, < •
1 2Ь
Для прибыли PRX условие второго порядка имеет вид
d*PRx
(8.7.4)
, = -2д<0.
Таким образом, объем выпуска первой фирмы, равный у
(см. (8.7.4)), максимизирует ее прибыль PRX в течение производ-
ственного периода, если выпуск второй фирмы равен у2.
Аналогично если выпуск первой фирмы равен ур то выпуск
второй фирмы, максимизирующий ее прибыль PR2 в течение про-
изводственного периода, равен y2(yj):
У2 =
а-с у,
2Ь 2 *
(8.7.5)
304
На основании равенств (8.7.4) и (8.7.5) выписываем систему
У1 =
а-с у2
2Ь 2 ’
У1 =
а-с У|
2Ь 2
линейных алгебраических уравнений, которая имеет единствен-
ное решение
« » а-с
Уг=У^^
которое позволяет переписать равенства (8.7.4) и (8.7.5) так:
*
У1 =
а-с У2
2Ь 2 ’
(8.7.6)
У1 =
а-с У,
2Ь 2
(8.7.6')
т.е. если у2=уг, то у} = у*, и если у = у*, то у2 = у2.
Таким образом, выпуск у(* первой фирмы максимизирует ее
прибыль, если вторая фирма имеет выпуску2, который максимизи-
рует ее прибыль при условии, что первая фирма имеет выпуск у[,
который максимизирует ее прибыль. Естественно такую пару вы-
пусков (у,, у2) первой и второй фирм назвать равновесием дуопо-
лии Курно или просто равновесием Курно. Ниже приведено под-
робное пояснение этого фундаментального понятия экономичес-
кой теории.
Напомним, что изопрофита — это линия постоянной прибыли
фирмы.
При объеме у=у(у2) выпуска первой фирмы ее максимальная
прибыль равна
РЛ](ур у2) = PR{ = (a-cjy-by*-byy2-d{ = xr (8.7.7)
Уравнение изопрофиты /,(Tj) имеет вид
РЛ1(уРУ2) = Т1
или в развернутом виде
(а - с)у, - by! - by{y2 -d{ = тр
откуда следует, что
а-с Ъ+d, 1
(8.7.8)
20 - 7620
305
т.е. получили, что уравнение изопрофиты есть уравнение
гиперболы, проходящей через точку (ур у2). У этой гиперболы
одна вертикальная асимптота (yj = 0) и одна наклонная, которая
проходит через точки GlnG2n которая имеет уравнение
У2 =
(8.7.9)
(рис. 8.33).
^ = _1+vt± 1 о,
4 У?
откуда следует, что
2 _ т, +4 <8-7-7>(а-с)у, -by2 . (а-с У8™> 2 -2-2
У'~ b ” b b У2 ~ У1 У'~У1
306
т.е. при j] = у производная dy2 /dyx = 0 и, следовательно, изопро-
фита (т,) в точке (ур у2) имеет горизонтальную касательную
(см. рис. 8.33).
Поскольку
Ь >з<0’
то при у, = У) изопрофита ^(tj) имеет максимум, равный у2, что
проверяется непосредственно:
а-с _ 1 (8Л7)д-с „ (a-c)yx-by*-by.y2 1
у2=——у,—1—L.— = —---------у--------1—— =
Ъ 1 b у, b 1 b у,
а-с _ а-с ~ Ьу.у~ _
Таким образом, в точке Н = (у,, у2) изопрофита /^tj) имеет
«шапочку» (см. рис. 8.33), т.е. самая высокая точка каждой изо-
профиты /|(Т|) первой фирмы расположена на линии Rx(yJ, име-
ющей уравнение
а-с у2
У1 2Ь 2 '
Линию Rx(y2) можно назвать линией реакции первой фирмы на
выпуск второй фирмы, ибо эту линию Rx(y^) заметают (от слова
«метла») все точки (у,, у2), первые координаты ух которых равны
выпуску, максимизирующему прибыль первой фирмы, если пер-
вая фирма полагает, что вторая фирма имеет выпуск у2.
Формальное дифференцирование функции ух = по
переменной y2(</yj /dy2 = -1/2) некорректно, ибо оно молчаливо
опирается на неявную предпосылку, что вторая фирма меняет
свой выпуск у2 в рассматриваемом производственном периоде,
что противоречит фундаментальной предпосылке Курно, что вто-
рая фирма не меняет свой выпуск у2 = у2 в рассматриваемом про-
изводственном периоде.
На рис. 8.33 показаны две другие изопрофиты /)(?,) первой
фирмы, а также изопрофита /,(т*), проходящая через точку £(Сои),
которая изображает равновесие (у,, у2) Курно. Очевидно,
т* = Р/?,(у*, у2) = (а - с)у* - Z>(y*)2 - byxy2 - dx.
20*
307
Абсциссы X и X" точек пересечения изопрофиты Z(Tj) с осью
О?! находим, положив в уравнении (8.7.8) изопрофиты /(ij) у2=0.
Тогда получим квадратное уравнение
2 а-с T.+J.
*у'+-‘-Г=а-
корни которого X и X' получаем по известной формуле решения
квадратного уравнения, которая после элементарных преобразо-
ваний приобретает вид
2Ь
(напомним, что 0 <
Имеем на основании формулы (8.7.3), что
ЭРЛ «. Л
-Ч=-1 = -АУ1 <0,
1
откуда следует, что с ростом выпуска у2 второй фирмы максималь-
ная прибыль РЛ( = PR^iy^yj) первой фирмы убывает, т.е. чем
выше изопрофита, тем меньшему значению прибыли первой
фирмы она соответствует.
Если в приведенных рассуждениях первую и вторую фирмы
поменять местами, то получим результаты, которые симметричны
только что приведенным (рис. 8.34).
Вернемся к точке (ур у2) (см- Рис- 8.33). На изопрофите /,(т,)
первой фирмы, проходящей через точку (ур у2), прибыль PRX рав-
на X (см. (8.7.7)).
На рис. 8.35 представлены изопрофиты /](т{), /((т^) пер-
вой фирмы, которые соответствуют значениям т{, тр т, прибыли
первой фирмы, таким, что т{ < т‘ < Аналогично на рис. 8.35
представлены изопрофиты /2(т2), /2(Х), втоР°й фирмы, кото-
рые соответствуют значениям т2, т2, т2 прибыли второй фирмы,
таким, что т2 < т2 < т^. В точке Et! пересекаются изопрофиты /, (rj)
и /2(т2), в точке £12 — изопрофиты ^(т}) и /2(т^), в точке Р21 — изо-
профиты ^(т,) и /2(т2), в точке Е22 — изопрофиты и 12(т%).
308
2b b
Рис. 8.34
Рис. 8.35
309
В точке £(Со") пересекаются изопрофиты /Дт*) и /2Сф. Таким
образом, в точках £п, £12, £21, £22 имеем следующие соотношения
между значениями прибыли обеих фирм: в точке Еп т} < т*, т2 < т2;
в точке £12 т[ < tp > ^; в точке £2) т* > т*, в точке £22 -q > т*
и т2 > т2.
Из всех точек £п, £12, £2р £22, £(С9И) только последняя точка
обладает свойством: если одна из фирм, скажем первая фирма,
меняет свой выпуск Ур уменьшая его до у{ или увеличивая его до у{,
а вторая фирма не изменяет свой выпуск у2, то первая фирма
уменьшает свою прибыль, переходя с изопрофиты //т’) на более
высокую изопрофиту Это означает, что первой фирме в оди-
ночку не выгодно менять свой выпуск у*, если другая фирма не
меняет свой выпуск у2. Ситуация, когда первая фирма не меняет
свой выпуск Ур а другая фирма меняет свой выпуск у2, уменьшая
его до у2 или увеличивая его до у2, поясняется на рис. 8.35 анало-
гично.
Отсюда следует, что точку Е{Сои) естественно считать равнове-
сием дуополии, в котором прибыль равновесия первой фирмы
равна т* и прибыль равновесия второй фирмы равна т2. В этом
равновесии ни одной фирме в одиночку не выгодно менять объем
выпускаемой продукции, если другая фирма этого не делает. Опи-
санное равновесие есть равновесие Курно дуополии. Оно представ-
ляет собой частный случай равновесия Нэша (см. параграф 9.7).
Равновесие (у*, у2) Курно — одна из первых реализаций фунда-
ментальной идеи экономического равновесия.
Отметим, что главным обстоятельством получения точки £(Сви)
является факт пересечения изопрофит //т*) и /2(т2)-
Таким образом, на основании равновесия Курно топ-менед-
жерам фирм можно дать конструктивную рекомендацию д ля при-
нятия ими рационального решения в условиях неопределенности
(когда каждая фирма не знает, какое решение об объеме выпуска
примет другая фирма): каждой фирме следует выпускать продук-
цию в объеме у* = у2 равновесия Курно. Отметим, что если обе
фирмы изменят свой выпуск у, = у2, уменьшив его, то они могут
прийти в точку £22 (см. рис. 8.35), в которой пересекаются изопро-
фиты, соответствующие большим значениям прибыли т* < = PRX
и т2 < т2 = PR2 и которые расположены соответственно ниже и ле-
вее изопрофит, проходящих через точку £(Сои).
310
Отмеченная оптимальность объемов производства у* и у* в
равновесии Курно имеет место в случае некооперативного пове-
дения фирм. Уменьшение объемов производства и увеличение
прибыли каждой фирмы возможны в случае кооперативного по-
ведения фирм, которое будет проанализировано ниже.
8.7.2. Если не принимать простейшую предпосылку о том, что
dy2ldyx = 0 (dyx /dy2 = 0), то для прибыли PRX первой фирмы
PRX = (а- с)ух - by2 - byxy2 -
условие первого порядка имеет вид
^^- = (a-c)-2byx-by2-byx-^- = 0. (8.7.10)
dyx
Выражение dPRx /dyx есть предельная прибыль первой фирмы.
Оно показывает, как изменится прибыль первой фирмы, если
объем ее выпуска ух изменится на одну единицу.
Производная dy2 /dyx формально показывает, на сколько еди-
ниц вторая фирма изменяет объем своего выпуска в производ-
ственном периоде, если первая фирма изменит объем своего выпус-
ка в том же периоде на одну единицу. В контексте формулы (8.7.10)
производную dy2 /dyx необходимо интерпретировать следующим
образом: первая фирма предполагает, что вторая фирма изменит
объем своего выпуска на dy2ldyx единиц, если первая фирма изме-
нит объем своего выпуска на одну единицу. Поэтому производ-
ную dy2 /dyx (а также производную dyx /dy2) принято кратко назы-
вать предполагаемой реакцией, ибо первая фирма предполагает,
как будет реагировать вторая фирма на изменение выпуска пер-
вой фирмы.
Выбор конкретной предпосылки о значении производной
dy2/dyx (производной dyx /dy2) означает выбор конкретной модели
количественной дуополии. Если предположить, что dy2 /dyx =
= dyx /dy2 = 0, то получим, как отмечалось выше, модель Курно.
Задачу максимизации прибыли PRX в предположении, что
у2 = у2, можно решать методом Лагранжа с использованием функ-
ции Лагранжа в виде
L(yx, у2, К) = (а - с)ух - by2 - byxy2 -dx + Х(у2 - у2).
Точка £(Сои) есть точка пересечения линий Rx(y2) и Я2(У1) реак-
ций первой и второй фирм соответственно на выпуск у2 второй
фирмы и выпуск ух первой фирмы. Поэтому координаты у* и у2
311
точки Е(Сои^ формально получаются как решение системы линей-
ных алгебраических уравнений
= (а ~ с> “ 2^1 ~ ^2 = °’
dPR/ypyJ
--2 = (а - с) - 2Ьуг - Ьух = О,
dy2
описывающих эти линии реакции
=^£-^0’2». (8.7.11)
* = ^-^(ВД). <8.7.12)
Для максимальной прибыли PRX = Р1\(у*х, у2) получаем
(8.?.7)
т’ = PR] (у*, у2) = (а - с)у* - b(y* )2 - by*y2-dx =
= (а-с)^--b-b^a~-)2 -d = ^а~С)2 -dx. (8.7.13)
3b (3b)2 (3b)2 1 9b *
Аналогично имеем и для максимальной прибыли РЯ2 = PR^yf, у2)
т2 = PR^yf, у2) = (a-c)y*2-b(y*)2-by*ly*2-d2 =
= ^i^—d2- (8714)
9b 2
Осталось найти
PR = PR. +PR, = 2^a C^-d.-d2,
1 2 9b 12
♦ » . 2a-c
y =y'+y^TT-
и
♦ , . , 2a-c 3a-2a + 2c a + 2c
p =a-by =a-b-—— =---------= ——.
3 b 3 3
Сопоставим цену p*, выпуск у* и общую максимальную при-
быль PR] + PR2 дуополии Курно с ценами, общим выпуском и об-
щей прибылью в случае чистой конкуренции и в случае чистой мо-
312
нополии при условии, что во всех трех случаях функция, обратная к
функции (отраслевого) спроса, имеет вид р = а - by (у=у, + у2).
В случае чистой конкуренции = с, поэтому с = а - Ду(с), от-
куда получаем, что суммарный отраслевой выпуск равен
(С) _ а-с
У b
и
РЯ(С) = р(с)у(с)-cy-dl-d2=-dl-d2.
В случае чистой монополии монопольный выпуск у(т) опреде-
ляется из уравнения MR = МС, которое в рассматриваемом случае
имеет вид MR = а - 2Ьу = с, ибо R=ру= (а - by)y = а - by2, МС=с.
Из уравнения а - 2Ьу = с следует, что
v(m) _ а~с
У 2Ь
и
(/я) » а + с
р' ’ = a-by'’ =a-b— =-------.
2Ь 2
Для общей максимальной монопольной прибыли имеем
PRX + PR2 = PRm} = р(т}у(т} - су(т) -d{-d2 =
l Am) -\„(m) j j (a + C Ad — C , , (d —c) , ,
= (P' '-<?)/ ---C)2b'~dx~d'i=~~4b-------di~dr
Сопоставляя цены, отраслевые выпуски и значения максималь-
ной прибыли, получаем, что
„(с) * а + ^С Ат) а + С
р'’ — с < р = з <р'
(ибо с < а),
Ат) = а~с • _ 2d-c (с) = а-с
У 2Ь У 3 b У b ’
^(с) 2 (а — с)2
PR =-d.-d,<PR —d,-d?<PR =
12 9 b 12
Сведем все эти величины в табл. 8.1.
313
Таблица 8.1
Р У PR
Чистая конкуренция С 1 1 Q 1 ~d\ “ d2
Дуополия Курно д + 2с 3 1 1 <3 1 сч I m 2 <°-С)2 Я J ах — d^ 9 b 12
Чистая монополия а+с Т" 1 а-с 1 b 1 (а-с)2 d, — di 4 b 12
Сопоставим данные таблицы с рис. 8.35. Точка Gt показывает
конкурентный выпуск = —— первой фирмы и нулевой выпуск
второй фирмы, т.е. в этой ситуации суммарный выпуск равен
-. С точкой G2 ситуация аналогична. Точка Я, показывает мо-
а—с
нопольный выпуск у. = —— первой фирмы и нулевой выпуск
2Ь
второй фирмы, т.е. в этой ситуации суммарный выпуск равен
С точкой Н2 ситуация аналогична.
8.7.3. Вернемся к толкованию линии реакции Rx (у2) первой фир-
мы на объем выпуска у2 второй фирмы. Согласно основной пред-
посылке дуополии Курно первая фирма предполагает, что вторая
фирма не реагирует на изменение выпуска первой фирмы в тече-
ние одного производственного периода, т.е. в статике. Формали-
зуется эта предпосылка так: dy2/dyx = 0. В связи с тем что в модели
дуополии Курно обе фирмы идентичны, имеет место аналогичное
равенство dyx /dy2 = 0. С другой стороны, из (8.7.11) и (8.7.12) фор-
мально следует, что
Луг1Лу{=-1г и dyx/dy2 = -xlv
что, на первый взгляд, явно противоречит равенствам dyx /dy2 = 0,
dy2/dyx = Q.
Это противоречие было преодолено в разделе 8.7.1. Здесь мы
продолжим анализ рассматриваемой ситуации.
314
Поскольку вторая фирма в течение одного производственного
периода не может одновременно не реагировать на изменение
выпуска первой фирмы (dy2/dyl = 0) и в то же самое время реаги-
ровать на него (dy2 /dy{ = —’/2), постольку естественно принять,
что вторая фирма реагирует уже в следующем производственном
периоде t + 1 на изменение выпуска первой фирмы в производ-
ственном периоде t, т.е. естественно перейти от статики к динами-
ке в толковании уравнений (8.7.11) и (8.7.12) (см. М. Интрилигатор,
1975; 2002): <8'715> <s-716)
Формально уравнения (8.7.15), (8.7.16) образуют неоднород-
ную систему линейных обыкновенных разностных уравнений с
постоянными коэффициентами.
Сначала решим эту систему графически (рис. 8.36), а затем
аналитически.
Рис. 8.36
315
Пусть в базовом периоде t = 0 выпуск второй фирмы равен
у2(0),тогда в силу (8.7.15) в первом периоде t = 1 выпуск первой
фирмы будет равен yt(l) (см. рис. 8.36, на котором показано, что
точка (У](1), У2(0)) расположена на линии реакции Rx(y2) первой
фирмы на выпуск у2(0) второй фирмы).
Далее рассуждения аналогичны. Если в первом периоде t = 1
выпуск первой фирмы равен _У,( 1), то во втором периоде t = 2 вы-
пуск второй фирмы будет равен у2(2) (см. рис. 8.36, на котором
показано, что точка (у2( 1), у2(2)) расположена на линии /?2(у,)
реакции второй фирмы на выпуску,(1) первой фирмы). И т.д.
Рисунок 8.36 наглядно показывает, что выпуски ух(1), ух(3),...
1 а-с
= —,авыпус-
j о
неограниченно приближаются (снизу) к точке у.
ки у2(0), у2(2), у2(4), ... неограниченно приближаются (сверху) к
♦ 1 а-с
точке у2 =
. Неограниченное приближение выпусков первой
и второй фирм к выпускам у* и у2 равновесия Курно свидетель-
ствует об устойчивости этого равновесия.
Для аналитического решения неоднородной системы (8.7.15),
(8.716) сначала найдем общее решение соответствующей ей одно-
родной системы, затем частное решение неоднородной системы и
выпишем общее решение неоднородной системы в виде суммы
полученных общего и частного решений.
Для однородной системы
(/ + !) = -
Z2(0
2
Z2(/ + l)
=_£i«
2
(8.7.17)
(8.7.18)
выпишем характеристическое уравнение
глеЛ = (-0,5
— матрица системы (8.7.17), (8.7.18).
316
Найдем правые собственные векторы матрицы Л, соответству-
ющие собственным числам Х( = 0,5, Xj = -0,5:
-0,5 -0,5^
-0,5 -O,sJ
откуда получаем, что
Общее решение однородной системы (8.7.17), (8.7.18) имеет вид
(в векторной форме)
z(O = Y1A1X{+y2A2X',
где Yi и — произвольные постоянные. В координатной форме
общее решение z(0 имеет вид
Z1(O = Y1(0,5)/+y2(-0,5)/,
Z2(O = -Y1(O,5)/+y2(-O,5)/.
Частное решение неоднородной системы (8.7.15), (8.7.16)
отыскиваем в виде у(/) =
Имеем
, где т| — скалярная величина.
а —с п а—с Т|
П =-------1 т] =-------
1 2Ь 2 ' 2Ь 2
откуда следует, что
Следовательно, общее решение неоднородной системы
(8.7.15), (8.7.16) имеет вид
MO = Yj(0,5)' + Y2(-0,5)'+^p (8.7.19)
y1(O = -Y1(0,5)/+Y2(-0,5)/+^. (8.7.20)
317
Если у,(0) = у°, _у2(0) = у\, то для определения значений произ-
вольных постоянных следует решить систему линейных алгебраи-
ческих уравнений
у*0 = 71+Т2+1Г (8Л21)
У°2 =-Yi+Y2+^£- (8.7.22)
При фиксированных Yj и у2 ПРИ * -* +°°
^(0^^ = /, (8.7.23)
^(0-^^ = ^. (8-7.24)
Таким образом, получено аналитическое решение неоднород-
ной системы (8.7.15), (8.7.16) и доказана устойчивость равновесия
Курно.
8.7.4. Рассмотрим дуополию Курно, когда издержки обеих
фирм имеют соответственно вид Ц = +dx, С2=с^2+d2 и сх * с2,
т.е. МСХ * МС2. Все остальное сохраняется без изменений, в част-
ности обратная функция спроса
p = a-d(yx+y2).
Выражения (8.7.1) и (8.7.2) для прибыли каждой фирмы пере-
пишутся так:
^(Ур У2) = (« “ С1)У1 “ by2i - byxy2 - dx,
Р1ЦУ\ > У2) = (а “ с2^2" brf ~ ЬУ\У2 ~ d2-
Повторив формальные построение начала параграфа 8.7 и при-
нимая во внимание предпосылку Курно dy2 /dyx = 0, dyx /dy2 = О,
получим систему линейных алгебраических уравнений
(a-cx)-2byx-by2 = 0,
(a-c^-2by2-byx-Q
для нахождения равновесия Курно
« а-2с.+с, . а-2с, +с.
*=—
318
Для максимальной прибыли PRX = PRx(yx, у2) имеем
. „„, • »v (а-2с.+с,)2
= W>W2) =-------2-----4’
для максимальной прибыли PR2 = PR^yx, У2) имеем
. „„ , • «, (о-2с, + с,)2
т2 = РЛ2(у1,у2) =--1----dv
Для остальных характеристик равновесия Курно (у*, у2) имеем
(а-2с.+с,)2 (о-2с,+с.)2
PR = PR, + PR2 = 2-JL-Jl. + J-^-12- - d, - d2,
. « . a-2c.+c, a-2c,+c, 2a-c.-c,
y #-L=—3^’
. , . ,2a-c.-c, a+c.+c,
P =a-by =a-b----—2. =-----—2-.
JU J
Если положить cx = c2 = с, то из только что выписанных выра-
жений получим равенства (8.7.12), (8.7.13), (8.7.14), а также зна-
чения
« 2 а-с
У ~3~
• а + 2с
/,=~
Рассмотрим дуополию Курно, когда издержки обеих фирм
имеют соответственно вид
Cj = Cjjp С2 = с^г, т.е. Cj = AfCp с2 = MCY
Пусть функция рыночного спроса имеет вид
у = ^+у2=4-
р
(а и у — положительные параметры), тогда обратная функция
спроса имеет следующее представление:
vl/a
319
В этом случае для прибыли каждой фирмы имеем выражение
РЩух, У2) =Р(У)У,- ~ С/У,. /=1,2.
Для нахождения равновесия Курно (у[, у*2) выпишем систему
алгебраических уравнений
1Л (,**)'*
-у 1
Ъ -У ' (,1+*)2/“
После элементарных преобразований этих уравнений и деле-
ния первого уравнения на второе получим равенство
(а-1)у,+ау2 = с,
ayj+(a-l)y2 с2’
откуда следует представление
afl~— V1
\ с1)
I С| «I
——1 a—L
kC2 ) С2
которое после подстановки, например, в уравнение ЭРЛ)(ур у2):
: Эу, = О позволит найти равновесие Курно (у,, у2). В целях упро-
щения выкладок положим сх = с2, тогда получим, чтоу1 =у2.
Преобразуем уравнение ЭРДСур у2)/Эу, = 0, положив у2 = ух,
тогда
,Л
у — Q
(2ух)1/а{2ух)
откуда следует, что
-a / 1 \а
320
Если a = 1, то выпуск второй и первой фирм в равновесии Кур-
но приобретут вид
• ♦ У
У2=У^^
В этом случае имеем
р/?!=рщу;, у2)=(X-с)У;=I=рл,
pr=pr.+pr,=1
1 2 2
8.7.5. Перейдем к модели олигополии Курно, которая аналогич-
на дуополии Курно.
На рынке в течение производственного периода функциони-
руют п фирм, функции издержек которых имеют вид
c^cy.+dp
где c = MCjt dt = FC', у, —объем выпуска фирмы Fp
у=ух +... +уп — совокупный (отраслевой) выпуск.
Функция, обратная к функции рыночного спроса, имеет вид
р = а - by = а - Ь(ух +... +ул),
где а и Ь — положительные параметры. Для прибыли PR( фирмы Fj
имеем представление
PIW = (a-by)y(-cy-dt, /=1,...,л. (8.7.25)
В рассматриваемом случае п фирм предполагается, что фир-
ма Р, полагает, что выпуск остальных фирм Рр ..., F/_v FM,..., Fn
в рассматриваемом периоде не меняется (даже если фирма Г,
изменит свой выпуск в этом периоде), т.е. ух » ур ...,yzl = yz_p
Ум = Ум, -->Уп = У„ И, следовательно, dyjdyi - dyjdyi = О,
i = 1, ..., л, j*i.
Тогда выражение (8.7.25) для прибыли PR/fy) фирмы Fp
/ = 1,..., л, перепишется так:
PIW)=<a-byx -•••-byt_x -byrbyM -.-Ьу^^-d/ =
=(о-с)у,-Ьуху,..-Aywyz-by?-ЬумУ1 -.. .-£улу, -dr (8 7 26)
321
21 -7620
Для решения задачи максимизации прибыли PR/у) следует
сначала использовать условие первого порядка
dPR^ = (°"^)"-••• -^/-1 -Щ -Ьум -...-Ьуп=0,
откуда получаем объем выпуска у, фирмы
Л _о-с 71 +- + У/-1 +У<+1 + ••• + ?„
У'~ 2Ь 2
который максимизирует ее прибыль PRt(y). Отметим, что в рас-
сматриваемом случае условие второго порядка имеет вид
</2РЛ(у.) ж
-----^- = -26<0.
ч2
Таким образом, точка (ур ...,yw,ypy/+p расположена
на (п - 1)-мерной плоскости Rt (ур ..., у(._р ум, ...,уп) реакции
фирмы на объем выпусков остальных фирм:
+ У /= (8 7 27)
' 2Ь 2
По аналогии со случаем дуополии Курно равновесие у =
= (у*, .... У*) олигополии Курно формально определяется как ре-
шение системы (8.7.27) п уравнений с п неизвестными у р ..., ул.
В силу предполагаемой симметрии все фирмы будут иметь
равные выпуски, максимизирующие их прибыли, поэтому
у, =... = у,_, =ум =... =у„ =yt и, следовательно, выражение (8.7.26)
перепишется так:
а-с (л-1)у,
У‘ 2Ь 2 ’
откуда следует, что
Таким образом, в случае п фирм равновесие Курно имеет вид
322
Отраслевой выпуску равен
• » • а-
У =>>1+••• + >'„=-£
п
Л + Г
а цена р* имеет представление
♦ , ♦ а-с п
р = а-Ьу =а-
а п
=----+ с---.
b л+1 л+1 л+1
Для максимальной прибыли PRf фирмы F., i = 1, п, имеем
выражение
PRi(У^) = (а-с)у* -b(y*)2n-d.= у. ((а-с)-by* п)-d, =
(п + 1)2 А
а суммарная максимальная прибыль (максимальная прибыль от-
расли) равна
га = га,(/)+...+гал(У;) = —
(п +1) О
При неограниченном росте числа п фирм цена/Г -> с, у* —> -—-
b
и суммарная максимальная прибыль становятся суммой числово-
го ряда — (dj +... + dn +...), т.е. при неограниченном росте числа п
основные характеристики олигополии Курно (цена р*, суммар-
ный выпуск р*) приближаются к основным характеристикам чис-
той конкуренции (цена с = МС? суммарный выпуск —т~)-
При п = 1 имеем случай чистой монополии: ь
» а + с • а-с -Ti 1 (а-с)2 .
р‘~у=^
Случаи п=1,п = 2ил сведем в табл. 8.2.
21*
323
Таблица 8.2
р У РЛ
п = 1 а + с ~Г а+с 2Ь 1 П ч.✓ к> 1
л = 2 а + 2с 3 2а-с 3 b 2 (а-с)2 . . 9 Ь
п а п + с л+1 л + 1 п а-с п {d + +d}
л+1 b (л+1)2 b <4+-+4.)
8.7.6. Вернемся к формуле (8.7.26), которая представляет при-
быль PRjiy) фирмы Ft, i = 1,..., п. Доход фирмы Fi в рассматрива-
емом случае равен
R^=pyP
фиксированы, т.е. уу. = уу., j = 1,..., л, / #/.
Имеем
MRM = =р+у>= р\1+~ тг I=
dyt [ Р dyj
(8.7.28)
У dp)
где s, — доля выпуска фирмы Fi в общем выпуске у = у, + ... + уя
отрасли; Ed—эластичность рыночного спроса по ценер (отметим,
что dp/dy. = (</р/</у)(Эу/Эу,.) = dp/dy).
В (8.7.28) положим MR/y) = MCt (условие максимизации при-
были фирмы F), тогда получим
МС, = р
324
откуда следует, что
Р Ed’
т.е. получено выражение для индекса Лернера фирмы Ft олигопо-
лии Курно. Из формулы (8.7.29) следует, что рыночная власть от-
дельной фирмы F. обратно пропорциональна эластичности ры-
ночного спроса и прямо пропорциональна доле объема выпуска
фирмы Ft (на рынке олигополии Курно).
Умножим обе части равенства (8.7.29) на sf и просуммируем по
всем фирмам от 1 до л включительно. Тогда получим
p(s. +...+s„)-(stMC. +... + з„МС) s, +...+S*
Р Ed ’
откуда следует равенство
£ = Р~МС = (8.7.30)
Р Ed
ибо Sj +... + sn = 1, $2 +... + s* = HHI (индекс Хиршмана—Херфин-
даля), МС — средневзвешенные издержки всех фирм, где роль ве-
сов играют доли .... sn этих фирм в общем объеме выпуска от-
расли.
Из формулы (8.7.30) следует, что индекс Лернера олигополии
Курно определяется числом фирм, их рыночными долями, т.е. ин-
дексом HHI, а также эластичностью рыночного спроса по цене.
8.8. Модели дуополии и олигополии Штакельберга
8.8.1. Модель дуополии Курно представляет собой симметрич-
ную количественную дуополию, ибо обе фирмы придерживаются
одного типа поведения на рынке. Первая (вторая) фирма полага-
ет, что конкурирующая с ней вторая (первая) фирма имеет фикси-
рованный выпуск в производственном периоде, т.е. она его не
изменяет в этом периоде, если даже первая (вторая) фирма изме-
нит свой выпуск, что формально выражается так:
±1 = 0, ±1 = 0.
dy2 dy\
325
Модель дуополии Штакельберга — модель асимметричной
количественной дуополии, ибо каждая из двух фирм придержи-
вается одного из двух типов поведения: стремится либо стать лиде-
ром по объему выпускаемой продукции, либо быть последовате-
лем, т.е. следовать за лидером.
В этом параграфе проанализирована ситуация, когда одна
фирма (например, первая фирма) является лидером (по объему
выпускаемой продукции), а другая фирма (вторая) — последовате-
лем. Случай ценовой войны, когда обе фирмы стремятся быть
лидером, рассматриваться не будет, ибо в этом последнем случае в
результате ценовой войны один из лидеров откажется от своих
притязаний либо фирмы вступят в сговор.
Согласно предпосылке Штакельберга вторая фирма полагает,
что выпуск первой фирмы фиксирован в производственном перио-
де, т.е. не изменится в данном периоде, что формально означает, что
^/^2 = 0, (8.8.1)
т.е. д ля второй фирмы сохраняется предпосылка Курно. Собствен-
но, эта предпосылка делает вторую фирму последователем. Первая
фирма, согласно предпосылке Штакельберга, полагает, что вторая
фирма сокращает в производственном периоде объем производ-
ства в два раза, если первая фирма увеличивает объем своего про-
изводства на одну единицу. Это формально означает, что
=“|- (8’8’2>
Собственно, предпосылка (8.8.2) делает первую фирму лидером.
Сначала рассмотрим дуополию, когда издержки обеих фирм
имеют соответственно вид Cx = cyx + dx, C2 = cy2 + d2, т.е. МСХ =
= МС2 = с. Как и раньше, символом ух обозначим объем выпуска
первой фирмы (фирмы-лидера), символом у2 — объем выпуска
второй фирмы (фирмы-последователя) в течение фиксированно-
го периода. Символом у обозначена сумма у, +ух=у.
Прибыль PRX первой фирмы имеет вид
РК[ =РУ[ ~ сух -dx = (a- byx - by2)yx - сух - dv
Для решения задачи максимизации прибыли PRX первой фир-
мы следует сначала использовать условие первого порядка
dPRx dyJ**» 3L t
—± = a-c-2byx-by2-byx-^ = a-c--byx-by2 =0,
т.е. первая фирма (фирма-лидер) учитывает в функции своей при-
были равенство (8.8.2).
326
Из последнего равенства получаем уравнение реакции первой
фирмы 7Jj5/,)(y2)
2 а—с 2
3 ь 3 (8.8.3.1)
на выпуску второй фирмы.
Прибыль Р/?2 второй фирмы имеет вид
Р1<2 =РУ2 - ^2 -d2 = (a- by2 - Ьу')у2 - су2 - d2.
Для решения задачи максимизации прибыли Р/?2 второй фир-
мы следует использовать условие первого порядка
dPIL dy. <8-81>
—-2- = a-c-2by2-byi-by2~p- = a-c-2by2-byx =0,
</y2
откуда получаем уравнение реакции второй фирмы
v-£z£_21 (8.8.3.2)
2 2b 2
на выпуску, первой фирмы (см. формулу (8.7.2) параграфа 8.7).
Подставив выражение (8.8.3.2) в (8.8.3.1), получим
_2 а-с 2(а-с У]^
У' "З’ b “з! 2Ь ~ 2 )’
откуда вытекает, что
Подставив (8.8.4)
(Л1) _ °~с
Л| 2Ь ‘
а-с У]
ву2= ——у, получим
V(«D=£Z£_1 а~с _ а~с
Уг 2Ъ 2 2b 4Ь ‘
(8.8.4)
Выпуски у}*'1) и у^Л1> образуют равновесие 1 Штакельберга,
когда первая фирма является лидером, а вторая фирма является
последователем.
Отметим, что в равновесии 1 Штакельберга объем выпуска
первой фирмы в 2 раза больше объема выпуска второй фирмы.
Найдем суммарный (отраслевой) выпуск
у(л1) = (Л1) (Л1) = О с а с = 3 (8.8.5)
1 2 2b 4Ь 4 b ’
327
ценур(л|) равновесия по обратной функции рыночного спроса
р(л,) = а - 6у.(л1) - by?" = а - Ь-~ (8.8.6)
1 1 4 b 4
Максимальная прибыль Рк^ первой фирмы (фирмы-лиде-
ра) равна
= /Л1>у<Л1) - су^1) -dx = (p(al) - c)y(ai} -dx =
(а+Зс ^о-с , 1 (а-с)2 .
Максимальная прибыль рЩяГ) второй фирмы (фирмы-после-
дователя) равна
PRffn = - су(я'} -d2= (p(sli) - с)у(я1) -d2 =
(а + Зс Aa-c , 1 (а-с)2 ,
=1,—
Суммарная максимальная прибыль равна
ш>(Я1) _ 3 (О —с) , ,
PR ь—12’
В случае когда лидером является вторая фирма, а последовате-
лем — первая фирма, равновесие 2 Штакельберга характеризуется
следующими величинами:
(й2) _ а~с (st2) _ а~с Asti) _ 3 а-С
У1 4Ь ’ Уг 2Ь ’ У' 4 b ’
/л2>=о-^2>-^2) = ^,
рр(^2) _ 1 (а~ с) , nn(st2) _ 1 (а — С) ,
PRi ----dv PR2 --—b--------d2.
Суммарная максимальная прибыль равна
dd(^2)______________3 (а—с) j _ j
PR "16 ь di dr
Сведем все характеристики равновесий 1 и 2 Штакельберга в
табл. 8.3, в которую также поместим все характеристики равнове-
сия Курно.
328
Таблица 8.3
/1 У p
Курно 1 а-с 3 b 1 а-с зТ" 2а-с 3 b a+2c 3
Штакельберг— 1 1 а-с 2 b 1 а-с 4 b За-с 4 b a+3c 4
Штакельберг—2 1 а-с 4 b 1 а-с 2 b За-с 4 b a + 3c 4
PR. pr2 PR. +PR2
Курно Цо-с)2 и 9 Ь -d' 1 (а-с)2 . 9 Ь 2(о-с)2 . . 9 Ь
Штакельберг -1 1(о-с)2 и 8 Ь 1 (а-с)2 16 4 з (а-с)* . , 16 ь -d'-^
Штакельберг—2 16 ь l-^-d2 8 b * 16 ь di d*
Прибыль PR. первой фирмы (фирмы-лидера) можно предста-
вить так:
PRt = РУ1 -cy.-d.=(a- с)у. - by* - by.y2 -d.=
(X 2
a-c yx I , а-с ,ух ,
~2b~~i'jdl=~2~y,~!>i~~dl'
Для решения задачи максимизации этой прибыли выписыва-
ются условия первого и второго порядков
dPR. а-с , Л d*PR. г Л
—----------by. =0 и ---т± = -Ь<0.
* 1 dy*
Из условия первого порядка сразу получаем объем выпуска
(8.8.4) первой фирмы (фирмы-лидера), который максимизирует
ее прибыль.
329
Задачу максимизации прибыли первой фирмы (фирмы-лиде-
ра) можно сформулировать как задачу на условный экстремум
PR, = (а - с)у{ -by}- by^2 - (max)
при наличии ограничения
^-21-у2=о
2Ь 2 1
в виде равенства и решать эту задачу методом Лагранжа с помо-
щью функции Лагранжа:
ДУ1, У2 > М = (° “ С)У1 “ by? - ЬУ\ у2 - dx + “ у “ У2 J
Уравнение изопрофиты ^(т,) первой фирмы (фирмы-лидера),
соответствующей ее максимальной прибыли PRX = х р имеет вид
2
(а - с)у, - by2 -byIy2-dl=^- , (8.8.7)
о и
откуда следует, что
а-с 1 (а-с)2 1
*=—< (8 8 8)
1 ^0.0.07
Получили уравнение гиперболы, у которой одна асимптота есть
ось Оу, (Xj = 0), а другая — прямая <7jG2 (рис. 8.37), имеющая урав-
а-с
нениеу2= ——
„ 1 а— с
Непосредственно проверяется, что при имеем
firn la-c. „ а-с 1 а-с 1 (а-с)2 2Ь
Уг = 7—Г~ (Действительно, у2 =——— -----------------=
4 b 2 b 2 b 8 ь2 (а-с)
1 а-с.
= 4—)И
4у2 г . 1 («~с) 1 = 1
<fyi 8 Ь2 у2 2
, „ ^2 1 1(о-с)2 4А2 1
(действительно, —- = -1+--—--------=—).
dyt 8 ь2 (а-с)2 2'
Из приведенных расчетов следует, что изопрофита (8.8.8) ка-
сается линии (8.8.3.2) в точке в равновесии 1 Штакельберга
(см. рис. 8.37). В задачах для самопроверки, помещенных в конце
330
главы 8, предлагается обосновать прохождение изопрофи-
ты соответствующей максимальной прибыли = Tj
„ (а-с д-сЛ „ „
через точку F = ——, —— , и доказать, что в этой точке FKaca-
\4b 4b )
ются изопрофиты, соответствующие прибыли PR^ = Tj и при-
были Р/?2*2) = Ъ-
рис. 8.37
8.8.2. Вернемся к исходным предпосылкам Штакельберга в слу-
чае Штакельберг — 1. Вторая фирма (фирма-последователь) пола-
гает, что выпуск первой фирмы (фирмы-лидера) фиксирован в
производственном периоде, т.е. не изменяется в производствен-
ном периоде (dyi /dy2 = 0), что означает выполнение предпосылки
Курно. В этом случае условие первого порядка
dPR. dy,
~Т~ = (а-с)~byi -2by2-by2-^- = (a-c)~by} -2by2 = 0
4^2
331
задачи максимизации прибыли PR2 второй фирмы дает выраже-
ние функции реакции второй фирмы на объем выпуска yt
первой фирмы
а-с
У1~ 2Ь 2’
Первая фирма (фирма-лидер), согласно предпосылке Штакель-
берга, знает о «подражательном» поведении второй фирмы (фир-
. ж а~с У\
мы-последователя) согласно ее функции реакции у2 = ----£
и поэтому принимает равенство dy2/dyx=~/2. В этом случае усло-
вие первого порядка
dPR. , . . л, dy^ v , 3,
= (а - с) - by2 - 2byx-byi-^- = (a-c)~ by2 - -Ьу{ = О
dyx ' 2
задачи максимизации прибыли PR{ первой фирмы дает выраже-
ние функции /?](л1)(у2) реакции первой фирмы на объем выпуска у2
второй фирмы
2 а-с 2
У'~3~Ь 3Уг
в а~с У\
В рассматриваемом случае из равенства у2 = —-следует,
что 2
dy2 = 1
2’
т.е. имеет место предпосылка Штакельберга о «подражательном»
поведении второй фирмы. Из равенства yt
что
2 а-с
т-7—-у2 следует.
э и 5
3'
что противоречит предпосылке dyx /dy2 = 0.
Как и в случае модели Курно, для элиминирования противо-
речия перейдем от статики к динамике, т.е. будем толковать урав-
2а-с 2 а-с У< .
нения у{ = ——у2 и у2 = как реакции фирм в произ-
водственном периоде t+1 на объемы выпусков своих конкурентов
в предыдущем периоде t
332
y1(/+i)=-jy2(O+j—,
y2a+D=-|y1(o+^£.
Общее решение полученной системы обыкновенных разно-
стных уравнений первого порядка найдем аналогично тому, как
было найдено общее решение системы (8.7.15), (8.7.16).
Для однородной системы
г1(/+1) = -|«2(0,
Zi(/+l) = -|z2(O
выпишем характеристическое уравнение
матрица однородной системы.
Найдем правые собственные векторы матрицы А, соответству-
ющие собственным числам 1] = 3“|/2,12 = 3-|/2:
"-3-1/2
< 2
-з-1/2 WJ
откуда получаем, что
Д -1 р Д 1 J
Общее решение однородной системы имеет вид (в векторной
форме)
г(/) = у1А|Х}+у2Л21^,
где Yj и у2 - произвольные постоянные. В координатной форме
общее решение z(f) имеет вид
?1(Г) = п(2 • 3-|/2) • 3"'/2 + у2(2 • 3-|/2) • (-3)“'/2,
г2(') = ?!(-!) г,/2+у2(-3)-'/2.
333
Частное решение неоднородной системы отыскиваем в виде
y(t) = I Т'1 , где т| j и Т)2 — скалярные величины.
vh )
Имеем
Подставив выражение т|2 в первое уравнение, получим
а-с
откуда имеем
1 а-с la-с а-с а-с
Я2 -“2^1 +^2Ь~~~21Г+~1Г~~4Ь~
Следовательно, общее решение неоднородной системы обык-
новенных разностных уравнений в аналитической форме имеет
вид
У((0 = у,(2 • 3-,/2) • 3-'/2 + т2 (2 • 3’1/2)(-3)-//2 +
У2(0 = Yi(-i)3“'/2 + у2(-3)‘,/2
Если ^[(0) =ур у2(0) =у2, то для определения значений произволь-
ных постоянных У] и у2 следует решить систему линейных алгебра-
ических уравнений
уо = у1(2.3-17Ъ + у2(2.3-17Ъ + ^,
о а-с
У2=-У1+У2 + -^--
При фиксированных у1 и у2 при t -> <»
У^-^У^0,
Таким образом, траектория (у((0, У2(0) выпусков первой и
второй фирм с ростом номера t обладает свойством устойчивости
334
и сходится к равновесию 1 Штакельберга (y{J,1\ yf'l)) (рис. 8.38,
на котором видно, что если у2(0) > y2(f/1), то у2(2), у2(4), ... стре-
мятся ку2(5,1) сверху, ауДО.уДЗ),... стремятся к у^0 снизу. Если
yt(0) > У^1), то> очевидно, выпуски у1 первой фирмы будут стре-
миться ку^1) сверху, а выпуски у2 второй фирмы будут стремиться
ку21П) снизу). Случай равновесия 2 Штакельберга рассматривает-
ся аналогично.
8.8.3. Рассмотрим дуополию, когда издержки обеих фирм имеют
соответственно вид
С, = cly{ + dl, C2 = c2y2 + d2 и С]<с2,
т.е. МС{ < МС2. Для символов у,, у2 и у сохраняется старое толкова-
ние.
Принимается предпосылка, что вторая фирма (фирма-после-
дователь) полагает, что выпуск первой фирмы (фирмы-лидера)
335
(8.8.9)
фиксирован в производственном периоде, т.е. не изменяется в
данном периоде (т.е. Jy, /t/y2 = 0), что означает выполнение пред-
посылки Курно.
Для максимизации прибыли PR2 второй фирмы
PRi =РУ2 ~ с2у2 -d2 = (a- byx - by2)y2 - с2у2 - d2
необходимо использовать условие первого порядка
В силу предпосылки Курно о том, что выпуску первой фирмы
не изменяется в рассматриваемом периоде, т.е. dyx /dy2 = 0, ра-
венство (8.8.9) перепишется так:
= (° - с2) - Ьух - 2Ьу2 = 0,
^2
откуда следует, что выражение функции реакции второй фирмы
на объем выпуска первой фирмы
у
2 2Ь 2
(8.8.10)
(Р PR~
Условие второго порядка---= -2Ь < 0 выполняется,
ф
Для максимизации прибыли PRX первой фирмы
PRi =РУХ ~ С\У\ -dx = {a- byx - byjyx - схух - dx
используем условие первого порядка
dPR. , ч , dy-.
——1 = (а - с,) - 2Ьух - Ьу2 - Ьух = 0.
(8.8.11)
В силу того что принимается предпосылка
dy2 = 1
2’
условие первого порядка (8.8.11) для первой фирмы перепишется
так:
^• = (a-c1)-|z>y1-^2=0,
1
336
откуда следует, что функция реакции первой фирмы на объем вы-
пуска у2 второй фирмы имеет вид
(8812)
Условие второго порядка
выполняется, следовательно, задача максимизации прибыли PRX
решена.
Подставив (8.8.10) в (8.8.12), получим
v = 2 °~ci 2f°~C2 ^11
1 3 b 3( 2Ь 2 J
откуда следует, что
CD _ 1 а-2с,+с2 (8.8.13)
1 2 b
Подставив (8.8.13) в (8.8.10), получим
Ог1)_1я-2с2 ifl а-2с1+с2\_1 а+2сх-3с2
У1 ~2 b “2(2' b J 4 b
Найдем остальные характеристики равновесия 1 Штакельбер-
га, когда с, < с2:
v(*i) _ V(*D + v(^2) _ 1. За-2с, -с2 (8.8.14)
У У1 У1 4 b ’
/>(tfl)=a-Zyw = a + 2^|+C\
1 - (р -><’ -<'.=!• (°-2с'+сг)2 - </,,
о и
М?" -(F-e,)//1’-d2 =±.<ii±Ll^-d2,
+ _ 2.. (°~2ci +сг) + 1 ф (a+2c, — 3c2) _
, , 1 3a2 + 12c? +1 1Cj - 4ac. - 2ac, - 20c. c7 , ,
~d2=Te---------«----------------2-----d2.
22-7620
337
Полагая ct=с2 в выраженияхУ},г>, а также во всех форму-
лах, которые выписаны после формулы (8.8.14), получим все вы-
ражения строки Штакельберга — 1 табл. 8.3.
8.8.4. Переходим к случаю п фирм и предположим, что у первой
фирмы (фирмы-лидера) предельные издержки ct строго меньше
предельных издержек с2, ...,сп остальных фирм (фирм-последова-
телей), которые предполагаются равными, т.е. с{ < с2 =... = сп =
Общие издержки фирм имеют соответственно вид
Cj = clyl + dl, C2 = c^y2 + d2, ..., Сп = cfyn + dn.
Как и выше, символы ур у2,..., уп означают объемы выпусков
фирм с первой по л-ю в фиксированном периоде времени, так что
функция, обратная к функции рыночного (отраслевого) спроса,
имеет вид
p = a-b(yl +...+уп) = а-Ьу, где у=у^ ...+у„.
Аналогично случаю двух фирм (п = 2) принимается предпо-
сылка, что каждая фирма-последователь полагает, что выпуск
первой фирмы (фирмы-лидера) и любой другой фирмы-после-
дователя фиксирован в производственном периоде, т.е. в данном
периоде не меняется (т.е. dy} /dy2 = 0, ..., dyx /dyn = 0, dy( /dyj = 0,
I * J, i> J = 2,..., n), что означает выполнение предпосылки Курно.
Предпосылка Штакельберга о том, что полагает первая фирма
(фирма-лидер), приведена ниже.
Для максимизации прибыли PR,, i =2, ..., п, каждой фирмы-
последователя
PR,=РУ1 ~ - d. = (а - b(yx +у2 +... +У„))У,- - ciyl -d.=
= Ц - cz)y, - byx yt - ... - by] -... - byn yf - d,
необходимо использовать условие первого порядка
^i- = (a-ci)-byl-by2-...-2byi-...-byn=0 (8.8.15)
(dy, /dyt =... = dyl{ /dy.=dyM /dyt =... = dyn /dy.=0 согласно сделан-
ному выше предположению о том, что для каждой фирмы-после-
дователя выполняется предпосылка Курно).
Условие второго порядка
«<•?
выполняется.
338
Следовательно, выпуски у2, ...,уп всех фирм-последователей,
которые максимизируют прибыль этих фирм, удовлетворяют сис-
теме п - 1 линейных алгебраических уравнений, получаемых из
уравнений (8.8.15) путем их деления на Ь:
a-cf
2уг+у3+...+уп^—^—ух,
a-cf
У2+2у3 + ... + уп-^--У1,
a-cf
y1+yi+... + 2yn=—^—yv
Непосредственно проверяется, что определитель этой систе-
мы из п -1 уравнений с п -1 неизвестными равен п и сама система
имеет решения
1 a-Cf 1
yf = y2 = ... = у =-—у (8.8.16)
Выражения (8.8.16) представляют собой функции реакций фирм-
последователей.
Согласно предпосылке Штакельберга фирма-лидер полагает,
что каждая фирма-последователь реагирует на изменение объема
выпуска у1 первой фирмы-лидера по формуле (8.8.16) (т.е. умень-
шает объем своего выпуска, если фирма-лидер его увеличивает,
или, наоборот, увеличивает объем своего выпуска, если фирма-
лидер его уменьшает).
Из (8.8.16) следует, что
^2- = ... = ^- = --. (8.8.17)
dyx <fyx п
Для максимизации прибыли PRX фирмы-лидера
PRi =РУХ ~ схух - dx = {а - с,)^ - by] - by{y2 - ... - byxyn - dx
используем условие первого порядка (принимая во внимание ра-
венства (8.8.17)):
-^- = a-cl-2byl-fy2-...-byn+^—^-byl =0. (8.8.18)
22»
339
Условие второго порядка
d2PRx
dyx
_ л-1). л+1. Л
-2 +-- 6 =-----6<0
п ) п
выполняется.
Из равенства (8.8.18) получаем функцию реакции фирмы-ли-
дера
а-с, л+1
откуда следует, что
п а-с. п . .
_ л а-с, л(л —1)
л + 1 b л + 1
(8.8.19)
Последнее равенство цепочки (8.8.19) написано на основании
(8.8.16).
Из (8.8.16) и (8.8.19) получим объемы выпусков фирмы-лиде-
ра и всех фирм-последователей в равновесии 1 Штакельберга
(равновесие 1 означает, что лидером является первая фирма).
Имеем из (8.8.19) и (8.8.16)
v п a~ci <n~l)n la~cf 1 =
1 л+1 b л+1 л b пх
п а-с. п-\а~с/ л-1
—_________!_________£. -|___у
л + 1 b л + 1 b л + 1 *’
откуда получаем
у,=л
а-с,
26
_^D (8.8.20)
Имеем на основании (8.8.16) и (8.8.20)
1 а cf _ cf_____5. _ v(«i)
л 26 26 yf ‘
(8.8.21)
340
Общий объем выпуска всех п фирм (фирмы-лидера и остальных
(п - 1) фирм последователей) равен
У(Л|) = и(Л1) + (п -1)//0 = — + -—--—
1 f 2b п 2b
(8.8.22)
а рыночная ценар(Л|) равна
(1/1) L. (1/1) l( ~ ^1 Л —Cf
о'1' = а - д/ ° = a-bl 1 +---------------
у 2b п 2d ;
a + cx n-la~cf
2 п 2
(8.8.23)
С ростом числа п фирм выпуску^'1* каждой фирмы последова-
теля убывает (см. (8.8.21)), общий выпуск всех фирм-последовате-
лей также убывает, ибо
общий выпуск y(i,1) растет и приближается снизу к дроби
2а-с( -Су
2Ь ’
цена равновесия неограниченно приближается к дроби
О + С| в Су С| +Су
~2 2~= 2 ’
которая расположена между ct и Су (с1 < (С] + Су)/2 < Су).
Если с( = Су, то формулы (8.8.20)—(8.8.22) перепишутся так:
v(i/i) _ a~ci V(i/D _ 1 °~ci vst _ 2л-1а-с,
71 2b ’ п 2Ь ’ У п 2Ь ’
„dM) = а + с1 _ и~1а~с1
Р 2 п 2 '
Сопоставление моделей олигополии Курно и Штакельберга
аналогично сопоставлению этих моделей в случае дуополии. Чи-
тателю предлагается в этом убедиться самостоятельно.
341
8.9. Модели сговора в дуополии и олигополии
8.9.1. В модели сговора (в модели картеля) фирмы объединяются
в целях совместного принятия решения относительно рыночной
цены и общего объема выпуска, т.е. в модели сговора фирмы функ-
ционируют в режиме кооперативного поведения. Другими слова-
ми, разные фирмы на рынке выступают в качестве (одного) моно-
полиста.
Функция, обратная к функции рыночного (отраслевого) спро-
са, имеет видр = a-by (у=yt +у2), функции издержек обеих фирм
соответственно равны
Cj = cyj —С2 = су2 — d2.
Постоянные издержки dl и d2 неотрицательны, остальные па-
раметры а, Ь, с положительны.
Общая (совокупная) прибыль обеих фирм равна
PR=ру - С, - С2 = {а - с - by)y - d{ - d2.
Для максимизации общей прибыли PR используем условие
первого порядка
^ = (а-с)-2Ау = 0. (8.9.1)
dy
Условие второго порядка выполняется всегда:
Из равенства (8.9.1) следует, что общий выпуск у(т\ максими-
зирующий общую прибыль PR, равен
(т) _ °~с
У 2Ь ’
рыночная ценар(т), очевидно, равна
р{т) =а-Ьу{т) =^-
и максимальная общая прибыль PR(m) такова:
рЛ(т> = Р(т) (т) _ (т) _d d- 1 _d _d .
1 1 4 b 12
342
Напомним, что общая максимальная прибыль дуополии Кур-
но, т.е. общая прибыль двух фирм в равновесии Курно, равна
^2(0^^
следовательно, PR(m} > PR*.
Правило распределения объема общего выпуска у(т} по выпус-
кам и у2 отдельных фирм определяется вне рассматриваемой
модели.
В связи с тем что фирмы отличаются только своими постоян-
ными издержками, наиболее естественным является равное рас-
пределение объема общего выпуска у(и,) по фирмам: у. = у- = ——-.
1 2 4Z>
Каждая фирма получает свою часть PR\m\ i = 1, 2, общей мак-
симальной прибыли PR(m\
Мр".рмУ1 _СУ:
о и
о и
На рис. 8.39 показана контрактная линия L, имеющая уравне-
ние
а также изопрофиты первой и второй фирм, которые проходят
через точки контрактной линии L. Каждая точка В (в том числе
точка 27О) контрактной линии L показывает возможное распреде-
ление yt и уг общего выпуска у(и,) = по обеим фирмам. В каж-
дой точке В изопрофиты первой и второй фирм касаются: в точ-
ке Во под углом, равным тс/4; в точках В, расположенных на ли-
нии L ниже точки Во, под углом, меньшем, чем тс/4; в точках В,
расположенных на линии L выше точки Во, под углом, большим,
чем тс/4.
Точки контрактной линии L образуют границу Парето, ибо
при переходе от одной точки к другой на этой прямой прибыль
одной фирмы будет строго возрастать, а прибыль другой фир-
мы — строго убывать (см. рис. 8.39).
343
8.9.2. Проанализируем ситуацию, когда одна из двух фирм (на-
пример, первая) нарушает договор и увеличивает свой выпуск, зная,
что другая фирма будет соблюдать договоренность. На рис. 8.40
точка 2Г = (yj, у£) принадлежит контрактной линии L. Это означа-
ет, что фирмы, вступившие в сговор, поделили общий выпуск
а-с _ .
у( +у2 = таким образом, что первая фирма выпускает про-
дукцию в объеме у', а вторая — в объеме у'2. В этом случае рыноч-
ная цена р' равна
, .а-с а+с
Р 2Ь 2
максимальная прибыль РЛ, первой и максимальная прибыль PR2
второй фирмы равны
PR{ = Р'у{ ~ су{ ~ ~ .
РК1 = “d2 = ~d2-
344
Рис. 8.40
Если первая фирма, зная, что вторая фирма будет соблюдать
договоренность, решила смошенничать и увеличить свою при-
быль за счет увеличения объема выпуска своей продукции, она
соответственно из точки В' перейдет в точку Н, расположенную
на линии В{(у2) реакции первой фирмы на выпуск второй фирмы,
ибо на горизонтальной прямой только в точке Я прибыль пер-
вой фирмы будет наибольшей (изопрофита /т» соответствует при-
были т", которая строго больше прибыли Тр соответствующей
изопрофите /т,). Приведем результаты необходимых в такой ситу-
ации вычислений:
1 2Ь 2 ’
Р" = a-b(y"+ у2) = -\Wi< Р\
J1+^(y')2 =PPf + |/>(y')2
Р^'= {pn-c)y"-d2 = а-^у'2-d2-\btf2)2 = РЩ -|z>(^)2 < РК,.
L L L
345
Если точка В' (см. рис. 8.40) совпадает с точкой Вй (см. рис. 8.39),
то приведенные общие формулы конкретизируются следующим
образом:
, , а-с , а + с 1(а-с)2 , DD, 1(а-с)2 ,
* = * = — РЛ> = 8-7—4’
3 а-с За + 5с pp,,= 9_(^cf_d
Л| 8 8 1 64 b 1 32 b г
Таким образом, в условиях сговора у каждой (в частности, у пер-
вой) фирмы есть соблазн смошенничать путем увеличения объема
выпуска своей продукции (у">у\) и своей прибыли (PR"> PR1)
даже при понижении рыночной цены (р" < р') при условии, что
другая фирма будет соблюдать договоренность. Отсюда следует,
что сговор (картель) не может быть устойчивым рыночным обра-
зованием.
Итак, с одной стороны, в условиях сговора общая прибыль
обеих фирм может быть строго больше общей прибыли фирм в
равновесии Курно. С другой стороны, равновесие Курно пред-
ставляет собой устойчивое рыночное образование в отличие от
сговора, которое не является устойчивым рыночным образовани-
ем. Отсюда следует, что принятие решения фирмами, функцио-
нирующими в дуополии, по своей сути нетривиально и зависит от
вероятности склонности к мошенничеству этих фирм.
8.9.3. В случае олигополии имеем функцию р=а- Ьу,у=ух + ... +уп,
обратную к функции рыночного (отраслевого) спроса; функции
издержек п фирм соответственно равны
Cx=cyx+dx,...,C„ = cyn + dn.
Постоянные издержки dx, ..., уп неотрицательны, остальные
параметры а, Ь, с положительны.
Общая (совокупная) прибыль всех фирм равна
PR =ру-Сх - ...-Сп = ((а-с)~ by)y-dx -...-dn.
Для ее максимизации используем условие первого порядка
^- = (а-с)-2Ьу = 0. (8.9.2)
dy
346
Условие второго порядка
^ = -2*<0
dy2
не зависит от у, поэтому решение у<т) = -—- уравнения (8.9.2)
2Ь
есть общий выпуск всех п фирм, который обеспечивает их общую
прибыль.
Как и в случае дуополии, определяем рыночную цену
р(т) =а-Ьу(т) =~-
и максимальную общую прибыль PR(m)
PRM = р(т)у(т) _ _^= -d{-...-dn.
Правило распределения объема общего выпуска у(т) = ° — по
2Ь
выпускамУр ..., уп отдельных фирм определяется вне рассматри-
ваемой модели.
Как и в случае дуополии, наиболее естественным является
правило равномерного распределения общего объема выпуска у(т)
по фирмам:
1 а-с
У' ~--Уп
Каждая фирма получает свою часть PR9"\ i = 1, ..., п, общей
максимальной прибыли PR^m}:
рд<т> =(п<т>-c)v -d = a—-d = — ^a~c^2 -d
‘ (P )У‘ 1 2 In b 1 4n b ’’
Z = l, ...,«.
Ситуация, когда одна из фирм нарушает договоренность, увели-
чивая свой выпуск, а остальные фирмы договоренности не наруша-
ют, аналогична ситуации, проанализированной в случае дуополии.
8.10. Модели дуополии и олигополии Бертрана
8.10.1. Модель дуополии Бертрана представляет собой модель
ценовой, а не количественной дуополии. Для фирмы в дуополии
Бертрана постоянным является не объем выпуска фирмы-конку-
347
рента, а назначаемая конкурентом цена. Как и в случае модели
Курно, пусть две фирмы производят однородные продукты, име-
ют равные предельные издержки с, но теперь фирмы выбирают
цены, а не объемы выпускаемой ими продукции. В связи с тем что
продукты однородны, потребители приобретают продукты той
фирмы, которая предлагает меньшую цену. Если цена у обеих
фирм одна и та же, то, естественно, объем продаж у каждой фир-
мы будет один и тот же.
В рассматриваемом случае равновесие в дуополии Бертрана
достигается, когда ценаpt каждой фирмы становится равной пре-
дельным издержкам с, т.е. pf® = - с.
Если функция, обратная к функции рыночного спроса, имеет
вид р = а-Ьу,у =у( +у2, то прибыль каждой фирмы PRt равна
=РУ/ ~ СУ/ ~ = -dp /=1,2,
ибо р = рх = р2 = с. Выпуск каждой фирмы при этом, очевидно,
равен
д —С (ПХ (В) ( Д —С ]
—- = |у = у1+у2=— .
Таким образом, дуополия Бертрана функционирует как ры-
нок совершенной конкуренции (такая ситуация называется пара-
доксом Бертрана).
Для сравнения в случае дуополии Курно
v(Cou) _ (Сои) _ а-с (Сои) _ а + 2с
У ~Уг ~ ЗЬ’ Р ~ 3 ’
pR(Cou) = (а-с)2 _d^ pR(Cou) = (а-с)2
В равновесии Бертрана (когда цены фирм устанавливаются на
уровне предельных издержек с) ни одна фирма не заинтересована
изменять свою цену, равную предельным издержкам, если другая
фирма не будет этого делать. Действительно, если одна фирма
повышает цену (а другая этого не делает), она потеряет всех своих
покупателей. Если одна фирма понизит цену, которая будет уже
ниже предельных издержек (а другая фирма не станет этого де-
лать), то первая фирма, получив в свое распоряжение всех поку-
пателей, будет терять деньги и торговать себе в убыток.
Таким образом, в случае когда фирмы производят однородные
продукты, более естественно конкурировать с помощью объемов
(как у Курно) выпускаемой продукции, а не цен (как у Бертрана).
348
Построим линию спроса на продукцию одной (скажем, пер-
вой) фирмы дуополии. Пусть функция рыночного спроса имеет
вид
в р
У=Ь"Ь> У =
Если цена рр устанавливаемая первой фирмой, строго боль-
ше, чем цена р2 (т.е. р{ > р2), то, очевидно, первая фирма потеряет
всех своих покупателей и при рх > р2 линия спроса на продукцию
первой фирмы есть вертикальный полупромежуток [а,р2) на оси Opt
(рис. 8.41). ЕслиР] =р2, то величину D(p}) рыночного спроса фир-
мы первая и вторая поделят поровну. Тогда точка G на рис. 8.41
есть фрагмент линии спроса на продукцию первой фирмы. Нако-
нец, если р, < р2, то фрагментом линии спроса на продукцию пер-
вой фирмы является отрезок [Н, К\. Поскольку случай < с эко-
номического смысла не имеет, постольку точка К — последняя
точка этой линии спроса.
8.10.2. В случае когда фирмы в условиях дуополии выпускают
дифференцированные продукты, ценовая конкуренция является
вполне уместной.
349
Пусть функции спроса на продукцию каждой фирмы имеют
одни и те же параметры и выглядят так:
yx=h-gp{ + kp2, y2 = h-gp2 + kpv
Все параметры h, g, к — положительные постоянные.
Для максимизации прибыли
PR\ =Р\У\ ~gP\ + kPi) ~ di
первой фирмы используем условие первого порядка
= h - gp, + кр2 + (р. - с)| -g+к^2-1 = -2gpl + h+кр2 + cgt = О
(по аналогии со случаем Курно в модели дуополии Бертрана при-
нимается предпосылка о том, что dp2 /dpx = Qv.dp{ /dp2 = 0. Это
содержательно означает, что каждая из фирм полагает, что в тече-
ние производственного периода другая фирма не меняет цену на
свою продукцию). Отсюда получаем функцию реакции R{(pJ) пер-
вой фирмы на цену р2, которую назначает вторая фирма:
А=А/’2+^(^(/’2))- (8.10.1)
Условие второго порядка
d2PR. dp-
——i- = -2g+k-p- = -2g<0
dp2 dPl
для точки максимума прибыли PR{ выполняется.
По аналогии на основании решения задачи максимизации
прибыли
PR2 =РтУ2 -^-d^fy- c)(h-gp{ + кр2) - d2
второй фирмы получаем функцию реакции R2(p^ второй фирмы
на цену pv которую назначает первая фирма:
к cg+h,B . ..
Pi = 2jP1 + 2F Л ’ (8.10.2)
Если к < 2g (с содержательной точки зрения естественно, что
к <g), графики функций R2(p{) и /?,(р2) должны иметь углы накло-
нов с осями Ор( и Ор2 соответственно, которые меньше л/4 (45’)
(рис. 8.42).
350
Рве. 8.42
Точка В пересечения графиков функций Л^) и Rx(p2) имеет
координаты и р^, которые по экономическому смыслу долж-
ны быть больше предельных издержек с.
Решая систему уравнений (8.10.1) и (8.10.2), найдем явное вы-
ражение для р^ и р^:
(В) _ cg+h _ (В)
р' -гг-к-ъ
Точка В = (р^,?^) (см. рис. 8.42) представляет собой геометри-
ческую интерпретацию равновесия Бертрана в дуополии Бертрана.
Отметим, что линии реакции (графики функций реакций
R2(px) и 7?j(p2)) являются восходящими. Это содержательно озна-
чает, что прибыль каждой фирмы растет с ростом цены на ее про-
дукцию. Напомним, что в случае дуополии Курно линия реакции
каждой фирмы была нисходящей. Это содержательно означало,
что прибыль фирмы растет по мере понижения ее выпуска.
8.10.3. Из (8.10.1) и (8.10.2) получаем, что
*L. *->0, ^. = ±>0.
Ф2 2g dpx 2g
Это противоречит предпосылке о том, что dp2 /dpx = Q,dpx /dp2 = 0.
351
Как и в случае дуополии Курно, противоречие элиминирует-
ся, если от статики в (8.10.1) и (8.10.2) перейти к динамике:
^0+D = ^ft(0+^, (8.10.3)
Р2(/ + 1) = ^р1(/)+^^. (8.10.4)
Для однородной системы, соответствующей неоднородной
системе (8.10.3), (8.10.4),
?1(/+1) = у-Р2(0»
«2<Г + 1) = ~«2(О,
выпишем характеристическое уравнение
ГДеЛ = С/2«
системы.
к/2g}
0 )
— матрица однородной (неоднородной)
Найдем правые собственные векторы матрицы А, соответству-
к к
ющие собственным числам X, = —, X, =-----:
1 2g 2 2g
откуда получаем, что
V1 — и2 — ( О
^1/ (-1/
Общее решение однородной системы имеет вид (в векторной
форме)
9(0 = У/1Х{ + у2И2Х',
где у( и у2 — произвольные.
352
В координатной форме общее решение q(f) имеет вид
( к \ ( к \
?1(О = гХ + у2Х'=у1 — + у2 ,
= У- у2*2 = Y1 - У2 •
Частное решение неоднородной системы (8.10.3), (8.10.4)
отыскиваем в виде p(t) = где т| — скалярная величина.
Имеем на основании (8.10.3), (8.10.4)
n = vn+—;—. n = Y~B+-z—.
2g 2g 2g 2g
откуда вытекает, что
^5 /V
Следовательно, общее решение неоднородной системы (8.10.3)
(8.10.4) имеет вид
а<')=т.(^] +л<'>’
,2<',=1',й) +р^'
Если/>](0) = p°t,р2(0) = р2, то для определения значений произ-
вольных постоянных у, и у2 следует решить систему линейных ал-
гебраических уравнений
Рх^х + Ъ+Рх*^
Р2=Ух~У2+Р2В)-
При фиксированных у, и у2 при t -> «> и при к < 2g
23 - 7620
353
Таким образом получено аналитическое решение неоднород-
ной системы (8.10.3), (8.10.4) и доказана устойчивость равновесия
Бертрана. Имеем ситуацию, аналогичную случаям равновесия
Курно и Штакельберга.
Рисунок 8.42 наглядно демонстрирует, как текущие цены
р2(0),р2(2),... приближаются к ценер^, а текущие цены р,(1),...
приближаются к цене р\в\
8.10.4. Если прибыль PRX = т,, то соответствующая изопрофи-
та /Т| первой фирмы имеет уравнение (р, - c)(h-gpx + кр2) -dx = т,.
Положим
F(px, Р2) = P\h ~ сЛ - gpl + cgpx + кр2рх - кср2,
тогда уравнение изопрофиты /Т| перепишется так:
F(px,pJ = \ + dv
Имеем
dF(px,p2) 2 + +к , dF(px,p2) _ _с).
ЭР1 Эр2
Если рх - с > 0, то уравнение F(px, р2) = т, + dx изопрофиты /т
определяет р2 как неявную функцию переменной рх. По теореме
о неявной функции
Ы\рх,р2)
dp2 _ Эр, _ h-2gpx +cg+kp2
dpx~ dF(px,p2) ~ k(px-c)
Ър2
Условие первого порядка в рассматриваемом случае имеет вид
^- = 0, т.е. h-2gp. +cg + kpj =0,
dp,
откуда следует, что
к , h+cg
Р'=2~^ + ЧГ’
что представляет собой функцию Л,(р2) реакции первой фирмы.
354
„ h h + cg dp, h h + cg
При p, < —p, + - имеем —- < 0, при p. > — p, +
л 2g 2 2g dpt и л 2g 2 2g
dp, ~
имеем —- > 0, т.е. выполнено первое достаточное условие мини-
4Р1
мума для изопрофиты /т первой фирмы, откуда следует, что изо-
профита PRX = Т| первой фирмы пересекает линию реакции Rx(p2)
в своей самой низкой точке, т.е. в минимальной точке.
На основании теоремы о неявной функции
d2p2 2~gP}+h + kp2
dp2 *(р,-с)2
Неравенство
£Л>0 (8-10.5)
ф2
является достаточным условием выпуклости вниз изопрофиты
PRX = X, первой фирмы. Неравенство (8.10.5) эквивалентно нера-
венству -gPj + h + кр2 > 0, множество решений которого состоит из
всех точек (р,, р2), расположенных левее и выше прямой -gp( + h +
, п „ к h
+ кр2 = 0, уравнение которой можно переписать так: р, = — р2 + —.
h к h 88
Если с < —, то прямая рх = — р2 +—расположена выше (по оси
прямой Rx(pJ) и имеет более крутой наклон относительно оси Ор2,
чем прямая Л,^), имеющая уравнение
к h+cg
(рис. 8.43).
Таким образом, все изопрофиты PRX = т, первой фирмы есть
линии, выпуклые вниз к оси Орр которые пересекают линию Rx(p^)
реакции первой фирмы в своих самых низких точках. Аналогично
все изопрофиты PR2 = т2 второй фирмы есть линии, выпуклые вле-
во к оси Ор2, которые пересекают линию Л2(р,) реакции второй
фирмы в своих самых крайних левых точках (рис. 8.44).
При движении по линии реакции Rx(p2) вверх мы переходим на
изопрофиты первой фирмы, которые соответствуют все большим
значениям прибыли первой фирмы. Это обстоятельство естествен-
ным образом аргументируется как содержательными (чем выше це-
ны, тем выше прибыль фирмы), так и формальными (можно найти
23*
355
рис. 8.44
производную прибыли PRt по направлению линии Л,(р2) реакции
первой фирмы в любой ее точке) соображениями (см. рис. 8.44). Для
изопрофит второй фирмы ситуация аналогичная (см. рис. 8.44).
Сопоставление дуополии Бертрана с дуополией Курно пока-
зывает, что эти дуополии представляют собой антиподы. В случае
дуополии Курно линии реакции фирм являются нисходящими,
изопрофиты выпуклы вверх и вправо и с ростом прибыли фирм
изопрофиты перемещаются вниз и влево.
В случае дуополии Бертрана линии реакции фирм являются
восходящими, изопрофиты выпуклы вниз и влево и с ростом при-
были фирм изопрофиты перемещаются вверх и вправо.
8.10.5. Проиллюстрируем суть равновесия Бертрана В = (р\в\ р^)
как частный случай равновесия Нэша на рис. 8.44. Если фирма
устанавливает цену р(2В\ а первая фирма уменьшает свою цену
(с />|Л) до Pj) или увеличивает ее (с р^ до Д), то первая фирма
уменьшает свою прибыль, переходя с изопрофиты (т|Л — при-
быль первой фирмы, если фирма устанавливает цену р\®) на более
низкую изопрофиту (содержащую точки (р(, р^), (р{, р^У). Это оз-
начает, что первой фирме в одиночку не выгодно менять цену р^,
если вторая фирма не меняет свою ценур^. Ситуация, когда пер-
вая фирма не меняет цену p,S), а вторая фирма меняет цену р^,
анализируется аналогично. Таким образом, равновесие Бертрана
В = (р\в\ р^) есть равновесие Нэша.
В случае когда параметры функции спроса обеих фирм отли-
чаются между собой:
У}=Ai SiPi+kiP2> у2=h2 ~s2p2+Vp
аналитические построения усложняются, но качественный харак-
тер результатов существенно не корректируется.
Напомним, что задача оценки параметров функций спроса
как отдельных фирм, так и рыночного спроса (в частности, в слу-
чаях Курно и Бертрана) представляет собой, как правило, серьез-
ную прикладную проблему.
При переходе от дуополии к олигополии Бертрана ситуация
качественным образом сильно не изменится. В случае однород-
ной продукции развитие рынка идет в режиме ценовой войны,
в которой все фирмы в конце концов установят цену на уровне
357
предельных издержек и олигополия превратится в рынок чистой
конкуренции. Общий объем выпуска определяется линией ры-
ночного спроса и равен -—объем выпуска каждой фирмы при
и “ с
этом будет равняться л-й части общего объема, т.е.-. Напом-
nb
ним, олигополия Курно переходит в рынок чистой конкуренции
только в случае, когда п -> +«>.
В случае дифференцированной продукции (как и в случае дуо-
полии) вводится понятие равновесия по Бертрану и демонстриру-
ется его устойчивость.
Вопросы для самоконтроля к главе 8
1. Что представляют собой условия первого и второго порядка для зада-
чи максимизации фирмой-монополистом своей прибыли?
2. Что представляет собой геометрическая интерпретация условия вто-
рого порядка для задачи максимизации фирмой-монополистом сво-
ей прибыли?
3. Что такое производственный период и временной промежуток в за-
даче максимизации фирмой-монополистом своей прибыли?
4. Что такое краткосрочный и долговременный промежутки в задаче
максимизации фирмой-монополистом своей прибыли? В чем сход-
ство и различие этих понятий?
5. Что представляет собой достаточное условие ухода фирмы-монопо-
листа со своего рынка в случае краткосрочного промежутка? Ответ
обоснуйте.
6. Каким образом фирма-монополист выбирает «оптимальный» вари-
ант своего функционирования в текущем периоде в случае долговре-
менного промежутка?
7. Что такое монопольная власть? Что представляют собой три источ-
ника монопольной власти?
8. Чему равен индекс Лернера монопольной власти?
9. Как на индекс Лернера фирмы влияют линия спроса и эластичность
спроса на продукцию фирмы?
10. Чему равен индекс Хиршмана-Херфиндаля концентрации фирм на
рынке?
11. Что такое естественная монополия?
12. Что представляет собой второе наилучшее решение регулирования
естественной монополии? Какие существуют альтернативные вари-
анты регулирования естественной монополии?
13. Что такое конкуренция по Демзетцу?
358
14. Что такое ценовая дискриминация первого рода? Идеальная ценовая
дискриминация? (Приведите примеры фрагментов экономической
реальности, которые допускают использование ценовой дискрими-
нации первого рода.)
15. Что представляет собой условие участия потребителя в рыночной
ситуации? Дайте содержательную экономическую интерпретацию
величин, фигурирующих в условии участия.
16. Что такое оптимальный контракт между фирмой-монополистом и
потребителем? Дайте содержательную экономическую интерпрета-
цию координатам оптимального контракта.
17. Что представляют собой линейная схема ценообразования (линей-
ный тариф) и нелинейная схема ценообразования (нелинейный та-
риф)? Что такое двухкомпонентный тариф?
18. Какова взаимосвязь между максимальной прибылью фирмы-моно-
полиста, не использующей и использующей ценовую дискримина-
цию первого рода (в случае предельных издержек)?
19. Что такое совокупная дополнительная прибыль фирмы-монопо-
листа?
20. Что такое ценовая дискриминация второго рода? (Приведите приме-
ры фрагментов экономической реальности, которые допускают ис-
пользование ценовой дискриминации второго рода.)
21. Что такое пакетная (ценовая) дискриминация?
22. Что такое условие самовыявления потребителя?
23. Задача максимизации прибыли монополии в случае пакетной дис-
криминации. Постановка задачи и ее решение.
24. Сформулируйте постановку и решение задачи максимизации в слу-
чае двухкомпонентного тарифа.
25. Приведите результаты сравнительного анализа максимизации при-
были фирмы-монополиста в случае пакетной дискриминации и
двухкомпонентного тарифа.
26. Какова взаимосвязь между максимальной прибылью фирмы-моно-
полиста, не использующей и использующей ценовую дискримина-
цию второго рода (в случае постоянных предельных издержек)?
27. Какова взаимосвязь между ценовыми дискриминациями первого и
второго рода?
28. Что такое ценовая дискриминация третьего рода? (Приведите при-
меры фрагментов экономической реальности, которые допускают
использование ценовой дискриминации третьего рода.)
29. Чему равна максимальная прибыль фирмы-монополиста, исполь-
зующей ценовую дискриминацию третьего рода на двух рыночных
сегментах (в случае постоянных и непостоянных предельных изде-
ржек)?
30. Какова взаимосвязь между ценами фирмы-монополиста на двух ры-
ночных сегментах и между эластичностями спроса по этим ценам?
359
31. Для описания функционирования каких фрагментов экономической
реальности целесообразно использовать модель монополистической
конкуренции?
32. Что представляет собой модель двух линий спроса фирмы, функцио-
нирующей в условиях монополистической конкуренции?
33. Как фирма, функционирующая в условиях монополистической кон-
куренции, решает задачу максимизации своей прибыли в случае
краткосрочного промежутка?
34. Как фирма, функционирующая в условиях монополистической кон-
куренции, решает задачу максимизации своей прибыли в случае
долговременного промежутка?
35. Как фирма решает задачу максимизации своей прибыли в случае
учета расходов на рекламу?
36. Могут ли меры по стимулированию спроса путем расходов на рек-
ламу привести к снижению цены на продукцию фирмы и повыше-
нию ее прибыли? (Ответ обоснуйте с помощью геометрических
построений.)
37. Могут ли меры по стимулированию спроса путем расходов на рек-
ламу привести к повышению цены на продукцию фирмы и сниже-
нию ее прибыли? (Ответ обоснуйте с помощью геометрических
построений.)
38. Могут ли меры по стимулированию спроса путем расходов на рек-
ламу привести к снижению цены на продукцию фирмы и сниже-
нию ее прибыли? (Ответ обоснуйте с помощью геометрических
построений.)
39. Могут ли меры по стимулированию спроса путем расходов на рекла-
му привести к повышению цены на продукцию фирмы и повыше-
нию ее прибыли? (Ответ обоснуйте с помощью геометрических по-
строений.)
40. Может ли выпуск фирмы упасть в результате принятых ею мер по
стимулированию спроса путем расходов на рекламу? (Ответ обос-
нуйте с помощью геометрических построений.)
41. Что представляет собой основная предпосылка Курно в модели дуо-
полии Курно? (Дайте экономическую интерпретацию этой предпо-
сылки.)
42. Что представляет собой функция реакции и линия реакции фирмы
на выпуск другой фирмы в дуополии Курно? (Рассмотрите статичес-
кий и динамический варианты.)
43. Что представляет собой изопрофита фирмы в модели количествен-
ной дуополии? Какая существует взаимосвязь между изопрофитами
и линиями реакции фирм в дуополии Курно?
44. Что такое равновесие Курно в случае двух фирм? (Дайте геометри-
ческую интерпретацию.) Докажите, что равновесие Курно - это
частный случай равновесия Нэша.
360
45. Как выглядят результаты сопоставления цены, общего выпуска и
максимальной прибыли дуополии Курно с ценами, общим выпуском
и общей прибылью в случае чистой конкуренции и чистой монопо-
лии?
46. Что представляет собой статический и динамический варианты функ-
ций (линий) реакции в случае дуополии Курно?
47. Что понимается под устойчивостью равновесия Курно? (Дайте гео-
метрическое пояснение и аналитическое обоснование.)
48. Что представляет собой модель олигополии Курно?
49. Как определяется равновесие олигополии Курно?
50. Как выглядят результаты сопоставления цен, общего выпуска и мак-
симальной прибыли олигополии Курно, когда число п фирм олиго-
полии равно п = 1 (случай чистой монополии), п = 2 (случай дуопо-
лии), п -»+оо (случай чистой конкуренции)?
51. Чему равен индекс Лернера олигополии Курно? Чем определяется
индекс Лернера олигополии Курно?
52. В чем экономическая суть предпосылок Штакельберга о поведении
фирм дуополии в производственном периоде?
53. Как определяется равновесие Штакельберга в случае дуополии?
54. Как выглядят основные характеристики равновесия по Штакельбер-
гу в случае дуополии (выпуски обеих фирм, цена равновесия, макси-
мальная прибыль каждой фирмы, суммарная максимальная при-
быль)?
55. Как выглядят результаты сопоставления основных характеристик
равновесий Курно и Штакельберга в случае дуополии (выпуски обе-
их фирм, цены равновесия, максимальная прибыль каждой фирмы,
суммарная максимальная прибыль)?
56. Что представляют собой изопрофиты обеих фирм в равновесии Кур-
но и Штакельберга?
57. Что представляют собой статический и динамический варианты
функций (линий) реакции фирм в случае дуополии Штакельберга?
58. Что понимается под устойчивостью равновесия Штакельберга?
(Дайте геометрическое и аналитическое обоснования.)
59. Как выглядят основные характеристики равновесия Штакельберга
в случае дуополии, в которой фирмы имеют разные предельные
издержки?
60. Что представляет собой модель олигополии Штакельберга?
61. Как определяется равновесие олигополии Штакельберга?
62. Как выглядят результаты сопоставления цен, выпусков и значений
максимальной прибыли олигополии Штакельберга, где число п
фирм олигополии меняется от двух до бесконечности?
63. Как выглядят результаты сопоставления основных характеристик
равновесия по Курно и по Штакельбергу в случае олигополии?
361
64. Что представляет собой модель сговора в случае двух (и большего
числа) фирм?
65. Как выглядят основные характеристики равновесия дуополии (оли-
гополии) в случае сговора (общий выпуск фирм, цена, общая макси-
мальная прибыль)? Покажите на примере неустойчивость равнове-
сия в случае сговора.
66. Что представляют собой изопрофиты фирм в равновесии в случае
сговора двух фирм?
67. Как выглядят результаты сопоставления основных характеристик
равновесия по Курно и по Штакельбергу в случае сговора для двух
(и большего числа) фирм?
68. Как формулируются основные предпосылки модели дуополии Берт-
рана в случае недифференцированных и дифференцированных про-
дуктов?
69. Как выглядит линия спроса на продукцию фирмы в случае дуополии
Бертрана? Ответ обоснуйте.
70. В чем суть парадокса Бертрана?
71. Как определяется равновесие по Бертрану в случае дифференциро-
ванных продуктов для двух фирм?
72. Что представляют собой статический и динамический варианты
функций (линий) реакции фирм в случае дуополии Бертрана?
73. Что понимается под устойчивостью равновесия по Бертрану? (Дайте
геометрическое и аналитическое обоснование.)
74. Что представляют собой изопрофиты обеих фирм в модели ценовой
дуополии?
75. Как выглядят результаты сопоставления основных характеристик
равновесия (для двух (и большего числа) фирм) Курно, Штакельбер-
га, Бертрана, а также в случае чистой конкуренции (п -» +<») и чистой
монополии (п = 1)?
Задачи и упражнения для самоконтроля к главе 8
1. У фирмы-монополиста функция АС имеет вид АС (у)=0,25(у - 2)2+9,25.
Функция AR(y) = 10 - (у/3):
а) определите: функции МС и MR, а также у(да) и р(т\ при которых
PR{m} будет максимальной;
б) дайте геометрическую интерпретацию функциям АС(у), МС(у),
AR(y), MR(y), а также величинам у(/я), р(да), Я(у(/я)), С(у(да)) и
РЯ(у(/я)).
2. Эластичность спроса на продукцию фирмы равна: a) Ed=-4; б) Ed=6.
Определите индекс Лернера монопольной власти фирмы в слу-
чаях а) и б).
362
3. Предельные издержки МС фирмы равны МС = 10, а цена (р) одной
единицы продукции фирмы равна 15. Определите индекс Лернера
монопольной власти фирмы.
4. Максимальная прибыль фирмы равна 1000 д.е., доход фирмы со-
ставляет 6000 д.е. Определите индекс Лернера монопольной власти
фирмы.
5. Максимальная прибыль фирмы равна 2000 д.е., объем продукции
фирмы равен 1000 д.е., каждая из которых реализуется по цене, рав-
ной 5 д.е. Определите индекс Лернера монопольной власти фирмы.
6. На рынке функционируют 10 фирм, имеющих следующие рыночные
доли: Sj = 0,2, s2 = s3 = 0,15, s4=s5 = s6 = 0,1, s7 = s8 = s9 = s10 = 0,05. Най-
дите индекс Хиршмана — Херфиндаля концентрации фирм на рынке.
7. Средние издержки АС(у) естественной монополии имеют вид АС(у) =
= 3у“1/2:
а) определите предельные издержки МС(у)\
б) решите задачу максимизации прибыли PR м естественной моно-
полии, определите у(да), р^т\ а также РА(л°;
в) определите у^г\ р^г\ и PR^ = р^у^ - С(у<0) (см. рис. 8.11);
г) определите у(я), р(п\ и РА(с) = р(с)у(с) - С(у(с)) (см. рис. 8.11).
8. Средний доход ЛА (у) фирмы-монополиста имеет вид AR=60 - (у/2),
предельные издержки МС(у) постоянны и равны МС(у) = 25:
а) решите задачу максимизации прибыли фирмы, определив y(w), р(т)
иРА(т);
б) определите прибыль фирмы, если она применяет ценовую дис-
криминацию первого рода.
9. Фирма-монополист имеет два сегмента рынка, на каждом из кото-
рых функция, обратная к функции спроса, имеет вид ARX = 18 -у} и
AR2 = 24 - 2уг Предельные издержки фирмы постоянны и равны
Ж?=13:
а) определите выпуску}"0, ценур}ш) и максимальную прибыль PR^
фирмы в первом сегменте;
б) определите выпуску}"0, ценур}"° и максимальную прибыль PR^
фирмы во втором сегменте;
в) определите суммарный выпуск у = у}"° + y}w) и суммарную при-
быль РА = РА<"° + РА}"°;
г) выпишите уравнение линии рыночного спроса ЛА (путем сложе-
ния по горизонтали линий спроса ЛА, и ЛА2) и линии предельно-
го дохода MR. Постройте эти линии ЛА и Л/А;
д) определите выпуск у("°, ценур("° и максимальную прибыль РВ№
фирмы в условиях отсутствия ценовой дискриминации третьего
рода;
е) сопоставьте величины у и y(w), а также РА и РВ№ и сделайте со-
держательные выводы на основании результатов сопоставления.
363
10.
Фирма-монополист имеет два сегмента рынка, в каждом из кото-
рых функция, обратная к функции спроса, имеет вид ЛЛ, = 18 -yj и
14
AR2 = 24 - 2ут Предельные издержки фирмы равны МС = 12 + —у:
а) постройте линии ARX и AR2,
б) выпишите уравнения линий MRX и MR2 и постройте их;
в) выпишите уравнение линии MR = MRX + MR2 и постройте ее;
г) далее выполните все пункты а)-е) предыдущей задачи 2.
Дайте геометрическую интерпретацию ситуации, когда меры по сти-
мулированию спроса путем расходов на рекламу приводят к повыше-
нию цены и прибыли.
12. Обоснуйте прохождение изопрофиты, соответствующей максималь-
- ~ м(*1) т- (а~с а-с । п u
нои прибыли PR , через точку F = -----,---- . Дайте геометри-
4b 4Ь )
ческую интерпретацию.
13. Найдите производную функции
а-с 1 (а-с)2 1
^=—-^"8—<
графиком которой является изопрофита, соответствующая макси-
мальной прибыли PR( , в точке у. =----. Дайте геометрическую
4Ь
интерпретацию.
14. Докажите, что изопрофиты, соответствующие максимальным при-
_ г (а-с а-сЛ п „
былям PR< и PR, , касаются в точке F = -----,---- . Дайте гео-
4b 4b J
метрическую интерпретацию.
15. Найдите для изопрофиты lx (t\) dy2 /dyx в точке ее пересечения с конт-
а — с ♦
рактной прямой ух + у2 = ——. Найдите для изопрофиты /2(/2) dy2/dyx
а —с
в точке ее пересечения с контрактной прямой ух + у2 =
16. В отрасли с функцией (отраслевого) спроса У= 2000 - ЗОр функцио-
нируют 100 фирм, которые выпускают однородный продукт и каждая
из которых имеет функцию предельных издержек, равную МС= 20+у.
Здесь Y — объем отраслевого выпуска; у — объем выпуска каждой
фирмы; р — цена одной единицы выпускаемой фирмами продукции.
Все эти величины «привязаны» к одному производственному перио-
ду (равному, например, одному году) (расчеты во всех пунктах про-
водите с тремя знаками после запятой):
а) пусть все фирмы отрасли объединились в картель. Картель максими-
зирует суммарную прибыль.
Определите рыночную цену одной единицы продукции фирм, вы-
пуск (отраслевого) картеля, его максимальную прибыль, выпуск
364
каждой фирмы, индекс Лернера картеля. Дайте геометрическую ин-
терпретацию для этого пункта;
б) пусть каждая фирма отрасли максимизирует прибыль в условиях
чистой конкуренции.
Определите рыночную цену одной единицы продукции фирм, вы-
пуск каждой фирмы, максимальную прибыль каждой фирмы, отрас-
левой выпуск, максимальную отраслевую прибыль. Дайте геометри-
ческую интерпретацию этого пункта;
в) пусть 25 фирм отрасли объединились в картель, а остальные фирмы
образуют конкурентное окружение картеля и действуют как фирмы-
последователи. Найдите рыночную цену одной единицы продукции
фирм, выпуск и прибыль каждой фирмы конкурентного окружения,
картеля, всей отрасли, индекс Лернера для картеля. Дайте геометри-
ческую интерпретацию этого пункта;
г) пусть 50 фирм отрасли объединились в картель, а остальные фирмы
образуют конкурентное окружение картеля и действуют как фирмы-
последователи. Найдите рыночную цену одной единицы продукции
фирм, выпуск и прибыль каждой фирмы конкурентного окружения,
картеля, всей отрасли, индекс Лернера для картеля. Дайте геометри-
ческую интерпретацию этого пункта;
д) пусть 75 фирм отрасли объединились в картель, а остальные фирмы
образуют конкурентное окружение картеля и действуют как фирмы-
последователи. Найдите рыночную цену одной единицы продукции
фирм, выпуск и прибыль каждой фирмы конкурентного окружения,
картеля, всей отрасли, индекс Лернера для картеля. Дайте геометри-
ческую интерпретацию этого пункта.
Вопросы и тесты для контрольных работ к главе 8
1. Функция, обратная к функции спроса на продукцию монополии,
имеет вид р = а-Ьу. Пусть y(w) и у— выпуски монополии, которые
соответственно максимизируют прибыль монополии и ее доход.
Тогда:
a) y(w) > у(w);
б)
в) у(т) < у(w);
г) нет однозначного ответа.
2. Точка Е пересечения линий MR и МС фирмы-монополиста опреде-
ляет объем выпуска/*0, максимизирующий ее прибыль, если:
а) касательные линий MR и МС в точке Е совпадают;
б) касательная к линии МС в точке Е Ьълее пологая относительно
горизонтальной оси Оу, чем касательная к линии MR в этой
точке;
365
в) касательная к линии MR в точке Е более пологая относительно
горизонтальной оси Оу, чем касательная к линии МС в этой
точке;
г) нет однозначного ответа.
3. Индекс Лернера монопольной власти равен:
а) /"> 5
б) норме прибыли фирмы (т.е. отношению максимальной прибыли
фирмы к ее доходу);
в) отношению средней прибыли фирмы к цене
г) варианты а)—в) верны;
д) варианты а)—в) не верны.
4. С ростом числа фирм на рынке индекс Хиршмана — Херфиндаля:
а) возрастет;
б) становится сколь угодно малым;
в) варианты а) и б) верны;
г) нет однозначного ответа.
5. Для регулирования естественной монополии второе наилучшее ре-
шение означает, что для определения объема выпуска продукции и
цены выбирается:
а) точка пересечения линий MR (у) и МС(у)\
б) точка пересечения линий АС(у) и AR(y);
в) точка пересечения линий МС(у) и AR(y)\
г) варианты а)—в) не верны.
6. Если фирма-монополист имеет постоянные предельные издержки, то:
а) ценовая дискриминация первого рода представляет собой асимп-
тотический непрерывный вариант дискретной дискриминации
второго рода;
б) ценовая дискриминация первого рода представляет собой асимп-
тотический непрерывный вариант дискретной дискриминации
третьего рода;
в) ценовая дискриминация второго рода есть частный случай цено-
вой дискриминации третьего рода;
г) ценовая дискриминация третьего рода есть частный случай це-
новой дискриминации второго рода;
д) все варианты а)—г) не верны.
7. Если фирма-монополист имеет растущие предельные издержки
МС(у), то при ценовой дискриминации третьего рода:
а) объем умаксимизирующий прибыль фирмы в первом сегмен-
те, строго больше объема у который представляет собой абс-
циссу точки пересечения линии предельного дохода MRx(y)
фирмы в первом сегменте с линией предельных издержек МС(у)
фирмы;
366
б) объем максимизирующий прибыль фирмы в первом сегмен-
те, строго больше объема у2(да), который представляет собой абс-
циссу точки пересечения линии предельного дохода MR2(y)
фирмы в первом сегменте с линией предельных издержек МС(у)
фирмы;
в) объем умаксимизирующий прибыль фирмы в первом сегмен-
те, строго меньше объема у который представляет собой абс-
циссу точки пересечения линии предельного дохода MRx(y)
фирмы в первом сегменте с линией предельных издержек МС(у)
фирмы;
г) объем у{”\ максимизирующий прибыль фирмы во втором сег-
менте, строго меньше объема у2(да), который представляет собой
абсциссу точки пересечения линии предельного дохода фирмы в
первом сегменте с линией предельных издержек МС(у) фирмы;
д) оба варианта б) и в) верны;
е) оба варианты в) и г) верны.
8. Фирма, функционирующая в условиях монополистической конку-
ренции, имеет две линии спроса, ибо:
а) продукт этой фирмы сильно отличается от продуктов, выпуска-
емых другими фирмами;
б) продукт этой фирмы слабо отличается от продуктов, выпуска-
емых другими фирмами;
в) другие фирмы не реагируют на изменение цены этой фирмой;
г) другие фирмы реагируют на изменение цены этой фирмой;
д) оба варианта а) и в) верны;
е) оба варианта в) и г) верны.
9. При стимулировании спроса путем рекламной кампании фирма в
случае долговременного промежутка:
а) может понизить цену и снизить свою прибыль;
б) может понизить цену и повысить свою прибыль;
в) может повысить цену и повысить свою прибыль;
г) может повысить цену и снизить свою прибыль;
д) все варианты а)-г) верны.
10. Изопрофиты фирмы (скажем, фирмы Т^), функционирующей в дуо-
полии Курно:
а) в своих самых высоких точках пересекают ее линию реакции
CKjO'P) на выпуск другой фирмы;
б) пересекают ее линию реакции (R{ (у2)) на выпуск другой фирмы в
своих самых высоких точках;
в) при движении вдоль линии реакции (R{ (у2)) сверху вниз перехо-
дят от изопрофит с большей прибылью к изопрофитам с мень-
шей прибылью;
г) в точках пересечения с линией реакции (R{(y2)) имеют верти-
кальные касательные.
367
11. Изопрофита первой фирмы, проходящая через точку равновесия Е™:
а) касается изопрофиты второй фирмы, проходящей через точку
равновесия £(5/2);
б) касается изопрофиты второй фирмы, проходящей через точку
g(cou).
в) расположена выше изопрофиты первой фирмы, проходящей че-
рез точку
12. Изопрофиты фирмы (скажем, фирмы Гр, функционирующей в дуо-
полии Бертрана:
а) пересекают ее линию реакции (Rx(pJ) в своих самых высоких
точках;
б) пересекают ее линию реакции (Лj (р2)) в своих самых низких точ-
ках;
в) при движении вдоль линии реакции (Rx(pJ) сверху вниз осу-
ществляется переход от изопрофит с меньшей прибылью к изо-
профитам с большей прибылью;
г) в точках пересечения с линией реакции {R^ip^)) имеют верти-
кальные касательные.
Задачи для контрольных работ к главе 8
1. Фирма-монополист имеет два сегмента рынка, в каждом из которых
функция спроса имеет вид = 18 -р, у2 = 24 - 2р. Предельные издер-
жки фирмы постоянные и равны МС = 10:
а) постройте линии AR{ и AR2,
б) выпишите уравнения линий MR{ и MR. и постройте их;
в) определите выпуски у{*\ у%*\ цены p{w), и максимальные
значения прибыли РЯ1(да) и PR™ в каждом из сегментов;
г) определите суммарный выпуск у = у1(да) + у%* и суммарную при-
быль PR = PR™ + PR™\
д) выпишите уравнение рыночного спроса AR (путем суммирова-
ния по горизонтали линий спроса АЛ, и ЛЛ2) и линии предельно-
го дохода MR. Постройте эти линии AR и MR\
е) определите выпуск у™, цену р™ и максимальную прибыль Pit™
фирмы в условиях отсутствия ценовой дискриминации третьего
ж)
2.
рода;
сопоставьте величины у и у™, а также PR и Pit™ и сделайте со-
держательные выводы на основании результатов сопоставления.
Фирма-монополист имеет два сегмента рынка, на каждом из кото-
рых функция спроса имеет вид yj = 18 - р, у2 = 24 - 2р. Предельные
издержки фирмы равны МС = -у:
6
а) постройте линии AR, и ЛЯ2;
368
б) выпишите уравнения линий MR{ и MR2 и постройте их;
в) выпишите уравнения линии MR = MR{ + MR2 и постройте ее;
г) далее выполните все пункты в)—ж) предыдущей задачи 1.
3. Дайте геометрическую интерпретацию ситуации, когда меры по сти-
мулированию спроса путем расходов на рекламу приводят к падению
и цены, и прибыли фирмы.
4. Проанализируйте случай дуополии, когда dy{ /dy2 = 0 (случай Курно)
и когда dy2/dyx = h (при h = -/2 имеем случай Штакельберга).
5. Докажите, что изопрофиты обеих фирм, проходящие через точку
„ (а-с а-с
пересекаются также в точке Fc координатами --—; ——
I 6Ь 6Ь
24 - 7620
Глава
ОСНОВЫ ТЕОРИИ
НЕКООПЕРАТИВНЫХ ИГР
9.1. Некоторые понятия теории игр
и их краткая характеристика
9.1.1. В теории игр описываются и анализируются ситуации при-
нятия решений о своих действиях (ходах) несколькими взаимо-
действующими индивидуумами, называемыми игроками. Такие
ситуации появляются в экономике, политике, учебном процессе
и во многих других областях человеческой (и не только человечес-
кой) деятельности. Многие задачи микроэкономики удобно фор-
мулировать и исследовать, используя язык и аппарат математи-
ческой теории игр, которая в настоящее время представляет собой
достаточно обширный раздел современной математики.
Специфика микроэкономических задач обусловливает отбор
таких положений математической теории игр, которые в наиболь-
шей степени сочетались бы с этой спецификой.
Существует достаточно подробная классификация составных
частей теории игр. Одним из самых общих критериев такой клас-
сификации является деление теории игр на теорию некоопера-
тивных игр, в которых субъектами принятия решений являются
собственно индивидуумы, и теорию кооперативных игр, в кото-
рых субъектами принятия решений являются группы, или коали-
ции индивидуумов. На сегодняшний день в панораме использова-
ния теоретико-игрового подхода для описания и решения микро-
экономических задач многие авторы отдают предпочтение
некооперативной теории игр.
370
В настоящей главе приведены основы теории некооператив-
ных игр. Для первоначального знакомства и изучения теории ко-
оперативных игр можно рекомендовать главу шестую книги
М. Интрилигатора (1975, 2002).
9.1.2. Некооперативные игры обычно представляют в нормаль-
ной (стратегической) и развернутой (экстенсивной) формах. Важ-
ным является вопрос о переходе описания игры от одной формы к
другой. В главе дано описание статических игр с полной и непол-
ной информацией. В статических играх индивидуумы принимают
решения о своих действиях (своих ходах) независимо друг от друга
в течение одного фиксированного периода времени. При перехо-
де от нормальной формы статической игры к ее развернутой фор-
ме появляется важное понятие информационного множества иг-
рока, которое позволяет формально описать состояние неопреде-
ленности игрока в связи с тем, что он не знает, какой конкретно
ход будет сделан другим (другими) игроком (игроками). Много
внимания в главе уделено важному частному случаю статических
игр с полной информацией в нормальной форме — теории бимат-
ричных игр, для которых нормальная форма имеет вид двойной
матрицы, элементы которой показывают размеры выигрышей
игроков, если игроки принимают определенные решения о своих
действиях (ходах). Специальный параграф (параграф 9.5) посвя-
щен биматричным играм с матрицами второго порядка.
В динамических играх игроки делают ходы поочередно, т.е. в
одном периоде времени принимает решения о своем действии
(ходе) один игрок, а в следующем периоде времени принимает
решения о своем действии (ходе) другой игрок и т.д.
Для динамических игр наиболее удобной является разверну-
тая (экстенсивная) форма представления, т.е. форма представле-
ния игры в виде дерева, вершины которого показывают положе-
ние (состояние) игрока, а дуги, выходящие из вершины, показы-
вают его возможные ходы (его возможные действия).
В статической игре каждый игрок, делая ход, получает опреде-
ленный выигрыш (он может быть как собственно выигрышем, так
и проигрышем), который зависит также от ходов, которые сдела-
ют другие игроки, т.е. каждый игрок делает ход в условиях полной
неопределенности, ибо не знает, какие ходы сделают другие игро-
ки. Естественно, каждый игрок стремится максимизировать свой
выигрыш, что непросто сделать в условиях полной неопределен-
24*
371
ности. Понятие оптимального решения (или просто — решения)
игры до сих пор определить не удалось. Поэтому предлагались
различные версии понятия решения игры. Основные версии это-
о понятия будут определены и проанализированы в этой главе
(равновесие в доминирующих стратегиях, равновесие Нэша, рав-
новесие Нэша — Байеса).
В случае динамической игры центральным понятием является
понятие оптимальной стратегии игрока. Основные версии этого
понятия будут определены и проанализированы: равновесие Нэ-
ша, совершенное в подыграх равновесие, совершенное байесов-
ское равновесие).
В главе предложены содержательные экономические задачи,
для описания и решения которых использовались приведенные ос-
новные положения теории игр. Познавательная полезность ряда
положений теории игр демонстрируется на приведенных примерах.
9.2. Статические игры с полной информацией
в нормальной форме. Биматричные игры
9.2.1. В статической игре каждый ее участник (игрок) Р прини-
мает решение (делает свой ход, выбирает стратегию своего пове-
дения) одновременно с другими игроками в некотором периоде
времени, не зная, какие решения принимаются другими участни-
ками (игроками). Отметим, что в этом параграфе понятия «реше-
ние игрока», «ход игрока», «стратегия поведения игрока» являют-
ся синонимами. Далее понятия «ход игрока», «стратегия поведе-
ния игрока» могут иметь разные толкования, что будет специально
оговариваться.
Везде в этой главе речь пойдет о случае игры G т лиц (2<т —
натуральное число), т.е. о случае игры, в которой участвует конеч-
ное число игроков Рр...,Рот. Символом 1={1,...,т} обозначим
множество номеров всех игроков. Каждый игрок Рк, к=1,...,т,
имеет множество Sk своих стратегий, т.е. множество своих воз-
можных действий. Стратегия игрока Рк обозначается символом
Упорядоченный набор s=(sp стратегий sp выбранных
игроками Рр ...,Рт, соответственно, называется профилем страте-
гий игры G т лиц. Термин полная информация означает, что каж-
дый игрок Рк знает множества Sj стратегий всех игроков Pj,
372
(в том числе и множество Sk своих стратегий), однако
игрок Рк не знает, какие конкретно стратегии выберут все осталь-
ные игроки Pj,j*k. (Понятие «неполная информация» приведено
ниже в параграфе 9.8.) Каждый игрок Рк имеет функцию своего
выигрыша (функцию полезности) uk(s), частное значение которой
равно выигрышу игрока Рк и зависит не только от стратегии sk,
выбранной игроком Рк, но и от стратегий s., выбранных всеми
другими игроками P^j^k, т.е. частное значение uk(s) функции
выигрыша игрока Рк зависит от профиля s стратегий игроков
..., Рт игры G. Частные значения функции выигрыша игрока Рк
не обязаны иметь стоимостную форму. Предполагается, что каж-
дый игрок Рк должен сам вести себя рационально, т.е. максимизи-
ровать (насколько возможно) функцию своего выигрыша.
Описание статической игры Gc полной информацией с указа-
нием множества 1= {1,..., т} всех номеров игроков Рк, множеств Sk
стратегий игроков Рк и функций uk(s) выигрыша игроков Рк,
к=1, называется нормальной (стратегической) формой игры
G т лиц, т.е. нормальная форма игры G есть представление этой
игры в виде
G = (Sk,uk(s),kel). (9.2.1)
Отметим, что профиль $=($р стратегий игры G т лиц
есть элемент декартова произведения 5=5! х ...х$т множеств
стратегий 5р игроков Рх,...,Рт т.е. seS.
Подчеркнем, что для описания игры G в нормальной форме
следует задать:
1) множество номеров всех игроков;
2) множество стратегий каждого игрока;
3) функцию выигрыша каждого игрока на множестве профи-
лей, состоящих из всех стратегий игроков.
Задача теории игр — найти оптимальное решение игры, т.е. опре-
делить, какие стратегии выберут игроки, так, чтобы соответству-
ющий профиль стратегий игроков был предпочитаемым некоторым
другим или всем профилям стратегий этой игры. Далее эта общая
постановка будет уточняться, однако до сих пор в литературе нет
конкретного рационального понятия оптимального решения игры.
В параграфе 9.3 описан один из возможных подходов опреде-
ления профиля стратегий, предпочитаемого остальным профилям
стратегий, который опирается на понятие доминирующей (строго
доминирующей) стратегии. К сожалению, существование доми-
373
нирующих (строго доминирующих) стратегий — достаточно ред-
кое явление в теории игр.
В параграфе 9.3 рассматривается также другой подход опреде-
ления профиля стратегий, предпочитаемого остальным профилям.
9.2.2. Определение 9.2.1. Если т=2, а множества 6’1 и S2 стратегий
игроков Р] и Р2 конечны, то статическая игра с полной информа-
цией называется биматричной игрой.
Если т > 2, а множества^, ...,Sm стратегий игроковPv ...,Рт—
конечны, что статическая игра с полной информацией называет-
ся конечной.
Биматричная игра может быть представлена двойной матри-
цей (Л|Р) (отсюда и термин «биматричная игра»)
(апЛ1) " (а1л5^л)
............................. (9.2.2)
(а/пл’^тл)’
построенной на основе матриц A = (a.j) и В=(Ьу) (с размерами
т х п) которые называются матрицами выигрышей игроков Р{ и Р2
соответственно. Поэтому говорят, что биматричная игра задается
матрицами А и В с одинаковыми размерами и обозначается симво-
лом G(A\B). Принято считать, что игрок Р{ имеет т стратегий,
а игрок Р2 имеет п стратегий. Если игрок Р{ выбирает стратегию с
номером /, а игрок Р2 выбирает стратегию с номеромJ, то выигрыш
игрока Рх будет равен а.., а выигрыш игрока Р2 будет равен by
т.е. выигрыши a.j и Ь.. образуют пару {ау,Ь^, расположенную в
двойной матрице (Л|5) на пересечении 7-й строки и у-го столбца.
7-ю строку двойной матрицы (Л|1?) называют 7-й стратегией игрока
Pj (символика: sj), ау-й столбец двойной матрицы (Л|2?) также на-
зывают у-й стратегией игрока Р2 (символика: Ц )и наглядно бимат-
ричную игру представляют в виде табл. 9.1, в которой двойная
матрица (т4|Б) выделяется двойной рамкой.
Таблица 9.1
Стратегии игрока Р2
4 ... sn
1 о (°пА1) ... <а1йАя)
fc S &£ а . ... .
и & S ... ^атп9 Ьтг)
374
Множество стратегий игрока Р, состоит из всех стратегий
511,...,5|т игрока Р{ т.е. 5(= s”}. Аналогично множество 52
стратегий игрока Р2 состоит из всех стратегий ,—,^2 игрока Р2,
т.е. 52 = {s2,..., ф.
Функция выигрыша игрока Pt принимает частные значения
Og=ul(Si , з2), функция выигрыша игрока Р2 принимает частные
значения by=u2 (s', s0.
Таким образом, нормальная форма биматричной игры с мат-
рицами А и В имеет вид
G(A,B) = {Sl,S2-,A,B).
По существу нормальной формой биматричной игры является
двойная матрица (9.2.2), все строки которой представляют все
стратегии игрока Р{, все столбцы которой представляют все стра-
тегии игрока Р2, все левые элементы представляют собой все
частные значения функции выигрыша игрока Pv а все правые
элементы by представляют собой все частные значения функции
выигрыша игрока Р2.
Таким образом, формально определенная биматричная игра
(см. определение 9.2.1) порождает двойную матрицу (9.2.1). Оче-
видно, верно и обратное. Любая двойная матрица (9.2.2) с разме-
рами (т х п) является порождением игры с полной информацией
с двумя игроками Р( и Р2 и с конечными множествами и 5, стра-
тегий игроков Pi и Р2.
9.3. Равновесие в статических играх
с полной информацией
9.3.1. Имеем статическую игру с полной информацией
G=<Sk,uk,(s),keГ>. Для профиля s=(sp ...,sp...,sm) стратегий
s1,...,s/,...,sm игроков Р1,...,Р.,...,Рт используется символика s=
= где символом s_.обозначен профиль
стратегий s1,...,s/_1,s/+1,...,sm игроков Pv...P._I,Pi+l,...,Pm. Симво-
лом S_. принято обозначать декартово произведение 5,х...х
'xS._^S.+^<.Sm. Переход от профиля стратегий s=(sr;s_z) к профилю
стратегий (s’f ;s_z) означает, что игрок Р( один отклонился от про-
филя стратегий (s(.;s_.), т.е. только он один поменял свою страте-
гию Sj на стратегию s/.
375
Определение 9.3.1. Говорят, что стратегия s.gS. игрока Р. силь-
но доминирует стратегию я.'е S. игрока Р., если для любого профи-
ля s_t еS_.справедливо строгое неравенство u.(s., > u^s'., s_i).
Если для любого профиля s_. 6 S_. справедливо нестрогое не-
равенство u.(s., S g) > u.(s!, s_.), то говорят, что стратегия s. игрока Р.
слабо доминирует стратегию s! игрока Р..
Определение 9.3.2. Стратегия s. е игрока Р. называется сильно
доминирующей стратегией (сильной доминантой) игрока Рр если
она сильно доминирует любую стратегию из S..
Стратегия s. е S. игрока Р. называется доминирующей стратеги-
ей (доминантой) игрока Р., если она (слабо) доминирует любую
стратегию из У.
Очевидно, если стратегия s. € S{ сильно доминирует стратегию
5.'е S., то стратегия s. е S. слабо доминирует стратегию s!e S.. Обрат-
ное, конечно, неверно. Если стратегия является сильно домини-
рующей, то она является доминирующей. Здесь также обратное
неверно.
Если у игрока Р. есть сильно доминирующая стратегия, то она
обязательно единственная (для доказательства следует использо-
вать метод от противного).
Если у каждого игрока Рр 1=1,..., т, есть своя сильно домини-
рующая стратегия, то, естественно, ее следует принять в качестве
оптимальной для этого игрока, а профиль из оптимальных страте-
гий также естественно назвать оптимальным. Таким образом,
в рассматриваемом случае существует единственный оптималь-
ный профиль у игры G из т лиц. Как отмечалось выше, к сожале-
нию, существование доминирующей стратегии у каждого игро-
ка — явление достаточно редкое.
Если у каждого игрока Рр i= 1,..., т, есть (слабо) доминиру-
ющая стратегия, она не обязательно является единственной.
В этом случае мы также имеем существование оптимального про-
филя у игры G из т лиц, который может быть не единственным.
Определение 9.3.3. Если стратегия каждого игрока в профиле
/е S является его доминирующей стратегией, то профиль s* назы-
вается равновесием в доминирующих стратегиях статической иг-
ры Gm лиц.
Пример 9.3.1. Рассмотрим известную игру «Голосование»-. В За-
конодательном собрании три фракции: правые, центристы и левые.
В каждой фракции равное число депутатов. При голосовании по
некоторому законопроекту каждая фракция (как единое целое) го-
376
лосует «за» или «против». Решение принимается большинством
голосов. Пусть правые и центристы выступают за принятие законо-
проекта, а левые — против. Если законопроект будет принят, пра-
вые и центристы получают в качестве выигрыша по 1, а левые полу-
чают выигрыш (—1), т.е. проигрыш. Если законопроект не будет
принят, у каждой фракции выигрыш будет равен нулю.
Обозначим символами Рр Р2, Р3 соответственно фракции ле-
вых, центристов и правых, тогда в профиле s= (sp s2, s3) — это
стратегия левых, s2 —стратегия центристов, $3 — стратегия правых.
Определим, существует ли в этой игре профиль равновесия в до-
минирующих стратегиях.
Первую стратегию (ЗА) игрока Р{ естественно представлять в
виде вектора s} = (1, 0), вторую стратегию (ПР) игрока Р, естест-
венно представлять в виде вектора = (0,1).
Аналогично первая стратегия (ЗА) игрока Р2 имеет вид s2 = (1,0),
вторая стратегия (ПР) игрока Р2 имеет вид s2 = (0,1). Для игрока Р3
имеем первую (ЗА) стратегию 5] = (1,0), вторую (ПР) s3 - (0,1).
Функция выигрыша w((sp s2, s3) игрока Р{ (фракция левых)
принимает следующие частные значения в зависимости от про-
филей s = (ip s2, s3):
«1С*1>4>5з) = -i. = -1 («1 (S1 >52>5з) = и1(*12,4>5з))>
^(s/.s^sj) = -1, u^,sl,sl3) = 0 (цЦ1,^,^) < Ui(sf,sl,^)),
Wj(^,^,^) = -1, u^s^s^s]) = 0 («1Ц2,^,^) < W1(S12,^)),
Uj(s|,S2,S3) = 0, Uj ($2, $2 , $2 ) = 0 («!(«},sj,sj) =
Профиль s = (sj, $2, sj) стратегий s[, s2, sj означает, что каждый
из игроков Рр Р2, Р3 выбирает свою первую стратегию (т.е. голосу-
ет ЗА). В этом случае законопроект проходит, и поэтому частное
значение и = (s{, $2, $3) функции выигрышей игрока Pj равно (-1).
Аналогично поясняются остальные частные значения функции
выигрышей игрока Рр
Из равенств и неравенств для частных значений функции вы-
игрыша игрока Р, вытекает, что стратегия $2 (ПР) для игрока Р{
(фракция левых) является доминирующей.
Функция выигрыша u2(sp s2, s3) игрока Р2 (фракция центрис-
тов) принимает следующие частные значения в зависимости от
профилей s = ($р s2, s3):
377
U^s},4,S3) = 1, U2(s},S2,s}) = 1 (^(4,4^) = «2(51>52«5з))>
= i» #2<«iM»*j) = 0 [^(5^4,33) > “2(512»52>5з))>
U2(s},s|,s|) = 1, U2(s{,s2,s3) = 0 (^(Xj1,^,^) > U^sf^sty,
Uj(s?,s^s|) = 0, ^(sf.sf,s|) = 0 (u^s^sf) = urfs^sty,
откуда вытекает, что стратегия х2’ (ЗА) для игрока Р2 (фракция
центристов) является доминирующей. Аналогично стратегия 5]
(ЗА) для игрока Р3 (фракция правых) является доминирующей.
На основании вышесказанного для игры «Голосование» суще-
ствует профиль равновесия в доминирующих стратегиях s =(sj, s], xj).
9.3.2. Определение 9.3.4. Стратегия хЛ' е Sk игрока Рк называется
сильно доминируемой, если существует стратегия ske Sk игрока
Рк, которая ее сильно доминирует, т.е. uk(sk, s_k)>uk(sk, s_k) для
любых стратегий Sj е SJt выбранных другими игроками Pj{j*k).
Отбрасывание сильно доминируемых стратегий называется
принципом сильного доминирования в теории статических игр т лиц
с полной информацией. Отбрасывая (элиминируя) сильно доми-
нируемые стратегии игрока, мы сужаем множество его стратегий.
При этом подмножество оставшихся стратегий, естественно, со-
держит стратегии, которые должны входить в решение игры. Если
после отбрасывания сильно доминируемых стратегий у каждого
игрока останется по одной стратегии, то, очевидно, профиль, со-
стоящий из всех этих стратегий, и будет решением игры. В этом
случае говорят, что статическая игра с полной информацией раз-
решима по доминированию.
К сожалению, такая идиллия в теории игр — достаточно ред-
кое явление. Однако последовательное сокращение множеств
стратегий игроков за счет отбрасывания сильно доминируемых
стратегий может упростить первоначально трудную задачу отыс-
кания решения игры.
Отметим, что тот факт, что каждый игрок исходит из того, что
каждый игрок не выберет доминируемую стратегию (и т.д. до бес-
конечности), принято называть общим знанием.
В рассматриваемом случае важно, что предполагается не толь-
ко рациональность поведения игроков (не выбирать доминиру-
емые стратегии), но их способность провести соответствующие
378
рассуждения, ибо цепочка рассуждений может быть достаточно
длинной (я знаю, что он знает, что я знаю...).
Пример 9.3.2. Биматричная игра G(A;B) задана табл. 9.2, в кото-
рой двойная матрица выделена двойной рамкой.
Таблица 9.2
Стратегии игрока Р2
4 s22 S2
Стратегии игрока Р{ 4 (1,2) (4, 3) (2,5)
(-1,0) (5, 3) (3,2)
«i (-1,7) (3,4) (1,6)
Проиллюстрируем на этой биматричной игре реализацию
принципа сильного доминирования.
Стратегия s{ = (1; 4; 2) игрока Р, сильно доминирует стратегию
sf = (—1; 3; 1) игрока Рр ибо каждая координата вектора s{ строго
больше соответствующей координаты вектора sp что содержа-
тельно интерпретируется так: каждое частное значение s2),
s2=s2,s$,s2 функции выигрыша игрока Рг при выборе им страте-
гии s’ строго меньше соответствующего частного значения
w1(s};s2),s2=s2,s%,s2 функции выигрыша игрока при выборе им
стратегииs!, т.е. и. (si;sl)= д..=1>—1=а,.= «.(«?; si), и. ($}; s?)= а.,=
=4 > 3=4, = 4),' 4) = «„-2 >1=4 = »,(«[; J’).
Таким образом, стратегия sf является сильно доминируемой,
и поэтому ее можно отбросить: игрок Р( не будет выбирать страте-
гию sp
После отбрасывания стратегии sj мы получим новую биматрич-
ную игру, задаваемую табл. 9.3. Говорят, что биматричная игра, за-
даваемая табл. 9.3, редуцируется к биматричной игре, задаваемой
табл. 9.3. В табл. 9.3 сохранена символика табл. 9.2, хотя в табл. 9.3
стратегии s2,s^,s2 игрока Р2 уже не те, что в табл. 9.2.
Таблица 9.3
Стратегии игрока Р2
S2 S2 S2
Страте- гии игрока Р{ (1,2) (4, 3) (2,5)
(-1, 0) (5, 3) (3,2)
379
В табл. 9.3 стратегия s2 игрока Р2 сильно доминирует стратегию
$2 игрока Р2, поэтому стратегия s2 является сильно доминируемой
и ее можно отбросить. После отбрасывания стратегии $2 получаем
новую биматричную игру, задаваемую табл. 9.4.
Таблица 9.4
Стратегии игрока Р2
S2 S2
6 S* й § s 1 (4, 3) (2,5)
§ ’J (5,3) (3,2)
В табл. 9.4 стратегия s? игрока Р( сильно доминирует стратегию
я} игрока Р], поэтому стратегия $} является сильно доминируемой и
ее можно отбросить. После отбрасывания стратегии получим
новую биматричную игру, задаваемую табл. 9.5.
Стратегии игрока Р2
Таблица 9.5
S2 S2
Стратегии игрока Р, (5,3) (3,2)
В табл. 9.5 стратегия s2 игрока Р2 сильно доминирует стратегию
$2 игрока Р2, поэтому стратегия s2 является сильно доминируемой и
ее можно отбросить. После отбрасывания стратегии s2 получим
новую биматричную игру, задаваемую одной клеткой (см.
табл. 9.6).
Таблица 9.6
Стратегии игрока Р2
S2
Стратегии игрока Л (5, 3)
380
Отсюда вытекает, что решение биматричной игры, заданной
первоначальной табл. 9.2 двойной матрицей третьего порядка,
будет получено, если игрок Pt выберет единственную стратегию
s*, а игрок Р2 выберет единственную стратегию s2, т.е. профиль
(sf,s2) первоначальной игры является единственным профилем,
(строго) предпочитаемым остальным профилям (sp s2) игры, зада-
ваемой табл. 9.2. Этот профиль (s[,s2) был получен с помощью
принципа сильного доминирования.
9.3.3. Приведем определение равновесия Нэша как профиля,
который предпочитается некоторым, но, вообще говоря, не всем
профилям игры G т лиц.
Определение 9.3.5. Пусть G={Sk, ик, (s), к е 7) — статическая иг-
ра т лиц в нормальной форме. Профиль s’ =(sp .... s£) € •... • Sm
стратегий sp..., игры G называется равновесием Нэша игры G,
если для любого номера к е /и любой стратегии sk е Sk справедли-
во неравенство uk(s°) > ик (sk, s’/).
Стратегия 5^, к = 1,... т, входящая в равновесие Нэша s’, назы-
вается стратегией равновесия Нэша.
Приведенное неравенство означает, что если каждый игрок
Рр * к) выбирает свою стратегию sy* равновесия Нэша, а игрок Рк
перейдет в одиночку (!) от своей стратегии зк равновесия Нэша к
другой своей стратегии sk, то выигрыш игрока Рк может только
уменьшиться. Другими словами, в равновесии Нэша s’ =(sp..., s£)
любому игроку Рк в одиночку не выгодно менять свою стратегию
s°k, если все остальные игроки Рр * к) этого не делают, т.е. не ме-
няют свои стратегии sy.’.
Если же в равновесии Нэша s’ =(s°,..., s’) поменяют свои стра-
тегии s’ два (или более) игрока, то они уже могут строго увеличить
свои выигрыши (см. далее пример 9.3.3).
Равновесие Нэша представляет собой вариант решения игры
G в нормальной форме.
Имеет место следующая важная теорема существования рав-
новесия Нэша для игры G т лиц.
Теорема 9.3.1 (X. Никайдо, К. Исода). Пусть в статической игре
т лиц G={Sk, ик, (s), к е I) в нормальной форме каждое множество
$к выпукло, замкнуто и ограничено в евклидовом пространстве
каждая функция выигрыш ups) непрерывна на S = х ... х Sm i-
выпукла вверх по sk при любых фиксированных sz, / * к. Тогда с\
шествует равновесие Нэша игры G из т лиц.
381
Для оиматричной игры G(A;B) с(тхп) матрицами выигрышей
А и В игроков Р] и Р2 соответственно простроим двойную матрицу
ИЯ).
(°1Р^1) • •• Ц„;АЯ)
(°<П1’^Л11) \ гПП7 тп'
В каждом столбце j двойной матрицы среди элементов а., вы-
берем наибольший и пометим его знаком v — «птичкой». Если
наибольших элементов будет несколько, «птичкой» пометим каж-
дый из них. Аналогично в каждой строке i двойной матрицы среди
элементов by выберем наибольший и пометим его л — «шляпкой».
Если наибольших элементов будет несколько, «шляпкой» поме-
тим каждый из них. Элемент (клетка) : ) двойной матрицы,
куда попали и «птичка», и «шляпка», соответствует равновесию
Нэша (sj°; 527°) данной биматричной игры. Если таких элементов
(клеток) несколько, то каждой из них соответствует свое равнове-
сие Нэша. Если нет такого элемента (клетки) двойной матрицы,
куда попадают одновременно «птичка» и «шляпка», то это означа-
ет, что биматричная игра не имеет ни одного равновесия Нэша.
Из сказанного следует, что если для элемента (клетки) (а/оЛ;
двойной матрицы (Д|2?) справедливы неравенства
% * = 1>.J =
то этому элементу (клетке) (в/оЛ; Ь^) соответствует равновесие
Нэша (д',0; s/°) биматричной игры.°(3чевидно, верно и обратное
утверждение.
Пример 9.3.3. На рынке функционируют конкурирующие
фирмы Fx и Г2 (скажем, два магазина, которые могут торговать в
течение некоторого фиксированного периода (например, в тече-
ние недели) по нормальной цене (НЦ) или по высокой цене
(ВЦ)). Если каждая фирма торгует по ВЦ, она получает прибыль
(выигрыш), равную 200 д.е., если каждая фирма торгует по НЦ,
она получает прибыль, равную 30 д.е. Если фирма торгует по
ВЦ, а фирма F2 по НЦ, то фирма Fx получает прибыль, равную
(-50 д.е.), т.е. будет в убытке, а фирма F2 получит прибыль 300 д.е.,
бо к ней придет много новых покупателей, которые ранее приоб-
щали товар у фирмы Fv Если фирма Fx торгует по НЦ, а фирма
f'2 по ВЦ, то фирма Fx получит прибыль 400 д.е., а фирма F2 полу-
|ит прибыль (-100 д.е.), т.е. будет в убытке.
382
Приведенное описание функционирования фирм Г, и F2 пере-
ведем на язык теории игр.
В примере 9.3.3 Р} = Р2 = F2, т =2. Каждое из множеств и
S2 состоит из двух стратегий: торговать по НЦ, торговать по ВЦ,
что формально можно записать так: = {НЦ, ВЦ,}, S2 = {НЦ,
ВЦ}. В связи с тем что т = 2, а множества и S2 — конечны, игра
этого примера является биматричной G(A, В).
Прибыли (выигрыши) фирм Ft и F2, которые могут быть как по-
ложительными, так и отрицательными, представим в виде табл. 9.7,
основным элементом которой является двойная матрица с размерами
2x2, обведенная двойной рамкой. Первая клетка двойной матрицы
есть профиль (точнее, соответствует профилю) из первой стратегии
(НЦ) игрока Р( и первой стратегии (НЦ) игрока Р2. Когда игрок Р1 и
игрок Р2 выбирают первую стратегию (НЦ), прибыль (выигрыш)
каждого из них равна 30 д.е., что и показано в первой клетке. Левое
число относится к игроку Рр правое число—к игроку Р2. Аналогично
поясняются клетки со второй по четвертую двойной матрицы.
Таблица 9.7
Стратегии игрока Р2
нц ВЦ
Страте- гии игрока л нц (30,30) 7^ (400,-100)
ВЦ (-50,300) Ч- Дх (200,200)
Аналогично тому, как это было сделано в примере 9.3.2, стра-
тегия НЦ игрока Р, сильно доминирует свою стратегию ВЦ,
а стратегия НЦ игрока Р2 сильно доминирует свою стратегию ВЦ.
Поэтому профиль стратегий НЦ игроков Р, и Р2 есть равновесие в
доминирующих стратегиях, которое является равновесием Нэша.
Если в рассматриваемом примере допустить смену своих стра-
тегий НЦ на стратегии ВЦ сразу двум игрокам Р{ и Р2, то каждый
из них увеличит свой выигрыш с 30 до 200 д.е.
Таблица 9.8
Стратегии игрока Р2
нц ВЦ
Страте- гии игрока л нц (30,30) (Г Тх (400,-100)
ВЦ (-50,100) U (200,200)
383
Пример 9.3.4. Рассмотрим биматричную игру G(A;B), заданную
табл. 9.8. Здесь стратегия НЦ игрока Р, сильно доминирует страте-
гию ВЦ игрока Рх. Среди стратегий НЦ и ВЦ игрока Р2 нет доми-
нирующей. Поэтому рассматриваемая игра не имеет равновесия в
доминирующих стратегиях. Как и в предыдущем примере 9.3.3,
профиль стратегий НЦ игроков Р, и Р2 есть равновесие Нэша.
Пример 9.3.3 отражает тот факт, что равновесие в доминиру-
ющих стратегиях есть равновесие Нэша; пример 9.3.4 показывает,
что равновесие Нэша не обязано быть равновесием в доминиру-
ющих стратегиях.
Пример 9.3.5. Биматричная игра G(A\B), представленная
табл. 9.9, не имеет ни одного равновесия Нэша, ибо ее двойная
матрица (А\В) не содержит ни одной клетки, в которой одновре-
менно были бы «птичка» и «шляпка».
Таблица 9.9
Стратегам игрока Р2
нц ВЦ
Страте- гии игрока Л нц (60,80) /Г" (70,-40)
ВЦ (150,60) 4/ (-70,200)
Взаимосвязь последовательного использования принципа
строгого доминирования и равновесия Нэша описывается следу-
ющими двумя теоремами.
Теорема 9.3.2. Пусть 5° — (s°,..., s£) — равновесие Нэша игры G
т лиц. Тогда ни одна из входящих в s° стратегий не может быть
отброшена в результате применения принципа сильного домини-
рования.
Теорема 9.3.3. Пусть в результате последовательного применения
принципа сильного доминирования у каждого игрока Рк, к=1,..., т,
остается единственная стратегия sk. Тогда профиль s°=(s°, ...,
s °) — равновесие Нэша игры G т лиц.
В примере 9.3.6 показано, что равновесие дуополии Курно
есть равновесие Нэша этой модели как статической игры с пол-
ной информацией. Для разбора примера 9.3.6 достаточно сведе-
ний об этой классической модели, которые описываются в пара-
графе 8.7 этой книги.
Пример 9.3.6. Модель дуополии Курно как статическая игра с
полной информацией.
384
Обозначим символом s. объем выпуска фирмы Fjf /=1,2, в не-
котором фиксированном периоде времени. Функция, обратная к
функции спроса, имеет вид p=a—b(sl+s2), где а и b — положи-
тельные параметры. Прибыль PRt фирмы F. имеет вид
PRi=psj—cpj—d., (9.3.1)
где с.=МС. — предельные издержки, a d.=FC. — постоянные
издержки фирмы F., i = 1, 2.
Прибыль PRt фирмы F. есть выигрыш и. фирмы F., которая
рассматривается в качестве игрока Рр i = 1,2. Игроки и Р2 ходы
делают одновременно, т.е. фирмы F, и F2 выпускают свою продук-
цию на рынок, не зная об объемах друг друга.
Покажем, что мы имеем дело со статической игрой с полной
информацией.
1. Число игроков равно двум. Как только что было отмечено,
игроком Рх является фирма F{, игроком Р2 — фирма FT
2. Множество £,= {$jO<s(. g есть множество возможных объ-
емов выпусков s. фирмы F., i = 1, 2.
3. Для игрока Pj функция Uj(s)=Uj(sv s2) выигрыша есть функция
прибыли PR. фирмы F. (см. (9.3.1)):
Uj(si,s2) = PRj =(а-b{s{ + s2))Sj - CjSt -d(. (9.3.2)
Для нахождения равновесия Нэша этой статической игры с
полной информацией следует максимизировать функции и((5) и
ux(s) выигрышей обоих игроков Рх и Р2.
Задача максимизации прибыли PRx(sv s2) фирмы F{ решается
путем отыскания ее первой производной по переменной 5] с уче-
том предпосылки модели Курно о том, что предполагаемая вариа-
ция <fc2/ife]=0.
Имеем уравнение
= чгя,м = _ _ =
ds{ ds{
откуда следует, что
d — *^2
5| = 2b = ~2Ь ~2~
Отметим, что
(9.3.3)
25 - 7620
385
Поскольку
= _24 < о,
ds{
постольку выражение (9.3.3) (глобально) максимизирует прибыль
R{ (sp s2) при фиксированном s2.
Аналогично имеем для объема выпуска s2 фирмы F2, максими-
зирующего прибыль R2 Ц, s2), при фиксированном
Из (9.3.3) и (9.3.4) следует, что
= 5» = °~2с»+\ (9.3.5)
3b 3b
и профиль (Sp ф есть равновесие Нэша модели Курно как стати-
ческой игры с полной информацией, ибо
И] (s']0, s2) = (а - С] )5|° - />(5]° )2 - bs°s2 ~dt >
> (a-Ci)st -bs* -bs^l -^ = и(($р52),
UjOu*?) = (a ~ C2^S2 ~ ^(52 )2 ~ ^s1°52 ~ d2 >
> (a - c2)S] - bs2 - bSiS2 ~d2= u2(s^,s2).
Последние два неравенства можно проверить непосредствен-
но, используя явные выражения (9.3.5).
При Cj= с2 = с имеем классическое равновесие Нэша дуополии
Курно.
Аналогично показывается, что модель дуополии Бертрана
представима как статическая игра с полной информацией, а рав-
новесие Бертрана есть частная версия равновесия Нэша.
Равновесия Курно и Бертрана в случае олигополии также яв-
ляются равновесиями Нэша.
9.4. Смешанное расширение биматричных игр
9.4.1. В этом параграфе уточняется и развивается понятийный
аппарат теории биматричных игр G(A;B), который был введен в
параграфе 9.2.
386
Таблица 9.1 дает наглядное представление биматричной игры
G(A, В), /-ю строку двойной матрицы (Л|Б) с этого момента будем
называть /-й чистой стратегией игрока Р{, i-я чистая стратегия
игрока Pj обозначается символом Аналогичноу-й столбец двой-
ной матрицы (Л|2?) с этого момента будет называтьу-й чистой стра-
тегией игрока Р2,у-я чистая стратегия игрока Р2 обозначается
символом з? Множество = {$},..., з”} всех строк двойной матри-
цы (Я|Р) — это множество всех чистых стратегий игрока Pv Мно-
жество 52 = {л2, всех столбцов двойной матрицы (Я|Р) — это
множество всех чистых стратегий игрока Р2.
В связи с тем что
Ь„„,
тп/
естественно вектор е;=(0, ...,0,1,0, ...,0) также назвать /-й чистой
стратегией игрока Р{.
Если игрок Р, использует свою первую чистую стратегию
е{ (1,0,...,0) с вероятностьюPj(0<p,^ 1),..., свою т-ю чистую стра-
тегию ет = (0,...,0,1) с вероятностьюpm(0<pm< 1), то произведение
р(Л|В) = ((po1;pZ>1),...,(po";pZ>"))
естественно толковать как смесь чистых стратегий игрока
Р{ с весовыми множителями рр..,рт, которую (смесь) следует на-
звать смешанной стратегией игрока Рр
Здесь символы c/,bi,J= означают столбцы матриц Я и В
соответственно, apj +... +рт = 1, ибо игрок Р{ обязательно должен
выбрать какую-то из своих чистых стратегий $}, ...,з”.
Термин «смешанная стратегия игрока» Р{ применяется не только
к смеси р(Я|5) чистых стратегий s[, ...,s” с весовыми множителями
25“
387
pv... pm, но и к самому вектору р=(рр.., />т) вероятностей Рх,-,Рт.
Отметим, что вектор ре &т\ где 5<m)={z=(zv .... Z^Zi 0, ...,^^0,^+
+zm~ И—(»*— 1)-мерный симплекс в zn-мерном пространстве Ет.
Очевидно, чистые стратегии ер..., ет игрока Рх являются част-
ными случаями смешанной стратегии р=(рр..,рж) этого игрока.
9.4.2. В связи с тем, что
ГА1
Л4 =
- Ь, - ‘i.YO'l
............... i
^mj *** Ътп> k6>
V
естественно вектор j£.=(0,...,0,l,0,...,0) также назвать у-й чистой
стратегией игрока Р2.
Если игрок Р2 использует свою первую чистую стратегию
/7=(1,0, ...,0) с вероятностью qx (0<<7( < 1),..., свою п-ю чистую стра-
тегию^ =(0,..., 0,1) с вероятностью qH(0<qn< 1), то произведение
И«)«-
естественно толковать как смесь чистых стратегий s2, ...» s2 игрока
Рг с весовыми множителями qx, ..., qn, которую (смесь) следует
назвать смешанной стратегией игрока Рг
Здесь символы а., Ь., /= 1,... т, означают строки матриц А и В
соответственно, a qx + ... +tf„=l, ибо игрок Рг обязательно должен
выбрать какую-то из своих чистых стратегий s],..., s*.
Термин «смешанная стратегия игрока» Рг применяется не только к
смеси (A\B)q чистых стратегий s2,..., s2 с весовыми множителями
qv...,qn, но и к самому вектору q={q[,—,qr) вероятностей^,...,^. От-
метим, что вектор где5(л)={г= (zp...,^)IZ|^0, ...,^>0, ...,zx +...
... =1} —(л—1)-мерный симплекс в «-мерном пространстве Еп.
388
Очевидно, чистые стратегии fx,—Jn игрока Р2 являются част-
ными случаями смешанной стратегии q = (qx,..., q^ игрока Р2.
9.4.3. Напомним, что ^-мерный вектор z = Zk), который
рассматривается сам по себе, можно представить как в виде векто-
ра-строки z~(zx, .... Zk), так и в виде вектора-столбца
Z =
&
где числа zx,..., Zk — координаты вектора z.
Если вектор z умножается на некоторую матрицу D и располо-
жен слева от нее, то в этом случае он обязательно есть вектор-
строка.
Если вектор z умножается на некоторую матрицу D и располо-
жен справа от нее, то в этом случае он обязательно есть вектор-
столбец.
Ожидаемый выигрыш (частное значение функции ожидаемо-
го выигрыша) игрока Рх, когда игрок Рх выбирает смешанную
стратегиюр = (рх,..., рт), а игрок Р2 выбирает смешанную страте-
гию q = (qx,..., qn), естественно определить так:
Ul(P^) = P^ = (Pl>->Pm)
ь&т! ''' &тп J \Яп у
Аналогично ожидаемый выигрыш (частное значение функции
ожидаемого выигрыша) игрока Р2, когда игрок Рх выбирает сме-
шанную стратегиюр = (рх, —,рт), а игрок Р2 выбирает смешанную
стратегию q = (qv ..., q^, определяется так:
«2(А9) = ^ = (/>!,...,/>„)
\^т\
bmn)\fln;
Игра G(A,B) = ^5(т),5(/,),м1(д^),«2(/’,?)^ называется смешан-
ным расширением биматричной игры G(A,B) = (5р S2, А, В)
(см. параграф 9.2).
Аналогично описанному определяется смешанное расшире-
ние конечной игры G. Смешанные расширения биматричной иг-
ры G(A, В) называются рандомизацией биматричной игры G(A,
В). В общем случае переход от чистых стратегий игры к ее сме-
389
шанным стратегиям называется рандомизацией соответствующей
игры. _
Для игры G(A,B) векторы р = (Р\,—,Рт) е 5(т) и^= (дх, ...,дп)
е являются стратегиями, вектор (р, q) — профиль стратегий р
и q, и, (р, q) и и2 (р, q) — функции выигрышей игроков Рх и Р2.
Однако принято все понятия, которые появляются в связи с
введением смешанного расширения G(A,B) биматричной игры
G(A, В), привязывать к биматричной игре G(A, В). Векторы р =
= (рр ..., ря) е 5(от) и q = (?р ..., qj е называются смешанными
стратегиями биматричной игры G(A, В), которые могут быть, в
частности, и чистыми стратегиями; вектор (р, д) называется профи-
лем смешанных стратегий биматричной игры G(A, В), а значения их
(р, q) и u2 (р, q) функций выигрышей игроков Р{ и Р2 называются
(ожидаемыми) выигрышами игроков Рх и Р2 биматричной игры
G(A, В).
Приведем определение равновесия Нэша в смешанных стра-
тегиях биматричной игры G(A, В).
Определение 9.4.1. Равновесие (р°, <?°) Нэша игры G(A, В) назы-
вается равновесием Нэша в смешанных стратегиях биматричной
игры G(A, В), что формально записывается так:
их(р, q°) (р°, q°) для любых ре Ет,
и2(р°, 9) - «2 Л Для лк,бых qe Ея.
Справедлива следующая важная лемма 9.4.1.
Для того чтобы профиль (р°, </°) был равновесием Нэша в сме-
шанных стратегиях биматричной игры G(A, В), необходимо и до-
статочно выполнение неравенств ux(ei,qQ)<ux(p{>,(f),i=\,...,m,
и2и2 q°)>J=l,—,n. Необходимость леммы 9.4.1 очевид-
на, ибо в определении 9.4.1 можно положить р = et е &т\ q =f. е
Для доказательства достаточности леммы 9.4.1 перепишем
неравенство их(е., q°) < их (р°, q°) в явном виде C/Aq0 £ pQAqQ,
i = \,...m. Умножив его обе части наpt> 0,/>1 + ...+/>ж= 1 и сложив
полученные неравенства, будем иметь
(?&+... +ртет)Ад° < +... + р^)р°Ад°,
р 1
т.е. pAq^<pQAq^.
Аналогично получается неравенство p^Bq^Bq®, а это означа-
ет, что профиль (р°, 9°) стратегий и ср есть равновесие Нэша
биматричной игры G(A,B).
390
Имеет место следующая важная теорема теории биматричных игр.
Теорема 9.4.1 (Дж. Нэш). Для любой биматричной игры G(A, В)
существует равновесие (р°, <?0) Нэша в смешанных стратегиях.
Для любой конечной игры существует равновесие Нэша в сме-
шанных стратегиях.
Доказательство первой части этой теоремы сразу следует из
теоремы 9.3.1. Действительно, множества 5(да) g Ет и g Еп, кото-
рые являются симплексами, выпуклы, замкнуты и ограничены.
Функции их(р, д) и и2(р, д) билинейны и, следовательно, непрерыв-
ны на 5(т) х &п\ Функция их(р, д) линейна по переменным
p=(Pp...,pm) при фиксированных переменных д={дх,...,д,) и по-
этому выпукла вверх на множестве 5<т); аналогично функция
иг(р, д) линейна по переменным д—(дх,...,д,) при фиксированных
переменныхР=(р],---,Рт) и, значит, выпукла вверх на множестве
5<я). По теореме 9.3.1 всего этого достаточно для существования
равновесия Нэша у игры G(A,B) и, значит, существования равно-
весия Нэша в смешанных стратегиях биматричной игры G(A, В).
Как было показано выше, биматричная игра G(A,B) в примере
9.3.5 не имела ни одного равновесия Нэша в чистых стратегиях.
Теорема 9.4.2 (условия дополняющей нежесткости). Пусть
(р°, 9°) — равновесие Нэша в смешанных стратегиях биматричной
игры G(A, В). Тогда
О р? > 0 => = их(р°,д°);
2) их(е„д°) < их(р0,д0) => р? = 0;
3) g°j > 0 => u^p^fj) = U2(p0,g0);
4) и2(р°,/у) < Чг(р°,?°) => д° = 0.
9.4.4. Приведем ряд полезных символов и понятий.
Положим M={l,...,m}=I,N={l,...,n}, Мхи Nx — непустые
множества, такие, что Мх £lM,Nx<^ N. Множество sp(p) (зр(д)) на-
зывается спектром (носителем) вектора р е Ет(д е Еп), если sp(p) =
=Mx = {ie Л^;>0}, sp(p)=Nx = {ie ЛЦХ)}).
Пусть at — i-я строка матрицы А и bJ' — у-й столбец матрицы В.
Обозначим символом АМ[ матрицу, строками которой являются
разности строк ах — а., где ix— первый (наименьший) номер во
множестве Мх, i*ix. Обозначим символом А'м матрицу, строками
которой являются разности строк а. — а.^, где /'й Мх. Символом
391
BN обозначим матрицу, столбцами которой являются разности
столбцов У—Ь^, где — первый (наименьший) номер во множест-
ве Nvj* jv Символом B'N' обозначим матрицу, столбцами кото-
рой являются разности столбцов bJ' — bJl, где/ £ Nv
Опишем метод нахождения всех равновесий Нэша в смешан-
ных стратегиях биматричной игры G(A, В).
Для нахождения всех равновесий Нэша в смешанных страте-
гиях биматричной игры G(A, В) с матрицами А и В:
1) зафиксируем два непустых множества и Д',, таких, что
2) обозначим символом Р(М\, NJ множество всех векторов
ре &т\ таких, что:
2Л)зр(р)=М1;
2.2) вектор р есть решение системы линейных алгебраических
уравнений5^ =0;
2.3) векторр есть решение системы линейных неравенствр B'N < 0;
3) обозначим символом 0(3/,,^) множество всех векторов
де таких, что:
3.l) sp(q)=Nl;
3.2) вектор q есть решение системы линейных алгебраических
уравнений Ам q=0;
3.3) вектор q есть решение системы линейных неравенств Ащ д = 0.
Множество всех векторов (р,д) е P(Mi,Ni)xQ(Ml,Nl) принад-
лежит множеству всех равновесий Нэша в смешанных стратегиях.
Для нахождения всех равновесий Нэша в смешанных страте-
гиях биматричной игры G(А, В) следует приведенную процедуру
1)—3) выполнить для всех непустых множеств и , т.е. осущест-
вить (полный) перебор непустых множеств М{ и и нахождение
множеств P(M1,Nl) и Q(Ml,Nl). Реально этот (полный) перебор
осуществим для биматричных игр G(A,B) с матрицами А и В не-
больших размеров.
Определение 9.4.2. Профиль (р, q) стратегий р и q биматричной
игры G(A, В) называется вполне смешанным, если спектры (носи-
тели) векторов р и q полностью совпадают со множествами
М = {1,...,т} и N— {1,...,п} соответственно.
Пусть в биматричной игре G(A, В) с матрицами второго поряд-
ка элементы, стоящие в одном столбце матрицы А, и элементы,
стоящие в одной строке матрицы В, попарно различны. Тогда в
биматричной игре G(A, В) равновесия Нэша могут быть либо чис-
тыми, либо вполне смешанными.
392
Действительно, пусть в равновесии Нэша, например, страте-
гия игрока является чистой, скажем p0=ep а стратегия q° игрока
Р2 является смешанной. Тогда по условию дополняющей нежест-
кости из ?°>0 следует равенство UjCep/i) = u^e^q0), а из q2>0
следует равенство u2(el,f2) = u2(el,q°), т.е. u2(el,fi) = u2(ei,f2),
откуда получаем
= (1;о)й W==“г,е‘м - W=г'2'
что противоречит предположению, что * Ь12.
9.5. Биматричные игры с матрицами второго порядка
9.5.1. Описанный кратко в параграфе 9.4 метод нахождения всех
равновесий Нэша в смешанных стратегиях, естественно, можно
применить для случая биматричной игры G(A,B) с матрицами
второго порядка. Однако проще рассмотреть прямой метод на-
хождения всех равновесий Нэша в смешанных стратегиях бимат-
ричной игры G(A,B) с матрицами второго порядка, опираясь на
определение 9.4.1 равновесия Нэша. По существу этот прямой
метод аналогичен описанному в параграфе 9.4 общему методу.
Для того чтобы вектор (р°, <?°) был равновесием Нэша в сме-
шанных стратегиях биматричной игры G(A, В) с (2 х 2)-матрицами
А и В, по лемме 9.4.1 необходимо и достаточно выполнение нера-
венств
<7°) «1(Р°,?°), Ui(e2,q°) < Ui(p°,q°),
u2(p°,fi) < u^p^q0), u2(p°,f2) < u^p^q0)-
Напомним, что р°=(р°{; р2), qQ=(^; <7°), P°i Р% P°i +Р° ~ 1 >
9«>0,?2°>0,^+92°=1.
Перепишем выражение w1 (р°, qQ) в развернутом виде, полагая
Р20==1-Рр«20=1-^
z \( (Л
МАА°'2 В +
\^21 a22j\q2 J
+ «21 />2^i° + a22p2q2 = (flu -a,2 -a2i + а21)Р\ч[ + (ai2 -a^p^ +
+ (a2i — a22)?l° +a22-
393
Аналогично для u2(p°, q°) имеем
и2(р°,?°) = P°Bq° = (^j-bi2-Ьц + Аг)А1° + (Аг “ Аг)Л° +
+(A1 “ Аг)?? + Аг-
Полагая p°—e{ =(1,0) (т.е./>®= 1 ,p2 =0), из выражения для ufo0, <?°)
получим
«|(«р Я ) («ц «i2 «2] + («2] «22^ ^1"^"«12‘
Полагая р°=е2=(1,0) (т.е. = 0, р2 =1), из выражения для ufo0, <f)
будем иметь ы1(е2,^°)=(д21 - д22) +д^.
Аналогично, полагая ^°=/J=(l,0) (т.е. q® = l,q2 = 0), из выраже-
ния для «2(р°, q°) получим
«г^0>/i) = (Ai — Аг “ Ai + Аг)А° + (Аг — Аг)А° + Ai-
Полагая ?°=^=(0,1) (т.е. ^=0, ?2 =1), из выражения для «2(р°, <7°)
получим
«2 (Р° >Ъ) = (Аг “ Аг)Pi + Аг •
Имеем
«1(/Л<7°) - «1(«рq°) = (°11 - % - % + О22)аЧ° + («12 - «22^1° + «22 ’
“(«И “«12 -«21 + «22)?1° - «12’
Ul(P°,q°) - u\(e2,q°) = (Дц - Д12 - Д21 + Д22)А0?10 + («12 - «22)А°-
Положим «ц—«12 —«21 + «22 = а, «12~«22 = —0’ тогда только что
полученные разности можно переписать так:
“i(P°,<l0) ~ u^q0) = apfo0 - Bp,0 - a?!0 + р =
-1) - ₽(А° -1) = (А° - D(a«® - Р),
Ui(p°,q°)-Ui(e2,q°) = apiqi -рр® = /^(а^0 -р). (9.5.2)
Аналогично выпишем разности
Ui(p0,q°) - иг(р0,Л) = (А1" Аг - А1 + А2)аЧ° + (А1 - Аг)?? + Аг "
~(А1 _Аг “ Ai + Аг)А° “ А1>
«г^0»?0)-«гО’О’./г)= (Ai “ Аг ~ Ai + A2)A°?i° +(Ai — Аг)??-
Каки в случае функции и,(р0, с/*), положим Ai _ Аг _ Ai + Аг = Y’
Аг — Ai = ’ ТОГДа только что выписанные разности можно пере-
писать так:
394
~U2(p°,fi) = TP?91° -8^1° - W + 8 =
= " 8) - (V? - 8) = («г® - 1)Ы - 8), (9.5.3)
MaW) - «гОЛ/г) = TA°?i° ~ 8^i° = A°(1A0 - 8). (9-5-4)
Для того чтобы вектор (р°, <?°) был равновесием Нэша в сме-
шанных стратегиях, необходимо и достаточно (см. начало этого
параграфа 9.5), чтобы левые разности четырех равенств ((9.5.1) —
(9.5.4)) были неотрицательны, т.е. необходимо и достаточно, что-
бы были справедливы неравенства
(А°-1)(а<7® -Р)>0,
Л°(о^1°-Р)>0,
(^°-l)()Pi0-8)>0,
910(^10-8)>0,
О < А° < 1,
О < ?i° < 1,
(9.5.5)
(9.5.6)
(9.5.7)
(9.5.8)
(9.5.9)
(9.5.10)
где коэффициенты а = о12—а21+а22, bl2—b2l+b22,
Р=а22—а12,8 = b22 — Z>21 были определены выше.
Таким образом, решение (р°, ^) системы неравенств
(P!-l)(o^i-P)>0,
Pi(a$i-P)£°,
(?1-1)(ТР1-8)£0,
91 (1А -8)^ 0,
0 < а° £1,
0 < q{ <, 1
(9.5.11)
(9.5.12)
(9.5.13)
(9.5.14)
(9.5.15)
(9.5.16)
порождает равновесие (р°,90) = ((А°5/,2)’(9?>92)) Нэшавсмешан-
ных стратегиях биматричной игры G(A, В) с (2х2)-матрицами А и В
и любое равновесие (р°, q°) Нэша порождается решением (р° ^)
приведенной системы неравенств.
395
9.5.2. Выпишем и найдем решения систем неравенств для приме-
ров биматричных игр G(A, В) с (2х2)-матрицами Ап В.
Пример 9.5.1 (продолжение той части примера 9.3.2, в которой
фигурирует двойная матрица второго порядка).
Двойная матрица выигрышей биматричной игры G(A,B) имеет
вид
(4; 3) (2; 5)
(5;3) (3;2)
Сразу получаем, что эта биматричная игра имеет равновесие
(е2’Л)((е2 = (0;l);/i =(1;0)) Нэша в чистых стратегиях. В этом рав-
новесии выигрыши игроков Р. и Р, соответственно равны и. (e-f.)
= 5,«2(е2;/1)=3.
В рассматриваемом примере ап =4; а12=2; а21 =5; а22=3; =3;
^12=^» ^21=^’ ^22=2-
Имеема=ап—а12—а21+а22=4—2—5+3=0,у=6п—612—621+622=
= 3—5—3+2=—3, Р = а22—а12,= 3—2=1,5=622—d21 = 2—3=—l.
Перепишем систему неравенств (9.5.11)—(9.5.16) для этого
конкретного примера:
(A-l)(0<7i-l)>0,
PilQ qi -1)>0,
(91-1)(-Зр,-(-!))> 0,
?1(-3А-(-1))>0,
0 < Pi < 1, 0^?!^1.
Рассмотрим сначала первые два неравенства -(/>!-1) > 0, - />] > 0
и цепочки 0</>!<!, O^q^ 1.
После элементарных преобразований получаем, что р(^0,
/>,<1,0^.
Отсюда следует, чтор{= 0. При этом 0<^j<1. На плоскости
Opj^j множество {а,901 Pi = 0,0 £ q{ < 1} изображается отрезком
OW, выделенным черной жирной линией (рис. 9.1).
Таким образом, множество, изображающее на плоскости
Ор^ систему из первых двух неравенств и неравенств
O<0j < 1, есть отрезок ОИ<
Рассмотрим теперь третье и четвертое неравенства (q{ — 1) (—3pt+
4-1) >0, $1(-Зр1 + 1)>0 и цепочки ()£/>!< 1,0 <q} < 1.
396
При <7j=0 имеем неравенство — (—Зр. +1) >0, т.е. Зр,—1 >0 и,
значит, (с учетом того, что р{ £ 1) 1 £ рj > /3. На плоскости Op{q(
множество 1 £р, £ 73, qt =1} изображается отрезком VXV,
расположенным на оси Opt и выделенным светлой жирной лини-
ей (см. рис. 9.1).
При ?! = 1 имеем неравенство —Зр, +1 >0, откуда следует, что
(с учетом, чтор,!>0) 1< р^х/3. На плоскости Qp{qx множество
{Рр^О^р^’/з» 0, =1} изображается отрезком WVQ, выделенным
светлой жирной линией (см. рис. 9.1).
ПриОС^С! имеем неравенство—Зр,+1 £0,£—Зр,+1 £0, от-
куда вытекает р, = х/у На плоскости Opvq{ множество {рp0t)| р{ =
= */3, 0 < 01 < 1} изображается промежутком Ио (без концов Vx и
Ио), выделенным светлой жирной линией (см. рис. 9.1).
Таким образом, множество, изображающее на плоскости
ОР101 все решения системы третьего и четвертого неравенств и
цепочки 0 <Р] < 1,0 < 0] 1, есть зигзаг
В рассматриваемом примере точка пересечения отрезка ОРК и
зигзага РКК0К, Vесть точка W— (0; 1) (показанная кружком),
T.e.pj = 0,0, = 0, откуда следует, что равновесие Нэша существует,
является единственным и имеет вид
(Л 0°) = (РрА < $ = <(0; 1), (1; 0)) = (е2;/1).
Других равновесий Нэша рассмотренная биматричная игра не
имеет. Выигрыши игроков Р, и Р2 были выписаны выше.
397
Пример 9.5.2. Двойная матрица выигрышей биматричной игры
G(A, В) имеет вид
(30; 30) (200; -100)
(-50;100) (300;200)
Сразу получаем, что эта биматричная игра имеет два равнове-
сия Нэша в чистых стратегиях: (е( = (1; 0);/j = (1; 0)) и (е2;/2)
(ех = (0; l);/j = (0; 1)). Выигрыши игроков Pj и Р2 в этих равнове-
сиях Нэша соответственно равны
и1<ерЛ) = 30« = 30’
^1(^2’-^) 300, u2{e2,f^) — 200.
В рассматриваемом примере ап = 30; о12 = 200; а21 = -50;
а22 = 300; />и = 30; Z>12 = -100; 621 = 100; Ь22 = 200.
Имеем а = й]! - в12- о21 + а22 = 30 - 200 + 50 + 300 = 180,
р = а22 - а12 = 300 - 200 = 100,
у = 6(1 - Z»12 - Ь2Х + Ь22 = 30 + 100- 100 + 200 = 230,
8 = Ь22 - Ь2Х = 200 - 100 = 100.
Система неравенств (9.5.11)—(9.5.16) для этого конкретного
примера 9.5.2 имеет вид
(Pj -1)(180^,- 100) >0,
^,(180?, -100)>0,
(?! -1)(230р, - 100) >0,
qx (230р, -100) >0,
0<р,<1,
0<q, < 1.
Сначала проанализируем систему из первого и второго нера-
венств с учетом цепочек O^p^l.O^j^l.
При рх = 0 из первого неравенства (с учетом того, что qx > 0)
имеем 0£qx< 5/9- На плоскости Oplql множество {р,, ?])|р1 = 0,
0 < <?, < 5/9} изображается отрезком OB',, выделенным черной жир-
ной линией (рис. 9.2).
При р{ = 1 из второго неравенства (с учетом того, что qx < 1)
имеем цепочку 1 > qx > 5/9.
На плоскости Opxqx множество {рр ^^IPj = 1, 5/9 > qx > 1} изоб-
ражается отрезком выделенным черной жирной линией
(см. рис. 9.2).
При 0 < рх < 1 из первого и второго неравенств следует, что
qx = 5/9- На плоскости Qpxqx множество {рр <7j)|0 < рх < 1, qx = 5/9}
398
изображается отрезком W2 (без концов и И^2), выделенным
черной жирной линией (см. рис. 9.2).
Таким образом, множество, изображающее на плоскости Oplql
все решения системы из двух неравенств (р, -l)(180^j - 100) > 0,
р,( 180^1 - 100) > 0 и цепочек O^pj^l, O^^j^l, есть зигзаг
ОИ'И'И'.
Переходим к анализу системы из третьего и четвертого нера-
венств:
(9, -1)(23р| - 10) * 0, <7,(23^ - 10) £ 0
и двух цепочек 0 1,0 1.
При qx = 0 из неравенства (qx -1)(23/>j - 10) £ 0 с учетом того,
что рх £ 0, имеем 0 < рх £ |0/23. На плоскости Opxqx множество
{рр ^i)|0 < Pi < 10/гз’ 91 = ЭД изображается отрезком ОИр располо-
женным на оси Ор( и выделенным светлой жирной линией (см.
рис. 9.2).
При qx = 1 имеем неравенство 23р( > 10, откуда следует с уче-
том того, что рх < 1, % <Pj < 1. На плоскости Ор1?1 множество
{рр 9i)|10/23 <Р\ < 1,9\ = 1} изображается отрезком EjWj, выделен-
ным светлой жирной линией (см. рис. 9.2).
При 0 < q{ < 1 из третьего и четвертого неравенств получаем
Pi = *°/23. На плоскости Qpxqx множество {рр qx)|pj = 10/23,0 < qx < 1}
изображается промежутком VXV2 (без концов Vx и К2), выделен-
ным светлой жирной линией (см. рис. 9.2).
399
Таким образом, множество, изображающее на плоскости
Opfli все решения системы из третьего и четвертого неравенств
(?i -1)(230р1 - 100) > 0, - 100) > 0 и из цепочек 0 <р{ < 1,
0 < qx < 1, есть зигзаг О/ Й21Г3.
В рассматриваемом примере зигзаги и OK(K1K3
имеют три точки пересечения О = (0; 0), 1К3 = (1; 1), К3 = (*/23;
79).
Точке О = (0; 0) соответствует равновесие Нэша ((0; 1); (0; 1)) =
= (е2>Л)в чистых стратегиях e2,f2. В этом равновесии Нэша выиг-
рыш игрока Р, равен u{(e2,fj = 300, выигрыш игрока Р2 равен
“2(e2,f2) = 200.
Точке = (1; 1) соответствует равновесие Нэша ((1; 0); (1; 0)) -
= (вр/j) в чистых стратегиях ер/г В этом равновесии Нэша выиг-
рыш игрока Р{ равен = 30, выигрыш игрока Р2 равен «2(вр
/,)-зо.
Точке К3= (10/23; 5/9) соответствует равновесие Нэша ((10/23;
/23), ( /9> /9)) в смешанных стратегиях
.(10 13Л . (5 4>
23’23 I’ д’ д I-
Ожидаемый выигрыш игрока Р, равен
“’((23’23/(9’9/Г(23’23/(-50
= — = 105,56.
9
Ожидаемый выигрыш игрока Р2 равен
[710.13 А (5. 4?|=(10.13 \( 30
*4123’ 23/(9’ 9JJ~ 123’ 23/(100
200А Г5/9Л
300/V4/9J
-100") (5/9Л
200 /(4/9,1
1600 _
23 ~
69,57.
Таким образом, биматричная игра G(A, В) этого примера
(9.5.2) имеет три равновесия Нэша — два равновесия Нэша в чис-
тых стратегиях и одно равновесие в смешанных стратегиях.
Пример 9.5.3. (В.В. Морозов (2002)). Двойная матрица выиг-
рышей биматричной игры G(A, В) имеет вид
400
(0;3) (1;3)
(1;-1) (0;2)
Сразу получаем, что эта биматричная игра имеет равновесие
Нэша в чистых стратегиях: (еру^) ((е, = (1; 0);^ = (0; 1)). В этом
равновесии Нэша выигрыши игроков Рх и Р2 соответственно рав-
ны
В данном примере ап = 0; а12 = 1; a2I = 1, а22 = 0; Z>n = 3; Z>12 =
= 3;/>2I = -1; b22 = 2.
Имеем а = - о12 - а21 + а22 = 0 - 1 - 1 + 0= -2, Р = а22 - а12 =
= 0 — 1 = —1, у= — />)2 — />2[ + Z>22 = 3 — 3 + 1 + 2 = 3,5 = b22 — Ь2Х =
= 2+1 = 3.
Перепишем систему неравенств (9.5.11)—(9.5.16) для этого
конкретного примера (9.5.3):
(р, -1)(-291 + 1) > 0,
^(-2^+ 1) > 0,
(?1-1)(3Л-3)>0,
^(3Л-3)>0,
0<р,<1,
Рассмотрим первое неравенство и цепочки O^Pj^ljO^j^l.
При рх = 0 имеем неравенство -(-2/^ + 1) > 0, откуда следует
неравенство 2qx - 1 > 0, т.е., принимая во внимание неравенство
qx < 1, имеем 1 > qx > */2. На плоскости Opxqx множество {рр =
= 0, */2 < ^] <1} изображается отрезком IF, 1К2, выделенным черной
жирной линией (рис. 9.3).
При рх = 1 имеем неравенство -2^1 + 1 > 0, т.е. (принимая во
внимание неравенство qx > 0) имеем 0 £ qx £ х/2. На плоскости
Opxqx множество {рр ^,)|р1 = 0,0 < qx £ */2} изображается отрезком
выделенным черной жирной линией (см. рис.9.3).
При 0 < рх < 1 из первого и второго неравенств следует, что
qx = х/2. На плоскости Qpxqx множество {рр 0j)| 0 < рх < 1, qx = */2}
изображается отрезком (без концов W2 и 1К3), выделенным
черной жирной линией (см. рис. 9.3).
26 - 7620
401
Таким образом, множество, изображающее на плоскости
все решения системы из неравенств (рх - 1)(-2^1 + 1) > О,
Р|(_2?1 + 1) > Ои цепочек 0 < рх < 1, 0 < qx £ 1, есть зигзаг
и'И'И'з»;.
Переходим к анализу системы из третьего и четвертого нера-
венств
(?, - 1)(3Л - 3) > 0, qx(3px - 3) £ О
и двух цепочек 0 <рх < 1, 0 < qx < 1.
При qx = 0 имеем неравенство -рх + 1 > 0, т.е. (принимая во
внимание неравенство рх £ 0) 0 <рх < 1. На плоскости Opxqx мно-
жество {рр 4г()| 0 <рх < 1, qx = 0} изображается отрезком ОИ^, выде-
ленным светлой жирной линией (см. рис. 9.3).
При q{ = 1 имеем неравенство рх - 1 > 0, тл.рх > 1, и следова-
тельно, рх = 1. На плоскости Qpxqx множество {рр ^)|рх = 1, qx = 1}
изображается точкой Vx = (1; 1) (см. рис. 9.3).
При 0 < qx < 1 имеем равенстворх = 1. На плоскости Ор1^1 мно-
жество 0j)|рх = 1, 0 < qx < 1} изображается промежутком W4VX
(без концов FK4 и Vx), выделенным светлой жирной линией
(см. рис. 9.3).
Следовательно, множество, изображающее на плоскости
Ор1?1 все решения системы из неравенств (qx - 1)(3р1 - 3) £ 0,
- 3) £ 0 и цепочек 0 £рх < 1,0 < qx < 1, есть зигзаг
402
В рассматриваемом примере зигзаги и пе-
ресекаются по отрезку Точке W4 = (1; 0) соответствует рав-
новесие Нэша (ej/j) в чистых стратегиях eltf2.
Выигрыши игроков Р] и Р2 в этом равновесии Нэша были вы-
писаны в начале текста этого примера.
Каждой точке (1, qx), 0 < qx< */2 полупромежутка W4V\ (без
конца В'Д соответствует равновесие Нэша ((1; 0); (qx, 1 - q^i),
0 < 4i < */2,в котором стратегия игрока Рх является е( = (1; 0), стра-
тегия игрока Р2 является смешанной (qx, 1 - 4,), 0 < q{ < ’/2.
Следует особо отметить, что в рассматриваемом примере 9.5.3
имеем бесконечно много (континуум) равновесий Нэша в сме-
шанных стратегиях.
В равновесии Нэша ((1; 0); (4,; 1 - 4,)), 0 < 4! < 1/2 ожидаемые
выигрыши игроков Рх и Р2 соответственно равны
Го 1Y <7. ( di Л
= 1-4ь 0<4i^X’
«2(е1;(41,1-41)) = (1;0)
= 34] +3-34] =3.
3¥ 91 1
=(3;3)
U-41
Замечание 9.5.1. Пример 9.5.3 корректирует одно ошибочное
утверждение в Замечании 2 на с. 407 книги «Количественные ме-
тоды в экономических исследованиях» (2004).
9.6. Парето-эффективность в статических играх
с полной информацией
9.6.1. Определение 9.6.1 Профиль /игры G = {sk, uk(s), ке 7) назы-
вается Парето-эффективным (Парето-оптимальным), если не су-
ществует профиля s игры G, чтобы были справедливы неравен-
ства
uk(s) > uk(s*), к = 1,..., т,
при этом хотя бы одно из этих неравенств должно быть строгим.
26*
403
Это определение естественным образом формулируется в слу-
чае биматричной игры G(A,B) в чистых стратегиях и в случае сме-
шанного расширения G(A,B) биматричной игры G(A,B).
Профиль (в чистых стратегиях e^ff биматричной игры
G(A,B) называется Парето-эффективным в чистых стратегиях, ес-
ли не существует ни одного профиля чистых стратегий e.,fj,
для которых одновременно были бы справедливы неравенства
м1(еГ’//)^и1(е/ «Л )> , среди которых хотя
бы одно должно быть строгим.
Профиль (р*, q*) в смешанных стратегиях р* и q биматричной
игры G(A,B) называется Парето-эффективным, если не суще-
ствует ни одного профиля (р, q) смешанных стратегий р и q (среди
них могут быть и чистые стратегии), для которых одновременно
были бы выполнены неравенства и}(р*, q*) < их(р, q) и2(р*, q*) <
< и2(р, q), среди которых хотя бы одно должно быть строгим.
Профиль равновесия Нэша биматричной игры G(A, В)
в чистых стратегиях обязательно остается равновесием Нэша би-
матричной игры G(A, В) в смешанных стратегиях. А профиль,
Парето-эффективный в чистых стратегиях биматричной
игры G(A, В), уже может не быть Парето-эффективным в смешан-
ных стратегиях (см. ниже пример 9.6.3). Понятие Парето-эффек-
тивного в чистых стратегиях профиля биматричной игры введено
в параграфе 9.6 скорее в учебных целях в связи с тем, что это поня-
тие допускает наглядную геометрическую интерпретацию в дву-
мерном пространстве (плоскости Оиги2 выигрышей и и2 игроков
Р] и Р2 соответственно). Это пространство Outu2 выигрышей при-
нято также называть критериальным.
Каждый элемент (а^; by) двойной матрицы (9.2.2) показывает
величины a.j и Ь.. выигрышей игроков Р, и Р2 для профиля (e,;j^)
(чистых) стратегий е. и fj, выбранных игроком Р{ и игроком Р2 со-
ответственно. Если на оси Ouj отложить выигрыш а у, а на оси
О«2 — выигрыш Ь.., то точка Му = (a.? by) в пространстве Ои{и2 вы-
игрышей наглядно геометрически проинтерпретирует пару (а у-,
by) выигрышей игроков Р, и Р2 для профиля (е.; fj) их (чистых)
стратегий e^fj.
Пример 9.6.1 (продолжение примера 9.3.2). Двойная матрица
(Л|5) биматричной игры G(A, В) имеет вид
404
(1;2) (4;3) (2; 5)
Н;0) (5;3) (3;2)
(-1;7) (3;4) (1;б)
Если игрок Р, выбирает стратегию = (1; 0; 0) (т.е. первую
чистую стратегию), а игрок Р2 выбирает стратегию fx = (1; 0; 0)
(свою первую чистую стратегию), то выигрыш игрока Рх равен 1,
а выигрыш игрока Р2 равен 2.
Как уже было сказано выше, в системе координат OujU? на оси
О«] следует откладывать выигрыши игрока Рх, а на оси О«2 — вы-
игрыши игрока Р2.
Построим в пространстве выигрышей ОИ]И2 вектор (точку)
(1; 2) = М] и остальные элементы данной двойной матрицы
(рис. 9.4). Каждую построенную точку следует толковать в ка-
честве вершины прямого угла с (короткими) сторонами, парал-
лельными осям Ouj и О«2 и уходящими вправо и вверх.
Угол, вершиной которого является точка М2 = (-1; 7), не со-
держит («не ловит») ни одной из точек М},..., М6, М8, М9, отлич-
ных от точки Мг Отсюда следует (см. двойную матрицу), что пара
405
чистых стратегий е3 = (0; 0; 1) и/j = (1; 0; 0) игроков Р( и Р2 соот-
ветственно образуют Парето-эффекгивный профиль дан-
ной биматричной игры G(A, В) в чистых стратегиях.
Угол, вершиной которого является точка М2 = (4; 3), содержит
точку Ms. Поэтому соответствующая точке М2 пара чистых страте-
гий е1 = (1; 0; 0) и/2 = (0; 1; 0) игроков и Р2 образует профиль
стратегий (ер/2), который не является Парето-эффективным в
чистых стратегиях.
Таким образом, пары чистых стратегий (е3;/(), (е3;^), (е(;/3),
(e3;f2) и (e2;f2), которые соответствуют точкам Л/7, Л/9, М3, Л/8, М5,
формируют Парето-эффективные профили чистых стратегий в
чистых стратегиях, а пары чистых стратегий (е2; е{), (е2,/3),
которые соответствуют точкам М4, М{, М6, М2, формируют
профили чистых стратегий, которые не являются Парето-эффек-
тивными в чистых стратегиях.
Отметим, что в рассматриваемом примере профиль (e2,f2) рав-
новесия Нэша в чистых стратегиях совпадает с Парето-эффектив-
ным профилем в чистых стратегиях, а Парето-эффективные про-
фили в чистых стратегиях (e3,/j), (e3,f3), (e3,f2) не являются
профилями равновесия Нэша в чистых стратегиях.
Равновесие Нэша в чистых стратегиях может и не быть Паре-
то-эффективным в чистых стратегиях.
Смешанное расширение биматричной игры этого примера
9.6.1 рассматривать не будем.
Пример 9.6.2 (продолжение примера 9.3.3). Двойная матрица
(Л|Д) биматричной игры G(A, В) имеет вид
(30; 30) (400;-100)
(-5О;ЗОО) (200; 200)
Построим в пространстве выигрышей Ои(«2 векторы (точки)
Л/, = (30, 30), М2 = (400, -100), М3 = (-50, 300), М4 = (200, 200),
(рис. 9.5).
Здесь пары чистых стратегий (e2;/j), (е2;/2), которые
соответствуют точкам М3, М4, М2, формируют профили в чистых
стратегиях, которые Парето-эффективны. Пара чистых стратегий
(ep/j), которая соответствует точке Mv формирует равновесие
406
Нэша в чистых стратегиях, которое не является Парето-эффек-
тивным, т.е. равновесия Нэша могут не быть эффективными.
Здесь = (1; 0), е2 = (0; 1),/, = (1; 0),/2 = (0; 1).
9.6.2. Пример 9.6.3. Двойная матрица биматричной игры G(A, В)
имеет вид
(50; 70) (60;-50)
(100; 50) (-50; 120)
Рассматриваемая игра не имеет ни одного равновесия Нэша в
чистых стратегиях.
Построим в пространстве выигрышей Ои}и2 векторы (точки)
Мх = (50, 70), М2 = (60, -50), М3 = (100, 50), М4 = (-50, 120)
(рис. 9.6).
Здесь пары чистых стратегий (е,;/^, (e2,f^, (e2‘f2) ((е, = (1; 0),
е2 = (0; l),/t = (1; 0),f2 = (0; 1)), которые соответствуют точкам Mv
М3 и М4, формируют профили чистых стратегий, которые Парето-
эффективны в чистых стратегиях. Пара чистых стратегий (е{;/2),
соответствующая точке М2, формирует профиль чистых страте-
гий, который не является Парето-эффективным.
407
Перейдем к смешанному расширению G(A,B) данной бимат-
ричной игры.
Сначала определим равновесия Нэша в смешанных стратеги-
ях.
Имеем ап = 50; а12 = 60; а21 = 100; а22 = -50; Ьц = 70; 612 = -50;
Z>21 = 50; Ь22 = 120.
Положим а = ах t - а12 - а21 + а22 — 50 - 60 - 100 - 50 = -160,
В = а,,-а., = -50-60 = -110, у= Ь,,-Ь,^-Ьэ, + Z>,, = 70 + 50-
50+ 120 = 190, 5 = b22 - b2l = 120 - 50 = 70.
Тогда система неравенств (9.5.11)—(9.5.16) запишется так:
(р1-1)(-160?, + 110)^0,
р1(-160?1 + 110) ^0,
408
(<7,-1X190/,,- 70) > 0,
<7,(100/?! - 70) > О,
О^р, < 1,
0<^ < 1.
Проанализируем первые два неравенства
(р( - 1)(-160^ + ПО) > O,Pj(-16O0j + ПО) > 0 и две цепочки
О^р, < 1, 0<?( < 1.
Прирх = 0 имеем -(-16?. + 11) > О, откуда с учетом неравенства
qx < 1 получаем 1 > qx > "/1б. На плоскости Opxqx множество
{РР?1)|Р1 = 0, п/1б < ^! < 1} изображается отрезком РК, выделен-
ным черной жирной линией (рис. 9.7).
При рх = 1 имеем -16</. + 11 > 0, откуда с учетом неравенства
qx > 0 получаем 0 * /16- На плоскости Opxqx множество
{рр ?i)l₽i= 1,н/1б} изображается отрезком 1К3И^, выделен-
ным черной жирной линией (см. рис. 9.7).
При 0 < Pj < 1 имеем qx = п/16. На плоскости Opxqx множество
{рр ?i)l 0 <Pi < 1, = 11/i6J изображается промежутком (^ез
концов 1F, и РК3), выделенным черной жирной линией
(см. рис. 9.7).
Таким образом, множество, изображающее на плоскости
Opxqx все решения системы из двух первых неравенств и цепочек
0<р1<1,0<^1<1, есть зигзаг
Переходим к анализу системы из третьего и четвертого нера-
венств:
409
(9, - l)(190jp( - 70) > 0, 190/>, - 70) > 0 и двух цепочек
0</>j < 1,0<^ < 1.
При <7, = 0 имеем неравенство -(19р, - 7) > 0, откуда с учетом
неравенства р{ > 0 получаем 0 <pj < 7/19- На плоскости Opxqx мно-
жество {рр 9()| 0 < р( < 7/19, qx = 0} изображается отрезком ОКр
выделенным светлой жирной линией (см. рис. 9.7).
При q{ = 1 имеем неравенство 19р1 - 7 > 0, откуда с учетом не-
равенства/^ < 1 получаем 7/19 <р{ < 1. На плоскости Oplqi множест-
во {рр 9,)| 7/19 < р( < 1, q{ = 1} изображается отрезком К2К3, выде-
ленным светлой жирной линией (см. рис. 9.7).
При 0 < qx < 1 имеем равенство р, = 7/19. На плоскости Ор^(
множество {рр ^plP] =7/19, 0 < < 1} изображается промежутком
К, V2 (без концов и К2), выделенным светлой жирной линией
(см. рис. 9.7).
Следовательно, множество, изображающее на плоскости
Opj?! все решения системы из третьего и четвертого неравенств и
из цепочек 0 <р{ < 1,0 <qx < 1, есть зигзаг
Зигзаги и ОК(К2К3 имеют единственную общую
точку К4 =
7 1П
19’16/
которой соответствует единственное равно-
тт (( 7 12Л (11 5 Y)
весне Нэша 11 19’19 1’1 II в смешанных стратегиях
Ожидаемый выигрыш игрока Р( равен
✓ _0 0 \
щр )=
50 60 1 16
119’19Д100 -50J 5
\16>
= 53,125.
Ожидаемый выигрыш игрока Р2 равен
«2(Р°,9°) =
_7_.12Y70 -50А 16
19’19^50 120 J _5_
ч16>
1090
19
= 57,368.
410
Построим в пространстве выигрышей OU]U2 точку
(850 1090Л . о
Мо = <см- Рис> 9 6)-
\ 10 17 J
Таким образом, биматричная игра G(A, В) этого примера име-
ет единственное равновесие Нэша в смешанных стратегиях.
Для того чтобы проанализировать Парето-эффективные про-
фили в смешанных стратегиях/» = (рх,р^) nq = (qx, </2), выпишем в
явном виде функции ожидаемых выигрышей игроков Рх и Р2 соот-
ветственно:
(50 60 Ya А
Ui(p,q) = (Pi,P2) inn ЬбО/зд + ЮО^+бО/^-бО/»^,
U2<P^) = (Pl‘,P2) 50
-50Y91
120 ? ^2
= 70^ +5O0j/>2 -5O/>!02 +120p292-
Из выписанных формул получим следующие представления
вектора и = (и{; и2), принадлежащего пространству выигрышей
Ow(«2:
(YA Г f50A
100А1 Г (60 A f-50A
50 J]+92|/\-5oJ+/412oJ
Pi
(50]
*70 Г72
60 Al Г flOOA f-50A'
-50Jj+P1 [*[50 J+*[ 120J
(9.6.1)
M\ M2 M3 M4
Если в выражении (9.6.1) qx = 1, q2 = 0, apx пробегает значения
от 0 до 1 (тогда р2 пробегает значения от 1 до 0, ибо рх + р2 = 1,
рх >0,р2> 0), точка и = (и,; и2) заметает (от слова «метла») отрезок
M3A/j (см. рис. 9.6).
Если в выражении (9.6.1) qx = 0, q2 = 1, а 0 £рх £ 1, 1 >р2 S 0,
точка и = (и,; и2) заметает отрезок М4М2 (см. рис. 9.6). Если в
(9.6.1)/», = 1,/>2 = 0, аО^#! < 1,1 > д2 >0, точка и = (их; и2) заметает
отрезок М2МХ. Если в (9.6.1) рх = 0, р2 = 1, а 0 < qx £ 1, 1 £ q2 £ 0,
точка и = (их, и2) заметает отрезок М4М3 (см. рис. 9.6).
Если 0 <рх £ 1,1 >р2 > 0,0 < qx £ 1,1 > q2 £ 0, то точка и = (их, и2)
заметает некоторое множество в пространстве выигрышей Оихи2,
которому принадлежат все построенные только что отрезки М3МХ,
М4М2, М2МХ, М4М3, однако внутренние точки отрезка М2М3 в это
411
множество не входят. Это можно доказать, взяв любую точку про-
межутка М2М3, скажем точку (80; 0), и доказав, что система урав-
нений ux(jr, q) = 80, и2(р; q) = 0 не имеет ни одного неотрицатель-
ного решениярх,р2, qx, q2, такого, чторх +р2 = 1, qx + q2 = 1.
Любая точка М = (их; и2) отрезка М3М4 соответствует Парето-
эффективному профилю (р; q) в смешанных стратегиях, ибо угол
этой точки не содержит (кроме нее самой) ни одной точки тре-
угольника МХМ3М4.
Как уже отмечалось выше, точка Мх = (50; 70), которая соот-
ветствует Парето-эффективному профилю (ex;fx) в чистых страте-
гиях ех и fx, не соответствует никакому Парето-эффективному
профилю (р; q) в смешанных стратегиях, ибо угол точки Мх (кроме
нее самой) содержит часть точек отрезка М3М4.
Точка Мо, соответствующая равновесию Нэша в смешанных
стратегиях, не соответствует Парето-эффективному профилю в
смешанных стратегиях, ибо точка Мо не принадлежит отрезку
М3М4, а расположена строго ниже него.
В заключение отметим, что четырехугольник МХМ3М4 М2МХ и
точка Мо, которая расположена вне его, принадлежат множеству
ожидаемых выигрышей рассматриваемой биматричной игры. Са-
мо множество ожидаемых выигрышей здесь не строится.
9.7. Динамические игры с совершенной
и несовершенной информацией
9.7.1. В динамической игре игроки делают свои ходы (т.е. прини-
мают решения о своих действиях) поочередно. Если каждый иг-
рок, делая ход, знает, какие ходы были сделаны до него, то такая
динамическая игра называется игрой с совершенной информацией.
В противном случае игра называется игрой с несовершенной инфор-
мацией (уточнение дается ниже).
В качестве примера динамической игры с совершенной ин-
формацией рассмотрим хорошо известную игру, которую называ-
ют «Вхождение фирмы на рынок». Отметим, что в изложении
разных авторов фигурируют разные условные цифры.
Пример 9.7.1 (Вхождение фирмы на рынок)
В отрасли функционирует фирма-монополист (,F2), и в эту от-
расль пытается войти другая фирма (Гх) и потеснить на рынке от-
412
расли фирму-монополиста F2. Фирма Fx (игрок Р,) имеет два воз-
можных хода (два варианта принятия решения о своих действиях):
вступить (В) в отрасль (в частности, построить завод по выпуску
продукции) или не вступить (НВ) в отрасль. Фирма F2 (игрок Р2)
имеет два своих возможных хода: сохранить (С) объем выпуска-
емой продукции или сократить (СКР) объем выпускаемой продук-
ции. Ходы фирмы делают поочередно: сначала ход делает фирма
Fx, потом ход делает фирма F2, и на этом игра заканчивается.
Если фирма Г] приняла решение В в отрасль, а фирма F2 при-
няла решение С объем выпускаемой продукции, то, естественно,
объем предложения в отрасли вырастет и цена на продукцию упа-
дет. В этой ситуации весьма вероятно, что фирма-новичок Fx по-
лучит вообще отрицательную прибыль, а прибыль фирмы F2 оста-
нется положительной, но меньше максимальной (равной 14).
Итак, в этом случае расклад прибылей фирм Fx и F2 будет, напри-
мер, таким (—3; 6).
Если фирма Fx приняла решение В в отрасль, а фирма F2 при-
няла решение СКР объем выпускаемой продукции, т.е. уступила
часть (возможно, половину) рынка фирме Fx, то расклад прибы-
лей фирм Fx и F2 будет таким: (7; 7).
Если фирма Fx приняла решение НВ в отрасль, а фирма F2
приняла решение С объем выпускаемой продукции, то, естест-
венно, фирма Fx в отрасли прибыли не получит, а у фирмы F2 бу-
дет максимальная монопольная прибыль, равная 14 (например,
14 млрд руб.). Таким образом, описанная последовательность хо-
дов НВ — С приводит к следующему набору выигрышей игроков
Рх и Р2 соответственно (к набору прибылей фирм Fx и F2): (0; 14).
Если фирма Fx приняла решение НВ в отрасль, а фирма F2
приняла решение СКР объем выпускаемой продукции, то эта по-
следовательность ходов НВ — СКР приводит к следующему набо-
ру прибылей фирм Fx и F2: (0; 8). Отметим, что причин и поводов
СКР объема выпускаемой фирмой F2 продукции может быть до-
статочно много, например в связи с ухудшением конъюнктуры в
данной отрасли (поэтому фирма Fx решила НВ, а фирма F2 реши-
ла СКР объем производства).
Динамическая игра, описывающая данную содержательную за-
дачу, представляет собой математическую модель этой содержатель-
ной задачи и называется игрой «Вхождение фирмы на рынок».
Изобразим динамическую игру в виде графа (рис. 9.8), кото-
рый называется деревом игры.
413
Представление игры в виде дерева является развернутой (рас-
ширенной, экстенсивной) формой игры.
Развернутая форма динамической игры с совершенной ин-
формацией включает:
1) дерево игры, которое имеет единственную начальную вер-
шину (позицию), в котором каждая вершина (позиция) имеет
только одну вершину (позицию), которая ей предшествует;
2) множество игроков;
3) единственную дугу, которая соединяет любую вершину
(кроме начальной) с той единственной вершиной, которая ей не-
посредственно предшествует;
4) конечные вершины, которые не предшествуют другим вер-
шинам и которые содержат векторы выигрышей всех игроков.
В каждой вершине дерева (т.е. в кружке) на рис. 9.8 указан иг-
рок, делающий ход из этой вершины (принимающий решение о
своих действиях). В квадратных скобках находятся номера вер-
шин. Дуга изображает сам ход. Дуга имеет направление от верши-
ны предшествующей к вершине, за ней следующей. В частности,
дуга (В), которая соединяет вершины Ш и [1], показывает, что иг-
рок Рх (фирма F,) делает свой ход (принимает решение В в от-
расль). Вершина с номером [1], куда упирается дуга (В), означает,
что теперь решение будет принимать игрок Р2 (фирма Г2), кото-
рый может сделать ход С (сохранить объем выпускаемой продук-
ции) или сделать ход СКР (сократить объем выпускаемой продук-
414
ции). После хода игрока Р2 (фирмы Г2) игра заканчивается. Кон-
цом каждой последней (из четырех) дуги является конечная
(висячая) вершина, в каждой из которых показаны прибыли
фирм Т7! и F2 (выигрыши игроков Р1 и Р2).
Отметим, что в рассматриваемом примере 9.7.1 начальная вер-
шина — это вершина Д], вершины [1] и [з] — вершины, которые
следуют за вершиной Щ.
Множество, состоящее из вершины Ш, называется множест-
вом очередности фирмы Ft (игрока Р,); множество, состоящее из
вершин [2] и[з], называется множеством очередности фирмы Р2
(игрока Р2). Остальные четыре вершины образуют множество ко-
нечных вершин. В каждой из них слева указана прибыль фирмы
Рр а справа — прибыль фирмы Р2 (т.е. слева указаны выигрыши
игрока Рр справа — выигрыши игрока Р2).
Последовательность ходов (действий), которые выбирают иг-
роки Р] и Р2 в каждой из своих вершин, называется траекторией
ходов (действий), т.е. траектория ходов начинается в начальной
вершине и заканчивается в одной из конечных вершин. Траекто-
рия ходов, предпочитаемая остальным траекториям, называется
решением динамической игры с совершенной информацией в
предположении, что игроки ведут себя рационально.
Решение игры в развернутой форме можно найти методом об-
ратной индукции, суть которого в том, что игра анализируется с ее
конца, т.е. с конечных вершин.
Если фирма F, сделала ход (В), т.е. вступила в отрасль, то фирма
F2 сделает ход (СКР), т.е. сократит объем выпускаемой продукции,
ибо прибыль, равная 7, больше прибыли, равной 6. Здесь формаль-
но сравниваются вторые координаты векторов (—3; 6) и (7; 7), ибо
анализируется фирма FT Подчеркнем вектор (7; 7) на рис. 9.8.
Если фирма F} сделала ход (НВ), т.е. решила не вступать в от-
расль, то фирма F2 сделает ход (С), т.е. сохранит объем выпуска-
емой продукции, ибо 14 > 8. Здесь формально сравниваются вто-
рые координаты векторов (0; 14) и (0; 8), ибо анализируется фирма
F2. Подчеркнем вектор (0; 14) на рис. 9.8.
Переходим к определению первого хода фирмы Fv Для этого
следует сравнить уже первые координаты двух подчеркнутых век-
торов (7; 7) и (0; 14). В связи с тем что фирма F{ ведет себя рацио-
нально, она сделает ход (В), ибо 7 > 0.
Таким образом, в предположении того, что оба игрока ведут
себя рационально, метод обратной индукции, который только что
415
был использован для построения решения игры в развернутой
форме, состоит из двух этапов. Сначала сопоставляются прибыли
фирмы F2 путем сравнения вторых координат двух пар векторов
прибылей: пары (—3; 6) и (7; 7) и пары (0; 14) и (0; 8). В результате
мы получаем из двух пар векторов одну пару векторов (7; 7) и
(0; 14), в которой сравниваем уже первые координаты 7 и 0. Реше-
нием рассматриваемой игры является траектория, состоящая из двух
ходов: хода (В), который делает фирма F, из вершины Щи который
приводит в единственную вершину 0; из вершины Щфирма F2
затем делает ход (СКР), который приводит только в одну конеч-
ную вершину с вектором прибылей (7; 7). В результате таких ходов
вектор прибылей фирм F{ и F2 (вектор выигрышей игроков Рх и
Р2) есть вектор (7; 7).
Метод обратной индукции, продемонстрированный на при-
мере 9.7.1, является общим методом решения конечных динами-
ческих игр с совершенной информацией, имеющих развернутую
форму, который позволяет получить хотя бы одно решение такой
игры. Если дополнительно предположить, что выигрыши игроков
во всех конечных вершинах различны, то такое решение (полу-
ченное методом обратной индукции) будет единственным. Метод
обратной индукции на дереве называется алгоритмом Куна
{Kuhn Н. (1953))
Отметим, что последовательность дуг дерева, такая, что вер-
шина, которая является концом предыдущей дуги, — это начало
следующей дуги, называется путем в дереве. Следовательно, тра-
ектория ходов, которая исходит из начальной вершины и закан-
чивается в одной из конечных вершин, является в дереве путем,
исходящим из начальной вершины и достигающим какую-то одну
из конечных (висячих) вершин. Этот путь принято называть пар-
тией игры (динамической игры с совершенной информацией в
развернутой форме). Траектория ходов (партия) однозначно реа-
лизует набор вершин дерева игры, исходящий из начальной вер-
шины и достигающий какую-то одну из конечных вершин в связи
с тем, что в дереве из каждой предыдущей вершины по дуге, выхо-
дящей из этой вершины, можно попасть только в единственную
следующую за ней вершину. В примере 9.7.1 в качестве партии
можно взять набор вершин [1], [5], (-3;6); 0, 0, (7; 7); 0, 0,
(0; 14); Щ, 0,(0; 8).
416
Каждой вершине дерева, которое представляет динамическую
игру с совершенной информацией, соответствует единственная
предыстория, т.е. траектория ходОв, которая приходит из началь-
ной вершины в данную.
Уточним термин «совершенная информация» в случае дина-
мической игры, используя представление в развернутой форме.
Совершенная информация означает, что каждый игрок знает всю
предысторию игры или, используя представление динамической
игры в виде дерева, каждый игрок знает, в какой вершине он на-
ходится.
9.7.2. От развернутой формы динамической игры с совершенной
информацией перейдем к представлению этой игры в нормальной
форме, которая позволяет получать решение игры в виде равнове-
сия Нэша.
Представление игры в нормальной форме состоит из: 1) зада-
ния множества номеров игроков; 2) множества стратегий (чистых)
для каждого игрока; 3) функции выигрыша каждого игрока.
Чистая стратегия игрока динамической модели с совершен-
ной информацией в развернутой форме определяется так. Фикси-
руются все вершины дерева, ходы из которых принадлежат опре-
деленному игроку (каждый ход имеет один и тот же номер t). Для
каждой фиксированной вершины из всех возможных ходов с но-
мером /данного игрока выбирается любой, но обязательно един-
ственный ход.
Далее берется совокупность этих выбранных единственных
ходов по всем зафиксированным вершинам данного игрока, ко-
торые соответствуют всем его ходам. Выбранная совокупность
ходов и есть его чистая стратегия.
Поясним понятие чистой стратегии игрока и взаимосвязь по-
нятий чистой стратегии и хода игрока в примере 9.7.2, который
является продолжением примера 9.7.1.
Пример 9.1.2
Из одной вершины [1] (см. рис. 9.8) первая фирма Fx (т.е. иг-
рок Pj) может сделать только два хода: ход (В) и ход (НВ), поэтому
для фирмы Fj имеем две чистые стратегии: стратегию (В) и страте-
гию (НВ).
Вершины [2] и [з] — это две вершины, из каждой фирма Р2 (иг-
рок Р2) может сделать по два своих хода (после хода фирмы F^.
27 - 7620
417
Если мы выберем какой-то ход фирмы F2 из вершины [2] и какой-
то ход фирмы F2 из вершины [з], то эту пару ходов следует толко-
вать в качестве чистой стратегии фирмы Fr В связи с тем что из
двух вершин ([2] и [з]) по одному ходу из каждой вершины можно
выбрать четырьмя способами, мы получаем четыре чистые страте-
гии фирмы F2 для нормальной формы динамической биматрич-
ной игры с совершенной информацией.
Первую чистую стратегию фирмы F2 построим путем выбора
хода (С) из вершины [2] и хода (С) из вершины [з]. Эта чистая стра-
тегия фирмы F2 имеет следующее формальное представление:
(В) (НВ) 00(C)
0 (С)
(-3;6)
(0; 14)
Если фирма F{ выбирает стратегию (В), т.е. она выбирает дугу,
соединяющую вершины [0 и [2], и фирма F2 делает свой ход (С) из
вершины [2], тогда дуга (С) дерева, выходящая из вершины [2], за-
канчивается вектором (—3; 6) (см. рис. 9.8). Число —3 равно при-
были (точнее, убытку) фирмы F{ (т.е. выигрышу (в данном случае
проигрышу) игрока Р(), число 6 равно прибыли фирмы F2
(т.е. выигрышу игрока Р2). Таким образом, пара чисел (—3; 6) есть
не что иное, как элемент двойной матрицы биматричной игры.
Остальные элементы этой двойной матрицы будут построены
постепенно дальше.
Если фирма F{ выбирает стратегию (НВ), т.е. она выбирает
дугу, соединяющую вершины [1] и [з], и фирма F2 делает свой ход
(С) уже из вершины [з], тогда дуга (С) дерева, выходящая из вер-
шины заканчивается вектором (0; 14) (см. рис. 9.8). Число 0
равно прибыли фирмы F{ (т.е. выигрышу игрока Р(), число 14 рав-
но прибыли фирмы F2 (т.е. выигрышу игрока Р2). Следовательно,
пара чисел (0; 14) есть следующий элемент двойной матрицы би-
матричной игры.
Вторую чистую стратегию фирмы F2 построим путем выбора
хода (СКР) из вершины [2] и хода (СКР) из вершины [з]. Эта чис-
тая стратегия фирмы F2 имеет формальное представление
418
(В)
(НВ)
@(СКР)
[з](СКР)
(7;7)
(0;8)
Пояснения этого представления аналогичны пояснениям
первой чистой стратегии фирмы F2 и поэтому здесь не приво-
дятся.
Третью чистую стратегию фирмы F2 построим путем выбора
хода (С) из вершины [2] и хода (СКР) из вершины [з]. Четвертую
чистую стратегию фирмы F2 построим путем выбора хода (СКР)
из вершины [5] и хода (С) из вершины [2]. Формально третья и чет-
вертая чистые стратегии фирмы F2 соответственно имеют вид
(В)
(НВ)
й (С) [2] (СКР)
@ (СКР) [з](С)
(-3;6) (7; 7)
(0; 8) (0; 14)
Пояснения этих представлений аналогичны пояснениям пер-
вой чистой стратегии и поэтому здесь не приводятся.
Отметим, что номера у этих четырех чистых стратегий фирмы
F2 можно было расставить иначе.
На этом заканчивается комплектование всех чистых стратегий
фирмы F2, которая каждый раз выбирает свои ходы после того,
как свой ход сделает фирма Fv Основанием для такого заверше-
ния является осуществление полного перебора всех пар возмож-
ных ходов фирмы F2, когда фирма F2 один ход делает из вершины
а другой — из вершины [з].
Сведем чистые стратегии фирм F{ и F2 в табл. 9.10, содержа-
щую двойную матрицу биматричной игры с матрицами 2x4.
Матрица Л выигрышей игрока Р, (фирмы F^ и матрица выиг-
рышей игрока Р2 (фирмы Р2) соответственно имеют вид
(-37-37^ 5_f6767>|
ДО 0 0 0/ Д148814/
27*
419
Таблица 9.10
Чистые стратегии фирмы F2
(i) 13(C) [3(C) (2) Ш(СКР) @(СКР) (3) [3 (С) 13 (скр) (4) [З(СКР) 13(C)
Чистые страте- ГИИ фирмы (В) (-3;6) (7; 7) (-3;6) (7; 7)
(НВ) (б; 14) (0;8) (б; 8) (б; 14)
Напомним (см. параграф 9.4), что первой (В) чистой стратеги-
ей фирмы Fj является также вектор et = (1; 0), второй (НВ) чистой
стратегией фирмы Ft — вектор е2 = (0; 1), первой чистой стратеги-
ей фирмы F2 — вектор /i = (1; 0; 0; 0), второй чистой стратегией
фирмы F2 — вектор/2 = (0; 1; 0; 0), третьей чистой стратегией фир-
мы F2 — вектор/3 = (б; 0; 1; 0), четвертой чистой стратегией фирмы
F2 — вектор f4 = (0; 0; 0; 1).
Построение двойной матрицы табл. 9.10 представляет собой
результат перехода от игры в развернутой форме к игре в нормаль-
ной форме. Это главное формальное обстоятельство. Менее важ-
но здесь то, что речь идет о динамической игре с совершенной
информацией.
В двойной матрице (Л|2?) табл. 9.10 расставим «птички» и
«шляпки» и получим три равновесия Нэша в чистых стратегиях
биматричной игры G(A, В) с выписанной в табл. 9.10 двойной мат-
рицей (Л|Б):
(^(«р/РЛерД)-
9.7.3. Как уже отмечалось, в результате использования метода
обратной индукции (см. пример 9.7.1) было получено на основа-
нии предпосылки о рациональном поведении фирм F{ и F2 реше-
ние динамической игры с совершенной информацией в виде тра-
ектории ходов (В) и (СКР) с вектором прибылей фирм Ft и F2,
равным (7; 7).
Проанализируем связь между решением динамической игры с
совершенной информацией, полученным методом обратной ин-
дукции, и тремя равновесиями Нэша.
420
Равновесие Нэша (e2;/j) интерпретируется следующим обра-
зом. Если фирма Fx делает ход (В), то фирма F2 делает ход (С), если
фирма делает ход (НВ), то фирма F2 делает ход (С) (см. рис. 9.8).
Последовательность ходов (В) и (С) противоречит предпосылке о
ряпиональном поведении фирм Fx и F2, ибо после хода (В) фирмы
Fx фирма F2 на основании предпосылки о ее рациональном пове-
дении должна сделать ход (СКР), ибо прибыль фирмы F2, рав-
ная 6, меньше прибыли фирмы F2, равной 7.
Противоречие предпосылке рациональности означает, что
траектория ходов (В) и (С) не может быть получена методом об-
ратной индукции, который опирается на предпосылку о рацио-
нальном поведении фирм Fx и F2. Таким образом, равновесие
Нэша (e2\fx) оказывается «лишним».
Равновесие Нэша (e2,fx) интерпретируется следующим обра-
зом. Если фирма Fx делает ход (В), то фирма F2 делает ход (СКР),
что соответствует предпосылке о рациональном поведении фир-
мы F2 (прибыль фирмы F2, равная 7, больше прибыли фирмы F2,
равной 6, — см. рис. 9.8). Если фирма Fx делает ход (НВ), то фирма
F2 делает ход (СКР), что противоречит предпосылке о рациональ-
ном поведении фирмы F2, ибо после хода (НВ) фирмы Fx фирма F2
должна сделать ход (С) в связи с тем, что прибыль фирмы F2, рав-
ная 8, меньше прибыли фирмы F2, равной 14. Поэтому траектория
ходов (НВ) и (СКР) не может быть получена методом обратной
индукции. Следовательно, равновесие Нэша (врД) (как и равно-
весие Нэша (ex,f^) является «лишним».
Осталось рассмотреть равновесие Нэша (е,; Д), для которого
мы имеем следующие утверждения. Если фирма Fx делает ход (В),
то фирма F2 делает ход (СКР). Если фирма Fx делает ход (НВ), то
фирма F2 делает ход (С). Обе траектории ходов ((В) и (СКР), (НВ)
и (С)) вполне содержательно состоятельны и соответствуют пред-
посылке о рациональном поведении фирм Fx и F2.
Таким образом, решение динамической игры с совершенной
информацией в виде траектории ходов (В) и (СКР) соответствует
равновесию Нэша (врД) в чистых стратегиях, а по существу и есть
равновесие Нэша (е,;Д) в чистых стратегиях.
Этот частный факт обобщается в виде следующей теоремы.
Теорема 9.7.1. Любое решение динамической игры с совер-
шенной информацией (с конечным числом ходов), полученное
методом обратной индукции, есть равновесие Нэша (в чистых
стратегиях).
421
Как показали только что приведенные рассуждения, обратное
утверждение о том, что любое равновесие Нэша может быть полу-
чено методом обратной индукции, является неверным.
Наличие «лишних» равновесий Нэша достаточно типично при
представлении динамических игр в нормальной форме. «Лиш-
ние» равновесия Нэша противоречат предпосылке о рациональ-
ном поведении игроков Р, и Р2 и поэтому могут дать смещенную
оценку ожидаемому решению динамической игры с совершенной
информацией.
9.7.4. Возникает вопрос о возможности элиминирования «лиш-
них» равновесий Нэша. Элиминирование «лишних» равновесий
Нэша называется рафинированием (от англ, refinement — усовер-
шенствование, уточнение).
Прежде чем описать и проанализировать один из возможных
подходов элиминирования «лишних» равновесий Нэша динами-
ческой игры с совершенной информацией путем усиления поня-
тия равновесия Нэша таких игр, сделаем одно замечание.
Замечание 9.7.1. С одной стороны, динамическая игра с совер-
шенной информацией (с двумя игроками и с конечным числом
ходов) может быть представлена в нормальной форме в виде двой-
ной матрицы (Л|Б) (в примере 9.7.2 в виде двойной матрицы
табл. 9.10). С другой стороны, двойная матрица (Я|7?) (в частности,
матрица табл. 9.10) является нормальной формой биматричной
игры, которая является частным случаем статической игры с пол-
ной информацией (см. параграф 9.2). Таким образом, каждая
двойная матрица (Л|7?) является представителем сразу двух игр:
динамической (с совершенной информацией) и статической (с
полной информацией). В статической игре с полной информаци-
ей среди равновесий Нэша (найденных с помощью двойной мат-
рицы) «лишних» не бывает. В динамической игре с совершенной
информацией среди равновесий Нэша могут быть «лишние».
Приведем определение важного понятия подыгры игры с со-
вершенной информацией в развернутой форме.
Определение 9.7.7. Подыгра игры с совершенной информацией
в развернутой форме — эта игра в развернутой форме, которая со-
держит в качестве начальной любую вершину дерева игры (кроме
конечных вершин), а также все вершины дерева игры, следующие
за этой выбранной в качестве начальной вершиной, вплоть до ко-
нечных вершин игры. Сама игра называется полной игрой.
422
Выигрыши игроков, которые показаны в конечных вершинах
подыгры, совпадают с выигрышами игроков в конечных верши-
нах полной игры.
Собственная подыгра — это подыгра, начальная вершина кото-
рой отлична от начальной вершины полной игры. Полная игра
называется также своей несобственной подыгрой.
У динамической игры с совершенной информацией, пред-
ставленной на рис. 9.8, есть три подыгры: сама игра с начальной
вершиной щ и две ее собственные подыгры с начальными верши-
нами [I] и [з].
Определение 9.7.2. Совершенным в подыграх равновесием называ-
ется такой набор стратегий игроков, который является равновеси-
ем Нэша в полной игре, а соответствующие части этого набора
стратегий являются равновесиями Нэша во всех собственных по-
дыграх полной игры.
Замечание 9.7.1. Понятие совершенного в подыграх равнове-
сия было предложено германским экономистом Р. Зельтеном в
работе Selten R. (1965).
Пример 9.7.3 (продолжение примеров 9.7.1 и 9.7.2). Предста-
вим первую собственную подыгру с начальной вершиной [5] в
нормальной форме.
Фирма в этой подыгре не функционирует, а фирма F2 может
сделать один из двух ходов (С) и (СКР). Двойная матрица рас-
сматриваемой подыгры имеет вид
@(С) m (скр)
(-3;6) (7; 7)
В этой двойной матрице имеет место одно равновесие Нэша
(«ь /2) (здесь ё} = (1), = (0; 1)). Оно предписывает фирме Г2 в вер-
шине [2] сделать ход (СКР). Для того чтобы равновесие Нэша в
полной игре было совершенным в подыграх равновесием, необхо-
димо, чтобы в вершине [2] фирма F2 сделала ход (СКР). А равнове-
сие Нэша (е2; /j) (здесь е2 — (0; 1),/.= (1; 0; 0; 0)) в полной игре
предписывает фирме F2 из вершины |2| сделать ход (С) (см. чистую
стратегию (1) фирмы F2 в двойной матрице с размерами (2 х 4) в
табл. 9.10). Следовательно, равновесие Нэша {e2,ff полной игры
не является совершенным в подыграх равновесием.
423
Равновесие Нэша (врД) (здесь е, = (1; 0),Д® (0; 0; 0; 1)) в пол-
ной игре предписывает фирме F2 из вершины |2] сделать ход (СКР)
(см. чистую стратегию (4) фирмы F2 в двойной матрице с размера-
ми (2 х 4), т.е. равновесие Нэша (ej Д) полной игры содержит в
качестве составной части равновесие Нэша подыгры с на-
чальной вершиной [2]).
Представим вторую собственную подыгру с начальной верши-
ной 0 в нормальной форме. Фирма Ft в этой подыгре не функци-
онирует, а фирма F2 может сделать один из двух ходов (С) и (СКР).
Двойная матрица рассматриваемой подыгры имеет вид
0(C) 0(СКР)
(0;14) (0;8)
В этой двойной матрице имеет место одно равновесие Нэша
Л) (здесь ё1 = (1), / = (1; 0)). Оно предписывает фирме F2 в вер-
шине 0 сделать ход (С). Для того чтобы равновесие Нэша в пол-
ной игре было совершенным в подыграх равновесия, необходимо,
чтобы в вершине 0 фирма F2 сделала ход (С). А равновесие Нэша
(врД) (здесь в] = (0; 1),Д = (0; 1; 0; 0)) в полной игре предписыва-
ет фирме F2 из вершины 0 сделать ход (СКР) (см. чистую страте-
гию (2) фирмы F2 в двойной матрице с размерами (2 х 4) в
табл. 9.10). Следовательно, равновесие Нэша (ex\f^ полной игры
не является совершенным в подыграх равновесием.
Равновесие Нэша (е(;Д) (здесь^ = (1; 0),Д = (0; 0; 0; 1)) в пол-
ной игре предписывает фирме F2 из вершины 0 сделать ход (С),
т.е. равновесие Нэша (e{; Д) полной игры содержит в качестве со-
ставной части равновесие Нэша (ё(; Д) подыгры с начальной вер-
шиной 0.
Из того, что равновесие Нэша (врД) в полной игре содержит в
качестве составных частей равновесия Нэша обеих подыгр, сле-
дует, что равновесие Нэша (вр Д) есть совершенное в подыграх
равновесие.
Таким образом, равновесие Нэша (вр Д) полной игры (дина-
мической игры с совершенной информацией), с одной стороны,
получается методом обратной индукции и, с другой стороны, оно
есть совершенное в подыграх равновесие, понятие которого уси-
ливает и уточняет понятие равновесия Нэша.
424
Отмеченное обстоятельство является частным случаем общей
теоремы о том, что в динамических играх с совершенной инфор-
мацией и конечным числом ходов множество решений, получа-
емых методом обратной индукции, совпадает с множеством со-
вершенных в подыграх равновесий.
В связи с тем что метод обратной индукции может быть проще
методов отыскания совершенных в подыграх равновесий (особен-
но в случае, когда нормальные формы игр являются громоздки-
ми), совершенные в подыграх равновесия следует отыскивать с
помощью метода обратной индукции (который к тому же может
иметь достаточно высокую степень наглядности).
9.7.5. Вернемся к табл. 9.10.
Чистые стратегии фирмы F2
(1)Ш(С) 0(C) (2) Щ (СКР) 0(СКР) (3)0 (С) 0(СКР) (4) |2] (СКР) 0(C)
Чистые страте- гии фирмы (В) (-3; 6) (7; 7) (-3;6) (7; 7)
(НВ) (б; 14) (0; 8) (б; 8) (0;14)
Выше уже отмечалось, что рассматриваемая динамическая
игра с совершенной информацией, представленная в нормальной
форме, имеет три равновесия Нэша — три клетки (0; 14), (7; 7), (7;
7), каждая из которых содержит «птичку» и «шляпку». Более фор-
мально эти три равновесия Нэша в чистых стратегиях легко пред-
ставить в виде трех векторов (e2,/j), (e{,f2) и (ерД), где е{ = (1; 0),
е2 = (0; 1),/! = (1; о; 0; 0),/2 = (0; 1; 0; 0),/4 = (0; 0; 0; 1).
Выявим Парето-эффективные профили (пары), используя
критериальное пространство OWjU2 (рис. 9.9).
Профили (пары) (e2,fx), (е2,/4), (е,,/2) и (ерД) чистых страте-
гий, которым соответствуют клетки М5 = и М2 = М4, Парето-
эффективны, остальные профили (пары) чистых стратегий Паре-
то-неэффективны.
Здесь имеет место как совпадение равновесия Нэша и Парето-
эффективности (см. точки М2 = М4 и М5 на рис. 9.9),так и несо-
425
впадение (см. точку Ms на рис. 9.9, которая соответствует Парето-
эффективному профилю (e2,f4), который не является равновесием
Нэша).
9.7.6. Выше был рассмотрен переход от игры в развернутой фор-
ме к игре в нормальной форме (конкретно в виде двойной матри-
цы выигрышей).
Теперь рассмотрим обратный переход — сначала на примере
статической игры с полной информацией.
Пример 9.7.4 (модификация примера 9.7.1). Пусть фирма-мо-
нополист (Р2) функционирует в некоторой отрасли, а фирма (Р()
пытается войти в эту отрасль. Фирма Fx (игрок Pt) имеет два воз-
можных хода (два варианта принятия решения о своих действиях):
вступить (В) в отрасль или не вступать (НВ) в отрасль. Фирма Р2
(игрок Р2) имеет два возможных хода: сохранить (С) объем выпус-
каемой продукции или сократить (СКР) объем выпускаемой про-
426
дукции. Ходы фирмы делают одновременно, в течение некоторого
периода времени, т.е., делая ход, ни одна из фирм не знает, какой
ход сделает другая.
Нормальная форма этой статической игры с полной информа-
цией имеет вид табл. 9.11.
Таблица 9.11
Чистые стратегии фирмы F2
(С) (СКР)
Чистые стратегии фирмы Т7! (В) (-3; 6) (7; 7)
(НВ) (0; 14) (0; 8)
Как уже отмечалось, в статической игре ход игрока и его стра-
тегия — это одно и то же.
Если фирма F{ выбирает стратегию (В), а фирма F2 выбирает
стратегию (С), то в этом случае прибыль фирмы Fx (выигрыш иг-
рока Р,) равен —3, а прибыль фирмы Р2 (выигрыш игрока Р2) ра-
вен 6, т.е. пара (—3; 6) образует первый (сверху и слева) элемент
двойной матрицы (9.7.1):
(-3; 6) (7; 7)
(0; 14) (0; 8)
Остальные элементы двойной матрицы (9.7.1) интерпретиру-
ются аналогично.
Одновременное выполнение ходов (выбор (чистых) страте-
гий) с помощью дерева игры можно представить в одном из двух
вариантов (эти варианты эквивалентны) (рис. 9.10).
Выбору фирмой Fx стратегии (В) и фирмой Р2 стратегии (С)
соответствует выбор дуг (В) и (С) на левом (правом) дереве
рис. 9.10, ибо решение о выборе этих стратегий фирмы F{ и F2
принимают одновременно, поэтому не важно, какая фирма нахо-
дится в вершине [1] — первая Fx или вторая F2. В конечной верши-
не стратегий (В) и (С) показаны прибыли фирм Fx и F2 согласно
табл. 9.11. Выбор остальных стратегий фирмами Fx и F2 интерпре-
тируются аналогично.
Если фирмы и F2 принимают решения (игроки Рх и Р2 дела-
ют ходы) одновременно, то фирма F2 не знает, в какой вершине
(|2j или [3]) левого дерева рис. 9.10 она находится, ибо фирма F2 не
427
знает, какое решение ((В) или (НВ)) примет фирма т.е. какой
ход ((В) или (НВ)) сделает фирма F{. Поэтому говорят, что верши-
ны [5]и Ц] левого дерева рис. 9.10 находятся в информационном
множестве фирмы Г2 (игрока Р2) Говорят, что информационное
множество фирмы Г2 (овал левого дерева рис. 9.10, охватывающий
вершины [2] и [з]) представляет несовершенную информацию фирмы
*2-
Пояснение, относящееся к правому дереву рис. 9.10, анало-
гично. Если фирмы Fx и F2 принимают решение одновременно, то
фирма F{ не знает, в какой вершине ([1] или [з|) правого дерева
рис. 9.10 она находится, ибо фирма F{ не знает, какое решение
((C) или (СКР)) примет фирма Fr То есть здесь информационное
множество фирмы F{ (игрока Р{) состоит из вершин [2J и [З].
Естественно считать, что фирма, которая находится в вершине
Ц] (см. левое или правое дерево на рис. 9.10), имеет информацион-
ное множество, состоящее из одной (первой) вершины.
В связи с введением важного понятия информационного мно-
жества игрока отметим следующее принципиальное обстоятель-
ство: информационное множество игрока может состоять из од-
ной вершины дерева игры или из более чем одной вершины дерева
игры. Дерево на рис. 9.8 содержит три информационных множес-
тва, каждое из которых состоит только из одной (своей) вершины.
Каждое дерево (левое и правое) рис. 9.10 содержит по два инфор-
мационных множества: информационное множество, состоящее
из одной вершины Ш, и информационное множество, состоящее
из вершин [1] и [з].
Рис. 9.10
428
С помощью понятия «информационное множество игрока»
можно четко определить понятие игры с совершенной информа-
цией и понятие игры с несовершенной информацией. Если каж-
дое информационное множество состоит только из одной (своей)
вершины, то соответствующая этому дереву игра является игрой с
совершенной информацией. Если в дереве хотя бы одно информаци-
онное множество состоит из двух (или более) вершин этого дере-
ва, то соответствующая этому дереву игра является игрой с несовер-
шенной информацией.
Используя понятие «информационное множество игрока»,
можно отметить, что дерево есть совокупность информационных
множеств игроков, такое, что каждая вершина дерева (кроме ко-
нечных вершин) принадлежит только одному (своему) информа-
ционному множеству, которое может содержать только ее или еще
какие-то другие вершины дерева. Далее все вершины информаци-
онного множества игрока — это вершины информационного мно-
жества только одного (какого-то) игрока, принадлежащие (в слу-
чае динамической игры) множеству определенной очередности
этого игрока. Наконец, в каждой вершине определенного инфор-
мационного множества игрока множество ходов этого игрока
должно быть одним и тем же.
Таким образом, каждая игра (статическая и динамическая)
имеет представление в нормальной и развернутой формах.
В примере 9.7.4 был осуществлен переход от табл. 9.11, кото-
рая является нормальной формой статической игры с полной ин-
формацией, к ее развернутой форме в виде левого или правого
дерева на рис. 9.10.
В следующем примере 9.7.5 осуществим переход от табл. 9.10,
которую можно толковать как нормальную форму некоторой ста-
тической игры, к развернутой форме в виде дерева.
Пример 9.7.5. (продолжение примера 9.7.4). Для статической
игры, имеющей в качестве нормальной формы табл. 9.10, постро-
им соответствующее ей дерево игры (рис. 9.11).
Одновременному выбору фирмой F2 (игроком Р2) стратегии
(1) и фирмой (игроком Д) стратегии (В) соответствует выбор
дуг (1) и (В) на дереве рис. 9.11. В конечной вершине цепочки
стратегий (1) и (В) показаны прибыли фирм F{ и Р2 (—3; 6) со-
гласно табл. 9.10. Выбор остальных пар стратегий фирмами F{ и Р2
интерпретируется аналогично.
429
Поскольку фирмы F, и F2 выбирают стратегии одновременно,
фирма F, не знает, в какой из вершин (0, 0, 0, [Ц) (см. рис. 9.11)
она находится, ибо она не знает, какую стратегию ((1), (2k (3), (4))
выберет фирма F2. Поэтому все четыре вершины 0, Й, ® об-
разуют информационное множество фирмы Ft на рис. 9.11.
В связи с тем что табл. 9.10 интерпретируется в качестве нор-
мальной формы некоторой статической игры и фирмы F{ и F2
выбирают свои стратегии одновременно, построим другое (отно-
сительно дерева рис. 9.11) дерево, представляющее табл. 9.10
(рис. 9.12).
Одновременному выбору фирмой Ft стратегии (В) и фирмой
F2 стратегии (1) соответствует выбор дуг (В) и (1) на дереве
рис. 9.12. В конечной вершине цепочки стратегий (В) и (1) пока-
заны прибыли фирм Ft и F2 (—3; 6) согласно табл. 9.10. Выбор ос-
тальных пар стратегий фирмами Ft и F2 интерпретируется анало-
гично.
Аналогично рассуждениям об информационном множестве
фирмы F} дерева на рис. 9.11 в случае дерева рис. 9.12 показывает-
ся, что вершины Щи [з] образуют информационное множество
фирмы F2.
9.7.7. От развернутой формы (см. рис. 9.8) динамической игры с
совершенной информацией (назовем ее ДИ1) сначала был осу-
ществлен переход к нормальной форме этой игры в виде табл. 9.10,
(В)/ \(НВ) (В)/ \(НВ) (В)/ \(НВ) (В)/ \(НВ)
(-з; 6) (о; 14) (7; 7) (о; 8) (-з; 6) (о; 8) (7; 7) (о; 14)
Рис. 9.11
430
а затем был сделан переход от этой нормальной формы к развер-
нутой форме в виде деревьев на рис. 9.11 и 9.12. Деревья на
рис. 9.11 и 9.12 представляют собой развернутую форму другой
динамической игры (с несовершенной информацией (назовем ее
ДИ2)), которая отличается от первоначальной динамической иг-
ры ДИ 1, развернутой формой которого было дерево на рис. 9.8.
Переход от ДИ1 к ДИ2 привел к потере информации, которая
выражается в появлении информационного множества фирмы F2
(игрока Р2), состоящего из двух вершин, в то время как в ДИ1 ин-
формационные множества фирмы F2 (игрока Р2) состоят из одной
вершины каждое.
Следовательно, одна и таже нормальная форма в видетабл. 9.10
представляет две разные динамические игры и поэтому не может
считаться адекватным представлением этих игр (ибо динамичес-
кие игры разные).
В случае статических игр (с полной информацией) нормаль-
ная и развернутая формы однозначно соответствуют друг другу.
В случае игры с совершенной информацией при определении
стратегии игрока (в отличие от определения хода игрока) необхо-
димо было указывать все ходы данного игрока, которые он сдела-
ет, находясь в своей очередной вершине. В случае игры с несовер-
шенной информацией это определение стратегии игрока следует
обобщить путем замены очередной вершины игрока на его оче-
редное информационное множество. Поскольку в определении
понятия равновесия Нэша фигурировали стратегии, постольку
(-з;б) (7; 7) (-з;б) (7; 7) (о; 14) (о; 8) (о; 8) (о; 14)
Рис. 9.12
431
это понятие дословно переносится на случай динамических игр с
несовершенной информацией.
Определение понятия совершенного в подыграх равновесия в
случае несовершенной информации дословно повторяет опреде-
ление этого понятия в случае совершенной информации при
условии корректировки определения подыгры при переносе его
на случай несовершенной информации. В этом случае при опре-
делении подыгры следует требовать, чтобы наряду с вершиной
дерева, содержащийся в подыгре, в этой подыгре принадлежало
все информационное множество, содержащее эту вершину. При
таком уточнении понятия подыгры для случая несовершенной
информации не всякая вершина дерева (исключая с самого нача-
ла его конечные вершины) может быть начальной для некоторой
подыгры. Например, в дереве на рис. 9.12 вершины [Ц и [з] не мо-
гут играть роль начальных вершин для подыгр игры, представлен-
ной этим деревом. Поэтому в случае дерева на рис. 9.12 существует
только одна подыгра, которая совпадает с полной игрой, пред-
ставленной деревом на рис. 9.12.
Не к любой игре с несовершенной информацией можно при-
менять метод обратной индукции для отыскания ее решения.
В частности, в случае игры, представленной деревом на рис. 9.12,
фирма f2 (игрок Р2) не может осуществить выбор хода, ибо не зна-
ет, в какой вершине она находится. Как было показано, в примере
9.7.1 в случае игры с совершенной информацией с помощью ме-
тода обратной индукции было найдено решение в виде траекто-
рии ходов (В) и (СКР).
Игры с несовершенной информацией, для анализа которых
можно использовать метод обратной индукции, называются игра-
ми с почти совершенной информацией. К числу таких относятся иг-
ры, в которых статические игры повторяются конечное число раз.
Такие игры называются повторяющимися. В связи с этим динами-
ческие игры называются также последовательными, ибо в этих иг-
рах игроки делают свои ходы последовательно.
Анализировать повторяющиеся игры мы не будем.
Замечание 9.7.2. При подготовке текста настоящего парагра-
фа 9.7 был использован текст параграфа 5.9 учебника «Количест-
венные методы в экономических исследованиях» (М.: ЮНИТИ-
ДАНА, 2004), в котором не всегда аккуратно сопоставлялись по-
нятия «ход» игрока и «стратегия» игрока. В настоящем параграфе 9.7
отмеченные неточности полностью устранены.
432
9.8. Статические игры с неполной информацией
9.8.1. В статической игре с полной информацией (см. параграф 9.2)
каждый игрок знает множество возможных ходов всех других иг-
роков и их функции выигрышей. Если игрок не знаком с особен-
ностями других игроков (с их функциями выигрышей и множест-
вом возможных ходов), то говорят, что этот игрок обладает непол-
ной информацией. Если в статической игре существует хотя бы
один игрок, обладающий неполной информацией о других игро-
ках, то такая игра называется статической игрой с неполной инфор-
мацией.
Далее рассматриваются статические игры, в которых предпоч-
тения каждого игрока определяются реализацией некоторой слу-
чайной переменной. Эту реализацию некоторой случайной пере-
менной выбирает нулевой игрок Ро (Природа). «Выбор» игроком
Ро определенной реализации означает, что осуществляется выбор
определенного типа предпочтений каждого игрока, т.е. каждый
игрок может реализоваться в нескольких вариантах, т.е. в не-
скольких своих типах. Каждый игрок может наблюдать реализа-
ции только своей случайной переменной, т.е. наблюдать только
свои типы. Вводя для каждого игрока Рк различные типы его
предпочтений, мы «расширяем» первоначальную игру. Такие ста-
тические игры с неполной информацией называются статически-
ми байесовскими играми.
Инструмент байесовских игр активно востребован в экономи-
ческих исследованиях, когда приходится учитывать случайные
факторы. Дадим формальное описание статической байесовской
игры.
В этой игре конечное число игроков Рр ..., Рт (т > 2 — нату-
ральное число) и нулевой игрок Ро — Природа. Обозначим симво-
лом G>k множество типов игрока Рк (множество ©к может быть не
только конечным или счетным, хотя дальше мы ограничимся
только конечным вариантом). Конкретный элемент 0Л е Qk соот-
ветствует определенному типу игрока Рк, к = 1, ..., т. Появление
конкретного элемента 0* — случайное событие. Поэтому должно
быть задано распределение вероятностей р(0) на 0 = ©j х ... х ©т,
известное всем игрокам Рр ..., Рт. Здесь 0 = (0р ..., 0т) е О. Веро-
ятности должны быть неотрицательными, а их сумма по всем
28 - 7620
433
0 е 0 должна равняться единице. После выбора типа 0А игрока Рк,
т.е. при выборе конкретного (типа) 0Л е @к, игрок Рк выбирает
свою стратегию (свой ход) sk(Qk) е Sk, где Sk — множество ходов
игрока Рк. Поэтому (чистая) стратегия sk(Qk) игрока Рк есть функ-
ция (отображение), аргумент которой пробегает множество Qk
типов игрока Рк, а ее частные значения пробегают множество Sk
ходов игрока Рк. Множество всех таких функций sk(Qk) обозначим
символом Sk(Qk). Тогда 5(0) = (5,(0,),..., sm(0OT)) есть профиль стра-
тегий игроков Р,, ..., Рт на множестве
5(0) = 5,(0^ х... х 5Ж(0Д т.е. 5(0) = (5,(0,),..., 5ж(0т)) е 5,(0,) х
... х5т(0ж) для любого© 6 0.
Выигрыш игрока Рк зависит не только от выбора ходов s,,..., sm
всех игроков Р{,..., Р , в том числе и от хода sk самого игрока Рк,
но и от их типов, т.е. выигрыш игрока Рк равен значению uk(s(Q),
0) его функции выигрыша на профиле 5(0) = (•s,,(0,), ..., «m(0m))
стратегий 5,(0,),..., sm(0m) игроков Р,,..., Р . Более подробно зна-
чение «а(5(0), 0) следует представить так «А(^(0Л), s_k(^_k), Qk, 0_Д
где 0_Л = (0_,,..., 0Л, 0А+1,..., 0Ж),s_k= (5_,,..., sk,sk+l5m).
Ожидаемый выигрыш игрока Рк, имеющего тип вк и выбравше-
го ход sk, в предположении, что остальные игроки Р,,..., РЛ_,, РЛ+,,
..., Рт выбрали стратегии (ходы) 5_,(0_,) = (5,(0,), ...,
WW ...,V0J)’PaBeH
где 0,, ..., 0Л_,, 0Л+1,..., 0т — типы остальных игроков Р,,..., РЛ_,,
Pk+V ..., Pm; и сумма имеет место быть, если множества 0,,..., 0от
не пусты, конечны или счетны. В противном случае вместо суммы
появится интеграл.
В связи с тем что игрок Рк знает свой тип 0Л, математическое
ожидание является условным по этому типу. Поскольку условные
вероятности в общем случае рассчитываются по формуле Байеса,
постольку атрибутом игры и далее равновесия является термин
«байесовский».
Кратко статическую байесовскую игру можно записать так:
{Sk, uk(s(&), 0), 0Л,р(0)>.
Таким образом, для описания статической байесовской игры
необходимо иметь: 1) множество всех игроков Р,, ..., Рот; 2) для
каждого игрока Рк — множество Qk всех его типов; 3) распределе-
434
ние вероятностей р(&) на множествах ©,, Qm типов, известное
всем игрокам; 4) для каждого игрока Рк множество Sk его возмож-
ных ходов sk и множество Sk(Q^ функций 5Л(0Л), преобразующих
множество Qk во множество Sk ходов игрока Рк, 5) для каждого
игрока Рк функцию uk(s(Q), 0) выигрыша на профиле 5(0) = (5,(0,),
9 т"
Определение 9.8.1. Равновесие Нэша — Байеса статической
байесовской игры (с конечным числом типов игроков) есть рав-
новесие Нэша в «расширенной игре», в которой множество (чис-
тых) стратегий каждого игрока Рк есть множество Sk(Q^) функций
(отображений) из @к в Sk, к = 1,.... т, а в качестве выигрыша игро-
ка Рк фигурирует его ожидаемый выигрыш.
Формально профиль 5(0) = (5,(0,),..., 5m(0m)) (чистых) страте-
гий 5,(0,),..., 5m(0m) называется равновесием Нэша — Байеса, если
для каждого номера к, к = 1,.... т, справедливы неравенства
Д V г W >-,«•-*>. ер
для любых Sk 6 Sk.
Аналогично определяется равновесие Нэша — Байеса в сме-
шанных стратегиях.
Замечание 9.8.1. В статической байесовской игре вместо одно-
го игрока Рк,к= 1, .... т, вводится множество его типов Qk, что
фактически резко увеличивает число игроков. Однако множество
Sk ходов (стратегий) каждого игрока остается неизменным. В свя-
зи с тем что каждый игрок Рк знает свой тип, а все другие игроки
его тип не знают, другие игроки должны знать его ходы во всех
случаях. Поэтому в качестве выигрыша игрока Рк предлагается
использовать его ожидаемый выигрыш.
Замечание 9.8.2. Понятие равновесие Нэша — Байеса было
предложено Дж. Харшаньи в серии работ, опубликованных в
1967-1968 гт. (см. HarsanyiJ.C. (1967-1968)).
Более точно равновесие Нэша — Байеса следовало бы назвать
байесовским равновесием Нэша, а еще более точно (и справедли-
во) — байесовским равновесием Харшаньи.
9.8.2. Пример 9.8.1. Модель дуополии Курно как статическая игра
с неполной информацией.
Обозначим символом 5, выпуск фирмы F., i = 1, 2, в некотором
фиксированном периоде времени. Функция, обратная к функции
28*
435
спроса, имеет вид р = а- b(sl + s2), где а и b — положительные па-
раметры. Прибыль PR) фирмы F, имеет вид
PRi=psj-cp-di, (9.8.1)
где с. = МС( — предельные издержки, ad. = FC( — постоянные из-
держки фирмы Fr
Фирма Fx имеет один тип предпочтения, а фирма F2 — два типа
предпочтения. Типы 02w характеризуются величиной c2w пре-
дельных издержек, т.е. 02w = c^\j= 1,2. Следовательно, предель-
ные издержки сх фирмы Fx неизменны. То есть предельные из-
держки сх фирмы Fx принимают сх с вероятностью единица,
а предельные издержки с2 фирмы F2 принимают значение с2(1) с
вероятностью рх (рх > 0) (это тип один фирмы Г2) и значение с2(2) с
вероятностью 1 — рх (это тип два фирмы F2). Содержательно это
интерпретируется следующим образом.
Фирма F2 имеет полную информацию о фирме Fv поэтому
предельные издержки сх неизменны. Фирма Fx полагает, что фир-
ма F2 имеет предельные издержки с2(1' с вероятностью рх, а пре-
дельные издержки с2(2) — с вероятностью qx = 1 -pv
Прибыль PR. фирмы F. есть выигрыш и, фирмы Fp которая
рассматривается в качестве игрока Рр /=1,2. Игроки Рх и Р2 ходы
делают одновременно, т.е. фирмы F{ и F2 выпускают свою продук-
цию, не зная о выпусках друг друга.
Покажем, что мы имеем дело со статической байесовской иг-
рой.
1. Число игроков равно двум. Игроком Рх является фирма Fv
игроком Р2 — фирма F2.
2. Для игрока Р{ множество ©j = Сх его типов состоит из одного
элемента — предельных издержек 0( = сх фирмы Fx, которые явля-
ются неизменными. Для игрока Р2 множество ©2 = С2 его типов
состоит из двух элементов: предельных издержек с2(1) и предель-
ных издержек с2(2) фирмы F2.
3. Распределение вероятностей на множестве С= Ct х С2 типов
(ср с2) игроков Рх и Р2 имеет вид
С (Ср с2(1)) (Ср С<2>)
р Pi
т.е. случайная величина С принимает значение (ср с2(1)) с вероят-
ностью Рр а значение (ср с2(2)) — с вероятностью qx = 1 - рг
436
4. Для игрока Р, множество S,(0,) = ^(Cj) функций ^,(0,) =
= состоит из функции 5,, равной объему выпуска фирмы F}
при предельных издержках с,. Для игрока Р2 множество 52(0.) =
= 52(С) функций состоит из з2(с2), таких, что 52(1) = 52(с^1)) и =
= s2(c^), т.е. 52(|) есть выпуск фирмы F2 при предельных издержках
а 5® — выпуск фирмы F2 при предельных издержках с^\
Следовательно, набор s стратегий 5. и 5, игроков Р. и Р, имеет
ВВД5=(51,^1и®).
5. Для игрока Р{ функция С/,(5) ожидаемого выигрыша имеет
вид прибыли PRt фирмы Fy
£А,(5) = РР,(5,,5<'),5<2>) =
= La - b(sl + р^1) + - c,5, -d{ =
=p^a - 6(5, + 52(1))5, — c,5, — J,J + (9.8.2)
+?,La - 6(5, + 52(2))5, — C,5, — </,J.
Третье звено приведенного выражения 9.8.2 можно обосно-
вать так.
В связи с тем что фирма Р, не знает, какой тип фирмы Р, будет
функционировать на рынке, и поэтому фирме Р, неизвестен вы-
пуск 52 фирмы Р2, но зато фирме Р, известно, что фирма Р2 может
иметь предельные издержки с2(1) с вероятностью р{ и, следова-
тельно, выпуск 52(1) с той же вероятностьюpv аналогично выпуск
52(2) с вероятностью ?,, поэтому фирме Р, естественно ориентиро-
ваться на ожидаемый выпуск + ?,5^2) Фирмы Р2, который и
был включен в формулу прибыли фирмы Р,
РЛ, = (а - 6(5, +р,52(1) + ?Л(2)))51 ~ ci5i ~di
вместо объема s2.
Последнее (четвертое) звено цепочки (9.8.2) следует обосно-
вать так.
Прибыль фирмы Р, есть ее ожидаемая прибыль, которая равна
произведению прибыли фирмы Р,
(а - 6(5, + 52(1)))5, - С,5, -di
(при условии, что выпуск фирмы Р2 равен 5,(1)) и вероятности р,
того, что фирма Р2 будет иметь выпуск 52(1\ плюс аналогичное
произведение прибыли фирмы Р,
(a-6(5, +52(2)))5,-C,5,-J,
(при условии, что выпуск фирмы Р2 равен 5®) и вероятности <?,
того, что фирма Р, будет иметь выпуск з^2\
437
Для игрока Р2, который знает свой тип, функция U2(s) имеет
вид
= ~ "I" ~ ^2^2
Если предельные издержки фирмы F2 равны с2(1), то мы имеем
первый тип фирмы Fr В этом случае
U2(s) = PR^, s™, 0) = (о - + s2(1))) s2(1) - c™ - d2.
Если предельные издержки фирмы F2 равны с2(2), то мы имеем
второй тип фирмы F2. В этом случае
U2(s) = PR2(sv 0, s2(2)) = (а - b(Sl + s2<2*)) 52(2) - с2(2) s2(2) - d2.
Для нахождения равновесия Нэша — Байеса этой статической
байесовской игры следует максимизировать функции U^s) и U2(s)
ожидаемых выигрышей обоих игроков Р, и А.
Задача максимизации прибыли PRfa, 52 , $2(2)) фирмы Р, ре-
шается путем отыскания ее первой производной по с учетом
важной предпосылки модели Курно о том, что предполагаемые
вариации ds2(l) / ds{ = 0 и </$22) / ds{ = 0.
Имеем уравнение
dU,(s) dPR^s^sP (1) (2). п
-"Г2-2 =---1V ’ 2 ’ 2 = а - с, - 2Ц - Ь(р$> + q/f) = 0,
dsx dsx
откуда следует, что
= (98 3)
Поскольку
^>=-24<0,
dsl
постольку выражение (9.8.3) (глобально) максимизирует прибыль
PRx(sv 52<2)) при фиксированных52(1) и s2<2).
Задача максимизации прибыли РР2(5р 52) фирмы Р2 решается
путем отыскания ее первой производной по переменной s2 с уче-
том важной предпосылки модели Курно о том, что предполагае-
мая вариация ds{ / ds2 = 0.
Имеем уравнение
= {а - с2) - 2Ц -2bs2= 0,
ds2
откуда получаем
438
_a-c2-bsx
‘-----~
Поскольку
^Й=-26<0,
as2
постольку вектор (sp s2) максимизирует (глобально) прибыль
U2(s) = PR^, s2) при фиксированных 5Г
Если с2 = с2(1\ то
Если с2 = с^2\ то di _ a-c(2)-bsi (9.8.4) 2 2b 52 " 2Ь • (9-8 5)
Подставив в (9.8.3) выражения (9.8.4) и (9.8.5), получим
;(1)=±2a+fl£+«l£ (9.8.6)
Подставив (9.8.4) и (9.8.5) в выражение (9.8.6), получим соот-
ветственно
о(1) 52 = 2а (3+)с?2) /а g j\ 6b
о(2) S2 - 2а—(3+д1 )сд2^ — PicP + 2С[ (9.8.8) 6Ь
Набор (9.8.6), (9.8.7) и (9.8.8.) представляет собой равновесие
Нэша — Байеса (в чистых стратегиях) дуополии Курно как стати-
ческой байесовской игры.
ПриPj = 1 ((Ц = 0) и С! = с2(1) формулы (9.8.6) и (9.8.7) дают клас-
сическое равновесие Нэша дуополии Курно
о а-с, о а-с,
51 =----L, 52 =---L.
3b 3b
Аналогично при рх = 0 = 1) и с1 = с2(2) формулы (9.8.6) и
(9.8.8) дают классическое равновесие Нэша дуополии Курно
о a Ci о а ““ Ct
51 = зь ’ 52 = ЗЬ '
439
9.8.3. Пример 9.8.2 (A. Mas-Colell, M.D. Winston, J.R. Green (1995)).
Рассмотрим сначала хорошо известную биматричную игру
«Дилемма заключенных» (в этом примере 9.8.2 игру 1), задавае-
мую табл. 9.12 (у разных авторов фигурируют разные цифры).
Таблица 9.12
Заключенный 2 (Р2)
НП п
Заключенный 1 (Л) НП (-2;-2) 'Г (-9; -1)
п 4/ (-4;-4)
Здесь и далее в этом примере буквы «П» и «НП» означают со-
ответственно «Признаться», «Не признаться».
Содержательная интерпретация клеток 1—4 табл. 9.12 хорошо
известна. Если оба заключенных не признаются, их выпускают на
свободу через два года, приписав им не слишком серьезное право-
нарушение в целях оправдания их задержания на время ведения
следствия. Если заключенный 1 признается, а заключенный 2 не
признается (клетка 3), то заключенного 1 отпускают на свободу
через один год. Заключенному 2 дают большой срок, равный
9 годам. Клетка 2 интерпретируется аналогично. Если оба заклю-
ченных признаются, им сокращают срок за признание и обоих
отпускают на свободу через 4 года.
Модификацию игры 1 представляет игра «Брат следователя»
(в этом примере игра 2), задаваемая табл. 9.13.
Таблица 9.13
Заключенный 2 (Л)
НП П
Заключенный 1 (Л) НП (б; -2) д'
п \ 3 (-1;-9) -^(-4;-4)
440
В игре 2 клетки со второй по четвертую интерпретируются так
же, как и в игре 1. Клетка первая в табл. 9.13 интерпретируется
так. Заключенный 1 является братом следователя, который ведет
дело этих заключенных. Если заключенные оба не признаются, то
следователь отпустит заключенного 1 на свободу. Как и в игре 1,
в игре 2 равновесие Нэша образуют стратегии (П, П).
Рассмотрим модификацию игра «Брат следователя» (в этом
примере игра 3), задаваемую табл. 9.14.
Таблица 9.14
Заключенный 2 (Р2)
НП П
Заключенный 1 (Л) НП (б; -2) Т\(-9; "7)
п - V (-1; -9) -Мн; -10)
В игре 3 клетки первая и третья такие же, как и в (предыдущей)
игре 2. Клетки вторая и четвертая интерпретируются так, что за-
ключенный 2, признаваясь (П), хочет задержаться в тюрьме до-
полнительно еще на 6 лет (в случае клетки 2: — 1 — 6 = —7, в случае
клетки 4: —4 — 6 = —10), чтобы, например, исповедоваться тюрем-
ному священнику. Возможно, такое желание у заключенного 2
появилось в связи с некоторым душевным расстройством. В игре
3 равновесие Нэша образуют стратегии (НП, НП).
В игре 4 игрок Р( имеет один тип предпочтений, игрок Р2 — два
типа предпочтений. Формально единственный тип игрока Р{ ха-
рактеризуется его матрицей выигрышей
-(-°. 3'
которая одна и та же в табл. 9.13 и 9.14. Это обстоятельство интер-
претируется так: игрок Р2 имеет полную информацию о предпоч-
тениях игрока Рг
Первый и второй типы игрока Р2 характеризуются двумя его
матрицами выигрыша
п (-2 -П п (-2 -7 А
Pi — I , р? = I I»
1-9 -4J 2 1-9 -10/
441
которые следует выписать из табл. 9.13 и 9.14 соответственно.
Игрок Р2 имеет первый тип предпочтений с вероятностью pv
а второй тип предпочтений с вероятностью qx = 1 — pv т.е. игрок
Р] полагает, что с вероятностью рх игрок Р2 имеет первый тип
предпочтений, с вероятностью q} игрок Р2 имеет второй тип пред-
почтений. Строгое толкование первого и второго типов предпоч-
тений игрока Р2 дается ниже.
Игра 4 в нормальной форме представлена в виде табл. 9.15.
Таблица 9.15
нп п нп п
Л нп (0;-2) (-1; 1) (0;-2) (-9;-7)
п (-4;-4) (-4;-10)
<h
Игра 4 в развернутой форме представлена на рис. 9.13. Выбор
реализации случайной величины, которая определяет тип пред-
почтений каждого игрока, целесообразно отдать в руки нулевого
игрока Ро, т.е. Природы (N), что и показано на рис. 9.13.
Рис. 9.13
442
Таким образом, игрок p0(N) делает первый ход, выбирая реа-
лизацию случайной величины, т.е. тип предпочтений каждого
игрока (в данном случае игрока Р2), причем каждый игрок наблю-
дает реализацию только собственной случайной величины.
Представим чистые стратегии игроков Р1 и Р2 в виде единич-
ных векторов е{ = (1; 0) (представление стратегии (НП) игрока Рх),
е2 = (0; 1) (представление стратегии (П) игрока Px),f}l) = (1, 0, 0,0)
(представление стратегии (НП) первого типа игрока P^,f^ =
= (0,1,0,0) (представление стратегии (П) первого типа игрока Р2),
//2) = (0.0,1,0) (представление стратегии (НП) второго типа игро-
ка Р2),^(2) = (0, 0,0,1) (представление стратегии (П) второго типа
игрока Р2).
Покажем, что игра 4 есть статическая байесовская игра.
1. Число игроков равно двум. Игроком Рх является заключен-
ный 1, игроком Р2 — заключенный 2. Нулевой игрок Ро — Приро-
да (N) в число игроков не включается.
2. Для игрока Р{ множество 0j = С, его типов состоит из одного
элемента 0j = с(, для игрока Р2 множество 02 = С2 его типов состоит
из двух элементов 02(1) = с2(1) и 02(2) = с2(2).
3. Распределение вероятностей на множестве С = Сх х С2 типов
(ср с2) игроков Pj и Р2 имеет вид
С (С|,С2(2>)
р Р1 2?
То есть случайная величина С принимает значение (ср с2(1)) с
вероятностью а значение (ср с2(2)) — с вероятностью qx = 1 -pv
4. Множество 5, возможных ходов игрока Рх имеет вид 5. = (е.,
е,), множество S2 возможных ходов игрока Р2 S2 = (/j(1),^(1 ,//2,
/М
Множество ^(0,) совпадает со множеством ибо у игрока Рх
только один тип предпочтений.
Множество 52(02) состоит из следующих четырех стратегий
$2(1), а2(2), л2(3), а2(4) статической байесовской игры:
*2(1) = (6<l),z,<2)>, *2(2) = (А(1),/2(2)), j2(3) = (Г2(1),/1(2)),
52(4) = «2(1),/2(2)).
5. Для игрока Рх ожидаемый выигрыш Ux(s(c)) принимает сле-
дующие значения:
443
( о — 9 0 —9
^1(e1^2(l)) = e1(^|^)(A/;<1>+91/i<2)) = (l;0) \ \
А
О
<h
О
( 0 -9 0 -9 А
^(е1,52(2)) = е1(ЛМ)(А/1<1)+?1/2<2>) = (1;0) л
= -9?!=-9+9а>
<0-90 —9
t/1(eI,s2(3)) = e1(^M)(A/2<1>+^2>) = (l;0)
у—1—4—1—4
<0—90 —9
^(е1,52(4)) = е1(Л|Л)(А^|)+^2)) = (1;0) , А , л
= -9 А “9а= “9-
=0,
А
0
О
Л1>
А
О
Аналогично имеем
U{(e2, s2(l)) = е2(ЛИ)(р/,0) + = -1,
и}(е2,52(2)) = е2(ЛИ)<М(,) + q^) = -4 + Зрр
Ut(e2,52(3)) = е2(А\А)(р/™ + 91//2)) = -1 - Зр,,
Ц(е2,52(4)) = е2(А\А)(р/™ + 9)/2<2>) = -4.
Для игрока Р2 U2(s(c)) ожидаемый выигрыш принимает следу-
ющие значения:
tf2(ep 52(2)) = e,(^| В2)(р/^ + 9/2<2>) = -7 + 5/>р
С/2(ер 52(3)) = ^(5,1 В2)(р/2^ + ?1//2>) = —2 +рр
52(4)) = B2)(p/2W + 91/2<2>) = -7 + 6рр
444
f—2—1—2 —7
{/г(е„5;(1»=е,(Д, |Дг)(йЛ,|и?,/;|2))=(1;0)1 , , , 10
Pl
о
91
о
= -2px-2ql=-2,
t/2(e„s2(D)=e2(«, |я2)(А/1||,+91/1га)=(О; 1)['^ “’'1
Ivy (ft
w
U2(e2, s2(2)) = e2(/?,| B2)(p/™ + qxf™) = -10 + pp
U2(e2,s2(3)) = e2(Bx\ B2)(p/2^ + qxf™) = -9 + 5px,
U2(e2, s2(4)) = e2(Bxl B2)(p/2<» + qx/™) = -10 + 6pp
Для отыскания равновесий Нэша-Байеса рассматриваемой
байесовской игры 4 следует попарно сравнить значения ожида-
емых выигрышей игроков Рх и Р2.
Имеем
Ц(ер^(1)) = 0>-1 = Ц(е2,^2(1)),
^2(ер j2(l)) = -2 > -7 + 5рх = U2(ex, ^(2)),
CZ2(ep 52(1)) = -2 > -2 + рх = tf2(ep 52(3)),
tf2(ep s2(l)) = -2 > -7 + 6рх = U2(ex, j2(4)).
Система линейных неравенств —2 > —7 + 5рр —2 > —2 + рх,
-2 > —7 + 6рх имеет единственное решение р. = 0. Отсюда следует,
что при рх - 0 профиль (ер $2(1)) = (ер //* ,/i(2)) стратегий s( и
л2(1) есть равновесие Нэша — Байеса рассматриваемой байесовс-
кой игры 4. Равенство рх = 0 содержательно означает, что в игре 4
с вероятностью единица участвует тип 2 игрока Р2. Если рх > 0, то
профиль ех, s2(l) не является равновесием Нэша — Байеса.
Прирх = 0 профиль (ex,f^,f^2)) содержательно интерпретиру-
ется так. Игрок Рх выбирает стратегию (НП), а стратегия игрока Р2
есть выбор хода (НП) во втором типе игрока Р2.
Далее имеем
Ux(ex, 52(2)) = -9 + 9рх > —4 + Зрх = Ux(e2,52(2)),
tf2(ep s2(2)) = -7 + 5рх > -2 = {72(ер з2( 1)),
445
U2(ep S2(2)) = —7 + 5p, > -2 + p{ = U2(ep j2(3)),
U2(ev 52(2)) = -7 + 5px > -7 + 6P1 = V2(ep 52(4)).
Система этих четырех линейных неравенств противоречива.
Отсюда следует, что профиль (ер $2(2)) = стратегий ех
и л2(2) не является равновесием Нэша — Байеса рассматриваемой
игры 4.
Аналогично анализируются профили (е,, s2(3)) = (epf2w,f^),
(е 52(4)) = (е,,/2(1),/2<2)), (е s (1)) = (е2, 5,(2)) = (е2,
Профиль (^],52(3)) = (el,/2<l),/j(2)) есть равновесие Нэша —
Байеса игры 4 при 0 <рх < 1.
Профиль (е2,52(3)) = (е2,^(1),/j(2)) есть равновесие Нэша —
Байеса при 1/6 <р} < 1.
Профиль (е2,?2(4)) = (е2,^(|),^2)) есть равновесие Нэша —
Байеса прир^ 1.
Остальные профили не являются равновесием Нэша — Байеса
игры 4.
Приведенный подробный анализ игры 4 можно сократить,
если воспользоваться частными особенностями этой игры 4. Если
игрок Р2 использует тип 1 с вероятностью единица, то оба игрока
должны выбрать стратегии ех = (П) и/2(1)(П), ибо пара этих страте-
гий есть равновесие Нэша в первом типе предпочтений игрока Р2.
Если игрок Р2 использует второй тип с вероятностью единица, то
оба игрока должны выбрать стратегии е{ = (НП) и/2(1)(НП), ибо
пара этих стратегий есть равновесие Нэша во втором типе пред-
почтений игрока Р2.
Замечание 9.8.3. Равновесие Нэша в смешанных стратегиях в
играх с полной информацией можно представить как равновесие
Нэша — Байеса (в чистых стратегиях) в играх с неполной инфор-
мацией.
9.9. О динамических играх с полной и неполной
информацией
9.9.1. Динамические игры с неполной информацией (динамичес-
кие байесовские игры) обобщают статические игры с неполной
информацией (статические байесовские игры). Здесь ситуация
аналогична той, что имеет место во взаимодействии динамичес-
446
ких и статических игр с полной информацией, которым были
посвящены параграфы 9.1—9.7.
Важная особенность динамических игр с неполной информа-
цией — наличие неизвестных вероятностей, с которыми игрок
находится в той или иной вершине своего информационного
множества, состоящего, естественно, более чем из одной верши-
ны. Поэтому игрок должен делать предположения относительно
того, с какой вероятностью он окажется в той или иной вершине
своего информационного множества. Если у игрока есть такие
предположения, то на их основе он выбирает стратегию, которая
может обеспечить ему наибольший ожидаемый выигрыш
Эта идея является основной в понятии совершенного байесов-
ского равновесия (СВР), для описания которого следует иметь:
1) набор стратегий (sp ..., sm) всех игроков Рр ..., Рот; 2) набор ожи-
даемых каждым игроком Рк стратегий s_k = (s', ..., sk_', sk+', ...,
sme) всех остальных игроков Рр ..., Pk_v Pk+l, ..., Рт, к = 1, ..., т;
3) для каждого игрока Рк в каждом информационном множестве,
в котором ему принадлежит ход, ожидаемое игроком Рк распреде-
ление вероятностей, заданное на вершинах этого информацион-
ного множества, к = 1,..., т.
Для того чтобы описанный набор стратегий и ожиданий со-
ставлял СВР, требуется выполнение следующих условий: а) ожи-
даемое распределение вероятностей на вершинах информацион-
ных множеств для каждого игрока Рк соответствует (согласова-
ны с) выбранной им стратегии sk и тем стратегиям s_k, которые,
как он (игрок РА) ожидает, выберут остальные игроки Рр ..., Рк_{,
Pk+i,..., Рт; б) выбранная стратегия последовательно оптимальна
при данных ожиданиях, т.е. выбор игрока Рк в каждом его инфор-
мационном множестве должен быть таким, чтобы максимизиро-
вать ожидаемый выигрыш в предположении, что после каждого
информационного множества игра будет продолжена в соответ-
ствии с набором стратегий (sk, s_k),k= 1,..., /и; в) ожидаемые стра-
тегии s_k совпадают с фактически выбранными стратегиями s_k,
т.е. s_k = s_k, к = 1,..., т.
Особенность СВР в том, что в общем случае для его поиска
невозможно использовать обратную индукцию, за исключением
игр с почти совершенной информацией. Если игра не имеет по-
дыгр, то СВР следует находить как решение системы уравнений:
ожидаемые распределения вероятностей на вершинах информа-
ционных множеств находятся в соответствии с набором стратегий
447
равновесия, а стратегия равновесия выбирается каждым игроком
на основе предположений об ожидаемых распределениях вероят-
ностей на вершинах информационных множеств.
Замечание 9.9.1. Неявное использование СБР содержалось в
работах ряда авторов, посвященных динамическим моделям,
в которых учитывалась неопределенность (ссылки даются по мо-
нографии Fudenberg and Tirole (2000)): Aumann and Maehler (1966)
(игра про разоружение), Akerlof (1970) (известная работа о рынке
«лимонов»), Spence (1974) (работа о рыночном сигнализирова-
нии), Ortega-Reichert (1967) (работа об анализе аукционов с повто-
ряющимся первым предложением). Первое формальное предло-
жение идеи СБР было дано в работе Мильгрома и Робертса (MU-
grom and Roberts (1982а). См. также: Kreps and Wilson (1982в) и
Milgrom and Roberts (1982в)).
9.9.2. Проиллюстрируем построение СБР на конкретном при-
мере.
Пример 9.9.1. (В.П. Бусыгин и др. (2000), О. Shy (1995)). В са-
молет, который должен лететь из пункта М в пункт G, попал тер-
рорист, который требует, чтобы самолет летел в пункт Н. В про-
тивном случае террорист угрожает взорвать самолет. Террорист не
может определить, куда летит самолет, но может определить, куда
он прилетел. Дерево игры показано на рис. 9.14.
В игре фигурирует два типа террористов: сумасшедший и
«нормальный». Террорист знает свой тип, а пилот его не знает.
Если террорист (независимо от его типа) не станет выдвигать свое
требование и угрожать, т.е. если p.j = 0 и ц2 = 0, то «выигрыш» пи-
лота и «выигрыш» террориста будут равны нулю. Если пилот по-
садит самолет в пункте Н, то «выигрыш» пилота будет равен -1,
а «выигрыш» террориста (независимо от его типа) будет равен 1.
Если пилот посадит самолет в пункте G, а сумасшедший террорист
взорвет самолет, то «выигрыш» пилота будет равен -100, а «выиг-
рыш» сумасшедшего террориста будет равен нулю. Если пилот
посадит самолет в пункте G, «нормальный» террорист не взорвет
самолет, т.е. «выигрыш» пилота будет равен 1, а выигрыш «нор-
мального» террориста будет равен -1.
СБР приведенной динамической игры с неполной информа-
цией должно состоять из следующих величин: 1) вероятности цр
с которой сумасшедший террорист проводит свою операцию,
т.е. выдвигает свои требования и угрожает, gj е [0; 1]; 2) вероят-
448
ности ц2, с которой «нормальный» террорист проводит свою опе-
рацию, ц2 е [0; 1]; 3) вероятности а, с которой пилот ожидает по-
явления сумасшедшего террориста, а е [0; 1]; 4) вероятности ц3, с
которой пилот летит в пункт G, ц3 е [0; 1]. Все остальные вероят-
ности рассчитываются как функции только что приведенных.
1°. Ожидаемые выигрыши пилота от двух его возможных ходов
равны —1а + (—1)(1 — а) = —1 в случае, если пилот посадит само-
лет в пункте Н, и а(—100) + (1 — а) = 1 в случае, если пилот поса-
дит самолет в пункте G.
Очевидно, формальное неравенство —1 < а(—100) + (1 — а) = 1
(т.е. а < 2/ю1) означает, что выигрыш пилота в пункте G выше, по-
этому пилот полетит в пункт G, т.е. ц3 = 1. Формальное неравенство
—1 > а(—100) + (1 — а) = 1 (т.е. а > 2/ю1) означает, что выигрыш пи-
лота в пункте G ниже, чем в пункте Н, поэтому пилот полетит в пункт
Н, т.е. ц3 = 0. В случае равенства —1 = а(—100) + (1 — а) = 1
(т.е. а=2/101) пилоту все равно куда лететь (0 < ц3 < 1).
Таким образом, зависимость стратегии пилота от вероятности
а его ожидания имеет вид
1, еслиа<%и
Нз(а) = )[О»Л> еслиа = Хо1»
0, еслиа>%)1
29 - 7620
449
2°. Опишем вероятность а ожидания пилота как функцию ве-
роятностей (J.J и ц2. Если |х( * 0 или ц2 * 0, то используем формулу
Байеса, считая, что событие Вх — это появление сумасшедшего
террориста, событие В2 — это появление «нормального» терро-
риста, событие А — пилот получил ход и должен сделать выбор,
куда лететь. Выпишем вероятности событий Вх, В2 и А, используя
введенную выше символику рассматриваемой модели: = v,
Р{В2} = 1 — v, /’{•BjH} = a, Р{Л|Я2} = ц2. По известной
формуле Байеса имеем
а = а(ц., ц,) = ЛДI -4} =----------------------=
vp,+(l-v)p2
при Ц) * 0 или ^2 * 0.
Напомним, что — это (условная) вероятность события
А при условии, что произошло событие В{ (если появился сума-
сшедший террорист (событие Вх), то условная вероятность собы-
тии А, т.е. P{>4|5j}, очевидно, равна Ц]). Аналогично Р{Л|Б2} — это
(условная) вероятность события А при условии, что произошло
событие В2 (если появился «нормальный» террорист (событие Р2),
то условная вероятность события А, т.е. Р{Л|Р2}, очевидно, рав-
на р2). Символ Р{Л]|Л} — это (условная) вероятность события Вх
при условии, что произошло событие Л.
Известная формула Байеса выше была использована обосно-
ванно, ибо, во-первых, события Вх и В2 несовместимы (террорист
либо сумасшедший, либо «нормальный») и, во-вторых, если про-
изошло хотя бы одно из событий Вх и В2, то произошло также
событие А (действительно, пилот самолета должен принимать
решение о месте посадки в случае появления террориста любого
типа).
Если Ц] = 0 и ц2 = 0, то, исходя из содержательных соображе-
ний, пилот может ожидать появление сумасшедшего террориста с
любой вероятностью 0 < а < 1.
3°. Проанализируем выбор террориста каждого (из двух) ти-
пов. Если террорист сумасшедший, то его ожидаемый выигрыш
при стратегии пилота лететь с вероятностью ц3 в пункт G и с веро-
ятностью 1 — ц3 — в пункт Н, очевидно, равен (1 — ц3) -1 + р3 - 0 =
= 1 ~ Из-
450
Если 1 — ц3 > О (тогда, очевидно, ц3 < 1), и поэтому Ц[ =1.
Если 1 — ц3 = 0 (тогда, очевидно, ц3 = 1), и поэтому 0 <, ц, < 1.
Случай 1 — ц3 < 0 (тогда, очевидно, ц3 > 1) невозможен, ибо
— вероятность.
Таким образом,
, к ( 1, если LL, < 1,
= [[0; 1], еслиЦз =1.
Если террорист «нормальный», то его ожидаемый выигрыш
при стратегии пилота лететь с вероятностью ц3 в пункт G и с веро-
ятностью 1 - ц3 — в пункт Н, очевидно, равен (1 — ц3) • (+1) + ц3 х
х(—1)=1 —2ц3.
Если 1 — 2ц3 > 0 (тогда, очевидно, ц3 < */2), и поэтому = 1.
Если 1 — 2ц3 = 0 (тогда, очевидно, ц3 = ’/2)> и поэтому 0 < < 1.
Если 1 — 2ц3 < 0 (тогда, очевидно, ц3 > 1/2), и поэтому ц2 = 0.
Таким образом,
1, если ц3
H2<U3) = iI°; 1],если g3=X.
0, если ц3 >Уг.
4°. Набор вероятностей (jij°, ц2°, ц3°, а0) задает СБР, если вы-
полнены условия
ц3° 6 Ц3(а°), Ц]0 е Ц,(Ц3°), а0 е «(цД Ц2°), р/ е Ц2(Ц3°).
Для решения этой системы целесообразно проанализировать
следующие варианты: ц2 = 0 («нормальный» террорист не прове-
дет операцию, т.е. не выдвигает свое требование и не угрожает),
Ц2 = 1 («нормальный» террорист проводит операцию, т.е. выдвига-
ет свое требование и угрожает), 0 < ц2 < 1 (у «нормального» терро-
риста невырожденная смешанная стратегия).
5°. Рассмотрим случай, когда gj = 0 и |12=0. Содержательно эти
равенства означают, что террорист (независимо от его типа) не
станет выдвигать свое требование и угрожать, поэтому пилот мо-
жет спокойно сажать самолет в пункте G. Это означает формаль-
но, что ц3 = 1. При этом а = 0, так как в рассматриваемом случае
пилот не ожидает встретить сумасшедшего террориста (ибо
h = 0).
29*
451
Таким образом, рассматриваемая динамическая игра с непол-
ной информацией имеет следующее СБР: pt° = 0, ц2° = 0, р3° = 1,
а° = 0.
В связи с тем что р,(а) = 1, если а < 2/101 (см. п. 1° этого при-
мера), СБР р,° = 0, р2 = 0, р ° = 1, а0 = 0 дополняется СБР вида
р.° = 0, р2° = 0, р3° = 1, 0 £ а® £ 2/101. Отметим, что неравенство
а° < 2/101 означает, что вероятность <х°, с которой пилот ожидает
появления сумасшедшего террориста, является малой (для срав-
нения сопоставьте это неравенство с неравенством v > 2/101 п. 6°
этого примера).
6°. Случай, когда р2 = 1 и р, = 1, содержательно означает, что
террорист (независимо от его типа) обязательно станет выдвигать
свое требование и угрожать. Тогда для пилота вероятность а иметь
на борту самолета сумасшедшего террориста, очевидно, будет
совпадать с вероятностью у, с какой сумасшедшие террористы
появляются вообще, т.е. а = у.
На основании п. 3° этого примера
р/Рз) = 1, если р3 < 1, и р2(р3) = 1, если р3 < 1/2,
т.е. в рассматриваемом случае р3 < */2.
Если v(=a) > 2/101, то p3(v) = 0, и если у(=а) = 2/101, то 0 < р3(у)<
< */2 (см. п. 1° этого примера).
Таким образом, если v(=a) > 2/101, то СБР имеет вид
Р]° = 1, р2° = 1, р3°=0, a° = v; если v(=a) = 2/101, то СБР имеет вид
Р!0 = 1, Р2° = 1, а° = у = 2/101,0 р3° < 72.
Отметим, что неравенство v > 2/101 содержательно означает,
что сумасшедшие террористы на свете встречаются, к сожалению,
не очень редко. Для реальной действительности это, скорее всего,
так и есть.
7°. Случай, когда р2 е (0; 1) — необходимое условие равенства
р3 = */2 (см. п. 3° этого примера), которое, в свою очередь, есть
необходимое условие равенства a = 2/101 (см. п. 1° этого примера).
Равенство р3 = '/2 влечет равенство Р[(р3) = 1 (см. п. 3° этого при-
мера). Используя вышеприведенную формулу Байеса (pj = 1)
2_ = a=.________________Y____
101 vpj+(l—v)p2 v+(l—v)p2
(cm. n. 2° этого примера), получим, что
99v
И2 2(l-v)’
452
откуда, принимая во внимание неравенство Ц2 < 1, получаем, что
у < 2/10), откуда следует, что природа порождает не так уж много
сумасшедших террористов, что, к сожалению, не совсем так, как
было отмечено в п. 6° этого примера.
Следовательно, при v < 2/t01 получаем еще одно СБР
о,о 99v о 1 о 2
’ И2 ” 2(1-v)’ Из “ 2’ “ " 101 ’
Таким образом, в п. 5°—7° этого примера выписаны все СБР
рассмотренной динамической игры с неполной информацией.
Замечание 9.9.2. Дальнейшее развитие концепции равновесия
в теории некооперативных игр (равновесие Нэша, совершенное в
подыграх равновесие, равновесие Нэша — Байеса, совершенное
байесовское равновесие) представлено в монографии D. Fudenberg
and I. Tirole (2000), в которой подробно проанализированы после-
довательное равновесие, совершенное равновесие относительно
дрожащей руки, правильное (рорег) равновесие и т.п. Широкий
спектр понятий равновесия в теории игр свидетельствует о том,
что в настоящее время вопрос о рациональном определении по-
нятия оптимального решения игры, по-видимому, еще не имеет
приемлемого ответа.
Вопросы для самоконтроля к главе 9
1. Дайте описание статической игры п лиц с полной информацией в
нормальной форме.
2. Что означает термин «полная информация» в теории статических
игр?
3. Что означают термины «стратегия игрока» и «профиль стратегий иг-
ры» в теории статических игр?
4. Дайте толкование понятий «задача теории игр» и «решение игры».
5. Сформулируйте определения биматричной игры и ее двойной мат-
рицы.
6. Сформулируйте определение доминирующей (сильно, слабо) стра-
тегии.
7. Сформулируйте определение равновесия в доминирующих стратеги-
ях статической игры с полной информацией.
8. Что представляет собой принцип сильного доминирования в теории
статических игр в нормальной форме?
9. Сформулируйте определение равновесия Нэша статической игры т
лиц в нормальной форме.
453
10. Сформулируйте теорему о достаточном условии существования рав-
новесия Нэша статической игры т лиц в нормальной форме.
11. Опишите взаимосвязь последовательного использования принципа
сильного доминирования и равновесия Нэша статической игры и
лиц в нормальной форме.
12. Сформулируйте определение понятий чистой стратегии, смешанной
стратегии и ожидаемого выигрыша игрока в теории биматричных
игр.
13. Что такое смешанное расширение (рандомизация) биматричной иг-
ры?
14. Сформулируйте определение и теорему существования равновесия
Нэша в смешанных стратегиях биматричной игры.
15. Сформулируйте условие дополняющей нежесткое™ равновесия Нэ-
ша в смешанных стратегиях биматричной игры.
16. Приведите систему неравенств для явного определения равновесия
Нэша в смешанных стратегиях биматричной игры с матрицами вы-
игрышей игроков второго порядка.
17. Сформулируйте понятие Парето-эффективного профиля статичес-
кой игры с полной информацией.
18. Что представляет собой «геометрический критерий» Парето-эффек-
тивности профиля чистых стратегий биматричной игры в критери-
альном пространстве выигрышей игроков?
19. Сформулируйте определение динамической игры с совершенной и
несовершенной информацией.
20. Что означают термины «совершенная» и «несовершенная информа-
ция»?
21. Что такое развернутая (расширенная) форма динамической игры с
совершенной информацией?
22. Сформулируйте понятие хода игрока, траектории ходов, пути в дере-
ве игры, партии динамической игры с совершенной информацией в
развернутой форме.
23. Что представляет собой метод обратаой индукции решения динами-
ческой игры в развернутой форме?
24. Что представляет собой динамическая игра с совершенной инфор-
мацией в нормальной форме?
25. Сформулируйте определение чистой стратегии игрока динамичес-
кой модели с совершенной информацией в развернутой форме.
26. Сформулируйте теорему о связи решения динамической игры с со-
вершенной информацией, полученного методом обратной индук-
ции, и равновесием Нэша.
27. Сформулируйте определение подыгры игры с совершенной инфор-
мацией в развернутой форме.
28. Сформулируйте определение совершенного в подыграх равновесия.
29. Сформулируйте определение информационного множества игрока.
454
30. Что представляет собой развернутая форма статической игры?
31. Сформулируйте понятие игр с совершенной и несовершенной ин-
формацией, используя понятие информационного множества.
32. Опишите ситуацию адекватности представления в виде нормальной
формы динамической игры.
33. Сформулируйте определение неполной информации и статической
игры с неполной информацией.
34. Дайте определение понятия типа предпочтений игрока.
35. Сформулируйте понятие статической байесовской игры.
36. Сформулируйте определение (чистой) стратегии игрока и ожидаемо-
го выигрыша игрока в случае статической байесовской игры.
37. Сформулируйте определение равновесия Нэша — Байеса статичес-
кой байесовской игры.
38. Представьте модель дуополии Курно как статическую игру с полной
информацией.
39. Покажите, что равновесие Курно — это равновесие Нэша.
40. Представьте модель дуополии Бертрана как статическую модель с
полной информацией. Покажите, что равновесие Бертрана — это
равновесие Нэша.
41. Представьте модель дуополии Курно как статическую игру с непол-
ной информацией.
42. Сформулируйте определение динамической игры с неполной ин-
формацией.
43. Сформулируйте основные требования к набору стратегий и ожида-
ний игроков, составляющих совершенное байесовское равновесие
динамической игры с неполной информацией.
Задачи и упражнения для самоконтроля к главе 9
1. Биматричная игра G(A, В) задана следующей информацией:
Таблица
Стратегии игрока Р2
S2 S2 S2
Стратегии игрока Л *1‘ (2; 3) (3;5) (7; 4)
512 (-2; 1) (2; 6) (4; 7)
513 (3; 2) (2; 3) (6; 4)
Реализуйте принцип сильного доминирования для этой биматричной
игры.
455
2. Покажите, что равновесие дуополии Курно есть равновесие Нэша этой
дуополии как статической игры с полной информацией.
3. Покажите, что равновесие Бертрана есть равновесие Нэша дуополии
как статической игры с полной информацией Бертрана.
4. На рынок однородной продукции поставляют продукцию две фирмы
F{ и F2. Для выпуска продукции каждая фирма может использовать
один (1Ц) или два (2Ц) своих цеха. Если в каждой фирме функцио-
нирует два цеха, то это приведет к перепроизводству продукции,
в результате каждая фирма понесет убытки в количестве 30 д.е. Если
в каждой фирме функционирует только один цех, то каждая из них
получит прибыль, равную 40 д.е. Если в одной фирме функциониру-
ет только один цех, а в другой — два цеха, то прибыль первой из этих
фирм будет равна 30 д.е., а прибыль другой составит 60 д.е.
Представьте описанную ситуацию в виде биматричной игры с явно
выписанной двойной матрицей выигрышей (проигрышей) фирм Fx
иГ2.
Представьте биматричную игру в развернутой форме, указав явно
информационные множества обеих фирм.
Для этой биматричной игры найдите равновесия Нэша в чистых и
смешанных стратегиях. В критериальном пространстве выигрышей
фирм F{ и F2 представьте множества выигрышей фирм F{ и F2 в слу-
чае чистых и в случае смешанных стратегий фирм Fx и F2 и выявите
Парето-эффективные профили (смешанных) стратегий.
Сопоставьте равновесие Нэша и Парето-эффективные профили
смешанных стратегий. Дайте содержательную экономическую ин-
терпретацию найденным равновесиям Нэша и Парето-эффекгив-
ным профилям смешанных стратегий.
5. Фирма Fx собирается продавать свою продукцию на одном из двух
рынков, которые контролируются фирмой F2. Если фирма Fx выйдет
со своей продукцией на первый рынок (Aft), она получит прибыль,
равную 4 д.е., а фирма F2 понесет убытки, равные 4 д.е. Если фирма
F{ выйдет со своей продукцией на второй рынок (Af2), она получит
прибыль, равную 2 д.е., а фирма F2 понесет убытки, равные 2 д.е.
Если фирма F2 принимает контрмеры и не пустит фирму Fx на рынок
М{9 то фирма F2 получит прибыль, равную 3 д.е., а фирма Fx понесет
большие убытки, равные 5 д.е. Наконец, если фирма F2 принимает
меры и не пустит фирму F{ на рынок М2, то фирма F2 получит при-
быль, равную 4 д.е., а фирма Fx понесет убытки, равные 1 д.е.
Представьте описанную ситуацию в виде биматричной игры с явно
выписанной двойной матрицей выиграшей (проигрышей) фирм F{
иГ2.
Представить биматричную игру в развернутой форме, указав явно
информационные множества обеих фирм.
456
Для этой биматричной игры найти равновесие Нэша в смешанных
стратегиях (равновесий Нэша в чистых стратегиях эта биматричная
игра не имеет).
В критериальном пространстве выигрышей фирм F{ и F2 представьте
множества выигрышей фирм F{ и F2 в случае чистых стратегий и в
случае смешанных стратегий фирм F{ и F2 и выявите Парето-эффек-
тивные профили (смешанных) стратегий.
Сопоставьте равновесие Нэша и Парето-эффективные профили
смешанных стратегий.
Дайте содержательную экономическую интерпретацию найденному
равновесию Нэша и Парето-эффективным профилям смешанных
стратегий.
6. Для следующих игр
(7; i)
(4; 3) (4; 1)
(6; 4)
(Л, л — игрок выбирает левую дугу;
П, п — игрок выбирает правую дугу)
сделайте переход от развернутой формы к нормальной форме, най-
дите равновесие Нэша (в чистых стратегиях), Парето-эффективные
профили (чистых) стратегий, опишите все подыгры (включая пол-
ную игру), из равновесий Нэша выделите (с обоснованием) совер-
шенное в подыграх равновесие, постройте их решения методом об-
ратной индукции.
7.1. Для статической игры с полной информацией нормальная форма
имеет следующий вид:
(Чистые) стратегии игрока Р2
(Л) (П)
(Чистые) стратегии игрока (Л) (-2; 8) (9; 9)
(П) (0; 12) (0; 10)
457
Постройте ее развернутую форму в двух вариантах (в одном варианте
в первой вершине находится игрок Р{9 в другом варианте в первой
вершине находится игрок Р2).
7.2. Для статической игры с полной информацией нормальная форма
имеет следующий вид:
(Чистые) стратегии игрока Р2
(Л) (П)
(Чистые) стратегии игрока Pj (Л) (1; 7) (8; 8)
(П) (2; П) (2; Ю)
Постройте ее развернутую форму в двух вариантах (в одном варианте
в первой вершине находится игрок Рр в другом варианте в первой
вершине находится игрок Р2).
8. Представьте модель дуополии Бертрана как статическую игру с пол-
ной информацией и докажите, что равновесие Бертрана есть равно-
весие Нэша.
9. От статических игр с полной информацией, имеющих в качестве
нормальных форм таблицы, которые следует построить, выполняя
задания 7.1 и 7.2, постройте соответствующие им деревья игр в двух
вариантах (в одном варианте в первой вершине находится игрок Р{,
в другом варианте в первой вершине находится игрок Р2).
Вопросы, тесты и задачи для контрольных работ к главе 9
1. Докажите, что пара сильно доминирующих стратегий игроков Р{ и Р2
составляет единственное равновесие Нэша.
2. Приведите пример биматричной игры, в которой равновесие Нэша
не является равновесием в доминирующих стратегиях.
3. Приведите пример биматричной игры, в которой существует един-
ственное равновесие Нэша (в чистых стратегиях).
4. Приведите пример биматричной игры, в которой существует два рав-
новесия Нэша (в чистых стратегиях). Исследуйте вопрос о существо-
вании у этой игры равновесия Нэша в смешанных стратегиях.
5. Для биматричной игры с матрицей выигрышей
(20; 20) <-1;30)
(40;-2) (5; 5)
найдите равновесия Нэша и профили Парето-эффективных страте-
гий.
Дайте геометрическую интерпретацию в критериальном простран-
стве выигрышей игроков Р{ и Р2.
458
6. В игре игрок Р( имеет два типа предпочтений, игрок Р2 — один тип
предпочтений. Формально первый и второй типы предпочтений иг-
рока Р1 характеризуются следующими матрицами выигрышей:
Л -
-3
-8
-5/ 2 ^-9 -nJ'
Единственный тип предпочтений игрока Р2 характеризуется его мат-
рицей выигрышей
в-Р -1»
-5 J
Игрок Р{ имеет первый тип предпочтений с вероятностьюр{, а вто-
рой тип предпочтения с вероятностью q{ = 1 — рр т.е. игрок Р2 пола-
гает, что с вероятностьюр{ игрок Р{ имеет первый тип предпочтений,
с вероятностью q{ игрок Р{ имеет второй тип предпочтений.
6.1. Представьте предложенную игру в нормальной форме.
6.2. Представьте предложенную игру в развернутой форме.
6.3. Покажите, что предложенная игра есть статическая байесовская
игра.
6.4. Выпишите значение ожидаемого выигрыша игрока Pv
6.5. Выпишите значение ожидаемого выигрыша игрока Рг
6.6. Отыщите равновесия Нэша — Байеса предложенной игры.
Глава
ТЕОРИЯ РЫНОЧНОЙ
КОНКУРЕНЦИИ
10.1. Толкование понятия рыночной конкуренции
10.1.1. Понятие конкуренции обсуждается и анализируется многи-
ми авторами. Отметим здесь только, что во введении ко второму
тому курса микроэкономики трех авторов (В.М. Гальперин,
С.М. Игнатьев, В.И. Моргунов (1997), с. 8), в частности, отмеча-
ется, что слова «конкуренция, konkurrenz, concurrence происходят от
латинского сопсигго — сбегаться, сталкиваться (соп — вместе, сиг-
го — бежать), тогда как английское competition восходит к латинс-
кому competitionem (сот — con + petito — стремление достать что-то,
добиться чего-либо, притязать на что-то)».
Понятие рыночной конкуренции означает борьбу за ограничен-
ный объем платежеспособного спроса потребителей, которая ве-
дется фирмами на доступных им сегментах рынка. Здесь следует
подчеркнуть, что речь идет о рыночной конкуренции, а не о кон-
куренции вообще. Понятие рыночной конкуренции можно тол-
ковать с позиций поведенческого, структурного и функционального
подходов. Если анализируются методы рыночной конкуренции,
стратегии конкуренции, используемые отдельными фирмами
и т.д., то это означает использование поведенческого подхода к
пониманию сути рыночной конкуренции. Если анализируются
проблемы уровня монополизации (или, напротив, ее отсутствия)
рынка, то это означает применение структурного подхода к пони-
манию сути рыночной конкуренции. Если речь идет об исследо-
460
вании роли рыночной конкуренции в экономике, то это означает
использование функционального подхода к пониманию сути ры-
ночной конкуренции (А.Ю. Юданов (2001)).
10.1.2. В следующем параграфе рассматриваются основные поло-
жения теории рыночной конкуренции, разработанной М. Порте-
ром (2000), в которой рыночная конкуренция толкуется как мо-
дель пяти сил конкуренции. При изложении этой теории здесь
активно используются материалы главы 15 книги А. Томпсона,
Д. Формби (1998). Изложение остальных параграфов нашей главы
10 следует в основном тексту главы 16 книги А. Томпсона,
Д. Формби (1998).
10.2. Модель пяти сил конкуренции
10.2.1. Рыночная конкуренция представляет собой систему, в ко-
торой взаимодействуют пять элементов (пять сил) конкуренции
(рис. 10.1).
Сначала проанализируем рыночную конкуренцию между
фирмами отрасли.
Каждая фирма должна иметь стратегию конкуренции, пред-
ставляющую план действий фирмы по занятию лучших позиций
на рынке и ее оборонительных действий по защите своих позиций
на рынке.
Рассмотрим действия и противодействия конкурентных фирм
отрасли на примере «Кока-кола» и «Пепси-кола» (см.: А. Томп-
сон, Д. Формби (1998), с. 432-434]).
В целях улучшения положения на рынке фирмы «Пепси» по
сравнению с позицией «Коки» руководство «Пепси» в период с
1950 по 1955 г. реализовало первый этап своей наступательной
программы. Прежде всего оно приняло целенаправленные меры
по улучшению вкуса самого напитка «Пепси» (исключение под-
слащивающих компонент, усиление контроля за разливом напит-
ка на местах, где к сиропу добавляли различное количество гази-
рованной воды). После повышения качества продукта фирма
«Пепси» провела рекламную кампанию в целях улучшения имид-
жа напитка. «Пепси» (на рекламных плакатах «Пепси» пили кра-
сивые, со вкусом одетые женщины и галантные мужчины, рекла-
му сопровождала тема о легком напитке «Пепси», что косвенно
461
Фирмы из других отраслей,
предлагающие продукты-заместители.
(Сила конкуренции возникает
в результате попыток фирм
завоевать покупателей
продуктами-заместителями.)
Конкуренция между
фирмами отрасли.
(Сила конкуренции возникает
в результате стремления
фирм-соперников занять
лучшие позиции на рынке
отрасли.)
Потенциально новые
на рынке фирмы.
(Сила конкуренции возникает
в результате попыток угрозы
появления на рынке отрасли
новых фирм.)
Рис. ЮЛ
означало, что «Кока» — тяжелый напиток). В этот же период вре-
мени фирма «Пепси» решила освоить тот рыночный сегмент, по-
купатели которого приобретали прохладительный напиток для
домашнего потребления. Наконец, важный элемент первого эта-
па наступательной программы фирмы «Пепси» состоял в выборе
25 городов, в которых была реализована специальная программа
стимулирования сбыта. Концентрация сил в этих 25 городах поз-
волила фирме «Пепси» увеличить свою долю рынка. К 1955 г.
итоги первого этапа наступательной программы фирмы «Пепси»
позволили ей приступить к реализации ее второго этапа — увели-
чению доли на рынке продаж в розлив, где прочно укрепилась
фирма «Кока». Фирма «Пепси» стала широко использовать авто-
маты по продаже напитков.
462
После того как второй этап наступления фирмы «Пепси» стал
демонстрировать признаки успеха, фирма «Кока», которая с юмо-
ром относилась к наступлению «Пепси» и которая не привыкла к
конкуренции, также стала действовать (проведение новой рек-
ламной кампании под лозунгом, что «Кока» освежает лучше,
и предложение бутылочек новых размеров), что позволило ей уве-
личить объем сбыта.
В начале 1960-х гг. темпы роста фирмы «Пепси» уменьшились
и она предприняла новые рекламные кампании под лозунгами:
«Будь общительным» и «Будь молодым». Фирма «Кока» ответила
лозунгом: «С «Кокой» дела идут лучше».
Далее рыночная конкуренция между фирмами «Пепси» и «Ко-
ка», которая ранее сосредоточивалась на вкусе напитка, рекламе,
размерах и формах бутылок, перешла в новые сферы. Первая сфе-
ра касалась использования одноразовых бутылок, алюминиевых и
стальных банок. Вторая и третья сферы рыночной конкуренции
касались новизны продукции (производство диетических прохла-
дительных напитков, а также других вкусных напитков, отличных
от знаменитых «кол»). Четвертая сфера рыночной конкуренции
возникла в 1980-х гг., когда обе фирмы («Кока» и «Пепси») пред-
ложили рынку традиционные диетические варианты своей про-
дукции, не содержащие кофеина.
В отрасли прохладительных напитков фирма «Кока» продол-
жает удерживать лидирующие позиции, а фирма «Пепси» занима-
ет прочное второе место.
10.2.2. Силу или слабость (т.е. интенсивность) рыночной конку-
ренции между фирмами отрасли объясняет ряд факторов. Рас-
смотрим факторы, которые усиливают рыночную конкуренцию
между фирмами отрасли:
1) рост числа конкурентов, уравнивание их размеров и мощ-
ностей;
2) медленный рост спроса на продукцию отрасли;
3) отраслевые условия таковы, что у конкурирующих фирм
возникает соблазн использовать снижение цен или другие ин-
струменты конкуренции в целях увеличения объема сбыта своей
продукции (в случае уменьшения рыночного спроса уровень ис-
пользования капитала начинает понижаться, рост удельных из-
держек заставляет конкурирующие фирмы прибегать к тайным
ценовым уступкам, специальным скидкам и другой повышающей
463
объем продаж тактике, что усиливает конкуренцию; аналогично в
случае скоропортящейся продукции конкуренция усиливается,
когда фирмы применяют демпинг);
4) покупатели не несут значительных издержек при замене
одного приобретаемого продукта другим (в этом случае конкури-
рующим фирмам легче перехватить потребителей друг у друга,
что, конечно, усиливает рыночную конкуренцию);
5) отраслевые условия таковы, что одна или ряд конкурирую-
щих фирм не удовлетворены занимаемым ими положением и
предпринимают меры для корректировки ситуации за счет конку-
рентов (к таким мерам можно отнести поглощение малых конку-
рентов, выпуск новой продукции, активизацию рекламной дея-
тельности, установление специальных цен);
6) рост размера отдачи от удачного стратегического шага (ко-
торая зависит от скорости, с которой предпринимаются ответные
меры другими фирмами: если реакция фирм-конкурентов будет
вялой, то инициатор стратегического шага может извлечь выгоды
и получит преимущество во времени);
7) отраслевые условия таковы, что дороже выйти из бизнеса,
чем в нем оставаться и конкурировать (чем выше издержки ухода
с рынка отрасли, тем сильнее желание фирмы остаться в отрасли
и конкурировать изо всех сил, даже если фирма будет функциони-
ровать с убытками);
8) сильные компании из других отраслей поглощают слабые
фирмы отрасли и предпринимают агрессивные действия для пре-
вращения своих приобретений в сильных соперников других
фирм отрасли.
10.2.3. На рыночную конкуренцию между фирмами отрасли ока-
зывает существенное влияние разнообразие стратегий конкурен-
ции отдельных фирм, индивидуальные особенности конкурентов,
их корпоративные приоритеты и национальная принадлежность.
Проанализируем силу конкуренции, которая возникает в резуль-
тате попыток фирм завоевать покупателей продуктами-замести-
телями. Конкурентная угроза со стороны продуктов-заместителей
сильна тогда, когда заместители имеют низкие цены, низкие из-
держки потребителей, связанные с переходом на продукты-замес-
тители, и при этом потребители уверены, что заместители облада-
ют не худшим качеством.
464
Фирмы, производящие прохладительные напитки, конкури-
руют с производителями фруктовых соков, чая, кофе. Производи-
тели пластиковой тары конкурируют с изготовителями стеклян-
ных бутылок и банок, бумажных пакетов, жестяных и алюминие-
вых банок.
10.2.4. Переходим к анализу силы конкуренции, которая возни-
кает в результате угрозы появления на рынке отрасли новых фирм.
Уровень угрозы со стороны новых фирм зависит от барьеров входа
и от ожидаемой реакции со стороны действующих на рынке от-
расли фирм.
Причины появления барьеров входа новых фирм в отрасль:
1) экономия от масштаба производства затрудняет вход но-
вых фирм в отрасль, ибо заставляет потенциальных новичков
входить в отрасль на базе широкомасштабного производства (что
сопряжено с большими издержками и большим риском) или со-
гласиться занять невыгодное по издержкам положение в отрасли
(т.е. согласиться столкнуться с барьерами не только в производ-
стве, но и в рекламе, маркетинге, распределении готовой продук-
ции, послепродажных услугах, приобретении сырья и проведении
НИОКР);
2) невозможность получить доступ к технологиям и специа-
лизированному ноу-хау (вход на отраслевой рынок могут пере-
крыть патенты, отсутствие высококвалифицированных кадров и
неспособность использовать сложные производственные мето-
ды);
3) наличие кривой обучения и опыта (снижение средних из-
держек частично или во многом есть функция опыта производства
продукции и других характеристик кривой обучения, поэтому
фирма-новичок, которая не имеет опыта, будет находиться в ме-
нее выгодном положении);
4) предпочтение и лояльность торговой марки (для преодо-
ления предпочтений покупателей и для формирования своей кли-
ентуры фирма-новичок должна сделать большие вложения в рек-
ламу, предложить покупателям более низкие цены, лучшее каче-
ство и дополнительные услуги; все это для фирмы-новичка
означает снижение прибыли, увеличение риска);
5) капиталоемкость (требования к объему инвестиций прямо
связаны с производственными площадями и оборудованием, обо-
ротным капиталом для финансирования складских запасов и про-
зе - 7620
465
дажи в кредит, рекламой и стимулированием сбыта в целях фор-
мирования круга клиентов, а также для покрытия издержек стар-
тового периода);
6) невыгодное положение по издержкам независимо от раз-
мера фирмы (фирмы отрасли могут иметь преимущества по из-
держкам, которые недоступны фирмам-новичкам независимо от
их размеров: доступ к лучшему и дешевому сырью, владение па-
тентами или технологическим ноу-хау, эффект кривой обучения
и опыта, наличие давно построенных с меньшими издержками
предприятий, наличие деловых кредитов);
7) доступ к каналам распределения продукции (вполне воз-
можно, что придется с нуля организовывать сеть розничной тор-
говли, ибо розничные торговцы и оптовики могут не пожелать
иметь дело с товарами (продуктами), которые не пользуются до-
статочным признанием со стороны потребителей; для преодоле-
ния барьера, препятствующего доступу фирмы-новичка к кана-
лам распределения продукции, ей придется специально оплатить
доступ к этим каналам; в связи с этим прибыль фирмы-новичка
может быть невысокой);
8) нормативно-правовая база (государственные органы мо-
гут ограничить или запретить вход на рынок, требуя лицензий или
разрешений; это прежде всего относится к таким отраслям, как
банковское и страховое дело, СМИ, розничная торговля алко-
гольной продукцией, железнодорожные перевозки; на междуна-
родных рынках национальные правительства обычно ограничи-
вают вход для иностранцев и утверждают все предложения по
иностранным инвестициям);
9) тарифы и международные торговые ограничения (госу-
дарственные органы стран используют тарифы и ограничения
торговли в качестве мер, повышающих барьеры для иностранных
фирм; в частности, европейские государства требуют, чтобы изго-
товленные в Европе детали и затраты труда европейских рабочих
составляли не менее 40% цены некоторых товаров из стран Азии,
например копировальной техники; для защиты европейских изго-
товителей электронных микросхем от дешевых азиатского произ-
водства европейские государства установили жесткую формулу
вычисления нижней цены чипов компьютерной памяти).
Отметим в заключение, что угроза входа фирм-новичков на
рынок отрасли как одна из сил конкуренции корректируется в
зависимости от перспектив развития отрасли, в частности перс-
466
пектив повышения и понижения барьеров. Например, окончание
срока действия ключевого патента скорее усиливает угрозу входа
в отрасль новых фирм. Повышение фирмами отрасли интенсив-
ности их рекламной деятельности, укрепление их отношений с
дилерами и дистрибьюторами, продвижение в сфере НИОКР,
повышение качества продукции могут повысить уровень барьеров
на пути в отрасль.
10.2.5. Переходим к анализу силы конкуренции, которая возни-
кает в связи с наличием контроля за условиями следок со стороны
поставщиков. Поставщики отрасли представляют собой значи-
тельную конкурентную силу, когда поставщики могут диктовать
цены на свою продукцию и влиять на благосостояние отрасли-по-
требителя посредством надежности своих поставок или качества и
технологических характеристик своей продукции. Поставщики
отрасли представляют собой слабую силу конкуренции, если поку-
патели могут приобрести продукт (товар) из многих других источ-
ников, если существуют хорошие товары-заместители и когда
благосостояние отрасли-покупателя важно для благосостояния ее
поставщиков.
В качестве примера рыночной отрасли рассмотрим сельское
хозяйство, а в качестве сильных поставщиков возьмем мощные
машиностроительные и химические компании, которые гораздо
сильнее фермеров, фермы которых образуют сельскохозяйствен-
ную отрасль. Прямым следствием дисбаланса существующих вза-
имосвязей между поставщиками (машиностроительными и хими-
ческими компаниями) и потребителями (фермерами) являются
наблюдаемые во многих странах (в том числе и в России) «ножни-
цы цен», когда цены на потребляемую сельским хозяйством про-
мышленную продукцию растут быстрее, чем отпускные цены
сельскохозяйственной продукции, в результате чего сельскохо-
зяйственные фермы несут убытки и поэтому нуждаются в госу-
дарственных субсидиях.
В качестве примера рыночной отрасли, которая сильнее своих
поставщиков, можно привести фармацевтическую промышлен-
ность. Другой пример дает отрасль прохладительных напитков,
которая сильнее своих поставщиков, производящих алюминие-
вые, пластиковые и стеклянные банки.
В заключение отметим, что, если рыночная отрасль сформи-
ровала тесные рабочие связи с основными поставщиками, она
30«
467
может получить значительные выгоды в виде комплектующих из-
делий более высокого качества, поставок точно в срок и снижения
в связи с этим издержек на складские расходы.
10.2.6. Нам осталось рассмотреть силу конкуренции, которая
возникает в связи с наличием контроля за условиями сделок со
стороны покупателей. Покупатели рыночной отрасли представля-
ют собой значительную конкурентную силу, если они способны
навязать продавцам цены и другие условия сделки. Они являются
слабой силой конкуренции, если рыночная отрасль способна дикто-
вать цены покупателям. Это, в частности, возможно, когда ры-
ночная отрасль достаточно крупная, а покупатели — мелкие и их
к тому же значительное количество.
В качестве примера покупателя, представляющего собой зна-
чительную конкурентную силу, можно рассмотреть крупные фир-
мы пищевой промышленности, а в качестве рыночной отрасли —
сельское хозяйство, состоящее из сельскохозяйственных фирм.
Здесь ситуация аналогична той, которую мы наблюдаем в случае,
когда поставщиками сельского хозяйства выступали крупные ма-
шиностроительные и химические фирмы.
За рыночную отрасль, которая способна диктовать свои цены
покупателям, опять можно принять фармацевтическую отрасль,
покупателей которой не пугают высокие цены, ибо здоровье до-
роже всего на свете.
Теория пяти сил конкуренции представляет собой реализа-
цию системного подхода к анализу экономических процессов,
когда фрагмент экономической реальности описывается с помо-
щью системы, состоящей из пяти элементов (см. рис. 10.1). Такая
структуризация фрагментов экономической реальности позволя-
ет анализировать уровни интенсивности конкуренции.
10.2.7. На рыночную конкуренцию оказывают влияние различ-
ные факторы, которые могут быть квалифицированы как движу-
щие силы конкуренции:
1) изменения в характере роста отрасли в долговременном
промежутке (скажем, увеличение спроса на продукцию отрасли в
долговременном промежутке поощряет фирмы отрасли к расши-
рению производства и привлекает в отрасль новые фирмы; сокра-
щение спроса (сужение рынка) приводит к спаду производства,
уходу фирм из отрасли);
468
2) изменения в категории покупателей продукции и способе
ее использования (широкое использование персональных ком-
пьютеров и мобильных телефонов радикально преобразовало от-
расли, производящие компьютеры и телекоммуникационные
системы, что привело к повышению интенсивности конкуренции
между фирмами в этих отраслях);
3) новая продукция (к отраслям, в которых ключевой движу-
щей силой конкуренции является инновация, относятся отрасли
копировального оборудования, вычислительной техники, теле-
коммуникационных систем, электронных видеоигр, лекарств,
свежезамороженных продуктов питания, продуктов питания для
домашних животных, программного обеспечения для персональ-
ных компьютеров);
4) технологические изменения (технические достижения мо-
гут серьезно изменить отрасль, расширить ее границы, повысить
качество выпускаемых продуктов и снизить их цену, радикально
изменить характер наемного труда (широкое распространение
современного вида паломничества);
5) инновации в области маркетинга (за счет новых способов
маркетинга своей продукции фирмы отрасли могут увеличить от-
раслевой спрос, повысить степень дифференциации продукции);
6) выход на рынок или уход с рынка ведущих фирм (выходя-
щие на рынок ведущие фирмы часто существенно корректируют
правила конкуренции и ключевых игроков; аналогичное справед-
ливо и для ситуации, связанной с уходом с рынка ведущих фирм,
например, в связи с ростом влияния остающихся в отрасли лиде-
ров);
7) распространение технического ноу-хау (ноу-хау распро-
страняется через научные журналы, торговые публикации, путем
посещения предприятий, в ходе межличностных контактов между
поставщиками и потребителями; одной из движущих сил конку-
ренции в последние годы стала международная передача техноло-
гий, происходящая в условиях глобализации рынков; передача
технологий превратила в глобальные такие ранее внутренние от-
расли, как автомобильная, бытовая электротехника, телекомму-
никации и вычислительная техника);
8) глобализация промышленности (в качестве движущей си-
лы конкуренции глобализация выступает в таких отраслях, как:
а) базовые отрасли (сырая нефть, медь, хлопок); б) отрасли, для
которых важны низкие издержки производства, что делает абсо-
469
лютно необходимым размещение производства в странах, где
можно добиться самых низких издержек (например, производ-
ство трудоемкой продукции переносится в страны Юго-Восточ-
ной Азии (Южная Корея, Тайвань, Малайзия, Сингапур) с деше-
вой квалифицированной рабочей силой);
9) изменение издержек и эффективности (как только в из-
держках или эффективности происходят значительные измене-
ния, сразу перед конкурирующими фирмами открываются воз-
можности радикального изменения своего положения с учетом
величины преимуществ по издержкам);
10) предпочтение потребителями товаров, обладающих инди-
видуальными качествами, перед стандартизированной продукци-
ей или, наоборот, предпочтение стандартизированной продукции
перед продукцией с индивидуальными качествами (когда покупа-
тели начинают полагать, что высокостандартизированная (и от-
носительно дешевая) продукция удовлетворяет их потребность
столь же эффективно, как и дорогая продукция, обладающая на-
бором дополнительных характеристик, то такое изменение спроса
потребителей может существенно скорректировать профиль про-
изводства в пользу относительно дешевой стандартизированной
продукции; может иметь место и обратная ситуация);
11) изменения государственной политики и нормативно-пра-
вовой базы (государственная политика, направленная на откры-
тие внутреннего рынка для иностранных фирм или закрывающая
его для них, может быть главным фактором, влияющим на между-
народных рынках на то, имеет ли место конкуренция между наци-
ональными и зарубежными фирмами на равных или одна из сто-
рон пользуется (незаслуженными) преимуществами);
12) социальные перемены, перемены в образе жизни (данные
изменения могут быть источником существенных структурных
сдвигов в развитых национальных экономиках; например, повы-
шение интереса к поддержанию хорошей физической формы
привело к появлению целой новой отрасли спортивных тренаже-
ров, одежды, обуви для пробежек, медицинских программ соблю-
дения диет; нарастающая борьба с курением в долгосрочной пер-
спективе представляет серьезную угрозу табачным фирмам);
13) снижение неопределенности и риска в бизнесе (для вновь
формирующейся фирмы характерна неустойчивая структура из-
держек и неопределенность относительно потенциального разме-
ра рынка, затрат времени и средств на преодоление технических
470
проблем и определение каналов сбыта продукции и привлечения
покупателей. Высокий риск в таких отраслях привлекает только
наиболее предприимчивые фирмы. Со временем, когда перво-
проходцы достигают успеха и снижается неопределенность,
в формирующуюся отрасль начинают постепенно входить более
консервативные фирмы).
10.3. Конкурентное преимущество. Стратегии,
используемые фирмами для получения конкурентного
преимущества
10.3.1. Конкурентное преимущество — одно из важных понятий
теории рыночной конкуренции. Фирма Л имеет конкурентное пре-
имущество перед фирмами В, С,.... если она расширяет свою до-
лю рынка за счет этих фирм.
К источникам конкурентного преимущества фирмы относят-
ся: производство продукции более высокого качества; предостав-
ление покупателям лучших услуг; достижение более низкого, чем
у конкурентов, уровня издержек; выгодное географическое рас-
положение, а также функционирование (полное или частичное) в
рамках теневого сектора национальной экономики или глобаль-
ной экономики.
Как уже отмечалось в параграфе 10.2, стратегия конкуренции
представляет собой совокупность действий фирмы, направлен-
ных на достижение успеха в рыночной конкуренции с другими
фирмами. Стратегия конкуренции должна содержать меры насту-
пательного и оборонительного характера в целях преодоления
или ослабления всех пяти сил конкуренции (см. параграф 10.2).
Степень разработанности стратегии конкуренции оценивается по
двум критериям: критерий получения конкурентного преимуще-
ства и наличие выгодной позиции на рынке в долгосрочной пер-
спективе и критерий высокой прибыли.
Стратегии конкуренции разрабатываются фирмами с учетом их
уникальных особенностей, поэтому реально существует столько
стратегий, сколько существует фирм. Однако число фундаменталь-
ных различий у стратегий конкуренции сравнительно невелико.
10.3.2. Принято выделять следующие пять стратегий, которые
используются фирмами для получения конкурентного преимуще-
ства-. стратегия лидерства по низким издержкам; стратегия диф-
471
ференциации; гибридная стратегия; стратегия рыночной ниши и
глобальная стратегия.
Стратегия лидерства по низким издержкам целесообразна на
рынках стандартизированной продукции, покупатели которой
чувствительны к ценам, т.е. в случае, когда доминирующим фак-
тором конкуренции является цена, а не характеристики или каче-
ство продукции. Если фирме удалось снизить издержки, то она
может использовать это обстоятельство для снижения цен по
сравнению с конкурентами. В этом случае фирма расширяет свою
долю рынка за счет конкурентов и, следовательно, получает кон-
курентное преимущество.
Стратегии лидерства по издержкам следуют такие известные
фирмы, как «Форд» при производстве тяжелых грузовиков, «Дже-
нерал электрик» в производстве бытового оборудования, «Ас» в
производстве шариковых ручек.
Стратегия лидерства по издержкам позволяет фирме активно
защищаться от всех пяти сил конкуренции (см. параграф 10.2).
Лидер по издержкам за счет конкурентов своей отрасли увеличи-
вает объем продаж (и следовательно, свою долю рынка), защища-
ется от ценовых войн (ибо может назначить самую низкую на
рынке цену). Лидер по издержкам имеет частичную защиту маржи
своей прибыли от воздействия со стороны крупных покупателей,
ибо последние редко сбивают цену ниже уровня выживания вто-
рого по издержкам продавца отрасли. Лидер по издержкам лучше
своих конкурентов защищен от обладающих мощной рыночной
силой поставщиков. Лидер по издержкам может использовать по-
нижение цены и тем самым создать дополнительный барьер для
фирм-новичков, которые являются кандидатами на вхождение в
отрасль. Наконец, лидер по издержкам лучше своих конкурентов
может использовать низкие цены от попыток товаров-замести-
телей пробиться на рынок данной отрасли.
Перечислим ряд условий, при выполнении которых высока
вероятность достижения конкурентного преимущества в резуль-
тате реализации стратегии лидерства по низким издержкам: доми-
нирующей силой конкуренции является ценовая конкуренция при
высокоэластичном спросе по цене; продукция отрасли в сильной
степени стандартизирована, и потребитель может ее приобретать
у разных продавцов (в том числе и у тех, кто предлагает ее по ми-
нимальной цене), дифференциация продукции менее значима
для потребителей, чем ее цена.
472
10.3.3. Стратегия дифференциации целесообразна, когда пред-
почтения потребителей слишком разнообразны, чтобы их могла
удовлетворить стандартизированная продукция. В результате
стратегии дифференциации фирма получает конкурентное пре-
имущество, если она наделяет свою продукцию такими характе-
ристиками, которые привлекают новых потребителей, которые
готовы платить за них больше (возможно, намного больше). Диф-
ференциация результативна, если выручка, полученная от прода-
жи дифференцированной продукции, превышает издержки, ко-
торые охватывают издержки, связанные с дифференциацией.
Дифференциация неудачна, если форма уникальности продук-
ции, выбранная фирмой, не привлекает достаточное число потре-
бителей и если повышенная цена дифференцированной продук-
ции не покрывает дополнительных издержек, связанных с диффе-
ренциацией.
Стратегии дифференциации следуют такие известные фирмы,
как «Federal Express» (доставка почты в течение одних суток), «Cat-
erpillar» (доставка запасных частей любому потребителю в любой
стране мира в течение 48 часов), «Rolex» (престижные часы),
«Johnson & Johnson» (товары для детей), «McDonnald’s» (высокое
качество картофеля-фри).
Стратегия дифференциации позволяет фирме активно защи-
щаться от всех пяти сил конкуренции (см. параграф 10.2). В рам-
ках своей отрасли фирма, следующая результативной стратегии
дифференциации, имеет защиту от силы конкуренции, возника-
ющей в результате стремления конкурентов занять лучшие пози-
ции на рынке этой отрасли, ибо фирма реализует свою продукцию
по повышенным ценам. Результативная дифференциация повы-
шает барьер проникновения на рынок отрасли для фирм-новичков,
ибо им трудно наладить выпуск дифференцированной (т.е., по
сути, уникальной) продукции и, следовательно, привлечь новых
покупателей, которые «избалованы» продукцией высокого качест-
ва. Результативная дифференциация уменьшает рыночную власть
крупных покупателей в связи с тем, что продукция конкурентов
менее привлекательна для них. Фирма, следующая результатив-
ной стратегии дифференциации, благодаря повышению цен на
выпускаемую продукцию может повышать цены на приобретае-
мые у поставщиков ресурсы и тем самым получить защиту от той
силы конкуренции, носителем которой являются поставщики.
473
Наконец, результативная стратегия дифференциации защищает
фирму от угрозы со стороны товаров-заместителей, ибо потреби-
тели предпочитают качественную продукцию фирмы любой ана-
логичной продукции.
Перечислим ряд условий, при выполнении которых высока
вероятность достижения конкурентного преимущества в резуль-
тате реализации стратегии дифференциации: существует много
способов дифференциации продуктов и услуг, с одной стороны,
и большое число потребителей, которые полагают для себя цен-
ными отличительные характеристики продуктов и услуг, наличие
разнообразных причин, по которым потребители приобретают
дифференцированную продукцию, относительно малое число
фирм реализует один и тот же подход к дифференциации, диффе-
ренцирующие продукцию качества не могут быть быстро и без
больших издержек имитированы.
Дифференциация продукции может базироваться на техноло-
гическом превосходстве, на качестве, на основе широкого спектра
услуг.
10.3.4. Гибридная стратегия соединяет конкурентные преимуще-
ства, которые фирма получит, используя стратегию лидерства по
издержкам и стратегию дифференциации. Если дифференциация
востребована на рынке, а значительное число потребителей чув-
ствительно к цене, то гибридная стратегия лучше двух крайнос-
тей: чистой стратегии низких издержек и чистой стратегии диф-
ференциации, ибо фирма может функционировать в состоянии,
близком к середине рынка, продавая либо продукцию среднего
достоинства по цене, ниже среднерыночной, либо высокого ка-
чества по среднерыночной цене.
Гибридная стратегия представляет собой метод конкуренции,
который принято называть стратегией производителя с наилуч-
шими издержками.
10.3.5. Стратегия рыночной ниши целесообразна тогда, когда
фирма не в состоянии получить конкурентное преимущество на
всем рынке в масштабах национальной экономики. Ниша может
быть определена с географической точки зрения, с точки зрения
специальных требований к использованию продукции или осо-
бенностей характеристик, важных в рамках ниши.
474
Основу конкурентного преимущества фирмы, реализующей
стратегию рыночной ниши, составляют либо низкие издержки на
обслуживание ниши, либо способность предложить потребите-
лям ниши нечто отличное от других конкурентов. Стратегия ры-
ночной ниши, основанная на низких издержках, зависит от нали-
чия сегмента потребителей, потребности которых удовлетворить
дешевле, чем потребности покупателей остальной части рынка.
Стратегия рыночной ниши, основанная на дифференциации, за-
висит от наличия сегмента покупателей, которым требуются уни-
кальные качества продукции.
Стратегии рыночной ниши следуют такие известные фирмы,
как «Роллс-Ройс» (сверхшикарные автомобили), «Apple Computer»
(настольные издательские системы), ряд авиакомпаний («Sky-
west», «Atlantic Southeast»), специализирующихся на местных авиа-
перевозках, на не сильно загруженных линиях и коротких марш-
рутах.
Стратегия рыночной ниши целесообразна тогда, когда разме-
ры ниши должны обеспечить прибыльность, когда ниша имеет
хороший потенциал роста, когда конкуренты не рассматривают
нишу в качестве критически важного фактора своего успеха, когда
фирма обладает необходимыми ресурсами, достаточными для эф-
фективного обслуживания ниши.
Стратегия рыночной ниши позволяет фирме активно защи-
щаться от всех пяти сил конкуренции (см. параграф 10.2). Фирмы
отрасли, действующие в нескольких рыночных нишах, не облада-
ют той же конкурентной способностью, что и фирма, которая
специализируется по обслуживанию целевой клиентуры. Специ-
ализированные знания и опыт фирмы, которая функционирует в
рыночной нише, являются барьерами для входа на рынок фирм-
новичков, а также для проникновения в нишу товаров-замести-
телей. Рыночная сила мощных покупателей снижается, ибо эти
покупатели не испытывают особого желания приобретать продук-
цию у фирмы, которая не в полной мере может удовлетворить их
потребности. Аналогично рыночная сила продавцов также сни-
жается, ибо они, как правило, не могут удовлетворить все своеоб-
разие потребностей фирмы, связанное с ее функционированием в
рыночной нише.
Конкурентному преимуществу на глобальных рынках посвящен
отдельный параграф 10.7.
475
10.4. Риски стратегий, используемых фирмами
для получения конкурентного преимущества
10.4.1. Стратегии, используемые фирмой для получения конку-
рентного преимущества, не являются безрисковыми. Остановим-
ся сначала на факторах риска стратегии лидерства по низким из-
держкам. Важным фактором снижения издержек являются, как
правило, крупные инвестиции. Однако прорыв в технологиях мо-
жет открыть перед конкурентами новые возможности снижения
издержек и фактически обесценить инвестиции, сделанные лиде-
ром ради снижения издержек.
Конкуренты могут также достаточно дешево имитировать ме-
тоды, примененные лидером для снижения издержек, и тем са-
мым сократить срок жизни конкурентного преимущества.
Скалярная целевая функция фирмы (быть лидером по низким
издержкам) может оказаться слишком узким критерием ее функ-
ционирования, в то время как фирма должна более активно реаги-
ровать также на текущие и радикальные перемены рыночной си-
туации, например на изменение покупательных предпочтений в
пользу качества, новых характеристик, которые могут появляться
в связи с научно-технологическим прогрессом.
10.4.2. К факторам риска стратегии дифференциации можно от-
нести прежде всего то обстоятельство, что в результате реализа-
ции стратегии дифференциации не обязательно будет достигнуто
конкурентное преимущество (т.е. не факт, что удастся привлечь
новых потребителей за счет фирм-конкурентов).
Конкуренты могут быстро скопировать стратегию дифферен-
циации. В этом случае стратегия дифференциации фирмы не бу-
дет результативной.
Слишком сильная степень дифференциации может привести
к тому, что цена на продукцию значительно превысит цену конку-
рентов или качество продукции или услуг превысит запросы по-
требителей.
Слишком высокая надбавка к цене на продукцию позволяет
конкурентам привлечь на их рыночный сектор тех покупателей,
которые были в секторе фирмы, использующей стратегию диффе-
ренциации.
476
10.4.3. К факторам риска стратегии рыночной ниши можно от-
нести прежде всего то обстоятельство, что конкуренты могут
отыскать пути обслуживания рыночной ниши с той же эффектив-
ностью, что данная фирма.
Предпочтения потребителей могут измениться в пользу ка-
честв продукции, которые присущи остальному рынку, что озна-
чает исчезновение границы между нишей и остальным рынком.
Рыночная ниша может оказаться настолько привлекательной, что
она переполнится конкурентами. Это приведет к снижению при-
быльности данного сегмента рынка. Наконец, реализация страте-
гии деятельности только в одной рыночной нише влечет за собой
риск, поскольку единственная ниша может исчезнуть.
Таким образом, факторы риска стратегий, используемых фир-
мами для получения конкурентного преимущества, могут быть
связаны с тем, что фирмы могут не иметь надежной защиты от
пяти сил конкуренции.
10.5. Достижение конкурентного преимущества на
основе стратегий лидерства по низким издержкам,
дифференциации и рыночной ниши
10.5.1. Конкурентное преимущество посредством лидерства по
низким издержкам достигается путем лучшего (чем у конкурен-
тов) контроля над факторами, влияющими на издержки, а также
путем преобразования цепи издержек производства так, чтобы
снижение издержек позволяло продавать потребителям более де-
шевые продукты или услуги.
Перечислим основные факторы, влияющие на издержки зве-
ньев цепи издержек производства.
1. Издержки от масштаба производства могут расти и сни-
жаться в зависимости от звеньев цепи издержек производства
(например, уменьшение числа моделей в массовом производстве
уменьшает издержки, переход фирмы с регионального рынка на
общенациональный может привести к росту издержек).
2. Эффекты кривых обучения и опыта (обучаемость зависит
от того, сколько внимания руководители фирмы уделяют анализу
опыта своей и других фирм; полученные знания и их обобщения
могут держаться в секрете, вплоть до жестких условий неразгла-
477
шения тайны, которые включаются в контракты, заключаемые с
персоналом).
3. Процент использования производственных мощностей
(увеличение степени использования мощностей повышает эф-
фективность использования основного производственного капи-
тала; демпфирование сезонных скачков использования производ-
ственных мощностей — важный источник преимущества по
издержкам).
4. Связи между видами деятельности цепи издержек произ-
водства (если издержки одного вида деятельности влияют на дру-
гой вид деятельности, то общие издержки можно снизить путем
координации данных видов деятельности; важным фактором
снижения издержек является активное использование телеком-
муникационных систем, в частности сети Интернет, например,
для решения задач материально-технического снабжения, когда
можно резко сократить издержки на содержание складских поме-
щений и на размеры запасов).
5. Совместное использование несколькими подразделениями
фирмы вновь открывающихся возможностей (сокращение издер-
жек достигается, когда деятельность одного подразделения может
выполняться совместно с родственным подразделением).
6. Степень вертикальной интеграции (вертикальная интегра-
ция может способствовать как снижению, так и росту издержек).
7. Соображения времени, связанные с преимуществами и не-
достатками первопроходца (фирма может выводить на рынок но-
вый товар благодаря снижению издержек его создания и поддер-
жания репутации фирменной марки; фирмы-последователи могут
снизить издержки за счет того, что они имеют меньшие затраты на
разработку нового товара и его вывода на рынок).
8. Выбор вариантов и оперативные решения (на издержки
фирмы влияют решения, принимаемые руководителями разных
уровней по следующим вопросам: расширение и свертывание но-
менклатуры продукции, предлагаемых потребителям услуг; уве-
личение/уменьшение характеристик качества продуктов; повы-
шение/снижение зарплаты наемных работников; увеличение/
уменьшение числа каналов сбыта готовой продукции; увеличе-
ние/уменьшение объемов НИОКР по сравнению с конкурента-
ми; внимание, уделяемое производительности труда; повышение/
понижение требований к качеству сырья и материалов).
478
9. Географические факторы (издержки могут быть снижены
путем перемещения производства, складов и головных подразде-
лений фирмы в другой регион).
10. Связь фирмы и теневого сектора (если объем теневого
сектора в ВВП страны значителен, многие операции горизонталь-
ной интеграции могут быть реализованы в рамках теневого секто-
ра, что позволит сократить официальные и фактические издержки
фирмы).
Приведем пример преобразования традиционной цепи издер-
жек производства, которое позволило фирме «Iowa Beef Packers»
(IBP) занять на рынке сильные конкурентные позиции (см.: А. Том-
псон, Д. Формби (1998), с. 464—465):
«Традиционный процесс производства мяса включает в себя
выращивание скота на разбросанных фермах и ранчо, доставку
скота в живом виде на бойни, где производство отличается высокой
трудоемкостью, а его условия находятся под жестким контролем
профсоюза, транспортировку говяжьих туш розничными продав-
цами мяса, где туши рубятся на части и фасуются, после чего они
поступают в продажу. Компания «Iowa Beef Packers» радикально
перестроила традиционную цепь. Рядом с экономичными постав-
щиками скота были построены автоматизированные бойни, на ко-
торые нанимались только не члены профсоюза. Здесь же мясо ру-
билось на части (которые запаивались в пластик и были готовы к
продаже), упаковывалось по ящикам и доставлялось розничным
продавцам. Стоимость поставки скота на бойню, которая является
традиционным источником основных издержек, была значительно
снижена в результате сокращения потерь веса в процессе перевозки
животных на далекие расстояния. Снизились и издержки сбыта,
источником которых традиционно служит большое количество от-
ходов при поставке продавцам целых туш. Стратегия компании
«Iowa Beef Packers» оказалась настолько успешной, что к 1985 г. она
стала крупнейшим производителем мяса в США, обойдя таких ли-
деров отрасли, как фирмы «Swift», «Wilson» и «Armour».
10.5.2. Конкурентное преимущество посредством дифференциа-
ции достигается путем использования возможностей для диффе-
ренциации в любом звене цепи издержек производства, а не толь-
ко в отделах маркетинга и рекламы фирмы.
Перечислим основные звенья цепи издержек производства,
которые могут быть источниками дифференциации.
479
1. Закупка сырья (сырье влияет на качество и характеристики
конечной продукции; например, фирма «McDonnald’s» избира-
тельнее своих конкурентов подходит к закупке картофеля).
2. НИОКР в области продукции (улучшение конструкции,
расширение спектра качества, сокращение времени разработки
новых моделей готовой продукции).
3. НИОКР в области производственных процессов (повыше-
ние качества, надежности и показателей продукции).
4. Производственный процесс (изготовление высококачест-
венной продукции).
5. Система сбыта и транспортировки продукции (поставки в
срок по необходимым адресам).
6. Маркетинг, продажа, послепродажное обслуживание поку-
пателей (обеспечение комфортных условий покупки продукции,
ремонт продукции в короткие сроки, предоставление потребите-
лям информации о новых изделиях, приемлемые условия прода-
жи в кредит).
Дифференциация означает нечто большее, чем качество про-
дукции и услуг фирмы. Качество есть функция физических харак-
теристик продукции, тогда как источники дифференциации ло-
кализуются в любом звене цепи издержек производства.
10.5.3. Конкурентное преимущество фирмы в рыночной нише
достигается путем снижения издержек или дифференциации в
избранной фирмой нише.
Если фирма будет лидировать по низким издержкам, то ей
следует применять в данной нише методы снижения издержек,
которые она применяет в отрасли. Если фирма решит дифферен-
цировать свою продукцию, то ей следует применять в данной ни-
ше методы дифференциации, которые она использует в отрасли.
Дополнительным источником конкурентного преимущества
стратегии рыночной ниши является различие между нишами.
При слабой разнице между нишами у небольшой фирмы нет за-
щиты от крупных конкурентов, ибо они не хуже специализиро-
ванной фирмы могут удовлетворять потребности ниши. Если цель
издержек небольшой специализированной фирмы значительно
отличается от цели издержек фирмы, которая следует стратегии
крупносерийного производства и низких издержек, то небольшая
фирма может эффективно функционировать в рыночной нише.
480
Для того чтобы стратегия рыночной ниши обеспечивала кон-
курентное преимущество, ниша должна обладать следующими
признаками: покупатели должны иметь разнообразные потреб-
ности; цель издержек производства должна отличаться от анало-
гичной цели, характерной для другой ниши. Если конкуренты
могут легко обслуживать многочисленные ниши, преимущества
стратегии рыночной ниши проблематичны.
10.6. О становлении и потере конкурентного
преимущества
10.6.1. Период становления (первый период) конкурентного пре-
имущества может быть как коротким (например, в сфере услуг),
так и длинным (например, в капиталоемких и технологически
сложных отраслях). Чем длиннее период становления конкурент-
ного преимущества, тем выше вероятность того, что конкуренты
заметят это становление и будут на него реагировать.
Размер преимущества может быть как значительным (как в
фармацевтической промышленности, где конкурентное преиму-
щество приносит патенты на новые препараты), так и достаточно
малым (как в производстве одежды, где новый фасон легко ско-
пировать).
10.6.2. За периодом становления конкурентного преимущества
следует период извлечения выгоды (второй период), в течение кото-
рого «пожинаются плоды конкурентного преимущества».
Продолжительность периода извлечения выгоды зависит от
того, сколько времени требуется конкурентам, чтобы они могли
ликвидировать конкурентное преимущество. Продолжительный
период извлечения выгоды представляет собой время, в течение
которого фирма получает хорошую прибыль и может вернуть ин-
вестиции, вложенные в создание преимущества. С началом
«контрнаступления» конкурентов начинается период исчезнове-
ния — «третий, последний период) конкурентного преимущества.
В связи с этим фирма-лидер, имеющая конкурентное преимущест-
во, должна постоянно поддерживать и развивать конкурентное
преимущество и идти по крайней мере на шаг впереди своих кон-
курентов.
31 - 7620
481
10.7. Конкурентное преимущество на глобальных
рынках
10.7.1. Фирма решает покинуть пределы рынка и конкурировать
на глобальных (мировых) рынках по следующим причинам: жела-
ние фирмы найти новые рынки сбыта своей продукции; осозна-
ние необходимости, вызванное конкуренцией снижения издер-
жек; желание использовать принадлежащие другим странам отно-
сительно дешевые ресурсы (в частности, труд и полезные
ископаемые).
При переходе с национального на глобальный уровень фирме
следует обратить внимание на различие между национальными
рынками в потребностях и привычках покупателей, в каналах рас-
пространения продукции, в потенциалах долговременного роста,
в особенностях конкуренции. Международные рынки характеризу-
ются следующими четырьмя факторами: различиями производ-
ственных издержек между странами; колебаниями валютных об-
менных курсов; государственной торговой политикой и структу-
рой международной конкуренции.
Различия в производственных издержках между странами зави-
сят от разницы в зарплатах, в производительности труда, в уровне
инфляции, в стоимости энергии, в налоговой политике. Фирмы,
чьи производственные мощности функционируют в странах с де-
шевыми ресурсами, в частности трудовыми, обладают значитель-
ным конкурентным преимуществом. Такие страны, как Тайвань,
Южная Корея, Мексика, Бразилия, давно являются раем для
фирм, производящих трудоемкие товары.
В глобально конкурирующей отрасли мощное конкурентное
преимущество обеспечивает мировое лидерство по низким це-
нам.
Колебания обменного курса валюты (в пределах от 20 до 40% в
год считается обычным) затрудняют достижение конкурентного
преимущества по издержкам от географического размещения
предприятий. Изменение пределов колебания обменного курса
может ликвидировать конкурентное преимущество страны по
низким издержкам или сделать дорогую страну дешевой. Слабая
национальная валюта выгодна фирмам-экспортерам страны и
невыгодна фирмам, которые в страну импортируют свою продук-
482
цию. Это означает, что иностранные производители, которые
импортируют свою продукцию в страну, теряют конкурентное
преимущество перед национальными фирмами, а национальные
фирмы, которые экспортируют свою продукцию, получают кон-
курентное преимущество перед национальными фирмами, рабо-
тающими на внутренний рынок.
Государственная торговая политика может оказывать сильное
влияние на участие страны в международных экономических от-
ношениях. Национальные органы власти и управления могут ус-
танавливать импортные тарифы и квоты, требования к продук-
ции, которая изготавливается иностранными фирмами на их тер-
риториях, регулировать цены на импортируемые товары. Кроме
того, они могут устанавливать стандарты, требования к сертифи-
кации продукции, заниматься предварительным одобрением ка-
питалоемких проектов, управлять вывозом капитала из страны.
Для оказания отечественным фирмам помощи в конкуренции с
иностранными фирмами государственные органы некоторых
стран предоставляют им субсидии или дешевые кредиты. В других
странах в целях привлечения зарубежных инвестиций и создания
новых рабочих мест субсидируются иностранные фирмы, им пре-
доставляют привилегированный доступ к рынку и техническую
помощь.
В глобально конкурирующей отрасли конкурентные позиции
фирмы в одной стране влияют и подвержены влиянию конкурен-
ции, имеющей место в других странах. В условиях глобальной
конкуренции общее конкурентное преимущество фирмы форми-
руется из всех ее международных отношений. Созданное фирмой
конкурентное преимущество на отечественном рынке дополняет-
ся преимуществами, достигнутыми в ходе деятельности в других
странах. Рыночная сила глобально конкурирующей фирмы прямо
пропорциональна количеству ее конкурентных преимуществ в
каждой стране. Глобальная конкуренция характерна для автомо-
бильной, авиационной промышленности, производства телеви-
зоров, шин, персональных компьютеров, телекоммуникационных
систем, копировальной техники, часов.
В отрасли могут быть сегменты, для которых характерна гло-
бальная конкуренция, и сегменты с конкуренцией на внутренних
рынках многих стран. В отрасли мотелей и отелей дешевые и сред-
ние по ценам сегменты характеризуются конкуренцией на внут-
ренних рынках многих стран, так как конкуренты обычно обслу-
31*
483
живают клиентов в пределах одной страны. Однако в дорогих
сегментах конкуренция глобальна. Отели таких фирм, как «Mar-
riott», «Sheraton», «Hilton», расположены в международных секто-
рах и в целях завоевания конкурентного преимущества в обслужи-
вании клиентов, которые совершают частые международные по-
ездки, используют всемирную систему бронирования и
одинаковые стандарты качества и услуг.
На рынках, на которых преобладает условие внутрирыночной
конкуренции, лидеры рынка — это национальные лидеры. В ус-
ловиях глобальной конкуренции лидеры рынка — это мировые
лидеры.
10.7.2. Отметим шесть видов международных стратегий конку-
ренции.
1. Продажа иностранным фирмам лицензий на использова-
ние технологии фирмы или на продажу ее продукции.
2. Создание производственной базы на национальном уровне
в одной стране и экспорт товаров на зарубежные рынки.
3. Использование международной стратегии конкуренции на
внутренних рынках многих стран (международная стратегия фир-
мы варьируется от страны к стране в соответствии с потребностя-
ми покупателей и с условиями конкуренции).
4. Использование глобальной стратегии низких издержек
(в целях снижения издержек по сравнению с конкурентами стра-
тегические усилия фирмы координируются в глобальных масшта-
бах; фирма является самым дешевым поставщиком продукции
покупателям на большинстве стратегически важных для нее рын-
ков мира).
5. Использование глобальной стратегии дифференциации
(имеется в виду дифференциация продукции на глобальных рын-
ках по одним и тем же критериям).
6. Использование стратегии глобальной ниши (стратегия
конкуренции фирмы направлена на обслуживание одинаковых
ниш на стратегически важных рынках различных стран, для обес-
печения целостной стратегии на каждом национальном рынке
конкурентные шаги фирмы координируются в глобальных мас-
штабах).
Чем больше разница между национальными рынками, тем
выгоднее стратегия конкуренции на внутренних рынках многих
484
стран, позволяющая фирме действовать с учетом ситуации на
каждом из национальных рынков. В этом случае международная
стратегия фирмы складывается из суммы ее стратегий в разных
странах.
10.7.3. Глобальная стратегия фирмы лучше всего подходит тем
отраслям, которым присуща глобальная конкуренция. Глобаль-
ная стратегия фирмы не зависит от национальных условий и
практически одинакова в разных странах. Межнациональная уни-
версальность глобальной стратегии позволяет фирме сконцент-
рироваться на завоевании стабильного конкурентного преимуще-
ства как над международными, так и над национальными конку-
рентами.
Глобальная стратегия фирмы позволяет ей достичь конкурент-
ного преимущества: 1) посредством концентрации или рассредо-
точения своей деятельности (НИОКР, производство комплекту-
ющих, сборка, распределение, сбыт, маркетинг продукции, цент-
ры обслуживания потребителей) в целях снижения издержек или
достижения большей дифференциации продукции, а также 2) пу-
тем координации своей концентрированной или рассредоточенной
деятельности и стратегических шагов.
Концентрация деятельности фирмы в одной (двух) стране
уместна, если может быть получена значительная экономия от
масштаба производства, достигнут высокий уровень координа-
ции. В частности, фирме выгоднее создать одно крупное предпри-
ятие (например, по производству карданных валов), которое будет
обслуживать несколько разных мировых рынков.
Рассредоточение фирме выгодно тогда, когда имеются виды
деятельности (например, поставка продукции дилерам, сбыт,
послепродажное обслуживание), которые должны быть располо-
жены рядом с потребителями.
Таким образом, глобальная фирма может получить конкурент-
ное преимущество над внутренними фирмами за счет концентра-
ции или размещения своих операций именно там, где это выгод-
нее всего. Наибольшая выгода — это прежде всего самые низкие
издержки.
Низкие издержки — не единственная причина рассредоточе-
ния деятельности глобальной фирмы. НИОКР следует локализо-
вать прежде всего там, где живут необходимые для этого специа-
листы, хотя возможна ситуация, когда целесообразно пересылать
485
специалистов. Процесс сборки может быть локализован в стране,
правительство которой разрешило беспошлинно или по низким
пошлинам импортировать комплектующие, производимые на
предприятиях других стран.
Практика рассредоточения фирмой своей деятельности полу-
чила широкое распространение в связи с революционными пре-
образованиями в телекоммуникационных системах и в компьюте-
ризации. Теперь рабочее место многих специалистов может быть
оборудовано где угодно, в том числе и по месту проживания. Го-
товая продукция (например, программный продукт, научно-ис-
следовательский текст, литературное произведение и т.п.) испол-
нителями может быть представлена руководству по электронной
почте. Причем исполнители и их руководители могут быть лока-
лизованы не только в разных городах, но и в разных странах и на
разных континентах. Современные формы практики рассредото-
чения фирмами своей деятельности стали возможны только в
эпоху тотальной глобализации экономических отношений, мате-
риальной основой которых была революция в телекоммуникаци-
онных системах и в компьютеризации. Косвенным (по сути, но не
значимости) эффектом современных форм практики рассредото-
чения фирмами своей деятельности стали такие значимые явле-
ния современной экономической реальности, как отсутствие не-
обходимости ездить, пользуясь общественным или личным
транспортом, работникам фирм на работу, что снижает нагрузку
на общественный транспорт и уменьшает пробки на улицах боль-
ших городов.
Примером современной формы практики рассредоточения
является кардинальное разделение в розничной и оптовой торгов-
ле информационных и материально-вещественных потоков, что
позволило сделать эффективной торговлю через Интернет.
В 1999 г. в США около 50% сделок по покупке автомобилей было
оформлено с помощью электронных средств, в частности через
Интернет.
Координация своей распределенной деятельности позволяет
фирме завоевать надежное конкурентное преимущество. Фирма
может передавать свои передовые технологии от одного филиала
другому, имея большую экономию на издержках. Фирма может
перемещать производство из одной страны в другую для получе-
ния выгоды от благоприятного обменного курса. Глобальный
конкурент может выбирать, где бросить вызов соперникам. Фир-
486
ма, которая конкурирует лишь на внутреннем рынке, не имеет
возможности воспользоваться ни одним конкурентным преиму-
ществом, связанным с географическим размещением или коорди-
нацией.
10.8. Стратегические намерения фирм,
«заповедники» прибыли, перекрестное
финансирование
10.8.1. Конкурирующие фирмы отличаются не только своими
стратегиями, но и своими долговременными целями или страте-
гическими намерениями. По характеру стратегических намерений
различают четыре типа фирм.
1. Фирмы, которые намерены доминировать глобально, по
крайней мере конкурировать с лидерами глобальных рынков. Эти
фирмы реализуют глобальную стратегию.
2. Фирмы, которые намерены защищать свое доминирующее
положение на внутреннем рынке несмотря на то, что некоторое
количество своей продукции (обычно менее 20%) они сбывают за
рубежом и действуют на нескольких или многих иностранных
рынках.
3. Фирмы, которые намерены увеличить мировую долю свое-
го сбыта и ориентированы главным образом на удовлетворение
потребностей рынка каждой страны, в которой эти фирмы при-
сутствуют; стратегия конкуренции таких фирм направлена на
внутренние рынки многих стран, где они получают большую
часть своих доходов.
4. Фирмы, работающие исключительно на внутреннем рынке
своей отрасли и не стремящиеся к укреплению своего положения
за границей. Происходящие на международных рынках события
такие фирмы рассматривают с точки зрения влияния этих собы-
тий на свои операции на внутреннем рынке.
Рассмотрим ситуацию, когда одна американская фирма рабо-
тает только на внутреннем рынке и конкурирует с японской фир-
мой, которая действует на рынках многих стран и которая стре-
мится к глобальному доминированию. Японская фирма может
снизить цены, чтобы за счет американской фирмы увеличить
свою долю на американском рынке. Потери японская фирма ком-
487
пенсирует за счет доходов, которые она имеет в других странах.
У американской фирмы нет возможности для адекватного ответа.
Этот пример иллюстрирует ситуацию, в которой глобальная
(японская) фирма имеет конкурентное преимущество перед на-
циональной (американской) фирмой за счет перераспределения
доходов, получаемых глобальной фирмой в разных странах. Если
же американская фирма также является глобальной и работает,
например, на рынках Японии, она может отреагировать на сниже-
ние цены японской фирмы в Америке снижением своей цены в
Японии. То есть в этом примере японская и американская фирмы
уже не имеют друг перед другом конкурентного преимущества.
10.8.2. «Заповедником» прибыли является рынок страны, в кото-
рой рыночные позиции фирмы хорошо защищены и приносят
значительную прибыль.
Для большинства японских фирм «заповедником» их прибыли
являются рынки Японии, ибо японское государство не позволяет
иностранным фирмам обладать в стране большой долей рынка.
Защита от угрозы иностранных конкурентов позволяет япон-
ским фирмам держать повышенные цены и, следовательно, полу-
чать приличную прибыль. В большинстве случаев «заповедником»
прибыли для фирмы является отечественный рынок, однако в
случае многонациональных фирм их «заповедниками» прибыли
являются рынки стран, в которых фирмы занимают прочные по-
зиции, имеют большие объемы продаж и получают высокие при-
были.
Фирмы, у которых есть большие и хорошо защищенные «за-
поведники» прибыли, имеют конкурентное преимущество перед
фирмами, у которых «заповедников» прибыли нет. Аналогично
обстоит дело в случае фирмы с несколькими «заповедниками»
прибыли и фирмы с одним «заповедником».
Критический рынок — важное понятие теории рыночной кон-
куренции. Критические рынки — это такие рынки:
1) которые являются «заповедниками» прибыли ключевых
конкурентов;
2) для которых характерны большие объемы сбыта;
3) где имеются престижные и стратегически важные для фир-
мы покупатели;
4) слабая конкуренция на которых позволяет получать ис-
ключительно высокую прибыль.
488
10.8.3. Перекрестное финансирование состоит в том, что прибыль,
заработанная фирмой в одной или нескольких странах, использу-
ется для финансирования наступления против конкурентов. По-
нятие типичного наступления означает, что продукция фирмы бу-
дет полностью или почти полностью соответствовать продукции
конкурентов по качеству и услугам, однако цена ее будет ниже
цены на продукцию конкурентов. Хотя более низкая цена означа-
ет снижение прибыли и даже наличие возможных убытков, фирма
может все-таки получить приемлемую совокупную прибыль за счет
доходов, извлекаемых из «заповедников» прибыли. Глобальная
стратегия побеждает стратегию внутреннего рынка, ибо фирма,
действующая только на внутреннем рынке, не может в долговре-
менном промежутке эффективно защитить свою долю рынка от
посягательств со стороны глобального конкурента, имеющего
возможности перекрестного финансирования. Глобальная фирма
может использовать низкие цены для завоевания покупателей,
для увеличения доли рынка, для укрепления позиций. Издержки
глобальной фирмы, обладающей крупным современным произ-
водством, почти наверняка будут меньше издержек фирмы, кото-
рая действует в нескольких странах и мелкосерийное специализи-
рованное производство которой рассредоточено по малым заво-
дам. Поэтому многонациональные фирмы должны сосредоточить
усилия на получении конкурентных преимуществ от деятельности
в рыночной нише и от дифференциации продукции с учетом по-
требностей местных рынков. Такой способ защиты от глобальных
конкурентов применим в тех сферах производства, в которых
большие национальные различия препятствуют использованию
глобальной стратегии. Но если эти различия не имеют значения
для глобальной фирмы, то она может победить фирму с многона-
циональной стратегией.
Вопросы для самоконтроля к главе 10
1 • Что такое рыночная конкуренция?
2. Что представляет собой модель пяти сил конкуренции?
3. В чем суть первого этапа наступательной программы фирмы «Пепси»
в 1950-1955 гг.?
4. В чем суть второго этапа наступательной программы фирмы «Пепси»
в 1955-1960 гг.?
5. Каковы факторы интенсивности рыночной конкуренции между
фирмами отрасли?
489
6. Почему возникает сила конкуренции в случае возможного появле-
ния на отраслевом рынке продуктов-заместителей?
7. Почему возникает сила конкуренции в случае возможного появле-
ния на отраслевом рынке фирм-новичков?
8. Каковы причины появления барьеров для входа на отраслевой ры-
нок фирм-новичков?
9. Почему возникает сила конкуренции в случае появления давления
на отраслевой рынок со стороны поставщиков?
10. Почему возникает сила конкуренции в случае появления давления
на отраслевой рынок со стороны покупателей?
11. Что такое движущие силы конкуренции?
12. Что представляют собой движущие силы конкуренции?
13. Что такое конкурентное преимущество?
14. Каковы источники конкурентного преимущества?
15. Что представляют собой основные стратегии, применяемые фирмой
для получения конкурентного преимущества?
16. В чем суть стратегии лидерства по низким издержкам?
17. При каких условиях целесообразна стратегия лидерства по низким
издержкам?
18. В чем суть стратегии дифференциации? Приведите примеры.
19. При каких условиях целесообразна стратегия дифференциации?
20. В чем суть гибридной стратегии? При каких условиях гибридная
стратегия целесообразна? Приведите примеры.
21. В чем суть стратегии рыночной ниши? Приведите примеры.
22. При каких условиях целесообразна стратегия рыночной ниши?
23. Каковы факторы риска стратегии лидерства по низким издержкам?
24. Каковы факторы риска стратегии дифференциации?
25. Каковы факторы риска стратегии рыночной ниши?
26. Каковы факторы, влияющие на издержки звеньев цепи издержек
производства?
27. Каковы основные звенья цепи издержек производства, которые мо-
гут быть источниками дифференциации?
28. Из каких периодов состоит траектория развития конкурентного пре-
имущества?
29. Каковы факторы, характеризующие международные рынки?
30. Каковы причины перехода фирмы с национального на глобальный
уровень функционирования?
31. Каковы виды международных стратегий конкуренции?
32. Каковы способы достижения конкурентного преимущества с помо-
щью глобальной стратегии?
33. Каковы материальные основы широкой практики рассредоточения
фирмой своей деятельности?
34. Что такое стратегическое намерение фирмы?
35. Что такое «заповедники» прибыли фирмы?
36. Что такое перекрестное финансирование?
490
Задачи и упражнения для самоконтроля к главе 10
Приведите собственный пример и проанализируйте возникновение
силы конкуренции в результате стремления фирм-соперников за-
нять лучшие позиции на рынке отрасли.
Приведите собственный пример и проанализируйте возникновение
силы конкуренции в связи с наличием контроля за условиями сделок
со стороны поставщиков.
Приведите собственный пример и проанализируйте возникновение
силы конкуренции в связи с наличием контроля за условиями сделок
со стороны покупателей.
Приведите собственный пример и проанализируйте возникновение
силы конкуренции в связи с угрозой появления на рынке отрасли
продукта-заместителя.
Приведите собственный пример и проанализируйте возникновение
силы конкуренции в связи с угрозой появления на рынке отрасли
фирм-новичков.
При каких условиях фирме следует выбрать стратегию по низким
издержкам? В чем сила данной стратегии? В чем слабость данной
стратегии?
Объясните, почему лидер по низким издержкам имеет защиту от пя-
ти сил конкуренции.
Каковы преимущества стратегии дифференциации? В чем слабость
данной стратегии?
Объясните, почему фирма, удачно реализующая стратегию диффе-
ренциации, успешно защищается от пяти сил конкуренции.
При каких условиях фирме следует выбрать стратегию рыночной
ниши? В чем сила такой стратегии? В чем ее слабость?
Объяснить, почему фирма, реализующая стратегию рыночной ни-
ши, успешно защищается от пяти сил конкуренции.
Тесты для контрольных работ к главе 10
Теория пяти сил конкуренции построена в рамках:
а) поведенческого подхода;
б) структурного подхода;
в) функционального подхода.
Рыночную конкуренцию между фирмами отрасли усиливает следу-
ющий фактор:
а) уравнивание размеров конкурентов;
б) медленный рост спроса на продукцию отрасли;
в) покупатели не несут значительных издержек при замене одного
продукта другим;
491
г) отраслевые условия таковы, что дороже выйти из отрасли, чем в
ней остаться;
д) ответы а)-г) верны.
3. Рыночную конкуренцию между фирмами отрасли усиливает следу-
ющий фактор (укажите неверный ответ):
а) рост размера отдачи от удачного стратегического шага;
б) сильные фирмы из других отраслей поглощают слабые фирмы
отрасли и превращают их в сильных отраслевых соперников;
в) отраслевые условия таковы, что все фирмы удовлетворены зани-
маемым ими положением и не пытаются скорректировать ситуа-
цию за счет конкурентов;
г) отраслевые условия таковы, что конкурирующие фирмы отрасли
снижают цены в целях увеличения сбыта своей продукции;
д) рост числа конкурентов.
4. Укажите причину появления барьеров для входа новых фирм в от-
расль:
а) невозможность получить доступ к передовым технологиям;
б) ограниченный доступ к каналам распределения продукции;
в) необходимость предъявления лицензий;
г) ответы а)-в) верны;
д) ответы а)-в) не верны.
5. К движущим силам конкуренции относятся (укажите неверный от-
вет):
а) появление новой продукции;
б) повышение уровня неопределенности в бизнесе;
в) снижение риска в бизнесе;
г) инновации в области маркетинга;
д) предпочтение потребителями дифференцированной продукции
перед стандартизированной.
6. К факторам риска стратегии лидерства фирмы по низким издержкам
относятся:
а) достижения научно-технологического прогресса, используемые
конкурентами для снижения их издержек;
б) дешевая имитация фирмами-конкурентами методов фирмы-ли-
дера по снижению издержек;
в) изменения предпочтений потребителей, которые появляются в
результате использования фирмами достижений научно-техно-
логического прогресса;
г) ответы а)—в) верны;
д) ответы а)—в) не верны.
7. К факторам риска стратегии дифференциации фирмы относятся
(укажите неверный ответ):
а) повышение качества дифференцированного продукта;
492
б) необязательное достижение конкурентного преимущества в ре-
зультате реализации стратегии дифференциации;
в) достигнутое качество дифференцированного продукта превысит
запросы потребителей;
г) цена дифференцированного продукта значительно превысит за-
просы потребителей;
д) цена дифференцированного продукта значительно превысит це-
ну конкурентов.
8. К факторам международного рынка относятся (укажите неверный
ответ):
а) различия в производственных издержках между странами;
б) колебания валютных обменных курсов;
в) торговая политика государств;
г) ответы а)—в) верны;
д) ответы а)-в) не верны.
9. К международной стратегии конкуренции относятся:
а) использование глобальной стратегии низких издержек;
б) использование глобальной стратегии дифференциации;
в) использование стратегии глобальной ниши;
г) ответы а)-в) верны;
д) ответы а)—в) не верны.
10. Стратегия низких издержек лучше всего работает в следующей ситу-
ации:
а) спрос эластичен по цене;
б) продукция отрасли не имеет существенных различий в зависи-
мости от производящей фирмы;
в) на рынке превалирует конкуренция по цене;
г) ответы а)—в) верны;
д) ответы а)—в) не верны.
Задания для контрольных работ к главе 10
1. Опишите и проанализируйте конкурентную силу перекрестного фи-
нансирования в краткосрочном и долговременном промежутках.
2. Опишите и проанализируйте два способа достижения конкурентно-
го преимущества фирмой, которая следует глобальной стратегии.
3. Опишите и проанализируйте составные элементы глобальной стра-
тегии фирмы.
4. Проанализируйте сходства и различия межстрановой и глобальной
стратегий фирмы.
5. Опишите и проанализируйте модель становления и потери конку-
рентного преимущества.
Глава И
МОДЕЛИРОВАНИЕ СТАТИЧЕСКОГО
ЭКОНОМИЧЕСКОГО РАВНОВЕСИЯ
11.1. Сфера производства модели Эрроу—Дебре.
Функция рыночного предложения и ее свойства
11.1.1. Модель Эрроу—Дебре (см.: К. Arrow, G. Debreu (1954)) пред-
ставляет собой вариант описания экономики с конкуренцией на-
ряду с моделями Вальраса (см. JI. Вальрас (2000)) и МакКензи
(см. L. W. McKenzie (1959)). Вальрас впервые дал подробное описа-
ние статического равновесия на основе своей модели. Эрроу и
Дебре (совместно) и МакКензи независимо впервые доказали су-
ществование статического экономического равновесия (общего
экономического равновесия) для своих общих моделей экономи-
ки с совершенной конкуренцией. Описание модели Эрроу—Дебре
(МЭД) начнем с ее сферы производства. Сферу производства
МЭД составляют фирмы. В МЭД фигурируют п фирм F(1),..., Г(я)
и г продуктов Gv ..., Gr. Каждая фирма F(J\j = 1,..., п, выпускает
продукты и затрачивает ресурсы. Если продукт Gt, i = 1,..., г, вы-
пускается фирмой Г(7) в количестве у.л единиц, то у^л > 0; если
продукт Gk, к = 1, ..., г, затрачивается фирмой /,(-/) в качестве ре-
сурса в количестве | укл | единиц, тоу^ < 0. Вектор
у(7> = (у\л,..., у(Л) е У(Л с Ег,
где У— технологическое множество фирмы Р(Л.
Технологическое множество У(7) удовлетворяет следующему
условию:
494
(1.1) Для всех/ (j = 1, п) множество У(у) а Ег ограничено,
замкнуто и об Y^\ т.е. фирма № может ничего не затрачивать и
ничего не выпускать. Разные фирмы № могут выпускать и затра-
чивать разные продукты. Алгебраическая сумма (сумма Минков-
ского) множеств У(1>,..., У(л), т.е. множество
у= у(0 + + уОО
(Y={y\y = yw +...+у(п\ y(j)e Y(J)a,Er, j—i,..., л})
называется технологическим множеством МЭД. Оно удовлетворя-
ет условию
(1.2) Y— выпуклое множество.
11.1.2. Пусть/» = (рр ...,р) вектор цен в МЭД. Каждая фирма F^,
j = 1,..., л, максимизирует свою прибыль
p.yW (max) (11.1.1)
при условии,что
у(У)е У0). (11.1.2)
Решение задачи максимизации прибыли фирмы F^ обозна-
чим символом y(i\p),j = 1, ..., л. Решение у^\р) всегда суще-
ствует, ибо множество У(7> ограничено и замкнуто. Решение
у^\р) называется локальным рыночным равновесием фирмы F(^
или предложением фирмы F^,j = 1,..., л, а также функцией предло-
жения фирмы F^,J = 1,..., л. Сумма
у(р)=у(1)(р) + ...+у(я)(/О (Н.1.3)
называется совокупным предложением (рыночным предложением),
а также функцией совокупного предложения.
Пример 11.1.1
Пусть г = 2.
Пусть
уО) = |у(У)|уО) = (у^\ у^ + y(2j} < 0, у? > -3, у^ > 0}.
Пусть вектор рыночных цен р = (1; 2). Задача максимизации
прибыли № фирмы № в этом случае имеет вид
ЛуР + РгУ^ =Ух) + = (max)
при наличии ограничений у\^ + < 0, у^ > -3, у^ > 0.
Тогда имеем
уиЧр) = (У1У)(р),У2У)(р))= (-3;3) (₽ис-111)-
495
Прямая l*0 — изопрофита, проходящая через точку (yxJ\p),
УрА/О)= (-3; 3), максимизирующую прибыль фирмы №.
Предложение /^(р) фирмы Г(у) есть функция, однородная
нулевой степени своей векторной переменнойр = (рр ...,р), ибо
у(У)(р) =у(У)(ур), (11.1.4)
где 0 < уе Ех, поскольку обе задачи (задача (11.1.1), (11.1.2) и зада-
чау- ру^ (max) при условии (11.1.2)) имеют одно и то же множест-
во максимальных решений.
Из равенств (11.1.3) и (11.1.4) следует, что
У(Р)=У(ЧР>- (11.1.5)
11.2. Сфера потребления модели Эрроу—Дебре.
Функция рыночного спроса и ее свойства
11.2.1. Сферу потребления МЭД составляют потребители (напри-
мер, домашние хозяйства). В МЭД фигурирует т потребителей
С(|),..., С(т). Каждый потребитель Cw максимизирует свою функ-
496
цию полезности и(,)(х) (хе Е*= {х|х = (хр хг), х1 £ 0,хг > 0})
при наличии бюджетного ограничения рх < М(\ где М® — доход
потребителя Cw, i = 1,...,т. Таким образом, каждый потребитель
С(/) решает задачу максимизации
м(/)(х(,)) (max) (11.2.1)
при условии,что
px(i)<M«\ х(,)>0. (11.2.2)
Решение задачи максимизации потребителя С(/) обозначается
символом xw(p) и называется локальным рыночным равновесием
потребителя С® или спросом потребителя С®, а также функцией
спроса потребителя С®, i = 1,..., т. Сумма
х(р) =х(1)(р) + ... +х(т)(р) (11.2.3)
называется совокупным спросом (рыночным спросом), а также функ-
цией совокупного спроса.
Функция полезности «(,)(х(,)), / = 1,..., т, удовлетворяет следу-
ющим условиям.
(2.1) Функция а(,)(х) имеет непрерывные частные производ-
ные по всем переменнымхр ..., хг.
(2.2) Множество Н‘= {х | х = (хр ..., хг), м(/)(х) > t} является стро-
го выпуклым. Каждый потребитель С(/), i = 1, ..., т, имеет запас
продуктов = (z®,..., z^), такой, что > 0, k = 1,..., т. Поло-
жим Z = z(l) + — + z^m).
(2.3) Каждый потребитель Cw, i = 1,..., т, получает долю а^. >0
прибыли PRW фирмы F(i\j = 1,..., п, и а1у. + ... + amj. = 1.
Доход М(Г> потребителя С(/), i=\,...,m, равен сумме М(Г> =
- М® + М®, где
=pz(l) = Piz{i) + ... + PrZ®,
п
М2} = ^аиРУи)(РУ
J=1
Спрос х('\р), i = 1,... , т, потребителя С(/) есть однородная функ-
ция нулевой степени своей векторной переменной р = (рх,рг),
ибо
х®(р) —х^(ур), i= 1,..., т, (11.2.4)
гдеОСуе Е{, поскольку обе задачи (задача (11.2.1), (11.2.2) и за-
дача и(,)(х(,)) (max)) при условии, что
32 - 7620
497
у • px(i} <, у • pz(i) + Xaj/Y • РУ(Г>(Р) (11.25) js
/=1 I
имеют одно и то же множество решений. I
Из равенств (11.2.3) и (11.2.4) следует, что
х(р)=х(ур).
11.2.2. Избыточный спрос (функция избыточного спроса) определя-
ется как разность совокупного спроса &(р) и суммы совокупного
предложения $(/>) и совокупного ликвидного запаса z, т.е.
F(p)=$(p)-$(p)-z, (11.2.6)
где $(/>) дается формулой (11.1.3), 5(р) — формулой (11.2.3),
az = z(1) +... + z(m).
Равенство
pF(p) = 0 (11.2.7) _
при любом векторе цен р > 0 называется законом Вальраса.
Перепишем равенство (11.2.7), представив избыточный спрос
F(p) в развернутой форме (11.2.6):
р%(р) = р$(р)+PZ. (11.2.8)
Равенство (11.2.8) содержательно интерпретируется следу-
ющим образом. Стоимость р%(р) совокупного спроса £(р) в ценах
р равна сумме стоимостей р$(р)+PZ совокупного предложения
р$(р) и совокупного ликвидного запаса pz.
11.3. Определение статического экономического
равновесия модели Эрроу — Дебре и формулировка
теоремы о его существовании
11.3.1. Статическое экономическое равновесие (конкурентное рав-
новесие) МЭД есть набор векторов
{р*,у*(1), ...,у*(л),х*(1), ...,х*(т)}, (11.3.1)
удовлетворяющих условиям:
1) векторр* > 0 и р* = Pi +...+р* = 1,
498
вектор р* = (р/,..., р*) называется вектором цен статического
экономического равновесия МЭД;
2) вектор = y^fp*), J = l,...,n, есть локальное рыночное
равновесие фирмы Р®, т.е. решение задачи максимизации при-
были PPV фирмы Р® при ценах/>р (р* = (р*, ...,р*))
р*уУ> _> (max)
при условии, что
у(/)е = j, >й.
3) вектор х(,) = х(|)(р*), i = l,...,m, есть локальное рыночное
равновесие потребителя С®, т.е. решение задачи максимизации
функции полезности и(/)(х) при ценахр^, ...,р*
uw(x) -> (max)
при условии, что
п
P*XU) < P*z+^ct9p*y(j);
J=i
4) имеет место следующее векторное неравенство:
х*^у +Z,
(которое означает отсутствие в МЭД дефицита по всем продук-
там) и условие дополняющей нежесткости
p*(xt-y-z) = 0, (Н.3.2)
где х* =х(1>+... + х(я,\ у* = *уМ+...+ *у^.
Условие дополняющей нежесткости в развернутом виде выпи-
сывается так:
Pi*(x* -У\ ~ zi> + - +Pr*(xr* -Уг* ~ = °- (Н-З.З)
В связи с тем что х' — у{* — z{ 0, ...,-х* — у* — zr£0,a вектор
Р £ 0, равенство (11.3.3) означает, что если рк' > 0, то обязательно
хк = У+ если же х < У + zk>то Нена р* = 0.
Равенство (11.3.2) представляет собой закон Вальраса в ценах
Р равновесия.
Отметим, что понятие статического экономического равнове-
сия содержит в качестве своего исходного элемента вектор цен
Равновесия, который является основополагающим для определе-
ния остальных элементов статического экономического равнове-
32*
499
сия. Несущей конструкцией понятия статического экономиче-
ского равновесия является пункт 4) который, как уже подчеркива-
лось, означает отсутствие дефицита по всем продуктам.
11.3.2. При выполнении условий (1.1), (1.2), (2.1)—(2.3) суще-
ствует статическое экономическое равновесие (см. раздел 11.3.1)
модели Эрроу—Дебре (теорема Эрроу—Дебре).
Сформулированная теорема существования статического эко-
номического равновесия была доказана Эрроу и Дебре (K.J. Arrow,
G. Debreu (1954)) с помощью построения точечно-множественно-
го отображения, которое удовлетворяет всем условиям теоремы
Какутани (5. Kakutani (1941)) о неподвижной точке точечно-мно-
жественного отображения. Неподвижная точка этого специаль-
ного точечно-множественного отображения и есть статическое
экономическое равновесие (см. раздел 11.3.1).
Доказательство теоремы Эрроу — Дебре в этом учебнике не
приводится. Далее сначала рассмотрим пример построения стати-
ческого экономического равновесия МЭД в случае, когда г = 2,
т = 2, п = 1.
11.4. Примеры модели Эрроу — Дебре
и цен равновесия
11.4.1. Пример 11.4.1 приведен и разобран в книге Алипрантис и
др. (1995). Пример 11.4.2, а также ряд заданий для самостоятель-
ной работы и для контрольных работ представляют собой моди-
фикации аналогичного примера в книге Алипрантис и др. (1995).
Пример 11.4.1. Рассмотрим следующую МЭД:
1) пространство продуктов £2;
2) два потребителя С**) и с характеристиками:
потребитель С*1) имеет начальный запас z(1) = (1; 2) и функцию
полезности «(1)(хр х2) = х,х2; потребитель С52) имеет начальный
запас /2) = (2; 2) и функцию полезности «(2)(хр х2) = х^х2;
3) фирма F имеет технологическое множество
^={(yPy2)l У\< 1 О);
4) доли потребителей и С® в прибыли фирмы равны a j =
= а2=1/2-
Технологическое множество /изображено на рис. 11.2.
500
Требуется найти для векторар = (р{, р2) локальное рыночное
равновесие, максимальную прибыль фирмы F, локальное рыноч-
ное равновесие для каждого потребителя С*1’ и С*2), избыточный
спрос, нормированные цены равновесия, статическое экономи-
ческое равновесие.
Локальное рыночное равновесие у(р) = (У1(р),у2(/’)) фирмы F
определяется как решение задачи на условный глобальный мак-
симум:
Р^+р^Спах) (11.4.1)
при условии, что
у2=^7. (11.4.2)
?1~1
Очевидно, вектор ценр = (pvp2) > 0 (Pj > 0,р2 > 0) (см. рис. 11.2).
Для решения задачи (11.4.1)—(11.4.2) выпишем для функции Лаг-
У1 "I
У\~Ч
ранжа Цу{, у2> X) = рхух + р2у2 + X -у2 +
условия первого по-
рядка
501
Из первых двух уравнений получаем (в этой задаче 1 — мно-
житель Лагранжа 1 # О, что легко доказывается от противного):
Р1
откуда вытекает, принимая во внимание неравенства
y/pi/Pi >о КУ1 < i’470
Полагая = t, имеем
yl(p) = \-t, °y2(p)=-^^- = l-k
Ш-i
у.
В силу строгой выпуклости к точке О границы у2 = — । тех-
0 0
нологического множества Уточка (У1(р),у2(р)) возможного ус-
ловного локального максимума является не только точкой ло-
кального, но и глобального условного максимума рассматривае-
мой задачи (11.4.1)—(11.4.2) на условный экстремум.
Предложение фирмы F— это вектор у(р)=(1-/, 1_~)-
Доход Л/1! потребителя С*** равен
Л/0) = р?1)+^ру(р)=Р1+2р2+|р1(1-/)+|р2(1-^).
Локальное рыночное равновесие (xi(p),x2(p)) потребителя
определяется как решение задачи на условный глобальный
максимум
«(1)(хр х2) = Х]Х2 (max) (11.4.3)
при бюджетном ограничении
рххх + р^с2 = (11.4.4)
502
Для решения задачи (11.4.3)—(11.4.4) выпишем для функции
Лагранжа L(x{, х2,X) = х{х2 + Х(Л/1) — р{х{ — р^с2) условия первого
порядка
|^ = х2-р1% = 0, ^ = х,-р2Х = 0, ^ = Л/(|)-р1х1-р2х2=0.
ОХ| иХ2 ОА
Из первых двух уравнений получаем, что р1х1 = р^с2 (в этой
задаче множитель Лагранжа X * О, что легко доказывается от про-
тивного). Из третьего уравнения имеем
О М(1) 3 5л 1 О Mw 5 3 1
2/^ 4 4 2 2р2 4 4/2 2t
В силу строгой выпуклости к точке О линий безразличия
функции полезности ufa, х2) = xtx2 точка (Х1(р),хг(р)) возмож-
ного условного локального максимума является точкой не только
локального, но и глобального условного максимума рассматрива-
емой задачи (11.4.3)—(11.4.4) на условный экстремум.
Таким образом, спрос потребителя — это вектор
7+Л-^-
4 4 2 4 4/ 2/
Перейдем ко второму потребителю С52). Его доход равен
/И(2) = р?2) + |ру(р) = 2р1+2р2+|р1(1-/)+|р2(1-у), и свою
функцию полезности w(2)(xp х2)=х2х2 этот потребитель максими-
зирует при бюджетном ограничении р(х( + р^х2 = Л/2). Вновь ис-
пользуя множитель Лагранжа, получаем, что для набора, макси-
мизирующего полезность, выполнено равенство = 2р^хг
Следовательно, М(2) = р1х1 + р2х2 = - Р]Х} = Зр2х2.
_ о(2) 2М(2} 5 5, 2
Отсюда вытекает, что xi = —------------= -+-/ -—/ и
й2> = Л^= 5+_5___1_ 3₽, 3 3 3
Зр2 6 6/2 3/
Следовательно, спрос второго потребителя С*2) выглядит так:
о(2). .5 5, 2 5 5 1
* ^“S + 3 3 ’ 6 + 6/2 3/ '
Избыточный спрос F(p) для этой МЭД задается формулой
503
F(p) = x(l\p)+x(2\p) -y(p)- z(1) - z(2) =
= ( 35t^-2t-19 35Г2 — 2r—19^ <
Д 12 ’ 12? )
Последнее неравенство означает, что в статическом экономи-
ческом равновесии не должно быть дефицита ни по одному из
продуктов.
Поскольку в рассматриваемом примере обязательно р > 0, по-
стольку (по закону Вальраса) избыточный спрос F(p) = 0, а для
этого необходимо и достаточно, чтобы 35? — 2t — 19 = 0.
Решая это квадратное уравнение и учитывая, что t > 0, получа-
1+>/666 _ _,,
ем t =------= 0,766.
35
Так как р2/ pl = t2^ 0,587, р{ + р2 = 1, то цены равновесия суть
р s (0,63; 0,37), р* = 0,63, р* г 0,37.
Соответствующий луч цен равновесия в плоскости цен изоб-
ражен на рис. 11.3.
Статическое экономическое равновесие рассматриваемой
МЭД есть набор
3 5,.ч2 1.3 1 5 1
’ 4 + 4 2 ’4 /,*?+4 2t
В примере 11.4.2 МЭД г = п = т = 2.
11.4.2. Пример 11.4.2. Рассмотрим следующую МЭД:
1) пространство продуктов (ресурсов) Е2,
2) технологическое множество фирмы № имеет вид
I*0 = {(Ур y2)h < Уг У“ !)}’
технологическое множество У-2* фирмы № имеет вид
^2) = {(УР У2)1У1 < 1, У2 £/(У,)}>
где $(.У1) =
1-^’,.^ <0,
1п(1-у1),0<у1 <1;
504
3) потребитель имеет начальный запас z(1) = (1; 3) и функ-
цию полезности Ux(x{, х2) = х,х2, потребитель С^2) имеет началь-
ный запас г(2) = (4; 2) и функцию полезности ^2(хр х2) = х 2х2;
4) доли потребителей С(1) и С(2) в прибыли фирмы равны
ап = 3/4 и а21 = в прибыли фирмы № равны а12 = */3
И а22 ~ /у
Требуется построить технологические множества и
найти для вектора ценр = (ррр2) локальное рыночное равновесие,
максимальную прибыль каждой фирмы 7*° и найти локаль-
ное рыночное равновесие для каждого потребителя С*0 и С®, вы-
писать избыточный спрос, найти нормированные цены равнове-
сия, статическое экономическое равновесие, построить множест-
ва 2^, /1)+У(1), }™+}<2>.
Г. Технологические множества и У^2) расположены левее и
У,
ниже линий, которые являются графиками функций Уг ~ и
^2 =$0'1) (рис. 11.4). 1
1 V
При у. < 0 имеем неравенство —Ц- < 1 - еу>, так как при у. < 0
У1-1
и близких к точке = 0 имеем представления
505
1-ел=-у,-^—....
При}'! < О
-й_<1-ем, (11.4.5)
У1-1
ибо при j] -> -оо экспонента — е’’1 приближается к оси Оу, снизу
быстрее, чем гипербола--.
Ji-1
При 0 < у} < 1 имеет место неравенство
——1—< 1п(1 — У]) >
я-1
так как при 0 < < 1 справедливы представления
10(1-^) = -^-^--....
506
2°. Локальное рыночное равновесие (предложение) фирмы 1*1)
былодановпримере11.4.1:у(1)(р) =[ ,гдет=^р2/р] >0.
Максимальная прибыль
PRm(p) = ft $1Чр)+Р2 ?2n(p) = Pi (1 - т)+р2 (1 -
V ^7
3°. Для фирмы следует рассмотреть два случая: т > 1 и
0 < т < 1. _____
При т > 1 (тогда ^/а/А -1> откуда следует, чтор2 >р{) необхо-
димо решить задачу на условный экстремум
Pixi +Р^2 <тах)
при условии, что
у2=1-<Л
Частные производные функции Лагранжа L = р1у1 + р^у2 +
+ Цу2 — 1 + е*'1) приравняем к нулю:
^- = Pi + 'key' =0, -^ = р2+Х = 0, ^- = у2-1+еу' =0,
0У2 дл
откуда следует, что
£2. = е~у'.
Pl
Полагая в последнем равенстве 7а/А = т’ будем иметь
Ж)</’)=-21пт’
а также
у¥\р) = 1-е~%П =1~.
х
Таким образом, при т > 1 локальное рыночное равновесие
(предложение) фирмы № имеет вид
y(2)(p)=f-21nt; 1—
\ г)
и максимальная прибыль фирмы № равна
507
PR{\p) = -2px\nz+p2\ 1-A-
При 0 < т < 1 (тогда 0 < Jp2/Pi < 1, откуда следует, чтоp2 < р})
необходимо решить задачу на условный экстремум
Р1У1 + Р-У2 <max>
при условии, что
^2 = ^(1-^).
Частные производные функции Лагранжа L = рху} + р^2 +
+ 1(у2 — 1п(1 —у,)) приравняем к нулю:
Э£ 1 л д£ . п 3L » л \ л
- = />,+- = 0, — = р2+1 = 0, — = у2-1п(1-у1) = 0,
Эу, l-У! Эу2 Эл
откуда следует, что
— = 1-У1,
Pi
т.е.
Й2)(/0=1-т2
И
^2)(р)=1п(1-у1(2)(р))=1пт2 = 21пт.
Таким образом, при 0 < т < 1 локальное рыночное равновесие
(предложение) фирмы имеет вид
у<2)(р)=(1-т2; 21пт)
и максимальная прибыль фирмы Т^2) равна
PR(2\p)=Pi(l - т2)+2р2 in т.
4°. Локальное рыночное равновесие (спрос)
#(1)(р)= ^(р); х2(р) потребителя имеет вид
k J
. = ОМ = = a2J/i =
' (oq+aj)/», 2pt’ (al+a2)p2 2р2
508
где Мх = М(1) + М\(2) = + Р2^+а11 -И?(1)+а12 /*Я(2) •
При т £ 1 имеем
S|,’W=^M-=^K+M'<2,)=
1 ( , _ , 3 . 3 Z1 1. 2 , 1 Г, 1
= х- А+Зр2+7А(1-'г)+7Л(1--)-тА1пг+-р2 1—у
2 Р\ 4 4 Т 3 З^т
17+49т2-18т-81пт
24
1 ( _ з 3 1. 2 , 1 Л 1 Y)
= Т— А+З^+тАО-^+тЛО—)-7А1п'г+Т/’2 1—2 Г
2 а V 4 4 Т 3 \ t J J
17+49?-18т-81пт
24-с2
При О < т < 1 имеем
=^-[ А+Зд+|(й(1-г)+й(1--»+|(Р|(1-т2)+2д1пт)
25+41т2 -18т+8т2 In т
24
в^П“[ А+За+7(а(1-т)+Р2(1--))+|(а(1-?)+2/’21п'О
2 а \ 4 Т 3 ,
_25+41т2-18т+8т21пт
24т2
509
5°. Локальное рыночное равновесие (спрос)
\ 7
потребителя С52) имеет вид
а‘^2 _ а2^2 _ ^2
(cq+aj)/?! Зд ’ (а,+а2)р2 Зр2’
где Мх = Mf» + А?2’ = p,z}2) + p2z(22>+a2i PRm+а22 РЯ(2).
При т > 1 имеем
«‘12,(р)=Ам2 = Л(л/о>+лг<«)=
2 ( 1 1
= т— 4р1 + 2р2+-(р1(1-т)+ р2(1—))+
*Р\\ Q ъ
2. _ , 1J 43+35т2-6т-161пт
+-(-2А 1пт+р2(1--)) =-----------------,
3 Ту 1о
= т^-f4?! + 2д + 7< А <1 -1)+Й<1 ~Ь)+
3 Р2 \ 4 Т
2 _ , ,t 1 Л 43+35?-6т-161пт
+-(-2А1пт+р2(1--)) =---------—-2-----.
3 X J 36т
При 0 < т < 1 имеем
2 ( 1 1
= т— 4pi+2p2 + -(p1(l-T)+p2(l—))+
3pj V 4 т
2 ,
+j(Pi(l-'r)+P2lnT)
59+19т2-6т+16т2 1пт
18
510
й%)=^м2=^+<>)=
1 12 i
= т— 4pl+2p2+-(pl(l-r)+p2(l—))+-(р1(1-?)+2р21пт) =
эр2 \ 4 T 3 J
59+19? - 6т+16? 1пт
36т2
6°. Выписываем первую (Fj(p)) и вторую (Г2(р)) координаты
избыточного спроса F(p).
При т > 1 имеем
г/ \ о(1), \ . о(2)/ \ о(1)/ \ о(2)/ \ (1) (2)
fi(p) = xi (p)+xi (р)-у{ (р)-У1 (p)-zr-zr =
17+49?-18т-81пт 43+35т2-6т-161пт ,
24 18
-209 + 287?-6т+561пт
72
^2(/’)=^1)(/’)+^22)(/’)-Й1)(/’)-Й2)(/’)-41) -42)=
17+49?-18т-81пт 43+35т2-6т-161пт , 1 , 1 с
24т2 18т2 т т2
_ 209-287?+6т-5б1пт
72т2
При 0 < т < 1 имеем
^(p)=xi (p)+xi (р)-У1 (р)-У1 (/>)-zr-4 -
25+41?-18т-8?1пт 39+19?-6т-16?1пт , , 2 <
----------24-------+---------18--------------1+т-1+?~5 =
_-193+271?-6т+88?1пт
72
511
п / \ o(Dz ч о(2) о(0 о(2)
Г2(р) = Х2 (р)+Х2 (р)-У2 (р)~У2 (p)-£}-zr =
25+41т2-18т-8т21пт 59+19т2-6т-16т2inn 1 _
24т2 36т2 т
_ 193-271т2 + 6т-88т2 In т
72т2
Таким образом, при т > 1 (р2 >р{) имеем
„z ч f-209+287т2-6т+56Inт -209+287т2-6т+561пт^
F( л) = -----------------.--------------------- .
При 0 < т < 1 (р2 < р{) имеем
„ ч (-193+271т2-6т+88т21пт -193+271т2-6т+88т21пт^
ад=[-------------72----------'-----------72?---------j
7°. Аналогично тому, что мы имели в примере 11.4.1, в рас-
сматриваемом примере 11.4.2 всегда р = (рр р2) > 0, поэтому (по
закону Вальраса) F(p) = 0, т.е. F{(p) = 0, F2(p) = 0.
При т > 1 имеем уравнение
-209 + 287т2 - 6т + 561пт = 0,
откуда следует, что
287т2 - 6т + 561пт = 209.
При т > 1 это уравнение не имеет решений, ибо при т = 1 име-
ем
287- 12-6- 1 + 561П1 = 287-6 = 281 >209
и производная левой части равенства 287т2 — 6т + 561пт = 209
287-2Т-6+ —
т
при т > 1 положительна, ибо уравнение 287т2 — Зт + 28 = 0 не име-
ет действительных корней и, следовательно, его левая часть поло-
жительна.
При 0 < т < 1 имеем уравнение
Дт) = 271т2 - 6т + 88т21пт = 193.
Путем перебора получаем, чтоД0,87) = 190,6215 < 193,ДО,88) =
« 195 > 193, откуда следует, что т* = 0,87, а (т*)2 = 0,7569 = p2/pv
512
Добавив к последнему равенству условие нормировки + р2 = 1,
получим, что р{* = 0,5692, р2 = 0,4308. Таким образом, вектор
р' — (р*, р2) цен статического экономического равновесия равен
р* s (0,5692; 0,4308), р* г 0,5692, р* s 0,4308.
Статическое экономическое равновесие рассматриваемой
МЭД есть набор
{р*,/(|),/(2),х‘(1),х‘<2>} =
=((А,Л), d-т*, 1--?j), (1-(т*)2; 21пт*),
I т’
25+41(т*)2 -18т*+8(т*)21пт* 25+41(т*)2 - 18т* +8(т*)2In т *'
< 24 ’ 24(т*)2 )’
Л59+19(т*)2-6т*+16т*1пт* 59+19(т*)2-6т*+16т*1пт*У
k 18 ’ 36т* JJ’
где т*=0,87.
8°. Для того чтобы построить множество Y= 2У(1), отметим,
что по определению
Y = 2Yw( = \у | у = 2у(1), у(|) е У(1)},
или более детально
= l(yi,3'2)l(3'i>Jz2) = (2>'i(i)>2^1)), У1(1)<1,У2°
У,(1)
Положив 2у^ =у(, 2у2(|) =у2, получим для множества У= 2У*1*
следующее представление:
2У(1) = |(у„ у,) I < 1А < У{!—
[ 2у I
=ИУ1.У2)1>'1<2’
I У J
Множество Y= 2J<1) изображено на рис. 11.5.
Для того чтобы построить множества Y= и Y= У*1) +
+ У<2), напомним определение алгебраической суммы множеств
(суммы Минковского):
зз - 7620
513
Y = Ym+У(1) (“i\y | у = y(1)+y(2), y(1) e Г(1), y(2) e У(1)},
Очевидно, что
у(П + у(2)= J (/)+у(2))= J (у(0+у<2)).
у<»€У<1> у2)еу<2)
Здесь символ у(1) + у<2)(У<*> + у(2)) означает сдвиг каждого эле-
мента у<2) в Y® (у(1) g У(,)) на вектор у(1) (на вектор у(2)). Следова-
тельно, алгебраическая сумма Z0 + /2) множеств и /2) пред-
ставляет собой объединение всех параллельных переносов мно-
жества И2) (множества на всевозможные векторы у(|) из
множества (на всевозможные векторы у(2) из множества №).
На рис. 11.6 линия /j изображает эффективную («северо-вос-
точную») границу множества которая имеет уравнение
* rf’-r
(пунктирная) линия /2 изображает эффективную границу множест-
ва которая имеет уравнение
У2(2) = g0,1(2)),
514
линия / изображает эффективную границу множества + №,
которая имеет уравнение
У2 = а0'1)-
Аналитическое представление й(у() будет получено ниже для
множеств и + №.
Далее на рис. 11.6 линия /2 получена из линии /2 путем ее (ли-
нии 12) сдвига параллельным переносом на вектор у(1) (изобра-
женный на рис. 11.6). Прямая Ко — касательная к линиям /р /2 и I
в точке О, прямая Кх — касательная к линии /2 в точке у(1) = (у/1*,
У2 ).
Очевидно, линия / есть огибающая семейства линий /2, когда
вектор у(1) пробегает всю эффективную границу множества У(,).
Сама линия /2 заметает (от слова метла) все множество + №.
Аналогично можно было бы выбрать вектор у(2), принадлежащий
33’
515
эффективной границе множества У®, который осуществлял бы
параллельный перенос линии_/р а затем построить линию / как
огибающую семейства линий \ (линия получается из линии
путем ее сдвига на вектору®), когда вектору® пробегает всю эф-
фективную границу множества У®. При этом сама линия \ будет
заметать все множество У® + У®.
Сначала получим уравнение огибающей линии / в случае, ког-
да вместо множества У® фигурирует множество У®, а множество
У® фигурирует в качестве самого себя.
Итак, имеем
У = У® + У< 11 = {у|у = у® + у®, у® е У®, у® е У®}, при этом
„(1) „(2)
^4-7.
УГ-1 У1 -1
Положим
У , =У1(1) +У1(2)»У2 =Уг(1) +Уг(2)- (11.4.6)
Очевидно, yt < 2.
Рассмотрим уравнение эффективной границы множества У®:
^1>=-фЛ rf’=-ra4>- (11.4.7)
У1 -1 У1 -1
Построим алгебраическую сумму (сумму Минковского) эф-
фективной границы множества J® и эффективной границы мно-
жества У®, используя метод построения огибающей однопара-
метрического семейства линий. Для этого перепишем равенства
(11.4.6) и (11.4.7) следующим образом:
v(l) v(2)
У1 _ v(l) _ v _ v(2) _ v У| v(l) _ v _ v(2)
— -_y2 _y2-y2 _y2 У1 -У1~У1 ,
У1 -1 У1 -1
откуда получаем уравнение
У1~уР У1(2)
У(-уР~1 2 уР"1
(11.4.8)
однопараметрического семейства линий, где переменная ур
(у® < 1) играет роль параметра.
Согласно теории огибающих (Математический энциклопеди-
ческий словарь (1988)) следует взять и приравнять производные
правой и левой частей уравнения (11.4.8) по параметру ур:
516
~(У1 -У12)-1)+(У1 -У12)) _ У12)-1-У12)
(У1-У12)-1)2 (У12)-1)2
откуда после необходимых сокращений и преобразований полу-
чаем уравнение
-У1(2) ~ О2 = (yt(2)- I)2. (11.4.9)
Осталось из системы уравнений (11.4.8) и (11.4.9) исключить
параметр у{2). Для этого сначала в уравнении (11.4.9) избавимся от
квадратов.
Если у1 - у[2) -1^0, то, извлекая из обеих частей уравнения
(11.4.9) квадратный корень, будем иметь (у<2) < 1)
У|—У|2) -1 = 1 — У|2),
откуда получаем У] = 2, что невозможно, ибоу1 < 2.
Если ух - у,2) - 1 < 0, то, извлекая из обеих частей уравнения
(11.4.9) квадратный корень, будем иметь
+У® +1 = 1 -у{2),
откуда получаем, чтоу, = у[2>/2. Подставив последнее равенство в
уравнение (11.4.8), получаем после элементарных преобразова-
ний
У2 =
2У1
У1-2-
Таким образом, если = У*1*, то у2 = h(yx) = -211
В рассматриваемом случае оказалось, что 2У<1) = У^ + У^.
Вообще говоря, справедливо включение 2 У0* с У*1' + У°\ что
подтверждается простым примером:
X -1
= у(0 + y(D
Построение уравнения огибающей в случае множеств У*1* и
У^2) аналогично только что рассмотренному случаю, когда вместо
множества /2) фигурировало множество У*1*.
517
Имеем
Y = /О + /2) = {у|у = y(D + у<2), У0 е /О, /2) 6 у(2)}>
„(1) ’ v(2>’
при этом 0 < у^ < 1, 0 £ < 1, у2^ < —, у^ £ —Д—
УГ~1 уг-i
Положим
У1 = у<’> + у[2),у2 = у2(1) + у2(2). (11.4.10)
Очевидно, у [ < 1.
Уравнения эффективных границ множеств и /2) соответ-
ственно имеют вид
„(1) „(2)
v(0 У1 v(2) — У1 /1 1 л 11 \
У1 ~ (1) ,» у2 “ (2) Т- (11.4.11)
уг -1 У1 -1
Как и в случае, когда вместо множества фигурировало
множество У0*, имеем
У1(1)=У1-У1(2).
v(2)
ln(l - yi + уР) = 1п(1 - у}1*) = у^ = у2- у<2) = у2 —. (11.4.12)
УГ -1
Оставив в (11.4.12) крайние звенья, будем иметь уравнение
v(2)
ln(l-y1+y<2>) = y2 —g—, (11.4.13)
У1 -1
содержащее переменные уру2 и параметру^.
Согласно теории огибающих возьмем и приравняем произ-
водные по параметру у,(2) правой и левой частей уравнения
(11.4.13):
/ ( (2) V
(ВД-л+уР)) ’
у' I У1 Vv!2»
откуда следует, что
1 (zP-D-z,»1
i-zi+zi® (X21-1)2
т.е.
(у1(2)_1)2=1_у1+у1(2) (11.4.14)
Для того чтобы получить уравнение огибающей у2 = h(y^, сле-
дует из системы уравнений (11.4.13), (11.4.14) исключить пара-
метру^ (0 yf2) < 1).
518
Раскроем скобки в (11.4.14) и решим квадратное уравнение
(у^У-Зу^+у^О
относительно параметра у*2’. Имеем, очевидно,
„<а_3±>/9-4Л
* - j
Корень
У!2) = 3+^~4у‘ > 1, (9-4у,) > О,
поэтому он является посторонним, ибо 0 < у*2) < 1.
Корень
o<yp=^z£4K<i>
1 2
(11.4.15)
откуда следует, что 0 < < 2, т.е. этот корень подходит.
Подставив выражение уj(2) в уравнение (11.4.13), будем иметь
In 1-У! +
откуда получаем, что
6-4*-2^К 5-2^-^
2 4(2-у,) 2
Таким образом, при 0 < у((1) < 1,0 < у*2) < 1,0 < уj < 2 уравнение
эффективной границы множества У= У^ + У^, которая является
огибающей однопараметрического семейства линий (11.4.13),
имеет вид (11.4.16).
Переходим к случаю у<1) < 0, у{2) £ 0, (yj = у[1) + у<2) < 0), тогда
0<у2(1)< 1и0<у2(2)< 1,(0<у2<2).
Положим, как и ранее, у^ = у((1) — у<2), у2(1) = у2 — у2(2).
В рассматриваемом случае получим
519
уР
г(2)= Ы2),^))|у1(2)<0,0^Р^-оГ-г.
Л"1 J
Выразим уР через у2(1) иур через у2(2):
у2° = 1-еу'" => У](|) = 1п(1-уР
д,<» = у'2’ => »«>=_j£!_
У2 Л2,-1 * И8-!'
Имеем
у-—<
= У\~ У1(2) = У1(,) = ln(l - у£>)=1п(1 - у2 + у™).
Выпишем крайние звенья приведенной цепочки
у(2)
У1—= 1п(1-у2 + уР). (11.4.17)
у2 -1
Согласно теории огибающих возьмем и приравняем произ-
водные по параметру у2(2) правой и левой частей уравнения
(11.4.17):
( v(2) Y / ч/
К. У1 lJyw Уг
откуда следует, что
(у2(2) - I)2 = 1 —у2 + у<2>. (11.4.18)
Для того чтобы получить уравнение огибающей, из системы
уравнений (11.4.17) и (11.4.18) следует исключить параметр у2(2)
(0^у2(2)<1).
В связи с тем что переменные у ру2 и параметр у2(2) в уравнени-
ях (11.4.17) и (11.4.18) соответствуют переменным у2, yt и парамет-
ру у^2), по аналогии с решением (11.4.16) системы уравнений
(11.4.13) и (11.4.14) выпишем решение
6-4y2-2J9-4y2 , 5-2y2-J9-4y2
4(2-1) +1П~^Т------------- <IL419>
520
Таким образом, при 0 <у2(2) < 1,0 <у?(|) < 1,0 £у2 < 2 уравнение
эффективной границы множества У= + Y™, которая является
огибающей однопараметрического семейства линий (11.4.17),
имеет вид (11.4.19).
11.5. Критические замечания по МЭД и ее обобщения
МЭД — чисто теоретическая конструкция, которая представ-
ляет собой абстрактную модель, ее параметры и экзогенные пе-
ременные не оцениваются на основании реальных или (и) экс-
пертных данных. Модель экономики называется вычислимой, если
ее параметры и экзогенные переменные оцениваются на основа-
нии реальных или (и) экспертных данных.
Теоретические модели могут быть как абстрактными, так и
вычислимыми. Прикладные модели — обязательно вычислимые
модели. Для решения конкретных теоретических задач построено
много абстрактных моделей. Абстрактные модели не являются
универсальными. Универсальных моделей не существует, как не
существует универсального транспортного средства, которое бы
решало разнообразные транспортные проблемы перемещения в
горах, по воде, в воздухе.
Как и всякая абстрактная модель, МЭД отражает многие ха-
рактерные черты экономической реальности, но не все. Так, на-
пример, авторская версия МЭД не учитывает зарплату в форми-
ровании дохода потребителей. У каждого потребителя в МЭД до-
ход формируется за счет ликвидного запаса и дивидендов из
прибыли тех фирм, где потребитель является собственником. Для
такого потребителя зарплата не нужна. Тогда в модели должны
быть другие потребители, в формировании дохода которых важ-
ную роль играет заработная плата, а таких потребителей в МЭД
нет. В МЭД нет динамики, и следовательно, в МЭД не представ-
лена такая важная компонента экономической реальности, как
инвестиционный процесс.
Если МЭД толковать как модель национальной экономики,
в этой модели никак не отражаются внешние экономические
связи.
Список таких замечаний может быть достаточно продолжи-
тельным. Но это обстоятельство, естественно, не умаляет главно-
го достоинства МЭД как модели, для которой было получено до-
521
казательство существования статического экономического рав-
новесия (общего экономического равновесия).
Работа Эрроу и Дебре стимулировала появление большого
числа работ, в которых развивались в разнообразных направлени-
ях основные положения МЭД.
В одной из версий МЭД в явном виде фигурируют труд и зар-
плата, в другой версии рассматривается динамический вариант
МЭД. Во многих работах авторы шли в направлении повышения
математического уровня абстракции МЭД за счет, в частности,
перехода от конечного числа продуктов и потребителей к беско-
нечному числу продуктов и потребителей, что требовало от авто-
ров весьма продвинутых математических средств, в частности
теории топологических векторных пространств.
Результаты недавних исследований представлены в книге:
General Equilibrium: Problems, Prospects and Alternatives (1999).
Абстрактные модели в экономической литературе выполняют
важную функцию. Они играют роль формальных каркасов, кото-
рые охватывают в качестве частных случаев широкие классы при-
кладных моделей экономики. Небольшой список важных аб-
страктных моделей составляют динамические модели в матрич-
ной и конической формах (модели Дж. фон Неймана и Д. Гейла) и
их обобщения, последние модели финансовой экономики. К это-
му списку «избранных» абстрактных моделей принадлежит и
МЭД.
Вопросы для самоконтроля к главе 11
1. Опишите: сферу производства; теорию фирмы, затрачивающей не-
сколько ресурсов и выпускающей несколько продуктов; технологи-
ческое множество фирмы и его свойства. Сформулируйте определе-
ние локального рыночного равновесия фирмы (определение предло-
жения фирмы). Докажите однородность нулевой степени
предложения фирмы как векторной функции цен.
2. Опишите технологическое множество сферы производства и сфор-
мулируйте его свойства. Дайте определение рыночного (совокупно-
го) предложения.
3. Опишите сферу потребления, функцию полезности потребителя и ее
свойства.
4. Опишите два слагаемых дохода потребителя. Сформулируйте ло-
кальное рыночное равновесие потребителя (спрос потребителя).
Докажите однородность нулевой степени спроса потребителя как
522
векторной функции цен. Сформулируйте определение рыночного
(совокупного) спроса.
Сформулируйте определение избыточного спроса. Докажите одно-
родность нулевой степени избыточного спроса.
Сформулируйте закон Вальраса.
Сформулируйте определение статического экономического (конку-
рентного) равновесия.
Приведите формулировку теоремы Эрроу — Дебре.
Для сферы производства, состоящей из одной фирмы и содержащей
два продукта, определите предложение фирмы как набор функций
рыночных цен.
Для сферы потребления, состоящей из двух потребителей и содержа-
щей два продукта, определите спрос первого и второго потребителей
как наборы функций рыночных цен.
Определите понятие абстрактной модели. Приведите примеры аб-
страктных моделей.
Определите понятие вычислимой модели. Приведите примеры вы-
числимых моделей.
Сформулируйте критические замечания по модели Эрроу — Дебре.
Определите направления обобщения модели Эрроу — Дебре.
Задачи и упражнения для самоконтроля к главе 11
Технологическое множество /фирмы F имеет вид
i,={(yi;y2)lj'i<1 * * * У;j'2^«(j'i)}> где ^.)= , J-*??*0’ >
1) постройте это множество на плоскости Оу{у2',
2) найдите сумму Y + У, опишите аналитически северо-восточную
(эффективную) границу множества У + У. Постройте множество
У + У. Ответ обоснуйте.
В моделируемой системе два продукта (продукт и ресурс), одна фир-
ма Fn два потребителя С0* и С52) Технологическое множество /фир-
мы дописано в предыдущей задаче 1. Доли потребителей в прибыли
фирмы Нравны оц = 74; а2 = 3/4. У потребителя начальный запас
(с/0; z2(I)) = (1; 3) и функция полезности t/j(xp х2) = х{ • х2. У потре-
бителя С(2) начальный запас (z/2); ^(2))= (2; 3) и функция полезности
U2(xl,x2)=xlx22;
а) найдите локальное рыночное равновесие фирмы F;
б) найдите локальное рыночное равновесие у каждого потребителя
С^иСЯ;
в) выпишите вектор избыточного спроса;
523
г) Найдите цены равновесия (нормированные). Выпишите стати-
ческое экономическое равновесие;
д) постройте множество У на плоскости Оуху2-
3. В экономической системе два продукта (продукт и ресурс), две фир-
мы и /*2) и два потребителя С*0 и С52). Технологическое множест-
во У0* фирмы имеет вид Iх0 = {(у,; у2)| < 1; у2 £ у{/(ух - 1)}.
Технологическое множество У<2) фирмы F™ имеет вид
= {(Ур У2)1 yt < 1; У2 * Я(У1)}. где $(?!) = 1 1-е ^°’
1п(1-у1),0<у1<1.
Доля потребителей в прибыли фирмы 7х0 и фирмы № соответ-
ственно равны (Xj j = 2/3; а21 = а12 = а22 = х/т У потребителя
С5!) начальный запас (z/!); z2(l)) = (3; 1) и функция полезности
Цхр х2) = х, • х22. У потребителя С^2) начальный запас (z/2); z2(2))
= (3; 2) и функция полезности U(xv х2) = xt • х2:
а) найдите локальное рыночное равновесие каждой фирмы;
б) найдите локальное рыночное равновесие для каждого потреби-
теля;
в) выпишите вектор избыточного спроса;
г) найдите цены равновесия (нормированные). Выпишите стати-
ческое экономическое равновесие;
д) постройте множества )^2,и У= Iх0 + У<2).
4. Технологические множества Iх0 и У(2) двух фирм № и 1*2) соответ-
ственно имеют вид
y4i) = ^(lyi) = ^(D, ув)9 о 1 у™ ± , у/1* £ 0)},
у<2) = ^(2) = ^(2), о у&) ^у(2^ У1(2) < 0)}>
где а, Рр Р2 — положительные параметры и 0 < а < 1:
а) постройте множества Iх0 и /2);
б) постройте множество
в) постройте множество У= Iх1) +
г) опишите аналитически эффективную границу множества У =
= + }<2)
Вопросы, тесты и задачи для контрольных работ к главе 11
1 Фирма сферы производства МЭД характеризуется:
а) своей производственной функцией вида у = Дур ..., уг), где у —
объем выпускаемой фирмой продукции; у. — количество затра-
чиваемого ресурса вида /, i = 1,..., г,
б) технологическим множеством, описывающим допустимые ком-
бинации затрачиваемых ресурсов и выпускаемых продуктов;
в) ответы а) и б) не верны.
2. Фирма сферы производства МЭД:
524
1-еу',у{ <0,
1п(1-у1),0<у1 <1:
а) допускает соединенные затраты (т.е. использование ряда ресур-
сов);
б) допускает соединенные выпуски (т.е. выпуск ряда продуктов);
в) максимизирует прибыль;
г) ответы а)—в) являются верными.
3. Доход потребителя сферы потребления МЭД включает:
а) «стоимость» ликвидного запаса;
б) заработную плату;
в) субсидии государства;
г) налоговые льготы;
д) ответы а)—г) не верны.
4. В понятии статического экономического (конкурентного) равнове-
сия исходным является понятие:
а) цен равновесия;
б) локального рыночного равновесия фирмы;
в) локального рыночного равновесия потребителя;
г) ответы а)—в) не верны.
5. Технологическое множество Yфирмы F имеет вид
1' = {(У1^2)1з,1 d^sO'i)}, гае g(yi) =
а) постройте это множество на плоскости Оу{у2;
б) Постройте множество 2 У, опишите аналитически северо-восточ-
ную (эффективную) границу множества 2У. Ответ обоснуйте.
6. В моделируемой системе два продукта (продукт и ресурс), одна фир-
ма Fn два потребителя <5° и С52). Технологическое множество Уфир-
мы F описано в задании 5. Доли потребителей в прибыли фирмы F
равны <Х| =а2 = 2/3. У потребителя С*0 начальный запас (z/0; z2(1))
= (2; 3) и функция полезности U{(xv х2) = х, • х2. У потребителя С52)
начальный запас (z/2); z2<2))= (3; 2) и функция полезности U2(x{, х2) =
Х12'Х2:
а) найдите локальное рыночное равновесие фирмы F;
б) найдите локальное рыночное равновесие каждого потребителя
(ЯиС<2>;
в) выпишите вектор избыточного спроса;
г) найдите цены равновесия (нормированные). Выпишите стати-
ческое экономическое равновесие;
д) постройте множество Уна плоскости Оу}у2.
7. В экономической системе два продукта (продукт и ресурс), две фир-
мы № и Т*2) и два потребителя С*1) и С52). Технологическое множест-
во У*0 фирмы F™ имеет вид Iх0 == {(у,; у2)| yj < 1; у2 < У{/(у{ - 1)}.
Технологическое множество /2) фирмы Т*2) имеет вид /2) = {(Ур у2)|
525
^1 < 1; У2 £ giy^}, где g(y,) =
1-еу,,У] <0,
1п(1—У|),0<у, <1.
Доля потребителей в
прибыли фирмы и фирмы /*2) соответственно равны ап = 3/4;
а21 = V4> а12 = V$> а22= У потребителя <5° начальный запас (с/0;
^(0) = (4- 2) и функция полезности U(xp х2) = • х2. У потребителя
С2) начальный запас (z/2); ^(2)) = (2; 3) и функция полезности U(xy
Х^) Xj • х2.
а) найдите локальное рыночное равновесие каждой фирмы;
б) найдите локальное рыночное равновесие для каждого потреби-
теля;
в) выпишите вектор избыточного спроса;
г) найдите цены равновесия (нормированные). Выпишите стати-
ческое экономическое равновесие;
д) постройте множества У*1* и У<2);
е) постройте множества У^ + Г*1), 2У<1\ Г*1) + + Y^2\
Глава 12
ЭКОНОМИЧЕСКАЯ ТЕОРИЯ
БЛАГОСОСТОЯНИЯ
12.1. Парето-эффективность и статическое
экономическое равновесие в экономике обмена.
Первая и вторая теоремы экономики благосостояния
12.1.1. В модели экономики обмена функционирует т потребите-
лей Ср Ст и г продуктов Ср ...» Сг. Для каждого продукта Gk,
к = 1,г, имеет место равенство
хк} +хк2) + - +хкт) = ак> (12.1.1)
где ак — общее количество продукта СЛ; — количество продукта
Gk, которое находится в распоряжении потребителя С., i = 1,..., т.
Каждый потребитель имеет функцию полезности и((хм)
е £/ = {х|х = (xj,...,*,),*! -0,...,хг О})- Потребители мо-
гут добровольно (без принуждения) обмениваться продуктами,
увеличивая (или не уменьшая) свою функцию полезности.
В модели экономики обмена вместо потребителей Ср ..., Ст
могут фигурировать фирмы Fx,..., Fn, а вместо продуктов (това-
ров) Ср ..., Сг фигурировать ресурсы Rv ..., Rr. Каждая фирма Fj
имеет производственную функцию
= 0,Л = 1,...,г,У = 1,...,л). Фир-
мы могут обмениваться ресурсами, увеличивая (или не уменьшая)
объем выпуска своей продукции.
Набор векторов называется Парето-эффектив-
ным (эффективным по Парето), если он допустим, т.е. удовлетво-
527
ряет равенствам (12.1.1), и не существует другого допустимого
набора векторов |х(1),...,х(т)|, такого, что
мДх^'^^мДх^),/ = 1, (12.1.2)
причем хотя бы одно неравенство является строгим.
Отметим, что в определении Парето-эффективности (эффек-
тивности по Парето) отсутствуют цены на продукты.
12.1.2. Парето-эффективность при т = 2 наглядно иллюстрирует-
ся с помощью диаграммы (ящика) Эджворта, которая строится
следующим образом.
Для каждого потребителя С\ и С2 имеем пространство потре-
бительских наборов и карту линий безразличия (рис. 12.1а (для
потребителя С,) и рис. 12.16 (для потребителя С2)). Если функции
полезности «](х(1)) и и2(х(Г>) строго выпуклы вверх и гладкие, то их
линии /т и 1д безразличия гладкие и выпуклы к точкам О(1) и О(2)
соответственно.
Поскольку X]1’ + х{2) = х|1} + хр = а2, постольку 0 < < ар
О < х^< а2„ i = 1, 2, что и показано на рис. 12.1.
Для построения диаграммы Эджворта следует весь рис. 12.16
развернуть на 180’ на плоскости О(2)хрхр и после этого совмес-
тить его с 12.1а так, чтобы точка О(2) попала в точку с координата-
ми (йр д2) (рис. 12.2). На рис. 12.2 точка В изображает два потре-
528
Рис. 12.2
бительских набора: х(1) = (хР\ хР*) и х(2) = (xl2), х!2)) и при этом
x^^a^+x^.
Очевидно, совокупность потребительских наборов {х(1),х(2)},
изображающая на рис. 12.2 точку В, не является Парето-эффек-
тивной, ибо из точки В, которая изображает потребительские на-
боры х(1) и х(2) потребителей С, и С2, можно перейти в точку Н,
которая изображает потребительские наборы Х^ — (xj \ Х2
^(2)_^(2) ^(2)^ При этом значение т функции полезности
первого потребителя С{ стало равным
, а значение а функции полезности
o=w(2)(x1(2),x^2)) второго потребителя С2 не изменилось. Переход
из точки В в точку Я содержательно означает обмен продуктами,
который осуществили потребители С, и С2. Потребитель С{ пере-
дал потребителю С2 (т.е. потребитель С2 получил от потребителя
Cj) первый продукт в количестве х^-х}1* =X](2)-xt(2) единиц.
Потребитель Ct получил от потребителя С2 (т.е. потребитель С2
передал потребителю С.) второй продукт в количестве
xV* -xl!) - V<2> -х<2> рпииип
л2 л2 — *2 — СДИНИЦ.
34 - 7620
529
Переход из точки В в точку Q анализируется аналогично.
Только в этом случае значение т функции полезности i/^xj0, х^!))
первого потребителя С\ остается неизменным, а значение ст функ-
ции полезности и2(х[2\ х^2)) второго потребителя С2 становится
равным ст>ст.
Точки Ни Q на рис. 12.2 изображают Парето-эффективные
наборы, ибо при переходе, скажем, из точки Нв точку Q значение
ст функции полезности и2(х^\ х22)) растет и становится равным
ст > ст, а значение t функции полезности х|^) убывает и
становится равным т<т. Выйти из точки Я так, чтобы значение
одной функции полезности строго выросло, а другой по крайней
мере осталось неизменным, невозможно.
Парето-эффективность можно наглядно проиллюстрировать
ситуацией двух козликов на мосту, которые упираются друг в дру-
га своими рожками. Один козлик может продвинуться вперед
только в том случае, если другой козлик отступит назад.
Линия L в диаграмме Эджворта, которая соединяет точки,
изображающие Парето-эффективные наборы, называется конт-
рактной линией. Криволинейный отрезок QH контрактной линии
L, который находится между двумя линиями безразличия, назы-
вается переговорным множеством. Линии безразличия, проходя-
щие через точки переговорного множества, соответствуют значе-
ниям функций полезности, которые больше (не меньше) значе-
ний функции полезности, соответствующих линиям безразличия,
проходящим через точку В (на рис. 12.3 более детально показан
фрагмент рис. 12.2, содержащий точки В, Н и Q. На рис. 12.3
т < т < т, ст < ст < ст. Линии безразличия 4 и /а на рис. 12.2 показа-
ны не были).
12.1.3. Пространство полезностей OUj«2 называется критериаль-
ным пространством экономики обмена. Образ множества О^х^а,,
О £ х2 < а2 в пространстве полезностей называется множеством U
достижимых полезностей. Эффективной границей dUмножества U
достижимых полезностей называется подмножество множества U
достижимых полезностей, такое, что если векторы и = («р и2) е dU
и it = (u{, и2) е Unit >и (покоординатно), то it = и.
Очевидно, эффективная граница dU множества Uявляется
образом контрактной линии L диаграммы Эджворта.
530
Рис. 12.3
Построим множество U достижимых полезностей в случае
т = 2.
ВточкеО(1) х|,)=д41)=О>^12)=Л1,л42)=<»2>поэтому
= <^(0, 0) = 0, и2(х[2\ хр}) = «Двр а2) = д, т.е. образом точки О(1) в
критериальном пространстве OWjW2 является точка
О(,) =(«i,u2)=(0, о) (рис. 12.4). Аналогично, в точке О(2) х,(,) = ар
х<» = а2, хх(2) =х2(2) = 0, поэтому их(х[1), х2(1)) = их(ах, а2) = т,
и2(х(2\ х22)) = Wj(0,0) = 0 ,т.е. образом точки О® в критериальном
пространстве Quxu2 является точка О(2) =(м1,«2) = (т,0)
(см. рис. 12.4).
Образом точки Я = (х1<1),х^)) в критериальном пространстве
Объявляется точка Н = (их,и2), где т =Ц = м1(х1(1),х^)),
о = «2 =и2(-х1<2),хР)) (см. рис. 12.4). Образом точки B^xf^xP),
которая не принадлежит контрактной линии и, следовательно,
потребительский набор (х^, х^) не является Парето-эффектив-
ным, в критериальном пространстве является точка В = (щ,и2),
которая не принадлежит эффективной границе д U. В случае точки
В = (их,и2), их= т = их (х*1*, х^°), и2= о = их (х,(2), х^2)), (см. рис. 12.4).
Образом точки Q в критериальном пространстве Ои1и2 является
точка Q = где их= т, и2= д (см. рис. 12.4).
34*
531
Геометрическая характеристика некоторой точки К (см.
рис. 12.4), принадлежащей эффективной границе 8Uмножества U
достижимых полезностей, формулируется так. Если прямой угол,
вершина которого находится в точке К множества U и стороны
которого параллельны осям Ои{ и Ои2, пересекается со множе-
ством Uтолько в самой вершине К, то точка К принадлежит эф-
фективной границе dU. Верно и обратное.
Точка А = (и,, ы2) расположена вне множества U. Содержатель-
но это означает, что потребители С\ и С2 не могут ее достигнуть,
ибо для этого недостаточно запасов at и а2 продуктов G{ и G2.
12.1.4. Пример 12.1.1
В модели экономики обмена функции полезности потребите-
лей Cj и С2 имеют соответственно вид '(х^) *♦
«2х22)) = (xf2)p (х^^1. (Функции полезности в мульти-
пликативной форме с одинаковыми показателями a j = 0 ] и а2 = р2
первых и вторых переменных предложил рассматривать
532
Я.И. Кротов, когда он был студентом экономического факультета
МГУ.) Имеем Х](1)+xj2) = ар х^ + х® = а2.
Требуется:
1) выписать необходимые и достаточные условия Парето-
эффективности;
2) выписать уравнение контрактной линии L и построить ее
на диаграмме Эджворта;
3) выписать уравнение эффективной границы dUмножества
{/достижимых полезностей (для ряда конкретных значений пара-
метров «j и а2).
Прежде чем выписать необходимое и достаточное условие
Парето-эффективности набора |x(1),x(2)J x(1)=(xj(1),xPj,
х(2) = (*i<2>,*22)), отметим, что уравнение t = и{ (х^, х^) линии без-
различия /х определяет х^!) как неявную функцию от переменной
xt(1). В рассматриваемом случае вообще из уравнения
[ у Г
v =a0^x1(1)j (х21>) 2 следует, что хР=-——), производная
(xi(1))^
которой по теореме о неявной функции имеет вид
Эи^хР, хР)
(Ьф Эх,(1)
dx^ Эи^х^, х<'>)
м»
Аналогично
ди2(х[2\ xl2))
Эх<2>
dx[2) Эм2(Х1(2),х^2))
Эх<2>
1. Поскольку необходимым и достаточным условием Парето-
эффективности набора {х<‘>, х(2)} является касание линий безраз-
личия 4 и в точке х^^Сх^^х^) (в точке х(2) = (Х]2),х^2))
(см. рис. 12.2), постольку эти линии безразличия имеют в этой
точке х(1) (х<2>) одинаковые угловые коэффициенты
533
^2 _^2 (12.1.3)
dbq(1) dx^
2. Используя теорему о неявной функции в случаях
t =Uj(xP,xP), o’ = w2(x1<2\x^2)), получим из (12.1.3) следующую
цепочку:
9«i(it(1),xP)
Эх,(2) dx™ ЭхР
d«2(xt(2),xP)) г/гр’ dx^} Эы2(х1(|,,х21))
Ъф 34»
Подставив частные производные
в правое и левое звенья цепочки (12.1.4), получим
w«W мМ~Ш
vz^'WT' зд^’ТИ’Г
Выполнив сокращения и использовав равенства
Х[2) = а, -хр, х<2) = а2 -хР, получим
Р1 02-^2° = «Г ^2°
P2-at-Xi(1) а2Х1(1)’
откуда следует, что уравнение контрактной линии L имеет вид
х(1) = «2Р1О2Х1(1) _
2 а^-^Рг-Р^хР’
Для того чтобы эта контрактная линия была отрезком 0(1) 0(2)
(рис. 12.5)
хР=^-хР, (12.1.6)
а1
необходимо и достаточно, чтобы имело место равенствоа^ = р,а2
для показателей степени мультипликативных функций полезности
«1(х1(1),хР), «г(х1(2),х^2))-
534
Рис. 12.5
Аналогично в переменных х{2) и xf2) уравнение контрактной
линии L имеет вид
^2> = ^,<2>. (12.1.7)
а1
3. Подставив в ui =flo(xi<1>) '(д41>) > w2 =A>(*i(2)p(x22))Pl выра-
жения (12.1.6) и (12.1.7), будем иметь
«1
откуда следует, что
1 <*г 1 Рг
«F7=*}2)f—У1*’’ (а, Д. (12.1.8)
k °1 J \al J
Полагая x}2) = получаем из (12.1.8)
1 1
= xf) W“,+“2 , «pfc =
kfll J
535
Полагая aQ = bQ, после сложения и выполнения элементарных
преобразований, принимая во внимание, что при at02 = P,a2
0С2 Р? Oti Bi жж
----— = ——— и ------i— = —, получаем уравнение эффек-
«i+a2 Bi+₽2 оц+аз В1+В2
тивной границы dUмножества U:
1 1 а, а2
. (12.1.9)
Само множество Uдопустимых полезностей описывается сле-
дующей системой неравенств:
1 1 Q] а2
<+а> +М₽1+Рг Ul >0,«2 >0.
3.1. В (12.1.9) положим а, = а2 = р, = Р2 = ^, а} = 4, а2 = 9, тогда
уравнение (12.1.9) перепишется так:
и1 +и2 =4*92 =6 (рис. 12.6).
536
3.2. В (12.1.9) положим а, = а2 = pj = р2 = ai = ^а2 = 9» Т0ГДа
уравнение (12.1.9) перепишется так:
£ £
ut+U2 = 4292 =6
(см. рис. 12.6).
3.3. В (12.1.9) положим а( = а2 = Р, = Р2 =1, а{ = 4, а2 = 9, тогда
уравнение перепишется так:
£ £ £ £
u2 =4292 = 6
(см. рис. 12.6).
3.4. В (12.1.9) положим а, = а2 = 2, р. =Р2 =•-, at = 4, а2 = 9, тог-
а, а2
да а,₽2= 24 = 3.02, a -^1— = _2?_ 1 a а1+а2 ец+а, =
4 1 2 Oj+a2 а1+о2 2 1
£
= (^,02)2 = 6, и поэтому уравнение (12.1.9) перепишется так:
£
«J4 +U2 =6
(рис. 12.7, на котором оси Out и Ои2 имеют разные масштабные
единицы).
537
12.1.5. Пример 12.1.2
В модели экономики обмена функции полезности потребите-
лей Ци С2 имеют соответственно вид
h
«l(xi(1),xi1)) = flo^i(x1(1)) ° + а2(хР) “,
к
Й!{.<»х<г>) = 4ь[(1(х«>Г + 6г(^,)-“уг.
Справедливы равенства х*^ + х}2) = gt, + хр = gv Общие
количества g, и g2 первого и второго продуктов положительны:
g1 > 0, g2 > 0. Показатель степени а * -1.
1. Выпишем необходимые и достаточные условия Парето-
эффективности.
2. Выпишем уравнение контрактной линии L.
3. Выпишем уравнение эффективной границы dUмножест-
ва Uдостижимых полезностей.
При разборе этого примера на параметры функций полезнос-
ти постепенно накладываются разнообразные ограничения.
Выражения (12.1.3) и (12.1.4), которые фигурировали в приме-
ре 12.1.1, в пример 12.1.2 переносятся без всяких корректировок.
Имеем
<fc«> Эх,™ / Эх™ 4*f"J
Аналогично получим, что
dx^2) _ bA х<2) Y+1
dxi(2) ^xpj
538
При = а2, bx = b2 уравнение контрактной линии L, имеющей
уравнение
dx^
dbC](1) dx^ ’
приобретает простой вид
x2l) =g2~x2l)
откуда вытекает, что контрактная линия L имеет уравнение
хр = —х^, 0 < х^ < gpO < х^ £ g2.
Si
По аналогии с этим уравнением имеем другое уравнение
(в переменных хр и х|2))
х(2) _ £2^(2), 0 < Х|2) <£[,()< Хр < g2
Si
контрактной линии L.
Перепишем выражение для функции и/х^, х^!>) полезности
потребителя С} следующим образом:
«1 Л =«o4«i(xi(1))_a+e2(xP)'0
Учитывая первое и последнее звенья цепочки, можно напи-
сать следующее равенство:
По аналогии имеем
539
При
1_1 1-1
a^aia=b^bla=r
имеем (напомним, что х{2)+х|2)=gj
Таким образом, уравнение эффективной границы Э ^множест-
ва Uдостижимых полезностей имеет вид
11 _1
«1А +U2 = г(^1"а +&2“) “ , «1 0, 0.
Само множество t/допустимых полезностей описывается сис-
темой неравенств
11 _1
Н]А +«£ £ +g£“) “ , 0, «2 > 0.
12.1.6. Статическое экономическое равновесие в экономике обме-
на есть набор векторов {/>*, х*(1),..., такой, что он удовлетво-
ряет условиям:
1) вектор цен равновесия р* =(pf,...,pj), р[ >0,..., р* >0,
X +...+ р'г =1;
2) вектор х*(,) = (х?‘\..., х*(,) j — локальное рыночное равнове-
сие потребителя Ср i = 1, ..., т, т.е. решение следующей задачи
рационального поведения потребителя С{ на рынке:
И/(х(,))(тах)
р* х(,) = р*х*(,);
3) для каждого продукта Gk, k= 1,..., г, имеет место равенство
х^ +...+х^ = ак.
540
В отличие от определения Парето-эффективности, в котором
цены на продукты не фигурируют, в статическом экономическом
равновесии обязательно присутствуют цены равновесия.
Взаимосвязь между Парето-эффективностью и статическим
экономическим равновесием описывается двумя теоремами эко-
номики благосостояния.
Первая теорема экономики благосостояния — это теорема о
том, что статическое экономическое равновесие Парето-эффек-
тивно. Говоря точнее, если набор {р", х*(1),..., x‘(m)} есть статичес-
кое экономическое равновесие, то набор |x*(1),...,x*(m)J является
Парето-эффективным.
Вторая теорема экономики благосостояния — это теорема о
том, что если набор |x(1),...,x(m)J Парето-эффективен, то суще-
ствует такой вектор р = (Д..Д) цен, что набор {р, х(1),..., x(m)J
есть статическое экономическое равновесие.
В случае экономики обмена при т = 2 обе теоремы экономики
благосостояния доказываются достаточно просто с помощью ис-
пользования диаграммы Эджворта.
Докажем сначала первую теорему экономики благосостояния,
т.е. если набор {//,х*(1\...,х*('")} есть статическое экономическое
равновесие, то набор {х*(1),...,х*<т)} является Парето-эффектив-
ным.
Согласно определению статического экономического равно-
весия для потребителя С(, i = 1,2, потребительский набор х’(/) есть
решение следующей задачи рационального поведения потреби-
теля Ср /= 1,2, на рынке
M/[x(/)J(max) (12.1.10)
А\(/) +ДхР = аХ(/)+Л^° (12.1.11)
Для этой экстремальной задачи выпишем функцию Лагранжа
541
Потребительский набор х*^ = (х^0, x^j как решение экстре-
мальной задачи (12.1.10), (12.1.11) удовлетворяет условиям перво-
го порядка для функции Лагранжа:
(12.1.12)
x*V> Э«, х*> „
'—к—=о,
Эх£> Эх£> П
dlAx^X^}
эх<-> = А ~ ~ = °-
(12.1.13)
Из (12.1.12) и (12.1.13) при i = 1 и i = 2 вытекает цепочка ра-
венств (здесь существенно, что ценыр\ ир2 являются общими для
потребителей С\ и С2)
Эм^х*^) ЭнДх**2^
Эх,(1) _Р\ _ дхр
Эи^х*0*) Рг Э«2(х*(2))’
ЭхР Эх<2>
что означает касание линий безразличия в точке x*(I) = (х^’^х^1^
(в точке х‘<2> = (х;<2>,х2*<2))),т.е. набор векторов |х‘(1),х*(2) J Парето-
эффективен.
Докажем, предполагая строгую выпуклость линий безразличия
обоих потребителей С( и С2, вторую теорему экономики благосо-
стояния.
Набор векторов |х(1),х<2)| Парето-эффективен, что означает,
что в точке х(1) диаграммы Эджворта касаются линии безразличия
потребителей CinC2, т.е. в точке х(1) (в точке х(2)) диаграммы Эдж-
ворта имеем цепочку равенств
542
Эи^х^, х^) ди2(х[2\х^))
дх}1» _ dxf?\ dx™ дх<2>
ЭиДх}1),*^) ^Xl<2) d«^(xf2), Х^2))
а^> а^>
Приравняв крайние звенья этой цепочки дроби pj Pi
(А > O,pj > О» А + А = 1), получим
3U,(x<M")=i,„ri| эи,са<‘М1>)=^1>/|. (12114)
OXj OX^
^М8)^. (12.1.15)
ОХ| ох^
Из условий (12.1.14) и (12.1.15) первого порядка следует, что
потребительские наборы х(1) =(x1(1),x^1)j и х<2) = ^Xj2),xpj являют-
ся локальными рыночными равновесиями потребителей и С2.
Равенства хр+х{2) = ах, х^ + х^2) = а2 следуют из того, что на-
бор векторов |х(|), х<2>} Парето-эффективен.
Таким образом, доказано существование вектора цен р и то,
что потребительские наборы х(1) и х(2) являются локальными ры-
ночными равновесиями потребителей С{ и С2, т.е. набор векторов
|p*,x‘(1),...,x*(m)J есть статическое экономическое равновесие в
экономике обмена.
12.2. Парето-эффективность и статическое
экономическое равновесие в экономике обмена.
Первая и вторая теоремы экономики благосостояния
(общий случай)
12.2.1. Рассмотрим модель экономики, состоящую из сферы про-
изводства (СПр) и сферы потребления (СПо), аналогичную моде-
ли главы 11.
Сфера производства состоит из фирм Fv ...,Fn, каждая из кото-
рых характеризуется своим технологическим множеством (техно-
логией) Y®.
543
Технологическое множество (технология) Y сферы производ-
ства представляет собой алгебраическую сумму (сумму по Мин-
ковскому) технологических множеств Y® фирм:
Y = Y(l) + ... + YM=[y\y = yw + ...+y(m),yU}eY(J},j = l,. ..,л}.
(1.1) Технологическое множество Y предполагается выпуклым
и ограниченным, что естественно с содержательной экономичес-
кой точки зрения.
Сфера потребления состоит из потребителей Ср..., Ст, каждый
из которых характеризуется своей функцией полезности и.(уР) и
множеством Е* = {х|х = (хр..., хг), xt > О, i = 1,..., г} потребитель-
ских наборов х(,) = (х^,..., х*'^, z = 1,..., т.
(2.1) Функция полезности i = 1, ..., т, предполагается
строго выпуклой вверх при х(,) е £*.
Любой вектор х = х(1) +...+ х(т\ для которого существует век-
тор у g Y, такой, что х < у (покоординатно), называется допусти-
мым.
Набор векторов |x(I),...,x(m)j называется Парето-эффектив-
ным, если, во-первых, он допустим и, во-вторых, не существует
допустимого набора векторов {х(|),..., x(m)j, такого, что
Uj (х0)) > и, (х(/) j, i = 1,..., т,
причем хотя бы для одного потребителя С, неравенство будет стро-
гим.
Таким образом, Парето-эффекгивность означает, что ни один
потребитель не может увеличить уровень удовлетворения своих
потребительских амбиций, не обедняя других потребителей.
Определение статического экономического равновесия до-
словно повторяет соответствующее определение параграфа 11.3
главы 11, с той лишь разницей, что в рассматриваемом здесь слу-
чае вектор запасов каждого потребителя принимается равным
нулю.
12.2.2. Первая теорема экономики благосостояния формулирует-
ся так.
Пусть набор |р*,х*(1),...,х*(л’),у*(1),...,у*(я)| есть статическое
экономическое равновесие.
544
Тогда набор Парето-эффективен.
Вторая теорема экономики благосостояния формулируется
так.
Пусть существуют векторы у°е Yи х°, такие, что у° - х° > 0.
Пусть для каждой функции полезности и/х^) выполняется
условие ненасыщаемости (т.е. для каждого потребительского на-
бора х(,) существует потребительский набор х(,), такой, что
Пусть выполнены условия (1.1) и (2.1) см. раздел 12.2.1).
Пусть набор векторов |х(1),х(т)} (х(/) — потребительские
наборы, /= 1,..., т) Парето-эффективен. Тогда существуют вектор
цен Р = (Р{,-..,Рг) (А >0,...,рг >0), |/>| = А+...+А = 1), отхл-мат-
рица(а,-,) (а,7>0, dly+...+dmy =1, 1 = 1,...,т, J = l,...,«) и векторы
У(1), —, У(л) (у<7) eYj, J = 1,..., л), такие, что набор
In* Г*^ Y*(m) V*(1)
есть статическое экономическое равновесие.
Доказательства этих общих теорем экономики благосостоя-
ния не являются обязательными и поэтому не приводятся.
При формулировках определений Парето-эффективности и
статического экономического равновесия присутствует неявное
допущение о наличии полной информации в моделируемой эко-
номической системе.
12.3. Функции общественного благосостояния
12.3.1. В теории потребления каждый потребитель С., i = 1,..., т,
имеет свою индивидуальную функцию полезности. Для выясне-
ния того, что является общественно желательным, целесообразно
агрегировать индивидуальные функции полезности и агрегиро-
ванную функции полезности естественно максимизировать. Ин-
дивидуальные функции полезности можно агрегировать по-раз-
ному, но при этом естественно требовать, чтобы с неубыванием
35 - 7620
545
каждой индивидуальной функции полезности агрегированная
функция полезности также не убывала. Агрегированная функция
полезности называется функцией общественного благосостояния.
В общем виде функцию общественного благосостояния целесо-
образно представить в виде функции B^(«p «т) т переменных
«р •••» где каждая переменная ир i = 1,т, есть индивидуаль-
ная функция полезности потребителя Ср I = 1, ..., т:
1К = Иг(м1(х(1)),...,«от(х(я’))), где х(,) =(х1(,),...,х^')) — некоторый
потребительский набор, i = 1,т.
Если
W = Ui(xw)+...+u„(x(m)),
то функция общественного благосостояния называется утилита-
ристской функцией или функцией Бентама. Максимизация этой
функции означает максимизацию суммарной полезности всех
потребителей. На рис. 12.8 для случая двух потребителей и С2
(т.е. т = 2) представлено выпуклое множество Uдостижимых по-
лезностей. Линия уровня утилитаристской функции обществен-
546
ного благосостояния Иг= и, + и2 представляет собой прямую /,
образующую с осями Ои} и Ом2 углы, равные 45’ (=л/4).Точка
И(м,; й2) касания линии уровня I и эффективной границы дUмно-
жества U есть точка максимума утилитаристской функции обще-
ственного благосостояния. В случае, представленном на рис. 12.8,
общественно желательной является ситуация й2), когда зна-
чение функции полезности их первого потребителя Сг
равно wb значение полезности «2 (xf2),x22)) второго потребителя С2
равно «г и при этом получилось, что й] > м2 (и весьма значитель-
но).
Точка касания V есть одна из точек эффективной границы dU
множества t/достижимых полезностей. Точка V является образом
точки ^диаграммы Эджворта (рис. 12.9), которая расположена на
контрактной линии L и, следовательно, изображает Парето-эф-
фективный набор векторов lx(1),x(2)) = (хР,х^),
х(2) = (х<2>,х<2>)).
Следовательно, общественно желаемая ситуация V = (м1;й2),
реализуется на Парето-эффективном наборе векторов |x(l),x(2)J.
Обратное, конечно, неверно. Например, Парето-эффективному
Рис. 12.9
35*
547
набору векторов (см. на рис. 12.9 точку V с координата-
ми (xP.Xj)) (или (х<2>,х<2>)) соответствует точка V' границы dU,
которая не максимизирует утилитаристскую функцию обще-
ственного благосостояния. Поскольку (в случае выпуклых вверх
функций полезности) Парето-эффективный набор порождает
статическое экономическое равновесие, постольку общественно
желаемая ситуация И = (ы1;й2) реализуется в статическом эконо-
мическом равновесии. Статическое экономическое равновесие
может и не реализовать общественно желаемую ситуацию V.
Здесь рассуждения аналогичны приведенным выше о том, что
Парето-эффективный набор векторов не обязательно реализует
общественно желаемую ситуацию.
Отметим, что в случае, когда уравнение границы dU множест-
ва достижимых полезностей имеет вид и2 +и% =6 (см. рис. 12.6),
9 9
имеем Wj =й2 = v3. Здесь х((1) = 2, х^=~, хр =2, х}2) =- (прове-
ряется непосредственно). В случае когда уравнение границы дU
548
имеет вид и1 + и2 = 6 имеем щ +й2 = 6, S 0, й2 > О (см. рис. 12.6).
В случае когда уравнение границы dU имеет вид «/2+«У2 =6
(см. рис. 12.6), имеем либо ц = 0, й2 = 36, либо щ =36, й2 = 0.
12.3.2. Обобщением утилитаристской функции общественного
благосостояния является функция
ir=pi«1+...+pmMm,
в которой обычно полагают р1 +... + Pm = 1 и р j £ 0,..., Pm £ 0.
Коэффициенты Рр.... Рт принято называть весовыми множи-
телями. Каждый такой коэффициент показывает относительную
значимость соответствующей функции полезности для совокуп-
ного общественного благосостояния. На рис. 12.10 для случая
двух потребителей и С2 (т.е. для случая т = 2) представлено вы-
пуклое множество U достижимых полезностей и показаны две
линии уровня двух версий обобщенной утилитаристской функ-
ции общественного благосостояния:
^pvvp^,
^2=₽Р«1+р(22Ч-
Точка касания е 3U есть точка глобального максиму-
ма функции И^, а точка касания (tf2),i$2)) € dU есть точка гло-
бального максимума функции W2. Очевидно, в случае выпуклого
множества Uдопустимых полезностей для каждой точки («1, й2),
границы д U достижимых полезностей можно подобрать весовые
множители р j и Р2 так, чтобы точка глобального максимума функ-
ции W = Р]+ p2«2 общественного благосостояния при фиксиро-
ванных запасах и а2 продуктов <7р (72 совпадала с точкой («о «г)-
Таким образом, в случаях выпуклого множества U если весовые
множители Р| и р2 пробегают (каждый) отрезок [0; 1] и при этом
Р] + Р2 = 1, то множество точек (иь «2), которые являются решени-
емзадачиглобальноймаксимизациифункции W(ux,u2) = Р^ + Р2ы2,
«заметает» (от слова «метла») всю эффективную границу dUмно-
жества Uдостижимых полезностей. Случай т = 2, проиллюстри-
рованный на рис. 12.10, естественным образом обобщается на
случай 1Г = р1м1+...+Ротиот.
549
12.3.3. Случай обобщенной утилитаристской функции обще-
ственного благосостояния И' = P,«| +...+POTwm представляет собой
важный частный случай скалярной свертки критериев задачи век-
торной оптимизации, в которой целевая функция векторная, а не
скалярная, что имеет место в теории скалярной оптимизации.
Задача векторной оптимизации имеет следующую постанов-
ку:
W (х) = (щ(х),...,иж(х)) (max)
при наличии ограничений
^(х)>0,...,^(х)>0.
Здесь х е М с Er, М— замкнутое и выпуклое множество, функ-
ции и1(х),...,ит(х), <7|(х),..., qp(x) выпуклы вверх на множестве М.
Вектор х g Мназывается допустимым, если он удовлетворяет
неравенствам ?1(х)>0,...,^/,(х)>0. Вектор х называется эффек-
тивным вектором задачи векторной оптимизации, если он допус-
тим и если не существует другого допустимого вектора х, для ко-
торого и^х) > их(х),..., ит(х) > ит(х), причем хотя бы одно из нера-
венств должно быть строгим.
Задача векторной оптимизации — это нахождение всех ее эф-
фективных векторов.
Имеет место следующее важное утверждение.
Пусть х — эффективный вектор задачи векторной оптимиза-
ции. Тогда существуют числа ..., 0т, такие, что
₽.+... +₽ = 1,р,>о,...,р >о
• 1 * т * 1 7 * т
и глобальный максимум функции Р1«1(х)+...+РЛ1«Л1(х) при нали-
чии ограничений ?1(х)>0,...,?/,(х)>0, хе Л/достигается при
х = х.
12.3.4. Примером функции общественного благосостояния явля-
ется следующая функция:
W (х) = min (wj (х),..., wm(x)),
которая называется функцией Роулза, или роулзианской функцией
общественного благосостояния.
550
Максимизация функции Роулза означает максимизацию
уровня благосостояния потребителя, имеющего минимальное
значение из значений остальных функций полезности.
На рис. 12.11 для случая двух потребителей С, и С2 (т.е. для
случая т = 2) представлено выпуклое множество U достижимых
полезностей и показана линия / уровня функции общественного
благосостояния min(wp и2). Точка V = (w(;i^) «касания» линии
уровня / и эффективной границы dUмножества Uесть точка гло-
бального максимума функции Роулза общественного благососто-
яния. Рассмотрим случаи, представленные на рис. 12.6.
В случае когда dU имеет уравнение uf +u2 =6 (см. рис. 12.6),
точка V имеет координаты Щ =2^ = >/з. В случае когда dU имеет
уравнение + «2 = 6, точка V имеет координаты й] =5^ =3
(см. рис. 12.6). В случае когда dU имеет уравнение itf2 + d[2 =6,
точка V имеет координаты й( = й2 = 9.
Если сопоставить полученные ответы с ответами в случае ути-
литаристской функции общественного благосостояния, то можно
551
отметить их совпадение в случае, когда граница д U имеет уравне-
ние wj2 + «2 = 6 - В остальных случаях ответы разные.
12.3.5. Выбор функции общественного благосостояния ассоци-
ируется с определенным толкованием понятия справедливости.
Например, согласно Роулзу, наиболее справедливым является та-
кое распределение продуктов Gt, ..., Gr между потребителями
Ср ..., Ст, при котором максимизируется полезность наименее
обеспеченных потребителей:
И^(хт,..., х(м)) = max min(U[ (х(1)),..., ит (х(т)).
Согласно утилитаристскому подходу наиболее справедливым
является такое распределение продуктов Ср..., Grмежду потреби-
телями Ср ..., Ст, при котором суммарная полезность
их(хт) + ..лит{х(т)) максимальна. В этом случае вполне могут
отличаться друг от друга значения «((х(1)),..., ит(х(п,)) функций по-
лезности разных потребителей Ср ..., Ст (см. рис. 12.8).
В рассмотренных выше примерах (см. рис. 12.11 и 12.6) спра-
ведливое распределение продуктов Ср G2 между потребителями
Ср С2 было Парето-эффективным и приводило к статическому
экономическому равновесию.
552
Согласно эгалитаристскому подходу наиболее справедливым
является такое распределение продуктов Gv Gr между потреби-
телями СрСт, при котором должно быть равное распределение
каждого продукта между всеми потребителями. На рис. 12.12 точ-
ка Л = (х1(|),х^1>) = (х1(2),х^2)) такова, что х,^ = xf2) =Oj/2,
х^ - =02/2. Точка А иллюстрирует справедливое распределе-
ние продуктов и G2 между потребителями С{ и С2 с точки зрения
эгалитаристского подхода при г = 2 и т = 2. Если контрактная ли-
ния L не проходит через точку А (рис. 12.12), то мы имеем случай,
когда ни один Парето-эффективный потребительский набор
(х^, х^Х*!2), не является справедливым (с точки зрения эга-
литаристского подхода). Поскольку Парето-эффективный набор
приводит к статическому экономическому равновесию (если все
функции полезности выпуклы вверх), постольку статическое эко-
номическое равновесие также может и не быть справедливым
(с точки зрения эгалитаристского подхода).
Было рассмотрено три подхода к толкованию понятия спра-
ведливости, которые в порядке уменьшения равенства следует
расположить так: эгалитаристский подход (каждый потребитель
получает поровну всех продуктов), роулзианский подход (макси-
мизируется минимальная функция полезности), утилитаристский
подход (максимизируется суммарная полезность всех потребите-
лей). К этим трем подходам следует добавить рыночно ориентиро-
ванный подход, согласно которому справедливость устанавливает
рынок.
12.4. Теорема о демократических групповых
рыночных решениях и ее значение для теории
общественного выбора
12.4.1. В параграфе 12.3 были рассмотрены конкретные примеры
функции общественного благосостояния, которая агрегировала
индивидуальные функции полезности. На самом деле вопрос о
согласовании предпочтений не исчерпывается рассмотренными в
параграфе 12.3 конкретными примерами.
Рассмотрим процедуру голосования в качестве способа согла-
сования индивидуальных предпочтений. В ходе голосования под-
считывают число индивидуумов (потребителей), предпочита-
553
ющих одно конкретное распределение х чего-то (например, про-
дуктов, телепрограмм) другому конкретному распределению у.
Вместо термина «конкретное распределение» (чего-то) использу-
ют термин «ситуация» (ситуация х, ситуация у). После подсчета
голосов воля большинства признается выбором общества (обще-
ственным выбором). Принцип большинства является основой для
принятия важнейших решений (политических, экономических,
социальных) не только в странах, которые называют себя демок-
ратическими, но и во многих международных организациях, на-
пример в таких, как ООН, МОК. Принцип большинства базиру-
ется на эгалитаристском принципе «один человек — один голос».
Еще в XVIII в. Бурда и Кондорсе обратили внимание на пара-
докс голосования, суть которого состоит в следующем. Представим
себе группу из трех студентов ($р s2, s3), каждый из которых имеет
собственную шкалу предпочтений относительно трех видов спор-
та: футбола (F), легкой атлетики (LA) и гимнастики (Н). Суть во-
проса в том, на соревнование по какому виду спорта должна пой-
ти вечером вся наша троица. Шкала предпочтений каждого сту-
дента имеет следующий вид:
*5. S. S. .
F LA Н
LA Н F
Н F LA
Шкала предпочтений каждого студента дана по убывающей
сверху вниз. В частности, студент 5] гимнастике предпочитает
легкую атлетику, а легкой атлетике футбол. Аналогично поясня-
ются шкалы предпочтений студентов S2 и 53.
При выборе между Fn LA большинство (5, и 53) высказывает-
ся в пользу F. При выборе между £Аи Н большинство (5, и 52)
высказывается в пользу LA. По аналогии со свойством транзитив-
ности индивидуальных предпочтений естественно ожидать, что
если Fпредпочитается LA, a LA предпочитается Н, то Fпредпочи-
тается Н. Однако в рассматриваемом примере при выборе между
Ни /’большинство (S2 и 53) высказывается в пользу Н. Таким об-
разом, свойство транзитивности здесь (т.е. в случае общественно-
го выбора) не выполняется, т.е. голосование имеет циклический
характер. В этом и состоит суть парадокса голосования.
554
Из-за нетранзитивности коллективных (групповых) предпоч-
тений общественный выбор зависит от очередности постановки
распределений (ситуаций) на голосование. Если сначала студенты
должны (большинством голосов и 53) сделать выбор между F и
LA, а затем выбранную ситуацию /’сравнить с Н, то будет выбрана
(большинством голосов S2 и 53) ситуация Н. Если же сначала сле-
дует выбрать из /и Н, а потом выбранную (большинством голосов
S2 и 53) ситуацию Я сравнить с LA, то большинством голосов (5( и
S2) будет выбрана ситуация LA. Зависимость общественного вы-
бора от очередности постановки ситуаций на голосование откры-
вает возможности для манипулирования этой очередностью.
12.4.2. В конце 40-х гг. XX в. К. Эрроу (К. Arrow (1950), К. Эрроу
(2004)) проанализировал проблему преобразования индивидуаль-
ных предпочтений в коллективные в общем случае.
Эрроу предположил, что принятие коллективных решений в
демократическом обществе должно удовлетворять ряду достаточ-
но очевидных условий. Эрроу отобрал следующие шесть усло-
вий.
1. Все ситуации вполне упорядочены при принятии любого
индивидуального (не коллективного) решения.
2. Все ситуации обладают свойством транзитивности при
принятии любого индивидуального решения.
3. Правило принятия любого коллективного решения должно
работать при любых индивидуальных предпочтениях (условие
универсальности).
4. Если каждый индивидуум предпочитает ситуацию х ситуа-
ции у, то ситуация х социально предпочтительнее ситуации у (ус-
ловие Парето-совместимости).
5. Не существует такого индивидуума (диктатора), предпочте-
ния которого автоматически индуцируют аналогичные групповые
(общественные) предпочтения независимо от индивидуальных
предпочтений других индивидуумов (условие отсутствия диктату-
ры).
6. Отношение индивидуумов к ситуациям х и у не должно за-
висеть от их отношения к ситуации z (условие независимости от
других ситуаций).
В своей работе Эрроу показал, что невозможно построить алго-
ритм принятия коллективных решений, который бы удовлетворял
всем перечисленным шести условиям. Это утверждение Эрроу
555
получило название теоремы о невозможности или теоремы о де-
мократических групповых решениях. Суть этой теоремы в том,
что любой коллективный выбор, удовлетворяющий всем перечис-
ленным шести условиям, превращает одного индивидуума в дик-
татора.
Реакция теоретиков на основополагающую работу Эрроу была
достаточно разноплановой. Некоторые теоретики считали необхо-
димым наличие «единообразия» индивидуальных предпочтений
для нормального функционирования демократических обществ.
Для этого требуется манипулировать общественным сознанием.
Другие теоретики обратили внимание на нерациональность удов-
летворения общественных предпочтений тем же условиям, кото-
рым удовлетворяют индивидуальные предпочтения, т.е. условиям
полной упорядоченности и транзитивности. Приписывать обще-
ству (коллективу) характеристики отдельного индивидуума — зна-
чит заниматься его олицетворением, что логически неправомерно.
Работа Эрроу показала, что построение функции обществен-
ного благосостояния представляет собой серьезную проблему.
В любом случае для преобразования индивидуальных предпочте-
ний в коллективные (общественные) следует отказаться или су-
щественно ослабить по крайней мере одно из перечисленных вы-
ше шести условий.
Вопросы для самоконтроля к главе 12
1. Что представляет собой модель экономики обмена?
2. В чем формальное отличие модели экономики обмена, в которой
фигурируют потребители, от модели экономики обмена, в которой
фигурируют фирмы?
3. Как определяется Парето-эффективность в модели экономики об-
мена?
4. Что представляет собой диаграмма (ящик) Эджворта?
5. Как с помощью диаграммы Эджворта описать процедуру обмена
продуктами (товарами) между двумя потребителями Cj и С2?
6. Что такое контрактная линия?
7. Что такое критериальное пространство модели экономики обмена?
8. Что такое множество достижимых полезностей и его эффективная
граница?
9. Как строятся множество достижимых полезностей и его эффектив-
ная граница в случае, когда степенные функции полезности потре-
556
бителей Cj и С2 имеют одинаковые показатели у первых и вторых пе-
ременных?
10. Как определяется статическое экономическое равновесие в эконо-
мике обмена?
11. Как формулируется первая теорема экономики благосостояния в
случае экономики обмена? Приведите доказательство первой теоре-
мы экономики благосостояния в случае экономики обмена.
12. Как формулируется вторая теорема экономики благосостояния в
случае экономики обмена? Привести ее доказательство.
13. Как определяется Парето-эффективность (в общем случае)?
14. В чем принципиальное отличие Парето-эффекгивности и статичес-
кого экономического равновесия?
15. Как формулируется первая теорема экономики благосостояния в
общем случае?
16. Как формулируется вторая теорема экономики благосостояния в
общем случае?
17. Как определяется функция общественного благосостояния?
18. Что такое утилитаристская функция общественного благосостоя-
ния?
19. Что такое роулзианская функция общественного благосостояния?
20. Как охарактеризовать взаимозависимость между общественно жела-
емой ситуацией, Парето-эффективностью и статическим экономи-
ческим равновесием?
21. Что такое обобщенная утилитаристская функция общественного
благосостояния?
22. Как формулируется задача векторной оптимизации?
23. Как характеризуется взаимосвязь между сверткой критериев задачи
векторной оптимизации и обобщенной утилитаристской функцией
общественного благосостония?
24. Как характеризуется эгалитаристский подход к понятию справедли-
вости?
25. Как характеризуется роулзианский подход к понятию справедливос-
ти?
26. Как характеризуется утилитаристский подход к понятию справедли-
вости?
27. Как характеризуется рыночно ориентированный подход к понятию
справедливости?
28. В чем суть парадокса голосования?
29. Как формулируются основные шесть условий теоремы Эрроу о не-
возможности?
30. Как формулируется теорема Эрроу о невозможности?
31. В чем состоит теоретическое значение теоремы Эрроу о невозмож-
ности?
557
32. В чем состоит практическое значение теоремы Эрроу о невозмож-
ности?
Задачи и упражнения для самоконтроля к главе 12
1. В экономике обмена w1(xi1)>^2)) = (xi(1>) '(х2°)
W2 (xj2), Х22^) = (х^)^ (х^)^ , *1(1)+*1(2)=Л1,
Параметры a2, ах и а2 равны:
а) oq = -, a2 = -, ах =32, а2 =1;
б) ai=p «2=1, =32, а2 = 1;
в) oq =1, a2 = 2, ах =32, а2 = 1.
Для каждого конкретного набора параметров:
а) постройте диаграмму (ящик) Эджворта;
б) выпишите уравнение контрактной линии L и постройте ее в диа-
грамме Эджворта;
в) постройте потребительский набор (xf^x^js (16; У^ в диаграм-
ме Эджворта. Выпишите уравнение линий безразличия функций
полезности их и «2, содержащих потребительские наборы
(xf0, х^°) = (16; У) и (хР, хр) = (16; %). Постройте в диаграмме
Эджворта эти линии безразличия (по не менее чем трем точкам,
включая обязательно точки (16; }/3) и (16; 2/3);
г) найдите точки пересечения линий безразличия с контрактной
линией и опишите полностью обмен продуктами между потре-
бителями Cj и С2, когда они перемещаются в точки, расположен-
ные на контрактной линии. Постройте точки пересечения в
диаграмме Эджворта;
д) выпишите уравнение эффективной границы dUмножества до-
стижимых полезностей Uи постройте dUи Uв критериальном
пространстве Ои{и2 модели экономики обмена;
е) найдите образы точки (16; х/3) и точек, найденных в 4), в крите-
риальном пространстве Ои{и2 и постройте эти образы в критери-
альном пространстве Оихи2;
ж) найдите и постройте в диаграмме Эджворта потребительский
набор (xf0,^0), который реализует эгалитаристский подход к
понятию справедливости. Постройте образ этого набора (х^, х^)
в критериальном пространстве Оихи2,
з) найдите и постройте в критериальном пространстве OwjW2 кон-
фигурацию (йх, w2) полезностей, которая максимизирует утилита-
558
ристскую и роулзианскую функции общественного благосостоя-
ния. Найдите и постройте в диаграмме Эджворта прообразы
(xf0,^0) » ((*i<2\*22>)) конфигураций (ц,й2) полезностей, кото-
рые реализуют утилитаристский и роулзианский подходы к
справедливости.
2. В экономике обмена w1(x1(1),x^l)) = (x1(1)) ' (х^°) 2,
«,(,<».= х<'’«Р=0„ х«>+,«=аг. Парамет-
ры ос j а2, р j р2, и а2 соответственно равны
а) «! =|, а2 =|, =3, р2 =2, at =в2 =32;
б) а,=3, а2=1, Р|=-, Рг=7, ^=16, а2 = 256.
2 6
Для каждого конкретного набора параметров выполнить п. 1)~8) за-
дания 1. Для варианта а) параметров рассмотреть два варианта потре-
бительского набора (хР,х<2>): вариант (х1(1),х^1)) = (4; 8) и вариант
(х|0), х^) = (16; 8). Для варианта б) параметров рассмотреть два вари-
анта потребительского набора (хр, хр): вариант (хР, хР) = (4; 64) и
вариант (хР,хр) = (16; 64).
3. Проанализируйте групповые (общественные) предпочтения в слу-
чае, если шкала индивидуальных предпочтений (шкала предпочте-
ний каждого студента) имеет вид
•S, S, S.
F LA Н
LA Н LA
Н F F
4. Приведите содержательный пример индивидуальных предпочтений,
объединение (агрегирование) которых в групповые предпочтения
приводит к парадоксу голосования.
Вопросы, тесты и задачи для контрольных работ к главе 12
1. Нетранзитивными являются следующие отношения:
а) отношение безразличия;
б) отношение предпочтения-безразличия;
в) отношение «вассал моего вассала не мой вассал».
559
2. Пусть функции полезности «1(хР,хР) = (хРр (хР)”2,
((2) (2)\ / (2) \tt| / (2)\а2
Х1 »х2 )= 1^1 J 1*2 J строго выпуклы вверх. Тогда множество
^достижимых полезностей модели экономики обмена:
а) выпукло;
б) не является неограниченным;
в) является неограниченным;
г) нет однозначного ответа.
3. Пусть функции полезности в модели экономики обмена имеют вид
«1 (хр, х<°) = (хРр , «2 (х1(2)> х22)) = (х1(2))а’ (х22))а2‘ Пусть гра-
ница 9U множества U достижимых полезностей строго выпукла к
точке О критериального пространства OWjW2.
Тогда:
а) функция их (хР, хР) выпукла вверх;
б) функция (хр, хр) выпукла вниз;
в) график функции их (хР, хР) — элемент седловой поверхности;
г) ответы а)-в) не верны.
4. Опишите взаимосвязь между контрактной линией диаграммы Эдж-
ворта и эффективной границей dUмножества Uдостижимых полез-
ностей.
5. Приведите пример, в котором справедливый (с точки зрения эгали-
таристского подхода) потребительский набор Парето-эффективен.
6. Приведите пример Парето-эффекгивного потребительского набора
(хР, х£2)) , который невозможно получить в процессе обмена на кон-
курентных рынках.
7. В экономике обмена ^(*Р,*Р) = (*Р)
Wi(xP,xP) = (xP)2(xP)^, хР+х1(2)=а1, Xj(2)+x^2) =д2, где ах = 8,
а2 =64:
а) выведите уравнение контрактной линии L и постройте ее в диа-
грамме Эджворта;
б) выведите уравнение эффективной границы д Uмножества дости-
жимых полезностей Uи постройте dUи U в критериальном про-
странстве Он ^экономики обмена.
Глава 13
МОДЕЛИРОВАНИЕ ДИНАМИКИ ЦЕН
13.1. Простейшая однопродуктовая модель
экономической динамики (паутинообразная модель)
и ее обобщения
13.1.1. В простейшей однопродуктовой модели экономической
динамики время дискретное. Единица времени (например, сутки,
неделя, декада, месяц, квартал, год) называется (производствен-
ным) периодом. Упорядоченная совокупность периодов называет-
ся временным промежутком. Базовый период называется нулевым
(t = 0), текущий период называется периодом t. Состояние моде-
лируемой системы в периоде t описывается одной (эндогенной)
переменной — ценой />(/) одной единицы продукта.
Функции рыночного предложения и рыночного спроса про-
стейшей однопродуктовой модели экономической динамики с
дискретным временем имеют вид
/(/) = ср(/-1)+р, yD(t) = -a p(t)+b, 7 = 1,2,..., (13.1.1)
где параметры а > 0, Ь>0, а > 0 и р не зависят от времени t.
В модели принята предпосылка, что величина y°(t) рыночного
спроса в период t определяется ценой р(0 этого же периода, ибо
продукт (товар) сегодня (в период I) покупают по текущей p(t),
а не по вчерашней (p(t- 1)) цене или по ценеp(t+ 1), которая будет
завтра.
Продукт (товар) следует еще произвести. В модели принята
предпосылка, что объем предложения сегодня (т.е. yfy)) опреде-
ляется вчерашней ценой (p(t - 1)) продукта. Тем самым предпола-
36 - 7620
561
гается, что периода хватит для производства и предложения про-
дукта сегодня, т.е. в периоде I, в объемеyfy).
Предполагается также, что произведенный в периоде t - 1 и
предлагаемый в периоде t продукт полностью реализуется в пери-
оде /, т.е. предполагается, чтоу*(/) =yD(J), т.е. в модели не создает-
ся запас продукта.
Таким образом, простейшая однопродуктовая модель эконо-
мической динамики в линейном варианте представляет собой
обыкновенное линейное разностное уравнение первого порядка
(неоднородное, с постоянными коэффициентами)
a-p(f)+a-p(t-l) = b-$, (13.1.2)
которое получается из равенства^/) = yD(t).
Сначала проанализируем поведение во времени t траектории
цен p(f) (удовлетворяющей начальному условию р(0) = р° —
рис. 13.1), используя наглядную геометрическую интерпретацию.
Если а<оиЛ>р,то прямая у=ар + Р(5) пересекает ось Ор под
углом <р, таким, что tgq> = а, а прямая у = -ар + b(D) пересекает ось
Ор под углом ф, таким, что (gy = а (см. рис. 13.1). Поскольку
tgy = а<а = tgy, постольку прямая D пересекает ось Ор под боль-
шим углом ф, чем угол ф, под которым 5 пересекает ось Ор. Точка
562
Е пересечения прямых Р и S имеет координаты уе (уе — величина
равновесия) и ре (ре — цена равновесия). На основании рис. 13.1
строим траекторию цен p(f), удовлетворяющую начальному усло-
вию р(0) = р°, следующим образом.
При/>(0) = р° имеем^(1) = а-р(О) + р, далее из равенства/*(1) =
=у^(1) = -о р(1) + b определим цену р(1) Этот цикл повторяется:
XD => /(2) = а-р(1) + Р => /(2) = /(2) = - а р(2) + р => р(2)
ИТ.Д.
На основании рис. 13.1 имеем с ростом времени t неограни-
ченное приближение текущей цены />(/) к цене равновесия ре (па-
утина «наматывается» на точку Е). В связи с тем что разность
ХО _ Ре фактически становится равной нулю, имеем фактическое
равенство p(t) = ре, начиная с какого-то конечного номера /.
Если а>яи/>>р,то прямая S пересекает ось Ор под углом <р,
таким, что tgq> = а, прямая D пересекает ось Ор под углом хр, таким,
что tgy = а, и угол <р больше угла у (рис. 13.2).
На основании рис. 13.2 строим траекторию цен/>(/) также, как
строилась траектория цен в первом случае (а < а). Во втором слу-
чае (а > а) паутина «разматывается» от точки Е и построение за-
канчивается при цене р(2), ибо вертикальная прямая у = у^(3) пе-
ресекает прямую D ниже оси Оу. Это означает в рассматриваемом
36*
563
втором случае выполнение неравенства р(3) < 0, что лишено эко-
номического смысла.
Если эндогенная переменная (во втором случае текущая цена
р(0) принимает значения, не имеющие экономического смысла,
то рассматриваемая модель теряет свою адекватность. Во втором
случае линии DviS могут быть прямыми лишь вблизи точки Е,
а далее они должны искривляться, т.е. линейная модель должна
превратиться в нелинейную.
Рассмотрим геометрическую версию второго случая (а > а),
которая более адекватна экономической реальности (рис. 13.3).
Здесь около точки Е наклоны линий 5 и D такие же, как и во вто-
ром случае (а > а). Однако с удалением от точки Е наклоны линий
SviD становятся похожими на наклоны этих линий в первом слу-
чае (а < а). В рассматриваемом сейчас варианте паутина также
разматывается, но не уходит в отрицательные значения цены,
а наматывается изнутри на некий прямоугольный контур (на
рис. 13.3 он не показан) и при четных номерах ценаpit) стремится
к пороговой величине р** > 0, а при нечетных номерах цена p(t)
стремится к пороговой величинер* (см. рис. 13.3).
564
Если а = а и b > р, то прямые 5и D пересекают ось Ор под рав-
ными углами ф = ф и мы имеем случай циклических колебаний
текущей ценыp(t) около цены равновесияре (рис. 13.4). Этот мо-
дельный вариант маловероятен в реализации.
13.1.2. Формально динамика текущей цены анализируется с по-
мощью аппарата теории обыкновенных линейных разностных
уравнений первого порядка.
В линейном варианте (при b > Р) имеем уравнение для отыска-
ния цены ре равновесия
вр+ар = д-р, (13.1.3)
откуда получаем
*"Р
Ре -----’
а+а (13.1.4)
Полагая q(t) = p(f) - ре, имеем после вычитания равенства
(13.1.3) из уравнения (13.1.2) следующее однородное обыкновен-
ное разностное уравнение первого порядка:
a q(t)+aq(t-l) = Q, (13.1.5)
общее решение которого имеет вид
565
?(/)= -- с, (13.1.6)
к а)
где с —произвольная постоянная. Тогда общее решение неодно-
родного разностного уравнения (13.1.2) имеет вид
АО = 0(0+&=(--] С+Ре- (13.1.7)
к а J
Если р(0) = р°, то имеем
с+Ре,
откуда
с=рй-ре.
Следовательно, частное решение уравнения (13.1.2), удовлет-
воряющее начальному условию р(0) = р°, имеет вид
А0 = (Р°-Л)("1 +Ре- (13.1.8)
Если а < а, то, очевидно, текущая ценаp(t) при t -> +оо неогра-
ниченно приближается к цене равновесия ре (см. рис. 13.1). Если
а = а, то имеем случай циклических колебаний
А0 = (Р° - Л)(-1)' + Ре- (см. рис. 13.4). (13.1.9)
Если а > а, то при t -> +оо текущая цена неограниченно растет
по модулю:
|А0-л|=|/’°-л|^
(см. рис. 13.2). (13.1.10)
13.1.3. Простейшая однопродуктовая модель экономической ди-
намики (13.1.2) обобщается в следующих направлениях.
1. Функция предложения у$(Г) может зависеть не только от
цены p(t - 1) предыдущего периода, но и от цен более ранних пе-
риодов:
/(0 = ar pit- 1) + а2А*-2) + ... + агА>-*) + ₽.
В этом случае простейшая однопродуктовая модель экономи-
ческой динамики (13.1.2) преобразуется в модель, описывающую-
ся неоднородным обыкновенным разностным уравнением поряд-
ка к с постоянными коэффициентами
566
a • pit) + a j -pit- 1) +... + a.k • p(t- k) = b - p.
Для решения этого уравнения следует использовать теорию
обыкновенных разностных уравнений порядка к с постоянными
коэффициентами.
2. В модели могут быть учтены запасы у°(/) = /у(/) +Дг).
Если /(/) > 0, то в моделируемую систему поступает извне
(т.е. имеет внемодельное происхождение) продукт в объеме Д/)
единиц. ЕслиДО < 0, то из моделируемой системы изымается про-
дукт в объеме (-ДО) единиц. Слагаемое ДГ) может быть как экзо-
генной переменной, так и некоторой функцией, зависящей от
эндогенной переменной pit).
3. В функциях (13.1.1) спроса и предложения параметры могут
зависеть от времени:
/(О = а(0 • Pit- 1) + р(0-/(О = -о(0Х0 + b(t), /= 1, 2,...
В этом случае (при отсутствии запасов) простейшая однопро-
дуктовая модель экономической динамики (13.1.2) преобразуется
в следующую модель:
ait)pit)+ait)pit-l)=bit)-^t). (13.1.11)
Частное решение уравнения (13.1.11), удовлетворяющее на-
чальному условию р(0) = р°, можно найти пошаговым методом,
который, к сожалению, не распространяется на обыкновенные
разностные уравнения с переменными коэффициентами порядка
выше первого
ait)pit) + a{it)pit- 1) +... + akit)pit-к) = bit) - р(/).
Приведем первые две итерации пошагового метода.
При t= 1 из (13.1.11) получаем
а(1) а(1)
где у(1) = (д(1) - 0(1)) / аЦ), р°=р(0).
При t= 2 имеем
A2)=_®xl)+i(2)=_«(2)C«a)&
аЦ) д(2) а(2)^ аЦ)Р аЦ)) a(2)
^a(2)a(l) о a(2) у(1) у(2)
ai2)ail)P ai2) a(l) a(2)’
где y(2) = (Z>(2) - p(2)) / a(2). И т.д.
567
4. Функции (13.1.1) спроса и предложения могут быть нели-
нейными. В этом случае имеем нелинейную версию простейшей
однопродуктовой модели экономической динамики (13.1.2)
/(XO)=g(A/-D). (13.3.12)
гдеДр(г))1))=/(0-
На рис. 13.3 приведено геометрическое решение нелинейной
версии (13.1.12).
13.2. Избыточный спрос и моделирование динамики
цен с использованием аппарата теории обыкновенных
дифференциальных уравнений
13.2.1. Разность между рыночным спросом х(р) (см. параграф
11.2) и рыночным предложением у(р) (см. параграф 11.1)
F(p) = х(р)~ у(р) и называется избыточным спросом при ценах р =
(j>q,Pv ...,р). (Здесь и далее в главе 13 полагаем, что число продук-
тов равно r+ 1 (а не г, как в главе 11) и что общий запас потребите-
лей z = = 0). Функция F(p) однородна нулевой степе-
ни, ибо функции х(р) и у(р) однородны нулевой степени
х(')р) = х(р), у(ур) = у(р), 0 < у е £, (см. параграфы 11.1 и 11.2).
Поскольку в этой главе речь идет о динамике цен, а по сущест-
ву об экономической динамике, постольку время t вводится явно.
С содержательной экономической точки зрения целесообразно
рассматривать дискретное время, однако с формальной точки
зрения более удобно непрерывное время, ибо аппарат теории
обыкновенных дифференциальных уравнений проще аппарата
теории обыкновенных разностных уравнений. Поэтому далее
предполагается, что время t непрерывно.
Неравенство Fk(p(t)) > 0 означает, что в момент t избыточный
спрос на продукт Gk, к= 0,1,..., г, положителен и поэтому текущая
ценаpk(f) должна расти, а ценаpk(t) растет, если ее производная по
времени t pk(f) положительна, т.е. pk(f) > 0.
Неравенство Fk(p(t)) < 0 означает, что в момент t избыточный
спрос на продукт Gk, к = 0,1,..., г, отрицателен и поэтому текущая
цена pk(t) должна падать, а цена pk(t) падает, если ее производная
по времени t pk(t) отрицательна, т.е. pk(t) < 0.
568
Следовательно, если допустить, что избыточный спрос Fk(p(fii)
на продукт Gk (к = 0, 1,..., г) пропорционален производной pk(t)
цены на этот продукт по времени, то получим систему обыкно-
венных дифференциальных уравнений
1 n 1 (13.2.1)
к = 0,1,..., г.
Траектория p(t) (t > 0) описывает динамику рыночных цен в
модели Эрроу — Дебре (МЭД), рост и падение во времени которых
зависит от знака и величины избыточного спроса.
13.2.2. Поскольку функции избыточного спроса Fk(pQ, pv ..., р^
однородны нулевой степени, постольку систему (13.2.1) можно
переписать так:
Л(0_ г f/%(0 А(0
р I р р р )
(13.2.2)
Л = 0,1,..., г.
Полагая в (13.2.2)
А(0/
/Р
= Л (0, получим
pk(t) = Fk(p0(f),Pi(t),...,pr(f)), к = 0,1,...,г.
Убрав волну, вернемся к старой символике Pk(t), к-0, 1,..., г,
т.е. для новой цены Pk(t) будем использовать прежнюю символику
Р/ОД = °, 1»
С помощью системы обыкновенных дифференциальных
уравнений
A(0=^(A)(0, Pl(t), -; PrW),
Л = 0,1,..., г
(13.2.3)
будем анализировать динамику текущих цен p(t) = (ро(О, />,(0, •••»
рг(/)). Напомним, что вектор ценp(f) характеризует состояние мо-
делируемой экономической системы в момент времени t.
569
13.3. Динамика цен в случае, когда они
не нормированы, и в случае, когда они нормированы
13.3.1. В пункте 4 определения общего экономического равнове-
сия (см. параграф 11.3) требуется, чтобы для цен р* = (р*0, р*х,...,
р*} равновесия имел место закон Вальраса p*F(p*) = 0.
Если вектор цен равновесия положителен р* > 0 (что естест-
венно с содержательной экономической точки зрения), то по ус-
ловию дополняющей нежесткости F(p') = 0, т.е.
Л)(Р*о’/р-’Л) = °’
Цр\,р\, -,Р*) = 0»
откуда следует, что вектор цен равновесия р* есть вектор равнове-
сия автономной системы (13.2.3), т.е. вектор р* есть постоянное
(стационарное) решение автономной системы (13.2.3).
Таким образом, анализ динамики текущих цен p(t) = (р0(/),
px(t), ..., pr(t)) сводится к анализу асимптотического поведения
траектории текущих цен p(t) при неограниченном возрастании
времени t.
Анализ асимптотического поведения текущих цен р(1) во вре-
мени проводится в предположении, что закон Вальраса pF(p) = 0
выполнен не только для цен равновесия р*, но и для текущих цен
p(/):p(0W)) = 0.
Вектору равновесия р* системы (13.2.3) соответствует точкар*
фазового пространства цен Ор0рр ...,рг (рис. 13.5).
В связи с тем что функции F0(p), Fx(p),..., Fr(p) однородны ну-
левой степени, вектором равновесия системы (13.2.3) будет также
вектор Хр‘, где X > 0 — любое число (см. рис. 13.5). Вектору равно-
весия р* системы (13.2.3) в эволюционном пространстве
ОФоРр—,/>г соответствует луч L**, параллельный оси Ot, выходя-
щий из точки р* фазового пространства ОРфР,,...^ а лучу£* натя-
нутому на вектор р* в фазовом пространстве Oplj>l,...,pr, в эволю-
ционном пространстве Otp$x,...,pr соответствует вертикальная
плоскость, параллельная оси Ot и проходящая через этот луч £*
(рис. 13.6).
Если начальный вектор цен р° не расположен на луче L*, то
существует (по теореме существования и единственности реше-
570
ния задачи Коши) единственная траектория текущих цен p(t, р°),
которая удовлетворяет системе (13.2.3) и начальному условию
P(G,P°)=P°-
График траектории цен p(t, р°) в эволюционном пространстве
О/рдРр...,^ также называется траекторией цен или интегральной
571
линией цен (рис. 13.7). График траектории цен p(t, р°) в фазовом
пространстве Ор0р1,...,рг называется фазовой траекторией цен
(рис. 13.8).
Если для любого начального вектора цен р°, близкого к лучу
£*, существует постоянная 1(р°), такая, что траектория />(/, р°) не-
ограниченно приближается к вектору 1(р°)р‘ при неограниченном
возрастании времени t, то говорят, что вектор равновесия р* сис-
темы (13.2.3) локально устойчив (см. рис. 13.7 и 13.8).
Если lim p(t, р°) = Х(р°)р* для любого начального вектора р°, то
говорят, что вектор равновесия р* системы (13.2.3) глобально ус-
тойчив.
13.3.2. Цены р0(/), р/0, •••> Pr(t) принято называть ненормирован-
ными. Переход к нормированным ценам осуществляется за счет то-
го, что цены />,(/),..., pr(t) делят на цену p0(f) нулевого продукта
(товара), в роли которого могут выступать деньги. В качестве нор-
мирующей цены может выступать любая другая цена px(t), ...,
Pr(fY
Итак, нормированные цены имеют вид
572
/>о(0 Ро(О
В силу однородности нулевой степени избыточного спроса на
каждый продукт имеем
Ш), Л(0) = Ft f 1,-^,.... = <7, (<* (0,.... qr(t)),
< Po\t) A)v))
где/ = 0,1, 2,
Для анализа динамики нормированных цен используется сле-
дующая система обыкновенных дифференциальных уравнений:
k = \,...,r.
Отметим, что системы (13.3.1) и (13.2.3) не являются эквива-
лентными в математическом смысле.
Аналогично случаю ненормированных цен используется по-
нятие вектора равновесия q системы (13.3.1) и анализируется по-
ведение траектории нормированных цен q(t) при неограниченном
возрастании времени t.
Вектор q* = (q“,..., q*) нормированных цен называется векто-
ром равновесия системы (13.3.1), если
<7*(91.->9г) = 0, (13.3.2)
к = \,...,г.
Вектор равновесия q представляет собой постоянное (стацио-
нарное) решение системы (13.3.1). В фазовом пространстве
, Яг вектор равновесия q изображается точкой (рис. 13.9),
в эволюционном пространстве Otyp ..., qr — лучом, параллельным
оси Ot и проходящим через точку q* в фазовом пространстве
—> 9г(рис. 13.10).
Если для любого вектора q°, близкого к вектору q*,
limq(t,q°) = q*, (13.3.3)
t
то говорят, что вектор равновесия q локальноустойчив (см. рис. 13.9
и 13.10). Символом q(t, обозначено решение системы (13.3.1),
удовлетворяющее начальному условию <?(0, qQ) = q°.
573
Если для любого начального вектора q° имеет место равенство
(13.3.3), то вектор равновесия q* называется глобально устойчи-
вым.
13.4. Достаточные условия локальной устойчивости
цен равновесия
13.4.1. Достаточные условие локальной и глобальной устойчи-
вости цен равновесия являются весьма жесткими. Для их форму-
лировки нам понадобятся некоторые понятия, которые сами по
себе также являются важными.
Квадратная матрица С = (су) называется матрицей Метцлера,
если все ее внедиагональные элементы Сд > 0, i ф j. Квадратная мат-
рица С = (с/у.) называется сильной матрицей Метцлера, если все
Cy>Q,i*J.
Говорят, что выполнено условие валовой заменимости, если
Bg(q) = ^^>0,i,J=l
574
Говорят, что выполнено условие сильной валовой заменимости,
если
О/>у
г, i*j,
W = ^T^>0’^==1
г, / *j.
С содержательной экономической точки зрения неравенство
ЭЛ(р) п . .( dG,(q) Л .
dpj dqj )
означает, что продукты (7, и G. являются взаимозаменяемыми (ес-
ли цена /х растет, то величина (избыточного) спроса на продукт G.
также растет).
Из условия валовой заменимости (сильной валовой замени-
мости) следует, что в моделируемой системе отсутствуют взаимо-
дополняемые продукты, что является сильным упрощением эко-
номической реальности.
13.4.2. В случае ненормированных цен достаточное условие ло-
кальной устойчивости цен равновесия формулируется так.
Пусть А(р) = Ау(р*)) — сильная матрица Метцлера. Пусть век-
тор равновесия р* > 0 и начальный вектор цен р° близок к лучу L* =
={1р1 0 <. 1 е £,}, тогда существует постоянная 1* = 1(р°), такая,
что
limp(/, р°) = 1*(р°)р*.
t
В случае нормированных цен достаточные условия локальной
устойчивости цен равновесия формулируются так:
1. Пусть B(q*) = (B^q)) — матрица Метцлера, i,J = 1,..., г.
Пусть
^>0,У=1,........
либо
^>го,у=1........г
и det#(<7*) = det(5..(/)) 0.
575
2. Пусть B(q') — матрица Метцлера, пусть число £ такое, что
матрица B(q*)+£/ > 0, а номер h такой, что (B(q) + ^Т)А > 0.
(*)
Пусть
эо0(^)>0 a?e(g*) Э(7О(/) ag0(/)
’ Э9| •" Ъг
Если выполнены условия пункта 1 или условия пункта 2, то
вектор равновесия q системы (13.3.1) локально устойчив.
Приведенные условия пунктов 1 и 2 являются достаточными
для использования теоремы Ляпунова о локальной устойчивости
по первому приближению вектора равновесия q* системы
(13.3.1).
Теорема Ляпунова об устойчивости по первому приближению
утверждает, что если нелинейную систему (13.3.1) заменить на
линейную однородную и если нулевой вектор линейной однород-
ной системы глобально устойчив, то вектор q* нелинейной систе-
мы (13.3.1) локально устойчив.
Суть линеаризации системы (13.3.1) состоит в следующем.
Для функции Gk(qv ..., q} выписываем разложение по формуле
Тейлора в окрестности точки q*'.
Ыч.....«З-СИ»!*...ft (?!-?. •)*
Э?| (13.4.1)
...^^ft-ft-)*^,..............г.
где слагаемое g означает остаточный член со вторыми частными
производными функции Gk(qv ..., q£.
В (13.4.1) Gk(q{,..., qk) = 0, ибо q = (q{,..., q*) — вектор равно-
весия системы (13.3.1), и следовательно, справедливы равенства
(13.3.2).
Полагая Zk = qk- qk и используя выражение
dqj
выпишем линеаризованный вариант системы (13.3.1) в виде одно-
родной линейной системы обыкновенных дифференциальных
уравнений первого порядка с постоянными коэффициентами
576
Zk=Bki(q*)Zi+...+Bkz(q*)zr, k = i,...,r. (13.4.2)
Если нулевой вектор z = (0, ..., 0) системы (13.4.2) глобально
устойчив, то вектор q* = (q{,.... q*) системы (13.3.1) локально ус-
тойчив.
Для глобальной устойчивости нулевого вектора z = 0 системы
(13.4.2) необходимо и достаточно, чтобы все собственные числа
матрицы B(q') = (By(q*)) имели отрицательные действительные
части.
В отличие от просто проверяемых условий пунктов 1 и 2 нача-
ла раздела 13.4.2 для использования приведенного необходимого
и достаточного условия следует отыскивать спектр матрицы B(q),
а это в общем случае требует больших вычислений. Однако при
решении примеров на анализ локальной устойчивости вектора q'
системы (13.3.1) целесообразно вычислять собственные значения
матрицы B(q‘) = (By(q')).
13.5. Достаточные условия глобальной устойчивости
цен равновесия
13.5.1. Приведем достаточные условия глобальной устойчивости
цен равновесия в случае ненормированных цен.
1. Пусть вектор цен равновесия р* и для любого вектора
Р = <Ро,Р\,Р2,...,Рг)>0, -^^->0, = i*j.
dpj
2. Пусть вектор цен равновесия р* > 0 п для любых // и pF,
рГ > 0, рР > 0, выполнена слабая аксиома выявленных предпочте-
ний, т.е. из неравенства pf F(pf) > pf F(p") следует, что рРF(p") <
<pPF(jf).
Если выполнены условия пункта 1 или условия пункта 2, то
вектор равновесия р глобально устойчив.
Замечание. Слабая аксиома выявленных предпочтений может
иметь место для векторов pf vipf, близких к вектору р*, но малове-
роятно, что она выполняется глобально.
13.5.2. Рассмотрим важное понятие доминирующей главной диа-
гонали квадратной матрицы Н.
37 - 7620
577
Квадратная матрица Н — матрица с доминирующей главной
диагональю, если существуют положительные постоянные ср
сг, такие, что при i = 1,..., г
Г
ci lA«1 > Т Cj \hij | (доминирование по /-й строке),
У=1
г
с, Ы > Xе; |М (доминирование по /-му столбцу).
/=1
/*'
Приведем достаточные условия глобальной устойчивости век-
тора равновесия д* в случае нормированных цен.
Пусть вектор равновесия д* системы (13.3.1) положителен.
Пусть существуют постоянные 0 < ср ..., сг, такие, что для любого
номера /, /= 1,..., г, и для любого вектора д > 0 справедливы нера-
венства
9 9G;(g) э?, V э<?,(?) , (13.5.1)
<7 эад С'' л М^д) Эд, (13.5.2)
Если выполнено неравенство (13.5.1) или (13.5.2), то вектор
равновесия д системы (13.3.1) глобально устойчив.
Замечание. Из (13.5.1) следует, что изменение на одну единицу
нормированной цены д. на продукт Gt, i = 1,..., г, меняет величину
избыточного спроса значительно сильнее, чем изменения на одну
единицу каждой из остальных нормированных цен.
13.6. Критические замечания по модели динамики цен
13.6.1. В теории динамики цен (в теории экономической динами-
ки) предполагалось, что технологические множества = 1,..., п,
фирм и функции полезности потребителей постоянны во времени,
откуда следует, что вектор цен равновесия р* не зависит от време-
ни. На самом деле это не так, ибо в реальной экономике и техноло-
578
гические множества № фирм, и функции полезности потребите-
лей меняются во времени и, следовательно, меняется вектор цен
равновесия р*(/). Тогда предлагается задача определения опти-
мальной траектории р(/, р°), удовлетворяющей начальному усло-
вию р(0,р°)=р(0), такой, что |р(ЛР°)~ Р*(0| О-
Эта задача называется задачей о погоне. Она относится к числу
трудных задач экономической динамики.
В моделях (13.2.3) и (13.3.1) динамики цен речь идет о траекто-
риях ненормированных и нормированных рыночных цен, кото-
рые формируются под влиянием рыночного спроса и предложе-
ния на каждый продукт. Под влиянием только рыночных сил те-
кущие цены должны двигаться к ценам равновесия.
В параграфах 13.4 и 13.5 приходится налагать на функции
Г0(р), •••’ Др) избыточного спроса достаточно жесткие ограниче-
ния для доказательства локальной и глобальной устойчивости цен
равновесия, что косвенно свидетельствует о том, что, скорее все-
го, одних рыночных сил недостаточно для обеспечения «правиль-
ной асимптотики» текущих цен, а возможно, требуются дополни-
тельные меры по жесткому регулированию механизма ценообра-
зования.
Вопросы для самоконтроля к главе 13
1. Каковы основные предпосылки простейшей линейной однопродук-
товой модели экономической динамики?
2. Какая существует связь между равенством y?(f) = y°(t) в простейшей
однопродуктовой модели экономической динамики и законом Валь-
раса в случае МЭД?
3. Что такое избыточный спрос?
4. На какой содержательной основе выписывается система обыкновен-
ных дифференциальных уравнений, описывающая поведение во
времени рыночных цен?
5. Какова взаимосвязь между вектором цен равновесия и вектором рав-
новесия системы обыкновенных дифференциальных уравнений,
описывающих динамику рыночных цен?
6. Каков экономический смысл нормирования текущих рыночных
цен?
7. Какое принципиальное отличие вектора равновесия в случае ненор-
мированных цен от вектора равновесия в случае нормированных
цен?
37*
579
8. Как формулируются определения локальной и глобальной устойчи-
вости вектора равновесия в случае ненормированных цен? Дайте
наглядную геометрическую интерпретацию локальной и глобальной
устойчивости в случае г = 1 (р = р0, р^ в фазовом и эволюционном
пространствах.
9. Как формулируются определения локальной и глобальной устойчи-
вости вектора равновесия в случае нормированных цен? Дайте на-
глядную геометрическую интерпретацию локальной и глобальной
устойчивости в случае г = 2 (q = (qv q2)) в фазовом и эволюционном
пространствах.
10. В чем суть содержательной интерпретации локальной устойчивости
вектора цен равновесия (в ненормированном и нормированном слу-
чаях)?
11. В чем суть содержательной интерпретации глобальной устойчивости
вектора цен равновесия (в ненормированном и нормированном ва-
риантах)?
12. Как формулируется условие валовой заменимости (сильной валовой
заменимости) в случае ненормированных (нормированных) цен?
Почему выполнение этого условия не вполне адекватно экономичес-
кой реальности?
13. Как формулируется достаточное условие локальной устойчивости
вектора равновесия в случае ненормированных цен? Дайте содержа-
тельную интерпретацию достаточного условия.
14. Как формулируется достаточное условие локальной устойчивости
вектора равновесия в случае нормированных цен?
15. Что представляет собой линеаризация нелинейной системы обыкно-
венных дифференциальных уравнений?
16. Как формулируются необходимое и достаточное условия глобальной
устойчивости нулевого вектора линейной однородной системы
обыкновенных дифференциальных уравнений с постоянными коэф-
фициентами?
17. Как формулируется теорема Ляпунова об устойчивости по первому
приближению?
18. Как формулируются достаточные условия глобальной устойчивости
вектора равновесия в случае ненормированных цен? Каков уровень
адекватности этих условий?
19. Как формулируются достаточные условия глобальной устойчивости
вектора равновесия в случае нормированных цен? Дайте содержа-
тельную интерпретацию этим условиям.
20. Как формулируется задача о погоне?
21. Какова взаимосвязь между жесткостью достаточных условий локаль-
ной и глобальной устойчивости вектора равновесия и реальной ди-
намикой нерегулируемых рыночных цен?
580
Задачи и упражнения для самоконтроля к главе 13
1. Найдите все векторы равновесия q > 0 у следующих систем вида
(13.3.1):
a) q=qtf-2), r= 1;
б) q=35^2-2^-19, r= 1;
в) q-q2-q-l, r= 1;
г) Щ = ~9i ~ql+q2, q2 = ~9? ~Ч2‘,
Д) 91 = (91 -1)(92 - О, 92 = 9i92 " 2;
e) qt = ln(-tf, +q2), q2 =qt-q2-l.
2. Опишите все векторы равновесия р* S 0 следующих систем вида
(13.2.1):
а) А)=®> A=A’_^l_^
Ро Ро
2
б) Ро = б, А =—2--2-^--3;
Ро Ро
в)
А) = °.
г)
А)=3>
• -Pl Pi а -К Р\ •
А = з“„ ’ р2 „—з’
Ро Ро Ро Ро
„3 „3 „2 и3
а h ~Р\____Рг_
и3 + и3 ’ Рг ” »2 »3 *
Ро Ро Ро Ро
3. Исследуйте на локальную и на глобальную устойчивость векторы
равновесия q > 0 следующих систем вида (13.3.1):
а) 9 = 9(93-2);
б) 0=35^2-2^-19;
в) 9 = 92-9-2;
г) 9 = 92 - 29 - 3;
Д) 9i=-9i“9i2 + 92> 92=391-92-92;
е) 91=1п(-91+9^), 92=9i-92-1-
581
Вопросы и тесты для контрольных работ к главе 13
1. Если в момент t избыточный спрос на продукт Gk строго положите-
лен, то ценаpk(t)\
а) строго убывает;
б) строго возрастает;
в) ведет себя неоднозначно.
2. Фазовые траектории цен q(f):
а) не пересекаются и не касаются друг друга;
б) могут касаться;
в) могут пересекаться;
г) могут и пересекаться, и касаться.
3. Условие сильной валовой заменимости в случае ненормированных
цен означает, что:
а) продукт Gq обязательно есть продукт Гиффена;
б) продукт Gq обязательно есть нормальный продукт;
в) среди пар продуктов (GQ, GJ, ..., (<70, GJ обязательно найдется
хотя бы одна пара взаимодополняемых продуктов;
г) все продукты взаимодополняемы.
4. Если у системы дифференциальных уравнений для нормированных
цен два (или более) вектора равновесия, то:
а) они оба обязательно локально устойчивы;
б) они оба обязательно локально неустойчивы;
в) обязательно один вектор локально устойчив, другой — локально
неустойчив;
г) для каждого из них нет глобальной устойчивости.
Задачи для контрольных работ к главе 13
1. Найдите все векторы равновесия q £ 0 у следующих систем, выпи-
санных для случая нормированных цен:
а) ? = (?-1)(д2-4);
б) q = q2-q-f>\
в) = ?2=912+?2-17;
г) ?i=?i02-4> ?2=912+02-17;
2. Исследуйте на локальную и глобальную устойчивость векторы рав-
новесия q* > 0 следующих систем, выписанных для случая нормиро-
ванных цен:
а) 4 = (9-2)(92-9);
582
6) q=q2+q-6;
в) qi=q?~ql~l5, q2=Qi+^~l7;
г) 71=ад-4> $2 = ?12+02-17-
Глава 14
МОДЕЛИРОВАНИЕ
ДИНАМИЧЕСКОГО РАВНОВЕСИЯ
14.1. Динамическая модель в матричной форме
и оптимизация ее траекторий
14.1.1. Динамическая модель в матричной форме (ДММФ), пред-
ложенная Дж. фон Нейманом, состоит из двух сфер: производ-
ственной (ПС) и монетарной (МС). Основными понятиями моде-
ли являются основной производственный процесс (для кратко-
сти — процесс), интенсивность (кратность) его использования,
продукт и цена продукта. В модели реализован принцип «затра-
ты — выпуск».
Предполагается, что существует конечное число (скажем, л)
основных производственных процессов. В каждом основном про-
изводственном процессе продукты затрачиваются и выпускаются
в определенных количествах. Формально основной производ-
ственный процесс Qt (/ = 1,..., п) представляет собой 2/и-мерный
вектор-строку (а., д.) = (а.р ..., а1т; Ьа,..., bjm), где т — число про-
дуктов G. (j = 1,..., т). Вектор-строка at = (ozl,..., а!т) называется
вектором затрат, вектор-строка Ь. = (Ь.{,..., bjm) — вектором выпус-
ка. Число ay (i = 1,..., n;j = 1,...» т) показывает, сколько единиц
продукта G. затрачивается в основном процессе Qt (если продукт G.
в процессе Q. затрачивается, то а.. > 0, если не затрачивается, то
Оу = 0). Аналогично число bt. (/ = 1,..., n;j = 1,..., т) показывает,
сколько единиц продукта Gj выпускается в основном процессе Q.
(если продукт Gj в процессе Ql выпускается, то by. > 0, если не вы-
пускается, то by = 0).
584
Количества затрачиваемых и выпускаемых продуктов «привя-
заны» к одному периоду времени («атому» времени), который на-
зывается производственным периодом и может, например, рав-
няться одному году, т.е. время предполагается дискретным. Упо-
рядоченная совокупность (производственных) периодов t
называется временном промежутком ДММФ. Число Т периодов
временнбго промежутка называется временном горизонтом
ДММФ. Предполагается, что число основных процессов п, число
m продуктов и количества затрачиваемых и выпускаемых в каж-
дом процессе продуктов от периода к периоду не меняются.
Предположения о возможности соединенных затрат (a.j > О,
aik > 0’-/ * и соединенных выпусков (Ьи > 0, д/г > 0, 1ф г) отражают
важные фрагменты экономической реальности. Например, в про-
цессе, описывающем функционирование доменной печи, затра-
чиваются в определенных количествах кокс, железная руда и чу-
гун, а выпускаются чугун и шлаки. Чугуна выпускается больше,
чем его затрачивается.
Если два основных процесса Qf и Qk используются одновре-
менно, то каждый продукт G. теперь затрачивается в количестве
а.. + ак. единиц и выпускается в количестве b.. + bkj, т.е. использо-
вание основных процессов Q. и Qk можно толковать как процесс
Qi + Qk, который равен покоординатной сумме процессов Q. и Qk.
Если основной процесс Q. используется с интенсивностью
(кратностью) Zj > 0, то каждый продукт G. теперь затрачивается и
выпускается в количествах zp9 и zfiy единиц соответственно,
т.е. основной процесс Q., используемый с интенсивностью zp
можно толковать как процесс ztQj, который равен покоординатно-
му произведению процесса Q. на число zr Если процесс Q. не ис-
пользуется, то его интенсивность z, = 0, верно и обратное.
Теперь естественно определить допустимый процесс Q как
неотрицательную линейную комбинацию +... + ZnQn основ-
ных процессов ..., Qn с неотрицательными коэффициентами
..., z„- Векторы затрат и выпуска этого допустимого процесса Q
соответственно имеют вид zA wzB, т.е. Q = (zA, zB). Здесь £ = (zp ...,
Z„) — неотрицательный вектор-строка, а (п х т) — матрицы А и В
составлены из строк fl- и bj (i = 1,..., л) соответственно. Матрица
А > 0 называется матрицей затрат, матрица В £ 0 — матрицей вы-
пуска.
Множество всех допустимых процессов (zA, zB) образует неот-
рицательный конус CN в неотрицательном ортанте пространства
585
Е2т, конус CN натянут на основные процессы (ор Z>(),(ап, Ья).
Этот конус называется технологическим множеством ПС ДММФ
или технологией ПС ДММФ.
Предполагается, что смежные периоды t и t + 1 между собой
связаны следующим образом:
Z(t + t = 0,1,Т- 1, (14.1.1)
где?(Г +1) = (z/Г +1),.... z„(t +1)) uztf) = (Zj(0, ...» Z„(0) - векторы
интенсивностей использования основных процессов Q{,..., Qn в
периоды t + 1 и t соответственно. Векторное неравенство (14.1.1)
означает, что в следующем периоде t + 1 можно затратить каждого
продукта G. в количестве z(t + 1)</, не большем, чем его было вы-
пущено в предыдущем периоде t в количестве z(t)bl,j = 1,..., /и.
Здесь а!'и У — j-е столбцы матриц А и В соответственно.
Формально ПС ДММФ представляет собой систему линей-
ных неравенств
2(1)Л< 2(0)5, (14.1.2)
z(t + 1)А —z(t)B<.O,t = O, 1,..., Т- 1, (14.1.3)
z(/)£0,/ = 0,1,..., Т-1. (14.1.4)
Равенство z(0) =z° (z° — заданный вектор) называется началь-
ным условием. Упорядоченная совокупность векторов интенсив-
ностей z(l),..., 2(7) называется допустимой траекторией интен-
сивностей ПС ДММФ (с начальным условием z(0) = 2°). Очевид-
но, модельное время ПС ДММФ совпадает с реальным
временем.
К неравенствам (14.1.2)—(14.1.4) можно добавить максимизи-
руемую целевую функцию
Д2(1),...,г(Т))(тах). (14.1.5)
Тогда получится задача математического программирования,
размерность которой будет зависеть не только от чисел п и т, но и
от временнбго горизонта Т ПС ДММФ. Допустимая траектория
2(1),..., z(T) интенсивностей, максимизирующая целевую функ-
цию, называется оптимальной траекторией интенсивностей ПС
ДММФ (с начальным условием 2(0) = z°). Оптимальная траекто-
рия интенсивностей обозначается символом 241), —, (сим-
вол «штрих» к производной отношения не имеет).
Целевая функция (14.1.5) может быть как терминальной
z(T)u(max), (14.1.6)
586
(14.1.7)
так и интегральной
z(l)u(l) z(2)u(2) ^z(T)u(T)
1+5 (1+5)2 (1+8)г
Здесь число — дисконтирующий множитель, а число
5 > 0 — норма дисконтирования.
Далее в основном рассматривается терминальная целевая
функция (14.1.6) с целевым вектором и — («р ..., «п).
ПС ДММФ и экстремальные задачи, построенные на ее основе,
имеют широкий класс содержательных областей на микро- и мак-
роэкономическом уровнях. Каждый основной процесс ПС ДММФ
может описывать производственный способ фирмы, которую тогда
следует толковать как совокупность основных производственных
процессов, которые могут конкурировать между собой. Каждый
основной производственный процесс ПС ДММФ может описы-
вать отрасль национальной экономики, производственную сферу
которой тогда следует толковать как совокупность своих отраслей.
Основной производственный процесс может описывать процесс
хранения, транспортировки продуктов. Если продукт Gj является
капиталом, то его можно включить в вектор выпуска bt с учетом
годовой нормы износа : b.. = (1 - ^.)а.. В конце этого параграфа
рассматриваются конкретные примеры ПС ДММФ.
14.1.2. Каждый продукт <^впериоде/имеетцену/>у.(/)>0,у = 1, ...,т.
Тогда скалярные произведения ap(t) и bp(t) представляют собой
общую «стоимость» затрат и общую «стоимость» выпуска в период
t соответственно. В связи с тем что вектор выпуска bt фактически
используется в следующем после выпуска периоде t + 1, естест-
венно прибыль, которую дает процесс Q., определить так:
bp(t + 1) - ap{t). (14.1.8)
Поскольку в условиях чистой конкуренции в долговременном
промежутке прибыль фирмы равна нулю, постольку естественно
предположить, что прибыль (14.1.8) процесса Q, неположительна:
bjpit+xy-aiplf)^, / = 1,..., л. (14.1.9)
Формально МС ДММФ представляет собой систему линей-
ных неравенств
Ap(t)-Bp(t+l)>Q, t = 0,1,...,Т-1, (14.1.10)
587
Ар(Г&Вр(Т+\),
(14.1.11)
p{f)>Q, / = 0,1,...,T. (14.1.12)
Равенствоp(T +1) = р° (р° — заданный вектор) называется на-
чальным условием. Упорядоченная совокупность векторов назы-
вается допустимой траекторией цен МС ДММФ (с начальным
условиемр(Т + 1) = р°). Формальная структура МС ДММФ тако-
ва, что ее модельное время противоположно реальному времени.
К неравенствам (14.1.10)—(14.1.12) можно добавить терми-
нальную целевую функцию
z(0)5p(l)(min). (14.1.13)
Если и = Вр(Т + 1), то задача линейного программирования
(14.1.13), (14.1.10)—(14.1.12) будет сопряженной к задаче линей-
ного программирования (14.1.6), (14.1.2)—(14.1.4).
Допустимая траектория цен р(Т),..., р(1), минимизирующая
целевую функцию (14.1.13), называется оптимальной траекторией
цен МС ДММФ (с начальным условиемр(Т+ 1) =р°). Оптималь-
ная траектория цен обозначается символом р'(Т), ..., р’(1)
(в модельном времени) или символом//(1), ...,//(7) (в реальном
времени). Отметим, что разнонаправленность модельного и реаль-
ного времени, которая имеет место для модели (14.1.10)—(14.1.12)
((14.1.13), (14.1.10)—(14.1.12)), существует для любой задачи, со-
пряженной к исходной динамической задаче (в математическом
программировании, теории оптимального управления).
Динамическая модель в матричной форме (ДММФ) представ-
ляет собой объединение своих производственной и монетарной
сфер, т.е. систему линейных неравенств (14.1.2)—(14.1.4) и
(14.1.10)—(14.1.12).
14.1.3. ПС ДММФ охватывает в качестве частных случаев широ-
кие классы динамических межотраслевых моделей (ДМОМ) с ла-
гом капитальных вложений продолжительностью в один год и
более одного года. Содержательными областями ДМОМ являют-
ся национальные и региональные экономики, так что с точки
зрения содержательных областей ДМОМ — это модели макроэко-
номические. С точки зрения структурно-математической ДМОМ
относятся к моделям микроэкономики подобно тому, как модель
общего экономического равновесия также относится к моделям
микроэкономики.
588
ДМОМ в замкнутом варианте с постоянными во времени мат-
рицами AL, Ни Fl (Al — матрица коэффициентов прямых матери-
альных затрат с учетом затрат на возмещение выбытия основного
производственного капитала, FL — матрица основного и оборот-
ного капитала, Н— матрица замыкания) имеет вид
FLx(l)<(I - AL-Н+FL)x(0), (14.1.14)
FLx(t+l)-(I-AL-H + FL)x(f)£Q, / = 0,1,...,Т-1, (14.1.15)
x(Z)>0, / = 0,1,...,Т, (14.1.16)
гдех(/) — вектор выпусков отраслей.
Полагая в (14.1.14)—(14.1.16)
A = Fl', B = (I-Al-H+Fl)', z(t)=x'(t) (14.1.17)
(здесь штрих —символ транспонирования), получаем, что ДМОМ
в замкнутом варианте укладывается в формальную схему ПС
ДММФ (14.1.2)—(14.1.4).
ДМОМ в замкнутом варианте, в которой учитывается эколо-
гический фактор, также укладывается в формальную схему ПС
ДММФ (14.1.2)—(14.1.4).
ДМОМ в замкнутом варианте с учетом затрат на борьбу с за-
грязнением окружающей среды имеет вид
(T^ + AF^ + fpW+l)^
£ [/ - (4° + АЛр + 42) + АЛ[2) + Н)+F^ + AF/° + Ff > ] х (14.1.18)
хх(О, / = 0,1,...,Т-1,
где F£(l) и FjW — матрицы основного и оборотного капитала;
Л£(1) — матрица коэффициентов прямых материальных затрат без
учета затрат на возмещение выбытия основного производствен-
ного капитала; Л£(2) — матрица амортизации; AF£(I) — матрица
прироста основного производственного капитала для устранения
загрязнений окружающей среды; АЛ£(2) — матрица прироста мат-
рицы амортизации в связи с приростом основного производ-
ственного капитала; А4£(1) — матрица прироста текущих матери-
альных затрат в связи с наличием дополнительных материальных
затрат для устранения загрязнений окружающей среды.
Полагая в (14.1.18), (14.1.16)
Л = (F£(1)+AF£(1)+F£(2)),
589
B = (I-(A,W + ДЛ ,(1) +Л,(2)+ДЛ,(2) + Н) + F.W + AF,(1) + F,(2>Y,
x Lt Lt la Lt Lt Lt Lt
zit) =y(0,
получаем, что ДМОМ в замкнутом варианте с учетом затрат на
борьбу с загрязнением окружающей среды укладывается в фор-
мальную схему ПС ДММФ (14.1.2)—(14.1.4).
14.1.4. ПС ДММФ допускает обобщения в разных направлениях.
В частности, возможен переход от постоянных во времени матриц
А и В к переменным Ait) и Bit), которые позволяют учитывать на-
учно-технологический прогресс в экзогенной форме. В этом слу-
чае ПС ДММФ описывается следующей системой линейных не-
равенств:
z(lM(l)£z(<W), (14.1.19)
г(/ + 1)Л(Г+1)-г(/)5(Г)<0, / = 0,1,...,Т-1, (14.1.20)
z(/)>0, / = 0,1,...,Т. (14.1.4)
Терминальная (14.1.6) и интегральная (14.1.7) целевые функ-
ции при этом не корректируются.
МС ДММФ описывается в этом случае такой системой линей-
ных неравенств:
Ait) pit) - Bit) pit +1) > 0, t = 0,1,..., Т -1, (14.1.21)
А(Т)р(Т)^и (14.1.22)
pit)>Q, / = 0,1,...,Т. (14.1.12)
Промежуточным вариантом между ДММФ с постоянными и
переменными во времени матрицами Ait) и Bit) является ДММФ
с асимптотически постоянными матрицами Ait) и Bit).
14.2. Стационарные траектории динамической
модели в матричной форме и их основные
характеристики
14.2.1. Упорядоченный набор векторов интенсивностей
z(l),..., ziT) такой, что для любого номера t, t = 1,..., Т- 1, имеет
место равенство z(f + l) = vz(0, называется стационарным (точ-
нее, квазистационарным) набором интенсивностей. Вектор zit)
590
называется элементом стационарного набора интенсивностей.
Очевидно, набор интенсивностей является стационарным, если
для любого номера t, t = 1,..., Т, имеет место равенство z(t) = q v's.
Здесь скалярные постоянные c{nv положительны и вектор s > О
такой, что его октаэдрическая норма И равна единице:
1$! = $!=1. Число v >0 и вектор5> 0 называются основны-
ми характеристиками стационарного набора интенсивностей.
Число v > 0 называется коэффициентом постоянного пропорцио-
нального (т.е. сбалансированного) роста стационарного набора
интенсивностей, вектор s £ 0 называется структурой стационар-
ного набора интенсивностей. Если число v > 1, то имеем случай
постоянно растущего стационарного набора; если число v = 1, то
имеем случай собственно стационарного набора
(qv=z(l)=...=z(T)); если число 0 < v < 1, то имеем случай посто-
янно убывающего стационарного набора. Стационарный набор
интенсивностей представляет собой набор сбалансированного
развития (изменения) интенсивностей во времени. Все элементы
стационарного набора интенсивностей расположены на луче Ls,
натянутом на вектор s (рис. 14.1). Стационарный набор называет-
ся стационарной траекторией интенсивностей ПС ДММФ, если
его элементы удовлетворяют неравенствам (14.1.3), (14.1.4). Вы-
полнение неравенства (14.1.2) не обязательно, т.е. стационарная
591
траектория интенсивностей ПС ДММФ может и не быть допусти-
мой траекторией интенсивностей ПС ДММФ.
Для стационарной траектории интенсивностей ПС ДММФ
имеем
c^nsA-cxVsB<A,t = Q, 1,..., Т- 1
или после сокращения на положительный множитель c}v*
vsA^sB. (14.2.1)
Верно, очевидно, и обратное. Если основные характеристики
v и s стационарного набора удовлетворяют векторному неравен-
ству (14.2.1), то этот набор есть стационарная траектория интен-
сивностей ПС ДММФ.
14.2.2. Из всех стационарных траекторий интенсив-
ностей ПС ДММФ интерес представляют траектории с макси-
мальным коэффициентом v постоянного пропорционального
роста интенсивностей, т.е. траектории максимального постоян-
ного пропорционального роста интенсивностей (ТрМсППРИ).
Для определения этих траекторий следует решить задачу квад-
ратичного программирования
v(max), (14.2.2)
vsAlsB, (14.2.3)
v>0, (14.2.4)
s>0, (14.2.5)
|л| = 1. (14.2.6)
Решение (v, s) этой задачи представляет собой основные ха-
рактеристики ТрМсППРИ г(/) = с1(у)'?, / = 0, 1,..., Т. Основные
характеристики определяются только матрицами А и В, т.е. техно-
логией ПС ДММФ. Задача (14.2.2)—(14.2.6) называется моделью
максимального постоянного пропорционального роста интен-
сивностей (ММсППРИ). Теория максимального постоянного
пропорционального роста интенсивностей (ТеМсППРИ) анали-
зирует ММсППРИиихоптимальныерешения(9, ?). ВТеМсППРИ
и в ММсППРИ цены не фигурируют.
Задача квадратичного программирования (14.2.2)—(14.2.6)
эквивалентна следующей задаче на максимин:
592
(14.2.7)
v = max min
s20
. (sb1
___ $6”
за1 ’ ’ sam
в которой дроби вида (0/6) и [sbJ/(ty не рассматриваются.
Переход от задачи (14.2.2)—(14.2.6) к задаче (14.2.7) осуще-
ствляется с помощью следующих простых рассуждений.
Векторное неравенство (14.2.3) переписывается в координат-
ной форме
vsa' < sb',..., vs(f < sbm. (14.2.8)
Получается система т неравенств с одной неизвестной v. Ре-
шение этой системы имеет вид
. . . (sb'
v($)=min —г,
$<г
sbm
sam
(14.2.9)
где дроби вида (0/0) и (sbJ/о) не рассматриваются, ибо они соот-
ветствуют неравенствам vsd < $У, которые удовлетворяются при
любых значениях v. Для отыскания v остается найти max v($).
И=1
14.2.3. Задачи вида (14.2.7) относятся к классу задач негладкой
оптимизации и в общем случае достаточно трудноразрешимы.
Однако при л = 2 задачи вида (14.2.7) легко решаются на основа-
нии элементарных геометрических соображений. Проиллюстри-
руем это обстоятельство на двух примерах.
Пример 14.2.1
Для матриц Л и В
л-Г0’3
10,6
°’4l 5-1 °’6
0,2/ ~[o,5
0,3
0,4
имеем
. [ sb' sb2
v = max min —r,—y
sa sa
Sj+S2=l
. Г 0,6$! + 0,5$з 0,3$]+0,4$2
max min ---------!----—---------!--------
s,+s2=i 10,3$,+0,6$, 0,4$,+0,2$2.
5,2:0,5,2:0 v
S2~ 1
= max min
oss,si
0,5+0,1$] 0,4-0,!$!
0,6-0,3$!’ 0,2+0,2$i
(/) (Я) )
38 - 7620
593
Нарисуем эскизы графиков обеих дробно-линейных функций
(I) и (II) (рис. 14.2). Очевидно, графиком функции
является линия FEG, ибо при
v(s) = min
0<5]<5( v(s) = min
0,54-0,15, 0,4-0,151
0,6-0,35] ’0,2+0,25] ?
0,5+0,15( 0,4-0,15] 0,5+0,15]
0,6-0,35] ’ 0,2+0,25] J~ 0,6-0,35] ’ а П Р И
, . [0,5+0,15] 0,4-0,15]] 0,4-0,15] „
5, <5, <1 v(5) = min —-----L,---------L ---------L. Изэлемен-
11 1^0,6-0,35] ’0,2+0,25] J 0,2+0,25]
тарных геометрических соображений max v(5) достигается при
0Ss,Sl
5] =5]. Для определения 5t следует решить уравнение
0,5+0,15] 0,4-0,15]
——- = ——— - , которое сводится к квадратичному уравне-
нию 52 — 305] + 14 = 0, корнями которого являются числа
5]=15+>/2П, 5]=15->/2ТТ.
Выбираем корень 5( =15-V211 =0,47, который попадает в от-
резок 0 £ 5] £ 1, второй корень 5t = 15+VzTT > 1 является посторон-
ним.
Осталось определить коэффициент роста:
594
- = 5+?i = 5+15-7211 = 7 + Т2П
V 6-3$i ~ 6-45+3-У2П ~ 18
= 1,1959.
Таким образом, задача на максимин имеет решение
v = 7-+^^ =1,1959, s{ = 15-/211 = 0,47;
s2 = 1-5] =/211-14 = 0,53.
Пример 14.2.2
Для матриц А и В
р,3 0,5Л /0,6 0,4Л
[о 0,3/ ДО 0,7/
имеем
. ( sb1 sb2
v= max mm —г,—у
*,+*2=1 sa sa .
*,го,*2&о v 7
= max min
0,65] 0,4.^ +0,7s2
/,35] ’ 0,55] +0,s2
max min
02s, 21
0,65] 0,7-0,35]
0,35]’0,3+0,25]
I (Z) (ZZ)
Нарисуем эскизы графиков обеих функций (I) и (И) (рис. 14.3).
Из элементарных геометрических соображений графиком функ-
ции v(s) = min
'0,6si 0,7-0,35/
/,35] ’ 0,3 + 0,25! ?
является множество, состоящее
из ломаной линии FGH (без точки F) и изолированной точки
Е = (0,7/3) Точка Г= (0,2) не рассматривается, ибо при 5] = 0 левая
дробь 0,б5]/0,35! имеет вид (0/0) и поэтому не учитывается. Самой
высокой точкой этого множества (графика функции v(s)) является
точка Е. Следовательно, задача на максимин имеет решение 5, = 0,
52 =1, v=J^. Непосредственно проверяется, что 5(=0,
v-0,35, <0,65. => •—0,30<0,60=> 0 = 0,
1 1 3
v(0,3+0,25])<(0,7-0,35])=> |0,3<0,7=>0,7 = 0,7.
38*
595
14.2.4. Упорядоченный набор векторов цен p(i),...,p(T), такой,
что для любого номера t, t = Т— 1,1, имеет место равенство
^p(t+l)=p(t), называется стационарным (точнее, квазистацио-
нарным) набором цен. Вектор p(t) называется элементом стацио-
нарного набора цен. Очевидно, набор цен является стационар-
ным, если для любого номера — Т, имеет место равенство
p(t) = с2£г+,~'г. Верно и обратное. Здесь скалярные постоянные ct
и £ положительны и вектор г > 0 такой, что его октаэдрическая
норма (г) равна единице: |r| = /i +...+г„ =1. Число £ > 0 и вектор
г > 0 называются основными характеристиками стационарного
набора цен. Число £ > О называется коэффициентом постоянного
пропорционального (т.е. сбалансированного) падения стацио-
нарного набора цен, вектор г > 0 называется структурой стацио-
нарного набора цен. Если число £ > 1, то цены падают в реальном
времени и растут в обратном времени; если число £ = 1, то цены
постоянны (случай истинно стационарного набора цен
с2г = р(1) =... = р(Т)); если число 0 < £ < 1, то цены растут в реаль-
ном времени и падают в обратном времени. Стационарный набор
цен представляет собой набор сбалансированного развития (из-
менения) цен во времени.
596
К вопросу о рациональности рассмотрения цен, падающих в
реальном времени, мы вернемся в следующем параграфе 14.3.
Все элементы стационарного набора цен расположены на луче
Lr, натянутом на вектор г. (рис. 14.4). Стационарный набор цен
р(1),...,р(7') называется стационарной траекторией цен МС
ДММФ, если его элементы удовлетворяют неравенствам (14.1.10),
(14.1.12). Выполнение неравенства (14.1.11) не обязательно,
т.е. стационарная траектория цен МС ДММФ может и не быть
допустимой траекторией цен МС ДММФ.
Для стационарной траектории цен МС ДММФ имеем
Ac£T-'^r>Bc£T~!r, t = 1,..., Т— 1
или после сокращения на положительный множитель с£т~*
t^r>Br. (14.2.10)
Верно, очевидно, и обратное. Если основные характеристики
и г стационарного набора цен удовлетворяют векторному нера-
венству (14.2.10), то этот набор есть стационарная траектория цен
МСДММФ.
14.2.5. Из всех стационарных траекторий р(1),..., р(Т) цен МС
ДММФ интерес представляют траектории с минимальным коэф-
фициентом | постоянного пропорционального падения цен в ре-
альном времени (т.е. с минимальным коэффициентом | постоян-
597
ного пропорционального роста цен в обратном к реальному вре-
мени), т.е. траектория минимального постоянного
пропорционального падения цен (ТрМиППРИ) в реальном вре-
мени.
Для определения этих траекторий следует решить задачу квад-
ратичного программирования
(14.2.11)
1-Аг*Вг, (14.2.12)
^>0, (14.2.13)
г>0, (14.2.14)
|г| = 1. (14.2.15)
Решение rj этой задачи представляет собой основные ха-
рактеристики ТрМиППРИ p(0 = c2(^)r+I-zr, t = 1,..., Т. Основные
характеристики | и г определяются только матрицами А и В,
т.е. технологией ПМ ДММФ.
Задача (14.2.11)—(14.2.15) эквивалентна следующей задаче на
минимакс:
| = minmax|(14.2.16)
/•го (a,r a„r j
И=1 v 1 " 7
в которой дроби вида (0/0) и (О/az) не рассматриваются.
Переход от задачи (14.2.11)—(14.2.15) к задаче (14.2.16) осуще-
ствляется с помощью следующих простых рассуждений.
Векторное неравенство (14.2.12) переписывается в координат-
ной форме
(14.2.17)
Получается система п неравенств с одной неизвестной Ре-
шение этой системы имеет вид
£(/•)=max -2- ,
апг) (14.2.18)
где дроби вида (0/0) и (0/<у) не рассматриваются, ибо они соот-
ветствуют неравенствам > bf, которые удовлетворяются при
любых значениях ij. Для отыскания | остается найти min^(r).
г£0
кН1
598
14.2.6. Задачи вида (14.2.16) аналогичны задаче (14.2.7), они от-
носятся к классу задач негладкой оптимизации и в общем виде
трудноразрешимы. Однако при т = 2 задачи вида (14.2.16) легко
решаются на основании элементарных геометрических соображе-
ний. Проиллюстрируем это обстоятельство на двух примерах.
Пример 14.2.3 (продолжение примера 14.2.1)
Для матриц
Г 0,3 0,4^)
[о,6 0,2/ ДО,5 0,4j
имеем
= min max
П+г2=1
^0,r2S0
/
min max
r^o’rjSO '
0,6г, + 0,3r2 0,5/j +0,4r2
0,3/j +0,4r2 ’0,6/j +0,2r2
' l\r
min max
0,3+0,3/j 0,4+0,1/i
0,4-0, Ц ’0,2+0,4/1
I (/) (Я)
Нарисуем эскизы графиков обеих дробно-линейных функций
(I) и (II) (рис. 14.5). Очевидно, графиком функции
599
t. . I О,3 + О,3л 0,4+0,1л
c(r) = max --------L,---------L
ъ V0,4-0,lr, 0,2+0,4r(
является линия FEG, ибо при
О< г( < /5 £(/•,) = max
q </, < 1 £(/]) = max
а при
0,3+0,3/] 0,4+0,1/11 0,4+0,1g
0,4-0,1/, ’ 0,2+0,4rJ~ 0,2+0,4r{ ’
0,3+0,3л 0,4+0,1л 1 0,3+0,Зл „
--------L,—----—L =---------L. Изэлемен-
0,4-0,1/j 0,2+0,4r, J 0,4-0,1/,
тарных геометрических соображений min £(r) достигается при
/1=4. Для определения q следует решить уравнение
0,3+0,Зл 0,4+0,1л
——уру = д 2+04* ’ котоРое сводится к квадратичному уравне-
нию 13г? + 18л, — 10 = 0, корнями которого являются числа
_ -9+>/2П _ ... _ -9-ЛП
Л =---------= 0,425, л =--------.
1 13 ’ ’ 1 13
Выбираем корень i\ =--—---= 0,425, который попадает в
„ - -9-V2TT .
отрезок 0 < rj < 1, второй корень г, =-—-< -1 является посто-
ронним.
Осталось определить коэффициент падения:
^-^959.
g З+3/j 3+3 13
4-/J -9+^
13
Таким образом, задача на минимакс имеет решение
| = v= 7+^1аЦ959 - = ~9+^П 0 425 22-2^П
5 18 ' 13 2 13
Пример 14.2.4 (продолжение примера 14.2.2)
Для матриц
<0,3 0,5^ o_f°>6 0,4'
[о 0,3/ V0 °,7>
имеем
600
ё I b,r Кг । . (0,6я+0,4а 0,7a ।
<; = min maxi—,-^-l = min maxi——1—2 =
г,+г2=1 lfl,r a7r I r,+r2=i l 0,3л +0,5a 0,3a J
v ' 41 1 i/
r>=1-'i . fo,4+O,2r, 0,7(1-/;)
= min max —-------—L, -L--:——
(Er,si 0,5-0,2?i 0,3(1-75)
I (/) (Я) )
Нарисуем графики обеих функций (I) и (II) (рис. 14.6). Из эле-
ментарных геометрических соображений графиком функции
£(r) = max
0,4+0,2/j 0,7(1-/;/
0,5-0,2/5’0,3(1-75),
является множество, состоящее
из горизонтальной линии FG (без точки б) и изолированной точки
£=(1,2). Точка G = (1,7/3) не рассматривается, ибо при r{ = 1
правая дробь 0,7(1-г()/0,3(1-Г1) имеет вид (0,0) и поэтому не учи-
тывается. Самой низкой точкой этого множества является точка
Е. Следовательно, задача на минимакс имеет решение = 1,
г2 = 0Д = 2.
Непосредственно проверяется, что
^O,3(l-/5)>O,7(l-/i)=>O = O,
^(0,5-0,2/i) > (О,4+О,2/5) =>
=» <0,3 > 0,6 => 2-0,3 >0,6.
601
Отметим, что в случае матриц А и В примеров 14.2.1 и 14.2.3
имеем v = | = (7 + V211)/18. В случае матриц А и В примеров 14.2.2
и 14.2.4 v = 7/3>2 = |.
Пример 14.2.5
Для матриц
<0,3 0,4А <0,6 0,ЗА
[о 0,2/ ^”[о O,3J
имеем
. [ sb1 sb2
v = max min —г, —=-
*,+*2=1 sa )
= max min
S|+S2=l
0,65] 0,35, +0,3s2 5
40,35, ’ 0,45] +0,2s2>
f2—i-i,
= max min
025,21
0,65t 0,3
0,3s2’0,2+0,251
l (Л (П)
Нарисуем эскизы графиков обеих дробно-линейных функций
(I) и (II) (рис. 14.7). Очевидно, графиком функции
v(5]) = min
0,65]
0,3
——,------------I является линия EG. Точка F = (0, 2)
0,351 0,2(1 + 5! )J
не рассматривается, ибо при 5j = 0 левая дробь 0,65/0,35] имеет
вид (0,0) и поэтому не учитывается. Самой высокой точкой линии
602
£6 является точка E= (0,3/2). Следовательно, задача на максимин
в рассматриваемом случае имеет вид v = 3/2,?, = 0, s2 = 1.
Непосредственное проверяется, что
3
v0,3?. < 0,6?. => — 0,3 0<0,6-0 => 0<0,
1 1 2
3
v(0,4S] + 0,2?2) < 0,3?! + 0,3?2 => ~ 0,2 • 1 <, 0,3-1 => 0,3 £ 0,3.
Для | имеем
й • (°ir
q= mm max —,——
'i+'j=i v a,r a,r,
hr . (0,6г, + 0,За 0,3а Y'i-1
-,-£- = mm maxi-2—!——-,-2—L -
>i+r2=i 10,3/;+0,4а 0,2a,
п20,г220 v 1 L
= min max
'i+'H
^20,r2S0
0,3+0,3/j 0,3(1-/j)
0,4-0,1Г]’0,2(1-q) '
(/) (//) J
Нарисуем графики обеих функций (I) и (II) (рис. 14.8). Оче-
видно, графиком функции Е(я)=max) 2*--21^11212
^0,4-0,1/10,2(1-^)
ется линия E}E2G. Точка F= (1, 3/2)не рассматривается, ибо при
fj = 1 правая дробь 0,3(1 — г()/0,2(1 — г() имеет вид (0/0) и поэтому
явля-
603
не учитывается. Самыми низкими точками графика функции £(г,)
являются точки отрезка ЕХЕ2 с координатами (rj, 3/2)» где 0 £ rt £ 2/3
(при г, = 2/3 линии (I) и (II) пересекаются, что проверяется непо-
средственно). Следовательно, задача на минимакс имеет решение
2
£ = 3/2, r2 = l-q.
Непосредственно проверяется, что
<3 Л Л
£(0,Зг, + 0,4г2) £ 0,6/j + 0,3r2 => I — • 0,4-0,3 lr2 +1 -• 0,3-0,6г, 1^0=^
2
=> (0,6 - 0,3)(1 - гх)+(0,45 - 0,6>|) > 0 => 0,6 £ 0,9г, => гх * 0.
3 3
£0,2(l-r,)>0,3(l-r,)=> j-0,2--|-0,2/i >О,3-О,3г, =>
=> 0,3-0,Зг, >0,3-0,Зг, => 0>0.
т> - й 3
В рассматриваемом примере v=£=-, и вектор г определяется
неоднозначно. 2
14.3. Динамическое равновесие динамической модели
в матричной форме
14.3.1. Динамическим равновесием (ДР) динамической модели в
матричной форме (ДММФ) называется пара стационарных тра-
екторий интенсивностей и цен
z(/) = c1(v,)/s, / = 1,...,Т, (14.3.1)
X(0 = C2(v‘)T+1'zr\ t = (14.3.2)
таких, что основные характеристики (v’,s‘)» (v’,r‘) этих траекто-
рий удовлетворяют условиям
vsA<sB, (14.3.3)
vAr>Br, (14.3.4)
v£0, (14.3.5)
s£0, (14.3.6)
M=b (14-3.7)
r£0, (14.3.8)
И=1. (14.3.9)
604
Таким образом, ДММФ находится в ДР, если развитие в ней
осуществляется по стационарным траекториям (т.е. по траектори-
ям сбалансированного развития) интенсивностей и цен.
Система неравенств и уравнений (14.3.3)—(14.3.9) называется
моделью динамического равновесия (МДР) ДММФ. Теория ди-
намического равновесия (ТДР) анализирует свойства МДР. Тра-
ектория (14.3.1) называется траекторией интенсивностей ДР,
траектория (14.3.2) называется траекторией цен ДР.
Коэффициент V* называется коэффициентом роста ДР, векто-
ры s' иг — векторами интенсивностей и цен ДР. Для краткости
ДР ДММФ называется набор из коэффициента роста v‘ и векто-
ров s' и г' интенсивностей и цен ДР, что символически показыва-
ется так: p(v‘) = {v‘; s'; г* J.
ДР с коэффициентом роста v* называется невырожденным,
если
s’Br’>0, (14.3.10)
и вырожденным, если
s'Br’=0. (14.3.11)
Для данного коэффициента роста V* могут быть ДР как невы-
рожденные, так и вырожденные. Содержательный интерес пред-
ставляют коэффициенты роста V*, для которых обязательно су-
ществуют невырожденные ДР. Для этих коэффициентов V* также
могут быть и вырожденные ДР.
Если ДР |v‘; s’; г’J невырожденное, то s'Br > 0, откуда следу-
ет, что z'(t)Bp'(t) = ci(y’)s'B(c2lv')T'¥{~tf =clc2(v')T+is'Br' >0,
т.е. «общая стоимость» z'(t)Bp’(t) в ценах равновесия p'(f) выпуска
z’(f)B равновесия положительна и постоянна во времени. Это оз-
начает, что в случае роста интенсивностей равновесия цены рав-
новесия должны падать в реальном времени: постоянство денеж-
ной массы в условиях экономического роста означает необходи-
мость падения цен во времени.
Множество всех коэффициентов роста V*, для которых обяза-
тельно существуют невырожденные ДР, называется невырожден-
ным спектром ДММФ. Множество всех коэффициентов роста v‘,
для которых существуют лишь вырожденные ДР, называется вы-
рожденным спектром ДММФ.
605
ДР ДММФ является важным понятием как с содержательной
экономической точки зрения, так и с формально математической
точки зрения.
С математической точки зрения МДР, точнее векторные нера-
венства (14.3.3) и (14.3.4), представляет собой нетривиальное
обобщение задачи на собственные числа и правые и левые соб-
ственные векторы как для матрицы
Dv =lv, wD = Xw,
так и для матричного пучка
Gv = XHv, wG = kwH.
14.3.2. В связи с ДР ДММФ возникают три вопроса: вопрос о су-
ществовании невырожденного ДР, вопрос о числе различных ко-
эффициентов роста X" в случае невырожденного и вырожденного
спектров и вопрос об условиях дополняющей нежесткости.
В предположении существования ДР p(v*) = |v’; s'; г* J, которое
может быть как невырожденным, так и вырожденным, для дока-
зательства условий дополняющей нежесткости не требуется на-
кладывать на матрицы А и В никаких условий.
В предположении существования ДР p(v’) = |v’; s'; f J для до-
казательства того, что невырожденный спектр ДММФ обязатель-
но содержит не более min(«, /и) различных коэффициентов роста
v*, также не требуется накладывать на матрицы Аи В никаких ус-
ловий.
Для доказательства существования ДР используются различ-
ные достаточные условия.
Первое достаточное условие было предложено Дж. фон Ней-
маном в1932 г. (опубликовано на немецком языке в 1938 г.)
(см. Neumann von J. (1945—1946): пусть матрицы А и В — матрицы
с неотрицательными элементами, т.е. А > О, В > 0, и пусть Л + В > 0.
Тогда существует единственный коэффициент v‘, который может
принадлежать как невырожденному, так и вырожденному спектру
и для которого справедливы равенства v’ = v = | (см. пара-
граф 14.2).
Если Л > 0 и В = 0, то V* =0; если А = 0 и В> 0, то v’ =+«> (си-
туация рога изобилия). Оба этих крайних варианта являются чис-
то формальными и не представляют интереса с содержательной
точки зрения.
606
Второе достаточное условие существования ДР было пред ло-
жено в работе трех авторов (Дж. Кемени, О. Моргенштерн,
Дж. Томпсон), опубликованной в журнале Econometrica в 1956 г.
(см.: J.G. Кетепу, О. Morgenstern, G.L. Thompson (1956)).
Пусть матрицы Ап В неотрицательны и в каждой строке мат-
рицы Лив каждом столбце матрицы В есть хотя бы один ненуле-
вой элемент. Тогда существует хотя бы один коэффициент v’,
принадлежащий невырожденному спектру, причем наибольший
из таких v* равен V, а наименьший равен | (см. параграф 14.2).
14.3.3. Если в ДР |v’; s’; г* J вектор г > 0, то v* = V. Приведем про-
стое достаточное условие существования коэффициента v’, при-
надлежащего невырожденному спектру.
Пусть п = т, detS # 0, матрица D = АВ~1 примитивна и правый
собственный вектор г матрицы G=В~1А, соответствующей числу
Перрона матрицы G (матрицы D и G имеют одинаковые спектры),
положителен.
Тогда существует единственный коэффициент V*, принадле-
жащей невырожденному спектру, с единственным ДР
p(v’)=|v’;s’;r’J.
Докажем это.
По теореме Г. Фробениуса примитивная матрица D = АВ~Х
имеет число Перрона X’ и левый вектор s’ Перрона, такие, что
s'D = X’ s', откуда следует, что (1/Х')5”Я = S'В, т.е. число v* = 1/Х* и
вектор s’ удовлетворяют неравенству (14.3.3) как равенству.
Аналогично для матрицы G имеем Gr’ =k’r, откуда вытекает
равенство
—Аг’ =Вг,
X'
т.е. число v' = 1/Х* и вектор г удовлетворяют неравенству (14.3.4)
как равенству.
Таким образом, набор •! v" = s', г’ > — ДР ДММФ.
IX J
Принадлежность v’ к невырожденному спектру следует из не-
равенства
s’Bf >0.
которое справедливо в силу того, что матрица В > 0 и векторы s’ и
г’ положительны.
607
Единственность v* вытекает из неравенств s’ >0 и г’ >0.
Пусть матрицы А и В имеют размеры п х т. Тогда может су-
ществовать не более min(« х т) различных коэффициентов роста
v’, принадлежащих невырожденному спектру ДММФ.
14.3.4. Пусть в ДР {v‘; s*; f J коэффициент роста v‘ принадлежит
невырожденному спектру ДММФ, тогда существует пара индек-
сов i и j, такая, что
s‘bj >0, rj >0 и s'jbjjfj >0.
Пусть коэффициенты роста v" и v' принадлежат невырожден-
ному спектру и таковы, что
v" > v' ({v", s", г"},{v', s', г'}).
Пусть две пары координат s", г" и s'k, гк таковы, что справедли-
вы неравенства з"1У > 0, г"> 0 и з'Ьк > 0, гк > 0.
Имеем
(ry5.°) (v">v')
v"s"aJ <s”bJ => v"s"?=s"i7>0=>s"?>0 =>
=> v’s”aJ < v"s”aJ = s”bJ => rj = 0.
Поскольку rk > 0 и r'j = 0, постолькуj * к. Следовательно, может
быть не более чем т различных коэффициентов роста v’, принад-
лежащих невырожденному спектру.
Аналогично показывается, что может быть не более чем п раз-
личных коэффициентов роста V*, принадлежащих невырожден-
ному спектру.
14.3.5. Условия дополняющей нежесткости для ДР |v‘, s’, r’j име-
ют вид:
Если sj >0, то v’azr’ =д(г’, если v’atf >bjr', то s/ =0 (первое
условие дополняющей нежесткости).
Если rj > 0, то v's‘aJ =s‘bJ, если v's'aJ <s'bJ, то rj = 0 (второе
условие дополняющей нежесткости).
Дадим содержательную интерпретацию первому условию до-
полняющей нежесткости.
Из равенства v’atf >Ь^‘ следует, что
О1Сг(у‘)Т~м =f ^bfC^iy')74 f, т.е. bip'(t+\)-alp'(t) = G. Верно и
608
обратное. Из неравенства у'ар'^г' следует, что
bjр (/ +1) - atр' (/) < 0. Верно и обратное.
Отсюда следует, что если основной процесс Q:- в ДР функцио-
нирует, то он дает максимальную прибыль в ценах равновесия.
Если основной процесс Q. в ДР не дает максимальной прибыли, то
он в ДР не функционирует, ибо s'; = 0.
Дадим содержательную интерпретацию второму условию до-
полняющей нежесткости.
Из равенства v’s'aJ =sbJ следует, что cl(v')>+ls'aJs'b1,
т.е. z (t+l)aj = z (t)bJ, т.е. продукт G. в периоде t + 1 затрачивается
ровно в том количестве, в котором он был выпущен в периоде t.
Верно и обратное. Из неравенства vs’aJ <s’bJ следует, что
z'(t + l)aJ < z’(t)bJ. Верно и обратное. Отсюда вытекает, что если в
ДР продукт G. имеет положительную цену р}(1) = с2(у)т+1~‘ /у >0,
то в периоде t + 1 он затрачивается ровно в том объеме, в котором
он был выпущен в предыдущем периоде t. Если же в ДР в периоде
t + 1 продукт G. затрачивается в меньшем объеме, чем он был вы-
пущен в предыдущем периоде /, то продукт G. является свободным
в ДР, т.е. его цена p'j(t) = c2(y‘)T+[~t rj = 0.
Выше уже отмечалось, что наибольший коэффициент v* роста
ДР равен v, а наименьший равен Отсюда следует, что среди тра-
екторий интенсивностей и цен ДР обязательно находятся
ТрМсППРИ и ТрМиПППЦ (см. параграф 14.2).
Верно и обратное. Пару v, s, которая является оптимальным
решением ММсППРИ, можно пополнить вектором г , таким, что
тройка {v, s, г} станет ДР ДММФ. Пару (|, г), которая является
оптимальным решением ММиПППЦ, можно пополнить векто-
ром s, таким, что тройка s, г} станет ДР ДММФ.
Таким образом, установится взаимосвязь между тремя моде-
лями: МДР, с одной стороны, и ММсППРИ и ММиПППЦ, с
другой стороны.
Эта взаимосвязь аналогична двум теоремам экономики благо-
состояния, которые описывают взаимосвязь между эффективнос-
тью по Парето (ее аналогом являются ММсППРИ и ММиПППЦ)
и конкурентным равновесием (его аналогом является ДР).
14.3.6. В заключение этого параграфа приведем доказательство
первого условия дополняющей нежесткости. Будут приведены
рассуждения, аналогичные рассуждениям, используемым для до-
39 - 7620
609
казательства второй теоремы двойственности в линейном про-
граммировании. Однако следует добавить, что исторически
двойственный подход в теории ДР ДММФ был предложен на ряд
лет раньше, чем появилась теория двойственности в линейном
программировании да и само линейное программирование.
Векторное неравенство
v's'A<s'B (14.3.12)
распишем покоординатно:
уУа1 <s'b1,...,vsa" <s‘bm.
Умножив каждое скалярное неравенство на соответствующую
координату /f £0,...,/£ >0 и сложив полученные неравенства,
будем иметь
v‘s’alri +...+n s’amr^ <,s'blr{ + ...+s‘bmr^,
откуда следует, что
v* s‘ (a1 rf +...+amrm ) < s’(blr\ +...+bmr^ ) • (14.3.13)
Принимая во внимание равенства a1r1*+...+a'”z£ = Аг,
bl/\ +...+Ьтг^ =Вг, перепишем неравенство (14.3.13) так:
v's'Ar <s’Br. (14.3.14)
Аналогично поступив с векторным неравенством
у’ Аг >Вг‘,
получим неравенство
v's’Ar’ >s’Br. (14.3.15)
Из (14.3.14) и (14.3.15) следует равенство
v’s’Ar’ =s'Br\ (14.3.16)
которое следует расписать в виде скалярного произведения
(v'a/ - bf )+...+з'п (у anr’ -bnr') = 0. (14.3.17)
В каждом слагаемом s’^v’^r" -bp), z = l,...,w, оба множителя
(s‘i и v’anr‘ -Ьпг’) неотрицательны. Следовательно, левая часть
равенства (14.3.17) содержит все слагаемые одного знака. Отсюда
следует, что каждое слагаемое левой части равенства (14.3.17) рав-
но нулю, т.е. s'iiv'Ojr -b/г), i — 1,..., п. Поэтому если s] >0, то
vatr -b;f = 0. Если же v’atr > Ь(г, то обязательно s’t = 0.
610
Таким образом, первое условие дополняющей нежесткости
доказано. Второе условие дополняющей нежесткости доказывает-
ся аналогично.
14.4. Взаимосвязь между оптимальными
траекториями и траекториями равновесия
динамической модели в матричной форме
14.4.1. На основе ПС ДММФ (14.1.2)—(14.1.4) (см. параграф 14.1)
строится ММсППРИ (14.2.2)—(14.2.6) (см. параграф 14.2), благо-
даря которой строятся ТрМсППРИ z(O = c1(v),s, t= 1,..., Т, кото-
рые являются траекториями интенсивностей равновесия. На ос-
нове ПС ДММФ строятся терминально оптимальные траектории
интенсивностей^(1), ...,^(7).
Оптимальная траектория интенсивностей ПС ДММФ зависит
от начального вектора г(0) = г°, целевого вектора и от матриц А и
В. Основные характеристики V и s ТрМсППРИ и, следовательно,
сама ТрМсППРИ зависят только от матриц А и В, т.е. от техноло-
гического множества ДММФ.
Говорят, что оптимальная траектория интенсивностей обла-
дает магистральным свойством, если она в своем развитии сначала
приближается (не обязательно монотонно) к лучу Ls, натянутому
на вектор s , затем в течение ряда периодов элементы оптималь-
ной траектории располагаются около луча Ls, мало отличаясь от
соответствующих элементов z(t) ТрМсППРИ, и в конце
временного промежутка ДММФ оптимальная траектория интен-
сивностей может отойти от луча Ls для того, чтобы попасть в тер-
минальную точку ^(7) (рис. 14.9, на котором точками (кляксами)
показаны элементы терминально оптимальной траектории,
а крестиками — элементы ТрМсППРИ, которые все расположе-
ны на луче Ls). Роль самой магистрали играет луч Ls.
Термин «магистраль» означает скоростную автомобильную
дорогу, по которой автомобилист передвигается с максимально
возможной скоростью. К магистрали автомобилист едет по мест-
ной дороге, от магистрали также по другой местной дороге, чтобы
попасть в требуемый пункт. Термин «магистральное свойство оп-
тимальной траектории» был введен (П. Сэмуэльсоном) в связи с
тем, что характер ее поведения похож на стратегию передвижения
39*
611
автомобилиста, который должен проехать из одного города в дру-
гой, используя магистраль, если расстояние между городами от-
носительно велико. (Если расстояние невелико, следует ехать по
местной дороге, не выезжая на магистраль.)
Отметим, что теоремы, которые дают достаточные условия
существования магистрального эффекта, называются теоремами
о магистрали. Существует много теорем о магистрали, доказан-
ных разными авторами. Совокупность теорем о магистрали со-
ставляет магистральную теорию. Магистральная теория включает
также теоремы о магистрали для оптимальных траекторий цен,
которые не только играют вспомогательную роль, но и представ-
ляют самостоятельный интерес.
14.4.2. Приведем достаточное условие существования магист-
рального свойства у терминально оптимальной траектории
ДММФ с квадратными матрицами А и В.
Пусть набор {v*, s', г* J —ДР ДММФ и нормированные векто-
ры s' >0 (р| = 1) и г* >0 (р’|=1) являются единственными. Пусть
число а* > 0 — простой корень характеристического уравнения
det(S - wA) = 0 и на окружности радиуса а нет других корней этого
уравнения.
Пусть матрица В > 0 (матрица А > 0).
612
Пусть вектор > 0 и его носитель включает носитель вектора
s’ А.
Пусть s’w>0 и существует постоянная с, такая, что и<сАг'.
Тогда для любого сколь угодно малого числа е > 0 найдутся номера
Tj (Tj = Т](е)) и Т3 (Т3 = Т3(е)), такие, что для любой терминально
оптимальной траектории ДММФ при всех номерах t, удовлетво-
ряющих неравенствам Т\ £ t< Т— Т3, справедливо неравенство
d(z'(f),s')<E.
Номера Tj и Т3 от Г не зависят. Номер 7’(7’> Тх + 7*3) может
быть любым. Из неравенств s’ >0 и г’ >0 следует (см. параграф
14.3), что коэффициент роста ДР v* = v, т.е. траектория интенсив-
ностей равновесия?*(/)=q(v*Уs’,t= 1,..., Г,являетсяТрМсППРИ
ДММФ 1,..., Т.
Векторы s’(=s) и г’(=г) называются магистральными векто-
рами интенсивностей и цен, коэффициент роста v’(= v) называет-
ся магистральным коэффициентом роста.
Символом обозначено угловое расстояние между
векторами ?'(0 и s’:
d[z'(f),s’)=
Z'(t)
k'(o|
где |?'(0| = ?i'(0+•••+zh(t) — октаэдрическая норма вектора ?'(0;
октаэдрическая норма вектора (z'(O/k'(O|)-s*.
Неравенство d(z'(f),s’}<£. означает, что все элементы
(7\<t<T— Т3) оптимальной траектории ^(1),..., г'(7) расположе-
ны внутри е — конуса, натянутого на октаэдрическую е-окрест-
ность вектора s’.
Номер Тх может зависеть от ?(0) = ?°, номер Т3 — от целевого
вектора и. С ростом номера Гудлиняется второй (основной) учас-
ток оптимальной траектории интенсивностей, а длины первого и
третьего участков с ростом номера Г не меняются.
Неравенство d(z'(t),s’^<E описывает поведение второго
участка оптимальной траектории интенсивностей ^(1),..., ^(7) и
означает, что этот второй участок близок к соответствующему
613
участку ТрМсППРИ. Таким образом, второй участок оптималь-
ной траектории аналогичен передвижению автомобилиста по ма-
гистрали с максимально возможной скоростью.
14.4.3. Поведение первого участка оптимальной траектории ин-
тенсивностей зависит от начального вектора г(0) = г°, поведение
последнего участка оптимальной траектории интенсивностей за-
висит от целевого вектора и. Характер поведения второго (основ-
ного) участка оптимальной траектории, по сути, регламентирует-
ся только технологическим множеством ПС ДММФ и не зависит
ни от начального вектора z(0) = z°, ни от целевого вектора и.
Отсюда можно сделать по крайней мере три важных теорети-
ческих вывода.
Во-первых, в ДММФ с продолжительным временном гори-
зонтом не требуется большая точность для определения терми-
нального целевого вектора и, ибо он влияет, по существу, только
на третий участок (т.е. на «хвост») оптимальной траектории, кото-
рый можно отбросить, уменьшив временной горизонт ТДММФ.
Во-вторых, решение задачи динамической оптимизации,
т.е. нахождение оптимальной траектории интенсивностей z'(l),
..., Z'(T) в случае продолжительного временнбго горизонта Т, по-
лучается лишь, по существу, благодаря максимальному постоян-
ному пропорциональному росту, основные характеристики
v’(= v) и 5*(= S) которого эндогенны и определяются лишь техно-
логическим множеством ДММФ. Итак, в случае продолжитель-
ного временнбго горизонта достижение оптимальности возможно
только через максимальный постоянный пропорциональный рост
с эндогенными основными характеристиками.
В-третьих, магистральное свойство можно использовать для
рационального решения так называемой проблемы «хвоста» в
экономической динамике, суть которой заключается в том, что
всякая динамическая модель с конечным временном горизонтом
Тимеет свой модельный «конец света» в последний период Т. По-
этому в последние годы временнбго промежутка оптимальная
траектория переходит в режим «после нас хоть потоп». В связи с
этим на элементы оптимальной траектории в последние годы вре-
менного промежутка следует накладывать дополнительные огра-
ничения, элиминирующие неадекватное реальности поведение
этой оптимальной траектории. Формирование этих дополнитель-
ных условий, особенно в задачах прогнозирования, представляет
614
собой нетривиальную задачу. На основании магистрального
свойства можно рекомендовать в качестве терминального вектора
интенсивностей магистральный вектор интенсивностей s‘(=s).
С прикладной точки зрения магистральное свойство полезно
тем, что на его основе можно строить траектории структурно ап-
проксимирующие оптимальные, которые искать проще опти-
мальных. Делается это так. Сначала решается ММсППРИ и опре-
деляются магистральный коэффициент v*(=v) и магистральная
структура интенсивностей s'(=s), а затем определяется только
первый участок выхода на магистраль. Второй и третий участ-
ки — это участки развития по магистрали с наибольшим коэффи-
циентом роста. Первый участок (участок выхода на магистраль)
естественно рассматривать как участок перехода из начального
состояния z(0) = z° ДММФ в сбалансированное состояние, опре-
деляемое вектором s*.
Обобщение теорем о магистрали на случай асимптотически
постоянных матриц основано на том, что в ММсППРИ
(14.2.2)—(14.2.6), с помощью которой определяются магистраль-
ный коэффициент и магистральный вектор интенсивностей,
в качестве матриц Л и В берутся предельные матрицы асимптоти-
чески постоянных матриц A(t) и B(t). В случае переменных во
времени матриц A(t) и B(f) «прямая» магистраль превращается в
«косую», на которой коэффициент и магистральная структура
вектора интенсивностей уже перестают быть постоянными, как в
классических теоремах о магистрали.
Вопросы для самоконтроля к главе 14
1. Назовите четыре базовых понятия динамической модели в матрич-
ной форме (ДММФ).
2. В какой форме в ДММФ реализован основополагающий принцип
«затраты — выпуск»?
3. Что представляет собой основной производственный процесс? При-
ведите примеры его содержательной интерпретации.
4. Дайте содержательное обоснование покоординатному сложению и
умножению на неотрицательное число основных производственных
процессов.
5. Как в производственной сфере (ПС) ДММФ учитывается научно-
технологический прогресс?
6. Что такое технологическое множество (технологический конус) ПС
ДММФ?
615
7. Как осуществляется переход от описания в матричной форме ПС
ДММФ к ее описанию в конической форме?
8. Как осуществляется переход от описания в конической форме ПС
ДММФ к ее описанию в матричной форме?
9. Как содержательно интерпретируется условие замкнутости ПС
ДММФ?
10. Как определяются допустимые и оптимальные траектории интен-
сивностей ПС ДММФ?
11. Как определяется прибыль основного производственного процесса?
12. Какова взаимосвязь между реальным и модельным временем в ПС и
монетарной сфере (МС) ДММФ?
13. Как определяются допустимые и оптимальные траектории цен МС
ДММФ?
14. Что такое стационарная траектория интенсивностей ПС ДММФ?
Каковы ее основные характеристики? Дайте геометрическую интер-
претацию стационарной траектории интенсивностей.
15. Что такое траектория максимального постоянного пропорциональ-
ного роста интенсивностей (ТМсППРИ)? Что такое модель макси-
мального постоянного пропорционального роста интенсивностей
(ММсППРИ) ПС ДММФ? Что такое теория максимального посто-
янного пропорционального роста интенсивностей (ТеМсППРИ)?
Преобразуйте ММсППРИ в задачу на максимин.
16. Что такое стационарная траектория цен МС ДММФ? Каковы ее ос-
новные характеристики? Дайте геометрическую интерпретацию ста-
ционарной траектории цен.
17. Что такое траектория минимального постоянного пропорциональ-
ного падения цен (ТМиПППЦ)? Что такое модель минимального
постоянного пропорционального падения цен (ММиПППЦ) МС
ДММФ? Что такое теория минимального постоянного пропорцио-
нального падения цен (ТеМиПППЦ)? Преобразуйте ММиПППЦ в
задачу на минимакс.
18. Как определяется динамическое равновесие (ДР) ДММФ? Дайте
развернутую и краткую версии ДР ДММФ.
19. Что такое траектория роста интенсивностей ДР и ее основные харак-
теристики?
20. Что такое траектория падения цен ДР и ее основные характеристи-
ки?
21. Что такое модель динамического равновесия (МДР) ДММФ? Что
такое теория динамического равновесия (ТеДР)?
22. Как можно охарактеризовать взаимосвязь между МДР ДММФ,
с одной стороны, и ММсППРИ ПС ДММФ и ММиПППЦ МС
ДММФ, с другой стороны?
23. Как определяются понятия невырожденного и вырожденного спект-
ров ДММФ?
616
24. Сформулируйте достаточные условия существования ДР ДММФ.
25. Каковы мощности невырожденного и вырожденного спектров
ДММФ?
26. Как формулируются условия дополняющей нежесткости ДР ДММФ?
Приведите доказательства условий дополняющей нежесткости.
27. Что такое магистральное свойство оптимальной траектории интен-
сивностей ПС ДММФ? Приведите формулировку одной из теорем о
магистрали.
28. В чем теоретическое значение магистрального свойства?
29. В чем заключается прикладное значение магистрального свойства?
Задачи и упражнения для самоконтроля к главе 14
1. Приведите конкретный пример фрагмента экономической реаль-
ности, который можно описать с помощью ПС ДММФ.
2. Покажите, что замкнутая динамическая межотраслевая модель
(ЗДМОМ) укладывается в формальную схему ПС ДММФ.
3. Докажите, что если г > 0, то V* = V (см. параграфы 14.2 и 14.3).
4. Докажите, что если з* > 0, то V* = £ (см. параграфы 14.2 и 14.3).
5. Пусть А — матрица затрат, В — матрица выпуска ДММФ.
Для каждой пары матриц
(0,3 0,5Л (0,6 0,2А
5Л‘ “[о,4 0,2]’ “[о,1 О,?]
Л в-
1
2
5.2. А
1
а) найдите основные характеристики (v,5) ТрМсППРИ, решив
задачу на максимин. Выпишите ТрМсППРИ;
б) найдите основные характеристики (£, г) ТрМиПППЦ, решив
задачу на минимакс. Выпишите ТрМиПППЦ;
в) в случае V = £ выпишите ДР |V*, 5*, г j. Проверьте условия до-
полняющей нежесткости;
г) в случае v>£ опишите вырожденный спектр ДММФ;
д) в случае v>£ опишите все ДР } {невырожденные и
вырожденные) ДММФ.
6. Приведите пример матриц Л и Б ДММФ, таких, что V* = V, но среди
векторов 5* нет положительных.
7. Приведите пример матриц Л и Б ДММФ, таких, что V* = но среди
векторов г нет положительных.
Тесты для контрольных работ к главе 14
1. Продолжительность траектории перехода из начального состояния в
сбалансированное для ПС ДММФ не зависит от:
а) начального состояния z°;
б) углового расстояния между начальным и сбалансированным со-
стоянием;
в) сбалансированного состояния;
г) продолжительности временнбго промежутка ПС ДММФ.
2. Коэффициент роста ДР ДММФ является наибольшим, если:
а) целевой вектор ПС ДММФ положителен;
б) вектор цен равновесия положителен;
в) вектор интенсивностей равновесия положителен;
г) вектор интенсивностей нулевого (базового) периода положите-
лен.
Из возможных ответов
1) только а); 4) только г), в);
2) только б); 5) только а), в);
3) только в); 6) только а), г)
выберите наилучший.
3. Коэффициент роста ДР ДММФ является наименьшим, если:
а) целевой вектор ПС ДММФ положителен;
б) вектор цен равновесия положителен;
в) вектор интенсивностей равновесия положителен;
г) вектор интенсивностей нулевого (базового) периода положите-
лен.
Из возможных ответов
1) только а);
2) только б);
3) только в);
выберите наилучший.
4) только г);
5) только а), б);
6) только а), г)
618
4. Коэффициент роста ДР ДММФ является единственным, если:
а) целевой вектор ПС ДММФ положителен;
б) вектор цен равновесия положителен;
в) вектор интенсивностей равновесия положителен.
Из возможных ответов
1) только а); 4) только а), б);
2) только б); 5) только б), в);
3) только в); 6) только а), в)
выберите наилучший.
5. Основные характеристики траектории максимального постоянного
пропорционального роста интенсивностей определяются:
а) начальными условиями (при t = 0);
б) конечными условиями (при t = 0);
в) структурными параметрами (матрицами АиВ);
г) целевой функцией (целевым терминальным вектором и);
д) длиной временнбго промежутка ПС ДММФ.
6. Теорема о магистрали для ПС ДММФ:
а) устанавливает связь на продолжительном временнбм промежут-
ке между оптимальной траекторией ПС ДММФ и траекторией
максимального постоянного пропорционального роста интен-
сивностей;
б) позволяет прогнозировать структурные параметры ПС ДММФ
на далекую перспективу;
в) дает рациональное решение проблемы выбора терминальной
целевой функции для ПС ДММФ в случае продолжительного
временнбго промежутка;
г) позволяет определить оптимальную продолжительность
временнбго промежутка модели.
Из возможных ответов
1) только а), б); 4) только б), в);
2) только а), в); 5) только в), г)
3) только а), г);
выберите наилучший.
7. Магистральный темп роста и структура магистрального вектора ин-
тенсивностей ПС ДММФ определяются:
а) ее начальным (базовым) вектором;
б) ее технологическим множеством; *
в) ее целевым вектором (вектором и);
г) первым участком ее оптимальной траектории.
8. Наиболее естественной является следующая (генетическая) связь
между теориями экономической динамики:
а) ТО-» ТеМсППРИ-> ТДР;
619
б) ТДР-> ТО-> ТеМсППРИ;
в) ТО-> ТДР-> ТеМсППРИ;
г) ТДР -> ТеМсППРИ -» ТО;
д) ТеМсППРИ-> ТО-> ТДР
(ТО — теория оптимизации).
9. В случае разрешимой модели максимального постоянного пропор-
ционального роста интенсивностей в ее решение в качестве элемента
входит:
а) конечное число различных коэффициентов роста, для которых
существуют невырожденные положения равновесия;
б) бесконечное число различных коэффициентов роста, для кото-
рых существуют вырожденные положения равновесия;
в) ни одного коэффициента роста;
г) только один коэффициент роста.
10. Если оптимальная траектория интенсивностей обладает магистраль-
ным свойством, то не следует:
а) задавать конечные условия;
б) сглаживать ее первый участок;
в) сглаживать ее второй участок;
г) сглаживать ее третий участок;
д) строить траекторию, которая ее аппроксимирует.
11. Модель максимального постоянного пропорционального роста ин-
тенсивностей представляет собой:
а) задачу линейного программирования;
б) двойственную пару задач линейного программирования;
в) задачу квадратичного программирования;
г) систему линейных неравенств;
д) задачу на собственное число и собственный вектор.
12. Погодовые структурные сдвиги на траектории интенсивностей наи-
более естественно оценивать с помощью следующего показателя:
а) наибольшее отношение одноименных координат векторов ин-
тенсивностей двух смежных периодов временндго промежутка;
б) отношение норм векторов интенсивностей двух смежных перио-
дов временндго промежутка;
в) угловое расстояние между векторами интенсивностей двух смеж-
ных периодов временндго промежутка;
г) косинус угла между векторами интенсивностей двух смежных
периодов временндго промежутка;
д) такого показателя не существует.
13. ПС ДММФ представляет собой:
а) задачу линейного программирования;
б) двойственную пару задач линейного программирования;
в) задачу квадратичного программирования;
620
г) систему линейных неравенств;
д) задачу на собственное число и собственный вектор.
14. МДР (матрицы затрат (А) и выпуска (В) таковы, что А £ О, В £ О,
Л + 5>0):
а) в динамическом равновесии свободный продукт имеет нулевую
цену;
б) функционирующие в динамическом равновесии основные про-
цессы дают максимальную (т.е. нулевую) прибыль;
в) для функционирования в динамическом равновесии безотноси-
тельно к длине временного промежутка необходимо наличие
неограниченных ресурсов (в том числе естественных факторов
производства).
Из возможных ответов
1) только а), б); 4) только а), в);
2) только б); 5) только б), в)
3) только а);
выберите наилучший.
15. Траектория максимального постоянного пропорционального роста
интенсивностей обладает следующим свойством:
а) ее погодовые элементы имеют разные структуры;
б) по всем интенсивностям она монотонна во времени;
в) в качестве ее начального вектора может быть взят любой ненуле-
вой неотрицательный вектор;
г) ее коэффициент роста зависит от целевого вектора (целевых век-
торов);
д) ее темп роста зависит от углового расстояния между структурами
ее начального вектора и начального вектора ПС ДММФ.
16. Элементы траектории максимального постоянного пропорциональ-
ного роста интенсивностей:
а) являются решением задачи линейного программирования;
б) определяются вектором интенсивностей базового года;
в) определяются вектором интенсивностей, задающим конечное
условие;
г) имеют постоянную структуру в течение всего временнбго проме-
жутка.
17. Если оптимальная траектория интенсивностей обладает магистраль-
ным свойством, то:
а) ее первый участок обязательно является монотонным;
б) ее второй участок обязательно является монотонным;
в) ее третий участок обязательно является монотонным;
г) первый участок траектории, которая ее аппроксимирует, обяза-
тельно является монотонным;
621
д) она позволяет определить оптимальную продолжительность
временнбго промежутка ПС ДММФ.
18. Теоретическую оценку продолжительности траектории перехода из
начального состояния в сбалансированное для ПС ДММФ дает:
а) длина временнбго промежутка;
б) длина третьего отрезка оптимальной траектории;
в) длина второго отрезка оптимальной траектории;
г) длина первого отрезка оптимальной траектории;
д) длина первого и второго отрезков оптимальной траектории.
19. На магистральный темп роста и структуру магистрального вектора
валовых выпусков существенно влияет:
а) продолжительность модельного временнбго промежутка;
б) целевой вектор;
в) начальное условие;
г) погодовая динамика угловых расстояний между векторами вало-
вых выпусков в первые годы временнбго промежутка;
д) матрица замыкания.
20. Теорема о магистрали для ПС ДММФ:
а) служит основанием для построения траектории, аппроксимиру-
ющей оптимальную в течение всего продолжительного
временнобго промежутка модели;
б) позволяет оценить уровень модельной сбалансированности эко-
номической системы в базовом году временнбго промежутка
модели;
в) дает рациональное решение проблемы «хвоста» в случае продол-
жительного временнбго промежутка ПС ДММФ;
г) дает рациональное решение проблемы сглаживания оптималь-
ной траектории на продолжительном временнбм промежутке
модели.
Из возможных ответов
1) только а), б), в); 4) только б), в), г);
2) только а), б), г); 5) только а), б)
3) только а), в), г);
выберите наилучший.
21. Комплексной характеристикой уровня сбалансированности в базо-
вом году развивающейся экономической системы, описываемой ПС
ДММФ, является:
а) выполнение начального условия;
б) коэффициент максимального постоянного пропорционального
роста интенсивностей;
в) угловое расстояние между базовым и магистральным векторами
интенсивностей;
622
г) угловое расстояние между векторами интенсивностей базового и
первого годов.
22. Процедура сглаживания оптимальной траектории интенсивностей
ПС ДММФ осуществляется в целях:
а) сохранения размерности ПС ДММФ;
б) усиления магистрального эффекта оптимальной траектории ПС
ДММФ;
в) корректировки магистрального вектора интенсивностей;
г) уменьшения разницы между интенсивностями смежных лет
временнбго промежутка;
д) корректировки магистрального коэффициента роста интенсив-
ностей.
23. Связь между двумя теориями экономической динамики осуществля-
ется посредством третьей теории экономической динамики:
а) ТДР, ТеМсППРИ, МТ;
б) ТДР, МТ, ТеМсППРИ;
в) ТО, МТ, ТеМсППРИ;
г) ТО, ТеМсППРИ, МТ;
д) МТ, ТеМсППРИ, ТО.
Задачи для контрольных работ к главе 14
1. Пусть А — матрица затрат, В — матрица выпуска ДММФ.
Для каждой пары матриц
Г 0,3 0.6А 5_р>5 0.2Л
1^0,4 0,2/ Д0,1 °>8J
1.2. А =
а) найдите основные характеристики (v, J) ТрМсППРИ, решив
задачу на максимин. Выпишите ТрМсППРИ;
623
б) найдите основные характеристики (£> ТрМиППРИ, решив
задачу на минимакс. Выпишите ТрМиППРИ;
в) в случае V = £ выпишите ДР {v’,s’,r’j. Проверьте условия до-
полняющей нежесткости;
г) в случае V > £ выпишите вырожденный спектр ДММФ;
д) в случае v>£ выпишите все ДР |v’,s’,r’} (невырожденные и
вырожденные) ДММФ.
2. Пусть в ДР |v’,s’,r’} вектор г таков, что Аг >0. Докажите, что
v* = V, и v’ принадлежит невырожденному спектру ДММФ.
3. Пусть в ДР |v’,s’,r’} вектор s' таков, что As' >0. Докажите, что
V* = £, и V* принадлежит невырожденному спектру ДММФ.
4. Пусть в ДР |v’, s’, г } векторы s’ и г таковы, что Аг > 0 и As* > 0.
Докажите, что V* — единственный коэффициент роста ДММФ и V*
принадлежит невырожденному спектру.
Глава 15
ВНЕШНИЕ ЭФФЕКТЫ
15.1. Отрицательные внешние эффекты
15.1.1. Внешними эффектами (экстерналиями) называются воз-
действия (неопосредованные рынком) одних экономических
агентов на результаты деятельности других. Внешний эффект на-
зывается отрицательным, если деятельность одного экономичес-
кого агента вызывает дополнительные издержки в деятельности
другого. Внешний эффект называется положительным, если дея-
тельность одного экономического агента уменьшает издержки в
деятельности другого. Таким образом, в случае отрицательных
внешних эффектов деятельность одних экономических агентов не
благоприятствует деятельности других. В случае положительных
внешних эффектов деятельность одних экономических агентов
благоприятствует деятельности других.
В этом параграфе рассматриваются отрицательные внешние
эффекты, в следующем — положительные.
Отрицательный внешний эффект имеет место, когда предпри-
ятия (металлургический завод, фирма по выращиванию поросят)
сбрасывает отходы в реку, используемую для рыбной ловли или
купания. В рассматриваемом примере внешний эффект представ-
ляет собой внешние издержки предприятия, загрязняющего реку.
Такие издержки выражаются в дополнительных издержках рыбо-
ловецких и туристических фирм, которые они имеют в связи с
тем, что должны принимать дополнительные меры по очистке
речной воды. Эти внешние издержки предприятием, загрязня-
ющим реку, не учитываются (поэтому они и называются внешни-
40 - 7620
625
ми). Следовательно, имеет место ситуация, когда предприятие,
загрязняющее реку, часть своих издержек (эта часть и есть внеш-
ние издержки) перекладывает (нерыночным способом) на другие
фирмы. Сокращая таким образом свои издержки, предприятие
получает конкурентное преимущество перед предприятиями, ко-
торые имеют дополнительные издержки для сокращения или
ликвидации своих отходов. Особо отметим, что это конкурентное
преимущество предприятие получает за счет деградации окружа-
ющей среды (в частности, загрязнения реки) и за счет переклады-
вания бремени дополнительных издержек на другие фирмы,
а также и на рядовых потребителей продуктов и услуг этих фирм.
Внешние издержки предприятия, загрязняющего окружа-
ющую среду отходами, которые оно выбрасывает в атмосферу че-
рез трубу, в которой нет очистных агрегатов, выражаются, в част-
ности, в дополнительных издержках граждан, которые вынуждены
чаще красить крыши, больше покупать лекарств, больше тратить
средств для временного переезда в рекреационные зоны и т.д.
15.1.2. Рассмотрим простейшую однопродуктовую модель, кото-
рая иллюстрирует суть отрицательных внешних издержек. Пусть
фирма функционирует в условиях чистой конкуренции и про-
изводит продукт (товар) 6^ в количестве единиц. Пустьр( — ры-
ночная цена одной единицы продукта Gv Если фирма макси-
мизирует прибыль при выпуске у} = у{, то
MC(yi) = pl,
где Л/С(у1) — частные предельные издержки фирмы Fj, которые
не включают дополнительные предельные издержки МЕС(у{), рав-
ные отрицательному внешнему эффекту (рис. 15.1). Сумма част-
ных предельных издержек МС(у{) и дополнительных предельных
издержек (внешних предельных издержек) МЕС(у^)
МС(у{) + МЕС(у{) = MSC(y{)
представляет собой предельные общественные издержки MSC(y})
(они по своей сути являются истинными предельными издержка-
ми фирмы Fj) На рис. 15.1 представлено также решение у уравне-
ния MSCiy^ =pv
На рис. 15.1 четко видно, что Я > yj. Это означает, что продукт
(7, фирма Fj производит в большем объеме уо чем у, т.е. в объеме
Ji фирма Fj производила бы продукт Gv если бы учитывала не
только частные предельные издержки МС(у{), но и внешние пре-
626
дельные издержки МЕС(у^). Объем Я естественно назвать эффек-
тивным с общественной точки зрения, объем yt — эффективным с
точки зрения фирмы Fv Таким образом, больший выпуск у, фир-
ма Fi обеспечивает за счет того, что часть МЕС(у{) своих истинных
издержек MSC(yx) она перекладывает на другие фирмы и на обще-
ство в целом.
15.1.3. Проблема внешних издержек может быть решена с помо-
щью так называемой интернализации внешнего эффекта, которая
достигается за счет объединения (слияния) фирм, производящих,
к примеру, продукты (7, (скажем, сталь) и G2 (скажем, рыбу). Здесь
предполагается, что все свои внешние издержки фирма цели-
ком перекладывает на фирму F2. До объединения каждая фирма F{
и F2 решала самостоятельно свою задачу максимизации прибыли
и, следовательно, задачу о максимальном объеме ух и у2 своей
продукции. После объединения фирма F3 совместно решает зада-
чу об объемах выпусков обоих продуктов Gt и (72. После объедине-
ния у фирмы F] уже нет внешних издержек, а ее общественные
издержки играют роль ее частных издержек, и поэтому фирма F{,
40*
627
сокращает свой максимальный выпуск. Сокращая максимальный
выпуск, фирма Г, сокращает свои общественные издержки и, сле-
довательно, объем загрязнений. Однако возможная неэффектив-
ность с ростом масштаба производства ставит пределы такому
способу решения проблемы внешних эффектов.
Другой вариант решения проблемы внешних эффектов за-
ключается в установлении специального налога (называемого на-
логом Пигу). Ставка 7 налога Пигу устанавливается в размере
7{=МЕС(у{)
(см. рис. 15.1).
После введения налога Пигу линия МС(ух) частных предель-
ных издержек сдвигается параллельно самой себе на величину tx
Новая линия МС(ух)+7х пересечет линию цены MR(yx) в точке
Е=(у,Pi), т.е. в точке, где ценарх равна предельным обществен-
ным издержкам MSC(yt). Теперь издержки фирмы Ft, генериру-
ющей отрицательный внешний эффект, равны сумме частных
издержек (площадь четырехугольника ONHyi и налоговых выплат
(площадь прямоугольника NBEH)._
На практике установить ставку налога Пигу довольно слож-
но, ибо величину МЕС(ух) оценить трудно. Для разных фирм эта
величина МЕС(ух) может быть существенно разной. Кроме того,
величина MECfy) может сильно варьироваться от хорошо разви-
тых к слаборазвитым регионам.
Третий вариант решения проблемы внешних эффектов дает
известная теорема Коуза, суть которой состоит в следующем.
Внешние эффекты можно интернализировать посредством за-
крепления прав собственности на порождающих внешние эффек-
ты экономических агентах и обмена этими правами, если это не
связано с большими трансакционными издержками.
Отметим, что права собственности — это установление зако-
ном правил, которые предписывают, что экономические агенты
(люди, фирмы) могут делать со своей собственностью. Например,
собственник земельного участка может на нем заниматься строи-
тельством, выращивать цветы, а может продать его целиком или
какую-то его часть.
Пусть фирма Fx (металлургический завод) загрязняет реку, на
которой фирма F2 (рыболовецкая артель) ловит рыбу. Рассмотрим
сначала ситуацию, когда право собственности на чистую воду
принадлежит фирме Fv Фирма Fv максимизирующая прибыль,
628
может согласиться сократить выпуск своей продукции, если ей
возместят потери (убытки), которые фирма Fx будет иметь в связи
с сокращением выпуска.
Если фирма F] выпускает/( единиц своей продукции, то раз-
ность/^ - MCxty = BN равна чистой прибыли фирмы Fx от про-
изводства/ -й единицы продукта Gx. Разность MSCX (/ ]) - МСХ (У, )=
= B/f представляет собой внешние предельные издержки, свя-
занные с производством у']-й единицы продукта Gx.
В рассматриваемом случае рх - МСХ(УХ) > MSCx(yx) - МСХ(У х)
(рис. 15.2). Величина MSCx(y х) - МСХ(УХ) — это максимально воз-
можная сумма, которую фирма F2 согласится заплатить фирме Fx
д ля того, чтобы фирма Fx не выпускала эту/-ю единицу продукта
6]. Поскольку максимально возможная сумма фирмы F2 меньше
чистой прибыли фирмы Fp фирма Fx не согласится с такой сум-
мой возмещения. Если фирма Fx выпускает единиц своей про-
дукции Gx, то разностьрх - МС{(у") = B'N' равна чистой прибыли
фирмы Fx от производства/;-й единицы продукта (7,. Разность
MSCx(yx) - МСХ(У[) = В11F представляет собой внешние предель-
ные издержки, связанные с производством/[-й единицы продук-
та Ср В рассматриваемом случае MSCx(yfi - МСХ(У'^ > рх- МСХ(У^
(см. рис. 15.2). Теперь фирма F2 не согласится выплачивать фирме
Fx такую большую компенсацию.
Очевидно, обе фирмы Fx и F2 могут достигнуть соглашения
при у, =ух, при котором рх -МСх(ух) = MSCx(yx)~МСх(ух). Это оз-
начает, что фирма Fx ограничит свой выпуск величиной у в обмен
на денежную компенсацию MSCx(yx)-MCx(yx) = BE, которая рав-
на рх-МСх(ух) чистой прибыли фирмы Fx от производства угй
единицы продукта С,.
Анализ ситуации, когда право собственности на чистую воду
принадлежит фирме F2, проводится аналогично. В этом случае
фирма Fx будет оплачивать фирме F2 и согласие на загрязнение
воды. Фирма F2 согласится дать такое разрешение на загрязнение,
если платежи фирмы Fx будут выше (точнее, не ниже) предельно-
го для F2 уровня загрязнения, равного МЕСх(ух) = MSCx(yx) -
- МСх(ух). Фирма Fx согласится платить за право увеличить вы-
пуск своей продукции на одну единицу, если этот платеж будет
ниже (точнее, не выше), чем разность MRx(yx) - МСх(ух). Согла-
шение будет достигнуто, когда фирма F2 продает фирме право
произвести продукцию в объеме ух единиц (см. рис. 15.2), кото-
рый является эффективным с общественной точки зрения. Этот
629
объем получается независимо от того, кто наделен правом собст-
венности, и без вмешательства органов управления на региональ-
ном и национальном уровнях.
Теорема Коуза привлекательна для либералов, которые счита-
ют, что органы управления на региональном и национальном
уровнях должны как можно меньше вмешиваться в экономичес-
кие проблемы и, в частности, в проблемы, порождаемые наличи-
ем отрицательных внешних эффектов. Однако с общественной
точки зрения решения, предлагаемые на основании теоремы Коу-
за (если, конечно, они состоятся), не всегда обязательно будут
рациональными.
Во-первых, решения на основании теоремы Коуза могут быть
конструктивными в ситуации, охватывающей ограниченное чис-
ло участников, и такой, что источники отрицательных внешних
эффектов легко определяются. В этом случае распределение прав
собственности на ресурсы влияет не на эффективный исход пере-
говоров, а на распределение доходов. Поэтому эффективное с
общественной точки зрения решение может и не быть справедли-
вым.
630
Во-вторых, решения на основании теоремы Коуза могут быть
конструктивными, если владельцы ресурсов могут четко иденти-
фицировать источники наносимого им ущерба и легально предо-
твратить этот ущерб. К сожалению, такая адресная определен-
ность далеко не всегда возможна (попробуйте определить истин-
ных виновников смога и парникового эффекта). Отсюда следует,
что не всегда ясно, как легально предотвращать ущерб, наноси-
мый отрицательными внешними эффектами, когда невозможна
локализация его источников. А если возможна, то по какому
принципу распределять меру ответственности за ущерб, наноси-
мый этими источниками отрицательных внешних эффектов.
В-третьих, теорема Коуза содержит важное условие о необхо-
димости невысокой стоимости переговоров, предметом которых
должно быть соглашение об эффективном с общественной точки
зрения решении конкретной проблемы внешних эффектов. Это
условие может не выполняться, когда, например, речь идет о про-
блемах отрицательных внешних эффектов, затрагивающих инте-
ресы миллионов граждан, владельцев личного автотранспорта —
основного источника загрязнения атмосферы больших городов,
и миллионов граждан, которые являются «потребителями» гряз-
ной атмосферы. Процесс таких переговоров непременно будет
политизированным и иметь высокую стоимость.
15.2. Положительные внешние эффекты
15.2.1. Напомним, что внешний эффект называется положитель-
ным, если один экономический агент так воздействует на другого
(других) экономического агента, что уменьшает издержки в его
(другого агента) деятельности. Классическим примером, иллюст-
рирующим наличие положительного эффекта, служит ситуация
«фруктовый сад — пасека».
Здесь фирма — это фруктовый (например, яблоневый) сад,
фирма F2 — пасека. Пчелы активно опыляют цветы, тем самым
значительно снижают издержки фирмы на опыление. Цветы
хорошо «кормят» пчел и тем самым значительно снижают из-
держки фирмы F2.
Рассмотрим пример с ремонтом дома и разбивкой цветника.
Символом у обозначим объем капиталовложений (например,
631
в руб.) владельца дома, которые он выделяет на ремонт дома и
разбивку цветника. Пусть расценки на ремонт дома и разбивку
цветника не зависят от объема ремонтных работ, поэтому линия
МС горизонтальна. Линия спроса D есть линия предельного част-
ного выигрыша владельца дома от объема ремонта. Но ремонт
также выгоден соседям, которым, например, будет достаточно
любоваться цветником владельца дома, чтобы не тратиться на
собственный цветник. Выгоды соседей отражает линия МЕВ пре-
дельных внешних выигрышей, которая является нисходящей, ибо
по мере расширения объема ремонтных работ предельный внеш-
ний выигрыш убывает (отметим, что предельный внешний выиг-
рыш здесь аналогичен предельной полезности потребителя, кото-
рая с ростом объема потребляемого продукта убывает). Линия MSB
предельного общественного выигрыша есть сумма линий D и
МЕВ, т.е. MSB = D + МЕВ (рис. 15.3). Владелец дома реально ин-
вестирует сумму у, которая является проекцией точки пересече-
ния линий D и МС. Эффективным с общественной точки зрения
(т.е. с точки зрения учета не только интересов владельца дома, но
632
и интересов соседей) является сумма у, которая есть проекция
точки пересечения линий MSB и МС. При более низкой цене
р (Р < Р) владелец дома будет реально инвестировать сумму У, ко-
торая эффективна с общественной точки зрения.
15.3. Модель для определения стандарта на вредные
выбросы и платы за вредные выбросы
15.3.1. Рассмотрим и проанализируем модель для определения
стандарта и размера платы за вредные выбросы для фирмы F. Мо-
дель состоит из линий MSC и MCA. Символом MSC обозначены
предельные общественные издержки фирмы от вредных выбросов,
символом MCA — предельные издержки от снижения вредных вы-
бросов, символом у обозначен объем вредных выбросов фирмы F
(рис. 15.4). Линия MSC эквивалентна линии МЕС (см. рис. 15.1).
С ростом объема у вредных выбросов растут предельные обще-
633
ственные издержки от этих выбросов, поэтому линия MSCявляет-
ся восходящей.
Если фирма F увеличила объем вредных выбросов с уровня у
по уровень у, это приведет к тому, что общественные издержки от
вредных выбросов возрастут на величину, равную определенному
интегралу
/'
J MSC{y)dy = \y'B'B"y"\v
у'
где символом 1у'В'В"у"12 обозначена площадь криволинейной
трапеции у’В'В"у".
Линия MCA имеет с осью Оу общую точку у, которая соответ-
ствует объему производства фирмы, максимизирующего ее при-
быль. Линия MCA является нисходящей, ибо при снижении объ-
ема вредных выбросов на небольшую величину (скажем, с у до у"
(см. рис. 15.4)) предельные издержки МСА{уГ) будут относительно
невелики. При снижении объема вредных выбросов на сравни-
тельно большую величину (скажем, с у до У (см. рис. 15.4)) пре-
дельные издержки MCA{yf) также станут значительными, ибо
большое снижение объема вредных выбросов требует относитель-
ного большего прироста издержек от снижения объема вредных
выбросов на единицу. Если фирма снизила объем вредных выбро-
сов с уровня У' до уровня У, это потребует от нее дополнительных
издержек, равных определенному интегралу
у”
J МС {y)dy = \y'H'H"y"\v
у'
где символом |у'//7/’"у"|2 обозначена площадь криволинейной
трапеции у'Н’Н"у".
Отметим, что чисто внешне рассматриваемая модель напоми-
нает крест Маршалла, в котором линия AfC4 есть линия спроса
(скажем, на арбузы), а линия MSC есть линия предложения (арбу-
зов). Точка пересечения £* изображает в «арбузной» модели точку
равновесия на рынке арбузов. В нашем (уже не арбузном) примере
точка £* = {у* ,р) есть также точка равновесия, абсциссу у* которой
естественно интерпретировать как стандарт {норматив) на объем
вредных выбросов для фирмы F, а ординату р — как налог {плату)
на одну единицу вредных выбросов, которые производит фирма
F.
634
Стандарту* на объем вредных выбросов и налогр* на одну еди-
ницу вредных выбросов рационально уравновешивают интересы
фирмы Fn общественные интересы. Отметим, что интересы фир-
мы Г необходимо учитывать, если фирма F выпускает обществен-
но значимый продукт, а его фирма может выпускать, только осу-
ществляя вредные выбросы, т.е. если не будет вредных выбросов,
то и не будет общественно значимого продукта.
Здесь уместно следующее важное замечание. Решение о введе-
нии стандарта (норматива) на объем вредных выбросов для фирмы
Гили налога (платы) на одну единицу вредных выбросов фирмы F
должно приниматься органом регионального или национального
управления. Иными словами, регулирование на региональном или
национальном уровне необходимо для устранения (или ослабле-
ния) потерь, которые порождаются внешними эффектами. Опи-
санная модель в принципе позволяет получить основу для приня-
тия такого решения, ибо позволяет получить количественные
оценки стандарта у* и налога р* для фирмы F. Серьезным является
вопрос о реализации этого принципа, о чем речь пойдет дальше,
когда будет обсуждаться вопрос, какой из показателей (у* или р‘)
более предпочтителен.
15.3.2. Если объем вредных выбросов фирмы Г равен у, то фирма
должна выплатить налог в размере, равном площади четырех-
угольника Ор*0'"у|2 = р* у.
Если объем вредных выбросов фирмы F равен у*, то фирма
должна выплатить налог в размере, равном площади прямоуголь-
ника |Ор*£*у*| = р*у*. К этому налогу р*у следует добавить из-
держки
]мСА(у)(1у = \у*Елу\2,
у’
равные площади криволинейного треугольника у*Е*у, которые
фирма Г будет иметь в связи с тем, что она снизила вредные вы-
бросы с объема, равного у, до объема у*. Таким образом, в рас-
сматриваемом случае «полные» издержки фирмы Г (сумма налога
р*у и издержек |у‘£*у|2 в связи со снижением объема вредных
выбросов с у до у‘) будут равны
635
У
р*у* + J MCA(y)dy.
у'
(15.3.1)
Если объем вредных выбросов фирмы /'равен/ (/), то фирма
должна выплатить налог в размере, равном площади прямоуголь-
ника |Op*0'yj2 = р*у'(|Ор*0"у"|2 = /Л/')- К этому налогу/"/ (/*/')
следует добавить издержки
у ( ? '
j MCA(y)dy = \у'Н'у\2 J MCA(y)dy = \y"H"y\2 ,
у’ V" 7
у
равные площади криволинейного треугольника у'Н'у (у"Н"у),
которые фирма £имеет в связи с тем, что она снижает объем вред-
ных выбросов с у до/ (доу"). Таким образом, в рассматриваемом
случае «полные» издержки фирмы F (сумма налога р*у (р*У) и
издержек \y'ff'y\2 (ly'Tf'J'k) в связи со снижением объема вредных
выбросов с у до у (до /')) будут равны
У
р*у'+ ] MCA(y)dy (15.3.2)
/
/>‘у"+
MCA(y)dy
(15.3.3)
Из четырех величин р*у, (15.3.1), (15.3.2) и (15.3.3) минималь-
ной является величина (15.3.1). Величина (15.3.2) больше величи-
ны (15.3.1) на площадь |0'Я'£*|2 криволинейного треугольника
Qfftf (см. рис. 15.4). Величина (15.3.3) больше величины (15.3.1)
на площадь |£*0"Я"|2 криволинейного треугольника
(см. рис. 15.4). Величина р*у больше величины (15.3.1) на пло-
щадь |Е*0"у| криволинейного треугольника E*Q”y (см. рис. 15.4).
Таким образом, у* вредных выбросов и налогр* на одну едини-
цу вредных выбросов совершенно равноправны, однако при реа-
лизации на практике, особенно в случае отсутствия достаточной
информации, величины у и р* теряют свое равноправие.
15.3.3. Сначала проанализируем ситуацию с налогом р* на одну
единицу вредных выбросов, который должен быть установлен для
636
всех фирм, ибо контролировать каждую фирму государство не
имеет возможности.
Рассмотрим две фирмы — фирму Fx и фирму F2, у которых
предельные издержки от снижения объема вредных выбросов раз-
ные (на рис. 15.5 — МСАХ и МСА2), а предельные общественные
издержки одинаковы (на рис. 15.5 они не показаны).
Если вводится стандарт у* на объем вредных выбросов, еди-
ный для фирм F] и Fv то каждая фирма снизит объем вредных
выбросов на величину у - у*, а обе фирмы — на величину 2(у - у’).
При этом издержки фирмы F, будут равны площади
кри-
волинейного треугольника у*Еху, а издержки фирмы F2 будут рав-
ны площади
криволинейного треугольника у*Е2у.
Если вводится налог р* на одну единицу вредных выбросов, то
фирма Fx снижает объем вредных выбросов на величину У~У\,
а фирма F2 — на величину у-у2, а обе фирмы снизят объем вред-
ных выбросов на величину 2у - у, - у2. При этом издержки фирмы
637
F{ будут равны площади |у1Я]у|2 криволинейного треугольника
ухНху, а издержки фирмы F2 — площади ^y2ff2yl2 криволинейного
треугольника УгН2у.
Сопоставим издержки фирм Fx и F2 при введении стандарта/
и налога р*. В случае стандарта у издержки фирмы Fx больше ее
издержек в случае налогар* на площадь |у*.Е'1Я1у1|2 криволинейно-
го четырехугольникау*ЕхНхух (см. рис. 15.5). В случае стандарта/
издержки фирмы F2 меньше ее издержек в случае налога р на пло-
щадь у*ЕхНхух криволинейного четырехугольника у2Е2Н^* (см.
>. Очевидно, площадь (/^Яр^ больше площади
2. Это означает, что в случае введения стандарта / сум-
марные издержки фирм Fx и F2 будут больше их суммарных издер-
жек при введении налогар. Этот результат имеет место и в случае,
когда у, + у2 = 2/, т.е. когда в обоих случаях (в случае р* и /) со-
кращение объема 2(у-у*) = 2у-ух-у2 вредных выбросов будет
одинаковым. Таким образом, в рассматриваемом примере налог
/ предпочтительнее стандарта/.
рис.
15.3.4. Проанализируем ситуацию влияния стандарта / на объем
вредных выбросов. Рассмотрим случай, когда линия MSC фирмы
Fx идет достаточно круто вверх, а линия MCA фирмы F — доста-
точно пологая. Тогда точка £* = (у*, /) пересечения этих линий
геометрически показывает стандарт / и налог/ (рис. 15.6).
Пусть из-за ограничений информации вместо стандарта / ус-
тановлен стандарту^ такой, чтоу! >у* (см. рис. 15.6). Тогда обще-
ственные издержки фирмы F вырастут на площадь у*£*Ду1|2 че-
тырехугольника у ЁВху,, а издержки от снижения объема вредных
выбросов уменьшатся на площадь у^’Я^Л четырехугольника
/^y(.
«Цена» погрешности в определении стандарта (в результате
установления стандарта у( вместо стандарта у*) равна площади
Е*ВХНХ 2
Е*ВХНХ 2
треугольника Е*ВХНХ,
=|/-г-дЛ|2-|/£,я|^||2.
которая равна разности
Пусть теперь из-за ограниченной информации ошибочно ус-
тановлен налог р2, который меньше налога /, и пусть порядки
ошибок в установлении налога р2 и стандарта у1 примерно одина-
ковы (см. рис. 15.6). Тогда цена погрешности в определении нало-
638
га (в результате установления налога р2 вместо налога р*) равна
площади |£*52Я2| треугольника ЁВ2Н2, которая равна разности
^В^^ =|у‘£*52у2|2-|у*Г*Я2у2|2. Рисунок 15.6 показывает,
что в рассматриваемом случае чистый рост общественных издер-
жек значительно больше в случае погрешности с налогом, чем в
случае погрешности со стандартом.
Приведенные выше случаи показывают, что нет основания
считать, что предпочтительнее: налог р* или стандарт у. В одних
ситуациях целесообразно ориентироваться на установление стан-
дарта, в других — на установление налога.
В заключение отметим, что в разных странах «золотого милли-
арда» исторические традиции являются разными. Например,
в США органы государственного управления больше ориентиру-
ются на стандарты при решении задач контроля за загрязнением
окружающей среды (заметим, что, вообще говоря, исторически
сложилось так, что в США помешаны на стандартах, и не только в
области контроля за загрязнением окружающей среды). Во мно-
639
гих европейских странах (в частности, в ФРГ) успешно использу-
ют практику налогов при решении задач контроля над загрязне-
нием окружающей среды.
15.3.5. Рассмотрим и проанализируем модель переработки отхо-
дов (например, стеклотары). Составными элементами модели яв-
ляются линии частных предельных издержек МС владельцев отхо-
дов, предельных общественных издержек MSC, предельных из-
держек переработки отходов MCR (отходы перерабатываются
местными властями или специальными фирмами). Символом у
обозначается объем отходов. Все элементы модели представлены
на рис. 15.7. С ростом объемов отходов частные предельные из-
держки МС и общественные предельные издержки MSC растут.
Предельные частные издержки МС, например, в связи с тем, что
отходы, если их не трогать, растут в объеме и здорово мешают
сбыту. Если заниматься их утилизацией, то эта процедура требует,
по крайней мере, какого-то времени, которое уже невозможно
потратить на что-то иное. С пониманием ситуации интенсивного
роста общественных предельных издержек MSC в связи с ростом
объема отходов дело обстоит достаточно просто, ибо растут горы
мусора, растет число порезанных осколками стекла ног, загрязня-
ется окружающая среда. Линии МС и MSC имеют тот же смысл,
что и на рис. 15.1. Символ У означает максимальное число отходов
(стеклотары) в течение некоторого фиксированного периода, на-
пример одного месяца. С увеличением объема перерабатываемых
отходов (при движении по рис. 15.7 справа налево) предельные
издержки MCR переработки отходов растут. Если в результате пе-
реработки объем отходов сократится с у до, например, у, то из-
держки такой переработки представляют собой интеграл
]Л/СЛ(у)^ = |уЦ,
У
где |у^|2 — площадь треугольника (вообще говоря, криволиней-
ного) уЁу.
Из рис. 15.7 следует, что фактически перерабатывается объем
отходов, равный у-у, т.е. после переработки остаются отходы в
объеме у единиц. В то же время должен быть переработан объем
отходов, который является эффективным с общественной точки
зрения, и этот объем равен У - У > У - У, т.е. эффективный с обще-
640
ственной точки зрения объем отходов должен быть равен у
(и у < у).
Реализовать объем у можно с помощью, например, введения
залога t, который покупатель уплачивает за одну единицу стекло-
тары, приобретая в ней товар, и который (залог) покупатель полу-
чает обратно, когда он эту стеклотару возвращает по месту покуп-
ки. В этом случае линия частных предельных издержек переходит
в линию МС +1, а объем у переходит в объем У, который эффек-
тивен с общественной точки зрения.
Пример 15.3.1
Линии MSC и MCA имеют уравнение MSC(y) = ay + Р MCA =
= -ay + b, где a > 0, b > 0, a > О, p > 0, p < b.
Найдем:
1) стандарту* и налогр*;
2) общественные издержки SC, если объем вредных выбро-
сов увеличился с у до у";
3) издержки СА от снижения объема вредных выбросов с у до
У'.
• Имеем уравнение MSC(y) = МСА(у),
-ay + 6 = ay + p,
откуда вытекает, что
41 - 7620
641
. d-P » » , . ad-ар
у =—р = -ау +Ь=-----—,
а+а а+а
SC(y'; у") = J MSC(y)dy = J (ay+p)rfy=у2 + py|J,
У У 2 У
=(//-/)Гу(Г+Г)+р1=|/^'У12,
У
СА(У,у”}= J MCA(y}dy= J (ау+Ыу=-±у2
У' у'
=(/,-У)|-^(Г+У)+*1=|/Я/яу'|2
(рис. 15.8).
642
15.4. Рынок прав на вредные выбросы
15.4.1. Предположим, что на региональном или национальном
уровне удалось получить оценку предельного (сверху) общего
объема вредных выбросов, который допустим в данном регионе
или в стране в целом в течение некоторого периода времени, ска-
жем в течение одного года. Пусть, однако, достоверная информа-
ция, достаточная для установления величины налога или стандар-
та, отсутствует. Тогда можно использовать метод лицензирования,
суть которого заключается в следующем. Каждая фирма отрасли
получает лицензию, в которой указывается разрешенный фирме
предельный (сверху) объем (т.е. квота) вредных выбросов. Общая
сумма этих квот должна, естественно, равняться предельному
(сверху) объему вредных выбросов. Квоты (целиком или частич-
но) могут продаваться и покупаться на рынке квот. Пусть, напри-
мер, каждая из фирм F{ и F2 получила лицензию на одну и ту же
(по объему) квоту, т.е. на одинаковый объем вредных выбросов в
течение фиксированного периода времени. Пусть фирма Fx имеет
относительно высокие предельные издержки МСАх(у) от сниже-
ния объема вредных выбросов, а фирма F2 — относительно низкие
предельные издержки МСА2(у) от снижения объема вредных вы-
бросов. Поэтому, естественно, фирма F2 может продать часть сво-
ей квоты (или всю квоту) фирме Fx по цене, меньшей (точнее, не
большей) предельных издержек МСАх(у).
Если число фирм (и следовательно, лицензий) в отрасли до-
статочно велико, возникает конкурентный рынок лицензий
(квот). В состоянии рыночного равновесия установится рыночная
цена лицензии (точнее, цена равновесия одной единицы объема
вредных выбросов). При этом фирмы с относительно низкими
предельными издержками от снижения объема вредных выбросов
будут сокращать вредные выбросы активнее других, а фирмы с
относительно высокими предельными издержками от снижения
объема вредных выбросов будут покупать больше лицензий (боль-
ше квот) и меньше сокращать вредные выбросы.
Описанный рыночный подход сочетает ряд преимуществ
стандартов с преимуществами налогов.
Определение общего объема вредных выбросов и общего чис-
ла лицензий аналогично установлению стандартов. Возможность
41*
643
торговли лицензиями позволяет достичь общего объема вредных
выбросов при минимальных издержках, что аналогично ситуа-
ции, когда вводятся налоги.
Вопросы для самоконтроля к главе 15
1. Что такое внешний эффект (экстерналия)?
2. Какой внешний эффект называется положительным? Приведите
экономический пример.
3. Какой внешний эффект называется отрицательным? Приведите эко-
номический пример.
4. Что такое частные предельные издержки фирмы?
5. Что такое объем выпуска фирмы, эффективной с точки зрения фир-
мы?
6. Что такое внешние предельные издержки фирмы?
7. Что такое предельные общественные издержки фирмы?
8. Что такое объем выпуска фирмы, эффективный с общественной точ-
ки зрения?
9. Что такое интернализация внешнего эффекта? Перечислите пробле-
мы интернализации внешнего эффекта.
10. Что такое налог Пигу? Назовите проблемы, связанные с реальным
установлением ставки налога Пигу.
11. Что такое права собственности?
12. В чем экономическая суть теоремы Коуза?
13. В чем суть проблем, связанных с реальным использованием теоремы
Коуза?
14. Каков экономический смысл линии MSC1 Как определить обще-
ственные издержки, если объем вредных выбросов растет?
15. Каков экономический смысл MCA — предельных издержек фирмы
от снижения объема вредных выбросов? Как определить издержки
фирмы от снижения объема вредных выбросов?
16. Что такое стандарт (норматив) на объем вредных выбросов для фир-
мы F> Как он определяется? Как формулируется основное свойство
стандарта?
17. Что такое налог (плата) на одну единицу вредных выбросов? Как он
определяется? Как формулируется основное свойство налога?
18. Чему равны полные издержки фирмы при ее переходе на стандарт на
объем вредных выбросов?
19. Чему равны полные издержки фирмы при ее переходе на объем вред-
ных выбросов, который не равен стандарту на объем вредных выбро-
сов?
20. Как оцениваются суммарные издержки двух фирм в случае введения
стандарта и налога?
644
21. Как оценивается погрешность в определении стандарта в случае кру-
той линии MSC и пологой линии MCA?
22. Как оценивается погрешность в определении налога в случае крутой
линии MSC и пологой линии MCA?
23. Что представляет собой модель переработки отходов?
24. В чем суть метода лицензирования объемов вредных выбросов?
25. Как работает рынок прав на вредные выбросы?
Задачи и упражнения для самоконтроля к главе 15
1. Опишите подробно использование теоремы Коуза при анализе ситу-
ации «металлургический завод» — «рыболовецкая артель» в случае,
когда право собственности на чистую воду принадлежит рыболовец-
кой артели.
2. Пусть МСАх(у) = МСА2(у) = / = b Р* = Найдите:
а) объем вредных выбросов у, при котором фирмы Fx и F2 максими-
зируют свою прибыль;
б) издержки САХ фирмы Fv которая снизила объем вредных выбро-
сов с у до у*;
в) издержки СА2 фирмы Г2, которая снизила объем вредных выбро-
сов с у до у*;
г) издержки САХ фирмы Fv которая снизила объем вредных выбро-
сов су до yj (см. рис. 15.5);
д) издержки СА2 фирмы F2, которая снизила объем вредных выбро-
сов су до у2 (см. рис. 15.5).
г) сопоставьте аналитически и графически совместные издержки
САХ и СА2 фирм Fx и F2 при введении стандарта у* и налогар*.
3. Пусть MSC = у + 10, MCA = -Зу + 110, погрешность Ау* в установле-
нии стандарта равна Ау* = +1, погрешность Ар* в установлении нало-
га равна Ар* = -1. Найдите:
а) стандарт у* и налог р*;
б) «цену» погрешности в определении стандарта (когда вместо
стандарта у* устанавливается стандарту* + 1);
в) «цену» погрешности в определении налога (когда вместо налога
р* устанавливается налогр* - 1);
г) сопоставьте аналитически и графически «цены» погрешности в
определении стандарта у* и налога р*.
4. Фирмы расположены в северной части города, жилые кварталы —
в южной. Фирмы выпускают один и тот же продукт и выбрасывают в
атмосферу вредный для жителей дым:
а) почему фирмы создают внешние эффекты?
645
б) могут ли в рассматриваемой ситуации переговоры решить про-
блему внешних эффектов?
в) как местные власти могли бы определить эффективный уровень
качества воздуха?
Вопросы и тесты для контрольных работ к главе 15
1. Какое из следующих предложений описывает внешний эффект,
а какое — нет? Ответ обоснуйте:
а) политика ограничения экспорта кофе из Бразилии приведет к
росту цены американского кофе, который вызовет рост цен на
чай;
б) реклама отвлекла водителя, и он попал в аварию.
2. Сопоставьте следующие три механизма борьбы с внешними эффек-
тами загрязнения, когда издержки и выигрыши от уменьшения за-
грязнения неопределенны:
а) налоги на выбросы;
б) стандарты на выбросы;
в) продаваемые лицензии на выбросы.
3. Когда внешние эффекты требуют государственного вмешательства,
а когда не требуют?
4. Приведите конкретные экономические примеры, когда применение
теоремы Коуза не является результативным.
Задачи для контрольных работ к главе 15
1. Пусть Л/СЛ,(у) = (у - 4)2, МСА2(у) = 0,75(у - 4)2,/ = 1,р* = 8. Найдите:
а) объем вредных выбросов у, при котором фирмы F{ и F2 максими-
зируют свою прибыль;
б) издержки СА{ фирмы которая снизила объем вредных выбро-
сов с у до у ;
в) издержки СА2 фирмы F2, которая снизила объем вредных выбро-
сов с у до у* ;
г) издержки СА{ фирмы F{, которая снизила объем вредных выбро-
сов с у доу1 (см. рис. 15.5);
д) издержки СА2 фирмы F2, которая снизила объем вредных выбро-
сов с у до у2 (см. рис. 15.5).
Сопоставьте аналитически и графически совместные издержки СА} и
СА2 фирм F{ и F2 при введении стандарта у* и налога р\
646
2. Пусть MSC = у + 20, MCA = -2у + 80, погрешность Ay* в установ-
лении стандарта равна Ау* = +2, погрешность Ар* в установлении
налога равна Ар* = -4.
Найдите:
а) стандарт у и налог р*;
б) «цену» погрешности в определении стандарта, (когда вместо
стандарта у* устанавливается стандарту* + 2);
в) «цену» погрешности в определении налога, (когда вместо налога
р* устанавливается налогр* - 4).
Сопоставьте аналитически и графически «цены» погрешностей в
определении стандарта у* и налога р*.
Глава 16
ОБЩЕСТВЕННЫЕ БЛАГА
16.1. Характеристики общественных благ
16.1.1. Обычные продукты и услуги представляют собой частные
блага. Они конкуренты и исключаемы, ибо приобретение частно-
го блага индивидуумом означает, что другой индивидуум его при-
обрести уже не может.
Общественные блага — товары и услуги, потребление которых
не изменяет их объем и доступно всем членам общества (услуги
радиовещания, телевидения, национальной обороны, дороги, го-
родские и национальные парки).
Общественные блага обладают двумя важными характеристи-
ками: они неконкурентны и неисключаемы. Неконкурентность бла-
га означает, что при любом заданном объеме его производства
предельные издержки его предоставления дополнительному по-
требителю равны нулю, т.е. дополнительное потребление некон-
курентного блага не увеличивает издержки. Если на шоссе нет
«пробок», дополнительные издержки проезда по этому шоссе рав-
ны нулю. Дополнительное морское судно не увеличивает эксплу-
атационные издержки маяка. Частные блага конкурентны в по-
треблении. Если, например, индивидуум приобрел костюм, то это
обстоятельство исключает возможность его приобретения другим
индивидуумом.
Неисключаемость блага означает, что потребители не могут
быть исключены из сферы его потребления. Примеры неисклю-
чаемого блага — национальная оборона, маяк, общественное ра-
дио и телевидение.
648
Некоторые блага исключаемы, но неконкурентны. Примером
такого блага является телевизионный сигнал. Когда сигнал пере-
дан в эфир, появление дополнительного пользователя не требует
дополнительных издержек. Это означает, что телевизионный сиг-
нал — неконкурентное благо. Однако телевизионный сигнал мо-
жет быть закодирован и поэтому недоступен тем потребителям,
которые не знают его кода, т.е. телевизионный сигнал — исклю-
чаемое благо.
Примером конкурентного, но неисключаемого блага является
обыкновенный воздух, неисключаемость которого очевидна. Од-
нако дополнительные потребители чистого воздуха должны его
дополнительно оплачивать, например в виде оплаты путевки в
экологически чистый регион.
К общественным относятся следующие блага: информацион-
ные (непрерывные, например радио и телевидение), локальные
(доступные представителям отдельного региона или социальной
группы, например районные библиотеки и ведомственные поли-
клиники), ограниченного пользования (т.е. такие, которые до-
ступны для одновременного использования ограниченному числу
потребителей, например шоссе в часы «пик»), дискретные (карти-
ны в музеях), бесплатные (услуги травмпунктов), с положитель-
ной ценой (общественный транспорт), с отрицательной ценой
(высшее образование).
Общественные блага требуют для своего производства част-
ных благ и услуг, объем которых лимитируется суммарными дохо-
дами государства, которые, в частности, образуются от поступле-
ния различных налогов.
16.1.2. Проанализируем простую модель определения объема
предоставления общественного блага с использованием функций
спроса и предложения общественного блага.
Функция спроса индивидуума на общественное благо опреде-
ляется как зависимость получаемой индивидуумом предельной
выгоды АН? от объема потребления общественного блага. Предель-
ная выгода равна полезности индивидуума (выраженной в денеж-
ной единице) от потребления дополнительной единицы обще-
ственного блага. Предельная выгода показывает, сколько готов
индивидуум заплатить за дополнительную единицу общественно-
го блага. Предполагается, что индивидуум не ведет себя, как «за-
649
яц» (или «безбилетник»), т.е. как потребитель, который использу-
ет общественное благо за счет других потребителей.
Линия индивидуального спроса на общественное благо явля-
ется нисходящей, ибо отражает убывающую предельную полез-
ность от потребления дополнительной единицы общественного
блага (рис. 16.1, на котором представлены линии D{ и D2 спроса
первого (Ц) и второго (С2) индивидуумов и линия D совокупного
спроса на общественное благо б). Ценыр\ ир*2 показывают полез-
ности (в денежной единице) индивидуумов первого (Ц) и второго
(С2) от потребления дополнительной (к у) единицы обществен-
ного блага.
Линия D совокупного спроса на общественное благо строится
путем суммирования по вертикали линий и D2 индивидуально-
го спроса, ибо каждый индивидуум потребляет весь объем обще-
ственного блага (ибо оно неконкурентно). Отметим здесь прин-
ципиальное отличие построения линии совокупного спроса на
общественное благо от построения линии совокупного спроса на
частное благо путем горизонтального суммирования линий инди-
видуального спроса на это частное благо.
Частное равновесие на рынке общественного блага определя-
ется в виде равенства суммарной предельной выгоды (величины
суммарного спроса) потребителей потребительской цене р* (пре-
дельным издержкам), по которой готов предложить производи-
тель (продавец) данное количество у* общественного блага. Рав-
новесие называется частным потому, что речь идет лишь о рынке
общественного блага (благ). Частные блага здесь не фигурируют.
На рис. 16.1 частное равновесие на рынке общественного блага
показано точкой Е.
16.2. Частное и общее равновесие в модели экономики
с общественными благами
16.2.1. Прежде чем рассматривать модель общего экономическо-
го равновесия, когда фигурирует два типа благ (частные и обще-
ственные), проанализируем графическое решение задачи опти-
мального распределения ресурсов при наличии частного блага и
общественного блага.
650
Рис. 16.1
Пусть в экономической системе только два потребительских
блага — частное Gx и общественное Gy. Имеется два потребителя
(индивидуума) (Cj и С2) со своими функциями полезности и1(х1 ,у)
и и2(х2 у), где Xj и х2 — количества частного блага Gx, потребляемо-
го соответственно индивидуумами С1иС2(х=х1 + х2),ау — коли-
чества общественного блага, потребляемого индивидуумами Cj и
С2. Символами и 1^ обозначим линии безразличия первого и
второго потребителей соответственно с уровнями полезности т, и
т2. Пусть граница Р множества производственных возможностей
задана и имеет уравнение F(x,y) = 0 (рис. 16.2).
Зафиксируем уровень т, полезности первого индивидуума Ср
тогда подучим конкретную линию безразличия (см. рис. 16.2).
Уравнение F(xy) = 0 определяет неявную функцию х =fly), гра-
фиком которой является линия Р. Уравнения uflx^yj = Tj и
и2(х2у2) = т2 определяют неявные функции х, = Л((у) и х2 = h2(y),
графиками которых являются линии безразличия и /*2) соот-
ветственно.
651
Рис. 16.2
Разность fly)—hx(y) = q(y) функций х = Ду) и хх = й((у) имеет в
качестве графика линию Q (см. рис. 16.2). Экономический смысл
линии Q. она показывает для каждого объема у общественного
блага объем частного блага х, которое доступно потребителю С2,
ибо х = fly) — общее количество частного блага, частное благо в
объеме X] = hx(y) получил потребитель Сх.
При фиксированном уровне полезности Tj первого потреби-
теля Сх второй потребитель С2 максимизирует свою функцию по-
лезности и2(х,у) при наличии ограничения в виде линии Q:
и2(х,у) (max) (16.2.1)
при условии, что
(x,y)eQ.
(16.2.2)
652
Из простых наглядных соображений (см. рис. 16.2) решением
этой задачи будет точка £* касания линии Q и некоторой фикси-
рованной линии /<2) безразличия второго потребителя.
Из того что точка £* есть точка касания линий Q и I™, следует,
что при у=у (у — абсцисса точки £*) имеет место равенство про-
изводных:
= (16.2.3)
dy dy dy
Производная dh^y/dy (dx\/dy) представляет собой предель-
ную норму замены при у- у (одной единицы) общественного
блага G частным благом Gx для первого индивидуума С., т.е.
^^=MRS%(y). (16.2.4)
dy
Аналогично
^l = MRS^(y). (16.2.5)
dy У2
Производная dfly)/dy представляет собой предельную норму
• трансформации при у = у частного блага Gx в (одну единицу) об-
щественного блага Gy т.е.
-j^ = -MRTyx(y*y. (16.2.6)
dy *
Подставив (16.2.4)—(16.2.6) в (16.2.3), получим
-M/Wg(/) = -M^‘(/)-(-WtS«(/)),
откуда вытекает важное равенство
(/)+MRS^y'y = MRT^y), (16.2.7)
которое показывает оптимальное (Парето-эффекгивное) распре-
деление ресурсов при наличии общественного блага в случае двух
благ (одного частного Gx, одного общественного Gy и двух потре-
бителей Cj и С2).
Содержательно формула (16.2.7) интерпретируется так. Пре-
дельная норма трансформации частного блага Gx в общественное
благо Gy равна сумме предельных норм замены общественного
блага Gv частным благом (7 для каждого индивидуума.
653
16.2.2. Формула (16.2.7) естественным образом обобщается в виде
MRS^ (/)+...+MRS$4y) = MRT„(y) (16.2.8)
на случай двух благ (одного частного Gx и одного общественного
(Ур и т потребителей Сх,...,Ст.
Частное благо Gx в количестве х единиц распределяется между
потребителями следующим образом:
х-х. + ...X .
1 пг
где xt — количество единиц частного блага Gx, которое доступно
потребителю Ср i =
Общественное благо Gy в количестве у единиц доступно каж-
дому потребителю в своем полном объеме у: у, = ... =ут =у.
Каждый потребитель Ц имеет свою функцию полезности
i=
По аналогии с задачей (16.2.1), (16.2.2) оптимального (Парето-
эффективного) распределения ресурсов при наличии обществен-
ного блага рассмотрим следующую экстремальную задачу:
M(l)(xpy) (max) (16.2.9)
при наличии ограничений
«<2>(х2,у) = т2, (16.2.10.1)
и(тЧхт,у) =тт, (16.2.10,/и)
F(x,y) = 0, (16.2.11)
где уровни т2,...,тт полезностей потребителей С2,...,Ст фиксирова-
ны.
Для решения задачи (16.2.9)—(16.2.11) составим функцию Лаг-
ранжа и приравняем все ее первые частные производны к нулю.
Имеем
£ = «(1)(х1,у)+Х2(«(2)(х2,у)-т2)+...+ 2
+Xm(u(m\xm,y)-xm)+$F(x,y)
И
= dtt(1>(x, ,у) + dF(x,y)Эх = 0> (16.2.12.1)
vXj ОХ
654
dL Э*/2)(х2,у) rdF(x,y) dx
Эх2 2 Эх2 + Эх Эх2
(16.2.12.2)
dZ dtt(w)(xm,y) dF(x,y) Эх
дхт т дхт Эх дхт
(16.2.12.т)
ЪЬ_Ъит(хх,у), Эи(2)(х2,у) ,
dy Эу 2 Эу
т Эу 4 Эу
^=«(2)(х2,у)-т2=0,
0^2
(16.2.13.1)
(16.2.13.2)
^- = «(m)(xm,y)-Tm=O,
^ = Г(х,у) = О.
(16.2.13./л)
(16.2.14)
Решением системы (16.2.12.1)—(16.2.14) является вектор
о;............ой-!»
Далее все аналитические преобразования выполняются на
векторе (16.2.15).
Из (16.2.12.1)—(16.2.12./л) вытекают равенства (дх/дхх = ...
= дх/дхт= 1)
Эи(1) /ЭГ
Эх, / Эх ’
g Э/7 /Эи(2) . £ ЭГ /Э«(л,)
2 Эх/ Эх2 ’’ ’ т дх/ Эх„
(16.2.16)
Подставив выражения (16.2.16) в (16.2.13.1), получим
655
dF
Э«(1) Э«(2) дх
Эу 4 Эу Эи(2)
дх2
^Э«(1) £Э/’Г Эи^/ду
Эу Эх <Эи(2)/Эх2
- дц(1) + Эи(1) ди^/Ъу
Эу + Эх] [д«(2)/Эх2
откуда следует, что
Эи(1)/Эу Ъит/Ъу Ъи(т}1Ъу dF/dy
Эм(1)/Эх1 Эм(2)/Эх2 Ъи(т)/Ъхт dF/dx
На основании теоремы о неявной функции и равенств
-dxx /dy = MRS™ ,...,-dxm/dy = MRS™, - dx/dy = MRT^
имеем
э«(от) аГ [£э/\
Эу Эи(д,) S Эу
ди(т}!Ъу Э/’/Эу^
Э«('я)/Эх„, bF/bx]
ди(т}!Ъу dF/dy'
dF/dx J’
(16.2.17)
ди(т)/дхт
^>L=_^L=MAs!i>,
Эи( /Эх( dy
...= (16.2.18)
Э«(2)/Эх2 dy fo(m}/Zxm dy 7
Э/7Эх dy
Подставив (16.2.18) в (16.2.17), получим важную формулу
(16.2.8)
MRS™ +...+MRS%> = MRTm,
утверждающую, что предельная норма трансформации частного
блага в общественное равна сумме предельных норм замены об-
щественного блага частным благом у каждого индивидуума.
Строго говоря, система уравнений (16.2.12.1)—(16.2.14) пред-
ставляет собой условия первого порядка. Решение системы есть
критическая точка (16.2.15) функции Лагранжа, которая после
656
элиминирования множителей Лагранжа Х2*, к*т, не обязана
быть точкой условного максимума функции (16.2.9) при наличии
ограничений (16.2.10.1)—(16.2.11).
Для того чтобы узнать, является ли точка (х^, ..., х*, у*) при
наличии ограничений (16.2.10.1)-(16.2.11) точкой условного мак-
симума функции (16.2.9), следует использовать условия второго
порядка.
Если функции полезности «^’(Хру),..., w(m)(xm,y) строго вогну-
ты (выпуклы вверх) при х( > 0, у > 0, i = 1,..., т, множество произ-
водственных ВОЗМОЖНОСТеЙ СТРОГО ВЫПУКЛО, ТО (Xj*,..., хот‘,
у) — единственная точка (глобального) максимума функции
(16.2.9) при наличии ограничений (16.2.10.1)—(16.2.11).
Существование общего равновесия при разных предпосылках
было доказано многими авторами (см. статью «Общественные
блага» в «Экономико-математическом энциклопедическом сло-
варе» (2003)).
16.2.3 . Общественное благо обладает свойством неисключаемос-
ти, ибо нельзя его предоставлять одним индивидуумам и не пре-
доставлять другим. Отсюда вытекает, что у потребителей (которых
может быть довольно много) нет стимула участвовать в финанси-
ровании производства общественного блага в объеме, который
соответствовал бы их оценкам общественного блага. Таким обра-
зом, эти индивидуумы ведут себя, как «зайцы» (пассажиры-безби-
летники в общественном транспорте), ибо они потребляют обще-
ственное благо и не собираются за него платить.
Если потребителей конкретного общественного блага относи-
тельно немного, появление среди них «зайцев» маловероятно в
связи с достаточной простотой их выявления. Однако с ростом
числа потребителей общественного блага «поголовье зайцев» бу-
дет расти в связи с возрастающими трудностями их выявления и в
связи с естественным соображением о том, что если число потре-
бителей общественного блага велико, то его можно потреблять
бесплатно.
Таким образом, рынок не может обеспечить эффективный
уровень наличия общественного блага из-за существования среди
его потребителей «зайцев». Поэтому, если общественное благо
социально значимо, эффективный уровень производства обще-
ственного блага должен субсидироваться или обеспечиваться го-
сударством.
42 - 7620
657
В экономической теории предложен ряд моделей в целях ре-
шения проблемы элиминирования «зайцев» среди потребителей
общественного блага. Эти модели следует оценивать с позиции
трех критериев: общественные блага должны быть предоставлены
в Парето-эффективном объеме; выявление истинных потребите-
лей должно быть в их интересах и издержки, связанные с произ-
водством общественных благ, должны покрываться (должны быть
равными) совокупными выплатами всех потребителей.
Ниже приводятся модель равновесия Линдаля и механизм
действия закона Кларка.
16.3. Равновесие Линдаля
16.3.1. Рассмотрим модель экономики с частными и обществен-
ными благами. Экономическое равновесие Линдаля — это такое
состояние экономики, в котором равенство спроса и предложе-
ния частных и общественных благ реализуется с помощью единых
(для всех потребителей) цен на частные блага и с помощью персо-
нальных цен (для каждого потребителя) на общественные блага.
Экономическое равновесие по Линдалю анализировалось многи-
ми авторами.
В модели экономики существует г частных благ 6Р...,СГ и Л
общественных благ Gv...,Gk. Вектор частных и общественных благ
имеет вид (х,у) = (хр ..., хг, ур ..., уА), где 0 < х. — количество част-
ного блага Q., i = 1,..., г, и 0 <у; — количество общественного блага
Gj,J= 1,...Л
В модели экономики функционирует/и потребителей Ср...,Ст.
Каждый потребитель С. имеет вектор w® = (h’1w,..., w®) началь-
ных запасов частных благ и функцию полезности ufx, у), опреде-
ленную на всех неотрицательных векторах х и у соответственно
частных и общественных благ. Символом X обозначим произ-
водственное множество, элементами которого являются векторы
предложения (г, у). Вектор предложения (г, у) представляет собой
пару из вектора z частных благ (без запасов) для производства век-
тора у общественных благ. Допустимым распределением в эконо-
мике называется такой набор (х(|),..., х(т), у), состоящий из векто-
ров (х(|),..., х(т) частных благ и вектора у общественных благ
(х(/) =Х](/), ...,х«, / = 1,..., т;у = у(ур ...,уЛ)), что
658
^(xP-v^y eX.
Вектор цен (p(x), p(yW),..., p(y<t>)) состоит из вектора общих
для всех потребителей Сх,...,Ст цен р(х) = (pjx), на частные
блага и персональных (для каждого потребителя С,) цен р^\
i = 1,т, на общественные блага.
Экономическим равновесием по Линдалю называется вектор
цен (р*(х),р*('’'">),...,р*(,''*>)) и допустимое распределение (х‘(1),...,
х(т\ у), такие, что для любого вектора предложения (z, у) е X
справедливо неравенство
р,(х), £p‘wo)Yf>‘(/)-w(/)), у
м /м‘=1
т
AZ/'*0’
(z,y);
если
то
р*(х)х(0 + р*(?°)у(О > + р*^у "'у*® = р^х\№.
Неравенство
р,(х), i р(хо) Y f(x’(,) - *(/)), /
< м Дм >
P*x,^P4y(i)) <z,y)
/=1 J
означает, что в целях равновесия ^p*(x),p‘(y">),...,p‘(-’'”>)j допусти-
мое распределение (х‘(1),..., х’(т), у) является самым выгодным для
предложения (т.е. для производства).
Импликация в определении экономического равновесия оз-
начает, что индивидуальный спрос (x’w, у) является наилучшим в
бюджетном множестве потребителя С., i = 1,..., т.
Величина p^‘^y=t. представляет собой налог, который по-
требитель С. готов заплатить за потребление набора общественных
благу, тогда стоимостный баланс по общественным благам имеет
вид ^/, =р(у)у, где р(у) =^р<у >),...,р(-‘''
/=i
42*
659
Доказательство теоремы о существовании экономического
равновесия Линдаля приведено в работе D. Foley (1970).
В экономическом равновесии Линдаля бюджет сбалансирован,
ибо издержки предоставления общественного блага равны налого-
вым сборам на эти цели. Однако потребители не имеют стимулов к
выявлению своих истинных предпочтений, а сущность проблемы
«зайцев» в том и состоит, что потребитель заинтересован дезин-
формировать общество о своих истинных предпочтениях.
16.4. О налоге Кларка
16.4.1. Суть налога Кларка и его действие здесь иллюстрируются
в случае трех индивидуумов.
Пусть три индивидуума решают вопрос о строительстве кафе
или тренажерного зала (предполагается, что затраты на их строи-
тельство одинаковы).
Для решения вопроса каждый индивидуум определяет, сколь-
ко он готов заплатить за сооружение того и другого объекта. На
основе информации о «готовности платить» осуществляется вы-
бор между кафе и тренажерным залом и определяется величина
налога Кларка.
Налог Кларка для конкретного индивидуума равен измене-
нию благосостояния остальных индивидуумов, которое произо-
шло бы, если бы этот конкретный индивидуум не принимал учас-
тия в голосовании. Помимо налога Кларка индивидуум платит
налог, равный стоимости общественного блага, поделенной на
число индивидуумов.
Пусть индивидуумы 1 и 2 предпочли бы кафе, а свою выгоду
(полезность) от его строительства они оценивают соответственно
в 10 и 15 д.е. Полезность от строительства зала тренажеров для
индивидуумов 1 и 2 равна нулю, ибо тренажерный зал они не по-
сещают. Индивидуум 3 предпочел бы тренажерный зал, свою вы-
году от строительства которого он оценивает в 20 д.е., а полезность
кафе для него нулевая, ибо он кафе не посещает. Приведенные
данные сведем в табл. 16.1.
На основании информации о готовности платить будет при-
нято решение о строительстве кафе, ибо 10 + 15 = 25 > 20. Налог
Кларка для индивидуума 1 равен 5 д.е., ибо на эту сумму изменит-
660
Таблица 16.1
Индивидуум Кафе Тренажерный зал Налог Кларка
1 10 0 5
2 15 0 10
3 0 20 0
Итого 25 20
ся состояние всех индивидуумов в результате неучастия индиви-
дуума 1 в голосовании. Действительно, если индивидуум 1 не го-
лосует, вопрос будет решен в пользу тренажерного зала, ибо
15 < 20. Выгода индивидуума 3 при этом увеличивается на 20 д.е.,
что дает в итоге + 20 — 15 = 5. Налог Кларка для индивидуума 2
равен 10 д.е., ибо на эту сумму изменится благосостояние всех
индивидуумов в результате неучастия индивидуума 2 в голосова-
нии. Действительно, если индивидуум 2 не голосует, вопрос ре-
шается в пользу тренажерного зала, ибо 10 < 20. Выгода индивиду-
ума 3 при этом увеличится на 20 д.е. (с 0 до 20), а выгода индиви-
дуума 1 снизится на 10 д.е., что дает в итоге + 20 — 10 = 10. Налог
Кларка для индивидуума 3 равен нулю, ибо его участие в голосо-
вании, как и его неучастие, ни на что не влияет.
Налог Кларка стимулирует честное поведение индивидуумов.
Чтобы в этом убедиться на примере, предположим, что индивиду-
ум 1 завысил оценку своей полезности от строительства кафе,
тогда налог Кларка для него не изменится. Если индивидуум 1
будет вести себя, как «заяц», и вместо кафе отдаст свою оценку
тренажерному залу, вопрос решается в пользу тренажерного зала.
«Заяц» будет наказан, ибо не получит никакой выгоды и упустит
свой шанс увеличить свою выгоду на 10 д.е. (см. табл. 16.1).
Если индивидуум 3 завысит оценку своей полезности до
30 д.е., то вопрос решится в пользу строительства тренажерного
зала. В этом случае индивидуумы 1 и 2 потеряют свою выгоду в
размере 25 д.е. и, следовательно, налог Кларка для индивидуума 3
составит 25 д.е., что больше его истинной оценки тренажерного
зала, равной 20 д.е. (см. табл. 16.1).
Из приведенных рассуждений следует, что искажение своей
оценки индивидуумом либо не влияет на результат голосования и
величину налога Кларка, либо снижает выгоду обманщика.
661
16.4.2. К сожалению, введение налога Кларка не решает пробле-
му «зайцев» по следующим причинам.
1. Индивидуумы в ходе голосования могут создавать коали-
ции, что может препятствовать выявлению истинных предпочте-
ний. В концепции налога Кларка существенно используется
предпосылка о желании всех индивидуумов участвовать в голосо-
вании. Однако в реальности часть индивидуумов может отказать-
ся участвовать в голосовании, считая, что издержки участия в го-
лосовании превосходят выгоды от участия в голосовании (напри-
мер, получение информации о различных альтернативах может
потребовать значительных средств).
2. На практике не соблюдается предположение о том, что ре-
шения о потреблении частных и общественных благ можно рас-
сматривать как независимые.
3. Неясно, смогут ли индивидуумы платить налог Кларка, если
в действительности он будет введен, ибо изменение благосостоя-
ния остальных индивидуумов может многократно перекрывать
материальные возможности индивидуума, который не участвует в
голосовании.
4. Схема действия налога Кларка соответствует первым двум
критериям, которым должны удовлетворять механизмы решения
проблемы «зайцев» (общественное благо должно предоставляться
в Парето-эффективном объеме, выявление истинных предпочте-
ний индивидуумов должно быть в интересах самих индивиду-
умов). Однако схема действия закона Кларка не согласуется с
третьим критерием, которому должны удовлетворять механизмы
решения проблемы «зайцев» (критерий сбалансированности рас-
ходов на общественное благо с уровнем налоговых изъятий). Сбо-
ры по налогу Кларка создают бюджетный профицит, который
нельзя вернуть индивидуумам, ибо это может привести к измене-
нию их поведения.
На основании вышеизложенного следует утверждать, что при-
веденные модели (экономическое равновесие и закон Кларка) не
дают решения (хотя бы принципиального) проблемы «зайцев».
Отсюда следует, что сегодня альтернативы необходимости вмеша-
тельства государства в предоставление и финансирование обще-
ственных благ не существует.
662
Вопросы для самоконтроля к главе 16
Какие блага называются неконкурентными? Приведите примеры.
Какие блага называются неисключаемыми? Приведите примеры.
Какие блага называются общественными? Приведите примеры.
Что такое выгода индивидуума?
Как связаны между собой понятия предельной выгоды индивидуума
и функция спроса на общественное благо со стороны индивидуума?
Как объяснить процедуру вертикального суммирования линий спро-
са на общественное благо?
В чем отличие частного и общего равновесия в экономической сис-
теме с общественными благами?
В чем экономический смысл равенства предельной нормы транс-
формации сумме предельных норм замены между частным и обще-
ственным благами в случае двух и более потребителей?
Что представляет собой проблема «зайцев»?
В чем проявляется неэффективность рыночных механизмов при
обеспечении потребления общественного блага?
Как формулируются критерии, которым должны удовлетворять ме-
ханизмы решения проблемы «зайцев»?
Как определяется экономическое равновесие Линдаля?
В чем сходство экономического равновесия Линдаля с общим эконо-
мическим равновесием?
В чем различие экономического равновесия Линдаля и общего эко-
номического равновесия?
Почему с помощью модели экономического равновесия Линдаля
нельзя решить проблему «зайцев»?
В чем суть налога Кларка?
В чем конкретно проявляется функция налога Кларка, стимулиру-
ющая честное поведение индивидуумов?
Каковы причины того, что введение налога Кларка не решает про-
блему «зайцев»?
Каким образом критериям (которым должны удовлетворять меха-
низмы решения проблемы «зайцев») соответствует схема действия
налога Кларка?
Задачи и упражнения для самоконтроля к главе 16
Общественные блага являются неконкурентными и неисключаемы-
ми. Дайте толкование каждого термина и сформулируйте явные раз-
личия между ними. Приведите примеры благ неконкурентных и не-
исключаемых, конкурентных и неисключаемых, конкурентных и
исключаемых и общественных благ.
663
2. В населенном пункте проживают 2000 граждан. Их интересует толь-
ко футбол и пиво. Футбольный матч устраивают один раз в неделю.
Ради посещения одного футбольного матча следует пожертвовать
10 бутылками пива. Функция полезности каждого жителя имеет вид
U(x.,G) =xt + G1/2/40,
где х. — количество бутылок пива, потребляемое в неделю одним
жителем; G — число посетителей футбольного матча.
Чему равно Парето-эффективное число посетителей футбольного
матча?
3. В комнате общежития проживают два студента. Функция полезности
одного студента аддитивная Ufa,G) — 3xj + 2G, функция полезности
другого студента мультипликативная Ufa2,G) == (х2(Т)1/2. Здесь Xj и
х2 — суммы, которые расходуют студенты (соответственно первый и
второй) на частные блага (еда, одежда); G — сумма, которую они оба
расходуют на общественные блага (холодильник, телевизор). Месяч-
ный доход студентов 6000 д.е., расходуемых на частные и обществен-
ные блага. Найти Парето-эффективное распределение этой суммы
на частные и общественные блага.
4. В условиях чистой конкуренции предельные издержки фирмы равны
МС = 6. Фирма готова предоставить любой объем услуги:
а) найдите оптимальный объем услуги, если она является частным
благом и если спрос на нее со стороны двух потребителей имеет
следующее представление:
= 60 — 20р, у2 = 30 — р.
Дайте геометрическую интерпретацию;
б) найдите оптимальный объем предоставляемой услуги, если она
представляет общественное благо при тех же функциях спроса на
него. Дайте геометрическую интерпретацию.
5. В экономике имеется два блага: частное (Q) и общественное (<7), два
потребителя с функциями полезности Ufa,у) = х^*у\ Ufa,у) =
= х2,/4у1/4. Линия производственных возможностей имеет вид х + 2у =
= 8.
Определите оптимальный объем потребления общественного блага
при условии, что первый потребитель имеет фиксированный уро-
вень полезности, равный Ц = тг
6. В населенном пункте проживают три группы граждан. Их линии
спроса на телевидение в часах t имеют вид
Ux = a{—t, U2 — a2—2t, U3 = a3-t.
Пусть общественное телевидение — чисто общественное благо, для
производства которого требуются постоянные предельные издержки
МС:
664
а) чему равно оптимальное число часов общественного вещания?
б) сколько часов вещания может обеспечить конкурентный ры-
нок?
Рассмотрите конкретный пример: ах = 200, а2 = 300, а3 = 400,
МС=300.
Дайте геометрическую интерпретацию.
Вопросы и тесты для контрольных работ к главе 16
1. Экономическое равновесие Линдаля отличается от общего экономи-
ческого равновесия:
а) наличием сферы производства;
б) наличием сферы потребления;
в) наличием общественных благ;
г) все пункты верны.
2. С ростом числа потребителей общественного блага число «зайцев»:
а) скорее убывает;
б) скорее растет;
в) нет однозначного ответа;
г) ответы а)—в) не верны;
д) ответы а)—в) верны.
3. Модель экономического равновесия Линдаля не элиминирует про-
блемы «зайцев» потому, что:
а) издержки предоставления общественного блага равны налого-
вым сборам на эти цели;
б) потребители не имеют стимулов к выявлению своих истинных
предпочтений;
в) общественные блага должны быть предоставлены в Парето-эф-
фективном объеме;
г) ответы а)—в) не верны;
д) ответы а)—в) верны.
4. Налог Кларка элиминирует проблему «зайцев» потому, что:
а) индивидуумы в ходе голосования могут создавать коалиции, что
может препятствовать выявлению истинных предпочтений по-
требителей;
б) неясно, смогут ли индивидуумы, не участвующие в голосовании,
платить налог Кларка, в связи с тем что его размер может быть
большим;
в) на практике не соблюдается предположение о том, что решения
о потреблении частных и общественных благ можно рассматри-
вать как независимые;
г) схема действия закона Кларка не согласуется с критерием сба-
лансированности расходов и на общественные блага с уровнем
налоговых изъятий;
д) ответы а)—г) не верны.
665
Задачи для контрольных работ к главе 16
1. Два потребителя имеют следующие функции полезности Ц(х1му) =
= 4xj + Зу, U2(xvy) =х21/4у1/4. ЗдесьXj их2 — суммы, которые расходу-
ют потребители (соответственно первый и второй) на частные блага,
у — сумма, которую они оба расходуют на общественные блага. Ме-
сячный доход потребителей — 10 000 д.е., расходуемых на частные и
общественные блага. Найдите Парето-эффективное распределение
этой суммы на частные и общественные блага.
2. В экономической системе два блага: частное (Q) и (G), два потреби-
теля с функциями полезности Ux(x{9y) = хх1/4у1/4, l/2(xlfy) = x21/2yl/2.
Линия производственных возможностей имеет вид х + 4у = 16. Опре-
делите оптимальный объем потребления общественного блага при
условии, что второй потребитель имеет фиксированный уровень по-
лезности, равный Z72 = т2.
3. В условиях чистой конкуренции предельные издержки фирмы равны
МС = 8. Фирма предоставляет любой объем услуг:
а) найдите оптимальный объем услуги, если она является частным
благом и если спрос на нее со стороны двух потребителей имеет
следующие представления:
yj = 80—4р, у2 = 40—2р.
Дайте геометрическую интерпретацию;
б) найдите оптимальный объем предоставляемой услуги, если она
представляет собой общественное благо при тех же функциях
спроса на него.
Дайте геометрическую интерпретацию.
Глава 17
АСИММЕТРИЧНАЯ ИНФОРМАЦИЯ
17.1. Неблагоприятный отбор на рынке товаров
и услуг
17.1.1. Если участники сделки (например, продавцы и покупате-
ли) на рынке имеют полную информацию о предмете сделки (что
имеет место, как правило, в экономической реальности достаточ-
но редко, если имеет место вообще), то говорят, что участники
сделки вступают в отношения в условиях симметричной инфор-
мации (СИ).
В этом и остальных параграфах главы 17 предполагается, что
участники экономической сделки (контракта) имеют разную ин-
формацию о предмете сделки, т.е. предполагается, что экономи-
ческие (в том числе рыночные) отношения имеют место в услови-
ях асимметричной информации (АСИ). Информированного в от-
носительно большей степени участника сделки принято называть
агентом, информированного в относительно меньшей степени
участника (сделки) — принципалом. (Вместо пары терминов
принципал — агент используется пара терминов заказчик — ис-
полнитель.) Говоря точнее, перед заключением сделки (контрак-
та) агент обладает большей информацией о предмете сделки
(о предмете контракта), чем принципал.
Если в условиях АСИ более информированный агент, стре-
мясь максимизировать свою полезность, совершает действия, ко-
торые негативно влияют на полезность принципала, то говорят,
что имеет место неблагоприятный отбор (возможно, по контрасту
с биологическим естественным отбором — отбором благоприят-
667
ных свойств). Неблагоприятный отбор базируется на ненаблюдае-
мых (для принципала) характеристиках предмета сделки.
Если в условиях АСИ наличие издержек контроля со стороны
принципала за поведением агента после заключения сделки со-
здает у агента стимулы к максимизации собственной полезности в
ущерб интересам принципала, то говорят, что возникает мораль-
ный риск, ибо после заключения сделки агент не чувствует необ-
ходимости находиться в каких-либо моральных рамках (отсюда
термин «моральный риск» (для принципала)). Более точным яв-
ляется термин «риск недобросовестных действий». Здесь слово
«риск» относится к принципалу, а слова «недобросовестные дей-
ствия» — к агенту. Недобросовестные действия (агента) являются
ненаблюдаемыми действиями для принципала. Вместо термина
«неблагоприятный отбор» используют термин предконтрактный
оппортунизм, а вместо термина «моральный риск» используют
термин постконтрактный оппортунизм.
АСИ приводит к несовершенному функционированию рын-
ков и порождает целый спектр теоретических и прикладных про-
блем.
Если сделка (контракт) заключена, то участники сделки нахо-
дятся в (рыночном) равновесии, которое, скорее всего, будет ло-
кальным. Если участники сделки заключили ее в условиях СИ, то
это равновесие оказывается Паретто-эффективным (на основа-
нии теоремы экономической теории благосостояния о том, что
при естественных предположениях равновесие Паретто-эффек-
тивно). Если же участники сделки заключили ее в условиях АСИ,
то равновесие уже не будет (скорее всего) Парето-эффективным.
Таким образом, имеет место потеря Парето-эффективности в ус-
ловиях АСИ. Из-за асимметрии одни участники могут получить
дополнительный выигрыш, а другие участники могут оказаться в
проигрыше. Равновесия, которые появляются в условиях АСИ,
требуют специального анализа.
Для (рыночного) равновесия, которое Парето-эффективно,
используют термин первое лучшее.
(Рыночное) равновесие называется условно Парето-эффек-
тивным, если не существует иного распределения ресурсов, кото-
рое будет Парето-доминировать данное равновесие при дополни-
тельном условии, что для этого иного распределения ресурсов
достаточно той информации, которая доступна участникам рын-
ка.
668
Для (рыночного) равновесия, которое условно Парето-эф-
фективно, используют термин второе лучшее.
17.1.2. Основы теории рынков, функционирующих в условиях
АСИ, были предложены в статье Дж. Акерлофа (1994), который
показал значение этой теории для анализа различных рынков
(рынка страховых услуг, рынка банковских кредитов, рынка труда
и т.д.). В качестве примера, на котором была продемонстрирована
суть теории АСИ, был использован пример рынка подержанных
автомобилей («лимонов»), который представляет собой ситуацию
с ненаблюдаемыми характеристиками. Отметим, что термин «ли-
мон» в Северной Америке используется для обозначения товаров
со скрытыми дефектами.
На рынке предлагают два типа подержанных автомобилей —
высокого и низкого качества. Пусть как продавцы, так и покупа-
тели могут определить тип автомобиля, т.е. они находятся в усло-
виях СИ. На рис. 17.1а SH — линия предложения высококачест-
венных автомобилей, aDH—линия спроса на них. Аналогично SL
и Z>£ на рис. 17.1 б—линии предложения и спроса для низкокачест-
венных автомобилей. Заметим, что ^расположена выше, чем SL,
669
ибо продавцы высококачественных автомобилей должны полу-
чить за них более высокую плату. Аналогично DH расположена
выше Dl, так как покупатели готовы заплатить больше за хорошее
качество. Как видно из рис. 17.1а и 17.16, рыночная цена высоко-
качественных машин — ряд.е., низкокачественных — pL д.е.,
и при этом продаются у экземпляров каждого типа. Таким обра-
зом, в условиях СИ, когда продавцы и покупатели одинаково ин-
формированы о выставленных на продажу автомобилях на каж-
дом из двух сегментов рынка автомобилей, продавцы и покупате-
ли могут заключать сделки. Итак, в условиях СИ (рыночное)
равновесие есть пара наборов (р№ у) и (pL, у).
В действительности продавец подержанного автомобиля мо-
жет знать больше о его качестве, чем покупатель. Пусть теперь
продавцы хорошо осведомлены о качестве автомобилей, а поку-
патели вообще ничего не знают о нем (последние знакомятся с
качеством автомобилей после их покупки и определенного пробе-
га), т.е. теперь продавцы и покупатели находятся в условиях асим-
метричной информации. Вначале покупатели могли полагать,
что шансы купить автомобиль хорошего качества равны 50%. Та-
670
ким образом, совершая покупку, они считают все автомобили
имеющими среднее качество. (Конечно, только купив машину,
покупатель определит ее настоящее качество.) Линия спроса DM
на автомобили среднего качества (см. на рис. 17.1а и 17.16) распо-
ложена ниже линии DH, но выше линии DL. Как видно из рис. 17.1а
и 17.16, теперь будет продано меньше (по сравнению су) высоко-
качественных автомобилей (ун) и больше низкокачественных
(УД
Как только потребители начинают понимать, что бдльшая
часть проданных автомобилей — низкого качества, их линия
спроса сдвигается. Как показано на рис. 17.1а и 17.16, новой ли-
нией спроса может быть линия DLM, которая отражает снижение
качества автомобилей ниже среднего уровня. Линия спроса пере-
двигается влево, перемещая всю совокупность высококачествен-
ных и низкокачественных автомобилей в сторону низкого ка-
чества. Это перемещение продолжается до тех пор, пока на рынке
не останутся только низкокачественные автомобили. При этом
рыночная цена pL окажется слишком низкой, чтобы осуществля-
лась продажа высококачественных автомобилей, так что потреби-
тели правильно полагают, что любой покупаемый ими автомо-
биль имеет низкое качество, и линия спроса совпадает с DL. Итак,
в условиях АСИ (рыночное) равновесие есть пара наборов (рн, 0),
(Р£,У), (Ph>Pl)-
17.1.3. В условиях АСИ рынок может прийти к равновесию и при
цене, обеспечивающей реализацию какой-то части высококачест-
венных автомобилей. Но эта часть будет заведомо меньше, чем в
том случае (СИ), когда потребителям известно качество автомо-
билей в момент покупки. Из-за асимметричности информации
низкокачественные товары вытесняют с рынка высококачествен-
ные, происходит фактическая «дебилизация» рынка. Явление
вытеснения с рынка высококачественных товаров товарами низ-
кокачественными — это и есть, по существу, неблагоприятный
отбор. Ущерб (потерю эффективности функционирования) от
неблагоприятного отбора терпят и продавцы хороших товаров,
и покупатели, и страховые фирмы, и страхователи — словом,
участники всех рынков, на которых эффект неблагоприятного
отбора оказывается значительным.
Следующий пример неблагоприятного отбора дает рынок
страхования. Люди, покупающие страховку, знают намного луч-
671
ше о своем общем состоянии здоровья, чем любая страховая ком-
пания, даже если последняя настаивает на медицинском освиде-
тельствовании. В результате возникает неблагоприятный отбор,
причем даже в большей мере, чем в случае с подержанными авто-
мобилями. Поскольку вероятнее всего, что именно нездоровые
люди желают быть страхователями и их доля в общем числе стра-
хователей возрастает. Это повышает цену страховки, так что более
здоровые люди, взвешивая риск, предпочитают уже не страхо-
ваться. Тем самым доля нездоровых еще больше увеличивается,
что опять повышает цену, и т.д. до тех пор, пока на рынке не оста-
нется лишь эта категория лиц; таким образом, страховая деятель-
ность становится невыгодной.
Неблагоприятный отбор может сделать проблематичным
функционирование рынка страхования и по другим причинам.
Допустим, например, что страховая компания собирается предло-
жить полис для конкретного случая — такого, как автокатастрофа.
Компания выбирает подходящую группу населения, скажем муж-
чин в возрасте до 25 лет, которой собирается продавать полисы, и
оценивает частоту подобных несчастных случае по данной группе.
Для некоторых ее представителей вероятность попасть в аварию
низка, существенно ниже 0,01; для других — высока, существенно
выше 0,01. Если страховая компания не может выделить группы
людей с высокой и низкой степенями риска, она установит размер
страховой премии для всех клиентов, исходя из вероятности про-
исшествия 0,01. Располагая лучшей информацией, некоторые
люди (с низкой вероятностью несчастного случая) предпочтут не
страховаться, тогда как другие (с высокой вероятностью попасть в
аварию) будут страховку покупать. Это, в свою очередь, повышает
вероятность аварии в группе тех, кто застраховался до уровня вы-
ше 0,01, провоцируя страховую компанию повышать страховую
премию. В конечном счете только наиболее вероятные жертвы
захотят страховаться, что представит серьезную угрозу доходам
страховой компании.
Рынки страхования социально значимы, и поэтому нельзя
допустить их самоликвидации. В связи с этим необходим субъект,
который своими действиями позволит сохранить рынок страхова-
ния в условиях неблагоприятного отбора. Таким субъектом в раз-
витых странах является государство. Обеспечивая страхование
всех пожилых людей (на Западе — старше 65 лет), государство уст-
раняет проблему неблагоприятного отбора.
672
Следующим примером рынка, функционирующего в условиях
неблагоприятного отбора, является рынок кредита на Западе. Ис-
пользуя кредитные карточки, граждане могут занимать деньги без
какого-либо обеспечения. Большинство кредитных карточек поз-
воляет их владельцам начислять на свой расчетный счет до не-
скольких тысяч долларов, и при этом многие люди имеют по не-
сколько таких карточек. Компании, выпускающие эти карточки,
получают доход, начисляя проценты на долг заемщика. Но как
может такая компания или банк отличить «высококачественных»
заемщиков (возвращающих долги) от «низкокачественных» (не
возвращающих долги)? Очевидно, должник лучше, чем компа-
ния, знает, будет он возвращать долг или нет. Снова возникает
проблема неблагоприятного отбора. Компании и банки должны
назначать одинаковый процент для всех заемщиков, и это больше
привлекает «низкокачественных» заемщиков. В свою очередь, это
приводит к повышению ставки процента, что опять-таки увели-
чивает долю данной группы, снова повышается процент и т.д.
В действительности компании, выпускающие кредитные кар-
точки, и банки могут в какой-то мере использовать хранящиеся в
компьютере ретроспективные данные о кредитах, которыми они
делятся друг с другом, чтобы научиться отличать «низкокачест-
венных» заемщиков от «высококачественных». Многие люди счи-
тают, что компьютеризация кредитной информации является
вторжением в частную жизнь. Это специальная юридическая про-
блема. С экономической точки зрения ретроспективная инфор-
мация о кредитах выполняет важную функцию. Она снимает или,
по крайней мере, существенно сглаживает проблемы неблагопри-
ятного отбора, которые иначе могли бы препятствовать функцио-
нированию кредитных рынков.
17.1.4. В параграфе 8.4 главы 8 была рассмотрена и проанализи-
рована модель идеальной (совершенной) ценовой дискримина-
ции, в которой фирма-монополист выбирает для себя оптималь-
ную схему ценообразования, т.е. такую схему, когда фирма-моно-
полист может предложить каждому потребителю Cjt i = 1, ..., k,
выпускаемый этой фирмой продукт в количестве у* единиц с оп-
латой (со стороны потребителя С;) в размере t* д.е. При этом су-
щественно, что фирма-монополист может индентифицировать
каждого потребителя (т.е. определить его тип). Это означает, что
43 - 7620
673
фирма-монополист функционирует (проводит на рынке идеаль-
ную (совершенную) ценовую дискриминацию) в условиях СИ.
Оптимальные контракты (у*, t*), i = 1,к, совокупность ко-
торых максимизирует прибыль фирмы при выполнении для каж-
дого потребителя С., 1=1,к, условия участия, являются конт-
рактами первого лучшего. Эти контракты образуют рыночное рав-
новесие в модели идеальной (совершенной) дискриминации
(каждый потребитель С. получил, что хотел, по оптимальной цене,
а фирма-монополист получила максимальную прибыль).
В случае АСИ фирма-монополист не может (не умеет) разли-
чать потребителей, т.е. не может определить тип потребителя.
В параграфе 8.4 главы 8 был рассмотрен и проанализирован
вариант ценовой дискриминации второго рода, называемой па-
кетной дискриминацией, которую фирма-монополист проводит в
условиях АСИ. Как было показано в параграфе 8.4, в случае па-
кетной дискриминации потребители и С2 первого и второго
типов соответственно были заинтересованы заключить с фирмой-
монополистом один и тот же контракт (уД /,’), что свидетельству-
ет о наличии неблагоприятного отбора на рынке в условиях АСИ.
Этот неблагоприятный отбор характеризуется тем, что потребите-
ли первого типа (с более скромными потребительскими амбиция-
ми) остаются потребителями первого типа, а потребители второго
типа (у которых более высокие потребительские амбиции) пре-
вращаются в потребителей первого типа, ибо они, как и потреби-
тели первого типа, выбирают контракт (у,*, т.е. наблюдается
«дебилизация» рынка (см. в начале этого параграфа 17.1 модель
рынка «лимонов» Дж. Акелофа), в которой не заинтересована
фирма-монополист. Причина этой незаинтересованности —
в понижении прибыли фирмы-монополиста, когда потребители
Ct и С2 выбирают один и тот же контракт (у(‘, (*).
Таким образом, в случае АСИ равновесие образует пара конт-
рактов (У]*, и (У]‘, t{*), которая понижает максимальную при-
быль фирмы-монополиста, которую она имеет на паре контрак-
тов (у/, /,*) и (у2‘, /2‘).
Как уже отмечалось в параграфе 8.4, для уменьшения информа-
ционной асимметрии на рынке фирма-монополист может исполь-
зовать механизм фильтрации, который в рассматриваемой ситуации
выглядит так: фирма-монополист, максимизируя свою прибыль,
имеет дело с теми потребителями, для которых выполнены не толь-
ко условия участия, но и условия самовыявления (самоотбора):
674
К](У]) — 0, К2(у2) — /2 > О (условие участия),
И О']) - ^(у2) “ *2’ ^2^2) ~l2~ ^,) - *i (условие самовы-
явления).
Условия участия являются естественными с содержательной
точки зрения, ибо для фирмы-монополиста не существует потре-
бителя, который не участвует в рыночной ситуации. Условие са-
мовыявления К2(у2) — /2 > K2(yj) — содержательно можно проин-
терпретировать так: фирма-монополист имеет дело только с теми
амбициозными потребителями, которые принципиально не поз-
волят себе превратиться в потребителей неамбициозных ни при
каких условиях. Условие самовыявления ^0]) — > Vx(y2) — t2
можно проинтерпретировать аналогично только что приведенной
содержательной интерпретации: фирма-монополист имеет дело
только с теми неамбициозными потребителями, которые принци-
пиально не готовы выдавать себя за амбициозных потребителей.
Множество контрактов между фирмой-монополистом и по-
требителями С, и С2 с учетом условий участия и условий самовы-
явления уже позволит фирме-монополисту определить типы по-
требителей и проводить пакетную дискриминацию (в условиях
АСИ).
Контракты (ур fj), (у2; /2), которые представляют собой опти-
мальное решение задачи (8.4.4.)—(8.4.8) (см. параграф 8.4) макси-
мизации прибыли фирмы-монополиста, являются контрактами
«второго лучшего». В параграфе 8.4 выполнено сопоставление
между собой обеих систем оптимальных контрактов «первого луч-
шего» (контрактов (У]*, t*), (у2‘, /2*)) и «второго лучшего» (конт-
рактов (у,; /j), (у2; /2)) (см. материал параграфа 8.4, относящийся к
пакетной дискриминации, включая пример 8.4.2).
17.2. Моральный риск
17.2.1. Общая характеристика морального риска была представ-
лена в начале параграфа 17.1. В этом параграфе описывается и
анализируется проблема морального риска на рынке труда, на
котором функционируют фирма-наниматель (принципал) и на-
емный работник (агент).
Функция полезности агента имеет вид u(w,e) = V(w) — е, где
w — его заработная плата; е— уровень усилий, прилагаемых аген-
«•
675
том на рабочем месте; слагаемое V(w) (которое принято называть
также функцией полезности) удовлетворяет стандартным услови-
ям К(0) = 0, V'(w) > 0 , V"(w) < 0 при любых и» > 0. Из неравенства
V'(w) > 0 следует, что с ростом заработной платы полезность
агента растет; из неравенства V"(w)<0 следует, что V'(w) строго
убывает с ростом w и функция V(w) строго выпукла вверх при
w> 0.
Альтернативная полезность агента равна й, т.е. неравенство
u(w, е) = V(w) — е>й, содержательно означает, что агент работает
по найму у принципала, а в случае неравенства u(w, е)<й агент по
найму у принципала не работает. Агент максимизирует свою функ-
цию полезности.
Взаимосвязь между доходом R фирмы-нанимателя и уровнем
усилий агента представлена в табл. 17.1.
Таблица 17.1
Доход Уровень усили1Г^~-~--^^^ *1 *2
ei Рц Pl2
е2 Р21 Р22
Для параметров табл. 17.1 выполнены следующие условия:
el < е2’ Rl < *2>/>11 +/’12 = 1>Р11 +Р22 = ЬРц >Pi2’P2l <Р2Т ПрИНЦИ-
пал максимизирует свою ожидаемую прибыль, что означает, что
он нейтрален к риску.
17.2.2. График функции K(w) представлен на рис. 17.2.
На рис. 17.2 Ew =pw{ + (1 — p)w2 — ожидаемая заработная пла-
та агента, Ew = pV(w{) + (1 — p)V(w2) — ожидаемая полезность
агента, р — вероятность, с которой агент получает заработную
плату wp (1 — р) — вероятность, с которой агент получает заработ-
ную плату w2.
Из строгой выпуклости вверх функции V(w) вытекает нера-
венство V(Ew) > EV(w), которое означает, что для агента полез-
ность ожидаемой заработной платы более значима, чем его ожи-
даемая полезность. Отсюда следует, что агент согласен отказаться
от своей ожидаемой (но рискованной) заработной платы в пользу
меньшей, но фиксированной заработной платы w*. Это означает,
что агент является рискофобом.
676
Потеря в зарплате Ew — w* > 0, на которую согласен агент в
целях избавления от необходимости нести бремя риска (бремя
неопределенности заработной платы), называется, как известно,
премией за риск. Потеря в полезности у агента в данном случае
равна V(Ew) — V(w*) > 0.
17.2.3. В условиях СИ усилия агента принципалом наблюдаемы.
Сначала рассмотрим случай, когда принципал стимулирует
агента трудиться усердно (случай, когда е = е2). В этих целях прин-
ципал предложит агенту следующий контракт:
/П2,еслие = е2,
/Пр если е = в]
Агент соглашается заключить контракт с принципалом, если
на основании предложения принципала полезность агента будет
не меньше его альтернативной полезности й, т.е.
u(w,e2) = V(w)-e2 ^й,
откуда следует, что V(mi)>u+e2. В силу того что функция V(w)
строго возрастает, уравнение V(m2)>'u + е2 имеет единственное
решение т2=т2. Таким образом, если заработная плата агента
w > «2, агент не покинет принципала (фирму-нанимателя).
677
Контракт, предлагаемый принципалом, стимулирующий
агента трудиться усердно, имеет вид:
/и2,еслие = е2,
/и1,еслие = е1.
Отметим, что заработная плата /л1 должна быть такой, что
V(т2) - е2 > ) - е}. Это содержательно означает, что агенту вы-
годнее получать зарплату л^, прилагая усилие е = е2, чем получать
зарплату /ир прилагая меньшее усилие ег Решением этого нера-
венства будет принадлежность зарплаты т1 некоторому проме-
жутку. Аналогичное неравенство фигурирует ниже в случае, когда
в условиях СИ принципал стимулирует агента трудиться с мини-
мумом усилий (т.е. в случае е = е^. Неравенства, подобные приве-
денному в случае АСИ (см. ниже), играют важную роль и называ-
ются условиями самовыявления (условия самоотбора).
В рассматриваемом случае, когда принципал стимулирует
агента трудиться усердно (е = е2), ожидаемый доход £Я(2) принци-
пала равен ER(V) = ^21^i + ожидаемая прибыль EPR^ прин-
ципала равна EPR^= ER^-ir^,, а полезность w^,^) агента
равна u(m2,e2) = V(m2)-e2=u.
Рассмотрим случай, когда принципал стимулирует агента тру-
диться с минимумом усилий (случай, когда е = et). Основанием
для рассмотрения такого, с позволения сказать, варианта является
то обстоятельство, что усердный труд агента приносит принципа-
лу бдлыпий доход, но и бблыпие издержки из-за высокой оплаты
труда.
В рассматриваемом случае е = е, принципалу естественно
предложить агенту следующий контракт:
ц.2,еслие=е2,
ц1,еслие = е1.
Агент согласится заключить контракт с принципалом, если на
основании предложения принципала полезность агента будет не
меньше его альтернативной полезности й, т.е.
u(w,ei) = V(w)-el ^й,
откуда следует, что У(ц.х)>й+е{. Уравнение имеет
единственное решение =Ц]. Таким образом, если заработная
плата агента w > агент не покинет принципала.
678
Отметим, что аналогично случаю стимулирования агента тру-
диться с усердием (е = е2) заработная плата ц2 должна быть такой,
что
К(Ц1)-е1>И(ц2)-е2.
Ожидаемый доход принципала равен + pi2R2,
ожидаемая прибыль принципала равна EPR^y = ER^ -ць а по-
лезность агента w(p(, ) = K(pj) - = й.
Разность -pj равна издержкам оплаты принципалом до-
полнительных усилий агента.
Разность ЕЛ(2) — ЕЯщ равна приросту ожидаемого дохода при-
нципала, обусловленного дополнительными усилиями агента.
Если £Я(2) — > w2 -gj, т.е. если EPR^ — EPR^ > 0, то прин-
ципалу выгоднее стимулировать агента трудиться усердно.
17.2.4. В условиях АСИ усилия агента принципалом не наблюда-
емы. Поэтому при составлении контрактов, предлагаемых прин-
ципалом агенту, принципиалу ничего не остается, как в первую
очередь руководствоваться собственным доходом, а также любой
другой доступной ему информацией.
Для стимулирования агента трудиться усердно принципал
предложит ему контракт вида
у,если/? = Л,
х, если Я = Я2.
Аналогично случаю СИ ожидаемая полезность агента в слу-
чае, когда он трудится усердно, равна
£"(2) =/,21М<Х’ е2> + Р22и^ ег) =/,21(Г(Х) - в2> + РпМ*) ~ в2> =
Р21И(х)+р22К(у)-е2
и она должна быть не меньше альтернативной полезности и, т.е.
£w(2) >й.
Это неравенство называется условием участия агента в конт-
ракте. Невыполнение этого неравенства означает, что агент не
будет участвовать в контракте.
Далее приоритетное участие агента в усердном труде означает,
что его ожидаемая полезность в случае усердного труда (е = е2)
должна быть больше (точнее, не меньше) ожидаемой полезности
679
в случае труда с минимальным усердием (е = е^, что формально
записывается так:
^U(2)~^U(l)
или в развернутом варианте
Р2Л(Х) +/>22PV) ~ е2 + Pi2^(y) - еГ
Это неравенство называется условием самовыявления (условием
самоотбора) агента, готового трудиться усердно. В экономичес-
кой реальности условие самовыявления выполняется для трудо-
голиков. Множество пар (х, у), удовлетворяющих условиям учас-
тия и самовыявления, представляет собой множество контрак-
тов, которые приемлемы для агента и стимулируют его трудиться
усердно.
Задача принципала найти такие значения х и у (х > 0, у > 0),
которые удовлетворяют условием участия и самовыявления и ко-
торые максимизируют его ожидаемую прибыль:
£Р/?(2) =/>21(Р1 -х) +/>22(Я2 —у).
Пусть решение задачи максимизации ожидаемой прибыли
принципала есть двумерный вектор (х', у'), откуда следует, что
оптимальный стимулирующий агента к усердному труду контракт
имеет вид
у’,еслиР = Р2 >Ri,
х’, если
Тогда ожидаемая заработная плата агента равна Ew' = р21х‘ +
+ р22у", ожидаемый доход принципала равен ER' = p2{Rl + p22R2,
ожидаемая прибыль принципала равна EPR' = ER' — Ew’, ожида-
емая полезность агента равна Ей ' =p2l V(x') + p22V(y') — е2.
Случай, когда принципалу необходимо нанять в условиях
АСИ агента, который будет трудиться с минимальным усердием,
совпадает со случаем, который имел место в условиях СИ. Глав-
ная забота принципала, чтобы агент не ушел от него. В таком слу-
чае агент как рациональный индивидуум, естественно, будет ра-
ботать с минимальным усердием е = ег
Снова выпишем контракт в случае, когда агент трудится с ми-
нимальным усердием:
М' = <
|12,еслие = е2,
ц1,еслие = е1 —
680
и повторим соответствующие выражения для ожидаемых дохода и
прибыли принципала и для полезности агента: £7?(1) = +
+р12/?2, EPR<р = ER^ - fij, u(ji,, ех) = Г(й,) - е, = й.
Если EPR* > EPR^, то заключение контракта, стимулирующе-
го усердный труд агента, целесообразно. Если EPR* < EPR^, то
заключение контракта, стимулирующего минимальное усердие
агента, целесообразно.
Пример 17.2.1. Пусть u(w, e) = Jw-e, й = 2, е, = 1, е2 = 3, R{ = 10,
R2 - 80, = 0,7, pi2 = 0,3, p2i = 0,3, p22 = 0,7.
Сначала проведем вычисление в случае СИ.
Для определения зарплаты решаем относительно т2 урав-
нение V(m2) = й+е2 или в нашем конкретном примере уравнение
= 2+3, откуда получаем = 25.
Найдем промежуток возможных значений заработной платы
тr Неравенство в рассматриваемом приме-
ре имеет вид 725 - 3 > у[щ -1, откуда следует, что т{ < 9.
Выпишем значения ER^, EPR^ и е2):
£Я(2) = 0,3- 10 + 0,7- 80 = 59,
EPR(2) = ERq) - «2 = 59 - 25 = 34,
«(/л2,е2) = 725-3 = 2 = и.
Для определения зарплаты Й1 решаем относительно урав-
нение К(й1) = й + е1, или ^йГ = 2+1, откуда получаем Й1 =9.
Найдем промежуток возможных значений заработной платы
ц2. Неравенство >К(й2)-е2 в рассматриваемом примере
имеет вид 79 -1 > 7^7- 3,, откуда следует, что ц2 < 25.
Имеем
£Л(1) = 0,7- 10 + 0,3- 80 = 31,
ЕРР^} = ER^-y^ =31-9 = 22,
и(Й1,е1) = л/9-1 = 3-1 = 2 = й.
Найдем разности - Й1 = 25 - 9 = 16, EPR^ - EPR^ =34-22 =
= 12, т.е. принципалу выгоднее стимулировать агента трудиться
усердно в условиях СИ.
681
Переходим к выполнению расчетов в случае АСИ. Для этого
выпишем задачу максимизации ожидаемой прибыли принципала
при условиях участия и самовыявления агента, которого принци-
пал стимулирует трудиться усердно:
0,3(10 - х) + 0,7(80 -у) = EPR(1} (max)
при условиях
0,3>/х + 0,77у-3>2,
0,3>/х + 0,7у[у - 3 > 0,7>/х +0,3^/у -1,
х>0,у>0.
Сделаем замену переменных 4х = a,Jy =Р,, тогда EPR,2. =
= 3 - 0,3а2 + 56 - 0,7р2 = 59 - 0,3а2 - 0,7р2, 0,3а + 0,7р > 5, 0,3а +
+ 0,7р - 3 > 0,7а + О,3р - 1.
Перепишем задачу максимизации в виде задачи минимиза-
ции:
0,3а2 + 0,7р2 (min)
при условиях
0,3а + 0,7р £ 5,
-0,4а + 0,4р > 2,
х>0,р >0.
Решим задачу минимизации графическим методом. Сначала
построим множество стимулирующих контрактов, описываемое
условиями задачи минимизации.
На плоскости Оар неравенство За + 7р > 50 изображает верх-
няя полуплоскость прямой За + 7р = 50 (рис. 17.3), неравенство
-4а + 4р > 20 изображает верхняя полуплоскость прямой -а + р =
= 5. Неравенства а > 0 и р > 0 изображают правую и верхнюю от-
крытые полуплоскости. Общая часть этих четырех полуплоскос-
тей есть заштрихованный на рис. 17.3 неограниченный двууголь-
ник.
Точка пересечения прямых За + 7р = 50 и —4а + 4р = 20 имеет
координаты а" = 1,5; Р' =6,5 (проверяется непосредственно).
Для построения линии уровня целевой функции За2 + 7р2 = у,
проходящей через точку (а’; р ‘), следует вычислить у' = 3(а ’) +
+ 7(Р ‘) = 302,5 и написать уравнение За2 + 7р2 = у', которое после
элементарных преобразований приобретает вид
682
Его графиком в положительном ортанте плоскости Осф явля-
ется «четвертушка» эллипса с полуосями, равными (приближен-
но) 10,04 и 6,57 (см. рис. 17.3).
Градиенты прямых За + 70 = 50 и -4а + 40 = 20 соответственно
равны (3; 7) и (—4; 4). Градиент целевой функции у = За2 + 702 в
точке (а ’; 0 *) = (1,5; 6,5) равен grad у(а *; 0 ‘) = (9; 91). Непосред-
ственно проверяется, что в линейной комбинации
X] = 10; Х2 = 21/4. Это означает, что grad y(a”; 0’) содержится в
неотрицательном конусе с вершиной в точке (а’; 0*), натянутом
на векторы (3,7) и (—4; 4), которые являются градиентами ограни-
чений (эти три градиента на рис. 17.3 не показаны).
Отсюда вытекает, что точка у(а‘; 0‘)= (1,5; 6,5) есть решение
задачи минимизации.
683
Возвращаясь к старым переменным х = а2иу = р2ик задаче
максимизации ожидаемой прибыли принципала, имеем опти-
мальный стимулирующий контракт
w'
х' = (а* )2 = 2,25, если R = R2 = 80,
У = (Р* )2 = 42,25, если R = Я, = 10,
ожидаемую заработную плату агента
Ew' = p2lx' + р22у' = 0.3 • 2,25 + 0,7 • 42,25 = 30,25,
ожидаемую полезность агента
Ей =р21Р(х°)+р22^(у)-е2 = 0,3-7^25 + 0,7-^42,25-3 = 2,
ожидаемый доход принципала
ER' = p2iRx + />22Я2 = 0,3 • 10 + 0,7 • 80 = 59,
ожидаемую прибыль принципала
EPR' = ER' - Ew' = 59 - 30,25 = 28,75.
Сопоставив ожидаемую прибыль EPR' = 28,75 с найденной
ранее EPR^ = 22, естественно сделать вывод, что в условиях АСИ
(как и в условиях СИ — см. выше EPR(2) = 34 и EPR^ = 22) прин-
ципалу выгоднее стимулировать агента трудиться усердно.
Для данного примера в целях сравнения ответов, полученных
в случае СИ и в случае АСИ, сведем эти ответы в табл. 17.3.
Таблица 17.3
СИ е2 т{ < 9 '”2 = 25 «0п2,е2) = й = 2 ERm = 59 £Р£(2)_= ££(2)~ »»2 = 34
е1 Й1=9 Ц2<25 ИЙ1,е1)= й = 2 £Л(1) = 31 £РЛ(1) = -£/?(!)-Ц1 - = 22
АСИ е2 х' = 2,25 / = = 42,25 £м’ = 2 £Г = 59 ЕРК = =EK-Ew* = 28,75 = 30,25
е1 II li Uj<25 «(Й1>е1) = й = 2 £Л(1) = 31 £РЛ(1Г £Л(^221-
В случае СИ и е = е2 зарплата агента равна /^=25 и
EPR(2y = £Л(2) - ^2 = 59 - 25 = 34. В случае АСИ и е = е2 ожидаемая
684
зарплата агента равна Ew' = 30,25 и EPR' = ER' - Ew' = 59 - 30,25 =
= 28,75. Следовательно, ожидаемая зарплата агента увеличивается
на 30,25 - 25 = 5,25 д.е., а ожидаемая прибыль принципала умень-
шается на 34 - 28,75 = 5,25 д.е.
На рис. 17.4, который представляет собой конкретизацию
рис. 17.2, показан ряд результатов расчетов, сведенных в табл. 17.3.
Для наглядности на осях абсцисс и ординат даны разные масшта-
бы. Линия OQ{QaQ2 — график функции полезности V(w)=4w,
прямая 0103С2 — хорда, соединяющая точки Qt и Qr Разность
Ew'-m2 = 30,25 - 25 = 5,25 между ожидаемой зарплатой Ew'vi
фиксированной зарплатой есть премия за риск, содержатель-
ная интерпретация которой была дана в начале этого параграфа.
При переходе от СИ к АСИ ожидаемая прибыль принципала
снижается в связи с тем, что он перестает наблюдать усилия аген-
та. И это снижение EPR^y - EPR' = 34 - 28,75 = 5,25 равно пре-
мии за риск.
Общественное благосостояние W(совокупное благосостояние
агента и принципала) определяется как сумма полезности агента
и прибыли принципала. В условиях СИ при стимулировании
агента трудиться усердно (случай е = е2) IF(2) = «(«2, е2)+ EPR^ =
= 2 + 34 = 36, при стимулировании агента трудиться с минималь-
ным усердием (случай е = =м(Ц1,е1)+.Е'Р./^1) = 2 + 22 = 24.
В условиях АСИ при стимулировании агента трудиться усердно
(случайе = е2) W' = Ей' + EPR' = 2 + 28,75 = 30,75, при стимули-
685
ровании агента трудиться с минимальным усердием (случай е = е{)
= «(Й„ е,)+ ЕРЯ^ = 2 + 22 = 24.
Таким образом, при переходе от СИ к АСИ в случае стимули-
рования агента трудиться усердно общественное благосостояние
понижается = W = 30-30,75 = 5,25 на величину 5,25. В случае
стимулирования агента трудиться с минимальным усердием обще-
ственное благосостояние остается неизменным — 1K(I) =
На этом разбор примера 17.2.1 заканчивается.
17.2.5. Рассмотрим на вербальном уровне проблему морального
риска на рынке страхования.
Если, например, собственник (агент) оптового магазина стои-
мостью 100 000 долл, реализует программу мер противопожарной
безопасности для своих сотрудников стоимостью 50 долл., то ве-
роятность пожара равна 0,005. Без такой программы вероятность
пожара повышается до 0,01. Зная об этом, страховая компания
(принципал), если она не может проследить за реализацией про-
граммы, сталкивается с дилеммой. В предлагаемый ею полис
нельзя включать пункт о выплате страховки лишь в случае выпол-
нения программы противопожарной безопасности. Если бы эта
программа была выполнена, страховая компания могла бы застра-
ховать оптовый магазин на сумму, равную ожидаемым потерям от
пожара, составляющим 500 долл. (0,005 • 100 000 долл.). Когда же
страховой полис куплен (агент и принципал заключили конт-
ракт), у собственника исчезает стимул к выполнению программы:
если произойдет несчастье, то их финансовый ущерб будет полно-
стью компенсирован. Невыполнение программы мер противопо-
жарной безопасности агентом (собственником магазина) есть
пример недобросовестного действия (точнее, бездействия), кото-
рое ненаблюдаемо для принципала (страховой компании). Таким
образом, продавая полис за 500 долл., страховая компания терпит
убытки, поскольку «ожидаемые потери» от пожара составляют не
500, а 1000 долл. (0,01 • 100 000 долл.).
Если какой-либо агент (страхователь) полностью застрахован
и принципал (страховая компания, т.е. страховщик), имеющий
ограниченную информацию, не может подвергнуть агента тща-
тельному наблюдению, то поведение агента (страхователя) может
измениться после покупки страхового полиса. Возникает пробле-
ма морального риска. Моральный риск имеет место, когда агент
может воздействовать на вероятность или значимость страхового
686
случая, т.е. события, обусловливающего выплату. Например, если
индивидуум застраховал свое здоровье на все случаи, то он может
посещать врача чаще, чем при ограниченном договоре. Если стра-
ховая компания в состоянии наблюдать за поведением своего
клиента, то она может назначить повышенную плату для тех, кто
посещает врачей чаще. Но если у компании нет такой возможнос-
ти, то ее выплаты, вероятно, окажутся больше ожидаемых. В связи
с моральным риском страховые компании вынуждены увеличи-
вать страховые взносы или вообще отказываться от заключения
подобных сделок.
Рынок страхования, в частности медицинского страхования,
социально значим. Однако вследствие неблагоприятного отбора
(увеличение страховых взносов в связи с тем, что на рынке оста-
ются менее здоровые и малоимущие индивидуумы) рынок меди-
цинского страхования содержит потенциал своей самоликвида-
ции. В параграфе 17.1 уже отмечалось, что в экономически разви-
тых странах действует практика обязательного государственного
медицинского страхования всех пожилых лиц. Благодаря такой
практике, а также другим социально-экономическим мерам дей-
ствие неблагоприятного отбора блокируется, что выражается в
нормальном функционировании рынка медицинского страхова-
ния.
Другой обширный класс ситуаций, связанных с моральным
риском, образуют продажи на условиях абонементной платы —
шведский стол, помесячная оплата телефона, газа и т.д.
Например, предельные расходы едока, оплатившего шведский
стол, равны нулю — оплачено любое количество еды. Если плата
ориентирована на средний аппетит, то она оттолкнет человека,
привыкшего есть мало, и привлечет любителя хорошо поесть. Да-
лее включается механизм неблагоприятного отбора, и в конце
концов установится такая цена, которая может быть привлека-
тельной лишь для обжор-рекордсменов. Такого в действитель-
ности не случается вследствие того, что возможность пользовать-
ся шведским столом не покупается отдельно, а предоставляется
обычно в комплекте с другими услугами при покупке туристиче-
ской путевки, найме гостиничного номера, заказе обслуживания
конференции, съезда и т.д. Тем самым действие неблагоприятно-
го отбора ослабляется или сводится на нет.
687
17.2.6. В 1934 г. во время Великой депрессии правительство Со-
единенных Штатов ввело широкомасштабную систему финансо-
вого страхования. Федеральная корпорация страхования депози-
тов обеспечила страхование депозитов коммерческих банков,
а Федеральная корпорация страхования займов и сбережений сде-
лала то же самое (до 100 000 долл, на счет) для депозитов в ссудо-
сберегательных ассоциациях. Эти программы страхования поро-
дили моральный риск у части вкладчиков, так как они могли те-
перьссужатьденьгилюбой финансовой организации, не принимая
во внимание рискованность этого кредита и не подвергаясь при
этом никакому риску.
Позднее моральный риск по депозитам соединился с мораль-
ным риском собственников сбережений и займов. Начиная с
1982 г. новые участники бизнеса убедились, что они могут привле-
кать крупные суммы капитала, застрахованного правительством,
и осуществлять фактически неограниченные высокоприбыльные
спекулятивные инвестиции. Поскольку вклады были застрахова-
ны, их мало интересовал сопряженный с этим риск.
По существу, страхование вкладов позволило совершать более
рискованные и крупные операции с займами и сбережениями,
чем это было бы возможно без него. Неблагоприятные обсто-
ятельства, связанные с моральным риском в сочетании с кризи-
сом в сфере недвижимого имущества в ряде штатов, привели к
потере многих сбережений и займов.
В 1990 г. затраты на спасение вкладчиков, чьи деньги были
потеряны, когда разорились более 1000 ссудосберегательных ас-
социаций, по скромной оценке, составили более 200 млрд долл.
Наибольшие потери имели место в Техасе, где к октябрю 1990 г.
было потрачено более 42 млрд долл. Полные затраты агентств,
занимающихся страхованием вкладов, составили около 100 млрд
долл, только за 1990 г.
Хотя перспективы на будущее не блестящие, имеются некото-
рые обнадеживающие признаки. Учитывая неблагоприятные
факторы, связанные с моральным риском, правительство преоб-
разовало свою систему страхования. Сегодня Федеральная корпо-
рация страхования депозитов регулирует ссудосберегательные
учреждения и банки так, что они подчиняются жестким требова-
ниям, которые вынуждают менеджеров проводить более ответ-
ственную инвестиционную политику. Рискуя собственными
688
деньгами; менеджеры в меньшей степени заинтересованы в спе-
кулятивных инвестициях.
В отрасли сбережений и займов устранению проблемы мо-
рального риска вкладчиков способствуют следующие меры воз-
действия на вкладчиков:
1) уменьшение размеров страхового покрытия;
2) применение принятого максимального покрытия к индиви-
дууму, а не к каждому его счету;
3) разрешение двойного страхования, предусматривающего
страхование депозита с возмещением потерь в соотношении
меньшем, чем один доллар за один доллар.
Устранению проблемы морального риска собственников паев
способствуют следующие меры воздействия на собственников:
1) взимание страховых премий в зависимости от портфельного
риска: чем выше риск, тем выше премия;
2) ограничение инвестиционных возможностей собственни-
ков паев.
17.3. Модели сигналов и фильтрации
17.3.1. В случае морального риска (риска недобросовестности, т.е. в
ситуации ненаблюдаемых действий) агент выбирает действия, ко-
торые максимизируют его собственное благосостояние, а не об-
щую прибыль. В случае неблагоприятного отбора агент выбирает
контракт, максимизирующий его выгоду, выдавая себя за агента с
другими характеристиками и увеличивая тем самым свою выгоду.
Однако не всегда агенту выгодно поступать так, чтобы его част-
ная информация была недоступна принципалу, ибо такое поведе-
ние агента связано с появлением для него дополнительных издер-
жек. Агенту выгоднее послать принципалу сигнал для того, чтобы
принципал выбрал именно этого агента. Таким образом, подавая
сигнал, агент уменьшает информационную асимметрию на рын-
ке. Согласно концепции рыночных сигналов на некоторых рын-
ках продавцы подают покупателям сигналы, содержащие инфор-
мацию о качестве товаров.
Действие рыночных сигналов проиллюстрируем на рынке
труда, который является характерным примером рынка с асим-
метричной информацией. Допустим, фирма намерена нанять ра-
44 - 7620
689
ботников. Работники (продавцы рабочей силы) знают гораздо
больше о качестве своего труда (о своей продуктивности), чем
фирма (покупатель рабочей силы). К примеру, работники пред-
ставляют, насколько добросовестно намерены трудиться, на-
сколько они ответственны, какова их квалификация-и т.п. Фирме
же удастся выяснить все это только после приема и какого-то пе-
риода их работы. В момент же найма фирме мало что известно об
их продуктивности.
Почему бы фирмам просто не нанять работников, посмотреть,
как они трудятся, а потом уволить тех, кто продемонстрирует
свою относительно низкую продуктивность? Потому, что это за-
частую обходится очень дорого. Во многих странах трудно уволить
человека, проработавшего свыше нескольких месяцев. (Фирме
требуется указать вескую причину или заплатить выходное посо-
бие.) Кроме того, на многих местах работники не достигают пол-
ной производительности, по крайней мере, в первые шесть меся-
цев. Возможно, потребуется обучать работников, на что фирма
должна будет выделить существенные средства. Таким образом,
фирма может не выявить уровень продуктивности работников в
период от шести месяцев до года. Так что было бы намного лучше,
если бы фирма знала заранее уровень продуктивности потенци-
альных работников.
Какие же сведения о продуктивности потенциальных работ-
ников фирма может получить еще до их найма? Могут ли они
сообщать данные об этом? Хорошая одежда и хорошо поставлен-
ная речь при собеседовании могли бы дать какую-то информа-
цию, но даже плохие работники иногда одеваются хорошо или
прекрасно говорят, чтобы получить работу. Таким образом, хоро-
шая одежда и хорошо поставленная речь — это недостоверные
сигналы, они не позволяют верно отличать относительно высо-
копродуктивных работников (работников с высокой производи-
тельностью) от относительно низкопродуктивных работников
(работников с низкой производительностью). Чтобы сигнал был
достоверным, необходимо, чтобы его с большей вероятностью
подавали относительно высокопродуктивные работники (чтобы
им было легче это сделать), чем относительно низкопродуктив-
ные работники.
Например, образование является достоверным сигналом на
рынке труда. Уровень образования работника может быть изме-
рен несколькими показателями: количеством лет обучения, полу-
690
ценными степенями, репутацией университета или колледжа,
давшего степень, средним баллом и т.д. Конечно, образование
может прямо или косвенно повысить продуктивность человека.
Во время обучения индивидуум часто попадает в ситуацию повы-
шенной интеллектуальной активности, когда пробелы в знании
необходимо хотя бы частично компенсировать интуицией, удач-
ной импровизацией, когда приходится принимать рациональное
решение в условиях жесткого цейтнота. Образование является
важным сигналом продуктивности работника еще и потому, что
более способному человеку проще достичь высокого уровня обра-
зования. (Способные люди, как правило, являются более интел-
лектуальными, целенаправленными, энергичными и трудолюби-
выми, а эти качества полезны и при обучении.) Следовательно,
более способные люди скорее могут получить хорошее образова-
ние, которое служит сигналом для фирм о возможностях работни-
ков, и тем самым рассчитывать на высокооплачиваемую работу.
И фирмы вполне обоснованно рассматривают образование как
сигнал о продуктивности.
17.3.2. Первую модель сигналов (модель о сигнализировании) на
рынке труда предложил А.Спенс в своей классической работе
(А.М. Spens (1973)). Далее при описании и анализе модели сигна-
лов мы будем следовать основным положениям этой работы.
На рынке труда представлены работники (агенты) и фирмы-
наниматели (принципалы), которые конкурируют по Бертрану.
Далее для простоты предполагается наличие одной фирмы-нани-
мателя Ги работников двух типов. Работник Lx первого типа ха-
рактеризуется относительно низкой продуктивностью (произво-
дительностью) 0(, работник Ь2 второго типа характеризуется от-
носительно высокой продуктивностью (производительностью)
02. Здесь 0Z, i = 1,2, — положительный скалярный параметр, кото-
рый является денежным эквивалентом продуктивности (произво-
дительности) Lr Следовательно, 0( < 02.
В случае СИ фирма-наниматель F предлагает работнику Lx
заработную плату в размере Wf = 0р работнику L2 заработную
плату в размере = 02. Таким образом, в рассматриваемом слу-
чае равновесие на рынке труда реализуется в виде = 0!, W2 = 02;
при этом прибыль фирмы-нанимателя F, которая наняла работ-
ника 1=1,2, равна нулю: PR. = Q. — Wx = 0. Здесь слагаемое 0.
интерпретируется как доход фирмы F, а слагаемое W. — как из-
44*
691
держки фирмы F. Равенство нулю прибыли фирмы-нанимателя F
является достаточно естественным с содержательной точки зре-
ния, например в связи с тем, что конкурентная фирма имеет нуле-
вую экономическую прибыль в случае долговременного проме-
жутка, а также нулевую прибыль получают фирмы, конкуриру-
ющие по Бертрану.
В случае АСИ, когда у работников отсутствует возможность
подачи сигналов, фирма-наниматель F готова платить каждому
работнику (независимо от его продуктивности) заработную плату
W, равную ожидаемой продуктивности
0,9 +(1-9)02,т.е. H^=qOI + (1 -q)Qr
Здесь скалярный множитель q, 0 < q £ 1, равен доле работников
£] на рынке труда, тогда скалярный множитель 1—q, 1^1 — q^O,
равен доле работников L2 на рынке труда.
В рассматриваемом случае (на основании неравенства 91 < 02)
для заработной платы И7, равной средней продуктивности, имеет
место следующая цепочка неравенств:
0! = ^6, + (1-9)0! ^^ + (1-9)02 =^902+ (1-9)02 = 02,
т.е. работник £, будет доволен тем, что он будет получать ббльшую
(точнее, не меньшую) зарплату Жпо сравнению с зарплатой 0р в
случае СИ, а работник L2 будет недоволен тем, что он будет полу-
чать меньшую (точнее, не большую) зарплату 1К по сравнению с
зарплатой 02 в случае СИ.
17.3.3. Переходим к разбору случая АСИ, когда работник имеет
возможность подавать сигнал об уровне своей продуктивности.
Речь идет о подаче достоверного сигнала, который фирма-нани-
матель F может (легко) проверить. В качестве такого сигнала в
работе М. Спенса был выбран уровень образования работника.
Свидетельством достоверности такого сигнала является, напри-
мер, наличие документа об образовании.
Получение образования работником связано с издержками
этого работника. Пусть е — уровень образования работника,
т.е. например, число лет, в течение которых обучался работник,
и пусть с(е, Q.) — издержки этого работника /, i = 1,2, связанные с
получением им образования в течение слет. Эти издержки с(е, 0Z)
есть издержки сигнализирования работника £.. Далее для крат-
кости символа с(е, 0.) будет использован краткий термин: из-
держки работника Lt, i = 1,2. На основании содержательных сооб-
692
ражений издержки с(е, 0;) как функция двух переменных е и 0
удовлетворяет неравенствами
дс д2с
^>0(>0), ^Ц->0(>0), с(е,01)>с(е,02). (17.3.1)
де де
Первые два из набора неравенств (17.3.1) означают, что с рос-
том продолжительности обучения е издержки с(е, 0), естественно,
растут и функция с(е, 0) по переменной е выпукла вниз. Третье
неравенство цепочки (17.3.1) означает, что у работника Lx из-
держки выше, чем у работника L2, что вполне согласуется с содер-
жательными соображениями, ибо работник L2, который более
продуктивен, как правило, является более способным и поэтому
обучается профессиональным навыкам быстрее и лучше, чем ме-
нее продуктивный работник Lv Третье неравенство цепочки
(17.3.1) можно обобщить в виде неравенства
которое означает, что предельные издержки по продуктивности
отрицательны, и дополнить неравенством
^<0,
ЭеЭ0
которое продолжим отношением конечных разностей (при отно-
сительно малой Де)
дс(е+Де, 0) дс(е, 0)
О > Э2с s Э0Э0
дедв Де
откуда следует, что при Де > 0 (т.е. с увеличением продолжитель-
ности обучения) предельные издержки Эе(е,0)/Э0 по продуктив-
ности должны убывать.
Отметим также очевидные с содержательной точки зрения
равенства с(0,0() = с(0,02) = 0. Если работник, имеющий продук-
тивность 0, обучался е лет и нанимается на ставку заработной
Платы W, то его функция полезности U(e, W, 0) приобретает вид
U(e, 1Г,0)= 1Г-с(е,0),
где, как уже отмечалось выше, с(е, 0) — издержки работника, свя-
занные с получением им образования.
693
Очевидно, с ростом заработной платы (дохода) W работника
значение его функции полезности растет, а с ростом уровня 0 об-
разования значение функции полезности работника убывает.
При фиксированных е и W имеем фиксированный уровень т
полезности работника, имеющего продуктивность 0:
U(e, W, 0) = т(е, ИО, т.е. W- с(е, 0) = т(е, W).
При фиксированном уровне т полезности множество пар
(е, ИО, удовлетворяющих уравнению W — с(е, 0) = т, представляет
собой линию /т безразличия уровня т полезности работника. Урав-
нение линии 1Х безразличия имеет вид
ИЛ=т + с(е, 0).
Для работника Lp i = 1,2, линия безразличия 4° уровня xt
имеет уравнение W(i) = т/. + с(е, 0,) (рис. 17.5, который показывает,
что линия безразличия является восходящей, что содержа-
тельно интерпретируется следующим образом: с ростом уровня е
образования должен расти доход, который необходим для покры-
тия растущих издержек с(е, 0), чтобы иметь один и тот же уровень
полезности.)
694
Поскольку работник фирме-нанимателю подает сигнал в фор-
ме уровня е своего образования, постольку естественно этот уро-
вень е образования толковать в качестве интенсивности сигнала.
Отметим, что продуктивность 0(. работника £. — его частная
информация, уровень е. образования работника — общедоступная
информация (которую принято называть общим знанием), фир-
ма-наниматель F может дифференцировать работников по уров-
ню их образования.
Действия работников и фирмы-нанимателя можно предста-
вить в виде последовательной игры.
Нулевой ход делает Природа, выбирая тип работника.
Первый ход делает «выбранный» Природой работник (агент,
т.е. информированный участник рынка), который подает фирме-
нанимателю F (принципалу, т.е. неинформированному участнику
рынка) сигнал об уровне своего образования.
Второй ход делает фирма-наниматель F, которая, получив сиг-
нал об уровне образования работника, относит этого работника к
одному из двух типов и предлагает соответствующую зарплату.
При отнесении работника к одному из двух типов фирма-нанима-
тель руководствуется своей оценкой представления о связи уров-
ня образования работника с его продуктивностью.
После предложения фирмой-нанимателем F зарплаты работ-
нику он (работник) определяет (оценивает) соответствующее зна-
чение своей функции полезности, а фирма-наниматель вычисля-
ет свою прибыль.
Для определения равновесия в рассматриваемом случае АСИ,
когда работник имеет возможность подавать сигнал о своей про-
дуктивности, необходимо иметь оценку представления фирмы-на-
нимателя Fo том, как связан уровень образования работника с его
продуктивностью. Эту оценку представления принято называть
верой (по аналогии с верой в Бога) фирмы-нанимателя F. Если
работники (агенты) разных типов ведут себя по-разному, имеем
случай разделяющего равновесия на рынке труда в условиях АСИ.
Если работники (агенты) разных типов ведут себя одинаково,
имеем случай объединяющего равновесия на рынке труда в условиях
АСИ.
17.3.4. Рассмотрим случай разделяющего равновесия.
Пусть фирма-наниматель F имеет следующее представление о
связи уровня образования работника и его продуктивности:
695
• работник Z( с уровнем образования е < е характеризуется от-
носительно низкой продуктивностью;
• работник L2 с уровнем образования е > е характеризуется от-
носительно высокой продуктивностью.
Здесь скалярная величина е есть оценка представления
(т.е. вера) фирмы-нанимателя F, о которой речь шла выше.
Минимальный промежуток, накрывающий величину е , будет
описан ниже. Этот промежуток характеризует область разделя-
ющих равновесий. Представление фирмы-нанимателя /"обуслов-
ливает возникновение разделяющего равновесия, если работник
Lx выбирает относительно низкий уровень образования, а работ-
ник Ь2 — относительно высокий уровень образования.
Работнику при данном представлении фирмы-нанимателя F
невыгодно выбирать уровень образования, отличный от нуля или
е . Действительно, если работник L{ имеет уровень образования е
(он связан с наличием издержек с(е, 0f)), такой, что е < е , то этот
работник не изменит представления фирмы-нанимателя F о нем
как о работнике с относительно низкой продуктивностью, кото-
рую он имел при е = 0 (с(0,0) = 0). Следовательно, работнику не
имеет смысла повышать уровень своего образования с е = 0 до
е < е , т.е. работнику не следует посылать фирме-нанимателю F
никакого сигнала. Аналогично работнику не имеет смысл по-
вышать уровень своего образования с е = е до е < е*, ибо он не
изменит представления фирмы-нанимателя F о нем как о работ-
нике с относительно высокой продуктивностью. Иными словами,
работнику достаточно послать фирме-нанимателю F сигнал с ин-
тенсивностью, равной е*.
Для того чтобы в разделяющем равновесии работники с различ-
ной продуктивностью выбирали разные уровни образования, необ-
ходимо выполнение условий самовыявления (самоотбора) fljin этих
работников: работник Lx не должен иметь стимулы для представле-
ния себя на рынке труда в качестве работника Ь2 (первое условие
самоотбора), а работник Ь2 не должен представлять себя на рынке
труда в качестве работника Lx (второе условие самоотбора).
Формально первое условие самоотбора имеет вид
0( >02 — с(е‘, 0j),
откуда вытекает, что с(е*, 0,) > 02 — 0Г В последнем неравенстве
левая часть с(е*, 0j) равна издержкам работника связанным с
получением им образования, правая часть 02 — 01 показывает до-
696
полнительный выигрыш работника L{ в случае, если этот работ-
ник становится работником Ь2. Неравенство с(е*, 0j) > 02 — 0] оз-
начает, что дополнительный выигрыш (02 — 0,) работника L{ не
покрывает его издержек с{е, 0j), поэтому работнику L{ не следует
на рынке труда представлять себя работником Lr
В связи с тем что функция издержек с(е, 0j) (строго) растет с
ростом е, начиная с нулевого значения с(0, 0j) = 0, и значение
с(е, 0р снизу подпирается положительной величиной 02 — 0j > О,
существует такое число ё < е и с(ё, 0]) = 02 - 0] > 0 (рис. 17.6).
Таким образом, получена нижняя граница ё для всех оценок е
представлений фирмы-нанимателя F о том, как связан уровень
образования работника L{ с его продуктивностью 0р
Формально второе условие самоотбора имеет вид
02 — с(е*, 02) > 0j - с(0,0j).
Левая часть этой цепочки есть значение t/(©2, е , 02) функции
полезности Z7( РИ, е, 02) работника L2, которое строго больше пра-
вой части цепочки, которая есть значение U(Q{, 0, 0j) функции
полезности U(W, е, 0j) работника Lv Таким образом, работнику
L2 не следует на рынке труда представлять себя работником Lv
В связи с тем что функция издержек с(е, 02) строго растет с ростом
е и значение с(е‘, 02) накрывается сверху положительным числом
02 - 0р существует такое число ё, что обязательно е <ё и
с(е, 02) = 02 -0j (см. рис. 17.6). Таким образом получена верхняя
граница ё для всех оценок е* представлений фирмы-нанимателя F
и, следовательно, промежуток (ё, ё), содержащий все оценки е*.
На рис. 17.6 т2 = 02 — ©1 — с(е‘, 02) и 0 т2 т2 = 02 -©j -с(ё, 02).
Сдвинутые вверх на величину ©j графики функций с(е, 0,), с(е, 02)
и с(е, 02) + т2 представлены на рис. 17.7, на котором линия /£2) есть
график функции = с(е, 0]) + 0р т.е. линия есть линия без-
различия уровня 0, работника £р которая имеет уравнение
Ux(e, W, 0р = 0р т.е. W- с(е, ©,) =0,. Линия 1^ есть график функ-
ции Wz(2) = с(е, 02) + 0р т.е. линия есть линия безразличия уров-
ня 0j работника Ь2, которая имеет уравнение U2(e, W, 02) = 0р т.е.
W - с(е, 02) = 0Р Линия есть график функции 1Г(2) =
= с(е, ©,) + 0.+ т,*, т.е. линия /»2> . есть линия безразличия уровня
0] + т2 работника L2, которая имеет уравнение U2(e, W, 02) =
= 01+ т2, т-е- ^(2) ~ с(е» + ®i+ т2’ 0^т2 <t2 =02 -0] -с(ё, 02).
697
На рис. 17.6 и 17.7 дан вариант оценки е представления фир-
мы-нанимателя F, ее нижней (ё) и верхней (е) границ, заработной
платы 6, работника и заработной платы 02 работника Ь2.
Таким образом, если представление фирмы-нанимателя о ра-
ботнике имеет вид:
— работник с уровнем образования е < е характеризуется от-
носительно низкой продуктивностью;
— работник с уровнем образования е > «‘характеризуется отно-
сительно высокой продуктивностью, где е е («,«), то на рынке
труда в условиях АСИ существует разделяющее равновесие:
«! = О, IF=Q1 для работников с относительно низкой продук-
тивностью;
е2 = е , е = (ё,е) , 1K= 02 для работника с относительно высо-
кой продуктивностью.
Поскольку ё < ё, существует континуум разделяющих равно-
весий с уровнем образования е* работника с относительно высо-
кой продуктивностью, е € (е,е)(см. рис. 17.7).
17.3.5 . Переходим к рассмотрению случая объединяющего равнове-
сия.
Пусть фирма-наниматель F имеет следующее представление о
связи уровня е образования работника и его продуктивности:
698
• если е < е*, работник характеризуется относительно низкой
продуктивностью с вероятностью 1;
• если е > е*, работник характеризуется относительно низкой
продуктивностью с вероятностью q или относительно высо-
кой продуктивностью с вероятностью (1 - q).
Как в случае разделяющего равновесия, каждый работник вы-
бирает уровень образования между 0 и е. Если величина е доста-
точно мала, то каждый работник скорее выберет получение обра-
зования на уровне е*. Для этого необходимо выполнение нера-
венств
qex + (1 - q)e2 - с(е‘, 0,) £ 0р (17.3.2)
?0] + (1 - q)Q2 - с(е, 02) £ 0Р (17.3.3)
Для содержательной интерпретации неравенства (17.3.2) пре-
образуем его следующим образом:
откуда вытекает, что работник Lx выбирает уровень е* образова-
ния, ибо дополнительный выигрыш 02 — 0] работника Lx при вы-
боре им уровня е образования строго больше издержек с(е‘, 0,),
связанных с выбором уровня е образования.
699
Для содержательной интерпретации неравенства (17.3.3) пре-
образуем его так:
02-0,>(1-дХ02-0,)^с(е.е2),
откуда следует, что работник Ь2 также выберет уровень е образо-
вания.
Итак, оба работника и £2) выберут один и тот же уровень е
образования, в этом случае фирма-наниматель /'предложит (ни-
чего другого ей не остается) зарплату, равную ожидаемой продук-
тивности:
^(б) = 901 + (1-?)02.
Таким образом, имеет место объединяющее равновесие
ех = е\ W=Eq(Q),
е2 = е\ W=Eq(Q).
В этом случае получение фирмой-нанимателем F сигнала с
интенсивностью е* не дает ей основания для идентификации ра-
ботника с относительно высокой продуктивностью.
Объединяющее равновесие было получено в предположении,
что справедливы неравенства (17.3.2) и (17.3.3).
Покажем сначала, что из неравенства (17.3.2) следует неравен-
ство (17.3.3). Для этого вспомним, что с(е*, 0j) > с(е, 02), откуда
следует, что — с(е*, 0j) > — с(е*, 02).
Рассмотрим теперь очевидную цепочку
+ (1 - <?)02 - с(е*, 02) > g0] + (1 - <?)02 - с(е*, 0]) > 0р
откуда получаем, что из (17.3.2) следует (17.3.3).
Далее, в связи с тем что функция с(е*, 0t) строго возрастает по
е (с(0,0 j)), с ростом величины е* в левой части неравенства (17.3.2)
эта левая часть убывает, поэтому найдется такая величина е° > О,
что неравенство (17.3.2) превратится в равенство
901 + (1-9)02-с(ео,01) = 01,
т.е. (1 - д)(02 - 0,) = с(е°, 0^ (рис. 17.8).
Следовательно, для выполнения неравенства (17.3.2) доста-
точно, чтобы величина е* была не больше этой величины е°
(см. рис. 17.8).
Таким образом, е* е [0, е0). Поскольку е0 > 0, существует кон-
тинуум объединяющих равновесий с уровнем е* образования ра-
ботников с относительно высокой и с относительно низкой про-
дуктивностью, е е [0, е0).
700
Геометрическая интерпретация описанного выше объединя-
ющего равновесия представлена на рис. 17.9. В связи с тем что при
е = е оба работника получат одну и ту же зарплату Eq(Q), линии
безразличия и /<2) работников £, и L2 должны пересечься в точ-
ке (е*,£(0)). ' ’
17.3.6 . Таким образом, в случае АСИ на рынке труда при отсут-
ствии возможности подачи сигналов (при отсутствии института
сигнализирования), как уже отмечалось выше, работник Lx полу-
чит зарплату W> 0р т.е. будет в выигрыше, а работник Z2 получит
701
зарплату W< 02, т.е. будет в проигрыше. В этом случае фирма-на-
ниматель /'’не может идентифицировать работников.
В случае АСИ на рынке труда при наличии возможности пода-
чи сигналов (при наличии института сигнализирования), как
только что было установлено, в случае разделяющего равновесия
работник L{ получит зарплату W\ = 0р работник L2 получит зар-
плату = 02. При этом зарплата работника Lx уменьшается с W,
которая была у него при отсутствии института сигнализирования,
до 0р а зарплата работника ^увеличивается с W, которая была у
него при отсутствии института сигнализирования, до 02. В этом
случае фирма-наниматель F может идентифицировать работни-
ков.
В случае объединяющего равновесия при 0 < е < е° имеем с
зарплатой W— ^0, + (1 — ?)02 ситуацию, аналогичную той, кото-
рая имела место в случае АСИ при отсутствии возможности пода-
чи сигналов.
В случае объединяющего равновесия при е = 0 (т.е. работники
не обучаются) работник Lx и работник L2 получают одну и ту же
зарплату W= <у0 j + (1 — <?)02 без издержек, связанных с получени-
ем образования, т.е. имеем ситуацию, аналогичную той, которая
имела место в случае АСИ при отсутствии возможности подачи
сигналов.
Выше было отмечено, что существует континуум разделя-
ющих равновесий е е (ё,е)и континуум объединяющих равнове-
сий е 6 [0, е°).
17.3.7 . Наличие неединственности равновесий стимулирует эко-
номистов на поиски таких равновесий, которые предпочитаются
(по тем или иным критериям) другим равновесиям. Элиминиро-
вание этих других равновесий принято называть операцией очи-
щения равновесий. Для очищения разделяющих равновесий мож-
но использовать критерий минимизации издержек (затрат) работ-
ника Ь2 за счет сокращения продолжительности е2 его обучения
при наличии ограничения е > ё . Напомним, что нижняя граница
ё величин е* определялась как решение уравнения с(е, 0j) = 02 -
-0] > 0, полученного в качестве «предельного» варианта первого
условия самоотбора 0, > 02 — с(е, 0,).
Назовем наименее затратным разделяющим равновесием та-
кое, что:
702
et = 0, W= 0 j для работника с относительно низкой продук-
тивностью;
е2 = * , ИЛ= 02 для работника с относительно высокой продук-
тивностью.
Из вышеизложенного следует, что наименее затратное разде-
ляющее равновесие существует и является единственным
(рис. 17.10, на котором наименее затратное разделяющее равнове-
сие представлено точками (контрактами между фирмой-нанима-
телем F п работниками Lx и Z2) Л(1) = (0, 0р и Л(2) =(ё,02),
т2=02-01-с(ё,02).
17.3.8 . Отметим, что разделяющим и объединяющим равновеси-
ям можно дать теоретико-игровую интерпретацию в виде равно-
весия Нэша — Байеса.
В рассматриваемой модели сигналов (сигнализирование — sig-
naling) первый ход делал работник (агент, т.е. информированный
игрок), второй ход делала фирма-наниматель (принципал,
т.е. неинформированный игрок), т.е. инициатива по преодоле-
нию информационной асимметрии принадлежит работникам.
Ниже рассматривается модель фильтрации (фильтрация (про-
сеивание) — screening), в которой первый ход делает фирма-нани-
703
матель (принципал, т.е. неинформированный игрок), предлагая
работнику (агенту, т.е. информированному игроку) выбрать наи-
лучшую (с точки зрения работника) из предлагаемых ему альтер-
натив (т.е. контрактов), т.е. инициатива по преодолению инфор-
мационной асимметрии принадлежит уже фирме-нанимателю.
Первыми работами по теории фильтрации принято считать
статьи М. Ротшильда и Дж.Е. Стиглица (М. Rothschild, J.E. Stiglitz
(1976)) и С. Вильсона (С. Wilson (1976)).
Действия фирмы-нанимателя и работников можно предста-
вить в виде последовательной игры.
Нулевой ход делает Природа, выбирая тип работника.
Первый ход делает фирма-наниматель (принципал, т.е. неин-
формированный игрок), который предлагает (выбранному При-
родой) работнику (агенту, т.е. информированному игроку) набор
альтернатив, т.е. набор контрактов.
Второй ход делает выбранный Природой работник, который
принимает один из предложенных фирмой-нанимателем конт-
рактов.
Все участники рынка вычисляют свои выигрыши (работник
подсчитывает значение своей функции полезности, фирма-нани-
матель — свою прибыль).
Как и в случае модели сигналов, в модели фильтрации пред-
ставлены работники (агенты) и фирмы-наниматели (принципалы),
которые конкурируют по Бертрану. Следовательно, фирмы-нани-
матели получают нулевую прибыль. Для простоты предполагается
(как и в модели сигналов) наличие одной фирмы-нанимателя F
(которая получает нулевую прибыль) и работников двух типов, ха-
рактеристики которых приведены в модели сигналов. Понятия
объединяющего и разделяющего равновесий в модели фильтрации
совпадают с аналогичными понятиями в модели сигналов.
В модели фильтрации любая пара неотрицательных чисел
(е, W) называется контрактом (между фирмой-нанимателем и
работником). Контракт (е, W) содержательно интерпретируется
следующим образом: при уровне е образования работника фирма-
наниматель предлагает работнику зарплату W. Предполагается,
что работник является лексиграфическим лодырем (ЛГ-лодырем),
т.е. из двух контрактов (е', W) и (е", W) (е’ < е") работник выберет
контракт (е', W). Отсюда следует, что работник, имеющий опре-
деленную продуктивность, выберет единственный контракт, та-
кой, что (ё, W), где ё = min е.
(е.^)
704
Фирма-наниматель может предлагать любые контракты,
т.е. любые пары (е, W) неотрицательных чисел е и W. Наличие
функциональных зависимостей зарплаты IK от уровня е образова-
ния не предполагается. Каждый работник из предлагаемых фир-
мой-нанимателем контрактов выбирает наилучший для себя,
т.е. контракт, максимизирующий его функцию полезности.
Как и в модели сигналов, фирме-нанимателю неизвестны
продуктивности работников. В модели фильтрации фирма-нани-
матель пытается оценить продуктивность работника на основа-
нии того, какой контракт из предложенных фирмой-нанимателем
этот работник выбрал.
В модели фильтрации равновесие на рынке труда должно
удовлетворять следующим условиям.
Во-первых, ни один из предлагаемых фирмой-нанимателем
контрактов равновесия не дает ей отрицательную ожидаемую
прибыль.
Во-вторых, не существует реализуемого контракта с положи-
тельной ожидаемой прибылью вне равновесия.
Покажем (методом от противного), что в модели фильтрации
не существует объединяющего равновесия.
Пусть в модели фильтрации существует (хотя бы одно) объ-
единяющее равновесие (геометрически интерпретируемое точкой
А = (е*,^(0)))
е( = е, Eq(B) = $0, + (1 - ?)02,
е2 = е, Eq(G) = $0, + (1 - ?)02,
(рис. 17.11, который следует сопоставить с рис. 17.9), где число
О < </ < 1 есть вероятность того, что при е > е работник характери-
зуется относительно низкой продуктивностью, а число 1 — q есть
вероятность того, что при е > е работник характеризуется относи-
тельно высокой продуктивностью.
Здесь £?(0) — ожидаемая продуктивность, W = Eq($) — зара-
ботная плата, предлагаемая фирмой-нанимателем работникам
и Ь2. Тогда ожидаемая прибыль фирмы-нанимателя равна нулю:
Eq(pR) = £?(0) - W= 0.
Рассмотрим контракт, предлагаемый фирмой-нанимателем,
который геометрически интерпретируется точкой В, которая рас-
положена строго ниже горизонтальной линии, проходящей через
точку 02 на оси OW, и строго выше горизонтальной линии, прохо-
45 - 7620
705
дящей через точку А, и, следовательно, строго выше горизонталь-
ной линии, проходящей через точку 0t на оси ОИ<
Точка В = (е, расположена между пересекающимися в
точке А линиями безразличия и работников Lx и Ь2 соответ-
ственно. Линия безразличия имеет уравнение Ux(e, W, 0j) = тр
где т t = Eq(B) — с(е, 6 (). Градиент функции полезности Ux(e, W, 0 j)
в точке А имеет вид
gradt/,0?*, jEy(0),0j) =
dc(e*,0[
Эе
,1
7
поэтому значение функции полезности Ц(е, W, 0j) в точке А стро-
го больше ее значения в точке В. Это означает, что работнику Lx
невыгодно переходить от контракта Л к контракту В.
Аналогично показывается, что работнику L2 переход от конт-
ракта А к контракту В выгоден. Контракт В = (е, И^) между фир-
мой-нанимателем и работником Ь2 обеспечивает фирме положи-
тельную прибыль PR2 = 02 — WB > 0, ибо 02 > WB (см. рис. 17.11).
Таким образом, существует реализуемый контракт В = (е, И^в)
между фирмой-нанимателем и работником L2, который фирме
обеспечивает положительную прибыль и который не совпадает с
контрактом Л = (е, £<д(0))(объединяющего равновесия).
Итак, предположение о том, что существует объединяющее
равновесие в модели фильтрации, привело нас к противоречию:
706
существование (объединяющего) равновесия, с одной стороны,
необходимо предполагает выполнение двух условий (см. выше),
а с другой стороны, из существования объединяющего равнове-
сия следует, что второе условие не выполняется. Следовательно,
объединяющего равновесия в модели фильтрации не существует.
Переходим к вопросу существования и единственности разде-
ляющего равновесия в модели фильтрации.
Пусть существует наименее затратное разделяющее равнове-
сие, которое было выписано в модели сигналов (рис. 17.12):
=0, для работника с относительно низкой продук-
тивностью;
е2 = ё, W= 02 для работника с относительно высокой продук-
тивностью.
Это разделяющее равновесие состоит из двух контрактов:
= (0,0,) и А(2) = (е,02) (см. рис. 17.12). Каждый из контрак-
тов.^1) и Л<2) приносит фирме-нанимателю нулевую прибыль:
PR{ = 0, - ^(=0,) = 0 и PR2 = 02 - ИХ=02) = 0.
В связи с тем что все работники — ЛГ-лодыри, наименее за-
тратное разделяющее равновесие (если оно существует) является
единственным.
45*
707
Осталось провести исследование существования наименее за-
тратного разделяющего равновесия.
Пусть фирма-наниматель предлагает работникам Д и L2 конт-
ракт D = (О, W^, где Ид = (рИС 1743)
Пусть число 0 < q < 1 — доля работников первого типа,
т.е. тех работников, которые характеризуются относительно низ-
кой продуктивностью. Тогда число 0 < <7 < 1 — доля работников L2
второго типа, т.е. тех работников, которые характеризуются отно-
сительно высокой продуктивностью. В этом случае ожидаемая
продуктивность работников, которые выберут контракт Д равна
^(е) = 9е, + (1-?)е2.
Если q = q' > - (в этом случае среди работников, которые вы-
берут контракт Д будут преобладать работники Д), то, очевидно,
0 +0
WD = 1 2 > Д-(6) и поэтому ожидаемая прибыль фирмы-на-
нимателя будет отрицательной (неположительной) Eq,(PR) =
=£9.(е)-и^<о.
708
Отрицательная (неположительная) прибыль будет также
иметь место для всех контрактов G = (е, и Н= (е, где е > О
и£/0)< И^02.
Таким образом, в рассматриваемом случае выполнены оба ус-
ловия существования равновесия, которое является разделяющим
и которое состоит из двух контрактов Л(1) и Л<2): во-первых, как
только что отмечено, каждый из контрактов Л(1) и Л(2) разделя-
ющего равновесия приносит фирме-нанимателю нулевую при-
быль; во-вторых, все реализуемые контракты D,G mH, рассматри-
ваемые вне разделяющего равновесия Л(1) и Л<2), приносят фирме-
нанимателю либо отрицательную, либо нулевую прибыль.
Следовательно, выполнены оба условия существования (разделя-
ющего) равновесия в модели фильтрации. Как уже отмечалось
выше, это равновесие является наименее затратным разделяю-
щим равновесием и оно единственное.
Если q = q" < — (в этом случае среди работников, которые вы-
берут контракт D = (О, Л^), преобладают работники L2), то, оче-
0 +0
видно, = 1 2 < £д-(0), и поэтому ожидаемая прибыль фир-
мы-нанимателя будет положительной.
£д,(РЛ) = £9.(0)-И^>О.
Положительная прибыль будет также иметь место для всех
контрактов G = (е, FK^) иЯ = (е, Л^), где е > 0 и Eq,(Q) > > 0r
Таким образом, в рассматриваемом случае каждый из контрактов
Л(1) и Л(2) разделяющего равновесия приносит фирме-нанимателю
нулевую прибыль, т.е. выполнено первое условие существования
(разделяющего) равновесия в модели фильтрации. Второе усло-
вие существования равновесия в рассматриваемом случае не вы-
полнено, ибо существуют реализуемые контракты D, би Я (доста-
точно существования одного из них) с положительной прибылью
фирмы-нанимателя. Отсюда следует важный вывод: в рассматри-
ваемом случае < q" < j в модели фильтрации (разделяющего)
равновесия не существует. Ранее было показано, что в моделях
фильтрации не существует объединяющих равновесий.
709
17.3.9 . Асимметричность информации присутствует на многих
рынках. Добавим здесь несколько примеров: розничные магази-
ны (устранит ли такой магазин дефект товара или вам разрешат
товар вернуть? Магазин лучше покупателя знает свою линию по-
ведения); торговцы редкими марками, монетами, книгами и кар-
тинами (подлинные или фальшивые эти предметы? Торговец
знает гораздо больше об их подлинности, чем покупатель); кро-
вельщики, водопроводчики, электрики (потребитель не полезет
на крышу, когда кровельщик ремонтирует или обновляет ее); рес-
тораны (часто ли его посетитель заходит там на кухню, чтобы
проверить свежесть используемых шеф-поваром продуктов и со-
блюдение им законов об охране здоровья?).
Во всех этих случаях продавец знает больше о качестве товара,
чем покупатель. И пока продавцы не смогут предоставить инфор-
мацию о качестве покупателям, низкокачественные товары и ус-
луги будут вытеснять высококачественные и рынок будет несо-
стоятельным. Поэтому продавцы весьма заинтересованы в том,
чтобы убедить потребителей, что качество предлагаемых товаров
на самом деле высокое. В приведенных выше случаях это достига-
ется в основном за счет репутации, которая является достоверным
сигналом о высоком качестве товара. Индивидуум делает покупки
именно в этом магазине, потому что он известен хорошим обслу-
живанием клиентов; нанимает тех кровельщика и водопроводчи-
ка, которые имеют репутацию хороших работников; идет именно
в тот ресторан, который славится свежестью используемых про-
дуктов и в котором никто из ваших знакомых не заболел после его
посещения.
Иногда бизнесмены не в состоянии создать репутацию. На-
пример, ббльшая часть клиентов закусочной или мотеля, находя-
щихся у скоростного шоссе, заходят туда всего один раз или из-
редка, во время путешествия, так что этот бизнес не имеет воз-
можности создать себе репутацию. Как в таком случае закусочным
и мотелям решить проблему «лимонов»? Один из путей ее реше-
ния — стандартизация, которая является достаточно достовер-
ным сигналом о высоком качестве товара. Живя в своем родном
городе, индивидуум, возможно, не питается в «Макдональдсе».
Однако, проезжая по скоростной трассе и решив позавтракать, он
выберет именно «Макдональдс». Дело в том, что «Макдональдс»
предлагает стандартизированный продукт; в любом «Макдональд-
710
се» по всему миру используются одни и те же ингредиенты и пода-
ется одна и та же пища.
Перечень рынков с АСИ можно продолжить за счет рынков
товаров длительного пользования, таких, как телевизоры, радио-
аппаратура, кино- и фототовары, холодильники. Многие фирмы
производят эти товары, но одни марки более надежны, чем дру-
гие. Если потребители не смогут определить, какая марка более
надежна, то лучшие марки невозможно продать по более высоким
ценам. Фирмы, производящие высококачественную, надежную
продукцию, могут проинформировать об этом потребителей, по-
давая им сигналы в виде гарантий и обязательств.
Гарантии и обязательства эффективно сигнализируют о ка-
честве товара, поскольку долгосрочные обязательства такого рода
обходятся дороже производителю низкокачественного товара,
чем высококачественного. (Низкокачественный товар чаще тре-
бует обслуживания по гарантии, которое производитель должен
оплачивать.) Вследствие этого производители низкокачественно-
го товара не заинтересованы в долгосрочных гарантиях. Таким
образом, потребители могут справедливо считать гарантии и обя-
зательства сигналами о высоком качестве товаров и будут платить
за такие товары больше.
17.4. О модели «принципал — агент»
17.4.1. В этом параграфе на содержательном уровне проанализи-
рованы фрагменты экономической реальности, охватываемые
моделью «принципал — агент». Интерпретация терминов «при-
нципал» и «агент» дана в параграфе 17.1.
Мониторинг производительности работников и менеджеров
требует, как правило, значительных издержек со стороны соб-
ственников. В большинстве фирм собственник (собственники)
не в состоянии осуществить этот мониторинг. О своей производи-
тельности работники и менеджеры знают лучше собственника
(собственников). Эта асимметричная информация приводит к
проблеме «принципал — агент».
Агент — лицо, которое действует, а принципал — та сторона,
на которую это действие влияет, так что менеджеры и рабочие
являются агентами, а собственник — принципалом. Проблема
711
«принципал — агент» состоит в том, что работники и менеджеры
могут преследовать собственные цели даже за счет снижения при-
были собственника (собственников).
Отношения такого рода широко распространены в обществе.
Например, врачи (врач — пример работника по найму) являются
агентами для больниц и как таковые могут отбирать пациентов и
делать процедуры, отвечающие их собственным предпочтениям,
а не обязательно целям лечебного учреждения. Аналогично уп-
равляющие недвижимостью могут управлять собственностью не
так, как хотели бы владельцы.
17.4.2. Пример 17.4.1. Проблема «принципал — агент» на частных
предприятиях. Отдельная семья или финансовая организация об-
ладает пакетом акций, превышающим 10%, лишь в 16 из 100 круп-
нейших промышленных корпораций США. Наиболее крупные
фирмы управляются менеджерами. То обстоятельство, что боль-
шинство держателей акций владеют лишь незначительным про-
центом общего капитала корпорации, затрудняет получение ими
информации о деятельности менеджеров. Одна из функций соб-
ственников (или их представителей) состоит в наблюдении за по-
ведением менеджеров. Но такой мониторинг требует затрат на
сбор и обработку информации, что недешево, особенно для отде-
льного лица.
Менеджеры частных корпораций могут преследовать свои
собственные цели. Согласно одной точке зрения они, по сущест-
ву, в большей степени добиваются роста объемов производства,
чем прибыли, более быстрый рост и большая доля корпорации на
рынке обеспечивают большие кассовые потоки, которые, в свою
очередь, позволяют менеджерам чувствовать себя более сильны-
ми. Другая точка зрения переносит акценты с роста на полезность,
получаемую менеджерами от их деятельности, имея в виду не
столько прибыли, сколько престиж, власть над корпорацией, до-
полнительные льготы и другие преимущества, а также длительные
сроки пребывания в должности.
Имеются, однако, некоторые важные факторы, ограничива-
ющие возможности менеджеров уклоняться от достижения целей
собственника (собственников). Во-первых, держатели акций мо-
гут недвусмысленно выражать недовольство, когда они чувству-
ют, что менеджеры ведут себя неподобающим образом, а в исклю-
чительных случаях — сменить их (возможно, при помощи совета
712
директоров корпорации, чья обязанность заключается в наблюде-
нии за поведением менеджеров). Во-вторых, в управлении корпо-
рацией могут развиваться сильные рыночные начала. Если при
плохом управлении корпорацией появляется угроза перехода уп-
равления в другие руки, то у менеджеров появляется серьезный
стимул к максимизации прибыли. В-третьих, может существовать
хорошо развитый рынок менеджеров. Если те из них, которые
максимизируют прибыль, пользуются спросом, то они будут по-
лучать высокие оклады, что, в свою очередь, вызовет у других ме-
неджеров желание придерживаться той же цели.
Пример 17.4.2. Проблема «принципал — агент» в государствен-
ных организациях. Модель «принципал — агент» может также по-
мочь понять поведение менеджеров в государственных организа-
циях. Здесь менеджеры могут быть заинтересованы во власти и
дополнительных доходах, которые можно получить благодаря
расширению организации за пределы эффективного уровня. По-
скольку поведение менеджеров в общественном секторе контро-
лировать также дорого, то и нет гарантий, что они обеспечат эф-
фективный выпуск. Проверки государственных учреждений,
проводимые в законодательном порядке, чаще всего бывают не-
эффективными, поскольку учреждения имеют лучшую информа-
цию о своих издержках, чем проверяющие органы.
Однако, хотя в государственном секторе отсутствуют рыноч-
ные силы, дисциплинирующие менеджеров на частных предпри-
ятиях, существуют важные факторы, ограничивающие возмож-
ности менеджеров уклоняться от достижения основных целей
государственных организаций. Во-первых, менеджеры государ-
ственных организаций заботятся не только об их размерах. Мно-
гие из них отдают предпочтение общественным работам с низки-
ми издержками, так как им небезразличны «общественные инте-
ресы». Во-вторых, менеджеры государственных организаций
(в не меньшей степени, чем частных) подчиняются строгим тре-
бованиям рынка менеджеров. Если выяснится, что они преследу-
ют несоответствующие цели, то их возможности получить в буду-
щем более высокие оклады сужаются. В-третьих, законодатель-
ные и другие государственные органы выполняют функцию
надзора. Например, в США Государственная бухгалтерская
служба, а также Управление менеджмента и бюджета тратят мно-
го сил на мониторинг других учреждений.
713
В США на местном уровне менеджеры в государственном сек-
торе подвергаются даже более строгому контролю, чем на феде-
ральном уровне. Пусть, например, какое-то городское управление
транспорта расширило автобусные перевозки сверх эффективно-
го уровня. Тогда жители города могут добиться смены руковод-
ства управления или же, если это не удастся, использовать альтер-
нативные виды транспорта. И конкуренция между различными
общественными службами может стать такой же эффективной,
как и между частными корпорациями, ограничивая тем самым
ориентацию менеджеров на цели, отличные от максимизации
прибыли.
Пример 17.4.3. Об эффективности деятельности менеджеров
некоммерческих и коммерческих фирм сферы медицинского об-
служивания. При обследовании в США 725 больниц из 14 основ-
ных лечебных сетей сравнивались прибыли и средние издержки в
коммерческом и некоммерческом секторах.
В ходе обследования установлено, что в 1977 и 1981 гг. нормы
прибыли в этих типах больниц действительно различались. На-
пример, в 1977 г. коммерческие больницы имели рентабельность
11,6%, тогда как некоммерческие — 8,8%. В 1981 г. прибыль пер-
вых составила 12,7%, а вторых — лишь 7,4%. Прямое сравнение
прибыли и издержек этих больниц, однако, не вполне корректно,
потому что они выполняют разные функции. Например, програм-
мы медицинского обслуживания по месту жительства осущест-
вляются в 24% некоммерческих лечебниц и лишь в 6% коммерчес-
ких. Аналогичные различия можно обнаружить в обеспечении
специальными услугами: 10% больниц первого типа и 5% второго
имели сердечно-сосудистые отделения. Кроме того, 43% неком-
мерческих больниц и лишь 29% коммерческих имели отделения
для недоношенных детей.
Используя регрессионный анализ, который определяет разли-
чия в предложении услуг, можно установить, объясняются ли эти
различия более высокими издержками. Такое исследование обна-
ружило, что после исключения различий в услугах средние из-
держки на одного пациента в день на 8% выше в некоммерческих
лечебницах, чем в коммерческих. Отсюда следует, что коммерчес-
кий статус больницы влияет на ее поведение в соответствии с мо-
делью «принципал — агент»: не сталкиваясь с конкуренцией, не-
коммерческие лечебные учреждения в отличие от коммерческих
714
могут ослабить внимание к издержкам и, следовательно, в недо-
статочной мере служить исполнителями для своих заказчиков и
общества в целом.
На основании приведенных результатов обследования нельзя
сделать вывод, что некоммерческие больницы бесполезны: они
оказывают услуги, которые общественно востребованы. Однако
при решении вопроса об освобождении их от уплаты налогов не-
обходимо принять во внимание дополнительные издержки, свя-
занные с управлением ими.
17.5. О теории эффективной заработной платы
17.5.1. В теории эффективной заработной платы базовой является
модель уклонения наемных работников от добросовестного выпол-
нения своих обязанностей, предложенная К. Шапиро и Дж. Стиг-
лицем (С. Shapiro, J.E. Stiglitz (1984)). В этом параграфе 17.5 пред-
ставлена на вербальном уровне основная идея этой модели. Де-
тально модель описывается и анализируется в курсе, посвященном
экономике труда.
Если рынок труда конкурентный, то всякий желающий рабо-
тать найдет себе место за оплату, равную его предельному продук-
ту. Однако большинство стран имеют высокую безработицу, не-
смотря на то что многие люди упорно ищут работу. Очевидно,
многие безработные работали бы и за более низкую заработную
плату, чем та, которую получают занятые. Однако фирмы не сни-
жают заработную плату, не повышают уровень занятости и не
увеличивают прибыль.
Производительность труда принято определять в зависимости
от способностей работников и инвестиций фирм в основной ка-
питал. Модели эффективной заработной платы предполагают,
что производительность труда зависит также от размеров его оп-
латы. Существуют различные объяснения этой связи.
В развивающихся странах, как полагают экономисты, произ-
водительность работников зависит от оплаты труда в той мере,
в какой они могут лучше питаться. Более высокооплачиваемые
работники имеют возможность купить больше еды и лучшего ка-
чества, отчего они меньше болеют и интенсивнее трудятся.
715
Более подходящее объяснение для развитых стран дает модель
уклонения наемных работников от добросовестного выполнения
своих обязанностей. Поскольку мониторинг работников стоит
дорого или вообще невозможен, фирмы в этих моделях имеют
несовершенную информацию о производительности работников,
что ставит проблему «принципал — агент». В простейшем виде
модель уклонения предполагает, что рынки конкурентны, так что
все работники одинаково производительны и получают одну и ту
же заработную плату. Будучи нанятыми, они могут либо эффек-
тивно трудиться, либо ослабить свои усилия (уклоняться от рабо-
ты). Но так как информация об их деятельности ограничена, ра-
ботники могут не потерять работу, работая спустя рукава.
Модель уклонения имеет следующий вид. Если фирма платит
своим работникам равновесную заработную плату то у работ-
ников есть стимул уклоняться от работы. Даже если это станет
известно и их уволят (а этого может и не случиться), они немед-
ленно устроятся где-нибудь еще за ту же заработную плату. В та-
кой ситуации угроза увольнения не действует на работников, по-
этому у них нет стимулов трудиться максимально эффективно.
Чтобы повысить эффективность труда, фирма должна предло-
жить работникам повышенную оплату We. При этом увольнение
за недобросовестную работу приведет к уменьшению заработка,
ибо тогда уволенные работники нанимаются другой фирмой, ко-
торая выплачивает заработную плату в размере < We). Ког-
да различие в оплате труда достаточно велико, работники станут
трудиться эффективно и фирма решит проблему уклонения путем
ее элиминирования. Уровень оплаты, позволяющий добиться
этого, называется эффективной заработной платой. С проблемой
уклонения сталкиваются все фирмы. Это значит, что все они захо-
тят предложить оплату труда We, превышающую равновесный
уровень. Повсеместное повышение заработной платы не приведет
к тому, что у работников исчезнет стимул к добросовестному вы-
полнению своих обязанностей в связи с тем, что другие фирмы
предлагают заработную плату, превышающую И^, ибо в этом слу-
чае спрос на рабочую силу окажется ниже равновесного уровня,
т.е. появится безработица. Это означает, что рабочие, уволенные
за уклонение от добросовестного выполнения своих обязаннос-
тей, какое-то время будут безработными, прежде чем им предло-
жат заработную плату We в другой фирме.
716
Рисунок 17.14 иллюстрирует явление уклонения от работы на
рынке труда. Линия спроса на труд DL, как правило, является нис-
ходящей. Еслибынебыло уклонения, тоточка(£*, Ил)пересечения
Dl с линией предложения SL труда показывала бы рыночную зара-
ботную плату IF* и полную занятость £*. Однако, учитывая укло-
нение, фирмы не согласны платить IF*. Им выгоднее при любом
уровне безработицы назначить несколько более высокую плату,
с тем чтобы работники стали эффективнее трудиться. Этот уро-
вень оплаты показан линией NSC, построенной с учетом условия
отсутствия уклонений (NSC — No shrinking condition). Эта линия
МУС показывает, какова минимальная заработная плата, при ко-
торой работники перестают уклоняться от работы, при каждом
уровне занятости L. Заметим, что чем ниже уровень занятости L
(т.е. чем выше уровень безработицы), тем меньше разница между
эффективной заработной платой W и IF*. Это объясняется тем,
что при высоком уровне безработицы лица, уклоняющиеся от вы-
полнения своих обязанностей, рискуют долго не найти работу и
поэтому не требуют большого вознаграждения за высокопроизво-
дительный труд (без уклонения).
Рис. 17.14
717
На рис. 17.14 равновесная заработная плата We находится на
пересечении линий NSC и с числом рабочих Le, получающих
заработную плату We. Это объясняется тем, что jV5C выражает ми-
нимальный уровень оплаты, при котором фирмы еще исключают
уклонения. Им не нужно платить больше, чтобы привлечь требу-
емую численность рабочих, но они не могут предложить и меньше
из опасения уклонений. Заметим, что линия NSC всегда располо-
жена выше линии предложения труда SL. Это означает, что в рав-
новесии (Le, We) всегда будет какая-то безработица (L* - Le).
17.5.2. Пример 17.5.1. Один из первых примеров использования
эффективной заработной платы можно найти в истории компа-
нии «Форд» — одного из самых крупных производителей автомо-
билей в США. До 1913 г. производство автомобилей в значитель-
ной степени зависело от высококвалифицированных рабочих. Но
применение сборочного конвейера коренным образом изменило
положение. Теперь требовались специалисты гораздо более низ-
кого уровня квалификации, а производство все больше стало за-
висеть от поддержания оборудования конвейера в рабочем состо-
янии. Это привело к падению уровня трудового энтузиазма рабо-
чих, и они стали активно увольняться. В 1913 г. текучесть кадров
на «Форде» составила 380%. В следующем году она достигла
1000%, что резко снизило рентабельность компании «Форд».
Компании необходимо было обеспечить себя стабильной ра-
бочей силой, и Генри Форду, а также его деловому партнеру
Джеймсу Казенсу удалось этого добиться. В 1914 г., когда дневная
оплата труда в отрасли в среднем составляла от 2 до 3 долл., ком-
пания «Форд» ввела для своих рабочих дневной заработок в 5 долл.
Эта мера была продиктована стремлением повысить эффектив-
ность труда (а не щедростью). Цель заключалась в привлечении
лучших работников, которые не оставляли бы компанию, и в ко-
нечном счете в увеличении прибыли компании.
Хотя Генри Форда и критиковали за это решение (и не без ос-
нования, ибо рост зарплаты приводит к росту издержек, однако
вопрос о росте заработной платы характеризуется не только прос-
тым эффектом (ростом издержек), но и составным эффектом
(ростом прибыли), что и имело место у фирмы «Форд»), оно ока-
залось вполне успешным. Кадровый состав стал более стабиль-
ным, а известность компании обеспечила реализацию продукции.
И поскольку Генри Форд получил возможность отбора рабочих,
718
он смог нанять более производительных. Как следует из расчетов
начальника отдела труда компании «Форд», производительность
труда компании выросла на 51%. Согласно другому исследова-
нию, число прогулов уменьшилось вдвое и пропуски по уважи-
тельным причинам также резко сократились. Итак, эффектив-
ность повысилась в большей степени, чем того требовало возме-
щение дополнительных затрат на оплату труда. В результате
прибыли у компании «Форд» существенно выросли — с 30 млн
долл, в 1914 г. до 60 млн в 1916 г.
Вопросы для самоконтроля к главе 17
1. Что такое асимметричная информация? принципал? агент?
2. Что такое неблагоприятный отбор?
3. Что такое моральный риск?
4. Как выглядит динамика линий спроса на высококачественные и
низкокачественные автомобили в модели рынка «лимонов»? Ответ
обоснуйте.
5. В чем суть неблагоприятного отбора на рынке медицинского страхо-
вания?
6. В чем суть неблагоприятного отбора на рынке кредита?
7. В чем суть связи между понятиями «идеальная (совершенная) цено-
вая дискриминация» и «симметричная информация»?
8. Как содержательно интерпретируется условие участия в модели па-
кетной дискриминации?
9. Как содержательно интерпретируется условие самовыявления в мо-
дели пакетной дискриминации?
10. Проблема морального риска на рынке труда: опишите понятийный
аппарат модели.
11. Как функционирует модель рынка труда в условиях симметричной
информации?
12. Как функционирует модель рынка труда в условиях асимметричной
информации?
13. Как меняется общественное благосостояние при переходе от сим-
метричной информации к асимметричной информации в случае
стимулирования агента трудиться усердно и в случае стимулирова-
ния агента трудиться с минимальным усилием?
14. В чем суть морального риска в отрасли сбережений и займов?
15. В чем суть концепции рыночных сигналов?
16. Какой сигнал является сильным на рынке труда? Ответ обоснуйте.
17. В чем суть веры принципала, т.е. оценки его представления о том,
как связан уровень образования агента с его продуктивностью?
719
18. В чем отличие ситуации на рынке труда в условиях асимметричной
информации, в которой работник имеет возможность подавать сиг-
нал о своей продуктивности, от ситуации, когда у работника отсут-
ствует возможность подавать сигнал о своей продуктивности?
19. Что такое разделяющее равновесие на рынке труда в условиях асим-
метричной информации?
20. Дайте содержательную интерпретацию первому и второму условиям
самовыявления (самоотбора) агента (работника).
21. Как получаются нижняя и верхняя оценки промежутка, содержаще-
го все веры принципала в случае разделяющего равновесия?
22. Что такое объединяющее равновесие на рынке труда в условиях
асимметричной информации?
23. Как получается верхняя оценка для значений продуктивности агента
объединяющего равновесия?
24. Что такое наименее затратное разделяющее равновесие? Раскройте
проблему существования и единственности наименее затратного
разделяющего равновесия.
25. В чем сходство и различие между моделью сигналов и моделью филь-
трации?
26. Что означает термин «лексикографический лодырь»?
27. Как формируются условия существования равновесия на рынке тру-
да в модели фильтрации?
28. Как обосновать, что в модели фильтрации не существует объединя-
ющего равновесия?
29. Как обосновать, что в модели фильтрации существует не более одно-
го разделяющего равновесия?
30. Что такое репутация фирмы? Прокомментируйте это понятие в рам-
ках концепции рыночных сигналов.
31. Что такое стандартизация продукции фирмы? Прокомментируйте
понятие гарантии в рамках концепции рыночных сигналов.
32. В чем суть отношения «заказчик — исполнитель»? Приведите приме-
ры отношения «заказчик — исполнитель».
33. Каковы факторы, ограничивающие возможности управляющих ук-
лоняться от достижения целей собственников?
34. Каковы факторы, ограничивающие возможности управляющих ук-
лоняться от достижения целей государственных организаций?
35. В чем суть модели уклонения?
36. Что такое линия NSC, построенная с учетом отсутствия уклонения?
Каково взаимное расположение линии NSC и линии предложения
труда SL?
37. Что такое эффективная заработная плата?
38. Какие эффекты (прямой и составной) имело резкое повышение за-
работной платы работникам фирмы «Форд» накануне Первой миро-
720
вой войны? Объясните, почему рост дохода резко опережал рост из-
держек.
Задачи и упражнения для самоконтроля к главе 17
1. Во многих университетах Запада используется следующая система
оценок (в порядке убывания их значимости): А, В, С9 D9 Е, F Круп-
ный университет запрещает ставить отметки Д £или F Он объясня-
ет это тем, что студенты стараются учиться выше среднего уровня,
когда они не испытывают опасений быть исключенными. Универси-
тет заявляет, что он хочет, чтобы все его студенты получали только
оценки А и В, Если цель состоит в том, чтобы поднять отметки в це-
лом до уровня В или выше, то является ли это эффективной полити-
кой? Ответьте, учитывая проблему морального риска.
2. Сталкиваясь с проблемой репутации производства автомобилей,
требующих редкого ремонта, ряд американских автомобильных ком-
паний предложили широкие гарантии покупателям машин (напри-
мер, семилетние гарантии на все детали и выполнение необходимого
ремонта):
а) с учетом ваших знаний о рынке «лимонов» почему это будет разум-
ной политикой?
б) будет ли эта политика создавать проблему морального иска? Объ-
ясните.
3. Чтобы стимулировать конкуренцию и повысить благосостояние по-
требителей, Федеральная комиссия по торговле США требует, чтобы
фирмы давали правдивую рекламу. Почему правдивая реклама бла-
гоприятствует конкуренции? Почему рынок менее конкурентен, ес-
ли фирмы обманывают при рекламе?
4. Страховая компания рассматривает выпуск трех типов страховок от
пожара:
а) с полным страховым покрытием;
б) с полным страховым покрытием за вычетом 10 000 долл.;
в) с 90%-м покрытием всех потерь. Какая страховка, скорее всего,
создаст проблему морального риска?
5. Для рынков с преобладанием асимметричной информации согласи-
лись бы вы с каждым из следующих утверждений? Дайте краткое
объяснение:
а) правительство должно субсидировать «Вестник потребителя»;
б) правительство должно установить стандарты качества: напри-
мер, фирмам должно быть запрещено продавать товары низкого
качества;
в) производитель качественного товара захочет, вероятно, предло-
жить широкие гарантии;
46 - 7620
721
г) правительство должно потребовать, чтобы все фирмы предложи-
ли широкие гарантии.
6. Доход фирмы за определенный короткий промежуток времени опи-
сывается формулой
Л=Юе-е2,
где е — затраты труда типичного рабочего (все рабочие предполага-
ются идентичными).
Рабочий выбирает свой уровень затрат труда так, чтобы максимизи-
ровать свою чистую заработную плату (т.е. за вычетом стоимости за-
трат) w — е (стоимость единицы затрат труда полагается равной 1).
Определите уровень затрат труда и уровень прибыли (доход минус
уплаченная заработная плата) для каждой из следующих систем зара-
ботной платы. Объясните, почему эти различные схемы стимулиро-
вания исполнителя дают различные результаты:
a) w = 2 для е > 1; в противном случае w = 0;
б) w = J?/2;
в) и> = Я-12,5.
7. Функция полезности агента (наемного работника) имеет вид
U(JK, е) = - е, где W — его заработная плата; е — уровень усилий
агента, прилагаемых на рабочем месте. Альтернативная полезность
агента U = 3. Взаимосвязь между доходом R принципала (фирмы-на-
нимателя) и уровнем усилий агента представлена в следующей таб-
лице:
Уровень усилий ' Доход Я, = 5 Л2 = 65
ei рп = °,8 Р|2
е2 = 4 р21 = 0,3 Р22 = 0,7
а) постройте на плоскости OW(U+e) график функции полезности
агента;
б) проведите необходимые расчеты в условиях симметричной ин-
формации:
— найдите заработную плату и промежуток возможных значений
заработной платы тх\
— найдите О(2), EPR^ и Щт2, е2);
— найдите заработную плату gj и промежуток возможных значений
заработной платы
— найдите £Я(1), EPR(X) и ЩЦр ех);
— найдите разности - fq и EPR^ — EPR^ и приведите их содер-
жательную экономическую интерпретацию;
722
в) проведите необходимые расчеты в условиях асимметричной ин-
формации:
— выпишите условия участия и самовыявления агента в случае, ког-
да его стимулируют трудиться усердно;
— выпишите ожидаемую прибыль принципала, который стимулиру-
ет агента трудиться усердно;
— решите задачу максимизации ожидаемой прибыли принципала,
который стимулирует агента трудиться усердно при выполнении
для агента условий участия и самовыявления, и выпишите опти-
мальный стимулирующий контракт;
— в случае оптимального стимулирующего контракта выпишите
ожидаемую заработную плату Ew агента, ожидаемую полезность
Ей агента, ожидаемый доход £7?* принципала и ожидаемую при-
быль ЕРЕ? принципала;
— сопоставьте ожидаемую прибыль ЕРЕ? с найденной ранее EPR^ и
сделайте содержательные выводы;
г) постройте таблицу, аналогичную табл. 17.3, и сопроводите эту таб-
лицу содержательными пояснениями;
д) постройте график, аналогичный графику на рис. 17.4, и сопрово-
дите его содержательными пояснениями;
е) оцените общественное благосостояние в условиях симметричной
и асимметричной информации. Сопоставьте общественное бла-
госостояние в случае, когда агента стимулируют трудиться усерд-
но и с минимальным усердием.
8. Пусть линия спроса на труд имеет уравнение у = 20 — 2w. Линия
предложения труда имеет уравнение у = 2w — 10. Линия NSC имеет
z \2
уравнение w = 0,5у + 5,5 + f 1 (цифры условные):
а) определите равновесную заработную плату ю* и равновесный
объем труда £*;
б) определите эффективную заработную плату wen эффективный
объем труда Ze;
в) дайте геометрическую интерпретацию пунктов а) и б).
Вопросы для контрольных работ к главе 17
1. В чем отличие неблагоприятного отбора и морального риска на рын-
ке страхования? Ответ обоснуйте.
2. Каковы меры устранения проблемы морального риска для собствен-
ников?
46*
723
3. Почему продавец может считать выгодным подавать сигналы о ка-
честве своей продукции? Почему гарантии и обязательства являются
рыночными сигналами?
4. Почему менеджеры фирм могут стремиться к достижению целей,
отличных от максимизации прибыли — цели акционеров фирмы?
5. Как модель «заказчик — исполнитель» объясняет, почему государ-
ственные предприятия, такие, как почты, часто преследуют цели,
отличные от максимизации прибыли?
Задачи для контрольных работ к главе 17
Пусть линия спроса на труд имеет уравнение у = 30 - 3w. Линия
3
предложения труда имеет уравнение y = -w-6. Линия NSC имеет
2 л < (У Y 2
уравнение w = -y+4,5+l — I :
2.
а) определите равновесную заработную плату w* и равновесный
объем труда Z*;
б) определите эффективную заработную плату we и эффективный
объем труда Ze;
в) дайте геометрическую интерпретацию пунктов а) и б).
Функция полезности агента (наемного работника) имеет вид
U(FK, ё) = tfw - е, где FK — его заработная плата; е — уровень усилий
агента, прилагаемых на рабочем месте. Альтернативная полезность
агента U = 4. Взаимосвязь между доходом R принципала (фирмы-на-
нимателя) и уровнем е усилий агента представлена в следующей
таблице:
Уровень усилий"" Доход А, = 4 r2 = 100
е1 Л1 = °.7 />12 = °>3
е2 = 5 />21 = 0,4 />22 = 0,6
Требуется выполнить задания а)—е) пункта 7 из раздела «Задачи и
упражнения для самоконтроля к главе 17.
Глава 181
СПЕЦИАЛЬНЫЕ
МИКРОЭКОНОМИЧЕСКИЕ
ПРОБЛЕМЫ
18.1. Влияние современных форм научно-
технологического прогресса (телекоммуникационных
систем и компьютеризации) на микроэкономические
процессы
18.1.1. В развитых странах фирмы практически всех секторов эко-
номики используют возможности, предоставляемые сетью Ин-
тернет, в целях снижения своих издержек, расширения связей с
поставщиками, повышения эффективности управления запаса-
ми, более адекватного учета в реальном времени плановых реше-
ний. Фактически появление сети Интернет породило новую эко-
номическую реальность.
Темпы развития телекоммуникационной отрасли (отрасли
высоких технологий) крайне высоки.
Объем информации, передаваемой через Интернет, удваива-
ется каждые 100 дней.
Темпы развития Интернета можно сравнить с темпами разви-
тия радио, телевидения и персональных компьютеров (ПК). Для
того чтобы охватить 50 млн своих поклонников, радио потребова-
лось 38 лет, телевидению — 13 лет, персональному компьютеру —
16 лет. Интернет пересек эту отметку всего за 4 года.
1 При подготовке параграфов 18.1—18.7 главы 18 были использованы мате-
риалы источников, приведенных в списке литературы к главе 18.
725
Цены на продукцию отрасли информационных технологий
(IT) в США, скорректированные на улучшение качества и произ-
водительности, падали, в то время как цены во всей остальной
экономике США росли. В частности, за 6 лет (с 1991 по 1997 г.)
цена условного микропроцессора MIPS {million instructions per
second), т.е. выполняющего 1 млн процессорных инструкций в
секунду, упала с 230 до 3,42 долл.
По закону Мура, производительность компьютеров удваива-
ется каждые 18 месяцев. Эмпирические данные показывают, что
этот закон выполняется последние 30 лет. Исключение составил
2002 г., когда для удвоения производительности потребовалось
менее 18 месяцев.
Экономический рост ускоряется не только в самой отрасли
информационных технологий, но и в других отраслях экономики,
ибо количество людей, имеющих выход в Интернет, постоянно
растет, стремительно увеличивается и коммерческое использова-
ние Интернета.
Можно выделить 4 составляющие экономического роста, по-
рождаемые НТП, в частности цифровой (электронной) револю-
цией:
• развитие сети Интернет значительно увеличивает инвестиции
в компьютеризацию и телекоммуникационные системы, со-
здание специальных видов услуг;
• электронная коммерция на уровне фирм: примерно с 1995 г.
фирмы (компании) стали использовать Интернет для взаимо-
выгодной торговли. Использование Интернета позволяет до-
стичь значительных улучшений в производительности от ис-
пользования электронных сетей в целях создания, покупки,
продажи, доставки продуктов и услуг;
• электронная доставка товаров и услуг: компьютерные про-
граммы, газеты, музыкальные компакт-диски теперь не обяза-
тельно упаковывать и доставлять напрямую клиентам и в тор-
говые точки. Можно получать электронные аналоги через
Интернет. На сегодня очень распространены электронные
сделки по покупке авиабилетов и операции с ценными бума-
гами. Такие услуги, как консалтинг, банковские услуги и стра-
хование, обучение и медицинская помощь, могут встретить
некоторые препятствия на своем пути, но уже сейчас предо-
ставляющие их фирмы начинают все шире использовать Ин-
тернет в целях изменения стиля ведения бизнеса. Через неко-
726
торое время электронные продажи и доставка электронных
товаров и услуг, скорее всего, станут основной движущей си-
лой новой цифровой (электронной) экономики;
• розничная торговля физическими товарами. Интернет может
быть также использован в целях продажи, хранения и физи-
ческой доставки продуктов. Объем электронных продаж опре-
деленной продукции, например компьютерной техники, про-
граммного обеспечения, автомобилей, книг и цветов, растет
очень быстрыми темпами.
Развитие собственно сети Интернет с чисто технологической
точки зрения обеспечивается появлением и внедрением новых
технологий.
Основной прогресс в телекоммуникациях состоит в повыше-
нии пропускной способности каналов связи. Возникла техноло-
гия DSL, позволяющая использовать кабельные соединения, но-
вые алгоритмы сжатия передаваемой информации, появились
оптико-волоконные сети.
Темпы инвестиций в телекоммуникационный сектор стреми-
тельно увеличиваются, достаточно посмотреть на некоторые чис-
ла. В США группа компаний проинвестировала 27 млрд долл, для
построения глобальной информационной сети, использующей
спутники связи в 1998—2002 гг. Инвестиции в спутники и ретран-
сляторы достигли достаточных размеров. Персональные компью-
теры, смарт-телефоны, часы смогут передавать и получать голосо-
вую и видеоинформацию, имея при этом выход в Интернет, не
привязанный физически к какой-то одной точке, что существен-
но повысит мобильность и производительность множества раз-
личных систем.
18.1.2. Электронная коммерция растет наивысшими темпами
среди всех остальных форм бизнеса. Одной из причин является не
только важность уровня В2В (business-to-business) и В2С (business-
to-consumer), но и внутрифирменный уровень. Информационные
технологии используются для координации закупочных операций
между фирмами и поставщиками, для оперативного сбора и до-
ставки информации в отделы планирования и логистики. Транс-
портные отделы располагают информацией о состояниях на скла-
дах и о текущем состоянии каждой транспортной операции.
Самые ранние компьютеры использовались исключительно в
научных и военных целях, но не для торговли. Компьютеры стали
727
использоваться в торговле, когда в 1960-х гг. была создана система
ERMA (the Electronic Recording Machine — Accounting). В то время
банки уже начали ощущать чрезмерный поток чеков, подлежащих
обработке. В период с 1943 по 1952 г. объем чеков в обращении
удвоился и вырос с 4 млрд подписанных чеков в год до 8 млрд.
Автоматизируя процесс их обработки с помощью ERMA, первый
банк (Bank of America), использующий компьютер, сообщил о том,
что 9 работников могли выполнять объем заданий, для которого
раньше требовалось 50 человек.
Коммерческое использование компьютеров стало быстро рас-
пространяться, когда компании различных секторов экономики
стали использовать информационные технологии в бухгалтер-
ском учете, административных задачах, создании проектных от-
четов, планировании производственного цикла.
В 1970-х и 1980-х гг. фирмы стали использовать информаци-
онные технологии за пределами их офисов, посылая и принимая
электронные дубликаты запросов на покупки, уведомления, по-
грузочные документы через систему EDI (Electronic Data
Interchange).
В 1980-х гг. произошло достаточно важное событие — были
введены в эксплуатацию С4Р-системы (computer-aided design),
С4£-системы (computer-aidedengineering), САМ-сжлылы (computer-
aided manufacturing), которые позволили инженерам, дизайнерам
и техническому персоналу получить доступ и работать с техничес-
кими спецификациями, инженерными проектами, дизайнерски-
ми разработками через внутренние корпоративные информаци-
онные сети (интрасети).
Однако стоимость установки и эксплуатации быстрых и тех-
нически сложных сетей была достаточно высокой, поэтому их
использование было доступно лишь большим фирмам. Боль-
шинство средних и мелких фирм предпочитали использовать те-
лефон и факс в качестве основного коммуникационного оборудо-
вания. Даже крупные фирмы, использующие системы EDI, не
всегда могли оценить в полной степени сокращение своих издер-
жек, так как далеко не все их партнеры устанавливали аналогич-
ные системы у себя.
Интернет сегодня делает электронную коммерцию и объем
информацией доступными даже для малого бизнеса (так называ-
емая категория SOHO — small office and home office).
728
Можно говорить о том, что рост электронной коммерции в
секторе В2В вызван снижением закупочных издержек, сокраще-
нием необходимых складских запасов из-за более оперативных
форм учета, более быстрой оборачиваемости средств (уменьше-
ния длительности бизнес-цикла), более эффективной системы
поддержки клиентов, меньшими издержками на продажи и мар-
кетинговые исследования и, наконец, из-за новых возможностей
по расширению продаж.
Покупка сырья, материалов или каких-либо специальных ус-
луг означает достаточно длинный процесс согласования сначала
со стороны покупателя, потом со стороны продавца, потом их
непосредственное взаимодействие, после чего начинается про-
цесс обмена обязательствами, уведомлениями, подтверждениями
и т.д. В реальности этот процесс может быть значительно более
запутанным и длительным. Фирмы снижают издержки по снаб-
жению, объединяя покупки и развивая отношения с главными
поставщиками в целях получения возможности использования
дисконтных схем и устанавливая более тесное взаимодействие с
партнерами во время производственного процесса. Фирмы, ис-
пользующие системы EDI в частных корпоративных сетях, сни-
жают издержки на наем персонала, издержки на печать бумажных
документов, почтовые издержки. Автоматизируя рутинные снаб-
женческие операции, фирма позволяет снизить число необходи-
мого персонала и переключить его, например, на переговоры и
поиск лучших ценовых условий и установление лучших взаимоот-
ношений с партнерами. Эксперты оценивают такую экономию в
среднем в 5—10% от издержек снабжения.
Интернет открывает возможности для дальнейшего снижения
такого рода издержек. Большие фирмы могут выигрывать от более
низких тарифов на передачу информации через Интернет по
сравнению с частными сетями, однако здесь возникает достаточ-
но серьезная проблема безопасности и конфиденциальности пе-
редаваемых коммерческих данных.
18.1.3, Одним из характерных примеров внедрения информаци-
онной системы и существенного снижения издержек снабжения
является фирма General Electric. Ее складское подразделение было
специально переоборудовано с тем, чтобы быстро и оперативно
отвечать на запросы других ее подразделений о наличии тех или
иных деталей на складе. Раньше специальный технический пер-
729
сонал должен был вручную заполнить форму запроса, доставить
ее в установленное место, фотокопировать, присоединить к бу-
мажному запросу, положить в конверт все документы и отправить
по почте. Процесс занимал в среднем 7 дней и был таким слож-
ным и длительным, что отдел снабжения обычно посылал заявки
не более чем 2—3 поставщикам за день.
В 1996 г. фирма GE установила первую онлайновую систему
снабжения. Теперь весь документооборот стал электронным,
и процесс, который занимал 7 дней, теперь стал занимать не более
2 часов. Издержки на наем персонала в отдел снабжения снизи-
лись примерно на 30%. 60% персонала отдела снабжения были
переспециализированы. Отдел по обработке запросов стал иметь
от 6 до 8 свободных дней каждый месяц, которые можно было ис-
пользовать на решение стратегических задач, а не на бумажную
работу.
Издержки на покупку оборудования и прочего имущества в
среднем снизились на 20% в связи с тем, что теперь фирма GE мог-
ла выйти на более широкий круг поставщиков, тем самым повы-
сив уровень конкуренции среди них и снизив цены на их продук-
цию.
Использовав систему APS {Advanced Planning System), фирме
IBM удалось существенно снизить свои издержки. Так, в первый
год использования данной системы оборот запасов увеличился на
40%, а объемы продаж увеличились на 30%. Снижение операци-
онных издержек и уменьшение необходимых инвестиций из-за
улучшенного оборота запасов вылились в экономию в размере
500 млн долл.
Другой показательный пример — это укорачивание полного
бизнес-цикла. Цикл — это время, необходимое для построения
продукта. Очевидно, что если уменьшить данную величину по
сравнению с конкурентами, то фирма получает конкурентное
преимущество в виде дополнительных покупателей. Производ-
ство новой продукции всегда связано с фиксированными издер-
жками, включающими амортизацию оборудования, издержки на
аренду зданий и сооружений и большинство управленческих из-
держек, в том числе и выражающихся в истраченном времени.
В 1980-е гг. меньшее время разработки конечного продукта позво-
лило японским фирмам получить существенное конкурентное
преимущество по сравнению с их американскими коллегами.
Японские фирмы стали разрушать барьеры между различными
730
департаментами фирмы, тем самым стараясь повысить эффектив-
ность. Самым главным нововведением стало более тесное взаимо-
действие между отделами дизайна, производства и отделом сбыта;
кроме того, были улучшены связи с внешними партнерами. Все
это позволило в первую очередь уменьшить время на необходи-
мые операции по взаимодействию, не говоря уже об остальных
преимуществах. Фирмы, рассматриваемые в данном примере,
специализировались на производстве автомашин. После созда-
ния прототипа они должны были проводить комплексное тести-
рование; и как правило, после этого специалисты дорабатывали
модель. Естественно, что подобные сертифицированные проце-
дуры тестирования достаточно дороги. Поэтому японские авто-
мобилестроительные фирмы внедрили специальные компьютер-
ные эмуляторы, имитирующие физические законы и поведение
каждого конкретного прототипа в зависимости от его техничес-
ких характеристик. Это позволило сделать качественный рывок
вперед и снизить издержки — как денежные, так и временные.
Сегодня на современных производствах повсеместно использу-
ются CAD-, САМ- и САЕ-программы, а также программы трехмер-
ного моделирования. Работа командой, разделение и обмен ин-
формационными потоками с помощью сетей позволяют разраба-
тывать и выпускать новый автомобиль уже через 30 месяцев.
18.1.4. Фирмы начинают использовать Интернет и для улучше-
ния поддержки своих клиентов. Имея перед глазами описание
продуктов, службу технической поддержки и информацию по за-
казу продукции онлайн, клиент фирмы поможет ей не только
снизить ее издержки, снизив потребности в техническом персо-
нале, который мог бы отвечать на сложные специализированные
вопросы, но эти возможности могли бы привести и к появлению
более серьезных клиентов у фирмы.
Например, компания Cisco Systems сообщает о том, что произ-
водительность ее службы по работе с клиентами выросла на
200—300%, что отразилось в падении издержек на 125 млн долл.
Dell оценивает свой выигрыш от использования аналогичной сис-
темы в несколько миллионов долларов в год.
Интернет действует вне временных и пространственных гра-
ниц по всему земному шару. Как результат фирмы, ведущие элек-
тронные продажи, могут завоевывать новые рынки, которые были
бы недоступны в традиционной экономике из-за дороговизны
731
рекламной кампании и огромного количества персонала для ин-
дивидуального продвижения своей продукции. Кроме того, фир-
ма физически не может присутствовать на иностранных рынках,
если она имеет единственное представительство в одной стране.
В Интернете электронный магазин находится как бы вне террито-
риальных рамок и доступен для любого пользователя в любое
время и из любой точки планеты.
Фирмы, которые используют Интернет для покупки, прода-
жи, доставки и обслуживания продуктов и услуг, действуют так
из-за снижения различного рода издержек, улучшения экономи-
ческой эффективности и получения новых стратегических ры-
ночных возможностей. И эти преимущества будут становиться все
более значимыми с дальнейшим развитием электронных сетей,
информационных технологий и электронной коммерции.
Сказанное следует кратко дополнить данными о специфике
информационных услуг, например таких, как представление мно-
гих туристических фирм в Интернете, услуги страхования, бан-
ковские услуги (home banking), возникновение виртуальных бир-
жевых площадок, проблемы безопасности в Сети. Кроме того, за
кадром остается вторая половина типичного взаимодействия —
потребитель — его характеристики, возникновение феномена
дистанционной занятости, изменения профессиональных требо-
ваний для работников, проекты по виртуальному обучению и
оказанию удаленной медицинской помощи. Отдельная группа
последствий — это влияние информационных технологий на мо-
нетарную сферу, в частности через Кембриджское уравнение де-
нег, влияние на макроэкономические показатели (инфляция, за-
нятость, экономический рост).
18.2. Рынок интернет-магазинов и его проблемы
в российской экономике
18.2.1. Интернет-торговля — это продажа товаров и услуг любому
пользователю Интернета. Можно добавить, что интернет-торгов-
ля — часть, причем совсем небольшая, более широкого поня-
тия — «электронная коммерция».
Электронная коммерция — одно из наиболее бурно развива-
ющихся направлений применения всемирной сети Интернет. Ее
732
технической основой являются современные сетевые технологии
(WWW, электронная почта, технологическая почта и т.п.). Суть
же электронной коммерции заключается в использовании едино-
го информационного пространства Интернета для повышения
эффективности общения между участниками коммерческих опе-
раций (продавцом и покупателем, между деловыми партнерами,
сотрудниками предприятия и т.д.). С точки зрения значимости
для наибольшего числа людей самой важной областью электрон-
ной коммерции следует признать электронную торговлю — тех-
нологию продвижения товаров и услуг на рынок с использовани-
ем сети Интернет.
Интернет-торговля является преемницей широко распростра-
ненной в мире торговли по каталогам, только на совершенно дру-
гой технической основе.
Немаловажной особенностью интернет-торговли является то,
что покупателю обычного магазина, чтобы найти более конкурен-
тоспособный желаемый товар, придется обойти не один магазин
(и не один рынок). Чаще всего, однако, бывает так: покупатель
остановится на ближайшем магазине и купит там желаемое, даже
осознавая, что немного переплатил, а умелого пользователя Ин-
тернета от конкурентоспособного товара в том или ином регионе
отделяет только несколько кликов мышью!
Рассмотрим интернет-торговлю с точки зрения продавца.
Продавец может использовать Интернет по-разному. Имея
реальный магазин, можно просто рекламировать свой товар в Ин-
тернете. Можно создать И'ей-каталог, что наиболее распростране-
но в России. Продавец также изначально может создавать интер-
нет-магазин.
В России, как показывает статистика, только 40% покупателей
удовлетворены выполнением своих заказов. Многие интернет-
торговцы проигрывают потому, что уделяют мало внимания со-
зданию инфраструктуры обработки заказов и последующей до-
ставки товаров. Западные консультанты выделяют три более или
менее четкие стратегии обработки заказов в интернет-торговле.
Первая — передача заказов дистрибьюторам или производите-
лям товаров, вторая — создание собственного склада, третья —
аутсорсинг (передача операций по обработке и доставке заказов
специализированным фирмам).
Рассмотрим интернет-торговлю с точки зрения покупателя.
733
Основное отличие интернет-торговли от обычного торгового
процесса в том, что в интернет-торговле нет прямого общения
покупателя с продавцом.
Единственным средством воздействия на покупателя в интер-
нет-магазине является информация. Можно выделить следующие
особенности интернет-торговли: психология прямого общения
(воздействия) должна быть заменена психологией подачи/вос-
приятия информации; знакомство или взаимодействие с товаром
должно быть заменено его информационным описанием.
В обычном магазине всегда есть люди, пришедшие просто по-
смотреть товар (прицениться к нему, сравнить с какими-то други-
ми и т.д.), а не купить его. В интернет-магазине таких посетителей,
не являющихся покупателями, существенно больше, их просто
интересует, что и, главное, как продается в том или ином магазине.
Такой покупатель может подробно рассматривать каталог товаров,
«складывать» их в «корзину» и даже выписывать счет, но не опла-
чивать его. На вопрос, зачем ему это, имеется ясный ответ: ему
просто интересно, как это все работает (и работает ли вообще).
Продавцу же важно понять, что подобного рода хаотичную и
безрезультатную активность покупателя необходимо использо-
вать в своих целях.
Во-первых, всегда следует анализировать маршруты таких по-
сетителей. Отслеживая места, куда они чаще всего направляются,
можно определить, какой товар пользуется потенциально повы-
шенным спросом, где дольше задерживаются покупатели. В наи-
более интересных для покупателей местах интернет-магазина
лучше всего размещать рекламу, в частности анонсировать новые
продукты, объявлять лотереи и т.д. В обычных магазинах инфор-
мация для ответа на подобные вопросы собирается с большим
трудом.
Во-вторых, покупатель обязательно купит что-нибудь (и не
раз!), если убедится, что в данном интернет-магазине есть не
просто «голый» список товаров, а полноценный торговый зал с
хорошим информационным наполнением, в котором имеется
подробное описание товаров, их сравнение с другими товарами,
различного рода «рекомендации продавцов» по выбору тех или
иных товаров и т.д. К сожалению, информационная ценность для
покупателя большинства российских интернет-магазинов прак-
тически равна нулю, ибо он в них никакого подробного описания
товаров не находит.
734
Итак, интернет-магазин — это не просто список товаров с це-
нами на них, а существенно более тонкий и сложный инструмент
для организации торгового процесса.
В целом для интернет-покупателей характерны две особен-
ности: привередливость (он будет покупать только в «удобном»
интернет-магазине, т.е. там, где ему обеспечен максимально дру-
жественный интерфейс или просто интересно), дотошность (ре-
шив что-то покупать у вас, он захочет получить всю имеющуюся
информацию о данном товаре, вашей фирме, гарантиях, которые
вы ему готовы предоставить, и т.д).
У интернет-покупателя есть и определенные положительные
черты: раскрепощенность (сидя дома за компьютером, практи-
чески все чувствуют себя значительно свободнее, чем в много-
людном торговом зале традиционного магазина), сверхлюбопыт-
ство (интернет-покупатель имеет больше времени на покупки,
и следовательно, ему можно (и нужно!) выдавать больше инфор-
мации, удовлетворяющей его любопытство).
18.2.2. Остановимся подробнее на особенностях и проблемах
рынка интернет-магазинов в российской экономике.
Основные обороты составляют товары, которые не приносят
прибыли, например компьютеры и комплектующие (норма при-
были от торговли компьютерной техникой составляет 2—3%).
Это объясняется тем, что развитие розничной интернет-тор-
говли находится на начальном этапе и потребитель приобретает
товар, который поддается полному описанию на страницах ин-
тернет-магазина. По мере вхождения интернет-торговли в жизнь
российского общества, увеличения положительного опыта об-
щения с виртуальными магазинами спрос будет смещаться в
сторону более дорогих товаров и в сторону товаров повседневно-
го спроса.
Самым популярным способом оплаты покупок в российских
интернет-магазинах по-прежнему остается оплата наличными
курьеру. Причинами этого являются невысокая степень распро-
странения кредитных и дебетовых карт в России, недоверие со
стороны покупателей к онлайновым способам оплаты (к элект-
ронным платежам). Такое отношение вызвано недоверием граж-
дан к банковской системе вообще, нестабильностью экономичес-
кой ситуации в стране, неурегулированностью организационных
735
и правовых вопросов электронных платежей, неуверенностью в
безопасности проведения платежей через Интернет.
Доставка — один из основных вопросов, без решения которо-
го невозможно повысить уровень предлагаемых услуг. Покупатель
прежде всего оценивает качество обслуживания в виртуальном
магазине по скорости доставки товара. Наиболее распространен-
ные способы доставки: курьерская — 55%, почтовая — 26%, дру-
гие —19%.
Наличие удачного бренда (широко известной торговой марки)
помогает увеличить не только эффективность взаимодействия с
клиентами, рекламодателями, поставщиками и инвесторами, но и
кредит доверия потенциальных клиентов. В Интернете конкури-
рующие проекты находятся на расстоянии одного клика друг от
друга — все это увеличивает важность наличия самого бренда и
лояльного отношения к нему пользователей.
Насколько сложно в настоящее время начать деятельность в
Интернете?
Большинство игроков на рынке интернет-магазинов не полу-
чают прибыли. Их основной задачей было «вхождение в рынок».
Открытие электронного магазина все еще не является очень доро-
гим удовольствием, несмотря на то, что «порог входа» в Интернет
становится выше (по разным оценкам, стоимость его увеличива-
ется от 50 до 100% в год). И если возможность «вхождения в ры-
нок» сохраняется, то для того, чтобы закрепиться на нем и конку-
рировать с его другими участниками, уже недостаточно просто
оформить И'ёй-сайт и привлечь посетителей. Сейчас необходимо
не только занять нишу, но и бороться за долю на рынке, совер-
шенствовать проект, привлекать новых и удерживать старых кли-
ентов.
Инфраструктура розничной интернет-торговли еще не сфор-
мирована: отсутствуют качественные услуги доставки товаров, не
прижились системы онлайновых микроплатежей, большинство
российских пользователей так и не стали доверять покупкам через
интернет-магазины. Общие проблемы российского Интернета
ограничивают возможности электронной торговли: низкая сте-
пень распространения Интернета среди населения, низкие дохо-
ды, неразвитость платежных систем, моральная неподготовлен-
ность населения совершать покупки в виртуальном магазине
ит.д.
736
18.3. Глобализация и микроэкономические
проблемы
18.3.1. Глобализация — тенденция к образованию всемирной ин-
вестиционной среды и интеграция национальных рынков капита-
лов.
На исходе XX столетия мировая экономика как совокупность
национальных хозяйств и их экономических и политических вза-
имоотношений обретает новое качество: важнейшей формой и
одновременно новым этапом интернационализации хозяйствен-
ной жизни становится глобализация. Она охватывает важнейшие
процессы социально-экономического развития мира, способ-
ствует ускорению экономического роста и модернизации. В то же
время глобализация рождает новые противоречия и проблемы в
мировой экономике. Сегодня все страны мира в разной степени
охвачены процессом глобализации.
На протяжении тысячелетий существует в мире международ-
ная торговля, чуть меньше — понятие инвестиций, т.е. долгосроч-
ного вложения капиталов в какое-либо дело или предприятие на
территории своего или иного государства. Всесторонний, пол-
ный, универсальный и всеобщий процесс глобализации, относя-
щийся к земному шару в целом, был подготовлен как раз самим
фактом роста инвестиций в конце XIX в., и особенно после миро-
вых войн XX в. Правда, все это называлось глобальными процес-
сами. Сам термин «глобализация» впервые появился в литературе
в 1983 г. в статье американского экономиста Т. Левита, опублико-
ванной в «Гарвард бизнес ревью». Широкое употребление термин
получил в начале 90-х гг. XX в. после распада СССР. Однако на-
иболее важной материально-вещественной предпосылкой явле-
ния глобализации была, конечно, научно-технологическая рево-
люция в телекоммуникационных системах и компьютеризации
(Интернет, электронная почта), которая радикально изменила
характер международных экономических отношений.
Речь идет не только о традиционной внешней торговле това-
рами и услугами, но и о валютных потоках, движении капитала,
обмене технологиями, информацией и идеями, перемещении лю-
дей. Мерой масштаба глобализации может служить объем между-
народных финансовых сделок, который только на валютных рын-
47 - 7620
737
ках Нью-Йорка ежедневно составляет 1,3 трлн долл., а на между-
народном рынке ценных бумаг даже превышает эту сумму.
В процессе глобализации одни усматривают серьезную угрозу
мировой экономической системе, а другие видят средство даль-
нейшего прогресса мировой экономики. Одни считают, что в ре-
зультате процесса глобализации произойдут общепланетарное
объединение национальных экономик и их универсализация, дру-
гие считают, что процесс глобализации закончится экологической
деградацией, чрезмерным ростом народонаселения и широкой
пропастью между богатыми и бедными странами. Характерной
особенностью процесса глобализации являются международные
потоки (в основном это потоки капитала и информации, а также
иммиграционные потоки), которые в условиях либерализации
почти или вовсе не контролируются национальными законода-
тельствами. Важным следствием информационной революции
становится нарастание раскола в развитых странах. В ближайшие
десятилетия в них завершится формирование отчужденного клас-
са лиц, не находящих применения своим способностям в области
информационной экономики. Разрыв в доходах между интеллек-
туальными работниками и остальной частью общества будет на-
растать. Именно поэтому на протяжении первой половины XXI в.
страны будут сконцентрированы не только на внешних, но и на
внутренних проблемах и степень их позитивного влияния на раз-
вивающийся мир неизбежно снизится. Условия конкуренции,
потребности клиентов, технологии и рынки изменяются быстрее,
масштабнее, неожиданнее, чем когда-либо раньше. Перманентное
обновление становится решающим для будущего фирм.
Глобализация — это наиболее яркое проявление научно-тех-
нологического прогресса, несущего экономические и социальные
новации не только по критерию изобилия неизвестных ранее благ
и услуг, но и с учетом уже проглядывающих очертаний нового
облика человечества. Вместе с тем глобализация уже в начальной
своей стадии выявила новые опасности и риски, причем довольно
грозные, представляющие вызовы всему человечеству. А это озна-
чает, что речь должна идти об общечеловеческой ответственности
за происходящее и об общих усилиях по гармонизации устройства
мира. Можно отметить, что глобализация — это соревнование не
только за рынки, но и за ценности. На сегодняшний момент ре-
шающим ресурсом в соревновании глобальных рынков являются
не запасы сырья, а неограниченные ресурсы знаний.
738
Глобализация затрагивает все области общественной жизни,
включая экономику, политику, социальную сферу, культуру, эко-
логию, безопасность и др. Глобализация является важнейшим
процессом, без учета которого невозможно прогнозировать, опре-
делять и осуществлять внешнюю и внутреннюю политику любого
государства.
18.3.2. О преимуществах глобализации
Если высказывания противников глобализации довольно лег-
ко найти в том же Интернете, то столь же активных сторонников
у этого явления нет.
Но как бы ни относились к глобализации ее противники и
сторонники, следует признать, что она уже явно изменила миро-
вую систему, порождая новые проблемы и открывая новые воз-
можности. Очевидно, что тенденции технологического, полити-
ческого, институционального, идеологического и культурного
развития активизируют глобализационный процесс, который в
будущем, видимо, ускорится. Важным аспектом этого процесса
станет рост международной торговли услугами. Ее объем уже
значительно возрос, а в будущем увеличится еще больше, осо-
бенно в области телекоммуникационных и финансовых услуг.
Мир станет более открытым, интегрированным, взаимозависи-
мым.
Что касается преимуществ глобализации, то она вызвала, во-
первых, обострение международной конкуренции, во-вторых,
экономию на масштабе производства, что потенциально может
привести к сокращению издержек и снижению цен, а следова-
тельно, к устойчивому экономическому росту. В-третьих, глоба-
лизация может привести к повышению производительности труда
в результате рационализации производства на глобальном уровне
и распространения передовой технологии, а также конкурентного
давления в пользу непрерывного внедрения инноваций в миро-
вом масштабе. В-четвертых, преимущества глобализации связаны
также с выигрышем от торговли на взаимовыгодной основе, удов-
летворяющей все стороны, в качестве которых могут выступать
отдельные лица, фирмы и другие организации, страны, торговые
союзы и даже целые континенты.
По идее, конечным результатом глобализации должно стать
общее повышение благосостояния в мире.
47*
739
18.3.3. 0 минусах глобализации
Глобализация чревата негативными последствиями или по-
тенциальными проблемами, в которых ряд ее критиков усматри-
вают большую опасность.
Первая из основных проблем связана с вопросом: кто оказы-
вается в выигрыше от глобализации? Некоторые оппоненты гово-
рят о возможности глобальной конвергенции доходов, аргументи-
руя это тем, что экономика бедных государств развивается более
высокими темпами, чем богатых. На самом же деле быстрый рост
характерен лишь для небольшой группы стран Юго-Восточной
Азии («азиатских тигров»), тогда как наименее развитые в эконо-
мическом отношении страны отличаются гораздо более низкими
темпами роста, чем богатые государства. Их выгоды от глобализа-
ции минимальные. Растущий разрыв в доходах вызывает недо-
вольство со стороны бедных стран, чреватое международными
конфликтами.
Вторая проблема связана с потенциальной региональной или
глобальной нестабильностью из-за взаимозависимости нацио-
нальных экономик на мировом уровне. Локальные экономичес-
кие колебания или кризисы в одной стране могут иметь регио-
нальные или даже глобальные последствия. Такая возможность
носит не только теоретический характер, а является вполне реаль-
ной, что подтверждает финансовый кризис в Азии, начавшийся
летом 1997 г. в Таиланде, а затем перекинувшийся на другие
страны Юго-Восточной Азии, дойдя до Южной Кореи.
Третья проблема вызвана опасением, что контроль над эконо-
микой отдельных стран может перейти от суверенных прави-
тельств в другие руки, в том числе к наиболее сильным государ-
ствам, многонациональным или глобальным корпорациям и
международным организациям. В силу этого некоторые усматри-
вают в глобализации попытку подрыва национального суверени-
тета. Такие настроения могут легко перейти в крайний национа-
лизм с призывами к протекционизму, повлечь за собой рост экс-
тремистских политических движений, что потенциально чревато
серьезными конфликтами. Укрепление государства и его инсти-
тутов — обязательное условие не только выживания, но и разви-
тия государства и нации в условиях глобализации.
К ряду издержек глобализации относят безработицу в эконо-
мически развитых странах с высоким уровнем заработной платы.
740
Но это утверждение опровергается низкой нормой безработицы
во многих из них и ее высоким уровнем в государствах с низкой
заработной платой. Национальная политика и научно-технологи-
ческий прогресс являются более важными факторами занятости,
чем факторы глобализации. С глобализацией увязывают и миф о
том, что она угрожает социальному благосостоянию некоторых
стран, однако значительно большее влияние на эту сферу оказы-
вают другие факторы, такие, как налоговая политика и демогра-
фические тенденции. В обоих случаях глобализация обычно ис-
пользуется для оправдания провалов в национальной политике
тех или иных государств.
Явление глобализации имеет последствия и неэкономическо-
го характера, сопряженные с огромными рисками, потенциаль-
ными издержками и даже возможностью катастрофы. Первой из
таких областей является сфера безопасности, где глобальные про-
цессы могут привести к возникновению конфликтов. Вторая об-
ласть — это политические кризисы, способные перерасти из ло-
кальных в крупномасштабные события, а если их вовремя не уст-
ранить, то они могут привести к катастрофе. Третьей областью
следует считать экологию и здравоохранение. Глобальные взаи-
мосвязи чреваты и глобальными экологическими бедствиями,
связанными, например, с всеобщим потеплением и изменением
климата, широкомасштабными эпидемиями.
В целом решение экономических, политических и прочих
проблем глобализации потребует реальных усилий но развитию
сотрудничества всех крупных государств, особенно стран ЕС,
США, Канады, Японии, России, Китая, Индии, Бразилии и др.
18.3.4. Об источниках глобализации
В течение последних десятилетий выявился ряд источников
глобализации.
Первый источник — научно-технологический прогресс, кото-
рый привел к резкому сокращению транспортных и коммуника-
ционных издержек, значительному снижению затрат на обработ-
ку, хранение и использование информации. Информационное
обслуживание непосредственно связано с успехами в электрони-
ке, созданием электронной почты, Интернета. Современный
компьютер стоимостью в 2 тыс. долл, во много раз мощнее, чем
компьютер стоимостью в 10 млн долл. 30 лет назад.
741
Второй источник глобализации — либерализация торговли и
другие формы экономической либерализации, вызвавшие огра-
ничение политики протекционизма и сделавшие мировую тор-
говлю более свободной. В результате были существенно снижены
тарифы, устранены многие иные барьеры в торговле товарами и
услугами. Другие меры либерализации привели к усилению дви-
жения капитала и остальных факторов производства.
Третьим источником глобализации можно считать значитель-
ное расширение сферы деятельности организаций, ставшее воз-
можным в результате научно-технологического прогресса. Мно-
гие фирмы, ориентировавшиеся раньше только на местные рын-
ки, расширили свои производственные и сбытовые возможности
и вышли на национальный, многонациональный, международ-
ный и даже глобальный уровень, что позволило им укрепить свои
позиции, увеличить их прибыль, повысить производительность,
выбирать источники сырья, открывать производства и осваивать
рынки в других странах, быстро приспосабливаясь к меняющимся
условиям. Практически все крупные предприятия располагают
сетью филиалов или стратегическими союзами, которые обеспе-
чивают им необходимое влияние и гибкость на рынке. В рамках
подобных многонациональных корпораций в настоящее время
осуществляется почти треть мировой торговли.
С появлением глобальных фирм международные конфликты в
значительной мере переместились со странового на фирменный
уровень, и борьба завязывается не между странами за территори-
альные владения, а между фирмами за долю на мировом рынке.
Некоторые усматривают в таких фирмах угрозу власти и автоно-
мии государства, однако пока власть и суверенитет сохраняют
силу, государство может спокойно выполнять свои традиционные
функции в мировой экономике и политике. Более широкие перс-
пективы открылись и перед неправительственными организация-
ми, вышедшими, как и в случае с глобальными фирмами, на мно-
гонациональный или мировой уровень. Новую глобальную роль
стали играть такие международные организации, как ООН, МВФ,
Всемирный банк, ВТО. Таким образом, многонациональные
фирмы и другие организации, как частные, так и государствен-
ные, превратились в основные действующие лица глобальной
экономики.
Четвертый источник глобализации — особенности культурно-
го развития. Речь идет о тенденции формирования глобальных
742
«однородных» средств массовой информации, искусства, культу-
ры, повсеместного использования английского языка в качестве
всеобщего средства общения. Частично из-за этого некоторые
страны, особенно Франция и ряд других европейских государств,
рассматривают глобализацию как попытку США добиться куль-
турной, экономической и политической гегемонии в мире.
Как бы ни относились к глобализации ее противники и сто-
ронники, следует признать, что она уже явно изменила мировую
систему, порождая новые проблемы и открывая новые возмож-
ности.
18.3.5. О влиянии глобализации на национальную экономику
Глобализация оказывает большое влияние на экономику всех
стран. Она затрагивает производство товаров и услуг, использова-
ние рабочей силы, инвестиции в человеческий капитал, техноло-
гии и их распространение из одних стран в другие. Все это в ко-
нечном счете отражается на эффективности производства, произ-
водительности труда и конкурентоспособности. Влияние
глобализации на национальную экономику проявляется прежде
всего в высоких темпах роста прямых иностранных инвестиций,
намного превосходящих темпы роста мировой торговли. Эти ка-
питаловложения играют ключевую роль в трансферте технологий,
промышленной реструктуризации, образовании глобальных
фирм, что оказывает непосредственное воздействие на нацио-
нальную экономику. Влияние глобализации проявляется в широ-
ком распространении технологических инноваций.
Новые технологии, как уже отмечалось, являются одной из
движущих сил глобализации, но она, в свою очередь, усиливая
конкуренцию, стимулирует их дальнейшее развитие и распро-
странение среди стран.
Глобализация способствует росту торговли и услуг, которые
превращаются в основной фактор международных торговых от-
ношений. Если в 1970 г. с экспортом услуг было связано менее
73 прямых иностранных инвестиций, то в настоящее время эта
доля возросла до 50%, причем интеллектуальный капитал стал
наиболее важным товаром на мировом рынке.
В начале XXI в. ожидается дальнейшее усиление взаимосвязей
и взаимозависимостей между национальными хозяйствами стран
мира. Весьма высокими темпами будет и впредь расти междуна-
родный обмен товарами, услугами и капиталом.
743
Необходимость адаптации отечественного народного хозяй-
ства к этим тенденциям, очевидно, требует такой стратегии взаи-
модействия с внешним миром, которая позволяла бы постепенно
улучшать позиции России и минимизировать, блокировать не-
благоприятные внешние воздействия.
Анализ показывает, что истоки внешнеэкономических про-
блем России находятся не где-то за пределами национальных
границ, а внутри национальной экономики. Сырьевая специали-
зация страны — следствие деформированной структуры промыш-
ленного производства и отсталости производственного аппарата.
Импортная зависимость — оборотная сторона недостаточной
конкурентоспособности отечественного производства. Утечка
капитала — реакция отечественного бизнеса на нестабильность
ситуации и неблагоприятный инвестиционный климат. Поэтому
для изменения роли России в мировой экономике важно скоррек-
тировать прежде всего макроэкономическую политику и затем на
новой основе строить внешнеэкономическую стратегию.
18.4. Технологический монополизм
и микроэкономические проблемы
18.4.1. Глобализация представляет собой процесс формирования
единого общемирового финансово-информационного простран-
ства на базе современных форм научно-технологического про-
гресса (телекоммуникационных систем и компьютеризации).
Наибольшее впечатление производят «финансовые цунами»
спекулятивных капиталов, сметающие национальные экономи-
ки (первый кризис глобальной экономики в 1997—1999 гг.),
и наконец, вершина всего — Интернет, виртуальная реальность,
интерактивность. Однако внешние атрибуты глобализации не
должны заслонять главного — влияния современных форм науч-
но-технологического прогресса на общество и на человечество в
целом.
В 1991 г. компьютеров с доступом в Интернет во всем мире
было около 5 млн, в 1996 г. — 60 млн, в 2001 г. их число достигло
300 млн. Беспрецедентный рост Всемирной информационной
паутины (Интернета) базируется на двух факторах — удешевле-
нии электронной техники и снижении стоимости услуг по переда-
744
че информации. Взаимодополняя и усиливая друг друга, они ведут
к лавинообразному разрастанию компьютерных сетей и потоков
информации. Объем информационного обмена посредством Ин-
тернета удваивается каждые 100 дней — ежегодный рост в 7,3 раза.
При этом цена компьютеров в течение жизни одного поколения
упала более чем в 10 тыс. раз и продолжает снижаться (в расчете на
единицу мощности) на 30—40% в год. С помощью спутников свя-
зи по мобильному телефону, телефаксу, Интернету можно об-
щаться из любой точки земного шара с абонентом в любой другой
его точке. Новейшие телекоммуникационные и компьютерные
технологии создали наднациональные мосты, благодаря которым
информация легко преодолевает на своем пути физические пре-
грады и государственные границы. Складывается глобальное ки-
берпространство.
Современный мир формируется на базе качественно новых
телекоммуникационных систем и компьютеров, которые породи-
ли новые информационные технологии, а те, в свою очередь, ка-
чественно изменили природу бизнеса.
Происходящее во всем мире обособление групп людей, рабо-
тающих с «информационными технологиями», в «информацион-
ное сообщество» неизбежно ведет к постепенной концентрации
этого сообщества в наиболее развитых странах (интеллект, хотя и
выживает, но не воспроизводится в условиях бедности и опаснос-
ти). Тем самым создается объективно обусловленный технологи-
ческий разрыв, в первую очередь, между развитыми и развивающи-
мися странами.
Данный разрыв закрепляется и становится практически не-
преодолимым в силу целого ряда факторов, важнейшими из кото-
рых являются так называемые метатехнологии — кардинально
новый тип технологий, само применение которых принципиаль-
но исключает возможность конкуренции с разработчиком.
В качестве примеров можно привести проект сетевого ком-
пьютера (рассредоточение его памяти в сети открывает разработ-
чику всю информацию пользователя) и современные технологии
связи, позволяющие анализировать в онлайновом режиме все те-
лефонные сообщения Европы (вялотекущий скандал вокруг сис-
темы «Эшелон» вызван именно коммерческим использованием
результатов этого анализа), а также технологии формирования
сознания, нуждающиеся в постоянном обновлении.
745
18.4.2. Появление и распространение метатехнологии снижают
значение финансов с точки зрения конкурентоспособности: если
раньше они были главным источником рыночной силы, то теперь
становятся лишь ее следствием. Конкурентоспособность все
больше определяется технологиями, которые часто нельзя ку-
пить.
Разработчики новых технологических принципов, а точнее
владельцы организационных и исследовательских технологий
разработки таких принципов, становятся наиболее влиятельными
субъектами современной мировой экономики, в наибольшей сте-
пени контролирующими рынки своей продукции и практически
избавленными от внешней конкуренции. Эффективность созда-
ния этих принципов связана не только с наибольшей долей добав-
ленной стоимости (которая неуклонно уменьшается от верхних
«этажей» технологической пирамиды к нижним, снижая соответ-
ственно эффективность бизнеса) и наибольшей степенью конт-
роля за рынком сбыта (которая прямо зависит от степени уни-
кальности товара — реальной или внедряемой в сознание, а также
снижается от верхних этажей к нижним), но и с тем, что на основе
этих принципов затем формируются технические и поведенческие
стандарты, дающие совершенно фантастическое конкурентное
преимущество тому, кто эти стандарты создает.
Признаком вырождения конкуренции является возникнове-
ние на едином мировом рынке глобальных монополий, почти не
поддающихся регулированию государствами и международной
бюрократией (последние были бессильны даже перед лицом тра-
диционных производственных ТНК; сейчас же им противостоят
во многом неформальные финансово-информационные группы,
которые почти явно ненаблюдаемы).
Существует два способа преодоления глобальных монополий.
Первый — расширение масштабов рынков.
Второй путь — качественный технологический рывок, и в от-
личие от первого он носит слабопредсказуемый, нерегулируемый
и весьма разрушительный характер. Эта разрушительность вызва-
на кардинальным повышением производительности труда, в ре-
зультате которого значительная часть занятых лишается работы и
средств к существованию в сроки, не позволяющие самостоятель-
но адаптироваться к изменению и освоить новую профессию.
746
18.5. Экономический национализм
и микроэкономические проблемы
18.5.1. Основная цель экономического национализма заключа-
ется в проведении экономической политики под контролем на-
ции и национальных интересов. Ключевые элементы такого конт-
роля следующие: поощрение индустриализации, национализация
капитала и широкая интервенция государства в экономику. На-
ционалисты всегда верят, что только через экономическую неза-
висимость можно достичь политической и культурной независи-
мости.
Очевидно, что с уровнем патриотизма в народе связана поддер-
жка потребителями национального производителя. Особенно это
чувствуется на таких рынках, как японский или американский.
Представители этих наций выберут отечественный товар. С наци-
ональной идеей связан и бизнес. Национальная идея проявляется
в том, что граждане покупают отечественные товары, отстаивают
свой язык, пропагандируют свой стиль жизни. Часть экономистов
считает, что в конечном итоге это приводит к росту благосостоя-
ния этих народов, а отсутствие национализма и патриотизма при-
водит к экономическим потерям.
Некоторые экономисты поддерживают идею, что экономи-
ческий национализм является жизненной альтернативой «либе-
рализации» торговой политики. Речь идет не об оживлении систе-
мы национального государства, а об интеграции мировой эконо-
мики разумным, демократическим образом.
Наиболее ярко в настоящее время экономический национа-
лизм проявляется в ситуации с транснациональными компания-
ми и глобальными брендами. И без антиглобалистов глобальные
бренды переживают сегодня не лучшие времена, и причинами
тому являются меняющиеся предпочтения потребителей и расту-
щая конкуренция со стороны местных производителей. Уже се-
годня британцы отправляются перекусить в забегаловки Pret-a-
Manger, малайзийцы ездят на отечественных автомобилях Proton,
китайцы пьют пиво Tsingtao, а россияне покупают одежду Тот
Klaim. Десятки тысяч небольших национальных брендов, возни-
кающие по всему миру, лишают гигантские транснациональные
корпорации надежд на процветание.
747
Еще в 90-е гг. XX в. в такое развитие событий сложно было бы
поверить. Тогда инвесторы рассматривали известные бренды как
легкий способ зарабатывания денег. Рынки развитых стран были
насыщены товарной массой, и продвигать новые торговые марки
для массового потребителя в США, Японии и Западной Европе
стало делом сложным и хлопотным. А вот выход со сложившими-
ся брендами на новые рынки открыл безграничные возможности
для экспансии, особенно после открытия для западных товаров
рынков стран бывшего соцлагеря. Запретный плод западных
брендов десятилетиями не был доступен в России, Китае и Вос-
точной Европе, поэтому ликвидация торговых барьеров привела к
быстрому завоеванию рынков этих стран западными торговыми
марками. Аналогичная ситуация складывалась на рынках многих
развивающихся стран (Латинской Америки, Юго-Восточной
Азии и Индии), которые лишь в начале 90-х гг. XX в. ослабили
торговые барьеры. Вместе с ростом объемов продаж резко росли и
котировки акций владельцев брендов.
Однако достигнутый успех международных корпораций ока-
зался явлением временным. Уже в конце 90-х гг. XX в. любовь
потребителей новых рынков к международным брендам стала
сходить на нет.
18.5.2. Призыв «Покупайте отечественное!», запущенный в Рос-
сии Ю.М. Лужковым, одновременно прозвучал и в других стра-
нах. Самое интересное, что и там, и в России он был услышан.
Свою роль сыграло удачное стечение обстоятельств. Во-первых,
одновременно с потерей потребителями первоначального инте-
реса к иностранным торговым маркам (приобретение «Кока-ко-
лы» и «биг-маков» вовсе не приближало их потребителей к стан-
дартам жизни западного среднего класса) в результате глобаль-
ного финансового кризиса 1997—1999 гг. в России, Бразилии и
Юго-Восточной Азии произошла девальвация. Она помогла
местным производителям в этих странах успешнее конкуриро-
вать по ценам с западными гигантами. Во-вторых, в условиях
жесткой конкуренции в середине 90-х гг. XX в. местным произ-
водителям пришлось подтянуть технологические стандарты до
международного уровня и брать на вооружение агрессивную
маркетинговую стратегию конкурентов. В-третьих, еще одним
фактором стала постепенная индивидуализация потребитель-
748
ского спроса в этих странах, которая протекала одновременно с
формированием среднего класса.
В результате рынки потребительских товаров были наводнены
многочисленными национальными товарами, среди которых ста-
ли формироваться бренды, потеснившие западных гигантов. На-
пример, сейчас в Китае, из десяти наиболее рекламируемых брен-
дов — все десять китайские, хотя еще несколько лет назад в десят-
ке были торговые марки Procter and Gamble и Coca-Cola. Наиболее
быстро растущим брендом в этой стране стали компьютеры Leg-
end. История компании Legend началась лишь в 1988 г., а собирать
компьютеры под этой маркой стали лишь два года спустя. Но уже
к 1997 г. Legend стала наиболее популярной маркой в Китае, не-
плохо продавались компьютеры этой марки и в соседних странах.
А в 2000 г. компания Legend заняла восьмую строчку в рейтинге
компьютерных брендов, опубликованном в журнале BusinessWeek.
Не последнюю роль в продвижении китайских брендов по всему
миру играет само правительство страны, принявшее специальное
постановление по рекламе на Западе примерно 100 национальных
брендов самого разного профиля.
Даже на рынке дорогих, эксклюзивных товаров международ-
ным брендам, которые согласно рейтингу BusinessWeek все еще
находятся на подъеме, все большую конкуренцию составляют
местные производители. Некоторым из них удается не только
стать популярными на родине, но и добиться признания в разви-
тых странах — как, например, бразильскому бренду Rosa Cha,
продающему летнюю одежду и купальники, или японскому про-
давцу модной одежды Uniqlo. Бразильцы выигрывают за счет того,
что представляют свои коллекции несколько раньше, чем это де-
лают американские и европейские дизайнеры. Кроме того, мест-
ная индустрия одежды смогла в последние годы «раскрутить» не-
сколько бразильских моделей международного уровня, например
Жизель Бундхен.
Секретом успеха японской фирмы Uniqlo стало то, что вла-
дельцы магазина, продающие одежду, не считают, что покупать ее
должны исключительно люди с фигурами Сталлоне или Шиффер.
Этот нестандартный для западных бутиков подход позволил при-
влечь в магазины Uniqlo как молодежь, так и взрослых людей.
Кроме того, большая часть одежды производится в Китае, а пото-
му ее можно приобрести по фантастически низким в сравнении с
западными брендами ценам. Годовой оборот сети Uniqlo уже пре-
749
высил 2 млрд долл., и недавно японцы открыли свой магазин в
Лондоне. Однако, даже если национальные бренды и не становят-
ся международными, они вполне неплохо чувствуют себя на на-
циональном рынке, как, например, российские (хотя и «косящие»
под иностранные) бренды по продаже одежды и обуви Devore,
Gregory, Carlo Pazolini, Desegni, OGGY.
Интересно, что экономический национализм охватил не толь-
ко рынок товаров, но и рынок услуг.
Благодаря тем же факторам, что и на товарном рынке (деваль-
вация, повышение качества, агрессивная реклама), вполне ус-
пешной оказалась раскрутка брендов авиакомпаний и гостинич-
ных сетей. В странах Азии некоторые авиакомпании (Cathay Pa-
cific, Singapore Airlines, Thai Air) и гостиничные сети (Marco Polo в
Гонконге, Meritus в Сингапуре, Dusit в Таиланде) стали выигры-
вать по популярности у своих западных конкурентов. Недавно
около 70 крупных азиатских отелей сформировали альянс, чтобы
совместно бороться с транснациональными сетями.
18.6. Об экономической безопасности фирмы
18.6.1. Процесс создания внутреннего рынка в России и на терри-
тории стран ближнего зарубежья, появление негосударственных
хозяйствующих субъектов и установление между ними отноше-
ний конкуренции делают актуальной такую проблему, как обес-
печение безопасности предпринимательской деятельности.
Основные проблемы безопасности отечественного бизнеса
заключаются в следующем. Во-первых, рыночная экономика,
построенная на конкуренции, очень динамичная система, а сле-
довательно, очень рискованная. Во-вторых, российский рынок
находится в стадии становления, и поэтому многие механизмы
еще просто не отработаны. В-третьих, в России пока отсутствуют
устойчивые нормы права защиты интересов предпринимателей.
Экономическая безопасность фирмы — это такое состояние ее
производственных, научно-технических, материально-техничес-
ких, кредитно-финансовых и информационно-аналитических
структур, которое обеспечивает защиту и дальнейшее эффектив-
ное использование имеющихся ресурсов в условиях конкуренции
как внутри России и СНГ, так и на мировом рынке.
750
Любое игнорирование законов рыночной экономики и требо-
ваний экономической безопасности очень часто приводит к тому,
что упускаются выгодные сделки, заключаются контракты с не-
добросовестными партнерами, принимаются на работу некомпе-
тентные сотрудники или сотрудники, являющиеся подставными
лицами недобросовестных конкурентов и даже организованной
преступности.
Легче, дешевле и выгоднее сохранять необходимый уровень
экономической безопасности, чем вести длительные, дорогостоя-
щие и не всегда перспективные судебные процессы, пытаясь зад-
ним числом отстоять свои права.
Безопасность фирмы зависит от разных причин. В частности,
ущерб интересам предпринимателя может быть нанесен в резуль-
тате недобросовестных действий конкурентов, невыполнения
партнерами, заказчиками, поставщиками, клиентами своих обя-
зательств по оплате контрактов, поставке товаров и т.п., а также в
результате кризисных явлений в экономике, непредсказуемых
изменений конъюнктуры рынка, стихийных бедствий, чрезвы-
чайных происшествий, управленческой некомпетентности, соци-
альной напряженности и, наконец, неблагоприятной экономи-
ческой политики государства.
Таким образом, факторы, влияющие на уровень безопасности
фирмы, могут быть внутренними и внешними, экономическими
и внеэкономическими, объективными и субъективными.
18.6.2. Чтобы дать полную картину обстановки в российской на-
циональной экономике, необходимо учитывать следующие осо-
бенности российского рынка (их следует толковать как внешние
факторы безопасности фирмы): структурное деформирование
национального хозяйства; размах промышленного и коммерчес-
кого шпионажа (со стороны различных структур, использующих
методы агентурного и технического проникновения в коммерчес-
кую тайну); отсутствие единой стратегии обеспечения безопас-
ности предпринимательских структур и, наконец, отсутствие ци-
вилизованных юридических гарантий для реализации коммерчес-
ких интересов предпринимателя.
Говоря о внутренних факторах, влияющих на безопасность
фирмы, следует подчеркнуть, что наиболее широкое распростра-
нение в российской действительности получили кражи, грабежи,
разбои, мошенничество, вымогательство, злоупотребление слу-
751
жебным положением, должностной подлог, а также различные
формы недобросовестной конкуренции и такие особо опасные
формы, как заказные убийства и захват заложников.
Кто в современных условиях может защитить предпринима-
теля?
Во всяком случае, на сегодняшний день российские правоох-
ранительные органы в силу разных причин практически утратили
способность профессионально защищать интересы предприни-
мателей. Произошло это в результате бесконечного реформирова-
ния органов и общего паралича, наступившего в результате такой
распространенной болезни, как коррупция.
Все это означает одно: экономическая безопасность в услови-
ях функционирования различных форм собственности — госу-
дарственной, коллективной и частной — уже не может быть обес-
печена силами только государственных правоохранительных ор-
ганов. В результате представители российского бизнеса
оказываются один на один с проблемой защиты своих жизненно
важных интересов. Остается одно — объединяться и защищать
свои интересы собственными силами.
Предприниматели должны осознать себя как клан, четко вы-
строить свои задачи и систематически финансировать их реше-
ние.
Похоже, что эту истину все усвоили, однако организацию та-
кой деятельности каждый понимает по-своему, расставляя при-
оритеты на свой вкус, страх и риск, без учета наработанных про-
фессионалами методик в ходе складывавшейся годами практики.
Анализ содержания бесед с экспертами наиболее крупных
коммерческих служб безопасности (только в Москве их более
2 тыс.) показывает, что многие фирмы, заинтересованные в обес-
печении собственной защиты, вынуждены сегодня действовать в
пространстве, где нет достаточной нормативной базы, регламен-
тирующей деятельность службы безопасности (СБ). Нет перечня
сведений, составляющих коммерческую тайну, системного под-
хода к организации безопасности предпринимательской деятель-
ности, налаженного информационно-аналитического сопровож-
дения мер безопасности, квалифицированных кадров; практичес-
ки отсутствуют научно обоснованные и проверенные практикой
механизмы и технологии обеспечения различных видов безопас-
ности (имеется в виду отсутствие наработанных методик по обес-
752
печению физической защиты персонала и имущества фирмы,
информационной безопасности, защиты коммерческой тайны).
Дальновидные и прибегающие к советам экспертов руководи-
тели могли бы с пользой для дела многие из перечисленных де-
фектов устранить уже сегодня (на практике почему-то это случа-
ется весьма редко).
Следует осознать, что обеспечение безопасности предприни-
мательской деятельности — весьма обширная проблема, включа-
ющая комплекс организационно-правовых, технико-технологи-
ческих, административных, воспитательных, финансовых и спе-
циальных мер, направленных на выявление, предупреждение и
пресечение угроз и посягательств на стабильность функциониро-
вания и развития фирмы.
Сегодня эффективная безопасность предпринимательской
деятельности, как и всей национальной экономики, представля-
ется специалистам как система мер, которая обеспечивается на
следующих взаимосвязанных направлениях: защита от преступ-
ного мира; защита от нарушений закона с тем, чтобы самим не
попасть под санкции; защита от недобросовестной конкуренции;
защита от противоправных действий собственных сотрудников.
Эти направления деятельности реализуются на участках: про-
изводственный (сохранность материальных ценностей); коммер-
ческий (оценка партнеров, юридическая защита интересов); ин-
формационный (определение значимости информации, порядка
поступления, пользования, передачи, защиты от хищения), кад-
рового обеспечения.
Идея применения метода системного подхода к проблемам
обеспечения экономической безопасности состоит в том, чтобы
пресечь, сократить или, по крайней мере, ограничить утечку тех
крупиц ценной информации, которые могут дать конкурентам
возможность заранее узнать о том, что руководство фирмы пред-
принимает и планирует.
К сожалению, в России почти полностью отсутствуют такие
необходимые для реализации системного подхода составляющие,
как: достаточно полная законодательная база, регулирующая ос-
новные отношения в сфере бизнеса (например, в России недоста-
точно еще развиты частное право и юридическое обеспечение
экономической деятельности); отлаженный реформой экономи-
ческий механизм на федеральном и региональном уровнях; доста-
точный уровень включения общества в процессы экономических
48 - 7620
753
преобразований; государственная программа борьбы с распро-
страняющейся коррупцией в национальной экономике; эффек-
тивная национальная статистика и контроль.
18.6.3. Какие же направления обеспечения экономической безо-
пасности предпринимательской деятельности с учетом всего из-
ложенного выше сегодня являются приоритетными?
При выработке концепции защиты следует в первую очередь
исходить из того, что конечной целью применения любых мер
противодействия угрозам является защита персонала, материаль-
ных и финансовых средств и информационных ресурсов от нане-
сения им материального и морального ущерба в результате слу-
чайных или преднамеренных действий.
По целям защитные мероприятия должны обеспечивать: пре-
дупреждение появления угроз; выявление возможных направле-
ний и степени нарастания опасности; обнаружение реальных
действий, приносящих ущерб предпринимательству; пресечение
разглашения и утечки информации и несанкционированного до-
ступа к ней; ликвидацию последствий неправомерного получения
информации и ее использования злоумышленниками.
Анализ состояния дел в области экономической безопасности
предпринимательства показывает, что:
• обеспечение безопасности не может быть одноразовым актом;
это непрерывный процесс, заключающийся в обосновании и
реализации наиболее рациональных форм, методов, способов
и путей создания, совершенствования и развития системы бе-
зопасности, непрерывном управлении ею, контроле, выявле-
нии ее узких и слабых мест и потенциально возможных угроз
бизнесу;
• безопасность может быть обеспечена лишь при комплексном
использовании всего арсенала средств защиты всех структур-
ных элементов производственной системы и на всех этапах
технологического цикла предпринимательской деятельности;
• требуемый уровень безопасности не может быть обеспечен без
надлежащей подготовки персонала фирмы и пользователей и
соблюдения ими всех установленных правил, направленных
на обеспечение безопасности.
Главным в безопасности предпринимательства являются эко-
номические рычаги по возмещению ущерба и предотвращению
негативных последствий для организации бизнеса. В этом заклю-
754
чается основной смысл обеспечения экономической безопаснос-
ти предпринимательства от противоправных действий.
Поддержание правопорядка в экономической сфере заключа-
ется в развитии судебной системы с ведущей ролью арбитражных
судов. Только арбитражные суды, а не административные и дру-
гие внешнеэкономические меры могут воссоздать нормальный
правопорядок в экономике и сделать предпринимательство циви-
лизованным.
Общепризнан тот факт, что приоритетным направлением в
оперативной деятельности любой службы безопасности хозяй-
ствующего субъекта является обеспечение его экономической
безопасности.
Основа экономического развития любой фирмы — научно-
технологический прогресс и ее способность осуществлять плав-
ный переход к передовым технологиям. В этой связи можно ут-
верждать, что стержнем экономической безопасности в современ-
ных условиях являются технико-экономическая независимость
хозяйствующего субъекта и его технико-экономическая неуязви-
мость.
Следует упомянуть, что, как свидетельствует практика, при
обеспечении экономической безопасности не всегда занимает
полагающееся ей место защита интеллектуальной собственности
фирмы. Кража интеллектуальной собственности может быть во
много раз серьезнее материальной. Фирма, лишившаяся ее, рис-
кует потерять место ’в конкурентной борьбе и будет вынуждена
сократить штат сотрудников, отказаться от планов развертывания
производства. Все это может в конце концов привести к банкрот-
ству.
Похоже, что сегодня российские предприниматели начинают
понимать, что коммерческая тайна является обязательной для
обеспечения безопасности фирмы.
Известно, что один из самых распространенных путей утечки
информации — небрежное обращение со служебными документа-
ми. Как правило, огромное число входящих и исходящих доку-
ментов в немалой степени затрудняет контроль за их сохраннос-
тью. Проводившаяся проверка на крупных российских отрасле-
вых фирмах показала, что порядок регистрации и хранения
документов у большинства из них не выдерживает критики.
Особо следует отметить, что большие возможности для неза-
конного распространения деловой информации предоставляет
48*
755
современная копировальная техника. Существенный ущерб несут
фирмы и от утечки информации в результате подслушивания кон-
курентами телефонных разговоров, а также регистрации излуче-
ний компьютерных терминалов. По мнению специалистов, не-
смотря на самые совершенные технические средства, наилучшей
защитой от промышленного (коммерческого) шпионажа является
поддержание порядка и соответствующего режима секретности
внутри фирмы.
Трудность обеспечения экономической безопасности любой
фирмы заключается в том, что внутри самой предприниматель-
ской структуры очень часто действуют скрытые от глаз противо-
речивые, если не взаимоисключающие, групповые и личные ин-
тересы. В связи с этим проблема службы экономической безопас-
ности фирмы заключается в том, чтобы найти такие сферы,
которые были бы выгодны (приемлемы) всем субъектам экономи-
ческой деятельности фирмы в равной мере. Сгладить их, не разо-
бравшись в существе, для субъектов обеспечения безопасности
представляется затруднительным.
В рыночных условиях стабильная работа любой фирмы невоз-
можна без надежной защиты от неправомерных посягательств на
ее права, собственность и персонал от различного рода внутрен-
них и внешних угроз. Следует заметить, что сегодня экономичес-
кая безопасность — это не только прерогатива государства и не
только деятельность государственных служб по охране собствен-
ности, но также право самих организаций бизнеса.
18.7. О теневой экономике и некоторых
микроэкономических проблемах
18.7.1. Понятие «теневая экономика» охватывает следующие че-
тыре относительно самостоятельных понятия: 1) «неофициальная
экономика» — включает легальные виды экономической деятель-
ности, в рамках которой осуществляется не отражаемое офици-
альной статистикой производство товаров и услуг в целях ухода от
оплаты налогов; 2) «криминальная экономика» — охватывает все
запрещенные законом виды экономической деятельности (тор-
говля наркотиками, коррупция, рэкет, грабежи, сутенерство, про-
ституция и т.д.); 3) «фиктивная экономика» — это экономика
756
спекулятивных сделок, приписок, взяточничества, мошенничест-
ва, а также деятельность, направленная на получение необосно-
ванных льгот субъектами хозяйствования; 4) «неформальная эко-
номика» — это деятельность по производству товаров и услуг се-
мьями и (или) коллективами друзей.
Субъекты теневой экономики образуют пирамиду, на верхней
части которой располагаются криминальные элементы: нелегаль-
ные торговцы наркотиками и оружием, рэкетиры, грабители, на-
емные убийцы, сутенеры, проститутки, коррумпированные пред-
ставители органов власти, которые берут крупные взятки, торгуют
государственными должностями и интересами. По оценкам экс-
пертов, численность криминальных элементов составляет от 5 до
25% всей пирамиды теневой экономики.
Среднюю часть пирамиды теневой экономики образуют тене-
вики-хозяйственники, коммерсанты, финансисты, «челноки»
ИТ.Д.
Подножие пирамиды теневой экономики представлено наем-
ными работниками физического и умственного труда, которые
получают зарплату в конвертах и к которым примыкают мелкие и
средние государственные служащие, в доходах которых, по оцен-
кам экспертов, до 60% составляют взятки.
По оценкам экспертов, до 75% российской экономики рабо-
тает в теневом секторе, хотя, конечно, точную цифру назвать
практически невозможно.
18.7.2. В настоящее время в Правительстве РФ имеются предста-
вители, которые отстаивают две диаметрально противоположные
точки зрения. Суть одной точки зрения — в необходимости прове-
дения политики протекционизма национальной промышленнос-
ти в целях укрепления положения российских национальных
компаний на отечественном рынке. Суть другой точки зрения —
в необходимости снижения таможенных барьеров в целях облег-
чения прихода иностранных компаний на российский рынок, что
особенно важно перед вступлением РФ в ВТО.
Наличие двух таких крайних точек зрения имеет своим резуль-
татом отсутствие четкой последовательной политики регулирова-
ния национальной экономики РФ.
Среднюю и нижнюю части пирамиды теневой экономики
можно вывести из тени, либо создав условия функционирования,
757
к которым стремятся ее субъекты (теневики-хозяйственники и
наемные работники), либо создав такие (невыполнимые) условия
функционирования, при которых субъекты сами побегут, уже не
думая куда.
По-видимому, Правительство РФ фактически стремилось
«выдавливать» фирмы из теневого сектора, однако эта политика
не дала серьезного эффекта.
Одна из причин отсутствия серьезного эффекта в том, что го-
сударственные структуры, которые должны заниматься «выдав-
ливанием» фирм из теневого сектора (Государственный таможен-
ный комитет РФ, Министерство по налогам и сборам РФ, Мин-
фин РФ, службы экономической безопасности ФСБ и МВД
и т.д.), не шли до конца, ибо существует такая точка зрения, что
если закрыть в РФ теневой сектор полностью, то российская эко-
номика тут же развалится.
Другая причина в том, что, выйдя на «легальную поверхность»,
почти каждая фирма тут же прекратит свое существование, ибо
«климат на легальной поверхности» совершенно непригоден для
нормального функционирования нормальной фирмы. Названное
обстоятельство имеет, в свою очередь, две причины, которые по-
казывают, как макроэкономическая политика влияет на функци-
онирование микроэкономических субъектов: нерациональный
налоговый режим и неустойчивая денежная политика в РФ.
Если по Налоговому кодексу РФ собирать все налоги, то фир-
ма (производственное предприятие) на рубль дохода (т.е. выруч-
ки) должна внести в виде налогов и сборов в кассы различных
организаций (от профсоюза до бюджета) 1 руб. 02 коп., т.е. фирме
не остается никаких денег не только для предпринимательского
дохода, но и для заработной платы персонала. В ходе подготовки
Налогового кодекса РФ было заявлено, что налоговую нагрузку
на производственные предприятия уменьшат. На самом деле про-
изошло следующее: число налогов и сборов сократилось, но объ-
ем налогового изъятия у фирмы (промышленного предприятия) в
среднем вырос, что, конечно, не стимулирует выход из тени как
фирм, так и предпринимателей.
18.7.3. Если финансовая политика стратегически не определена
(на сколько-нибудь длительный временной промежуток, хотя бы
на 5—7 лет), то нет оснований для принятия микроэкономических
решений радикального характера — инвестировать или изымать
758
прибыль, осваивать новые продукты или нет. По оценкам экспер-
тов, сформировавшийся в России класс собственников и пред-
принимателей (получивших собственность в ходе приватизации)
в основном оказался неэффективным. За исключением несколь-
ких сотен, максимум тысячи компаний, остальные (примерно
3 млн хозяйствующих субъектов) оказались неэффективными в
том смысле, что они не имеют потенциала для удержания своей
собственности на конкурентоспособном уровне. Они не могут в
рамках своей собственности материализовать ни новые техноло-
гии, ни новый менеджмент. Для этого, к сожалению, часто не
хватает знаний и нет денег. Необходимо отметить, что для эффек-
тивного функционирования фирмы не столь важно, кто является
ее собственником, а важно, кто управляет собственностью.
Для создания предпосылок формирования внутренних источ-
ников накопления у микроэкономических субъектов необходима
корректировка налоговой политики. В последние годы советской
власти накопления предприятий составляли примерно 30%.
В настоящее время аналогичный показатель в 2,3—2,5 раза ниже,
что означает фактическое отсутствие внутренних источников ин-
новационных процессов для инвестиций.
Внешние источники накопления (не обязательно иностран-
ные) должны прийти в основном с рынка, на котором новые ин-
весторы будут покупать акции, облигации и прочие активы фирм.
Однако новых инвесторов фактически не наблюдается: в течение
ряда лет объем «голубых» фишек колеблется по годам, но новые
субъекты не появляются.
На основании вышесказанного необходима корректировка
средств макроэкономической политики в целях сокращения объ-
ема теневого сектора и создания нормальных условий функцио-
нирования фирм, выходящих из тени на «поверхность»: измене-
ния налоговой системы, которая создавала бы фирмам условия,
благоприятствующие их выходу из тени и проведению рациональ-
ной политики накопления, проведения стабильной по годам фи-
нансовой политики, преобразования административной системы
путем перевода от разрешительного режима функционирования
фирм к регистрационному режиму их функционирования.
В заключение отметим, что согласно утвержденной ООН в
1993 г. новой версии национальных счетов каждой стране было
рекомендовано учитывать объем теневого сектора в объемах про-
изводства ее национальной экономики.
759
Вопросы для самоконтроля к главе 18
1. Что представляют собой современные формы научно-технологичес-
кого прогресса?
2. С каким темпом роста растет объем передаваемой через Интернет
информации?
3. Как можно охарактеризовать динамику в экономике США отрасли
информационных технологий в последней четверти XX в.?
4. Как формулируется закон Мура?
5. Как можно охарактеризовать динамику цен на микропроцессоры в
последнее десятилетие XX в.?
6. Что представляют собой составляющие экономического роста, по-
рождаемые НТП и, в частности, цифровой революцией?
7. В каких операциях микроэкономического уровня используются ин-
формационные технологии?
8. Какой фактор был определяющим для быстрого роста коммерческо-
го использования компьютеров?
9. За счет чего фирмы, использующие Интернет, снижают свои из-
держки? Приведите конкретные примеры.
10. Каковы основные проблемы российских интернет-магазинов?
11. В чем суть современного толкования понятия «глобализация»?
12. Что представляет собой материально-вещественная база современ-
ной глобализации?
13. Что представляют собой положительные последствия глобализа-
ции?
14. Что представляют собой негативные последствия глобализации?
15. Что представляют собой материальные и нематериальные источники
глобализации?
16. В чем проявляется влияние глобализации на национальные эконо-
мики?
17. В чем суть технологического монополизма?
18. В чем суть современного толкования понятия «метатехнология»?
19. Что такое экономический национализм? Приведите конкретные
примеры.
20. Что следует понимать под экономической безопасностью фирмы?
21. Каковы особенности современного (конец XX — начало XXI в.) рос-
сийского рынка?
22. Каковы внешние факторы безопасности фирмы?
23. Каковы внутренние факторы безопасности фирмы?
24. Что представляет собой система мер, которая обеспечивает эффек-
тивную экономическую безопасность фирмы?
25. Что представляет собой современное толкование понятия «теневая
экономика»?
760
26. Что представляет собой пирамида современной теневой экономи-
ки?
27. В чем суть двух крайних точек зрения о мерах государственного регу-
лирования национальной экономики России?
28. Как следует корректировать средства макроэкономической полити-
ки в целях сокращения объема теневого сектора и создания нормаль-
ных условий для функционирования фирм, выходящих из тени на
«поверхность»?
Вопросы для контрольных работ к главе 18
1. Опишите и проанализируйте составляющие экономического роста,
порождаемые цифровой (электронной) революцией.
2. Опишите и проанализируйте факторы снижения издержек тех фирм,
которые используют Интернет.
3. Объясните, почему в российских условиях основным способом оп-
латы покупок в интернет-магазинах является оплата наличными ку-
рьеру.
4. Опишите и проанализируйте проблемы российских интернет-мага-
зинов.
5. Опишите и проанализируйте материально-вещественные основания
современной глобализации.
6. Укажите на сходства и различия между глобальными процессами в
прошлом и современной глобализацией.
7. Укажите и проанализируйте позитивные последствия глобализации.
8. Укажите и проанализируйте негативные последствия глобализации.
9. Укажите и проанализируйте основные экономические проблемы
России в условиях глобализации.
10. Опишите суть феномена технологического монополизма.
11. Опишите и проанализируйте феномен экономического национализ-
ма.
12. Опишите исторические примеры экономического национализма.
13. Приведите современные примеры экономического национализма.
14. Укажите факторы современного подъема экономического национа-
лизма.
15. Опишите суть понятия экономической безопасности фирмы.
16. Назовите внешние и внутренние факторы понижения уровня эконо-
мической безопасности фирмы.
17. Опишите и проанализируйте четыре относительно самостоятельных
фрагмента теневой экономики.
18. Проанализируйте влияние финансовой политики (краткосрочной и
долговременной) правительства на принятие микроэкономических
решений.
Приложение
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ
ПОНЯТИЯ И РЕЗУЛЬТАТЫ,
ИСПОЛЬЗУЕМЫЕ В КУРСЕ
«МИКРОЭКОНОМИКА.
ПРОДВИНУТЫЙ УРОВЕНЬ»
П 1. Множества и отображения
П.1.1. Множество — начальное понятие в математике, которое
строго не определяется, а только поясняется примерами: множест-
во домов в городском квартале, множество точек прямой на плос-
кости. Немецкий математик Г. Кантор писал, что он под множест-
вом понимает всякое многое, мыслимое как единое, т.е. всякую
совокупность определенных элементов, которую можно связать в
единое целое с помощью некоторого закона. Объекты, составля-
ющие множество, называются его элементами. Множество зада-
но, если указано свойство, которым обладают все его элементы и
которым объекты, не принадлежащие множеству, не обладают.
То, что объект х является элементом множества М, записывается
так: хе Ми читается: «х принадлежит М». То, что z не является
элементом множества М, записывается так: z£ Ми читается: «z не
принадлежит М». Множество М, состоящее из элементов*, и, v...,
записывается так: М = {*, и, v...}. В частности, множество Мможет
состоять из одного элемента: М= {т}. Множество, содержащее
конечное число элементов, называется конечным, в противном
случае — бесконечным. Множество товаров одной партии — ко-
762
нечное множество; множество точек прямой на плоскости — бес-
конечное. Множество называется пустым, если оно не содержит
ни одного элемента. Пустое множество обозначается символом 0.
Пусть А и М — два множества и пусть все элементы множества А
являются элементами множества М, тогда множество Л называет-
ся подмножеством (или частью) множества М, что записывается
так: А с М (или М 2 А) и читается: «А включено в М» (рис. П.1).
Если хе М, то {х} а М. Множество М является своим подмножест-
вом. По определению пустое множество 0 есть подмножество
любого множества, 0 и М называются несобственными подмно-
жествами множества М, все остальные его подмножества называ-
ются собственными. Множество всех подмножеств множества М
обозначается символом 2м. Множества А и В называются равны-
ми, если А а В и А 2 В, их равенство обозначается так: А = В.
П.1.2. Теория множеств изучает понятие «множество», операции
над множествами и свойства этих операций. Приведем определе-
ния трех операций над множествами (объединения, пересечения
и разности) и их свойства.
Объединением двух множеств А и В называется множество С
(обозначаемое символом А и В), состоящее из всех тех элементов,
которые принадлежат хотя бы одному из множеств А и В (рис. П.2).
В общем случае объединение произвольной совокупности мно-
жеств Аа (а е Г), где I— некоторое множество (конечное или бес-
763
C=AvB
Рис. П.2
конечное) индексов, есть множество С (обозначаемое символом
U Дх),состоящее из всех тех элементов, которые принадлежат
clgI
хотя бы одному из множеств Ла (а е 7). Вместо термина «объеди-
нение» иногда используют термин «теоретико-множественная
сумма».
Пересечением двух множеств А и В называется множество С
(обозначаемое символами А п В), состоящее из всех тех элемен-
тов, которые принадлежат каждому из множеств А и В. Иными
словами, пересечение — это общая часть множеств А и В (рис. П.З).
Например, множество всех квадратов есть пересечение множест-
ва всех ромбов и множества всех прямоугольников. Если множест-
ва Л и Б не имеют общих элементов, то говорят, что эти множества
не пересекаются (или имеют пустое пересечение). В общем случае
пересечение произвольной совокупности множеств Аа (а е 7) есть
множество С (обозначаемое символом П 4х), состоящее из всех
ае/
элементов, которые принадлежат каждому из множеств Ла (а е 7).
Вместо термина «пересечение» иногда используют термин «тео-
ретико-множественное произведение».
Разностью двух множеств Л и В называется множество С, кото-
рое обозначается символом Л \ В и состоит из всех тех элементов
множества Л, которые не принадлежат множеству В (рис. П.4).
Разность между множеством М и его подмножеством Л называет-
ся дополнением множества Л во множестве М.
Непосредственно проверяется, что:
1) A<jВ= B<jА, Ао В= Вг> А (коммутативность);
764
C=Ar\B
Рис. П.3
2) (А иВ)иС=А и(ДиС), (Аг< B)riC=Ar> (Вг>А) (ассоциатив-
ность);
3) А и (В n Q = (A В) n (A С), А п (В u Q = (А п В) о (A n С)
(дистрибутивность);
4) A<jA=A,Ar>A=A(идемпотентность);
5) А^0=А,Аг10 = 0;еслиАаЕ,то A<j Е= Е,Аг\ Е=А;
6) еслиЛа£,то£\(£\Л)=Л;
7) еслиЛс£,тоЛо(£\Л) = £;Ап(£\Л) = 0;
8) если Л а Е, В с Е, то (А и (Е\А)) пВ = В,(Аг> (£\А)) иВ=
= В;
9) (A<jB)oB = B, (Аг\В)иВ=В;
10) если Л а Е, В а Е, то Е\(А и В) = (Е\А) п (£\ В), Е\(А п В)
= (Е\А)и(Е\В).
Свойства 2), 3), 4), 10) естественным образом обобщаются на
случай произвольной (конечной или бесконечной) совокупности
множеств.
П.1.3. Пусть А и В — непустые множества, элементами которых
могут быть любые объекты. Отображение g из Л в В есть правило,
ставящее в соответствие каждому элементу х множества А один
вполне определенный (для каждого х свой) элемент у множества
В. Элемент у, который отображение g ставит в соответствие эле-
менту х, обозначается символом g(x) и называется частным значе-
нием (или просто значением) отображения g на элементе х,
т.е. у=g(x). Элементу называется также образом элемента х, а эле-
мент х — прообразом элемента у = g(x). Множество А называется
областью определения отображения g. Множество всех значений
отображения g обозначается символом g(A) и называется областью
765
значений отображения g. Таким образом, g(A) с В. Отображение
полностью определено, если: 1) задано множество Л (которое
отображается); 2) задано множество В (в которое отображается
множество А); 3) задано правило (закон) g, по которому для каж-
дого элемента хе А задается определенный элемент у е В (для
каждого х свой у). Если g(A) = В, то вместо термина «отображение
g из А в В» используют термин «отображение g из А на В».Часто
вместо длинной (но правильной) терминологии:... отображение g
из А в (на) В... применяют краткую (не совсем правильную) тер-
минологию: ...отображение g... не называя явно множества А и В.
Используемая в литературе для записи отображения символика
g: А -> В включает все три составные части (g, А, В) понятия отоб-
ражения. Символиках -»g(x), хе А (илиg: х->g(x), хе А) пред-
почтительнее, ибо здесь прямо показано, что элемент хе А отоб-
ражается в свой образ g(x) е В. Наиболее употребительным явля-
ется такое (укороченное) обозначение отображения: g(x), хе А,
которое обычно и применяется. Вместо слова «отображение» ис-
пользуется также термин оператор.
Если g(A) с А, то отображение g называется преобразованием
множества А. Пусть g(A) с А. Элемент х е А, такой, что g(x) = х,
называется неподвижной точкой отображения А.
Отображение g называется тождественным, если А = g(A)
и g(x) = х для всех х из А, т.е. в случае тождественного отображения
все элементы х из А являются неподвижными.
Отображение называется обратимым, если из того, что х' # х"
(х7 е А, х!' е А), следует, что g(x') * g(x") (т.е. каждый образах)
имеет единственный прообраз х), а отображение h :g(A) А назы-
вается обратным к отображению g. Иными словами, обратным
называется отображение, ставящее в соответствие каждому образу
g(x) его прообраз х. Обратимость отображения g означает, что у
этого отображения имеется обратное отображение h. Говорят, что
обратимое отображение g устанавливает взаимно однозначное
соответствие между множествами A ng(A). Очевидно, область зна-
чений отображения g есть область определения обратного отобра-
жения h, а область определения отображения g — область значе-
ний отображения h. Обратное отображение также обратимо,
и обратным для него является само отображение g. Отображение,
обратное к отображению g, обозначается символом g-1.
Если между множествами А и В можно установить взаимно од-
нозначное соответствие, т.е. если существует хотя бы одно обра-
766
тимое отображение g: А —> В, такое, что g(A) = В, то говорят, что
множества А и В имеют одинаковую мощность. Множества, име-
ющие одинаковую мощность, называются также эквивалентными
множествами. Очевидно, множества^ и В, эквивалентные одному
и тому же множеству С, эквивалентны между собой. Два конечных
множества эквивалентны тогда и только тогда, когда они состоят
из одного и того же числа элементов. Всякое бесконечное мно-
жество имеет хотя бы одно собственное подмножество, ему экви-
валентное. Верно и обратное. Множество, эквивалентное мно-
жеству всех натуральных чисел {1, 2, 3,...}, называется счетным.
Все счетные множества эквивалентны между собой. Понятие
мощности в применении к бесконечным множествам является
аналогом понятия количества для конечных множеств.
ПЛ.4. Пусть даны два отображения g: А —> В nf: В -> С (очевидно,
g(A) с В), т.е. отображение сопоставляет каждому элементу х из А
один вполне определенный элементу = g(x) из В, а отображение f
сопоставляет каждому элементу у из В один вполне определенный
элемент z = Ду) (рис. П.5). Отображение s из А в С, сопоставля-
ющее каждому элементу х из А элемент z =flg(x)) из С, обозначает-
ся символом^ (или/g) и называется композицией (суперпозици-
ей или произведением) отображения g и /(см. рис. П.5). Таким
Рис. П.5
767
образом,: х->/(g(x)), хе А. Очевидно, отображениеgg 1 иg lg
являются тождественными.
Отображение называется функционалом, если В есть множест-
во действительных чисел Ev Функционал называется функцией,
если его область определения А представляет собой множество
«-мерного пространства или, в частности, множество из Ех (ряд
авторов используют термины «отображение» и «функция» как
синонимы). Иногда, чтобы подчеркнуть, что речь идет об отобра-
жении во множество действительных чисел, говорят скалярная
(или числовая) функция. Для отображения множества «-мерного
пространства Еп в /«-мерное пространство Ет (т > 1) используют
термин векторная (или векторно-значная) функция (при т = 1 име-
ем скалярную функцию). В случае функции (скалярной или век-
торной) элемент х из А с Е1 называется независимой переменной
(аргументом), а сама функция (скалярная или векторная) называ-
ется функцией одной переменной, или функцией скалярного аргумен-
та. В случае когда элемент хе А с Еп, функцию (скалярную или
векторную) называют функцией нескольких переменных х = (хр ...,
хи), или функцией векторного аргументах.
П 2. Векторы и множества векторов
П.2.1. «-мерный вектор — упорядоченный набор из п действи-
тельных чисел. Эти числа называются координатами (или компо-
нентами) вектора. Вектор х = (хр х2), имеющий две координаты,
называется двумерным, пять координат (х= (хр х2 х3, х4, х5)) — пя-
тимерным, п координат (х= (хр ..., хя)) «-мерным. Одномерный
вектор (т.е. вектор, имеющий одну координату) есть число.
Вектор, у которого все координаты равны нулю, называется
нулевым 0 = (0,..., 0). Два вектора называются равными, если они
имеют одно и то же число координат и если их соответствующие
координаты равны. Координаты вектора нельзя менять местами,
ибо после их перестановки может получиться новый вектор, на-
пример (3, 2,6,9,4) * (2, 3,6, 9,4). Для «-мерных векторов опре-
делена операция умножения на действительные числа и операция
сложения. Обе эти операции являются «покоординатными». Про-
изведением векторах= (хр..., хя) на действительное число X назы-
вается вектор Хх = (Ххр ..., Ххя). Суммой векторов х= (хр ..., хя) и
у= (ур ...,уя) называется векторх + у= (Xj +ур ...,хя + уя). Опера-
ции сложения и умножения векторов обладают следующими
свойствами (проверяются непосредственно):
1) х + у=у + х;
2) (x + y) + z=x+(y + z);
3) х + 0=х;
4) х + (-х) = 0 (—х = (-хр ..., -хя));
5) а(рх) = (сф)х;
6) (а+ Р)х = ах + Рх;
7) а(х + у) = ах + ау;
8) 1х=х.
Множество всех «-мерных векторов с определенными выше
операциями сложения и умножения на действительные числа на-
зывается «-мерным пространством (символика: Еп), точнее
«-мерным координатным пространством или «-мерным арифме-
тическим пространством, «-мерные векторы являются элемента-
49 - 7620
769
ми пространства Еп. Элементы пространства Еп называют его
точками; следовательно, термины «вектор» и «точка» используют-
ся как синонимы.
ПустьХр хк — л-мерные векторы, а ар ..., ак — числа. Век-
тор у = а! х, + ... + а^ск называется линейной комбинацией векто-
ров хр ..., хк с коэффициентами ар ..., ак. Линейной оболочкой
векторовХр..., хк называется совокупность всех линейных комби-
наций этих векторов. Набор (система) векторовхр ...,хк называет-
ся линейно зависимым, если существуют числа ар ..., ак, не все
равные нулю, такие, что af х} + ... + аккк = 0. В противном случае
набор векторов называется линейно независимым. В простран-
стве Еп всякий набор, содержащий более чем л векторов, обяза-
тельно линейно зависим. Легко проверяется, что набор из векто-
ров
е, = (1,0,0,..., 0), е2 = (0,1,0,..., 0),..., еп = (0,..., 0,1)
пространства Еп линейно независим. Следовательно, всякий ли-
нейно независимый набор векторов в пространстве Еп содержит л
векторов или меньше.
Набор из л линейно независимых векторов называется бази-
сом пространства £я, а число векторов в базисе — размерностью
(рангом) пространства Еп. Таким образом, размерность (ранг)
пространства Еп равна л. Базис ер ..., еп называется стандартным.
Пусть набор векторов/ f является базисом пространства Еп,
тогда всякий вектор х е Еп представляется в виде линейной ком-
бинации векторов базиса х = + ... + и это представление
единственно. Поэтому говорят, что базис порождает простран-
ство Еп, ибо пространство Еп совпадает с линейной оболочкой
своего базиса. Коэффициенты ..., £я в представлении векторах
в виде линейной комбинации векторов базиса/р называются
координатами вектора/относительно базиса/р •••,/„• Поскольку
представление вектора х= (хр ...,хя) в виде линейной комбинации
векторов стандартного базиса ev..., еп имеет вид х=х)е) +... + хпеп,
постольку координаты (компоненты) хр ..., хя вектора х суть не
что иное, как координаты этого вектора относительно стандарт-
ного базиса ..., еп пространства Еп. В приложениях используют-
ся базисы пространства Еп, не являющиеся стандартным базисом,
и осуществляются переходы от одних базисов к другим.
770
П.2.2. Евклидовой нормой (длиной) вектора х = (хр ...,хд) назы-
вается число, равное квадратному корню из суммы квадратов всех
его координат, т.е.
Используются также октаэдрическая норма векторах = (хр ...,
хд): I х 10 = IX] | + ... +1 хя | и кубическая норма вектора
х = (х|,...,х„):|х|1 =тах|х,|.
Каждая из этих норм удовлетворяет следующим трем услови-
ям:
I) |х + у|<|х| + |у| (неравенствотреугольника);
2) | ах | = | a I | х | (а — действительно число, I а | — его мо-
дуль);
3) | х | > 0, если х * 0, и I х | =0, если х = 0.
Расстоянием между двумя л-мерными векторами х = (хр ...,хд)
иу-(ур —,У„) называется норма |х-у| векторах-у. Таким об-
разом,
к - у| = 'l(xi-y02+-+(x„-y„)2.
Это расстояние называется также евклидовым, ибо оно опре-
делено с помощью евклидовой нормы. Иногда для обозначения
расстояния между л-мерными векторами х и у используют символ
Скалярным произведением векторов х = (хр —,х) и у = (ур ...,
уд) называется число, обозначаемое символом (х, у) или ху и рав-
ное сумме произведений соответствующих координат этих векто-
ров, т.е. (х, у) = Х|У| + ... + х^п. Свойства скалярного произведе-
ния: (х, х) > 0; (х, у) = (у, х); (х + у) z = (х, z) + (у, z); (Ах, у) = А.(х, у).
Векторы х и у называются ортогональными, если их скалярное
произведение равно нулю, т.е. (х, у) = 0. Нулевой вектор 0 ортого-
нален любому вектору: (0, х) = 0. л-мерное пространство, в кото-
ром определено скалярное произведение, называется л-мерным
евклидовым пространством. Символика та же: Еп. В л-мерном
евклидовом пространстве Еп базис/р ...,fn называется ортогональ-
ным, если {fpfp = 0, /*/, /,/= 1,.... л. Базис/р ...,fn называется ор-
тонормированным, если = 0, \fj | = 1, i*j, i,j= 1,..., л. Очевид-
49*
771
но, стандартный базис является ортонормированным. Евклидова
норма |х| вектора х = (хр ...,хя) равна
|х| = 7(х,х).
Для любых двух л-мерных векторовх и у справедливо неравен-
ство Коши- Буняковского | (х, у) | < |х| |у|, где |х| и |у| —ев-
клидовы нормы векторовх и у соответственно, a I (х, у) | — модуль
скалярного произведения (х, у).
Последовательность х’.х2, ...,х* л-мерных векторовх* = (Xj*,...,
хя*) называется сходящейся к л-мерному вектору х° = (Х]°, ..., хя°),
если lim |х* - х°| = 0, к = 1,2,....
П.2.3, л-мерный вектор х = (хр ..., хя) называется неотрицатель-
ным, есди все его координаты неотрицательны, т.е. х. > 0, i = 1,.., л
(символика: х > 0). л-мерный вектор х = (хр ..., хя) называется по-
ложительным, если все его координаты положительны, т.е. х. > 0,
i = 1, ..., л (символика: х > 0).
Если х > 0, то (х, х) > 0, если же х > 0 (* 0), то (х, х) > 0. Пусть
(х, у) = 0 и х > 0, у > 0, тогда из х. > 0 (у(. > 0) следует, что у;. = 0 (х. = 0).
Если векторы х и у имеют равное число координат, то пишутх > у,
х > у в зависимости от того, положительна или неотрицательна
разность х - у. Отношение > есть отношение порядка на множест-
ве всех л-мерных векторов, ибо:
1) х > х для любого вектора х = (Х],..., хя);
2) из х > у, у > z следует, что х > z',
3) из х > у, у > z следует, что х = z-
Множество всех л-мерных векторов частично упорядочено
отношением >, поскольку неравенство х > у (или симметричное
ему х < у) выполняется только для некоторых пар векторов х и у
(если, например,х(.>ур а ху.<у^. (/*/), то них>у, них<у не выпол-
няется). В то же время отношение > на множестве всех действи-
тельных чисел есть отношение линейной упорядоченности, ибо
для любых двух чисел аир всегда справедливо либо а < р, либо
а>р.
П.2.4. Для изображения двумерных векторов введем на плоскос-
ти прямоугольную декартову систему координат. Двумерный век-
тор х = (х,, х2), т.е. упорядоченная пара (х(, х2) действительных
чисел X] и х2, изображается на плоскости точкой X=(xv х2) с коор-
динатами Х( и х2 (первая геометрическая интерпретация упорядо-
772
ценной пары (хр х2) — рис. П.6) или направленным отрезком ОХ,
начало которого совпадает с началом координат — точкой
О = (0, 0), а конец — с точкой Х= (хр х2) (вторая геометрическая
интерпретация упорядоченной пары (хр х2) — рис. П.7). Двумер-
ный вектор х = (хр х2) изображается также в виде произвольного
направленного отрезка АВ, равного направленному отрезку ОХ
(равенство направленных отрезков АВ и ОХ означает, что они па-
раллельны, одинаково направлены и имеют равные длины — см.
рис. П.7). Если точки Хи Yизображают векторы х = (хр х2) и
У = (Ур У2) соответственно, то суммах+у этих векторов изобража-
ется точкой R, такой, что OXRY — параллелограмм, если точки О,
Хи Уне лежат на одной прямой (см. рис. П.6). Если число 1 > 0,
вектор Ах = (Ахр 1х2) изображается точкой S = (Ахр Ах2) луча ОХ,
такой, что отношение длин отрезков 05 и ОХ равно 1. Если 1' < О,
то вектор 1'х= (1'хр 1'х2) изображается точкой S = (А'хр 1'х2), ле-
жащей на продолжении луча ОХ за точку О и такой, что отноше-
ние длин отрезков 05 и ОХравно числу -1' > 0. Если число 1 = 0,
то вектор Ах = (0, 0) изображается точкой О. Рассмотрим первую
геометрическую интерпретацию двумерных векторов х = (хр х2),
Рис. П6
773
таких, что х > у (вектор у = (ур у2) — фиксированный), векторов
Z = (zp z2), таких, что у < z, и векторов v = (vp v2), для которых ни
неравенство v > у, ни неравенство v < у не выполняются. На
рис. П.8 часть плоскости, заштрихованная горизонтально, изоб-
ражает множество всех векторов х; часть плоскости, заштрихован-
ная вертикально, изображает множество всех векторов z', часть
незаштрихованной плоскости изображает множество всех векто-
ров v. Вторая геометрическая интерпретация суммы двух векто-
ров, произведения вектора на число и векторных неравенств рас-
сматривается аналогично (см. рис. П.8 и П.9).
Одномерные векторы изображаются точками или направлен-
ными отрезками на координатной прямой, трехмерные векто-
ры — точками или направленными отрезками в трехмерном про-
странстве, в котором введена прямоугольная декартова система
координат, «-мерные векторы (л > 4) не имеют наглядной геомет-
рической интерпретации. Если координаты «-мерного вектора х
774
А"= (лс,; ж2)< е
ж¥=(х[;х2):
(хр
г=(у,;У1)
• K=(v,;v2)
K=(v,;v2)
>Z=(z,;z2)
*
Рис. П8
записываются в виде строки х = (х(, хп), вектор называется век-
тором-строкой, если в виде столбца
\XnJ
вектор называется вектором-столбцом. Вектор-столбец есть
транспонированный вектор-строка, поэтому его иногда обозна-
чают символом^. Разделение на векторы-строки и векторы-столб-
цы необходимо при рассмотрении векторов в комбинации с мат-
рицами. В этом случае разделение каждый раз оговаривается.
Приведенные выше определения произведения вектора на
число, суммы двух (и более) векторов, нормы вектора, расстояния
между векторами и утверждения относительно этих операций
применимы и для комплексных векторов, т.е. векторов, координа-
775
Рис. П9
тами которых являются комплексные числа. Исключение состав-
ляет скалярное произведение, которое для комплексных векторов
х= (хр хя), иу = (ур ...,уя) вводится следующим образом:
(х,у) = х1у1+...+хяуя,
где yt — числа, комплексно сопряженные с числами у, (i= 1,..., л).
Свойства скалярного произведения для любых комплексных век-
торов х, у, z и любого комплексного числа X:
(х,х)>0,(х,у) = (у,х),
(х+у,г)=(х,г)+(у,г),
(Хх,у)=Х(х,у).
Вектор с координатами у, (/= 1,л) обозначается символом у
и называется вектором, сопряженным с вектором у. Скалярное
произведение, введенное для комплексных векторов, на действи-
776
тельных векторах совпадает со скалярным произведением, опре-
деленным для действительных векторов.
Кроме векторов с действительными (и комплексными) коор-
динатами в экономико-математическом моделировании исполь-
зуются векторы, координаты которых — функции.
В теории «-мерного пространства применяется геометричес-
кая терминология, хотя при п > 4 пространство Еп не имеет на-
глядной геометрической интерпретации. Использование геомет-
рической терминологии при описании множеств пространства Еп
(л > 4), задаваемых аналитически, оправдано тем, что эти множест-
ва сохраняют ряд существенных свойств аналогичных им мно-
жеств пространства Еп (п = 1, 2, 3), которые уже имеют наглядную
геометрическую интерпретацию и свое геометрическое «имя».
Это важное обстоятельство позволяет при исследовании (весьма
абстрактных) объектов пространства Еп использовать богатый
геометрический опыт, который приобретается естественным об-
разом при изучении пространства Еп (п = 1, 2, 3). В дальнейшем
для краткости вместо слов «множество векторов (точек) х из Еп,
координаты хр ..., хп которых удовлетворяют уравнению (системе
уравнений, неравенству, системе неравенств)», будем говорить
«множество векторов (точек) х, удовлетворяющих уравнению
(системе уравнений, неравенству, системе неравенств)».
П.2.5. Непустое множество векторов из Еп называется подпро-
странством L пространства £л; если хе Лиге L и а и р — произ-
вольные действительные числа, то ах + Pz е L. Отсюда вытекает,
что подпространство L обязательно содержит нулевой вектор и
вместе с любыми своими векторами содержит все их линейные
комбинации. Очевидно, множество, состоящее только из нулево-
го вектора, а также все пространство Еп являются подпростран-
ствами. Эти подпространства называются несобственными, все
остальные подпространства — собственными подпространствами
пространства Еп. Набор, содержащий максимальное число линей-
но независимых векторов из L, называется базисом подпро-
странства L, а само максимальное число — размерностью (рангом)
подпространства L. Собственное подпространство пространства
Еп может иметь размерность от 1 до п - 1 включительно. Размер-
ность нулевого подпространства равна нулю. Любой вектор х из L
представляется в виде линейной комбинации векторов базиса
подпространства L, и это представление для вектора х единствен-
777
но. Отсюда следует, что подпространство есть линейная оболочка
векторов своего базиса. Пересечение любого числа подпро-
странств есть подпространство пространства Еп. Множество всех
векторов пространства Еп, ортогональных подпространству L
(т.е. ортогональных любому вектору из подпространства L), обо-
значается символом Z1 и называется ортогональным дополнением
подпространства L. Ортогональное дополнение подпространства
L является подпространством пространства Еп (проверяется непо-
средственно). Ортогональным дополнением нулевого подпро-
странства является все пространство Еп, и наоборот. Ортогональ-
ное дополнение ортогонального дополнения подпространства L
есть само подпространство L. Если/р ...,fk — базис подпростран-
ства L, а Ар ..., hm — базис его ортогонального дополнения L, то
обязательно к + т = п и набор/р ...,fk, h{,..., hm является базисом
пространства Еп. Множество всех векторов х, удовлетворяющих
однородной системе линейных алгебраических уравнений Ах = О,
есть подпространство пространства Еп (проверяется непосред-
ственно). Размерность этого подпространства равна к = п - г, где
г — ранг матрицы А (см. ниже). Базис этого подпространства L
называется фундаментальным набором решений системы Ах = 0.
Базис ортогонального дополнения Z1 образует г линейно незави-
симых строк матрицы А.
Множество С л-мерных векторов х, у,... называется конусом в
пространстве Еп, если для любых векторов х и у из С и любых дей-
ствительных чисел а > 0, р > 0 справедливо ах + Ру е С.
«-мерный вектор (точка) Xх, такой, что Xх = (1 - 1)х° + Лх1, где
число 0 < X < 1, называется выпуклой комбинацией векторов (то-
чек) х° и х*. Множество всех выпуклых комбинаций векторов х° и
х1 называется отрезком К, соединяющим векторы (точки) х°, х*.
Множество Л/л-мерных векторов называется выпуклым, если оно
вместе с любыми двумя своими векторами (точками) целиком
содержит отрезок, который их соединяет. Выпуклое множест-
во — это множество, не имеющее вмятин и дыр.
Пусть L — подпространство пространства Еп и пусть х° е Еп —
фиксированный вектор, который может как принадлежать, так и
не принадлежать подпространству L. Рассмотрим множество М
всех векторов х=z + х°, где вектор z «пробегает» все подпростран-
ство L. Это множество называется линейным многообразием про-
странства Еп. Говорят, что линейное многообразие М есть резуль-
тат сдвига подпространства L вдоль вектора х°. Линейное много-
778
образие может и не быть подпространством. Непустое пересечение
любого числа линейных многообразий есть линейное многообра-
зие. Множество всех векторов х, удовлетворяющих системе ли-
нейных алгебраических уравнений Ах=Ь, есть линейное многооб-
разие М. Обратно, линейное многообразие М есть множество всех
векторов х, удовлетворяющих системе уравнений Ах = Ь, строки
матрицы А которой суть векторы базиса ортогонального дополне-
ния £* подпространства L, сдвигом которого получилось линей-
ное многообразие М. Размерностью (рангом) линейного многооб-
разия Л/называется размерность (ранг) подпространства L, сдви-
гом которого было получено линейное многообразие М.
Нульмерное многообразие состоит из единственного фиксиро-
ванного вектора (точки); если этот вектор нулевой, нульмерное
многообразие есть нулевое подпространство. Одномерное линей-
ное многообразие называется прямой, двумерное — плоскос-
тью, ..., ^-мерное линейное многообразие — ^-мерной плоскос-
тью (к > 3). Линейное многообразие размерности (ранга) п - 1 на-
зывают гиперплоскостью пространства Еп и обозначают символом
Нп[ или просто Н. Гиперплоскость есть множество всех векторов
х, удовлетворяющих уравнению а{х{ + ... + алхл = Ь, где вектор
а = (а{,..., ап) * 0. Гиперплоскость Н{ изображается на плоскости;
эта прямая имеет уравнение + а^с2 = b (первая геометрическая
интерпретация — рис. П. 10). Кроме того, гиперплоскость Н1 мож-
но понимать как множество (геометрическое место) концов на-
правленных отрезков, координаты которых удовлетворяют урав-
нению fljXj + а^х2 = Ьи начала которых находятся в точке О (вторая
геометрическая интерпретация — см. рис. П.10). Гиперплоскость
Я порождает два замкнутых полупространства IT К.Н* простран-
ства Еп. Замкнутое полупространство есть множество то-
чекхе Еп, удовлетворяющих неравенству а^ + ... + апхп < b (а1х1
+... + ajcn > Ь) Очевидно, Hn_v Н* и Н~ = Еп. Полупрост-
ранство порождаемое прямой 2х{ + х2 = 2, изображается
полуплоскостью, содержащей эту прямую и расположенной ниже
(выше) этой прямой (рис. П.11). Гиперплоскость Я порождает
также два открытых полупространства Н~ и Я+. Открытое полу-
пространство Я~(Я+) есть множество точек х е Еп, удовлетворя-
ющих неравенству +... + ах < b (alxi +... + апхп > Ь). Очевидно,
что Н~ п Я+ = 0 и Н~ и Я и Я^ = Еп. Полупространство Я~(Я+),
порождаемое прямой 2xj + х2 = 2, изображается полуплоскостью,
779
не содержащей этой прямой и расположенной ниже (выше) этой
прямой (см. рис. П.11).
Размерностью множества А с Еп называется размерность ли-
нейного многообразия, которое есть пересечение всех линейных
многообразий, включающих множество Л.
В приводимых ниже определениях вместо термина «вектор»
обычно используется эквивалентный ему термин «точка».
П.2.6. Пусть ее £я и г > 0 — число. Множество точек хе Еп, об-
ладающих свойством |х - а\ < г, называется открытым «-мерным
шаром радиуса г с центром в точке а (символика: CZ (г, а)). Напом-
ним, что |х - а| = ^(хх - ах )2+...+(х„ - а„ )2. Множество точекх е Еп,
обладающих свойством |х - а| = г, называется «-мерной сферой
радиуса г с центром в точке а (символика: Sn(r, а)). На плоскости
множество U2(r, а) изображается кругом (без периферии) радиу-
са г с центром в точке а, а множество S2(r, а) — окружностью радиу-
са г с центром в точке а (рис. П.12), «-мерный открытый шар
780
Un(r, a) — выпуклое множество, не имеющее крайних точек,
л-мерный замкнутый шар Un(r, а) и 5я(г, а) — выпуклое множест-
во, множество крайних точек которого совпадает с Sn(r, а). Мно-
жество Sn(r, а) не является выпуклым.
а-окрестностью точки а называется открытый л-мерный шар
радиуса £ с центром в точке а. Точка а множества А с Еп называет-
ся внутренней, если она принадлежит множеству Л вместе со все-
ми близкими к ней точками, т.е. если она принадлежит множеству
А вместе с некоторой своей £-окрестностью Un(e, а) (рис. ПЛЗ,
л = 2). Множество внутренних точек множества А обозначается
символом А и называется внутренностью множества Л. Множест-
во, все точки которого внутренние, называется открытым. Объ-
единение двух и более открытых множеств есть множество откры-
тое. Пересечение конечного числа открытых множеств есть мно-
жество открытое. Пространство Еп, л-мерный шар, открытое
полупространство — примеры открытых множеств. Благодаря
свойствам открытых множеств множество всех открытых мно-
жеств пространства Еп вместе с пустым множеством образует то-
пологию в пространстве Еп (эта топология называется естествен-
ной). Следовательно, пространство Еп — это пример топологичес-
кого пространства.
Точка а е Еп называется граничной точкой множества Л, если
для любого числа £ > 0 открытый шар Un(z, а) содержит точки, как
принадлежащие множеству Л, так и не принадлежащие множест-
ву Л (рис. П.14, п = 2). Множество граничных точек множества Л
обозначается символом Л и называется границей множества Л.
Объединение Л и Л обозначается символом Л и называется замы-
канием множества Л. Множество Л, содержащее все свои гранич-
ные точки, называется замкнутым. Множество, не имеющее гра-
ничных точек, по определению является замкнутым. Пересечение
двух и более замкнутых множеств есть множество замкнутое. Объ-
единение конечного числа замкнутых множеств есть множество
замкнутое. Пространство Еп, множество, содержащее только ко-
нечное число точек, «-мерная сфера, множество Un(r,a)\jSn(r,a)
(это «-мерный замкнутый шар), линейное многообразие, замкну-
тое полупространство, множества Л и Л (если они не пусты) —
примеры замкнутых множеств.
Если Л — множество открытое, то Еп \ Л — множество замкну-
тое; если Л — множество замкнутое, то Еп \ Л — множество откры-
тое (теорема о дополнении). Множество Л с Еп называется огра-
ниченным, если существует такое число г >0, что Л с Un(r, 0),
в противном случае множество Л называется неограниченным,
«-мерный шар (открытый и замкнутый), «-мерная сфера — при-
меры ограниченных множеств; пространство Еп, подпространство
(не нулевое), линейное многообразие (не нульмерное), полупрост-
ранство — примеры неограниченных множеств. Множество
Л с Еп называется компактом, если оно замкнуто и ограничено.
Пусть Л1 и Л2 — непустые множества в пространстве Еп. Век-
торной суммой (суммой по Минковскому) множеств Л1 и Л2 назы-
вается множество всех векторов z вида z=х + у, где вектор х «про-
бегает» все множество Л], а вектору — все множество Л2. Вектор-
ная сумма множеств и Л2 обозначается символом Л1 + Л2.
Например, линейное многообразие М есть векторная сумма под-
пространства L и вектора х°, вдоль которого подпространство
сдвигается: М= {х0} + L. Векторную суммуЛ, + Л2 множествЛ] иЛ2
не следует путать с объединением (теоретико-множественной
суммой) Л( U Л2 этих множеств. Пусть Л — непустое множество в
пространстве Еп. Произведением множества Л на число а называ-
ется множество всех векторов z вида z = сиг, где вектор х «пробега-
782
ет» все множество А. Произведение множества А на число а обо-
значается символом аА. Всегда 2А а А + А, легко построить при-
мер, когда 2А Ф А + А. Пусть множество
Тогда множество
а множество
т.е. 2А с А + А (рис. П. 15).
Рис. П14
Рис. П15
П 3. Матрицы и операции над матрицами
П.3.1. Матрица — прямоугольная таблица
kaml ‘‘ amj ‘' атп у
действительных чисел а.., /= 1,т; i= 1,п. Такая таблица на-
зывается также матрицей с размерами т*п или (т х л)-матрицей.
л-мерный вектор а(. = (ааа1п) называется /-й строкой матрицы А,
а m-мерный вектор aJ
называетсяJ-м столбцом матрицы Л.
Число а., называется элементом матрицы А: индекс i показывает
номер строки, а индекс j — номер столбца, на пересечении кото-
рых находится элемент ау. Используется следующая символика:
А = (а.) (или А=|| ау\\). Если т = п, то А называется квадратной мат-
рицей, число л — ее порядком, а совокупность ап,..., апп элемен-
тов квадратной матрицы А — главной диагональю матрицы А.
(тхп) — матрица, у которой все элементы равны нулю, назы-
вается нулевой. Нулевая матрица обозначается символом 0.
(1 х л)-матрица есть л-мерный вектор-строка, (т х 1)-матрица
есть л»-мерный вектор-столбец, (1 х 1)-матрица есть число ап.
л-мерный вектор-строку можно понимать как (1 х л)-матрицу,
а /и-мерный вектор-столбец — как (т х 1)-матрицу.
Две матрицы Л и В называются равными, если они имеют оди-
наковые размеры и если их соответствующие элементы равны.
Равенство матриц Аи В записывается так: А = В. Элементы матри-
цы переставлять нельзя, ибо после их перестановки может полу-
читься, вообще говоря, новая матрица.
784
Для матриц определены операции сложения, умножения и
умножения на числа.
Произведением матрицы А = (а~) на число а называется мат-
рица, каждый элемент которой равен соответствующему элементу
Оу матрицы А, умноженному на число а, т.е. аА = а(бг.) = (аа.р.
Матрицы можно складывать, если они имеют одинаковые
размеры. Суммой матриц А и В называется матрица С, каждый
элемент Су которой равен сумме соответствующих элементов atJ и
Ь.. матриц Л и Д: с.. = ау + bir Непосредственно проверяется, что:
1)А + В= В + А; 2) (А + В) + С=А + (В + Q; 3)а(Л + В) = аА + аД
4) (а + 0)Л = аА + 0Л; 5) а(рЛ) = (а0)Л. Здесь Л, В, С — матрицы с
размерами mxn, ааир — числа.
Произведением двух прямоугольных матриц — (/их ^-матри-
цы Л на (и х р)-матрицу В — называется (/и х р)-матрица С, каждый
элемент Су которой вычисляется по формуле
cv = taikb,, i = l, . ,т-, j = l,...,p.
*=i
Если число столбцов матрицы Л не равно числу строк матрицы
Д произведение АВ не определяется. Непосредственно проверя-
ется, что: 1) (АВ)С = А(ВС); 2) (Л + В)С = АС+ ВС; 3) А(В + С) =
= АВ + АС; 4) а{АВ) = (аЛ)5 = Л(аД). Здесь матрицы Л, В и С
соответствующих размеров, а а — число.
Произведение двух квадратных матриц порядка л есть квад-
ратная матрица порядка л. Если Л и В — квадратные матрицы, то,
вообще говоря, АВ ВА.
Умножение (т х л)-матрицы Л на л—мерный вектор-столбец х
и умножение /и-мерного вектора-строки у на (т х л)-матрицу Л
выполняется по правилу умножения прямоугольных матриц, ког-
да одна из них является (п х 1)-матрицей (т.е. «-мерным вектором-
столбцом) или (1 х /и)-матрицей (т.е. m-мерным вектором-стро-
кой).
Произведение (т х л)-матрицы Л на л-мерный вектор-столбец
х есть «/-мерный вектор-столбец, а произведение /и-мерного век-
тора-строки у на (т х л)— матрицу Л есть л-мерный вектор-строка.
Очевидно, что Ах = х{а1 + ... + хял", уА = у1а1 + ... + Утат, т.е. Ах —
линейная комбинация столбцов матрицы Л, ауЛ —линейная ком-
бинация строк матрицы Л.
50 - 7620
785
Матрица, полученная из матрицы А заменой строк на столб-
цы, обозначается символом А' и называется транспонированной
по отношению к матрицей. Если х — вектор-строка, то очевидно
У — вектор-столбец, и наоборот. Легко проверяются свойства
операции транспонирования: 1) (А)' = А; 2) (аЛ)' = аА; 3) (А + Ву =
= А + В\4) (АВ)' = ВА; 5) (Ах)' =*А.
В математическом анализе экономических процессов сущест-
венное применение находят матрицы с неотрицательными эле-
ментами. Матрица А = (а^ i= 1,..., m;J = 1,..., п, называется неот-
рицательной, если все ее элементы неотрицательны (обозначе-
ние: А > 0). Матрица А = (а.р называется положительной, если все
ее элементы положительны (обозначение: А > 0). Квадратная мат-
рица М, такая, что /и.. > 0 (т^ > 0), / j, i,J = 1, ..., л, называется
матрицей (строгой) Метцлера. Знаки диагональных элементов лг.,
/= 1,..., л, не регламентируются. Если матрицы Ап В имеют оди-
наковые размеры, то пишут А > В, А > В в зависимости от того,
неотрицательна или положительна разность А - В. Множество
всех матриц с одинаковыми размерами тх п частично упорядоче-
но соотношением >. Положение здесь такое же, как и в случае
множества всех л-мерных векторов.
П.3.2. Пусть А — матрица с размерами т х л. Ранг матрицы А
обозначается символом р(А) и равен максимальному числу ли-
нейно независимых строк (или столбцов) матрицы Л, таким обра-
зом, всегда р(Л) < тш(л», л). Если А = 0, то р(А) = 0, в противном
случае р(А) > 1. Очевидно, р(А) = р(А). Если произведение двух
матриц определено, то ранг этого произведения не больше ранга
любого из сомножителей, т.е. р(АВ) < тш{р(Л), р(В)}. Ранг суммы
двух матриц не больше суммы рангов слагаемых, т.е. р(А + В) <
<,р(А) + р(В).
Квадратная матрица А порядка л называется вырожденной,
если ее ранг р(А) < л, и невырожденной, если ее ранг равен л.
Все строки (или все столбцы) невырожденной матрицы А по-
рядка л могут быть взяты в качестве базиса пространства ЕП. Если
В — (т х л)-матрица, Ти S — невырожденные матрицы порядков
т и л соответственно, то р(В) = р(ТВ) = p(BS) = r(TBS), т.е. при
умножении (т х л)-матрицы В на невырожденную матрицу слева
(справа или и слева и справа) ранг р(В) матрицы В не меняется.
Каждая невырожденная матрица А порядка л имеет един-
ственную обратную матрицу Л-1 того же порядка, такую, что
786
А~ХА = АА~Х = I, где символом I обозначена единичная матрица,
т.е. матрица I, такая, что ее элементы е..= 1, е..= 0, / * J, i,j = 1,..., п.
Справедливы равенства (Л-1)-1 = А, (Л')-1 = (А~1)'.
Если А и В — невырожденные матрицы одного порядка, то
матрица АВ также невырожденна и (АВ)~1 = 2Г14"1. Обратную мат-
рицу АГ1 можно построить, решив п систем линейных алгебраи-
ческих уравнений Ах* = е7, где х7 — у-й столбец искомой обратной
матрицы АГ1, а е7 — л-мерный орт-столбец, т.е. л-мерный единич-
ный вектор-столбец, у которого одна (конкретноу-я координата)
равна единице, а все остальные координаты равны нулю. Все сис-
темы Axj = е7,у = 1, ..., л, можно решать одновременно методом
Гаусса — Жордана. При больших л обратные матрицы строят
именно таким способом.
Если А — квадратная матрица, то символ А2 означает произве-
дение АА матрицы А на себя, т.е. Л2 = АА, вообще для любого нату-
рального к (т.е. k = 1, 2, ...) Ак = А-... А. Матрица Л* называется
к
к-й степенью матрицы А. Для любых натуральных чисел р и q
справедливы равенства АР*4 = АРА4, (АР)4 = АР4. Если р — натураль-
ное число, то символ АГР означает матрицу (Л-1/, т.е. АГР = (A~iyf.
Нулевая степень квадратной матрицы А есть единичная матрица,
т.е. А° = I. Если А — невырожденная матрица, то для любых целых
чисел (положительных, отрицательных и нуля) р и q справедливы
равенства АР*4 = АРА4, (АР)4 = АР4.
Все приведенные здесь определения и утверждения (исключая
понятия положительных матриц и матриц с неотрицательными
элементами) дословно повторяются для матриц и векторов, эле-
ментами которых являются комплексные числа.
50*
П 4. Определитель матрицы и его свойства
П.4.1. Квадратная матрица А индуцирует три важных числа:
след матрицы А — trA = ап + ... + авд, ранг матрицы А — р(А) и
определитель матрицы А — det А.
Определитель det А матрицы А определяется индуктивно сле-
дующим образом. Определитель det Л матрицы Л первого порядка
(матрица первого порядка есть число аи) равен числу лп.
Определитель det Л матрицы
^_<*11 *12
1*21 *22
есть число det Л = дпо22 “ а\2а2г
Определитель det Л матрицы
*и
Л- ^21
<*31
*12 *13
*22 *23
*32 *33?
третьего порядка
есть число det Л = апа22 а33 + а12о23 а31 + а21а32 а13 - а{3а22 a3i -
- л12а21 а33- о2з*з2 *1г
Если в матрице
41 *12 *13 *14 >
л= *21 *22 *23 *24
*31 *32 *33 *34
<*41 *42 *43 *44 >
четвертого порядка вычеркнуть /-го строку at и у-й столбец d,
i,j = 1,2, 3,4, то получим матрицу третьего порядка, определитель
Му которой называется минором (третьего порядка) элемента а...
Число (~1)'^Му обозначается символом А., и называется алгебраи-
ческим дополнением элемента а у матрицы Л. Определитель det Л
матрицы Л четвертого порядка определяется так:
det Л = в]|Лц + ^12^12 *13^13 + *14^14’
788
т.е. путем разложения по первой строке матрицы А. Вместо пер-
вой строки можно было взять любую другую строку или любой
столбец
det А = йуАу + ОуАу + ЯуАу + а^А^.
Для матрицы А пятого (л) порядка вычисляются миноры ее
элементов четвертого порядка (порядка п - 1), а определитель
det А матрицы пятого (л) порядка вычисляется разложением по
(любой) строке матрицы А или по (любому) столбцу матрицы А.
П 5. Основные результаты теории квадратных
матриц
П.5.1. Вектор v * 0 называется (правым) собственным вектором
(квадратной) матрицы А, если существует число X, такое, что
Av= Xv. Число X называется собственным числом матрицы Л.
Вектор w* 0 называется (левым) собственным вектором (квад-
ратной) матрицы А, если существует число X, такое, что wA = Xw.
Число X называется собственным числом матрицы А. Число X и
векторы w и v могут быть как действительными, так и комплекс-
ными.
Если А — квадратная матрица порядка п, матрица X/- А, где
X — независимая скалярная переменная, называется характерис-
тической для матрицы А. Определитель det(X/- А) характеристи-
ческой матрицы X/- А является многочленом относительно пере-
менной X. Он называется характеристическим многочленом мат-
рицы А. Степень характеристического многочлена det(X/ - А)
матрицы А равна порядку матрицы А, т.е. натуральному числу п
(это можно проверить, непосредственно вычислив определитель
det(X/-/l)).
Уравнение det(X/ - А) = 0 называется характеристическим
уравнением матрицы А. Среди корней характеристического урав-
нения могут быть комплексные корни (даже если матрица Л имеет
только действительные элементы a.., i,j = 1, ..., л). Поэтому при
достаточно полном разборе таких важных понятий, как собствен-
ное число и собственный вектор матрицы Л, нельзя обойтись без
использования комплексных чисел, ибо собственное число мат-
рицы Л является корнем характеристического многочлена
det(X/- Л) этой матрицы Л; и наоборот, корень характеристичес-
кого многочлена является собственным числом матрицы Л. По-
скольку многочлен det(X/-Л) имеет не более п различных корней,
постольку матрица Л имеет не более п различных собственных
чисел. Множество всех собственных чисел матрицы Л называется
спектром матрицы Л. Если матрица имеет собственное число, рав-
ное нулю, она вырожденная; и наоборот, вырожденная матрица
обязательно имеет собственное число, равное нулю. Алгебраичес-
790
кой кратностью (или просто кратностью) собственного числа Хо
матрицы А называется кратность числа Хо как корня характерис-
тического многочлена det(X7- А).
Выпишем в виде набора Х,(Л),ХЯ(Л) все собственные числа
матрицы Л порядка п так, что каждое собственное число в наборе
повторяется столько раз, какова его кратность, тогда: 1) собствен-
ные числа Х/аЛ + 07) (/= 1,..., п) матрицы аА + 0/(а и 0 — числа)
равны Х/аЛ + 07) = аХ(.(Л) + 0 (/ = 1,..., л); 2) собственные числа
Х/Л*) (/= 1,..., и) матрицы Ак (к= 1,..., л) равны X.(Л)* (/= 1,..., л);
3) собственные числа ХДЛ^) (/ = 1,л) матрицы АР (р — целое чис-
ло, которое не равно нулю) равны ХДЛ) (/ = 1,..., л), если Л — не-
вырожденная матрица.
Если матрица Л с действительными элементами a.., (i,j= 1,..., л)
имеет комплексное собственное число £0, то матрица Л имеет обя-
зательно собственное число комплексно сопряженное с чис-
лом £0. Паре комплексно сопряженных собственных чисел и
соответствует пара комплексно сопряженных собственных векто-
ров и° и й° матрицы Л: Аи° = £ои°, = ЪМ)- Умножение действи-
тельной матрицы на комплексный вектор-столбец производится
по обычному правилу умножения матрицы на вектор-столбец.
Собственные векторы, соответствующие различным соб-
ственным числам матрицы Л, линейно независимы. Если среди
собственных векторов есть комплексные, то необходимо прирав-
нивать к нулю всевозможные линейные комбинации этих векто-
ров с комплексными коэффициентами; в случае линейной неза-
висимости все эти коэффициенты должны равняться нулю. Гео-
метрической кратностью собственного числа матрицы Л
называется максимальное число линейно независимых собствен-
ных векторов матрицы Л, соответствующих этому собственному
числу. Всегда геометрическая кратность не больше алгебраичес-
кой. Если алгебраическая кратность равна единице, то и геомет-
рическая кратность равна единице.
П.5.2. Важный частный случай квадратных матриц — класс мат-
риц с неотрицательными элементами, которые часто применяют-
ся в математическом анализе моделей экономических состояний
и процессов.
Квадратная матрица Л называется разложимой, если переста-
новками строк и такими же перестановками столбцов ее можно
привести к блочному (клеточному) виду
791
0>|
^Л2 А3 J
где At и А3 — квадратные подматрицы (не обязательно одного по-
рядка) матрицы А. В противном случае квадратная матрица А на-
зывается неразложимой. Например, квадратная матрица А > О
неразложима, а матрица I — разложима. Если перестановками
матрицу Л > 0 можно привести к блочному (клеточному) виду (вид
называется циклическим разложением)
г О Л] 0 ••• О"
О О Л2 • •• О
О 0 0 ••• Л*ч
Ак 0 0 ••• 0 .
\ А- /
где к >. 2 и нули на главной диагонали означают нулевые квадрат-
ные подматрицы, которые могут иметь разные порядки, то матри-
ца Л > 0 называется циклической (импримитивной), в противном
случае — примитивной. Отметим, что у циклической (имприми-
тивной) матрицы может существовать несколько циклических
разложений. Натуральное число & > 2 называется индексом цик-
личности (или индексом импримитивности) матрицы Л. Если
Л 0 (* 0) неразложима, то и матрица Л' > 0 (# 0) также неразложи-
ма. Если Л 0 (* 0) неразложима, а В > 0, то АВ > 0.
Квадратная матрица примитивна тогда, когда существует на-
туральное число р > 1, такое, что А? > 0, т.е. матрица Л > 0 — част-
ный случай примитивной матрицы. Для наименьшего номера
р = рА, для которого справедливо неравенство АР > 0, имеет место
неравенство рл < (л - I)2 + 1, где п — порядок матрицы Л. Если Л
примитивна и натуральное число т >р, то Ат > 0. Степень Л* при-
митивной матрицы Л есть примитивная матрица (1 < к — нату-
ральное число).
Квадратная матрица Л > 0 (примитивная матрица Л) имеет по-
ложительное собственное число А*, кратность которого равна
единице и которое строго больше модулей остальных собствен-
ных чисел матрицы Л. Собственный вектор (как правый v, так и
левый w*), соответствующий собственному числу А*, можно вы-
792
брать положительным (для А > 0 — это теорема Перрона, для при-
митивной матрицы А — теорема Фробениуса).
Собственное число X* называется максимальным числом (или
числом Перрона) положительной (примитивной) матрицы, соот-
ветствующие ему положительные собственные векторы v и w* —
векторами Перрона квадратной матрицы А > 0 (обычно в качестве
векторов Перрона v и w* фигурируют положительные нормиро-
ванные векторы: |v*| = 1, |w*| = 1).
Пусть матрица Л > 0 (^ 0) порядка п примитивна и пусть вектор
Z° > 0 (^ 0) (z° е Еп), тогда существует число с > 0, зависящее только
от вектора z°, такое, что
lim Ак z°/(X*)* = cv* (к = 0,1,...),
к->оо
где X* > 0 и v* > 0 (|v*| =1) соответственно число Перрона и правый
вектор Перрона матрицы А (предельная теорема Фробениуса).
Квадратная матрица Р > 0 (^ 0) называется стохастической,
если сумма элементов каждой строки матрицы Р равна единице.
Стохастическая матрица является частным случаем квадратной
неотрицательной матрицы. Квадратная матрица Р> 0 (^ 0) являет-
ся стохастической тогда и только тогда, когда вектор (1,...» 1) яв-
ляется собственным вектором этой матрицы, соответствующим
собственному числу, равному единице. Все собственные числа
стохастической матрицы Рпо модулю не превосходят единицы.
Квадратная матрица А > 0 (^ 0) называется продуктивной, если
существует вектор х > 0 (* 0), такой, что х > хА. Из последнего не-
равенства следует, что на самом деле вектор х > 0. Если матрица Л
является продуктивной, то матрица I- А невырожденная. Для то-
го чтобы матрица Л > 0 была продуктивной, необходимо и доста-
точно, чтобы матрица (/- Л)-1 > 0 (^ 0). Если матрица Л продук-
тивная, то lim Ак = 0(Х = 0,1,...).
П.5.3. Квадратная матрица с действительными элементами назы-
вается ортогональной, если А' = Л-1. Ортогональная матрица Л
обладает следующими свойствами: 1) матрица, обратная к ортого-
нальной, является ортогональной; 2) 1= А А=АА (это сразу следу-
ет из определения А = Л-1), откуда вытекает, что скалярные квад-
раты всех строк (столбцов) равны единице и скалярные произве-
дения попарно различных строк (попарно различных столбцов)
равны нулю, т.е. попарно различные строки (попарно различные
793
столбцы) ортогональны, их длины равны единице, и поэтому все
строки (все столбцы) ортогональной матрицы могут быть взяты в
качестве ортонормированного базиса в «-мерном пространстве
£л; 3) длина (евклидова норма) вектора Ах равна длине вектора х,
т.е. |4х| = |х|; 4) произведение двух ортогональных матриц есть ор-
тогональная матрица; 5) определитель ортогональной матрицы
равен ±1; 6) все собственные числа ортогональной матрицы по
модулю равны единице.
П.5.4. Квадратная матрица В называется подобной квадратной
матрицей, если существует невырожденная матрица Т, такая, что
В = Т~1 А Т. Очевидно, из подобия Вс А вытекает подобие Ас В, ибо
А = S~lBS, где 5= Т~1. Каждая квадратная матрица подобна сама
себе; две матрицы, подобные третьей, подобны между собой.
Приведем ряд свойств подобных матриц:
1) trCT'AT) = tr(A); 2) det(r'/17) = беЦЛ); 3) р(Г1Л7) = р(А);
4) спектры подобных матриц совпадают, т.е. если Х^Я),..., ХЯ(Л) —
собственные числа матрицы А порядка п, где каждое собственное
число выписано столько раз, какова его кратность, то Х/Т^’ЛТ) =
=Х.(Л); /= 1,..., и.
Для произвольной квадратной матрицы А существует невы-
рожденная матрица Т, такая, что матрица J= Г1АТ имеет нор-
мальную жорданову форму, т.е. имеет следующий квазидиаго-
нальный (блочно-диагональный) вид:
Х( 1 0 ... О
О Xj 1 ... О
О 0 0 ... X!
X, 1 о ... О
О X, 1 ... о
О О О ... X,
794
Диагональные блоки матрицы / имеют специальный вид, они
называются жордановыми блоками (жордановыми клетками).
Число блоков (клеток), соответствующих одному и тому же соб-
ственному числу 1(. (/ = 1,л) квадратной матрицы А, равно гео-
метрической кратности собственного числа к.. Собственное число
X; квадратной матрицы А на главной диагонали матрицы / повто-
ряется столько раз, какова его алгебраическая кратность.
Квадратная матрица подобна диагональной матрице Л - И-1Л V
(элементами главной диагонали матрицы Л являются собствен-
ные числа квадратной матрицы А, выписанные с учетом их крат-
ностей)
%
(П
Л =
0 ••• Хл>
тогда и только тогда, когда квадратная матрица А имеет ровно п
(п — порядок квадратной матрицы А) линейно независимых соб-
ственных векторов у1, ..., v", что, в свою очередь, эквивалентно
тому, что алгебраические кратности всех собственных чисел квад-
ратной матрицы А равны геометрическим кратностям этих чисел.
ИзравенстваЛ= К'ЛИследует, чтоЛК= ИЛ,т.е. столбцы матрицы
И составлены из правых собственных векторов v1, ..., v" квадрат-
ной матрицы А.
П.5.5. Квадратная матрица А называется симметрической, если
a.j= a.., i,j= 1,..., п (п — порядок матрицы^).
Все собственные числа симметрической матрицы являются
действительными числами, и для каждой симметрической матри-
цы А существует такая ортогональная матрица Т, что матрица
ТХАТ = Л является диагональной матрицей Л. (Напомним, что
для ортогональной матрицы Т-1 = Г). Если в квадратичной фор-
ме
f=Yaijxixi
i,J=l
с матрицей А положить х = Tz, то получим канонический вид
/= l,z(2 + ... + X„z„2 квадратичной формы. Здесь Хр ..., 1я — спектр
симметрической матрицы А, каждое собственное число повторя-
ется столько раз, какова его алгебраическая кратность.
795
Симметрическая матрица А = (а^, i,J = 1,л, называется по-
ложительно (отрицательно) определенной, если соответствующая
ей квадратичная форма
/(*) = X anxixj
i,j=\
является положительно (отрицательно) определенной, т.е. Дх) > О
(Дх) < 0) при любых х е Еп, х * 0. Для того чтобы симметрическая
матрица Л (соответствующая ей квадратичная форма Дх)) была
положительно (отрицательно) определенной, необходимо и до-
статочно, чтобы все ее собственные числа были положительными
(отрицательными). Другим необходимым и достаточным услови-
ем положительной (отрицательной) определенности симметри-
ческой матрицы А является выполнение неравенств det^) > 0
((-l)*det(jp > 0), к= 1,2,..., п, где подматрицы Ак= (а^, i,j= 1.к,
симметричны относительно главной диагонали лп,..., атт квад-
ратной матрицы Л. Миноры det^), к= 1,..., п, называются после-
довательно повышающими порядок главными минорами матри-
цы (критерий Сильвестра).
Симметрическая матрица Л = (а^), i,J = 1,..., п, называется не-
отрицательно (неположительно) определенной, если квадратич-
ная форма
/(*)= X a^xj
является неотрицательно (неположительно) определенной,
т.е. Дх) > 0 (Дх) < 0) для любого х е Еп. Для того чтобы симметри-
ческая матрица Л (соответствующая ей квадратичная форма Дх))
была неотрицательно (неположительно) определенной, необхо-
димо и достаточно, чтобы все ее собственные числа были неотри-
цательны (неположительны). Другим необходимым и достаточ-
ным условием неотрицательной (неположительной) определен-
ности симметрической матрицы Л является выполнение при
к= 1...п неравенствdet(A/p> 0 ((-l)*det(AQ), где det(Mk) — глав-
ные миноры матрицы Л порядка к (т.е. определители всех подмат-
риц Мк порядка к, симметричных относительно главной диагона-
ли квадратной матрицы Л). В этом утверждении неотрицательнос-
ти только последовательно повышающих порядок миноров
det(Ak), к= 1,..., п, квадратной матрицы Л недостаточно.
796
( " izV
П.5.6. Число |Л| = У, |aj
называется нормой |Л| квадратной
матрицы А. Свойство нормы: 1) |Л| > О, если А * 0 и |Л| = 0, если А=0;
2) |л + 24 - И1 +М; 3) М = |а|И1; 4) |лл| <, ИМ; 5) ИМ * И11М. ИМ.
|М — евклидовы нормы векторов Ах и х соответственно.
Используются и другие определения нормы квадратных,
а также и прямоугольных матриц:
л п т
/,у=1
Известно, что если модуль |а| числа а строго меньше единицы
(т.е. |4 < 1), то справедливо равенство (1 - а)'1 = 1 + а +а2 + ... +
+ в* + ... Аналогичное равенство имеет место и для квадратной
матрицы А, норма которой строго меньше единицы (т.е. И| < 1):
(/- A)~l = 1 + А +А2 + ... + Ак + ... Последнее равенство находит ।
широкое применение в анализе межотраслевых моделей, в кото-
рых А — матрица коэффициентов прямых материальных затрат,
а (/-Л)-1 — матрица коэффициентов полных материальных за-
трат.
П 6. Основные результаты теории экстремума
функций одной и нескольких переменных
П.6.1. Экстремум функции — это частное значение функции f
одной или нескольких переменных, являющееся ее максимумом
или минимумом.
Функция Дх) одной переменной имеет в точке х° е М g Е{ ло-
кальный максимумах0) (локальный минимум Дх0)), если суще-
ствует 5-окрестность Ц(5, х°) точки х°(Ux(5, х°) cz М)), такая, что
для любой точки хе Ц(5, х°) справедливо неравенствоДх°) >Дх)
(Дх°) < Дх)). Точка х° называется точкой локального максимума
(локального минимума) функции Дх). Если для любой точки
хе ^(З.х0) и такой, чтох*х°, справедливо неравенствоДх°) >Дх)
(Дх°) < Дх)), то говорят о сильном локальном максимуме Дх°)
(сильном локальном минимуме Дх°). Если локальный экстремум
не является сильным, он называется слабым.
Если для любой точки хе М с Е{ справедливо неравенство
Дх°) >Дх) (Дх0) <Дх)), то говорят о глобальном максимуме Дх°)
(глобальном минимуме Дх0)) функции Дх) на множестве М с Ev
Если глобальный экстремум не является сильным, он называется
слабым. На рис. П.16 х2 — точка локального максимума, х4 — точ-
ка глобального максимума, точки х3 — точки локального миниму-
ма, х6 — точка глобального минимума. Точки х2, х4, хб — точки
сильного экстремума (х2, х4 — точки сильного локального и силь-
ного глобального максимума соответственно, х6 — точка сильного
глобального минимума). Точки х3 — точки слабого локального
минимума.
Если существует (сколь угодно малое) число 5 > 0 и х°
(х° е Ц(5, х°) g Мс Е.) — точка экстремума (локального или гло-
бального) и в точке х° функция Дх) непрерывна, то/(х°) = 0 или
/(х°) = оо или/(х°) не существует ни конечная, ни бесконечная
(необходимое условие экстремума функции Дх), непрерывной в
точке х°). На рис. П.16/(х2) = 0,/(х3) = 0,/(хб) = оо,/(х4) — не су-
ществует ни конечной, ни бесконечной производной. В 8-окрест-
ности точки х2 график F функции имеет форму «шапочки» с
«макушкой» (х2; Дх2)), в 5-окрестности точки х6 график F имеет
798
форму «клюва», острие которого направлено вниз; точкух4 естест-
венно назвать «угловой», ибо график F функции fix) в точке (х4;
Дх4)) не имеет касательной, а имеет слева и справа разные каса-
тельные.
Точка х°, в которой/'(х°) = 0 или/'(*°) =00 или/(х°) не суще-
ствует ни конечная, ни бесконечная (функция Дх) непрерывна в
точке х°), называется критической (стационарной) точкой функ-
ции Дх). Часто термин «критическая точка» (стационарная точка)
используют только в случае, когда/(х°) = 0. Критические точки
называются подозрительными на экстремум, ибо экстремум мо-
жет быть только в критических точках. Проверяют критическую
точку на предмет наличия (или отсутствия) в ней экстремума с
помощью достаточных условий экстремума функцииДх), опреде-
ленной в промежутке (конечном или бесконечном).
Если при переходе через точку х° производная/(х) меняет знак
(через нуль, <ю или через несуществование), а функцияДх) непре-
рывна в точке х°, точка х° есть точка локального сильного экстре-
мума (достаточное условие сильного экстремума функции Дх),
непрерывной в точке х°). Если знак меняется с + на -, то х° — точ-
ка сильного локального максимума (на рис. П.16 точки х2 и х4,
799
точка х4 — точка не только локального, но и глобального макси-
мума).
Если знак у первой производной/(х) меняется с - на +, то
х0 — точка сильного локального минимума, который может быть
глобальным (на рис. П. 16 точка х6). Если знак у первой производ-
ной/(х) не меняется, функция Дх) в точке х° экстремума не имеет
(на рис. П. 16 точки х5 и х7).
На рис. П. 16 точка х( — точка краевого (локального) миниму-
ма функции Дх), х8 — точка краевого (локального) максимума
функции Дх) на множестве М (М = [Хр х8]), остальные точки —
точки внутреннего экстремума.
П.6.2. ФункцияДх) нескольких переменных х = (хр ..., хя) имеет
в точке х° = (хД ..., хя°) абсолютный локальный максимум Дх°)
(абсолютный локальный минимум Дх0)), если существует 5-ок-
рестность Un(8, х°) точки х° (х° е U„(8, х°) с Мс £я), такая, что для
любой точки х е Ц,(5, х°) с М с Еп справедливо неравенство
Дх°) £Дх) (Дх°) < Дх). Точка х° называется точкой абсолютного
локального максимума (абсолютного локального минимума)
функции Дх). Если для любой точки х е Un(b, х°) и такой, что
х*х°, справедливо неравенство Дх°) >Дх) Дх°) <Дх), то говорят
об абсолютном сильном локальном максимуме Дх°) (абсолютном
сильном локальном минимуме Дх0)). Если абсолютный локаль-
ный экстремум не является сильным, он называется слабым.
Если для любой точки х е М а Еп справедливо неравенство
Дх°) >Дх) Дх0) < Дх)), то говорят об абсолютном глобальном мак-
симуме Дх°) (об абсолютном глобальном минимумеДх°) функции
Дх) на множестве Мс Ен). Точках0 называется в этом случае точ-
кой абсолютного глобального максимума (абсолютного глобаль-
ного минимума) функции Дх) на множестве Мс Еп. Если при
х # х°Дх°) > Дх) Дх°) < Дх)), то говорят об абсолютном сильном
глобальном максимуме Дх°) (абсолютном сильном глобальном
минимуме Дх0)). Если абсолютный глобальный экстремум не яв-
ляется сильным, то он называется слабым.
Функция Дх) нескольких переменных х= (хр ..., хя) имеет в
точке х° = (Xj°,..., хя°) условный локальный максимумДх°) (услов-
ный локальный минимум Дх0)) при наличии ограничений в виде
равенств
g1(x) = 0, ...,gm(x) = 0 (П6.1)
800
(т < л), если существует 8-окрестность Un(8, х°) точки
х° = (х,0, хя°), такая, что для любой точки х е Un(8, х°) и
удовлетворяющей ограничениям (П 6.1) справедливо неравенство
Дх°) >Дх) Дх°) < Дх)). Точка х° называется точкой условного ло-
кального максимума (условного локального минимума) функции
Дх) при наличии ограничения (П 6.1). Если для любой точки
х е 17 (8, х°), удовлетворяющей ограничениям (П 6.1), и такой, что
х*х , справедливо неравенствоДх°) >Дх) Дх°) <Дх)), то говорят
об условном сильном локальном максимумеДх°) (условном силь-
ном локальном минимуме Дх0)) функции Дх) при наличии огра-
ничений (П 6.1). Если условный локальный экстремум не являет-
ся сильным, он называется слабым. Если для любой точки
хе Мс Еп и удовлетворяющей ограничениям (П 6.1) справедливо
неравенство Дх°) > Дх) (Дх°) < Дх)), то говорят об условном гло-
бальном максимуме Дх°) (условном глобальном минимуме Дх0))
функции Дх) на множестве М с Еп при наличии ограничений
(П 6.1). Точках0 называется в этом случае точкой условного гло-
бального максимума (условного глобального минимума) функции
Дх)) на множестве М с Еп. Если при х # х° Дх°) >Дх) Дх°) <Дх)),
то говорят об условном сильном глобальном максимуме Дх°) (ус-
ловном сильном глобальном минимуме Дх0)) функции Дх) при
наличии ограничений (П 6.1). Если условный глобальный экстре-
мум не является сильным, то он называется слабым.
Необходимые условия абсолютного локального экстремума и
условного локального экстремума для функции нескольких пере-
менных имеют, как правило, форму условий первого порядка.
П.6.3. Условия первого порядка для функции у =Дх) (хе МсЕ^),
имеющей конечные частные производные первого порядка по
всем переменным х = (хр ..., хя), — это равенство нулю всех част-
ных производных первого порядка этой функции:
У(х) Q Э/(х) _0
Эх, ’ ’ Эхя
Для функции одной переменной условие первого порядка
имеет вид/(х) = 0. Условия первого порядка
_ (П6.2)
51 - 7620
801
необходимые условия абсолютного локального экстремума функ-
ции у =fix) (хе МсЕ^, имеющей в точке х° (х°=(хД ,хп°) конеч-
ные частные производные по всем переменнымх= (хр ...,хл), когда
х° — внутренняя точка множества М. Точка х° е М с Еп, для кото-
рой выполнены условия первого порядка (П 6.2), называется кри-
тической (стационарной) точкой функции у =Дх) (хе Мс Еп). Если
функция у =flx) дифференцируема и выпукла (вниз) на открытом
выпуклом множестве Мс Еп, то условия первого порядка (П 6.2) —
достаточные условия (абсолютного) глобального минимума Дх°)
функции у =f(x) на множестве М, достигаемого в точке х°.
Функция Лагранжа задачи на условный локальный максимум
(минимум)
Дх) (шах)
при наличии ограничений в виде равенств
gt(x) = 0, ...,gOT(x) = 0
(х = (хр ..., хд), т < п) имеет вид
£(х, X) =Дх) + Х^](х) + ... +
Пусть функции Дх), gj(x), ..., gm(x) непрерывны и имеют не-
прерывные первые частные производные по всем переменным
х= (хр ..., х ) на открытом множестве Мс Еп.
Пусть х° - точка условного локального максимума (миниму-
ма) и пусть градиенты gradgjx0),..., gradgm(x°) линейно независи-
мы. Тогда существует единственный вектор Х° = (ХД ..., Хот°), та-
кой, что для «длинной» точки (х°; Х°) имеют место условия перво-
го порядка для функции Лагранжа Z(x, X):
Э£(х°;Х°) Q Э£(х°;Х°) 0 Э£(х°;Х°) Q Э£(х°;Х°) 0
dxj Эхл ’ ЭХ! ЭХОТ
П.6.4. Достаточные условия абсолютного локального экстрему-
ма и условного локального экстремума функции нескольких пе-
ременных имеют, как правило, форму условий второго порядка.
Условия второго порядка для функции у =Дх) (х е Л/с £л), име-
ющей непрерывные вторые частные производные по всем пере-
менным х = (X], ..., хл), это совокупность неравенств
det(Ak(x))<Ъ,к = \,...,п, где det(J*(x)), к = 1,..., п, последовательно
повышающие порядок главные диагональные миноры симметри-
802
ческой матрицы А = А(х) вторых частных производных функции
У = fix')-
Э2/(х) Э2/(Х) э2/(х<
Эх2 9xj9x2 3xjdx„
Э2/(х) Э2/(х) Э2/(х)
Л(х)= Эх2ЭХ] Эх2 Эх2Эх„
Э2/(х) Э2/(х) Э2/(х)
^X„dx, Эх„Эх2 К }
Пусть М — открытое множество (М а Еп) и пусть для точки
х° = (хД хя°) выполнены условия первого порядка, т.е. пусть
х° — стационарная точка функции у =f(x) (хе Л/с £я).
1. Тогда условия второго порядка det(^(x0)) > 0, к = 1,...»л, —
это достаточные условия того, чтох0 — точка абсолютного локаль-
ного сильного минимума функции у =Дх) на открытом множестве
Мс£л.
2. Тогда условия второго порядка (-1)Аде1(ЛДх°)) > 0, к = 1,...,
п — это достаточные условия того, что х° — точка абсолютного
локального сильного максимума функции у =Дх) на открытом
множестве М с Еп.
3. Тогда условия второго порядка в виде беЦЛДх0)) 0 и невы-
полнения условий второго порядка в виде 1) и в виде 2) — доста-
точные условия того, что х° — седловая точка, т.е. в точке х° абсо-
лютного локального экстремума нет.
Функция Лагранжа задачи на условный локальный максимум
(минимум)
Дх) (max)
при наличии ограничений в виде равенств
gj(x) = 0, ...,gm(x) = 0
(х= (хр ..., хя), т < п) имеет вид
Цх, X) =Дх) + Xjg/x) + ... + к^т(х).
Пусть функцииДх), gj(x),..., gOT(x) имеют непрерывные вторые
частные производные по всем переменным х = (хр ..., хя) на от-
крытом множестве М s Еп. Пусть для точки (х°; Х°) выполнены
51*
803
условия первого порядка для функции Лагранжа, т.е. пусть
(х°; 1°) — стационарная точка функции Лагранжа £(х; 1).
1. Тогда условия второго порядка (-l)mdet5*(x°; Х°) > О,
к = т+ достаточные условия того, чтох0 — точка услов-
ного локального сильного минимума.
2. Тогда условия второго порядка (-l)*detl?*(x0; 1°) > О,
к = т + 1,..., п, — достаточные условия того, чтох0 — точка услов-
ного локального сильного максимума. Здесь
0 0 д&(х°) Эх( д&(х°) Эх*
detJ?*(x°;X°)= 0 0 dgm(x°) Эх) dgm(x°)
dgt(x°) .. Э^<х°) Э2£(х°;Х°) Э2£(х°;Х°)
Эх( Эх2 Эх(Эх*
dgi(x°) dgm(x°) Э2£(х°;1°) Э2£(х°;Х°)
Эх* ^хк дхкдх1 Эх*
(к = т + 1,..., п) — главный минор окаймленной матрицы Гессе
0 0 dgi(x°) Э^1(лг°) Эх*
0 0 dgm(x°) dgm(x°)
Эх( Эх„
dgi(x°) dgm(x°) Э2£(х°;Х°) Э2£(х°Д°)
Эх, 3xj Эх2 Эх(Эх„
dg|(x°) 3gw(x°) Э2£(х°;Х°) Э2£(х°;1°)
Эхл Эхл ЭхяЭх] Эх2 .
функции Лагранжа £(х°; Х°) в точке (х°; Х°).
П 7. Теоремы об огибающей
П.7.1. Теорема об огибающей (теорема о покрытии) — это теоре-
ма о частных производных по параметрам (локального) экстрему-
ма как функции параметров задачи на экстремум. Рассмотрим три
версии теоремы об огибающей.
Случай задачи на абсолютный (локальный) экстремум функ-
ции Дх, а) переменных х = (х,,хя) и параметров а = (а{,ак).
Пусть при а = а0 задача максимизации (минимизации) функции
Дх, а) на множестве М а Еп имеет единственное решение х°(а°).
Пусть функция Дх, а) непрерывна и имеет непрерывные частные
производные первого порядка по всем переменным х; (/= 1,..., п)
и параметрам а. (/= 1,..., к) в некоторой окрестности точки (х°(а°),
Л
Пусть К(о)=(/)тах/(х,а)(Й(а)=(/)тт/(х,о)), тогда
хеМ хеМ
3f(a°)_3f(x°,a°) (ЭЙОЛ-ЭЛХ’У)']
~3^~ За, [ За, ~ За, J’7 <п7|>
Случай задачи на условный (локальный) экстремум с парамет-
рами а = (ар ..., ак). Рассмотрим задачу на условный экстремум
(для определенности — задачу на условный локальный максимум,
задача на условный локальный минимум рассматривается анало-
гично)
(max) Дх, а)
при наличии ограничений в виде равенств
qx(x, а) = 0,..., qm(x, а) = О,
х= (Хр ...,хя), а = (Ор ..., аЛ), т < п.
Пусть при а = а° задача на условный (локальный) максимум
имеет единственное решение х° = х°(а°). Обозначим символом
К(о°) сам локальный условный максимум К(а°) = Дх°, о0). Пусть
найдутся шар
805
Sk (a; a°) = |a|| a - a01 < a j
(|o - a01 = 7ц-а®)2+...+(а*-а®)2)
и такое число 0 > О, что для любой точки а е 5^(а, о0) задача на
условный экстремум имеет решение х(а) из шара 5т(0, х°) =
={х||х—х°| < 0}.
Пусть целевая функцияДх, о0) и функции ограничений непре-
рывны и имеют непрерывные частные производные первого по-
рядка по всем переменным*, (/=1,..., л) и параметрам а. (/ = 1,Л)
в некоторой окрестности точки (х°(а°), а0). Пусть градиен-
ты grad g1(x°(a°), а0), grad gm(x°(a°), а0) линейно независимы.
Тогда функция К(а) в точке а0 имеет частные производные перво-
го порядка и
......................к, (П.7.2)
dOj dOj
где Цх, а) =Дх, а) + Х^х, а) + ... + Xmgm(x, а) — функция Лагран-
жа задачи на условный экстремум.
Случай задачи математического программирования с пара-
метрами а = (ар ..., ак).
Рассмотрим задачу (локальной) максимизации (случай задачи
(локальной) минимизации рассматривается аналогично)
(max) Дх, а)
при наличии ограничений в виде равенств
^(х, а) < 0,..., gm(x, а) < О,
х= (хр ...,хя), а = (ар ..., аЛ).
Пусть при а = а0 задача (локальной) максимизации имеет
единственное решение х° = х°(а°). Обозначим символом К(а°) сам
локальный условный максимум К(а°) =Дх°(в0), а0). Пусть найдут-
ся шар Sk(a, а0) и такое число 0 > 0, что для любой точки ее $к (а,
а0) задача локальной максимизации имеет решение х(а) из шара
5л(0, х°). Пусть целевая функция Дх, а) и функции ограничений
g](x, а), ..., gm(x, а) непрерывны и имеют непрерывные частные
производные по всем переменным х(х = х.,..., хл) и параметрам а
(а = ах,..., ар. Пусть градиенты gradg1(x°(ab), а0), ..., grad р(х°(а°),
а0), соответствующие тем ограничениям, которые при (х”(а°), а0)
806
являются равенствами, линейно независимы. Тогда функция V(a)
в точке а° имеет частные производные первого порядка
ЭК(в°)_ Э£(х°,в°)
да, ~
где Цх, a) =flx, а) + Х^х, а) +... + \£т(х, а) — функция Лагран-
жа задачи математического программирования.
П.7.2. Рассмотрим задачу максимизации функции полезности
«(Хр х2) при бюджетном ограничении р1х1 + р^с2 = М, где ^—до-
ход потребителя; (xt; х2) — потребительский набор; (р^ р2) — ры-
ночные цены за единицу первого и второго продукта соответ-
ственно. Функция Лагранжа задачи максимизации имеет вид
Z(Xp х2; X) = w(Xp х2) + Х(Л/-р1х1 -р2х2)- Условия первого порядка
для функции Лагранжа имеют вид
Э£(Х|, х2; X) _ Q Э.£(Х], х2, X) _ ЪЦхх, Х2, X) _ д у 3)
Эх, Эх2 ЭХ
Если линии безразличия функции полезности u(xt; х2) строго
выпуклы к точке 0 = (0; 0) в пространстве продуктов, то система
(П. 7.3) имеет единственное решение (xf; х2;Х0)=(Х];х2;Х).
Функции X] =хх(рх;р2;М), х2=х2(рх;р2;М) называются
функциями спроса по Маршаллу на первый и второй продукты
соответственно. Условный максимум v(pp р2; М) функции полез-
ности w(Xp х2) равен
у(^;Р2;Л/) = «(х1;х2)=«(х1(р1;р2;Л/); хх(рх;р2;М)),
т.е. он зависит от параметроврр р2; Л/задачи максимизации функ-
ции полезности. Для функции Лагранжа имеем
ЦА (р,; р2; М); х2(рх; р2; М), X)=v(рх; р2; М)+ЦМ - рххх - р2х2).
Полагая в (П.7.2) ах =М, а2=рх, а2 = р2, получаем
<М.Р\>Р£М) _ dZ(xt;x2;X) с
ЪМ ” ЪМ
(предельная полезность по доходу равна множителю Лагранжа X),
3v(pj; р2; М) _ dL(xx; х2; X)
Эд дрх
- XX!
807
(предельная полезность по цене первого продукта равна -Ьх^,
dv(Pi‘,p2‘,M) _ dL(xx;х2; X)
Э/>2 Эр2
-Хх2
(предельная полезность по цене первого продукта равна -Хх2)-
Два последних равенства называются тождествами Роя (при
п = 2). Функция v(pp р2; М) называется косвенной функцией по-
лезности.
П.7.3. Рассмотрим задачу минимизации расходар1х1 + р^с2 потре-
бителя при фиксированном уровне й полезности и(х(; х2), т.е. при
w(x,, х2) = й. функция Лагранжа задачи минимизации имеет вид
N(xx, х2, v)=рххх + р2х2 + v(u - и(хх, х2)).
Условия первого порядка для этой функции имеют вид
Э(У(х„Х2,у) = 0> ЭМхрХг.г) ^ Э#(х„х2>у)^0 щ.7.4)
Эх1 ’ Эх2 ’ Эу
Если линии безразличия функции полезности и(хх; х2) строго
выпуклы к точке 0 = (0; 0) в пространстве продуктов, то система
(П. 7.4) имеет единственное решение (х1°;х2;Х°)=(х1;^;Х). Функ-
ции х1=х1(р1,р2,й), х2=х2(р1,р2,й) называются функциями
спроса по Хиксу на первый и второй продукты соответственно.
Условный минимум т(рх,р2,й) расходов потребителяр1х) + р^с2
называется функцией расходов (по переменным />|,р2,й). Этот
минимум равен
m(Pi,P2^) = Р\х{(рх,р2,й)+Р2х2{рх,р2,й).
Для функции Лагранжа имеем
Н(хх (рх, р2,й), х2 (А, р2, й), у) = рхх1 + р2х + v(u - и(хх; х2)).
Полагая в (П.7.2) ах =й, <$ = рх, а2 =р2, получаем
bm{Pi',p2',U) _ Э1(х!;х2;у) _ _
Эй " Эй ~V
(предельный расход по полезности равен множителю Лагранжа у),
Ът(рх,р2‘,и) _ ЭМХ];х2;у) _ - Эт(Р];р2,й) _ bN(xx,x2,v) _ _
Эр, dpi ” др2 др2 2
808
(предельный расход по цене равен величине спроса по Хиксу на
соответствующий продукт). Два последних равенства представля-
ют собой лемму Шепарда.
Рассмотренные задачи максимизации функции полезности и
минимизации расходов естественным образом обобщаются на
случай п > 2.
П 8. Функции выпуклые, вогнутые, квазивогнутые,
псевдовогнутые
П.8.1. Выпуклая функция — функция, графиком которой являет-
ся выпуклая кривая (поверхность). ФункцияДх), определенная на
выпуклом множестве М пространства Еп, называется выпуклой
(выпуклой вниз) на М, если для любых векторов (точек) х° и х1,
принадлежащих М, и для любого числа X (0 > X £ 1) справедливо
неравенство
Д(1 - Х)х° + Хх1) < (1 - ХИ*0) + ХДх1). (П.8.1)
Например, функции Дх) = + ... + ajcn (линейная форма),
Дх) = х,2 + ... + хп_2 (неотрицательно определенная квадратичная
форма) выпуклы на всем пространстве Еп, функцияДх) = InXj вы-
пукла на полупространстве х, > 0 пространства Еп. Если функция
Дх) выпукла на множестве М, то она выпукла на любом выпуклом
подмножестве множества М. График выпуклой функции Дх) рас-
положен ниже (точнее — не выше) любой своей хорды
(рис. П.17).
Если функцияДх) выпукла на выпуклом множестве Л/с Еп, то
множество {х|х е M,f(x) < Ь} выпукло (если оно не пусто). Пусть
Дх) дифференцируема и выпукла на Еп, пусть ее градиент
Э/(х°), , Э/(х°)\ о,
Эх, ..... Эхл J
Я*°) =
тогда (п - 1)-мерная плоскость
1д(х°)(х,.-х«) = 0
(А(Х°) =
Э/(х°)
Эх,
) в пространстве Еп будет касательной к поверх-
ности уровняДх) =Дх°) в точкех° и опорной к выпуклому множест-
ву {х|хе En,f{x) <Дх0)}. Если функцииД(х) (/= 1,..., к) выпуклы на
множестве Л/и числа X, > 0 (z= 1,..., к), то функция
810
Рис. П17
к
1=1
выпукла на множестве М. Функция Дх), выпуклая на множестве
М, непрерывна в каждой внутренней (и относительно внутрен-
ней) точке множества М. Отсюда следует, что функция Дх), вы-
пуклая на открытом множестве М, непрерывна на этом множест-
ве. ФункцияДх), выпуклая на множестве М, которое не является
открытым, может иметь точки разрыва, и эти точки обязательно
принадлежат границе множества М.
811
Выпуклая функция может быть недифференцируемой даже во
внутренних точках множества М. Пусть функция Дх) дифферен-
цируема на открытом выпуклом множестве М. Для того чтобы эта
функция была выпуклой на множестве М, необходимо и доста-
точно, чтобы для любых векторов (точек) х° и х из множества М
выполнялось неравенство
п
лх)>/(х0)+ХА(^0)(^-^)-
/=1
Это неравенство означает, что график выпуклой дифференци-
руемой функцииДх) расположен выше (точнее — не ниже) любой
своей касательной плоскости К:
п
К = /(х°)+ХД(х0)(х/.-х/°),
/=1
т.е. любая касательная плоскость к графику выпуклой дифферен-
цируемой функцииДх) является опорной для надграфика .Тэтой
функции (рис. П.18).
Пусть функция Дх) имеет все непрерывные вторые частные
производные на открытом выпуклом множестве М о Еп. Для того
чтобы эта функция была выпуклой на множестве М, необходимо и
достаточно, чтобы квадратичная форма
п
'J=l
<fX,XjM =
д2Лх)}
dXjdXj
была неотрицательно определенной на мно-
жестве М, т.е. чтобы для любых векторов хе = ...,£л)е Еп
квадратичная форма была неотрицательной. Критерий неотрица-
тельной определенности приведен в параграфе П5.
Выпуклая на множестве М а Еп функция Дх) может не иметь
локального (и следовательно, глобального) минимума (например,
если М — открытое выпуклое множество, а функцияДх) = а1х1 + ...+
+ а^сп, где а,2 + ... + а2 > 0). Если функцияДх) выпукла на мно-
жестве М и если она имеет локальный минимум на множестве М,
то этот минимум обязательно является глобальным. Таким обра-
зом, задача минимизации выпуклой функции на выпуклом мно-
жестве является одноэкстремальной (если она имеет решение).
812
Множество точек из М, в которых выпуклая функция Дх) имеет
глобальный минимум, есть выпуклое множество. Если функция
Дх) выпукла на множестве М а Еп, дифференцируема в точке х° е
М и если/(х°) = 0, то х° — точка глобального минимума функции
Дх) на множестве М. Если выпуклая функция Дх) имеет на огра-
ниченном замкнутом множестве М глобальный максимум, то этот
максимум достигается в одной (или более) крайней точке этого
множества. Локальные максимумы этой функции также достига-
ются в крайних точках множества М, однако они не обязательно
будут глобальными, т.е. задача максимизации выпуклой функции
на замкнутом ограниченном выпуклом множестве является мно-
гоэкстремальной (если она имеет решение).
Выпуклая функция называется строго выпуклой на множестве
А/с Еп, если для любого числа X (0 < X < 1) и для любых векторов
(точек) х° и х* из множества М, таких, что х° * х’, неравенство
(П.8.1) превращается в строгое неравенство. Для того чтобы диф-
813
ференцируемая функция Дх) была строго выпуклой на открытом
выпуклом множестве Мс Еп, необходимо и достаточно, чтобы для
любых векторов (точек) х° и х из Л/(х° # х) выполнялось неравен-
ство
/(х)>/(х°)+^Д(х°)(х/-х,°).
/=1
Положительно определенная квадратичная форма является
строго выпуклой на всем пространстве Ен. Пусть функция Дх)
имеет все непрерывные вторые частные производные на откры-
том выпуклом множестве М; если квадратичная форма
«1
положительно определена на множестве М, то функцияДх) строго
выпукла на множестве М. Обратное, вообще говоря, не верно.
Если строго выпуклая на множестве М функция Дх) имеет локаль-
ный (и следовательно, глобальный) минимум, то он достигается в
единственной точке из множества М.
Функция Дх), определенная на выпуклом множестве М про-
странства Еп, называется вогнутой (строго вогнутой) на множест-
ве М, если функция — Дх) выпукла (строго выпукла) на множестве
М. Приведенные утверждения можно переформулировать для
вогнутых (строго вогнутых) функций. Иногда выпуклые (строго
выпуклые) функции называются выпуклыми (строго выпуклыми)
вниз, а вогнутые (строго вогнутые) — выпуклыми (строго выпук-
лыми) вверх функциями.
П.8.2. Квазивогнутая функция Дх) на выпуклом множестве
Л/с Еп — функцияДх), такая, что множество {х|хе Л/с En,fix) >т}
выпукло (если оно не пусто) для любого действительного числа т.
Функция Дх) квазивогнута на выпуклом множестве М с Еп
тогда и только тогда, когда из неравенстваДх) >Дх°) следует нера-
венство ДХх + (1 - Х)х° >Дх°) для любых векторов х, х° е М и лю-
бого числа Хе (0; 1).
Функция Дх) квазивогнута строго на выпуклом множестве
М с Еп, если из неравенстваДх) >Дх°) следует неравенство ДХх +
+ (1 - Х)х°) >Дх°) для любых векторов х * х° из М и любого числа
Хе (0; 1).
814
Функция -Дх) квазивыпукла (квазивыпукла строго) на выпук-
лом множестве М £ Ен, если функция Дх) квазивогнута (квазиво-
гнута строго) на выпуклом множестве М а Еп.
Свойства квазивогнутых и квазивыпуклых функций:
1) если функцияДх) вогнута (выпукла вверх), тоДх) квазиво-
гнута; 2) если функцияДх) выпукла (выпукла вниз), тоДх) квази-
выпукла; 3) еслиДх) (х е Ма возрастает или убывает, тоДх)
квазивогнута или квазивыпукла; 4) сумма квазивогнутых функций
не обязательно квазивогнутая функция (^(х)=х3 и/2(х) = -х—ква-
зивогнутые функции, однако функция Д(х) = х3 - х не обладает
этим свойством); 5) сумма квазивыпуклых функций не обязатель-
но квазивыпуклаяфункция; 6) если функцияДх) (хе Мс £,) ква-
зивогнута (квазивыпукла), а функция F(f) (te £t) возрастает (убы-
вает), то функция £Дх)) квазивогнута (квазивыпукла) [квазивы-
пукла (квазивогнута)]; 7) если функция Дх) > 0, х е К а Еп
(К — выпуклый конус) однородна степени 1 и квазивогнута на К,
то функцияДх) вогнута на £; 8) функцияДх), непрерывная и име-
ющая непрерывные частные производные первого порядка по
всем переменным, квазивогнута на открытом выпуклом множест-
ве Мс Ен тогда и только тогда, когда из неравенства Дх) >Дх°)
следует неравенство gra<V(x0)(x - х°) > 0 для любых х и х°из Ма Еп.
Пусть
бДх) =
О
Э/(х)
Эх,
э/(х)
Эхг
Э/(х) Э/(х)
Эх( дхг
d2f(x) Э2/(х)
Эх3 ЭХ)Эхг
э2/(х) э2/(х)
ЭхгЭх! Эх3
Пусть функцияДх) непрерывна и имеет непрерывные частные
производные по всем переменным до второго порядка включи-
тельно; 9) если функцияДх) квазивогнута на открытом выпуклом
множестве М с Еп, то
(-l/G/x) > 0, r= 1,..., п,
для любых х е М (необходимые условия квазивогнутости);
10) если (-l/GXx) > Оприг= 1, ...,ядлялюбыххе MczEn (М-суг-
815
крытое выпуклое множество), то функция Дх) квазивогнута на
множестве М (достаточные условия квазивогнутости); 11) если
функция Дх) квазивыпукла на открытом выпуклом множестве
М с Еп, то
G.(x)<0, r= 1,...,«,
для любых хе М g Еп (необходимые условия квазивыпуклости);
12) если Gr(x) < 0 при r= 1,п для любыххе Me Еп (М— откры-
тое выпуклое множество), то функция Дх) квазивыпукла на мно-
жестве М (достаточные условия квазивыпуклости).
П.8.3. Псевдовогнутая функция Дх) в точке х° выпуклого мно-
жества Мс Еп — функцияДх) такая, чтоДх) непрерывна со всеми
своими частными производными первого порядка на множестве
М с Е'и из неравенства Дх) > Дх°) следует неравенство
ёгадДх(5)(х - х°) > 0 для любой точки хе МсЕп. ФункцияДх) псев-
довогнута ца выпуклом множестве М, если функция Дх) псевдо-
вогнута в каждой точке множества М g Еп, т.е. для любых точек х
и х° из множества Л/из неравенстваДх) >Дх°) следует неравенство
gra<V(x0)(x - х°) > 0. ФункцияДх) псевдовыпукла в точке х° выпук-
лого множества М с Еп, еслиДх) непрерывна со всеми своими
частными производными первого порядка на множестве Мс Еп и
если из неравенстваДх) > Дх°) следует неравенство 8гадДх°)(х - х°) < 0
для любой точки хе МсЕп. Функция Дх) псевдовыпукла на вы-
пуклом множестве М с Еп, если функция Дх) псевдовыпукла в
каждой точке множества М.
Свойства псевдовогнутых функций (свойства псевдовыпук-
лых функций аналогичны):
1) пусть функция Дх) непрерывна со всеми своими частными
производными первого порядка на множестве Мс Еп. Тогда:
1.1) если функция Дх) псевдовогнута на множестве М а Еп, то
Дх) квазивогнута на М‘,
1.2) если множество М открыто и бгадДх) * 0 для любой точки
хе Мс Еп, то функцияДх) на множестве Мпсевдовогнутатогда и
только тогда, когда функцияДх) квазивогнута на М с £я;
2) пусть функцияДх) псевдовогнута на открытом выпуклом мно-
жестве Л/с Еп. Пусть точка х° е Л/такова, что вгадДх®)(х - х°) < 0 для
любой точки х е М (что совпадает со случаем §гас1Дх0) = 0). Тогда
х° — точка глобального максимума функции Дх) на множестве
Л/с£„.
П 9. Дифференциальные уравнения и системы
дифференциальных уравнений
П.9.1. Дифференциальное уравнение — это уравнение, содержа-
щее неизвестную функцию, ее производные различных порядков
и независимую переменную (независимые переменные). В эконо-
мических приложениях независимые переменные и функции
принимают действительные значения.
Многие процессы описываются дифференциальными уравне-
ниями (например, процесс возрастания денежной суммы при не-
прерывном начислении процентов), поэтому их интенсивно при-
меняют в самых разнообразных теоретических и прикладных
экономико-математических исследованиях. С помощью диффе-
ренциальных уравнений во многих случаях удается получить ана-
литические выражения различных законов.
Порядком дифференциального уравнения называется поря-
док наивысшей производной, входящей в уравнение. Обыкновен-
ные дифференциальные уравнения содержат неизвестные функ-
ции только одной независимой переменной, которую обозначают
символом t. Это объясняется тем, что в ряде важных приложений
независимой переменной является время. Дифференциальные
уравнения в частных производных содержат неизвестные функ-
ции нескольких независимых переменных. Дифференциальные
уравнения в частных производных в экономических приложениях
встречаются достаточно редко. Обыкновенное дифференциаль-
ное уравнение порядка п имеет вид
Г(/, х(Г), У (/),..., х(й)(0) = О, (П.9.1)
гдех=х(/) — неизвестная функция: x!(t) — ее первая производная;
х(п)(/) — производная порядка п неизвестной функции х(/); F— за-
данная функция п + 2 переменных.
Решением (частным решением) уравнения (П.9.1) называется
всякая функция, удовлетворяющая этому уравнению (т.е. при
подстановке обращает его в тождество) для всех значений t в неко-
тором конечном или бесконечном промежутке (интервале). Гра-
фик решения в плоскости переменных /, х называется интеграль-
52 - 7620
817
ной линией уравнения (П.9.1). Дифференциальное уравнение
имеет, вообще говоря, бесконечное множество решений.
Общее решение уравнения (П.9.1) представляет собой семей-
ство функций х = ф(/, ср ..., ся), зависящих от п произвольных по-
стоянных. Выбирая надлежащим образом значение этих постоян-
ных, можно получить любое частное решение уравнения (П.9.1)
(за исключением так называемых особых решений). Отыскание
решений дифференциального уравнения называется его интегри-
рованием.
В задаче с начальными условиями (называемой также задачей
Коши) требуется найти частное решение x(f) уравнения (П.9.1),
удовлетворяющее п начальным условиям
х0о)=х0’*,^о)=ХР =
где t0, х0, Хр ..., хя_! — заданные числа. На основании этих условий
находятся соответствующие значения произвольных постоянных
с,....с .
1 ’ ’ п
В краевой задаче требуется найти частное решение x(t) уравне-
ния, удовлетворяющее п краевым условиям, накладываемым на
функцию и ее производные в двух точках tQ и Вопрос о сущест-
вовании (и единственности) решения задачи Коши решают тео-
ремы существования и единственности решения. Приведем фор-
мулировку теоремы существования и единственности решения
задачи Коши для обыкновенного дифференциального уравнения
первого порядка х*(О =ЛЛ разрешенного относительно про-
изводной x'(Z): пусть функция fit, х) непрерывна и имеет непре-
рывную частную производную///, х) в открытом прямоугольнике
Q = {(/, х)|а <t<b,c<x<d], расположенном в плоскости перемен-
ных /, х; тогда для любой точки (/0, х0) € Q существует единствен-
ное частное решение х(/) уравнения х'(/) =Д/, х(/)), и это частное
решение удовлетворяет начальному условию х(/0) = х0 и определе-
но на некотором отрезке [/° — Р + Л]. Геометрическая интерпре-
тация теоремы: при выполнении условия теоремы через каждую
точку (t0, х0) прямоугольника Q проходит (для каждой точки
(/*, х°) своя) единственная интегральная линия уравнения x'(Z) =
х°) (рис. П. 19). Множество всех интегральных линий в откры-
том прямоугольнике Q изображает общее решение дифференци-
ального уравнения первого порядках'(О =Д/, х(/)).
818
Рис. П19
П.9.2. В математической экономике большое применение нахо-
дят линейные дифференциальные уравнения. Уравнение (П.9.1)
называется линейным, если оно имеет вид
о0(/)х(л)(/) + + ... + a^it) + ай(/)х(0 = b(t), (П.9.2)
где а0(/),..., ал(0, b(t) — данные функции. Если b(t) = 0, уравнение
называется однородным, в противном случае — неоднородным.
Общее решение уравнения (П.9.2) есть сумма какого-либо его
частного решения x(t) и общего решения z(t) соответствующего
ему однородного уравнения
a0(t)z(n4t) + at(^)(0 + - + + an(t)z(t) = 0. (П.9.3)
Если коэффициенты а0(/), .... ая(0 постоянные, уравнение
(П.9.2) приобретает вид
V<">(0 + а/и-1)(0 + ... + о„_/(0 + оХО = *(')• (П.9.4)
и называется линейным дифференциальным уравнением по-
рядка п с постоянными коэффициентами (а0 * 0). Соответству-
ющее однородное уравнение имеет вид
a^n\t) + + ... + a^zUt) + anz(t) = 0. (П.9.5)
Многочлен Ф(1) = а^," + а^"-1 + ... + ап1к + ап называется
характеристическим многочленом дифференциального уравне-
52- 819
ния (П.9.4 или П.9.5), а уравнение Ф(Х) = 0 называется характе-
ристическим уравнением дифференциального уравнения (П.9.4
или П.9.5). Если многочлен Ф(Х) имеет п действительных корней
Хр .... Хя, общее решение ?(/) однородного линейного дифферен-
циального уравнения (П.9.5) записывается так:
?(/) = с1еХ1' + ...+сяА', (П.9.6)
где Ср..., сп — произвольные постоянные. В случае комплексных и
кратных корней многочлена Ф(Х) запись общего решения услож-
няется:
г(/) = ^(/)?1' + ...+Ру(/)Л'+...+РЯ1(/)?-' (т<п), (П.9.7)
где Ру(/)=Су0+су1/+...+Суо = — кратность (дей-
ствительного или комплексного) корня Ху. (а,. £ 1, а,++ аж = л);
Су — произвольные постоянные (Z = 1,..., т; v=0,1,..., а.у-1). Если
в случае действительных коэффициентов а0, ар ..., ап характерис-
тический многочлен Ф(Х) имеет комплексный корень Ху = Оу + /Ту
(здесь I2 = -1) кратности a,. (Оу > 1), то многочлен Ф(Х) обязательно
имеет комплексно сопряженный корень Хл =Ху =Gy -/Ту той же
самой кратности ак = ау, В случае комплексно сопряженных кор-
ней Ху и Хл = Ху произвольные постоянные Су0,..., cja/ ,ск0,..., ска* (
в слагаемых Pjtfie* и Рл(/)ех*' выражения (П.9.7) должны быть
комплексными с. = dJv + /с"^. Положив сь =Cyv =c'v -ic"v и при-
менив формулу Эйлера
en,t = cos Ту/ + / sin Ту/,
после элементарных преобразований в сумме
Ру (/)?'' +Р*(/)Л'
выражения (П.9.7) мы избавимся от мнимой единицы /. Проделав
то же самое во всех других парах Pr(t)ex,t и РД/)еХ'\ соответству-
ющих остальным парам комплексно сопряженных корней Хг и
Х5 (Х5 = Хг), мы получим для общего решения уравнения (П.9.5)
новое выражение (П.9.7), уже не содержащее мнимой единицы /.
Таким образом, описанная процедура позволяет из общего комп-
лексного решения (П.9.7) уравнения (П.9.5) с действительными
коэффициентами а0, ар ..., ап выделить действительное общее ре-
шение уравнения (П.9.5).
820
Частное решение x(f) неоднородного уравнения (П.9.4) может
быть найдено, например, методом вариации произвольных по-
стоянных, методом неопределенных коэффициентов или с помо-
щью операционного исчисления.
П.9.3. Система обыкновенных дифференциальных уравнений
связывает неизвестные функции хД/),..., хя(/), их производные и
независимую переменную /. Обычно рассматривают системы, со-
держащие столько уравнений, сколько в них имеется неизвестных
функций. Основные понятия, введенные для дифференциальных
уравнений, переносятся на случай системы естественным обра-
зом. Системы весьма общего вида обычно удается свести к систе-
ме обыкновенных дифференциальных уравнений первого поряд-
ка, имеющей по Коши нормальную форму
...,х„(0). (П.9.8)
Система вида (П.9.8) представляет собой обобщение уравне-
ния У (О =flf, хД/), которое было рассмотрено выше. Утверждения
для этого уравнения переносятся на систему (П.9.8), в частности
теорема существования и единственности решения задачи Коши.
Линейная система (П.9.8) имеет вид
х[ (О = а, 1 (/)х, (Г)+...+aln (t)x„ (Г)+(/),
....................................... (П.9.9)
ХП (О = ап1 (0*1 (0+• • •+а„„ (0х„ (0+Ьп (/),
или в векторно-матричной форме x!(t) = A(t)x(t) + b(t), где x(Z) —
«-мерный вектор-столбец с координатами хД/), ..., хя(Г); A(t) =
= — матрица порядка п и b(t) — вектор-столбец с координа-
тами^/), ...,bn(f).
Для однородной системы (П.9.9) с постоянными коэффици-
ентами (т.е. b(t) = 0; s ал J = 1,..., л) z'(Z) = Az(t) в случае неот-
рицательной неразложимой матрицы А имеет место следующий
аналог теоремы Фробениуса. Пусть вектор z° > 0 (=£ 0) и пусть век-
тор z(t) — решение системы г' (0 = Az(t), удовлетворяющее началь-
ному условию z(/°) = z°, тогда
lim zif)/ekJ =cv*,
/->+«>
821
где с > 0 — скалярный множитель, зависящий только от начально-
го вектора z°, а А.» и v‘(|v*| = 1) — число Перрона и правый вектор
Перрона соответственно матрицы А.
В рамках общей теории дифференциальных уравнений боль-
шое значение имеют результаты качественного исследования ре-
шений систем обыкновенных дифференциальных уравнений,
т.е. исследования существенных свойств решений без явного зна-
ния этих решений. В качественной теории дифференциальных
уравнений важное место занимают такие ее разделы, как устойчи-
вость по А.М. Ляпунову и асимптотика решений по малому пара-
метру. Материалы этих разделов находят применение для реше-
ния теоретических и прикладных задач математической экономи-
ки.
В общей теории дифференциальных уравнений рассматрива-
ются также уравнения и системы, содержащие комплексные
функции комплексных переменных.
П.9.4. Система (П.9.8) обыкновенных дифференциальных урав-
нений называется автономной, если ее правые части явно не зави-
сят от времени t
...,хя(0). (П.9.10)
Постоянное решение х//) др..., хя(/) « ап системы (П.9.10)
называется равновесием этой системы.
Для того чтобы л-мерный вектор а = (а,,..., ап) был равновеси-
ем системы (П.9.10), необходимо и достаточно, чтобы вектор
а = (др ..., дя) был решением (нелинейной) системы алгебраичес-
ких уравнений
//Хр ...,хя) = 0, ...,/я(Хр ...,хя) = 0. (П.9.11)
Равновесие д = (др ..., дя) системы (П.9.10) называется устой-
чивым по Ляпунову, если для любого числа s > 0 найдется число
8 = 8(е, д) > 0, такое, что как только |х,° - aJ < 8, i = 1, ..., п, то
|х,(/, х°) - flj < s, i = 1,..., п, гдех;(/, х°) — решение системы (П.9.10),
удовлетворяющее начальным условиям
х,(0, х°) = х,0,..., хя(0, х°) = х„°. (П.9.12)
Решение х(/, х°) = (х,(/, х°),..., xn(t, х0)), которое сравнивается с
равновесием д = (др ..., дя), называется возмущенным решением
системы (П.9.10).
822
Равновесие а = (др дя) системы (П.9.10) называется асимп-
тотически устойчивым, если оно, во-первых, устойчиво по Ляпу-
нову и, во-вторых, существует такое число ст > 0, что при [хР - aj<
< ст, 1= 1,...,«,
limxz(/,x°) = ah i = (П.9.13)
Приведенные определения — это определения локальной ус-
тойчивости. Если постоянные 8 и ст могут быть сколь угодно вели-
ки, то приведенные определения будут определениями глобаль-
ной устойчивости.
В первом методе Ляпунова вопрос об устойчивости и асимпто-
тической устойчивости равновесия а = (др..., оя) системы (П.9.10)
исследуется с помощью вспомогательной линейной системы
обыкновенных дифференциальных уравнений первого порядка с
постоянными коэффициентами, которая называется системой
первого приближения системы (П.9.10).
Система первого приближения системы (П.9.10) строится
так.
Предполагая, что в некоторой т|-окрестности точки а = (др ...,
ая) функции=(хр ..., хя), / = 1,...,л, обладают частными произ-
водными до второго порядка включительно, напишем представ-
ленные функции^.(хр ..., хя), i = 1,..., п, по формуле Тейлора:
^(хр...,хя) = Х(Д1,...,ая)+Р^а',"‘,ай)(х1-О1)+...
+ Э/(а1„..,дя)(^_^Л (П.9.14)
. V э2/Ц+6(*1-«1)>-,ап + 0(хя-а„))
+ -------------5---------------\xj ~aJ>\xk ~ак>-
j,k=l dXjk
Полагая
OXj
напишем однородную систему обыкновенных линейных диффе-
ренциальных уравнений с постоянными коэффициентами:
823
г'(0 =ft^,(O + •••+ ginzn(t),.... z„'(0=ад(О +... +ft„V'). (П.9.15)
которую можно толковать как полученную из систем (П.9.10) пу-
тем отбрасывания остаточных членов второго порядка (П.9.14);
отметим также, что/^ар ..., дл) = 0,/= 1, ...,я(см. (П.9.11)).
Система (П.9.15) и есть вспомогательная система первого
приближения системы (П.9.10).
Пусть все собственные числа 1= а. + р/,У = 1,..., п, /2 = -1, мат-
рицы
>11 - ft?
G = ...........
^Snl ft» у
системы (П.9.15) имеют отрицательные действительные части
Оу < 0,/ = 1,..., я. Тогда равновесие а = (av ..., ап) системы (П.9.10)
(локально) асимптотически устойчиво. Отметим, что в рассмат-
риваемом случае система (П.9.15) имеет единственное равновесие
= 0, ..., zn = 0, которое глобально асимптотически устойчиво.
Если хотя бы одно собственное число матрицы G имеет положи-
тельную действительную часть а?- > 0, то положение равновесия
а = (Ор ..., оя) системы (П.9.10) не является устойчивым по Ляпу-
нову.
Во втором методе Ляпунова вопрос об устойчивости равнове-
сия а = (Яр ..., яд) системы (П.9.10) исследуется с помощью функ-
ции Ляпунова.
П 10. Задача оптимального управления и принцип
максимума Л.С. Понтрягина
П.10.1. Задача оптимального управления с непрерывным време-
нем формулируется следующим образом.
Процесс управления описывается обыкновенными диффе-
ренциальными уравнениями
*1 *1,"-,*„,«1,...,Иг),
................................. (П.10.1)
гдех= (хр ..., хл) — вектор состояния управляемой системы — эле-
мент фазового пространства; траектория состояний х(/) = (хД?),...,
хл(/)) называется фазовой траекторией, она описывает поведение
управляемой системы во времени; и = (ыр ..., ип) — вектор управ-
ления системой; пара (х, и) = (хр ..., хл; «р ..., мл) называется про-
цессом управления. Точка здесь и далее — символ производной по
времени /.
Вектор управления и принадлежит области U возможных зна-
чений управления, область Uможет меняться во времени.
Таким образом,
ы(0е U(t). (П.10.2)
Заданы начальные условия траектории состояний
х1Оо)=*Ю’ = Хл0 (П.10.3)
и конечные условия траектории состояний
х,(Л) = х|Р ...,x(t.) = xm.,m<n. (П.10.4)
Неравенство т<п может быть строгим: т < п .
Качество процесса управления (х(Г), «(0) оценивается целе-
вым функционалом
J = \f^t,xx,...,xn,ux,...,ur)dt+F{x{tx))(mm). (П.10.5)
Процесс управления (х(/), «(/)) называется допустимым про-
цессом задачи оптимального управления (П.10.1)—(П.10.5), если
825
он удовлетворяет условиям (П.10.1—(П.10.4). Допустимый про-
цесс (x(t), u(t)) называется оптимальным процессом задачи опти-
мального управления (П.10.1)—(П.10.5), если он минимизирует
целевой функционал (П.10.5).
Если правый конец траектории x(f) = (xx(t),..., хп(0) зафикси-
рован полностью, то слагаемое F(x(tx)) является постоянным, не
оказывает влияния на нахождение оптимального процесса
(х(О,й(О).
Прежде чем приводить формулировку теоремы, отметим, что
функции./^, х, u),fx(t, х, и), ...,fn(t, х, и) непрерывны и имеют не-
прерывные частные производные по переменным t, хр ..., хп в об-
ласти их определения.
Теорема (принцип максимума Понтрягина). Пусть (x(t), u(t)) —
оптимальный процесс задачи оптимального управления (П. 10.1 )—
(П.10.5).
Тогда существует векторная функция \|/(0 = (^(Г), ..., V„(0),
такая, что:
1) функция H(t, х, и) = Wjfjit, х, и) + ... + \|/„/я(/, х, и) -
м) Достигает максимального значения при всех t е [?0, Г,],
при x = x(t), v = v(0, по переменным и= (wp ..., иг), равным
и —и = (ux(t), ...,ur(t)), т.е.
H(t,x(t),xu(t),u(t))= max
u(t)eU{t)
2) векторная функция у(/) = (ц///). —, V„(0) удовлетворяет сис-
теме обыкновенных дифференциальных уравнений
. (0=_ ЭЯ(/,х(0,у(/),й(/))
' Эх,
, '=1
x=x(t)
ж
3) в конечный момент t = выполнено условие трансверсаль-
ности
,, ч Э7?<х)
, i = m+l,...,n.
x=x(t)
Приведенная теорема дает необходимые условия оптимально-
го процесса (x(t), u(t)). Полученные необходимые условия позво-
ляют сузить исходное множество допустимых процессов (x(t),
u(t)) путем выделения из этого множества только тех процессов,
которые удовлетворяют необходимым условиям. Совокупность
826
приведенных необходимых условий, как правило, позволяет вы-
делить единственную траекторию x(t) из множества допустимых.
Если при этом еще известно (например, из содержательных сооб-
ражений), что оптимальная траектория существует, тогда эта
единственная траектория х(/) и отвечающее ей оптимальное уп-
равление «(/) образуют оптимальный процесс, который и есть ре-
шение задачи оптимального управления (П.10.1)—(П.10.5).
Функцию H(t, х, v, и) принято называть функцией Гамильто-
на — Понтрягина, она является аналогом функции Лагранжа;
функции у//), •••, W„(t) являются аналогами множителей Лагран-
жа Хр ..., в теории экстремальных задач.
СПИСОК ЛИТЕРАТУРЫ
Глава 1
Винер Дж. (1925; 2000). Концепция полезности в теории ценности и
ее критики // Вехи экономической мысли. Теория потребитель-
ского поведения и спроса. Т. 1. СПб.: Экономическая школа.
Воркуев Б.Л. (2002). Модели микроэкономики. М.: ТЕИС.
Воркуев БД. (2007). Количественные методы исследования в микро-
и макроэкономике. М.: ТЕИС.
Гальперин В.М., Игнатьев С.М., Моргунов В.И. (1996). Микроэконо-
мика. Т. 1. СПб.: Экономическая школа.
Горбунов В.К. (2004). Математическая модель потребительского рын-
ка: теория и прикладной потенциал. М.: Экономика.
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. (1997, 1999, 2001,
2003). Математические методы в экономике. М.: ДИС.
Интрилигатор М. (1975,2002). Математические методы оптимизации
и экономическая теория. М.: Прогресс.
Пиндайк Р., РубинфельдД. (2000). Микроэкономика. М.: Экономика:
Дело.
Слуцкий Е.Е. (1999). Экономическая школа: Журнал-учебник. Вы-
пуск 5.
Тарануха Ю.В. (2006). Микроэкономика. М.: ДИС.
Хикс Дж.Р. (1941; 2000). Реабилитация потребительского излишка//
Вехи экономической мысли. Теория потребительского поведения
и спроса. Т. 1. СПб.: Экономическая школа.
Хикс Дж.Р., Аллен Р.Г.Д. (1934; 2000). Пересмотр теории ценности //
Вехи экономической мысли. Теория потребительского поведения
и спроса. Т. 1. СПб.: Экономическая школа.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
Экономическая школа. Периодический научно-популярный журнал
(1992). Выпуск 2.
828
'Gravelle H., Rees R. (1992). Microeconomic. Longman Group UK
Limited.
Gravelle H., Rees R. (1994). Microeconomic. Solutions Manuel and Work-
book. Longman Group UK Limited.
Kreps D. (1990). A Gorse in Microeconomic Theory. Harvester
Wheatsheaf.
* Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Varian H.R. (1992). Microeconomic Analysis. W.W. Norton and
Company.
Глава 2
'Gravelle H., Rees R. (1992). Microeconomic. Longman Group UK
Limited.
Gravelle H., Rees R. (1994). Microeconomic. Solutions Manuel and Work-
book. Longman Group UK Limited.
Kreps D. (1990). A Gorse in Microeconomic Theory. Harvester
Wheatsheaf.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Varian H.R. (1992). Microeconomic Analysis. W.W. Norton and
Company.
Глава 3
Гальперин B.M., Игнатьев C.M., Моргунов В.И. (1996). Микроэконо-
мика. Т. 1. СПб.: Экономическая школа.
Горбунов В.К. (2004). Математическая модель потребительского рын-
ка: теория и прикладной потенциал. М.: Экономика.
Интрилигатор М. (1975,2002). Математические методы оптимизации
и экономическая теория. М.: Прогресс.
'Gravelle Н., Rees R. (1992). Microeconomic. Longman Group UK
Limited.
Gravelle H., Rees R. (1994). Microeconomic. Solutions Manuel and Work-
book. Longman Group UK Limited.
* Звездочкой отмечены те позиции списка литературы, материалы которых
существенно были использованы при подготовке и написании текстов
глав 1—18 и приложения настоящего учебника по микроэкономике.
829
Kahneman D., Tversky A. (1984). Choices, values and frames. American
Psychologist, 39, pp. 341—350.
Kreps D. (1990). A Gorse in Microeconomic Theory. Harvester
Wheatsheaf.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Varian H.R. (1992). Microeconomic Analysis. W.W. Norton and
Company.
Глава 4
* Гальперин B.M., Игнатьев C.M., Моргунов В.И. (1996). Микроэконо-
мика. Т. 1. СПб.: Экономическая школа.
Ланкастер К. (1966; 2000). Перемены и новаторство в теории потреб-
ления И Вехи экономической мысли. Теория потребительского
поведения и спроса. Т. 1. СПб.: Экономическая школа.
Глава 5
Выбор в условиях рынка. (1999) // Экономическая школа. Журнал-
учебник. Выпуск 5. С. 391-409.
* Гранатуров В.М. (1999; 2002). Экономический риск: сущность, ме-
тоды измерения, пути снижения. М.: ДИС.
* Интрилигатор М. (1975, 2002). Математические методы оптимиза-
ции и экономическая теория. М.: Прогресс.
* Пиндайк Р., Рубинфельд Д. (2000). Микроэкономика. М.: Экономи-
ка: Дело.
Фридмен М., Сэвидж Дж. (1948; 2000). Анализ полезности при выборе
среди альтернатив, предполагающих риск // Вехи экономической
мысли. Теория потребительского поведения и спроса. Т. 1. СПб.:
Экономическая школа.
Хей Дж. (2002). Неопределенность в экономической теории // Пано-
рама экономической мысли конца XX столетия. Т. 1. СПб.: Эко-
номическая школа: СПГУЭ: ГУ ВШЭ.
Kahneman D., Tversky А. (1979). Prospect Theory: An Analysis of Decision
under Risk. Econometrica 47, pp. 263—292.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
830
Глава 6
Алчиан А. (1959; 2000). Затраты и выпуски // Вехи экономической
мысли. Теория фирмы. Т. 2. СПб.: Экономическая школа.
Гальперин В.М., Игнатьев С.М., Моргунов В.И. (1996; 1997). Микро-
экономика. Т. 1,2. СПб.: Экономическая школа.
' Замков О.О., Толстопятенко А.В., Черемных Ю.Н. (1997, 1999, 2001,
2003). Математические методы в экономике. М.: ДИС.
Количественные методы в экономических исследованиях (2004) /
Под ред. М.В. Грачевой. Л.Н. Фадеевой, Ю.Н. Черемных. М.:
ЮНИТИ-ДАНА.
Коуз Р.Г. (1937; 2000). Природа фирмы // Вехи экономической мыс-
ли. Теория фирмы. Т. 2. СПб.: Экономическая школа.
* Моделирование экономических процессов (2005) / Под ред.
М.В. Грачевой, Л.Н. Фадеевой, Ю.Н. Черемных. М.:
ЮНИТИ-ДАНА.
Махлуп Ф. (1967; 2000). Теория фирмы: маржиналистские, бихевио-
ристические и управленческие // Вехи экономической мысли. Те-
ория фирмы. Т. 2. СПб.: Экономическая школа.
‘ Томпсон А., ФормбиД. (1998). Экономика фирмы. М.: БИНОМ.
Уолтерс А.А. (1963; 2000). Производственные функции и функции за-
трат: экономический обзор // Вехи экономической мысли. Тео-
рия фирмы. Т. 2. СПб.: Экономическая школа.
Экономическая школа. Периодический научно-популярный журнал
(1993). Выпуск 3.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
Gravelle Н., Rees R. (1992). Microeconomic. Longman Group UK
Limited.
Gravelle H., Rees R. (1994). Microeconomic. Solutions Manuel and Work-
book. Longman Group UK Limited.
Kreps D. (1990). A Gorse in Microeconomic Theory. Harvester
Wheatsheaf.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Varian H.R. (1992). Microeconomic Analysis. W.W. Norton and
Company.
831
Глава 7
Антипов Е.В. (2002). Оптимальные вложения в научно-технический
прогресс // Моделирование и прогнозирование социально-эко-
номических процессов. М.: Экономический факультет МГУ.
* Аршакуни К.В. (2001). Вывод функции с постоянной эластичностью
замещения // Современные проблемы экономико-математиче-
ского моделирования: Сборник научных трудов. М.: Экономиче-
ский факультет МГУ: ТЕИС.
Вагапова Я.Я. (2007). Моделирование экономического роста с учетом
экологического и социального факторов. М.: МАКС-Пресс.
Голиченко О.Б. (1999). Экономическое развитие в условиях несовер-
шенной конкуренции. Подходы к многоуровнему моделирова-
нию. М.: Наука.
Замков О.О., Толстопятенко А.В., Черемных Ю.Н. (1997, 1999, 2001,
2003). Математические методы в экономике. М.: ДИС.
Интрилигатор М. (1975,2002). Математические методы оптимизации
и экономическая теория. М.: Прогресс.
Клейнер Г.Б. (1986). Производственные функции: Теория, методы,
применения. М.: Финансы и статистика.
Лагоша Б.А. (2003). Оптимальное уравнение в экономике. М.: Фи-
нансы и статистика.
* Лотов А. В. (1984). Введение в экономико-математическое модели-
рование. М.: Наука.
Моисеев А.Н. (2002). Двухсекторная модель НТП с закупкой техноло-
гий // Моделирование экономических процессов: Сборник науч-
ных работ молодых ученых / Под ред. М.В. Грачевой. М.: Эконо-
мический факультет МГУ: ТЕИС.
* Моисеев А.Н. (2004). Построение оптимальных траекторий управля-
емых процессов в экономических задачах. Автореферат дис. ...
канд. физ.-мат. наук. Саратов.
Смирнова А.К. (2001). Анализ агрегированных динамических моде-
лей. М.: МАКС-Пресс.
Уолтерс А.А. (1963; 2000). Производственные функции и функции за-
трат: экономический обзор // Вехи экономической мысли. Тео-
рия фирмы. Т. 2. СПб.: Экономическая школа.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
832
Bucci A. (2001). Scale Effects, Market Power and Growth when Human
and Technological Capital are Complements. — International Review
of Economics and Business, vol. 48, №1.
Глава 8
Алчиан А. А., Демсец Г. (1972; 2003). Производство, стоимость инфор-
мации и экономическая организация // Вехи экономической
мысли. Теория отраслевых рынков. Т. 5. СПб.: Экономическая
школа.
* Бусыгин В.П., Желободько Е.В., Коковин С.Г., Цыплаков А.А. (1998).
Лекции по микроэкономической теории. Новосибирск.
* Бусыгин В.П., Желободько Е.В., Коковин С.Г., Цыплаков А.А. (2000)
Микроэкономический анализ несовершенных рынков.
Новосибирск.
Бусыгин В.П., Желободько Е.В., Цыплаков А.А. (2003) Микроэкономи-
ка — третий уровень. Новосибирск.
Васин А.А., Морозов В.В. (2005). Теория игр и модели математической
экономики. М.: МАКС-Пресс.
ВуросА., Розанова Н. (2000). Экономика отраслевых рынков. М.: Эко-
номический факультет МГУ: ТЕИС.
* Гальперин В.М., Игнатьев С.М., Моргунов В.И. (1997). Микроэконо-
мика. Т. 2. СПб.: Экономическая школа.
Дюсуше О.М. (2003). К вопросу о модели нелинейных тарифов. Эко-
номика и математические методы. 39. Вып. 1.
Дюсуше О.М. (2003). Особенности моделирования монопольного
рынка дифференцированного продукта // Формирование россий-
ской модели рыночной экономики: Противоречия и перспекти-
вы. Часть 2 / Под ред.К.А. Хубиева. М.: Экономический факультет
МГУ: ТЕИС.
Клюкин П.Н. (2001). Научные комментарии к «Экономическим очер-
кам» В.К. Дмитриева. Комментарий 52 к очерку 2 // Дмитриев
В.К. Экономические очерки. М.: ГУ ВШЭ.
Милгром П., Робертс Дж. (2000). Ценовые и рекламные сигналы ка-
чества продукции // Вехи экономической мысли. Теория отрасле-
вых рынков. Т. 5. СПб.: Экономическая школа.
Самуэлсон П.Э. (1967; 2000). Монополистическая конкуренция — ре-
волюция в теории // Вехи экономической мысли. Теория фирмы.
Т. 2. СПб.: Экономическая школа.
53 - 7620
833
Стиглер Дж. Дж. (1964; 2000). Теория олигополии // Вехи экономи-
ческой мысли. Теория фирмы. Т. 2. СПб.: Экономическая школа.
Стиглер Дж. Дж. (1964; 2000). Ломаная кривая спроса олигополиста
и жесткие цены // Вехи экономической мысли. Теория фирмы.
Т. 2. СПб.: Экономическая школа.
Тарануха Ю.В. (2006). Микроэкономика. М.: ДИС.
* ТомпсонА., ФормбиД. (1998). Экономика фирмы. М.: БИНОМ.
Хикс Дж.Р. (1935; 2000). Годовой обзор экономической теории: тео-
рия монополии // Вехи экономической мысли. Теория фирмы.
Т. 2. СПб.: Экономическая школа.
Чахоян В.А. (2001). Об одном применении метода Лангранжа // Со-
временные проблемы экономико-математического моделирова-
ния. М.: ТЕИС.
ЧеканскийА.Н., Фролова Н.Л. (2005). Микроэкономика. Промежуточ-
ный уровень: Учебник. М.: ИНФРА-М.
Чеканский А.Н., Фролова НЛ. (2005). Микроэкономика. Промежу-
точный уровень: Учеб, пособие. М.: ИНФРА-М.
* Шерер Ф.М., Росс Д. (1997). Структура отраслевых рынков. М.:
ИНФРА-М.
Шмалензи Р. (2003). Реклама и рыночная структура // Вехи экономи-
ческой мысли. Теория отраслевых рынков. Т. 5. СПб.: Экономи-
ческая школа.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
Экономическая школа. Периодический научно-популярный журнал
(1993). Выпуск 3.
Bertrand J. (1883). Review of theorie mathematique de la richesse sociale
reacherches sur les principes mathematiques de la theorie des richesses
// Journal ofdes Savants, 68, pp. 449-508.
Bowly A. (1924). Groundwork of Economics. Oxford: Oxford University
Press.
Bresnahan T. (1981, 1983). Duopoly Models with Consistent Conjectures
/I American Economic Review, p. 934-945; p. 240-241.
Cournot A. (1838). Recherches sur, les principes mathematiques de la
theorie des richesses. Paris.
Cournot A. (1863). Rrincipes de la'theorie des richesses. Paris.
Fisher I. (1898). Cournot and Mathematical Economics. // Quarterly Jour-
nal of Economics, 12(2), p. 119-138.
834
FrishR. (1933). Monopole—Polypole-La Notion de force dans L’Economie,
Festschrift til Harold Westergaard. Supplement to natiooalerooomisk
Tidsskrift.
Gravelle H., Rees R. (1992). Microeconomic. Longman Group UK
Limited.
Gravelle H., Rees R. (1994). Microeconomic. Solutions Manuel and Work-
book. Longman Group UK Limited.
Kreps D. (1990). A Gorse in Microeconomic Theory. Harvester
Wheatsheaf.
LeontiefW. (1936). Stackelberg on Monopolistic Competition. I I Journal
of Political Economy, p. 554-559.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Stackelberg H. von (1934). Marktform und Gleichgewicht. Wien, Springer.
Vartan H.R. (1992). Microeconomic Analysis. W.W. Norton and
Company.
Глава 9
БабешкоЛ.О., ЛабскерЛ.Г. (2003). Основы теории игр // Экономико-
математическое моделирование. М.: Экзамен.
* Бусыгин В.П., Желободько Е.В., Коковин С.Г., Цыплаков А.А. (2000)
Микроэкономический анализ несовершенных рынков.
Новосибирск.
Бусыгин В.П., Желободько Е.В., Цыплаков А.А. (2003) Микроэкономи-
ка — третий уровень. Новосибирск.
Васин А.А., Морозов В.В. (2005). Теория игр и модели математической
экономики. М.: МАКС-Пресс.
Данилов В.И. (2002). Лекции по теории игр. М.: Российская экономи-
ческая школа.
Интрилигатор М. (1975; 2002). Математические методы оптимизации
и экономическая теория. М.: Прогресс.
Крепе Д.М., Уилсон Р. (2003). Репутация и несовершенная информа-
ция // Вехи экономической мысли. Теория отраслевых рынков.
Т. 5. СПб.: Экономическая школа.
Монте К. (2002). Теория игр и стратегическое поведение // Панорама
экономической мысли конца XX столетия. Т. 1. СПб.: Экономи-
ческая школа: ГУЭиФ: ГУ ВШЭ.
53*
835
Морозов В.В. (2002). Основы теории игр. М.: ФВМК МГУ.
Мулен Э. (1985). Теория игр с примерами из математической эконо-
мики. М.: Мир.
ПетросянЛ.А., Зенкевич Н.А., Семина Е.А. (1998). Теория игр. М.: Вы-
сшая школа: Университет.
* Розен В.В. (2002). Модели принятия решений в экономике. М.: Выс-
шая школа: Университет.
Харшаньи Д., Зельтен Р. (2001). Общая теория выбора равновесия в
играх. СПб.: Экономическая школа: СПб.ГУ.
Черемных Ю.Н. (2004). Элементы теории игр // Количественные ме-
тоды в экономических исследованиях. М.: ЮНИТИ-ДАНА.
* Шикин Е.В. (1997). От игр к играм. Математическое введение. М.:
Эдиториал УРСС.
Akerlof G. (1970). The market for “Lemons”. // Quarterly Journal of Econ-
omies, 90, pp. 629-650.
Aumann R., Maehler M. (1966). Game-theoretic aspects of gradual disar-
mament. —Mathematica ST-80, Chapter V, 1—55.
' Fudenberg D., Tirole J. (2000). Game Theory. The MIT Press.
* Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
NY, Oxford, Part two. Game Theory.
HarsanyiJ.C. (1967—1968). Games with Incomplete Information Played by
“Bayesian” Players. Parts I — III. // Management Science, V. 14, pp.
159-182, 320-334,486-502.
Kuhn H. (1953). Extensive Games and the Problem of Information. Annals
Mathematical Studies of Princeton University Press, № 28.
Milgrom P., Roberts J. (1982a). Limit pricing and entry under incomplete
information. // Econometrica 50, pp. 443-460.
Milgrom P., Roberts J. (1982b). Predation, reputation, and entry deterrence.
// Journal of Economic Theory 27, P. 280—312.
Nash J.F. (1950). Equilibrium Points iin N-Pperson Games. // Proceedings
of the National Academy of Sciences of the United States of America, v.
36, pp. 48-49.
Nash J.F. (1951). Non-Cooperative Games. // Annals of Mathematics,
v.54, pp. 286-295.
Ortega-Reichert A. (1967). Models for competitive bidding under uncer-
tainty, Ph. D. thesis, Stanford University.
836
Selten R. (1965). Spieltheoretische Behandlung eines Oligopolmodells mit
Nachfragetragheit. Parts I-II. // Zeitschrift fur die Gesamte Staatswis-
senschaft, 121, S. 301-324,667-689.
* Shy O. (1995). Industrial Organization. Theory and Applications. The
MIT Press.
Spence A.M. (1974). Market Signaling. Harvard University Press.
Глава 10
Гальперин B.M., Игнатьев C.M., Моргунов В.И. (1997). Микроэконо-
мика. Т. 2. СПб.: Экономическая школа.
* Портер М. (2000). Конкуренция. СПб.; М.; Киев: Вильямс.
Стиглер Дж. (1957; 2000). Совершенная конкуренция: исторический
ракурс // Вехи экономической мысли. Теория фирмы. Т. 2. СПб.:
Экономическая школа.
* Томпсон А., Формби Д. (1998). Экономика фирмы. М.: БИНОМ.
* Юданов А.Ю. (2001). Конкуренция: Теория и практика. М.
Глава И
* Алипрантис К., Браун Д., Бёркекшо О. (1995). Существование и опти-
мальность конкурентного равновесия. М.: Мир.
Белоусов Е.Г., Курош Н.А. (2003). Линейная алгебра: операции над
множествами. М.: ТЕИС.
Блауг М. (1994). Экономическая мысль в ретроспективе. М.: Дело.
Вальрас Л. (2000). Элементы чистой политической экономии, или
Теория общественного богатства. М.: Изограф.
Вереникин А.О. (2004). Общее экономическое равновесие при возрас-
тающей отдаче от масштабов производства. // Вестник Москов-
ского университета. Серия 6. Экономика. № 5.
Гильдебранд В. (1986). Ядро и равновесие в большой экономике. М.:
Наука.
* Данилов-Данильян В.И. (2003). Экономического равновесия моде-
ли // Экономико-математический энциклопедический словарь.
М.: БРЭ: ИНФРА-М.
* Карлин С. (1964). Математические методы в теории игр, программи-
ровании и экономике. М.: Мир.
Макаров В.Л. (1982). Экономическое равновесие: существование и
экстремальное свойство // Итоги науки техники. Современные
проблемы математики. Т. 19. М.
837
Математический энциклопедический словарь. (1988). М.: Советская
энциклопедия. Статья Огибающая.
Негиши Т. (1995). История экономической теории. М.: Аспект-
Пресс.
* Никайдо X. (1972). Выпуклые структуры и математическая экономи-
ка. М.: Мир.
Полтерович В.М. (1990). Экономическое равновесие и хозяйствен-
ный механизм. М.: Наука.
Полтерович В.М. (2003). Экономического равновесия теория // Эко-
номико-математический энциклопедический словарь. М.: БРЭ:
ИНФРА-М.
Селигмен Б. (1968). Основные течения современной экономической
мысли. М.: Прогресс.
УзллиДж. (2002). Прикладные модели общего равновесия // Панора-
ма экономической мысли конца XX столетия. Т. 2. СПб.
Экланд И. (1983). Элементы математической экономики. М.: Наука.
Arrow K.J., Debreu G. (1954). Existence of an equilibrium for a competitive
economy. // Econometrica, v. 22, No. 3.
Gale D. (1955). The law of supply and demand. // Journal of Mathematical
Economics, v. 3.
General equilibrium: Problems, Prospects and Alternatives. (1999). XXI
Workshop. Italy, Siena.
Kakutani S. (1941). A generalization of Brouwer’s fixed point theorem. I I
Duke Mathematical Journal, v. 8, p. 281-314.
McKenzie L.W. (1954). On equilibrium in Graham’s model of trade and
other competitive systems. // Econometrica, v. 22, No. 2.
McKenzie L. W. (1959). On the existence of general equilibrium for a com-
petitive market. // Econometrica, 27, pp. 54-71.
Sonnenschein H. (1973). Do Walras’ identity and continuity characterize
the class of community excess demand functions? // Journal of Eco-
nomic Theory, v. 6, pp. 345-354.
Глава 12
Вехи экономической мысли. Экономика благосостояния и обще-
ственный выбор. Т. 4. (2004). СПб.: Экономическая школа.
838
Гаврилец Ю.Н. (2003). Общественного благосостояния функция //
Экономико-математический энциклопедический словарь. М.:
БРЭ: ИНФРА-М.
* Гальперин В.М., Игнатьев С.М., Моргунов В.И. (1997). Микроэконо-
мика. В 2 т. Т. 2. СПб.: Экономическая школа: ГУЭИ: ГУ ВШЭ.
'Интрилигатор М. (1975, 2002). Математические методы оптимиза-
ции и экономическая теория. М.: Прогресс.
'Карлин С. (1964). Математические методы в теории игр, программи-
ровании и экономике. М.: Мир.
Кац М., Роузен X. (2004). Микроэкономика. Минск: Новое знание.
Мюллер Д. (2002). Теория общественного выбора // Панорама эконо-
мической мысли конца XX столетия. В 2 т. Т. 1. СПб.: Экономи-
ческая школа: ГУЭИ: ГУ ВШЭ.
* Никайдо X. (1972). Выпуклые структуры и математическая экономи-
ка. М.: Мир.
Нуреев Р.М. (2005). Теория общественного выбора. М.: ГУ ВШЭ.
Роулз Дж. (1995). Теория справедливости. Н.
'Стиглиц Дж.Ю. (1997). Экономика государственного сектора. М.:
Изд-во МГУ: ИНФРА-М.
Эрроу КДж. (2004). Коллективный выбор и индивидуальные ценнос-
ти. М.: ГУ ВШЭ.
Arrow К. (1950). A Difficulty in the Concept of Social Welfare. // Journal of
Political Economy, 58, N 3.
Mas-ColellA., Whinston M.D., Green J.R. (1995). Microeconomic Theory.
N-Y, Oxford: Oxford University Press.
Глава 13
Вальрас Л. (2000). Элементы чистой политической экономии, или
Теория общественного богатства. М.: Изограф.
'Интрилигатор М. (1975, 2002). Математические методы оптимиза-
ции и экономическая теория. М.: Прогресс.
'Карлин С. (1964). Математические методы в теории игр, программи-
ровании и экономике. М.: Мир.
Allais М. (1952). Traite d’economie pure. Paris: Impremerie Nationale.
Arrow K.J., Block D., Hurwicz L. (1959). On the stability of the competitive
equilibrium, II. // Econometrica, 27, pp. 82—109.
839
General Equilibrium: Problems, Prospects and Alternatives. (1999). XII
Workshop. Italy, Siena.
Hahn F.H. (1958). Gross substitutes and the dynamic stability of general
equilibrium. // Econometrica, 26, pp. 169—170.
Hicks J.R. (1953). Value and capital. Oxford.
McKenzie L.W. (1956—1957). Demand theory without an utility index. //
Review of Economic Studies, 24, pp. 185—189.
Metzler L.A. (1945). Stability of multiple markets: the Hicks conditions. //
Econometrica, 13, pp. 277—292.
Mosak J.L. (1944). General equilibrium theory in international trade.
Bloomington (Indiana).
Negishi T. (1962). The stability of a competitive economy: a survey article.
I I Econometrica, 30, pp. 635-669.
Uzawa H. (1960). Walras tatonnement in the theory of exchange. // Review
of Economic Studies, 27, pp. 182—194.
Uzawa H. (1961). The stability of dynamic processes. // Econometrica, 29,
pp. 617-631.
Глава 14
Алъсевич В.В. (2004). Введение в математическую экономику. Кон-
структивная теория. М.: Едиториал УРСС.
* Черемных Ю.Н. (1987). Математическое моделирование народнохо-
зяйственной динамики. М.: Знание.
* Черемных Ю.Н. (1982). Анализ траекторий динамики народнохо-
зяйственных моделей. М.: Наука.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
Кетепу J.G., Morgenstern О., Thompson G.L. (1956). A Generalization of
the von Neumann Model of an Expanding Economy. // Econometrika,
v. 24, № 2.
Neumann J. von (1945—1946). A Model of General Economic Equilibrium.
//Review of Economic Studies, v. 13(1), № 33.
Глава 15
* Гальперин B.M., Игнатьев C.M., Моргунов В.И. (1997). Микроэконо-
мика. Т. 2. СПб.: Экономическая школа.
840
* Пиндайк Р., Рубинфелъд Д. (2000). Микроэкономика. М.: Экономи-
ка: Дело.
ПирсД.У. (2002). Экономика окружающей среды // Панорама эконо-
мической мысли конца XX столетия. Т. 1. СПб.: Экономическая
школа: ГУЭИ: ГУ ВШЭ.
Экономическая школа. Журнал-учебник (1995). Выпуск 5.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Глава 16
* Гальперин B.M., Игнатьев C.M., Моргунов В.И. (1997). Микроэконо-
мика. Т. 2. СПб.: Экономическая школа.
* Пиндайк Р., Рубинфелъд Д. (2000). Микроэкономика. М.: Экономи-
ка: Дело.
Полищук Л.И. (2003). Микроэкономическая теория: проблемы асим-
метричной информации и общественных благ. М.: Российская
экономическая школа.
* Экономическая школа: Журнал-учебник (1999). Выпуск 5.
Foley D.K. (1970). Lindahl’s Solution and the Core of an Economy with
Public Goods. I I Econometrica, vol. 38, Issue 1.
Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Глава 17
Акерлоф Дж. (1970; 1994). Рынок «лимонов»: неопределенность ка-
чества и рыночный механизм // THESIS. № 5.
* Пиндайк Р., Рубинфелъд Д. (2000). Микроэкономика. М.: Экономи-
ка: Дело.
Полищук Л.И. (2003). Микроэкономическая теория: проблемы асим-
метричной информации и общественных благ. Препринт
№ KL/2003/009. М.: Российская экономическая школа.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
Экономическая школа. Журнал-учебник (1999). Выпуск 5.
* Юдкевич М.М., Подколзина Е.А., Рябинина А.Ю. (2002). Основы тео-
рии контрактов: модели и задачи: Учеб, пособие. М.: ГУ ВШЭ.
841
* Mas-Colell A., Winston M.D., Green J.R. (1995). Microeconomic Theory.
Oxford University Press.
Rothschild M., Stiglitz J.E. (1976). Equilibrium incompletitive insurance
markets: An essay in the economics of imperfect information. // Quar-
terly Journal of Economics, 80, pp. 629—649.
Salanie B. (1997). The Economics of Contracts: A Primer. Boston, Mass.:
MIT Press.
SpensA.M. Job Market Signaling// Quarterly Journal of Econom-
ics, № 87, pp. 355-374.
Shapiro C., Stiglitz J.E. (1984). Equilibrium unemployment as a worker
displine device I I American Economic Review, V. 74, № 3.
Wilson C. (1976). A model of insurance markets with incomplete informa-
tion // Journal of Economic Theory, 16, pp. 167—207.
Глава 18
Барсукова С.Ю. (2004). Неформальная экономика: экономико-соци-
ологический анализ. М.: ГУ ВШЭ.
Богданович А. (2001). Покупайте отечественное//Эксперт. № 31.
Глинкина С.П. (2001) Теневая экономика в глобализирующемся мире
И Проблемы прогнозирования. № 4.
Глобализация мирового хозяйства и национальные интересы России
(2002) / Под ред. В.П. Колесова. М.: Экономический факультет
МГУ: ТЕИС.
Джунусов М.С. (1998). Национализм: Словарь-справочник. М.
Загашвили В.С. (1997). Экономическая безопасность России. М.:
Юристь.
Исправников В.О., Куликов В.В. (1997). Теневая экономика в России:
иной путь и третья сила // Российский экономический журнал:
Фонд «За экономическую грамотность».
Мишель Л. Экономический национализм против мировой экономи-
ки, http://elem2000.virtualave.net.4econat.html
Некипелов А.Д. (2001). Глобализация и стратегия развития экономики
России // Проблемы прогнозирования. № 4.
Практика глобализации: игры и правила новой эпохи (2000). М.:
ИНФРА-М.
Рокер Р. Опасность национальной идеологии, http://elem2000.virtuala-
ve.net.4econat.html
842
Савченко А. Я сделал бы ставку на экономический национализм,
http://gs.com.ua/rus/gs/nomer/2000/2000-34/34tema2.html
* Судоплатов А.П., Лекарев С.В. (2001). Безопасность предпринима-
тельской деятельности. М.: ОЛМА-ПРЕСС.
Черемных Ю.Н. (2000). О влиянии научно-технического прогресса в
компьютеризации и информатике на современную экономику //
Философия хозяйства. № 6 (12).
Шишков А. (2001). Внешнеэкономические связи в XX в. — от упадка к
глобализации // Мировая экономика и международные отноше-
ния. № 8.
Щербаков В.И. (2003). Проблемы выработки промышленной полити-
ки в России. Международная Академия Менеджмента. Научные
труды. Выпуск IV. М.
Р.А. Эксперт, http://www.raexpert.ru
Magazine.ru, www.magazine.ru
“The emeiging digital economy”
Приложение
Математический энциклопедический словарь (1988). М.: Советская
энциклопедия.
СюдсетерК., Стрем А., Берк П. (2000). Справочник по математике для
экономистов. СПб.: Экономическая школа.
Экономико-математический энциклопедический словарь (2003). М.:
Большая Российская Энциклопедия: ИНФРА-М.
По вопросам приобретения книг обращайтесь:
Отдел продаж «ИНФРА-М» (оптовая продажа):
127282, Москва, ул. Полярная, д. 31 в, тел.: (495) 380-4260; факс: (495) 363-9212
E-mail: books@infra-m.ru
•
Магазин «Библиосфера» (розничная продажа):
109147, Москва, ул. Марксистская, д. 9, тел. (495) 670-5218, 670-5219
•
Отдел «Книга—почтой»:
тел. (495) 363-4260 (цоб. 232,246)
•
Центр комплектования библиотек:
119019, Москва, ул. Моховая, д. 16, (Российская государственная библиотека, кор. К)
тел. (495) 202-9315
Учебное издание
Юрий Николаевич Черемных
МИКРОЭКОНОМИКА
Продвинутый уровень
Учебник
Редактор З.А. Басырова
Корректор Л.С, Куликова
Компьютерная верстка О.В. Савостиной, С.М. Майорова
* ЛР№ 070824 от 21.01.93.
Сдано в набор 10.12.2006. Подписано в печать 20.06.07.
Формат 60 х 90!/16. Бумага офсетная. Гарнитура Newton.
Печать офсетная. Усл. печ. л. 53,0. Уч.-изд. л. 48,1.
Тираж 30 000 экз. (1 — 2500 экз.). Заказ № 7620.
Цена свободная.
Издательский Дом «ИНФРА-М»
127282, Москва, Полярная ул., д. 31 в.
Тел.: (495) 380-05-40, 380-05-43. Факс: (495) 363-92-12.
E-mail: books@infra-m.ru; http://www.infra-m.ru
Отпечатано с готовых диапозитивов в ОАО ордена «Знак Почета»
«Смоленская областная типография им. В. И. Смирнова».
214000, г. Смоленск, проспект им. Ю. Гагарина, 2.
книги
ИНФРА-М
ПОЧТОЙ
ООО «Издательский Дом ИНФРА-М» осуществляет рассылку книг по почте
на территории Российской Федерации.
Информацию о наличии книг можно получить, воспользовавшись прайс-листом
Издательского Дома «ИНФРА-М», который можно бесплатно заказать и получить
по почте. Также информацию о книгах можно посмотреть
на сайте http.//www.infra-m.ru в разделах «Прайс-лист»
и «Иллюстрированный каталог».
Для оформления заказа необходимо прислать заявку, где следует указать:
- для организаций;
название, полный почтовый адрес, банковские реквизиты (ИНН/КПП). номера
телефона, факса, контактное лицо (получателя), наименование книг.
их количество;
- для частных лиц;
Ф.И.О., полный почтовый адрес, номер телефона для связи, наименование книг,
их количество.
шннпнмммннннншнм
При заполнении заявки необходимо указывать код книги, что значительно
ускорит оформление Вашего заказа.
Заказ оформляется по оптовым ценам, указанным в прайс-листе. На основании
заявки Вам будет выставлен счет на имеющуюся в наличии литературу с учетом
почтовых расходов (при сумме заказа свыше 5000 рублей, предоставляются скидки).
Произвести оплату вы можете:
по безналичному расчету:
перечислите сумму на расчетный счет ООО «Издательский Дом ИНФРА-М»;
за наличный расчет;
- на почте: почтовым переводом отправьте сумму на расчетный счет
ООО «Издательский Дом ИНФРА-М»:
- в отделении Сбербанка: по квитанции-извещению на сумму счета, где получатель
платежа - ООО «Издательский Дом ИНФРА-М».
В течение 5 рабочих дней с момента зачисления денежных средств на расчетный счет
заказ будет подобран и отправлен по указанному в заявке адресу
с сопроводительными документами (счет-фактура, накладная).
Заявку можно прислать по факсу или по адресу, указанным ниже.
127282, г, Москва, ул. Полярная, д. 31 в
Телефон: (495) 363-4260 (доб.: 246,247)
Факс: (495) 363-4260 (доб. 232)
E-mail: podplska@lnfra-m.ru
С 2004 года
ИЗДАТЕЛЬСКИЙ ДОМ
«ИНфРА-М»
ВЫПУСКАЕТ СЕРИЮ
«УЧЕБНИКИ ЭКОНОМИЧЕСКОГО
ФАКУЛЬТЕТА МГУ
им. М.В. ЛОМОНОСОВА»
Я Я WWhoc.M .....—«
ичси» *л1>«к«е*
________ ЭКОНОМИКА
—иша^памЗОВАНИЛ
«вдижна# **^*ysgg^ -»wrH
А.Й
жюзшоша
ГЖЦЯК
«аскмимй >xx»irc*rn
г---— «... И«0К>Ш4 ——]
ммяхтамй *миш<
Ии»
ВП. К«ш«*»МВ- Кчъ.- ч
иипПйЛ/м: £ 0, (Д *ч4ф«Л •-'
МАКРОЭКОНОМИКА
ЮУВАРОДШ
ЭКОНОМИКА
ЗДьнмш
о ЭКОНОМИКА
ПРИРОДОПОЛЬЗОВАНИЯ
о ИНСТИТУЦИОНАЛЬНЫЕ АСПЕКТЫ
ОРГАНИЗАЦИИ МАЛОГО БИЗНЕСА
В РАЗВИТЫХ СТРАНАХ И В РОССИИ
О ИНСТИТУЦИОНАЛЬНЫЕ
СОГЛАШЕНИЯ В УСЛОВИЯХ
ЕСТЕСТВЕННОЙ МОНОПОЛИИ
О ВВЕДЕНИЕ В ЭКОНОМИЧЕСКУЮ
ТЕОРИЮ КОНТРАКТОВ
О КОНКУРЕНТОСПОСОБНОСТЬ
КООПЕРАЦИИ В ПЕРЕХОДНОЙ
ЭКОНОМИКЕ: ИНСТИТУЦИОНАЛЬНЫЙ
ПОДХОД
О ПРОЕКТНЫЙ АНАЛИЗ:
ПРОДВИНУТЫЙ КУРС
о МЕЖДУНАРОДНАЯ ПРАКТИКА УЧЕТА
И ОТЧЕТНОСТИ
О МАКРОЭКОНОМИКА. ЭЛЕМЕНТЫ
ПРОДВИНУТОГО ПОДХОДА
Учебники и учебные пособия серии -
новое поколение учебников для университетского
экономического образования.
По многим дисциплинам они выпускаются впервые
в стране и создают основу для полноценной подготовки
экономистов высшего звена.
О ФИНАНСЫ ПРЕДПРИЯТИЙ-. МЕНЕДЖМЕНТ И АНАЛИЗ
О ЭКОНОМИЧЕСКАЯ ИНФОРМАТИКА. ВВЕДЕНИЕ
В ЭКОНОМИЧЕСКИЙ АНАЛИЗ ИНФОРМАЦИОННЫХ СИСТЕМ
О ОСНОВЫ ИНСТИТУЦИОНАЛЬНОЮ ПРОЕКТИРОВАНИЯ
О ПРАВО И ЭКОНОМИЧЕСКАЯ ТЕОРИЯ
О ПЕРВЫЕ СИСТЕМЫ ПОЛИТИЧЕСКОЙ ЭКОНОМИИ
О ЭКОНОМИЧЕСКОЕ МЫШЛЕНИЕ-. ФИЛОСОФСКИЕ ПРЕДПОСЫЛКИ
О МИКРОЭКОНОМИКА-. ПРОМЕЖУТОЧНЫЙ УРОВЕНЬ
О СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЕ ПРОБЛЕМЫ РОССИИ
О ИНСТИТУЦИОНАЛЬНЫЙ АНАЛИЗ ИНТЕЛЛЕКТУАЛЬНОЙ
СОБСТВЕННОСТИ
О ЭКОНОМИЧЕСКАЯ ДЕМОГРАФИЯ
О НАЦИОНАЛЬНЫЕ БАНКОВСКИЕ СИСТЕМ
О ЭКОНОМИЧЕСКАЯ КОМПАРАТИВИСТИКА
О ПУТИ РАЗВИТИЯ ЭКОНОМИКИ РОССИИ
О ИСТОРИЯ УПРАВЛЕНЧЕСКОЙ МЫСЛИ
О ЦЕНООБРАЗОВАНИЕ
О МИКРОЭКОНОМИКА
О БУХГАЛТЕРСКИЙ УЧЕТ
О АНАЛИЗ ОТРАСЛЕВЫХ РЫНКОВ
О МЕЖДУНАРОДНАЯ ЭКОНОМИКА
О ИНСТИТУЦИОНАЛЬНАЯ ЭКОНОМИКА
О САМОРЕГУЛИРОВАНИЕ БИЗНЕСА
О ТЕОРИИ ИНСТИТУЦИОНАЛЬНЫХ ИЗМЕНЕНИЙ
I
ПРОЕКТНЫЙ
АНАЛИЗ
УЧЕЯНЖ
С И
О В :
Более 60 000
наименований
литературы
Более 10 000
канцелярских
товаров
Скидки
покупателям
Принимаются
к оплате кредитные
карты
КНИЖНЫЙ СУПЕРМАРКЕТ
Адрес: м. “Пролетарская”,
ул. Марксистская, д.9,
выход из метро к Абельмановской ул.
Контактные телефоны:
(495) 670-52-17
(495) 670-52-18
(495) 670-52-19
Часы работы:
с 10.00 до 20.00
воскресенье:
с 10.00 до 19.00
без перерыва на обед
Сайт в интернете: www.bibliosfera-DDK.ru