Дж.А. Джейли
Ф.Дж. Рени
МИКРО
ЭКОНОМИКА

Geoffrey A. Jehle
Vassar College
Philip J. Reny
University of Chicago
ADVANCED
MICROECONOMIC
THEORY
Second edition

Дж.А. Джейли
Ф.Дж. Рени
МИКРО
ЭКОНОМИКА
Продвинутый
уровень
Учебник
Перевод с английского под научной редакцией
В.П. Бусыгина, М.И. Левина, Е.В. Покатович
ш
Издательский дом
Государственного университета — Высшей школы экономики
Москва, 2011

УДК 330.101.542
ББК 65.012.1
Д40
Подготовлено при содействии НФПК —
Национального фонда подготовки кадров в рамках
программы «Совершенствование преподавания
социально-экономических дисциплин в вузах»
Перевод с английского:
Е.В. Покатович (предисловие, гл. 1, 2, 3, 5), Е.И. Фатеева (гл. 4, 8),
Г.Г. Покатович (гл. 6, 9), ЕЛ. Левина (гл. 7), КЛ. Букин (гл. Al, A2)
Научные редакторы
В.П. Бусыгин, М.И. Левин, Е.В. Покатович
Authorized translation from the English language edition, entitled
ADVANCED MICROECONOMIC THEORY, 2nd Edition, ISBN 0321079167,
by Jehle, Geoffrey A. and Reny, Philip J., published by Pearson Education, Inc.
publishing as Addison->\fesley.
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any
means, electronic or mechanical, including photocopying, recording by any information storage
retrieval system, without permission from Pearson Education, Inc.
Russian language edition published by the University — Higher School of Economics.
Авторизованный перевод с английского языка книги
Джеффри А. Джейли и Филипа Дж. Рени «Микроэкономика: продвинутый уровень», 2-е изд.,
ISBN 0321079167, изданной Pearson Education, Inc. и опубликованной Addison-Wesley.
ISBN 0-321-07916-7 (англ.) Copyright © 2001 Geoffrey A. Jehle and Philip J. Reny
ISBN 978-5-7598-0362-1 (рус.) © Перевод на русский язык.
Государственный университет —
Высшая школа экономики, 2011
© Оформление. Издательский дом
Государственного университета —
Высшей школы экономики, 2011

ОГЛАВЛЕНИЕ
Предисловие (перевод Е.В. Покатович) 9
Часть I. Экономические агенты
Глава 1. Теория потребителя (перевод Е.В. Покатович) 13
1.1. Базовые понятия 13
1.2. Предпочтения и полезность 15
1.2.1. Отношение предпочтения 16
1.2.2. Функция полезности 26
1.3. Задача потребителя 34
1.4. Косвенная полезность и расходы 44
1.4.1. Косвенная функция полезности 44
1.4.2. Функция расходов 51
1.4.3. Связь между косвенной функцией полезности
и функцией расходов 60
1.5. Свойства потребительского спроса 68
1.5.1. Относительные цены и реальный доход 68
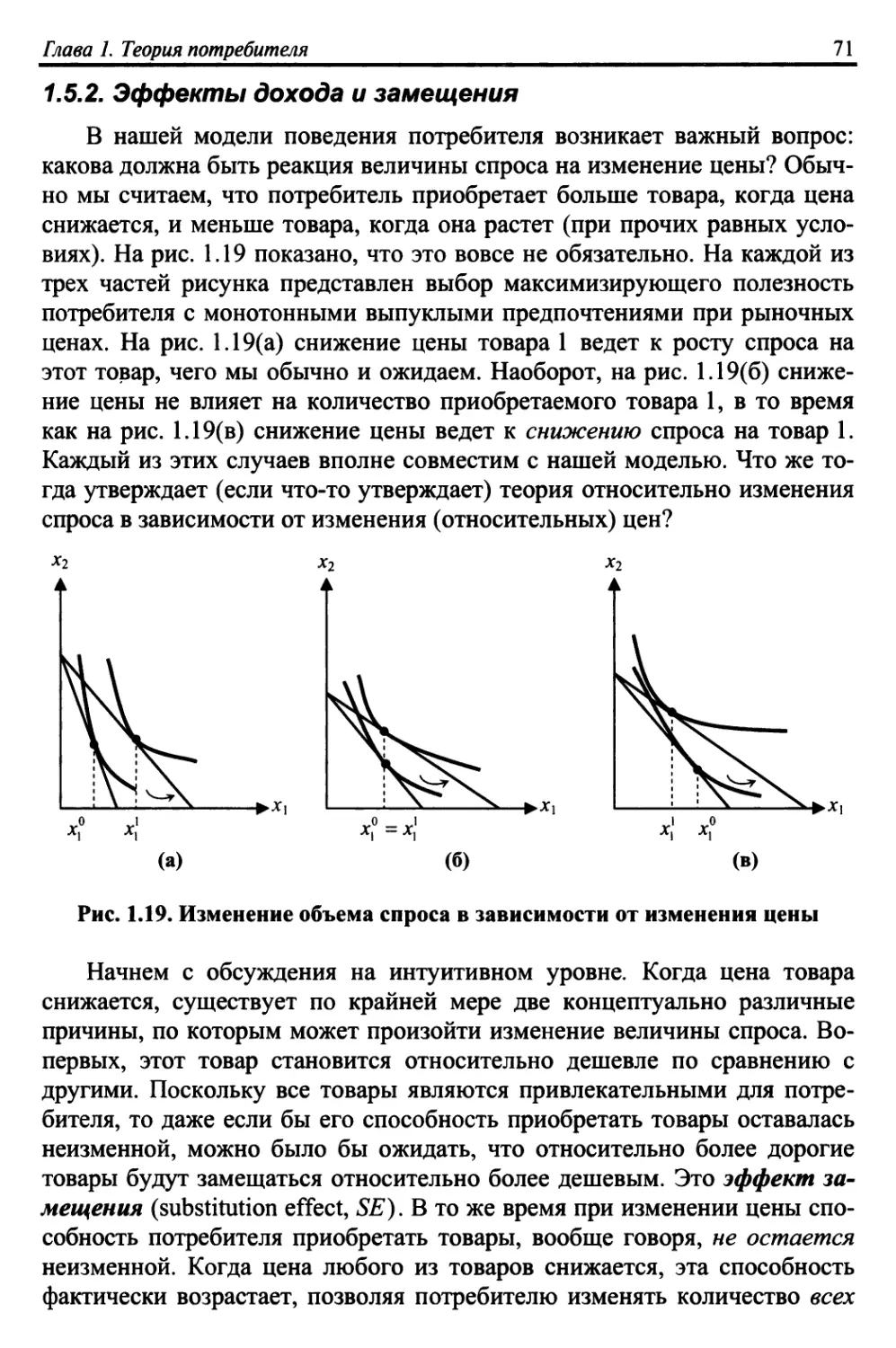
1.5.2. Эффекты дохода и замещения 71
1.5.3. Некоторые соотношения между эластичностями 82
1.6. Упражнения 86
Глава 2. Продолжение теории потребителя (перевод Е.В. Покатович) 97
2.1. Подробнее о двойственности 97
2.1.1. Расходы и предпочтения потребителя 97
2.1.2. Выпуклость и монотонность 103
2.1.3. Косвенная полезность и предпочтения потребителя 106
2.2. Восстановление функции полезности 111
2.3. Выявленные предпочтения 118
2.4. Неопределенность 126
2.4.1. Предпочтения 127
2.4.2. Функция полезности фон Неймана — Моргенштерна 132
2.4.3. Несклонность к риску 143
2.5. Упражнения 153
Глава 3. Теория фирмы (перевод Е.В. Покатович) 160
3.1. Базовые понятия 160
3.2. Производство 161
3.2.1. Отдача от масштаба и изменения пропорций 168
3.3. Издержки 171
3.4. Двойственность в производстве 182
3.5. Конкурентная фирма 183
3.5.1. Максимизация прибыли 184
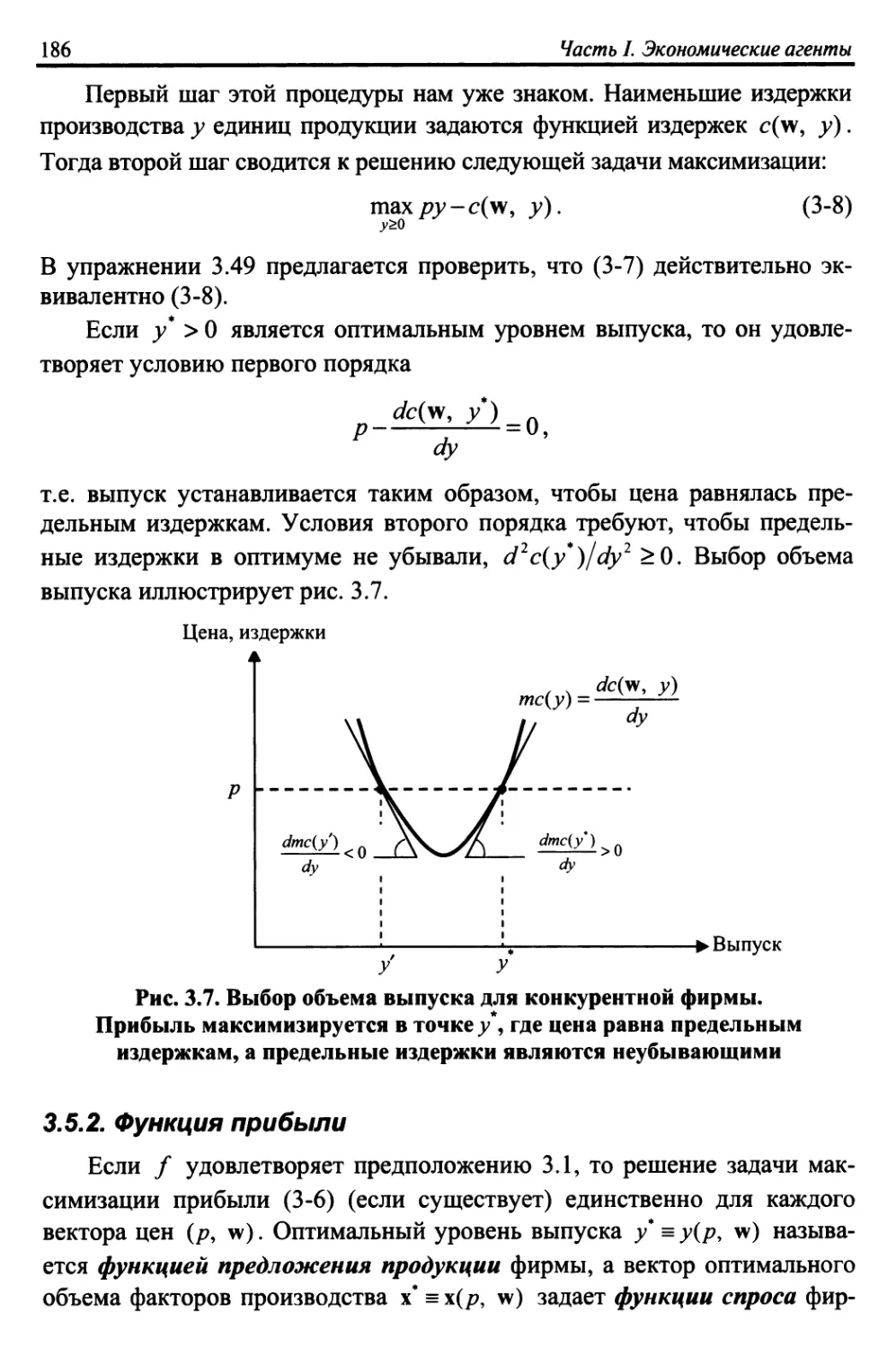
3.5.2. Функция прибыли 186
3.6. Упражнения 195

6 Оглавление
Часть II. Рынки и благосостояние
Глава 4. Частичное равновесие {перевод Е.И. Фатеевой) 207
4.1. Совершенная конкуренция 207
4.2. Несовершенная конкуренция 213
4.2.1. Олигополия Курно 217
4.2.2. Олигополия Бертрана 219
4.2.3. Монополистическая конкуренция 221
4.3. Равновесие и благосостояние 224
4.3.1. Цена и индивидуальное благосостояние 224
4.3.2. Эффективность конкурентного рынка 230
4.3.3. Эффективность и максимизация совокупного излишка 233
4.4. Упражнения 236
Глава 5. Общее равновесие (перевод Е.В. Покатович) 245
5.1. Равновесие в экономике обмена 246
5.2. Равновесие в конкурентных рыночных системах 253
5.2.1. Существование равновесия 254
5.2.2. Эффективность 266
5.3. Равновесие в экономике с производством 276
5.3.1. Производители 276
5.3.2. Потребители 280
5.3.3. Равновесие 282
5.3.4. Благосостояние 291
5.4. Ядро и равновесия 296
5.4.1. Реплицированные экономики 297
5.5. Упражнения 311
Глава 6. Общественный выбор и благосостояние
(перевод Г.Г. Покатовича) 321
6.1. Суть проблемы 321
6.2. Общественный выбор и теорема Эрроу 323
6.2.1. Графическое доказательство 330
6.3. Измеримость, сравнимость и дополнительные возможности 337
6.3.1. Роулзианская форма 340
6.3.2. Утилитаристская форма 343
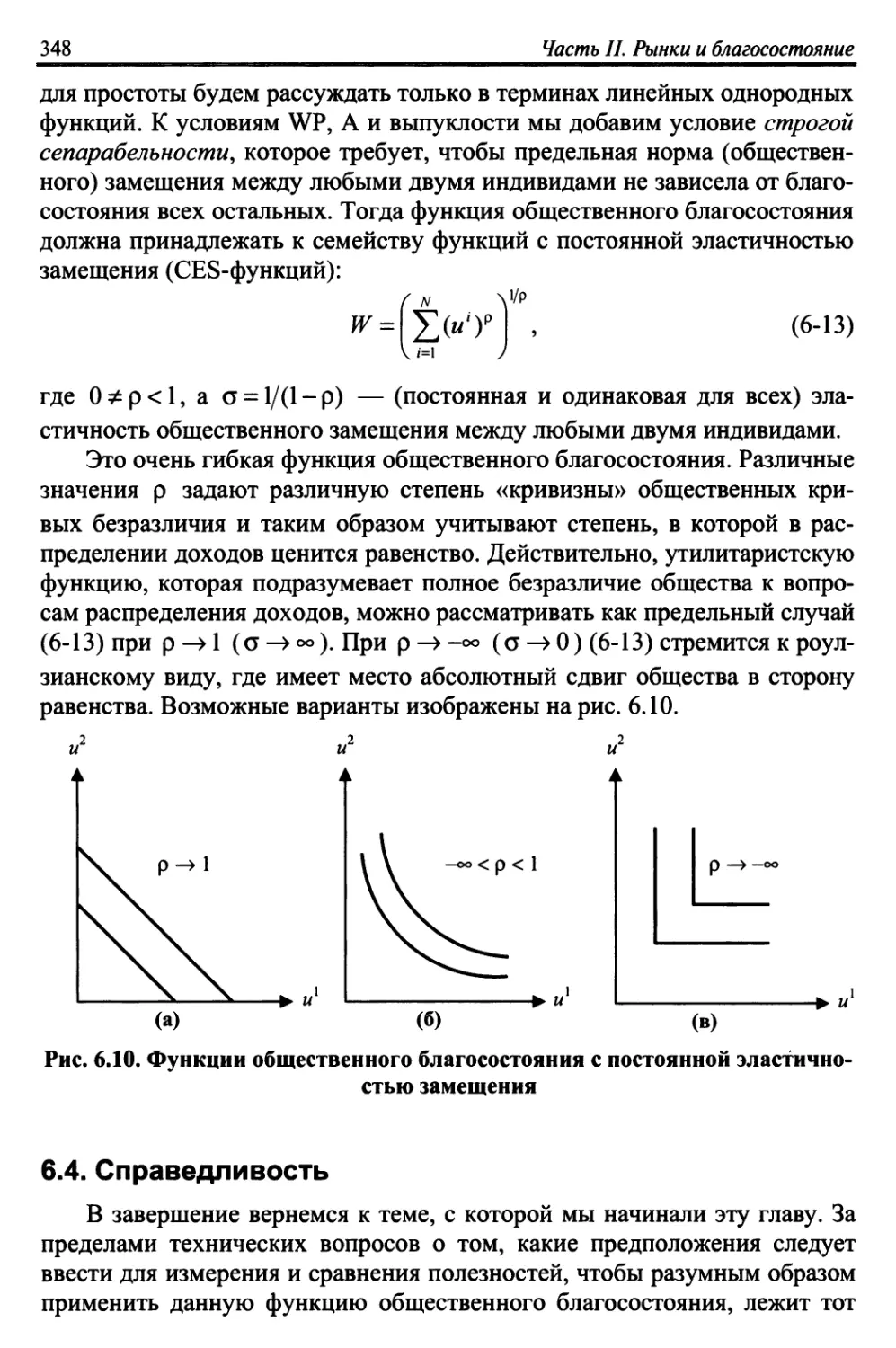
6.3.3. Гибкие формы .. 345
6.4. Справедливость 348
6.5. Упражнения 351
Часть III. Стратегическое поведение
Глава 7. Теория игр (перевод Е.А. Левиной) 359
7.1. Стратегическое принятие решения 359
7.2. Игры в стратегической форме 362
7.2.1. Доминирующие стратегии 363

Оглавление 7
7.2.2. Равновесие по Нэшу 368
7.2.3. Неполная информация 378
7.3. Игры в развернутой форме 385
7.3.1. Дерево игры: графическое представление 389
7.3.2. Неформальный анализ игры «Кто последний» 391
7.3.3. Стратегии в играх в развернутой форме 393
7.3.4. Стратегии и выигрыши 394
7.3.5. Игры с совершенной информацией и стратегии,
полученные обратной индукцией 395
7.3.6. Игры с несовершенной информацией и совершенное
в подыграх равновесие 401
7.3.7. Секвенциальное равновесие 415
7.4. Упражнения 436
Глава 8. Экономика информации (перевод Е.И. Фатеевой) 444
8.1. Неблагоприятный отбор 445
8.1.1. Информация и эффективность рыночных исходов 445
8.1.2. Рыночные сигналы 453
8.1.3. Скрининг 477
8.2. Моральный риск и модель контрактных отношений 489
8.2.1. Симметричная информация 491
8.2.2. Асимметричная информация 493
8.3. Информация и функционирование рынка 498
8.4. Упражнения 499
Глава 9. Аукционы и создание механизмов (перевод Г.Г. Покатовича) .... 504
9.1. Четыре стандартных аукциона 504
9.2. Модель независимых частных оценок 505
9.2.1. Поведение на аукционе первой цены 506
9.2.2. Поведение на голландском аукционе 510
9.2.3. Поведение на аукционе второй (скрытой) цены 511
9.2.4. Поведение на английском аукционе 513
9.2.5. Сравнение доходов 514
9.3. Теорема об эквивалентности доходов 517
9.3.1. Совместимые по стимулам механизмы прямой продажи 519
9.3.2. Эффективность 524
9.4. Максимизация дохода: приложение теории
создания механизмов 524
9.4.1. Индивидуальная рациональность 525
9.4.2. Оптимальный механизм продажи 526
9.4.3. Оптимальный механизм продажи: детали 531
9.4.4. Эффективность, симметрия и сравнение с четырьмя
стандартными аукционами 534
9.5. Упражнения 537

8 Оглавление
Математическое приложение
Глава А1. Множества и отображения (перевод К.А. Букина) 547
А1.1. Элементы логики 547
А1.1.1. Необходимость и достаточность 547
А1.1.2. Теоремы и доказательства 548
А1.2. Элементы теории множеств 550
А1.2.1. Обозначения и основные понятия 550
А.1.2.2. Выпуклые множества 553
А1.2.3. Отношения и функции 557
А1.3. Немного топологии 561
А1.3.1. Непрерывность 573
А1.3.2. Некоторые теоремы существования 581
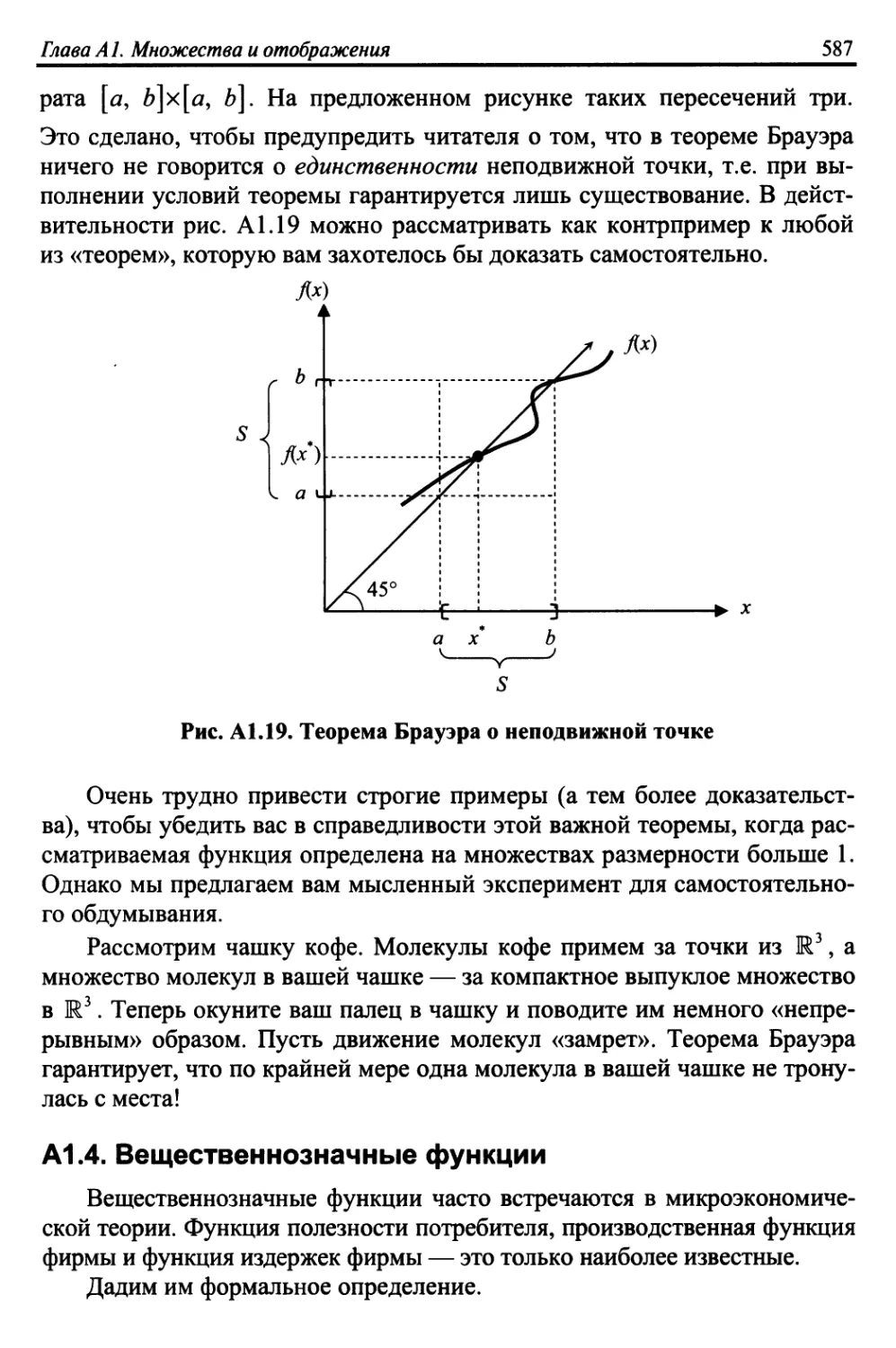
А1.4. Вещественнозначные функции 587
А1.4.1. Соответствующие множества 589
А1.4.2. Вогнутые функции 594
А1.4.3. Квазивогнутые функции 600
А1.4.4. Выпуклые и квазивыпуклые функции 605
А1.5. Упражнения 609
Глава А2. Математический анализ и оптимизация
(перевод К.А. Букина) 616
А2.1. Математический анализ 616
А2.1.1. Функции одной переменной 616
А2.1.2. Функции многих переменных 619
А2.1.3. Однородные функции 629
А2.2. Оптимизация 633
А2.2.1. Вещественнозначные функции многих переменных 636
А2.2.2. Условия второго порядка 639
А2.3. Условная оптимизация 647
А2.3.1. Ограничения в виде равенств 648
А2.3.2. Метод Лагранжа 649
А2.3.3. Геометрическая интерпретация 657
А2.3.4. Условия второго порядка 661
А2.3.5. Ограничения в виде неравенств 665
А2.3.6. Условия Куна — Таккера 669
А2.4. Функции значений 672
А2.5, Упражнения 678
Список теорем 684
Список определений 689
Ответы и указания 692
Список литературы 702
Предметный указатель 707

Посвящается
Ране и Камрану (B.A.J.);
Диане, Лизе и Элизабет (P.T.R.)
ПРЕДИСЛОВИЕ
В каждой главе нового издания книги нашей целью остается
изложение современного ядра микроэкономической науки. Мы по-прежнему
полагаем, что такой подход позволяет внимательному читателю добиться
глубокого понимания оснований современной микроэкономики и увидеть
взаимосвязи между ними. Мы благодарны многочисленному отряду
студентов и коллег, которые поддерживают нас в этом.
В конце каждой главы есть упражнения, и проработка максимально
возможного числа из них является самым надежным способом освоения
материала. Подсказки и ответы к некоторым упражнениям приведены в
конце книги вместе со списками теорем и определений, встречающихся
в тексте. Мы также планируем вести форум в Интернете, где
читатели смогут обмениваться решениями задач из книги (адрес форума:
http://alfred.vassar.edu).
При подготовке второго издания мы воспользовались возможностью
внести одно крупное структурное изменение. Поскольку все больше
студентов поступают на магистерские программы, имея хорошую
математическую подготовку, мы решили, что необходимую чистую математику
можно вынести в приложение. Таким образом, она по-прежнему будет
доступна тем, кому нужно освежить знания или восполнить пробелы в
подготовке, но не станет помехой преподавателям, которые чувствуют,
что их студенты достаточно подготовлены, чтобы погрузиться в
микроэкономическую теорию. Две полноценные главы математического
приложения по-прежнему содержат подробное и практически
самостоятельное изложение теории множеств? элементов математического анализа,
топологии и современной теории оптимизации, которые являются
неотъемлемыми частями современной микроэкономики. Изложение
ведется формально, но не требует особых предварительных знаний помимо
сведений из теории функций одной переменной и простой линейной
алгебры. Даже студентам с очень хорошей математической подготовкой мы
рекомендуем вначале просмотреть обе главы приложения. Тогда, если
потребуется что-то уточнить или повторить, читатель будет знать, как
организован этот материал.
Основная структура остального текста не изменилась.
Часть I посвящена современной теории поведения потребителя и
производителя. Вначале мы рассматриваем теорию поведения потребите-

10
Предисловие
ля, причем довольно подробно — по причине ее важности как таковой, а
также потому, что ее методы и результаты применяются во многих
других областях микроэкономики. Далее следует теория поведения
производителя, и мы обращаем внимание на формальное сходство между
многими элементами этих важных разделов современной микроэкономики.
В части II мы изучаем поведение экономических агентов, когда они
взаимодействуют на рынках. Мы дадим исчерпывающую характеристику
неоклассических моделей конкурентных и неконкурентных рыночных
структур и в общих чертах покажем взаимосвязь структуры рынка,
рыночного равновесия и экономической эффективности. Затем последует
теория общего равновесия, в которой некоторые из этих вопросов
рассматриваются на уровне экономической системы в целом. Глава об
общественном выборе и благосостоянии представляет собой доступное
введение в нормативный анализ.
Предметом части III является стратегическое поведение. Объемная
глава по теории игр содержит тщательное и подробное описание игр в
стратегической и развернутой форме. Далее идет глава по экономике
информации, где мы применяем теоретико-игровой подход к этой
актуальной области. В заключительной главе дается детальное изложение
современной теории аукционов, которая находится на переднем крае
сегодняшних теоретических исследований.
По счастью, мы получили целый ряд полезных предложений от
многих внимательных читателей предыдущего издания. Большинство из них
(как и все указания на ошибки) учтены в настоящем издании. Текст стал
сильнее благодаря добровольной помощи коллег, друзей и студентов.
Всем им мы искренне признательны.

Часть I
ЭКОНОМИЧЕСКИЕ АГЕНТЫ

I Глава 1
ТЕОРИЯ ПОТРЕБИТЕЛЯ
1.1. Базовые понятия
В первых двух главах этой книги мы рассмотрим основные
положения современной теории потребителя— фундамента, на котором
построены многочисленные теоретико-экономические структуры. Позднее,
изучая экономику, вы начнете понимать, какую огромную роль эта теория
играет в образе мышления экономистов. Ее эхо будет не раз слышаться
практически в любых разделах экономической науки — в их
возникновении, структуре и приложениях.
Прежде чем переходить к самой теории, нельзя не упомянуть о роли в
ней математики. Вы заметите, что некоторые предположения в тексте
делаются исключительно ради математической целесообразности. Тому
есть простое объяснение, и в любой другой науке оно точно такое же:
абстрагирование от «реальности» открывает нам доступ к мощным
математическим методам, которые благодаря своей строгости помогают
заглянуть дальше, чем позволяют интуиция и опыт. В физическом мире «не
бывает» плоскостей без трения или абсолютного вакуума, но в
экономике, как и в физике, возможность подобных предположений позволяет
сконцентрироваться на более важных аспектах проблемы и с помощью
этого создать теоретические ориентиры для того, чтобы соотносить с
ними опыт и наблюдения реального мира. Это ничуть не означает, что
нужно без сомнений принимать любое нереалистичное или чисто формальное
теоретическое положение. Если оно возникает, то на него всегда стоит
бросить критический взгляд и выяснить, что дает и чего требует такая
абстракция. Понимание этих вопросов и размышления над ними и
составляют тот материал, благодаря которому происходит развитие
теоретических знаний. Далее, однако, мы будем воспринимать и стремиться понять
теорию «как есть», оставляя большинство критических оценок за
рамками этой книги.
В любой модели потребительского выбора имеются четыре основных
элемента: это потребительское множество, допустимое множество,
отношение предпочтения и поведенческая предпосылка. Они концептуально
отличны друг от друга, хотя даже экономисты нередко упускают это из
вида. Такая базовая структура является очень общей и поэтому крайне
гибкой. Специфицируя каждый из этих элементов для соответствующих
задач, можно формально описать и проанализировать множество ситуа-

14
Часть I. Экономические агенты
ций, связанных с выбором. Хотя далее мы будем заниматься
преимущественно конкретными формализациями, которые доминируют во взглядах
экономистов на поведение отдельного потребителя, хорошо бы иметь в
виду, что «теория потребителя» как таковая — это фактически очень
богатая и гибкая теория выбора.
Понятие потребительского множества вводится очевидным
образом: потребительское множество X представляет собой множество всех
альтернатив, или вполне специфицированных потребительских планов,
которые потребитель способен вообразить, независимо от того, можно ли
их реализовать. Таким образом мы хотим отразить множество
всевозможных альтернатив без учета ограничений реального мира.
Потребительское множество иногда еще называют множеством выбора.
Пусть каждый товар измеряется в бесконечно делимых единицах.
Пусть xt € R представляет число единиц /-го товара. Мы предполагаем,
что имеет смысл только неотрицательное количество единиц товара и что
всегда можно представить себе возможность отсутствия любого товара.
Далее предположим, что имеется конечное, фиксированное, но
произвольное число п различных товаров. Пусть х = (х15...,хл) является
вектором, содержащим соответствующие количества каждого из п товаров.
Назовем х потребительским набором, или потребительским планом.
Потребительский набор х е X, таким образом, представлен точкой
х€ R". Обычно мы в целях упрощения будем представлять
потребительское множество как весь неотрицательный ортант, X = Ш"+. Легко видеть,
что в этом случае выполнено каждое из следующих основных
требований.
Предположение 1.1. Свойства потребительского множества X.
Минимальные условия на потребительское множество:
1) 0*ХсМп+;
2) X замкнуто;
3) X выпукло;
4) ОеХ.
Понятие допустимого множества также интуитивно понятно. Пусть
В — множество таких потребительских планов, которые не только можно
себе вообразить, но и которые, что важнее, являются реально
достижимыми при тех экономических условиях, с которыми сталкивается
потребитель. Допустимое множество В, таким образом, является подмножеством
потребительского множества X, состоящим из тех потребительских
планов, которые остаются после того, как мы приняли во внимание все
ограничения на доступ потребителя к благам, возникающие как следствие

Глава 1. Теория потребителя
15
практических, институциональных или экономических реалий
окружающего мира. Спецификация этих реалий в той или иной ситуации
определяет конкретный вид и дополнительные свойства, которыми будет обладать
множество В. Пока мы ограничимся утверждением, что В с X.
Отношение предпочтения обычно отражает ограничения (если они
есть) восприятия потребителя в ситуациях, связанных с выбором,
противоречивость или непротиворечивость его выбора и информацию о его
вкусах по отношению к различным объектам выбора. Отношение
предпочтения играет ключевую роль в любой теории выбора. Его особый вид
в теории потребительского поведения заслуживает отдельного изучения.
Наконец, модель «замыкается» путем введения некоторой
поведенческой предпосылки. Она выражает основной принцип, которому
потребитель следует при выборе, и определяет основную цель такого выбора.
Предполагается, что потребитель стремится найти и выбрать ту из
доступных ему альтернатив, которая является наиболее
предпочтительной с точки зрения его личных вкусов.
1.2. Предпочтения и полезность
В данном разделе мы рассмотрим отношение предпочтения
потребителя и исследуем его связь с современным пониманием термина
«полезность». Однако прежде скажем несколько слов о развитии экономической
мысли, которые помогут поместить дальнейшее изложение в правильный
контекст.
Так называемый закон спроса поначалу строился да некоторых
крайне сильных предположениях. В классической .теории Эджворта, Милля и
других сторонников утилитаристского направления в философии
«полезность» считалась некоей субстанцией, а «удовольствие» и «страдание»
различных индивидов — четко определенными явлениями, которые
можно измерять и сравнивать. Помимо этого, «принцип убывающей
предельной полезности» принимался в качестве псиаддогического «закона», а
ранние формулировки закона спроса существенным образом на него
опирались. Все это представляло собой исключительно сильные
предположения о внутреннем мире человека.
Дальнейшая история теории потребителя была отмечена
настойчивыми усилиями сделать ее основания как можно более общими.
Экономисты стремились исключить максимальное количество традиционных
допущений, явных или неявных, и при этом сохранить логически
последовательную теорию, обладающую прогностической способностью. Пи-
рето [Pareto, 1896], по-видимому, первым заподозрил, что предположение
об измеримости «полезности» несущественно для теории cnpDca
Слуцкий [Slutsky, 1915] провел первое систематическое исследование теории
спроса без использования понятия измеримой субстанции под названием

16
Часть L Экономические агенты
«полезность». Хикс [Hicks, 1939] продемонстрировал, что принцип
убывающей предельной полезности не является ни необходимым, ни
достаточным условием для того, чтобы выполнялся закон спроса. Наконец,
Дебре [Debreu, 1959] завершил сведение стандартной теории потребителя
к тем основам, которые мы здесь рассмотрим. Сегодняшняя теория тесно
связана со своими предшественницами, но является более стройной,
более строгой и более общей.
1.2.1. Отношение предпочтения
Предпочтения потребителя характеризуются аксиоматически. При
таком способе моделирования, для того чтобы охарактеризовать
структуру и свойства предпочтений, принимается минимально необходимое
число явных аксиом. Остальная теория и выводы о поведении агентов
логически следуют из этих аксиом.
Аксиомы потребительского выбора математически выражают
фундаментальные характеристики потребительского поведения и отношения
к объектам выбора. Вместе они формализуют точку зрения, согласно
которой потребитель способен делать выбор и что этот выбор является в
известном смысле непротиворечивым.
Предпочтения потребителя формально представляются бинарным
отношением )z, определенным на потребительском множестве X. В ситуации,
когда х1 Ь х2, мы говорим, что для этого потребителя « х1 не хуже х2».
Тот факт, что мы используем бинарное отношение для описания
предпочтений, существенен и заслуживает небольшого обсуждения. Он
отражает точку зрения, что с самого начала нашей теории требуется
относительно немного информации о потребителе. Нам необходимо только,
чтобы потребитель делал попарные сравнения, т.е. чтобы он каждый раз
рассматривал только два потребительских плана и принимал относящееся
к ним решение. Следующие аксиомы задают базовые критерии, которым
должны соответствовать эти попарные сравнения.
Аксиома 1. Полнота. Для любых х1 и х2 из X либо х1 ^х2, либо
х2 ьх1.
Аксиома 1 формализует идею о том, что потребитель может делать
сравнения, т.е. что он способен различать и обладает необходимыми
знаниями для оценки альтернатив. Аксиома утверждает, что потребитель
может сравнить любые два потребительских плана х1 и х2 и определить,
является ли для него х1 не хуже х2 или х2 не хуже х1.
Аксиома 2. Транзитивность. Для любых трех элементов х1, х2 и
х3 из X из соотношений хЧх2их2^ х\ следует х1 ;ь х .

Глава 1. Теория потребителя
17
Аксиома 2 — особая форма требования непротиворечивости
потребительского выбора. Хотя по нашему условию потребитель способен
каждый раз сравнивать только две альтернативы, предположение о
транзитивности требует, чтобы эти сравнения были непротиворечивым образом
связаны друг с другом. На первый взгляд такое условие кажется простым
и естественным. Действительно, не будь предпочтения транзитивными,
наши чувства подсказывали бы нам, что в них есть что-то странное. Тем
не менее это, вероятно, наиболее спорная из всех аксиом, описывающих
потребительский выбор. Эксперименты показали, что в различных
ситуациях выбор реальных людей не всегда удовлетворяет условию
транзитивности. Все же мы оставим это условие в нашем описании потребителя,
хотя и не без некоторых сомнений.
Из двух этих аксиом следует, что потребитель может полностью
упорядочить любое конечное число элементов потребительского множества
X от наилучшего к наихудшему, причем некоторые элементы могут
оказаться эквивалентными друг другу. (Попробуйте доказать это.)
Предпочтения, позволяющие потребителю так ранжировать альтернативы, можно
представить отношением предпочтения.
Определение 1.1. Отношение предпочтения.
Бинарное отношение >z на потребительском множестве X
называется отношением предпочтения, если оно удовлетворяет аксиомам 1 и 2.
Существуют два других отношения, которые мы будем использовать
для анализа потребительских предпочтений. Они определяются с
помощью предпочтения >г и формализуют понятия строгого предпочтения и
безразличия.
Определение 1.2. Отношение строгого предпочтения.
Бинарное отношение >- на потребительском множестве X
определяется следующим образом:
х1 >- х2 тогда и только тогда, когда х'ьх2 w неверно, что х2ьх'
(будем записывать это так: х2^х').
Отношение >- называется отношением строгого предпочтения,
порожденным >:, или просто отношением строгого предпочтения, если
ясно, какое отношение имеется в виду. Выражение х1 >- х2 читается как
«х1 строго предпочитается х2».
Определение 1.3. Отношение безразличия.
Бинарное отношение ~ на потребительском множестве X
определяется следующим образом:
х1 - х2 тогда и только тогда, когда х'^х^х^х1.

18
Часть I. Экономические агенты
Отношение ~ называется отношением безразличия, порожденным
>z, или просто отношением безразличия, если ясно, какое отношение
имеется в виду. Выражение х1 ~ х2 читается как «х1 эквивалентно х2».
И отношение строгого предпочтения, и отношение безразличия
отражают обычный смысл, в котором термины «строгое предпочтение» и
«безразличие» используются в повседневной речи. Поскольку они
построены на основе отношения предпочтения, можно ожидать, что они
должны обладать некоторыми (на самом деле не всеми) его свойствами:
для обоих отношений выполняется свойство ^гранзитивности, но не
выполняется свойство полноты.
Используя эти два введенных бинарных отношения, мы можем
охарактеризовать ранжирование потребителем любых двух альтернатив. Для
любой щры х1 и х2 имеет место ровно одна из трех взаимоисключающих
ситуаций1: х1 >- х2, х2 >- х1 или х1 - х2.
На данный момент мы просто формализовали предположение, что
предпочтения отражают способность потребителя делать выбор и
характеризуются определенной непротиворечивостью. Рассмотрим, как можно
графически описать набор предпочтений, удовлетворяющих только этим
аксиомам. Для этого (а также в целях упрощения дальнейшего
изложения) определим с помощью отношения предпочтения некоторые
связанные с ним множества. Эти множества строятся по одной из имеющихся в
потребительском множестве альтернатив и ранжируют относительно нее
все остальные альтернативы.
Определение 1.4. Множества в X, основанные на отношении
предпочтения.
Пусть х° — произвольная точка в потребительском множестве X.
По отношению к любой такой точке можно определить следующие
подмножества X:
1) ъ (х°) = {х | х е X, х Ъ х0} (множество «не хуже чем»).
2) ¦< (х°) = {х | хе X, х° ъ х} (множество «не лучше чем»).
3) -< (х°) = {х | хе X, х° У х} (множество «хуже чем»).
4) ^(х°) = {х|хе X, хух0} (множество «лучше чем»).
5) ~ (х°) = {х | хе X, х ~ х0} (множество «безразличия»).
Гипотетическое множество предпочтений, удовлетворяющих
аксиомам 1 и 2, изображено на рис. 1.1 для X = М2. Любая точка такого потре-
1 Понятно, это справедливо в предположении, что У является отношением
предпочтения, т.е. полным и транзитивным бинарным отношением. — Примеч. ред.

Глава 1. Теория потребителя
19
бительского множества, например х° = (jc,0,^) , представляет собой
потребительский план, состоящий из некоторого количества х^ товара 1 и
некоторого количества jc^ товара 2. По аксиоме 1, потребитель может
сравнить х° с любым другим планом х в множестве X и решить,
является ли х не хуже, чем х°, или х° не хуже, чем х. Согласно
определениям подмножеств и аксиомам 1 и 2, потребитель должен отнести каждую
точку множества X к одной из трех взаимоисключающих категорий:
любая другая точка хуже х°, эквивалентна х° или предпочитается х°.
Таким образом, для любого набора х° потребительское множество
разбивается на три подмножества -< (х°), - (х°) и У (х°).
Рис. 1.1. Гипотетические предпочтения, удовлетворяющие аксиомам 1 и 2
Предпочтения на рис. 1.1 могут показаться довольно странными. Они
обладают лишь минимальной структурой, но вместе с тем ничем не
противоречат первым двум аксиомам. Ни одно из наших предположений не
запрещает изображенные на рисунке «неправильности» — «толстые»
зоны безразличия или «разрывы» и «изгибы» множества безразличия
~ (х°), которые можно исключить только путем дополнительных
ограничений на предпочтения.
Рассмотрим некоторые новые предположения. Одно из них очень
слабо связано с поведением потребителя и преимущественно
характеризует чисто математические аспекты представления предпочтений;
остальные описывают вкусы потребителя по отношению к объектам из
потребительского множества.
Первая аксиома является своего рода условием топологической
регулярности предпочтений. Ее назначение прояснится немного позже.

20
Часть I. Экономические агенты
Здесь и далее мы предполагаем, что X = W+.
Аксиома 3. Непрерывность. Для каждого xgR" множество «не
хуже чем» (^(х0)) и множество «не лучше чем» (^:(х0)) являются
замкнутыми в W+.
Вспомним, что множество замкнуто, если его дополнение открыто,
т.е. замкнутость ь (х°) в R" означает, что его дополнение -< (х°)
открыто в R".
Аксиома непрерывности гарантирует невозможность резких
изменений предпочтений на противоположные. Действительно, ее
эквивалентная формулировка следующая: если каждый элемент у"
последовательности потребительских наборов не хуже (не лучше) х,ау" сходится к у,
то у не хуже (не лучше) х. Заметим, что поскольку множества ^ (х°) и
^ (х°) замкнуты^ то и множество ~ (х°) замкнуто, так как оно является их
пересечением. Следовательно, с аксиомой 3 несовместимо наличие
открытой области в множестве безразличия в левой верхней части рис. 1.1.
Дополнительные предположения о вкусах потребителя придают
предпочтениям более структурированный вид, ту регулярность, с которой
вы, возможно, уже знакомы по предшествующим курсам экономической
теории. Их следует подбирать исходя из особенностей анализируемой
задачи потребительского выбора. Мы последовательно рассмотрим
некоторые ключевые предположения относительно вкусов, которые обычно
делаются в «стандартной» теории потребителя, и попробуем понять, какое
влияние они по отдельности или все вместе оказывают на структуру
предпочтений. В каждом классе предположений мы будем двигаться от
менее жестких ограничений к более жестким и в дальнейшем, как
правило, будем использовать последние. Номерами со штрихом обозначены
аксиомы, соответствующие концептуально близким, но менее жестким
ограничениям, чем соответствующие аксиомы без штриха.
Представляя предпочтения на множестве обычных потребительских
благ, мы хотели бы отразить тот основополагающий факт, что
«потребности» по существу не ограничены. Весьма приближенно это можно
выразить как предположение о том, что всегда найдется такое изменение в
структуре (любого) потребительского плана данного потребителя,
которое после его осуществления приведет к более предпочтительному плану,
который этот потребитель предпочитает первоначальному. Оно может
включать увеличение объема одних товаров и уменьшение объема
других, увеличение объема всех товаров или даже уменьшение объема всех
товаров. Благодаря данному предположению мы лишаем потребителя

Глава 1. Теория потребителя
21
возможности вообразить, что все его прихоти и потребности в товарах
полностью удовлетворены. Формально это предположение имеет вид1:
Аксиома 4'. Локальная ненасыщаемость. Для любых х°еМ" и
?>0 существует xeZ??(x°)nR" такой, что х^х°, где 5е(х°)
обозначает открытую окрестность радиуса г с центром в точке х°.
Аксиома 4' гласит, что в сколь угодно малой окрестности данной
точки х° всегда найдется хотя бы одна отличная от нее точка х, которую
потребитель предпочтет х°. Эта аксиома существенным образом влияет
на структуру возможных множеств безразличия. Она исключает
появление «зон безразличия», подобных окрестности точки х1 на рис. 1.2.
Чтобы убедиться в этом, заметим, что на рис. 1.2 всегда можно найти
некоторое 8 > 0 и окрестность Ве(\1), в которой будут содержаться только
точки, эквивалентные х1. Тогда, конечно, нарушается аксиома 4', поскольку
она требует, чтобы независимо от выбранного е > 0 в соответствующей
окрестности всегда имелась хотя бы одна точка, строго предпочитаемая
точке х1. Предпочтения, изображенные на рис. 1.3, удовлетворяют
аксиоме 4', а также аксиомам 1—3.
Рис. 1.2. Гипотетические предпочтения, удовлетворяющие аксиомам 1,2 и 3
Весьма распространено и другое, более жесткое ограничительное
представление о потребностях, согласно которому больше всегда лучше,
чем меньше. Хотя свойство локальной ненасыщаемости требует, чтобы
вблизи каждой точки всегда имелась более предпочтительная
альтернатива, оно не исключает возможности того, что количество одного или всех
товаров в этой альтернативе будет меньше. Точнее, из него не следует,
1 См. определение А 1.4 в математическом приложении.

22
Часть I. Экономические агенты
что потребителю будет лучше, если он получит больше каждого товара.
Альтернативная точка зрения предполагает, что потребитель всегда
предпочтет план с большим количеством товаров плану с меньшим
количеством товаров, и формулируется в виде аксиомы монотонности. Введем
следующие обозначения: если набор х° содержит не меньше каждого
товара, чем х1, то это записывается как х° > х1, а если х° содержит строго
больше каждого товара, чем х1, то это записывается как х° » х1.
Рис. 1.3. Гипотетические предпочтения, удовлетворяющие
аксиомам 1, 2,3 и 4'
Аксиома 4. Монотонность. Для любых х°, х'еМ" если х° >х', то
х° ^х1, а если х° »х\ то х° ^х1.
Аксиома 4 утверждает, что если один набор х° содержит не меньше
каждого товара, чем другой набор х1, то х° не хуже х1. Более того, х°
строго лучше, если в нем строго больше каждого товара. Влияние этой
аксиомы на структуру множества безразличия и других определенных
выше множеств также существенно. Во-первых, должно быть ясно, что из
аксиомы 4 следует аксиома 4', т.е. если предпочтения удовлетворяют
аксиоме 4, они автоматически удовлетворяют аксиоме 4'. Тем самым
аксиома 4 оказывает тот же эффект на структуру множества безразличия, а
также других множеств («лучше чем» и «хуже чем»), что и аксиома 4', но
с небольшими дополнениями. В частности, аксиома 4 исключает для
множеств безразличия в W+ возможность «загибаться вверх», или
содержать сегменты с положительным наклоном. Она также требует, чтобы
множества «лучше чем» находились «над» множествами безразличия, а
множества «хуже чем» — «под» ними.

Глава 1. Теория потребителя
23
Продемонстрируем это на рис. 1.4. Согласно аксиоме 4, точки выше и
правее х° и точки ниже и левее х° не могут находиться в том же
множестве безразличия, что их0. Любая точка выше и правее х°, например х1,
содержит больше каждого товара по сравнению с х°. Все такие точки
должны строго предпочитаться х°. Аналогично любая точка ниже и левее
х°, например х2, содержит меньше каждого товара. По аксиоме 4, х°
должна строго предпочитаться х2 и всем остальным точкам этого
квадранта, поэтому ни одна из них не может находиться в том же множестве
безразличия, что и х°. Для любого х° точки выше и правее множества
безразличия войдут в множество У (х°), точки ниже и левее — в
множество -<(х°). Множество предпочтений, удовлетворяющих аксиомам 1, 2,
3 и 4, изображено на рис. 1.5.
*>*!
Рис. 1.4. Гипотетические предпочтения, удовлетворяющие
аксиомам 1,2,3 и 4'
*2
^(Х°)
V)
>*!
Рис. 1.5. Гипотетические предпочтения, удовлетворяющие
аксиомам 1, 2,3 и 4

24
Часть I. Экономические агенты
Предпочтения на рис. 1.5 ближе всего к тем, которые вам,
несомненно, встречались в предшествующих курсах экономики. Тем не менее они
отличаются от уже знакомых вам предпочтений очень важной
особенностью: обычно области невыпуклости типа северо-западной части
предпочтений не допускаются. Это достигается путем использования
последней аксиомы, которую мы сформулируем в двух вариантах, а затем
рассмотрим их смысл и назначение.
Аксиома 5'. Выпуклость. Если х1 ьх°, то /х1 +A-/)х° ьх° для
любых te [О, 1].
Чуть более сильный вариант звучит так.
Аксиома 5. Строгая выпуклость. Если х'^х0 и х^х0, то
txl +A-0х° ^х° для любых te (О, 1).
Прежде всего заметим, что и аксиома 5', и аксиома 5 — в сочетании с
аксиомами 1, 2, 3 и 4 — исключают появление вогнутых к началу
координат участков во множествах безразличия, таких, как в левой верхней части
рис. 1.5. Чтобы убедиться в этом, выберем две различные точки на
множестве безразличия, изображенном на рисунке. Поскольку и х1, и х2
эквивалентны х°, то х'ьх2. Выпуклые комбинации двух этих точек, такие, как
х', будут лежать в множестве -< (х°), нарушая условия аксиом 5' и 5.
Оказывается, аксиому 5' можно ввести без ущерба для целей
развиваемой здесь теории (поведения) потребителя: предсказательное
содержание будет тем же как с данной аксиомой, так и без нее. Хотя подобное
утверждение для чуть более сильной аксиомы 5 не вполне верно, она
значительно упрощает анализ.
Существует по крайней мере два способа понять на интуитивном
уровне значение выпуклости потребительских предпочтений.
Предпочтения, изображенные на рис. 1.6, удовлетворяют и аксиоме 5', и аксиоме 5.
Снова предположим, что мы выбрали различные точки х1 - х2. Точка х1
представляет собой набор, в котором доля товара х2 относительно велика
по сравнению с набором х2. Набор х2, напротив, содержит относительно
большую по сравнению с х1 долю товара д:,. Тем не менее для
потребителя эти наборы эквивалентны. Любая выпуклая комбинация х1 и х2,
например х', будет содержать более «сбалансированное» сочетание х, и
х2, чем каждый из них в отдельности. Смысл аксиом 5' и 5 сводится к
тому, чтобы запретить потребителю впадать в крайности: аксиома 5'
требует, чтобы любой относительно сбалансированный набор (например, х')
был для потребителя не хуже экстремальных наборов, а аксиома 5 — чтобы

Глава 1. Теория потребителя
25
он был строго лучше. И в том, и в другом случае от предпочтений требуется
некоторое «смещение» в сторону сбалансированного потребления.
х2
I ^.Х\
Рис. 1.6. Гипотетические предпочтения, удовлетворяющие
аксиомам 1,2,3,4 и 5' или 5
Второй способ описать значение выпуклости связан с «кривизной»
самих множеств безразличия. Если Х = Ж2+9 то модуль наклона кривой
безразличия называется предельной нормой замещения. В каждой точке
кривой эта величина показывает, от какого количества товара х2
потребитель готов отказаться в обмен на единицу товара хх, оказавшись при
этом с эквивалентным потребительским набором.
Если предпочтения монотонны, то любая форма выпуклости требует,
чтобы кривые безразличия были хотя бы слабо выпуклыми к началу
координат. Это эквивалентно условию невозрастания предельной нормы
замещения при движении от наборов с относительно высокой долей
товара х2 (таких, как х1) к наборам с относительно высокой долей товара хх
(таким, как х2). Можно сказать, что когда у потребителя относительно
мало товара х2 и много товара хх, он не более склонен к обмену х2 на хх,
чем в ситуации, когда у него относительно много х2 и мало jCj. Согласно
аксиоме 5', пропорция, в которой потребитель обменивает х2 на х{9
оставаясь при этом на той же кривой безразличия, является либо постоянной,
либо убывает при движении по кривой безразличия слева направо.
Аксиома 5 выдвигает более сильное требование строгого убывания этой
пропорции. На рис. 1.6 изображены предпочтения, удовлетворяющие

26
Часть L Экономические агенты
данному свойству, которое иногда называется принципом убывания
предельной нормы замещения в потреблении.
Итак, мы рассмотрели ряд аксиом, описывающих предпочтения
потребителя. Наша цель заключалась в том, чтобы выяснить влияние
каждой из них по отдельности и всех вместе на структуру и представление
предпочтений. Подведем краткие итоги этого анализа. Аксиомы о
потребительских предпочтениях можно разбить на следующие группы.
Аксиомы полноты и транзитивности описывают потребителя, который может
непротиворечивым образом сравнивать различные альтернативы.
Аксиома непрерывности обеспечивает существование топологически
приемлемых множеств «не хуже чем» и «не лучше чем» и вводится
преимущественно из математических соображений. Все остальные аксиомы служат
для того, чтобы охарактеризовать вкусы потребителя по отношению к
объектам выбора. Обычно мы предполагаем, что вкусы демонстрируют
некоторую форму ненасыщаемости (слабую или сильную), а также
некоторую смещенность в сторону сбалансированного потребления (слабую
или сильную).
1.2.2. Функция полезности
В современной теории функция полезности является просто удобным
инструментом для обобщения информации об отношении предпочтения
потребителя — не больше и не меньше. Иногда удобнее работать
напрямую с отношением предпочтения и соответствующими множествами.
В других случаях, особенно если использовать методы математического
анализа, удобнее работать с функцией полезности. Отношение
предпочтения считается базовой, наиболее фундаментальной характеристикой
предпочтений, а функция полезности лишь «представляет», или
обобщает, передаваемую им информацию. Формально функция полезности
определяется следующим образом.
Определение 1.5. Функция полезности, представляющая
отношение предпочтения ъ.
Вещественнозначная функция и : R" —> R называется функцией
полезности, представляющей отношение предпочтения ^, если для любых
Тем самым функция полезности представляет отношение
предпочтения потребителя, если более предпочтительным наборам она ставит в
соответствие большие числа.

Глава 1. Теория потребителя
27
Вопрос» который ранее привлекал внимание теоретиков, касался
свойств, которыми должно обладать отношение предпочтения, чтобы
гарантировать его представимость в виде непрерывной вещественнознач-
ной функции. Он весьма важен, поскольку анализ многих проблем в
теории потребителя крайне упрощается, если есть возможность работать с
функцией полезности, а не с самим отношением предпочтения.
С математической точки зрения это вопрос существования
непрерывной функции полезности, представляющей отношение предпочтения.
Оказывается, некоторые из уже рассмотренных нами аксиом — как раз
то, что требуется для существования такой функции. Можно показать,
что любое бинарное отношение, которое является полным,
транзитивным и непрерывным, можно представить непрерывной вещественнознач-
ной функцией полезности1. (В упражнениях вам предлагается показать,
что эти три аксиомы являются также необходимым условием для такого
представления.) Все вместе эти аксиомы требуют, чтобы потребитель
умел делать непротиворечивый бинарный выбор, а отношение
предпочтения отвечало некоторым условиям топологической «регулярности».
В частности, возможность представить предпочтения функцией
полезности не зависит от предположений о вкусах потребителя, таких, как
выпуклость или даже монотонность, что открывает путь к использованию
непрерывных функций полезности для анализа и решения исключительно
широкого круга задач.
Здесь мы подробно рассмотрим чуть менее общий результат. В
дополнение к трем вышеупомянутым основополагающим аксиомам мы
введем условие монотонности предпочтений. Оно не существенно для
представимости, но упрощает чисто математические тонкости задачи и делает
доказательство утверждения интуитивно более ясным. Заметим при этом,
что нам не потребуется ни одна из форм выпуклости.
Теорема 1.1. Существование вещественнозначной функции,
представляющей отношение предпочтения.
Если бинарное отношение Ь является полным, транзитивным,
непрерывным и монотонным, то существует непрерывная вещественно-
значная функция и: R" —> М, представляющая >z.
Обратите внимание на то, что это исключительно теорема
существования. Она утверждает, что при указанных условиях гарантируется
существование хотя бы одной непрерывной вещественнозначной функции,
представляющей отношение предпочтения. Такая функция может быть (и
на самом деле всегда будет) не единственной. Однако сама теорема ниче-
1 См., например, работы Бартена и Бёма [Barten, Bohm, 1982]. Классическим источником
является работа Дебре [Debreu, 1954].

28
Часть I. Экономические агенты
го не говорит о том, как много таких функций и какой вид они имеют.
Тем самым если мы сможем придумать всего лишь одну непрерывную
функцию, представляющую данные предпочтения, то теорема будет
доказана. В доказательстве, приведенном ниже, применена именно такая
стратегия.
Доказательство. Пусть отношение >г является полным,
транзитивным, непрерывным и монотонным и пусть е = A, ...,l)eR" — вектор,
состоящий из единиц. Рассмотрим отображение и: R" -» Е,
определенное таким образом, что выполняется следующее условие1:
w(x)e~x. (P-1)
*2
и(х)
1
1 и(х)
Рис. 1.7. Построение отображения и: М" —»R
Убедимся, что мы правильно понимаем это выражение. Оно означает:
«возьмем любой х из множества Шп+ и сопоставим ему число и(х) такое,
что набор м(х)е, содержащий и{\) единиц каждого товара,
эквивалентен х».
1 Для t > О вектор te будет некоторой точкой в Ш"+, каждая из координат которой равна
/, поскольку te = t(\, ...,1) = (/, ...,/). Если / = 0,то № = @, ...,0) совпадает с началом
координат. Если / = 1, то /е = A, ..., 1) совпадает с е. Если / > 1, то точка te лежит
дальше от начала координат, чем е. При 0 < t < 1 точка te лежит между началом
координат и е. Отсюда должно быть ясно, что при любом / > 0 te будет точкой в R" ,
лежащей на луче, выходящем из начала координат и проходящем через точку е, т.е.
некоторой точкой на биссектрисе координатного угла на рис. 1.7.

Глава 1. Теория потребителя
29
Сразу же возникают два вопроса. Во-первых, всегда ли существует
число м(х), удовлетворяющее (Р-1)? Во-вторых, является ли оно
единственным, так что функция и(х) корректно определена?
Чтобы ответить на первый вопрос, зафиксируем xg R" и рассмотрим
два подмножества в множестве вещественных чисел:
А = {/ > 01 te ъ х}
В s {/ > 01 /е з х}.
Заметим, что если t* e Аг\В9 то /*е~х, так что можно положить
u(x) = t\ и это будет удовлетворять (Р-1). Тем самым на первый вопрос
можно ответить утвердительно, если мы покажем, что An В всегда не
пусто. Именно это мы сейчас и сделаем.
Из упражнения 1.11 следует, что непрерывность ь означает
замкнутость А и В в R+. Согласно монотонности из te А следует, что t'e A
для всех t' > t. Тогда А должно быть замкнутым интервалом вида [/, °°].
Аналогично, монотонность и замкнутость В в М+ означают, что В
должно быть замкнутым интервалом вида [О, Т]. Далее, для любого / > О
из полноты )- следует, что либо /е^х, либо te ^ х, т.е. что te A u В. Но
отсюда R+ =AkjB = [О, 7]и[/, <*>], поэтому /</ и Лп5*0 .
Обратимся ко второму вопросу. Нам необходимо показать, что
существует только одно число t > О такое, что te ~ х . Но это легко видеть из
того, что если txe ~ х и t2e ~ х, то по транзитивности - (см.
упражнение 1.4) /,е ~ t2e. Из монотонности следует, что tx = t2.
Мы приходим к выводу, что для любого xeW+=X существует
единственное число w(x), для которого выполняется (Р-1). Покажем
теперь, что предпочтения ь представимы с помощью этой функции.
Рассмотрим два набора х1 и х2 и соответствующие им значения по-
лезностей и(х1) и w(x2), которые по определению удовлетворяют
условиям u(xl)e ~ х1 и w(x2)e ~ х2. Тогда мы получаем следующее:
х1 ъ х2 <=> (Р-2)
» и(х1 )е-х'^гх2~ и(х2 )е <=> (Р-3)
<=> и(х1 )е ъ и(х2 )е <=» (Р-4)
&u(xl)>u(x2). (P-5)

30
Часть L Экономические агенты
Здесь (Р-2) <=> (Р-3) по определению функции и; (Р-3) <=> (Р-4) следует
из транзитивности ^г, транзитивности и определения - и определения и;
(Р-4) <=> (Р-5) следует из монотонности ь. Вместе выражения (Р-2) — (Р-5)
означают, что (Р-2) <=> (Р-5), поэтому х1 ^х2 тогда и только тогда, когда
и(х1) > и(х2), что и требовалось доказать.
Остается только показать непрерывность функции полезности
u:Rn+ -»R, представляющей ^г. По теореме А 1.6 для этого достаточно
показать, что для функции и прообраз любой открытой окрестности
является открытым в R". Поскольку открытые окрестности в R — это
просто открытые интервалы, нужно показать, что и~х((а,Ь)) открыто в
Ш"+ для любых а < Ь.
Имеем:
и~\(а,Ь)) = {х€ R^ | а < и(х) < Ъ)
= {xeR"+\ae<u(x)e<be}
= {xeRn+\ae<x<be}.
Первое равенство следует из определения прообраза, второе— из
монотонности ;ь, а третье — из условия и(х)е - х и упражнения 1.4.
Перепишем последнее выражение так:
и ((а, Ь)) = у (ае)п -< (be). (Р-6)
Вследствие непрерывности ;ь, множества ^ (ае) и k (be) замкнуты в
X = W+. Два множества в правой части (Р-6) представляют собой
дополнения к ним и поэтому открыты в R"+, а по упражнению А 1.28 u~l((a,b))
как пересечение открытых множеств само является открытым вМ". ¦
Теорема 1.1 очень важна. Она позволяет нам описывать предпочтения
либо с помощью отношения предпочтения и базовых множеств, либо в
числовом виде с помощью непрерывной функции полезности. Но
представление функцией полезности данного отношения предпочтения
никогда не является единственным. Если некоторая функция и представляет
предпочтения потребителя, то их будет представлять и функция v = и + 5,
и функция v = t/3, поскольку каждая из них ранжирует наборы благ точно
так же, как и и. Это важная особенность функций полезности. Если от
отношения предпочтения нам требуется только то, чтобы оно
упорядочивало наборы из потребительского множества, а от функции полезности —
чтобы она отражала этот порядок с помощью чисел, сопоставляемых на-

Глава 1. Теория потребителя
31
борам, то любая другая функция, которая сопоставляет потребительским
наборам числа в том же порядке, что и функция и, тоже будет
представлять отношение предпочтения и не хуже и сможет выступать в качестве
функции полезности.
Это свойство называется по-разному. Иногда говорят, что функция
полезности инвариантна относительно положительных монотонных
преобразований или что она единственна с точностью до
положительного монотонного преобразования. В любом случае суть такова: если от
отношения предпочтения нам требуется только осмысленное
ранжирование наборов, то любая функция полезности, представляющая это
предпочтение, может дать нам только порядковую информацию, не более, но и
не менее. Если мы знаем, что некоторая функция корректно отражает
порядок наборов, то любое ее преобразование, сохраняющее этот порядок,
также может служить в качестве функции полезности.
Это свойство дает нам свободу и одновременно ограничивает ее.
Если у нас есть функция и, представляющая предпочтения некоторого
потребителя, то мы можем преобразовать и в другую, возможно, более
удобную, форму при условии сохранения ранжирования наборов. В то же
время мы ограничены тем, что числа, сопоставляемые данной функцией
полезности конкретным наборам, не имеют никакого значения — важен
только порядок этих чисел1. Хотя этот вывод достаточно прост, он
заслуживает отдельной формулировки. Его доказательство оставлено в
качестве упражнения.
Теорема 1.2. Инвариантность функции полезности
относительно положительных монотонных преобразований.
Пусть ^ является отношением предпочтения в R". Предположим,
что оно представимо функцией полезности и(х). Другая функция v(x)
может представлять это отношение предпочтения тогда и только
тогда, когда v(x) = f(u(x)) для любого х, где /: К —» R строго
возрастает на множестве значений функции и.
Чтобы завершить описание потребительских предпочтений, мы, как
правило, будем вводить для них некоторые дополнительные
предположения. Естественно, это будет отражаться на свойствах соответствующей
им функции полезности. И наоборот, если мы предположим, что функция
полезности обладает некоторыми свойствами помимо непрерывности, это
Некоторые теоретики настолько опасаются возможного смешения современного
термина «функция полезности» и классического утилитаристского понятия «полезность»
как измеримого количества удовольствия или неудовольствия, что полностью
отказываются от устаревшей терминологии и говорят только об отношениях предпочтения и их
«функциях представления».

32
Часть I. Экономические агенты
будет означать наличие дополнительных условий на соответствующее ей
отношение предпочтения. Таким образом, аксиомы о предпочтениях
эквивалентны конкретным математическим свойствам функции полезности.
В завершение данного раздела мы перечислим некоторые из них.
Следующая теорема крайне проста, поскольку сразу же следует из
определений. Однако ее утверждения стоит проверить, поэтому доказательство
оставлено в качестве упражнения. (См. в математическом приложении
определения строго возрастающей, квазивогнутой и строго квазивогнутой
функций.)
Теорема 1.3. Свойства предпочтений и функции полезности.
Пусть отношение предпочтения Ь представимо функцией
u:R"->R. Тогда:
1) и(х) строго возрастает тогда и только тогда, когда >=
монотонно;
2) и{\) квазивогнута тогда и только тогда, когда )z выпукло;
3) и{\) строго квазивогнута тогда и только тогда, когда >= строго
выпукло.
Далее будем анализировать задачи, используя аппарат
математического анализа. До сих пор мы ограничивались непрерывностью функции
полезности и гарантирующими ее свойствами отношения предпочтения.
Дифференцируемость, конечно, представляет собой более сильное
условие, чем непрерывность. В интуитивном понимании непрерывность
требует, чтобы в предпочтениях не было внезапных резких изменений на
противоположные, но не противоречит, например, наличию «изломов».
Дифференцируемость исключает возможность такого поведения и
обеспечивает не только непрерывность, но и «гладкость» кривых безразличия,
поэтому она требует более жесткого ограничения на предпочтения.
Аналогично аксиоме непрерывности, все, что требуется, — это правильное
математическое условие. Мы не будем его выводить, а отошлем читателя
к работе Дебре [Debreu, 1972]. Здесь же нам достаточно просто
предположить, что представляющая предпочтения функция полезности
дифференцируема в тех случаях, когда это необходимо.
В случае, когда функция полезности дифференцируема, используется
особый набор терминов. Приведем их. Первая частная производная и{\)
по xi называется предельной полезностью i-го товара. В случае двух
товаров мы определяли предельную норму замещения как модуль
наклона кривой безразличия. Можно выразить ее в терминах предельных по-
лезностей двух товаров. Для этого рассмотрим произвольный набор
х1 = (х,1, х\). Поскольку кривая безразличия, проходящая через точку х1,

Глава 1. Теория потребителя
33
является функцией на плоскости (xl, х2), предположим, что она задается
выражением х2 = /(х,). Тогда при изменении хх точка
(хр х2) = (хр /(х,)) описывает кривую безразличия, содержащую х1.
Следовательно, для любых х,
w(xp f(xl)) = const. A-1)
Предельная норма замещения первого блага на второе в точке
х1 =(х[, х\) обозначается MRSl2(x{, x\) и равна модулю наклона кривой
безразличия, проходящей через (xj, x\):
MRSl2(xl x\)=\f'(xl)\=-fX*l), A-2)
поскольку /'< 0. Но по A-1) м(Хр /(х,)) является константой по jc, ,
поэтому ее производная по х, должна быть равна нулю:
ди(х{, х2) Эм(хр х2) ,
Эх, Эх2
¦f(xl) = 0. A-3)
Из A-2) и A-3) следует, что
MRSi2(x') =
,,ч_Э»(х')/Эу
ди(х1)/дх2
Аналогично, если число товаров больше двух, то предельная норма
замещения блага / благом j определяется как отношение их предельных
полезностей
х)=Э«(х)/^
du(x)/dXj
Если предельные полезности положительны, MRSy(x) является
положительным числом и показывает, в каком соотношении х,. можно заменить
на Xj без изменения полезности потребителя.
Если функция и(х) дифференцируема на М"+, а предпочтения
монотонны, предельная полезность каждого товара почти всегда строго
положительна, т.е. Эи(х)/Эх, > 0 для «почти всех» наборов х и всех
1 Соответствующее выражение можно получить напрямую, рассматривая дифференциал
функции м(х). — Примеч. ред.

34
Часть I. Экономические агенты
/ = 1,...,и . Когда предпочтения строго выпуклы, предельная норма
замещения двух товаров всегда строго убывает вдоль любой поверхности
уровня функции полезности. Вообще, для любой квазивогнутой функции
полезности ее гессиан Н(х) будет удовлетворять условию
угН(х)у < 0 для всех векторов у таких, что Vw(x) • у = 0.
Если неравенство строгое, то это выражение означает, что движение из
точки х в направлении у по касательной к поверхности безразличия,
проходящей через х (Vw(x)y = 0), приводит к снижению полезности
(т.е. угН(х)у<0).
1.3. Задача потребителя
Мы занимались структурой и представлением предпочтений, но это
только одна из четырех составных частей теории потребительского
выбора. В данном разделе мы рассмотрим все остальные части и построим из
них формальное описание поведения центральной фигуры многих
разделов экономической теории — простого атомистического потребителя.
На самом абстрактном уровне мы предполагаем, что у потребителя
есть потребительское множество X = R"+, содержащее все альтернативы,
которые он только может себе представить. Его восприятие этих
альтернатив описывается отношением предпочтения ^, определенным на
множестве R". Реальные условия, в которых находится потребитель,
ограничивают набор доступных ему альтернатив допустимым множеством
В с R". Наконец, мы предполагаем, что потребитель стремится выбрать
наиболее предпочтительную из доступных ему альтернатив в
соответствии со своим отношением предпочтения. Формально, он выбирает
х* е В такое, что х* >=х для всех х е В. A-4)
Чтобы преуспеть в достижении поставленной цели, введем следующие
предположения, которые будем считать выполненными, если не указано
иное.
Если читателю интересно, термин «почти все» означает все наборы, кроме множества,
мера Лебега которого равна нулю. Правда, нет необходимости знать о мере Лебега,
чтобы понимать необходимость подобного ослабления формулировки. Рассмотрим случай
единственного товара х и функцию полезности и(х) = х + sin(x). Поскольку функция и
строго возрастает, она представляет монотонные предпочтения. Однако хотя и'(х)
строго положительна для большинства значений jc, она равна нулю при
х = к + 2лк, к = 0, 1, 2, ... .

Глава 1. Теория потребителя
35
Предположение 1.2. Потребительские предпочтения.
Отношение предпочтения потребителя ^ является полным,
транзитивным, непрерывным, монотонным и строго выпуклым в R". Тогда
по теоремам 1.1 и 1.3 оно представимо с помощью вещественнозначной
функции полезности и, которая непрерывна, строго возрастает и
строго квазивогнута в Ш"+.
Для случая с двумя товарами подобные предпочтения можно
представить с помощью карты безразличия, линии уровня которой не
пересекаются, строго выпуклы к началу координат и возрастают по
направлению вправо-вверх, как показано на рис. 1.8.
Рис. 1.8. Карта безразличия для предпочтений, удовлетворяющих
предположению 1.2
Далее мы рассмотрим условия, в которых находится потребитель, и
определим структуру допустимого множества. Нас интересует
индивидуальный потребитель, который действует в рамках рыночной экономики.
Под рыночной экономикой мы понимаем экономическую систему, в
которой взаимодействия между агентами опосредованы рынками. Для
каждого товара существует свой рынок, на этих рынках / -му товару
соответствует цена pf. Мы предполагаем, что цены строго положительны, т.е.
р.х >0, / = 1, ...,«. Кроме того, предполагается, что отдельный
потребитель является несущественной силой на каждом из рынков. Под этим
понимается то, что размер каждого рынка по отношению к потенциальной
величине покупки отдельного потребителя настолько велик, что
независимо от того, сколько товара он приобретет, рыночная цена не изменится.
Формально это означает, что вектор рыночных цен р » 0 является
фиксированным с точки зрения потребителя.

36
Часть I. Экономические агенты
Потребитель располагает фиксированным денежным доходом у > О.
Поскольку на приобретение xt единиц / -го товара по цене /?, (долларов)
необходимо потратить pixi долларов, условие того, что расходы не
превышают доходов, можно записать как 2Г=1/?,*, ^ У или более компактно
как р • х < у. Мы суммируем эти предположения, определив допустимое
множество 5, которое будет называться бюджетным множеством,
следующим образом:
Я = {х|хеМ% р-х<у}.
В случае с двумя товарами множество В состоит из всех наборов,
лежащих внутри или на границах заштрихованной области на рис. 1.9.
х2
У/Р2
Уф\
Рис, 1.9. Бюджетное множество В = {х | хе R", р • х < у} в случае
двух товаров
При желании можно переформулировать задачу потребителя в
привычных терминах. В условиях предположения 1.2 предпочтения предста-
вимы с помощью строго возрастающей и строго квазивогнутой функции
полезности и(х), определенной на потребительском множестве R". При
наших предположениях о допустимом множестве совокупные расходы не
должны превышать доходов. Тогда задачу потребителя A-4) можно
переписать эквивалентным образом как задачу максимизации функции
полезности при бюджетном ограничении. Формально задача максимизации
полезности потребителя выглядит как
maxw(x) при рх<у. A-5)
xeR"

Глава 1. Теория потребителя
37
Заметим, что если х* является решением этой задачи, то и{\) > и(х) для
всех хе 5, а это означает, что х* ^ х для всех хей. То есть решения
задачи A-5) действительно являются решениями задачи A-4). Обратное
также верно.
Остановимся на математической структуре этой задачи. Как мы
заметили, при некоторых предположениях относительно предпочтений
функция полезности и(\) вещественнозначна и непрерывна. Бюджетное
множество В является непустым (оно содержит Ое R"), замкнутым,
ограниченным (поскольку все цены строго положительны) и поэтому
компактным подмножеством Ш". Теорема Вейерштрасса (теорема А 1.10)
гарантирует существование максимума и(х) на В. Далее, поскольку В
выпукло, а целевая функция строго квазивогнута, решение задачи
максимизации м(х) на В единственно. Так как предпочтения монотонны, то
решение х* будет удовлетворять бюджетному ограничению как
равенству, т.е. будет лежать не внутри, а на границе бюджетного множества. Тем
самым, если j/>0 и поскольку х* >0, но х* Ф0, то jc* >0 хотя бы для
одного товара. Типичное решение этой задачи в случае двух товаров
изображено на рис. 1.10.
х2
У/Р2
> *1
Рис. 1.10. Решение задачи максимизации полезности потребителя
Ясно, что вектор решений х* зависит от параметров задачи
потребителя. Поскольку он будет единственным для данных значений р и у,
решение задачи A-5) корректно рассматривать как функцию,
отображающую цены и доход во множество объемов товаров, Х = Шп+. Поэтому мы
часто будем писать jc*=x;(p, у\ / = 1, ...,« или в векторных обозначени-

38
Часть I. Экономические агенты
ях х* = х(р, у). Когда решения задачи максимизации полезности
рассматриваются как функции р и у, их называют обыкновенными или
маршалловскими функциями спроса (функциями спроса по Маршаллу).
Если доход и цены всех товаров, кроме данного, зафиксированы, то
график зависимости между объемом спроса на этот товар х{ и его ценой р.{
является стандартной кривой спроса на него.
х2
/ 0 0 0\
Х2(Р\>Р2>У )
Х2(Р\,Р2>У0)
**1
**1
*(л°,а°У) ъ(р1р1у°)
(б)
Рис. 1.11. Задача потребителя и поведение потребительского спроса
Связь между задачей потребителя и поведением потребительского
спроса проиллюстрирована на рис. 1.11. На рис. 1.11(a) потребитель
сталкивается с ценами /?,° и/J°и располагает доходом у0. Объемы товаров
Х\(Р\9 Р*9 У°) и х2(р*9 р\, у0) являются решениями задачи
потребителя и максимизируют его полезность при данных ценах и доходе. Прямо
под этим рисунком, на рис. 1.11F), цена товара 1 откладывается по
вертикальной оси, а объем спроса на товар 1 — по горизонтальной оси. Если
изобразить цену р® и соответствующий объем спроса на товар 1 (при

Глава 1. Теория потребителя
39
данных цене р2 и доходе у ), то мы получим одну точку маршалловской
кривой спроса потребителя на товар 1. При том же доходе и цене
товара 2, но другой цене товара 1 (р\ < рх) объемы товаров хх{р\, р\, у0) и
х2(р{, р\, у0) также являются решениями задачи потребителя и
максимизируют полезность. Если изобразить цену р\ и соответствующий ей
объем спроса на товар 1, то мы получим другую точку маршалловской
кривой спроса на товар 1 на рис. 1.11F). Рассмотрев все возможные
значения рх, мы построим всю кривую спроса на товар 1, как изображено на
рис. 1.11F). Как легко проверить, при других уровнях дохода и других
ценах товара 2 положение и форма кривой спроса на товар 1 будут
другими. Положение и форма этих кривых, однако, всегда будут
определяться свойствами отношения предпочтения потребителя.
Дополнительно будем предполагать, что если и{\)
дифференцируема, то для дальнейшей характеризации спроса можно будет
воспользоваться методами математического анализа. Вспомним, что задача
потребителя формулируется как
maxw(x) при р • х < у. A-6)
хеК"
Это задача нелинейного программирования с одним ограничением в
форме неравенства. Как мы отмечали, ее решение х* существует и
единственно. Если мы перепишем ограничение как у - р • х > 0, а затем
построим лагранжиан, то получим
?(х, у) = и(х) + Х[у-рх].
Предполагая, что решение х* строго положительно, можно применить
для его описания методы Куна — Таккера. Если х* » 0 является
решением A.6), то по теореме А2.20 существует А,* >0 такое, что (х*, X*)
удовлетворяют следующим условиям Куна — Таккера:
д? ди(\) .. .
V = — А,/?,. =0, i = l, ...,«, A-7)
dxi dxi
у-р х>0, A-8)
%-р-х>0. A-9)
По условию монотонности A-8) должно выполняться как равенство,
поэтому ограничение A-9) становится избыточным. Следовательно, эти
условия сводятся к таким:

40
Часть I. Экономические агенты
дх1 ах1
MJjfl-XPn=o, (i-io)
дхп дхп
Что это говорит нам о решении задачи A-6)? Есть два варианта: либо
Vw(x*) = 0, либо Vw(x*)*0. При монотонности первый вариант
возможен, но весьма маловероятен. Поэтому мы просто предположим, что
Vw(x*) Ф 0. Тогда из условия монотонности ди(\*)/дх{ > 0 для некоторого
/ = 1, ...,и. Поскольку р{ >0 для всех /, из A-7) ясно, что в решении
множитель Лагранжа будет строго положительным, так как
A,* =i/f.(x*)//?,. >0. Следовательно, для всех j du(x*)/dxj=Xpj>0J т.е.
для всех товаров в оптимуме предельная полезность пропорциональна
цене. Иначе говоря, для любых двух товаров j и к мы получаем условие
M*)foJ=Pj ^ (М1)
ди(х*)/дхк рк '
Оно утверждает, что в оптимуме предельная норма замещения двух
любых товаров должна быть равна отношению цен этих товаров. В случае
двух товаров условия A-10) требуют, чтобы наклон кривой безразличия,
проходящей через точку х*, равнялся наклону бюджетного ограничения
и чтобы точка х* лежала на бюджетной линии, как на рис. 1.10 и 1.11(a).
Вообще говоря, условия A.10) являются только необходимыми
условиями локального оптимума (см. конец раздела А2.3). Однако для данной
конкретной задачи эти необходимые условия первого порядка на самом
деле являются и достаточными для глобального оптимума. Это
утверждение заслуживает отдельной формулировки.
Теорема 1.4. Достаточность условий первого порядка для
задачи потребителя.
Предположим, что и(\) непрерывна и квазивогнута на W+ и
(р, у)»0. Если и(\) дифференцируема в точке х*, а (х*, А,*)»0
является решением A-10), то х* является решением задачи максимизации
полезности потребителя при ценах р и доходе у.

Глава 1. Теория потребителя
41
Доказательство. Воспользуемся следующим фактом, который
приведем без доказательства: поскольку и квазивогнута и дифференцируема
в точке х, то Vu(\)(\l - х) > 0 для всех х,х!>0 при условии, что
и(х1)>и(х).
Теперь предположим, что Vw(x*) существуете (х*, Х*)»0
является решением A-10). Тогда
Vw(x*) = ?t*p, (P-1)
рх=у. (Р-2)
Если х* не максимизирует полезность, то должно существовать
некоторое х° > 0 такое, что
н(х°)>м(х*),
рх°<у.
Поскольку и непрерывна и у > 0, из этих неравенств следует, что
u(tx°)>u(x*), (P-3)
ptx°<y (P-4)
для некоторого te[0, 1], достаточно близкого к единице. Положив
х1 =/х°, получаем
Ум(х*)(х' -х*) = Д'рМ*1 -х*) =
= Г(р х-р х*)< (Р-5)
<Х*(у-у) =
= 0,
где первое равенство следует из (Р-1), а неравенство— из (Р-2) и (Р-4).
Однако так как и(х1)>и(х*) по (Р-3), (Р-5) противоречит утверждению,
приведенному в начале доказательства. ¦
Таким образом, на основе этого утверждения для нахождения
решения задачи A-6) достаточно найти решение (х*, А,*)»0 системы
уравнений A-10), системы из п +1 уравнений с п +1 неизвестной jc,*,..., х*п Д *.
Обычно эти уравнения можно использовать для нахождения функций
спроса xi (р, у), / = 1, ...,«, что мы и покажем на следующем примере.

42
Часть I. Экономические агенты
Пример 1.1. Функция */(*,, х2) = (х* +jc?I/p, где 0*р<1 известна
как функция полезности с постоянной эластичностью замещения
(CES-функция). Легко проверить, что эта функция полезности описывает
монотонные и строго выпуклые предпочтения.
Потребителю требуется найти неотрицательный потребительский
набор, являющийся решением следующей задачи:
тах(х,р + х2 I/Р ПРИ У - Р\х\ ~ Pixi ^ 0. (Е-1)
хх,х2
Для этого выпишем соответствующий лагранжиан:
?(x1? х2, Х) = (хх + x2I/p + \(у-р1х1 -р2х2).
Поскольку предпочтения монотонны, то в решении бюджетное
ограничение будет выполняться как равенство. В предположении внутреннего
решения условия Куна — Таккера совпадают с обычными условиями
первого порядка для лагранжиана, поэтому для значений jci, Jt2, и А,,
являющихся решениями, должны выполняться следующие равенства:
^ = (*f + xl I/p"' *{"-' - V, = 0, (Е-2)
ахх
^ = (хр +;сРI/р-'х2р-' -Яр2 =0, (Е-3)
ох2
~Ч1=У- Р\Х\ " P2X2 = 0 • (Б)
Преобразовав (Е-2) и (Е-3), разделив одно на другое и снова
преобразовав, мы сведем эти три уравнения с тремя неизвестными к двум уравнениям
с двумя неизвестными jc, и х2, представляющими для нас особый интерес:
\i/(P-i)
(Е-5)
y = plxl+p2x2. (E-6)
Сначала подставим jc, из (Е-5) в (Е-6), чтобы получить уравнение
относительно Х2'.
( y/(p-D
+ Ах2=х2(Ар^1)+Л^1))Л-^1). (Е-7)
у = рхх2
Pi
Pi
Выразив х2 из (Е-7), найдем решение:
рГ1)у
(Р,Р/(Р"')+АР/(Н))
(Е-8)

Глава 1. Теория потребителя
43
Чтобы найти хх, подставим (Е-8) в (Е-5) и получим
хЛ =
рГХ)у
(pf^+pf^)
(Е-9)
Равенства (Е-8) и (Е-9) — решения задачи потребителя (Е-1) —
представляют собой маршалловские функции спроса. Определив параметр
г = р/(р -1), можно упростить (Е-8) и (Е-9) и записать их как
Р\ +Рг
Рх+Рг
(Е-10)
(Е-11)
Отметим, что решения задачи потребителя зависят только от ее
параметров, р]9 р2 и у . При различных ценах и доходе (Е-10) и (Е-11)
дадут различные объемы спроса на каждый товар. Проиллюстрируем
проведенный анализ на рис. 1.12. При ценах рх, р2 и доходе у решениями
задачи потребителя будут указанные на рисунке объемы товаров х, и х2.
Пара (/?,, Xj(/?,, р2, у)) будет точкой на (одной из) кривых спроса
потребителя на товар х,. ?
х2
рг2-1уКр;+ю
+Хх
**1
рГ]уКрГ1+рг2)
Рис. 1.12. Потребительский спрос в случае, когда предпочтения
описываются CES-функцией полезности

44
Часть I. Экономические агенты
В завершение несколько слов о свойствах функции спроса х(р, у),
выведенной из задачи максимизации полезности потребителя. Мы
приняли достаточно предположений для того, чтобы гарантировать (по теореме
о максимуме) непрерывность х(р, у) в R"+. Мало того, нам хотелось бы
рассмотреть наклон кривых спроса, а для этого требуется дифференци-
руемость х(р, у). С этого момента мы будем просто предполагать, что
функция х(р, у) дифференцируема там, где это нужно. Но для того
чтобы вы знали, за счет чего это достигается, мы сформулируем без
доказательства следующий результат.
Теорема 1.5. Дифференцируемость функции спроса.
Пусть х* » 0 является решением задачи максимизации полезности
потребителя при ценах р° » 0 и доходе у0 > О. Если
• и дважды непрерывно дифференцируема на Ш"++,
• du(\*)/dxi > О для некоторого i = 1, ...,«,
• окаймленный гессиан и имеет ненулевой определитель в х ,
то функция х(р, у) дифференцируема в (р°, у0).
1.4. Косвенная полезность и расходы
1.4.1. Косвенная функция полезности
Обычная функция полезности и{\) определена на потребительском
множестве X и напрямую представляет предпочтения потребителя.
Поэтому она называется прямой функцией полезности. При данных ценах
р и доходе у потребитель выбирает набор х(р, у), максимизирующий
его полезность. Уровень полезности, достигаемый при выборе х(р, у),
будет наивысшим из всех, которые допускаются бюджетным
ограничением потребителя при данных ценах р и доходе у. Различные цены или
доход будут задавать различные бюджетные ограничения, что в общем
случае повлияет на выбор потребителя и итоговый уровень полезности.
Соотношение между ценами, доходом и значением полезности можно
определить с помощью вещественнозначной функции v:M"xIR+->R
следующим образом:
V(P> 7) = maxw(x) при px<j/, A-12)
Функция v(p, у) называется косвенной функцией полезности. Это
функция максимального значения, соответствующая задаче максимиза-

Глава 1. Теория потребителя
45
ции полезности потребителя. Если и(х) непрерывна, то v(p, у)
корректно определена для всех р » 0 и у > О, поскольку гарантируется
существование решения задачи A-12). Если кроме того и(х) строго квазивогну-
та, то решение единственно и записывается как х(р, у), т.е. как значение
функции спроса потребителя. Максимально возможный уровень
полезности, который может быть достигнут при ценах р и доходе у, будет,
таким образом, достигаться при выборе х(р, у). Итак,
v(p, y) = u(x(p, у)).
A-13)
Геометрически можно представить, что v(p, у) задает уровень
полезности, соответствующий самой высокой кривой безразличия, достижимой
потребителем при данных ценах р и доходе у, как изображено на
рис. 1.13.
х2
у/р2
Рис. 1.13. Косвенная полезность при ценах р и доходе у
Косвенная функция полезности будет обладать несколькими
свойствами. Непрерывности функции ограничения по р и у достаточно для
того, чтобы обеспечить непрерывность v(p, у) по р и у на R"+xM+ (см.
раздел А2.4). В сущности, непрерывность v(p, у) следует из того факта,
что при положительных ценах «малые изменения» любого из параметров
(Р> У)> определяющих положение бюджетного ограничения, приведут к
«малым изменениям» максимального уровня полезности, достижимого
потребителем. В следующей теореме мы сформулируем ряд других
свойств v(p, у).

46
Часть I. Экономические агенты
Теорема 1.6. Свойства косвенной функции полезности .
Если и(х) непрерывна и строго возрастает на Ш"+, то функция
v(p, у), определенная в A-12):
1) непрерывна на R"+ xR+ ;
2) однородна нулевой степени по (р, у);
3) строго возрастает по у;
4) не возрастает по р.
Кроме того она:
5) квазивыпукла по (р, у);
6) удовлетворяет тождеству Роя: если v(p, у) дифференцируема в
точке (р°, у0) и 9v(p°, у°)/ду*0, то
Wp« о) = _Эу(Р°, /)/»,
Доказательство. Свойство 1) следует из теоремы о максимуме,
упомянутой в разделе А2.4. Вдаваться в детали мы не будем.
Второе свойство легко доказать. Требуется показать, что
V(P> У) = V(*P> С) Для всех * > 0 • Но v(p, j;) = [max м(х) при ф • х < ty],
что, конечно, эквивалентно [maxw(x) при р-х<хЬ потому что мы
можем разделить обе стороны ограничения на t > О, не влияя на множество
удовлетворяющих ему наборов (см. рис. 1.14). Следовательно,
v(/p, ty) = [max и(\) при р • х < у] = v(p, у).
*2
ty/tp2=y/pi
v(fp,fv) = v(p,v)
-**i
HjPl/^2 = -/^1^2 У^ ty/tp\ = >ф|
Рис. 1.14. Однородность косвенной функции полезности по ценам и доходу
Эта теорема (как и многие последующие утверждения книги) остается справедливой и
при более слабых предположениях, в частности при замене условия строгого
возрастания функции полезности на условие ее локальной ненасыщаемости. Авторы
представляют экспозицию теории в максимально упрощенном виде, избегая деталей, которые
можно опустить при первом (серьезном) знакомстве с этой теорией. — Примеч. ред.

Глава 1. Теория потребителя
47
Интуитивный смысл свойств 3) и 4) заключается в том, что любое
ослабление бюджетного ограничения потребителя никогда не приведет к
снижению максимально достижимого уровня полезности, в то время как
любое ужесточение бюджетного ограничения никогда не приведет к его
повышению.
Чтобы доказать свойство 3) (и попрактиковаться в использовании
метода Лагранжа), мы введем некоторые дополнительные предположения,
хотя можно обойтись и без них. Для простоты предположим, что решение
задачи A-12) строго положительно и дифференцируемо, (р, у)»0, а
функция и() дифференцируема, причем du(x)/dxi >О для всех х»0.
Как мы отмечали выше, поскольку и() строго возрастает,
ограничение в A-12) в оптимуме должно выполняться как равенство.
Следовательно, A-12) эквивалентно задаче
V(P> 7) = maxw(x) при рх = у. (Р-1)
xeR"
Лагранжиан для (Р-1) выглядит как
Дх, Х) = и(х) + Х(у-рх). (Р-2)
Пусть х*=х(р, у) является решением (Р-1) для некоторого
(Р> >0 » 0 • По нашему дополнительному предположению х* » 0,
поэтому можно применить теорему Лагранжа и прийти к заключению, что
существует X* е R такое, что
д?(х\ X*) ди(х*)
Эх, Эх
--АДр, =0,1 = 1, ...,". (Р-3)
Заметим, что, поскольку и рпи du{x)/dxi положительны, X тоже
положительно.
Дополнительные предположения о дифференцируемости позволяют
нам применить теорему об огибающей (теорема А2.21), чтобы увидеть,
что v(p, у) строго возрастает по у. По теореме об огибающей частная
производная функции v(p, у) по у равна частной производной
лагранжиана по у в точке (х\ X*):
МР,у) = д?(*\Г) = х.>0 (р4)
ду ду
Таким образом, v(p, у) строго возрастает при у > 0, а значит, поскольку
v непрерывна, она возрастает при у > 0.

48
Часть I. Экономические агенты
Для свойства 4) также можно использовать теорему об огибающей.
Однако мы приведем более элементарное доказательство, которое не
задействует никакие дополнительные гипотезы. Рассмотрим р°>р!, и
пусть х° является решением A-12) при р = р°. Поскольку х°>0,
(р° -р^-х0 >0. Тогда р1 -х° <р° -х° <у, так что х° является
допустимым набором для A-12) при р = р!. Можно заключить, что
v(p', у) > и(х°) = v(p°, у), что и требовалось доказать.
Свойство 5) утверждает, что потребитель предпочтет одно из двух
экстремальных бюджетных множеств любому их среднему. Нам нужно
показать, что v(p,y) квазивыпукла по вектору цен и доходу (р,У).
Пусть В1, В2 и В1 представляют собой бюджетные множества при
ценах и доходах соответственно (р1, у1), (р2, у2) и (р', У), где
р' =/р* +A-/)р2, а У =tyl +A-0/. То есть
^{xlp'-x^y},
52={х|р2.х</},
Я'={х|р'-х<У}.
Предположим, что любой выбор, который потребитель может сделать
в бюджетном множестве В1, мог также быть сделан либо в бюджетном
множестве В1, либо в бюджетном множестве В2. Это значит, что любой
уровень полезности, достижимый в бюджетном множестве В1, мог быть
достигнут либо в В1, либо в В2. Тогда, конечно, максимальный уровень
полезности, достижимый в В', не может быть больше, чем максимальный
уровень полезности, достижимый в В], или же максимальный уровень
полезности, достижимый в В2. Но если это так, то максимальная
полезность, достижимая в множестве В1, не может превышать наибольшего из
этих уровней. Если наше предположение верно, то мы получаем, что
v(p', У^тахКр1, У), v(p2, /)] V>e [0, 1].
Это эквивалентно утверждению, что v(p, ;;) квазивыпукла по (р, у).
Теперь нам достаточно показать, что наше предположение о бюджетных
множествах верно, т.е. что если хе В1, то либо хе В1, либо хе В2 для всех
te [0, 1]. Если в качестве / мы выберем одно из граничных значений, то В1
совпадет с В1 или с В2, и нужные соотношения будут тривиальными.
Остается доказать, что они будут выполняться для всех t е @, 1).

Глава 1. Теория потребителя
49
Предположим, что утверждение неверно. Тогда можно найти некоторое
te (О, 1) и хе В1 такое, что х<? В1 их^52. Но если xg 51 их^В2, то
р1 • х > У
р2 х>/
соответственно. Поскольку / е @, 1), можно умножить первое
неравенство на /, а второе — на A - /), что дает
tpl-x>tyl
и
A-/)р2-ж>A-0/.
Сложив их, получим
(/р'+A-0р2)х>у+A-0у2,
или
р' х>/.
Но из этого соотношения следует, что xg В1, а это противоречит
исходному предположению. Поэтому мы делаем вывод о том, что если хе Я',
то хе В1 или хей2 для всех tG [О, 1]. Из предшествующих рассуждений
можно заключить, что v(p, у) квазивыпукла по (р, у).
Наконец, обратимся к свойству 6), тождеству Роя. Оно гласит, что
маршалловский спрос потребителя на 1-й товар равен отношению
частных производных косвенной функции полезности по pi и по у с
обратным знаком. (Обратите внимание на знак «минус» в свойстве 6).)
Мы снова используем дополнительные предположения, введенные
выше, поскольку еще раз обратимся к теореме об огибающей. (См. в
упражнении 1.35 доказательство, которое не требует этих предположений.)
В предположении, что х* = х(р, у) — решение A-12) — является строго
положительным, как доказывалось выше, должно существовать X,
удовлетворяющее (Р-3). Используя теорему об огибающей для нахождения
3v(p, y)/bpi, получим
ЩЛ=Щ1*1=-хх-. (р_5)

50
Часть I. Экономические агенты
Однако по (Р-4) X* = 9v(p, у)/ду > 0. Поэтому (Р-5) принимает вид
_Мр, >0/Эл=х»=х(р yh
5v(p, у)/ду
что и требовалось доказать. ¦
Пример 1.2. В примере 1.1 прямая функция полезности имела CES-
форму, w(jc,, jc2) = (x,p+^I/p, где 0*р<1. Мы нашли маршалловские
функции спроса
~г-К
(Е-1)
Р\ +Р2
*2(р, У)^4^7
Рх+Рг
при г = р/(р-1). По A-13) мы можем построить косвенную функцию
полезности, подставив их в прямую функцию полезности. После
преобразований получаем
v(p, J) = [(*,(P, у)У+(х2(р, у)У?> =
А У +\JbJL
= У
Р\+Рг) УР\+Рг
w j. „- ¦1/р
Р\ +Рг
1/р
(Е-2)
Нам нужно проверить, что (Е-2) удовлетворяет всем свойствам
косвенной функции полезности, перечисленным в теореме 1.6. Легко видеть,
что v(p, у) однородна нулевой степени по ценам и доходу, потому что
для любого t > 0
v(tp,ty) = ty((tPiy+(tp2yr/r =
= ty(fprl+trp'2)-l/r =
=tyt-\p;+pr2r/r =
=у(р:+рг2уУг =
= Чр, у)-

Глава 1. Теория потребителя
51
Чтобы убедиться в ее возрастании по у и убывании по р,
продифференцируем (Е-2) по доходу и любой из цен:
<Мр, У) _,„г_^ Mr4-i/r
ду
= (аг+/>2Т/г>о, (е-з)
^^ = -<Л' + аТ'гНЛ>Г' <0, / = 1,2. (Е-4)
dPi
Для проверки выполнения тождества Роя поделим (Е-4) на (Е-З) и
вспомним (Е-1):
Эу(р, у)/дР, _( х,Лр[+р[Г1г)-хурГ _
Мр, у)/дУ (p;+pr2rl/r
ург'х
Pi +P2
Доказательство квазивыпуклости (Е-2) по (р, у) мы оставляем в качестве
упражнения. ?
1.4.2. Функция расходов
Косвенная функция полезности дает эффективный способ описания
поведения потребителя на рынке. Не менее нужным инструментом
является функция расходов. Чтобы построить косвенную функцию полезности,
мы фиксировали рыночные цены и доход и искали максимальный уровень
полезности, достижимый потребителем при этих ценах и доходе. Чтобы
построить функцию расходов, мы фиксируем цены и уровень полезности и
задаем другой вопрос: какой минимальный объем денеэюных расходов
обеспечивает потребителю при данных ценах достижение заданного
уровня полезности? При этом мы игнорируем любые ограничения, связанные с
доходом потребителя, и просто спрашиваем: сколько потребителю
придется потратить, чтобы получить некоторый уровень полезности?
Чтобы лучше понимать характер изучаемой проблемы, рассмотрим
рис. 1.15 и сравним его с рис. 1.13. Каждая из параллельных прямых на
рис. 1.15 изображает все наборы х, для приобретения которых требуется
один и тот же объем совокупных расходов при ценах р = (/?р р2). Каждая
из этих кривых постоянных расходов неявно задается уравнением
е = рххх + р2х2 для различных объемов совокупных расходов е > О. Таким
образом, все они имеют одинаковый наклон — Р\/р2 > но пересекают
горизонтальную и вертикальную оси в разных точках, соответственно, е/р{ и

52 Часть I. Экономические агенты
е/р2. Кривые постоянных расходов, более удаленные от начала координат,
содержат более дорогие наборы, менее удаленные — более дешевые
наборы. Если зафиксировать уровень полезности и, то кривая безразличия
и(х) = и даст все наборы, приносящие потребителю именно эту полезность.
*i*(P,w) еъ/рх е/рх е{/рх е2/рх
Рис. 1.15. Поиск наименьшего уровня расходов, необходимого
для достижения уровня полезности и
Отсутствие общих точек у кривой постоянных расходов еъ и кривой
безразличия и указывает на то, что еъ долларов при данных ценах
недостаточно для того, чтобы достичь полезности и. Однако каждая из кривых
е1, е2 и е имеет по крайней мере одну общую точку с и, и это значит,
что любого из этих объемов расходов достаточно для того, чтобы
потребитель получил полезность и. Для построения функции расходов нам
нужен минимальный объем расходов, необходимый потребителю для
достижения уровня полезности и, или самая низкая кривая постоянных
расходов, которая имеет хотя бы одну общую точку с кривой безразличия и.
Очевидно, что это будет объем расходов е , а самым дешевым набором,
который обеспечивает полезность и при ценах р, будет набор
xA=(jc*(p, u\ лг*(р, и)). Если обозначить минимальный объем расходов,
необходимый для достижения полезности и при ценах р, через е(р, и),
то он будет равен стоимости набора хЛ, т.е. е(р, u) = plxlh(p, u) +
+p2xh2(p, u) = e.
В общем виде функция расходов определяется как функция
минимального значения
е(р, w) = minpx при и(х)>и A-14)
X€R"

Глава 1. Теория потребителя
53
для всех р » 0 и всех достижимых уровней полезности и. Для удобства
обозначим множество достижимых уровней полезности как
11 = {и(х)\хе R"+}. Таким образом, областью определения е() является
множество Щ+х!1.
Заметим, что функция е(р, и) корректно определена, поскольку при
ре R"++ и xgR" имеет место рх>0. Следовательно, множество чисел
{е | е = р • х для некоторого х, такого, что и(х) > и}, ограничено снизу
нулем. Кроме того, поскольку р » 0, можно показать, что это множество
замкнуто, а значит, содержит наименьший элемент. Значение е(р, и) в
точности равно этому наименьшему числу1. Заметим, что любое решение
этой задачи минимизации будет неотрицательным и будет зависеть от
параметров р и и. Заметим также, что если функция и(х) непрерывна и
строго квазивогнута, то решение будет единственным и его можно
обозначить как функцию хЛ(р, м)>0. Как мы видели, если хЛ(р, и)
является решением этой задачи, то наименьший объем расходов, необходимый
для достижения полезности и при ценах р будет в точности равен
стоимости набора хЛ(р, м),или
е(р, и) = р.хл(р, и). A-15)
Мы видели, насколько тесно задача максимизации полезности
потребителя связана с его наблюдаемым спросом на рынке. Точнее, сами
решения этой задачи — маршалловские функции спроса — подсказывают,
какое именно количество каждого товара потребитель будет реально
покупать при различных ценах и доходе. Решение задачи минимизации
расходов хл(р, и) мы будем интерпретировать как другой вид «функции
спроса», но такой, который ненаблюдаем напрямую.
Проведем следующий мысленный эксперимент. Если зафиксировать
полезность, которую может получить потребитель, на некотором
произвольном уровне и, то как будет изменяться объем каждого из
приобретаемых товаров при изменении цен? «Функции спроса», о которых идет речь,
являются функциями спроса с постоянной полезностью. Мы полностью
игнорируем объем денежных доходов потребителя и уровень полезности,
1 Заметим, что е(р, и) = minр• х при xeUJ9 где U- = {хе R" | р• х < р• х}, а х —
любой потребительский набор такой, что и(х)>и. Формально: пусть xeU и
Uж ={хе ?/|р-х<р-х}. При этом и^ — непустое компактное множество и
е(р, и) = min р • х при х е U- для любого х такого, что и(Т) >и. — Примеч. ред.

54
Часть I. Экономические агенты
которого он действительно может достичь. Нам известно, что если у
потребителя имеется некоторый доход и происходит изменение цен, то объем
его покупок, как правило, изменяется, как изменяется и уровень
достигаемой им полезности. Чтобы представить, как нам построить наши
гипотетические функции спроса, нужно вообразить процесс, при котором любое
снижение цены и соответствующий прирост полезности потребителя
компенсируются снижением его дохода и соответствующим снижением
полезности до исходного уровня. Аналогично, увеличение одной из цен,
приводящее к снижению полезности, должно быть компенсировано таким
увеличением дохода, чтобы сопровождающий его прирост полезности был
равен ее снижению. Поскольку в этом процессе любое изменение
полезности, связанное с изменением цен, компенсируется изменением полезности
за счет гипотетического изменения дохода, описываемые здесь
гипотетические функции спроса часто называются функциями компенсированного
спроса. Первым в таком виде их описал Джон Хикс A939), поэтому эти
функции более известны как хиксовские функции спроса (функции спроса
по Хиксу). Как мы покажем ниже, решение задачи минимизации расходов
хЛ(р, и) в точности равно вектору спроса по Хиксу потребителя.
Чтобы прояснить эту идею, рассмотрим рис. 1.16. Если зафиксировать
достижимую потребителем полезность на уровне и, как показано на
рис. 1.16(a), и задать цены /?,° и р\, то бюджетное ограничение будет
иметь наклон — p\j р\ • Заметим, что максимизация полезности и
минимизация расходов достигаются тогда в одной и той же точке с
координатами х\{р\,р\9и) и X2(pi,p2,u). Если снизить цену товара 1 до р\ <р1°,
оставляя потребителя на кривой безразличия с уровнем полезности и,
путем соответствующего снижения дохода, то новая бюджетная линия будет
иметь наклон — р\1 р\ > а точка> максимизирующая полезность, -
координаты х*(р\9р\,и) и хь2{р\,р1,и). Если зафиксировать цену р\ и
изобразить, как показано на рис. 1.16F), цены товара 1 и соответствующие
гипотетические количества товара 1, которые потребитель «приобретет» при
этих ценах, при условии, что если его полезность ограничена уровнем и,
то получится «псевдокривая спроса». Это построение и есть кривая спроса
по Хиксу на товар 1 при уровне полезности и. Очевидно, что кривые
спроса по Хиксу будут различными для разных уровней полезности, т.е. для
разных кривых безразличия. Форма и положения каждой из них при этом
будут определяться потребительскими предпочтениями.
Короче говоря, решение задачи минимизации расходов хЛ(р, и) —
это в точности вектор спроса по Хиксу, так как каждое из гипотетических
«бюджетных ограничений» потребителя, представленных на рис. 1.16,

Глава 1. Теория потребителя 55
соответствует минимальному объему расходов, необходимому для
достижения заданного уровня полезности при данных ценах.
A{pIpIu)
4{р1р»
J(pIp» xf(p\9p°29u)
P\
p\
x^plplu) x^pIpIu)
F)
Рис. 1.16. Хиксовский спрос на товар 1
Таким образом, функция расходов, определенная в A-14), содержит
важную информацию о спросе по Хиксу. Хотя ее аналитическая ценность
станет очевидной немного позднее, здесь можно обратить внимание на ту
легкость, с которой эта информация из нее извлекается: спрос по Хиксу
можно получить из функции расходов простым дифференцированием.
Это и другие важные свойства функции расходов детализированы в
следующей теореме.
Теорема 1.7. Свойства функции расходов.
Если функция и() непрерывна и строго возрастает, то функция
е(р, и), определенная в A-14), обладает следующими свойствами:
1) равна нулю, когда «(•) принимает наименьшее значение из
множества 11;

56
Часть I. Экономические агенты
2) непрерывна на множестве определения Ш"++ хТ/;
3) для всех р » 0 строго возрастает и не ограничена сверху по и ;
4) возрастает по р;
5) однородна первой степени по р;
6) вогнута по р.
Если, кроме того, w(-) квазивогнута, то выполняется:
7)лемма Шепарда: е(р,и) дифференцируема по р в точке (р°, и0),
р°»0, и
Эе(р°, и°)_ h о о
Доказательство. Для доказательства свойства 1) заметим, что
наименьшее значение в множестве 1/ равно и@), потому что и() строго
возрастает в R"+. Следовательно, е(р, м@)) = 0, так как при х = 0
уровень полезности и@) достигается при объеме расходов, равном р • 0 = 0.
Свойство 2) — непрерывность — снова следует из теоремы о
максимуме.
Хотя свойство 3) выполняется и без дальнейших предположений, мы
удовлетворимся его доказательством при дополнительных гипотезах о
том, что хЛ(р,н)»0 и дифференцируема Vp»0, u>u@) и что и()
дифференцируема, причем du(x)/dxj > 0, V/ на R"++.
Функция и() непрерывна, строго возрастает и р »0, поэтому
ограничение в A-14) должно выполняться как равенство, так как если
w(x1)>w, то найдется такое te@,1), достаточно близкое к 1, что
u(txl) > и. Далее, и > и@) означает, что w(x') > w@), поэтому х1 Ф 0.
Таким образом, поскольку рх'>0, р(Гх1)<рх1. Следовательно, если
ограничение не выполняется как равенство, то найдется более дешевый
набор, который также будет удовлетворять этому ограничению. Поэтому
в оптимуме ограничение должно выполняться как равенство, и A-14)
можно записать как
е(р, w) = minpx при и(х) = и. (Р-1)
xeR"
Лагранжиан для этой задачи:
Дх, 1) = р-х + Чм-ф)]. (Р-2)
При р » 0 и и > и@) решением (Р-1) является х* = хл(р, и)» 0 (по
предположению). Поэтому по теореме Лагранжа существует такое А,*, что

Глава 1. Теория потребителя 57
= Pi~^ — = 0, / = !,...,«. (Р-3)
dx, dx,
Заметим, что pi и ди(х*)/дх{ положительны, поэтому А,* тоже
положительно. При наших дополнительных предположениях можно применить
теорему об огибающей, для того чтобы показать, что е(р, и) строго
возрастает по и.
По теореме об огибающей частная производная функции
минимального значения е(р, и) по и равна частной производной лагранжиана по
и в точке (х*Д*). Отсюда
Эе(р, и) = Э?(х*, А,*)=д.^0
ди ди
Поскольку это верно для всех и > м@) и поскольку е(-) непрерывна,
можно сделать вывод о том, что для всех р » 0 функция е(р, и) строго
возрастает по и на множестве X/, которое включает м@).
Можно показать, что неограниченность е по и следует из
непрерывности и строгого возрастания и(\). В упражнении 1.33 вам предлагается
это проделать.
Свойство 4) следует из свойства 7), поэтому мы вернемся к нему чуть
позже. Доказательство свойства 5) будет оставлено в качестве упражнения.
В свойстве 6) необходимо доказать, что е(р, и) является вогнутой
функцией цен. Для начала вспомним определение вогнутости. Пусть р1
и р2— некоторые положительные векторы цен, /е[0, 1], и
р; =tpl +(l-/)p2 является любой выпуклой комбинацией р1 и р2. Тогда
функция расходов будет вогнутой по ценам, если
te(pl, и) + A - t)e(p2, и) < е(р', и). (Р-5)
Чтобы убедиться в том, что это свойство имеет место, посмотрим, что
означает минимизация расходов при заданных ценах. Предположим, что
набор х1 минимизирует расходы, необходимые для достижения уровня
полезности и при ценах р1, х2 минимизирует эти расходы при ценах р2,
а х* - при ценах р'. Тогда стоимость х1 при ценах р1 не должна
превышать стоимости при ценах р1 любого другого набора х, который
позволяет получить полезность и . Аналогично стоимость набора х2 при ценах
р2 не должна превышать стоимости при ценах р2 любого другого

58
Часть L Экономические агенты
набора х, который позволяет получить ту же полезность и . Если, как мы
сказали, соотношения
р1 х1 <р! х
и
р2 х2 <р2 х
имеют место для всех х, позволяющих достичь полезности и, то эти
соотношения должны также выполняться и для х*, поскольку х*
позволяет получить полезность и . Таким образом,
р1 х1 <р* х*
и
р2 х2<р2 х*.
Поскольку t>0 и A-/)>0, мы можем умножить первое из этих
неравенств на t, второе — на A-0 и сложить их. Использовав определение
р', получим неравенство
ф1 -х'+а-ор'-х^р'-х*.
Левая часть является выпуклой комбинацией минимальных расходов,
необходимых для достижения полезности и при ценах р1 и р2, а правая
часть представляет собой минимальные расходы, необходимые для
достижения полезности и при ценах, являющихся выпуклой комбинацией
р1 и р2. Иными словами, это в точности то же самое, что (Р-5), т.е.
te(p\ u) + (l-t)e(p\ и)<е(р', и) V7e[0, 1]
то, что мы и намеревались показать.
Для доказательства свойства 7) снова обратимся к теореме об
огибающей, но дифференцировать будем по /?,. Это дает
М^и1=ЭЩ±Г1 = х>х^и),
Щ др,
что и требовалось доказать. Поскольку хл(р, и) > 0, это также доказывает
свойство 4). (См. в упражнении 1.36 доказательство свойства 7), не
требующее никаких дополнительных предположений. Попытайтесь
самостоятельно доказать свойство 4) без дополнительных предположений.) ¦
Пример 1.3. Снова предположим, что прямая функция полезности
имеет CES-форму, w(jcp х2) = (jc,p +х*)]/р, где 0 * р < 1. Выведем соответст-

Глава 1. Теория потребителя
59
вующую функцию расходов для этого случая. Поскольку предпочтения
монотонны, можно сформулировать задачу минимизации расходов A-15) в виде
ттрххх + р2х2 при и-(х% +х?I/р =0, хх >0, х2 >0.
Xj ,Х2
Ее лагранжиан
?(х1? х29 X) = plxl + p2x2 + \[u-(Xi+х2у/р]. (E-l)
В предположении внутреннего решения для обоих товаров
оптимальные значения х{9 х2 и А, должны удовлетворять следующим условиям
первого порядка:
|^ = />2-5i«+x2pH/pHx2p-1=0,
ох2
|? = м-(*Г+*2р),/р=о.
(Е-2)
(Е-3)
(Е-4)
Исключив X, их можно свести к двум уравнениям с двумя неизвестными:
/ n1/(p-D
ДС,=*2Р- , (Е-5)
\Рг)
u = (x*+xp2)l/p. (E-6)
Подставив (Е-5) в (Е-6), получим
м =
\р/(р-1)
,р П.
.Рг)
+ хр2
1/р
= х,
\р/(р-|)
П1/Р
.Pi.
+1
Выразим отсюда х2 и, положив г = р/(р -1), найдем
X, =14
/ \P/(P-1>
П-1/Р
хР + 1
= W[AP/(P-" +/>2Р/(р-|)Г1/(>2/<Р~') =
=«(лг+лг)<1/г)>Г'-
Подстановка (Е-7) в (Е-5) дает
хх=ирГ-Х)р^Лр[+рГгГ1г)-'рг2-Х =
=M(K+^)A/rHK"'
(Е-7)
(Е-8)

60
Часть I. Экономические агенты
Решения (Е-7) и (Е-8) зависят от параметров задачи минимизации, величин
р и и. Это хиксовские функции спроса, поэтому обозначим (Е-7) и (Е-8) как
х*(р, и) = и{р[+рг2)т-хр[-\ (Е-9)
*2Л(р, u) = u{p[+pr2flr)-xp[-\ (Е-10)
Чтобы построить функцию расходов, воспользуемся уравнением
A-15) и подставим (Е-9) и (Е-10) в целевую функцию (Е-1):
е(р,и) = ptx* (р,и) + р2х2(р,и) =
= upi(prl+pr2fr)-lprl+up2W+p2-yl/r)-lp2-,= (E-ll)
=«(K+/>2)(K+pD(l/rH =
= u(p[+pr2t.
Выражение (Е-11) представляет собой искомую функцию расходов.
Доказательство наличия у нее обычных свойств мы оставляем в качестве
упражнения. ?
1.4.3. Связь между косвенной функцией полезности
и функцией расходов
Хотя косвенная функция полезности и функция расходов
концептуально различны, между ними, очевидно, существует тесная связь. То же
самое можно сказать о функциях спроса по Маршаллу и Хиксу.
В частности, зафиксируем (р, у) и положим и = v(p, у). По
определению функции v это означает, что при ценах р уровень полезности и
является максимально достижимым, если доход потребителя равен у.
Следовательно, если бы при ценах р потребитель хотел достичь уровня
полезности не ниже, чем и, то доход у позволил бы ему сделать это. Но
вспомним, что е(р, и) — это минимальный объем расходов, необходимый
для того, чтобы достичь уровня полезности не ниже и. Тогда е(р, и) < у.
Следовательно, определения функций v и е приводят нас к неравенству
е(р, v(p, y))<y, V(p,j;)»0. A-16)
Далее, зафиксируем (р, и) и положим у = е(р, и). По определению
функции е это означает, что при ценах р доход у — это наименьший
доход, который позволяет потребителю достичь уровня полезности не
ниже и. Следовательно, если бы при ценах р доход потребителя состав-

Глава 1. Теория потребителя
61
лял у, то он мог бы достичь уровня полезности не ниже и . Но поскольку
v(p, у) является максимальным уровнем полезности, достижимым при
ценах р и доходе у, отсюда следует, что v(p, у) > и. Таким образом,
определения функций v и е также означают, что
v(p, e(p, u))>u9 V(p, u)eW++xll. A-17)
Следующая теорема показывает, что при некоторых уже знакомых
нам условиях относительно предпочтений оба эти неравенства на самом
деле должны выполняться как равенства.
Теорема 1.8. Связь между косвенной функцией полезности и
функцией расходов.
Пусть v(p, у) и е(р, и) являются косвенной функцией полезности и
функцией расходов для некоторого потребителя, функция полезности
которого непрерывна и строго возрастает. Тогда для всех р » 0, у > О и
uell:
1) *(Рэ v(p> у)) = у;
2) v(p, е(р, и)) = и.
Доказательство. Поскольку и() строго возрастает на Ш"+, она
достигает минимума в точке х = 0, но не достигает максимума. Кроме того, так
как м() непрерывна, множество 1/ достижимых значений полезности
должно представлять собой интервал. Следовательно, 1/ = [и@), й] при
й > и@), где й может быть конечным или стремиться к + <*>.
Для доказательства первого утверждения возьмем (р, j>)€3R^.+ xR+.
По A-16) е(р, v(p, y))<y. Нам нужно показать, что на самом деле
выполняется равенство. Предположим обратное, т.е. что е(р, и)<у, где
и = v(p, у). Заметим, что по определению v() uell, так что и<й.
По непрерывности е() (теорема 1.7) можно выбрать такое достаточно
малое ?>0, что и + е<й и е(р, и + е)<у. Пусть уг=е(р, w + е), тогда из
A-17) следует, что v(p, уе)>и + г. Поскольку уе <у9 a v строго
возрастает по доходу по теореме 1.6, v(p, >0>v(p, уг)>и + е. Но w = v(p, у),
так что мы получаем противоречие: и>и + г. Таким образом,
е(Р> v(p, у)) = у\
По-видимому, это тот случай, когда дополнительные предположения, скорее,
усложняют доказательство. — Примеч. ред.

62
Часть I. Экономические агенты
Для доказательства второго утверждения возьмем (р, w)gR"++x
x[t/@), и]. По A-17) v(p, e(p, и))>и. Чтобы показать, что A-17)
выполняется как равенство, снова предположим обратное, т.е. что
v(p,e(p,w))>M. Нужно рассмотреть два случая: и = и@) и w>w@). Мы
разберем только второй из них, оставив первый в качестве упражнения.
Положив у = е(р, w), получим v(p, y)>u. Поскольку е(р, w@)) = 0, a
е() строго возрастает по полезности (теорема 1.7), у = е(р, и)>0. Так
как v(-) непрерывна по теореме 1.6, можно выбрать такое достаточно
малое 8 > 0, что у-г > О и v(p, у-г)> и. Таким образом, при ценах р
доход у-г является достаточным для достижения уровня полезности,
превышающего и . Поэтому должно выполняться неравенство е(р, и) < у-г,
а это противоречит тому факту, что у = е(р, и). ¦
До сих пор, если мы хотели вывести функции косвенной полезности
и расходов потребителя, нам приходилось решать две отдельные задачи
условной оптимизации: задачу на максимум и задачу на минимум. Данная
теорема указывает простой путь, как получить одну из этих функций,
зная другую, т.е. теперь достаточно будет решить только одну
оптимизационную задачу, причем не важно, какую именно.
Чтобы посмотреть, как это работает, предположим, что задача
максимизации полезности решена и косвенная функция полезности
построена. Одно из известных нам свойств косвенной функции полезности —
строгое возрастание по доходу. Но тогда, если считать цены
постоянными и рассматривать ее только как функцию от дохода, для нее будет
существовать обратная функция по доходу. Имея
v(p, e(p, и)) = и9
мы можем применить эту обратную функцию (обозначим ее v_1(p:/)) к
обеим частям данного равенства, откуда
е(р, u) = v-\p:u). . A-18)
Что бы ни стояло в правой части равенства A-18), нам известно, что оно
будет в точности совпадать с выражением для функции расходов
потребителя — выражением, которое мы бы в конечном счете получили, решив
задачу минимизации расходов и подставив результат в целевую функцию.
Предположим теперь, что мы решили задачу минимизации расходов
и построили функцию расходов е(р, и). Мы знаем, что е(р, и) строго
возрастает по и . В предположении о постоянных ценах для нее сущест-

Глава 1. Теория потребителя
63
вует обратная функция по полезности, которую мы можем обозначить
е_1(р:/). Применив ее к обеим частям первого соотношения теоремы 1.8,
мы увидим, что косвенная функция полезности будет равна обратной
функции расходов по полезности при любом уровне дохода у :
v(p, y) = e-\p:y). A-19)
Равенства A-18) и A-19) снова иллюстрируют тесную связь между
максимизацией полезности и минимизацией расходов. Концептуально это
две стороны одной медали, а математически — косвенная функция
полезности и функция расходов являются (соответствующим образом
подобранными) обратными функциями по отношению друг к другу.
Пример 1.4. Эту технику можно продемонстрировать на основе
результатов предыдущих примеров. В примере 1.2 мы обнаружили, что
прямая CES-функция полезности порождает косвенную функцию
полезности вида
v(p, У) = У(Р[+РГ2У'Г (E-l)
для любых цен р и уровня дохода у. Таким образом, для дохода, равного
е(р, и) долларов, должно выполняться следующее равенство:
v(p, е(р, u)) = e(p, u)(p;+pr2yl/r. (E-2)
Далее, из второго утверждения теоремы 1.8 нам известно, что для любых
р и и
v(p, е(р, и)) = и. (Е-3)
(Е-2) и (Е-3) вместе дают
*(Р, u){p[+PlVlr=u. (E-4)
Найдя отсюда е(р, и), получаем выражение
е(р, u) = u(P;+pr2)l/r (E-5)
для функции расходов. Пример 1.3 подтверждает, что это в точности то
же самое выражение, которое было получено напрямую путем решения
задачи минимизации расходов потребителя.
Предположим теперь, что мы знаем функцию расходов и хотим
вывести косвенную функцию полезности. Для прямой CES-функции
полезности нам известно из примера 1.3, что
е(р, u) = u(p[ + p[t (E-6)

64
Часть I. Экономические агенты
для любых цен р и уровня полезности и. Тогда для уровня полезности
v(p, у) мы получим
е(р, v(p,y) = v(p,j)(K + рг2У/г. (Е-7)
Из первого утверждения теоремы 1.8, для любых pay
е(р, v(p, у)) = у. (Е-8)
Из (Е-7) и (Е-8) получаем
v(p, y)(p[+pr2t=y. (E-9)
Решая (Е-9), находим выражение для косвенной функции полезности:
v(p, У) = У(р;+рг2УУг. (Е-10)
С помощью примера 1.2 можно проверить, что (Е-10) совпадает с тем
выражением, которое было найдено напрямую путем решения задачи
максимизации полезности потребителя. ?
Изучим взаимоотношения между максимизацией полезности и
минимизацией расходов чуть глубже, обратив внимание на решения
соответствующих задач. Решения задачи максимизации полезности — это функции
спроса по Маршаллу, а решения задачи минимизации расходов— это
функции спроса по Хиксу. Учитывая тесную связь между самими
задачами, естественно предположить наличие тесной связи между их
решениями. Следующая теорема проясняет связь между спросом по Маршаллу и
спросом по Хиксу.
Теорема 1.9. Двойственность между функциями спроса по
Маршаллу и по Хиксу.
По предположению 1.2 при р»0, у>0, uell и / = 1,...,л между
функциями спроса по Маршаллу и по Хиксу выполняются следующие
соотношения:
1) *,(Р> J0 = *f(p, V(P> У))-
2) х*(р, w) = x;.(p, e(p, и)).
Первое соотношение означает, что маршалловский спрос при ценах
р и доходе у равен хиксовскому спросу при ценах р и максимальном
уровне полезности, достижимом при ценах р и доходе у. Второе гласит,
что хиксовский спрос при любых ценах р и уровне полезности и
совпадает с маршалловским спросом при тех же ценах и доходе, равном
минимальным расходам, необходимым при этих ценах для достижения уровня
полезности и.

Глава 1. Теория потребителя
65
Другими словами, теорема 1.9 утверждает, что решения задачи A-12)
являются решениями задачи A-14), и наоборот. Точнее, если х* является
решением задачи A-12) при (р,.у), то согласно данной теореме х*
является решением задачи A-14) при (р,и), где и -и{\). Наоборот, если х*
является решением A-14) при (р,и), то х* является решением A-12) при
(р, у), где у = р • х*. Теорема проиллюстрирована на рис. 1.17, из
которого ясно, что х* может рассматриваться либо как решение задачи A-12),
либо как решение задачи A-14), и именно в этом смысле х* обладает
двойственной природой.
У/Р2
У*Р\
Рис. 1.17. Минимизация расходов и максимизация полезности
Доказательство. Мы докажем, что выполняется первое
соотношение, оставляя доказательство второго в качестве упражнения.
Заметим, что по предположению 1-2 функция и() непрерывна и
строго квазивогнута, поэтому решения задач A-12) и A-14) существуют и
единственны. Следовательно, функции спроса по Маршаллу и по Хиксу
определены корректно.
Для доказательства первого соотношения положим х° =х(р°, у0) и
w°=w(x°). Тогда v(p°, y°) = u° по определению функции v(), a
р° -х° = у0 в силу строгого возрастания и() по предположению 1-2. По
теореме 1.8 е(р°, v(p°, у°)) = у0, или, что то же самое, е(р°, и°) = у°. Но
так как и(\°) = и° и р0-х0=>>0, то х° является решением A-14) при
(р, н) = (р°, и0). Таким образом, х°=хЛ(р°, м°), т.е. х(р°, ^°) =
= ж*<р°, v(p°, /)). ¦
и{\ ) = и
^Tfi

66
Часть I. Экономические агенты
Пример 1.5. Подтвердим утверждение теоремы 1.9 для
потребителя с CES-функцией полезности. Как было показано ранее (пример 1.3),
функции спроса по Хиксу равны
*?(р, и) = и(р;+рг2Г/г)-1рГ\ / = 1,2. (Е-1)
Косвенная функция полезности (пример 1.2) имеет вид
v(p, У) = У(Р;+РГ2Г/Г. (Е-2)
Подставляя (Е-2) вместо и в (Е-1), получаем
*?(р, v(P, ^))=v(p, уМ+рг2Г'г)-}рГ =
= ЯК + Р2Г1/г(К + К)<,/гНрГ' =
= урГ\р; + рг2Г*= (е-З)
Последнее выражение в правой части (Е-З) представляет собой функции
спроса по Маршаллу, выведенные нами в примере 1.1 напрямую путем
решения задачи максимизации полезности потребителя, что
подтверждает первое соотношение теоремы 1.9.
Чтобы подтвердить второе соотношение, возьмем функции спроса по
Маршаллу (пример 1.1)
*,(Р. jO = -^Hr,/ = 1,2, (Е-4)
Pi + А
и функцию расходов (пример 1.3)
е(р, tt) = n(K+Ar)Vr- (E-5)
Подставляя (E-5) вместо у в (E-4), находим
е(р, и)/?Г' _
дг,(р, е(р, и)) = -
А +Рг
= u(prl+pr2)Vr-^—r = (E-6)
Л + />2
=uPr\p;+pr2f,r)-\i=i,2.
Последнее выражение в правой части (Е-6) совпадает с функциями спроса
по Хиксу, полученными в примере 1.3 напрямую путем решения задачи
минимизации расходов потребителя. ?

Глава 1. Теория потребителя
67
В завершение этого раздела проиллюстрируем четыре соотношения
из теорем 1.8 и 1.9. На рис. 1.18(a) потребитель с доходом у достигает
максимального уровня полезности и при ценах р, выбирая х\ и х*2.
Соответствующая кривая безразличия функции полезности и(х) дает
полезность w = v(p, у), и на рис. 1.18F) точка (р,, дс*) лежит на маршаллов-
ской кривой спроса на товар 1. Далее рассмотрим задачу минимизации
расходов потребителя и предположим, что мы минимизируем расходы,
необходимые для достижения полезности и. Очевидно, что тогда самая
нижняя кривая постоянных расходов, позволяющая получить полезность
и при ценах р, совпадет с бюджетным ограничением в задаче
максимизации полезности, а минимизирующий расходы объем спроса на товары
снова составит jc* и х*2, в результате чего точка (р19х*) на рис. 1.18 (б)
будет лежать и на кривой спроса по Хиксу на товар 1.
и = v(p, у) = v(p, e(p, и))
у = е(р, v(p, у))
А Р
(а)
*>*!
xi(p,y)=xl(v,u(p,y))
х,А(р, и)= **(р,е(р,и))
х* = х,А(р, и) = х*(р, \4р,у))=хх(р,у)
(б)
Рис. 1.18. Иллюстрация теорем 1.8 и 1.9
->*i

68
Часть I. Экономические агенты
Рассматривая обе задачи одновременно, из того факта, что
бюджетное ограничение и линия постоянных расходов пересекаются в одних и
тех же точках, легко видеть, что доход у равен минимальному объему
расходов, необходимому для получения полезности v(p, у), т.е. что
у = е(р, v(p, у)). Уровень полезности и является максимально
достижимым как при ценах р и доходе у, в силу чего и = v(p, у), так и при
ценах р и доходе, равном минимально необходимым для достижения и
расходам, т.е. w = v(p, e(p, и)). Наконец, заметим, что точка (р19х*)
лежит на всех трех кривых — на кривой хиксовского спроса на товар 1 при
ценах р и уровне полезности и, кривой хиксовского спроса на товар 1
при ценах р и уровне полезности v(p, у), кривой маршалловского спроса
на товар 1 при ценах р и доходе у. Тем самым, х,(р, у) = х*(р9 v(p, у)) и
jc^p, w) = jc,(p, e(p, и)), как мы и предполагали.
1.5. Свойства потребительского спроса
Теория потребительского поведения позволяет строить определенные
прогнозы относительного рыночного поведения. Мы увидим, что если
предпочтения, цели и обстоятельства, в которых потребители принимают
решение, таковы, какими мы их смоделировали, то поведение рыночного
спроса должно обладать некоторыми наблюдаемыми характеристиками.
Тогда теорию можно проверить, сопоставив теоретические ограничения
на поведение спроса с фактическими. Если в результате теория завоюет
определенное доверие, то ее можно применять и далее. Например,
теоретические выводы можно использовать при статистической оценке
потребительского спроса в качестве ограничений на значения оцениваемых
параметров. Такое приложение теории помогает повысить статистическую
точность полученных оценок. Поэтому и для теоретических, и для
эмпирических целей крайне важно «выжать» из нашей модели
максимизирующего полезность потребителя все возможные выводы, относящиеся к
наблюдаемому поведению спроса. В этом и состоит задача данного
раздела.
1.5.1. Относительные цены и реальный доход
Экономисты предпочитают измерять существенные переменные в
реальном, а не денежном выражении, потому что «деньги — это туман»,
который только скрывает то, что на самом деле волнует (или должно
волновать) людей, а именно: реальные товары. Относительные цены и
реальный доход и есть два таких измерителя.

Глава L Теория потребителя 69
Под относительной ценой товара / мы понимаем количество
единиц некоторого другого товара j, от которых надо отказаться ради
приобретения одной единицы /-го товара. Если р{ — денежная цена /-го
товара, то она будет измеряться в долларах за единицу товара. Денежная
цена j -го товара также будет показывать количество долларов за
единицу товара. Относительная цена /-го товара в единицах у-го измеряет
число единиц j -го товара, от которых следует отказаться, чтобы
приобрести единицу /-го товара. Она определяется отношением цен Pi/pj,
поскольку
/?7 _ долл./единица i _ долл. единица j _ количество j
Pj долл./единица j единица i долл. единица i
Под реальным доходом мы понимаем максимальное количество
единиц некоторого товара, которое потребитель мог бы приобрести, если бы
он потратил на него весь свой денежный доход. Реальный доход должен
отражать способность потребителя распоряжаться всеми ресурсами путем
измерения его способности распоряжаться одним реальным благом. Если
денежный доход потребителя равен у, то отношение y/pj называется
его реальным доходом, выраженным в j -м товаре, и измеряется в
единицах j -го товара, потому что
у долл.
— = = количество j .
pi долл./ единица j
Простейший вывод, который следует из модели максимизирующего
полезность потребителя, заключается в том, что на его поведение влияют
только относительные цены и реальный доход. Он формулируется как
утверждение о том, что поведение потребительского спроса
демонстрирует отсутствие денежной иллюзии. Чтобы убедиться в этом, обратимся
к рис. 1.14. Мы видим, что изменение денежного дохода и уровня всех
цен в равных пропорциях не влияет на наклон бюджетной линии
(относительные цены) и ее пересечения с координатными осями (на реальный
доход, выраженный в терминах каждого из товаров), а значит, и на спрос.
Математически это означает, что функции спроса положительно
однородны нулевой степени по ценам и доходу. Поскольку деньги в нашей
модели играют только роль единицы измерения, что-то иное вряд ли
было бы возможно.
Для использования в дальнейшем мы объединим эти свойства с тем
фактом, что потребитель обычно тратит весь свой доход, и дадим
название обоим результатам.

70
Часть I. Экономические агенты
Теорема 1.10. Однородность и сбалансированность бюджета.
При выполнении предположения 1.2 функция спроса потребителя
xi(f>> У)> *' = 1, ...,и однородна нулевой степени по ценам и доходу и
удовлетворяет условию сбалансированности бюджета рх(р, у) = у
для всех (р, у).
Доказательство. Однородность мы, в сущности, уже доказали в
первой части теоремы 1.6, где было показано, что косвенная функция
полезности однородна нулевой степени, т.е.
v(p> у) = у(ф> ty) дая всех * > о •
Это эквивалентно утверждению, что
w(x(p, у)) = w(x(/p, ty)) для всех / > 0.
Далее, поскольку бюджетные множества при (р, у) и (tp, ty)
одинаковы, объем спроса х(р, у) является допустимым, если выбран объем
спроса х(ф, ty), и наоборот. Поэтому предыдущее равенство и строгая
квазивогнутость и означают, что
Х(Р> У)= Х(Ф> ty) Для всех t > 0,
или что спрос на каждый товар jc,(p, у), / = 1, ...,и, является
однородным нулевой степени по ценам и доходу.
Мы уже не раз упоминали о том, что, поскольку и() строго
возрастает, при объеме спроса х(р, у) должен расходоваться весь доход
потребителя. В противном случае он может приобрести строго больше каждого
товара и увеличить свою полезность. Далее мы будем называть это
условие сбалансированностью бюджета. ¦
Однородность позволяет нам полностью исключить из анализа
спроса деньги как единицу измерения. Обычно это делается путем
произвольного выбора одного из п товаров в качестве единицы счета (numeraire)
вместо денег. Если его цена в денежном выражении составляет /?„, то
можно положить / = \/рп и, используя однородность, заключить, что
(
х(р, y) = \(tp, ty) = x
А Рп-\ 1 У
> • • • 5 5 1>
Таким образом, спрос на каждый из п товаров зависит только от «-1
относительной цены и реального дохода потребителя.

Глава 1. Теория потребителя
71
1.5.2. Эффекты дохода и замещения
В нашей модели поведения потребителя возникает важный вопрос:
какова должна быть реакция величины спроса на изменение цены?
Обычно мы считаем, что потребитель приобретает больше товара, когда цена
снижается, и меньше товара, когда она растет (при прочих равных
условиях). На рис. 1.19 показано, что это вовсе не обязательно. На каждой из
трех частей рисунка представлен выбор максимизирующего полезность
потребителя с монотонными выпуклыми предпочтениями при рыночных
ценах. На рис. 1.19(a) снижение цены товара 1 ведет к росту спроса на
этот товар, чего мы обычно и ожидаем. Наоборот, на рис. 1.19F)
снижение цены не влияет на количество приобретаемого товара 1, в то время
как на рис. 1.19(b) снижение цены ведет к снижению спроса на товар 1.
Каждый из этих случаев вполне совместим с нашей моделью. Что же
тогда утверждает (если что-то утверждает) теория относительно изменения
спроса в зависимости от изменения (относительных) цен?
*2 Х2 Х2
(а) (б) (в)
Рис. 1.19. Изменение объема спроса в зависимости от изменения цены
Начнем с обсуждения на интуитивном уровне. Когда цена товара
снижается, существует по крайней мере две концептуально различные
причины, по которым может произойти изменение величины спроса. Во-
первых, этот товар становится относительно дешевле по сравнению с
другими. Поскольку все товары являются привлекательными для
потребителя, то даже если бы его способность приобретать товары оставалась
неизменной, можно было бы ожидать, что относительно более дорогие
товары будут замещаться относительно более дешевым. Это эффект
замещения (substitution effect, SE). В то же время при изменении цены
способность потребителя приобретать товары, вообще говоря, не остается
неизменной. Когда цена любого из товаров снижается, эта способность
фактически возрастает, позволяя потребителю изменять количество всех

72
Часть I. Экономические агенты
покупаемых товаров (любым) подходящим способом. Влияние общего
увеличения покупательной способности на объем спроса называется
эффектом дохода (income effect, IE).
Хотя интуиция подсказывает, что мы можем в некотором смысле
разложить общий эффект изменения цены (total effect, ТЕ) на эти два
концептуально различных компонента, нам потребуется сформулировать эти
идеи гораздо строже, чтобы сделать их аналитически полезными. Чтобы
формализовать интуитивные понятия эффектов дохода и замещения,
можно воспользоваться различными способами. Мы будем следовать
способу, предложенному Хиксом [Hicks, 1939].
Декомпозиция общего эффекта изменения цены по Хиксу начинается с
наблюдения, что потребитель достигает некоторого уровня полезности при
исходных ценах (до каких-либо изменений). Формальное изложение
интуитивного понятия эффекта замещения таково: эффект замещения
представляет собой такое (гипотетическое) изменение потребления, которое произошло
бы, если бы относительные цены изменились, но максимально достижимый
потребителем уровень полезности остался тем же, что и до изменения цен.
Эффект дохода определяется как то, что остается от общего эффекта после
вычитания эффекта замещения. Обратите внимание, что в силу определения
эффекта дохода как остаточного общий эффект всегда в точности равен
сумме эффекта замещения и эффекта дохода. На первый взгляд такой
подход может показаться странным, но рис. 1.20 должен убедить вас по крайней
мере в том, что это, с одной стороны, нетривиальное аналитическое
построение и что, с другой стороны, оно в достаточной мере соответствует
интуитивным представлениям об эффектах дохода и замещения.
Посмотрим сначала на рис. 1.20(a) и предположим, что потребитель
изначально сталкивается с ценами р\ и р\ и имеет доход у. Он
приобретает товары в объеме jc,° их2°и достигает уровня полезности и0.
Предположим, что цена товара 1 падает до величины р\ < /?,° и что общий
эффект от этого заключается в увеличении потребления товара 1 до х\ и
снижении потребления товара 2 до х\. Чтобы применить декомпозицию
по Хиксу, нам необходимо сначала провести мысленный эксперимент,
при котором цена товара 1 снижается до своего нового уровня р\, а
потребителю предоставляется возможность осуществлять выбор на
прежней кривой безразличия и0. Это выглядит так, как будто мы
поставили потребителя перед новыми относительными ценами, но сократили
его доход (соответствующая бюджетная линия показана пунктиром) и
предложили максимизировать полезность при этом ограничении. В этой
ситуации потребитель увеличит потребление товара 1, который стал
относительно дешевле, с jc,° до jc* и сократит потребление товара 2, кото-

Глава 1. Теория потребителя
73
рый стал относительно дороже, с х2 до xs2. Эти гипотетические
изменения потребления представляют собой эффекты замещения по Хиксу для
товаров 1 и 2, и мы считаем, что они связаны исключительно с
изменением относительных цен при неизменном благосостоянии потребителя.
(а)
(б)
»J / «°
-Px'Pi
+Х\
*\(Ри р\,у)
х!(рир1и°)
> *!
Рис. 1.20. Декомпозиция по Хиксу при изменении цены
Теперь посмотрим, что остается от общего эффекта. После
гипотетических изменений от х,° и х2 до х,5 и xs2 нужно объяснить изменения от х,5
и *2 до х,1 и х\. Заметим, что это как раз те изменения, которые
произошли бы, если бы при новых ценах и первоначальном уровне полезно-

74
Часть I. Экономические агенты
сти и0 реальный доход потребителя увеличился, тем самым сдвинув
гипотетическое бюджетное ограничение, обозначенное пунктирной линией,
до уровня окончательной бюджетной линии, отражающей изменение
цены и касающейся кривой безразличия и1. Именно в этом смысле эффект
дохода по Хиксу представляет изменения в потребление как следствие
исключительно изменения в цене.
Теперь посмотрим на рис. 1.20F), где игнорируется все
происходящее с товаром 2 и фокусируется внимание только на товаре 1. Очевидно,
что точки (р°, х,°) и (р\, х\) лежат на маршалловской кривой спроса на
товар 1. Аналогично точки (р^, jCj0) и (р\, х*) лежат на хиксовской
кривой спроса на товар 1 при исходном уровне полезности и0. Как видно,
хиксовская кривая спроса на товар в точности отражает эффект
замещения по Хиксу от изменения цены на этот товар. (Понятно ли это?) Мар-
шалловская кривая спроса отражает общий эффект изменения цены на
товар. Эти две кривые вследствие наличия эффекта дохода по Хиксу
отклоняются друг от друга на расстояние, равное величине этого эффекта.
Декомпозиция по Хиксу позволяет строгим аналитическим способом
разделить две различные силы, изменяющие спрос вследствие изменения
цены. Эту же идею можно выразить гораздо точнее, в более общей и
удобной форме. Связь между общим эффектом, эффектом замещения и
эффектом дохода задается уравнением Слуцкого. Его иногда называют
«фундаментальным уравнением теории спроса», поэтому дальнейшее
изложение заслуживает тщательного осмысления.
До конца этой главы мы будем опираться на предположение 1.2 и в
случае необходимости предполагать дифференцируемость
соответствующих функций.
Теорема 1.11. Уравнение Слуцкого.
Пусть х(р, у) — маршалловский спрос потребителя. Пусть и* —
уровень полезности, который достигается потребителем при ценах р и
доходе у. Тогда
Эх,(р, >р_Эх*(р, и) гдЭх,(р, у)
dpj dp j qy
ТЕ SE &
Доказательство. Доказательство этой замечательной теоремы
довольно простое, но требует определенного внимания. Для начала
вспомним одно из соотношений между функциями спроса по Маршаллу и по
Хиксу. Из теоремы 1.9 нам известно, что
xf(p, i/*) = x,.(p, e(p, и*))

Глава 1. Теория потребителя
75
для любых цен и уровня полезности и*. Поскольку это верно для всех
р » 0, обе части можно продифференцировать по ру, причем равенство
сохранится. Спрос по Хиксу в левой части равенства дифференцировать
легко, поскольку он зависит от цен только напрямую. Спрос по
Маршаллу зависит от цен напрямую через первый аргумент и косвенно через
функцию расходов во втором аргументе, поэтому в правой части
равенства потребуется применить правило дифференцирования сложной
функции, из которого мы получаем
a*f(p, i/') = a*,(p, е(р, и*)) t ЭдгДр, е(р, и))де(р, и*)
dp; dpj ду dpj
Если теперь внимательно взглянуть на (Р-1) и вспомнить, как была
определена величина и\ то можно сделать несколько важных замен. По
предположению, и* — это уровень полезности, который достигается
потребителем при ценах р и доходе у, т.е. и* = v(p, у). Поэтому
минимальные расходы при ценах р и полезности и* будут равны
минимальным расходам при ценах р и полезности v(p, у). Однако из теоремы 1.8
мы знаем, что минимальные расходы при ценах р и максимальной
полезности, достижимой при ценах р и доходе у, равны доходу у. Таким
образом, мы имеем
е(р, и) = е(р9 v(p, y)) = y. (P-2)
Кроме того, теорема 1.7 гласит, что частная производная функции
расходов в (Р.1) по Pj равна хиксовскому спросу на j -й товар при уровне
полезности и*. Поскольку и* =v(p, у), она равна хиксовскому спросу на
j -й товар при уровне полезности v(p, у), или
Эе(р, и*) h * h
—^ - = х,.(р, и ) = х (р, v(p, у)).
OPj
Но посмотрим на крайний правый член в этом равенстве. Из теоремы 1.9
мы знаем, что хиксовский спрос при р и максимальной полезности,
достижимой при р и у, в свою очередь, равен маршалловскому спросу при
риу! Отсюда мы имеем
^КЧ(Р, У). (Р-3)

76
Часть I. Экономические агенты
(Здесь будьте внимательны: мы показали, что частная производная
функции расходов по цене в (Р-1) равна маршалловскому спросу на j -й, а не
на / -й товар.)
Чтобы завершить доказательство, подставим (Р-2) и (Р-3) в (Р-1):
Эх*(р, г/) = ЭхДр, у) [ Эх,(р, у)
dpj dp j ду J
После небольшого преобразования получаем требуемое:
Э*,(Р, у)_Эх*(р, и) .ЭхДр, у)
Эр, dpj ду
Уравнения Слуцкого дают строгие аналитические выражения для
эффектов дохода и замещения. Они также создают схему, подробно
описывающую, как комбинировать эти эффекты, чтобы объяснить общий
эффект от любого изменения цен. Но сами по себе уравнения не отвечают
на поставленные нами вопросы. Может показаться, что они только
мешают делать выводы из нашей теории, которые относятся к
наблюдаемому поведению. В конце концов все, что мы сделали на данный момент,
сводится к тому, что мы разложили наблюдаемый общий эффект на
наблюдаемый эффект дохода и ненаблюдаемый эффект замещения. Вот что
уравнение Слуцкого, к примеру, дает нам в особом случае изменения
цены самого товара /. Из теоремы 1.11 мы имеем
Э*ДР, 7) = Э*»(р, к*)_х(р? у)дх^у) A20)
Эр, Эр,. ' ду
Левая часть этого равенства представляет собой наклон маршалловской
кривой спроса на i -й товар — реакцию объема спроса на изменение цены
товара, т.е. как раз то, что мы хотим объяснить. Для этого нам, очевидно,
требуется знать что-то о первом члене выражения в правой части. Это
наклон хиксовской кривой спроса, а она не наблюдаема напрямую. Что же
мы можем узнать о хиксовских кривых спроса, если мы не можем их даже
наблюдать?
Поразительно, но наша теория способна немало сообщить нам о
спросе по Хиксу, а значит, и о коэффициентах замещения независимо от
того, наблюдаемы они или нет. Все, что нам известно о коэффициентах
замещения, можно с помощью уравнений Слуцкого преобразовать в
информацию о наблюдаемом маршалловском спросе. Именно так мы и
будем действовать. Начнем с формулировки следующего результата об
эффекте изменения цены.

Глава 1. Теория потребителя
77
Теорема 1.12. Отрицательные собственные коэффициенты
замещения.
Пусть jcf(p, и) — спрос по Хиксу на i -й товар. Тогда
*?flt4so. 1-1.......
dp,
Доказательство. Эта теорема утверждает, что хиксовские кривые
спроса должны всегда быть такими, как они изображены на рис. 1.16 и
др., т.е. должны иметь отрицательный (неположительный) наклон по
своей цене. Доказательство несложно.
По свойству производной функции расходов (теорема 1.7,
свойство 7)) при любых р и и
^И->, и).
др,
Повторно дифференцируя по /?,, получаем
Э2е(р, ц)_Эх*(р, и)
Эр! ' bPi >'~['¦¦¦>"¦
Согласно свойству 6) теоремы 1.7 функция расходов вогнута по р. Тогда
по теореме А2.5 все ее частные производные второго порядка
неположительны, что и доказывает теорему. ¦
Теперь у нас есть все, что нужно для того, чтобы сформулировать
современную версию так называемого закона спроса. Экономисты-
классики, такие, как Эджворт и Маршалл, предполагали, что
«полезность» можно измерить, и верили в принцип убывающей предельной
полезности. Поэтому классический вариант закона спроса звучит очень
категорично: «Если цена снижается, объем спроса возрастает». Это в целом
согласовалось с наблюдениями о реальном поведении людей, но
оставались некоторые неприятные исключения. Самым известным из них был
знаменитый парадокс Гиффена. Оказывалось, что для некоторых, хотя и
немногочисленных, товаров за снижением цены следовало снижение
объема спроса. Это противоречило принятой доктрине, и классическая
теория не могла объяснить этого.
Современная теория накладывает меньше ограничений на
предпочтения, чем классическая. В этом смысле она менее жесткая и применима
гораздо шире. Более того, она даже способна разрешить парадокс
Гиффена. Взгляните на рис. 1.19(b) и обратите внимание, что величина спроса
на первое благо jc, действительно снижается при снижении цены. Ничто
не запрещает такого поведения, поэтому в современном контексте в пара-

78
Часть I. Экономические агенты
доксе Гиффена нет ничего парадоксального. Но за большую общность
приходится расплачиваться: современный закон спроса менее прозрачен,
чем его классический предшественник.
В формулировке закона мы будем пользоваться знакомой
терминологией. Благо называется нормальным, если его потребление возрастает с
ростом дохода при неизменных ценах. Благо называется инфериорным,
если его потребление снижается с ростом дохода при неизменных ценах.
Теорема 1.13. Закон спроса.
Снижение цены нормального блага приводит к увеличению объема
спроса на него. Если снижение цены длага приводит к снижению объема
спроса на него, то это инфериорное благо.
Доказательство. Утверждение легко следует из теоремы 1.12, если
воспользоваться теоремой 1.11. Мы оставляем его доказательство в
качестве упражнения. ¦
На самом деле мы знаем о хиксовских коэффициентах замещения
гораздо больше, чем говорится в теореме 1.12, а о маршалловском спросе —
гораздо больше, чем говорится в теореме 1.13. Чтобы продвинуться далее
по сравнению с простыми утверждениями, сделанными на данный
момент, нам придется немного глубже изучить систему коэффициентов
замещения. Прежде всего мы докажем, что «перекрестные коэффициенты
замещения» являются симметричными.
Теорема 1.14. Симметричность коэффициентов замещения.
Пусть хл(р, и) — функция спроса по Хиксу и пусть функция е(-)
дважды непрерывно дифференцируема. Тогда
Эх*(р, и) Эхл(р, и) .
—^ = —^т , I, 7 = 1, ...,л.
oPj dpj
Доказательство. Сразу понять значение этого результата довольно
непросто. Примечательно, однако, что можно показать, что условие
симметричности тесно связано с предположением о транзитивности
отношения предпочтения потребителя! Мы не будем здесь углубляться в эту
связь, но затронем ее в дальнейшем.
При доказательстве теоремы 1.12 мы заметили, что первые частные
производные функции расходов по цене дают нам хиксовские функции
спроса, поэтому из вторых частных производных функции расходов по
цене мы получим первые частные производные хиксовских функций
спроса по этой цене:
Э (де(р, и)]_ Э h
др\ др, ) др.

Глава 1. Теория потребителя
79
или
Э2е(р, н)_Эх*(р, и)
(Р-1)
dpjdpj dpj
для всех / и j. По теореме Юнга порядок дифференцирования функции
расходов не имеет значения, поэтому
Э2е(р, и) _ Э2е(р, и)
dptdpj dpfa
Вместе с (Р-1) это приводит нас к выводу о том, что
Э^(р, и) Эх*(р, и)
ЧРУ ор,
Если мы представим, что все п2 коэффициентов замещения в системе
функций потребительского спроса помещены в матрицу размера п х п, то
собственные коэффициенты замещения будут находиться на ее
диагонали, а перекрестные коэффициенты замещения — вне диагонали.
Теоремы 1.12 и 1.14 дают нам довольно полное представление о том, как будет
выглядеть эта матрица. Согласно теореме 1.12, все элементы на главной
диагонали будут неположительными, а по теореме 1.14 матрица будет
симметричной. О матрице коэффициентов замещения можно на самом
деле сказать даже больше: она должна быть также отрицательно
полуопределенной.
Теорема 1.15. Отрицательная полуопределенность матрицы
замещения.
Пусть хЛ(р, и) — функция спроса по Хиксу и пусть матрица заме-
щения
Э-х^Ср, и)
а(р, и) =
содерэюит все хиксовские коэффициенты замещения. Тогда матрица
а(р, и) отрицательно полуопределена.
Доказательство. Доказательство очевидно, если из доказательства
предыдущей теоремы мы вспомним, что каждый элемент матрицы равен
Эх^р, и)

80
Часть L Экономические агенты
одной из вторых частных производных функции расходов по цене. В
частности, мы видели, что 3jcf(p, u)/dpj =d2e(p, u)/dpjdpi для всех / и j,
поэтому в матричном виде получаем
(дх*(р9 и) Эх*(р, и)} (д2е(р, и) Э2е(р, и)}
dPi "' дрп др2 '" дрндрх
Эх*(р, и) Э**(р, и) Э2е(р, и) д2е(р, и)
[ Эр, "" дря ) У др,дрп '" др2н )
Матрица в правой части представляет собой матрицу Гессе функции
расходов. По теореме 1.7 функция расходов вогнута по ценам, а по
теореме А2.4 матрица Гессе вогнутой функции отрицательно полу
определена. Поскольку две матрицы совпадают, матрица замещения будет
отрицательно полуопределена. ¦
Потратив так много времени на исследование свойств
ненаблюдаемых функций спроса по Хиксу, мы наконец можем применить
полученные знания для того, чтобы сделать какие-либо конкретные выводы о
наблюдаемом спросе потребителя. Способ, который можно использовать
для этой цели, уже рассматривался при обсуждении «закона спроса». Там
мы задавались вопросом о том, что же модель поведения потребителя
сообщает нам о ненаблюдаемых собственных эффектах замещения, а затем
с помощью уравнения Слуцкого искали связь между производными
наблюдаемых маршалловских функций спроса на некоторый товар по цене
этого товара и доходу. Учитывая то, что мы теперь знаем обо всей
системе коэффициентов замещения, нам необязательно ограничиваться
утверждениями о влиянии на спрос изменений в доходе и цене этого товара.
Мы можем использовать матрицу замещения для того, чтобы делать
полноценные выводы о влиянии всех цен и дохода на наблюдаемые мар-
шалловские функции спроса на все товары.
Теорема 1.16. Симметричность и отрицательная
полуопределенность матрицы Слуцкого.
Пусть х(р, у) — маршалловская функция спроса. Определим ij -и
коэффициент Слуцкого как
dpj ду
и построим матрицу Слуцкого размерности пхп:

Глава 1. Теория потребителя
81
s(p, у) =
oPi оу дрп ду
Тогда матрица s(p, у) симметрична и отрицательно полуопределена.
Доказательство. Доказательство очень простое. Пусть и* —
максимально достижимый уровень полезности при ценах р и доходе у, так что
и* = V(P> у)- Из уравнения Слуцкого в теореме 1.11 найдем у-й
коэффициент замещения:
Эх*(р, Ц*) = Эх,(р, У) , х /р чЭ*/(Р> -У)
Если мы теперь построим матрицу s(p, у), становится ясно, что каждый
ее элемент в точности равен соответствующему элементу матрицы
замещения по Хиксу о(р, и*). По теореме 1.14 матрица замещения
симметрична для всех и, а по теореме 1.15 она отрицательно полу определена
для всех и; поэтому в и* она будет и симметрична, и отрицательно
полуопределена. Поскольку две матрицы совпадают, матрица Слуцкого
S(P> У) тоже будет симметрична и отрицательно полуопределена. ¦
Теоремы 1.10 и 1.16 можно использовать в качестве исходной точки
для проверки или эмпирического приложения разработанной теории.
Условия сбалансированности бюджета и однородности потребительского
спроса, а также симметричности и отрицательной полуопределенности
соответствующей матрицы Слуцкого дают набор ограничений на
допустимые значения параметров любой эмпирически оцененной системы
маршалловских функций спроса, если предполагается, что эта система
построена для потребителя, который максимизирует свою полезность и
принимает цены как данные. Существуют ли другие вытекающие из
теории и поддающиеся тестированию ограничения? Этим вопросом мы
займемся в следующей главе, но сначала рассмотрим некоторые важные
соотношения между эластичностями.

82
Часть I. Экономические агенты
1.5.3. Некоторые соотношения между эластичностями
Чтобы завершить обсуждение потребительского спроса, посмотрим
внимательнее, какое влияние оказывает условие сбалансированности
бюджета на то, как потребитель реагирует на изменение цен и дохода.
«Тяжелая артиллерия», к которой мы обращались ранее, здесь не
потребуется. Достаточно вспомнить, что бюджетное ограничение некоторым
образом упорядочивает и дисциплинирует эту реакцию.
Если х(р, у) — маршалловская функция спроса, то согласно
условию сбалансированности бюджета бюджетное ограничение должно
выполняться как равенство при любом наборе цен и дохода, т.е.
п
y = ^Pi*,(P> У)-
Поскольку это тождество выполняется для всех р и у, то при изменении
одной из цен или дохода потребителя оно будет верным и до, и после
этого изменения. Поэтому все изменения спроса в ответ на изменение цен и
дохода должны складываться, или агрегироваться таким образом, чтобы
бюджетное ограничение выполнялось как равенство. Существует
несколько таких экспериментов по сравнительной статике, которые
можно осуществить с бюджетным ограничением для определения того,
как должны агрегироваться изменения величины спроса. Иногда они
формулируются напрямую в терминах соотношений между
производными различных функций спроса, но мы представим их в терминах
соотношений между эластичностями спроса по цене и доходу. Это позволит
получить те же самые результаты, но в более удобном и ясном виде.
Начнем с некоторых определений.
Определение 1.6. Эластичности спроса и доли в доходе.
Пусть лсДр, у) —маршалловский спрос на 1-й товар. Тогда пусть
л =дх,(р, у) у
ду *,(р, У)'
с =Эх,(р, у) Pj
9 dPj *,(P> У)
и пусть
s РЯЬ, У\такчто s >0 и ySj =1
У ы\

Глава 1. Теория потребителя
83
Символ г\. обозначает эластичность спроса на /*-й товар по доходу
и измеряет изменение величины спроса на /'-й товар (в процентах) при
изменении дохода на 1%. Символ гу обозначает эластичность спроса
на / -й товар по цене и измеряет процентное изменение объема спроса на
/"-й товар при изменении цены р} на 1%. Если j = i9 то е|у называется
эластичностью спроса на /-й товар по своей цене1. Если j Ф i, то е~
называется перекрестной эластичностью спроса на / -й товар ля цене
Pj. Символ я,, обозначает долю в доходе, т.е. часть дохода потребителя,
израсходованную на покупку /-го товара. Эти доли, конечно, должны
быть неотрицательными и в сумме давать единицу.
Теорема 1.17. Агрегирование потребительского спроса.
Пусть х(р, у) —маршалловская функция спроса. Пусть r\it гу и s(
при /, j = 1, ..., п — определенные выше величины. Тогда между долями в
доходе и эластичностями по цене и доходу должны выполняться
следующие соотношения:
п
1) агрегирование по Энгелю: ]^?/П, = 1»
п
2) агрегирование по Курно: ^ $.?., = -s., j = l9 ...,«.
/=i
Доказательство. Вспомним сначала, что выбор потребителя должен
удовлетворять бюджетному ограничению
у = р х(р, у) (Р-1)
для всех р и у.
Теорема утверждает, что при агрегировании по Энгелю взвешенная
сумма эластичностей по доходу должна равняться единице. Для
доказательства этого утверждения продифференцируем обе части (Р-1) по
доходу и получим
ы ау
Умножим и разделим каждое слагаемое на xty и преобразуем:
х = у Рг*> &/ У
ы\ У Ьу х,
1 Обратите внимание: в приведенном определении не гарантируется (как иногда
делается), что эластичность по своей цене будет положительной при отрицательном наклоне
кривой спроса на товар.

84
Часть I. Экономические агенты
В соответствии с определением величин s{ и ri, это соотношение
записывается как
п
При агрегировании по Курно взвешенная (по долям в доходе) сумма
эластичностей спроса на любое благо по цене некоторого блага j должна
равняться взятой со знаком «минус» доле расходов на это благо (благо
j). Для доказательства этого утверждения рассмотрим воздействие на
величину спроса изменения цены блага j, р.. Дифференцируя обе части
(Р-1) по pj, получим
Л I ^ Эх,
dp j
где j -й член суммы записан отдельно, чтобы подчеркнуть, что при
дифференцировании произведения PjXj(p, у) необходимо использовать
правило дифференцирования произведения. Учитывая это, приведем данное
выражение к виду
А Эх,.
-xj=LPi^-'
Умножим обе части равенства на р. /у :
PjXj _»Pi dxt я
У /=i У dp j
затем умножим и разделим каждый элемент под знаком суммы на х,.:
Pjxj =уРЛ дх* Р\
У ы У ^Р j x, '
Вспоминая определение соответствующих величин (эластичностей и долей
дохода), получаем требуемое соотношение, что и доказывает теорему:
-Sj =Х5/е// ' J = l> •••'"•
Теоремы 1.10—1.17 содержат описание логических следствий
поведения, ориентированного на максимизацию полезности. Однородность
показывает, что спрос не должен реагировать на одновременное
изменение всех цен и дохода в одинаковой пропорции, а условие
сбалансированности бюджета требует, чтобы на потребление расходовался весь
доход потребителя. Уравнения Слуцкого обеспечивают нас качественной

Глава 1. Теория потребителя
85
информацией, или «ограничениями на знаки», из которых мы узнаем, как
изменяется спрос в ответ на самые разные изменения цен, а также
позволяют анализировать ненаблюдаемые компоненты этих ответных
изменений — эффекты дохода и замещения. Наконец, формулы агрегирования
показывают, как изменения объема спроса — сначала в ответ на
изменение дохода, а затем в ответ на изменение одной из цен — должны быть
согласованы друг с другом в рамках системы функций потребительского
спроса. В следующей главе мы зададимся вопросом о том, нет ли у
изложенной нами теории других следствий, а в завершение данной главы
подведем итог тому, что мы знаем на данный момент (см. табл. 1.1).
Таблица 1.1
Свойства потребительского спроса1
Спрос по Маршаллу
Однородность
Симметричность
Отрицательная

полуопределенность

Сбалансированность бюджета
Агрегирование
Энгеля
Агрегирование
Курно
х(р, у) = х(ф, ty) для всех (р, у) и / > 0
Эх,(р, у) | х >а*,(р, У)= Для всех (р, у) и
dpj J ' By i, 7 = 1, ...,n
Эх (р, у) Эх,.(р, у)
= ^ +*,(р» у)—4
ар/ оу
zrs(p, у)ъ < 0 для всех (р, у) и z
р • х(р, у) = у для всех (р, у)
/=1
Л для у = 1, ...9п
Спрос по Хиксу
Однородность
Симметричность
Отрицательная

полуопределенность
хА(/р, и) = хл(р, и) для всех (р, и) и />0
аьс,*(р, и) _дхн;(р, и) для U 7 = 1, ...,«
dpj Bpi
zro(p, w)z < 0 для всех (р, и) и z
Связь между спросом по Маршаллу и по Хиксу
Уравнение
Слуцкого
Эх,(р, ,у)_Э.х*(р, и) ^ Эх,(р, 7) для всех (р, у), и =
Эр j Эр j j ' Эу =у(р,>>)и/,
7 = 1, ...,и
Заметим, что величина спроса определена только при положительных ценах; в
соотношениях, где участвуют производные по доходу, следует считать, что у > О . — Примеч. ред.

86
Часть I. Экономические агенты
1.6. Упражнения
1.1. Пусть X = R2+. Проверьте, что потребительское множество X
удовлетворяет всем условиям предположения 1.1.
1.2. Рассмотрите отношение предпочтения >=. Докажите, что
а) Уаъ;
б) ~с>т;
в) у и ~=У;
г) у п ~ = 0.
1.3. Приведите доказательство или убедительно аргументируйте
каждое из следующих утверждений, сформулированных в тексте.
а) Ни >-, ни - не являются полными.
б) Для любых х1 и х2 из множества X выполняется только одно из
следующих условий: х1 >- х2, или х2 >- х1, или х1 ~ х2.
1.4. Докажите, что если ^ — отношение предпочтения, то отношения
>- и ~ являются транзитивными. Покажите также, что если х'~х2^х3,
то х1 ь х3.
1.5. Пусть у — отношение предпочтения. Докажите следующие
соотношения для любого х° е X :
а)~(х0)=Их°)п^(х0);
б)Их0)=~(х°)иКх0);
в)~(х°)пКх°) = 0;
г)~(х°)п^(х°) = 0;
дН(хо)пКхо) = 0;
е) <(х°)п~(х°)пу(х°) = 0;
ж) ^(х°)и - (х°)и>- (х°) = X.
1.6. Приведите пример предпочтений «обычного потребителя», не
удовлетворяющих аксиоме выпуклости.
1.7. Докажите, что при выполнении аксиомы 5' множество ь (х°)
является выпуклым для любого х° е X.
1.8. Изобразите карту кривых безразличия, являющихся
параллельными прямыми с отрицательным наклоном, для предпочтений,
возрастающих вправо-вверх. Известно, что предпочтения, подобные данным,
удовлетворяют аксиомам 1, 2, 3 и 4. Докажите, что они также
удовлетворяют аксиоме 5' и не удовлетворяют аксиоме 5.
1.9. Изобразите карту кривых безразличия, являющихся
параллельными прямыми углами с вершинами на линии я;, = х2. Если предпочтения

Глава L Теория потребителя
87
возрастают вправо-вверх, то данные предпочтения удовлетворяют
аксиомам 1, 2, 3 и 4'. Докажите, что они также будут удовлетворять аксиоме 5'.
Будут ли они удовлетворять аксиомам 4 и 5?
1.10. Изобразите такие предпочтения, удовлетворяющие аксиомам 1,
2, 3 и 4, что их множества безразличия частично выпуклы к началу
координат, а частично линейны. Докажите, что предпочтения, подобные
данным, удовлетворяют аксиоме 5, но не согласуются с аксиомой 5.
1.11. Покажите, что если отношение предпочтения ^ непрерывно, то
множества А и В, определенные в доказательстве теоремы 1.1, являются
замкнутыми подмножествами множества R .
1.12. Рассмотрите две функции полезности u{xv х2) и v(jcp x2).
а) Докажите, что если функции и(х{, х2) и v(xp x2) однородны
степени г, то функция s(xp jc2) = w(jc,, x2) + v(xp x2) также однородна
степени г.
б) Докажите, что если функции м(хр х2) и v(xp x2) квазивогнуты, то
функция w(jcp x2) = min{w(xp x2), v(xp х2)} также квазивогнута.
1.13. Потребитель имеет лексикографические предпочтения
относительно хеМ2+, если отношение предпочтения ^ таково, что х1 ^ х2, если
либо х\ > х,2, либо л:,1 = х2 и х\ > х\.
а) Изобразите карту кривых безразличия для данных предпочтений.
б) Представимы ли данные предпочтения с помощью непрерывной
функции полезности? Обоснуйте свой ответ.
1.14. Пусть предпочтения >- представимы непрерывной функцией
полезности. Покажите, что они удовлетворяют аксиомам 1, 2 и 3.
1.15. Докажите, что бюджетное множество В является выпуклым
компактом для любых р » 0.
1.16. Докажите сформулированное в тексте утверждение о том, что
при выполнении предположения 1.2:
а) если решение задачи потребителя х существует, то оно
единственно;
б) на покупку набора х* будет расходоваться весь доход потребителя,
т.е. у = рх*.
1.17. Рассмотрите выпуклые, но не строго выпуклые предпочтения.
Дайте ясную, убедительную аргументацию того, что решение задачи
потребителя по-прежнему существует, но не обязательно единственно.
Проиллюстрируйте ваши рассуждения, приведя пример для случая двух
товаров.
1.18. Рассмотрите экономику с двумя товарами, где х* > 0 и х*2 = 0 —
решение задачи потребителя. Приведите условия, подобные A-11), харак-

88
Часть I. Экономические агенты
теризующие это решение, и проиллюстрируйте ваш ответ рисунком,
аналогичным рис. 1.10.
1.19. Докажите теорему 1.2.
1.20. Пусть предпочтения потребителя описываются функцией
полезности Кобба—Дугласа вида w(xp х2) = Ах*х\~а, 0<ос<1, А>0.
Предполагая, что решение внутреннее, найдите функции спроса по
Маршаллу.
1.21. Мы отмечали, что функция полезности и(х) инвариантна
относительно положительных монотонных преобразований. Одним из часто
используемых преобразований является логарифмическое
преобразование ln(w(x)). Проведите логарифмическое преобразование функции из
предыдущего упражнения и, используя полученную функцию как
функцию полезности, найдите функции спроса по Маршаллу. Убедитесь, что
они совпадают с найденными в предыдущем упражнении.
1.22. Мы можем и далее обобщить результат предыдущего
упражнения. Пусть предпочтения потребителя описываются функцией полезности
и(х). Предположив внутреннее решение, мы можем неявно определить
функции спроса потребителя x(p,j>) из условий A-10). Рассмотрите
функцию полезности f(u(\)), где /' > 0, и покажите, что условия первого
порядка, характеризующие решение задачи потребителя, в обоих случаях
могут быть сведены к одному и тому же набору уравнений. Объясните, как из
этого следует, что спрос потребителя инвариантен относительно
положительного монотонного преобразования функции полезности.
1.23. Докажите теорему 1.3.
1.24. Пусть функция и(\) представляет монотонные предпочтения
некоторого потребителя на наборах xel". Какие из нижеследующих
функций f(x) также могут представлять предпочтения данного
потребителя, а какие — нет? В каждом из случаев обоснуйте свой ответ,
приведя либо доказательство, либо контрпример.
а)Дх) = и(х) + (М(х)K.
б)Дх) = и(х)-(«(х)J.
п
в) /(x) = w(x) + I>,.
1=1
1.25. Пусть потребитель, предпочтения которого выпуклы и
монотонны, потребляет неотрицательное количество хх и х2.
а) Если предпочтения потребителя описываются функцией
полезности и(х]9 x2) = х"х{21/2)~а, то какие ограничения должны быть наложены на
параметр а? Объясните.

Глава 1. Теория потребителя
89
б) Вычислите функции маршалловского спроса при найденных
ограничениях.
1.26. Пусть в экономике с двумя товарами цены товаров
положительны, и потребитель имеет положительный доход. Найдите функции
маршалловского спроса потребителя, если его полезность имеет вид
w(x,, х2) = х1.
1.27. Пусть в экономике с двумя товарами цены товаров
положительны и потребитель имеет положительный доход. Найдите функции
маршалловского спроса потребителя, если его полезность имеет вид
и(х{, х2) = тах[ахр ах2] + minfjc,, х2], где 0<я<1.
1.28. Пусть бесконечно живущий агент владеет 1 потребляемого им
товара. Предположим, что этот товар совершенно не портится, и у
потребителя нет возможности пополнять его запас. Обозначим потребление
данного товара в период t через х,. Пусть функция полезности
потребителя имеет вид
и(х09 х1? х29 ...) = ]Гр'1п(.х;,),где 0<р<1.
Найдите оптимальный уровень потребления в каждом периоде.
1.29. В случае двух товаров множества линий уровня
косвенной функции полезности в пространстве цен имеют вид
{(А> Рг)\ v(Pi> Рг> У) = у°} 9 где v°e M . Иногда они называются
кривыми безразличия в пространстве цен. Изобразите карту кривых
безразличия в пространстве цен и обоснуйте их наклон, кривизну и направление
возрастания полезности.
1.30. Покажите, что косвенная функция полезности из примера 1.2
является квазивыпуклой функцией от цен и дохода.
1.31. В формулировке теоремы 1.6 мы требовали, чтобы функция
полезности и(\) являлась возрастающей. Как должны быть
переформулированы условия 1)—6) (если это возможно), чтобы мы могли опустить это
требование на предпочтения потребителя? Объясните и
проиллюстрируйте свой ответ для случая двух товаров.
1.32. Пусть v(p, у) — косвенная функция полезности некоторого
потребителя. Покажите, что спрос потребителя инвариантен относительно
произвольного монотонного преобразования функции v(p, у) и поэтому
любое такое преобразование косвенной функции полезности само по себе
может рассматриваться как косвенная функция полезности потребителя.

90
Часть I. Экономические агенты
1.33. Покажите, что если и(х) непрерывна и строго возрастает, то для
любых р » 0 е(р, и) не ограничена сверху по и .
1.34. Завершите доказательство теоремы 1.7, доказав свойство 5).
1.35. Приведите альтернативное доказательство тождества Роя,
выполнив следующие шаги.
а) Используя определение v, покажите, что если р»0 и
х° = х(р°, /),то v(p, p-x°)>v(p0, p°.x0) Vp»0.
б) Проверьте, что функция /(p) = v(p, px°) достигает минимума на
множестве R"++ при р = р°.
в) Предположим, что функция / дифференцируема в точке р°.
Каково будет значение ее градиента в точке р° ?
г) Докажите тождество Роя, используя пункты а)—в).
1.36. Приведите альтернативное доказательство леммы Шепарда,
выполнив следующие шаги.
а) Используя определение, покажите, что если р»0 и
х° = хЛ(р°, и0), то е(р, и0) < р • х° Vp » 0 и е(р, и0) = р • х° при р = р°.
б) Проверьте, что функция /(р) = е(Р> м)-р-х° достигает
максимума на множестве Rn++ при р = р°.
в) Предположим, что функция / дифференцируема в точке р°.
Каково будет значение ее градиента в точке р° ?
г) Предполагая, что функция е(р, и) дифференцируема по р, и
используя пункты а)—в), докажите лемму Шепарда.
1.37. Убедитесь, что функция расходов, полученная для прямой
функции полезности с постоянной эластичностью замещения в примере
1.3, удовлетворяет всем условиям теоремы 1.7.
1.38. Завершите доказательство теоремы 1.9, показав, что
хЛ(р, w) = x(p, e(p, w)).
1.39. Используйте тождество Роя и теорему А2.6 для альтернативного
доказательства того, что функция х;(р, у) однородна нулевой степени по
ценам и доходу.
1.40. Докажите, что хиксовский спрос однороден нулевой степени по
ценам.
1.41. Докажите закон спроса, сформулированный в теореме 1.13.
Докажите также, что обратные утверждения не верны.
1.42. Для наглядности мы вместо одного утверждения
сформулировали две теоремы 1.14 и 1.15, хотя в действительности из первой следует

Глава 1. Теория потребителя
91
вторая. Покажите, что если матрица замещения с(р, и) отрицательно
полуопределена, то все собственные коэффициенты замещения
Эх*(р, и)/др; должны быть неположительны.
1.43. Для случая двух благ покажите, что если одно из благ является
инфериорным, то другое благо должно быть нормальным.
1.44. Зафиксируем х° е R" и определим функцию
компенсированного спроса по Слуцкому в точке х°, х5(р, х°),как х5(р, х°) = х(р, рх°).
Таким образом, компенсированный спрос по Слуцкому в точке х° — это
такой спрос, который будет предъявлять потребитель при изменении цен,
если доход потребителя компенсируется так, что он всегда может себе
позволить набор х°. Пусть х° = х(р°, у0). Покажите, что
Эх*(р°, х°) = ЭхУ, и0)
Эр,. Эр,.
где и0 =«(х°), т.е. наклоны кривых хиксовского спроса и
компенсированного спроса по Слуцкому совпадают. Наконец, матрица Слуцкого
является матрицей наклонов функций компенсированного спроса по
Слуцкому, чем и объясняется название таких функций спроса.
1.45. Мы можем получить еще один набор соотношений, которым
должны удовлетворять эластичности по цене и по доходу в системе
потребительского спроса. Одно из них непосредственно следует из
однородности и может рассматриваться просто как другая формулировка это-
п
го принципа. Докажите, что ^е,у +Г|, = 0, / = 1, ..., п.
1.46. Пусть и(х) — линейно однородная функция полезности.
а) Покажите, что функция расходов мультипликативно сепарабельна
по р и и и может быть представлена в виде е(р, и) = е(р, \)и .
б) Покажите, что предельная полезность дохода зависит от р, но не
зависит от у.
1.47. Пусть функция расходов мультипликативно сепарабельна по р
ими имеет следующий вид: е(р, и) = k(u)g(p), где функция к()
является некоторой положительной монотонной функцией одной переменной, а
g:R"->М+. Покажите, что эластичность по доходу (маршалловского)
спроса на каждый товар равна единице.
1.48. Пусть вам известна следующая информация о функциях спроса
и расходах потребителя, который тратит весь свой доход на два товара:
1) при текущих ценах на оба товара тратятся одинаковые суммы; 2) при

92
Часть I. Экономические агенты
текущих ценах эластичность спроса на первый товар по своей цене
равна - 3.
а) Какова эластичность спроса на второй товар по цене первого при
текущих ценах?
б) Могут ли условия 1) и 2) выполняться при любых ценах?
Объясните свой ответ.
1.49. Рассмотрите индивида, который потребляет только один товар
х и имеет косвенную функцию полезности вида
v(p, y) = G\A(p) + }^lmeA(p) = ]x& y)dt>
и G(-) — положительная монотонная функция одной переменной.
а) Найдите спрос потребителя на товар х и покажите, что
эластичность спроса по доходу постоянна и равна Г|.
б) Пусть доход потребителя равен у, и цена товара х возрастает от
р до р' > р. Покажите, что изменение полезности потребителя,
вызванное изменением цены, можно измерить с помощью величины
р
-\ л:(?, y)dt, < О. Проинтерпретируйте эту величину.
р
1.50. Рассмотрите функцию полезности и{хх, х2) = (х,I/2 +(х2I/2.
а) Найдите функции спроса *,(/?,, р2, у), / = 1,2.
б) Найдите коэффициент замещения в уравнении Слуцкого,
отражающий влияние изменения цены р2 на хх.
в) Охарактеризуйте хх и х2 как (валовые) взаимозаменяемые или
взаимодополняющие блага.
1.51. Пусть Г| и г\ — нижняя и верхняя границы эластичности спроса
по доходу для товара xi при всех ценах и доходе соответственно. Тогда
ду х,(р, у)
для всех цен и доходов. Покажите, что для любых у и у0
?? < */(р. у) А уЛЛ
1.52. Предположим, что потребители А и В имеют функции
расходов, приведенные ниже. В каждом из случаев ответьте на вопрос: будет

Глава 1. Теория потребителя
93
ли их наблюдаемое поведение на рынке идентичным? Обоснуйте свой
ответ.
а) еА(р9 и) и е5(р, и) = еА(р9 2и).
б) еА(р, и) = k(u)g(p), где к'(и)>0 и ев(р, u) = 2eA(p, и).
1.53. Рассмотрите функцию полезности Кобба — Дугласа для п
товаров следующего вида:
«00=41*;",
п
где А >0 и ^ос,. =1.
/=1
а) Найдите функции маршалловского спроса.
б) Найдите косвенную функцию полезности.
в) Найдите функцию расходов.
г) Найдите функции хиксовского спроса.
1.54. Пусть функция
и(х) = ?/,(*,)
/=1
является строго квазивогнутой и /,>0 для всех /. Потребитель
сталкивается с фиксированными ценами р » 0 и обладает доходом у > 0.
Будем предполагать, что х(р, у)» 0.
а) Покажите, что если предельная полезность одного товара в точке
х(р, у) возрастает, то предельные полезности всех других товаров в этой
точке должны убывать.
б) Докажите, что если предельная полезность одного товара в точке
х(р, у) возрастает, а предельные полезности всех других товаров при
х(р, у) убывают, то это благо является нормальным, а все остальные —
инфериорными.
в) Покажите, что если предельные полезности всех товаров в точке
х(р,>>) убывают, то все товары являются нормальными.
1.55. Каким условиям должны удовлетворять а;, f(y), w{px, p2) и
z{pv p2), чтобы приведенные ниже функции были косвенными
функциями полезности?
a)v(/7p p29 рЪ9 y) = f(y)p?p?p?.
б) v(p,, p2, y) = w(pl9 p2) + z(pl9 p2)/y.

94
Часть I. Экономические агенты
1.56. Функция полезности Стоуна — Гири имеет вид
и(х) = П(х,-а/)\
1=1
и
где bi > О и ^&, = 1. Параметры я, > О часто интерпретируют как «про-
i=i
житочный минимум» по соответствующим товарам.
а) Найдите функцию расходов и косвенную функцию полезности.
Заметьте, что первая линейна по полезности, тогда как вторая пропорцио-
п
нальна величине «оставшегося дохода» y-^PjOf .
/=i
б) Покажите, что bf измеряют доли «оставшегося дохода»,
затрачиваемого на необязательные покупки товаров х. сверх прожиточного
минимума ai.
1.57. Функция расходов Стоуна — Гири, полученная в пункте а)
предыдущего упражнения, представляет собой частный случай функции
расходов в форме Гормана:
е(р, и) = а(р) + м&(р),
где функции я(р) и Ь(р) — линейно однородны и вогнуты. Покажите,
что для потребителя с такой функцией расходов эластичность спроса по
доходу на каждый товар стремится к нулю при ^0 и стремится к
единице при у -» ©о.
1.58. При каких условиях на z(pl9 p2) функция е(р, и) =
= z(pl9 р2)Рзи-> гДе w>0, является функцией расходов для некоторого
потребителя?
1.59. Предположим, что при (р°, у0) эластичность спроса по доходу
для x1(p,j>) и х2(р,у) одинакова. Покажите, что dxjdp2 =дх2/др1 в точ-
ке (р°, /).
1.60. Покажите, что уравнение Слуцкого можно записать в эластич-
ностях как
? = Eh-s л ,
где Еу — эластичность хиксовского спроса на товар xi по цене ру, а все
остальные члены уравнения описаны в определении 1.6.

Глава 1. Теория потребителя
95
1.61. В соответствии с третьим законом Хикса
?*ЙЬ4,,..,,., „
или в терминах эластичностей
Xej=0,i = l л.
Докажите этот закон и убедитесь в его выполнении для потребителя,
имеющего функцию полезности Кобба — Дугласа для п товаров из
упражнения 1.53.
1.62. Матрица замещения максимизирующего полезность
потребителя при ценах (8, р) имеет вид
(а Ъ
\г -1/2
Найдите значения параметров а, Ъ и р .
1.63. Верны ли следующие утверждения?
а) Если отношение потребляемых товаров х^х- не зависит от уровня
дохода для любых i и j, то коэффициенты эластичности по доходу для
всех товаров равны единице.
б) Если все коэффициенты эластичности по доходу постоянны и
равны, то они должны быть равны единице.
в) Если функция полезности гомотетична, то предельная полезность
дохода не зависит от цен, а зависит только от дохода.
1.64. Покажите, что функция полезности гомотетична тогда и только
тогда, когда все функции спроса мультипликативно сепарабельны по
ценам и доходу, х(р, у) = ф(>>)х(р, 1) •
1.65. Потребитель с доходом у0 сталкивается с ценами р° и имеет
полезность и° = v(p°, y°), но при изменении цен до уровня р1 стоимость
жизни также изменяется. Для измерения влияния изменения цен мы
можем использовать индекс стоимости жизни, который определяется
следующим образом:
а) Покажите, что 7(р°, р1, и0) больше (меньше) единицы, если
затраты, необходимые для поддержания начального уровня полезности м°,
увеличиваются (снижаются).

96
Часть I. Экономические агенты
б) Предположим, что доход потребителя также изменяется от у0 до
У. Покажите, что положение потребителя улучшится (ухудшится) в
конечном периоде, если у1/у0 больше (меньше), чем 7(р°, р1, и0).
1.66. Пусть функция полезности потребителя имеет вид
а) Пусть в начальном периоде цены равны р° = A, 2), а доход
у0 = 10. Предположим также, что р1 = B, 1). Подсчитайте индекс I
(определенный в предыдущем упражнении).
б) Пусть цены начального и конечного периодов будут такими же,
как в пункте а), и начальный уровень полезности равен и0. Покажите, что
значение индекса I будет изменяться в зависимости от изменения
начальной полезности.
в) Покажите, что если предпочтения потребителя гомотетичны, то
индекс / не зависит от начального уровня полезности для любых цен р°
и р1.
1.67. Покажите, что долю дохода, расходуемого на благо *,., можно
измерить как Э1п[е(р, и*)]/дЪ(р,), где и* = v(p, у).

ц
I Глава 2
ПРОДОЛЖЕНИЕ ТЕОРИИ ПОТРЕБИТЕЛЯ
В этой главе мы исследуем некоторые дополнительные разделы
теории потребителя. Мы начнем с теории двойственности и более полно
изучим связи между прямыми функциями полезности, косвенными
функциями полезности и функциями расходов. Затем мы займемся
классической «задачей восстановления» и узнаем, каким условиям должна
удовлетворять функция, зависящая от цен и дохода, чтобы являться функцией
спроса некоторого максимизирующего полезность потребителя. Ответ на
этот вопрос позволит дать всеобъемлющую характеристику
ограничениям, накладываемым нашей теорией на наблюдаемый спрос. После этого
мы остановимся на «выявленных предпочтениях»— альтернативном
подходе к теории спроса. Наше изучение индивидуального потребителя
завершится рассмотрением задачи выбора в условиях неопределенности.
2.1. Подробнее о двойственности
Как мы видели, решения задач максимизации полезности и
минимизации расходов в некотором смысле оказываются одними и теми же. Эта
идея формализована в теореме 1.9. В данном разделе мы продолжим
изучение связей между прямыми функциями полезности, косвенными
функциями полезности и функциями расходов. Мы покажем, что, хотя наша
теория потребителя самым естественным образом основывалась на
аксиомах о предпочтениях потребителя, эквивалентная ей теория может
быть построена на базе аксиом о его расходах. В частности, будет
показано, что любая функция цен и полезности, обладающая всеми указанными
выше свойствами функции расходов, действительно является функцией
расходов, т.е. что существует функция полезности, которая ее порождает.
Хотя этот результат интересен и сам по себе, его истинная роль
проясняется, когда он используется для характеристики наблюдаемых следствий
нашей теории потребительского спроса. Эта характеристика будет
следовать из так называемой теоремы о восстановлении, рассматриваемой в
разделе 2.2. Учитывая важность этой теоремы, данный раздел вполне
может рассматриваться как вводный к следующему разделу.
2.1.1. Расходы и предпочтения потребителя
Рассмотрим произвольную функцию цен и полезности ?(р, и),
которая может быть (хотя и не обязательно) функцией расходов. Предполо-

98
Часть I. Экономические агенты
жим, что Е обладает свойствами функции расходов 1)—7),
перечисленными в теореме 1.7, т.е. является непрерывной, строго возрастающей и
неограниченной сверху по w, а также возрастающей, однородной первой
степени, вогнутой и дифференцируемой по р. Тогда Е «похожа» на
функцию расходов. Мы покажем, что Е должна быть функцией расходов.
Точнее, мы покажем, что в R" должна существовать такая функция
полезности, что соответствующая ей функция расходов будет совпадать с Е, и
опишем в явном виде процедуру построения такой функции полезности.
Х2 Х2
(а) (б)
Рис. 2.1. (а) — Замкнутое полупространство А(р°, и0);
(б) — пересечение конечного набора множеств Л(р, и°)
Чтобы понять, как она «работает», выберем точку (р°, и°)е R"+ xM+,
и вычислим Е в этой точке для получения числа ?(р°, и0)- Теперь
используем его для построения (замкнутого) полупространства в
потребительском множестве
А(р\и°)= {xgM;|p°.x>?(p0,W0)},
как показано на рис. 2.1(a). Заметим, что А(р°, и0) является замкнутым
выпуклым множеством, содержащим все точки над гиперплоскостью
р°х = ?,(р°, и0) и на ней самой. Теперь выберем другие цены р1,
оставим и0 неизменным и построим замкнутое выпуклое множество
А(р\ и°)= {xelTJp'.x^p1, и0)}.
Представим, что мы проделали это для всех цен р » 0 и нашли
пересечение (бесконечного множества) всех таких множеств

Глава 2. Продолжение теории потребителя
99
А(и°)= n Л(р, M°) = {xeR" |р х>?(р, и0) для всех р»0}. B.1)
р»0
Заштрихованная область на рис. 2.1F) иллюстрирует пересечение
конечного числа множеств А(р°, и0) и дает представление о том, как
будет выглядеть А(и°). Понятно, что чем больше цен рассматривается и
чем больше множеств добавляется к пересечению, тем больше
заштрихованная область будет напоминать супериорное множество1 для
некоторой квазивогнутой вещественнозначной функции. Можно предположить,
что с помощью этих множеств строится что-то очень похожее на прямую
функцию полезности, представляющую «хорошие» выпуклые и
монотонные предпочтения. Это действительно так, что и доказывает следующая
теорема.
Теорема 2.1. Построение функции полезности на основе
функции расходов.
Пусть ?:М"+хМ+ —»М+ удовлетворяет свойствам 1)—7) функции
расходов, приведенным в теореме 1.7. Пусть А(и) определено формулой
B-1). Тогда функция и: Ж"+ —> R+, определенная как
и(х) = max {и > 01 хе А(и)},
является возрастающей, неограниченной сверху и квазивогнутой.
Почему и(х) определена именно так? В конце концов, есть много
способов использовать ?(р, и) для того, чтобы сопоставить число
каждому хеЕ". Чтобы разобраться в этом, забудем приведенное
определение и(х) и на минуту предположим, что ?(р, и) действительно является
функцией расходов, порожденной некоторой функцией полезности и(х).
Как нам восстановить и(х), зная ?(р, и) ? Заметим, что по определению
функции расходов р х > ?(р, и(х)) для всех цен р » 0, и обычно для
некоторой цены это соотношение выполняется как равенство2. Отсюда, так
как Е строго возрастает по и, и(х) будет наибольшим значением и,
таким, что р • х > ?(р, и) для всех р » 0. То есть и(х) — наибольшее
значение и такое, что хе А(и). Следовательно, наше построение позволяет
восстановить функцию полезности, породившую ^(р, и), если ?(р, и)
действительно является функцией расходов. Во-первых, покажем, что
То есть множество, лежащее выше некоторой кривой безразличия некоторой функции
f(\): {х | /(х) > const}. — Примеч. ред.
2 Что далее и предполагается. — Примеч. ред.

100
Часть I. Экономические агенты
w(x), определенная в соответствии с формулировкой теоремы 2.1,
представляет собой функцию полезности, удовлетворяющую нашим аксиомам
(теорема 2.1). Во-вторых, покажем, что Е действительно является
функцией расходов, порожденной и{\) (теорема 2.2). Докажем теорему 2.1.
Доказательство. Заметим, что по определению А(и) функцию и(х)
можно записать как
w(x) = max{tt>0|p-x>?(p, w)Vp»0}.
Прежде всего нужно показать, что и(х) корректно определена, т.е.
что множество {и > 01 р • х > ?(р, и) Vp » 0} содержит наибольший
элемент. Наметим основные шаги. Во-первых, это множество — назовем его
В(х) — должно быть ограничено сверху, потому что функция ?(р, и) не
ограничена сверху и возрастает по и. Тогда В(х) имеет верхнюю грань, а
значит, и наименьшую верхнюю грань и. Требуется показать, что
и е В(х). Это следует из замкнутости В(х), которую мы доказывать не
будем.
Рассмотрим утверждение о том, что и(х) возрастает. Пусть х1 > х2.
Тогда
р х>р х2 Vp»0, (Р-1)
поскольку все компоненты вектора х1 не меньше соответствующих
компонент х2. По определению и(х2),
р х2 > ?(р, и(х2)) Vp » 0 . (Р-2)
Вместе (Р-1) и (Р-2) означают, что
р х1 > ?(р, и(х2)) Vp » 0. (Р-3)
Следовательно, и(х2) удовлетворяет условию х1 е А(и(х2)). Но и(х1)
является наибольшим и, удовлетворяющим условию х1 е А{и). Поэтому
u(x1)>u(x2)9t.q. u(x) возрастает.
Неограниченность и() на Ш"+ можно показать, используя свойства
вогнутости, однородности и дифференцируемости Е() по р, а также то
обстоятельство, что ее областью определения по и является все
множество R". Доказательство мы приводить здесь не будем (хотя его основные
моменты отражены в нижеследующем доказательстве теоремы 2.2).
Для доказательства квазивогнутости и() нам необходимо показать,
что для любых х1, х2 и их выпуклых комбинаций х' выполняется соот-

Глава 2. Продолжение теории потребителя 101
ношение и(х')>тт[и(х1\ и(х2)]. Чтобы установить это, предположим,
что w(x1) = min[w(x1), и(х2)]. Поскольку Е строго возрастает по и, нам
известно, что ?(р, и(х1)) < ?(р, м(х2)), и тогда
tE(p, и(*1))Н1-*)Е<р, и(х2))>Е(р, и(х{)) We [0,1]. (P-4)
Из определений и(х1) и и(х2) мы знаем, что
р х>?(р, и(х1)) Vp»0,
рх2>?(р, и(х2)) Vp»0.
Умножая эти неравенства соответственно на t > 0 и A-/) > 0, складывая
их и используя (Р-4), получаем
рх'>?(р, и(х')) Vp»0 и /е[0, 1].
Следовательно, по определению w(x'), w(x/)>w(x1) = min[w(x1), w(x2)],
что и требовалось доказать. ¦
Теорема 2.1 утверждает, что мы можем взять функцию расходов и
использовать ее для построения прямой функции полезности,
описывающей некоторые выпуклые монотонные предпочтения. На самом деле мы
знаем об этих предпочтениях немного больше. Если выводить
соответствующую им функцию расходов, то мы придем к той же самой функции
Е(), с которой и начинали.
Теорема 2.2. Функция расходов, соответствующая построенной
функции полезности м9 представляет собой Е.
Пусть ?(р, и), определенная на R"++xR"+, удовлетворяет
свойствам 1)—7) функции расходов из теоремы 1.7, и пусть и(х) построена на
основе Е в соответствии с теоремой 2.1. Тогда для всех положительных
цен и неотрицательных уровней полезности выполняется соотношение
?(р, и) = min р • х при и(х) > и ,
х
т.е. ?(р, и) является функцией расходов, порожденной и(х).
Доказательство. Зафиксируем р° » 0 и и0 > 0 и предположим, что
xeR" удовлетворяет условию и(х)>и°. Заметим, что поскольку и()
построена на основе Е в соответствии с теоремой 2.1, должно выполняться
неравенство
р х>?(р, и(х)) Vp»0.

102
Часть 1. Экономические агенты
Кроме того, поскольку Е возрастает по уровню полезности, а и(х) > и ,
должно также выполняться условие
рх>?(р, и0) Vp»0. (P-1)
Следовательно, для данного вектора цен р° верно, что
?(р°, w°)<p°-x VxeM"+ при и(х)>и°. (Р-2)
Но из (Р-2) следует, что
?(р°, w°)<minp°x при и(х)>и°. (Р-3)
xeR"
Мы хотим показать, что первое неравенство в (Р-3) является равенством.
Для этого достаточно найти х° е R"+ такой, что
р0-х°<?(р0, и0) и и(х°)>и\ (Р-4)
поскольку это и будет означать, что минимум правой части (Р-3) не
может быть больше Е(р°, и0).
Для доказательства (Р-4) заметим, что по теореме Эйлера
(теорема А2.7), поскольку Е дифференцируема и однородна первой степени по р,
?(р, и) = ^^Р VP»0, (P-5)
Эр
где Э?(р, м)/Эр = (Э?(р, и)/дрх, ...,д?(р, и)/дрп) — вектор частных
производных функции Е. Кроме того, в силу вогнутости ?(р, и) по р,
из теоремы А2.4 следует, что для всех р » 0
?(р, и«)<Е(р\ цо) + Э?(р0^0)<(р_р0)< (р_6)
Эр
Но если вычислить (Р-5) в точке (р°, и0) и подставить в (Р-6), то мы
получим
?(р, и0)<(Э?(р°, «°)/Эр).р Vp»0 (Р-7)
Положив х°=Э?,(р°, и°)/др, заметим, что х°еМ", поскольку Е
возрастает по р. Тогда (Р-7) можно переписать как
р-х°>?(р, и0) Vp»0. (P-8)
Но тогда по определению и(-) должно выполняться неравенство
и(х°)>и°. Далее, вычислив (Р-5) в точке (р°, м°), мы получаем

Глава 2. Продолжение теории потребителя
103
Е(р°, и0) = р° -х°. Таким образом, мы доказали (Р-4) для выбранного
нами х° и тем самым показали, что
?(р°, w°) = minp°x при и(х)>и°.
Поскольку р° »0 и и0 > 0 произвольны, то ?(р, и) совпадает с
функцией расходов для функции полезности и(\) на R"++ xR+ . ¦
Две последние теоремы утверждают, что мы можем взять
произвольную функцию цен и полезности, удовлетворяющую свойствам 1)—7)
теоремы 1.7, и она будет (полноценной) функцией расходов для некоторых
предпочтений, которые удовлетворяют многим из обычных аксиом о
предпочтениях. Затем мы, конечно, можем продифференцировать эту функцию
по ценам (товаров) и получить систему функций спроса по Хиксу. Если
предпочтения непрерывны и строго возрастают, такую функцию расходов
можно обратить по и, получить тем самым косвенную функцию
полезности, вывести систему функций спроса по Маршаллу и применить
тождество Роя. При этом на каждом шаге гарантируется, что итоговые функции
спроса обладают всеми свойствами, которые следуют из максимизации
полезности. Таким образом, при теоретических построениях у нас есть
выбор. Можно начать с прямой функции полезности и выводить хиксовские и
маршалловские функции спроса, решая соответствующие
оптимизационные задачи. Или же можно взять функцию расходов и выводить функции
спроса более легким способом, используя переход к обратной функции и
простое дифференцирование.
2.1.2. Выпуклость и монотонность
Как вы помните, после введения аксиомы о выпуклости
предпочтений в главе 1 мы говорили о том, что основные выводы теории не
изменятся и при отказе от предположения о выпуклости рассматриваемых
предпочтений. Сейчас самое время доказать это утверждение, а также
остановиться на предположении о монотонности предпочтений.
Для этого предположим, что функция и{\) непрерывна (т.е. она не
обязана быть ни возрастающей, ни квазивогнутой).
Пусть е(р, и) — функция расходов, порождаемая и(х). Как нам
известно, непрерывности и(\) достаточно для того, чтобы гарантировать,
что е(р, и) корректно определена. Кроме того, е(р, и) непрерывна.
Теперь рассмотрим функцию полезности — назовем ее w(x), —
порожденную функцией расходов е() уже знакомым нам способом, т.е.
w(x) = max {и > 01 р х > е(р, и) Vp » 0}.

104
Часть I. Экономические агенты
Обратившись к доказательству теоремы 2.1, можно убедиться в том,
что w(x) возрастает и квазивогнута, причем это не зависит от того,
является и(х) квазивогнутой и возрастающей или нет. Тогда очевидно, что
и(х) и и>(х) не обязательно совпадают. Как они связаны между собой?
Легко заметить, что w(x)>u(x) для всех хеК". Это следует из
определения функции е(), согласно которому е(р, w(x))<px Vp»0.
Нужное неравенство, таким образом, следует из определения w(x).
Таким образом, для любого и > 0 супериорное множество уровня и
для функции и(х) — скажем, S(u) — будет содержаться в аналогичном
множестве для w(x) — скажем, Т(и). Кроме того, поскольку w(x)
квазивогнута, то множество Т(и) выпукло.
Рассмотрим теперь рис. 2.2. Если и(х) окажется возрастающей и
квазивогнутой, то граница S(u) будет представлять собой выпуклую к началу
координат кривую безразличия с отрицательным наклоном, и(х) = и на
рис. 2.2(a). Заметим, что каждая точка на этой границе соответствует
набору, который позволяет при некотором векторе цен р » 0 минимизировать
расходы при достижении уровня полезности и. Следовательно, если
w(x°) = и, то для некоторого р° » 0 мы получим, что е(р°, и) = р° • х°. Но
так как е() строго возрастает по и, это означает, что w>(x°)<w = w(x°).
Поскольку неравенство w(x°)>w(x°) всегда верно, мы должны получить
w(x°) = w(x0). Так как и выбиралось произвольно, отсюда следует, что
w(x) = w(x) для всех х. В свете теорем 2.1 и 2.2 и предположений о
квазивогнутости и возрастании и(х) в этом нет ничего удивительного.
Более интересен случай, изображенный на рис. 2.2F), когда функция
и(х) не является ни возрастающей, ни квазивогнутой. Здесь снова
граница S(u) дает кривую безразличия и(х) = и .
Заметим, что некоторые наборы на кривой безразличия ни при каких
ценах не минимизируют расходы при уровне полезности и. Жирными
фрагментами на рис. 2.2(b) показаны те наборы, которые действительно
минимизируют расходы при некотором положительном векторе цен. Для
них, как и ранее, w(x) = и(х) = и. Но поскольку w(x) квазивогнута и
возрастает, кривая безразличия w(x) = и должна выглядеть так, как показано
на рис. 2.2(г). Тем самым функция и>(х) отличается от и(х) ровно
настолько, насколько этого требуют свойства строгого возрастания и
квазивогнутости.

Глава 2. Продолжение теории потребителя
105
*2
Х2
(и)-Ци) 4v*v
w(x) = и
-+Х1
(б)
*2
и(\) = и
(в)
->*1
*2
А
(Г)
w(x) = и
->*!
м(х) = w
Бюджетная линия
Рис. 2.2. Двойственность расходов и полезности

106
Часть I. Экономические агенты
Из связи между кривыми безразличия функций w(x) и и{\) ясно, что
если некоторый набор максимизирует и(\) при условии р • х < у, то тот
же самый набор максимизирует w(x) при условии р\<у. (Внимание!
Обратное неверно.) Следовательно, любой наблюдаемый спрос может
быть порожден невозрастающей и неквазивогнутой функцией
полезности, такой, как и(х), а также — некоторой возрастающей и
квазивогнутой функцией полезности, такой, как w{\). Именно в этом смысле
предположения монотонности и выпуклости предпочтений не имеют
наблюдаемых последствий для нашей теории потребительского спроса1.
2.1.3. Косвенная полезность и предпочтения потребителя
Мы видели, как двойственность позволяет нам от функции расходов
перейти к прямой функции полезности. Поскольку функции расходов и
косвенной полезности тесно связаны (т.е. являются взаимно обратными),
не должен вызывать удивления тот факт, что можно из косвенной
функции полезности вывести прямую функцию полезности, на основе которой
косвенная функция полезности была получена. В этом разделе мы
сформулируем соотношения двойственности между прямой и косвенной
функциями полезности.
Предположим, что и(х) порождает косвенную функцию полезности
v(p, у). Тогда по определению для каждого хеМ" и р » 0 верно
неравенство v(p, р • х) > и(\). Кроме того, обычно существует некоторый
вектор цен, для которого неравенство выполняется как равенство. Очевидно,
в этом случае мы можем записать
и(\) = min v(p, p • х), B-2)
т.е. B-2) дает нам способ восстановления функции полезности и(х), если
известна только порожденная ею косвенная функция полезности. В
следующей теореме представлен один из вариантов этого результата.
Прежде чем закончить обсуждение этой темы, сделаем оговорку относительно
выводов, касающихся предположений о монотонности. Вывод о том, что рассмотренный в
предыдущем случае спрос, порождаемый функцией полезности и(\), может
порождаться и возрастающей функцией w(x), основан на предположении о неотрицательности
цен. Но если бы, например, для двух товаров одна из цен — скажем, р2 — была
отрицательной, мы получили бы ситуацию, аналогичную изображенной на рис. 2.2(д), где х*
является оптимальным набором при функции полезности и(х), но не является таковым
при w(x). Таким образом, если допустить, что цены могут быть отрицательными,
условие монотонности оказывается существенным.

Глава 2. Продолжение теории потребителя
107
Теорема 2.3. Двойственность между прямой и косвенной
полезностью.
Предположим, что и(х) квазивогнута и дифференцируема на Ш"++,
причем ее частные производные положительны. Тогда для всех х е R"+
v(p, p • х) — косвенная функция полезности, порожденная и{\), —
достигает минимума по р на Ш"++ и
и(\) = min v(p, p • х). (Т-1)
Доказательство. Как мы помним по обсуждению, предшествующему
теореме 2.3, левая часть (Т-1) никогда не превосходит правую часть.
Поэтому достаточно показать, что для каждого х»0 существует вектор
цен р » 0 такой, что
w(x) = v(p, р х). (Р-1)
Так что рассмотрим х° » 0 и положим р° = Vw(x°). Тогда, по
предположению, р° » 0. Кроме того, положив А,0 = 1 и у0 = р° • х°, мы имеем
^!>-XV=0,i = l,...,n (P-2)
Эх,
и
Р°-х°=/. (Р-3)
Следовательно, (х°, Х°) удовлетворяют условиям первого порядка для
задачи потребителя max и(х) при р° • х = у0. Более того, в силу
квазивогнутости и(х) по теореме 1.4 этих условий достаточно, чтобы гарантировать,
что х° является решением задачи потребителя при р = р° и у = у°.
Поэтому и(х°) = v(p°, у0) = v(p°, р° • х°), т.е. (Р-1) выполняется для (р°, х°), но
поскольку х° произвольно, можно заключить, что для каждого х»0
(Р-1) верно при некотором р » 0. ¦
Как и в случае функции расходов, используя (Т-1), можно показать,
что если некоторая функция К(р, у) обладает всеми свойствами
косвенной функции полезности, приведенными в теореме 1.6, то F(p, у)
действительно является косвенной функцией полезности. Мы не будем
разбирать здесь этот результат, а отошлем заинтересованного читателя к работе
Диверта [Diewert, 1974].

108
Часть I. Экономические агенты
Наконец, заметим, что (Т-1) можно записать в другой форме, которая
иногда бывает более удобной. Так как v(p, у) однородна нулевой
степени по (р, у), при р • х > 0 мы имеем равенство v(p, р • х) = v(p/(p • х), 1).
Следовательно, если х » 0, а р* »0 доставляет минимум функции
v(p, р• х) на ре R"++, то р = р*/(р* • х)» 0 минимизирует функцию
v(p, 1) на ре R"+, таких, что рх = 1. Кроме того, v(p\ p*x*) = v(p, l),
поэтому (Т-1) можно переписать как
и(\) = min v(p, 1) при р • х = 1. (Т-Г)
Не имеет значения, (Т-1) или (Т-Г) используется для восстановления
м(х) на основе v(p, у), нужно просто выбрать более удобный вариант.
Один из недостатков задачи (Т-1) заключается в том, что она всегда имеет
много решений в силу однородности v (т.е. если р* является решением
(Т-1), то решением будет и /р* для всех />0). Поэтому, в частности,
нельзя применять теорему об огибающей, которой мы воспользуемся в
следующем примере. В этом случае задача (Т-Г) однозначно
предпочтительнее. ¦
Пример 2.1. Рассмотрим частный случай косвенной функции
полезности и выведем из нее прямую функцию полезности. Предположим,
что v(p, у) = у{р[ + р2)'1/г • Из последней части примера 1.2 нам известно,
что это выражение обладает всеми необходимыми свойствами косвенной
функции полезности. Воспользуемся (Т-Г) для восстановления и(\).
Положив у = 1, получим v(p, 1) = (р[ + р\)~1/г. Тогда прямая функция
полезности будет решением следующей задачи:
м(х,, х2) = min(/?,/' + р[)/г при рххх + р2х2 = 1.
Сначала решим задачу минимизации, а затем вычислим целевую
функцию в точке оптимума, чтобы получить функцию значения задачи
минимизации. Условия первого порядка для лагранжиана требуют, чтобы
оптимальные р\ и р\ удовлетворяли равенствам
-((p'j+(p2yti/r)'\p; г1 -***,=о, (е-1)
-((А У НРг)гГИ-\рТ' -Ь\ = 0, (Е-2)
1-р*х1-р*2х2=0. (Е-3)

Глава 2. Продолжение теории потребителя
109
Исключая X* из (Е-1) и (Е-2), получаем
\1/(г-1)
Р\ =Р2 \ —
(Е-4)
v2/
Подставив (Е-4) в (Е-3) и снова воспользовавшись (Е-4), после некоторых
преобразований находим решение
Р\ =¦
xfr-l)
Slir-l) . ^/(r-l)
Ч
+ Х'1
(Е-5)
J/(r-l)
Pl =
x[l{r-X)+xfr-{)
(E-6)
Подставив оптимальные р\ и р\ в целевую функцию, получим w(jtp jc2) :
w(x,, x2) =
M'-l)+Jcr/(r-l)
-,-1/r
*1
(J^(r-,)+^,,)r
"(^l)+^(r-,))'"
'A
(r-l)/r
Если определить p s r/(r -1), то выражение принимает вид
и(*„ x2) = (jc,p+^)I/p-
(Е-7)
Это прямая функция полезности с постоянной эластичностью замещения,
с которой мы начинали анализ в примере 1.2, как, собственно, это и
должно быть. ¦
Последняя теорема о двойственности, которую мы докажем, касается
обратных функций спроса потребителя. До сих пор мы ограничивались
обычными маршалловскими функциями спроса, где объем спроса являлся
функцией от цен и дохода, но иногда удобнее работать с обратными
функциями спроса. Здесь мы рассматриваем цену на / -й товар как
функцию от количества /-го и всех остальных товаров и записываем ее как
Pi =Р,(Х)- Теория двойственности, как показывает следующая теорема,
предлагает простой способ получения обратных функций спроса. Мы
предполагаем, что используемые функции дифференцируемы, когда это
необходимо.

по
Часть I. Экономические агенты
Теорема 2.4. (Теорема Хотеллинга, Уолда) Двойственность и
обратные функции спроса.
Пусть и(\) — прямая функция полезности потребителя. Тогда
обратная функция спроса на 1-й товар, соответствующая доходу у-\,
может быть рассчитана по формуле
ди(\)/дх{
А(х) = —
?"=1ху(Эм(х)/Эх;)
Доказательство. По определению р(х), мы имеем w(x) = v(p(x), 1) и
[р(х)] • х = 1 для всех х. Следовательно, согласно обсуждению,
предшествовавшему теореме 2.3,
w(x) = v(p(x), l) = minv(p, 1) при р*х = 1. (Р-1)
Рассмотрим теперь лагранжиан, соответствующий задаче минимизации
(Р-1):
Ар, i) = v(P, i)+Mi-px).
Применяя теорему об огибающей, получим
Эи(х) дЦр, X*)
Эх
= -X'p*,i = \, ...,«, (Р-2)
где р* = р(х), а X* — оптимальное значение множителя Лагранжа.
Предполагая, что Эи(х)/Эх; > 0, имеем X" < О.
Умножив (Р-2) на х и суммируя по /, находим
2><-т-=-х2><*,=
/=1 ОХ, м
= -X*fdpi(x)xi= (P-3)
/=1
поскольку [р(х)] • х = 1. Объединяя (Р-2) и (Р-3) и учитывая, что р] = р, (х),
получаем искомый результат. ¦
Пример 2.2. Снова рассмотрим случай функции с постоянной эла-
j, Х2 ) = (Xj + X2 j
стичностью замещения (CES-функции). Если м(хр х2) = (хр + х2 I/р, то
^ = К+х2р)A/рнхГ1,
dXj

Глава 2. Продолжение теории потребителя
111
Умножая это выражение на х. и суммируя по j = 1, 2, получим
необходимые соотношения и, применив теорему 2.4, придем к следующим
обратным функциям спроса при доходе у = 1:
р2=хр2-1(х>+х>Г1.
Обратите внимание, что это не что иное, как решения (Е-5) и (Е-6) для
соотношений первого порядка в примере 2.1 после замены р = г/(г-1).
Это не простое совпадение: решения задачи максимизации полезности
потребителя дают маршалловский спрос как функцию от цены, а решения
двойственной задачи минимизации (нормализованной) косвенной
полезности дают обратные функции спроса, зависящие от объема. ?
2.2. Восстановление функции полезности
В главе 1 мы показали, что максимизирующая полезность функция
потребительского спроса должна удовлетворять условиям однородности
нулевой степени, сбалансированности бюджета, симметричности и
отрицательной полуопределенности, а также условиям агрегирования по Курно и
Энгелю. На самом деле в этих условиях присутствует некоторая
избыточность. В частности, из теоремы 1.17 нам известно, что обе формулы
агрегирования напрямую следуют из условия сбалансированности бюджета.
Кроме того, из четырех оставшихся условий действительно независимыми
являются только условия сбалансированности бюджета, симметричности и
отрицательной полуопределенности, а однородность нулевой степени
следует из них. Точнее, однородность следует только из сбалансированности
бюджета и симметричности, как показывает следующая теорема.
Теорема 2.5. Однородность следует из сбалансированности
бюджета и симметричности.
Если х(р, у) удовлетворяет условию сбалансированности
бюджета, а его матрица Слуцкого симметрична, то он является однородным
нулевой степени по р и у.
Доказательство. Вспомним из доказательства теоремы 1.17, что если
выполняется условие сбалансированности бюджета, то бюджетное
ограничение можно продифференцировать по ценам и доходу.
Дифференцирование по цене p., i = 1, ...,л, дает
^ дх,(р, у)
У=1 Щ

112
Часть I. Экономические агенты
а по доходу
р^ч.
(Р-2)
Зафиксируем р и у и положим fi(t) = xj(tp, ty) для всех t>0.
Необходимо показать, что ff(t) не зависит от t, или что f'{t) - О для всех / > 0.
Продифференцируем f, no t:
гъ = у^(Ф. ty) ЭхДф, (у)
/,u ? эЛ Л эу '
(Р-3)
Из условия сбалансированности бюджета следует, что
fp • х(/р, ty) = ty, поэтому, разделив на t > О, получим:
/7
(Р-4)
У=1
Подставим ^ из (Р-4) в (Р-3) и после преобразования придем к
следующему соотношению:
До=2>,
У=1
ах/(ф>(у)+аУ|(щ>»)х(ф> ^
dpj ду J
Но в квадратных скобках стоит if -й элемент матрицы Слуцкого,
которая симметрична по определению. Поэтому внутри скобок мы можем
поменять / и j местами, сохраняя при этом равенство. Отсюда
до=2>у
7=1
Эх(/р, ty) Эх(/р, ty)
—^ +^ */(Ф. (к)
п
2>
7=1
1'Л
7=1
ЭхДф, Гу)
Эр,
dxj(tp, ty)
+ *,(Ф. (У)
5>у
У=1
ЭР/
+ */(Ф. 00"
Эх//р, (у)
Эу
ЭхД/р, fy)
§*' *
= -[-*,(ф, fy)] + x,(fp, <y)-[l] =
= 0,

Глава 2. Продолжение теории потребителя
113
причем предпоследнее равенство следует из (Р-1) и (Р-2), где в качестве
аргументов (/р, ty). ¦
Таким образом, если х(р, у) представляет собой набор функций
спроса для максимизирующего полезность потребителя, то полученные
нами выводы, относящиеся к наблюдаемому спросу, можно (кратко)
сформулировать с помощью всего лишь трех свойств:
• сбалансированности бюджета (р • х(р, у) - у );
• отрицательной полуопределенности (соответствующая матрица
Слуцкого s(p, у) должна быть отрицательно полуопределена);
• симметричности (матрица s(p, у) должна быть симметричной).
Нам хотелось бы знать, является ли этот список исчерпывающим, т.е.
только ли эти выводы относительно наблюдаемого спроса вытекают из
нашей модели поведения потребителя? Может быть, есть и другие, к
которым мы еще не пришли? Оказывается, можно доказать, что этот список
является полным: не существует других независимых ограничений,
накладываемых теорией максимизирующего полезность потребителя на
поведение спроса.
Но как же подступиться к доказательству этого результата? Способ
решения довольно оригинален и восходит к работе Антонелли [Antonelli,
1886]. Его идея такова. Предположим, что у нас есть векторнозначная
функция цен и дохода и что мы можем каким-то образом построить
функцию полезности, которая порождает в точности эту же функцию
спроса. Тогда, конечно, исходная функция должна соответствовать нашей
теории потребителя, потому что она является функцией спроса
потребителя с построенной нами функцией полезности. Антонелли обнаружил,
что если векторнозначная функция цен и дохода удовлетворяет трем
указанным условиям, то должна существовать функция полезности, которая
порождает данную функцию спроса. Задача восстановления функции
полезности по функции спроса известна под названием задачи
восстановления (интегрирования).
Трудно переоценить важность этого вывода. Согласно Антонелли, если
функция цен и дохода удовлетворяет трем перечисленным условиям, то
она является функцией спроса для некоторого максимизирующего
полезность потребителя. Нам уже известно, что функция цен и дохода будет
функцией спроса только если она удовлетворяет тем же условиям.
Объединяя эти два утверждения, мы приходим к выводу о том, что три
указанных условия позволяют протестировать нашу теорию потребительского
поведения: поведение спроса согласуется с теорией максимизации
полезности тогда и только тогда, когда оно удовлетворяет условиям
сбалансированности бюджета, отрицательной полуопределенности и симмет-

114
Часть I. Экономические агенты
ричности. Этот замечательный результат заслуживает строгой
формулировки.
Теорема 2.6. Теорема о восстановлении.
Непрерывно дифференцируемая функция х: Ш"*+ —»R" является
функцией спроса, порожденной некоторой возрастающей квазивогнутой
функцией полезности, тогда (и только тогда, если функция полезности
непрерывна, строго возрастает и строго квазивогнута), когда она
удовлетворяет условиям сбалансированности бюджета, симметричности и
отрицательной полуопределенности.
Ниже мы приведем лишь схематичное доказательство результата Ан-
тонелли, воспользовавшись современным подходом к этой проблеме,
изложенным в работе Гурвица и У завы [Hurwitz, Uzawa, 1971]. Ход их
доказательства является превосходной иллюстрацией возможностей теории
двойственности.
Доказательство (схематично). Поскольку мы уже доказали теорему в
одну сторону, то достаточно показать, что верно и обратное утверждение.
Предположим, что некоторая функция х(р, у) удовлетворяет условиям
сбалансированности бюджета, симметричности и отрицательной
полуопределенности. Нам необходимо показать, что существует такая функция
полезности, для которой х() является функцией спроса.
Рассмотрим произвольную функцию расходов е(р, и), порожденную
некоторой возрастающей квазивогнутой функцией м(х), и предположим,
что и(х) порождает маршалловскую функцию спроса хт(р, у). На этом
этапе между х() и е(), х() и м(-) или х() и хт() не обязательно должна
существовать какая-то связь.
Исключительно в целях доказательства предположим, что х() и е()
оказываются связанными следующими соотношениями:
Эв(Р' ц)=х,(р, e(p, „)), V(p, и), i = l, ...9n. (Р-1)
др,
Можем ли мы тогда сказать что-нибудь о связи между х(р, у) и
функцией полезности и(х), на основе которой была получена функция е(р, и) ?
На самом деле, можем. Если (Р-1) верно, то х(р, у) является функцией
спроса для функции полезности м(х),т.е. х(р, ^) = х"Чр, У)-
Почему это так? Заметим, что если бы была применима лемма Ше-
парда, то левая часть (Р-1) равнялась бы х/7(р, у), так что из (Р-1)
следовало бы равенство
хл(р, 7) = х(р, е(р, и)) V(p, и). (Р-2)

Глава 2. Продолжение теории потребителя
115
Кроме того, если бы была применима теорема 1.9, то функции спроса по
Хиксу и по Маршаллу были бы связаны следующим образом:
ж*(р, у) = хт(р, е(р, и)) V(p, и). (Р-3)
Объединяя (Р-2) и (Р-3), получим
х(р, е(р, i/)) = xm(p, е(р, и)) V(p, и). (Р-4)
Вспомним, что е(р, и) является функцией расходов и поэтому для
каждого фиксированного р принимает все неотрицательные значения, если
и принимает все значения из области определения. Следовательно, (Р-4)
эквивалентно равенству
х(р, у) = хт(р, у) V(p,w),
что мы и намеревались показать. (Это можно утверждать, даже если ни
лемма Шепарда, ни теорема 1.9 неприменимы.)
Таким образом, если функция х(р, у) связана с функцией расходов
соотношением (Р-1), то х(р, у) является функцией спроса, порожденной
некоторой возрастающей квазивогнутой функцией полезности (т.е. такой,
которая в соответствии с теоремой 2.1 порождает функцию расходов).
Тем самым мы свели нашу задачу к доказательству существования
функции расходов е(р, и), связанной с х(р, у) так, как показано в (Р-1).
Найти такую функцию расходов, чтобы выполнялось (Р-1), непросто.
Выражение (Р-1) известно в математической литературе как система
дифференциальных уравнений в частных производных. Хотя решать
такие системы, как правило, довольно трудно, существует результат,
гарантирующий существование решения при определенных условиях. Для
наших целей этого достаточно.
Но прежде чем использовать его, заметим следующее. Если (Р-1)
имеет решение е(р, и), то после дифференцирования обеих частей по Pj
мы получим
Э2е(р, ц)^Эх,(р, g(p, и)) | Эе(р, ц)ЭхДр, е(р, и))
dpjdpi dpj dpj ду
Используя лемму Шепарда, (Р-2) и положив у = е(р, и), перепишем это
выражение следующим образом:
opjop, dpj ду

116
Часть I. Экономические агенты
Теперь заметим, что левая часть согласно теореме Юнга симметрична
по / и j. Из (Р-5) следует, что правая часть тоже должна быть
симметричной по i и j. Таким образом, симметричность правой части по i и j
является необходимым условием существования решения (Р-1).
Оказывается, это условие является также и достаточным для
существования решения. По теореме Фробениуса решение (Р-1) существует
тогда и только тогда, когда правая часть (Р-5) симметрична по / и j.
Посмотрим внимательно на правую часть (Р-5). Это в точности ij -й элемент
матрицы Слуцкого, соответствующей функции спроса х(р, у).
Следовательно, поскольку матрица Слуцкого симметрична, функция е(р, и),
удовлетворяющая (Р-1), существует.
Но будет ли она настоящей функцией расходов? Теорема Фробениуса
об этом ничего не говорит, но по теореме 2.2 она будет функцией
расходов, потому что обладает всеми необходимыми свойствами,
перечисленными в теореме 1.7. Попробуем проверить каждое из этих свойств.
Во-первых, заметим, что поскольку е(р, и) удовлетворяет (Р-1), а
вектор х(р, у) неотрицателен, то е(р, и) автоматически является
возрастающей по р, и выполнение леммы Шепарда гарантировано по
построению. Можно доказать, что е(р, и) непрерывна по (р, и), строго
возрастает и неограничена по weE" и е(«, и) = О при и = 0. Если
выполняется (Р-1) и условие сбалансированности бюджета, функция е()
однородна первой степени по р. Это вам будет предложено доказать в
упражнении 2.4, и, таким образом, остается доказать только одно свойство
функции расходов — вогнутость по р.
По теореме А2.4 е(-) будет вогнутой по р тогда и только тогда, когда
ее матрица Гессе по р отрицательно полуопределена. Но согласно (Р-5)
это имеет место тогда и только тогда, когда матрица Слуцкого,
соответствующая х(р, у), отрицательно полуопределена, что верно по
предположению.
В итоге мы установили следующее: решение е(-) задачи (Р-1) суще-
ствует и является функцией расходов тогда и только тогда, когда
Х(Р> У) удовлетворяет условиям сбалансированности бюджета,
симметричности и отрицательной полуопределенности. Именно это мы и
хотели показать. ¦
Хотя мы подчеркивали важность этого результата для самой теории,
он имеет и практическое значение. Например, если оценивать функцию
потребительского спроса на ограниченном массиве данных, предполагая
при этом, что функция спроса порождается функцией полезности, то для

Глава 2. Продолжение теории потребителя
117
спроса можно выбирать произвольную функциональную форму,
удовлетворяющую условиям сбалансированности бюджета, симметричности и
отрицательной полуопределенности. Любая такая функция, как мы теперь
знаем, будет порождаться функцией полезности.
Чтобы продемонстрировать, как функция расходов выводится из
функции спроса, рассмотрим пример для трех товаров.
Пример 2.3. Предположим, что есть три товара, и спрос
потребителя задается функциями
xi(PnP2>P3>y) = -L-> 1 = 1,2,3,
Pi
где ос, > О и а, + а2 + а3 = 1.
Легко проверить, что вектор спроса х(р, у) удовлетворяет условиям
сбалансированности бюджета, симметричности и отрицательной
полуопределенности. Следовательно, по теореме 2.6 х(р, у) должен быть
порожден функцией полезности.
Нам будет достаточно вывести функцию расходов, удовлетворяющую
условию (Р-1) из вышеприведенного доказательства. В упражнении 2.5 вам
предлагается сделать следующий шаг и использовать теорему 2.1 для
восстановления функции полезности, порождающей полученную здесь
функцию расходов. Построенная таким образом функция полезности будет
порождать функции спроса, с которых мы и начинаем этот пример.
Наша задача тогда заключается в том, чтобы найти е(рх, р2, /?3, w),
являющуюся решением следующей системы дифференциальных
уравнений в частных производных:
МР\> А>> Ръ> u)_aie(pl, p2, ръ, и)
Щ Pi
Прежде всего, заметим, что ее можно переписать как
дЩе(р,р2,Рз,и)) = а1^ ЫХ2Ъ (Е1)
fy Pi
Если бы вам потребовалось найти f(x), зная, что f\x) = а/х, вы бы
легко получили, что /(jc) = a ln(x) +const. Но (Е-1) утверждает именно это,
причем / = 1п(е). Следует только иметь в виду, что при нахождении
частной производной по одной из переменных, скажем, рх, все остальные
переменные — р2, ръ и и — должны считаться константами. Таким
образом, легко заметить, что из трех уравнений (Е-1) следует три других:

118
Часть I. Экономические агенты
ln(e(p, u)) = alln(pl) + cl(p29 p3, м),
1п(е(р, и)) = а21п(р2) + с2(р1, р3, и), (Е-2)
ln(e(p, u)) = a3ln(p3) + c3(pl, р2, и),
где функции сД) выступают в роли констант, добавляемых к f(x).
Однако с,() требуется выбрать таким образом, чтобы все три уравнения
выполнялись одновременно. Нетрудно увидеть, что тогда из (Е-2) следует, что
1п(е(р, и)) = ос, 1п(р,) + а2 \п(р2) + а31п(/?3) + с(и),
где с(и) — некоторая функция и . Но это означает, что
е(р, и) = ф)р?р?р?.
Поскольку необходимо обеспечить строгое возрастание е() по и,
с(и) может быть любой строго возрастающей функцией. Не имеет
значения, какой именно окажется эта функция, потому что спрос будет
инвариантным к таким строго возрастающим преобразованиям. Например,
можно положить с(и) = и и получить окончательное решение
е(р, и) = ир?р?р«\
Мы оставляем вам проверку того, что эта функция удовлетворяет
исходной системе дифференциальных уравнений в частных производных и
обладает всеми необходимыми свойствами функции расходов. п
2.3. Выявленные предпочтения
До сих пор мы изучали теорию спроса исходя из предположения о
том, что потребитель имеет предпочтения, обладающие определенными
свойствами (полноты, транзитивности и монотонности), и пытались
вывести наблюдаемые свойства рыночного спроса, которые следуют из них
(сбалансированность бюджета, симметричность и отрицательная
полуопределенность матрицы Слуцкого). Другими словами, мы начинали с
предположений о чем-то, что не можем наблюдать,— о
предпочтениях — для того, чтобы в конечном счете строить прогнозы о наблюдаемом
явлении — потребительском спросе.
В своей выдающейся книге «Основания экономического анализа»
A947) Пол Самуэльсон предложил альтернативный подход. Почему бы
не начать с наблюдаемых явлений и не закончить ими же? Самуэльсон
показал, что почти любой прогноз традиционной теории потребителя
относительно наблюдаемого спроса потребителя может также быть получен

Глава 2. Продолжение теории потребителя
119
из нескольких простых и разумных предположений не о ненаблюдаемых
предпочтениях потребителя, а о самом выборе, который он делает и
который можно наблюдать.
Основная идея проста: если потребитель приобретает какой-то набор
товаров вместо другого, доступного ему набора, то первый набор
выявление предпочитается второму. Действительно, выбирая один набор вместо
другого, потребитель передает важную информацию о своих вкусах, и
тогда вместо того, чтобы, как мы это делали до сих пор, формулировать
предположения о предпочтениях, мы можем строить гипотезы о
согласованности выбора потребителя. Выразим эту мысль более формально.
Определение 2.1. Слабая аксиома выявленных предпочтений
(weak axiom of revealed preference, WARP).
Выбор потребителя удовлетворяет WARP, если для каждой
различной пары наборов х°, х1, где х° был выбран при ценах р°, а х1 был
выбран при ценах р1,
p^x'^V^p'-x^p'-x1.
Другими словами, WARP выполняется, если при условии, что х° выяв-
ленно предпочитается х1, не верно, что х1 выявленно предпочитается х°.
Чтобы лучше понять смысл этого определения, взгляните на рис. 2.3.
На обеих частях рисунка потребитель выбирает х° при ценах р° и х1 при
ценах р1. На рис. 2.3(a) выбор удовлетворяет WARP. На нем
представлена ситуация, когда выбирается набор х° при доступном х1, а когда
выбирается х1, набор х° недоступен. Напротив, на рис. 2.3F) х° снова
выбирается при доступном х1, но когда выбирается х1, потребитель мог бы
выбрать х°, но не сделал этого, тем самым нарушив WARP.
Х2 Х2
(а) (б)
Рис. 2.3. Слабая аксиома выявленных предпочтений (WARP)

120
Часть I. Экономические агенты
Теперь предположим, что выбор потребителя удовлетворяет WARP.
Пусть х(р, у) обозначает выбор, сделанный потребителем при ценах р и
доходе у. Заметим, что х(р, у) не является функцией спроса (потому
что мы даже не упоминали о полезности или максимизации полезности),
она просто обозначает объем товаров, который потребитель выбирает при
ценах р и доходе у. Для ясности будем называть х(р, у) функцией
выбора. Помимо WARP, сделаем еще одно предположение о
потребительском выборе, а именно, что при р » 0 х(р, у) удовлетворяет условию
сбалансированности бюджета, т.е. р • х(р, у) - у. Эти два довольно
слабых ограничения имеют замечательные следствия.
Первое следствие WARP и сбалансированности бюджета заключается
в том, что функция выбора х(р, у) должна быть однородна нулевой
степени по (р, у). Чтобы установить это, предположим, что х° выбирается
при ценах р° и доходе j>°, a x1 выбирается при ценах р1 = /р° и доходе
У = ty° для любого / > 0. Поскольку у1 = ty°, то когда расходуется весь
доход, должно выполняться равенство р1 х1 =/р°х°. Заменим здесь р1
на /р°, разделим на t и получим
рО-х'^.х0. B-3)
Затем заменим в том же равенстве tp° на р1 и получим
р1 х'=р' х°. B-4)
Если х° и х1 различны и для них выполняется соотношение B-3), то
согласно WARP левая часть B-4) должна быть строго меньше правой, что
противоречит соотношению B-4). Значит, эти наборы не могут быть
различными, и, следовательно, функция выбора потребителя должна быть
однородной нулевой степени по ценам и доходу.
Таким образом, функция выбора х(р, у) должна демонстрировать
одно из дополнительных свойств функции спроса. Как мы сейчас
докажем, она обладает еще одним из этих свойств.
В упражнении 1.44 было введено понятие компенсированного спроса
по Слуцкому. Рассмотрим влияние компенсации по Слуцкому на выбор
потребителя. Если вы пропустили это упражнение, напомним, что
компенсация по Слуцкому относится к некоторому заданному набору,
например х°. Идея заключается в том, чтобы определить потребительский
выбор в ситуации, когда цены меняются произвольным образом, но доход
потребителя компенсируется так, чтобы стоимость набора х° оказалась
равной этому компенсированному доходу (см. рис. 2.4). Другими слова-

Глава 2. Продолжение теории потребителя
121
ми, при ценах р доход потребителя составит р • х°, а его выбор будет
определяться как х(р, р • х°).
>> Х\
Рис. 2.4. Компенсированный доход по Слуцкому
Зафиксируем р° »0, у0 >0 и положим х° = х(р°, у0). Тогда, если
р1 представляет собой любой другой вектор цен, а х1 = х(р', р1 х°), то из
WARP следует, что
р^х^р^х1. B-5)
Действительно, если х1 = х°, то B-5) выполняется как равенство. А если
х1 Ф х°, то, поскольку набор х1 выбирался, когда набор х° был доступен
(т.е. при ценах р1 и доходе р1 х°), согласно WARP набор х1 недоступен,
когда выбирается набор х°. Следовательно, неравенство в B-5) будет
строгим.
Заметим, что в силу сбалансированности бюджета
р1-х°=р,.х(р1,р,.х0). B-6)
Вычитая B-5) из B-6), получим, что для всех цен р1
(р,-р0).х0>(р1-р°).х(р1, p'V). B-7)
Поскольку B-7) выполняется для всех цен р1, то, положив р1 =p°+/z,
можно записать B-7) в виде
t[z-x°]>t[z-x(p\ p'-x0)], />0, zeR". B-8)
Разделив левую и правую части этого неравенства на />0 и произведя
замену р1 = р° + tz, получим

122
Часть L Экономические агенты
z-x°>z-x(p°+/z, (p°+/z)-x°). B-9)
Для фиксированного z мы можем выбрать такое достаточно малое
Т > О, что р° +/z » 0 для всех te [О, Т], поскольку р° » 0. Учитывая,
что B-9) выполняется как равенство при / = 0, из B-9) следует, что
функция /: [О, Т) —» R, определяемая правой частью B-9), т.е.
/@ = z-x(p°+/z, (p0+/z).x°),
достигает максимума на [0, 7") при / = 0. Тогда должно выполняться
(необходимое) условие (первого порядка) /'@)<0. Находя производную
f(t) и вычисляя ее в точке t = О (в предположении, что х()
дифференцируема), мы получаем
/<о) = Е2>,
dpj +Х+Р>У) ду
z;<0. B-10)
Поскольку ze R" было выбрано произвольно, B-10) показывает, что
матрица, Ц -й элемент которой равен
ЩЛ„&. у')Щ^1, B-М)
должна быть отрицательно полу определенной. Но это и есть матрица
Слуцкого, соответствующая функции выбора х(р, у)\
Таким образом, мы показали, что если функция выбора
удовлетворяет WARP и условию сбалансированности бюджета, то она должна
удовлетворять и двум другим свойствам, которые являются следствием
максимизации полезности, а именно однородности нулевой степени и
отрицательной полуопределенности матрицы Слуцкого.
Если бы помимо этого мы сумели показать, что матрица Слуцкого
для функции выбора симметрична, то по теореме о восстановлении
функция выбора действительно была бы функцией спроса, потому что тогда
мы могли бы построить порождающую ее функцию полезности.
Прежде чем развивать эту идею, стоит заметить, что если х(р, у)
была бы функцией спроса, порожденной максимизацией полезности, то
х(р, у) должна была бы удовлетворять WARP. Чтобы убедиться в этом,
предположим, что максимизирующий полезность потребитель имеет
монотонные и строго выпуклые предпочтения. Тогда, как нам известно, при
каждом наборе цен будет существовать единственный набор, на который
будет предъявляться спрос, и на этот набор будет полностью расходо-

Глава 2. Продолжение теории потребителя
123
ваться весь доход потребителя (см. упражнение 1.16). Пусть набор х°
максимизирует полезность при ценах р°, а набор х1 — при ценах р1, и
пусть р° • х1 < р° • х°. Набор х1 не выбирается, хотя и является доступным;
это значит, что w(x°)>w(x1). Соответственно, если х1 выбирается при
ценах р1, то это означает, что х° недоступен, или, другими словами,
р1 • х° > р1 • х1. Таким образом, из р° • х1 < р° • х° следует, что р1 х° > р1 • х1,
поэтому WARP выполняется.
Будет ли верным обратное утверждение? То есть если функция
выбора потребителя всегда удовлетворяет WARP, обязательно ли такое
поведение должно порождаться максимизацией полезности? Другими
словами, должна ли существовать функция полезности, которая в результате
максимизации приводит к тому выбору, который мы наблюдаем? Если
ответ положительный, то говорят, что функция полезности
рационализирует наблюдаемое поведение.
Оказывается, что ответ — и да, и нет. Если товаров всего два, то из
WARP следует, что всегда будет существовать функция полезности,
рационализирующая выбор; если число товаров превышает два, то, даже
если WARP выполняется, такая функция может не существовать.
Причина исключительности случая с двумя товарами связана с
симметричностью матрицы Слуцкого и с транзитивностью.
Оказывается, в случае с двумя товарами сбалансированность
бюджета вместе с однородностью означает, что матрица Слуцкого должна быть
симметричной (см. упражнение 2.9). Следовательно, поскольку из WARP
и сбалансированности бюджета следует однородность (как и
отрицательная полуопределенность), то в случае с двумя товарами WARP и
сбалансированность бюджета гарантируют симметричность матрицы Слуцкого,
а тогда по теореме о восстановлении функция выбора должна
порождаться функцией полезности.
Хотя и кажущееся иным, однако в конечном счете эквивалентное
объяснение этой исключительности случая с двумя товарами состоит в
том, что при попарном упорядочении наборов, подразумеваемом
концепцией выявленных предпочтений, не возникают нетранзитивных циклов.
(Доказать это вам предлагается в упражнении 2.9.) А если это так, то
будет существовать функция полезности, порождающая функцию выбора.
Поэтому, как мы упоминали выше, между симметричностью матрицы
Слуцкого и транзитивностью потребительских предпочтений существует
глубокая связь.
Если число товаров превышает два, то из WARP и
сбалансированности бюджета не следуют ни симметричность матрицы Слуцкого, ни
отсутствие нетранзитивных циклов для выявленных предпочтений. Следо-

124 Часть I. Экономические агенты
вательно, в ситуации с более чем двумя благами WARP и
сбалансированность бюджета не эквивалентны гипотезе максимизации полезности.
Это, естественно, приводит к вопросу: как усилить WARP таким
образом, чтобы получить теорию выявленных предпочтений,
эквивалентную теории максимизации полезности? Ответ кроется в сильной аксиоме
выявленных предпочтений.
Сильная аксиома выявленных предпочтений (strong axiom of
revealed preference, SARP) выполняется, если для каждой
последовательности различных наборов х°, х1, ...,х* таких, что х° предпочитается х1, х1
предпочитается х2,..., х* предпочитается х*, следует, что утверждение
о том, что х* предпочитается х°, неверно. SARP исключает
нетранзитивные выявленные предпочтения и поэтому может использоваться для того,
чтобы вывести полное и транзитивное отношение предпочтения ъ, для
которого будет существовать функция полезности, рационализирующая
наблюдаемое поведение потребителя. Мы опускаем доказательство этого
результата и отсылаем читателя к статьям Хаутаккера [Houthakker, 1950]
и Рихтера [Richter, 1966], содержащим соответственно базовое и более
изящное доказательства.
Легко видеть, что SARP следует из максимизации полезности. Теперь
мы также знаем, что из SARP следует существование
рационализирующей функции полезности, а значит, и симметричность матрицы Слуцкого.
Поэтому теория спроса, построенная только на базе SARP —
ограничении на наблюдаемый выбор, в сущности, эквивалентна теории спроса,
основанной на максимизации полезности. Как при гипотезе о
максимизации полезности, так и при выполнении SARP потребительский спрос
будет однородным, а матрица Слуцкого — отрицательно полуопределенной
и симметричной.
До сих пор мы анализировали аксиомы выявленных предпочтений и
функции потребительского выбора. По сути, мы действовали так, как
будто в нашем распоряжении был бесконечно большой набор данных о ценах
и объемах спроса. Для многих экономистов привлекательность теории
выявленных предпочтений изначально и была связана с потенциальной
возможностью получить на основе фактических данных
«подразумеваемую» функцию полезности потребителя, чтобы прогнозировать его
поведение. Но поскольку реальные массивы данных всегда конечны,
дальнейшее развитие теории выявленных предпочтений было направлено на
преодоление возникающих вследствие этого проблем.
С. Африат [Afriat, 1976] предложил обобщенную аксиому
выявленных предпочтений (generalized axiom of revealed preference, GARP),
несколько более слабое условие, чем SARP, и доказал аналог теоремы о
восстановлении (теоремы 2.6). Согласно теореме Африата конечное

Глава 2. Продолжение теории потребителя
125
множество наблюдений о ценах и объемах спроса удовлетворяет GARP
тогда и только тогда, когда существует локально ненасыщаемая,
непрерывная, возрастающая и вогнутая функция полезности, которая
рационализирует имеющиеся данные. Однако конечный массив данных не
определяет предпочтения потребителя вне элементов выборки, поэтому может
существовать много различных функций полезности,
рационализирующих сделанный этим потребителем выбор.
В отдельных случаях выявленные предпочтения позволяют нам
проводить некоторые сравнения в пределах выборки. Посмотрим, к примеру,
на рис. 2.5. Предположим, что потребитель выбрал х° при ценах р° и х1
при ценах р1. Легко заметить, что х° выявленно предпочитается х1.
Поэтому для любой функции полезности, рационализирующей эти данные,
должно по определению выполняться неравенство w(x°)>w(xi). Теперь
предположим, что мы хотим сравнить два набора, х и у, которые не
входят в нашу выборку. Поскольку набор у стоит дешевле х1 в ценах, при
которых потребитель выбирает х1, можно сделать вывод, что
м(х°) > и(\1) > и(у). Кроме того, если большее предпочитается меньшему,
функция полезности должна быть возрастающей, так что должно
выполняться соотношение w(x)>w(x°). В результате мы приходим к тому, что
и(х) > и(х°) > и(х1) > и(у) для любой возрастающей функции полезности,
которая рационализирует наблюдаемые данные, и поэтому можем
напрямую сравнить наши два не входящих в выборку набора, заключая, что
и(х) > и(у) для любой возрастающей функции полезности, которая могла
бы породить наблюдаемые данные.
х2
1 >*!
Рис. 2.5. Восстановление предпочтений, удовлетворяющих GARP

126
Часть I. Экономические агенты
Но такое сравнение сделать бывает не всегда просто. Для примера
предположим, что потребитель приобретает единственный набор
х1 = A, 1) при ценах р1 = B, 1). Функция полезности и(х) = х\х2
рационализирует наблюдаемый выбор, поскольку соответствующая кривая
безразличия, как легко проверить, касается в точке х1 бюджетного
ограничения 2х, + х2 - 3 . В то же время функция полезности v(x) = х{ (х2 +1) тоже
будет рационализировать выбор х1 при ценах р1, поскольку кривая
безразличия этой функции полезности, проходящая через точку х1, также
будет касаться в х1 этого бюджетного ограничения. Это не было бы
проблемой, будь и(х) и v(x) просто монотонными преобразованиями друг
друга, — но это не так. И когда мы сравниваем не входящие в выборку
наборы х = C, 1) и у = A, 7), в одном случае мы получаем, что
мC, 1) > мA, 7), т.е. потребитель предпочитает х, а в другом случае —
что vC, 1) < v(l, 7), т.е. потребитель предпочитает у.
Можем ли мы для данного набора у найти все такие наборы х, что
соотношение и{\) > и(у) выполняется для всех функций полезности,
рационализирующих массив данных? Частичное решение было предложено
Вэрианом [Varian, 1982]. Вэриан описал такое множество наборов, что
любой х из этого множества удовлетворяет условию и(\) > и(у) для
любой функции полезности w(), рационализирующей данные. Кноблаух
[Knoblauch, 1992] затем показал, что множество Вэриана является полным
решением, т.е. что оно содержит все такие наборы.
К сожалению, на реальных данных о потребительском поведении GARP
обычно не выполняется, и поэтому в настоящее время идет поиск критериев,
помогающих определить, когда можно игнорировать эти нарушения, а также
разрабатываются практические алгоритмы, которые позволяют строить
функции полезности по данным с небольшими нарушениями GARP.
2.4. Неопределенность
Вплоть до настоящего момента мы предполагали, что агенты
действуют в условиях абсолютной определенности: потребители знают цены всех
товаров и знают, что любой доступный набор товаров может
гарантированно быть получен. Очевидно, в реальном мире такие идеальные условия
выполняются не всегда. Многие экономические решения содержат элемент
неопределенности. Например, покупая автомобиль, потребитель должен
учитывать будущую цену бензина, расходы на ремонт и цену, по которой
он сможет через несколько лет автомобиль перепродать. Ничего этого в
момент принятия решения он с уверенностью не знает. В подобных реше-

Глава 2. Продолжение теории потребителя
127
ниях присутствует неопределенность относительно результатов сделанного
выбора. Хотя агент может знать вероятность возможных исходов,
окончательный исход остается неизвестным, пока он не реализуется.
Может показаться, что ситуации с неопределенностью недоступны
для экономического анализа, однако это не так. Аналитический подход к
неопределенности опирается на основополагающую статью фон Неймана
и Моргенштерна [von Neumann, Morgenstern, 1944].
2.4.1. Предпочтения
До сих пор предполагалось, что потребитель имеет предпочтения
относительно потребительских наборов х из потребительского
множества X. Чтобы учесть неопределенность, необходимо лишь немного
изменить точку зрения. Мы по-прежнему будем опираться на понятие
отношения предпочтения, но будем предполагать, что вместо
потребительских наборов потребитель сравнивает лотереи.
Формализуем это. Пусть А = {а{, ...,я„} обозначает конечное
множество исходов. Элемент я, может быть потребительским набором, суммой
денег (положительной или отрицательной) или вообще чем угодно.
Основная идея заключается в том, что а. сами по себе не связаны с
неопределенностью. В то же время мы воспользуемся множеством А как
основой для создания лотерей.
Например, пусть А - {1, -1}, где 1 — исход «выиграть один доллар»,
а -1 — исход «проиграть один доллар». Предположим, что вы играете со
своим другом в такую игру: если после подбрасывания правильной
(симметричной) монеты выпадает орел, друг платит вам один доллар, а если
решка — то один доллар платите вы ему. С вашей точки зрения, эта игра
приводит к одному из двух исходов, содержащихся в множестве А: 1
(выиграть доллар) и -1 (проиграть доллар), и каждый из них выпадает с
вероятностью 1/2, потому что монета симметрична.
В общем случае простая лотерея сопоставляет вероятность р}.
каждому исходу а. из множества^1. Конечно, поскольку pi являются
вероятностями, они должны быть неотрицательными, а поскольку лотерея
должна приводить к одному из исходов из множества А, то р1 в сумме
должны давать единицу. Обозначим эту простую лотерею как
(/7joa,, ...ypn°an). Определим множество простых лотерей (gs
следующим образом.
1 Обычно при определении простых лотерей не ограничиваются ситуацией, когда А —
конечное множество. Требуется, грубо говоря, чтобы в каждой лотерее с положительной
вероятностью могло реализоваться лишь конечное число исходов. — Примеч. ред.

128
Часть I. Экономические агенты
Определение 2.2. Простые лотереи.
Пусть А = {ах, ...,я„} является множеством исходов. Тогда (gs,
множество простых лотерей (на А), задается как
Если одна или несколько вероятностей pt равны нулю, то можно
исключить соответствующие компоненты. Например, простую лотерею
(а°я,, 0оа2,..., Ootfw p (l-a)oaw) можно записать как (осояр
(\-а)°ап). Заметим, что Qs содержит А, потому что для каждого / во
множестве (gs содержится лотерея A°я,), которая с единичной
вероятностью приводит к исходу ai. Чтобы еще больше упростить обозначения,
будем писать а. вместо A°я,) для лотереи, приводящей к исходу ai с
определенностью.
Возвращаясь к нашему примеру с подбрасыванием монеты, где
А = {1, -1}, каждый из агентов тогда сталкивается с простой лотереей
(\ 1 ^
— ol, —о—1 I. Конечно, не все лотереи являются простыми. Например, в
v2 2 J
некоторых лотереях в качестве выигрыша часто выдаются билеты
следующей лотереи! Лотереи, в которых исходы сами являются лотереями,
называются сложными лотереями.
Заметим, что у сложной лотереи не существует предела усложнения.
Экстремальным случаем является как раз предыдущий пример, поскольку
каждый лотерейный билет в качестве выигрыша может принести другой
лотерейный билет, количество уровней вложенности может быть
бесконечным. То есть если продолжать выигрывать лотерейные билеты, то для
реализации исхода первоначального лотерейного билета может
потребоваться произвольное число розыгрышей.
Для простоты мы исключим бесконечно вложенные сложные лотереи
и будем рассматривать только такие сложные лотереи, которые приводят
к одному из исходов из множества А после конечного числа шагов.
Пусть тогда (д обозначает множество всех лотерей, как простых, так
и сложных. Хотя множеству сложных лотерей, а соответственно и (д,
можно дать более формальное описание, для наших целей этого не
требуется. Лотерея может рассматриваться просто как лотерейный билет, по
которому можно выиграть один из нескольких других (возможно, самых
разнообразных) лотерейных билетов, и так далее. Но, в конце концов,
после того как сыграно конечное число лотерей, должен наступить один из

Глава 2. Продолжение теории потребителя
129
исходов из множества А. То есть если g является произвольной
лотереей из (д , то g = {рх о g1,..., рк о gk) для некоторого к > 1 и некоторых
лотерей g' e (д, где g' могут быть сложными лотереями, простыми
лотереями или исходами. Конечно, pi должны быть неотрицательными и в
сумме давать единицу1.
Объектами выбора в условиях неопределенности являются лотереи.
Аналогично теории потребителя, мы будем предполагать, что агент имеет
предпочтения ь на множестве лотерей (д . Далее мы сформулируем
набор аксиом, которые называются аксиомами потребительского выбора
в условиях неопределенности, для отношения предпочтения этого
агента. Как и ранее, ~ и >- обозначают отношения безразличия и строгого
предпочтения, порождаемые отношением >=. Первые несколько аксиом
будут хорошо нам знакомы и поэтому не потребуют дополнительных
комментариев.
Аксиома G1. Полнота. Для любых двух лотерей g и g из (д либо
g^g\ либо g'bg.
Аксиома G2. Транзитивность. Для любых трех лотерей g, g' и
g" из §, если gbg и g')z g", то gb g".
Поскольку каждый исход я, из множества А представлен в (д как
вырожденная лотерея, аксиомы G1 и G2, в частности, означают, что
конечное число элементов А упорядочивается с помощью ь (см.
упражнение 2.14). Поэтому предположим без ограничения общности, что
элементы А проранжированы таким образом, что ах >=аг ъ ...ъап.
Представляется разумным, что наилучшей лотереей является та,
которая гарантированно дает ах, а наихудшей — та, что гарантированно
дает ап (хотя мы не предполагаем этого явно). То есть для любой лотереи
g вполне оправданно утверждение о том, что (а о а,, {\-а)°ап)ъ g при
а = 1 и gh(a°ax, (l-a)°an) при а = 0. Следующая аксиома
утверждает, что если отношение безразличия не имеет места при крайних
значениях а (т.е. при а = 0 или а = 1), то оно должно выполняться для
некоторого промежуточного значения а.
1 Чтобы получить формальное определение (д , нужно действовать следующим образом.
Положим (д0 = А и для каждого j = 1,2, ... пусть Q. = {(/?, о g1, ..., pk о gk) | k > 1; pi> О
к
и g' е G_, V/ = 1, ...,*; и Ypi = 1}. Тогда $=п§

130
Часть I. Экономические агенты
Аксиома G3. Непрерывность. Для любой лотереи g из (д
существует некоторая вероятность осе[0, 1] такая, что
g~(ocoap (l-oc)oaj.
Следствия из аксиомы G3 на первый взгляд могут показаться
странными. Например, предположим, что А = {1000 долл., 10 долл., «смерть»}.
Для большинства из нас эти исходы строго упорядочены следующим
образом: 1000 долл. У 10 долл. У смерть. Рассмотрим простую лотерею,
которая гарантированно приносит 10 долл. Согласно G3 должна
существовать такая вероятность а, которая делает лотереи (ос© 1000 долл.,
A-ос)° «смерть»} и 10 долл. одинаково привлекательными. А если не
существует такой а, при которой вы бы сочли гарантированные 10 долл.
и лотерею (а© 1000 долл., A-а)о «смерть»} одинаково
привлекательными, то ваши предпочтения на лотереях не удовлетворяют G3.
Не является ли тогда аксиома G3 излишне строгим ограничением на
возможные предпочтения? Не стоит спешить с выводами. Если бы вы
согласились проехать по городу за 1000 долл. — действие, с которым
связана некоторая положительная, хоть и мизерная, вероятность погибнуть, —
вместо того, чтобы остаться дома за 10 долл., вы бы с уверенностью
предпочли некоторую лотерею рассматриваемого типа данной небольшой
сумме денег. Предположим, что мы увеличивали бы вероятность аварии
со смертельным исходом до тех пор, пока эти два варианта не стали бы
для вас в точности эквивалентными. В этот момент мы найдем ту самую
вероятность, существование которой предполагается в G3.
Следующая аксиома формализует идею о том, что если каждая из
двух простых лотерей потенциально приводит только к наилучшему и
наихудшему исходам, то предпочтительной является та из них, которая
приводит к наилучшему исходу с более высокой вероятностью.
Аксиома G4. Монотонность. Для всех вероятностей ос,Cе[0,1]
(осоя,, A-ос)оа„)^(рояр (l-p)oaj
тогда и только тогда, когда ос > C.
Заметим, что из монотонности следует, что я, >¦ ап, и поэтому
исключается тот случай, когда все исходы из множества А для агента
эквивалентны.
Большинство людей обычно предпочитает лотереи, приводящие к
лучшим исходам с более высокой вероятностью, как того требует
аксиома монотонности, однако это не всегда верно. Например, для любителя
сафари гибель может быть наихудшим результатом охоты, но возмож-

Глава 2. Продолжение теории потребителя
131
ность погибнуть увеличивает удовольствие от нее. Охота с небольшой
вероятностью гибели будет предпочитаться охоте с нулевой
вероятностью гибели, что представляет собой явное нарушение монотонности.
Следующая аксиома утверждает, что две лотереи эквивалентны для
агента, если для него эквивалентны их исходы и эти исходы реализуются
с одинаковыми вероятностями.
Аксиома G5. Замещение. Если g = (Pi°g\ ---,pk°gk) и
h = (ploh\ ...,pkohk) принадлежат (д и К ~gl для каждого i, то
h~g.
Вместе с G1 аксиома G5 означает, что если две лотереи для агента
эквивалентны, то для него эквивалентны и все их выпуклые комбинации. То
есть если g ~ h, то поскольку по Gl g ~ g, из аксиомы G5 следует, что
(ccog, (l-a)oA)~(aog,(l-oc)og) = g.
Наша следующая и последняя аксиома говорит, что, рассматривая
конкретную лотерею, агент заботится только об эффективных
вероятностях, сопоставляемых каждому исходу из множества А. Это утверждение
заслуживает некоторого обсуждения.
Например, предположим, что А = {ах, а2}. Рассмотрим сложную
лотерею, которая с вероятностью а приводит к исходу ах,ас вероятностью
1 - а дает лотерейный билет, который сам по себе является простой
лотереей и приводит к исходу ах с вероятностью Р и к исходу а2 с
вероятностью 1-р.
Тогда какова эффективная вероятность исхода ах ? Исход ах может
возникнуть двумя взаимоисключающими способами: непосредственно как
результат реализации первого исхода из множества А = {ах,а2} и
опосредованно как результат реализации второго исхода — лотерейного билета.
Вероятность получить ах первым путем, очевидно, равна a. Вероятность
получить его вторым путем равна A - а)C, поскольку, чтобы прийти к
нему через лотерейный билет, ах должен быть результатом этого
лотерейного билета, но не должен быть непосредственным итогом сложной лотереи.
Таким образом, вероятность исхода ах равна a + A - a)p. Аналогично
эффективная вероятность исхода а2 составляет A — а)A — Р).
Утверждение о том, что в сложной лотерее агента интересуют только
эффективные вероятности исходов ап равносильно утверждению, что
сложная лотерея и порождаемая ею простая лотерея (a + (l-a)f3oa,,
A - a)(l - Р) о а2) для агента эквивалентны.

132
Часть I. Экономические агенты
Ясно, что аналогичным образом можно вывести (единственные)
эффективные вероятности исходов ап порожденные любой сложной
лотереей. Мы не будем подробно описывать эту процедуру, но по крайней
мере концептуально она очевидна.
Пусть рх обозначает эффективные вероятности исходов я, в лотерее
geQ. Тогда говорят, что g порождает простую лотерею
{рхоах, ...,рп°ап)е:(д5. Подчеркнем, что каждая лотерея g e (д
порождает единственную простую лотерею. Тогда наша последняя аксиома
формулируется так1.
Аксиома G6. Сведение к простым лотереям. Если для любой лоте-
реи ge(g О?!0*?,, ...,рп°ап) является простой лотереей, порожденной
g,mo (до а„ ...,/?„ otfJ~g.
Заметим, что по G6 (и транзитивности G2) предпочтения индивида на
всех лотереях — сложных или простых — полностью определяются его
предпочтениями на простых лотереях.
Сколь разумной ни казалась бы нам аксиома G6, она все же
ограничивает сферу нашего анализа. В частности, она не подходит для
моделирования поведения отдыхающих в Лас-Вегасе. Для них есть разница
между игрой на различных автоматах и участием в одной-единственной
лотерее, определяемой эффективными вероятностями выигрыша и
проигрыша. Вместе с тем большое число решений в условиях
неопределенности принимаются за пределами Лас-Вегаса, и для многих из них
аксиома G6 вполне уместна.
2А.2. Функция полезности фон Неймана — Моргенштерна
Сформулировав аксиомы, которым должны подчиняться
предпочтения на лотереях, мы снова зададим вопрос о том, можно ли представить
эти предпочтения с помощью непрерывной вещественнозначной
функции. Ответ на него положительный, что не должно вызывать удивления.
Из свойств предпочтений в условиях определенности нам известно, что
аксиом Gl, G2 и некоторого предположения о непрерывности должно
быть достаточно, чтобы гарантировать существование непрерывной
функции, представляющей предпочтения ь. Вместе с тем помимо Gl, G2
и непрерывности мы делали и другие предположения, поэтому можно
попытаться получить функцию полезности, которая будет не просто
непрерывной. Действительно, мы покажем, что существует не только не-
1 В некоторых изложениях аксиомы G5 и G6 объединяются в аксиому «независимости»,
(см. упражнение 2.18).

Глава 2. Продолжение теории потребителя
133
прерывная функция полезности, представляющая ь на (д , но и функция,
которая будет линейной по эффективным вероятностям исходов.
Для большей определенности предположим, что и: (д —> Ж является
функцией полезности, представляющей >= на (д \ Тогда для любой ge (д
u(g) — это значение полезности, соответствующее данной лотерее.
В частности, каждому i функция и сопоставляет число м(я;), причем
исход ai может рассматриваться как вырожденная лотерея A°я,), которая
дает этот исход с определенностью. Число и(а{) мы часто будем
называть просто полезностью исхода аг Теперь мы готовы сформулировать
свойство линейности, упомянутое выше.
Определение 2.3. Свойство ожидаемой полезности.
Функция полезности и\(д —> R обладает свойством ожидаемой
полезности, если для любой лотереи geQ
п
где {рхоах, ...,рпоап) является простой лотереей, порожденной g.
Таким образом, наличие у функции и свойства ожидаемой
полезности означает, что она сопоставляет каждой лотерее ожидаемое значение
полезностеи, к которым эта лотерея может привести, причем для каждой
такой полезности приписывается эффективная вероятность ее
получения2. Очевидно, эффективная вероятность того, что лотерея g принесет
полезность и(я,), равна pt — эффективной вероятности того, что она
приведет к исходу at.
Заметим, что если и обладает свойством ожидаемой полезности и
8*-(Р\°а\9 '•">Рп°ап) является простой лотереей, то, поскольку gs
порождена самой gs, должно иметь место равенство
1 Функция и() представляет предпочтения у, если g> g тогда и только тогда, когда
u(g)>u(g') (см. определение 1.5).
2 Ожидаемое значение функции jc , принимающей значения х{, ...,*„ с вероятностями
/?,, ...,/?„ соответственно, по определению равно ^/?,*,. Здесь величины u{at) играют
роль Xt, так что мы рассматриваем ожидаемое значение полезности.

134
Часть I. Экономические агенты
и(рх°ах, ..., рп о ап) = ? /?.м(я.) V векторов вероятности (рх, ...9р„).
Следовательно, функция и полностью определена на всем (д теми
значениями, которые она принимает на конечном множестве исходов А.
Если предпочтения индивида представимы функцией полезности,
обладающей свойством ожидаемой полезности, и если этот индивид всегда
выбирает наиболее предпочитаемую из имеющихся альтернатив, то он
отдаст предпочтение одной лотерее перед другой тогда и только тогда,
когда ожидаемая полезность одной превосходит ожидаемую полезность
другой. Следовательно, такой индивид, осуществляя выбор среди
лотерей, максимизирует ожидаемую полезность.
Любая подобная функция будет иметь некоторые очевидные
аналитические преимущества, потому что полезность любой лотереи можно
будет выразить как линейную сумму, в которую входят только
полезности исходов и соответствующие им вероятности. Вместе с тем свойство
ожидаемой полезности предполагает достаточно сильные требования к
функции, представляющей ь, которые отличаются от требований к
обычным функциям полезности в условиях определенности. Чтобы не
забыть о важных различиях между этими двумя классами функций, будем
называть функции полезности, обладающие свойством ожидаемой
полезности, функциями полезности фон Неймана — Моргенштерна (von
Neumann—Morgenstern utility functions, VNM).
Приведем фундаментальную теорему теории выбора в условиях
неопределенности.
Теорема 2.7. Существование функции полезности фон
Неймана — Моргенштерна на (д .
Пусть предпочтения >z на лотереях из (д удовлетворяют
аксиомам Gl—G6. Тогда существует такая функция полезности
и: (д —» Ш, представляющая эти ^ на (д , которая обладает свойством
ожидаемой полезности.
Доказательство. Аналогично доказательству существования
функции полезности, представляющей предпочтения потребителя,
приведенному в главе 1, доказательство этой теоремы будет конструктивным.
Рассмотрим произвольную лотерею g из множества (д . Определим
u(g) как число, удовлетворяющее условию
g~(u(g)oa{, (l-u(g))oan).
По аксиоме G3 такое число должно существовать, и в
упражнении 2.17 вам предлагается показать, что в соответствии с G4 это число

Глава 2. Продолжение теории потребителя
135
единственно. Тем самым определяется вещественнозначная функция и
на (д . (Кстати, по определению, u(g) e [О, 1] для всех g.)
Остается показать, что и представляет ъ и обладает свойством
ожидаемой полезности. Начнем с первого утверждения.
Рассмотрим произвольные лотереи g,g'e(g. Мы утверждаем, что
верно следующее:
g*g (P-1)
тогда и только тогда, когда
(t/(g)ofl„ (l-M(g))oa„)^(M(g>a„ {\-u{g'))oan) (P-2)
тогда и только тогда, когда
u(g)>u(g'). (Р-3)
Чтобы убедиться в этом, заметим, что (Р-1) эквивалентно (Р-2),
поскольку * транзитивно, g~(w(g)°a„ (l-w(g))°a„), g'~("(g')°ap
(l-u(g'))oan), и оба эти соотношения следуют из определения и . Кроме
того, эквивалентность (Р-2) и (Р-3) напрямую следует из монотонности
(аксиома G4).
Следовательно, g >= g тогда и только тогда, когда u{g) > u(g'), так
что и представляет ^на§.
Для завершения доказательства необходимо показать, что и обладает
свойством ожидаемой полезности. Пусть g e (д — произвольная лотерея
и gs ={px °tfp .--,р„ °ап)е (д$ — порождаемая ею простая лотерея.
Требуется показать, что
п
/=1
Поскольку согласно G6 g ~ gs и поскольку и представляет ь, должно
выполняться равенство u(g) = u(gs). Поэтому достаточно показать, что
«(*,)=5>м*,). (р-4>
Для каждого / = 1,...,п u{at) по определению удовлетворяет условию
а,.~(М(а,.)оа„ {\-„(а,))оав). (Р-5)
Обозначим через q' простую лотерею в правой части (Р-5),
ql = (u(ai)°a{, A -u{ai))°ап) для каждого / = 1,...,п. Следовательно,
ql ~ а. для каждого /, и по аксиоме о замещении (G5)

136
Часть I. Экономические агенты
g' = (pl°q\...,pnoqn)~(ploal9...,pnoa„) = gs. (P-6)
Теперь мы хотим найти простую лотерею, порожденную сложной
лотереей g'. Заметим, что так как каждое q' может привести только к
одному из двух исходов — ах или ап, то g тоже должна приводить к
одному из этих двух исходов. Какова эффективная вероятность наступления
исхода ах, согласно лотерее g ? Исход ах реализуется, если для любого
/ случится ql (с вероятностью /?,), и ах будет исходом лотереи ql (с
вероятностью */(#,)). Поэтому для каждого /' вероятность исхода ах равна
/7,1/@,-). Поскольку исходы лотереи q' взаимно исключают друг друга,
п
эффективная вероятность исхода ах равна сумме ^p/w(^/). Аналогично,
п
эффективная вероятность исхода ап равна ^# 0-«(#,•))> или
п
1-^Р/И(я;), поскольку pi в сумме дают единицу. Тогда простая лоте-
рея, порожденная g\ будет такой:
Ss =
( " ^ ( " ^
\i=\ J V /=1 )
°a„
По аксиоме G6 о сведении к простым лотереям должно выполняться
соотношение g ~ gs. Но транзитивность - и (Р-6) означают, что
gs =
((» \
2^pMai) hi.
^V /=i J
( л >
i-5>,«(«,)
V /=i )
\
oa„
J
(P-7)
Однако по определению (и в соответствии с результатом, полученным в
упражнении 2.17) u(gs) — единственное число, удовлетворяющее
соотношению
g,~(u(g,)°ai> (!-«(&))«>«.). (Р-8)
Поэтому, сравнивая (Р-7) и (Р-8), мы приходим к равенству
п
u(gs) = T,PMai)>
1=1
что и требовалось доказать. ¦
Внимательный читатель мог заметить, что в доказательстве
теоремы 2.7 аксиома G1 не использовалась. Действительно, в присутствии дру-

Глава 2. Продолжение теории потребителя
137
гих аксиом она является избыточной. В упражнении 2.20 вам
предлагается показать, что G1 следует из аксиом G2, G3 и G4, и поэтому мы могли
бы вообще не упоминать здесь свойство полноты в явном виде. В то же
время предположение о транзитивности предпочтений без
предположения о полноте привело бы к появлению у читателя излишних вопросов.
Чтобы избавить вас от этого, мы выбрали представленный здесь подход.
Вывод из теоремы 2.7 таков: если предпочтения индивида на лотереях
удовлетворяют аксиомам Gl—G6, то существуют значения полезностей,
которые могут быть приписаны исходам из множества А таким образом,
что индивид предпочтет одну лотерею другой тогда и только тогда, когда
ожидаемая полезность первой больше ожидаемой полезности второй.
Доказательство теоремы 2.7 не только устанавливает существование
функции полезности, обладающей свойством ожидаемой полезности, но и
демонстрирует шаги, которые необходимо предпринять для построения
такой функции на практике. Чтобы определить полезность любого исхода
а{, необходимо только спросить у индивида, какой будет вероятность
наступления наилучшего исхода, при которой лотерея из наилучшего и
наихудшего исходов (аоа19 A-а)°я„) окажется для него эквивалентной
гарантированному исходу я.. Повторяя этот шаг для каждого исхода ai; е А,
мы можем рассчитать полезность, соответствующую каждой лотерее
g e (д , просто как ее ожидаемую полезность. И если предпочтения
индивида удовлетворяют аксиомам Gl—G6, теорема 2.7 гарантирует, что
полученная таким образом функция полезности представляет эти предпочтения.
Пример 2.4. Предположим, что А- {10 долл., 4 долл. -2 долл.},
где каждое из чисел обозначает тысячи долларов. Разумно предположить,
что наилучшим исходом является 10 долл., а наихудшим -2 долл.
Чтобы построить функцию полезности фон Неймана — Моргенш-
терна, использованную в доказательстве теоремы 2.7, нам сначала
необходимо найти вероятности, которые порождают лотереи указанного выше
вида, эквивалентные каждому из трех исходов. Для этого мы образуем
лотереи из наилучшего и наихудшего исходов, в которых 10 долл. и -2 долл.
выпадают с неизвестными пока еще вероятностями, в сумме дающими
единицу. Затем относительно каждого из трех исходов индивиду задается
вопрос: «При какой вероятности наилучшего исхода построенная таким
образом лотерея будет эквивалентна гарантированному исходу я,?»
Полученные ответы станут теми значениями полезности, которые мы ставим
в соответствие каждому из трех рассматриваемых исходов.
Предположим, что мы приходим к следующим результатам:
10 долл.- A о Ю долл., 0о -2 долл.), мA0 долл.) =1, (Е-1)

138
Часть I. Экономические агенты
4 долл.- @,6о 10 долл., 0,4о -2 долл.), мD долл.) = 0,6, (Е-2)
-2 долл. ~ @ о 10 долл., 1 о -2 долл.), и{-2 долл.) = 0. (Е-3)
Обратите внимание, что при таком отображении полезность наилучшего
исхода всегда должна быть равна 1, а полезность наихудшего — 0. Однако
полезность, соответствующая промежуточным исходам, таким, как 4 долл.,
в этом примере, будет зависеть от отношения индивида к риску.
Получив значения полезности для каждого из трех возможных
исходов, мы теперь располагаем информацией, необходимой для
ранжирования всех лотерей, включающих эти исходы. Рассмотрим, например,
gx = @,2 о 4 долл., 0,8 о 10 долл.), (Е-4)
g2 =@,07 о -2 долл., 0,03 о 4 долл., 0,9 о 10 долл.). (Е-5)
Какую из этих лотерей индивид предпочтет? Предполагая, что его
предпочтения на лотереях удовлетворяют аксиомам Gl—G6, мы можем
обратиться к теореме 2.7. Она утверждает, что для ответа на этот вопрос нам
достаточно вычислить ожидаемую полезность каждой из лотерей,
используя значения, полученные в (Е-1)—(Е-3). Найдем ее:
u(gx) = 0,2wD долл.) + 0,8иA0 долл.) = 0,92,
u{g2) = 0,07w(-2 долл.) + 0,03wD долл.) + 0,9и(\ 0 долл.) = 0,918.
Поскольку лотерея gl дает большую ожидаемую полезность, она и будет
выбрана индивидом с такими предпочтениями на лотереях. Аналогичным
образом, используя только значения полезности из (Е-1)—(Е-3), мы
можем проранжировать любые из бесконечного числа лотерей, которые
можно построить на основе трех исходов из множества А.
Обдумайте то, что мы узнали из этого примера. Взгляните еще раз на
ответ, полученный при сравнении гарантированных 4 долл. и лотереи
(Е-2). Предлагаемая лотерея g приносит ожидаемый выигрыш
E(g) = @,6)A0 долл.) + @,4)(-2 долл.) = 5,2 долл. Это превосходит
ожидаемый выигрыш 4 долл., который дает простая лотерея с
гарантированным выигрышем в 4 долл., и при этом две лотереи эквивалентны.
Поскольку предполагается монотонность предпочтений, мы немедленно приходим
к выводу о том, что для индивида, чьи предпочтения мы анализируем,
гарантированные 4 долл. будут строго предпочитаться любой лотерее из
наилучшего и наихудшего исходов, в которой нам лучший исход выпадает с
вероятностью ниже 0,6. Сюда, конечно, входит и лотерея, в которой
10 долл. и -2 долл. выпадают с одинаковыми вероятностями 0,5, хотя
ожидаемый выигрыш по ней тот же, что и по лотерее с гарантированным вы-

Глава 2. Продолжение теории потребителя
139
игрышем в 4 долл. Таким образом, в некотором смысле потребитель
предпочитает избегать риска. Такое отношение к риску отражается и на
ранжировании лотерей gj и g2 в (Е-4) и (Е-5): лотерея gx предпочитается g2,
хотя ожидаемый выигрыш от первой, E(gx) = 8,80 долл., меньше, чем от
второй, ?'(g2) = 8,98 долл. Индивид избегает участия в лотерее g2 при
возможном выборе между gx и g2, поскольку в отличие от gx в ней
слишком велик риск худшего исхода. Далее мы поговорим о несклонности к
риску и ее измерении в более строгих терминах, но этот пример позволяет
увидеть, что функция полезности фон Неймана — Моргенштерна
суммирует важные аспекты, касающиеся отношения индивида к риску. ?
Вернемся на минуту на шаг назад, чтобы посмотреть, как на самом
деле работает функция полезности фон Неймана — Моргенштерна и как
она соотносится с обычной функцией полезности в условиях
определенности. В стандартном случае, если два товарных набора для потребителя
эквивалентны, то им соответствует одно и то же значение полезности, а
если один предпочитается другому, то для первого значение полезности
должно быть больше. Это верно и для функции полезности фон
Неймана — Моргенштерна u(g), хотя термин «товарный набор» следует
заменить термином «лотерея».
Однако в теории потребителя сами по себе значения полезности лишь
ранжируют потребительские наборы. Любое строго монотонное
преобразование функции полезности даст другую функцию полезности,
представляющую те же предпочтения. Значения полезности, соответствующие
представлению предпочтений на лотереях в виде функции
фон Неймана — Моргенштерна, напротив, имеют и другое содержание.
Чтобы увидеть это, предположим, что А = {а,Ь,с}, где а>-Ъ>с, и
что предпочтения ь удовлетворяют аксиомам Gl—G6. По G3 и G4,
существует осе @, 1), удовлетворяющее условию
b~(aoa, (l-cc)oc).
Заметим, что вероятность ос отражает предпочтения индивида и
определяется ими. Эта вероятность имеет значение и сама по себе. Ее нельзя
удвоить, прибавить к ней константу или преобразовать ее любым
способом, не изменив при этом предпочтения, с которыми она связана.
Теперь пусть и представляет ъ в виде функции фон Неймана —
Моргенштерна. Тогда предыдущее отношение безразличия означает, что
и(Ь) = и(аоа, A-ос)ос) =
= аи(а) + A-а)и(с),

140
Часть I. Экономические агенты
где второе равенство следует из свойства ожидаемой полезности
(функции и). Но его можно преобразовать к виду
и{а)-и{Ь) __ 1-ос
u(b)-u(c) a
Следовательно, отношение разностей между значениями полезностей
однозначно определяется а. Но поскольку а сама единственным
образом определяется предпочтениями индивида, то это же верно и для
отношения разностей.
Мы приходим к выводу, что отношение разностей полезностей имеет
особый смысл, определяемый предпочтениями индивида, и что оно должно
принимать одно и то же значение для каждой функции фон Неймана —
Моргенштерна, представляющей предпочтения ь. Таким образом,
представление предпочтений функцией полезности фон Неймана —
Моргенштерна дает нам не только порядковую информацию о предпочтениях,
потому что иначе в результате соответствующих монотонных
преобразований отношение разностей могло бы принимать различные значения.
Тогда очевидно, что строго возрастающее преобразование функции
фон Неймана — Моргенштерна может не дать другую функцию
фон Неймана — Моргенштерна. (Конечно, это будет функция
полезности, представляющая предпочтения, но у нее не обязательно будет
свойство ожидаемой полезности.) Поэтому возникает вопрос: какой класс
функций полезности фон Неймана — Моргенштерна представляет
данные предпочтения? Из вышеприведенных рассуждений следует, что
каждая из этих функций должна сохранять отношение разностей между
значениями полезностей. Как показывает следующая теорема, это свойство
полностью характеризует данный класс функций.
Теорема 2.8. Единственность функций фон Неймана —
Моргенштерна с точностью до положительных аффинных преобразований.
Предположим, что функция полезности фон Неймана —
Моргенштерна и() представляет предпочтения Ь. Тогда функция
полезности фон Неймана — Моргенштерна v() представляет те же самые
предпочтения тогда и только тогда, когда для некоторого числа а и
некоторого числа р > 0
v(g) = cc + pw(g)
для всех лотерей g.
Доказательство. Достаточность очевидна (убедитесь в этом
самостоятельно), поэтому здесь мы докажем только необходимость. Более
того, мы предположим, что g является простой лотереей. Вам останется

Глава 2. Продолжение теории потребителя
141
показать, что если и и v связаны линейным преобразованием на
множестве всех простых лотерей, то они линейно связаны и на множестве всех
лотерей. Как и ранее, будем рассматривать
А = {а19 ...,я„} ng = {pxoav p2°a2, ...,р„оап),
где я, Ь ... У ап и ах У ап.
Поскольку и() представляет предпочтения ^, выполняются
неравенства u(al)>...>u(ai)>...>u(an) и и{ах) > и{ап). Тогда для каждого
/ = 1, ..., п существует единственное ос; е [0,1], такое, что
«(fl/) = a/w(aI) + (l-a/)i/(?ill). (Р-1)
Заметим, что ос, > 0 тогда и только тогда, когда я, >- ап.
Так как и() обладает свойством ожидаемой полезности, из (Р-1)
следует, что
u(ai) = u(aioal, (l-a;)oaJ,
а поскольку и() представляет у, это означает, что
я,.~(а,одр A-а,)оа„). (P-2)
Функция v() тоже представляет У, поэтому должно выполняться
равенство
v(fl/) = v(a/o?i1,(l-al.)oflJ.
Кроме того, v(-) обладает свойством ожидаемой полезности, поэтому
v(ai) = aiv(al) + (l-aiM<*n)- (P-3)
Вместе (Р-1) и (Р-3) означают, что
цЦ )-!/(<!,) = !-<*/ = v^-v^,) .р4)
и(а,)-и{ап) a, у(я,)-у(я„)
для каждого / = 1, ...,« такого, что а. У ап (т.е. такого, что ос, > 0).
Из (Р-4) можно заключить, что
(u(al)-u(aMM)-^„)) = (v(a{)-v(ai))(u(ai)-u(a„)) (P-5)
при ai У ап. Однако (Р-5) выполняется даже при at ~ ап, потому что в
этом случае и{а^-и{ап) и v(aj) = v(an). Следовательно, (Р-5)
выполняется для всех /' = 1, ...,«.

142
Часть I. Экономические агенты
После преобразований (Р-5) можно записать в виде
v(a/.) = a + Pw(a/) для всех / = 1, ...,и, (Р-6)
где
a_u{ax)v{an)-v{ax)u{an) ^ v(ax)-v(an)
и(ах)-и(ап) и(ах)-и(ап)'
Заметим, что а и Р являются константами (т.е. не зависят от /) и что Р
положительное число.
Поэтому для любой лотереи g, если (рх°ах, ...,/?„ о#J — простая
лотерея, порожденная g,
п
v(g) = SAv(fl/) =
1=1
= 2>,(а+ри(*,)) =
п
= а + р]Г/?,и(я,.) =
= a + pw(g),
где первое и последнее равенства следуют из того, что и() и v() обладают
свойством ожидаемой полезности, а второе равенство следует из (Р-6). ¦
Прежде чем сформулировать теорему 2.8, мы утверждали, что класс
представлений одного и того же отношения предпочтения в виде
функции полезности фон Неймана — Моргенштерна характеризуется
постоянством отношения разности значений полезностей. Это следствие
теоремы 2.8, что вам и предлагается показать в упражнении.
Согласно теореме 2.8 мы можем найти бесконечное число функций
фон Неймана — Моргенштерна, которые будут ранжировать лотереи
одним и тем же образом и при этом будут обладать свойством ожидаемой
полезности. Но в отличие от обычных функций полезности, от которых
требуется сохраняющее ранжирование наборов численное
масштабирование, здесь, если мы хотим сохранить свойство ожидаемой полезности,
мы должны ограничиться преобразованиями, при которых функция
умножается на положительное число и(или) к ней прибавляется константа.
Тем не менее не следует придавать излишнего значения абсолютной
величине полезности от лотерей или разности между полезностями от двух
лотерей. При столь слабых ограничениях на попарные сравнения лотерей
функцию полезности фон Неймана — Моргенштерна нельзя использовать

Глава 2. Продолжение теории потребителя
143
для сравнения благосостояния разных индивидов или для измерения
«интенсивности» предпочтения одной лотереи другой.
2.4.3. Несклонность к риску
В примере 2.4 мы утверждали, что построенная там функция
полезности фон Неймана — Моргенштерна отражает известное желание
избежать риска. Теперь мы готовы определить и описать несклонность к
риску более формально. Для этого ограничимся рассмотрением лотерей,
исходами которых являются различные уровни богатства. Кроме того,
удобнее взять в качестве множества исходов А все неотрицательные
уровни богатства, т.е. А = R+. Хотя множество исходов теперь содержит
бесконечно много элементов, мы будем рассматривать лотереи, в которых
положительная вероятность соответствует только конечному числу
исходов. Таким образом, простая лотерея принимает вид (/?, °и>р ...,/?„ ° w„),
где п — некоторое целое положительное число, wf — неотрицательные
уровни богатства, а неотрицательные вероятности /?,,...,/?„ в сумме
дают единицу1. Наконец, предположим, что функция полезности
фон Неймана — Моргенштерна индивида и() дифференцируема, причем
u\w) > О для всех уровней богатства w.
Исследуем связь между свойствами функции полезности фон
Неймана — Моргенштерна и отношением агента к риску. Ожидаемый
выигрыш от простой лотереи g, в соответствии с которой сумму денег wt
п
можно получить с вероятностью р(, равен E(g) = ^Р№ • Предположим,
что агенту предоставлен выбор между участием в лотерее g и
гарантированным получением ожидаемого выигрыша от g. Если и() — функция
полезности фон Неймана — Моргенштерна для данного агента, то эти две
альтернативы можно оценить следующим образом:
п
u(E(g)) = uу?р№ V
V /=i J
В рамках этих предпосылок можно доказать теорему о существовании ожидаемой
полезности аналогично тому, как была доказана теорема 2.7, модифицировав аксиомы так,
чтобы отразить тот факт, что множество А не является конечным.

144
Часть I. Экономические агенты
Первое из этих выражений — полезность фон Неймана — Моргенштерна
от лотереи, а второе — полезность фон Неймана — Моргенштерна от
ожидаемого выигрыша лотереи. Нам известно, что если предпочтения
удовлетворяют аксиомам Gl—G6, то агент предпочтет альтернативу с
более высоким уровнем ожидаемой полезности. Будем называть
несклонным к риску индивида, который предпочитает гарантированное
получение ожидаемого выигрыша от лотереи риску участия в ней. Конечно, риск
может вообще не волновать людей или даже быть для них
привлекательным, но их предпочтения будут по-прежнему удовлетворять
аксиомам Gl—G6. Далее мы перечислим все возможные варианты отношения
к риску и строго определим соответствующие понятия.
Как отмечалось в комментариях к определению 2.3, функция
полезности фон Неймана — Моргенштерна на (д полностью определяется
своими значениями на множестве исходов А. Следовательно,
характеристика функции фон Неймана — Моргенштерна для индивида на
множестве простых лотерей обеспечивает полное описание предпочтений
индивида на всех лотереях. Поэтому, чтобы узнать отношение индивида к
риску, достаточно ограничиться поведением и на (gs.
Определение 2.4. Несклонность к риску, нейтральность к
риску и склонность к риску.
Пусть и{-) — функция полезности фон Неймана — Моргенштерна
индивида для лотерей, определенных на неотрицательных уровнях
богатства. Тогда, если g = (pl°wl, ...,p/ww) —простая лотерея, то
индивида называют:
1) несклонным к риску относительно лотереи g, если
u(E(g))>u(g);
2) нейтральным к риску относительно лотереи g, если
u(E(g)) = u(g);
3) склонным к риску относительно лотереи g, если u(E(g)) < u(g).
Если для любой невырожденной простой лотереи g индивид,
например, является несклонным к риску относительно нее, то говорят,
что он несклонен к риску (или несклонен к риску на всем пространстве
лотерей (д). Аналогично, индивида можно определить как нейтрального
к риску и склонного к риску (на (д ).
Каждое из этих отношений к риску эквивалентно конкретному
свойству функции полезности фон Неймана — Моргенштерна. В упражнени-
Простая лотерея невырожденна, если она приписывает положительные вероятности
хотя бы двум различным уровням богатства.

Глава 2. Продолжение теории потребителя
145
ях вам предлагается показать, что агент является несклонным,
нейтральным или склонным к риску на некотором подмножестве лотерей тогда и
только тогда, когда его функция полезности фон Неймана — Морген-
штерна строго вогнута, линейна или строго выпукла соответственно в
своей области определения (на множестве значений богатства).
Чтобы проиллюстрировать первое из этих утверждений, рассмотрим
простую лотерею с двумя исходами:
gs(p°wp (l-/?)ow2).
Предположим, что индивиду предлагается выбор между участием в
лотерее g и гарантированным получением ожидаемого выигрыша от этой
лотереи, равного E(g) = pwx + (l-p)w2. Оценить альтернативы можно
следующим образом:
u(g) = pu(wx) + A - p)u(w2),
u{E{g)) = u{pw{ + A - P)w2) •
Теперь посмотрим на рис. 2.6. На нем изображена хорда,
соединяющая две точки R = (w,, w(w,)) и S = (w2, u(w2)), и отмечена их выпуклая
комбинация Т = pR + A - p)S . Абсцисса Т должна быть равна E(g), a
ордината — u(g). (Убедитесь в этом.) Тогда мы можем найти u(E(g)) на
вертикальной оси, используя график функции u(w), как показано на
рисунке. Изображенная на рис. 2.6 функция полезности фон Неймана —
Моргенштерна строго вогнута в соответствующей области, и легко
заметить, что u(E(g)) > u{g), поэтому индивид несклонен к риску.
u{w)
+ W
w\ CE E(g)
Wi
Рис. 2.6. Несклонность к риску и строгая вогнутость функции полезности
фон Неймана — Моргенштерна

146
Часть I. Экономические агенты
На рис. 2.6 индивид предпочитает гарантированное получение
ожидаемого выигрыша E(g) самой лотерее g. Однако ему можно (с
определенностью) предложить некоторую сумму денег, такую, что ему будет
безразлично, участвовать в лотерее g или получить соответствующий
гарантированный доход. Такая сумма денег называется
гарантированным эквивалентом лотереи g. Если агент несклонен к риску и большее
количество денег строго предпочитает меньшему, то легко показать, что
гарантированный эквивалент меньше ожидаемого выигрыша от лотереи
(это вам предлагается проделать в упражнениях). По сути, несклонный к
риску индивид готов «заплатить» некоторую положительную сумму за то,
чтобы избежать сопутствующего лотерее риска, и эта сумма называется
премией за риск. Определения гарантированного эквивалента и премии
за риск, изображенных на рис. 2.6, приведены ниже.
Определение 2.5. Гарантированный эквивалент и премия за
риск.
Гарантированный эквивалент любой простой денежной лотереи g
для индивида— это такая сумма денег, СЕ, полученная с
определенностью, что u(g) = u(CE). Премия за риск— это такая сумма денег Р,
что u(g) = u(E(g) -Р),т.е. Р = E(g) - СЕ.
Пример 2.5. Предположим u(w) = ln(w). Поскольку данная
функция полезности строго вогнута по богатству, то индивид несклонен к
риску. Пусть по лотерее g можно с шансами 50 на 50 приобрести или
потерять некоторую сумму денег h, так что если начальное богатство
индивида равно и>0, то
g = ((l/2)o(w0+A), (l/2)°(w0-/0).
Легко заметить, что ожидаемый выигрыш E(g) от этой лотереи будет
равен w0. Гарантированный эквивалент лотереи g должен удовлетворять
условию
ЩСЕ) = A/2) ln(w0 + И) + A/2) ln(w0 - h) = \n(w20 - h1 I/2.
Отсюда CE = (w20-h2y/2<E(g) и Р = w0 -(w20 -A2)I/2 >0. ?
Во многих случаях нам нужно знать не только сам факт несклонности
индивида к риску, но и то, насколько несклонным к риску он является.
Идеальным был бы такой показатель, который позволял бы сравнивать
степень несклонности к риску у различных индивидов и одновременно
измерять, как у данного индивида отношение к риску изменяется в
зависимости от уровня дохода. Поскольку несклонность к риску и вогнутость

Глава 2. Продолжение теории потребителя
147
функции полезности фон Неймана — Моргенштерна по богатству
эквивалентны, наиболее естественным «кандидатом», по-видимому, могла бы
стать вторая производная u"{w) как характеристика «кривизны»
функции. Можно было бы предположить, что чем больше абсолютное
значение производной, тем больше степень несклонности к риску.
Однако это не так. Хотя знак второй производной сигнализирует нам
о склонности, несклонности или нейтральности индивида к риску, ее
величина абсолютно произвольна. В теореме 2.8 показано, что функции
полезности фон Неймана — Моргенштерна единственны с точностью до
аффинных преобразований. Это означает, что для любых данных
предпочтений мы можем получить практически любую величину второй
производной, умножая и() на соответствующим образом выбранную
положительную константу. Учитывая это и другие соображения, Эрроу
[Arrow, 1970] и Пратт [Pratt, 1964] предложили следующую меру
несклонности к риску.
Определение 2.6. Мера Эрроу — Пратта абсолютной
несклонности к риску.
Мера Эрроу — Пратта абсолютной несклонности к риску задается как
и (w)
Заметим, что знак этого показателя немедленно сообщает нам об
отношении к риску: Ra(w) положительна, отрицательна или равна нулю,
если агент несклонен, склонен или нейтрален к риску соответственно.
Кроме того, произвольное аффинное преобразование полезности не
изменит значение этой меры: добавление константы не влияет ни на
числитель, ни на знаменатель; умножение на положительную константу влияет
и на тот, и на другой, но не отражается на их отношении.
Чтобы продемонстрировать эффективность меры Эрроу — Пратта,
мы покажем, что индивиды, у которых ее значение больше,
действительно более несклонны к риску в том смысле, что для них гарантированный
эквивалент лотереи меньше и они реже соглашаются на участие в игре.
Предположим, что имеются два потребителя — 1 и 2; потребитель 1
имеет функцию полезности фон Неймана — Моргенштерна u(w), а
потребитель 2 — v(w). Богатство w может принимать любое
неотрицательное значение. Предположим, что при любом уровне богатства мера
Эрроу — Пратта у потребителя 1 больше, чем у потребителя 2, т.е.
KM = ~!^>-^T = R2aM длявсех w>0, B-12)
и (w) v (w)
где мы предполагаем, что и' и v всегда строго положительны.

148
Часть I. Экономические агенты
Для простоты предположим, что v(w) принимает любые значения на
[О,©о). Поэтому можно определить отображение Л:[0,°о)—>М
следующим образом:
h(x) = u(v~l(x)) для всех х > О. B-13)
Функция h является дважды дифференцируемой, как и и w, причем
^) = 4^>0,и
vVW)
[v'(v-\x))f
для всех х > О, где первое неравенство следует из того, что и\ v > О, а
второе — из B-12). Таким образом, h является строго возрастающей и
строго вогнутой функцией.
Рассмотрим лотерею (р, ° w,, ...,jpflowJ. Можно воспользоваться
B-13) и строгой вогнутостью h для того, чтобы показать, что
гарантированный эквивалент данной лотереи у потребителя 1 меньше, чем у
потребителя 2.
Обозначим гарантированный эквивалент лотереи для / -го
потребителя через wt:
5>Mw/) = «(*i)> B-14)
!>,v(h>,.) = v(w2). B-15)
/=1
Мы хотим показать, что щ < w2.
Положив х = v(w) в B-13) и используя B-14), получим
п
"(m,i) = EaAWw,))<
/=1
( "
V м
= h(v(w2)) =
= u(w2),

Глава 2. Продолжение теории потребителя
149
где неравенство, которое называется неравенством Йенсена, следует из
строгой вогнутости А, а два последних равенства следуют из B-13) и
B-15) соответственно. Следовательно, w(h>,) < u(w2), а поскольку и
строго возрастает, то wx < w2, что и требовалось доказать.
Мы приходим к выводу о том, что у потребителя 1 гарантированный
эквивалент любой данной лотереи меньше, чем у потребителя 2.
Непосредственно из этого следует, что если начальное богатство у
потребителей одинаково, то потребитель 2 (у которого абсолютная мера Эрроу —
Пратта меньше) примет участие в любой лотерее, в которой примет
участие потребитель 1. (Убедитесь в этом.) То есть потребитель 1 будет реже
соглашаться на участие в лотереях, чем потребитель 2.
Заметим, наконец, что в ходе обсуждения мы также показали, что из
B-12) следует, что функция полезности фон Неймана — Моргенштерна у
потребителя 1 более вогнута, чем у потребителя 2, в том смысле, что
(снова положим х = v(w) в B-13))
u(w) = h(v(w)) для всех w > О, B-16)
где, как вы помните, h является строго вогнутой функцией. Поэтому
согласно B.16) и является вогнутым преобразованием v. Это еще одно
(эквивалентное) выражение идеи о том, что потребитель 1 более несклонен к
риску, чем потребитель 2.
Ra(w) является всего лишь локальной мерой несклонности к риску,
поэтому она не обязательно должна быть одной и той же для всех
уровней дохода. Действительно, можно ожидать, что отношение к риску, а
значит, и мера Эрроу — Пратта, будет «разумным» образом меняться в
зависимости от величины богатства. Эрроу предложил простую
классификацию функций полезности фон Неймана — Моргенштерна в
соответствии с зависимостью Ra(w) от уровня богатства. Так, будем говорить,
что функция полезности фон Неймана — Моргенштерна демонстрирует
постоянную, убывающую или возрастающую степень абсолютной
несклонности к риску для некоторых уровней богатства, если Ra(w) в этой
области остается соответственно постоянной, убывает или возрастает с
ростом богатства.
Условие убывания абсолютной несклонности к риску (decreasing
absolute risk aversion, DARA), вообще говоря, является разумным. При
постоянной абсолютной несклонности к риску с ростом дохода потребитель
не будет чаще соглашаться на небольшие лотереи, а при возрастающей
абсолютной несклонности к риску поведение становится странным: чем
больше доход, тем менее потребитель склонен участвовать в одной и той
же небольшой лотерее. DARA вводит более осмысленное ограничение:

150
Часть I. Экономические агенты
индивид будет менее несклонен соглашаться на небольшие риски при
росте уровня дохода.
Пример 2.6. Рассмотрим инвестора, который решает, какую часть
своего начального богатства w вложить в рисковый актив. Рисковый
актив может иметь положительную или отрицательную норму доходности
г; с вероятностью рп / = 1, ...,и. Если р — объем инвестиций в
рисковый актив, то при реализации / -го исхода богатство инвестора составит
(w-P) + (l + 7*)p = w+P^ . Задача инвестора заключается в том, чтобы
путем выбора р максимизировать ожидаемую полезность. Формально ее
можно записать как оптимизационную задачу вида
п
maxVp^w+p^.) при 0<P<w. (E-1)
Сначала мы найдем, при каких условиях несклонный к риску
инвестор решит не вкладывать средства в рисковый актив. В этом случае мы
получаем угловое решение, когда целевая функция из (Е-1) достигает
максимума при р* = 0, поэтому ее первая производная не должна быть
положительной в этой точке. Дифференцируя ожидаемую полезность из
(Е-1) по р и вычислив ее в р* = 0, мы получим
п п
Сумма в правой части этого выражения равна ожидаемой норме
доходности рискового актива. Поскольку u(w) должна быть
положительной, то ожидаемая доходность будет неположительной. Легко проверить,
что вогнутости функции и по богатству достаточно, чтобы гарантировать
вогнутость функции из (Е-1) по р, и поэтому мы заключаем, что
несклонный к риску индивид воздержится от инвестиций в рисковый актив
тогда и только тогда, когда этот актив имеет неположительную
ожидаемую доходность. Другими словами, можно сказать, что несклонный к
риску инвестор всегда предпочтет вложить некоторые средства в
рисковый актив со строго положительной ожидаемой доходностью.
Предположим, что рисковый актив имеет положительную
ожидаемую доходность. Как мы видели, это позволяет нам исключить случай
Р* = 0. Предположим также, что р* < w. Условия первого и второго
порядка для внутреннего решения задачи максимизации (Е-1) имеют вид:

Глава 2. Продолжение теории потребителя
151
XA"'(w + P4)^=0 (Е-2)
Xa«V+P4K2<o (е-з)
соответственно, где неравенство (Е-З) является строгим вследствие
несклонности к риску.
Что же происходит с объемом инвестиций в рисковый актив, если
богатство инвестора увеличивается? Опыт подсказывает, что при росте
богатства в рисковый актив вкладывается все больше средств в абсолютном
выражении, т.е. что рисковый актив является «нормальным», а не «инфе-
риорным» благом. Мы покажем, что при условии DARA это действительно
так. Рассматривая р* как функцию w, продифференцируем (Е-2) по w:
п
^- = ^ . (Е-4)
Из несклонности к риску следует, что знаменатель (Е-4) будет
отрицательным, так что рисковый актив будет «нормальным», только если
числитель также отрицателен (для выполнения последнего условия
достаточно того, чтобы выполнялось условие убывания абсолютной
несклонности к риску).
Чтобы убедиться в этом, заметим, что из определения Ra(w+^*rf)
следует
-i/"(w+p7,)r,, ^^(w+pV^ryCw+pV,), / = 1, ...,л. (Е-5)
При условии DARA Ra(w) >Ra(w+$*rt) при г{>0 и Ra(w)<Ra(w+^*ri)
при rt < О. Умножив обе части этих неравенств на г.;, в том и другом
случаях мы получим
Ra(w)r, >Дв(и>+р7,)г„ i = l, ...,n. (E-6)
Подставив в (Е-5) Ra(w+^*ri) вместо Ra(w) и воспользовавшись (Е-6),
получим
-i/"(w+pV}>;r</?^w>;w'(w+pV}), / = 1, ...,«.

152
Часть I. Экономические агенты
Наконец, взяв математические ожидания от обеих частей, мы придем к
соотношению
-?,piu"(w+pri)ri<Ra(w)?piriu'(w+Fri) = 0, (E-7)
/=1 1=1
где последнее равенство следует из (Е-2).
Таким образом, если поведение инвестора характеризуется DARA, то
(Е-4) положительно и при росте богатства в рисковый актив будет
вкладываться больше средств. ?
Пример 2.7. Несклонный к риску индивид с начальным богатством
и>0 и функцией полезности фон Неймана — Моргенштерна и(-) решает,
страховать ли ему автомобиль и сколько на это потратить. Вероятность
аварии и денежного ущерба L равна осе @,1). Каков оптимальный объем
страхового покрытия х ?
Конечно, ответ зависит от цены страхования. Предположим, что
страховой полис предлагается по актуарно справедливой цене, т.е. такой,
которая приносит страховой компании нулевую ожидаемую прибыль.
Если р обозначает цену одного доллара страхового покрытия (единицы
страховки), то ожидаемая прибыль страховой компании в расчете на один
доллар страхового покрытия равна ос(р -1) + A - ос)р. Приравняв ее к
нулю, получаем р = а.
Тогда каков оптимальный объем покрытия для несклонного к риску
индивида при цене одного доллара страхового покрытия, равной а ?
Индивид выберет такой объем покрытия х, который максимизирует его
ожидаемую полезность
au(w0 -ax-L + x) + (l-a)u(w0 -ax). (E-1)
Продифференцировав (Е-1) по х и приравняв результат к нулю, мы
получим
A - a)au'(w0 -ajc-L + x)-a(l- a)u'(w0 - ах) = 0,
откуда, разделив на A - а)а, придем к равенству
u'(w0 -ax-L + x) = u'(w0 - ах).
Но поскольку индивид несклонен к риску, w"<0, то предельная
полезность строго убывает по богатству, а из равенства предельных полезно-
стей богатства следует равенство самих уровней богатства, т.е.
w0-ax-L + x = wQ-ax,
откуда
x = L.

Глава 2. Продолжение теории потребителя
153
Следовательно, в случае актуарно справедливой страховки
несклонный к риску индивид полностью страхуется от всех рисков. Заметим, что
в оптимуме благосостояние индивида постоянно и равно w0 - oL
независимо от того, произошла авария или нет.
2.5. Упражнения
2.1. Покажите, что условия сбалансированности бюджета и
однородности х(р, у) не связаны друг с другом в том смысле, что ни одно из них
не следует из другого.
2.2. Пусть функция х(р, у) е R"+ удовлетворяет условию
сбалансированности бюджета и является однородной на множестве М"*1. Покажите,
что для всех (р, у)е М"++' выполняется условие s(p, у)р = 0, где
S(P> У) — матрица Слуцкого, соответствующая х(р, у).
2.3. Найдите прямую функцию полезности индивида, если его
косвенная функция полезности имеет вид v(p, у) = ур\р\, где а < 0 и Р < 0.
2.4. Рассмотрите некоторую функцию е(р, и)е R+ (которая не
обязательно является функцией расходов) и функцию х(р, у)е R"+ (которая не
обязательно является функцией спроса). Пусть эти функции
удовлетворяют системе дифференциальных уравнений в частных производных,
приведенной в разделе 2.2. Покажите, что:
а) если х(р, у) удовлетворяет условию сбалансированности
бюджета, то функция е(р, и) должна быть однородной первой степени по р;
б) если функция е(р, и) однородна первой степени по р и при
каждом р принимает любые неотрицательные значения при изменении и, то
функция х(р, у) должна быть однородной нулевой степени по (р, у).
2.5. Рассмотрите функцию расходов е(р, и) = ир"] р%2 р"*,
полученную в примере 2.3.
а) Найдите косвенную функцию полезности, используя соотношение
е(Р> V(P> У)) - У 9 и проверьте выполнение тождества Роя.
б) Используя схему доказательства теоремы 2.1, восстановите
соответствующую функцию полезности. Покажите, что полученная функция
полезности порождает функции спроса, приведенные в примере 2.3.
2.6. Пусть функция расходов потребителя имеет вид е(рХ9 р2, и) =
= ирхр2 /(/?, + р2). Найдите прямую функцию полезности, и{хх, х2),
согласующуюся с рациональным поведением данного потребителя.

154
Часть I. Экономические агенты
2.7. Получите обратные функции спроса потребителя, /?,(*,, х2) и
/72(jc,, д:2), если функция полезности потребителя имеет вид
м(хр х2) = Ах"х1~а, где 0 < а < 1.
2.8. Предположим, что потребитель приобретает набор х' при ценах
р', / = 0, 1. Для каждого из следующих случаев проверьте, удовлетворяет
ли спрос потребителя WARP:
а) р° =A, 3), х° =D, 2); р1 =C, 5), х1 =C, 1);
б) р°=A, 6), х°=A0, 5); р'=C, 5), х'=(8, 4);
в) р°=A, 2), х°=C, 1); р'=B, 2), ^=A, 2);
г) р° = B, 6), х° = B0, 10); р1 = C, 5), х1 = A8, 4).
2.9. Предположим, что в экономике только два блага, и функция
выбора потребителя, х(р, у), удовлетворяет условию сбалансированности
бюджета, р • х(р, у) = у, V(p, у). Покажите, что:
а) если функция х(р, у) однородна нулевой степени по (р, у), то
матрица Слуцкого, соответствующая х(р, у), симметрична;
б) если х(р, у) удовлетворяет WARP, то отношение выявленного
предпочтения, R, не содержит нетранзитивных циклов. (По определению
\lRx2 тогда и только тогда, когда х1 выявленно предпочитается х2.)
2.10. Хикс [Hicks, 1956)] предложил следующий пример того, что
выполнение WARP не гарантирует транзитивности выявленных
предпочтений, если число товаров больше двух. Пусть потребитель выбирает набор
х' при ценах р', / = 0, 1, 2, где
A)
1
UI
х° =
f5l
19
W
т
1
W
х' =
(п)
12
W
A) BЛ
р2= 2 х°= 11 .
1и Ы

Глава 2. Продолжение теории потребителя
155
а) Покажите, что приведенные данные удовлетворяют WARP,
проводя попарное сравнение всех возможных пар наборов и показывая, что в
каждом из случаев один из наборов выявленно предпочитается другому.
б) Укажите нетранзитивность выявленных предпочтений.
2.11. Ответьте на следующие вопросы.
а) Предположим, что функция выбора х(р, >>)€^+ однородна
нулевой степени по (р, у). Покажите, что WARP выполняется для любых
(р, у) тогда и только тогда, когда она выполняется для {(р, 1)|ре М"+}.
б) Предположим, что функция выбора х(р, у) е Ш"+ удовлетворяет
свойствам однородности и сбалансированности бюджета. Предположим
также, что для любого р1, не пропорционального р°, выполняется
условие (p1)rs(p°, y)pl < 0. Покажите, что х(р, у) удовлетворяет WARP.
2.12. Рассмотрите задачу страхования некоторого актива от
похищения, вероятность которого равна р. Стоимость актива составляет D долл., а
страховка стоит /долл. в год. Перечислите все четыре исхода из
множества^, соответствующие данной рисковой ситуации. Охарактеризуйте выбор
между тем, страховать актив или нет, как выбор между двумя лотереями,
исходами которых являются все элементы множества А, предполагая, что
лотереи отличаются только вероятностями наступления исходов.
2.13. Мы предполагали, что множество исходов А содержит
конечное число элементов п. Покажите, что для п > 2 пространство (д всегда
будет содержать бесконечное число лотерей.
2.14. Используя аксиомы G1 и G2, докажите, что в любом конечном
множестве исходов А = {ах, ...,#„} при п>\ содержатся по крайней мере
один наилучший и по крайней мере один наихудший исходы.
2.15. Пусть А = {ах,а2,аъ}, где ах >- а2 >- аъ. Лотерея g дает исход а2
с определенностью. Докажите, что если g~(ocoap A-а)°я3), то
вероятность а должна быть строго больше нуля и меньше единицы.
2.16. В тексте утверждалось, что для любителя сафари гибель может
быть наихудшим исходом охоты, но тем не менее именно охота с
некоторой вероятностью погибнуть предпочитается безопасному сафари (когда
смерть охотника невозможна). Охарактеризуйте соответствующее
множество исходов и докажите, что такое поведение индивида не согласуется
с аксиомами G3 и G4.
2.17. В аксиоме G3 утверждается существование вероятности,
порождающей эквивалентную лотерею на множестве (д . Используя G4,
докажите, что для заданной лотереи g e (д вероятность, порождающая
эквивалентную лотерею, единственна.

156
Часть I. Экономические агенты
2.18. Рассмотрите следующую «аксиому независимости» для
предпочтений >: потребителя на лотереях, если:
(flea,, ...,ftofl|f)~(9loflp ...9qnoan)9
то для любого осе [О, 1] и любой простой лотереи (г, о#р ...,гиоаи),
((од+A-0)^H^, ...,(од+A-а)гя)оАя)
((од+О-ау^од,, ...,(а?я+A-а)ги)оди).
(Обратите внимание, что эта аксиома утверждает, что когда мы
комбинируем каждую из двух лотерей с третьей одним и тем же способом,
упорядочивание предпочтений потребителя между двумя новыми лотереями не
зависит от того, какая лотерея используется в качестве третьей.)
Покажите, что эта аксиома следует из аксиом G5 и G6.
2.19. Используя определение несклонности к риску, приведенное в
тексте, докажите, что индивид демонстрирует несклонность к риску на
денежных лотереях тогда и только тогда, когда его функция полезности
фон Неймана — Моргенштерна строго вогнута на множестве Ш+.
2.20. Пусть ъ является бинарным отношением на лотереях из
множества (д, удовлетворяющим аксиомам G2, G3 и G4. Покажите, что
предпочтения ъ также удовлетворяют и аксиоме G1.
2.21. Пусть и и v — некоторые функции полезности (не обязательно
фон Неймана — Моргенштерна), представляющие предпочтения
потребителя >z на множестве (д . Покажите, что v является положительным
аффинным преобразованием и тогда и только тогда, когда для всех
лотерей g\g29g3 e (д (ни одна из которых не эквивалентна другой)
выполняется соотношение
»(g')-a(g2) = v(g')-v(g2)
u(g2)~u(g3) v(g2)-v(g3)'
2.22. Обратитесь вновь к примеру 2.7 и покажите, что индивид будет
страховаться на сумму, меньшую потерь, если цена единицы страховки р
превышает вероятность наступления страхового случая а.
2.23. Рассмотрите квадратичную функцию полезности фон
Неймана — Моргенштерна вида U(w) = я + bw+cw2.
а) Укажите, при каких условиях (если это возможно) на параметры а,
b и с данная функция будет отражать предпочтения несклонного к риску
индивида.

Глава 2. Продолжение теории потребителя
157
б) Укажите область определения (уровни богатства) данной
квадратичной функции полезности фон Неймана — Моргенштерна.
в) Рассмотрите лотерею
g = ((l/2)o(w+A), (l/2)o(w-A))
и покажите, что для нее СЕ < E(g) и Р > О.
г) Покажите, что данная функция, удовлетворяя условиям из пункта
а), не моэюет описывать предпочтения, характеризующиеся убывающей
абсолютной несклонностью к риску.
2.24. Пусть u(w) = -(b - w)c. При каких условиях на w, Ъ и с можно
гарантировать строгое возрастание и строгую вогнутость функции u{w)l
Покажите, что при этих условиях u(w) демонстрирует убывающую
абсолютную несклонность к риску.
2.25. Покажите, что при C > О функция полезности фон Неймана —
Моргенштерна w(w) = oc + pln(w) демонстрирует убывающую
абсолютную несклонность к риску.
2.26. Пусть w(x,, x2) = ln(x,) + 2b(x2). Если рх = р2 =1, то будет ли
индивид склонным, нейтральным или несклонным к риску при различных
уровнях дохода?
2.27. Используя определения несклонности к риску,
гарантированного эквивалента и премии за риск, докажите, что условие СЕ < E(g) (или
Р > О) для всех geCj является необходимым и достаточным условием
несклонности к риску.
2.28. Докажите, что индивид нейтрален к риску тогда и только тогда,
когда выполняются следующие условия:
а) функция полезности фон Неймана — Моргенштерна линейна по
богатству;
б) С = E(g) для всех g e Cj;
в) Р - 0 для всех g e (д .
Каковы три аналогичных необходимых и достаточных условия для
склонности к риску?
2.29. Докажите, что для любой функции полезности фон Неймана —
Моргенштерна условие u~(w) > 0 является необходимым, но не
достаточным для убывания абсолютной несклонности к риску (DARA).
2.30. Если функция полезности фон Неймана — Моргенштерна
демонстрирует постоянную абсолютную несклонность к риску, т.е.
Ra (w) = а для всех w, то каков должен быть ее функциональный вид?
2.31. Введем еще одну меру несклонности к риску, предложенную
Эрроу и Праттом, которая называется мерой относительной несклонно-

158
Часть I. Экономические агенты
emu к риску, Rr (w) = Ra (w)w. Объясните, почему Rr(w) можно
рассматривать как «эластичность»? Если u(w) демонстрирует постоянную
относительную несклонность к риску, то каков должен быть ее
функциональный вид?
2.32. Инвестор должен принять решение о том, какую часть своего
первоначального богатства w инвестировать в рисковый актив с
неизвестной нормой доходности г, если каждый исход rt реализуется с
вероятностью рп / = 1, ...,и. Используя пример 2.6, докажите, что если
предпочтения инвестора характеризуются возрастающей абсолютной
несклонностью к риску, то рисковый актив должен быть инфериорным
благом.
2.33. Пусть S' — множество всех вероятностей выигрыша, таких, что
индивид / будет принимать участие в лотерее, позволяющей выиграть
или проиграть небольшую сумму денег h. Покажите, что для любых двух
индивидов / и j, таких, что R'a(w) > RJa (w), должно выполняться условие
S' с SJ, т.е. покажите, что чем индивид более несклонен к риску, тем
меньше множество лотерей, в которых он согласится принять участие.
2.34. Рассмотрите бесконечно живущего агента, который должен
выбрать план своего потребления. Обозначим через xt его расходы на
потребление в период /, через yt — ожидаемый доход в период /, а через
г > 0 — рыночную ставку процента, по которой агент может свободно
занимать или давать в долг. Многопериодная функция полезности агента
аддитивно сепарабельна и имеет вид
u\xQ9xl9x29 ...) = ?P'w(*,),
где и(х) — возрастающая строго вогнутая функция и 0 < р < 1. Многопе-
риодное бюджетное ограничение требует, чтобы текущая стоимость
расходов не превосходила текущую стоимость дохода:
Y 1 V _=_/^ 1 V
/=0
1 + г
t=0
1 + г
У,-
а) Как вы проинтерпретируете параметр р ?
б) Выпишите условия первого порядка, характеризующие
оптимальный потребительский набор в период /.
в) Изобразите кривую безразличия, отражающую выбор только
между х, и jc/+i , предположив, что потребление в остальных периодах остает-

Глава 2. Продолжение теории потребителя
159
ся неизменным. Объясните, каковы будут наклон и кривизна
изображенной вами кривой безразличия.
г) Как изменится потребление в период t при изменении рыночной
ставки процента?
д) Покажите, что в любом периоде полезность является
возрастающей функцией от дохода.
е) Если р = 1/A + г), то каков будет потребительский план агента?
ж) Опишите потребительский план агента, если C > 1/A н- г) и
Р<1/0 + г).
2.35. Рассмотрите двухпериодный вариант предыдущего упражнения,
где
u(xt) = -(V2)(xt-2)\t = 0, 1.
а) При у0 = 1, ух = 1 и р = 1/A + г) найдите оптимальный объем
потребления в каждом периоде и вычислите соответствующий уровень
полезности агента.
Предположим теперь, что агенту известно, что в начальном периоде
его доход будет равен у0 = 1. Однако ему неизвестно, какой доход он
получит в следующем периоде: он может быть либо высоким — у" = 3/2,
либо низким — у\ -1/2 . Предположим, что агенту известна вероятность
получения высокого дохода, равная 1/2. Теперь задача потребителя
состоит в том, чтобы выбрать уровень потребления в начальном периоде
jc0 , потребление в следующем периоде при высоком доходе х" и
потребление в следующем периоде х[, если доход будет низким, таким образом,
чтобы максимизировать свою (многопериодную) ожидаемую полезность.
б) Полагая, что р = 1/A + г), сформулируйте оптимизационную задачу
агента и найдите оптимальный план потребления и уровень полезности.
в) Как вы объясните любые различия и сходство результатов,
полученных в пунктах а) и б)?

Глава 3
ТЕОРИЯ ФИРМЫ
3.1. Базовые понятия
Вторым важным объектом в микроэкономике является фирма. Мы
начнем эту главу с обсуждения производства и издержек — вопросов, с
которыми сталкивается любая фирма, а затем рассмотрим поведение
фирм в условиях совершенной конкуренции (специфический, но крайне
важный случай). По этому материалу мы сможем продвигаться довольно
быстро благодаря тому, что между теорией производителя и только что
изложенной теорией потребителя существует большое формальное
сходство.
Напомним, что такое фирма. В простейшем понимании это —
организационная единица, создаваемая индивидами для некоторой цели.
Обычно она занимается тем, что приобретает факторы производства и
использует их для выпуска продукции. Факторы производства
покупаются на рынках факторов производства, а расходы на них являются
издержками фирмы. Продукция продается на товарных рынках, а фирма
получает от этого доход.
Зачем вообще создавать фирму и что помогает принимать
многочисленные решения, необходимые для ее функционирования? Любой
экономист скорее всего ответит, что все это делается для максимизации
прибыли, — и будет абсолютно прав. Прибыль равна разнице между доходами,
которые фирма получает, продавая свою продукцию, и расходами,
которые она несет, покупая факторы производства, и представляет собой
доход владельцев фирмы. Они же одновременно являются потребителями,
получающими удовлетворение от товаров и услуг, которые могут купить
на свой доход. Ясно, что чем больше прибыль фирмы, тем больше
товаров и услуг могут приобрести ее владельцы. Поэтому они будут
стремиться к тому, чтобы все решения о приобретении факторов
производства, их использовании и продаже продукции служили цели максимизации
прибыли.
Это, конечно, не единственный мотив поведения фирмы. Экономисты
рассматривают и многие другие варианты, в том числе максимизацию
объема продаж, доли на рынке и даже престижа. Каждый из этих
вариантов наряду с другими обладает определенной внешней
привлекательностью, но большинство экономистов в своих работах, как правило,
продолжают использовать гипотезу максимизации прибыли.

Глава 3. Теория фирмы
161
Подобное упорство имеет веские основания. С эмпирической точки
зрения на основе предположения о максимизации прибыли делаются
прогнозы, которые вновь и вновь подтверждаются фактами. С теоретической
точки зрения оно, во-первых, отличается простотой и согласованностью с
гипотезой максимизации полезности рациональными потребителями.
Кроме того, многие альтернативные гипотезы, например максимизацию
продаж или рыночной доли, лучше рассматривать не как
самостоятельные цели, а как краткосрочную тактику в рамках долгосрочной стратегии,
ориентированной на максимизацию прибыли. Наконец, существуют
объективные рыночные силы, заставляющие фирму максимизировать
прибыль, даже если ее владельцы или менеджеры сами по себе к этому не
склонны. Предположим, что некая фирма не максимизирует прибыль.
Если в этом виноваты менеджеры и если хотя бы простое большинство
владельцев фирмы являются потребителями с ненасыщаемой полезностью,
тогда это большинство будет заинтересовано в том, чтобы заменить таких
менеджеров на тех, кто будет максимизировать прибыль. Если же в этом
виноваты владельцы, то у любого другого предпринимателя с
ненасыщаемой полезностью появится стимул завладеть фирмой и направить ее
деятельность на максимизацию прибыли.
Аналогично гипотезе максимизации полезности для потребителей,
максимизация прибыли является самым надежным предположением,
которое мы можем сделать, начиная изучать, а затем и предсказывать
поведение фирм. Таким образом, мы будем предполагать, что любое решение
фирмы обусловлено целью максимизации прибыли. Конкретные
действия, направленные на достижение этой цели, будут зависеть от
обстоятельств: во-первых, от технологических возможностей фирмы, во-вторых,
от ситуации на рынках факторов производства и, наконец, от ситуации на
рынке ее продукции. Для понимания поведения фирмы потребуется
также четко различать цель фирмы, которая всегда одна и та же, и
ограничения, которые изменяются и определяются рыночными факторами,
находящимися за пределами ее влияния.
3.2. Производство
Производство — это процесс преобразования факторов производства
в продукцию. Реальностью, с которой при этом сталкивается фирма,
является проблема технологической допустимости. Технология определяет
и ограничивает возможности комбинирования факторов производства для
выпуска продукции, и соответствующие ограничения могут быть
формализованы различными способами. В самом общем случае технологию
можно описать посредством множества производственных
возможностей YсШт, где каждый вектор у = (yl9 ...jJg7 — это производств

162
Часть I. Экономические агенты
венный план, компоненты которого обозначают количества различных
факторов производства и видов продукции. В этой записи считается, что
yi < О, если / -й элемент является фактором производства, и у.> О, если
/ -й элемент представляет собой выпуск фирмы.
Множество производственных возможностей является наиболее
общим способом описания технологии фирмы; с его помощью можно
описать технологию со многими факторами производства и многими видами
выпуска. Нам, однако, часто придется рассматривать фирмы,
производящие единственный продукт из многих факторов. В этом случае технологию
фирмы удобнее описывать производственной функцией.
Если с помощью многих факторов производится только один продукт,
будем обозначать объем выпуска через у, а объем / -го фактора через xi,
так что для п факторов весь вектор факторов будет обозначаться как
x = (jcp ...9хя). Конечно, вектор факторов и объем выпуска должны быть
неотрицательными, поэтому требуется, чтобы х > О и у > О.
Для каждого вектора факторов производства производственная
функция описывает максимально возможный объем выпуска. Таким образом,
производственная функция / является отображением R" в К+. Запись
у = /(х) означает, что с использованием вектора х может быть
произведено у единиц продукции (и не больше). Мы будем придерживаться
следующего предположения о производственной функции /1.
Предположение 3.1. Свойства производственной функции.
Производственная функция /:М"-»М+ является непрерывной,
строго возрастающей и строго квазивогнутой на множестве R",
причем /@) = 0.
Непрерывность / гарантирует, что небольшие изменения затрат
факторов производства ведут к небольшим изменениям объема выпуска.
Условие строгого возрастания f обеспечивает возрастание объема
выпуска при увеличении затрат любого из факторов. Условие строгой
квазивогнутости / вводится, в сущности, для упрощения анализа. Без него
можно обойтись без значимых изменений в результатах, как и без
предположения о строгой выпуклости потребительских предпочтений (и
квазивогнутости функции и), введенного в предыдущей главе. Тем не менее
оно имеет определенный смысл. Одно из объяснений связано с тем, что
строгая квазивогнутость обеспечивает взаимодополняемость факторов в
производстве. Интуитивно это означает, что два фактора — скажем, ка-
1 Ср. с предположением 1.2 в главе 1.

Глава 3. Теория фирмы
163
питал и труд — являются в некоторой степени взаимодополняющими,
если объем выпуска очень низок при малом количестве одного из
факторов, даже если используется большой объем другого фактора. В этом
смысле для производства важно использование обоих факторов. В такой
ситуации среднее двух производственных векторов, в одном из которых
много труда и мало капитала, а в другом мало труда и много капитала,
позволит произвести больше продукции, чем каждый из этих векторов в
отдельности. Предположение о строгой квазивогнутости распространяет
эту идею на средние всех различных пар векторов факторов производства.
Последнее условие предположения 3.1 означает, что производство данной
продукции нельзя осуществить без каких-либо затрат факторов
производства.
Если производственная функция дифференцируема, то ее частная
производная, Э/(х)/Эх; , называется предельным продуктом i -го
фактора производства и показывает изменение выпуска при использовании
дополнительной (малой) единицы / -го фактора. Если / строго возрастает и
всюду дифференцируема, то Э/(х)/Эх/ > 0 для «почти всех» векторов
факторов производства. Для простоты мы часто будем использовать
предположение о том, что здесь всегда имеет место строгое неравенство.
Для заданного уровня выпуска у множество векторов факторов
производства, из которых производится у единиц продукта, называется изо-
квантой уровня у\ изокванты представляют собой множество линий
уровня функции /. Обозначим это множество через Q{y):
Q(y) = {x>0\f(x) = y}.
Для заданного вектора факторов производства х изокванта,
проходящая через точку х, — это множество векторов факторов производства,
каждый из которых позволяет произвести такой же объем выпуска, как и
х, а именно Q(f(x)).
Аналогом предельной нормы замещения в теории потребителя в
теории производителя является предельная норма технологического
замещения (marginal rate of technical substitution, MRTS). Она измеряет
степень, в которой один фактор может замещаться другим без изменения
объема выпуска. Формально предельная норма технологического
замещения между / -м и j -м факторами при векторе факторов х обозначается
MRTSyfx) и определяется как отношение предельных продуктов:
'А ЭДх)/Э*.

164
Часть I. Экономические агенты
В случае с двумя факторами производства (рис. 3.1) MRTSn(x*)
равна модулю наклона изокванты, проходящей через х , вычисленному в
точке х
х2
ewx1))
Наклон в х
М?Г512(х1) = |наклонв х11 =
Э/(х')/Эх
ЭДх'уЭх,
ЭДх')/Э*2
>*!
Рис. 3.1. Предельная норма технологического замещения
MRTS любых двух факторов производства, вообще говоря, зависит от
количества всех используемых факторов. В эмпирических работах,
однако, часто предполагается, что факторы производства можно разбить на
относительно небольшое число типов, причем степень замещаемости
между факторами одного типа отличается от степени замещаемости между
факторами разных типов. Производственные функции, обладающие этим
свойством, называются сепарабельными, причем существует не менее
двух основных видов сепарабельности.
Определение 3.1. Сепарабельные производственные функции.
Пусть N = {1, ...,и} — количество факторов производства и
предположим, что это множество можно разбить на S > 1
непересекающихся подмножеств Nv ...,N5. Производственная функция называется
нестрого сепарабельной, если MRTS между двумя факторами одной
группы не зависит от факторов, входящих в другую группу:
ЭШх)//у(х))
дхк
= 0 для всех /, je Ns, кё Ns,
где fi и fj — предельные продукты i -го и j -го факторов. При S > 2
производственная функция называется строго сепарабельной, если MRTS
между двумя факторами из разных групп не зависит от факторов за
пределами этих групп:
дШх)//:(х))
= 0 для всех IE Ns,je Nt, k? NsuNt.
дх.

Глава 3. Теория фирмы
165
MRTS является одной из локальных мер замещаемости факторов при
данном объеме выпуска. Однако экономисты предпочитают измерять
подобные параметры с помощью безразмерных эластичностей. Хотя
существует несколько таких показателей, наиболее распространенным из них
является эластичность замещения а. Для двух факторов х, и Xj при
фиксированном уровне выпуска и объеме всех остальных факторов она
показывает, на сколько процентов изменится отношение между
факторами Xj/xj в результате изменения MRTS на 1%.
Определение 3.2. Эластичность замещения.
Для производственной функции f(\) эластичность замещения
между i -м uj-м факторами в точке х определяется как
d\n(Xj/Xi) =d(Xj/x,) Щ/fjW
°>j dHfW/fjd)) xj/x, </Шх)//,(х))'
где f. и fj — предельные продукты i -го и j -го факторов.
Если производственная функция квазивогнута, то эластичность
замещения не может быть отрицательной, т.е. ау > О. Чем ближе она к
нулю, тем «труднее» будет происходить замещение факторов; чем она
больше — тем «легче» замещение между ними. Смысл этого проще всего
увидеть в случае двух факторов. На рис. 3.2(a) изокванта линейна, между
факторами имеется совершенная замещаемость, с бесконечна. На
рис. 3.2F) изображен промежуточный случай, где о не равна ни нулю, ни
бесконечности, а изокванты не являются ни прямыми, ни прямыми
углами. Чем ближе о к нулю, тем больше форма изоквант приближается к
прямому углу и тем «труднее» замещение между факторами; чем а
больше, тем более гладкими являются изокванты и тем «легче» замещение
между факторами.
Х2 Х2 Х2
+Х\
0<О<оо
600
->*i
о = 0
¦GO0
W)
(а) (б) (в)
Рис. 3.2. (а) — о бесконечна, факторы полностью взаимозаменяемы;
(б) — а конечна, но больше нуля, замещаемость неполная;
(в) — а равна нулю, факторы не взаимозаменяемы
>> JCi

166
Часть I. Экономические агенты
Пример 3.1. Из теории спроса нам знакома функция с постоянной
эластичностью замещения. Сейчас мы увидим, откуда появилось это
название. Для этого рассмотрим производственную функцию с постоянной
эластичностью замещения
при О Ф р < 1.
Чтобы рассчитать эластичность замещения, заметим, что
1п(х2 /х,) = 1п(д:2) - ln(Xj), поэтому, если взять полный дифференциал
числителя а, мы получим
^х
1 J
= d\n(x2) - dln(x]) = —dx2 dxx =
1' \ i Л
—dxx dx2
\x\
(E-l)
7
Вычислив частные производные функции /, поделив их друг на друга и
взяв логарифмы, получим
In
^
Л
( vP-l ^
= 1п
\J2J
\л2
= (p-l)[ln(jc,)-ln(x2)].
Взяв полный дифференциал, найдем знаменатель а:
d In
А
=(p-i)
vx,
—<abc, dx2
х-,
(E-2)
Поделив (Е-1) на (Е-2), получаем эластичность замещения
1
1-р
которая является константой, отсюда и аббревиатура CES — постоянная
эластичность замещения (constant elasticity of substitution). ?
Для CES-функций степень замещения между факторами всегда одна
и та же независимо от уровня выпуска или соотношения факторов. Это
ограничивает диапазон технологий, описываемых такими функциями.
Вместе с тем с помощью различных значений параметра р, а значит, и
различных значений параметра а, можно задавать технологии с самой
разной (но всюду постоянной) эластичностью замещения факторов. Чем
ближе р к единице, тем больше а; если р равно единице, то с бесконечна,

Глава 3. Теория фирмы
167
производственная функция является линейной, а ее изокванты
аналогичны тем, что изображены на рис. 3.2(a).
Другие популярные производственные функции также можно
рассматривать как частные случаи некоторых CES-функций. В частности,
легко проверить, что
У =
V/=i
?а,.х;р , где Ха,.=1,
является функцией с постоянной эластичностью замещения, у которой
oiy =l/(t-p) для всех 1Ф j. Можно показать, что о;> —»1 при р-»0, и
эта функция сводится к однородной первой степени (линейно
однородной) функции Кобба — Дугласа
^=П
*а'
Если р —»-©о , то а/у —> 1, что дает леонтьевскую производственную
функцию в качестве предельного случая:
<y = min{x1, ...,*„}
с изоквантами, аналогичными представленным на рис. 3.2(b).
Все производственные функции с постоянной эластичностью
замещения (включая предельные случаи функций Кобба — Дугласа и
Леонтьева) входят в класс однородных первой степени производственных
функций, который играет большую роль в теоретических и прикладных
исследованиях. Однородность первой степени дополнительно структурирует
производственную функцию; помимо прочего, однородные первой
степени функции всегда вогнуты.
Теорема 3.1. (Теорема Шепарда) Вогнутость однородных
первой степени производственных функций.
Пусть /(х) — производственная функция, удовлетворяющая
предположению 3.1, является однородной первой степени. Тогда f(\)
является вогнутой функцией по х.
Доказательство. Пусть для некоторых х1 » 0 и х2 » 0 у1 = /(х1) и
у2 =/(х2). Тогда У, у2 >0, поскольку /@) = 0 и / строго возрастает.
Отсюда, так как / однородна первой степени,
/I*.
л Л
/^ 2
=А
71"-

168
Часть I. Экономические агенты
Функция / (строго) квазивогнута, поэтому
/рТ+A~?Х Ь1 Для всех/е [0, 1]. (Р-1)
Теперь возьмем /* = у1/(у1 + у2) и (l-t*) = у2 /(у1 +у2). Тогда из (Р-1)
следует
Г х1 х2 ^
Снова используя однородность / и неравенство (Р-2), получим
f(xl+x2)>y*+y2=f(xl) + f(x2). (Р-3)
Таким образом, (Р-3) выполняется для любых х1, х2 »0. Но из
непрерывности / следует, что (Р-3) выполняется для всех х1, х2 > 0.
Чтобы завершить доказательство, рассмотрим два произвольных
вектора х1 > 0 и х2 > 0 и произвольное t е [О, 1]. Вспомним, что
однородность первой степени означает, что
/(ft') = «f(x'), (P-4)
ДA-Ох2) = A-0/(х2). (Р-5)
Применив (Р-3) и воспользовавшись равенствами (Р-4) и (Р-5), получим
Д/х1 + A - t)x2) > tf(xl) + A - t)f(x2),
что и требовалось доказать. ¦
3.2.1. Отдача от масштаба и изменения пропорций
Нам часто необходимо знать, как выпуск реагирует на изменения
объемов использования тех или иных факторов производства. Например,
в краткосрочном периоде, т.е. таком периоде времени, в течение
которого по крайней мере затраты одного фактора производства постоянны,
влиять на объем выпуска можно, только варьируя определенные (но не
любые) факторы. При изменении объема переменного фактора
изменяется и соотношение между используемыми постоянными и переменными
факторами. Отдача от изменения пропорций характеризует реакцию
выпуска в этой ситуации. В долгосрочном периоде фирма может
варьировать все факторы производства, и одним из способов описания реакции
выпуска является классификация производственных функций по их от-

Глава 3. Теория фирмы
169
даче от масштаба. Точнее, отдача от масштаба призвана
характеризовать изменение выпусков как реакцию на изменение затрат в той лее
пропорции, т.е. когда масштаб деятельности пропорционально
уменьшается или увеличивается. В двухфакторном случае различие между этими
двумя характеристиками производственной функции легче всего увидеть
на рис. 3.3. Отдача от изменения пропорций относится к поведению
выпуска при движении по карте изоквант вдоль горизонтальной прямой х2,
когда х2 остается постоянным, а количество хх изменяется. Отдача от
масштаба связана с поведением выпуска при движении вдоль луча,
такого, как ОА, на котором количество факторов хх и х2 изменяется
одновременно, при этом оставаясь в соотношении х2/хх = а.
х2
А |
L^?
1 \ 4*^
~ ео-1)
^^ есЛ
" 'W
>
О
Рис. 3.3. Отдача от масштаба и изменения пропорций
Элементарные показатели отдачи от изменения пропорций
включают предельный продукт (MPi(x) = fi(x)) и средний продукт
(APj(x) = f(x)/xi) каждого фактора. Эластичность выпуска по i-му
фактору, измеряющая процентное изменение выпуска в ответ на
изменение затрат /-го фактора на 1%, определяется как
\ii(x) = fi(x)xi/f(x) = MPj(x)/APi(x). Это все локальные показатели,
определенные в точке. Отдачу технологии от масштаба можно определить
локально или глобально. Свойства постоянной, возрастающей или
убывающей отдачи от масштаба характеризует следующее определение.
Определение 3.3. (Глобальная) Отдача от масштаба.
Производственная функция f(x) характеризуется (глобальной):
1) постоянной отдачей от масштаба, если f(tx) = tf(x) для всех
t>0 и всех х;

170
Часть I. Экономические агенты
2) возрастающей отдачей от масштаба, если f(tx) > tf{\) для всех
t>\ и всех х;
3) убывающей отдачей от масштаба, если f(tx) < tf(\) для всех t > 1
и всех х.
Из этих определений отдачи от масштаба видно, что
производственная функция имеет постоянную отдачу, если она является (положительно)
однородной первой степени. Заметим также, что любая однородная
производственная функция степени больше (меньше) единицы имеет
возрастающую (убывающую) отдачу, хотя обратное, вообще говоря, не верно.
Следует отметить, что многие производственные функции,
удовлетворяющие предположению 3.1, не попадают ни в одну из трех указанных
категорий. Ряд технологий демонстрирует возрастающую, постоянную и
убывающую отдачу от масштаба только в определенных диапазонах
объема выпуска. Поэтому полезно иметь локальную меру отдачи от
масштаба. Одна из них определяется в точке и показывает процентное изменение
объема выпуска в ответ на увеличение объема всех факторов
производства на 1%. Ее называют эластичностью масштаба или (общей)
эластичностью выпуска и определяют следующим образом.
Определение 3.4. (Локальная) Отдача от масштаба.
Эластичность масштаба в точке х по определению равна
, ч г dln[f(tx)] 1^(Х)Х<
u(x) = hm LJ = — .
-i dln(t) Дх)
Отдача от масштаба является локально постоянной, возрастающей или
убывающей, когда |i(x) равна, больше или меньше единицы.
Эластичность масштаба и эластичности выпуска по факторам связаны
следующим соотношением:
д(х) = 2>,.(х).
1=1
Пример 3.2. Рассмотрим производственную функцию с
переменной отдачей от масштаба:
y = k(l + x;ax-2*y\ (E-1)
где а>0, C>0, a i — верхняя грань уровня выпуска, т.е. 0<у<к.
Найдем эластичности выпуска по каждому фактору:
(I, (X) = 0СA + *Га*2 Р Г1 *Га*2 Р >

Глава 3. Теория фирмы
171
Каждая из них, очевидно, зависит и от масштаба, и от пропорций
факторов. Складывая их, получим следующее выражение для эластичности
масштаба:
ц(х) = (а + Р)A + хГах-рГ1^а^?
которое также зависит от х.
Гораздо более простые выражения можно получить, если
рассматривать эластичности как функции от уровня выпуска. Из (Е-1) имеем
Подставляя (Е-1)
получим
и
*г
(Е-2) в
а*-р=--1.
У
выражение для
эластичностей
(Е-2)
выпуска,
ц;оо=а
к
Ц*2G) = Р|1-^
Снова складывая эти выражения, найдем
\i (у) = (<*+$)
\-L
Отсюда ясно, что отдача каждого фактора и общая отдача от
масштаба монотонно убывают с ростом объема выпуска. При у = 0
Ц*О0 = (сс + Р) > 0, а при у -> к \1*(у) -> 0. Если a + р > 1, то
производственная функция демонстрирует возрастающую отдачу от масштаба при
низких уровнях выпуска 0<>><&[l-l/(a + p)], локально постоянную
отдачу при 7 = &[l-l/(a + p)] и убывающую отдачу при высоких уровнях
выпуска ?[l - l/(a + p)] < у < к. ?
3.3. Издержки
Издержки выпуска для фирмы в точности равны расходам, которые
она несет на приобретение факторов производства. Технология, вообще
говоря, допускает, что любой возможный уровень выпуска может быть
достигнут с помощью различных векторов факторов производства, и эта
возможность отражена в множествах уровня производственной функции.

172
Часть I. Экономические агенты
Таким образом, фирме необходимо решить, какие из допустимых
производственных планов она будет использовать. Если цель фирмы —
максимизировать прибыль, то она обязательно выберет наименее затратный,
или минимизирующий издержки, производственный план для каждого
уровня выпуска. Отметим, что это будет верно для любой фирмы —
монополистической, совершенно конкурентной или какой-то другой.
Чтобы определить наименее затратный способ производства, фирма
должна учитывать условия, на которых она покупает факторы
производства, а также технологические возможности производства. Эти условия, в
свою очередь, зависят от ситуации на рынках факторов. Например,
кривые предложения на некоторые или все факторы, необходимые фирме,
могут иметь положительный наклон, т.е. чем больше фирма приобретает,
тем выше (для нее) цена фактора. Напротив, фирма может быть
маленькой и незаметной на рынках факторов и соответственно приобретать
любое количество фактора, не влияя на сложившиеся рыночные цены. Тогда
о фирме говорят, что она является совершенно конкурентной на рынках
факторов производства, поскольку не обладает возможностью влиять на
цены на этих рынках. В любом случае фирмы должны учитывать эти
обстоятельства.
Далее мы будем предполагать, что фирмы совершенно конкурентны
на рынках факторов производства, и поэтому цены на факторы
фиксированы. Пусть w = (w1? ...,w„)>0 — вектор сложившихся рыночных цен,
по которым фирма может покупать факторы х = (х,, ...,хп). Поскольку
фирма максимизирует прибыль, она будет производить некоторый объем
продукции, используя тот вектор факторов, который связан с
наименьшими денежными расходами. Поэтому можно говорить об издержках
производства у единиц продукции — это будут издержки на
приобретение по ценам w наименее затратного набора факторов, с помощью
которого можно произвести у единиц продукции.
Определение 3.5. Функция издержек.
При любых ценах факторов производства w » 0 и любых объемах
выпуска ye f(M."+) функция издержек определяется следующим образом:
c(w, x) = minw-x ПРИ f(x)^y>
X€R"
т.е. если вектор x(w, у) является решением задачи минимизации
издержек, то
c(w, j/) = w-x(w, у).

Глава 3. Теория фирмы
173
Рассмотрим задачу минимизации издержек фирмы подробнее.
Функция / строго возрастает, поэтому на решении ограничение всегда будет
выполняться как равенство. Следовательно, задача минимизации
издержек эквивалентна следующей задаче:
minwx при y = f(x). C-1)
xeR"
Обозначим решение C-1) через х*. Для простоты будем предполагать,
что х* »0 и что функция / дифференцируема в точке х*, причем
V/(x*)» 0. Тогда, по теореме Лагранжа, существует ^*gR такое, что
ах,
Поскольку w, > 0, / = 1, ..., п, можно разделить приведенное выше / -е
соотношение на j -e, откуда
д/(х)/дх; = wi
ЭДх*)/Эху wj
Таким образом, минимизация издержек означает, что предельная норма
замещения между двумя факторами производства равна отношению их
цен.
Из условий первого порядка ясно, что решение зависит от параметров
w и у. Более того, оно единственно, поскольку w » 0, а / квазивогну-
та. В упражнении 3.16 это требуется доказать, как и то, что решение
всегда существует. Через х* = x(w, у) можно обозначить вектор факторов
производства, минимизирующий издержки выпуска у единиц продукции
при ценах факторов w. Его называют условным спросом фирмы на
факторы производства, поскольку он обусловлен уровнем выпуска у,
который пока считается произвольным и поэтому может обеспечивать
или не обеспечивать максимизацию прибыли.
Решение задачи минимизации издержек изображено на рис. 3.4. Для
двух факторов производства внутреннее решение соответствует точке
касания >>-изокванты и изокосты, представляющей собой прямую вида
wx = a для некоторого ос>0. Если (^(w, y\ *2(w, у)) является
решением задачи, то c(w, y) = wlxl(yv9 y) + w2x2(yv, у).

174
Часть I. Экономические агенты
c(vf9y)/w2
x2(w,y)
x\(w,y) c(vf9y)/wi
{x I w- x = a'}
^j?^ {x I w- x = a = c(w, y)}
> x\
Рис. З.4. Решение задачи минимизации издержек фирмы
(на рисунке a < a')
Пример 3.3. Пусть технология фирмы описывается двухфакторной
производственной функцией с постоянной эластичностью замещения.
Тогда задача минимизации издержек C-1) имеет вид
min wlxl+w2x2 при ixf + *?) >у .
x,>0,x2>0
Предположим, что рО и решение внутреннее. Тогда условия первого
порядка имеют следующий вид:
w,
1 _
W,
^Лр"'
\XU
У-&+4Г.
(E-l)
(Е-2)
Выразив х, из (Е-1) и подставив в (Е-2), после преобразований получим
7 = Ar2w2-|/(p-1)(w1p/(p-1)+w2p/(p-1))l/P.
Найдя отсюда х2 и проделав аналогичные выкладки для х{, получаем
условный спрос на факторы:
xx=yw{
i<
iap-dLMp-1)
+ w\
p/(p
¦"Г1/р,
(E-3)

Глава 3. Теория фирмы
175
х2 = ywf»~X) (wf>-X) + w2p/(p-1} )/P. (E-4)
Чтобы найти функцию издержек, подставим (Е-3) и (Е-4) в целевую
функцию задачи минимизации, откуда
c(w, у) = W]Xi (W? у) + w2x2(W, у) = y(wf9~l) + wp/(p4) )(P",)/P. n
Здесь может быть замечено некоторое сходство с теорией
потребителя, и это неслучайно, поскольку задача минимизации издержек
аналогична задаче минимизации расходов в теории потребителя. Действительно,
по определению
функция расходов: е(р, w) = minp-x при и(х)>и;
xeR"
функция издержек: c(w, у) = min w • х при f{\) > у.
xeR"
С математической точки зрения эти задачи одинаковы. Следовательно,
для каждой теоремы, доказанной нами для функции расходов, существует
аналогичная теорема для функции издержек. Мы сформулируем эти
утверждения без доказательств, поскольку они могут быть доказаны так же,
как соответствующие утверждения в теории потребителя.
Теорема 3.2. Свойства функции издержек.
Если f непрерывна и строго возрастает, то c(w, у) обладает еле-
дующими свойствами:
1) равна нулю при у = 0;
2) непрерывна в области определения;
3) для любых w » 0 строго возрастает и не ограничена по у сверху.
4) возрастает по w ;
5) однородна первой степени по w ;
6) вогнута по w.
Если f строго квазивогнута, то выполняется также
7) лемма Шепарда: c(w, у) дифференцируема по w в точке
(w°, y°) для любого w° »0 и
OWj
Пример 3.4. Рассмотрим функцию издержек Кобба — Дугласа,
?(w> у) = Aw*w\y. По свойству 7) теоремы 3.2 условный спрос на факто-

176
Часть I. Экономические агенты
ры производства можно получить путем ее дифференцирования по ценам
факторов, т.е.
, ч 9c(w, у) а_! в occ(w, у)
,(w, у)= \ " =aAw*lwly= ",
w,
(E-l)
^(w> ^^^^>^ (E-2)
ow2 w2
Если взять отношение функций условного спроса, мы увидим, что
x2(w, >>) р w, "
Это означает, что пропорции, при которых фирма с такой функцией
издержек будет использовать факторы производства, зависят только от
относительных цен факторов и не зависят от объема выпуска.
Определим долю фактора производства я,. = w;jc,.(w, y)/c(w, у),
как долю расходов на /-й фактор в общем объеме расходов фирмы.
Из (Е-1) и (Е-2) следует, что эти величины всегда постоянны и
s{ =а,
?
Будучи решениями задачи минимизации издержек фирмы, функции
условного спроса на факторы обладают некоторыми общими свойствами.
Эти свойства аналогичны свойствам функций компенсированного спроса
по Хиксу, поэтому нет необходимости повторять доказательства снова.
Теорема 3.3. Свойства функций условного спроса на факторы
производства.
Пусть производственная функция удовлетворяет
предположению 3.1, а соответствующая ей функция издержек дважды непрерывно
дифференцируема. Тогда:
1) функция x(w, у) однородна нулевой степени по w ;
2) матрица замещения, определяемая как
(дхх{у/, у) ax,(w, >>)Л
G*(W, y) =

Глава 3. Теория фирмы
177
симметрична и отрицательно полуопределена. В частности, свойство
отрицательной полуопределенности означает, что дх{(У?9 y)/dwi <0 для
всех i.
Однородные, или в более общей формулировке гомотетичные,
технологии производства часто встречаются в теоретических и прикладных
работах. Функции издержек и условного спроса на факторы производства,
соответствующие этим технологиям, обладают рядом свойств, некоторые
из которых перечислены ниже.
Теорема 3.4. Функции издержек и условного спроса на факторы
при гомотетичных технологиях производства.
1) Если производственная функция удовлетворяет
предположению 3.1 и является гомотетичной, то:
а) функция издержек является мультипликативно сепарабельной по
ценам факторов и выпуску и может быть записана как
c(w> У) - Ну)с(™> 1)> г&е Ку)— строго возрастающая функция, а
c(w, 1) — функция удельных (единичных) издержек, или издержек на
производство единицы выпуска;
б) функции условного спроса на факторы производства
мультипликативно сепарабельны по ценам факторов и выпуску и могут быть
записаны как x(w, у) = h(y)\(w, I), где h\y)>0, a x(w, 1)— условный
спрос на факторы для производства единицы выпуска.
2) Если производственная функция однородна степени ос > О, то:
а)с(^ y) = y/ac(w, 1);
6)x(w, j;) = y/ax(W, 1).
Доказательство. Вторую часть теоремы можно доказать аналогично
первой, и читателю предлагается проделать это самостоятельно в
качестве упражнения. Пункт б) первой части следует из леммы Шепарда,
поэтому необходимо доказать только пункт а).
Обозначим производственную функцию через F. Она гомотетична,
поэтому ее можно записать в виде F(x) = f(g(x)), где / строго
возрастает, а g однородна первой степени.
Для простоты предположим, что образом F является все множество
R+. Следовательно, как требуется показать в упражнении 3.5, f~\y) > О
для всех у>0. Для некоторого у>0 возьмем t = f~l(l)/f~l(y)>0.
Теперь заметим, что f(g(x))>y <=> g(x)>f~l(y) <=>
g(tx)>tf~\y) = f~\\) <=> f(g(tx))>l. Тогда функцию издержек,
соответствующую F, можно выразить следующим образом.

178
Часть I. Экономические агенты
c(w, у) = min w • х при /(g(x)) > у
Х€К"
= min w • х при f(g(tx)) > 1
xeR"
= - min w • tx при f(g(tx)) > 1
t xeR"
= - min w • z при f(g(z)) > 1
t zeR+
= •* У c(w I)
где в предпоследней строке производится замена z = tx.
Из строгого возрастания / следует строгое возрастание f~l, поэтому
требуемое утверждение выполняется для всех у > 0. Чтобы увидеть, что
оно выполняется и при у = 09 вспомним, что c(w, 0) = 0, и заметим, что
g@) = 0, где первое равенство следует из условия F@) = 0, а второе —
из однородности первой степени функции g. ¦
Общий вид функции издержек, который мы рассматривали до этого
момента, правильнее всего понимать как функцию, задающую издержки
фирмы в долгосрочном периоде. Ранее мы предполагали, что, выбирая
производственный план для минимизации издержек, фирма может менять
количество любого используемого ею фактора. В краткосрочном периоде
у нее такой возможности нет. Обычно фирма имеет некоторые
фиксированные обязательства, скажем, по аренде завода определенного размера
или оборудования определенного типа. Поскольку в краткосрочном
периоде фирма «связана» обязательством использовать некоторые факторы
в заранее установленном количестве и не может выбирать это количество
оптимальным образом, как в долгосрочном периоде, ее издержки в
краткосрочном периоде скорее всего будут отличаться от издержек в
долгосрочном периоде. Чтобы исследовать соотношение между этими двумя
типами издержек, определим ограниченную функцию издержек фирмы,
или функцию издержек фирмы в краткосрочном периоде.
Определение 3.6. Ограниченная функция издержек (функция
издержек в краткосрочном периоде).
Пусть производственная функция имеет вид /(z), где z = (x, x).
Пусть х является подвектором переменных факторов производства, а
х — подвектором постоянных факторов. Пусть www —
соответствующие этим подвектором цены переменных и постоянных факторов.

Глава 3. Теория фирмы
179
Ограниченная функция совокупных издержек, или функция издержек в
краткосрочном периоде, определяется как
sc(w,w,^; x) = minwx + wx при f(x,x)>y.
X
То есть, если x(w,w,y; x) является решением этой минимизационной
задачи, то
sc(yv,\v,y; x) = wx(w,w9<y; x) + w-x.
Оптимальные издержки на переменные факторы w-x(w,w,j>; x)
называются совокупными переменными издержками. Издержки на
фиксированные факторы, wx, называются совокупными постоянными
издержками.
Рассмотрим это определение внимательнее. Заметим, что функция
издержек в краткосрочном периоде отличается от обобщенных, или
долгосрочных, издержек только тем, что постоянные факторы входят в нее
не как выбираемые фирмой переменные, а как параметры. Отсюда
должно быть ясно, что для любого данного уровня выпуска издержки в
долгосрочном периоде, когда фирма может устанавливать объем
использования всех факторов оптимальным образом, не могут превышать издержки
в краткосрочном периоде, когда оптимальным образом выбирается объем
только некоторых, а не всех факторов производства.
Это проиллюстрировано на рис. 3.5 с использованием изоквант и изо-
кост (здесь для простоты мы предположили, что wx = 1; лишние параметры
функций издержек на рисунке не показаны). Если в краткосрочном
периоде фирма имеет х2 единиц постоянного фактора, то она должна
использовать комбинации факторов А, С и Е для производства у\ у1 и уъ
единиц продукции и нести краткосрочные издержки sc(y]), sc(y2) и sc(y3)
соответственно. В долгосрочном периоде, когда фирма может выбирать
объемы использования обоих факторов оптимальным образом, она будет
использовать комбинации факторов В, С и D, а ее издержки составят
соответственно с(У), с(у2) и с(у3). Заметим, что sc(yl) и sc(y3) строго
больше, чем с(у1) и с(у3) соответственно, и sc(y2) = c(y2).
Еще раз посмотрим на рис. 3.5. Является ли случайным совпадение
долгосрочных и краткосрочных издержек при уровне выпуска у2? Нет,
не является. Почему же два вида издержек равны? Из рисунка легко
увидеть, что фиксированный объем второго (постоянного) фактора х2 в
точности совпадает с объемом х2, который фирма выбрала бы в
долгосрочном периоде для производства у2 при действующих ценах на факторы,

180
Часть I. Экономические агенты
т.е. х2, по сути, является элементом оптимального вектора факторов.
Поэтому при объеме выпуска у2 различия между издержками
краткосрочного и долгосрочного периода быть не может. Заметим далее, что в
подобной связи между х2 и у2 ничего особенного нет. Издержки
производства У в краткосрочном и долгосрочном периодах совпали бы при
наличии у фирмы только х2 единиц постоянного фактора, а для
производства уъ издержки в краткосрочном и долгосрочном периодах совпали
бы, если бы у фирмы было только х2 единиц фиксированного фактора.
Различные объемы постоянного фактора порождают различные функции
краткосрочных издержек, но в каждом случае при некотором уровне
выпуска издержки в краткосрочном и долгосрочном периодах совпадут.
С(у3) 5ф3)
c(yl) sc(yl) c(y') = sc(yz)
Рис. 3.5. sc(w,w,j; x)>c(w,\v,y) для любых уровней выпуска у
*> *i
Продолжая изучать эту связь, обозначим через х(у) оптимальный
объем постоянных факторов, выбираемый так, что краткосрочные
издержки выпуска у при данных ценах минимальны. Тогда тождество
c(w,w,jO = sc(w,w,>>; х(у))
C-3)
верно для любых у. Далее, поскольку объем постоянных факторов
выбран так, чтобы минимизировать краткосрочные издержки, оптимальное
значение х(у) должно быть таким, чтобы условия первого порядка на
минимум выполнялись как тождества:
dsc(w,w,y; xQ0)_0
Эх.
C-4)

Глава 3. Теория фирмы
181
для каждого постоянного фактора /. Продифференцируем тождество
C-3) и используем C-4), чтобы убедиться в том, что
<fc(w,w,у) _ dsc(w,w9y; х(у)) | у dsc(w,\v9y; х(у)) дх^у) _
dy ду i dxi ду
dsc(w,w9y; xQQ)
C-5)
Обобщим все то, что нам удалось показать. Во-первых, задача
минимизации издержек в краткосрочном периоде связана с большим числом
ограничений, чем в долгосрочном, поэтому sc(w,\v,y; x)>c(w,w,}>) для
любых объемов выпуска и постоянных факторов. Во-вторых, для любого
уровня выпуска тождество C-3) утверждает, что краткосрочные и
долгосрочные издержки совпадут для некоторого значения функции издержек в
краткосрочном периоде, соответствующего определенному уровню
постоянного фактора. Наконец, C-5) гласит, что наклон этой краткосрочной
функции издержек будет равен наклону долгосрочной функции издержек в
пространстве «издержки — выпуск». (Этот вывод, конечно, можно было
получить и напрямую, воспользовавшись теоремой об огибающей). Если
две функции принимают одно и то же значение в одной и той же точке на
плоскости, а их наклоны равны, то они касаются. Таким образом, мы
приходим к выводу, знакомому из курса микроэкономики промежуточного
уровня: кривая долгосрочных совокупных издержек является нижней
огибающей всего семейства кривых краткосрочных совокупных издержек! Эта
ситуация изображена на рис. 3.6.
Издержки
sc{y\x)
c(w, у)
Рис. 3.6. Кривая совокупных издержек в долгосрочном периоде,
являющаяся огибающей кривых совокупных издержек в краткосрочном периоде

182
Часть L Экономические агенты
3.4. Двойственность в производстве
Учитывая очевидное структурное сходство между задачами
минимизации издержек фирмы и минимизации расходов индивида, нет ничего
удивительного в том, что между производством и издержками, как и
между полезностью и расходами, существует двойственность. Принцип тот
же самый: если взять производственную функцию и получить
соответствующую функцию издержек, то можно из этой функции издержек снова
получить производственную функцию. Если исходная производственная
функция квазивогнута, то полученная производственная функция
совпадает с исходной. Если же исходная функция не квазивогнута, то
полученная производственная функция будет ее «вогнутой модификацией». Более
того, любая функция, обладающая всеми свойствами функции издержек,
порождает некоторую производственную функцию, для которой она
является функцией издержек.
Этот вывод является одним из важнейших достижений современной
теории и имеет огромное значение для прикладных исследований.
Экономистам больше не нужно начинать изучение фирмы с ее технологии и
запутанных технических данных. Вместо этого можно оценить функцию
издержек фирмы, используя наблюдаемые рыночные цены факторов
производства и объемы выпуска, а затем «восстановить» по ней
соответствующую производственную функцию.
Мы снова воспользуемся сходством между функциями издержек и
расходов и сформулируем теорему, которая представляет аналог
теорем 2.1 и 2.2 и доказательство которой следует из их доказательства.
Теорема 3.5. Восстановление производственной функции из
функции издержек.
Пусть отображение c:M"+xR+ —»М+ удовлетворяет свойствам
1)—7) функции издержек, перечисленным в теореме 3.2. Тогда функция
f: W+ —> М+, определенная как
/(x) = max{j>>0|wx>c(w, y\ Vw»0},
является возрастающей, неограниченной сверху и квазивогнутой. Кроме
того, с является функцией издержек, порождаемой функцией f.
Наконец, можно также сформулировать теорему о восстановлении
для спроса на факторы производства. Главный вопрос при этом таков:
если функция x(w,j/) характеризует спрос некоторой фирмы на факторы
производства, то при каких условиях мы можем сделать вывод о том, что
ее поведение соответствует гипотезе минимизации издержек при каждом
уровне выпуска?

Глава 3. Теория фирмы
183
Как и в случае с потребительским спросом, ответ будет зависеть от
возможности восстановить функцию издержек, порождающую данный
спрос на факторы производства. То есть спрос на факторы будет
соответствовать требованию минимизации издержек при каждом уровне выпуска
тогда и только тогда, когда существует функция издержек с,
удовлетворяющая условию
3C(W, у) 4 1
г—— = xi(w, у), 1 = 1 ...,л.
Не должен вызывать удивления следующий результат, в
справедливости которого читателю предлагается убедиться самостоятельно,
повторив доказательство теоремы о восстановлении для случая
потребительского спроса.
Теорема 3.6. Восстановление функции издержек на основе
функции условного спроса.
Непрерывно дифференцируемая функция x(w, у), отображающая
М"+хМ+ в R"+, является функцией условного спроса на факторы
производства, порожденной некоторой возрастающей квазивогнутой
производственной функцией, тогда и только тогда, когда она однородна
нулевой степени по w, а ее матрица замещения (ij -й элемент которой равен
ux,(w, y)/d\Vj) симметрична и отрицательно полуопределена.
3.5. Конкурентная фирма
В данном разделе мы рассмотрим поведение фирмы, которая является
совершенно конкурентной как на рынках факторов производства, так и на
рынке готовой продукции. Фирма является совершенно конкурентной на
рынке продукции, если она считает, что объем ее производства и продаж
не оказывает влияния на сложившиеся рыночные цены. Конкурентная
фирма наблюдает рыночную цену своей продукции, предполагая, что она
не изменится в зависимости от ее объема продаж, и соответствующим
образом планирует свою работу. Такая фирма-цено получатель
воспринимает цену как данную и на рынке факторов, и на рынке готовой продукции.
Одна из интерпретаций этого заключается в том, что хотя фирма
может выбирать цену, по которой она продает свою продукцию (и цены, по
которым она приобретает факторы производства), если она попытается
продать продукцию по цене выше рыночной, то ей не удастся этого
сделать, поскольку на конкурентном рынке продукции потребители
полностью информированы о том, что другие фирмы продают тот же самый
продукт по более низкой цене. В то же время, если фирма может продать

184
Часть I. Экономические агенты
сколько угодно продукции по рыночной цене, ей нет необходимости
снижать цену. Следовательно, для фирмы лучше всего всегда устанавливать
цену на свою продукцию, равную рыночной. Таким образом, фирма
действует так, как если бы она воспринимала цену своей продукции как
данную. Аналогично фирма не может платить за факторы производства по
цене ниже рыночной, поскольку на конкурентном рынке факторов владельцы
этих факторов могут продать их другим фирмам по более высокой,
рыночной цене. И поскольку у фирмы снова нет стимула платить больше,
оптимальное решение для нее — предлагать рыночную цену за факторы.
Хотя и само предположение о том, что цена воспринимается как
некая данность, и его условия крайне далеки от реальности, они дают
возможность построить простую модель фирмы, позволяющую прийти к
очень важным выводам. Конкурентная фирма, таким образом,
заслуживает самого внимательного изучения.
3.5.1. Максимизация прибыли
Прибыль фирмы равна разнице между доходом (выручкой) от
продажи готовой продукции и расходами на приобретение факторов для ее
производства. Конкурентная фирма может продать каждую единицу
продукции по рыночной цене р, поэтому ее доход является линейной
функцией выпуска R(y) = ру. Предположим, что фирма собирается выпустить
у0 единиц продукции. Если вектор х° факторов производства позволяет
произвести у0 единиц продукции, а вектор w задает цены факторов, то
издержки использования х° для производства у0 равны w • х°. Таким
образом, прибыль фирмы составит ру° -w-x°. Здесь стоит отметить две
вещи. Во-первых, у° может не быть наилучшим вариантом выпуска для
фирмы. Во-вторых, даже если бы он и был наилучшим, вектор
используемых факторов х° может не быть наилучшим способом его
производства. Поэтому фирме приходится принимать решения и об объеме
выпуска, и о том, сколько и каких факторов использовать для производства.
Как обычно, мы предполагаем, что основная цель фирмы — это
максимизация прибыли. Тогда она выберет такой уровень выпуска и такую
комбинацию факторов, которые будут решением следующей задачи:
maxp^-wx при /(х)>у, C-6)
(х,у)>0
где f(x) — производственная функция, удовлетворяющая
предположению 3.1. Решение этой задачи показывает, сколько продукции фирма
продаст и сколько и каких факторов производства приобретет.

Глава 3. Теория фирмы
185
Мы снова можем заменить в ограничении неравенство на равенство в
силу строгого возрастания производственной функции. Следовательно,
поскольку у = f(\), данную задачу максимизации можно переписать как
задачу выбора вектора факторов производства:
max pf(x) - w • х. C-7)
X€R"
Предположим, что эта задача имеет внутреннее решение (вектор
факторов х* » 0; при этом объем выпуска, максимизирующий прибыль,
равен у* = /(х*)). Тогда, поскольку отсутствуют ограничения, согласно
условиям первого порядка градиент максимизируемой функции при х = х*
равен нулю, или
№*) . f
p-^-z = w, для каждого/ = 1, ...,и.
Левую часть равенства — произведение цены продукции на
предельный продукт /-го фактора — часто называют предельным доходом от
i -го фактора. Он задает скорость увеличения дохода при увеличении
затрат /-го фактора (увеличение дохода при добавлении (малой единицы)
/-го фактора). В оптимуме эта величина должна равняться издержкам на
единицу / -го фактора, а именно — wi.
Предполагая далее, что все wi положительны, можно
воспользоваться условиями первого порядка, чтобы получить соотношение
df(\)/dxi u>, . .
г-^—- = —- для всех /, j ,
ЭДх )/dxj Wj
которые означают, что предельная норма технологического замещения
(MRTS) любых двух факторов производства равна отношению их цен.
Они в точности повторяют условия выбора факторов при минимизации
издержек, которые мы получили в C-2). Тем самым подтверждается наше
интуитивное представление о том, что максимизация прибыли требует
минимизации издержек производства.
Задачу максимизации прибыли фирмы можно сформулировать и
таким образом, чтобы подчеркнуть, что при этом необходимо
минимизировать издержки. Вместо того чтобы максимизировать прибыль в один шаг,
как это делалось раньше, рассмотрим двухшаговую процедуру. Сначала
для каждого из возможных уровней выпуска рассчитаем (наименьшие)
издержки производства, а затем выберем уровень выпуска,
максимизирующий разницу между доходом, который он приносит, и издержками.

186
Часть I. Экономические агенты
Первый шаг этой процедуры нам уже знаком. Наименьшие издержки
производства у единиц продукции задаются функцией издержек c(w, у).
Тогда второй шаг сводится к решению следующей задачи максимизации:
maxz?v-c(w, у). C-8)
>->о
В упражнении 3.49 предлагается проверить, что C-7) действительно
эквивалентно C-8).
Если у* > О является оптимальным уровнем выпуска, то он
удовлетворяет условию первого порядка
<fc(w, /)_n
Р ~ = °>
dy
т.е. выпуск устанавливается таким образом, чтобы цена равнялась
предельным издержкам. Условия второго порядка требуют, чтобы
предельные издержки в оптимуме не убывали, d2c(y*)/dy2 >0. Выбор объема
выпуска иллюстрирует рис. 3.7.
Цена, издержки
А
dc(w, у)
тс(у) =
dy dy
I ¦ ^ > Выпуск
/ у
Рис. 3.7. Выбор объема выпуска для конкурентной фирмы.
Прибыль максимизируется в точке у , где цена равна предельным
издержкам, а предельные издержки являются неубывающими
3.5.2. Функция прибыли
Если / удовлетворяет предположению 3.1, то решение задачи
максимизации прибыли C-6) (если существует) единственно для каждого
вектора цен (/?, w). Оптимальный уровень выпуска у* = у(р, w)
называется функцией предложения продукции фирмы, а вектор оптимального
объема факторов производства х* = х(р, w) задает функции спроса фир-

Глава 3. Теория фирмы
187
мы на факторы производства. Последние являются полноценными
функциями спроса, поскольку в отличие от функций условного спроса на
факторы, зависящих от выпуска, они обеспечивают достижение главной
цели фирмы — максимизацию прибыли. Функция прибыли,
определенная ниже, представляет собой полезный инструмент для изучения этих
функций спроса и предложения.
Определение 3.7. Функция прибыли.
Функция прибыли фирмы зависит только от цен на продукцию и
факторы производства и определяется как решение следующей задачи:
к(р, w) = max py - w • х при /(х) > у.
(х,^)>0
Ценность функции прибыли зависит от выполнения некоторых
непременных условий. Среди них немаловажным является сам факт
существования решения задачи максимизации прибыли. Это не просто
придирка, как может показаться. Пусть технология имеет возрастающую
отдачу от масштаба и пусть х; и / = /(х') максимизируют прибыль при
ценах р и w. Возрастающая отдача означает, что
f(tx) > tf{x) для всех t > 1.
Умножим это неравенство на р > О, вычтем w • tx из обеих частей,
преобразуем и, используя условие />1 и неотрицательность прибыли, получим
pf(tx) - w • /х' > pf{x) - w • х' для всех t>\.
Это означает, что увеличение объема факторов в пропорции t > 1
приводит к росту прибыли, что противоречит нашему предположению о том,
что при х и f{x) прибыль уже была максимальной. Заметим, что в
случае постоянной отдачи от масштаба эта проблема не возникает, если
максимальный уровень прибыли оказывается равным нулю. Однако тогда
неопределенным является масштаб деятельности фирмы, потому что для
всех t>\ комбинации (./Ж) и (ty\ tx) обеспечивают один и тот же —
нулевой — уровень прибыли.
Если функция прибыли определена корректно, то она обладает
некоторыми полезными свойствами, каждое из которых должно казаться
знакомым и вполне разумным.
Теорема 3.7. Свойства функции прибыли.
Если функция f удовлетворяет предположению 3.7, тогда при
р>0 и w > 0 функция прибыли (на том множестве, где она корректно
определена) непрерывна и

188
Часть I. Экономические агенты
1) возрастает по р ;
2) убывает по w;
3) однородна первой степени по (/?, w);
4) выпукла по (/?, w);
5) дифференцируема по (/?, w) » 0. Кроме того (лемма Хотеллинга),
дк(р, w) , ч -Эя(/?, w) / ч . , .
—^—L = y(p, w) и lp_Z = X/(A W), j = 1,2, ...,л.
dp dw,.
Доказательство. Доказательства каждого свойства проводятся по
знакомым схемам, и поэтому большинство из них оставлено в качестве
упражнений. Ниже мы приведем только краткое доказательство выпуклости.
Пусть объем выпуска у и вектор факторов производства х
обеспечивают максимизацию прибыли при ценах продукции р и факторов w, a
у и х'— при ценах p'w w'. Определим р* =#? + A-/)// и
w' = tv/ + A -t)yt' для 0 < t < 1, и пусть у* и х* максимизируют прибыль
при ценах /hw'. Тогда
я(р, w) = py - w • х > /ту* - w • х*,
Следовательно, для 0 < / < 1
m(/7, W) + A - t)n(P\ w') > ftp + A - t)p)y - (/W + A - ОW') • X* = 7l(//, w') ,
что доказывает выпуклость. ¦
Заметим, что по лемме Хотеллинга предложение фирмы и ее спрос на
факторы могут быть получены напрямую простым дифференцированием.
Отсюда можно вывести ограничения на поведение фирмы, которые
следуют из гипотезы максимизации прибыли. Они перечислены в
следующей теореме.
Теорема 3.8. Свойства функций предложения фирмы и спроса
на факторы производства.
Пусть к(р, w) — дважды непрерывно дифференцируемая функция
прибыли для некоторой конкурентной фирмы. Тогда для всех р > О и
w » 0 (на том множестве, где функция корректно определена):
1) имеет место однородность нулевой степени:
y(tp, tw) = y(p, w) для всех t > О,

Глава 3. Теория фирмы
189
x.(tp, t\v) = xj(p, w) для всех t>0 и / = 1, ...,и;
2) выполняются законы спроса и предложения :
ЭхД/?, w)
7W.
Эр '
< 0 для всех /' = 1, ..., и;
5) матрица замещения
f ду(р, w) Эу(р, w)
dp
dw<
-Эх, О, w) -Эх, (/7, w)
dp
dw,
-dxt(p, w)
-bxn{p, w) -Эх„(/7, w) -Эхи(р, w)
dp
dwx
dw„
симметрична и положительно полу определена.
Доказательство. Однородность функций предложения продукции и
спроса на факторы следует из леммы Хотеллинга и однородности первой
степени функции прибыли. Свойство 2) гласит, что предложение
продукции возрастает по ее цене, а спрос на каждый фактор убывает по его цене.
Чтобы убедиться в этом, воспользуемся леммой Хотеллинга и выразим
функции спроса и предложения как
у(р, w) =
MP, w)
dp
< \ / п^Л W) • 1
х,(р9 w) = (-l)—^ , 1 = 1, ...,«.
dw,
Поскольку эти равенства верны для всех р и w, продифференцируем
обе части каждого из них, что дает
Эу(р, w) _ д2к(р, w)
dp
dp2
>0,
1 Хотя это свойство следует из п. 3), мы выделили его в отдельный пункт, чтобы
подчеркнуть его значение.

190
Часть I. Экономические агенты
Каждая производная в правой части с точностью до знака равна второй
частной производной функции к{р9 w). Поскольку к{р, w) выпукла по
р и по w, ее вторые частные производные неотрицательны, что с учетом
указанных знаков доказывает пункт 2).
Матрица замещения в пункте 3), как уже должно быть ясно,
совпадает с матрицей Гессе (матрицей вторых частных производных) функции
прибыли. Она симметрична по теореме Юнга и положительно
полуопределена вследствие выпуклости функции прибыли. {Примечание: обратите
внимание на знак каждого члена, включающего функцию спроса на
фактор производства.) ¦
Аналогично случаю потребительского спроса и условного спроса на
факторы, для функций спроса на факторы и предложения готовой
продукции также существует теорема о восстановлении. Читателю
предлагается разобраться с этим вопросом самостоятельно в качестве упражнения.
Пример 3.5. Рассмотрим производственную функцию с постоянной
эластичностью замещения:
В упражнении 3.11 вам будет предложено показать, что при р < 1 она
характеризуется убывающей отдачей от масштаба. Предположим, что
р<1 и 0*р<1.
В предположении о том, что решение задачи максимизации прибыли
C-6) является внутренним, условия первого порядка сводятся к
следующему виду:
- w, + /?Р(хр + хр2 )(р~р)/р хр~1 = 0, (Е-1)
- w2 + /?Р(хр + х[ )(Р_Р)/Р jcp_1 = 0, (Е-2)
(х,р+*2р)р/р-;у = 0. (Е-З)
Из отношения (Е-1) и (Е-2) получим хх = x2{wjw2)xl{9_1). Подставив его в
(Е-З), после простых преобразований получим
Xj =^(^/(p-i)+^/(p-i))-VpwV(p-i) s / = lf 2. (E-4)
Подставив этот результат в (Е-1) и выразив у, найдем функцию
предложения

Глава 3. Теория фирмы
191
у = (pP^AM^pAp-i) + ^/(p-DjKp-D/pCP-d (Е.5)
Из (Е-4) и (Е-5) найдем функции спроса на факторы производства:
*, =^1/(M)(^Pr1/(M)D/(p-,) + w2p/(р-П)(р-Р)/р(Р-1)? / = 12 (Е-6)
Чтобы получить функцию прибыли, подставим последние два
равенства в целевую функцию:
к(р, w) = /7/(М)(Ч + wOP/r(M)p-p/(M)(l-P), (Е-7)
где г = р/(р-1).
Заметим, что если |3 = 1, то производственная функция имеет
постоянную отдачу от масштаба, а функция прибыли не определена, как мы
видели раньше. Если р>1 и производственная функция имеет
возрастающую отдачу от масштаба, то мы, несомненно, можем получить
соотношение (Е-7), формально проведя те же преобразования, но что это нам
дает? Если посмотреть внимательнее и проверить условия второго
порядка, то мы увидим, что (Е-5) и (Е-6) обеспечивают локальный минимум
прибыли, а не максимум. Таким образом, максимум прибыли при
возрастающей отдаче также не определен. ?
Рассмотренную нами функцию прибыли лучше всего понимать как
функцию прибыли в долгосрочном периоде, поскольку мы предположили,
что фирма может устанавливать уровень выпуска и объем используемых
факторов по своему усмотрению. Как и для функции издержек, мы можем
построить ограниченную функцию прибыли, или функцию прибыли в
краткосрочном периоде, описывающую поведение фирмы, когда
некоторые из факторов производства постоянны, а некоторые являются
переменными.
Ограниченная функция прибыли может быть эффективным
инструментом по нескольким причинам. Во-первых, во многих приложениях
разумно предполагать, что предложение по крайней мере некоторых
факторов производства фиксировано. При обычных предположениях
относительно технологии наличие постоянных факторов обычно гарантирует
существование решения задачи максимизации прибыли фирмы. Наконец,
большинство свойств обобщенной функции прибыли, связанных с ценами
на продукцию и факторы производства, сохраняются, но относятся к
ценам на продукцию и переменные факторы производства.
Теорема 3.9. Ограниченная функция прибыли (функция
прибыли в краткосрочном периоде).
Пусть производственная функция имеет вид /(х, х), где х —
подвектор переменных факторов, ах — подвектор постоянных факторов

192
Часть I. Экономические агенты
производства. Пусть www — соответствующие векторы цен на
переменные и постоянные факторы. Ограниченная функция прибыли
(функция прибыли в краткосрочном периоде) определяется как
к(р, w, w, x) = max#y-wx-wx при f{x,x)>y.
Решения у(р, w, w, x) и х(р9 w, w, x) этой задачи (при различных
значениях (р, w, w, x)) называются соответственно функциями
краткосрочного, или ограниченного, предложения и спроса на переменные
факторы производства.
Для всех р>0 и w » 0 функция к(р9 w, w, x) (на множестве, где
она корректно определена) непрерывна по р и w, возрастает по р,
убывает по w и выпукла по (/?, w). Если к(р, w, w, x) дважды
непрерывно дифференцируема, то функции у{р, w, w, х) и х(р, w, w, x)
обладают всеми тремя свойствами, приведенными в теореме 3.8 для
выпуска и цен на переменные факторы производства.
Доказательство. Доказательство свойств к(р, w, w, x) повторяет
доказательство аналогичных свойств, сформулированных в теореме 3.7.
Однородность по ценам переменных факторов является единственным
свойством, которое не переносится на случай функции прибыли в
краткосрочном периоде. Свойства функций краткосрочного спроса и
предложения доказываются аналогично доказательству теореме 3.8, за
исключением однородности, требующей некоторой модификации доказательства и
оставленной в качестве упражнения. ¦
Пример 3.6. Выведем краткосрочную функцию прибыли для
технологии Кобба — Дугласа с постоянной отдачей от масштаба. Если
зафиксировать х2 на уровне х2, то наша задача принимает вид:
max ру - w,jc, - w2х2 при х"х12~а > у,
у*
где 0 < а < 1. В предположении, что решение внутреннее, ограничение
выполняется как равенство, поэтому его можно подставить вместо у в
целевую функцию. Тогда задача сводится к выбору значения переменной х,:
maxрх"х2~а - wxxx - w2x2. (Е-1)
Условие первого порядка по дс, требует, чтобы
apx^xxx2a-wx = 0.

Глава 3. Теория фирмы
193
Выразив х,, получим
Х1=р1/{1-а^-})а1/A-а)х2. (Е-2)
Подставив это выражение в (Е-1) и упростив, найдем краткосрочную
функцию прибыли:
к(р, wp w2, x2) = p,/A-aV^/(a-1)aa/A-a4l-a)J2-vv23c2. (Е-3)
Заметим, что, поскольку a < 1, краткосрочная прибыль корректно
определена даже при том, что производственная функция демонстрирует
постоянную отдачу от масштаба (в долгосрочном периоде).
По лемме Хотеллинга краткосрочное предложение можно найти,
дифференцируя (Е-3) по р :
у(р9 wl9 w29 х2) = Ыр> "¦' *" ^ =р«™^1)а«™х2.
Эр
Можно ожидать, что функция предложения будет иметь положительный
наклон. Для проверки убедимся в этом:
<ty(P> Wp VP2, 3C2)_ a Ba-i)/(l-a)H,a/(a-»)a«/(l-«)j >Q Q
dp 1-oc ' 2
В последний раз посмотрим на поведение фирмы в краткосрочном
периоде. Отвлечемся от спроса на факторы производства и обратим
внимание на предложение готовой продукции. Задачу определения объема
факторов производства можно включить в краткосрочную функцию
издержек и выразить прибыль в краткосрочном периоде как
л(/?, w, w, x) = maxpy-sc(y, w, w, x).
v
По условию первого порядка при оптимальном положительном объеме
выпуска у*
dscjy*)
р = —1 '
dy
т.е. цена равняется (краткосрочным) предельным издержкам.
Является ли это утверждение универсальным правилом, которому
должна следовать конкурентная фирма при определении объема выпуска
в краткосрочном периоде? Предположим, что цена равна предельным
издержкам при некотором у1 > О. Тогда совокупные краткосрочные
издержки можно выразить как сумму совокупных переменных издержек

194
Часть I. Экономические агенты
tvc(y) и совокупных постоянных издержек tfc, где первая формула задает
оптимальные затраты на переменные факторы производства, а вторая — на
постоянные факторы. Опуская параметры, прибыль в краткосрочном
периоде можно записать как
Я1 = pyl -tvc(yx)-tfc.
Что будет, если я1 отрицательна! Фирме по-прежнему лучше
производить У, даже если это приносит убытки? Вышеприведенное условие
первого порядка гласит, что если фирма намерена выпускать
положительный объем продукции, то уровень выпуска, максимизирующий
прибыль (или минимизирующий убытки), составит у1, где цена равна
предельным издержкам. Однако фирма всегда может закрыться и не
производить ничего. Если она произведет у = О, то не получит доходов и не
будет приобретать переменные факторы производства, поэтому
переменные издержки будут равны нулю. При этом фирме по-прежнему
необходимо нести постоянные издержки, поэтому прибыль (убытки) при
закрытии составит
я0 =p.Q-tvc@)-tfc = -tfc<0.
Очевидно, что фирма, максимизирующая прибыль, будет выбирать между
производством _у'>0 с убытками и «производством» у = 0 с убытками в
зависимости от того, какой вариант приносит большую прибыль
(меньшие убытки). Таким образом, фирма произведет у1 > О, только если
я1 - я0 > 0, или если
pyl-tvc(yl)>0,
что, в свою очередь, эквивалентно условию
У
Теперь у нас есть полное описание процесса выбора фирмой объема
выпуска в краткосрочном периоде. Если фирма производит
положительный объем продукции, то она будет производить его на таком уровне,
чтобы цена равнялась предельным издержкам (при неубывающих
предельных издержках) и не была ниже средних переменных издержек. Если
при равенстве предельным издержкам цена окажется ниже средних
переменных издержек, то фирма закроется и не будет производить ничего.
В заключение добавим, что между функциями прибыли и
производственными функциями, так же как и в случае с функциями издержек, су-

Глава 3. Теория фирмы
195
ществует полный набор отношений двойственности. Как для
долгосрочного, так и для краткосрочного периода каждая функция с необходимыми
свойствами является функцией прибыли для некоторой производственной
функции, соответствующей обычным требованиям. Таким образом,
исследователь может выбирать, начинать ли ему работу со спецификации
технологии фирмы или со спецификации ее функции прибыли. (Более
подробно об этом см. в статье Диверта [Diewert, 1974], а также теорему о
восстановлении в упражнении 3.51.)
3.6. Упражнения
3.1. Эластичность среднего продукта определяется как
(dAPt;(х) / dxt)(xi I APi(x)). Покажите, что она равна цДх) — 1. Покажите
также, что средний продукт является возрастающим (постоянным,
убывающим), если предельный продукт больше (равен, меньше) среднего
продукта.
3.2. Пусть y = f(x{, x2) — производственная функция технологии с
постоянной отдачей от масштаба. Покажите, что если средний продукт
первого фактора х{ возрастает, то предельный продукт второго фактора
х2 отрицателен.
3.3. Покажите, что однородная первой степени производственная функ-
п
ция может быть представлена в виде f(x) = y^MPi(x)xi, где MFJ(x) —
/=i
предельный продукт / -го фактора.
3.4. Пусть производственная функция F(x) является гомотетичной,
т.е. представима в виде F(x) = f(g(x)), где / — строго возрастающая, а
g — однородная первой степени функции. Покажите, что х1 = t*x°, где
/* =f~l(y)/fl(l)9 если точка х° принадлежит единичной изокванте, т.е.
/г(х°) = 1, ах1 — это точка на луче, проходящем через точку х°, и
F(xl) = j, т.е. х1 принадлежит изокванте, соответствующей выпуску у.
3.5. Пусть производственная функция F(x) является гомотетичной,
т.е. представима в виде F(x) = f(g(x)), где / — строго возрастающая, а
g — однородная первой степени функции. Покажите, что если образом
функции F является R+, то /_1 (у) > 0 для всех у > 0.
3.6. Пусть производственная функция f(x{9 x2) не убывает и
однородна первой степени. Покажите, что изокванты функции / обобщенно
параллельны (вдоль луча), т.е. имеют одинаковый наклон в каждой точке
вдоль любого луча, выходящего из начала координат. Используя этот факт,

196
Часть I. Экономические агенты
покажите, что предельная норма технологического замещения зависит
только от пропорции используемых факторов производства. Покажите
также, что МРХ является неубывающей, а МР2 невозрастающей функцией
от отношения факторов производства R = x2/xl. Докажите, что эти
результаты имеют место и для гомотетичной производственной функции.
3.7. Голдман и Узава [Goldman, Uzawa, 1964] показали, что
производственная функция является нестрого сепарабельной относительно
распределения {TV,, ...,NS} тогда и только тогда, когда она может быть
представлена в виде
/(x) = g(/'(x<'>), ...,/5(х<*>)),
где g — некоторая функция S переменных и для каждого / /'(х(/)) —
функция от подвектора факторов х(/) только из группы i. Они также
показали, что производственная функция будет строго сепарабельной тогда
и только тогда, когда она может быть записана в виде
/(x) = G(/1(xA)) + ... + /5(xE))),
где G — строго возрастающая функция одной переменной и все
предположения относительно подфункций и подвекторов сохраняются.
Удостоверьтесь в том, что эти утверждения верны, показав, что производственные
функции являются соответственно нестрого и строго сепарабельными.
3.8. Рассмотрите леонтъевскую производственную функцию вида
j> = min{ajcp px>},
где a > 0 и E > 0. Изобразите карту изоквант для данной технологии и
покажите, что в точках, где эластичность замещения с определена, она
равна нулю.
3.9. Вычислите эластичность замещения а для производственной
функции Кобба — Дугласа вида у = Ах*х\, где А>0, ос>0 и C > 0.
3.10. Рассмотрите производственную функцию с постоянными
предельными долями факторов производства (CMS) вида у = Ах*х1{* - тх2.
Вычислите эластичность замещения о для этой функции и покажите, что
при т Ф 0 и а Ф1 АР2 возрастает, если a —И. При каких условиях
данная функция сводится к линейной производственной функции?
3.11. Обобщенная производственная функция с постоянной
эластичностью замещения (CES) имеет следующий вид:
7 = л1а0+?а,.х,р
р/р

Глава 3. Теория фирмы
197
где Л > 0, сс0 > 0, а, > О и 0^р< 1. Вычислите эластичность замещения
GfJ для этой функции и покажите, что при ос0 = 0 эластичность масштаба
определяется параметром р.
3.12. Вычислите эластичность замещения для производственной
функции из примера 3.2.
3.13. Покажите, что эластичность замещения для любой
гомотетичной производственной функции равна эластичности замещения для
однородной первой степени части этой функции.
3.14. Рассмотрите производственную функцию
(п Y/p
у= Za<*4 ' где Za/=1 и °^р<1-
V /=i ) /=i
Покажите, что а„ = для любых i' Ф j.
4 1-р J
3.15. Для производственной функции с постоянной эластичностью
замещения из предыдущего примера докажите следующие утверждения,
которые были сформулированы в тексте:
п
а) limj^JJx,0' ;
б) lim^ = min{xp ...,x„}.
3.16. Пусть функция/удовлетворяет всем условиям предположения 3.1.
а) Покажите, что задача минимизации издержек C-1) имеет решение,
х* для всех (w, у) > 0 таких, что ye /(R+).
б) Покажите, что решение задачи C-1) единственно, если, кроме того,
w»0.
3.17. Докажите пункты 1)—4) теоремы 3.2 (при доказательстве можно
считать, что функция издержек c(w, у) дифференцируема).
3.18. Докажите пункты 1)—4) теоремы 3.2 (не предполагая
дифференцируемое™ функции издержек c(w, у)).
3.19. При каких ограничениях на параметры А, а и C функция
c(w> у) = Aw"\^y из примера 3.4 является функцией издержек для
некоторой технологии?
3.20. Докажите теорему 3.3.
3.21. Вещественнозначная функция называется супераддитивной,
если /(z1 +z2)>/(zl) + /(z2). Покажите, что любая функция издержек
является супераддитивной по ценам факторов. Используя этот факт, по-

198
Часть I. Экономические агенты
кажите также, что функция издержек не убывает по ценам факторов, не
предполагая ее дифференцируемость.
3.22. Верно ли следующее утверждение: «Если A,(w, у) —
множитель Лагранжа в задаче минимизации издержек фирмы, то
wc(w, j>) = A,(w, X)»?
3.23. Покажите, что тс(у) = wi I MPi для каждого фактора /,
используемого фирмой, и тс(у) < Wj I MPj для каждого фактора j, не
используемого фирмой, если фирма производит выпуск у > О.
3.24. Вычислите функцию издержек и условный спрос на факторы
для леонтьевской производственной функции из упражнения 3.8.
3.25. Докажите части 16), 2а) и 26) теоремы 3.4.
3.26. Пусть фирма, технология которой обладает всеми стандартными
свойствами, выпускает продукцию, используя три фактора производства.
Условный спрос фирмы на факторы производства описывается функциями
xi (w\ > w2, и>з; у), / = 1,2,3. Некоторые из следующих случаев согласуются с
задачей минимизации издержек, а некоторые — нет. Если, по вашему
мнению, указанный случай не согласуется с задачей минимизацией издержек,
то объясните почему; если же утверждение верно, то приведите пример
соответствующей производственной функции или функции издержек:
а) дх2 /dw, > 0 и дх3 /Эи>, > О;
б) дх2 /dw, > 0 и дх3 /дн>, < 0;
в) Эх,/Эу<0, дх2/ду <0 и Эх3/Эу <0;
г) Эх, /ду = 0;
д) Э(Х /x2)/dw3 =0.
3.27. На рис. 3.8 изображены графики функций издержек фирм А и
В в зависимости от цены первого фактора w, при фиксированных
значениях w2 и у.
S.c»
А
I cA(wuw2,y)
cB(w\, w2,y)
—' ; > w,
Рис. 3.8

Глава 3. Теория фирмы
199
а) Какая из фирм при wQx использует первый фактор в большем
объеме? При w[ ? Обоснуйте свой ответ.
б) Производственная функция какой фирмы характеризуется большей
эластичностью замещения? Обоснуйте свой ответ.
3.28. Пусть первая фирма имеет функцию издержек с\мч, у). Будут
ли фирмы иметь одинаковый спрос на факторы и предложение готовой
продукции, если вторая фирма имеет функцию издержек вида:
ч 2 c'Bw, у)
а) с (w, у) = у^>
6)c2(w, y) = cl(w, 2y)l
3.29. Определим эластичность выпуска по спросу на фактор
производства х( следующим образом:
?,>(w, 7) = (^(w, y)/dy)(y/xt(vr9 у)).
а) Покажите, что 6(v(w, J>) = (to0e,>(w> 1), если производственная
функция гомотетична.
б) Покажите, что ziy =1 при / = 1, ...,«, если производственная
функция характеризуется постоянной отдачей от масштаба.
3.30. Покажите, что если средние издержки убывают, то предельные
издержки должны быть меньше средних; если средние издержки
постоянны, то предельные издержки равны средним; если средние издержки
возрастают, то предельные издержки должны быть выше средних.
3.31. Пусть 5, — доля фактора производства i. Покажите, что для
любой функции издержек 5/=31n(c(w, >>))/Э1п(мл). Убедитесь в этом,
вычислив доли факторов производства для функции издержек Кобба —
Дугласа.
3.32. В тексте было показано, что транслогарифмическая функция
издержек представляет собой (локальную) аппроксимацию второго
порядка любой произвольной функции издержек. В неявном виде она
описывается линейной относительно логарифмов функцией вида
П 1 П П
1п(с) = а0 + ? а, ln(w,) + - X Z Y/, 4*i) ln( w,) + ln(y).
1=1 ^ /=1 /=1
п
Пусть 7,у = 7У7 и Х^> =^' / = 1' —»w> тогда матрица замещения, как
/=1
оно и требуется, симметрична.
а) При каких ограничениях на параметры ОС/ можно гарантировать
однородность функции?

200
Часть I. Экономические агенты
б) При каких значениях параметров данная транслогарифмическая
функция издержек сводится к функции издержек Кобба — Дугласа?
в) Покажите, что доли факторов производства для
транслогарифмической функции издержек линейны по логарифмам цен факторов и выпуска.
3.33. Вычислите функцию издержек и функции условного спроса
на факторы производства для линейной производственной функции
п
/=1
3.34. Найдите функцию издержек для двухфакторной технологии
вида Кобба — Дугласа с постоянной отдачей от масштаба. Зафиксируйте
один из факторов и найдите функцию издержек в краткосрочном периоде.
Покажите, что долгосрочные средние и предельные издержки постоянны
и равны. Покажите также, что при любом объеме фиксированного
фактора производства краткосрочные средние издержки и долгосрочные
средние издержки равны при минимальном значении краткосрочных средних
издержек. Проиллюстрируйте полученные результаты в пространстве
«издержки — выпуск».
3.35. Докажите все результаты, полученные в предыдущем
упражнении, в общем случае, т.е. для любой технологии с постоянной отдачей от
масштаба.
3.36. Покажите, что если производственная функция гомотетична, то
пропорция, в которой фирма использует любую пару факторов
производства, будет одинаковой при любом уровне выпуска.
3.37. Покажите, что если производственная функция гомотетична, то
условный спрос на факторы производства не возрастает по своей цене.
3.38. Если фирма сталкивается с кривой предложения одного из
факторов производства &, имеющей положительный наклон, то мы можем
записать цену этого фактора как wk = wk (хк), где w'k > 0.
а) Определите функцию издержек фирмы в этом случае и выпишите
условия первого порядка, характеризующие оптимальный объем
использования факторов производства.
б) Определим эластичность предложения фактора к следующим
образом: гк =(dxk(wk)/dwk)(wk Iхк) и предположим, что в равновесий фирма
использует фактор к в положительном количестве. Покажите, что лемма
Шепарда применима только в том случае, если ек -» °°.
3.39. Рассмотрите производственную функцию, удовлетворяющую
всем условиям предположения 3.1. Докажите, что функция издержек
линейна по выпуску c(w, у) = j>(|)(w) тогда и только тогда, когда
производственная функция характеризуется постоянной отдачей от масштаба.

Глава 3. Теория фирмы
201
3.40. Как мы видели, производственной функции Кобба — Дугласа
у = Ах*х2~а соответствует функция издержек Кобба — Дугласа
c(w, у) = Aw"wl2~ay; производственной функции с постоянной
эластичностью замещения (CES) у = А\хх? + х92) соответствует функция
издержек с постоянной эластичностью замещения c(w, у) = уА{у/х+\/2} .
Для каждой пары функций покажите, что обратное также верно, т.е.
восстановите производственную функцию из функции издержек и покажите,
что она имеет соответствующий вид. Обоснуйте используемый метод
восстановления.
3.41. Покажите, что кривая долгосрочных средних издержек
lac(y) = c(w,yi,y)/ у является нижней огибающей кривых
краткосрочных средних издержек sac(^) = sc(w,w5>y; *)ly в пространстве
«издержки — выпуск». Изобразите полученный результат графически,
учитывая взаимосвязь долгосрочных предельных издержек
lmc(y) = dc(yv, w,y)/dy и краткосрочных предельных издержек
smc(y:x) = dsc(w, w,j>; x)/dy.
3.42. Найдите функцию прибыли для фирмы, имеющей технологию
вида Кобба — Дугласа, у = ххах2. При каких условиях на параметры а и
Р можно гарантировать, что полученная функция прибыли корректно
определена? Обоснуйте свой ответ.
3.43. Рассмотрите аддитивно сепарабельную производственную
функцию вида f(xx,x2) = g(xx) + h(x2). При каких условиях на функции
g и h функции спроса на факторы, хх(р, w) и х2(р9 w), однородны
степени 1/2 по ценам факторов производства w ?
3.44. Проверьте, выполняется ли теорема 3.7 для функции прибыли из
примера 3.5. Проверьте также, выполняется ли теорема 3.8 для
соответствующих функций предложения и спроса на факторы.
3.45. При получении функции предложения фирмы в краткосрочном
периоде в примере 3.6 мы не учитывали возможность бездействия,
предполагая внутреннее решение задачи максимизации прибыли фирмы.
Приведите полное описание предложения фирмы в краткосрочном периоде для
случая, когда производственная функция имеет вид Кобба — Дугласа.
3.46. Пусть производственная функция имеет вид:
Г Л
у = х2\ sin|
где 0 < хх < 2л, 0 < х2 < 2тс и у = 0 при х2 = 0.
а) Какой отдачей от масштаба характеризуется данная технология?

202
Часть I. Экономические агенты
б) Изобразите кривые предельного и среднего продукта первого
фактора jc, при х2 = 1 на одном графике.
в) Найдите функцию издержек в краткосрочном периоде и функцию
прибыли при wx = 1, w2 = 2 и х2 = 1.
3.47. Найдите функцию издержек для производственной функции из
примера 3.5. Затем решите задачу max/?y-c(w, у) и сравните ее реше-
V
ние у(р, w) с решением (Е-5). Проверьте, что к(р, w)= ру(р, w)-
-c(w, y(p, w)). Пусть C > 1. Докажите, что условия первого порядка
действительно характеризуют минимум прибыли (для этого покажите, что в
оптимуме предельные издержки убывают). Изобразите решение графически.
3.48. Докажите, что предложение и спрос фирмы на переменные
факторы производства в краткосрочном периоде однородны нулевой степени
по р и w.
3.49. Пусть функция c(w, у) является функцией издержек для
технологии, описываемой производственной функцией /. Предположим,
что задачи: 1) max/?y-c(w, у) и 2) max/?/(x)-wx —имеют решения
у>0 xeR'l
/>0их*>0 соответственно.
а) Покажите, что у = f{\) является решением задачи 1).
б) Покажите, что если c(w, y*) = wx и у* = /(х), то х является
решением задачи 2).
в) Воспользовавшись результатами из пунктов а) и б), покажите, что
py-c(yv, y) = pf(x)-wx.
3.50. Обобщим понятие функции прибыли для случая фирмы,
производящей много видов готовой продукции, а не один. Пусть фирма
производит вектор выпусков у = 0>р —9ут)9 используя вектор факторов
производства x = (Xj, ...,*„)• Взаимосвязь между эффективным выпуском и
объемом используемых факторов производства в неявном виде может
быть описана с помощью трансформационной функции Г(у, х) = 0.
Тогда если через р обозначить вектор цен готовой продукции, то
обобщенная функция прибыли определяется как: я(р, w) = maxpy-wx при
Г(у, х) = 0. Покажите, что такая обобщенная функция прибыли обладает
всеми свойствами, перечисленными в теореме 3.7. Покажите также, что
для нее справедлив обобщенный вариант леммы Хотеллинга.
3.51. Приведите схему доказательства следующей теоремы о
восстановлении для конкурентной фирмы, максимизирущей прибыль.

Глава 3. Теория фирмы
203
Непрерывно дифференцируемые неотрицательные функции х{(р, w),
/ = 1, ...,п, и у(р, w), определенные на множестве R"*1 являются
функциями спроса на факторы и функцией предложения соответственно,
порожденными некоторой возрастающей квазивогнутой
производственной функцией, тогда и только тогда, когда они однородны нулевой
степени по (р, w) и их матрица замещения, приведенная в пункте 3)
теоремы 3.8, является симметричной и положительно полу определенной.
В частности, покажите, что если матрица замещения симметрична и
положительно полуопределена, то существует выпуклая функция
П(/?, w), производные которой равны -xt{p, w) и у(р, w). Покажите
также, что функция П(р, w) однородна первой степени по (/?, w).
3.52. Рассмотрите следующую функцию издержек:
с(щ,™2>У) = У2(™1+™2)-
а) Изобразите кривые предельных издержек, средних совокупных
издержек и предложения фирмы на одном графике.
б) На отдельном графике изобразите кривую спроса на первый
фактор хх в зависимости от цены этого фактора и>,.
в) Используя оба рисунка, проиллюстрируйте эффект увеличения
цены второго фактора.
3.53. Электростанция производит электроэнергию для города. Цена,
по которой электроэнергия может продаваться, фиксирована, и при этой
цене весь спрос на нее должен удовлетворяться. Совокупный объем
спроса на электроэнергию за сутки постоянен, однако дневной (с 6 утра до 6
вечера) и ночной (с 6 вечера до 6 утра) спрос различается: в течение дня
требуется 4 единицы электроэнергии, тогда как ночью — лишь 3
единицы. Таким образом, совокупный спрос на электроэнергию за сутки
составляет 7 единиц. Предположим, что электростанция производит
электроэнергию в соответствии с производственной функцией
yi = {KFjI12, i = день, ночь,
где К — это мощность электростанции, Ft — требуемое топливо
(тонны). Фирма, владеющая электростанцией, не может изменять ее
мощность в зависимости от времени суток. Если единица мощности
электростанции стоит wk в сутки, а тонна топлива стоит Wj, то какова должна
быть мощность электростанции?

Часть II
РЫНКИ И БЛАГОСОСТОЯНИЕ

Глава 4
ЧАСТИЧНОЕ РАВНОВЕСИЕ
В предыдущих главах мы изучали поведение индивидуальных
потребителей и фирм, описывая оптимальное поведение в ситуациях, когда
рыночные цены фиксированы и установлены без контроля со стороны
экономических агентов. Теперь мы начинаем анализировать последствия
такого поведения, когда потребители и фирмы объединяются в рынки.
Сначала мы рассмотрим, как устанавливаются цены и определяется
количество товара на одном рынке или группе взаимосвязанных рынков.
Затем мы оценим эти рынки с точки зрения интересов общества. При этом
мы обратим особое внимание на тесную взаимосвязь между
конкурентной структурой рынка и общественной оценкой его «функционирования».
4.1. Совершенная конкуренция
На совершенно конкурентных рынках действует достаточно много
покупателей и продавцов товара для того, чтобы ни один из них не имел
возможности самостоятельно устанавливать цену на рынке. Покупатели и
продавцы принимают цены как заданные, и каждый выбирает наилучший
способ действия с учетом своих индивидуальных обстоятельств и целей.
Спрос покупателя на отдельный товар, как мы уже видели, является
результатом задачи максимизации полезности по всем товарам при
выполнении бюджетного ограничения. Точно так же предложение продавцом
какого-либо товара — результат задачи максимизации прибыли при
данной отпускной цене товара» технологических возможностях и ценах на
факторы производства. Равновесие конкурентного рынка, таким образом,
требует согласования часто противоречивых намерений большого числа
различных агентов.
Спрос на рынке формируется всеми потенциальными покупателями
товара, каждый из которых имеет свои собственные предпочтения,
потребительское множество и доход. Пусть J ={l, ...,/} — набор индексов,
обозначающий множество индивидуальных покупателей, a ql(p, p, у1) —
неотрицательный спрос /-го покупателя на товар q как функция
собственной цены товара р, дохода покупателя у1 и цен на другие товары р.
Рыночный спрос на товар q есть просто сумма индивидуальных спросов всех
покупателей
?'0>) = 2>'(АР, У)- D-1)
/е/

208
Часть II Рынки и благосостояние
Есть несколько моментов при определении рыночного спроса,
которые стоит оговорить особо. Во-первых, qd(p) характеризует совокупное
количество товара q9 которое требуется всем покупателям на рынке.
Во-вторых, так как спрос каждого покупателя на товар q зависит не
только от цены товара q, но и от цен на все другие товары, рыночный
спрос на товар q ведет себя так же, однако в большинстве случаев мы не
будем акцентировать на этом внимание. В-третьих, в то время как спрос
отдельного покупателя зависит от уровня его собственного дохода,
рыночный спрос зависит как от совокупного уровня дохода на рынке, так и
от распределения этого дохода между покупателями. И наконец, так как
индивидуальный спрос является однородным (нулевой степени) по всем
ценам и индивидуальному доходу покупателя, то и рыночный спрос
будет однородным (нулевой степени) по всем ценам и вектору доходов
покупателей; несмотря на то что в результате решения задачи максимизации
полезности мы получаем несколько ограничений на систему
индивидуального спроса, однородность является единственным ограничением на
рыночный спрос для отдельного товара.
Предложение на рынке формируется всеми потенциальными
продавцами товара q. Однако мы иногда будем проводить различие между
фирмами, которые являются потенциальными продавцами в
краткосрочном периоде, и фирмами, которые являются потенциальными продавцами
в долгосрочном периоде. Ранее мы определили краткосрочный период
как период времени, в течение которого по крайней мере один фактор
производства (например, размер завода) для фирмы фиксирован.
Согласно этому определению в краткосрочном периоде количество
потенциальных продавцов на рынке фиксировано, конечно и ограничено теми
фирмами, которые «уже существуют» и которые до некоторой степени
способны и увеличивать производство, и функционировать, просто
приобретая необходимые ресурсы. Пусть индексами / ={l, ...,./}
обозначены такие фирмы; тогда функция краткосрочного рыночного
предложения есть сумма функций краткосрочных предложений отдельных
фирм qJ (p, w):
?'(/>)= 5У(A w). D-2)
Рыночный спрос и рыночное предложение совместно определяют
цену и совокупное количество товара, продаваемого на рынке. Будем
говорить, что конкурентный рынок находится в краткосрочном равновесии
при цене р* 9 если qd(p*) = qs(p). Геометрически это соответствует уже
знакомому нам пересечению кривых рыночного спроса и рыночного

Глава 4. Частичное равновесие
209
предложения, изображенных на плоскости (/?, q). Отметим, что
рыночное равновесие имеет некоторые интересные и важные особенности:
каждый покупатель, принимая цену как заданную, приобретает оптимальное
для него количество товара по этой цене, и каждая фирма, принимая цену
как заданную, продает готовую продукцию, максимизируя свою прибыль,
по той же цене. Таким образом, мы имеем равновесие в том смысле, что
ни у одного агента на рынке нет стимулов менять свое поведение —
каждый получил наилучший возможный исход в тех обстоятельствах, с
которыми он столкнулся.
Пример 4.1. Рассмотрим конкурентную отрасль, состоящую из J
одинаковых фирм. Фирмы производят выпуск согласно технологии с
производственной функцией Кобба — Дугласа q = xakl'a, где х —
переменный фактор производства (например, рабочая сила), а А: — фактор
производства (например, размер завода, который зафиксирован в
краткосрочном периоде), и 0 < а < 1. В примере 3.6 мы вывели формулу
краткосрочной прибыли и функцию предложения для фирмы с этой
производственной функцией. При ценах р, wx и wk максимальная прибыль равна
nJ = р»'о-«у'<«-V'^O " <*)* " Щк, (Е-1)
а предложение готовой продукции составляет
qJ = рИ1-«у/(«-i)aa/(i-«)? ^ (Е_2)
Если a = 1 / 2, wx = 4 и wk = 1, то, предполагая, что у каждой фирмы
размер завода к = 1, приводим формулу для предложения готовой
продукции одной фирмой к простому виду qJ = р/8. Функция рыночного
предложения для рынка, на котором существуют J = 48 фирм, имеет вид тогда:
qs =4S(p/S) = 6p. (E-3)
Пусть рыночный спрос задается как
qd =294/р. (Е-4)
Тогда, используя (ЕЛ) — (Е.4), можно определить равновесную цену в
краткосрочном периоде, количество товара на рынке, а также выпуск
готовой продукции и прибыль отдельной фирмы:
p=i
q =42

210
Часть II. Рынки и благосостояние
qj =7/8
тгу=2,0625>0
Это равновесие и для всего рынка, и для отдельной фирмы
проиллюстрировано на рис. 4.1. (Заметим, что кривые издержек в краткосрочном
периоде для фирм с подобной технологией могут быть получены из
упражнения 3.34.) D
Цена
Цена, издержки
Рынок
i
7
4,64
а
i
Фирма
ySmc(q)
,л/">0 /
/л8
//sac(q)
i ь
»> q v.—i . 1 *> q
42 1/2 7/8
Рис. 4.1. Краткосрочное равновесие на одном рынке
В долгосрочном периоде никакие факторы производства для фирмы
не фиксированы. Уже существующие фирмы — те, которые уже
производят, — свободны в выборе объемов использования всех факторов
производства, включая, например, размер завода. Они также могут покинуть
отрасль. Более того, в долгосрочном периоде новые фирмы могут решить
начать производство рассматриваемого товара. Таким образом, в
долгосрочном периоде у фирм есть возможность входа в отрасль и выхода из
отрасли. Фирмы входят в отрасль, реагируя на положительную
экономическую прибыль в долгосрочном периоде, и выходят — реагируя на
отрицательную прибыль (потери) в долгосрочном периоде.
В долгосрочном равновесии ни у одной из фирм нет стимулов для
входа в отрасль или выхода из нее. Ясно, что в этом случае долгосрочная
прибыль должна быть неотрицательной; иначе фирмы будут стремиться
выйти из отрасли. В то же время, так как все фирмы имеют свободный
доступ к технологиям друг друга (в частности, у фирм, в настоящее время
не занимающихся производством, есть возможность воспользоваться
технологией любой производящей фирмы), никакая фирма не может
претендовать на получение положительной прибыли в долгосрочном периоде.

Глава 4. Частичное равновесие
211
Иначе фирмы, находящиеся вне данной отрасли, усвоили бы технологию
фирмы, имеющей положительную прибыль, и вошли в отрасль.
Итак, два условия характеризуют долгосрочное равновесие на
конкурентном рынке:
я'(р) = 0, 7 = 1, ...J. D-3)
Первое условие просто говорит о том, что рынок должен прийти в
равновесие. Второе говорит о том, что долгосрочная прибыль для всех фирм
отрасли должна равняться нулю, чтобы ни у одной из фирм не возникало
желания входить в отрасль или выходить из нее. В краткосрочном
периоде число фирм задано, и балансовое условие определяет равновесную
цену в краткосрочном периоде. Заметим, однако, что в долгосрочном
периоде условия рыночного равновесия и нулевой прибыли совместно
определяют и равновесную цену, и равновесное число фирм J в отрасли.
Пример 4.2. Предположим, что обратная функция рыночного
спроса линейна
/7 = 39-0,009?. (Е-1)
Технология производства товара q одинакова для всех фирм, и все
фирмы сталкиваются с одинаковыми ценами на факторы производства.
Функция прибыли в долгосрочном периоде для репрезентативной фирмы
задается как
nJ\p) = p2 -2/7-399, (Е-2)
так что функция предложения готовой продукции имеет вид
y=f^)=2/7-2. (Е-3)
Ф
Заметим, что условие yJ > 0 требует, чтобы р > 1.
В долгосрочном периоде равновесная рыночная цена р и число фирм в
равновесии J должны удовлетворять двум условиям D-3). Таким образом:
A000/9)C9-р) = УBр-2),
?2-2?-399 = 0.
Из требования нулевой прибыли мы получаем /7 = 21. Подстановка в
балансовое условие дает J = 50. Из (Е-3) имеем, что каждая фирма произ-

212
Часть II. Рынки и благосостояние
водит 40 единиц готовой продукции в долгосрочном равновесии. Это
рыночное равновесие проиллюстрировано на рис. 4.2. ?
Цена, издержки
Фирма
-> q ¦ ' > q
2,000 40
Рис. 4.2. Долгосрочное равновесие на конкурентном рынке
Пример 4.3. Исследуем долгосрочное равновесие на рынке из
примера 4.1. В этом примере рассматривалась технология с постоянной
отдачей от масштаба, q = xak]~a, где х — переменная, а к — фиксированная
величина в краткосрочном периоде. Для а = 1/2, wx =4 и wk = 1
прибыль и функция предложения в краткосрочном периоде имеют вид
п'(р, к) = р2к/16-к, (Е-1)
qf =pk/S. (E-2)
При рыночном спросе
qd =294/р
(Е-3)
и 48 фирмах в отрасли мы получили равновесную цену краткосрочного
периода р* = 7 и прибыль отдельной фирмы nJ = 2,0625 > 0.
В долгосрочном периоде фирмы могут входить в отрасль, если
прибыль положительна, а уже существующие фирмы могут выбирать
оптимальный размер завода. Рыночная цена будет стремиться к уровню, при
котором максимальная прибыль фирм равна нулю. Из (Е-1) мы видим,
что независимо от выбранного фирмами размера заводов это произойдет
только при р = 4, потому что
п(р,к) = к(р2 /16-1) = 0
(Е-4)

Глава 4. Частичное равновесие
213
при любых к > О, только если р = 4. Условие сбалансированности рынка с
J фирмами, каждая из которых управляет заводом размера к, требует, чтобы
я"(р) = я'(р),
ИЛИ
4 8
Преобразовав, получим
147 = Л. (Е-5)
Так как при р = 4 прибыль фирм равна нулю независимо от размера
завода к, долгосрочное равновесие на самом деле совместимо с широким
диапазоном рыночных структур. Из (Е-4) и (Е-5) следует, что
долгосрочное равновесие может существовать для единственной фирмы,
управляющей заводом размера к = 147, для двух фирм, каждая из которых
управляет заводом к = 147/2, для трех фирм — с заводами к = 147/3 и
для J фирм, каждая из которых управляет заводом размера k = l47/J.
Эта неопределенность в равновесном числе фирм в долгосрочном
периоде — явление, обычное во всех отраслях с постоянной отдачей от
масштаба. В упражнениях вам будет предложено показать это. ?
4.2. Несовершенная конкуренция
Совершенная конкуренция представляет собой один из крайних
случаев в спектре возможных рыночных структур, проранжированных от
«более» к «менее» конкурентным. На противоположном полюсе
находится чистая монополия —- самая неконкурентная структура рынка,
которую можно себе представить. Чистая монополия предполагает, что
существует единственный продавец товара, у этого товара нет никаких
близких заменителей в потреблении, а вход на рынок блокирован
технологическими, финансовыми или юридическими барьерами.
Монополист воспринимает функцию рыночного спроса как данную и
выбирает цену и объем выпуска так, чтобы максимизировать свою
прибыль. Так как самая высокая цена, которую монополист может назначить
для любого данного количества произведенного им товара q, является
обратной функцией спроса p(q), то фирма может ограничиться только
выбором q. Затем фирма просто устанавливает цену, равную p(q).
Прибыль как функция от q является разностью между доходом
r{q) = p(q)q и издержками c(q). Таким образом, П(#) = r(q)-c(q). Если

214
Часть II Рынки и благосостояние
выпуск q > О максимизирует прибыль, то он удовлетворяет условию
первого порядка W\q*) = r{q*)-c\q*) = 0. Это, в свою очередь,
аналогично требованию равенства предельного дохода предельным издержкам:
mr(q*) = mc(q*). D-4)
Равновесная цена при этом определяется как р = p(q), где p(q) —
обратная функция рыночного спроса.
Исследуем выбор монополистом объема выпуска подробнее.
Поскольку r{q) = p(q)q, то, дифференцируя, чтобы получить предельный
доход, имеем
mr(q) = p(q) + q^- = p(q)\
dq
1 +
dp(q) q
= p{q)\
l-i
1
Ш
D-5)
dq p(q)
где e(q) — эластичность рыночного спроса при выпуске q, и
\s(q)\ = -(dq/dp)(p/q)>0 всякий раз, когда наклон кривой рыночного
спроса отрицателен. Комбинируя D-4) и D-5), получаем, что q
удовлетворяет соотношению
1
Piq)
1-7
Кя)\
= mc(q)>0,
D-6)
поскольку предельные издержки всегда неотрицательны. Цена также
неотрицательна, поэтому ?(<?*) ^ 0. Таким образом, монополист никогда не
выбирает объем выпуска продукции в неэластичном диапазоне
рыночного спроса, что показано на рис. 4.3.
Цена, издержки
Р(Я)
mriq)' =mc(q')
+1
О
mc(q)
*¦ q
1е(<7I>1 | \1е(<7I<1
| ?(?) | = i mr(q)
Рис. 4.3. Равновесие при чистой монополии

Глава 4. Частичное равновесие
215
Преобразуя D-6), мы можем получить выражение для процентного
отклонения цены от предельных издержек в равновесии при монополии:
p{q*)-mc{q) ^ 1 „?.
Р(Я*) |е(?*)|
Если рыночный спрос — не бесконечно эластичен, то \г(д*)\ будет
конечной величиной, и в равновесии цена, назначаемая монополистом,
превысит предельные издержки. Кроме того, при прочих равных условиях цена
превысит предельные издержки тем в большей степени, чем более
неэластичен рыночный спрос.
Как мы уже отмечали, совершенная конкуренция и чистая монополия
являются крайними (и противоположными) случаями рыночных
структур. Тем не менее они имеют одну общую важную особенность: ни
совершенно конкурентной фирме, ни чистому монополисту не надо
учитывать действия других фирм при решении собственной задачи
максимизации прибыли. Совершенно конкурентная фирма не может влиять на
рыночную цену и, следовательно, на действия других фирм, поэтому она
заботится только о влиянии собственных действий на свою прибыль.
Чистый монополист полностью управляет рыночной ценой и выпуском
продукции, и его не волнует возможность входа на рынок конкурентов,
поскольку вход на рынок полностью блокирован.
Многие рынки представляют собой некую смесь монополии и
конкуренции. Фирмы становятся тем более взаимозависимыми* чем меньше
число фирм в отрасли, чем легче вход в отрасль и чем доступнее
взаимозаменяемые товары для потребителей. Когда фирмы чувствуют свою
взаимозависимость, у них появляется стимул принять во внимание
действия своих конкурентов и формировать свои планы стратегически. В
главе 7 мы подробнее расскажем о стратегическом поведении и о том, как
его анализировать, здесь же мы остановимся лишь на некоторых из
основных концепций.
При стратегическом поведении фирм мы в первую очередь должны
задаться вопросом: как характеризовать равновесие в подобных
ситуациях? Отвечая на этот вопрос, можно рассуждать следующим образом.
Поскольку фирмы знают о своей взаимозависимости и действия одной
фирмы могут уменьшить прибыль других фирм, то почему бы им просто не
сотрудничать или не вступить в сговор, чтобы получить максимальную
суммарную прибыль и затем поделить ее между собой? В конце концов,
если они соглашаются работать вместе, чтобы сделать прибыльный пирог
настолько большим, насколько это возможно, неужели они не смогут
разделить этот пирог так, чтобы каждый получил по крайней мере столь же

216
Часть II. Рынки и благосостояние
большой кусок, какой бы ему достался в противном случае? Оставляя в
стороне законность такого сговора, можно констатировать, что есть нечто
привлекательное в идее равновесия, основанного на сговоре этого типа.
Если бы не следующая проблема.
Рассмотрим рынок одного товара, состоящий из J фирм, каждая из
которых производит qj единиц этого товара. Предположим, что на
прибыль каждой фирмы неблагоприятно влияет увеличение выпуска
продукции любой другой фирмы, так что
Ylj=UJ(q\ ...,qJ\ ...,qJ) иЭГГ/Э?* <0, j*k. D-8)
Теперь предположим, что фирмы скооперировались, чтобы
максимизировать совокупную прибыль. Если выпуск q максимизирует ^ Y\J,
он должен удовлетворять условиям первого порядка
ЭП*(д),^ЭГГ(д)
¦ +
dqk j*k dq
Заметим, что из D-8) и D-9) следует, что
ЭП*(ф
Z-^-P^0' * = L -'J- С4"9)
V
>0, it = l, ...,J.
Посмотрим, что это означает. Поскольку прибыль каждой фирмы
увеличивается с увеличением ее выпуска при векторе выпуска q, то каждая
фирма может увеличить свою прибыль, увеличивая выпуск своей
продукции относительно заданного в q, при условии, конечно, что все
остальные продолжают производить количества, обусловленные вектором q!
Если хотя бы одна фирма уступит этому искушению, q не будет
равновесным вектором выпуска на данном рынке.
Фактически в таких ситуациях все основанные на сговоре соглашения
порождают у вовлеченных в сговор экономических агентов стимул
нарушить эти соглашения. Поэтому трудно ожидать, что основанный.на
сговоре исход окажется «равновесным». Более разумно считать фирмы с
меркантильными целями некооперирующимися. Любое описание
равновесия на несовершенно конкурентных рынках, чтобы быть
непротиворечивым, должно принимать это во внимание.
Наиболее общая концепция некооперативного равновесия была
выдвинута Джоном Нэшем в 1951 г. В равновесии по Нэшу каждый агент
выбирает наиболее предпочтительный исход при данных действиях всех
других агентов. Как нетрудно заметить, когда все агенты достигают
этого состояния, ни одному из них невыгодно изменять свои решения в од-

Глава 4. Частичное равновесие
217
ностороннем порядке, поэтому такое состояние разумно рассматривать
как равновесие.
В рыночной ситуации, подобной той, которую мы обсуждаем,
рассматриваемые агенты — это фирмы. Так, объемы выпусков всех фирм не
составляют равновесие по Нэшу, пока каждая фирма не максимизирует
свою собственную прибыль при данных максимизирующих прибыль
действиях всех других4шрмЛ Очевидно, что максимизирующий совокупную
прибыль вектор выпуска готовой продукции q в D-9) не удовлетворяет
требованиям равновесия по Нэшу, поскольку, как мы заметили,
индивидуальная прибыль никакой фирмы не максимизируется при выпуске,
соответствующем q, при данном выборе выпуска продукции другими
фирмами (также соответствующем q). Действительно, если q* —равновесие
по Нэшу, то выпуск каждой фирмы должен максимизировать ее прибыль
при данном выборе выпусков другими фирмами. Таким образом, q*
должен удовлетворять условиям первого порядка:
^^ = 0,^1, ...,У. D-10)
Различие между D-9) и D-10) очевидно. Вообще говоря, эти соотношения
определяют совершенно различные векторы выпуска готовой продукции.
В дальнейшем мы будем использовать понятие равновесия по Нэшу
во множестве различных ситуаций, в которых решения фирм являются
взаимозависимыми.
4.2.1. Олигополия Курно
Следующая модель олигополии восходит к 1838 г. и обязана своим
происхождением французскому экономисту Огюсту Курно. Здесь мы
рассмотрим простой пример олигополии Курно на рынке однородного
товара. Предположим, что есть J одинаковых фирм, вход для других фирм на
рынок надежно закрыт и все фирмы имеют одну и ту же линейную
функцию издержек:
C(qJ) = CqJ9 c>0 и у = 1, ...,J. D-11)
Фирмы продают выпускаемую продукцию на одном и том же рынке, так
что рыночная цена зависит от совокупного выпуска готовой продукции,
реализованной всеми фирмами на рынке. Предположим, что функция
обратного рыночного спроса линейна,
р = а-Ь?д', D-12)
У=1

218
Часть II Рынки и благосостояние
где я>0, 6>0, причем а>с. Согласно D-11) и D-12) прибыль
фирмы j имеет вид:
к
к=\ J
\
qJ-cqJ. D-13)
Требуется найти такой вектор выпуска (ql9 ...,^y), что объем
выпуска каждой фирмы максимизирует ее прибыль при заданном выпуске других
фирм. Такой вектор выпуска называют равновесием Курно — Нэша. Это
название отдает должное Курно, который нашел решение для олигополии, и
Нэшу, который позже развил идею Курно для более общего случая.
Так, если (ql9 ...,#у) — равновесие Курно — Нэша, то объем
выпуска <7/ должен доставлять максимум прибыли D-13) при qk =qk для всех
к * j. Следовательно, производная выражения D-13) по q} должна быть
равна нулю при qk = qk для всех к = 1, ..., J. Таким образом,
a-2bqj-b?qk-c = 0,
k*j
что можно переписать как
j
bqj=a-c-b^qk . D-14)
*=i
Заметим, что правая часть D-14) не зависит от того, какую именно фирму
мы рассматриваем, следовательно, все фирмы должны в равновесии иметь
одинаковый объем выпуска. Обозначая этот совокупный равновесный
выпуск через q , из D-14) получаем bq =a-c- Jbq , откуда следует, что
" а~С D-15)
6(У + 1)
Используя D-15) и произведя ряд вычислений, получим полный набор
величин, характеризующих рыночное равновесие, а именно, объем
выпуска фирмы, совокупный выпуск готовой продукции, рыночную цену и
прибыль фирмы:
9y=(*-c)/6(j + i),y = i, ...,</;
р = а- J (а - c)/(J +1) < а;
ГР =(a-cJ/(J + lJb.

Глава 4. Частичное равновесие
219
Равновесие в модели олигополии Курно имеет некоторые интересные
характеристики. Вычислив отклонение цены от предельных издержек
р-с = ^Ц>0, С4'16)
можно заметить, что равновесная цена обычно превышает предельные
издержки каждой (идентичной) фирмы. Когда J = 1 и эта единственная
фирма является чистым монополистом, отклонение цены от предельных
издержек будет наибольшим. В другом крайнем случае, когда число фирм
J -> оо 9 из D-16) следует
lim(p-c) = 0. D-17)
J—»оо
Уравнение D-17) говорит о том, что цена приближается к предельным
издержкам по мере увеличения числа фирм-конкурентов. Действительно,
этот предельный результат соответствует тому, что получилось бы, если
бы любое конечное число фирм вело себя как совершенные конкуренты.
Таким образом, эта простая модель обеспечивает другую интерпретацию
совершенной конкуренции. Она предлагает рассматривать совершенную
конкуренцию как предельный случай несовершенной конкуренции, если
количество фирм становится большим.
4.2.2. Олигополия Бертрана
Спустя почти 50 лет после Курно другой французский экономист —
Жозеф Бертран A883), предложил иной взгляд на соперничество фирм в
условиях несовершенной конкуренции. Бертран утверждал, что намного
более естественно полагать, что фирмы конкурируют, выбирая цены, а не
количества. Этого маленького различия достаточно, чтобы полностью
изменить характер рыночного равновесия.
Возникающие здесь проблемы лучше всего видны на примере
конкуренции между двумя фирмами. В простой модели дуополии Бертрана
две фирмы, имеющие одинаковые предельные издержки о 0
(постоянные издержки отсутствуют), производят однородный товар. Хотя это и
не важно, для того чтобы проще было сравнить эту ситуацию со случаем
дуополии по Курно, снова предположим, что рыночный спрос есть
линейная функция совокупного выпуска Q двух фирм:
где р — рыночная цена.

220
Часть II. Рынки и благосостояние
Фирмы одновременно объявляют цены, которые они назначат, и
готовы поставлять любое количество товара, которое потребуется при этой
цене. Потребители покупают по самой низкой цене. Таким образом,
фирма, назначившая самую низкую цену, удовлетворит весь спрос на рынке
по объявленной ею цене, тогда как на продукцию фирмы, назначившей
более высокую цену, спроса не будет. Если обе фирмы объявляют
одинаковую цену, то они разделят рыночный спрос на данный товар поровну, и
каждая обслужит половину потребителей.
Здесь прибыль каждой фирмы, очевидно, зависит от цены
конкурента, так же как и от своей собственной. Рассмотрим, например, прибыль
фирмы 1 для всех неотрицательных цен ниже а/C (цена, при которой
рыночный спрос равен нулю). Эта прибыль равна
V-cXa-p/?1), с<р] <р2;
^(У-сХсс-РУ), с<р]=р2;
0, в противном случае.
Заметим, что прибыль фирмы 1 неотрицательна, пока ее цена
превышает предельные издержки. Конечно, при прочих равных условиях
прибыль будет наибольшей, если цена фирмы 1 ниже, чем цена фирмы 2, и
составит только половину этой величины, если обе фирмы назначат одну
и ту же цену. Однако прибыль фирмы не может быть отрицательной,
потому что фирма может всегда назначить цену, равную предельным
издержкам, т.е. в худшем случае обеспечить себе нулевую прибыль. Для
фирмы 2 ситуация будет симметричной. Таким образом, мы
предполагаем, что каждая фирма /ограничивает свое внимание ценами р1 >с.
Что будет равновесием по Нэшу на этом рынке? Может показаться
немного удивительным, но в единственном равновесии по Нэшу обе
фирмы назначают цену, равную предельным издержкам, и обе получают
нулевую прибыль. Поскольку функции прибыли в этом случае
разрывные, мы не можем для характеристики равновесия использовать условия
первого порядка. Вместо этого обратимся к здравому смыслу.
Заметим, что так как фирма с наименьшей ценой обслуживает весь
рынок, то у каждой фирмы есть стимул предлагать товар по более низкой
цене, чем конкурент. Именно этот эффект в конечном счете приводит к
равенству равновесной цены и предельных издержек. Теперь приведем
формальное обоснование этого утверждения.
Обратим внимание сначала на то, что, если каждая фирма выбирает
цену, равную с, то это — равновесие по Нэшу. Тогда каждая фирма
обслуживает половину рынка и получает нулевую прибыль, потому что ка-
nW) =

Глава 4. Частичное равновесие
221
ждая единица продана по цене, равной издержкам производства. Более
того, увеличивая цену, фирма столкнется с нулевым спросом, потому что
цена другой фирмы в этом случае ниже. В результате прибыль увеличить
невозможно. Следовательно, выбор цены фирмой является
максимизирующим прибыль при заданном выборе цен другими фирмами.
Теперь докажем, что другого равновесия по Нэшу не существует.
Поскольку каждая фирма / выбирает pf > с, то достаточно показать, что не
существует равновесия, в котором р1 > с хотя бы для одного /. Итак,
пусть (/?,, р2) является равновесием.
Если рх > с, то, так как р2 максимизирует прибыль фирмы 2 при
заданном выборе цены фирмой 1, р2е(с, рх], поскольку подобный выбор
цен позволяет фирме 2 получить положительную прибыль, тогда как при
любом другом выборе прибыль фирмы 2 будет нулевой. Кроме того,
р2 Ф рх, потому что, если фирма 2 может получить положительную
прибыль, выбирая р2 = рх, то она может получить большую прибыль,
выбирая р2 немного ниже рх и обеспечивая себе целый рынок фактически по
той же самой цене, Поэтому
Р\ > с => р2 > с и р2 < рх.
Но, меняя ролями фирмы 1 и 2 и используя аналогичные аргументы, мы
получаем, что
Pi > с => Р\ > с и Р\ < Pi •
Следовательно, если в равновесии цена одной фирмы выше предельных
издержек, то обе цены должны быть выше предельных издержек и цена
каждой фирмы должна быть выше цены другой, что невозможно.
В модели Бертрана цена совпадает с предельными издержками
благодаря конкуренции только между двумя фирмами. Это поразительно, и это
сильно контрастирует с тем, что происходит в модели Курно, где
различие между ценой и предельными издержками уменьшается только при
возрастании числа фирм на рынке.
4.2.3. Монополистическая конкуренция
Фирмы и в олигополии Курно, и в олигополии Бертрана продают
одну и ту же (однородную) продукцию. В модели монополистической
конкуренции «относительно большая» группа фирм продает различные
товары, которые рассматриваются покупателями как близкие хотя и
несовершенные заменители друг друга. Каждая фирма поэтому имеет
ограниченную монопольную власть на рынке своей специфической модифика-

222
Часть II Рынки и благосостояние
ции товара, хотя рынки различных модификаций взаимосвязаны. Фирмы
производят свои товары с помощью «подобных» технологий. В
монополистически конкурирующей группе вход на рынок возможен, если новая
фирма предлагает ранее несуществующую модификацию товара.
Предположим потенциально бесконечное число возможных
модификаций товара 7 = 1, 2, .... Спрос на товар j зависит от его собственной
цены и цен на все другие модификации. Запишем спрос на j как
qj = ^(р), где dqj/dpj < 0 и dqJ/dpk > О для к Ф j D-18)
и р = (р\ ...,РУ> ...)• Кроме того, предположим, что всегда существует
некоторая цена pJ > О, при которой спрос на j будет нулевым,
независимо от цен на другие товары.
Ясно, что прибыль одной фирмы зависит от цен на все модификации
и является разностью между доходом и издержками:
nj(i>) = qj(p)pJ-cJ(qJ(p)). D-19)
При монополистической конкуренции различают два типа
равновесия: краткосрочное и долгосрочное. В краткосрочном равновесии
фиксированное число активных фирм выбирает цену так, чтобы
максимизировать прибыль, учитывая при этом цены, выбранные другими. В
долгосрочном равновесии также может быть принято решение о входе на
рынок и выходе с него. Рассмотрим по очереди каждый тип равновесия.
Пусть j = 1, ...,У — число активных фирм в краткосрочном периоде.
Для простоты будем считать, что каждая бездействующая фирма к »
назначает» цену рк (гарантируя тем самым, что ни одна из них ничего не
производит).
Теперь предположим, что р = (р\ "-,pJ) — равновесие по Нэшу в
краткосрочном периоде. Если pJ = pJ\ то qJ(p) = 0 и фирма j несет
потери, равные краткосрочным фиксированным издержкам, П; =-су@).
Однако если 0<pj <р\ то выпуск фирмы j положителен, и вектор р
должен удовлетворять условиям первого порядка для внутреннего
максимума D-19), которые могут быть переписаны с учетом D-5) в виде
^Р Wj (qj (p)) - mcj (q' (p))] = 0. D-20)
dpJ
Поскольку dqj /dpJ <0, то это сводится к знакомому нам требованию,
что цена и выпуск выбираются из условия равенства предельного дохода
предельным издержкам. Как обычно, монополистический конкурент мо-

Глава 4. Частичное равновесие
223
жет иметь положительную, отрицательную или нулевую краткосрочную
прибыль.
В долгосрочном периоде фирмы выйдут из отрасли, если их прибыль
отрицательна. Чтобы проанализировать долгосрочное равновесие,
предположим, что у каждой модификации товара есть сколь угодно близкие
заменители, которые могут быть произведены с теми же самыми
издержками. Согласно этому предположению положительная долгосрочная
прибыль любой отдельной фирмы приведет к входу на рынок сколь угодно
большого числа фирм, производящих близкие заменители. Как обычно,
одно из. условий долгосрочного равновесия заключается в отсутствии
стимулов для входа на рынок или выхода с него. Следовательно,
максимально достижимая прибыль для всех фирм должна быть отрицательной
или нулевой и прибыль каждой активной фирмы также должна быть
нулевой.
Предположим, что р* — вектор цен в долгосрочном равновесии по
Нэшу. Тогда для всех активных фирм j должны выполняться следующие
два условия:
^^[mr V(P*))->^(q V))] = 0,
nW))=o.
D-21)
D-22)
Краткосрочное и долгосрочное равновесия для репрезентативной
активной фирмы проиллюстрированы на рис. 4.4, где точка касания кривых
спроса и средних издержек характеризует долгосрочное равновесие,
описываемое соотношениями D-21) и D-22).
Цена, издержки Цена, издержки
П;(р)>0
nd= тп
a* md = тг*\
* Я
+ Ч
Рис. 4.4. Краткосрочное (а) и долгосрочное (б) равновесие при
монополистической конкуренции

224
Часть II. Рынки и благосостояние
4.3. Равновесие и благосостояние
До этого момента мы занимались вопросами определения цены и
количества для различных рыночных структур. Мы изучили стимулы
экономических агентов в условиях конкуренции, монополии и при других
формах несовершенной конкуренции и определили соответствующий
равновесный совокупный выпуск готовой продукции. В этом разделе мы
сосредоточимся на «оценке», а не на «предсказании» и ответим на разные
типы вопросов, показав, что различные структуры рынка обусловливают
различные совокупные выпуски. Означает ли это, что мы оценили
рыночные исходы с социальной точки зрения? Можем ли мы судить, что
некоторые из них «лучше» или «хуже», чем другие? Чтобы ответить на
подобные вопросы, наш угол зрения должен переместиться от чисто
позитивного к преимущественно нормативному подходу.
Нормативные суждения неизменно мотивируют и направляют
экономическую политику в ранжировании вопросов начиная с
налогообложения заканчивая регулированием фирм и отраслей промышленности.
Когда правительство вмешивается с целью изменения рыночного исхода.
Это по-разному влияет на различных экономических агентов. Как
правило, одни от этого «выигрывают», в то время как другие «проигрывают».
Если благосостояние отдельного экономического агента признается
ключевым моментом социальной политики, то неизбежно возникают две
проблемы. Во-первых, мы должны задать позитивный вопрос: как
предложенная политика отразится на благосостоянии человека? Во-вторых, мы
должны задать намного более трудный нормативный вопрос: как мы
должны взвешивать влияние, оказываемое на различных людей, чтобы
прийти к заключению об интересах «общества»? Здесь мы
сконцентрируемся на первом наборе проблем, второго — лишь коснемся, оставляя его
более полное рассмотрение для следующей главы.
4.3.1. Цена и индивидуальное благосостояние
Часто так бывает, что результаты новой политики по существу
сводятся к изменению цен, с которыми сталкивается потребитель. Налоги и
субсидии— очевидные тому примеры. Чтобы проанализировать изменения
благосостояния, мы должны понять, как цена товара влияет на
благосостояние индивида. Чтобы упростить рассуждения, предположим, что цены
всех товаров, кроме товара q, остаются фиксированными на время нашего
исследования. Это — подход с точки зрения частичного равновесия.
Так, если цена товара q есть р, а вектор остальных цен — р, то
вместо того чтобы описывать косвенную полезность потребителя как
v(p, p, у), мы просто запишем ее как v(/?, у). Точно так же мы уберем

Глава 4. Частичное равновесие
225
вектор остальных цен р из аргументов функции расходов потребителя и
функций спроса по Хиксу и по Маршаллу. Фактически будет удобнее
ввести агрегированный товар т как доход, потраченный на все товары
кроме q. Если х(р, р, у) — это вектор спроса на все другие товары, то
спрос на композитный товар составит т(р, р, у) = р • х(/?, р, у), и мы
обозначим его просто как т(р, у). В упражнении 4.16 вас попросят
показать, что, если функция полезности потребителя u(q, x) по всем
товарам удовлетворяет нашим стандартным предположениям, то функция
полезности по двум товарам q и т u(q, m) = maxx u(q, x) при
ограничении р • х < т также удовлетворяет тем же предположениям. Кроме того,
мы можем использовать й, чтобы анализировать проблему потребителя
так, как будто есть только два товара q и т. Таким образом, спрос
потребителя на q и т (величины q(p, у) и т(р, у) соответственно)
является решением задачи
maxw(<7,m) при pq + m<y,
q,m
причем значение й на решении задачи есть v(p,y).
Рассмотрим теперь следующую типичную ситуацию, в которой
может оказаться экономист. Местный орган власти рассматривает планы по
модернизации устройства для очистки воды для всего сообщества.
Запланированная реконструкция увеличит эффективность установки и, как
результат, удешевит воду. Затраты на реконструкцию будут возмещены
единовременным «водным налогом». Возникает вопрос: надо ли
проводить реконструкцию? Если руководствоваться только предпочтениями
сообщества, то вопрос можно переформулировать так: захотят ли
потребители платить дополнительный налог, чтобы «получить» снижение цены
на воду?
Чтобы ответить на этот вопрос, предположим, что наш экономист
имеет данные по спросу на воду для каждого потребителя. В частности,
ему известна для каждого потребителя кривая спроса по Маршаллу,
соответствующая текущему уровню его дохода. Оказывается, что из этого
экономист может определить весьма точно, сколько каждый потребитель
желал бы платить за снижение цены. Посмотрим, как это делается. Возьмем
отдельного потребителя, доход которого равен у0. Предположим, что
начальная цена на воду была равна р° и что она упадет в результате
реконструкции до р]. Пусть v — косвенная функция полезности потребителя,
v(p°, у0) — его полезность до снижения цены, a v(p\ у0) — его
полезность после снижения. Максимальная сумма дохода, которую потреби-

226
Часть II. Рынки и благосостояние
тель готов потратить с целью уменьшения цены, будет такой, что при
более низких уровнях цен и дохода положение потребителя окажется таким
же, как и при начальных цене и доходе. Обозначив через CV такое
изменение дохода потребителя, при котором он после изменения цены
достигает того же уровня благосостояния, что и прежде, имеем
v(p\ y°+CV) = v(p\ /). D-23)
Заметим, что в данном примере CV неположительна, потому что v не
возрастает по /?, возрастает по у и р1 < р°. CV была бы неотрицательной
при увеличении цены (р1 > р°). В любом случае D-23) остается
справедливым. CV — компенсирующая вариация (compensating variation) — это
изменение в доходе, требуемое для поддержания полезности потребителя при
изменении цен на прежнем уровне. Это понятие было введено Хиксом.
т (долл.)
<kpV)=<,V,v°)
Рис. 4.5. Цены, благосостояние и спрос потребителя

Глава 4. Частичное равновесие
227
Идею компенсирующей вариации легко проиллюстрировать
графически, что и сделано в верхней части рис. 4.5, где изображены кривые
безразличия для й(q, m). Первоначально потребитель находится в точке А,
которая характеризуется полезностью v(/?°, y°). Когда цена падает до/?1, спрос
потребителя сдвигается в точку В, и полезность возрастает до v(p\ y°).
При новой цене р1 мы должны уменьшить доход этого потребителя до
у0 + CV (напомним, что здесь CV < 0), чтобы вернуться к начальному
уровню полезности v(/?°, y°) в точке С.
Уравнение D-23) и рис. 4.5 предлагают другой взгляд на CV.
Используя известное тождество, связывающее косвенную функцию
полезности и функцию расходов, и подставляя выражение из D-23), получим
е(р\ v(p\ У°)) = е(р\ v{p\ y° + CV)) = y° + CV. D-24)
Так как у0 =е(р°, v(/?°, у0)), то D-24) можно преобразовать следующим
образом:
СУ = е(р\у°)-е(р°У), D-25)
где v° =v°(p°, y°) обозначает базовый уровень полезности потребителя
при исходных ценах и доходе.
Мы знаем, что спрос на товар q по Хиксу задается частной
производной функции расходов по цене (лемма Шепарда). Из этого факта и
выражения D-25) имеем
ПЛ, /1 оч /о (к Г'1 де(р, v°)
CV = e(p , v )-е(р , v )=] 0—^ ф =
jp dp
= lU"(py)dP- D-26)
Jp
Заметим, что когда рх < р°, CV равна со знаком минус площади области,
расположенной слева от кривой спроса по Хиксу для базового уровня
полезности v° между р{ и /7°, а если рх > р°, то CV — положительна и
равна площади этой области. Этот факт следует из D-26), так как, когда
меняются местами пределы интегрирования, нужно изменить знак
интеграла. Поэтому на рис. 4.5 CV равна (равна со знаком «минус») светлой
заштрихованной области между р1 и р°. Рассмотрим D-26) и рис. 4.5
внимательно. Мы видим, что, как и следовало ожидать исходя из здравого
смысла, если цена растет (р>р°), то для восстановления исходного

228
Часть II. Рынки и благосостояние
уровня полезности необходимо увеличение дохода (CV > 0), а если цена
уменьшается (р > р°), то для восстановления исходного уровня
полезности необходимо уменьшение дохода (СК < 0).
Компенсирующая вариация является мерой изменения
благосостояния, вызванного изменением цены. К сожалению, однако, как мы только
что узнали, CV всегда будет определяться площадью, слева от некоторой
кривой спроса по Хиксу, а хиксовский спрос ненаблюдаем в отличие от
маршалловского. Конечно, имея достаточно данных относительно спроса
потребителя по Маршаллу, систематизированных по различным ценам и
уровням дохода, можно восстановить с помощью методов интегрирования
спрос потребителя по Хиксу и непосредственно вычислить CV. Между
тем наш экономист имеет доступ только к кривой потребительского спроса
для данного товара, соответствующей одному фиксированному уровню
дохода. А этого недостаточно для восстановления спроса по Хиксу.
Несмотря на это, для получения оценки CV мы все же можем
использовать связь между спросом по Хиксу и спросом по Маршаллу,
описываемую уравнением Слуцкого. Напомним, что маршалловский спрос отражает
полный эффект изменения цен, а хиксовский отражает только эффект
замещения. Поэтому, вообще говоря, они будут различаться, и различаться при
изменении цен в точности из-за эффекта дохода. Это проиллюстрировано
для случая, когда q — нормальный товар, в нижней части рис. 4.5
горизонтальным расхождением между двумя кривыми всюду, кроме точки р°.
Мы хотели бы связать идею Хикса о компенсирующей вариации с
понятием излишка потребителя, потому что последний легко
измеряется непосредственно с помощью маршалловского спроса. Напомним, что в
координатах «цена — доход» (р°, у0) излишек потребителя CS(p°, y°)
является площадью, ограниченной сверху кривой спроса (при заданном
у0) и снизу — ценой р°. Следовательно, объединение заштрихованных
областей на рис. 4.5 равняется приросту излишка потребителя,
обусловленному падением цены от р° до рх. Так,
ACV = CS(p\ y°)-CS(p°, y°)=\P°q(p, y°)dp. D-27)
J p
Как видно, ACS всегда противоположен по знаку CV и отличается
по абсолютной величине от CV благодаря эффекту дохода,
появляющемуся при изменении цен всякий раз, когда спрос зависит от дохода
потребителя. Поскольку мы хотим определить CV , но можем вычислить
только ACS, то возникает естественный вопрос: насколько хорошее
приближение CV обеспечивает ACS?

Глава 4. Частичное равновесие
229
Виллиг [Willig, 1976] изучил этот вопрос и получил некоторые
полезные результаты. Он нашел, что когда эластичность спроса по доходу
не зависит от цены, абсолютная величина CV отличается от абсолютной
величины ACS, но первая может быть точно рассчитана на основе
последней1. Более того, Виллиг показал для произвольных функций спроса,
что можно вычислить верхний и нижний пределы ошибки, которую мы
допускаем, когда используем -ACS как приближение для CV . Основной
вывод, полученный Виллигом, заключается в следующем: для небольших
изменений в цене ошибка, допускаемая при использовании -ACS вместо
CV, является обычно настолько малой, что можно ее просто
игнорировать. Некоторые из численных результатов Виллига воспроизведены в
табл. 4.1. Каждая графа таблицы дает ошибку как долю в излишке
потребителя (CV - ACS)/ACS для различных значений эластичности спроса по
доходу г| и излишка потребителя как доли основного дохода
а = |ACS,|/j>°. Изучите внимательно эти данные и помните, что для
небольших изменений в цене единственного товара в бюджете потребителя
доля а = IACaSJ/jk0 действительно будет незначительной.
Таблица 4.1
\. а
-1,01
0,50
0,70
0,90
1,01
1,10
1,20
1,50
2,00
0,005
-0,003
0,001
0,002
0,002
0,003
0,003
0,003
0,004
0,005
0,010
-0,005
0,003
0,004
0,005
0,005
0,006
0,006
0,008
0,010
0,020
-0,010
0,005
0,007
0,009
0,010
0,011
0,012
0,015
0,020
0,030
-0,015
0,008
0,011
0,014
0,015
0,017
0,018
0,023
0,031
0,040
-0,019
0,010
0,014
0,018
0,020
0,022
0,024
0,031
0,042
0,050
-0,024
0,013
0,018
0,023
0,026
0,028
0,031
0,039
0,053
0,075
-0,035
0,019
0,027
0,034
0,039
0,043
0,047
0,059
0,081
0,100
-0,046
0,025
0,035
0,046
0,052
0,057
0,063
0,080
0,111
0,150
-0,066
0,038
0,054
0,070
0,08
0,088
0,097
0,125
0,176
Источник: [Willig, 1976].
Теперь вернемся к нашему примеру. Из вышесказанного следует, что,
до тех пор пока уменьшение цены от р° до р1 не слишком велико, наш
экономист может легко оценить действительную готовность каждого
потребителя заплатить за такое уменьшение. Основываясь на этом, может
быть принято обоснованное решение относительно того, кто должен
заплатить налог и в каком размере.
1 См. упражнение 4.18.

230
Часть II Рынки и благосостояние
Перед тем как пойти дальше, стоит предупредить, что когда известна
только рыночная кривая спроса как альтернатива индивидуальным
кривым спроса, изменение в излишке потребителя (скажем, снова при
небольшом падении цены) обеспечит хорошую аппроксимацию
совокупного дохода всех потребителей, который они готовы потратить ради
уменьшения цены. Однако вполне может случиться так, что одни потребители
будут готовы потратить на это больше дохода, чем другие (крупные
водопользователи, например). Следовательно, анализ рыночного спроса мог
бы верно указать на то, что общая готовность заплатить превышает
общую стоимость проекта, и это означало бы, что есть некоторый способ
распределить стоимость проекта среди потребителей так, чтобы каждый
был в лучшем положении после выплаты своей части и получения воды
по более низкой цене. Однако это не помогло бы ответить на вопрос: как
эта общая стоимость должна быть распределена среди потребителей в
действительности?
4.3.2. Эффективность конкурентного рынка
В примере, который только что был рассмотрен, казалось ясным, что
проект должен быть осуществлен, если, принимая во внимание и затраты,
и выгоды, положение каждого потребителя могло бы стать лучше. В
общем случае, когда чье-то положение можно улучшить, не ухудшая
положения остальных, мы говорим, что имеет место Парето-улучшение. Если
нет никакого способа улучшить ситуацию по Парето, мы говорим, что
ситуация Парето-эффективна (оптимальна). Таким образом, ситуация
Парето-эффективна, если нет никакого способа улучшить положение
одного, не ухудшая положения других.
Идея Парето-эффективности довольно популярна в экономике и
часто используется как один из способов оценить работу экономической
системы. Ее суть заключается в том, что экономическая система считается
хорошо функционирующей, если данное распределение ресурсов
невозможно изменить таким образом, чтобы получить Парето-улучшение. Мы
разовьем эту мысль более систематически в главе 5. А пока ограничимся
следующим вопросом: какие (если таковые вообще имеются) из трех
типов рыночной конкуренции — совершенная конкуренция, монополия или
олигополия Курно — функционируют хорошо в том смысле, что
приводят к Парето-эффективному результату?
Заметим, что различие между тремя формами конкуренции— это
просто цены и объемы выпуска, которые определяются ими. Например,
если бы совершенно конкурентная отрасль была захвачена
монополистом, то цена повысилась бы (относительно цены в совершенно
конкурентном равновесии) до уровня, максимизирующего прибыль монополи-

Глава 4. Частичное равновесие
231
ста, а количество произведенного и потребленного товара упало бы.
Заметим, однако, что в обоих случаях пара «цена—количество» является
точкой на кривой рыночного спроса. То же самое верно для модели
олигополии Курно. Следовательно, мы могли бы точно так же спросить: какие
пары «цена—количество» на кривой рыночного спроса дают Парето-
эффективный исход? Попробуем найти ответ на этот вопрос.
Чтобы упростить обсуждение, предположим с этого момента, что есть
только один производитель и один потребитель. (Доказательство можно
обобщить.) Обратимся теперь к рис. 4.6, на котором изображен маршал-
ловский спрос потребителя (и поэтому рынка) q(p,y°), его хиксовский
(компенсированный) спрос qh(p, v°), где v°=v(/?0, у0), и кривая
предельных издержек фирмы mc{q). Заметим, что если бы эта фирма вела
себя как совершенно конкурентная, пара «цена—количество» в равновесии
определялась бы пересечением двух кривых, потому что выше минимума
средних переменных издержек кривая предложения конкурентной фирмы
совпадает с кривой ее предельных издержек. (Мы предположили, что
средние переменные издержки достигают минимума при q = 0.)
Р
Р°
Р1
Рис. 4.6. Неэффективность монополистического равновесия
Рассмотрим теперь на рис. 4.6 пару «цена—количество» (р°, q°) на
кривой спроса потребителя выше конкурентной точки. Покажем, что эта
точка не является Парето-эффективной. Для этого мы должны
предложить такой способ перераспределения ресурсов, который бы позволил
улучшить положение одного агента, не ухудшая положения другого.
i
с
Г
?V
с\
D\
v°)
у mc{q)

232
Часть II Рынки и благосостояние
Рассмотрим сокращение цены товара q с р° до рх. Что потребитель
готов заплатить за это сокращение? Как мы теперь знаем, ответ — это
абсолютная величина компенсирующей вариации, которая в данном случае
равна сумме площадей А и В на рис. 4.6. Уменьшим теперь цену до рх и
заберем у потребителя А + В единиц дохода. Следовательно, теперь он
находится в том же положении, в котором был прежде, и согласно кривой
компенсированного спроса предъявляет спрос на qx единиц товара.
Чтобы обеспечить дополнительный спрос на товар q, допустим, что
фирма произвела достаточно дополнительной продукции для
удовлетворения этого спроса.
Итак, к данному моменту мы понизили цену до рх, увеличили
производство товара до qx и забрали А + В долларов у потребителя.
Потребитель при этом находится точно в таком же положении, как и прежде,
когда эти изменения еще не произошли. Конечно, изменения в цене и
количестве будут влиять на прибыль, получаемую фирмой. В частности, если
через c(q) обозначить издержки производства q единиц готовой
продукции, то изменение прибыли фирмы составит
[pV-cfo')]-[^^
= [pW-pV]-^mc(q)dq =
= [C + D-A]-D =
= С-А.
Следовательно, если после проведения всех этих изменений мы
дадим фирме А долларов из суммы А + В, взятой у потребителя, то фирма
окажется в положении лучшем, чем раньше. Мы можем тогда вернуть
потребителю сумму В, и тогда оба — и потребитель, и фирма — окажутся в
лучшем положении.
Таким образом, по сравнению с рыночным исходом (р°, q°),
перераспределяя доступные ресурсы, мы улучшили положение и потребителя, и
фирмы. Следовательно, начальная ситуация не была Парето-эффективной.
Подобное доказательство применимо и к парам «цена—количество»
на кривой маршалловского спроса потребителя, лежащим ниже
конкурентной точки1. Следовательно, единственная пара «цена—количество»,
которая, возможно, является Парето-эффективным результатом,— это
1 См. упражнение 4.21.

Глава 4. Частичное равновесие
233
точка равновесия при совершенной конкуренции. И это действительно
так. Мы не будем приводить здесь доказательство, потому что этот
результат будет следовать из более общего анализа в главе 5. Однако
советуем читателю проверить, что детальная схема, которая использовалась
прежде, чтобы получить Парето-улучшение, не работает, когда мы
начинаем процесс в точке конкурентного равновесия. (Никакая другая схема
также не произведет улучшения по Парето.)
Таким образом, наш вывод заключается в следующем: единственная
пара «цена—количество», дающая Парето-эффективный исход, — это
точка равновесия при совершенной конкуренции. В частности, ни
монополия, ни олигополия Курно не приводят к Парето-эффективному
исходу.
Обратите внимание: мы не можем заключить из данного анализа, что
вынуждая монополию изменить линию поведения, мы обязательно
придем к улучшению по Парето. Вполне можно понизить цену и увеличить
объем поставляемой продукции, но если потребители, положение
которых в результате этих перемен улучшилось, не выплатят компенсацию
монополисту, положение которого ухудшилось, это не будет Парето-
улучшением.
4.3.3. Эффективность и максимизация совокупного излишка
Как мы видели, излишек потребителя — это оценка меры выгоды (в
долларах), получаемой потребителем в результате покупки
рассматриваемого товара. Гораздо легче найти точный способ измерить в долларах
ценность, которую приносит производителю продажа товара
потребителю. Эта величина, называемая излишком производителя, представляет
собой разницу между доходом фирмы и ее переменными издержками.
Теперь, казалось бы, для получения эффективного исхода нужно
максимизировать совокупный излишек — сумму излишка потребителя и
производителя. В противном случае положение и производителя, и
потребителя можно улучшить, перераспределяя ресурсы таким образом, чтобы
сначала увеличить совокупный излишек, а затем поделить возросший излишек
между ними так, чтобы каждый получил больше, чем прежде.
Но мы должны быть осторожны. Излишек потребителя завышает
долларовые выгоды потребителя всякий раз, когда присутствует эффект
дохода и товар — нормальный. Несмотря на это, в предположении, что
кривая спроса имеет отрицательный наклон, а предельные издержки
фирмы являются возрастающей функцией, эффективность действительно
не будет достигнута, пока сумма излишка потребителя и производителя
не будет достигать максимума.
Чтобы убедиться в этом, вернемся снова к случаю единственного
потребителя и единственного производителя, как показано на рис. 4.7, и

234
Часть II. Рынки и благосостояние
рассмотрим произвольную пару «цена—количество» (/?, q) на кривой
спроса (причем р = p{q), где /?(•) — обратная функция спроса). Ранее
мы определили излишек потребителя при (р, q) как площадь области
под кривой спроса и выше цены р. Легко увидеть, что мы можем
выразить ту же самую площадь и соответственно излишек потребителя как
площадь под кривой обратного спроса до q за вычетом площади
прямоугольника p(q)q. Таким образом, мы можем записать сумму
потребительского излишка и излишка производителя в следующем виде1:
CS + PS = [\gop(№-p(q)qy[p(q)q-tvc(q)] =
= \lp^)dk-tvc(q) =
= \1[р^)-тфЩ.
Выбирая q так, чтобы максимизировать это выражение, приходим к
условию первого порядка
p(q) = mc(q),
которое в точности выполняется при равновесном объеме выпуска в
условиях совершенной конкуренции, когда кривая спроса имеет отрицательный
наклон и предельные издержки возрастают, как это изображено на рис. 4.7.
Цена
* Ч
Ч Ч
Рис. 4.7. Максимизация совокупного излишка потребителя и производителя
при конкурентном рыночном равновесии
1 Последняя строка следует из J mc(^)d^ = c(q) - с@) и так как с@) — постоянные
издержки, a c(q) — совокупные издержки, то разность c(q)-c@) — это совокупные
переменные издержки, т.е. tvc{q).

Глава 4. Частичное равновесие
235
Фактически именно отношение между ценой и предельными
издержками отвечает за связь между нашим анализом в предыдущем параграфе
и анализом, проводимым здесь. Всякий раз, когда цена и предельные
издержки различаются, может быть осуществлено Парето-улучшение,
аналогичное тому, как это делалось выше. И, как мы только что видели,
всякий раз, когда цена и предельные издержки различаются, совокупный
излишек может быть увеличен.
Еще раз предупредим: хотя Парето-эффективность предполагает, что
совокупный излишек достигает максимума, Парето-улучшение
необязательно сводится к простому увеличению совокупного излишка. Если те, кто
извлекает из этого выгоду, не компенсируют потери тех, кто «проиграл» в
результате изменения, то изменение не является улучшением по Парето.
Мы видели, что, когда рынки несовершенно конкурентны, как
правило, в равновесии цены превышают предельные издержки. Однако
равенство цены предельным издержкам является необходимым условием
максимизации излишка потребителя и производителя. Поэтому не должен
удивлять тот факт, что равновесные распределения на рынках с
несовершенной конкуренцией не являются Парето-эффективными.
Пример 4.4. Рассмотрим модель олигополии Курно из
параграфа 4.2.1. Пусть рыночный спрос на совокупный выпуск готовой
продукции q равен p = a-bq. Фирмы имеют одинаковые предельные издержки
с > О. Если все фирмы производят одинаковый объем выпуска q/J,
то совокупный излишек W = cs-\- ps — как функция совокупного
выпуска — будет равен
W(q) = \qo(a-b№-Jjqo'Jcdt;,
ИЛИ
W(q) = aq-(b/2)q2-cq. (E-1)
Поскольку функция из (Е-1) является строго вогнутой, то совокупный
излишек достигает максимума при q = (a-c)/b, когда W\q*) = 0. Таким
образом, максимальный потенциальный излишек на этом рынке будет
следующим:
W{q) = {^t. (E-2)
В равновесии Курно — Нэша мы видели, что совокупный выпуск рынка
составляет q = J {а - с)/(J + l)b. Ясно, что q <q\ так что олигополия
Курно производит слишком малый объем продукции по сравнению с
общественно оптимальным. Совокупный излишек в равновесии Курно равен

236
Часть II. Рынки и благосостояние
r^_(a-cJ J2+2J
2b (J + l)
а безвозвратные потери —
пч)=у\:;:,:::, (е-з>
W(q )-W(q) = ^ С} > 0. (Е-4)
Используя (Е-3), легко показать, что совокупный излишек
увеличивается по мере того, как растет число фирм на рынке. Ранее мы отмечали,
что рыночная цена стремится к предельным издержкам, по мере того как
возрастает число фирм в модели олигополии. Следовательно, совокупный
излишек увеличивается до своего максимального уровня (Е-2), а
безвозвратные потери (Е-4) уменьшаются до нуля при J —> «>. ?
4.4. Упражнения
4.1. Предположим, что предпочтения потребителей одинаковы и
гомотетичны. Покажите, что рыночный спрос на любой товар не зависит от
распределения дохода. Покажите также, что эластичность рыночного
спроса относительно уровня рыночного дохода равна единице.
4.2. Предположим, что предпочтения потребителей гомотетичны, но
не одинаковы. Гарантирует ли это независимость рыночного спроса от
распределения дохода?
4.3. Покажите, что если q — нормальный товар для каждого
потребителя, то кривая рыночного спроса на q будет иметь отрицательный
наклон по своей цене.
4.4. Предположим, что х и у являются взаимозаменяемыми
товарами для всех потребителей, кроме одного. Следует ли из этого, что
рыночный спрос на товар х будет увеличиваться с ростом цены товара у ?
4.5. Покажите, что число фирм в долгосрочном равновесии
неопределенно, если все фирмы в отрасли совместно используют одинаковую
технологию с постоянной отдачей от масштаба и сталкиваются с одними и
теми же ценами на факторы производства.
4.6. Фирма j в конкурентной отрасли имеет функцию совокупных
издержек cJ (q) = aq + bjq2, где а > 0, q — выпуск фирмы, а Ь} — некий
параметр, характеризующий фирму j.
а) Если bj > 0 для всех фирм, то чем регулируется количество,
произведенное каждой из них? Будут ли они производить равные объемы
продукции? Объясните свой ответ.
б) Что произойдет, если Ь} < 0 для всех фирм?

Глава 4. Частичное равновесие
237
4.7. Технология производства товара q описывается функцией
издержек c(q) = aq + bq2. Рыночный спрос на товар q составляет
а) Если я > О и />< О ив отрасли J фирм, то каковы будут цена в
краткосрочном равновесии и выпуск репрезентативной фирмы?
б) Если а > О и 6 < 0, то каковы будут цена в долгосрочном
равновесии и число фирм? Объясните свой ответ.
в) Если я > О и fc > 0, то какова будет цена в долгосрочном
равновесии и число фирм? Объясните свой ответ.
4.8. Пусть в олигополии Курно, рассмотренной в параграфе 4.2.1,
J = 2. Пусть каждый дуополист имеет постоянные средние и предельные
издержки, как прежде, но 0 < с1 < с2. Покажите, что в равновесии по Нэ-
шу фирма 1 будет иметь большую прибыль и производить большую долю
совокупного выпуска, чем фирма 2.
4.9. В дуополии Штакельберга одна из фирм — «лидер», другая —
«последователь». Обе фирмы знают издержки друг друга и рыночный
спрос. Последователь принимает выпуск лидера как заданный и выбирает
свой собственный выпуск, учитывая это (т.е. действия последователя
аналогичны поведению в модели Курно). Лидер, выбирая свой собственный
выпуск, принимает реакцию последователя как заданную. Предположим,
что фирмы 1 и 2 сталкиваются с рыночным спросом p = WQ-(ql+q2).
Издержки фирм равны с, = 10д, и с2 = q\.
а) Вычислите рыночную цену и прибыль каждой фирмы,
предполагая, что фирма 1 является лидером, а фирма 2 — последователем.
б) Сделайте то же самое, предполагая, что фирма 2 является лидером,
а фирма 1 — последователем.
в) Учитывая ответы на пункты а) и б), объясните, кого фирма 1 хотела
бы видеть лидером рынка? Кого хотела бы видеть лидером рынка фирма 2?
г) Если каждая фирма согласно пункту в) занимает то место, которое
хотела бы, то каковы будут равновесная цена на рынке и прибыль фирм?
Как это соотносится с равновесием Курно — Нэша на этом рынке?
4.10. (Экономическая война по Штакельбергу) Пусть на рынке,
описанном в параграфе 4.2.1, J = 2.
а) Покажите, что если, например, фирма 1 — лидер, а фирма 2 —
последователь, то лидер получает большую, а последователь — меньшую
прибыль, чем в равновесии в модели Курно. Сделайте вывод о том, что
каждая фирма хотела бы стать лидером.
б) Если обе фирмы решают действовать как лидер и каждая
предполагает, что вторая фирма будет последователем, то может ли быть
определено равновесие? Что произойдет на таком рынке?

238
Часть II. Рынки и благосостояние
4.11. Пусть в модели конкуренции по Курно из параграфа 4.2.1
каждая фирма имеет функцию издержек c(q) -кл-cq, где к > 0 —
постоянные издержки.
а) Каковы будут равновесная цена, объем выпуска готовой продукции и
прибыль каждой фирмы при J действующих фирмах на рынке?
б) Если существуют свободный вход на рынок и выход с него, то
каково будет число фирм на рынке в долгосрочном равновесии?
4.12. В дуополии по Бертрану из параграфа 4.2.2 рыночный спрос
равен 2 = а-Р/?, и фирмы имеют одинаковые предельные издержки
(постоянные издержки отсутствуют). Найдите в равновесии по Бертрану пары
цен (pl9 p2) и объемов выпуска (#,, q2) при следующих предпосылках:
а) Фирма 1 имеет фиксированные издержки F > 0.
б) Обе фирмы имеют фиксированные издержки F > 0.
в) Фиксированные издержки — нулевые, но фирма 1 имеет более
низкие предельные издержки, чем фирма 2, так что с2 > с, > 0. (Считайте,
что фирма с низкими издержками получает весь рыночный спрос всякий
раз, когда фирмы назначают равные цены.)
4.13. Дуополисты, производящие взаимозаменяемые товары qx и q2,
сталкиваются с обратным спросом:
Pi =2(> + -Р2-<1\
и
Pl=20 + -P\-<l2
соответственно. Каждая фирма имеет постоянные предельные издержки,
равные 20, постоянные издержки отсутствуют. Фирмы конкурируют по
Курно по цене, а не по объему выпуска продукции. Найдите равновесие
по Курно на этом рынке, вычислив равновесную цену и объем выпуска
для каждого товара.
4.14. Отрасль состоит из большого числа одинаковых фирм, каждая из
которых имеет функцию издержек c{q) = q2 +1. При J действующих
фирмах каждая из них сталкивается с одинаковым обратным рыночным спросом
р = 10 -15q - (J - \)q , когда каждая из оставшихся (J -1) действующих
фирм производит объем продукции q .
а) При J действующих фирмах и невозможности входа или выхода с
рынка каков будет в краткосрочном равновесии объем выпуска готовой
продукции репрезентативной фирмы q*, если фирмы действуют как
конкуренты по Курно при выборе объема выпуска?

Глава 4. Частичное равновесие
239
б) Сколько фирм останется в отрасли в долгосрочном периоде?
4.15. Пусть фирмы у = 1, ...,*/ действуют на монополистически
конкурентном рынке, фирма j сталкивается со следующей функцией спроса:
QJ=(PJ)
Л-2
( V2
j
-1/2
Т.рг
/=1
К* J
7=1, ...,У.
Действующая или нет, каждая фирма из числа у = 1,2... имеет
одинаковые издержки,
c(q) = cq + k,
где о 0 и к > О. Каждая фирма выбирает цену, чтобы максимизировать
свою прибыль, учитывая цены, выбранные другими.
а) Покажите, что кривая спроса каждой фирмы имеет отрицательный
наклон, характеризуется постоянной эластичностью по своей цене, и что
все товары являются взаимозаменяемыми.
б) Покажите, что если все фирмы повышают цены пропорционально,
то спрос на любой товар снижается.
в) Найдите количество фирм в долгосрочном равновесии по Нэшу.
4.16. Предположим, что функция полезности потребителя u(q, x) по
всем товарам является непрерывной, строго возрастающей и строго
квазивогнутой и что вектор цен р на вектор товаров х фиксирован. Пусть
т обозначает агрегированный товар р • х так, что т — это доход,
потраченный на х. Определим функцию полезности й по этим двум
товарам q и т следующим образом:
й(#, т) = max u(q, х) при р • х < т.
X
а) Покажите, что u(q, m) строго возрастающая и строго
квазивогнутая. Если сможете, то обратитесь к теореме, которая позволит вам сделать
вывод, что она также и непрерывна.
б) Покажите, что если q(p, p, у) и х(р, р, >>) обозначают маршал-
лианский спрос потребителя на товары q и х, то q(p, p, у) и
т(Р> Р> У) = Х(Р> Р> У) являются решениями задачи
maxw(g, m) при pq + m<y.
q,m
Покажите, что максимальное значение й есть v(p, p, у).

240
Часть II Рынки и благосостояние
в) Сделайте вывод, что, когда цены на все товары, кроме одного,
фиксированы, можно анализировать потребителя так, как будто было
только два товара, товар, цена на который не установлена, и композитный
товар — «деньги, потраченные на все другие товары».
4.17. Пусть (д°, х°)»0 максимизирует u{q, x) при условии
p°q + р° • х < у0. Покажите, что если и дифференцируема в точке
(#°, х°) и Vw(#°, x°)»0, то потребитель готов заплатить больше, чем
(р° - pl)q°, за сокращение цены товара q до р].
4.18. Виллиг показал, что когда эластичность спроса по доходу не
зависит от цены, так что
ду q(p, У)
для любых р и у в допустимой области, тогда для исходной цены р° и
дохода у0 CS и CV связаны следующим соотношением:
-ACS = J7expU;^
а) Покажите, что, когда эластичность спроса по доходу постоянна, но
не равна единице,
-|1/0-П)
CV = y°\
A-Л) + 1
/
¦/.
б) Используя этот факт, покажите, что, когда спрос не зависит от
дохода, то - ACS = CV, так что излишек потребителя может использоваться
для получения точной меры воздействия изменения цен на благосостояние.
в) Получите связь между CV и ACS в случае, когда эластичность по
доходу равна единице.
г) Наконец, мы можем использовать результат пункта а), чтобы
установить удобное эмпирическое правило, которым можно пользоваться для
оценки величины отклонения между изменением в излишке потребителя и
компенсирующей вариацией в случае, когда эластичность по доходу
является постоянной. Покажите, что когда эластичность по доходу является
постоянной и не равной единице, (CF — |АС*^!)/!ACS|«(г||АС5'|)/2^0.
4.19. Предпочтения потребителя относительно единственного товара
х и всех других товаров т описываются функцией полезности
w(jc, т) = 1п(*) + т. Пусть цена х равна р, цена т равна единице, и
пусть доход потребителя равен у.

Глава 4. Частичное равновесие
241
а) Выведите спрос по Маршаллу на товары х и т .
б) Выведите косвенную функцию полезности v(p, у).
в) Используя уравнение Слуцкого, разложите эффект изменения цены
товара х на эффекты замещения и дохода. Проинтерпретируйте
полученный результат.
г) Предположим, что цена товара х возрастает от р° до р1 > р°.
Покажите, что площадь излишка потребителя между р° и рх дает точную
меру эффекта изменения цен на благосостояние потребителя.
д) Аккуратно проиллюстрируйте полученные результаты на двух
диаграммах: верхней — в терминах кривых безразличия и бюджетных
ограничений, нижней — в терминах кривых спроса по Маршаллу и по Хиксу.
Убедитесь, что ваши диаграммы отражают всю качественную
информацию относительно предпочтений и спроса, которую вы получили.
Убедитесь, что рассмотрели две цены р° и р1 и идентифицировали спрос по
Маршаллу и по Хиксу.
4.20. Спрос потребителя на единственный товар х задается
выражением х(р, у) = у/р, где р — цена товара, а у — доход потребителя.
Пусть доход равен 7 долл. Найдите компенсирующую вариацию при
возрастании цены товара от 1 до 4 долл.
4.21. Используя рисунок, подобный рис. 4.6, объясните, почему пары
«цена—количество» на кривой спроса ниже точки конкурентного
равновесия не являются Парето-эффективными.
4.22. Монополист сталкивается с линейным спросом p = a-$q и
имеет издержки C = cq + F, где все параметры положительны, а>с и
(cc-cJ>4pF.
а) Вычислите монопольный объем выпуска, цену и прибыль.
б) Вычислите безвозвратные потери и покажите, что они
положительны.
в) Если правительство потребует, чтобы монополист установил цену,
которая максимизирует сумму излишков потребителя и производителя, и
обеспечил всех покупателей товаром по этой цене, то какая цена будет
назначена? Покажите, что при этом прибыль фирмы будет
отрицательной, а значит, эта форма регулирования нежизнеспособна в долгосрочном
периоде.
4.23. (Правило Рамсея.) Основываясь на предыдущем упражнении,
предположим, что монополист сталкивается с кривой спроса с
отрицательным наклоном р = p{q) и имеет издержки С = cq + F. Теперь
предположим, что правительство требует, чтобы монополист установил цену
р*, которая максимизирует сумму излишков потребителя и производите-

242
Часть II Рынки и благосостояние
ля при условии, что прибыль фирмы неотрицательна (так, чтобы
регулирование было жизнеспособно в долгосрочном периоде). Покажите, что
при этой форме регулирования фирма назначит цену, превышающую
предельные издержки, и что процентное отклонение цены от предельных
издержек (р*-с)/р* будет пропорционально l/e*, где е*—
эластичность спроса фирмы по выбираемой цене и объему выпуска.
Проинтерпретируйте полученный результат.
4.24. Предположим, что (р, q) — равновесная рыночная цена и
объем выпуска готовой продукции на совершенно конкурентном рынке, на
котором действуют только две фирмы. Покажите, что если кривая спроса
имеет отрицательный наклон и предельные издержки возрастают, то
(Р> Я) удовлетворяют условиям второго порядка задачи максимизации
суммы излишков потребителя и производителя.
4.25. (Смещение благосостояния при выборе продукции.)
Монополист должен выбрать один из двух проектов выпуска своей продукции.
Каждый проект будет иметь различный рыночный спрос и различные
издержки производства. Если будет принят проект jc, , то рыночный спрос и
издержки будут равны
2 7 7
— + 6--рх, если 0<р{<6-,
рх 8 8
х, =
2 S
—, если рх >6—,
Р, 8
/ ч с1
cl(*l) = 5g+*l-
Если будет принят проект %г, то рыночный спрос и издержки будут
следующими:
i1 11
х2 =7 —1-/?2,
2 8 Г2
с2С*2) = 4:: + *2-
Обратите внимание, что функции издержек двух проектов отличаются
только постоянными издержками.
а) Вычислите цену, которую фирма назначила бы, и прибыль,
которую она получила бы, если будет принят каждый проект. Какой проект
будет одобрен фирмой?

Глава 4. Частичное равновесие
243
б) Схематично изобразите кривые спроса и кривые предельных
издержек для обоих проектов на одном рисунке. Максимизирует ли выбор
фирмы сумму излишков потребителя и производителя? Эффективен ли
результат по Парето?
4.26. Конкурентная отрасль находится в долгосрочном равновесии.
Рыночный спрос линеен и равен p = a-bQ, где я > 0, 6 > 0, и Q —
совокупный объем выпуска. Все фирмы в отрасли имеют одну и ту же
технологию с функцией издержек c(q) = k2 +q2.
а) Какова цена в долгосрочном равновесии? (Введите необходимые
предпосылки на параметры, чтобы гарантировать, что она положительна
и меньше а.)
б) Предположим, что правительство вводит потоварный налог / > О
на каждую фирму, работающую в отрасли. Опишите то, что случится в
долгосрочном периоде с количеством фирм в отрасли. Какова будет
равновесная рыночная цена после введения налога? (Введите снова все
необходимые предпосылки, чтобы гарантировать, что цена будет
положительна и меньше а.)
в) Вычислить долгосрочный эффект этого налога на излишек
потребителя. Покажите, что безвозвратные потери от данного налога
превышают объем налогового дохода, собранного правительством в условиях
рыночного равновесия после введения налога.
г) Был бы паушальный налог на производителей, позволяющий
собрать тот же самый объем налогового дохода, более предпочтителен для
потребителей? Поясните свой ответ.
д) Приведите условия, при которых паушальный налог на
потребителей, позволяющий собрать тот же самый объем дохода, будет для
потребителей предпочтительнее любой предыдущей формы налога.
4.27. Пусть на выпуск монополиста введен потоварный налог / > 0.
Монополист сталкивается со спросом q = р~г, где 8 > 1 и имеет
постоянные средние издержки. Покажите, что монополист увеличит цену на
большую величину, чем объем потоварного налога.
4.28. Фирма в условиях неопределенности сталкивается с лотереями
q = (pl°nl9 ...,/?„ оrcj, где л,. — прибыль, а р( — вероятность ее
получения. Предпочтения владельца фирмы описываются функцией
полезности фон Неймана— Моргенштерна на этих лотереях; считайте, что он
руководствуется максимизацией ожидаемой полезности. Докажите, что
владелец фирмы будет всегда действовать так, чтобы максимизировать
ожидаемую прибыль тогда и только тогда, когда он нейтрален к риску.
4.29. Рассмотрим монополию в двухпериодной модели,
сталкивающуюся с кривой обратного спроса р( = p(qt) с отрицательным наклоном

244
Часть II. Рынки и благосостояние
в каждом периоде t = 1, 2. Фирма максимизирует текущую дисконтиро-
ванную прибыль PDV = ^A-г)~'7с,, где г > О — рыночная процентная
ставка, а я, — прибыль периода /. Предположим, что издержки в каждом
периоде являются возрастающей функцией от объема выпуска этого
периода и строго выпуклы и что PDV является строго вогнутой.
а) Если издержки с, = c(qt) для t = 0, 1, покажите, что фирма будет
«максимизировать прибыль в краткосрочном периоде» в каждый период,
таким образом выбирая объем выпуска, чтобы уравнять предельные
издержки и предельный доход в каждом периоде.
б) Теперь предположим, что фирма может «учиться в процессе
работы». Ее издержки первого периода равны с0 = c0(q0). Ее издержки
второго периода, однако, зависят от объема выпуска первого периода;
с\ =ci(<7p #o)> где dcjdq0 <0. Будет ли фирма продолжать
«максимизировать прибыль в краткосрочном периоде» в каждый период? Да или нет?
Почему? Проинтерпретируйте полученные результаты.

Глава 5
ОБЩЕЕ РАВНОВЕСИЕ
II
Многие исследователи возводят зарождение экономической теории к
публикации «Богатства народов» Адама Смита A776). За видимым
хаосом бесчисленных взаимодействий экономических агентов,
преследующих свои эгоистические интересы, Смит разглядел объединяющую силу,
которая служит обществу. Эта невидимая рука ведет рыночную систему к
равновесию, которое, как полагал Смит, обладает полезными для
общества характеристиками.
Из множества вопросов о конкурентной рыночной системе сразу же
выделяется один, фундаментальный: является ли логически
последовательным взгляд Смита на нее как на отлаженный механизм, состоящий из
многочисленных индивидов, которые участвуют в функционировании
рынков, не интересуясь ничем кроме собственной выгоды? Если это так,
то существует ли одно конкретное состояние, к которому будет двигаться
такая система, или таких состояний много? Являются ли они
устойчивыми или их легко нарушить?
Это вопросы существования, единственности и устойчивости общего
конкурентного равновесия. Все они важны, но мы обратимся только к
первому из них — вопросу существования, который во многих
отношениях заслуживает нашего особого внимания.
Нас интересует прежде всего само логически последовательное
понятие конкурентной рыночной системы. Но вопрос существования,
однако, обычно формулируется как вопрос о существовании таких цен, при
которых спрос и предложение приходят в соответствие одновременно для
каждого товара и услуги. Рыночные цены на все, что мы покупаем и
продаем, определяют наше возможное потребление, а значит, и достижимый
уровень благосостояния. Поэтому от цен в значительной степени зависит,
«что и кому достается» в рыночной экономике.
В этой главе мы не просто попытаемся выяснить, при каких условиях
существует набор цен, который приводит рынки в равновесие. Нас
интересует и то, насколько хорошо рыночная система решает основную
задачу экономики — задачу распределения. Мы начнем изучать ее в очень
общей постановке, а затем будем рассматривать саму проблему
существования общего конкурентного равновесия. По ходу дела мы проверим
утверждение Смита о том, что конкурентная рыночная система
способствует увеличению общественного благосостояния без какого-либо
сознательного коллективного замысла членов общества.

246
Часть II. Рынки и благосостояние
5.1. Равновесие в экономике обмена
Здесь мы рассмотрим задачу распределения в очень простом
обществе без организованных рынков. Наша цель — описать, к каким исходам
может привести процесс добровольного обмена. Изучив их, мы сможем
получить точку отсчета, с которой будем сравнивать равновесия в
конкурентной рыночной системе.
Рассматриваемое нами общество является очень простым. Во-первых,
в нем нет производства. Товары имеются, но пока мы не спрашиваем,
откуда они взялись. Вместо этого мы просто предполагаем, что каждый
потребитель «наделен» природой некоторым запасом потребительских
товаров. У каждого потребителя есть предпочтения относительно
доступных потребительских наборов, и каждого заботит только его собственное
благосостояние. Члены этого общества (агенты) могут потреблять свои
начальные запасы или участвовать в бартерном обмене с остальными.
В данном обществе мы допускаем наличие института частной
собственности и предполагаем, что соблюдается принцип добровольной торговли.
При отсутствии принуждения и по причине корыстных интересов
потребителей добровольный обмен является единственным способом
перераспределения товаров по сравнению с первоначальным распределением.
Каких исходов можно ожидать в этих условиях? Или, перефразируя
вопрос, к какому устойчивому состоянию эта система придет путем
добровольного обмена? Такие состояния мы будем называть бартерными
равновесиями.
Для простоты предположим, что в этом обществе только два
потребителя — потребитель 1 и потребитель 2, и два товара — хх и х2.
Обозначим неотрицательный первоначальный запас двух товаров
потребителя 1 как е1=(е\, е\), а первоначальный запас потребителя 2 — как
е2 =(е2, е]). Совокупное количество каждого товара, имеющегося в
обществе, можно выразить вектором е1 +е2 = {е\ + ех2, е\+е\). (Далее верхние
индексы будут обозначать потребителей, а нижние индексы — товары.)
Важные особенности такой экономики можно проанализировать с
помощью такого инструмента, как ящик Эджворта, знакомого вам по
промежуточным курсам микроэкономики. На рис. 5.1 по каждой
горизонтали откладывается количество я:,, а по каждой вертикали — количество
х2. Нижний левый угол является началом координат для потребителя 1, а
верхний правый — для потребителя 2. Количество хх для потребителя 1
возрастает от О1 вправо по нижней стороне, а для потребителя 2 — от О2
по верхней стороне. Аналогично, х2 для потребителя 1 возрастает от О1

Глава 5. Общее равновесие
247
по вертикали вверх слева, а для потребителя 2 — от О2 по вертикали вниз
справа. Ящик строится таким образом, чтобы его ширина равнялась
суммарному начальному запасу х,, а высота — суммарному начальному
запасу х2.
e\+e] х] е\ <— 02
(х\х2)
О1 — .1
е = (е\е2)
о, с, т^,
Рис. 5.1. Ящик Эджворта
Обратите внимание, что каждая точка ящика имеет четыре
координаты— две показывают количество каждого товара у потребителя 1, а
две — у потребителя 2. Поскольку размеры ящика жестко задаются
величиной начальных запасов, каждый набор из четырех координат
соответствует некоторому распределению общего количества каждого товара
между двумя потребителями. Например, точка е обозначает пару
начальных запасов е1 и е2. Любая другая точка ящика отражает какой-либо
другой способ распределения запасов между потребителями, а любому
возможному распределению запасов соответствует некоторая точка
ящика. Таким образом, ящик содержит все допустимые распределения
имеющихся товаров между потребителями.
Чтобы завершить описание экономики обмена с двумя участниками,
предположим, что предпочтения потребителей выпуклы. На рис. 5.2
кривые безразличия потребителя 1 возрастают по направлению вправо-вверх,
а кривые безразличия потребителя 2 — влево-вниз. Через каждую точку в
ящике Эджворта проходит по одной кривой безразличия каждого
потребителя. Кривая, обозначенная СС, является подмножеством
распределений, в которых кривые безразличия потребителей, проходящие через
одну точку, касаются друг друга, и называется контрактной кривой
(contract curve, cc). В любой точке не на контрактной кривой проходящие
через эту точку кривые безразличия должны пересекаться.

248
Часть II. Рынки и благосостояние
О1 *¦
Рис. 5.2. Равновесие при обмене между двумя участниками
Если начальные запасы задаются точкой е, то какие распределения
могут быть бартерными равновесиями в этой экономике обмена?
Очевидно, первое условие связано с тем, что они должны лежать «в ящике»,
поскольку только такие распределения являются допустимыми. Но
бартерным равновесием может быть не любое допустимое распределение.
Например, предположим, что происходит перераспределение, приводящее
из точки е в точку А . Потребитель 2 улучшает свое положение, а
потребитель 1 ухудшает. Рассматриваемая экономика основана на
добровольном обмене, и потребителей заботит только их собственное
благосостояние, поэтому перераспределение в точку А будет «заблокировано»
потребителем 1 и не станет равновесием при данных начальных запасах (и
предпочтениях). Аналогично, все распределения влево от кривой
безразличия потребителя 1, проходящей через точку е, будут заблокированы
им, а все распределения вправо от кривой безразличия потребителя 2,
проходящей через точку е, будут заблокированы потребителем 2.
Таким образом, потенциальными бартерными равновесиями могут
быть только распределения внутри и на границе области, имеющей
форму линзы, которая ограничена кривыми безразличия потребителей,
проходящими через точку е. В каждой граничной точке одному потребителю
будет лучше, а второму — не хуже, чем в е. В каждой внутренней точке
обоим потребителям будет строго лучше, чем в е. Чтобы добиться этого,
потребителям необходимо договориться: потребитель 1 должен отдать
часть хх в обмен на часть х2 потребителя 2, а потребитель 2 должен
отдать часть х2 в обмен на часть хх потребителя 1.

Глава 5. Общее равновесие 249
Но являются ли все распределения внутри «линзы» бартерными
равновесиями? Предположим, что происходит перераспределение в точку В.
В не лежит на контрактной кривой, поэтому проходящие через нее кривые
безразличия должны пересекаться, образуя еще одну область в форме
линзы, которая целиком лежит в первоначальной «линзе». Следовательно,
положение обоих потребителей можно снова улучшить, с помощью
соответствующего обмена перейдя из точки В в какую-либо другую точку внутри
новой «линзы». Поэтому В и все подобные точки, которые лежат внутри
области, ограниченной кривыми безразличия, проходящими через е, но не
на контрактной кривой, не могут быть бартерными равновесиями.
Теперь рассмотрим точку D на отрезке се контрактной кривой.
Переход от е к любой такой точке обязательно улучшит положение обеих
сторон. Более того, если потребители приходят в точку D, допустимых
взаимовыгодных обменов больше быть не может, и D является
бартерным равновесием. На самом деле любая точка, принадлежащая ее,
является бартерным равновесием. Если потребители в результате обмена
придут к любому распределению из отрезка на се, то любое дальнейшее
перераспределение в пределах ящика будет заблокировано одним или
обоими потребителями. (Включая, конечно, и движение от одной точки
отрезка се к другой.) Выберите любую точку се, рассмотрите несколько
возможных перераспределений и убедитесь в этом. Оказавшись на
отрезке се, можно быть уверенным в том, что уйти с него уже не удастся.
Конечно, существует много бартерных равновесий, к которым может
прийти система, но нам достаточно только обозначить все эти
возможности. Заметим, что все они обладают тем свойством, что из них нельзя
перейти к другой точке ящика, не ухудшив положения по крайней мере
одного из потребителей. Таким образом, любое равновесие обмена является
Парето-эффективным в том смысле, в котором это описано в главе 4.
Рассмотрим случай многих потребителей и многих товаров. Пусть
/ = {1 ...,/}
обозначает множество потребителей, и пусть имеется п товаров. У
каждого потребителя /е I имеется отношение предпочтения ъ' и
неотрицательный вектор первоначального запаса, включающий п товаров
е' = (е\, ..., е1п). Весь набор Е = (ъ1, е' )/е/ определяет экономику обмена.
Какими условиями характеризуются бартерные равновесия в
экономике обмена? Как и ранее, первое условие заключается в том, чтобы
суммарный объем товаров, достающийся индивидам, не превышал
имеющегося количества. Пусть
е^(е\ ...У)

250
Часть II. Рынки и благосостояние
обозначает вектор начальных запасов в экономике, а распределение мы
определим как вектор
х = (х', ...,ху),
где х1 =(*,', ...,-0 обозначает набор /-го потребителя в соответствии с
распределением. Множество допустимых распределений в этой
экономике задается формулой
7Че)-{х|2>'=5>'1 E-D
I iel iel J
и содержит все такие распределения товаров среди индивидов, которые
исчерпывают весь имеющийся объем каждого товара. Таким образом,
первое условие бартерного равновесия относительно х заключается в
том, что х е F(e).
В случае двух потребителей мы замечали, что в бартерном
равновесии Парето-улучшения невозможны. Это распространяется и на более
общий случай. Начнем со следующего определения.
Определение 5.1. Парето-эффективные распределения.
Допустимое распределение хе F(e) является Парето-эффектив-
ным, если не существует другого допустимого распределения у е F(e)
такого, что у1 ъ' х1 для всех потребителей i, причем предпочтение
является строгим хотя бы для одного из них.
Таким образом, распределение Парето-эффективно, если положение
ни одного индивида невозможно улучшить, не ухудшив положение кого-
либо другого.
Если х е F(e) не Парето-эффективно, то существует другое
допустимое распределение у, при котором какому-то потребителю строго лучше
и никому не хуже. Следовательно, потребитель, положение которого
улучшается, может произвести обмен с другими, объявив: «Я дам /-му
потребителю набор у' в обмен на набор х'». Поскольку распределения х
и у являются допустимыми, такой обмен возможен. Никто не будет
возражать, потому что каждому будет по крайней мере не хуже, чем раньше.
Кроме того, по крайней мере одному потребителю будет строго лучше.
Следовательно, распределение х не могло быть равновесным, т.е., чтобы
оказаться бартерным равновесием, х должно быть допустимым и Парето-
эффективным.
Предположим, что распределение х Парето-эффективно. Можем ли
мы уйти от него? Нет, не можем. Поскольку х Парето-эффективно,
любое другое допустимое распределение, при котором кому-то лучше,

Глава 5. Общее равновесие
251
должно ухудшать положение по крайней мере одного из остальных
потребителей, а он не согласится на соответствующий обмен.
Итак, теперь мы знаем, что только Парето-эффективные
распределения могут быть кандидатами на бартерное равновесие, и, когда Парето-
эффективное распределение достигнуто, оно будет равновесием в нашем
процессе добровольного обмена. Поэтому нам остается описать
множество Парето-эффективных распределений, которые могут быть достигнуты
путем добровольного обмена.
Вспомним, что в случае с двумя потребителями не все Парето-
эффективные распределения были равновесиями. Равновесными
оказались только те распределения, которые лежали на контрактной кривой
внутри области («линзы»), ограниченной кривыми безразличия,
проходящими через точку первоначального запаса. Причина этого в том, что
другие Парето-эффективные распределения, лежавшие на контрактной
кривой, но за пределами «линзы», приводили к ухудшению положения по
крайней мере одного из индивидов по сравнению с тем, как если бы он
просто потребил свой начальный запас. Каждое такое Парето-эффек-
тивное распределение было бы «заблокировано» одним из потребителей.
Аналогично, если число потребителей больше двух, никакое
равновесное распределение не должно приводить к ухудшению положения
любого из потребителей по сравнению с начальным. Такой потребитель
просто отказался бы участвовать в обмене. Есть и другие причины отказаться
от участия в обмене, который приводит к Парето-эффективному
распределению. Действительно, хотя вы могли бы предпочесть начальному
запасу набор, являющийся результатом некоторого перераспределения,
можно было бы найти другого потребителя и договориться с ним о таком
обмене, при котором вы выиграли бы еще больше, а он — не меньше, чем
в случае этого перераспределения. Следовательно, хотя вы не можете
заблокировать его сами, его можно заблокировать вместе с кем-то другим.
Конечно, заблокировать распределение может коалиция не только из
двух, но и из трех или более участников. Имея это в виду, введем
следующее определение.
Определение 5.2. Блокирующие коалиции.
Пусть Sal обозначает коалицию потребителей. Говорят, что S
блокирует Х€ F(e), если существует распределение у такое, что1:
1 Заметим, что нет необходимости настаивать на условии у е F(e), поскольку его
выполнения всегда можно добиться, заменив наборы, которые достаются потребителям
j'? S, на eJ.

252
Часть II. Рынки и благосостояние
2) у' ъ* х' для всех ie S, причем хотя бы для одного из них
предпочтение является строгим.
Вместе первый и второй пункты определения означают, что
потребители из коалиции S могут разделить между собой все, что у них имеется,
таким образом, что ни у кого из них положение не ухудшится, а у хотя бы
у одного — улучшится по сравнению с распределением х. То есть
распределение х блокируется, если некоторая группа потребителей может
улучшить свое положение по сравнению с х, действуя самостоятельно.
Наоборот, говорят, что распределение «не блокируется», если никакая
коалиция не может его заблокировать. Последнее условие равновесия
поэтому заключается в том, чтобы распределение не блокировалось.
Заметим, что это определение охватывает и случай двух
потребителей, потому что все распределения вне «линзы» блокируются
коалициями, состоящими из одного потребителя (потребителя 1 или
потребителя 2). Кроме того, заметим, что, вообще говоря, если х е F(e) не
блокируется, то оно должно быть Парето-эффективным, поскольку в
противном случае оно блокировалось бы большой коалицией S = I.
Благодаря этому мы можем кратко сформулировать условия равновесия при
обмене.
Итак, распределение х е F(e) является равновесием в экономике
обмена с начальными запасами е, если х не блокируется никакой коалицией
потребителей. Убедитесь в том, что это определение сводится к
приведенному выше для случая двух товаров и двух потребителей.
Множество распределений, которые являются равновесиями в
процессе добровольного обмена, называется ядром. Приведем определение
этого термина.
Определение 5.3. Ядро экономики обмена.
Ядром экономики обмена с начальным запасом е является
множество всех допустимых неблокируемых распределений С(е).
Можем ли мы гарантировать, что в каждой экономике обмена хотя
бы одно распределение принадлежит ядру? То есть должно ли
существовать хотя бы одно допустимое и неблокируемое распределение? Как мы
покажем ниже, ответ будет положительным при соблюдении некоторых
знакомых нам условий.
Мы доказали, что в идеальной ситуации, в которой формирование
коалиций и сбор информации для организации взаимовыгодных обменов
не связаны с издержками, потребители путем добровольного обмена
приходят к распределениям, принадлежащим ядру. В реальной экономике
воплотить такие распределения, скорее всего, не удастся. Обычно у нас

Глава 5. Общее равновесие
253
практически нет связей с подавляющим большинством других
потребителей, поэтому удивительно, если выигрыш от обмена все-таки
реализуется независимо от организации экономической системы —
централизованно-плановой, рыночной или иной. В следующем разделе мы
рассмотрим экономику, состоящую из конкурентных рынков.
5.2. Равновесие в конкурентных рыночных системах
В предыдущем разделе мы изучали самую простую экономическую
систему, целиком основанную на добровольном бартерном обмене. Здесь
мы начнем рассматривать более сложную — совершенно конкурентную
рыночную систему. В ней все сделки между индивидами опосредованы
обезличенными рынками. Поведение потребителей на рынке
определяется исключительно их эгоистическими интересами, и каждый потребитель,
будь то продавец или покупатель, сам по себе не влияет на сложившиеся
цены. Равновесие достигается на каждом рынке по отдельности, когда
совокупность решений покупателей согласуется с совокупностью
решений продавцов при сложившейся цене. Равновесие в системе
конкурентных рынков достигается, когда при сложившихся ценах спрос
покупателей совпадает с предложением продавцов одновременно на всех рынках.
В рассматриваемой модели заслуживает внимания ее
децентрализованный характер. Каждый потребитель, полностью осведомленный о
ценах на всех рынках, предъявляет спрос на набор, который является для
него наилучшим, без всякой необходимости учитывать спрос других
потребителей и будучи твердо уверенным в том, что нужный набор будет
ему доступен. Аналогично, производители, также полностью
осведомленные о сложившихся ценах на все товары (как на факторы
производства, так и на готовую продукцию), выбирают такие объемы производства,
которые максимизируют их прибыль, без всякой необходимости
учитывать предложение других производителей и будучи твердо уверенными в
том, что их продукция будет куплена.
То, что модель является децентрализованной, т.е. что каждый агент
действует в своих корыстных интересах, игнорируя действия остальных,
представляет собой ее сильную сторону. Поскольку в равновесии спрос
потребителей будет удовлетворен, а произведенная продукция будет
куплена, действия остальных агентов можно игнорировать, и единственной
информацией, необходимой потребителям и производителям, становятся
сложившиеся цены. Следовательно, информационные потребности модели
минимальны. Это разительно отличает ее от представленной в разделе 5.1
модели бартерного обмена, в которой каждому потребителю требовалась
очень подробная информация о предпочтениях и наборах, имеющихся у
всех остальных потребителей.

254
Часть II Рынки и благосостояние
Очевидно, что игнорировать действия остальных агентов можно
только при условии, что при действующих ценах потребительский спрос
удовлетворен, а произведенная продукция распродается. Поэтому
существенно, чтобы цены приводили все рынки к равновесию одновременно.
Не слишком ли смелым является предположение о том, что подходящий
вектор цен обеспечит точное совпадение разнообразных вкусов
потребителей, объединенных их итоговым спросом, и предложения, которое
формируется многочисленными и разнородными фирмами, которые
(хорошо или не очень) производят различные товары? Существование такого
вектора цен, вообще говоря, не очевидно, но обусловлено внутренней
структурой нашей конкурентной модели.
Чтобы проиллюстрировать потенциальные масштабы проблемы,
предположим, что имеются всего три товара и что при текущих ценах
спрос на товар 1 равен его предложению, так что этот рынок находится в
равновесии. Допустим, что име.тся избыточный спрос на товар 2 и
избыточное предложение товара 3. Естественно предположить, что достичь
равновесие на этих рынках можно, увеличив цену товара 1 и снизив цену
товара 3. Хотя таким образом можно сократить разрыв между спросом и
предложением на этих рынках, изменение цен легко может повлиять на
спрос на товар 1! В конце концов, если товары 1 и 2 являются
взаимозаменяемыми, то увеличение цены товара 2 приведет к увеличению спроса
на товар 1. Поэтому изменение цен на товары 1 и 2 в попытке
уравновесить эти рынки может нарушить равновесие на рынке товара 1.
Взаимозависимость рынков превращает вопрос о существовании
равновесного вектора цен в весьма тонкую проблему. Вспомним, что
именно существование вектора цен, который одновременно приводит все
рынки к равновесию, необходимо для того, чтобы можно было
использовать модели потребителя и производителя, рассмотренные в главах 1 и 3,
где мы предполагали, что спрос всегда удовлетворяется, а произведенная
продукция всегда раскупается. К счастью, хотя это совсем не очевидно,
можно показать (ценой изрядных усилий), что при некоторых условиях
существует хотя бы один вектор цен, который одновременно приводит к
равновесию на всех рынках. Мы начнем именно с этого
основополагающего вопроса.
5.2.1. Существование равновесия
Для простоты сначала рассмотрим экономику без производства.
Обозначим множество потребителей через / = {1, ...,/} и предположим, что
каждый из них располагает неотрицательным набором (вектором) е' из п
товаров. Далее, предположим, что предпочтения каждого потребителя на

Глава 5. Общее равновесие
255
потребительском множестве Rn+ представимы функцией полезности и',
удовлетворяющей следующим условиям1.
Предположение 5.1. Полезность потребителя.
Функция полезности и1 непрерывна, строго возрастает (в сильном
смысле) и строго квазивогнута на Ж"+.
На конкурентных рынках каждый потребитель воспринимает цены
как данные независимо от того, выступает он в качестве покупателя или
продавца. Если р = (/?,, ...,рп)» О представляет собой вектор рыночных
цен, то каждый потребитель решает задачу
max и' (х') при р • х1 < р • е'. E-2)
Ограничение в E-2) соответствует обычному бюджетному ограничению
потребителя, но явно указывает на источник его дохода. Интуитивно
можно представить, что потребитель продает весь свой начальный запас
по действующим рыночным ценам, получая доход ре', а затем
сталкивается с обычным ограничением на то, чтобы его расходы р • х' не
превышали доход. Решение E-2) — х'(р, ре') является тем самым набором,
который требуется потребителю и который зависит от рыночных цен и
первоначального дохода. Сформулируем здесь уже знакомый нам
результат, который понадобится позже.
Теорема 5.1. Основные свойства спроса.
Если и' удовлетворяет предположению 5.1, то для каждого р » О
задача потребителя имеет единственное решение х'(р, ре'). Кроме
того, функция х'(р, ре') непрерывна по р на R"++.
Вспомним, что существование решения следует из ограниченности
бюджетного множества в силу р » 0, а единственность — из строгой
квазивогнутости и1. Непрерывность в точке р следует из теоремы о
максимуме, и для этого также требуется условие р » 0. Подчеркнем, что
функция х'(р, ре') не является непрерывной по р на всем R", потому
1 Напомним, что функция называется строго возрастающей (в сильном смысле), если
увеличение одного компонента вектора аргумента при условии, что остальные
компоненты по крайней мере не сокращаются, приводит к возрастанию функции. Заметим
также, что функция Кобба — Дугласа не является ни строго возрастающей (в сильном
смысле), ни строго квазивогнутой на R" и поэтому исключается предположением 5.1.
(См. также определение А 1.17 в математическом приложении.)

256
Часть II. Рынки и благосостояние
что спрос может быть бесконечным, если одна из цен равна нулю. Ниже
нам потребуется приложить некоторые усилия для того, чтобы
справиться с этой неприятной, но неизбежной трудностью.
Начальный запас потребителя е' можно интерпретировать как
неэластичное предложение некоторого количества каждого из п товаров на
различных рынках.
Теперь мы можем начать описание системы рынков, которую мы
собираемся анализировать. Рыночный спрос на некоторый товар будет
равен суммарному индивидуальному спросу всех потребителей на этот
товар. При п товарах система будет состоять из п рынков, каждый со
своими спросом и предложением. Поскольку спрос потребителей на
любой товар зависит от цен всех товаров, построенная таким образом
система рынков будет взаимосвязанной, т.е. состояние любого из рынков в ней
влияет на остальные и, в свою очередь, подвергается их влиянию.
Самый ранний анализ рыночных систем, предпринятый Леоном
Вальрасом A874), двигался именно в этом направлении: каждый рынок
описывался своими функциями спроса и предложения. В настоящее
время, в основном для удобства и простоты обозначений, каждый рынок
описывается своей функцией избыточного спроса, т.е. рыночную систему
можно компактно описать п -мерным вектором избыточного спроса,
каждый из элементов которого является функцией избыточного спроса для
одного из п рынков.
Определение 5.4. Избыточный спрос.
Функция совокупного избыточного спроса на k-й товар является
вещественнозначной функцией
z*(P)s2X<P» Р'е'Ь?4-
is I is I
Функция совокупного избыточного спроса является векторнозначной
функцией
z(p) = (z,(p), ...,z„(p)).
Если zk (p) > 0, то совокупный спрос на k -й товар превышает его
совокупный запас, вследствие чего возникает избыточный спрос на к -й
товар. Если zk (р) < 0, то возникает избыточное предложение к -го товара.
Функции совокупного избыточного спроса обладают рядом свойств,
которые перечислены ниже.

Глава 5. Общее равновесие
257
Теорема 5.2. Свойства функций совокупного избыточного
спроса.
Если для каждого потребителя i функция и1 удовлетворяет
предположению 5.1, то при любых р » 0 для функций совокупного
избыточного спроса выполняются следующие свойства:
1) непрерывность (z() непрерывна в точке р);
2) однородность (z(A,p) = z(p) для всех X > О);
3) закон Вальраса (р • z(p) = 0).
Доказательство. Непрерывность следует из теоремы 5.1.
Однородность. Достаточно одного взгляда на ограничение в задаче
E-2), чтобы убедиться, что индивидуальный и избыточный спрос
однороден нулевой степени по ценам. Из этого сразу же следует, что
совокупный избыточный спрос также однороден нулевой степени по ценам.
Закон Вальраса. Это важное свойство. Оно утверждает, что величина
совокупного избыточного спроса всегда будет равна нулю при любых
положительных ценах. Закон Вальраса следует из того, что бюджетное
ограничение каждого потребителя выполняется как равенство, если и1
строго возрастает (в сильном смысле).
Если бюджетное ограничение в E-2) выполняется как равенство, то
Zft(*J(P> P-e')-4) = 0.
Суммирование по всем индивидам дает
Z2>*D(P> p-e/)-<) = 0.
iel k=\
Поскольку порядок суммирования роли не играет, поменяем его и
запишем это равенство как
ZZaD(P> P-e'W) = 0.
*=1 /б/
Но оно, в свою очередь, эквивалентно выражению
?а(Е4(Р. Р-е')-5>{1 = 0.
По определению 5.4 выражение в скобках равно совокупному
избыточному спросу на к -й товар, поэтому мы получаем
п
к=\
что и доказывает теорему. ¦

258
Часть II. Рынки и благосостояние
Закон Вальраса имеет интересные следствия. Например, рассмотрим
экономику с двумя товарами и предположим, что цены строго
положительны. Из закона Вальраса нам известно, что
PMp) = -p2z2(p).
Если на рынке 1 наблюдается избыточный спрос, т.е. z, (р) > 0, то на
рынке 2 должно быть избыточное предложение, т.е. z2(p) < 0.
Аналогично, если рынок 1 при ценах р находится в равновесии — z, (р) = 0, то
закон Вальраса гарантирует, что рынок 2 тоже находится в равновесии и
z2 (р) = 0. Эти идеи обобщаются для случая п рынков. Любой
избыточный спрос в системе рынков должен в точности уравновешиваться
избыточным предложением такой же величины при данных ценах на других
рынках. Более того, если при некоторых ценах в равновесии находится
п -1 рынок, по закону Вальраса в равновесии будет и п -й рынок. Это
полезно запомнить.
Рассмотрим рыночную систему, описываемую некоторой функцией
избыточного спроса z(p). Мы знаем, что избыточный спрос на каждом
отдельном рынке zk (p) может зависеть от цен на всех рынках, поэтому
мы имеем систему взаимосвязанных рынков. Частичное равновесие на
некотором рынке к возникает, когда объем спроса на к равен
предложению к при действующих ценах, или zk (р) = 0. Если при некоторых ценах
р выполняется равенство z(p) = 0, т.е. спрос равен предложению на
каждом рынке, то в системе рынков имеет место общее равновесие. Цены,
которые уравновешивают спрос и предложение на каждом рынке,
называются вальрасовскими1.
Определение 5.5. Вальрасовское равновесие.
Вектор р* е Ш"++ называется вальрасовским равновесием, если
z(p*) = 0.
Обратимся к вопросу о существовании вальрасовского равновесия,
который напрямую связан с тем, насколько логически последовательным
является взгляд Адама Смита на рыночную экономику. Конечно,
невозможно изучать социально-экономические свойства равновесий в
экономике, не будучи уверенным в том, что они существуют, и не зная, при
каких условиях можно гарантировать их существование. Этот вопрос при-
Заметим, что мы ограничиваемся положительными ценами. Строго говоря, для этого
нет причин. Однако в предположении о строгом (в сильном смысле) возрастании
функций полезности потребителей совокупный избыточный спрос может равняться нулю,
только если все цены положительны. См. упражнение 5.3.

Глава 5. Общее равновесие
259
тягивал множество теоретиков, и мы уже упоминали о том, что первым на
него попытался ответить Вальрас, сведя проблему к поиску решения
системы уравнений для рыночного спроса и предложения. Однако его ответ
нельзя назвать удовлетворительным, потому что он опирался на неверное
предположение о том, что любая система уравнений, в которой число
уравнений равно числу неизвестных, всегда имеет решение. Абрахам
Вальд [Wald, 1936] первым указал на эту ошибку, приведя простой
контрпример: система из двух уравнений с двумя неизвестными,
х2 +у2 = 0 и х2 -у2 = 1, как легко проверить, решения не имеет.
Считается, что Вальд привел первое математически корректное доказательство
существования равновесия, но оно включало излишне жесткие условия на
предпочтения потребителя. По сути, он требовал, чтобы предпочтения
были строго сепарабельными, а каждое благо имело «убывающую
предельную полезность». Маккензи и Эрроу в соавторстве с Дебре первыми
предложили гораздо более общие доказательства. В них поиск
равновесных цен сводился к поиску неподвижной точки специально подобранного
отображения и опирался на мощные теоремы о неподвижной точке. Ниже
мы тоже воспользуемся этим методом для того, чтобы показать
существование равновесия. Однако за более полным изложением мы предлагаем
читателю обратиться к работам и Маккензи [McKenzie, 1954], и Эрроу и
Дебре [Arrow, Debreu, 1954].
Начнем с набора условий на совокупный спрос, которые гарантируют
существование равновесного вектора цен.
Теорема 5.3. Совокупный избыточный спрос и вальрасовское
равновесие.
Пусть z(p) удовлетворяет следующим трем условиям:
1) z(-) непрерывна на Ш"++;
2) р • z(p) = 0 для всех р » 0;
3) если {рт} — последовательность векторов цен в W++, сходящихся
к р * 0, и рк = О для некоторого товара к, то для некоторого товара
к' с pk> =0 соответствующая последовательность значений совокупного
избыточного спроса на рынке товара к' {zk>(pm)} не ограничена сверху.
Тогда существует вектор цен р* » 0 такой, что z(p*) = 0.
Прежде чем приступить к доказательству, обсудим условия теоремы.
Первые два нам уже знакомы и гарантированно выполняются в рамках
предположений теоремы 5.2. Новым является только третье, которое
выглядит весьма запутанным. Но его смысл на самом деле вполне ясен: если
цены некоторых, но не всех товаров неограниченно близки к нулю, то

260
Часть II Рынки и благосостояние
(избыточный) спрос хотя бы на один из них неограниченно высок. В
такой формулировке условие выглядит вполне понятным. Далее мы
покажем, что в условиях предположения 5.1 оно выполняется.
Помимо этого заметим, что именно отсутствие непрерывности
потребительского спроса, а значит, и совокупного избыточного спроса, на
границе неотрицательного ортанта цен потребует от нас некоторых усилий.
В частности, во многих местах нам придется вводить дополнительные
ограничения, чтобы не оказаться на этой границе.
Доказательство. Пусть для каждого товара k Jk (p) = min(zk (p), 1)
для всех р»0, и пусть z(p) = (z,(p), ...,zw(p)), т.е. zk(p) ограничено
сверху единицей.
Выберем ? е @,1) и положим
*Нр
Аг=1 1 +
2л
V*
В поисках р*, для которого z(p*) = 0, мы ограничимся множеством
Se. На рис. 5.3 оно изображено для двух товаров. Заметим, что цены на
границе неотрицательного ортанта и около нее исключены из Se.
Заметим также, что по мере приближения ? к нулю Se включает все больше и
больше цен. Поэтому мы можем расширить круг нашего поиска,
устремив ? к нулю. Это мы сделаем несколько позднее, а пока ? останется
фиксированным.
{(риР2)\Р\+Рг= U р\,р2*Е/5}
0 е/5
-*> Pi
Рис. 5.3. Множество SE в R2+

Глава 5. Общее равновесие
261
Отметим следующие свойства множества Se: оно компактно,
выпукло и непусто. Компактность следует из замкнутости и ограниченности
(докажите), а выпуклость легко проверить. Для доказательства непустоты
достаточно заметить, что вектор цен, в котором все компоненты равны
B + 1/л)/A + 2п), всегда является элементом множества, потому что ? < 1.
Для каждого товара к и вектора р е St определим fk (p) следующим
образом:
_ е + рк +max@,z,(p))
w8+1+L.=imax@'z-(p))
и положим Др) = Шр), ...,/„(р)). Следовательно, ?/Др) = 1 и
fk (р) > ?/(и? +1 + и • 1), поскольку zw (р) < 1 для каждого w . Далее,
fk(p) > e/(l + 2n), так как ? < 1. Поэтому f:Se->St.
Каждая функция fk непрерывна на 5е, потому что по условию 1)
теоремы zk (•), а значит, и zk (•), непрерывны на Se, так что числитель и
знаменатель в определении fk непрерывны на Se. Кроме того,
знаменатель всегда принимает значения не меньше 1.
Таким образом, / является непрерывной функцией, отображающей
непустое компактное выпуклое множество Se в себя. Поэтому мы можем
воспользоваться теоремой Брауэра о неподвижной точке (теорема А 1.11),
из которой следует, что существует вектор ре е SE, такой, что /(ре) = ре,
или, что то же самое, fk(p*) = pt для всех ? = 1, ...,«. Но это означает,
если воспользоваться определением /Дре), что для каждого к
Рк
п
и? + ?тах@, zw(pe))
= ? + max@, z,(pe)). (P-1)
Итак, мы показали, что для каждого ? е @,1) существует вектор цен из
множества Se, удовлетворяющий (Р-1).
Теперь устремим ? к нулю и рассмотрим соответствующую
последовательность векторов цен {ре}, удовлетворяющих (Р-1). Заметим, что она
ограничена, потому что если ре € Se, то цена каждого товара лежит
между нулем и единицей. Следовательно, по теореме А 1.8 некоторая
подпоследовательность {ре} должна сходиться. Для простоты обозначений
предположим, что мы с самого начала выбрали ее так, что сама последо-

262
Часть II. Рынки и благосостояние
вательность {ре} сходится, скажем, к р*. Конечно, р* >0 и р* *0,
потому что компоненты этого вектора в сумме дают единицу. Мы хотим
доказать, что на самом деле р* » 0. Здесь нам и пригодится условие 3).
Будем доказывать от противного. Предположим, что соотношение
р* » 0 не выполняется. Тогда для некоторого к р*к- - 0 и из условия 3)
теоремы следует, что должен найтись такой товар к', что р\> = 0 и
z^(pe) не ограничено сверху, если ? стремится к нулю.
Заметим, что, так как ре -> р*, из равенства рк> - 0 следует, что
р\, -»0. Тогда левая часть (Р-1) при к-к' должна стремиться к нулю,
потому что выражение в скобках ограничено сверху по определению z.
Однако правая часть, очевидно, не стремится к нулю, потому что из
неограниченности zk>(p?) сверху следует, что zr(pe) принимает свое
максимальное значение — единицу — бесконечно часто (начиная с некоторого
достаточно малого 8). Конечно, это противоречие, потому что две части
равны при всех значениях 8, поэтому р* » 0.
Таким образом, ре —>р* »0 при е —> 0. Поскольку z() наследует
непрерывность на Ш"++ от z(), можно взять предел от (Р-1) при е—>0 и
получить
п
/?;?max@, zm(p*)) = max@, z,(p*)) (Р-2)
т=\
для всех к = 1,2, ...,«. Умножив обе части на zk(p*) и просуммировав по
к, получим
Р*-*(Р) Xmax(°' 5"m(p*)) =Xz*(P*)max(°> ?*(P*))-
\т=\ J k=\
По условию 2) теоремы (закону Вальраса) p*z(p*) = 0, поэтому левая,
а значит, и правая части соотношения равны нулю. Но поскольку знак
zk(p*) совпадает со знаком zk(p*), сумма в правой части может
равняться нулю только при zk(p*)<0 для всех к. С учетом условия р* »0 и
закона Вальраса это означает, что zk(p*) = 0 для всех к, что и
требовалось доказать. ¦
Итак, равновесие Вальраса (в котором цены всех благ строго
положительны) существует, если на Ш"++ совокупный избыточный спрос непре-

Глава 5. Общее равновесие
263
рывен, удовлетворяет закону Вальраса и не ограничен сверху, когда
некоторые (но не все) цены стремятся к нулю.
Может возникнуть соблазн попытаться получить этот результат без
условия 3) на неограниченность избыточного спроса, однако в
упражнении 5.7 вам будет предложено показать, что в таком случае он просто
неверен.
Нам уже известно, что если функция полезности каждого
потребителя удовлетворяет предположению 5.1, то выполняются условия 1) и 2)
теоремы 5.3. (В этом и состоит теорема 5.2.) Остается показать, когда же
выполняется условие 3.)
Теорема 5.4. Полезность и совокупный избыточный спрос.
Если функция полезности каждого потребителя удовлетворяет
предположению 5.1 и если совокупный запас каждого товара
положителен (т.е. ^/=1е' »0), то совокупный избыточный спрос удовлетворяет
условиям 1)—3) теоремы 5.3.
Доказательство. Условия 1) и 2) следуют из теоремы 5.2. Остается
проверить только условие 3). Рассмотрим последовательность строго
положительных векторов цен {рт}, сходящуюся к р Ф 0 такому, что рк = О
для некоторого товара к. Поскольку ^ е' »0, должно выполняться
условие P'X,=ie >^- Следовательно, P*X,=ie =S,=iP'e >^' П0ЭТ0МУ
должен иметься хотя бы один потребитель / такой, для которого
ре'>0.
Рассмотрим спрос /-го потребителя x'(pw, pw -e'), вычисленный для
этой последовательности цен. Предположим, что такая
последовательность векторов спроса ограничена. Тогда по теореме А 1.8 у нее должна
быть сходящаяся подпоследовательность, и без потери общности
(например, перенумеровав подпоследовательность) можно предположить, что
исходная последовательность векторов спроса сходится, скажем, к х*, т.е.
х'*(р"\ pw-e'*)->x\
Для простоты обозначим xm=x'(pw, pwe') для любого т.
Поскольку \т максимизирует и1 при бюджетном ограничении и данных ценах
рт и поскольку и1 строго возрастает (в сильном смысле), бюджетное
ограничение должно выполняться как равенство, т.е.
рт -хт =рт e;
для любого т.

264
Часть II. Рынки и благосостояние
Взяв предел при т —> ©о 9 получим
р х* = р е>0, (Р-1)
где строгое неравенство следует из нашего выбора потребителя /.
Теперь пусть х = х*+@, ..., 0,1,0, ...,0), т.е. все компоненты
векторов х и х* совпадают, а k-я компонента вектора х больше к -й
компоненты вектора х* на единицу. Тогда, поскольку и' строго возрастает (в
сильном смысле) на W+,
ui(x)>ui(x). (P-2)
Кроме того, так как рк = 0, из (Р-1) следует, что
р х = р е>0. (Р-З)
Поскольку и1 непрерывна, (Р-2) и (Р-З) означают, что существует
/ е @,1) такое, что
ui(tx)>ui(x)9
р (/х)<р е'.
Но так как pw —> р , хт —» х*, а и1 непрерывна, то для достаточно
большого т эти неравенства означают, что
u\ti)>ul(TLm)9
p"-(^)<Pm*e/5
а это противоречит тому факту, что \т является решением задачи
потребителя при рт. Поэтому последовательность векторов спроса для /-го
потребителя должна быть неограниченной.
Так как последовательность {\т} является неограниченной и при
этом неотрицательной, должен найтись товар ?', такой, что {х™} не
ограничена сверху. Но последовательность доходов /-го потребителя
{рт • е'} ограничена, потому что его доход сходится кре' (см.
упражнение 5.8). Следовательно, должно выполняться соотношение р™ —>0,
потому что только так спрос на товар к' может быть не ограниченным
сверху и при этом удовлетворять бюджетному ограничению. Таким
образом, ^ = limw/7;=0.
Наконец, заметим, что, поскольку совокупное предложение товара к'
фиксировано и равно его совокупному запасу и все потребители предъяв-

Глава 5. Общее равновесие
265
ляют спрос на неотрицательное количество товара к', из того факта, что
спрос / -го потребителя на к' не ограничен сверху, следует
неограниченность сверху совокупного избыточного спроса на к'. Следовательно,
предположив, что pw -» р * О и рк=0 для некоторого к, мы показали,
что существует некоторый товар к', для которого рк, - О и совокупный
избыточный спрос на него, определяемый последовательностью цен
{рт}, также не ограничен сверху, что и требовалось доказать. ¦
Теперь мы можем сформулировать условие существования
равновесия в терминах более простых элементов модели. Следующая теорема
напрямую следует из теорем 5.4 и 5.3.
Теорема 5.5. Существование вальрасовского равновесия.
Если функция полезности каждого потребителя удовлетворяет
предположению 5.1 и ^..е1 » 0, то существует (хотя бы один) вектор
цен р* » 0, такой, что z(p*) = 0.
Предположение о строгом возрастании (в сильном смысле) функций
полезности является довольно сильным ограничением, хотя оно
позволило нам сделать анализ относительно простым. Как упоминалось ранее,
функция Кобба — Дугласа, обладающая практически всеми
необходимыми свойствами, не является строго возрастающей (в сильном смысле) в
Ш"+. В упражнении 5.14 вам предлагается показать, что, несмотря на это,
для нее можно гарантировать существование вальрасовского равновесия.
Если функции полезности удовлетворяют предположению 5.1, то, как
нам известно, по теореме 5.2 вектор избыточного спроса будет
однородным нулевой степени. Это важно, поскольку в таком случае на выбор
потребителя влияют только относительные цены. То есть если р* является
вальрасовским равновесием в этой экономике, то для любых X > О будет
выполняться равенство z(p*) = z(A,p*) = 0. Поэтому если найдется такой
набор цен, при котором рынки будут сбалансированы, то они останутся
сбалансированными при любом другом наборе цен, полученном путем
умножения данного вектора на некоторую положительную константу.
Этим фактом нередко можно воспользоваться для того, чтобы упростить
вычисления при поиске вальрасовских равновесий.
Пример 5.1. Рассмотрим простую экономику с двумя участниками
и найдем вальрасовское равновесие. Пусть у потребителей 1 и 2
одинаковые функции полезности с постоянной эластичностью замещения (CES),
м \Ж% , Л"} J -~ Л] i Лл , I ~— 1, jL ,

266
Часть II. Рынки и благосостояние
где 0 < р < 1. Пусть имеется по одной единице каждого товара и пусть
весь товар одного вида принадлежит одному потребителю, т.е. начальные
запасы равны е1 = A,0) и е2 = @,1). Поскольку совокупный запас
каждого товара строго положителен, а CES-функция полезности строго
возрастает (в сильном смысле) и строго квазивогнута на Ш"+ при 0 < р < 1,
условия теоремы 5.3 выполняются, поэтому в этой экономике должно
существовать вальрасовское равновесие.
Согласно (Е-10) и (Е-11) из примера 1.1, спрос /-го потребителя на
У-й товар при ценах р равен л^.(р, у1)-pr~xyxj(p[ + pr2), где
г = р/(р -1), а у' — доход потребителя. Здесь доход равен рыночной
стоимости начального запаса, т.е. у1 = р • е1 = рх и у2 = р • е2 = р2.
Поскольку имеют значение только относительные цены и поскольку
из теоремы 5.5 нам известно, что существует равновесие, в котором все
цены строго положительны, для простоты вычислений можно
соответствующим образом нормировать цены. Пусть р = A//?2)р • Здесь рх = рх/р2
и р2 = 1, так что рх — это просто относительная цена товара jc, .
Поскольку спрос каждого потребителя при ценах р точно такой же, как и
при ценах р, нашу задачу можно сформулировать как задачу поиска
равновесного набора относительных цен р .
Рассмотрим рынок товара 1. В предположении внутреннего решения
равновесный вектор р* должен быть таким, чтобы совокупный объем
спроса равнялся совокупному объему предложения, т.е.
1 /—* —* 1 \ 2 /—* —* 2 \ 1 2
*,(р , р •е) + дс,(р , р е ) = ех+ех .
Проделав все подстановки, получаем уравнение
*г-Х * *г-Х
Р\ А_ + _А 1
Рх +1 Рх +1
Решая его, находим р\ = 1. Таким образом, любой вектор р*, в котором
Р\ = Pi •> уравновешивает спрос и предложение на рынке 1. По закону
Вальраса, те же самые цены должны уравновешивать спрос и
предложение на рынке 2, так что задача решена. ?
5.2.2. Эффективность
Описание экономики с двумя участниками с помощью ящика Эд-
жворта можно использовать для иллюстрации сути вальрасовского рав-

Глава 5. Общее равновесие
267
новесия. На рис. 5.4 представлена экономика, в которой предпочтения
удовлетворяют условиям теоремы 5.5. Начальные запасы равны (е\, е\) и
(е2, el) у что соответствуют точке е на рисунке. При относительных
ценах р*/р*2 бюджетное ограничение потребителя 1 представляет собой
прямую, проходящую через е. При тех же ценах бюджетное ограничение
потребителя 2 совпадет с той же самой прямой (если смотреть из начала
координат потребителя 2). Наиболее предпочтительным набором
потребителя 1 в его бюджетном множестве является вектор (х|, х*) , задающий
количество каждого из товаров, на которые потребитель 1 предъявляет
спрос при ценах p\f р\ и доходе, равном рыночной стоимости его
начального запаса, р\е\+р*2е\. Аналогично, (х2, х2) — соответствующий
набор потребителя 2 при тех же ценах и доходе, равном стоимости его
начального запаса. Условие равновесия на рынке товара 1 требует, чтобы
х\ + х2 = е\ + е\, или чтобы величина совокупного спроса равнялась
величине совокупного предложения. Это, конечно, эквивалентно условию
х,2 - е,2 = е\ - х\, т.е. условию, что чистый спрос потребителя 2 равен
чистому предложению товара 1 потребителем 1. Можно дать аналогичное
описание равновесия и на рынке товара 2.
х2 -е
л_
2
х2
О1
С
of
i
i
*v 1
С ' V
i ^
X
1
1
1
1
1
1
1
с****0000
"\ 1
* i
,. i
С
\гл'а
Х\
Рис. 5.4. Вальрасовское равновесие в ящике Эджворта

268
Часть II. Рынки и благосостояние
Небольшая проверка для разных относительных цен и разных
бюджетных множеств для двух потребителей убедит вас в том, что эти условия
рыночного равновесия будут выполняться только тогда, когда требуемые
наборы, рассматриваемые из начала координат соответственно
потребителя 1 и потребителя 2, окажутся в одной точке ящика, как на рис. 5.4.
Поскольку по построению через каждую точку ящика проходит по одной
кривой безразличия для каждого потребителя, а в равновесии точки,
соответствующие требуемым наборам, должны совпадать, очевидно, что
кривые безразличия потребителей, проходящие через эти точки, должны
касаться друг друга, как показано на рисунке.
Рисунок раскрывает также некоторые интересные особенности валь-
расовского равновесия. Во-первых, как мы заметили, предложение и
спрос потребителей зависят только от относительных цен. Удвоение или
утроение цен не изменит бюджетных множеств потребителей и не
повлияет на их выбор. Во-вторых, рис. 5.4 еще раз подтверждает, что в
равновесии на рынке действия независимых, децентрализованных,
ориентированных на максимизацию полезности потребителей одновременно
оказываются согласованными.
Наконец, рис. 5.4 иллюстрирует распределительные особенности
конкурентного рыночного равновесия. Мы обратили внимание на то, что
равновесие характеризуется касанием кривых безразличия потребителей,
проходящих через предпочтительные для них наборы товаров. Эти
наборы, в свою очередь, окончательно определяют количество товаров,
которое принадлежит каждому потребителю в равновесии. Таким образом, из
некоторого исходного распределения товаров, заданного е, действия
потребителей, направленные на максимизацию полезности, привели к
такому перераспределению товаров, которое находится на «контрактной
кривой» и «внутри линзы», образованной кривыми безразличия каждого
потребителя, проходящими через точки начальных запасов. В предыдущем
разделе мы называли такие распределения распределениями из «ядра»
экономики с начальными запасами е. Поэтому, несмотря на то что для
рассматриваемого здесь конкурентного рынка потребителям не требуется
знать предпочтения и запасы других потребителей, распределение,
соответствующее вальрасовскому равновесию, оказывается в ядре, по крайней
мере в экономике, описываемой при помощи «ящика Эджворта». Как мы
покажем далее, это замечательное свойство распространяется не только
на этот частный случай. Начнем с обозначений.
Определение 5.6. Распределения, равновесные по Вальрасу.
Пусть р* является вальрасовским равновесием для некоторой
экономики с начальными запасами е и пусть

Глава 5. Общее равновесие
269
x(p*) = (xJ(p\ р* е),...,х7(р\ ре7)),
где i -му компоненту соответствует п -мерный вектор товаров, на
которые предъявляет спрос и которые приобретает i -й потребитель при
ценах р*. Тогда х(р*) называется распределением, равновесным по
Вальрасу (Walrasian equilibrium allocation, WEA).
Рассмотрим экономику с начальными запасами е и допустимыми
распределениями F(e), определенную в E-1). Следует отметить ряд
важных свойств вальрасовских равновесий в таких экономиках. Во-первых,
очевидно, что любое распределение, равновесное по Вальрасу, в такой
экономике будет допустимым. Во-вторых, из рис. 5.4 ясно, что набор,
который достается каждому потребителю в равновесии по Вальрасу,
является наиболее предпочтительным при его бюджетном множестве,
определяемом равновесными ценами. Отсюда следует, что любое другое
распределение, которое является допустимым и более предпочтительным по
сравнению с равновесным, должно быть слишком дорогим для
потребителя. На самом деле это верно, даже если вектор цен не является вальра-
совским равновесием. Сформулируем эти два факта в виде лемм и
оставим доказательство первой из них и части второй в качестве упражнений.
Лемма 5.1. Пусть р* является вальрасовским равновесием для
некоторой экономики с начальными запасами е. Пусть х(р*) является
соответствующим ему равновесным распределением. Тогда х(р*)е F(e).
Лемма 5.2. Предположим, что и1 строго возрастает на Щ., спрос
i -го потребителя корректно определен при р > 0 и равен х',ах'еМ".
а) Если м'(х')> и'(х1), то рх' >рх'.
б) Если и'(х')>и'(х1), шрх'>рх'.
Доказательство. Доказательство пункта а) мы оставляем вам в
качестве упражнения, поэтому предположим, что а) верно, и воспользуемся
им для доказательства б).
Докажем это утверждение от противного. Предположим, что б)
неверно. Тогда и'(х')> и'(х!) и рхЧр х'. Следовательно, начиная с х',
можно немного увеличить потребление каждого товара по сравнению с
набором х' так, чтобы новый набор х' оставался все еще менее дорогим,
чем х'. Поскольку и1 строго возрастает, мы получаем, что
и'(х')>и'(х')>и'(х1) и рх' <р х'. Но это противоречит а), если х'
заменить на х'. ¦

270
Часть II. Рынки и благосостояние
Стоит отметить, что, вообще говоря, нет оснований ожидать
единственности равновесного по Вальрасу распределения, если оно существует.
Даже в ящике Эджворта легко построить примеры, в которых
предпочтения удовлетворяют самым обычным свойствам и при этом существует
несколько равновесных распределений. Такой случай иллюстрируется на
рис. 5.5. Следует иметь это в виду и не склоняться к мысли о том, что
вальрасовское равновесие «обычно» единственно. Введем обозначение
для множества равновесных по Вальрасу распределений в экономике.
Рис. 5.5. Множественность равновесий в рыночной экономике
с двумя участниками
Определение 5.7. Множество распределений, равновесных по
Вальрасу.
Для любой экономики с начальными запасами е пусть W(e)
обозначает множество распределений, равновесных по Вальрасу.
Теперь мы подходим к основной проблеме. Из рис. 5.4 и 5.5 ясно, что
к равновесным по Вальрасу относятся такие распределения, которые
лежат на отрезке ее контрактной кривой, соответствующем ядру этих
экономик. Остается показать, что вальрасовские равновесия обладают этим
свойством в любых экономиках. Вспомним, что С(е) обозначает
множество распределений из ядра.
Теорема 5.6. Ядро и равновесия в конкурентных экономиках.
Рассмотрим экономику обмена (У, е')/б/. Если функция полезности
каждого потребителя и1 строго возрастает на Ж\, то любое
равновесное по Вальрасу распределение принадлежит ядру,
^(е)сС(е).

Глава 5. Общее равновесие
271
Доказательство. Теорема утверждает, что если х(р*) является
равновесным распределением при ценах р*, то х(р*)е С(е). Для
доказательства предположим, что х(р*) является равновесным по Вальрасу
распределением и что x(p*)g C(e).
Поскольку х(р*) является равновесным по Вальрасу распределением,
из леммы 5.1 следует, что х(р*)е F(e), т.е. х(р*) является допустимым.
Однако поскольку x(p*)g C(e), мы можем найти коалицию S и другое
распределение у, такое, что
1у'=2У (р-1)
isS ieS
И
и1 (у7) > и1 (х'" (р*, р* • е')) для всех i е S, (Р-2)
причем хотя бы одно неравенство является строгим. Из (Р-1) следует, что
р* 2>=р* 2> (р-з)
isS ieS
Из (Р-2) и леммы 5.2 нам известно, что для каждого ie S должно
выполняться соотношение
р* у>р* Х(р*,р* е') = р* е', (Р-4)
причем хотя бы одно неравенство является строгим. Суммируя по всем
потребителям из коалиции S, получаем
/eS i€S
что противоречит (Р-З). Отсюда следует, что х(р*)€ С(е) и теорема
доказана. ¦
Заметим, что в качестве следствия теоремы 5.5 мы немедленно
получаем, что ядро непусто. То есть в условиях теоремы 5.5 существует
распределение, равновесное по Вальрасу, а по теореме 5.6 оно принадлежит
ядру. Следовательно, условия теоремы 5.5 гарантируют непустоту ядра.
Прежде чем двигаться далее, обсудим то, что мы уже здесь показали.
В вальрасовском равновесии каждый потребитель действует абсолютно
независимо от всех остальных потребителей в том смысле, что он просто
предъявляет спрос на набор, который максимизирует его полезность при
действующих ценах и доходе, зависящем от стоимости его начального
запаса. В частности, потребитель не учитывает ни объем спроса других по-

272
Часть II. Рынки и благосостояние
требителей, ни объем предложения любого товара. Ему известны только
его собственные предпочтения и цены, по которым могут осуществляться
сделки.
Чистый бартерный обмен, с которого мы начали эту главу, выглядит
полной противоположностью этой системе. Там было важно, чтобы
потребители могли собраться, оценить имеющиеся у них ресурсы и
получить все потенциально возможные выгоды от обмена. В частности,
каждый потребитель должен был точно знать, когда возникает возможность
взаимовыгодного обмена с другим потребителем — любым другим
потребителем! Как мы уже отмечали, было бы удивительно, если бы
удалось хотя бы приблизиться к такой степени координации, не говоря уже о
ее практическом воплощении. И даже если какое-то подобие такой
системы удалось бы организовать, неизбежно потребовался бы какой-нибудь
центральный орган, занимающийся согласованием процессов
образования соответствующих коалиций и обменов.
Но в теореме 5.6 мы показали, что получить распределения,
принадлежащие ядру, можно и без помощи центрального планирующего органа.
Действительно, ни одному из участников нашей конкурентной экономики
не требуются указания или советы других. Каждый потребитель просто
наблюдает цены и предъявляет свой спрос (максимизирующий его
полезность) или предложение на рынке. В этом смысле конкурентный
рыночный механизм называют децентрализованным.
Заметим, в частности, что поскольку все распределения из ядра
являются Парето-эффективными, такими же должны быть и все
распределения, равновесные по Вальрасу. Хотя мы доказали еще более сильные
утверждения, уже одно это заслуживает внимания. Представьте, что перед
вами стоит задача распределения всех ресурсов в экономике и что
итоговое распределение должно быть Парето-эффективным. Чтобы избежать
ситуации, когда все ресурсы достаются одному участнику, потребуем
также, чтобы в итоге благосостояние каждого было не ниже, чем если бы
он просто потребил свой начальный запас товаров. Как этого можно было
бы добиться? Сначала необходимо выяснить предпочтения всех
потребителей в экономике. (Нелегкая задача!) Только после этого можно было бы
попытаться перераспределить товары так, чтобы использовать все
возможные выгоды от обмена. При всей невероятной сложности этой задачи,
конкурентный рыночный механизм решает ее, и не только ее. Чтобы
подчеркнуть, что конкурентные исходы являются Парето-эффективными, мы
сформулируем теорему, которая называется первой теоремой
благосостояния.
Теорема 5.7. Первая теорема благосостояния.
В предположениях теоремы 5.6 любое распределение, равновесное по
Вальрасу, является Парето-эффективным.

Глава 5. Общее равновесие
273
Доказательство. Доказательство следует из теоремы 5.6 и того
факта, что все распределения из ядра — Парето-эффективны. ¦
Теорема 5.7 является конкретным подтверждением мнения
Адама Смита, согласно которому интересам общества лучше всего служит
экономическая система, в которой эгоистические действия индивидов
опосредованы обезличенными рынками. Если параметры экономической
системы допускают существование вальрасовских равновесий, то
независимо от первоначального распределения ресурсов распределение, которое
реализуется в равновесии, будет Парето-эффективным.
Крайне важно должным образом оценить применимость этого
утверждения к конкурентным рыночным системам. Не менее важно осознать
его ограничения и устоять перед искушением приписать ему некий
дополнительный смысл. Ни одно из доказанных нами до сих пор положений
не должно приводить нас к мысли о том, что равновесные по Вальрасу
распределения являются «общественно оптимальными», если включить в
понятие общественной оптимальности соображения «равенства» и
«справедливости» при распределении. Большинство из вас согласится с тем,
что распределение, не являющееся Парето-эффективным, не должно быть
даже среди кандидатов на общественный оптимум, потому что в этом
случае всегда можно будет перераспределить ресурсы так, что кому-то
станет лучше и никому не хуже. В то же время едва ли можно
убедительно показать, что любое Парето-эффективное распределение с одинаковым
основанием может считаться наилучшим или «наиболее справедливым» с
точки зрения общества.
В следующей главе мы подробнее рассмотрим нормативные вопросы,
подобные этому. А пока для иллюстрации вышесказанного обратимся к
простому примеру. Рассмотрим рис. 5.6, где проиллюстрирована
экономика, описываемая «ящиком Эджворта». Предположим, что каким-то
способом общество выбрало распределение х в качестве общественного
оптимума. Предположим, кроме того, что начальные запасы задаются
распределением е. По теореме5.6 равновесное распределение, например х', в
конкурентной рыночной системе будет лежать в С(е) и, конечно, будет
отличным от х. То есть хотя конкурентные рыночные системы могут
улучшить первоначальное распределение, которое само по себе не является
Парето-эффективным, нет гарантии того, что конкурентная система
самостоятельно придет к окончательному распределению, которое будет
считаться наилучшим для общества в целом.
Прежде чем впадать в излишний пессимизм, поставим вопрос чуть
по-другому. Если нам каким-то образом удалось найти желаемое
распределение, можно ли достичь его с помощью децентрализованной системы?
Из рис. 5.6 видно, что, вероятно, можно. Если перераспределить началь-

274
Часть II. Рынки и благосостояние
ные запасы так, чтобы они оказались в точке е*, становится ясно, что
х оказывается распределением, которое будет достигнуто в
конкурентном равновесии при этих запасах и ценах р*.
Рис. 5.6. Эффективность и общественный оптимум в экономике
с двумя участниками
На самом деле это пример довольно общего принципа. Можно
показать, что при некоторых условиях любое Парето-эффективное
распределение может быть достигнуто конкурентными рынками при некоторых
начальных запасах. Этот результат называется второй теоремой
благосостояния.
Теорема 5.8. Вторая теорема благосостояния.
Рассмотрим экономику обмена (и1, e')/G/ с совокупными запасами
^.=1е' »0 и функциями полезности и', удовлетворяющими
предположению 5.1. Предположим, что х является Парето-эффективным
распределением для (и1, е')/е/ и что запасы перераспределяются таким
образом, что новый вектор запасов равен х. Тогда х является
равновесным по Валърасу распределением в получившейся экономике обмена
(«', х%7.
Доказательство. Поскольку х Парето-эффективно, оно является
допустимым, поэтому X/=i^ =S/=ie >:>0- Следовательно, можно
применить теорему 5.5 и прийти к выводу о том, что в экономике обмена
(У, х')/е/ существует равновесие по Вальрасу с распределением х.
Остается показать, что х = х.

Глава 5. Общее равновесие
275
В вальрасовском равновесии спрос каждого потребителя
максимизирует его полезность при бюджетном ограничении. Следовательно,
поскольку i -й потребитель предъявляет спрос х' и имеет запас х', должно
выполняться условие
и1 (х') > и1 (Г) для всех / е J. (Р-1)
Но поскольку х является равновесным распределением, оно должно быть
допустимым для экономики (У, х')/е/. Следовательно, X,=i*'=
= ^мх' =X/=ie ' так что * является допустимым и для исходной
экономики.
Это означает, что в распределении х ни одному из потребителей не
хуже, чем в Парето-эффективном (для исходной экономики)
распределении х. Тогда в х ни одному из потребителей не должно быть строго
лучше, потому что в противном случае х не будет Парето-эффективным.
Поэтому в (Р-1) все неравенства должны выполняться как равенства.
Чтобы убедиться в том, что х; = х' для всех i, заметим, что если бы
для некоторого потребителя это было не так, то в равновесии по Вальрасу
в новой экономике этот потребитель мог бы позволить себе приобрести
набор, средний между х'их',ив силу строгой квазивогнутости
увеличить свою полезность, а это противоречит тому, что в вальрасовском
равновесии х' максимизирует полезность. ¦
Вторую теорему благосостояния можно рассматривать как
утвердительный ответ на следующий вопрос: способно ли возникнуть
«наилучшее» с точки зрения общества распределение ресурсов, если удастся
договориться о том, что считать наилучшим, в децентрализованной системе,
основанной на эгоистических решениях большого-числа потребителей?
Вторая теорема благосостояния отвечает, что способно, при
перечисленных выше условиях и если общественный «оптимум» требует хотя бы
Парето-эффективности.
Хотя мы не упоминали цены ни в формулировке, ни в доказательстве
второй теоремы благосостояния, они все же неявно в ней присутствуют.
А именно, теорема утверждает, что в равновесии по Вальрасу
существуют цены р, такие, что, если начальное распределение задается вектором
х, каждый потребитель / будет максимизировать */(х')при ограничении
р • х' < р • х', выбирая х' = х1. По этой причине иногда говорят, что
распределение х поддерживается ценами р .
Мы начали обсуждение второй теоремы благосостояния с вопроса о
том, может ли перераспределение, например, в точку е* на рис. 5.6 при-

276
Часть II. Рынки и благосостояние
вести к тому, что распределение х будет равновесным по Вальрасу.
В теореме мы показали, что если начальные запасы перераспределяются в
саму точку х, то ответ положительный. Однако из рис. 5.6 должно быть
ясно, что распределение х станет равновесным по Вальрасу при ценах р,
если начальные запасы будут перераспределены в любую точку на линии
цен, проходящей через х, включая, конечно, точку е*. Этот принцип
выполняется и в общем случае, поэтому мы сразу же получаем следствие из
теоремы 5.8, доказательство которого оставлено в качестве упражнения.
Следствие 5.1. Другой взгляд на вторую теорему
благосостояния.
В предположениях предыдущей теоремы, если х Парето-эффек-
тивно, то х является равновесным распределением для некоторого
вальрасовского равновесия р после перераспределения начальных запасов
в любую точку е* е F(e), такую, что ре* = р • х' для всех ie I.
5.3. Равновесие в экономике с производством
В данном разделе мы расширим наше описание экономики, включив
в него не только потребление, но и производство. Большинство
найденных ранее основных свойств конкурентных рыночных систем останутся в
силе, но с производством будет связано несколько новых проблем.
Например, прибыль, полученная фирмами, должна быть
распределена между потребителями, которым эти фирмы принадлежат. Кроме того,
если в одной фирме различие между факторами производства и готовой
продукцией обычно довольно очевидно, то при анализе всего
производства в экономике оно гораздо менее четкое. Фактор производства одной
фирмы легко может оказаться готовой продукцией другой. Чтобы
окончательно не запутаться в обозначениях, лучше всего априори их не
различать и поставить все в зависимость от контекста, т.е. рассматривать
каждый вид товара или услуги нейтрально, как товар. Мы будем
предполагать, что имеется фиксированное и конечное число п таких товаров.
Применительно к производителям мы будем различать факторы
производства и готовую продукцию.
Конкурентную структуру экономики мы снова будем формализовать
исходя из предположения о том, что потребители стремятся
максимизировать свою полезность при бюджетном ограничении, а фирмы стремятся
максимизировать прибыль. И те, и другие воспринимают цены как данные.
5.3.1. Производители
Для описания производственного сектора предположим, что имеется
фиксированное число J фирм, которые обозначим с помощью множества

Глава 5. Общее равновесие
277
Обозначим через ууеК" производственный план для некоторой фирмы и
условимся записывать у[ < О, если к -й товар используется в
производственном плане как фактор производства, и у[ > О, если этот товар является
готовой продукцией. Если, например, есть два товара и yJ = (-7, 3), то
производственный план требует 7 единиц первого товара в качестве
фактора производства для получения 3 единиц второго товара в качестве
готовой продукции.
Чтобы охарактеризовать технологические возможности производства,
вернемся к самому общему описанию технологии фирмы, с которым мы
впервые столкнулись в разделе 3.2, и предположим, что фирма обладает
множеством производственных возможностей Yj при j e J. Примем
следующие предположения о множествах производственных возможностей.
Предположение 5.2. Фирма.
1) ОеУ'сК";
2) YJ замкнуто и ограничено;
3) YJ строго выпукло. То есть для любых различных у1, у2 g У; и
любого te (О, 1) существует ye Yj такое, что y^ty1 +(l-t)y2, причем
данное соотношение не выполняется как равенство.
Первое из этих условий гарантирует, что прибыль фирмы ограничена
снизу нулем, а второе — что для производства всегда требуются некоторые
ресурсы. Замкнутость во втором условии означает непрерывность, т.е. то,
что пределы производственных планов являются производственными
планами. Ограниченность здесь является очень жестким условием и введена
лишь для простоты анализа. Не стоит думать, что она просто выражает
идею ограниченности ресурсов. Пока считайте ее упрощающим
предположением, от которого, впрочем, можно отказаться. Далее мы обсудим
важность отказа от этого условия. Третье условие — строгая выпуклость —
является новым. В отличие от всех остальных — довольно слабых —
ограничений на технологию, строгая выпуклость является более сильным
условием. По сути, она исключает постоянную и возрастающую отдачу от
масштаба в производстве и гарантирует единственность
производственного плана, максимизирующего прибыль. Все наши дальнейшие результаты
исходят из принципа «бесплатного производства не бывает» (т.е.
YJ nR" = {0}), хотя он и не вводится в предположении 5.2.
Каждая фирма, сталкиваясь с фиксированными ценами товаров р > 0,
выбирает производственный план, который максимизирует ее прибыль,
т.е. каждая фирма решает задачу

278
Часть II. Рынки и благосостояние
тахрУ. E-3)
yJeYJ
Заметим, что наше соглашение о знаках компонент вектора yJ
гарантирует, что факторы производства учитываются в прибыли как затраты, а
готовая продукция — как выпуск. Поскольку целевая функция непрерывна,
а множество ограничений замкнуто и ограничено, то будет существовать
максимум прибыли фирмы. Поэтому пусть для всех р > О
Пу(р) = тахру7
yJeYj
обозначает функцию прибыли у-й фирмы. По теореме о максимуме
Пу(р) является непрерывной на R". Как вам предлагается показать в
упражнении 5.21, строгая выпуклость гарантирует, что максимизирующий
прибыль производственный план уу(р) будет единственным при р»0.
Наконец, по теореме о максимуме уу(р) будет непрерывной на R"++.
Заметим, что при р»0 уу(р) является векторнозначной функцией,
компоненты которой представляют собой функции предложения готовой
продукции и спроса на факторы производства. Однако мы часто будем
называть функцию у7(Р) просто функцией предложения у'-й фирмы.
Сформулируем эти свойства в виде теоремы.
Теорема 5.9. Основные свойства предложения и прибыли.
Если Yj удовлетворяет условиям 1)—3) предположения 5.2, то для
любого р»0 решение задачи фирмы E-3) является единственным и
обозначается как уу(р). Кроме того, уу(р) непрерывно на М"+. Помимо
этого, функция П7(р) корректно определена и непрерывна на Е".
Наконец, заметим, что функция прибыли фирмы однородна первой
степени по ценам на товары. Каждая функция предложения готовой
продукции и спроса на факторы производства будет однородной нулевой
степени по цене (см. теоремы 3.7 и 3.8).
Далее мы рассмотрим совокупные производственные возможности в
экономике в целом. Предполагается, что экстерналии в производстве
между фирмами отсутствуют. Определим совокупное множество
производственных возможностей как
^|у|у = ЕуУ> где у'егА.
Множество Y унаследует все свойства индивидуальных
производственных множеств, что может быть выражено формально.

Глава 5. Общее равновесие
279
Теорема 5.10. Свойства Y.
Если каждое Yj удовлетворяет предположению 5.2, то совокупное
множество производственных возможностей Y также удовлетворяет
предположению 5.2.
Мы оставим доказательство этой теоремы в качестве упражнения.
Свойства 1), 3) и ограниченность Y напрямую следуют из аналогичных
свойств YJ. Замкнутость Y не следует из замкнутости отдельных YJ, но
при дополнительном предположении о том, что Yj ограничены, можно
показать, что Y замкнуто.
Теперь рассмотрим задачу максимизации совокупных доходов. По
теореме 5.10 максимум р у на совокупном производственном множестве
Y будет существовать и будет единственным при р » 0 . Помимо этого,
совокупный производственный план, максимизирующий прибыль, у(р)
будет непрерывной функцией от цен р. Наконец, обратим внимание на
тесную связь между совокупным оптимальным производственным
планом и оптимальными производственными планами отдельных фирм.
Теорема 5.11. Максимизация совокупной прибыли.
Для любых цен р > 0 выполнено
р у > р у для всех у е Y
тогда и только тогда, когда для некоторых yJ eYJ, je J, можно
записать, что у = ]jT уJ и
р • уJ >р уJ для всех уJ е YJ, je J.
Иначе говоря, теорема утверждает, что вектор у е Y максимизирует
совокупную прибыль тогда и только тогда, когда его можно разложить на
оптимальные производственные планы отдельных фирм. Доказательство
очевидно.
Доказательство. Пусть у € Y максимизирует совокупную прибыль
при ценах р. Предположим, что у = ^ уj для уj е Yj. Если
производственный план у* не максимизирует прибыль к -й фирмы, то существует
другой производственный план у * е Yk, который приносит к -й фирме
большую прибыль. Но тогда и совокупный производственный вектор
ye Y, построенный на основе у* и суммы yj для j±к, должен
приносить более высокую совокупную прибыль по сравнению с вектором у , а
это противоречит предположению о том, что у максимизирует
совокупную прибыль при ценах р.

280
Часть II Рынки и благосостояние
Далее, предположим, что допустимые производственные планы
у1, ...,yJ максимизируют прибыль отдельных фирм из J при ценах р1.
Тогда
р уу >руу для ууе Yj и je J .
Суммируя по всем фирмам, получаем
^pf>^pyj для yJeYj и jej.
iej iej
Это можно преобразовать как
р ]Гуу >р ]Гу; для yJeYJ и je J.
Но по определению у иГ это просто означает что
р у>р у для уеУ,
и, таким образом, у максимизирует совокупную прибыль при ценах р,
что и требовалось доказать. ¦
5.3.2. Потребители
Формально описание потребителей остается тем же, что и ранее.
Однако нам потребуется модифицировать некоторые детали, чтобы учесть
распределение прибыли фирм, потому что они принадлежат
потребителям. Как и раньше,
обозначает множество потребителей, aw' — функцию полезности /-го
потребителя на потребительском множестве R".
Прежде чем продолжить, заметим, что наше предположение о
неотрицательности потребительских наборов не исключает для потребителей
возможности поставлять товары и услуги на рынок. Действительно,
предложение труда легко включить в модель, предоставив потребителю
фиксированное количество часов, которое он может использовать по своему
усмотрению. Те часы, которые не используются в качестве «досуга»,
потребитель тратит на труд. Если единственным источником дохода
потребителя является начальный запас, то потребитель становится либо
чистым потребителем, либо чистым поставщиком товара в зависимости от
1 И пусть у е Y, тогда существуют yJ, уJ e YJ, je J такие, что ^yJ = у . — Примеч.
ред.

Глава 5. Общее равновесие
281
того, превосходит его спрос на данный товар объем первоначального
запаса товара или нет.
Конечно, необходимо учесть и тот факт, что доход потребителей
включает и прибыль принадлежащих им фирм. В экономике с частной
собственностью, которую мы здесь рассмотрим, потребители владеют
акциями фирм, и прибыли фирм распределяются среди акционеров.
Принадлежащие / -му потребителю акции j -й фирмы дают ему право на
некоторую долю 0 < 0V < 1 прибыли j -й фирмы. В сумме по всем
потребителям в экономике эти доли должны равняться единице, т.е.
О < 6V < 1 для всех /€ / и je J,
где
^(У = 1 для всех je J.
В нашей экономике с производством и частной собственностью
потребитель может получать доход из двух источников — от продажи
запаса уже имеющихся товаров и от доли в прибыли фирм, акциями которых
он владеет. Если р > О — вектор рыночных цен, то бюджетное
ограничение потребителя выглядит как
рх^реЧ^в^Ср). E-4)
Обозначив правую часть E-4) через т1(р), запишем задачу
потребителя как
max и' (х') при р • х; < т1 (р). E-5)
х'еМ"
По предположению 5.2, каждая фирма будет получать
неотрицательную прибыль, потому что может выбрать нулевой производственный
вектор. Следовательно, m'(p)>0, потому что р>0 и е' >0. Поэтому в
условиях предположений 5.1 и 5.2 решение E-5) будет существовать и
будет единственным при р»0. Мы снова обозначим его через
х'(р, т' (р)), где т'(р) —доход потребителя.
Вспомним, что при условиях, сформулированных в данной главе и
главе 1, функция х'(р, у) непрерывна по (р, у)е R"+xM".
Следовательно, если т'(р) непрерывна по р, то х'(р, т'(р)) тоже будет непрерывна
по р. Используя теорему 5.9, можно увидеть, что т'(р) непрерывна на
К" в условиях предположения 5.2. Объединив все эти утверждения, мы
получаем следующую теорему.

282
Часть II. Рынки и благосостояние
Теорема 5.12. Основное свойство функции спроса при условии
участия потребителя в прибыли фирм.
Если каждое YJ удовлетворяет предположению 5.2, а и'
удовлетворяет предположению 5.1, то решение задачи потребителя E-5)
существует и единственно для всех р»0. Обозначив его через
х'(р, т'(р)), мы также имеем, что х'(р, т'(р)) непрерывно по р на
М"+. Кроме того, т' (р) непрерывно на R".
Этим заканчивается описание экономики. В итоге ее можно
представить как набор (У, е', Q'\ YJ)ieIj€j.
5.3.3. Равновесие
Как и в случае без производства, можно снова определить вещест-
веннозначную функцию совокупного избыточного спроса для каждого
рынка и векторнозначную функцию совокупного избыточного спроса для
экономики в целом. Совокупный избыточный спрос на k -й товар равен
**(p)=E*i(p. »»'(p))-2>/(p)-5>i,
iel jej iel
а вектор совокупного избыточного спроса имеет вид
z(p) = (^(p),...,z„(p)).
Как и ранее (см. определение 5.5), равновесный по Вальрасу вектор цен
р* » 0 обеспечивает сбалансированность всех рынков, т.е. z(p*) = 0.
Теорема 5.13. Существование вальрасовского равновесия в
экономике с производством.
Рассмотрим экономику {и1 ,е' ,0'7 ,YJ)ieIJeJ. Если каждое и1
удовлетворяет предположению 5.1, каждое Yj удовлетворяет
предположению 5.2 и У + ^ е'»0 для некоторого производственного вектора
у е ^ YJ', то существует хотя бы один вектор цен р* » 0 такой,
что z(p*) = 0.
Вспомним, что при отсутствии производства для существования
равновесия нам требовалась строгая положительность вектора совокупных
начальных запасов. Если производство присутствует, это условие можно
ослабить: достаточно, чтобы для данной экономики имелся допустимый
производственный вектор, для которого чистая продукция (с учетом
начальных запасов) была бы строго положительной (т.е. для некоторого
совокупного производственного вектора у у + ^ е' » 0).

Глава 5. Общее равновесие
283
Доказательство. Мы приведем только часть доказательства, оставив
его завершение в качестве упражнения. Идея заключается в том, чтобы
показать, что при перечисленных предположениях функция совокупного
избыточного спроса удовлетворяет условиям теоремы 5.3. Поскольку
производственные множества ограничены, а потребление
неотрицательно, задача сводится к доказательству того, что спрос некоторого
потребителя на некоторый товар неограничен, если некоторые (но не все) цены
стремятся к нулю. (Заканчивая доказательство самостоятельно, вам
следует проверить и этот переход.) Поэтому нам требуется только следовать
доказательству теоремы 5.4.
Рассмотрим последовательность строго положительных векторов цен
{рт}, сходящуюся к р Ф 0 такому, что рк = О для некоторого к. Мы
хотим показать, что для некоторого, может быть, отличного от к, товара к',
такого, что рк> = 0, последовательность функций избыточного спроса на
товар к' {zk>(pm)} неограниченна.
Вспомним, что на первом шаге доказательства теоремы 5.4 нам
нужно было найти потребителя, доход которого положителен при предельном
векторе цен р. Здесь мы воспользуемся новым условием применительно
к чистому совокупному производству.
Поскольку y + X,=ie >:>® Д™ некоторого совокупного
производственного вектора у и поскольку у ненулевого вектора цен р нет
отрицательных компонент, должно выполняться соотношение
р • (у + ]? е') > 0. Следовательно, помня о том, что для всех р > 0
функции т'(р) и П7(р) корректно определены, получим
( \
2>'(Р) = Е ^e' + 5>W(p) =
/е/ iel \ jej )
=Ер-еЧЕПУ(р)^
>?р е'+р у =
/б/
= Р- У + 1У
>
>о,
где первое равенство следует из определения т'(р), второе— из того,
что доход, не связанный с начальными запасами, просто равен совокуп-

284
Часть II. Рынки и благосостояние
ной прибыли, а нестрогое неравенство — из теоремы 5.11, согласно
которой сумма максимальной прибыли у отдельных фирм должна быть не
меньше максимальной совокупной прибыли, а значит, и совокупной
прибыли от у. Поэтому должен быть хотя бы один потребитель, доход
которого при ценах р, w'(p), строго положителен. Оставшаяся часть
доказательства аналогична доказательству теоремы 5.4, и ее мы оставляем вам в
качестве упражнения. (Вам потребуется один из результатов
теоремы 5.12, согласно которому функция т1(р) непрерывна по р.) ¦
Как и ранее, поскольку избыточный спрос (положительно) однороден
нулевой степени, если равновесные по Вальрасу цены существуют, то они
не будут единственными. Заметим также, что предположению о строгом
возрастании (в сильном смысле) (и строгой квазивогнутости) функций и1
на всем R" не удовлетворяют функции полезности вида Кобба —
Дугласа. Однако в упражнении 5.14 вас просят показать, что в условиях
предположения 5.2 функция совокупного избыточного спроса тем не
менее удовлетворяет всем условиям теоремы 5.3, даже если функции
полезности имеют форму Кобба — Дугласа.
Пример 5.2. В классической экономике Робинзона Крузо все
производство и потребление осуществляется единственным потребителем.
Робинзон-потребитель продает свое рабочее время h (в часах)
Робинзону-производителю, использующему труд потребителя в течение этого
периода для производства кокосовых орехов у, которые он затем продает
Робинзону-потребителю. Вся прибыль от производства и продажи
кокосовых орехов остается у Робинзона-потребителя.
Если фирма только одна, то множество производственных
возможностей фирмы совпадает с множеством производственных возможностей
всей экономики. Пусть это множество выглядит как
Y = {(-h, y)\0<h<bnO<y<ha},
где b>0 и осе @,1).
Так, например, производственный вектор (-2, 2а) принадлежит
производственному множеству, т.е., затратив 2 часа времени Робинзона,
можно произвести 2а кокосовых орехов. Легко проверить, что множество У,
изображенное на рис. 5.7 (а), удовлетворяет всем требованиям
предположения 5.2. Заметим, что параметр Ъ используется для описания
ограничения производственного множества. Это ограничение вызвано главным
образом техническими причинами, поэтому на него не стоит обращать
особого внимания (для этого мы далее представим его достаточно большим).

Глава 5. Общее равновесие
285
Бюджетная линия
без учета прибыли:
ру + wh = wT
е = (Г, 0)
n/w
(в)
Рис. 5.7. Множество производственных возможностей Y, бюджетная линия
без учета прибыли и бюджетная линия с учетом прибыли в экономике
Робинзона Крузо
Как обычно, потребительское множество Робинзона-потребителя
представляет собой просто неотрицательный ортант, т.е. Ш2+ для случая
двух товаров. Функция полезности Робинзона
где Ре @,1). Параметр h обозначает количество часов, потребленных
Робинзоном (отведенных на досуг, если угодно), а у — количество
потребленных кокосовых орехов. Предположим, что у Робинзона есть Т > 0
единиц h (т.е. Т часов) и нет орехов, т.е. е = (Г, 0).
Выберем достаточно большое Ъ так, чтобы Ъ > Т. Следовательно, в
любом вальрасовском равновесии ограничение h<b не будет жестким,
потому что в равновесии необходимое фирме количество часов не может
превосходить общего количества часов Т.

286 Часть II. Рынки и благосостояние
Данная экономика удовлетворяет всем условиям теоремы 5.13 кроме
условия, что функция полезности имеет вид Кобба — Дугласа и поэтому
не является ни строго возрастающей (в сильном смысле), ни строго
квазивогнутой на всем R". Однако, как вас просят показать в
упражнении 5.14, итоговая функция совокупного избыточного спроса все же
удовлетворяет условиям теоремы 5.3. Следовательно, гарантируется
существование вальрасовского равновесия со строго положительными
ценами, которое мы и будем искать.
Пусть р > 0 обозначает цену кокосовых орехов у, a w > 0 — цену
1 часа времени Робинзона h (т.е. имеет смысл считать w его почасовой
заработной платой). Бюджетное множество Робинзона-потребителя, не
включающее прибыль от производства, изображено на рис. 5.7F), а на
рис. 5.7(b) показано его бюджетное множество, когда он получает свою
долю A00%) прибыли фирмы, равной я на рисунке.
Чтобы определить цены в вальрасовском равновесии (w*,p*), найдем
функцию предложения фирмы (которое в нашей терминологии также
включает спрос фирмы на труд), функцию спроса потребителя и на их
основе найдем цены, которые приводят рынки в равновесие. Начнем с
Робинзона-фирмы. С этого момента мы будем говорить о фирме и
потребителе, но вам следует помнить о том, что и то, и другое — это Робинзон.
Поскольку фирма не может позволить себе терять приобретенное
рабочее время впустую, она всегда выберет (-/*, y)eY, так что y = ha.
Следовательно, поскольку мы взяли Ъ таким, чтобы ограничение было
нежестким, при выборе h > 0 фирма будет максимизировать
pha - wh.
При а < 1 h = 0 не будет доставлять максимум прибыли (как мы
увидим), поэтому согласно условиям первого порядка производная по h
должна равняться нулю, т.е. apha~l - w = 0. Переписав это выражение и
вспомнив о том, что y = ha, получим спрос фирмы на рабочее время,
обозначенный и ее предложение готовой продукции, обозначенное yJ,
как функции цен w, р х:
V ^У
1 Если вы следите за соглашением о знаках компонент вектора производственного плана
это означает, что {-hf, yf)eY.

Глава 5. Общее равновесие
287
w j
Следовательно, прибыль фирмы равна
11#л1/A_а)
7T(W, р) = -——w\
а v w )
1 - а (ар
А —
Заметим, что прибыль положительна, если положительны цены. (Это
доказывает, что А = 0 не максимизирует прибыль, как мы и утверждали
выше.)
Обратимся теперь к задаче потребителя. Доход Робинзона равен сумме
его начального дохода (w, p)(T, 0) = wT и дохода от 100%-й доли в
фирме, равного всей прибыли фирмы я(и>, р). Поэтому бюджетное
ограничение Робинзона, которое в силу строгого возрастания функции
полезности будет выполняться как равенство, выглядит следующим образом:
ру + wh = wT + Ti{w,p).
Он выбирает (Л, у) > @, 0) так, чтобы максимизировать полезность
при этом ограничении. Функции спроса для функции полезности в форме
Кобба — Дугласа вам уже знакомы: потребитель потратит долю 1-Р
своего совокупного дохода на А и долю Р на у. Поэтому, если
обозначить спрос через hc и/, мы получим
y = (l-P)(wr + it(w9p))
У =
w
Р(>уГ + 71(>У,р))
р
Все эти выражения можно объединить для того, чтобы найти вектор
равновесных цен (w,/?), но сначала введем два упрощения. Во-первых,
поскольку совокупный избыточный спрос однороден нулевой степени и
нам гарантировано существование вальрасовского равновесия со строго
положительными ценами, без ограничений общности можно приравнять
равновесную цену у - р* к единице. Во-вторых, нам требуется найти
только равновесную цену w* для рынка h, потому что по закону Вальра-
са рынок j/ также придет в равновесие.
Таким образом, остается найти w\ такое, что hc+hf =Г, т.е.,
используя вышеприведенные выражения и положив р* = 1,

288
Часть II. Рынки и благосостояние
(l-P)(wr + 7t(wM))+r_aV/(,-a)=:r5
w \w
или
('-w->f»rif=pr,
a \wJ \wJ
куда мы подставили выражение для прибыли фирмы для того, чтобы
получить второе равенство. Отсюда легко можно выразить равновесную
заработную плату w*:
* fl-p(l-a)
w =ос —^ -
арг .
>0.
Предлагаем вам проверить, что при этом значении w* и р* = 1 оба рынка
действительно уравновешиваются.
Равновесие можно проиллюстрировать графически. На рис. 5.8(a)
показано оптимальное решение фирмы. Прямая, задаваемая уравнением
к = py + wh, является изопрофитой (линия постоянной прибыли)
фирмы, потому что для любых точек (А, у) на этой линии прибыль фирмы в
них остается неизменной и равной тс*. Заметим, что если (А, у)е У, то
h < О, так что ру + wh действительно является корректной формулой для
прибыли, изображенной на рисунке. Заметим также, что эта изопрофита
(как и любые другие) имеет наклон -w/p. Более того, изображенная
изопрофита приносит фирме максимально возможную прибыль: для ее
дальнейшего увеличения потребуется производственный план, лежащий
выше изопрофиты к*, который уже не будет принадлежать
производственному множеству. Поэтому к* = tc(w*,1) •
На рис. 5.8F) показано оптимальное решение потребителя при
бюджетном ограничении ру + wh = wT + к . Заметим, что наклон бюджетного
ограничения потребителя равен -w/p и совпадает с наклоном
изопрофиты.
Рис. 5.8(b) объединяет рис. 5.8 (а) и 5.8 (б). Рисунок для потребителя
накладывается на рисунок для фирмы, причем точка Т на первом
попадает в начало координат на втором. Начало координат для потребителя
обозначено 0С, а для фирмы 0f. Точка А показывает равновесное по Валь-
расу распределение.

Глава 5. Общее равновесие
289
ру + wh = wT + к*
(в)
Рис. 5.8. Равновесие в экономике Робинзона Крузо
Рис. 5.8(b) приводит нас к выводу о том, что это конкурентное
равновесие с производством является Парето-эффективным. Рассмотрим
заштрихованную область на рисунке. Заштрихованная область с началом
координат в точке 0f обозначает множество допустимых
производственных планов, которые могут быть реализованы в данной экономике с
учетом имеющихся ресурсов. Любой производственный план из этой
области может быть осуществлен, потому что он требует не более Т часов, т.е.
не более имеющегося количества часов. Вместе с тем такой
производственный план, как точка В, технологически возможен, потому что он
принадлежит производственному множеству, но недоступен, потому что
требует более Т часов.
Если рассматривать точку 0С как начало координат, то
заштрихованная область обозначает множество допустимых потребительских наборов

290
Часть II. Рынки и благосостояние
для этой экономики. С учетом этого ясно, что вальрасовское
распределение в точке А Парето-эффективно. Оно максимизирует полезность
Робинзона по сравнению со всеми остальными допустимыми
потребительскими наборами.
Вскоре мы покажем, что, как и в случае чистой экономики обмена,
это общий результат, который распространяется на случай экономики с
производством. ?
Вернемся к предположению об ограниченности производственных
множеств фирм. Как упоминалось ранее, без этого предположения можно
обойтись и, более того, есть веская причина отказаться от него.
Множество производственных возможностей предназначено для
описания технологии фирмы и ничего более. Оно показывает, сколько и
какой продукции можно произвести из различных факторов производства.
Поэтому если объем используемых факторов производства
неограниченно возрастает, то же самое может происходить и с объемом выпуска. То
есть прежде всего следует отметить, что в описании самой технологии
просто нет места для ограничений на объем имеющихся факторов
производства.
Однако это едва ли произведет впечатление на практика. В конце
концов, что с того, что Вселенную можно было бы заполнить перьевыми
ручками, если бы большая ее часть была наполнена чернилами! Разве не
достаточно описать технологию только для действительно допустимых
производственных планов? С одной стороны, это верно, потому что в
равновесии производственные планы должны быть допустимыми. Но
есть более тонкая и важная проблема. Если мы вводим ограничения на
производственные возможности, основываясь на совокупном
предложении ресурсов, то неявно предполагается, что фирма в своих
оптимизационных решениях учитывает эти ограничения на совокупный объем
факторов производства. Например, если ограничить производственное
множество производителя ручек, потому что предложение чернил конечно, то
при очень низких ценах на чернила спрос со стороны производителя
будет сдерживаться этим условием. Но если бы не ограничение, то при
низкой цене производитель предъявлял бы спрос на большее количество
чернил. Таким образом, введя кажущееся невинным ограничение
допустимости на производственные возможности, мы нарушили важнейшую
связь между ценой и (избыточным) спросом, которая является основой
конкурентной модели. Производители (и потребители) принимают
решения исходя из действующих цен, а не из того, достаточно ли в экономике
товара для удовлетворения их спроса. Поэтому условие ограниченности
производственных множеств полностью противоречит
децентрализованной природе конкурентного рынка, которую мы пытаемся отразить. (Ана-

Глава 5. Общее равновесие
291
логичные аргументы можно привести против установления верхних
границ на потребительское множество.)
К счастью, предположение об ограниченности не требуется. Но и все
наши труды не пропали даром. Оказывается, стандартный метод
доказательства существования без использования ограниченности
производственных множеств заключается в том, чтобы сначала доказать его, введя
искусственные границы для множеств (в сущности то, что мы и
проделали), а затем сделать эти границы достаточно большими (чего мы делать
не будем). При подходящих условиях это приведет нас к конкурентному
равновесию в экономике с неограниченными производственными
множествами.
Отметим, что строгая выпуклость предпочтений и производственных
множеств фирмы в условиях теоремы 5.13 является более жестким
ограничением, чем необходимо для доказательства существования
равновесия. Если вместо этого предположить просто выпуклость предпочтений и
множеств производственных возможностей, существование все равно
можно доказать, хотя это потребует применения математических
методов, которые выходят за рамки этой книги. Если множества
производственных возможностей выпуклы, то мы допускаем постоянную отдачу от
масштаба у фирм. Постоянная отдача создает возможность для того,
чтобы функции предложения продукции фирмы и спроса на факторы
производства имели своими значениями множества и не являлись
непрерывными в обычном смысле. Аналогично, простая выпуклость допускает
функции спроса, имеющие множества в качестве значений и те же
проблемы с непрерывностью. Со всем этим можно справиться, используя
обобщенные функции (называемые соответствиями) и обобщенное
понятие непрерывности, а затем применяя теорему Какутани [Kakutani,
1941] — обобщенную версию теоремы Брауэра о неподвижной точке. На
самом деле можно обойтись вообще без выпуклости множеств
производственных возможностей отдельных фирм, если совокупное множество
производственных возможностей является выпуклым. Заинтересованного
читателя мы отсылаем к книге Дебре [Debreu, 1959].
5.3.4. Благосостояние
Здесь мы покажем, как теоремы 5.7 и 5.8 можно распространить на
экономику с производством. Как и ранее, мы сконцентрируемся на
свойствах распределений, соответствующих вальрасовским равновесиям.
В экономике с производством наше прежнее определение равновесного
по Вальрасу распределения расширяется следующим образом.

292
Часть II. Рынки и благосостояние
Определение 5.8. Равновесное по Вальрасу распределение в
экономике с производством.
Пусть р* »0 является вальрасовским равновесием в экономике
(и1, е', 9У, YJ)i€ljeJ. Тогда пара (х(р*), у(р*)) является равновесным по
Вальрасу распределением, где х(р*) обозначает вектор (х1, х2, ...,х7),
/ -я компонента которого является максимизирующим полезность
набором i-го потребителя при ценах р* и доходе т'(р*), и где у(р*)
обозначает вектор (у1,у2, .-.?уУ) максимизирующих прибыль
производственных планов фирм при ценах р*. Заметим, что поскольку р* является
вальрасовским равновесием, ^ х' =]|Г re +S г У7 •
Иными словами, распределение в потреблении и в производстве
является равновесным по Вальрасу при ценах р*, если: 1) потребительский
набор товаров каждого потребителя является наиболее предпочтительным в
его бюджетном множестве при ценах р*; 2) производственный план каждой
фирмы максимизирует прибыль на множестве ее производственных
возможностей при ценах р*; 3) на каждом рынке спрос равен предложению.
Теперь мы готовы к тому, чтобы распространить первую теорему
благосостояния на экономику с производством. Вспомним, что в нашем
примере с Робинзоном Крузо распределение в вальрасовском равновесии
было таким, что никакое другое допустимое распределение не могло
улучшить положение Робинзона. Основываясь на той же самой идее,
определим Парето-эффективность для случая многих потребителей и фирм.
До конца этого раздела будем действовать в рамках экономики
(и1, е', &\ Yj)j€lj(_j, и все определения и теоремы будут относиться
именно к ней.
Распределение (х, у) = ((х1, ...jX7),^1, ...,y7)) наборов среди
потребителей и производственных планов среди фирм является
допустимым, если x'gR" для всех z, yJ e Y1 для всех j и
Определение 5.9. Парето-эффективное распределение в
экономике с производством.
Допустимое распределение (х,у) является Парето-эффективным,
если не существует другого допустимого распределения (х, у) такого,
что ul(xl)>ul{xl) для всех ie I, причем хотя бы одно неравенство
является строгим.

Глава 5. Общее равновесие
293
Тем самым допустимое распределение наборов потребителей и
производственных планов фирм является Парето-эффективным, если не
существует другого допустимого распределения, которое строго улучшает
положение хотя бы одного потребителя и не ухудшает положение ни
одного из потребителей.
Распределить ресурсы Парето-эффективным образом —
действительно непростая задача. Для ее решения потребуется не только информация
о предпочтениях потребителей, но и точное знание технологии всех фирм
и производительности всех факторов производства. В частности,
индивидов с конкретными навыками необходимо будет направить в те фирмы,
которым требуются именно эти навыки. А распределения,
соответствующие вальрасовским равновесиям, будут Парето-эффективными без
всякого централизованного контроля, как мы сейчас покажем.
Теорема 5.14. Первая теорема благосостояния для экономики с
производством.
Если каждое и1 строго возрастает на W+, то любое равновесное по
Вальрасу распределение является Парето-эффективным.
Доказательство. Предположим, что распределение (х, у) является
равновесным по Вальрасу при ценах р*, но не эффективным по Парето, и
придем к противоречию.
Поскольку (х, у) — равновесное распределение, оно является
допустимым, поэтому
iel iel jej
Поскольку (х, у) не является Парето-эффективным, существует
некоторое допустимое распределение (х, у), такое, что
w4x')>w'(x'), iel, (P-2)
причем хотя бы одно неравенство строгое. По лемме 5.2 из этого следует,
что
р* х>р* х\ iel, (Р-3)
причем хотя бы одно неравенство строгое. Суммируя (Р-3) по
потребителям и преобразуя, получаем
iel iej
Выражение (Р-4) вместе с (Р-1) и допустимостью (х, у) дает нам
неравенство
p*ily7+Ze']>p*ilyy+Ie'
KjeJ iel J
\jej iel J

294
Часть II. Рынки и благосостояние
откуда
р* Еу>р* 1У
Однако это означает, что р* • уj > р* • уJ для некоторой фирмы j, yj e YJ.
Это противоречит тому, что в вальрасовском равновесии yJ
максимизирует прибыль j -й фирмы при ценах р*. ¦
Далее мы покажем, что конкурентные рынки могут поддерживать
Парето-эффективные распределения при соответствующих трансфертах.
Теорема 5.15. Вторая теорема благосостояния для экономики с
производством.
Предположим, что: а) каждое и1 удовлетворяет
предположению 5.1; б) каждое YJ удовлетворяет предположению 5.2;
в) у + ^Г е' » 0 для некоторого совокупного производственного
вектора у; г) распределение (х, у) — Парето-эффективно.
Тогда существуют трансферты Тх, ...,7), удовлетворяющие
условию ^Г V = 0, и вектор цен р такие, что:
1) х' максимизирует и'(\1), р -х' < m'(p) + Tif ie J;
2) у1 максимизирует pyj, yJ eYj, je J.
Доказательство. Пусть для каждого je J Yj =YJ -{yj}. Заметим,
что при таком определении каждое YJ удовлетворяет
предположению 5.2. Рассмотрим экономику X =(w/,x/,0{/,77)/6/jej? полученную из
исходной экономики путем замены запаса /-го потребителя е' запасом
х' и каждого производственного множества Yj производственным
множеством YJ. Используя предположения а)—в), легко показать, что Ъ
удовлетворяет всем условиям теоремы 5.13. Следовательно, в *Е
существуют вальрасовское равновесие р » 0 и соответствующее распределение
(х, у).
Поскольку Ое Yj для каждой фирмы j, прибыль каждой фирмы в
равновесии неотрицательна, поэтому каждому потребителю доступен его
вектор начальных запасов. Следовательно,
*/(x0>w'(x'M *€ J. (Р-1)
Далее мы докажем, что для некоторой совокупности
производственных планов у распределение (х, у) является допустимым. Для этого за-

Глава 5. Общее равновесие
295
метим, что по определению YJ каждый ye YJ имеет вид у7 = у7 -у7
для некоторого у7 € YJ. А поскольку (х, у) является равновесным по
Вальрасу распределением для экономики Т , оно должно быть
допустимым в ней. Тогда
/е/ . /е/ y'ej
=Ii'-Zyy+Zyy =
fe/ ye J jej
=Z*,+Zyy.
где последнее равенство следует из допустимости (х, у) в исходной
экономике. Следовательно, (х, у) допустимо в исходной экономике, причем
y=Z^yy-
Можно заключить, что каждое неравенство в (Р-1) должно быть
равенством, потому что в противном случае (х, у) не будет Парето-
эффективным. Но в силу квазивогнутости и'
X' =Х', /G /,
поскольку иначе некоторый потребитель предпочтет не х7, а среднее из
двух наборов, которое будет удовлетворять его бюджетному
ограничению при ценах р, потому что каждый из этих наборов сам удовлетворяет
бюджетному ограничению. Тогда возникнет противоречие с тем, что
распределение (х, у) является равновесным по Вальрасу в экономике Ъ
при ценах р . Таким образом, можно сделать вывод о том, что
х' максимизирует и'(\') при р • х' < р • х' + ^ 6,7р у7, ie I.
Но поскольку полезность строго возрастает (в сильном смысле),
бюджетное ограничение выполняется как равенство при х' = х'. Это
означает, что доход / -го потребителя от участия в прибыли фирм равен
нулю. Поэтому каждая фирма должна получать нулевую прибыль, т.е.
у7 = 0 для каждой фирмы j.
В качестве упражнения мы оставляем такое утверждение: поскольку
у7 = 0 максимизирует прибыль j -й фирмы при ценах р на производст-

296
Часть II. Рынки и благосостояние
венном множестве YJ\ то (по определению Yj) у' максимизирует
прибыль j -й фирмы при ценах р на производственном множестве YJ (т.е. в
исходной экономике).
В итоге мы показали следующее:
х' максимизирует и1 (х') при р • х' < р • х', / е I, (Р-2)
у' максимизирует р уу при yj gYj , je J. (P-3)
Заметим также, что необходимые трансферты вычисляются, если
установить 7] = р • х' - т'(р), где т'(р) = р • е' + ]Г 6'7р • уJ равно доходу
/ -го потребителя в исходной экономике при ценах р . В силу
допустимости (х, у) эти трансферты в сумме дают нуль, и если они применяются в
исходной экономике, то задача потребителя сводится к задаче (Р-2).
Таким образом, выполняются и утверждение 1), и утверждение 2). ¦
5.4. Ядро и равновесия
В этом заключительном разделе мы вернемся в мир экономики
чистого обмена и глубже изучим взаимосвязь между ядром экономики и
множеством равновесных по Вальрасу распределений. Как мы видели,
каждое равновесное по Вальрасу распределение принадлежит ядру. Вместе с
тем в ящике Эджворта можно построить простые примеры, в которых
распределения из ядра не будут равновесными по Вальрасу. Таким
образом, по-видимому, связь между двумя понятиями ограничена.
Однако Эджворт [Edgeworth, 1881] высказал догадку о наличии более
глубоких взаимоотношений между вальрасовскими распределениями и
ядром. Он предположил, что если экономика «большая» (т.е. если идея о
том, что потребители воспринимают цены как данные, наиболее
оправданна), различие между распределениями из ядра и распределениями,
равновесными по Вальрасу, исчезает. По-новому взглянув на эту
возможность, Дебре и Скарф [Debreu, Scarf, 1963] расширили схему Эджворта и
доказали, что она верна. Короче говоря, они показали, что, когда
экономика становится «больше», ее ядро «сжимается» и в конечном счете
включает только распределения, равновесные по Вальрасу!
Их вывод вдохновляет тех, кто верит в особые свойства рыночной
системы, где единственной информацией, необходимой потребителю,
признается набор рыночных цен. Этот результат предполагает сравнение
двух противоположных парадигм в очень больших экономических
системах — централизованного планирования и свободной конкуренции. Если
цель планирования заключается в том, чтобы определить, а затем
реализовать некоторое распределение, принадлежащее ядру, и если в ядре нет

Глава 5. Общее равновесие
297
других распределений, кроме тех, которые реализуются конкурентной
рыночной системой, то зачем вообще планировать и нести все связанные
с этим издержки? Чтобы найти ядро, планирующему органу требуется
информация о предпочтениях потребителей, а у потребителей есть
стимулы быть не вполне честными, сообщая ему эту информацию. Рынку же
не нужно ничего знать о потребительских предпочтениях, он зависит от
эгоистических интересов потребителей. Недостаток в одном случае
превращается в некое достоинство в другом.
В этой дискуссии, конечно, довольно много обобщений. В широком
плане выбор между плановыми и рыночными системами никогда не
определяется исключительно соображениями эффективности. Помимо
этого, нам известно, что распределения из ядра при определенных начальных
запасах не обязательно будут справедливыми в любом смысле слова.
Планирование может быть оправданно как способ достижения желаемого
перераспределения начальных запасов. В более узком плане имеется ряд
технических проблем при проведении такого сравнения. Что значит —
экономика «большая» или «больше», чем другая? Кроме того, поскольку
«распределение» подразумевает вектор товаров для каждого потребителя
и поскольку предполагается, что в большой экономике потребителей
много, не отличается ли «размерность» ядра в больших экономиках от
«размерности» ядра в малых? Если да, то как можно говорить о «сжатии»
ядра? Мы ответим на эти вопросы в ходе дальнейшего изложения.
5.4.1. Реплицированные экономики
Чтобы конкретизировать анализ, мы будем следовать Дебре и Скар-
фу, формализуя понятие большой экономики вполне определенным
образом. Начнем с идеи базовой экономики обмена, состоящей из конечного
(произвольно большого) числа / потребителей, каждый из которых
имеет собственные предпочтения и обладает начальными запасами. Теперь
представим, что предпочтения и(или) запасы каждого потребителя
превращают его в иной «тип» потребителя, отличный от других. Два
потребителя с различными предпочтениями, но одинаковыми начальными
запасами считаются потребителями разных типов. То же самое верно для
двух потребителей с одинаковыми предпочтениями, но разными
начальными запасами1. Таким образом, мы считаем, что имеется конечное число
различных типов потребителей и базовая экономика обмена состоит из
одного потребителя каждого типа.
На самом деле мы назовем потребителями различного типа потребителей с
одинаковыми предпочтениями и начальными запасами даже, несмотря на то что различие будет
чисто формальным. Но пока лучше всего считать, что никакие два потребителя не могут
иметь одновременно одинаковые предпочтения и одинаковые начальные запасы.

298
Часть II. Рынки и благосостояние
Теперь представим, что у каждого потребителя появляется двойник.
Двойники полностью идентичны, имеют одинаковые предпочтения и
начальные запасы. В новой экономике, состоящей из всех первоначальных
потребителей и их двойников, теперь присутствует по два потребителя
каждого типа вместо одного. Новая экономика, конечно, больше
исходной, потому что в ней ровно в два раза больше потребителей. Эта
экономика называется дважды реплицированной. Если потребителя каждого
типа «утроить» или «учетверить», то мы сможем аналогичным образом
построить трижды или четырежды реплицированную экономику, каждая из
которых больше предыдущей в четко определенном соотношении. Идея
реплицированной экономики заключается в том, что в экономике
существует конечное число «типов» потребителей, одинаковое число
потребителей каждого типа и все индивиды одного типа идентичны в том
смысле, что у них одинаковые предпочтения и одинаковые начальные запасы.
Введем следующее формальное определение и предположения.
Определение 5.10. Реплицированная экономика (г -реплика).
Пусть в базовой экономике обмена имеется I типов потребителей,
которые составляют множество / = {1, ...,1}.Под г-репликой,
обозначаемой Хг, мы понимаем экономику с г потребителями каэюдого типа и
общим числом потребителей rl. Для каэюдого типа ie I все г
потребителей этого типа имеют одни и те же предпочтения ъ' на Ш"+ и
одинаковые начальные запасы е' » 0. Кроме того, для ie I мы
предполагаем, что предпочтения >=' представимы функцией полезности и',
удовлетворяющей предположению 5.1.
Таким образом, сравнивая две реплицированные экономики, мы
можем сказать, какая из них больше, — это та экономика, в которой больше
потребителей каждого типа.
Поговорим о ядре г -кратно раз реплицированной экономики Тг. При
сделанных предположениях все условия теоремы 5.5 будут выполнены.
Следовательно, будет существовать распределение, равновесное по Валь-
расу, и по теореме 5.5 оно будет принадлежать ядру, т.е. наших
предположений достаточно для того, чтобы обеспечить непустоту ядра Хг.
Чтобы отслеживать всех потребителей в каждой реплицированной
экономике, мы будем обозначать их с помощью двух индексов, i и q, где
/ = 1, ...,/ — индекс типа потребителя, a q = \, ...,r — индекс
потребителя конкретного типа. Например, индекс iq = 23 относится к
потребителю типа 2 под номером 3, или просто к третьему потребителю второго
типа. Поэтому распределение в Хг принимает вид

Глава 5. Общее равновесие
299
х = (хп, х12, ..., х\ ..., х71, ..., х7"), E-6)
где \'q обозначает набор q -го потребителя типа /. Тогда распределение
является допустимым, если
S5>*=r5>', E-7)
isl q=\ iel
поскольку каждый из г потребителей типа i имеет вектор начальных
запасов е'.
Этот факт, а также строгая выпуклость предпочтений используются в
следующей теореме.
Теорема 5.16. Одинаковый подход в ядре.
Если распределение х принадлежит ядру ГЕГ, то каждый потреби-
тель типа i должен иметь один и тот же набор в соответствии с х.
То есть для каждого / = 1, ...,/ xiq =xiq для каждого q', q = l, ...,r.
В этой теореме с приятным демократическим названием
формулируется ключевое свойство распределений, принадлежащих ядру в реплици-
рованных экономиках. Поэтому важно, чтобы мы не просто полагали, что
в ядре соблюдается принцип одинакового подхода к потребителям одного
и того же типа, но и хорошо понимали, почему это действительно так. Из
этих соображений мы рассмотрим «доказательство» теоремы для
простейшего случая экономики с двумя типами и четырьмя участниками.
Доказательство. Пусть / = 2. Рассмотрим 12 — реплицированную
экономику с двумя типами потребителей и двумя потребителями каждого
типа, т.е. всего с четырьмя потребителями. Предположим, что
распределение
х = (хп, х12, х21, х22)
принадлежит ядру Т2. Во-первых, заметим, что поскольку х лежит в
ядре, оно должно быть допустимым. Поэтому
хп +х12 н-х21 + х22 = 2е' +2е2, (Р-1)
так как оба потребителя каждого типа имеют одинаковые начальные
запасы.
Теперь предположим, что в распределении х паре потребителей
одного типа достаются разные наборы. Пусть это будут потребители 11 и
12, так что х11 и х12 различны. Вспомним, что предпочтения у этих
потребителей одни и те же >=1.

300
Часть II. Рынки и благосостояние
Поскольку ^г1 являются полными, эти наборы сравнимы, так что один
из двух наборов по крайней мере не хуже второго. Допустим, что
х11 ^х12.
(Р-2)
Предпочтение может быть строгим или два набора могут оказаться
эквивалентными. На рис. 5.9(a) и 5.9F) изображены обе эти возможности
соответственно. В любом случае мы хотим показать, что так как х11 и х12
различны, х не может лежать в ядре 2Г2. Для этого мы покажем, что х
можно заблокировать.
0»
х2
-> *i
-> *i
(а)
(б)
Рис. 5.9. Демонстрация одинакового подхода в ядре
Рассмотрим двух потребителей типа 2. Оба они имеют предпочтения
^г2, и в соответствии с распределением х их наборы равны х21 и х22.
Допустим (без ограничения общности), что
х21^2х22,
(Р-3)
Таким образом, потребитель 2 типа 1 находится в наихудшем положении
из всех потребителей типа 1, а потребитель 2 типа 2 — в наихудшем
положении из всех потребителей типа 2. Посмотрим, могут ли находящиеся
в наихудшем положении потребители каждого типа объединиться и
заблокировать распределение х.
Определим наборы х12 и х22 следующим образом:
_12 хи +х12
х = ,
_22 х2,+х22
х =

Глава 5. Общее равновесие
301
Первый набор равен среднему из наборов, достающихся потребителям
типа 1, а второй — среднему из наборов, достающихся потребителям
типа 2 (расположение х12 см. на рис. 5.9).
Предположим, что набор х12 можно отдать потребителю 12. Какой
набор предпочтет потребитель: этот или набор х12, который он получает
в распределении х? Вспомним, что согласно (Р-2) потребитель 12
находился в наихудшем положении из всех потребителей типа 1.
Следовательно, поскольку наборы х11 и х12 различны, потребитель 12 строго
предпочтет х12, потому что его предпочтения ъ1 строго выпуклы. Таким
образом,
x'Vx12.
Это показано на рис. 5.9.
Аналогично строгая выпуклость предпочтений потребителя 22 ;ь2
вместе с (Р-3) означает, что
х22^2х22,
где предпочтение необязательно будет строгим, потому что может
выполняться равенство х21 = х22.
Таким образом, пара наборов (х12, х22) строго улучшает положение
потребителя 12 и не ухудшает положение потребителя 22 по сравнению с
распределением х. Если потребители 12 и 22 сами смогут сформировать
такие наборы, то они заблокируют распределение х и доказательство
будет завершено.
Для того чтобы показать это, заметим, что
11 , 12 21 ,22
IT ТТ Л ТА А ТА
X +Х + =
2 2
= -(хп+Х,2+х2|+х22) =
2
= -Bе'+2е2) =
2
= е +е ,
где третье равенство следует из (Р-1). Следовательно, два находящихся в
наихудшем положении потребителя каждого типа могут вместе
сформировать такую пару наборов, которая строго улучшает положение одного из
них и не ухудшает положение второго. Поэтому коалиция S = {12, 22}
может заблокировать х, а это противоречит тому, что х принадлежит ядру.
Итак, приходим к выводу, что в распределении х потребителям
одного и того же типа должны доставаться одинаковые наборы. ¦

302
Часть II. Рынки и благосостояние
Теперь, когда мы выяснили, что значит «одна экономика больше
другой», и продемонстрировали принцип одинакового подхода в ядре реплици-
рованной экономики, посмотрим, что такое «сжатие» ядра при увеличении
экономики путем реплицирования. Прежде всего отметим, что, реплицируя
базовую экономику, мы увеличиваем число потребителей в ней, а
соответственно и число наборов в распределении. Однако когда мы рассматриваем
только распределения, принадлежащие ядру этих экономик, одинаковый
подход позволяет нам полностью описать любое распределение из ядра Тг
с помощью аналогичного распределения в базовой экономике *ЕХ.
Чтобы увидеть, как это происходит, предположим, что х
принадлежит ядру Тг. Тогда согласно теореме об одинаковом подходе х должно
выглядеть как
( \
х =
х1 х1 х2 х2 х7 х7
л. , . . . , л. , л , . . . , л. , ..., л. , . .. , л.
/
потому что все потребители одного типа должны иметь одинаковые
наборы. Следовательно, распределения из ядра *ЕГ являются г раз
скопированными распределениями из *ЕХ, т.е. вышеприведенное распределение
из ядра представляет собой г -кратное распределение из ?",
(х1, х2, ..., х7). E-8)
Это распределение является допустимым в Тх. Для доказательства
сначала заметим, что, поскольку х принадлежит ядру Хг, оно является
допустимым в Хг. Поэтому мы имеем
/е/ fej
что при делении на г показывает, что распределение E-8) является
допустимым в базовой экономике Т{.
Таким образом, мы показали, что каждое распределение из ядра
г-реплики получается r-кратным реплицированием некоторого
допустимого распределения из базовой экономики ?,. Следовательно, можно
контролировать изменение ядра при реплицировании экономики, просто
отслеживая распределения в ?,, соответствующие ядру каждой г -реплики.
С учетом этого определим Сг следующим образом:
Cr=\x = (x\x2,...,xJ)eF(e)
принадлежит
ядру

Глава 5. Общее равновесие
303
Теперь можно формально описать идею «сжатия» ядра при реплици-
ровании экономики.
Лемма 5.3. Последовательность множеств СХ,С2, ... убывает,
т.е. С, э С2 з ... з Сг з....
Доказательство. Достаточно показать, что для г>\ Сг с Сг_,.
Поэтому предположим, что х = (х1,...,х/)е Сг. Это означает, что в
г -реплике г -кратную копию этого распределения заблокировать нельзя.
Нам необходимо показать, что (г -1) -кратную копию нельзя
заблокировать в (У -1) -реплике. Для этого достаточно обратить внимание на то, что
любая коалиция, которая блокирует (г-1)-кратную копию в Тг_]9
заблокировала бы и г -кратную копию в Ъг — в конце концов все участники
этой коалиции присутствуют ив Тг, а их запасы (наборы) не
изменились. ¦
Таким образом, отслеживая в базовой экономике распределения,
г-кратные копии которых принадлежат ядру г-реплики, лемма 5.3
утверждает, что это множество не будет расти с увеличением г. Чтобы
увидеть, что ядро на самом деле сжимается при реплицировании
экономики, снова посмотрим на экономику с двумя типами потребителей.
Поскольку нас интересуют только распределения из ядра, мы воспользуемся
теоремой об одинаковом подходе и проиллюстрируем наши аргументы с
помощью ящика Эджворта, изображенного на рис. 5.10. На этот раз
будем считать предпочтения и начальные запасы в ящике предпочтениями и
начальными запасами репрезентативного потребителя каждого типа.
о2
о1
Рис. 5.10. Ящик Эджворта для реплицированной экономики
с двумя типами

304
Часть II. Рынки и благосостояние
В базовой экономике с одним потребителем каждого типа ядро ?",
представлено волнистой линией, соединяющей кривые безразличия двух
потребителей, которые проходят через точку начальных запасов е. Ядро
Г, содержит распределения, которые являются равновесными по Вальра-
су, и распределения, которые таковыми не являются. Распределение,
обозначенное х, не является равновесным по Вальрасу, потому что линия
цен, проходящая через х и е, не касается кривых безразличия
потребителей в точке х . Заметим, что х лежит на кривой безразличия
потребителя 11, проходящей через точку его начальных запасов. Если мы один
раз реплицируем эту экономику, может ли реплика этого распределения
оказаться в ядре большой экономики с четырьмя потребителями?
Нет, не может. Обратим внимание на то, что любая точка на прямой,
соединяющей е и х, предпочитается обоими (теперь их два)
потребителями типа 1, потому что их предпочтения строго выпуклы. В частности,
этим свойством обладает и середина отрезка х. Теперь рассмотрим
коалицию из трех потребителей, S = {11,12,21}, состоящую из обоих
потребителей типа 1 и одного (любого) потребителя типа 2. Пусть у каждого
потребителя типа 1 имеется набор, соответствующий набору типа 1 в
точке х, а у единственного потребителя типа 2 — набор,
соответствующий набору типа 2 в точке х . Нам известно, что каждый потребитель
типа 1 предпочтет свой набор набору типа 1 в точке х, а благосостояние
потребителя типа 2 не изменится. А именно:
i,1si(e,+x>,i,,>
2
^Е1(еЧх,2)^х12,
2
х21~2х21.
Являются ли наборы {хп,х12,х21} допустимыми для S? Из
определений и того факта, что х11 = х12, мы получаем, что
хм+х|2 + х21=2
-е +-Х1
V2 2 ,
+ х =е'+х"+х". E-9)
Затем вспомним, что х принадлежит ядру экономики 2Г, и поэтому
должно быть допустимым в экономике с двумя потребителями, т.е.
х"+х21=е'+е2. E-10)
Из E-9) и E-10) получаем
х"+х|2 + х21=2е'+е2,

Глава 5. Общее равновесие
305
так что предлагаемое распределение действительно является допустимым
для коалиции S из двух потребителей типа 1 и одного потребителя
типа 2. Поскольку мы нашли коалицию и распределение, которое приводит
к строгому улучшению положения двух участников и не ухудшает
положение оставшегося по сравнению с их наборами согласно распределению
х, эта коалиция блокирует х в экономике с четырьмя потребителями,
исключая его из ядра 2Г2.
Если мы продолжим реплицировать экономику, так что новые
потребители смогут формировать новые коалиции, можем ли мы еще больше
«сжать» ядро? Если да, то существуют ли распределения, которые
никогда не исключаются и поэтому остаются в ядре любой реплицированной
экономики? Ответ на оба вопроса положительный, и мы докажем это в
общем случае.
Мы хотим показать, что с увеличением г множество распределений
из ядра экономики *ЕГ сходится к множеству распределений,
равновесных по Вальрасу в этой экономике. Благодаря теореме об одинаковом
подходе мы смогли описать распределения в ядре Хг как г -кратные
копии распределений базовой экономики. Теперь мы проделаем то же самое
для множества вальрасовских равновесий экономики Тг.
Лемма 5.4. Распределение х является равновесным по Вальрасу в
экономике Хг тогда и только тогда, когда оно имеет вид
( \
х =
А, . . . , X , X , ...,Х , ..., X , ...,Х
г раз г раз г раз
а распределение (х1, х2, ..., х7) является равновесным по Вальрасу в
экономике Х{.
Доказательство. Если х является равновесным по Вальрасу
распределением в *ЕГ, то по теореме 5.5 оно принадлежит ядру Хг, поэтому по
теореме 5.16 оно должно удовлетворять свойству одинакового подхода.
Тогда оно должно быть г-кратной копией некоторого распределения в
Ъх. В качестве упражнения покажите, что это распределение в 2Г, будет
равновесным по Вальрасу. Обратное утверждение мы также оставляем в
качестве упражнения. ¦
Лемма 5.4 гласит, что когда мы реплицируем экономику, множество
вальрасовских равновесий остается «постоянным» в том смысле, что оно
состоит только из копий соответствующей кратности вальрасовских
равновесий в базовой экономике. Следовательно, множество вальрасовских

306
Часть II. Рынки и благосостояние
равновесий в базовой экономике в точности отражает множество вальра-
совских равновесий в ее г-репликах.
Теперь мы можем сравнить множество распределений из ядра Хг с
множеством распределений, равновесных по Вальрасу, т.е. множество
Сг, элементы которого являются распределениями из Хх, с множеством
равновесных по Вальрасу распределений в Тх.
Поскольку С, з С2 з..., ядро сжимается, как мы уже видели. Более
того, С, з С2 з ... з Wx (e) — множество распределений, равновесных по
Вальрасу, в *ЕХ. Это так, потому что по лемме 5.4 г-я копия
распределения, равновесного по Вальрасу, в экономике Хх лежит в ядре экономики
Тг, что по определению Сг означает, что исходное распределение,
равновесное по Вальрасу, в Тх принадлежит Сг.
Если рассматривать Сг и реплицировать экономику, в пределе
останутся только распределения, удовлетворяющие условию хе Сг для
каждого г = 1,2,.... Таким образом, утверждение о том, что ядро сжимается
до множества конкурентных равновесий, равносильно утверждению о
том, что если х е Сг для каждого г, то х является конкурентным
равновесием в экономике Хх. Именно это и показали Дебре и Скарф.
Теорема 5.17. (Теорема Эджворта — Дебре — Скарфа)
Предельная теорема о ядре.
Если хе Сг для каждого г = 1, 2,..., то х является равновесным по
Вальрасу распределением в Хх.
Прежде чем приступать к изложению общего доказательства,
рассмотрим случай с двумя типами в ящике Эджворта на рис. 5.11.
Предположим обратное, т.е. что некоторое распределение, не являющееся
равновесным по Вальрасу, х принадлежит Сг для каждого г. Тогда, в
частности, х лежит в ядре базовой экономики с двумя потребителями, в
которой присутствует один потребитель каждого типа. На рис. 5.11 это
означает, что х должно лежать внутри линзы и на контрактной кривой.
То есть оно должно лежать на волнистой линии, а кривые безразличия
потребителей, проходящие через х , должны касаться друг друга. ,
Теперь рассмотрим прямую, соединяющую точку начальных запасов
е и х. Она соответствует бюджетной линии для обоих потребителей и
паре цен р19 р2 двух товаров. Поскольку MRS]X2(xl) = MRSx22(x), то либо
рх Iр2 > MRS\2 (х1), либо р21рх > MRSX2 (х2). Заметим, что равенства
быть не может, потому что тогда эти цены представляли бы собой валь-
расовское равновесие, а х было бы соответствующим равновесным рас-

Глава 5. Общее равновесие
307
пределением. На рис. 5.11 изображен первый случай. Второй можно
изобразить аналогично, поменяв местами типы 1 и 2.
О2
Рис. 5.11. Иллюстрация доказательства теоремы 5.17
Как видно, прямая, проходящая через е и х, пересекает кривую
безразличия типа 1 в точке А ив силу строгой выпуклости лежит выше нее
на всем промежутке между А и х . Тогда на отрезке между А и х
существует некоторая точка х, которую потребитель типа 1 строго предпочтет
своему набору в точке х. Поскольку точка х принадлежит отрезку,
соединяющему точки е и х, ее можно выразить как выпуклую
комбинацию е и х. Немного забегая вперед, запишем набор типа 1 в точке х
следующим образом:
м 1 , г-1^
х =-е + х
E-11)
для некоторого г > 1. Заметим, что это действительно выпуклая
комбинация нужного вида, потому что 1/г + (г - 1)/г = 1. Заодно вспомним, что
х1 у1 х1.
E-12)
Предположим, как это всегда можно сделать, что г целое, и
рассмотрим fEr — экономику с г потребителями каждого типа. Поскольку мы
предположили, что х б Сг, это означает, что г -кратная копия х
принадлежит ядру Хг. Но может ли это быть так? Нет, если мы найдем
коалицию и блокирующее распределение, а именно это мы и сделаем.
На этот раз наша коалиция S состоит из всех г потребителей типа 1
и г-\ потребителя типа 2. Если каждому потребителю типа 1
предоставить набор х1, то по E-12) он предпочтет его своему набору в
распределении х. Если каждому потребителю типа 2, вошедшему в коалицию,
предоставить набор х2, совпадающий с его набором в х, то эти наборы
будут для него эквивалентны. То есть мы получим

308
Часть II. Рынки и благосостояние
х1 >-1 х1 для каждого из г потребителей типа 1,
х2 ~2 х2 для каждого из г-\ потребителя типа 2.
Является ли такое распределение допустимым для S ? Суммируя по
всем потребителям из 5, мы видим, что в совокупности они получат
гх1 +(г-1)х2. Из определения х1 в E-11)
+ (г-1)х2 = е' + (г-1)(х1 + х2). E-14)
Вспомним, что х1 и х2 по определению принадлежат ядру базовой
экономики с двумя потребителями. Поэтому для нее они должны быть
допустимыми, так что
х1 + х2=е' + е2. E-15)
Используя E-14) и E-15), находим
гх1 +(г-1)х2 =е' +(г-1)(х1 + х2) =
= е1+(г-1)(е1+е2) =
= геЧ(г-1)е2,
что подтверждает, что предлагаемое в E-13) распределение
действительно является допустимым для коалиции из г потребителей типа 1 и г -1
потребителя типа 2. Поскольку оно допустимо и строго предпочитается
некоторыми участниками коалиции S, и для любого участника коалиции
оно не хуже, чем г -кратная копия х, S блокирует г -кратную копию х ,
которая поэтому не принадлежит ядру Хг. Таким образом, если х е Сг
для каждого г, то это должно быть распределение, равновесное по Валь-
расу, в базовой экономике.
Приведем общее доказательство при двух дополнительных гипотезах.
Первая заключается в том, что если х е С,, то х » 0. Вторая — что для
каждого is I функция полезности и1, представляющая ь',
дифференцируема на Ш"++ и имеет строго положительный градиент.
Доказательство. Предположим, что х е Сг для каждого г. Требуется
показать, что х является распределением, равновесным по Вальрасу,
для Тх.
Сначала мы докажем, что
w4(l-0x'+'e0<w'(x')> V/e[0,l] и V,e J. (P-1)
гх1 +(г-1)х2 =г\
1 , г-1^,
-е + х1
г г

Глава 5. Общее равновесие
309
Чтобы убедиться в том, что это неравенство верно, предположим
обратное и придем к противоречию. Так, пусть для некоторого / е [0,1] и
некоторого ie /
ul((l-i)xl+h')>ul(ll).
Строгая квазивогнутость и' требует, чтобы
и1 (A -/)х' + te') > и1 (х') для всех t е @,1].
Следовательно, в силу непрерывности и1 существует достаточно
большое положительное целое г, такое, что выполняется неравенство
и
1--1хЧ-е' |>и'(х').
Г J Г
Но теперь мы можем воспользоваться тем же самым аргументом,
который мы приводили выше для доказательства того, что г -кратная копия
х не принадлежит ядру Хг. А это противоречит тому факту, что х е Сг,
поэтому (Р-1) должно выполняться.
Взглянем внимательно на (Р-1). Если рассматривать левую часть
этого соотношения как вещественнозначную функцию от / на [0,1], то эта
функция достигает максимума при / = 0. Поскольку / = 0 — левая
граница отрезка [0,1], это значит, что производная левой части в точке t = 0 не
положительна. Взяв производную и вычислив ее в / = 0, получим
Уи\х1)(е -х1)<0 длявсех iel. (Р-2)
Поскольку х принадлежит ядру Т1, оно Парето-эффективно. Кроме
того, по нашим дополнительным гипотезам х»0 и каждый
Vw;(x')»0. Следовательно, как вам предлагается показать в
упражнении 5.25, строго положительные градиенты Vw^x1),...,Vw7(x7)
пропорциональны друг другу, а значит, и общему вектору р » 0. Тогда
существуют строго положительные числа Х1,... Д7, такие, что
W (х;) = А,;р для всех i е I. (Р-3)
Вместе (Р-2), (Р-3) и положительность каждого из А,, дают
р • х' > р • е' для всех /е /. (Р-4)
Заметим, что доказательство было бы закончено, если бы каждое
неравенство в (Р-4) было равенством. В этом случае х' удовлетворял бы
условиям первого порядка задачи максимизации полезности потребителя

310
Часть II. Рынки и благосостояние
так что
при бюджетном ограничении при ценах р. Кроме того, при сделанных
нами гипотезах условия первого порядка являются также и достаточными
(см. теорему 1.4), поэтому х' являлся бы распределением, равновесным
по Вальрасу, в Т].
Покажем, что каждое неравенство в (Р-4) действительно является
равенством. Заметим, что, так как х е Сг, оно должно быть допустимым в
2?,. То есть
Однако это неравенство не выполнялось бы, если хотя бы для одного
потребителя / неравенство в (Р-4) было бы строгим. ¦
Мы показали, что для достаточно больших экономик в ядре будут
только распределения, равновесные по Вальрасу. Этот удивительный
результат свидетельствует об уникальности больших рыночных экономик и
может являться неким окончательным «доказательством» идей Адама
Смита об эффективности конкурентных рыночных систем. Однако здесь
есть некоторые тонкости. Прежде всего, данный результат был получен
при довольно жестких ограничениях в виде реплицированных экономик с
одинаковым количеством потребителей каждого типа. Далее, нельзя
упускать из вида тот факт, что само ядро является слабой концепцией
решения с сомнительными свойствами с точки зрения равенства. В той
степени, в которой «хорошее» с точки зрения общества решение задачи
распределения включает соображения равенства, даже самая широкая
интерпретация этого результата не дает аргументов в поддержку чисто
рыночной экономики (laissez-faire). «Равенство» любого распределения из
ядра, а значит, и для любого распределения, равновесного по Вальрасу,
зависит от начальных запасов.
Первое из этих возражений можно оспорить, что и было сделано.
Отказавшись от реплицированных экономик в пользу экономик более
гибких— с континуумом участников, Ауманн [Aumann, 1964], Хильден-
бранд [Hildenbrand, 1974] и другие доказали еще более сильные
утверждения, не используя предположение об одинаковом числе потребителей
каждого типа. Что же со вторым из упомянутых возражений? Если мы
хотим воспользоваться рыночной системой для того, чтобы получить
«хорошее общество», вторая теорема благосостояния утверждает, что мы
можем этого добиться. Все, что нужно, — это решить, в каком распреде-

Глава 5. Общее равновесие
311
лении из ядра мы хотим оказаться, перераспределить «запасы» и
«доходы» и воспользоваться рынком для того, чтобы «поддержать» это
распределение. Есть препятствие: как же нам принять решение? Как «общество»
может решить, какое из распределений в ядре оно «предпочитает»?
Этими вопросами мы займемся в главе 6.
5.5. Упражнения
5.1. Для решения следующих упражнений используйте ящик Эджворта.
а) Изобразите ситуацию, когда равновесие по Вальрасу не
существует, если предпочтения не являются ни выпуклыми, ни монотонными.
б) Изобразите ситуацию, когда равновесие по Вальрасу существует,
если предпочтения не являются ни выпуклыми, ни монотонными.
в) Выполните пункты а) и б), предполагая, что предпочтения не
непрерывны.
5.2. Пусть некоторый потребитель обладает первоначальным запасом
е и сталкивается с ценами р. Пусть v(p, ре) — косвенная функция
полезности потребителя. Покажите, что при небольшом увеличении цены
некоторого товара положение потребителя ухудшится, если
первоначально он был чистым покупателем этого товара (т.е. его спрос на товар
превышал запас), и, наоборот, улучшится, если первоначально он был
чистым продавцом этого товара. Как изменится ваш ответ, если цена товара
возрастет значительно!
5.3. Рассмотрите экономику обмена. Пусть р — вектор цен, и цена по
крайней мере одного блага неположительна. Покажите, что если функции
полезности потребителей являются строго возрастающими (в сильном
смысле), то совокупный избыточный спрос не может быть равен нулю на
всех рынках.
5.4. Найдите функцию избыточного спроса z(p) для экономики из
примера 5.1 и проверьте выполнение закона Вальраса.
5.5. Для экономики из примера 5.1 найдите равновесные
распределения и проиллюстрируйте решение в ящике Эджворта. Изобразите также
контрактную кривую и ядро.
5.6. Докажите лемму 5.1 и завершите доказательство леммы 5.2.
5.7. Рассмотрите экономику обмена с двумя товарами. Пусть функция
совокупного избыточного спроса имеет вид z(/?,, p2) = (-l, рх1 р2) для
всех (/?,, /?2)»@, 0).
а) Покажите, что данная функция удовлетворяет условиям 1) и 2)
теоремы 5.3, но не удовлетворяет условию 3).
б) Покажите, что результат теоремы 5.3 здесь не выполнен, т.е.
покажите, что не существует таких (/?*, р*2)»@, 0), что z(j?*, p*2) = @, 0).

312
Часть II. Рынки и благосостояние
5.8. Пусть р™ — последовательность строго положительных цен,
сходящаяся к р. Предположим также, что потребитель обладает
первоначальным запасом товаров е. Покажите, что последовательность {рт -е}
дохода потребителя ограничена. Докажите и более общий результат: если
последовательность действительных чисел сходится, то она должна быть
ограничена.
5.9. Докажите следствие теоремы 5.8. А именно: покажите, что при
тех же предположениях любое Парето-эффективное распределение может
быть реализовано как распределение, равновесное по Вальрасу, при
некоторых равновесных ценах р и некотором распределении дохода
(/?',...,R1), где R' —доход потребителя /.
5.10. Рассмотрите экономику обмена с двумя товарами и двумя
потребителями, имеющими строго возрастающие функции полезности.
а) Покажите, что распределение х е F(e) Парето-эффективно тогда и
только тогда, когда х' является решением следующей задачи:
maxw'(x') при uJ{\J)> uJ(\J),
х'
х\+х22=е\+е22
при У = 1,2 и i Ф j.
б) Обобщите это эквивалентное определение Парето-эффективного
распределения на случай п благ и / потребителей и докажите его.
5.11. Рассмотрите экономику обмена с двумя потребителями и двумя
благами. Пусть функции полезности потребителей и их начальные запасы
имеют следующий вид:
u\xv jc2) = (jcjjc2J и е1 =A8, 4),
u2(xl9 jc2) = ln(;c1) + 2b(x2) и е2=C, 6).
а) Как можно более полно опишите множество Парето-эффективных
распределений.
б) Опишите ядро данной экономики.
в) Найдите равновесие по Вальрасу и равновесное распределение.
г) Проверьте, что равновесное распределение, найденное в пункте в),
принадлежит ядру.
5.12. Рассмотрите экономику обмена с двумя товарами и двумя
потребителями. Пусть предпочтения потребителей и их начальные запасы
описываются соответственно как

Глава 5. Общее равновесие 313
ul(x]9 jc2) = min{jc,, x2} и е'=C0, 0),
v2(p, y) = y/2yfcf2 ие2=@, 20).
а) Найдите равновесие по Вальрасу и равновесное распределение в
данной экономике.
б) Найдите равновесие по Вальрасу для случая, когда запас первого
потребителя равен е1 = E, 0), а запас второго потребителя остался
неизменным, е2 = @, 20).
5.13. Пусть в экономике обмена функции расходов потребителей
имеют вид:
el(p, w) = C(l,5J/?2/?2exp(w)) ,
е\р, w) = C(l,5Jp2p1exp(w)) .
Найдите равновесие по Вальрасу при первоначальных запасах е1 = A0, 0)
ие2=@, 10).
5.14. Пусть каждый потребитель / имеет строго положительный
вектор запасов е' и определенную на множестве R" функцию полезности
вида Кобба — Дугласа и1 (х) = xf* х22 ...х"'п, где ос^ >0 для всех потреби-
п
телей / и благ к, и ]Г а* = 1 для всех /.
а) Покажите, что функции полезности потребителей не являются
строго возрастающими (в сильном смысле) на R", т.е. теорема 5.5 в
данной экономике неприменима для того, чтобы гарантировать
существование равновесия по Вальрасу.
б) Покажите, что условия 1), 2) и 3) теоремы 5.3 выполняются, т.е.
непосредственно из теоремы 5.3 можно сделать вывод, что равновесие по
Вальрасу в данной экономике существует.
в) Докажите, что равновесие по Вальрасу также будет существовать в
данной экономике в случае наличия производства, если все
производственные множества удовлетворяют предположению 5.2 (для этого
используйте ту же стратегию, что и ранее).
5.15. Пусть в экономике 100 единиц х, и 100 единиц х2.
Предположим также, что потребители 1 и 2 каждый имеют по 50 единиц каждого
товара. Пусть первый потребитель говорит «я люблю хХ9 но могу либо
потреблять х2, либо отказаться от него», а второй потребитель говорит «я
люблю х2, но могу либо потреблять jc, , либо отказаться от него».

314
Часть II. Рынки и благосостояние
а) Изобразите в ящике Эджворта предпочтения этих потребителей и
производимые обмены.
б) Укажите ядро данной экономики.
в) Найдите все равновесия по Вальрасу в данной экономике.
5.16. Рассмотрите простую экономику обмена, в которой первый
потребитель имеет функцию расходов
е1(р, и) =
~(Р\+Р2)и> если Р2/2<Р\< 2Pi>
ир2, если/?! >2р2,
ир}, если рх<р212,
а второй потребитель имеет функцию расходов
е2(Р> и) = (Р\+Р2)и Для всех (р,, р2).
а) Изобразите ящик Эджворта для данной экономики, если
совокупный начальный запас благ равен A, 1), и опишите множество Парето-
эффективных распределений.
б) Изобразите ящик Эджворта для данной экономики, если
совокупный начальный запас благ равен B, 1), и опишите множество Парето-
эффективных распределений.
5.17. Рассмотрите экономику обмена с двумя одинаковыми
потребителями, предпочтения которых описываются функцией полезности
u'(x{, х2) = х*х12~а, где 0 < а < 1. Пусть в экономике имеется 10 единиц х,
и 10 единиц х2. Укажите векторы первоначальных запасов е1 и е2,
е1 Ф е2, и равновесные цены, при которых распределение, в котором оба
потребителя имеют одинаковое количество благ E, 5), может быть
реализовано как равновесное.
5.18. Рассмотрите экономику обмена с двумя благами и двумя
потребителями, функции полезности которых имеют вид
U \Х\, Х2 ) — Xj (^2 / 5
u2{xv x2) = (xlJx2.
Пусть совокупный начальный запас благ составляет A0, 20).
а) Предположим, что некий плановик решает распределить блага так,
чтобы максимизировать полезность первого потребителя при уровне
полезности второго потребителя, равном и2 =8000/27. Найдите распреде-

Глава 5. Общее равновесие
315
ление благ между потребителями, являющееся решением задачи
плановика, и покажите, что оно эффективно по Парето.
б) Предположим, что плановик решает поделить запасы так, чтобы
е1 =A0, 0) и е2 =@, 20), а затем позволяет потребителям производить
обмены на совершенно конкурентных рынках. Найдите равновесие по
Вальрасу и покажите, что равновесное распределение будет таким же, как
и в пункте а).
5.19. (Скарф) Рассмотрите экономику обмена с тремя потребителями
и тремя благами. Пусть функции полезности потребителей и их
первоначальные запасы имеют вид
u\xv х2, x3) = min(x,, х2) е!=A, 0, 0),
w2(xp x29 x3) = min(x2, х3) е2=@, 1, 0),
иъ{хх, х>, jc3) = min(x1, хъ) е3=@, 0, 1).
Найдите равновесие по Вальрасу и равновесное распределение в данной
экономике.
5.20. Пусть в экономике обмена с двумя потребителями совокупный
начальный запас благ равен (el9 е2) = {e\ +ef, e2+el). Предположим, что
функции полезности потребителей имеют вид и' =(х[ -s[)a + (х2 -sl2)a,
где 0<сс<1 и / = 1, 2, причем (s\9 s2)*(s{2, si).
а) Пусть в экономике действует единственный гипотетический
потребитель, имеющий первоначальный запас (е19 е2) и функцию
полезности и1 = (х{ -s,)a +(x2 -s2)a, где Sj =s\ +5y, 7 = 1, 2 . Вычислите
отношение (диIдхх)/(диIдх2) для этого потребителя и найдите ее значение в
точке (ос,, jc2) = (ep e2). Назовем его р\
б) Покажите, что р*, полученное в пункте а), является относительной
равновесной ценой первого блага хх в описанной выше экономике
обмена.
5.21. Покажите, что если производственное множество фирмы строго
выпукло, а вектор цен строго положителен, то существует не более
одного производственного плана, максимизирующего прибыль.
5.22. Приведите доказательство теоремы 5.10.
5.23. Завершите доказательство теоремы 5.13, показав, что z(p) в
экономике с производством удовлетворяет всем свойствам теоремы 5.3.
5.24. Предположим, что в экономике с единственным потребителем
потребитель не обладает запасом потребительского блага у, но обладает

316
Часть II. Рынки и благосостояние
24-часовым запасом времени h, т.е. е = B4, 0). Предположим также, что
его предпочтения определены на множестве Ш2+ и описываются
функцией полезности u(h, y) = hy, а производственное множество имеет вид
Y = {(-h, y)\0<h<b9 0<y<y[h}, где b — некоторое достаточно
большое положительное число. Пусть ру и ph — цены потребительского
блага и досуга соответственно.
а) Найдите относительные цены pyl ph, при которых рынки
потребительского блага и досуга сбалансированы.
б) Найдите равновесное потребление и производственные планы и
изобразите полученные результаты в пространстве R2+.
в) Сколько времени в день потребитель тратит на работу?
5.25. Рассмотрите экономику обмена (и', е')/е/, в которой все
функции полезности и' непрерывны и квазивогнуты на множестве R".
Предположим, что х = (х!, х2,..., х7)»0 — Парето-эффективное
распределение и все и1 дифференцируемы в точке х' и Vw'(x')»0. При этих
условиях (которые несколько отличаются от условий теоремы 5.8), следуя
приведенным ниже пунктам, докажите другой вариант второй теоремы
благосостояния.
а) Покажите, что для любых двух потребителей / и j градиенты
Vw'(x') и VuJ(\J) должны быть пропорциональны, т.е. существует такое
а>0 (которое может зависеть от / и у), что Vw'(x') = aVw7(xy).
Проинтерпретируйте это условие для случая двух потребителей.
б) Пусть р = Vw1 (х1) » 0. Покажите, что для каждого потребителя /
существует А,, > 0, такое, что Vul (х;) = А,,.р.
в) Используя теорему 1.4, покажите, что для каждого потребителя /
набор х' является решением задачи
тахм^х1) при рх' <рх'.
х'
5.26. Предположим, что выполнены все условия упражнения 5.25 за
исключением строгой положительности набора х и градиентов Vw'(x').
Приведите пример в ящике Эджворта, когда, отказавшись от этих
предпосылок, нельзя реализовать распределение х как равновесное.
Поскольку теорема 5.8 не требует строгой положительности вектора х, укажите,
какая предпосылка теоремы 5.8 нарушается в вашем примере.

Глава 5. Общее равновесие 317
5.27. Рассмотрите двухпериодную модель с двумя потребителями и
единственным потребительским благом х. Обозначим потребление блага
в период / через хп t = 1, 2. Пусть многопериодные функции полезности
потребителей имеют вид:
и'(х]9 x2) = ln(xl) + ln(x2), / = 1,2,
а начальные запасы потребителей заданы векторами е!=A0, 0) и
е2 = B0, 5). Предположим, что рассматриваемый товар является
непортящимся, и поэтому то, что не было потреблено в первом периоде, может
быть сохранено и использовано в следующем периоде.
а) Пусть торговля между потребителями запрещена. Найдите объемы
потребления для каждого потребителя в каждом периоде и
соответствующие уровни полезности.
б) Теперь предположим, что существуют конкурентный спот-рынок и
фьючерсный рынок блага. Пусть рх — цена единицы блага (на спот-
рынке) в первом периоде, р2 — действующая в первом периоде
(фьючерсная) цена поставки единицы блага во втором периоде. Найдите
равновесное соотношение цен р2 /р1 .
5.28. Пусть у = 0 является решением задачи
тахру при ye Y-y°.
у
Покажите, что у0 является решением задачи
тахру при ye Y.
у
5.29. Рассмотрите экономику с производством, в которой
выпускается много товаров, но каждая отдельная фирма выпускает лишь один
товар. Предположим также, что технология каждой фирмы описывается
дифференцируемой производственной функцией, и функции полезности
потребителей также дифференцируемы. Пусть данная экономика
находится в состоянии равновесия при строго положительных ценах;
предельные полезности (потребительских товаров) для всех потребителей и
предельные продукты (факторов) для всех фирм строго положительны.
а) Покажите, что предельные нормы замещения между любыми
двумя потребительскими товарами одинаковы для всех потребителей и
равны отношению цен этих товаров.
б) Покажите, что предельные нормы технологического замещения
между любыми двумя факторами одинаковы для всех фирм и равны
отношению цен этих факторов.
в) Как вы проинтерпретируете результаты пунктов а) и б)? Какую
информационную нагрузку несут цены в равновесии по Вальрасу?

318
Часть II. Рынки и благосостояние
5.30. Завершите доказательство леммы 5.4.
а) Покажите, что, если распределение х является г-репликой
распределения (х1, х2, ..., х7) экономики Хг и х —распределение,
равновесное по Вальрасу, в экономике 2ГГ, то (х1, х2, ..., х7) — равновесное
распределение в экономике Хх.
б) Покажите, что если (х1, х2, ..., х7) —равновесное распределение
в экономике 2Г,, то его г -реплика является равновесным распределением
в экономике 2ГГ.
5.31. Приведите доказательство теоремы 5.16 в общем виде для
случая произвольного числа / типов потребителей и произвольного числа г
потребителей каждого типа.
5.32. (Корнуолл) В экономике с потребителями двух типов каждый тип
имеет соответствующую функцию полезности и первоначальные запасы
uXq{xx, х2) = ххх2 и е1 =(8, 2),
u2q(xx, х2) = ххх2 и е2=B, 8).
а) Изобразите ящик Эджворта для данной экономики в случае одного
потребителя каждого типа.
б) Опишите как можно более полно множество распределений,
принадлежащих ядру данной экономики с двумя потребителями.
в) Покажите, что распределение х11 =D, 4) и х21 =F, 6)
принадлежит ядру.
г) Теперь рассмотрите реплицированную экономику с четырьмя
потребителями, в которой по два потребителя каждого типа. Покажите, что
распределение хп=х12=D, 4) и х21=х22=F, 6) «в принадлежит ядру
реплицированной экономики.
5.33. Пусть в экономике чистого обмена потребитель / завидует
потребителю j, если \J >¦' х' (т.е. / завидует j, если потребителю /
нравится набор потребителя j больше его собственного). Таким образом,
распределение х не вызывает зависти, если х' >=l \J для всех / и j. Известно,
что не вызывающие зависти распределения всегда существуют. Таким,
например, является распределение, где каждому потребителю достается
одинаковое количество благ х = A//)е. Распределение называется
справедливым, если оно не вызывает зависти и эффективно по Парето.
а) Изобразите в ящике Эджворта распределения, которые не
вызывают зависти, но не эффективны по Парето.

Глава 5. Общее равновесие
319
б) При выполнении предположения 5.1 докажите, что в любой
экономике обмена со строго положительным вектором совокупных запасов
существует по крайней мере одно справедливое распределение.
5.34. Рассмотрите двух потребителей со следующими
характеристиками:
u\xl9 x2) = eXlx2 и е1 =A, 1),
w2(jc,, х2) = еХхх\ и е2=E, 5).
а) Найдите уравнение контрактной кривой и изобразите ее график в
ящике Эджворта.
б) Найдите справедливое распределение благ между потребителями в
этой экономике.
в) Теперь рассмотрите трижды реплицированную экономику.
Найдите справедливое распределение благ между потребителями в этой
новой экономике.
5.35. Рассмотрите двух потребителей со следующими
характеристиками:
и\хх, jc2) = 2jc,+x2 ие'=A, 6),
и2{хх, х2) = х1+х2 и е2=C, 4).
Найдите справедливое распределение благ.
5.36. До сих пор мы предполагали, что полезность потребителя
зависит только от объемов потребляемых им благ. Теперь предположим, что
полезности потребителей взаимозависимы, т.е. зависят как от
собственного потребления, так и от объемов потребления других участников.
Например, пусть в экономике с двумя благами, двумя потребителями и
совокупным запасом благ е, их =и\х\, х2, х2, я:2) и и2 = и2(х2, х2,
Xj1, х2),где ди'/дх{ ФО и ди'/дх^ ФО при /, ; = 1, 2 и/^;.
а) Каковы необходимые условия Парето-эффективности
распределения благ между потребителями?
б) Будет ли распределение, равновесное по Вальрасу, Парето-эффек-
тивным в такой экономике? Обоснуйте свой ответ.
5.37. В тексте мы называем распределение х Парето-эффективным,
если не существует другого допустимого распределения х, такого, что
х' ^' х' для всех i и \J yJ xJ по крайней мере для одного потребителя j.
Иногда распределение х называют Парето-эффективным, если не
существует другого допустимого распределения х, такого, что х1 >-' х' для всех /.
а) Покажите, что если предпочтения непрерывны и монотонны, то
два приведенных определения эквивалентны.

320
Часть II. Рынки и благосостояние
б) Приведите пример, когда эти два определения неэквивалентны, и
проиллюстрируйте его в ящике Эджворта.
5.38. (Теорема Эйзенберга) Как правило, система рыночных функций
спроса не удовлетворяет таким свойствам индивидуальных функций
спроса, как уравнение Слуцкого, отрицательная полуопределенность матрицы
замещения и т.д. Однако иногда полезно знать, при каких условиях
рыночный спрос ведет себя так, как будто он порожден одним гипотетическим
потребителем, максимизирующим свою полезность. Эйзенберг [Eisenberg,
1961] показал, что это возможно, когда предпочтения потребителей предста-
вимы с помощью линейно однородных функций полезности (не обязательно
одинаковых), а распределение дохода фиксировано и не зависит от цен.
В частности, предположим, что х'(р, у') является решением задачи
maxw'(x') при р-х'=/, где /е/, а х(р, у*)— решением задачи
\'еШ"+
тах?/(х) при р • х = у*. Если: 1) функции и'(х') линейно однородны для
xeR"
всех / е I; 2) у* — агрегированный доход, и доли дохода фиксированы
так, что у'=Ъ'у*, где 0<5'<1 и ^81=1;
/е/
3) U(\) = maxYl(ui(xi))S при x = ^V ,
то х(р, У) = ^х1(р, У), т.е. рыночный спрос ведет себя так, как будто
он был получен из единственной задачи максимизации полезности.
а) Рассмотрите экономику обмена с двумя благами и двумя
потребителями, первоначальные запасы которых описываются векторами
е1 = (81, 81) и е2 = (82, 82), где 0 < 81 < 1 и 81 + 82 = 1. Покажите, что
доли дохода фиксированы и не зависят от цен р = (р,, р2) -
б) Найдите U(x) для экономики из пункта а), если
u\s)=(xmx2j-\
гдеО<ос<1иО<р<1.
в) Проверьте выполнение теоремы Эйзенберга для данной экономики.
5.39. Рассмотрите экономику обмена с первоначальным запасом благ
е, докажите, что вектор совокупного избыточного спроса z(p) не
зависит от первоначального распределения запасов благ между
потребителями тогда и только тогда, когда предпочтения потребителей одинаковы и
гомотетичны.

Глава 6
ОБЩЕСТВЕННЫЙ ВЫБОР
И БЛАГОСОСТОЯНИЕ
6.1. Суть проблемы
До сих пор, за редким исключением, мы занимались
преимущественно вопросами «позитивной экономики». Как правило, нам было
достаточно выдвинуть предположения о мотивах и обстоятельствах действий
агентов и на этой основе сделать вывод о последствиях их
индивидуальных и коллективных действий. В сущности, мы описывали и
предсказывали эти действия, а не оценивали или каким-либо образом диктовали их.
В этой главе мы изменим нашу точку зрения с позитивной на
нормативную и вкратце рассмотрим некоторые важные проблемы экономики
благосостояния.
Когда мы оцениваем некую ситуацию, например рыночное равновесие,
как «хорошую» или «плохую» либо считаем ее «лучше» или «хуже»
другой, мы неизбежно, по крайней мере неявно, опираемся на некий этический
стандарт. Люди различаются по своим этическим представлениям, а
значит, и по своим суждениям о тех или иных ситуациях. Этот очевидный
факт не должен нас смущать и вызывать сожаление о том, что нормативная
экономика «только вопрос мнений». Напротив, переход от предпосылок к
выводам, а от них — к рекомендациям оказывается согласованным
(непротиворечивым). Экономика благосостояния создает теоретическую основу
для дискуссии по общественным проблемам, открывая этические
принципы нашей аргументации и позволяя нам увидеть их следствия.
В широком смысле наша цель в данной главе заключается в том,
чтобы изучить методы, с помощью которых можно непротиворечиво
упорядочить различные социальные ситуации, или «социальные состояния»,
опираясь на явные и корректно определенные этические предпосылки. На
том уровне обобщения, на котором мы будем этим заниматься,
«социальным состоянием» может быть практически все что угодно: выбор
определенного кандидата на политическую должность, конкретный способ
поделить пирог между несколькими людьми, принятие рыночно
ориентированной формы организации общества или конкретный способ
распределения общественных ресурсов между членами общества.
Проблема общественного выбора возникает, когда группе индивидов
приходится делать коллективный выбор из множества имеющихся альтернатив.

322
Часть II. Рынки и благосостояние
Чтобы на время конкретизировать обсуждение, рассмотрим проблему
распределения в простой экономике обмена с двумя индивидами и двумя
товарами, представимой ящиком Эджворта, подобным изображенному на
рис. 6.1. Каждая точка ящика представляет собой некоторый способ
разделить фиксированный запас принадлежащих обществу благ между
двумя его членами и поэтому может рассматриваться как одно из
(взаимоисключающих) альтернативных социальных состояний, которые могут
возникнуть. У каждого из агентов есть свои предпочтения относительно этих
альтернатив, и, конечно, эти предпочтения часто противоречат друг
другу. Легко поставить соответствующую проблему общественного выбора:
какое из возможных альтернативных распределений является наилучшим
для общества?
Рис. 6.1. Проблема распределения
Ответить на этот вопрос не так просто, как задать его. Вероятно, без
особых возражений точки за пределами контрактной кривой можно
исключить. Если бы одна из них считалась наилучшей, было бы легко найти
некоторую другую точку на контрактной кривой, которую предпочтет
каждый из агентов. Поскольку трудно что-то возразить против такого
совпадения мнений членов сообщества, можно, видимо, ограничиться при
поиске наилучшей альтернативы Парето-эффективными распределениями.
Но какое из них является наилучшим? Многие легко согласятся с тем,
что явно несправедливые альтернативы, такие как х, также должны быть
исключены, несмотря на то что они являются Парето-эффективными. При
этом используется некий этический стандарт, дополняющий простой
принцип Парето, поскольку последний не дает ответа на существенный
вопрос: в какой степени можно пожертвовать благосостоянием второго
участника с целью увеличить благосостояние первого в интересах
общества в целом? Имеет ли значение интенсивность предпочтений при
попытке осуществить такое изменение? Если считать, что имеет, то возни-

Глава 6. Общественный выбор и благосостояние
323
кают другие вопросы. Можно ли выявить интенсивность предпочтений?
Могут ли люди сказать, насколько сильно их отношение к тем или иным
альтернативам? Можно ли сравнивать интенсивность предпочтений
разных людей для того, чтобы сбалансировать выигрыши и потери?
Подобные вопросы многочисленны, и они затрагивают глубокие
проблемы. Чтобы продвинуться в их понимании, нам понадобятся
концептуальные рамки их изучения. Такие рамки предложил Эрроу [Arrow, 1951],
и мы начнем с его новаторского анализа некоторых из этих проблем.
6.2. Общественный выбор и теорема Эрроу
Принимаемая нами формальная структура является весьма простой и
общей. Существует некоторое непустое множество X
взаимоисключающих социальных состояний. Иногда мы будем требовать конечности X,
но чаще оно будет предполагаться бесконечным. Общество состоит из N
индивидов, N>2.Y индивида / есть отношение предпочтения R1,
определенное на альтернативах X, с соответствующими отношениями
строгого предпочтения Р' и безразличия /'. Будучи отношением
предпочтения, каждое R1 является полным и транзитивным. Интуитивно ясно, что
нам требуется только то, чтобы люди могли попарно сравнивать любые
элементы X и чтобы эти сравнения были непротиворечивы, т.е. транзи-
тивны. Множество X определено очень широко, поэтому следует иметь
в виду, что его элементы могут быть как чисто материальными, так и
чисто духовными. Поэтому отношения R1 также должны трактоваться
довольно широко. Они не обязаны ограничиваться эгоистическим
отношением к материальным объектам и могут также отражать человеческий
альтруизм, доброту и даже религиозные воззрения.
Теперь вспомним, что если предпочтения являются полными и
транзитивными, а X конечно, то индивид может полностью упорядочить
элементы Хот лучшего к худшему. Отношения R1, таким образом, содержат
всю необходимую информацию для того, чтобы определить выбор
индивида из множества альтернатив X. Однако, чтобы определить
общественный выбор, нам понадобится некоторое ранжирование социальных
состояний X, отражающее предпочтения общества. В идеальном случае нам
бы хотелось уметь сравнивать две любые альтернативы из X с
общественной точки зрения, а также чтобы эти сравнения были
непротиворечивыми в обычном смысле этого слова. Так мы приходим к следующему
определению.
Определение 6.1. Отношение общественного предпочтения.
Отношение общественного предпочтения R является полным и
транзитивным бинарным отношением на множестве социальных со-

324
Часть II. Рынки и благосостояние
стояний X. Для х и у из множества X выражение xRy читается как
утверждение «х не хуже у с точки зрения общества». Р и I являются
соответствующими отношениями строгого общественного
предпочтения и общественного безразличия.
Мы принимаем как данность то, что ранжирование альтернатив с
общественной точки зрения должно зависеть от их оценки индивидами.
Проблема, рассмотренная Эрроу, формулируется просто: каким образом
мы можем перейти от зачастую разнородных, но внутренне
непротиворечивых взглядов отдельных членов общества к единому и внутренне
непротиворечивому общественному взгляду?
На этот вопрос совсем не легко ответить. Если мы настаиваем на
транзитивности как критерии непротиворечивости общественного
выбора, возникают некоторые хорошо известные трудности. Например,
парадокс Кондорсе иллюстрирует ситуацию, когда знакомый метод
голосования по правилу простого большинства не удовлетворяет требованию
транзитивности R. Чтобы убедиться в этом, предположим, что N = 3,
X = {х, у, z}, а индивидуальные (строгие) предпочтения на X таковы:
Агент 1 Агент 2 Агент 3
х у z
у z х
z х у
При выборе между х и у альтернатива х получит два голоса, а у —
один, поэтому общественное предпочтение по правилу простого
большинства будет выглядеть как хРу. При выборе между у и z результатом
голосования будет yPz. Поскольку имеют место отношения хРу и yPz,
то транзитивность общественных предпочтений требует выполнения
отношения xPz. Однако при данных индивидуальных предпочтениях z
против х получит два голоса против одного, что дает общественное
предпочтение zPx и нарушает условие транзитивности. Заметим, что в
этом примере механизм голосования по правилу простого большинства
является «полным» в том смысле, что он указывает наилучшую
альтернативу при любом попарном сравнении элементов множества X. Но
отсутствие транзитивности означает, что по правилу простого большинства
нельзя определить единственную наилучшую из трех альтернатив.
Условия полноты и транзитивности требуют, чтобы отношение общественного
предпочтения ранжировало все элементы множества X.
Непротиворечивость, необходимая для наличия транзитивности, таким образом,
существенно влияет на возможность решения этой проблемы.
При этом сама по себе непротиворечивость не столь интересная и
убедительная характеристика для общественного выбора. Можно быть

Глава 6. Общественный выбор и благосостояние
325
абсолютно последовательным и при этом нарушать все действующие в
обществе моральные заповеди. Более интересный вопрос ставится так:
каким образом мы можем перейти от непротиворечивых индивидуальных
взглядов к общественному взгляду, который является непротиворечивым
и который также соответствует некоторым базовым ценностям,
разделяемым членами сообщества? Поскольку разногласия между индивидами
по вопросам «базовых ценностей» на деле являются той самой причиной,
по которой вообще возникает проблема общественного выбора, нам
придется соблюдать осторожность, называя эти ценности, если мы хотим
избежать тривиализации задачи с самого начала.
Имея в виду подобные предосторожности, мы можем поставить
задачу нахождения «правила», или функции, которая согласует и агрегирует
различные индивидуальные взгляды, представленные индивидуальными
отношениями предпочтения R!, в единое отношение общественного
предпочтения, удовлетворяющее некоторым этическим принципам. То
есть формально мы ищем функцию общественного благосостояния f,
где
R = f(Rl9...,RN).
Таким образом, / превращает N индивидуальных отношений
предпочтения на множестве X в отношение общественного предпочтения на X.
До конца подраздела 6.2 мы будем предполагать, что множество
социальных состояний X конечно.
Эрроу предложил набор из четырех условий, которые можно считать
минимально необходимыми свойствами функции общественного
благосостояния.
Предположение 6.1. Условия Эрроу для функции
общественного благосостояния.
U. Неограниченная область определения (unrestricted domain).
Область определения функции f должна включать все возможные
комбинации индивидуальных отношений предпочтения на множестве X.
WP. Слабый принцип Парето (weak Pareto Principle). Для любой пары
альтернатив х и у из множества X, если хР'у для всех i, то хРу.
НА. Независимость от посторонних альтернатив (independence of
irrelevant alternatives). Пусть R = f{Rx,...,RN), R = f(Rl,...9RN),u пусть х
и у — две альтернативы из X. Если для каждого индивида i Rl и R'
упорядочивают х и у одинаковым образом, то порядок хиус точки
зрения общества при R и при R также одинаков.
D. Отсутствие диктатора (nondictatorship). He существует такого
индивида /, что для всех х и у из множества X из предпочтения хР1у

326
Часть II. Рынки и благосостояние
следует хРу независимо от предпочтений Rj любого другого индивида
j(j*0.
Условие U утверждает, что функция / может порождать
упорядоченные общественные предпочтения независимо от того, какими
оказываются индивидуальные отношения предпочтения. Оно формализует тот
принцип, что способность механизма к осуществлению общественного
выбора не должна зависеть от того, какие именно взгляды разделяют
члены общества. Как мы видели выше, это условие вместе с требованием
транзитивности R исключает голосование по правилу простого
большинства из числа подходящих механизмов, поскольку в тех случаях,
когда число альтернатив превышает три, это правило может не приводить к
транзитивным общественным предпочтениям.
Условие WP вполне очевидно, и с ним соглашаются по крайней мере
экономисты. Оно гласит, что общество должно предпочесть х
альтернативе у, если каждый член общества предпочитает х, а не у. Заметим,
что это слабое условие Парето, потому что оно не требует, чтобы
общество предпочитало х в том случае, если, скажем, все, кроме одного,
предпочитают х, а для одного участника х и у эквивалентны.
Условие ПА, возможно, труднее всего интерпретировать, поэтому
перечитаем его еще раз. Короче говоря, оно утверждает, что общественное
ранжирование х и у должно зависеть только от индивидуального
ранжирования х и у. Заметим, что индивидуальные предпочтения R' и R1
могут отличаться по ранжированию других пар, отличных от х, у.
Подумайте, что могло бы произойти, если бы условие НА не выполнялось.
Например, предположим, что утром все индивиды ранжируют z ниже,
чем х и у, но одни предпочитают х альтернативе у, а другие — у
альтернативе х. Теперь предположим, что при таких индивидуальных
предпочтениях функция общественного благосостояния порождает
общественное предпочтение, при котором х строго предпочитается у . Так что
если бы выбор между х и у производился с утра, то «общество» выбрало
бы х. Однако пусть, как это бывает, выбор между х и у откладывается
до обеда. Предположим, что к тому времени индивидуальные
предпочтения изменились так, что все индивиды ранжируют z выше, чем х и у,
однако индивидуальное ранжирование х по отношению к у остается
неизменным. Разумно ли то, что общественные предпочтения будут теперь
ранжировать у выше, чем х ? НА дает отрицательный ответ.
Условие D на самом деле очень мягкое. Оно просто требует, чтобы ни
один индивид не мог навязывать всем свои предпочтения в любой ситуа-

Глава 6. Общественный выбор и благосостояние
327
ции общественного выбора, независимо от взглядов остальных членов
общества. Таким образом, явно исключается лишь наиболее
экстремальная и абсолютная форма диктатуры. Это условие допускает даже наличие
квазидиктатора, который добивается своего по всем социальным
альтернативам, кроме одной пары.
Посмотрите еще раз на эти условия. Проанализируйте их и
попробуйте представить ситуации, которые могут породить проблему
общественного выбора, если одно или более из этих условий не выполняется. Если в
конце концов вы согласитесь, что это действительно мягкие и
минимальные условия, налагаемые на разумную функцию общественного
благосостояния, следующая теорема удивит вас и, может быть, разочарует.
Теорема 6.1. Теорема о невозможности Эрроу.
Если существуют по крайней мере три социальных состояния (т.е.
множество X содержит не менее трех элементов), то не существует
такой функции общественного благосостояния f, которая одновременно
удовлетворяет условиям U, WP, НА и D.
Доказательство. Стратегия доказательства заключается в том, чтобы
показать, что условия U, WP и НА гарантируют существование
диктатора. Следовательно, если U, WP и НА выполняются, то D не выполняется,
и поэтому не существует функции общественного благосостояния,
удовлетворяющей всем четырем условиям.
Доказательство, которое представлено в работе Геанакоплоса [Geana-
koplos, 1996], производится в четыре шага. Отметим, что аксиома U
используется на каждом шаге при выборе или изменении рассматриваемого
профиля предпочтений. Неограниченность области определения
гарантирует, что любой такой профиль предпочтений является допустимым.
Шаг 1. Рассмотрим некоторое социальное состояние с.
Предположим, что в предпочтениях каждого индивида с занимает последнее
место. По условию WP в общественных предпочтениях с также будет на
последнем месте (см. рис. 6.2).
Rl R2 ... RN R
х х' ... х" хт
у у' ... / ут
с с ... с с
Рис. 6.2. Следствие условий WP и U в доказательстве
теоремы Эрроу

328
Часть II Рынки и благосостояние
Шаг 2. Представим, что с перемещается на первое место в
предпочтениях первого индивида, причем положение остальных социальных
состояний остается неизменным. Далее проделаем то же самое со вторым
индивидом, переместив с на первое место в его предпочтениях. Будем
повторять это для каждого индивида, имея в виду, что изменения в
индивидуальных предпочтениях могут влиять на общественные предпочтения.
В конце концов с окажется на первом месте в предпочтениях каждого
индивида, а согласно WP — и на вершине общественных предпочтений.
Следовательно, в какой-то момент общественный ранг с повысится в
первый раз. Пусть п -й индивид будет первым, для которого перемещение
с на первое (с последнего) место в его предпочтениях приводит к
повышению общественного ранга с.
Мы утверждаем, что если с оказывается на первом месте в
предпочтениях и-го индивида, то с не только повышает свой общественный
ранг, но и занимает в общественных предпочтениях первое место, как
показано на рис. 6.3.
Rl R2 ... Д" ... RN R
с с ... с ... х" с
х х' ... ... /
У у' ¦
w w' ... ... с W"
Рис. 6.3. Аксиомы WP, U и ПА порождают главного индивида
Чтобы убедиться в этом, предположим обратное: ранг с в
общественных предпочтениях повышается, но не до первого места, т.е. aRc и
cR$ для некоторых состояний а, Р Ф с.
Тогда, поскольку с находится на первом или последнем месте в
предпочтениях каждого индивида, мы можем изменить предпочтения
индивида / таким образом, чтобы (ЗР'а, но положение с для этого
индивида осталось прежним. Это и приводит к противоречию, поскольку, с
одной стороны, рР'ос по условию WP означает, что общество строго
предпочитает Р по сравнению с а, т.е. рРа. Но с другой — так как
положение с относительно а и положение с относительно р в
предпочтениях каждого индивида не изменилось, условие НА означает, что и в
общественных предпочтениях положение с относительно а и с
относительно р должно остаться неизменным, т.е., как изначально предполага-

Глава 6. Общественный выбор и благосостояние
329
лось, имеют место отношения аЛс и с/?р. Но тогда по транзитивности
имеет место отношение ос/?р, что противоречит тому факту, что (ЗРос.
Это доказывает наше утверждение о том, что с должно переместиться на
первое место в общественных предпочтениях, как на рис. 6.3.
Шаг 3. Рассмотрим два различных социальных состояния а и Ъ,
каждое из которых отлично от с. На рис. 6.3 изменим профиль
предпочтений следующим образом: изменим ранжирование социальных состояний
п -м индивидом так, чтобы аРпсРпЪ, а в предпочтениях остальных
индивидов расположим а и Ъ произвольно, но так, чтобы положение с для
каждого из них осталось прежним. Заметим, что в новом профиле
предпочтений положение а относительно с у каждого индивида то же самое,
каким оно было до перемещения с на первое место в предпочтениях п -го
индивида на шаге 2. Следовательно, согласно условию ПА положение а
относительно с в общественных предпочтениях должно быть таким же,
каким оно было в тот момент. Но это означает, что аРс, поскольку в тот
момент социальное состояние с все еще находилось на последнем месте
в общественных предпочтениях.
Аналогично в новом профиле предпочтений положение с
относительно Ъ для каждого индивида такое же, каким оно было сразу после
перемещения с на первое место в предпочтениях п -го индивида на шаге 2.
Следовательно, согласно условию ПА положение с и Ъ в общественных
предпочтениях должно быть таким же, каким оно было в тот момент. Но
это означает, что сРЬ, поскольку в тот момент социальное состояние с
поднялось на первое место в общественных предпочтениях.
Итак, поскольку аРс и сРЬ, по транзитивности можно заключить,
что аРЬ. Заметим, что независимо от предпочтений других индивидов
относительно а и Ъ общественное ранжирование этих альтернатив
соответствует предпочтениям п -го индивида. По условию НА, а также
потому, что а и Ъ произвольны, мы можем сделать вывод, что для всех
социальных состояний а и Ь, отличных от с, из отношения аРпЪ следует
аРЬ. То есть п -й индивид является диктатором по всем парам
социальных состояний, не включающим с. Последний шаг показывает, что п -й
индивид действительно является диктатором.
Шаг 4. Пусть а отлично от с. Мы можем повторить
вышеприведенные шаги, используя а в роли с, и прийти к выводу о том, что некоторый
индивид является диктатором по всем парам, не включающим а. Однако
вспомним, что положение с в предпочтениях п -го индивида (на первом
или последнем месте) на рис. 6.3 определяет положение с в
общественных предпочтениях (на первом или последнем месте). Следовательно,
именно п -й индивид должен быть диктатором по всем парам, не вклю-

330
Часть II. Рынки и благосостояние
чающим а. А поскольку а — произвольное состояние, отличное от с, то
наряду с вышеприведенным выводом об п -м индивиде это означает, что
он является диктатором. ¦
Хотя теорема Эрроу называется теоремой о «невозможности»,
приведенное доказательство предполагает, что она может быть
сформулирована как теорема о «возможности». Мы показали, что любая функция
общественного благосостояния, удовлетворяющая трем условиям — U, WP и
НА, должна порождать отношение общественного предпочтения, которое
в точности совпадает с отношением предпочтения отдельного индивида,
и поэтому должна являться диктаторской функцией общественного
благосостояния. Это на самом деле единственная «возможность».
6.2.1. Графическое доказательство
Учитывая важность теоремы Эрроу, мы приведем еще одно — более
простое — доказательство — графическое для случая двух индивидов.
Мы надеемся, что два доказательства вместе будут способствовать более
глубокому понимание сути этого замечательного результата.
Следуя работе Блэкорби, Дональдсона и Веймарка [Blackorby,
Donaldson and Weymark, 1984], мы сохраним все условия Эрроу
относительно /?', R и /, но усилим некоторые из них следующим образом. Во-
первых, к списку требований, предъявляемых к индивидуальным
предпочтениям R' и общественным предпочтениям R, мы добавим
непрерывность. Нам известно, что полные транзитивные и непрерывные
бинарные отношения на некоторых множествах (т.е. конечных ; или
замкнутых и выпуклых) могут быть представлены непрерывными
вещественнозначными функциями (полезности). Поэтому предположим,
что каждое допустимое индивидуальное отношение предпочтения R1
представимо непрерывной функцией полезности и'(-). Мы хотим
агрегировать их в общественную функцию полезности К(). Тогда в данном
контексте наша задача заключается в том, чтобы найти такую функцию
общественного благосостояния /, которая для каждого вектора
непрерывных индивидуальных функций полезности (м1 (•),...,«*(•)) давала бы
общественную функцию полезности
V(x) = [f(u\),...,uN())](x), F-1)
удовлетворяющую условиям предположения 6.1.
Для конечных множеств условие непрерывности выполняется для всех
рассматриваемых отношений предпочтения. Так что в «старой» постановке задачи усиление
требований в действительности не имеет места. — Примеч. ред.

Глава 6. Общественный выбор и благосостояние
331
Условие U в этой ситуации означает, что любой из возможных
векторов непрерывных функций полезности является допустимым в F-1).
Условие ПА означает в точности то же, что и раньше. Отметим, что
согласно ему, в частности, соотношение между V(x) и V{y) может зависеть
только от векторов (*/(*),...,uN(x)) и (и1 (у),...,uN(y)), но ни от каких
других значений, принимаемых векторной функцией (и] (•),..., и N (•))].
Смысл условий WP и D остается прежним.
Рассмотрим дополнительное условие, налагаемое на /.
PL Принцип безразличия по Парето (Pareto indifference). Если
и'(х) = и'(у) для всех / = 1, ...,iV, то V(x) = V(y).
Можно показать (см. упражнение 6.3, а также работу Сена [Sen,
1977]), что если общественная функция полезности К(), порожденная /
в соответствии с F-1), непрерывна на X, а функция / удовлетворяет
принципам «теории благосостояния» (welfarism), т.е. условиям U, ПА и
PI, то должна существовать непрерывная функция W: RN —> R, такая, что
для любых альтернатив х, у
V(x) > V{y) тогда и только тогда, когда
W(u\x\..MN{x))>W(u\y\...uN(y)). F-2)
Это означает, что отношение общественного предпочтения можно
выразить с помощью функции W, которая просто упорядочивает векторы
значений индивидуальной полезности, соответствующие различным
альтернативам. Следовательно, мы можем ограничиться такой формой
функции общественного благосостояния. Ее простота связана с тем, что
общественная полезность какой-либо альтернативы в ней явным образом
ставится в зависимость только от вектора индивидуальных полезностей
этой альтернативы.
Тем самым наша задача сводится к нахождению такой непрерывной
вещественнозначной функции
W{u\...9uN)
на RN, что функция общественного благосостояния /, порождаемая ею
через соотношение
1 Заметим, что F-1) допускает, что общественная полезность V(x), сопоставленная
альтернативе х, может зависеть от самой функции полезности каждого индивида, а не
только от ее значения, соответствующего х. Условие ПА фактически требует, чтобы V(x)
зависело только от вектора полезностей (w1 (x), ...,uN(x)).

332
Часть II Рынки и благосостояние
удовлетворяет условиям предположения 6.1. Иногда мы будем называть
функцией общественного благосостояния саму функцию W. Благодаря ее
форме мы можем сконцентрироваться исключительно на влиянии
перечисленных условий на то, как W должна «обрабатывать» информацию,
содержащуюся в векторах значений функций полезности (и\ ...,uN). Как
вам предлагается показать в упражнении 6.4, если функция /
удовлетворяет условиям WP и НА предположения 6.1, то W должна быть строго
возрастающей. Далее мы воспользуемся этим фактом.
В ходе наших рассуждений важно будет помнить о том, что наша
конечная цель — охарактеризовать общественные предпочтения
относительно социальных состояний на множестве X. Принципы «теории
благосостояния» позволяют нам сконцентрировать усилия на информации об этих
состояниях, которая содержится в функциях полезности индивидов и
векторах их значений (u\...9uN). Какая же информация о социальных
состояниях из множества X действительно отражается в векторе
полезностей при минимальных ограничениях на индивидуальные отношения R' ?
Поскольку от R1 мы требуем только того, чтобы они упорядочивали
альтернативы на множестве X от наилучшей к наихудшей, то от функции
полезности, представляющей R', нам требуется только, чтобы она
отражала эту же самую информацию на порядковой числовой шкале. Более
того, Эрроу полностью исключает возможность сравнения полезностей у
различных индивидов. Предположения Эрроу относительно R' означают,
что полезности измеримы только на порядковой шкале (ordinal scale, OS)
и что полезности разных людей несравнимы (noncomparable, NC). Тогда,
как и в нашем анализе обычных потребительских предпочтений, если
и'(х) представляет предпочтения R', то и любая функция \\f'(u'(x))
представляет эти предпочтения при условии, что \|/' (.) — строго возрастающее
преобразование. Если полезности различных индивидов несравнимы, то
преобразование \|/' может быть выбрано произвольным образом.
Предположение OS/NC имеет большое значение для нашей
агрегирующей функции W. Предположим, что (u\...,uN) и (u\...yuN)
—векторы полезностей, соответствующие двум социальным состояниям х и
у. Функция W должна быть инвариантной к любому положительному
монотонному преобразованию функций полезности индивидов или к
любому «перенумерованию кривых безразличия индивидов». Таким
образом, если, например, согласно W альтернатива х для общества лучше
альтернативы у, т.е. если

Глава 6. Общественный выбор и благосостояние
333
W(u\...9uN)>W(u\...9uN)9
то отсюда неравенство
^(V(W,),...,^(W^))>^(i|/,(i/1),...,x|/;v(^))
имеет место для любых N функций \|/', различных или совпадающих (по
условию NC), при ограничении, что \|/' > 0 (по условию OS), / = 1, ...,N.
Этот факт будет ключевым в дальнейшем изложении.
Для графического доказательства мы предполагаем, что N = 2, и
поэтому можем действовать на плоскости. Задачу поиска непрерывной
функции общественного благосостояния W можно свести к поиску ее
множеств уровня, или общественных кривых безразличия, покрывающих
плоскость Ш2. Стратегия будет той же самой, что и в предыдущем
доказательстве. Мы воспользуемся информационными ограничениями на
полезность, условиями упорядоченности, непрерывности и монотонности
W для того, чтобы выявить диктатора и тем самым установить
невозможность существования функции общественного благосостояния,
отвечающей предположению 6.1.
Для начала рассмотрим произвольную точку И на рис. 6.4 и
попробуем вообразить общественную кривую безразличия, на которой она лежит.
Для удобства пространство полезностей разделено на четыре области
относительно П, причем пунктирные линии в эти области не входят.
Прежде всего заметим, что по условию WP общество предпочитает точке И
все точки области I. Аналогично и должна предпочитаться всем точкам
области III. Наша задача, таким образом, заключается в том, чтобы
ранжировать точки областей II, IV и исключенных границ относительно П.
•* ! i
и •'
i u
III i IV
1 >«'
Рис. 6.4. Графическое доказательство теоремы Эрроу

334
Часть II. Рынки и благосостояние
Рассмотрим произвольную точку и в области II. Должно
выполняться одно из следующих соотношений:
W(u) > W(u), F-3)
W(n) = W(u), F-4)
W(u) < W(u). F-5)
Предположим, что W(u) < W(u). Тогда при условиях OS/NC, налагаемых
на полезность, тот же самый порядок должен сохраниться, если мы
применим любые положительные монотонные преобразования к полезностям
индивидов. Допустим, что мы выбрали две строго возрастающие
функции — ц/1 и \|/2, причем
\|/V) = w, \\г2(й2) = й2. F-6)
Применим эти функции к координатам точки и. Поскольку и лежит в
области II, нам известно, что и1 <й1 и и2 >й2. Так как \|/' строго
возрастают, то, применяя их к и , мы должны получить
v1 =\|/l(w,)<\|/1(w1) = w1, v2 =\|/2(w2)>\|/2(w2) = w2. F-7)
Соотношения F-6) и F-7) вместе означают, что точка \ = (vl, v2) также
должна находиться где-то в области И. Поскольку условие OS/NC дает
нам полную свободу выбора 1|/', то, соответственным образом подобрав
эти функции, мы можем отобразить и в любую точку области И1. Но
тогда, поскольку общественное ранжирование соответствующих
социальных состояний должно быть инвариантным к таким преобразованиям
полезности индивидов, каждая точка области II должна занимать в
общественных предпочтениях такое же место относительно И! Если, как мы
предполагали, W(u) < W(u), то любая точка области II должна
предпочитаться й. Заметим, что мы нигде не использовали тот факт, что
W(u) < W(vl) . Мы могли бы начать с любого из предположений F-3),
F-4) или F-5) и прийти к тому же самому выводу с помощью тех же
аргументов. Таким образом, при условиях инвариантности индивидуальной
1 Например, чтобы получить \\f'(u') = u' и у'(«') = и', мы можем выбрать
и' -и'
й' -и'
t +
и' -и'
й' -и'
т.е. функцию, имеющую вид \|/'@ = a'f + |3'. Заметим, что при любом выборе (и\ и2) в
области II величины а1 и а2 положительны.

Глава 6. Общественный выбор и благосостояние
335
полезности каждая точка области II должна ранжироваться относительно
й одним из трех способов в общественных предпочтениях, т.е. ТГ может
являться более предпочтительной, менее предпочтительной или
эквивалентной любой точке области И. Мы запишем этот вывод как условие
того, что должно выполняться одно из следующих соотношений:
W(u) > W{\\), F-8)
W(u) = W(ll), F-9)
W(u)<W(ll). F-10)
Заметим, что равенство F-9) не может быть верным, так как это
означало бы, что точка U для общества эквивалентна любой точке из
области II (согласно условию WP), а значит, что все точки области II
эквивалентны друг другу. Но это противоречит строгому возрастанию
функции W, поскольку точка v » u области II (см. рис. 6.4) строго
предпочитается точке и.
Поэтому либо W(u) > W{\\), либо W(u) < W(Il). Проведя
рассуждения, аналогичные вышеизложенным, мы могли бы рассмотреть точки
области IV и показать, что либо W(u) > W(TV), либо W(u) < W(TV).
Предположим, что W(u)<W(ll). Тогда, в частности,
W(U)< W(ul -1, й2 +1). Рассмотрим пару строго возрастающих функций
\|/1(w1) = w1 +1, \\f2(u2) = u2 -1. Будучи примененными к точкам И и
(й1 -1, й2 +1), эти функции отобразят их в (й] +1, и2 -1) и й
соответственно. Но поскольку функция W должна быть инвариантной к таким
преобразованиям, эти варианты должны быть упорядочены так же, как их
прообразы. Следовательно, мы должны получить неравенство W(ul+1,
й2 -1) < W(u). Но это означает, что общество строго предпочитает и
точке (й1 +1, й2 -1) области IV. Следовательно, общество строго
предпочитает й любой точке области IV.
Мы показали, что если W(И) < W(II), то W(u) > W(IV). Аналогичные
рассуждения доказывают, что если W(u) > W(ll), то W(u)<W(W).
Таким образом, на данный момент мы имеем следующие неравенства:
либо W(W) < W(u) < W(ll), F-11)
либо W{\\) < W(u) < W(W). F-12)
Теперь заметим, что если точки в смежных областях одинаково
ранжируются по отношению к й, то и пунктирная линия, разделяющая
области, должна занимать в предпочтениях такое же место относительно II.

336
Часть II Рынки и благосостояние
Например, предположим, что точки области I и II ранжируются выше,
чем точка П. Поскольку, согласно условию WP любая точка выше ТГ на
пунктирной линии ранжируется выше точек области II, которые
находятся строго ниже ее, то по транзитивности эта точка на пунктирной линии
должна ранжироваться выше, чем П.
Следовательно, если F-11) выполняется, то, поскольку точки области I
ранжируются выше, чем й, а точки области III — ниже, то общественные
предпочтения выглядят так, как показано на рис. 6.5(a), где «+» («-»)
обозначает векторы полезности u = (i/, w2), при которых W(u) принимает
значение большее (меньшее), чем W(и). Но тогда непрерывность W
означает, что кривая безразличия, проходящая через точку й, является
горизонтальной прямой. Вместе с тем если имеет место F-12), т.е. ситуация
такова, как изображено на рис. 6.5F), то кривая безразличия, проходящая
через точку П, является вертикальной прямой.
и2
i I I I I I
1
1 1 1 1 1
1 1 1 1 1
<
> + +
>
> + +
>
>и+ +
i
» + +
t + +
W
9
> + +
i
+
+
Ч
1
+ + +
+ + +
ь
W
г
Рис. 6.5. Общественное благосостояние при условиях Эрроу
Итак, поскольку точка П была выбрана произвольно, мы можем
сделать вывод, что кривая безразличия, проходящая через любой вектор
полезности, является либо горизонтальной, либо вертикальной прямой.
Однако, поскольку кривые безразличия не пересекаются, это означает, что
либо все кривые безразличия представляют собой горизонтальные
прямые, и тогда индивид 2 является диктатором, или все кривые безразличия
представляют собой вертикальные прямые, и тогда диктатором является
индивид 1. В любом случае мы установили наличие диктатора и
завершили доказательство.

Глава 6. Общественный выбор и благосостояние
337
6.3. Измеримость, сравнимость и дополнительные
возможности
Теорема Эрроу поразительна. Внимательное изучение убеждает в
корректности каждого из ее условий по отдельности и всех вместе
взятых. Чтобы осмелиться опустить или ослабить одно из них, нужно быть
очень самоуверенным. Тем не менее суть теоремы и состоит в том, что
мы должны быть готовы сделать именно это.
Предпринимались многочисленные попытки вырвать анализ
общественного благосостояния из тисков теоремы Эрроу. Один из
вариантов заключался в том, чтобы ослабить условия, налагаемые на отношение
общественного предпочтения Л. Например, если заменить транзитивность
более слабым свойством под названием «ацикличность» и потребовать,
чтобы R не упорядочивало все альтернативы от наилучшей к
наихудшей, а позволяло лишь находить наилучшую альтернативу в любом
подмножестве, то открывается путь к нескольким механизмам выбора,
каждый из которых удовлетворяет всем остальным условиям Эрроу.
Аналогично, если сохранить транзитивность, но заменить условие U
предположением об «однопиковости» предпочтений, то, как показал Блэк [Black,
1948], голосование по правилу большинства удовлетворяет остальным
условиям Эрроу при нечетном числе индивидов.
Другая попытка была предпринята в ином направлении и принесла
весьма интересные результаты. Вместо того чтобы оспаривать
ограничения Эрроу на отношения общественного предпочтения или его
требования к допустимости любых «разумных» профилей предпочтений,
внимание было сконцентрировано на информации, которая содержится в
предпочтениях индивидов. В схеме Эрроу мера полезности задает только
порядок альтернатив и не подлежит сравнению у разных индивидов. Если
ослабить эти ограничения, допустить некоторую измеримость полезности
и в определенных пределах возможность ее сравнения между
индивидами, то в теории общественного благосостояния возникают интересные
возможности, особенно в сочетании с требованиями «равенства»,
налагаемыми на отношения общественного предпочтения. Первоисточниками
этого анализа являются работы Хэммонда [Hammond, 1976], д'Аспремона
и Жевера [d'Aspremont, Gevers, 1977], Робертса [Roberts, 1980], Сена [Sen,
1984]. Ниже мы рассмотрим только отдельные результаты для того,
чтобы оценить логику и ход мысли их авторов.
В предположении OS возможны утверждения наподобие
«благосостояние индивида / выше в состоянии х, чем в состоянии у». В сочетании с
условием NC, как в схеме Эрроу, оно не допускает сравнения
благосостояния индивидов / и у. Ограничения Эрроу на сравнение полезности
между индивидами можно ослабить и предположить, что всю
существенную информацию о полезности индивида можно полностью сравнивать

338
Часть II. Рынки и благосостояние
(fully comparable, FC) у разных индивидов. При условиях OS и FC можно
утверждать, например, что «благосостояние индивида i выше в состоянии
х, чем благосостояние индивидау в состоянии^».
Вместо того чтобы ограничиваться уровнями полезности для
отдельного индивида и в сравнении с другими, как это делается при условиях
OS/FC, предположим, что нас интересуют приращения полезности. То
есть предположим, что индивидуальная полезность измеряется на
числовой шкале (cardinal scale, CS), причем понятие приращения полезности
для индивида имеет смысл, и что сравниваются приращения полезности
различных индивидов (incrementally comparable, 1С) . В предположении
CS об индивидуальной полезности возможны такие утверждения, как
«индивид / увеличивает в большей степени полезность при переходе от
состояния х к состоянию у, чем при переходе от состояния w к состоянию
z». Сочетание условий CS и 1С позволяет сравнивать приращения
полезности у различных индивидов, и поэтому допускаются такие
утверждения, как «индивид / увеличивает в большей степени полезность при
переходе от состояния х к состоянию у, чем индивиду».
Можно придумать и использовать в различных комбинациях много
других способов измерения полезности и сравнения ее у разных
индивидов, но мы ограничимся парами OS/FC и CS/IC. В рамках принципов
«теории благосостояния» каждая из них накладывает на функции
общественного благосостояния некоторые условия инвариантности. Мы видели,
что при условиях Эрроу (OS/NC) ранжирование социальных состояний
должно быть инвариантным к произвольным положительным
монотонным преобразованиям индивидуальных полезностей, которые могут
различаться для разных индивидов. Когда мы используем комбинацию
OS/FC, можно сравнивать уровни полезности различных индивидов.
Условие OS, как мы знаем, эквивалентно требованию, чтобы функции
полезности были инвариантны по отношению к произвольным
положительным монотонным преобразованиям. Добавление условия FC означает, что
общественные предпочтения должны оставаться неизменными, только
когда одно и то же преобразование применяется к функции полезности
каждого индивида. Если мы, напротив, предположим, что полезность
удовлетворяет свойствам CS/IC, т.е. что могут сравниваться приращения
полезности, то тем самым мы также ограничим класс преобразований,
относительно которых общественные предпочтения должны быть
инвариантны. Условие CS требует, чтобы полезность сохранялась при
положительных аффинных преобразованиях, а по условию 1С единицы
измерения у различных индивидов должны быть сравнимы, поэтому
общественные предпочтения должны быть инвариантны по отношению к таким
1 Блэкорби, Дональдсон и Веймарк [Blackorby, Donaldson, Weymark, 1984] используют
термин «сравнение на единицу полезности» вместо «сравнения приращения полезности».

Глава 6. Общественный выбор и благосостояние
339
аффинным преобразованиям, при которых единицы измерения
приращения полезности («наклон») являются одними и теми же. Подытожим все
вышесказанное в следующем определении.
Определение 6.2. Измерение, сравнение и инвариантность.
1) В условиях OS/FC имеет смысл измерение уровней полезности,
которые могут сравниваться у различных индивидов. Общественное
ранжирование состояний, таким образом, долэюно быть инвариантным по
отношению к произвольному положительному преобразованию \|/,
примененному к функции полезности каждого индивида.
2) В условиях CS/IC имеет смысл измерение приращений уровня
полезности, которые могут сравниваться у различных индивидов.
Общественное ранжирование состояний, таким образом, долэюно быть
инвариантным по отношению к положительным аффинным преобразованиям
вида \|/' = а1 + Ьих, где Ь>0 одно и то же для каждого преобразования.
Возможность измерять и сравнивать полезность у различных
индивидов лучше всего рассматривать как вопрос о том, сколько информации
может «использовать» общество при выборе из нескольких альтернатив.
Такая постановка существенно отличается от этических ограничений,
которым, по нашим представлениям, этот выбор должен следовать. В
условиях Эрроу U, WP и ИА присутствует определенное этическое
содержание, однако некоторые исследователи стремятся пойти дальше и встроить
больше этических принципов в отношение общественного предпочтения.
Как можно догадаться, предложений на этот счет поступило немало.
Каждое из них сводится к дополнительным ограничениям на функцию
общественного благосостояния W помимо основных условий теории
благосостояния. Здесь мы рассмотрим только два.
Определение 6.3. Два дополнительных этических
предположения о функции общественного благосостояния.
А. Анонимность (anonymity). Пусть й — N -вектор полезностей, и
пусть и — другой вектор, полученный из й некоторой перестановкой
элементов. Тогда W(u) = W(u).
НЕ. Равенство по Хаммонду (Hammond equity). Пусть й и и — два
различных N -мерных вектора полезностей. Предположим, что йк - ик
для всех к, кроме i и j. Если и' > й' > uj > uj, то W(vl) > W(u).
Условие А утверждает только то, что с людьми следует обращаться
симметрично, т.е. ранжирование социальных состояний должно зависеть
не от самих индивидов, а только от уровня их благосостояния. Условие
НЕ более противоречиво. Оно отражает идею о том, что общество
предпочитает снижение дисперсии полезностей различных индивидов.
(Заметим, что дисперсия полезностей для П ниже, чем для и .) Далее мы вое-

340
Часть II. Рынки и благосостояние
пользуемся этими условиями для того, чтобы проиллюстрировать, как
можно аксиоматически охарактеризовать некоторые хорошо известные
функции общественного благосостояния.
6.3.1. Роулзианская форма
В этической системе, предложенной Роулзом [Rawls, 1971], решения
общества определяются благосостоянием его беднейшего члена. В
следующей теореме мы дадим аксиоматическую характеристику этого
критерия общественного благосостояния, верную только для случая N = 2.
Аналогичные результаты можно получить и для N > 2, но предлагаемое
изложение позволяет воспользоваться графическим подходом, к
которому мы прибегали ранее.
До конца этой главы мы будем предполагать, что все
рассматриваемые функции общественного выбора / удовлетворяют принципам
«теории благосостояния» (т.е. условиям U, PI, IIA) и непрерывны.
Следовательно (см. упражнение 6.4),/можно выразить с помощью непрерывной
функции W: RN -* R, где
[Аи\\...УШх)*[Аи\\...У(Жу)^
<*W(u\x\...y{x))>W{u\y\...,uN{y)).
Теорема 6.2. Роулзианские функции общественного
благосостояния.
Предположим, что выполняются условия OS/FC, так что функция
общественного благосостояния W удовлетворяет условию инвариант-
ности 1 из определения 6.2. W удовлетворяет также условиям WP, А и
НЕ тогда и только тогда, когда она может принимать роулзианскую
форму: W = min[u\...,uN].
Рис. 6.6. Доказательство теоремы 6.2

Глава 6. Общественный выбор и благосостояние
341
Доказательство. Во-первых, заметим, что если W = min[w1,...,w^v],
то условия теоремы выполняются. Остается показать обратное.
Мы докажем это графически только для N = 2, снова попытавшись
охарактеризовать карту общественных кривых безразличия. Для начала
выберем произвольную точку П на рис. 6.6 и заметим, что в этой точке
благосостояние первого участника выше, чем благосостояние второго,
поскольку й находится правее биссектрисы координатного угла. Точка
йТ с другой стороны этой линии получена перестановкой элементов П.
По условию А точка йт в предпочтениях должна иметь тот же ранг, что
и й, т.е. W(u) = W(uT). По условию WP любая точка правее и выше П
должна предпочитаться точке й. Аналогично любая точка правее и выше
Пг должна предпочитаться точке Пг . Тогда, по транзитивности
отношения общественного предпочтения, все точки из окрашенной темным
области справа вверху должны предпочитаться точке И. Далее заметим, что
любая точка левее и ниже й должна быть хуже, чем й, а любая точка
левее и ниже Пг — хуже, чем ur, опять-таки по условию WP. Тогда,
следуя приведенным рассуждениям, й должно предпочитаться всем точкам
из окрашенной светлым области слева внизу. Таким образом, мы
получаем области I, II, III и IV вместе с их границами.
Теперь выберем любую точку и из области III. Она должна
удовлетворять неравенствам й2 <и2 <их <йх (обдумайте это). Согласно
условиям OS/FC относительное положение состояний, соответствующих И и
и, в предпочтениях должно оставаться неизменным, когда к полезности
каждого агента применяется одно и то же положительное монотонное
преобразование. Предположим, что, как и раньше, мы выбрали некоторое
такое преобразование \|/, которое отображает П в себя. Тогда из
только что рассмотренных неравенств мы должны получить и2 <\\f(u2)<
< ^(й1) < й1. Но это говорит о том, что и должно отобразиться в
некоторую точку области III. Поскольку \|/ можно выбрать так, чтобы
отобразить ее в любую точку области III, мы заключаем, что все точки
области III должны занимать в предпочтениях одинаковое место
относительно П. Путем аналогичных рассуждений мы придем к тому, что все
точки области II должны занимать в предпочтениях одинаковое место
относительно йг. Поскольку й и йт должны быть одинаково
предпочтительными, то это означает, что все точки области II и III имеют ранг либо
выше, либо ниже и П и йт. (Как исключить эквивалентность?
Подсказка: благодаря транзитивности и условию WP, как в доказательстве
теоремы Эрроу.)

342
Часть II. Рынки и благосостояние
Теперь обратимся к областям I и IV. Рассматривая сначала
область IV, как и выше, получим, что либо W(u) > W(YV), либо
W(u) < W{W). (Эквивалентность мы снова можем исключить.) Далее
заметим, что любую точку области I можно получить перестановкой
элементов некоторой точки области IV. Тогда по условию А точки в
областях I и IV должны иметь в предпочтениях одинаковый ранг относительно
й. То есть обе области имеют ранг либо выше й, либо ниже й. Легко
видеть, что при допустимых преобразованиях й по отношению к точкам
области IV имеет тот же ранг, что и точки области III по отношению к й.
Следовательно, должно выполняться либо неравенство 0^A11) >
> W{n) > W(TV), либо неравенство W(III) < W(u) < W(TV), которые
означают, что области III и IV должны находиться по разные стороны от П.
Поскольку мы помимо этого знаем, что области II и III должны
находиться по одну сторону от П, так же как и области I и IV, то остается только
две возможности:
либо ^(П) и 0^A11) > W(u) > W(\) и W(IV), (P-l)
либо W{\) и W(W) > W(u) > W(ll) и W{\\\). (Р-2)
До сих пор мы не говорили о границах. Из приводившихся ранее
аргументов ясно, что любая граница между областями, находящимися
согласно предпочтениям с одной и той же стороны от П, должна занимать
это же самое положение. Поскольку функция W непрерывна, то точка П
и границы областей, находящихся с разных сторон от й, должны быть
эквивалентны для общества. Так что если верно (Р-1), то общественная
кривая безразличия должна представлять собой прямой угол (границу),
проходящий через точки йг,а ий. Если же верно (Р-2), то
общественной кривой безразличия должен являться другой прямой угол (граница),
проходящий через точки йг, b и й.В любом случае по условию WP
общественная полезность возрастает на карте по направлению вправо
вверх.
Это показано на рис. 6.7. Если имеет место (Р-1), то общественные
кривые безразличия, проходящие через й, а значит, и все общественные
кривые безразличия (так как они не пересекаются), имеют роулзианский
вид (рис. 6.7(a)), и соответствующая функция общественного
благосостояния может быть задана в виде максимина, W = min[u\ и2]. Если
же мы приходим к (Р-2), то общественные кривые безразличия должны
быть такими, как показано на рис. 6.7F), а соответствующая функция
общественного благосостояния может быть задана как максимакс,
W = тъх[и\ и1].

Глава 6. Общественный выбор и благосостояние
343
45°
(а)
-> w
+> и
(б)
Рис. 6.7. Кривые общественного безразличия для (роулзианских) функций
общественного благосостояния максимин и максимакс
До сих пор возможными были как максимин, так и максимакс.
Согласно максимаксу общественный выбор определяется в первую очередь
благосостоянием самого богатого индивида. Максимин, или роулзиан-
ская функция, наоборот, отдает приоритет интересам самого бедного
индивида. Чтобы исключить довольно неприятный вариант максимакса и
завершить аксиоматизацию максимина, нам остается воспользоваться
последним условием — НЕ. Представим себе прямую, соединяющую точки
й и йг на рис. 6.7. По условию НЕ, все точки на этой прямой, лежащие
ниже биссектрисы координатного угла и отличные от й, должны строго
предпочитаться ей. (Проверьте.) Таким образом, НЕ исключает (Р-2) и
соответственно функцию общественного благосостояния в виде
максимакса, оставляя нам только (Р-1) и максимин. ¦
Еще раз отметим, что приведенное здесь доказательство
действительно только для рассмотренного случая двух участников.
Доказательство для случая N участников является более сложным (см. [Roberts, 1980]).
6.3.2. Утилитаристская форма
Утилитаристская функция является наиболее распространенной и
широко используемой функцией общественного благосостояния в
экономической теории. Согласно ей социальные состояния ранжируются в
соответствии с суммой полезностей индивидов. Чтобы суммирование
вообще было возможным, полезность, очевидно, должна измеряться в
одинаковых единицах. Кроме того, должны иметь смысл утверждения типа
«при переходе от х к у /-й индивид приобретает больше, чем теряету-й».
Вместе эти условия означают, что должны иметь смысл приращения
полезности для отдельного индивида и должна допускаться возможность их

344
Часть II. Рынки и благосостояние
сравнения у разных индивидов. Таким образом, для утилитаристской
функции требуется выполнение условий CS/IC. В следующей теореме мы
дадим аксиоматическое описание утилитаристской функции. Теорема
верна для любого числа индивидов.
Теорема 6.3. Утилитаристские функции общественного
благосостояния.
Предположим, что выполняются условия CS/IC, так что функция
общественного благосостояния W удовлетворяет условию
инвариантности 2 из определения 6.2. W удовлетворяет также условиям WP и А
тогда и только тогда, когда она может принимать утилитаристскую
N
форму: W = ^и' .
N
Доказательство. Снова ясно, что если W = JV , то условия теоремы
/=1
выполнены. Остается показать обратное. Мы приведем графическое
доказательство для случая двух участников, которое может быть
распространено на любое их число.
На рис. 6.8 выберем произвольную точку u = (wI, й), лежащую на
биссектрисе координатного угла. Определим константу у = м1 + й2 и
рассмотрим множество точек ?2 = {(и1, и2)\и1 +и2 =у}. Это все точки,
лежащие на прямой, которая проходит через й и имеет наклон -1.
Выберем любую точку из множества Q, отличную от й, например и . Точка
иТ получается перестановкой элементов и, поэтому ur =(w2,w1) также
должна принадлежать множеству Q. По условию А и и ит должны
занимать одинаковое место в предпочтениях по отношению к й.
.2
>> I/'
Рис. 6.8. Утилитаристская функция общественного благосостояния

Глава 6. Общественный выбор и благосостояние
345
Теперь предположим, что W(u) > W(u). По условиям CS/IC этот
порядок должен быть инвариантным по отношению к преобразованиям вида
а' + Ьи1. Пусть \|/' {и1) = (й' - и1) + и' для / = 1,2. Обратите внимание, что
оба преобразования имеют допустимый вид. Отметим, что 2й' = и1 +и2,
так как й лежит на биссектрисе, а П и и принадлежат Q,, и применим
эти преобразования к и и П, что дает соответственно (\\fl(ul),
\|/2(й2)) = П и (у1 (и1), \|/2(й2)) = йг, т.е. эти преобразования отображают
и вй,айв иг. Тем самым, если W(n) > W(u), как мы предположили,
то по условию инвариантности должно выполняться и соотношение
W(uT)>W(u). Но вместе два эти неравенства означают, что
W(uT)> W(u), что нарушает условие А, и поэтому неравенство
W(й) > W(u) не может быть верным. Если мы, напротив, предположим,
что ^(Н) > ^(П), то аналогичными рассуждениями придем к
противоречию. Таким образом, заключаем, что W(u) = W(u). Тогда по условию А
W(uT) = ^(й) = ^(и). Теперь вспомним, что точка и выбиралась в
множестве Q произвольно, и поэтому те же рассуждения можно применить к
любой точке из этого множества, а следовательно, W(Q) = W(u).
С помощью условий транзитивности и WP можно показать, что
любая точка правее и выше Q должна предпочитаться любой точке из Q, а
каждая точка левее и ниже должна быть хуже. Таким образом, Q
является общественной кривой безразличия, а общественная карта безразличия
представляет собой множество параллельных прямых с наклоном -1,
причем общественная полезность возрастает по направлению вправо вверх.
Это, само собой, означает, что функцию общественного благосостояния
можно задать в виде W -их +и2, что и завершает доказательство. ¦
Если мы проигнорируем требование анонимности, то допустимым
становится целый класс обобщенных утилитаристских способов
ранжирования альтернатив. Он представлен линейными функциями
общественного благосостояния вида W = ^а'и', где а' > 0 для всех / и aJ > 0 для
некоторого j. При обобщенном утилитаристском критерии сумма благо-
состояний остается важным показателем, но благосостоянию отдельных
индивидов можно придавать разный «вес» в глазах общества.
6.3.3. Гибкие формы
Чем больше возможности по измерению и сравнению полезностей,
тем до некоторых пределов шире набор допустимых функций обществен-

346
Часть II. Рынки и благосостояние
ного благосостояния. Если предположить, что полезность измерима на
относительной шкале (ratio scale, RS), то появляется масса
дополнительных возможностей. При измеримости по RS предполагается, что
имеют смысл такие утверждения, как в процентном отношении
увеличение полезности i -го индивида больше при переходе от х к у, чем от х к
z». Если полезности различных индивидов еще и пропорционально
сравнимы (proportionally comparable, PC), то возможны утверждения вида
ui(x)-ui(y)^uJ(x)-uj(y)
и\х) uj{x)
которые также будут иметь смысл. Поскольку неизменность таких
сравнений гарантируется только при одинаковых возрастающих линейных
преобразованиях полезности (т.е. для некоторого Ъ > О преобразования
вида \\f(u') = bul для всех /), то в условиях RS/PC функция
общественного благосостояния должна быть инвариантной по отношению к
одинаковым возрастающим линейным преобразованиям полезности.
Следовательно, здесь допускаются и роулзианская, и утилитаристская функции
общественного благосостояния. Более того, допустимым становится
целый класс функций. Если непрерывная функция общественного
благосостояния удовлетворяет принципам «теории благосостояния», условию WP
и инвариантна по отношению к одинаковым положительным линейным
преобразованиям полезностей, то общественные кривые безразличия
должны быть обобщенно параллельными (вдоль луча) и иметь
отрицательный наклон.
Чтобы убедиться в этом, рассмотрим рис. 6.9. Прежде всего выберем
произвольную точку П. Ясно, что по условию WP общественная кривая
безразличия, проходящая через й, должна иметь отрицательный наклон,
как на изображенном примере. Теперь выберем любую другую точку на
луче ОА, проходящем через П. Эта точка должна иметь вид Ьй для
некоторой константы Ъ . Теперь выберем любую другую точку В, в которой
W(u) = W(u). По условию инвариантности должно также выполняться
равенство W{bu) = W(bu), где и и Ьй лежат на луче ОВ, как показано
на рисунке.
Мы хотим убедиться в том, что наклон касательной к общественной
кривой безразличия в точке И равен наклону касательной в точке Ьй. Во-
первых, заметим, что наклон хорды СС приближается к наклону
касательной в точке U, а наклон хорды DD приближается к наклону
касательной в точке Ьй. Легко рассчитать, что наклон СС и наклон DD
равны. Далее представим себе, что точка и выбирается все ближе и ближе к
й вдоль общественной кривой безразличия, проходящей через П. По ме-

Глава 6. Общественный выбор и благосостояние
341
ре того как и приближается кй,й соответственно приближается к Ьй
вдоль общественной кривой безразличия, проходящей через Ьй, а наклон
хорд СС и DD остается равным. В пределе наклон СС сходится к
наклону касательной в точке П, а наклон DD сходится к наклону
касательной в точке Ьй. Таким образом, наклон общественной кривой
безразличия в точке й должен быть равен наклону кривой в точке Ьй. Поскольку
П и Ъ выбирались произвольно, наклон каждой общественной кривой
безразличия должен быть одинаковым в любой точке вдоль данного луча,
хотя, конечно, наклоны разных лучей могут различаться.
D%bu
cv"
С
О
Рис. 6.9. Полезность RS/PC и обобщенно параллельные общественные
кривые безразличия
Линии уровня функции будут обобщенно параллельными в
вышеописанном смысле тогда и только тогда, когда функция является
гомотетичной. Тем самым условия RS/PC и WP допускают любую неубывающую
гомотетичную функцию общественного благосостояния. Если
добавляется условие А, то функция должна быть симметричной, т.е. ее
общественные кривые безразличия должны быть «зеркальными отражениями» друг
друга относительно биссектрисы координатного угла. Иногда
добавляется и условие выпуклости. Если функция общественного благосостояния
квазивогнута, то множества нестрого предпочитаемых обществом
альтернатив выпуклы, а с точки зрения этики неравенство в распределении
доходов само по себе для общества не важно. При строгой
квазивогнутости возникает сильное смещение в сторону равенства. (Понятно ли,
почему это так?)
Поскольку при некотором положительном монотонном
преобразовании любая гомотетичная функция превращается в линейную однородную,

348
Часть II Рынки и благосостояние
для простоты будем рассуждать только в терминах линейных однородных
функций. К условиям WP, А и выпуклости мы добавим условие строгой
сепарабельности, которое требует, чтобы предельная норма
(общественного) замещения между любыми двумя индивидами не зависела от
благосостояния всех остальных. Тогда функция общественного благосостояния
должна принадлежать к семейству функций с постоянной эластичностью
замещения (CES-функций):
^=1|>')р1 , F-13)
где 0^р<15 а с = 1/A -р) — (постоянная и одинаковая для всех)
эластичность общественного замещения между любыми двумя индивидами.
Это очень гибкая функция общественного благосостояния. Различные
значения р задают различную степень «кривизны» общественных
кривых безразличия и таким образом учитывают степень, в которой в
распределении доходов ценится равенство. Действительно, утилитаристскую
функцию, которая подразумевает полное безразличие общества к
вопросам распределения доходов, можно рассматривать как предельный случай
F-13) при р —»1 (а —» оо). При р —> -°о (а —> 0) F-13) стремится к роул-
зианскому виду, где имеет место абсолютный сдвиг общества в сторону
равенства. Возможные варианты изображены на рис. 6.10.
и2 и2
р —> —о©
(а) (б) (в)
Рис. 6.10. Функции общественного благосостояния с постоянной
эластичностью замещения
6.4. Справедливость
В завершение вернемся к теме, с которой мы начинали эту главу. За
пределами технических вопросов о том, какие предположения следует
ввести для измерения и сравнения полезностей, чтобы разумным образом
применить данную функцию общественного благосостояния, лежит тот
<р< 1
-ь. и

Глава 6. Общественный выбор и благосостояние
349
факт, что выбор между функциями, в сущности, и является выбором
между альтернативными наборами этических ценностей. С этой точки
зрения имеет большое значение проблема субъективности мнений. Она с
полным правом относится к первому этапу любого анализа,
направленного на оценку значения для общества экономической политики или
институтов, — этапу выбора функции общественного благосостояния.
Экономические и философские воззрения, до Адама Смита
представлявшие собой единое целое, вновь объединились для изучения
особенностей этого выбора с позиции морали. В основу были положены
аксиоматические теории справедливости, в своем подходе к общественному
выбору опиравшиеся на показатели общественного благосостояния.
Применительно к ним сложились две мощные исторические традиции.
Первая из них— утилитаристская, связанная с именами Юма, Смита,
Бентама и Милля. Вторая — традиция «общественного договора»,
которую связывают с Локком, Руссо и Кантом. Впоследствии эти концепции
были отшлифованы и изложены в работах Харшаньи [Harsanyi, 1953,
1955, 1975] и Роулза [Rawls, 1971] соответственно.
И Харшаньи, и Роулз принимают положение о том, что
«справедливым» критерием общественного благосостояния должен быть такой,
который выбрал бы рациональный человек, если бы судил «по
справедливости». Чтобы обеспечить «справедливость» его решения, они вводят
понятие «исходного состояния» (скрытого, по выражению Роулза, «покровом
неведения»), в котором индивид обдумывает свой выбор, не зная о том,
какие роль и место в обществе будут ему отведены на самом деле. Таким
образом, оба автора предполагают, что этот выбор делается в условиях
неопределенности относительно того, кем человек в итоге станет в
обществе, создаваемом по его рецепту. Однако взгляды Харшаньи и Роулза на
правило, которое определяет выбор индивида в «исходном состоянии»,
различаются.
Подход Харшаньи отличается прямолинейностью. Прежде всего, он
принимает аксиоматическое описание фон Неймана — Моргенштерна
для рациональности в условиях неопределенности. Тогда предпочтения
индивида можно представить функцией полезности фон Неймана —
Моргенштерна на социальных состояниях w'(x), инвариантной по
отношению к положительным аффинным преобразованиям. Затем согласно
принципу недостаточного обоснования он предполагает, что
рациональный индивид в исходном состоянии оценивает возможность
оказаться на месте любого другого члена общества как равновероятную. Если в
обществе N индивидов, вероятность того, что /-й индивид окажется в
положении j -го, равна 1/N. Индивид / соответственно должен
вообразить себе это положение и то, каковы будут предпочтения uj(x). По-

350
Часть II. Рынки и благосостояние
скольку индивид может оказаться на месте любого из N участников, то
социальное состояние х можно «рационально» оценить в соответствии с
его ожидаемой полезностью:
ХA/ЛГ)и'(*). F-14)
При общественном выборе между состояниями х и у должно
предпочитаться то из них, которое имеет более высокую ожидаемую полезность
F-14). Но это эквивалентно утверждению, что общество предпочитает х
по сравнению с у тогда и только тогда, когда
2>ч*)>2>ч>о,
i=i /=i
т.е. согласно чисто утилитаристскому критерию.
Роулз отвергает утилитаристское правило Харшаньи по нескольким
причинам. В частности, он отрицает назначение каких бы то ни было
вероятностей, одинаковых или нет, потому, что один индивид окажется на
чужом месте, поскольку в исходном состоянии для этого нет
эмпирических оснований. Таким образом, Роулз отвергает саму идею выбора на
основе ожидаемой полезности. Вместо этого он рассматривает проблему
выбора в исходном состоянии как проблему выбора при полном
неведении. Предполагая, что люди не склонны к риску, он доказывает, что при
полном неведении рациональный индивид будет ранжировать
социальные состояния, основываясь на том, как бы он их оценил с позиции
самого бедного члена общества. Тем самым х будет предпочитаться у, когда
тт[и1(х\...У(х)]>тт[и\у\...У(у)], F-15)
т.е. в соответствии с критерием максимина.
В конечном счете аргументация Роулза в пользу максимина по
сравнению с утилитаристским правилом основывается на мнении, что люди
не склонны к риску. Но, как указал Эрроу [Arrow, 1973], это не может
быть окончательным доводом хотя бы потому, что в функциях
полезности фон Неймана — Моргенштерна в построении Харшаньи можно
учесть любую степень несклонности к риску, т.е. в схеме Харшаньи
ничто не мешает индивидам в исходном состоянии быть несклонными к
риску. Кроме того, чтобы прийти к критерию Роулза, необязательно
отказываться от критерия ожидаемой полезности.
Чтобы увидеть это, возьмем произвольную функцию полезности на
социальных состояниях в условиях определенности и'(х). Эти же самые
предпочтения, конечно, можно представить и с помощью положительно-

Глава 6. Общественный выбор и благосостояние
351
го монотонного преобразования v'(x) = -и'(х) а, где а > 0. Теперь
предположим, что v' (х) является функцией полезности фон Неймана — Мор-
генштерна z-го индивида на неопределенных исходах. Легко убедиться,
что степень несклонности к риску, демонстрируемая v(x), возрастает по
параметру а. Предположим, как это делает Харшаньи, что: 1) вероятность
оказаться в положении любого индивида одинакова; 2) социальные
состояния ранжируются каждым индивидом в соответствии с его ожидаемой
полезностью; 3) функция общественного благосостояния имеет вид
W = ftv'(x)S-fiu'(xr. F-16)
1=1 /=1
Поскольку ранжирование состояний, задаваемое функцией F-16), имеет
значение только с точки зрения порядка, оно останется тем же при
положительном монотонном преобразовании W, задаваемом формулой
( N уЧа
W* =-(Wyl/a = ?и'(хГ F-17)
V /=i J
При р = -а<0 это выражение имеет вид F-13). Мы уже замечали, что
при р—>-оо (д—>оо) оно приближается к критерию максимина F-15) в
предельном случае. Таким образом, критерий максимина Роулза не
только не является несовместимым с утилитаризмом Харшаньи, но, напротив,
может рассматриваться как его частный случай, в котором индивиды
бесконечно не склонны к риску.
По размышлении понятно, что все это имеет смысл. Правила
максимина привлекательны в стратегических ситуациях, где интересы
некоторого рационального и полностью информированного оппонента
диаметрально противоположны вашим собственным. В мысленном
эксперименте, необходимом для исходного состояния, немного очевидных
оправданий для принятия такого правила, если только, конечно, вы не
являетесь абсолютным (и иррациональным?) пессимистом.
Повторимся: выбор функции общественного благосостояния— это
выбор приоритетов в распределении, а тем самым и этической системы.
Этот выбор — за вами.
6.5. Упражнения
6.1. Эрроу [Arrow, 1951] показал, что когда множество X содержит
только две альтернативы, метод голосования по правилу простого
большинства действительно приводит к функции общественного
благосостояния, которая удовлетворяет всем условиям предположения 6.1. Убедитесь
в этом, построив пример или приведя доказательство.

352
Часть II. Рынки и благосостояние
6.2. Пусть / — функция общественного благосостояния,
представляющая собой отображение всех векторов непрерывных функций
полезности (u\)9...9uN())9 каждая из которых определена на множестве X, в
общественную функцию полезности V(-), определенную на X. То есть
для каждого xg X выполнено V(x) = [f(ul()9...9uN(•))](jc) . Предположим
также, что V() непрерывна наХ9 и/удовлетворяет условиям U, НА и PL
Определим бинарное отношение ъ на множестве RN следующим
образом: (а1,...,^):^^1,...,^), если для некоторого вектора
непрерывных функций полезности (w1 (•),...,w^()) и некоторой пары альтернатив
х9уе X, удовлетворяющих условиям и1(х) = а' и и'(у) = Ь' для всех i
выполнено [/(и1 (•),...,И())](х)>[Ди\)9...,*/"(•))](у).
а) Покажите, что отношение ъ удовлетворяет свойствам полноты и
транзитивности.
б) Пусть отношение ь является непрерывным. Покажите, что оно
может быть представлено непрерывной вещественнозначной функцией
W (в качестве задания повышенной сложности покажите, что отношение
Ъ непрерывно).
в) Покажите, что для любых непрерывных функций полезности и1 и
для любых пар альтернатив х и у
[Дм1 ()> ...,«"(•))] (х) >[f(u\)9 ...,*/(•))] (у) тогда и только тогда, когда
W{{u\x)9 ...,*/"(*)) > W((u\y\ ...9uN(y)).
6.3. Пусть W: RN —> R, и функция общественного благосостояния /,
определенная как [f(ul(-)9...9uN())](x) = W((ul(x)9...9uN(x))9
удовлетворяет свойствам WP и ПА. Покажите, что функция W должна быть строго
возрастающей.
6.4. Предположим, что в теореме Эрроу мы заменили WP на SP
{сильный принцип Парето, strong Pareto requirement — SP), который
формулируется следующим образом: «Если хР'у для всех i и xPJу по
крайней мере для одного j, то хРу ». Каковы тогда возможные функции
общественного благосостояния, удовлетворяющие условиям U, ПА и SP?
6.5. При графическом доказательстве теоремы Эрроу утверждалось,
что с помощью рис. 6.4 мы можем показать, что либо И^(и) < ^(IV), либо
W(u) > W(TV). Обоснуйте это утверждение.
6.6. Докажите, что если W инвариантна при условиях OS/FC или
CS/IC, то она также инвариантна при условиях RS/PC. Покажите, что
обратное неверно.

Глава 6. Общественный выбор и благосостояние
353
6.7. Пусть R — правило общественного выбора. Рассмотрите
сообщество, состоящее из трех человек {1, 2, 3}, и пусть существует три
альтернативы {x,j>, z},a Pl и Г обозначают строгое предпочтение и отношение
безразличия для индивида /. Предположим также, что область
определения R неограниченна и правило R формулируется следующим образом.
1) Если голосование по правилу простого большинства приводит к
транзитивному отношению общественного предпочтения с единственной
наилучшей альтернативой, то выбирается наилучшая альтернатива.
2) Если голосование по правилу простого большинства приводит к
транзитивному отношению общественного предпочтения без
единственной наилучшей альтернативы, то в случае равного числа голосов выбор
производится по правилу «х лучшее, а у лучше z».
3) Если голосование по правилу простого большинства не приводит к
транзитивному отношению общественного предпочтения, то выбирается
альтернатива х.
а) Рассмотрите следующие индивидуальные предпочтения:
Агент 1: xPlyPlz
Агент 2: yP2zP2x
Агент 3: zP3xP3y.
Какая из альтернатив является наилучшей с точки зрения общества в
соответствии с правилом Л?
б) Удовлетворяет ли R условию WP? Обоснуйте свой ответ.
в) Докажите, что правило R не является диктаторским.
6.8. Пусть агрегированный доход у > О распределен между I
потребителями так, чтобы максимизировать утилитаристскую функцию
общественного благосостояния W = ^и' . Предположим также, что
и1 = ос'(/У, где а' >0 для всех ie I.
а) Покажите, что если 0 < р < 1, то доход должен быть распределен
поровну тогда и только тогда, когда а' = aJ для всех /и;.
б) Предположим, что а' Ф aJ для всех / и j. Что произойдет в
пределе при Р -» 0 и при р —> 1 ? Проинтерпретируйте полученный результат.
6.9. Пусть функции полезности всех потребителей в экономике
обмена с п благами и совокупным первоначальным запасом е » 0 являются
строго возрастающими, строго вогнутыми и дифференцируемыми.
а) Покажите, что если х* » 0 является распределением,
равновесным по Вальрасу, то при некоторых соответствующим образом
подобранных весах а1,...,а7 >0 х* доставляет максимум (обобщенной)
утилитаристской функции общественного благосостояния

354
Часть II Рынки и благосостояние
^ = ?ocV(x')
при ресурсных ограничениях
Z*J-Це) ПРИ J = l->"-
fe/ fe/
б) Используя результат пункта а), приведите альтернативное
доказательство первой теоремы благосостояния 5.7.
6.10. Правило Борда широко применяется для определения
коллективного выбора. Пусть общество состоит из N индивидов, и множество
X содержит конечное число альтернатив. Индивид / приписывает ранг
Борда В1(х) каждой альтернативе х,где В'(х) —это число альтернатив
из множества X, которым индивид i предпочитает альтернативу х.
Таким образом, альтернативы ранжируются в соответствии с совокупным
рангом следующим образом:
хИу^В!(х)>^В'(у).
/=1 /=1
а) Покажите, что правило Борда удовлетворяет условиям U, WP и D
предположения 6.1.
б) Покажите, что правило Борда не удовлетворяет условию ПА.
6.11. Сен [Sen, 1970b] интерпретировал «либеральные ценности» как
определенный общественный выбор, с которым согласен каждый
отдельный индивид. Например, при общественном выборе между тем, чтобы
индивид i читал или не читал определенную книгу, предпочтения
индивида / определяют общественные предпочтения. Таким образом, мы
можем рассматривать либерализм как условие, налагаемое на отношения
предпочтения общества и требующее, чтобы каждый индивид имел
решающий голос при выборе по крайней мере между одной парой
альтернатив. Сен несколько ослабил это требование, введя условие, которое он
назвал минимальным либерализмом.
L*: существует по крайней мере два человека к и j и две пары
различных альтернатив (х, у) и (z, w), таких, что предпочтения к и j играют
решающую роль при выборе между (jc, у) и (z, w) соответственно.
Докажите, что не существует отношения предпочтения общества, которое
удовлетворяет (только) условиям U, WP и L .
6.12. Аткинсон [Atkinson, 1970] предложил индекс равенства
распределения доходов, который основан на принципе «поровну
распределенного эквивалентного дохода», обозначенного уе. Для любой строго
возрастающей, симметричной и квазивогнутой функции общественного
благосостояния на векторах доходов W{y\ ...,yN) доход уе определяется как

Глава 6. Общественный выбор и благосостояние
355
величина дохода, которая, будучи распределенной между всеми
потребителями, будет приводить к тому же уровню общественного
благосостояния, что и данное распределение. Таким образом, при е = A,...,1) и
У = (У,...,>>") имеем
W(y9*) = W(y).
Пусть |1 — среднее распределения доходов у. Тогда индекс равенства
распределения доходов можно определить следующим образом:
/(у)^.
И
а) Покажите, что 0 < /(у) < 1 для любых у1 > О при всех /.
б) Покажите, что индекс /(у) всегда «нормативно значим» в том
смысле, что для любых двух распределений дохода у1 и у2 с одинаковым
средним, /(у1) больше, чем (равен или меньше, чем) /(у2) тогда и
только тогда, когда W(yx) больше, чем (равен или меньше, чем) И^(у2).
6.13. Блэкорби и Доналдсон [Blackorby, Donaldson, 1978] развивали
работу Аткинсона, описанную в предыдущем упражнении. Пусть W{y) —
строго возрастающая, симметричная и квазивогнутая функция
общественного благосостояния, определенная на распределениях дохода.
Авторы определяют «однородное неявное представление функции W»
следующим образом:
F(w, у) = max Я > 0| W(y/X) > w),
где we E — произвольный «контрольный уровень» исходной функции
общественного благосостояния. Затем они определяют свой индекс
равенства распределения доходов как
_, л F(w9 у)
E(w, у) = - J
F(w, це)
где (I, как и прежде, среднее распределения у, а е — единичный вектор.
а) Покажите, что функция F(w, у) однородна первой степени по
вектору дохода. Покажите также, что F(w, у) больше (равна или меньше)
единицы, если W(y) больше (равна или меньше), чем w соответственно.
б) Покажите, что если W(y) гомотетична, то «контрольный уровень»
функции E(w9 у) не имеет значения, т.е. E(w, у) = ?*(у) для всех у.
в) Покажите, что если W(y) гомотетична, то E(w, у) = /(у), где
/(у) — индекс Аткинсона, определенный в предыдущем примере.
Покажите, что из этого следует, что при этих условиях индекс E(w9 у) также
«нормативно значим» и принадлежит интервалу от 0 до 1.

356
Часть II. Рынки и благосостояние
г) Предположим, что функция общественного благосостояния являет-
N
ся утилитаристской и имеет вид W = ^у'. Покажите, что E(w, y) = l,
/=i
что означает «абсолютное равенство» независимо от распределения
дохода. Какой вывод вы можете из этого сделать?
д) Найдите индекс E(w, у) для случая, когда функция общественного
благосостояния характеризуется постоянной эластичностью замещения:
( N У;Р
W(y) =
Х(У)Р ,о*Р<1.
v /=i )
6.14. Пусть x = (x1,...,xAf) — распределение благ между агентами.
Обозначим множество допустимых распределений в этой экономике
через Г. Предположим, что х доставляет максимум утилитаристской функ-
n
ции общественного благосостояния W = ^м'(х') при хеТ.
/=i
а) Пусть \|/' при i = l,...9N — произвольное множество
возрастающих функций одной переменной. Будет ли х* доставлять максимум
функции W = ^Гуди^х')) при хе Г? Обоснуйте свой ответ.
б) Как изменится ваш ответ на вопрос пункта а), если \|/' = \|/ для
всех i?
в) Как изменится ваш ответ на вопрос пункта а), если
\|/' =а' +Ь'и'(х') при произвольных а' и Ь' >0?
г) Как изменится ваш ответ на вопрос пункта а), если
\|/; =al +bul(\l) при произвольных а' и 6>0?
д) Как вы объясните результаты, полученные в пунктах а)—г)?
6.15. Продолжая предыдущий пример, пусть х* доставляет максимум
роулзианской функции общественного благосостояния W = min[ul(xl),...,
uN(xN)]9 xeT.
а) Если \|/; при / = 1, ...,N —произвольное множество возрастающих
функций одной переменной, то будет ли х* доставлять максимум
функции W = minty1^1 (x1)), ...,\\fN(uN(xN))]7 Обоснуйте свой ответ.
б) Как изменится ваш ответ на вопрос пункта а), если \|/' = \|/ для
всех /?
в) Как вы объясните результаты пунктов а) и б)?
г) Как вы объясните сходство и различие ответов на вопросы данного
и предыдущего упражнений?

Часть III
СТРАТЕГИЧЕСКОЕ
ПОВЕДЕНИЕ

Глава 7
ТЕОРИЯ ИГР
Как происходит торг потребителя с продавцом, когда потребитель
покупает новую машину? Если две страны ведут переговоры о
заключении торгового договора, каков будет исход этих переговоров? Каких
стратегий будут придерживаться нефтяные компании, участвующие в
аукционе первой цены, на котором выставляются нефтяные
месторождения в прибрежном шлейфе?
Во всех описанных ситуациях действия, предпринятые одним агентом,
влекут за собой определенные последствия для других. Поэтому агентам
имеет смысл действовать стратегически. Теория игр исследует, как ведут
себя агенты в стратегических ситуациях, или в играх, когда каждый агент
для принятия лучшего для него решения должен знать о решениях других
агентов. Такая взаимозависимость и является характерной особенностью
теории игр, а в этой главе соответственно анализируется, каким образом
рациональный агент должен вести себя в подобных ситуациях.
Глава начинается с детального изучения игр в стратегической форме,
затем рассматриваются игры в развернутой форме. Игры в
стратегической форме — это игры, в которых агенты делают свой выбор однократно
и одновременно, в то время как в играх в развернутой форме игроки
принимают решения последовательно.
Мы рассмотрим различные методы определения исходов игры.
Вы увидите, что каждый из рассмотренных методов приводит к
некоторой мшащий ррцйРиця щры_ (solution concept). Концепции решения,
которые мы изучаем, включают концепции, основанные на принципе
доминирования; равновесие по Нэшу; равновесие Байеса — Нэша; обратную
индукцию; совершенное в подыграх равновесие и секвенциальное
равновесие. Каждая из этих концепций решения является некоторым развитием
предыдущих. Знание того, какую из концепций использовать в каждом
конкретном случае, — важная характеристика хорошего экономиста-
прикладника.
7.1. Стратегическое принятие решения
Существенным отличием стратегического решения от
нестратегического является то, что последнее можно принимать «в изоляции», не
учитывая те решения, которые могут принять другие. Например, теория
поведения потребителя, рассмотренная в главе 1, описывает нестратегиче-

360
Часть III. Стратегическое поведение
ское поведение. При заданных ценах и доходе потребитель действует
вполне независимо, не принимая во внимание поведение других. Вместе с
тем в рассмотренных в главе 4 моделях дуополии Курно и Бертрана
описано стратегическое поведение двух фирм. Каждая фирма вполне
осознает, что ее оптимальный выбор зависит от выбора другой фирмы.
В качестве еще одного примера, демонстрирующего значимость
стратегического принятия решения, рассмотрим классическую дуэль между
отбивающим и подающим в бейсболе. Для простоты предположим, что у
подающего есть только два возможных действия: прямой бросок и
крученый. Предположим также, всем известно, что прямой бросок у
подающего — лучший в лиге, а крученый — весьма посредственный. Может
показаться, что лучшее, что может сделать подающий, — это всегда
использовать прямой бросок. Однако такое нестратегическое решение подающего
не учитывает поведения отбивающего. Поскольку, если отбивающий
ожидает, что подающий воспользуется прямым броском, он будет всегда
готов к этому и отобьет. Следовательно, с точки зрения подающего, было
бы мудрее при выборе броска учесть решение, принимаемое
отбивающим.
Для того чтобы продвинуться в анализе ситуации, припишем
некоторые значения различным исходам. Для простоты предположим, что
выигрыш одного из участников равносилен проигрышу другого. Это можно
трактовать следующим образом. Идет 9 ининг, т.е. последний, команда
подающего выигрывает, у команды подающего все игроки на базах, два
аута. Предположим также, что отбивающий может либо отбить (и
выиграть игру), либо промахнуться (и проиграть игру). Следовательно,
остается единственный бросок, который решит исход игры. Наконец,
предположим, что выигрыш каждого игрока в случае победы составит 1 и -1 —
в случае поражения. Мы можем представить эту ситуацию с помощью
матрицы, изображенной на рис. 7.1.
"\^ в
р ^\
F
С
F
-1,1
1,-1
С
1,-1
-1,1
Рис. 7.1. Игра «Дуэль отбивающего и подающего»
На этом рисунке подающий (Р— pitcher) выбирает строку, F
(fastball— прямой бросок) или С (curve— крученый бросок), и
отбивающий (В — batter) выбирает столбец. Отбивающий отражает удар, если
он готов к броску, выбранному подающим, и промахивается в противном
случае. Цифры в клетках таблицы означают выигрыши, которые получат

Глава 7. Теория игр
361
игроки в зависимости от того, что каждый из них предпринял. Первое
число означает выигрыш подающего, второе — выигрыш отбивающего.
Таким образом, запись (l, -l) на пересечении первой строки и второго
столбца означает, что, если подающий воспользуется прямым броском и
отбивающий не будет к этому готов, то выигрыш подающего равен 1, а
отбивающего -1. Записи в других клетках интерпретируются таким же
образом.
Хотя мы до сих пор рассуждали о том, как должен вести себя
подающий, очевидно, что позиция отбивающего симметрична. Как подающий
должен решить, каким броском воспользоваться, и точно так же
отбивающий должен определить, к какому броску готовиться. Что можно
сказать об их поведении при такой постановке проблемы? Даже если вам
кажется, что вы уже ответили для себя на этот вопрос, мы еще не
проанализировали игру полностью.
Тем не менее мы можем сразу же сделать весьма важный вывод,
основываясь только на идее, что каждый игрок должен максимизировать
собственный выигрыш, рассуждая при этом стратегически. В этой игре
участники должны быть «непредсказуемы». Почему? Потому что, если
поведение подающего прогнозируемо в том, что он, скажем, все время
выбирает прямой бросок, то отбивающий, выбирая F, гарантировал бы
себе победу. Но это означало бы, что поведение отбивающего также
предсказуемо: он всегда готов к прямому броску. Следовательно,
поскольку подающий ведет себя стратегически, ему было бы выгодно
выбрать бросок С, к которому отбивающий не готов, и тем самым выиграть.
Но это противоречит первоначальному нашему предположению о том,
что подающий всегда использует прямой бросок. Таким образом, мы
пришли к выводу, что неверно было бы предполагать, что подающий
всегда использует F. Аналогично неверно полагать, что он всегда использует
С. Таким образом, в поведении подающего должна присутствовать
некоторая непредсказуемость. По тем же причинам в поведении отбивающего
также должна присутствовать неопределенность относительно того, к
какому броску он подготовится.
Таким образом, когда рациональные индивиды принимают решение
стратегически, т.е. когда каждый учитывает решение, принимаемое
другими, они иногда ведут себя непредсказуемо. Любой хороший карточный
игрок отлично понимает, что это неотъемлемый элемент успешного
блефа. Тем не менее обратите внимание, что в нестратегической постановке
задачи, когда вы предоставлены самому себе и нет необходимости
обводить кого-либо вокруг пальца, этот аспект не имеет никакого значения.
Это только один пример того, что исходы, если решения принимаются
стратегически мыслящими индивидами, могут существенно отличаться

362
Часть III. Стратегическое поведение
от исходов, если решения принимаются нестратегически. Теперь, когда
мы оценили преимущества стратегического принятия решений, можно
переходить к изложению теоретических концепций.
7.2. Игры в стратегической форме
Дуэль отбивающего и подающего, как и дуополии Курно и
Бертрана, — это всего лишь три примера стратегических ситуаций, которые
желают изучать экономисты. В качестве других примеров можно привести
переговоры между профсоюзом и фирмой, торговые войны между двумя
странами, конкуренцию компаний в области исследований и разработок и
т.д. Нам нужна единая схема, позволяющая включить в анализ ключевые
особенности этих и других ситуаций. Таким образом, мы должны найти
элементы, общие для всех этих ситуаций. Что же их объединяет? А вот
что. В каждой ситуации имеется несколько участников (будем называть
их «игроки»); у каждого из них в арсенале есть множество возможных
действий, которые могут быть предприняты (будем называть эти
действия «стратегии»), и каждый из них получает выигрыш, который зависит и
от выбранной им стратегии, и от стратегий других игроков. Традиционно
такие ситуации называются играми, даже если анализируемый вопрос
весьма серьезен. Учитывая все это, приведем следующее определение.
Определение 7.1. Игра в стратегической форме.
Игра в стратегической форме — это набор G = (St, нД=1, где St —
мноэюество стратегий, доступных игроку i, a ui '.x"=lSj —>R описывает
выигрыш игрока i как функцию стратегий, выбранных всеми игроками.
Игра в стратегической форме называется конечной, если мноэюество
стратегий каждого игрока содержит конечное множество элементов.
Заметим, что это определение достаточно общее, и мы можем
воспользоваться им, чтобы описать нашу дуэль отбивающего и подающего
как игру в стратегической форме. Пусть подающий будет игроком 1.
Тогда игра в стратегической форме, описывающая эту ситуацию, задается
следующим образом:
Sx=S2={Ff С},
ux{F, F) = Ul{C, C) = -l,
ux(F, С) = щ{С, F) = 1,h
u2(sx, s2) = ~u\{s\> si) для всех E1? s2)e SxxS2.

Глава 7. Теория игр
363
Заметим, что игра в стратегической форме с двумя участниками и с
конечными множествами стратегий всегда может быть представлена в
матричной форме, где строки соответствуют стратегиям игрока 1, столбцы —
стратегиям игрока 2, а в клетках таблицы записаны выигрыши игроков.
7.2.1. Доминирующие стратегии
Всякий раз, когда мы пытаемся предсказать исход игры,
предпочтительнее делать это, не предполагая, что игрокам слишком много известно
о поведении их оппонентов. Это не всегда возможно. Но в тех случаях,
когда возможно, полученное решение игры особенно убедительно. В этом
подразделе мы рассмотрим различные виды стратегического
доминирования и способы их использования, чтобы решить игру (когда это
возможно) или сузить множество возможных решений.
Начнем с анализа игры в стратегической форме с двумя участниками,
изображенной на рис. 7.2. В этой игре максимизирующий выигрыш
выбор игрока 2 зависит от выбора, сделанного игроком 1. Если игрок 1
выберет U (up), то лучший ответ игрока 2 — выбрать L (left), если же игрок 1
выберет D (down), то лучшим ответом игрока 2 будет R (right). Поэтому
игрок 2 должен принимать решение стратегически: он должен понять,
какое решение примет игрок 1, прежде чем что-то предпримет сам.
\. 2
1 ^\
и
D
L
3,0
2,4
R
0,^
-1,8
Рис. 7.2. Строго доминирующие стратегии
Как же будет действовать игрок 1? Посмотрите на его выигрыши, и
вы увидите, что наилучший выбор игрока 1 в действительности не
зависит от выбора игрока 2. Каким бы ни был выбор игрока 2, U—
наилучшая стратегия игрока 1. Следовательно, игрок 1 выберет U. Поняв это,
игрок 2 тогда выберет L. Таким образом, единственный разумный
прогноз в игре — это пара стратегий (U,L), которой соответствует вектор
выигрышей C,0).
Особенность этой игры, позволяющая ее «решить», т.е. предсказать
исход игры, когда игроки рациональны, состоит в том, что у игрока 1 есть
стратегия, использование которой для него предпочтительнее независимо
от стратегии, выбранной другим игроком. Как только решение игрока 1
понятно, становится очевидным и решение игрока 2. Таким образом, если
у одного из игроков в игре с двумя участниками есть такая
доминирующая стратегия, то предсказать исход довольно просто.

364
Часть III. Стратегическое поведение
Чтобы представить этот вывод чуть более формально, введем
следующие обозначения. Пусть S = SX x...xSN — множество всех чистых
стратегий. Символ -/ обозначает «всех игроков кроме игрока /». Таким
образом, например, $_. обозначает элемент множества ?_., что, в свою
очередь, обозначает множество Sx x.^xS^ xSi+l x...xSN. Теперь
сформулируем следующее определение.
Определение 7.2. Строго доминирующие стратегии.
Стратегия 5. игрока i называется строго доминирующей, если
неравенство ut{sn s_i)>ui(si9 s_;) имеет место для всех (si9s_t)eSf при
s,*3r
Случаи, когда в игре существует строго доминирующая стратегия,
т.е. стратегия, которая лучше всех других стратегий игрока, весьма редки.
Тем не менее, даже когда в игре ни у одного игрока нет строго
доминирующих стратегий, все еще остается возможность упростить анализ игры,
исключив все те стратегии игрока, которые для него очевидно
непривлекательны.
Рассмотрим пример, изображенный на рис. 7.3. Ни у одного из
игроков нет строго доминирующей стратегии. Чтобы убедиться в этом,
заметим, что, когда игрок 2 выбирает L, то лучший ответ игрока 1 — это U, а
когда игрок 2 играет М9 то лучший ответ игрока 1 — Д если игрок 1
выбирает U, то лучший ответ игрока 2 — Z,, если же игрок 1 выбирает Д то
лучший ответ игрока 2 — играть R. Тем не менее у каждого из игроков
есть стратегии, которые особо непривлекательны. Стратегия С игрока 1
всегда менее предпочтительна, чем Д в том смысле, что выигрыши
игрока 1 всегда будут выше при выборе Д чем при выборе С, независимо от
того, какую стратегию выберет игрок 2. Таким образом, С мы можем не
рассматривать как кандидата на выбор игроком 1. Игрок 1 никогда ее не
выберет. Аналогично стратегия М игрока 2 менее привлекательна, чем
стратегия R (убедитесь, что это так), и ее мы также можем исключить из
анализа. Теперь, после исключения стратегий С и М, мы получим
редуцированную игру, уже знакомую нам по рис. 7.2. Таким образом, как и
раньше, единственный разумный исход — это C,0). Мы снова
воспользовались идеей доминирования, чтобы решить игру. Но в этот раз мы
обратили внимание на доминирование одной стратегии над другой, а не над
всеми другими.

Глава 7. Теория игр
365
^\ 2
1 ^\
и
С
D
L
3,0
1,-1
2,4
М
0,-5
3,3
4,1
R
0,-4
-2,4
-1,8
Рис. 7.3. Строго доминируемые стратегии
Определение 7.3. Строго доминируемые стратегии.
Стратегия st игрока i строго доминирует стратегию Jjf
если ui(sn s_i)>ui(Jn s4) для всех s^eS^. В этом случае мы такэюе
говорим, что стратегия J. строго доминируема на множестве
стратегий S.
Как мы уже отметили, существование строго доминирующих или
строго доминируемых стратегий может упростить анализ игры вплоть до
ее полного решения. Весьма полезно еще раз рассмотреть нашу методику
решения игр, изображенных на рис. 7.2 и 7.3.
В игре на рис. 7.2 мы заметили, что Uявляется строго доминирующей
стратегией / игрока 1. Таким образом, мы смогли исключить D из
дальнейшего анализа. После этого мы смогли сделать вывод, что игрок 2
будет использовать L, или, что то же самое, мы смогли исключить R.
Заметим, что хотя R не является строго доминируемой в исходной игре, она
строго доминируется (стратегией L) в редуцированной игре, в которой
исключена стратегия D игрока 1. Это привело нас к единственному
решению {и,Ь). В игре, представленной на рис. 7.3, мы сперва исключили
стратегию С игрока 1 и стратегию М игрока 2 (каждая из них строго до-
минировалась); затем (следуя анализу игры, представленной на рис. 7.2)
исключили стратегию D игрока 1; затем исключили стратегию R игрока 2.
И снова получили единственную пару стратегий ([/, L). Как и в
предыдущем случае, стратегия D не была строго доминируемой в исходной
игре, однако она стала строго доминируемой в редуцированной игре,
полученной исключением стратегии М Аналогично R стала строго
доминируемой только после того, как стратегии С и D были исключены. Теперь
мы формализуем эту процедуру итеративного исключения строго
доминируемых стратегий.
Пусть S? = St для каждого игрока /', и для любого п > 1 через S"
обозначим множество стратегий игрока /, оставшихся после п шагов
процедуры исключения. Таким образом, стратегия si e S", если si e S"~l не
является строго доминируемой в S"~l.

366
Часть III. Стратегическое поведение
Определение 7.4. Итеративно строго недоминируемые
стратегии.
Стратегия si игрока i итеративно строго недоминируема на
множестве стратегий S (т.е. остается в результате последовательного
исключения строго доминируемых стратегий), если st e S" для всех п>\.
До сих пор мы рассматривали только понятие строгого
доминирования. Существует также понятие слабого доминирования. Ниже даются
соответствующие аналоги определений 7.3 и 7.4.
Определение 7.5. Слабо доминируемые стратегии.
Стратегия ${ игрока i слабо доминирует стратегию Jif если
Uj(si9 ^_(.)>wf.EJ, s4) для всех s^eS^ и по крайней мере для одного
профиля s_j неравенство строгое. В этом случае мы также говорим,
что стратегия li слабо доминируема на множестве стратегий S.
Разница между слабым и строгим доминированием поясняется на
примере игры, представленной на рис. 7.4. В этой игре ни у одного игрока
нет строго доминируемой стратегии. Тем не менее и D и R слабо домини-
руются стратегиями U и L соответственно. Таким образом, исключение
строго доминируемых стратегий здесь ничего не дает, в то время как
исключение слабо доминируемых стратегий приводит к единственной паре
стратегий {U,L). Как и в случае строгого доминирования, мы также
можем итеративно исключить слабо доминируемые стратегии.
\. 2
1 \^
и
D
L
1,1
0,0
R
0,0
0,0
Рис. 7.4. Слабо доминируемые стратегии
Учитывая сказанное, обозначим через W" стратегии игрока /,
оставшиеся после п периодов исключения слабо доминируемых стратегий, и
пусть Wj° = St. То есть sj e W", если si e W"~l не является слабо
доминируемой в wn~x = wrx х...х^;4.
Определение 7.6. Итеративно слабо недоминируемые стратегии.
Стратегия si игрока i итеративно слабо недоминируема на
множестве стратегий S (т.е. остается в результате итеративного
исключения слабо доминируемых стратегий), если st e W" для всех п>\.

Глава 7. Теория игр
367
Вы должны понимать, что множество стратегий, остающихся после
применения процедуры итеративного исключения слабо доминирумых
стратегий, содержится в множестве стратегий, остающихся после
применения процедуры итеративного исключения строго доминируемых
стратегий. Вас попросят показать это в одном из упражнений.
Чтобы получить представление о подчас поражающих воображение
возможностях итеративного доминирования, рассмотрим игру «Угадай
среднее», в которой участвуют N>2 игроков, пытающихся превзойти
друг друга в отгадывании. Игроки должны одновременно выбрать любое
целое число между 1 и 100. Тот, кто назовет число, наиболее близкое к
одной трети среднего от выбранных, выиграет 100 долл., а другие не
получат ничего. Если несколько игроков назвали числа, одинаково близкие
к среднему, то 100 долл. делятся поровну между ними. (Перед тем как
продолжить чтение, подумайте, как бы вы сыграли в этой игре, если бы в
ней участвовало, скажем, 20 игроков.)
Давайте воспользуемся процедурой исключения слабо
доминируемых стратегий. Заметим, что выбор числа 33 слабо доминирует выбор
всех чисел больше 33, поскольку одна треть от среднего всех названных
чисел должна быть меньше или равна 33-. Следовательно, независимо от
3
того, какие числа назвали другие игроки, число 33 — не худший выбор,
чем любое большее число, и если бы вдруг все другие игроки выбрали
число 34, то выбор числа 33 был бы лучше, чем выбор любого большего
числа. Таким образом, для всех игроков мы можем исключить из анализа
все числа больше 33. Следовательно, W) с{1, 2, ..., 33} \ Но
рассуждения, подобные приведенным, показывают, что все числа больше 11 также
доминируемы в W[. Следовательно, й^2с{1, 2, ..., И}. Продолжая в
том же духе, приходим к выводу, что для каждого участника игры
единственная стратегия, остающаяся после применения последовательного
исключения слабо доминируемых стратегий, — это выбор числа 1.
Если вы еще не забыли о дуэли между отбивающим и подающим, то
можете заметить, что ни одна из стратегий там не является слабо
доминируемой. Следовательно, ни одна из описанных нами процедур в этой игре
не может исключить ни одну стратегию. И хотя процедуры исключения,
несомненно, бывают весьма полезны в ряде случаев, мы ничуть не
приблизились к решению игры «Дуэль отбивающего и подающего». Пришло
время изменить ситуацию.
В зависимости от количества участников игры другие числа могут также оказаться
слабо доминируемыми. Это исследуется в упражнениях.

368
Часть III. Стратегическое поведение
7.2.2. Равновесие по Нэшу
В соответствии с теорией спроса и предложения концепция
рыночного равновесия, т.е. состояния, в котором спрос равен предложению,
является ключевой. Теоретическая привлекательность этой концепции
состоит в том, что ни у кого из участников нет ни стимулов, ни необходимости
менять свое поведение. Эти закономерности в поведении дают
возможность строить прогнозы.
Намереваясь прогнозировать исход игры, опишем для начала
потенциальные закономерности в поведении, которые могут возникать в
стратегической ситуации. При этом мы включим в анализ идею о том, что
игроки «рациональны», в том смысле, что они действуют в своих
собственных интересах и вполне осознают закономерности в поведении других
игроков. В стратегической ситуации, как и в случае с теорией спроса и
предложения, закономерности в поведении игроков, которые могут быть
«рационально» обоснованы, будем называть равновесиями. В главе 4 мы
уже сталкивались с понятием равновесия по Нэшу в стратегической
ситуации, а именно в дуополии Курно. Эту концепцию можно обобщить
для любых игр в стратегической форме. В самом деле равновесие по
Нэшу, предложенное в работе [Nash, 1951], представляет собой
единственную важнейшую концепцию равновесия во всей теории игр.
Неформально профиль стратегий se S является равновесием по
Нэшу, когда ни один из участников игры, зная поведение других игроков, не
заинтересован изменять свое собственное поведение. Таким образом,
равновесие по Нэшу описывает поведение, которое может быть
рационально обосновано. Формально эта концепция определяется следующим
образом.
Определение 7.7. Равновесие по Нэшу в чистых стратегиях.
Для игры в стратегической форме G = [Sn w;)/=1, профиль
стратегий se S составляет равновесие по Нэшу в чистых стратегиях в игре G,
если для каждого игрока i соотношение ui(s)>ui[si9 ?_,) выполняется
для всех sf 6 Sf.
Обратите внимание, что в играх, представленных на рис. 7.2—7.4,
пара стратегий (С/, L) является равновесием по Нэшу в чистых
стратегиях. Чтобы убедиться в этом, например, для игры, показанной на рис. 7.2,
рассмотрим сначала, сможет ли игрок 1 увеличить свой выигрыш,
изменив свой выбор, при условии, что стратегия игрока 2 не изменилась.
Выбрав Д игрок 1 получит 2 вместо 3. Следовательно, игрок 1 не может
увеличить свой выигрыш. Аналогично игрок 2 не может увеличить свой
выигрыш, изменив свою стратегию, если стратегия игрока 1 остается не-

Глава 7. Теория игр
369
изменной. Следовательно, (t/, L) действительно является равновесием по
Нэшу в игре на рис. 7.2. Остальные примеры можно (и нужно) проверить
таким же образом.
В игре может быть более одного равновесия по Нэшу. Например, в
игре, изображенной на рис. 7.4, (Д R) также равновесие по Нэшу в
чистых стратегиях, поскольку ни один игрок не сможет увеличить свой
выигрыш, выбрав другую стратегию, если выбор другого игрока остается
неизменным. В некоторых играх нет равновесий по Нэшу в чистых
стратегиях. Как вы могли уже догадаться, речь идет об игре «Дуэль
отбивающего и подающего», представленной на рис. 7.1 и воспроизведенной на
рис. 7.5.
\^ в
р ^\
F
С
F
-1,1
1,-1
С
1,-1
-1,1
Рис. 7.5. Игра «Дуэль отбивающего и подающего»
Давайте убедимся, что в этой игре действительно нет равновесия по
Нэшу в чистых стратегиях. Возможны только четыре варианта: (F,F),
(F,C), (C,F) и {С,С). Мы проверим один вариант, и оставляем вам
проверить оставшиеся самостоятельно. Может ли (F, F) быть
равновесием по Нэшу в чистых стратегиях? Только в том случае, если ни один из
игроков не сможет увеличить свой выигрыш, в одностороннем порядке
отклонившись от своей стратегии в профиле стратегий {F,F). Начнем с
отбивающего. Когда разыгрывается профиль стратегий (F,F),
отбивающий получает 1. Если он отклонится, переключившись на С, то
разыгрываемый профиль стратегий (F9 С) (не забудьте, что мы должны оставить
неизменной стратегию подающего), а отбивающий получит -1.
Следовательно, отбивающий не может увеличить свой выигрыш,
переключившись на другую стратегию. А что можно сказать о подающем? При игре в
соответствии с профилем стратегий {F,F) подающий получает -1.
Выбрав С, тогда профиль стратегий будет (C,F), подающий получит 1, т.е.
увеличит выигрыш. Таким образом, подающий может увеличить
выигрыш, изменив в одностороннем порядке свою стратегию, и,
следовательно, профиль стратегий (F, F) не является равновесием по Нэшу в чистых
стратегиях. Аналогичные рассуждения можно провести и для оставшихся
трех вариантов.

370
Часть III. Стратегическое поведение
Конечно, в свете нашего эвристического анализа дуэли между
отбивающим и подающим в самом начале главы этого следовало ожидать. Мы
же пришли к заключению, что и отбивающий, и подающий должны вести
себя непредсказуемо. А определение равновесия по Нэшу в чистых
стратегиях воплощает идею, что каждый игрок точно знает, какую стратегию
будут использовать другие игроки. Иными словами, в равновесии по
Нэшу в чистых стратегиях выбор каждого полностью предсказуем. Нам
снова не удалось разобраться с дуэлью отбивающего и подающего. Но мы
уже близки к решению этой проблемы.
Смешанные стратегии и равновесие по Нэшу
Самый верный способ сделать свой выбор непредсказуемым для
других — это сделать его непредсказуемым для себя. А простейший способ
этого добиться —рандомизировать свой выбор. Например, в дуэли
между отбивающим и подающим и отбивающий, и подающий, чтобы сделать
свой выбор непредсказуемым для другого игрока, могут принимать
решение, подбрасывая монету.
Остановимся на минутку, чтобы обсудить, каким образом это
поможет разобраться с дуэлью между отбивающим и подающим.
Предположим, что и отбивающий, и подающий имеют по «правильной» монете.
Перед тем как сделать свой выбор, каждый (независимо от другого)
подбрасывает свою монету. Если выпадает «орел», ее хозяин выбирает F9 a
если «решка», то С. Более того, предположим, что каждый из них знает,
что контрагент принимает решение таким же образом. Можно ли этот
набор стратегий определить как равновесие в том смысле, который мы
описывали выше? Да, можно. При таком механизме выбора никто из игроков
не может увеличить свой выигрыш, в одностороннем порядке изменив
свое правило принятия решения. Покажем это.
Начнем с подающего. Он знает, что отбивающий подбрасывает
«правильную» монету, чтобы решить, приготовиться ли ему к прямому броску
(F) или к крученому (Q. Таким образом, он знает, что отбивающий
выберет или F, или С с вероятностью 1/2. Следовательно, любой выбор
подающего порождает лотерею на множестве возможных исходов в. игре.
В связи с этим давайте предположим, что выигрыши игроков
рассчитываются как полезности фон Неймана — Моргенштерна и что выбор
каждого игрока максимизирует его ожидаемую полезность.
Какую же ожидаемую полезность получит подающий, выбрав ту или
иную стратегию? Если бы он просто выбрал F (не используя монету), то
его ожидаемый выигрыш составил бы — (-l)+ —(l) = 0, в то время как,

Глава 7. Теория игр
371
если бы он выбрал С, то получил бы — (l)+—(~l) = 0. Следовательно, при
условии, что отбивающий выбирает F и С с вероятностью 1/2,
подающему безразлично, какую из стратегий F или С использовать. Таким
образом, поскольку и выбор F, и выбор С дают подающему равный нулю
выигрыш, тот же выигрыш он получит, выбирая и F, и С с вероятностью
1/2. Аналогично, если подающий рандомизирует между F и С с
вероятностью 1/2, то отбивающий может также максимизировать свою
ожидаемую полезность, рандомизируя между F и С с равными
вероятностями. Иначе говоря, такие рандомизированные стратегии игроков
составляют равновесие: каждый из участников знает способ рандомизации
выбора другого игрока, и ни один из них не может увеличить свой
ожидаемый выигрыш, выбрав другой способ рандомизации.
Перед тем как использовать эту идею для всех игр в стратегической
форме, введем определение смешанной стратегии.
Определение 7.8. Смешанные стратегии.
В конечной игре в стратегической форме G = (Sn и.) смешанная
стратегия игрока i — это распределение вероятностей на множестве
Si. Множество смешанных стратегий игрока i будем обозначать через
Мп а множество S, будем называть теперь множеством чистых
стратегий игрока i.
Таким образом, смешанная стратегия для игрока — это способ
рандомизации своего выбора. Каждую смешанную стратегию можно
рассматривать как рулетку с названиями чистых стратегий на секторах
колеса. У разных рулеток могут быть разные по величине секторы, на которых
написаны названия чистых стратегий. Это приводит к тому, что чистые
стратегии выбираются с разной вероятностью. Тогда множество
смешанных стратегий — это множество таких рулеток.
Каждый игрок / теперь может выбирать из множества смешанных
стратегий Mf, а не только из множества чистых стратегий S.. Заметим,
что это предоставляет ему гораздо более широкий выбор, чем раньше, так
как любая чистая стратегия st e Sf содержится в Mt, поскольку ее можно
трактовать как (вырожденную) смешанную стратегию, в соответствии с
которой чистая стратегия Si выбирается с вероятностью 1.
Пусть М = x?j M. обозначает множество профилей смешанных
стратегий. В дальнейшем мы будем опускать слово «смешанный» и просто
называть те М профилем стратегий, а т{ е А/, — стратегией игрока /.

372
Часть III. Стратегическое поведение
Если ui — полезность фон Неймана — Моргенштерна на
множестве S и игроки используют профиль стратегий те М, то ожидаемая
полезность игрока /
seS
где m^Sj) обозначает вероятность, с которой выбирается чистая
стратегия st игроком /и,. Это следует из того факта, что игроки выбирают свои
стратегии независимо друг от друга. Следовательно, вероятность того,
что игроками будет использоваться профиль чистых стратегий
s = (sl9 ...9sN)e S, равна произведению вероятностей выбора каждой
компоненты, а именно юДя,)--^^). Сформулируем теперь основную
концепцию равновесия для игр в стратегической форме.
Определение 7.9. Равновесие по Нэшу.
В конечной игре в стратегической форме G = [Sn w.) профиль
стратегий те Мявляется равновесием по Нэшу, если для каждого
игрока i соотношение и;(т)>и;(тп тч) выполняется для всех mfe Mr
Таким образом, в равновесии по Нэшу каждый игрок может рандоми-
зировать свой выбор, но каждый знает, как рандомизируют остальные.
Более того, ни один из игроков не может увеличить свой ожидаемый
выигрыш, отклонившись в одностороннем порядке от своего способа
рандомизации.
Может показаться, что, для того чтобы понять, является ли профиль
стратегий (тй., т_{) равновесием по Нэшу, нужно для каждого игрока /
сопоставить выигрыш, который дает стратегия тх, с выигрышами любой
другой стратегии из бесконечного множества стратегий Mi. Следующее
утверждение, возможное вследствие линейности и{ по тп упрощает
задачу.
Теорема 7.1. Упрощенный поиск равновесия по Нэшу.
Следующие утверждения эквивалентны.
а) те М является равновесием по Нэшу.
б) Для любого игрока i ui(m) = ui^si, тч) для любой j.eS,.,
выбираемой игроком в т1 с положительной вероятностью, и

Глава 7. Теория игр
373
и. (т) > их (si9 т_х) для любой st. e Si, выбираемой в тх с нулевой
вероятностью.
в) Для каждого игрока i их(т)> ui (si, т_х) для любой sx. e ?..
По теореме 7.1 утверждения б) и в) дают альтернативные методы
проверки равновесия по Нэшу. Утверждение б) наиболее полезно для
поиска равновесия по Нэшу. В нем говорится, что выигрыш игрока должен
быть одинаков для любой чистой стратегии, выбираемой с
положительной вероятностью, и что каждая из них не должна давать выигрыш
меньший, чем любая чистая стратегия, выбираемая с вероятностью, равной
нулю. В утверждении в) говорится, что, для того чтобы профиль
смешанных стратегий являлся равновесием по Нэшу, достаточно, чтобы ни для
одного из игроков не существовало чистой стратегии, дающей ему
больший ожидаемый выигрыш, чем его смешанная стратегия из этого
профиля.
Доказательство. Сперва покажем, что из утверждения а) следует
утверждение б). Предположим, что т — равновесие по Нэшу. Следовательно,
их (т) > и, (mt, т_х) для всех mi e Мх.. В частности, для любой si e St мы
можем выбрать тх такую, что sx. выбирается с вероятностью, равной единице,
так что и. (т) > их [si9 т_х) выполняется для всех sx. e Si. Осталось показать,
что и. (т) = их (s;, т_х) для всех чистых стратегий st. e Sx., которые
выбираются с положительной вероятностью при использовании тх. Теперь, если
любое из этих чисел отличается от м;(т), то по крайней мере одно будет
строго больше, поскольку их{т) — их выпуклая комбинация. Но это
противоречит неравенству, которое только что было доказано.
Поскольку очевидно, что из утверждения б) следует утверждение в),
осталось только доказать, что из в) следует а). Итак, предположим, что
для каждого игрока j u\m)>их($., т_х) для всех ste Sx.. Рассмотрим
игрока / и стратегию тхе Мг Поскольку их{т0 т_х) — выпуклая
комбинация чисел {ux(sn w_;)} , то должно выполняться соотношение
м;(/й)>м.(/и., т_х). Поскольку и игрок, и стратегия были выбраны
произвольно, т — равновесие по Нэшу в игре G . ¦

374
Часть III. Стратегическое поведение
Пример 7.1. Чтобы показать, как можно использовать это
утверждение, рассмотрим следующий пример. Вам и вашему коллеге дано
задание — в течение часа подготовить отчет. Вы согласны разделить работу
пополам. К вашему взаимному огорчению, вы обнаруживаете, что ваши
текстовые редакторы не совместимы друг с другом. Чтобы соединить обе
части отчета, один из вас должен поменять текстовый редактор. Конечно,
поскольку привыкнуть к новому редактору нелегко, каждый из вас
предпочел бы, чтобы его сменил коллега. В то же время каждый из вас скорее
предпочел бы сменить редактор, чем не иметь возможности
координироваться. Наконец, предположим, что у вас нет времени на обсуждение
вопроса координации. Каждый должен сам решить, какой текстовый
редактор использовать в своем офисе.
Эта ситуация представлена игрой, матрица выигрышей которой
изображена на рис. 7.6. Текстовый редактор игрока 1 — WP, а игрока 2 —
MW. Выигрыш игрока равен 0, если у обоих игроков разные текстовые
редакторы, 1 — если одинаковые, но игрок редактор поменял, и 2 — если
текстовые редакторы одинаковые и игрок не менял редактор. В этой игре
существуют два равновесия по Нэшу в чистых стратегиях, а именно (WP,
WP) и (MW, MW).
\ 2
1 ^\
WP
MW
WP
2,1
0,0
MW
0,0
1,2
Рис. 7.6. Координационная игра
Существуют ли в игре равновесия по Нэшу в смешанных стратегиях?
Если да, то, как видно из рис. 7.6, оба игрока должны выбирать все свои
чистые стратегии с положительной вероятностью. Пусть тогда р > 0
обозначает вероятность, с которой игрок 1 выбирает текстовый редактор MW
своего коллеги, и пусть q > 0 обозначает вероятность, что игрок 2
выбирает текстовый редактор WP своего коллеги. В соответствии с пунктом б)
теоремы 7.1 каждому из игроков должно быть все равно, какую из чистых
стратегий использовать. Для игрока 1 это означает, что
gB) + (l-q)@) = q@) + (l-q)(l),
а для игрока 2 — что
A-р№ + р@) = A-р)(.0) + рB).
Решив эти уравнения, получим, что p = q = l/3. Таким образом,
профиль (смешанных) стратегий, в котором каждый игрок выбирает тексто-

Глава 7. Теория игр
375
вый редактор своего коллеги с вероятностью 1/3 и свой собственный
текстовый редактор с вероятностью 2/3, — третье равновесие по Нэшу в
этой игре. Других равновесий в игре нет. ?
Игра из примера 7.1 интересна в нескольких аспектах. Во-первых, в
ней существует несколько равновесий по Нэшу. Это равновесия и в
чистых стратегиях, и в смешанных стратегиях. Во-вторых, одно из этих
равновесий неэффективно. Обратите внимание, что в равновесии в
смешанных стратегиях ожидаемый выигрыш каждого игрока 2/3, т.е. выигрыш
обоих игроков был бы выше в любом из равновесий в чистых стратегиях.
В-третьих, в игре существует равновесие в смешанных стратегиях, хотя в
этой игре никто из игроков не хотел бы, чтобы его поведение было
непредсказуемо.
Должны ли мы игнорировать обнаруженное равновесие в смешанных
стратегиях по той причине, что в этой игре смешанные стратегии не
служат цели, с которой мы их вводили? Нет. Хотя мы ввели понятие
смешанных стратегий для того, чтобы позволить игрокам действовать
непредсказуемо, если они этого хотят, существует другая интерпретация
смешанной стратегии. Вместо того чтобы трактовать смешанную
стратегию игрока 1 как обдуманную рандомизацию своего выбора, ее можно
интерпретировать как ожидание другого игрока относительно того,
какую чистую стратегию выберет игрок 1. Например, в игре,
представленной на рис. 7.6, равновесную стратегию игрока 1, в соответствии с
которой он выбирает текстовый редактор MW с вероятностью 1/3 и с
вероятностью 2/3 — текстовый редактор WP, можно трактовать как отражение
неопределенности, которая имеется у игрока 2 относительно того, какая
именно чистая стратегия будет использоваться игроком 1. Игрок 2
полагает, что игрок 1 выберет MW с вероятностью 1/3, a WP с вероятностью
2/3. Аналогично равновесная смешанная стратегия игрока 2 не
обязательно должна означать, что игрок 2 сознательно рандомизирует между
WP и MW: она может трактоваться как ожидания игрока 1 относительно
того, какую чистую стратегию будет использовать игрок 2.
Таким образом, в нашем распоряжении теперь две возможные
интерпретации смешанных стратегий. С одной стороны, они могут представлять
реальный физический механизм (колесо рулетки), который используют
игроки, чтобы сознательно рандомизировать свой выбор. С другой стороны,
смешанная стратегия игрока может просто отражать ожидания другого
игрока относительно того, какая чистая стратегия может быть выбрана.
Какую из интерпретаций мы выберем, в значительной степени зависит от
контекста. Обычно интерпретация рандомизации как колеса рулетки
подходит для таких игр, как «Дуэль отбивающего и подающего», в которой
интересы игроков противоположны, тогда как основанная на ожиданиях

376
Часть III. Стратегическое поведение
интерпретация лучше подходит для игр, подобных игре, показанной на
рис. 7.6, в которой интересы игроков до какой-то степени совпадают.
В каждой ли игре существует равновесие по Нэшу? Напомним, что,
если речь идет о равновесии в чистых стратегиях, то ответ — «нет»
(например, «Дуэль отбивающего и подающего»). Однако если рассматривать
и смешанные стратегии, то, как правило, ответ будет «да».
Теорема 7.2 (Теорема Нэша). Существование равновесия по
Нэшу.
В любой конечной игре в стратегической форме существует по
крайней мере одно равновесие по Нэшу.
Доказательство. Пусть G = [Sj9 w,).=1 — игра в стратегической
форме. Чтобы упростить запись, предположим, что все игроки имеют
одинаковое число чистых стратегий п. Таким образом, для каждого игрока /
мы можем перенумеровать все чистые стратегии от 1 до п и записать, что
Si. = {l,2,...,«}. Следовательно, ut(j\9 j29 ..., jN) обозначает выигрыш
игрока /, если игрок 1 выбрал чистую стратегию у,, игрок 2 выбрал
чистую стратегию у2, ..., и игрок N выбрал чистую стратегию jN.
Множество смешанных стратегий игрока / — это
M;=Umn9 ..., aw/w)gR"| ^w/y=lL где mi} обозначает вероятность, с
которой игрок / выбирает у-ю чистую стратегию. Обратите внимание,
что множество Mi не пусто, компактно и выпукло.
Мы покажем, что равновесие по Нэшу в игре G существует,
продемонстрировав существование неподвижной точки функции, чьи
неподвижные точки являются равновесиями в игре G . Таким образом, для
доказательства мы должны: 1) построить функцию; 2) доказать, что у нее
есть неподвижная точка; 3) показать, что неподвижная точка является
равновесием по Нэшу в G .
Шаг 1. Определим f'.M-^M следующим образом. Для каждой
те М, каждого игрока / и каждой чистой стратегии j
, v= m..+max@, ut(j, m^-u^m))
l + ?max@, и.(у1, тч)-и,(т))
Пусть fl(m) = (Jn(m)9...,fb,(m))9 i = l9...9N и пусть f(m) =
= (fl(m)9 ..., fN(m)). Заметим, что для каждого игрока / ^/y(w) = l и
У=1

Глава 7. Теория игр
Ъ11
что fijim) > О для любого j. Следовательно, /(w)e M. для всех i, и,
таким образом, f(m)e M.
ZZ/аг 2. Поскольку числитель в определении ftj непрерывен по т, а
знаменатель непрерывен по т и не равен нулю (в самом деле, он никогда
не будет меньше единицы), fy — непрерывная функция т для любых /
и j. Следовательно, / — непрерывная функция, отображающая
непустое, компактное и выпуклое множества М в себя. Таким образом, мы
можем воспользоваться теоремой Брауэра о неподвижной точке (теорема
А1.11), чтобы сделать вывод о том, что у / есть неподвижная точка т .
Шаг 3. Поскольку f(m) = m, то fij(th) = ihij для всех игроков / и
чистых стратегий j. Следовательно, по определению fy
Ар + max@, и, (у, *&_,)-«,• (А))
W//= п >
l + ?max@, ut(j\ m4)-ut(m)
r=\
или
п
w(/.^max@, w,.(yf, w_/)-w/(m)) = max@, и.(у, w_;.)-w,.(w))-
Умножая левую и правую части этого уравнения на и. (у, Л_, )-!#,(/») и
суммируя по у , получим:
я п
= ZbU ^-^(™)]тах(°> uiU> rh^-u^m)). (P-l)
Теперь обратим внимание на то, что левая часть равна нулю,
поскольку
п п
Z Ч [м/ U> ™-i) - и>(*)]=Z4"i (•/» Л-/)"м< (*)=
= м,(/и)-м,(/и)=
= 0,

378
Часть III. Стратегическое поведение
где первое равенство следует из того, что сумма ту по j равна единице.
Следовательно, (Р-1) можно переписать как
п
° = ZbU w_,.)~w/(w)]max@, и,(у, /w_;)-w,(w)).
7=1
Но сумма в правой части может обратиться в ноль, только если
и,-(у, й_, )-!/,.(/!!)< О Для любого у. (Если ut(j9 m_i)-ui(fh)>0 для
некоторого j, то у -й член в сумме строго больше нуля. Поскольку ни один
член суммы не является отрицательным, это означало бы, что сумма
строго положительна.) Следовательно, по утверждению в) теоремы 7.1 т
является равновесием по Нэшу.
Теорема 7.2 весьма примечательна. В ней утверждается, что
независимо от того, сколько игроков участвуют в игре, до тех пор пока у
каждого игрока есть конечное число чистых стратегий, в игре существует по
крайней мере одно равновесие по Нэшу. С практической точки зрения это
означает, что поиск равновесия по Нэшу не окажется безрезультатным.
Однако, что еще более важно, теорема устанавливает непротиворечивость
концепции равновесия по Нэшу. Если бы равновесие по Нэшу
существовало достаточно редко, это означало бы, что в определении заложена
фундаментальная несогласованность. То, что равновесие по Нэшу в
конечных играх существует всегда, — одно из свидетельств осмысленности
идеи, лежащей в его основе.
7.2.3. Неполная информация
Хотя множество разнообразных ситуаций можно моделировать как
игры в стратегической форме, до сих пор при анализе этих игр мы делали
важное ограничивающее предположение: когда для того, чтобы
спрогнозировать исход игры, мы использовали последовательное отбрасывание
строго или слабо доминируемых стратегий или концепцию равновесия по
Нэшу, мы всегда предполагали, что каждый игрок полностью
информирован о выигрышах всех других игроков. В противном случае игроки не
могли бы произвести вычисления, необходимые для поиска оптимальной
стратегии.
Но во многих жизненных ситуациях информация о выигрыше
оппонентов может быть неполной. Например, рассмотрим две фирмы,
конкурирующие на одном рынке. Весьма вероятно, что одна из них или они обе
не в полной мере информированы об издержках конкурента. Как
анализировать такую ситуацию? Идея состоит в том, чтобы добавить некий
компонент, чтобы свести ситуацию к игре в стратегической форме. И
тогда мы сможем воспользоваться любой из уже рассмотренных нами кон-

Глава 7. Теория игр
379
цепций решения. Эта идея впервые появилась в работах Харшаньи [Наг-
sanyi, 1967—1968].
Дополнительный компонент — это спецификация ожиданий фирмы 1
в форме вероятностного распределения относительно издержек фирмы 2.
Например, мы можем установить, что фирма 1 допускает предположение
о том, что издержки фирмы 2 с равной вероятностью могут быть низкими
или высокими. Прежде чем двигаться дальше, стоит формализовать идею,
которую мы только что сформулировали.
Рассмотрим класс стратегических ситуаций с неполной информацией.
Как обычно, в игре участвует конечное число игроков / = 1,..., N, у
каждого из которых есть множество чистых стратегий Si. Кроме того, может
существовать неопределенность относительно предпочтений некоторых
из игроков. Чтобы учесть это, введем для каждого игрока / конечное
множество Тп характеризующее все возможные «типы» игроков. Как
обычно, выигрыш игрока зависит от профиля стратегий, но также и от его
собственного типа, и от типов других игроков. То есть функция
выигрыша м, отображает S х Т в R, где Т = х^ Tf и S — множество профилей
чистых стратегий.
Наконец, мы вводим дополнительный компонент, который позволит
использовать концепции решения, изложенные в предыдущих
подразделах. Пусть р — распределение вероятностей на множестве типов
игроков Т, такое, что p{t)> О для каждого te T. Это распределение
вероятностей р часто называют общеизвестным распределением
вероятностей, поскольку его используют все игроки, чтобы оценить вероятность
появления того или иного типа игроков.
Предположение об общеизвестном распределении вероятностей
можно интерпретировать по крайней мере двумя способами. Первая
интерпретация состоит в том, что р — просто объективное эмпирическое
распределение на множестве типов игроков, которое было получено
ранее посредством многократных наблюдений. Вторая — в том, что
общеизвестное распределение вероятностей отражает идею, согласно которой
разница в ожиданиях возникает только из различий в
информированности. Следовательно, до того как игроки узнают свой собственный тип —
и пока они находятся в симметричных позициях, — ожидания каждого
игрока относительно возможного типа любого другого игрока должны
быть одинаковы и равны р .
Пусть Tte Тх — тип игрока /. Тогда неопределенность относительно
типов других игроков для него будет отражена с помощью условного

380
Часть III. Стратегическое поведение
распределения вероятностей на Г_;, полученного из р при заданном /..
То есть если Tt — тип игрока /, то он приписывает вероятность
тому факту, что типы других игроков есть f_.. (Это не что иное, как
правило Байеса, которое можно найти в любом хорошем учебнике по теории
вероятностей; см. также параграф 7.3.7.)
Предваряя анализ таких ситуаций, сведем все их элементы воедино.
Определение 7.10. Игра с неполной информацией.
Игра с неполной информацией — это набор G = yp, TL Sn utj , где
p — распределение вероятностей на Т, приписывающее
положительную вероятность каждому элементу этого множества для каждого
игрока i = 1,..., N, множество 7] конечно и ut: SxT —> R. Если, кроме
того, для каждого игрока i множество стратегий St конечно, то G
называется конечной игрой с неполной информацией.
Остался вопрос: как мы можем использовать уже рассмотренные
концепции решений для нахождения решения в играх с неполной
информацией? Ответ: игру нужно переинтерпретировать следующим образом.
Будем рассматривать каждый тип каждого игрока в игре с неполной
информацией как отдельного игрока и предполагать, что Природа
случайным образом, в соответствии с вероятностным распределением р,
выбирает, какой из типов в действительности примет участие в игре. Кроме
того, в этой переинтерпретации каждый тип каждого игрока должен
выбрать свою стратегию еще до того, как Природа сделает свой случайный
выбор. Как мы увидим, такая переинтерпретация приведет нас к игре в
стратегической форме (определение 7.1), которую можно анализировать,
как и раньше. Более того, эта игра в стратегической форме превосходно
отражает все относящиеся к делу аспекты первоначальной игры с
неполной информацией. Рассмотрим следующий пример.
Пример 7.2. Две фирмы конкурируют по Бертрану, как это описано
в главе 4, за исключением того обстоятельства, что одна из них точно не
знает, каковы постоянные предельные издержки другой фирмы.
Предельные издержки фирмы 1 известны, а предельные издержки фирмы 2 с
равной вероятностью либо высокие, либо низкие. Постоянных издержек нет.
Таким образом, фирма 1 может быть лишь одного типа, а фирма 2 — двух
типов: с высокими издержками или с низкими издержками. У обеих фирм
одно и то же множество стратегий, а именно — множество неотрицатель-

Глава 7. Теория игр
381
ных цен. Выигрыш фирмы 2 зависит от ее типа, но выигрыш фирмы 1 не
зависит от типа фирмы 2; он зависит только от выбранных цен.
Чтобы получить игру в стратегической форме на основе игры с
неполной информацией, предположим, что в игре участвуют три, а не две
фирмы, а именно фирма 1, фирма 2 с высокими издержками и фирма 2 с
низкими издержками. Предположим также, что каждая из этих трех
фирм одновременно с другими должна выбрать цену, после чего Природа
выберет один из двух типов фирмы 2 (каждый с вероятностью 1/2),
который будет конкурировать с фирмой 1 в соответствии с уже выбранной
ценой. Хотя это может показаться несколько причудливым, однако,
поразмыслив, вы убедитесь, что полученная игра вполне отражает все
относящиеся к делу аспекты первоначальной игры с неполной информацией.
В частности, фирма 1 должна назначить цену, не зная, высокие или
низкие издержки у конкурента. Более того, фирма 1 понимает, что цена
конкурента может различаться в зависимости от его издержек. ?
Таким образом, мы хотим для каждой игры с неполной информацией
построить соответствующую игру в стратегической форме, отражающую
ее существенные особенности. Это делается следующим образом.
Определение 7.11. Ассоциированная игра в стратегической
форме.
Пусть (? = (/?, T; Si9 w,). — игра с неполной информацией и пусть
G* = \Rj9Vj). j — игРа в стратегической форме, множество игроков
которой J — это множество, помеченное индексами j, где j = (/, /.),
tfe Ti и i-\, 2, ..., N; множество стратегий и функция выигрыша
игрока j = (i9 tf) определяются соответственно как
и
где rexleJRr Тогда мы будем называть G* игрой в стратегической
форме, ассоциированной с игрой с неполной информацией G.
Построив для каждой игры с неполной информацией
соответствующую игру в стратегической форме, мы свели изучение игр с неполной
информацией к изучению игр с полной информацией, т.е. в
стратегической форме. Следовательно, мы можем использовать любые уже рассмот-

382
Часть III. Стратегическое поведение
ренные концепции решения для изучения ассоциированных игр в
стратегической форме. В частности, мы можем проанализировать множество
равновесий по Нэшу в ассоциированной игре. В самом деле это будет
чрезвычайно полезно.
Определение 7.12. Равновесие Байеса — Нэша.
Равновесие Байеса — Нэша в игре с неполной информацией — это
равновесие по Нэшу в ассоциированной игре в стратегической форме.
Опираясь на изложенный выше инструментарий, легко ответить на
вопрос о существовании равновесия Байеса — Нэша.
Теорема 7.3. Существование равновесия Байеса — Нэша.
В любой конечной игре с неполной информацией существует по
крайней мере одно равновесие Байеса — Нэша.
Доказательство. По определению 7.12 достаточно показать, что в
ассоциированной игре в стратегической форме существует равновесие по
Нэшу. Поскольку игра в стратегической форме, ассоциированная с
конечной игрой с неполной информацией, также конечна, то мы можем
воспользоваться теоремой 7.2, чтобы сделать вывод о том, что в
ассоциированной игре в стратегической форме существует равновесие по Нэшу.
Пример 7.3. Чтобы увидеть, как работают эти идеи на практике,
давайте рассмотрим более детально две фирмы, обсуждавшиеся в
примере 7.2. Предположим, что предельные издержки фирмы 1 равны 0. Кроме
того, предположим, что предельные издержки фирмы 2 равны либо 1,
либо 4 и что вероятность появления каждого из этих типов фирмы 2 равна
1/2. Если наименьшая назначенная цена равна р, то рыночный спрос
равен 8-/7. Чтобы упростить ситуацию, предположим, что каждая из
фирм может выбрать только одну из трех цен: 1, 4 или 6. Выигрыши
фирм показаны на рис. 7.7. Выигрыш фирмы 1 всегда первое число, а
выигрыш фирмы 2, когда ее издержки низкие (высокие), указан вторым
числом в матрице слева (справа).
1 ^\
Pi = 6
Pi = 4
Р.= 1
Pi =6
6,5
16,0
7,0
pi = 4
0,12
8,6
7,0
P,= l
0,0
0,0
7,0
^\ 2Л
1 ^\
Pi = 6
Р.=4
pi=l
Рн=6
6,2
16,0
7,0
Pa = 4
0,0
16,0
7,0
pA=l
0,-21
0,-21
7,0
Рис. 7.7. Игра с неполной информацией — конкуренция по Бертрану

Глава 7. Теория игр
383
Ориентируясь на знания о действии механизма конкуренции по
Бертрану, будем придерживаться следующего соглашения относительно
выигрышей в случае, если фирмы выбрали одинаковые цены. Если
издержки обеих фирм строго меньше, чем назначенная ими обеими цена, то
рынок делится между ними поровну. В противном случае фирма 1
захватывает весь рынок, продавая свою продукцию по этой цене. Такое
неравное распределение отражает идею о том, что, если цена выше
издержек фирмы 1, но не выше издержек фирмы 2, то фирма 1 может
захватить весь рынок, немного понизив свою цену (именно это фирма и
сделает, если ей будет позволено, поскольку цена все еще превышает ее
издержки). В то же время фирма 2 не может снизить цену (даже если ей это
позволить), поскольку такое снижение приведет к убыткам.
Тем самым мы описали игру с неполной информацией. В
ассоциированной игре в стратегической форме участвуют три игрока: фирма 1,
фирма 2/ (с низкими издержками) и фирма 2h (с высокими издержками).
Множества чистых стратегий участников одинаковы, а именно — это
множество цен {l, 4, б}. Пусть рх, рп ph обозначают цену, выбранную
фирмами 1, 2/ и 2Л соответственно.
На рис. 7.8 изображена эта игра. Так как в игре три участника, то
выбор цены игроком 1 определяет матрицу, а цене, назначенной фирмами 2/
и 2Л, соответствуют строка и столбец выбранной матрицы. Например, как
видно на рис. 7.8, если фирма 1 выбирает рх = 4, фирма 2/ выбирает
р,=4 и фирма 2А выбирает ph =4, то их выигрыши составят 12, 6 и О
соответственно.
Фирма 1 выбирает/?! = 6 Фирма 1 выбирает р\ = 4
\2й
2/ \,
Pi =6
р, = А
р,= \
Рн = 6
6,5,2
3,12,2
3,0,2
Ph = 4
3,5,0
0, 12,0
0,0,0
Рн=\
3,5,-21
0,12,-21
0,0,-21
\2й
2/ \^
Pi =6
Р/ = 4
р/=1
Ph = t>
16, 0, 0
12,6,0
8,0,0
Ph = 4
16, 0, 0
12, 6,0
8,0,0
Ph= 1
8,0,-21
4,6,-21
0,0,-21
Фирма 1 выбирает/71 = 1
"~-\^ 2Л
2/ ^\
Pi =6
Pi = 4
Р,= \
Ph = 6
7,0,0
7,0,0
7,0,0
Ph = 4
7,0,0
7,0,0
7,0,0
Ра= 1
7,0,0
7,0,0
7,0,0
Рис. 7.8. Ассоциированная игра в стратегической форме

384
Часть III. Стратегическое поведение
Согласно определению 7.11 сумму выигрыша в игре в стратегической
форме, изображенной на рис. 7.8 для фирм 2/ и 2Л, благодаря тому что
существует только один тип фирмы 1, можно просто взять из матриц на
рис. 7.7. Например, как показано на рис. 7.7, когда Природа выбирает
фирму 2/, которая, в свою очередь, выбирает р1 = 6, то выигрыш фирмы
2/ равен 5 в случае, если фирма 1 выбирает рх = 6, независимо от того,
какой выбор делает фирма 2Л.
Выигрыши фирмы 1 в ассоциированной игре в стратегической форме,
изображенной на рис. 7.8, подсчитаны на основе априорного
распределения вероятностей издержек фирмы 2. Рассмотрим, например, стратегию,
при которой фирма 2/ выбирает р{ = 1, фирма 2Л выбирает ph = 6, а
фирма 1 выбирает рх = 4. Теперь, если Природой выбрана фирма 2/, то в
соответствии с матрицей на рис. 7.7 выигрыш фирмы 1 равен 0. Если же
выбрана фирма 2А, то выигрыш фирмы 1 равен 16. Поскольку оба типа
фирмы 2 выбираются согласно априорному распределению с
вероятностью 1/2, ожидаемый выигрыш фирмы 1 равен 8. Именно этот выигрыш
указан на рис. 7.8 при рх = 4, р{ = 1 и ph=6. Аналогично
рассчитываются и другие (ожидаемые) выигрыши фирмы 1 в ассоциированной игре в
стратегической форме при всех других возможных профилях стратегий.
Чтобы найти равновесие Байеса — Нэша в игре с неполной
информацией, описывающей конкуренцию по Бертрану, мы должны найти
равновесие по Нэшу в ассоциированной игре в стратегической форме,
изображенной на рис. 7.8.
Одно равновесие по Нэшу в этой игре найти довольно легко.
Обратите внимание, что у фирм 2/ и 2Л есть слабо доминирующие стратегии.
У фирмы 2/ слабо доминирующая стратегия — это цена 4, а у
фирмы 2Л — цена 6. Но если отбросить остальные стратегии этих фирм, то у
фирмы 1 есть строго доминирующая стратегия: назначить цену 4. Чтобы
убедиться в этом, предположим, что р( = 4 и ph=6. Тогда согласно
рис. 7.8 выигрыш фирмы 1 равен 3, если она выберет рх =6; 12 — если
она выберет рх = 4; и 7 — если она выберет рх=1.
Следовательно, в игре существует равновесие Байеса — Нэша в
чистых стратегиях, в котором две из трех фирм выбирают цену 4, а третья
выбирает цену 6. В одном из упражнений вас попросят проанализировать,
существуют ли другие равновесия Байеса — Нэша в игре. Обратите
внимание, что, в отличие от случая конкуренции по Бертрану с полной
информацией, не у всех фирм прибыль здесь равна нулю. Действительно, в
рассмотренном нами равновесии только у фирмы 2 с высокими
издержками нулевая прибыль. ?

Глава 7. Теория игр
385
7.3. Игры в развернутой форме
До сих пор мы рассматривали стратегические ситуации, в которых
игроки должны были выбирать свои стратегии одновременно. Теперь мы
добавим в анализ динамику, рассматривая стратегические ситуации, в
которых игроки должны делать свой выбор последовательно.
В игре «Кто последний» на столе разложена 21 монета. Вы и ваш
оппонент по очереди берете монеты со стола. Единственное
ограничение состоит в том, что каждый раз можно взять одну, две или три
монеты. Пропускать свой ход нельзя. Проиграл тот, кто забирает последнюю
монету. Какое поведение в игре будет оптимальным и, если оба игрока
ведут себя оптимально, кто выиграет? Со временем мы ответим на эти
вопросы.
Обратите внимание, что в игре «Кто последний» игроки ходят
последовательно, зная все ходы, которые уже были сделаны. Таким образом,
модель игры в стратегической форме, когда игроки делают свои ходы
одновременно, не зная ходов других игроков, не подходит для анализа этой
игры.
Во многих настольных играх, таких, как эта, игроки делают ходы
друг за другом, и, когда каждый из них должен ходить, он полностью
информирован обо всех предыдущих ходах. Но в других играх — ив
настольных, и в экономических — игроки могут не иметь всей информации
о предыдущих ходах контрагентов.
Рассмотрим, например, покупку подержанной машины. Продавец
может отремонтировать машину, а может этого не делать. После того
как он принял решение, касающееся ремонта машины, он назначает на
нее цену. Затем он сообщает цену покупателю. Однако у покупателя нет
возможности узнать, была ли отремонтирована машина . Будет ли
высокая цена сигналом, что машина отремонтирована? И если да, каким
образом будет себя вести недобросовестный продавец? Сейчас, однако, мы
хотим только заметить, что в этой достаточно стандартной
экономической ситуации игроки ходят последовательно, однако второй игрок
(покупатель) только частично информирован о выборе, сделанном первым
игроком.
Существует стандартная общая схема, в рамках которой можно
моделировать оба типа динамических ситуаций (как и многие другие). Она
называется игрой в развернутой форме. Неформально элементы игры в
развернутой форме — это: 1) игроки; 2) Природа (или случай); 3) «правила»
игры, включая порядок игры и информацию, которой каждый игрок рас-
1 Это означает, что продавец подержанных машин не может доказать, был ли произведен
ремонт машины. В действительности это не так далеко от истины.

386
Часть III Стратегическое поведение
полагает относительно предыдущих ходов; и 4) выигрыши игроков.
Формально же все эти элементы содержатся в следующем определении1.
Определение 7.13. Игра в развернутой форме.
Игра в развернутой форме, обозначенная через Г, состоит из
следующих элементов:
1) конечного множества игроков N;
2) множества (не обязательно конечного) действий А, включающего
все возможные действия, которые потенциально могут быть
предприняты в какой-то из моментов игры;
3) множества узлов, или историй, X, где:
а) X содержит особый элемент х0, называемый начальным узлом
или пустой историей;
б) каждый хеХ\{х0} имеет вид х = (а19 а2, ..., ак) для некоторого
конечного множества действий а{ е А ;
в) если (яр а2, ..., ак)е Х\{х0} для некоторого к>\, то
(я,, а2, ..., ak_i)eX\{x0}.
Узел, или история, тогда представляет собой просто полное
описание действий, которые были уже предприняты в игре.
Мы будем использовать термины «история» и «узел» как
взаимозаменяемые. Для удобства обозначим через
А(х) = {ае А | (х, a)e X}
множество действий, доступных игроку, чья очередь сделать ход после
истории х е X \ {х0};
4) множества действий А(хH с: А и распределения вероятностей л
на А(х0) для описания роли Природы (случая) в игре. Природа всегда
ходит первой и только один раз, выбирая в соответствии с законом
распределения к действие из А(х0). Таким образом, (яр а2, ..., а^е Х\{х0}
подразумевает, что ах е А(х0) для i = \,u только для / = 1 ;
Соглашение относительно использования последовательности действий для
определения «истории» игры взято из работы Осборна и Рубинштейна [Osborne, Rubinstein,
1994]. Классическую трактовку можно найти в работе фон Неймана и Моргенштерна
[Neumann, Morgenstern, 1944].
2 Может показаться, что предположение о том, что Природа делает только один ход в
начале игры, оказывается ограничительным. Но это не так. Рассмотрим, например,
настольную игру «Монополия». Предположим, что в игре, длящейся обычно часа два, кубики
кидаются не чаще, чем каждые 5 секунд. Таким образом, приблизительная верхняя граница
числа бросков кубиков равна 2000. С таким же успехом мы могли бы играть в эту игру,
поручив независимому арбитру перед ее началом бросить кубики 2000 раз, с тем чтобы

Глава 7. Теория игр
387
5) множества терминальных узлов Е = {хе X |(дг, а)? X для всех
я€ А }. Каждый терминальный узел полностью описывает один
розыгрыш игры от начала до конца;
6) функции l:X\(Eu{x0}) —> N, которая в каждом узле решений из
X определяет, чья очередь делать ход. Для удобства обозначим через
X, ={xeX\Eu{x0}\l(x) = i}
множество узлов решений, принадлежащих игроку i;
7)разбиения I множества узлов решения X\(E\j{x0}) такого,
что, если х и ху принадлежат одному и тому же элементу разбиения,
то a) i(jc) = i(jc') и б) А(х) = А(х') . I разбивает мноэюество узлов ре-
шений на информационные множества. Информационное множество,
содержащее узел х, обозначается через 1(х). Когда в игре достигается
узел х, игрок l(x) должен предпринять действие, будучи
информированным, что история игры — это один из элементов множества 1{х).
Таким образом, 1{х) описывает информацию, доступную игроку \{х) в
момент игры, когда он должен ходить после истории х. Условия а) и б)
гарантируют, что игрок l(x) не может различать истории в 1(х),
основываясь на информации о том, его или не его очередь делать ход, или
на информации о том, какие действия ему доступны, соответственно.
Для удобства обозначим через
1,={1{х)\ l(x) = i, хеХ\(Еи{х0})}
множество информационных множеств игрока i;
8) для каждого i € N функции выигрыша фон Неймана —
Моргенштерна и,: ? —> М область определения которой — множество
терминальных узлов. Данная функция описывает выигрыш каждого
игрока для любого возможного завершения игры.
Мы записываем игру Г как r = (N,A,X9E9 % тс,/,(«,.)fe^V Если
множество действий А и мноэюество узлов X конечны, то игра Г
называется конечной игрой в развернутой форме.
выбрать 2000 чисел между 1 и 12, а затем открывать эти числа по очереди в тот момент,
когда это необходимо. Таким образом, можно считать, что Природа сделала ход один раз в
самом начале игры.
1 Разбиением множества называется совокупность непересекающихся непустых
подмножеств, объединение которых представляет собой первоначальное множество. Таким
образом, элемент разбиения сам является множеством.

388
Часть III. Стратегическое поведение
Вполне возможно, что это определение покажется довольно
сложным, но перечитайте его два или три раза. Вы вскоре оцените, насколько
оно сжато, особенно когда вы осознаете, что под него подходят
фактически все существующие настольные игры, не говоря уже о громадном
количестве приложений из общественных наук! Тем не менее, чтобы
помочь вам это лучше прочувствовать, приведем несколько примеров.
Пример 7.4. Начнем с описанной ранее игры «Кто последний».
В игре участвуют два игрока, т.е. N = {1, 2}. В свой ход игрок может
взять до трех монет. Так что пусть г{, г2 и гъ обозначают, что игрок взял
одну, две или три монетки соответственно. Чтобы формально указать, что
случай в этой игре не играет никакой роли, положим А(х0) = {а} (т.е. у
Природы только один ход). Таким образом, множество действий в игре
А = {а, гр г2, г3}. Типичный элемент множества Х\{х0} тогда может
иметь такой вид: х = (а, г19 г2, гр г3, г3). Это означает, что к этому
моменту в игре игроки по очереди взяли 1,2, 1, 3 и 3 монеты.
Следовательно, осталось 11 монет, и сейчас ход игрока 2 (поскольку игрок 1 сделал
первый ход). Таким образом, l(x) = 2. Кроме того, поскольку каждый
игрок полностью информирован обо всех предыдущих ходах, то 1(х) = {х}
для каждого хеХ. Два примера терминальных узлов в игре
ех =(я, гр г2, Гр г3, г3, г3, г3, г3, г2) и е2 =(а, г3, г3, г3, г3, г3, г3, г2, г,),
в каждом игроки по очереди взяли все 21 монету. Первый из этих двух
узлов показывает, что выиграл игрок 2 (поскольку игрок 1 забрал
последние две монеты), а второй показывает, что выиграл игрок 1. Таким
образом, если выигрыш победителя равен 1, а выигрыш проигравшего равен
(-1),то ul(el) = u2(e2) = -l и ul(e2) = u2(el) = l. ?
Пример 7.5. Во втором примере рассмотрим взаимоотношения
покупателя и продавца подержанной машины. Чтобы упростить ситуацию,
предположим, что у продавца при назначении цены есть только две
возможности: он может назначить либо высокую цену, либо низкую. В этой
игре два игрока, т.е. N = {5, В}, где S означает продавца (seller), а В —
покупателя (buyer), и следующее множество действий: А =
{ремонтировать, не ремонтировать, высокая цена, низкая цена, принять предложение,
отклонить предложение}. Поскольку действия Природы здесь не играют
никакой роли, вместо того чтобы указать для нее единственное действие,
мы просто исключим ее из анализа. Пример узла в этой игре: х =
(ремонтировать, высокая цена). В узле х должен сделать ход покупатель, т.е.
l(x) = B. Поскольку в этом узле покупатель информирован о цене,
выбранной продавцом, но не знает, была ли починена машина, то

Глава 7. Теория игр
389
1{х) = {(ремонтировать, высокая цена), (не ремонтировать, высокая
цена)}. Иными словами, когда достигается узел х9 покупатель
информирован только о том, что имела место одна из двух возможных историй в
1(х), однако он не знает, какая именно. ?
7.3.1. Дерево игры: графическое представление
Игру в развернутой форме также можно представить графически с
помощью диаграммы «дерево игры». Чтобы лучше разобраться с этим
понятием, рассмотрим версию игры «Кто последний» с четырьмя
монетами. На рис. 7.9 изображена эта упрощенная игра.
Рис. 7.9. Дерево игры в развернутой форме
Маленькими темными кружками отмечены узлы; линии,
соединяющие их, представляют предпринятые действия. Например, узел х имеет
вид л; = (я, гр г2) и обозначает историю игры, в которой игрок 1 взял
одну монету, а игрок 2 — две монеты. Следовательно, в узле х осталась
одна монета, и ходить должен игрок 1. Каждый узел отмечен номером
игрока, чтобы было понятно, чей ход, если этот узел достигнут. Начальный
узел обозначен буквой С (chance), показывающей, что игра начинается с
хода Природы. Поскольку Природа фактически не играет никакой роли в
этой игре (формально это выражено тем, что у Природы только одно
действие), можем упростить дерево игры, удалив этот узел. В дальнейшем
мы будем следовать этому принципу каждый раз, когда Природа не
играет никакой роли.

390
Часть III. Стратегическое поведение
За каждым терминальным узлом следует вектор выигрышей. По
соглашению i-я компонента вектора означает выигрыш /-го игрока.
Например, и}(е) = -\ и w2(e) = l, где е — терминальный узел, показанный на
рис. 7.9.
Дерево игры «Покупатель и продавец» изображено на рис. 7.10,
однако на нем отсутствуют выигрыши игроков. Здесь появилась новая
деталь, а именно эллипсы, проведенные пунктирной линией, которыми
обведены различные узлы. Каждый из этих эллипсов представляет собой
информационное множество. На рисунке мы видим два таких
информационных множества. Обычно тривиальные информационные
множества, т.е. множества, содержащие только один узел, пунктиром не
обводятся1. Например, и первоначальный узел jc0, и узел (*0, ремонтировать) —
каждый является единственным элементом двух различных
информационных множеств. Каждому информационному множеству приписан
индекс того единственного игрока, который должен сделать ход, если узел в
информационном множестве будет достигнут. В этой игре
информационные множества покупателя являются нетривиальными.
S
Ремонтировать^^Т^Х^ Не ремонтировать
S ^ \ S
Низкая />v Низкая
^ цена / ^VjeHa
Высокая
цена / ! х В
Принять
предложение «
Принять Отклонить / Отклонить
предложение предложение / предложение
'Высокая
цена
В
Принять Отклонить
предложение предложение
Принять
предложение
Отклонить
предложение
Рис. 7.10. Игра «Покупатель и продавец»
1 Обратите внимание, что дерево игры на рис. 7.9 изображено с учетом этого
соглашения, поскольку все информационные множества в нем — тривиальные.

Глава 7. Теория игр
391
Игры в развернутой форме, в которых все информационные
множества тривиальные, как в игре «Кто последний», называются играми с
совершенной информацией. Все другие игры, как игра «Покупатель и
продавец», называются играми с несовершенной информацией.
7.3.2. Неформальный анализ игры «Кто последний»
Мы хотим дать неформальное описание двух фундаментальных идей,
появившихся в ходе анализа игры «Кто последний». Первая — это
понятие стратегии в игре в развернутой форме, вторая — это понятие
обратной индукции. Ясное понимание этих двух идей в данном контексте
весьма важно для того, чтобы и о более сложных идеях данного раздела
тоже имелось ясное представление.
Цель нашего систематического анализа игры «Кто последний»
состоит в том, чтобы понять, как играли бы два «эксперта». В частности, мы
хотим найти «самый лучший» алгоритм действий для каждой возможной
ситуации. На языке игр в развернутой форме это означает, что мы хотим
определить оптимальное действие каждого игрока в каждом узле решения.
Спецификация действий в каждом узле решения для каждого игрока
составляет то, что мы будем называть (чистой) стратегией игрока. Это
понятие формально будет введено ниже. А сейчас достаточно отметить,
что стратегия игрока 1 в игре «Кто последний» должна указать, что он
будет делать на первом ходу; что нужно делать на втором ходу в
зависимости от того, какой ход был выбран на первом ходу и какой ход был
предпринят в ответ игроком 2, и т.д. Следовательно, вооруженный
стратегией игрок может сверяться с ней, чтобы определить, что ему нужно
делать, когда приходит его очередь сделать ход, и она предлагает ход для
каждой истории игры. В частности, стратегия игрока продолжает
предлагать ему, что делать, даже если он (ошибочно или обдуманно) в прошлом
отклонился от нее. Например, рассмотрим следующую простую
стратегию игрока 1: «Брать одну монету, если число остающихся монет будет
нечетным, и две, если число оставшихся монет будет четным». Даже если
игрок 1 отклонится от своей стратегии, взяв две монеты в свой первый
ход, стратегия продолжает предлагать ему, как поступать до конца игры.
Теперь мы вернемся к вопросу, какие же стратегии было бы разумно
использовать в этой игре.
Возможно, у вас уже было достаточно времени поразмыслить над
тем, как нужно действовать в игре «Кто последний». Тем не менее, когда
на столе 21 монета, на первый взгляд вовсе не очевидно, сколько монет
должен взять первый игрок. Конечно, он должен взять одну, две или три.
Но какой ход будет лучшим? Трудно немедленно ответить на этот
вопрос, поскольку в игре еще очень много ходов. Таким образом, мы не

392
Часть III. Стратегическое поведение
можем судить о том, насколько хорош первый ход, не зная, как будет
развиваться игра в дальнейшем.
Чтобы упростить задачу, рассмотрим ситуацию, когда монет на столе
осталось гораздо меньше. В самом деле, если бы на столе оставалась одна
монета, то игрок, чья очередь сделать ход, проиграл бы, поскольку по
правилам игры он должен был сделать ход. Таким образом, одна монета
(оставшаяся на столе) — это проигрышная позиция. А если монет две?
Это выигрышная позиция, поскольку тот игрок, чья очередь сделать ход,
может забрать одну монету, оставляя вторую, что, как мы уже знаем,
будет проигрышной позицией для другого игрока. Аналогично, и три и
четыре монеты на столе — это тоже выигрышная позиция, поскольку,
забрав две и три монеты соответственно, игрок оставляет оппонента в
проигрышной позиции, когда на столе остается одна монета. А что можно
сказать о пяти монетах? Это, должно быть, проигрышная позиция,
поскольку, забрав одну, две или три монеты, игрок оставляет оппонента в
выигрышной позиции, оставляя соответственно четыре, три и одну
монету. Продолжая рассуждать таким образом, двигаясь с конца игры к
началу, можно показать, что, если остается 1, 5, 9, 13, 17, 21 монета — это
проигрышные позиции, все остальные — выигрышные.
Следовательно, если два эксперта участвуют в игре «Кто последний»
с 21 монетой, то второй игрок всегда может гарантировать себе выигрыш,
независимо от того, какой первый ход сделает игрок 1. Чтобы убедиться в
этом, рассмотрим следующую стратегию второго игрока, которая
сформирована по результатам нашего анализа выигрышных и проигрышных
позиций: «Везде, где возможно, всегда забирайте столько монет, чтобы
количество оставшихся монет соответствовало проигрышной позиции, а
именно — 1, 5, 9, 13, 17, 21; в противном случае забирайте одну монету».
Мы предоставляем читателю возможность проверить, что, если второй
игрок поступал таким образом на каждом из своих предыдущих ходов, он
всегда может привести оппонента в проигрышную позицию. Поскольку
оппонент начинает с проигрышной позиции, то доказательство можно
считать оконченным.
Обратите внимание на метод, который мы использовали при анализе
игры. Вместо того чтобы анализировать игру с самого начала, когда на
столе была 21 монета, мы начали анализ с конца игры, когда на столе
оставалась одна монета, затем две и так далее. Этот метод лежит в основе
многочисленных концепций решения игр в развернутой форме. Он
называется обратной индукцией. Мы вернемся к нему чуть позже. Но, перед
тем как идти дальше, мы формализуем идею стратегии для игры в
развернутой форме.

Глава 7. Теория игр
393
7.3.3. Стратегии в играх в развернутой форме
Как уже было сказано, (чистая) стратегия участника игры в
развернутой форме — это полное описание поведения игрока в любых
обстоятельствах, которые могут возникнуть в ходе игры; это полный набор
инструкций, которые может выполнять кто-нибудь еще от имени игрока.
Определение 7.14. Стратегия в игре в развернутой форме.
Рассмотрим игру в развернутой форме Г, удовлетворяющую
определению 7.13. Формально чистая стратегия игрока i в игре Г — это
функция Sj: It —> А, для которой выполнено s{ (I(x))e А(х) для всех х, таких,
что l(x) = i. И пусть S. обозначает множество чистых стратегий
игрока i в игре Г.
Таким образом, чистая стратегия игрока указывает, какое из
доступных действий должно быть предпринято в каждом из его
информационных множеств. Тот факт, что выбор игрока может зависеть только от того,
в каком информационном множестве он сейчас находится (а не, скажем,
от историй в этом информационном множестве), гарантирует, что
стратегия должным образом отражает информационные ограничения, с
которыми сталкивается игрок.
Чистую стратегию игрока можно легко изобразить с помощью дерева
игры, указывая стрелками действия, которые должен предпринять игрок в
каждом информационном множестве, когда оно достигнуто. Например,
на рис. 7.11 изображена следующая чистая стратегия игрока 2: выбрать /,
если достигается /(*), и выбрать г, если достигается 1(у).
1 R
Рис. 7.11. Стратегия для игры в развернутой форме

394
Часть III. Стратегическое поведение
Важно отметить, что чистая стратегия игрока действительно
полностью описывает то, как он должен играть. Например, предположим, что
вы играете в шахматы черными. Ваша стратегия, кроме всего прочего,
должна содержать указания, как вам нужно ходить йосле первого хода
белых. Недостаточно решить, как вы будете ходить после какого-то
одного хода белых (скажем, Р — К4), даже если вы фактически уверены, что
именно таким будет первый ход белых. Определение чистой стратегии
требует, чтобы вы указали, как будете ходить после любого возможного
первого хода белых. И вы должны указать, как будете действовать в ответ
на любую возможную (допустимую) последовательность ходов,
заканчивающуюся ходом белых. Только тогда вы специфицируете некоторую
чистую стратегию черных в шахматах. В упражнениях вас попросят указать
чистые стратегии для игр, которые мы анализировали. Вы убедитесь, что
это уже само по себе может представлять непростую задачу.
7.2.4. Стратегии и выигрыши
По определению 7.14 Ss для каждого игрока / обозначает множество
его чистых стратегий в игре Г. Предположим, что игра Г конечна.
Следовательно, каждое из множеств S. также конечно. Обратите внимание,
что если чистая стратегия для каждого игрока выбрана, то действия
игроков в ходе игры полностью определены, если не считать влияния на них
ходов Природы. Таким образом, если Природа сделала свой выбор, то
исход игры однозначно обусловливается чистыми стратегиями игроков.
Чтобы убедиться в этом, предположим, что а0 — ход Природы. Этим
определяются история игры хх = а0 и информационное множество 1(х){,
принадлежащее, скажем, игроку l(x1) = l. При заданной стратегии sx
игрока 1 игрок 1 предпринимает действие ах = s{ (/(хХ), тем самым
определяя историю х2=(х19 ах) и информационное множество 1(хJ,
принадлежащее теперь, например, игроку г{х2) = 2 . Теперь при заданной
стратегии s2 игрока 2 игрок 2 предпринимает действие а2 =52(J(x2)), тем
самым определяя историю хъ =(х2, а2). Можно продолжать эти
рассуждения до тех пор, пока мы неизбежно (поскольку игра конечная) не
достигнем терминального узла е, в котором выигрыши игроков, положим,
и.(е) для каждого ie N. Следовательно, для любого профиля стратегий
sg x^S., ход Природы в соответствии с распределением вероятностей я
на множестве А(х0) определяет ожидаемую полезность игрока /,
которую мы будем обозначать u^s).

Глава 7. Теория игр
395
Обратите внимание, что тогда набор E,.,«,.)^ представляет игру в
стратегической форме. Он называется стратегической формой игры Г
и мы еще вернемся к этому понятию чуть позже1. Сейчас достаточно
отметить, что для игр в развернутой форме мы можем использовать все
концепции решения игр в стратегической форме. Например,
доминирующая стратегия в игре в развернутой форме Г — это просто
доминирующая стратегия в игре Г в стратегической форме. А равновесие по Нэшу в
игре в развернутой форме Г — это просто профиль стратегий,
составляющий равновесие по Нэшу для игры Г в стратегической форме, и т.д.
7.3.5. Игры с совершенной информацией и стратегии,
полученные обратной индукцией
Важным подклассом игр в развернутой форме являются игры, в
которых игроки в момент своего хода полностью информированы обо всех
предыдущих действиях, т.е. в которых 1(х) = {х} для всех узлов
решения х. Эти игры называются играми с совершенной информацией.
«Кто последний» — это игра с совершенной информацией, так же как
и шахматы, шашки, крестики-нолики и многие другие настольные игры.
В качестве примера простой игры с совершенной информацией из
экономики рассмотрим следующую ситуацию в отрасли, в которой конкурируют
две фирмы. Одна уже закрепилась на рынке (закрепившаяся
фирма — incumbent), а вторая еще нет (новичок — entrant). Новичок должен
решить, выходить ему на рынок или нет. Если он не выйдет на рынок, то
сохраняется статус-кво и игра заканчивается. Если же он выходит на
рынок, то закрепившаяся фирма должна решить, начинать ли ей торговую
войну, резко увеличив предложение своего товара и тем самым снизив цену
на него, или смириться и не делать этого. В ситуации статус-кво выигрыш
закрепившейся фирмы составит 2, а новичка — 0. Если же новичок войдет
на рынок, а закрепившаяся фирма объявит торговую войну, то выигрыш
обоих составит -1. Если же фирма смирится, то выигрыш каждой фирмы
составит 1. Дерево игры входа на рынок изображено на рис. 7.12.
Заметим, что мы преобразовали любую конечную игру в развернутой форме (которая
может отражать очень сложную, динамическую стратегическую ситуацию) в игру в
стратегической форме. Таким образом, наше раннее впечатление, что игры в
стратегической форме полезны только для моделирования ситуаций, в которых нет динамики,
было достаточно наивным. В самом деле, поскольку мы можем построить игру в
стратегической форме для любой игры в развернутой форме, можно утверждать в точности
обратное; с теоретической точки зрения можно ограничиться лишь рассмотрением игр в
стратегической форме, поскольку все игры в развернутой форме могут быть сведены к
ним! Но достаточно ли только стратегической формы для анализа игр в развернутой
форме — это одно из направлений исследований, которые ведут специалисты в области
теории игр. Но мы не будем касаться здесь этой темы.

396
Часть III. Стратегическое поведение
Новичок
Не входить v'Nw Входить
Закрепившаяся фирма
Смириться
Рис. 7.12. Игра «Закрепившаяся фирма и новичок»
Очевидно, что закрепившаяся фирма не хотела бы пускать новичка на
рынок, чтобы и дальше получать монопольную прибыль, равную 2. Но
откажется ли новичок от входа? Очевидно, что это зависит от того, как
отреагирует на вход закрепившаяся фирма. Если она начнет торговую
войну, то выигрыш новичка составит -1, и в этом случае ему лучше не
входить на рынок. Если же закрепившаяся фирма смирится с его входом
на рынок, то новичок должен войти. Таким образом, все сводится к
вопросу, каким образом закрепившаяся фирма отреагирует на вход1.
Итак, давайте просто предположим, что новичок вошел. Какое
действие является наилучшим для закрепившейся фирмы в этой ситуации?
Очевидно, что ей лучше смириться, поскольку в этом случае ее выигрыш
составит 1, а не -1. Следовательно, с точки зрения новичка игру можно
упростить так, как это сделано на рис. 7.13, где узел решения
закрепившейся фирмы замещен вектором выигрышей, которые будут получены
игроками после того, как этот узел достигнут. Очевидно, что новичок
войдет на рынок, поскольку это даст ему выигрыш 1, а не 0. Таким
образом, мы снова получили пару стратегий для обоих игроков, решая игру с
конца. Эти стратегии — новичок войдет на рынок, а закрепившаяся
фирма с этим смирится.
Новичок
Не входить
Входить
Рис. 7.13. Редуцированная игра «Закрепившаяся фирма и новичок»
1 Обратите внимание на сходство с исследованием игры «Кто последний». Здесь, как и
там, невозможно оценить ход, не проанализировав, как игра будет проходить в
дальнейшем.

Глава 7. Теория игр
397
Попробуем воспользоваться методом обратной индукции, чтобы
решить несколько более сложную игру с совершенной информацией,
дерево игры которой изображено на рис. 7.14. Начнем с анализа узлов
решений, которые предшествуют только терминальным узлам. В игре есть два
таких предпоследних узла, они обозначены х и у. Оба узла принадлежат
игроку 1. Лучший выбор игрока 1 в узле х — это R1, а в узле у — L".
Следовательно, игру на рис. 7.14 можно упростить так, как показано на
рис. 7.15, где узлы х и у, а. также те, что следуют за ними, заменены на
выигрыши, которые непременно будут получены игроками, если узлы х
и у будут достигнуты. Повторим этот прием с редуцированной формой
игры. Теперь предпоследние узлы — это w и z (принадлежат игроку 2).
Если достигнут узел w, то лучший выбор игрока 2 — г, а если достигнут
узел z, то — /'. Воспользуемся этим, чтобы снова редуцировать игру так,
как это показано на рис. 7.16, после чего ясно, что игрок 1 выберет R.
Таким образом, мы пришли к заключению, что игрок 1 выберет
стратегию (/?, R\ L"), а игрок 2 выберет стратегию (г, 71I. В результате
использования этих двух стратегий выигрыш каждого игрока будет равен 0.
(°1
W
У)
L" /
f4]
1-lJ
.1
\Л"
Р1
ы
Рис. 7.14. Упражнение на применение обратной индукции
1 Запись (R9R\ L") означает, что игрок 1 в свой первый ход выберет R ; если будет
достигнут узел решения х, то он выберет R'; если будет достигнут узел у, то — L".
Стратегия игрока 2 (г, /') интерпретируется аналогично.

398
Часть III Стратегическое поведение
Рис. 7.15. Использование обратной индукции для упрощения дерева игры
Рис. 7.16. Последний шаг обратной индукции
Может показаться несколько странным, что решение игры
прогнозирует исход, в котором каждый из игроков получает 0, тогда как выигрыш
обоих может составить 3, если оба они будут выбирать «правую ветвь»,
когда это возможно. Однако для игрока 2 было бы несомненной ошибкой
выбрать г , если бы он оказался в узле z, поскольку рациональный выбор
игрока 1 в узле;; — это L", а не Л", так как L" дает игроку 1 более
высокий выигрыш. Таким образом, игрок 2, предвидя подобный исход, скорее,
выберет /', поскольку это даст ему 0, что больше, чем -Xх.
Описанную процедуру можно использовать для получения стратегии
игроков в любой игре с совершенной информацией. Такие стратегии
называются стратегиями, полученными обратной индукцией. Перед тем
как дать формальное определение, введем следующие понятия. Будем
говорить, что у строго следует за х, если y = (x9al9...,ak) для некоторых
1 Можно возразить, что игрокам следует заключить такое связывающее друг друга
соглашение, чтобы гарантировать получение вектора выигрышей C,3). Тем не менее, по
определению, игра в развернутой форме включает все возможные действия, доступные
игрокам. Следовательно, если бы игроки могли заключить обязывающее соглашение,
это должно было бы быть включено в описание игры в развернутой форме. Поскольку в
игре это не представлено, такие соглашения просто невозможны.

Глава 7. Теория игр
399
ах,..., ак е А, и что >> непосредственно следует за х, если А: = 1. Мы
говорим, что ^ с/ш00 следует за х, если ^ = л: или j; строго следует за х.
Определение 7.15. Стратегии, полученные обратной индукцией.
Профиль чистых стратегий s называется профилем стратегий,
полученных обратной индукцией для конечной игры Г в развернутой форме
с совершенной информацией, если он определяется следующим образом.
Будем называть узел х предпоследним в игре Г, если все узлы,
непосредственно следующие за ним, являются терминальными. Для каждого
предпоследнего узла х пусть sx,x) (jc) обозначает действие, ведущее к
терминальному узлу, которое максимизирует (из всех доступных
действий в узле х) выигрыш игрока i(x). Обозначим через их результирующий
вектор выигрышей. Удалим узлы и действия, строго следующие за
каждым предпоследним узлом в игре Г, и припишем выигрыши узлу х,
который становится, таким образом, терминальным узлом в Г. Будем
повторять этот процесс до тех пор, пока каждому узлу не будут
предписаны действия^. Тогда это даст профиль чистых стратегий s,
полученных обратной индукцией.
Этот метод построения профиля стратегий, полученного обратной
индукцией, называется алгоритмом обратной индукции. Такой способ
поиска решения отражает следующую идею: решения, принятые на
ранних этапах игры, должны учитывать оптимальное поведение игроков в
дальнейшем. Мы обобщим эту идею в следующем параграфе. В
заключение этого параграфа мы покажем связь между стратегиями, полученными
с помощью алгоритма обратной индукции, и равновесием по Нэшу.
Теорема 7.4 (Теорема Куна). Обратная индукция и равновесие
по Нэшу.
Если s — профиль стратегий, полученных обратной индукцией в
конечной игре в развернутой форме с совершенной информацией Г, то s
является равновесием по Нэшу игры Г.
Доказательство. Поскольку равновесие по Нэшу в игре Г — это
просто равновесие по Нэшу для ее стратегической формы (S,, мДеЛ,,
достаточно показать, что и.(s)>ut (s'ns4) для любого игрока / и любой
стратегии s'eS,.
Предположим, что это не так. Тогда для некоторого игрока / и
стратегии s'eS; выполнено w,(s', s_i)>ui(s). Следовательно, существует
1 Так как игра конечна, эта процедура тоже конечна.

400
Часть III. Стратегическое поведение
ход природы ах, такой, что выигрыши игрока в терминальных узлах е и
е , которыми оканчивается игра в случае использования профиля
стратегий s и s' = (s', 5_;) соответственно, удовлетворяют следующему
неравенству: ui (e) > и{ (е).
Следовательно, множество узлов х, в которых, если игра достигнет
узла, игрок i может увеличить свой выигрыш, отклонившись от
стратегии si, не пусто, поскольку х = ах — элемент этого множества.
Обозначим через х элемент этого множества, не имеющий строгих
последователей в этом множестве1.
Таким образом, когда игра достигает х и другие игроки используют
набор стратегий s_i9 выигрыш игрока / будет строго больше, если он
воспользуется некоей стратегией s", а не s{. Более того, поскольку х не
имеет строгих последователей среди элементов множества, из которого
он был выбран, то: 1) J принадлежит игроку /; 2) все действия,
диктуемые стратегией st в узлах, принадлежащих i, строго следующие за х , не
могут быть улучшены.
Таким образом, когда игра достигает х и другие игроки используют
s4 выигрыш игрока / в случае, если он в узле, следующем за х ,
выбирает действия, соответствующие стратегии sf, а до этого играл в
соответствии с s;., будет выше, чем в случае, когда он во всех узлах, где должен
делать ход, выбирает действия, соответствующие стратегии st. Но
поскольку s — это профиль стратегий, полученный обратной индукцией, то
выигрыш игрока / будет максимальным из возможных при достижении
узла х и использовании стратегии sf во всей игре. Следовательно, мы
пришли к противоречию. ¦
Таким образом, любой профиль стратегий, полученный обратной
индукцией, является равновесием по Нэшу. Поскольку алгоритм обратной
индукции всегда имеет конечное число итераций в конечных играх с
совершенной информацией, мы также доказали следующее утверждение.
Следствие 7.1. Существование равновесия по Нэшу в чистых
стратегиях.
В любой конечной игре в развернутой форме с совершенной
информацией существует равновесие по Нэшу в чистых стратегиях.
1 Такой узел х существует (возможно, не единственный), поскольку множество узлов, из
которого он выбран, конечное и непустое (см. упражнения).

Глава 7. Теория игр
401
Хотя любой профиль стратегий, полученный обратной индукцией,
является равновесием по Нэшу, не всякое равновесие по Нэшу может быть
получено обратной индукцией. Чтобы убедиться в этом, обратите внимание, что,
хотя в соответствии с единственным профилем стратегий, полученным с
помощью алгоритма обратной индукции в игре, изображенной на рис. 7.12,
новичок входит на рынок и закрепившаяся фирма мирится с этим, следующий
профиль стратегий также является равновесием в игре. Новичок не входит,
закрепившаяся фирма начинает торговую войну в случае, если вход
состоялся. При данной стратегии другого игрока ни один из участников игры не
может увеличить свой выигрыш, изменив свою стратегию. Таким образом,
указанный профиль стратегий действительно является равновесием по Нэшу.
Однако это последнее равновесие по Нэшу представляется плохим
прогнозом игры, поскольку оно предполагает угрозу вступления в борьбу со
стороны закрепившейся фирмы, что неправдоподобно. А неправдоподобно
потому, что выполнение этой угрозы вовсе не в интересах закрепившейся
фирмы. Новичок должен понимать это, а следовательно, входить на рынок.
Это именно та логика рассуждений, на которой базируется алгоритм
обратной индукции.
Как мы еще увидим, если в игре много равновесий по Нэшу, то часто
можно отбросить некоторые из них, поскольку они основаны на
неправдоподобных угрозах, подобных только что рассмотренной.
7.3.6. Игры с несовершенной информацией и совершенное
в подыграх равновесие
Метод обратной индукции оказывается вполне безупречным, если его
применять к играм с совершенной информацией. Однако он
непосредственно не обобщается для других игр. Например, рассмотрим игру, дерево
которой изображено на рис. 7.17. В ней у игрока 1 есть выбор —
поучаствовать в координационной игре с игроком 2 (ход IN) или не участвовать
(ход OUT). Попробуем использовать метод обратной индукции в этой игре.
1 OUT BЛ
IN
1
f1]
lv
1 ./^
i /Г
/ \r
f°l
loj
2
/7 ~\
f°l
W
r
(i\
IU
Рис. 7.17. Координационная игра, в которой у игрока 1 есть возможность
выйти из игры

402
Часть III. Стратегическое поведение
Как и раньше, первый шаг заключается в определении всех
информационных множеств, в узлах которых любые действия ведут к окончанию
игры1. В игре, показанной на рис. 7.17, такое информационное множество
принадлежит игроку 2. Это множество достигается в игре после того, как
игрок 1 выберет (IN), а затем L или R.
Обратите внимание, что, если ход получает игрок 2, то, какое бы
действие он ни предпринял — / или г, игра закончится. Теперь, в
соответствии с алгоритмом обратной индукции, следующий шаг — выбрать
действие, оптимальное с точки зрения игрока 2. Но здесь мы сталкиваемся с
затруднением, поскольку неясно, какое же из действий для игрока 2 будет
оптимальным. Чтобы определить это, необходимо знать, что предпримет
игрок 1. Если игрок 1 выбрал L, то лучший ответ игрока 2 — это /, в то
время как если игрок 1 выбрал R, то игроку 2 следует выбрать г. Но в
соответствии с определением информационного множества игрок 2 не
знает, как поступил игрок 1.
Вспомним, почему для решения игры мы воспользовались методом
обратной индукции. Мы применили его, поскольку для определения
оптимального хода в информационном множестве необходимо понять,
какие ходы будут сделаны в последующих информационных множествах.
Но в рассматриваемом примере верно также и обратное: чтобы
определить оптимальный ход в информационном множестве (принадлежащем
игроку 2), мы должны понять, как шла игра до этого (т.е. что выбрал
игрок 1 — L или R). Таким образом, в этой игре (и довольно часто в играх с
несовершенной информацией) мы должны, по крайней мере, в какой-то
степени, одновременно определить оптимальные ходы, и
предшествующие, и последующие за данным ходом.
Продолжим анализ игры, изображенной на рис. 7.17. Несмотря на то
что для начала нам бы хотелось понять, как игрок будет вести себя в
«последнем» информационном множестве, по вышеизложенным причинам
мы пока откажемся от этого и займемся следующим. Поднявшись по
дереву игры на один ход выше, мы окажемся во втором информационном
множестве игрока 1. Можем ли мы определить, как будет развиваться
игра, начиная с этой точки? Если да, то мы сможем заменить эту «часть»
игры, или подыгру, результирующим вектором выигрышей, так же как
мы делали при использовании алгоритма обратной индукции. Но каким
образом определить ход игры в подыгре, начинающейся со второго
информационного множества игрока 2?
Такие информационные множества всегда существуют в конечных играх с полной
информацией. Однако в (конечных) играх с неполной информацией их может и не быть.
Вас попросят проанализировать это в одном из упражнений.

Глава 7. Теория игр
403
Идея, впервые выдвинутая в работах Зельтена [Selten, 1965; Selten
1975], состоит в том, чтобы рассматривать подыгру как самостоятельную
игру (см. рис. 7.18). Воспользуемся концепцией равновесия по Нэшу для
игры, изображенной на рис. 7.18. В этой игре два равновесия по Нэшу в
чистых стратегиях: (L, I) и (R, гI. Предположим, что, если подыгра
достигается в ходе первоначальной игры, в ней будет разыграно одно из
этих равновесий. Предположим, например, что это будет (L, /).
Следовательно, результирующий вектор выигрышей A, 3) (см. рис. 7.19). 1еперь
очевидно, что игрок 1 выберет OUT в первом узле решения, поскольку
при заданном поведении в подыгре игроку 1 выгоднее выбрать ход OUT,
что даст ему выигрыш 2, чем ход IN, дающий ему в конечном счете
выигрыш, равный 1.
Рис. 7.18. Подыгра
OUT
IN
кЬ
OUT
V^y
(а)
(б)
Рис. 7.19. (а) — Поведение в подыгре; (б) — редуцированная игра
при данном поведении в подыгре
1 Существует также равновесие по Нэшу в смешанных стратегиях, но, чтобы не
усложнять обсуждение, мы его пока опускаем.

404
Часть III. Стратегическое поведение
В целом построенные стратегии выглядят следующим образом. Для
игрока 1 — OUT в первом узле решения и L во втором; для игрока 2 — /в
его единственном информационном множестве.
Следует отметить два сходства со случаем совершенной информации.
Во-первых, эти стратегии отражают способность игрока 1 смотреть
вперед в том смысле, что его выбор в первом узле решения оптимален при
условии, что в последующем играется равновесие по Нэшу. Таким
образом, игрок 1 не просто смотрит вперед, он осознает, что в дальнейшем
игра будет «рациональной» в том смысле, что она оказывается
равновесием по Нэшу в этой подыгре. Во-вторых, эти стратегии являются
равновесием по Нэшу в исходной игре.
Полученные стратегии называются стратегиями,
соответствующими совершенному в подыграхравновесию. Вспомним, в подыгре было
два равновесия и мы произвольно выбрали одно из них. Если бы мы
выбрали другое, то в результате получили бы и другие стратегии. Тем не
менее и эти стратегии также являются совершенным в подыграх
равновесием в соответствии с определением, которое будет приведено чуть ниже.
(Убедитесь в этом, сделав одно из упражнений.)
Перед тем как дать формальное определение стратегий,
соответствующих совершенному в подыграх равновесию, мы должны ввести ряд
терминов.
Определение 7.16. Подыгры.
Говорят, что узел х определяет подыгру игры в развернутой форме,
если для любого узла решения у, слабого последователя х и узла решения
z, находящегося в том же информационном множестве, что и узел у,
верно, что z является слабым последователем х.
Таким образом, узел х определяет подыгру, если каждый игрок,
который должен сделать ход, знает, был ли достигнут узел х. Заметим, что
поскольку в определении 7.16 допускается возможность, что у = х, то х
может определять игру только в случае, если х формирует одноточечное
(вырожденное) информационное множество, т.е. только если 1(х) = {х}.
На рис. 7.20(a) указан узел х, определяющий подыгру, а на рис. 7.20F) —
узел jc, который подыгру не определяет. В игре, изображенной на
рис. 7.20(a), каждый узел в неодноточечном информационном множестве
игрока 1 является последователем узла х. Напротив, на рис. 7.20F) узлы
у и z принадлежат информационному множеству игрока 3, но только у
является последователем х.

Глава 7. Теория игр
405
р]
1
ы
(°)
0
W
f°]
0
W
f1]
3
w
f4]
4
w
f1!
i
bJ
Рис. 7.20. (a) — Узел х определяет подыгру; (б) — узел х не определяет
подыгру
Подыгру, определяемую узлом, таким, как х на рис. 7.20(a),
обозначим Гх. Гх содержит все узлы, следующие за х, и наследует
информационную структуру и выигрыши исходной игры Г. На рис. 7.21 изображена
подыгра Гх игры Г, представленной на рис. 7.20(a).
2
B)
[о)
Рис. 7.21. Подыгра Гх игры Г, изображенной на рис. 7.20(a)

406
Часть III. Стратегическое поведение
Заметим, что профиль чистых стратегий s игры Г естественным
образом индуцирует и профиль чистых стратегий любой подыгры Гх в Г. То
есть в любом информационном множестве / в Гх индуцированная чистая
стратегия предписывает в / те же действия, что и s.
Определение 7.17. Совершенное в подыграх равновесие в
чистых стратегиях.
Профиль чистых стратегий s является совершенным в подыграх
равновесием в чистых стратегиях игры в развернутой форме Г, если s
индуцирует равновесие по Нэшу в каждой подыгре игры Г.
Заметим, что, поскольку любая игра в развернутой форме Г сама
является подыгрой, совершенное в подыграх равновесие в чистых
стратегиях в Г также является равновесием по Нэшу в чистых стратегиях в Г.
Следовательно, концепция совершенного в подыграх равновесия является
усилением концепции равновесия по Нэшу. Более того, это усиление
является строгим, как показывает пример, приведенный на рис. 7.22.
(а)
(б)
Рис. 7.22. (а) — Равновесие по Нэшу, которое не является совершенным
в подыграх; (б) — оптимальный ответ игрока 2 в подыгре
Чистые стратегии, отмеченные стрелками на рис. 7.22(a), являются
равновесными по Нэшу, поскольку ни один из игроков не может
увеличить свой выигрыш, переключившись на другую стратегию, при
заданных стратегиях другого игрока. Тем не менее они не являются
совершенным в подыграх равновесием. Чтобы убедиться в этом, обратите
внимание, что стратегии, показанные на рис. 7.22(a), в подыгре не составляют
равновесие по Нэшу. Это видно из рис. 7.22F), где подыгра изображена

Глава 7. Теория игр
407
отдельно и двойными стрелками показано отклонение, которое увеличит
выигрыш игрока 2 в подыгре1.
Сформулированная ниже теорема показывает, что концепция
совершенного в подыграх равновесия, применимая ко всем играм в
развернутой форме, представляет собой обобщение обратной индукции, которая
применима только к играм с совершенной информацией.
Теорема 7.5. Обобщение обратной индукции в концепции
совершенного в подыграх равновесия.
В любой конечной игре в развернутой форме с совершенной
информацией множество стратегий, полученных с помощью метода обратной
индукции, совпадает с множеством совершенных в подыграх равновесий
в чистых стратегиях.
Доказательство. Сначала мы покажем, что любой профиль
стратегий, полученный методом обратной индукции, является совершенным в
подыграх равновесием. Так, обозначим через s профиль стратегий,
полученный методом обратной индукции. Поскольку в игре с совершенной
информацией каждый узел определяет подыгру (см. упражнения), мы
должны показать, что s индуцирует равновесие по Нэшу в подыгре,
определенной узлом решения х для всех jc . Но для каждого узла х подыгра
Гх, определенная х, сама является игрой с совершенной информацией, а
стратегии, индуцируемые s, являются стратегиями, полученными
методом обратной индукции в подыгре. (Чтобы убедиться в этом, вспомните,
каким образом был получен профиль стратегий s, а затем, какой профиль
стратегий получился бы, если бы обратная индукция использовалась для
решения подыгры.) Следовательно, воспользовавшись теоремой 7.4,
делаем вывод о том, что соответствующие части профиля стратегий s
являются равновесием по Нэшу в Гх.
Теперь покажем, что каждое совершенное в подыграх равновесие в
чистых стратегиях может быть получено методом обратной индукции.
Пусть профиль стратегий s — совершенное в подыграх равновесие.
Достаточно проверить, что s может быть получен обратной индукцией.
Рассмотрим любой предпоследний узел. Этот узел определяет подыгру с
одним игроком. Поскольку профиль s — совершенное в подыграх
равновесие, он должен предписать игроку, чья очередь делать ход, выбор
максимизирующий выигрыш этого игрока (в противном случае это не
было бы равновесием по Нэшу в этой подыгре одного игрока). Следова-
1 Обратите внимание, что хотя игрок 2 может увеличить выигрыш в подыгре, он не
может сделать этого в исходной игре. Причина заключается в том, что рассматриваемая
подыгра не достигается при указанных стратегиях. В самом деле, равновесные по Нэшу
стратегии в исходной игре индуцируют равновесия по Нэшу в подыграх, которые
достигаются при первоначальных стратегиях. (См. упражнения.)

408
Часть III. Стратегическое поведение
тельно, выбор, сделанный в соответствии с s, согласуется с методом
обратной индукции. Рассмотрим теперь любой узел решения,
последователи которого — только предпоследние узлы. Этот узел определяет подыг-
ру, в которой во всех узлах, следующих за ним, стратегия s
специфицирует выбор, получаемый обратной индукцией. Поскольку s индуцирует
равновесие по Нэшу в этой подыгре, то он должен указать
максимизирующий выигрыш ход игрока г{х) в узле х при условии, что выбор во
всех последующих узлах — это выбор, сделанный согласно методу
обратной индукции (т.е. выбор, индуцированный s). Следовательно, выбор,
точно определенный в каждом таком х, также согласуется с методом
обратной индукции. Двигаясь подобным образом вверх по дереву игры, мы
получим желаемый результат. ¦
Совершенное в подыграх равновесие в чистых стратегиях существует
не всегда, как не всегда существует равновесие по Нэшу в чистых
стратегиях в играх в стратегической форме. Например, рассмотрим игру,
изображенную на рис. 7.23. Поскольку единственная подыгра — это сама
игра, множество совершенных в подыграх равновесий в чистых стратегиях
совпадает с множеством равновесий по Нэшу в чистых стратегиях в этой
игре. Легко убедиться, однако, в том, что ни один из четырех профилей
чистых стратегий не является равновесием по Нэшу.
1
L ^*\/?
1 / V 1 / \г
(',) {1) {-:) С)
Рис. 7.23. Игра, в которой отсутствует совершенное в подыграх равновесие
в чистых стратегиях
Чтобы гарантировать существование по крайней мере одного
совершенного в подыграх равновесия, мы должны дать возможность игрокам
рандомизировать свой выбор. Следующий раздел рассматривает
рандомизацию в игре в развернутой форме.
Смешанные стратегии, поведенческие стратегии
и совершенная память
Для игр в стратегической форме существует единственный
естественный способ рандомизировать поведение — приписать каждой чистой

Глава 7. Теория игр
409
стратегии вероятность и затем использовать механизм рандомизации,
который выбирает каждую стратегию с этой приписанной вероятностью.
Для игр же в развернутой форме есть два способа рандомизации
поведения. Первый — это прямой аналог способа, используемого для игр в
стратегической форме: припишите каждой стратегии вероятность и перед
началом игры воспользуйтесь подходящим механизмом рандомизации
для выбора одной из ваших чистых стратегий. Таким способом ваш
выбор определяется единожды и в самом начале игры. Как только чистая
стратегия выбрана, на протяжении всей игры ваше поведение
определяется этой чистой стратегией; никакая рандомизация в дальнейшем не
предпринимается.
Второй способ — использовать механизм рандомизации, когда вы
должны сделать ход. Вместо того чтобы рандомизировать поведение
единожды в начале игры на множестве чистых стратегий, вы рандомизи-
руете при каждом ходе на множестве доступных вам в рассматриваемый
момент действий. Так, если на протяжении всей игры вы должны ходить
более одного раза, то и использовать механизм рандомизации вы будете
более одного раза. При каждом ходе вы можете воспользоваться разными
механизмами рандомизации.
Первый способ рандомизации называется смешанной стратегией,
чтобы придерживаться терминологии, принятой для игр в стратегической
форме. Второй называется поведенческой стратегией.
Формально смешанная стратегия mi игрока i — это, как и раньше,
вероятностное распределение на множестве чистых стратегий St игрока
/. То есть для каждой чистой стратегии st е Si, /иД-у,.) обозначает
вероятность выбора чистой стратегии sr Следовательно, /H.(,s.)e [0, 1] и
SjeSj
В то же время поведенческая стратегия bi задает для каждого
информационного множества игрока / вероятностное распределение на
множестве действий, доступных в этом множестве. То есть
Ь;(а, /)е[0, 1] и X МЛ' ^) = 1 Для каждого информационного множе-
аеА{1)
ства /, принадлежащего игроку /, где A(l) обозначает множество
действий, доступных в информационном множестве / .
В дереве игры мы обозначаем поведенческую стратегию, указывая
для каждого действия вероятность, с которой оно выбирается (в скобках).
Например, на рис. 7.24(г) указана поведенческая стратегия игрока 1, в
соответствии с которой в своем первом информационном множестве он вы-

410
Часть III. Стратегическое поведение
бирает и L, и R с вероятностью 1/2, а во втором — L с вероятностью
2/3, a R с вероятностью 1/3.
1 1
(в) (г)
Рис. 7.24. Эквивалентные поведенческие стратегии.
Смешанная стратегия, в которой игрок 1 выбирает чистую стратегию LL
(на рис. (а) отмечена стрелками) с вероятностью 1/2, чистую стратегию RL
(на рис. (б) отмечена двойными стрелками) с вероятностью 1/3 и чистую
стратегию RR (на рис. (в) отмечена тройными стрелками) с вероятностью
1/6, эквивалентна поведенческой стратегии, показанной на рис. (г), где
вероятности, приписанные действиям, приведены в скобках
Оказывается, хотя мы и не будем это доказывать, во всех играх,
рассматриваемых в этом учебнике, не имеет значения, какую стратегию —
смешанную или поведенческую — будут использовать игроки. Со
стратегической точки зрения они эквивалентны. То есть для каждой смешанной
стратегии mi игрока / существует поведенческая стратегия, дающая
игроку i точно такой же ожидаемый выигрыш, как и стратегия mi,
независимо от стратегий (смешанных или поведенческих), используемых дру-

Глава 7. Теория игр 411
¦»^™"»»»^^^^'»"'""»^^^^^""""^»^"^^^^»»'"™^^ ¦=—*^^™
гими игроками. Аналогично для каждой поведенческой стратегии
существует эквивалентная смешанная стратегия1.
Пример 7.6. На рис. 7.24(а—в) указаны три чистых стратегии
игрока 1 в игре в развернутой форме, а именно ZZ, RL и RR. Рассмотрим
смешанную стратегию, приписывающую этим чистым стратегиям вероятности
1/2, 1/3 и 1/6 соответственно. Что же тогда представляет собой
поведенческая стратегия, эквивалентная данной смешанной стратегии? Чтобы
выяснить это, мы просто вычислим вероятности, с которыми будут
предприниматься действия в случае, если достигается информационное множество,
в котором они могут быть выбраны. Например, поскольку первое
информационное множество игрока 1 непременно будет достигнуто,
индуцированная вероятность, с которой будет выбрано действие Z,, равна 1/2, как и
вероятность действия R (см. рис. 7.24 (г)). Что касается второго
информационного множества игрока 1, заметим, что оно достигается в игре только
при чистых стратегиях RL и RR. Следовательно, при условии, что будет
выбрана одна из этих стратегий, вероятность выбора L игроком 1 в его
втором информационном множестве равна 2/3, а вероятность выбора R —
соответственно 1/3. Объединим полученные результаты. На рис. 7.24(г)
показана эквивалентная поведенческая стратегия. ¦
Как уже упоминалось выше, всем играм, которые будут
рассматриваться в этом учебнике, свойственна эквивалентность смешанных и
поведенческих стратегий. Этим качеством обладают все игры с совершенной
памятью.
Определение 7.18. Совершенная память.
Игра в развернутой форме имеет совершенную память, если всякий
раз, когда два узла х и у = (х, а, а19 ..., ак) принадлежат одному
игроку, каждый узел из того же информационного множества, что и у,
имеет вид w = (z, а, Яр..., а\) для некоторого узла z в том же
информационном множестве, что и х.
Совершенная память говорит о том, что каждый игрок всегда помнит
то, что он знал в прошлом об истории игры. В частности, по
определению 7.18, если игрок не может провести различия между двумя
историями у и w, то они могут отличаться только действиями, предпринятыми
другими игроками. В частности, ни один из игроков не забывает то, что
он делал раньше.
1 Для некоторых смешанных (поведенческих) стратегий могут существовать несколько
эквивалентных поведенческих (смешанных) стратегий. Детальный анализ
эквивалентности смешанных и поведенческих стратегий можно найти в статье Куна [Kuhn, 1953].

412
Часть III. Стратегическое поведение
На рис. 7.25 изображена игра в развернутой форме, не обладающая
свойством совершенной памяти. Заметим, что в игре не существует
поведенческой стратегии, эквивалентной смешанной стратегии,
приписывающей вероятность 1/2 обеим чистым стратегиям Ы и Лг, поскольку любая
такая поведенческая стратегия должна приписывать положительные
вероятности обоим выборам L и R в первом информационном множестве
игрока 1, и она также должна приписывать положительные вероятности
обоим выборам / и г во втором информационном множестве игрока 1. Но
она тогда так же приписывает положительные вероятности
терминальным узлам (Z,, г) и (Л, /), тогда как указанная смешанная стратегия
этого не делает.
10 0 1
Рис. 7.25. Игра в развернутой форме, не обладающая свойством
совершенной памяти. Это свойство нарушено, поскольку узлы х
и у = (х9 L) принадлежат игроку 1, однако узел w = (x, R) находится
в том же информационном множестве, что и у. Таким образом, игрок 1 не
видит различий между двумя историями у = (х9 L) и w = (x, Л), хотя они
отличаются предыдущим его действием
Поскольку смешанные и поведенческие стратегии в играх с
совершенной памятью эквивалентны, мы можем позволить себе использовать
то понятие, которое более удобно. Поэтому в дальнейшем ограничимся
множеством поведенческих стратегий игроков.
Совершенное в подыграх равновесие с рандомизацией действий
Хотя в игре может не быть совершенного в подыграх равновесия в
чистых стратегиях (см. пример на рис. 7.23), совершенное в подыграх
равновесие в поведенческих стратегиях существует при довольно общих
условиях. По аналогии с определением 7.17 дадим следующее
определение.

Глава 7. Теория игр 413
Определение 7.19. Совершенное в подыграх равновесие.
Профиль поведенческих стратегий Ь называется совершенным в
подыграх равновесием в конечной игре в развернутой форме Г, если он
индуцирует (составляет) равновесие по Нэгиу в каждой подыгре игры Г.
Заметим, что, поскольку поведенческие и смешанные стратегии
эквивалентны в играх в развернутой форме с совершенной памятью, то по
теореме 7.1 профиль смешанных стратегий является равновесием по Нэ-
шу в игре (или подыгре), если ни у одного игрока нет чистой стратегии,
дающей ему больший выигрыш при заданных поведенческих стратегиях
других игроков. Этот факт полезен как при поиске совершенного в
подыграх равновесия, так и при проверке того, будет ли профиль стратегий
совершенным в подыграх равновесием. Эквивалентность смешанных и
поведенческих стратегий гарантирует также, что в играх с совершенной
памятью любое совершенное в подыграх равновесие является и
равновесием по Нэшу.
Ниже мы установим, что совершенные в подыграх равновесия
существуют при довольно общих условиях.
Теорема 7.6 (Теорема Зельтена). Существование совершенного в
подыграх равновесия.
В любой конечной игре в развернутой форме с совершенной памятью
существует совершенное в подыграх равновесие.
Доказательство. В доказательстве используется метод, сходный с
алгоритмом обратной индукции. Мы построим искомую поведенческую
стратегию с помощью пошаговой процедуры, продвигаясь от конца игры
к началу.
Выберем подыгру, не содержащую других подыгр кроме себя самой.
Это всегда возможно, поскольку игра конечна. По теореме 7.2 в этой
подыгре существует равновесие по Нэшу в смешанных стратегиях.
Поскольку исходная игра — игра с совершенной памятью, то подыгра также
обладает этим свойством, а для любой смешанной стратегии (в подыгре)
найдется эквивалентная поведенческая стратегия. Поскольку стратегии
эквивалентны, профиль поведенческих стратегий также является
равновесием по Нэшу в подыгре.
Теперь заменим подыгру на вектор выигрышей, определяемый
равновесными стратегиями подыгры. Тем самым мы редуцировали игру и
определили в подыгре часть совокупной поведенческой стратегии.
Теперь мы можем повторить процедуру для редуцированной игры и
действовать таким же образом до тех пор, пока полностью не определим
профиль равновесных смешанных стратегий в исходной игре. Заметим, что
такая процедура должна иметь конечное число шагов, поскольку игра
конечна.

414
Часть III. Стратегическое поведение
То, что полученный таким образом профиль поведенческих
стратегий — совершенное в подыграх равновесие, доказывается по аналогии с
первой половиной доказательства теоремы 7.5. Вас попросят уточнить
детали в одном из упражнений. ' ¦
Важно отметить, что нельзя отбрасывать предположение о
совершенной памяти. В играх, не обладающих этим свойством, совершенное в
подыграх равновесие может не существовать. Этот вопрос также будет
рассмотрен в одном из упражнений.
На рис. 7.26 (а—в) проиллюстрирован алгоритм доказательства.
Обратите внимание, как концепция совершенного в подыграх равновесия
перекликается с идеей обратной индукции, а именно: оптимальный выбор
в начале игры определяется оптимальным выбором в дальнейшем. В
следующем подразделе мы рассмотрим дальнейшее усиление концепции
равновесия по Нэшу, чтобы более плодотворно применять эту
центральную идею.
'°1 {
(а)
(б)

Глава 7. Теория игр
415
Рис. 7.26. (а) Поиск совершенных в подыграх равновесий. В подыгре,
определенной одноточечным информационным множеством игрока 2, нет
других подыгр, кроме нее самой. Стрелки изображают равновесие по Нэшу в
этой подыгре. Заменив подыгру соответствующими выигрышами, получим
дерево редуцированной игры на рис. (б); (б) Редуцированная игра. В этой
игре только одна подыгра — сама игра. Несложно проверить, что в этой
игре существует единственное равновесие по Нэшу: игрок 1 выбирает М и
R с вероятностями 1/2; игрок 2 выбирает /иге вероятностями 1/2; (в)
Совершенное в подыграх равновесие. (Существует ли в игре другое
совершенное в подыграх равновесие?)
7.3.7. Секвенциальное равновесие
В игре, изображенной на рис. 7.27, существует несколько равновесий
по Нэшу. А поскольку в ней нет собственных подыгр, то каждое из этих
равновесий совершенно в подыграх. Но все ли из этих равновесий
являются разумными?
№
А
т (
Рис. 7.27. Не все совершенные в подыграх равновесия являются разумными

416
Часть III. Стратегическое поведение
Рассмотрим совершенное в подыграх равновесие в чистых стратегиях,
в котором игрок 1 выбирает L, а игрок 2 выбирает т. Очевидно, что этот
набор стратегий является равновесием по Нэшу (и, следовательно,
совершенным в подыграх равновесием), поскольку ни один из игроков не может
увеличить выигрыш, изменив свою стратегию. В частности, игрок 1 не
выбирает Мили R, поскольку в соответствии со своей равновесной
стратегией игрок 2 ответит выбором т, что приведет к выигрышу первого игрока,
равному -1, вместо 0, как в случае выбора L. Таким образом, угрозы
игрока 2 играть w, если у него будет возможность сделать ход, достаточно,
чтобы убедить игрока 1 выбрать L. Но правдоподобна ли угроза игрока 2?
Имеет ли смысл игроку 1 верить, что игрок 2 выберет т, если у него будет
возможность сделать ход? Чтобы ответить на этот вопрос, мы должны
рассмотреть, какой выбор сделал бы игрок 2, если бы 1 не выбрал L.
Итак, предположим, что игрок 2 должен сделать ход. Как он может
решить, какое действие выбрать? В конечном счете, его выбор зависит от
хода игрока 1. Если игрок 1 выберет М, то лучший ответ игрока 2 — это г,
в случае же, если игрок 1 выберет R, то лучший ответ игрока 2 — это /.
Теперь, поскольку игрок 2 не знает хода игрока 1, но ему известно
только, что игрок 1 выбрал либо М, либо Л, то игрок 2 должен
сформировать ожидания относительно хода игрока 1. Пусть р(х) и р(у)
обозначают вероятности, которые игрок 2 приписывает событиям, что
достигнуты узлы х и у, при предположении, что он имеет ход (следовательно,
р(х) + р(у) = 1). При заданных ожиданиях игрока 2 мы можем найти его
ожидаемые полезности выбора /, т или г. Эти ожидаемые полезности
равны соответственно 4р(у), 1 и 4р(х). Конечно же игрок 2 сделает
выбор, максимизирующий его ожидаемую полезность.
Поскольку на этом этапе мы не знаем ожиданий игрока 2 (т.е.
значений р(х) и р(у)), мы не можем определить его выбор. Однако мы можем
сказать, что это не т. То есть независимо от того, каковы значения р(х) и
р{у), ход т никогда не будет максимизировать ожидаемую полезность
игрока 2. Чтобы убедиться в этом, просто заметим, что смешанная
стратегия, в которой игрок 2 выбирает и /, и г с вероятностями 1/2, дает ему
ожидаемую полезность
р(х)
~@) + iD)уР(у)(|D) + |@) | = 2(р(х) + р(у)) = 2,
что больше, чем ожидаемая полезность при выборе w, равная 1. Таким
образом, независимо от ожиданий игрока 2 по крайней мере одна из
стратегий / или г даст ему строго бблыыую ожидаемую полезность, чем
стратегия т.

Глава 7. Теория игр
417
Следовательно, в противоречие с указанным совершенным в поды-
грах равновесием игрок 2, получив ход, не выберет т. Следовательно, это
совершенное в подыграх равновесие не является разумным.
Причина неразумности такого совершенного в подыграх равновесия
состоит в том, что эта концепция не накладывает никаких ограничений на
поведение игрока 2 в информационном множестве, которое не
достигается. Поведение игрока 2 в этом информационном множестве никак не
регламентируется, поскольку недостигнутое информационное множество не
является тривиальным и, следовательно, не определяет подыгру.
Тем не менее, как мы видели, введя ожидания игрока 2 относительно
того, в каком узле в информационном множестве он находится при
условии, что оно достигнуто, мы можем разумным образом регламентировать
его поведение в этом информационном множестве. Это может оказать
существенное влияние на множество равновесных исходов. Вас попросят
показать в одном из упражнений, что единственным совершенным в
подыграх равновесием, в котором игрок 2 выбирает т с нулевой
вероятностью (что и будет соответствовать проведенному выше анализу), является
равновесие, в котором игрок 1 выбирает L с вероятностью 0.
Теперь мы формально введем ожидания игроков на множестве узлов
нетривиальных информационных множеств, чтобы усилить концепцию
совершенного в подыграх равновесия, используя идею обратной индукции.
Ожидания и их связь со стратегиями
Как было показано на примере игры, изображенной на рис. 7.27,
имеет смысл учитывать ожидания игроков в их информационных множествах
относительно истории игры вплоть до этих информационных множеств.
Для заданной игры в развернутой форме Г и узла х обозначим через
р(х) вероятность, которую игрок l(x) приписывает истории х при
условии, что достигнуто информационное множество 1(х). Таким образом,
для любого узла у выполняется равенство ^ р(х) = 1. Функция /?(•) на-
xeJ(y)
зывается системой ожиданий, поскольку она представляет ожидания
всех игроков во всех их информационных множествах относительно
истории игры вплоть до этих информационных множеств.
Изображая дерево игры, мы будем приводить систему ожиданий р,
указывая вероятности, приписанные каждому узлу в каждом
нетривиальном информационном множестве, рядом с соответствующим узлом в
квадратных скобках.
Поскольку ожидания игрока относительно истории игры обычно
оказывают влияние на его поведение, важно, чтобы формирование этих
ожиданий происходило осмысленно.

418
Часть III. Стратегическое поведение
Нас интересует ответ на следующий вопрос. Какая система ожиданий
р будет разумной для заданного профиля поведенческих стратегий Ы Для
удобства назовем пару «система ожиданий — профиль поведенческих
стратегий» (р, Ь) стратегическим набором. Для заданной пары (р, Ь)
р интерпретируется как ожидания, которые формирует игрок при
заданном профиле поведенческих стратегий Ъ. Таким образом, наш вопрос
можно переформулировать так: какие стратегические наборы разумны!
Например, рассмотрим игру, изображенную на рис. 7.28, где
показаны поведенческая стратегия игрока 1 и ожидания игрока 2 (а, |3 и
уметавшиеся неопределенными). При заданной стратегии игрока 1 игрок 2
может вычислить вероятности достижения каждого узла в своем
информационном множестве при условии, что он достиг хотя бы одного из них,
просто используя правило Байеса. Таким образом, единственно
разумными ожиданиями игрока 2 (если задана стратегия игрока 1) будут а = 1/3,
C = 1/9 и у = 5/9.
1
Рис. 7.28. Использование правила Байеса. Чтобы понять, почему
использование правила Байеса разумно, предположим, что эта игра разыгрывается
1 500 раз и при этом игрок 1 использует указанную на рисунке стратегию.
В среднем из 1500 раз игрок 1 выбирает две самые левые ветви
400 + 200 = 600 раз, а остальные выборы делаются 300 + 100 + 500 = 900 раз.
Следовательно, информационное множество игрока 2 будет достигнуто в
игре 900 раз. За эти 900 раз левый узел информационного множества будет
достигнут 300 раз, средний узел — 100 раз и правый узел — 500 раз. Таким
образом, при условии, что информационное множество игрока 2 достигнуто,
вероятность того, что игрок 2 оказался в левом узле своего информацион-
300 1/1 а 10° 1/о
ного множества, равна а = = 1/3; в среднем узле р = = 1/9 и в пра-
900 900
вом узле у = = 5/9.
J ' 900
Таким образом, для того чтобы стратегический набор (р, Ь) был
разумным, система ожиданий р , где это возможно, должна быть получена

Глава 7. Теория игр
419
при заданном профиле поведенческих стратегий Ъ по правилу Байеса. То
есть если Р(х \ Ъ) обозначает вероятность того, что узел х будет
достигнут в игре при использовании профиля поведенческой стратегии Ь, то
правило Байеса утверждает, что для любого информационного множества
/ и для каждого хе I соотношение
Р(х\Ь)
р(х) =
yel
выполняется всякий раз, когда знаменатель положителен, т.е. когда
информационное множество достигается с положительной вероятностью
при использовании Ь \
Мы сформулируем это как наш первый принцип.
Правило Байеса: Ожидания должны быть получены из стратегий
по правилу Байеса, когда это возможно.
Выражение «когда возможно» означает «во всех информационных
множествах, которые достигаются с положительной вероятностью при
заданном профиле стратегий». Следовательно, правило Байеса может быть
использовано не всегда. Например, в игре, изображенной на рис. 7.29, при
заданных поведенческих стратегиях игроков 1 и 2 информационное
множество игрока 3 не достигается (т.е. достигается с нулевой вероятностью).
Таким образом, мы не можем формально использовать правило Байеса в
этой ситуации для того, чтобы получить ожидания игрока 3. Тем не менее
при заданной стратегии игрока 2 единственно разумным для игрока 3
будет а = 1 / 3 .
1
Рис. 7.29. Ограничения на ожидания, когда правило Байеса не используется
1 Для простоты обозначений мы не стали подчеркивать тот факт, что Р(х \ Ь) также
зависит и от распределения вероятностей ходов природы к.

420
Часть III. Стратегическое поведение
Причина, по которой это — единственно разумные ожидания,
заключается в следующем: поведенческая стратегия игрока 2 в строгом
понимании предполагает, что он будет выбирать левую ветку с вероятностью
1/3, если игрок 1 выберет правую ветку, даже когда предполагается, что
игрок 1 выбирает левую ветку с вероятностью 1. Таким образом, выбор
игроком 2 смешанной стратегии уже предполагает, что игрок 1 должен
отклониться от своей стратегии для того, чтобы стратегия игрока 2
«сыграла». Следовательно, когда достигается информационное множество
игрока 3, единственно разумным для него будет предположить, что с
вероятностью 1/3 игрок 2 выбрал левую ветку.
Есть ли еще ограничения, которые мы могли бы ввести для ожиданий
при заданных поведенческих стратегиях? Да, есть. Рассмотрим игры,
изображенные на рис. 7.30 и 7.31, где указаны поведенческие стратегии
игроков 1 и 2. В каждой игре при любых значениях а и C из интервала от 0
до 1 результирующий стратегический набор согласуется с правилом Бай-
еса. Более того, доводы, подобные использовавшимся при анализе игры,
изображенной на рис. 7.29, здесь не могут быть приведены. Тем не менее
есть основание настаивать, что в каждом из этих случаев а = р. В самом
деле это равенство следует из следующих двух принципов, которые
намеренно описываются неформально.
1 OUT
Рис. 7.30. Ограничение, налагаемое принципами одинаковых ожиданий
и независимости

Глава 7. Теория игр
421
1 A)
Рис. 7.31. Ограничение, налагаемое принципом независимости
Независимость: Ожидания должны отражать независимость
выбора игроками своих стратегий.
Одинаковые ожидания: У игроков с одинаковой информацией
ожидания совпадают.
Чтобы понять, каким образом из этих двух принципов следует, что
ос = Р, рассмотрим рис. 7.30. Когда достигается информационное
множество игрока 2, а — это вероятность, которую игрок 2 приписывает
событию «игрок 1 выбрал L». Теперь, хотя это и не показано на рисунке,
принцип одинаковых ожиданий подразумевает, что игрок 3 в своем
информационном множестве также приписывает вероятность а событию
«игрок 1 выбрал L» (т.е. когда игрок 3 обладает той же информацией, что
и игрок 2). Но в силу независимости стратегий игроков знание стратегии
игрока 2 не дает игроку 3 никакой дополнительной информации о выборе
игрока I1. Следовательно, ожидания игрока 3 относительно игрока 1 не
1 Обратите внимание, что принцип независимости применим, даже если
информационное множество игрока 2 разделить на два одноточечных информационных множества.
В этом случае выбор игрока 2 (/ или г) может зависеть от выбора игрока 1 (L или R).
Следовательно, знание выбора игрока 2 (/ или г) дает игроку 3 дополнительную
информацию о выборе игрока 1. Тем не менее это не нарушает принципа независимости,
поскольку в новой игре множество стратегий игрока 2 — это {//, /г, г/, гг}, а не {/, г} , и в
соответствии с принципом независимости знание того, какую стратегию игрок 2
выбрал, не дает игроку 3 информации о выборе игрока 1. Поможет ли вам при
прогнозировании поведения игрока 1 информация о том, что стратегия игрока 2 «выбирать /, если
игрок 1 выберет L, и выбирать г, если игрок 1 выбирает Я»?

422
Часть III. Стратегическое поведение
должны измениться (т.е. игрок 3 полагает, что с вероятностью а игроком
1 выбран ход L). Но это и означает, что р = а.
Аналогичные рассуждения можно привести и для игры на рис. 7.31.
Знание того, выбрал ли игрок 1 L или Л, не влияет (согласно принципу
независимости) на ожидания игрока 3 относительно вероятности выбора
игроком 2 L или М9 т.е. а = р. Заметим, что в принципе одинаковых
ожиданий здесь нет нужды, поскольку два рассматриваемых
информационных множества принадлежат одному и тому же игроку.
Эти три принципа — правило Байеса, независимость и одинаковые
ожидания — обеспечивают все ограничения на ожидания, которые мы
анализировали в предыдущих примерах. (Вас попросят в одном из
упражнений показать, что в игре, изображенной на рис. 7.29, независимость
приводит к ограничению а = 1/3.) Может возникнуть вопрос: какие
ограничения на ожидания для игр в развернутой форме следуют из этих идей?
Мы удовлетворимся ответом, не вдаваясь в детальное обсуждение.
Хотя доказательство здесь не приводится, можно показать, что
стратегический набор удовлетворяет правилу Байеса, а также принципам
независимости и одинаковых ожиданий тогда и только тогда, когда он
согласован, в том смысле, как мы определим ниже.
Введем еще одно понятие. Поведенческая стратегия в конечной игре
в развернутой форме называется (полностью) вполне смешанной, если
она всем действиям приписывает положительные вероятности. В одном
из упражнений вас попросят показать, что при полностью смешанных
стратегиях каждое информационное множество достигается с
положительной вероятностью. Следовательно, при таких стратегиях правило
Байеса однозначно определяет ожидания игроков.
Определение 7.20. Согласованные стратегические наборы.
Стратегический набор (/?, Ь) для конечной игры в развернутой
форме Г согласован, если существует последовательность полностью
смешанных поведенческих стратегий Ьп, сходящихся к Ь, такая, что
соответствующая последовательность индуцированных правилом
Байеса ожиданий р" сходится к р.
Согласованность — более сильное ограничение, чем правило Байеса,
причем даже более сильное ограничение, чем правило Байеса в каждой
подыгре. Чтобы как-то «прочувствовать» понятие согласованности,
применим введенное определение к анализу примера, который мы уже
рассматривали.
Пусть для игры, изображенной на рис. 7.28 Ъ обозначает профиль
поведенческих стратегий, указанных на рисунке (поведенческая стратегия

Глава 7. Теория игр
423
игрока 2 в данном случае к делу не относится), и пусть р = (а, р, у)
обозначают систему ожиданий. Для того чтобы стратегический набор был
согласованным, должна существовать последовательность
стратегических наборов (рп, Ь")—>(/?, Ь), где Ъп — профиль полностью
смешанных стратегий для каждого пир" получены из Ь" по правилу Байеса.
Но это означает, что последовательность стратегий первого участника
такова, что вероятности, с которыми он выбирает три правые ветки
(ведущие к информационному множеству игрока 2), сходятся,
соответственно к 3/15, 1/15 и 5/15. Поскольку последовательность ожиданий
рассчитывается по правилу Байеса, то а" IР" -> 3, C" / у" —> 1 / 5 и
f /ос" ->5/3. Таким образом, а" ->1/3, р" -П/9 и у" ->5/9.
Следовательно, согласованность стратегического набора требует, чтобы
выполнялось равенство р = (а, р, у) = A / 3, 1/9, 5 / 9), как мы и утверждали выше.
На рис. 7.29 для заданных поведенческих стратегий согласованность
означает, что а = 1/3. Действительно, для любой последовательности
полностью смешанных стратегий, сходящейся к единице, вероятность
того, что игрок 1 выберет правую ветку и игрок 2 — тоже правую, в пределе
в 2 раза больше, чем вероятность, что игрок 1 выберет правую ветку, а
игрок 2 — левую. А ожидания в игре — это предел последовательности
ожиданий, выводимых по правилу Байеса из этой последовательности.
Мы оставляем в качестве упражнения проверку того, что из
согласованности следуют ограничения, о которых говорилось применительно к
примерам, приведенным на рис. 7.30 и 7.31.
Хотя формальное определение согласованного стратегического
набора представляется довольно техничным и даже ad hoc предположением,
важно иметь в виду, что согласованность выражает три идеи: правило
Байеса, принцип независимости и принцип общности ожиданий. Иными
словами, стратегический набор не согласован в смысле определения 7.20
тогда и только тогда, когда он не удовлетворяет правилу Байеса, а также
принципам независимости или общности ожиданий1.
Секвенциальная рациональность
Исследовав взаимосвязь между ожиданиями и стратегиями, мы
можем вернуться к осмыслению понятия обратной индукции для любой
игры в развернутой форме.
Более подробно эта интерпретация согласованности рассматривается в работе Коль-
берга и Рени [Kohlberg, Reny, 1997].

424
Часть III Стратегическое поведение
Применение метода обратной индукции к играм с совершенной
информацией равнозначно предположению о том, что все игроки делают
максимизирующий выигрыши выбор каждый раз, когда получают ход.
Концепция совершенного в подыграх равновесия обобщает эту идею и на
более широкий класс игр. Однако, как видно на примере игры на
рис. 7.27, эта концепция недостаточно строгая для того, чтобы исключить
поведение, которое не является оптимальным в каждом информационном
множестве.
Теперь, после того как мы наделили всех игроков ожиданиями по
поводу истории игры в каждой ситуации, когда наступает его черед делать
ход, логично потребовать, чтобы любой выбор, сделанный конкретным
игроком в каждом информационном множестве, был оптимальным
выбором. Далее мы соответствующим образом обобщим идею обратной
индукции для любой игры в развернутой форме. А пока изложим все это
формально.
Рассмотрим конечную игру в развернутой форме, стратегический
набор (р, Ь) и информационное множество /, принадлежащее игроку i.
Чтобы проверить тот факт, что поведенческая стратегия bi игрока i будет
для него оптимальной, когда достигается его информационное
множество /, нам надо вычислить выигрыш / для любой другой стратегии,
которую он может использовать, когда достигается /.
Найдем выигрыш игрока i при стратегическом наборе (/?, Ь) при
условии, что достигнуто информационное множество /. Для каждого узла
х в / мы можем использовать Ъ, чтобы определить выигрыш игрока /
начиная с узла х. Будем рассуждать так, как если бы узел х определял
подыгру. Пусть для всех таких х ut(b\x) обозначает этот выигрыш.
Таким образом, и.F| х) — это величина выигрыша игрока /, если
достигнут узел х в информационном множестве /. Конечно, игрок / не знает,
какой именно узел информационного множества / достигнут. Но
система ожиданий р описывает вероятности, которые игрок i приписывает
каждому узлу в /. Следовательно, выигрыш игрока / в соответствии со
стратегическим набором (р, Ь) при условии, что достигнуто
информационное множество /, — это просто среднее (ожидаемое) значение чисел
ut{b | х) в соответствии с системой ожиданий р, а именно
2>(*)И,0|Х).
jce/
Обозначим этот выигрыш через v;(/?, Ъ \ I). На рис. 7.32 и 7.33
приведен пример игры, для которой вычислены v.(p, b\I).

Глава 7. Теория игр
425
B/5) ^^ C/2) \ "Ч. A/10)
B/5^/\B/5)
2 *^ \'х/[\12] у\[\1Ъ] 1 >»[1/6]
0)/ \@) A/3) / N/2/3) / V2/3) A/3)/ \B/3)
1Л 5 6 3 /A/3) 0 6
A/2)/ \A/2) ГТ- з
1 4
C/4) / \ A/4) C/4) / \ A/4)
8 12 4 12
Рис. 7.32. Выигрыши, обусловленные информационным множеством.
На рис. 7.33 показаны шаги вычисления этого выигрыша при условии
достижения информационного множества /
/3)/ \B/3)
/ \
6 3
(а)
A/3)/ \B/3)
Л о
C/4)/\A/4)
8 12
(б)
A/3)-
6
1 V2/3)
C/4)/\
4
(в)
,A/4)
12
Рис. 7.33. Вычисление выигрышей в информационном множестве.
Рассмотрим по отдельности узлы х, у и z информационного множества
1 2
игрока 1, обозначенного на рис. 7.32 как / : а) их(Ь \ х) = -F)+-C) = 4;
б)и1(Ь\у) =
-(8)н-—A2)
8 4
+ |[0] = 3;b)WiF|z) = ±[6] + |
Следовательно,
1
3
4 4
= 6.
1
1
v,(/7, b\I) = p(xX(b|х) + р(у)щ(Ь|y) + p(z)ux{b| z) = -D) + -C) + -F) = 4

426
Часть III. Стратегическое поведение
Теперь, когда мы знаем, каким образом найти выигрыш игрока / для
произвольного стратегического набора при условии, что достигнуто одно
из его информационных множеств, нетрудно сравнить этот выигрыш с
выигрышем, который получит игрок, если изменит свою стратегию в этой
точке игры. Вышесказанное позволяет сформулировать основное
определение этого раздела.
Определение 7.21. Секвенциальная рациональность.
Стратегический набор (/?, Ъ) для конечной игры в развернутой
форме секвенциально рационален, если для любого игрока i, любого
информационного множества I y принадлежащего игроку i, и любой
поведенческой стратегии Ъ\ игрока i имеет место
v,ip, b\i)>Vi(P(b;, b_,)\i).
Мы также будем называть профиль поведенческих стратегий Ъ
секвенциально рациональным, если для некоторой системы ожиданий р
стратегический набор (р, Ь) секвенциально рационален.
Таким образом, стратегический набор секвенциально рационален,
если ни в каком из моментов игры ни один из игроков не имеет стимула
изменить свою стратегию. Заметим, что выделенная курсивом фраза «ни в
каком из моментов игры» относится не только к информационным
множествам, достигаемым при поведенческой стратегии Ъ с положительной
вероятностью, но и ко всем информационным множествам вообще.
Значение этого уточнения становится очевидным при анализе игры,
приведенной на рис. 7.27. Как вы помните, совершенное в подыграх
равновесие, в котором игрок 1 выбирает L, а игрок 2 выбирает w, не является
разумным именно потому, что игрок 2, если бы он достиг своего
информационного множества, уклонился бы от w. Мы бы не отбросили это
неразумное равновесие, если бы не настаивали на проверке оптимальности
поведения во всех информационных множествах, а ограничились только
проверкой оптимальности поведения в информационных множествах,
которые при заданных стратегиях достигаются с положительной
вероятностью. Однако, как только мы потребовали, чтобы поведение было
оптимальным во всех информационных множествах, нам пришлось отбросить
это совершенное в подыграх равновесие. Более формально, если Ь
обозначает профиль поведенческих стратегий, указанных на рис. 7.27, то не
существует системы ожиданий р такой, что стратегический набор (р, Ь)
секвенциально рационален. (Смотрите упражнения.)
Таким образом, не все совершенные в подыграх равновесия (а
следовательно, и не все равновесия по Нэшу) секвенциально рациональны.

Глава 7. Теория игр
427
Существуют ли игры с секвенциально рациональными стратегиями,
которые не составляют совершенное в подыграх равновесие? Да, существуют.
Следующий пример служит еще одной иллюстрацией того, насколько
важно установить надлежащую связь между ожиданиями и стратегиями.
Игра, изображенная на рис. 7.34, называется «Сравнение монеток».
У каждого игрока есть монетка, которую он выкладывает решкой или
орлом вверх. Если оба игрока выложили монетки решкой вверх или орлом
вверх, то игрок 1 выигрывает у игрока 2 монетку. В противном случае
выигрывает игрок 2. Первый выбор делает игрок 1, но не разжимает
ладони до тех пор, пока игрок 2 не сделает свой выбор. Таким образом,
игрок 2 должен выложить монетку, не зная выбора игрока I1.
м
,1,
A\
Рис. 7.Э4. Секвенциально рациональный стратегический набор, который не
является секвенциальным равновесием. Ожидания игрока 2 не выведены
из стратегий с использованием правила Байеса
В единственном равновесии по Нэшу в этой игре и, следовательно, в
единственном совершенном в подыграх равновесии оба игрока рандоми-
зируют путем выбора орла и решки с вероятностью 1/2. Рассмотрите,
однако, стратегический набор, указанный на рисунке, при котором оба
игрока выбирают орла с вероятностью, равной 1, и ожидания игрока 2
приписывают вероятность 1 выбору игроком 1 решки. Этот
стратегический набор, хотя и не является равновесием по Нэшу, секвенциально ра-
В сущности, игроки делают свой выбор одновременно. Таким образом, эта игра в
развернутой форме эквивалентна игре в стратегической форме, в которой игроки делают
свой выбор одновременно (т.е. игре в стратегической форме из раздела 7.2, которую мы
называли дуэлью отбивающего и подающего; в литературе по теории игр игра такого
вида гораздо чаще называется «Сравнение монеток»). В этом смысле любую игру в
стратегической форме можно моделировать как игру в развернутой форме, в которой
каждый игрок ходит один раз в произвольно выбранном порядке и в которой ни один из
игроков не информирован о выборе, сделанном другими игроками на предыдущих
ходах.

428
Часть III. Стратегическое поведение
ционален, поскольку игрок 1 получает свой максимально возможный
выигрыш, и игрок 2 в соответствии со своими ожиданиями, когда
достигается его информационное множество, также получает свой наибольший
выигрыш. Так происходит потому, что в соответствии с ожиданиями
игрока 2 игрок 1 выбрал решку с вероятностью 1. Следовательно, выбирая орла,
игрок 2 максимизирует свой выигрыш на основании своих ожиданий.
Таким образом, секвенциально рациональные стратегические наборы
не обязаны быть равновесиями по Нэшу. Очевидно, что возникшая в
только что рассмотренном примере проблема заключается в том, что
ожидания не выводятся из стратегий по правилу Байеса.
Объединение понятия секвенциальной рациональности с тремя
принципами, связывающими ожидания со стратегиями, которые мы обсудили
в предыдущем подразделе, — правилом Байеса, независимостью и
общностью ожиданий — ведет к следующей важной концепции равновесия,
предложенной в работе Крепса и Уилсона [Kreps, Wilson, 1982].
Определение 7.22. Секвенциальное равновесие.
Стратегический набор для конечной игры в развернутой форме
является секвенциальным равновесием, если он одновременно согласован и
секвенциально рационален.
Поскольку согласованный стратегический набор действительно
удовлетворяет правилу Байеса (вас попросят проверить это в одном из
упражнений), в единственном секвенциальном равновесии в игре «Сравнение
монеток», изображенной на рис. 7.34, оба игрока выбирают орла с
вероятностью 1/2.
Любопытно применить концепцию секвенциального равновесия к
менее очевидному примеру.
Пример 7.7. Рассмотрим вариант игры «Сравнение монеток»,
который назовем усложненным вариантом сравнения монеток. В игре
участвуют три игрока, у каждого из которых по монетке. Игроки преследуют
следующие цели. Игрок 3 должен сделать тот же выбор, что и игрок 1, а
игрок 1, наоборот, хочет противоположного. Роль игрока 2 в том, чтобы
«помочь» игроку 3 угадать ход игрока 1. Таким образом, можно считать,
что игроки 2 и 3 — это одна команда (хотя они делают свой выбор
независимо друг от друга), играющая против игрока 1. На кону в игре 4
доллара.
Насколько точно игрок 2 сможет помочь игроку 3 угадать, что
выберет игрок 1 — орла или решку? Очевидно, что ответ на этот вопрос мы
получим, когда сформулируем четкие правила игры. Правила такие.
Игрок 1 выкладывает монетку орлом или решкой вверх так, чтобы этого
никто не видел. Затем то же самое делает игрок 2. Затем игроки 1 и 2 откры-

Глава 7. Теория игр
429
вают свои монетки арбитру (оставляя при этом игрока 3 по-прежнему в
неведении). Арбитр объявляет игроку 3, одинаковый или различный
выбор сделали игроки 1 и 2. Затем игрок 3 решает, каким образом выложить
монетку — орлом или решкой. Если игрок 3 угадывает выбор игрока 1, то
игрок 1 выплачивает игрокам 2 и 3 по 2 доллара каждому. В противном
случае каждый из игроков 2 и 3 платит игроку 1 по 2 доллара. Чтобы
сделать игру еще интереснее, мы дадим возможность игрокам 1 и 2 выйти из
игры. Выход из игры стоит 2 доллара. Таким образом, если игрок 1
выходит из игры, то он платит игрокам 2 и 3 по 1 доллару каждому. Если же из
игры выходит игрок 2, то каждый из игроков 2 и 3 платит игроку 1 по
1 доллару. Дерево игры изображено на рис. 7.35. Убедитесь, что оно
полностью соответствует только что данному описанию игры.
D]
-2
l-v
f-4!
2
UJ
Рис. 7.35. Усложненный вариант сравнения монеток
В этой игре существует несколько секвенциальных равновесий.
Полезно продемонстрировать, как находится одно из них. Остальные вас
попросят найти в одном из упражнений.

430
Часть III. Стратегическое поведение
На рис. 7.35 мы обозначили ожидания игрока 2 через ос,, игрока 3 —
через р; и у.. Для простоты изложения будем называть информационное
множество игрока 3, ожидания в котором обозначены Р,,
информационным множеством «бета», а его второе информационное
множество — информационным множеством «гамма».
Пусть х и у обозначают вероятности того, что игроки 1 и 2
соответственно сыграют орла, и пусть х и у обозначают вероятности того, что они
выберут решку. Пусть zp и zy — это вероятности, с которыми игрок 3
выбирает орла в своих информационных множествах бета и гамма
соответственно.
Таким образом, стратегический набор в игре — это вектор
@Ср (Зр Ур х, х, у, у, zp, zy). Мы найдем секвенциальное равновесие,
в котором величины х, х, у, у, zp, zy строго больше нуля и меньше
единицы и в котором игроки 1 и 2 никогда не выходят из игры. Конечно,
нет никакой гарантии, что такое равновесие существует. Но если оно
существует, то наш анализ даст возможность его найти.
Предположим, что х, х , у, у, zp, zy строго больше нуля и меньше
единицы и что х + х=у + у = 1. Следовательно, каждое информационное
множество достигается с положительной вероятностью, и, таким образом,
для того чтобы стратегический набор был согласован, достаточно, чтобы
ожидания были получены по правилу Байеса (см. упражнения). Таким
образом, для согласованности, должно выполняться
а, =х, Р, =-^= и у, =—^=. (Е-1)
ху + ух ху + х у
Осталось воспользоваться свойством секвенциальной рациональности.
Секвенциальная рациональность требует, чтобы стратегия каждого
игрока максимизировала его выигрыш в каждом из его информационных
множеств при заданных ожиданиях и стратегиях других игроков.
Напомним важный факт, касающийся смешанных стратегий. Если игрок
максимизирует свой выигрыш и при этом использует смешанную стратегию, то
использование чистых стратегий, которые играются с положительной
вероятностью при этой смешанной стратегии, дают ему одинаковый
выигрыш. Мы воспользуемся этим для того, чтобы найти стратегии игроков.
Подсчитав выигрыши от использования чистых стратегий, с учетом
(Е-1) получим
у,(Я|/|) = Я-4гт+4A-гт)) + Я-4^+4A-2р)), (Е-2)

Глава 7. Теория игр 431
v1(r|/1) = yDzp-4(l-zp)) + K4zr-4(l-zy)),
v2(Я | /2) = xBzy - 2A -zy))+ x(-2zp + 2A -z„)),
v2(r|/2) = xBzp-2(l-zp)) + J(-2zr+2(l-zr)),
v3(# | /3p) = _2L_B)+-=22L_(-2),
xy + yx xy + yx
v,(T I /3P) = -^-г(-2)+^-=B), (Е-3)
xy + yx xy + yx
^(Я|/1г) = —^гзB)+-Ц^(-2),
xy + x>> xy + xy
v3G-|/3y) = ^^(-2)+^^B),
xy + xy xy + x у
где, например, формула (Е-2) дает выигрыш игрока 1, если он выберет
орла в своем информационном множестве, которое мы обозначили 1Х, и
(Е-3) дает выигрыш игрока 3, если он выберет решку в своем
информационном множестве бета, обозначенном /зр •
Теперь, как уже отмечалось, х, х , у, у, zp и zy должны давать
следующие соотношения:
у1(Я|/1) = у1(Г|/1),
у2(#|/2) = у2(Г|/2),
у3(Я|/зр) = У3(Г|/зр),
у3(Я|/3у) = У3(Г|/3у).
Поскольку мы предполагаем, что ни один из игроков в равновесии не
выходит из игры, то х = 1 - х и у = 1-у. Имея это в виду, мы можем
использовать последние два соотношения, чтобы найти х, у, получая
х = х = у = у = 1/2. Тогда из первых двух соотношений найдем
zp=zy=l/2.
Поскольку в каждом своем информационном множестве игрок 3
имеет точно две альтернативы и поскольку выбор любой из них дает ему
один и тот же выигрыш, он максимизирует свой выигрыш во всех своих
информационных множествах. Осталось только показать, что игроки 1

432
Часть III Стратегическое поведение
и 2 также максимизируют свои выигрыши. Иными словами, мы должны
убедиться, что никто из них не выиграет, выйдя из игры. Это
действительно так, поскольку, если кто-нибудь из них выйдет из игры, он
получит отрицательный выигрыш, тогда как выбор орла или решки дает ему
выигрыш, равный нулю.
Таким образом, стратегический набор (а,, E,, у,; jc, Зс, у, у,
zp, zy), в котором все компоненты равны 1/2, является секвенциальным
равновесием.
Обратите внимание, что в этом секвенциальном равновесии выигрыш
каждого игрока равен нулю. Таким образом, игрок 3 не получил
существенной помощи от игрока 2, поскольку без игрока 2 игра превратилась бы в
стандартную игру сравнения монеток между игроками 1 и 3. В
упражнениях вас попросят найти остальные секвенциальные равновесия. Вы
увидите, что в других равновесиях выигрыши игроков 2 и 3 будут выше. ?
Этот пример нам еще пригодится, чтобы понять важную вещь.
В самом деле рассмотрим стратегический набор (а,, РР %;
х, х9 у, у9 zp, zy) = (l, 0, 0; 1, 0, 0, 0, 0, 0), в котором игрок 1 с
вероятностью 1 выбирает орла, игрок 2 с вероятностью 1 выходит из игры и
игрок 3 с вероятностью 1 выбирает решку.
Этот стратегический набор кажется довольно бессмысленным,
поскольку, хотя игрок 1 детерминированно выбирает орла, а игрок 3 хотел
бы угадать его ход, он почему-то выбирает решку независимо от выбора
игрока 2. Несмотря на это, стратегический набор секвенциально
рационален и удовлетворяет правилу Байеса! Чтобы убедиться в том, что
действительно выполняется свойство секвенциальной рациональности,
заметим, что игрок 1 максимизирует свой выигрыш, поскольку игрок 2
предпочитает выйти из игры. Игрок 2 также максимизирует выигрыш в своем
информационном множестве, поскольку при заданных ожиданиях (в
соответствии с которыми игрок 2 полагает, что игрок 1 детерминированно
выбирает орла) и стратегии игрока 3 (выбирать решку в любых
ситуациях) игрок 3 наверняка не угадывает, какой выбор сделал игрок 1. Таким
образом, лучшее, что игрок 2 может предпринять, — это выйти из игры.
Наконец, при условии, что игрок 3 ожидает, что в каждом из своих
информационных множеств (если оно достигается) игрок 1 выбирает решку,
его лучший выбор — также выбрать решку. Чтобы проверить выполнение
правила Байеса, просто заметим, что единственное нетривиальное
информационное множество, которого достигают участники при данном
профиле поведенческих стратегий, — это информационное множество
игрока 2, и его ожидания действительно индуцируются по правилу Байеса
из этой стратегии.

Глава 7. Теория игр 433
Хотя этот стратегический набор удовлетворяет правилу Байесу и
является секвенциально рациональным, он не будет секвенциальным
равновесием. В самом деле, он не согласован. Интуитивно понятно, что
проблема связана с ожиданиями игрока 3. Перед тем как формально
убедиться в том, что стратегический набор не удовлетворяет свойству
согласованности, сформулированному в определении 7.20, мы попробуем
оценить ситуацию на уровне интуиции. Начнем с напоминания о том, что
согласованность подразумевает выполнение трех условий — правила
Байеса, принципа независимости и принципа одинаковых ожиданий. Хотя
стратегический набор удовлетворяет правилу Байеса, он не удовлетворяет
принципу независимости. Действительно, мы утверждаем: из принципа
независимости следует, что величина либо Р2, либо у2 должна быть равна
нулю. (Однако в рассматриваемом наборе обе величины равны единице.)
Пусть bx{b2) обозначает левый (правый) узел информационного
множества бета игрока 3 и пусть gx (g2) обозначает левый (правый) узел
информационного множества гамма. Представим, какой вопрос
обдумывал игрок 3 при заданных стратегиях, до того как они были реализованы.
«Насколько больше вероятность того, что я попаду в узел gx, а не в узел
Ь2 ?» Мы хотим убедиться, что ответ игрока 3 заключается в следующем:
«Попадание в узел gx бесконечно более вероятно, чем в узел Ъ2 »1.
Причина в следующем. Заметим, что для рис. 7.35 вопрос можно
переформулировать так: «При условии, что игрок 2 выбирает орла,
насколько более вероятно, что игрок 1 выбирает орла, а не решку?» Но согласно
принципу независимости игрок 3 не получает информации о том, какую
стратегию выбрал игрок 1, узнав, какую стратегию выбрал игрок 2.
Следовательно, ответ на поставленный выше вопрос должен совпадать с
ответом на следующий вопрос: «При условии, что игрок 2 выбирает выход
из игры, насколько более вероятно, что игрок 1 выбирает орла, а не
решку?» Но ответ на последний вопрос состоит в том, что выбор орла
игроком 1 бесконечно более вероятен, чем выбор решки, поскольку это
непосредственно следует из заданных стратегий. Следовательно, согласно
принципу независимости ответ на первоначально поставленный вопрос
должен быть тем же: попадание в gx бесконечно более вероятно, чем
в Ь,.
1 Выражение «одно событие бесконечно более вероятно, чем другое» означает, что если
происходит одно из них, то первому приписывается вероятность 1, а второму —
вероятность 0. Так, например, при заданных стратегиях игроков перед началом игры мы
скажем, что выбор решки игроком 1 бесконечно более вероятен, чем выбор орла, поскольку
первый имеет вероятность 1, а последний — вероятность 0.

434
Часть III. Стратегическое поведение
Аналогичные рассуждения приведут нас к ответу на вопрос,
насколько более вероятно попадание в узел Ьх, чем в узел g2: попадание в узел
Ьх бесконечно более вероятно, чем в g2. (Покажите это самостоятельно).
Наконец, ответим на вопрос игрока 3: «Насколько более вероятно
попадание в узел gx, чем в Ьх ?» И хотя мы не можем быть уверены
относительно ответа игрока 3, возможны только два варианта. Либо более
вероятно попадание в g,, чем в Ьх (это событие не обязательно должно быть
бесконечно более вероятным), либо наоборот. Если более вероятно
попадание в g,, то поскольку попадание в Ьх бесконечно более вероятно, чем
попадание в g2, то gx должно быть бесконечно более вероятно, чем g2.
Но это эквивалентно тому, что у, = 1 и у2 = 0. Поэтому в этом случае
у2=0.
В то же время если Ьх по крайней мере на столько же вероятно, что и
g,, то, поскольку g1 бесконечно более вероятно, чем Ь2, то Ьх должно
быть бесконечно более вероятно, чем Ь2. Но это эквивалентно тому, что
Р,=1иР2=0.
Следовательно, независимость означает, что либо у2 = 0, либо Р2 = 0.
Таким образом, мы показали, что заданный стратегический набор не
удовлетворяет принципу независимости.
Этот интуитивный ответ, не является формальным доказательством
того, что стратегический набор не согласован. Он приведен здесь только
ради того, чтобы лучше почувствовать суть проблемы. Теперь формально
покажем, что стратегический набор не удовлетворяет принципу
согласованности, а следовательно, не является секвенциальным равновесием,
доказав следующее утверждение.
Утверждение. Если стратегический набор (оср рр ур
х, х, у, у, Zp, z ) в усложненном варианте сравнения монеток
согласован, то ожидания должны удовлетворять следующему соотношению:
(a,Jp2Y2=(a2JpiYl.
Прежде чем привести доказательство этого утверждения, заметим,
что если а, = 1 (как в стратегическом наборе, который мы анализируем),
то в соответствии с соотношением, заданным в утверждении, либо
величина Р2, либо у2 должна быть равна нулю, как мы и показали выше,
используя принцип независимости. Следовательно, доказать
утверждение — в действительности означает продемонстрировать, что заданный
секвенциально рациональный стратегический набор не согласован и,
следовательно, не является секвенциальным равновесием.

Глава 7. Теория игр 435
1 U
Доказательство утверждения. Если стратегический набор
(ар РР YP х, Зс, у, у, zp, z) согласован, то по определению 7.20
существует последовательность полностью смешанных поведенческих
стратегий х", хп, у", у", z", z", сходящаяся к х, х , у, у, z^, zy
соответственно, чья ассоциированная последовательность индуцированных
правилом Байеса ожиданий а", р" и у" сходится кар Р, и у, соответственно.
Далее, поскольку вероятности всех поведенческих стратегий
положительны для всех членов последовательности, то
(х"JТу"х"У
— —-l ^— = 1 дЛЯ всех п.
[х") х"Ух"у"
Но в силу правила Байеса мы имеем
а~Г'
р;_зсу
ft" х-у'
К=гу_
для всех п. Следовательно, подставляя полученные выражения в
уравнение выше и перегруппировав, получаем
«Jр2^ = (atfWH для всех п.
Искомый результат найдем, взяв предел левой и правой частей
выражения при п, стремящемся к бесконечности. ¦
Мы закончим этот раздел формулировкой следующей теоремы,
которая, показывает, с одной стороны, общую согласованность концепции
секвенциального равновесия, а с другой — что секвенциальное равновесие
в действительности является обобщением обратной индукции для любых
игр в развернутой форме.
Теорема 7.7 (Теорема Крепса — Уилсона). Существование
секвенциального равновесия.
В каждой конечной игре в развернутой форме с совершенной
памятью существует по крайней мере одно секвенциальное равновесие. Более
того, если стратегический набор (р, Ъ) является секвенциальным рае-

436
Часть III. Стратегическое поведение
новесием, то профиль поведенческих стратегий Ь является
совершенным в подыграх равновесием.
В этой главе мы рассмотрели множество идей — от доминирования и
равновесия по Нэшу вплоть до секвенциального равновесия. Надеемся, что
нам удалось продемонстрировать читателю все богатство теории игр, как и
ее громадные возможности, позволяющие пролить свет на исходы
стратегических ситуаций, в которых участвуют рациональные игроки.
В следующей главе мы непременно используем изложенные здесь
теоретико-игровые идеи, чтобы разобраться в важных экономических
последствиях асимметрии информации.
7.4. Упражнения
7.1. Представьте дуополию Курно и Бертрана как игру в
стратегической форме.
7.2. Покажите, что для конечной игры алгоритм итеративного
исключения строго доминируемых стратегий имеет конечное число шагов, если
игра конечна. Покажите также, что соответствующие множества
доминируемых стратегий являются вложенными. Если возможно, найдите
оценки для точной верхней грани необходимого числа шагов (итераций).
7.3. Наш алгоритм итеративного исключения (слабо или строго)
доминируемых стратегий на каждом этапе исключает все соответствующие
стратегии. Можно рассмотреть исключение только некоторых из тех
стратегий, которые доминируются на этом этапе. В этом смысле можно
установить порядок исключения стратегий.
а) Используя следующую игру, покажите, что порядок исключения
слабо доминируемых стратегий может влиять на исход игры.
1 ^\
и
С
D
L
2,1
1,2
2,-2
М
1,1
3,1
1,-1
R
0,0
2,1
-1,-1
б) Докажите, что в конечной игре порядок исключения строго
доминируемых стратегий не влияет на исход игры.
7.4. Мы уже видели, что одна чистая стратегия может строго
доминировать другую чистую стратегию. Смешанные стратегии могут также
строго доминировать как чистые стратегии, так и другие смешанные
стратегии. В качестве примера рассмотрим следующую игру двух
участников.

Глава 7. Теория игр
431
\\ 2
1 \
и
D
L
3,0
2,4
М
о,-з
4,5
R
0,-4
-1,8
а) Убедитесь, что чистые стратегии L и R игрока 2 не доминируют
чистую стратегию М
б) Покажите, что чистая стратегия М строго доминируется
смешанной стратегией, в которой игрок 2 выбирает и L, и R с вероятностью 1/2.
7.5. Рассмотрите игру «Угадай среднее», изложенную в конце
раздела 7.2.1.
а) Покажите, что ни одна чистая стратегия не является строго
доминирующей для любой другой чистой стратегии.
б) Найдите смешанную стратегию, которая строго доминирует
стратегию 100.
в) Покажите, что стратегия 99 не является строго доминируемой.
г) Покажите, что итеративное исключение строго доминируемых
стратегий оставляет единственную стратегию для каждого игрока —
назвать 1 — и что для этого необходимо 99 раундов.
д) Покажите, что если в игре три игрока, т.е. N = 3, и используется
процедура итеративного исключения слабо доминируемых стратегий, то
Wtl={l 2, ..., 14}, Щ2={19 2} и ^3={l} для всех игроков /, где W?
обозначает множество стратегий игрока /, оставшиеся после п раундов
исключения слабо доминируемых стратегий, и W? = Si.
7.6. Покажите, что любая стратегия, оставшаяся после применения
процедуры итеративного исключения слабо доминируемых стратегий,
останется также и после применения последовательного отбрасывания
строго доминируемых стратегий.
7.7. Игра, в которой принимают участие два игрока, называется игрой
с нулевой суммой, если сумма выигрышей игроков при любом исходе
равна нулю. Пусть и(х, у) обозначает выигрыш игрока 1 в такой игре,
если игрок 1 выбирает хе X, а игрок 2 выбирает ye Y; следовательно,
выигрыш игрока 2 составит -м(х, у). И X, и Y - конечные множества
чистых стратегий. Все следующие вопросы касаются описанной игры
двух участников с нулевой суммой.
а) Докажите теорему о минимаксе. То есть докажите, что
существует пара смешанных стратегий т\, т*2 такая, что
max min w(w,, т2) = и(т*, т*2)= min maxu(mv m2).
/и(бЛ/| пг2еМ2 т2еМ2 mieMi
Проинтерпретируйте этот результат.

438
Часть III. Стратегическое поведение
б) Покажите, что равновесия по Нэшу взаимозаменяемы в том
смысле, что, если (w*, т*2) и (/й,, т2) — два равновесия по Нэшу, то
{т\ , т2) и (/й,, т*2) — также равновесия по Нэшу. Отсюда сделайте
вывод, что если в игре двух участников с нулевой суммой имеется
несколько равновесий по Нэшу, то ни одному из игроков не нужно знать,
какую равновесную стратегию использует его контрагент.
в) Покажите, что выигрыш игрока 1 (и, следовательно, выигрыш
игрока 2) одинаков во всех равновесиях по Нэшу. Это число называется
ценой игры.
7.8. Говорят, что игра симметрична, если множество чистых
стратегий у всех игроков одинаково и un(i)(sn{l), ..., sK{N)) = ui(sl9 ..., sN) для
всех игроков /, где N-мерный вектор (лA), ..., n(N)) является
перестановкой вектора A, ..., N). Докажите, что в конечной симметричной игре
существует симметричное равновесие по Нэшу, т.е. равновесие, в
котором все игроки выбирают одну и ту же стратегию.
7.9. Докажите, что цена симметричной игры с нулевой суммой, в
которой участвуют два игрока, равна нулю.
7.10. Найдите все равновесия по Нэшу в следующих играх:
\ 2
1 ^\
и
D
L
1,1
0,0
R
0,0
0,0
Покажите также, что в игре два равновесия по Нэшу, но только в одном
из них ни один из игроков не использует слабо доминируемую стратегию.
б)
\. 2
1 ^\
и
D
L
1,1
1,0
R
0,1
-1,-1
Покажите также, что в игре существует бесконечно много равновесий по
Нэшу в чистых стратегиях, но только в одном из них ни один из игроков
не использует слабо доминируемую стратегию.
в) .

Глава 7. Теорця игр
439
Покажите также, что в результате использования процедуры
итеративного исключения слабо доминируемых стратегий останется единственная
стратегия.
7.11. Покажите, что во всех конечных играх существует равновесие
по Нэшу, в котором ни один из игроков не приписывает положительную
вероятность слабо доминируемой чистой стратегии.
а) Дополните этот результат, показав, что в любой конечной игре
существует равновесие по Нэшу m такое, что для всех игроков / mi не
является слабо доминируемой.
б) Покажите, что вывод, полученный в пункте а), перестает быть
верным без предположения о том, что игра конечна, рассмотрев дуополию
Бертрана, изложенную в главе 4.
7.12. Покажите, что в конечной игре в стратегической форме
множество стратегий, остающихся после применения процедуры итеративного
исключения слабо доминируемых стратегий, непусто.
7.13. Покажите, что в игре с двумя фирмами, конкурирующими по
Бертрану, рассмотренной в примере 7.3, существуют другие равновесия
Байеса — Нэша.
7.14. Рассмотрите аукцион первой скрытой цены, в котором
участники одновременно подают запечатанные конверты с заявками и лот уходит
к тому, чья ставка окажется больше, при этом он платит заявленную цену.
Предположим, что в аукционе принимают участие два игрока, чьи оценки
являются независимыми случайными величинами, равномерно
распределенными на интервале [0, 1]. Тип игрока — это его оценка. Выигрыш
игрока равен v - b, если он выигрывает на аукционе, заявив b при оценке
v, и 0, если он не выигрывает на аукционе.
а) Опишите эту ситуацию как байесовскую игру и постройте
соответствующую игру в стратегической форме. Обратите внимание, что в игре в
стратегической форме число игроков бесконечно.
б)Пусть Ь;(у) обозначает заявку, которую подает игрок / типа v.
Покажите, что в игре существует равновесие Байеса — Нэша, в котором
Ъх (у) = а + pv для всех / и v. Найдите значения коэффициентов а и р.
7.15. Модифицируйте аукцион, описанный в предыдущем
упражнении, таким образом, что проигравший также платит величину, которую
он заявил (но не получает лот). Этот модифицированный аукцион
называется аукционом, где платят все.
а) Покажите, что существует равновесие Байеса — Нэша, в котором
bi(v) = y+8v + <\>v2 для всех / и v.
б) Как соотносятся заявки участников в этом аукционе с заявками в
аукционе первой цены? Проинтерпретируйте полученный результат.

440
Часть III. Стратегическое поведение
в) Покажите, что ex ante в аукционе первой цены и аукционе, где
платят все, ожидаемый доход продавца одинаков.
7.16. Опишите полностью две различные чистые стратегии для
каждого игрока в игре «Покупатель—продавец» и упрощенной игре «Кто
последний?». Вычислите выигрыши, получаемые игроками при
использовании всех четырех пар стратегий.
7.17. Перечислите все чистые стратегии обоих игроков в играх в
развернутой форме, изображенных на рис. 7.12 и 7.14. Кроме того,
изобразите ассоциированные игры в стратегической форме в виде матричной
диаграммы.
7.18. Примените алгоритм обратной индукции к играм,
изображенным на рис. 7.36.
С) 0 С) 0 0 О
(а) (б)
f0'
f0>
,0,
(в)
Рис. 7.36
а) В какой из игр использование алгоритма обратной индукции
приводит к множеству профилей?

Глава 7. Теория игр 441
б) Докажите, что, если в конечной игре с совершенной информацией
выигрыши каждого игрока различны, использование алгоритма обратной
индукции приводит к единственному профилю стратегий.
в) Приведите пример конечной игры с совершенной информацией, в
которой использование алгоритма обратной индукции не приводит к
единственному профилю стратегий, однако вектор выигрышей
единственен.
7.19. Рассмотрите дерево игры без указания выигрышей,
изображенное на рис. 7.37. Предположим, что игра заканчивается либо победой
одного из игроков и поражением другого, либо ничьей. То есть в игре
возможны только три вектора выигрышей: @, 0), A, -1) и (-1, 1).
Придумайте четыре различные игры, тем или иным способом приписав эти
векторы выигрышей терминальным узлам этой игры.
Рис. 7.37
а) Покажите, что во всех придуманных вами играх один из игроков
может обеспечить себе победу, или оба могут гарантировать ничью.
б) Можете ли вы обобщить этот результат для нескольких известных
настольных игр (крестики-нолики, шашки, шахматы)?
7.20. Пусть Y обозначает конечное подмножество узлов некоторой
игры в развернутой форме. Докажите, что Y содержит узлы, не имеющие
строгих последователей в Y.
7.21. Приведите пример конечной игры с несовершенной
информацией и совершенной памятью, в которой нет «последнего»
информационного множества. То есть в любом информационном множестве существует
узел х такой, что (х, а) е X не является терминальным узлом для
некоторого действия а .
7.22. Найдите все совершенные в подыграх равновесия в игре,
изображенной на рис. 7.17.

442
Часть III. Стратегическое поведение
7.23. Докажите, что для любой игры в развернутой форме сама игра
также является подыгрой.
7.24. Покажите, что если s является равновесием по Нэшу в чистых
стратегиях, то s индуцирует равновесие по Нэшу в тех подыграх,
которые достигаются, если игроки используют s.
7.25. Докажите, что во всех играх с совершенной информацией
каждый узел определяет подыгру.
7.26. Ответьте на следующие вопросы.
а) Докажите, что во всех конечных играх в развернутой форме с
совершенной информацией существует по крайней мере одно совершенное
в подыграх равновесие в чистых стратегиях.
б) Приведите пример конечной игры в развернутой форме, в которой
не существует совершенного в подыграх равновесия в чистых стратегиях.
7.27. Завершите доказательство теоремы 7.6 о существовании
совершенного в подыграх равновесия.
7.28. Найдите все совершенные в подыграх равновесия в игре,
изображенной на рис. 7.26(a).
7.29. Ответьте на следующие вопросы об игре, представленной на
рис. 7.38.
1 И
J w
С)
(о]
Рис. 7.38
а) Найдите равновесие по Нэшу в этой игре.
б) Покажите, что в этой игре не существует равновесия по Нэшу в
поведенческих стратегиях.
в) Покажите, что в этой игре нет совершенного в подыграх
равновесия в чистых стратегиях.
г) В чем причина отсутствия такого равновесия?
7.30. Докажите, что для конечной игры в развернутой форме, если
профиль поведенческих стратегий Ъ является полностью смешанным, то:

Глава 7. Теория игр 443
а) любое информационное множество достигается с положительной
вероятностью;
б) стратегический набор (р, Ъ) согласован тогда и только тогда,
когда р получены из Ь по правилу Байеса.
7.31. Ответьте на следующие вопросы.
а) Докажите, что согласно принципу независимости при указанных на
рис. 7.29 поведенческих стратегиях величина а равна 1/3.
б) Убедитесь, что при указанных на рис. 7.30 и 7.31 поведенческих
стратегиях по принципу согласованности в обоих случаях а = Р.
7.32. Докажите, что, если стратегический набор согласован, он
удовлетворяет правилу Байеса, более того, он удовлетворяет правилу Байеса в
каэюдой подыгре. (Исходный стратегический набор игры индуцирует
стратегические наборы для подыгр. Говорят, что исходный
стратегический набор удовлетворяет правилу Байеса в каждой подыгре, если каждая
подыгра трактуется как самостоятельная игра, и индуцированный
стратегический набор в этой игре удовлетворяет правилу Байеса.)
7.33. Рассмотрите игру, представленную на рис. 7.27. Пусть Ь
обозначает профиль поведенческих стратегий, при котором игрок 1 выбирает
L, а игрок 2 выбирает т. Докажите, что для любой системы ожиданий р
стратегический набор (р, Ъ) не является секвенциально рациональным.
Найдите все секвенциально рациональные стратегические наборы.
7.34. Найдите все секвенциально рациональные равновесия в игре,
представленной на рис. 7.35.

Глава 8
ЭКОНОМИКА ИНФОРМАЦИИ
В неоклассической теории поведения потребителя и фирмы
потребители обладают совершенной информацией о существенных свойствах
приобретаемых ими товаров — таких, как качество и долговечность.
Фирмы обладают совершенной информацией о производительности
факторов, которые им необходимы для производства. Это позволило
разработать отдельно теорию спроса потребителей и теорию предложения
производителей и после этого просто объединить их, предполагая, что
цены приводят рынки в равновесие.
Можно было бы надеяться, что расширить теорию потребителя и
производителя так, чтобы учесть несовершенную информацию, будет
столь же просто, как и включить задачу принятия решений в условиях
неопределенности в эти неоклассические модели поведения потребителя
и производителя. Можно было бы тогда вывести теорию спроса и
предложения при несовершенной информации и снова объединить эти две
теории, чтобы создать теорию рыночного равновесия. К сожалению, этот
подход имел бы смысл, только если бы источники неопределенности с
обеих сторон рынка были экзогенными и поэтому находились вне
влияния всех участников сделок.
Конечно, качество и долговечность товара, например, не являются
экзогенными. Это характеристики, которые в конечном счете выбирает
производитель. Если потребители не могут непосредственно проверить
качество товара перед тем, как совершить покупку, то вполне может
быть, что в интересах производителя — выпускать только
низкокачественные изделия. Конечно, зная это, потребители смогут сделать вывод о
том, что качество товара должно быть низким, и будут действовать
соответственно. Таким образом, мы не можем предложить адекватную
равновесную теорию ценности в условиях несовершенной информации, не
предполагая в явном виде существование соответствующих
стратегических возможностей, доступных участвующим агентам. Примечательно,
что эти стратегические возможности связаны с распределением
информации среди экономических агентов.
Говорят, что ситуация, при которой различные агенты обладают
различной информацией, является ситуацией асимметричной информации.
Как мы увидим, стратегические возможности, которые возникают при
наличии асимметричной информации, обычно приводят к неэффективным
рыночным исходам — провалам рынка. В условиях асимметричной ин-

Глава 8. Экономика информации
445
формации первая теорема благосостояния, вообще говоря, больше не
имеет места.
Таким образом, главная тема этой главы — влияние, которое
асимметричная информация оказывает на эффективность рыночных исходов.
Для простоты и ясности мы рассмотрим эту тему на примере одного
рынка — рынка страхования. Изучая наши модели рынка страхования, вы
можете понять, как теоретики моделировали бы другие рынки с подобной
асимметрией информации. Наконец, надеемся настроить вас на поиск
аналогий и приложений в области ваших профессиональных интересов.
8.1. Неблагоприятный отбор
8.1.1. Информация и эффективность рыночных исходов
Рассмотрим рынок страхования автомобилей, на котором множество
страховых компаний продают услуги по страхованию большому числу
потребителей.
Потребители страховых услуг идентичны во всем, кроме экзогенно
заданной вероятности попасть в автомобильную аварию. Предположим,
что вероятность несчастного случая для /-го страхователя равна
я;€[0, 1], / = 1, 2,...,w и что наступление несчастного случая является
независимым событием среди страхователей1. Во всем остальном
страхователи одинаковы. Каждый из них вначале обладает богатством w; если
он попадает в аварию, то теряет L долларов, и его функция полезности
от богатства и() является непрерывной, строго возрастающей, строго
вогнутой функцией полезности фон Неймана — Моргенштерна.
Страхователи руководствуются максимизацией ожидаемой полезности.
Страховые компании тоже одинаковы. Каждая предлагает только
полное страхование от несчастного случая. То есть за некоторую цену
они обещают выплатить страхователям L долларов, если те попадут в
аварию, и ничего — в противном случае. Здесь мы предполагаем, что этот
полный страховой полис выступает цельным продуктом, т.е. его дробные
части не могут быть ни проданы, ни куплены. Мы также предполагаем,
что издержки по предоставлению услуг страхования являются нулевыми.
Таким образом, если полный страховой полис продается за р долларов и
куплен страхователем /, то ожидаемая прибыль страховой компании от
этой сделки равна р - n.L . Считаем, что страховые компании
максимизируют свою ожидаемую прибыль.
Иными словами, несчастным случаем мы будем считать «удар о дерево», а не
«столкновение с другим автомобилем».

446
Часть III. Стратегическое поведение
Симметричная информация
Рассмотрим ситуацию, когда вероятность несчастного случая может
быть определена страховыми компаниями для каждого страхователя.
Понятно, что здесь никакой асимметрии информации нет. Каков тогда
конкурентный (вальрасовский) исход при таких начальных условиях,
когда вся информация является общедоступной?
Чтобы понять, каким будет конкурентный исход в данном случае,
важно осознать тот факт, что цена любого товара может зависеть от
«состояния мира». Например, зонт в состоянии «дождь» — совсем другой
товар, нежели зонт в состоянии «солнечно». Следовательно, эти
различные товары могли бы иметь разные цены.
То же самое можно сказать и о ситуации, когда состояние мира
определяет подмножество страхователей, у которых произойдет несчастный
случай. Поскольку состояние, в котором страхователь i попадает в
аварию, отличается от того, в котором в аварию попадет страхователь j, то
товар (полис), под которым имеется в виду оплата L долларов i -му
страхователю при условии, что он попадает в аварию, отличается от полиса,
по которому выплачивается L долларов j -му страхователю, когда
несчастный случай происходит с ним. Следовательно, полисы, приносящие
пользу различным страхователям, являются, по сути, различными
товарами и могут, следовательно, иметь разные цены.
Итак, пусть pi обозначает цену полиса, по которому L долларов
выплачивается страхователю / в случае, если он попадает в аварию. Для
простоты будем именовать этот полис / -м. Мы хотели бы далее
определить для каждого i = l, 2, ...,w равновесную цену /-го полиса р* в
условиях конкуренции.
Давайте сначала рассмотрим предложение полиса i. Если р{ меньше,
чем %.L, то продажа такого полиса приведет к ожидаемым потерям.
Следовательно, предложение полиса / будет в таком случае нулевым. В то же
время если pt больше, чем n.L, то продажа каждого такого полиса дает
положительную ожидаемую прибыль, так что предложение таких полисов
будет бесконечно. Наконец, если р. = П;Ь, то страховые компании
получают нулевую ожидаемую прибыль по каждому проданному полису / и,
следовательно, могут предложить любое количество подобных полисов.
Рассмотрим ситуацию со стороны спроса. Если pi меньше, чем ntL,
то страхователь /, будучи не склонным к риску, предъявит спрос по
крайней мере на один полис /. Это следует из нашего анализа в главе 2,
где мы показали что не склонные к риску потребители предпочитают
полностью застраховаться, чем не страховаться вообще всякий раз, когда

Глава 8. Экондмика информации
447
условия страхования актуарно справедливы (т.е. когда р. = к}Ь). Тот же
самый анализ показывает, что если pt превышает л,Х, то /-й
потребитель приобретет самое большее один полис /. (Напомним, что полисы
частичного страхования недоступны.)
Если рассмотреть спрос и предложение вместе, то получится, что
единственная возможность существования равновесия — выполнение
условия р.х - л,Х. В этом случае каждый потребитель / предъявляет спрос
точно на один полис /, который и предлагается только одной (любой)
страховой компанией. Все другие страховые компании предлагают
нулевое количество полисов i, все они при цене pi - n.L имеют
максимальные (нулевые) ожидаемые прибыли.
Таким образом, когда информация является общедоступной, то
существует единственное конкурентное равновесие. При этом р* = П/L для
каждого полиса / = 1, 2,..., т. Заметим, что в таком конкурентном
равновесии все страховые компании получают нулевые ожидаемые прибыли, а
все потребители полностью застрахованы.
Мы хотим доказать, что конкурентный исход Парето-эффективен, т.е.
нельзя улучшить состояние ни одного страхователя или страховой
компании, не ухудшая состояния какого-то другого страхователя или
страховой компании. Можно прийти к этому заключению, обращаясь к первой
теореме благосостояния и конструируя соответствующую экономику
чистого обмена. Вас попросят сделать это в упражнении 8.1. Здесь же мы
приведем прямое доказательство.
В данном случае под распределением имеется в виду распределение
богатства среди страхователей и страховых компаний в каждом
состоянии. Распределение допустимо, если в каждом состоянии данное
совокупное богатство равно совокупному богатству страхователей.
Покажем теперь, что никакое допустимое распределение не является
Парето-доминирующим по отношению к конкурентному распределению.
Проведем доказательство от противного. Предположим, что некоторое
допустимое распределение Парето-доминирует конкурентное
распределение. Без потери общности мы можем предположить, что конкурентное
распределение доминируется допустимым распределением, в котором
богатство каждого страхователя остается неизменным независимо от того,
попадает он в аварию или нет (см. упражнение 8.5). Следовательно,
доминирующий исход гарантирует каждому /-му страхователю богатство
w,. Чтобы это распределение было доминирующим по отношению к
распределению в конкурентном равновесии, для любого / должно
выполняться условие й>. > w-itfL .

448
Часть III. Стратегическое поведение
Теперь, так как богатство каждого потребителя не зависит от
состояния мира, без потери общности можно легко предположить, что
доминирующее распределение не означает передачу богатства от одного
страхователя другому в любом состоянии (снова см. упражнение 8.5). Поэтому
богатство каждого страхователя всегда прямо переходит только к
страховым компаниям (или от них — страхователю).
Рассмотрим теперь страхователя / и страховые компании, которые
предоставляют этому страхователю услуги страхования в доминирующем
распределении. Их совокупные ожидаемые прибыли от страхователя /
равны
(l-nj)(w-^) + ni(w-L-wi) = w-niL-wi9 (8-1)
поскольку величина Щ - w (или w. + L - w) добавляется к богатству
/-го страхователя в состояниях, когда он не попадает (или попадает) в
аварию, а из допустимости распределения следует, что это
дополнительное богатство должно компенсироваться соответствующим изменением
совокупного богатства страховых компаний.
Но мы уже определили, что правая часть (8-1)— неположительна.
Так что, обозначая через ЕР/ ожидаемую прибыль у-й компании от
потребителя /, мы показали для доминирующего распределения, что
w- KjL - w. - ^ ЕР/ < О для любого потребителя /. (8-2)
j
Но ожидаемая прибыль каждой страховой компании при
доминирующем распределении должна быть неотрицательной, так как каждая из
них получает нулевую ожидаемую прибыль при конкурентном
распределении. Следовательно, должно быть также выполнено
^ ЕР/ > О для любой страховой компании j. (8-3)
Суммируя (8-2) по i и (8-3) по j, получаем, что каждое из этих двух
неравенств должно быть равенством для каждого / и j. Следовательно,
(не зависящее от состояния мира) богатство каждого страхователя и
ожидаемая прибыль каждой фирмы при доминирующем распределении
равны их аналогам при конкурентном распределении. Но это противоречит
определению доминирующего распределения и завершает доказательство
того, что конкурентное распределение эффективно.
Асимметричная информация и неблагоприятный отбор
Обратимся теперь к более реалистичной картине, когда страховые
компании не в состоянии определить вероятность несчастного случая для
потребителей. Хотя страховые компании могут и действительно исполь-

Глава 8. Экономика информации
449
зуют данные за прошлые годы, чтобы хотя бы отчасти оценить
вероятность аварии для страхователя, для простоты мы все же рассмотрим этот
крайний случай. Предположим, что страховым компаниям известно
только распределение вероятностей несчастного случая среди страхователей и
ничего больше.
Так, пусть невырожденный интервал [л, Щ содержит множество всех
вероятностей несчастного случая для страхователей, и пусть F —
функция распределения на [я, Щ, известная страховой компании. Такая
постановка задачи позволяет рассматривать и конечное множество, и
континуум потребителей (что удобно для примеров). Предположим также,
что и тс, и я принадлежат носителю F1. Следовательно, для каждого
ке[к, к] F(n) обозначает долю страхователей, имеющих вероятность
аварии, меньшую или равную к. Или, что то же самое, F(n) обозначает
вероятность того, что для любого конкретного страхователя вероятность
аварии равна я или ниже. В остальном страховые компании точно такие
же, как и прежде. В частности, каждая из них продает только полис
полного страхования.
Влияние асимметрии информации оказывается весьма
существенным. В самом деле, даже при том, что полисы, проданные различным
страхователям, потенциально могут иметь разные цены, в равновесии они
разными не будут. Причина совершенно очевидна. Чтобы увидеть это,
предположим обратное, т.е. что равновесная цена, по которой приобрел
полис страхователь /, выше цены, по которой приобрел полис
страхователь j. Поскольку оба страхователя фактически приобрели полис,
ожидаемая прибыль от каждой продажи должна быть неотрицательной, иначе
страховая компания, предлагающая невыгодный полис, не
максимизировала бы прибыль. Следовательно, так как страхователи / и j идентичны
для страховой компании с точки зрения вероятности несчастного случая,
полис, проданный страхователю /, должен принести строго
положительную ожидаемую прибыль. Но тогда каждая страховая компания желала
бы предложить бесконечное количество подобных полисов, что не может
иметь место в равновесии. Это противоречие приводит к следующему
выводу: для полиса полного страхования существует единственная рае-
новесная цена для всех страхователей.
1 Для конечного множества потребителей и, следовательно, конечного множества
вероятностей несчастного случая это просто означает, что на я и я F задает
положительную вероятность. В общем случае это означает, что на всех невырожденных интервалах
вида [тс, а) и (Ь, Щ F задает положительную вероятность.

450
Часть III. Стратегическое поведение
Обозначим через р эту единственную цену полиса полного
страхования. Теперь мы хотели бы определить ее равновесное значение р*.
Поскольку положительная ожидаемая прибыль приводит к
бесконечному предложению, а отрицательная ожидаемая прибыль — к нулевому,
то естественно предположить, что р = E(n)L, где Е(к) = я dF(n) —
ожидаемая вероятность несчастного случая. Может показаться, что такая
цена приведет к нулевой ожидаемой прибыли страховых компаний. Но
так ли это на самом деле?
Чтобы понять, что это вовсе не обязательно, заметим, что данная цена
может быть настолько велика, что только потребители с относительно
высокими вероятностями несчастного случая захотят купить страховку.
Следовательно, компании недооценили бы ожидаемую вероятность
несчастного случая, используя безусловное ожидание Е(п) вместо оэюидания
условной вероятности несчастного случая на множестве тех
потребителей, которые фактически желают купить полис по этой цене. При
подобной недооценке прибыль в среднем была бы отрицательной. Таким
образом, при нахождении величины р мы должны принимать во
внимание это обстоятельство.
При любой вероятности несчастного случая я страхователь
приобретает полис по цене р, только если ожидаемая полезность от этой
покупки превышает ожидаемую полезность в том случае, если он останется
незастрахованным1, т.е. если
u(w- р) > я u{w-L) + A - я) u(w).
Перегруппировав и определив функцию h(p), находим, что полис
будет куплен, только если
u(w)-u(w-L)
Далее мы будем называть р* конкурентной равновесной ценой в
условиях асимметричной информации, если она удовлетворяет следующему
условию:
p=E(n\n>h(p))L. (8-4)
* м
Здесь выражение Е(п | я > h(p ))=\ . я dF{n) — это ожидаемая ус-
J И(р )
ловная вероятность несчастного случая на множестве я > h(p*).
Для простоты предположим, что потребитель, которому все равно, покупать полис или
нет, в действительности покупает его.

Глава 8. Экономика информации
451
Заметим, что страхователь с вероятностью несчастного случая я
приобретет полис полного страхования по цене р тогда и только тогда,
когда к > h(p). Условие (8-4) гарантирует, что фирмы получат нулевую
ожидаемую прибыль от каждого проданного полиса. Предложение
полисов тогда может быть равным количеству, затребованному
страхователями. Таким образом, условие, приведенное выше, действительно
описывает равновесие.
Непосредственный интерес представляет вопрос о существовании
такого равновесия. То есть обязательно ли существует р*,
удовлетворяющее (8-4)? Ответ: да, и вот почему.
Пусть g(p) = Е(к | к > h{p))L для любого р € [0, я L], где п — самая
высокая вероятность несчастного случая среди всех потребителей.
Заметим, что условное ожидание является вполне определенным, потому что
h(p)<n для любого ре [О, я!] (проверьте это). Кроме того, так как
Е(к | к > h{p)) е [0, я], функция g отображает интервал [0, я L] на себя.
Наконец, так как h — функция, возрастающая по р, то g — функция,
неубывающая по р. Следовательно, g — неубывающая функция,
отображающая замкнутый интервал в себя. Как вас попросят доказать в
упражнениях, даже в том случае, когда g не является непрерывной, она
должна тем не менее иметь неподвижную точку р е [0, я L] .По
определению g эта неподвижная точка и является равновесием.
Разрешив вопрос о существовании, обратимся теперь к свойствам
равновесия. Во-первых, нет никакой причины считать, что равновесие
единственно. Действительно, можно легко придумать примеры с
множеством равновесий. Но, что еще более важно, равновесие в данном случае
не обязано быть эффективным.
Рассмотрим, например, ситуацию, когда F равномерно распределена
на отрезке [я, я] = [0, 1]. Тогда g(p) = (l + h(p)) L/2 — возрастающая и
строго вогнутая функция, потому что такова h(p). Следовательно,
существует единственная равновесная цена р*, и она удовлетворяет равенству
р* =A + h(p*))L/22. Но так как A(L) = 1, то мы должны иметь p*=L.
1 Конечно, если g непрерывна, мы можем применить теорему Брауэра о неподвижной
точке. Однако (вы покажете это в упражнении) в случае конечного множества
потребителей g не может быть непрерывной.
2 Здесь в рассуждениях авторов допущена ошибка. Функция g(p) = (\ + h(p))L/2 в дей-
*( \
ствительности является строго выпуклой, поскольку h"(p) = —— > 0 в силу
u(w)-u(w-L)

452
Часть III. Стратегическое поведение
Однако, когда р* = L, (8-4) говорит нам, что ожидаемая вероятность
несчастного случая для тех, кто покупает страховку, должна быть
Е(п | я > h{L)) -1. Таким образом, в равновесии все потребители
останутся незастрахованными, кроме тех, кто уверен, что попадет в аварию. Но
даже эти потребители имеют страховку только формально, потому что
они должны оплатить полный объем потери L, чтобы получить полис.
Таким образом, их богатство (и, следовательно, их полезность) остается
тем же самым, как если бы они не покупали полис вообще.
Ясно, этот исход крайне неэффективен. Конкурентный исход при
условии симметричной информации дает каждому потребителю (кроме тех,
кто уверен, что попадет в аварию) более высокую полезность, гарантируя
также, что ожидаемая прибыль каждой страховой компании является
нулевой. Здесь асимметрия информации приводит к провалу рынка
страхования. Фактически никаких сделок не происходит, и поэтому
возможности для Парето-улучшения остаются нереализованными.
Чтобы понять, почему цены не способны привести в данном случае к
эффективному равновесию, рассмотрим цену, при которой ожидаемая
прибыль страховых компаний отрицательна. Тогда, при прочих равных
условиях, можно было бы предположить, что повышение цены приведет
к увеличению ожидаемой прибыли. Но на рынках страхования прочие
условия не остаются равными. В общем случае всякий раз, когда цена
страховки возрастает, ожидаемая полезность, которую потребитель
получает от приобретения страховки, падает, тогда как ожидаемая полезность,
которую он получает, не приобретая страховку, остается той же самой
при росте цены. Для некоторых потребителей покупка страховки
перестает быть привлекательной альтернативой, и они откажутся от ее
приобретения. Но кто будет тогда приобретать полисы, если цена возросла?
Только те, для кого ожидаемые потери от неприобретения страховки наиболее
велики, а это и есть потребители с самыми высокими вероятностями
несчастных случаев. Всякий раз, когда цена страховки возрастает, выборка
страхователей, которые продолжают приобретать страховку, становится в
среднем более рискованной.
Это — пример неблагоприятного отбора, и этот отбор в
рассматриваемой ситуации оказывает негативное влияние на ожидаемую прибыль.
Если, как в нашем примере, негативное влияние неблагоприятного отбора
на ожидаемую прибыль перевешивает позитивное влияние более высоких
цен страхования, никакого эффективного равновесия может не
возникнуть, а потенциально взаимовыгодные сделки между страховыми компа-
возрастания и строгой вогнутости функции м(-). Таким образом, равновесная цена р ,
вообще говоря, не единственна: наряду с р* = L может существовать еще одно
равновесное значение р <L . — Примеч. ред.

Глава 8. Экономика информации
453
ниями и страхователями с относительно низкими рисками могут не
осуществиться.
Вывод ясен. В условиях асимметричной информации и
неблагоприятного отбора конкурентный исход не обязан быть эффективным. В
действительности он может быть поразительно неэффективен.
Одно из преимуществ свободных рынков заключается в их
способности «эволюционировать». Можно было бы ожидать, что рынок
страхования так или иначе перестроится, чтобы совладать с неблагоприятным
отбором. Фактически реальные рынки страхования действительно
справляются с этой проблемой намного лучше, чем тот рынок, который мы
только что проанализировали. Следующий раздел посвящен объяснению
того, как это может быть достигнуто.
8.1.2. Рыночные сигналы
Вообразите себя страхователем с низкой степенью риска,
оказавшимся в неэффективном равновесии, которое мы только что описали.
Равновесная цена страховки настолько высока, что вы предпочитаете не
приобретать полис. Вот если бы существовал какой-нибудь способ, с помощью
которого вы могли убедить одну из страховых компаний в том, что
являетесь страхователем с низким риском, тогда бы она продала вам полис по
той цене, которую вы готовы были заплатить.
На самом деле страхователи всегда могут найти множество путей,
чтобы достоверно сообщить страховым компаниям, насколько рисковыми
они являются. Мы называем такое поведение использованием рыночных
сигналов. На реальных рынках страховых услуг страхователи могут и
действительно демонстрируют свое отличие от других, и делают они это,
покупая полисы различных типов. Хотя в предыдущем анализе мы
исходили из существования только одного типа полиса, теперь мы можем
учесть данное обстоятельство.
Для простоты предположим, что существуют только две
возможности наступления несчастного случая — л и я, где 0<к< к< 1.
Предположим также, что доля страхователей, имеющих вероятность несчастного
случая я, равна ае (О, 1). Страхователей с вероятностью несчастного
случая к назовем страхователями с низким риском, а страхователей с
вероятностью несчастного случая к — страхователями с высоким риском.
Чтобы смоделировать ситуацию, когда страхователи пытаются
выделиться из общей массы, выбирая различные полисы, воспользуемся
теоретико-игровым подходом.
Рассмотрим следующую игру в развернутой форме, которую мы
будем называть игрой с сигналами на рынке страхования. В ней участвуют
два страхователя (с низким и высоким риском) и единственная страховая
компания.

454
Часть III. Стратегическое поведение
• Природа начинает первой и определяет, какой страхователь
обратится с предложением к страховой компании. Страхователь с низким
риском выбирается с вероятностью а, а страхователь с высоким риском — с
вероятностью 1-ос.
• Назначенный страхователь делает ход вторым. Он выбирает полис
(В, р), состоящий из страховых выплат В > О, которые страховая
компания выплатит ему, если он попадет в аварию, и страховой премии
0<p<w, которую страхователь выплатит страховой компании
независимо от того, попадет он в аварию или нет1.
• Затем делает ход страховая компания, не зная, какой страхователь
был назначен Природой, но зная, какой полис предложен выбранным
страхователем. Страховая компания или соглашается принять условия
страхователя относительно полиса, или отклоняет их.
Развернутая форма этой игры приведена на рис. 8.1. При
интерпретации игры представляйте себе страховую компанию как одну из многих
конкурирующих компаний, а назначенного страхователя — как случайно
выбранный элемент из множества всех страхователей, среди которых
доля а принадлежит к типу с низким риском, а доля 1 - а — к типу с
высоким риском.
Природа
Низкий риск (ос)^
Страхователь
с низким риском
Высокий риск A - а)
Страхователь
с высоким риском
(я-,/) (в,Р) /\(в\р')
Страховая компания
Рис. 8.1. Игра с сигналами на рынке страхования: схематичное
изображение использования сигналов в игре в развернутой форме. На рисунке
показан выбор только из двух полисов (В, р)п{В',р\ тогда как страхователю
фактически доступно бесконечное множество полисов
1 Отметим, что, используя термин «полис», мы теперь имеем в виду пару «выплаты—
премия» (В, р), а не просто страховые выплаты. Ограничение на /?, заключающееся в
том, чтобы оно было не больше, чем w, гарантирует, что страхователь не обанкротится.

Глава 8. Экономика информации
455
Чистая стратегия для страхователя с низким риском — это выбор
полиса у, =(?,, /?,), а для страхователя с высоким риском— полиса
Чистая стратегия для страховой компании должна определять одну из
двух реакций — А (принять) или R (отклонить) — для каждого
потенциально предложенного полиса. Таким образом, чистая стратегия для
страховой компании— функция реакции с, где аE, р)е {A, R} для
каждого полиса (В, р). Заметим, что с зависит только от
предложенного полиса, а не от того, является ли страхователь, выбравший его,
страхователем с низким или высоким риском. Это соответствует
предположению, что страховая компания не знает, со страхователем какого типа она
имеет дело.
Как только полис предложен, страховая компания должна
сформировать ожидания относительно вероятности несчастного случая для
страхователя. Пусть вероятность CE, р) обозначает ожидания страховой
компании относительно того, что страхователь, который выбрал полис
E, р), принадлежит к типу с низким риском.
Мы хотели бы определить чистую стратегию секвенциального
равновесия в данной игре . Однако при этом появляется чисто техническая
трудность. По определению секвенциального равновесия игра должна
быть конечной, но рассматриваемая игра таковой не является —
страхователь может выбрать любой полис из континуума полисов.
Определение секвенциального равновесия требует, чтобы игра была
конечной, только потому, что условие согласованности не определяется
простым способом для бесконечных игр. Однако, как вам предстоит
показать в упражнении, когда множество выборов страхователя ограничено
любым конечным множеством полисов так, чтобы игра стала конечной,
каждый стратегический набор, удовлетворяющий правилу Байеса, также
удовлетворяет условию согласованности. Следовательно, в каждой
конечной версии игры с сигналами на рынке страхования стратегический
набор является секвенциальным равновесием тогда и только тогда, когда
он секвенциально рационален и удовлетворяет правилу Байеса.
Имея это в виду, мы определим секвенциальное равновесие для
(бесконечной) игры с сигналами на рынке страхования в терминах
секвенциальной рациональности и правила Байеса следующим образом.
1 См. главу 7, где подробно обсуждается секвенциальное равновесие. Мы будем
использовать здесь понятие секвенциального равновесия, потому что хотим подчеркнуть
рациональность поведения страховой компании в каждом из ее информационных
множеств, а также то обстоятельство, что страхователи принимают это во внимание.

456
Часть III. Стратегическое поведение
Определение 8.1. Секвенциальное равновесие в чистых
стратегиях в игре с рыночными сигналами.
Набор (\|//9 \|/Л, а(), Р()) является секвенциальным равновесием в
чистых стратегиях в игре с рыночными сигналами на рынке
страхования, если:
1) при заданной стратегии страховой компании а(-) выбранный
полис \\fj максимизирует ожидаемую полезность страхователя с низким
риском, а выбранный полис \|/А максимизирует ожидаемую полезность
страхователя с высоким риском;
2) ожидания страховой компании удовлетворяют правилу Байеса, т.е.
а) Р(у)е [0? 1] для любых полисов \|/ = E, р),
б) если у, Ф \|/А, то P(i|/,) = 1 и р(\|/Л) = 0,
в) если \|/7 = \|/Л, то Р(\|/,) = Р(\|/Л) = а;
3) для каждого полиса \|/ = (В, р) реакция страховой компании о(\|/)
максимизирует ее ожидаемую прибыль при заданных ожиданиях
Р(Я, р).
Условия 1) и 3) гарантируют, что набор секвенциально рационален,
тогда как условие 2) гарантирует, что ожидания страховой компании
удовлетворяют правилу Байеса. Поскольку мы ограничиваемся чистыми
стратегиями, правило Байеса сводится к некоторому достаточно простому
утверждению. Если страхователи с различными рисками выбирают в
равновесии различные полисы, то, сталкиваясь с полисом страхователя с
низким (высоким) риском, страховая компания делает вывод, что имеет
дело со страхователем с низким (высоким) риском. Это условие 26).
Однако, если страхователи с двумя разными рисками выбирают в
равновесии один и тот же полис, то апостериорные ожидания страховой
компании оказываются равными ее априорным ожиданиям. Это условие 2в).
Основной вопрос заключается в следующем: может ли страхователь с
низким риском выявить различие между собой и страхователем с
высоким риском и в результате добиться более эффективного исхода?
Неочевидно, что ответ будет положительным. Заметим, что нет никакой прямой
связи между типом страхователя и полисом, который он предлагает. То
есть факт приобретения меньшей страховки не уменьшает вероятности
того, что несчастный случай произойдет. В этом смысле сигналы,
используемые страхователями (т.е. полисы, которые они предлагают), являются
непродуктивными.
Однако, несмотря на это, страхователь с низким риском еще может
попытаться просигнализировать, что он — страхователь с низким риском,
показывая свою готовность согласиться на меньшую выгоду (от страхов-

Глава 8. Экономика информации 457
ки) при компенсирующем понижении страховой премии на величину,
меньшую, чем та, на которую согласится страхователь с высоким риском.
Конечно, для того чтобы этот вид передачи сигналов (непродуктивный)
был эффективным, страхователи различных типов должны иметь
различные предельные нормы замещения между уровнем выгоды В и
страховой премией р. Как мы скоро покажем, такая ключевая разница в
предельных нормах замещения действительно существует.
Анализ игры
Для начала удобно определить для каждого типа страхователей
ожидаемую полезность некоторого полиса E, р). Итак, пусть
и1 E, р) = nu(w-L + B-p) + (l-n)u(w-p),
uh(B, p) = nu(w-L + B-p) + (l-n)u(w-p)
обозначают ожидаемую полезность полиса E, р) для страхователей с
низким и высоким риском соответственно.
Легко устанавливаются следующие факты:
а) н;E, р) и uh(B, p) непрерывны, дифференцируемы, строго
вогнуты по E, р), возрастают по В и убывают по р ;
б) MRS^B, p) больше, равна или меньше я, если В меньше, равно
или больше L соответственно. MRSh(B, p) больше, равна или меньше
я, если В меньше, равно или больше L;
в) MRS,{B, p)<MRSh(B, p) при любых (В, р).
Последнее соотношение часто называют свойством
единственности пересечения. И, как видно по его названию, оно подразумевает, что
кривые безразличия страхователей разных типов пересекаются самое
большее один раз. Столь же важно и то, что оно показывает, что
предельные нормы замещения, соответствующие одним и тем же полисам у
страхователей, различны.
Рисунок 8.2 иллюстрирует факты а) и в). В соответствии с фактом в)
крутые кривые безразличия — кривые безразличия страхователя с
высоким риском, а более пологие — страхователя с низким риском. Разница в
их предельных нормах замещения означает, что для данного полиса
(В\ р") страхователь с низким риском готов принять сокращение
страховых выплат до В" за меньшее компенсирующее уменьшение страховой
премии, чем страхователь с высоким риском. При этом сокращение
страховых выплат является менее затратным для страхователя с низким
риском, потому что он попадает в аварию с меньшей вероятностью.

458
Часть III. Стратегическое поведение
Р
щ = const
w/ = const
Направление роста
полезности
> В
О В" В'
Рис. 8.2. Свойство единственности пересечения. Относительно данного
полиса (В\ /?') страховые выплаты сокращаются до В". Чтобы
страхователь с низким риском оказался в положении не худшем, чем раньше, цена
полиса должна упасть до р". Она же должна сократиться до р[, чтобы и
страхователю с высоким риском было не хуже, чем раньше
Страховая компания максимизирует ожидаемую прибыль. В случае
если ей известно, что страхователь — с низким риском, она примет
любой полис (В, р), удовлетворяющий условию р>пВ, потому что такой
полис приносит ей положительную прибыль. Рассуждая аналогичным
образом, она отклонит полис, если р < кВ. И страховой компании
безразлично, принять или отклонить полис, при р = пВ. Если страховая
компания знает, что она имеет дело со страхователем с высоким риском, то она
примет полис E, р), если р>кВ, и отклонит его, если р<кВ.
На рис. 8.3 показаны две линии нулевой прибыли страховой
компании. Линия р = пВ содержит полисы E,р), приносящие нулевую
ожидаемую прибыль страховой компании, если их приобретает страхователь
с низким риском. Линия р = кВ содержит полисы, приносящие нулевую
ожидаемую прибыль, если они приобретены страхователем с высоким
риском. Эти две линии будут играть важную роль в нашем анализе.
Заметим, что линия нулевой прибыли от страхователя с низким риском имеет
наклон я, а линия нулевой прибыли от страхователя с высоким риском
имеет наклон я.
Р
Pi
Ph

Глава 8. Экономика информации
459
р = кВ — линия нулевой
прибыли от страхователя
с высоким риском
р = пВ — линия нулевой
прибыли от страхователя
с низким риском
¦+В
О
Рис. 8.3. Линии нулевой прибыли. Полис \\f\ приносит страховой компании
положительную прибыль от обоих типов страхователей; \|/2 приносит
положительную прибыль, если его приобретает страхователь с низким риском,
и отрицательную прибыль от страхователя с высоким риском; \|/з приносит
отрицательную прибыль от обоих типов страхователей
Вернемся к конкурентному равновесию в случае, когда страховая
компания может идентифицировать типы страхователей по степени риска. Мы
показали, что в единственном конкурентном равновесии цена полной
страховки, т.е. такой, что B = L, равна кЬ для страхователя с низким риском и
HL — для страхователя с высоким риском. Этот исход показан на рис. 8.4.
Страховая компания получает нулевую прибыль от любого страхователя,
каждый страхователь приобретает полную страховку, и по
вышеупомянутому факту б) кривые безразличия страхователей обоих типов касаются
соответствующей линии нулевой прибыли страховой компании.
р = пВ — линия нулевой
прибыли от страхователя
с высоким риском
р = кВ — линия нулевой
прибыли от страхователя
с низким риском
x\fc, = (L, nL)
О
-+в
Рис. 8.4. Конкурентный исход; \|/, и \\fch — это полисы для двух типов
страхователей с низким и высоким риском соответственно, в конкурентном
равновесии в ситуации, когда страховая компания может определить типы
страхователей. Равновесный исход здесь эффективен

460
Часть III. Стратегическое поведение
Возвращаясь к нашей игре, опишем ее секвенциальное равновесие,
определив нижние границы для ожидаемой полезности каждого страхователя
при условии, что он был выбран Природой. Заметим, что самые
пессимистические ожидания, которые могли бы возникнуть у страховой компании,
связаны с тем, что она может иметь дело со страхователем с высоким
риском. Следовательно, полезности обоих типов страхователей должны быть
ограничены снизу максимальной полезностью, которую они могли бы
получить, если бы страховая компания полагала, что они оба являются
страхователями с высоким риском. Этот факт нашел отражение в следующей лемме.
Лемма 8.1. Пусть (v|//9 \|/л, а(), Р()) является секвенциальным
равновесием, и пусть и* и и\ обозначают равновесную полезность
страхователя с низким или высоким риском соответственно при условии, что
он выбран Природой. Тогда
1) и] > й,;
2)щ>и1
где u^max^^UjiB, p) при p = nB<w, a uch=uh(L, kL) обозначает
полезность страхователя с высоким риском в конкурентном равновесии
при полной информации.
Доказательство. Рассмотрим полис E, /?), лежащий выше линии
нулевой прибыли от страхователя с высоким риском, так что р>кВ. Мы
хотим доказать, что в равновесии страховая компания должна принять
этот полис.
Чтобы понять это, заметим, что если полис принят, то ожидаемая
прибыль компании при ожиданиях РE, р) равна
Р-Ф(В, р)я + A-р(Я, р))ЩВ>р-кВ>0.
Следовательно, страховая компания предпочтет принять предложение
(В, р), поскольку его отклонение приводит к нулевой прибыли.
Следовательно, все полисы E, /?), лежащие выше линии нулевой прибыли,
полученной от страхователя с высоким риском, принимаются страховой
компанией.
Таким образом, выбрав любой полис, удовлетворяющий условию
кВ < р < w, страхователь с низким риском может обеспечить себе
полезность и,(Я, /?), а страхователь с высоким риском — полезность uh(B, p).
Следовательно, так как в равновесии страхователи обоих типов
максимизируют ожидаемую полезность, для всех полисов, удовлетворяющих
условию кВ< p<w, должны выполняться следующие неравенства:

Глава 8. Экономика информации
461
щ>и,(В9 р), (Р-1)
uh>uh(B, р). (Р-2)
Из непрерывности и{ и uh следует, что (Р-1) и (Р-2) должны
выполняться и для всех полисов, удовлетворяющих нестрогому неравенству
ИВ < р < w. Таким образом, (Р-1) и (Р-2) можно переписать как
и* >Uj(B, p) при всех кВ<p<w, (P-3)
и\ > uh(B, р) при всех ИВ < р < w. (P-4)
Но (Р-3) эквивалентно условию 1), так как полезность— невозрас-
тающая функция от р \ а (Р-4) эквивалентно условию 2), потому что
среди всех полисов, которые не лучше, чем актуарно справедливые
страховые полисы, только полис полного страхования максимизирует
полезность страхователя с высоким риском. ¦
Рисунок 8.5 иллюстрирует лемму 8.1. Из рисунка видно, что, как
следствие леммы, в равновесии страхователь с высоким риском должен
приобретать страховку: без страховки его полезность была бы равна
uh@, 0), что в силу его строгой несклонности к риску строго меньше,
чем и\ — нижняя граница его полезности в равновесии.
Р
^
/45°
/ Линия нулевой прибыли
/ от страхователя с высоким
Линия нулевой прибыли
от страхователя с низким
риском
Рис. 8.5. Нижние границы. Так как в равновесии любые полисы (В,р),
которые лежат выше линии нулевой прибыли от страхователя с высоким
риском, принимаются страховой компанией, то страхователь с низким
риском должен иметь в результате полезность не меньше, чем ul =ul(\\fl),a
полезность страхователя с высоким риском должна быть не меньше, чем
ul = ui(Vh) • Заметим, что хотя на рисунке \j/, * @, 0), ситуация, когда
\j/, = @, 0), возможна
1 Для доказательства утверждения достаточно заметить, что условие 1) является
следствием (Р-3). — Примеч. ред.

462
Часть III. Стратегическое поведение
Сказать то же самое для страхователя с низким риском нельзя, хотя
на рис. 8.5 это имеет место. На рис. 8.5 представлен случай, когда
MRSjiO, 0)>S, так что и, (О, 0)<йг Однако возможна ситуация, когда
MRS, (О, 0)<1, тогда г/ДО, 0)>й1. Здесь страхователь с низким риском
может и не захотеть приобретать страховку в равновесии (делая
предложение, которое будет отклонено), не нарушая при этом выводов леммы 8.1.
Эта лемма имеет место для каждого секвенциального равновесия.
Разделим множество равновесий на два типа: разделяющие и
объединяющие.
Равновесие называют разделяющим, если страхователи разных типов
выбирают различные полисы. Таким образом, страхователи выдают свой
тип и теперь могут быть идентифицированы страховой компанией на
основании выбранного полиса. Напротив, объединяющее равновесие
предполагает, что страхователи обоих типов выбирают один и тот же полис.
Следовательно, страхователей нельзя различить по выбранным ими
полисам. Отсюда получаем следующее определение.
Определение 8.2. Разделяющее и объединяющее равновесия
при использовании рыночных сигналов.
Секвенциальное равновесие в чистых стратегиях (у,, 1|/Л, о(-), Р())
называется разделяющим, если у, Ф \\fh, и объединяющим — в противном
случае.
Если существует только два возможных типа страхователей, то
секвенциальное равновесие в чистых стратегиях будет либо разделяющим,
либо объединяющим. Сказанного вполне достаточно, чтобы
характеризовать множества разделяющих и объединяющих равновесий. Начнем с
первого.
Разделяющее равновесие
В разделяющем равновесии страхователи разного типа выбирают
различные полисы, и на основании этого страховая компания сумеет их
идентифицировать. Конечно, страхователь одного типа мог бы при этом
выдать себя за страхователя другого типа, просто ведя себя
соответствующим образом в равновесии1. Ключевым моментом для понимания
здесь является то обстоятельство, что в разделяющем равновесии
имитировать поведение другого типа не должно быть выгодно ни одному из
страхователей. Основываясь на этой идее, мы можем охарактеризовать
Есть и другие способы симулировать сходство с другим типом. Например,
страхователь с низким риском мог бы выбрать предложение, которое вообще никакой тип, как
предполагается, не выбирает в равновесии. Но тем не менее это предложение заставило
бы страховую компанию поверить, что перед ней страхователь с высоким риском.

Глава 8. Экономика информации 463
полисы, предложенные и принятые в разделяющем секвенциальном
равновесии в чистых стратегиях, следующим образом.
Теорема 8.1. Свойства разделяющего равновесия.
Полисы у, =E/, Pj) и \\fh=(Bh, ph) выбираются страхователями с
низким и высоким риском соответственно и принимаются страховой
компанией в некотором разделяющем равновесии тогда и только тогда,
когда:
2) р, > пВ(;
3) мДу/^й/^тах^мДЯ, р) при p = nB<w;
4) «JsiiA(yJ^iiA(V/).
Доказательство. Предположим сначала, что \|/7 = (^, /77) и
\|/А =(L, kL) удовлетворяют условиям 1)—4). Мы должны придумать
такую стратегию о() и такие ожидания Р() страховой компании, чтобы
набор (\|//5 \\fh, с(), р()) являлся секвенциальным равновесием. Тогда
такое равновесие будет разделяющим. В частности, можно выбрать
следующие ожидания и стратегии страховой компании:
|Х если (В, р) = уп
[О, если (В, p)*x\fr
Р(Я, Р) = -
С(Я, р) =
\А, если (В, p) = \\ffWiu р>лВ,
[R в противном случае.
Согласно ожиданиям Р(-) при любом полисе, отличном от у,,
страховая компания решит с вероятностью, равной единице, что перед ней
страхователь с высоким риском. В то же время, когда предложен полис
\|/7, страховая компания уверена, что имеет дело со страхователем с
низким риском. Следовательно, ожидания страховой компании
удовлетворяют правилу Байеса.
Кроме того, при таких ожиданиях стратегия страховой компании
максимизирует ее ожидаемую прибыль, поскольку согласно этой
стратегии компания принимает полис тогда и только тогда, когда это приводит
к неотрицательной ожидаемой прибыли.
Например, предложение у, = (Вп pt) принимается, потому что
страховая компания полагает с вероятностью, равной единице, что она имеет
дело со страхователем с низким риском. Следовательно, ожидаемая при-

464
Часть III. Стратегическое поведение
быль страховой компании от принятия полиса равна величине р{-тфп
которая согласно условию 2) теоремы является неотрицательной. Точно
так же предложение V|/A = (Z,, HL) принимается, потому что оно с
вероятностью, равной единице, приводит страховую компанию к заключению,
что перед ней страхователь с высоким риском. В этом случае ожидаемая
прибыль от принятия полиса будет равна kL-kL = 0.
Все другие предложения относительно полисов E, р) заставляют
страховую компанию полагать (также с вероятностью, равной единице),
что она столкнулась со страхователем с высоким риском. Тогда ее
ожидаемая прибыль от принятия таких полисов составит р-ИВ. Таким
образом, эти полисы также принимаются только в том случае, если они при
данных ожиданиях страховой компании приносят неотрицательную
ожидаемую прибыль.
Мы показали, что при любом из рассматриваемых полисов E, р)
стратегия страховой компании максимизирует ее ожидаемую прибыль
(при данных ожиданиях). Осталось только доказать, что при заданной
стратегии страховой компании оба страхователя выбирают полисы,
которые максимизируют их полезность.
Для завершения этой части доказательства покажем, что любой полис
не приносит страхователю с низким риском большую полезность, чем
полис у,, а страхователю с высоким риском — большую, чем полис \|/Л.
Заметим, что, так как страховая компания принимает полис @, 0) и этот
полис эквивалентен отклонению полиса страховой компанией
(независимо от того, какой полис был отклонен), оба страхователя могут
максимизировать свою полезность, делая предложение, которое будет принято
страховой компанией. Следовательно, мы можем ограничиться
рассмотрением следующего множества полисов (обозначим его JA):
Л = {у1}и{(В, р)\р>кВ}.
Таким образом, достаточно показать, что для любых (В, р)е JA при
p<w
кДх^иДЯ, р), (Р-1)
uh(yh)>uh(B, p). (P-2)
Но (Р-1) следует из условия 3), а (Р-2) — из условий 1), 3) и 4), так как
(L, кЬ) является наилучшим полисом для страхователя с высоким
риском среди всех полисов, которые для него не лучше, чем актуарно
справедливые полисы.

Глава 8. Экономика информации
465
Докажем теперь обратное утверждение. Предположим, что
(V/> ?*> а(*)> PQ) — разделяющее равновесие, в котором равновесные
полисы принимаются страховой компанией. Покажем, что условия 1)—4)
выполняются. Рассмотрим каждое из них.
1). По определению разделяющего равновесия 1|/,*\|/Л. Чтобы
показать, что \\fh=(Bh, ph) = (L, Ж/), вспомним, что по лемме 8.1
uh(\\fh) = uh(Bh, ph)>uh(L, nL). Далее, так как страховая компания
принимает это предложение, оно должно приносить неотрицательную
прибыль. Следовательно, ph > HBh, поскольку в разделяющем равновесии
страховая компания ожидает с вероятностью, равной единице, что
предложение \\fh делает страхователь с высоким риском. Но, как мы уже
доказывали прежде, два эти неравенства приводят к тому, что \|/Л = (L, HL)
(см., например, рис. 8.4).
2). В равновесии страховая компания ожидает (в соответствии с
правилом Байеса с вероятностью, равной единице), что предложение (Вп pt)
сделано страхователем с низким риском. Если бы страховая компания
приняла данное предложение, то это принесло бы ожидаемую прибыль,
равную р{ -яВ7. Поскольку, в соответствии с гипотезой, страховая компания
принимает это предложение, то эта величина должна быть неотрицательной.
3). Это условие следует из пункта 1) леммы 8.1.
4). Согласно стратегии страховой компании, она принимает полис
\|/,. Поскольку uh(\\fh) является равновесной полезностью страхователя с
высоким риском, то должно выполняться соотношение uh(\\fh) > wA(\|/7). ¦
На рис. 8.6 показаны полисы, которые согласно теореме 8.1 могут
соответствовать разделяющему равновесию. Страхователь с высоким риском
получает полис \\fch = (Z,, HL), а страхователь с низким риском получает
полис у, = (Вп pt), лежащий в затемненной области.
Отметим важные свойства множества полисов страхователей с
низким риском. Каждый из этих полисов лежит выше линии нулевой
прибыли от страхователя с низким риском, чтобы страховая компания его
приняла, выше кривой безразличия страхователя с высоким риском при его
равновесном полисе, чтобы гарантировать, что у того не будет стимула
выдавать себя за страхователя с низким риском, и ниже кривой
безразличия, соответствующей полезности й1 страхователя с низким риском,
чтобы гарантировать, что у него не будет стимула отклониться, выдавая себя
за страхователя с высоким риском.

466
Часть III. Стратегическое поведение
Р
^
/45°
/
/
/ Линия нулевой прибыли от
/ страхователя с высоким риском
Линия нулевой прибыли
от страхователя
с низким риском
Рис. 8.6. Потенциальные разделяющие равновесия. В разделяющем
равновесии, в котором оба типа страхователей предлагают принимаемые
страховой компанией полисы, полис страхователя с высоким риском
должен быть \\fch, а полис страхователя с низким риском vj/, должен
находиться в затемненной области. Здесь MRS, (О, 0) > к. Аналогично
можно проиллюстрировать и альтернативный случай (обратите внимание,
что соотношение MRS^O, 0)>я всегда выполнено)
Теорема 8.1 ограничивается описанием тех равновесий, в которых оба
страхователя выбирают только те полисы, которые страховая компания
принимает. Согласно лемме 8.1 это ограничение на предложение полисов
распространяется только на страхователя с низким риском. Когда
MRS,@, 0)<й, тогда существуют разделяющие равновесия, в которых
предложение страхователя с низким риском отклоняется. Однако, как вас
попросят показать в упражнении, каждое из этих равновесий эквивалентно
некоторому разделяющему равновесию, в котором предложение
страхователя с низким риском принимается. Наконец, можно показать, что
затемненная область на рис. 8.6 всегда непуста, даже когда MRS,@, 0) < я,
поскольку MRS,@, 0)>я. Следовательно, разделяющее равновесие в
чистых стратегиях всегда существует.
Теперь, охарактеризовав полисы, соответствующие возможным
разделяющим равновесиям, мы можем оценить, как влияет возможность
предлагать такие страховые полисы как сигнал об уровне риска. Заметим,
что, поскольку разделяющее равновесие всегда существует, возможность
такого сигнализирования всегда эффективна, в том смысле, что она
позволяет страхователям с низким риском отличить себя от страхователей с
высоким риском.

Глава 8. Экономика информации
467
В то же время не следует ожидать особого улучшения с точки зрения
эффективности. Например, если MRS^O, 0)<7C, то существует
разделяющее равновесие, в котором страхователь с низким риском получает
(нулевой) полис @, 0), а страхователь с высоким риском получает полис
(L, uL). To есть только страхователь с высоким риском оказывается
застрахованным. Более того, этот исход является равновесным независимо
от доли страхователей с высоким риском! Таким образом, наличие
гнилого яблока — даже с очень низкой вероятностью — тем не менее может
«испортить» исход точно так же, как в конкурентном равновесии при
асимметричной информации.
Несмотря на существование равновесий, столь же неэффективных, как
и в модели без сигналов, когда рыночные сигналы имеют место, всегда
есть равновесия, в которых страхователь с низким риском приобретает
некоторую страховку. В том из них, которое является наилучшим для
страхователя с низким риском и наихудшим для страховой компании,
страхователь с низким риском приобретает полис, обозначенный как \j/z на рис. 8.7.
Р
р = пВ — линия нулевой прибыли
от страхователя с высоким риском
р-тфЛ-а — линия
постоянной прибыли от страхователя
с низким риском
р = пВ — линия нулевой
прибыли от страхователя с
низким риском
чт-ь
-+в
0 L
Рис. 8.7. Разделяющие равновесия. Пара полисов (\\fn \\fch) является
исходом разделяющего равновесия тогда и только тогда, когда \|/, Ф \\fh и \\f,
находится в затемненной области. Заметим, что (\\f% \\fch) Парето-доминирует
(\|/р \\fch). Страхователь с высоким риском безразличен между этими
парами, равно как и страховая компания (\|/^ и щ находятся на одной и той же
линии постоянной прибыли <?>0, полученной от страхователя с низким
риском). Но страхователь с низким риском предпочитает полис \|/" полису
\|//, потому что из факта б) следует, что MRSl(\\f')>n. Следовательно, среди
разделяющих равновесий только те, у которых \|/, лежит между \j/, и \|f , не
доминируются по Парето другими разделяющими равновесиями

468
Часть III. Стратегическое поведение
Поскольку страхователь с высоким риском получает тот же самый
полис \\fch и имеет одинаковую полезность в любом разделяющем
равновесии, то равновесный исход (\j7/9 \\fch) является Парето-эффективным
среди разделяющих равновесий и обеспечивает нулевую прибыль
страховой компании. Этот исход присутствует на рис. 8.7 независимо от
вероятности, с которой «выбирается» страхователь с низким риском. Таким
образом, даже когда в единственном конкурентном равновесии в условиях
асимметричной информации страхователь с низким риском не страхуется
(что происходит при достаточно малом а) в случае, если допускается
использование рыночных сигналов, тогда страхователь с низким риском
может получить страховку и эффективность рынка может быть повышена.
Теперь обратим свое внимание на равновесия второго типа.
Объединяющее равновесие
Напомним, что равновесие называется объединяющим, если оба типа
страхователей выбирают одинаковый полис. Из-за этого страховая
компания не может различить их. Следовательно, к страхователю с низким
риском будут относиться отчасти как к страхователю с высоким риском,
и наоборот. Заметим, что в таком равновесии страхователь с высоким
риском выдает себя за страхователя с низким риском.
Чтобы охарактеризовать множество объединяющих равновесий, давайте
сначала рассмотрим поведение страховой компании. Если оба страхователя
предлагают ей в равновесии один и тот же полис E, р), то при получении
предложения страховая компания не узнает ничего нового о вероятности
несчастного случая для страхователя. Следовательно, принятие такого
предложения принесло бы страховой компании ожидаемую прибыль, равную
р-(ак + {\-аУк)В.
Напомним, что здесь а — вероятность того, что страхователь
характеризуется низкой степенью риска.
Пусть
я = ая + A-а)я.
Тогда полис будет принят при р>пВ, отклонен при р<кВ,и
страховой компании будет безразлично, принять или отклонить данное
предложение, если р = кВ.
По этой причине множество полисов (В, р), удовлетворяющих
условию p = ftB, будет играть важную роль в анализе объединяющего
равновесия. На рис. 8.8 показано множество таких полисов. Они лежат на
луче, выходящем из начала координат, называемом объединяющей линией
нулевой прибыли.

Глава 8. Экономика информации
469
45°
р = кВ — линия нулевой прибыли
от страхователя с высоким риском
В —объединяющая
нулевой прибыли
р = пВ — линия нулевой
прибыли от страхователя с
низким риском
>?
О
Рис. 8.8. Объединяющая линия нулевой прибыли
Теперь пусть (В,р) — равновесный полис в объединяющем
равновесии. Тогда согласно лемме 8.1
и, (Я, р)>йп
uh(B, p)>uch.
(8-5)
Кроме того, как было отмечено в обсуждении, следующем за леммой, этот
полис должен быть принят страховой компанией. Поэтому он должен
лежать на объединяющей линии нулевой прибыли или выше нее, так что
р>кВ. (8-6)
Полисы, удовлетворяющие трем предыдущим неравенствам,
изображены на рис. 8.9 в виде затемненной области. Теперь покажем, что
именно эти полисы и будут исходами объединяющего равновесия.
Р
45 Линия нулевой прибыли от стра-
/ хователя с высоким риском
Объединяющая линия
нулевой прибыли
и,
Линия нулевой прибыли
от страхователя с низким
риском
>#
Рис. 8.9. Объединяющие равновесия. Затемненная область — это множество
полисов, которые могут иметь место в объединяющем равновесии

470
Часть III. Стратегическое поведение
Теорема 8.2. Свойства объединяющего равновесия.
Полис \|/ = (В\ р') является исходом объединяющего равновесия
тогда и только тогда, когда он удовлетворяет неравенствам (8-5) и (8-6).
Доказательство. Обсуждение, предшествующее формулировке теоремы,
показывает, что, для того чтобы полис \|/ был исходом некоторого
объединяющего равновесия, пара (В\ р') должна удовлетворять неравенствам (8-5)
и (8-6). Поэтому нам достаточно доказать только обратное утверждение.
Предположим, что \|/' = E', р) удовлетворяет (8-5) и (8-6). Мы
должны определить ожидания р() и стратегию о(-) страховой компании
так, чтобы набор (i|/'? \|/, о(), р()) представлял собой секвенциальное
равновесие.
Как и в доказательстве теоремы 8.1, предположим, что
[0, если (В, р)*у';
[А, если (В, p) = \\f\ или р>кВ,
[К в противном случае.
Таким образом, как мы видели и при доказательстве теоремы 8.1,
страховая компания считает, что любое отклонение от равновесного
предложения исходит от страхователя с высоким риском. Следовательно, чтобы
максимизировать прибыль, компания должна будет принять предложение
(В, р) Ф \|/ только в том случае, если р>кВ, как и предписывает о().
Вместе с тем если предложен равновесный полис \|/, то по правилу
Байеса ожидания страховой компании должны оставаться теми же
(априорными), так как это предложение делается обоими типами
страхователей. Поскольку Р(\|/) = а, ожидания действительно удовлетворяют
правилу Байеса. И при этих ожиданиях поведение, максимизирующее
прибыль, предполагает, что принимается полис \|/, поскольку согласно (8-6)
он приносит неотрицательную ожидаемую прибыль.
Таким образом, ожидания страховой компании удовлетворяют правилу
Байеса, и при этих ожиданиях поведение страховой компании согласуется
с максимизацией ожидаемой прибыли при данном предложении
страхователя. Осталось только показать, что оба типа страхователей
максимизируют свою полезность при заданной стратегии страховой компании.
Предлагая \|/, страхователь (с высоким или низким риском) получает
этот полис. Отклоняясь от этой стратегии (предлагая полис E, р)*у'),
страхователь получает полис @, 0), если страховая компания отклоняет

Глава 8. Экономика информации
471
предложение (т.е. при р<кВ), и получает полис (В, р), если он
принимается страховой компанией (т.е. при р>кВ). Таким образом,
предложение \|/ является оптимальным для страхователя типа / = /, h, если
и,(х|/')^,@, 0)
и
мДу')>ut(B, р) для всех кВ<p<w.
Но эти неравенства следуют из (8-5) (см. рис. 8.9). Поэтому
(\|/, \|/', а(), р()) является секвенциальным равновесием. ¦
Как показано на рис. 8.9, возможно существование множества
объединяющих равновесий. Интересно посмотреть, как влияют на это
множество изменения а — вероятности того, что «выбирается» страхователь с
низким риском.
При уменьшении а затемненная область на рис. 8.9 сокращается,
поскольку наклон объединяющей линии нулевой прибыли возрастает, тогда
как все остальное остается неизменным. В конечном счете, затемненная
область вообще исчезнет. Таким образом, если вероятность того, что
страхователь характеризуется высоким риском, достаточно велика,
объединяющего равновесия не существует.
При увеличении а затемненная область на рис. 8.9 расширяется,
потому что наклон объединяющей линии нулевой прибыли уменьшается.
Рисунок 8.10 показывает, что при достаточно большом а существуют
Р
Линия нулевой прибыли от
страхователя с высоким риском
Объединяющая линия нулевой прибыли
Линия нулевой прибыли от
страхователя с низким риском
0
X
-+В
V/
Рис. 8.10. Объединяющее равновесие может доминировать разделяющее.
Лучшее разделяющее равновесие обеспечивает страхователям полисы
\|/, = ij// и \|/л = \\fch. Исход объединяющего равновесия \|/, = \\fh = \|/ в
затемненной области предпочитается обоими типами страхователей. Для исходов
других объединяющих равновесий, например \|/, = \\fh = \|/*, Это неверно

472
Часть III. Стратегическое поведение
объединяющие равновесия, при которых обоим типам страхователей
(даже страхователю с низким риском) лучше, чем им было бы в любом
разделяющем равновесии. Этот факт не кажется неожиданным в отношении
страхователя с высоким риском. Причина же, по которой это
распространяется и на страхователя с низким риском, кроется в том, что для него
процесс «самовыявления» оказывается весьма дорогостоящим.
Эффективное разделение предполагает, что страхователь с низким
риском выбирает тот полис, которому страхователь с высоким риском
предпочтет полис \|/?. Это ограничивает выбор страхователя с низким
риском и, конечно, уменьшает его полезность относительно той, которую
он имел бы, если бы страхователя с высоким риском не было. Когда а
достаточно велико и равновесие является объединяющим, это очень
напоминает ситуацию при отсутствии страхователя с высоким риском.
Издержки страхователя с низким риском в объединяющем равновесии —
это тогда просто чуть более высокие предельные издержки на единицу
страховых выплат (т.е. it) по сравнению с теми издержками, которые он
понес бы, если бы его тип был известен (т.е. я). Эти издержки стремятся к
нулю по мере того, как а приближается к единице. С другой стороны, в
разделяющем равновесии страхователь с низким риском несет издержки,
связанные с выявлением своего типа, и эти издержки отличны от нуля.
Читатель, возможно, обратил внимание, что при доказательстве
теорем 8.1 и 8.2 был общий (и не очень привлекательный) момент. В каждом
случае при построении равновесного набора ожидания страховой
компании были достаточно причудливыми.
Напомним, что в обоих доказательствах ожидания страховой
компании были сконструированы таким образом, чтобы каждое отклонение от
равновесия интерпретировалось как предложение страхователя с высоким
риском. Хотя формально в этом нет ничего некорректного, возможно,
стоит рассмотреть, действительно ли подобные ожидания обоснованны.
Перед тем как двигаться дальше, следует сделать одну оговорку. При
доказательстве теорем 8.1 и 8.2 ожидания сконструированы вполне в духе
нашего определения секвенциального равновесия в играх с сигналами на
рынке страхования. Мы собираемся обсудить, действительно ли мы хотим
ввести дополнительные ограничения на ожидания страховой компании.
Пояснения
Являются ли ожидания, предписанные страховой компании при
доказательстве теорем 8.1 и 8.2, обоснованными? Чтобы убедиться в
обратном, рассмотрим типичный полис, соответствующий объединяющему
равновесию \|/, изображенному на рис. 8.11.

Глава 8. Экономика информации
473
Р
^
45°
, Линия нулевой прибыли от страхо-
/ вателя с высоким риском
и* Объединяющая линия
нулевой прибыли
Линия нулевой прибыли
от страхователя с низким
риском
¦> В
Рис. 8.11. Являются ли ожидания фирмы логичными? Если \|/ является
исходом объединяющего равновесия, то предложение \|/" предпочитается
только страхователем с низким риском. Оно также лежит выше линии
нулевой прибыли от страхователя с низким риском. Такой полис \|/" всегда
существует, потому что \|/ лежит на объединяющей линии нулевой
прибыли или выше нее, и MRS,(\\f') < MRSh(\\f')
По условию равновесия, сконструированного при доказательстве
теоремы 8.2, что бы страхователь ни предложил вместо полиса 1|/\
страховая компания будет полагать, что этот страхователь характеризуется
высокой вероятностью несчастного случая, и отклонит такое предложение.
Но правомерны ли такие ожидания при равновесном полисе 1|/'?
Заметим, что, предлагая равновесный полис \|/, страхователь с низким риском
получает полезность и*, а страхователь с высоким риском — полезность
и\. Более того, и] <и{{^) и uh{vf")<u*h. Поэтому независимо от того,
принимает страховая компания предложение \|/* или отклоняет его,
страхователь с высоким риском, делая это предложение, оказывается в
худшей ситуации, чем та, которая сложилась бы, предложи он равновесный
полис \|/. Вместе с тем если бы страховая компания приняла
предложение у", то страхователь с низким риском был бы в лучшем положении,
сделав это предложение, чем предложив равновесный полис \|/. Проще
говоря, только у страхователя с низким риском есть стимул предлагать
полис \\f" при условии, что \|/ является равновесным предложением.
Имея это в виду, кажется, нет никакой логики в том, что страховая
компания, получив предложение \|/", вдруг решит, что его сделал страхо-

474
Часть III. Стратегическое поведение
ватель с высоким риском. Гораздо более обоснованным было бы
предположение, что этот полис предложил страхователь с низким риском.
Соответственно мы вводим еще одно ограничение на ожидания страховой
компании. Оно применимо не только к объединяющим, но и ко всем
секвенциальным равновесиям.
Определение 8.3. Интуитивный критерий Хо — Крепса.
Секвенциальное равновесие (\|/,, \|/л, о(), ($(•)), обеспечивающее
равновесные полезности и] и и\ для страхователей с низким и высоким рис-
ком соответственно, удовлетворяет интуитивному критерию, если для
любого полиса 1|/*\|/, или \|/л выполнено следующее условие:
Если ui(\y)>u* и Uj(\\f)<u*j, тогда E(\|/) приписывает вероятность,
равную единице, страхователю типа i, так что
f 1, если i = /,
т = \п • *
[О, если i = п.
Ограничиваясь секвенциальными равновесиями, удовлетворяющими
интуитивному критерию, мы значительно уменьшаем множество
равновесных полисов. Действительно, имеет место следующая теорема.
Теорема 8.3. Равновесие, удовлетворяющее интуитивному
критерию.
Существует единственная пара полисов (\|//5 \|/л), совместимая с
секвенциальным равновесием, которое удовлетворяет интуитивному
критерию. Более того, это равновесие — наилучшее разделяющее равновесие
для страхователя с низким риском (т.е. \|/, = \j/, и \\fh = \\fch; см. рис. 8.7).
Доказательство. Сначала докажем, что не существует
объединяющего равновесия, удовлетворяющего интуитивному критерию. Фактически
мы почти уже сделали это при обсуждении рис. 8.11, предшествовавшем
определению 8.3. Там было доказано, что если \|/ — исход
объединяющего равновесия, то существует полис \|/*, который предпочитается только
страхователем с низким риском и который, кроме того, находится выше
линии нулевой прибыли от страхователя с низким риском (см. рис. 8.11).
Следовательно, если страхователь с низким риском выбирает этот полис,
то в соответствии с интуитивным критерием страховая компания должна
полагать, что имеет дело со страхователем с низким риском. Так как
полис \|/" лежит выше линии нулевой прибыли от страхователя с низким
риском, страховая компания должна его принять (по условию
секвенциальной рациональности). Но это означает, что страхователь с низким
риском может увеличить свой выигрыш, отклоняясь от \|/' к \|/'. Это проти-

Глава 8. Экономика информации 475
воречие доказывает утверждение, что не существует объединяющего
равновесия, удовлетворяющего интуитивному критерию.
Предположим теперь, что (у,, \|/А, о(), р()) — разделяющее
равновесие, удовлетворяющее интуитивному критерию. Тогда согласно
лемме 8.1 предложение страхователя с высоким риском должно быть принято
страховой компанией и его равновесная полезность щ должна быть не
ниже и\ (см. рис. 8.12).
Далее предположим от противного, что равновесная полезность
страхователя с низким риском и* удовлетворяет неравенству и* <w/(\j//). Пусть
^(=(Bl9 Pi) и \|/, =(?,-?, /?,+?), где 8 — достаточно малое
положительное число. Тогда вследствие непрерывности и1 (•), если ? достаточно
мало, выполняются следующие неравенства (см. рис. 8.12):
ul(\\fel)>ul,
р1+г>к(В1-г).
Первые два неравенства вместе с интуитивным критерием означают,
что, получая предложение \|/*, страховая компания полагает, что его
делает страхователь с низким риском. Из третьего неравенства и свойства
секвенциальной рациональности стратегического набора следует, что
страховая компания должна принять предложение \|/,, потому что она
получает при этом положительную ожидаемую прибыль.
Следовательно, страхователь с низким риском может обеспечить себе
полезность мД\|/*)>м*, предлагая полис \|/,. Но тогда и* не может быть
равновесной полезностью страхователя с низким риском. Это
противоречие говорит о том, что равновесная полезность страхователя с низким
риском должна быть не ниже иДу,). Таким образом, мы показали, что
равновесные полезности страхователей обоих типов должны
удовлетворять неравенствам
Эти неравенства означают, что предложения, сделанные
страхователями обоих типов, принимаются страховой компанией. Следовательно,
выполняются условия теоремы 8.1. Но согласно теореме 8.1 эти два
неравенства могут иметь место в секвенциальном равновесии, только если
\\fj=\\fn Vh=Yh (см. рис. 8.7).

476
Часть III. Стратегическое поведение
45°
Линия нулевой прибыли
от страхователя с высоким риском
Линия нулевой прибыли
от страхователя с низким
риском
\
¦+В
Ч>/
Рис. 8.12. Страхователь с низким риском может получить полис \|/,
Осталось только показать, что разделяющее равновесие,
удовлетворяющее интуитивному критерию, существует. Представим одно такое
равновесие.
Пусть \|/, = vj/, и \|/л = \\fch. Чтобы определить ожидания страховой
компании Р(-) способом, совместимым с интуитивным критерием,
рассмотрим следующее множество полисов (см. рис. 8.13):
A = {y\ul(\\f)>ul(\\fl) и uh(\\f)<uh(\\fch)}.
Это — множество полисов, которые только страхователь с низким
риском предпочитает своему равновесному полису.
Р
Линия нулевой прибыли
от страхователя с высоким риском
Линия нулевой прибыли
от страхователя с низким
риском
>В
Рис. 8.13. Равновесие, удовлетворяющее интуитивному критерию

Глава 8. Экономика информации 477
Определим теперь р() и о(-) следующим образом:
а(в ) = [1> если (Я> />)еЛи{у,}
[О, если (Z?, р)? ^и{\|//};
\А, если {B,p)-\fl или р>ЖВ,
[/с в противном случае.
Можно легко проверить, что эти ожидания удовлетворяют
интуитивному критерию. Кроме того, фактически повторив соответствующую
часть доказательства теоремы 8.1, можно заключить, что набор
(V/> Va» a(')> P@) является разделяющим равновесием. ¦
Следствием дополнительного ограничения на ожидания страховой
компании, представленной интуитивным критерием, является то, что
наилучшее разделяющее равновесие становится наиболее вероятным
исходом игры с рыночными сигналами. Как мы установили ранее, этот
исход может доминировать конкурентный исход при асимметричной
информации. Таким образом, использование сигналов — действительно
один из способов повысить эффективность данного рынка.
Существует и другой путь к повышению эффективности конкурентных
исходов при асимметричной информации. В действительности на реальном
рынке страхования наиболее распространен альтернативный подход.
8.1.3. Скрининг
Когда большинство потребителей приобретают услуги
автострахования, они не передают на рассмотрение страховой компании полис и не
ждут от нее ответа, как в модели, которую мы описали в предыдущем
разделе. Обычно страховая компания предлагает страхователю меню
полисов, а страхователь просто делает свой выбор. При этом страховые
компании могут (косвенным образом) сортировать страхователей,
составляя меню так, чтобы страхователи с высоким риском были
заинтересованы выбирать один полис, а страхователи с низким риском — другой.
Перейдем к анализу такой модели.
В данном случае мы снова сформулируем рассматриваемую
ситуацию как игру в развернутой форме. Для иллюстрации существенных
свойств модели с сигналами достаточно было рассмотреть только одну
страховую компанию, однако, чтобы выявить нюансы модели скрининга,
требуются две страховые компании. Поэтому добавим в модель еще одну
страховую компанию1.
В модель с рыночными сигналами мы также могли бы включить две страховые
компании. Это не изменило бы результата сколь-нибудь заметным образом.

478
Часть III. Стратегическое поведение
Как и прежде, имеются два страхователя — с низким и высоким
риском, «выбираемые» Природой с вероятностью а и 1 - а соответственно.
И снова это можно интерпретировать как существование многих
страхователей, доля которых (а) — это страхователи с низким риском.
Рассмотрим следующую игру, включающую две страховые компании
и двух страхователей. На рис. 8.14 показана развернутая форма этой игры.
Страховая компания А
Высокий риск A - а)
Страхователь
с низким риском
У
Рис. 8.14. Модель скрининга на рынке страхования. Отметим, что в
отличие от рисунка, на самом деле страховые компании имеют континуум
действий. Так что это игра не является конечной
• Две страховые компании делают ход первыми, одновременно
выбирая конечный набор (меню) полисов.
• Природа делает ход второй и определяет тип страхователя, с
которым столкнутся страховые компании. Страхователь с низким риском
выбирается с вероятностью а, а страхователь с высоким риском — с
вероятностью 1-ос.
• Выбранный страхователь делает ход последним, отдавая
предпочтение одному полису из какого-либо набора, предложенного страховыми
компаниями.
Поскольку есть только два возможных типа страхователей,
ограничимся анализом ситуаций, когда страховые компании предлагают меню не
более чем с двумя полисами. Таким образом, чистая стратегия для страховой
компании j = А, В — это пара полисов *?J =(\|//, \|/^). Под \|//
(соответственно, \\fJh) мы подразумеваем полис, который страховая компания j
предназначает для страхователя с низким (соответственно с высоким)
риском. Однако имейте в виду, что страхователь с низким (соответственно с
высоким) риском не обязательно выберет этот полис, так как страховая

Глава 8. Экономика информации 479
компания не может идентифицировать его тип. Из полисов, предложенных
этими двумя страховыми компаниями, страхователь предпочтет тот полис,
который обеспечит ему наибольшую полезность.
Чистая стратегия для страхователя / = /, h — это функция выбора
сД), определяющая для каждой пары из пар полисов Q?A, Ч*в)
страховую компанию и один из предлагаемых ею полисов (или «нулевой
полис»). Таким образом, мы всегда даем страхователям возможность
выбирать нулевой полис любой страховой компании, даже если этот полис
формально не включен в меню ни одной компании. Это просто удобный
способ предоставить страхователям право не приобретать страховку.
Таким образом, сДЧ''4, x?B) = (j\ \|/),где j = A илиу =5, и где \|/ = у/, \|/j[
или @, 0).
Из рис. 8.14 очевидно следует, что единственное неодноточечное
информационное множество принадлежит страховой компании В. Однако
заметим, что независимо от того, какие стратегии используют игроки, это
информационное множество всегда имеет место. Следовательно,
достаточно рассмотреть совершенное в подыграх равновесие этой игры. Вас
попросят показать в упражнении, что если бы игра была конечной (так
что можно было использовать понятие секвенциального равновесия),
множество исходов для секвенциальных равновесий этой игры совпадало
бы с множеством исходов совершенных в подыграх равновесий.
И снова мы можем разбить множество совершенных в подыграх
равновесий в чистых стратегиях на два вида: разделяющие и объединяющие.
В разделяющем равновесии два страхователя выбирают различные полисы,
тогда как в объединяющем равновесии они выбирают один и тот же полис.
Определение 8.4. Разделяющее и объединяющее равновесия в
модели скрининга.
Совершенное в подыграх равновесие в чистых стратегиях
Q?A, Ч^, сД), ch(-)) является разделяющим, если У/^Уа? г&е
Ui> V|//) = c/D/^, Ч*в) и (jh, \\fh) = chC?A, ?*), и объединяющим — в
противном случае.
Заметим, что в объединяющем равновесии, хотя страхователи двух
типов должны выбрать один и тот же полис, они не обязаны покупать его
у одной и той же страховой компании.
Анализ игры
Мы хотим охарактеризовать множество совершенных в подыграх
равновесий в модели скрининга на рынке страхования. Важный элемент
данного анализа — феномен, называемый снятием сливок.

480 Часть III. Стратегическое поведение
Снятие сливок происходит, когда одна страховая компания получает
стратегическое преимущество от множества полисов другой компании,
предлагая, в свою очередь, такой полис, который «увел» бы у компании-
конкурента только страхователей с низким риском. Такая страховая
компания привлекает только наилучших страхователей (сливки), в то
время как ее конкурент остается с наихудшими страхователями. В
равновесии обе компании должны гарантировать, что конкурент не сможет
снимать сливки подобным образом. Заметим, что, для того чтобы
феномен снятия сливок мог стать стратегической возможностью, требуется по
крайней мере две фирмы. Именно это обстоятельство обусловило
введение в модель второй страховой компании.
Сначала приведем лемму, которая применима ко всем совершенным в
подыграх равновесиям в чистых стратегиях.
Лемма 8.2. Обе страховые компании получают нулевую
ожидаемую прибыль в любом совершенном в подыграх равновесии в чистых
стратегиях.
Доказательство. Доказательство этого вывода аналогично
доказательству подобного результата в модели Бертрана (см. главу 4).
Для начала заметим, что в равновесии каждая страховая компания
должна получать неотрицательную прибыль, поскольку любая из них
может гарантировать себе нулевую прибыль, предлагая пару нулевых
полисов В = /? = 0. Таким образом, достаточно показать, что ни одна из
страховых компаний не получит положительную ожидаемую прибыль.
Предположим от противного, что компания А получает
положительную ожидаемую прибыль и что прибыль компании В не превышает
прибыль компании А. Пусть \|/* =(/?,*, р*) и \y*h=(B*h9 p*h) обозначают
полисы, выбранные в равновесии страхователями с низким и высоким
риском соответственно. Тогда совокупную ожидаемую прибыль двух фирм
можно записать в виде
n = a(P;-i&;) + (\-a)(ph-KBl)>0.
Очевидно, что П превышает ожидаемую прибыль компании В.
Рассмотрим теперь два случая.
Случай 1: \|/* =\\f*h =(В\ р*). Рассмотрим следующее отклонение
компании В. Компания В предлагает пару полисов
{(В* +е, />*), (В* +е, р*)}, где ? > 0. Очевидно, что страхователь
каждого типа тогда предпочтет выбрать полис (В* +е, р*) компании В при
любом 8 > 0; а если е — достаточно малая величина, ожидаемая
прибыль компании В будет достаточно близка к П и тем самым будет пре-

Глава 8. Экондмика информации
481
вышать ее прибыль в равновесии. Но это противоречит свойствам
равновесия.
Случай 2: \|/* = (В*, р]) *\\f*h=(B*h, p*h). По условию равновесия
страхователь любого типа не может увеличить свой выигрыш, выбирая полис
другого страхователя. Тогда из свойства единственности пересечения
следует, что по крайней мере один из страхователей строго предпочтет
свой полис; т.е. либо
«/(?/) Ж/(чО, (Р-1)
либо
"ЛчО^Л^)- (Р-2)
Предположим тогда, что выполняется (Р-1). Рассмотрим стратегию
компании 5, при которой она предлагает пару полисов \|/, =(В* + е, р]) и
\|/*=(Я;+р, А),гдее, Р>0.
Очевидно, что каждый страхователь /' = /, h предпочтет полис \|/*
полису \|/*. Кроме того, мы утверждаем, что числа е, Р > 0 могут быть
достаточно малыми, чтобы выполнялись неравенства
ulW)>ul(yl), (Р-3)
«М)>«№). (Р-4)
Чтобы понять это, заметим, что согласно (Р-1) неравенство (Р-3) будет
выполняться для всех достаточно малых е и Р. Неравенство (Р-4) тогда
можно гарантировать, фиксируя Р и выбирая достаточно малое 8,
поскольку для фиксированного Р > 0 мы имеем
е-»0
Здесь нестрогое неравенство— следствие того, что в равновесии
страхователь с высоким риском не может предпочесть никакой другой
полис, нежели тот, который он сам выбрал (см. рис. 8.15).
Но (Р-3) и (Р-4) говорят о том, что при таком отклонении компании
В страхователь с низким риском выберет полис \|/,, а страхователь с
высоким риском выберет полис V|/^. Если 8 и Р достаточно малы, это дает
ожидаемую прибыль компании В, сколь угодно близкую к П и,
следовательно, выше ее равновесной ожидаемой прибыли, что противоречит
условию.

482
Часть III. Стратегическое поведение
->Я
О
Рис. 8.15. Трудный случай. Изображен наиболее трудный для анализа
случай, при котором (Р-1) и* = и, (\|/* )>и1 (\|/*) выполняется, но
щ =uh(\\f*h) = uh(\\f])9 так что (Р-2) не выполняется. Для каждого (J>0
существует достаточно малое е > 0, такое, что и\ = uh(yl)> и) = uh{\y)). Когда
полисы \|/, и \|/д оказываются доступными, Vj/' предпочитается
страхователем с низким риском, а \|/Ц* — страхователем с высоким риском
Аналогичная аргументация приводит к противоречию и в ситуации,
когда выполняется (Р-2), так что можно сделать вывод, что обе страховые
компании должны получить нулевую ожидаемую прибыль в каждом
совершенном в подыграх равновесии. ¦
Объединяющее равновесие
Можно предположить, что множество объединяющих равновесий
перестанет существовать благодаря феномену снятия сливок. В самом деле,
если оба типа страхователей поступают одинаково, ситуация кажется
вполне подходящей для снятия сливок. Это предположение более чем
оправдывается. Действительно, следствием феномена снятия сливок
оказывается отсутствие объединяющего равновесия.
Теорема 8.4. Отсутствие объединяющих равновесий.
В модели скрининга на рынке страхования объединяющего
равновесия в чистых стратегиях не существует.
Доказательство. Докажем это утверждение от противного.
Предположим, что это не так и полис \|/* =(В\ р*) выбран обоими
страхователями в совершенном в подыграх равновесии. По лемме 8.2 со-

Глава 8. Экономика информации
483
вокупная ожидаемая прибыль двух страховых компаний должна быть
нулевой, т.е.
а(р* -кВ*) + (\-а)(р* -кВ*) = 0. (Р-1)
Рассмотрим сначала случай, когда В* > О. Тогда из (Р-1) следует, что
/-7cS*>0. (P-2)
Следовательно, р* > О, так что \\f* не лежит ни на одной из осей
координат, как показано на рис. 8.16.
Р
-* в
Рис. 8.16. Полис \|/* не лежит на осях
По свойству единственности пересечения существует область R (см.
рис. 8.16), такая, что полис \\f* является пределом полисов в Л. Пусть
\|/ — полис в R, лежащий достаточно близко к \\f*.
Предположим теперь, что в равновесии страховая компания А
предлагает полис i|/. Если страховая компания В предлагает только полис
\|Л то страхователь с высоким риском выберет полис \|/* (или один из
полисов, эквивалентный \|/*), предложенный первой страховой
компанией, тогда как страхователь с низким риском приобретет полис \|/,
предложенный страховой компанией В. Если \|/ достаточно близок к \|/*, то в
соответствии с (Р-2) страховая компания В получит положительную
прибыль от этого отклонения, поэтому должна получать положительную
прибыль в равновесии. Но это противоречит лемме 8.2.

484
Часть III. Стратегическое поведение
Рассмотрим теперь случай, когда В* = О. Из (Р-1) следует, что р* = О.
Таким образом, \|/ — нулевой полис, как показано на рис. 8.17. Любая
компания теперь может получить положительную прибыль, предлагая
единственный полис (Z,, HL + г), где е — достаточно малая
положительная величина. Предложившая его страховая компания имеет
положительную прибыль, потому что положительную прибыль приносят
страхователи обоих типов (этот полис находится выше линии нулевой прибыли,
полученной как от страхователя с высоким риском, так и от страхователя с
низким риском). Но страхователь с высоким риском при достаточно
малом г предпочтет этот полис нулевому полису. Это заключительное
противоречие завершает доказательство. ¦
Линия нулевой прибыли
от страхователя с
высоким риском
О L
Рис. 8.17. Полис \|/— нулевой
Отметим важность феномена снятия сливок для предшествующих
результатов. Это характерная черта конкурентных моделей скрининга, где
многочисленные агенты, представляющие одну сторону рынка,
конкурируют за привлечение общего пула агентов с другой стороны рынка,
одновременно предлагая набор «контрактов», из которых агенты из этого пула
могут выбирать подходящие им контракты.
Разделяющее равновесие
Конкурентная природа нашей модели скрининга, как мы сейчас
покажем, оказывает заметное влияние на множество разделяющих равновесий.
Теорема 8.5. Свойства разделяющего равновесия.
Предположим, что щ и \\f*h — полисы, выбранные страхователями с
низким и высоким риском соответственно в разделяющем равновесии в
чистых стратегиях. Тогда \|/* =\j77 и \\f*h =\\fch, как показано на рис. 8.18.

Глава 8. Экондмика информации
485
Р
т 45° Линия нулевой прибыли
/ от страхователя
' с высоким риском
Линия нулевой прибыли
от страхователя с низким
риском
Рис. 8.18. Единственно возможное разделяющее равновесие. Оно совпадает
с наилучшим разделяющим равновесием в игре с сигналами на рынке
страхования, рассмотренной в разделе 8.1.2
Отметим, что это единственно возможное разделяющее равновесие в
модели скрининга на рынке страхования совпадает с наилучшим
равновесием в игре с сигналами на рынке страхования, рассмотренной в
разделе 8.1.1. По теореме 8.4 оно будет единственно возможным равновесием в
игре.
Доказательство. Доказательство состоит из нескольких
утверждений.
Утверждение 1. Страхователь с высоким риском должен получить
полезность не ниже и\ (см. рис. 8.18).
По лемме 8.2 прибыль страховых компаний равна нулю.
Следовательно, ситуация, когда страхователь с высоким риском строго
предпочтет полис (L, кЬ + е) полису \\f*h возникнуть не может. Поскольку в этом
случае одна из страховых компаний могла бы, предложив только этот
полис, получить положительную прибыль. (Отметим, что этот полис
приносит положительную прибыль от страхователей обоих типов.) Но это
означает, что
uh(\\f*h) > uh(L9 nL + г) для любого е > 0.
Взяв предел от правой части неравенства при е-H и учитывая, что
ин(-) непрерывна, получим: \\fch=(L, HL).

486
Часть III. Стратегическое поведение
Утверждение 2. Полис \|/* должен принадлежать линии нулевой
прибыли, полученной от страхователя с низким риском.
Заметим, что согласно утверждению 1 полис \\f*h должен лежать на
линии нулевой прибыли от страхователя с высоким риском или ниже нее.
Так что от страхователя с высоким риском прибыль неположительна. По
лемме 8.2 совокупная прибыль страховых компаний равна нулю. Это
означает, что \|/* принадлежит линии нулевой прибыли от страхователя с
низким риском или лежит выше нее.
Итак, предположим от противного, что V|/* =E*, p]) находится выше
линии нулевой прибыли от страхователя с низким риском. Тогда р* > О.
Но это означает, что и В* > О, поскольку страхователь с низким риском в
противном случае выбрал бы нулевой полис (который всегда доступен).
Таким образом, полис \|/* лежит выше линии нулевой прибыли от
страхователя с низким риском, а не на вертикальной оси, как показано на рис. 8.19.
Линия нулевой прибыли
от страхователя
с низким риском
Рис. 8.19. Область снятия сливок
Следовательно, область R на рис. 8.19 не пуста. Если страховая
компания, которая не продает полис страхователю с высоким риском, будет
предлагать полис только в пределах области R, тогда лишь страхователь
с низким риском приобретет такой полис у этой страховой компании,
поскольку он более предпочтителен для страхователя с низким риском, чем
полис щ, и хуже, чем \|/* (который не лучше \y*h) для страхователя с
высоким риском. Такое отклонение принесло бы положительную прибыль
этой страховой компании, поскольку все такие полисы лежат выше линии

Глава 8. Экономика информации
487
нулевой прибыли от страхователя с низким риском. Искомый результат
следует из этого противоречия.
Утверждение 3. \\f*h = \\fch.
Согласно утверждению 2 и лемме 8.2 \|/* должен лежать на линии
нулевой прибыли от страхователя с высоким риском. Но по утверждению
1 uh(yf\)^uh(yCh)' Вместе два этих утверждения позволяют сделать
вывод, что \|/* =\|/? (см. рис. 8.18).
Утверждение 4. \|/* = \j/z.
Посмотрим на рис. 8.20. Согласно утверждению 2 достаточно
показать, что \|/* не может лежать на линии нулевой прибыли от страхователя
с низким риском строго ниже vj/, (подобно \|/*) или строго выше xj/,
(подобно \|/').
Линия нулевой прибыли от
45° страхователя с высоким риском
Линия нулевой прибыли
от страхователя
с низким риском
-> В
Рис. 8.20. Область снятия сливок: еще один вариант
Итак, предположим сначала, что \|/* = \|/. Страхователь с высоким
риском тогда предпочел бы полис \|/ полису \\fch и, таким образом, не
выбрал бы \\fch, вопреки утверждению 3.
Теперь, предположим, что \|/* = \|/". Тогда страхователь с низким
риском получает равновесную полезность и* (см. рис. 8.20). Кроме того,
область R в этом случае не пуста. Рассмотрим страховую компанию, кото-

488
Часть III. Стратегическое поведение
рая не продает полис \\fch страхователю с высоким риском. Если эта
страховая компания предложит полис в пределах области R, то он будет
куплен только страхователем с низким риском и принесет предложившей его
компании положительную прибыль. Это противоречие доказывает
утверждение 4 и завершает доказательство. ¦
Отметим, что теорема 8.5 не утверждает, что разделяющее
равновесие в модели скрининга существует. Вместе с теоремой 8.4 она говорит
только о том, что, если существует совершенное в подыграх равновесие в
чистых стратегиях, то оно должно быть разделяющим, а полисы,
выбранные страхователями, единственны.
Снятие сливок — мощный механизм в данной модели скрининга для
исключения равновесий. Но, возможно, он даже слишком мощный.
Действительно, иногда имеют место случаи, когда совершенное в подыграх
равновесие в чистых стратегиях вообще не существует.
Посмотрим ситуацию, представленную на рис. 8.21. Это как раз тот
случай, когда не существует равновесия в чистых стратегиях. Чтобы
убедиться в этом, достаточно показать, что ситуация, при которой
страхователи с низким и высоким риском получают полисы ij/, и \|/'Л, как описано
в теореме 8.5, не является равновесием. Это действительно так, поскольку
45° Линия нулевой прибыли
от страхователя
/ с высоким риском
Объединяющая линия
нулевой прибыли
Линия нулевой прибыли
от страхователя с низким
риском
О
-+В
Рис. 8.21. Равновесие не существует. Если наилучшие полисы, доступные
для страхователей с низким и высоким риском, равны \j// и \\fch
соответственно, то предложение полиса \|/' привлечет страхователей обоих типов и
позволит получить положительную прибыль, поскольку этот полис лежит
выше объединяющей линии нулевой прибыли. В этом случае не существует
совершенного в подыграх равновесия в чистых стратегиях

Глава 8. Экономика информации
489
любая страховая компания может отклониться, предлагая только полис
\|/', который будет куплен обоими типами страхователей (потому что они
строго предпочтут его своим равновесным полисам). Следовательно, эта
компания получит положительную ожидаемую прибыль, потому что \|/
лежит строго выше объединяющей линии нулевой прибыли и этот полис
приобретают страхователи обоих типов. Но это противоречит лемме 8.2.
Таким образом, когда а достаточно близко к единице, так что
объединяющая линия нулевой прибыли пересекает кривую безразличия и,
(см. рис. 8.21), в модели скрининга нет совершенного в подыграх
равновесия в чистых стратегиях1. Можно показать, что всегда существует
совершенное в подыграх равновесие в поведенческих стратегиях, но мы не
будем его рассматривать. Заметим только, что равновесие (в чистых
стратегиях) в данной модели отсутствует, только когда асимметрия
информации распространена относительно слабо и, в частности, когда
страхователей с высоким риском мало.
Теперь мы рассмотрим проблему, которую до сих пор игнорировали.
Каково влияние страховки на поведение страхователя?
8.2. Моральный риск и модель контрактных отношений
Страховые компании не наивны. Они хорошо понимают, что, как
только потребитель их услуг приобрел автомобильную страховку, он
может и не управлять автомобилем так же аккуратно, как прежде, пока не
застраховался. Более того, заинтересованность страхователя в
осторожной езде, вероятно, уменьшается с увеличением суммы возмещения по
договору страхования. К несчастью, страховые компании не видят усилий
потребителей по обеспечению безопасности движения. Поэтому они
вынуждены конструировать свои полисы так, чтобы сами полисы
побуждали страхователей соблюдать все меры предосторожности.
Когда принципал, или заказчик (подобно страховой компании),
заинтересован в результатах действий, предпринятых агентом, или
исполнителем (в данном случае — страхователем), но действия исполнителя
неочевидны для заказчика, то говорят, что имеет место моральный риск.
Модель контрактных отношений сводится к тому, что принципал
должен разработать такие условия стимулирования, которые заставили бы
Даже когда объединяющая линия нулевой прибыли не пересекает кривую безразличия
W,, нет гарантий, что равновесие будет существовать, поскольку может существовать
пара полисов, таких, что один привлекает страхователей с низким риском, принося
положительную прибыль, а другой — страхователей с высоким риском (удерживая их от
принятия первого полиса), принося отрицательную прибыль. При этом совокупная
ожидаемая прибыль положительна.

490
Часть III. Стратегическое поведение
агента придерживаться линии поведения, отвечающей его (принципала)
интересам. Применим эти идеи к нашему рынку страхования.
Для простоты рассмотрим модель с одной страховой компанией и
единственным страхователем. Со страхователем может произойти
несчастный случай, который повлечет за собой различные суммы потерь. Есть
L уровней потерь в пределах от 1 до L долл. в зависимости от
серьезности аварии. Возможно также, что несчастный случай вообще не
произойдет. Логично трактовать этот исход как несчастный случай, приводящий к
потере 0 долл.
Вероятность аварии, когда потери равны /е {0, 1, ...,Z,}, составляет
щ(е) > 0, где е — это усилия, предпринятые для обеспечения
безопасности движения. Как утверждалось выше, естественно предположить, что
эти вероятности зависят от подобных усилий. Заметим, что У?1Щ(е) = 1
для любого фиксированного уровня усилий е.
Чтобы не усложнять анализ, предположим, что страхователь может
предпринимать два уровня усилий. Пусть е = 0 обозначает низкий
уровень усилий, а е = 1 — высокий. Для того чтобы выразить идею, что
более высокий уровень усилий приводит к более низкой вероятности того,
что со страхователем произойдет более серьезная (т.е. влекущая за собой
большие затраты) авария, введем следующее предположение.
Предположение 8.1. Монотонность отношения правдоподобия.
яДО)/^^) возрастает по /е {0, 1, ...,Z,}.
Монотонность отношения правдоподобия означает, что условная по
наблюдаемым потерям / относительная вероятность того, что был
приложен низкий уровень усилий, возрастает по /. Таким образом, чем
выше наблюдаемые при аварии потери, тем выше вероятность того, что
страхователь приложил низкий уровень усилий.
Как и в наших предыдущих моделях, страхователь имеет
возрастающую, строго вогнутую функцию полезности от богатства фон Неймана —
Моргенштерна и(), и первоначальное богатство w>L. Обозначим через
d(e) отрицательную полезность страхователя от уровня усилий е .Таким
образом, для заданного уровня усилий е функция полезности фон
Неймана— Моргенштерна, зависящая от богатства, равна u()-d(e), где
d(l)>d@I.
Предположим, что страховая компания может наблюдать объем
потерь / в результате аварии, но не усилия страхователя е по предотвраще-
1 Весь последующий анализ обобщается на случай, когда функция полезности имеет вид
м(и>, ё), где w(w, 0) > u(w, 1) для любых уровней богатства w .

Глава 8. Экономика информации
491
нию несчастного случая. Следовательно, страховая компания может
только соотнести объем страховых выплат с объемом потерь. Обозначим
выплаты страховой компании страхователю через В1, где / — потери от
несчастного случая. Таким образом, полис — это набор
(/?, В09 5,, ...,5L), где р — это цена, полученная страховой компанией
взамен на гарантию выплатить страхователю сумму в В1 долл., если
потери при аварии составят / долл.
Возникает интересный вопрос: какой же тип полиса страховая
компания предложит страхователю и будет ли он эффективным?
8.2.1. Симметричная информация
Чтобы оценить влияние ненаблюдаемости усилий страхователя по
предотвращению несчастного случая, рассмотрим сначала ситуацию,
когда страховая компания может наблюдать уровень усилий страхователя.
Страховая компания может предложить полис, по которому
выплачиваются страховые выплаты только в том случае, если страхователь
обеспечит заранее оговоренный (в контракте) уровень усилий. Фактически
страховая компания может выбирать уровень усилий страхователя.
Таким образом, страховая компания решает следующую задачу:
L L
max р-У]п1(е)В1 при Vщ(е)и(\^-p-l + Bj)-d(e)>u, (8-7)
где й обозначает резервную полезность страхователя1.
В соответствии с задачей (8-7) страховая компания выбирает полис и
уровень усилий, максимизирующий ее ожидаемую прибыль при
ограничении, что полис обеспечивает страхователю полезность не ниже
резервной. Следовательно, страхователь заинтересован принять условия
страхования и обеспечить заданный уровень усилий.
Легче всего решить задачу (8-7), предположив, что уровень усилий
ее {О, 1} фиксирован. Функция Лагранжа такой задачи, зависящая от
переменных p,BQ,...,BL, имеет вид:
? = р-У?к,(е)В1+Х
^nl(e)u(w-p-l-\-Bl)-d(e)-u
Поскольку страхователь всегда может решить не покупать страховку, й должно быть
по крайней мере не ниже, чем тах^ 1} ^1=0Щ(е)и(м?-1)-с1(е). Однако й может быть и
больше этой величины, если, например, существуют другие страховые компании, тоже
предлагающие полисы страхователю.

492
Часть IIL Стратегическое поведение
Условия первого порядка
М.1-х
др
^(eWiw-p-l + B,)
1=0
= 0, (8-8)
^ = -nl(e) + Xn!(e)u'(w-p-l + Bl) = 09 V/>0, (8-9)
oBt
— ^n^eMw-p-l + B;)- d(e)-u>0, (8-10)
ok /=o
где (8-10) выполняется как равенство, если X * 0.
Отметим, что первое условие (8-8) является избыточным, поскольку
следует из L +1 уравнения (8-9). Таким образом, вышеприведенные
условия определяют систему самое большее из L + 2 независимых уравнений
с1 + 3 неизвестными.
Из (8-9) следует, что X > 0 и
u'(w-p-l + Bl) = l/X, V/>0.
Следовательно, величина Bt-l должна быть постоянной для всех
/ = 0, 1, ...,1.
Поскольку X > 0, то ограничение задачи на решение должно
выполняться как равенство, т.е.
u{w-p-l + Bl) = d{e) + u, V/>0. (8-11)
Поскольку мы имеем только L + 2 независимых уравнения с L + 3
неизвестными, можно без ограничения общности положить В0=0\
Полагая 1 = 0 в (8-11), мы получаем уравнение, из которого находим р.
Кроме того, так как В{ - / является константой при любых / = 0, 1, ..., L и
50-0 = 0,то Bj =/, при любых / = 0, 1, ...,L.
Следовательно, при том или другом фиксированном уровне усилий
ее {0, 1} симметричная информация обеспечивает страхователю полное
страхование независимо от величины ущерба. Это не удивительно,
потому что страхователь характеризуется несклонностью к риску, а страховая
компания нейтральна к риску. Такой страховой контракт является приме-
Действительно, с самого начала было ясно, что можно положить В0 = 0, потому что
изменения В0 всегда могут быть компенсированы изменениями цены р и размером
выплат В19 ...,BL, не влияя при этом на полезность страхователя или прибыль
страховой компании.

Глава 8. Экономика информации
493
ром эффективного распределения риска. К тому же цена, назначенная
страховой компанией, позволяет страхователю при данном уровне усилий
получить полезность, равную резервной.
Теперь, когда мы определили оптимальный полис для каждого
уровня усилий, можно непосредственно выбрать и сам уровень усилий. При
заданном ее {О, 1} оптимальный размер страховых выплат составит
В( =1 для любого /. Таким образом, используя (8-11), оптимальную цену
р(е) можно определить неявным образом как
u(w-p(e)) = d(e) + u. (8-12)
Следовательно, страховая компания выберет такой уровень усилий
ее {О, 1}, где ожидаемая прибыль
L
р(е)-^Щ(еI
1=0
максимальна.
Отметим, что, выбирая между высоким и низким уровнем усилий,
надо искать компромиссное решение. Поскольку d@)<d(l), то из (8-12)
следует, что требование более низкого уровня усилий позволяет
страховой компании устанавливать более высокую цену, тем самым увеличивая
прибыль. В то же время требование более высокого уровня усилий
сокращает ожидаемые потери при несчастном случае (согласно свойству
монотонности отношения правдоподобия; см. упражнения), что также
увеличивает ожидаемую прибыль. Просто в любом конкретном случае
нужно проверять, какой уровень усилий для страховой компании
является наилучшим.
Однако здесь важно иметь в виду, что, независимо от того, какой
уровень усилий является наилучшим для фирмы, полис, доставляющий
максимум прибыли, всегда предполагает полное страхование. Из этого
следует, что исход в данной ситуации Парето-эффективен. Прежде мы
уже сталкивались с результатами подобного рода, так что здесь не будем
еще раз доказывать это утверждение.
8.2.2. Асимметричная информация
Обратимся теперь к более интересному случаю, когда выбор
страхователя относительно усилий по предотвращению наступления
несчастного случая не может наблюдаться страховой компанией. Страховая
компания по-прежнему предлагает полис, который максимизирует ожидаемую
прибыль. Однако, если теперь уровень усилий ненаблюдаем, как
страховой компании выбрать оптимальный полис?

494
Часть III. Стратегическое поведение
Представим себе эту проблему таким образом. Страховая компания
должна заложить в полис желаемый уровень усилий страхователя по
предотвращению несчастного случая. Однако, так как уровень усилий
страхователя не может непосредственно наблюдаться, страховая компания
должна гарантировать, что характер выплат по полису оптимален для
страхователя, тем самым подталкивая его добровольно выбирать
желаемый уровень усилий.
Этим фактически вводится дополнительное ограничение в задачу
максимизации прибыли страховой компании. Полис и уровень усилий
должны выбираться, не только чтобы обеспечить страхователю по
крайней мере резервную полезность; полис должен побуждать страхователя
добровольно выбирать тот уровень усилий, в котором заинтересована
страховая компания. Таким образом, задача страховой компании будет
иметь следующий вид:
L
max р-У4П1(ё)В1 (8-13)
е, р, В0, .,BL ~
при
^nl(e)u(w-p-l + Bl)-d(e)>u (8-14)
/=о
и
Х^/(^)^-р-/ + 5/)-^)>ХяДе>(м;-^-/ + 5/)-^), (8-15)
/=0 /=0
где е,е'е {О, 1} и еФе .
Неравенство (8-15)— это и есть новое ограничение. Оно
гарантирует, что уровень усилий е, который страховая компания имеет в виду при
вычислении своей прибыли, будет фактически выбран страхователем,
поскольку этот уровень усилий для данного полиса максимизирует его
ожидаемую полезность.
При решении этой задачи мы будем следовать той же самой
процедуре, как и в ситуации симметричной информации. То есть сначала
зафиксируем уровень усилий е, а затем определим для этого уровня
оптимальный полис. Как только это будет сделано для обоих уровней усилий,
просто проверим, какой уровень усилий и связанный с ним оптимальный
полис максимизируют прибыль страховой компании.
Оптимальный полис при е = О
Предположим, что страховая компания хотела бы, чтобы уровень
усилий страхователя был низким. Какой из полисов, стимулирующий
этот уровень усилий, будет наилучшим для страховой компании? Хотя

Глава 8. Экономика информации
495
мы могли бы выписать функцию Лагранжа для этой задачи, проще
применить другую процедуру.
Напомним, что если бы условие совместимости стимулов (8-15)
отсутствовало, то оптимальный полис при е = 0 определялся бы набором
р, В0, ..., BL, удовлетворяющим соотношениям
u(w-p) = d@) + u,
Я,=/, / = 0, 1, ...,L. (8-16)
Добавление условия совместимости стимулов к задаче не может
увеличить максимальную прибыль страховой компании. Поэтому если
решение (8-16) удовлетворяет условию совместимости стимулов, то это и
должен быть желаемый оптимальный полис. Но, очевидно, решение
действительно удовлетворяет (8-15). Для полиса, определенного
соотношениями (8-16), условие совместимости стимулов при е = 0 сводится к
неравенству
d@)>d(l),
которое выполняется согласно введенному предположению.
Следовательно, если страховой компании вдруг окажется выгодно,
чтобы усилия страхователя по предупреждению несчастного случая
оставались на низком уровне, то она должна предложить тот же самый полис,
который был бы предложен ею, если бы эти усилия были наблюдаемы.
Оптимальный полис при е = 1
Предположим теперь, что страховая компания заинтересована в
высоком уровне усилий со стороны страхователя. Чтобы найти
оптимальный полис для страховой компании в этой ситуации, зафиксируем е = 1
в задаче (8-13). Максимизация осуществляется по переменным
р, 50, ...,5L. К тому же, так как е = 1, в условии совместимости
стимулов (8-15) е' = 0. Тогда функция Лагранжа для этой задачи будет
следующей:
? = p-yj?nl(l)Bl+X
/=0
ZmiMw-p-l + BJ-dW-u
+
+р
^(IMw-p-l + B^-dM-l^ntOMw-p-l + BJ-diO)
1=0
,(8-17)
V/=o
где X и Р — множители Лагранжа, относящиеся к условиям (8-14) и
(8-15) соответственно.

496
Часть III Стратегическое поведение
Условия первого порядка тогда имеют вид:
dp
?(ji/(e) + P(K/(l)-n/@)))«'(w-p-/ + 5/)
/=о
= 0,
эх
эд
= -я;A)+[Яя;A)+Р(я;A)-я;@))]||,(^-/»-/+5,) = 0,У/,
— = ?Jc/(l)M(w-p-/ + 5/)-^(l)-«>0,
/=0
L
(8-18)
(8-19)
(8-20)
(8-21)
/=0
где (8-20) и (8-21) выполняются как равенства, если Х*0 и р*0
соответственно.
Как и в предыдущей задаче, первое из этих условий (8-18) вытекает
из следующих L + 1 условий (8-19). Как и прежде, эта избыточность
позволяет положить В0 = 0 без потери общности.
Теперь (8-19) может быть переписано в виде
1
¦ = ^ + Р
1-
Я;@)
11,A).
(8-22)
u'(w-p + B,-l)
Покажем, что и X и Р отличны от нуля.
Предположим, что р = 0. Тогда из (8-22) следовало бы, что левая
часть не зависит от /. Это означает, что w—p + Bt—l тоже не зависит
от /. Но этого не может быть, поскольку тогда не выполняется условие
(8-21), так как его левая часть вырождается до соотношения d@)-d(Y),
которое отрицательно. Отсюда мы заключаем, что р * 0.
Чтобы доказать, что X Ф 0, сначала заметим следующее: из свойства
монотонности отношения правдоподобия следует существование /
такого, что 71,@)^71/A). Поскольку ^/7С/@) = ^7 7С/ A) = 1, то должны суще-
ствовать / и /', такие, что 7Г/@)>7С,A) и тсг@)<ягA). Следовательно,
выражение в квадратных скобках в уравнении (8-22) принимает как
положительные, так и отрицательные значения.
Поэтому, если X = 0, то, так как р Ф 0, правая часть (8-22) принимает
и положительные, и отрицательные значения. Однако левая часть всегда
положительна, поэтому X Ф 0. Следовательно, X > 0.
Из того факта, что и X и Р отличны от нуля, следует, что условия
(8-20) и (8-21) выполняются как равенства на решении задачи. Таким об-

Глава 8. Экономика информации
497
разом, страхователь получает резервный уровень полезности и
безразличен между выбором высокого и низкого уровня усилий.
Чтобы лучше понять, что же такое оптимальный полис при е = 1,
полезно показать, что Р > 0. Предположим противное: пусть р < 0. Из
свойства монотонности отношения правдоподобия тогда следует, что правая
часть (8-22) возрастает по /. Следовательно, u/(w-p-\-Bl -/) убывает по
/, так что В{-1 и, следовательно, u(w- p + B^l) возрастают по /.Но
последнее вместе со свойством монотонности отношения правдоподобия
означает, что ^ (я,(l)-7i7@))w(w-p + Bf-l)<О (см. упражнение 8.11).
Это противоречит (8.21), поскольку d@)<d(l). Отсюда мы приходим к
выводу, что р > 0.
Заметим теперь, что, так как Р > 0, из свойства монотонности
отношения правдоподобия следует, что правая часть (8-22) убывает по /, так
что u(w- p + Bf -/) возрастает. Следовательно, оптимальный полис
должен обладать следующим свойством:
/ - В( — возрастающая функция по /, / = 0, 1, ..., L. (8-23)
Напомним, что без потери общности можно положить В0 = 0. Тогда из
условия (8-23) следует, что оптимальный полис при высоком уровне
усилий не обеспечивает полное страхование — скорее, он устанавливает
размер удерживаемых платежей, которые растут вместе с величиной потерь.
Все это, конечно, очень интуитивно. Для того чтобы у страхователя
появился стимул выбирать высокий уровень усилий, в этом для него
должно быть что-то особенное. Когда 1-В1 возрастает, то приложение
высокого уровня усилий приносит выигрыш:
fd(nl(\)-nl@))u(w-p-l + Bl)>0,
1=0
Из (8-23) и свойства монотонности отношения правдоподобия следует,
что эта величина положительна (см. упражнение 8.11). Конечно, есть
также издержки, обусловленные высоким уровнем усилий, т.е.
d(l) - d@) > О. Оптимальный полис составлен таким образом, что выгода
при высоком уровне усилий в точности равна издержкам.
Оптимальный полис и эффективность
Таким образом, в зависимости от того, какой уровень усилий по
предотвращению несчастного случая — высокий или низкий — страховая
компания хочет заставить выбрать страхователя, тот полис и будет для
нее оптимальным. В общем и целом оптимальный полис (решение задачи

498
Часть III. Стратегическое поведение
максимизации (8-13)) — это просто тот полис, который приносит
наибольшую ожидаемую прибыль.
Предположим теперь, что в случае симметричной информации
оптимальный уровень усилий, предлагаемый страхователю страховой
компанией, низкий. Тогда точно тот же самый (полное страхование) полис
будет оптимален и в случае асимметричной информации. Это следует из
того, что данный полис приносит ту же ожидаемую прибыль, что и в
случае симметричной информации, а максимум ожидаемой прибыли при
е = 1 — в случае асимметричной информации не выше, чем в случае
симметричной информации, поскольку при асимметричной информации
возникает дополнительное ограничение. Следовательно, так как исход при
симметричной информации Парето-эффективен, в данной ситуации будет
эффективен и исход при асимметричной информации.
Теперь предположим, что в условиях симметричной информации
высокий уровень усилий страхователя с точки зрения страховой компании
является оптимальным. Тогда может случиться, что максимальная
ожидаемая прибыль страховой компании будет существенно ниже, если она
вдруг попытается стимулировать тот же высокий уровень усилий при
асимметричной информации. Поскольку ожидаемая прибыль, если
выбран низкий уровень усилий, одинакова в случае и симметричной, и
асимметричной информации, то, может быть, лучше всего для страховой
компании при асимметричной информации было бы навязать
страхователю низкий уровень усилий, предложив полный страховой полис. Хотя
такая сделка оптимальна для страховой компании, ее результат не будет
Парето-эффективным. По сравнению с решением при симметричной
информации полезность страхователя не изменится (и равна и ), а прибыль
страховой компании окажется ниже.
Таким образом, еще раз заметим: влияние асимметричной
информации может проявиться в Парето-неэффективных исходах.
8.3. Информация и функционирование рынка
Распространение информации среди участников рынка может
оказывать значительное воздействие на рыночное равновесие. Действительно,
как мы видели в этой главе, равновесие при асимметричной информации
может приводить к провалам рынка, так что взаимовыгодные сделки
остаются нереализованными. Эта возможная неэффективность рыночных
исходов — наиболее беспокоящий аспект с нормативной точки зрения.
Мы посвятили данную главу изучению только одного рынка —
рынка страховых услуг1. Но проблемы, с которыми мы при этом столкнулись,
1 Большая часть анализа была заимствована у Ротшильда и Стиглица [Rothschild, Stiglitz,
1976].

Глава 8. Экономика информации
499
существуют также на многих других рынках. Неблагоприятный отбор
возникает на рынке подержанных автомобилей и на рынке рабочей силы .
Проблема морального риска возникает в отношениях «работодатель—
служащий», «доктор—пациент» и даже при заключении брака2.
В этой главе главным образом мы сконцентрировались на болезни и
ее симптомах, только иногда намекая на возможное лечение. Мы
заканчиваем главу замечанием, что очень часто эти информационные
проблемы могут быть ослаблены, если не полностью преодолены. Если
проблема в неблагоприятном отборе — может помочь использование рыночных
сигналов или скрининг. Если проблема в моральном риске — могут быть
предложены контракты, стимулирующие предпринимать усилия, которые
приводили бы к Парето-эффективным исходам.
Анализ рынков с асимметричной информацией поднимает новые
вопросы в экономике. Это область, где существует мало простых и широко
применимых ответов, но это и область, где весь творческий потенциал
аналитика, проникновение в суть и логическая строгость могут дать
значительные результаты.
8.4. Упражнения
8.1. Рассмотрим модель страхования из раздела 8.1, но будем
трактовать каждую страховую компанию как нейтрального к риску потребителя с
богатством w > L в каждом состоянии, где L — величина потерь, если один
из т не склонных к риску потребителей попадает в аварию. Предположим
также, что число нейтральных к риску потребителей превышает число не
склонных к риску. Покажите, что конкурентное равновесие, полученное в
разделе 8.1, является конкурентным равновесием в экономике обмена.
8.2. Предположим, что в модели страхования при асимметричной
информации вероятность несчастного случая для потребителя страховых
услуг есть функция его богатства, т.е. к = f(w). Предположим также, что
различные потребители имеют различные уровни богатства и что /' > 0.
Обязательно ли при этом имеет место неблагоприятный отбор?
8.3. В нашей модели страхования из раздела 8.1 множество
страхователей могут иметь одинаковую вероятность несчастного случая.
Предположим теперь, что цена полиса индивидуальна для каждого потребителя.
Покажите, что при симметричной информации равновесные цены
полисов зависят только от вероятностей, а не от конкретных индивидов,
приобретающих их.
1 См. работы Акерлофа и Спенса: [Akerlof, 1970], [Spence, 1973].
2 См. работы Гроссмана и Харта: [Grossman, Hart, 1983], а также Холмстрома
[Holmstrom, 1979, 1982].

500
Часть III. Стратегическое поведение
8.4. Ответьте на следующие вопросы, связанные с моделью
страхования при неблагоприятном отборе.
а) Если множество страхователей конечно, то распределение
вероятностей несчастного случая среди них F является кусочно-постоянной
функцией. Покажите, что тогда g :[0,я?] —>[0,я?] также является
неубывающей кусочно-постоянной функцией.
б) Покажите, что g должна иметь неподвижную точку.
в) Покажите, что неубывающая функция, отображающая единичный
интервал в себя, имеет неподвижную точку. (Заметим, что функция не
должна быть непрерывной! Это — частный случай теоремы о
неподвижной точки Тарского [Tarski, 1955].)
8.5. Предположим, что есть два состояния — 1 и 2. Состояние 1
наступает с вероятностью к, и wi обозначает богатство страхователя в
состоянии /.
а) Покажите, что если страхователь строго не склонен к риску и
wl^w2, то страховая компания может предоставить ему страховку,
гарантирующую одно и то же богатство в обоих состояниях, которая
улучшает положение страхователя и дает при этом положительную прибыль
страховой компании.
б) Предположим, что существует множество страхователей и
множество страховых компаний и что допустимое распределение таково, что
богатство каждого страхователя постоянно в обоих состояниях.
Предположим также, что при этом распределении некоторые страхователи
страхуют других. Покажите, что те же самые уровни богатства
страхователей и ожидаемой прибыли страховых компаний могут быть достигнуты
при допустимом распределении, в котором никто из страхователей не
может страховать кого-либо другого.
8.6. (Акерлоф) Рассмотрим рынок подержанных автомобилей.
Каждый продавец выставляет на продажу только один подержанный
автомобиль и характеризуется качеством подержанного автомобиля, который он
желает продать. Пусть 9е [0, 1] — показатель качества подержанного
автомобиля. Предположим, что параметр G равномерно распределен на
отрезке [0, 1]. Если продавец типа в продает свой автомобиль (качества
9) за цену /?, его полезность равна us(p, 9). Если он не продает свой
автомобиль, то его полезность равна 0. Покупатели подержанных
автомобилей получают полезность 9-р, если они приобретают автомобиль
качества 9 по цене р, и полезность 0, если они не приобретают
автомобиль. Информация относительно качества подержанных автомобилей
асимметрична. Продавцы знают о качестве автомобиля, который они

Глава 8. Экономика информации
501
предлагают, но покупателям о нем не известно. Предположим, что
автомобилей недостаточно, чтобы обеспечить всех потенциальных к
покупателей.
а) Докажите, что в конкурентном равновесии при асимметричной
информации мы должны иметь ^(б! р) = р.
б) Покажите, что если us(p, в) = /?-9/2, то любое ре@, 1/2] —
равновесная цена.
в) Найдите равновесную цену, если us(p, Q) = p . Опишите
полученное равновесие. В частности, укажите: какие автомобили будут
проданы в равновесии?
г) Найдите равновесную цену, если us{p, 0) = /?-63. Сколько
равновесий существует в этом случае?
д) Являются ли какие-нибудь из найденных исходов Парето-эффек-
тивными? Опишите Парето-улучшения, если они возможны.
8.7. Покажите, что в игре с сигналами на рынке страхования, если
страхователи имеют конечное множество полисов для выбора, то
стратегический набор является равновесным тогда и только тогда, когда он
удовлетворяет правилу Байеса. Сделайте вывод, что секвенциальное
равновесие тогда представляет собой стратегический набор, который
удовлетворяет правилу Байеса и секвенциально рационален.
8.8. Проанализируйте игру с сигналами на рынке страхования, когда
страховые выплаты В равны L.
а) Покажите, что в состояниях, в которых страховая компания
получает нулевую прибыль, существует единственное секвенциальное
равновесие.
б) Покажите, что среди всех секвенциальных равновесий не
существует разделяющего равновесия. Насколько это интуитивно ясно?
в) Покажите, что существуют объединяющие равновесия, в которых
страховая компания получает положительную прибыль.
8.9. Рассмотрите игру с сигналами на рынке страхования.
а) Покажите, что существуют разделяющие равновесия, в которых
страхователь с низким риском предлагает полис, отклоняемый в
равновесии, тогда и только тогда, когда MRS^O, 0) < тс.
б) При заданном разделяющем равновесии, когда предложение
полиса от страхователя с низким риском отклонено, постройте разделяющее
равновесие, в котором это предложение будет принято, не изменяя при
этом равновесные выплаты всех игроков.
в) Предположим теперь, что на рынке действуют одна страховая
компания и два типа страхователей. Предположим также, что страхователи с
низким риском скорее предпочтут вовсе не страховаться, чем полностью

502
Часть III. Стратегическое поведение
застраховаться по конкурентной цене для страхователей с высоким
риском. Покажите, что когда а (доля страхователей с низким риском)
достаточно мала, в единственном конкурентном равновесии при
асимметричной информации страхователь с низким риском не будет страховаться, а
страхователь с высоким риском приобретает полную страховку.
г) Возвращаясь к описанной ранее игре с сигналами на рынке
страхования, покажите, что любое разделяющее равновесие Парето-доминирует
конкурентное равновесие, описанное в предыдущем пункте в).
8.10. Рассмотрим модель скрининга на рынке страхования.
Предположим, что страховые компании располагают большим, но конечным
числом полисов, из которых можно составлять меню полисов. Покажите,
что совместная стратегия есть совершенное в подыграх равновесие тогда
и только тогда, когда существуют ожидания, при которых
соответствующий стратегический набор является секвенциальным равновесием.
8.11. Рассмотрите модель морального риска в страховании, где
страхователь может прилагать два уровня усилий, чтобы избежать аварии
(е = 0 или е = 1). Напомним, что к1(е)>0 означает вероятность потери
/ долл. в результате аварии. Покажите, что если свойство монотонности
отношения правдоподобия выполнено, так что я/@)/я/A) возрастает по
L L
I, тогда ^лДО)*/ >^л/A)х/ для каждой неубывающей
последовательно /=о
ности действительных чисел хх < х2 < • • • < xL.
8.12. Рассмотрите модель морального риска в страховании.
а) Покажите, что если информация симметрична, то цена полиса,
максимизирующая прибыль, выше в том случае, когда стимулируется
низкий уровень усилий по предотвращению аварии, чем когда
стимулируется высокий уровень усилий.
б) Пусть резервная полезность страхователя и — наибольшая
величина, которая может быть обещана при уровне усилий,
максимизирующем полезность в ситуации, когда страховка недоступна. Предположим,
что когда информация асимметрична, страховая компания не может
получить неотрицательную прибыль, заставляя страхователей прилагать
высокий уровень усилий. Покажите, что, когда страхование недоступно,
страхователь будет прилагать низкий уровень усилий.
8.13. Рассмотрим модель морального риска в страховании. Пусть
страхователь имеет функцию полезности фон Неймана — Моргенштерна
от богатства вида w(w) = vw, пусть его начальное богатство
w0 = 100 долл., и пусть существует два уровня потерь / = 0 и / = 51 долл.
Как обычно, есть два уровня усилий по предотвращению несчастного
случаям = 0 и е = 1. Отрицательная полезность страхователя в зависимо-

Глава 8. Экономика информации
503
сти от уровня усилий задается функцией d(e), где d@) = 0 и d{\) = 1/3.
Наконец, предположим, что вероятности потерь заданы следующей
таблицей, где строки соответствуют уровням усилий, а столбцы — потерям.
е ^\
е = 0
е = \
1 = 0
1/3
2/3
/ = 51
2/3
1/3
Так, например, вероятность потери в 51 долл., когда от страхователя
требуется высокий уровень усилий, равна 1/3.
а) Проверьте, удовлетворяют ли вероятности, заданные в таблице,
свойству монотонности отношения правдоподобия.
б) Найдите резервную полезность страхователя, предположив, что
существует только одна страховая компания и что у страхователя есть
еще только одна возможность — это самострахование.
в) Какой уровень усилий приложит страхователь, если страхование
недоступно?
г) Покажите, что если информация симметрична, то оптимальным для
страховой компании является полис, который стимулирует высокий
уровень усилий.
д) Покажите, что полис, рассмотренный в предыдущем пункте г), не
будет стимулировать высокий уровень усилий, если информация
асимметрична.
е) Найдите оптимальный полис в условиях асимметричной
информации.
ж) Сравните прибыль страховой компании при симметричной и
асимметричной информации. Сравните также полезность страхователя в
этих двух случаях. Покажите, что решение при симметричной
информации Парето-доминирует решение при асимметричной информации.

I Глава 9
АУКЦИОНЫ И СОЗДАНИЕ МЕХАНИЗМОВ
В отличие от предположения, которому мы до сих пор следовали в
данной книге, на большинстве реальных рынков продавцы не обладают
полной информацией о рыночном спросе. Вместо этого они обычно
располагают только статистической информацией, и лишь сами
покупатели точно знают, какое количество данного товара они хотят приобрести
при той или иной цене. В данной главе мы рассмотрим задачу монополии
в этих типичных случаях.
Вероятно, простейшая ситуация, в которой присутствуют указанные
элементы, возникает, когда некий предмет (объект) выставляется на
аукцион. На нем продавец обычно не знает, как покупатели оценивают этот
предмет, но может иметь некоторую информацию о распределении их
оценок. Для таких ситуаций существует ряд стандартных видов аукциона,
которыми продавец может воспользоваться, — аукционы первой цены,
второй цены, голландский, английский. Приносит ли каждый из этих
стандартных аукционов одинаковый доход продавцу? Если нет, то какой
из них лучше? Существует ли нестандартный, но более выгодный для
продавца механизм продажи? Чтобы ответить на эти и другие вопросы,
мы введем и используем некоторые инструменты теории создания
механизмов (mechanism design).
Создание механизмов — это общая теория о том, как и когда
конструирование подходящих институтов позволяет достичь определенных
целей. Она особенно уместна в тех случаях, когда создателю механизма для
достижения своей цели требуется информация, которая оказывается в
распоряжении других индивидов. Тонкость в построении хорошего
механизма заключается в том, чтобы при этом заинтересовать обладателей
нужной информации, раскрыть ее. Хотя мы не будем здесь заниматься
общей теорией создания механизмов, использование ее техники для
изучения аукционов, максимизирующих доход, чему будет посвящена эта
глава, послужит введением в проблему.
9.1. Четыре стандартных аукциона
Рассмотрим продавца, который хочет продать единственный предмет
(объект) одному из N покупателей по максимально возможной цене. Как
продавец должен действовать, чтобы достичь этой цели? Один из
возможных ответов — провести аукцион. Существует множество различных

Глава 9. Аукционы и создание механизмов
505
видов аукционов, но мы ограничимся следующими четырьмя
стандартными типами1.
• Аукцион первой (скрытой) цены. Каждый участник подает заявку
в запечатанном конверте. Тот, кто предлагает самую высокую цену,
выигрывает и платит эту цену за объект.
• Аукцион второй (скрытой) цены. Каждый участник подает заявку
в запечатанном конверте. Тот, кто предлагает самую высокую цену,
выигрывает и платит за объект вторую по величине цену.
• Голландский аукцион. Продавец начинает с очень высокой цены и
постепенно ее снижает. Выигрывает и получает объект тот участник,
который первым выразит готовность заплатить объявленную цену.
• Английский аукцион. Продавец начинает с очень низкой цены
(возможно, равной нулю) и постепенно ее повышает. Каждый участник
подает знак, если хочет отказаться от дальнейшего участия в аукционе.
Отказавшись, он уже не может участвовать в дальнейших торгах. Когда
остается только один участник, он становится победителем и платит
объявленную цену.
Можем ли мы определить, какой из четырех перечисленных
аукционов является наилучшим с точки зрения продавца? Для ответа на этот
вопрос нам потребуется модель.
9.2. Модель независимых частных оценок
Предположим, что нейтральный к риску продавец хочет продать
неделимый объект одному из N нейтральных к риску покупателей.
Продавец оценивает объект в ноль долларов2. Оценка объекта / -м
покупателем v, принимает значение из интервала [0,1] в соответствии с
функцией распределения F.(v.), имеющей функцию плотности /](v,K. Будем
предполагать, что оценки покупателей взаимно независимы. Каждый
покупатель знает свою оценку, но не знает оценок остальных. Однако
функции плотности /J, ...9fN являются публичной информацией и поэтому
1 Далее, если не указано иное, мы будем предполагать, что на всех аукционах в случае
равенства ставок победитель определяется случайным образом, т.е. получить предмет с
равной вероятностью может каждый из участников, предложивших одинаковую цену.
2 Это эквивалентно предположению о том, что объект уже произведен и ценность его
использования продавцом равна нулю.
3 Напомним, что /^(v,.) обозначает вероятность того, что оценка объекта i -м
покупателем меньше или равна v, и что /(v,.) = /^'(v,). Последнее равенство можно также запи-
сать как F;(v.) = ^(х)с1х, поэтому мы иногда будем ссылаться на f., а иногда на Fi,
J о
поскольку одно определяется другим.

506
Часть III. Стратегическое поведение
известны продавцу и всем покупателям. В частности, хотя продавец не
знает точных оценок покупателей, ему известно распределение каждой из
этих оценок. Если оценка / -го покупателя равна v, и если он выигрывает
аукцион и платит за объект цену р, то его выигрыш (т.е. полезность фон
Неймана — Моргенштерна) равен v, - р, а если он платит р , но не
получает объект, его выигрыш составляет - рх.
Это называется моделью независимых частных оценок.
Независимость подразумевает, что частная информация каждого покупателя (в
данном случае его оценка) не зависит от частной информации любого
другого участника. Частный характер оценок означает, что если
покупатель воспользовался своей частной информацией, чтобы оценить объект,
эта оценка не изменится, даже если он позднее получит доступ к частной
информации любого другого покупателя, т.е. каждому покупателю
достаточно его собственной частной информации для того, чтобы
сформировать свою оценку2.
В данной главе мы будем предполагать, что условия, в которых
оказывается наш монополист, хорошо описываются моделью независимых
частных оценок. Теперь можно начинать изучение того, как прибыль
продавца изменяется в зависимости от формата аукциона. Заметим, что,
поскольку производственное решение уже было принято продавцом, а его
собственная оценка равна нулю, максимизация прибыли эквивалентна
максимизации дохода.
Прежде чем определять доходы продавца в любом из четырех
стандартных случаев, нам необходимо понять, как ведут себя участники в
каждом аукционе. Начнем с аукциона первой цены.
9.2.1. Поведение на аукционе первой цены
При анализе поведения покупателей на аукционе первой цены будем
для простоты предполагать, что они ex ante симметричны, т.е. что для
всех участников i = l,...,N fl (v) = f(v) для всех ve [0,1].
Очевидно, главная трудность при определении дохода продавца
заключается в том, чтобы выяснить, как покупатели (назовем их
участниками) будут делать ставки. Но заметим, что, если вы — один из участни-
1 Хотя подобный исход невозможен ни в одном из четырех перечисленных аукционов,
существуют и другие типы аукционов, в которых платить необходимо независимо от
того, кто победил (т.е. аукционы, в которых платят все участники).
2 Существуют более общие модели, в которых покупатели, обладающие частной
информацией, потенциально могут получить дополнительную информацию о ценности
объекта, если они будут иметь доступ к частной информации других покупателей, но такие
модели мы здесь не рассматриваем.

Глава 9. Аукционы и создание механизмов
507
ков, то, поскольку вам хотелось бы получить объект по возможно более
низкой цене, вы пожелаете объявить низкую цену, когда остальные
объявляют низкие цены, и высокую — когда у остальных ставки высоки.
Конечно, ставки остальных вам неизвестны, потому что они подаются в
запечатанных конвертах. И тем не менее ваша оптимальная ставка
зависит от ставок других участников. Таким образом, участники находятся в
ситуации, когда оптимальные действия (ставка) одного зависят от
действий остальных. Следовательно, чтобы определить поведение участников,
нам необходимо воспользоваться инструментами теории игр,
описанными в главе 7.
Рассмотрим проблему выбора оптимальной ставки с точки зрения
/ -го участника. Предположим, что его оценка равна vi. Он должен подать
заявку bi в запечатанном конверте. Поскольку, вообще говоря, bt будет
зависеть от оценки / -го участника, обозначим заявку участника /, когда
его оценка равна v,, как bi (v,). Так как / -й участник должен быть готов
подать заявку 6,(v;) для каждой из своих потенциально возможных
оценок v,. e [0,1], его стратегию можно рассматривать как функцию ставок
bi: [0,1] —> Ш+, которая отображает каждую из оценок в неотрицательную
ставку (возможно, разную для разных оценок).
Прежде чем обсуждать выигрыши, полезно определить естественный
класс функций, к которому будут принадлежать стратегии участников.
Естественно предположить, что участники с более высокими оценками
будут делать более высокие ставки, поэтому ограничимся строго
возрастающими функциями ставок. Далее, поскольку участники
предполагаются ex ante симметричными, также естественно предположить, что
участники с одинаковыми оценками будут делать одинаковые ставки. Имея это
в виду, будем искать строго возрастающую функцию ставок
6: [0,1] —> 1R+, использование которой оптимально для каждого участника
при условии, что все остальные используют эту же функцию. Иными
словами, нашей целью является симметричное равновесие по Нэшу в классе
строго возрастающих функций ставок.
Теперь предположим, что мы нашли такое симметричное равновесие
по Нэшу, которое задано строго возрастающей функцией ставок Ь(-). По
определению, участник (скажем, / -й) с оценкой v должен
максимизировать свой выигрыш, делая ставку b(v) при условии, что остальные
участники используют ту же самую функцию ставок Ь(). Имея это в виду, мы
можем проделать полезный, но на первый взгляд загадочный
эксперимент.

508
Часть III. Стратегическое поведение
Он заключается в следующем. Представим, что / -й участник не
может присутствовать на аукционе и посылает своего приятеля делать
ставки за него. Приятель знает равновесную функцию ставок б(-), но не знает
оценки / -го участника. Если оценка / -го участника равна v, то он хотел
бы, чтобы приятель от его имени сделал ставку b(v). Тот может это
сделать, если / -й участник позвонит и сообщит ему свою оценку. Очевидно,
что /-й участник не заинтересован сообщать неверную оценку. То есть
выигрыш будет максимальным, если из всех возможных оценок г € [0,1]
/ -й участник сообщит свою истинную оценку v. Так происходит потому,
что, если он сообщит другу некоторую оценку г, тот от его имени
сделает ставку b(r), в то время как сам участник сделал бы ставку b(v).
Найдем ожидаемый выигрыш /-го участника, если он сообщит
своему другу произвольную оценку г вместо истинной оценки v и если все
остальные участники используют функцию ставок Ь(). Для этого
необходимо заметить две вещи. Во-первых, / -й участник победит, только если
сделанная за него ставка окажется самой высокой, т.е. если b{r) > b(vj)
для всех )Ф1. Поскольку />(•) строго возрастает, это произойдет в
точности тогда, когда г превысит оценки всех остальных N-1 участников.
Если принять, что F — это функция распределения, соответствующая
/, вероятность этого события составит (F(r))N~l, мы обозначим ее через
FN~l(r). Во-вторых, 1-й участник платит только в случае победы, и его
платеж равен его ставке b(r). Следовательно, ожидаемый выигрыш / -го
участника, если он сообщает своему другу оценку г вместо истинной
оценки v при условии, что все остальные участники используют
функцию ставок Ь(), можно записать как
u(r9 v) = FN~](r)(v-b(r)). (9-1)
Как мы уже знаем, поскольку Ь() является равновесием, ставка,
максимизирующая ожидаемый выигрыш /-го участника, равна 6(v), если
оценка участника равна v. Следовательно, (9-1) достигает максимума при
г = v, т.е. когда / -й участник сообщает своему другу истинную оценку v.
Поэтому правую часть можно продифференцировать по г и приравнять
производную к нулю при г = v. После дифференцирования получаем
dF»-\r)(v-b(r)) =(N_ {)F N_2 ^ _ ?(r)) _ p „_, (r)?,(r) (92)
dr

Глава 9. Аукционы и создание механизмов
509
Приравняв это выражение к нулю при г = v, после преобразований
получим
(N - 1)F" (v)/(vN(v) + FN~l (v)b'(v) = (N- W(v)FN~2 (v). (9-3)
Левая часть (9-3) представляет собой производную произведения
FN~l (v)b(v) no v. Тогда мы можем переписать (9-3) как
^">ЖУ> = (N- l)v/(v)F »-> (v). (9-4)
dv
Поскольку (9-4) должно выполняться для каждого v, имеет место
также соотношение
F" (v)b{ v) = (N -1) fV xf(x)FN~2 (x)dx + const.
J 0
Заметим, что участник с нулевой оценкой сделает нулевую ставку,
поэтому константа должна равняться нулю. Тогда
*v)=t^№x>fH~2№>
что можно в более сжатой форме^лаписать как
kv) = j±^roxdF"(x). (9-5)
О функции ставок (9-5) следует заметить, что, во-первых, как мы и
предполагали, она строго возрастает по v (см. упражнение 9.1), а во-
вторых, она определена единственным образом. Итак, мы доказали
следующую теорему.
Теорема 9.1. Симметричное равновесие на аукционе первой
цены.
Если N участников имеют независимые частные оценки с единым
распределением F, то ставка
b(v) = —Д—\VxdFN-\x)
для участника, имеющего оценку v, представляет собой симметричное
равновесие по Нэшу на аукционе первой (скрытой) цены. Более того, это
единственное симметричное равновесие по Нэшу .
1 Строго говоря, мы не показали, что это равновесие. Мы показали, что если
симметричное равновесие существует, то оно имеет указанный вид. В упражнении вам
предлагается доказать, что это действительно равновесие. Возникает также вопрос о
существовании асимметричных равновесий. Можно показать, что их нет, хотя мы и не будем здесь
этого делать.

510
Часть III. Стратегическое поведение
Пример 9.1. Предположим, что оценки участников равномерно
распределены на отрезке [0,1]. Тогда F(v) = v и /(v) = 1. Следовательно,
если число участников равно N
Таким образом, каждый участник скрывает свою ставку, предлагая цену
меньшую, чем его оценка. Заметим, что участники делают ставки более
агрессивно, по мере того как их число растет. ?
Поскольку FN~l() является функцией распределения наивысшей
оценки среди N -1 соперников, стратегия поведения, сформулированная
в теореме 9.1, означает, что ставка каждого участника равна ожидаемому
значению второй по величине оценки при условии, что его собственная
оценка является наивысшей. Но так как участники используют одну и ту
же строго возрастающую функцию ставок, наивысшая оценка
эквивалентна наивысшей ставке, а значит, и победе на аукционе. Поэтому
можно сказать, что в единственном симметричном равновесии на аукционе
первой скрытой цены ставка каэюдого участника равна ожидаемому
значению второй по величине оценки при условии победы на аукционе.
Идея о том, что ставка определяется при условии победы, интуитивно
возникает на аукционе первой цены потому, что ставка участника имеет
значение только в случае его победы. Эта особенность присутствует и на
других аукционах, и поэтому данная идея должна рассматриваться как
одна из основ нашего анализа.
После изучения аукциона первой цены легко описать стратегию
поведения и на голландском аукционе.
9.2.2. Поведение на голландском аукционе
На голландском аукционе каждый участник принимает единственное
решение: «При какой цене мне поднимать руку, если я хочу просигнали-
, то каждый использует функцию ставок
у"'1 N
_ V
AT '

Глава 9. Аукционы и создание механизмов
511
зировать о своем желании купить товар по этой цене?» Кроме того,
участник, выбирающий максимальную цену, выигрывает на аукционе и
платит эту цену. Следовательно, заменив в предыдущем предложении слово
«цена» на слово «ставка», мы увидим, что этот аукцион эквивалентен
аукциону первой цены. Отсюда немедленно следует вывод.
Теорема 9.2. Симметричное равновесие на голландском
аукционе.
Если N участников имеют независимые частные оценки с единым
распределением F, то набор стратегий, при которых участник,
имеющий оценку v, соглашается с ценой, когда она достигает величины
—Д—\VxdFN-\x),
FN~\vy*
представляет собой симметричное равновесие по Нэшу на голландском
аукционе. Более того, это единственное симметричное равновесие по
Нэшу.
Отсюда очевидно, что аукцион первой цены и голландский аукцион
приносят продавцу одинаковый доход expost (т.е. для каждой реализации
оценок участников v,,..., v^).
Теперь обратимся к аукциону второй (скрытой) цены.
9.2.3. Поведение на аукционе второй (скрытой) цены
Может возникнуть вопрос о том, зачем мы вообще рассматриваем
аукцион второй цены. Разве не очевидно, что аукцион первой цены
должен приносить продавцу больший доход? В конце концов на аукционе
первой цены продавец получает наивысшую ставку, а на аукционе второй
цены — только вторую по величине ставку.
Это звучит убедительно, но не учитывает ключевого обстоятельства:
на этих аукционах ставки будут делаться по-разному. На аукционе
первой цены у участника есть стимул повышать свою ставку, чтобы увеличить
шансы на победу, и в то же время — стимул понижать ее, чтобы сократить
цену, которую придется платить за объект в случае победы. На аукционе
второй цены последний эффект отсутствует, потому что если участник
побеждает, то размер платежа не зависит от величины ставки. Поэтому на
аукционе второй цены участники, вероятно, будут делать ставки более
агрессивно, чем на аукционе первой цены. Следовательно, есть шанс, что
аукцион второй цены принесет продавцу больший ожидаемый доход, чем
аукцион первой цены. Если признать, что стратегия поведения участников
меняется с изменением формата аукциона, ответ на вопрос о том, какой из
них приносит больший доход, становится не столь очевидным.

512
Часть III. Стратегическое поведение
К счастью, анализ поведения участников на аукционе второй цены
оказывается весьма прямолинейным. В отличие от анализа аукциона
первой цены нам не требуется ограничиваться случаем симметричных
участников, т.е. мы допускаем различные функции плотности распределений
fx,..., fN, из которых независимо выбираются оценки участников1.
Рассмотрим /-го участника с оценкой v, и обозначим через В
наивысшую ставку среди остальных участников. Конечно, В не известно
/-му участнику, поскольку заявки подаются в запечатанных конвертах.
Если ставка / -го участника максимальна, а ставка В — вторая по
величине, то он победит на аукционе и заплатит цену В. Следовательно, / -й
участник заплатил бы за объект цену В. Таким образом, / -й участник
должен заплатить за объект цену, равную максимальной из ставок
остальных участников.
Поскольку оценка i -го участника равна v;, он предпочтет победить
на аукционе, если его оценка превышает цену, которую ему придется
заплатить, т.е. если v, > 5, и предпочтет проиграть, если vi < В. Если
v, = В, то ему безразлично, выигрывать или проигрывать. Существует ли
для / -го участника стратегия, гарантирующая ему победу при vi > В и
проигрыш при v, < В, даже если он не знает В ? Ответ: да. Он может
добиться этого, делая ставку, равную его оценке v,.
Делая ставку v,, / -й участник выигрывает при vi > В и проигрывает
при vi < В. Следовательно, его оценка является ставкой,
максимизирующей выигрыш независимо от ставок остальных участников (вспомним,
что В было наибольшей ставкой, сделанной остальными участниками).
Более того, ставка ниже оценки влечет за собой риск проигрыша в
ситуации, когда участник предпочел бы выиграть, а ставка, превышающая
оценку, связана с риском выиграть аукцион и заплатить слишком
высокую цену. Поэтому стратегия делать ставку, равную своей оценке,
является для участника слабо доминирующей, и мы можем утверждать
следующее.
Теорема 9.3. Равновесие на аукционе второй цены.
Если N участников имеют независимые частные оценки, то на
аукционе второй цены для каждого участника стратегия делать ставку,
равную его оценке, является слабо доминирующей.
Это приводит нас к английскому аукциону.
На самом деле можно опустить даже предположение о независимости (см.
упражнение 9.3).

Глава 9. Аукционы и создание механизмов
513
9.2.4. Поведение на английском аукционе
По сравнению с рассмотренными аукционами на английском
аукционе участнику приходится принимать более разнообразные решения.
Например, если цена очень низкая, он должен решать, при какой цене
выходить из игры, если еще никто не вышел. Если кто-то другой уже вышел из
игры, то участнику необходимо решать, при какой цене выходить самому,
учитывая действия оставшихся активных участников, и т.д. Несмотря на
это, между английским аукционом и аукционом второй цены существует
тесная связь.
На английском аукционе, как и на аукционе второй цены,
доминирующей стратегией каждого участника оказывается выход из игры в тот
момент, когда цена достигает его оценки независимо от того, кто остается
в игре. Причина довольно ясна. Участник с оценкой vf., зная историю
игры и текущую цену р < v, и рассматривая возможность выхода, ничего не
теряет, если остается немного дольше — вплоть до тех пор, пока цена не
достигнет v;. В худшем случае он откажется от участия в тот момент,
когда цена действительно достигнет его оценки. Тогда выигрыш будет
равен нулю, как и в ситуации, при которой он выходит из игры при цене р .
Однако может случиться так, что участник останется в игре, а все
остальные выйдут из нее до того, как цена достигнет v,. Тогда / -му участнику
выгоднее остаться, поскольку он приобретет объект по цене, строго
меньшей его оценки v,, и получит положительный выигрыш. Мы
приходим к следующему утверждению.
Теорема 9.4. Равновесие на английском аукционе.
Если N участников имеют независимые частные оценки, то на
английском аукционе для каждого участника стратегия выходить из игры в
тот момент, когда цена достигает его оценки, является слабо
доминирующее.
Используя этот результат, легко увидеть, что участник с
максимальной оценкой победит на английском аукционе. Но сколько он заплатит за
объект? Это, конечно, зависит от цены, при которой его последний
оставшийся соперник выйдет из аукциона. Но последний оставшийся
соперник будет участником со второй по величине оценкой, и он, как и
другие, выйдет из игры, когда цена достигнет его оценки. Следовательно,
участник с наибольшей оценкой выигрывает и платит цену, равную вто-
Как и в случае аукциона второй цены, этот результат не использует независимость
оценок участников и выполняется, даже если они коррелируют. Важно, однако, то, что
оценки являются частными.

514
Часть III. Стратегическое поведение
рой по величине оценке. Таким образом, мы видим, что исход
английского аукциона совпадает с исходом аукциона второй цены. В частности, они
в итоге приносят продавцу один и тот же доход.
9.2.5. Сравнение доходов
Поскольку голландский аукцион и аукцион первой цены приносят в
итоге одинаковый доход, и то же самое верно для пары «английский
аукцион и аукцион второй цены», остается только сравнить доход,
генерируемый аукционами первой цены и второй цены. Ясно, что он не
обязательно будет одинаковым. Например, если максимальная оценка
довольно велика, а следующая по величине довольно мала, аукцион первой цены
принесет больший доход. В то же время, когда первая и вторая по
величине оценки близки, больший доход принесет аукцион второй цены.
Конечно, когда продавцу приходится решать, какой из видов
аукциона использовать, ему не известны оценки участников. Однако, зная их
стратегии как функции от оценок и распределение оценок, продавец
может рассчитать ожидаемый доход от каждого аукциона и определить,
какой из аукционов — первой цены или второй цены — приносит более
высокий ожидаемый доход. Поскольку в анализе аукциона первой цены мы
использовали симметрию участников, для сравнимости величины
ожидаемого дохода введем это предположение и для аукциона второй цены.
Далее /(•) будет обозначать одинаковую для всех плотность
распределения оценки каждого участника, a F(-) — соответствующую функцию
распределения.
Начнем с ожидаемого дохода от аукциона первой цены RFPA .
Поскольку максимальная ставка выигрывает аукцион первой цены и поскольку
участник с максимальной оценкой делает максимальную ставку, доход
продавца составит b(v), если максимальная ставка среди всех N
участников равна v. Если максимальная оценка распределена в соответствии с
плотностью g(v), ожидаемый доход продавца можно записать как
RFPA=fob(v)g(v)dv.
Поскольку плотность g максимума из N независимых случайных
переменных с одинаковой плотностью / и распределением F равна
NfFN~x , получаем
1 Чтобы убедиться в этом, заметим, что наибольшая оценка меньше или равна v тогда и
только тогда, когда все N оценок меньше или равны v и вероятность этого равна F*(v).
Следовательно, функция распределения наибольшей оценки равна F*. Требуемый результат
следует из того, что функция плотности является производной функции распределения.

Глава 9. Аукционы и создание механизмов
515
RFPA=Nfob(v)f(v)FN-\v)dv.
(9-6)
Мы видели, что на аукционе второй цены сумма, которую получит
продавец в качестве платы за товар, равна второй по величине оценке из
N оценок участников, так как каждый участник делает ставку, равную
его оценке. Поэтому если h(v) — плотность распределения этой оценки,
то ожидаемый доход продавца на аукционе второй цены RSPA можно
записать как
^=J/A(v)rfv.
Поскольку плотность h второй по величине переменной из N
независимых случайных переменных с одинаковой плотностью / и
распределением F равна N(N-l)FN'2f(l-F)], то мы имеем
Rspa =^(^-l)jVFw-2(v)/(v)(l-F(v))rfv.
(9-7)
Теперь сравним величины ожидаемых доходов от обоих аукционов.
Из (9-5) и (9-6)
RFPA=N
^—VxdFN-\x)
(v) J °
= N(N-\)
f(v)FN-\v)dv =
fiy)dv =
\\FN-\x)f(x)dx
= N(N-l)j,jVo[xFN-\x)f(x)Av)]dxdv =
= N(N-l)jlfx[xFN-2(x)f(x)f(v)]dvcIx =
= N(N -1) J' xFN~2 (*)/(*)(! - F(x))dx =
= R
SPA'
Один из способов увидеть это заключается в том, чтобы понимать плотность
вероятности как вероятность. Тогда вероятность того, что оценка некоторого участника равна v,
составляет f(v), а вероятность того, что ровно одна из оставшихся N -1 оценок ее
превышает, составляет (N-\)FN'2(v)(l-F(v)). Следовательно, вероятность того, что
оценка этого участника равна v и является второй по величине, составляет
(N-\)f(v)FN'2(v)(l-F(y)). Поскольку всего участников N, вероятность (т.е.
плотность вероятности) того, что вторая по величине оценка равна v, составляет
tf(tf-lXAv)Fw-2(v)(l-F(v)).

516
Часть III. Стратегическое поведение
где четвертая строка получается изменением порядка интегрирования (с
dxdv на dvdx), а последнее равенство следует из (9-7).
Пример 9.2. Рассмотрим случай, когда оценки участников
равномерно распределены на отрезке [0,1], так что F(v) = v и /(v) = 1.
Ожидаемый доход от аукциона первой цены равен
RFPA=Nllob(v)Av)FN-,(v)dv =
= N
v
v
N
'dv =
= (N-l)fovNdv =
N-l
N + \
В то же время ожидаемый доход от аукциона второй цены равен
RSPA = N(N -1) Jo' vFN-2 (v) Д v)(l - F(v))dv =
= N(N-l)fvN-l(l-v)dv =
= N(N-1)
_N-l
' 1 1
_N N + l_
N + l
п
Мы получили замечательный результат: аукционы первой цены и
второй цены приносят одинаковый доход независимо от распределения
оценок всех участников! Поэтому можно утверждать следующее: если N
участников имеют независимые частные оценки с единым
распределением F, то все четыре стандартных вида аукционов (первой цены, второй
цены, голландский, английский) приносят продавцу одинаковый
ожидаемый доход.
Эта эквивалентность дохода помогает понять, почему все четыре
вида аукционов встречаются на практике. Если бы один из них в среднем
приносил больший доход, то всегда использовался бы именно он. Но как
объяснить совпадение ожидаемого дохода во всех четырех случаях? Наша
следующая цель заключается в том, чтобы это выяснить.

Глава 9. Аукционы и создание механизмов
517
9.3. Теорема об эквивалентности доходов
Чтобы объяснить эквивалентность дохода в четырех стандартных
аукционах, необходимо сначала найти способ объединить их в единую
схему. Учитывая это, введем понятие механизма прямой продажи1.
Механизм прямой продажи представляет собой набор из N
функций вероятностей рх {vx,..., v^),..., pN (v,,..., v^) и N функций издержек
cx(vX9...9vN)9...9cN(vv...9vN). Для каждого / и любого набора значений
(v,,...,vN) величина p.(vl9...9vN)e [О,1] обозначает вероятность
получения объекта z-м участником, a ci(vl9...9vN)e'R — сумму, которую /-й
участник должен заплатить продавцу2. Следовательно, сумма
вероятностей pl(vl9...9vN) + ... + pN(vl9...9vN) не должна превосходить единицу.
Вместе с тем она может быть меньше единицы, поскольку мы даем
продавцу возможность оставить объект у себя3.
Механизм прямой продажи работает следующим образом. Поскольку
продавец не знает оценок участников, он просит их одновременно
сообщить ему свои оценки гг Получив эти сообщения rl9...9rN9 которые не
обязательно являются правдивыми, продавец отдает объект одному из
участников в соответствии с вероятностями Pj(rl9...9rN)9 где / = 1,...9N9
или с соответствующей вероятностью сохраняет его у себя, получая от
каждого участника / = 1,...9N платеж cf(rl9...9rN). Предполагается, что
весь механизм прямой продажи — функции вероятности и функции
издержек — является общеизвестным, и продавец должен действовать в
соответствии с ним, зная сообщенный ему вектор оценок.
Очевидно, что доход продавца будет зависеть от того, что ему
сообщат участники. Удастся ли заставить их говорить правду? Если нет, то
как они будут действовать? Это хорошие вопросы, но пока мы их
оставим, а вместо этого рассмотрим еще один: как четыре стандартных
аукциона связаны с механизмами прямой продажи?
Мы покажем, что любой из них может эквивалентным образом
рассматриваться как совместимый по стимулам механизм прямой
продажи, т.е. такой механизм, в котором стратегия сообщать свои истинные
оценки является равновесной для участников. Эти механизмы окажутся
1 Наше изложение основано на книге Майерсона [Myerson, 1981].
2 Заметим, что, во-первых, издержки участника могут быть отрицательными, и,
во-вторых, они могут быть положительными, даже если участник не получает объект
(т.е. когда вероятность получить объект для него равна нулю).
3 Такого рода обобщение в данный момент нам не требуется, потому что ни в одном из
четырех стандартных аукционов продавец не оставляет объект себе, однако далее оно
окажется весьма полезным.

518
Часть III. Стратегическое поведение
центральными, потому что они не только позволят нам увидеть связи
между четырьмя стандартными аукционами, но и будут способствовать
изучению максимизирующих доход аукционов в целом.
Рассмотрим аукцион первой цены с симметричными участниками.
Нам бы хотелось построить «эквивалентный» механизм прямой продажи,
в котором стратегия говорить правду является равновесной. Для этого мы
воспользуемся функцией ставок аукциона первой цены />(•). Идея такого
построения проста. Вместо того чтобы делать ставки, рассчитанные
путем подстановки оценок в равновесную функцию ставок, участникам
будет предложено сообщить свои оценки, на основе которых продавец
затем рассчитает равновесные ставки. Вспомним, что, поскольку Ь()
строго возрастает, на аукционе первой цены участник может получить объект
тогда и только тогда, когда его оценка максимальна.
Рассмотрим следующий механизм прямой продажи, где Ь() является
равновесной функцией ставок для аукциона первой цены, приведенной в
(9-5):
\\, если vj > v для всех) Ф i
Pi(yv...,vN) = \
\у в противном случае,
Ь(у,), если v. > v,. для всех] Ф i
c,(v„...,vw) = J >
(9-8)
[О в противном случае.
Заметим, что участник, сообщающий максимальную оценку v,
получает объект и платит за него &(•), как это было бы на аукционе первой
цены. Поэтому если участники сообщают свои истинные оценки, то
участник с максимальной оценкой v выигрывает и платит продавцу за
объект &(•). Следовательно, если данный механизм совместим по стимулам,
то продавец в итоге получит тот же самый доход, что и на аукционе
первой цены.
Для доказательства нам необходимо убедиться* что говорить лрав-
ду — это равновесие по Нэшу. Предположим, что все остальные
участники сообщают свои истинные оценки и что оставшийся участник имеет
оценку v. Нам требуется показать, что для этого участника выгоднее
всего тоже сообщить продавцу свою истинную оценку. Но предположим, что
вместо этого он собирается сообщить продавцу, что его оценка равна г.
В таком случае он выигрывает и платит за объект b(r), только если г > Vj
для всех остальных j. Поскольку оценки других N -1 участников рас-

Глава 9. Аукционы и создание механизмов
519
пределены независимо в соответствии с F, это событие происходит с
вероятностью FN~l(r). Следовательно, ожидаемый выигрыш
рассматриваемого участника, если он сообщает г вместо своей истинной оценки v,
равен
F">)(v-6(r)).
Но это в точности выигрыш из формулы (9-1), который, как нам уже
известно, максимален при г = v. Поэтому механизм прямой продажи (9-8)
действительно совместим по стимулам.
Подытожим полученные нами результаты. Начав с равновесия на
аукционе первой цены, мы построили совместимый по стимулам
механизм прямой продажи, в котором «правдивое» равновесие в итоге
приводит к попаданию объекта к тому же участнику за ту же самую плату.
В частности, это означает, что и доход продавца будет таким же. Более
того, сам способ построения прямого механизма является довольно
общим. Действительно, начиная с равновесия на любом из четырех
стандартных аукционов, мы аналогичным образом можем построить
совместимый по стимулам механизм прямой продажи, в котором объект будет
передаваться тем же участникам, а платежи будут теми же самыми. (Вам
будет предложено сделать это в одном из упражнений.)
В сущности, мы доказали, что каждый из четырех стандартных
аукционов эквивалентен некоторому совместимому по стимулам механизму
прямой продажи. По этой причине мы можем узнать что-то о первых,
изучая второй.
9.3.1. Совместимые по стимулам механизмы прямой
продажи
Рассмотрим совместимый по стимулам механизм прямой продажи с
функциями вероятности рД) и функциями издержек сД), / = 1, ...,Л/\
По условию совместимости стимулов каждый участник должен считать
для себя оптимальным сообщать свою истинную оценку при условии, что
так же поступают все остальные. Рассмотрим следствия из этого факта.
Предположим, что оценка i -го участника равна vi, но он собирается
сообщать оценку rt. Если все остальные сообщают свои истинные
оценки, то ожидаемый выигрыш / -го участника составляет
и' Ь' v<J = j0' *' Jo (p* h' V"')V/" c* h' V"' ))^"/ (v"')rfv"''
где
/_;(v_/) = /(vl).../(vM)/(v/+l).../(v^) и dv_,=dvl...dvi_ldvM...dvN.

520
Часть III. Стратегическое поведение
Для каждого rf e [0,1] положим
и
?/(r/) = Jo-JoC'(f1, у-')/-/(у-/>Л-/ •
Таким образом, рДг;) равно вероятности, с которой /-й участник
получает объект, сообщая ri9 a cj(^) — его ожидаемый платеж в этой ситуации
при условии истинности оценок, сообщаемых остальными участниками.
Следовательно, ожидаемый выигрыш / -го участника при истинной
оценке v, и сообщаемой оценке г,, если остальные участники сообщают свои
истинные оценки, можно записать как
Ч(Г» v/) = ^(r/)v,-cl(ri). (9-9)
Итак, механизм является совместимым по стимулам тогда и только
тогда, когда для каждого v, функция u.(rj9 v;) достигает максимума по г{
при г, =v/5 т.е. f/.(v„ v,) >*/,(*;, v.) для всех ^g[0,1].
Следующий результат оказывается очень полезным. Он полностью
характеризует совместимые по стимулам механизмы прямой продажи.
Теорема 9.5. Совместимые по стимулам механизмы прямой
продажи.
Механизм прямой продажи (/?,(•), C/(-))/Ii является совместимым по
стимулам тогда и только тогда, когда для каждого участника i
а) функция /?,(v;.) не убывает по v,;
б) с" (v;.) = сх @) + pt (v;. )v/ - JJ' pt (x)dx для всех v, e [0,1].
Доказательство. Предположим, что механизм совместим по
стимулам. Нам требуется показать, что выполняются условия а) и б).
Чтобы убедиться в а), заметим, что при условии совместимости
стимулов для всех rj9 vi e [0, 1]
PMi>i-ci(ri) = ui(rn vf)<Ui{vn vi) = pi(yi)vi-ci(vl).
Если добавить и вычесть pi (v,.)?;. из правой части, получим
Выражение в квадратных скобках равно w,(v;, т;), ожидаемому
выигрышу i -го участника, сообщающего vt при истинной оценке rt. По условию

Глава 9. Аукционы и создание механизмов
521
совместимости стимулов он не должен превышать ut{rn rt) —
ожидаемого выигрыша, если сообщается истинная оценка rt. Следовательно,
^Щ{г» l) + A(v,Xv,-r,) =
= [A(l)';-ci(r/)] + p/(v/)(v/-r/).
То есть
Переписав это соотношение, получим
Итак, если ^>г/5 должно выполняться неравенство J?,(v, )>#(/;),
откуда мы заключаем, что /?.(•) не убывает, т.е. условие а) выполняется.
Для доказательства б) заметим, что, поскольку ожидаемый выигрыш
/-го участника должен быть максимальным, если сообщается истинная
оценка, то производная ut(rn v,.) по гг должна равняться нулю при
1
г, = v, . Рассчитаем производную
3w,(^, v,.) _, _/
dr.,
и приравняем ее к нулю при rt = vt:
cXn) = m>i- (9-Ю)
Поскольку v, было произвольным, (9-10) должно выполняться для
всех v,. e [0, 1]. Следовательно,
ci(vi)-ci@) = ^c;(x)dx =
= fQ p'(x)xdx =
= A(v,)v/-JoV'p/(x)A,
1 Здесь мы игнорируем два момента. Первый заключается в том, действительно ли
функция ufa, v,) является дифференцируемой по г,. Хотя ей не требуется быть всюду
дифференцируемой, условие совместимости по стимулам означает, что она должна быть
дифференцируемой почти всюду и что проводимый анализ можно сделать абсолютно
строгим. Этими подробностями мы заниматься не будем. Второй момент — это условие
первого порядка в граничных точках v; = 0 или v, = 1. Строго говоря, производная в них
не обязательно равна нулю. Но ничего страшного в этом нет, потому что обе эти оценки
встречаются с нулевой вероятностью.

522
Часть III. Стратегическое поведение
где первое равенство следует из основной теоремы математического
анализа, второе — из (9-10), а третье — из интегрирования по частям.
Следовательно, для каждого участника / и всех v, e [0,1]
сДу/) = с/@) + л(у,)у/-/оУ'л(дг)Л, (9-11)
что доказывает б).
Теперь необходимо доказать обратное, поэтому предположим, что
условия а) и б) выполняются. Требуется показать, что и fa, v,.) достигает
максимума по rt при ri = v,. Для этого подставим выражение из б) в (9-9):
Щ% vi) = p^r>/-[c;@) + p^ri)ri-Jo>/(x)A]. (9-12)
Его можно переписать как
и,(г„ v,) = -с,@) +JJй(*)A-{JJЙМ-Й^Ц,
причем это выражение имеет смысл и при гг < v;, и при г, > v,Л
Поскольку по условию а) функция р.(-) не убывает, интеграл в фигурных скобках
неотрицателен при всех г. и vt. Следовательно,
ufa, vJZ-cW + ^PtWdx. (9-13)
Но по (9-12) правая часть (9-13) равна ufa, vy). Следовательно,
ufa, vjuufa, v;),
так что и fa 9 v,) действительно достигает максимума по /* при rx = v;. ¦
Часть б) теоремы 9.5 говорит о том, что если прямой механизм
совместим по стимулам, то должна существовать связь между функциями
вероятности и функциями издержек. Утверждается, в частности, что если
известны функция вероятности и ожидаемые издержки участника при Нулевой
оценке, то известно и значение функции издержек при всех других
оценках. Иными словами, при условии совместимости стимулов зависимость
ожидаемого платежа участника от его оценки полностью определяется его
ожидаемыми издержками при нулевой оценке и функцией вероятности.
Это наблюдение существенно для понимания следующего результата.
1 Вспомним принятое в математике соглашение о том, что для а < Ъ

Глава 9. Аукционы и создание механизмов
523
Теорема 9.6. Эквивалентность доходов.
Если два совместимых по стимулам механизма прямой продажи
имеют одинаковые функции вероятности и для каждого участника с
нулевой оценкой эти механизмы эквивалентны, то они приносят продавцу
одинаковый ожидаемый доход.
Доказательство. Ожидаемый доход продавца равен
* = Jo-L'?C<(v" •••>v„)Av,).../(v„)<V--^ =
/=1
= 2j0-J0c'(v" •••»vA-)/(v,).../(vA,)«frI...<fyr =
/=1
=ZLN(°)+A(v.)v,-f0>,w^
/=1 I-
№№,=
1=1 I- -J /=1
где четвертое равенство следует из определения с. (vf.), а пятое — из (9-11).
Следовательно, ожидаемый доход продавца зависит только от
функций вероятности и величины сумм, которые участники готовы заплатить,
если их оценки равны нулю. Нужный результат следует из того факта, что
ожидаемый выигрыш участника с нулевой оценкой полностью
определяется его ожидаемым платежом при нулевой оценке. ¦
Теорема об эквивалентности доходов объясняет кажущееся
случайным равенство между ожидаемыми доходами, получаемыми на всех
четырех стандартных аукционах. Как мы видим, оно следует из того, что
при симметричных участниках функции вероятности одинаковы во всех
четырех стандартных аукционах (т.е. объект отдается участнику с
наивысшей оценкой), и в каждом из них участник с нулевой оценкой
получает нулевую ожидаемую полезность.
Теорема об эквивалентности доходов является очень общей и
позволяет расширить список аукционов, приносящих тот же ожидаемый доход,
что и любой из четырех стандартных типов. Например, к нему добавится
аукцион первой цены, на котором платят все участники (победившей

524
Часть III. Стратегическое поведение
объявляется максимальная из всех закрытых ставок, но каждый участник
платит сумму, равную своей ставке). При симметричных участниках он
приносит тот же самый ожидаемый доход. В упражнениях вам
предлагается изучить этот и другие аукционы.
9.3.2. Эффективность
Прежде чем закончить этот раздел, остановимся кратко на
распределительных свойствах четырех стандартных аукционов. Как мы уже не раз
отмечали, в каждом из них объект передается тому участнику, который
его ценит больше, чем все другие, т.е. все стандартные аукционы
эффективны. В случае голландского аукциона и аукциона первой цены это
связано с симметрией участников. Без нее различные участники, скажем, на
аукционе первой цены будут использовать различные строго
возрастающие функции ставок; следовательно, участник может проиграть аукцион
при более высокой, чем у других участников, оценке выставленного на
аукцион объекта.
9.4. Максимизация дохода: приложение теории создания
механизмов
К настоящему моменту нам уже хорошо знакомы четыре
стандартных аукциона, их равновесные состояния, ожидаемый доход и
соотношения между ними. Но при том, что все они генерируют одинаковый доход
(если участники симметричны), будет ли он максимальным? Или
существует более выгодный для продавца механизм продажи? Если да, то какой
вид он имеет? Подаются ли заявки в запечатанных конвертах? Подаются
ли они последовательно? Или имеет место и то и другое? Является ли
аукцион наилучшим механизмом продажи?
По всей видимости, поиск максимизирующего доход механизма
продажи будет трудной задачей. Если мы можем выбрать любую процедуру,
с чего начинать? Главное здесь — вспомнить, как нам удалось построить
совместимый по стимулам механизм прямой продажи на основе
равновесия на аукционе первой цены и как исход аукциона первой цены в
точности повторился в «правдивом» равновесии механизма прямой продажи.
Оказывается, аналогичное построение можно применить к любой
процедуре продажи, т.е. при данной произвольной процедуре продажи и
равновесии по Нэшу, в котором каждый участник использует стратегию,
отображающую его оценку в действия, направленные на максимизацию
выигрыша, мы можем построить эквивалентный совместимый по стимулам
механизм прямой продажи. Соответствующие функции вероятностей и
издержек отображают вектор оценок в вероятности и издержки, с
которыми каждый участник столкнулся бы, используя равновесную стратегию

Глава 9. Аукционы и создание механизмов
525
в исходной процедуре. Построенный таким образом механизм совместим
по стимулам и обеспечивает то же самое (вероятностное) распределение
объекта, те же ожидаемые издержки участников и тот же самый
ожидаемый доход продавца.
Следовательно, если некоторая процедура продажи приносит
продавцу ожидаемый доход в размере Л, то же самое происходит и при
некотором совместимом по стимулам механизме прямой продажи. Но это
означает, что ни один из всевозможных механизмов продажи не приносит
продавцу большего дохода, чем максимизирующий доход и совместимый
по стимулам механизм прямой продажи. Поэтому можно ограничить наш
поиск максимизирующей доход процедуры продажи множеством
совместимых по стимулам механизмов прямой продажи. Тем самым мы
значительно упростили задачу, ничего при этом не потеряв.
9.4.1. Индивидуальная рациональность
Существует еще одно ограничение, которое нам необходимо
рассмотреть. Поскольку участники вступают в игру абсолютно добровольно, их
ожидаемый выигрыш при заданной оценке не может быть отрицательным.
В противном случае независимо от своих оценок они просто не будут
участвовать. Поэтому мы должны ограничиться совместимыми по стимулам
механизмами прямой продажи, которые являются индивидуально
рациональными, т.е. теми, которые в правдивом равновесии приносят каждому
участнику неотрицательный ожидаемый выигрыш независимо от его оценки.
Пусть / -й участник совместимого по стимулам механизма с оценкой
v; получает в правдивом равновесии ожидаемый выигрыш ut(vi9 v,.).
Тогда совместимый по стимулам механизм прямой продажи является
индивидуально рациональным, если этот выигрыш всегда неотрицательный,
т.е. если
Щ(Уп v/) = A(v/)v/ -^(v/) ^ 0 Для всех vt G [0,1].
Однако по условию совместимости стимулов часть б) теоремы 9.5
говорит, что
ct (v,) = с, @) + р, (v,)v, - JJ' p, (x)dx для всех v, e [0,1].
Следовательно, совместимый по стимулам механизм прямой продажи
является индивидуально рациональным тогда и только тогда, когда
Щ(Уп v/) = S-(v>/-c;.(vi) = -c/@) + JoV,p/(x)&>0 для всех v,€[0,l],
что, конечно, верно, в свою очередь, тогда и только тогда, когда
с,@)<0. (9-14)

526
Часть III. Стратегическое поведение
Следовательно, совместимый по стимулам механизм прямой продажи
является индивидуально рациональным тогда и только тогда, когда
ожидаемые издержки каждого участника при нулевой оценке неположительны.
9.4.2. Оптимальный механизм продажи
Итак, мы свели задачу поиска оптимального механизма продажи к
максимизации ожидаемого дохода продавца по всем индивидуально
рациональным и совместимым по стимулам механизмам прямой продажи
Pi (•) и с/ (•), / = 1,..., N. Поскольку теорема 9.5 характеризует все
совместимые по стимулам механизмы продажи, а совместимые по стимулам
механизмы прямой продажи индивидуально рациональны тогда и только
тогда, когда сД0)<0, наша задача выглядит так: найти механизм прямой
продажи pt (•), с; (•), i = 1,..., N, который максимизирует величину
при условиях
а) Д(у/) не убывает по vj9
б) с, (v,.) = с, @) + р, (v, )v,. - JJ' pt (x)dx для всех v, e [0,1],
в)с;.@)<0,
где выражение для ожидаемого дохода продавца следует из условия
совместимости стимулов точно так же, как в доказательстве теоремы 9.6.
Преобразуем это выражение:
R=z L'Nv<)v< "Jo p> <*)A~U<v< vh+fe«»=
/=i *- -* /=i
=z[Jo^(v/)vi/(vi)^/-j07ov'^w>'(v')d^'l+i?/(o)-
/=1 L. J ,=i
Изменив порядок интегрирования в двойном интеграле (с dxdvi на
dVjdx), получим
^ = Z[/0,A(v,)v,y;(v/)<ft;/-Jo7x,p/W/(v,)*A] + X^@) =
/=1 *- -* /=1
=zrj0,A(v/)v/y;(v/)*/-jo,^(Jcxi-/:;w)&l+f;c,(o).
/=i I- -J /=i

Глава 9. Аукционы и создание механизмов
527
После замены переменной интегрирования х на v;. это можно записать
как
/=1 I- -J /=1
Наконец, вспомнив, что
рМ) = \0---Ц,р,(п>*-1)/-,(*-№-,.
можно записать:
* = Zj0...JeA(v„...,vw)
/=1
V; -
1-^(у,)
yi(v,)...AK)^,...^+?c;.@)
ИЛИ
^=J0,...J0,|Ip,(vi,...,vw)
+ ?с,.@).
>fl(Vl)---fN(VN)dvr--dvN +
(9-15)
Таким образом, наша задача— максимизировать (9-15) при
ограничениях а)—в). Сконцентрируемся пока на первом слагаемом из (9-15), а
именно
Jo-Ji Ia(v„-,v„)
V;-
l-^(v,)
•yi(v,)...AK)^,...^. (9-16)
Ясно, что (9-16) достигнет максимума, если выражение в фигурных
скобках будет принимать максимальное значение при любом векторе
оценок v,,...,v^. Поскольку /7/(v1,...,v;v) неотрицательны и в сумме
меньше или равны единице, N + 1 число /?,(у,,...,у^),..., pN{vv...,vN),
N
1 - 2] # (Vj,..., v^) неотрицательно и в сумме эти величины равны единице.
/=i
Поэтому выражение в фигурных скобках, которое можно переписать как
EA(vi'-'vtf)
v, -
i-^(y,)
+ 1-1р,(П,...,у^) -О,

528
Часть III. Стратегическое поведение
равно взвешенному среднему N +1 числа
i-^.(y.)
/i(v.)
Л К)
,0.
Но тогда сумма в фигурных скобках не может превышать наибольшего из
этих чисел, если хотя бы одно из них положительно, и не может быть
больше нуля, если все они отрицательны. Предположим теперь, что
никакие два члена в скобках не равны друг другу. Тогда если определить
/>*(v,,...,v„) как
P,*(v„...,v„) =
l-F(v)
1, если v; ..' ,' > max
(
f,iy,)
[0 в противном случае,
то должно выполняться неравенство
0,v
lMvi.»..v#)
v,--
' /(v,)
^EaVi v»)
v,-
для всех j Ф i,
(9-17)
I-^(v,)~
Таким образом, если выражения в скобках различаются с вероятностью,
равной единице, мы получим
+ fo@)
v..-
>yi(v,)...A(vwWv,...rfvJV +
V, -
i-*;(v/)
/(V/)
^(у,)...ЛЮЛ1...л^ +
для всех совместимых по стимулам механизмов прямой продажи />,(•),
сД). На минуту предположим, что все члены в скобках различаются с
вероятностью, равной единице. Вскоре мы введем предположение
относительно распределений участников, которое будет гарантировать это1.
1 Это предположение приведено в (9-22).

Глава 9. Аукционы и создание механизмов
529
Поскольку условие в) означает, что сД0)<0, мы также можем
сказать, что для всех совместимых по стимулам механизмов прямой продажи
Л О 9 с,() Д°Х°Д продавца не может превышать верхнюю грань, т.е.
«J.4.1 2»,.-.v,)
V; -
l-*)(vi)
^/i(v,)...A(vJ*.-^.(9-18)
Теперь мы построим совместимый по стимулам механизм прямой
продажи, достигающий этой верхней грани. Следовательно, такой
механизм будет максимизировать доход продавца и поэтому будет для него
оптимальным.
Для построения этого оптимального механизма положим, что
функции вероятности равны p*(vl9...9vN)9 i = l9...9N из (9-17). Необходимо
определить и функции издержек c*(v,,...,v^), / = 1,...9N. Но условие б)
требует, чтобы для каждого v. ожидаемые издержки и вероятности
получить объект для /-го участника — ^*(v;) и p*(v.) — были связаны
следующим образом:
с>,) = с/ДО + лО^у, - JoV' p*{x)dx.
Так как ZT* и р* являются средними для значений с* и /?*, это
соотношение между средними будет выполняться, если оно верно для любого и
каждого вектора оценок v,,...,v^. To есть б) гарантированно
выполняется, если мы определим с] следующим образом: для любого vp..., v^
c.(vp...,v^)=c;(o,v_/)+p;(vp...,v^)v/.-JJ>;(x,v_/)cfc. (9-19)
Чтобы закончить определение функций издержек и выполнить
условие (в), положим с*@, v_i9..., v_,) = 0 для всех / и всех v29...9vN.
Поэтому наш кандидат на роль максимизирующего доход и совместимого по
стимулам механизма прямой продажи таков: для каждого / = 1, ...9N и
каждого vl9...9vN
p'(V\*->Vn) = \
l-/^(v,) ( l-Fj(Vj)
1, если v; jr/ \ > max 0, vy L-J—
\
0 в противном случае,
f№
для всех j * /,
(9-20)
и

530
Часть III. Стратегическое поведение
c-(Vp...,v^) = ^(vp...,vAr)v.-JoV>/,(x,v./)A. (9-21)
По построению, этот механизм удовлетворяет ограничениям б) и в) и
достигает верхней грани доходов, установленной в (9-18). Чтобы
убедиться в этом, просто подставим р* в (9-15) и вспомним, что опять же по
построению "с*@) = 0 для всех i. В результате доход продавца равен
максимально возможному значению, т.е.
*=j0'-j; \tpM^N)
l-^(v,)
^1^).../^^)*,...^
Итак, если мы сумеем показать, что функции вероятности,
определенные в (9-20), удовлетворяют условию а), то наш механизм
действительно будет искомым решением.
К сожалению, р* в определении (9-20) не обязательно удовлетворяет
а). Чтобы обеспечить выполнение этого условия, нам придется
ограничить распределения оценок участников. Рассмотрим следующее
предположение: для каждого i = l,...,N
l-F(v)
v, —— строго возрастает по v;. (9-22)
//(v,-)
Это предположение верно для многих распределений, включая
равномерное. Более того, в упражнении вам будет предложено показать, что оно
выполняется всякий раз, когда F. является произвольной выпуклой
функцией, а не только когда приходится иметь дело с равномерным
распределением1. Заметим, что это предположение обеспечивает выполнение
условия а), но также гарантирует, что числа v, -(l-Fx{vx))/fx{vx),...,
vN -(l-FN(vN))/fN(vN) различны с единичной вероятностью. Это
требование использовалось нами ранее, но до сих пор не было объяснено.
Посмотрим, почему из (9-22) следует а). Рассмотрим некоторого
участника / и некоторый фиксированный вектор оценок других участников
v_,. Предположим, что v; > v; и p*(vi9 v_f.) = 1. Тогда по определению р*
выражение vir- A - Ft(v, ))jfl(v,) положительно и строго больше, чем
Vj -A -Fj(Vj))/fj(Vj) для всех )Фг. Следовательно, так как
1 Если это допущение не выполняется, то предложенный здесь механизм не является
оптимальным. Тем не менее построить оптимальный механизм все же можно, но делать
этого мы не будем. Тем самым дополнительное предположение вводится только для
простоты.

Глава 9. Аукционы и создание механизмов
531
v,-(l-i^Cv,.))//,^) строго возрастает, величины v, -(l-^(v;))//(v,)
также положительны и строго больше, чем vy-(l-F^vy))//y(vy), для
всех j*i9 откуда следует p*(vn v_.) = l. Таким образом, мы показали,
что если p](vn v_.) = 1, то /?*(v',v_,) = 1 для всех v' > vf.. Но поскольку />*
принимает значение 0 или 1, p*(v.9 v_.) не убывает по vf. при любых v_;.
Это, в свою очередь, означает, что p*(vf.) не убывает по v;, так что
условие а) действительно выполняется.
Итак, наши усилия в конце концов полностью оправдались, и мы
можем утверждать следующее.
Теорема 9.7. Оптимальный механизм продажи.
Если N участников имеют независимые частные оценки, причем
функция распределения оценки i -го участника имеет непрерывную
положительную функцию плотности f., удовлетворяющую (9-22), то
механизм прямой продажи, определенный в (9-20) и (9-21), приносит
продавцу максимально возможный ожидаемый доход.
9.4.3. Оптимальный механизм продажи: детали
Посмотрим, можно ли упростить описание оптимального механизма
продажи, изучив его подробнее. Механизм состоит из двух частей -
процедуры передачи объекта, которая характеризуется функцией /?*, и
процедуры определения платежей с*.
Первая часть оптимального механизма проста. При данных
сообщаемых оценках v,,...^ объект передается /-му участнику, у которого
v. - A - Fi.(v,;))// (v,) максимально и положительно. В противном случае
продавец оставляет объект у себя. Эту схему полезно попытаться
проанализировать.
Мы докажем, что v, -A -Fi,(v,))//,-(v,.) представляет собой
предельный доход Aff?,(v;), который продавец получает, увеличивая вероятность
передачи объекта / -му участнику с оценкой v,. Чтобы убедиться в этом
без длинных выкладок, приведем интуитивное доказательство.
Рассмотрим эффект от увеличения вероятности того, что объект получит / -й
участник с оценкой v,. Это позволяет продавцу увеличить плату за объект до
v,, оставляя полезность участника без изменений. Поскольку плотность
распределения v, равна /(v,), доход продавца в результате этого
увеличения возрастает со скоростью v./.(v.). В то же время условие совмести-

532
Часть III. Стратегическое поведение
мости стимулов требует наличия связи между вероятностью отдать
объект / -му участнику и издержками, приписываемыми всем более высоким
оценкам v' > v;. Действительно, в соответствии с условием б) увеличение
вероятности того, что объект получат игроки с низкими оценками, в той
же пропорции снижает издержки, которые должны нести игроки с
высокими оценками. Поскольку над v. лежит масса распределения l-i^v,.),
общее снижение дохода составит l-J^v,.). В целом доход продавца
вырастет на vifi (v,) - A - Ft (v7)). Но это общий эффект, который относится к
плотности fiivi) оценок, равных vr
Следовательно, предельный доход, соответствующий каждому v/9 равен
MRi(vi) = vi-(l-Fi(vi))/fi(vi).
Правило передачи объекта теперь абсолютно ясно. Если
МКДу,) > MRj(Vj), то продавец может увеличить доход, уменьшая
вероятность отдать объект j -му участнику и увеличивая эту вероятность для
/-го участника. Тогда, очевидно, продавец максимизирует свой доход,
приписывая всю вероятность (т.е. единичную) участнику с максимальным
MR;(vy), если он положителен. Если все предельные доходы
отрицательны, то продавцу лучше всего понизить вероятности для всех участников
до нуля, т.е. оставить объект себе.
Немного менее прозрачна часть механизма, связанная с оплатой.
Чтобы прояснить картину, предположим, что если (правдивые)
сообщаемые оценки равны Vj,...,^, то i-й участник не получает объект, т.е.
jp*(v,,v_/) = 0. Сколько он должен заплатить в соответствии с
механизмом? По (9-21) ответ такой:
с*(У» v_/) = ft(v/, v_y)v;.-joV>;(x, v_,)A =
= 0-v/-J0V>*(^v./>fc.
Но вспомним, что благодаря предположению (9-22) р*(-> у_.) не убывает.
Следовательно, поскольку p*(yi9 v_,.) = 0, равенство р*{х, v_;) = 0 должно
выполняться для всех x<vr Поэтому вышеприведенный интеграл
должен быть равен нулю, откуда
c,(vl9 v_,) = 0.
Итак, мы показали, что в соответствии с оптимальным механизмом /-й
участник, не получающий объект, ничего не платит.

Глава 9. Аукционы и создание механизмов
533
Предположим теперь, что он получает объект, т.е. p*(vj9 v_,.) = 1.
Согласно (9-21) в этом случае он платит
c'(yl9 v_,.) = /?>,, v_>,-JoV,/?;(x, v_t)dx =
Так как р* принимает значение 0 или 1, не убывает и непрерывна слева
от оценки /-го участника, a /?*(v, »v-,) = 1, для /-го участника должна
существовать наибольшая оценка г* <v,, такая, что р*г(г*9 v_,) = 0.
Заметим, что, вообще говоря, г* будет зависеть от v_,, так что правильнее
было бы написать r/(v_f.). Заметим также, что по определению r*(v4)
величина р*(х, v_7) равна 1 для всех х > r*(v_f) и равна 0 для всех х < r*(v_t).
Но это означает, что
с>,> V-') = V'-Jr;(v,I* =
= vi-(vi-r'(v_i)) =
Таким образом, если /-й участник получает объект, он платит цену
P*(v4), которая не зависит от той оценки, которую сообщает он сам.
Более того, цена, которую он платит, равна максимальной оценке,
которую он мог бы сообщить при данных (сообщаемых) оценках остальных,
не получая объект.
Сводя все это вместе, мы можем переформулировать определение
максимизирующего доход механизма продаж, приведенное в (9-20) и
(9-21), следующим образом.
Теорема 9.8. Упрощенный оптимальный механизм продажи.
Если N участников имеют независимые частные оценки, причем
функция распределения оценки i-го участника имеет непрерывную
положительную функцию плотности fi и каждое vi.-Fi(yi))/fi(vi)
строго возрастает, то максимально возможный ожидаемый доход про-
давцу приносит следующий механизм прямой продажи.
Для каждого сообщаемого вектора оценок v,,...,v^ продавец
отдает объект такому участнику i, у которого величина

534
Часть III. Стратегическое поведение
v,. - A - Fi(vi ))/fi (vi) максимальна и строго положительна. Если такого
участника нет, то продавец оставляет объект себе, и никакие платеэюи
не производятся. Если же такой участник есть, тогда он и только он
платит продавцу сумму г*, где г* -(\-F.(r*))l f.(r*)t или max .,,. v. -A-
~Fj(vj))lfj(vj) 6 зависимости от того, что больше. Платеж: i-го
участника г*, таким образом, является максимальной оценкой, которую он
мог бы сообщить при данных сообщаемых оценках других, не получая
объект.
Как мы знаем, этот механизм является совместимым по стимулам, т.е.
говорить правду — это равновесие по Нэшу. Но на самом деле стимул
говорить правду здесь гораздо сильнее: для каждого участника стратегия
сообщать продавцу свою истинную оценку является доминирующей; даже
если остальные участники не сообщают своих истинных оценок, для / -го
участника это самый лучший вариант. Вам будет предложено показать
это в упражнении.
Одним из недостатков такого механизма является то, что для его
реализации продавцу необходимо знать распределения оценок участников
Fi. Этим он отличается от стандартных аукционов, которые можно
организовать, не имея вообще никакой информации об участниках. Тем не
менее между оптимальным механизмом и этими аукционами существует
связь, изучением которой мы сейчас займемся.
9АЛ. Эффективность, симметрия и сравнение с четырьмя
стандартными аукционами
В оптимальном механизме продажи объект не всегда передается
участникам эффективным образом. Иногда участник с максимальной
оценкой не получает объект. Неэффективность в оптимальном механизме
может возникать по двум причинам. Во-первых, исход может быть
неэффективным, потому что продавец иногда оставляет объект у себя, даже если
оценка объекта у него равна нулю, а у всех участников — положительна.
Это происходит в том случае, если для всех i оценка i -го участника v,
такова, что vf. — A — ^Cv/))/^Cv,-) — 0 - Во-вторых, даже если продавец
передает объект одному из участников, это может быть не участник с
максимальной оценкой. Чтобы убедиться в этом, рассмотрим случай с двумя
участниками. Если ситуация несимметрична, то для некоторого ve [0,1]
v-(\-Fx{v))l/х{у)Фv-A~jF2(v))//2(v). Предположим, что для данного
конкретного v v - A - Fx (v))//j (v) > v - A - F2 (v))/f2 (v) > 0.
Следовательно, если оценки обоих участников равны v, объект получит участник 1.

Глава 9. Аукционы и создание механизмов
535
Но по условию непрерывности, даже если оценка участника 1
уменьшается до v'<v, пока v достаточно близко к v, неравенство
v - A - Fx (v'))//j (v') > v - A - F2 (v))//2 (v) > 0 будет выполняться. Поэтому
участник 1 получит объект, хотя его оценка строго меньше оценки
участника 2.
Отсутствие эффективности неудивительно. В конце концов, продавец
является монополистом, стремящимся к максимальной прибыли. В
главе 4 мы видели, что монополист установит объем выпуска на уровне ниже
эффективного, чтобы добиться более высокой цены. Ту же самую
картину можно наблюдать и здесь, но поскольку продается только один
неделимый объект, продавец ограничивает предложение, иногда оставляя
объект у себя, в зависимости от сообщаемых оценок. Однако это
объясняет только первый вид неэффективности. Возникающий здесь второй ее
вид не встречался в нашем кратком анализе монополии в главе 4.
Причина в том, что там мы предполагали, что монополист не может отличить
одного покупателя от другого и поэтому вынужден взимать со всех
одинаковую плату. Здесь же мы считаем, что монополист может отличить
i -го участника от j -го и знает, что распределение оценок первого Ft, a
второго Fj. Эта дополнительная информация позволяет монополисту
дискриминировать участников, что ведет к повышению прибыли.
Исключим второй источник неэффективности, предположив, что
участники симметричны. Поскольку в этом случае все четыре стандартных
аукциона приносят продавцу одинаковый ожидаемый доход, мы также
сможем сравнить их с оптимальным механизмом продажи.
Как симметрия влияет на оптимальный механизм? Если ситуация
симметрична, то /; = / и Fi,= F для каждого участника /.
Следовательно, оптимальный механизм таков: если вектор сообщаемых оценок равен
(vp...,v^), то участник / с максимальным и положительным
v.-(I-Fjty))/fity) получает объект и платит продавцу сумму г*9
равную максимальной оценке, которую он мог бы сообщить при данных
сообщаемых оценках остальных участников, не получая объект. Если
такого участника нет, то продавец оставляет объект у себя и платежи не
производятся.
Но давайте задумаемся над этим. Поскольку мы предполагаем, что
v-(l-F(v))//(v) строго возрастает по v, то объект действительно
передается участнику i с максимальной оценкой vi при условии, что
v,. -(l-^(v,))/y;(v;.) > 0, т.е. если v, > р* е [0,1], где

536
Часть III. Стратегическое поведение
р--ЬО1>=0. (9-23)
Др)
(В упражнении вам предлагается показать, что такое р* существует и
единственно.)
Насколько велика может быть сообщаемая / -м участником оценка до
передачи ему объекта? Он не получит объект до тех пор, пока не сообщит
оценку, которая максимальна и больше р*. Поэтому оценка, которую
участник может сообщить, не получая объект, равна либо максимуму
оценок других участников, либо р* в зависимости от того, что больше.
Следовательно, получая объект, /-й участник платит либо р*, либо
максимальную из оценок, сообщаемых остальными, в зависимости от того,
что больше.
С учетом этого оптимальный механизм продажи принимает
следующий вид. Участник, сообщаемая оценка которого является максимальной
и строго большей р*, получает объект и платит большую величину из р*
и максимума оценок, сообщаемых другими участниками.
Примечательно, что этот механизм можно имитировать с помощью
аукциона второй цены с резервной ценой р , т.е. аукциона, в котором
участник с максимальной ставкой, превышающей резервную цену,
выигрывает и платит за объект сумму, равную второй по величине ставке или
резервной цене в зависимости от того, что больше. Если ни одна из ставок не
превышает резервную цену, продавец оставляет объект у себя и платежи не
производятся. Это оптимум, поскольку, точно так же как в стандартном
аукционе второй цены, на аукционе второй цены с резервной ценой
стратегия делать ставку, равную оценке участника, является доминирующей.
Данное заключение стоит сформулировать отдельно.
Теорема 9.9. Оптимальный аукцион при симметричных
участниках.
Если N участников имеют независимые частные оценки, причем
функция распределения оценки i -го участника имеет непрерывную
положительную функцию плотности f, a v-(l-F(v))//(v) строго
возрастает, то аукцион второй цены с резервной ценой р*,
удовлетворяющей условию p*-(l-F(p*))//(p*) = 0, максимизирует ожидаемый доход
продавца.
А что же остальные три стандартных аукциона? Можно ли их тоже
сделать оптимальными для продавца, добавив соответствующую
резервную цену? Ответ — да, можно, но объяснение оставлено вам в качестве
упражнения.

Глава 9. Аукционы и создание механизмов
537
Итак, мы вернулись к началу. Четыре стандартных аукциона —
первой цены, второй цены, голландский и английский — при симметричных
участниках приносят одинаковый доход. Если дополнить каждый из них
соответствующей резервной ценой, то продавец будет максимизировать
свой ожидаемый доход. Поэтому нет ничего удивительного в том, что эти
аукционы так широко распространены. На этом выводе мы и остановимся.
9.5. Упражнения
9.1. Покажите, что функция ставок в (9-5) строго возрастает.
9.2. Покажите двумя способами, что стратегию ставок в
симметричном равновесии на аукционе первой цены с N симметричными
участниками, оценки которых распределены по закону F, можно записать как
6(v) = v-
F(v)
В первом способе воспользуйтесь нашим решением, приведенным в
тексте, и примените интегрирование по частям.
Во втором способе воспользуйтесь тем фактом, что FN~\r){v-b{r))
максимизируется по г при г = v, а затем примените теорему об
огибающей и получите, что d(FN~](v)(v-b(v)))/dv = FNl(v). После этого
проинтегрируйте обе части от 0 до v.
9.3. Это упражнение проведет вас через доказательство того, что
функция ставок в (9-5) является симметричным равновесием на аукционе
первой цены.
а) Вспомните из (9-2), что
^i^ = (N-l)FN-\r)f(r)(v-b(r))-FN-,(r)b\r).
dr
Используя (9-3), покажите, что
^^ = (yV-l)FA'-2(A-)/(A-)(v-6(r))-(iV-l)FA'-2(r)/(r)(r-6(r)) =
dr
= (N-\)FN-\r)f(r)(v-r).
б) С помощью результата, полученного в пункте а), покажите, что
du(r, v)/dr положительна при г < v и отрицательна при г > v, так что
w(r, v) достигает максимума при г = v.

538
Часть III. Стратегическое поведение
9.4. В тексте мы предполагали, что продавец и все участники
нейтральны к риску. В этом упражнении мы рассмотрим, к каким
последствиям приводит несклонность к риску у некоторых участников.
Пусть на аукционе первой цены N участников. Оценка каждого
участника независимо выбирается из отрезка [0,1] в соответствии с
функцией распределения F, обладающей непрерывной и строго положительной
функцией плотности /. Если оценка участника равна v и он выигрывает
объект при ставке b< v, то его полезность фон Неймана — Моргенштер-
на равна (v-b)a, где а > 1 фиксировано и одинаково для всех
участников. Следовательно, участники не склонны к риску при а > 1 и
нейтральны к риску при а = 1. (Понятно, почему?) При данном показателе
несклонности к риску а пусть ba(v) обозначает равновесную ставку
участника с оценкой v (в симметричном равновесии). С помощью
следующих шагов найдите ba (v) и некоторые его свойства.
а) Пусть u(r, v) обозначает ожидаемую полезность участника от
ставки ba(v) при оценке v и при условии, что все остальные участники
используют Ьа(-). Покажите, что
и(г, v) = FN-\r)(v-ba(r)r.
Почему w(r, v) должно достигать максимума по г при г = v ?
б) Используя пункт а), докажите, что
[и(г, у)Г=[/г>)Г>Ч('0)
должно достигать максимума по г при г = v.
в) Используя пункт б), докажите, что аукцион первой цены с N -1 не
склонным к риску участники (см. определение выше), оценки которого
независимы и распределены по закону F(v), эквивалентен аукциону
первой цены с N -1 нейтральным к риску участником, оценки которого
независимы и распределены по закону Fa(v). Воспользуйтесь нашим
решением для случая нейтральности к риску (см. упражнение 9.2) для того,
чтобы доказать, что
ba(v) = v-
F(xf
,U(v)
dx.

Глава 9. Аукционы и создание механизмов
539
г) Докажите, что ba(v) строго возрастает по ос>1.
Проинтерпретируйте этот рузультат. Убедитесь в том, что с ростом несклонности
участников к риску доход продавца от аукциона первой цены возрастает.
д) Используя пункт г) и теорему об эквивалентности доходов для
стандартных аукционов в случае нейтральности к риску, докажите, что, если
участники не склонны к риску, аукцион первой цены приносит продавцу
больший доход, чем аукцион второй цены. То есть в случае несклонности к
риску два стандартных аукциона приносят различный доход.
е) Что произойдет с доходом продавца, если участники станут
бесконечно не склонными к риску (т.е. при а —> <*>)?
9.5. В модели частных оценок докажите, что стратегия делать ставку,
равную оценке, является для участника слабо доминирующей, даже если
совместное распределение оценок участников коррелированно.
9.6. Используя равновесия аукциона второй цены, а также
голландского и английского, постройте для каждого из них совместимый по
стимулам механизм прямой продажи, в котором фактическое распределение
объекта среди участников и фактические платежи продавцу неизменны.
9.7. На аукционе первой цены, где платят все участники, заявки
подаются в запечатанных конвертах. Выигрывает участник, предложивший
наибольшую ставку, и каждый участник выплачивает продавцу величину
своей ставки. Рассмотрите модель независимых частных оценок с
симметричными участниками, оценки которых распределены согласно
закону F с плотностью /.
а) Найдите единственную функцию ставок в симметричном
равновесии. Объясните свой ответ.
б) Выше или ниже будут ставки по сравнению с аукционом первой
цены?
в) Найдите выражение для ожидаемого дохода продавца.
г) Используя и не используя теорему об эквивалентности доходов,
покажите, что ожидаемый доход продавца совпадает с его ожидаемым
доходом на аукционе первой цены.
9.8. Предположим, что участников всего два. На аукционе второй
цены, где платят все, участники одновременно подают заявки в
запечатанных конвертах. Выигрывает участник с наибольшей ставкой, и оба
участника платят вторую по величине ставку.
а) Найдите единственную функцию ставок в симметричном
равновесии. Объясните свой ответ.
б) Выше или ниже ставок на аукционе первой цены, где платят все,
будут искомые ставки?
в) Выведите формулу для ожидаемого дохода продавца.

540
Часть III. Стратегическое поведение
г) Используя и не используя теорему об эквивалентности доходов,
покажите, что ожидаемый доход продавца совпадает с его ожидаемым
доходом на аукционе первой цены.
9.9. Рассмотрите следующий вариант аукциона первой цены. Заявки
подаются в запечатанных конвертах. Участник с наибольшей ставкой
платит равную ей сумму, но получает объект, если при бросании
правильной монеты выпадает орел. Если выпадает решка, продавец
оставляет себе объект и ставку этого участника. Считайте, что участники
симметричны.
а) Найдите единственную функцию ставок в симметричном
равновесии. Объясните свой ответ.
б) Выше или ниже будут искомые ставки по сравнению со ставками
на аукционе первой цены?
в) Выведите формулу для ожидаемого дохода продавца.
г) Используя и не используя теорему об эквивалентности доходов,
покажите, что ожидаемый доход продавца в точности равен половине его
ожидаемого дохода на аукционе первой цены.
9.10. Пусть оценки всех участников равномерно распределены на
отрезке [0,1]. Постройте аукцион, максимизирующий доход. Какова в нем
будет резервная цена?
9.11. Снова рассмотрите случай оценок, равномерно распределенных
на отрезке [0,1]. Является ли оптимальным для продавца аукцион первой
цены с той же резервной ценой, что и в предыдущей задаче? Докажите
свое утверждение с использованием теоремы об эквивалентности доходов.
9.12. Пусть оценки участников независимы и равномерно
распределены на отрезке [1, 2]. Постройте аукцион, максимизирующий доход
продавца.
9.13. Пусть имеется N участников с независимыми частными
оценками, причем оценка i -го участника равномерно распределена на отрезке
[ai, bi ]. Покажите, что максимизирующим доход и совместимым по
стимулам механизмом прямой продажи является следующий механизм.
Каждый участник сообщает свою оценку. При данных сообщаемых оценках
vp...,v^ /-й участник выигрывает объект, если v. строго больше, чем
N-1 число вида 6./2 + max@, Vj-bj/2) для у'*/. Тогда j'-й участник
платит продавцу сумму, равную наибольшему из этих N-1 чисел. Все
остальные участники ничего не платят.
9.14. Недостатком прямых механизмов является то, что для
построения оптимального аукциона продавцу необходимо знать распределение
оценок участников. В этом упражнении мы предложим оптимальный
аукцион, который не требует знания распределения в случае двух асим-

Глава 9. Аукционы и создание механизмов
541
метричных участников с независимыми частными оценками. Строго
положительная и непрерывная плотность оценок / -го участника на отрезке
[0,1] задается функцией / при распределении Fr Будем предполагать,
что vi ~(l-Fi (vi ))lfi (v;) строго возрастает для / = 1, 2.
Аукцион организован следующим образом. На первом шаге
участники одновременно подают заявки в запечатанных конвертах. Перед вторым
шагом заявки вскрываются и объявляются всем. На втором шаге
участники должны одновременно заявить, готов ли каждый из них купить объект
по цене заявки другого участника. Если один из них говорит «да», а
второй «нет», то объект достается первому из них по этой цене. Если они оба
говорят «да» или оба говорят «нет», то продавец оставляет объект у себя
и никто ничего не платит. Заметим, что продавец может провести этот
аукцион, не зная распределений оценок участников.
а) Рассмотрите следующие стратегии участников: на первом шаге
участник 1Ф] с оценкой v. подает в запечатанном конверте заявку
Ь*(У;) = Ьп где bf является решением уравнения
Ь, = max 0,v,. '^-LL .
(Хотя такое bi не обязательно существует, оно всегда будет иметь место,
если функции v,-(l-^(v,))/yj(v,) и v2-(l-F2(v2))//2(v2) имеют
одинаковые области значений. Предположим, что это именно тот случай.)
На втором шаге каждый из участников говорит «да» тогда и только
тогда, когда оценка одного из них превышает ставку, сделанную другим
на первом шаге.
Покажите, что эти стратегии составляют равновесие на данном
аукционе. (Также обратите внимание на то, что, хотя продавцу не требуется
знать распределение оценок участников, участникам нужно знать
распределение оценок друг друга, чтобы следовать своим стратегиям. Тем самым
аукцион переносит информационное бремя с продавца на участников.)
б)A) Покажите, что в этом равновесии ожидаемый доход продавца
максимален.
B) Всегда ли исход является эффективным?
в) A) Покажите, что для каждого участника стратегия делать ставку,
равную его оценке, а затем говорить «да», является равновесной тогда и
только тогда, когда его оценка превышает ставку другого участника на
первом шаге.
B) Всегда ли в этом равновесии исход является эффективным?

542
Часть III. Стратегическое поведение
г) Покажите, что доход продавца во втором равновесии не
максимален.
д) К сожалению, на данном аукционе имеется много равновесий.
Выберем две произвольные строго возрастающие функции g,:[0, 1]—>R2,
/ = 1,2 с одной и той же областью значений. Предположим, что на первом
шаге участник i' Ф j с оценкой v. делает ставку ^(v,) = bt, где bi является
решением уравнения gyF,) = g/Cv,.), а на втором шаге говорит «да» тогда
и только тогда, когда его оценка строго выше ставки другого участника.
Покажите, что такая стратегия является равновесной. Покажите также,
что исход всегда эффективен тогда и только тогда, когда g. = gy.
9.15. Покажите, что условие (9-22) выполняется, если каждая из
функций Ft выпукла. Является ли выпуклость Fi необходимым условием?
9.16. Рассмотрим модель независимых частных оценок с N
участниками, которые могут быть асимметричными. Ограничим наше внимание
эффективными индивидуально рациональными и совместимыми по
стимулам механизмами прямой продажи, т.е. такими, в которых объект
отдается участнику, сообщившему наибольшую оценку.
а) Каковы в этом случае функции вероятности?
б) Каковы функции издержек?
в) Какие из этих функций издержек максимизируют доход продавца?
г) Покажите, что среди эффективных индивидуально рациональных
и совместимых по стимулам механизмов прямой продажи ожидаемый
доход продавца будет оптимальным на аукционе второй цены. (Что можно
сказать о трех других стандартных видах аукционов?)
9.17. Назовем механизм прямой продажи /?,(•), с(), / = 1, ...,7V
детерминированным, если р{ принимают только значения 0 или 1.
а) Предположив независимость частных оценок, покажите, что для
любого совместимого по стимулам детерминированного механизма
прямой продажи, функции вероятности которого pt(vn v_.) не убывают
по v, для любых v_., существует другой совместимый по стимулам
механизм прямой продажи, с теми же функциями вероятности (а значит,
тоже детерминированный) и функциями издержек, обладающими
следующим свойством: участник платит, только если он получает объект, и
в случае выигрыша платеж не зависит от сообщаемой участником
оценки. Кроме того, покажите, что новый механизм можно построить так,
что ожидаемый доход продавца в нем останется тем же, что и в старом
механизме.

Глава 9. Аукционы и создание механизмов
543
б) Как этот результат можно применить к аукциону первой цены с
симметричными участниками, когда платеж участника зависит от его
ставки?
в) Как этот результат можно применить к аукциону первой цены с
симметричными участниками, когда платят все, независимо от того, кто
побеждает?
9.18. Покажите, что в оптимальном механизме прямой продажи,
который мы вывели в данной главе, стратегия сообщать свою истинную
оценку является слабо доминирующей для каждого участника.
9.19. Пусть плотность распределения оценок каждого
участника f. непрерывна и строго положительна, а каждая функция
vy -(l-Fi (vi))/ fi (vt) строго возрастает.
а) Покажите, что в оптимальном механизме продажи вероятность
того, что продавец оставит объект себе, строго положительна,
б) Покажите, что существует ровно одно р* е [0,1], удовлетворяющее
соотношению р* -A -F(p*))/f(p*) = 0.
9.20. Покажите, что если участники симметричны, то аукцион первой
цены, а также голландский и английский аукционы являются
оптимальными для продавца при соответствующим образом выбранной резервной
цене. Покажите, что оптимальная резервная цена одинакова для всех
четырех стандартных аукционов.

МАТЕМАТИЧЕСКОЕ
ПРИЛОЖЕНИЕ

Глава А1. Множества и отображения
А1.1. Элементы логики
Важные идеи в экономической литературе часто формулируются в
виде теорем. Теорема — это просто утверждение, выводимое из других
утверждений, и вы должны быть знакомы с ними из изученных вами
математических курсов. Теоремы дают компактный и точный формат для
предложенных предположений и важных выводов, вытекающих из
зачастую запутанных аргументов, и таким образом помогают определить
величину и пределы предложенного результата. Однако теоремы должны
быть доказаны, и доказательство требует установления справедливости
утверждения теоремы в соответствии с правилами логики. В этом разделе
мы объясним некоторые положения языка логики и ее простые правила.
МАЛ. Необходимость и достаточность
Необходимость и достаточность — это основные понятия логики.
В обыденном языке, когда вы утверждаете «А необходимо для В», что вы
имеете в виду? А когда вы утверждаете «А достаточно для В»? Стоит
потратить немного времени, чтобы разобраться в различных значениях этих
двух утверждений.
Рассмотрим любые два утверждения А и В. Когда мы говорим, что
«А необходимо для В», мы имеем в виду, что А должно выполняться или
быть справедливым, чтобы В выполнялось или было справедливым.
Чтобы В было справедливым, требуется, чтобы справедливым было А, стало
быть, всякий раз, когда В верно, мы знаем, что А должно быть верным.
Мы могли бы сказать иначе: «А верно, если верно В» или просто «из В
вытекает А» (А <= В), и поэтому есть соответствие между обыденным
языком и логикой, если сравнивать фразы «А необходимо для В», «А,
если В» и «А вытекает из В».
Предположим, мы знаем, что «А«=В» — верное утверждение. Но
что, если А не является верным? Так как А необходимо для В, то если А
неверно, то В тоже неверно. Не означает ли это, что «В неверно» есть
необходимое условие для «А неверно»? Или что «не А» вытекает из «не В»?
(~В<=~А)? Это последнее утверждение называется утверждением в
контрапозитивной форме. Контрапозиция аргументов в утверждении
меняет направление импликации на противоположное в верном
утверждении.
Рассмотрим простую иллюстрацию этих идей. Пусть утверждение
А — «л: — целое число меньше 10». Пусть утверждение В — «х — целое

548
Математическое приложение
число меньше 8». Ясно, что А необходимо для В, так как «х — целое
число меньше 10» следует из утверждения «х — целое число меньше 8».
Если мы образуем утверждения, контрапозитивные к исходным, то
утверждение ~А становится «х не является целым числом меньше 10», а
утверждение -В становится «х не является целым числом меньше 8».
Обратите внимание, что утверждение «~А <= ~В»ложно. Число jc может
быть равно 9. Мы должны изменить на противоположное направление
импликации, чтобы получить верное контрапозитивное утверждение.
Поэтому надлежащим контрапозитивным утверждением будет следующее:
«х не является целым числом меньше 8» вытекает из «jc не является
целым числом меньше 10», или ~ В <=~ А.
Понятие необходимости следует отличать от понятия
достаточности. Всякий раз, когда мы говорим, что «А достаточно для В», мы
подразумеваем, что если А верно, то и В верно. Мы можем сказать «А верно,
только если верно В», или «из А вытекает В» (А => В). Снова мы
получаем, что всякий раз, когда утверждение А => В верно, то и ~ В =>- А
тоже верно.
Обе импликации А => В и А <= В могут оказаться верными. Когда
это случается, мы говорим «А необходимо и достаточно для В», или
«А верно тогда и только тогда, когда верно В». Когда А является
необходимым и достаточным условием для В, то мы говорим, что утверждения
А и В являются эквивалентными, и пишем «А<=> В».
Чтобы вкратце проиллюстрировать сказанное, предположим, что А и
В следующие утверждения: А=«Х — желтого цвета», В = «Х — лимон».
Конечно, если X — лимон, то он желтый. Здесь А является
необходимым условием для В. В то же время из того, что X — желтого цвета, не
вытекает, что X — лимон. X может быть бананом. Следовательно, А не
является достаточным для В. Предположим теперь, что утверждения
таковы: А =«Х — кислый фрукт с желтой кожурой» и В =«Х — лимон».
Здесь А вытекает из В, или А необходимо для В. Если X — лимон, то
он должен быть желтым и кислым фруктом. В то же время А влечет В,
или А необходимо для В, потому что если X — это желтый и кислый
фрукт, то он должен быть лимоном. Так как А необходимо и достаточно
для В, то должна быть эквивалентность между лимонами и кислыми
фруктами с желтой кожурой.
А1.1.2. Теоремы и доказательства
Математические теоремы обычно имеют вид импликаций или
эквивалентных утверждений, в которых предполагается, что одно или
несколько утверждений взаимосвязаны определенным образом.
Предположим, мы рассматриваем теорему «А=>В». Здесь А называется предпо-

Глава А1. Множества и отображения
549
сыпкой, а В — выводом. Для доказательства теоремы надо установить
верность вывода, основываясь на справедливости предпосылки, и этого
можно достичь разными методами.
В конструктивном доказательстве мы предполагаем, что А верно,
выводим разные следствия из этого и используем их, чтобы показать, что
В должно быть тоже верным. Такой метод иногда называется прямым
доказательством, понятно почему. Есть также контрапозитивное
доказательство. В контрапозитивном доказательстве мы допускаем, что В
несправедливо, а затем показываем, что тогда А не может быть
справедливым. Этот подход использует преимущество логической
эквивалентности между утверждениями А=>Ви -В =>~ А, только что
рассмотренной нами, и, по сути, предполагает построение конструктивного
доказательства к контрапозитивному по отношению к исходному утверждению.
Наконец, есть доказательство от противного, или reductio ad
absurdum. Здесь стратегия состоит, чтобы допустить, что А справедливо,
также допустить, что В несправедливо, и пытаться вывести логическое
противоречие. Этот подход основывается на том, что если импликация
А =>~ В ложна, то импликация А => В должна быть верной. Иногда
доказательства сведением к противоречию работают весьма эффективно, но
в силу того что они не используют цепь конструктивных рассуждений
между А и В, так как это делают два других способа, они редко
проясняют взаимосвязь между предпосылкой и выводом.
Если мы настаиваем, что А необходимо и достаточно для В, или
А <=> В, мы должны доказать утверждения теоремы «в обе стороны». То
есть оба утверждения А => В и В => А должны быть доказаны, иначе
доказательство не будет полным.
Здесь стоит вспомнить старую поговорку «Доказательство с
помощью примера не является доказательством». Предположим, даны
утверждения А =<а — студент» и В =«у х рыжие волосы», и мы высказываем
утверждение, что А=>В.
Тогда, найдя рыжеволосого студента и показав на него, мы не
убедимся в том, что утверждение справедливо. Примеры хороши для
иллюстраций, но обычно не годятся для доказательств. В этой книге мы ни
разу не претендовали на доказательство, приводя пример, служащий лишь
для иллюстрации. Однако время от времени бывает необходимо
сформулировать некоторые теоремы без доказательства. Мы надеемся, что
принятие результата на веру лишь ободрит читателя в его стремлении
продолжать исследования вне рамок этой книги.
Наконец, приведем утверждение, в некоторой степени
противоположное к высказанному утверждению о соотношении доказательств и
примеров. В то время как цитирование сотен примеров не доказывает
справедливости некоторого утверждения, один-единственный контр-

550
Математическое приложение
пример позволяет доказать, что данное утверждение верно не всегда.
Например, чтобы опровергнуть высказывание о цвете волос студента,
следует всего лишь найти студента, у которого каштановые волосы.
Контрпример показывает, что вывод не может быть верным всегда, так
как найден по крайней мере один пример, противоречащий ему.
А1.2. Элементы теории множеств
А1.2.1. Обозначения и основные понятия
Язык и методы теории множеств глубоко проникли в
микроэкономическую теорию. Не вызывает сомнений, что понятие множества и
основные правила работы с множествами вам известны. Тем не менее, так как
некоторые из них мы будем использовать вновь и вновь, имеет смысл
повторить основы.
Множеством называется любая совокупность элементов.
Множества могут быть определены перечислением всех своих элементов,
например, S = {2, 4, 6, 8}; описанием всех своих элементов, например S = {х\ х
положительное, четное, целое число больше нуля и меньше 10}. Когда
мы хотим обозначить принадлежность множеству, или то, что элемент
включен в множество, мы используем знак е. Например, если
S = {2, 5, 7}, мы говорим 5 е S .
Множество S является подмножеством другого множества Т, если
любой элемент изSпринадлежит также Т. Мы пишем 5сГ E
содержится в Т ) или Г z> S (Т содержите ). Если S aT, TOxeS=>xeT.
Два множества называются равными, если они имеют одинаковые
элементы. Мы пишем S = T в том случае, если хе S=>xeT и
хе Г=> хе S . Таким образом, S и Т равные множества тогда и только
тогда, когда если S с Т и Т aS. Например, если S = {целые, х | х = 1} и
Г = {-1, 1}, тогда S = Т.
Множество S пусто, или является пустым множеством, если оно
не содержит элементов. Например, если А = {jc \х2 = 0 и х > 1}, то А —
пусто. Мы будем обозначать пустое множество символом 0 и писать
А = 0.
Дополнением множества S до универсального множества U
называется множество всех элементов из U, не принадлежащих S, оно
обозначается 5е. Если U = {2, 4, 6, 8} и S = {4, б], то Sc ={2, 8}. В общем
случае для любых двух множеств S и Т из универсального множества U
мы определим разность множеств, обозначаемую S \ Т или S - Т, как

Глава А1. Множества и отображения
551
множество всех элементов из 5, не принадлежащих Г. Таким образом,
мы можем считать, что дополнением S до U является разность множеств
sc = u\s.
Основными операциями над множествами являются объединение и
пересечение. Они соответствуют логическим понятиям «или» и «и»
соответственно1. Для двух множеств S и Т мы определим объединение Sn T
как множество SuT = {x\xe S или хеТ}. Мы определим пересечение
S и Г как множество SnT = {x\xeS и хеТ}. Некоторые из этих
множеств изображены на рис. А1.1.
и— и
и
Рис. А1.1. Диаграммы Венна
Иногда нам требуется исследовать множества, образованные из
произвольного набора других множеств. Мы могли бы использовать символы
{5Р S29 S3, ...}, чтобы обозначить интересующее нас множество, но
чаще составляют необходимое (возможно бесконечное) множество целых
чисел начиная с 1 / = {l, 2, 3, ...} , называемое индексным множеством,
и обозначают совокупность множеств просто как {^Д^. Мы будем
обозначать объединение всех множеств из совокупности как и/6/5 , а
пересечение всех множеств из совокупности как r\ielS .
1 В обычном языке слово «или» может использоваться в двух смыслах. Первый,
называемый исключающим «или», имеет смысл как «любое из двух, но не то и другое
вместе». В математике слово «или» используется во включающем смысле. Включающее
«или» означает«любое из двух, или то и другое».

552
Математическое приложение
Произведением двух множеств S и Т называется множество
«упорядоченных пар» в виде (s, t), где первый элемент пары принадлежит 5, а
второй — принадлежит Г. Произведение S и Т обозначается
SxT = {(s, t)\seS9 teT}.
Наиболее известное произведение множеств называется декартовой
плоскостью. Это именно та плоскость, на которой вы обычно что-либо
изображаете. Плоскость является графическим представлением
произведения двух множеств всех действительных чисел. Для обозначения
множества всех действительных чисел есть специальный символ R, и это
множество определяется как
Если мы образуем произведение множеств
RxRs{(jc„ jc2)| Xj6R, jc26R},
тогда любой точке этого множества (любой паре чисел) можно поставить
в соответствие точку декартовой плоскости, как это изображено на
рис. А1.2. Множество RxR иногда называют двумерным евклидовым
пространством и обычно обозначают R2.
Рис. А1.2. Декартова плоскость R2
В общем случае п -мерный набор чисел, или вектор, — это просто
упорядоченный набор (хр...,хп) размерности п, и можно считать, что это
«точка» в п -мерном евклидовом пространстве, или в «пространстве раз-

Глава А1. Множества и отображения
553
мерности п ». Как и ранее, п -мерное пространство определяется с
помощью произведения множеств
RnsRxRx...xRs{fa, ...,хп)\ x,e R, i = 1, ...,«}.
п раз
Обычно мы обозначаем векторы или точки в Rn жирным шрифтом, так
что х = (х19...,хп).
Часто мы хотим сконцентрировать внимание на подмножестве R",
называемом неотрицательным ортантом и обозначаемом R\, где
Rl = {(xl9...9xn)\xt>0, / = 1,...,и}сГ.
Для векторов в R"+ мы используем обозначение х > 0, у которых каждая
компонента х. больше или равна нулю. Мы используем
обозначение х » 0, чтобы отличать векторы, у которых все компоненты строго
больше нуля. В общем случае для любых двух векторов х иу изМ", мы
будем говорить, что х>у тогда и только тогда, когда я:. >уп / = 1, ...,«.
Мы будем говорить, что х » у, если х. >уп / = 1, ...,п.
А. 1.2.2. Выпуклые множества
Выпуклые множества являются основными элементами моделей
практически в каждой области микроэкономики. В теоретических
исследованиях выпуклость чаще всего предполагается, чтобы проводимый
анализ с математической точки зрения проходил беспрепятственно и
давал ясные, «хорошие» результаты. Вы увидите, что существует простой
интуитивный способ мысленного представления выпуклости. Как только
вы уловите идею, вы почувствуете, насколько всеобъемлющим является
понятие выпуклости в теории. Позже вы оцените важность выпуклости и
ее роль в некоторых фундаментальных задачах оптимизации в
микроэкономике. Сейчас мы начинаем с формального определения выпуклого
множества, а затем постараемся развить то, что определили.
Определение А1.1. Выпуклые множества в R".
Множество S с R" называется выпуклым множеством, если для
всех х1 g S и х2 € S выполнено
txl+(l-t)x2eS
при любых t из интервала 0 < / < 1.

554
Математическое приложение
Это определение не настолько трудно, как это кажется на первый
взгляд, вы быстро освоите то, что в нем утверждается. Его суть сводится
к тому, что множество является выпуклым, если для любых двух точек из
этого множества все взвешенные средние этих двух точек (т.е. с суммой
весов, равной 1) также принадлежат этому множеству. Давайте
рассмотрим это определение поэтапно, а потом составим полную картину из
рассмотренных деталей.
Взвешенная сумма, используемая в определении, называется
выпуклой комбинацией. Будем говорить, что z является выпуклой
комбинацией, если z= ts} + A-/)х2для некоторого числа /, находящегося между О
и 1. Так как t находится между 0 и 1, 1-/ лежит там же, а сумма весов
/ + A - /) всегда равна 1. Выпуклая комбинация z , таким образом,
является точкой, которая в некотором смысле «лежит между» двумя точками
х1 их2.
Чтобы легче понять изложенное, приведем простой пример.
Рассмотрим две точки УеМ и x2eR, где х1 =8 и х2 =2, изображенные на
рис. А1.3. Выпуклая комбинация z = txx + A - t)x2 может быть переписана
в виде
z = x2 +t(xl -х2).
Если мы будем считать точку х2 «начальной», а разность (х1 -х2)
«расстоянием» от х2до х1, тогда это выражение показывает, что z находится
в точке с координатой х2плюс некоторая доля t, меньшая или равная 1,
расстояния между х2и х1. Если мы предположим, что t принимает
нулевое значение, тогда в нашем примере z = х2 = 2. Если t принимает
значение 1, то z = xl =8. Таким образом, при крайних значениях 0 и 1
выпуклая комбинация любых двух точек совпадает с одной из этих
точек. При значениях / от 0 до 1 выпуклая комбинация примет
некоторое значение между этими точками. Если / = 1 / 2, то
z = х2 + A / 2)(х* -х2) = 2 + 3 = 5, что является средней точкой интервала
между х1 и х2. Если / = 2/3, то z = х2 +B/3)(х1 -х2) = 2 + 4 = 6,что
является точкой, расположенной на расстоянии двух третей величины
разности между х2 и х1. Как видно, до тех пор пока мы выбираем значение
t из интервала 0 < / < 1, выпуклая комбинация будет всегда лежать где-то
строго между точками или совпадет с одной из них.

Глава А1. Множества и отображения
555
точка z при
f = 0 /=1/2 / = 2/3 t=\
х2 х1
< • • • • >
2 5 6 8
V s
Рис. А1.3. Выпуклые комбинации в Ш
Вторая часть определения выпуклого множества относится не к
некоторой выпуклой комбинации двух точек, а ко всем выпуклым
комбинациям этих точек. Заметим, что в нашем примере, рассмотренном в случае
действительной прямой, х1, х2и любая точка между х1 и х2 могут быть
выражены как выпуклые комбинации х1 и х2для некоторого значения /,
лежащего между 0 и 1. Поэтому множество всех выпуклых комбинаций
точек х1 и х2 будет образовывать целый отрезок между х1 и х2, включая
эти точки.
Эти основные идеи точно так же можно распространить на
двумерный случай. Рассмотрим два вектора в R2, обозначаемые х1 =(х\, х\)и
х2 = (х2, х2). Когда мы образуем выпуклую комбинацию векторов, мы
должны внимательно соблюдать правила скалярного умножения и
векторного сложения. Когда вектор умножается на скаляр, произведение
является вектором, каждая компонента которого умножается на этот
скаляр. Когда два вектора складываются, сумма является вектором, причем
каждая его компонента является суммой соответствующих компонент
суммируемых векторов. Так что выпуклая комбинация х1 и х2 будет
выглядеть как
z = fx!+(l-/)x2 =
= (/*;, tx\) + ((\-t)x2, (l-t)x22) =
На рис. А 1.4, х1 и х2 имеют координаты (х|, х\) и (х,2, х2)
соответственно. Их выпуклая комбинация z имеет абсциссу
tx\ + A - t)x2 = х2 + t{x\ - х2), или х2 плюс доля t расстояния между
абсциссами х1 и х2. Аналогично ордината z равняется

556
Математическое приложение
tx\ + A - t)x\ = х\ + t{x\ - х\), или я;2 плюс доля t расстояния между
ординатами х1 и х2. Так как каждая координата является одной и той же
долей / расстояния между соответствующими абсциссами и ординатами,
точка z разбивает отрезок, соединяющий х1 и х2, в той же пропорции.
При изменении доли / координаты точки z будут варьировать между jcJ и
х2 по горизонтали и между х\ и jc2 по вертикали. При этом абсцисса и
ордината z будут находиться в той же пропорции к расстоянию между
соответствующими координатами х1 и х2. Таким образом, мы будем получать
разные точки, лежащие на отрезке, соединяющем х1 и х2. Как и ранее,
любая точка отрезка может быть описана как выпуклая комбинация х1 и х2
для некоторого значения /, лежащего между 0 и 1. Поэтому множество
всех выпуклых комбинаций векторов х1 и х2 в точности образует
множество всех точек отрезка, соединяющего х1 и х2, включая его концы.
*2
х\
z2=tx2+(\-t)x22
Л2
х2 z\ =tx\ + (l-t)x2 x\
Рис. А 1.4. Некоторые выпуклые комбинации в Ш2
Теперь вернемся к определению выпуклого множества. Прочитайте
его внимательно, и вы увидите, что мы с таким же успехом могли бы
сказать, что множество выпукло, если оно содержит все выпуклые
комбинации любой пары точек множества. Так мы получаем очень простое
интуитивное правило, определяющее выпуклые множества: множество
выпуклое тогда и только тогда, когда мы можем соединить.любые две его
точки отрезком, полностью лежащим внутри множества. Примеры
выпуклых и невыпуклых множеств приведены на рис. А 1.5. Заметьте, что
все выпуклые множества отличаются «примерным поведением». В них
нет дыр, нет разрывов, на их границах нет уродливых кривых. Это
хорошие множества.
^ г,

Глава AL Множества и отображения
557
Рис. А1.5. Выпуклые и невыпуклые множества в М2
Мы завершим наше обсуждение выпуклых множеств на этом этапе,
обратив внимание на одно простое, но важное свойство множеств,
образованных из выпуклых множеств.
Теорема А1.1. Выпуклость пересечения выпуклых множеств
Пусть S и Т — выпуклые множества в Мп. Тогда SnT —
выпуклое множество.
Доказательство. Пусть SnT — выпуклые множества. Пусть х1 и
х2 любые две точки из SnT. Так как xl e SnT, то х1 е S и х2 еТ. Так
как x2eSnT, то х2 е S и х2еТ. Пусть z = txl +(l-/)x2 для любого
/е[0, 1] — произвольная выпуклая комбинация х1 и х2. Так как S
выпуклое множество, то z е S . Так как Т выпуклое множество, то z е T.
Так как ze S и z е Г, то ze SnT. В силу того, что всякая выпуклая
комбинация любых двух точек из S пТтакже лежит в S пТ, то S пТ —
выпуклое множество. ¦
А1.2.3. Отношения и функции
Мы видели, что любая упорядоченная пара (s, t) определяет
соответствие между элементом se S и элементом teT. Множества SnT
необязательно состоят из чисел, они могут состоять из чего угодно.
Говорят, что любая совокупность упорядоченных пар образует бинарное
отношение между SnT.
Бинарное отношение будет определено установлением осмысленной
связи между элементами пары. Например, пусть S — множество городов
{Вашингтон, Лондон, Марсель, Париж} и Г — множество стран
{Соединенные Штаты, Англия, Франция, Германия}. Тогда утверждение
«является столицей» определяет отношение между двумя этими множествами,

558
Математическое приложение
состоящее из элементов {(Вашингтон, Соединенные Штаты), (Лондон,
Англия), (Париж, Франция)}. Как показывает этот пример, бинарное
отношение R на SхТвсегда является подмножеством SxT. Когда
se Sсвязано определенным отношением с te Г, мы обозначаем
принадлежность отношению 21 одним из двух способов: или мы пишем
E, t)e !R, или (что встречается чаще) мы просто пишем sJlt.
Много знакомых бинарных отношений содержится в произведении
какого-либо множества на себя. Например, пусть S — замкнутый
единичный интервал, S = [0, 1]. Тогда бинарное отношение >, изображенное
на рис. А 1.6, состоит из всех упорядоченных пар чисел из S, у которых
первое число пары больше второго числа или равно ему. Если, как в этом
случае, бинарное отношение является подмножеством произведения
множества S на себя, то мы говорим, что это отношение на множестве S.
1 •-
>с5х5
0 1
Рис. А1.6. Отношение > на 5 = [0, 1]
Мы можем выстроить структуру для бинарного отношения на
некотором множестве, если потребуем, чтобы оно обладало определенными
свойствами.
Определение А1.2. Полнота.
Отношение Л на S полно, если для всех элементов х и у из S,
xRy или уЛх.
Предположим, что ? = {1, 2,..., 10}, и рассмотрим отношение,
определенное утверждением «больше чем». Это отношение не является
полным, потому что легко найти некоторое х е S и некоторое у е S, для
которых не выполняется ни х>у, ни у>х: например, можно выбрать
х = у = 1, или х = у = 2 и т.д. В определении не требуется, чтобы
элементы х и у различались, так что ничего не мешает нам выбрать их
одинаковыми. Так как никакое целое число не может быть больше или меньше
себя самого, отношение «больше чем» не является полным. Однако от-

Глава А1. Множества и отображения
559
ношение на S, определенное утверждением «по меньшей мере равное»
полно: для любых двух целых чисел, независимо от того, совпадают они
или нет, одно из них всегда будет по меньшей мере равным другому, как
того и требует полнота.
Определение А1.3. Транзитивность.
Отношение 71 на S транзитивно, если для любых трех элементов
х, у и z, принадлежащих S, из хЛу и yTlz следует x3lz.
Оба только что рассмотренных отношения транзитивны. Если х
больше, чем у, и у больше, чем z, то х определенно больше, чем z. То же
верно для отношения определенного фразой «по меньшей мере, равное».
Функция очень распространенное, но и очень специфическое
отношение. Особенность функции заключается в том, что она является
отношением, связывающим каждый элемент одного множества с одним-
единственным элементом другого множества. Мы говорим, что функция
/ является отображением множества D в другое множество R и
пишем /:/)—>/?. Мы называем множество D областью определения и
множество R областью значений отображения. Если точка у из области
значений является отображением точки х из области определения, то мы
записываем это так: у = f(x). Чтобы обозначить целое множество А в
области значений, получаемое в результате отображения множества точек
В из области определения, мы пишем А = f(B). Для иллюстрации
рассмотрим рис. А1.7. На рис. A 1.7(a) изображена не функция, так как более
одной точки из области значений соответствует точкам из области
определения, например точке хх. На рис. А 1.7F) действительно изображена
функция, так как каждой точке области определения соответствует
единственная точка из области значений.
^ А
Рис. А1.7. Функции и не функции

560
Математическое приложение
Образом /служит множество таких точек из области значений,
которые являются отображениями некоторых точек из области
определения, т.е. I = {y\ y = f{x\ для некоторого хе D}czR. Прообраз (или
обратный образ) множества точек 5с/ определяется как
f~\S) = {x\ хе Д/(х)е S}. График функции /определяется привычным
образом и представляет множество упорядоченных пар
G = {(*,у) | хе D,y = f(x)}. Некоторые из этих идей проиллюстрированы
на рис. А1.8. На рис. А1.8(а) R = R, D = R, и изображен график функции
>> = sin(jt). Функция синуса, однако, никогда не принимает значений
больше 1 или меньше -1. Поэтому ее образ является подмножеством
области значений и состоит из отрезка / = [-1, 1]. На рис. А1.8(б) мы видим
функцию /: [0, 1] —> [0, 1], задаваемую как у = — х. Здесь область
определения и область значений выбраны так, что они совпадают с
единичным отрезком. Образом функции служит подмножество области значений
Рис. А1.8. Область определения, область значений и образ
Нет ничего такого в определении функции, что запрещало бы более
одному элементу из области определения отображаться в один и тот же
элемент из области значений. На рис. А 1.7F), например, два элемента хх
и х2 отображаются в один ух, и все-таки отображение удовлетворяет
требованиям, накладываемым на функцию. Если же любой точке из об-

Глава А1. Множества и отображения
561
ласти значений соответствует не более одной точки из области
определения, то функция называется взаимооднозначной. Если образ функции
совпадает с областью значений, т.е. каждая точка из образа является
отображением некоторой точки из области определения, то говорят, что это
отображение на себя. Если функция взаимооднозначна и является
отображением на себя, тогда обратная функция f~x :R—>D существует,
взаимооднозначна и также является отображением на себя.
А1.3. Немного топологии
Топология — это исследование фундаментальных свойств множеств и
отображений. В этом разделе мы введем несколько основных
топологических понятий и будем пользоваться ими, чтобы выявить некоторые важные
свойства множеств и непрерывных функций, отображающих множества в
множества. Хотя многие из идей, рассматриваемых здесь, могут быть
обобщены для случая произвольных типов множеств, мы ограничимся
рассмотрением множеств из R", т.е. множеств, состоящих из действительных
чисел или векторов, компоненты которых — действительные числа.
Мы начнем с описания понятия метрики и метрического
пространства. Метрика — это просто мера расстояния. Метрическое
пространство — это множество с введенным понятием расстояния между точками
множества. Действительная прямая Е, для которой введена функция,
измеряющая расстояние, является метрическим пространством. Одна из
таких функций расстояния, или метрика, — это функция абсолютного
значения. Для любых двух точек jc1 и х2из R расстояние между ними,
обозначаемое d(x\ х2), будет иметь вид
Декартова плоскость R2 — также метрическое пространство.
Естественное понятие расстояния, определенное на плоскости, унаследовано от
Пифагора. Рассмотрим любые две точки из R2 х1 =(х\, х\) и
х2 =(jc2, jc2), как показано на рис. А 1.9. Образуем прямоугольный
треугольник, соединив две точки. Если длина горизонтального катета
равная , а длина вертикального катета равна Ъ, то по теореме Пифагора
длина гипотенузы, т.е. расстояние между точками х1 и х2, равна \а2 +Ь2 .
Пусть теперь а2 — квадрат разности между двумя компонентами х,, а
Ъ2 — квадрат разности между двумя компонентами х2. Тогда длина
гипотенузы, или d{\\ х2), может быть найдена следующим образом:
d(x\x2) = y/a2+b2 =t](x2-xIJ+(x22-x\J .

562
Математическое приложение
*2
^
л \ -

^У\
d{\\ x2) = yla2+b2 yS j
i ^ "!
i jc,2 -x,1 =a :
i !
>x\-x\=b
>
*1
Рис. А1.9. Расстояние на плоскости
Может это и неочевидно на первый взгляд, но обе формулы
расстояния являются разновидностями одной и той же формулы. Для х1 и х2 из
R абсолютное значение х1 -х2 может быть получено как квадратный
корень из произведения (х*-х2) на себя. Мы могли написать
d{x\ x2) = \xl-x2\ = yj(xl-х2)(х]-х2). Для х1 и х2 из Ш2 мы можем
сначала применить правила векторного вычитания, чтобы получить
разность (х1 -х2) = (х11 -х2, х\ -х2), а затем применить правила скалярного
произведения векторов, чтобы умножить эту разность на себя. Тогда мы
получим
I А """" Л. I V Л "—™ Л. I ~~ \"^\ "^ " 5 9 "™"" 9 / * V 1 ~"~ 1 9 9 ~~ 9 / ^—
= (х\ -х2J + (х[ -x22f = (-1J(х,2 -х,1J + (-1J(х22 -х\J =
= (x2-xlJ+(x22-x2J.
Заметьте, что это произведение векторов дает скаляр, который неотличим
от скаляра, стоящего под знаком квадратного корня в формуле Пифагора.
Теорема Пифагора, следовательно, говорит нам, что мы теперь сможем
измерять расстояние между двумя точками как квадратный корень из
произведения разности двух точек, на этот раз векторного произведения
векторных разностей двух точек плоскости. Аналогично случаю точек на
прямой мы можем поэтому записать, что d(x\ х2) = у](х1 -х2)-(х1 -х2)
для х1 и х2
-1 " ~2 из R2.

Глава А1. Множества и отображения
563
Понятие расстояния между двумя точками из R" является прямым
развитием этих идей. В общем случае, для х1 и х2 из R"
что мы перепишем в виде ^(х1, х2)= х1 -х2 . Мы назовем эту формулу
евклидовой метрикой или евклидовой нормой. Вполне естественно, что
метрические пространства R", которые используют эту меру расстояния,
называются евклидовыми пространствами.
Как только мы ввели понятие метрики, можно сформулировать, что
означает для точек быть «близкими» друг к другу. Если мы возьмем
любую точку х° е R", мы определим множество точек, лежащих от х° на
расстоянии меньшем, чем ?>0, как открытую г-окрестность точки
х°. Множество точек, расположенных от х° на расстоянии, равном или
меньшем е, называется замкнутой г -окрестностью точки х°. Обратите
внимание, что любая ? -окрестность является множеством точек.
Приведем формальное определение.
Определение А1.4. Открытые и замкнутые е-окрестности.
1) Открытая г-окрестность точки х°, где ?>0 (действительное
число), есть подмножество точек в R":
BE(x°) = {xeRn\d(x\ х)<е}.
строго меньше
2) Замкнутая ? -окрестность точки х°, где е > О, есть
подмножество точек в R" :
Bl(x°) = {хе Rn\d(x\ x)<?}.
меньше или равно
Некоторые примеры открытых и замкнутых окрестностей даны на
рис. А 1.10. На действительной прямой открытая е-окрестность точки
х0 — это просто открытый интервал Ве(х°) = (х° -?, х°+е).
Соответствующая замкнутая окрестность — это отрезок 5*(jc°) = [jc°-?, x°+e].
В R2 открытая окрестность 58(х°) является диском, состоящим из
внутренних точек, или внутренности, круга радиуса ? с центром в х°.
Соответствующая замкнутая окрестность 5*(х°) на плоскости состоит из
точек, лежащих внутри и на границе круга. В трехмерном пространстве от-

564
Математическое приложение
крытая окрестность Ве(х°) состоит из точек, лежащих внутри сферы
радиуса е. Замкнутая окрестность 5*(х°)является множеством, состоящим
из точек, лежащих внутри и на границе сферы. В К4 и в пространствах
высоких размерностей геометрическая интуиция не очень помогает, но
идея остается прежней.
Вг(х°)
х°-г
в;(х°)
\#?(х°)с/Я2/
Рис. А1.10. Окрестности в R и
Мы очень хорошо представляем себе, чем отличаются открытые и
замкнутые интервалы на действительной прямой. Понятие
Е -окрестностей позволяет формализовать это различие и применять его к
пространствам высоких размерностей. Мы используем г -окрестности для
определения открытых и замкнутых множеств, чтобы получить
некоторые важные результаты относительно них.
Определение А1.5. Открытые множества в Ш".
5сМл является открытым множеством, если для всех хе S
найдется такое е > 0, что Ве(х)сS.
Иными словами, речь идет о том, что множество открыто, если
вокруг каждой его точки существует некоторая открытая сколь угодно
малая окрестность такая, что все ее точки лежат целиком внутри множества.
Этот способ формализации описывает существенные свойства
привычного нам открытого интервала на действительной прямой. Так как
открытый интервал (а, Ь) содержит все точки между а и Ь кроме самих а и
Ъ, мы можем выбрать любую точку х из этого интервала, сколь угодно
близкую к а или Ъ, и найти любое маленькое, но положительное 8, та-

Глава А1. Множества и отображения
565
кое, что открытая окрестность (в нашем случае это открытый интервал)
Ве(х) = (х-г, х + г) лежит целиком внутри интервала (а, Ь). Таким
образом, любой интервал на действительной прямой является открытым
множеством. Аналогично открытые диски и открытые сферы являются
открытыми множествами по определению. Вообще, любая открытая
окрестность является открытым множеством.
Чтобы в этом убедиться, предположим, что S на рис. А 1.11 — это
открытая г -окрестность точки х°. Если мы возьмем любую другую точку
х в S, то всегда возможно найти такую открытую окрестность х, точки
которой лежат внутри S. Так как х лежит в S, мы знаем,
что t/(x°, x)<8. Поэтому е-б/(х°, х)>0. Если мы положим
?' = ?-d(x°, х) > 0, то всегда будет выполняться условие B?,(x)aS при
этом неважно, насколько близко к «краю» круга будет расположено х.
Именно в этом мы хотели убедиться. Следующая теорема является
принципиально важной.
Теорема А1.2. Об открытых множествах в R".
1) Пустое множество 0 является открытым.
2) Все пространство W является открытым множеством.
3) Объединение открытых множеств является открытым
множеством.
4) Пересечение любого конечного числа открытых множеств
является открытым множеством.
Доказательство. Доказывать второе утверждение вряд ли требуется.
Короче говоря, если мы возьмем любую точку в R" и любое е > 0, то
множество Ве (х), конечно, будет состоять исключительно из точек в R"
согласно определению открытой окрестности. Стало быть, Bg(x)cR",
так что Ш" открыто. Точно так же первое утверждение очевидно. Если в
0 нет точек, то, конечно, верным будет утверждение, что «для любой
точки из 0 мы можем найти г...», что и будет означать открытость.
Два последних утверждения стоит доказать. Мы докажем третье
утверждение, оставляя доказательство четвертого в качестве упражнения.
Пусть St — открытые множества для всех / е /, где / — некоторое
множество индексов. Мы должны показать, что ufe/S'l. является
открытым. Возьмем хе ufe/S,. Тогда хе Sf для некоторого /'е /. Так как Sr
открыто, то Be(\)(zSr для некоторого е>0. Тем самым BE(x)cufe/S/}
что и показывает, что u^S,. открыто. ¦

566
Математическое приложение
У открытых множеств есть интересное и замечательное свойство.
Они всегда могут быть точно описаны как объединение различных
открытых множеств. Потребуется немного времени, чтобы убедиться в
этом. Предположим, мы выбираем некоторое открытое множество. Так
как наше множество открыто, то можно взять любую из точек и
«окружить» ее открытой окрестностью, все точки которой лежат в этом
множестве. Каждая из таких открытых окрестностей сама по себе является
открытым множеством (см. рис. А 1.11). Теперь рассмотрим объединение
всех этих окрестностей. По теореме А 1.2 такое объединение открытых
окрестностей должно быть открытым множеством. Вы можете себе
представить, что точка, с выбора которой мы начали, не принадлежит
этому объединению открытых окрестностей? Вы можете себе
представить, что найдется точка из объединения открытых окрестностей, не
принадлежащая исходному множеству? Если вы ответите «нет» на оба
эти вопроса, то это значит, вы убедились в том, что эти множества
совпадают! Это свойство открытых множеств настолько важно, что оно
имеет статус теоремы.
х2
А
/"ГХ
х°
S =
j/ 0
Вг(х°)
х) !
*
*1
Рис. Al.ll. Открытая окружность как открытое множество
Теорема А1.3. Любое открытое множество является
объединением открытых окружностей.
Пусть S — открытое множество. Для любого х е S выберем
некоторое 8Х >0, такое, чтобы Ве (х)сХ. Тогда
?=ч*А(х).

Глава А1. Множества и отображения
567
Доказательство. Идея доказательства нам уже знакома, поэтому
проведем его быстро. Пусть S с R" открыто. Тогда для любого х е S
найдется такое ?х > 0, что Ве (х) с S, потому что S — открытое
множество. Мы должны показать, что из xeS следует хе uxG5Be (x), и,
наоборот, из хе ихе55е (х) следует хе S.
Если хе 5, то хе Ве (х) по определению открытой окрестности
точки х. Но тогда х принадлежит любому объединению, содержащему эту
открытую окрестность, в частности, должно быть выполнено условие
хе ихб55е (х), что завершает доказательство первой части.
Теперь, если хе uX€SBe (х), то хе Ве (s) для некоторого se S. Но
мы выбираем каждую 8 -окрестность так, чтобы она целиком содержалась
в S. Поэтому, если хе Ве (s) с S, то хе S, что завершает вторую часть
доказательства. ¦
Мы используем открытые множества для определения замкнутых
множеств.
Определение А1.6. Замкнутые множества в R".
S — замкнутое множество, если его дополнение Sc является
открытым множеством.
На этом месте стоит ненадолго задержаться, чтобы посмотреть, как
«работает» это определение, давая результаты, которые согласуются с нашим
интуитивным представлением. Для этого рассмотрим простейший пример.
Мы знаем, что отрезок на действительной прямой является (или должен
быть) замкнутым множеством. Удовлетворяет ли отрезок определению
замкнутого множества? Рассмотрим отрезок [я, Ь] = {х | хе R, а < х < Ь),
как показано на рис. А 1.12. Теперь рассмотрим два множества
А = {х\хеЖ, -оо<х<а} и В = {х | хе М, b< jc<+°°} . А и В
—открытые интервалы по обе стороны от [а, Ь]. Так как интервалы открыты, то А
и В — открытые множества. По теореме А 1.2 объединение открытых
множеств является открытым множеством, так что
AuB = {x\xsR, -оо<х<а или Ь< х < +°°} открыто. Но А и В является
дополнением множества [а, Ь] до R . Так как [а, Ь]с — открытое
множество, то [а, Ь] — замкнутое множество по определению замкнутых множеств,
что мы и хотели показать. В пространствах высоких размерностей любая
замкнутая окрестность замкнута. В R2 замкнутый круг является замкнутым
множеством, а в Е3 замкнутая сфера замкнута.

568
Математическое приложение
( )[ к )
—оо а Ъ +оо
Рис. А1.12. Отрезок как замкнутое множество
Проще говоря, множество в W открыто, если оно не содержит точки
своей границы, и замкнуто, если оно содержит все точки своей границы.
Точнее, точка х называется граничной точкой множества S вКя,
если любая е -окрестность х содержит как точки, принадлежащие S, так и
точки, не принадлежащие S. Множество всех граничных точек S
обозначается dS. Множество открыто, если оно не содержит ни одной своей
граничной точки; оно замкнуто, если оно содержит все свои граничные
точки. Продолжая в том же духе, мы можем определить внутреннюю
точку множества. Точка х е S называется внутренней точкой S, если
найдется некоторая ?-окрестность х, которая полностью лежит в S, или
найдется такое е>0, что Ве(х)с5. Множество всех внутренних точек
множества S называется его внутренностью и обозначается intS. Если
воспользоваться этим понятием, то можно сказать, что множество
открыто, если оно не содержит ничего кроме внутренних точек, или S = intS.
В противоположность сказанному множество S замкнуто, если оно
содержит все свои внутренние точки, плюс все свои, граничные точки, или
S = intSudS. Рисунок А 1.13 иллюстрирует некоторые из этих идей для
множеств из R2. Мы завершим обсуждение открытых и замкнутых
множеств, отметив свойства замкнутых множеств, аналогичные тем, которые
были установлены для открытых множеств в теореме А 1.2.
х2
Рис. А1.13. S n dS = 0 ; S — открытое множество; S U dS —

Глава А1. Множества и отображения
569
Теорема А1.4. О замкнутых множествах в W.
1) Пустое множество 0 является замкнутым.
2) Все пространство W является замкнутым множеством.
3) Объединение любой конечной совокупности замкнутых множеств
является замкнутым множеством.
4) Пересечение замкнутых множеств является замкнутым
множеством.
Доказательство. Пустое множество и все пространство R" — это
единственные два множества, которые одновременно открыты и
замкнуты в R". То, что они открыты, было показано в теореме А 1.2. Чтобы
доказать их замкнутость, заметим, что каждое из них является дополнением
другого до R". Так как 0 = {R"}c и Ш" открыто, то 0 должно быть
замкнуто в силу определения А 1.6. Аналогично, так как R"=0C и0
открыто, W должно быть замкнуто.
Мы снова докажем третье утверждение, оставляя доказательство
четвертого в качестве упражнения. Пусть S. — замкнутые множества в R"
для всех / е /, где / — некоторое конечное множество индексов. Мы
хотим показать, что u/e/5f. — замкнутое множество. Так как Sf замкнуто,
его дополнение S* открыто в силу определения А1.6. По теореме А1.2
пересечение n^S. также открыто, так как пересечение конечного набора
открытых множеств открыто. По закону де Моргана (см. упражнение
А 1.4) дополнение пересечения совокупности множеств равно
объединению дополнений множеств из этой совокупности, так что
(n/e/S7)c =\jtelSr Так как nfe/S* открыто, его дополнение ufe/ Sf
замкнуто согласно определению замкнутых множеств. ¦
Следующее важное понятие — понятие ограниченного множества.
Проще говоря, множество ограничено, если его можно «заключить» в
окрестность. Следующее определение уточняет эту идею.
Определение А1.7. Ограниченные множества.
Множество S в W называется ограниченным, если оно полностью
содержится внутри некоторой ? -окрестности (открытой или
замкнутой). То есть S будет ограниченным множеством, если найдется такое
г > 0, что S с Ве(х) для некоторого xeR".
По этому определению множество ограничено, если мы всегда можем
найти некоторую заключающую его 8-окрестность. Определение
становится интуитивно понятнее, если мы возьмем лишь е -окрестности начала

570
Математическое приложение
координат, Ое Е". С этой позиции S ограничено, если найдется
некоторое число е, такое, что все точки S находятся на расстоянии не далее 8
от начала координат.
Открытая окрестность Ве,(х°), показанная на рис. А 1.14, является
ограниченным множеством, потому что она может быть полностью
помещена внутрь окрестности с центром в х°и радиусом е = ?/ + 1. Можно
также сказать, что 5е>(х°) ограничен, потому что никакая из ее точек не
лежит на расстоянии, превышающем г" от начала координат. Также
заметим, что любой открытый интервал на действительной прямой
(a, i)cl является ограниченным множеством. На рис. А 1.14 мы можем
полностью заключить интервал (а, Ь) внутрь окрестности с центром в
точке jc € R и радиусом, например, г = be - (а -1 )|.
**i
Рис. А1.14. Ограниченные множества в Е и
Для ограниченных множеств на действительной прямой введена
специальная терминология. Пусть S с Е — любое непустое множество
действительных чисел. Любое действительное число / (не важно,
принадлежащее S или нет), для которого / < х при всех х е S, называется
нижней гранью множества чисел S. Например, если S = {4, 6, 8}, то число 1
является нижней гранью для S, как и число 4. Подобным образом любое
действительное число и (не важно, и в S или нет), для которого х < и
при всех х € S, называется верхней гранью для S. В нашем предыдущем
примере 27 ? S является верхней гранью для S, так же как и 8 е S.
Множество чисел S с Е ограничено снизу, если оно имеет нижнюю
грань, и ограничено сверху, если оно имеет верхнюю грань. Интервал

Глава А1. Множества и отображения
571
(-оо5 4) ограничен сверху, но не ограничен снизу. Любое числовое
множество, которое одновременно ограничено сверху и снизу, является
ограниченным в смысле определения А 1.7 (разберитесь, почему).
Мы видели, что любое подмножество S действительных чисел обычно
имеет много нижних граней и много верхних граней. Наибольшее число из
нижних граней называется точной нижней гранью (greatest lower bound,
g.l.b.) множества S. Наименьшее число из верхних граней называется
точной верхней гранью (least upper bound, l.u.b.) множества S. Можно
применить основные аксиомы действительных чисел, чтобы показать, что
для любого ограниченного подмножества в R существуют^Lb. и l.u.b.
Рассмотрим интервал (а, Ь) и отрезок [а, Ь], изображенные на
рис. А 1.15. Из рисунка ясно, и это нетрудно доказать, что любое
замкнутое подмножество в Е будет содержать свои g.l.b. и l.u.b. Напротив,
любое открытое подмножество bR не будет содержать свои g.l.b. или l.u.b.
На рис. Al.15(a) а — это g.l.b. и b — это l.u.b. открытого интервала
(а, Ь), и ни то, ни другое число не содержится в этом интервале. На
рис. А1.15(б) а — это g.l.b. и b — это l.u.b. отрезка [а, Ь], и оба числа
принадлежат ему. Этот результат стоит иметь в виду в дальнейшем.
—С )— —? 3—*
а Ъ а Ь
(а) (б)
Рис. А1.15. Верхние и нижние грани для подмножеств
действительных чисел
Теорема А1.5. Верхние и нижние грани подмножеств
действительных чисел.
1) Пусть S — ограниченное открытое множество в Ж и пусть а
является g.l.b. множества Sub — Lu.b. множества S. Тогда аё S и
btS.
2) Пусть S — ограниченное замкнутое множество в Ш и пусть
а является g.l.b. множества Sub — Lub. множества S. Тогда ае S и
beS.
Доказательство. Мы остановимся здесь настолько подробно,
насколько этого будет достаточно, чтобы показать способ, которым можно
было бы доказать эту теорему. Доказательство обоих утверждений будет
проведено для g.l.b., для l.u.b. оба утверждения вам предстоит доказать
самостоятельно в качестве упражнений.

572
Математическое приложение
Пусть ScR открыто, и пусть а является g.l.b. для множества S.
Теорема утверждает, что а € S . Мы допустим, что а е S, и придем к
противоречию.
Пусть а е S . Так как а е S и S открыто, найдется такое 8 > 0, что
открытая окрестность Ве(а) с5, потому что это верно для всех точек
открытого множества. В частности, точка а—ге S. Но в силу того, что
а—6<а и а—ее 5, а не может быть нижней гранью для S. Так как
она не является нижней гранью, она не может быть точной нижней
гранью, потому что мы нашли по меньшей мере одну точку в 5, которая
меньше а. Допустив, что gib, а лежит в S, мы пришли к противоречию.
Таким образом, нам остается заключить, что а g S, что и требовалось
доказать.
Чтобы провести доказательство теоремы для замкнутых множеств,
предположим, что S aR замкнутое и ограниченное множество, и пусть
а является g.l.b. множества S. Тогда по определению любой нижней
грани а<х для всеххе S. Если а = х для некоторого хе S, то ае S,
что и требуется. Поэтому предположим, что а строго меньше любой
точки из S.
Если а < х для всех хе S, то а? S , так что ае Sc. В силу того что
S — замкнутое множество, его дополнение открыто. Если ае Sc и Sc
открыто, то найдется такое ?>0, что все точки открытой окрестности
Ве(а) = (а-г, а + г) содержатся в Sc по определению открытых
множеств. Если а < х для всех хе S и Be(a)<zSc, то каждая точка интервала
(а-г, а + г) должна быть строго меньше любой точки из S. (Если бы это
было не так, то мы получили бы х<а-е<а для некоторого хе 5, что
противоречило бы утверждению, что а — нижняя грань для S, или
получили бы хе Be(a)czSc, что противоречит хе S.) В частности, точка
1 / 1 о тт 1
а+—ге (а-е, а + г) и а +—г<х для всех хе S. Но тогда а+—г явля-
2 2 2
ется нижней гранью для S и а +—е>а, так что а не является точной
нижней гранью S, что противоречит нашему первоначальному
предположению. Поэтому нам остается только заключить, что а е S . ¦
Мы обсудили открытые и замкнутые множества. Подмножества в
Ш", одновременно замкнутые и ограниченные, называются компактны-

Глава Л1. Множества и отображения
573
ми множествами, и эти множества весьма популярны в экономических
приложениях. Для дальнейшего нам потребуется следующее
определение1.
Определение А1.8 (Гейне — Бореля). Компактные множества.
Множество S из W называется компактным (компактом), если
оно замкнуто и ограничено.
Любой открытый интервал в R не является компактным множеством.
Он может быть ограниченным, как мы видели, но он не замкнут.
Аналогично открытый шар в R" не является компактом. Однако любой
замкнутый и ограниченный интервал в Е является компактом, как и любая
окрестность конечного радиуса в Е". Все пространство в Е" не является
компактом, так как хотя оно может быть замкнутым, оно не ограничено.
А1.3.1. Непрерывность
Непрерывность — это последнее из топологических понятий, которое
мы рассмотрим. В большинстве экономических приложений мы будем
или допускать, что функции, с которыми мы работаем, непрерывны, или
нам потребуется их исследовать на непрерывность, если нам будет
недостаточно одного лишь предположения. В любом случае следует
хорошо понимать, что означает непрерывность функции и каковы свойства
непрерывных функций.
7^>7° 7Та х°
(а) (б)
Рис. А1.16. Непрерывность и разрывность
Компактность сама по себе является топологическим свойством. Однако теорема
Гейне — Бореля показывает, что для множеств из Ш" она эквивалентна замкнутости и
ограниченности.

574
Математическое приложение
Интуитивно мы представляем, какой должна быть непрерывная
функция. Функция на рис. А 1.16(a) непрерывна, в то время как функция
на рис. А 1.16F) — нет. Основная идея в том, что функция непрерывна,
если «небольшое изменение» аргумента не вызывает «большого скачка»
значения функции. Мы, однако, можем уточнить это понятие. Для
простых функций, типа изображенных на рис. А 1.16, приведенное ниже
определение должно быть вам знакомо из курса математического анализа
одной переменной.
Функция /: R —> R непрерывна в точке х°, если для любого 8 > О
найдется такое 8> 0, что из d(x, х°) < 8 следует, что d(f(x), f(x0))<8.
Функция называется непрерывной, если она непрерывна в любой точке
своей области определения.
Потратим немного времени, чтобы увидеть, как это определение
согласуется с нашим интуитивным представлением о функциях вроде тех,
которые изображены на рис. А1.16. Рассмотрим сначала рис. А1.16(б), и
обсудим, почему эта функция не удовлетворяет определению
непрерывности в точке jc° . Определение требует, чтобы для любого 8 > 0 мы смогли
найти некоторое 8 > 0, такое, что для любой точки х, лежащей на
расстоянии меньшем 5 от х°, ее образ f(x) будет лежать на расстоянии
меньшем е от f(x°). Предположим, мы выбираем некоторое е'>0.
Мгновенно убеждаемся, что нет такого 8>0, удовлетворяющего этому
определению. Чтобы увидеть это, обратим внимание, что на любом
расстоянии от х°, меньше положительного 8, например на расстоянии 8',
будут находиться точки, лежащие справа от х°, например jc1. Любая точка
вида х1 отображается функцией в точку вида f(xl), лежащую на верхнем
участке кривой на расстоянии, заведомо превышающем расстояние е' от
образа точки jc° , т.е. f(x°). Так как мы нашли по меньшей мере одну точку
jc° e R и 8 > 0, для которых не существует соответствующего 8 > 0,
функция не может быть непрерывной в соответствии с данным определением.
Вместе с тем ясно, что функция на рис. А 1.16(a) действительно
удовлетворяет определению. Чтобы убедиться в этом, предположим, что мы
выбираем некоторое х° е R и некоторое 8 > 0, например е'. Точки f(x°) + e' и
/(х°)-е' являются образами точек х°+я, х° -Ь соответственно. Теперь,
если для этого е' > О мы выбираем 8, равное наименьшему из чисел а > О и
Ъ > О (на рисунке это а), мы можем быть уверены, что образ любой точки,
лежащей на расстоянии, меньшем 8' = а , по обе стороны от х°, будет
отображаться в точку, лежащую не далее расстояния е' от f(x°)! Таким
образом, / удовлетворяет условию непрерывности в точке х°.

Глава AL Множества и отображения
575
Определение непрерывности, которое мы привели, хорошо подходит
для описания простых функций, рассмотренных ранее. Оно логически
точно описывает поведение непрерывных функций, так, как мы себе это
интуитивно представляли. Однако, если мы посмотрим на это
определение более пристально, увидим, что в состоянии выразить те же самые
идеи более компактно и на языке, который позволит применять эти идеи
к гораздо более широкому классу функций.
По существу, понятие непрерывности означает, что функция
непрерывна в точке х° из области определения, если для любого г > О
найдется 5 > О такое, что любая точка, лежащая на расстоянии меньше 8 от х°
(а следовательно, все такие точки, лежащие на расстоянии меньше 8 от
лс°), отображается функцией / в некоторую точку множества значений,
лежащую на расстоянии меньше г от f(x°). Теперь мы знаем, как
характеризовать все множество точек из области определения, лежащих на
расстоянии меньше 8 от х°. Это открытая 8-окрестность точки х°, т.е.
Вь(х°). Используя обозначение теории множеств, обозначим множество
значений, являющееся образом точек из Вь(х°), как /E5(jc0)).
Аналогично, если f(x°) — образ точки х°, то мы можем обозначить
множество точек из множества значений, которые лежат на расстоянии меньше
б от f(x°), как Be(f(x0)). Чтобы выразить идею о том, что каждая точка
из Вь(х°) отображается функцией / в некоторую точку, лежащую на
расстоянии меньше е от /(х°), мы можем с таким же успехом сказать, что
любая точка из f(Bb(x0)) принадлежит множеству 5е(/(лс0)), или
f(Bb(x0))с5e(/(jc0)). Рисунок А1.17, повторяющий рис. Al.16(a),
показывает, как эти множества соотносятся с более привычной терминологией.
Вг(А*°)) 1
Рис. А1.17. Непрерывность по Коши

576
Математическое приложение
Рисунок А 1.17 полезен, но мы должны, опираясь на его суть,
продолжить обобщение идей непрерывности. Во-первых, нам потребуется
характеристика непрерывности, которая применима к функциям с
областями определения из Шт, а не только из R . Во-вторых, нам понадобятся
функции, у которых области определения — это подмножества Rm, т.е.
не все пространство Rw 1. Ранее мы неявно предполагали, что областью
определения / было все R. Тогда мы были уверены в том, что для
любого jc°gR и любого 5>0 окрестность Вь(х°) целиком содержится в
области определения /, так что /E6(х0)) хорошо определено. Однако,
когда область определения D некоторой функции / — всего лишь
подмножество, нам не следует рассматривать все точки из Rm, лежащие на
расстоянии меньше 8 от х°. В этом случае мы будем брать только те
точки из D, которые находятся на расстоянии меньше 8 от х°, а именно
Bb(x°)nD. Следующее определение обобщает понятие непрерывности
для этих двух направлений.
Определение А1.9 (Коши). Непрерывность.
Пусть D — подмножество в W" и пусть f :D —>R". Функция f
непрерывна в точке х° е D, если для любого г > О найдется 8 > 0, такое,
что
ДЯ5(х°)п?>)сЯе(Дх0)).
Если /непрерывна в каждой точке хе D, то она называется
непрерывной функцией.
Это определение непрерывности фокусирует внимание на связи
между одним множеством в пространстве образов (образ открытого
множества из области определения) и другим открытым множеством из
пространства образов. Неплохо было бы знать, какие свойства множеств
сохраняются при непрерывных отображениях (если вообще что-то сохраняется) в
процессе отображения области определения в пространство образов и
обратно. Наша интуиция подсказывает, что непрерывная функция вполне
«правильная» и ведет себя предсказуемым образом, возможно даже, такие
свойства, как открытость и замкнутость, сохраняются при отображении
области определения в область значений. К сожалению, бывают
ситуации, когда интуиция подводит. Кроме одного специального случая, о
котором речь пойдет ниже, мы не можем принимать на веру, что любое
1 Например, область определения функции f(x) = у[х — это R+cR.

Глава Ah Множества и отображения
577
свойство множеств из области определения будет сохранено при
отображении, если это отображение осуществляется непрерывными функциями.
В частности, неверно, что непрерывная функция всегда отображает
открытое множество из области определения в открытое множество из
области значений или что замкнутые множества всегда отображаются в
замкнутые. Например, непрерывная функция f(x) = а отображает
каждую точку из области определения, тем самым каждое открытое
множество точек из области определения, в изолированную точку а из области
значений. Выполнив упражнение А1.25, вы убедитесь, что изолированная
точка является замкнутым множеством, т.е. оно не открыто; таким
образом, интуиция нас не обманула.
Если, как в определении А 1.9, мы допускаем, что область определения
функции является подмножеством D (возможно, строгим) из Rw, то
больше не имеет смысла представлять открытое множество из области
определения в терминах открытых окрестностей в Шт, так как эти
окрестности могут лежать частично или полностью вне D. Нам нужно развивать и
использовать подходящий язык, который объяснял бы такого рода
возможности. Поэтому естественным образом мы подошли к следующей идее.
Определение А 1.10, Открытые множества в D.
Пусть D — подмножество в Шт. Тогда подмножество S из D
будет открытым в D, если для любого хе S найдется ?>0, такое, что
Bz(x)nDaS.
Так, множество открыто в D, если для любой точки множества все
близлежащие точки либо принадлежат множеству, либо находятся вне D.
Заметим, что при D = Rm это определение совпадает с определением
открытого множества в Шт. Также заметим, что D всегда открыто в D.
Как и ранее, мы определим замкнутость через открытость.
Определение Al.ll. Замкнутые множества вD.
Пусть D — подмножество в Шт. Подмножество S из D будет
замкнутым в D, если его дополнение в D, т.е. множество {хе D\x? S],
открыто в D.
Хотя, в общем, мы не можем наверняка знать, что произойдет, когда
мы отобразим область определения в область значений посредством
непрерывной функции, но мы можем сказать кое-что о том, что произойдет
при движении в обратном направлении — из области значений в область
определения. На самом деле существует тесная связь между
непрерывностью функции и свойствами множеств из области значений, с одной
стороны, и свойствами их обратных образов (прообразов) из области опре-

578
Математическое приложение
деления — с другой. Следующая теорема устанавливает ряд соотношений
между непрерывностью функции и сохранением основных свойств
множеств под воздействием обратного отображения.
Теорема А 1.6. Непрерывность и обратные отображения.
Пусть D — подмножество в Rw. Следующие условия являются
эквивалентными:
1) /:D—>IR" непрерывна',
2) для любой открытой окрестности В из W f~l (В) открыто
в D;
3) для любого открытого множества S из R" f~x (S) открыто
в D.
Доказательство. Мы покажем, что 1) => 2) => 3) => 1).
1)=>2). Предположим, что 1) справедливо и В - открытая
окрестность в R". Выберем любую точку xg f~\B). Ясно, что тогда f(x)e В.
Так как В открыто в R", то найдется такое е>0, что Bz(f{x))aB.
И вследствие непрерывности / найдется такое 5>0, что
/(S6(x)nZ))c5e(/(x))cB. В результате 58(x)nZ)c/E). Так как
хе f~x{B) было выбрано произвольным, мы заключаем, что f~\B)
открыто в D, так что 2) справедливо.
2)=>3). Предположим, что 2) справедливо и S открыто в Ш".
По теореме А 1.3 S может быть представлено в виде объединения
открытых окрестностей Вп ie I, так что S - и/е/ В.. Поэтому
f-\S) = f~\ui&IBi) = uieIf'](Bi). В силу 2) каждое множество /"'(Я,)
открыто в D, тогда f~l (S) является объединением открытых множеств в
D. Следовательно, по упражнению А 1.28 /_1(^) также открыто в D.
Так как S — произвольное открытое множество вК", это доказывает 3).
3) => 1). Предположим, что 3) справедливо, и выберем хе D и е > 0.
Так как 5е(/(х))открыто в R", из 3) следует, что f~l(Be(f(x))) открыто
в D. Так как xg f~\Bzf(x))), то отсюда следует, что найдется 8> 0,
такое, что B8(x)nDc/_1(j??(/(x))). Но из этого следует, что
/E8(х)п/))с5?(/(х)). Поэтому / непрерывна в точке х. Так как х
было выбрано произвольно из D, то 1) справедливо и доказательство
завершено. ¦

Глава Ah Множества и отображения
579
Это очень общая и очень сильная теорема. Если мы знаем что-либо
об обратных отображениях открытых множеств или открытых
окрестностей из области значений, то мы можем использовать эту теорему, чтобы
сделать вывод о непрерывности функции. Таким же приемом можно
воспользоваться, если нам известно, что функция непрерывна, тогда мы
можем с помощью этой теоремы показать, какими свойствами должны
обладать обратные отображения открытых множеств и окрестностей из
области значений. Все равно было бы здорово, если бы нам удалось
выяснить хоть что-то о том, что происходит с множествами из области
определения, когда они отображаются в множества из области значений.
Как вам уже известно, мы не можем сказать так много, как этого бы
хотелось. Тем не менее кое-что у нас все-таки есть. В частности, можно
показать, что если S — компактное подмножество из области определения и
/ непрерывна, то образ множества f(S), лежащий в области значений,
также является компактом. Наконец-то мы получили результат, который
интуитивно ожидали. К сожалению, доказательство выходит далеко за
рамки того, чем бы мы хотели ограничиться. Так как это важный
результат, стоит привести его здесь для последующего использования.
Заинтересованный (и подготовленный) читатель может найти доказательство в
приведенной ниже библиографической ссылке.
Теорема А 1.7. Непрерывное отображение компактного
множества является компактным множеством.
Пусть D — подмножество в Шт и пусть f :D—>Rn —
непрерывная функция. Если S aD компактно в D (т.е. замкнуто в D и
ограничено), то его образ f(S) с Ж" компактен в R".
Доказательство. См. книгу Ройдена [Royden, 1963], где приведено
полное доказательство. ¦
Наконец, мы можем ввести понятие последовательности.
Определение А1.12. Последовательности в Ш".
Последовательность в W — это функция, отображающая
некоторое бесконечное подмножество I положительных целых чисел в Шп. Мы
будем обозначать последовательность через \xk\kGl, где xk e Ш" для
любого ке I.
Если члены последовательности {х*} приближаются сколь угодно
близко к некоторой точке из R" при достаточно больших к, то мы
говорим, что последовательность сходится к этой точке. Дадим формальное
определение.

580
Математическое приложение
Определение А1.13. Сходящиеся последовательности.
Последовательность \&k\kGl сходится к хеШ", если для любого
? > 0 найдется такое к, что \к е Вг(х) для всех ке I, превышающих к .
В М1, например, последовательность 1, —, -, ••• сходится к нулю,
хотя нуль и не является членом последовательности. Вместе с тем
последовательность 1, 2, 3, ... не сходится ни к какому действительному числу.
Таким образом, не все последовательности являются сходящимися. На
самом деле даже последовательности, все члены которых ограничены,
необязательно сходятся. Например, последовательность 1, -1, 1, -1, ...
ограничена, но не является сходящейся. В то же время, если мы
рассмотрим члены последовательности через один, начиная с первого, мы
получим подпоследовательность 1, 1, 1, ..., которая заведомо сходится к 1.
Этот пример может быть обобщен в виде важного следствия. Но чтобы
его сформулировать, нам понадобится еще несколько определений.
Определение А1.14. Ограниченные последовательности.
Последовательность {х* \keI из R" является ограниченной, если для
некоторого MeR х* < М для всех ке I.
и
Определение А1.15. Подпоследовательности.
ш является подпоследовательностью последовательности
7, если J является бесконечным подмножеством I.
и«
Теперь мы готовы сформулировать следующий важный результат.
Теорема А1.8. Об ограниченных последовательностях.
Из любой ограниченной последовательности в W можно выделить
сходящуюся подпоследовательность.
Доказательство. Доказательство приведено в книге Ройдена
[Royden, 1963], или его можно найти в любом другом хорошем учебнике
по вещественному анализу. ¦
Оказывается, мы могли бы определить открытые и замкнутые
множества в терминах последовательностей. Так что мы завершаем этот раздел
теоремой, которую вам предлагается доказать самостоятельно.
Теорема А1.9. Последовательности, множества и непрерывные
функции.
Пусть D - подмножество в Ж", и пусть f: D —> Rm. Тогда:

Глава AL Множества и отображения
581
1) D открыто тогда и только тогда, когда для любого хе D из
сходимости |х*] к х следует, что найдется такое к, что хк е D для
всех к>к;
2) D замкнуто тогда и только тогда, когда для любой
последовательности {х*| точек из D, сходящейся к некоторой xgR", вытека-
em, что х € D;
3) f непрерывна тогда и только тогда, когда для любой
последовательности \хк} точек из D, сходящейся к xeD, следует, что
х* Н сходится к /(х).
А1.3.2. Некоторые теоремы существования
Чтобы завершить этот раздел, мы рассмотрим некоторые очень
сильные топологические результаты, каждый из которых имеет важные
приложения в микроэкономической теории. Все они из класса теорем,
который носит название «теоремы существования». В теореме из этого класса
утверждается, что при выполнении некоторых условий что-то
существует. При обсуждении теорем существования следует обращать внимание
на два момента. Во-первых, условия в таких теоремах обычно
достаточные, они не необходимые. Это означает, что если они выполнены, то
существование гарантируется. В то же время, если в каком-то случае
условия не выполняются, то существование все равно могло бы иметь место.
Вообще говоря, в этом мы не можем быть уверены a priori. Во-вторых,
хотя эти теоремы убеждают нас в существовании чего-либо, они обычно
не дают никакой подсказки, как это выглядит и как его найти!
Следовательно, они обеспечивают мощную и неоценимую поддержку при
построении строгих «абстрактных» результатов, но очень слабо помогают
при решении «практических» задач.
Первая из теорем, которую мы рассмотрим, является
фундаментальным результатом в теории оптимизации. Во многих экономических
задачах требуется максимизировать или минимизировать функцию,
определенную на некотором подмножестве из Ж". В последующих разделах мы
исследуем, как методы математического анализа помогают описать и
найти решения задач подобного типа. Мы уделим особое внимание проблемам
максимизации или минимизации функций, которые отображают векторы
из W в действительные числа. Функции такого типа называются вещест-
веннозначными, и мы приступим к детальному исследованию этого класса
функций в разделе А 1.4. Однако здесь мы можем использовать некоторые
знания топологии, чтобы доказать одну из наиболее широко используемых
/<

582
Математическое приложение
теорем существования, известную как теорема Вейергитрасса. В теореме
Вейерштрасса определяются достаточные условия, выполнение которых
гарантирует существование максимума и минимума функции.
Теорема А1.10 (Вейерштрасса). Существование экстремальных
значений.
Пусть f: S —> Ж — непрерывное вещественнозначное отображение,
где S — непустое компактное подмножество в Ж". Тогда найдутся
векторы х* е S и х е S, такие, что
/(х) < /(х) < /(х*) для всех х е S.
Доказательство. Так как / непрерывна и S компактно, то по
теореме А 1.7 f(S) является компактным множеством. А в силу того что
/ — вещественнозначная функция, выполнено/^) cR. Так как f(S)
компактно, то оно замкнуто и ограничено. По теореме А 1.5 любое
замкнутое ограниченное подмножество действительных чисел содержит свою
точную нижнюю грань, назовем ее а, и точную верхнюю грань, назовем
ее Ь. По определению области значений существует некоторое х* е S,
такое, что f{\) = Ье f(S) и некоторое хе S, такое, что f(x) = ae f(S).
По определению точных верхней и нижней граней имеем f(\) < f(\) и
/(х) < /(х*) для всех х е S. ¦
Смысл теоремы А1.10 иллюстрируется на рис. А1.18. В обоих
случаях, (а) и (б), /: R —> Ж — непрерывная вещественнозначная функция. На
рис. Al. 18(a) подмножество 5 = [1, 2] замкнуто, ограничено и,
следовательно, компактно. Так как / непрерывна, минимум /Eс) и максимум
/(**) будут соответственно совпадать с точной нижней и точной верхней
гранями из области значений f(S). Чтобы выяснить, когда это будет
неверно, рассмотрим, например, рис. А 1.18F). Область определения
теперь — это подмножество S' = (l9 2), которое не является компактом.
Оно ограничено, но не замкнуто. Ясно, что в этом случае у функции / на
?' нет ни минимума, ни максимума. Так как S' открыто, мы можем
перемещаться все ближе и ближе к любому из концов открытого интервала
без всякой надежды когда-либо достичь концевой точки. Эти движения
отображаются в нижние значения и соответственно в верхние значения
функции, при этом функция никогда не принимает максимальное или
минимальное значение.

Глава А1. Множества и отображения
583
(б)
Рис. А1.18. Теорема Вейерштрасса: (а) — гарантированно существуют
максимум и минимум, (б) — не существует ни минимума, ни максимума
Теперь давайте обратимся к одному более специальному классу
функций. В дальнейшем изложении мы ограничим свое внимание век-
торнозначными функциями, отображающими некоторое подмножество
из R". Если ScR" и / \S -> S, тогда / отображает векторы из S
обратно в другие векторы из того же множества S.
Линейные и нелинейные системы уравнений определяют функции
этого типа. Например, система уравнений, записываемая в виде
yx=fl(xl9 ...,*„)
: (А1-1)
отображает точки (дс,, ..., хп) е К" в точки {ух, ..., уп) е R", так что это —
отображение из одного множества в то же множество. Много раз нас
интересовало решение подобных систем в случае, когда у.} принимали
конкретные значения. В частном случае, когда yt=xi9 / = 1, ...,«, решением
системы (А 1 -1) будет некоторый вектор (х*, ..., jc* ) e R", где
(А1-2)
Хп ~~ J п \Х\ ' * • •' Хп Г

584
Математическое приложение
Вектор х*, который является решением системы (А 1-2), называется
неподвижной точкой отображения f: R" —> R". Выражение
«неподвижная точка» используется потому, что, если бы такая точка
существовала, то она оставалась бы невозмущенной, или «несдвинутой», при
отображении области определения в область значений. Отображение /
всего лишь отображает х* на себя.
Предположим, мы записали некоторую систему уравнений в виде
(А 1-2). Было бы неплохо выяснить, является ли эта система логически
непротиворечивой, или, наоборот, условие, накладываемое на какое-либо
уравнение, логически противоречит условию, требуемому от другого
уравнения. Фундаментальный вопрос, является ли система вида (А 1-2)
внутренне непротиворечивой или внутренне противоречивой, может быть
легко перефразирован в вопрос, существует ли решение у системы
(А 1-2)? Это, в свою очередь, эквивалентно вопросу, существует ли
неподвижная точка у системы (А 1-1).
На многие глубокие вопросы о фундаментальной
непротиворечивости микроэкономических систем были найдены ответы благодаря
сведению этих вопросов к задаче о существовании неподвижной точки. С ее
помощью было показано, что представление о конкурентной экономике
как системе взаимосвязанных рынков логически состоятельно.
Знаменитая теория о минимаксе из теории игр была также доказана этим методом.
В этих и других случаях некоторые варианты теоремы о неподвижной
точке играют центральную роль. Достаточные условия, обеспечивающие
существование неподвижной точки в системах уравнений вида (А1-1),
были выведены из следующей сильной теоремы.
Теорема Al.ll. Теорема Брауэра о неподвижной точке.
Пусть SаШ" — непустое, компактное и выпуклое множество.
Пусть /*:?—>? — непрерывное отображение. Тогда существует по
крайней мере одна неподвижная точка функции f в S. То есть
существует по крайней мере одна х* е S, такая, что х* = f(x*).
Доказательство. К несчастью, даже так называемые простые
доказательства этой глубокой теоремы должны увести нас в область топологии,
которая далеко выходит за рамки этой книги. Читатели могут обратиться
к работе Никайдо [Nikaido, 1968], где приводится полное доказательство
этой теоремы. Чтобы не остаться с пустыми руками, мы дадим
доказательство для специального случая отображения точек действительной
прямой в точки действительной прямой. (Для отображений /: R" —>R"
теорема Брауэра сводится к теореме о промежуточных значениях из
вещественного анализа.)

Глава AL Множества и отображения
585
Пусть ScR компактно и выпукло. В силу того что любое
замкнутое, ограниченное и выпуклое подмножество из R должно быть
отрезком, мы упростим ситуацию, если будем считать S = [a, b]. Пусть
/: [я, Ь] —> [я, b] — любое непрерывное отображение множества [а, Ь]
в себя.
Так как / отображает [а, b] в [а, Ь]9 то мы знаем, что для всех
хе [a, b] /00 е [a, Ь]. Рассмотрим значения / на концах отрезка. Так
как а < f{x) < Ъ для всех хе [а, Ь], то должны выполняться неравенства
a<f(a)nb>f(b). (P-1)
Теперь определим новую функцию g, где
g(x) = x-f(x)9 (P-2)
и область определения g — тот же самый отрезок [а, Ь]. Заметим, что g
непрерывна, так как / непрерывна по условию теоремы, функция у = х
очевидно непрерывна, а разность непрерывных функций также
непрерывна. Заметим далее, что в силу (Р-1) мы можем оценить g на концах
области определения и сделать вывод, что g(a) = а - f(a) < 0 и
g(b)-b- f{b)>0. Если какое-либо из этих неравенств обращается в
равенство, то наше дело сделано, так как если g(a) = 0, то f(a) = а, и,
стало быть, а есть неподвижная точка функции /, а если g{b) = 0, то
f(b) = b, и b есть неподвижная точка. На этом, к сожалению, мы не
можем остановиться. Нам придется рассмотреть случай, когда g(a) < 0,
g(b)>0.
Предположим, что g(a) < 0 и g(b) > 0. Так как g{a) < 0, мы знаем,
что найдется по крайней мере одно число о а, такое, что g(x) < 0 для
всех хе [а, с). (Заметим, что это не отрезок. Всегда обращайте внимание
на то, является ли множество открытым, замкнутым или ни тем ни
другим!) Например, если мы положим г = -g(a) > 0, то непрерывность g
гарантирует, что найдется некоторое 8>0, такое, что из
хе[а, а + 8]аВь(а) будет следовать, что g(x)eBg(a), 0) = 5e(g(a)).
Так как все точки из последнего интервала отрицательны, то, полагая
с = а + 8 > а, получим, что с и будет одним из этих чисел. Более того, так
как g(b) > 0, мы знаем, что любое из таких чисел с должно быть строго
меньше b по той же причине. Снова, используя непрерывность g, мы

586
Математическое приложение
получаем, что при выборе г = g(b) > О найдется некоторое 6 > 0, такое,
что из хе F-8, Ь) с В8(Ь) мы получим g(x)e @, 2g(b)) = Be(g(b)) и все
числа из последнего интервала положительны. Так как определение с
предполагает g(x)<Q для всех хе [а, с), любое с должно быть меньше
или равно Ъ - 8, что, в свою очередь, влечет с < Ь .
Каждое число с определяет интервал вида [а, с), на котором g
везде отрицательно. Давайте выберем наибольший из таких интервалов и
предположим, что это интервал [я, с*). Так как с* <Ь, то мы знаем, что
интервал ограничен. По определению с* мы также знаем, что
g(x)<0,Vxe[a, с*). (Р-З)
Что мы можем сказать о значении g в точке с*? Невозможно, чтобы
g(c*) > 0. Если бы это имело место, мы могли бы выбрать ? = g(c*) > 0, а
в силу непрерывности g нашлось бы 8>0, такое, что из
хе(с*-Ь, с*]сВ8(с*) следовало бы g(x)e@, 2g(c*)) = Be(g(c*))9 что
противоречит (Р-З). Точно так же невозможно, чтобы g(c*)<0. Если бы
это было так, мы могли бы выбрать e = -g(c*)>0, и вследствие
непрерывности g нашлось бы 8 > 0, такое, что из хе [с*, с*+8)сЯ6(с*)
следовало бы g(x)eBg(c*% 0). Так как g(x)<0 для всех хе (я, с*), это
означает, что g(x) < 0 для всех хе (я, с* + 8). Но это противоречит
определению с*. Мы должны сделать вывод, что g(c*) = 0. Но тогда с*— это
неподвижная точка, которую мы искали, так как из g(c*) = 0 следует в
силу (Р-2), что
c=f(c),
что и требовалось доказать. ¦
Доказательство теоремы Брауэра даже для отображений точек
действительной прямой в действительную прямую требует значительных
усилий. К счастью, его геометрический смысл легко уяснить. Ситуация,
рассмотренная в доказательстве, проиллюстрирована на рис. А 1.19. Короче
говоря, если / — непрерывное отображение одного отрезка на тот же
отрезок, то теорема Брауэра гарантирует, что график / пересечет
прямую, проведенную под углом 45° к оси х, хотя бы один раз внутри квад-

Глава Л L Множества и отображения
587
рата [я, b]x[a, b]. На предложенном рисунке таких пересечений три.
Это сделано, чтобы предупредить читателя о том, что в теореме Брауэра
ничего не говорится о единственности неподвижной точки, т.е. при
выполнении условий теоремы гарантируется лишь существование. В
действительности рис. А 1.19 можно рассматривать как контрпример к любой
из «теорем», которую вам захотелось бы доказать самостоятельно.
* х
Рис. А1.19. Теорема Брауэра о неподвижной точке
Очень трудно привести строгие примеры (а тем более
доказательства), чтобы убедить вас в справедливости этой важной теоремы, когда
рассматриваемая функция определена на множествах размерности больше 1.
Однако мы предлагаем вам мысленный эксперимент для
самостоятельного обдумывания.
Рассмотрим чашку кофе. Молекулы кофе примем за точки из R3, а
множество молекул в вашей чашке — за компактное выпуклое множество
в Ш2. Теперь окуните ваш палец в чашку и поводите им немного
«непрерывным» образом. Пусть движение молекул «замрет». Теорема Брауэра
гарантирует, что по крайней мере одна молекула в вашей чашке не
тронулась с места!
А1.4. Вещественнозначные функции
Вещественнозначные функции часто встречаются в
микроэкономической теории. Функция полезности потребителя, производственная функция
фирмы и функция издержек фирмы — это только наиболее известные.
Дадим им формальное определение.

588
Математическое приложение
Определение А1.16. Вещественнозначные функции.
/: D —> Е — вещественнозначная функция, если D является
произвольным множеством мйсЕ.
Проще говоря, / вещественнозначна, если она отображает элементы
своей области определения в точки действительной прямой. Если область
определения является подмножеством в Е", вещественнозначная
функция отображает векторы из R" в точки из Е. Функции у = ах{+Ьх2,
y = Tjz2+w2 и y = ^djxf являются примерами вещественнозначных
функций, так как в любом из случаев левая часть выражения —
действительное число. Конечно, класс вещественнозначных функций очень
широк. В этом разделе мы рассмотрим некоторые частные виды
вещественнозначных функций и исследуем их важные свойства.
В обычных экономических приложениях вещественнозначные
функции, как правило, возрастают или убывают на своей области определения.
Они называются возрастающими и убывающими, и нам следует
тщательно определить эти понятия, чтобы ссылаться на них в будущем. В данный
момент мы будем различать три типа возрастающих функций.
Определение А1.17. Возрастающие, строго возрастающие и
строго возрастающие (в сильном смысле) функции.
Пусть /:D—>Е, где D — подмножество в Ж". Функция f
называется возрастающей, если f(x°) > /(х1) при х° > х1. Если, кроме того,
неравенство /(х°)>/(х1) строгое при х° »х!, то функция f строго
возрастающая. Если же f(\°)>f(\l) выполняется для различных х° и
х1 и таких, что х° > х1, то будем говорить, что f строго возрастает
(в сильном смысле).
Внимательно посмотрим на эти определения и вспомним, как мы
использовали символы > и » при сравнении векторов. Мы определили
функцию как возрастающую в том случае, если возрастание одной или
нескольких компонент xt вектора x = (jcp ...,jc„) не приводит к
убыванию значений функции. Мы назвали функцию строго возрастающей, если
увеличение всех компонент х приводит к строгому возрастанию
значения функции. Мы определили функцию как строго возрастающую (в
сильном смысле), если увеличение одной или нескольких х. приводит к
строгому возрастанию функции. Прежде чем продолжить чтение,
обратите внимание на иерархию свойств: возрастающая функция не обязана
быть строго возрастающей, и строго возрастающая функция не обязана

Глава AL Множества и отображения
589
быть строго возрастающей (в сильном смысле), но всякая строго
возрастающая (в сильном смысле) функция является строго возрастающей, и
всякая строго возрастающая функция является возрастающей.
Убывающие функции определяются аналогично, и мы проведем
подобное различие.
Определение А1.18. Убывающие, строго убывающие и строго
убывающие (в сильном смысле) функции.
Пусть f : D -» R, где D — подмножество в W. Функция f
называется убывающей, если /(х°)</(х1) при х° >х\ Если, кроме того,
неравенство f(x°)<f(xl) строгое при х° »х!, то функция f строго
убывающая. Если же f(x°)<f(xl) выполняется для различных х° и х1
и таких, что х°>х\ то будем говорить, что f строго убывает
(в сильном смысле).
А1.4.1. Соответствующие множества
Мы видели, что функция — это особый вид отношения между двумя
множествами. Мы также обратили внимание на то, что график функции
является множеством, позволяющим зачастую легко и интуитивно
воспринять функцию. Есть и другие множества, связанные с функциями,
множества, которые входят в привычный арсенал и словарь
экономической теории. Как и графики, некоторые из них имеют простые
геометрические представления, и они часто дают нам эквивалентные, но
упрощенные способы описания и манипуляций с функциями. Это особенно верно
для вещественнозначных функций, для которых множество значений есть
некоторое подмножество действительной прямой. После определения
некоторых множеств, связанных с функциями, и пояснения как этой связи,
так и связи между самими множествами мы рассмотрим некоторые
частные виды вещественнозначных функций и специфические свойства
множеств, определяемые этими функциями.
Понятие множества уровня (или линии уровня), несомненно, вам
вполне известно, хотя, быть может, и под другим названием. Многие
привычные объекты микроэкономики, такие, как кривые безразличия, изо-
кванты, изопрофиты и т.д., являются множествами уровня
вещественнозначных функций. Множество уровня — это множество всех элементов в
области определения функции, которое отображается в одно число,
«уровень», из множества значений. Таким образом, любые два элемента из
одного множества уровня будут согласно определению порождать одно и то
же число из множества значений при подстановке в аргументы функции.
Дадим формальное определение.

590
Математическое приложение
Определение А1.19. Множества уровня.
L(y°) является множеством уровня вещественнозначной функции
f :D —> R тогда и только тогда, когда L(y°) = {х | хе Д f(x) = у0}, где
y°eRc:R.
Заметим, что эти множества лежат в области определения функции.
Так как мы можем построить одно множество уровня для любого
значения из ее образа, мы можем полностью представить функцию этими
множествами из области определения и тем самым уменьшить на
единицу величину размерности, требуемой для представления функции. Это
свойство множеств уровня часто использовалось при построении карт
кривых безразличия, карт изоквант и т.д.: множества уровня позволяют
нам исследовать функции трех переменных, что обычно требует
построения громоздких трехмерных графиков, путем изучения множеств на
простой плоскости двух переменных. Некоторые множества уровня для
функции трех переменных изображены на рис. А 1.20.
хг
'L(y°)={(xhx2)\Ax>,x2)=y0}
-+> *i
Рис. А1.20. Множества уровня в
Следует отметить и другое свойство множеств уровня. Ранее мы
видели, что отображение / :D —> R является функцией тогда и только
тогда, когда оно ставит в соответствие любому элементу из области
определения единственное число из области значений. Поэтому два разных
множества уровня никогда не пересекаются. Если бы они пересекались,
то это означало бы, что два разных числа поставлены в соответствие
одному элементу из области определения, являющемуся пересечением. Это,
разумеется, противоречит определению функции.
Наконец, следует сделать замечание об обозначениях. Для многих
целей удобнее связывать множества уровня с конкретными точками из
области определения, а не из области значений. Так как вещественнознач-

Глава AL Множества и отображения
591
ная функция отображает любую точку х° из своей области определения в
некоторую точку или уровень /(х°) = у0 из своей области значений, то
это просто вопрос удобства обозначений, не более того. Таким образом, в
соответствии с нашим прежним представлением, мы можем определить
множество уровня, относящееся к точке х°, как множество всех точек из
области определения, отображаемых в тот же уровень области значений,
что и точка х°.
Дадим формальное определение.
Определение А1.20. Множества уровня, относящиеся к точке.
-С(х°) является множеством уровня, относящимся к х°, если
Дх°) = {х|хеД Дх) = Дх0)}.
Рассмотрим множество уровня для /(х) = у0 на рис. А 1.21. Так как
точка х° принадлежит множеству уровня у0 для /(х), то понятно, что
f(x°) = y°. Что нам известно о других точках из области определения,
таких, как х1 и х2? Если Дх) строго возрастающая функция, то мы
знаем, что Дх1) > Дх°) и Дх2) < Дх°). Это ясно, потому что обе
координаты вектора х'(х2) строго больше (меньше), чем координаты х°, а
строго возрастающая функция принимает большие (меньшие) значения,
отображая векторы с большими (меньшими) компонентами. Это довольно
просто. Но что можно сказать о других точках, лежащих по ту же сторону
от L(y°), что и х1 или х2, например х3 или х4? Ясно, что если функция
возрастает или убывает, то точки, такие, как х3 или х4 должны
приводить к такому же росту функции по отношению к у0, что и наблюдаемый
рост функции в точках х1 и х2 соответственно. Если /(х) строго
возрастает, f(x{)<y°, f(x3)<y° и f(x2)>y°, f(x4)>y°. Это тоже ясно,
потому что, например, х3 находится в том же отношении к некоторой
другой точке из L(y°), такой, как х5, что и х1 в отношении х°. Так как обе
точки — х° и х5 — лежат на L(y°), то Дх°) = f(x5) = у0. Аналогично
рассуждая, мы сможем определить, будет ли значение функции в х3
больше или меньше значения в х5, в зависимости от того, возрастает ли
строго Дх) или же она строго убывает. Если /(х) строго убывает, то
Дх!)> Дх°) = >>0 и /(х3)>/(х5) = У\ Если f(x) строго убывает, то
/(х1)</(ж°) = /и/(х3)</(х5) = /.

592 Математическое приложение
х2
L(y°)
> *i
Рис. А1.21. Множество уровня относительно точки х°
Продолжая рассуждать подобным образом, мы сможем найти
некоторые дополнительные множества, которые помогут разделить область
определения функции на удобные множества.
Определение А1.21. Супериорные и инфериорные множества.
1) S(y°) = {х | хе D, /(х) > у0} называется супериорным
множеством для у0.
2) 1(у°) = {х | хе D, f(x) <y0} называется инфериорным
множеством для у0.
V S'(y°) = {х | хе Д f(x) > у0} называется строго супериорным
множеством для у0.
4) I'(y°) = {x \xe D, /(х)<^0} называется строго инфериорным
множеством для у0.
Супериорное множество содержит все точки из D, для которых
функция принимает значения, равные или больше у0; строго супериорное
множество содержит все точки, для которых функция принимает
значения строго больше у0. Инфериорное множество содержит все точки, в
которых функция принимает значения, меньшие или равные у0; строго
инфериорное множество содержит все точки, в которых функция
принимает значения строго меньше у0. Так как множество уровня само
определено как множество, для всех точек которого функция принимает
значения у0, то все эти множества тесно связаны. Следующая теорема
устанавливает взаимосвязь между этими множествами. Доказательство этой
теоремы предлагается в качестве упражнения.

Глава А1. Множества и отображения
593
Теорема А1.12. Супериорные, инфериорные множества и
множества уровня.
Для любой f:D^>R иу°е R:
1) L(y°)<zS(y°);
2)L(y°)<zI(y°);
3)L(y°) = S(y°)nI(y0);
4)S'(y0)<zS(y0y,
5;/'(/)c/(/);
6j5V)nl(j°) = 0;
7) lXy°)nL(yo) = 0-
8) 5V)n/'(/) = 0-
Рисунок А 1.22 иллюстрирует супериорные и инфериорные
множества для двух разных функций, одна из которых возрастающая, а другая —
убывающая. Когда /(х) возрастает, S(y°) будет всегда лежать на и
выше множества уровня L(y°), а 1(у°) будет всегда лежать на и ниже
L(y°). S'(y°), если оно не пусто, будет всегда лежать строго выше
множества уровня L(y°), a I'(y°) будет всегда лежать строго ниже его. Когда
f(\) убывает, S(y°) будет лежать на и ниже множества уровня L(y°), a
1(у°) будет лежать на и выше его. S'(y°), если оно не пусто, будет
лежать строго ниже L(y°), а 1'(у°) будет лежать строго выше L(y°).
/(v°)
* *i
* *i
(a)
F)
Рис. А1.22. Множества уровня, супериорные и инфериорные множества для
(а) возрастающей функции и (б) убывающей функции

594
Математическое приложение
А1.4.2. Вогнутые функции
До конца раздела А 1.4 мы будем заниматься вещественнозначными
функциями, чьи области определения — выпуклые множества. В
последующем изложении это также почти всегда будет иметь место, если даже
явным образом не оговаривается. В данный момент, однако, мы
постараемся быть аккуратными, четко формулировать предположения и вводить
обозначения.
Предположение А1.1. Вещественнозначные функции на
выпуклых множествах.
На протяжении всего этого раздела, всякий раз, когда определяется
вещественнозначная функция f :D —»R, мы будем полагать, что
Z)cK" — выпуклое множество. Когда мы будем выбирать х1 е D и
х2 е D, будем считать, что вектор х' s/x1 +(l-/)x2 npu te [0> l]>
обозначает выпуклую комбинацию х1 и х2. Так как D — выпуклое
множество, то мы знаем, что х' е D.
В экономике мы часто встречаемся с вогнутыми
вещественнозначными функциями, определенными на выпуклых областях. Вогнутыми мы
будем называть следующие функции.
Определение А1.22. Вогнутые функции.
/ :D —> R — вогнутая функция, если для всех х1, х2 е D
Дх')>1Дх[) + A-0Ах2) V/€[0, 1].
Следуя этому определению, будем считать, что / вогнута, если ее
значение в точке, являющейся выпуклой комбинацией двух точек, не
меньше выпуклой комбинации ее двух значений. Это определение
становится особенно понятным при графической иллюстрации.
Рассмотрим простую вогнутую функцию одной переменной, график
которой изображен на рис. А 1.23. Теперь выберем две точки на
графике — (х1, У) и (х2, у2) — и соединим их хордой. Из предыдущего
анализа выпуклых множеств следует, что, когда мы образуем любую
выпуклую комбинацию элементов из области определения х1 и х2, мы
получаем точку х1, делящую расстояние между jc1 и х2 в некоторой пропорции.
Если мы составим соответствующую комбинацию точек из области
значений yl=f(xl) и у2=/(х2)9 то получим точку у'=tf(xl) +
+A-/)/(х2), делящая расстояние между f(xl) и f(x2) в той же
пропорции, что и х* делит расстояние между х1 их2. Если мы нанесем точку
(У, у1) на плоскость, то тогда она будет лежать на хорде, соединяющей

Глава Ah Множества и отображения
595
(У, /(jc1)) и (х2, f(x2)). Абсцисса точки (jc', у') является выпуклой
комбинацией jc1 и х2 , а ее ордината — это выпуклая комбинация
значений функции / в точках х1 их2. Чтобы / была вогнутой, ордината
точки (У, /(*')) должна быть, по меньшей мере, такой же, что и ордината
точки (У, у1), т.е. должно выполняться неравенство /(*')> У = tf(xl) +
+A-/)/(jc2). На графике первая ордината больше второй, так что это
требование выполнено.
к
У
У
У
L
/1
/ 1
' 1
>^^ ' ^^
*,-Ят)
^^^¦^^^^.Z W
1 ь
*> х
Рис. А1.23. Вогнутая функция
Теперь, если мы рассмотрим все значения te [О, 1], то получим
абсциссы всех точек между jc1 и х2. Для каждого / все предыдущие
рассуждения справедливы. Вертикальное расстояние до графика превышает
вертикальное расстояние до хорды для каждого значения х*. Из этого
вытекает очень простое и интуитивно понятное правило: функция вогнута
тогда и только тогда, когда для любой пары точек на ее графике хорда,
их соединяющая, лежит на или ниже графика.
Чтобы увидеть, что произойдет, если вогнутость отсутствует,
рассмотрим функцию на рис. А 1.24. Эта функция вогнута на участках [0, х1]
и [л:2, ©о), как вы легко увидите, соединив хордами точки графика в
указанных промежутках. Однако она не является вогнутой на участке
[У, х2]. Мы можем построить хорду между точками (У, /(х1)) и
(jc2, /(jc2)) и найти такое t (скажем, t = —), для которого выпуклая ком-

596
Математическое приложение
бинация точек графика (У, у') лежит строго над (У, /(У)) • Так как мы
нашли две точки из области определения и по крайней мере одно
te [О, 1], такое, что /(х')<^(У) + A-/)/(х2), то определение
вогнутости нарушено.
у
У
Л*)
х1 х' х2
Рис. А 1.24. Вогнутые и невогнутые области
Посмотрите снова на рис. А1.23 и А1.24. Вы понимаете, чем
отличается вогнутая функция на рис. А 1.23 от невогнутой функции на
рис. А 1.24? Посмотрите на области под графиком на рис. А 1.23 и под
вогнутыми участками графика на рис. А 1.24. Сравните их с областью под
невогнутой частью на рис. А 1.24. Точки под вогнутыми участками
графиков демонстрируют «примерное поведение» в рассмотренном ранее
смысле. В частности, множества точек под графиком на обоих вогнутых
участках являются выпуклыми множествами. Множество точек под
невогнутой областью рис. А 1.24 не является выпуклым множеством. Эта
взаимосвязь между вогнутой функцией и множеством точек под ее
графиком в действительности является довольно общей и довольно
характерной. Она справедлива для всех вогнутых функций, а не только для
функций одной переменной. Довольно важно сформулировать этот
результат в виде теоремы.
Теорема А 1.13. Точки на графике вогнутой функции и ниже
него всегда образуют выпуклое множество.
Пусть ^4={(x,j)|xe Z), f(x)>y} есть множество точек «на и
ниже» графика f :D —> R, где DcR" — выпуклое множество и R сR.
Тогда
f — вогнутая функция <=> А — выпуклое множество.

Глава А1. Множества и отображения
597
Скоро мы столкнемся с несколькими теоремами подобного типа,
устанавливающими эквивалентность между определенным типом функций
и соответствующим выпуклым множеством. Доказательства одних
теорем будут опущены, а других — предложены в качестве упражнений. Так
как важно развить вашу интуицию в отношении этих взаимосвязей,
доказательство этой теоремы мы приведем полностью. Чтобы сделать
доказательство максимально ясным, мы не будем экономить на деталях.
Доказательство (подробное). Так как теорема устанавливает
эквивалентность между вогнутостью функции и выпуклостью множества А,
мы разобьем ее доказательство на две части и проведем доказательства в
обе стороны. Нам придется показать, что / вогнута => А выпукло и что
А выпукло => / вогнута.
Первая часть: / вогнута => А выпукло.
Предположим, что / — вогнутая функция. Тогда для векторов
х' = /х1 + A - /)х2 в силу определения вогнутых функций имеем
/(х')>//(х') + A-0Дх2) длявсех х\х2 е D и *е[0, l]. (P-1)
Возьмем любые две точки (х1, у1)е А и (х2, у2)е А . Из определения А
следует, что
Дх')>У и/(х2)>.у2. (P-2)
Чтобы доказать выпуклость А, мы должны убедиться в том, что
выпуклая комбинация (х', y() = (txl +(l-t)x2, tyx +(\-t)y2) также
принадлежит А при любых te [0, 1]. Так как D выпукло по условию теоремы, мы
знаем, что х' е D для всех /е [0, 1]. Таким образом, нам нужно всего
лишь показать, что /(х')>У для всех te [О, 1], чтобы установить, что
(х', У)е А. Но это легко. Из (Р-2), как мы знаем, следует /(х1) > у1 и
/(x2)>j/2. Умножая первое из этих неравенств на />0, а второе на
A -t)>0, получаем tf{xx)>tyx и (l-0/(x2)>(l-/)/ V/e[0, 1].
Суммируя эти неравенства, получим
tf{i}) + (\-t)f{x2)>ty'+(\-t)y2.
Используя (Р-1) и вспоминая, что у1 = ty] + A - t)y2, выводим
/{*')> у'.

598
Математическое приложение
Таким образом, (х', у1 )g А, так что А —выпуклое множество.
Это завершает первую часть доказательства и устанавливает
импликацию: / вогнута => А — выпуклое множество. Теперь нужно доказать
вторую часть.
Вторая часть: А выпукло => f вогнута.
Здесь мы предполагаем, что А — выпуклое множество, и надо
показать, что тогда / — вогнутая функция. Стратегия этой части
доказательства состоит в том, что мы выбираем любые две точки в области
определения D функции /, но в то же время выбор точек из А будет
специальным, а именно: две точки из А будут лежать не под графиком, а на
графике функции / и при этом будут соответствовать выбранным
точкам из области определения. Если мы сможем воспользоваться
выпуклостью множества А, чтобы установить, что / удовлетворяет определению
вогнутой функции для этих двух точек из области определения, то нам
удастся доказать общее утверждение теоремы, потому что выбор точек из
области определения произволен.
Выберем х1 е D и х2 е D, и пусть у1 и у2 удовлетворяют
следующим условиям:
У=/(х')и/=Лх2). (Р-3)
Точки (х1, у1) и (х2, у2), таким образом, лежат в А, потому что xl e D
и Дх') > у' для каждого i. Теперь образуем выпуклую комбинацию этих
двух точек (х'? у'). Так как А — выпуклое множество, (х', у1) тоже
лежит в А при любых te [О, 1]. Таким образом,
Дх')>/. (Р-4)
Теперь у1 =ty] +A-/)>>2, и мы можем подставить у\ пользуясь (Р-3).
Тогда
/^Дх'НО-ОДх2). (Р-5)
Объединив (Р-4) и (Р-5), получим Дх') > Дх') + A-0/(х2) V/e[0, l],
а значит, f — вогнутая функция.
Так как мы доказали утверждение теоремы в обе стороны (=> и ф=),
то доказательство завершено. ¦
Теперь у нас есть два эквивалентных способа описания вогнутых
функций: один способ использует значения функции, принимаемые в

Глава А1. Множества и отображения
599
точках выпуклых комбинаций любых двух точек, а второй — использует
«вид» множества, заданного графиком функции. Любой из подходов
полностью характеризует вогнутую функцию.
В соответствии с определением вогнутых функций на рис. А 1.25
изображена вогнутая функция. Ничто в этом определении или в теореме
А 1.13 не отрицает наличия линейных участков графика функции.
Множество под графиком все еще выпукло. В точке х* значение функции в
точности равняется выпуклой комбинации f(xl) и f(x2), так что
неравенство f(xl)>tf(xl) + (l-t)f(x2) все еще справедливо. Геометрически
точка (У, /(*')) просто лежит на хорде (а не строго над хордой),
соединяющей х1 и х2, так что все в порядке.
у
у2
У
хх х' х2
Рис. А1.25. / — вогнутая, но не строго вогнутая функция
Иногда бывает удобно исключить возможность линейных участков
на графиках функций. Строгая вогнутость позволяет это сделать.
Определение А1.23. Строго вогнутые функции.
/ : D —> R является строго вогнутой функцией тогда и только
тогда, когда при любых х1 Ф\2 из D
f(x')>tf(xl) + (l-t)f(x2) для всех te @, 1).
Обратите внимание на то, что различия между определениями
вогнутых и строго вогнутых функций хотя и незначительны, но важны.
Во-первых, строгая вогнутость требует от Дх'), чтобы значение было
строго больше, чем выпуклая комбинация /(х1) и /(х2), в отличие от
определения вогнутых функций, в котором знак неравенства — больше

600
Математическое приложение
или равно. Во-вторых, строгое неравенство должно быть выполнено для
всех t из открытого интервала @, 1), а не из отрезка [0, 1], как было
ранее. Это вполне разумно, так как, если t равняется или нулю, или
единице, то выпуклая комбинация совпадает с х2 или х1, тогда строгое
неравенство в определении не выполняется.
Геометрически эти модификации требуют, чтобы график функции
лежал строго над хордой, соединяющей любые две его точки, за
исключением их самих. Это приводит к невозможности появления линейных
участков на графике функции.
А1.4.3. Квазивогнутые функции
Вогнутость, строгая или нет — не важно какая, — является довольно
серьезным ограничением, накладываемым на функцию. Часто одной из
целей теоретической работы является поиск по возможности наиболее
слабых ограничений, необходимых для справедливости желаемого результата.
Квазивогнутость является близким, но более слабым свойством, чем
вогнутость, требованием которого зачастую можно ограничиться.
Определение А1.24. Квазивогнутые функции1.
Функция f :D —> R квазивогнута тогда и только тогда, когда для
всех х1 и х2 из D,
/(х')>тт\/(х1\ /(х2I при всех /е[0, 1].
Надо признать, что это определение на первый взгляд выглядит
крайне неуклюже. Оно говорит о том, что, если мы возьмем любые две точки
из области определения и образуем их выпуклую комбинацию, то
значение функции в этой точке должно быть не меньше наименьшего из
значений, принимаемых функцией в этих точках. Другим способом описания
квазивогнутых функций являются множества уровня.
Предположим, мы рассматриваем функцию у = /(*,, х2) и выбираем
любые две точки х1 и х2 из ее области определения. В каждой из этих
точек функция принимает какое-то значение, так что любая из них лежит в
некотором множестве уровня в области определения. Когда мы образуем
любую выпуклую комбинацию этих двух точек, мы получаем точку х',
лежащую где-то на хорде, соединяющей х1 и х2. Кроме того, функция
принимает какое-то значение в х', поэтому х' вдобавок лежит в некото-
Выражение min[tf, b] просто означает «наименьшее из чисел а и Ъ ». Если а > Ь, то
min[a, b] = b . Если а = b, то min[a, b] равняется и а, и b .

Глава AL Множества и отображения
601
ром множестве уровня. Теперь рассмотрим функции, множества уровня
которых изображены на рис. А 1.26. Для обоих рисунков будем считать,
что/(х')>Дх2).
х2
А
Ах1)
-> *i
->*!
(а)
(б)
Рис. А1.26. Множества уровня для квазивогнутых функций:
(а) — функция квазивогнутая и возрастающая; (б) — функция
квазивогнутая и убывающая
Если f(x) — возрастающая функция, она будет квазивогнутой
всякий раз, когда множество уровня, соответствующее любой выпуклой
комбинации из точек ?{\*), всегда находится на или выше ниболее низко
расположенного из множеств уровня ?{\х) и -Z~(x2). Этот случай
приведен на рис. Al.26(a). Если f(x) — убывающая функция, она будет
квазивогнутой всякий раз, когда множество уровня, соответствующее любой
выпуклой комбинации двух точек лежит всегда на или ниже наиболее
высоко расположенного из двух множеств уровня. Этот случай показан
на рис. А 1.26F).
Множества уровня на рис. А1.26 изображены гладкими по
определенной причине. Помимо того что они должны быть правильно
расположены по отношению друг к другу, квазивогнутость требует очень
правильного поведения ее супериорных множеств. Как можно догадаться,
они должны быть выпуклыми.
Теорема А1.14. Квазивогнутость и супериорные множества.
Функция f :D —»R. является квазивогнутой тогда и только тогда,
когда S(y) — выпуклое множество для всех у е R.

602
Математическое приложение
Доказательство. Достаточность. Сначала мы хотим показать, что,
если / квазивогнута, то S(y) будет выпуклым множеством для всех
ye R. Пусть у — любая точка из R и пусть S(y) — супериорное
множество по отношению к у. Пусть х1 и х2 — любые две точки из S(y).
(Если S(y) пусто, то результат очевиден, так как пустое множество
выпукло.) Мы хотим показать, что, если / квазивогнута, то все точки вида
х' = txl +(l-t)x2, /е[0, 1] также лежат в S(y).
Так как х1 е S(y) и х2 е S(y), то из определения супериорного
множества следует, что х1 и х2 обе из D и удовлетворяют
f(xl)>yaf(x2)>y. (P-1)
Теперь рассмотрим любую х'. Мы знаем, что x'eD, потому что мы
считаем, что D — выпуклое множество. Если / квазивогнута, то
f(x')>min[f(xl), f(x2)]>y. (P-2)
Первое неравенство — это определение квазивогнутости, а второе —
следует из (Р-1). Но если х'еАи f(x')> у, то х' удовлетворяет
требованиям принадлежности к S(y), так что S(y) должно быть выпукло. Это
завершает доказательство достаточности.
Необходимость. Здесь мы должны показать, что, если S(y) —
выпуклое множество для всех j>eR, то /(х) — квазивогнутая функция.
Чтобы это проделать, возьмем любые две точки из D — х1 и х2. Без
ограничения общности примем
f(xl)>f(x2). (P-3)
Из предложения выпуклости S(y) для любого yeR ясно, что
«S(/(x2)) должно быть тоже выпукло. Очевидно, х2 е S(f(x2)) и в силу
(Р-3) х1 е S(f(x2)). Тогда для любой выпуклой комбинации х1 и х2
х* е S(f(x2)). Из определения S(f(x2)) следует /(х')>/(х2), но из
(Р-3) вытекает
f(x')>mm[f(xll /(х2)],
так что f(x) квазивогнута, что и требовалось доказать. ¦
Эта теорема устанавливает эквивалентность между квазивогнутыми
функциями и выпуклыми супериорными множествами. Предположение,
что / квазивогнута, таким образом, аналогично предположению, что су-

Глава А1. Множества и отображения
603
периорные множества выпуклы, и наоборот. Заметим, однако, что из
всего, что было сказано, ничто не исключает возможности появления
«линейных участков», только на этот раз в множествах уровня. И
определение квазивогнутости, и теорема А 1.14 вполне согласуются с тем, что
изображено на рис. А 1.27: точки х1 и х2 лежат на плоской части одного и
того же множества уровня; хорда, их соединяющая, совпадает с
линейным участком множества, так что все выпуклые комбинации также будут
лежать на линейном участке. Здесь /(х1) = /(х2) = /(х/), так что
неравенство /(x/)>min[/(x1), /(x2)J выполняется, но в виде равенства.
Естественно, эта возможность исключается при условии строгой
квазивогнутости.
*2
> Дх1) = Ах2) = А\1)
I > *\
Рис. А1.27. Квазивогнутость и линейные участки множеств уровня
Определение А1.25. Строго квазивогнутые функции.
Функция f :D —» R строго квазивогнута тогда и только тогда,
когда для всех хх Фх2 из D, f(xx)>mm[f(xl), /(х2)] для всех te @, 1).
Мы снова требуем, чтобы / было из открытого интервала и
неравенство было строгим.
Полагая / принадлежащим открытому интервалу, мы тем самым
избегаем тривиальных случаев. Знак строгого неравенства запрещает
выпуклым комбинациям двух точек из одного и того же множества уровня
принадлежать тому же множеству уровня, т.е. ситуация, изображенная на
рис. А 1.27, становится невозможной. Таким образом, подобные выпуклые
комбинации должны лежать в строго супериорных множествах уровня,
например как на рис. А1.28. Тем самым, у строго квазивогнутых функций
супериорные множества не могут иметь плоских участков границы.

604
Математическое приложение
(а)
(б)
Рис. А1.28. (а) Функция строго квазивогнута и возрастает;
(б) — функция строго квазивогнута и убывает
> Xi
Мы начали обсуждение квазивогнутых функций, отметив, что
квазивогнутость является более слабым ограничением по сравнению с
вогнутостью. Поэтому можно предположить, что, если функция вогнута, она
будет обладать всеми свойствами квазивогнутых функций. Это
действительно верно, и мы завершим исследование квазивогнутости
доказательством этого факта. (При этом заметим, что обратное утверждение не
имеет силы. Квазивогнутая функция не обязательно вогнута.)
Теорема А1.15. Вогнутость предполагает квазивогнутость.
Вогнутая функция всегда квазивогнута. Строго вогнутая функция
всегда строго квазивогнута.
Доказательство. Теорема утверждает, что если / (строго) вогнута,
то / также (строго) квазивогнута. Мы приведем доказательство для
случая вогнутости, оставляя утверждение для строгой вогнутости в качестве
упражнения.
Допустим, что функция /: D —> R является вогнутой. Выберем
любые точки х1 и х2 из D и предположим без ограничения общности, что
Дх')>Дх2). (Р-1)
Из определения вогнутости для х' = tx1 + A - t)x2 мы должны получить
Дх') > гДх1) + A - 0Дх2) при всех t е [0, 1].
(Р-2)
Раскроем скобки в правой части неравенства, перегруппируем, вынесем
за скобки (>0и выразим (Р-2) в виде
Дх')*/(х2) + /(/(*')-/(i2)) длявсех/е[0, I]. (Р-З)

Глава А1. Множества и отображения
605
Теперь рассмотрим второе слагаемое из правой части неравенства
(Р-3). Мы знаем, что />0 и что в силу (Р-1) /(х1)-/(х2)>0, поэтому
это произведение неотрицательно и может быть строго больше нуля.
В том или другом случае правая часть должна быть больше или равна
fix2). В то же время мы знаем из (Р-1), что /(x2) = min[/(x1), fix2)].
Поэтому из (Р-1) и (Р-3), вместе взятых, следует, что
Дх')>тт[/(х1\ fix2)] для всех/е[0, 1],
а значит, / удовлетворяет определению квазивогнутой функции. ¦
А1.4.4. Выпуклые и квазивыпуклые функции
Последний из типов вещественнозначных функций, который мы
рассмотрим, это выпуклые и квазивыпуклые функции. Хотя терминология
может внести путаницу, нам следует различать термин «выпуклость» в
том смысле, в котором он применялся к множествам, и тот же термин
применительно к функциям. Как правило, выпуклость функции — это
всего лишь «обратная сторона» вогнутости. Так как понятию вогнутости
мы посвятили достаточно времени, а наиболее важные понятия уже были
проработаны, этот раздел будет короче предыдущего. Мы начнем с
некоторых определений.
Определение А1.26. Выпуклые и строго выпуклые функции.
1) f :D —> R является выпуклой функцией тогда и только тогда,
когда для любых х1, х2 из D
fix()<tfix]) + i\-t)fix2) при ecexte[0, I].
2) f : D —> R является строго выпуклой функцией тогда и только
тогда, когда для любых х1 ^х2 из D
f{xl) < /Дх1) + A - 0f{x2) при всех t е @, 1).
Рассмотрим /*:?>—>/?, где DcR. Определение выпуклой функции
требует, чтобы ее значение, принимаемое в любой выпуклой комбинации
двух точек, было не больше, чем образованная выпуклая комбинация из
значений fixl)n fix2). Геометрически это означает, что точка
(xl9 tfix]) + ([-t)fix2)) на хорде, соединяющей (х1, fix1)) и
(х2, fix2)), лежит не ниже, чем точка (*', fix1)). Некоторые примеры
выпуклых и невыпуклых функций приведены на рис. А1.29. Как видно на
рисунке, выпуклые функции могут иметь «линейные участки» на своих

606
Математическое приложение
графиках. Как и прежде, строгая выпуклость должна исключить
появление таких участков.
у
У
-+> х
-> х
(а)
(б)
-> х
-> х
(в) (г)
Рис. А1.29. Выпуклые функции (а) и (б); невыпуклые функции (в) и (г);
строго выпуклая функция (а)
Вогнутые и выпуклые функции тесно связаны, и это действительно
так. Мы уже упоминали, что одну из другой можно получить «зеркальным
отражением». Точнее говоря, между вогнутостью функции и выпуклостью
той же функции существует эквивалентность, но со знаком минус.
Теорема А 1.16. Вогнутые и выпуклые функции.
f{\) является (строго) вогнутой функцией тогда и только тогда,
когда — f(x) (строго) выпуклая.
Доказательство. Для доказательства нам потребуется произвести
некоторые манипуляции с определениями. Мы докажем достаточность и
оставим доказательство необходимости читателю.
Если /(х) вогнута, то f{xt)>tf{xx) + (\-t)f{x2) для всех х1 и х2 из
?>, и /е[0, 1]. Умножение на -1 дает -f(x')<t(-f(xl)) +
+(l-t)(-f(x2)), так что — f(x) — выпукла.
В то время как вогнутость требует от точек, лежащих под графиком
функции, чтобы они образовывали выпуклое множество, выпуклость
требует, чтобы множество точек на графике и над ним было выпукло.

Глава А1. Множества и отображения
607
Теорема А1.17. Точки на графике выпуклой функции и над
ним всегда образуют выпуклое множество.
Пусть А* = {(х, у)\хе D, /(Х)-У) —множество точек, лежащих
«на графике и над графиком функции» f: D —> R, где DczR" —
выпуклое множество и R с К. Тогда
f —выпуклая функция <=> А*—выпуклое множество.
Доказательство. По теореме А 1.16 /(х) выпукла тогда и только
тогда, когда - f{x) вогнута, и по теореме А 1.13 последнее имеет место в
том и только в том случае, если множество
Аш{(х, y)\xeD, -f(x)>y}
выпукло. Заметим, что, поскольку у может быть как положительным, так
и отрицательным числом, мы можем переписать множество А в виде
Л = {(х, -y)\xeD, -Дх)>->;}ее{(х, -у)\ке D, f(x)<y}.
Таким образом, мы показали, что f(x) выпукла тогда и только тогда,
когда множество Л = {(х, -у)\хе D, f(x)<y} выпукло.
В заключение заметим, что А выпукло тогда и только тогда, когда
А* выпукло, потому что (х, у)е А* тогда и только тогда, когда
(х, -у)е А . Мы заключаем, что f(x) является выпуклой функцией тогда
и только тогда, когда А* — выпуклое множество. ¦
Функция также может быть квазивыпуклой. Как следует из названия,
квазивыпуклость является более слабым условием, чем выпуклость.
Определение, следующее ниже, похоже по форме на то, что было ранее, но
советуем следить за деталями.
Определение А1.27. Квазивыпуклые и строго квазивыпуклые
функции1.
1) Функция f :D -» R квазивыпукла тогда и только тогда, когда
для любых х1, х2 из D
Дх')<тах[Дх'), Дх2)] Vfe[0, 1].
2) Функция f :D —> R строго квазивыпукла тогда и только тогда,
когда для любых х1 Фх2 из D
/(х/)<тах[/(х1), Дх2)] V/e@, 1).
1 Выражение тах[д, Ь] означает «наибольшее из а и Ь ». Если а > Ъ, то max [а, Ъ\-а .
Если а = Ъ, то max [a, b] равняется и а, и Ъ .

608
Математическое приложение
Все эти формулы здесь снова могут выглядеть неуклюже. К счастью,
мы знаем кое-что о множествах уровня и других множествах, связанных с
квазивыпуклыми функциями. Результаты будут противоположны тем, что
мы получили ранее. Для квазивыпуклой функции выпуклыми являются
инфериорные множества. Если квазивыпуклая функция возрастает, то
это будет множество точек, лежащих ниже множества уровня. Если она
убывает, то это будет множество точек, лежащих выше множества
уровня. Это проиллюстрировано на рис. А 1.30 и детально будет рассматрено
далее. Доказательство следующей теоремы мы оставляем в качестве
упражнения.
Х2 Xj
-> Х\
¦> *1
(а)
(б)
Рис. А1.30. У квазивыпуклых функций выпуклые инфериорные
множества; у строго квазивыпуклых функций нет линейных участков в их
множествах уровня; (а) — строго квазивыпуклая и возрастающая функция;
(б) — строго квазивыпуклая и убывающая функция
Теорема А 1.18. Квазивыпуклость и инфериорные множества.
f :D —>R является квазивыпуклой функцией тогда и только тогда,
когда 1(у) — выпуклое множество для всех ye R.
Как мы уже видели, между вогнутостью функции и выпуклостью
функции со знаком «минус» существует эквивалентность. Аналогичная
эквивалентность связывает квазивогнутые и квазивыпуклые функции.
Теорема А 1.19. Квазивогнутые и квазивыпуклые функции.
f(x) является (строго) квазивогнутой функцией тогда и только
тогда, когда— f(\) является (строго) квазивыпуклой функцией.
Доказательство. И на этот раз мы докажем лишь достаточность.
Если f{\) квазивогнутая функция, то /(x/)>min[/(x1), /(x2)]. Умножив
на -1, получим -f(x')<min[-f(xl), -/(x2)] = max[/(x1), Дх2)], так

Глава Ah Множества и отображения
609
что -/(х) квазивыпуклая функция. Необходимость доказывается столь
же просто. ¦
Наконец, некоторые из важных взаимосвязей между различными ве-
щественнозначными функциями, изученные нами, сведены в рис. А 1.31.
f вогнутая ^ множество точек под графиком выпукло
/ выпуклая <=> множество точек над графиком выпукло
/ квазивогнутая <=> супериорные множества выпуклы
/ квазивыпуклая <=> инфериорные множества выпуклы
/ вогнутая => /квазивогнутая
/ выпуклая => /квазивыпуклая
/ (строго) вогнутая <=> -/ (строго) выпуклая
/ (строго) квазивогнутая О -/ (строго) квазивыпуклая
Рис. А 1.31. Основные результаты
А1.5. Упражнения
А1.1. Операции объединения и пересечения множеств подчиняются
коммутативному и дистрибутивному законам. Коммутативный закон
для объединений множеств утверждает, что S и Г = Г u S, а для
пересечений SnT = TnS. Дистрибутивный закон для пересечений говорит,
что для трех множеств R, S и Т Rn(SпТ) = (R nS)пТ), а, для
объединений Ли^иГ^СЯиЗ'ЭиГ. Проверьте эти законы, используя
диаграммы, аналогичные изображенным на рис. А 1.1.
А1.2. Следующие утверждения интуитивно «очевидны». Докажите
каждое из них.
аMсEиГ).
б) Tcz(SuT).
B)(SnT)dS.
r)(SnT)czT.
А1.3. Законы де Моргана говорят нам, о том, что
(SnT)c=ScvTc
(SKjT)c=ScnTc.
Докажите эти законы.

610
Математическое приложение
А1.4. Распространите законы де Моргана на случай произвольного
набора множеств. Докажите, что для любого индексного множества /
(ns,.)c = us;
\/€/ '/ 16/ '
Kiel '/ /€/ '
А1.5. Пусть А и В — выпуклые множества. Докажите, приведя
контрпример, что АиВ, вообще говоря, невыпуклое множество.
А1.6. Распространите теорему А 1.1 на случай произвольного набора
выпуклых множеств.
А1.7. Нарисуйте указанные ниже множества. Если множество
выпукло, то докажите это. Если невыпукло, то приведите контрпример.
а){(х, у)\у = ех}.
б){(х, у)\у>ех].
в) {(*> у)\у>2х-х2; х>0, ^>0}.
г){(*, У)\ху>\\ *>0, у>0}.
д){(*, у)\у<Ы(х)}.
А1.8. Пусть S — множество людей, живущих на Земле. Пусть
отношение R означает «любит». Будет ли Л полным? А транзитивным?
А1.9. Пусть А и В — два множества из области определения D\
предположим, что В с: А. Докажите, что f(B) с f(A) для любого
отображения /:?>—»#.
ALIO. Пусть А и В — два множества из множества значений R;
предположим, что В а А. Докажите, что f~x{B)af~\A) для любого
отображения /: D -> R.
Al.ll. Рассмотрим функцию f(x) = x2. Опишите образ функции и
определите, является ли функция взаимооднозначной и является ли она
отображением на себя, если:
а) D = R, R = R;
б) D = E, Л = М+;
в) ?> = Е+, Л = М;
г) D = R+9 R = R+;

Глава А1. Множества и отображения
611
А1.12. Существует ли функция, обратная функции, изображенной на
рис. A 1.8(a)? Ответьте на тот же вопрос относительно функции,
изображенной на рис. А1.8(б). Обоснуйте ответ.
А1.13. Пусть /: D —> R — любое отображение, и пусть В — любое
множество из множества значений R. Докажите, что f~l(Bc) = (f~l(B))c.
А1.14. Для любого отображения f:D—>R и любых двух множеств
А и В из множества значений R докажите, что
Г\АиВ) = Г1(А)иГ\В)
Г!(АпВ) = Г1(А)пГ1(В).
А1.15. Пусть {i4,}fe/ с Л — любой набор (конечный или
бесконечный) множеств из множества значений отображения /. Используйте
доказательство из предыдущего упражнения, чтобы показать, что
А1.16. Пусть S и Т — выпуклые множества. Докажите, что каждое
из приведенных ниже множеств выпукло.
а) -5 = {x|x = -s, seS).
б) 5-r = {x|x = s-t, seS, t<=r}.
A1.17. Пусть Ai <zW — выпуклые множества, / = 1, ...,«. Докажите,
что приведенные ниже множества являются выпуклыми.
а)п;ш14.
б) х"=1 Ai (декартово произведение).
в) ^Aiг^^^.Це Ап / = 1, ...9п> (сумма множеств).
г) ^аЦ sj^Ta'a,. oc'e R, ate Ап / = 1, ...,п> (линейная
комбинация множеств).
А1.18. Пусть /; (х) = а' • х + Ь' для а' € R", bi е R. Рассмотрим
неравенства /'(х)>0 для / = 1, ...,«. Пусть Q = {x|/'(x)>0, / = 1, ...,и} —
множество решений этих п линейных неравенств. Покажите, что Q, —
выпуклое множество.

612
Математическое приложение
А1.19. Мы иногда пишем ||х|| = |х-0||, чтобы обозначить расстояние
от начала координат в Ш" до точки х. Рассмотрим любой вектор tx, где
/ > 0 является неотрицательным скаляром. Докажите, что ||/х| = /|х|.
А1.20. Рассмотрите любой открытый интервал (я, Ь). Покажите, что
(д, 6) = 1?.Г^1гдее = F-а)/2.
А1.21. Докажите часть 4 из теоремы А1.2. Будет ли пересечение
бесконечного множества открытых множеств открытым множеством?
А1.22. Рассмотрим любые две точки х1 и х2из R". Пусть Ве(х1) —
любая окрестность точки х1.
а) Пусть Z ={z|z = txx + (l-t)x2, *e [0, 1]} — множество всех
выпуклых комбинаций х1 и х2. Докажите, что fi?(x1)nZ^0.
б) Пусть Z* ={z\z = txl +(l-t)x2, te@, l)J — подмножество Z, не
содержащее х1 и х2. Докажите, что fi?(x')nZ*^0.
А1.23. Докажите часть 4 из теоремы А 1.4.
А1.24. Рассмотрите интервалы из R вида [а, -н») и (-<», Ь].
Докажите, что оба эти множества замкнуты. Будет ли этот результат верен,
если заменить данные интервалы на [я, с) и (-с, Ь] для конечного с ?
А 1.25. Пусть ScR — множество, состоящее из одной точки S = {s}.
Докажите, что S является замкнутым, выпуклым множеством.
А1.26. Пусть (a, i)cR — любой открытый интервал. Докажите, что
его дополнением является множество (а, Ь)с =(-°°, я]и[6, -н»).
Докажите, что дополнение любого открытого интервала — это объединение
двух замкнутых множеств.
А1.27. Любое замкнутое множество действительных чисел обладает
специфическим свойством: его можно представить в виде пересечения
(возможно, бесконечного) объединений простых замкнутых интервалов.
Точнее, для любого замкнутого множества S a R
S = n((-oo, я,]и[6,., +оо))
для некоторых действительных чисел ai < bf и некоторого индексного
множества / . Приведите доказательство этого утверждения.
А1.28. Пусть D — подмножество R". Докажите аналоги теорем А1.2
и А 1.4 для открытых и замкнутых множеств из D. Например, аналог
третьего утверждения теоремы А 1.2 будет звучать так: «объединение от-

Глава А1. Множества и отображения
613
крытых множеств из D является открытым множеством в ?>».
Формулировки остальных аналогов выглядят похоже.
А1.29. Рассмотрите следующие утверждения.
а) Покажите, что [0, 1) открыто в R+, но не в R .
б) В пункте а) вы увидели, что открытые множества в R+ не
обязательно открыты в R. Покажите, что тем не менее замкнутые множества
R+ являются замкнутыми в R .
в) Докажите более общий результат. Покажите, что если D —
подмножество из R" и D открыто (замкнуто) в W, то SaD открыто
(замкнуто) в D тогда и только тогда, когда оно открыто (замкнуто) в R".
А1.30. Докажите, что если b является точной верхней гранью
множества S с R и S — открытое множество, то b€ S. Докажите, что если Ъ
является точной верхней гранью множества SczR и S — замкнутое
множество, то be S.
А1.31. Пусть о^ >0, ос2>0 и C>0 — действительные числа.
Рассмотрим подмножество точек из R2, заданное Q = {х€ Ш2+ \а^ +
+а2х2 < Р}. Докажите, что Q — выпуклое множество. Нарисуйте Q на
плоскости. Если х{ = 0, какое наибольшее значение может принять х2 ?
Если х2 = 0, какое наибольшее значение может принять х{ ? Изобразите
найденные точки на той же координатной плоскости. (Ничего не
напоминает?) Докажите, что Q ограничено.
А1.32. Множество S"~l = < х
]Гл:;=1, jcf. > 0, / = 1, ...,п> называется
(п -1) -мерным единичным симплексом.
а) Изобразите это множество для п = 2 .
б) Докажите, что S"~l —выпуклое множество.
в) Докажите, что S"~l —компактное множество.
А1.33. Докажите аналог теоремы А1.6 для замкнутых множеств. То
есть покажите, что следующие утверждения эквивалентны:
а) Отображение/:D ->R" непрерывно.
б) Для любой замкнутой окрестности В в R" ее прообраз для /
замкнут в D.
в) Для любого замкнутого подмножества S в R" его прообраз для /
замкнут в D.

614
Математическое приложение
А1.34. Докажите, что отображение/:D->R" непрерывно тогда и
только тогда, когда f~l(T) является компактом в области Z)cRm для
любого компактного множества Т из множества значений R".
А1.35. Чтобы убедиться в том, что условия теоремы А 1.10
достаточны, но не являются необходимыми, приведем простой пример,
проиллюстрированный на рис. А 1.18, на котором функция / вещественнозначна
и непрерывна, SczD не является компактом, однако оба значения —
максимум и минимум — на S существуют. Придумайте пример, в
котором S не является компактом, / не является непрерывной функцией,
однако у / на множестве S максимум и минимум существуют.
А1.36. Любая гиперплоскость делит R" на два «полупространства»:
множество точек «на гиперплоскости и над ней», Н+ = {х|а-х>а}, и
множество точек «на гиперплоскости и под ней», Н~ ={х|а-х<а}.
Докажите, что эти полупространства являются замкнутыми, выпуклыми
множествами.
А1.37. Убедитесь в том, что условия теоремы Брауэра достаточны, но
не необходимы для существования неподвижной точки, построив
следующие примеры:
а) S компактно, S выпукло, / не является непрерывной функцией,
но неподвижная точка / существует;
б) S компактно, S не выпукло, / является непрерывной функцией,
но неподвижная точка / существует;
в) S не компактно, S выпукло, / является непрерывной функцией,
но неподвижная точка / существует;
г) S не компактно, S не выпукло, / не является непрерывной, но
неподвижная точка / существует.
А1.38. Пусть f(x) = x2, предположим, что S = (О, 1). Покажите, что
/ не имеет неподвижной точки, хотя и является непрерывным
отображением из S на S. Противоречит ли этот пример теореме Брауэра или нет?
А1.39. Покажите с помощью теоремы Брауэра, что уравнение
cos(x) -jc-1/2 = 0 имеет решение на интервале 0 < х < л 14.
А1.40. Нарисуйте несколько линий уровня следующих функций:
а) у = х1х2;
б) у = х{ +х2;
в) у = тш[х19 дг2].

Глава А1. Множества и отображения
615
А1.41. Докажите теорему А1.12. Не забудьте, что для утверждений 3,
6—8 следует доказать, что А с В и В с: А.
А1.42. Пусть ?> = [-2, 2] и /:?>-»/? задана формулой у = 4-х2.
Аккуратно постройте ее график. Используя определение вогнутой
функции, докажите, что / вогнута. Продемонстрируйте, что множество А
является выпуклым.
А1.43. Завершите доказательство теоремы А 1.15.
А1.44. Докажите теорему А1.18.
А1.45. Завершите доказательства теорем А1.16 и А1.19.
А1.46. Рассмотрите произвольную линейную функцию f(\) = а • х + 6
для аеГийеМ.
а) Покажите, что любая линейная функция одновременно выпукла и
вогнута, хотя и не является ни строго вогнутой, ним строго выпуклой.
б) Покажите, что любая линейная функция одновременно квазивы-
пукла и квазивогнута, хотя и не является ни строго квазивогнутой, ни
строго квазивыпуклой.
А1.47. Пусть /(х) — вогнутая (выпуклая) вещественнозначная
функция. Пусть g(t) — возрастающая вогнутая (выпуклая) функция
одной переменной. Покажите, что сложная функция h{\) = g(/(x)) —
вогнутая (выпуклая) функция.
А1.48. Пусть /(*,, х2) = -(х1 -5J -(х2 -5J. Докажите, что /
квазивогнутая функция.
А1.49. Ответьте на каждый из ниже приведенных вопросов «да» или
«нет» и обоснуйте свой ответ.
а) Предположим, f(x) — возрастающая функция одной переменной.
Является ли f(x) квазивогнутой?
б) Предположим, f(x) — убывающая функция одной переменной.
Является ли f(x) квазивогнутой?
в) Предположим, f(x) — функция одной переменной и существует
такое число b, что функция f(x) убывает на интервале (-©о, Ь] и
возрастает на интервале [Ь, -н»). Является ли f(x) квазивогнутой?
г) Предположим, f(x) — функция одной переменной и существует
такое число Ь, что функция f(x) возрастает на интервале (-<*>, Ь] и
убывает на интервале [Ь, +«>). Является ли f(x) квазивогнутой?
д) Теперь вы должны быть готовы к тому, чтобы охарактеризовать
квазивогнутые функции одной переменной, используя слова
«возрастание» и «убывание».

Глава А2. Математический анализ
и оптимизация
А2.1. Математический анализ
II
А2ш1.1. Функции одной переменной
Грубо говоря, функция у = f(x) дифференцируема, если она
одновременно является непрерывной и «гладкой», т.е. не имеет скачков и
изломов. Функция на рис. А2.1(б) дифференцируема везде, в то время как
функция на рис. А2.1(а) не дифференцируема в точке jc°. Таким образом,
дафференцируемость — это более жесткое требование^ чем
непрерывность. Мы часто налагаем это условие, также потому что дифференци-
руемость позволяет использовать хорошо известную нам технику
математического анализа.
У У
¦> х
-> х
(а)
(б)
Рис. А2.1. Недифференцируемая (а) и дифференцируемая (б) функции
одной переменной
Понятие производной f'(x), без сомнения, вам знакомо.
Производная является функцией, показывающей для каждого х наклон
касательной, или мгновенную скорость изменения f(x). Поэтому мы иногда
пишем:
dy
dx
= f\x),
(А2-1)
тем самым показывая, что f\x) дает нам (мгновенную) величину
отношения dy к dx, где dy есть изменение у, a dx есть изменение х. Если

Глава А2. Математический анализ и оптимизация
617
(первая) производная дифференцируема, то мы можем взять производную
от нее, получив вторую производную первоначальной функции
ТГ = /*(*)• (А2-2)
ах
Если функция обладает непрерывными производными /', /", ..../*% то
она называется п раз непрерывно дифференцируемой, или функцией
класса С". Некоторые правила дифференцирования приведены в таблице
А2.1 для справки.
Таблица А2.1
Правила дифференцирования
Правило дифференцирования константы, a d
Правило дифференцирования суммы d x
—[f(x) ± g(x)\ = f(x)±g (х)
Правило дифференцирования степенной d ,
функции "? (а-хя) = па-х-
Правило дифференцирования произведения d г п , ,
¦т-1/W' ?(*)] = /(*)? (*) + / (x)g(x)
dx
Правило дифференцирования отношения d
~dx~
fM
g(x)
g{x)f\x)-f{x)g\x)
ШJ
Правило дифференцирования сложной d г 4-i r/ ,
функции -f L/(«W)J = / (*(*))•*(*)
Аналогично тому как производная f\x) дает (мгновенную) скорость
изменения f(x) за единицу изменения л:, точно так же f"(x) дает
скорость изменения f\x) за единицу изменения х. То есть f\x) дает
скорость, с которой меняется наклон касательной к графику /.
Впоследствии мы увидим, что вторая производная связана с кривизной графика
функции /.
Например, на рис. А2.2 изображена вогнутая функция. Тот факт, что
ее график «изогнут кверху», характеризуется уменьшением угла наклона
касательной с ростом х, т.е. неположительностью второй щюизводной.
(Заметим, что f'(x°), наклон прямой /0, больше, чем /'(V), угол
наклона прямой /j.)
Из рис. А2.2 ясно, что функция вогнута, если ее вторая производная
неположительная на некотором интервале. Позже мы докажем теорему о
связи между вогнутостью и неположительностью второй производной.
Нарисуйте несколько графиков, чтобы убедиться в этом.

618
Математическое приложение
У
А
-> х
Рис. А2.2. Кривизна и вторая производная
Из рис. А2.2 следует еще кое-что. Заметим, что обе касательные /0 и
1Х лежат полностью выше графика (иногда лишь чуть-чуть выше).
Рассмотрим прямую /0. Это прямая с наклоном f'(x°), проходящая через
точку ( х°, f(x°)). Можно получить уравнение касательной
10(х) = Г(х0)(х-х0) + Дх°).
Когда мы говорим, что прямая /0 лежит над графиком /, имеем в
виду, что /0(х) > f{x) для всех х. Отсюда следует неравенство
f(x)<f(x°) + f'(x°)(x-x0)
для всех х. Таким образом, это неравенство следует из вогнутости /.
Теорема А2.1, которую мы сформулируем без доказательства,
обобщает указанные наблюдения и характеризует вогнутые функции одной
переменной двумя способами: первый способ — это описание вогнутых
функций с помощью второй производной, второй — с помощью первой
производной и уравнения касательной.
Теорема А2 Л. Вогнутость и первая и вторая производные.
Пусть D — невырожденный интервал действительной прямой, на
котором f дважды непрерывно дифференцируема. Утверждения 1)—3)
эквивалентны:
1) f вогнута;
2) f\x)<0 VxeD;
3) для всех x°eD: f{x)<f{x*) + f'{x0){x-xQ), VxeD.

Глава А2. Математический анализ и оптимизация
619
Более того:
4) если f"{x) < О Vjce D, тогда f строго вогнута.
В силу того что функция / является выпуклой, если / вогнута,
теорема А2.1 помогает описать выпуклые функции. Достаточно заменить
слово «вогнутый» на слово «выпуклый» и поменять на противоположные
знаки всех неравенств. Можно было бы предположить, что утверждение,
обратное утверждению 4, справедливо, т.е., если / строго вогнута, ее
вторая производная должна быть строго отрицательна на интервале
вогнутости. Вам будет предложено показать, что это не так, в упражнении А2.20.
А2.1.2. Функции многих переменных
Как правило, мы рассматриваем вещественнозначные функции
многих переменных, и идеи, которые только что были обсуждены, легко
переносятся на случай со многими переменными.
В одномерном случае удобно рассматривать производную функции
как наклон, или скорость изменения у относительно изменения х. Если
единственным аргументом функции является х, то любое изменение
значения у связано с изменением jc . Однако у вещественнозначных
функций п переменных, у зависит от всех п переменных jc, ,...,*„. Поэтому в
этом случае представить себе наклон, или скорость изменения у, гораздо
труднее, нежели в одномерном случае. Хотя вполне естественно найти
сначала наклон при изменении х{, затем наклон при изменении х2 и так
далее для всех п переменных, от которых зависит у. Вместо
единственного наклона функция п переменных имеет п частных наклонов,
каждый из которых показывает скорость изменения функции при изменении
лишь только одной из переменных х.. Любой из этих частных наклонов
называется частной производной. Иными словами, частные производные
определяются как обыкновенные производные, т.е. как предел отношения
приращения значения функции к приращению одного из аргументов
функции.
Определение А2.1. Частные производные.
Пусть y = f(xl9 ...,xn). Частная производная f no Xt определяется как
д/(*) _ Ит/(*р -, *, + *, -, *„)-/(*!, ..., xi9 ...» хп)
Эх,. *-*<> h
Для обозначения частной производной используется такэюе запись
ду/дх(, или просто yj(x).

620
Математическое приложение
Сделаем несколько важных замечаний о частных производных.
Во-первых, если имеется п производных, то каждая из них вычисляется по
своей переменной х,.. Во-вторых, как и в случае с функцией одной
переменной, любая из частных производных является функцией. В частности,
каждая частная производная является функцией, зависящей от значений
всех переменных х,, ...9хп. Наконец заметим, что частная производная
определяется в каждой точке области, чтобы оценить, насколько изменится
значение функции при изменении одного xi, если значения всех остальных
(и-1) переменных остаются неизменными. Таким образом, чтобы
вычислить частную производную, скажем, по х,. следует вычислить
обыкновенную производную по х,., полагая все прочие переменные х., j' * i
константами. Рассмотрим пример функции двух переменных.
Пример А2.1. Пусть /(х,, jc2) = jc,2 + Зх,х2 -х2 . Эта функция двух
переменных, поэтому у нее две частные производные. Мы вычислим
частную производную по хх, дифференцируя по хх и считая х2 постоянной
величиной. Таким образом, мы получим:
Эх,
В формуле, задающей исходную функцию, мы считали множители 3 и х2
константами. В третьем слагаемом этой формулы х, совсем не
присутствует, так что данный член считается константой. Поскольку производная
константы равна нулю, в выражении для производной вклад третьего
члена нулевой.
Следуя этому принципу, мы можем продифференцировать исходную
функцию по х2, на этот раз считая, что хх — константа. Частная
производная по х2 будет равна
Ш^Ы = Зх{-2х2.
дх2
Обратите внимание, что каждая из частных производных в этом
примере является функцией обеих переменных х, и х2. Поэтому
значения, принимаемые частными производными, будут, вообще говоря,
различны для разных х, и х2. В точке A,2) значения производных
составляют /|A, 2) = 8 и /2A, 2) = -1. В точке B, 1) они соответственно равны
/B, 1) = 7и/2B, 1) = 4. ?

Глава А2. Математический анализ и оптимизация
621
Легко увидеть, что каждая частная производная говорит нам о том,
является функция возрастающей или убывающей, если мы будем
изменять одну эту переменную, оставляя все остальные переменные
фиксированными. Другими словами, значение частной производной показывает,
как изменяется функция при изменении аргумента в направлении одного
из п единичных векторов. Иногда полезно знать, растет или убывает
значение функции, если мы движемся в каком-либо направлении от
некоторой точки из области определения.
Давайте зафиксируем точку х = (лгр ...,хп)еКй из области
определения/ Предположим, мы хотим выяснить, как изменяется значение
функции/по отношению к /(х) при удалении от х в сторону z = (z,, ...,zw).
Функция
g(t) = f(x + tz),
определенная для / е R, поможет нам в этом деле. Заметим, что g(t)
принимает значение f(x) при / = 0 и при росте /, начиная с нуля, x + /z
движется в сторону z . Если в результате мы получим, что g(t)
возрастает при возрастании / в сторону положительных значений, то мы сделаем
вывод о возрастании / при движении от х в сторону z . Таким образом,
нам следует выяснить, будет производная g'@) положительной,
отрицательной или равной нулю.
Сейчас мы предложим эвристическое описание вычисления g'@).
Сначала заметим, что согласно определению g'@) — всего лишь
скорость, с которой/изменяется за единицу изменения t. Далее, xt —
координата в области определения/— возрастает со скоростью zi за единицу
изменения t. Более того, скорость изменения/за единицу изменения /-й
координаты равняется ff(x), /-й частной производной/в точке х. Затем
скорость изменения/за единицу изменения t обусловлена изменением /-й
координаты и равна /(x)z;. Суммарная скорость изменения/просто
равняется сумме всех изменений, порожденных каждой из координат. Таким
образом,
/=i
Выражение в правой части уравнения известно как производная по
направлению /в точке х в направлении z1. Это выражение можно записать
компактнее, используя векторное обозначение.
Строго говоря, чтобы вычисления были справедливы,/должна быть непрерывно
дифференцируемой.

622
Математическое приложение
Прежде чем сделать это, несколько слов о принятых векторных
обозначениях. Все векторы считаются векторами-столбцами, если не
оговорено противное. Мы будем писать х = (хр ...,*„), даже если х вектор-
столбец. Это избавит нас от неудобства постоянно использовать символы,
означающие транспонирование, т.е. х = (хр ...,хп)Т.
Имея это в виду, запишем все п частных производных как вектор-
строку V/(x) = (/J(x), ...,/w(x)). Вектор-строка V/(x) называется
градиентом / в точке х. Тогда производная по направлению / в точке х в
направлении z может быть записана следующим образом:
g'@) = V/(x)z. (A2-3)
Заметим, что частная производная / по xi тем самым
становится просто производной по направлению / в направлении
(О, ..., О, 1, 0, ...,0), где 1 стоит на i-m месте. Таким образом, все
частные производные — это просто специальный случай производных по
направлению. Вместе с тем (А2-3) дает нам информацию о том, что
скорость, с которой / изменяется в любом направлении, определяется
вектором частных производных, т.е. градиентом /. Таким образом, полезно
представлять градиент V/ как аналог производной функции одной
переменной. Как и ранее, градиент сам по себе является функцией, потому что
он отображает каждую точку х из области определения в вектор,
состоящий из п «частных наклонов». Мы также можем взять производную от
этих производных и получить нечто близкое ко второй производной.
Давайте рассмотрим одну из частных производных функций,
например по переменной хх. Прежде всего, заметим, что
ЗА*,, ...,*„)
сама является функцией п переменных. Изменение любой координаты х,
в принципе может повлиять на ее значение. Таким образом, fx{\) сама
имеет п частных производных.
Нет принципиальной трудности в вычислении п частных
производных от производной (первого порядка) /|(х). Каждая из этих
производных будет получена дифференцированием по своей переменной, при этом
все прочие переменные будут считаться константами; правила
дифференцирования функций одной переменной вполне применимы. Результат
дифференцирования (он тоже сам по себе будет функцией п переменных)
называется частной производной второго порядка. Когда /|(х) диффе-

Глава Л2. Математический анализ и оптимизация
623
ренцируется по х/5 то получается частная производная второго порядка
по х, и х;. , обозначаемая
Э ГЭ/(х)Л
Эх
7 V
Эх,
или
1 У
Эх.Эх,
, или /.(х).
Так как мы получили п частных производных от частной
производной по х,, каждая из которых является производной по одной из х, при
/ = 1, ...,«, то эти производные можно записать в виде градиента. На этот
раз вектор будет градиентом частной производной по х,, т.е. fx(x). Мы
можем записать этот градиент как
УЛ(х) =
Э2Дх) Э2ДхI_
Эх Эх,
Ц^Сх),...,/;„(х)).
Теперь нами получены п частных производных первого порядка от
исходного градиента V/J(x). Мы можем повторить процедуру,
проделанную с /рив совокупности получить п градиентов V/J(x), где / = 1, ...,«.
В сущности, когда мы это проделываем, мы берем «градиент от
градиента» исходной функции /, при этом не забывая, что любая из частных
производных в «-мерном векторе градиента сама имеет п частных
производных. Если мы представим все векторы V/j(x), где каждый вектор
состоит из частных производных второго порядка, в виде матрицы,
располагая один вектор над другим построчно, то мы получим
(fu{x) fl2(x) ... /и(х^
„, Л /2i00 /22оо - /2*00
ЩХ) -
Ui« /я2оо - /*„(х)>
Заметим, что Н(х) содержит все возможные частные производные
второго порядка исходной функции. Н(х) называется матрицей Гессе
функции f(x). Теперь вспомним аналогии между градиентом и первой
производной. Матрица Гессе была получена взятием градиента от
градиента, поэтому мы можем считать Н(х) аналогом второй производной
функции одной переменной.
Время от времени мы будем ссылаться на следующую важную
теорему о частных производных второго порядка. Она будет приведена без
доказательства.

624
Математическое приложение
Теорема А2.2. Теорема Юнга.
Для любой дважды непрерывно дифференцируемой функции f(x)
Хотя мы не даем доказательства теоремы Юнга, ее суть мы
проиллюстрируем следующим примером.
Пример А2.2. Рассмотрим функцию f(xv x2) = xlxl+xlx2, которая
имеет следующие частные производные первого порядка:
Т- = /(х) = *2 +*2 И "Г—= /2(x) = 2xiX2+X1.
ох1 ох2
Если мы продифференцируем /| по х2, то получим
а2/ _
Эх,Эх
= f12(x) = 2x2 + l.
Дифференцируя f2 по х{, получаем
:>2
Э/ ^/21(х) = 2*2+1
oXjdx2
Ясно, что /, = /2 для любого х, о чем и шла речь в теореме Юнга. ?
Как и вторая производная, матрица Гессе является функцией. Она
отображает любое х из области определения в множество значений
пхп = п2 частных производных второго порядка, и значения,
принимаемые каждым элементом матрицы Н(х), будут, вообще говоря,
различаться в зависимости от х. Теорема Юнга утверждает, что матрица Гессе
симметрична. Можно было бы ожидать, что по аналогии с одномерным
случаем матрица, составленная из частных производных второго порядка
функции /, содержит информацию о кривизне функции. Так оно и есть,
и сейчас мы займемся изучением этого факта.
В случае одной переменной теорема А2.1 устанавливает тот факт, что
кривизна вогнутой функции может быть выражена посредством ее второй
производной, или же расположением графика функции по отношению к
ее касательной. Такой же вывод можно сделать для случая со многими
переменными. Чтобы легче это было понять, приведем сначала
следующий результат.

Глава А2. Математический анализ и оптимизация
625
Теорема А2.3. Одномерная и многомерная вогнутость.
Пусть / — вещественнозначная функция, определенная на выпуклом
подмножестве D из Шп. Функция f (строго) вогнута тогда и только
тогда, когда для любого хе D и любого не нулевого z€Rn функция
g(t) = /(х + tz) (строго) вогнута на {t e R |х + /z e D}.
Доказательство. Мы докажем теорему только для вогнутого случая,
оставляя доказательства прочих утверждений в качестве упражнения
А2.21. Предположим, что / — вогнутая функция. Пусть хе D и zgR".
Мы должны показать, что g(/) = /(x + fz) вогнута на
C = {teR\x + tzeD}.
Выберем t0, /,еС и осе [0, 1]. Мы должны показать также, что
я(ш0+A-а)О>ая(/0) + A-а)я(О. (Р-1)
Сначала заметим, что С — выпуклое множество, поэтому
Ш0 + A-ос)^ g С, и в силу этого g определена на нем. Чтобы установить
требуемое неравенство, нам достаточно всего лишь воспользоваться
определением g. Действительно,
g(o/0+(l-a)/1) = /(x+(a/0+(l-a)/I)z)=
= /(a(x + f0z) + (l-aXx + /1z))?
> ссД х + t0z) + A - ос) Дх + t{t) =
где неравенство следует из вогнутости / (заметьте, поскольку /, е С, то
x + /,zeZ) для / = 1, 2). ¦
На самом деле, теорема А2.3 говорит о том, что для проверки на
вогнутость многомерной функции достаточно проверить в каждой точке х
из области определения и для каждого направления z вогнутость
функции одной переменной той функции, которая принимает значения на
прямой, проходящей через точку х в направлении z. Так как теорема А2.1
описывает вогнутые функции одной переменной, мы можем объединить
теоремы А2.1 и А2.3, чтобы охарактеризовать вогнутые функции многих
переменных.
До этого объединения будет удобно ввести некоторую терминологию
из матричной алгебры. Матрица пхп называется отрицательно
полуопределенной, если для всех векторов zgKw,

626
Математическое приложение
zTAz<0.
Если неравенство строгое для всех ненулевых z , то А называется
отрицательно определенной1. Матрица А называется положительно
полуопределенной (соответственно положительно определенной), если — А
отрицательно полуопределена (отрицательно определена).
Отрицательную полуопределенность можно рассматривать как обобщение понятия
неположительных чисел на случай матриц. Действительно, заметим, что
матрица 1x1 (т.е. число) отрицательно полуопределена тогда и только
тогда, когда ее единственный элемент неположителен.
Приняв сказанное во внимание, видим, что аналогом
неположительной второй производной функции одной переменной будет
отрицательно полуопределенная матрица частных производных второго порядка (т.е.
матрица Гессе) функции многих переменных. Теперь нам пора
объединить теоремы А2.1 и А2.3, с тем чтобы убедиться в этом.
Теорема А2.4. Наклон, кривизна и вогнутость функций многих
переменных.
Пусть D — непустое выпуклое подмножество W, на котором f
дважды непрерывно дифференцируема. Утверждения 1)—3)
эквивалентны:
l)f вогнута;
2) Н(х) отрицательно полуопределена для всех х на D;
3) для всех x°eD: Дх)</(х0) + У/(х0)(х-х°) VxgD.
Более того,
4) если Н(х) отрицательно определена для всех х из Д то/строго
вогнута.
Доказательство. Так как / дважды непрерывно дифференцируема,
достаточно доказать теорему для внутренних точек D. По непрерывности
можно распространить результат на граничные точки. Зафиксируем
xeintD и zeR\ Пусть С = {teR\x + tze D} и пусть g(t) = f(x + tz) для
всех te С. Заметим, что g наследует дважды непрерывную дифференци-
руемость от /.
Теперь предположим, что утверждение 1) справедливо, так что /
вогнута. Тогда в силу теоремы А2.3 g вогнута на С. Заметим также, что,
Если а у обозначает элемент, стоящий на пересечении /-й строки иу-го столбца матри-
п п
цы А, тогда zrAz = ^^zjaijzr

Глава А2. Математический анализ и оптимизация
627
так как х принадлежит внутренности D, то С — невырожденный
интервал, поэтому по теореме А2.1 имеем:
g"(t)<0 V/eC, (P-1)
g(t)<g(t0) + g'(t0)(t-tQ) V/, /0еС. (P-2)
Чтобы воспользоваться этими результатами, нам потребуется выразить
первую и вторую производные g через /.
Теперь g\t) просто является производной функции / по
направлению в точке х + йв направлении z . Далее получаем
g'(t) = Vf(x + tz)z. (P-3)
Чтобы найти g"(t), проще всего написать g\t) в виде
а затем продифференцировать сумму. Так как производная ffa + tz)
по t — это всего лишь производная по направлению /. в х + й в
направлении z, то ее можно записать как
fdfij(x + tz)zj.
7=1
Умножая каждую из этих сумм на z; и суммируя по /, получаем
*'(о=ЕЕ*,лA+й)гу,
что можно записать в виде
g"@ = zrH(x + /z)z. (P-4)
Теперь заметим, что Об С. В силу (Р-1) у нас должно быть g*@)< 0.
Используя (Р-4), получаем
zrH(x)z<0.
Но так как выбор z был произвольным, это означает, что Н(х)
отрицательно полуопределена для всех х.
Таким образом, мы показали, что из 1) => 2).
Заметим, что тем самым мы доказали утверждение 4), так как, если
Н(х) отрицательно определена для всех х, то независимо от выбранных
х и z, до тех пор пока z — ненулевой вектор, g"{t) < О для всех /, так
что по теореме А2.3 / должна быть строго вогнутой.

628
Математическое приложение
Чтобы увидеть, что 1) => 3), мы должны использовать (Р-2). Выберем
любую точку х° € D, и пусть z равняется х° - х. (Напомним, что точка
zelR" выбрана произвольно.) Тогда оба значения 0, 1еС. Далее, из
(Р-2) следует, что
g@)<g(l)-g'(l).
Но, если использовать (Р-1) и определение g, то окажется, что это
неравенство означает
Ах)<Дх0) + УЯх°)(х-х0).
Поэтому утверждение 3) справедливо, так как выбор обеих точек был
произвольным. Отсюда 1)=>3). Доказательства утверждений 2)=>1) и
3) => 1) аналогичны, и мы оставляем их в качестве упражнения. ¦
Согласно теореме, функция вогнута тогда и только тогда, когда ее
матрица Гессе отрицательно полуопределена во всех точках области
определения. Поэтому она выпукла тогда и только тогда, когда ее матрица
Гессе положительно полуопределена во всех точках области определения.
В то же время мы знаем, что функция будет строго вогнутой (выпуклой),
когда матрица Гессе отрицательно (положительно) определена в области
определения, хотя обратное утверждение неверно.
Существует много тестов, применимых напрямую к матрице Гессе, с
помощью которых породившая ее функция исследуется на вогнутость,
выпуклость, квазивогнутость или квазивыпуклость. Правила и методы
исследования в этой области печально известны своей сложностью. Их
надо применять в контексте задач оптимизации, о чем речь пойдет далее в
этой главе. Поэтому представляется разумным отложить пока изучение
соответствующих тестов.
Есть довольно ясная интуитивная связь между вогнутостью
(выпуклостью) функции и ее частными производными второго порядка; эта
связь заслуживает упоминания. В одномерном случае необходимым и
достаточным условием того, что функция вогнута (выпукла), является
знак ее второй производной. В многомерном случае, заметим, знаки всех
вторых производных будут давать необходимое, но недостаточное
условие вогнутости или выпуклости. Доказательство этого факта мы
оставляем в качестве упражнения.
Теорема А2.5. Вогнутость, выпуклость и частные производные
второго порядка.
Пусть f :D —» R — дважды дифференцируемая функция.
1) Если f вогнута, то Vx /Дх)<0, / = 1, ...,«.
2) Если f выпукла, то Vx ^.(х)>0, / = 1, ...,«.

Глава А2. Математический анализ и оптимизация
629
А2.1.3. Однородные функции
Однородные вещественнозначные функции довольно часто
встречаются в микроэкономических приложениях. В этом разделе мы кратко
остановимся на функциях этого вида и используем методы математического
анализа, чтобы установить некоторые их важные свойства.
Определение А2.2. Однородные функции.
Вещественнозначная функция f(x) называется однородной степени
к, если
f(tx) = tkf{\) для всех t > О.
Следует обратить особое внимание на два специальных случая: f(\)
однородна первой степени, или линейно однородна, если f{tx) = tf(x) для
всех t > О; /(х) однородна нулевой степени, если f(tx) = f(x) для всех
/>0.
Однородные функции демонстрируют регулярное поведение, если
все ее переменные одновременно увеличиваются в одной и той же
пропорции. Когда функция однородна первой степени, то, например,
удвоение или утроение всех переменных удваивает или утраивает значение
функции. Когда функция однородна нулевой степени, то
пропорциональное изменение всех аргументов не меняет значения функции.
Пример А2.3. Функция вида
/(*,, х2) = Ах?х%, Л>0, ос>0, Р>0
известна как функция Кобба—Дугласа. Проверим, является ли эта
функция однородной, умножая все ее переменные на один и тот же
множитель t. Мы получим, что
f(txx, tx2) = A(txx )a {tx2 )p = ft*Ax*x\ = f^f{xx, x2).
Согласно определению функция Кобба — Дугласа однородна степени
сс + Р>0. Если коэффициенты выбраны таким образом, что ос+р = 1, то
она линейно однородна. ?
Частные производные однородных функций также однородны, о чем
и говорит следующая теорема.
Теорема А2.6. Частные производные однородных функций.
Если /(х) однородна степени к, то ее частные производные
однородны степени к-1.

630
Математическое приложение
Доказательство. Допустим, /(х) однородна степени k. Тогда
f(tx) = tkf(x) V/>0. (Р-1)
Продифференцируем левую часть по х,. и получим
*(/№).загць.*!!й1. ,Р-2)
dx, dx,. dxj dx,.
Продифференцируем правую часть по х;. и получим
?.(/*/(х))=г*Ш. (Р.з)
Так как (Р-1) — тождество, то (Р-2) должно равняться (Р-3), поэтому
df(tx)(^tkdf(x)
Эх, Эх,.
Поделив обе части на t, получим
a/«»)=ft-,yw>
Эх,. Эх,.
для / = 1, ...,« и / > 0, что и требовалось доказать. ¦
Особенно часто этот результат применяется в случае однородных
функций первой степени. Если f{\) однородна первой степени, теорема
говорит нам о том, что ее частные производные удовлетворяют соотношению
2Х*)=Ш V/>o.
Эх,. Эх,.
Другими словами, увеличение (или уменьшение) всех переменных в
одной и той же пропорции оставляет все п частных производных
неизменными. Проверим это на примере функции Кобба — Дугласа.
Пример А2.4. Пусть /(*,, х2) = Ах^. Предположим ос + Р = 1,так
что функция линейно однородна. Частная производная по хх равна
Эх,

Глава А2. Математический анализ и оптимизация
631
Умножим обе переменные х, и х2 на множитель t и оценим частную
производную в точке (/х,, tx2). Мы получим
df{tx^ ^ =aA{txxr\tx2f=
охх
= /а+на<'х2р =
Э/(х1? х2)
Эх,
что и требовалось, поскольку а + Р = 1 и /а+р ' = t° = 1. ?
Наконец, теорема Эйлера, иногда также называемая теоремой о
суммировании, дает нам интересный способ полностью охарактеризовать
однородные функции. Она говорит о том, что функция однородна тогда и
только тогда, когда ее всегда можно представить через частные
производные и степень однородности.
Теорема А2.7. Теорема Эйлера.
f{\) однородна степени к тогда и только тогда, когда
kf(\) = У х. для всех х.
Доказательство. Определим следующую функцию от /
g@ = f(K) (P-1)
и рассмотрим некоторые ее свойства. В частности, для
фиксированного х, продифференцировав по /, получим1
•«.да,. (и,
ы Эх;.
1 Если это не понятно, то вспомните, что, поскольку g(t) = f(txl9 ...,/*„), на t
умножаются все п переменных, так что эффект от умножения распространяется на каждую
переменную. Чтобы найти производную g(-) по /, мы должны просуммировать
отдельные эффекты от изменения t, которые действуют на /(•), по этим переменным.
Более того, при подсчете производной мы должны воспользоваться правилом
дифференцирования сложной функции. Таким образом,
,() = у ЭЯ**р ...,*,) Эр*,)
tt Эх,. д/ '
Но Э(/х,) / Эг = х. , откуда следует (Р-2).

632
Математическое приложение
Это выражение при / = 1 имеет вид:
*'(!) = 1^*,- (Р-3)
Для того чтобы доказать необходимость, предположим, что f(\)
однородна степени ?, так что f(tx) = tkf(\) для всех />0 и любого х.
Из (Р-1) мы имеем g(t) = tkf(\). Дифференцирование дает
g\t) = ktk~xf{\); подставляя f = l, мы получаем g'(l) = //(х). Поэтому,
если использовать (Р-3), тогда
*П*) = Щ&х„ (Р-4)
/=1 ОХ.
что и доказывает необходимость.
Чтобы доказать достаточность, предположим, что (Р-4) выполнено.
Подставим /х вместо х, тогда
kf(tx) = ±^tXi. (P-5)
ы Эх,.
Умножим обе части выражения (Р-2) на /, сравним результат с (Р-5): как
нетрудно заметить, выполнено соотношение tg\t) = kf(tx). После
подстановки (Р-1) мы получаем
tg'(t) = kg(t). (P-6)
Теперь рассмотрим функцию t~kg{t). Если мы продифференцируем ее по
t, то получим —[t~kg(t)] = t~k~l[tg'(t)-kg(t)]. В силу (Р-6) эта
производив
ная должна равняться нулю, отсюда мы заключаем, что t~kg(t) = c9 где
с — некоторая константа. Перепишем эту формулу как g{t) = tkc. Чтобы
найти с , подставим t = 1 и получим g(l) = с. Теперь воспользуемся
определением (Р-1), чтобы получить с = /(х). Теперь мы знаем, что
g(t) = tkf(x). Делая подстановку (Р-1) еще раз, приходим к выводу, что
/(ft) = f*/W
для любого х, что и требовалось доказать. ¦

Глава А2. Математический анализ и оптимизация
633
Нам бы хотелось получить следствие из теоремы Эйлера для линейно
однородных функций. При k = l по теореме Эйлера f(x) можно
следующим образом представить через ее частные производные:
ы Эх,
Давайте проверим эту формулу для функции Кобба — Дугласа.
Пример А2.5. Пусть /(jcp x2) = Ax?xl и пусть а + C = 1. Найдем
частные производные
ЭЯ*„ х2)=аАх«-1х»
ОХ,
Умножим первую формулу на jc, , вторую — на х2 и сложим. Тогда,
учитывая, что a+р = 1, получим
Э/(*" *2)*, + Э/(*" Xl)x2 =aAx^xlxx +$Ах;х$-1х2 =
aXj дх2
= (a + p)^jc,ax2p =
= /(*„ х2),
как и должно быть по теореме Эйлера. ?
А2.2. Оптимизация
Этот раздел посвящен методам решения оптимизационных задач, т.е.
тех задач, которые наиболее часто встречаются в микроэкономической
теории. После краткого обзора хорошо знакомых нам результатов из
анализа одной переменной мы рассмотрим, в какой мере их можно
распространить на многомерный случай. После чего мы исследуем методы,
которые помогают решать проблемы оптимизации с ограничениями, часто
встречающимися в теоретической экономике. Хотя мы и не ставим своей
целью описание всех тонкостей, но и не ограничимся изложением
методов на уровне рецептов из поваренной книги. На основе глубокого знания
методов одномерного анализа мы разовьем интуитивные представления о
некоторых непростых методах решения оптимизационных задач, а заодно

634
Математическое приложение
приобретем навыки в их практическом использовании. Начнем с обзора
известных результатов.
Рассмотрим функцию одной переменной у = /(х) и предположим, что
она дифференцируема. Когда мы говорим, что функция достигает
локального максимума в точке х*, мы имеем в виду, что /(х*) > /(х) для всех х
из некоторой окрестности х*. Когда мы говорим, что функция достигает
глобального максимума в х*, то это значит, что f(x*) > f(x) для всех х
из области определения функции. Функция достигает единственного
локального максимума в точке х*, если f(x*) > /(х) для всех х Ф х* из
некоторой окрестности х*. Она достигает единственного глобального
максимума, когда /(х*)> /(х) для всех х*х* из области определения.
Совершенно аналогично, функция достигает локального минимума
(единственного локального минимума) в х , если f(x) < /(х) (/(х) < f(x))
для всех х Ф х из некоторой окрестности х , и достигает глобального
минимума (единственного глобального минимума) в х, если
f{x) < /(x) (f(x) < /(х)) для всех х Ф х из области определения.
Различные типы оптимумов показаны на рис. А2.3. На рисунке
функция достигает локальных максимумов в точках х1, х3 и х5; глобальный
максимум достигается в х3. Однако глобальный максимум в х3 не
единственен. Локальные максимумы в х1 и х3 называются внутренними
максимумами, так как х1 и х3 лежат в области определения Д а не на ее
«границах». Максимум типа того, что достигается в х5, называется граничным
максимумом. Совершенно аналогично, в точках х°, х2 и х4 достигаются
локальные минимумы, в х4 — глобальный минимум. Минимумы в точках
х2 и х4 — внутренние, а в точке х° — минимум граничный.
А*)
х° х1 х2 ? 7 х5
ч '
D
Рис. А2.3. Локальные и глобальные оптимумы

Глава А2. Математический анализ и оптимизация
635
Вам известен подход к решению задач максимизации и минимизации
функций одной переменной, развитый в математическом анализе. В
изученных вами курсах математического анализа вас знакомили с логикой
«тестов первой и второй производных», и вы решали практические задачи
по отысканию оптимальных значений функций. Упор делался на
применение этих тестов. Однако в теоретической экономике нам в
действительности редко приходится вычислять оптимальные значения. Взамен нам
обычно нужно их охарактеризовать с точки зрения условий,
обеспечивающих оптимальные значения, и, скорее, приходится работать с этими
условиями, чем с конкретными численными значениями.
Для полноты картины мы напомним известные необходимые условия
первого порядка (first-order necessary conditions, FONC) и необходимые
условия второго порядка (second-order necessary conditions, SONC),
описывающие оптимальные значения произвольных дважды непрерывно
дифференцируемых функций одной переменной. Геометрическое
содержание этой теоремы изображено на рис. А2.4.
А*) Ах)
/(**) = о
/\\
•' : 4W /V) < о
*> х
f(x2)>0
*> х
(а)
(б)
Рис. А2.4. f'(x*) = 0n f\x) убывает там, где f(x) достигает максимума (а);
f'(x) = 0 и f\x) возрастает там, где f(x) достигает минимума (б)
Теорема А2.8. Необходимые условия локального внутреннего
оптимума функции одной переменной.
Пусть f(x) дважды непрерывно дифференцируемая функция одной
переменной. Тогда если f(x) достигает локального внутреннего
оптимума, то:
1) максимум в х* => /'(**) = О (FONC),
=>/V)^0 (SONC);

636
Математическое приложение
2) минимум в 5с =>/'(*) = О (FONC),
^f\x)>0 (SONC).
А2.2.1. Вещественнозначные функции многих переменных
Большая часть интуитивных представлений и привычной
терминологии переносится на случай многих переменных. Предположим, что
Del", и пусть /:?>—>/? — дважды непрерывно дифференцируемая
вещественнозначная функция п переменных. Функция достигает
локального максимума в х*, если при малом смещении из точки х* в любом из
направлений значение функции не возрастает. В R" некоторая
е -окрестность с центром в х*, 5е(х), содержит все близкие точки к х*.
Таким образом, функция достигает локального максимума в х* всякий раз,
когда существует такое е>0, что /(х*)>/(х) для всех х€#е(х*).
Функция достигает глобального максимума в х*, если /(х*)>/(х) для
всех х из области определения. Максимум является единственным
локальным (глобальным), если найдется такое е>0, что
/(х*)>/(х) Vxe Be(\*) (Vxe Z)), х*х*. Аналогично локальный
(глобальный) минимум достигается в х тогда и только тогда, когда
/(х)</(х) Vxe5g(x) (Vxe D), х*х. Минимум единственен, если
неравенства строгие.
Мы хотели бы обобщить необходимые условия первого и второго
порядка для максимума и минимума функций одной переменной на случай
многих переменных. Уже было показано, насколько полезно
использование функции g(t) = f{\ + tz) при различных векторах х и z для сведения
исследования функции многих переменных к изучению функции,
зависящей лишь от одной переменной. Этот метод будет применен снова.
Заметим, что если функция / многих переменных, например,
достигает максимума в точке х*, тогда эта функция для любого вектора z
будет функцией одной переменной, т.е. g(t) = f(\ +/z), и она будет
достигать максимума при / = 0. Таким образом, мы можем необходимые
условия первого и второго порядка, найденные для функций одной
переменной, применить к g в точке / = 0. Тогда получим условия на
градиент и гессиан функции / в точке х*.
Можно ожидать, что есть аналогия между производной функции
одной переменной, обращающейся в ноль в точке оптимума, и вектором-
градиентом функции многих переменных, равным нулю в точке
оптимума. Это интуитивно ясно, так как, если / достигает максимума в х*, то,

Глава А2. Математический анализ и оптимизация
637
меняя любую из переменных в отдельности и фиксируя остальные, мы не
сможем увеличить значение функции.
Таким образом, условие первого порядка, характеризующее оптимум
функции одной переменной /'(х*) = 0, превращается в систему из п
одновременных уравнений У/Хх*) = 0, характеризующих оптимум функции
п переменных. Тем самым мы получили необходимое условие первого
порядка для внутреннего оптимума вещественнозначных функций.
Теорема А2.9. Необходимые условия первого порядка
локальных внутренних оптимумов вещественнозначных функций.
Если дифференцируемая функция f(x) достигает локального
внутреннего максимума или минимума в точке х*, то х* является решением
системы уравнений
Эх,
дх2
№) = 0
дхп
Доказательство. Предположим, что /(х) достигает локального
внутреннего максимума в х*, и хотим показать, что V/(x*) = 0.
Доказательство, предлагаемое нами, не из простых, но оно пригодится, когда мы
будем рассматривать условия второго порядка. Для начала возьмем
любой вектор zeR". Тогда для любого скалярного / образуем знакомую
нам функцию
g(t) = f(x+tz). (Р-1)
Вспомним важные свойства g. Во-первых, для t Ф 0 х* + Vl есть некоторый
вектор, отличный от х*, так что g(t) принимает те же значения, что и /.
При / = 0 выражение (х* +tz) равно х*, поэтому g@) имеет то же
значение, что и / в х*. Так как для любого t g(t) принимает те же значения,
что и /, и /(х*) при / = 0, то g(t) достигает локального максимума при
/ = 0, так как мы предположили, что / достигает экстремума в х*. Из
теоремы А2.8 мы знаем, что, если g(t) достигает локального экстремума при

638
Математическое приложение
t = 0, то g'@) = 0. Как и раньше, здесь мы можем продифференцировать
(Р-1), используя правило дифференцирования сложной функции, чтобы
получить
^df(x+tz)
/=i Эх,.
*'(о=1-
для любого /. Подставляя в эту формулу / = 0и считая g'@) = О,
получаем, что из локального экстремума g в нуле следует
= V/(x> = 0.
Так как это должно быть справедливо для любого z из W и, в частности,
для любого из п единичных векторов, то мы получили, что все частные
производные (первого порядка) функции / равны нулю, т.е.
V/(x') = 0,
что и требовалось доказать. ¦
Пример А2.6. Пусть у-х2 — 4jcf + Ъххх2 -х\. Чтобы найти
критическую точку этой функции, вычислим ее частные производные:
д/(*Р х2) _
Эх
• — —oXj ¦+¦ 5х2)
-VJ
Э/(*Р х2)
Эх,
— = 1н-3х1 -2х2.
Критическая точка — это вектор (**, х*2), для которого обе эти
производные одновременно равны нулю. Чтобы ее найти, приравняем каждую
из производных к нулю
ЭЖ, *2)=_8jCi*+3x2*=o
ах{
эл^;, х2)
дх2
= 1 + Зх,*-2л:2*=0 (Е-1)
и решим эту систему относительно х1 и х2.
Существует много способов сделать это. Самый «грубый» состоит в
том, чтобы решить одно из уравнений относительно х*{ , затем подставить

Глава А2. Математический анализ и оптимизация
639
хх во второе уравнение, получив уравнение, содержащее лишь х2, и
решить его. Найдя х*2, подставим его в первое уравнение и найдем х*. Так
как система состоит из линейных уравнений, что удобно, мы можем
поступить более изящно. Сначала перепишем (Е-1) в виде
- 8х,* + Ъх1 = О
Зх* -2х*2 =-1,
или в матричной форме
^-8 3
. 3 -2
"а
Если мы обратим А, то получим
l-i J
(Е-2)
. 1 (-2 -3^1 Г-2/7 -3/7
А =т—г
А -3 -8
-У
,-3/7 -8/7,
так как детерминант |AJ = 16—9 = 7. Если мы слева умножим обе части
(Е-2) на А ' и перегруппируем, то получим
'-2/7 -3/7У0^| C/7Л
ЧЛ
\хи
-3/7 -8/7
-L
8/7.
Таким образом, критической точкой функции является х\ =3/7 и х*2 =8/7.
Однако пока не ясно, нашли мы максимум или минимум, так как для
этого следует применить условия второго порядка. ?
А2.2.2. Условия второго порядка
Опять интуитивно кажется, что условия второго порядка в
многомерном случае такие же, что и в одномерном. Как только мы нашли точку, в
которой V/(x) = 0, мы получим в ней максимум, если функция «локально
вогнута» в окрестности, или минимум, если функция «локально выпукла».
Теорема А2.4 подчеркивает связь между кривизной и
знакоопределенностью гессиана /. Интуитивно ясно, что функция будет локально
вогнутой вблизи х, если Н(х) отрицательно полуопределена, и локально
выпуклой — если положительно полуопределена. Тем самым мы
предлагаем следующее необходимое условие второго порядка для локального
внутреннего оптимума.

640
Математическое приложение
Теорема А2.10. Необходимые условия второго порядка
локального внутреннего оптимума вещественнозначных функций.
Пусть /(х) — дважды непрерывно дифференцируемая функция.
1) Если f(x) достигает локального внутреннего максимума в х*, то
Н(х*) отрицательно полуопределена.
2) Если f(x) достигает локального внутреннего минимума в х, то
Н(х) положительно полуопределена.
Доказательство. Доказательство этой теоремы будем строить на
основе доказательства теоремы А2.9. Вспомним, что мы определили
функцию
где zeR" их — критическая точка /. Мы заметили, что если /
достигает критического значения в х, то g достигает критического значения в
t = 0. Далее, мы заметили, что для любого t
,=1 ОХ}
Дифференцируя еще раз по t и применяя правило дифференцирования
сложной функции, получаем вторую производную
Теперь предположим, что / достигает максимума при х = х*. Согласно
теореме А2.8 должно быть выполнено g"@) < 0. Подстановка х* и / = 0 в
(Р-1) дает
g'(o)=II^p^o,
или что zrH(x)z < 0. Так как выбор z произволен, это означает
отрицательную полуопределенность Н(х*). Аналогично, если / достигает
максимума при х = х , тогда g"@) > 0, так что Н(х) положительно
полуопределена, что завершает доказательство. ¦
Теоремы А2.9 и А2.10 важны и полезны. Мы можем использовать их,
чтобы исследовать (внутренние) оптимумы в том случае, когда мы знаем
или предполагаем их существование. Обе теоремы являются необходи-

Глава А2. Математический анализ и оптимизация
641
мыми, т.е. они звучат таким образом: «Если в точке х* /(х) достигает
максимума, тогда fi(x*) = 0, / = 1, ...,п и Н(х*) отрицательно
полуопределена». Эти условия помогают в поиске потенциальных кандидатов на
точки максимума (или минимума) конкретных функций, но для проверки,
являются ли эти точки действительно таковыми, нам потребуются
достаточные условия.
Достаточные условия позволяют нам утверждать, что «если что-то
выполнено в х, то х — оптимум функции». Условия подобного рода
позволяют гарантировать оптимизацию функции в х. Нам несложно
вывести достаточные условия для оптимума функции, но можно
предположить, что они являются более жесткими, чем необходимые условия.
Несколько упрощая, можно сформулировать достаточные условия для
внутреннего оптимума следующим образом: 1)если /{(х*) = 0 для / = 1, ...,« и
Н(х*) отрицательно определена в х*,то f(x) достигает локального
максимума в х*; 2) если /(х) = 0 для / = 1, ...,п и Н(х) положительно
определена в х , то /(х) достигает локального минимума в х . Достаточные
условия требуют, чтобы точка была критической, а от условий
кривизны — выполнения в строгой форме. (Это сделано с целью исключения
точек перегиба, которые ошибочно могут быть приняты за точки
оптимума.) Например, когда Н(х*) отрицательно определена, тогда функция
будет строго вогнутой в некоторой окрестности с центром в х*.
Найти критические точки довольно легко. Мы просто полагаем все
первые частные производные равными нулю и решаем систему из п
уравнений. Исследования гессиана на положительную или отрицательную
определенность — задача посложнее.
Всевозможные тесты на знаковую определенность гессиана
основываются на характере чередования знаков детерминантов определенных
подматриц, образуемых из исходной матрицы, причем вычисления
проводятся в некоторой точке (или области). Эти детерминанты называются
главными минорами гессиана. Выпишем первые п главных миноров
Н(х) в точке х:
Щ*) = \/п\ = /и
D2(x) = \fu M
\J2l J22\

642
Математическое приложение
А00 =
/п ••• J и
Ji\ '•' J ii
АЮ =
/ll ••* Ли
где каждая из частных производных ftj вычисляется в точке х. Любой из
написанных детерминантов получен вычеркиванием из матрицы Н(х)
последних n-i строк и столбцов для / = 1, ...,л. Они называются
главными минорами потому, что получены из подматриц, образованных при
движении вниз и вправо вдоль главной диагонали матрицы Гессе.
Следующая теорема определяет ограничения, накладываемые на
главные миноры гессиана, чтобы гарантировать его определенность.
Теорема A2.ll. Достаточные условия отрицательной и
положительной определенности гессиана.
Пусть f(x) дважды непрерывно дифференцируема и пусть Ц(х) —
главный минор i -го порядка матрицы Гессе Н(х).
1)Если (-l)'Z)/(x)>0, / = l, ...,п, то Н(х) отрицательно определена.
2) Если Z)(x)>0, / = 1, ...,«, тогда Н(х) положительно определена.
Если условие 1) справедливо для всех х в области определения, то f
строго вогнута. Если условие 2) справедливо для всех х в области
определения, то f строго выпукла.
Эта теорема, в частности, говорит о том, что функция будет строго
вогнутой, если главные миноры матрицы Гессе чередуют свой знак,
начиная с отрицательного знака. Функция будет строго выпуклой, если все
главные миноры матрицы Гессе положительны.
Доказательство. Доказательство в общем случае опирается на
утверждение 4) теоремы А2.4, а затем сводит задачу к следующей: доказать,
что если главные миноры матрицы чередуют свой знак, то
соответствующая квадратичная форма отрицательно определена, а если все
главные миноры положительны, то соответствующая квадратичная форма
положительно определена. Это, в свою очередь, есть хорошо известный
результат из линейной алгебры. Заинтересованный читатель может
свериться с любым стандартным учебником по линейной алгебре (напри-

Глава Л2. Математический анализ и оптимизация
643
мер, см. [Hohn, 1973]). Здесь мы приведем простое доказательство для
случая двух переменных.
Предположим, что y = f(x{, x2) дважды непрерывно
дифференцируема. Первые и вторые миноры таковы:
Aw=|yiil=y;.
А00 =
У11 J12
Ji\ J г:
~~ Ли 22 (У 12/
(P-l)
Здесь мы использовали тот факт, что fn = /21. Для
z = (zp z2)*@, 0) zrH(x)z можно записать в виде
2 2
zrH(x)z = YLfijzizj = fxx(zxf+2fX2zxz2+f22(z2f.
j=\ /=i
(P-2)
Если мы сможем доказать, что zrH(x)z<0 всякий раз, когда главные
миноры в (Р-1) чередуют свой знак, начиная с отрицательного, а также
что zrH(x)z > 0 всякий раз, когда все главные миноры положительны, то
теорема будет «доказана».
Так как (z,, z2) — не нулевой вектор, то хотя бы одна из координат
zp z2 не равна нулю. Предположим, что z2 *0. Заметим, что мы можем
одновременно добавить и вычесть одно и то же выражение в правой
части формулы (Р-2) без изменений чего-либо. Добавляя и вычитая величину
(fnfi^f/fn >мы получаем
z'H(x)z = fxx(zxf+2fX2zxz2 +^^ + /22(z2J -Unfibl.
У и У п
После вынесения за скобки /п и (z2J мы получаем
zrH(x)z = y;1
\2 , О У12
(z1)z+2^2-z1z2 +
У и
У12
\f\\J
(z2J
J22
ш
у;
2 Л
(Z2J
п У
Заметим, что первое слагаемое является квадратом суммы, а второе — мы
приведем к общему знаменателю. Тогда можно записать
zrH(x)z=d
, /l2
V
11 J
jwin \J\i)
2\
\(z2J
(P-3)

644
Математическое приложение
Предположим, что главные миноры в (Р-1) чередуют знак, начиная с
отрицательного. Тогда первое произведение в (Р-3) неположительно, а
последнее — строго отрицательно, потому что z2 Ф О и потому что
числитель и знаменатель в том выражении, на которое умножается (z2J,
имеют разные знаки по предположению. Следовательно, zrH(x)z<0.
Аналогично, если оба главных минора в (Р-1) положительны, то оба члена
в (Р-3) неотрицательны, и хотя бы один положителен, так что
zrH(x)z>0. ¦
Мы теперь готовы сформулировать достаточное условие первого и
второго порядка для локального внутреннего оптимума. Эти условия
непосредственно следуют из того, что было установлено, так что они не
нуждаются в дальнейшей проверке. Мы просто объединим предыдущие
результаты вместе и запишем условия компактно, чтобы облегчить их
использование в последующем.
Теорема А2.12. Достаточные условия локального внутреннего
оптимума вещественнозначных функций.
Пусть f(\) дважды непрерывно дифференцируема.
1)Если fi(x*) = 0 и (-1)'Д(х*)>0, / = 1, ...,«, то f(x) достигает
локального максимума в х*.
2) Если ^(х) = 0 и Z)(x)>0, / = 1, ...,я, то f(x) достигает
локального минимума в х.
Пример А2.7. Давайте проверим, будет ли критическая точка,
найденная нами в предыдущем примере, максимумом или минимумом. У нас
была функция
и мы нашли, что
J- = -SXl+3x2 и -^- = 1 + 3jCj-2x2.
дх1 ох2
Вычислим производные второго порядка.

Глава А2. Математический анализ и оптимизация
645
а2/ _
ох2дх1
а2/_
Эх,2
*«>-(?
3
-2
3
и образуем матрицу Гессе.
Ранее мы нашли критическую точку х* = C/7, 8/7). Проверка на знак
главных миноров дает
Д(х) = |-8| = -8<0
1-8 3
D2(x) =
3 -2
= 16-9 = 7>0.
Так как у них чередуется знак, начиная с отрицательного, то по теореме
А2.12 точка х* = C/7, 8/7) — это локальный максимум. ?
Вы, возможно, заметили в этом примере, что матрица Гессе
совершенно не зависела от х. Поэтому мы получили бы то же самое
чередование знаков главных миноров, вне зависимости от того, где мы их
вычисляли. Согласно теореме А2.11, мы знаем, что этого достаточно, чтобы
гарантировать строгую вогнутость функции. Теперь давайте представим
себе график некоторой такой строго вогнутой функции в трехмерном
пространстве. Если такая поверхность имеет вершины, то, видимо она
может иметь лишь одну такую вершину, где она должна принимать
единственное наибольшее значение.
Конечно, из рис. А2.4 интуитивно ясно, что любой локальный
максимум (минимум) вогнутой (выпуклой) функции должен также быть
глобальным максимумом (минимумом). Эта интуиция точно так же
распространяется на многомерный случай. В многомерной (безусловной)
оптимизации локальные и глобальные оптимумы совпадают, когда функция
является либо вогнутой, либо выпуклой. Как обычно, мы рассмотрим
лишь случай вогнутых функций.
Теорема 2.13 (Безусловная). Локально-глобальная теорема.
Пусть / — дважды непрерывно дифференцируемая, вещественно-
значная вогнутая функция на D. Следующие утверждения
эквивалентны, где х* — внутренняя точка D:

646
Математическое приложение
1) V/(x*) = 0;
2)/достигает локального максимума в х*;
3)f достигает глобального максимума в х* .
Доказательство. Ясно, что 3) => 2) и 2)=> 1) по теореме А2.9.
Следовательно, нам только остается показать, что 1) => 3).
Предположим, что
W) = 0.
Так как / вогнута, из теоремы А2.4 следует, что для всех х из области
определения
Дх)<Дх*) + У/(х*)(х-х*).
Вместе эти два условия означают, что для всех х
/(х)</(х*),
поэтому / достигает глобального максимума в х*. ¦
Теорема А2.13 говорит о том, что наличие выпуклости или вогнутости
превращает локальный оптимум в глобальный. Однако заметим, что все
еще возможно, чтобы наименьшее (наибольшее) значение достигалось в
более чем одной точке области. Если мы хотим, чтобы наибольшее или
наименьшее значение функции достигалось в единственной точке, мы
должны наложить условие строгой вогнутости или строгой выпуклости.
Теорема А2.14. Строгая вогнутость (выпуклость) и
единственность глобального оптимума.
1) Если строго вогнутая функция f достигает максимума в точке
х*, то х* — единственная такая точка, т.е. f(x*)<f(x) Vxe D,
хФх*.
2) Если строго выпуклая функция f достигает минимума в точке
х, то х — единственная такая точка, т.е. /(х) < /(х) Vxe D, хФ х .
Доказательство. Снова мы докажем теорему для строго вогнутых
функций. Предположим, как и раньше, противное и выведем противоречие.
Если в точке х* достигается глобальный максимум функции /их*
не является единственной точкой, то в этом случае существует некоторая
другая точка х *х*, такая, что f{x) = /(х*). Положим х! = tx + A -/)х*,
тогда в силу строгой вогнутости
f{xt)>tf{x) + (\-t)f{x*) для всех /е@, 1).

Глава А2. Математический анализ и оптимизация
647
Так как f{\) = /(х*), то
/(х>/Дх') + A-0Ах*),
или просто
Дх')>/(х').
Однако это противоречит предположению, что в точке х' достигается
глобальный максимум /. Таким образом, точка, в которой достигается
глобальный максимум строго вогнутой функции, может быть только
одна.
Теорема А2.15. Достаточные условия единственности
глобального оптимума.
Пусть f(\) — дважды непрерывно дифференцируемая функция.
1) Если /(х) строго вогнута и fj(\*) = 0, / = 1, ...,и, то х* —
единственная точка глобального максимума /(х).
2) Если /(х) строго выпукла и /(х) = 0, / = 1, ...,«, то х
—единственная точка глобального минимума /(х).
Доказательство. Эта теорема интуитивно является совершенно
прозрачной. Как обычно, мы рассмотрим лишь случай строго вогнутых
функций, оставляя доказательство для случая строго выпуклых функций
для самостоятельной работы.
Если / строго вогнута, то по теореме А2.13 в силу V/(x*) = 0
/ достигает глобального максимума в х*. Тогда из теоремы А2.14
следует, что х* — единственная точка глобального максимума. ¦
А2.3. Условная оптимизация
До сих пор мы просто старались охарактеризовать точки, в которых
функция достигает локального оптимума, в том случае, когда есть
свобода в выборе переменных х. В экономике мы не можем позволить себе
такой роскоши. Дефицит является фактом, неотъемлемым от экономики.
Можно даже определить экономику как исследование поведения при
наличии дефицита. Дефицит обычно выражается в виде ограничений на
допустимые значения экономических переменных. Тогда экономическим
агентам приходится искать наилучшее решение (в том смысле, который
наиболее подходит к конкретной ситуации) с учетом имеющихся
ограничений. Это задача, с которой мы будем постоянно сталкиваться. Нам
необходимо соответственно модифицировать наши методы оптимизации, а
также условия, которые характеризуют оптимум в этих случаях. Сущест-

648
Математическое приложение
вуют три основных типа ограничений, с которыми мы будем встречаться.
Это ограничения в виде равенств, ограничения неотрицательности и
более общий случай ограничений — ограничения в виде неравенств. Мы
разработаем методы для решения задач в каждом из этих случаев по
очереди, ограничившись при этом обсуждением задач максимизации, делая
замечания о тех модификациях (если нужно), которые нужно произвести
в случае минимизации.
А2.3.1. Ограничения в виде равенств
Пусть нам предстоит выбрать хх, х2, чтобы максимизировать
f(xx, х2) в том случае, когда jCj и х2 должны удовлетворять некоторому
соотношению, имеющему неявный вид g(xx, jc2) = 0. Формально мы
можем записать эту задачу таким образом:
maxf(xx, х2) при g(xx, jc2) = 0. (А2-4)
Здесь f(xx, x2) называется целевой функцией или максимандом, хх
и х2 называются выбираемыми переменными, и обычно их пишут под
оператором «max», чтобы напомнить о том, что именно их значения и
следует найти. Функция g(xx, x2) называется ограничением', она
определяет допустимые значения переменных, т.е. те, которые разрешено
использовать при решении задачи. Множество всех значений хх и х2,
удовлетворяющих ограничению, иногда называются набором ограничений
или допустимым множеством.
Одним из способов решения такой задачи является метод
подстановки. Если ограничение допускает решение уравнения относительно хп
причем эта переменная выражена через остальные, то мы сведем задачу
на условный экстремум с двумя переменными к задаче с одной
переменной без ограничений. Например, предположим, что g{xx, х2) = 0 может
быть записана так, чтобы можно было выразить х2 слева, т.е.
x2=g(xx). (A2-5)
Мы можем подставить это выражение непосредственно в целевую
функцию и быть уверенными, что х2 требуемым образом связана с хх. Таким
образом, задача на условный экстремум с двумя переменными может
быть переформулирована в виде задачи на безусловный экстремум с
одной переменной:
max/(x,, g(xx)). (A2-6)

Глава А2. Математический анализ и оптимизация
649
Теперь мы просто максимизируем эту функцию известными
методами. Обычные условия первого порядка требуют, чтобы мы приравняли
полную производную df /dxx к нулю и решили это уравнение
относительно оптимального х*. Вычисляя производную, следует иметь в виду, что
хх действует на / двояким образом: «непосредственно» через свое
(собственное) участие в / и «косвенно» через присутствие / в х2. Таким
образом, при дифференцировании (А2-6) мы должны помнить, что у /
две частные производные, и следует не забывать воспользоваться
правилом дифференцирования сложной функции. Нам нужно найти х*х из
уравнения
д/(*Г, g(**)) Э/(*;, g(x*x)) dg(x*x)
Эх, Эх2 dxx
V ->
по правилу дифференцирования
сложной функции
После нахождения х* нам нужно подставить х,* в ограничение (А2-5) и
найти х*2 = g(x*). Пара (х*, х*2) тогда является решением задачи с
ограничением, если известно, что надлежащее условие второго порядка
выполнено.
К сожалению, легко представить себе случай, когда ограничение
выглядит довольно сложно и из него не так просто выразить одну
переменную через другую. Более того, во многих интересных задачах бывает
более двух переменных и более одного ограничения. Метод подстановки не
очень хорошо подходит для таких задач. В некоторых случаях
подстановка будет неоправданно затруднять решение. В других — будет просто
невозможна. К счастью, есть способ получше, и этот способ позволяет
решить гораздо более широкий класс задач.
А2.3.2. Метод Лагранжа
Метод Лагранжа — это мощное средство решения задач условной
оптимизации. В этом разделе мы сконцентрируем свое внимание на
отработке этого метода и докажем его состоятельность в относительно
простом случае задач типа (А2-4). Как только мы освоим принципы метода,
его распространение на более общий случай будет делом нетрудным.
Метод Лагранжа родился из простого вопроса: как мы можем
использовать то, что применяется к решению безусловных задач оптимизации
многих переменных, для решения задач с ограничениями? Мы знаем, что
решение задач без ограничений — дело несложное. Нам нужно найти
частные производные первого порядка, приравнять их к нулю и решить

650
Математическое приложение
систему уравнений. Проницательность Лагранжа позволила ему увидеть,
что всегда существует некоторая задача на безусловный экстремум,
которая решается обычными методами и в виде побочного продукта дает нам
решение задачи на условный экстремум.
Чтобы в этом убедиться, рассмотрим снова исходную задачу:
max/0P x2) при g(x{9 x2) = 0.
Предположим, мы умножаем уравнение ограничения на новую
переменную, назовем ее X (лямбда). Если мы добавим это произведение к
целевой функции, мы построим новую функцию, называемую функцией
Лагранжа, или лагранжианом для краткости, и обозначаемую значком ?(•).
У этой новой функции есть три переменные вместо двух, а именно хх, х2
и X:
?(х19 х29 А,) = /0Р x2) + Xg(xl9 x2).
Как бы мы теперь стали находить критические точки ?(•), если бы
она была обычной функцией трех переменных? Мы нашли бы все три
частные производные и приравняли их нулю. Проделав это, получаем
д? = ЭД*;, х*2) | ^ 9g(*;, x*2) =()
дх{ ЭХ, Эд^
d?jf(x;,x2)+rdg(x;,x2)=0 (A28)
дх2 дх2 дх2
— = g(x,\ x2) = 0. (A2-9)
Это система из трех уравнений с тремя неизвестными xvx2 и X. Метод
Лагранжа утверждает, что, если мы можем найти значения дс*, х2 и X* 9
являющиеся решениями этих трех уравнений, то мы получим
критическую точку функции /(;СрХ2), удовлетворяющую ограничению
g(xp x2) = 0.
Предположим, мы можем найти **, х*2 и X* 9 которые удовлетворяют
(А2-7), (А2-8), (А2-9). Заметим важное обстоятельство. Так как они
являются решением (А2-9), то *,*, х*2 одновременно удовлетворяют
ограничению g(x^9 xl) = 0. Показать, что f(xl9 x2) точно так Dice принимает для

Глава Л2. Математический анализ и оптимизация
651
этих значений наибольшее (или наименьшее) значение, хотя и несколько
труднее, но все-таки можно.
Рассмотрим нашу придуманную функцию ?(•) и найдем ее первый
дифференциал, помня, что X — это полноценная переменная функции:
. п о? , о? , о? ,*
d? = -—dx, + -—dx, + —-dX.
дх1
дх.
дХ
По предположению х*9 х2 и X* удовлетворяют условиям первого
порядка (А2Т7), (А2-8), (А2-9), являющимся условиями оптимума ?, так что
d? должен равняться нулю. Подставляя условия первого порядка,
получаем
d? =
У(*Г, *2*) ^ , УСлс*, х*2)
Эх,
-dxx+-
дх.
dx2+g(x\, x*2)dX +
+Г
dg(s*, xp^ | 9g(s*, x2*)
Э^! Эх2
<&0
= 0
(A2-10)
для всех dx{, dx2 и dX. Чтобы убедить вас в том, что решения условий
первого порядка, дающие оптимум функции Лагранжа, точно так же
оптимизируют целевую функцию /(*,, x2) при ограничении g(x{9 х2),мы
должны показать, что в точке (х*9 х*2, X*) первый дифференциал целевой
функции /(дгр х2) также равняется нулю — по крайней мере для всех
допустимых dxl9 dx2, dX, которые удовлетворяют уравнению
ограничения g. В сущности, мы хотим показать, что из d? = 0 для всех
dxv dx2, dX следует df = 0 для всех допустимых dxx, dx2.
Одно наблюдение можно сделать сразу же для упрощения; заметим
снова, что (А2-9) говорит нам, что ограничение выполнено в х*9 х*2, так
что g(x*9 х2) = 0. Это означает, что третье слагаемое в (А2-10) равно
нулю, и нам предстоит показать, что из равенства нулю сокращенного
выражения
d? =
Э/Qf, х*2) j , Э/(х*, х*2)
Эх
-dx, +-
Эх,
dx2 +
+Г
MwiU +
Эх,
9g(x;, л?)
Эх,
etc,
= 0
(А2-11)

652
Математическое приложение
для всех dxi будет следовать df = О для тех dxt, которые удовлетворяют
ограничению g.
Далее, мы хотим понять, каковы допустимые значения dxx, dx2.
Посмотрим снова на уравнение ограничения. Ясно, что если g(jcp x2) должна
всегда равняться нулю, то после изменения д:, и jc2, ее значение по-
прежнему должно быть нулем. Другими словами, допустимые изменения
хх и х2 таковы, что они не приводят к изменению значения функции
ограничения g(jcp x2). Пусть dxx и dx2 обозначают эти «допустимые
изменения» хх и х2 от значений переменных х* и х2 соответственно. Вместо того
чтобы сказать, что значение g не изменяется, можно сказать, что его
первый дифференциал должен равняться нулю. Имея это в виду, мы найдем те
изменения dxx и dx2, для которых dg = О, продифференцировав
ограничение и приравняв его к нулю. Выполнив это, мы увидим, что допустимые
изменения должны удовлетворять следующему соотношению:
dg=?^LjOdx+dg(x;,x;)dx^^ (A2_12)
дхх дх2
где dxx и dx2 — допустимые изменения х*х и х2 соответственно.
Учитывая одновременно (А2-11) и (А2-12), мы получим искомый
результат. Если мы рассматриваем лишь те изменения переменных, которые
удовлетворяют (А2-12), тогда третье слагаемое в (А2-11) должно
равняться нулю. Поэтому в (х*, х2) (А2-11) сводится к
ох1 дх2
для всех dxx и dx2, удовлетворяющих ограничению. Но это именно то,
что нам нужно: решения (jc*, x*29 X*) условий первого порядка задачи на
безусловный экстремум функции Лагранжа гарантируют, что значение
целевой функции / не может быть увеличено или уменьшено при малых
изменениях jc* и х*2, удовлетворяющих ограничению. Поэтому мы
должны находиться в точке максимума или минимума целевой функции вдоль
ограничения.
Снова повторим то, что мы проделали: мы показали, что,
если (хх\ х*2, X*) является решением d?(xx\ x2, А,*) = 0 для всех
(dxx, dx2, dX), то df(xx\ x*2) = 0 для всех dxx и dx2, удовлетворяющих

Глава Л2. Математический анализ и оптимизация
653
ограничению. То есть, если (х*, х*2) — критическая точка / при условии,
что переменные должны удовлетворять ограничению и что любое
движение от (х*, х*2) должно быть движением вдоль ограничения. Условия
первого порядка (А2-7), (А2-8), (А2-9) тем самым характеризуют
критические точки целевой функции вдоль ограничения. Будут ли эти
критические точки решениями условной задачи на максимум или минимум,
сказать невозможно, исходя лишь из условий первого порядка. Чтобы
разделить эти два случая, нам потребуется знание «кривизны» целевой
функции и ограничения в рассматриваемой критической точке. Мы
исследуем эти вопросы позже.
Пример А2.8. Давайте рассмотрим задачу такого типа, которую мы
обсуждали, и применим метод Лагранжа для ее решения. Предположим,
задача формулируется следующим образом:
max(-axf -bx22) при х{ + х2 -1 = 0, (Е-1)
ДГ|, Х2
где а > О и Ь > О.
Сначала образуем лагранжиан
-?(*,, х2, X) =-axf - bx^ +X{xx +х2-1).
Затем приравняем все его первые частные производные нулю:
^ = -20*,+^ = О (Е-2)
дхх
?± = -2Ьх2+Х = 0 (Е-3)
ох2
— = х]+х2-1 = 0. (Е-4)
Чтобы решить задачу относительно
(Е-3) следует
или
Подставляя (Е-5) в (Е-4),
2ах1 =
Ъ
а
получаем
Ъ
х2+ — •
а
1' 2'
2fox2,
•х2.
х, =1,
к
заметим,
что
из
(Е-2) и
(Е-5)

654
Математическое приложение
или
а
х2= -. (Е-6)
а + Ь
Чтобы найти дс,, подставим (Е-6) в (Е-5) и получим
b
х. = .
1 а + Ь
(Е-7)
Чтобы найти X, мы можем подставить (Е-6) или (Е-7) в (Е-3) или в (Е-2)
соответственно. Так или иначе, мы получаем
-2ь(—]+\ = 0,
[а + Ь)
ИЛИ
Ь~. (Е-8)
а + Ь
Решив уравнения с (Е-2) по (Е-5), найдем следующие три значения
х{= -, х2 = -, А = -. (Е-9)
а + Ь а + Ь а + Ь
Только х{ и х2 в (Е-9) представляют интерес как возможные решения
задачи (Е-1). Дополнительная информация, получаемая нами, —
величина множителя Лагранжа — всего лишь «побочный» продукт. Мы можем
найти значение целевой функции, которого она достигает вдоль
ограничения, подставляя значения х, и х2 в целевую функцию (Е-1):
( h ^
у =-а
\<-
-Ъ
а+Ь) Уа+Ь
-М^р.. (Е.,0)
Помните, что из одних лишь условий первого порядка мы не можем
сделать вывод о том, будет ли это значение целевой функции
максимальным или минимальным при наличии ограничения. D
Метод Лагранжа адресуется гораздо более широкому классу задач,
нежели тот, который мы уже рассмотрели. Метод Лагранжа «хорош» для
функций с любым числом переменных, а также для задач с любым
числом ограничений до тех пор, пока число ограничений меньше числа
выбираемых переменных.
Предположим, дана функция п переменных и т ограничений, где
т<п. Задача поставлена следующим образом:

Глава Л2. Математический анализ и оптимизация
655
max/(*„ ...,*„) при gl(xl9 ...,*„) = О
g\xv ...,xj = 0 (A2-13)
gm{xv ...,хп) = 0.
Чтобы ее решить, образуем лагранжиан, умножая каждое уравнение
ограничения gJ на свой множитель Лагранжа Xj и добавляя их все к
целевой функции /.Для x = (jcp ...,х„) и А = (А,Р ...Д,,,) мы получаем
функцию т + п переменных.
т
Дх, A) = /(x) + ?byg'(x). (A2-14)
Согласно условиям первого порядка все частные производные ?
должны равняться нулю в точке оптимума. Так как ? имеет т + п
переменных, то мы получим систему из т + п уравнений, определяющую т + п
неизвестных х* и Л*:
OXj OX{ j=\ OXj
^ = «J(i>0 j = l..,m. (A2-15)
oKj
В принципе, эта система может быть решена относительно т + п
неизвестных, х* и Л*. Все векторы решения х* будут кандидатами на
решение задачи условной оптимизации (А2-13).
Метод Лагранжа очень полезен и продуман. На самом деле он
предлагает нам алгоритм по нахождению условных оптимумов в широком
классе практических задач. Приведенная задача сразу же ставит перед
нами ряд вопросов: прежде всего, возникает вопрос о существовании
решений задач условной оптимизации (А2-4) или (А2-13). В большинстве
случаев на этот вопрос легко ответить. Если целевая функция веществен-
нозначная и непрерывная (а она должна быть непрерывной, если
дифференцируема) и если множество, заданное ограничениями, компактно, то
теорема Вейерштрасса (теорема А1-10) гарантирует существование
оптимума целевой функции на множестве, заданном ограничениями.
Как только мы ответили на этот вопрос, следует ответить на другой —
более тонкий, оставшийся пока за рамками обсуждения метода Лагранжа.
Например, откуда мы знаем, что множители Лагранжа, которые мы толь-

656
Математическое приложение
ко что «взяли с потолка», вообще существуют? Точнее, откуда нам
известно, что существуют такие Л*, что критические точки функции
?(•, Л*) совпадают с условным оптимумом / на множестве, заданном
ограничениями? Ясно, что должны быть некие условия, при выполнении
которых существование гарантируется.
Действительно, есть некоторые условия, и они в основном являются
требованиями, накладываемыми на множество ограничений. В
простейшем случае двух переменных и одного ограничения это сводится к
требованию отличия от нуля хотя бы одной частной производной функции
ограничения. Обоснованность такого требования станет яснее в
дальнейшем, когда мы исследуем геометрию этой простой задачи в разделе
А2.3.3. В общем случае это требование становится шире и формулируется
следующим образом: векторы-градиенты т ограничений, т.е.
Vgy, j = 1, ..., т , должны быть линейно независимыми.
Для полноты картины, не говоря уже о пользе просвещения, мы
сформулируем теорему Лагранжа, в которой рассматриваются эти
вопросы. Доказательство требует более продвинутых методов, чем те, которые
мы применяли здесь, и поэтому будет опущено. Заинтересованный
читатель найдет это доказательство в любом хорошем учебнике по
математическому анализу многих переменных.
Теорема А2.16. Теорема Лагранжа.
Пусть f{\) и gj{\\ j = h ...,т, вещественнозначные, непрерывно
дифференцируемые функции с одной и той лее областью определения
DcR". Пусть х* — внутренняя точка D, предположим, что х* —
оптимум (максимум или минимум) при ограничениях gJ (х*) = 0, j = 1, ...,m.
Если векторы-градиенты Vgy(x*), j = l, ...,т, линейно независимы, то
существуют такие единственные т чисел А,*, у = 1, ...,w, что
выполняется условие
ЭДж', A*)Jf(x)^frdgJ(x)_Q . = 1 ^
Эх, дх; % J Эх,
Несколько опережая события, мы должны здесь отметить, что теорема
недвусмысленно избегает упоминания важности Л для оптимальности
L. Ранее в нашем описании метода Лагранжа мы связали критическую
точку / по переменной х из множества, удовлетворяющего
ограничениям, с критической точкой L по переменным х и Л. Это было
обосновано, однако критические точки функции ? по Л в задачах максимизации
не будут давать максимумы; в задачах же минимизации они не будут да-

Глава А2. Математический анализ и оптимизация
657
вать минимумы. Мы надеемся, что это удастся пояснить в дальнейшем.
В следующем разделе мы вернемся к случаю двух переменных и одного
ограничения и постараемся представить графическую иллюстрацию.
А2.3.3. Геометрическая интерпретация
Условия, характеризующие решение задач условной оптимизации с
помощью лагранжиана, имеют геометрическую интерпретацию, и вы
должны быть знакомы с ней из промежуточного курса экономической
теории. Стоит потратить некоторое время, чтобы научиться
интерпретировать эти вещи стандартными графическими средствами.
Рассмотрим снова задачу (А2-4). Целевую функцию мы можем
геометрически представить через ее множества уровня
?(у°) = {(х]9 x2)\f(x], х2) = у0} для некоторого у0 из множества
значений. (Имейте в виду, что каждое значение у, принимаемое функцией,
имеет свое множество уровня.) По определению все точки множества
должны удовлетворять уравнению
/(*,, х2) = у°.
Если мы будем изменять х{ и х2, оставаясь на множестве уровня, dxl и
dx2 должны быть такими, чтобы и значение / неизменно равнялось у0.
Поэтому они должны удовлетворять уравнению
fa)^ , d/(s„ х2)
aXj ox2
-dxl+JK» 2jdx2=0, (A2-16)
получаемому путем полного дифференцирования обеих частей уравнения
множества уровня с учетом того, что первый дифференциал константы
у0 равен нулю. Это условие должно выполняться для любой точки
множества уровня функции.
Мы можем вывести выражение для наклона любой из кривых уровня
в произвольной точке. На плоскости (jcp х2), угол наклона любой кривой
уровня будет равняться отношению вертикального приращения (dx2) к
горизонтальному приращению (dfr,) для dxx и dx2, удовлетворяющих
dx
(А2-16). Решая (А2-16) относительно —-, угол наклона линий уровня в
dx{
точке (jc15 x2) будет равен
dx2
dxl
= (_1)Л(*1» ^) (А2-17)
вдоль?(/) /г(хР хг)

658
Математическое приложение
Обозначение |вдоль использовано, чтобы напомнить вам о специальных
изменениях dxx и dx2. Таким образом, как это изображено на рис. А2.5,
наклон линий уровня в точке (хр х2) равен (отрицательному) отношению
частных производных первого порядка в (*,, х2).
^
х2
-У!(х)//2(х)
./::-. L{/)
-> Xi
Х\
Рис. А2.5. Наклон линий уровня
Используем тот же прием и предположим, что ограничение g
выглядит так, как изображено на рис. А2.6, причем кривая изображена на той
же плоскости. Мы можем считать, что функция ограничения тоже
является некоторым множеством уровня. Это множество всех точек (х,, х2),
таких,что
g(*p x2) = 0.
> *i
Рис. А2.6. Наклон ограничения

Глава А2. Математический анализ и оптимизация
659
Как и прежде, мы можем вывести угол наклона кривой ограничения
полным дифференцированием в точке обеих частей уравнения, помня о
том, что дифференциал константы равен нулю. Следовательно, для любой
(jcp х2), удовлетворяющей ограничению, уравнение
ах1 ах2
должно выполняться для изменений dxx и dx2 вдоль ограничения.
После перегруппировки слагаемых мы снова получим выражение для
угла наклона в точке (jc, , х2):
dx2
dxl
= (-l)gi(*" x^ . (А2-18)
вдоль g()=0 ?г(*Р Xl)
Теперь вспомним нашу задачу (А2-4) и посмотрим на условия
первого порядка для критической точки лагранжиана, выписанные в (А2-7),
(А2-8), (А2-9). По методу Лагранжа эти условия определяют решения
нашей задачи (х*, х2) плюс «побочный» продукт — множитель
Лагранжа X*. Так как мы интересуемся лишь значениями переменных и у нас
нет непосредственного интереса к значению множителя Лагранжа, мы
можем переписать (А2-7), (А2-8), (А2-9), чтобы избавиться от X*, и
получить выражение, содержащее лишь jcj" и х*2. Простая перегруппировка
условий (А2-7), (А2-8), (А2-9) тогда дает
У(*Г, *г)= ^*dgC<, x2)
дхх Эх,
д/(*Г, *2*) = _^* dg(x*, x2)
дх2 дх2
g(x{\ x*2) = 0.
Для простоты будем считать, что X* *¦ О. Тогда деление первого
выражения на второе позволяет избавиться от Г, и у нас остаются всего два
уравнения, позволяющие определить переменные х\ и х*2:
j\ \х\ •> х2) _ Si \х\ ^ х2) СА2-19)
J 2 \Х\ 5 Х2 ) &2 \Х\ ' Х2 )

660
Математическое приложение
g(x*9 х*2) = 0.
(А2-20)
О чем говорят эти два уравнения? Взглянем снова на (А2-17) и
(А2-18) и рассмотрим первое условие (А2-19). Левая часть (А2-19) равна
произведению (-1) на наклон линий уровня целевой функции в точке
(jc*, х2). Правая часть равна произведению (-1) на наклон линии уровня
ограничения. Условие говорит о том, что решения х\ и х*2 являются
координатами точки, в которой совпадут наклоны линий уровня целевой
функции ограничения, но это еще не все. Из второго условия (А2-20)
следует, что мы должны находиться на линии уровня ограничения. То, что
точка находится на ограничении и наклоны равны, по определению
означает, что данная точка является точкой касания ограничения и линии
уровня целевой функции.
Ситуация с максимумом целевой функции при ограничении
изображена на рис. А2.7(а). Ясно, что наибольшее значение / вдоль
ограничения достигается в точке касания, которая может быть найдена из (А2-19)
и (А2-20), а стало быть, из условий первого порядка для безусловного
экстремума лагранжиана, т.е. (А2-7), (А2-8), (А2-9). Те же идеи
применимы к задаче минимизации, как это изображено на рис. А2.7(б).
х2
Наклон в точке касания
r/i@//2@=-gi(«V&@
Наклон в точке касания
-/,(x)//2(x)=-gl(x)/g2(x)
g(x) = 0
* *i
(а)
(б)
Рис. А2.7. Условия первого порядка для решения задачи Лагранжа
определяют точку касания линии уровня
целевой функции и ограничения

Глава А2. Математический анализ и оптимизация
661
А2.3.4. Условия второго порядка
Условия второго порядка для задач с лагранжианом весьма в духе
условий первого порядка. С самого начала есть соблазн рассуждать
следующим образом: если (х*, Л*) удовлетворяют условиям второго
порядка для безусловного максимума функции ?, тогда мы знаем, что при
наличии ограничений у функции / есть локальный максимум. Эта гипотеза
верна, но оказывается, что эти условия избыточны по сравнению с тем,
что действительно требуется для проверки оптимума. На самом деле мы
можем учесть взаимосвязь между х-ми в ограничении. Чтобы убедиться в
том, что мы имеем максимум, нам необходимо выявить убывание вдоль
ограничения второго дифференциала целевой функции в точке,
удовлетворяющей условиям первого порядка.
Когда у нас две переменные и одно ограничение, условия легко могут
быть получены из соотношения между х, и х2, накладываемого
ограничением. Давайте считать, что х1 — свободная переменная, принимающая
любое значение, и х2(хх) — требуемое значение х2, соответствующее
ограничению. Ограничение можно считать тождеством
g(x1,x2(x1)) = 0.
Уравнение ограничения задает неявным образом х2 как функцию *,.
Дифференцируя по jc, и решая относительно —-, мы получим знакомое
dxl
соотношение
(А2-21)
наклона
ограничения
d*2 = -g\
dxx g2
на плоскости
для наклона ограничения на плоскости (х,,х2). Полагая
y = f(xl9 jc2(x,)) и считая, что тем самым целевая функция учитывает
ограничение, мы получим функцию одной переменной jc, .
Дифференцируя по дс,, получаем dy/dx] = fl+f2(ck2/dxl). Подстановка (А2-21) дает
^Г = А-/2 — • (А2-22)
Дифференцируем снова, помня, что х2 — функция от хх и f. и g.
зависят от х, как непосредственно, так и косвенно через х2. Получаем
вторую производную

662
Математическое приложение
d У _ f , г dx2
dxx dxx
dx
dx,
Ml
g2
_ r fg2[gll+gl2(^2Ml)]-gl[g21+g22(A2Ml)]] (A2_23)
Необходимые условия максимума второго порядка для одной
переменной требуют, чтобы эта вторая производная была неотрицательна в
точке, где выполнены условия первого порядка. Достаточные условия
требуют строгого неравенства в этой точке. Из условий первого порядка
(А2-7), (А2-8), (А2-9) следует fx = -Xgx и f2 = -Xg2. По теореме Юнга
f\i~fi\ и 8п -Six- Учитывая это, а также используя (А2-21) и затем
преобразовывая, можем переписать (А2-23) в виде
d2y= 1
dxx2 (g2)
[(/и +ten)(g2J -2(/2 +bgn)gxg2 +(/a + ?Lg22)(g1J]. (А2-24)
Теперь посмотрим внимательно на выражения в скобках, содержащие
X. Вспомним, что, когда мы выписывали условия первого порядка
(А2-7), (А2-8), (А2-9), мы нашли частные производные лагранжиана по
переменным jcf.
Тогда частные производные второго порядка будут равны
^=/22+^22 (А25)
Ясно, что слагаемые с X внутри скобок — всего лишь частные
производные второго порядка лагранжиана по переменным xt. Все выражение в
квадратных скобках представляет собой комбинацию производных
второго порядка плюс производные первого порядка функции ограничения.
Для опытного глаза это квадратичное выражение представляет собой
детерминант симметричной матрицы. Предположим, мы образуем
симметричную матрицу

Глава А2. Математический анализ и оптимизация
663
Н =
'О
У%2
§2
#1
А
? ? ,
г
-11 -^12
Эта матрица называется окаймленным гессианом функции
Лагранжа, так как она состоит из частных производных второго порядка ? с
каймой из производных первого порядка уравнения ограничения и нуля.
Если мы вычислим ее детерминант (например, разложением по
последнему столбцу), то увидим, что
D =
0
Si
gl
g,
А.
А^
gi
Аг
Аг
= -[rn(g2f-2?ngxg2+?22{gxJ]. (A2-26)
Комбинируя вместе (А2-24), (A2-25), (A2-26), получаем, что вторая
производная целевой функции при ограничении может быть записана в
терминах окаймленного гессиана функции Лагранжа следующим образом:
d2y = (-1)
dx2
D.
(А2-27)
*. <ЯгГ
Таким образом, кривизна целевой функции вдоль ограничения
определяется знаком детерминанта окаймленного гессиана функции Лагранжа
(в предположении, что g2 Ф О). Следует отметить, что знак одной
величины будет всегда противополоэюен знаку другой, так как детерминант в
(А2-27) умножается на -1. Мы теперь готовы сформулировать
достаточное условие для задачи с двумя переменными и одним ограничением.
Теорема А2.17. Достаточное условие локального оптимума
задачи оптимизации с двумя переменными и одним ограничением.
Если (**, х2, А,*) является решением условий первого порядка (А2-7),
(А2-8), (А2-9) и если D>0 (<0) в (А2-26), причем значение D найдено
при (х*, х*2, X*), то точка (х*, х*2) является точкой локального
максимума (минимума) функции /X*p х2) при ограничении g(xp x2) = 0.
Пример А2.9. Давайте исследуем критическую точку, найденную в
примере (А2-8), на максимум или минимум. Возвращаясь к условию
примера, легко находим -?,, = -2а, -?,2 = 0, 1^ = О и ?22= -2Ъ. Из уравнения
ограничения известно, что gx = 1 и g2 = 1. Образуем окаймленный
гессиан; его детерминант равен

664
Математическое приложение
D =
-2а О 1
0 -26 1
1 1 О
= 2(а + Ь)>0.
(А2-28)
Так как здесь D > О для всех значений хх , х2 и X, то тот же знак будет
для решений (Е-9) условий первого порядка примера А2.8. Таким
образом, значение целевой функции в (Е-10) должно быть максимумом при
данном ограничении. ?
В случае п переменных и т < п ограничений достаточные условия
второго порядка снова дают нам информацию о максимуме (минимуме),
если второй дифференциал целевой функции меньше нуля (больше нуля)
в точке, где выполнены условия первого порядка. Исследование знака
второго дифференциала может быть сведено к анализу
знакоопределенности, окаймленного гессиана лагранжиана. В случае многих переменных
и ограничений, окаймленный гессиан снова формируется окаймлением
матрицы вторых производных частными производными первого порядка
ограничений и нулями в нужном количестве, чтобы получилась
симметричная матрица. Чтобы проверить на знакоопределенность, следует
проверить чередование знаков, соответствующих главных миноров этой
(чудовищно выглядящей) окаймленной матрицы:
Н =
Ее главные миноры являются детерминантами подматриц, получаемых
движением вниз по главной диагонали. Представляют интерес лишь
п - т главных миноров, начиная с минора порядка 2т+ \ и заканчивая
минором порядка т + п, т.е. детерминантом Н. То есть речь идет о
главных минорах
D* =
0 •
0 •
g\ ¦
s\ ¦
¦¦ 0
• 0
•• «г
•• *;
g\ ¦
§: ¦
Ax ¦
Ax ¦
¦ s\
¦¦ g:
•• A
•• a
, k = m + \, ...,«.
(A2-29)

Глава А2. Математический анализ и оптимизация
665
Мы можем подытожить сказанное о достаточных условиях для опти-
мумов в общем случае в виде следующей теоремы.
Теорема А2.18. Достаточные условия локальных оптимумов с
ограничениями в виде равенств.
Пусть заданы целевая функция f(x) и ограничения gJ(\) = 0,
j = 1, ...,/w при т<п. Пусть лагранжиан задан формулой (А2-14). Пусть
(х*, Л*) —решения условий первого порядка в (А2-15). Тогда:
1) х* является локальным максимумом f(\) при ограничениях, если
п-т главных миноров в (А2-29) чередуют свой знак, начиная с
положительного Dm+l >0, Dm+2 <0, ..., причем все миноры вычислены в (х*,Л*);
2) х* является локальным минимумом f(x) при ограничениях, если
п-т главных миноров в (А2-29) все отрицательны Dm+l < О, Dm+2 < О, ...,
причем все миноры вычислены в (х*,Л*).
А2.3.5. Ограничения в виде неравенств
Во многих экономических приложениях нам приходится
максимизировать или минимизировать что-либо при наличии ограничений, когда
эти ограничения — неравенства, а не уравнения, или же в добавление к
уравнениям. Например, в большинстве задач ограничение здравого
смысла состоит в неотрицательности экономических переменных. Метод Ла-
гранжа следует модифицировать так, чтобы он позволил решать такие
задачи, и даже с более сложными ограничениями на переменные в виде
неравенств.
Чтобы развить интуицию, которой позже воспользуемся для решения
трудных задач, мы начнем с наиболее простой задачи: максимизируем
функцию одной переменной при наличии ограничения
неотрицательности этой переменной. Формально мы можем записать эту задачу
следующим образом:
max/(jc) при лс>0. (A2-30)
X
Как и ранее, нас интересуют условия, характеризующие решение х*.
Если мы внимательно отнесемся к этой задаче, не забывая о том, что об-
ласть допустимых значений для решения — это неотрицательная
полуось действительной прямой, то, видимо, может встретиться любая из трех
ситуаций, изображенных на рис. А2.8.

666
Математическое приложение
А*)
/ги
Ах)
^
Д**)<о
»^AA>^n»S^
f\x) = 0
К«А^^«^Г^^»*
= 0
(а)
= 0
/>о
(б)
(в)
Рис. А2.8. Три возможные ситуации при максимизации с ограничениями
неотрицательности: (а) — случай 1, ограничение связывающее;
(б) — случай 2, ограничение связывающее, но неработающее;
(в) — случай 3, ограничение не является связывающим
Давайте рассмотрим каждый случай в отдельности и постараемся
охарактеризовать решения по каждому из них. В случае 1 (глобальный)
максимум достигается в х1. Но ситуация х1 < 0 недопустима, так как при этом
нарушается условие неотрицательности. Ясно, что максимум /, если х > 0,
достигается на границе допустимого множества в точке х* = 0. Здесь мы
говорим, что ограничение является связывающим. Относительно точки jc* = 0
справедливы два факта: х* равняется нулю и наклон / отрицательный.
Таким образом, два условия — х* = 0 и /'(**) < 0 — характеризуют решение
в первом случае. В случае 2 глобальный максимум достигается, но на самом
краю. Функция достигает максимума прямо в точке х* = 0, лежащей на
границе допустимого множества. Ограничение снова является связывающим,
но это не имеет значения. Снова два условия характеризуют решение в этом
случае: х* = 0 и f'(x*) = 0. Лишь случай 3 отвечает ситуации, которую мы
встречали ранее. Здесь максимум достигается в точке х* > 0, находящейся
внутри допустимого множества. Ограничение не является связывающим, и
мы говорим, что задача допускает существование внутреннего решения, так
как решение находится строго внутри допустимого множества. Снова мы
получаем два условия: х* > 0 и /'(jc*) = 0.
Теперь поставим вопрос: существует ли удобная комбинация
условий, объединяющая все три случая? Выпишем снова все три варианта:
Случай 1. jc*=0 и /V)<0.
Случай 2. х* = 0 и /'(**) = 0.
Случай 3. jc* > 0 и /'(**) = 0.

Глава А2. Математический анализ и оптимизация
667
Есть ли что-то общее для всех трех случаев? Посмотрим повнимательнее.
В каждом из случаев при перемножении двух условий мы получаем ноль!
Таким образом, во всех трех случаях x*[f'(x*)] = 0.
Однако одного этого условия недостаточно. Взглянем снова на
случай 3. Ясно, что в точке х* = О максимум функции не достигается. В этой
точке f'(x) > 0, и поэтому по мере увеличения х и смещения внутрь
допустимой области значение функции будет расти. Тем не менее
произведение x[f'(х)] = 0, несмотря на то что при условии х > О в точке х
достигается минимум, а не максимум. Мы можем исключить эту
нежелательную возможность, потребовав от функции, чтобы она не возрастала с
ростом х.
Тем самым мы нашли три условия, характеризующих решение
простой задачи на максимум с ограничением неотрицательности. Если х*
является решением (А2-30), тогда должны быть выполнены следующие три
условия:
Условие 1. /'(**) < О.
Условие 2. x*[f'(x)] = 0. (А2-31)
Условие 3. jc* > 0.
Заметим, что все три условия, рассмотренных вместе, исключают
проблему «минимизации», описанную только что. В точке Зс = 0, хотя и
выполнено xf'(x) = 0, условие 1 нарушено, так как f\x) > О.
Пример А2.10. Рассмотрим задачу
max F-х2 -Ах) при х > О.
X
Дифференцируя, мы получаем f'(x) = -2x-4. Согласно условиям
(А2-31) точка х* должна удовлетворять следующим требованиям:
1) -2х*-4<0;
2) x*[-2jc*-4] = 0;
3) jc* >0. х
Иногда решение такой системы является довольно запутанным и
сложным. Правило, облегчающее решение подобных систем, таково:
начинать решение следует с условия, записанного в виде произведения B).
Решив его, надо заняться остальными условиями. Умножим это условие
на -1, вынесем общий множитель 2 и получим
2*V+2] = 0.
Единственные решения этого уравнения — это х = 0 и х = -2. Однако
условие 3 исключает jc = -2, оставляя лишь х = 0в качества кандидата на

668
Математическое приложение
решение. Проверяем, что это решение также удовлетворяет условию 1,
поскольку 0 - 4 = -4 < 0, так что решением должно быть х* = 0. ?
Условия минимизации f(x), если jc>0, вывести тоже несложно.
Рассуждения здесь практически аналогичны предыдущим с тем
исключением, что затруднительный случай возникает, когда функция убывает на
границе допустимого множества. Мы исключим этот случай, потребовав,
чтобы производная функции была неотрицательной в рассматриваемой
точке. Если х* является решением задачи минимизации с ограничением
неотрицательности, то выполняются следующие условия:
Условие 1. /'(**) > 0.
Условие 2. x[f{x)] = 0. (А2-32)
Условие 3. х* > О.
Условия (А2-31) и (А2-32) легко обобщаются на случай оптимизации
вещественнозначных функций любого числа переменных при условии
неотрицательности всех этих переменных. В случае многих переменных эти
три условия должны выполняться для каждой переменной в отдельности,
причем вместо обыкновенной производной нужно подставить
соответствующую частную производную. Следующая теорема формализует
сказанное, и ее доказательство предлагается в качестве упражнения.
Теорема А2.19. Необходимые условия оптимума
вещественнозначных функций при условиях неотрицательности.
Пусть f{\) непрерывно дифференцируема.
1) Если в точке х* достигается максимум функции f(\) при х > О,
то х* удовлетворяет условиям:
Эх
б)х]
Э/(х*)
= 0, / = 1, ...,«;
Эх,
в) х] >0, / = 1, ...,«.
2) Если в точке х* достигается минимум функции f(\) при х > 0, то
удовлетворяет условиям:
a)m±l>0,i = l,...,n;
Эх
б)х]
ЭДх*)
Эх,
в) х* >0, / = 1, ...,«
= 0, / = 1, ...,«;

Глава А2. Математический анализ и оптимизация
669
А2.3.б. Условия Куна — Танкера
До сих пор нам на самом деле не приходилось использовать метод
Лагранжа, так как ограничения в виде неравенств были слишком
элементарными. Мы теперь рассмотрим задачу оптимизации с двумя
переменными, в которой единственным ограничением является неравенство
g(jc,, х2) > 0. Формально поставленная задача выглядит так:
max/(x,, х2) при g(x,, х2)>0. (A2-33)
дг,, х2
Это часто встречающаяся задача нелинейного программирования.
В задачах линейного программирования линейная функция
оптимизируется при наличии ограничений в виде линейных неравенств. В (А2-33) нет
подобных ограничений ни на вид целевой функции, ни на вид
ограничений, так что можно увидеть, что задачи линейного программирования
являются всего лишь специальными случаями нелинейных задач. Методы,
предлагаемые для решения общих нелинейных задач, обязаны своим
появлением хорошо нам известному линейному случаю.
Мы исследуем этот новый для нас случай, пробуя
переформулировать задачу в более привычных терминах. Наше исследование метода
Лагранжа научило нас, как рассматривать задачи с ограничениями в виде
равенств, а недавно мы разобрались со случаем ограничений
неотрицательности. Чтобы решить (А2-33), мы преобразуем ее в задачу с
ограничениями в виде равенств и ограничений неотрицательности, а затем
применим наши знания.
Прием, который мы хотим использовать, довольно прост.
Ограничение в (А2-33) требует от g неотрицательности. Введем новую
переменную, назовем ее z, определим ее как величину, на которую g превышает
ноль. Так как g должна быть неотрицательной, то z должна быть
неотрицательной по определению. Тогда мы сможем переписать единственное
ограничение в (А2-33) в виде неравенства заново, теперь в виде двух но-
1 вых условий: g(x,, x2)-z = 0 и z>0. За счет введения новой
переменной z нам удалось превратить условие в виде неравенства в условие в
виде равенства и еще одно условие неотрицательности. Таким образом,
задача с двумя переменными (А2-33) и одним неравенством превратилась
в эквивалентную задаче с тремя переменными с ограничениями в виде
равенства и неравенства:
max/(*„ х2) при g(x{9 x2)-z = 0,
z>0.
(А2-34)

670
Математическое приложение
Теорема А2.16 говорит нам, что максимум по х функции / при
ограничении равенства совпадает с безусловным максимумом по х
соответствующего лагранжиана в отсутствие ограничений неотрицательности.
А теорема А2.19 помогает нам модифицировать условия первого порядка
для максимума безусловного лагранжиана, чтобы учесть условия
неотрицательности. Давайте воспользуемся обеими этими теоремами.
Сначала мы образуем лагранжиан для задачи (А2-34):
?{х{, х2, z, X) = f(xl9 x2) + X[g(x{, x2)-z].
Помня о теореме Лагранжа, мы хотим максимизировать ? по переменным
jcp x2, z при условии z > 0. Так как хх и х2 не связаны ограничениями, а
z должна быть неотрицательной, то условия первого порядка по
переменным могут быть получены комбинированием теорем А2.16 и А2.19:
A^fi+Xg^O; О)
A=f2+Xg2=0; B)
А=-Х<0; C)
z2>zHt) = 0; D)
z>0. E)
Условие первого порядка на (свободный) выбор X, если ограничение
неотрицательности не вводится, таково:
Asg(x\> x2)-z = 0. F)
Заметьте, что условия с C) по E) являются условиями на частные
производные, произведения и знаки выражений при условии
неотрицательности z . Условия A), B) и F) возникли из-за ограничений в виде равенств,
следовательно, соответствующих произведений нет. Это результат того,
что мы не ввели никаких ограничений на знаки х,, х2 или X, и поэтому
воспользовались обычными условиями в задачах с лагранжианом и
ограничениями в виде равенств.
Эти условия характеризуют решение, которое мы ищем, но в
действительности нужды в придуманной переменной z нет. Если мы взглянем
внимательнее на условия D), E) и F), то увидим, что можно исключить
z . Умножая D) на -1 и переписывая заново E) и D), мы получаем
zA = 0
z>0
z = g(*„ х2).
Если мы используем третье из этих условий, с тем чтобы подставить z в
первые два, то мы можем ограничиться этими двумя условиями, не
содержащими z:

Глава А2. Математический анализ и оптимизация
671
g(xp x2)>0.
Возвращаясь к исходным условиям, с учетом последних двух мы
получаем минимальный набор условий, который называется условиями Куна —
Танкера:
/+tei=0 A)
Л+^2=0 B)
Xg{xx, х2) = 0 C0
?L>0, g(xl9 х2)>0. D0
Исследуем их внимательно. Условия A) и B) легко узнаваемы, как
обычные условия первого порядка для безусловного экстремума ?.
Чтобы проинтерпретировать условия C0 и D0, вернемся к теореме А2.19 и
выясним, что бы мы получили, если бы пытались минимизировать ? по
X, при условии неотрицательности X. Условия C0 и D0 в точности
повторяют условия ?х > О, Х?Х = О и X > О, которые возникли бы при
минимизации лагранжиана по X, если X > О.
Нетрудно заметить, что условия с A) по D0 являются необходимыми
для максимизации лагранжиана по переменным jtf. и минимизации
лагранжиана по множителю X. Если в некоторой точке (х*, х2, X*) ?
максимизируется по х, и х2, а по X минимизируется, то эта точка
(л:*, х2, X*) называется седловой точкой функции Лагранжа. Все это,
конечно, можно обобщить на случай многих переменных и любое число
ограничений при условии, что удовлетворены необременительные
требования к функциям ограничений.
Мы также можем вывести похожие, но не идентичные условия для
задач минимизации с условиями в виде равенств и неравенств. При
минимизации договоримся записывать ограничения в виде
неположительных неравенств g()<0 в отличие от неотрицательных неравенств,
используемых при максимизации. Тогда мы сможем повторить рассуждения
и методы, примененные ранее, с тем чтобы получить совпадение седло-
вой точки лагранжиана с решением условной задачи минимизации. На
этот раз, однако, седловая точка будет давать минимум лагранжиана по
пространственным переменным и максимум — по множителям Лагранжа.
У вас есть шанс проверить справедливость этого утверждения в
упражнении. А мы просто соберем воедино эти результаты, расширив теорему
Лагранжа (теорема А2.16).

672
Математическое приложение
Теорема А2.20 (Куна — Таккера). Необходимые условия
оптимума вещественнозначных функций с ограничениями в виде
неравенств.
Пусть /(х) и gJ(x)9 y = l, ...,/и непрерывно дифференцируемые ве-
щественнозначные функции, определенные на некоторой области
DcR", и пусть х* — внутренняя точка в D. Предположим, что в х*
достигается оптимум (максимум или минимум) f при ограничениях
gJ(x)>09 j = l9...9m.
Если векторы-градиенты WgJ(x*), вычисленные для существенных
ограничений, линейно независимы, то существует такой единственный
вектор Л*, что (х*, Л*) удовлетворяет условиям Куна—Таккера:
Эх, dxf jrf J dx;
X]gJ(x) = 09 gJ(x)>09 y = l, ...9m.
Более того, вектор Л* неотрицателен, если х — точка максимума, и
неположителен, если х — точка минимума.
Доказательство. Подробное доказательство этой теоремы уведет нас
в тот раздел математики, который нами не был рассмотрен. Полные
доказательства можно найти в работах Люнбергера [Luenberger, 1973] и
Мураты [Murata, 1977]. ¦
Условия Куна — Таккера теоремы А2.20 — всего лишь необходимые
условия первого порядка для локальных оптимумов, достаточные условия
получены для случая, когда целевая функция вогнута или квазивогнута.
Заинтересованного читателя мы отсылаем к Люнбергеру [Luenberger,
1973] или к Эрроу и Энтховену [Arrow, Enthoven, 1961]. Для наших целей
необходимых условий теоремы А2.20 вполне достаточно.
А2.4. Функции значений
Нам часто приходится встречаться с задачами оптимизации вида
max /(х, а) при g(x, а) = 0 и х > 0, (А2-35)
X
где вектор х является вектором переменных задачи, а а = (ар ...,ат)
является вектором параметров, возможно, входящих или в целевую
функцию, или в ограничения, или во все эти функции. Разумеется, решения
этой задачи будут зависеть некоторым образом от вектора параметров а.
Предположим, для каждого вектора а решение единственно и может
быть обозначено через х(а).

Глава Л2. Математический анализ и оптимизация
673
Мы можем определить новую функцию М(а), которая дает значение,
достигаемое целевой функцией в точке х, доставляющей максимум
функции / при ограничениях задачи. М(а) называется функцией
максимального значения и формально определяется следующим образом:
М(а) = max /(х, а) при g(x, а) = 0 и х > 0 .
Если мы найдем значение оптимизируемой функции/(х, а) на решении
задачи х(а), то значение этой функции будет наибольшим из возможных с
учетом ограничения. Это изображено на рис. А2.9.
Поэтому мы можем определить М(а) эквивалентным образом, как
Д/(а)«/(ж(а), а). (А2-36)
*2
\ ! V ^ Цу)\ У =/х(а), а)
Я(х, а) = 0 \
I ' \
I ' \
I ! А + х\
*,(а)
Рис. А2.9. Максимальное значение /(х, а) при ограничении g(x, a) = О
Довольно часто нам приходится выяснять, как изменяется
максимальное значение функции при изменении одного или нескольких параметров
задачи. Иногда нам также важно выяснить, как изменяются решения
задачи максимизации с изменением параметров. Теорема о максимуме1
говорит нам (в общих чертах), что если целевая функция и ограничения
непрерывны по своим параметрам и если область определения является
компактным множеством, то М(а) и х(а) — непрерывные функции от
параметров а (при условии, конечно, что решение единственно). Если же
целевая функция, ограничение и решения дифференцируемы по
параметрам, то можно доказать очень мощную теорему, позволяющую проанали-
1 См. книгу Бержа [Berge, 1963, р. 116], где даны полная формулировка и доказательство.

674
Математическое приложение
зировать, как ведет себя функция максимального значения при изменении
параметров. Она известна как теорема об огибающей.
Теорема А2.21. Теорема об огибающей.
Рассмотрим задачу (А2-35) и предположим, что целевая функция и
ограничение являются непрерывно дифференцируемыми функциями по а.
Пусть для любого а х(а)»0 является единственным решением
(А2-35). Предположим, что х(а) также непрерывно дифференцируема по
параметрам а. Пусть ?(х, а, X) — функция Лагранжа задачи и пусть
точки (х(а), Ца)) удовлетворяют условиям Куна — Таккера,
приведенным в теореме А2.20. Наконец, пусть М(а) — функция максимального
значения задачи. Тогда теорема об огибающей утверждает, что
ЭМ(а) д?
да j daj
j = h ~.9*n9
х(а), Ца)
где правая часть выражения обозначает частную производную функции
Лагранжа по параметру а} в точке (х(а), Ца)).
Теорема говорит о том, что совокупный эффект изменения
параметров на оптимальное значение целевой функции (на самом деле при
изменении параметров нужно решать задачу заново) можно найти, просто взяв
частную производную функции Лагранжа по параметру. Затем в эту
производную надо подставить решение исходной задачи, найденное с
помощью условий Куна — Таккера. Хотя мы ограничились формулировкой
теоремы, в которой у нас было только одно ограничение, теорема
справедлива и для произвольного числа ограничений, если только число
ограничений меньше числа переменных. Так как эта теорема важна и
неочевидна, то ее доказательство будет очень подробным.
Доказательство. Сначала построим лагранжиан для задачи
максимизации
?ее/(ж, a) + ?l[g(x, a)].
Если х(а) является решением (А2-35), то по теореме А2.20 найдется
такое А,(а), которое удовлетворяет условиям первого порядка Куна —
Таккера, изученным ранее. Если х(а) » 0, то легко видеть, что они сводятся
к и + 1 условиям:
ЩкЛ+Чш)Щ^Ля01/=i, ...,„ (P-D
axj oxt
g(x(a), a)aO,

Глава А2. Математический анализ и оптимизация
675
которые записаны нами как тождества, потому что они служат для
определения решений х(а) и А,(а).
Частная производная ? по параметру яу равна
д? _ЭДх, я) ^3g(x, a)
да,.
да;
да,
j j j
Если мы найдем значение этой производной в точке (х(а), Х(а)), то
получим
д?\
да,
ЭДх(а), a)i + 9g(x(a), a)
(Р-2)
Эя,. Эа;.
Если нам удастся показать, что частная производная по а} функции
максимального значения равна правой части выражения в (Р-2), то теорема
будет доказана.
Мы начнем с непосредственного вычисления производной по aj
функции М(а). Так как а} воздействует на / прямо и косвенно за счет
всех переменных xt (a), то следует воспользоваться правилом
дифференцирования сложной функции. Мы получаем
ЭМ(а)
да,
= Х
Э/(х(а), а)
Эх
Эх,(а) ( Э/(х(а), а)
daj daj
по правилу дифференцирования
сложной функции
Теперь вернемся к условиям первого порядка (Р-1). Перенос одного
слагаемого в другую сторону дает
Э/(х(а), а) _ ^43g(x(a), a)
ОХ{ OX j
Подстановка в выражение, стоящее в квадратных скобках, позволяет
получить новое представление для частной производной М(а)
ЭМ(а)
да,.
= Ма)?
9g(x(a), а) Эх. (а)
Эх, Эа,
Э/(х(а), а)
• да,
(Р-3)
Заключительный «трюк» состоит в том, что нам предстоит
продифференцировать второе тождество из условий первого порядка (Р-1). Так
как g(x(a), а) = 0, производные по а} от обеих частей тождества должны
быть равны. Так как производная константы равна нулю, мы получаем

676
Математическое приложение
9g(x(a), а)Эл:,(а)
Эх
да,
, dg(x(a), a)_Q
да,
по правилу дифференцирования
сложной функции
Перенося в другую сторону, получаем
9g(x(a), а) _ ^
да, ^
/=1
3g(x(a), а)Эх,(а)
Эх да;
Внесем минус под знак суммы, а затем подставим правую часть этого
тождества в выражение (Р-3), чтобы получить
(Р-4)
ЭМ(а) ag(i(a),«) | Э/(х(а),а)
да j daj да j
Правые части (Р-2) и (Р-4) совпадают. Таким образом,
ЭМ(а) = д?
да. да{
J J lx(a), Ця)
что и требовалось доказать. ¦
Пример A2.ll. Решим задачу на теорему об огибающей;
Пусть даны функция /(*,, х2) = ххх2 и простое ограничение
g(x,, х2) = а - 2хх - 4х2. Поставлена задача
max ххх2 при а - 2хх - 4х2 = 0,
дг,, х2
и мы хотим знать, как изменяется максимальное значение целевой
функции с изменением (единственного, скалярного) параметра а. Мы решим
задачу двумя способами: сначала найдем функцию М(а) непосредственно,
а затем продифференцируем ее, чтобы получить ответ. Далее мы
воспользуемся теоремой об огибающей, чтобы сравнить полученные результаты.
Чтобы найти М{а), нам следует найти оптимальные значения
переменных как функции параметра, после чего, подставив их в целевую
функцию, как это сделано в (А2-36), получим выражение для М(а). Заметим,
что эта задача слегка отличается от задачи в (А2-35), так как мы не требуем
неотрицательности от переменных. Таким образом, мы можем не
привлекать условия Куна — Таккера, а использовать простой метод Лагранжа.
Выпишем лагранжиан
? = х{х2 + Х[а-2хх -4х2]

Глава А2. Математический анализ и оптимизация
677
и условия первого порядка
?[=х2-2Х = 0
4=^-4^ = 0 (Е-1)
1^ -а-2хх -4х2 = 0.
Решив эту систему, получим хх (а) = а 14, х2 (а) = а 18 и Х(а) = а/16. Мы
найдем функцию максимального значения, если подставим найденные
значения х, и х2 в целевую функцию. Таким образом, получаем
Дифференцирование М(а) по а дает информацию о том, как
максимальное значение целевой функции меняется с изменением а.
Продифференцировав, получаем
dM{a) = a
da ~16*
Теперь давайте проверим этот результат, используя теорему об
огибающей. Теорема говорит о том, что, для того чтобы узнать, как меняется
максимальное значение функции с изменением параметра, всего лишь
требуется продифференцировать лагранжиан задачи максимизации по
параметру и найти значение этой производной в точке, являющейся
решением условий первого порядка (Е-1). Применяя теорему, мы сначала
получаем
dM(a)_d?
da da
Затем мы подставляем в это выражение решение системы (Е-1), т.е.
Х(а) = а 116. Это дает нам
da W 16
что совпадает с ранее найденным значением. ?
Кроме выполненной проверки теоремы об огибающей, этот пример
полезен с точки зрения интерпретации «побочных» переменных, т.е.
множителей Лагранжа. Интерпретации множителей Лагранжа будет
уделено больше внимания в упражнениях. Хотя в этом разделе мы
сконцентрировали свое внимание на задачах максимизации и функциях
максимального значения, но совершенно ясно, что мы можем аналогично
построить функции минимального значения, и теорема об огибающей будет
применима и к таким функциям.

678
Математическое приложение
А2.5. Упражнения
А1.1. Продифференцируйте следующие функции. Сделайте вывод о
том, является ли исследуемая функция возрастающей, убывающей или
имеет нулевое значение производной в точке х = 2. Классифицируйте
также исследуемую функцию на локальную выпуклость, вогнутость или
линейность в точке х = 2 .
а) 11jc3-6jc + 8.
б) Cjc2-jc)Fjc + 1).
в) х2-A/х3).
г) (jc2+2jcK.
д)[Зх/0с3+1)]2.
е)[A/х2+2)-A/х-2)]4.
1
ж) уг л.
х
А2.2. Найдите все частные производные первого порядка.
а) j\x\9 х2/ — 2*i —Х\ —х2.
б) f(xl9 х2) = х{2 + 2х\-4х2.
В) J\X\9 Х2 ) = Х\ ~~ Х2 "~ ^Х2 *
г) /(*,, x2) = 4xx +2x2 -х2 + ххх2 -х\ .
д) /(*,, х2) = х\ -6х,х> + х\.
е) /(*„ *2) = Зх2 -ххх2 + х2.
ж) g(x„ х2, Хз) = 1п(х2-х2х3-Хз).
А2.3. Пусть g(xa9 xh) = f(xa+xb, хв-х6),где /
—дифференцируемая функция двух переменных, например / = f(xu, xv). Покажите, что
дхадхь [дхи;
2 ( -vr V
Э/
уЪх„,
А2.4. Покажите, что функция у = х2х2 + х\хг + х]хх удовлетворяет
уравнению
ду ду ду , .,
-f- + -f- + -i- = (х, + х2 + хъJ.
охх dx2 dx3
А2.5. Найдите матрицу Гессе и постройте квадратичную форму
zrH(x)z для функций:
а) у = 2х, - х2 - х2.

Глава А2. Математический анализ и оптимизация
679
б) у = х2х + 2х\ - 4х2.
в) У = х\ ~" х1 ~ 2Х2 •
г) у = 4х, + 2х2 - х2 + jc,jc2 - х\.
Д) ^ = Х13 -б^^ + х\.
А2.6. Докажите, что частные производные второго порядка (не
смешанные) выпуклой функции должны быть всюду неотрицательными.
А2.7. Завершите пример А2.4 для частных производных иох2.
А2.8. Предположим, что f{xv х2) = yjx2 + х\ .
а) Покажите, что /(ягр x2) однородна первой степени.
б) По теореме Эйлера должно выполняться f(x{9 x2)=(df/dxx)xl +
+(df/dx2)x2. Проверьте это.
А2.9. Предположим, что f{xv jc2) = (jCjjc2J и g(jcp x2) = (x2x2f.
а) /(jcp x2) однородна. Какова степень однородности?
б) g(*P х2) однородна. Какова степень однородности?
в) Л(х,, x2) = f(xl9 x2)g(xl9 x2)однородна. Какова степень
однородности?
г) ?(jcp x2) = g(f(xl, jc2), /(xp х2)) однородна. Какова степень
однородности?
д) Докажите, что если f{xv x2) однородна степени т и g(xl9 x2)
однородна степени и, то k(x{9 x2) = g(f(xx, x2), f(x{9 x2)) однородна
степени тп.
А2.10. Вещественнозначная функция Л на Del" называется
гомотетичной, если она может быть представлена в виде g(/(x)), где
g: Е —> Е строго возрастающая и /: D —> Е однородна первой степени.
Покажите, что если дифференцируемая функция h: D —»Е гомотетична,
то для любого х g D и для любых i и у отношение
ЭА(/х)/Эдс,
ЭА(/х)/Эл:у
постоянно при t > О. Что можно сказать о множествах уровня функции h ?
A2.ll. Пусть F{z) — возрастающая функция одной переменной z.
Постройте сложную функцию F(/(x)). Покажите, что х* является
локальным максимумом (минимумом) /(х) тогда и только тогда, когда х*
является локальным максимумом (минимумом) F(/(x)).

680
Математическое приложение
А2.12. Предположим, f(\) — вогнутая функция и М — множество
всех точек в!л,в которых достигается глобальный максимум /.
Докажите, что М — выпуклое множество.
А2.13. Пусть /(х) — выпуклая функция. Докажите, что /(х)
достигает локального минимума в х тогда и только тогда, когда/(х)
достигает глобального минимума в х .
А2.14. Докажите, что если f(x) — строго выпуклая их — точка, в
которой достигается глобальный минимум /(х), то в х достигается
единственный глобальный минимум /(х).
А2.15. Проверьте вычисления примера А2.6, используя метод
подстановки, с тем чтобы решить систему из первых частных производных.
Затем найдите значение функции при я;,* =3/7 и ^=8/7 и найдите у*.
Проверьте, что мы нашли локальный максимум (см. пример А2.7),
вычислением значения функции в любой другой точке и сравнением с у*.
А2.16. Найдите критические точки следующих функций:
а) J \х\ » х2)= 2*i ~~ х\ ~х2.
б)/(*,, x2) = xf +2xl -4x2 •
в) Я*р х2) = х*-х%+2х2.
г) /С*р х2) = 4х{ + 2х2 -х* +ххх2 -х\ .
Д) /С*р х2) = х\-6ххх2+хъ2.
А2.17. Докажите теорему А2.15 для случая строго выпуклых
функций.
А2.18. Пусть f{\) — вещественнозначная функция, определенная на
R". Рассмотрим матрицу
Го
Г
^Л
а •
/и ¦
/.. •
J п
• J\n
J пп J
Это другой тип окаймленного гессиана, чем тот, который мы рассмотрели
в главе А.2. Здесь матрица из вторых производных окаймлена частными
производными первого порядка и нулем (так, чтобы матрица стала
квадратной). Главные миноры этой матрицы являются детерминантами

Глава А2. Математический анализ и оптимизация
681
D2 =
О /,
\J\ J\\
,А =
/. /.. /.2.-Д.=|н*|.
\J2 /21 J22\
Эрроу и Энтховен [Arrow, Enthoven, 1961] использовали разные варианты
чередования знаков главных миноров, чтобы установить следующие
полезные результаты.
1) Если f(x) квазивогнутая функция, то знаки главных миноров
чередуются в таком порядке: D2 < 0, D3 > 0,...
2) Если для всех х > 0 эти главные миноры (которые зависят от х)
чередуют знаки, начиная со строго отрицательного — D2 < 0, D3 > 0,..., —
тогда f(x) квазивогнутая на неотрицательном ортанте. Далее, можно
показать, что если для всех х » 0 знаки главных миноров чередуются
таким же образом, то f{\) — строго квазивогнутая на (строго)
положительном ортанте.
а) Функция /(*,, x2) = x]x2+xl квазивогнута на Ш2+. Проверьте, что
ее главные миноры чередуют свои знаки по типу 2).
б) Пусть /(*,, х2) = а\п(х{ +х2) + Ь, где а > О. Будет ли эта функция
строго квазивогнутой при х » 0 ? Является ли она квазивогнутой? А
если ее рассмотреть при х > 0 ? Обоснуйте свой ответ.
А2Д9. Пусть /(хр х2) = (х,л:2J. Является ли /(х) вогнутой на R+ ?
А квазивогнутой на R2+ ?
А2.20. Покажите, что обратное утверждение к утверждению 4)
теорем А2.1 и А2.4 неверно, используя пример функции f(x) = -х4, которая
строго вогнута на R, но ее вторая производная не везде строго
положительная.
А2.21. Завершите доказательство теоремы А2.3.
А2.22. Завершите доказательство теоремы А2.4.
А2.23. Используйте часть 2) теоремы А2.4, чтобы доказать теорему
А2.5. В частности, рассмотрите произведение zrH(x)z, когда z — один
из п единичных векторов в R".
А2.24. Найдите локальные экстремальные значения и
классифицируйте стационарные точки на точки максимума, минимума и прочие.
а) /(*„ х2) = 2хх-х2-х22.
б) /С*р х2)-х2 Л-2х\ -4х2.
в) /С*р jc2) = jc13-x22 + 2jc2.

682
Математическое приложение
Д) /О,, Х2) = х] -6XjX2 + *2 .
А2.25. Решите следующие задачи. Классифицируйте найденные
оптимальные значения функций.
а) min {х2 + х2) при ххх2 = 1.
X,, ДГ2
б) min jCjjc2 при х2 + х2 = 1.
Jf,, Х2
в) min л,** при х2 /a2 +x2 /b2 = 1.
х,, х2
г) min (jc, + jc2) при л;* +х2 = 1.
х,, х2
д) min jCjX2x33 при jcj + x2 + х3 = 1.
А2.26. Нарисуйте график функции /(*) = 6 - х2 - 4х. Найдите точку,
в которой функция достигает своего безусловного (глобального)
максимума, и вычислите значение функции в этой точке. Сравните найденное
значение с тем максимальным значением, которого она достигает при
условии неотрицательности х > О.
А2.27. При нахождении минимального значения функции f(x) при
х > О возможны три случая. Ограничение может являться связывающим,
но неработающим, или не являться связывающим. Постройте три
графика, аналогичные изображенным на рис. А2.8, чтобы проиллюстрировать
эти три случая. Убедитесь в том, что три условия (А2-32) учитывают все
эти три случая. Постройте четвертый случай, вызывающий
«затруднения», о котором упоминалось в главе А.2, и объясните, почему условия
(А2-32) делают его появление невозможным.
А2.28. Воспроизведите технику, использованную в главе А.2 для
вывода условий Куна — Таккера, для решения задачи
min /(*,, х2) при g(jcp jc2)<0 и х, >0, х2 >0.
х,, х2
А2.29. Рассмотрим задачу с двумя переменными (А2-33).
Предположим, что точка (jcj\ х2, А,*) является седловой точкой лагранжиана.
Выпишите условия Куна — Таккера, характеризующие это решение.
Предположим, нам известно, что условия неотрицательности не являются
связывающими, так что х* > 0, /' = 1, 2 и X* > О. Покажите, что условия
Куна — Таккера сводятся к обычным условиям Лагранжа для задачи без
ограничений неотрицательности или ограничений в виде неравенств.
А2.30. Вернитесь к задаче из упражнения А2.29. Используйте
условия Куна — Таккера, чтобы показать, что при X* > О ограничение в виде

Глава А2. Математический анализ и оптимизация
683
неравенства становится связывающим и обращается в равенство.
Покажите, что всякий раз, когда ограничение в виде неравенства не является
связывающим, множитель Лагранжа при этом ограничении должен
обращаться в нуль.
А2.31.Эрроу и Энтховен (см.: [Arrow, Enthoven, 1961]) рассмотрели
задачу квазивогнутого программирования вида
max /(х) при g(x) < 0 и х > 0,
X
где f(\) — квазивогнутая функция, a g(x) — квазивыпуклая.
а) Покажите, что если х* — точка локального максимума, то она
является также точкой глобального максимума.
б) Покажите, что если /(х) — строго квазивогнутая, то глобальный
максимум единственен.
А2.32. Рассмотрите задачу максимизации, в которой заданы целевая
функция /(jcp ...,*„) и т ограничений в виде aj-gJ(xl9 ...,*„) = О,
у = 1, ...,w. Здесь ни один из параметров а} не входит в целевую
функцию и, напротив, каждый из этих параметров входит ровно в одно
ограничение. В задачах подобного типа а} называется константой в
ограничении для j -го ограничения. Предполагая, что решение внутреннее,
покажите, что мы можем интерпретировать множитель Лагранжа,
соответствующий любому из ограничений, как эффект изменения
максимального значения целевой функции при изменении соответствующей
константы ограничения.
А2.33. Рассмотрим задачу нелинейного программирования вида
max/(jc,, x2) при a-g(xl9 x2)>0, х, >0, х2 >0.
дг,, х2
Используйте условия Куна — Таккера, чтобы показать, что в случае
внутреннего решения и при связывающем ограничении максимальное
значение целевой функции не будет убывать при смягчении ограничения
(т.е. при росте а).
А2.34. Покажите, что теорема А2.19 является специальным случаем
теоремы А2.20.

Список теорем
Глава 1
1.1. Существование вещественнозначной функции, представляющей
отношение предпочтения
1.2. Инвариантность функции полезности относительно
положительных монотонных преобразований
1.3. Свойства предпочтений и функции полезности
1.4. Достаточность условий первого порядка для задачи потребителя
1.5. Дифференцируемость функции спроса
1.6. Свойства косвенной функции полезности
1.7. Свойства функции расходов
1.8. Связь между косвенной функцией полезности и функцией расходов
1.9. Двойственность между функциями спроса по Маршаллу и по
Хиксу
1.10. Однородность и сбалансированность бюджета
1.11. Уравнение Слуцкого
1.12. Отрицательные собственные коэффициенты замещения
1.13. Закон спроса
1.14. Симметричность коэффициентов замещения
1.15. Отрицательная полу определенность матрицы замещения
1.16. Симметричность и отрицательная полуопределенность матрицы
Слуцкого
1.17. Агрегирование потребительского спроса
Глава 2
2.1. Построение функции полезности на основе функции расходов
2.2. Функция расходов, соответствующая построенной функции
полезности и, представляет собой Е
2.3. Двойственность между прямой и косвенной полезностью
2.4. (Теорема Хотеллинга, Уолда). Двойственность и обратные
функции спроса
2.5. Однородность следует из сбалансированности бюджета и
симметричности
2.6. Теорема о восстановлении
2.7. Существование функции полезности фон Неймана — Морген-
штерна на (д
2.8. Единственность функций фон Неймана — Моргенштерна с
точностью до положительных аффинных преобразований

Список теорем
685
Глава 3
3.1. (Теорема Шепарда). Вогнутость однородных первой степени
производственных функций
3.2. Свойства функции издержек
3.3. Свойства функций условного спроса на факторы производства
3.4. Функции издержек и условного спроса на факторы при
гомотетичных технологиях производства
3.5. Восстановление производственной функции из функции издержек
3.6. Восстановление функции издержек на основе функции условного
спроса
3.7. Свойства функции прибыли
3.8. Свойства функций предложения фирмы и спроса на факторы
производства
3.9. Ограниченная функция прибыли (функция прибыли в
краткосрочном периоде)
Глава 4
Глава 5
5.1. Основные свойства спроса
5.2. Свойства функций совокупного избыточного спроса
5.3. Совокупный избыточный спрос и вальрасовское равновесие
5.4. Полезность и совокупный избыточный спрос
5.5. Существование вальрасовского равновесия
5.6. Ядро и равновесия в конкурентных экономиках
5.7. Первая теорема благосостояния
5.8. Вторая теорема благосостояния
Следствие 5.1. Другой взгляд на вторую теорему благосостояния
5.9. Основные свойства предложения и прибыли
5.10. Свойства Y
5.11. Максимизация совокупной прибыли
5.12. Основное свойство функции спроса при условии участия
потребителя в прибыли фирм
5.13. Существование вальрасовского равновесия в экономике с
производством
5.14. Первая теорема благосостояния для экономики с производством
5.15. Вторая теорема благосостояния для экономики с производством
5.16. Принцип равноправия в ядре
5.17. (Теорема Эджворта — Дебре — Скарфа). Предельная теорема о
ядре

686
Список теорем
Глава 6
6.1. Теорема о невозможности Эрроу
6.2. Роулзианские функции общественного благосостояния
6.3. Утилитаристские функции общественного благосостояния
Глава 7
7.1. Упрощенный поиск равновесия по Нэшу
7.2. (Теорема Нэша). Существование равновесия по Нэшу
7.3. Существование равновесия Байеса — Нэша
7.4. (Теорема Куна). Обратная индукция и р>авновесие по Нэшу
Следствие 7.1. Существование равновесия по Нэшу в чистых
стратегиях
7.5. Обобщение обратной индукции в концепции совершенного в
подыграх равновесия
7.6. (Теорема Зельтена). Существование совершенного в подыграх
равновесия
7.7. (Теорема Крепса — Уилсона). Существование секвенциального
равновесия
Глава 8
8.1. Свойства разделяющего равновесия
8.2. Свойства объединяющего равновесия
8.3. Равновесие, удовлетворяющее интуитивному критерию
8.4. Отсутствие объединяющих равновесий
8.5. Свойства разделяющего равновесия
Глава 9
9.1. Симметричное равновесие на аукционе первой цены
9.2. Симметричное равновесие на голландском аукционе
9.3. Равновесие на аукционе второй цены
9.4. Равновесие на английском аукционе
9.5. Совместимые по стимулам механизмы прямой продажи
9.6. Эквивалентность доходов
9.7. Оптимальный механизм продажи
9.8. Упрощенный оптимальный механизм продажи
9.9. Оптимальный аукцион при симметричных участниках

Список теорем 687
Математическое приложение
Глава А1
А 1.1. Выпуклость пересечения выпуклых множеств
А1.2. Об открытых множествах в Ш"
А 1.3. Любое открытое множество является объединением открытых
окружностей
А 1.4. О замкнутых множествах в R"
А 1.5. Верхние и нижние грани подмножеств действительных чисел
А 1.6. Непрерывность и обратные отображения
А 1.7. Непрерывное отображение компактного множества является
компактным множеством
А 1.8. Об ограниченных последовательностях
А1.9. Последовательности, множества и непрерывные функции
А 1.10. (Теорема Вейерштрасса). Существование экстремальных
значений
А1.11. Теорема Брауэра о неподвижной точке
А 1.12. Супериорные, инфериорные множества и множества уровня
А 1.13. Точки на графике вогнутой функции и ниже него всегда
образуют выпуклое множество
А 1.14. Квазивогнутость и супериорные множества
А 1.15. Вогнутость предполагает квазивогнутость
А 1.16. Вогнутые и выпуклые функции
А 1.17. Точки на графике выпуклой функции и над ним всегда
образуют выпуклое множество
А 1.18. Квазивыпуклость и инфериорные множества
А 1.19. Квазивогнутые и квазивыпуклые функции
Глава А2
А2.1. Вогнутость и первая и вторая производные
А2.2. Теорема Юнга
А2.3. Одномерная и многомерная вогнутость
А2.4. Наклон, кривизна и вогнутость функций многих переменных
А2.5. Вогнутость, выпуклость и частные производные второго порядка
А2.6. Частные производные однородных функций
А2.7. Теорема Эйлера
А2.8. Необходимые условия локального внутреннего оптимума
функции в одной переменной
А2.9. Необходимые условия первого порядка локальных внутренних
оптимумов вещественнозначных функций

688
Список теорем
А2.10. Необходимые условия второго порядка локального
внутреннего оптимума вещественнозначных функций
А2.11. Достаточные условия для отрицательной и положительной
определенности гессиана
А2Л 2. Достаточные условия локального внутреннего оптимума
вещественнозначных функций
А2.13. (Безусловная). Локально-глобальная теорема
А2.14. Строгая вогнутость (выпуклость) и единственность
глобального оптимума
А2.15. Достаточные условия единственности глобального оптимума
А2.16. Теорема Лагранжа
А2.17. Достаточное условие локального оптимума для задачи
оптимизации с двумя переменными и одним ограничением
А2.18. Достаточные условия локальных оптимумов с ограничениями
в виде равенств
А2.19. Необходимые условия оптимума вещественнозначных
функций при условии неотрицательности
А2.20. (Теорема Куна — Таккера). Необходимые условия оптимума
вещественнозначных функций с ограничениями в виде неравенств
А2.21. Теорема об огибающей

Список определений
Глава 1
1.1. Отношение предпочтения
1.2. Отношение строгого предпочтения
1.3. Отношение безразличия
1.4. Множества в X, основанные на отношении предпочтения
1.5. Функция полезности, представляющая отношение предпочтения >=
1.6. Эластичности спроса и доли в доходе
Глава 2
2.1. Слабая аксиома выявленных предпочтений (weak axiom of
revealed preference, WARP)
2.2. Простые лотереи
2.3. Свойство ожидаемой полезности
2.4. Несклонность к риску, нейтральность к риску и склонность к риску
2.5. Гарантированный эквивалент и премия за риск
2.6. Мера Эрроу — Пратта абсолютной несклонности к риску
Глава 3
3.1. Сепарабельные производственные функции
3.2. Эластичность замещения
3.3. (Глобальная) Отдача от масштаба
3.4. (Локальная) Отдача от масштаба
3.5. Функция издержек
3.6. Ограниченная функция издержек (функция издержек в
краткосрочном периоде)
3.7. Функция прибыли
Глава 4
Глава 5
5.1. Парето-эффективные распределения
5.2. Блокирующие коалиции
5.3. Ядро экономики обмена
5.4. Избыточный спрос
5.5. Вальрасовское равновесие
5.6. Распределения, равновесные по Вальрасу

690
Список определений
5.7. Множество распределений, равновесных по Вальрасу
5.8. Равновесное по Вальрасу распределение в экономике с
производством
5.9. Парето-эффективное распределение в экономике с производством
5.10. Реплицированная экономика (г-реплика)
Глава 6
6.1. Отношение общественного предпочтения
6.2. Измерение, сравнение и инвариантность
6.3. Два дополнительных этических предположения о функции
общественного благосостояния
Глава 7
7.1. Игра в стратегической форме
7.2. Строго доминирующие стратегии
7.3. Строго доминируемые стратегии
7.4. Итеративно строго недоминируемые стратегии
7.5. Слабо доминируемые стратегии
7.6. Итеративно слабо недоминируемые стратегии
7.7. Равновесие по Нэшу в чистых стратегиях
7.8. Смешанные стратегии
7.9. Равновесие по Нэшу
7.10. Игра с неполной информацией
7.11. Ассоциированная игра в стратегической форме
7.12. Равновесие Байеса — Нэша
7.13. Игра в развернутой форме
7.14. Стратегия в игре в развернутой форме
7.15. Стратегии, полученные обратной индукцией
7.16. Подыгры
7.17. Совершенное в подыграх равновесие в чистых стратегиях
7.18. Совершенная память
7.19. Совершенное в подыграх равновесие
7.20. Согласованные стратегические наборы
7.21. Секвенциальная рациональность
7.22. Секвенциальное равновесие
Глава 8
8.1. Секвенциальное равновесие в чистых стратегиях в игре с
рыночными сигналами
8.2. Разделяющее и объединяющее равновесия при использовании
рыночных сигналов

Список определений
691
8.3. Интуитивный критерий (Хо — Крепса)
8.4. Разделяющее и объединяющее равновесия в модели скрининга
Глава 9
Математическое приложение
Глава А1
А1.1. Выпуклые множества в W
А 1.2. Полнота
А1.3. Транзитивность
А 1.4. Открытые и замкнутые е-окрестности
А1.5. Открытые множества в R"
А 1.6. Замкнутые множества в W
А 1.7. Ограниченные множества
А1.8. (Гейне — Борель). Компактные множества
А 1.9. (Коши). Непрерывность
А1.10. Открытые множества в D
А1.11. Замкнутые множества в D
А 1.12. Последовательности в R"
А 1.13. Сходящиеся последовательности
А 1.14. Ограниченные последовательности
А1.15. Подпоследовательности
А 1.16. Вещественнозначные функции
А 1.17. Возрастающие, строго возрастающие и строго возрастающие
(в сильном смысле) функции
А1.18. Убывающие, строго убывающие и строго убывающие (в
сильном смысле) функции
А1.19. Множества уровня
А 1.20. Множества уровня, относящиеся к точке
А 1.21. Супериорные и инфериорные множества
А 1.22. Вогнутые функции
А 1.23. Строго вогнутые функции
А 1.24. Квазивогнутые функции
А 1.25. Строго квазивогнутые функции
А 1.26. Выпуклые и строго выпуклые функции
А 1.27. Квазивыпуклые и строго квазивыпуклые функции
Глава А2
А2.1. Частные производные
А2.2. Однородные функции

Ответы и указания
Глава 1
1.2. Воспользуйтесь определениями.
1.4. Для начала рассмотрите отношение безразличия. Возьмите
любые три точки х' е X, / = 1, 2, 3, такие, что х1 ~ х2 и х2 ~ х3. Мы хотим
показать, что если х1 ~ х2 и х2 - х3, то х1 - х3. По определению
отношения безразличия, если х1 ~х2, то х'^х2 и х2 ^х1. Аналогично, если
х2~х3, то х2^х3 и х3;ьх2. По транзитивности >z, если х'^х2 и
х2 ^х3, то х1 ьх3. Используя аналогичные рассуждения, вы получите
требуемый результат.
1.16. В пункте а) предположите, что существует другой допустимый
набор х', х'~ х*. Используя выпуклость множества В и строгую
выпуклость предпочтений, получите противоречие. В пункте б) используйте
доказательство от противного, т.е. предположите, что утверждение не
верно. Тогда, используя монотонность, придете к противоречию.
1.22. Используйте метод, аналогичный тому, что был использован в
A.11), для исключения множителя Лагранжа, и сведите (и + 1) условие к
п условиям.
1.23. В пункте 2) воспользуйтесь аксиомой 5': заметьте, что
множества ^г(х) являются супериорными множествами для функции и(х).
Вспомните теорему А 1.14.
1.27. Нарисуйте карту кривых безразличия.
1.28. Выпишите все условия первого порядка и рассмотрите условие,
определяющее jc^. Используя его, постройте геометрическую
прогрессию. Будет ли этот ряд сходиться?
1.31. Предположите, что все необходимые производные существуют.
1.32. Тождество Роя.
1.40. Теорема А2.6.
1.45. Теорема Эйлера и любая функция спроса, лс;(р, у).
1.46. В пункте а) начните с определения е(р, 1). Умножьте
ограничение на» и воспользуйтесь однородностью. Предположите, что z = их и
представьте целевую функцию как функцию от z .
1.51. Рассмотрите каждое неравенство по отдельности. Запишите
одно из них как
Э*Др, у)/ду^Ц
*,(Р> У) У'

Ответы и указания
693
Проинтегрируйте обе части неравенства от у до у, а затем
прологарифмируйте.
1.53. В пункте б)
v(p,y) = A'yflp;a',
1=1
где А* = А\[а« .
/=1
1.59. Воспользуйтесь уравнением Слуцкого.
1.62. Никаких подсказок по этой задаче.
1.65. В пункте б) и0 должна быть равна v(p°, y°)9 не правда ли?
Перепишите знаменатель.
1.66. А пункте а) вам необходима функция расходов и нужно
вычислить и0. В пункте б) I = (и° - 1/8)/Bи° -1). В пункте в), если вы сможете
показать, что функция расходов должна быть мультипликативно сепара-
бельной по ценам и полезности, то остальное доказать легко.
Глава 2
2.3. Это должна быть функция полезности вида Кобба — Дугласа.
2.9. Воспользуйтесь графиком.
2.10. Для начала покажите, что х2 выявленно предпочитается х1.
2.11. Пусть х°=х(р°, 1) и х1=х(р1, 1). Рассмотрите функцию
f(t) = (p°-pl)-x(pl+t(p°-pl), (рЧ^рО-р'^х^где /€[0, 1], и
покажите, что если х° выявленно предпочитается х1 при ценах (р°, 1), то /
достигает единственного максимума на отрезке [0, 1] при t = 0.
2.12. В каждой из двух лотерей некоторый исход из множества А
будет иметь нулевую вероятность.
2.14. Вспомните, что каждый исход из множества А также является
лотереей из множества (д , гарантированно приводящей к данному исходу.
2.15. Аксиома G4.
2.17. Какая из аксиом будет нарушена, если существуют две
неравные вероятности, порождающие одну и ту же эквивалентную лотерею?
2.26. Несклонным к риску.
2.30. Воспользовавшись определением, выпишите дифференциальное
уравнение и решите его относительно u(w).
2.31. w(w) = wa+1/(a + l).
2.35. В пункте а) х0 = х{ = 1. В пункте б) агент имеет два
ограничения, и jc0 = 1, х" = 3/2, а jcf = 1/2. В пункте в) заметьте, что будущий до-

694
Ответы и указания
ход при гарантированном исходе равен ожидаемому доходу в случае,
когда исход не определен.
Глава 3
3.14. Сначала найдите отношение {fjfj), затем заметьте, что
^ln(jc./x/) = (-l)^ln(jc./x/).
3.15. В пункте а) сначала прологарифмируйте выражение, чтобы
получить
1п(>0 = -1п
Р
1 ( п ^
!«,.*?
V/=i
Заметьте, что liming) = @/0), и поэтому можно применить правило Ло-
р-»0
питаля. Использовав это правило, найдите limln(>>), а затем перейдите к
р-»0
выражению limj;. Пункт б) довольно труден. Если вам не удается его
р->0
сделать, советуем обратиться к учебнику Харди, Литлвуда и Поля [Hardy,
Littlewood, Polya, 1934], теорема 4.
3.18. Просто воспользуйтесь определениями и свойствами
производственной функции.
3.21. Во втором пункте положите z2 = z1 + Az, где Az > 0.
3.30. с(у) = atc{y)y.
3.41. Уравнения C-3) и C-4).
3.43. Используйте условия первого порядка.
3.48. Определим функцию
nv(p, w, x) = max/ту- w x при /(х, \)>у,
У, *
которая иногда называется функцией переменной прибыли, и заметим,
что nv(P> w> х) = яСр> w> w, x) + wx. Отметим также, что nv обладает
всеми свойствами, перечисленными в теореме 3.7, и частные производные
функций nv и к(р, w, w, x) no p и w совпадают.
3.53. K*=(wf/wk)(y2+y22)V2.
Глава 4
4.1. Упражнение 1.64.
4.2. Попытайтесь построить контрпример.
4.9. В пункте б) qx = 215/6, q2 = 110/6 и р = 275/6.
4.13. р\ =р*2 =80/3.
4.14. Воспользуйтесь симметричностью.

Ответы и указания
695
4.18. В пункте а) положите г\(у) = Г|, где Г| Ф1. В пункте б) положите
Г| = 0. В пункте в) начните все сначала и положите Г|(>>) = 1. В
пункте г) вспомните теорему Тейлора: /@~/('о) + //('оХ'~~'о) +
+(l/2)/"(/0)(/-/0J для произвольного ^.Рассмотрите CV + у0 как
функцию от y°[t + 1]1/A"л) и воспользуйтесь разложением в ряд Тейлора в точке
/0=0.
4.19. В пункте б) v(p, у) - 1пA1 р) + у-1. При решении пункта г) вам
может помочь упражнение 4.18.
4.20. Упражнение 4.18.
4.25. В пункте а) р1 = р2 = 4. В пункте б) начните с конца.
4.26. Изобразите решение графически на рисунках, подобных
рис. 4.2. Пункт г): есть ли разница для потребителя? Пункт д): введите
предположение, что все потребители одинаковы. Тем не менее у вас по-
прежнему останется много вопросов, над которыми надо подумать.
Глава 5
5.2. Продифференцируйте косвенную функцию полезности по той
цене, которая возрастает, и воспользуйтесь тождеством Роя.
5.10. Не стоит углубляться в математику. Просто подумайте, что
означает Парето-эффективность и что означает найти решение данной
системы уравнений.
5.12. Используйте х2 как единицу счета. В пункте б) не забудьте, что
ни потребительский набор, ни цены не могут быть отрицательными.
5.15. Найдите функции спроса потребителей.
5.16. Функция и2(\) является леонтьевской.
5.17. Относительная цена х{ равна а/A-ос).
5.18. В пункте а) х1 =A0/3, 40/3).
5.19. Найдите z(p) и убедитесь, что если р* — равновесие по Валь-
расу, то р* » 0. Решите систему функций избыточного спроса.
5.20. В пункте б) вспомните, что совокупное потребление каждого
блага должно быть равно совокупному начальному запасу благ.
Предположив, что р — относительная цена блага лг,, уравновешивающая рынок,
и р Ф р*, вы придете к противоречию.
5.21. Обратитесь к определению строгой выпуклости в
предположении 5.2.
5.24. (pv IрнУ = 4V2 , и он работает 8 часов в день.

696
Ответы и указания
5.25. Для того чтобы показать пропорциональность градиентов,
воспользуйтесь доказательством от противного, т.е. предположите, что это
не так. Положите z = (Vu\t)/\\Wu\t)\\)-(Vu\\J)/\\Vuj(\j)\\) и
покажите, что u'(x'+tz) и uJ(\J -tz) строго возрастают по / при / = 0.
Здесь вы можете использовать неравенство Коши — Шварца, согласно
которому для любых двух векторов vhw vw<||v||||w||, причем это
условие выполняется как равенство тогда и только тогда, когда векторы
пропорциональны.
5.27. Изобразите ситуацию графически. Для ответа на пункт б) вы
должны спросить себя: почему потребители захотят торговать?
Убедитесь, что ваш ответ осмыслен. Проверьте свои выводы, сравнив
полезность потребителей, если они не торгуют и если торгуют.
5.31. Внимательно ознакомьтесь с доказательством, приведенным в
тексте. Постройте коалицию из тех потребителей каждого типа, которые
находятся в наихудшем положении, и дайте члену каждой коалиции
«среднее» распределение для его типа.
5.32. В пункте б) опишите в терминах функций полезности и
первоначальных запасов выражения: 1) «в ящике Эджворта»; 2) «внутри
линзы»; 3) «на контрактной кривой». В пункте г) рассмотрите коалицию
S = {11, 12, 21} и найдите допустимое распределение благ между
потребителями, предпочитаемое потребителями из коалиции S.
5.33. Перераспределите первоначальные запасы поровну: такое
распределение не будет вызывать зависти. Воспользуйтесь теоремой 5.5 и
рассмотрите равновесное по Вальрасу распределение х*. Воспользуйтесь
теоремой 5.7. Теперь докажите, что х* также является распределением,
не вызывающим зависти.
5.34. В пункте б) воспользуйтесь предыдущим упражнением.
5.35. Определение справедливого распределения приведено в
упражнении 5.33.
5.36. Пункт а): кривые безразличия должны касаться друг друга, и все
блага должны быть распределены между потребителями. Пункт б):
вообще говоря, нет.
5.39. Упражнения 1.64 и 4.1. На самом деле в упражнении приведен
неполный вариант утверждения. Из теоремы Антонелли следует, что z(p)
не зависит от распределения первоначальных запасов и ведет себя как
система избыточного спроса одного потребителя тогда и только тогда, когда
предпочтения потребителей одинаковы и гомотетичны (см. доказательство
в статье Шафера и Сонненшейна [Shafer and Sonnenschein, 1982]).

Ответы и указания
697
Глава 6
6.4. Попробуйте «лексикографическую диктатуру».
6.7. В пункте в) предположите обратное. Найдите множество
профилей, ведущее к противоречию. Обоснуйте.
6.9. Пункт а): если х* » 0 — равновесное по Вальрасу
распределение, то должны существовать п цен (р*, ..., /?*), таких, что каждый
набор (х')* максимизирует полезность агента / на его бюджетном
множестве. Рассмотрите условия первого порядка и вспомните, что множитель
Лагранжа для агента / равен предельной полезности дохода агента / в
равновесии по Вальрасу, dv'(p*, р*е')/Эу. Затем заметьте, что функция
W должна быть строго вогнута. Таким образом, если у нас есть
некоторое множество весов а' при ie I и п-мерный вектор чисел
9 = F,, ..., 0„), такой, что oc'Vtt'((x') j=6 и х* удовлетворяет
ограничениям, то х* — максимум функции W при данных ограничениях. А если
выбрать а' равными величине, обратной предельной полезности дохода
для агента / в равновесии по Вальрасу? Каким выбрать вектор 8 ?
6.10. Пункт б): рассмотрите этот случай с тремя индивидами и тремя
альтернативами, так, как это было сделано в работе Сена [Sen, 1970a].
Сначала пусть xPlyPlz9 zP2xP2y и zP3xP3y. Определим ранжирование
х по сравнению с z согласно правилу Борда. Далее, пусть предпочтения
2 и 3 остаются неизменными, но для первого индивида xPlzPly. Теперь
проведите то же самое сравнение между х и z и докажите утверждение.
6.11. Сначала найдите в доказательстве теоремы Эрроу определение
«решающего голоса». Почему (х, у) и (z, w) не могут быть одной и той
же парой? При x = z воспользуйтесь U и предположите, что хРку,
wPJx и yP'w для всех /. Используйте L* и WP, чтобы показать
нарушение транзитивности. Если х, у, z и w — все различны, то пусть хРку,
zPjw, wP'x и yPlz для всех /'. Начните с этого.
6.13. Для решения пунктов б) и в) обратитесь к упражнению А2.10 за
необходимыми определениями. В пункте д)
( n , / ,vY/p
E(w, y) =
N 1
v^y
6.14. Нет, нет, нет, да.
6.15. Нет, да.

698
Ответы и указания
Глава 7
7.3. Сначала покажите, что если стратегия строго доминируется на
некотором шаге, то она остается строго доминируемой некоторой другой
оставшейся стратегией на каждом последующем шаге.
7.5. Пункт в): в каком случае выбор 99 является наилучшим ответом?
Для нахождения W] используйте следующие шаги. Шаг 1: покажите, что,
если 14 приводит к ничьей, то 15, 16, ..., 100 приводят либо к проигрышу,
либо к ничьей. Шаг 2: покажите, что выбор 14 ведет к выигрышу, если
все остальные игроки выбрали число строго больше 14. Шаг 3: покажите,
что выбор 14 ведет к проигрышу, только если одна треть от среднего
строго меньше 14. Сделайте из шагов 2 и 3 вывод, что если выбор 14
ведет к проигрышу, то и выбор 15, 16, ..., 100 также ведет к проигрышу.
7.7. В пункте а) используйте теорему существования равновесия по
Нэшу.
7.8. Используйте функцию с неподвижной точкой (подобно тому, как
это было сделано при доказательстве существования равновесия по
Нэшу) для доказательства существования стратегии rn e А/, для игрока 1,
который максимизирует w,(w, m\ ..., гп) при те Мх. Затем
воспользуйтесь симметричностью.
7.9. Найдите в пункте в) упражнения 7.7 определение цены игры, а в
упражнении 7.8 — определение симметричной игры.
7.13. Не исключайте слабо доминируемые стратегии. Будут ли все
равновесия равновесиями в чистых стратегиях? Убедитесь, что вторая
фирма в случае высоких издержек имеет нулевую прибыль в каждом
равновесии Байеса — Нэша.
7.21. Пусть информационные множества «пересекают» друг друга.
7.31. Может ли выбор первого игрока влиять на ожидания третьего
игрока относительно второго?
Глава 8
8.1. Вспомните, что богатство в разных состояниях представляет
собой разные блага, и состояние, в котором несчастный случай происходит
только с потребителем /, отличается от состояния, когда несчастный
случай происходит только с потребителем )Ф1. Проверьте выполнение
предпосылок первой теоремы благосостояния и убедитесь, что
конкурентный исход, получаемый в разделе 8.1, эффективен в описанном в
тексте смысле.
8.6. Пункт а): предположите, что это не так. Может ли спрос на
подержанные машины равняться предложению?

Ответы и указания
699
8.11. Сначала покажите, что ^(тс/@)-тс/A))>0 для всех &>0, пе-
реписав эту сумму в виде ^
i=k
я,A)
я,@) ^
|тс/ A) и применив доказательство
L
от противного. Затем примените тождество ^Я/6, =^П ^я, F* -&*_,)
/=0 к=0 V /=А /
для каждой пары элементов последовательностей действительных чисел
Ш/to и {&/}?о>где *_, =0.
Глава 9
9.3. Заметьте, что (9-3) выполняется для всех v, включая v = г.
9.12. Существенно ли для результата то, что оценки принадлежат
интервалу [0, 1]?
9.14. (б) Какой механизм продажи при этом возникает?
9.16. (б) Используйте теорему 9.5 и не забудьте об индивидуальной
рациональности.
9.18. Необходимо использовать предположение, что
V,. - A - Ft (v,))//. (v;) строго возрастает.
Математическое приложение
Глава А1
А1.2. Просто воспользуйтесь определениями подмножества,
объединения и пересечения.
А1.3. Для начала рассмотрите первое выражение. Возьмите любой
хе (SпТ)с. Если хе (SпТ)с, то х? Sс\Т. Если х? Sс\Т, то х? S или
х? Т (не забудьте, что это включающее «или»). Если х? 5, то хе Sc.
Если х?Т, то хеТс. Поскольку хе Sc или хеТс, то хе Sc kjTc .
Поскольку х было выбрано произвольно, то полученное соотношение
выполняется для всех xe(S пТ)с. Таким образом,
х е (S п Т)с => х е Sc u Т, и мы показали, что {S n Т)с с 5е иГ. Чтобы
завершить доказательство первого закона, нам осталось показать, что
ХсиГс(ХпГ)с.
А1.13. Пусть xef~\Bc). По определению прообраза хе D и
f(x)e Вс. По определению дополнения В до R хе D и f{x)? В. По
определению прообраза jcg D и х? f~l(B). По определению дополнения

700
Ответы и указания
Г1 (В) до D xeD и хе {/'1(В))\ таким образом, f~\Bc)(z(f-\B))c.
Завершите доказательство.
А1.18. Положите Q! = {х а' -х + Ь1 >0} и воспользуйтесь пунктом б)
упражнения А1.17.
А1.21. Сначала докажите утверждения 1)—3). Затем рассмотрите
П~=14,где Д. =(-!/'*, I/O-
А1.22. Начните с рисунка.
А1.24. Посмотрите на дополнение каждого множества.
А1.25. Используйте теорему А 1.2 для описания дополнения S до R.
А1.26. Для решения первого пункта воспользуйтесь графическим
представлением, подобным рис. А 1.12, и результатом упражнения А 1.24.
Вторая часть не должна вызывать трудностей.
А1.27. Для начала заметьте, что дополнение S является открытым, а
затем примените теорему А 1.3. Открытые окрестности в R представляют
собой открытые интервалы. Воспользуйтесь упражнением А 1.26.
А1.31. Центр окрестности лежит в начале координат.
А1.32. В пункте в) вы должны показать, что множество ограничено и
замкнуто. Для того чтобы показать первое, заметьте, что центр
окрестности лежит в начале координат. Чтобы показать последнее, рассмотрите
множества F0 = < хе
X*,=U, ^={хе]Г|я;,. >0}, / = 1, ...,
«.Убедитесь, что дополнение каждого множества открыто. Заметьте также, что
?„-\ _ р|^о/г Учтите все вышесказанное.
А1.38. Присмотритесь повнимательнее к множеству S.
А1.39. Проверьте образ f(x) = cos(jc) -1/2.
А1.40. Выберите значение у и несколько значений для jc,. и найдите
значения х2. Изобразите решение на графике.
А 1.46. В пункте б) вам поможет то, что х1 и х2 могут быть выбраны
так, что f(xl)> Дх2) и что //(x1) + (l-0/(x2) = /(x2) + /(/(x1)- Дх2)).
А1.49. Да, да, нет, да. Ищите выпуклые множества. В пункте д) ответ
может различаться в зависимости от того, является функция f(x)
непрерывной или нет.
Глава А2
А2.1. Пункт ж): f'(x) = -ехр(*2) < 0.
А2.2. Пункт а): /, = 2 - 2хх и /2 = -2х2.
Пункт д): /, = 3xf - 6х2 и /2 = -бя^ + Ъх\.

Ответы и указания 701
А2.3. Правило дифференцирования сложной функции.
А2.5. Пункт а):
(-2 0Л
Н(х) =
[О -2)
A2.ll. Используйте определение возрастающей функции и
определение локального оптимума.
А2.19. Квазивогнутость следует из строгой квазивогнутости.
А2.24. Пункт а): х* = A, 0) — максимум. Пункт б): х* = @, 1) —
минимум. .
А2.25.Пункта): A, 1) и (-1, -1); /A, 1) = /(-1, -1) = 2.
Пункт б): (-л/Т72, л/172) и (VT72, ->/Г72).
Пункт в): (х/^Тз, л/262/з) и (л/^7з, -л/262/з).
Пункт г): (A/2I/4, A/2I/4).
Пунктд): A/6, 2/6, 3/6).
А2.32. Теорема об огибающей.

Список литературы
Afriat S. The Combinatorial Theory of Demand. L.: Input-Output
Publishing, 1976.
Akerlof G. The Market for Lemons: Quality Uncertainty and the Market
Mechanism // Quarterly Journal of Economics. 1970. Vol. 89. P. 488—500
(русск. перевод: Акерлоф Дж. Рынок «лимонов»: неопределенность
качества и рыночный механизм // THESIS. 1994. Вып. 5. С. 31-104).
Antonelli G. Sulla Teoria Matematica della Economia Politica. Pisa, 1886.
Transl. as On the Mathematical Theory of Political Economy // Preferences
Utility and Demand: A Minnesota Symposium. J.L. Chipman et al. (eds.).
N.-Y.: Harcourt Brace Jovanovich, 1971. P. 333—364.
Arrow K. Social Choice and Individual Values. N.-Y.: John Wiley, 1951
(рус. перевод: Эрроу К.Д. Коллективный выбор и социальные ценности.
М.: Изд. дом ГУ ВШЭ, 1951).
Arrow К. The Theory of Risk Aversion // Essays in the Theory of Risk
Bearing. K. Arrow (ed.). Chicago: Markham, 1970. P. 90—109.
Arrow K. Some Ordinalist Utilitarian Notes on Rawls' Theory of Justice //
Journal of Philosophy. 1973. Vol. 70. P. 245—263.
Arrow K., Debreu G. Existence of Equilibrium for a Competitive
Economy // Econometrica. 1954. Vol. 22. P. 265—290.
Arrow K., Enthoven A. Quasi-Concave Programming // Econometrica,
1961. Vol. 29. P. 779—800.
Atkinson A. On the Measurement of Inequality // Journal of Economic
Theory. 1970. Vol. 2. P. 244—263.
Aumann R.J. Markets with a Continuum of Traders // Econometrica. 1964.
Vol. 32. P. 39—50.
Barten A., Bohm V. Consumer Theory // Handbook of Mathematical
Economics /K. Arrow, M. Intrilligator (eds.). Amsterdam: North Holland, 1982.
P. 2: 382^*29.
Berge С Topological Spaces: Trans. E. Patterson. Edinburgh: Oliver and
Boyd, 1963.
Bertrand J. Review of Theorie Mathematique de la Richesse Sociale and
Recherches sur les Principes Mathematiques de la Theorie des Richesses //
Journal des Savants. 1883. P. 499—508.
Black D. On the Rationale of Group Decision-Making // Journal of
Political Economy. 1948. Vol. 56. P. 23—34.
Blackorby C, Donaldson D. Measures of Relative Equality and Their
Meaning in Terms of Social Welfare // Journal of Economic Theory. 1978.
Vol. 18. P. 59—80.

Список литературы
703
Blackorby С, Donaldson D., Weymark J. Social Choice with Interpersonal
Utility Comparisons: A Diagrammatic Introduction // International Economic
Review. 1984. Vol. 25. P. 327—356.
Cho I.K., Kreps D.M. Signaling Games and Stable Equilibria // Quarterly
Journal of Economics. 1987. Vol. 102. P. 179—221.
Cornwall R. Introduction to the Use of General Equilibrium Analysis.
Amsterdam: North Holland, 1984.
Cournot A. Recherches sur les principes mathematiques de la theorie des
richesses. Paris: Hachette, 1838 (англ. перевод: Bacon N. Researches into the
Mathematical Principles of the Theory of Wealth: trans. N. Bacon. N.-Y.: Kel-
ley, 1960).
D'Aspremont C, Gevers L. Equity and the Informational Basis of
Collective Choice // Review of Economic Studies. 1977. Vol. 44. P. 199—209.
Debreu G. Representation of a Preference Ordering by a Numerical
Function // Decision Processes I R.M. Thrall et al. (eds.). N.-Y.: John Wiley, 1954.
P. 159—165.
Debreu G. Theory of Value. N.-Y.: John Wiley, 1959.
Debreu G. Smooth Preferences // Econometrica. 1972. Vol. 40. P. 603—
615.
Debreu G., Scarf H. A Limit Theorem on the Core of an Economy //
International Economic Review. 1963. Vol. 4. P. 235—246.
Diewert W.E. Applications of Duality Theory // Frontiers of Quantitative
Economics I M.D. Intrilligator, D.A. Kendrick (eds.). Amsterdam: North
Holland, 1974. P. 2: 106—199.
Edgeworth F.Y. Mathematical Psychics. L.: Paul Kegan, 1881.
Eisenberg B. Aggregation of Utility Functions // Management Science.
1961. Vol. 7. P. 337—350.
Geanakoplos J. Three Brief Proofs of Arrow's Impossibility Theorem /
[mimeo]. Cowles Foundation, Yale University, 1996.
Goldman S.M., Uzawa H. A Note on Separability in Demand Analysis //
Econometrica. 1964. Vol. 32. P. 387—398.
Grossman S.J., Hart O.D. An Analysis of the Principal-Agent Problem //
Econometrica. 1983. Vol. 51. P. 7—45.
Hammond P.J. Equity, Arrow's Conditions, and Rawls' Difference
Principle // Econometrica. 1976. Vol. 44. P. 793—804.
Hardy G., Littlewood J., Polya G. Inequalities. Cambridge: Oxford
University Press, 1934.
Harsanyi J. Cardinal Utility in Welfare Economics and in the Theory of
Risk-Taking II Journal of Political Economy. 1953. Vol. 61. P. 434—435.
Harsanyi J. Cardinal Welfare, Individualistic Ethics, and Interpersonal
Comparisons of Utility // Journal of Political Economy. 1955. Vol. 63.
P. 309—321.

704
Список литературы
Harsanyi J. Games with Incomplete Information Played by 'Bayesian'
Players. Parts I, II, III // Management Science. 1967—1968. Vol. 14. P. 159—
182, 320—334, 486—502.
Harsanyi J. Can the Maximin Principle Serve as a Basis for Morality?
A Critique of John Rawls's Theory // American Political Science Review. 1975.
Vol. 69. P. 594—606.
Hicks J. Value and Capital. Oxford: Clarendon Press, 1939.
Hicks J. A Revision of Demand Theory. Oxford: Clarendon Press, 1956.
Hildenbrand W. Core and Equilibria of a Large Economy. Princeton:
Princeton University Press, 1974.
Hohn F. Elementary Matrix Algebra. 3rd ed. N.-Y.: Macmillan, 1973.
Holmstrom B. Moral Hazard and Observability // Bell Journal of
Economics. 1979. Vol. 10. P. 74—91.
Holmstrom B. Moral Hazard in Teams // Bell Journal of Economics. 1982.
Vol. 13. P. 324—340.
Houthakker H. Revealed Preference and the Utility Function // Economica.
1950. Vol. 17F6). P. 159—174.
Hurwicz L., Uzawa H. On the Integrability of Demand Functions // Utility
Preferences and Demand: A Minnesota Symposium I J.S. Chipman et al. (eds).
N.-Y.: Harcourt Brace Jovanovich, 1971. P. 114—148.
Kakutani S. A Generalization of Brouwer's Fixed-Point Theorem // Duke
Mathematical Journal. 1941. Vol. 8. P. 451—459.
Knoblauch V. A Tight Upper Bound on the Money Metric Utility Function //
American Economic Review. 1992. Vol. 82. № 3. P. 660—663.
Kohlberg E., Reny P.J. Independence on Relative Probability Spaces and
Consistent Assessments in Game Trees // Journal of Economic Theory. 1997.
Vol. 75. P. 280—313.
Kreps D.M., Wilson B.D. Sequential Equilibria // Econometrica. 1982.
Vol. 50. P. 863—894.
Kuhn H. Extensive Games and the Problem of Information //
Contributions to the Theory of Games. H.W. Kuhn, A.W. Tucker (eds). Vol. II (Annals
of Mathematics Studies 28). Princeton: Princeton University Press. 1953. P. 2:
193—216.
Kuhn H., Tucker A.W. Nonlinear Programming // Proceedings of the
Second Berkeley Symposium on Mathematical Statistics and Probability.
J. Neyman (ed.). Berkeley: University of California Press, 1951. P. 481—492.
Luenberger D.G. Introduction to Linear and Nonlinear Programming.
N.-Y.: John Wiley, 1973.
McKenzie L. On Equilibrium in Graham's Model of World Trade and
Other Competitive Systems // Econometrica. 1954. Vol. 22. P. 147—161.
Myerson R. Optimal Auction Design // Mathematics of Operations
Research. 1981. Vol. 6. P. 58—73.

Список литературы
705
Murata Y. Mathematics for Stability and Optimization of Economic
Systems. N.-Y.: Academic Press, 1977.
Nash J. Non-cooperative Games // Annals of Mathematics. 1951. Vol. 54.
P. 286—295.
Osborne M.J., Rubinstein A. A Course in Game Theory. Cambridge, MA:
The MIT Press, 1994.
Pareto V. Cours d'economie politique. Lausanne: Rouge, 1896.
Pratt J. Risk Aversion in the Small and in the Large // Econometrica. 1964.
Vol. 32, P. 122—136.
Rawls J. A Theory of Justice. Cambridge, MA: Harvard University Press,
1971.
Richter M. Revealed Preference Theory // Econometrica. 1966. Vol. 34.
№ 3. P. 635—645.
Roberts K.W. S. Possibility Theorems with Interpersonally Comparable
Welfare Levels II Review of Economic Studies. 1980. Vol. 47. P. 409—420.
Rothschild M., Stiglitz J.E. Equilibrium in Competitive Insurance Markets:
An Essay in the Economics of Imperfect Information // Quarterly Journal of
Economics. 1976. Vol. 80. P. 629—649.
Roy R. De Vutilite: contribution a la theorie des choix. Paris: Hermann,
1942.
Royden H. Real Analysis. N.-Y.: Macmillan, 1963.
Samuelson P.A. Foundations of Economic Analysis. Cambridge, MA:
Harvard University Press, 1947.
Selten R. Spieltheoretische Behandlung eines Oligopolmodells mit Nach-
fragetragheit // Zeitschrift fur die Gesamte Staatswissenschaft. 1965. Bd. 12.
S. 301—324, 667—689.
Selten R. Reexamination of the Perfectness Concept for Equilibrium
Points in Extensive Games // International Journal of Game Theory. 1975.
Vol. 4. P. 25—55.
Sen A. The Impossibility of a Paretian Liberal // Journal of Political
Economy. 1970b. Vol. 78. P. 152—157.
Sen A. On Weights and Measures: Informational Constraints in Social
Welfare Analysis /I Econometrica. 1977. Vol. 45. P. 1539—1572.
Sen A. Social Choice Theory // Handbook of Mathematical Economics I
K. Arrow and M. Intrilligator (eds.). Amsterdam: North Holland, 1984. Vol. 3.
P. 1073—1181.
Shafer W., Sonnenschein H. Market Demand and Excess Demand
Functions // Handbook of Mathematical Economics I K. Arrow, M. Intrilligator
(eds.). Amsterdam: North Holland, 1982. Vol. 2. P. 671—693.
Shephard R.W. Theory of Cost and Production Functions. Princeton:
Princeton University Press, 1970.

706
Список литературы
Slutsky E. Sulla Teoria del Bilancie del Consumatore // Giornale degli
Economist. 1915. Vol. 51. № 1. P. 26 (англ. перевод: On the Theory of the
Budget of the Consumer // Readings in Price Theory I G.J. Stigler, K.E. Bould-
ing (eds). L.: Allen and Unwin, 1953. P. 27—56.
Smith A. The Wealth of Nations [1776]. Cannan Ed. Chicago: University
of Chicago Press, 1976.
Sonnenschien H. Demand Theory without Transitive Preferences, with
Applications to the Theory of Competitive Equilibrium // Utility, Preference
and Demand: A Minnesota Symposium / J.S. Chipman et al. (eds). N.-Y.: Har-
court Brace Jovanovich, 1971. P. 215—223.
Spence A.M. Job Market Signaling // Quarterly Journal of Economics.
1973. Vol. 87. P. 355—374.
Spence A.M. Product Selection, Fixed Costs, and Monopolistic
Competition // Review of Economic Studies. 1976. Vol. 43. P. 217—235.
Tarski A. A Lattice-Theoretical Fix Point Theorem and its Applications //
Pacific Journal of Mathematics. 1955. Vol. 5. P. 285—309.
Varian H. The Nonparametric Approach to Demand Analysis // Econome-
trica. 1982. Vol. 50. № 4. P. 945—973.
Neumann von J., Morgenstern O. Theory of Games and Economic
Behavior. Princeton: Princeton University Press, 1944.
Wald A. Uber einige Gleiehungssysteme der mathematischen Okonomie //
Zeitschrift fur Nationalokonomie. 1936. Bd. 7. S. 637—670 (англ. перевод:
Some Systems of Equations of Mathematical Economics // Econometrica.
Vol. 19. P. 368—403).
Walras L. Elements d'economie politique pure. Lausanne: L. Corbaz, 1874
(англ. перевод: W. Jaffe Element of Pure Economics: transl. W. Jaffe. L.:
Allen and Unwin, 1954: русск. перевод: Вальрас Л.)
Willig R.D. Consumer's Surplus without Apology // American Economic
Review. 1976. Vol. 66. P. 589—597.

Предметный указатель
А
Аксиома
выпуклости 24 , 103 - 106 , 291
замещения 131
локальной ненасыщаемости 21
монотонности (см. Монотонность)
непрерывности (см. Непрерывность)
полноты (см. Полнота)
транзитивности (см. Транзитивность)
Аксиоматическое моделирование 15 - 17 , 19 - 20
Аксиомы потребительского выбора 15 - 26
в условиях неопределенности 129 - 131
Аткинсона индекс 354 - 355
Аукцион
где платят все 439
максимизация доходов 524 - 537
модель независимых частных оценок 505 - 506
оптимальный аукцион при симметричных участниках 536
и создание механизмов 504 - 537
сравнение доходов 514 - 516
стандартный
английский 505 , 513 - 514
поведение при подаче заявок на 513 - 514
равновесие 513
первой скрытой цены 505 , 506 - 510
поведение при подаче заявок на 506 - 510
симметричное равновесие 509
второй скрытой цены 505 , 511 - 512
поведение при подаче заявок на 511 - 512
равновесие 512
голландский 505 , 510 - 511
поведение при подаче заявок на 510 - 511
симметричное равновесие 511
теорема об эквивалентности доходов 517 - 524
эффективность , симметрия и сравнение 534 - 537
Б
Байеса — Нэша равновесие 382 - 384 , 439
Байеса правило 380 , 418 - 419 , 420 , 422- 423 , 443 , 427 - 428 , 430 , 432 - 433 ,
435 , 443 , 455 - 456 , 463 , 465 , 470 , 501

708 Предметный указатель
Безвозвратные потери 236 , 241 , 243
Бертрана дуополия 219 - 221 , 238 , 360 , 362 , 380 , 382 - 383 , 436 , 439
Благо (см. Товар)
Благосостояние потребителя 224 - 236
Блэкорби — Дональдсона индекс неравенства 355
Борда
правило 354
ранг 354
Брауэра теорема 261 , 291 , 377 , 451 , 584 - 587 , 614
Бюджетное ограничение 36
изменение цен и дохода 82
многопериодное 158 - 159
в экономике обмена 255 , 257 , 263 , 267 , 275 - 276
в экономике с производством 281 , 285 , 287 - 288 , 295
в
Вальраса закон 257 - 258 , 262 - 263 , 266 , 287 , 311
Вальрасовское равновесие 258 - 262
и общественное благосостояние
в экономике обмена 272 - 276
в экономике с производством 291 - 296
определение
в экономике обмена 258
в экономике с производством 291 - 292
существование
в экономике обмена 265 - 266
в экономике с производством 282 - 290
Вейерштрасса теорема 37 , 582 - 583 , 655
Вектор 552
Включающее «или» 551
Вкусы 20 - 26
Восстановление (интегрируемость) 111 - 118
задача восстановления (интегрирования) 113
и предложение готовой продукции 203
спрос на фактор производства и 183 , 203
функции издержек 183
Вход в отрасль 210
Выбираемые переменные 648
Вывод 549

Предметный указатель
Выигрыш 394 - 395 , 437 - 441
Выпуклая комбинация 554 - 555
Выход из отрасли 210
Выявленные предпочтения 118 - 126
обобщенная аксиома выявленных предпочтений (GARP) 124 - 125
сильная аксиома выявленных предпочтений (SARP) 124
слабая аксиома выявленных предпочтений (WARP) 119 - 124 , 154 - 155
Г
Гарантированный эквивалент 145 - 146 , 157
Гейне — Бореля компактные множества 573 - 576
Гессе матрица 80 , 116 , 190 , 623 - 624 , 626 , 628 , 642 , 645 , 678
Гиперплоскость 614
Гипотенуза 561 - 563
Гиффена парадокс 77 - 78
Главный минор 641 - 642 , 663 - 665
Гормана форма 94
Градиент 622
Грань
верхняя 570
в подмножестве действительных чисел 571 - 572
нижняя 570
в подмножестве действительных чисел 571 - 572
точная верхняя 571 , 582
точная нижняя 571 , 582
д
Двойственность
производство и издержки 182 - 183
производство и прибыль 193 - 195
в теории потребителя 97 - 111
и обратная функция спроса 110 - 111
Действительные числа 552
Декартова
плоскость 552
произведение множеств 552 , 611
Денежная иллюзия 69
Дистрибутивный закон 609
Дифференциальные уравнения в частных производных 115

710 Предметный указатель
Долгосрочный период
кривая совокупных издержек 178 - 181
при монополистической конкуренции 222 - 223
определение 168 - 169
при совершенной конкуренции 210 - 212
средние и предельные издержки в 200
Доказательство
конструктивное 549
контрпозитивное 549
с помощью контрпримера 549 - 550
от противного 549
прямое 549
Достаточность 547 - 549
Доход
доля в 83
максимизация
на аукционах 524 - 537 , 540
индивидуальная рациональность 525 - 526
оптимальный механизм продажи 526 - 534
предельный 214
от фактора производства 185
и предельные издержки 214
и эластичность 214
реальный 69
Дуополия (см. Бертрана дуополия , Курно дуополия , Штакельберга дуополия)
Е
Евклидова
метрика 563
норма 563
пространство 553 - 563
Единицы измерения реальные и номинальные 69
Единичный симплекс 613
з
Задача восстановления (рационализации) 124 - 126
И
Игра
с нулевой суммой 437
в стратегической форме 362 - 384

Предметный указатель 711
определение 362 - 363
с неполной информацией 378 - 384
равновесие по Нэшу 368 - 378
Йенсена неравенство 149
Издержки 160 , 171 - 181 (см. также Функция издержек)
минимизация 171 - 182
в долгосрочном и краткосрочном периоде 178 - 181
и максимизация прибыли 185 - 186
переменные 178 - 179
постоянные 178 - 179
средние (краткосрочные и долгосрочные) 200
Излишек
потребителя 228
и компенсирующая вариация (см. Компенсирующая вариация)
и общественное благосостояние 233 - 235
как функция от количества товара 233 - 234
производителя 233 - 234
Изокванта 163
наклон и замещаемость факторов 163 - 164
обобщенно параллельные (вдоль луча) 195
Изокоста 173 , 179
Изопрофита 288
Индекс стоимости жизни 95
Интуитивный критерий 474
Информация (см. также Экономика информации)
асимметричная 444 , 448 - 453 , 493 - 498 , 499 , 500 - 503
симметричная 446 - 448 , 491 - 493
Исключающее «или» 551
Исходы 127
наилучший и наихудший 129 - 130
К
Квадратичная форма 625 - 626 , 642 , 678
Коалиция 251 - 252
блокирующая 251 - 252
Кобба — Дугласа форма
краткосрочной функции прибыли 192 - 193
производственной функции 167 , 192 - 193 , 196 , 200 - 201 , 209
прямой функции полезности 88 , 93 , 95
степень однородности 629 - 631 , 633

712 Предметный указатель
функции издержек 175 - 176 , 199 - 200
функции прибыли 201
как частный случай CES - функции 167
Коммутативный закон 609
Компенсирующая вариация 226 - 227
аппроксимация с помощью потребительского излишка 228 - 230
с постоянной эластичностью по доходу 229 - 230
и потребительский излишек 228 - 229
с эластичностью по доходу , зависящей от цен 228 - 229
Кондорсе парадокс 324
Конкуренция
монополистическая 221 - 223
несовершенная 213 - 223
общее равновесие 253 - 272
Контрактная кривая 247
Контрпозитивная форма логического утверждения 547 - 548
Косвенная функция полезности 44 - 68
двойственность между прямой функцией полезности и 107 - 109
и положительное монотонное преобразование 88
и предпочтения потребителя 106 - 111
связь со спросом 49 - 51
свойства 44 - 51
и функция расходов (см. Функция расходов)
Коэффициент замещения
отрицательная полуопределенность 79 - 81
симметричность 78 - 79 , 80 - 81
собственный 77
Краткосрочный период
определение 168
при совершенной конкуренции 208 - 210
средние и предельные издержки в 200
функция издержек в 178 - 181
функция предложения готовой продукции в 193
функция прибыли в 191 - 193
Кривая спроса по Хиксу (см. Хиксовский спрос)
Кривые безразличия (см. также Множество безразличия)
общественные 332 - 333 , 336 , 341 - 343 , 345
диктатура 336
максимакс 342 - 343
максимин 432 - 343 , 350 - 351

Предметный указатель 713
обобщенно параллельные (вдоль луча) 346
Роулзианские 340 - 343
утилитаристские 343 - 345
в пространстве цен 89
наклон 25 (см. также Предельная норма замещения)
Кривые постоянных расходов 51
Куна теорема 399 - 400
Куна — Таккера
теорема 39 , 672
условия 39 , 42 , 669 - 672 , 674 , 682 - 683
Курно
агрегирование 83 - 84
дуополия 237 - 238 , 360 , 436
олигополия 217 - 219 , 235 - 236
Курно — Нэша равновесие 218 , 235
Л
Лагранжа
метод 39 , 42 , 47 , 56 - 57 , 108 , 110 , 198 , 495 , 649 - 657 , 669 , 676
(см. также Оптимизация)
теорема 47 , 56 , 173 , 656 - 657
функция (лагранжиан) 39 , 42 , 47 , 56 - 57 , 59 , 108 , 110 , 174 , 491 , 495 ,
649 - 665 , 670 - 671 , 674 , 676 - 677 , 682
Либерализм 354
минимальный 354
Линейные участки
на графике вогнутой функции 599 , 606
в множествах уровня квазивогнутой функции 603
Лотерея 127 - 132
наилучшая и наихудшая 129
простая 127 - 132
сложная 127 - 132
м
Максимакс как функция общественного благосостояния 342 - 343
Максимин как функция общественного благосостояния 342 - 343 , 350 - 351
Максимум
внутренний 634
глобальный 634 , 636 , 646
граничный 634
локальный 634 - 636 , 646

714 Предметный указатель
Маршалловский спрос (спрос по Маршаллу)
(см. также Спрос маршалловский)
свойства 103
функция 37 - 39 , 44 , 225 , 228
и хиксовский спрос (спрос по Хиксу) (см. Хиксовский спрос)
Матрица
Гессе (см. Гессе матрица)
отрицательно определенная 626
отрицательно полуопределенная 79 - 81 , 626
положительно определенная 626
положительно полуопределенная 626
замещения 79 - 80 , 176 - 177 , 183 , 189 - 190 , 199 , 203
Метрика 561 - 562 (см. также Евклидова метрика)
Метрическое пространство 561 - 562
Механизм продажи
оптимальный 526 - 534
прямой 517 , 539 - 540 , 542 - 543
совместимость стимулов 517 , 519 - 524 , 542
Минимизация расходов 51 - 60
Минимум
глобальный 634
локальный 634 - 636
Множество
безразличия 17 - 26
бюджетное 36
внутренняя точка 568
выбора 14 (см. также Множество потребительское)
выпуклое 553 - 557
вещественнозначные функции на 594
выпуклость пересечения 557 , 611
геометрическая интерпретация в R и R2 554 - 556
и график вогнутой функции 596 - 598
и график выпуклой функции 607
и инфериорные множества квазивыпуклой функции 608
и супериорные множества квазивогнутой функции 601 - 602
граничная точка 568
дополнение 550 , 567
допустимое 14 , 648
замкнутое
и внутренние точки 568
и граничные точки 567 - 568

Предметный указатель 715
и непрерывное отображение 577
определение 567
основные свойства 568 - 569
и открытое множество 567
индексное 551
инфериорное 592
квазивыпуклой функции 608
информационное 390
компактное (компакт) 572 - 573 , 579
объединение 551
ограничений 648
ограниченное 569 - 571
сверху 570
снизу 570
основные концепции 550 - 553
открытое
и внутренние точки 568
и граничные точки 568
и замкнутое множество 567
и непрерывные отображения 577
определение 564
основные свойства 565 - 566
совокупность открытых множества 566 - 567
пересечение 551
потребительское 14 , 36
графическое представление 19
в модели предложения труда 280 - 281
свойства 14 - 15
производственных возможностей 161 - 162
в общем равновесии 277
предположения 277
свойства 279
совокупное 279
строго выпуклое 277
пустое 550
разность 550
строго выпуклое 277
супериорное 592
квазивогнутой функции 601 - 602
уровня 590 - 592

716 Предметный указатель
для квазивогнутой функции 600 - 601
по отношению к точке 591
и супериорные и инфериорные множества 592 - 593
Модель контрактных отношений 489 - 498
Модель независимых частных оценок 505 - 506 , 538 - 540
Монополистическая конкуренция (см. Конкуренция)
Монополия 213 - 215
двухпериодная 243 - 244
с потоварным налогом 243
равновесие 213 - 216
регулирование и благосостояние 241 - 242
Монотонность
аксиома отношения предпочтения 22
аксиома предпочтений на лотереях 130
отношения правдоподобия 490
и потребительский спрос 103 - 106
Моральный риск 489 - 498 , 498 - 499 , 502
де Моргана закон 569 , 609 - 610
н
Неблагоприятный отбор 445 - 489 , 499 - 500
асимметричная информация и 448 - 453
игра с рыночными сигналами на рынке страхования 453 - 477
использование рыночных сигналов 453 - 477
симметричная информация 446 - 448
Независимая оценка на аукционах 506
Независимость от посторонних альтернатив 325 - 326
Нейтральность к риску 144 , 492 , 499 , 538
Необходимое и достаточное (условие) 549
Необходимость 547 - 549
Неограниченная область определения 325 - 326
Неопределенность 126 - 153
Непрерывность
аксиома отношения предпочтения 20 , 26
аксиома предпочтений на лотереях 130
по Коши 576 - 577
общественных предпочтений 330 , 352
отображения 573 - 581
и образ компактных множеств 579
и прообраз открытых множеств 578
функции полезности (см. Функция полезности)

Предметный указатель 717
Несклонность к риску 143 - 153 , 446 , 461 , 492 , 499 - 500
на аукционах 538 - 539
возрастающая абсолютная 157
мера Эрроу — Пратта
абсолютная 147 - 152
относительная 157 - 158
постоянная абсолютная 157
убывающая абсолютная 149 - 152 , 157 - 158
и функция общественного благосостояния 351
Нэша равновесие 216 - 2178 , 220 - 223 , 235 , 237 , 239
Байеса — Нэша 382 - 384 , 439
вычисление 438 - 439
в играх в стратегической форме 368 - 378
обратная индукция и 392 , 399 , 407 - 411 , 440
существование 376 - 378
в смешанных стратегиях 371 - 376 , 409 , 436 - 437
в чистых стратегиях 368 , 399 - 401 , 404 - 415
упрощенный поиск 372 - 375
о
Обобщенные утилитаристские способы ранжирования альтернатив 345
Обратная индукция 392 , 395 - 401 , 407 - 411 , 440
Общественное благосостояние 224 - 236 , 321 - 351
анализ частичного равновесия 224 - 236
и общественный выбор 321 - 351
и экономическая справедливость 348 - 351
Общественный выбор 321 - 351
Объединяющая линия нулевой прибыли 468 - 471
Ограничение 647
бюджетное (см. Бюджетное ограничение)
в виде неравенства 648 , 665 - 672
в виде равенства 648 - 649
константа в 683
неотрицательности 648
Окаймленный гессиан 662 - 664 , 680 - 681
Окрестность (эпсилон - окрестность) 563
замкнутая 563
и ограниченное множество 569 - 570
открытая 563
и открытые множества 565 - 567

718 Предметный указатель
Олигополия (см. Бертрана дуополия , Курно олигополия , Штакельберга
дуополия)
Оптимизация 581 , 633 - 677
и геометрическая интерпретация условий Лагранжа 657 - 660
и достаточные условия единственности глобального оптимума 647
и достаточное условие локального оптимума для задачи с одним
ограничением в виде равенства 663 - 664
и достаточные условия единственного глобального оптимума
(при безусловной оптимизации вещественнозначной функции) 647
достаточные условия локального внутреннего оптимума
(при безусловной оптимизации вещественнозначной функции) 644 - 646
и достаточные условия локального оптимума для задачи
с ограничениями в виде равенств 665
и метод Лагранжа 39 , 42 , 47 , 56 - 57 , 108 , 110 , 198 , 495 , 649 - 657 , 669 , 676
и необходимые условия локального внутреннего оптимума (при
безусловной оптимизации функции одной переменной) 635 - 636
и необходимые условия первого порядка локального внутреннего
оптимума (при безусловной оптимизации вещественнозначной
функции) 637 - 639
и необходимые условия второго порядка локального внутреннего
оптимума (при безусловной оптимизации вещественнозначной
функцииN40
и необходимые условия оптимума для задачи с ограничениями
неотрицательности 668
и необходимые условия оптимума для задачи с ограничениями в виде
неравенств 672
условия Куна — Таккера 39 , 42 , 669 - 672 , 674 , 682 - 683
условная 647 - 672
функции нескольких переменных 636 - 677
функции одной переменной 633 - 636 , 665 - 668
Ортант 553
неотрицательный 553
Отдача от масштаба 168 - 171
возрастающая 168 - 171 , 187 , 191 , 277
глобальная 169 - 170
локальная 170 - 171
постоянная 169 - 171 , 187 , 191 - 193 , 195 , 199 , 200 , 277 , 291
убывающая 169 - 171 , 190 , 277
Отношение
безразличия 17 - 18
бинарное 15 - 26 , 557

Предметный указатель
общественного предпочтения 323 - 324
условия Эрроу 325 - 326
этические предпосылки 339
предпочтения 15 , 15 - 34
аксиоматическая структура 15 - 26
множество безразличия 17 - 18
множество «лучше , чем» 18
множество «не лучше , чем» 18 , 19 - 20
множество «не хуже , чем» 18 , 19 - 20
множество «хуже , чем» 18
определение 17
отношение строгого предпочтения 17 , 22 - 24
свойства 16 - 18
и функция полезности 26 - 30
Отображение
область значений 559
область определения 559
образ 560
прообраз 560 , 577 - 578
Отсутствие диктатуры 325 - 326
п
Параметрическая зависимость значения целевой функции экстремальной
задачи (значение задачи , функция значения) 672 - 677
Парето - безразличие 331
Парето принцип
сильный 352
слабый , 325 - 326 352
Парето - улучшение 230
Парето - эффективность (оптимальность) 230 , 250
вальрасовского равновесия 272 - 274 , 293 - 294
конкурентного рыночного распределения 233 - 234
максимизация совокупного излишка 234
и максимумы благосостояния 232 - 233
распределения 250 , 272 - 273 , 289 - 290 , 312 , 314 - 16 , 318 - 319 , 322 , 447
Первоначальный запас 246 - 247
Пифагора формула 561 - 562
Подмножество 550
Полезность 15 (см. также Функция полезности)
в конкурентной рыночной системе 255

720 Предметный указатель
ожидаемая (см. Функция ожидаемой полезности)
относительная шкала 346
полностью сравнимые полезности 337 - 338
порядковая шкала 332 , 338
пропорционально сравнимая 346
предельная 32
и цены 41 - 43
сравнимая в терминах приращений 338
убывающая предельная 15
числовая (кардинальная) шкала 338
Полнота
аксиома отношения общественного предпочтения 323 - 324
аксиома отношения предпочтения 16 , 26
аксиома предпочтений на лотереях 129
произвольного отношения 558
Полупространство 614
Последовательность 579 - 581
ограниченная 580
и подпоследовательность 580
сходимость 579 - 580
Постоянная эластичность замещения (CES - функция)
косвенная функция полезности 50 - 51 , 63 - 64 , 108 - 109
минимизация издержек 174 - 175
параметр замещения 166 - 167
производственная функция 166 - 167 , 190 - 191 , 197
прямая функция полезности 42 - 43 , 50 - 51 , 108 - 109
функция общественного благосостояния 348 , 356
функция расходов 58 - 60 , 63 - 64
в экономике обмена 265 - 266
Посылка 548
Потребитель
благосостояние (см. Благосостояние потребителя)
задача максимизации полезности 34 - 44
задача минимизации расходов 51 - 60
предпочтения (см. Предпочтения)
равновесие 36 - 41
ранжирование альтернатив 17 - 18 , 30 - 31
спрос (см. Спрос)
в экономике с производством 280 - 282
Потребительский набор 14

Предметный указатель 721
Потребительский план 14
Прибыль 160 (см. также Функция прибыли)
максимизация 160 - 161
при несовершенной конкуренции 213 - 217
совершенно конкурентной фирмы 184 - 186
совокупной 279 - 280
условия для 184 - 186
Правило закрытия фирмы 194 - 195
Правило равенства цены предельным издержкам 193
Предельная норма замещения
при конкуренции 25 - 26
принцип убывания 25
Предельная норма технологического замещения 163 - 164 , 185 , 196
Предельный продукт фактора производства 163 - 165 , 169 , 185 , 195
Предпочтения
аксиоматическая структура 15 - 26
как бинарное отношение 15 - 16
выявленные 118 - 126 (см. также Выявленные предпочтения)
графическое представление 19 - 25
в задаче общественного выбора 323 - 324 , 329 - 330
косвенная полезность и 106 - 111
лексикографические 87
математические свойства 32 - 34
в модели обмена 249 - 250 , 253 - 254
в модели общего равновесия 253 - 255
в реплицированной экономике 297 - 300
символическое представление 16 - 17
в условиях неопределенности 127 - 132
Преобразование
логарифмическое 88
монотонное 88
косвенной функции полезности 88
прямой функции полезности 31
функции ожидаемой полезности 140 - 142
Премия за риск 145 - 146 , 157
Принцип недостаточного обоснования 349
Принципы теории благосостояния 331
Производная 616
по направлению 621
и правила дифференцирования 617

722
Предметный указатель
частная 619
второго порядка 622
и градиент 621 - 622
и матрица Гессе 623
однородной функции 629 - 630
первого порядка 619
и теорема Юнга 624
Провал рынка 444 , 452 , 498
Программирование
квазивогнутое 683
нелинейное 669
Производственная функция 161 - 171
восстановление из функции издержек 182
гомотетичная 177 , 195 - 197 , 199 - 200
квазивогнутая 162 - 163 , 165 , 168 , 173 , 175 , 182 - 183 , 203
Кобба — Дугласа (см. Кобба — Дугласа форма)
Леонтьевская 167 , 196 , 198
линейная 196 , 200
обобщенная CES - форма 196 - 197
однородная 167 - 168 , 170 , 177 - 178 , 195 , 197
с постоянными предельными долями факторов производства 196
сепарабельная 164
CES - форма 166 - 167 , 190 - 191 , 197 (см. также Постоянная
эластичность замещения)
Производственный план 161 - 162 , 172 , 178 , 277 - 280 , 292
Производство 161 - 171
Р
Равновесие
на английском аукционе 513
на аукционе первой скрытой цены 509
на аукционе второй скрытой цены 512
Байеса — Нэша (см. Байеса — Нэша равновесие)
при бартерном обмене 246 - 253
вальрасовское (см. Вальрасовское равновесие)
на голландском аукционе 511
конкурентное 208 - 210 (см. также Совершенная конкуренция)
в конкурентной рыночной системе 253 - 311
Курно — Нэша (см. Курно — Нэша равновесие)
при монополистической конкуренции 222 - 223

Предметный указатель
по Нэшу 216 - 217 (см. также Нэша равновесие)
объединяющее 462 , 468 - 473 , 479 - 484
общее 245 - 311
в конкурентной рыночной системе 253 - 276
в экономике Робинзона Крузо 284 - 290
ядро и 296 - 311
в олигополии Бертрана 219 - 221
в олигополии Курно 217 - 219
при сговоре 216
разделяющее 462 - 468 , 484 - 489
при сговоре 216
секвенциальное равновесие 415 - 436
в игре с сигналами на рынке страхования 453 - 477
определение 428
и секвенциальная рациональность 423 - 428
существование 435 - 436
в случае монополии 213 - 215
частичное равновесие 258
в экономике обмена (см. Вальрасовское равновесие)
Рамсея правило 241 - 242
Распределение
в вальрасовском равновесии 268 - 270
ядро и 270 , 296 - 311
допустимое 250 , 292
определение 250
Парето - эффективное (см. Парето - эффективность (оптимальность
первоначальных запасов 274 - 275 , 294 - 296
и равенство 310
распределение , не вызывающее зависть (справедливое) 31 - 319
Расстояние в пространстве Rn 561 - 563
Рациональность 16 , 26
индивидуальная 525 - 526
секвенциальная 423 - 428
Реплицированные экономики 297 - 298
Робинзона Крузо экономика 284 - 290
Роулзианская справедливость (см. Общественное благосостояние)
Роя тождество 46 , 49 - 51 , 90
Рыночная структура 207 - 236
Рыночная экономика 35
Рыночное предложение 208

724 Предметный указатель
Рыночные сигналы 453 - 477 , 501 - 502
Рыночный спрос 207 - 208
С
Сбалансированность бюджета 70 , 82 , 119 - 124 , 153 - 155
симметричность и 111 - 113
Свойство единственности пересечения 457
Сепарабельность
нестрогая и строгая 196
производственной функции 164
функции общественного благосостояния 348
Симметричность
на аукционе 534 - 537
игры 438
информации 446 - 448 , 491 - 493
сбалансированность бюджета и 111 - 113
Симплекс (см. Единичный симплекс)
Система ожиданий 417 - 422
Склонность к риску 144 - 145
Скрининг 477 - 489
в модели страхования 477 - 489 , 502
объединяющее равновесие 479 - 484
снятие сливок 479 - 489
Слуцкого матрица 80 - 81 , 118 , 122 - 124 , 153 - 154
Слуцкого уравнение 74 - 76 , 111 - 113
в терминах эластичности 94
Снятие сливок 479 - 489
Совершенная конкуренция 183 - 195 , 207 - 213
выбор выпуска фирмой 184 - 195
долгосрочное равновесие 210 - 212
краткосрочное равновесие 208 - 210
и максимизация прибыли 184 - 186
на рынках готовой продукции 183 - 184
при постоянной отдаче от масштаба 212 - 213
правило закрытия 194 - 195
эффект потоварного налога 243
Создание механизмов (см. Аукцион)
Справедливость (см. также Общественное благосостояние)
по Хаммонду 339
и общественное благосостояние 348

предметный указатель
Спрос
дифференцируемый 44
закон 78
избыточный 256 - 258 , 282
компенсированный (по Хиксу) 54 (см. также Хиксовский спрос)
и косвенная функция полезности 49
маршалловский 38 - 39 , 43 , 49 - 50 , 53 , 60 , 64 - 68 , 74 - 76 , 78 , 80 - 83 , 85 ,
88 - 89 , 91 , 93 , 103 , 109 , 111 , 114 - 115 , 225 , 228 , 231 - 232 , 239 , 241
(см. также Маршалловский спрос)
маршалловский и хиксовский 74 - 76 , 225
обратная функция 109 - 111
однородность 70
при неизменном уровне полезности 53
порожденный функцией полезности с постоянной эластичностью
замещения 42 - 43
проверка теории 68
и рыночное предложение 209 - 213
рыночный 207 - 208
свойства потребительской системы 68 - 85 , 114 - 118 , 253 - 254
современная теория 77 , 80
хиксовский 54 - 55 , 60 , 64 - 68 , 74 - 80 , 85 , 90 - 91 , 93 - 94 , 103 , 115 ,
(см. также Хиксовский спрос)
Средний продукт 169
эластичность 195
Стратегия
слабо доминируемая 366 , 436 , 438 - 439
строго доминирующая 364 , 437
строго доминируемая 365 , 436
итеративно строго недоминируемая 366
итеративно слабо недоминируемая 366
итеративное исключение 365 - 367 , 436
при подаче заявок на аукцион 507 , 537
соответствующая равновесию , совершенному в подыграх 404 - 415
существование 413 - 141
поведенческая стратегия 409
система ожиданий и 417 - 422
вполне (полностью) смешанная 422
Стратегическая форма игры в развернутой форме 394 - 395 , 399 - 400 , 406
Стратегический набор 418
согласованный 422 - 423

726
Предметный указатель
Страхование 152 - 153 , 155 - 156
в игре с сигналами 453 - 477
модель контрактных отношений 489 - 498
моральный риск 489 - 498 , 498 - 499 , 502
неблагоприятный отбор 445 - 489 , 499 - 500
скрининг 477 - 489
Строгая выпуклость
аксиома отношения предпочтения 24 - 25
кривых безразличия общества 347
функции (см. Функция)
т
Теорема
благосостояния
вторая
в экономике обмена 274 - 275
в экономике с производством 294 - 296
первая
в экономике обмена 272 - 273
в экономике с производством 293 - 294
доказательство 548 - 550
Брауэра (см. Брауэра теорема)
Вейерштрасса (см. Вейерштрасса теорема)
о восстановлении (интегрируемости) 114 - 118
Какутани (см. Теоремы о неподвижной точке)
Куна (см. Куна теорема)
Куна — Таккера (см. Куна — Таккера теорема)
Лагранжа (см. Лагранжа теорема)
о локально - глобальном (экстремуме) 645 - 646
о максимуме 46 , 56 , 255 , 278 , 673
о минимаксе 437
о невозможности Эрроу 323 - 336
графическое доказательство 330 - 336
доказательство в общем виде 327 - 330
требования к предпочтениям общества 327 - 330
формулировка 327
об огибающей 47 - 49 , 57 - 58 , 108 , 110 , 674 - 677
понятие 547
Фробениуса (см. Фробениуса теорема)
Эйзенберга (см. Эйзенберга теорема)

Предметный указатель 727
Эйлера (см. Эйлера теорема)
об эквивалентности доходов на аукционах (см. Аукцион)
Эрроу (см. Теорема о невозможности Эрроу)
Юнга (см. Юнга теорема)
Теоремы
о неподвижной точке
Брауэра (см. Брауэра теорема)
Какутани 291
и равновесие в игре п лиц 376
и существование вальрасовского равновесия 259 , 291
существования 581 - 587
Теория выбора (см. Теория потребителя)
Теория игр 359 - 436
игры в развернутой форме 385 - 436
игры в стратегической форме 362 - 384
игры с совершенной информацией 385 , 391 - 392 , 395 - 398
неполная информация 378 - 384 , 401 - 404
смешанные стратегии 370 - 372 , 371 - 376 , 409 , 436 - 437
стратегическое принятие решений 359 - 362
Теория потребителя
восстановление (интегрируемость) в 111 - 118
выводы для наблюдаемого поведения 68 - 85
выявленные предпочтения 118 - 126
в условиях неопределенности 126 - 153
Теория производителя 160 - 195 , 276 - 280
двойственность в производстве 182 - 183
конкуренция 183 - 195
минимизация издержек 171 - 181
Технология
двойственность по отношению к функции издержек 182 - 183
и производство 161
Товар 14 , 276
агрегированный 225 , 239
инфериорный 78
нормальный 78
Топология 561
Точка
внутренняя 568
граничная 568
неподвижная 584 - 587 (см. также Брауэра теорема)
седловая 671

728 Предметный указатель
Транзитивность
аксиома отношения общественного предпочтения 323 - 324 , 345
аксиома отношения предпочтения 16 , 26
аксиома предпочтений на лотереях 129
произвольного отношения 559
У
Упорядоченная пара 552 , 557 - 558 , 560
Условия оптимизации второго порядка (см. Оптимизация)
Условия оптимизации первого порядка (см. Оптимизация)
Условное распределение вероятности 379 - 380
Условный спрос на факторы производства 173
для гомотетичной производственной функции 177 - 178
и лемма Шепарда 175
мультипликативная сепарабельность 177
для однородной производственной функции 177
свойства 176 - 177
для функции издержек Кобба — Дугласа 175 - 176
Ф
Фактор производства
доля 176
замещение 163 - 167
Фирма 160
теория (см. Теория производителя)
цели 160 - 161
ценополучатель 184
Фробениуса теорема 116
Функция 559 - 561
вещественнозначная 582 , 588 - 609
и оптимизация 636 - 642 , 666 - 668
взаимнооднозначная 561
вогнутая 594 - 605 , 615
и вторая производная 617 - 619
и выпуклые функции 606
график 594 - 596
линейные участки на графиках 599
локальный и глобальный максимум 636
и матрица Гессе 623
и первая производная 618 - 619
и частные производные второго порядка 628

Предметный указатель 729
возрастающая 437 , 451
выпуклая 605 - 609
и вогнутые функции 606
и вторая производная 617 - 619
график 606
локальный и глобальный минимум 636
и матрица Гессе 623
и первая производная 618 - 619
и частные производные второго порядка 628
гомотетичная 347 , 679
дифференцируемая 616 - 617
значения (см. Параметрическая зависимость значения целевой
функции экстремальной задачи)
квазивогнутая 600 - 609
и квазивыпуклая функция 608 - 609
квазивыпуклая 605 , 607
и квазивогнутая функция 608 - 609
линейная 615
линейно однородная 629
обратная 561
однородная 188 - 189 , 629 - 633
строго вогнутая 599 , 605
и единственный глобальный максимум 634 , 635 - 636 , 645 - 647
и матрица Гессе 626 - 628
и частные производные второго порядка 628
строго возрастающая 588
строго возрастающая (в сильном смысле) 588
строго выпуклая 605 - 606
и единственный глобальный минимум 634 , 635 - 636 , 645 - 647
и матрица Гессе 628
и частные производные второго порядка 628
строго квазивогнутая 603
строго квазивыпуклая 607
строго убывающая 589
строго убывающая (в сильном смысле) 589
супераддитивная 197
убывающая 589
целевая 648 , 660
Функция издержек
восстановление производственной функции из 182
для гомотетичной производственной функции 177

730 Предметный указатель
в краткосрочном периоде 178 - 181
для однородной производственной функции 177
мультипликативная сепарабельность 177
ограниченная (см. Функция издержек в краткосрочном периоде)
определение 172
производства единицы выпуска 177
свойства 176 - 177
транслогарифмическая форма 199 - 200
Функция общественного благосостояния
в рамках принципов теории благосостояния 331 - 332
гомотетичная 347 - 348
и обобщенные утилитаристские способы ранжирования 345
максимакс 342 - 343
максимин 342 - 343 , 350 - 351
Роулзианская форма 340 - 343
строгая сепарабельность 348
условия Эрроу 325 - 326
утилитаристская форма 343 - 345
CES - форма 348 , 356
Функция ожидаемой полезности 132 - 140
доказательство существования 134 - 136
единственность 140 - 142
и несклонность к риску 143 - 153 , 351
и обычная функция полезности 137 - 139
и общественное благосостояние 350
квадратичная форма 156 - 157
многопериодная 158 - 159
Функция полезности 26 - 27 (см. также Полезность)
единственность 31
из функции расходов 99 - 101
Кобба — Дугласа 88
косвенная 44 - 68 (см. также Косвенная функция полезности)
максимизация 36 - 44
математические свойства 32 - 34
многопериодная 158 - 159
и мультипликативно - сепарабельный спрос 91
непрерывность 31 - 32
и представление предпочтений 26 - 27
прямая 44 , 50 - 51
Стоуна — Гири 94
существование 27 - 30
CES - формы 42 - 43 (см. также Постоянная эластичность замещения)

Предметный указатель 73J
Функция полезности фон Неймана — Моргенштерна (см. Функция
ожидаемой полезности)
Функция предложения готовой продукции 186
Функция прибыли 186 - 195
как двойственная к производственной функции 193 - 195
долгосрочная и краткосрочная 191 - 192
для технологии Кобба — Дугласа 192 - 193 , 201
краткосрочная 191 - 195
ограниченная (см. Функция прибыли краткосрочная)
обобщенная форма 202
свойства 187 - 188
Функция расходов 51 - 68
задача минимизации 52 - 53
и косвенная функция полезности 61 - 63
мультипликативная сепарабельность 91
и построение прямой функции полезности 99 - 101
предпочтения потребителя и 97 - 103
из прямой функции полезности 58 - 60
свойства 55 - 58
свойство производной 57
и хиксовский спрос 54
формы Гормана 94
CES - формы (с постоянной эластичностью замещения) 58 - 60
Функция совокупного избыточного спроса 256 - 257 , 259 - 262 , 282
свойства 256 - 257
Функция спроса
на переменный фактор производства 191
обратная 108 - 109 , 154 , 211 - 213
на фактор производства 186 - 187
свойства 188 - 190
Функция трансформационная 202
X
Хикса декомпозиция при изменении цены 72 - 74
Хикса третий закон 95
Хиксовский спрос (спрос по Хиксу) 54 (см. также Спрос хиксовский)
и компенсирующая вариация 225 - 228
кривая 54 - 55 , 76
и маршалловский спрос (спрос по Маршаллу) 64 - 66 , 74 - 76 , 224 - 229
свойства 103

732 Предметный указатель
Хо — Крепса критерий (см. Интуитивный критерий)
Хотеллинга лемма 188 - 189 , 193 , 202
ц
Цена
игры 438
относительная 68 - 69
фьючерсная 317
ч
Частная оценка на аукционе 506
Чистая монополия 213 - 215 (см. также Монополия)
ш
Шепардалемма 56 , 90 , 114 - 116 , 175 , 177 , 200 , 227
Штакельберга
война 237
дуополия 237
лидер 237
э
Эджворта ящик 246 - 247
и вальрасовское равновесие 248 , 267 , 270 , 274
и ядро 303 , 307
Эйзенберга теорема 320
Эйлера теорема 102 , 631 - 633
Эквивалентность доходов на аукционах 523 - 524
Эквивалентность , логическая 548
Экономика информации 444 - 499
асимметричная информация 444 , 448 - 453 , 493 - 498 , 499 , 500 - 503
использование сигналов 453 - 477 , 501 - 502
модель контрактных отношений 489 - 498
моральный риск 489 - 498 , 498 - 499 , 502
неблагоприятный отбор 445 - 489 , 499 - 500
провалы рынка 444 , 452 , 498
симметричная информация 446 - 448 , 491 - 493
скрининг 477 - 489 , 502
Экономика обмена
общее равновесие в 245 - 253
определение 249

Предметный указатель 733
Экономика с континуумом участников 310
Экономическая справедливость (см. Общественное благосостояние)
Экстремум 582 - 583
Эластичность
агрегирование по Курно 83 - 84
агрегирование по Энгелю 83 - 84
выпуска
по спросу на фактор производства 199
по фактору производства 169 - 170
и эластичность масштаба 170 - 171
замещения 165 - 167 , 174 , 190 , 196 - 197 , 199 , 201
масштаба 170 - 171 , 197
спроса 82 - 84
перекрестная по цене 83
по доходу 83 , 91
по цене 83 , 91
спроса на фактор производства (см. Эластичность выпуска)
среднего продукта 195
формула однородности 91
Эрроу теорема (см. Теорема о невозможности Эрроу)
Эффект замещения 71 - 81
и декомпозиция по Хиксу при изменении цены 71 - 74
Эффект дохода 71 - 81
в декомпозиции по Хиксу 71 - 74
Эффективность (см. также Парето - эффективность)
на аукционах 324 , 534 - 537
ю
Юнга теорема 624
Я
Ядро
и равновесное вальрасовское распределение 296 - 311
теорема об одинаковом подходе в 299 - 301
экономики обмена 251 - 252

Джейли , Дж. А. Микроэкономика: продвинутый уровень [Текст] : учеб -
Д40 ник / Джеффри А. Джейли , Филип Дж. Рени ; пер. с англ. ; под науч. ред.
В. П. Бусыгина , М. И. Левина , Е. В. Покатович ; Гос. ун - т — Высшая школа
экономики. — М: Изд. дом Гос. ун - та — Высшей школы экономики , 2011. —
733 , [3] с. — Перевод изд.: Advanced Microeconomic Theory / Geoffrey A. Jehle ,
Philip J. Reny. Second edition. The Addison - Wesley , 2001. — (The Addison - Wesley
Series in Economics). — 2000 экз. — ISBN 978 - 5 - 7598 - 0362 - 1 (в пер.)
Учебник двух выдающихся экономистов и высокопрофессиональных
преподавателей из США — профессора Джеффри А. Джейли (Колледж Вассар , По -
кипси) и профессора Филипа Дж. Рени (Университет Чикаго) — превосходное
пособие по изучению микроэкономического анализа. В нем рассматриваются
теория потребителя и производителя , частичное и общее равновесие ,
общественное благосостояние , теория игр и экономика информации. В
математическом приложении подробно изложены теория множеств , элементы
математического анализа и теория оптимизации , являющиеся неотъемлемыми частями
современной микроэкономики. Продуманный отбор материала — ничего
лишнего , но все необходимое , точность формулировок , доказательность выводов ,
плюс необходимый инструментарий — таков стиль этой книги. Учебник
содержит не только теорию , но и примеры , а также многочисленные упражнения , к
которым приведены указания и ответы , что превращает его еще и в отличный
обучающий задачник.
Для студентов старших курсов университетов и аналитиков - экономистов , а
также всех , кто хотел бы знать современную микроэкономическую теорию , ее
методы и результаты применения.
УДК 330.101.542
ББК 65.012.1

Учебное издание
Джеффри А. Джейли , Филип Дж. Рени
Микроэкономика:
продвинутый уровень
Зав. редакцией ЕЛ. Бережнова
Редактор ЕЛ. Рязанцева
Художественный редактор А. М. Павлов
Компьютерная верстка и графика: ОЛ. Христенко
Корректор И.В. Андрианова
Подписано в печать 14.12.2010. Формат 70х100'/16
Гарнитура Times New Roman. Усл. печ. л. 59 , 8. Уч. - изд. л. 49 , 9
Тираж 2000 экз. Изд. № 551. Заказ 4313.
Государственный университет — Высшая школа экономики
125319 , Москва , Кочновский проезд , д. 3
Тел./факс: D95) 772 - 95 - 71
Отпечатано в ОАО «Можайский полиграфический комбинат».
143200 , г. Можайск , ул. Мира , 93.
www.oaompk ru , www.oaoMnK - рф тел.: D95) 745 - 84 - 28 , D9638) 20 - 685
ISBN 978 - 5 - 7598 - 0362 - 1
9