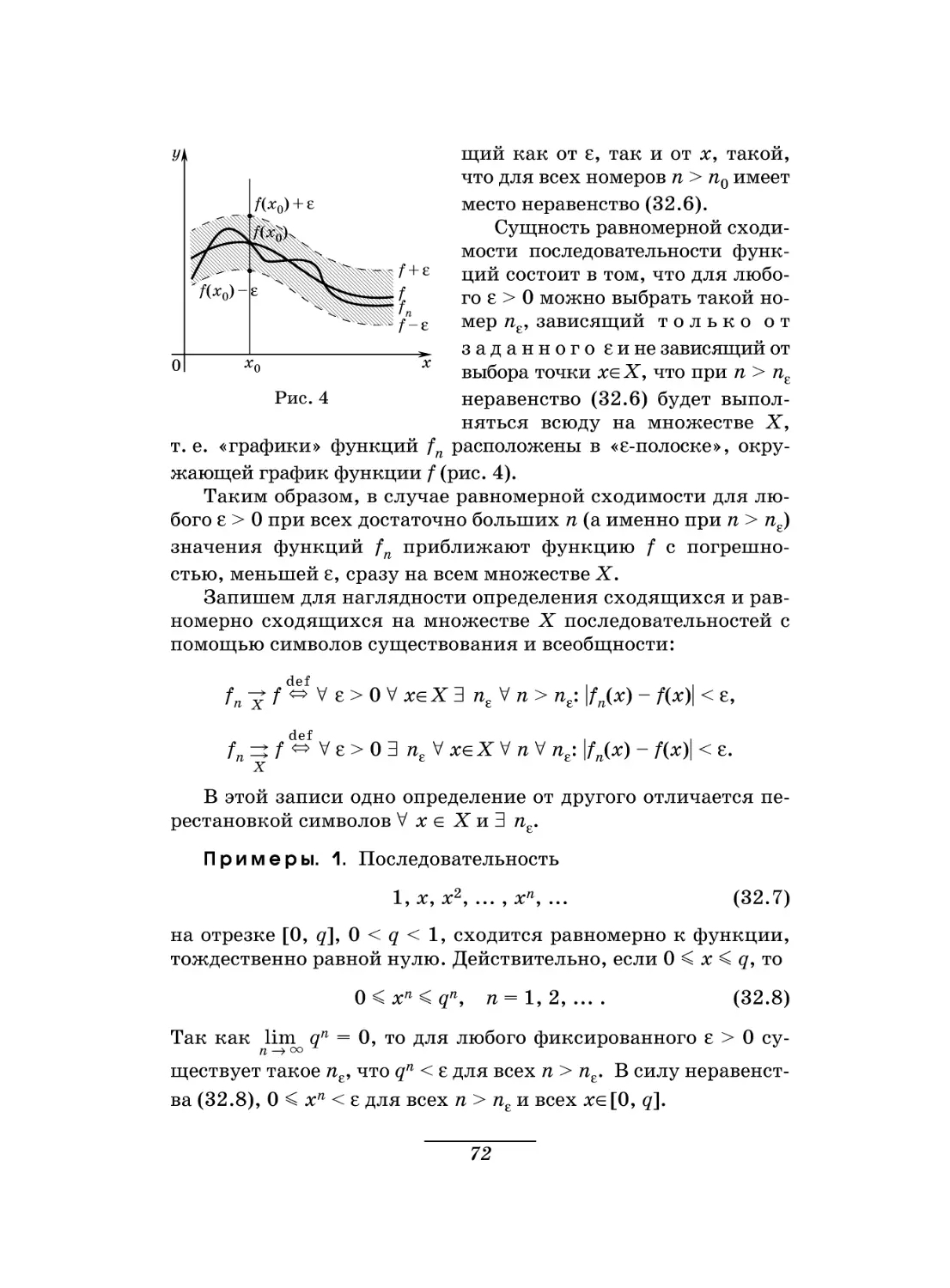
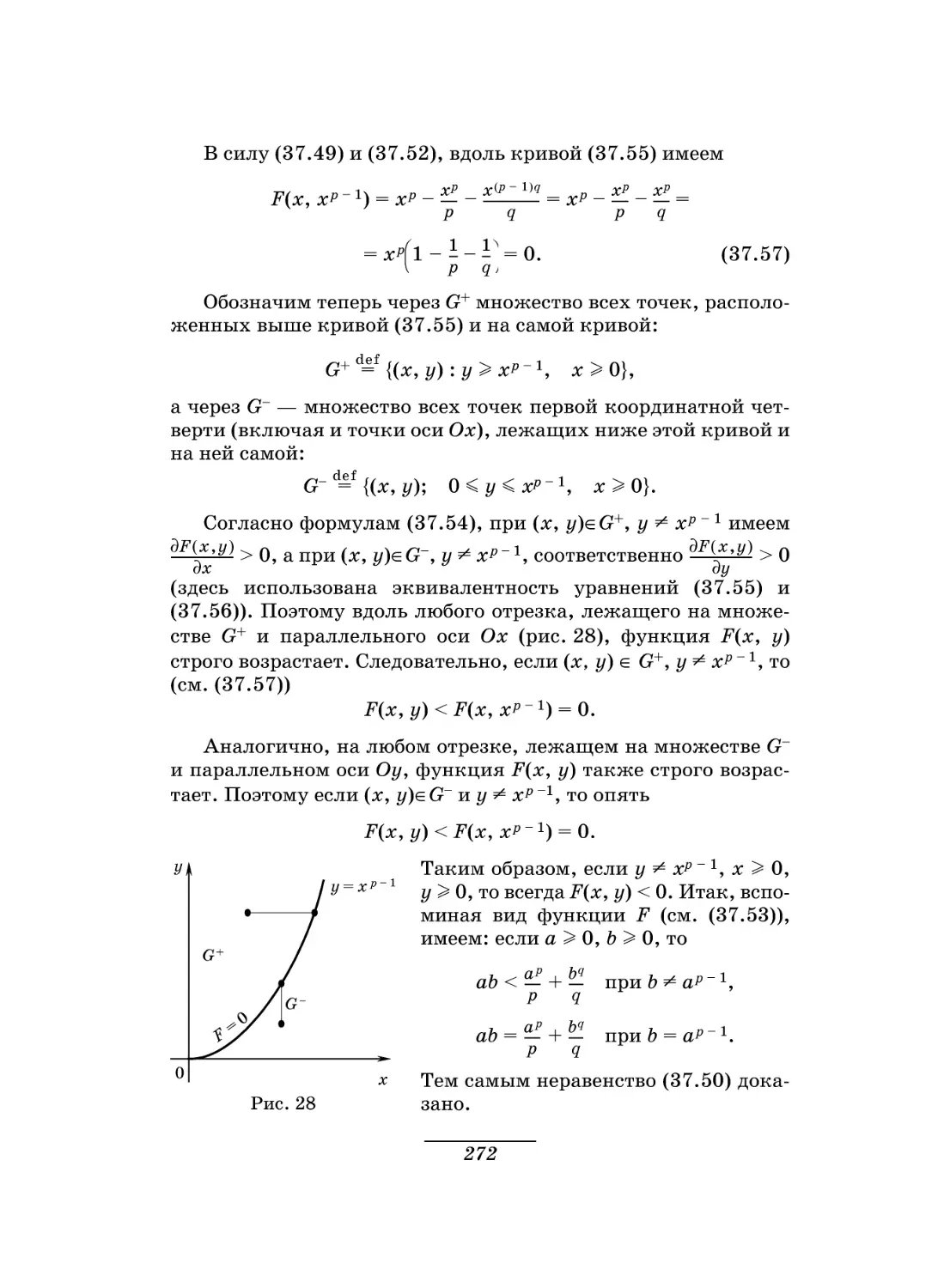
Текст
Предисловие
Во втором томе излагаются теория рядов,
дифференциальное и интегральное исчисления функций многих переменных.
В главе 3 изучаются числовые и функциональные ряды"^.
Больпюе внимание уделяется степенным рядам и методам
разложения в них функций. Даются начальные сведения из
теории асимптотических рядов по отрицательным степеням
аргумента. Изучаются также бесконечные произведения и
некоторые их приложения. Кратко излагается теория кратных рядов.
В главе 4 рассматривается та часть теории функций
многих переменных, которая относится к их дифференциальным
свойствам. Глава начинается с изучения некоторых вопросов
теоретико-множественной топологии многомерных
евклидовых пространств. Особое внимание уделено свойствам
компактов. Доказывается, в частности, супа;ествование числа Лебега
и лемма Гейне—Бореля о выделении конечного покрытия из
любого покрытия компакта открытыми множествами.
Обпа;ие свойства функций, связанные понятиями предела и
непрерывности, рассматриваются сразу для отображений
множеств из я-мерного пространства в т-мерное. Доказывается,
например, что образ компакта есть снова компакт, а также
что непрерывное отображение компакта является и
равномерно непрерывным, а непрерывное взаимно однозначное
отображение компакта представляет собой гомеоморфизм. Соответ-
ствуюгцие свойства функций многих переменных получаются
из свойств рассмотренных отображений как частный случай
при т = 1.
Собственно дифференциальное исчисление излагается более
традиционным способом: для функций многих переменных,
принимаюгцих числовые значения, вводятся понятия частных
производных и дифференциалов, изучаются их свойства,
выводится формула Тейлора с остаточными членами в форме Пеано и
* Во втором томе нумерация глав и параграфов продолжает
нумерацию первого тома.
Лагранжа, устанавливаются необходимые и достаточные
условия наличия у функции локального экстремума в данной точке.
Затем доказываются теоремы о сугцествовании неявных
функций. Они применяются к нахождению необходимых и
достаточных условий, которым удовлетворяют точки относительного
локального экстремума функций многих переменных, к
исследованию вопроса о зависимости функций и к изучению свойств
дифференцируемых отображений.
Для дифференцируемого отображения с неравным нулю
якобианом из одного пространства в другое устанавливается
локальный диффеоморфизм и, как его следствие, дается
принцип сохранения области при рассматриваемых отображениях.
Глава 5 посвягцена интегральному исчислению функций
многих переменных. В ней вводится понятие кратного
интеграла Римана, устанавливаются различные критерии его су-
гцествования, приводятся формула сведения кратного
интеграла к повторному и формула замены переменного в кратном
интеграле для взаимно однозначных дифференцируемых
отображений измеримых по Жордану множеств.
Определяется также несобственный интеграл и
доказывается, что при введенном его определении понятия сходимости
и абсолютной сходимости несобственного кратного интеграла
равносильны. Затем рассматриваются понятия
криволинейных интегралов первого и второго рода.
В этой же главе даются краткие сведения о
дифференциальной геометрии двумерной поверхности, связанные с ее
первой и второй квадратичной формой. Вводится понятие плогца-
ди поверхности.
Далее изучаются поверхностные интегралы первого и
второго рода, доказываются теоремы Гаусса—Остроградского и
Стокса. Построенная теория применяется к изучению
векторных полей, в частности, устанавливаются критерии их соле-
ноидальности и потенциальности.
Заканчивается пятая глава изложением теории
собственных и несобственных интегралов, зависягцих от параметра,
теории асимптотических рядов обгцего вида и их
приложениями, например, для установления асимптотических формул
для полной и неполной гамма-функции Эйлера.
Глава
3
Ряды
§30
Числовые ряды
30.1. Определение ряда и его сходимость
В настоягцем параграфе понятие суммы обобгцается на
некоторые случаи бесконечного множества слагаемых и изучаются
свойства таких обобгценных сумм. Многие из
рассматриваемых ниже вопросов справедливы не только для
действительных чисел, но и для комплексных. Поэтому, в отличие от пре-
дыдупа;его, в настояпа;ей главе будем вести рассмотрение в
комплексной области.
Аналитическое выражение, имеюпа;ее формально вид
суммы, содержапа;ей бесконечно много слагаемых, называется
бесконечным рядом или, короче, рядом. Дадим строгое
определение ряда и его суммы.
Определение 1. ili/cmb задана последовательность
комплексных чисел и^у я = 1, 2, ... . Составим новую
последовательность чисел s^, п = 1, 2, ... , следующим образом:
ор U-t "i Unj
S^ = и^ + U2^ + г/3.
S^ = U^ + U^ + ... + U^,
Пара последовательностей {u^ и {s^ называется
числовым рядом {подробнее: числовым рядом с общим членом и^) и
обозначается через
u^ + U2 + ... + г/^+ ... , C0.1)
или
оо
Е "„• C0.2)
Д = 1
Элементы исходной последовательности {г/^}
называются членами ряда C0.1), а элементы последовательности
{s^} — частичными суммами этого ряда, при этом и^
называется п-м членом ряда, а конечная сумма s^ — п-й
частичной суммой ряда, п = 1, 2, ... ,
Если последовательность частичных сумм ряда C0.1)
сходится, то он называется сходящимся рядом, а если она
расходится, то расходящимся.
Определение 2. Ряд, членами которого являются члены ряда
C0.1), начиная с {п + 1)-го взятые в том же порядке, что и в
исходном ряде, называется п-м остатком ряда C0.1) и
обозначается через
оо
£ и^ или ц„ + 1 + ы„ + 2 + -•
Определение 3. ^слг/р^E C0.1) сходится, то предел
S = lim s„
называется его суммой.
В этом случае пишут
S = и^ + U2+ --- + Uj^+ ... ,
ИЛИ
оо
S = £ и„. C0.3)
п = \
Таким образом, мы будем употреблять один и тот же сим-
оо
вол Y, ^п ^^^ Д-^^ обозначения самого ряда C0.1), так и для
п = 1
обозначения его суммы, если он сходится.
Если lim s„ = оо^ или lim s„ = +оо^ или lim s„ = -оо, то со-
ответственно пигаут
оо оо оо
Е "« = °°' Е "« = +°° или £ и„ = -оо.
Итак, каждый ряд является парой двух
последовательностей таких, что первая может быть взята произвольной
(последовательность членов ряда), а вторая составлена
определенным образом из членов первой (последовательность
частичных сумм членов ряда). Однако ряд однозначно определяется
каждой из этих последовательностей. Действительно, если
задана последовательность членов и^ ряда, то члены
последовательности его частичных сумм находятся, согласно определе-
6
нию 1, по формулам s^^ = и-^ -\- U2 + ... + г/^, п = 1, 2, ... . Если
же задана последовательность {s^} частичных сумм ряда, то
его члены определяются по формулам и^ = s^, ^п ^ ^п ~ ^п- v
п = 2, 3, ... . Отсюда следует, что для всякой
последовательности всегда можно найти такой ряд, что она будет
последовательностью его частичных сумм.
В самом деле, пусть дана последовательность комплексных
чисел {z^}. Положим
и
1 ^19 "-2 "^2 '^l'
И рассмотрим ряд
г/1 + г/2 + ... + г/^ +
Тогда для его частичных сумм имеем
= 2^ + (^2 - 2^) + Bз - 2^) + ... + B^ -2^_^) = 2^.
Это означает, что рассмотрение рядов эквивалентно
рассмотрению последовательностей. Всякий вопрос, сформулированный
в терминах рядов, можно перефразировать в вопрос,
сформулированный в терминах последовательностей, и наоборот.
Например, задача изучения сходимости рядов равносильна
задаче изучения сходимости последовательностей.
Подчеркнем, что всюду, где не оговорено противное, члены
рассматриваемых рядов подразумеваются комплексными.
Если п-й остаток ряда C0.1) (см. определение 2) сходится,
то его сумму будем обозначать через г^:
оо
г„= Е и„ C0.4)
k = П+ 1
И называть для краткости просто остатком ряда.
Всякую сумму конечного числа слагаемых
МОЖНО рассматривать как ряд, добавив к ней члены
Сумма получивп1егося ряда, очевидно, совпадает с заданной
суммой, так как при всех п> п^ его частичные суммы равны s^ .
Если заранее неизвестно, содержит сумма конечное или
бесконечное число слагаемых, то иногда удобно в обоих
случаях называть ее рядом, считая, что конечная сумма является
рядом в указанном выгае смысле.
Отметим одно супа;ественное свойство сходяпа;ихся рядов.
ТЕОРЕМА 1 (необходимое условие сходимости ряда). Если
ряд (ЗОЛ) сходится, то
lim и„ = 0. C0.5)
Доказательство. Если ряд C0.1) сходится, то
последовательности его частичных сумм s^, п = 1, 2, ... , И8^_^, п = 2,
3, ... , очевидно, имеют один и тот же предел, равный сумме s
этого ряда. Поэтому, замечая, что и^ = s^ - s^ _ -^^ п = 2, 3, ... ,
имеем
lim и^ = lim (s„ - s„ _ .) = lim s„ - lim s„ _. = 0. П
л ^ oo '^'^ л ^ oo '^'^ '^'^ ^ л ^ oo '^'^ л ^ oo '^'^ ^
с помогцью теоремы 1 иногда удается установить
расходимость рассматриваемого ряда: если для данного ряда условие
C0.5) не выполняется, то он расходится.
Примеры. 1. Пусть q— комплексное число и |д| < 1.
Тогда ряд l + g + g^ + g^ + ... + д^+... с членами и^ = q^,
я = О, 1, 2, ... , образуюгцими бесконечную убывающую
геометрическую прогрессию, сходится.
Действительно,
s^=l + q + q^ + ... + q^= ^ =-^ - 2 ,
^ 1 - q 1 - q 1 - q
пП + 1
и так как lim ^ = О, то
л^оо 1 — q
lim s^= -^.
2 . Ряд, члены которого образуют геометрическую
прогрессию 1 + g + д^ + д^ + ... + д^ + ... , при \q\ > 1 расходится, так
как его обпа;ий член и^ = q^ не стремится к нулю: \uj = \q\^ > 1.
3 . Ряд 1-1 + 1-1 + ...+ (-1)^ + 1 + ... с членами и^ = (-1)^ + 4
п= 1, 2, ... , расходится.
В самом деле, в этом случае
^2^^^' ^^1?^?***? ^2^ + 1^-*-' ^^0, 1, ...,
поэтому последовательность частичных сумм {s^} не имеет
предела.
Расходимость рассматриваемого ряда следует, конечно, и
из того, что все его члены по абсолютной величине равны
единице, и поэтому не выполняется необходимое условие C0.5)
сходимости ряда.
8
30.2. Свойства сходящихся рядов
оо
ТЕОРЕМА 2. Пусть с — комплексное число. Если ряд ^ г/^,
п = \
оо
г/^G С, сходится, то ряд ^ си^, называемый произведением
п = 1
данного ряда на число с, также сходится и
оо оо
1,си^ = с1^ и„. C0.6)
п = 1 п = \
Эта теорема означает, что числовой множитель «можно
выносить за скобку» и в случае бесконечного множества
слагаемых, если они образуют сходягцийся ряд. «Можно» в том
смысле, что справедливо равенство C0.6).
п п
Доказательство. Пусть s^= Y. ^k^ ^п^ L ^^k- По ус-
ловию lim s^ сугцествует, поэтому, в силу очевидного равен-
ства s^ = cs^, сугцествует предел lim s^ и
lim s'= с lim s„,
д ^ оо ^'- д ^ оо 't^
Согласно определению суммы ряда, отсюда сразу следует
C0.6). П
оо оо
ТЕОРЕМА 3. Пусть ряды Y, ^п^ И ^п сходятся; тогда ряд
п = 1 п = 1
оо
^ (и^ + vj, называемый суммой данных рядов, также схо-
п = 1
дится и
оо оо оо
ЕК + ^„)= !"„+ L^n- C0.7)
Эта теорема означает, что сходягциеся ряды «можно
складывать почленно» (я-й член с п-ш), «можно» в том смысле, что
справедливо равенство C0.7).
Доказательство. Пусть
тогда E^ = s^ + s^, и так как lim s^ и lim s^ no условию cy-
гцествуют, TO lim a^ также сугцествует и
lim a = lim (s„ + s") = lim s„ + lim s'.
Это равенство эквивалентно равенству C0.7). П
9
Пример. Найдем сумму ряда У , сведя его к сум-
п = 0 6"
мам членов бесконечно убываюгцих геометрических прогрессий
^ 2^ + 3^ _ vf— + —^= V—+ V—= 1 + 1 _ 7
^л f\n ^Л Чп On L^^on L^^on 1 12*
3 2
ТЕОРЕМА 4. ^слг/ р^E сходится, то любой его остаток
сходится. Если какой-либо остаток ряда C0.1) сходится,
то и сам ряд также сходится. При этом если
оо т оо
«=!"&' «т = Е "ft' ^m = Е "ft'
mo
^ = ^т + Гт^ m=l,2,... .
Доказательство. Пустьs^ = щ + U2 + ... + u^,n= 1, 2,..., —
oo
частичные суммы ряда ^ г/^, a
д = 1
частичные суммы его т-го остатка:
Очевидно, что при п> т имеем
^^ = ^^ + 4"^^ n = m + k, C0.8)
откуда при произвольно фиксированном т следует, что
предел lim s„ супа;ествует тогда и только тогда, когда супа;ествует
предел lim si^\
Иначе говоря, ряд сходится тогда и только тогда, когда
сходится некоторый его остаток г^ = lim s^^^. Поскольку
натуральное число т было произвольным, первая часть теоремы
доказана.
Наконец, переходя к пределу в равенстве C0.8) при й ^ оо
и фиксированном т, имеем s = s^-\- r^, так как п = т -\- k ^ ^
при й ^ оо а lim s„ = s, lim si^^ = r^. П
Из этой теоремы следует, что отбрасывание или
добавление конечного числа членов к данному ряду не влияет на его
сходимость.
То
Из формулы S = s^ -\- г^, очевидно, следует, что если ряд
сходится, то его остаток стремится к нулю:
lim г = lim (s - sj = 0. C0.9)
Отметим, что само собой разумеется, что условие C0.9)
нельзя принять в качестве определения сходяпа;егося ряда, так как
остаток ряда сам является рядом, и говорить о его стремлении к
нулю можно лип1ь уже зная определение сходимости ряда.
30.3. Критерий Коши сходимости ряда
Критерий Коп1и сходимости последовательностей может быть
легко перефразирован применительно к рядам.
Действительно, как известно (см. п. 4.7 и 19.3), для того чтобы
последовательность комплексных чисел {s^} была сходягцейся,
необходимо и достаточно, чтобы для каждого 8 > О сугцествовал
такой номер п^, что для любых номеров п > п^, п = 1, 2, ... , и
любых целых р > О выполнялось неравенство
Для удобства использования этого критерия в случае рядов
мы пип1ем здесь разность s^ + - s^ _ ^ вместо разности s^ + - s^,
которую писали раньпхе в п. 4.7. Это, конечно, не влияет на
суть дела. При этом, поскольку сумма Sq не определена, мы
всегда будем считать по определению, что Sq = 0.
Если теперь под {s^} подразумевать последовательность
частичных сумм ряда C0.1), то
\+р -\-l = Un^ ^я + 1 + ••• + ^п+р
и сформулированный в этих обозначениях критерий
принимает следуюпа;ий вид.
оо
ТЕОРЕМА 5 (критерий Коши). Для того чтобы ряд ^ г/^ схо-
п = 1
дился, необходимо и достаточно, чтобы для любого 8 > О
существовал такой номер п^, что при любом п > п^и любом
целом р>0 выполнялось неравенство
К + г/, + 1 + ... + г/,+д<8. C0.10)
Из критерия Коп1и сходимости ряда легко можно
получить снова необходимое условие C0.5) сходимости ряда.
Действительно, в этом случае неравенство C0.10) выполняется
для любого р > О и, в частности, для р = 0. Поэтому для всех
П
n> n^ имеем \u^ < 8, a это, в силу произвольности 8 > О, и
означает, что lim г/„ = 0.
Свойство C0.5) означает, что «общий член сходящегося
ряда стремится к нулю».
Пример. Рассмотрим гармонический ряд
1 + 1 + ... + ! + ...
2 п
и докажем, что он расходится (факт, установленный епа;е
Н. Оресмом).
Действительно, для любого п= 1, 2, ... имеем
= - + -^ + ••• + 7Г^ >7^ + 7^ + --- + Л = 7^ = ^. C0.11)
п п + 1 2п-1 2п 2п 2п 2п 2 ^ ^
т. е. для любого п при 8 = 1/2 j^p = п - 1 неравенство C0.10) не
выполняется.
Таким образом, из критерия Konin следует, что
гармонический ряд расходится.
В гармоническом ряде его п-й член и^ = 1/п стремится к
нулю при я ^ оо. Таким образом, пример гармонического
ряда показывает, что условие стремления к нулю
последовательности членов ряда, являясь необходимым условием
сходимости ряда (теорема 1), не является достаточным.
Из рассмотренного примера следует также, что ряд
1 + - + — + ... + — + ... C0.12)
2а 3^^ ДОС
при а < 1 расходится. В самом деле, замечая, что при а < 1 для
любого п = 2, 3, ... справедливо неравенство п^ < п, имеем, в
силу C0.11), неравенства
^ + 1 +... + 1 > 1 + ^- +... + -J— > 1.
ДОС (я + 1)ос Bя-1)о^ п п + 1 2п+1 2
Поэтому в случае ряда C0.12) при а < 1 для любого п = 1, 2, ...
при 8 = 1/2 л р = п — 1 неравенство C0.11) не выполняется и,
следовательно, в силу критерия Konin, ряд C0.12) при а < 1
также расходится.
оо
Задача 1. Доказать, что для всякого сходящегося ряда ^ а^ с не-
п = 1
отрицательными членами а^ > О существует такая возрастающая
бесконечно большая последовательность {bj, lim Ь^ = +оо, Ь^<Ь^ + ^, я = 1, 2, ... ,
оо
что ряд ^ (^rfin также сходится.
п = 1
12
30.4. Ряды с неотрицательными членами
В этом пункте рассмотрим ряды, все члены которых —
неотрицательные действительные числа.
ЛЕММА 1. Пусть все члены ряда C0.1) неотрицательны:
и^>0, я = 1,2, ... . C0.13)
Для того чтобы этот ряд сходился, необходимо и
достаточно, чтобы существовала хотя бы одна сходящаяся
подпоследовательность последовательности его частичных
сумм.
Действительно, из условия C0.13) следует, что
k = 1
т. е. последовательность частичных сумм {s^}
рассматриваемого ряда является возрастаюпа;ей. Монотонная же
последовательность сходится в том и только в том случае, когда
сходится хотя бы одна ее подпоследовательность (см. замечание
после теоремы 3 в п. 4.5). П
ЛЕММА 2.Для того чтобы ряд C0.1) с неотрицательными
членами сходился, необходимо, чтобы последовательность
его частичных сумм была ограниченной сверху, и
достаточно, чтобы была ограниченной сверху хотя бы одна
подпоследовательность {s^ } последовательности {s^ его частичных
сумм, причем если
s = sup{s^ },
то s является суммой ряда C0.1).
В самом деле, сходимость ряда означает сходимость
последовательности его частичных сумм, а всякая сходягцаяся
последовательность ограничена, в частности ограничена сверху.
Таким образом, первая часть леммы справедлива и без
предположения неотрицательности членов ряда.
Однако в обгцем случае условие ограниченности даже всех
частичных сумм ряда (а не только некоторой их
подпоследовательности) не является достаточным для сходимости ряда, как
это показывает, например, пример 3, разобранный в п. 30.1.
Поэтому условие неотрицательности членов ряда сугцественно
для справедливости второй части леммы 2. Докажем ее.
Из неотрицательности членов ряда, как мы убедились при
доказательстве предыдугцей леммы, следует, что последова-
Тз
тельность его частичных сумм — возрастаюгцая. Поэтому,
если сугцествует ограниченная сверху подпоследовательность
{s^ } последовательности частичных сумм {s^}
рассматриваемого ряда, то она тоже возрастаюгцая (как всякая
подпоследовательность возрастаюгцей последовательности) и,
следовательно (см. теорему 3 в п. 4.5), сходится, причем
S = sup{s„ } = lim s„ .
Согласно предыдугцей лемме, из сходимости
подпоследовательности частичных сумм {s^ } следует сходимость ряда, т. е.
сугцествование конечного предела lim s„, а так как предел
сходягцейся последовательности совпадает с пределом любой
ее подпоследовательности, то
lim s„ = lim s„ = s. П
Из леммы 2 следует, что если ряд с неотрицательными
членами расходится, то последовательность его частичных сумм не
ограничена сверху и в силу ее монотонности lim s^ = +оо.
Поэтому для расходягцихся рядов с неотрицательными членами,
оо
согласно сделанному в п. 30.1 соглагаению, пигаут ^ г/^ = -\-оо,
п = 1
Доказанные леммы по своей формулировке внегане
напоминают соответствуюгцие утверждения для несобственных
интегралов (см. п. 29.3). Между сходимостью рядов с
неотрицательными членами и сходимостью несобственных
интегралов от неотрицательных функций можно иногда установить и
более непосредственную связь. Для убываюгцих функций это
сделано в п. 30.7.
Пример. Рассмотрим теперь ряд C0.12) при а > 1.
Покажем, что в этом случае он сходится. Возьмем сначала
частичные суммы этого ряда порядков n = 2^-l,k = l,2, ...,
объединив их слагаемые в k групп, которые имеют следуюгций вид:
— + + + ... + —-i , р = 0, 1, ... ,й-1,
т. е.
2а 3^ J v4^ 5^ 6^ 7^
2(^- 1)а B^ - 1)^
Заметив, что для каждого слагаемого р-й группы справедливо
неравенство
<7^. т = 0, 1, ...,2^-1
и что в этой группе 2^ слагаемых, получим
9 92 ok - \
^ -л _| ^ _| ^ _| _| ^ ^^
+ 00 1 1 оа- 1
< У = = — .
2а-1
Таким образом, последовательность частичных сумм s^
ряда C0.12) при а > 1 ограничена сверху. Далее, в силу
положительности членов рассматриваемого ряда,
последовательность его частичных сумм возрастает. Поэтому супа;ествует
конечный или бесконечный предел lim s„ = s. Но тогда и любая
подпоследовательность {s^}, в частности последовательность
{s^ }, имеет тот же предел s, а так как по доказанному эта
последовательность ограничена, то предел s конечен.
оо -|
Отметим, что в случае а = 2 сходимость ряда У —^ доказы-
вается значительно прогце. Действительно, для любого п =
= 1, 2, ... имеем
5„ = 1 + Л + Л + --- + Л <1 + ^— + ^— + ••• + 7—Кг- =
^ 22 32 я2 1.22-3 (п-1)п
I 2 J l2 Зу [п-1 п) п ' ' ' '
оо -1
т.е. частичные суммы ряда У —- ограничены сверху и, следова-
тельно, согласно лемме 2, он сходится. Отсюда для любого а > 2
в силу неравенства
\<\, «=1,2,....
оо -|
сразу следует ограниченность частичных сумм ряда У — при
п = \ ^^'
а > 2, поэтому и его сходимость (подобный метод
установления сходимости ряда с неотрицательными членами
рассмотрен в обгцем случае в следуюгцем пункте). Таким образом,
только из-за случая 1 < а < 2 пригалось применить выгае более
оо -1
сложный способ оценки частичных сумм ряда У —, а > 1
ДЛЯ установления его сходимости.
Тз
Сумма ряда C0.12) при а > 1 является, очевидно, функцией
от а. Эта функция называется дзета-функцией Римана и
обозначается греческой буквой ^. Обычно ее аргумент обозначают
буквой S. Таким образом,
30.5. Признак сравнения для рядов
с неотрицательными членами.
Метод выделения главной части члена ряда
Рассмотрим теперь признаки сравнения рядов, также по своей
форме весьма напоминаюгцие соответствуюгцие признаки
сходимости несобственных интегралов.
ТЕОРЕМА 6 (признаксравнения). Пусть
и^>0, v^>0, я = 1,2,..., C0.14)
u^ = 0(vj\ C0.15)
Тогда если ряд
оо
Е Vn C0.16)
сходится, то сходится и ряд
t "я' C0.17)
п = \
а если ряд C0.17) расходится, то расходится и ряд C0.16).
Доказательство. Пусть выполнено условие C0.15).
Тогда сугцествует такое с > О, что
Uj^<cvj^, й = 1,2, .... C0.18)
Если теперь ряд C0.16) сходится, то, согласно лемме 2,
последовательность {s^} его частичных сумм ограничена, т. е. су-
па;ествует такая постоянная М > О, что
^п= t^k^M, я=1,2, .... C0.19)
Обозначим через а^ частичную сумму ряда C0.17). Тогда, в
силу неравенств C0.18) и C0.19),
<^п= t^k<^t^k = ^^n<^M, П= 1, 2, ... .
В частности, и^ < v^. Объяснение обозначения О см. т. 1, п. 23.3.
Согласно лемме 2, из ограниченности сверху частичных сумм
ряда C0.17) следует его сходимость. Итак, если ряд C0.16)
сходится, то ряд C0.17) также сходится.
Если же ряд C0.17) расходится, то и ряд C0.16)
расходится, так как если бы он сходился, то, по доказанному, сходился
бы и ряд C0.17), что противоречит условию. П
СЛЕДСТВИЕ. Пусть v^^ О, я = 1, 2, ... , и
lim ^ = й, C0.20)
тогда:
1) если ряд C0.16) сходится и О < k < -\-оо, то ряд C0.17)
также сходится;
2) если ряд C0.16) расходится и О < k < +оо, то ряд
C0.17) также расходится.
В частности, если и^ ~ v^ (и^ и v^ эквивалентны, см.
п. 19.3), то ряды C0.16) и C0.17) сходятся или расходятся
одновременно.
Из выполнения условия C0.20) для О < й < +оо следует су-
гцествование такого п^, что если п > п^, то
^<й + 1, T.e.u^<(k + l)v^,
а это означает, что г/^ = 0(i;^). Поэтому утверждение 1
следствия непосредственно вытекает из утверждения 1 теоремы.
Из выполнения условия C0.20) для О < й < +оо следует,
что если зафиксировать такое k\ что О < й^ < й, то сугцествует
номер tIq = п^(к'), обладаюгций тем свойством, что если п > п^,
то — > k\ т. е. v^ < -pU^, а это означает, что v^ = 0(и^). Поэто-
му утверждение 2 следствия непосредственно вытекает из
утверждения 2 теоремы. П
Примеры. 1. Пусть и^ = ёнЦ^. Тогда О < и^ < \,
оо -|
п = 1, 2, ... , и так как ряд ^ — сходится (см. п. 30.1), то схо-
дитсяиряд £ ^i^^.
°° 1 11
2. Ряд Y, р расходится, так как — > ——,
оо -1
п = 1, 2, ... , а ряд Y, ~р' ^^^ было показано (см. исследова-
ние ряда C0.12)), расходится.
1?
Приведем егце один способ доказательства сходимости ря-
оо -1
да C0.12), т. е. ряда У —, при а > 1, основанный на признаке
сравнения рядов.
3. Рассмотрим ряд
его члены положительны, и он сходится. В самом деле, для
него легко находятся его частичные суммы:
откуда следует, что lim s^= 1, Применив теперь формулу конеч-
п —^ '-^
пых прирагцений Лагранжа к функции на отрезке [п- 1, п],
получим
-^—-—-—- = -—^^—^—, о<е<1.
Следовательно,
1 1 _ а - 1 ^ а - 1
(я-1)^-1 я^-1 (я-1 + 0)^
поэтому
Из этого неравенства, в силу признака сравнения рядов, следует
сходимость ряда C0.12), так как исходный ряд C0.21) сходится.
Эффективность использования критерия сравнения для
исследования сходимости ряда зависит, конечно, от запаса
«рядов сравнения», т. е. рядов, о которых уже известно,
сходятся ли они или расходятся, и которые мы можем пытаться
использовать для исследования сходимости данного ряда.
оо -1
Если в качестве «ряда сравнения» C0.16) взять ряд У —,
о котором уже известно, при каких а он сходится, то из
теоремы 6 непосредственно следует справедливость следую-
па;ей теоремы.
ТЕОРЕМА 7. Пусть и^>0,п=1, 2, ... . Тогда если и^ = о(\)
иа> 1, то ряд
£ и, C0.22)
П = 1
сходится; если же — = 0(uj г/ а < 1, то ряд C0,22)расходится.
Is
СЛЕДСТВИЕ. Пусть lim п^и^ = k, тогда:
1) если а> 1 иО < k < +00, то ряд C0.22) сходится;
2) если а< 1 иО < k < +00, то ряд C0,22) расходится,
В частности, если и^ ~ —, то ряд C0.22) сходится при
а> 1 и расходится при а < 1.
Если члены и^ ряда C0.22) с неотрицательными членами
заданы с помопа;ью формулы, пред став ляюпа;ей собой функцию
от п, которая имеет смысл для всех действительных
достаточно больп1их неотрицательных значений переменной п и, более
того, является «достаточно гладкой» функцией этой
переменной, то для практического применения теоремы 7 обычно
бывает целесообразно разложить член и^ с помогцью формулы
Тейлора по степеням -.
п
Если главный член получивгаегося разложения имеет вид
1 оо ^
—, то, беря в качестве ряда сравнения ряд У — и применяя
теорему 7, можно определить, сходится ли данный ряд или
расходится. В известном смысле можно сказать, что этот
метод исследования сходимости ряда, называемый методом
выделения главной части обгцего члена ряда, является наиболее
удобным и вместе с тем достаточно обгцим.
Примеры. Исследуем сходимость рядов, обгцие члены и^
которых задаются указанными ниже формулами.
1. и^ = 1- cos -. Очевидно, г/„ > 0. Так как (см. замечание в
конце п. 13.3) cos х= \ + О(х^), х ^ О, и, следовательно,
то, в силу теоремы 7, ряд с обгцим членом и^ сходится.
2. и^ = In cos -. Здесь и^ < О, Вспомнив, что In A -\- х) = 0(х),
X ^ О, и, применив последовательно формулу Тейлора для
косинуса и логарифма, получим
u„^lncosi^ln[l + of-i]]^of-L) „^00,
И поэтому, в силу теоремы 7, ряд с положительными членами
оо оо
^ (-и J сходится, а вместе с ним сходится и ряд ^ и^,
п = \ п = \
То
3. ц = In -, n = 3, 4, ... . Имеем u„ > 0 и tg-
l-tg5
n
- + o[ - I я ^ oo, поэтому
n J n \ n) n \n
„, = l„(l + tgS]-l„(l-.gS] = 2tgI + „(tgS)==L« + o(
Таким образом, u^ ~ —; так как ряд ^ - расходится, то
расходится и ряд ^ In
п = г 1 _ f«.5
30.6. Признаки Даламбера и Коши
для рядов с неотрицательными членами
Иногда оказываются полезными некоторые специальные
признаки сходимости ряда. Отметим среди них так называемый
признак Даламбера"^ и признак Konin, непосредственно полу-
чаюпа;иеся из признака сравнения, если в качестве ряда
сравнения взять соответствуюпа;им образом выбранную
геометрическую прогрессию.
ТЕОРЕМА 8 (признакДаламбера). ili/cmb дан ряд с
положительными членами
оо
Х: и^, г/^>0, я =1,2,... . C0.23)
Тогда:
1) если существует такое число q, О < q < 1, что
выполняется неравенство
'^^^<q, я=1,2, ...,
то данный ряд сходится;
2) если выполняется неравенство
^^^>1, я=1,2,...,
то данный ряд расходится.
' Ж. Даламбер A717—1783) — французский философ и математик.
Доказательство. Пусть О < g < 1 и пусть
^^ <д, т. е. u„ + i<gu„, п = 1,2,....
Тогда
г/3 ^ u^q ^ г/^д^.
и так как ряд u^q + г/^g^ + ... + u^q^ " ^ + ... , являясь суммой
бесконечной убываюгцей геометрической прогрессии со
знаменателем g (О < g < 1), сходится, то, по признаку сравнения,
сходится ряд и исходный ряд C0.23).
Если же выполняется неравенство -Л±1 >1,я = 1,2, ...,то
И так как, по предположению, и^ > О, то п-й член ряда, будучи
ограничен снизу положительной постоянной, не стремится к
нулю. Следовательно, не выполняется необходимое условие
сходимости ряда (см. теорему 1 этого параграфа), поэтому ряд
C0.23) расходится. П
СЛЕДСТВИЕ. Пусть существует lim -Л-Ll = I, Тогда если
I < 1, то ряд C0.23) сходится, а если I > 1, то ряд C0.23)рас-
ходится.
Это вытекает непосредственно из доказанной теоремы.
°° 1 1
В качестве примера рассмотрим ряд ^ —. Здесь и^ = — vl
lim -JLll = lim _ = О, поэтому, согласно следствию
теоремы 10, данный ряд сходится. Его сходимость, конечно,
можно установить и сравнив его, например, со сходяпа;имся
оо -1
рядом у —.
Более содержательные примеры на применение признака
Даламбера приведены в дальнейпхем (см., например, п. 32.1).
Yl
ТЕОРЕМА 9 (признак Коши). Пусть дан ряд
оо
^ и„, и„>0, п = 1,2, ... . C0.24)
Д = 1
Тог^а:
1) если существует такое д, О < g < 1, что для всех п =
= 1,2,... выполняется неравенство ^fiT^ ^ q, то данный ряд
сходится;
2) если для всех п = 1, 2, ... выполняется неравенство
^JiTji > 1, то данный ряд расходится.
Доказательство. Если при ^^yil^ < g, т. е. u^<q'^, п=1,2,...,
то, по признаку сравнения, ряд C0.24) сходится, так как ряд
оо
^ q^ при О < g < 1 сходится.
п = 1
Если же \[й~^ > 1, то и^> 1, п = 1, 2, ..., и, следовательно,
ряд C0.24) расходится (см. теорему 1). П
СЛЕДСТВИЕ. Пусть существует
lim rif^„ = L
Тогда, если Z < 1, то ряд C0.24) сходится, а если 1> 1, он
расходится.
Доказательство следствия очевидно.
оо -1 I -1
Рассмотрим ряд У —. Так как lim ^i и = Ит - = О,
ТО, согласно следствию из теоремы 9, данный ряд сходится.
Его сходимость легко устанавливается и с помогцью
теоремы 7.
оо
Замечание. Если о ряде ^ и^, и^ > О, п = 1, 2, ...,
п = 1
известно лип1ь, что
lim ^^:i±i = 1 или lim ^,/Z = 1, C0.25)
ТО ничего определенного о его сходимости сказать нельзя: ряд
может как сходиться, так и расходиться. Например, ряды
оо -1 оо -1
удовлетворяют обоим условиям C0.25), однако первый из них
расходится, а второй сходится.
22
30.7. Интегральный признак
сходимости рядов с неотрицательными членами
Если для данного ряда C0.1) с неотрицательными членами
удается подобрать функцию, определенную при х > 1 и такую,
что f(n) = и^у то при определенных условиях по сходимости
+ 00
или расходимости интеграла | f(x)dx можно судить и о сходи-
1
мости или расходимости ряда C0.1).
ТЕОРЕМА 10 (интегральный признак сходимости рядов). Если
функция f(x), определенная при всех х> 1, неотрицательна и
убывает, то ряд
L fix)
C0.26)
сходится тогда и только тогда, когда сходится интеграл
I f(x)dx.
C0.27)
Доказательство. Прежде всего заметим, что, в силу
монотонности функции / на промежутке [1, +оо), она
интегрируема по Риману на любом конечном отрезке [1, Г|], и поэтому
имеет смысл говорить о несобственном интеграле C0.27).
Если й<х<й + 1, то,в силу убывания функции f(x)
(рис. 1), f(k) > f(x) > f(k + l),k = 1, 2, ... ; поэтому, интегрируя
эти неравенства по отрезку \k, k + 1], будем иметь
f{k)> ] f{x)dx>f{k + l), й = 1,2, ....
k
Суммируя от k = \ д,ок = п (рис. 2), получим
f f{k)>^Yf{x)dx> f /(й + 1).
23
n
и, полагая s^= У f(k), будем иметь
k- 1
s,>"|V(x)dx>s, +1-/A), я = 1,2, .... C0.28)
1
Если интеграл C0.27) сходится, то, в силу неотрицательности
функции /, согласно лемме п. 29.3, при любом п = 1, 2, ...
П + 1 +00
I f(x) dx < I f(x) dx,
1 1
Отсюда и из неравенства C0.28) следует, что
+ 00
s^ + 1 </(!)+ \fix)dx,
1
т. е. последовательность частичных сумм ряда C0.26)
ограничена сверху, а значит, согласно лемме 2 п. 30.4, этот ряд сходится.
Если ряд C0.26) сходится и его сумма равна s, то, согласно
той же лемме, s^ ^ s для всех п = 1, 2, ..., и, следовательно, в
силу неравенства C0.28), для всех п = 1, 2, ...
п + 1
I f(x) dx < s.
1
Если теперь ^ > 1, то, беря п так, чтобы я > ^, получим,
в силу неотрицательности функции /,
I /(х) dx < I /(х) dx < S.
1 1
Итак, совокупность всех интегралов | /(х) dx, ^ ^ 1, огра-
1
ничена сверху, поэтому интеграл C0.27) сходится (см. лемму
п. 29.3). П
Эта теорема часто значительно облегчает исследование
сходимости рядов, так как если для данного ряда удается подобрать
соответствуюпа;ую функцию / и, следовательно, свести вопрос об
изучении сходимости ряда к изучению сходимости интеграла,
то это дает возможность применить развитый в предгаествую-
гцей главе аппарат интегрального исчисления.
Примеры. 1. Рассмотрим снова (см. п. 30.3 и п. 30.5)
ряд C0.12)
1 + —+ — + ... + — + ...
С п-ш членом г/^ = я"^, я = 1, 2, .... В данном случае при а > О
функция /(х), указанная в теореме, подбирается легко:
f(x) = ±, х>1.
24
Tdx
Так как интеграл J — сходится при а > 1 и расходится при а < 1,
то и ряд C0.12) сходится при а > 1 и расходится при О < а < 1.
Расходимость ряда C0.12) при а < О очевидна сразу — его об-
гций член не стремится к нулю, поскольку — > 1, а < 0. Эти
факты были установлены в п. 30.3, 30.4 и 30.5 другим методом.
Как видно из изложенного выпхе, применение к изучению ряда
C0.12) интегрального признака сходимости рядов значительно
упростило задачу исследования сходимости этого ряда.
2. Рассмотрим ряд
оо -1
у . C0.29)
Этот ряд легко можно исследовать с помопа;ью
интегрального признака сходимости: из того, что интеграл
{ (х+1Iп(х+1) ^2 ^
расходится, следует, что и ряд C0.29) расходится.
Сформулируем теперь простое, но часто полезное в
приложениях следствие из теоремы 10.
Если существует такое натуральное п^, что неотрица-
оо
тельная функция f убывает при х > п^, то ряд ^ f(n) сходит-
П = Uq
+ 00
ся тогда и только тогда, когда сходится интеграл | f(x) dx.
Этот случай сводится к рассмотренному в теореме заменой
переменного х = у + п^- \.
30.8''. Неравенства Гёльдера и Минковского
для конечных и бесконечных сумм
Пусть заданы числа (вообгце говоря, комплексные) х^, ... , х^,
у^, ... , у^, 1 <р < +00, и число q определяется равенством - + - =
= 1 (см. B8.16) в п. 28.2"^). Тогда справедливы неравенства
^|x,z/J<^|xJ^' [1^ЫЛ C0.30)
(неравенство Гёльдера) и
Iki + yJ^ < EW^ + ЕЫЛ C0.31)
(неравенство Минковского).
25
Их доказательство проводится по той же схеме, что и в
случае соответствуюпа;их интегральных неравенств (см. п. 28.2"^).
Введем для краткости обозначения
и и def f ^ \ I Л1/-Р и и def f ^ \ \ Л^/^
H = fi:kN , 1Ы|/=(Е|г/Л . C0.32)
Применив неравенство B8.17) аЬ< — + —,а>0, Ь>Ок
^^ГГТГ'^^^'^^1'2, ...,я,имеем1^1 ^ <i^ +i^
Ikll;, Цг/Нд Ikll^, ||г/||^ v\\x\\l q\\y\\l
Просуммировав эти неравенства по / от 1 до я, в силу C0.32) и
условия - + - = 1, получим
1 "| I 1 "|| 1"|| 11
откуда
Е k^yj < Ikiyiyllg;
i = 1
тем самым неравенство C0.30) доказано.
Неравенство Минковского C0.31) следует из неравенства
Гёльдера C0.30): из очевидного соотногаения
i = 1 i = 1 i = 1
применив к каждому слагаемому в правой части неравенство
Гёльдера, получим
Xj^» + yJ''<(X,W'') (Xjk + yJ^^"'^J +
/ п \l/q/ п Л1/^
Если левая часть неравенства равна нулю, то неравенство
Минковского, очевидно, справедливо; если же она не равна нулю, то,
сокрагцая обе части неравенства на множитель 2^ |л:^ + У if
^ i = 1
И заметив, что - + - = 1, q(p - 1) = р, получим неравенство
C0.31). П
Для любых двух рядов Y, ^п^ l2 Уп справедливы аналогич-
п ^ 1 п = \
ные неравенства
Е Куп\ < Е К\Л Е кМ ' C0.33)
п = \ ^ п = \ ' ^ п=\ '
ЪК^у^Л < Ек1Л + Ек1^ .C0.34)
Действительно, для всех частичных сумм одного и того же
порядка заданных рядов справедливы неравенства Гёльдера и
Минковского. Переходя в них к пределу при я ^ оо^ мы и
получим неравенства C0.33) и C0.34).
Из доказанных неравенств следует, в частности, что если
оо оо оо
ряды ^ kj^, ^ |i/J^ сходятся, то ряд ^ |х^г/J сходится, а если
п = \ п = \ п = \
оо оо °° I
СХОДЯТСЯ ряды ^ \xj, Y. 1^дГ' '^^ сходится ряд ^ \х^ + г/^р.
30.9. Знакопеременные ряды
В этом пункте рассматриваются ряды с действительными
членами, знаки которых, вообгце говоря, изменяются при
изменении номера; такие ряды называются знакопеременными.
Рассмотрим прежде всего знакочередующиеся ряды, т. е.
ряды, члены которых поочередно то положительны, то
отрицательны.
ТЕОРЕМА 1 (теорема Лейбница), ^сл г/
lim г/„ = О C0.35)
и
^я>^я + 1>0' п=1,2,„,, C0.36)
то знакочередующийся ряд
оо
£(-!)« +X C0.37)
П = 1
сходится. При этом любая частичная сумма s^ ряда C0.37)
отличается от его суммы s на величину, меньшую
следующего члена г/^ + 1, иначе говоря, абсолютная величина
остатка ряда г^ в этом случае не превышает абсолютной
величины его первого члена, т, е,
~27
Доказательство. Рассмотрим частичные суммы четного
порядка ряда C0.37)
2k
п = \
Их можно записать в виде
В силу условия C0.36), выражения в круглых скобках
неотрицательны и поэтому s^j^ < s^j^ + 2' ^- ®- последовательность
частичных сумм четного порядка ряда C0.37) возрастает.
Замечая, что частичные суммы s^j^ можно записать также в
виде
^2k ^ ^1 ~ (^2 ~ ^з) ~ ••• ~ \Ц2к-2 ~ ^2k-V ~ ^2k^ Й = 1, 2, ... ,
И ЧТО выражения в круглых скобках, в силу условия C0.36),
неотрицательны, а г/2у^ ^ О? получаем, что §2)^ ^ ^i? т. е.
последовательность {§2)^} ограничена сверху. Из возрастания и
ограниченности сверху последовательности {^2^^} следует, что она
сходится:
,1™о«2. = «- C0.38)
Покажем, что и частичные суммы нечетного порядка ряда
C0.37) стремятся к тому же пределу. Действительно,
52^ + 1 = ^2^ + ^2^ + 1' ^=1, 2, ... , C0.39)
C0.39), имеем
и так как, согласно C0.35), lim г/^^, , i = О, то, в силу C0.38) и
^ —^ со ^'^ "■" -■-
Дт^^2. + 1 = ^. C0.40)
Из C0.38) и C0.40) следует, что
lim s„ = s.
Теперь отметим, что для ряда C0.37) справедливо неравенство
^2у^<^<^2у^-1' ^=1,2,.... C0.41)
Действительно, с одной стороны, уже было показано, что s
является пределом возрастаюпа;ей последовательности [s^j^,
поэтому s^j^ < S. С другой стороны,
^2^ + 1 ^ ^2^-1 ~ \^2k ~ ^2fe + l) ^ ^2^-1' ^ ^ 1' 2, ... ,
~28
т. е. последовательность {s2f^ _ 1} убывает, и так как s является
пределом и последовательности {s2f^ _ 1} (см. C4.40)), то s < §2)^ -1-
Из неравенства C0.41) следует
^ ~ ^2fe ^ ^2fe + 1 ~ ^2k ^ ^2k + 1'
^2^-1 ~ ^ ^ ^2^-1 ~ ^2fe ^ ^2^' Й = 1, 2, ... ,
а это и означает, что для всех я = 1, 2, ... выполняется
неравенство |s - s^l < г/^ + ^. П
Если условия чередования знаков ряда и монотонности
выполняются не с первого члена, а лигаь начиная с некоторого
номера tIq, то при выполнении условия C0.35), т. е. при
стремлении обгцего члена ряда к нулю, рассматриваемый ряд будет
также сходиться. Это следует из того, что отбрасывание конечного
числа членов ряда не влияет на его сходимость (см. теорему 4
в п. 30.2).
В качестве примера рассмотрим ряд
У ЬУ . C0.42)
Его члены удовлетворяют, очевидно, условиям теоремы 11, и
поэтому он сходится. Замечая, что здесь s^ = 1 и Sg = -, для
суммы S ряда имеем оценку
1<S<1. C0.43)
На ряды переносятся не все свойства конечных сумм.
Поясним это на примере того же ряда C0.42). Если
S=l-^ + ^-7 + ^-^+^-K + ---. C0.44)
2 3 4 5 6 7 8 ' ^ ^
то
1с-1Г1_1 + 1_1+ V1-1 + 1-1+ •
г'^-г!^ 2 + 3 4 + -J 4 + 6 8 + -'
сложив почленно этот ряд с рядом C0.44), получим равенство
2 325749 11 6 '^ ^
т. е. ряд, составленный из тех же членов, что и данный ряд
C0.44), взятых только в другом порядке, поэтому -aS = aS,
откуда следует, что aS = О, что противоречит неравенству C0.43).
Несмотря на кажупа;уюся очевидность справедливости
проведенных рассуждений, где-то соверпхена грубая оп1ибка.
Подробный анализ причин, породивп1их эту оп1ибку, дан в
одном из следуюпа;их пунктов.
2^
30.10. Абсолютно сходящиеся ряды.
Применение абсолютно сходящихся рядов
к исследованию сходимости произвольных рядов
В этом пункте снова рассматриваются ряды, члены которых,
вообш;е говоря, комплексные числа.
Определение 4. Ряд
оо
1 w„, u„G С, C0.46)
называется абсолютно сходящимся, если ряд, составленный
из абсолютных значений его членов, т, е, ряд
t к1' C0.47)
п = \
сходится.
Применяя критерий Konin сходимости ряда к ряду C0.47),
получим: для того чтобы ряд C0.46) абсолютно сходился,
необходимо и достаточно, чтобы для любого 8 > О
существовал такой номер п^, чтобы для всех п> п^и всех целыхр > О
выполнялось неравенство ^ |г/^| < 8.
k = п
Примеры. 1. Ряд Y, ~^^^ абсолютно сходится, так
как
2" я + 1
1 оо ^
< —, а ряд £ — сходится.
2. Ряд У -— , как доказано выпхе, сходится, однако
СХОДИТСЯ он не абсолютно, ибо ряд, составленный из абсолют-
оо -I
ных величин его членов, т. е. гармонический ряд ^ - , расхо-
дится.
ТЕОРЕМА 12. Если ряд абсолютно сходится, то он и
просто сходится.
Доказательство. Пусть ряд C0.46) абсолютно сходится,
т. е. ряд C0.47) сходится. Тогда, в силу необходимости
выполнения условия Коп1и для сходимости ряда (см. теорему 5), для
любого 8 > О сугцествует такое п^, что для всех п> п^и всех
целых р > О выполняется неравенство
п+ р.
1 К\ < е.
k = п
30
Отсюда и из неравенства
п+р I п+ р
Y, ^Щ^ Y, \^k\ следует, что для всех
k = п I k = п
номеров п> n^vi всехр = О, 1, 2, ... выполняется неравенство
< 8. А это и означает, в силу достаточности выполнения
п+ р
k = п
условия Коп1и для сходимости ряда, что ряд C0.46)
сходится. П
Замечание. Следует иметь в виду, что свойство
абсолютной величины суммы не превыгаать сумму абсолютных
величин слагаемых остается справедливым и для сходягцихся
рядов:
г = 1
< Е К\-
п = 1
C0.48)
Это неравенство содержательно, когда его правая часть конечна,
т. е. когда рассматриваемый ряд абсолютно сходится. В этом
случае левая часть неравенства всегда имеет смысл, так как из
абсолютной сходимости ряда следует и его обычная сходимость.
Формально неравенство C0.48), по принятому нами соглагае-
нию об употреблении символа +оо (см. п. 3.1 и 30.1), верно и для
любого сходяпа;егося ряда, у которого ряд в правой части C0.48)
расходится.
Для доказательства неравенства C0.48) в случае сходяпа;е-
оо
гося ряда Y, ^п заметим, что для любого натурального т
п = 1
\ т I т
Е "J < Е К\-
m = 1 I д = 1
Переходя к пределу при m ^ оо, получаем неравенство C0.48).
Обозначим через
Е < C0.49)
т = 1
ряд, составленный из тех же членов, что и ряд C0.46), но
взятых, вообпа;е говоря, в другом порядке.
ТЕОРЕМА 13. Если ряд C0.46) абсолютно сходится, то ряд
C0.49) также абсолютно сходится и имеет ту же сумму.
Доказательство. Пусть ряд C0.46) абсолютно сходится,
т. е. сходится ряд C0.47), и пусть сумма ряда C0.46) равна s:
Е "я-
п= \
C0.50)
31
Покажем сначала, что ряд C0.49) также сходится и, более
того, что его сумма равна сумме ряда C0.46), т. е. s.
Обозначим частичные суммы ряда C0.46) через s^:
\= t ^k^ я =1,2, ... ,
k = 1
а частичные суммы ряда C0.49) — через s^:
т
k- 1
И ПОЛОЖИМ
оо П
*= Е К1 Щг= L к1' « = 1,2,....
п= 1 k= 1
Зафиксируем произвольно 8 > 0; тогда, в силу сходимости
ряда C0.47), сугцествует такой номер п^, что
£ К| = ^-И<|, C0.51)
следовательно, выполняется и неравенство
\s- s^ \--
е
п = п^+ 1
< Е К\<1 C0.52)
п = п^+ 1 ^
Выберем далее номер т^ так, чтобы частичная сумма s'^
ряда C0.49) содержала в качестве слагаемых все члены ряда
C0.46), входягцие в сумму s^ (иначе говоря, номер т^ таков, что
все члены ряда C0.46) с номерами, не превып1аюпа;ими п^,
имеют в ряде C0.49) номера, не превып1аюпа;ие т^). Пусть т > т^.
Положим
Поскольку |s^*| не превып1ает сумму абсолютных величин
слагаемых, входяпа;их в s^, и так как номера этих слагаемых
больп1е, чем п^, а следовательно, все их абсолютные значения
со
содержатся в сумме ^ \uj, то, в силу C0.51), имеем
п = п^+ 1
оо , , о
1С1< Е к1<|- C0.53)
п = п^+ 1 ^
Используя C0.52) и C0.53), получаем при т> т^
оо
Это и означает, что ^ и^^ = s,
т = \
32
Осталось доказать, что ряд C0.49) также абсолютно
сходится. Это сразу следует из только что доказанного
утверждения, если его применить к ряду C0.47). Действительно, этот
ряд, очевидно, абсолютно сходится (как и всякий сходягцийся
ряд с неотрицательными членами), и поэтому, согласно дока-
оо . .
занному, ряд Y, l^ml' составленный из абсолютных величин
т = 1
ряда C0.49), не только сходится (что и означает абсолютную
сходимость ряда C0.49)), но, более того, его сумма совпадает
с суммой ряда C0.47). П
ТЕОРЕМА 14. Если ряд C0.46) абсолютно сходится и
оо
с — какое-либо число, то ряд ^ си^ также абсолютно схо-
п = 1
дится.
Это следует из критерия Konin сходимости рядов и равенства
^+ р, ^+ р
Е \cuk\ = \с\ i: iuj.
k = п k = п
оо оо
ТЕОРЕМА 15. Если ряды Y, ^п ^ И ^п (абсолютно сходят-
п = \ п = \
оо
сяу то их сумма ^ (и^ + v^ также абсолютно сходится,
п = 1
Это следует из критерия Konin сходимости рядов и из
неравенства
п+ р п+ р п+ р
Е к + Vk\< Е К\ + Е К\-
k = п k = п k = п
ТЕОРЕМА 16. Если ряды
оо оо
Е "™ " Е ^« C0.54)
щ = 1 д = 1
абсолютно сходятся, то ряд, составленный из
всевозможных попарных произведений u^v^ членов этих рядов,
расположенных в произвольном порядке, также абсолютно
сходится. Если сумма этого ряда равна s, а сумма рядов C0.54)
равна соответственно s' и s'\ т, е.
оо оо
Е "т = S'. LVn = «"'
т = 1 п = 1
то
s = s's'\ C0.55)
Короче говоря, утверждение теоремы означает, что
абсолютно сходягциеся ряды можно перемножать почленно.
33
Доказательство. Покажем, что ряд, составленный из
всевозможных попарных произведений u^v^ членов рядов
C0.54), абсолютно сходится. Заметим, что если показать, что
ряд из этих произведений абсолютно сходится при каком-
то их порядке, то, согласно теореме 13, отсюда будет
следовать его абсолютная сходимость и при любом другом порядке
членов. Поэтому расположим произведения u^v^ в порядке,
удобном для доказательства теоремы. Для его описания
составим следуюпа;ую таблицу попарных произведений членов
рядов C0.54):
П""!
Ur,V
2У\
Ur,Vr, ... Ur,V
^г'^г
2^^д-
u^v
m^^2
Составим из элементов этой таблицы ряд
u^v^ + u^V2 + U2V2 + г/2^1 + ••• ?
C0.56)
в котором ее элементы расположены в порядке, показанном
на следуюпа;ей ниже схеме, где на месте каждого
произведения из таблицы указан его порядковый номер как члена ряда
C0.56):
^.1
4 3
9 8
5
6
7
16 15 14
<
10
11
12
13
Докажем, что ряд C0.56) абсолютно сходится, т. е. что
сходится ряд
\u-^v-^\ + \u-^v-^\ + |г/2^21 "^ l^2^il "^ ••• C0.57)
Для этого, в силу неотрицательности его членов, достаточно
доказать, что супа;ествует по крайней мере одна ограниченная
сверху подпоследовательность его частичных сумм (см.
лемму 2 п. 30.4).
Положим
i'
т = \
1 К1 4= Е
-/г!'
53'
34
и через §\ обозначим частичные суммы ряда C0.57). Тогда для
этих частичных сумм порядка n^^ будем иметь
п
5{ = \u^v^\ = 5{Sl<^^\
(\u^\ + \uMvi\ + K\)= ^§1<^^',
2 - i"ii'il + ... + KvJ + ... + \u^vj + ... + |u„i;i
(K| + ... + |uJ)(|i;i| + ... + |i;J)
"n n
J <
причем, в силу абсолютной сходимости рядов C0.54), в
правых частях этих неравенств стоят конечные величины.
Итак, подпоследовательность частичных сумм {Д 2} ряда
C0.57) ограничена сверху, и, следовательно, он сходится. Это
означает абсолютную сходимость ряда C0.56) и любого ряда,
полученного произвольной перестановкой его членов (см.
теорему 13). Таким образом, любой ряд
Ё v^v C0.58)
k = l ^ ^
составленный из всевозможных попарных произведений u^v^
членов рядов C0.54), сходится, и притом абсолютно.
Для доказательства C0.55) воспользуемся тем, что сумма
ряда C0.58) в силу его абсолютной сходимости не зависит от
порядка его членов, и снова расположим их наиболее удобным
способом; именно, рассмотрим снова ряд C0.56).
Обозначим через s^ его частичные суммы и положим
<= t ^k^ < = t ^k-
Аналогично тому, как это сделано Bbinie, получаем
s„2 = (ui + ... + ujiv^ + ... + и J = sy;. C0.59)
Поскольку уже доказано, что ряд C0.56) абсолютно сходится,
следовательно, и просто сходится, то супа;ествует конечный
предел lim s^ = s и, следовательно, lim s 2 ^ -s- Согласно же
условиям теоремы, имеют место равенства
lim s' = s\ lim s'' = s'\
Поэтому, перейдя к пределу в равенстве C0.59) при я ^ оо^
получим S = s's'\ т. е. C0.55). П
35
Теоремы 13—16 показывают, что свойства абсолютно схо-
дягцихся рядов во многом похожи на свойства конечных
сумм: величина суммы такого ряда не зависит от порядка
слагаемых, абсолютно сходягциеся ряды можно перемножать
почленно и т. п. В следуюгцем пункте будет доказано, что для
сходягцихся рядов, не сходягцихся абсолютно, эти свойства не
имеют места.
Замечание. В заключение этого пункта подчеркнем,
что, когда члены ряда комплексные или действительные, но
меняюпа;ие знак, вопрос о сходимости этого ряда нельзя реп1ить
только с помопа;ью определения «порядка убывания» п-то чле-
оо -1 оо / -1 \^ ~'~ ^
на. Например, п-е члены рядов ^ - и ^ ^^— имеют оди-
п = 1 ^ п = 1 ^
паковый порядок (см. п. 8.2 в т. 1) при я ^ оо^ однако первый
ряд расходится, а второй — сходится.
оо
Более того, нетрудно привести пример двух рядов ^ г/^ и
п = 1
оо
^ v^, п-е члены которых эквивалентны (и^ - v^, п = 1, 2, ...),
п = 1
НО один ряд сходится, а другой расходится.
В качестве таких рядов можно взять, например, ряд с п-ш
членом
и ряд с п-ш членом
V ^tlfll + I .
^ п (я + 1Iп(я + 1)
с одной стороны, здесь и^- v^, п = 1, 2, ... , так как
(-1)^"^ I 1
Vn _ п (я + 1Iп(я + 1) =1_^ {-If^'^n
и^ (-1)" + ^ (я +1Iп(я +1) '
п
V °°
и поэтому lim — = 1. С другой стороны, У и^ является ря-
П^оо и^ д= 1
оо
дом вида C0.37), поэтому он сходится. Ряд же ^ v^ расходит-
п = \
ся. в самом деле, если бы он сходился, то сходился бы и ряд
оо оо -1
т. е. ряд C0.29), который, как мы видели, расходится.
Было бы оп1ибкой, однако, считать, что метод выделения
главной части годится лигаь в случае рядов с
действительными членами, имеюгцими один и тот же знак. Метод выделения
главной части может с успехом применяться для выяснения
сходимости любых рядов. Суть этого метода в
рассматриваемом случае основана на следуюгцем замечании: пусть дан ряд
оо
^ г/^. Если представить его члены в виде г/^ = у^ + i^^, где ряд
п = 1
оо оо
^ w^ сходится, то ряд Y, ^п сходится и расходится одновре-
п ^ 1 п = \
оо
менно с рядом ^ v^ (почему?). Поэтому для исследования
д = 1
оо
сходимости ряда ^ и^ целесообразно попытаться представить
д = 1
его члены, например, в виде и^ = v^ + w^, так чтобы w = 0(—^
оо
при а > 1. Тогда, поскольку ряд ^ w^^ сходится (и даже абсо-
п = 1
лютно), сходимость данного ряда сводится к исследованию
оо
сходимости ряда ^ v^. Этот прием, конечно, целесообразен
Д ^ оо
оо
в том случае, если получивп1ийся ряд ^ v^ пропа;е исследо-
п = 1
вать на сходимость, чем данный ряд (ср. с аналогичным
исследованием сходимости интегралов в п. 29.6).
Рассмотрим, например, ряд с обгцим членом
Так как (см. замечание в п. 13.3)
In A + х) = X - ^ + О(х^), X ^ О,
(_1^_ 1^ .1 ^_^^_
то
Положим v^ = ' - — vLW^ = u^-v^. Ряд ^ v^ расхо-
ДИТСЯ как разность рядов, из которых один сходится, а другой
оо
расходится. Ряд же ^ w^ сходится, и даже абсолютно, так как
п = \
Таким образом, данный ряд ^ и^ расходится, хотя его
д = 1
оо /_-| \П+\
«главная часть» ^ ^^—^—— и представляет собой сходягцийся
ряд. Тем самым эти ряды являются егце одним примером двух
рядов, члены которых образуют эквивалентные
последовательности и из которых один сходится, а другой расходится.
30.11. Признаки Даламбера и Коши
для произвольных числовых рядов
Если в случае числового ряда C0.1) и^^ О, и^е С, я = 1, 2, ... ,
сугцествует такое д, О < g < 1, что для всех п выполняется
неравенство
1^^^ < q или nj\^\ < g,
ТО, согласно признаку Даламбера, соответственно Konin (см.
п. 30.6), данный ряд сходится, и притом абсолютно.
Если же для всех п имеет место неравенство
> 1 C0.60)
или
"лЯ > 1' C0.61)
то по признакам Даламбера и Konin можно лигаь утверждать,
что в этом случае ряд из абсолютных величин членов ряда
оо
C0.1), т. е. ряд Y, Wn\^ расходится, что лигаь означает, что за-
п = 1
данный ряд не сходится абсолютно.
На самом деле из C0.60) и из C0.61) следует, что данный
ряд C0.1) вообгце расходится. Действительно, как видно из
доказательства признака Даламбера, соответственно призна-
оо
ка Коп1и, применительно к ряду ^ \uj (см. теоремы 8 и 9
п = 1
В П. 30.6) при выполнении каждого из условий C0.60) и
C0.61) в отдельности последовательность {\uj} не стремится
к нулю, следовательно, не стремится к нулю и
последовательность {г/^}, т. е. не выполняется необходимое условие
сходимости ряда.
Полученные признаки расходимости ряда также обычно
называются признаками Даламбера и Коши,
38
30.12. Сходящиеся ряды, не сходящиеся абсолютно.
Теорема Римана
Если ряд сходится, но не абсолютно (такие ряды иногда
называют условно сходящимися), то, как ниже будет показано,
уже нельзя утверждать, что, переставив его члены в другом
порядке, получим сходягцийся к той же сумме ряд. Парадокс
в конце п. 30.9 и объясняется этим обстоятельством:
рассмотренный там ряд C0.45) отличался порядком членов от
заданного сходяпа;егося, но не абсолютно, ряда C0.42), и поэтому
нельзя было утверждать, что его сумма также равна S. Более
того, получивп1ееся противоречие показывает, что это
заведомо не так.
Итак, сумма ряда зависит от порядка слагаемых, т. е.
коммутативный закон сложения не имеет места для не абсолютно
сходяпа;ихся рядов.
Если в данном ряде сгруппировать каким-либо образом его
члены, не нарупхая их порядка, и сложить, то
последовательность частичных сумм получивпхегося ряда является
подпоследовательностью частичных сумм исходного ряда. Поэтому
если исходный ряд сходится, то будет сходиться и вновь
полученный, причем суммы обоих рядов одинаковы. Однако если
данный ряд расходится, то второй ряд может сходиться.
Например, ряд 1-1 + 1-1 + 1-1 + ... расходится. Объединив
же попарно его члены: A - 1) + A - 1) + A - 1) + ... , получим
сходяпа;ийся ряд. Таким образом, вообпа;е говоря, для рядов
неверен и ассоциативный закон сложения.
Рассмотрим некоторые свойства сходягцихся, но не
абсолютно, рядов с действительными членами. Пусть дан ряд
оо
Е и„, C0.62)
П= \
где u^j я = 1, 2, ... , — действительные числа.
Обозначим через и\, и^, ... , г/+, ... его неотрицательные
члены: г/+ > О, а через -и^, ~U2^ ••• ' ~^п^ ••• ®^^ отрицательные
члены: и~ > О, взятые в том порядке, в каком они расположены
в ряде C0.62). Рассмотрим ряды с неотрицательными членами
оо
1 и+; C0.63)
П = 1
t U-. C0.64)
Отметим, что если ряд C0.63) содержит лишь конечное
число членов, отличных от нуля, или ряд C0.64), все члены
которого, по определению, отличны от нуля, состоит лигаь
из конечного числа членов, то начиная с некоторого номера
все члены исходного ряда C0.62) имеют один и тот же знак и,
следовательно, его сходимость равносильна абсолютной
сходимости.
Таким образом, если ряд C0.62) сходится, но не
абсолютно, то оба множества {г/+} и {и~} бесконечные.
ЛЕММА 3. Если ряд C0.62) сходится, но не абсолютно, то оба
ряда C0.63) и C0,64)расходятся.
Доказательство. Положим
^.= 1: ч^ ^п= t к1' C0.65)
k-1 k-1
Все слагаемые последних трех сумм 5^, s+ и s~
неотрицательны, поэтому последовательности этих сумм возрастают и,
следовательно, имеют конечные или бесконечные пределы.
Суммы s^ и 5^ можно представить в следуюпа;ем виде:
S, = S+ - S,-; C0.66)
fl, = s++s,-; C0.67)
n = m + k C0.68)
(m и й зависят от п для данного ряда), при этом условие
стремления п к бесконечности равносильно одновременному
стремлению к бесконечности k и т. Действительно, если бы при
п ^ оо номера т = т(п) (номера k = k(n)) не стремились бы к
бесконечности, то это означало бы, что в ряде C0.62) имеется
лип1ь конечное число неотрицательных (отрицательных)
членов, а в этом случае ряд C0.62) сходился бы абсолютно, что
противоречило бы условию леммы.
Обратное утверждение, что при й ^ оо и m ^ оо имеет
место я ^ оо^ очевидно в силу равенства C0.68).
По условию, ряд C0.62) не сходится абсолютно, а это
означает, что
lim Д^ = +оо. C0.69)
40
Поэтому, в силу равенства C0.67), по крайней мере один из
пределов
lim S+, lim s' C0.70)
также равен +оо. Но тогда из соотноп1ения C0.66), в котором
частичные суммы s^ стремятся к конечному пределу (ряд
C0.62) сходится), явствует, что и другой из указанных
пределов C0.70) также равен +оо. Это и означает, что ряды C0.63)
и C0.64) расходятся. П
ТЕОРЕМА 17 (теорема Римана). Если ряд C0.62) сходится,
но не абсолютно, то, каково бы ни было число А, можно
так переставить члены этого ряда, что сумма
получившегося ряда будет равна А.
Доказательство. Снова рассмотрим ряды C0.63) и
C0.64). Согласно лемме,
£ и+=+оо; C0.71)
т = \
оо
Е Щ = +°°- C0.72)
k= 1
Пусть задано число А. Выберем из ряда C0.71) подряд
столько членов, чтобы их сумма превып1ала А и чтобы меньп1ее число
таких членов не обладало этим свойством, т. е. их сумма была не
больп1еА.
Точнее, выберем число п^ так, чтобы
и^ + и^ + ... + г/+ > А, C0.73)
причем в том случае, когда номер п^ = 1 не удовлетворяет
этому условию, выбор п-^ произведем егце таким образом, чтобы
при этом выполнялось также и неравенство
z/j^ + z/J + ... + z/+ _1<А. C0.74)
Сугцествование номеров п-^, для которых выполняется условие
C0.73), следует из условия C0.71); для того чтобы при этом
выполнялось и условие C0.74), надо взять наименыаий из
этих номеров п^.
Выберем теперь из ряда C0.72) подряд столько членов,
чтобы, вычтя их сумму из суммы уже набранных из ряда C0.71)
членов, получить значение, меныаее А, и чтобы меныаее число
членов ряда C0.72) уже не обладало этим свойством.
Tl
Таким образом, выберем из ряда C0.72) п^ первых членов
так, чтобы
г/++... + г/+^-г/1-...-г/-^<А,
причем в том случае, когда номер ^2 = 1 не удовлетворяет
этому условию, выберем п^ таким образом, чтобы при этом
выполнялось егце и неравенство
ul + ... + г/+^ _ 1 - г/i - ... - г/-^ _ 1 > А.
Сугцествование такого номера ^2 доказывается исходя из
C0.72), аналогично сугцествованию номера п^.
Снова выберем подряд из ряда C0.71) члены до некоторого
номера ^3 так, чтобы выполнялось неравенство
ul + ... + и+^ -щ- ... - и-^ + г/+^ + 1 + ... + и^^>А
и (при п^> п^-\- 1) неравенство
и^ + ... + К^ -щ- ... - и-^ + г/+^ + 1 + ... + г/+^ _ 1 < А.
Продолжая этот процесс далее, получим ряд
ul + ... + и+^ -щ- ... - и-^ + г/+^ + 1 + ... + г/+з "
-г/,^ + 1-...-г/-^ + .... C0.75)
Для последовательности его частичных сумм
^п^у^п^ + п^у^п^ + п^у ••• ' ^я^ + я^ + i' ••• ' ^^ 1' 2, ... ,
в силу построения, выполняются неравенства
причем отклонение от числа А каждой из указанных
частичных сумм s^ + д не превыгаает ее последнего члена:
Здесь и^ является абсолютной величиной члена ряда C0.75)
с номером Tif^ _^ ^ и соответствуюпа;им верхним индексом « + »
или «-».
В силу сходимости исходного ряда C0.62), имеем lim и^ = О,
п —^ '-^
И так как при й ^ оо номер члена и^ в ряде C0.62) также
стремится к оо^ то
lim и^ = 0.
72
Поэтому из C0.76) следует, что
lim s^ , ^ =А. C0.77)
Если теперь взять любую частичную сумму s^ ряда C0.75),
п> п^ + n^j то, в силу конструкции этого ряда, всегда можно
найти такой номер k = k(n), что будет иметь место либо неравенство
^^^ + ^^ + 1 ^ ^^ ^ ^^^ + 1 + ^^ + 2'
либо неравенство
^^^ + ^^ + 1 ^ ^^ ^ ^^^ + 1 + ^^ + 2'
поэтому из C0.77) следует, что и
lim s^=A.n
УПРАЖНЕНИЕ. Доказать, что если ряд C0.62) сходится, но не
абсолютно, то можно так переставить его члены, что полученный ряд будет
расходиться. В частности, можно сделать так, чтобы его сумма была
равна +00, -оо, а также и так, чтобы последовательность его частичных
сумм не имела ни конечного, ни бесконечного предела.
30.13. Преобразование Абеля.
Признаки сходимости Дирихле и Абеля
В этом пункте будут доказаны достаточные признаки
сходимости числовых рядов, пригодные и для рядов с
комплексными членами.
Предварительно рассмотрим одно преобразование сумм вида
S = а^Ъ^ + ajb^ + ... + aj)^, C0.78)
где а., Ь., / = 1, 2, ... , я, — комплексные числа. Положим
El = bi, B^ = b^ + b^, ... ,B^ = b^ + b^+ ... + b^;
тогда
и
S = a,B, + a^iB^-B^) + ... + а„(Б„ -5„_i).
Раскрыв скобки и группируя по-новому члены, получим
равенство
S = (a^- а^)В^ + (а^ - а^)В^ + ... + (а^_ ^ - aJB^_ ^ + а^В^.
Таким образом, окончательно имеем
t «А = "I («« - »i + i)Bi + »пВп- C0.79)
i = 1 i = 1
43
Преобразование сумм вида C0.78) называется
преобразованием Абеля; оно является в известном смысле аналогом
интегрирования по частям. Эта аналогия особенно бросается в глаза,
если формулу C0.79) записать в виде
п-\
Докажем с помопа;ью преобразования Абеля лемму.
Л Е М М А 4 (неравенство Абеля). Если
или
то
а.> а.^^, i=l,2, ... ,п- 1,
а. < а. + 1, i=l,2, ... ,п- 1\
|Ь1 + ... + Ь.|<Б, Ь.е С, /=1, 2, .
^ afi] < В(\а,\ + 2|aJ).
i = 1 I
, п.
C0.80)
C0.81)
C0.82)
C0.83)
Доказательство. Согласно условиям C0.80) или C0.81),
все разности а^ - а^.,. ^ в формуле C0.79) одного знака, поэтому,
в силу этой формулы и условия C0.82), имеем
1 afiil < X !«'
i,_il|Sj + |aJ|Bj<S
i = 1
+ \a„
: B(|ai - aj + |aj) < B{\a^\ + 2|aJ). П
Важно обратить внимание на то, что в неравенстве Абеля
оценка рассматриваемой суммы дается через первый и
последний ее члены и не зависит от числа слагаемых в этой сумме.
ТЕОРЕМА 18 (признак Дирихле). Пусть дан ряд
оо
п=\
C0.84)
такой, что последовательность {а^} монотонно стремится
к нулю, а последовательность частичных сумм {В^ ряда
оо
£ Ь„, Ь„еС, п = 1,2, ... ,
ограничена; тогда ряд C0.84) сходится.
* Из этих неравенств следует, что числа а^, i = 1, 2, ... , п,
действительны.
44
Доказательство. В силу ограниченности
последовательности {В^}, сугцествует такое число Б > О, что \В^\ < Б для всех
я = 1, 2, ... . Отсюда следует, что для любого я = 2, 3, ... и
любого целого р > О
п+ р
\в
п + р
B„_il<|B„ + J + |5„_i|<2B. C0.85)
Пусть задано 8 > 0. Из условия lim а„ = О следует сугцест-
вование такого номера п^, что для всех п> п^ выполняется
неравенство
C0.86)
\aj <
6В'
п+ р
Теперь, применив неравенство Абеля C0.83) к сумме ^ а-Ь-,
i = 1
где я > я^, и приняв во внимание неравенства C0.85) и C0.86),
получим
£''a,bJ<2B(|aJ + 2|a„+g)<8,
i ^ п I
отсюда, согласно критерию Konin, и следует, что ряд C0.84)
сходится. П
В качестве примера рассмотрим ряд
sm па
C0.87)
Прежде всего, если а ^ 2пт, т = О, ±1, ±2, ... , то
^ sin ka= Y,
ос
2 sin -sin ka
2K.
sm-
n г
COS \ k - ^ \a - cos I k +
m
COS -a - cos \n + - \a
2sin-
О • ОС
2sin-
. Я + 1 . n
sm —-—a sm -a
2 2_
. a
sm-
И, следовательно.
£^ sin йа
<r
1
. a
Если же a = 2пт, m = О, ±1, ±2, ... , то все члены сумм
п
у sin ka равны нулю, поэтому эти суммы при любом п равны
k- 1
нулю и, следовательно, ограничены. Таким образом, при всех а
п
суммы у sin ka ограничены.
45
с другой стороны, последовательность \ - 1 монотонно
убывает и стремится к нулю, поэтому, по признаку Дирихле, ряд
C0.87) сходится при любом а.
Аналогично ряду C0.87) исследуется ряд
f ^21Л:^, C0.88)
Так как при а ^ 2пт, т = О, ±1, ±2, ... , справедливо
равенство
п 1 " г/
у со8Йа= у 2sin^cosfta =
/г 1 2sin -^ ^
= -^^[-nf/. + i>-sinf/.-i>] =
2 sm ^
sm I я + - la - sm - sm — cos —-—a
2 sm - sm -
2 2
TO для указанных a выполняется неравенство
1
C0.89)
^ cos ka\
<
. a
И, следовательно, no принципу Дирихле, ряд C0.88) сходится
при всех а ^ 2%т, т = О, ±1, ±2, ... .
Если же а = 2пт, т = О, ±1, ±2, ... , то ряд C0.88) в
отличие от ряда C0.87) расходится, так как он преврагцается в
гармонический ряд.
Заметим, что признак Лейбница (см. п. 30.9) следует из
признака Дирихле. Действительно, если в ряде
оо
Е (-1)Х. C0.90)
П = 1
где а^ > а^ + ^ > О, положить Ь^ = (~1)^? то, очевидно, суммы
Ь^ + ... + Ь^, я = 1, 2, ... , равны нулю или единице и поэтому
ограничены и, значит, по признаку Дирихле, ряд C0.90) сходится.
Из неравенства Абеля C0.83) можно получить егце один
признак сходимости ряда.
ТЕОРЕМА 19 (признак Абеля), ^сл г/ последовательность {а J
оо
монотонна и ограничена, а ряд ^ Ь^, Ь^е С, я = 1, 2, ... , схо-
п = 1
дится, то ряд C0.84) также сходится.
16
< ^ По-
SM
Доказательство. В силу ограниченности
последовательности {а^} сугцествует такое М > О, что для всех п = 1, 2, ...
выполняется неравенство \aj < М,
оо
Пусть теперь задано 8 > 0. Из сходимости ряда ^ Ь^ следу-
п = 1
ет сугцествование такого номера п^, что для всех номеров п> п^
\п + р I
И всех целых р > Q выполняется неравенство ^ Ъл
\i = п I
этому для всех номеров п > п^ и всех целых р > О, согласно
лемме 4, справедливо неравенство
В силу критерия Konin сходимости рядов, это означает, что
ряд C0.84) сходится. П
Отметим, что теорема 19 может быть получена и из
теоремы 18. Действительно, если выполнены условия теоремы 19,
то, в силу монотонности и ограниченности
последовательности {а^}, сугцествует конечный предел а = lim а^ и, следова-
п —^ '^^
тельно, последовательность с^ = а^- а, п= 1, 2, ... , монотонно
стремится к нулю. Последовательность же частичных сумм
оо
ряда Y, ^п ограничена, так как этот ряд, по условию, сходит-
п = 1
оо
ся. Поэтому, согласно теореме 18, ряд ^ cj)^ сходится. Но
п = 1
оо оо
cj)^ = aj)^ - ab^ и ряд ^ аЬ^ ^ ^ Т, ^п также сходится. Сле-
п = 1 п = 1
довательно, как сумма двух сходягцихся рядов сходится и ряд
оо оо оо
п = \ п = \ п = \
Пример. Исследуем сходимость ряда
sm па cos -
1. ^ТьТТГ^- C0.91)
п-2
QQ СП "ХЛ Т1 fl
Заметим, что ряд У —-— сходится согласно признаку
„%2 In In Я
Дирихле: последовательность —-— монотонно стремится к
тшп
оо
нулю, а последовательность частичных сумм ряда ^ sin па
п = 2
ограничена (см. предыдугций пример). Последовательность
же cos -, я = 2, 3, ... , монотонна, поэтому, по признаку
Абеля, ряд C0.91) сходится при всех а.
47
30.14*. Асимптотическое поведение
остатков сходящихся рядов
и частичных сумм расходящихся рядов
Подобно несобственным интегралам, для рядов бывает нужно
ответить не только на вопрос об их сходимости, но в случае
сходимости ряда оценить ее скорость, а в случае расходимости
выяснить характер поведения его частичных сумм при
возрастании их номера.
оо
в случае рядов вида ^ fin), где / — неотрицательная убы-
п = 1
ваюгцая функция, на подобные вопросы иногда удается
получить ответы с помогцью метода, примененного при
доказательстве интегрального признака сходимости рядов (см. п. 30.7).
оо
Действительно, если ряд ^ f(n) сходится, следовательно, схо-
п = 1
оо
дится и интеграл | f(x) dx, то, обозначив, как обычно, через г^
1
остаток рассматриваемого ряда, получим неравенство
оо оо ^ +00
Гп= 1 f(k) < i: I fix) dx = J /(X) dx. C0.92)
k ^ n + 1 k = n+\^_-^ n
Это И есть искомая оценка остатка ряда, показываюпа;ая, что
при я ^ оо этот остаток убывает не медленнее, чем интеграл
+ 00
I f{x) dx.
п
Аналогично получается и оценка снизу для остатка ряда:
оо оо ^ + 1 °°
Гп= L Я^)^ L I f(^)d^= \ f(x)dx. C0.93)
k = n + l k = n + l f^ ^+1
Если f(x) — неотрицательная убываюпа;ая функция при х > 1,
то можно получить полезные оценки для частичных сумм ря-
оо
да Y, fin), не зависяпа;ие от того, сходится этот ряд или нет
п = 1
(следовательно, и не зависягцие от того, сходится или расхо-
+ 00
дится интеграл | f(x) dx).
1
Заметив, что
О < f(k) - ] f(x) dx < f(k) - f(k + 1),
k
и просуммировав эти неравенства по й от 1 до п, получим
Е /(^) - Т fix) dx < fil) - fin + 1) < /A).
A- 1 1
48
Из приведенных неравенств следует, что последовательность
t Я^)- fMdx, я=1,2, ...,
монотонно возрастает и ограничена сверху, поэтому
стремится к конечному пределу. Иначе говоря, сугцествует такая
постоянная с, что
lim Г У fik)-''] fix)dx] = c. C0.94)
Это равенство можно переписать в виде
1; fik) = ''\ fix)dx + c + E^, я=1,2, ..., C0.95)
оо
где lim 8^ = 0. Оно показывает, что если ряд ^ f(n) рас-
П
ХОДИТСЯ, то его частичные суммы У f{k) с точностью до
k = 1
бесконечно малой последовательности растут так же, как
п+1
I /(х) dx + с, где с — некоторая постоянная. Отсюда следует,
1
п п + 1
что частичные суммы У f(k) и интеграл [ f{x) dx асимпто-
тически равны при п -^ оо^ т. е. их отноп1ение стремится к
единице при я ^ оо:
t Я^)~"| Kx)dx, П^оо,
k = l \
п 1
Примеры. 1. Рассмотрим гармонический ряд ^ -, ко-
п ^ 1 ^
-1 оо
торый, полагая f(x) = -, х> 1, запипхем в виде ^ f(n).
X
п = 1
Функция f{x) = -, X > 1, удовлетворяет условиям
X
теоремы 10, и, поскольку f — = In (я + 1), из доказанного
^ X
следует, что супа;ествует такая постоянная С, что
1 + 1 + i + ... + 1 = In (я + 1) + С + 8^, я = 1, 2, ... ,
Z о Т1
где lim 8„ = 0. Эта постоянная С называется постоянной Эйле-
ра. Замечая, что In (я + 1) - In я = In f 1 + - ] ^ О при п ^ ^,
49
в полученной формуле можно заменить In (п + 1) на In п (при
этом, конечно, изменится и последовательность 8^, но она
останется бесконечно малой последовательностью):
1 + i + i + ... + i = In я + С + 8^, я = 1, 2, ... . C0.96)
Любопытно заметить, что до сих пор не удается выяснить
природу эйлеровой постоянной в том смысле, что неизвестно
даже, является ли она рациональным числом или нет.
Из формулы C0.96), очевидно, следует асимптотическое
равенство
1 + 1 + ... + 1~1пя, п^ оо,
2 п
оо -1
2. Рассмотрим ряд ^ —, О < а < 1.
п = 1 ^
Возьмем функцию f(x) = —, х > 1; тогда
1 х" 1-«
Из формул C0.94) и C0.95) для данного случая следует, что
сугцествует такая постоянная с^, что
2^^ ДОС 1 - (X ад'
где lim 8„ = 0. Отсюда получаем асимптотическое равенство
П^ оо '1^
1 1 я1 -ОС
1 + _L + ... + _L~ 1 .
2^ до^ 1 - а
оо -1
3. Рассмотрим сходягцийся ряд У —, а > 1.
Взяв снова в качестве функции / функцию — и замечая, что
х^
+ 00 т -,
г dx_ ^
J у-а
х^ (а-1)я^-1'
в силу формул C0.92) и C0.93), получаем
< £^< 1
(а-1)(я +1)^-1 к^пп"" (а-1)я^-1'
откуда
оо -1 1
г = у — ~
4. Рассмотрим ряд
£ h- C0.97)
50"
Мы уже знаем, что этот ряд сходится и что его предел
равен числу е (см. пример 6 в п. 4.9):
оо -1
е= Y к C0.98)
Оценим остаток г^ этого ряда:
^ ^^д(^ + 1)' (я+1)!1 я + 2 (я + 2)(я + 3) J
<^—Г1 + ^-+ 1 +...1^
(я + 1)!1 я + 2 (я+ 2J J
= —3^ ^ = "^^^ < —. C0.99)
я + 2
Следовательно, если s^ — частичная сумма ряда C0.98), то
^ = ^п^^п C0.100)
и, в силу неравенства C0.99), справедлива следуюгцая оценка
погреп1ности при замене е на s^\
^ п\п
Таким образом, число е можно приближенно вычислять
в виде суммы
1 + 1 + 1 + ... + 1,
1! 2! я!'
причем полученная оценка указывает точность получаюгцих-
ся приближений.
def
Замечание. Если положить 9^ = r^nln, то из C0.99)
получим О < 9^ < 1 и, следовательно, в силу формулы C0.100),
^^1+Г! + 1! + - + ^ + ^' 0<^«<1' '^^ 1,2, ....C0.101)
Отсюда легко следует, что число е является иррациональным.
Действительно, если бы е было рациональным числом: е = —,
meN, neN, то, в силу C0.101), было бы справедливо равенство
^ = 1 + 1+ 1 + ... + ! + -^^,
п 1! 2! п1 п\п'
откуда
«!"г-A + 1 + 1 + ... + 1>!я = е„.
Но это равенство невозможно, так как слева стоит целое
число, а справа 9^, где О < 9^ < 1. П
Л
30.15. О суммируемости рядов
методом средних арифметических
Иногда представляет интерес изучение расходягцихся рядов,
т. е. рядов, частичные суммы которых не стремятся к
конечному пределу. Как было уже показано, подобные ряды дают
возможность получать асимптотические формулы (см. п. 30.14"^,
а также далее п. 33.10"^). Изучение расходягцихся рядов
целесообразно, в частности, в том случае, когда для них удается
определить надлежагцим способом понятие суммы. Различные
методы определения сумм рядов называются методами
суммирования рядов. Метод суммирования ряда называется
регулярным, если для сходягцегося ряда его сумма, определенная
по этому методу, совпадает с обычной его суммой (в этом
случае говорят: регулярный метод суммирует сходягцийся ряд к
его сумме).
Рассмотрим метод суммирования ряда средними
арифметическими его частичных сумм. Пусть дан ряд
и^ + U2+ --- + и^+ ...
И пусть
s^ = г/i + г/2 + ... + и^, п= 1, 2, ..., —
последовательность его частичных сумм. Обозначим через а^
среднее арифметическое первых п членов этой
последовательности:
Si + So + ... + S„
^ п
Определение 5. Ряд называется суммируемым методом
средних арифметических к числу а, если последовательность {а^}
средних арифметических его частичных сумм сходится к а:
lim а„ = а.
Метод суммирования средними арифметическими
является регулярным методом суммирования, так как из того, что
некоторая последовательность {х^ имеет предел, следует, что
последовательность, составленная из средних
арифметических первых ее п членов:
я = 1, 2, ... ,
п
имеет тот же предел (см. пример 5 в п. 4.1).
~52
с другой стороны, сугцествуют расходягциеся ряды, которые
суммируются методом средних арифметических. Таким
примером является ряд
1-1 + 1-1 + .... C0.102)
В этом случае s^^ = ^. 4k-i= 1' ^2k = \^ ^2k - i = 2Г^'
й = 1, 2, ... . Следовательно, lim а = -, т. е. ряд C0.102) сум-
П^ оо ^1^ Z
мируется методом средних арифметических.
С применением суммирования рядов методом средних
арифметических мы встретимся в п. 55.6.
Задача 2 (признак Дюбуа—Реймона сходимости ряда).
оо
Доказать, что ряд У а^Ь^ (а^ и Ь^ — комплексные числа) сходится, ес-
п = 1
оо оо
ли ряд ^ Ь^ СХОДИТСЯ, а ряд ^ (а^ ~ ^д + i) абсолютно сходится.
п ^ 1 п = \
Задача 3 (признак Дедекинда сходимости ряда). Дока-
оо
зать, что ряд У а^Ь^ (а^ и Ь^ — комплексные числа) сходится, если ряд
п = \
оо
^ (а^ ~ ^д + i) абсолютно сходится, lim^ а^ = О и частичные суммы ряда
д = 1 "^
оо
у Ъ^ ограничены.
§31
Бесконечные произведения
31.1. Основные определения.
Простейшие свойства бесконечных произведений
Аналитическое выражение, имеюш;ее вид произведения
бесконечного множества сомножителей, называется
бесконечным произведением. Дадим более детальное и строгое
определение этого понятия.
Определение 1. ilopa последовательностей комплексных
чисел {а^ и {р^}, где
Рп = ЧЧ--^п^ я = 1,2, ..., C1.1)
называется бесконечным произведением и обозначается
оо
П «п- C1.2)
п- 1
Члены последовательности {а^ называются
сомножителями бесконечного произведения C1.2), а члены
последовательности {р^ — его частичными произведениями
{порядка п).
Если последовательность частичных произведений {р^
имеет конечный или определенного знака бесконечный пределу:
р= lim р^= lim Па., C1.3)
то ЭТОТ предел называют значением бесконечного
произведения C1.2) и пигаут
оо
р = а^а^...а^...= Ц а^.
п = 1
Таким образом, аналогично случаю ряда, здесь одним и
тем же символом обозначают как само бесконечное
произведение, так и его значение, если оно сугцествует.
Если хотя бы один из сомножителей бесконечного
произведения равен нулю, то и значение этого бесконечного произве-
оо
дения равно нулю: ]^ а^ = 0. Поэтому естественно предпо-
п=1
лагать, что все сомножители рассматриваемых бесконечных
произведений отличны от нуля. Это всегда и будем делать, не
оговаривая специально, в дальнейпхем.
Для таких бесконечных произведений можно построить
теорию, аналогичную теории сходяпа;ихся рядов. Этим
оправдывается следуюпа;ее определение.
Определение 2. Бесконечное произведение называется
сходящимся, если оно имеет конечное значение, отличное от
нуля.
В противном случае бесконечное произведение называется
расходящимся. Таким образом, бесконечное произведение
называется расходяпа;имся, если предел последовательности его
частичных произведений либо равен нулю, либо +оо^ либо не
супа;ествует. В частности, если
оо
оо
то произведение Y\ ^п ^^^^^^^^"^^^расходящимся к нулю.
п- 1
Примеры. 1. Бесконечное произведение 1-1- ... -1 ...
сходится, и его значение равно 1.
54
2. Бесконечное произведение (-1)(-1) ... (-1) ...
расходится, так как для нетор^ = (-1)^, а последовательность {(-1)^} не
имеет предела.
ОО X -j^ \
3. Бесконечное произведение Г[ 1 + - расходится, так
какр„ = я + 1 и, следовательно, lim р„ = +оо.
''^ д _^ ОО ''^
ОО X -j^ \
4. Бесконечное произведение Г[ 1 - - расходится к ну-
лю, так как здесьр^ = 1/п.
ОО X -j^ X
5. Для бесконечного произведения Y[ -'^ ~ " имеем
= LlI llA (я- 1)(я + 1) _ 1я+ 1
22 32 *** я2 2 Я *
1 °° /^ 1
Поэтому lim р^ = -,т. е. бесконечное произведение П М^ ~ ~2
сходится и его значение равно 1/2.
6. Формулу Валлиса (см. пример 1 в п. 26.2)
^=1^^ 1 Г Bя)!!
lim
2 д^оо 2я + 11B^- 1)!!.
можно рассматривать как разложение числа 7г/2 в
бесконечное произведение:
тс _ 2 2 4 4 2п 2п
2 1 3 3 5 *** 2я- 12я+ 1 *** *
7. Покажем, что бесконечное произведение
1
оо П
п ^
д-11 + i
сходится, и найдем его значение. Имеем
_ g 2 _ е - _ ^ с^с^п
^^ я+1 я + 1 я + 1
где С — постоянная Эйлера (см. п. 30.14^), а {е^} — бесконечно
малая последовательность, поэтому
П
Если в бесконечном произведении C1.2) отбросить первые п
сомножителей, то получивпхееся бесконечное произведение
оо
П «я + ^ C1-4)
называется п-м остаточным произведением.
Отметим простейп1ие свойства бесконечных произведений.
1^. Если бесконечное произведение сходится, то и все его
остаточные произведения сходятся.
Если какое-либо остаточное произведение сходится, то
и само бесконечное произведение сходится.
Эти утверждения легко доказываются аналогично соответ-
ствуюгцей теореме об остатках ряда (см. п. 30.2).
Таким образом, для бесконечного произведения как
отбрасывание конечного множества первых сомножителей, так и
присоединение конечного множества отличных от нуля
первых сомножителей не влияют на его сходимость.
УПРАЖНЕНИЯ 1. Доказать, что как отбрасывание конечного
множества сомножителей, не обязательно первых, бесконечного произведения,
так и добавление конечного множества отличных от нуля сомножителей
не влияют на его сходимость.
2^. Если бесконечное произведение C1.2) сходится, то
последовательность его остаточных произведений
оо
<1п= и ^п + и C1.5)
имеет пределом единицу:
lim q=l. C1.6)
Доказательство. Если
П ^п=Р^ C1.7)
то
п + т
i 1 D
^^ C1.5) m^oo j,-U-i ^^^ А т^оо ЛК ^ C1.7) п
^-1 [] а^ ^-1 C1.1) "
k- 1
Так как
то
Л^оо^МзГт)^^^,
lim g„ = lim Р- = Р = 1,п
3^ (необходимое условие сходимости бесконечного
произведения). Если бесконечное произведение C1.2) сходится, то
последовательность его сомножителей стремится к единице:
lim а=1. C1.8)
5ё
Доказательство. В самом деле, а„ = _^^ п = 2,3, ..., по-
Рп-1
этому
lim а= lim -1^ = Р=1.и
Отметим, что выполнение условия C1.8), т. е. стремление
последовательности сомножителей бесконечного произведения
к единице, недостаточно для его сходимости. Это видно,
например, из рассмотренных выгае примеров 3 и 4, в которых у рас-
ходягцихся бесконечных произведений последовательности
сомножителей стремятся к единице.
31.2. Критерий Коши
сходимости бесконечных произведений
Установим необходимые и достаточные условия сходимости
бесконечных произведений.
ТЕОРЕМА 1 (критерий Коши). Дл^ того чтобы бесконечное
произведение {31.2) сходилось, необходимо и достаточно,
чтобы для любого 8 > О нашлось такое п^, что для всех п > п^
и всех т> О выполняется неравенство
^iL±£i-l|<£. C1.9)
Рп I
Доказательство. Необходимость. Пусть
бесконечное произведение C1.2) сходится, и, следовательно, не равно
оо
нулю: Да^ = \im^p^=p^ 0.
Поэтому супа;ествует такой номер п^, что для всех п> п^
выполняется неравенство \pj > Lffl > О, т. е. последовательность
\Рп +k\^ k = 1, 2, ... , ограничена снизу, а так как все
сомножители а^ ^ О, я = 1, 2, ... , то и вся последовательность {|р^|}
ограничена снизу положительной постоянной: сугцествует такое
число с > О, что
|pj>c, я = 1,2,.... C1.10)
Зададим произвольно 8 > 0. Из сходимости
последовательности {Pjj}, согласно критерию Konin для последовательности,
следует, что найдется такой номер п^, что для всех номеров
п> HqH всех m > О выполняется неравенство
\Рп + т-Рп\<^^^ C1.11)
J?
тогда
\Рп-
Рп
-1
J_l
^ C1.10) с
C1.11)
е,
т. е. выполнено условие C1.9).
Достаточность. Пусть выполнено условие C1.9). Тогда
для 8=1 сугцествует такой номер п^, что для всех m > О
выполняется неравенство
\Рп,
откуда
\Рп^ + т\
\Р п-^ + т
Рп,
-1 + 1
Рп,
Рп,
<
<1,
\Рп-^ + т
Рп,
- 1
Ря.1 + 1Ря.1<2|р^|,
и, следовательно, последовательность [р^} ограничена, т. е.
сугцествует такое с > О, что
|р„|<с, /г = 1, 2, ... . C1.12)
Зададим произвольно 8 > 0. В силу условия теоремы,
найдется такой номер п^, что для всех номеров п> n^vi всех m > О
будет выполняться неравенство
\Рп-
Рп
<
C1.13)
т. е.
\Рп + т Рп\ C1^13) с^Рп\ C27^2) ^*
Это означает, что числовая последовательность {р^}
удовлетворяет критерию Коп1и сходимости числовых
последовательностей и, следовательно, сходится.
Покажем, что ее пределу = lim р^ не равен нулю. Если бы
п —^ '-^
он был равен нулю, то, перейдя к пределу в неравенстве
C1.13) при т ^ ^^ (п фиксировано), мы получили бы
неравенство 1 ^ -, что противоречит произвольному выбору 8 > 0. П
с
31.3. Бесконечные произведения
с действительными сомножителями
До сих пор все доказанные для бесконечных произведений
теоремы были справедливы независимо от того, являлись ли
их сомножители комплексными или только действительными
58
числами. Перейдем теперь к изучению бесконечных
произведений, сомножители которых являются только
действительными числами. В этом случае из необходимого условия
сходимости C1.8) бесконечного произведения C1.2) следует, что
все его сомножители начиная с некоторого номера
положительны. Согласно же свойству 1^ п. 31.1, отбрасывание
конечного множества сомножителей не влияет на сходимость
бесконечного произведения, поэтому дополнительное
предположение о том, что все сомножители бесконечного произведения
положительны, не будет ограничивать обпа;ности изучения
сходимости бесконечных произведений с действительными
сомножителями.
Взаимно обратную связь между бесконечными
произведениями с положительными сомножителями и рядами
устанавливает следуюпа;ее утверждение.
ТЕОРЕМА 2. Для того чтобы бесконечное произведение
оо
П а^, a^>0, я = 1,2,..., C1.14)
п = \
сходилось, необходимо и достаточно, чтобы сходился ряд
оо
Е 1па„. C1.15)
Д = 1
Если при сходимости ряда C1.15) число s является его
суммой, а число р — значением бесконечного произведения
C1.14), то
р = е'. C1.16)
Доказательство. В самом деле, если s^ — частичная
сумма порядка п для ряда C1.15), ар^ — частичное произведение
того же порядка для бесконечного произведения C1.14), то
^п= t ^^^k = ^^ и ^k = Inp^, п=1,2, ... ,
следовательно, p^ = e ^. Перейдя здесь к пределу при я ^ оо^
получим формулу C1.16). П
При исследовании бесконечного произведения C1.2) часто
бывает удобным его сомножители а^ представлять в виде
«я=1 + ^я' п=1,2, ... .
В случае сходягцегося бесконечного произведения C1.2), в
силу его свойства 3^ (см. п. 31.1), последовательность {и^
является бесконечно малой.
~59
ТЕОРЕМА 3. Если все и^, п = 1, 2, ..., знакопостоянны (т. е.
все и^> Q или все и^ < 0), то, для того чтобы сходилось
бесконечное произведение
оо
ПA + и„), C1.17)
необходимо и достаточно, чтобы сходился ряд
£ и„. C1.18)
д = 1
Доказательство. Согласно необходимому условию
сходимости бесконечного произведения (см. свойство 3^ в п. 31.1) и
необходимому условию сходимости ряда (теорема 1 в п. 30.1),
из сходимости бесконечного произведения C1.17), так же, как
и из сходимости ряда C1.18), следует, что
lim u=Q. C1.19)
Поэтому будем предполагать это условие выполненным.
Сходимость бесконечного произведения C1.17), согласно
теореме 1, равносильна сходимости ряда
оо
Е ln(l + u„). C1.20)
Д = 1
В силу же C1.19), имеет место эквивалентность
In A + г/J ~ г/^, п^ оо,
и так как все и^ одного знака, то, согласно признаку
сравнения рядов (см. следствие теоремы 6 в п. 30.4), ряд C1.20)
сходится и расходится одновременно с рядом C1.18)). П
Отметим, что нами уже было непосредственно и очень
оо X -j^ \
просто показано, что бесконечное произведение П М^ ~^ ~
расходится (см. пример 3 в п. 31.1). Из этого утверждения, в
оо -1
силу теоремы 3, следует, что ряд ^ - расходится, — епа;е од-
га = i '^
но доказательство расходимости гармонического ряда.
В случае знакопеременных и^ имеет место следуюпа;ее
достаточное условие сходимости ряда C1.17).
ТЕОРЕМА 4. Если сходятся ряды
1
"„, Е ul, C1.21)
п = \
оо
то бесконечное произведение П ^-'^ "^ ^т) сходится.
п = \
'бО
Доказательство. Прежде всего из сходимости рядов C1.21)
следует выполнение условия C1.19). Тогда, согласно формуле
Тейлора,
In A + и J = и^- \ul + о(г/2), я ^ оо,
и, следовательно.
Из этого равенства, согласно признаку сравнения рядов,
явствует, что ряд
оо
£ u„-ln(l + u„) C1.22)
П = 1
сходится, так как, по условию, сходится ряд ^ и^. По усло-
п = 1
оо
ВИЮ, сходится и ряд Y, ^д' поэтому из сходимости ряда
п = 1
оо
C1.22) следует и сходимость ряда ^ In A + и^), что, в силу
п = 1
теоремы 2, означает сходимость бесконечного произведения
C1.17). П
Примеры. 1. Произведение
П fi + ^\ ^>о,
Л1 ^ ^"^ ^
сходится при X > 1 и расходится при х < 1. Согласно теореме 3,
оо -1
это следует из того, что ряд У — сходится при х > 1 и
расходах п""
дится при X < 1.
2. Имеет место равенство Эйлера
оо -I
ПA + д^) = ^^ , о<д<1.
оо оо
Произведения JI A + д^) и П ^-'^ ~ ^^^ ^) сходятся, так как
п ^ 1 п = \
оо оо
СХОДЯТСЯ соответственно ряды ^ д^ и ^ q^^~^ (см. теорему 3).
п ^ 1 п = \
Заметим епа;е, что в силу аналогичных соображений сходится и
оо
бесконечное произведение П ^-'^ ~ Ф^)^ следовательно, в силу
критерия Коп1и сходимости бесконечных произведений,
выполняется условие
lim ft (l-g2fe) = l. C1.23)
n —^ со , А ± ^
61
Теперь имеем
оо
П A + Q") = Ит П A + я'') = lim ГГ -
2w , ^ 2п -^ _ 2k
q.
2п
П A-^'') .
= lim i^iL±i = i .
fe = 1 fe = 1
оо
УПРАЖНЕНИЯ. 2. Доказать, что, для того чтобы ]^ а^ = О, а^ > О,
п= 1, 2, ... , необходимо и достаточно, чтобы
оо
£ 1па„ = -оо.
П = 1
оо оо
3. Доказать, чтоесли w^ < о, я = 1, 2, ... , и ^ w^ = -oo, то Y[ A + О ^ ^*
д = 1 д = 1
Д = 1 П = 1
П A + ".) = о.
4. Доказать, что если ряд У и^ сходится, а ряд У и^ расходится, то
^ п = 1 п = \
5. Построить пример сходящегося бесконечного произведения Y[ A + ^д)>
оо
у которого ряд ^ и^ расходится.
п-1
п = \
6. Построить пример сходящегося бесконечного произведения ГТ A + w^),
оо "^1
у которого оба ряда ^ w^ и ^ и^ расходятся.
п = \ п = \
31.4. Абсолютно сходящиеся
бесконечные произведения
Вернемся снова к изучению бесконечных произведений, вооб-
па;е говоря, с комплексными сомножителями. Подобно рядам
для бесконечных произведений вводится понятие абсолютной
сходимости.
Определение 3. Бесконечное произведение
оо
П A + "п) C1.24)
называется абсолютно сходящимся, если сходится
произведение
П A + к1)- C1.25)
'62
ТЕОРЕМА 5. Для того чтобы бесконечное произведение
(^1.24) абсолютно сходилось, необходимо и достаточно,
чтобы сходился знакопостоянный ряд
£ 1пA + К|), C1.26)
д = 1
а также необходимо и достаточно, чтобы абсолютно
сходился каждый из рядов
оо
1 ln(l + u„) C1.27)
П = \
и
t "«• C1-28)
п = \
Доказательство. Равносильность сходимости
бесконечного произведения C1.24) и ряда C1.26) сразу следует из
определения абсолютной сходимости бесконечного
произведения и из теоремы 3.
Из сходимости каждого из рядов C1.26), C1.27) и C1.28)
следует, что lim г/„ = О, а при выполнении этого условия име-
ет место эквивалентность
In A + |u„|) ~ |и„| ~ |1п A + и„)|, /г - оо.
Поэтому все ряды
оо оо оо
£ 1пA + |и„|), £ \иХ Е |ln(l + u„)|
одновременно сходятся или расходятся. Это и означает, что
сходимость ряда C1.26) равносильна абсолютной сходимости
каждого из рядов C1.27) и C1.28). П
Замечание. Если сходится бесконечное произведение
C1.24), то сходится и бесконечное произведение
оо -1
П ГТТГ' ^^1-2^^
причем
оо -I
Д 1 + и«
П^ + ^-г)
Это следует из того, что если р^, п = 1, 2, ... , является
частичным произведением порядка п бесконечного
произведения C1.24), то обратная величина 1/р^ является частичным
^3
произведением того же порядка бесконечного произведения
C1.29).
Бесконечные произведения C1.24) и C1.29) одновременно
сходятся абсолютно или нет, так как абсолютная сходимость
и того и другого произведения равносильна абсолютной
сходимости ряда C1.27).
ТЕОРЕМА 6. Из абсолютной сходимости бесконечного
произведения следует его сходимость.
Доказательство. Если бесконечное произведение C1.24)
абсолютно сходится, то, согласно теореме 5, сходится, и даже
абсолютно, ряд C1.27), что, согласно теореме 2, равносильно
сходимости бесконечного произведения C1.24). П
ТЕОРЕМА 7. Значение абсолютно сходящегося
произведения не зависит от порядка сомножителей.
Это сразу следует из формулы C1.16), ибо если
бесконечное произведение C1.24) абсолютно сходится, то
абсолютно сходится и ряд C1.15) (он совпадает с рядом C1.27)),
а следовательно, его сумма s не зависит от порядка
слагаемых. П
Если бесконечное произведение сходится, но не абсолютно,
то его значение зависит от порядка сомножителей. В этом
легко убедиться, сведя тем же методом, что и при доказательстве
теоремы 7, рассмотрение бесконечных произведений к соот-
ветствуюгцим рядам.
Пример. Выясним, при каких х сходится, абсолютно
сходится и расходится бесконечное произведение
При X > 1 это произведение абсолютно сходится, так как
°° 1 1
сходится ряд у —. При - < X < 1 оно сходится, но не абсо-
п = \ п"" 2
оо ( — \ЛП - 1 °° 1 /
лютно, ибо сходятся ряды Y, ——— и Y, —2^ (с^- теоре-
му 4).
Наконец, при О < х < - оно расходится к нулю, поскольку
°° ( — 1)П - 1 оо ^
ряд у -— сходится, а ряд У —г- расходится (см. уп-
ражнение 4).
31.5*. Дзета-функция Римана и простые числа
Функция
ОО 1
^(х)= £ \, C1.30)
п ^ 1 ^
определенная этой формулой для х > 1 (см. п. 30.3), как
известно, называется дзета-функцией Римана. Она играет боль-
П1ую роль во многих вопросах математического анализа.
Докажем, что для нее имеется следуюгцее разложение в
бесконечное произведение:
k 1-±
Pk
где произведение берется по всем простым числамр^, й = 1, 2, ... ,
взятым в порядке возрастания (впрочем, как это будет
показано ниже, это бесконечное произведение сходится
абсолютно и поэтому не зависит от порядка сомножителей).
Отметим, что во всех проводимых ниже рассуждениях не будет
предполагаться, что простых чисел бесконечно много (т. е.
все сказанное верно и в случае, если произведение C1.31)
было бы конечно, а не бесконечно). Бесконечность
множества простых чисел будет отдельно доказана в конце этого
раздела.
Так как
Vi-1 nfi--
ps V^ Pi
и ряд у — при х> 1 сходится (это следует из сходимости ряда
k Pk
C1.30) при X > 1), то, согласно теореме 5, абсолютно сходится
бесконечное произведение П ( ^ ~ ~ ]' следовательно, и
произведение C1.31) (см. замечание после теоремы 5).
По формуле для суммы геометрической прогрессии имеем
^ - ^ ^ , й = 1,2, ... , C1.32)
1_J_ r/^liP^)
Pk
где ряды в правых частях равенств, очевидно, абсолютно
сходятся. Зафиксируем некоторое натуральное число N и перем-
65
ножим равенства C1.32), отвечаюпа;ие всем простым числам
р^, P2J ... , не превып1аюпа;им N\ тогда
def 1 ^1 оо * -1
Рм(^)= П ^ (ЗГ32) I, i-x + I h' ^^^-^^^
Pk
где знак «звездочка» у суммы означает, что суммирование
распространяется только на те натуральные числа п> N + 1, в
разложении которых на простые множители участвуют
только простые числа р^ < Л/' и которые получаются при
умножении отобранных рядов C1.32). Этими двумя свойствами
заведомо обладают все натуральные числа 1, 2, ... , N.
Так как
N 1 оо * -1 оо -1
0<Р^(х)- 1^ \ = ^ J-< ^ J- C1.34)
и ряд C1.30) сходится, следовательно.
iV^ оо
то
оо -1
lim у — = О,
оо -1 N -I -1
Т. е. представление C1.31) доказано.
Заметим, что при х = 1 равенство C1.33) (в его правой
части стоит конечная сумма) остается верным, поэтому
Рь< N 1 - — п = 1 '^ n-N +1 "■ п = 1 '^
Pk
ОО -1 N -I
а так как гармонический ряд У - расходится, то lim У - =
= +00 и, следовательно,
П ^- = +оо. C1.35)
k 1-1-
Pk
Из этого равенства следует, что простых чисел бесконечно
много, так как если бы их было конечное множество, то
произведение Y[ 7- было бы конечным. Это доказательство бес-
k 1-1
Pk
конечности простых чисел было дано епа;е Эйлером.
66
Из равенства C1.35) следует больше, чем просто констатация
того, что множество простых чисел бесконечно. Этот факт можно
установить и более простым способом. В самом деле, допустим,
что простых чисел конечное множествор^,Р2? ••• уРп- Тогда число
п = Р1Р2 --- Рп^ 1 больше каждого из чиселр^,р2? ---•> Рп^^
следовательно, не равно никакому из них, а вместе с тем оно
простое: если бы оно было не простым, то оно делилось бы на одно
из чисел р^, p^j ... , p^j так как, по предположению, других
простых чисел нет. Но это не так: число п не делится ни на
одно из чисел р^, P2J ... , Pj^j ибо при делении его на любое из них
остаток от деления равен 1.
Запишем равенство C1.35) в виде
Из него, согласно теореме 3, следует, что ряд
оо -1
у - C1.36)
k^l Pk
расходится. Это утверждение сильнее утверждения о том, что
гармонический ряд расходится, так как здесь идет речь лишь
о некоторых его членах. Расходимость ряда C1.36) содержит
информацию о росте простых чисел р^ при й ^ оо.
§32
Функциональные последовательности и ряды
32.1. Сходимость функциональных
последовательностей и рядов
В настояпа;ем параграфе будут рассматриваться
последовательности и ряды, членами которых являются некоторые, вообпа;е
говоря, комплекснозначные функции, т.е. последовательности
/„(x)gC, /г = 1,2, ... , C2.1)
И соответственно ряды
оо
£ и„(х), и„(х) е С, п = 1, 2, ... . C2.2)
При каждом фиксированном значении аргумента х эти
последовательности и ряды, очевидно, представляют собой уже рас-
сматривавп1иеся числовые последовательности и ряды.
'67
Пусть X — некоторое множество элементов, в частности
множество точек прямой, плоскости, пространства или вообпа;е
элементов произвольной природы, и пусть C2.1) —
последовательность функций, которые определены на множестве X и
значениями которых являются, вообпа;е говоря, комплексные числа.
Определение 1. Последовательность C2.1) называется
ограниченной на множестве X, если существует такая
постоянная М > О, что для всех хеХ и всех п = 1, 2, ,,,
выполняются неравенства
\Ux)\ < М.
(Иногда в этом случае последовательность C2.1) называют tslk-
же равномерно ограниченной,)
Определение 2. Последовательность C2.1) называется
убывающей (возрастающей) на множестве X, если для всех хеХ
и всех п = 1,2, ... выполняются неравенства
(соответственно если для всех хеХ и всех п = 1,2, ...
выполняются неравенства
Это определение, очевидно, предполагает, что функции
fj^x), п = 1, 2, ... , принимают действительные значения.
Определение3. Последовательность C2.1) называется
сходящейся в точке* XqgX, если числовая последовательность
{/^Xq)} сходится.
Последовательность C2.1) называется сходящейся на
множестве X, если она сходится в каждой точке множества X.
Если lim fji(x) = f(x), то говорят, что последовательность
C2.1) на множестве X сходится к функции f(x), xgX.
Аналогичные определения можно дать и для ряда C2.2).
Определение4. Ряд C2.2) называется сходящимся в точке
оо
XqgX, если сходится числовой ряд ^ uj^x^).
п = 1
Ряд C2.2) называется сходящимся на множестве X,
если он сходится в каждой точке этого множества.
Мы называем элементы множества X точками.
'68
Определение5. Ряд C2.2) называется абсолютно
сходящимся на множестве X, если на множестве X сходится ряд
оо
Е \Un(x)\.
Подобно случаю числовых рядов, сумма
k = 1
называется п-й частичной суммой ряда C1.2); предел
частичных сумм сходяш;егося на множестве X ряда C2.2)
называется его суммой s{x):
six) = lim sJx).
При ЭТОМ пишут
оо
s(x)= ^ ц„(х)
п = 1
оо
и говорят, что функция s(x) раскладывается в ряд ^ и^(х).
п = 1
Ряд
оо
Е Ч(^) C2.3)
^ = Д + 1
называется п-м остатком ряда C2.2). Остаток ряда сходится
на X тогда и только тогда, когда на X сходится сам ряд C2.2).
Если в этом случае сумму остатка ряда обозначить через rj^x), то
s(x) = s^(x) + r^(x).
Как и в случае числовых рядов, согласно определению,
каждый функциональный ряд является парой
последовательностей {г/^(х)} и {s^(x)}, где г/^(х) — его члены, а s^(x) —
частичные суммы:
При этом для каждой функциональной
последовательности C2.1) супа;ествует ряд C2.2), для которого она является
последовательностью его частичных сумм. Члены этого ряда
определяются однозначно:
Ui(^) = /i(^:), и^(х) = fj,x) - 4_i(x), я = 2, 3, ... .
Поэтому всякую теорему, доказанную для
функциональных рядов, можно перефразировать в соответствуюпа;ую
теорему для функциональных последовательностей, и наоборот.
Это обстоятельство неоднократно будет использоваться в даль-
нейп1ем.
'69
Примеры. 1. Пусть дан ряд
где г — комплексное число. Исследуем его абсолютную сходи-
мость, т. е. сходимость ряда с п-ж членом и^= ^-^, Применив
признак Даламбера, получим
lim \}^JL±A =
п\
lim ^
д ^ ОО Д + 1
о
при любом комплексном г. Таким образом, ряд C2.4)
абсолютно, а значит, и просто сходится при любом комплексном 2,
или, как обычно говорят, на всей комплексной плоскости.
2. Изучим сходимость ряда
х2 + ^_ + ... + —^i_ + ... , C2.5)
где X — действительное число. Этот ряд сходится при всех х.
Действительно, если х ^ О, то имеем сумму геометрической
прогрессии со знаменателем q =
-, О < g < 1. В этом случае
сумма s(x) ряда C2.5) легко вычисляется:
^^ = 1 + Х2.
s(x)
1 + х2
Если же X = О, то все члены ряда C2.5) равны нулю, поэтому
он, очевидно, сходится и s@) = 0.
Таким образом,
0 для X = О,
1 + х^ для X ^ 0.
s(x) ■
|\
1
1
1
-1
2
\1
0
1
i/
/\
ж '
1
S@)|
1
X
График функции s(x) изображен на рис. 3.
Как видно, несмотря на то что все члены
ряда C2.5) — непрерывные функции и ряд
сходится во всех точках действительной оси,
его сумма является разрывной функцией.
Следовательно, в случае сходяпа;егося ряда
C2.2), члены которого непрерывные
действительные функции г/^(х), его сумма s(x), во-
обпа;е говоря, не является непрерывной, т. е.
Рис. 3
lim s(x) ^ s(Xq)
д = 1
70
или, что то же,
оо оо
lim ^ и(х) ^ ^ lim и^(х).
Таким образом, предел суммы бесконечного числа слагаемых
не обязательно равен сумме их пределов.
Рассмотренный ряд C2.5) показывает, как при
предельных процессах (суммирование геометрической прогрессии) из
простых непрерывных функций образуются функции
значительно более сложной природы — разрывные функции.
В дальнейгаем будут выяснены условия, при которых
можно гарантировать непрерывность суммы сходягцегося ряда
непрерывных функций.
32.2. Равномерная сходимость
функциональных последовательностей
Определение 6. Пусть заданы последовательность функций
C2.1) и функция /, определенные на множестве X, Будем
говорить, что указанная последовательность сходится к
функции f равномерно на множестве X, если для любого 8 > О
существует такой номер п^, что если п > п^, то для всех
хеХ выполняется неравенство
|/,(х) -/(х)| < 8. C2.6)
Последовательность C2.1) называется равномерно
сходящейся на множестве X, если существует функция /, к
которой она равномерно сходится на X,
Очевидно, что если последовательность C2.1) равномерно
сходится к функции / на множестве X, то она и просто
сходится к этой функции на X.
Если последовательность {/^} сходится на множестве X к
функции /, то символически будем записывать это следую-
па;им образом: /^ ^ /.
Если же эта последовательность равномерно сходится на X
к функции /, то будем писать /^ ^ /.
Заметим, что если последовательность C2.1) просто
сходится к функции / на множестве X, то это означает, что для
любого 8 > О и любого XG X сугцествует номер п^ = п^(г, х), завися-
71
Рис. 4
па;ий как от 8, так и от х, такой,
что для всех номеров п> п^ имеет
место неравенство C2.6).
Супа;ность равномерной
сходимости последовательности
функций состоит в том, что для
любого 8 > О можно выбрать такой
номер п^, зависягций только от
заданного 8ине зависягций от
выбора точки хе X, что при п> п^
неравенство C2.6) будет
выполняться всюду на множестве X,
т. е. «графики» функций /^ расположены в «8-полоске», окру-
жаюгцей график функции / (рис. 4).
Таким образом, в случае равномерной сходимости для
любого 8 > О при всех достаточно больгаих п (а именно при п > п^)
значения функций /^ приближают функцию / с norpenino-
стью, меньгаей 8, сразу на всем множестве X.
Запигаем для наглядности определения сходягцихся и
равномерно сходягцихся на множестве X последовательностей с
помогцью символов сугцествования и всеобгцности:
fn^ f^^ ^ ^> ОУ хеХ 3 п^У п> п^: \f^(x) - f(x)\ < 8,
f^^f^^ У Е> 03 п^У хеХУ пУ п^: |/^(х) - /(х)| < 8.
в этой записи одно определение от другого отличается
перестановкой символов У X G X л 3 п^.
Примеры. 1. Последовательность
« *л^« *л^ « • • • « *л^ « • • •
C2.7)
на отрезке [О, д], О < g < 1, сходится равномерно к функции,
тождественно равной нулю. Действительно, если О < х < д, то
0<х^<д^, я =1,2,.... C2.8)
Так как lim g^ = О, то для любого фиксированного 8 > О су-
гцествует такое п^, что д^ < 8 для всех п> п^. В силу
неравенства C2.8), О < х^ < 8 для всех п> п^и всех хе [О, д].
72
Рис. 5
2. Та же последовательность C2.7)
на полуинтервале [О, 1) также,
очевидно, сходится к функции,
тождественно равной нулю: lim х^ = О,
О < X < 1. Однако в этом случае
сходимость уже не является
равномерной (рис. 5). Действительно, если
последовательность х^, я = 1, 2, ... ,
равномерно сходилась бы на
полуинтервале [О, 1) к некоторой функции,
то она и просто сходилась бы к этой
функции. В силу этого,
последовательность C2.7) может равномерно на полуинтервале [О, 1)
сходиться только к функции, равной нулю во всех точках
этого полуинтервала.
Заметим, что lim х^ = \ при любом фиксированном нату-
X ^ 1
ральном п. Следовательно, каково бы ни было 8, О < 8 < 1, при
фиксированном п найдется такое х^, О < х^ < 1, что х^ > 8
(например, при х„ имеем х^ = г). Поэтому при
фиксированном 8, О < 8 < 1, не сугцествует такого номера п^, что для всех
я > ^0 и всех xg[0, 1) будет выполняться неравенство C2.6)
при fj,x) = х^, /(х) = О, О < X < 1. Более того, какое бы N ни
взять, для каждого п> N найдется такое хе [О, 1), что для
него выполняется неравенство, противоположное неравенству
C2.6), т. е. |/^(х) - /(х)| > 8 (в качестве конкретного х здесь
можно взять, например, указанное выпхе х^).
Итак, неравномерная сходимость последовательности C2.7)
на полуинтервале [О, 1) доказана. Заметим, что из приведенных
рассуждений следует, что последовательность C2.7) не сходится
равномерно и на любом интервале вида (г, 1), где О < г < 1, в
частности на интервале (О, 1).
Следует обратить внимание на то, что если
последовательность функций /^(х), определенных на множестве X, не
сходится равномерно на некотором его подмножестве Xq ^ X,
то она заведомо не сходится равномерно и на самом
множестве X: если условия определения 1 не выполняются для
всех точек xgXq, то они заведомо не выполняются и для всех
точек множества X. Вместе с тем если последовательность
функций равномерно сходится на некотором множестве, то
73
она и подавно равномерно сходится на каждом его
подмножестве.
Отсюда следует, например, что последовательность C2.7),
сходягцаяся на отрезке [О, 1] к функции
f(^) = \^ "Р^ 0<х<1,
'^ ^ 1 1 при X = 1,
не сходится на нем равномерно, так как она уже не сходится
равномерно на полуинтервале [О, 1).
УПРАЖНЕНИЕ 1. Доказать, что для последовательности fj^x) = х^, п =
= 1, 2, ... , не суш;ествует максимального множества равномерной
сходимости, т. е. такого множества Xq, что заданная на нем
последовательность сходится равномерно, а на каждом множестве X, на котором эта
последовательность сходится и которое содержит в себе множество Xq в
качестве собственного подмножества, она сходится неравномерно.
Перейдем к описанию критериев равномерной сходимости.
Для функции / и последовательности функций {/^}, заданных
на некотором множестве X, будем рассматривать
последовательность чисел (конечных или бесконечных)
sup |/^(х) -/(х)|, я = 1,2, ..., C2.9)
хеХ
принадлежагцих, вообгце говоря, расгаиренному множеству
действительных чисел R (см. п. 2.5), и ее предел (см. п. 3.2).
Если последовательность {/^} равномерно сходится на
множестве Х к функции /, то сугцествует такой номер п^, что для
всех п> tIq верхние грани C2.9) конечны. Действительно, если
/^ ^ /, то, согласно определению равномерной сходимости, для
любого 8 > о, например, для 8=1, сугцествует такой номер п^,
что для всех хеХ л всех п> п^ выполняется неравенство
|/„(х) - f(x)\ < 1,
следовательно, и неравенство
sup|4(x)-/(x)|<l.
хеХ
Поэтому при п> tIq все верхние грани C2.9) конечны.
ТЕОРЕМА А. Последовательность функций {fj,
определенных на множестве X, равномерно сходится на этом
множестве к функции f в том и только том случае, когда
lim sup |/^(х) -/(х)| = 0. C2.10)
74
СЛЕДСТВИЕ. Для того чтобы последовательность {/^}
равномерно сходилась на множестве X к функции /,
необходимо и достаточно, чтобы нашлась такая числовая
последовательность {а^}, что
lim а„ = 0, а >0, я=1,2, ..., C2.11)
и существовал такой номер п^, что для всех п> п^и всех
xgX выполняется неравенство
|4(х) -/(х)| < а„. C2.12)
Доказательство теоремы. Если выполнены условия
определения 6, то для каждого 8 > О сугцествует такой номер п^,
что для всех п> n^vi всех xg X выполняется неравенство
|4(х)-Дх)|<|.
Тогда для всех п> п^ будем иметь
sup |/^(х) - /(Х)| < I < 8,
а это, согласно определению предела числовой
последовательности, и означает выполнение условия C2.10).
Обратно: если условие C2.10) выполнено, то, по
определению конечного предела последовательности элементов из R, для
любого 8 > О сугцествует такой номер п^, что для всех п> п^
выполняется неравенство
sup \f^(x) - f(x)\ < 8.
хеХ
Отсюда следует, что для всех п > п^и всех хеХ справедливо
неравенство
|4(Х) - f(x)\ < 8,
Т. е. выполняются условия определения 6. П
В силу того что почти все члены последовательности верхних
граней C2.9) для равномерно сходягцихся последовательностей
функций конечны, критерий C2.10), по сугцеству, сводит
понятие равномерной сходимости функциональной
последовательности к понятию сходимости числовой последовательности.
Доказательство следствия. Если /„ ^ /, то, согласно
X
сказанному выгае, сугцествует такой номер п^, что для всех п> п^
все верхние грани C2.9) конечны. Поэтому за
последовательность {а^} можно взять
а^ = sup \f^(x) - f(x)\, п = п^+1,п^ + 2, ...
хеХ
75
(очевидно, а^ > 0), выбрав первые члены а^, ... , а^
произвольно. Тогда при п > tIq условие C2.12) очевидно
выполняется, а в силу C2.10), имеем lim а^ = 0.
Если же сугцествует числовая последовательность {а^}, удов-
летворяюгцая условиям C2.11) и C2.12), то, в силу C2.12), для
любого п> tIq выполняется неравенство
sup \f^(x) - fix)\ < а^.
хеХ
Перейдя в этом неравенстве к пределу при я ^ оо^ получим,
согласно C2.11), что
lim sup \f^(x) - fix)\ = 0.
Выполнение этого условия и означает (см. теорему 1)
равномерную сходимость последовательности {/^} к функции / на
множестве X. П
Примеры. 3. Докажем егце раз с помогцью условия
C2.10), что последовательность х^, п = 1, 2, ..., не сходится
равномерно на полуинтервале [О, 1). Предел указанной
последовательности на рассматриваемом полуинтервале равен
нулю, поэтому утверждение сразу следует из очевидного (при
любом фиксированном п = 1, 2, ...) равенства sup \х^ - 0| = 1,
0<х<1
ИЗ которого явствует, что условие C2.10) равномерной
сходимости в данном случае не выполняется.
4. Последовательность fJx) = -х^, я=1,2,...,0<х<1,
^ п
сходится равномерно на отрезке [О, 1] (рис. 6).
Действительно, так как
У {
1
0
\
п = 2
п = 3
п = 4.
п = Ъ
п=10
1 X
lim i
OHO<ix^<i,
п п
Рис. 6
о < X < 1, я = 1, 2, ... ,
высказанное утверждение следует из
следствия теоремы 1.
Сформулируем и докажем
критерий равномерной
сходимости последовательности,
обычно называемый
критерием Коп1и.
76
ТЕОРЕМА 2 (критерий Коши равномерной сходимости
последовательностей). Для того чтобы последовательность
функций /^, я = 1, 2, ... , определенных на некотором множестве X,
равномерно сходилась на этом множестве, необходимо и
достаточно, чтобы для любого 8 > О существовал такой номер
п^, что для всех номеров п > п^, всех целых р> О и всех точек
хе X выполнялось неравенство
\fn^pM-fn(^)\<^' C2.13)
Доказательство необходимости. Пусть
последовательность {fj равномерно сходится на множестве X. Тогда,
согласно определению равномерной сходимости, сугцествует
функция / такая, что для любого 8 > О сугцествует такой номер п^, что
для всех п> п^и всех хе X выполняется неравенство
|Дх)-/„(х)|<|.
Поэтому если п> п^ир ^ О, то для всех хеХ получим
Доказательство достаточности. Если выполнено
условие C2.13), то при любом фиксированном хеХ
последовательность
/„(X), п=1,2,..., C2.14)
является числовой последовательностью, удовлетворяюгцей
критерию Когаи (см. п. 3.7 и 19.3), и потому она сходится.
Обозначим предел последовательности C2.14) на множестве
X через f(x). Покажем, что последовательность {fj сходится
равномерно к функции / на множестве X. Действительно, в силу
условия C2.13), для любого 8 > О сугцествует такое п^, что для всех
п > п^, всех целых р > О и всех хе X справедливо неравенство
\fn+p(^)-U^)\<l- C2.15)
Заметив, что lim /„ , (х) = f(x), перейдем к пределу в неравенст-
п —^ со II- ^ Р
ве C2.15) прир -^ оо; тогда для всех п> n^vi всех xgX получим
\КХ) - /„(Х)| < I < 8,
а это и означает, что /„ ^ /. П
Г7
в заключение отметим следуюш;ие два свойства
равномерно сходяш;ихся последовательностей.
1^. Если последовательности {fj и {gJ равномерно на
множестве X сходятся соответственно к функциям fug, то
любая их линейная комбинация {Xf^ + \xgj, ХеС, \хеС, также
равномерно на этом множестве сходится к такой же
линейной комбинации предельных функций, т, е, KXf -\- [ig.
Доказательство. Если Я. = ц = О, то утверждение
очевидно. Пусть хотя бы одно из чисел X или [i отлично от нуля, т. е.
|Я.| + ||а| > 0. Зафиксируем произвольно 8 > 0. В силу условий
f^^fvig^^g, супа;ествует такой номер п^, что для всех п> п^
уС уС
и всех хе X выполняются неравенства
а поэтому и неравенство
|[Щх) + ц^„(х)] - [Щх) + ngix)]\ <
< |Я| |/„(х) - f(x)\ + \ii\ \g^(x) - g(x)\ < l^lp^ + IHp^ = e.
Согласно определению равномерной сходимости, это и
означает, что Xf^ + [ig^ ^ V + [ig- □
2^. Если последовательность {f^^} равномерно сходится на
множестве X к функции f, а функция g ограничена на этом
множестве, то последовательность {gfj также равномерно
сходится на X к функции gf.
Доказательство. Ограниченность функции g на
множестве означает, что сугцествует такое М > О, что для всех хеХ
выполняется неравенство |^(х)| < М, В силу же равномерной
сходимости на множестве X последовательности {/^} к
функции /, сугцествует такой номер п^, что для всех я > ^q и всех
XG X выполняется неравенство
|/„(х)-/(х)|<^,
а следовательно,и неравенство
\g(x)f^(x) - g(x)f(x)\ = \g(x)\ \f^(x) - f(x)\ < 8.
Это и означает, что gf„ ^ gf, П
^ X
78
32.3. Равномерно сходящиеся функциональные ряды
Для рядов можно также ввести понятие равномерной
сходимости.
Определение 7. Ряд
оо
Е и„(х), C2.16)
п = \
члены которого являются функциями, определенными на
множестве X, называется равномерно сходящимся на этом
множестве, если последовательность его частичных сумм
равномерно сходится на X,
Таким образом, равномерная сходимость ряда C2.16)
означает сугцествование такой функции s(x), что
s^{x)^s{x) C2.17)
(здесь, как всегда, sj^x) — частичная сумма порядка п ряда
C2.16), я = 1,2, ...).
Из C2.17) следует, что sj^x) -^ s{x) на X, поэтому s{x)
является суммой ряда C2.16).
Положим
оо
k = П+ 1
Тогда s(x) - s^(x) = r^(x) и условие C2.17) для сходягцегося на
множестве Е ряда можно переписать в эквивалентной форме:
г,(х)-0, C2.18)
откуда, в силу эквивалентности определения 6 равномерной
сходимости последовательности функций и условия C2.10), следует,
что, для того чтобы сходящийся на X ряд C2,16) равномерно
сходился на множестве X, необходимо и достаточно, чтобы
lim sup|r(x)| = 0. C2.19)
^^"^ хеХ
Таким образом, из равномерной сходимости ряда, в
частности, вытекает, что начиная с некоторого номера верхние
грани sup |г^(х)| конечны, а условие C2.19) сводит понятие равно-
хеХ
мерной сходимости ряда к стремлению к нулю числовой
последовательности этих верхних граней.
Важное свойство равномерно сходяпа;ихся рядов
составляет содержание следуюпа;ей теоремы.
79
ТЕОРЕМА 3 (необходимое условие равномерной сходимости
ряда). Если ряд C2.16) равномерно сходится на множестве
X, то последовательность его членов и^(х), п = 1, 2, ,,,
,равномерно стремится к нулю на множестве X, т, е.
и^(х) zt 0.
Коротко это свойство выражается следуюш;им образом:
у равномерно сходящегося ряда общий член равномерно
стремится к нулю.
Доказательство. Пусть ряд C2.16) равномерно
сходится на множестве X. Обозначим его частичные суммы, как
обычно, через s^(x), а его сумму — через s(x), xgX. Тогда для
любого 8 > О сугцествует такой номер п^, что для всех п > п^и
всех хе X выполняется неравенство
|s^(x)-s(x)|<|.
Поэтому для всех п> n^vi всех хе X справедливо также
неравенство
к+i(^)H к+1(^) - М^)Н
= |[S^ + i(x) - S(X)] + [S(X) - S^(X)]| < I + I = 8.
Это и означает равномерную (на множестве X) сходимость к
нулю и последовательности членов равномерно сходягцегося
на этом множестве ряда. П
Отметим, что, в силу условия C2.10), равномерное
стремление к нулю обгцего члена ряда C2.16) означает, что
lim sup |г/„(х)| = 0.
Замечание. Теорема 3 следует также из свойства 1^
равномерно сходягцихся последовательностей (см. п. 32.2).
Действительно, если ряд C2.16) равномерно сходится, т. е.
выполняется условие C2.17), а следовательно, и условие
s^_^{x) ^ s(x). Отсюда, в силу указанного свойства 1^, имеем
с помогцью теоремы 3 иногда удается установить, что рас-
оо
сматриваемый ряд не сходится равномерно. Так, ряд ^ х^,
п = 0
члены которого образуют геометрическую прогрессию, не
сходится равномерно на интервале (О, 1), поскольку, как это
было показано в п. 32.2 (см. пример 2), последовательность х^.
я = о, 1, 2, ... , членов этого ряда не сходится равномерно к ну-
оо
лю на этом интервале. Отсюда, кстати, следует, что ряд ^ 2^,
п = 0
где 2 — комплексное число, также не сходится равномерно в
единичном круге 1^1 < 1, так как он не сходится равномерно
уже на подмножестве (О, 1) этого круга.
Часто бывает полезным следуюпа;ий достаточный признак
равномерной сходимости.
ТЕОРЕМА 4 (признак Вейерштрасса). Пусть даны два ряда:
функциональный C2.16), членами которого являются
функции и^(х), определенные на множестве X, и числовой
оо
£ а„, а„>0, п = 1,2, .... C2.20)
П = 1
Если ряд C2.20) сходится и для любого xgX
выполняются неравенства
\и^(х)\<а^, я = 1,2, ..., C2.21)
то ряд C2.16) абсолютно и равномерно сходится на
множестве X.
Абсолютная сходимость ряда C2.16) на X в случае
сходимости ряда C2.20) сразу следует, по признаку сравнения, из
неравенства C2.21). Равномерная же сходимость этого ряда
легко следует из следствия теоремы 1 п. 32.2. Приведем и
непосредственное доказательство.
Пусть s(x) — сумма ряда C2.16) и s^(x) — его частичная
сумма. В силу сходимости ряда C2.20), для любого 8 > О су-
па;ествует такой номер п^, что для всех п > п^ выполняется не-
оо
равенство (см. 30.9) ^ а^ < г. Но тогда для всех п > п^и
т = п + 1
всех хе X для разности s(x) - s^(x) будем иметь
I оо I оо оо
Их) - s„(x)| = £ ujx)\< £ \ujx)\< £ а„<8,
\т ^ п + 1 I т ^ п + 1 т = п + \
Т. е. sj^x) ^ s(x). Это и означает, согласно определению 7, рав-
номерную сходимость ряда C2.16) на множестве X. П
Отметим, что ряд C2.20) называется рядом, мажорирую-
гцим ряд C2.16).
оо
в качестве примера возьмем снова ряд ^ 2^, члены которого
д = о
образуют геометрическую прогрессию. Рассмотрим его в круге
оо
радиуса г : 1^1 < г, где О < г < 1. Числовой ряд ^ г^ с неотрица-
п = 0
5i
тельными членами, образуюпа;ими бесконечно убываюпа;ую
геометрическую последовательность, сходится, а для членов
данного функционального ряда справедлива оценка \2^\ < г^, так как
1^1 < г, поэтому он, согласно признаку Вейергатрасса, равномерно
сходится во всяком круге 1^1 < г < 1. Вместе с тем, как это было
показано выгае, этот ряд не сходится равномерно в круге 1^1 < 1.
Признак Вейергатрасса дает только достаточные условия
равномерной сходимости ряда, которые не являются
необходимыми. Убедиться в этом для рядов, у которых с
возрастанием номеров членов чередуются их знаки, достаточно легко.
Действительно, сходягцийся ряд ^ ^^—— (как и всякий схо-
п = 1 ^
дягцийся числовой ряд) можно рассматривать как равномерно
сходягцийся, например, на всей числовой оси R ряд: его члены
и„ = -—— являются функциями, постоянными на R. Вместе с
^ п
оо
тем всякий числовой ряд ^ а^, удовлетворяюгций условию
п = 1
\uj < а^, т. е. в данном случае условию - < а^, я = 1, 2, ... , рас-
ходится по признаку сравнения. Таким образом, ряд ^ ^^——
п = 1 ^
оо
СХОДИТСЯ равномерно, а сходягцегося ряда ^ а^, удовлетво-
п = 1
ряюгцего условиям признака Вейергатрасса, не сугцествует.
Можно показать, что, более того, условия признака
Вейергатрасса не являются необходимыми для равномерной сходимости
даже рядов, все члены которых неотрицательны. Чтобы в этом
убедиться, приведем пример равномерно сходягцегося на отрезке
оо
[О, 1] ряда Y, ^д(^) с неотрицательными членами, для которого
п = 1
оо
также не сугцествует сходягцегося числового ряда ^ а^, удов-
га = i
летворяюгцего условию C2.21).
Определим член ряда uj^x) следую-
гцим образом: г/^(х) = О на отрезках
и функция uj^x) линейна и
непрерывна на каждом из отрезков
1С. 7 Ее график изображен на рисунке 7.
'82
Ряд Y, ^д(^) сходится равномерно на отрезке [О, 1]. Дей-
п = 1
оо
ствительно, если г^(х) = ^ Uk(^) — остаток этого ряда, п =
k = п + 1
= 1, 2, ... , ТО для любого xg[0, 1] среди его членов сугцествует
не более одного, для которого Uj^(x) ^0, k> п-\- 1, При этом,
очевидно, О < uJx) < - < -, поэтому О < г(х) < и, следова-
^ k п + 1 ^ п + 1
тельно, г(х) ^ О при я ^ оо^ т. е. рассматриваемый ряд рав-
[0, 1]
номерно сходится на отрезке [О, 1].
оо
Если Y, ^п — такой числовой ряд, что для всех xg[0, 1]
п = 1
выполняется неравенство О < и^(х) < а^, то
- = max и(х) < а„.
^ [0,1] ^ ^
оо -1
Гармонический ряд ^ - расходится, поэтому расходится и
п= 1 ^
оо
ряд Y, ^п- Таким образом, в рассмотренном случае числового
п = 1
ряда, удовлетворяюпа;его по отнопхению к функциональному
оо
ряду Y, ^д(^) условиям признака Вейерп1трасса, заведомо нет.
п = 1
Перейдем теперь к условиям равномерной сходимости
ряда, являюпа;имся одновременно необходимыми и
достаточными. Замечая, что
^п+р(х) - ^п- i(x) = "l" Щ(х), C2.22)
k = П
ИЗ теоремы 2 получаем следуюпа;ий критерий равномерной
сходимости.
ТЕОРЕМА 5 (критерий Коши равномерной сходимости рядов).
Для того чтобы ряд C2,16) равномерно сходился на
множестве X, необходимо и достаточно, чтобы для любого 8 > О
существовал такой номер п^, что для всех п > п^, всех
целых р> О и всех хе X выполняется неравенство
п + р I
k = п I
<8. C2.23)
Очевидно, что из критерия Konin равномерной сходимости
ряда епа;е раз (если в C2.23) положить р = 0) получается
теорема 3, т. е. необходимое условие равномерной сходимости
ряда C2.16).
оо
УПРАЖНЕНИЕ 2. Выяснить, может ли ряд вида ^ а^г" (а^ л z —
п = 0
комплексные числа), у которого бесконечно много коэффициентов
отличны от нуля, равномерно сходиться на всей комплексной плоскости.
'83
Примеры. 1. Рассмотрим снова ряд C2.4)
1 +2+ ^ + ... + ^ + ...
2 п\
и покажем, что, каково бы ни было число г > О, ряд C2.4)
сходится равномерно в круге 1^1 < г.
Как было показано, ряд C2.4) сходится при любом
комплексном 2, в частности при 2 = г, т. е. числовой ряд
1 + Г+ ^ + ... + ^ + ...
сходится. Возьмем его в качестве ряда сравнения C2.20) для
ряда C2.4), тогда при 1^1 < г имеем
< —. Поэтому
утверждение о равномерной сходимости ряда C2.4) непосредственно
следует из теоремы 4.
Покажем, что ряд C2.4) не сходится равномерно на всей
комплексной плоскости. Это следует из невыполнения в данном
случае необходимого условия равномерной сходимости ряда
(см. теорему 3). Действительно, при любом фиксированном п^
lim
щ\
= +00.
C2.24)
Поэтому если задано 8 > О, то, каково бы ни было ^q > О, в силу
C2.24), можно подобрать г^ так, чтобы
щ\
> 8, Т. е. — не стре-
мится равномерно к нулю на всей комплексной плоскости
2. Исследуем равномерную сходимость ряда
^ X sin пх
Прежде всего заметим, что
- оо < X < +00.
л/1 + Я2A + ях2)
<
л/1 +Я2A + ЯХ2)
C2.25)
C2.26)
Далее, 1 + пх^ > '2\x\4ri'\ поэтому
<
<
л/1 + я2A + ях2) 24п{\ + я2) 2яЗ/2-
C2.27)
* Мы воспользовались здесь неравенством 2аЬ < а^ + Ь^, которое
сразу получается из очевидного неравенства (а - Ь^ > 0.
84
Так как ряд У ——г сходится, то, согласно признаку Вейер-
штрасса, в силу неравенств C2.26) и C2.27), исходный ряд
C2.25) равномерно сходится на всей действительной оси.
3. Рассмотрим ряд
оо _п^'у^
^ е sin пх. C2.28)
п = 1
I —П X I I I —П X
Очевидно, \е sin пх\ < п\х\е . Найдем максимум
функции v^(x) = п\х\е~^ ^ при фиксированном п. Функция vj,x)
четная, поэтому достаточно рассмотреть лигаь случай х > О (поче-
5 2
му?). Производная v'J,x) = п{\ - 2п^х'^)е~^ ^ обрагцается в нуль
в точке Xq = — . Так как vj^x) > О для всех х, i^^(O) = О и
lim vJx) = О, то в точке Хг. функция vJx) имеет максимум
X ^ + оо 't^ "^ 'I-
(почему?).
Таким образом,
ОО -1
И так как ряд У ^-— сходится, что согласно признаку Вейер-
HiTpacca, ряд C2.28) равномерно сходится на всей
действительной оси.
Метод, примененный для установления равномерной
сходимости ряда C2.28) (исследование на экстремум модуля об-
гцего члена или его мажоранты методами дифференциального
исчисления), является достаточно обгцим и часто
применяется на практике. С помогцью этого метода можно было бы
исследовать и равномерную сходимость ряда C2.25), однако
примененный выпхе способ исследования данного ряда
значительно быстрее приводит к цели.
4. Рассмотрим ряд
Согласно признаку Лейбница (см. п. 31.5), он сходится при
любом действительном х и, как было отмечено там же,
остаток ряда оценивается первым своим членом
\г (х)\ < ^ < ^—.
Из этого следует, что rj^x) ^ О при -оо < х < +оо^ т. е. ряд
C2.29) равномерно сходится на всей действительной оси.
^5
Покажем, что этот ряд не сходится абсолютно во всех
точках. Действительно, выберем для данного числа х какое-либо
натуральное п^ так, чтобы х^ < п^. Тогда для всех п > п^ будет
выполняться неравенство x^• < п, следовательно, и неравенст-
11 оо ^
во —Z > -—. А так как ряд У - расходится, то, в силу при-
х^ + п 2п „^1 п
знака сравнения, ряд C2.29) не сходится абсолютно.
УПРАЖНЕНИЕ 3. Привести пример ряда, который абсолютно сходится
во всех точках некоторого множества, но не сходится на этом множестве
равномерно.
Указание. См. пример 2 из п. 36.1.
оо
5. Ряд Y, ^^' zeC, сходится в открытом круге К = {z :\2\< 1}
п = 0
И при любом г, о < г < 1, сходится равномерно в замкнутом
круге К^= {z : \z\ < г}. Это следует, например, из признака
равномерной сходимости Вейерп1трасса, так как при 1^1 < г имеем
оо
\z^\ = \z\^ < r^, а ряд Y, ^^ сходится. Было показано, что в
круга = о
ге К заданный ряд не сходится равномерно. Это следует и из
того, что
lim sup \z^\ = lim sup \z\^ = lim 1 = 1,
^ ^ °° 1^1 < 1 ^ ^ °° 1^1 < 1 ^ ^ °°
И, следовательно, в круге К не выполняется необходимое
условие равномерной сходимости ряда (см. теорему 3).
оо
При 1^1 < 1 члены ряда ^ z^ образуют убываюпа;ую геомет-
п = 0
оо -1
рическую прогрессию, поэтому V 2^ = .
п^О 1 - ^
Если Z = г (cos ф + / sin ф), то z^ = r^(cos яф + sin яф) и
f г«(со8Пф + г8тпф)=- ^ ^ ^ 1 - rcoscp + ir sin ф^
„^0 1 - г COS ф - jr sm ф 1 - 2г cos ф + г^
О < Г < 1, -оо < ф < +00.
Приравняв действительную и мнимую части этого
равенства, получим
У r-^cosяф= l-гcosф f ^.sinяф= '-^^^ -.
п^о l-2гcosф + г2 „^1 ^ l-2гcosф + г2
При фиксированном г, О < г < 1, эти ряды, как функции
переменной ф, равномерно сходятся на множестве всех
действительных чисел. Это следует, например, из признака равно-
86
мерной сходимости Вейерштрасса, так как |r^cos яф| < г^,
|r^sin щ\ <. г^ VL при о < г < 1 ряд Y, ^^ сходится.
д = о
оо -1
УПРАЖНЕНИЕ 4. Используя формулу У (-1)^2:" = —!—, \z\ < 1, най-
ти суммы рядов у (~1)" ^ ^r^sin яф и У (-1) V^cos яф, О < г < 1. Ис-
п = \ п = О
следовать их равномерную сходимость на числовой прямой.
Докажем теперь достаточный признак равномерной
сходимости, применимый в отличие от признака Вейергатрасса и к
не абсолютно сходягцимся рядам. Его формулировка
напоминает признак Дирихле для сходимости числовых рядов (см.
п. 30.13) и впервые встречается в работах Харди"^.
ТЕОРЕМА 6. Пусть дан ряд
оо
£ а„(х)Ь„(х), C2.30)
Д = 1
в котором функции aj^x) и bj^x), п = 1, 2, ... , определены на
множестве X и таковы, что:
1) последовательность {а^(х)} монотонна при каждом
х^Х и равномерно стремится к нулю на X;
2) последовательность частичных сумм BJ^x), п= 1,2, ... ,
оо
ряда Y, ^д(^) ограничена на множестве X.
п = 1
Тогда ряд C2.30)равномерно сходится на множестве X.
Доказательство. В силу условия 2 теоремы, сугцествует
такое Б > О, что |Б^(х)| < В для всех хеХ и всех п = 1, 2, ... и
поэтому
Ге' hD = К+р(х) - B,.i(x)\ < К+р(х)\ + |В„_ i(x)| < 2В
\k = п I
для всех xgX, всех я = 2, 3, ... и всех целыхр > 0. Из условия
же 1 теоремы следует, что для любого фиксированного 8 > О
сугцествует такой номер п^, что для всех xgX и всех п> п^
выполняется неравенство О < |а (х)| < ^. Теперь, применив нера-
венство Абеля (см. п. 30.13), получим, что
\п + р
Е а&(^)М^)
k = п
<2В[|а„(х)| + 2|а„+р(х)|]<8
ДЛЯ всех хеХ, всех п> п^и всех целых р > 0. Это и доказывает
равномерную сходимость ряда C2.30). П
Г. Харди A877—1947) — английский математик.
'87
в качестве примера использования теоремы 6 рассмотрим ряд
^ sm пх^ Согласно теореме 6, этот ряд равномерно сходится на
д = 1 ^
любом отрезке [а, Ь], не содержагцем точек вида 27гт, m = О, ±1,
±2, ... . Действительно, последовательность а„ = -, я = 1, 2, ..., в
^ п
данном случае является числовой последовательностью, она
монотонно убывает и стремится к нулю (значит, и равномерно стре-
п
мится к нулю), а суммы У sin kx удовлетворяют неравенству
k = 1
^ sin kx\
<
1
. х\
<
< +00
max -
[а, Ъ] gij^ X
(см. п. 30.13), т. е. ограничены на любом указанном отрезке.
На всяком отрезке, содержагцем точки вида х = 2Й7Г,
рассматриваемый ряд не сходится равномерно. В силу свойств
синуса, это достаточно доказать для отрезка [О, тг]. Положим
х„ = -—; тогда для всех k = п -\- 1, п -\- 2, ... , 2п имеем О < kx„ <
< 1 < ^. Следовательно, в силу неравенства ^i^ > -, О < а < ^
2 а тг 2
(см. A4.1)), получим
sm /гх„
sin kx^ 1 ^ 2 J_ _ J_
kx„ 2n 7z2n тгя'
k = n-\- 1, ..., 2n.
Отсюда
sin (n + l)x„ sin (я + 2)x„
я + 1
n + 2
+
sin 2ях„
2я
> J- +
тгя
тгя тг
п раз
Поэтому ни для какого 8 < - на отрезке [О, тг] не выполняется
тг
критерий Коп1и равномерной сходимости.
Заметим, что доказать равномерную сходимость
рассматриваемого ряда на отрезке, не содержагцем точек вида х = 2йтг,
с помогцью признака Вейергатрасса нельзя. Например, для
отрезка
Гтг Зтг]
L2' 2 J
имеем max
[71/2, 371/2]
sm пх
-. Поэтому не сугцест-
sm пх
<
вует такого сходягцегося числового ряда ^ а^, что
п = 1
< а^ на ^, -^ , ибо тогда а^ > -, а ряд ^ - расходится.
LZZJ П j^ ^ -^ П
Подобно случаю числовых рядов, применяя неравенство
Абеля, можно получить егце один признак равномерной схо-
88
димости функциональных рядов, аналогичный признаку
Абеля для числовых рядов. Он также впервые встречается в
работах Харди.
ТЕОРЕМА 7. Если:
1) последовательность {а^(х)} ограничена на множестве X:
\а^(х)\<М, хеХ, я =1,2,...,
и убывает или возрастает при каждом xgX;
оо
2) ряд Y, ^д(^) равномерно сходится на множестве X,
то ряд C2.30) также равномерно сходится на X.
Доказательство. Пусть задано 8 > 0. В силу равномер-
оо
ной сходимости ряда ^ bj^x), сугцествует такой номер п^, что
п = 1
ДЛЯ всех номеров п > п^, всех целых р > О и всех точек xgX
выполняется неравенство
8
SM'
Отсюда, в силу неравенства Абеля (см. 30.77), для всех
номеров п > п^, всех целых р > О и всех точек хе X справедливо
неравенство
f а„ + ,(х)&„ + ,(х)\ < ^(К(х)\ + 2|а„+^(х)|) < е.
^ = О
Согласно критерию Konin, это и означает равномерную
сходимость ряда C2.30). П
X
_ sin^xcos-
п
Пример. Рассмотрим ряд ^
2 In In Я
На любом отрезке, не содержагцем точек вида 2пт, т =
оо СП ТЛ Т1 'У*
= о, ±1, ... , ряд Y, r~i—' согласно теореме 6, равномерно
сходится, а числовая последовательность cos -, я = 2, 3, ... ,
п
ограничена на всей числовой оси и при любом фиксированном
значении х возрастает начиная с некоторого номера (причем
можно выбрать такой номер, что начиная с этого номера эта
последовательность возрастает во всех точках указанного
отрезка). Поэтому на отрезке, не содержапа;ем точек вида 27гт,
т = О, ±1, ... , рассматриваемый ряд, в силу теоремы 7,
равномерно сходится.
89
в заключение заметим, что из двух свойств равномерно схо-
дяш;ихся последовательностей, доказанных в конце п. 32.2,
непосредственно следует справедливость соответствуюпа;их свойств
для равномерно сходяпа;ихся рядов.
оо оо
1^, Если ряды Y, uj^x)u Y, v^(x) сходятся равномерно на
п = 1 п = 1
оо
множестве X, то для любых чисел ХеС и [leC ряд ^ XuJ^x) +
п = 1
+ [iv^(x) также сходится равномерно на множестве X,
оо
2^. Если ряд Y, ^д(^) равномерно сходится на множест-
п = 1
ее X, а функция g(x) ограничена на этом множестве, то ряд
оо
^ g{x)uj^x) также равномерно сходится на X.
п = 1
32.4. Свойства равномерно сходящихся
рядов и последовательностей
Как было показано вып1е (см. пример 2 в п. 32.1), сумма схо-
дяпа;егося ряда, все члены которого непрерывные функции,
может и не быть непрерывной функцией. Следуюпа;ая ниже
теорема 8 содержит достаточные условия непрерывности
суммы ряда.
Следует обратить внимание, что рассмотрение
непрерывных на некотором множестве функций накладывает
дополнительные ограничения на само множество — оно уже не может
быть множеством произвольной природы (каковым до сих пор
было множество X, на котором были заданы члены
рассматриваемых рядов, элементы последовательностей и т. д.), а
должно быть таким, что для функций, заданных на нем,
определено понятие непрерывности. Когда речь пойдет о производных и
интегралах, придется егце более сузить класс допустимых
множеств X.
При изучении вопроса о непрерывности суммы ряда будем
оо
рассматривать ряды ^ uj^x), где хеХ ^R, uj^x)e С, я = 1, 2, ... ,
п = 1
т. е. ряды, члены которых являются функциями
действительного аргумента, принимаюпа;ие, вообпа;е говоря, комплексные
значения.
ТЕОРЕМА 8. Если ряд равномерно сходится на некотором
множестве и в какой-то точке этого множества все члены
ряда непрерывны, то и сумма ряда непрерывна в этой точке,
90
Доказательство. Пусть ряд ^ г/^(х) равномерно
сходится на множестве X, s(x) = ^ и^(х) — его сумма, а s^(x)
= £ г/^(х), я = 1, 2,
fe = 1
ловию теоремы.
его частичные суммы. Согласно ус-
S^(x) ^ S(x), П^оо,
Зафиксируем произвольно 8 > 0. Для него сугцествует
такой номер п^, что для всех хеХ л всех п > п^ выполняется
неравенство
|s(x)-s„(x)|<|. C2.31)
Выберем произвольно п^ > п^. Функция s^ (х), как сумма
конечного числа непрерывных в точке Xq функций Uf^(x), k =
= 1, 2, ... , jIq, также непрерывна в этой точке. Поэтому
сугцествует 6 = 6 (е) > О такое, что для всех точек xgX, удовлет-
воряюгцих условию |х - XqI < 6, выполняется неравенство
\^п^(Ч)-^п^(^)\<1-
C2.32)
и о
Теперь, заметив (рис. 8), что
s(x) - s(Xq) = [s(x) - s^^(x)] + [s^^(x) - s^^(Xo)] + [s^^(Xo) - s(Xo)],
из неравенства C2.31), взятого в точках Xq и х, и неравенства
C2.32) получим при |х - Xq| < 6 и xgX
|s(x) - s(Xo)| < |s(x) - s^^(x)| + |s^^(x) - s^^(Xo)| + |s^^(Xo) - s(Xo)| <
< I + - + ^
e,
3 3 3
это и доказывает непрерывность функции s(x) в точке Xq. □
Утверждению теоремы можно придать следуюгций вид:
оо
lim Y, ^д(^) ^ 1™ s(x) =
^^ ^0 П= 1 Х^ Xq
ОО
= S(X(,)= ^ и„(Хо),
п = 1
а так как каждая функция г/(х),
п = 1, 2, ... , непрерывна в точке
XqGX, то u^(Xq) = lim и^(х),
поэтому
оо оо
lim У uJx) = У lim uJx).
91
Таким образом, в условиях теоремы 8 предел суммы ряда
равен сумме пределов его членов, т. е. в рассматриваемом ряде
допустим почленный переход к пределу.
Здесь, как и ниже, все пределы функций при х ^ Xq
берутся по множеству задания рассматриваемых функций (если,
конечно, не оговорено что-либо другое), т. е. в данном случае
по множеству X.
Bbinie отмечалось, что каждой последовательности
функций соответствует функциональный ряд, для которого она
является последовательностью частичных сумм. При этом если
данная последовательность равномерно сходится на
некотором множестве, то и указанный ряд также, очевидно,
равномерно сходится на этом множестве. Это обстоятельство
позволяет перефразировать теоремы о равномерно сходягцихся
рядах в соответствуюгцие теоремы о равномерно сходягцихся
последовательностях.
Будем рассматривать последовательности {f^(x)}, xgX ^ R,
fJ^x)eC, п = 1, 2, ... . Теорема 8 в терминах
последовательностей равносильна следуюгцей теореме.
ТЕОРЕМА 8^ Если последовательность функций
равномерно сходится на некотором множестве и в некоторой его
точке все члены последовательности непрерывны, то и
предельная функция последовательности непрерывна в этой
точке.
Таким образом, если /^ ^ /, XqGX ^ й и функции /^, п =
= 1, 2, ... , непрерывны в точке Xq, то и функция / непрерывна
в этой точке, поэтому
lim lim fJx) = lim lim fJx),
T. e. предельные переходы по я и по x можно переставлять.
Действительно, предел /последовательности /^, п= 1, 2, ... ,
является, в силу теоремы 8^ непрерывной в точке XqGX
функцией, поэтому левая часть равенства равна /(Xq):
lim lim fJx) = lim fix) = f(Xf.),
X^XqU^OO ri X^ Xq ^
HO И правая часть рассматриваемого равенства, в силу
непрерывности функций /^, также равна /(Xq):
lim lim /^(х) = lim /^(Xq) = /(Xq). D
92
в случае, когда члены ряда неотрицательны и
непрерывны, а сумма ряда является непрерывной функцией, имеет
место утверждение, в некотором смысле обратное к теореме 8: ряд
оказывается равномерно сходящимся. Сформулируем это
утверждение более точно.
ТЕОРЕМА 9 (Дини''). Если члены сходящегося на отрезке
ряда неотрицательны и непрерывны и его сумма также
является непрерывной функцией, то ряд на этом отрезке
сходится равномерно.
Доказательство. Пусть функции и^{х) непрерывны и неот-
оо
рицательны, х g [а, Ь], я = 1, 2, ... , ряд ^ и^{х) сходится и его
п = \
сумма s{x) непрерывна на отрезке [а, Ь]. Из условия и^{х) > О
слега
дует, что частичные суммы sj^x) = У uj^x) данного ряда в каж-
дой точке х^\а,Ъ\ представляют собой возрастающую числовую
последовательность и, следовательно, остатки г^(х) = s{x) - sj^x)
ряда— убывающую последовательность: гДх)|. Очевидно, что
s^{x) < s(x), поэтому гДх) > о, X G [а, Ь], я = 1, 2, ... .
Для доказательства равномерной сходимости на отрезке [а, Ь\
рассматриваемого ряда достаточно доказать, что для любого 8 > О
существует такой номер п, что для всех точек xg [а, Ь]
выполняется неравенство rj^x) < 8, так как в этом случае для всех т> п,
в силу условий г^(хI и rj^x) > О, будет выполняться
неравенство О < Г^(х) < Г^(х) < 8.
Допустим противное: пусть существует такое 8q > О, что для
любого номера п существует точка х^, для которой rj^x^) > 8q.
Выделим из последовательности {х^} сходящуюся
подпоследовательность {х„ }, и пусть lim х„ = Хп.
оо
в силу сходимости ряда ^ г/^(х) в точке Xq, существует
п = 1
такой номер п^, что для остатка г^ (х) ряда справедливо
неравенство г„ (Хп) < -^.
Остаток г^ (х) = s(x) - s^ (х) непрерывен в точке Xq как
разность непрерывных в этой точке функций s(x) и s^ (х). Поэто-
У. Дини A845—1918) — итальянский математик.
93
му суш;ествует такая 6 > О, что для всех х g [а, Ь], \х - х^\ < 6,
выполняется неравенство \г^ (х) - г^ (Xq)| < -^. Следовательно,
для всех таких точек х справедливо неравенство
Отсюда, в силу неотрицательности и убывания остатков г^(х) во
всех точках отрезка [а, Ь], явствует, что для всех точек х g
G [а, Ь], |х - XqI < 6 и всех номеров п> п^ выполняется
неравенство О < г^(х) < 8q.
Из того, что lim х^ = Xq, следует супа;ествование такого
номера я^, что nj^> n^vi \х^ - х^ < 6, поэтому для этого номера
имеет место неравенство О < г^ (х^ ) < 8q, которое
противоречит выбору точек х^, согласно которому г^ (х^ ) > Eg.
Полученное противоречие доказывает теорему.П
Теорему 9 также можно перефразировать в терминах
последовательностей .
ТЕОРЕМА 9\ Если сходящаяся на отрезке
последовательность непрерывных функций в каждой точке возрастает
(б каждой точке убывает) и предел последовательности
также является непрерывной функцией, то
последовательность сходится равномерно.
Теперь перейдем к вопросу о почленном интегрировании и
дифференцировании рядов. Производная и интеграл
определялись только в действительной области, поэтому, начиная с
этого момента и до конца параграфа, будем считать, что все
рассматриваемые функции определены на промежутках
действительной оси и принимают действительные значения.
ТЕОРЕМА 10. Пусть функции и^(х), я = 1, 2, ... ,
непрерывны на отрезке [а, Ь] и ряд
оо
1 uj^x) C2.33)
Д = 1
равномерно сходится на [а, Ь]. Тогда, какова бы ни была
точка с g [а, Щ,ряд
оо ^
Е 1 u,it)dt C2.34)
п = \ с
также равномерно сходится на [а, Ь], и если
оо
s{x)= Y, uj,x).
то
C2.35)
C2.36)
j s{t) dt= Y, \ МО ^^' a < X < Ь.
с n=\ с
Если формулу C2.36) переписать в виде
•'^ р оо —I оо •'^
С 1-^ = 1 J n = \ с
TO ВИДНО, ЧТО она означает законность при условиях,
перечисленных в теореме 9, почленного интегрирования ряда.
Доказательство. В силу равномерной сходимости ряда
C2.33) и непрерывности его членов на отрезке [а, Ь], согласно
теореме 8, его сумма s{x) также непрерывна на этом отрезке,
поэтому она интегрируется на любом отрезке с концами в
точках CG [а, Ь] и XG [а, Ь].
Покажем, что ряд C2.34) равномерно сходится на отрезке
[а, Ь] к функции
о{х) = ] s(t)dt. C2.37)
с
Пусть
М^)^ L М^)' г^(л:) = s(x) - s^(x).
fe = 1
Обозначим через о^(х) частичные суммы ряда C2.34):
Теперь для любого х g [а, Ь] имеем
|а(х) - с^(х)\ = I 8@ dt - I s^@ rff
<
<
I |s@ - sM dt\ = J |r^@ \dt\ < sup |r^@| N dt
<
< |x - c| sup \r^(t)\ <(b-a) sup |r^(x)|. C2.38)
[a,&] [a,b]
Последовательность sup |r^(x)|, я = 1, 2, ... , является чис-
[a,b]
ЛОВОЙ последовательностью. В силу равномерной сходимости
ряда C2.33), имеем
lim sup |r^(x)| = О
95
(см. п. 32.3); поэтому из неравенства C2.38), согласно
следствию теоремы 1, явствует, что последовательность частичных
сумм ряда C2.34) равномерно сходится к функции C2.37), а
это и означает равномерную сходимость ряда C2.34) к функции
C2.37). Теорема и, в частности, формула C2.36) доказаны. П
Перефразируем полученный результат для
последовательностей функций.
ТЕОРЕМА ^0\ Если последовательность непрерывных на
отрезке [а, Ь] функций /^, я = 1, 2, ... , wa этом отрезке
равномерно сходится к функции /, то, какова бы ни была
точка с ^ [а, Ь],
1 f^{t) dt ^ 1 fit) dt на [а, Ь],
с с
в частности
lirn^ I т dt - J [ Идп^ ит dt.
с с
Покажем теперь, что равенство
b Ъ
lim [ fJx) dx = f lim fJx) dx
a a
справедливо не всегда, когда на отрезке [а, Ь] сугцествует
предел lim fj^x) и все рассматриваемые функции интегрируемы,
т. е. что в этом случае не всегда можно переходить к пределу
под знаком интеграла. Таким образом, требование
равномерной сходимости в теореме 10' (так же как и в теореме 10)
является супа;ественным.
Пусть /^(х) = пхе'''''^', я = 1, 2, ... , О < X < 1. Тогда /^@) = О
и при любом X ^ 0: lim fJx) = 0. Таким образом, /„ ^ О и,
^ п^оо'пУ ^ ^ ' '^ [О, 1]
следовательно, интеграл от предельной функции, т. е. от
нуля, также равен нулю. Однако
1 1 _ 2 1" 1
I f^(x) dx = я| хе ^^ dx = -| е~^ dt = -A - е^),
0 0 о
Поэтому lim f /„(х) dx = -, т, е, действительно, для рассмот-
о
ренной последовательности {/^(х)} имеет место неравенство
1 о
lim f fJx) dx ^ f lim fJx) dx = 0,
0 1
'96
Если построить ряд Y, ^д(^)' Д-^^ которого рассмотренная
п = 1
последовательность {fj,x)} является последовательностью
частичных сумм, т. е. положить и-^(х) = /^(х), г/^(х) = fni^) ~ fn- i(^)'
я = 2, 3, ... , то для этого ряда будем иметь
1 оо оо 1
I ^ и^(х) dx^ Y. \ ^п(^) ^^•
УПРАЖНЕНИЕ 4. Показать, что если
2п при X = —,
I п
и функция fJx) линейна на отрезках О, -— и -—, - , то для всех х е [О, 1]
" L 2nj 12п nj
1
имеет место равенство lim fJx) = О, а lim f fJx) dx = 1.
0
Рассмотрим теперь вопрос дифференцирования рядов.
ТЕОРЕМА 11. Пусть функции uj,x), п=1,2, ... , непрерывно
дифференцируемы на отрезке [а, Ь] и ряд, составленный из
их производных
оо
Е К(^)^ C2.39)
П = 1
оо
равномерно сходится на отрезке [а, Ь]. Тогда если ряд ^ uj^x)
п = 1
сходится хотя бы в одной точке се[а, Ь], то он сходится
равномерно на всем отрезке [а,Ь], его сумма
оо
8(х)= £ и„(х) C2.40)
П = 1
непрерывно дифференцируема и
оо
sXx)= £ u;(x). C2.41)
П = 1
Если эту формулу переписать в виде
[оо -]/■ оо
1 и,(х)\ = £ и;(х),
п = 1 -1 п = 1
то видно, ЧТО она означает законность при сделанных
предположениях почленного дифференцирования ряда.
^7
Доказательство. Пусть
оо
о(х)= ^ и;(х). C2.42)
Д = 1
В силу равномерной сходимости этого ряда, его сумма
является непрерывной функцией, а сам ряд можно почленно
интегрировать:
X QQ X ОО
\G(t)dt= ^ I u'^(t)dt= ^ [г/Дх) - г/Дс)], а < х < Ь. C2.43)
По теореме 10, ряд
оо
£ [u„(x) - и„(с)], a<x<& C2.44)
д = 1
— сходягцийся. Сходится, по условию теоремы, и ряд
оо
Е и„(с), C2.45)
Д = 1
поэтому сходится и сумма рядов C2.44) и C2.45), т. е. ряд
оо
^ г/Дх), а < X < Ь. C2.46)
Отсюда следует, что равенство C2.43) можно переписать в виде
^ оо оо
\o{t)dt= £ u„(x)- £ и^{с)
или, ЧТО ТО же (см. C2.40)), в виде
]G{t)dt = s{x)-s{c). C2.47)
с
функция в левой части равенства имеет производную по х,
следовательно, и функция s(x) имеет производную.
Дифференцируя равенство C2.47), получаем (см. п. 25.2)
s'(x) = a(x), C2.48)
где функция а(х) непрерывна на отрезке [а, Ь], так как
представляет собой сумму равномерно сходягцегося ряда C2.39),
члены которого — непрерывные функции. Поэтому сумма s(x)
ряда C2.46) имеет на отрезке [а, Ь] непрерывную производную
s'(x), т. е. непрерывно дифференцируема. Подставляя C2.42)
в C2.48), и получим искомую формулу C2.41).
Остается лигаь отметить, что из равенства C2.43), в силу
доказанной сходимости рядов C2.44) и C2.45), следует, что
оо оо ^ оо
Е и„(х)= Е \Ki.t)dt+ Е "«(^)-
Д=1 П ^ \ с П = 1
98
Ряд 12 I ^я (^) ^^ равномерно сходится на отрезке [а, Ь] (см.
п= 1 с
оо
теорему 10), а ^ ^д(<^) — числовой ряд, поэтому и их сумма,
п = 1
Т. е. ряд C2.40), равномерно сходится на отрезке [а, Ь]. П
Итак, если сходягцийся ряд непрерывно
дифференцируемых функций таков, что ряд, составленный из его
производных, равномерно сходится, то сумма ряда является
непрерывно дифференцируемой функцией и ее производная получается
почленным дифференцированием ряда.
Из предпосылок этой теоремы следует равномерная
сходимость ряда, поэтому, не ограничивая обгцности теоремы, ее
можно перефразировать следуюгцим образом.
Если ряд непрерывно дифференцируемых функций и ряд,
составленный из их производных, равномерно сходятся, то
сумма исходного ряда непрерывно дифференцируема и ее
производная равна сумме производных членов данного ряда
{т, е, ряд можно почленно дифференцировать).
Заметим, что в теореме 10 условие равномерной сходимости
ряда, членами которого являются производные членов
заданного ряда, является супа;ественным: если члены ряда непрерывно
дифференцируемы, а равномерно сходится только сам ряд, то,
вообпа;е говоря, его нельзя почленно дифференцировать. Напри-
^ sin пх
мер, ряд у — равномерно сходится на всей числовой оси.
поскольку
sm пх
<!-
П
, а ряд, полученный его почленным диф-
'-'*-' / sin ТЪЗС\ '~^ 0OS ТЪЗС
ференцированием, т. е. ряд У — = У , расходится
в точках X = %т, т = О, ±1, ±2, ... .
Необходимо также в теореме 11 и условие о сходимости
самого ряда в некоторой точке, так как одной равномерной
оо
сходимости ряда из производных, т. е. ряда ^ u'J^x), недо-
п = \
статочно для того, чтобы гарантировать сходимость самого
оо
ряда Y, ^д(^)- Так, ряд, полученный из производных членов
ряда 1 + 1 + 1 + + 1 + ... , т. е. ряд О + О + О + ... + О + ... ,
конечно, равномерно сходится на всей числовой оси, а сам
исходный ряд расходится.
Перефразируем теперь теорему 11 для
последовательностей.
'99
ТЕОРЕМА ^Y. Пусть последовательность непрерывно
дифференцируемых на отрезке [а, Ь] функций
/,, я=1,2, ..., C2.49)
сходится хотя бы в одной точке с g [а, Ь], а
последовательность их производных /^, я = 1, 2, ... , равномерно сходится
на [а, Ь]. Тогда последовательность C2Л9) равномерно
сходится на [а, Ь], ее предел является непрерывно
дифференцируемой на этом отрезке функцией и
lim ^1^ = Л. lim fix), a<x<b.
Аналогично случаю рядов, это утверждение равносильно
следуюш;ему.
Если функции /^ непрерывно дифференцируемы на
отрезке [а, Ь] и f^ ^ /, /^ ^ ф, то существует f и f = (р на
[а, Ь] [а, Ь]
отрезке [а, Ь].
Примеры применения этих теорем приведены в § 33.
УПРАЖНЕНИЯ. 5. Выяснить, будет ли справедливым равенство
1 1
lim f х^ dx= [ ( lim х") dx.
О о
Можно ли это установить с помопдью теоремы 10?
6. Доказать, что при х > 1 для дзета-функции Римана ^ (см. C0.4) и
п. 31.5*) справедлива формула
/ ОО ^ Л'' ОО ,
§33
Степенные ряды
33.1. Радиус сходимости
и круг сходимости степенного ряда
Определение 1. Функциональные ряды вида
оо
£ а„(г-го)", C3.1)
д = О
где а^ и 2q — заданные комплексные числа, а z —
комплексное переменное, называются степенными рядами. Числа а^,
Ш
я =0, 1,2, ... , называются коэффициентами степенного
ряда C3 Л).
Предполагая, что коэффициенты ряда и число Zq
фиксированы, будем исследовать поведение ряда C3.1) при
различных Z.
Если в ряде C3.1) выполнить замену переменного,
положив С^ = Z - Zq, то получим ряд
L «яС^
C3.2)
Очевидно, что исследование сходимости ряда C3.1)
эквивалентно исследованию сходимости ряда C3.2), поэтому
в дальнейгаем будем рассматривать ряды вида C3.2),
используя, как правило, для обозначения переменной букву z,
а не С,,
ТЕОРЕМА 1 (первая теорема Абеля). Если степенной ряд
L «.^"
C3.3)
сходится при z = Zq^ О, то он сходится, и притом
абсолютно, при любом Z, для которого \z\ < \zq\.
Доказательство. Пусть ряд
L ^n^S
C3.4)
сходится. Тогда его п-й член a^zg стремится к нулю при я ^ оо
(см. п. 30.1), поэтому последовательность {a^^z^} ограничена,
т. е. сугцествует такая постоянная М > О, что
\a^z^\ <М, п = 0,1, 2, ... .
В силу этого, для п-то члена ряда C3.3)
имеет место оценка
КП = 1«я^о1
"<м
Если 1^1 < I^qI (рис. 9), то ряд Y,
ЯВЛЯЯСЬ суммой геометрической
прогрессии со знаменателем q
< 1, схо-
Рис. 9
101
дится. Поэтому, согласно признаку сравнения (см. п. 30.5),
оо
сходится и ряд Y, \^п^\у ^ ^^^ означает абсолютную сходи-
п = 0
мость ряда C3.3) при \z\ < \z^. П
СЛЕДСТВИЕ. Если степенной ряд C3,3) расходится при z =
= Zq, то он расходится и при всяком z, для которого \z\ > \zq\.
Действительно, если 1^1 > \zq\ и ряд C3.4) расходится, то
расходится и ряд C3.3), так как если бы он сходился, то, в
силу доказанного, сходился бы и ряд C3.4).
Неравенство 1^1 < R задает на комплексной плоскости С
замкнутый круг радиуса R с центром в точке z = 0.
оо
Определение 2. Пусть задан ряд ^ ^п^^- ^^-^^ ^ — неотри-
п = о
цателъное число или +оо обладает тем свойством, что при
всех Z, для которых \z\ < R, ряд C3.3) сходится, а при всех
Z, для которых \z\ > R, ряд C3.3) расходится, то R
называется радиусом сходимости степенного ряда C3.3).
Множество точек z, для которых \z\ < R, называется
кругом сходимости ряда C3.3).
Если i? = О, то круг сходимости вырождается в точку z = Q,
а если R = +оо^ то круг сходимости совпадает со всей
комплексной плоскостью С.
ТЕОРЕМА 2. У всякого степенного ряда C3.3) существует
радиус сходимости R, Внутри круга сходимости, т, е, при
любом Z, для которого \z\ < R, ряд C3.3) сходится абсолютно.
На любом круге \z\ < < г, где г фиксировано и г< R, ряд C3.3)
сходится равномерно.
Доказательство. Обозначим через А множество всех
неотрицательных чисел X, в которых ряд
оо
1 a„x'^ C3.5)
СХОДИТСЯ. При X = о этот ряд заведомо сходится, поэтому
множество А не пусто и, следовательно, имеет конечную или
бесконечную верхнюю грань. Пусть sup А = R. Покажем, что R —
радиус сходимости ряда C3.3). Действительно, пусть 2gC и
1^1 < R. Согласно определению верхней грани, супа;ествует
такое хеА, что 1^1 < X < i? (см. определение 4' в п. 3.4). В силу
определения множества А, для указанного х ряд C3.5) сходится,
поэтому, согласно первой теореме Абеля, в выбранной точке z
оо
сходится абсолютно ряд ^ ^п^^-
п = 0
102
Если 1^1 > R, то выберем такое действительное число х, что
i? < X < 1^1; тогда снова, в силу определения множества А, ряд
C3.5) в такой точке х расходится — она лежит на
действительной оси правее всех точек, в которых ряд C3.5) сходится.
Поэтому, согласно следствию из первой теоремы Абеля, для
оо
выбранного 2 расходится и ряд ^ ^п^"^*
п = 0
Итак, действительно, R является радиусом сходимости ря-
да C3.3).
Если теперь О < г < R, то, по доказанному, ряд C3.3) при 2 = г
оо
абсолютно сходится, т. е. сходится числовой ряд ^ к^к^» А так
п = 0
как для любой точки 2 круга \2\ < г (рис. 10)
|a^2^|<|aJr^ я = 0,1,2, ... ,
то, согласно признаку Вейерп1трасса (см. п. 32.3), на этом
круге ряд C3.3) сходится равномерно. П
Таким образом, областью сходимости всякого степенного
ряда является всегда «круг», т. е. обычный круг, исключая,
быть может, некоторое множество точек ограничиваюгцей его
окружности (будем для краткости называть ее границей круга
сходимости), в которых он может расходиться (см. следуюгцие
ниже примеры).
Подчеркнем, что радиус сходимости степенного ряда C3.3)
обладает следуюгцим свойством: для каждого числа 2 такого,
что 1^1 < i?, указанный ряд абсолютно сходится, а для
каждого 2 такого, что 1^1 > i?, он просто, а следовательно, и подавно
абсолютно расходится (расходится ряд, составленный из
абсолютных величин членов данного ряда). Это следует,
очевидно, из определения радиуса сходимости и теоремы 2.
Члены степенного ряда являются непрерывными функциями
и, как было показано, на всяком круге, лежагцем вместе со своей
границей внутри круга сходимости,
степенной ряд сходится равномерно, z/A
поэтому его сумма непрерывна на
всяком указанном круге. Очевидно, что
для любой точки 2 круга сходимости,
1^1 < i?, можно подобрать круг, содержа- /
гции эту точку и лежагции вместе с гра- \ \ о|
ницей в круге сходимости (достаточно \
взять его радиус г таким, что 1^1 < г <
< i?), поэтому степенной ряд
непрерывен в каждой точке 2, лежащей
внутри его круга сходимости: \2\ < R, Рис. 10
Тоз
I
Рассмотрим теперь случай, когда степенной ряд сходится в
точке Z = R, лежагцей на границе его круга сходимости.
Отметим, что случай Z = -R может быть сведен к случаю z = R
простой заменой переменного ^ = -2.
ТЕОРЕМА 3 (вторая теорема Абеля). Если R — радиус сходи-
оо
мости ряда ^ a^z^ и этот ряд сходится при z = R, то он
п = о
сходится равномерно на отрезке [О, i?] действительной оси.
СЛЕДСТВИЕ. Если степенной ряд C3.3) сходится при z = R,
то его сумма непрерывна на отрезке [О, i?] действительной
оси.
Доказательство. Пусть О < х < i?. Представим ряд
оо оо °° f X Л^ °°
Е а„х„ в виде £ а„х„ = £ а„Д" - . Члены ряда £ а„Л«
п = 0 п = 0 п = 0 КП, J „_о
не зависят от х, поэтому его сходимость означает и его
равномерную сходимость. Последовательность же \[ъ] \ ограничена
на отрезке [О, R], ее члены неотрицательны: О ^ б ^ 1? и она
убывает в каждой точке (при х = R она не строго убывает,
точнее, является стационарной). Поэтому, в силу признака Абеля
равномерной сходимости рядов (см. теорему 7 в п. 32.3), ряд
C3.3) равномерно сходится на отрезке [О, R]. П
Следствие вытекает из того, что сумма равномерно сходя-
па;егося ряда непрерывных функций является также
непрерывной функцией.
Все сказанное с помопа;ью преобразования типа z = С, - C^q
(^ — новая переменная, ^q фиксировано) переносится и на обпа;ие
степенные ряды вида C3.1). В частности, областью сходимости
такого степенного ряда всегда является круг вида \z - Zq\ < R,
конечно, как и Bbinie, с точностью до точек ограничиваюгцей его
окружности. Этот круг называется кругом сходимости (ряда
C3.1)), а i? — его радиусом сходимости.
оо
Примеры. 1. Радиус сходимости R ряда ^ nlz^ равен
■к " ^ ^
нулю, т. е. этот ряд сходится только при Z = о .
Действительно, исследуя абсолютную сходимость этого
ряда по признаку Даламбера, при любом z ^ О получим
lim 1("У)'^'Ч = lim (п + l)\z\ = +00.
П^оо \п\2^\ П^оо ^
При 2 = 0, очевидно, сходится любой ряд вида C3.3).
104
Таким образом, рассматриваемый ряд не сходится
абсолютно при любом 2^0; отсюда, в силу следствия из первой
теоремы Абеля, он расходится при любом 2^0.
2. Радиус сходимости ряда ^ — равен +оо^ так как было
jj^ ^ Q п.
показано (см. п. 32.1), что этот ряд сходится при любом 2.
3. Сумма бесконечной геометрической прогрессии
оо
Е 2" C3.6)
п = 0
сходится при 1^1 < 1 И расходится при \2\> 1. Поэтому ее радиус
сходимости R= 1. Отметим, что во всех точках границы круга
сходимости, т. е. во всех точках окружности 1^1 = 1, ряд C3.6)
расходится, так как для обпа;его члена ряда имеем \2^\ = 1 и,
следовательно, он не стремится к нулю при я ^ оо,
4. Ряд
оо ~п
1 -, C3.7)
сходится при 1^1 < 1, так как при выполнении этого условия
£!| < ^, а ряд У ^ сходится.
При 1^1 > 1 ряд C3.7) расходится, поскольку в этом случае
I ^1 д
lim Ц- = +00 , т. е. не выполняется необходимое условие схо-
димости ряда. Радиус сходимости ряда C3.7), как и ряда
C3.6), равен единице, однако в каждой точке границы круга
сходимости ряд C3.7), в отличие от ряда C3.6), сходится.
оо ~п
5. Ряд Y, ~ имеет радиус сходимости R= 1.
п= 1 ^
Действительно, применив признак Даламбера для
определения 2, при которых ряд абсолютно сходится (расходится),
получим
lim
(я+1)
Ь| lim
►оо д + 1
Д ^ оо г^"
I п\
и, следовательно, при 1^1 < 1 данный ряд сходится, причем
абсолютно, а при 1^1 > 1 он расходится. При 2=1 получается рас-
* Действительно, легко, например с помощью правила Лопиталя,
убедиться, что lim —^ = +оо (см. пример 2 в п. 12.2).
X ^ оо y.Z
Тоб
oo -1
ходягцийся гармонический ряд ^ -, а при 2 = -1 — сходя-
гцийся ряд Y, — (^^' п. 30.3 и 30.9). Таким образом, в этом
п = 0 ^
примере на границе круга сходимости есть точки, в которых
ряд сходится, и точки, в которых он расходится.
Таким образом, область сходимости степенного ряда не
совпадает, вообпа;е говоря, с его кругом сходимости, а состоит
из внутренности этого круга, т. е. множества {z : \2\ < R}, и,
быть может, егце из некоторого множества точек, лежагцих на
его границе.
Из рассмотренных примеров (см. также п. 32.1) видно, что
иногда радиус сходимости R степенного ряда находится с по-
могцью признака Даламбера сходимости рядов с
положительными членами (см. теорему 8 в п. 30.6). Действительно,
справедливо следуюгцее утверждение: если существует предел
(конечный или бесконечный) lim ' ^"
Ы + \
то
R= lim
'"-д + 1
C3.8)
В самом деле, если число R определено этой формулой и
1^1 < R, то
,. \С1„л_л2 111* Г^га + 1 \z\ ^ 1
lim ' ^ ^ = b lim ' ,^ , ' = Р: < 1,
п^оо a^z"" ' 'д^оо |а^| \R\
поэтому ряд C3.3) для такого z сходится (и притом
абсолютно).
1^ 2П + 1| II
Если же \z\ > R, то lim LJLll—.—! = 1Л > i^ и,
следовательское |а„2;"| \R\
но, ряд C3.3) абсолютно расходится. Таким образом, R
действительно является радиусом сходимости ряда C3.3).
Аналогично можно найти величину радиуса сходимости R
и с помогцью признака Когаи (см. теорему 9 в п. 30.6),
если только сугцествует предел (конечный или бесконечный)
lim ^J\aJ. В этом случае
R = -. C3.80
lim ",/[а~
Действительно, если число R задается этой формулой и
если 1^1 < R, то
lim "iflalz^ = \z\ lim ^/[aJ = )|i < 1
\R\
~To6
и поэтому ряд C3.3) сходится. Если же 1^1 > R, то
lim а/к^ = г4 > 1
и, следовательно, ряд C3.3) абсолютно не сходится.
Таким образом, R является радиусом сходимости ряда C3.3).
Затруднения при использовании таких методов
определения радиуса сходимости степенного ряда могут возникнуть,
например, уже в том случае, когда в рассматриваемом ряде
имеются коэффициенты со сколь угодно болыаими номерами,
равные нулю. Тогда можно попробовать применить один из
этих методов, предварительно перенумеровав подряд все
члены ряда с отличными от нуля коэффициентами (отчего его
сходимость и сумма в случае, если он сходится, не изменяются).
Поясним сказанное на примере. Пусть требуется
определить радиус сходимости ряда
£ a,.^ где a, = \h если я = 1, 3, 5, ... ,
" = о [ О, если п = 0,2, 4, ... .
Признак Даламбера неприменим для определения
сходная+i
мости этого ряда, так как отнопхение -^—- не имеет смысла
для четных номеров п. Не дает ответа здесь и признак Konin,
поскольку нетрудно проверить, что здесь предел lim ^J\a„\ не
супа;ествует. Однако если положить Ь^
и записать данный ряд в виде
L ^^^ L 9ГТТ'
'>' 2feTI' * ~~
22k + 1
= 0,1,2,.,
• • ?
ТО, исследовав абсолютную сходимость этого ряда с помопа;ью
признака Даламбера, получим
lim ' , ,, ,, ' = br lim =Г7—7i = b •
Отсюда следует, что рассматриваемый ряд абсолютно
сходится, когда l^^l < 1, т. е. когда 1^1 < 1, и абсолютно расходится,
когда 1^1 > 1. Таким образом, радиус сходимости этого
степенного ряда равен 1.
Подчеркнем, что с помогцью признака Даламбера и признака
Коп1и можно найти радиус сходимости не для произвольного
степенного ряда, а лип1ь для такого, у которого сугцествуют
указанные Bbinie пределы (быть может, после новой нумерации членов).
Т07
УПРАЖНЕНИЯ. Определить радиусы сходимости рядов:
ОО ОО «Д ОО /" гу \П ОО / -1 _ АЛПгуП ОО
1. у пЧ^.2. у i-.З. у - .4. у . ^\! ^.-5. у 2"^2^
.^0 .^1 яз ,4^1 U J ,4^0 (^ + 1)(^ + 2) ,4^1
33.2*. Формула Коши—Адамара
для радиуса сходимости степенного ряда
Найдем теперь формулу для определения радиуса сходимости
произвольного степенного ряда через его коэффициенты в об-
гцем случае.
ТЕОРЕМА 4. Пусть R — радиус сходимости степенного ряда
ОО
д = О
тогда
R= ^ ^ C3.9)
lim ^JlaJ
д ^ ОО 'V I 'М
Формула C3.9) называется формулой Коши—Адамара**.
Доказательство. Положим р= lim ^/а„. Рассмотрим сна-
чала случай р = 0. Покажем, что в этом случае ряд C3.3)
сходится при любом Z. Возьмем какое-либо 2 ^ О и такое 8, что О < 8 < 1.
Тогда (см. теорему 10 п. 4.12"^) сугцествует такое N-^, что
^J\a„\ < Д для всех п> N^,
л/1 щ 1^1
т. е.
|а^| 1^1^ < 8^ для всех n>N^.
Отсюда по признаку сравнения следует, что ряд C3.3)
абсолютно, значит, и просто сходится при данном z, а так как z
было произвольно, то это означает, что R = +оо.
Возьмем другой крайний случай: пусть р = +оо. Покажем,
что в этом случае ряд C3.3) расходится при любом z ^ 0.
Действительно, если р = +оо^ то сугцествует последовательность
я^, й = 1, 2, ... , натурального ряда такая, что lim^ ^^/|а^ 1 = +оо.
Поэтому, каково бы ни было z ^ О, сугцествует такой номер k^,
что при k> k^
1
Wa„ >г-г, т. е.
а„ Z
>1.
О верхнем пределе см. в п. 3.12*.
^ Ж. Адамар A865—1963) — французский математик.
Т08
Таким образом, не выполняется необходимое условие
сходимости ряда — стремление к нулю п-то члена, поэтому при
данном 2^0 ряд расходится, а так как 2^0 было
произвольно, то это означает, что R = 0.
Пусть теперь О < р < +оо. Покажем, что при всяком 2 таком,
что Ь| < -, ряд C3.3) сходится. Выберем 8 > О так, чтобы Ь| <
Р
< ; тогда число д, определяемое равенством ^ = (р + 8)|2|,
будет удовлетворять неравенству g < 1. Согласно свойству
верхнего предела, сугцествует такой номер N-^, что при п> N^
п \п I < П + F
поэтому при п > N-^
\2\nJ\a^\<\2\(p-\-г) = q, т.е. \a^2'^\<q'^, 0<д<1,
и по признаку сравнения ряд C3.3) при рассматриваемом 2
абсолютно, а значит, и просто сходится.
Покажем теперь, что ряд C3.3) при всяком 2 таком, что
Ь| > -, расходится. Выберем 8 > О так, чтобы
Р
И>^>о, C3.10)
р-8
тогда \2\(р - 8) > 1. Согласно свойству верхнего предела
(см. теорему 10 п. 4.12"^), супа;ествует подпоследовательность я^,
й = 1, 2, ... , натуральных чисел такая, что
4j\^\>p-E, й = 1,2, ....
Из этого, в силу C3.10), следует, что
\2\^kJ\^\>\2\ip-E)>l
И, следовательно,
т. е. в этом случае не выполняется необходимое условие
сходимости ряда — стремление к нулю его п-то члена, и поэтому
для рассматриваемого 2 ряд C3.3) расходится.
Таким образом, ряд C3.3) сходится, если Ь| < -, и расходится,
Р
если Ь| > -, а это и означает, что его радиус сходимости R= -.П
Р Р
' Для этого достаточно взять 8 < р-, - р.
\2\
109
Отметим, что из доказанной теоремы егце раз следует, что для
каждого степенного ряда C3.3) сугцествует такое конечное или
бесконечное число R > О, что для всех zeC, для которых 1^1 < R,
ряд C3.3) сходится, а для которых 1^1 > R, — расходится, т. е. что
для каждого степенного ряда сугцествует радиус сходимости: им
является i?= ^ .
lim «^/ol
33.3. Аналитические функции
Определение 3. Функция f{z) называется аналитической в
точке 2q, если существует такое i? > О, что в круге \z - z^< R
она представима степенным рядом вида C3.1), т, е,
существуют такие комплексные числа а^, п = О, 1, 2, ... , что
оо
П2)= £ а„(г-2о)", \2-2o\<R. C3.11)
Сумма, разность и произведение аналитических в точке
функций снова являются аналитическими в этой точке
функциями (почему?).
ЛЕММА Л. Если R —радиус сходимости ряда C3.11), R> О и
оо
k- п+ 1
— остаток ряда C3.11), то
r^(z) = 0((z - 2o)- + i), z - 2o C3.12)
и, следовательно,
r^(z) = o((z-z^r),z^z^. C3.13)
Доказательство. Если \z - Zq\ < R, то
оо
k = n+ 1
и ряд, получивгаийся после вынесения множителя (z - Zq)^ + ^,
оо
сходится. Поэтому функция (p(z) = Y, ^k(^ ~ ^о)^ - п-1^ j^aj^
k = п + 1
сумма степенного ряда, непрерывна в круге \z - Zq\ < R.
Если теперь О < г < i?, то функция фB), будучи непрерывной
на замкнутом круге \z — Zq\ < г, является ограниченной на нем,
Ш
т. е. найдется такая постоянная М > О, что при \г - г^<^г
выполняется неравенство |фB)| < М. Поскольку rj^z) = (г - г^^^ ^фB)?
при \г - ZqI < г получим
|г^B)| = \z- z^ + 1|фB) < M\z - z^ +1,
а это и означает C3.12). Условие C3.13) непосредственно
следует из C3.12). П
ТЕОРЕМА 5. Разложение аналитической в точке Zq
функции в степенной ряд вида C3.11) единственно, т. е. если
оо оо
£ а„B-2о)«= £ bj^z-z^r, \z-z^\<R, R>0, C3.14)
п=0 п=0
то а^ = Ь^, п = О, 1, 2, ... .
Доказательство. Из равенства C3.14) (при п = 0),в силу
формулы C3.12), следует, что при z ^ Zq
а^ + 0(z - Zq) = Ьо + 0(z - Zq).
Переходя в этом равенстве к пределу при z -^ Zq, получаем,
что а^ = Ъ^.
Пусть уже доказано, что а^ = Ь^, j = О, 1,2, ... , п - 1; тогда,
в силу C3.12) и C3.14),
ао + a^(z - 2o) + ... + a^(z - z^r + 0((z - z^ +1) =
= bo + 4^ - ^o) + ... + b^iz - z^ + Oiiz - 2o)^ +1).
Уничтожая одинаковые члены в обеих частях этого равенства
и разделив обе его части на (z - Zq)^, имеем
а^ + Oiz - Zq) = Ъ^ + 0{z - 2о), z^ Zq, z^ z^.
Отсюда в пределе при z ^ Zq получим, что а^ = Ъ^ (ср.
с теоремой 2 в п. 13.2). П
Может оказаться, что лигаь рассмотрение ряда в области
комплексных чисел может объяснить величину его радиуса
сходимости. Например, ряд ^ (-l)^x^^, являюгцийся суммой
п = 0
геометрической прогрессии со знаменателем -х^, сходится при
|х| < 1 и расходится при |х| > 1. Его сумма на интервале (-1; 1)
равна -. Функция определена и бесконечно диффе-
1 + х^ 1 + х^
Тп
ренцируема на всей действительной оси и непонятно почему,
раскладывая ее в ряд
(—1 \Плг2п
1 оо
-^—= у (-1)^X2
1 + Х2 ,%о
МЫ получаем ряд, сходяпа;ийся только при |х| < 1. Это
разложение делается соверп1енно естественным, если рассмотреть эту
функцию в области комплексных чисел, поскольку функция
имеет «особую точку» при 2 = i (в этой точке функция не
1 + х^
определена и при приближении к ней стремится к
бесконечности), т. е. как раз на границе круга 1^1 < 1.
33.4. Аналитические функции в действительной области
В настоягцем пункте будут в основном рассматриваться
степенные ряды с действительными членами. Однако
предварительно докажем лемму, справедливую для степенных рядов и
в комплексной области.
ЛЕММА 2. Радиусы сходимости рядов
оо
C3.15)
оо а„г" + 1
к
п + 1
C3.16)
i: /га„2"-1 C3.17)
равны.
Таким образом, ряды C3.16) и C3.17), получаемые из
ряда C3.15) соответственно с помогцью «формального
интегрирования и дифференцирования», имеют те же радиусы
сходимости, что и исходный ряд. Интегрирование и
дифференцирование названы здесь формальными, поскольку для функций
комплексного аргумента эти операции не были определены, и
они выполнялись так, как если бы 2 было действительным
числом, т. е. в действительной области ряд C3.16) получается
из ряда C3.15) почленным интегрированием, а ряд C3.13) —
почленным дифференцированием.
Доказательство. Пусть R — радиус сходимости ряда
C3.15), R^ — радиус сходимости ряда C3.16), а i?2 — радиус
сходимости ряда C3.17). Из неравенств
pf!^ < 1^1 |а^2^|< \2^\ \па^2''-\ п = 1,2, ... ,
\ п + 1 \
172
и теоремы сравнения (см. теорему 6 в п. 30.5) следует, что если в
некоторой точке г сходится ряд C3.17), то в этой точке сходится
и ряд C3.15), и если в некоторой точке z сходится ряд C3.15), то
в той же точке сходится и ряд C3.16). Отсюда следует, что
i?2<i?<i?i. C3.18)
Покажем теперь, что
i?i<i?2. C3.19)
Возьмем какую-либо точку 2q ^ О из круга сходимости ряда
C3.16) и покажем, что в ней сходится ряд C3.17). Так как
l^ol < i?i, то найдется такое действительное число г, что I^qI < г <
< i?^. Запигаем абсолютную величину члена ряда C3.17) сле-
дуюгцим образом:
Щ^пЧ
п{п + 1)
а.г"
lim
0.
В силу сходимости ряда C3.16) при z =
ряда при Z = г стремится к нулю, когда п
й^дГ^ + 1
Я + 1
Следовательно, последовательность
чена, т.е. сугцествует такое М > О, что для всех п
полняется неравенство
= 1,2, ... . C3.20)
г, обгций член этого
а„г
71+1
п + 1
, п= 1, 2, ..
1,
. , ограни-
2, ... , вы-
уП + 1
<М.
Положив q
я + 1
, из C3.20) получим неравенство
\na„z
^,Q i\^!lilL±^Mq^ + \ 0<q<l.
ro|
Ряд с обгцим членом —^——-^Mq^ + ^ сходится (в этом легко
го|
убедиться, например, по признаку Даламбера), поэтому при
Z = Zq сходится и ряд C3.17). Таким образом, из сходимости в
точке z = Zq ряда C3.16) следует сходимость в ней и ряда C3.17).
Это и означает справедливость неравенства C3.19). Из
неравенств C3.18) и C3.19) следует, что R = R^ = Щ.П
Замечание. Утверждение леммы может быть доказано
прогце, если использовать формулу Konin—Адамара для
радиуса сходимости степенного ряда (см. п. 33.2"^). Это не сделано,
так как приведенное доказательство также не сложно, а п. 33.2"^
113
можно пропустить при первом чтении (на что и указывает
звездочка при его номере).
Далее в этом параграфе везде, где не оговорено противное,
будем предполагать, что коэффициенты всех рассматриваемых
рядов действительны и что переменные 2 и Zq также
действительны (в этом случае будем их обозначать х и Xq). Правда, все
рассматриваемые ниже свойства степенных рядов переносятся
в определенном смысле и на степенные ряды в комплексной
области, однако для осупа;ествления этого нам прип1лось бы обоб-
па;ить понятие производной и интеграла на функции
комплексного аргумента, а это не входит в задачу настояпа;его курса.
Итак, будет рассматривать ряды
оо
^ a„(x-Xo)«, C3.21)
где а^ (я = О, 1, 2, ...), х и Xq действительны. Если R — радиус
оо
сходимости ряда ^ aj^z - Xq), где z — комплексное число, т.е.
п = 1
ряда с теми же коэффициентами, что и у ряда C3.21), но
рассматриваемого в комплексной области, то, очевидно, ряд C3.21)
сходится, если |х - XqI < i?, и расходится, если |х - XqI > R.
В этом случае R по-прежнему называется радиусом
сходимости ряда C3.21), а интервал (Xq - i?, Xq + i?) — его
интервалом сходимости.
ТЕОРЕМА 6. Если R — радиус сходимости степенного ряда
оо
Кх)= £ a„(x-Xo)«, C3.22)
i? > О, то:
1) функция f имеет в интервале (Xq - i?, Xq + R)
производные всех порядков, и они находятся из ряда C3.22)
почленным дифференцированием;
2) для любого xg (Xq - i?, Xq + R)
X оо (у — у \П ~т \
Xq П-0 a ^ ±
m, e, внутри интервала сходимости степенной ряд можно
почленно интегрировать;
3) степенные ряды, получающиеся из ряда C3.22) в
результате почленного дифференцирования или интегрирования,
имеют тот же радиус сходимости, что и сам ряд C3.22).
Короче, внутри интервала сходимости степенного ряда его
можно почленно интегрировать и дифференцировать любое
число раз.
Доказательство. В силу леммы, доказанной в начале
оо
этого пункта, радиусы сходимости ряда ^ naj^x - x^Y ~ ? по-
п = 1
лучаюгцегося из ряда C3.22) почленным дифференцировани-
°° и (х ~ Хп)^ ^ ^
ем, и ряда ^ — ^ , получаюгцегося из того же ряда
п = 0 П + 1
почленным интегрированием, равны радиусу сходимости
ряда C3.22) (чтобы в этом убедиться, достаточно сделать замену
переменного х - х^ = z).
Всякий степенной ряд вида C3.22) с радиусом
сходимости R равномерно сходится на отрезке [Xq - г, Xq + г], О < г < i?
(см. теорему 2 в п. 33.1), поэтому утверждение теоремы о
возможности почленного дифференцирования и интегрирования
вепа;ественных степенных рядов непосредственно следует из
соответствуюпа;их теорем о дифференцируемости и
интегрируемости функциональных рядов, доказанных в п. 32.4. П
Заметим, что, например, возможность почленного
интегрирования степенного ряда C3.22) внутри интервала
сходимости (Xq - i?, Xq + К) сразу вытекает (см. теорему 10 в п. 32.4)
из того, что степенной ряд равномерно сходится на всяком
отрезке [Xq - г, Xq + г], о < г < i?. Отсюда следует, что при
почленном интегрировании радиус сходимости степенного ряда
не уменыаается. Доказанная теорема содержит более полное
утверждение, что указанный радиус сходимости, кроме того,
и не увеличивается, т. е. остается прежним.
ТЕОРЕМА 7. Если функция f аналитическая в точке Xq,
т, е, представима в окрестности этой точки рядом C3.22)
с радиусом сходимости i? > О, то
/(-)(хо)^ ^ = 0,1,..., C3.23)
f(^)= n^-^i^-^r-
т, е.
Доказательство. Продифференцировав п раз обе части
равенства C3.22), получим (см. теорему 6)
f^x) = n(n- 1) ... 2 • 1 • а^ + (я + 1)п ... 2a^ + i(x-Xo) +
+ (я + 2)(я+ 1) ... За^ + 2(^ - ХоJ + ... .
Отсюда при X = Xq и вытекает формула C3.23). П
ТТз
Заметим, что из доказанной теоремы следует еш;е раз
свойство единственности разложения функции в степенной ряд
(правда, на этот раз, в силу сделанных ограничений, только в
действительной области (ср. с п. 33.3)).
33.5. Разложение функций в степенные ряды.
Различные способы записи
остаточного члена формулы Тейлора
Определение 4. Пусть функция f определена в некоторой
окрестности точки Xq и имеет в этой точке производные всех
порядков. Тогда ряд
1 ЧгГ^(^-^о)" C3.24)
называется рядом Тейлора функции f в точке Xq.
При Xq = О ряд C3.24) называется т^кжерядом Маклорена
функции f(x).
Как известно, всякая аналитическая в точке Xq функция
бесконечно дифференцируема в некоторой окрестности этой
точки и равна в этой окрестности сумме своего ряда Тейлора.
Вместе с тем оказывается, что супа;ествуют функции,
бесконечно дифференцируемые, но не аналитические и, значит, не
представимые своим рядом Тейлора.
Примером является функция
А^)-|п''''' '''''' ""^п' C3.25)
^ ^ [О для х = 0. ^ ^
При X ^ О эта функция имеет производные всех порядков,
которые легко вычисляются:
Пх) = А,-1/-\ Пх) = -^.е-'^'"' + У'\
И вообгце
1Щх) = Р^1у"^\
где Р^ - I — многочлен некоторой степени относительно -
(п — порядковый номер, а не степень многочлена), т. е.
f^^\x) — линейная комбинация слагаемых вида
\е-'^''\ т = 0,1,2,.... C3.26)
ТТб
Это легко проверяется по индукции. Сделав замену
переменного t = —Z, найдем, применив правило Лопиталя, предел мо-
дуля выражения C3.26) при х ^ 0:
lim
+ 171/2
= lim ^—= 0.
Отсюда следует, что и предел выражения C3.26) при х ^ О
также равен нулю и что при любом п = О, 1, 2, ...
lim ГЩх) = lim Р/IV'/"' = 0. C3.27)
х^±0 х^О "'Ух)
Из формулы C3.27) при п = О }лп= 1 следует, что функция
/ непрерывна в точке х = О и lim fix) = О, поэтому (см.
х^±0
следствие 2 из теоремы 3 п. 11.2) /'@) сугцествует и /'@) = 0.
По индукции легко аналогично убедиться, что /^^^@) = О,
п = 0,1, 2, ... .
Таким образом, все члены ряда Тейлора функции C3.25) в
точке Xq = О равны нулю, поэтому его сумма при всех х также
равна нулю и, следовательно, не совпадает с самой функцией.
Заметим егце, что, согласно теореме 5 п. 33.3, функция C3.25)
не может быть разложена ни в какой степенной ряд (так как
если бы это было возможно, то он оказался бы рядом Тейлора),
а это и означает, что она не является аналитической.
УПРАЖНЕНИЯ. 6. Установить, можно ли разложить функцию f(x) =
= е~^/^, X > О, /@) = О, на отрезке [О, 1] в ряд Маклорена.
7. Пусть
1 при X > О,
^ ' |-1 при X < 0.
Доказать, что функцию 0(x)e-i/^^ можно так доопределить при х = О,
что в результате получится бесконечно дифференцируемая на всей
числовой оси функция.
Заметим, что если функция раскладывается в некоторой
окрестности данной точки в степенной ряд, то такой ряд
единствен (см. теорему 5 или теорему 7) и является ее рядом
Тейлора в этой точке. Однако один и тот же степенной ряд может
служить рядом Тейлора для разных функций. Так, степенной
оо
ряд с нулевыми коэффициентами ^ Ох^ является как рядом
п = 0
Тейлора функции, тождественно равной нулю на всей число-
и?
вой оси: f(x) = О, xeR, так и рядом Тейлора функции C3.25) в
точке X = 0.
Возникает вопрос: когда ряд Тейлора C3.24) бесконечно
дифференцируемой в точке Xq функции f(x) сходится на
некотором интервале к /(х)? Чтобы исследовать этот вопрос, напи-
П1ем формулу Тейлора для функции / (см. п. 13.1)
f(x)= £ ^1!^(х - хо)^ + г„(х) C3.28)
(она справедлива при любом п = О, 1, 2, ...). В этой формуле
г^(х) — остаточный член формулы Тейлора, а не остаток ряда
Тейлора, так как с остатком ряда нельзя оперировать до тех
пор, пока не будет установлено, что ряд сходится, и лип1ь в
случае, когда его сумма равна функции /(х), можно
утверждать, что остаточный член формулы Тейлора совпадает с
остатком ряда Тейлора. Полагая
перепигаем формулу C3.28) в виде
fix) = s^ix) + r^ix), C3.29)
где s^(x) — п-я частичная сумма ряда Тейлора. Отсюда
следует, что, для того чтобы функция / была равна на
рассматриваемом интервале сумме своего ряда Тейлора, т. е. чтобы
lim sJx) = f(x), необходимо и достаточно, чтобы для всех х
л ^ оо ''-
из этого интервала ее остаточный член в формуле Тейлора
стремился к нулю:
lim r(x) = Q. C3.30)
Если это имеет место, то из формулы C3.29) следует, что
остаточный член формулы Тейлора rj^x) является также и
суммой п-то остатка ряда Тейлора C3.24).
Для того чтобы найти условия, при которых остаточный
член в формуле Тейлора стремится к нулю в окрестности
данной точки, предварительно установим некоторые формы его
возможной записи.
ТЕОРЕМА 8. Пусть функция f определена и непрерывна
вместе со всеми своими производными до порядка п + \
включительно на интервале (Xq - Л, Xq + Л), Л > 0. Тогда
остаточный член г^(х) ее формулы Тейлора C3.29) для всех
TTs
xe(xQ - h, Xq + h) можно записать любым из следующих трех
способов:
г^(х) = 1 1 (х - t)''f^'' + '^\t) dt, C3.31)
nl
^-^^^ ^ oTTlf ^^ " ^оГ ^ \ C3.32)
где ^ принадлежит интервалу с концами в точках х^и х, и
^^(^) ^ /(^^1)[хо + 9(х-Хо)]^^ _ Q^,^^ _ ^^^,^1^ ^33.33)
гдеО<^<1.
Формула C3.31) называется остаточным членом
формулы Тейлора в интегральной форме, формула C3.32) — в
форме Лагранжа, а C3.33) — в форме Коши,
Доказательство. Из основной теоремы
дифференциального и интегрального исчисления (см. теорему 4 п. 25.3) имеем
f(x) = /(Хо) + 1 nt) dt = /(Хо) - } nt) d(x - t).
Xq Xq
Проинтегрировав no частям интеграл в правой части
равенства, получим
f{x) = /(хо) + {-nt){x - t))\l + I r{t){x -t)dt =
X
= /(Xq) + f\xQ)(x - Xq) + I f\t)(x - t) dt.
Xq
Пусть для некоторого m <: n уже доказано, что
fix)= £ L^(x-Xo)'^+-^—-]f^'^Kt)ix-tr-^t. C3.34)
Проинтегрируем по частям последний член:
1—. 1 fM{t){x - f)'» -1 df = -i- f f^t) d{x - 0'» =
~ 1)! i тп\ I
(m-l)!
./""'ft)(x- t)"
Л'"'(-«о)
TYlA *'
m
"-0
(X - Xq)"^ + —^ \ fim + l){t){x - t)"^ dt
TYlA *'
и подставим это выражение в C3.34):
fix) = £ Цр(х - x^f + J- 1 /СП + i)@(x - tr dt.
119
в результате получилась формула C3.34), в которой т
заменено на m + 1.
Таким образом, формула C3.34) доказана методом
математической индукции для всех т <. п. При т = п ее остаточный
член имеет вид C3.31).
Применим теперь первую интегральную теорему о среднем
значении к интегралу C3.31). Заметив, что функция (х — tY
не меняет знака на промежутке интегрирования, вынесем за
знак интеграла «среднее значение» производной fi^i + i) (см.
следствие из теоремы 1 в п. 24.2):
г (х) = 1 j /(^ + 1)@(х - t)^ dt = 1^!113М J (х - ty dt =
nl [ n + 1
Г±1^Ш(х-х)п + 1
где ^ лежит на интервале с концами в точках Xq и х. Формула
C3.32) доказана.
Если же применить интегральную теорему о среднем к
интегралу C3.31), вынося за знак интеграла «среднее значение»
всей подынтегральной функции (см. п. 24.2), то получим
г (х) = 1 J /(^ + 1)@(х - t)^ dt = t^^^lpSl(x - ^)^(х - Xq), C3.35)
Xq
где ^, как и вып1е, лежит на интервале с концами в точках
XqH X, т. е.
^ = Xq + е(х - Xq), о < е < 1.
Отсюда x-^ = x-Xq- 9(х - Xq) = (х - Xq)A - 9). Подставив это
выражение в C3.35), получим формулу C3.33). П
Приведем достаточное условие разложимости функции в
степенной ряд.
ТЕОРЕМА 9. Пусть функция f бесконечно
дифференцируема и все ее производные ограничены в совокупности на
интервале (Xq - л, Xq + Л), т. е. существует такая постоянная
М > О, что для всех xg(Xq - Л, Xq + Л) г/ всех я = О, 1, 2, ...
выполняется неравенство
|/(^)(х)| < М. C3.36)
Тогда на интервале (Xq - Л, Xq + К) функция f
раскладывается в ряд Тейлора:
п = 0
f(x)= ^ ^_^^(x-XQ)^ |x-Xq|<A. C3.37)
120
Доказательство. Прежде всего заметим, что, каково бы
ни было число а,
lim ^ = 0 C3.38)
(см. пример 4 в п. 4.9, впрочем, это равенство следует и
непосредственно из того, что выражение обгций член сходя-
гцегося ряда ^ —; см. C2.4)).
Для того чтобы доказать формулу C3.37), достаточно
убедиться (см. C3.30)), что
lim г(х) = 0, C3.39)
где г^(х) — остаточный член в формуле Тейлора функции /.
Возьмем г^(х) в форме Лагранжа (см. C3.32)). Из неравенства
C3.36) следует, что
где 1^ - XqI <\х - Xq\< h и, следовательно, ^ g (Xq - Л, Xq + h). На
основании C3.38) при а = \х - Xq\ имеем
I 'У 'У \ Т1 \ 1.
lim ^^4 = 0,
поэтому при \х - Xq\< h выполняется условие C3.39). П
УПРАЖНЕНИЕ 8. Заменим в теореме 8 условие ограниченности
производных f^^\x), я = 1, 2, ... , на интервале (xq - h, Xq-\- h) условием их
ограниченности только в точке Xq, т. е. пусть супдествует такое М > О, что
для всех п выполняется неравенство l/^^H-^o)! ^ ^- Тогда, очевидно, ряд
C3.37) сходится, и притом абсолютно, на всей действительной оси, так
как \—j^Kxq)(x - Xq)" < —^^, а ряд 2^ --^— сходится при всех х
\п. \ п. ^_Q п.
(см. ряд C2.4)). Следует ли отсюда утверждение теоремы 9?
33.6. Разложение элементарных функций
в ряд Тейлора
Прежде всего найдем разложение в ряд некоторых основных
элементарных функций.
1.Разложение в ряд функции f(x) = е^. Так как
f{n)(^x) = е^, то для любого фиксированного h > О при всех
xe(-h. К) и всех п = Q, 1, ...
О < /(^)(х) < е^.
121
Таким образом, условия теоремы 9 выполнены (Xq = 0),
поэтому функция е^ раскладывается в ряд Тейлора C3.34) на
любом конечном интервале, а следовательно, и на всей
действительной оси. Так как в данном случае /^^^@) = 1, то,
согласно формуле C3.37), разложение е^ имеет вид
е^= У —^. C3.40)
Напомним, что в п. 32.1 было установлено, что ряд ^ —
^^^ п.
абсолютно сходится на всей комплексной плоскости. Теперь
показано, что для действительных г = х его сумма равна е^,
В случае сугцественно комплексных г его сумму, по аналогии,
обозначают е^\ таким образом, формула
е'= У ^ C3.41)
ДЛЯ комплексных 2 является определением функции е^.
Данное определение естественно, во-первых, потому, что в
случае действительного 2 = х эта функция совпадает с
показательной функцией е^, sl во-вторых, функция е^ сохраняет ряд
характерных свойств функции е^. Покажем, например, что
g^ig^2 = g^i + ^2 C3.42)
для любых комплексных 2^ и ^2.
Ряд C3.41) абсолютно сходится, поэтому ряды
_ оо 2V^ 'У оо 2,V}
можно почленно перемножить (см. п. 30.10), а так как получаю-
гцийся при этом ряд также абсолютно сходится, то его члены
можно располагать в произвольном порядке. Соберем все члены,
содержапа;ие произведения 2^2^ с одинаковой суммой я + т, и
расположим эти группы членов по ее возрастанию:
е^^е '^ = У У —^ • — =
п + т = 0 k = Q (П + m-k)\ Ы
(я + 771)! ^n + m.-k ^k =
.О (я + 771)! k = o {п + т- k)\k\ 1
122
2.Разложение в ряд shxnchx. Заменив в формуле
C3.40) X на -X (это означает просто изменение обозначения),
получаем
е-^= у bLl^. C3.43)
Складывая и вычитая равенства C3.40) и C3.43), а затем
разделив их на два, получим
оХ — о-Х оо ^2k + 1
В силу единственности разложения функций в степенные
ряды, правые части этих формул являются рядами Тейлора
функций ch X и sh х.
Функция е^ определена теперь для всех комплексных z,
поэтому на сугцественно комплексные значения аргумента
можно распространить и гиперболические функции ch х и
sh X, положив
Определенные таким образом ch 2 и sh 2 для комплексных
Z раскладываются в степенные ряды C3.44) и C3.45), сходя-
гциеся на всей комплексной плоскости (под х в них в этом
случае понимается комплексное число).
3. Разложение в ряд sin х и cos х. Формулы
Эйлера. Если /(х) = sin х, то f^^\x) = sin [х + ^| ] (см.
пример 3, п. 10.1), поэтому |/^^^(х)| < 1 для всех
действительных X. Согласно теореме 9, отсюда следует, что функция sin х
раскладывается в степенной ряд на всей действительной оси.
Вспоминая формулу Тейлора для синуса (см. п. 13.3),
получаем ряд Тейлора для sin х:
ОО / 1 \ky.2k + 1
Рассуждая аналогично и используя формулу Тейлора для
косинуса (см. п. 13.3), получаем и для него ряд Тейлора
<^os^= Е Ц^' C3.47)
также сходяпа;ийся на всей действительной оси.
123
в силу теоремы Абеля (см. п. 33.1), ряды в правых частях
формул C3.46) и C3.47) сходятся также и при любом
комплексном х; это позволяет дать определение синуса и косинуса
для комплексных значений аргумента, положив для любого
комплексного 2
def оо / -1 \ky2k + 1
def оо / -\\ky.2k
В комплексной области легко установить связь между
показательной и тригонометрическими функциями. Заменив 2 в
ряде C3.41) сначала на i2, sl затем на -i2, получим
giz= у гг g-j2= у {-i.) г г _ C3.50)
В силу равенств i^* = (-1)*, ^г = 1, 2, ... , и, следовательно,
i2* + i = (-l)*i, й = 0, 1, ... , из C3.50) имеем
giz -)- g-iz _ оо (_]^)ftg2ft giz - g-iz _ оо (_X)tg2t+l
2 .■^o Bfe)! ' 2i .■^o Bfe + l)! *
Сравнив последние формулы с формулами C3.48) и C3.49),
получим
COS2 = ^^l±^, Sin 2 = ^^!^. C3.51)
Отсюда непосредственно следует также формула
cos 2 + /sin 2 = е^^ C3.52)
Равенства C3.51) и C3.52) называются формулами Эйлера.
Они справедливы, в частности, и для действительных 2.
Если в формуле C3.52) 2 = ф — действительное число, то
cos ф + /sin ф = е^^.
Отсюда, во-первых, следует, что
\е''^\ = 1,
так как \е^^\ = Jcos ^ф + sin ^ф = 1, и, во-вторых, что
комплексное число 2 с модулем г и аргументом ф, т.е. 2 = r(cosф +
+ / sin ф), можно записать в виде
2 = ге^^,
называемом показательной формой записи комплексного числа.
124
Положив 2 = -1 и, следовательно, ф = тг, получим
Эта формула показывает, что числа -1, е, тг и / связаны между
собой.
Напомним, что числа -1, тг, е и / были открыты
математиками при изучении весьма далеких друг от друга задач: число -1
было введено для того, чтобы операция вычитания имела смысл
для любых натуральных чисел (кроме того, введение
отрицательных чисел оказалось удобным при сравнении температур тел с
температурой замерзания воды, при измерении высот и низин на
Земле относительно уровня моря и т. п.); число тг найдено как от-
ногаение длины окружности к ее диаметру, е — как такое
основание показательной функции, при котором производная
функция совпадает с самой функцией, а мнимая единица / введена для
того, чтобы каждое квадратное уравнение имело регаение.
С помогцью формул Эйлера легко находятся модуль и
аргумент числа е^, где 2 = х -\- iy. Действительно (см. C3.42)),
^2 = ^x + iy = ^x^iy = gX^cOS У -\- i sin у),
Т. е. \е^\ = е^, Arg е^ = у.
Синус и косинус в комплексной области обладают
многими, однако далеко не всеми свойствами, которыми они
обладают и в действительной области. Появляются и новые
свойства, не имеюпа;ие аналогов в действительной области.
УПРАЖНЕНИЯ. Доказать, что при любом комплексном z:
9. sin (-z) = -sin z, cos (-z) = cos z.
10. sin^ z + cos^ z = 1.
11. sin {z + 27c) = sin z, cos {z + 2%) = cos z.
12. Для всех геС справедливо неравенство е^ ^ 0.
def •
13. Пусть ig Z = .ЁН1£. Доказать, что для всех геС выполняется неравен-
C0S2
ство ig z^ ±i.
Указание. Выразить ig z через показательную функцию е^.
14. Можно ли разложить функции л/г, sin л/г, cos Jz в степенной ряд C3.3)?
Покажем, что абсолютные величины синуса и косинуса в
комплексной области могут быть больп1е единицы и, более
того, не ограничены по абсолютной величине.
125
Заменим в рядах C3.48) и C3.49) z на iz\
U" 2ЛП -1-1 "" 2'^п
sin iz = 1\ , cos iz = У
Сравнив получивп1иеся ряды с рядами C3.44) и C3.45) (при
X = z), получим
i shz = sin iz, ch z = cos iz.
В частности, при действительном z = у имеем
|sin/г/| = |sh г/| и \cos iy\ = ch у,
откуда и следует, что на мнимой оси функции sin z и cos z не
ограничены по абсолютной величине.
Заметим, что функции ch 2 и cos z в силу формулы ch z =
= cos iz получаются одна из другой умножением их аргумента
на число /. Геометрически это означает поворот координатных
осей в комплексной плоскости на прямой угол. Иначе говоря, в
комплексной области функции ch 2 и cos z, как функции
точки, являются одной и той же функцией, записанной в разных
координатных системах, получаюгцихся одна из другой
поворотом на прямой угол! Подобное обстоятельство имеет место и
для функций sh 2 и sin z.
В качестве свойства нового типа у показательной функции
в комплексной области укажем епа;е на ее периодичность"^.
Именно, докажем, что функция е^ имеет период 2% i:
^2 + 27zi = e^e^T^i = e^(cos 271 + / sin 2n) = e^.
@0.4Z) yoo.oA)
Покажем ena;e, что множеством значений показательной
функции W = е^ является вся комплексная плоскость за
исключением точки Z = 0.
В самом деле, каково бы ни было число w = ре^^, р ^ О, су-
па;ествует такое z = х + yi, что w = е^, т. е. ре^^ = е^е^У. Очевидно,
что это имеет место, например, при х = In р, г/ = \|/.
4. Разложение в ряд функции 1пA + х).
Формула Тейлора для 1пA + х) имеет вид (см. п. 13.3)
1пA + х) = х-^ +^-... + (-1)^ + 1— + г^(х).
* Если функция / определена на некотором множестве чисел (вообще
говоря, комплексных)X, то число ТеС называется ее периодом, если для
каждого хеХ имеем х ± ТеХ и f(x + Т) = f(x). Функция, имеющая
период, называется периодической.
126
Запигаем остаточный член г^(х) в форме Лагранжа.
Заметив, что
[1пA + х)](^ + 1) = (-1Г-
т
A + х)" + 1'
получим
г(х) = (-1)^ ^^^ -, о < е < 1.
Если О < X < 1,тоО< -—-- < 1 и поэтому \г (х)\ < -, откуда
1 + 9х 71+1
lim г(х) = 0. C3.53)
Если же -1 < X < О, то целесообразно записать остаточный
член г^(х) в форме Konin:
г(х) = (-1)^ A-е)^ ^х^ + Ч
в этом случае
0< ^ "^ = ^ "^ < 1
1 + 0Х 1-0|х|
так как в числителе дроби -—-|—: из единицы вычитается чис-
ло болыаее, чем в знаменателе; кроме того,
1 - 1 <-1 .
1 + 0Х 1-0|х|
поэтому
|г,(х)| <
1-0
X
п + 1 <
X
п+1
1 + 0х|' ' 1-\х\
0х|
откуда при -1 < X < о также получаем C3.53).
Таким образом, для любой точки х полуинтервала (-1, +1]
имеет место разложение
1пA + х)= £ (-1)^ + 1^. C3.54)
71^1 ^
При X = -1 ряд в правой части равенства C3.54) отличается
от гармонического ряда лигаь множителем -1 и поэтому
расходится. Расходится он также и при всех х таких, что |х| > 1, так
как в этом случае п-й член ряда C3.54) не стремится к нулю,
более того (см. п. 12.2),
lim \^\ = +00.
5. Разложение в ряд степени бинома A + х)^.
Формула Тейлора для степени бинома имеет вид (см. п. 13.3)
A + х)« = 1 + ах + 5fcJ^x2 + ...
... + «(а-1)-(а-ге + 1)^„ ^ ^^^^^^ a^R,x>-l. C3.55)
J27
Рассмотрим соответствуюгций ряд (называемый
биномиальным рядом с показателем а):
1+ £ Ш+1)...(а-п+1)^п^ C3.56)
п ^ 1 ^'
Если а — неотрицательное целое, то ряд C3.56) содержит
конечное число членов, отличных от нуля, и, следовательно,
сходится при всех х.
Рассмотрим теперь случай, когда а не является
неотрицательным целым. В этом случае в ряде C3.56) все члены
отличны от нуля при X ^ 0.
Для исследования абсолютной сходимости ряда C3.56)
используем признак Даламбера. Иначе говоря, применим
признак Даламбера к ряду с п-ш членом
а(а+ 1) ... {а- п + 1)^^
Замечая, что lim -Л-Ll = Цщ
х\
... = \х\, получаем, что ряд
C3.56) абсолютно, а значит, и просто сходится при |х| < 1 и
расходится при |х| > 1.
Однако из одного лигаь факта сходимости биномиального
ряда C3.56) при |х| < 1 нельзя егце сделать заключение о том,
что его сумма равна A + х)^. Для этого надо доказать, что в
формуле C3.55) г^(х) -^ О при я ^ оо и |х| < 1.
Замечая, что
(A + х)«)(^ + 1) = а(а - 1)...(а - п)A + х)«-^- Ч
запип1ем остаточный член г^(х) формулы C3.55) в форме Konin:
г„(х) = сс(а-1)-(а-/г)A + ех)«-"-1^^ _ ^^„^^ +1^ О < Э < 1
п
(Э зависит от X и от п). Положим
А (х) = («-1)-[(а-1)-(га-1)]-у«^
S„(x) = ax(l + Qxr-\ C„(x) = [^^
тогда
г„(х)=А„(х)Б„(х)С„(х).
Очевидно, А^(х) является обпа;им членом биномиального
ряда с показателем а - 1 и, следовательно, в силу доказанной вы-
nie сходимости биномиального ряда при |х| < 1,
lim А(х) = О, 1x1 < 1.
128
Далее, из того, что 1 - |х| < 1 + 9х < 1 + |х|, следует, что
значения |Б^(х)| заключены между величинами
|ах|A-|х|)^-1 и |ах|A+ |х|)^-1,
не зависягцими от 9, т. е. последовательность {В^(х)} при
фиксированном xg(-1, 1) ограничена. Наконец,
К(х)\
1 -01x1
|1 + 0х|
Из установленных свойств АДх), В^(х) и С^(х) следует, что
lim г(х) = О, 1x1 < 1.
Таким образом, для любого xg(-1, 1) справедливо равенство
A+ХГ=1+ у «(«-1)-(«-^+1);,».
д = 1 '*"
Задача 4. Доказать, что: 1) в точке х = 1 при а > -1 биномиальный
ряд сходится, а при а < -1 — расходится;
2) в точке X = -1 при а > О биномиальный ряд абсолютно сходится, а
при а < О — расходится.
При этом каждый раз, когда биномиальный ряд C3.56) сходится,
его сумма равна A + х)^.
6. Л огарифмическ ая функция в комплексной
области. Функция w = wB), обратная показательной
функции е^,т. е. определяемая равенством е^ = 2, называется
логарифмической и обозначается Ln 2.
Таким образом, для любого 2^0 имеем е^^^ = 2.
Bbinie было показано, что множеством значений
показательной функции е^ является вся комплексная плоскость за
исключением точки 2 = 0, поэтому это же множество является
и областью определения логарифмической функции.
В силу периодичности показательной функции,
логарифмическая функция является многозначной: если при данном 2^0
комплексное число w — значение Ln 2, то всякое комплексное
число вида W + 27zni, п = О, ±1, ±2, ... , также является
значением Ln 2, так как
^w + 2nni = pW
Если w = и + iv, то
2 = е^ = е^^^^ = е^е^^ = e"(cos v + / sin v),
поэтому
1^1 = e^, Arg 2 = V Л- 2nn, n = 0, ±1, ±2, ... .
Следовательно, г/ = In 1^1, и если ф — какое-либо значение
аргумента 2,Tov = (p-\- 2т1п, п = О, ±1, ±2, ... .
129
Таким образом, все значения Ln 2, 2 ^ О, задаются формулой
Ln 2 = In 1^1 + (ф + 27zn)i, п = 0, ±1, ±2, ... , z^ 0.
Если значение аргумента ф числа z ^ О выбирать всегда на
полуинтервале (-тг, тг], т. е. считать, что ф = arg z (см. п. 19.1),
то значение логарифма Ln z определяется однозначно.
Однозначная функция, ставягцая в соответствие числу z указанное
значение Ln z, обозначается In 2 и называется главной ветвью
логарифма. Итак, если z^ Он
Z = г (cos ф + / sin ф), -7Г< ф < 71, C3.57)
то
1п2 = 1пг+/ф. C3.58)
Отсюда следует, что если 2 = х + /г/ и -тг < г/ < тг, то
In е^ = Z.
Если z^ = r^(cos ф^ + / sin ф^), -| < Ф1 ^ |? ^2 ^ r2(cos Ф2 +
+ /Sinф2), -^<ф2<^,ТО
In z^Z2 = ln z^-\- In ^2, In — = lii z^- In ^2. C3.59)
Эти формулы непосредственно вытекают из формулы
C3.58) и правил умножения и деления комплексных чисел.
Например, для первой формулы C3.59) имеем
-тг < arg z^ + arg ^2 = arg z^Z2 < тг,
поэтому
In z^Z2 = In \z^Z2\ + i arg z^Z2 = In \z^\ + In I22I + i (arg z^ + arg Z2) =
= (In \z^\ + / arg z^) + (In I22I + i arg Z2) = \n z^-\- In ^2.
Если 1^ - l| < 1, 2 ^ 0, TO можно показать, что функция In z
раскладывается в ряд по степеням z - 1:
1п2= £ (-1)^-1(^-1)"^ |2-1|<1, z^O.
п = 1 ^
Заменив в этом разложении 2 на 1 + 2, получим равносильную
формулу
1пA + 2)= £ (-1)^-1£!, И<1, z^-1. C3.60)
Естественный вывод этой формулы производится с помогцью
методов комплексного анализа, изложение которых выходит за
рамки данной книги. Впрочем, ее можно получить и методами,
рассматриваемыми в нашем курсе. Это будет сделано в п. 55.13.
Тзд
Зная для комплексного переменного z функции е^ и Ln 2,
можно определить степень w^ комплексного числа w с
комплексным показателем г по формуле
в силу многозначности логарифма, степень w^ является
многозначной функцией от z.
УПРАЖНЕНИЕ 15. Доказать, что все значения i^ являются
действительными числами.
33.7. Методы разложения функций в степенные ряды
Дифференцируя или интегрируя известные разложения в ряд
Тейлора, можно получать разложения новых функций в
степенные ряды. Так, например, интегрируя формулу
геометрической прогрессии
-^ = l-t + t'^- ... + {-1L'' + ...
1 + ^ ^ ^
в пределах от О до х, |х| < 1 (что законно, так как ряд в правой
части этого равенства равномерно сходится на отрезке с
концами в точках О и X при |х| < 1), получим известную уже
формулу C3.54):
Раныае эта формула была доказана на полуинтервале (-1; 1],
теперь только для интервала (-1; 1). Однако, в силу второй
теоремы Абеля о степенных рядах (п. 33.1), из
справедливости формулы C3.54) на интервале (-1; 1) сразу следует ее
справедливость и при X = 1. Действительно, ряд в правой части
этой формулы сходится при X = 1 и, следовательно, его сумма
непрерывна в этой точке (см. теорему 3 в п. 33.1), функция
In A + х) также непрерывна при х = 1, поэтому в обеих частях
равенства C3.54) (если известно, что оно справедливо на
интервале (-1; 1)) можно перейти к пределу при х ^ 1 - О и тем
самым доказать его справедливость и при х = 1:
In 2
(_1)д + 1
В результате дифференцирования или интегрирования
заданного степенного ряда иногда удается получить ряд, сумма
которого уже известна; это позволяет вычислить и сумму
исходного степенного ряда.
Примеры. 1. Найдем разложение функции arcsin х в
ряд. Заметив, что
(arcsin)" = ,
разложим (arcsin xY в ряд по формуле разложения степени
бинома (см. п. 33.6):
(arcsin х)^ =—^^ = 1 + У Bя-1)!!^2я^ C3.61)
7Г^2 п^1 2-я!
Радиус сходимости получивгаегося ряда равен единице (см.
там же). Интегрируя ряд C3.61) от О до |х| < 1, получим
arcsm X = = х + у ^—-—-^- -.
J уГ3^2 А Bя)!! 2я + 1
2. Разложим функцию arctg х в степенной ряд и с по-
могцью него найдем числовой ряд, сумма которого равна тт.
Поступая при |х| < 1 аналогично примеру 1, имеем
arctg - - I ГТ^ - I (£„ (-т^"] dt - £^ (-1)" 1^. C3.62)
Заметим, что полученный ряд при х = ±1 по признаку
Лейбница (см. теорему 11 п. 30.9) сходится, поскольку сходится
знакопеременный ряд ^ -^—^-—.
Функция arctg X непрерывна при х = ±1, поэтому,
согласно второй теореме Абеля для степенных рядов (см. теорему 3
п. 33.1), сумма ряда C3.62), являясь непрерывной функцией
на отрезке [-1; 1] и совпадая с arctg х на интервале (-1; + 1),
совпадает с ним и в концевых точках х = ±1. Иначе говоря,
разложение C3.62) справедливо для отрезка [-1, +1]. Взяв в
этом разложении, например, х = 1 и заметив, что arctg 1 ^ ^?
получим
7г_ ^ (-1)"
C3.63)
4 „^0 2я + 1
Этот ряд называется р^Eож Лейбница.
Отметим, что арктангенс определен на всей
действительной числовой оси, в частности и вне отрезка [-1, 1]. Однако
его разложение в степенной ряд C3.63) справедливо только на
этом отрезке. Вне этого отрезка ряд C3.63) расходится, в чем
легко убедиться, найдя его радиус сходимости, например, по
формуле C3.9). Анализ этого явления проводится в теории
функций комплексного переменного.
132
3. Найдем сумму ряда
оо
S(x)= Y, п^""' C3.64)
п = \
Радиус сходимости этого ряда равен единице. В этом легко
убедиться, например, по признаку Даламбера
lim
(п + 1)х" + 1
\х\.
пх
Следовательно, ряд C3.64) абсолютно сходится при |х| < 1 и
расходится при |х| > 1. Из C3.64) следует, что
^^= у ях^-1, \х\< 1.
•^ п = \
Проинтегрируем этот ряд почленно от О до х, |х| < 1,
^' S(t)
it ,4^1 1-х
и затем продифференцируем получивгаееся тождество:
S(x) ^ d X ^ 1
X dxl - X A - х)^'
В результате получаем
S(x)= ^ |х|<1.
A -ХJ
4. Найдем сумму ряда:
S(x)= £ ^;. C3.65)
Радиус сходимости этого ряда равен единице; в этом легко
убедиться, например, тем же способом, что и в случае ряда
C3.64). Продифференцировав ряд C3.65) почленно
оо „
S\x)= £ ^
п-\
п=1 П
И использовав разложение логарифма (см. п. 33.6), получим
xS\x)= £ — = -1пA-х), Н<1, или SXx) =-^"^^^ ~''\
Принимая во внимание, что aS@) = О, окончательно имеем
Six) = -} М1-Л dt.
Таким образом, здесь ответ выражается не в элементарных
функциях.
Тзз
УПРАЖНЕНИЯ. 16. Разложить в степенной ряд функцию (arcsin х)^.
оо
17. Найти сумму ряда ^ п^х^.
п = 1
5. При разложении рациональных функций в ряд Тейлора
удобно использовать их разложение на элементарные дроби
(см. п. 19.6). Поясним этот метод на примере: найдем
разложение функции
т
2
{2-1){2-2)
В ряд Тейлора в окрестностях точек 2^ = О, 2^= - и 2^ = 4.
Разложив функцию fB) на элементарные дроби, получим
2 _ 1 _ 2
B-1)B-2) 1-2 2-2
Найдем сначала ряд Тейлора для /(г) в окрестности 2q = 0. Для
этого заметим, что дроби и = — представляют
\- 2 2-2 1- 2/2
оо
собой суммы бесконечных геометрических прогрессий ^ 2^
п = о
И Y, 9 ^^ знаменателями 2 и - при условии, что \2\ < 1 и, со-
п = о
ответственно, что
< 1. Оба этих условия выполняются,
когда выполняется первое. Таким образом,
у оо oo^oox-ix
Это и есть разложение функции fB) в ряд Тейлора в
окрестности точки 2q = 0, причем радиус сходимости получивгаегося ряда
равен 1. Действительно, в силу доказанного, он не может быть
меныае 1 (полученный степенной ряд сходится при 1^1 < 1), с
другой стороны, он не может быть и болыае 1, так как на
расстоянии, равном единице от точки 2q = О, имеется точка 2^ = 1,
для которой lim fix) = оо^ и поэтому разложение функции fB)
В степенной ряд не может сходиться в точке 2^.
Для получения ряда Тейлора функции /(г) в окрестности
3
точки 2q= - снова воспользуемся суммой бесконечно убываю-
гцей геометрической прогрессии, но проделаем это иначе, вы-
134
деляя в знаменателях элементарных дробей, на которые
разложена дробь /(г), члены ^ ~ о-
B-
-1)B
-2)
2
l + 2(z-
1
1]
- Z
1 -
2-
4
-2^2
Z
-1)
1
2
оо
2 ^ (-1)"
п-0
1
2
2^
-1)
2J
4Е 2«Гг-|1"= £ 2" + i[(-l)" + ^-2]f2-|
д = О ^ -^ ^ д = О ^
Эта выкладка справедлива при условии, что 2
-1
< 1
(абсолютная величина знаменателя рассматриваемых геометри-
<i.Pac-
ческих прогрессий меньпхе единицы), т. е. если \2 -
суждая, как и в случае Zq = О, получим, что радиус сходимос
ти получивп1егося ряда равен -.
Наконец, в случае 2q = 4 имеем
2 _ 1 2 _ 1 2 _
B-1)B-2) 1-2 2-2 -3-(г-4) -2-B-4)
+
3 1 +
2-4
1 + :
п^о L 3^ + 1 2"J^ ^
Все это справедливо, когда
5 ц < 1, т. е. при 1^ - 4| < 2.
Отсюда, как и выгае, следует, что радиус сходимости получивгаего-
ся ряда равен 2.
Обратим внимание на то, что во всех трех случаях радиус
сходимости получивп1ихся степенных рядов равен расстоянию
от точки 2q, в окрестности которой искалось указанное
разложение, до ближайгаей от нее «особой точки» функции. В
данном случае до такой точки z., что lim /B) = 00. в случае 2г. = О
такой точкой является 1 и |2q - 2^| = 1; в случае Zq = 3/2 это
точка 2^ = 1 или z^ = 2 и здесь \z-^ - Zq\ = 1/2; наконец, при Zq = 4
имеем z^ = 2 -H.\z^ - Zq\ = 2. Это не случайное явление, оно
подробно изучается в теории функций комплексного переменного.
135
Рассмотренным методом можно раскладывать в соответст-
вуюпа;их областях рациональные функции в ряды не только по
положительным, но и по отрицательным степеням г.
Например, при 1^1 > 2 имеем
1 о 1 1
1 оо -1 -1 оо (уп оо -1
= --Е - + -Е -= Е B"-1)^,
а в кольце 1 < |2| < 2
B-1)B-2) Л 1Л 1_2 2 „%о 2
2l-i 1-
2
-1 оо -1
- Е -- Е
п-0
2
оо 1 оо «д
В первом случае получивпхееся разложение содержит
только отрицательные степени 2, во втором — как
положительные, так и отрицательные. Обпа;ая теория подобных
разложений также изучается в теории функций комплексного
переменного.
К разложению рациональных дробей в степенные ряды
сводится и разложение в такие ряды функций вида In 7^?
Q{x)
Р(х) Р(х)
arctg —^ и arctg 7^? где Р(х) и Q(x) — некоторые многочле-
Q(x) Q(x)
ны. Для получения нужных разложений можно
продифференцировать данные функции, в результате получатся
рациональные дроби. Разложив эти рациональные дроби в
степенные ряды и проинтегрировав их, будем иметь искомые
разложения.
Иногда сумму ряда удается найти, применив какой-нибудь
искусственный прием. Впрочем, следует отдавать отчет в том,
что понятие «искусственный прием» весьма относительно: по
поводу этого Г. Полна и Г. Сеге в предисловии к своему
задачнику (Полна Г., Сеге Г. Задачи и теоремы из анализа. — М.:
Наука, 1956) писали: «Идея, примененная однажды,
порождает искусственный прием, примененная дважды, она
становится методом».
6. Найдем сумму ряда
п - о ^" "■" ■^
Тзб
и область его сходимости. При |х| < 1 этот ряд сходится
абсолютно, так как
(-1)^
< |xh.
2п + 1|
при |х| > 1 он расходится, поскольку его обгций член не
стремится к нулю; при X = 1 он сходится по признаку Лейбница;
при х = -\ расходится, что, например, следует, согласно
интегральному признаку сходимости рядов, из расходимости интег-
рала I -—^. Заметим (это и есть искусственный прием), что
о 2^ + 1
1
2я + 1
I ^2я at.
О
И преобразуем ряд C3.66) следуюгцим образом:
Для любого ^g[1, 1] выполняется неравенство |-х^^|^ < |х|^.
Поэтому если |х| < 1, то, по признаку Вейергатрасса, ряд
£ {-xt^Y C3.68)
д = о
равномерно сходится (по f) на отрезке [О, 1], следовательно, его
можно почленно интегрировать. Его можно почленно интегри-
ровать и при х=1у хотя в этом случае ряд ^ {-t^Y не сходится
п = 0
равномерно на отрезке [О, 1], так как он даже расходится при
t=\. Возможность почленного дифференцирования ряда C3.68)
при х= \ можно проверить, например, непосредственно:
О
1
О
ж
4'
(-1)" _
?.1«-'^>"*^?„ё^<ззЪ,3
О
(при интегрировании функции ^ (-t^Y по отрезку [О, 1]
дога = о
статочно рассматривать ее значения только на полуинтервале
[О, 1), которые по формуле для бесконечно убываюпа;ей геомет-
J_
1 + ^2
ны на указанном полуинтервале. Значение этой функции в
точке t = 1 можно выбирать произвольно, так как это не
влияет ни на интегрируемость функции, ни на значение интеграла,
когда функция интегрируема).
Т37
рическои прогрессии равны и, следовательно, ограниче-
-1 I j-Z
Итак, для всех xg(-1, 1] имеем
^^0 2я + 1 C3.67) ^^Q J J ^^Q n 1 + -^
если 0 < X < 1,
2
1 j^ du ^ arctgVx
7^ J ГТ^2 7S '
1, еслих = 0, C3.69)
,^t^ = ^lnl±^, если -1<х<0.
[ J\x\ i 1 - w^ 2л/|х1 1 - VW
При выводе этой формулы было использовано соотноп1ение
C3.63), т. е. известное ранее частное значение суммы ряда
C3.66) при X = \. Это можно было и не делать, но тогда мы
получили бы формулу C3.69) только при |х| < 1, из которой
следует, что сумма s{x) степенного ряда C3.66) является
непрерывной на интервале (-1, 1) функцией и имеет конечный предел
lim s{x) = lim EI£i|^/^ = arctg 1 = ^. C3.70)
Ряд C3.66) сходится при X = 1, поэтому, в силу второй
теоремы Абеля (см. теорему 3 в п. 33.1), его сумма непрерывна на
отрезке [О, 1] и, следовательно, при х = 1 совпадает со значением
предела C3.70), т. е.
^ (-1)^ _ ж
и мы тем самым, наоборот, получили из формулы C3.69),
доказанной только при |х| < 1, разложение C3.63).
УПРАЖНЕНИЕ 18. Найти сумму ряда > -^ в области его сходимости.
п = 2 ^' - 1
Указание. Воспользоваться соотношением
д2-1 2\п-1 п +
33.8. Формула Стирлинга
С помогцью разложения логарифмической функции в
степенной ряд можно легко найти формулу, описываюгцую
асимптотическое поведение факториала п\ при я ^ оо. Она называется
формулой Стирлинга* и может быть записана в виде
, 1
^;^л/27Ш 1^ п^ОО; C3.71)
' Дж. Стирлинг A692—1770) — английский математик.
Т38
согласно определению асимптотического равенства для
последовательностей (см. п. 19.3), это означает, что
lim ^ = 1.
«^°° л/ЗТГП" + 1/26-"
Из разложения
ln(l + x)= £ (-!)« +1^, -1<х<1,
следует, что
In 1±^ = In A + х) - In A-х) =
1-х
П оо X у.п\ оо y.2k
Е,(-""*'т-„?Л-1г) = ^?.2Гп
Положив здесь х = -, п = 1, 2, ... , получим
1+ 1
rij ^ 1 2я + 11 3Bя + 1J 5Bя + 1L J
In
V п J ^ _
2п + 1
> 2
откуда
2п + 1 ^1'
"^2
п + 1]1п[1 + 1\>1,
или, потенцируя и принимая во внимание, что функция
In X — возрастаюгцая,
1 \п + {1/2)
1 + ij >е. C3.72)
Положим
def _я!е"
так как, согласно C3.72),
-п--^,; C3.73)
х„ -ifi+n-<^^%i.
то х^ > ^д +1? т. е. последовательность {х^} убывает и, кроме того,
она ограничена снизу х^> 0. Следовательно, супа;ествует предел
т def
lim х„ = а.
Поэтому
x, = a(l + 8j, C3.74)
где lim 8„ = 0.
Тзэ
Покажем, что а ^ 0. Так как
3Bя+1J 5Bя + 1L 3
+ : +
Bя + 1J Bя + 1L
_ 1 Bя + 1J _ 1
3^ 1 12я(я + 1)'
Bя + 1J
то
^ + illnfl + il<l +
12я(я+ 1)'
следовательно,
^ 1
п + - 1
1 л 2 1 + ^
1 + - < е 12«(«+ 1).
Поэтому
,1 J_
1/ 1Л" 2 1 -12«
- 1 + - <б12д(д + 1) = _^_
gl2(w+ 1)
т. е.
1 1
Х^е 12д< Х^+1 е 12(^+1).
1
Таким образом, последовательность г/^ = х^^е 12^^ я = 1, 2, ...,
возрастает, и так как, очевидно, г/^ < х^, то она ограничена
сверху и, следовательно, имеет предел
1
lim г/„ = lim х„ lim е i2« = а.
Кроме того, при любом п справедливо неравенство а> у^> Q,
поэтому а > 0.
Подставим C3.74) в C3.73):
я! = а^A + 8,). C3.75)
Для того чтобы получить формулу C3.71), осталось лигаь
показать, что а = л/27Г. По формуле Валлиса (см. B6.8) в п. 26.2),
а согласно C3.75),
Bя)!! _ [Bя)!!]2 _ 22^(я!J _ /^^A + £^J
Bп- 1)!! Bя)! Bя)! ^2 1 + г^^ '
Лд
Подставив это выражение в C3.76), получим
^= lim 1 ^2яA + е,L_а^
2 п^оо2п+1 2A + 82^J 4'
откуда а = л/27Г. П
33.9*. Формула и ряд Тейлора
для векторных функций
Рассмотрим векторную функцию /: [а, Ь] -^ R^, где R^ —
трехмерное векторное пространство. Как уже отмечалось, на
векторные функции обобгцаются понятия предела,
непрерывности, производной, дифференциала и интеграла (см. § 15),
на которые переносятся многие свойства этих понятий,
справедливые для числовых функций. Однако далеко не для всех
свойств это имеет место. Так, в п. 15.2 было показано, что
утверждение, аналогичное формуле конечных прирагцений Лаг-
ранжа, уже не справедливо для векторных функций. Поэтому
не справедливо, конечно, и ее обобгцение в виде формулы
Тейлора с остаточным членом в форме Лагранжа. Покажем, что
для векторных функций справедлива формула Тейлора с
остаточным членом в интегральной форме.
ТЕОРЕМА 10. Пусть функция /: (^q -\- h, t^ - h) ^ R^
непрерывна вместе со всеми своими производными до порядка
п -\- 1 включительно на интервале (t^ - h, t^-l- h), h> 0. Тогда
для любого te(tQ - h, t^-l- h) справедлива формула
f(i)= t y^'\t^)(t-tor + -,] (t-xrf(-^^b)dx. C3.77)
СЛЕДСТВИЕ.
Я0 - t y^^\4)it - hf\ <-st- ЧГ ^' sup 1/^" ^ 'b)l
k = 0 ^J I ^J {t^-h, t^+h)
где fG (^Q - h, tQ + h).
Доказательство теоремы. Прежде всего напомним, что
если
/(О = (/i@,/#),/з@), C3.78)
то
nt) = if{it),r2it),f^it)), teito-h,to + h), C3.79)
I fix) dx = (] f-^ix) dx, I f2{x) dx, I /з(х) dx \. C3.80)
tg \ tg tg tg
Ш
Из предположений теоремы следует, что каждая
координатная функция /., / = 1, 2, 3, непрерывна на интервале
(^Q — h, tQ-\- h) вместе со всеми своими производными до
порядка я + 1 включительно, поэтому для нее справедлива формула
Тейлора с остаточным членом в интегральной форме
W) = t ]Jf/^Р^(*о)(* - Ч)" + h\ (^- ^)"А^" ^ '^(^) ^^' J = 1' 2,3.
Отсюда, в силу формул C3.79) и C3.80), и следует сразу
справедливость формулы C3.77). П
Следствие вытекает из неравенства
j (^-тO^^ + 1)(т)йт
<\t
f F
j /(^ + i)(T)dT
<
<\t- t^Y sup |/(^ + i)(t)|
\dx
\f — f \n + l
sup |/(^ + 1)(т)|.П
Для векторных функций, как и для скалярных,
справедлива формула Тейлора и с остаточным членом в форме Пеано:
если функция /: (^q - Л, fq + Л) ^ R^ имеет в точке ^q
производную порядка п, то
Я*)= t T,f4h)it-hf + o({t~t^r). C3.81)
Это также сразу следует из того, что для каждой
координатной функции /., / = 1, 2, 3, в предположениях теоремы имеет
место формула Тейлора с остаточным членом в форме Пеано в
окрестности точки ^q (см. п. 13.1).
Если векторная функция /: (^q - Л, ^q + Л) ^ R^ имеет в
точке ^0 производные всех порядков и для любого fg (fq - Л, ^q + К)
выполняется условие
то на интервале (^q - Л, ^q + К) функция / раскладывается в
степенной ряд с векторными коэффициентами
называемый ее р^Eож Тейлора.
142
33.10*. Асимптотические степенные ряды
Известно (см. п. 13.1), что если функция / определена в
окрестности точки XqU п раз в ней дифференцируема, то супа;ест-
вует такой многочлен Р^(х) степени, не болыаей п, а именно
многочлен Тейлора, что
/(х) = Р^(х) + о((х - Xq)^), x^Xq, х=1,2, .... C3.82)
При этом
Р,(х) = Р, _ i(x) + ^^(х - х^Г. C3.83)
Из C3.82) и C3.83) следует, что разность f(x) - Р^_ i(x) пред-
ставима в виде
f(x) - Р^ _ i(x) = ^^^(х - Хо)^ + о((х - Хо)^), X ^ Хо,
и тем самым имеет место асимптотическое равенство
дх) — -Г ^ _ ]^(х) ~ j—(X — Xq) , X ~^ Xq.
Таким образом, члены многочлена Тейлора Р^(х) (ряда
Тейлора, если функция / бесконечно дифференцируема в
точке Xq) можно последовательно определить как слагаемые вида
а^(х - Xq)^, асимптотически равные разности /(х) - Р^ _ i(x)
при X -^ Xq.
Аналогично можно поступать и при изучении функции
при стремлении ее аргумента к бесконечности. Пусть, для
определенности, функция / определена при х > а и супа;ествует
конечный предел
lim /(х) = ао, C3.84)
следовательно, lim [/(х) - а^] = 0.
Иногда возникает вопрос: как именно разность /(х) - а^
стремится к нулю, каков порядок убывания этой разности?
Может случиться, что указанная разность имеет по крайней мере
порядок - и, более того, что супа;ествует такое число а^, что
/(х)-ап~-, х^+оо, C3.85)
X
т. е. (см. теорему 1 в п. 8.3)
/(х) -аг,= ^ + о(-\ X -^ +00, C3.86)
X \ X )
Из
откуда
^[/(^) ~ %] = (ii + хо(- ], X ^ +00,
. X
а так как, в силу определения символа о, хо(-] -^ О при
X -^ +00, то
а^= lim х[/(х)-ао]. C3.87)
X -^ +00
Наоборот, из C3.87) следует, что
^иМ ~ ^о] = <^1 + ^(х), lim е(х) = О,
и, следовательно.
Т. е. выполняется асимптотическое равенство C3.86). Если
указанное а^ найдено, то часто бывает нужно найти, как
говорят, «следуюгций член асимптотического разложения»
функции /, т. е. асимптотическое поведение разности f(x) - (а^ + —
X
при X -^ +00. Эта разность, согласно C3.86), представляет
собой не что иное, как о(-\х^ +оо. Может случиться, что
указанная разность имеет по крайней мере порядок — и, более то-
го, что сугцествует такое число аз, что
или, что то же.
Это условие равносильно сугцествованию предела
lim x^' f(x) - (а^ -\- — \\ = а^.
х^ +00 L ^ X и
Вообгце, если
S„_i(x) = ao+5 + 5 + - + ^' п = 1,2,..., C3.88)
— такой многочлен степени, не болыаей п - 1, относительно
переменной -, что
х
/(х)-Гао + ^ + Ч + ... + ^]~^, x^+oo,n = 2,S,...,
\ X Х^ Х" ^ ^ Х" ^
144
то может случиться, что суш;ествует такая постоянная а^, для
которой имеет место асимптотическое равенство
/(x)-S„_i(x)~^, х-+00. C3.89)
Это условие равносильно следуюпа;ему условию:
f(x)-S,_^(x)=^+o(\\ х-+00, C3.90)
X V X )
которое, полагая
S„(x) = S„_i(x) + ^„= t ?' C3.91)
можно переписать в виде
f{x)-S^{x) = o[l^y х-+00, C3.92)
ИЛИ, что то же, в виде
lim^ х^[/(х) - S^(x)] = 0. C3.93)
Как и Bbinie при п = 1, легко показать, что условие C3.90)
равносильно сугцествованию конечного предела
^lim^ х«[/(х) - S„ _ i(x)] = а„. C3.94)
Если указанные пределы а^ сугцествуют для всех я = 0, 1,2, ...,
то можно образовать ряд
ао + ^ + ^ + ... + ^ + ... . C3.95)
^ X Х^ Х'^
Ряды такого вида можно также назвать степенными рядами,
точнее, степенными рядами по целым отрицательным
степеням переменной х.
Определение 5. Пусть функция f определена при х > а и
lim f(x) = а^. Если существует ряд вида C3.95),
частичные суммы C3.98) которого удовлетворяют условию C3.89),
либо, что равносильно, одному из условий C3.92) или C3.93),
то этот ряд называется асимптотическим рядом
{асимптотическим разложением) в смысле Пуанкаре^ функции f
при X -^ +00.
В этом случае пигаут
ОО /7
/~ У ^, х^+оо. C3.96)
п = о л:"
' А. Пуанкаре A854—1912) — французский математик.
145
Подчеркнем, что здесь знак ~ означает не асимптотическое
равенство в том смысле, как оно, например, понимается в
формуле C3.89), т. е. в смысле определения 3 п. 8.2, а
соответствие: ряд C3.95) соответствует функции /.
Как было отмечено вып1е, условие C3.90) равносильно
условию C3.94), поэтому если у функции / супа;ествует при
X -^ +00 асимптотический ряд C3.95), то его коэффициенты а^,
п= 1, 2, ..., могут быть последовательно найдены по формулам
C3.94). При п = О следует воспользоваться формулой C3.84).
Отсюда следует, что если у функции имеется при х -^ +оо
асимптотический ряд, то он единствен и его коэффициенты
выражаются по формулам C3.84) и C3.94).
При разложении функции в степенной ряд была доказана
также единственность степенного ряда, в который
раскладывается функция, а именно было доказано совпадение этого ряда с
ее рядом Тейлора. Однако там было отмечено, что один и тот
же степенной ряд может являться рядом Тейлора разных
функций. Подобная ситуация имеет место и для
асимптотических рядов: один и тот же ряд вида C3.95) может оказаться
асимптотическим рядом при х -^ +оо разных функций.
Например, нулевой ряд, т. е. ряд, все коэффициенты которого равны
нулю: а^ = О, я = О, 1, 2, ... , является при х -^ +оо как
асимптотическим рядом функции, равной нулю во всех точках
числовой оси: /i(x) = О, -оо < X < +00, так и функции f^i^) = е~^, в
чем легко убедиться, вычислив в этих случаях
последовательно пределы C3.94).
В отличие от разложения функции в степенной ряд по
неотрицательным целым степеням аргумента, при котором
суммой степенного ряда является заданная функция и,
следовательно, рассматриваемый степенной ряд сходится, при
построении асимптотического ряда функции может случиться, что
полученный ряд не только не сходится к данной функции, а во-
обпа;е расходится во всех точках. Тем не менее асимптотический
ряд C3.96) функции является полезным инструментом для ее
изучения, в частности для вычисления ее значений. Это,
очевидно, связано с тем, что частные суммы асимптотического
ряда C3.96) функции, в силу условия C3.92), достаточно хороню
приближают саму функцию, причем тем лучп1е, чем больп1е х.
Принципиальное отличие разложения функции в
асимптотический ряд от разложения в обычный функциональный ряд
состоит в том, что при обычном разложении функции в ряд его
остаток в каждой точке стремится к нулю при п -^ оо^ т. е.
стремится к нулю абсолютная погреганость приближения функ-
Tie
ции частичными суммами ряда, тогда как при разложении в
асимптотический ряд этого может не быть, но заведомо
стремится к нулю при X ^ +00 относительная погреганость приближения
функции частичными суммами асимптотического ряда, т. е.:
^^+оо х-^ C3.93)
Разность f{x) - SJ,x) бесконечно мала при я ^ оо по сравнению
с каждым (в том числе и последним) членом частичной суммы
SJ^x) асимптотического ряда, причем увеличение числа
членов приводит к более точным асимптотическим формулам.
Поясним сказанное на примере функции
+ 00 X - t
f(x)= ^—dt, х>0. C3.97)
t
X
Интегрируя п раз по частям, получаем
л*' 4 -? + ?-■■• + '-"'":i°""' + <-«""' Т ^ *• C3.98)
Ряд
£ (-^Г-Чп-1)\ C3.99)
п = \ ^
является асимптотическим разложением функции C3.97).
" (—Л\^ - l(h — 1I
Действительно, если aS^(x) = ^ ^^— ^ -, п = 1, 2, ... ,
т. е. S^(x) — частичные суммы ряда C3.99), то, в силу C3.98),
+ 00 X - t
имеем |/(х) - aS^(x)| = ti\ ^ ~;ГТ\ ^^* Проинтегрировав епа;е раз по
X ^
частям, получим
+ 00 X — t
|/(x)-S„(x)| = n! \'-^,dt =
X ''
= ^-(„ + 1)!Т£1_^й,<^ = оГ^\
Х^ + 1 ^ J +п + 2 ллп +1 \^ лгП I
Т. е. выполняется C3.92).
Вместе с тем по признаку Даламбера легко убедиться, что
ряд C3.99) расходится при всех xg(-oo, +оо). Действительно,
полагая и = -—^—^ -, п = 1, 2, ... , получим при х^О
lim
п+ 1
lim А = +00.
1^+оо \х\
Поэтому ряд C3.99) абсолютно расходится при всех х ^ 0.
Отсюда после замены х = 1/у следует, что степенной ряд
оо
^ (-1)^ (п - 1)! г/^ также абсолютно, следовательно, и просто
п = 1
147
расходится при г/ ^ 0. Сделав обратную замену у = 1/х,
получим расходимость ряда C3.99) для всех х ^ 0.
Итак, асимптотический ряд C3.99) функции C3.97)
расходится во всех точках. Однако, несмотря на это, значения
функции C3.97), в силу условия C3.92), могут быть
вычислены с болыаой степенью точности с помогцью частичных сумм
этого ряда.
Покажем, что если ряд C3.95) сходится к некоторой
функции
/(х)= у ^, х>а>0, C3.100)
п = о л:"
ТО он является и асимптотическим рядом этой функции при
X -^ +00. в самом деле, пусть RJx) = У -^ и, следователь-
НО, f{x) = S^(x) + R^(x). Покажем, что
R,(x) = o[-^^], Х-+00, C3.101)
а потому, тем более, что
т. е. что выполняется условие C3.92). Для этого рассмотрим
функцию F(t) = ffl\o<t<:-.B силу C3.100), получим ра-
оо
венство F(t) = Y, ^д^^' ^ котором ряд в правой части сходится
п = 0
при о < t < -, откуда, по теореме Абеля, следует, что он
сходится и при всех таких t, что к| < -. Если
а
оо 7 I I 1
r„{t)= ^ a,f^ \t\<^
k = n + 1 ' ^
ТО (см. лемму 1 в п. 33.3) r^(t) = 0(f^ + ^), t ^ 0. Выполнив здесь
замену переменного t = -, получим C3.101).
X
В заключение отметим, что условие C3.92) разложения
функции в степенной асимптотический ряд можно заменить
другим, внеп1не более сильным, но по сугцеству
эквивалентным условием. Сформулируем его в виде леммы.
ЛЕММА 3. Для того чтобы ряд C3.95) являлся
асимптотическим при X -^ +00, для функции f необходимо и
достаточно, чтобы
f(x)-S^(x) = o[-^^y Х-+00, я = 1,2, .... C3.102)
148
Достаточность этого условия очевидна, так как 0\—-.
= о[— I (напомним, что подобные равенства читаются только
слева направо), следовательно, при выполнении условия
C3.102) выполняется C3.92).
Наоборот, если выполнено условие C3.92):
/(x)-S^ + i(x) = o[-^], я = 0,1,2,..., х^+оо,
то, поскольку aS^ + ^(х) = S^(x) + ^1^, получим
f(x)-S^(x) = ^^ + o(^) = o(^], х^+оо.п
33.11*. Свойства асимптотических степенных рядов
В этом пункте будут сформулированы и доказаны некоторые
основные свойства разложений функций в асимптотические
степенные ряды. В дальнейпхем (см. п. 54.6) будут
рассмотрены более обпа;ие, не обязательно степенные, асимптотические
ряды. В настояпа;ем пункте будут изучаться только
асимптотические разложения функций при х -^ +оо в степенные ряды
вида C3.95), поэтому будем их называть просто
асимптотическими разложениями.
I. Если
-1 ОО /7 ОО h
J- 1^ ^ g{x)- ^ ^^, Х-+00, C3.103)
то для любых чисел Xu\i
т, е, асимптотическое разложение линейной комбинации
функций, имеющих асимптотическое разложение, равно
такой же линейной комбинации асимптотических
разложений этих функций.
Действительно, если
Кх)= t -* + of^l. ё(^)= t ^ + «f^l' х^+00,C3.104)
ТО для любых чисел Я. и ц
k = 0 ^ V X" J
149
II. Если имеют место асимптотические разложения
C3.103), то
оо п
д^о л:"
где с^ = а^Ъ^ + а^Ъ^_ ^ + ... + а^Ъ^, т, е, асимптотическое
разложение произведения функций, имеющих асимптотические
разложения, равно произведению этих разложений,
расположенных по возрастающим степеням -.
В самом деле, если имеет место C3.104), то
X X" \Х^ } }\ ^ X
/(х)Жх) = Гао + ^ + ... + 5+<^11К + ^ + - + ^„ + <^11=
III. Если
«1^0
+... +
Ё О-кЬп-
к = 0
f(x)~ у ^, X
+ 1]^1'
+ 00,
X ■
+00. п
C3.105)
и а^^ О, то функция 1//(х) также имеет асимптотическое
разложение
1 1
оо и
fix) Uq „^1 X"'
+ 00,
и коэффициент d^ этого разложения выражается через
коэффициенты а^, а^, ... , а^разложения C3.105), я = О, 1, 2, ... .
Действительно, из C3.105) следует (см. C3.84)), что
lim fix) = ar.. Поэтому суш;ествует предел
■у \ -I-00 ^
lim -^
«О*
Далее, можно последовательно показать супа;ествование
пределов C3.94) для функции 1//(х), непосредственно вычисляя
их. Например,
lim х\ —- - — = lim х\
Х^+оо [f(x) Uq ) Х^+оо
Uq + — + 0| -
«о
- lim
хо\ -
ух
«oi«o+5+^u
Т. е. d^ = -а^/а^.
Аналогично вычисляются (^2? d^, ... . П
150
IV. Если функция f непрерывна при х > а > О и имеет
асимптотическое разложение, начинающееся с члена
порядка—,
fix)- £ -п^ Х-+00, C3.106)
то
+ °° ОО /7
I /(Orf^~ L z rfir^, Х-+00, C3.107)
i д^2 (я- 1)л:" 1
т, е, в указанном случае асимптотические ряды можно
почленно интегрировать.
Докажем это. Пусть
Sn(^)^= t Ч^ i?,(x) ^^'/(X) - S,(x), я = 2,3,....
Функции / и aS^ непрерывны при х > а, поэтому и функция R^
непрерывна при х> а.В силу C3.106),
Следовательно, для любого 8 > О сугцествует такое х^ > а, что
для всех X > х^ выполняется неравенство
+ 00
Отсюда вытекает, во-первых, что интеграл | R^it) dt, поэтому
+ 00
И интеграл | R^it) dt, х > х^, сугцествуют, а во-вторых, что
X
при х> х^ имеет место неравенство
х^-1 I i?^@<i^ <x^"^| \R^it)\dt<Ex''-^ \ Щ. = ^-,
и так как 8 > О произвольно, то
+ 00
lim х^-^ \ RJ(^t)dt = 0. C3.108)
Теперь, интегрируя равенство f{x) = SJ,x) + RJ,x), получим
+ 00 д ^ +00
в силу выполнения условия C3.108) для всех п = 2, 3, ... ,
равенство C3.109) и означает справедливость асимптотического
разложения C3.107) (см. C3.93)). П
Ш
V. Если функция f раскладывается в асимптотический ряд
ОО /7
А^)~ Е ^' х^+^, C3.110)
г/ еслг/ она имеет при х> а непрерывную производную,
которая также при х -^ +оо раскладывается в
асимптотический ряд, то этот ряд получается формальным почленным
дифференцированием ряда C3.110):
П^)~-1 ^. ^^+-- C3.111)
в самом деле, пусть
П:^)~ £ -п^ Х-+00. C3.112)
По формуле Ньютона—Лейбница для любых х > а и г/ > а
f{y) - fix) = ] nt) dt = ][b^ + ^-l + [at) - bo - у ]] dt =
= b^(y - X) + biln M. + I ^fXt) -bo-j] dt. C3.113)
Согласно C3.112), fit) -Ь^-- = o(-\ t -^ +oo.
Следовательно, интеграл
+ 00 г- и -,
I [nt)-\-'-i\dt
сходится, в силу C3.110), сугцествует конечный предел
lim f(y) = an..
Поэтому, переходя к пределу при у -^ +оо в C3.113),
убеждаемся в том, что для каждого х > а сугцествует конечный предел
Дш^[ь,{у-х) + Ъ,\пУ^.
Это возможно только в случае, когда Ъ^ = Ъ^ = 0. Таким
образом, равенство C3.113) в пределе перейдет в равенство
+ 00
aQ-f{x)= I f(x)dt;
X
при ЭТОМ, в силу условия Ъ^ = Ъ^ = о, из C3.112) имеем
отсюда, интегрируя почленно в пределах от х до +оо^ согласно
свойству IV, получим
152
Но из C3.110) следует, что
«о-/(^)~ Е ^-
д = 1 -^
Принимая во внимание, что разложение функции при
X -^ +00 в асимптотический степенной ряд единственно, и
сравнивая получивп1иеся для функции а^ - f(x) ряды, найдем, что
Замечание. Если непрерывно дифференцируемая при
X > а функция / раскладывается при х ^ +оо в асимптотический
ряд, то ее производная может не иметь при х ^ +оо
асимптотического разложения. Тем самым требование сугцествования
асимптотического разложения у производной в предложении V
является существенным. В качестве примера рассмотрим функцию
/(х) = e"^sin е^, -оо < X < +00. Нетрудно с помощью формул
C3.94) убедиться, что функция / при х -^ +оо раскладывается
в нулевой асимптотический ряд, т. е. ряд C3.95), у которого
а^ = О, п = О, 1, 2, ... . Ее производная f(x) = -e"^sin е^ + cos е^
заведомо не имеет асимптотического разложения при х -^ +оо^
так как она даже не имеет предела при х -^ +оо.
УПРАЖНЕНИЕ 19. Доказать, что:
^^1г
dt~i-il + ^-,..., Х^+оо;
+ 00
б) f C^'-t' dt- '^ - ^ +1 - 3_1 ■ 3 ■ 5 х^+оо
§зг
Кратные ряды
34.1. Кратные числовые ряды
В настоягцем параграфе рассматриваются так называемые
кратные ряды вида
оо
i: %....,' C4.1)
где и^ ^ — заданные числа (вообпа;е говоря, комплексные),
занумерованные k индексами п-, i = 1, 2, ... , k, каждый из
которых независимо от другого пробегает натуральный ряд
чисел: п- = 1, 2, ... . Ряд C4.1) называется й-кратным рядом, а
153
Определим четко эти понятия. Предварительно введем
понятие кратной последовательности.
Определение 1. ili/cmb X— некоторое множество; k-крат-
ной последовательностью элементов множества X
называется отображение f: NXNX ... XN -^ X (N, как всегда, обо-
V
k раз
значает множество натуральных чисел).
Элемент х = f(n-^, ... , я^), n-^eN, ... , Tif^eN, обозначается
через х„ „ , а сама последовательность — через {х„ „ }.
Однократная последовательность называется просто
последовательностью.
Итак, элементы й-кратной последовательности
«занумерованы» п натуральными индексами. Мы будем рассматривать
числовые кратные последовательности, т. е.
последовательности, элементами которых являются комплексные, в
частности действительные, числа. Для простоты обозначений
ограничимся случаем й = 2. В этом случае й-кратная
последовательность называется двойной.
Обобгцение на случай произвольного натурального keN не
представляет трудности.
Определение 2. Число аеС называют пределом двойной
последовательности {х^„} и пишут а = lim х^„, если для
любого 8 > О существует такое n^eN, что для всех т > п^,
п > п^, meN, neN, выполняется неравенство \х^^ - а\< г.
Если двойная последовательность имеет предел, то она
называется сходящейся.
Отметим, что не все свойства пределов обычных
последовательностей переносятся на двойные. Так, например,
последовательность и^^ = п, и^^ = О, т ^ 1, п = 1, 2, ... , т = 2, 3, ... ,
сходится: lim г/^„ = О, однако эта последовательность, оче-
т,п ^ оо "'''''
ВИДНО, не ограничена.
Замечание 1. Предел кратной последовательности
можно определить и другим не эквивалентным данному выгае
способом: например, назвать пределом двойной
последовательности {и^^} такое число а, что для любого 8 > О найдется такое
натуральное п^, что для всех я и т, для которых п + т > п^,
выполняется неравенство \и^^ - а| < 8.
При таком определении предела двойной
последовательности члены последовательности, имеюпа;ей предел, будут уже
ограничены (докажите это). Мы будем в дальнейп1ем
придерживаться определения 2 предела кратной последовательности.
154
Определение 3. Дбой«г/ю последовательность называют
последовательностью, стремящейся к +оо, и пишут lim х^^ =
= +00, если для любого г > О существует такое n^eN, что
для всех т > п^, п > п^, meN, neN, выполняется
неравенство Х^^ > 8.
Аналогично определяются бесконечные пределы
lim X = —оо и lim х = оо.
Как обычно, под пределом (в данном случае двойной
последовательности) понимается конечный предел, если не
оговорено что-либо другое.
Определим теперь двойной ряд.
Определение 4. Пусть задана двойная последовательность
{г/^^}. Составим двойную числовую последовательность:
т п
Smn= Y. Е ^ы- C4.2)
Пара последовательностей {г/^^}, {aS^^} называется двойным
рядом и обозначается через
оо
Е Umn- C4.3)
т,п = 1
Элементы двойной последовательности {и^^ называются
членами ряда C4.3), а элементы двойной последовательности
{aS^^} — частичными суммами этого ряда.
Определение 5. Двойкой р^E C4.3) называется сходящимся,
если последовательность его частичных сумм сходится. Ее
предел называется суммой ряда; причем если
lim S^^ = S, C4.4)
то пишут
оо
Е ^mn = S.
т,п = 1
Если конечного предела C4.4) не существует, то ряд C4.3)
называется расходящимся. Если существует один из
бесконечных пределов
lim S^^ = +oo^ lim S^ =-оо, C4.5)
то соответственно пишут
оо оо
т,п = 1 т,п = 1
155
Замечание 2. Содержательность определения ряда как
пары последовательностей хороню видна на примере кратных
рядов. Например, если задана последовательность {г/^^}, то
соответствуюгцую ей последовательность «частичных сумм»
можно задавать не только указанным выгае способом C4.2),
но и по-другому. Наряду с суммами C4.2), которые
определены BbiHie и называются прямоугольными (в них
суммируются элементы г/^^, которым соответствуют точки (k, I)
плоскости ху, содержагциеся в прямоугольнике О < х < т,
О < г/ < я), рассматриваются треугольные суммы
Т^ = Y, ^ы^ ^ ^ ^^ 2' ••• (точка (k, I) лежит в треугольнике
k + Кг
X > О, у > О, X -\- у < г), сферические суммы aS^ = ^ г/^^,
г = 1, 2, ... (точка (k, I) лежит в круге х^ -\- у^ < г^) и др. Таким
образом, для одной и той же последовательности {и^^}
имеются разные последовательности частичных сумм. Кроме того,
для этих последовательностей частичных сумм понятие
предела естественно определять по-разному. Например, для
треугольных частичных сумм таким определением является
определение предела, сформулированное в замечании 1. Поэтому
естественно рассматривать каждую пару, состояпа;ую из
последовательности {г/^^} членов ряда и каких-то его «частичных
сумм» как самостоятельный ряд. При этом может случиться,
что частичные суммы одного вида, составленные из членов
ряда, имеют предел, а другие его не имеют.
Последовательности частичных сумм кратных рядов
(например, частичных сумм Т^ или aS^) в отличие от
последовательностей частичных сумм однократных рядов не всегда
однозначно определяют последовательность обгцих членов ряда.
Обгцее определение ряда имеет следуюгций вид.
Рядом называется пара, состоягцая из (кратной)
последовательности, называемой последовательностью его членов, с соот-
ветствуюгцим понятием предела последовательностей такого
вида и некоторого множества {aS^}, аеШ, сумм aS^ его членов.
Здесь Ш — некоторое множество, элементами а которого
являются наборы мультииндексов (п-^, ... , я^) (в частности, обычных
индексов), и
'^а ^ 2^ ^п. ... д, •
Следует отметить, что иногда два разных в смысле данного
определения ряда, имеюгцих одну и ту же последовательность
членов ряда, называют одним и тем же рядом, но с разными
способами его «суммирования».
Тзб
в дальнейп1ем при изучении кратных рядов будут
рассматриваться только прямоугольные частичные суммы, в
частности для двойных рядов суммы aS^^.
Пример. Пусть ^|<1, 1^1 <1, Р^С, qeC; тогда ряд
оо
^ p^q^ сходится. Действительно, в этом случае
т,п = О
Поэтому супдествует предел lim aS^„ = — . Таким
образом.
Ряд свойств обычных (однократных) рядов переносится на
кратные ряды.
оо
1^^. Если ряд Y, ^тп сходится и S — его сумма, то
т,п = 1
оо
^ 'ки^^ = XS для любого числа Я..
т,п = 1
оо оо
2^. Если ряды Y, ^тп ^ S' и Y, ^тп ^ '^'' сходятся, то
т,п = 1 т,п = 1
оо
Е «n + <n) = s' + s-.
т,п = 1
Эти утверждения легко доказываются аналогично случаю
однократных рядов. Их доказательства могут быть проведены
читателем самостоятельно.
Докажем теперь несколько теорем о кратных рядах.
ТЕОРЕМА 1. Если ряд C4.3) сходится, то
lim г/^ = 0.
Это сразу следует из равенства
^тп ~ *^тп ~ *^т -1п~ *^тп - 1 ~^ *^т -1п-1
И условия C4.4). П
ТЕОРЕМА 2. Если все члены ряда C4.3) неотрицательны,
и^^>0, т,п= 1,2,..., C4.6)
то всегда существует конечный или бесконечный предел его
частичных сумм S^^, причем
гг}1'^оо^шп= sup S^^. C4.7)
Доказательство. Если выполняется условие C4.6) и
т' >т,п'> п, то S^.^. > S^^.
J57
Далее, если S = sup aS^^ и aS' < aS, to, в силу определения
т,п = 1, 2, ...
верхней грани, сугцествуют такие номера т^ип^, что aS^ ^ > aS'.
Положим N = max {т^, щ}, тогда при т> N и п> N
И так как aS^„ < aS, то lim aS^„ = aS, т. е. выполняется усло-
та YYi^ji^oo ran
вне C4.7). П
СЛЕДСТВИЕ. В предположениях теоремы ряд C4.3)
сходится тогда и только тогда, когда его частичные суммы
ограничены.
Доказательство следствия очевидно.
Для двойных рядов с неотрицательными членами
справедлив признак сравнения.
оо
ТЕОРЕМА 3. Если ряд ^ а^^ сходится и существует
тага,п = 1
кое с > О, что для всех т, я = 1, 2, ... , выполняется неравен-
оо
ство О < и^^ < са^^, то ряд ^ и^^ также сходится.
т,п = 1
Это сразу следует из следствия теоремы 2, так как для
любых натуральных тип выполняются неравенства
оо оо
т,п = 1 т,п = 1
Из двукратного ряда C4.3) можно формально образовать
два повторных ряда. Для этого следует сначала
просуммировать по одному индексу, зафиксировав другой, а затем
выполнить суммирование по оставгаемуся индексу:
оо оо оо оо
Е Е "тп' Е Е "mn- C4.8)
п = 1т = 1 т = In = 1
Ответ на вопрос, как связана сходимость кратного ряда с
получаюпа;имися из него повторными рядами, дает следуюпа;ая
теорема.
ТЕОРЕМА 4. Если сходится двойной ряд C4.3) и для всех п =
оо оо оо
= 1,2, ...сходятся ряды ^ и^^, то повторный ряд ^ ^ и^^
т = \ п = \т = \
также сходится и его сумма равна сумме данного двойного
ряда.
оо
Доказательство. Если s= ^ г/^^, то, согласно опреде-
т,п = 1
лению суммы двойного ряда, для любого 8 > О супа;ествует
такой номер п^, что для всех номеров т> п^ и п> п^
выполняется неравенство
п т I с
1 ii=i
158
< .
2
Перейдя здесь к пределу при m ^ оо^ получим, что при всех
п> п^ справедливо неравенство
V = 1 ц = 1
<1<е.
Таким образом, положив и^ = Y, ^i^v ^/^ = 1? 2, ... , при п> п^
[1 = 1
будем иметь
L и.
<8.
Это означает, что ^ и^ = s,t. е. сумма ряда ^ ^ и равна s:
V = 1 V=lU=l
оо оо
Определение 6. Ряд C4.3) называется абсолютно сходящимся,
если сходится ряд, составленный из абсолютных величин его
членов, т. е. ряд
оо
Е l"J- C4.9)
т,п = 1
Отметим, что если ряд C4.3) абсолютно сходится, то его
обгций член стремится к нулю при неограниченном
возрастании хотя бы одного из индексов: lim и^^ = 0.
тах{т,д} -^ оо
~ оо
в самом деле, пусть S= ^ \^тФ тогда для любого 8 > О су-
т,п = 1
гцествует натуральное п^такое, что при т> п^ип>
п^выполняется неравенство
~ т п
0<S- ^ ^ |uj<8.
k- 1 I- 1
Поэтому если номера ти.п таковы, что max {т; п} > п^-\- 1,то
l"J< Е K\<S- £ £ К\<г.
{|i>m}U{v>w} k=l 1=1
Из стремления обгцего члена абсолютно сходягцегося ряда
к нулю при неограниченном возрастании хотя бы одного из
его индексов, очевидно, следует, что члены этого ряда
ограничены. Отметим, что у сходяпа;егося, но не абсолютно, ряда это
может не иметь места. Примером такого ряда является,
например, рассмотренный ниже ряд C4.17) в точке A, 1).
ТЕОРЕМА 5. Если ряд C4.3) абсолютно сходится, то
сходится и любой ряд (однократный, двукратный или
повторный), полученный перестановкой членов данного ряда (в
частности, сходится и сам заданный ряд). При этом сумма
любого такого ряда совпадает с суммой исходного ряда {^А.^).
Т59
Доказательство. Расположим члены ряда C4.3) в
бесконечную прямоугольную матрицу, поместив в т-ю ее строку
члены ряда с данным фиксированным первым номером т,
расположенные по возрастанию второго индекса п:
^11 ^12 ^13 ••• ^1п
^21 ^22 ^23 ••• ^2п
^ml ^т2 ^тЗ ••• ^тп *••
Занумеруем теперь элементы этой таблицы согласно сле-
дуюгцей схеме:
^.1
4 3
9 8
5 1
6
Т
7
Член ряда C4.3), получивгаий при такой нумерации номер k,
обозначим Vf^. Рассмотрим ряд
Ё Vk C4.10)
k= 1
И покажем, что он абсолютно сходится, т. е. что сходится ряд
£ К\. C4.11)
k- 1
Обозначим частичные суммы ряда C4.9) через aS^^, его
сумму — через aS, а частичные суммы ряда C4.11) — через aS^.
Прежде всего заметим, что для любой суммы S^ найдутся
такие номера тип, что все члены ряда C4.11), входяпа;ие в
сумму aS^, войдут и в сумму aS^^, тогда aS^ < aS^^ < S. Отсюда и
следует (см. п.31.4) сходимость ряда C4.11).
Из абсолютной сходимости ряда C4.10) следует, что и
любой другой однократный ряд, составленный из членов ряда
C4.3), также сходится и его сумма равна сумме ряда C4.10)
оо
(см. п. 30.10). Пусть У Vf^ = S. Покажем теперь, что любой
двойной ряд
£ <п^ C4.12)
т,п = 1
полученный некоторой перенумерацией двойными индексами
членов данного ряда C4.3), абсолютно сходится и что его
сумма также равна S.
Тбд
Абсолютная сходимость ряда C4.12) легко следует из
абсолютной сходимости ряда C4.3), т. е. из сходимости ряда
C4.9), и доказывается тем же приемом, с помогцью которого
была доказана абсолютная сходимость ряда C4.10). Докажем
теперь, что сумма ряда C4.12) равна S. Обозначим его
частичные суммы через aS^^, а частичные суммы ряда C4.10) —
через aS^. Пусть фиксировано число 8 > 0. В силу сходимости
ряда C4.11), сугцествует такой номер k^, что
тогда и подавно
Е К1<|, C4.13)
< £ \v^<\. C4.14)
Выберем номер N^ так, чтобы частичная сумма S^ ^ ряда
C4.12) содержала в качестве слагаемых все члены ряда C4.10),
входяпа;ие в сумму aS^ . Пусть m > Л/^^ и я > N^, Положим
тогда, использовав C4.13) и C4.14), получим
Итак, S является суммой любого ряда C4.12), в частности
суммой самого ряда C4.3).
Покажем, наконец, что S является и суммой повторных
рядов C4.8). В самом деле, при любом фиксированном п
оо оо ~
т = \ k = 1
оо
Следовательно, все ряды ^ г/^^, п= 1, 2, ..., сходятся, и при-
т = 1
ТОМ абсолютно.
Положим
оо
"„= Е "т„- C4.15)
т = 1
Зафиксируем снова произвольное число 8 > 0. Выберем
номер k^ так, чтобы выполнялось условие C4.13), а
следовательно, и условие C4.14). Далее, подобно тому, как это было
сделано Bbinie, выберем номер N^ так, чтобы частичная сумма S^^^^
ряда C4.3) содержала в качестве слагаемых все члены ряда
C4.10), входяпа;ие в сумму aS^ . Тогда при всех т> N^iin> N^
.ЕХ"у-ЧН I W
е
<5.
■ *, +1
161
Перейдя в этом неравенстве к пределу при m ^ оо^ получим
(см. C4.15))
Отсюда, в силу C4.14), следует, что при п > N^ выполняется
неравенство
Это и означает, что
I I; = 1 '
+ \S^ -S\<e.
оо оо
п = \ т = \ п = \
УПРАЖНЕНИЕ 1. Обобщить критерий Коши сходимости однократных
рядов на случай кратных рядов.
34.2. Кратные функциональные ряды
Определение 7. Ряд вида
£ %....>)' C4.16)
где функции и^ ^ (х) определены на некотором
множестве X, называется k-кратным функциональным рядом, а
суммы вида
— его частичными суммами.
Определеннее. Ряд C4.16) называется сходящимся на
множестве X, если при каждом фиксированном х^еХ сходится
кратный числовой ряд
оо
i: ^п,... пЛч)'
Если ряд C4.16) сходится на X, то функция
оо
называется его суммой.
На кратные функциональные ряды легко переносятся
понятия равномерной сходимости ряда, критерий Konin для
равномерной сходимости ряда, признак Вейерп1трасса
равномерной сходимости и т. п. Мы не будем на этом останавливаться.
УПРАЖНЕНИЕ 2. Определив понятие равномерной сходимости
двойного ряда, доказать, что если ряд C4.16) сходится равномерно и если его
члены являются непрерывными функциями на множестве X ^ i2, то и
сумма ряда C4.16) является непрерывной на множестве X функцией.
162
Определение 9. Ряды вида
где с^ ^ — комплексные числа, называются кратными
степенными рядами.
Хотя, как это видно из предыдупа;его, многие утверждения,
справедливые для однократных рядов, обобгцаются и на
кратные ряды, последние имеют и много своих специфических
особенностей, сугцественно отличаюгцих их от однократных рядов.
В качестве примера приведем двойной степенной ряд с
действительными коэффициентами, который, если он
рассматривается в действительной области, сходится лигаь в двух точках
плоскости, а именно в точках (О, 0) и A, 1). Таким образом,
аналога теоремы Абеля для степенных рядов (см. п. 33.1), во
всяком случае в прямом смысле, для двойных рядов нет. Этот
пример показывает опасность использования аналогий, не
подкрепленных математическими доказательствами.
Рассмотрим ряд
оо
£ с„„х'"г/«, C4.17)
т,п = О
где Соо = О, Со„ = с„о = п1,п = 1, 2,...; с^^ = с^^ = -ml, т = 1, 2,...;
^тп = 0,т>2,га>2. Его частичные суммы имеют вид
S^,(x, г/) = A - у) f klx>' + y + (l-x)j: П уК C4.18)
k- 1 1 = 2
Очевидно, что aS^^@, 0) = О и aS^^A, 1) = 1, m, я = 1, 2, ... , и
поэтому ряд C4.17) сходится в точках (О, 0) и A,1).
оо
Заметим теперь, что радиус сходимости ряда ^ п\ г^ ра-
вен нулю (см. пример 1 в п. 33.1), при этом его частичные сум-
п
МЫ SJ^z) = У Ы 2^, п = 1, 2, ... , при действительных 2 > О,
очевидно, стремятся к +оо.
Покажем, что при 2 <0 его четные частичные суммы aS2^B)
также стремятся к +оо. в самом деле, объединив при 2 < О
попарно соседние члены, получим
«2пB)= Е B/г-1)!|гр-1B/г|2|-1).
k= 1
Далее заметим, что при любом фиксированном 2^0 для
номеров k> т—^ выполняется неравенство Bk - 1)! Ь|^^ " ^ Bk Ь| - 1) >
оо
> Bk - 1)! I^p^ " ^ и что при 2^0 ряд У Bk - 1)! 2^^ ~ ^ расходится
k = 1
(это, например, легко доказывается тем же способом, каким до-
ТбЗ
казывалась при 2^0 расходимость ряда в примере 1 п. 33.1) и,
следовательно, при 2 > О его сумма равна +оо, поэтому и
lim 82^B) = +00, 2^0. Из сказанного и из равенства C4.18)
следует, что если (х, у) ^ (О, 0) или (х, г/) ^ A, 1), то, каковы бы ни
были числа 8 > О и натуральное N, всегда можно подобрать
такие номера т > N и п > N, что |aS^^x, у)\ > 8. А это и означает,
что ряд C4.17) для указанных (х, у) расходится.
Заметим, что хотя в точке A,1) рассматриваемый ряд
сходится, его члены (т. е. в данном случае коэффициенты) не
ограничены. Если у степенного ряда C4.17) в некоторой
точке (Xq, Уо) его члены образуют ограниченное множество (это
имеет место, например, если ряд сходится абсолютно (см.
п. 34.1)), то для такого ряда справедлив двумерный аналог
первой теоремы Абеля (см. п. 33.1).
ТЕОРЕМА 6. Если в точке (Xq, у^) члены ряда C4.17)
ограничены, то в любой точке (х, у) такой, что |х| < |xq|, \у\ < \у^,ряд
C4.17) сходится абсолютно.
Доказательство. Если супа;ествует такое М > О, что для всех
натуральных mvin выполняется неравенство \с^^ xg^ у^\ < М, то
при |х| < |xq|, \у\ < |i/q| получим
X
Xq
т
У
Уо
п
<м
X
—
Xq
т
У
Уо
Отсюда, в силу признака сравнения (см. теорему 3) и
сходимости ряда вида ^ p^q^, \р\ < 1, \q\ < 1 (см. пример в п. 34.1),
т,п = 1
И следует утверждение теоремы. П
оо
УПРАЖНЕНИЯ 3. Назовем число S суммой ряда ^ w^ ^, если для
т,п = 1
любого 8 > о существует такой номер N, что для всех номеров тип,
удовлетворяющих условию т + п> N, выполняется неравенство |aS^^ ~ 'S| <
< 8. Выяснить, эквивалентно или нет это определение определению 5
п. 34.1.
оо
4. Назовем число S суммой ряда У ^тп^ если для любого 8 > О су-
т,п = 1
ществует такое конечное множество Й^ = {{т, п)) пар индексов т, п
членов данного ряда, что, каково бы ни было другое конечное множество Й
пар индексов членов этого ряда, содержащее множество Й^ : Й =) Й^,
выполняется неравенство
{т,п) е ft
<8.
Выяснить, эквивалентно или нет это определение определению 5 п. 34.1
и определению, сформулированному в предыдущем упражнении.
164
4
Глава
Дифференциальное исчисление
функций многих переменных
§35
Многомерные пространства
35.1. Окрестности точек.
Пределы последовательностей точек
Прежде чем перейти к изучению функций многих
переменных, ознакомимся с некоторыми свойствами множеств, на
которых эти функции задаются. Будем предполагать, что на
рассматриваемой плоскости или в пространстве всегда
задана некоторая прямоугольная система декартовых координат.
Точки будем, как правило, обозначать следуюгцими
буквами: а, Ь, ... , X, г/, 2, ...*, а их координаты — теми же буквами
с индексами, т. е. в случае плоскости будем писать х = (х^, Хз),
У = (г/i, г/2)? а в случае пространства — писать х = (х^, Хз, Xg),
У ^ (^1? ^2' Уз)' Расстояние между точками х и г/ будем
обозначать р(х, у). Как известно, формула для расстояния между
точками X и г/ в случае плоскости имеет вид
Р(л:, у) = 7(^1 -yi)^ + (^2-^2)^'
а в случае пространства —
Р(л:, у) = 7(^1 " уО^ + (^2 - У2)^ + (^3 " Уг)^ •
В дальнейгаем придется иметь дело не только с функциями
двух и трех переменных, но и с функциями болыаего числа
переменных, поэтому полезно ввести понятие я-мерного
пространства для любого п = 1, 2, 3, ... .
* Иногда точки обозначаются и больп1ими буквами, например М, N, Р,
а их координаты — буквами х, у, 2.
Тб5
Определение 1. Точкой х п-мерного пространства
называется упорядоченная совокупность п действительных чисел
\Х-^у ... , Х^) X»
Число X. называется i-координатой точки х, i = 1, 2, ... , п.
Расстояние между двумя точками (х^, ... , х^) и (г/^, ... , у^)
определяется по формуле
р(х, у) = 7(:^1-г/1J + ... + (х,-г/,J. C5.1)
Совокупность всех точек п-мерного пространства, в
котором определено расстояние согласно формуле C5.1),
называется п-мерным евклидовым пространством (или, более
полно, п-мерным точечным арифметическим евклидовым
пространством) и обозначается через R^ или R^.
Иногда для краткости вместо х = (х-^, ... , х^) будем писать
X = (х.).
В случае п = 1 пространство R^ совпадает с прямой, в
случае п = 2 — с плоскостью, а в случае п = 3 — с
пространством, изучаемым в элементарной и аналитической геометрии.
В случае произвольного я > 3 не следует искать в
приведенном определении скрытый физический или геометрический
смысл. Нап1ей целью является лип1ь построение некоторого
математического аппарата, удобного для изучения функций
многих переменных; определения и терминологию мы
заимствуем из обычной геометрии, так как это позволяет включить
прямую, плоскость и трехмерное пространство в одну более
обгцую схему.
Расстояние между точками в я-мерном евклидовом
пространстве R^ обладает следуюгцими свойствами.
1^. р(х, у) > о, причем р(х, у) = О в том и только том
случае, когда х = у.
2^. р(х, у) = р(г/, х) для любых двух точек хиу из R^.
3^. р(х, z) < р(х, у) + р(г/, z) для любых точек х, у и z из R^.
Свойства 1^ и 2^ непосредственно следуют из формулы
C5.1), третье же, обычно называемое «неравенством
треугольника» и хороню известное для обычного трехмерного
пространства, в обгцем случае (при произвольном п) требует
доказательства.
Тб6
Докажем предварительно лемму.
ЛЕММА 1 (лемма Коши—Шварца"^). Для любых
действительных чисел Uj^ и bj^, k = 1, ... , п, выполняется неравенство
СЛЕДСТВИЕ.
Х^(а, + Ь,J < jl^af + jX^bf. C5.3)
Неравенство C5.2) является частным случаем неравенства
Гёльдера, а неравенство C5.3) — частным случаем
неравенства Минковского (см. п. 30.8"^) прир = 2. Однако в этом случае
их доказательство значительно прогце, и поэтому мы его здесь
приведем.
Доказательство. Если всеа^ = О, / = 1, 2, ... , п, то
неравенство C5.2) очевидно — обе его части преврагцаются в нуль.
Если же af + ... + а^ > О, то рассмотрим квадратичную функцию
Fit) = t {a,t + &,J = f2 £ af + 2f £ «A + t Ч- C5.4)
i = \ i = \ i = \ i = \
Очевидно, что F(t) > 0. Из этого условия следует, что
квадратный трехчлен C5.4) имеет либо совпадаюгцие действительные
корни, либо сугцественно комплексные корни, поэтому его
дискриминант не положителен:
Перенося второе слагаемое в правую часть и извлекая
квадратный корень, получим C5.2). П
Для доказательства неравенства C5.3) оценим сумму
п
^ (а. + Ь.)^, применяя неравенство C5.2):
i = 1
£ (а, + Ь,J- £ а,2+ £ 6,2 + 2 £ а,!>, <
<X,'-? + ,E/? + 2jX,<-?^£^6f = (^£_.f+j£_6f).
Извлекая из обеих частей квадратный корень, получим
C5.3). П
Г. Шварц A843—1921) — немецкий математик.
167
Вернемся теперь к свойству 3^ расстояния между точками
в пространстве R^.
Пусть X = (Xi, ... , xj, у = (i/i, ... , г/J и 2 = (z^, ... , zj.
Положим а. = X. - у., Ь- = у. - z- и, значит, а. -\- Ь- = х- - z-,
i= 1, 2, ... , п. Тогда неравенство C5.3) можно переписать сле-
дуюгцим образом:
ИЛИ, согласно C5.1), р(х, z) < р(х, у) + р(г/, z). П
В дальнейгаем в этом параграфе пространство й^ будем
считать фиксированным (т. е. считать фиксированным число п).
Определение 2. Множество точек х = (х^, ... , х^) п-мерного
евклидова пространства R^ таких, что х^ = Х2 = ... = х._^ =
= Х- ^ -^ = ... = Xj^ = О, называется i-u координатной осью
(/ = 1, 2, ... , я) этого пространства. Точка О = (О, О, ... , 0)
называется началом координат.
Очевидно, в случае я = 2 и я = 3 приведенное определение
дает обычные координатные оси.
Пусть Q < k < п. Пространства R^ и R^ состоят
соответственно из точек (х^, ... , х^) и (х^, ... , х^). Между множеством
всех точек пространства й^ вида (х^, ... , х^. О, ... , 0) и
множеством всех точек (х^, ... , х^^) пространства R^ сугцествует
взаимно-однозначное соответствие (х^, ... , х^. О, ... , 0) ^ (х^, ... , х^),
при котором сохраняется расстояние между точками.
Поэтому естественно множество всех точек (х^, ... , х^. О, ... , 0)
пространства R^ обозначать также R^, и, следовательно, при этом
соглагаении R^ ^ R^, k<. п.
Замечание. Пусть на плоскости заданы две
прямоугольные системы координат, точка М в одной системе имеет
координаты (х, г/), а в другой (^, Г|), т. е. М = (х, у) = (^, Г|).
Ставя в соответствие упорядоченной паре чисел (х, у)
упорядоченную пару (^, Г|), получаем взаимно-однозначное соответствие
между множеством всех упорядоченных пар (х, у) и
множеством всех упорядоченных пар (^, Г|). При этом если
М' = {х', у') = (^', л'), М" = ix", у") = а", л"),
1б8
то
Этот пример делает естественным следуюпа;ее определение.
Пусть каждой точке х = (х^, ... , x^)eR^ поставлен в
соответствие упорядоченный комплекс из п действительных чисел
^(х) = (^^, ... , ^^) таким образом, что для любых двух точек
х' = (х^, ... , х^) и х'' = (х^', ... , х^') и соответствуюпа;их им
комплексов ^(х') = (^р ... , Ь,[) и ^(х'') = (^^', ... , ^^') выполняется
равенство
i = 1 i = 1
тогда числа, входяпа;ие в совокупность (^^, ... , ^^), также
называются координатами точки х («в другой системе
координат»). При таком определении координат расстояние между
двумя данными точками не меняется при изменении систем
координат, т. е. при замене одной системы координат другой.
В дальнейгаем, если не оговорено что-либо другое, система
координат считается фиксированной.
Если точка х задается координатами (х^, ... , х^), то иногда
для ясности пространство R^ будем обозначать R^ ^ .
Определение 3. ili/cmb xeR^ и 8 > 0. Совокупность всех
точек yeR^ таких, что р(х, у) < 8, называется п-мерным
шаром с центром в точке х и радиусом 8 или г-окрестностъю
(а иногда сферической или, правильнее, шаровой
окрестностью) точки X в пространстве R^ и обозначается С/(х; 8).
Таким образом,
Щх; г) = 1у = (г/1, ... , у J : Х^ (У, " х,)^ < г^\, C5.6)
X 1Х-|, ... , Х„1, С/ ^ \j.
В случае прямой, т. е. при п= 1 (рис. 11), х = х^, у = у^,
поэтому
Щх;е) = {у : \у- х\<е}.
Таким образом, U(x; г) является
—* • * ^
интервалом длины Z8 с центром в точ- х-г х х + е
ке X, т. е. окрестностью точки х в
рассмотренном Bbinie смысле (см. п. 3.2). Рис. 11
Тб9
\ X
\
\
\
/
Рис. 12
В случае плоскости, т. е. при п = 2
(рис. 12), X = (Xi, Х2), у = (г/1, г/з) и
С/(х; 8) = {г/ = (г/1, г/з): (г/^ - Xi)^ +
+ (г/2 - Хз)^ < 8 < 8^}, 8 > О,
т. е. U(x; 8) — круг радиуса 8 с центром в точ-
ке X = (х^, Хз) (круговая окрестность), а в
случае пространства, т. е. при п = 3, окрестность
точки X = (х^, Х2, Xg) задается формулой
Щх; г) = {у = (г/1, у^, Уз) : (г/i - х^)^ + (г/з - Хз)^ + (г/д - Xg)^ < 8^},
8>0
и является niapoM радиуса 8 с центром в точке (Xi, Х2, Х3).
Таким образом, понятие окрестности обобгцено на случай
я-мерного евклидова пространства R^. Однако наряду с
указанным обобгцением бывает полезно и другое обобгцение этого
понятия, а именно понятие так называемой прямоугольной
окрестности.
Определение4. ТТг/сть х = (х^, ... , xJgB^, 6. > О, / = 1, 2,... , я.
Множество
Р(х; 6i, ... , 8J =
= {у = (г/i, ... , у J : |г/. - х.| < 6-, / = 1, 2, ... , п} C5.7)
называется п-мерным параллелепипедом (точнее, п-мерным
параллелепипедом с ребрами, параллельными
координатным осям), а точка х — его центром.
Определение5. Если 5^ = 82 = ... = 5^ = 5, то Р(х; 6, 6, ... , 6)
называется п-мерным кубом с ребрами длины 26 (точнее,
п-мерным кубом с ребрами указанной длины и параллельными
осям координат) с центром в точке х и обозначается Р(х; 6).
Очевидно, что если для чисел 6i, 63, ... , 6^ положить
6q = min {61, ... , 5J, 6 = max {61, ... , 5J,
TO
P(x; 60) ^ P(x; 61, ... , 61) ^ P(x; 6). C5.8)
Если n= l,TO множество P(x; 6) является интервалом с
центром в точке X длины 26; если п = 2, то множество Р(х; 6i, 63) яв-
Ттд
ляется прямоугольником со сторонами, параллельными осям
координат (их длины равны соответственно 26^ и 262); при п = 3
множество Р(х; 5^, 63, 63) представляет собой прямоугольный
параллелепипед с ребрами, параллельными осям координат (их
длины соответственно равны 26^, 262, 263).
Под я-мерным параллелепипедом, соответственно я-мерным
кубом, понимается также множество, определенное
указанными Bbinie условиями хотя бы в одной системе координат (а не
обязательно в данной, как это было сделано выгае). В дальней-
П1ем я-мерный параллелепипед и я-мерный куб понимаются
лип1ь в узком смысле, т. е. в смысле данного выгае определения
при фиксированной системе координат, если, конечно,
специально не оговорено что-либо другое.
Определение6. Всякий п-мерный параллелепипед Р{х; 6^,... ,6^)
называется прямоугольной окрестностью точки х.
Если прямоугольная окрестность точки является я-мер-
ным кубом, то она называется также и кубической
окрестностью этой точки.
ЛЕММА 2. Любая сферическая окрестность точки
пространства содержит прямоугольную окрестность и содержится в
прямоугольной окрестности этой точки.
Любая прямоугольная окрестность точки содержит
сферическую окрестность и содержится в сферической
окрестности этой точки.
Эти утверждения геометрически очевидны при я = 1, 2, 3.
Действительно, при п= \ понятия сферической и
прямоугольной окрестностей совпадают. При п = 2 лемма означает, что во
всякий круг можно вписать прямоугольник и около всякого
круга описать прямоугольник так, что центры
прямоугольников будут совпадать с центром круга. Соответственно во
всякий прямоугольник можно вписать круг с
центром в центре прямоугольника и около
всякого прямоугольника можно описать
круг с центром в центре прямоугольника
(рис. 13). Аналогичный смысл имеет
лемма и при я = 3, следует только круги
заменить гаарами, а прямоугольники —
параллелепипедами. Нетрудно записать и
доказать эти утверждения в аналитической
форме, использовав координатную запись. Рис. 13
Тп
Этот способ, как это сейчас будет показано, легко обобгцается
и на случай пространства любой размерности.
Доказательство. Прежде всего отметим, что для любых
чисел а^, а^, ... , а^ справедливо неравенство
|а.| < 7«1+«| + «з + ••• + ^д ^
< \а^ + \а^ + \а^ + ... + |а^|, /=1,2, ... , п. C5.9)
Справедливость этого неравенства доказывается
возведением обеих его частей в квадрат.
В силу данного неравенства, для координат двух любых
точек X = (х^, ^2, ... , xj И г/ = (г/^, г/2, ... , г/J пространства Ш
справедливо неравенство
\У1 - ^:J < р(г/, х) = 7(г/1 - ^:iJ + (г/2 - Хз)^ + ... + (г/^ - х^J <
^ |г/1 - ^:i| + |г/2 - X2I + ... + \у^ - xj, /=1,2, ... , п. C5.10)
Из этого неравенства следует, что для любого 8 > О имеет место
вложение
Р х; - ^ C/(x; 8) ^ Р(х; 8) ^ C/(x; Я8). C5.11)
Действительно, если г/еР[х; - ], то |г/. - х.| < -, / = 1, 2, ... , я,
поэтому (рис. 14)
A/i^l C5.10) j^i j^i Я
Т. е. yeU(x, г).
Если уеЩх, 8), то |г/. - х.| < р(г/, х) < 8, / = 1, 2, ... , п, а
(o5.ll))
ЭТО означает, что уеР(х; 8) (рис. 15).
1
•^2
"о
1
8/
е
2
/х
У=(У^У2) \
1
1 У^
1 ^,^/
—:
1 ^^
^1
Рис. 14
Рис. 15
i72
Наконец, если уеР(х; г), то из первого включения C5.11),
заменив 8 на пе, получим, что yeU(x; пе). Из включений
C5.11) утверждение леммы следует очевидным образом. П
УПРАЖНЕНИЕ 1. Доказать, что для любого 8 > О и любой точки x^R
справедливы включения
Pfx; -^ V и{х, 8) ^ Р(х, 8) ^ и{х, 8л/я).
Лемма 2 показывает, что определения в я-мерном
пространстве выбираются таким образом, чтобы в нем имели
место утверждения, аналогичные некоторым простейгаим
утверждениям в трехмерном пространстве. От nocneninoro
использования аналогий, не подкрепленных математическими
доказательствами, предостерегает пример, содержагцийся в
следуюгцем ниже упражнении.
УПРАЖНЕНИЕ 2. Выяснить, при всех ли я = 1, 2, ... в пространстве R^
выполняется включение
Р{а; 1) CZ Ща; 1),
т. е. всегда ли я-мерный куб с ребром единичной длины вкладывается в
шар единичного радиуса.
Определение 7. Пусть каждому натуральному числу т
поставлена в соответствие некоторая точка x^^^^g R^ (не
обязательно разные точки для разных т). Отображение т -^ х^^\
т е N, х^^^ G R^, множества натуральных чисел N в
пространство R^ называется последовательностью {х^^^} точек
пространства R^,
Множество значений этого отображения, т. е. множество
{х^^^ : т = 1, 2, ...} ^ R^ называется множеством значений
последовательности {х^^^}. Последовательность {х^^^}
обозначается также х^^\ т = 1, 2, ... .
Последовательность {х ^^ }, образованная из членов данной
последовательности {х^^^} с сохранением порядка их следования,
называется подпоследовательностью последовательности {х^^Ц.
Таким образом, если — подпоследовательность
последовательности {х^^^}, то условие k^ < ^2 равносильно
условию т^ < mj^ .
Определеннее. Точку xeR^ называют пределом
последовательности {х^^^} и пишут
X = lim х^^\
ш —> со
если lim р(х^^\ х) = 0.
Ттз
Если X = lim х^^\ то говорят, что последовательность
{х^^^^} сходится к точке х. Последовательность, которая
сходится к некоторой точке, называется сходящейся.
Используя понятие окрестности, легко установить, что
X = lim х^^^ тогда и только тогда, когда для любого 8 > О
сугцествует такое т^, что для всех т > т^ выполняется
включение x^^^eU(x; 8). Согласно лемме 2, получаем также:
X = lim х^^^ в том и только том случае, когда для любой
m ^ оо
прямоугольной окрестности Р(х; 6^, ... , 6^) супа;ествует
номер т^ (зависяпа;ий от этой окрестности) такой, что для всех
т> т^ выполняется включение
^(т)^ P(x;6i, ... ,6J. C5.12)
В силу включений C5.8), при определении предела можно
ограничиться и только одними кубическими окрестностями.
В случае п = 1 определение 8 преврапа;ается в обычное
определение предела числовой последовательности.
При п = 2 сходимость последовательности {х^^^} точек
плоскости R^^ к точке xeR^^ означает, что, каков бы ни был круг
с центром в точке х, начиная с некоторого номера, зависяпа;его
от радиуса этого круга, все члены данной последовательности
лежат в этом круге (рис. 16). В случае п = 3 сходимость
последовательности точек {х^^^} пространства к точке xeR^
означает, что, каков бы ни был обычный трехмерный niap с
центром в точке X, начиная с некоторого номера, зависягцего от
радиуса niapa, все члены данной последовательности лежат в
этом niape.
Как и в случае числовых последовательностей, можно
X, x^^^eR^, m = 1, 2, ... , если всякая
8-окрестность точки X содержит
почти все точки данной
последовательности, т. е. все, за
исключением конечного их множества.
Понятие предела
последовательности {х^^^} точек пространства R^
может быть сведено к понятию пре-
___. ^ дела числовых последовательностей
Рис. 16 координат точек х^^\ т= 1, 2, ... .
174
сказать, что lim х^^^ =
х^
/
1
\
\
\
\
ч
m ^ оо
^\
^(т) \ Х^1)
.• \
.;•• J >
• • /
• /
У
ТЕОРЕМА 1. Для того чтобы последовательность х^^^ =
= (х^^\ ... , x^^^)eR^, m = 1, 2, ... , сходилась к точке х =
= (х-^, ... , xJeR^, необходимо и достаточно, чтобы
lim х(^) = Х;, i=l,2, ... ,п. C5.13)
Доказательство. Докажем необходимость условия C5.13).
Пусть lim х^"^^ = X. Зафиксируем произвольное 8 > 0; тогда,
corn ^ оо
гласно C5.12), сугцествует такое т^, что при всех т> т^
выполняется включение х^^^еР(х; г), т.е. для любого i = 1, 2, ... , п
и при т> т^ справедливо неравенство |х[^^ - х.\ < 8, а это и
означает, что lim х^^^ = Х-, /=1,2, ... , п.
Докажем достаточность условия C5.13). Пусть lim х/"^^ =
= X., / = 1, 2, ... , я, и Р(х; 8^, ... , 8^) — заданная
прямоугольная окрестность точки х. Тогда для каждого 8- > О (/ = 1, 2, ... , я)
сугцествует такой номер т- = т- (8-), что для всех т > т-
выполняется неравенство
|х[^) - х.\ < 8., i= 1, 2, ... , п. C5.14)
Обозначим через т^ наибольгаий из номеров т^, ... , т^, т. е.
т^ = max {т^, ... , mj; тогда при т> т^и всех / = 1, 2, ... , п
будут одновременно выполнены условия C5.14) и, следовательно
(см. C5.7)), при т > т^ имеем включение х^^^еР(х; 8^, ... , 8^),
что и означает, согласно C5.12), что lim х^^^ = х.П
Из теоремы 1 и свойств пределов числовых
последовательностей следует, что если последовательность точек имеет
предел, то он единствен, и что всякая подпоследовательность схо-
дягцейся последовательности сходится к тому же пределу, что
и вся последовательность.
УПРАЖНЕНИЕ 3. Сформулировать и доказать необходимое и
достаточное условие сходимости последовательности точек пространства R^,
аналогичное критерию Коши для числовых последовательностей.
Определение 9. Множество X ^ R^ называется
ограниченным, если существует п-мерный куб Р@; а) с центром в
начале координат О такой, что X ^ Р@; а).
Согласно лемме 2, можно дать епа;е одно эквивалентное
предыдупа;ему определение ограниченного множества.
Ттз
Определение 9\ Множество X ^ R^ называется
ограниченным, если существует п-мерный шар U@; г) такой, что
X CZ ЩО; 8).
ОпреА^^е^^е ^0-Последовательность точек х^^^е R^, т =
= 1, 2, ... , называется ограниченной, если множество ее
значений, т, е, множество {х^^^ : т = 1, 2, ...}, ограничено в
пространстве R^,
Если последовательность х^^^ = {х^^\ ... , х^^^), т = 1,2, ... ,
сходится, то она ограничена, ибо каждая из координатных
последовательностей х\^\ т = 1, 2, ... (/ фиксировано, i = 1, 2, ... , п) в
этом случае также сходится и, значит, ограничена.
ТЕОРЕМА 2. Из любой ограниченной последовательности
точек пространства R^ можно выделить сходящуюся
подпоследовательность.
Эта теорема, как и в одномерном случае, обычно
называется теоремой Больцано—Вейерштрасса.
Доказательство. Пусть задана ограниченная
последовательность точек х^^^ = (х^^\ ... , х^^^), т = 1, 2, ... ,
пространства R^. Тогда, согласно определению 9, супа;ествует такой куб
Р@; а), что при всех т = 1, 2, ... , выполняется включение
хМеР@; а), sl следовательно, и включения х1^^е(-а, а), т. е.
каждая из п координатных числовых последовательностей {х^^^},
i= 1, 2, ..., п также ограничена. Поэтому, по теореме Больцано—
Вейерп1трасса (см. п. 4.6) последовательность {х^^^} содержит
сходяпа;уюся подпоследовательность; пусть это последователь-
ность х-^ ^ , k-^ = 1, 2, ... . Последовательность {х2 ^ }, как
подпоследовательность последовательности {х^^^}, также ограничена
и поэтому содержит сходяпа;уюся подпоследовательность. Пусть
это последовательность Х2 ^' ^ , k2 = 1, 2, ... . Последователь-
ность {х-^ ^' 2 }, как подпоследовательность сходяпа;ейся после-
(rtij^ )
довательности {х-^ ^ }, очевидно, также является сходяпа;ейся.
Продолжая этот процесс, через п niaroB получим п сходяпа;ихся
числовых последовательностей х- ^' 2"'" "^ , i = 1, 2, ... , п,
каждая из которых является подпоследовательностью соответ-
Ттб
ственно последовательности {х[^^}. Тогда (теорема 1) последова-
(т. , , ) {т. , , ) {т. , , )
тельность точек х ^ ^ ^ = ух^ ^ ^ ^,...,х^ ^ ^ ^)
пространства й^ будет также сходяпа;ейся. П
Аналогично одномерному случаю, предел
подпоследовательности последовательности точек я-мерного пространства
называется частичным пределом. Теорема 2 показывает, что
множество частичных пределов ограниченной
последовательности точек из R^ всегда не пусто.
Иногда бывает удобно рассматривать последовательности
точек, стремягциеся к бесконечности.
Определение 11. Последовательность точек х^^^е R^, т =
= 1, 2, ... , называется стремящейся к бесконечности, если
расстояние ее членов от начала координат О = (О, О, ... , 0)
стремится к бесконечности, т, е, если
lim р(х("^). О) =+00. C5.15)
В этом случае пигаут lim х^"^^ = оо. Для любого aeR^, в си-
лу неравенства треугольника р(х^^\ О) < р(х^^\ а) + р(а. О),
справедливо неравенство
р(х("^), а) > р(х("^). О) - р(а. О), C5.16)
и при выполнении A4.15) lim р(х^^\ а) = +оо, т. е. если
lim х^^^ = оо^ то расстояния от точек последовательности {х^^^}
т ^ оо
ДО любой фиксированной точки aeR^ стремятся к бесконечности.
УПРАЖНЕНИЯ. 4. Последовательность х^'^^еД", тп = 1, 2, ...,
называется неограниченной, если множество ее значений не ограничено.
Доказать, что всякая неограниченная последовательность точек я-мерного
пространства содержит подпоследовательность, стремящуюся к
бесконечности.
5. Для того чтобы последовательность х^^^ = (х^^\ ..., xjf^^), т = 1, 2, ...,
стремилась к бесконечности, необходимо и достаточно, чтобы
существовал номер i, для которого
lim х(^) = оо
По аналогии со случаем прямой, бесконечность оо
называется также и бесконечно удаленной точкой я-мерного
пространства. В отличие от случаев прямой, на которой имеется
два направления и поэтому можно ввести понятия
бесконечностей со знаком, для пространства й^, я > 1, вводится только
бесконечность без знака.
Тт?
35.2. Различные типы множеств
В настоягцем пункте рассматриваются вспомогательные для
дальнейгаего изложения математического анализа вопросы,
связанные с геометрией я-мерного пространства.
Определение 12. ili/cmb X— некоторое множество точек
евклидова пространства R^, Точка хеХ называется
внутренней точкой этого множества {относительно
пространства R^), если существует г-окрестность этой точки,
содержащаяся в множестве X, т. е. существует такое 8 > О, что
Щх; 8) ^ X.
Совокупность внутренних точек множества называется
его внутренностью. Внутренность множества X
обозначается Х.^^\
УПРАЖНЕНИЕ 6. Если пересечение Х^ЛУ^Х^К'^^У ^ Д", содержит хотя
бы одну точку, являющуюся внутренней как для множества X, так и для
множества Y, то множество внутренних точек пересечения X П Y не пусто.
Определение 13. Множество, каждая точка которого
является его внутренней точкой {относительно рассматриваемого
пространства R^), называется открытым множеством.
Таким образом, открытыми являются множества, которые
совпадают со своими внутренностями.
Мы уже встречались с понятиями внутренней точки и
открытого множества в случае плоских множеств (см. п. 27.1).
Следует иметь в виду, что одна и та же точка одного и того
же множества может быть его внутренней точкой
относительно одного пространства, содержапа;его это множество, и не быть
внутренней точкой рассматриваемого множества относительно
другого пространства, также содержапа;его это множество.
Рассмотрим, например, пространство R'^y, т. е. плоскость с
некоторой фиксированной системой декартовых координат,
которые будем обозначать х и г/. Ось Ох этой плоскости, как всякая
числовая ось, является евклидовым пространством R]..
Каждая точка какого-либо интервала (а, Ъ) этой оси, т. е. множество
точек {(х, у): а< X <Ъ, у = 0} плоскости R'^y, является
внутренней точкой этого интервала относительно указанного простран-
int — начало латинского слова interior — внутренний.
Т78
/
8^^-
\
ч
'^
V
У-
" X
5/
Уу
\
1 \
/ \
/ 1
i
/
/
/
ства Rl (оси Ox) и не является внутренней
точкой этого интервала относительно всей
плоскости R^y. Таким образом, интервал
(а, Ь) является открытым множеством
пространства й^ и не является открытым
множеством пространства R^y
Важный класс открытых множеств ус- ^ ~—-^
танавливается следуюпа;ей леммой. Рис. 17
ЛЕММА 3. Всякая г-окрестностъ С/(х; 8)
любой точки xeR^ является открытым множеством.
Доказательство. Пусть задана некоторая окрестность
U(x; 8) и пусть уе U(x; 8). Положим
8 = г-р(у,х) C5.17)
и покажем, что U(y; 6) ^ U(x; 8) (рис. 17).
Если 2е U(y; 6) и, значит, рB; у) < 6, то, применив
неравенство треугольника и C5.17), получим
рB, х) < рB, у) + р(г/, х) < 6 + р(г/, х) = 8,
т.е. 2gC/(x; 8). Так как 2— произвольная точка множества
U(y; 6), то это означает, что U(y; 6) ^ U(x; 8). П
На примере доказательства этой леммы хороню видно, как,
используя для наглядности плоский чертеж, можно проводить
доказательства в я-мерном пространстве.
Открытые множества пространства R^ будем обозначать,
как правило, буквой G. Пустое множество будем по
определению считать открытым.
УПРАЖНЕНИЯ. 7. Доказать, что внутренность всякого множества
является открытым множеством.
8. Доказать, что прямоугольная окрестность точки является открытым
множеством.
ЛЕММА 4. Пересечение конечного числа, так же как и
объединение любой совокупности открытых множеств,
является открытым множеством.
Доказательство. Пусть G^, G^, ... , G^ — открытые мно-
k
жества пространства R^. Если их пересечение Q G — пустое
множество, то оно, согласно договоренности, является откры-
Ттэ
тым. Если же указанное пересечение не пусто и xg П ^ G , то, в
силу открытости множеств G, для каждого j = 1, 2, ... , k сугцест-
вует такое 8^ > О, что Щх, 8^) с Gj. Полагая 8 = min {8^, ... , 8^},
получим, что для каждого у справедливо включение U(x, 8) с G
k
(у = 1, 2, ... , k). Следовательно, U(x, 8) ^ П^ Gj, т. е. точка х
k
является внутренней для пересечения П G . Поскольку х —
произвольная точка этого пересечения, оно является
открытым множеством.
Пусть теперь дана произвольная система открытых множеств
{GJ, аеШ, где Ш — некоторое множество индексов и G = осУ^^а-
Покажем, что G — открытое множество. Действительно, какова
бы ни была точка xeG, существует такой индекс адеШ, что
xeG^ . Поскольку G^ — открытое множество, найдется такое
8 > О, ЧТО Щх; е) (Z G^ . Но тогда Щх; ^) ^ ^с Уш ^ос ^ ^' т. е. х —
внутренняя точка множества G и, значит, это множество
открыто. П
Очень удобным оказывается следуюгцее определение.
Определение 14. Всякое открытое множество, содержащее
точку, называется ее окрестностью.
Окрестность точки х будем, как правило, обозначать
через и = U(x), быть может, с теми или иными индексами, а
иногда, как и в одномерном случае, другими буквами,
например V, W.
Пересечение двух открытых множеств снова является
открытым множеством (лемма 4). Поэтому пересечение двух
окрестностей точки также является ее окрестностью.
Замечание. Во всякой окрестности U(x) точки х,
очевидно, содержится как сферическая, так и прямоугольная
окрестность этой точки. Далее, если окрестность точки
понимать в смысле определения 14, то точка х является пределом
последовательности {х^^Ц тогда и только тогда, когда для
каждой ее окрестности U(x) супа;ествует такой номер т^, что для
всех т > т^ выполняется включение х^^^е U(x).
Определение 15. Точка xeR^ называется точкой
прикосновения множества X ^ R^, если любая окрестность этой
точки содержит по крайней мере одну точку множества X.
Тзд
Очевидно, что каждая точка множества X является его
точкой прикосновения, ибо всякая окрестность точки хеХ
содержит саму точку X. Вместе с тем могут, конечно, сугцество-
вать и точки прикосновения данного множества, не принадле-
жагцие ему (например, концы интервала на прямой являются
его точками прикосновения).
УПРАЖНЕНИЕ 9. Доказать, что, для того чтобы точка xeR^ была
точкой прикосновения множества X ^ R^, необходимо и достаточно, чтобы
существовала последовательность точек х^^^еХ, т = 1, 2, ... , такая, что
lim х^^^ = X.
т ^ о°
Определение 16. Если у точки хеХ существует
окрестность, не содержащая никаких других точек множества X,
кроме самой точки х, то эта точка называется
изолированной точкой множества X,
Определение 17. Точка xeR^ называется предельной
точкой множества X, если любая окрестность точки х
содержит по крайней мере одну точку множества X, отличную
от X,
Очевидно, что предельная точка множества является и его
точкой прикосновения.
Определение предельной точки удобно сформулировать
с помогцью понятия проколотой окрестности точки я-мерного
пространства, которое вводится по аналогии со случаем
числовой прямой.
о
Определение 18. Проколотой окрестностью U(x^^^) точки
xi^)eR^ называется всякое множество, получающееся
удалением точки х^^) из некоторой окрестности С/(х^^)) этой
точки:
^(х@)) %^ С/(х@))\{х@)}.
Используя термин проколотой окрестности, предельную
точку множества можно определить как точку, любая проколотая
окрестность которой пересекается с данным множеством (в то
время как у точки прикосновения любая ее (целая) окрестность
обязана пересекаться с рассматриваемым множеством).
Мы уже встречались с понятиями точек прикосновения,
предельных и изолированных в одномерном случае (см. п. 5.4
и 5.5). Напомним некоторые их свойства.
Tsi
у всякой точки прикосновения Xq множества X либо супа;ест-
вует окрестность, содержапа;ая лип1ь одну точку из X (в этом
случае этой точкой является сама точка Xq), либо такой
окрестности нет, т. е. в каждой окрестности точки Xq имеется по
крайней мере две точки множества X (следовательно, по крайней
мере одна из них отлична от Xq). Поэтому всякая точка
прикосновения множества X является либо его изолированной точкой,
либо его предельной точкой (в последнем случае она может как
принадлежать, так и не принадлежать самому множеству).
Если х^^^ — предельная точка множества X ^ R^, то сугцест-
вует последовательность точек x^^^^gX таких, что lim х^^^ = х^^\
у.{т') ^ у.{т) ^ j^@)^ ^ ^ у1^'^ meN, m'eN, т. е. последовательность
{х^^^} состоит из различных точек множества X, отличных от
точки х^^\ и сходится к этой точке. В самом деле, поскольку
х@) — предельная точка множества X, для окрестности U(x^^\ 1)
сугцествует точка (обозначим ее через х^^^) такая, что х^^^е
еЩх^^К 1) ПХ и хA) ^ х@). Пусть б^ = min |i, р(х^^\ x^D)!. Для
окрестности U(x^^\ 6^) найдется такая точка (обозначим ее через
хB)), что х^^^е Щх^^\ 8) П X, х^ ^ х^^\ ясно, что х^^^ ^ х^^^.
Продолжая этот процесс, мы получим искомую последовательность.
Из доказанного следует, что любая окрестность
предельной точки множества содержит бесконечно много точек этого
множества (ими, например, являются точки построенной вы-
nie последовательности).
Пример. Пусть п = 1, X = (О, 1) — интервал. Каждая
точка отрезка [О, 1] является точкой прикосновения и
предельной точкой множества X, при этом точки О и 1 не
принадлежат самому множеству X. Если X = [О, 1] — отрезок, то
множество точек прикосновения множества X совпадает с самим
множеством. Наконец, если множество X состоит из
интервала (О, 1) и точки 2, т. е. X = (О, 1) U {2}, то точка 2 является его
изолированной точкой, а множеством его точек
прикосновения является множество [О, 1] U {2}.
Определение 19. Совокупность всех точек прикосновения
множества X ^ R^ называется замыканием множества X и
обозначается X.
Как уже отмечалось, каждая точка множества X является
его точкой прикосновения, поэтому
Х^ X. C5.18)
182
Определение 20. Множество X называется замкнутым, если
X = X, т, е, если оно содержит все свои точки прикосновения.
Например, при п = \ интервал (О, 1) не является
замкнутым множеством, а отрезок [О, 1] — замкнутое
множество. Пустое множество будем считать по определению
замкнутым.
Все пространство и пустое множество являются
одновременно замкнутыми и открытыми в R^ множествами
(проверьте это). Можно показать, что в пространстве R^ не супа;ествует
других одновременно замкнутых и открытых множеств.
Всякая точка прикосновения множества является либо его
предельной, либо его изолированной точкой, а изолированная
точка, в силу своего определения, принадлежит множеству,
поэтому требование принадлежности каждой точки
прикосновения к множеству эквивалентно требованию
принадлежности к этому множеству каждой его предельной точки. Иначе
говоря, множество замкнуто тогда и только тогда, когда
оно содержит все свои предельные точки.
УПРАЖНЕНИЯ. 10. Доказать, что из включения X ^Y следует
включение X^Y.
11. Пусть X ^ R^^ R^. Доказать, что xeR^ является точкой прикосновения
множества X в пространстве R^ тогда и только тогда, когда она
принадлежит пространству R^ и является в нем точкой прикосновения множества X.
Отсюда следует, что множество X является замкнутым множеством
пространства R^ тогда и только тогда, когда оно является замкнутым
множеством пространства R^. Таким образом, свойство множества быть замкнутым
в некотором пространстве R^ является «внутренним» свойством этого
множества, т. е. свойством, которое не зависит от выбора пространства i2", в
котором лежит рассматриваемое множество. Как было отмечено выше,
свойство множества быть открытым не является «внутренним» свойством в
указанном смысле, одно и то же множество может быть открытым в одном
пространстве R^ и не быть открытым в другом.
Отметим очевидное свойство замкнутых множеств:
Если F — замкнутое множество, а {х^^Ц — сходящаяся
последовательность, все члены которой принадлежат
множеству F: x^^^eF, m = 1, 2, ... , то ее предел также
принадлежит множеству F.
Действительно, если х^^^ = lim х^^\ то из определения
предела последовательности точек следует, что в любой
окрестности точки х^^^ имеются точки данной
последовательности (и, более того, там лежат почти все точки последователь-
J83
ности, т. е. все, за исключением конечного их множества), яв-
ляюгциеся, по предположению, и точками множества F.
Таким образом, точка х^^^ является точкой прикосновения
множества F, и так как F — замкнутое множество, то x^^^gF.
ЛЕММА 5. Точка прикосновения замыкания множества
является и точкой прикосновения самого множества.
СЛЕДСТВИЕ. Замыкание всякого множества является
замкнутым множеством.
Доказательство леммы. Пусть X ^ й^, X —
замыкание множества X и х — точка прикосновения множества X,
т. е. xgX. Покажем, что xgX.
Из условия xgX следует, что любой окрестности U = U{x)
точки X принадлежит хотя бы одна точка у множества X:
i/gC/ П X. Поскольку С/, как всякая окрестность, является
открытым множеством, она является и окрестностью содер-
жагцейся в ней точки у. Но уе. X, следовательно, в любой
окрестности точки г/, в частности в С/, имеется точка z из
множества X: Z&U Г\ X.
Итак, в любой окрестности U точки хе. X имеется точка из X.
Это означает, что х является точкой прикосновения
множествах: xgX. П
Доказательство следствия. В лемме 5 доказано, что
Х^Х,
и так как, согласно C5.18), X ^ X, то
Х = Х. C5.19)
Примеры. 1. Всякий я-мерный niap
Q^=\x = (Xi, ... , xj: 1^{х, - a.J < r^ I C5.20)
является открытым множеством (см. лемму 1), поэтому его часто
называют также п-мерным открытым шаром. Множество же
Q" =\х = (xi, ... , xj: 1^{х, - а,J < г^ I, C5.21)
замкнуто, так как нестрогие неравенства сохраняются при
предельном переходе. Оно является замыканием открытого niapa Q^
184
и называется п-мерным замкнутым шаром. В случае п = 2:
Q2 — открытый круг, Q — замкнутый круг; в случае п = 1:
Q^ — интервал, Q^ — отрезок.
2. Замкнутый шар Q^ получается из открытого шара Q^
присоединением к нему множества
X = (xi, ... , xj: f (х. - а.J = г^
i = 1
называемого (п - 1)-мерной сферой радиуса г с центром в
точке а = (а^, ... , а^) и обозначаемого aS^ " ^. В случае п = 2
множество aS^ — окружность, в случае п = 1 множество aS^ —
пара точек.
Сфера
S--i = ^x = (Xi, ...,xj: Х^(х.-а.J = г2 \ C5.22)
также служит примером замкнутого множества (почему?).
Заметим еш;е, что я-мерный niap радиуса 1 с центром в
начале координат обычно называется п-мерным единичным
шаром (замкнутым или открытым), а (я - 1)-мерная сфера
радиуса 1 с центром в начале координат — {п - 1)-мерной
единичной сферой.
3. Всякий я-мерный параллелепипед
Р^ = Р^ (а, 6i, ... , 6J = {х: |х. - а.| < 6., i= 1, 2, ... , п}
X = (Xi, ... , xj, а = (а^, ... , aj
является, как это уже отмечалось (см. упражнение 7),
открытым множеством, поэтому его называют также я-мерным
открытым параллелепипедом. Его замыкание
Рп = {х: |х. - а.\ < 6., / = 1, 2, ... , п}
является замкнутым множеством и называется я-мерным
замкнутым параллелепипедом. В частности, замыкание Q^
открытого куба Q^ = {х: \х- - а-\ < 5, i = 1, 2, ... , п} называется
замкнутым кубом.
Определение 21. Дл^ всякого множества X ^ R^
множество R^\X называется его дополнением в пространстве R^
(см. п. 1.1).
Т85
ЛЕММА 6. Для того чтобы множество было открытым,
необходимо и достаточно, чтобы его дополнение было
замкнутым.
Доказательство необходимости. Пусть G —
открытое множество. Тогда никакая точка x^G не является точкой
прикосновения его дополнения F = R^\G, так как множество G,
будучи открытым, является окрестностью точки х и не
содержит точек множества F. Следовательно, все точки
прикосновения множества F содержатся в F, что и означает замкнутость
множества F.
Доказательство достаточности. Пусть F —
замкнутое множество, G = R^\F и xgG. В силу замкнутости F,
точка X не является его точкой прикосновения, поэтому су-
гцествует ее окрестность С/(х), не пересекаюгцаяся с
множеством F и, следовательно, такая, что U{x) ^ G. Таким образом,
любая точка множества G является внутренней, т. е. G
открыто. П
СЛЕДСТВИЕ 1. Множество замкнуто тогда и только
тогда, когда его дополнение открыто.
Это сразу следует из леммы 6, так как если множество В
является дополнением множества А в R^, т. е. В = Й^\А, то
и, наоборот, множество А является дополнением В в R^:
A = R''\B.
СЛЕДСТВИЕ 2. Пересечение любой совокупности и
объединение конечного числа замкнутых множеств являются
замкнутыми множествами.
В самом деле, пусть F^ — замкнутые множества, тогда, по
лемме 6, множества G^ = R^\F^, аеШ, являются открытыми.
Согласно формуле A.1) (см. том 1), имеем
Множество UG^, по лемме 4, открыто как объединение
открытых множеств. Следовательно, его дополнение fiF^ = R^\JG^,
согласно лемме 6, замкнуто.
Аналогично с помопа;ью формулы A.2) доказывается
замкнутость объединения конечного числа замкнутых
множеств. П
УПРАЖНЕНИЕ 12. Доказать, что если G — открытое множество, а F —
замкнутое, G ^ i2", F ^ i2", то G\F — открытое множество.
Т86
ЛЕММА 7. Пусть X и Y — замкнутые непустые
непересекающиеся множества из R^ и множество X ограничено;
тогда существует такое число d > О, что для любых двух
точек хеХ и yeY выполняется неравенство р(х, у) > d.
Доказательство. Допустим, что такое число d не су-
па;ествует. Тогда для любого т = 1, 2, ... сугцествует пара
точек х^^^еХ и y^^^eY таких, что р(х^^\ У^^^) < — • Поскольку
X — ограниченное множество, из последовательности {х^^Ц
можно выделить сходягцуюся подпоследовательность {х ^^ }.
Пусть lim X ^^ = х^^\ В силу замкнутости множества X, име-
с ^ ■■
ем х^^^еХ. Из неравенства
р(х@), 1/^^^^) < р(х@), х^^^^) + р(х^^^\ 1/^^^^) < р(х@), х^^^^) + ^
следует, что lim р(х^^\ у ^^ ) = 0. Поэтому точка х^^^ является
точкой прикосновения множества Y и, в силу его
замкнутости, x^^^eY. Таким образом, х^^^еХ и x^^^eY, sl это противоречит
тому, что X и Y не пересекаются. П
Определение 22. Дл^ двух множеств X и Y величина
р(Х, Y)= inf ^р(х,у)
хе X, у е Y
называется расстоянием между X и Y. В частности, если
X состоит из одной точки х, то р(Х, Y) = р(х, Y)
называется расстоянием от точки х до множества Y.
Применяя этот термин, лемму 7 можно сформулировать
следуюгцим образом.
Если два замкнутых непустых множества не
пересекаются и по крайней мере одно из них ограничено, то
расстояние между ними положительно.
Удобным является не только понятие окрестности точки,
но и понятие окрестности множества.
Определение 23. Всякое открытое в R^ множество G,
содержащее множество X ^ R^, называется окрестностью
множества X и обозначается С/(Х).
Объединение г-окрестностей всех точек множества X
называется г-окрестностью этого множества и
обозначается U(X; г).
J87
Таким образом.
ЩХ,г)=ии(х;г).
X е X
Очевидно, 8-окрестность множества, являясь суммой 8-ок-
рестностей точек данного множества, являюгцихся открытыми
множествами, также является открытым множеством и,
следовательно, его окрестностью.
В терминах окрестностей множеств лемму 7 можно
перефразировать следуюгцим образом.
Если два непустых замкнутых множества не
пересекаются и по крайней мере одно из них ограничено, то они
имеют непересекающиеся г-окрестности.
В самом деле, если X и Y — непустые замкнутые
множества и X ограничено, то, согласно лемме 7, расстояние между
def
НИМИ больп1е нуля: d = р(Х, Y) > О — и достаточно взять,
например, е = ^-
УПРАЖНЕНИЯ. 13. Привести пример двух непересекающихся
непустых замкнутых множеств, расстояние между которыми равно нулю.
14. Доказать, что два любых непересекаюпдихся непустых замкнутых
множества имеют непересекаюпдиеся окрестности. Привести пример
двух непустых непересекаюпдихся множеств, у которых нет непересе-
каюпдихся окрестностей.
ЛЕММА 8. Если F — замкнутое множество, F ^ R^, х ^ R^ и
р(х, F) = d, то существует такая точка yeF, что р(х, у) = d.
Доказательство. Если р(х, F) = inf р(х, у) = d, то для
уе F
любого т = 1, 2, ... найдется такая точка y^^^eF, что р(х, у^^^) <
< d -\- —. Очевидно, для каждого т справедливо включение
т
у(т)^ С/(х, d + 1), поэтому последовательность {у^^^} ограничена
и, следовательно, из нее можно выделить сходягцуюся
подпоследовательность {у ^^ }. Пусть lim у ^^ = у^^\ В силу замкну-
тости множества F, имеем y^^^eF, далее,
Р(Х, Г/@)) < р(х, у""*') + р(г/<'"*', у^) < d + J_ + р(у('"/.', у@)).
Переходя здесь к пределу при й ^ оо^ получим р(х, г/д) ^ d.
С другой стороны, р(х, Уо) > р(х, F) = d, следовательно,
р(х, y@)) = d.n
188
Определение 24. Точка xeR^ называется граничной точкой
множества X ^ R^, если в любой ее окрестности существуют
точки, как принадлежащие множеству X, так и не
принадлежащие ему.
Совокупность всех граничных точек множества X
называется его границей и обозначается ЭХ.
Очевидно, что граничная точка множества является и его
точкой прикосновения: ЭХ ^ X, но не является его
внутренней точкой: ЭХ П X-j^^ = 0.
Каждая точка множества является либо его внутренней
точкой, либо граничной, при этом множество может не
содержать все или некоторые граничные точки:
Каждая точка замыкания X множества X также является
либо внутренней, либо граничной точкой самого множества X,
но его замыкание X содержит в себе уже все граничные точки
множества: ЭХ ^ X. Поэтому X = Х^^^^ U ЭХ.
Справедливо, конечно, и равенство X = X U ЭХ, но в нем
слагаемые правой части равенства, вообпа;е говоря,
пересекаются. Они не пересекаются тогда и только тогда, когда
множество X является открытым. В самом деле, если множество
открыто, то каждая его точка является внутренней и, тем
самым, не принадлежит его границе.
Отметим егце, что граница всякого множества является
замкнутым множеством. Действительно, в окрестности точки
прикосновения границы имеется точка самой границы,
поэтому в этой окрестности есть как точки, принадлежагцие
множеству, так и не принадлежагцие ему.
Примеры. Пусть п = 2, X = Q^ = {(х^, Хз): xf + х| < 1} —
открытый круг. Любая точка окружности
А^ |\^Х-|, Хп)» X-I \ Хп J.|
является граничной точкой множества X, и других
граничных точек нет, т. е. aS^ = ЭХ. В этом случае граница множества
X не принадлежит ему.
Пусть X = Q — замкнутый круг, и в этом случае
окружность aS^ также является границей для X, причем теперь ЭХ ^ X.
Наконец, если X = aS^ — окружность, то каждая точка
множества X является его граничной точкой и других граничных
точек нет, т. е. X = ЭХ.
J89
Вообгце, (п - 1)-мерная сфера C5.22) является границей
как я-мерного открытого niapa C5.20), так и замкнутого
C5.21), а также совпадает со своей собственной границей
(почему?).
УПРАЖНЕНИЕ 15. Доказать, что, для того чтобы множество X ^ R^
было замкнутым, необходимо и достаточно, чтобы ЭХ ^ X.
В дальнейгаем понадобится егце понятие кривой в я-мерном
пространстве. Обобгцим данное выгае определение кривой в
трехмерном пространстве как класса эквивалентных путей.
Предварительно заметим, что отображение x(t) = (x^(f), ... , xj^t))
отрезка [а, b] в пространство R^ называется непрерывным,
если все числовые функции x-^(t), ... , xj^t) непрерывны на
отрезке [а, Ь].
Определение 25. Непрерывное отображение отрезка в
пространство R^ называется путем в этом пространстве.
Два пути x(t)eR^, а < t < b, и y(x)eR^, а < т < р,
называются эквивалентными, если существует такая
непрерывная строго монотонная числовая функция t = ф(т), а < т < р,
отображающая отрезок [а, Р] на отрезок [а, Ь], что для
всех те [а, Р] выполняется равенство
х(ф(т)) = г/(т).
Класс эквивалентных путей в пространстве R^
называется кривой в этом пространстве.
Все изложенное в п. 16.1 и 16.2 о кривой в трехмерном
пространстве естественным образом переносится на случай
произвольного я-мерного пространства.
Для дальнейп1его является важным также понятие
прямой в я-мерном пространстве.
Определение26. ili/cmb х^^^ = {х^^\ ... , x^^^)g/2 и а^, ... , а^ —
п
некоторые фиксированные числа ^ af > 0. Множество то-
i = 1
чек X = {х^, ... , xj пространства R^, координаты которых
представимы в виде
X. = xf^ + a.t, i=l,2, ... , п, -оо <t < +00,
называется прямой в пространстве R^, проходящей через
точку х^^\
Тэд
Очевидно, что в случае п = 3 получается прямая в обычном
трехмерном пространстве, а (а^, аз, cl^) является направляю-
гцим вектором этой прямой.
Часть прямой, соответствуюгцая изменению параметра t в
некотором отрезке [t\ f], называется отрезком в пространстве R^.
Точки х' и х'' этого отрезка, соответствуюгцие значениям
параметра f и f\ называются его концами, и рассматриваемый
отрезок обозначается [х\ х'']. Расстояние р(х\ х'') между концами
отрезка называется его длиной.
Часть прямой, соответствуюгцая изменению параметра t
в бесконечном промежутке числовой оси, называется лучом
в пространстве R^.
Если даны две различные точки (х[, ... , х^) и (х^', ... , х^'),
то уравнение прямой, проходягцей через эти точки, имеет вид
Х. = Xl + i {x'l - X\)t, / = 1, 2, ... , я, -оо < ^ < + оо.
Пример. Пусть а = (а^, ... , aJeR"^, d > О и
Q^ = {х = (х^, ... , х^): а^< х^< а^-\- d, i= 1, 2, ... , п}
— я-мерный открытый куб. Каждая точка вида (а^ + E^d, ...
... , а^ + 8^rf), где 8., / = 1, 2, ... , п, могут принимать только
значения О и 1, называется вергаиной как открытого куба Q^,
так и его замыкания, т. е. замкнутого куба Q^. Две вергаины
куба, которые отличаются только значением одного 8-,
называются соседними. Отрезок, соединяюгций соседние вергаины
куба, называется его ребром. Длина ребра куба Q^,
следовательно, и куба Q^ равна d. Две вергаины куба, у которых все
значения 8- различны, называются противоположными.
Отрезок, соединяюгций противоположные вергаины куба,
называется его диагональю; ее длина равна dл/n. Нетрудно
убедиться, что
d^/n = sup р(х, у) = sup р(х, у).
Определение 27. Множество X ^ R^, любые две точки
которого можно соединить целиком лежащей в нем непрерывной
кривой, называется линейно связным*.
* Кроме понятия линейной связности суш;ествует понятие связности
множества, которое будет рассмотрено в § 57.
Ш
Иначе говоря, множество X называется линейно связным,
если, каковы бы ни были точки xgX и х''еХ, супа;ествует
непрерывная кривая x(t) = {x-(t): а < f < Ь} такая, что ее началом
является точка х\ т. е. х(а) = х\ концом — точка х'\ х(Ь) = х'\
и все точки этой кривой принадлежат множеству X: х(^)еХ
для всех ^е[а, Ь].
Примерами линейно связных множеств являются точка,
отрезок, а примером линейно несвязного множества — пара
различных точек.
ЛЕММА 9. Если линейно связное множество пересекается с
некоторым множеством и с его дополнением в R^, то оно
пересекается и с границей этого множества.
Доказательство. Пусть X — линейно связное множество
X ^ R^y Y — некоторое множество, Y ^ й^, и пусть пересечения
X П Y и X П (B^\Y) не пусты. Пусть xA)gX П Y и xB)gX П (B^\Y).
Поскольку X — линейно связное множество, сугцествует такая
непрерывная кривая x(t), а <. t <. Ъ, что х{а) = х^^\ х(Ь) = х^^^
и x(t)eX для всех te[a; b]. Обозначим через т верхнюю грань
тех te[a, Ь], для которых x(t)eY. Очевидно, а < т < Ь. В
любой окрестности точки х(т) содержатся как точки, принад-
лежагцие Y, так и не принадлежагцие Y (почему?).
Следовательно, x(t)g3Y. Поскольку x(t)gX, пересечение 3Y П X не
пусто.П
Определение 28. Открытое линейно связное множество
называется областью^
Примеры. В случае п = \ всякий интервал является
областью, а множество, состоягцее из двух (или более) попарно не-
пересекаюгцихся интервалов (рис. 18), хотя и представляет
собой открытое множество, не является областью.
-4 ^i^ 4 ^i^
Рис.18
/ •^\ / \
I \ I \
\ I \ I
\ / \ ^'У
х^__х х^__х
Рис. 19
* Не следует смешивать понятие области в смысле этого определения
с понятием области определения функции.
192
в случае п = 2 всякий открытый круг есть область, а
множество, состоягцее из двух (или более) попарно непересекаюгцихся
открытых кругов (рис. 19), хотя и открыто, но не является
областью, так как две точки х и г/, принадлежагцие разным
кругам, нельзя соединить непрерывной кривой, лежагцей целиком
внутри рассматриваемого множества.
Всякий я-мерный открытый niap является областью.
Определение 29. Множество, любые две точки которого
можно соединить отрезком, целиком в нем лежащим, называется
выпуклым.
Всякий я-мерный открытый или замкнутый niap является
выпуклым множеством.
Определение 30. Множество, лежащее в пространстве R^ и
являющееся замыканием некоторой области, называется
замкнутой областью.
Замкнутый я-мерный niap является замкнутой областью.
УПРАЖНЕНИЯ. 16. Доказать, что я-мерный шар и я-мерный
параллелепипед являются выпуклыми множествами.
17. Построить пример невыпуклой области.
Задача 5 (теорема Жордана*). Доказать, что всякий простой
контур (см. п. 16.1) на плоскости разбивает плоскость на две области
(ограниченную и неограниченную); это означает, во-первых, что он
является границей каждой из этих областей, во-вторых, что никакие две точки,
принадлежащие различным указанным областям, нельзя соединить
кривой, не пересекающей данный контур.
35.3. Компакты
В этом пункте будут рассмотрены некоторые свойства
множеств, называемых компактами и играюпа;их важную роль
в математическом анализе.
Определение 31. Множество А^Ш называется компактом,
если из любой последовательности его точек можно
выделить сходящуюся подпоследовательность, предел которой
принадлежит множеству А.
Пример. Из теоремы Больцано—Вейерп1трасса (п. 4.6) и
возможности перехода к пределу в неравенствах (п. 4.3)
следует, что отрезок числовой прямой является компактом.
К. Жордан A838—1922) — французский математик.
Тэз
Важное свойство, характеризуюгцее компакты в R^,
устанавливает следуюгцая теорема.
ТЕОРЕМА 3. Для того чтобы множество X ^ R^ было
компактом, необходимо и достаточно, чтобы оно было
ограниченным и замкнутым.
Доказательство необходимости. Пусть А ^ й^ и
А — компакт. Если множество А было бы неограниченным, то
для любого натурального числа т нагалась бы такая точка
x("^)g а, что р@, х^^^) > т, т = 1, 2, ... . Здесь, как всегда,
О = (О, О, ..., 0). Очевидно, lim х^^^ = оо. Поэтому любая под-
последовательность последовательности {х^^^} также имеет
пределом оо^ и, следовательно, из {х^^^} нельзя выбрать сходя-
па;уюся подпоследовательность, что противоречит тому, что
А — компакт. Итак, А — ограниченное множество.
Если множество А не было бы замкнутым, то у него су-
па;ествовала бы точка прикосновения х, которая в нем бы не
содержалась: х ^ А. Для этой точки нап1лась бы такая
последовательность х^^^ ^А,т = 1,2,..., что lim х^^^ = х. Ясно,
ЧТО любая ее подпоследовательность также имеет своим
пределом ту же точку X € А. Поэтому из последовательности {х^^Ц
точек множества А нельзя выделить подпоследовательность, схо-
дяпа;уюся к точке этого множества, т.е. множество А снова не
было бы компактом. Следовательно, А — замкнутое множество.
Доказательство достаточности. Пусть X —
ограниченное замкнутое множество, {х^^^} — какая-либо
последовательность его точек: х^^^еХ, m = 1, 2, .... В силу
ограниченности множества X, эта последовательность также ограничена.
Следовательно, по теореме 2 п. 35.1, из нее можно выделить
сходяпа;уюся подпоследовательность {х^^}. Обозначим ее
предел через х: lim х ^^ = х. Очевидно, что х — точка прикосно-
вения множества X, ибо х ^^ еХ, sl так как X — замкнутое
множество, то хеХ, т. е. X действительно компакт. П
Доказанная теорема позволяет легко устанавливать
компактность многих часто встречаюгцихся множеств, например
отрезков, замкнутых niapoB и параллелепипедов, сфер в
пространствах й^ любой размерности, — все перечисленные
множества, будучи ограниченными и замкнутыми, являются
компактами. Так же легко с помогцью теоремы 3 устанавливается
и некомпактность многих множеств. Например, конечные
интервалы, не будучи замкнутыми, а бесконечные, не будучи
ограниченными множествами, не являются компактами.
194
Отметим, что, в силу той же теоремы 3, лемму 7 из п. 35.2
можно сформулировать следуюпа;им образом: если два
замкнутых непустых множества не пересекаются и по
крайней мере одно из них является компактом, то расстояние
между ними больше нуля.
Прежде чем перейти к другим характеристическим
свойствам компактов, введем ряд определений и докажем одно
вспомогательное утверждение.
Последовательность я-мерных кубов {Qy^}, й = 1, 2, ... ,
называется последовательностью вложенных кубов, если
ЛЕММА 10. Для последовательности замкнутых
вложенных кубов {Qj^y длины ребер которых стремятся к нулю при
й ^ оо^ существует одна и только одна точка,
принадлежащая всем кубам рассматриваемой последовательности.
Доказательство. Пусть кубы
Qj, = {x = (х.): ар) < х- < а\^^ + d^^); /=1,2, ... , п) C5.23)
с ребрами длин d^^^ образуют последовательность вложенных
кубов"^ и пусть lim dP^"^ = 0. Тогда отрезки \ai^\ ар) + A^Щ,
/г —> со L L
k = 1, 2, ... , образуют систему вложенных отрезков, длины d^^^
которых стремятся к нулю при й ^ оо. Поэтому сугцествуют, и
притом единственные, числа ^. такие, что при фиксированном
i (i = 1, 2, ... , п) и любом й = 1, 2, ... имеет место включение
^.е[ар), ар) + d^^)]. Отсюда следует, что точка ^ = (Ь,^, ... , ^J
принадлежит всем кубам рассматриваемой
последовательности: ^^Qf^, й = 1, 2, ... , и эта точка единственна. П
Определение 32. Пусть X ^ й^. Система
Sl = {XJ, аеШ, C5.24)
множеств Х^ ^ R^ (Ш = {а} — некоторая совокупность
индексов а) называется покрытием множества X, если
х^ их..
* Напомним, что мы договорились (см. п. 35.1) под кубом, если не
оговорено что-либо другое, всегда понимать липеь кубы, задаваемые
неравенствами вида C5.23) при данной фиксированной системе
координат.
Т95
Таким образом, система A4.24) называется покрытием
множества X, если каждая точка этого множества
принадлежит хотя бы одному множеству Х^ системы Q..
Покрытие C5.24) множества X, состоягцее из конечного
числа множеств Х^, называется конечным покрытием этого
множества.
В том случае, когда все множества системы О. открытые,
покрытие С1 называется открытым покрытием множества X.
Ранее была доказана лемма Гейне—Бореля для покрытий
отрезка интервалами. Докажем теперь ее обобпа;ение для
покрытий компактов открытыми множествами.
ТЕОРЕМА 4. Для того чтобы множество X ^ R^ было
компактом, необходимо и достаточно, чтобы из любого его
открытого покрытия можно было выделить конечное
покрытие.
Доказательство необходимости. Пусть А —
компакт и пусть система
^ = {GJ, аеШ, C5.25)
— его открытое покрытие. Допустим, что из этого покрытия
нельзя выделить конечного покрытия компакта А. Согласно
теореме 3, из того что множество А является компактом,
следует его ограниченность. Поэтому супа;ествует замкнутый куб
Q, содержапа;ий множество А.
Пусть
Q = {х = (х-): а. < X. < а. + d, i= \, 2, ... , п).
Разобьем куб Q на 2^ равных замкнутых кубов Q^, определеляе-
мых набором п неравенств вида
а, + ^ < X, < а, + d, а. < х- < а• + ^
{i,j= 1, 2, ... , п)
(на рис. 20 изображен случай,
когда я = 2), тогда
Q= .^^Qj. C5.26)
Система C5.25) образует
открытое покрытие каждого из
множеств А П Q- (у = 1, 2, ... , 2^). Среди
этих множеств сугцествует такое
непустое множество (обозначим его
Q
^
1
;/
±
- ■
^
^
Рис. 20
196
через A П Q ), что из покрытия C5.25) нельзя выделить конеч-
■' 1
ное покрытие этого множества — в противном случае из
системы C5.25) можно было бы, в силу равенства C5.26), выделить
конечное покрытие и всего множества А, что противоречило бы
сделанному предположению.
Разобьем куб Q снова на 2^ равных замкнутых кубов Q
(j = 1, 2, ... , 2^). Обозначим через Q тот из кубов Q , пере-
сечение которого с компактом А нельзя покрыть конечным
числом множеств системы ^ и т. д. В результате получим
последовательность вложенных замкнутых кубов
длины ребер которых равны соответственно -,-,...,—,... и,
2 4 2^
следовательно, стремятся к нулю при й ^ оо.
Каждый из кубов Q последовательности C5.27) обла-
/1/2 ••• Jk
дает тем свойством, что из системы C5.25) нельзя выделить
конечное покрытие непустого множества А П Q- • ; , Уу прини-
/1/2 *** •'k
мает одно из значений 1, 2, 3, ... , 2^; v = 1, 2, ... , k; k = 1, 2, ... .
Согласно лемме 10, сугцествует, и притом единственная, точка ^,
принадлежагцая всем кубам системы C5.27). Ребра кубов этой
системы стремятся к нулю, и каждый куб имеет непустое
пересечение с множеством А, поэтому в любой окрестности точки ^
имеются точки множества А. Действительно, заметим, что
длина диагонали куба Qj j j равна (dJn)/2^.
Далее, каково бы ни было 8 > О, выберем k^ так, что
^<8. C5.28)
2 0
Это возможно, так как lim -^ = 0. Теперь, замечая, что лю-
бая точка хеО- ■ ■ находится от точки teO- ■ ■ на рас-
%'
стоянии, не превып1аюпа;ем длины диагонали куба Q
/1/2
будем иметь р(х, ^) < -^ < 8. Это означает, что х лежит в 8-ок-
2 0
рестности точки ^. Следовательно, весь куб Q , в том чис-
/1/2 ••• //г
ле его точки, принадлежапа;ие множеству А, содержится в
рассматриваемой 8-окрестности точки ^. Таким образом, ^
является точкой прикосновения множества А. Согласно же теореме 3,
множество А, будучи компактом, замкнуто, и поэтому Ь^еА.
J97
Построенная вспомогательная последовательность кубов
C5.27) позволяет легко показать невозможность выполнения
сделанного предположения о том, что из покрытия C5.25)
компакта А нельзя выделить конечного покрытия этого компакта.
В самом деле, система C5.25) является покрытием
множества А, поэтому сугцествует такой индекс адеШ, что ^&G^ .
Множество G^ открыто, следовательно, найдется такое число 8 > О,
что 8-окрестность С/(^; 8) точки ^ будет целиком содержаться
Щ^; 8) ^ G^^. C5.29)
Заметим, что для любого 8 > О, в частности для 8, удовлет-
воряюгцего условию C5.29), найдется, как показано выгае,
такой номер ^Q, что будет выполнено включение
Из C5.29) и C5.30) имеем
А П Q. . . CZ Q CZ Щ^; 8) с G^ ,
^hh '" h^ ^hh '" h^ C5.30) ^^ ^ C5.29) S
И, следовательно, из системы C5.25) можно выделить
конечное покрытие множества А П Q , , а именно покрытие, со-
/1/2 ••• Jk^
стоягцее только из одного множества G^ . Это противоречит до-
пупа;ению, в соответствии с которым выбраны кубы Q
Таким образом, предположив, что из системы C5.25) нельзя
выделить конечного покрытия компакта, мы прип1ли к
противоречию. Тем самым необходимость условия доказана.
Доказательство достаточности. Пусть X п й^ и пусть
из любого открытого покрытия множества X можно выделить
конечное покрытие. Допустим, что X не является компактом.
Это, согласно определению 29, означает, что супа;ествует
последовательность х^^^еХ, m = 1, 2, ... , из которой нельзя выделить
сходяпа;уюся к некоторой точке из X подпоследовательность.
Следовательно, какова бы ни была точка хеХ, она не является
частичным пределом последовательности {х^^^}. Поэтому у
каждой точки xgX найдется окрестность (обозначим ее через GJ, со-
держагцая лип1ь конечное число элементов последовательности
{х^^^}; в противном случае из последовательности {х^^^} можно
было бы выделить сходяпа;уюся к х подпоследовательность.
В силу выбора окрестностей G^, каждая точка х множества X
принадлежит соответствуюпа;ей окрестности: xeG^. Поэтому со-
J98
вокупность Q. = {GJ, xeX, всех таких окрестностей образует
открытое покрытие множества X. Согласно условию теоремы, из
него можно выделить конечное покрытие. Пусть это покрытие
^0^ {^х^' ^^2' ••• ' ^xj-
Каждый элемент этого покрытия содержит конечное число
членов последовательности {х^^Ц. Следовательно, все
элементы покрытия ^Q также содержат конечное число членов
последовательности {х^^Ц. Это, однако, невозможно, так как,
покрывая все множество X, элементы конечного покрытия ^q
должны содержать все члены последовательности {х^^^},
которых бесконечно много. Полученное противоречие доказывает
достаточность условий теоремы. П
Замечание. Необходимость условий теоремы, т. е.
утверждение, что из всякого открытого покрытия компакта
можно выделить конечное покрытие, как и в случае покрытия
отрезка интервалами, обычно называют леммой Гейне—Бореля.
Подчеркнем, что в теореме 4 супа;ественным является то, что
рассматриваются покрытия, состояпа;ие именно из открытых
множеств. Так, например, из покрытия отрезка [О, 1] (который,
как уже отмечалось, будучи ограниченным замкнутым
множеством, является компактом) отрезками -, -,я=1, 2, ...,и
Ln + 1 nJ
отрезком [-1,0] нельзя выделить конечного покрытия. Это
объясняется тем, что здесь покрытие состоит не из открытых, а из
замкнутых множеств.
Докажем епа;е одно полезное для дальнейп1его свойство
открытых покрытий компактов. Нам понадобится для этого
понятие диаметра множества.
Определение 33. Число конечное или бесконечное
sup р(х, у)
X, у е X
называется диаметром множества X ^ R^ и обозначается
diam X, т, е,
diamX= sup р(х, г/). C5.31)
X, у е X
Ясно, что о < diam X < +оо^ diam X = diam X.
Из определения диаметра множества, очевидно, следует,
что для любых двух его точек xg X и г/е Y выполняется
неравенство р(х, у) < diam X.
По определению будем считать, что диаметр пустого
множества равен нулю:
diam 0 = 0.
J99
Примеры. 1. Диаметр открытого я-мерного шара U (х^^^; г)
радиуса г равен 2 г.
Действительно, если х, у е U (х^^^; г) и, следовательно,
р (х, х^^)) < г, р (г/, х^^)) < г,
то
р (х, г/) < р (х, х@) + р (х@), г/) < 2 г. C5.32)
С другой стороны, если х^^^ = (x^i\ ^^2^, ••• ' ^^п^)^ ^^^^ ^ (^1^^ - г +
+ 1, Х<20\ ... , X(f)), yW = (Х<0) + г- 1, Х2, ... , Х<„«)), то
р (х(*), х@)) = р (г/(*), х@)) = г - i < г, /г = 1, 2, ... ,
и поэтому х**^ г/**' е ?7 (х*"); г). Поскольку
p(xW, yW) = 2r-|,
ТО
lirn^ р (х(^), г/(^)) = 2 г. C5.33)
Из C5.32) и C5.33) следует, что
diam U (х^^); г) = 2 г.
2. Пусть
Q. = Qnf^iO). ^] = \х = (X.): |х. - xW| < ^, /=1,2, ... , п] C5.34)
— замкнутый я-мерный куб с центром в точке х^^^ = (х^^^) и
ребром длины а, тогда
diam Q^ = ajn. C5.35)
Действительно, для любых точек х = (x-)eQ^ и г/ = (y-)eQ^
имеем
к- - г/;| < к- - x^o^l + 1x^0^ -у.\ < ^ + ^ = а, / = 1, 2, ... , п. C5.36)
Поэтому
Р(л:, г/) = 7(^1 " ^i)^ + (^2 - г/2)^ + ••• + (^n - Уп)^' C5^3g) «V^-
C5.37)
С другой стороны, при х- = х^^ ~ т^у у] ^ ^Р^ + ^? ^ ^
= 1, 2, ... , я, х' = (х^), у = (у1), получим
р(х', г/0 = aV^. C5.38)
Из соотношений C5.37) и C5.38) и следует равенство C5.35).
УПРАЖНЕНИЕ 18. Доказать, что диаметр любого множества совпадает
с диаметром его замыкания.
^00
с помогцью понятия диаметра
множества можно, например, описать свойство
множества быть ограниченным:
множество ограничено тогда и только тогда,
когда его диаметр конечен.
Действительно, если множество X
ограничено, то оно содержится в
некотором я-мерном кубе Q^ (см. определение 9
в п. 35.1). Если длина ребра куба Q^
равна а, то
2 diam X
diam X < diam Q^ = ajn. Рис. 21
Обратно, если диаметр множества X
конечен, то оно содержится в замкнутом кубе Q^, центром
которого является произвольно выбранная точка множества X, а
длина а ребра этого куба равна 2 diam X, так как все точки
множества X находятся от центра куба х на расстоянии, не
больп1ем diam X, т. е. половины длины ребра куба (на рис. 21
изображен случай п = 2).
ТЕОРЕМА 5. Для любого открытого покрытия компакта
существует такое положительное число {называемое
числом Лебега данного покрытия), что любое подмножество
компакта с диаметром, меньшим этого числа, содержится
по крайней мере в одном элементе покрытия.
Доказательство. Допустим противное. Пусть супа;ествует
такое открытое покрытие Q. = {GJ, аеШ, некоторого компакта
X, что для любого 6 > О найдется множество Е ^ X, diam Е < 5,
которое не содержится ни в одном элементе покрытия О..
Возьмем 6 = —, meN, и пусть Е^ — подмножество компакта X,
т ^
diamE <1, C5.39)
не содержагцееся ни в одном элементе покрытия О..
Выберем произвольно точку
х^^^еЕ^, т=1,2, ... . C5.40)
Поскольку множество X является компактом, то из
последовательности {х^^^} можно выделить сходягцуюся
подпоследовательность {х ^^ }, причем
lim x^'^^^ = x@)gX. C5.41)
Система Q. является покрытием компакта X. Поэтому сугцест-
вует по крайней мере один элемент G^ этого покрытия, содержа-
гций точку х^^\ В силу открытости множества G^ найдется
сферическая окрестность Щх^^^; г), 8 > О, точки х^^\ содержагцаяся в G^:
C/(x@); 8) ^ G^. C5.42)
Выберем номер k^ так, чтобы
J- < |. C5.43)
в силу условия C5.39) сугцествует такое
k>kQ, C5.44)
что
|^(^Р _ ^@)| < 8^ C5.45)
Тогда для любой точки хе Е^ будем иметь
\х - хЩ <\х- x^^^^l + |х^^^^ - хЩ <
C5.39), C5.40),
C5.45)
< — +1 < 1 + 1 = е. C5.46)
C5.39), C5.40), rJlj^ 2 C5.43), C5.44) 2 2
C5.45)
Таким образом,
Е^ с C/(x@);8) с G^,
^k C5.46) ^ ^ C5.42) ^
Т. е. нап1лось множество G^eQ., содержагцее множество Е^ —
противоречие. П
В заключение этого пункта докажем одно вспомогательное
утверждение. Предварительно введем следуюгцее
обозначение: для всякого множества X ^ й^ обозначим через X , где
Г| > О, совокупность всех точек, расстояния которых от X не
превосходят числа Г|, т. е. положим, что
Х^ "^^ {х : р(х, X) < л}.
ЛЕММА 11. Если А — компакт, А ^ R^, то при любом Г| > О
множество А также является компактом.
Доказательство. Согласно теореме 3, множество А,
будучи компактом, ограничено и замкнуто. Ограниченность
множества А означает, что супа;ествует такое а > О, что А
содержится в niape С/@, а).
^02
Покажем, что А ^ С/@, а + Г|). Если хеА , то, согласно
лемме 8, найдется такая точка г/еА, что р(х, у) = р(х. А) < Г|.
Из условия А ^ С/@, а) следует, что р@, г/) < а, поэтому
р@, х) < р@, у) + р(г/, х) < а + Г|.
Таким образом, хе U@, а + Г|). Точка х является произвольной
точкой множества А . Следовательно, А^ ^ U@, а + Г|), и
поэтому множество А ограничено.
Покажем теперь, что А — замкнутое множество. Если
X — точка прикосновения множества А : хе А , то для любого
8 > О сугцествует такая точка уеЛ^, что р(х, у) < 8. Из
определения множества А и леммы 8 следует, что сугцествует такая
точка 2q ^ А, что р(г/, Zq) = р(г/. А) < Г|; поэтому
р(х. А) = inf р(х, 2) < р(х, 2q) < р(х, у) + р(г/, 2q) < 8 + Г|.
2 G л
Это неравенство верно для любого 8 > 0. Устремляя 8 к нулю,
получаем р(х. А) < Г|, т. е. хеА , что и доказывает замкнутость
множества А .
Итак, множество А ограничено и замкнуто,
следовательно, в силу той же теоремы 3, является компактом. П
35.4. Многомерные векторные пространства
В п. 15.1 т. 1 отмечалось, что при фиксированной системе
координат в трехмерном пространстве задание вектора
равносильно заданию трех его координат. При сложении векторов
и их умножении на числа те же действия выполняются и с их
координатами. В я-мерном случае вектор можно определить
с помогцью его координат.
Определение 34. Упорядоченная система п действительных
чисел
(Xj, ... , X^Yj X^ElKj I = 1, Z, ... , n,
называется п-мерным действительным вектором х, а
числа х^, ,,,, х^ — его координатами. Число п называется
размерностью вектора.
Суммой х + у векторов х = (х^, ... , xj и у = (г/^, ... , г/J
называется вектор (Xj + г/i, ... , х^ + г/^), т. е.
х + у = (Xi + i/i, ... ,x^ + i/J,
а произведением вектора х на число Хе R называется вектор
кх = хК = (Лх^, ... , Лх„).
203
Множество всех я-мерных векторов, в котором введены
операции сложения векторов и умножения вектора на
действительное число, называется п-мерным действительным
векторным пространством или, более полно, п-мерным
арифметическим векторным пространством над полем действительных
чисел. Как в случае векторного, так и в случае точечного я-мер-
ного пространства число п называется размерностью этого
пространства. Вектор О = (О, О, ... , 0) называется нулевым
вектором или нулем п-мерного векторного пространства.
По определению, вектор -х = (-1)х называют
противоположным вектору X.
УПРАЖНЕНИЕ 19. Доказать, что если х, у, z — любые векторы, а числа
\, |aei2 произвольны, то: 1) л: + i/ = i/ + л:; 2) (л: + i/) + 2 = л: + (i/ + г); 3) л: + О =
= л:; 4) 1 • х = х\Ъ) Ц}^х) = (X[i)x; 6) (к + [i)x = Хх + [ix; 7) Х(х + у) = Хх + Ху.
Таким образом, я-мерное арифметическое точечное
пространство (см. определение 1 в п. 18.1) преврагцается в я-мер-
ное арифметическое векторное пространство, если в нем
ввести операции сложения его элементов и умножения их на
число, согласно определению 34.
В трехмерном случае связь между точками пространства
и векторами в нем можно установить (считая, как всегда,
систему координат фиксированной), сопоставляя каждой точке
М = (Xj, ^2, Х3) этого пространства ее радиус-вектор, т. е.
вектор ОМ = (Xj, Х2, Х3). Это сопоставление является
взаимно-однозначным соответствием между точками трехмерного
пространства и векторами в нем.
Итак, как я-мерное точечное, так и я-мерное векторное
пространства состоят из одних и тех же элементов — из
упорядоченных совокупностей п действительных чисел. Поэтому
как то, так и другое пространство будет обозначаться одним и
тем же символом R^. Они отличаются друг от друга тем, что в
точечном арифметическом я-мерном пространстве вводится
понятие расстояния между его элементами (см. определение 1
в п. 35.1), а в я-мерном векторном определяются операции
сложения векторов и умножения их на действительные числа
(см. определение 34 этого пункта).
Если обозначить через в^ я-мерный вектор, все координаты
которого равны нулю, кроме й-й, равной единице, k —
фиксированное натуральное число (ke{l, 2, ... , п}), то для любого
я-мерного вектора х = (х^, ... , х^) справедливо равенство
X = х^е^ + ... + х^е^, C5.47)
^04
правая часть которого называется разложением вектора х по
векторам в^, ... , е^. При этом коэффициенты х^, ... , х^ этого
разложения единственны, т. е. однозначно определяются
самим вектором X, и, следовательно, в силу равенства C5.47),
совпадают с его координатами х^, ... , х^.
Векторы в^, й = 1, 2, ... , я, называются координатными
или базисными векторами, а их упорядоченная
совокупность {е-^, ^2, ... , ej — стандартным (или каноническим)
базисом пространства R^ (обгцее определение базиса будет дано
ниже).
Подмножество L векторного пространства й^ называется
подпространством пространства R^, если для любых
векторов xeL, yeL л любых чисел XeR, [leR имеет место
включение Хх + [lyeL.
Определение 35. Скалярным произведением двух векторов
X = (Xj, ... , xj и у = (i/j, ... , i/J, я > 3, называется число,
обозначаемое через (х, у) и определяемое по формуле
(х, у) = Xji/i + ... + х^у^. C5.48)
Иногда при обозначении скалярного произведения скобки
опускают, т. е. вместо (х, у) пипхут ху.
Из элементарной математики известно, что формула
C5.48) справедлива и при обычном определении скалярного
произведения векторов, т. е. и для я < 3.
Всякое я-мерное векторное пространство, в котором
введено скалярное произведение, называется евклидовым.
Число л/(л:, х) = Jx\ + ... + х^ называется длиной вектора
X и обозначается через |х|:
|х| ^= Jxf + ... + х2. C5.49)
Очевидно, что для любого вектора хей и любого числа XeR
имеет место равенство
|;lx| = |;l| |х|, C5.50)
а из неравенства C5.3) (см. п. 35.1) следует, что для любых
хей^, y^R^ выполняется неравенство
|х + у|< |х| + |у|, C5.51)
называемое неравенством треугольника.
Из C5.51) следует, что
||х|-|у||< \х-у\. C5.52)
~205
Действительно, |jc| = |jc - у + i/| < |jc - i/| + \y\, поэтому
W - \y\ <\x- yl
В силу равноправия jc и у, имеем также
|у|-к1^ \у -^\ = \^-у1
Из двух последних неравенств и следует C5.52). П
Если X = (Xi, ... , XJ и у = (i/i, ... , yj, то имеем х - у =
= (Xj - i/i, ... , х^ - у J и поэтому
\х-у\ = 7(^1 -^/i)^ + ... + (х^-1/^J = р(х, г/), C5.53)
где X и г/ — точки точечного я-мерного пространства с теми же
координатами, что и векторы х и у. Таким образом, в я-мер-
ном векторном пространстве со скалярным произведением
определено расстояние \х - у\ между его элементами, совпадаю-
гцее с расстоянием р(х, у), определенным в п. 35.1. Поэтому
все понятия, введенные в п. 35.1—35.3 для точечных
пространств, имеют смысл и для векторных пространств со
скалярным произведением.
В качестве примера использования векторной символики
отметим, что замкнутый niap Q^ (Xq, г) радиуса г с центром в
точке Xq в векторных обозначениях определяется равенством
Q^(Xo, г) = {х: \х - Xq\ < г},
а ограничиваюгцая его (п - 1)-мерная сфера aS^ " ^(Xq, г) —
равенством
aS^ " 1(Xq, г) = {х: \х - XqI = г}.
Скалярное произведение обладает следуюгцими
непосредственно проверяемыми свойствами:
1^. Коммутативность. Для любых xeR^, yeR^
(х, у) = (у, х).
2^. Дистрибутивность. Для любых xeR^, y^R^, zeR^
(х + y,z) = (х, z) + (у, z).
3^. Однородность. Для любого xeR^ и любого числа
X^R""
(Хх, у) = Х(х, у).
4^. Невырожденность. Для любого xeR^
выполняется неравенство (х, х) > О, причем
(х, х) = О ^ X = 0.
~206
Дистрибутивность и однородность скалярного
произведения образуют вместе свойство, называемое линейностью
скалярного произведения.
Если в^, ... , в^ — координатные векторы в R^, то, согласно
C5.48),
( 1 при / = у.
(^^' ^i)
О при 1^ J, ''
Поэтому для любого вектора х = (х^, ... , х^), в силу свойств
скалярного произведения, получим
(х, е.) = (х^е^ + ... + х^е^, е.) =
= Xi(ei, е.) + ... + х^(е^, е.) = х.(е.е.) = х-, C5.54)
т. е. i-я координата вектора х равна скалярному
произведению (х, е-).
Используя обозначения скалярного произведения
векторов C5.48) и длины вектора C5.49), можно упростить запись
и доказательство ряда формул. Например, неравенство Ко-
П1И—Шварца (см. C5.2) в п. 35.1) для векторов х = (х^, ... , х^)
и у = (i/j, ... , у^) записывается в виде
(х, у) < |х| \у\. C5.55)
Запись формулы C5.3) с использованием обозначения длины
вектора была приведена выгае (см. C5.51)).
УПРАЖНЕНИЕ 20. Провести доказательство леммы 1 и ее следствия
(см. п. 35.1), используя обозначения скалярного произведения векторов
и их длин.
Углом ф между векторами xeR"^ и yeR"^, п > 3, называется
угол ф, О < ф < 71, определяемый равенством
со8ф=^^^. C5.56)
В силу неравенства Konin—Шварца C5.55), это
определение корректно, поскольку, согласно C5.55), для ф,
определяемого формулой C5.56), имеет место неравенство |cos ф| < 1.
Здесь снова, как и в случае определения скалярного
произведения, за исходное определение принимается
высказывание, аналогичное которому в пространстве й^, я < 3, является
доказываемым утверждением. Благодаря этому формулы
C5.48) и C5.56) оказываются справедливыми во всех
пространствах R^, п = 1, 2, ,,, ,
^07
Векторы, скалярное произведение которых равно нулю,
называются ортогональными.
Ненулевые ортогональные векторы называются
перпендикулярными.
Вектор единичной длины кратко называют единичным
вектором.
Если а VI Ъ — единичные векторы, то для косинуса угла
между ними из формулы C5.56) получаем
со8ф = (а, Ь), |а| = |Ь| = 1. C5.57)
Если а = (а^, ... , а^) — единичный вектор, то, обозначая через
а. угол между векторами а и е-, согласно C5.54) и C5.57), имеем
а. = (а, е.) = cos а., т. е.
а = (cos а^, ... , cos aj.
Косинусы COS а-, i = 1, ... , п, называются направляющими
косинусами вектора а.
Поскольку |а| = 1, в силу C5.49), имеем
cos2 ai + ... + cos2 а^ = 1. C5.58)
Если а не единичный вектор и а ^ О, то, очевидно, вектор
7^ уже единичный и его направляюпа;ие косинусы называются
\а\
также и направляюпа;ими косинусами вектора а.
Векторы стандартного базиса ортогональны друг другу, и
длины их равны единице.
Всякое упорядоченное множество п единичных векторов
{е[, ^2, ... , б^}, попарно ортогональных друг другу:
\e.\ = l,(e.,ej) = 0, i^j,i, у = 1,2, ...,я,
называется базисом векторного пространства R^ или, более
подробно, ортонормированным базисом этого пространства.
Из линейной алгебры известно, что каждый вектор
раскладывается и при этом единственным образом в линейную
комбинацию векторов базиса. Коэффициенты этого
разложения называются координатами вектора относительно данного
базиса. Поэтому переход от одного базиса к другому
называется переходом от одной системы координат к другой.
Из линейной алгебры известно также, что векторы любого
ортонормированного базиса {е[, ^2, ... , е'^} выражаются через
векторы другого такого базиса {е'^, ^2, ... , е'^} (в частности,
через векторы стандартного базиса) с помогцью матрицы С =
= {c.j}, i, j = 1, 2, ... , я, у которой обратная матрица С"^ совпа-
^08
дает с транспонированной С* (такие матрицы называются
ортогональными) :
i = 1
Верно и обратное утверждение: если упорядоченная
система векторов выражается через некоторый ортонормирован-
ный базис с помогцью ортогональной матрицы, то эта система
также является ортонормированным базисом.
Уравнение прямой в пространстве R^ (см. определение 26 в
п. 35.2) в векторной записи имеет вид
jc = jc@) + fa, -оо<^<+оо, C5.59)
л: = (х1, ... , xj, л:@) = (х<з^\ ... , х^О)), а = {а^, ... , а^)
(при сложении координат векторов сами векторы также
складываются, а при умножении их координат на число они
умножаются на то же число). Прямая C5.59) называется прямой,
проходящей через точку х^^^ = {х^^\ ..., х^^^) точечного
пространства в направлении вектора а.
Вектор а называется направляющим вектором прямой
X = х^^^ + at. Две несовпадаюгцие прямые, уравнение которых
можно записать с одним и тем же направляюгцим вектором,
называются параллельными.
Если а — единичный вектор, \а\ = 1 и, следовательно,
а = (cos а^, ... , cos а^) (cos а. — направляюгцие косинусы
вектора а; / = 1, 2, ... , п), то прямая C5.59) в координатной
записи имеет вид
X. = х}^^ + fcos а.; i=l,2, ... ,п; -оо < ^ <+оо. C5.60)
Пусть заданы две точки х' = (х{, ... , х^) и х'' = (х'{, ... , х^)
точечного пространства; обозначим через х' и х'' векторы с
теми же координатами. Тогда уравнение прямой, проходяпа;ей
через точки х' и х'' (см. п. 35.2), в векторной записи имеет вид
х = х' + (х'' -хУ, -оо<^<+оо. C5.61)
Если {е[, ^2, ..., е'^} — базис пространства R^, то множество
векторов X = e\t, -оо < t < +оо^ называется /-й координатной
осью для рассматриваемого базиса, /=1,2,...,я.
По аналогии с § 15 можно рассмотреть я-мерную
векторную функцию
r{t) = (Xi@, ... , xj^t)), teX^R
(R, как всегда, множество всех действительных чисел).
Аналогично тому, как это было сделано в § 15 т. 1, при любом на-
^09
туральном п определяются понятия предела, непрерывности и
производной векторной функции r(t)eR^. Как и для я < 3, при
дифференцировании векторной функции дифференцируются
ее координаты: r\t) = ix[(t), ... , x'^(t)).
§36
Предел и непрерывность функций
многих переменных и отображений
36.1. Функции многих переменных
Рассмотрим сначала функции, которые определены на
множествах я-мерного арифметического евклидова пространства R^
и значениями которых являются действительные числа.
Таким образом, эти функции являются функциями точек
пространства. Это означает, что если имеется какая-либо
функция /(Xj, ... , х^) и в пространстве R^ задана система координат
Xj, ... , х^, то в другой системе координат ^^, ... , ^^, связанной
с исходной преобразованием
^i = ^i(^v ••• 'У' i=l,2, ... ,п,
под той же функцией понимается не Д^^, ... , ^^), а функция
/(Xi(^i, ... ,у, ... ,x^i, ... ,У).
Рассматриваемые функции будем обозначать либо одной
буквой, например /, либо более подробно, с указанием аргумента,
через /(х) или /(Xj, ... , х^). При п> 1 они называются функциями
многих переменных. В случае п = 2 вместо /(х^, Хз) будем писать
также /(х, г/), в случае п = 3 вместо /(х^, Хз, Xg) также /(х, г/, г).
Для функции /(х) = /(Xj, Х2, ... , х^) ее аргументом
называют как точку X, так и каждую из ее координат х^, Хз, ... , х^.
Всякой функции г/ = /(х., „) я переменных
Xj, Х2, ... , х^ соответствует ее график в (п + 1)-мерном
пространстве точек (х., г/). Определим это понятие.
Определение 1. Пусть на множестве X евклидова
пространства R^ определена функция у = /(х), х = (х^, ... , xJgX,
и пусть R^^ ^ — {п + 1)-мерное евклидово пространство
точек (х, у) = (х^, ..., х^, у). Множество точек вида (х, /(х)) =
= (Xj, ... , х^, /(х)) пространства R^^ ^, гEе xgX, называется
графиком функции /.
2i^
Рис. 22
График функции многих
переменных, так же как и график функции
одной переменной, удобно использовать
для геометрической интерпретации
вводимых понятий и доказываемых
утверждений. Конечно, изображение
графика на рисунке в случае, когда число
независимых переменных больпхе
единицы, сложнее, чем в одномерном
случае. На рис. 22 изображен вид графика
функции двух переменных у = /(х^, Хз).
Сформулированное здесь
определение графика функции п
переменных является частным случаем обпа;его определения графика
функции, сформулированного в п. 1.2"^.
Пусть снова функция / определена на множестве X ^ й^.
Множество точек х = (х^, ... , х^) пространства R^, удовлетво-
ряюгцих уравнению
/(Xj, ... , Х^) = с,
где с — некоторая постоянная, называется множеством
уровня функции /, соответствуюпа;им данному значению с.
В случае п = 2 множество уровня называется также линией
уровня, в случае я = 3 — поверхностью уровня, а при я > 3 —
гиперповерхностью уровня.
Изучение функций многих переменных начнем с понятия их
предела. Для того чтобы не рассматривать отдельно случаи,
когда аргумент функции стремится к точке пространства или
«неограниченно возрастает», удобно, как и в случае пределов
последовательностей точек я-мерного пространства, использовать
понятие его бесконечно удаленной точки (см. конец п. 35.1).
Определим понятие окрестности бесконечно удаленной
точки оо пространства.
Окрестностью С/(оо) бесконечно удаленной точки оо в
пространстве R^ называется дополнение в R^ до любого лежагцего
в нем компакта.
Нередко встречается частный вид окрестностей бесконечно
удаленной точки — так называемые ее 8-окрестности.
Внеп1ность я-мерного замкнутого niapa с центром в начале
координат О и радиусом, равным -, т. е.
C/(oo;8L£f Jx:p(x,0)>i|,
называется Е-окрестностью бесконечно удаленной точки оо.
211
Бесконечность оо будем называть бесконечно удаленной
точкой прикосновения всякого неограниченного множества. Это
естественно, так как если X — неограниченное множество в R^, то
пересечение любой окрестности С/(оо) бесконечно удаленной
точки оо с множеством X не пусто. Это равносильно тому, что су-
гцествует такая последовательность x^^^^gX, т = 1, 2, ... , что
lim х("^) = оо.
m ^ оо
в отличие от бесконечно удаленной точки оо пространства
R^ его обычные точки будем называть также конечными
точками. Просто под точкой пространства всегда будем понимать
его конечную точку.
Понятие числовой функции многих переменных является
частным случаем понятия отображения множества из
пространства R^ в пространство R^. Чтобы в дальнейп1ем не
повторять аналогичные рассуждения для числовых функций и
отображений, перейдем сразу к изучению последних.
36.2. Отображения. Предел отображений
Пусть X = (Xj, Х2, ... , xj и г/ = (г/^, г/з, ... , у J- Тогда
Р(л:, у) = 7(^1 - Уг)^ + (^2 - У2)^ + ••• + (^п - Уп)^ = \^- у1
Здесь слева элементы х и г/ рассматриваются как точки, а
справа — как векторы пространства R^. В силу этого
равенства для обозначения расстояния между точками х и г/
правомерно наряду с обозначением р(х, у) использовать и
обозначение |х - г/|. Так и будет делаться в дальнейпхем для облегчения
понимания аналогий в определениях ниже рассматриваемых
понятий для отображений с соответствуюпа;ими
определениями для случая функций одной переменной.
Пусть R^ и R^ — соответственно я-мерное и т-мерное
точечные пространства, X ^ R^ и отображение / отображает
множество X в пространство R^: f : X ^ R^, т. е. у = f(x)eR^,
хеХ ^ й^.
Если т = 1, Si п > 1, то отображение / называется
действительной функцией многих переменных х^, Хз, ... , х^:
У ~ Д^1? ^2' ••• ' *^д/*
Если m > 1, то каждая координата у- точки у = f(x)eR^
является действительной функцией точки х. Обозначим эти
функции /., у = 1, 2, ... , т: Дх) = (/i(x), f^ix), ... , /Jx)).
Jl2
функции f-iX^R называются координатными
функциями отображения /. Они являются, вообш;е говоря (а точнее
при п > 1), функциями многих переменных.
Определим понятие предела отображений, которое
является обобгцением понятия предела функции одной переменной.
Пусть х^^^ и а — конечные или бесконечно удаленные
точки соответственно пространств R^ и R^, Для п = 1 или т = 1 в
случае бесконечно удаленных точек х^^^ и а они могут быть и
бесконечностями со знаком +оо или -оо. Пусть егце точка х^^^
является точкой прикосновения множества X.
Определение 2. Точка а называется пределом отображения
f: X ^ R^, X ^ R^, при X -^ х^^^ (или в точке х = х^^^), если для
любой последовательности х^^^еХ, й = 1, 2, ... , такой, что
lim х^^^ = х^^\ имеет место равенство
lim f(x^^y) = a.
Для предела отображения / в точке х^^^ используется
обозначение lim f(x),
В символической записи определение 2 выглядит следую-
гцим образом:
def
lim fix) = а ^
def
^ Vx(%X, й = 1, 2, ... , lim х(^) = х(О): lim /(х^^)) = а.
По аналогии с пределом функции одной переменной
определение предела отображения можно сформулировать в
терминах окрестностей.
Определение 2'. Точка а называется пределом отображения
f:X ^ R^, X ^ R^, при X -^ х^^^ (или в точке х = х^^^), если для
любой окрестности U(d) точки а существует такая
окрестность С/(х^^^) точки х^^\ что
f(X П C/(x@))) CZ и (а).
В символической записи:
lim f(x) = а ^^ \/U(a) ЗЩх^^^): f(X П ЩхЩ ^ Ща). C6.2)
Иначе говоря,
lim f(x) = а^^ У и (а) 3C/(x@)) VxgX П [/(х^^)): f(x)e Ща).
Лз
Определения 2 и 2' предела отображения равносильны.
Действительно, из сравнения записей определений предела
функций одной переменной E.4)—E.5) в п. 5.4 и E.23) в
п. 5.7 с определениями C6.1) и C6.2) предела отображений
видно, что они полностью совпадают по форме записи (только
точка, в которой берется предел, обозначается теперь х^^\ sl не
Xq, так как нижний индекс обозначает в пространственном
случае номер координаты точки). Поэтому доказательство
равносильности двух определений предела функций одной
переменной (см. теорему 1 в п. 5.7) дословно переносится на
случай пределов отображений, если только под точками и
окрестностями понимать точки и окрестности в пространстве.
Наряду с записью lim f(x) для предела отображения / в
точке х^^^ употребляются как равноправные записи lim f(x)
И lim f(x),
\х-хЩ^О
Если х^^^ и. а — конечные точки пространств R^ и R^, то
определение C6.3) можно записать в виде
def
lim f(x) = а ^
def
^ V8 > О 36 > О VxgX, \х -х@)| < 6: |/(х) - а| < 8. C6.4)
На этом примере епа;е раз хороню видно, как разумно
выбраны обозначения в многомерных пространствах: формула
C6.4) по записи ничем не отличается от случая числовых
функций одной переменной. Но, конечно, в случае числовых
функций одной переменной \х - х^^^\ и |/(х) - а\ означают
абсолютные величины чисел, а в формуле C6.4) — расстояния
между точками в я-мерном и т-мерном пространствах.
Поскольку функции многих переменных являются частным
случаем рассматриваемых отображений, то определение предела
отображения содержит в себе, в частности, определение предела
функций, принимаюгцих действительные числовые значения.
С другой стороны, из определения C6.2) видно, что
понятие предела отображения сводится к понятию предела
числовой функции |/(х) - а\ при aeR^ и функции |/(х)| при а = ^:
lim f(x) = a^ lim |/(х) - а| = О, aeR"^,
и
lim f(x) = oo ^ lim |/(x)| = oo.
Jl4
Укажем епа;е на одну связь понятий пределов числовых
функций и отображений.
Если точка а является конечной точкой пространства
R"^: а = (а^, а^, ... , aj; если f(x) = (f^(x), f^ix), ... , /Jx)),
f: X ^ R^, X ^ R^, TO в силу эквивалентности сходимости
точек пространства со сходимостью их координат (см. теорему 1
в п. 35.1) определение 2 предела lim f(x) = а отображения
f равносильно тому, что для любой последовательности точек
х^^^еХ, й = 1, 2, ... , lim х^^^ = х^^\ все координатные функции /•
этого отображения имеют пределы
^lirn^/.(х(^)) = а., у=1,2, ...,т.
Таким образом, отображение / имеет предел lim f(x) = а
тогда и только тогда, когда для всех у = 1, 2, ... , m сугцествуют
пределы lim fix) = а .
В символической записи это выглядит следуюгцим образом:
lim fix) = а ^yj=l, 2, ... , т: lim /.(х) = а-. C6.5)
х^х^^^ х^х^^^
в этом смысле понятие предела рассматриваемых
отображений снова сводится к понятию предела числовых
функций — предела его координатных функций.
Если отображение / задано на множестве X ^ R^, Е ^ X и.
х@) — точка прикосновения (конечная или бесконечно
удаленная) множества Е, то предел в точке х^^^ сужения /^
отображения / на множество Е называется пределом lim f(x)
X -^ х^^\ хе Е
отображения / по множеству Е. Таким образом,
lim f(x) = lim /^(х).
X -^ х^^\ хе Е X ^ х^^^
Очевидно, что если в точке х^^^ сугцествует предел lim /(х),
X —^ Х^^
то В ЭТОЙ точке сугцествуют и пределы отображения / по любым
множествам Е ^ X, для которых точка х^^^ является точкой
прикосновения, и все эти пределы равны между собой.
В случае п > 1 в качестве множества Е часто берутся
пересечения кривых, прямых или лучей (направлений), прохо-
дягцие через точку х^^\ с отображаемым множеством X.
Естественно, что при рассмотрении пределов отображения по разным
подмножествам множества X в случае, когда предела по
множеству не сугцествует, могут получаться разные результаты.
Jl5
Если множество X содержит некоторую окрестность или
проколотую окрестность точки х^^\ то предел отображения в
этой точке по этим окрестностям называется также и
всесторонним пределом,
Супа;ествование предела отображения в некоторой точке, а
если он супа;ествует, то и его значение полностью
определяются значениями отображения на пересечении произвольной
окрестности точки, в которой рассматривается предел, с
отображаемым множеством, т. е. не зависят от выбора указанной
окрестности. Точная формулировка этого утверждения имеет
следуюгций вид.
Если отображение f: X ^ R^, X ^ R^, имеет предел
lim fix), то для любой окрестности U(x^^^) точки х^^^ оно име-
ет тот же предел по множеству U (х^^^) П X:
lim fix)= lim fix). C6.6)
XE C/(jc@))nX
Если же отображение f: X ^ R^, X ^ R^, имеет предел
lim f(x) хотя бы для одной окрестности U(x^^^) точки х^^\
ТО ОНО имеет предел в этой точке и по множеству X при этом в
силу уже первого утверждения выполняется равенство C6.6).
Все это легко проверить и потому может быть в
случае внутренней потребности самостоятельно проделано
читателем.
Свойство отображения, не зависягцее от выбора достаточно
малой окрестности, содержагцей данную точку, называется
локальным свойством отображения в данной точке. В силу
сказанного выгае сугцествование предела отображения в
точке, являюгцейся точкой прикосновения отображаемого
множества, и значение предела (если он, конечно, супа;ествует)
являются локальными свойствами отображения.
УПРАЖНЕНИЯ. 1. Доказать эквивалентность определений 2 и 2^
предела отображений.
2. По аналогии со случаем функций одной переменной сформулировать
и доказать критерий Коши существования предела отображения.
2
Пример. Пусть /(х, у) = f ^ ^. Эта формула задает функ-
цию во всех точках плоскости, кроме начала координат (О, 0).
Исследуем пределы этой функции по различным направлениям
в точке (О, 0). Уравнение прямой, проходягцей через начало
координат (О, 0) в направлении вектора (а, Р), имеет вид
x = at, у = pf, а^ + р2 > 0.
Имеем f{aty ^t) = . , ^ ^- -^ О при f ^ О, т. е. предел по лю-
a^t^ + р^
бому направлению сугцествует и равен нулю. Если же г/ = х^, то
/(х, х^) = 1/2 и, следовательно, предел вдоль параболы у = х'^
также сугцествует, но равен 1/2.
Таким образом, для рассмотренной функции сугцествует
один и тот же предел по любому направлению, а предел по
указанной параболе, хотя и сугцествует, отличен от обгцего
значения пределов по направлениям; тем самым просто
предел в точке (О, 0) не сугцествует.
УПРАЖНЕНИЕ 3. Исследовать пределы по направлению в точке (О, 0)
функции fix, у) = J^f .
Замечание. Если множество X ^ R^, на котором
определена функция /, состоит только из точек X, координаты
которых являются натуральными числами: х = (ш-^, ... , ш^),
m-eN, / = 1, 2, ... , я, то функция / называется, как мы
знаем, я-кратной последовательностью (см. 34.1) и ее значения
у = f(m-^, ... , m^) обозначаются у^ ^ .
Определение предела двойной последовательности, данное
в п. 34.1 (см. там определение 2), отличается от ее предела,
если его рассматривать как частный случай предела функции в
смысле определения 2 этого пункта. Поясним это различие
подробнее на примере двойных последовательностей.
Если lim г/^ ^ = ав смысле предела функции, то это оз-
начает, что для любого 8 > О сугцествует такое 6 > О, что для
всех номеров meN и.пеМ таких, что Jm^^ -\- п^> 5, имеет место
неравенство |г/^ ^ - а| < 8. Условие Jm^' + n^' > 6 может
выполняться при выборе лигаь одного достаточно больгаого номера
т или п, другой же может оставаться даже постоянным. При
определении же предела lim у^ „, данном в п. 34.1, оба но-
т,п ^> <^ "''' '^'^
мера т VI п должны быть достаточно больгаими для того,
чтобы выполнялось неравенство |г/^ ^ - а| < 8 при достаточно
малом 8 > 0.
Л?
36.3. Непрерывность отображений в точке
При рассмотрении предела отображения в данной точке эта
точка может как принадлежать отображаемому множеству, так и
не принадлежать ему.
Если f: X ^ R^y X ^ R^, х^^^еХ и супа;ествует предел
lim f(x), то lim f(x) = f(x^^^).
Действительно, выбрав стационарную последовательность
xik) = x@)gX, й = 1, 2, ... , C6.7)
получим, согласно определению C6.1),
^ !i^<o, ^^^) Ci:i) ii?L f(^'%T.b, iiPoo f(^'''^ = f(^'''^- C6.8)
Определение 3. Если предел отображения в точке равен его
значению в этой точке, то отображение называется
непрерывным в ней.
Иначе говоря, равенство
lim /(х) = /(х@)) C6.9)
является определением непрерывности отображения в точке.
В символической записи определение непрерывности
отображения / в точке х^^^ выглядит в силу C6.4) следуюгцим образом:
V8 > О 36 > О VxgX, \х - х@)| < 6: |/(х) - /(х@))| < е. C6.10)
В терминах окрестностей определение указанной
непрерывности выглядит следуюгцим образом:
VC/(/(x@))) 3C/(x@)): /(X n C/(x@))) cz ЩГ(хЩ. C6.11)
Таким образом, понятие непрерывности отображения
является частным случаем понятия предела отображения при х^^^еХ,
Если х^^^ = (х^^\ х^^\ ... , х^^^), X = (Xj, ^2, ... , х^), Ах^ =
= X.- х^^\ i = 1, 2, ... , п, Ах = (Axj, Ах2, ... , AxJ, Аг/ = /(х^^^ +
+ Ах) - /(х^^)), то, перенеся в равенстве C6.9) значение /(х^^^) в
левую его часть под знак предела, получим
lim Ау = 0, C6.12)
Ах^ о
ЧТО, таким образом, является другой записью определения
непрерывности отображения / в точке х^^\
Можно, конечно, сформулировать понятие непрерывности
отображения и в терминах пределов последовательностей.
Jl8
Отображение f: X ^ R^, X ^ R^ непрерывно в точке х^^^еХ в
том и только том случае, когда для любой последовательности
точек х^^^еХ, й = 1, 2, ... , сходяпа;ейся к точке х^^^: lim х^^^ = х^^\
выполняется условие
lim /(х(^)) =/(х@)). C6.13)
k ^ оо
Это сразу следует из равносильности определений 2 и 2'
предела отображения.
Если f(x) = (fi(x), /зС^)' ••• ' /m(^))' ^^ ^^ C6.5) при а = f(x^^^)
следует, что отображение непрерывно в некоторой точке в том
и только том случае, когда все его координатные функции /.
непрерывны в этой точке.
Отсюда, в частности, следует, что определение
непрерывных отображений отрезка, данных при рассмотрении понятия
кривой в п. 16.1 (для случая отображений отрезка в
трехмерное пространство) и в п. 35.2 (для случая отображения отрезка
в произвольное я-мерное евклидово пространство) как
отображений, координатные функции которых непрерывны,
равносильны в случае отображения отрезка данному здесь
определению непрерывных отображений.
Ясно, что если отображение непрерывно в какой-либо
точке, то и его сужение по каждому множеству, содержагцему эту
точку, непрерывно в ней.
Отображение f: X ^ R^ называется непрерывным в точке
х^^^ по некоторому множеству Е, х^^^еЕ ^ X, если сужение /^
отображения / на множество Е непрерывно в этой точке.
Если а(х) — числовая функция, определенная на множестве
X ^ R^, Р(х) — отображение этого множества в пространство R^,
а х^^^ является конечной или бесконечно удаленной точкой
прикосновения множества X, то отображение Р(х) называют
бесконечно малым по сравнению с функцией а(х) при х -^ х^^^ и пигаут
Р = о(а), х^х(О), C6.14)
если сугцествует такое отображение е(х) множества X в
пространство R^, что
р(х) = 8(х)а(х), хеХ, C6.15)
и
lim Е(х) = 0. C6.16)
Если x^^^gX, то из условия C6.16) следует (см. C6.7)), что
8(х@)) = 0.
Jl9
Для отображений, в частности для функций многих
переменных /(Xj, ... , х^), п> 1, наряду с их непрерывностью в
определенном Bbinie смысле, которую называют также
непрерывностью по совокупности переменных х^, ... , х^, можно
рассматривать и непрерывность по отдельным переменным х-.
Функция /(Xj, ... , х^), определенная, например, в
некоторой окрестности точки х^^^ = {^^i\ ••• ? ^^^^)? называется
непрерывной в точке х^^^ по переменной х., если функция
Ф(х,) ''=' /(х<0', ... , x^oji, x^, xi«)i, ... , х(,0))
ОДНОЙ переменной х- непрерывна в точке xf^\ Очевидно, что
функция ф является сужением функции / на пересечение
прямой Ху = х^^^, у = 1,2,...,/-!,/ + 1, ... , п, с множеством
определения функции /, тем самым непрерывность функции по
некоторому переменному означает непрерывность ее сужения по
соответствуюпа;ему множеству.
Отметим, что из непрерывности функции по всем
переменным в отдельности не следует ее непрерывность по их
совокупности. Например, функция
f ^^' ^с™ х2 + 1/2 > О,
[ О, если х = у = Qy
непрерывна по каждой переменной х и г/ в отдельности в
каждой точке плоскости, но не непрерывна по их совокупности в
точке (О, 0), так как не имеет в этой точке даже предела
(проверьте это).
36.4. Свойства пределов отображений
Поскольку определение предела и непрерывности
отображений дословно совпадают с соответствуюпа;ими определениями
для функций одной переменной, то для случая отображений
сохраняются многие свойства пределов функций и свойства
непрерывных функций, доказанные в § 5. Если элементы
пространства R^ рассматривать как векторы, то их можно
складывать и умножать на числа. Аналогично случаю числовых
функций одной переменной доказывается, что если f: X ^ R^,
g: X ^ R^, X ^ R^, XeR, [leR, и если сугцествуют пределы
lim /(х) и lim ^(х), то сугцествует и предел
X —^ Х^^ X —^ Х^^
lim (Xf(x) + lig (х)) = X lim f(x) + u lim ^(x).
120
Если fug — числовые функции, т.е. если m = 1, то для их
пределов имеют место свойства, аналогичные свойствам
пределов функций одной переменной, связанные с
неравенствами, с произведением и делением функций (см. п. 5.10).
Формулировка этих свойств и их доказательства остаются
прежними, следует только под множествами понимать множества,
лежапа;ие в я-мерном пространстве.
Конечно, при я > 1 на случай отображений
непосредственно не обобпа;аются утверждения о пределах функций одной
переменной, связанные с упорядоченностью их аргумента, т. е.
утверждения об односторонних пределах и пределах
монотонных функций.
36.5. Повторные пределы
Для отображений f: X ^ R^, X ^ R^, при п> 1 наряду с
пределом в смысле определения 2 можно рассматривать пределы
другого вида, а именно связанные с последовательным переходом к
пределу по разным координатам точки х = (х^, ^2, ... , х^), т. е.
пределы вида
lim /(Xj, ^2, ... , xj,
где /j, ^2? ••• ? ^n — некоторая перестановка чисел 1, 2, ... , n, a
отображение /определено, например, в некоторой проколотой
или обычной окрестности точки х^^^ = (л:^^\ ^2^^ ••• ? ^1^^)-
Такие пределы называются повторными пределами.
Повторный переход к пределу в силу своего определения
сводится к последовательному нахождению пределов
отображений по одному переменному. Так, lim /(х^, Х2, ... , х^) оз-
начает, что у отображения f: X ^ R, фиксированы все
значения координат Ху, у ^ /, ее аргумента х = (х^, Х2, ... , х^) и тем
самым указанный предел означает предел отображения по
множеству {х = (х^, Х2, ... , х^): х^ = х^^\ j ^ i} П X,
Аналогично пределу в смысле определения 2 повторные
пределы отображения сводятся к повторным пределам
координатных функций этого отображения. Поэтому
ограничимся рассмотрением только повторных пределов числовых
функций.
22i
X
lim
lim
h h
'^2 ''2
lim fix, y) = 0. Повторные пределы
И
Пример. Рассмотрим определенную на всей плоскости
функцию
X sin - + г/ sin -, если х ^ О и г/ ^ О,
Пх,у) = \ у ^ х' ^ '
[ о, если X = О или у = 0.
Исследуем различные ее пределы в точке @,0). Очевидно,
) = 0. Повторные пределы
lim lim х sin - + lim у sin -
lim lim x sin - + lim у sin -
не супа;ествуют, так как не супа;ествуют даже пределы
lim у sin - (г/ ^ 0) и lim х sin - (х^ 0), а lim х sin - = О (у ^ 0)
и lim у sin - = О (х ^ 0).
1/^0 X
Для функции же /(х, у) = ^^ ^, определенной этой фор-
х^ + у^
мулой на всей плоскости, кроме начала координат, оба
повторных предела в точке (О, 0) супа;ествуют и
lim lim /(х, г/) = lim lim /(х, г/) = 0.
1/^0x^0 JC ^ О I/^ О
Однако предела функции / в точке (О, 0) не супа;ествует, так
как предел вдоль координатных осей равен нулю, а вдоль
прямой г/ = X он равен ^I^,
Таким образом, из одного лип1ь супа;ествования предела
функции в данной точке не следует супа;ествования повторных
пределов в этой точке и, наоборот, из супа;ествования
повторных пределов не следует супа;ествования предела в соответст-
вуюпа;ей точке. Тем не менее определенная связь между этими
понятиями может быть установлена.
ТЕОРЕМА 1. Пусть функция /(х, г/) определена на
множестве X, содержащем все точки некоторой прямоугольной
окрестности Р((Хо, г/д); 6^, 62) точки (Xq, г/д), кроме, быть
может, точек прямых х = х^и у = у^. Если существует
предел функции f в точке (Xq, i/q) по множеству X и при любом
уе(у^ - 52, z/q + 62) существует предел
lmijix,y) = giy), C6.17)
J22
то повторный предел lim lim f(x, у) существует и
lim lim f(x,y)= lim f(x, у). C6.18)
ix,y)EX
Доказательство. Пусть
lim f(x, y) = a
(x, y)^ixQ, у^),{х,у)е X
И пусть фиксировано произвольное 8 > 0. Сугцествует
прямоугольная окрестность Р = P((Xq, i/q); Г|^, ^2), О < Г|^ < 6^, О < Г|2 < 62
такая, что если (х, у)еР П X, то
|/(х,г/)-а|<|. C6.19)
В силу сугцествования предела C6.17), для любого числа
у такого, что (х, у)еР П X и, следовательно, \у - Уо\ < Л2' ^^
C6.19) имеем \g(y) - а| < | < 8 (для этого достаточно перейти к
пределу при х ^ х^в равенстве C6.19)), а это и означает, что
lim giy) = а,П
У->Уо
Пример. Рассмотрим функцию /(х, у) = х sin -, г/ ^ 0. Эта
функция определена во всей плоскости, кроме точек оси Ох.
Обозначим ее область определения через X. Очевидно, супа;ест-
вуют пределы
lim /(х, у) = 0 и lim /(х, г/) = О, г/ ^ О, C6.20)
{х, у) ^@, 0) х^О
хе X
поэтому, согласно доказанной теореме, супа;ествует и
повторный предел lim lim /(х, у) = 0. Это ясно и непосредственно.
у ^Ох ^0
Заметим, что другой повторный предел lim lim /(х, у) в этом
X ^0 у ^0
случае не супа;ествует.
36.6. Предел и непрерывность
композиции отображений
Композиция функций многих переменных и отображений
множеств многомерных пространств имеет ряд
специфических особенностей, связанных как с самой многомерностью,
123
так и с возможностью наличия разных размерностей у
пространств, в которых лежат отображаемые множества.
Пусть п, тгтр — произвольные, вообпа;е говоря, различные
натуральные числа, X ^ R^, f — отображение множества X в
множество Y ^ R^, sl g — отображение множества Y в
пространство RP, т. е.
fiX^Y ^ R^, X^R^, giY^RP. C6.21)
В этом случае имеет смысл композиция g ^ f отображений
/ и ^, задаваемая, как известно (см. п. 1.2"^), формулой
(g о f)(x) = g(f(x)), хеХ.
В этой ситуации отображение у = f(x) часто называют
заменой (независимой) переменной в отображении g(y).
Отметим, что если отображение f(x) множества X
непрерывно в точке х^^^е X, а отображение g(y) определено в
некоторой окрестности точки у^^^ = f(x^^^), то всегда сугцествует такая
окрестность U^ точки х^^\ что на множестве X П U^ имеет
смысл композиция g ^ f. Действительно, пусть U —
окрестность точки у^^\ на которой определено отображение g(y).
Согласно определению непрерывности отображения, для U
сугцествует такая окрестность U^ точки х^^\ что f(U^ П X) ^ Uy.
Очевидно, что для всех точек xg С/^ П X и имеет смысл
композиция g ^ f.
Пусть х^^\ а и b — конечные или бесконечно удаленные
точки соответственно пространств R^, R^ и Rp, причем если
какое-то из чисел п, т или р равно единице, то соответствую-
гцая ему из указанных точек может быть и бесконечностью со
знаком.
ТЕОРЕМА 2. Если имеет смысл композиция g(f(x)), хеХ, и
существуют пределы
lim fix) = a, C6.22)
lim giy) = b, C6.23)
то существует и предел
lim g(f(x)) = b. C6.24)
Объединив формулы C6.23) и C6.24), получим
lim gifix)) = lim giy). C6.25)
124
Эта формула называется формулой замены переменного для
пределов отображений (функций).
СЛЕДСТВИЕ. Если отображение f непрерывно в точке
х@)еХ ^ R^, а отображение g непрерывно в точке у^^^ = f(x^^^),
то их композиция gifix)) также непрерывна в точке х^^\
Короче: композиция непрерывных отображений
непрерывна.
Теорема 3 аналогична теореме о пределе композиции
пределов функций одного переменного. Для разнообразия
выберем метод ее доказательства, основанный на определении
предела функции в терминах последовательностей.
Доказательство. Возьмем произвольную
последовательность точек x^^^gX, й = 1, 2, ... , стремягцуюся к точке х^^^:
lim х(^) = х@). C6.26)
Тогда, в силу условия C6.22), будем иметь
lim /(х(^)) = а.
Поэтому, согласно предположению C6.23),
lim g{Kx^^^) = b. C6.27)
Поскольку последовательность х^^^ была произвольной
последовательностью, удовлетворяюгцей условиям C6.26),
равенство C6.27), согласно определению предела отображения,
и означает справедливость формулы C6.24).
Для доказательства следствия достаточно заметить, что в
силу непрерывности отображений fug соответственно в
точках х^^^ и у^^^ = f(x^^^) точка х^^^ принадлежит области
определения композиции g(f(x)). П
С помопа;ью теоремы 2 можно легко установить
непрерывность функций, наиболее часто встречаюпа;ихся на практике,
а именно элементарных функций многих переменных.
Определение 4. Функции, получающиеся из переменных
х^, ... , х^с помощью конечного числа композиций
элементарных функций одного переменного, операций сложения,
умножения и деления, называются элементарными функциями
переменных х^, ... , х^.
225
xy
у sm —^—
Например, функция /(х, у) = хе ^^у является
элементарной функцией двух переменных х и г/. Действительно,
/(х, у) = XW, W = е^, V = yz, Z = sin t, t = ъ^у ос = xy, ^ = х + у.
Из теоремы 2 и сохранения непрерывности в соответствую-
па;их точках при арифметических операциях над
непрерывными функциями (см. п. 36.4) следует, что всякая
элементарная функция любого числа переменных непрерывна в каждой
точке области своего определения.
36.7. Непрерывные отображения компактов
Отображение, непрерывное в каждой точке отображаемого
множества, называется непрерывным на этом множестве.
ТЕОРЕМА 3. Непрерывный образ компакта является
компактом.
СЛЕДСТВИЕ. Числовая непрерывная на компакте функция
ограничена и достигает своих экстремальных {наибольшего
и наименьшего) значений.
Доказательство. Пусть множество X является компактом,
X ^ R^ VL отображение f: X ^ R^ непрерывно на X. Покажем,
что из любой последовательности точек образа /(X) компакта X
можно выделить сходяпа;уюся к точке из /(X)
подпоследовательность. Это и будет означать, что множество /(X) — компакт.
Пусть y^^^ef(X). Тогда супа;ествуют такие точки х^^^еХ, что
f(^x^k)) = y{k)^ k = 1, 2, ... . Поскольку множество X — компакт,
супа;ествует сходяпа;аяся подпоследовательность {х ^ }
последовательности {х^^Ц, предел которой принадлежит множеству X:
lim х^^^^ = x@)gX. Пусть г/@) = /(х^^)).
у^ ОО
В силу непрерывности отображения / в точке х^^^ имеем
lim у J = lim f(x J) = f(x^^^) = y^^\ Таким образом, подпосле-
7 ^ CO 7 ^ CO
довательность {у ^} последовательности {у^^Ц сходится к
точке г/(%/(Х). П
Докажем следствие.
Если f: X ^ R, X — компакт, X ^ й^, то в силу доказанной
теоремы, множество /(X) является компактом на числовой
оси, т. е. ограниченным и замкнутым числовым множеством.
126
в силу своего определения, нижняя и верхняя грани
множества являются точками прикосновения этого множества. Из
ограниченности множества /(X) следует, что его нижняя и
верхняя грани конечны. Поскольку /(X) — замкнутое множество,
они содержатся в нем. Это и означает, что функция /
достигает на компакте X наибольпхего и наименьпхего значений. П
Замечание. Если функция определена на некотором
множестве X я-мерного пространства и ее значениями
являются комплексные числа, то она называется ограниченной
на этом множестве, если на нем ограничена ее абсолютная
величина.
Таким образом, ограниченность комплекснозначной
функции сводится к ограниченности функции, принимаюпа;ей
только действительные значения — ее абсолютной величине.
Из этого, в силу теоремы 3, сразу следует, что всякая комп-
лекснозначная функция, непрерывная в каждой точке
некоторого компакта, ограничена на нем.
Напомним, что, согласно введенной для отображений
терминологии (см. п. 1.2"^), отображение /: X ^ R^, X ^ R^,
называется взаимно-однозначным или инъекцией, если разным
точкам множества X соответствуют при этом отображении также
разные точки. В этом случае говорят также, что множество X
взаимно-однозначно отображается посредством этого
отображения на множество /(X), т. е. /: X ^ /(X) является биекцией.
При выполнении этого условия на множестве /(X) сугцествует
однозначное обратное отображение (однозначная обратная
функция) f~^(y) = X, где х таково, что f(x) = у, т. е. /"^ (f(x)) = х;
иначе говоря, отображение f~^f является тождественным
отображением (тождественным отображением множества X
называется отображение, которое каждой точке хеХ ставит в
соответствие эту же точку).
Важным является понятие гомеоморфного отображения.
Определение 5. Если отображение f множества X ^ R^ в
пространство R^ взаимно-однозначно и непрерывно на X и
обратное ему отображение f~^ непрерывно на множестве /(X), то f
называется гомеоморфным отображением или
гомеоморфизмом, а множество /(X) — гомеоморфным образом множества X
или, что то же, множеством, гомеоморфным множеству X.
Ясно, что если / — гомеоморфизм множества X, то
обратное ему отображение /"^ является гомеоморфизмом
множества /(X).
~227
ТЕОРЕМА 4. Непрерывное взаимно-однозначное
отображение компакта является гомеоморфизмом.
Доказательство. Пусть X — компакт, X ^ й^, и / — его
непрерывное взаимно-однозначное отображение в
пространство R^. Докажем, что обратное ему отображение f~^ множества
/(X) ^ R^ в пространство R^ также непрерывно.
Пусть у^^\ y^^^ef(X), тогда
х@) = /-1(г/@))еХ, х(^) = Г\у(^))еХ, й = 1, 2, ... , C6.28)
и пусть
Покажем, что
lirn^ г/(^) = 1/@). C6.29)
lim х(^) = х@). C6.30)
Если бы это было не так, то сугцествовало бы такое 8 > О,
что для любого натурального т нагалось бы натуральное
к^>тп, C6.31)
для которого выполнялось бы неравенство
|х(V - х@)| > 8, C6.32)
при этом из C6.31) следовало бы, что
lim k^ = оо.
В силу компактности множества X из
последовательности х^ G X, m = 1, 2, ... , можно выделить сходягцуюся подпос-
т
ледовательность х "^/,7 = 1,2,..., предел которой
принадлежал бы X:
lim x^V = xgX. C6.33)
Из неравенства C6.32) следует, в частности, что \х "^i - х^^^\ > 8,
7=1,2,.... Переходя к пределу при j ^ ^, получим \х - х^^^\ > 8.
Следовательно, х ^ х^^\ а это в силу взаимной однозначности
отображения / означает, что
fix) ^ /(х@)) = г/@). C6.34)
Однако последовательность {у "^i} является
подпоследовательностью последовательности {г/^^^}, имеюгцей своим
пределом точку г/^^^ и поэтому
lim i/^S^= lim г/(^) = г/@). C6.35)
228
Но в силу непрерывности отображения / в точке х, согласно
C6.33), имеем
lim у^^"^? = lim fix^^"^?) = f(x) ^ у^^\
у ^ оо у ^ °° C6.34)
ЧТО противоречит равенству C6.35). Таким образом,
справедливо равенство C6.30), т. е.
Дгп^ Г\у^^)) = Г\у^^\
Это и означает непрерывность отображения /"^ в любой точке
Г/@)£/(Х).П
Доказанная теорема является обобпа;ением теоремы о
непрерывности функции, обратной к непрерывной строго
монотонной на отрезке функции.
36.8. Равномерная непрерывность
В пункте 6.4 т. 1 было введено понятие равномерно
непрерывной функции на отрезке. Это определение можно обобгцить на
случай отображений f: X ^ R^, X ^ R^. Если отображение /
непрерывно на множестве X, то для любого 8 > О и для любой
точки хеХ сугцествует такое 6 > О (тем самым зависягцее от 8 и х),
что для всех точек х'е X, для которых \х' - х| < 6, выполняется
неравенство \f(x') - f(x)\ < 8.
Как и в случае функций одной переменной, отказ от
зависимости числа 6 от точки множества приводит к понятию
равномерной непрерывности.
Определение 6. Отображение f: X ^ R^, X ^ R^, называется
равномерно непрерывным, если для любого 8 > О существует
такое 6 > О, что для любых двух точек хеХ и х'еХ таких,
что \х' - х| < 6, выполняется неравенство
|/(хО - fix)\ < 8.
В символической записи это определение выглядит сле-
дуюгцим образом:
V8 > О 36 > О Ух, х'еХ, \х' - х| < 6: \f(x') - f(x)\ < 8, C6.36)
т.е. снова буквальное повторение записи определения
равномерной непрерывности функции одной переменной (см. т. 1, п. 6.4).
Вспомнив определение диаметра множества (см.
определение 33 в п. 35.3), по аналогии со случаем числовых
функций одной переменной легко убедиться, что определение рав-
129
номерной непрерывности отображения можно
сформулировать следуюш;им образом.
Определение Ь\ Отображение f\X ^ R^, X ^ R^, называется
равномерно непрерывным, если для любого 8 > О существует
такое 6 > О, что для каждого множества Е ^ X
диаметра, меньшего, чем 6: diam X < 6, выполняется неравенство
diam f{E) < 8.
Свойство отображения быть равномерно непрерывным на
множестве снова по аналогии со случаем функций одной
переменной можно описать в терминах колебания на этот раз
отображения на множестве.
Определение 7. Для отображения f: X ^ R"^, X ^ й^, его
колебанием на множестве X называется число {конечное или
бесконечное)
ш(/; X) ^= diam /(X).
В этих терминах определение C6.36) равномерной
непрерывности отображения в символической записи имеет вид
V8 > О 36 > О V^ ^ X, diam ^ < 6: ш(/; Е) < 8. C6.37)
ТЕОРЕМА 5. Непрерывное отображение компакта
равномерно непрерывно.
СЛЕДСТВИЕ. Если числовая функция непрерывна на
компакте, то она равномерно непрерывна.
Доказательство. Если /: X ^ R^ — непрерывное
отображение компакта X ^ R^, то для любого 8 > О и любой точки
xgX супа;ествует такое 6^ > О, что для всех точек x'gX, удов-
летворяюпа;их условию \х' - х\< Ъ^, выполняется неравенство
|/(х')-Дх)|<|. C6.38)
Система всех сферических окрестностей Q. = {U(x; 6^)},
хеХ, образует покрытие компакта X. Если Г| — лебегово число
этого покрытия (см. теорему 5 в п. 35.3), то для любых точек
x'gX и х''еХ, для которых \х'' - х'| < Г|, найдется такой элемент
покрытия О., обозначим его U(x^^^; 6 (Q))? что x'eU(x^^\ 6 (Q)) и
x''g U(x^^\ 5 @))? поэтому
\f(x-) - f(x')\ < \f(x-) - /(X@))| + |/(x@)) - f(x')\ < I + I = 8.
Это и означает равномерную непрерывность отображения /. П
230
Следствие является частным случаем теоремы при т = 1.
Для функций, непрерывных на отрезке, оно было доказано
panbHie (см. т. 1, п. 6.4).
В теореме 5 требование того, что отображаемое множество
является компактом, супа;ественно. Например, непрерывная и
ограниченная на интервале (О, 1) функция f(x) = sin - не явля-
X
ется равномерно непрерывной, так как при любом п = 1, 2, ...
имеем diam /[О, -1=2.
В самом деле, с одной стороны, для любых х\ x''g@, 1) для
функции f(x) = sin - имеет место неравенство
|/(х") - Дх')| =
sin ^> - sin —
X X
<
sin —^^
X
+
sin —
X
< 2.
С другой — для любого neN найдется такое meN, что
0<
Тогда при х'
7С/2 + 271771 П
1
<-, 0<
<
-7С/2 + 271771 П
C6.39)
7с/2 + 2жт
\f(x-) - f(x')\
-ж/2 + 2жт
будем иметь
sm - - sm
Li
i\
2 и x\ x"
C6.39)
0,1
n
Это и означает, что diam /[ О,
sup |/(х-)-/(хОН2
^> jc',jc"g @,1/д)
И, следовательно, сколь угодно малым по диаметру
множествам Е = (О, 1/п) не соответствуют достаточно малые по
диаметру множества f(E),
Аналогично определению модуля непрерывности числовой
функции одной переменной (см. т. 1, п. 6.4) вводится понятие
модуля непрерывности отображения.
Определение 8. Для отображения f: X ^ R"^, X ^ й^,
функция
(DE;f;X)= sup \f(x')-f(x)\, х,х'еХ, 6 > О, C6.40)
называется модулем непрерывности этого отображения.
231
Как и в случае функций одной переменной, модуль
непрерывности отображения является неотрицательной возрастаю-
па;ей функцией при 6 > 0.
Отметим очевидную связь понятий колебания
отображения и его модуля непрерывности на множестве: колебание
отображения / на множестве X равно значению его модуля
непрерывности соF; /; X) на этом множестве при 6 = diam X, т. е.
со(/; X) = co(diam X; /; X), а модуль непрерывности соF; /; X)
равен верхней грани диаметров образов f(E) множеств Е ^ X,
диаметры которых не превыгаают числа 6: соF; /; X) =
= sup diam f(E), diam E < 8.
Аналогично случаю функции одной переменной имеет
место следуюгцая теорема.
ТЕОРЕМА 6. Для того чтобы отображение f: X ^ R^,
X ^ R^, было равномерно непрерывно на множестве X,
необходимо и достаточно, чтобы lim соF; /; X) = 0.
Теорема 6 доказывается почти дословным повторением
доказательства соответствуюгцего утверждения для функций
одной переменной (см. т. 1, п. 6.4), поэтому в случае внутренней
потребности проведение ее доказательства может быть
предоставлено читателю.
Мы видели Bbinie (см. п. 6.4), что на отрезке [О, 1] соF; х^) =
= 26 - 6^, поэтому lim соF; х^) = О и, следовательно, функция x^'
6 -^ +0
равномерно непрерывна на этом отрезке, как и должно быть,
согласно теореме 5. Модуль непрерывности той же функции х^,
но уже рассматриваемой на всей вегцественной оси, так же как
и модули непрерывности со[ 6; sin - ], х ^ О, и со[ 6; - ], О < х < 1,
не стремится к нулю при 6^ + 0, поэтому все эти функции не
являются равномерно непрерывными на соответствуюгцих
множествах.
Задача 6. Пусть G — область в R"- и f: G ^ R. Доказать, что если
lim ^^ '/'—^ = О, то / — постоянная функция.
С помогцью доказанных свойств непрерывных отображений
можно получить одно полезное для дальнейгаего свойство
областей (т. е. открытых линейно связных множеств, см. п. 35.2).
Сформулируем это свойство в виде леммы.
132
h^MM к л. Открытое множество является областью тогда
и только тогда, когда любые две его точки можно
соединить целиком лежащей в нем ломаной.
Доказательство. Достаточность сформулированного
условия не требует доказательства. В самом деле, если у некоторого
открытого множества G ^ R^ любые две точки можно
соединить некоторой ломаной, целиком лежагцей в нем, то,
поскольку всякая ломаная является кривой (см. т. 1, п. 16.5), любые
две точки множества G оказываются соединимыми в нем
кривой, что и означает, согласно определению (см. определение 27
в п. 35.2), что открытое множество G линейно связно, т. е.
является областью (см. определение 28 там же).
Докажем необходимость условий леммы. Пусть G —
область пространства й^. Рассмотрим точки xgG и y^G.
Согласно определению области, сугцествует кривая Г = {r(f), а < f < Ь},
соединяюгцая в G точки х и у, т, е. г(а) = х, гф) = г/ и r(t)eG,
а < f < Ь. Кривая Г представляет собой непрерывный образ при
отображении r(t) отрезка [а, Ь], являюгцегося компактом, и
поэтому (см. теорему 3) сама будет компактом. Так как
компакт Г не пересекается с замкнутым множеством /2^\G, то
расстояние между ними болыае нуля (см. лемму 7 в п. 35.2).
Следовательно, сугцествует такое число Г| > О, что р(Г, R^\G) > г\.
Отображение r(t), а < f < Ь отрезка [а, Ь], будучи
непрерывным, является и равномерно непрерывным (см. теорему 5).
Поэтому сугцествует такое 6 > О, что для любых двух точек fe [а, Ь]
и f G [а, Ь], удовлетворяюгцих условию \f' - f\ < 6, выполняется
неравенство p(r(f'), r(f)) < r\. Отсюда вытекает, что для любого
разбиения T = {t^}lZQ отрезка [а, Ь] мелкости |т| < 6 все точки
ломаной \ с вергаинами r(t.), i = О, 1, ... , k, будут содержаться в G
(почему?). Следовательно, \ ^ G.
Началом и концом ломаной Х^ являются соответственно
начало и конец кривой Г, т. е. произвольно заданные точки хну
из G, поэтому нами доказано, что любые две точки области
могут быть соединены в ней ломаной. П
36.9. Непрерывные отображения
линейно связных множеств
Прежде всего определим, что будем понимать под образом
кривой при заданном непрерывном отображении.
Пусть Г = {x(t); а< t <b} — кривая в пространстве R^vif —
непрерывное отображение ее носителя в пространство R^.
~233
Кривая в пространстве R^, представлением которой является
отображение f(x(t)), а < f < Ь отрезка [а, Ь] в пространство R^,
называется образом /(Г) кривой Г при отображении f.
Докажем теперь следуюпа;ую простую теорему.
ТЕОРЕМА 7. Непрерывный образ линейно связного
множества является линейно связным множеством.
Доказательство. Пусть X — линейно связное
множество, X ^ R^ VI f — его непрерывное отображение в
пространство R^, Пусть Y = /(X) и г/'е Y, г/''е Y. Тогда сугцествуют такие
точки x'gX и x''gX, что f{x') = у\ fix'') = у'\ в силу
линейной связности множествах сугцествует такая кривая Г = {x(t)\
а <: t <: b}, что х(а) = х\ х(Ь) = х'' и для всех te[a, b]
выполняется включение x(t)eX. Очевидно, что кривая /(Г) = {f(x(t));
а <: t <: b} соединяет точки у' и у'' в множестве Y, т. е. f(x(a)) =
= f(x') = у\ f(x(b)) = f(x'') = у'' и для всех te[a, b] выполняется
включение fix(t)) = f(x)eY. Это и означает, что множество Y
линейно связно. П
Докажем теперь теорему о непрерывных числовых
функциях на линейно связных множествах, обобгцаюгцую теорему
Коп1и о промежуточных значениях непрерывных на отрезке
функций.
ТЕОРЕМА 8. Функция, непрерывная на линейно связном
множестве, принимая какие-либо два значения, принимает
и любое промежуточное между ними значение.
СЛЕДСТВИЕ 1. Функция, непрерывная на замыкании
линейно связного множества, принимая какие-либо два значения,
принимает и любое промежуточное между ними значение.
СЛЕДСТВИЕ 2. Функция, непрерывная на области или на
замыкании области, принимая какие-либо два значения,
принимает и любое промежуточное между ними значение.
Доказательство. Пусть X — линейно связное
множество, X ^ R^, функция f: X ^ R непрерывна на X, x^^^gX,
xB)gX, /(xA)) = А, /(хB)) = В и, например, А< С < В.В силу
линейной связности множества X, сугцествует такая кривая
Г = {x(t); а <: t <: b}, лежагцая в X, что х^^^ является началом, а
j^B) — QQ концом: х(а) = х^'^\ х(Ь) = х^^К Функция F(t) = f(x(t)),
а <: t <: b, непрерывна на отрезке [а, Ь] как композиция
непрерывных функций f(x) и x(t). Кроме того,
F(a) = f(x(a)) = /(x(i)) = А, F(b) = f(x(b)) = /(xB)) = В.
134
Поэтому, согласно теореме Коши о промежуточных значениях
непрерывных на отрезке функций (см. т. 1, п. 6.2), сугцеству-
ет такое ^о^[а, Ь], что i^(^o) ^ ^- Полагая х^^^ = х(^о)' получим
Докажем первое следствие. Пусть функция / непрерывна
на замыкании X линейно связного множества X ^ R^, х^^^е X,
хB)е X, /(x^i)) = А, /(хB)) = Б и, например, А < С < Б. В силу
непрерывности функции / в точке х^^^ для Е = С —А> О сугцеству-
ет такое 6 > О, что для всех хеХ П U(x^^^; 6) выполняется
неравенство \f(x) -А|<8 = С-Аи, следовательно, неравенство
fix) < С. C6.41)
Поскольку х^^^ — точка прикосновения множества X, в ее
6-окрестности U(x^^^; 6) сугцествует точка у^^\ принадлежагцая
множеству X:
i/(i)GXnC/(x(i);6).
Для нее, в силу C6.41), выполняется неравенство
/A/A)) < С. C6.42)
Аналогично сугцествует такая точка г/^^^е X, что
/A/B)) > С. C6.43)
Таким образом, /(г/A) < С < /(г/^^)) и мы находимся в
условиях теоремы 8 и поэтому из условий C6.42) и C6.43) следует,
что сугцествует такая точка x(^)gX, что /(х(^)) = С. П
Второе следствие теоремы непосредственно вытекает из
первого, так как область является линейно связным
множеством (см. определение 28 в п. 35.2). П
УПРАЖНЕНИЕ 4. Пусть функция / непрерывна и принимает значения
разных знаков на открытом множестве. Доказать, что множество точек, в
которых / ^ О, является открытым множеством, но не является областью.
Задача 7. Построить пример области G, в замыкании G которой
существуют две точки, не соединяемые в G непрерывной кривой.
36.10. Свойства непрерывных отображений
При непрерывных отображениях образ открытого множества
не является, вообпа;е говоря, открытым, а замкнутого —
замкнутым. Это видно уже на примере числовых функций
одной переменной. Так, отображение у = sin х отображает
интервал @,7г) — открытое множество — на полуинтервал (О, 1],
235
который не является открытым множеством, а отображение
у = arctg X отображает числовую прямую — замкнутое
множество — на интервал (-7г/2,7г/2), не являюпа;ийся замкнутым
множеством. То, что в последнем примере в качестве
замкнутого множества взято неограниченное множество, не является
случайным, так как ограниченное замкнутое множество,
будучи компактом, согласно теореме 3, при непрерывном
отображении отображается в компакт и, следовательно, в
замкнутое множество. Покажем, что для прообразов открытых и
замкнутых множеств дело обстоит иначе.
ЛЕММА 2. Если отображение f:G^ R^, G ^ R^, задано на
открытом множестве G, то оно непрерывно в точке х^^^еО
тогда и только тогда, когда для любой окрестности V
точки f(x^^^) существует такая окрестность U точки х^^\ что
f(U) ^ F, С/ ^ G. C6.44)
Таким образом, в отличие от обгцего случая (см. C6.11))
здесь можно не брать пересечение окрестности U точки х^^^ с
отображаемым множеством G.
Доказательство. Если f:G^ R"^, где G — открытое в
пространстве й^ множество, и отображение / непрерывно в точке
х^^^е G, т. е. lim f(x) = f(x^^^), то, согласно определению 2 пре-
дела для любой окрестности V точки f(x^^^) сугцествует такая
окрестность Uq точки х^^\ что для нее выполняется условие
C6.2), т. е. в данном случае /(G П C/q) ^ V,
Поскольку пересечение U = Опи^ открытых множеств G и C/q
является открытым множеством и содержит точку х^^\ оно
также является окрестностью этой точки и f(U) ^ V. Включение
C6.44) доказано.
Обратное утверждение, т. е. что из выполнения условия
C6.44) вытекает непрерывность отображения / в точке х^^\
следует непосредственно из определения непрерывности
C6.11), так как U ^ Gn, следовательно, G П С/ = С/. П
ТЕОРЕМА 9. Отображение f:G^ R^ открытого
множества G ^ R^ непрерывно тогда и только тогда, когда прообраз
всякого открытого множества является открытым
множеством.
Доказательство. Пусть отображение / непрерывно на
открытом множестве G,V — открытое в R^ множество и хе f~^(V).
Множество V, в силу своей открытости, является окрестностью
^36
точки у = f(x)eV. Согласно лемме, сугцествует такая
окрестность и точки X, что f(U) ^ Fh, следовательно, U ^ f~^(V), т. е.
для каждой точки х прообраза f~^(V) открытого множества F
сугцествует ее окрестность С/, содержагцаяся в этом прообразе. Это
и означает, что множество f~^(V) является открытым.
Пусть теперь при отображении / прообраз всякого
открытого множества — открытое множество и хе G. Тогда, какова
бы ни была окрестность V точки /(х), она, будучи открытым
множеством, имеет своим прообразом
U = f-\V) C6.45)
— также открытое множество, которое поэтому является
окрестностью точки хе и. Из равенства C6.45) следует, что f(U) =
= V, и, следовательно, отображение / непрерывно в точке
x@)gG. П
Пример. Рассмотрим непрерывное отображение /: R^ -^ R,
заданное формулой
/(x,z/) = ^ + g-l.
Согласно лемме 2, прообраз открытого множества (-^о, 0),
Т. е. множество точек (х, у), удовлетворяюгцих неравенству —- +
+ ^ < 1 (и, следовательно, составляюгцих внутренность эллип-
са), а также прообраз открытого множества (О, +оо), т. е.
множество таких точек (х, г/), что ^ + ^ > 1 (эти точки образуют
внеп1ность эллипса), являются открытыми множествами.
Вообгце, если f: R^ ^ R — непрерывная на R^ функция, то
для любого числа aeR множества {х: /(х) < а, xeR^} и {х: /(х) > а,
XG R^} являются открытыми множествами как прообразы
открытых множеств (-00, а) и (а, +оо).
При гомеоморфном отображении (см. определение 5 в п. 36.7)
открытого множества на открытое образы открытых
подмножеств также открыты. Действительно, если /— гомеоморфное
отображение открытого множества G на открытое /(G), U —
открытое подмножество множества G и F= /(С/), то в силу
взаимной однозначности отображения / имеем U = f~^(V), sl это
означает, что множество U представляет собой образ множества V
при отображении f~^. Следовательно, множество Fявляется
прообразом при отображении /"^ открытого множества U. Согласно
определению гомеоморфизма, отображение /"^ непрерывно.
Таким образом, множество V является прообразом открытого мно-
237
жества U при непрерывном отображении /"^ открытого
множества /(G), поэтому, в силу теоремы, множество F открыто.
Отметим, что в топологии доказывается, что гомеоморф-
ный образ открытого множества я-мерного пространства
может быть открытым множеством только в пространстве того
же числа измерений.
ТЕОРЕМА 10. Отображение f: X ^ R^ замкнутого
множества X ^ R^ непрерывно тогда и только тогда, когда
прообраз всякого замкнутого множества является замкнутым
множеством.
Доказательство. Пусть отображение / непрерывно на
замкнутом множестве X, Y — замкнутое множество в
пространстве R^ их — точка прикосновения прообраза
f-\Y) CZ X C6.46)
множества Y:
xef-\Y). C6.47)
Множество X — замкнуто: X = X, поэтому
X G /-i(Y) _С1 Х = Х
C6.47) ^ ^ C6.46)
И, следовательно, отображение / определено в точке х.
Покажем, что f(x)eY. Из того, что х — точка
прикосновения множества /"^(Y), следует, что сугцествует такая
последовательность точек
x(%/-i(Y), й = 1, 2, ... , C6.48)
что
lim х(^) = х. C6.49)
Последовательность у^^^ = f(x^^^), й = 1, 2, ... , имеет предел,
так как в силу непрерывности отображения / в точке х имеем
lim yW = lim /(х(^)) = fix). C6.50)
/г ^ СО j^ ^ оо («зо.4У)
Поскольку множество Y замкнуто и у^^^ = /(x^^^)gY, то
fix) G Y, следовательно, xef~^(Y). Это и означает замкну-
C6.50)
тость множества /"^(Y).
Пусть теперь f: X ^ R^ — отображение замкнутого
множества X ^ R^, при котором прообраз всякого замкнутого
множества также является замкнутым множеством. Пусть х^^^еХ и
V— какая-либо окрестность точки у^^^ = f(x^^^) в пространст-
^38
ве R^, y^^^eU. Поскольку V— открытое множество, множество
R^\V является замкнутым и, следовательно, замкнутым будет и
его прообраз f~'^(R^\V). Поэтому дополнение U = R^\f~\R^\V) в
пространстве й^ этого прообраза является открытым
множеством. Оно содержит точку х^^\ Действительно, х^^^ = f~^(y^^^) е
G f~^(V). Множества V и й"^\^не пересекаются, поэтому не
пересекаются их прообразы: f~^(V) П f~'^(R^\V) = 0.
Следовательно, х(О) ^ f-^R'^XV), а поэтому х^^) g R'^Xf-^R'^XV) = U.B силу
открытости множества С/, оно является окрестностью точки х^^\
При этом f (U nX)^V.
В самом деле, если xeU ПХ, то, очевидно, f(x) i R^\V(b
противном случае xef~'^(R^\V), тогда как xeU = R^\f~'^(R^\V)),
Следовательно, f(x)eV,
Итак, для любой окрестности V точки у^^^ = f(x^^^) сугцест-
вует такая окрестность U точки х^^\ что f (U nX)^V. Это и
означает непрерывность отображения / в точке хеХ. П
УПРАЖНЕНИЕ 5. Доказать теорему 4 с помощью теорем 3 и 10.
Замечание 1. При рассмотрении отображений f: X ^ R^,
X ^ R, было видно, в частности, что специфику ряда вопросов
можно в достаточной мере усмотреть уже на примере
отображений плоских или лежагцих в трехмерном пространстве
множеств, а специфику функций многих переменных на примере
функций двух или трех переменных. Благодаря удачно
выбранным определениям и обозначениям доказательства теорем для
указанных частных случаев без особого труда переносятся на об-
па;ий случай. Вместе с тем доказательства в этих частных
случаях имеют преимупа;ество наглядности и простоты записи.
Поэтому в дальнейп1ем будем иногда для больпхей ясности и простоты
изложения ограничиваться подробным рассмотрением лип1ь
двумерного или трехмерного случая, а в обпа;ем случае будем
только формулировать соответствуюпа;ие результаты или даже
ограничиваться указанием на возможность их обобгцения.
Однако если при изучении какого-либо вопроса в многомерном
случае возникают какие-то специфические трудности, то этот
вопрос будет детально рассматриваться в обгцем случае.
Замечание 2. Для отображений / множеств из
комплексного пространства С^ в комплексное пространство С^, т. е.
для отображений f: X ^ С^, X ^ С^, можно ввести многие
понятия, определенные нами для отображений множеств
действительного пространства й^ в действительное пространство R^,
^39
Например, понятие предела отображения, его непрерывности,
равномерной непрерывности отображения, колебания
отображения, его модуля непрерывности. В случае необходимости
читатель сможет без труда сформулировать определение
подобных нужных ему понятий.
Для отображений f: X ^ С^, X ^ С^, справедливы и
аналоги многих из доказанных выгае теорем, например о том, что
непрерывный образ компакта является компактом, что
непрерывное отображение компакта равномерно непрерывно,
следовательно, и их частные случаи для комплекснозначных
функций многих комплексных переменных, например, о том,
что непрерывная на компакте функция ограничена.
Справедливость всего этого следует из того, что для
рассматриваемых вопросов их изучение в комплексных
пространствах С^, состояпа;их из точек z = (z-^, 22, ... , z^, Zj^ = Xj^ + iy^^,
Xf^, yj^^R, k = 1, 2, ,,, , n, можно заменить изучением в
действительных пространствах R^^ с точками
(х, у) = (Xj, ^2, ... , х^, i/j, г/2, ... , Ул).
§37
Частные производные.
Дифференцируемость функций
многих переменных
37.1. Частные производные и частные дифференциалы
Рассмотрим сначала случай функций трех переменных.
Определение 1. Пусть в некоторой окрестности точки
(^0' ^0' ^о) задана функция и = и(х, у, z). Фиксируя
переменные у и z: у = у^, Z = Zq, получим функцию одного
переменного х: и = и(х, г/о, Zq). Обычная производная (см. т. 1, п. 9.1)
этой функции в точке х = х^ называется частной
производной функции и(х, у, z) в точке (Xq, i/q, 2q) по х и обозначается
du{xQ, yQ, Zq)
через
дх
Таким образом,
dujXQ, yQ, Zq) def dujx, yQ, Zq)
dx dx
^40
Заметим, что обозначение частной производной по пере-
fiU (у 77 2^ ^
менной X через ^1 ^'—— традиционно. Правильнее было
ох
бы писать ^(Xq, i/q, 2q), так как ^ является единым симво-
лом, обозначаюпа;им новую функцию, значение которой и
рассматривается в точке (Xq, i/q, 2q).
Если вспомнить определение обычной производной -^ (см.
ах
п. 9.1), то, согласно этому определению, можно написать
dujXQ, i/q, Zq) ^ i^(Xo + Ах, i/q, Zq) - u{Xq, i/q, ^q)
Эх Ax^O Ax
или, если ввести обозначение u(Xq + Ах, i/q, 2q) - z/(Xq, i/q, Zq) =
= A^u (A^u — прирагцение функции по переменной х),
^ = lim ^.
ох Ах^О Ах
Аналогично вводятся частные производные ноу viz:
du{xQ, г/о, Zq) _ du{xQ,yQ,ZQ)\
ду dy
du{xQ, г/о, Zq) _ du{xQ,yQ,z)
у-Уо
или, короче.
dz dz
^ = lim ^, ^ = lim ^,
Эг/ Ai/^0 Аг/' Эг Аг^О Аг'
где А г/ и А^г/ — прирагцения функции соответственно по
переменным у л Z,
Частным дифференциалом d^u функции и(х, у, z) в
данной точке называется ее дифференциал по переменной х
при условии, что переменные у и z фиксированы.
Из свойств дифференциала функции одного переменного
следует, что dji = т^ dx.
^ Эх
Аналогично определяются частные дифференциалы d и,
d^u. Для них имеют место формулы d и = ^ dy, d^u = -^ dz.
Подобные определения имеют место для любого числа
переменных.
'241
Если функция у = /(Xj, ... , х^) определена в некоторой
окрестности точки х^^^ = (х^^\ ... , х^^^), то, по определению,
df{x['\ ... , x(Q)) def df{x[^\ ... , xl^_\, x„ xf^,, ... , x(Q))
dx.
,C7.1)
@)
ИЛИ, что то же, если опустить обозначение аргумента,
|^= Иш ^,
где А,^г/ = /(х^, ... , х^^, х^ + Ах,, х^^, ... , х^) - /(^W, ...
... , х[^\, х[^\ ^i^+v ••• ' ^д^^)- Д-^^ обозначения частной
производной ^ применяются также обозначения у^ или /^ .
Частным дифференциалом d^y функции у = /(х^, ... , xj
называется дифференциал этой функции, рассматриваемой
как функция только одной переменной х-, остальные
переменные фиксированы.
Из свойств дифференциала функций одного переменного
следует, что
d^y = ^dx,, i=l,2,...,n, C7.2)
где dx- = Ax-, и тем самым частный дифференциал d^y
является линейной функцией переменной dx-, называемой
дифференциалом независимой переменной х-. Здесь везде i= 1, 2, ,,, , п,
В случае п = 1 частная производная совпадает с обычной
производной, а частный дифференциал — с обычным
дифференциалом.
Подчеркнем, что ^-^ — единый символ, т. е. в нем числи-
dXi
тель и знаменатель не имеют самостоятельного смысла. С
другой стороны, частная производная т-^, может быть записана и
дх^
В виде дроби: частного двух дифференциалов: =г-^ = —^.
ах^ ах^
Из определения частных производных, как обычных
производных при условии фиксирования всех переменных, кроме
одной, по которой берется производная, следует, что при
вычислении частных производных можно использовать правила
'242
вычисления обычных производных. Пусть, например,
требуется найти производную ^ функции z = хуе^^У. Для этого,
зафиксировав в этой формуле X, получим функцию одной
переменной г/; вычисляя ее производную, будем иметь
ду ""' ^""^^ ду[у] у •
в заключение этого пункта отметим, что из непрерывности в
данной точке функции п переменных не вытекает сугцествова-
ние у нее в этой точке частных производных. Соответствуюгций
пример в случае п= 1 был приведен ранее (см. п. 9.2). Важно
заметить, что при я > 2 из сугцествования даже всех частных
производных в некоторой точке не следует непрерывность функции
в этой точке"^. Это естественно, поскольку условие
непрерывности функции нескольких переменных в точке накладывает
определенное ограничение на ее поведение при приближении к этой
точке по всем направлениям, в то время как сугцествование
частных производных в точке означает, что функция
удовлетворяет определенным условиям при приближении к указанной
точке лип1ь в направлении координатных осей.
Чтобы в этом наглядно убедиться, рассмотрим функцию
/(х, г/), равную нулю, если хг/ = О, и единице, если ху ^ 0.
Очевидно, /(х, 0) = /(О, г/) = О и, следовательно,
Э/@,0)_Э/@,0)_р^
Эх ду
Однако эта функция разрывна в точке (О, 0), так как,
например, ее предел вдоль прямой у = х с удаленной из нее
точкой (О, 0) при (х, у) -^ (О, 0) равен 1, а /(О, 0) = 0. Более того,
сугцествуют функции, имеюгцие частные производные во всех
точках и все-таки разрывные. Примером является функция
f ^^ при х2 + г/2 > о,
fix,y) = \^'-'y' ^ C7.3)
[ О при X = у = 0.
Эта функция имеет частные производные во всей плоскости и
разрывна в точке (О, 0) (почему?).
* Напомним, что при я = 1, т. е. для функции одной переменной из
супдествования в точке производной, вытекает и непрерывность
функции в этой точке (см. п. 9.2).
243
37.2. Дифференцируемость
функций в точке
По аналогии с функцией одного переменного, функция а(х),
X = (Xj, ..., х^), многих переменных, заданная на
множестве X, называется бесконечно малой при х -^ х^^^ по
сравнению с функцией Р(х), заданной на том же множестве X ^ й^,
если сугцествует такая функция ф(х), определенная также
на множестве X, что в некоторой окрестности точки х^^^
для всех точек х множества X выполняется равенство а(х) =
= ф(х)Р(х) и lim ф(х) = 0. В этом случае пигаут а = о(Р),
X —^ Х^^\
Как и для функции одного переменного, если х^^^еХ, т. е.
если функции а, Р и ф определены в точке х^^\ то из
приведенного определения «о-малого» следует непрерывность функции
ф в точке х^^\ а поэтому и равенство ф(х^^^) = 0.
Само собой разумеется, что данное здесь определение а = о(Р)
при X -^ х^^^ является частным случаем соответствуюпа;его
определения для отображений из й в R^ (см. в п. 36.3 формулы
C6.14) —C6.16)).
При определении дифференцируемости функций многих
переменных рассмотрим сначала случай двух переменных:
здесь хороню видна супа;ность понятия дифференцируемости,
а соответствуюпа;ие формулы, естественно, выглядят короче и
пропа;е, чем в обпа;ем случае.
Пусть функция 2 = f(x, у) определена в некоторой
6-окрестности U = C/(Mq, 6) точки М^ = (Xq, i/q) и пусть
(рис. 23) М = (х, у)е U(Mq; 8), А х = х - Xq, А у = у - у^,
следовательно,
р = р(М, Mq) = VAx2 + Аг/2 < 6.
/ ^У] \ Пусть, наконец,
I ^^AxJ \ Аг = /(Xq + Ах, г/о + Ау) - /(х^, г/^).
\ Мо(хо,1/о) I
\ I Обычно Аг называется полным
приращением функции; это название объясняется
тем, что здесь, вообпа;е говоря, все независи-
Vi
\ /
^ мые переменные получают прирагцения, от-
Рис. 23 личные от нуля.
'2Л4
Определение 2. Функция г = f(x, у) называется
дифференцируемой в точке (Xq, i/q), если существуют два такие числа
А и В, что
А2 = A^x + B^y + о(р), р ^ 0. C7.4)
Определение 3. В случае дифференцируемости функции f в
точке (Xq, i/q) линейная функция ААх + БАг/ переменных Ах
и iSy называется полным дифференциалом или просто
дифференциалом функции f в точке (Xq, у^) и обозначается
через dz.
Таким образом, dz = ААх + БАг/.
Вместо Ах и Аг/ используют также равнозначные обозначения
def def
dx и dy, т. е. dx = Ах, dy = Ay. Таким образом, dz =Adx + Bdy,
функцию o(p), согласно определению символа «о-малое», можно
представить в виде о(р) = 8(Ах, Аг/)р, где
lim 8(Ах, Аг/) = 0, C7.5)
р ^0
и функция 8(Ах, Аг/) определена, согласно тому же
определению, в точке (О, 0), так как в этой точке определены функции
р и о(р) = Az - ААх - БАг/. Поэтому
8@, 0) = 0. C7.6)
Таким образом,
Az=AAx + БАг/ + 8(Ах, Аг/)р, C7.7)
причем выполняется условие C7.5), следовательно, и условие
C7.6).
Запигаем соотногаение C7.7) в другой форме, при этом все
ниже написанные пределы будут браться по целой
окрестности точки (О, 0).
ЛЕММА 1. Условие C7.7) эквивалентно условию
Az = ААх + БАг/ + г^(Ах, Ау)Ах + 82(Ах, Аг/)Аг/, C7.8)
где lim 8i = lim 89 = 0.
Доказательство. Пусть выполнено условие C7.7) и а = 8р,
где 8^0 при р ^ 0; тогда при р ^ О
а^
■■ 8р = 8/УАх^~+~А^
— Ах + г ^ —Ау = г^Ах + 82Аг/,
JAx^ + Аг/2 л/Ах2 + Аг/2
245
где 8i = F , ^^ 8p = F , ^^ Заметив, что ^^^^ < 1,
VAx2 + Аг/2 VAx2 + Аг/2 TAx^Ta^
L_^! < 1, имеем |8j| < |8|, I82I < И при p ^ 0. Если же p = О, то
л/Ах2 + Аг/2
положим 8^ = 82 = 0. в результате lim 8^ = lim 83 = О, т. е. полу-
р ^ о р ^ о
чилось представление функции а в виде а = е^Ах + 82Аг/, lim 8^ =
= lim 89 = 0.
р^О
2
Пусть, наоборот, выполнено условие C7.8) и а = 8^Ах + 82Аг/,
где 8j ^ О и 82 ^ О при р ^ 0. Тогда при р ^ О имеем
^^ F, + ^У F,\/A.r2 + A7y2 = ер,
л/Ах2 + Аг/2 л/Ах2 + Аг/2 ^>
А АЛ А уд I I I I I I
где 8 = —F-I + ^ —Fo и, следовательно, 8 < 8i + 89
VAx2 + Аг/2 VAx2 + Аг/2
при р ^ 0. Если же р = О, то положим 8 = 0. В результате
получим, что 8^0 при р ^ О, а это означает, что функция а
представлена в виде а = 8р, lim 8 = 0. П
р^О
ТЕОРЕМА 1. Если функция z = f(x, у) дифференцируема в
точке (Xq, i/q), то она непрерывна в этой точке.
Действительно, так как |Ах| < р и \Ау\ < р, то из формулы
C7.7) и следует, что при р ^ О имеет место Az -^ 0. Это и
означает непрерывность функции / в точке (Xq, i/q). П
ТЕОРЕМА 2. Если функция z = /(х, у) дифференцируема в
точке (Xq, у^) и dz = Adx + Bdy — ее дифференциал в этой
точке, то в точке (Xq, i/q) у функции f существуют все
частные производные и
^fixp, у о) _^^ Э/(хо, уо) _ ^ C7 9)
Эх ' Эг/ *
Таким образом,
dz = ^dx + ^dy. C7.10)
Доказательство. Согласно определению дифференциру-
емости (см. C7.4) и C7.8)), Az =ААх + ВАу + 8^Ах + 8^Аг/, где
lim 81 = lim 8^ = 0. C7.11)
р^О ^ р^О ^
^46
Если Аг/ = О, то Аг = А^2 = ААх + Е^Ах, где lim 81 = О (это сле-
дует из C7.11), поскольку, полагая Аг/ = О, получим р = |Ах|).
Отсюда, разделив на Ах при Ах ^ О, имеем
^ =A + 8i, C7.12)
Ах ^
где при Ах ^ О правая часть стремится к пределу, равному А,
поэтому и левая часть при Ах -^ О имеет тот же предел. Это
означает (см. C7.1)), что в точке (Xq, z/q) сугцествует производная
^ = А. Аналогично, полагая в C7.8) Ах = О, поделив на Аг/ и
перейдя к пределу при Аг/ ^ О, Аг/ ^ О, получим — = В.П
СЛЕДСТВИЕ. Если функция /(х, у) дифференцируема в точке
(Xq, z/q), то она имеет единственный дифференциал.
Единственность дифференциала непосредственно вытекает
из формул C7.9), так как частные производные в данной
точке определяются однозначно.
Вспоминая определения частных дифференциалов (см.
C7.2)), формулу C7.10) можно переписать в виде dz = d^z + d z,
т. е. полный дифференциал функции (когда он сугцествует)
является суммой ее частных дифференциалов.
Заметим, что утверждение, обратное теореме 2, не имеет
места: сугцествуют функции, имеюгцие все частные
производные во всех точках плоскости, но не дифференцируемые в
некоторой точке. Примером может служить функция C7.3),
приведенная в конце предыдугцего пункта: в точке (О, 0) эта
функция не непрерывна, откуда, в силу теоремы 1, вытекает,
что в точке (О, 0) она и не дифференцируема.
Из сказанного следует, что не всегда выражение d^z + d z,
когда оно имеет смысл, является полным дифференциалом
функции. Связь между дифференцируемостью функции в
точке и сугцествованием в этой точке частных производных
сложнее, чем связь между дифференцируемостью и
сугцествованием производной функции одной переменной.
Сформулируем достаточные условия в терминах свойств
частных производных для дифференцируемости функции.
ТЕОРЕМА 3. Пусть функция z = /(х, у) в некоторой ок-
рестности точки (Xq, z/q) имеет частные производные — и
247
^, которые непрерывны в самой точке (Xq, i/q); тогда
функция Z = f(x, у) дифференцируема в этой точке,
СЛЕДСТВИЕ. Если функция z = /(х, г/) имеет в некоторой
окрестности точки (Xq, Уо) частные производные ^ и ^, при-
чем эти частные производные непрерывны в самой точке
(Xq, i/q), то и функция z = /(х, г/) также непрерывна в этой
точке.
Доказательство теоремы. Обозначим через С/F) 6-ок-
рестность точки (Xq, i/q), в которой определена вместе со
своими частными производными f^ и / функция /. Выберем Ах и
Аг/ так, чтобы (Xq + Ах, у^ + Аг/)е С/F). Замечая, что
Az = fixQ + Ах, г/о + Аг/) - /(Xq, у^) =
= [/(Xq + Ах, г/о + Аг/) - Дх^, у^ + Аг/)] + [Дх^, у^ + Аг/) - Дх^, г/^)],
применим к выражениям в квадратных скобках, являюпа;им-
ся прирапа;ениями функций только одной переменной,
формулу конечных прирапа;ений Лагранжа (см. п. 11.2). Это
возможно, поскольку функция /(х, г/о + Аг/), рассматриваемая как
функция одного переменного х, имеет на отрезке с концами в
точках Xq и Xq + Ах производную (являюгцуюся частной
производной по X функции /), откуда следует непрерывность этой
функции на указанном отрезке и, таким образом, функция
/(х, z/q + Аг/) удовлетворяет всем условиям, при которых была
доказана формула конечных прирагцений Лагранжа.
Аналогично проверяется и возможность применения формулы
Лагранжа к функции /(Xq, г/), рассматриваемой как функция
одного переменного у на отрезке с концами в точках z/q и z/q + Аг/.
В результате получим
Az = 4(Xq + е^Ах, г/Q + Аг/)Ах + /^(Xq, z/q + е2Аг/)Аг/, C7.13)
o<ei< 1, о<е2< 1,
причем 9j и 02 зависят от выбора точки (Xq + Ах, z/q + Аг/), т. е.
от Ах и Аг/.
Если
C7.14)
4(^0' ^0 + б2Аг/) - /^(Xq, z/q) = 82,
^48
где 8^ = 8i(Ax, Аг/), 83 = 82(Ах, Аг/), то, в силу непрерывности
частных производных /^ и / в точке (Xq, i/q), имеем
lim 81 = lim 82 = 0. C7.15)
Найдя из C7.14) выражения для fj^x^ + Э^Ах, i/q + Аг/) и
fy(xQ, i/q + ЭзАг/) и подставив их в C7.13), получим
Az = f^ix^, г/о)Ах + fyix^, у^)Ау + 8iAx + е^Ау, C7.16)
что, в силу выполнения условий C7.15), и означает дифферен-
цируемость функции / в точке (Xq, у^) (см. C7.4) и C7.8)). П
Следствие из теоремы вытекает из того обстоятельства, что
функция, дифференцируемая в некоторой точке, является и
непрерывной в ней (см. теорему 1).
Теорема 3 имеет важное значение, поскольку понятие диф-
ференцируемости функции играет первостепенную роль в ряде
разделов теории функций многих переменных. Однако
непосредственная проверка дифференцируемости функции
(например, для выяснения возможности применения тех или иных
теорем) часто бывает затруднительна, проверка же
непрерывности частных производных, для вычислений которых
имеется удобный аналитический аппарат, оказывается прогце.
Определение 4. Функция, имеющая в некоторой точке (на
некотором множестве) непрерывные частные производные,
называется непрерывно дифференцируемой в этой точке
{на этом множестве).
Сопоставим определение дифференцируемости функции
(определение 2) и определение непрерывной
дифференцируемости (определение 4). Дифференцируемость функции в
точке означает сугцествование в этой точке дифференциала, т. е.
справедливость для этой точки формулы C7.4). Непрерывная
же дифференцируемость функции в точке означает
непрерывность в этой точке ее частных производных. Таким образом,
дифференцируемость функции связана с понятием
дифференциала, а непрерывная дифференцируемость — с понятием
частных производных. Вместе с тем из непрерывной
дифференцируемости в точке (на открытом множестве) следует
дифференцируемость в этой точке (на этом множестве); в этом
состоит утверждение теоремы 3.
В дальнейгаем понадобятся некоторые дополнительные
свойства функции 8^ и 82 из формулы C7.16).
'249
Определение 5. Пусть А и В— два плоских множества,
А ^ R'^y, В ^ й^у, и пусть функция f = /(х, г/, и, v)
определена для (х, i/)g а, (г/, 1;)еБ.
Функция f называется равномерно стремящейся к нулю
на множестве А точек (х, у) при (и, v) -^ (z/q, Vq), если для
любого 8 > О существует такое 6 > О, что для всех (и, v) е Б,
удовлетворяющих условию J(u - г/д)^ + (v - Уд)^ < 5, и всех
(х, у)еА выполняется условие |/(х, г/, и, v)\ < 8.
Обш;ее определение равномерного стремления функции к
пределу будет дано в п. 39.4.
ТЕОРЕМА 4. Пусть функция z = /(х, у) непрерывно
дифференцируема на открытом множестве G ^ R^, Тогда
Az = 4(х, у)Ах + fy(x, у)Ау + 8iAx + г^^у, C7.17)
где функции 8^ = 8^(х, у, Ах, Ау) г/ 83 = 82(х, у, Ах, Ау)
равномерно стремятся к нулю при р = JAx^' + Ay^' ^ О на любом
компакте А ^ G,
Доказательство. Пусть А — компакт, лежагций в G.
Тогда замкнутые множества А и R^\G не пересекаются, и так
как А ограничено (см. теорему 3 п. 35.3), то d = р(А, R^\G) > О
(см. лемму 7 п. 35.2).
Множество А^^2 ^ {(^' УУ- Р((^' У)^ ^) ^ <^/2} содержится в
множестве G и является компактом (см. лемму 11 п. 35.3).
Пусть теперь р = JAx^' + Ay^' < -. Поскольку точки
(Xq + Э^Ах, г/о + Ау) и (Xq, у^ + ЭзАг/) находятся от точки (Xq, г/д)
на расстоянии, меныаем -, при (Xq, z/q)^ А имеем
(Хо + е^Ах, г/о + Ау)е А^/^, (Xq, у^ + е2Аг/)е А^/2'
o<ei<i, о<е2<1,
и, следовательно, согласно формулам C7.14), имеем
неравенства |8j| < со(р; fyT, A^i^, I82I < со(р; /^; А^^2)' ^Д® ^ их правых
частях стоят соответственно модули непрерывности функций /^
и / . Из непрерывности частных производных /^ и / на
компакте А^/2 следует, что
lim ш(р; 4; А^/2) = О и lim ш(р; / ; А^/2) = 0.
р ^ о ' р ^ о i^ /
250
Поэтому для любого 8 > о сугцествует 6 > О такое, что для всех
р < 6 выполняются неравенства со(р; f^; ^d/2) ^ ^' ^(Р' fy''> ^d/2) ^ ^•
Следовательно, для всех р < 6 и всех (Xq, Уо)^А справедливы
неравенства |8j| < 8, I82I < 8.
Это и означает равномерное стремление к нулю при р ^ О
функций 8j и 82 на компакте А. П
Замечание. В предположениях теоремы 4 прирагце-
ние функции Az представимо также в виде
Az = 4(х, у) Ах + fy(x, у)Ау + 8р, C7.18)
где 8 = 8(х, г/. Ах, Аг/) равномерно на каждом компакте А ^ G и
стремится к нулю, когда р = vAx^ + Аг/^ -^ 0. Для
доказательства достаточно в формуле C7.18) положить 8 = 8i— + 89-^
Р Р
при р ^ о и 8 = о при р = о (сравните с доказательством леммы
в начале этого пункта).
Все определения и утверждения этого пункта переносятся и
на случай функции у = /(х), х = (х^, ... , х^) любого числа п
переменных, определенной в некоторой окрестности точки х^^К
Например, условие дифференцируемости в данной точке х^^^ в
обгцем случае выглядит так:
Аг/ = AjAxj + ... + А^Ах^ + о(р), р ^ О, C7.19)
где
р = Jt^f, Аг/ = fix,, ... , xj - /(х^О), ... , xW),
Za Xj Xj X- , L J-, ^, ... , fZ.
Таким образом, если функция /дифференцируема, то
fix) =/(х@)) + A(xi - х^^^) + ... + А^(х^ - х^^о)) + о(р), р -^ 0,C7.20)
т. е. функция / в окрестности данной точки с точностью до
бесконечно малых более высокого порядка, чем Р = Y, ^-^t ~ ^i^^)^y
равна линейной функции"^. Образно говоря, дифференциру-
емость функции в данной точке означает, что функция / «по-
* Функция вида у = Cq + с^х + ... + с^х^, где с^ — постоянные, i = О, 1,
2, ..., я, называются линейными (однородными) функциями п переменных
или, что то же самое, линейными функциями точки х = (х^, ... , xJeR^.
чти линейна» в окрестности этой точки; точный смысл
выражения «почти линейна» заключается в формуле C7.20).
Если функция /дифференцируема, т. е. имеет место
равенство C7.19), то у нее супа;ествуют все частные производные
-^-^ ^, и они равны коэффициентам А-:
Э/(х@))
ЭХ;
-А., i=l,2, ... ,п.
df(x) df(x)
Линейная функция '^ ^Ах-^ + ... + '^ Ах^ от переменных
Axj, ... , Ах^ (здесь вместо х^^^ написано х) называется
дифференциалом дифференцируемой функции или, подробнее, ее
полным дифференциалом в данной точке х и
обозначается df(x):
^^^^^ = l^^^i + - +1|^^^«- ^^^-^^^
Дифференциал, как и всякая линейная функция п
переменных, определен на всем я-мерном пространстве R^.
Таким образом, формула C7.21) имеет смысл для всех
значений Ах., / = 1, 2, ..., я, в то время как формула C7.19) —
только для тех, которые не выводят за область определения
функции f.
Переменные Ах- называются также дифференциалами
переменных X. и обозначаются dx-, i= 1, 2, ... , п.В этих
обозначениях дифференциал функции / записывается в виде
Очевидно, что А/(х) = df(x) + о(р) при р ^ 0.
Если функция / дифференцируема в данной точке, то ее
дифференциал является суммой всех ее частных
дифференциалов (см. п. 37.1) в этой точке:
df(x) = f d^. f(x).
i = 1 ^
Однако не всегда, когда сугцествуют все частные
дифференциалы d^f(x), i= 1, 2, ... , п, функция /дифференцируема
(соответствуюгцие примеры для случая функций двух
переменных были рассмотрены выгае).
252
Если же рассматривать дифференциал и при изменении
точки X = (Xj, ... , х^), то он уже является функцией от 2п
переменных: Xj, ... , х^, dxj, ... , dx^.
Теоремы 1—4 этого параграфа очевидным образом обобгца-
ются на функции любого числа п переменных (п = 1, 2, ...),
поэтому их формулировки не приводятся.
37.3. Дифференцирование сложной функции
ТЕОРЕМА 5. Пусть функции x(t) и y(t) одного переменного t
дифференцируемы в точке t^ (что, как мы знаем,
эквивалентно существованию у них производных в точке t^ (см. п. 9.2)) г/
пусть Xq = х(^0), i/q = г/(^о)- ^^-^^ функция г = /(х, у)
дифференцируема в точке (Xq, i/q), то сложная функция z = f(x(t), y(t))
определена в некоторой окрестности точки t^, имеет в t^
производную и эта производная выражается формулой
или подробнее
dz ^ d2_dx_ I d2_dy_ /оу оо^
dt dxdt dydt^
dfixjio), yito)) ^ Э/(Хо, yQ)dx{tQ) dfjXQ, yQ)dy{tQ)
dt dx dt dy dt
Доказательство. Функция /(x, у), согласно определению
дифференцируемости функции, определена в некоторой
окрестности точки (Xq, г/о). Из дифференцируемости же функций
х(^) и y(t) следует их непрерывность в точке ^q. Поэтому,
согласно замечанию перед теоремой 2 в п. 36.6, в некоторой
окрестности точки ^Q определена сложная функция f(x(t), y(t)).
Дифференцируемость функции z = /(х, у) в точке (Xq, у^)
означает, что ее полное прирагцение Az = /(Xq + Ах, у^ + Ау) -
- /(Xq, i/q) представимо в виде
Az = ^Ах + рАу + 8лУАх2 + Аг/2, C7.23)
где функция 8 = 8(Ах, Ау) определена в некоторой окрестности
точки (О, 0), непрерывна
обычно, р = л/Ах^ + А^.
точки (О, 0), непрерывна в ней и lim 8(Ах, Ау) = 0. Здесь, как
р ^0
253
Пусть теперь At — прирапа;ение переменной f и Ах =
= x(tQ + At) - x(t^. Ay = y(tQ + Ax) - yito). Разделим обе
части равенства C7.23) на At:
Az ^ д2_Ах , д2_Ау I /fAx Y (Ау^^
(при At > о берется знак плюс, а при At < О — знак минус).
При Af ^ О, в силу непрерывности функций х(^) и y(t) в точке
tQ, получим Ах ^ О и Аг/ ^ О, а значит, lim р = 0. Отсюда, по
А^ ^ о
теореме о пределе композиций функции lim 8(Ах, Ау) = 0. За-
метим, наконец, что супа;ествует конечный предел
Из всего этого следует, что при At ^ О правая часть формулы
C7.24) стремится к конечному пределу ^^ + ^^ (в точке
dxat ду at
Az
t = to), поэтому и левая часть этой формулы, т. е. —,
стремится к тому же пределу, а это и означает, что в точке ^q сугцест-
dz
вует производная — и выражается формулой C7.22). П
Отметим, что, хотя в окончательную формулу производной
сложной функции C7.22) входят только частные производные
=г^ и гг^ функции 2 = /(х, у), по ходу доказательства использо-
ох ду
валось более сильное свойство этой функции, чем сугцествова-
ние частных производных, а именно ее дифференцируемость.
УПРАЖНЕНИЕ. Показать, что при отказе от требования дифферен-
цируемости функции z = f(x, у) в точке (Xq, z/q), лишь при
предположении супдествования в этой точке частных производных г-^ и г-^ и су-
дх ду
ществования производных — и -^ в точке t^ формула C7.22), вообще го-
воря, несправедлива и, более того, сложная функция f (x(t), y(t))
(предполагается, что она имеет смысл), вообпде говоря, не имеет производной
в точке ^0-
СЛЕДСТВИЕ. Если функции х = х(и, v) и у = у(и, v)
непрерывны в точке (z/q, Vq) и имеют в ней частные производные ^,
^, а функция 2 = f(x, у) дифференцируема в точке (Xq, г/д), где
Xq = x(uq, Vq), i/q = y(uQ, Vq), mo в точке (z/q, Vq) существует ча-
254
dz
стная производная ^ сложной функции z = fix(u, v), у(и, v)),
причем
dz _ dz дх , dz ду /or? ок\
au axau дуди
Доказательство. Функция / дифференцируема в
точке (Xq, г/о) и, следовательно, определена в некоторой ее
окрестности. В силу непрерывности функции х(и, v), у(и, v) в точке
(Uq, Vq), в некоторой окрестности этой точки имеет смысл
сложная функция f(x(u, v), у(и, v)) (см. п. 36.6).
Зафиксируем v = Vq и рассмотрим сложную функцию z =
= f(x(u, Vq), у(и, Vq)) одного переменного и. Согласно теореме 5,
эта функция определена в некоторой окрестности точки Uq и
имеет в этой точке производную. Таким образом, производная
dz
— В точке (uq, Vq) сугцествует и из формулы C7.22) вытекает
формула C7.25). П
Аналогично, если в точке (Uq, Vq) сугцествуют частные
производные тг^ и .г^, то у сложной функции Z = f(x(u, v), у(и, v))
dv dv
сугцествует в точке (uq, Vq) частная производная по i; и для нее
справедлива формула
dz ^ dz дх , dz ду
dv dxdv dydv'
Замечание. Рассмотрим обгций я-мерный случай.
Пусть в окрестности точки х^^^ = (х^^\ ... , х^^^) задана
функция у = у (х), X = (Xj, ... , х^), а на некоторой
окрестности точки t^^^ = (t^^^\ ... , tf^^^^)eR^— функции
X. = X. (t), t = (t^, ... , tf), / = 1,2, ... , n, такие, что x.(f^^^) = x[^\
Если функция у = y(x) дифференцируема в точке х^^^ и если в
дх ■
точке t^^^ существуют частные производные —', у = 1, 2, ... , й,
/ = 1, 2, ... , Я, то сложная функция yix(t)) имеет в точке t^^^
частные производные ^, j = 1, 2, ,,, , k, причем
^= f d^p у=1,2, ...,й. C7.26)
Заметим, что если при сделанных предположениях част-
-\ д X
ные производные ^-^ и ^г—', /=1,2, ... , п, j = 1, 2, ... , k, непре-
ОХ; dti
J
255
рывны соответственно в точках х^^^ и t^^\ то, в силу формулы
C7.26), частные производные сложной функции у = y(x(t))
также непрерывны в точке t^^^ и, следовательно, она будет
дифференцируемой в этой точке (см. теорему 3 п. 37.2). В сле-
дуюпа;ем пункте будет доказана дифференцируемость
композиций функций при более слабых предположениях.
37.4. Инвариантность формы первого дифференциала
относительно выбора переменных.
Правила вычисления дифференциалов
ТЕОРЕМА 6. Пусть функция f(x), х = (х^, ... , xj, определена
в некоторой окрестности точки х^^^ = {х[^\ ... , х^^^), а
функции Х- = x-(t), t = (t-^, ... , tf^), / = 1,2, ... , n, определены в
некоторой окрестности точки t^^^ = (t^^\ ... , f^^^) и пусть х^^ = х.(^^^^),
/ = 1, 2, ... , п.
Тогда если функция f(x) дифференцируема в точке х^^\ а
функции X. = x.(t), i = 1, 2, ,,, , п, дифференцируемы в точке t^^\
то сложная функция f(x(t)) = f(x^(t), ... , xj^t)) определена в
некоторой окрестности точки t^^^ и дифференцируема в этой
точке. При этом дифференциал df функции f(x(t)) в точке t^^^
может быть записан как в виде
так и в виде
аг=1ЩЁ^сИ^, C7.27)
]
где dx. = dx.(t)\^ _ ^(О).
Доказательство. Функции x.(t), i= 1, 2, ,,, , п, определены
в некоторой окрестности точки t^^\ и так как из дифференциру-
емости функций следует их непрерывность, то сложная
функция fix(t)) определена в некоторой окрестности точки t^^^ (см.
замечание перед теоремой 2 п. 36.6). Зафиксируем какие-либо два
числа 6 > О и Г| > О так, чтобы функция f(x) была определена на
Г|-окрестности точки х^^\ функции x-(t), / = 1, 2, ... , я, на 6-ок-
рестности точки t^^^ и чтобы x(t) = (x^(t), ... , xj^t))e U(x^^^; r\) при
teU(t^^^; 6). Тогда на окрестности U(t^^^; 6) определена сложная
функция f(x(t)). Возможность выбора таких чисел 6 и Г| (очевид-
256^
но, 5 зависит от выбора Г|) была показана в н. 36.6. Функция f(x)
дифференцируема в точке х^^^; поэтому при т'= ^, ^^t < Л имеем
А/ = Ах(«> + ДХ1, ... , х^О) + Ах„) - /(х@\ ... , х(^0)) =
1^ М^дх, + ег, C7.29)
i= 1
где функция 8 = 8(Axj, Ахз, ... , Ах^) определена в некоторой
окрестности точки (О, О, ... , 0), непрерывна в ней и lim 8 = 0.
г^ О
В силу дифференцируемости функций х- = x-(t), / = 1, 2, ... , я.
в точке t^^\ при Р = Y, ^^f ^ ^ получим
Ах, = х,а@) + А^1, ... , ^0) + А^,) - x,it[^\ ... , 4'^)
;^1 ^^;
-Af. + 8,р, /=1,2, ... , п, C7.30)
где lim 8,- = О, / = 1, 2, ... , я. Подставив значения Ах,- из C7.30)
в C7.29), имеем
Af^y^J^l'.^^A.+^, C7.31)
где
Р= £ ^Zl^£.p + £r. C7.32)
Переставив порядок суммирования в C7.31), найдем
Теперь, для того чтобы доказать, что сложная функция
f(x(t)) дифференцируема в точке t^^\ надо показать, что Р = о(р)
при р ^ 0. В силу непрерывности функций x-(t), /=1,2, ... , п,
в точке t^^\ имеем lim Ах, = О и, следовательно, lim г = 0. От-
р^О р^О
сюда, в силу теоремы о композиции непрерывных функций
(см. п. 36.6),
lim 8 = 0. C7.34)
р^О
Заметим, что
р ^ f ^е, + ЕГ. C7.35)
р C7.32) jt^i dXt ^ р
Докажем ограниченность отнонгения -. Использовав
формулы C7.30), получим
г_1 /^ л„я^ 1 ^ 1л.,1* ^ ^ f ^ \dxdt(°>)\M^^\
р р ^М ^ pjt-i' " C7.30) М[ 1^1
^h
Из условия lim В- = О вытекает, что в некоторой
окрестности точки ^^^^ функции 8- ограничены, а так как ■—^ < 1, то и
функция - ограничена в некоторой окрестности точки t^^\ По-
Р
этому из равенств lim 8- = О, / = 1, 2, ... , я, C7.34) и C7.35)
р ^0
следует, что lim !^ = О, т. е. что Р = о(р) при р ^ 0. Дифферен-
Р^о р
цируемость сложной функции f{x{t)) в точке ^^^^ доказана.
Из формулы C7.31) имеем
Отсюда, замечая, что ^ —'-^ Atj = dt-, / = 1, 2, ... , я, мы и
получаем формулу C7.28). Формула же C7.27) является
обычной формулой для дифференциала (см. C7.21)). П
Формально обе записи C7.27) и C7.28) дифференциала
функции выглядят одинаково: в обеих формулах
дифференциал равен сумме произведений частных производных на со-
ответствуюгцие дифференциалы, однако в формуле C7.27)
dtj — дифференциалы независимых переменных, а в формуле
C7.28) dx. — дифференциалы функций. Свойство
дифференциала функции, выражаемое формулами C7.27) и C7.28),
называется инвариантностью формы первого дифференциала
относительно выбора переменных.
Замечание 1. Из формулы C7.33) следует, что
Но коэффициенты дифференциала функции при
дифференциалах независимых переменных определяются однозначно и рав-
* Мы воспользовались неравенством / V ^f ^ V |^J> которое являет-
ся следствием очевидного неравенства ^ <^f ^ ^ I^J (см. C5.9)).
i= 1 V J = 1 '
25S
ны соответствуюпа;им частным производным, поэтому,
сравнивая эту формулу с формулой C7.27), получаем
т. е. снова формулу C7.26). Правда, она выведена при более
сильных ограничениях, чем раныае: на этот раз
предполагалась дифференцируемость функций x-(t), i = 1, 2, ... , я, в то
время как в п. 37.3 — лигаь сугцествование у этих функций
соответствуюгцих частных производных.
Замечание 2. Если функции /(х^, ... , х^) и х- = x.(t),
t = (t^, ... , tf^)eR^, i = 1, 2, ... , n, имеют непрерывные частные
производные соответственно в точке (х^^\ ... , x^'^)eR^ и в точке
t^^^eR^, где х|^^ = x-(t^^^), то эти функции, будучи
дифференцируемы в указанных точках, удовлетворяют условиям теоремы 6.
Следовательно, как это уже отмечалось в конце п. 37.3, для них
справедливы утверждение этой теоремы и вытекаюгцая из него
формула для вычисления частной производной сложной
функции (см. предыдугцее замечание).
Инвариантность формы первого дифференциала гаироко
используется при практическом вычислении дифференциалов
и частных производных. Если г/ и г; — функции какого-то
числа переменных, то с помопа;ью формулы C7.28) легко
получаются следуюпа;ие формулы:
1. d(u -\- v) = du -\- dv.
2. d(uv) = vdu + udv. C7.36)
q л(иЛ ^ vdu - udv
\v ] i;2
Докажем, например, формулу 3. Пусть 2 = -, где и =
= и(х^, ... , х„), V = v(x^, ... , х„). Замечая, что ^ = -и ^ = --^,
^ '^ 1 я ди V av v^
согласно формуле C7.28), имеем
d2 = Uu-^dv = ^^^^i^-^^.n
V V^ V^
При вычислении конкретных дифференциалов
элементарных функций многих переменных можно использовать
формулы, полученные раньпхе (см. § 9) для дифференциалов
элементарных функций одной переменной. При этом следует
заметить, что если функция у = г/(х^, ... , х^) представлена в виде
у = F(u), где и = и(х-^, ... , х^), то при соответствуюпа;их
предположениях, согласно формуле C7.28), dy = F\u) du, и = г/(х^, ... , х^).
^59
Например, если у = sin и, то dy = cos и du; если у = 1пи, то
dy = —; если у = arctg и, то di/ = —^ и т. д. (подчеркнем, что
и 1 + w^
здесь везде и = и(х^, ... , х^)),
В качестве примера найдем дифференциал функции 2 =
= arctg ^. Вычисления произведем в следуюпа;ем порядке:
X
dz = dfarctg У]= -J—d(y]= f xdy-ydx ^ xdy - ydx^
1 + E^ X^ + Z/^ X^ X^ + Z/^
x^
При вычислении дифференциала di У- ] мы воспользовались
т " л(иЛ vdu — udv
формулой d\ - \= , доказанной выпхе для случая, ког-
\v ) v^
да г/ и i; являются функциями одних и тех же переменных.
Использование этой формулы в указанном случае правомерно,
так как можно считать, что у дроби ^ и числитель и знамена-
X
тель являются функциями одних и тех же переменных х и г/,
что можно даже выразить, например, следуюпа;ей формулой:
у _ у + 0х^
X X + Оу'
Если требуется найти частные производные функции
многих переменных, особенно если надо вычислить все
производные, то целесообразно вычислить дифференциал этой
функции, тогда искомыми частными производными являются
коэффициенты при соответствуюгцих дифференциалах.
Так, в рассмотренном примере 2 = arctg ^, беря коэффици-
X
енты при dx и dy из найденного для дифференциала
выражения, получим
Э£ ^ _ у д2_ ^ X
Эх х^ + г/^' ду х^ + г/^*
Замечание 3. Всякую функцию у = f(x^, ... , xj от п
переменных можно рассматривать в определенном смысле и как
функцию от любого числа п + т > п переменных х-^, ^2, ...
... , х^, ... , л:^ + ^. Именно для всякой функции /(х^, ... , х^),
заданной на множестве X ^ R^, определим функцию f\x-^, ...
... , х^, ... , x^ + ^) на множестве точек (х^, ... , х^, ... , x^ + ^)
таких, что (Xj, ... , xJgX, -оо < Xj< +00, j = п-\- 1, ,,, , п-\- т, сле-
дуюгцим образом:
/ (^1? ••• ? ^д? ••• ? ^п + т) ^ Д^1' ••• ' ^п)' C7.37)
^60
Таким образом, рассмотрение функции п переменных как
функции п -\- т переменных означает фактически
продолжение по формуле C7.37) функции / с множества ее определения
X ^ Д^ на множество
X' = {(xi, ... ,x^ + J:(Xi, ... ,xJgX, -оо<х.< + оо,
j = п-\- 1, ,,, , п-\- т},
лежаш;ее уже в пространстве R^ + ^. Для функции f,
полученной после такого продолжения, имеем
дх^ дх^
af (х^, ..., х^ + ^)
/= 1, 2, ... , п,
О, j = п -\- 1, ,,, , п -\- т,
dXj
поэтому
1
Эх,-
Э/(Х1, ..., xj
Например, когда мы говорим, что функцию одного
переменного 2 = /(х), определенную на некотором интервале (а, Ь), мы
рассматриваем как функцию двух переменных f(x) = F(x, у),
хе (а, Ь),- ^ <у < +00; это означает, что функция F(x, у)
является постоянной, равной f(x) на любой прямой, проходящей через
точку X интервала (а, Ь) оси Ох параллельно оси Оу, При этом
dFjx, у) _ л/, ч dFjx, у) _ г.
дх '^^^' ду ^'
dF(x, у) = df(x), a<x<b, -оо <у <-\-оо.
Полезно для дальнейгаего отметить обратный факт. Пусть
X ^ R^. Если функция f\x-^, ... , х^, х^ + ^) определена на
множестве
X = {(Xj, ... , х^, х^ + j) : (Xj, ... , x^)gX, а < х^ + J < Ь}
и
ЭГ(Х1 х^, x^ + i) _^ C7.38)
^^п+ 1
— наХ"^, то существует такая функция /(х^, ... , х^) от п
переменных, определенная на множестве X, что f\x-^, ... , х^, л:^ + i) =
= /(Xj, ... , xj для всех (Xj, ... , xJgX, x^ + iG(a, b), В этом
случае говорят, что функция f* фактически не зависит от
переменной х^ + ^. В самом деле, из условия C7.38) сле-
дует, что функция f^ постоянна как функция л:^ + i (см.
следствие 1 теоремы 3 из п. 11.2) при фиксированной точке
(Xj, ... , х^), т. е., зафиксировав какое-либо се (а, Ъ) для любой
точки (Xj, ... , x^)gXи х^^^^{а, Ь), имеем f^{x^, ... , х^, х^^^ =
= f*(^i^ ••• ? ^п^ с). Искомая функция /, очевидно,
определяется равенством /(х^, ... , х^) = f\x-^, ... , х^, с), причем она не
зависит от выбора се(а, Ь).
Из сказанного, в частности, следует, что формулы C7.36)
для дифференциалов остаются справедливыми и в том случае,
когда функции и и v зависят от разного числа переменных,
так как всегда, в силу указанного приема, этот случай можно
свести к разобранному вып1е случаю функций одного числа
переменных.
37.5. Геометрический смысл
частных производных и полного дифференциала
Для больп1ей геометрической наглядности и для того, чтобы
не вводить новых понятий, в этом пункте ограничимся
рассмотрением функций двух переменных.
Рассмотрим функцию 2 = /(х, г/), определенную на плоском
открытом множестве G, т. е. открытом множестве G, лежапа;ем
на плоскости R^. Пусть (Xq, z/o)gG, и пусть в точке (Xq, z/q) су-
dz
па;ествует частная производная .г—. Ее геометрический смысл
ах
сразу получается из определения частной производной т-^ как
ох
обычной производной функции /(х, у) по X при
фиксированном г/ и из геометрического смысла обычной производной (см.
п. 9.3). В самом деле, возьмем замкнутый круг Q радиуса г с
центром в точке (Xq, i/q) и лежагций в G*. Пусть Г — кривая,
заданная представлением z = /(х, г/д), г/ = г/д, Xq - г < х < Xq + г,
т. е. кривая, которая получается в результате сечения
графика функции 2 = /(х, у), (х, y)eQ плоскостью у = у^ (рис. 24).
^/(•^0' Уо) _ ^f(^^ Уо)\
Как известно.
Эх dx
tg а, где а — угол.
* Такой круг Q всегда существует. Действительно, в силу определения
открытого множества, существует такая 5-окрестность U точки (Xq, z/q),
что и ^ G. Тогда замкнутый круг Q радиуса 5/2 с центром в точке (Xq, z/q)
будет заведомо лежать в G.
^62
Рис. 24
образованный касательной к графику функции /(х, г/д) в точке
(Xq, /(Xq, г/о)) с осью Ох, т. е. угол, образованный касательной к
кривой Г в точке (Xq, у^, fi^o^ Уо)) ^ осью Ох.
Таким образом, ^—— = tg а; в этом и состоит
геометриях
ческии смысл частной производной т-^,
ох
Аналогично устанавливается и геометрический смысл ча-
стнои производной
^У
как тангенса угла наклона,
образованного с осью Оу касательной в точке (Xq, i/q, /(Xq, у^)) к
кривой, получаюпа;ейся в результате сечения графика
функции 2 = /(х, у), (х, y)eQ, плоскостью х = Xq.
Что же касается геометрического смысла дифференциала,
то из формулы C7.4) получим
/(X, у) = 2^+ А(х - Хо) + В(у - г/о) + о(р), р - О, C7.39)
Уравнение
р = J(x - Xq)^ + (г/-г/оJ, 2о = /(Хо, г/о).
2 = 2q+ А(х - Хо) + В(у - г/о)
C7.40)
является уравнением плоскости, проходягцеи через точку
(Хо, г/о, 2q) и не параллельной оси 02. Как известно,
коэффициенты А и В однозначно определяются из соотногаения C7.39),
причем
А^_ Э/(Хо, 1/о) ^ _ Э/(Хо, 1/о)
Эх ' Эг/
C7.41)
2^3
и, значит, плоскость C7.40) однозначно определена cooTHonie-
нием C7.39). Эта плоскость называется касательной
плоскостью к графику функции z = f(x, у) в точке (Xq, z/q? ^q)-
Таким образом, мы прип1ли к следуюпа;ему определению.
Определение 6. Касательной плоскостью к графику функции
f(x, у) в данной точке называется такая плоскость, что
разность ее аппликаты и значения функции f(x, у)
является величиной, бесконечно малой по сравнению с р при р ^ 0.
В силу C7.41), уравнение этой касательной плоскости
имеет вид
Z- Zn
дх
уХ "^0/ '
dfiXp, Уо)
Ьу
(у-Уо). C7.42)
В дальнейп1ем (см. п. 50.5) мы познакомимся с другим
подходом к понятию касательной плоскости.
Полагая Ах = х - Xq, Ay = у - у^, правую часть уравнения
C7.42) запигаем в виде
Э/(Хо, г/о) д^ ^ Э/(Хо, Уо)
дх
Эг/
Это есть обычная запись дифференциала dz функции z = f(x, у)
в точке (Xq, Уо), поэтому уравнение C7.42) можно переписать в
виде Z - Zq = dz.
Таким образом, геометрический
смысл полного дифференциала
функции в точке (Xq, Уо) состоит в том, что
он равен прирагцению аппликаты
плоскости, касательной к графику
функции (рис. 25).
Более подробно дифференциал
дх дх
Ах = Х- Хо,Ау = у- Уо,
совпадает с прирагцением в точке
X = Xq -\- Ах, у = Уо -\- Ау аппликаты
плоскости, касательной к графику
функции в точке
Ах, i/o + Ai/)
Рис. 25
(Xq, i/q, /(Xq, Уо))*
264
37.6. Градиент функции
Пусть функция F(x, у) дифференцируема в точке (Xq, z/q), а
кривая Г такова, что функции х = x(t), у = y(t), а < t < b, с по-
могцью которых она задана в параметрической форме,
удовлетворяют уравнению F(x, у) = О, т. е. с его помогцью осугцеств-
ляется неявное задание кривой Г. Пусть ^о^[а, Ь], Xq = x(tQ),
Уо ^ ^(^о)' ^ функции x(t) и y(t) дифференцируемы при t = t^.
Дифференцируя при t = tQ тождество F(x(t), y(t)) = 0, a<t<b,
получим
г ч^ \ ч^ \\ (^F{x^, г/о) Э^(Хо, у^)\
т. е. векторы (х yt^^ у yt^) и -^——^ ^——
ортогональны. Вектор а = (х^, г/^) в случае, когда он не равен нулю,
является, как известно, касательным вектором к кривой Г в точке
(Xq, г/о) = (х(^о), г/(^о)). Вектор (^—^^-^' —^ilo_^ называется
градиентом функции F в точке (Xq, г/д) и обозначается через
grad F(Xq, Уо). Из сказанного следует, что градиент функции F
ортогонален касательной к кривой, неявно задаваемой
уравнением F(x, у) = 0. Прямая, перпендикулярная касательной к
плоской кривой и лежапа;ая в одной плоскости с ней,
называется (см. п. 17.3) нормалью к данной кривой.
Таким образом, градиент функции F коллинеарен нормали
в соответствуюпа;ей точке к кривой, задаваемой уравнением
Fix, у) = 0.
В случае дифференцируемой функции /(х^, ... , х^) ее
градиентом называется вектор [^, --- , ^ \
37.7. Производная по направлению
Частные производные от функции являются производными
«в направлениях координатных осей». Естественно поставить
вопрос об определении и вычислении производной по любому
фиксированному направлению. Определим это понятие,
рассмотрев этот вопрос на примере функций трех переменных.
Пусть, как всегда, в пространстве зафиксирована система
координат X, г/, 2, заданы точка Mq = (Xq, i/q, Zq) и ненулевой
^65
вектор I. Обозначим через cos а, cos Р, cos у направляюпа;ие
косинусы вектора I. Как известно,
cos^ а + cos^ Р + cos^ У = 1,
и если ^Q — единичный вектор в направлении вектора I, то
^Q = 7-7 = (cos а, cos р, cos у).
Проведем из точки М^ луч в направлении вектора I. Его
уравнение в координатной форме имеет вид
X = Xq-\- tcos а, у = у^ + tcos р, z = 2^-\- tcos у, t > о, C7.43)
где параметр t равен расстоянию от точки М до точки М^:
\М^М\ = J{x - ХоJ + (г/ - г/оJ + (г - 2^)^ =
= tjcos ^а + cos 2р + cos ^у = t. C7.44)
Пусть функция f(M), где М = (х, г/, z), определена на
некотором отрезке [Mq, М^] с концами в точках М^ и М^
рассматриваемого луча. Ее производная -J- в точке Mq в направлении
вектора I определяется (рис. 26) равенством
a/(Mo)def ^.^ f(M)-f(M^)
dl
М^М,
О
\MqM\
в силу равенств C7.43) и C7.44), это определение можно
записать в следуюгцем виде:
Э/(Мо)
lim
/(xq + ^cosa, г/о + ^cosp, Zq + ^cosy) - /(xq, z/q, ^q)
dl Г-Т+0 t
Таким образом, производная функции / в точке Mq по
направлению вектора I является производной справа сложной
функции /(Xq + tcos а, у^ + tcos р,
Zq + tcos у) в точке f = 0:
'-^-if(^o + tcosa,y,+
+ fcos р, 2q + tcos y)|^ ^ Q. C7.45)
Если функция /(x, г/, z)
определена в некоторой окрестности точки
Mq = (Xq, i/q, Zq) и дифференциру-
Рис. 26 ема в этой точке, то, заметив, что
266
вдоль луча C7.43) -^ = cos а, -^ = cos Р, -^ = cos у, и продиф-
CVL LLv LLv
ференцировав по f в точке t = Q сложную функцию /(Xq + ^cos а,
г/о + ^cos Р, ^0 + ^cos у), получим
dl C7.45) Эх dt ду dt dz dt
Э/(Мо) , Э/(Мо) р , Э/(Мо)
= ; "cos а + ; "cos В + \ "cos у
ах ду 02
или, короче, опустив обозначения аргумента,
^ = |^cosa+ ^cosB + ^cosy. C7.46)
dl дх ду dz
Эта формула при сделанных предположениях имеет место
для любого ненулевого вектора I. С ее помогцью производная
по направлению вектора I выражается через частные
производные по координатам х, г/, 2 и направляюгцие косинусы
вектора I с координатными осями.
Таким образом, доказана следуюгцая теорема.
ТЕОРЕМА 7. Пусть функция f дифференцируема в точке
(Xq, i/q, 2q). Тогда в этой точке функция f имеет
производную по любому направлению и эта производная находится
по формуле C7.46).
Любопытно отметить, что из полученной формулы C7.46)
для производной по направлению сразу не видно, что эта
производная не зависит от выбора системы координат. Эта
независимость непосредственно следует из самого определения
производной по направлению, откуда, в свою очередь,
вытекает, что правая часть формулы C7.46) не зависит от выбора
прямоугольной декартовой системы координат, а
определяется только вектором I.
^ ЩМ^) df(M^) df(M^)
Вектор с координатами —^-^, —^-^? —^-^ называется,
дх ду dz
как отмечалось выгае, градиентом функции /(М) в точке М^ и
обозначается grad /. (Мы уже встречались с понятием
градиента функций при рассмотрении кривых, заданных неявным
образом; см. п. 37.6.)
Таким образом, если i, / и fe — координатные орты, то
'267
Часто оказывается удобно использовать символический
вектор Гамильтона"^
ах ду 0Z \ дх ду 0Z )
называемый наблой, Набла является обозначением
определенной операции, которую следует произвести над той или иной
функцией.
Для функции /, по определению, полагаем
ах ду 02
Формально это равенство можно рассматривать как
«произведение» вектора V на число /. Итак, grad / и V/ являются
обозначениями одного и того же выражения.
Пусть теперь вектор I является единичным и,
следовательно, I = (cos а, cos Р, cos у). С помогцью градиента формула для
производной функции / по направлению вектора I запигается
следуюгцим образом:
Ц = cos а^ + cos В^ + cos у^ = (I, grad /), C7.48)
dl дх ду dz
где в правой части стоит скалярное произведение векторов I
и grad /. Отсюда, поскольку I — единичный вектор,
^ = Igrad /|cos ф,
где ф — угол, образованный вектором I и grad /. Из этой
формулы видно, что если в данной точке
то производная дифференцируемой функции по направлению
достигает наибольп1его значения в единственном
направлении, а именно том, при котором cos ф = 1, т. е. в направлении
градиента. Из этого следует, что для заданной функции точки
/(М) градиент в каждой точке однозначно определяется самой
функцией и не зависит от выбора системы координат, как это
могло бы сначала показаться из формулы C7.47).
Действительно, прежде всего, если градиент равен нулю
в одной декартовой системе координат, то он равен нулю и
в каждой другой подобной системе координат. В самом деле.
У. Гамильтон A805—1865) — ирландский математик.
~268
равенство нулю градиента в некоторой точке, согласно
формуле C7.48), равносильно равенству нулю в этой точке
производных по всем направлениям, последнее же не зависит от
выбора декартовой системы координат, поскольку от этого
выбора не зависит производная по направлению. Если же градиент
не равен нулю, то его независимость от выбора декартовой
системы координат следует непосредственно из доказанного
Bbinie его геометрического смысла: направление градиента
показывает направление наибыстрейпхего роста функции (оно
единственно), а его величина равна производной в этом
направлении.
Возьмем теперь любую непрерывно дифференцируемую
кривую без особых точек, проходяпа;их через точку (Xq, i/q, 2q),
и такую, что вектор I является ее касательным вектором.
Обозначим через S переменную длину дуги этой кривой,
отсчитываемую от точки Mq в таком направлении, чтобы вектор I
давал положительное направление на касательной. Если х = x(s),
у = y(s), 2 = 2(s) — представление этой кривой, то, как
известно (см. п. 16.5), -^ = cos а, -^ = cos В, -^ = cos у, т. е. справед-
ds ds ds
ЛИВЫ те же формулы, что и для луча C7.43). Поэтому если
взять производную в точке Mq(Xq, i/q, Zq) от
дифференцируемой функции /(х, г/, z) по данной кривой в направлении
возрастания длины дуги S, т. е. производную по s сложной
функции f(x(s), y(s), z(s)), s > о, при s = о, то для этой производной,
если ее также обозначить через т^, справедлива формула C7.46).
61
Это означает, что производная в некоторой точке от функции
вдоль кривой, проходяпа;ей через указанную точку, совпадает с
производной по направлению касательной к кривой в той же
точке.
Все сказанное переносится на функции любого числа п
переменных (я > 2). Сформулируем лигаь для этого случая
определение производной по направлению.
Пусть в некоторой окрестности точки х^^^ = (х^^\ ... , х^^^)
определена функция f(x) и пусть х^^^ = (х[^\ ... , х^^^) — точка
этой окрестности, х^^^ ^ х^^\
Проведем прямую через точки х^^^ и х^^К Ее уравнение (см.
C5.44) и C5.45)) имеет вид
X. = х\^^ + t COS а., /=1,2, ... , п, -оо <t< +00,
^69
где cos а. — направляюгцие косинусы вектора
I = (х[
A)
X
@)
х<0)).
Рассмотрим функцию / только на точках этой прямой, т. е.
рассмотрим функцию
f(x^^^ + t COS а^, ... , х^^^ + t cos а J.
Производная ^ функции /(х^, ... , х^) в точке х^^^ в
направлении точки х^^^ или, что то же, в направлении вектора I
определяется как производная ^ от сложной функции
ot
f(x[^^ + f COS а^, ... , x^o) + t cos aj, t > 0.
В TOM случае, если функция / дифференцируема в точке х^^\
согласно формуле для производной сложной функции, в этой
точке имеем
Э/ ^^^ Э/
dl dt
^cos а^ +
+ Д-cos а„
Эх,
Вспоминая определение градиента функции п переменных
(см. п. 37.6), с помогцью скалярного произведения я-мерных
векторов (см. C5.32)) формулу производной функции / по
направлению вектора I для любого я-мерного пространства R^
можно записать в виде C7.48), т. е.
^ = (grad /, Iq), где 1^ = (cos а^, ... , cos aj = ^.
В заключение отметим, что из того, что функция в некоторой
точке имеет производные по всем направлениям, не следует, что
функция в этой точке дифференциру-
ук ема или даже непрерывна.
Например, функция
Jo, если у ^ х^ или х = у = О,
т, У)-\^^ ^^^^ 1/ = х2 и х2 + г/2 > о,
имеет в точке (О, 0) по любому
направлению производную, равную
нулю. Однако в точке (О, 0) функция /
разрывна и тем более не
дифференцируема (рис. 27).
0|
Рис. 27
270
37.8. Пример исследования функций двух переменных
С помопа;ью частных производных можно изучать поведение
функций многих переменных, подобно тому как
исследовалось поведение функции одной переменной с помогцью ее
производной. Вопрос отыскания наиболыаих и наименыаих
значений рассмотрен в § 40 и § 43, здесь же ограничимся одним
примером изучения функции двух переменных, с помогцью
которого получим егце одно доказательство установленного в
п. 28.2"^ числового неравенства B8.17). Напомним его.
Пусть р > 1 и число q определяется равенством
i + i = l. C7.49)
р q
Тогда для любых чисел а > О и Ь > О имеет место неравенство
аЬ<^ + ^-. C7.50)
р q
Прежде всего отметим, что уравнение C7.49), связываюгцее
числа р и q, равносильно соотногаению
(p-l)(g-l) = l, C7.51)
которое эквивалентно условию
q=^ri' C7.52)
Это устанавливается непосредственной проверкой.
Для доказательства неравенства C7.50) рассмотрим функцию
Г(х,у) = ху-^-^, х>0, у>0. C7.53)
Вычислим ее частные производные:
^ИШ=у-хР-\ ^ЛШ = х-у<1-К C7.54)
Из C7.51) следует, что при х > О и г/ > О уравнения
y-xP-^ = Q C7.55)
и
^-yq-l = Q C7.56)
равносильны. Таким образом, точки (х, г/), удовлетворяюгцие
как условию —L^i^ = о, так и условию —^^^ = О, лежат на
ох оу
кривой C7.55) или, что то же, на кривой C7.56).
в силу C7.49) и C7.52), вдоль кривой C7.55) имеем
F(x,xP-'^) = xP-
= xp(l
р q
р ^>
= хР-
_ ХР _
р
_ ХР
C7.57)
Обозначим теперь через G+ множество всех точек,
расположенных Bbinie кривой C7.55) и на самой кривой:
G+'^={{x,y):y>xP-\ х>0},
а через G~ — множество всех точек первой координатной
четверти (включая и точки оси Ох), лежапа;их ниже этой кривой и
на ней самой:
G- = {(х, у); 0<у<хР-\ х> 0}.
Согласно формулам C7.54), при (х, y)eG^, у ^ хр~^ имеем
соответственно —L^i^ > О
^-^^^§f^ > О, а при (х, y)&G-, у^хР-^,
(здесь использована эквивалентность уравнений C7.55) и
C7.56)). Поэтому вдоль любого отрезка, лежагцего на
множестве G+ и параллельного оси Ох (рис. 28), функция F(x, у)
строго возрастает. Следовательно, если (х, у) е G+, г/ ^ х^"^, то
(см. C7.57))
Fix, у) < Fix, хР-^) = 0.
Аналогично, на любом отрезке, лежагцем на множестве G~
и параллельном оси Оу, функция Fix, у) также строго
возрастает. Поэтому если (х, у)е G" и г/ ^ х^ "^, то опять
Fix,y)<Fix,xP-^) = 0.
Таким образом, если у ^ хр~^, х > О,
г/ > О, то всегда Fix, у) < 0. Итак,
вспоминая вид функции F (см. C7.53)),
имеем: если а > О, Ь > О, то
аЪ<^ + ^- приЬ^а^-1,
Р q
У:
0
\
G+
1 у = хР-^
G-
1
X
аЪ = ^ + ^- приЬ
р q
аР-
Рис. 28
Тем самым неравенство C7.50)
доказано.
272
§38
Частные производные
и дифференциалы высших порядков
38.1. Частные производные высших порядков
Пусть задана функция /(х, у). Тогда каждая из ее частных
производных (если они, конечно, супа;ествуют) '^^'^^ и -Ii^-iMl^
ах ду
которые называются также частными производными первого
порядка, снова является функцией независимых переменных
X, г/ и может, следовательно, также иметь частные
производные. Частная производная ^-[т^ ] обозначается через —-^ или
/^^, а — 1 .г^ 1 через .^-^ или / . Таким образом,
^^ духах ) ауах ^у
дх\дх ) дx^' ^^' дуУдх ) дудх ^У
И, аналогично,
дх[ду I дхду 'У"' ду[ду I Эг/2 ^уУ
Производные /^^, / , / и / называются частными
производными второго порядка. Рассматривая частные
производные от них, получим всевозможные частные производные
d^f d^f d^f
третьего порядка: —^, ^-зЧ' ТТГ ^ ^- ^^
dx'^ ayax"^ ау^ах
Аналогично определяются частные производные
произвольного порядка и для функций любого числа переменных.
Определение 1. Частная производная (по любой из
независимых переменных) от частной производной порядка т - 1,
т = 1, 2, ,,, ,* называется частной производной порядка т.
Частная производная, полученная дифференцированием
по различным переменным, называется смешанной частной
производной. Частная же производная, полученная
дифференцированием только по одной переменной, называется
чистой частной производной.
* Частной производной нулевого порядка для удобства обозначений
считают саму функцию.
~273
Число различных производных при увеличении т,
очевидно, возрастает, однако оказывается, что при определенных
предположениях многие из них совпадают, а именно смепхан-
ные частные производные по одним и тем же переменным не
зависят от порядка дифференцирования.
Более точно имеет место следуюпа;ая теорема.
ТЕОРЕМА 1. Пусть функция f(x, у) определена вместе со
своими частными производными f^, f , f и f в некоторой
окрестности точки (Xq, i/q), причем f и f непрерывны в этой
точке; тогда
fxyD^ у о) = fyxD^ У о)' C8.1)
Доказательство. Пусть функция f(x, у) определена
вместе с производными /^, / , / и / в 6-окрестности точки
(Xq, i/q), и пусть Ах и Аг/ фиксированы так, что Ах^ + Ау^ < 6^.
Будем обозначать, как и раньпхе (см. п. 37.1), символом А^,
соответственно А , прирапа;ение функции / по аргументу х,
соответственно г/, в точке (Xq, Уо)*- Введем обозначения А / =
= K(\f)y ^yxf = VV) и покажем, что
Ky=^xf^ C8.2)
Действительно,
Kyf = Ki^yf) = KUiH^ у о + ^У) - Я^о' ^о)] = Я^о + ^^' у о + ^У) -
- /(Хо + Ах, г/о)] - [/(Xq, г/о + Аг/) - /(Xq, у^)]; C8.3)
аналогично
\xf = ^y(Kf) = [Я^о + ^^' У О + ^У) - f(^o^ у о + ^^)] -
- [/(Хо + Ах, г/о) - /(Хо, г/о)]. C8.4)
Сравнивая C8.3) и C8.4), убеждаемся в справедливости соот-
ногаения C8.2).
Положим теперь ф(х) = /(х, у^ + Аг/) - /(х, г/о); тогда C8.3)
можно переписать в виде
^х/=ф(^0 + ^^)-ф(^о)-
* Напомним (см. п. 37.1), что для заданной функции F(x, у) ее
приращения А^ и А в данной точке (xq, z/q) определяются по формулам
A^FixQ, г/о) = FixQ + Ах, z/q) - FixQ, z/q),
AyF(xQ, уо) = F(xq, yQ + Ay) - FixQ, y^).
274
в силу того что в рассматриваемой окрестности точки (Xq, z/q)
сугцествует частная производная /^, функция ф(х)
дифференцируема на отрезке с концами в точках Xq и Xq + Ах. Из
теоремы Лагранжа о конечных прирагцениях следует, что
Kyf = Ф'(^о + eiAx)Ax, О < е^ < 1.
Но ф'(х) = 4(х, i/q + Ay) - 4(х, i/q), поэтому
Kyf = UxD + QjAx, г/о + Ay) - 4(Xo + Э^Ах, г/о)]Ах.
Применяя егце раз ту же теорему о конечных
прирагцениях, но теперь уже по переменной г/, имеем
Kyf = fxy(^ + ^1^^' Уо + %^у)^хАу,
o<ei<i, о<е2<1. C8.5)
Аналогично, полагая \|/(г/) = /(Xq + Ах, у) - fix^, у), имеем
\xf = ¥(г/о + Аг/) - \|/(г/о) = "^Ьо + ^3^^)^^ =
= [fyD + А^' Уо + ^зАг/) - /^(Xq, г/о + езАг/)]Аг/ =
=/^^(Хо + е4Ах, г/о + езАг/)АхАг/, 0<ез<1, 0<е4<1. C8.6)
Согласно C8.2), левые части равенства C8.5) и C8.6)
равны между собой, значит, равны и правые; приравнивая их и
сокрагцая на АхАу при Ах ^ О и Аг/ ^ О, получаем
fxyi^o + QjAx, г/о + ЭзАг/) = fyj^x^ + е4Ах, г/о + %Ау),
0<е.<1, /=1,2,3,4. C8.7)
В силу непрерывности частных производных /„„ и /„„ в точ-
ху ух
ке Хо, г/о, переходя в C8.7) к пределу при Ах^ + Аг/^ -^ О,
получаем C8.1). П
Замечание 1. Из доказанной теоремы по индукции
следует, что если у функции п переменных смегаанные частные
производные т-го порядка непрерывны в некоторой точке, а
производные низгаих порядков непрерывны в ее окрестности,
то производные порядка т в этой точке не зависят от порядка
дифференцирования. Это следует из того, что любые две
последовательности дифференцирования, отличаюгциеся только
порядком дифференцирования (т. е. такие, что по каждому
фиксированному аргументу они содержат одно и то же суммарное
число дифференцирований), можно перевести одну в другую
конечным числом гаагов, при каждом из которых меняется
порядок дифференцирования только по двум переменным, а дру-
~275
гие остаются фиксированными. Таким образом, при каждом nia-
ге фактически рассматривается изменение порядка
дифференцирования у функции лип1ь двух переменных, а в этом случае
выполняются условия доказанной выгае теоремы. Тем самым
обгций случай и сводится к случаю функций двух переменных.
Поясним это на примере. Докажем, например, что / = / .
Согласно сказанному выгае, последовательно имеем
/ =(f ) =(f ) =(f ) =(f ) =(f) =(f) =f .
' xyz V' x^yz V' x^zy V' xz^y V' zx^y V' z^xy V'z^yx ' zyx
Замечание 2. В заключение этого пункта отметим,
что на первый взгляд доказанная теорема может показаться
не очень содержательной: для того чтобы судить о том, имеет
ли место равенство / = / , надо, согласно этой теореме,
проверить непрерывность функций / и / , а для этого надо,
казалось бы, их знать, но если они уже известны, то без всякой
теоремы можно сказать, равны они или нет. Тем не менее
теорема 1 все-таки содержательна. Дело в том, что о
непрерывности функции можно иногда судить на основании
некоторых обгцих теорем, не прибегая к конкретному вычислению
и исследованию самой функции. Так, все элементарные
функции многих переменных непрерывны в своей области
определения (см. п. 36.5). С другой стороны, частные производные
элементарных функций сами являются элементарными,
поэтому если, например, частная производная некоторой
элементарной функции определена на некоторой окрестности
какой-либо точки, то эта производная и непрерывна в каждой
точке указанной окрестности.
Задача 8. Доказать, что если функция /(х, у) определена вместе со
своими частными производными /^, / и / в некоторой окрестности
точки (Xq, г/о), причем частная производная / непрерывна в точке (Xq, z/q), то
в этой точке существует частная производная f^^ и fyj^x^, z/q) = f^yi^o^ Уо)-
Функция, имеюпа;ая в некоторой точке (на некотором
открытом множестве) непрерывные частные производные всех
порядков до некоторого порядка т включительно, называется т раз
непрерывно дифференцируемой в этой точке (на этом множестве).
Заметим, что, для того чтобы функция имела в точке (на
открытом множестве) непрерывные частные производные всех
порядков до некоторого порядка т включительно, достаточно,
чтобы она имела в этой точке (на этом множестве)
непрерывные частные производные порядка т. Действительно, из
непрерывности всех частных производных порядка т в точке (на
^76
открытом множестве), согласно следствию из теоремы 3 в
п. 37.2, вытекает непрерывность всех частных производных
порядка т - 1 в рассматриваемой точке (на рассматриваемом
множестве). Из непрерывности же частных производных
порядка т - 1 вытекает (в случае т > 1) непрерывность частных
производных порядка m - 2 и т. д.
38.2. Дифференциалы высших порядков
Функция от 2п переменных х^, ... , х^, г/^, ... , г/^, или, что то
же, от упорядоченной пары (х, у) точек я-мерного
пространства х = (Xi, ... , xj, у = (i/i, ... , у J вида
А(х, у)=А(х^, ... , х^; i/i, ... ,yj= f а^^лг-г/^,
i,k = 1
где a-f^ — заданные числа (/, й = 1, 2, ... , я), называется
билинейной формой от X и г/. Это название объясняется тем, что
если одну из точек х и г/ зафиксировать, то функция будет
линейной относительно координат оставп1ейся точки.
Функция А(х, х) называется квадратичной формой, соот-
ветствуюпа;ей данной билинейной форме А(х, у):
п
i,k - 1
В случае, когда а-^ = а^., i, k = 1, 2, ... , п, билинейная форма
А(х, у) называется симметричной.
Так, например, скалярное произведение двух векторов
X = (Xj, Х2, ... , х^) и у = (i/j, г/2, ... , г/^) я-мерного евклидова
пространства R^
ху = х^у^ + х^у^ + ... + х^у^
является симметричной билинейной формой точек х =
= (Xj, Х2, ... , xj и г/ = (i/i, г/2, ... , г/J, а квадрат длины вектора
|х| — соответствуюгцей ей квадратичной формой
\лл\^ /\^ ^ I Л^ ^ I I /4^^
В дальнейгаем для удобства изложения будем обозначать
дифференциалы не только символом d, но и символом 6,
например писать не только dz = ^ dx + ^ dy, но и 62 = ^ 6х +
+ — 6г/, причем дифференциал какой-либо функции будем
называть также и ее первым дифференциалом.
^77
Пусть функция Z = 2(х, у) имеет непрерывные первые и
вторые частные производные на некотором открытом плоском
множестве G (такие функции, согласно определению предыдугцего
пункта, называются дважды непрерывно дифференцируемыми
на множестве G). Из непрерывности на множестве G частных
производных .-? и =г^ следует, как мы знаем (см. теорему 3 в
ох ду
П. 37.2), дифференцируемость самой функции z{x, у) в каждой
точке этого множества. Таким образом, для всех точек (х, г/)е G
определен дифференциал
аг = Щ1У1ах + Щ1У1ау.
дх ду ^
Согласно сделанным предположениям, частные
производные ^ и ^ имеют на открытом множестве непрерывные
частные производные
Э ГдгЛд^г
дх\ дх ) Эх^'
д2_Гд2_Л
ду\дх )
дЧ
Эг/Эх'
d_rdi
дх\ду
И
dzfdz Л ^ d^'Z
дхду ду[ ду ) Эг/^'
поэтому, в силу той же теоремы Зизп.37.2, г-^и.-? также
дх ду
дифференцируемы на множестве G. Поэтому дифференциал
dz, рассматриваемый как функция только переменных х и г/, в
свою очередь является дифференцируемой на множестве G
функцией. Вычислим дифференциал от первого
дифференциала dZj считая dx и dy фиксированными, а точку (х, у) — при-
надлежагцей области G: (х, y)eG, при этом новое
дифференцирование обозначим символом 6:
= ^dx5x + ^(dx 5y + 6x dy) + ^,dy Ъу.
дх^ дхду ду^
Обратим внимание на то, что непрерывность вторых
производных была использована не только для того, чтобы
проведенные вычисления имели смысл [т. е. для того, чтобы во всех
рассматриваемых точках супа;ествовали дифференциалы 6 т^
дх
dz Л
и 6 =г- , но и ДЛЯ того, чтобы в процессе вычислений не обрагцать
ду )
внимания на порядок дифференцирования. Действительно,
было показано (см. п. 38.1), что в случае непрерывности сме-
^78
гаанных частных производных ^-^ и ^-^ они совпадают, по-
дхду дудх
этому для их обозначения может быть использован один и тот
же символ, что и было сделано при указанных вычислениях.
В результате получилась симметричная билинейная форма
переменных dx, dy, 5х, Ъу. Полагая Ъх = dx, Ъу = dy, получим
соответствуюгцую ей квадратичную форму, которая и
называется вторым дифференциалом функции z = z(x, у) в данной
точке (х, y)eG и обозначается d^z.
Таким образом, мы пригали к следуюгцему определению.
Определение 2. Вторым дифференциалом d^z функции z = f(x, у)
в данной точке называется квадратичная форма от
дифференциалов dx и dy независимых переменных,
соответствующая билинейной форме дифференциала от первого
дифференциала, т. е.
аЧ = ^йх2 + 2 =^ dxdy + ^^ dy^. C8.8)
Эх2 дхду ^ Эг/2 ^ ^ ^
На практике при конкретном вычислении дифференциалов
обычно совмегцаются оба niara — вычисление дифференциала
от дифференциала Ъ(dz) и приравнивание дифференциалов
аргументов при последовательных дифференцированиях: Ъх = dx,
Ъу = dy. Например, пусть z = x^cos^ у и требуется найти d^z.
Последовательно имеем:
dz = 3x^cos^ у dx - x^sin 2г/ dy,
d^z = 6x cos^ у dx^ - Bx^sin 2y dx dy - Sx^sin 2y dx dy -
- 2x^cos 2y dy^ = 6x cos^ у dx^ - 6x^sin 2y dx dy - 2x^cos^ 2y dy^.
Аналогичным образом при непрерывности частных
производных третьего порядка можно вычислить и дифференциал
от второго дифференциала Ъ(d^z), после чего, полагая 6х = dx
иЪу = dy, мы получим по определению третий дифференциал.
По индукции определяется и дифференциал (т + 1)-го
порядка d^ ^^z, т = 1, 2, ... . Именно, чтобы в предположении
непрерывности у рассматриваемой функции z{x, у) всех ее
частных производных до порядка m + 1 включительно на
некотором открытом множестве получить ее дифференциал d^ ^ ^z,
надо взять дифференциал от дифференциала d^z порядка т:
Ъ(d^z) и положить 6х = dx, Ъу = dy. При этом для
дифференциалов порядка т = 1, 2, ... справедлива формула
d'^z= у Cl.-^^^—dx'^-^dy^, C8.9)
^79
ее обычно символически записывают с помогцью
«символической» степени {т} (см. п. 10.2) в следуюгцем виде, более
удобном для запоминания:
d^z = [^А dx + |- dy^"^f{x, у). C8.10)
Докажем формулу C8.9) по индукции. При т= \ она,
очевидно, верна. Пусть она справедлива при некотором т,
покажем ее справедливость при m + 1. Имеем
Положим 5х = dx Ji 5у = dy; тогда
dm + i2= у d^ ^"^11^-. ,dx^-^ + ^dy^ +
+ f CP^ Э^ + 1г dx'^-PdyP + K
Заменим во второй сумме индекс суммирования р usl k - 1
и заметим, что С^ + С^~ ^ = С^ + ^; окончательно получим
dm + i2= у с^ ^"^11^,^ dx'^-^ + ^dy^ +
+ у clr^-^—-^dx^-^^^dy^ =
'^^■^ 7 7)т+ \ ,-.77
k
^0 ^^^Эх^^ + ^-^Эг/
Замечание. Следует иметь в виду, что, как и в случае
функций одного переменного, для функций больгаего числа
переменных дифференциалы порядка выгае первого не
обладают свойством инвариантности формы записи относительно
выбора переменных. Например, для сложной функции z = /(х, у),
где X = х(и, v), у = у(и, v), второй дифференциал функции /,
записанный через дифференциалы переменных х и г/, уже не
будет, вообгце говоря, иметь вид C8.8), а, как правило,
выглядит сложнее. Чтобы в этом убедиться, вычислим в
рассматриваемом случае второй дифференциал функции z = /(х, у), где
X = х(и, и), у = у(и, и). В силу инвариантности формы первого
дифференциала, имеем
dz = ^dx + ^ dy.
Эх ду ^
Далее вычислим дифференциал 5(dz), считая, что 5и = du,
5v = dv. Использовав инвариантность формы первого диффе-
^80
ренциала относительно выбора переменных при вычислении
ах ) \ду
бГ^ЧбГ^имеем
5^ =^Sx + ^5r/,
V ах ) дх^ ауах
"'' ix + рЛу;
т
. ду J дхду ду^
заметив, что дифференциал 5(dx) является дифференциалом
функции и, значит, вообпа;е говоря, не нуль, получим
d^2 = 5(d2)
= бГ^ dx+^dy
bu = du \ ах ay
bv = dv
6u = du
bv = dv
^ , СЧИ-
bx = dx
by = dy
Эх2 дхду ^ Эг/2 ^ Эх ду ^
На практике и в этом случае обе операции: вычисление
дифференциалов и приравнивание дифференциалов Ъи = du, 5v =
= dv — выполняют одновременно, т. е. запись 5(d2)\
тается равноправной записи d{dz).
Все сказанное, в частности определение дифференциалов выс-
П1ИХ порядков, естественным образом переносится на функции
больп1его числа переменных. Отметим, что дифференциал т-то
порядка от функций п переменных у = у(х^, ... , х^) имеет вид
или в символической записи
^""У = (э! '^^i + - ^ 4 ^^y^Wi, ... , х„). C8.11)
Доказывается эта формула аналогично формуле C8.10).
§39
Формула Тейлора и ряд Тейлора
для функций многих переменных
39.1. Формула Тейлора
для функций многих переменных
Если функция многих переменных имеет достаточное число
непрерывных производных в окрестности некоторой точки, то
эту функцию в указанной окрестности можно (подобно тому,
как это было сделано для функций одного переменного)
представить в виде суммы некоторого многочлена и остатка,
который «мал» в определенном смысле.
ТЕОРЕМА 1. Пусть функция г = f(x, у) определена и
непрерывна вместе со всеми своими частными производными до
порядка т включительно (т > 1) в некоторой Ъ-окрестнос-
ти точки (Xq, i/q). Тогда для всех Ах и ISy, удовлетворяющих
условию р = л/Ах^ + Аг/^ < 6, существует такое 9 = 9(Ах, Аг/),
О < 9 < 1, что справедлива формула
А2 = /(хо + ^x, г/о + Ау) - /(хо, г/о) = Щ^^^ + Щ^Ау +
- l[^!^<g^Ax^ . 2^^^А.А, . ^!^ А,^] .
- + (^(^^Э^ + ""y^T'^'f^^o, Уо) + '-.-iCAx, Ay),
г/лг/, короче,
^ = Ж ^(^^^^ ^ ^^|У**^^^0' Уо) + ^^-i(A^. Ay), C9.1)
где
г^_ i(Ax, Ay) = ;^fAx|: + Ay^T'f(x^ + ЭАх, Уо + ЭАу). C9.2)
/nil Эх ду 1
Формула C9.1) называется формулой Тейлора (порядка
т - 1) для функции /.
Пусть X = Xq + Ах, у = у^ + Аг/. Многочлен
Рп(^^У)= t ^Г(^-^о)^ + (^-^о)|:Г'Лхо,г/о), я = 0,1, 2,...,
Эх ^ ду 1
называется многочленом Тейлора степени п функции / в точке
(Xq, i/q), разность /(х, у) - PJ,x, у) — остаточным членом гДх, у)
формулы Тейлора. Таким образом, формула Тейлора C9.1)
имеет вид
/(х, у) = Рт- i(^:, У) + г^_ i(x, у).
Запись г^ _ i(Ax, Аг/) в виде C9.2) называется остаточным
членом формулы Тейлора в форме Лагранжа.
При m = 1 в C9.1) требует разъяснения смысл первого члена
правой части, поскольку в этом случае верхний индекс
суммирования равен нулю. В этом случае, по определению,
полагается, что этот член равен нулю, т. е. что формула C9.1) имеет вид
Az = Гд(Ах, Аг/).
^82
в дальнейп1ем всегда, когда встретится выражение,
записанное с помогцью символа Е, у которого значение верхнего
индекса суммирования меныае значения нижнего индекса,
будем также считать, что это выражение равно нулю.
Доказательство. Пусть Ах и Аг/ зафиксированы так, что
р = л/Ах^ + Аг/2 < 6; тогда все точки вида (Xq + f Ах, у^ + tAy), где
О < f < 1, лежат на отрезке, соединяюпа;ем точки (Xq, у^) и
(Xq + Ах, г/о + Аг/), и поэтому все они принадлежат 6-окрестнос-
ти точки (Xq, г/о). Вследствие этого имеет смысл композиция
функций 2 = /(х, г/) и X = Xq + ^Ах, у = у^ + tAy, О < f < 1, т. е.
сложная функция
F(t) = fixQ + tAx, г/о + tAy), О < f < 1. C9.3)
Очевидно, что
Az = fix^ + Ах, г/о + Ay) - fix^, у^) = F(l) - F(O). C9.4)
Поскольку функция / имеет в 6-окрестности точки (Хо, г/о)
т непрерывных частных производных, согласно теореме о
производных сложной функции (см. п. 37.3), функция F также
имеет на отрезке [О, 1] т непрерывных производных и поэтому
для нее справедлива формула Тейлора порядка т - 1 с
остаточным членом в форме Лагранжа
Fit) - Fjo)=F\o)t+^t^+...+^"":у ^'"-^+go^f'",
0<e<l, C9.5)
и в рассматриваемой окрестности точки (Хо, г/о) функцию C9.3)
можно т раз продифференцировать по правилу
дифференцирования сложной функции (см. замечание 2 в п. 37.4), причем
значения получаюпа;ихся смеп1анных частных производных
не зависят от порядка дифференцирования (см. п. 38.1).
Выразив производные F^^\t) через производные функции
/(х, у) и положив в формуле C9.5) t = \ (см. C9.4)), получим
требуемую формулу Тейлора для функции /(х, г/).
Действительно, из C9.3) следует, что
jr^(^)_df dx_^dfdy_^fi^o + tAx, I/O + tAy)^^_^df{xQ + tAx, y^ + tAy)
dxdt dy dt dx dy
Отсюда для F'\t), опустив для краткости обозначения
аргументов, получим
'283
Вообпа;е по индукции легко установить, что
F^t) = Гах|- + Аг/|- Y^V(^:o + tAx, у^ + fAx),
й = 1, 2, ... , т. C9.6)
Положив в формулах C9.6) t = О при й = 1, 2, ... , m - 1, будем
иметь
^ ^ Эх Эг/ ^
дх^ дхду ду^
И вообпа;е
FW@) = [Ax|^ + Ay|y*V(Xo,r/o)' ^ = 1,2, ... ,m-l. C9.7)
При k = т, заменив t на 9^, получим
F^et) = (Ах^ + Аг/|- Y''V(^:o + 6^Ах, у^ + QtAy). C9.8)
Подставим теперь C9.7) и C9.8) в C9.5) и положим t = 1;
тогда, в силу соотногаения C9.4), получим
+ —\Ах^ + Аг/|- /(Xq + ЭАх, у^ + ЭАг/), О < 9 < 1. П
СЛЕДСТВИЕ. В предположениях теоремы 1 справедлива
формула
А2 = ^^ 1(Дх1 + Ду| y*V(Xo, г/о) + ^^(А^. Ау), C9.9)
причем остаточный член г^(Ах, Аг/) может быть записан как
в виде
т
rJAx,Ay)= У 8^(Ах, Аг/)Ах^Аг/"^-^, C9.10)
^ = 0
где
lim 8у^(Ах, Аг/) = 0, й = О, 1, ... , т, р = л/Ах^ + Аг/^,
так и в виде
rJAx, Ay) = 8(Ах, Аг/)р^, C9.11)
^84
где lim 8(Ах, Аг/) = О, т, е.
rJAx, Аг/) = о(р"^), р ^ 0. C9.12)
Представление остаточного члена формулы Тейлора в
форме C9.12) называется его записью в форме Пеано.
Доказательство. Положим
8,(Ах,Аг/)- Эх^Э^--^ Эх^Э^-^- ^^^'^^^
В силу непрерывности всех частных производных порядка т,
имеем lim 8у1(Ах, Аг/) = 0.
Преобразуем остаток г^_ ^(Ах, Аг/) (см. C9.2)), использовав
выражение C9.13), следуюгцим образом:
= _L у eg, , ,7^ТАх^Аг/^-^ + — У С^8;(Ах, Ау)Ах^Ау^-^ =
Э , л Э V'^>
fe = 0
= ^{^x± + Ay| ] " /(^0' Уо) + Д £ft(A^' Дг/)Дх'^Ду'» " ^ C9.14)
где 8^(Ax, Ay) = ^8^(Ax, Аг/), поэтому
lim 8^(Ax, Ay) = 0. C9.15)
Подставляя C9.14) в C9.1), получим формулу Тейлора C9.9)
с остаточным членом в виде C9.10).
Покажем, что остаточный член C9.10) можно записать в
виде C9.11). Для этого положим
г(Ах, Аг/) = Д 8,(Ах, Ау){^ ]*(^ J'". C9.16)
Тогда
т
г^(Ах, Ау)= Y, ^k(Ax, Ау)Ах^Ау'^~^ =
k = Q
= р'"Д 8,(Ах, Ayf[^ ]\^ J'" = E(Ax, Ar/)p'»,
И так как
Ах
< 1и
< 1, то из C9.15) следует, что
lim 8(Ах, Аг/) = 0. П
285
Используя понятие дифференциалов высп1их порядков,
формуле Тейлора для функций двух переменных можно
придать более компактную форму, внеп1не идентичную
формуле Тейлора для функций одной переменной, записанной
также с помопа;ью дифференциалов. В самом деле, так как
(см. п. 38.2)
#/(х, у) = [Ах^ + Аг/| У V(x, у), й = О, 1, 2, ... , т,
то, полагая для краткости Mq = (Xq, z/q) и М = (Xq + Ах, у^ + Аг/),
формулу C9.9) можно записать в виде
Д2= £ ldV(Mo) + г^М). C9.17)
k-1
kl
Эта форма записи формулы Тейлора наиболее проста и
поэтому удобна для запоминания.
Сделаем несколько замечаний к доказательствам
теоремы 1 и ее следствия. Прежде всего в условиях этой
теоремы было потребовано, чтобы функция / имела непрерывные
производные до порядка т включительно в некоторой 6-ок-
рестности точки (Xq, i/q). Можно было бы потребовать
непрерывность в указанной окрестности только производных
порядка т, поскольку из их непрерывности вытекает и
непрерывность в этой окрестности всех младгаих производных
данной функции, т. е. производных порядков k = О, 1, ... , т - 1
(см. п. 37.2).
Подчеркнем, что непрерывность частных производных в
6-окрестности точки (Xq, у^) была использована, во-первых,
для того чтобы встречаюгциеся частные производные не
зависели от порядка дифференцирования (это было использовано
как при доказательстве формулы Тейлора C9.1), так и в
самой форме записи этой формулы), и, во-вторых, для того
чтобы функцию C9.3) можно было т раз дифференцировать по
правилу дифференцирования сложной функции. Обратим
внимание на то, что при т = 1 смегаанные производные
отсутствуют; для возможности же один раз дифференцировать
функцию C9.3) по правилу сложной функции, следовательно,
и для справедливости теоремы 1 достаточно более слабого
предположения о рассматриваемой функции /. Именно,
вместо предположения о непрерывной дифференцируемости в вы-
п1еуказанной 6-окрестности точки (Xq, г/д) функции /
достаточно ее дифференцируемости в этой окрестности (см.
определения 2 и4 вп. 37.2).
Непрерывность частных производных порядка т (в точке
(Xq, i/q)) использована также при доказательстве следствия
теоремы 1: она нужна для того, чтобы функции 8у^(Ах, Аг/),
определенные формулами C9.13), стремились к нулю при р ^ 0.
Подчеркнем епа;е, что при сделанных предположениях в
формуле C9.9) доказано, что г^(Ах, Аг/) = о(р"^) при р ^ О не в
смысле предела по любому фиксированному направлению, как
может показаться на первый взгляд из приведенного
доказательства, а в более сильном смысле — в смысле предела в точке
(Xq, г/о) (почему?).
Формулу C9.1) можно несколько обобгцить, если не
стремиться к тому, чтобы она была справедливой для всех точек
(Xq + Axq, z/q + Аг/) 6-окрестности точки (Xq, z/q), а
рассматривать эту формулу лип1ь при фиксированных Ах и Аг/. Именно,
если функция / определена и имеет непрерывные частные
производные порядка т на открытом множестве, содержа-
гцем отрезок с концами (Xq, г/д) и (Xq + Ах, г/д + Аг/), то формула
C9.1) также остается справедливой вместе с ее
доказательством. Из этого следует, что если функция / определена в
выпуклой области G (см. п. 14.2) и имеет в G непрерывные
частные производные порядка т, то для любых двух точек
(Xq, Уо)еС и (Xq + Ах, z/q + Ay)eG справедлива формула
Тейлора C9.1).
Все сказанное переносится и на случай функции любого
числа переменных.
ТЕОРЕМА 1'. Если функция п переменных у = /(х^, ... , xj
определена и непрерывна вместе со всеми своими частными
производными до порядка т, т> 1, включительно в
некоторой Ъ-окрестности точки х^^^ = (л:^^\ ... , х^^^), то
справедлива формула
Аг/ = /(х^О) + Axi, ... , х^О) + AxJ - f{xf\ ... , х^^)) =
'287
где
^.-i(Ax) = ^fAxiA + ...+Ax^_|_y'^V(xi«^ ... ,x@) + eAxJ,
0<е<1, Ax = (Axi, ... , AxJ, C9.19)
a также формула
^y = Д U^-rl; + - + ^-ni-f Ax@)) + rJAx), C9.20)
где г^(Ах) можно записать как в виде
rJAx)= ^ 8 ..^(Дх)ДхГ1...Ах^, C9.21)
lim 8^ ^ (Ах) = О, р = У Axf, так и в виде
rJAx) = 8(Ах)р"^, lim 8(Ах) = О, C9.22)
р^О
т. е.
rJAx) = oip^), р-0.
Наконец, через дифференциалы формулу C9.20) можно
записать в виде
т -1
ДУ= Е УЧ{х(^Ь + г^{^х). C9.23)
Раскроем теперь скобки в формулах C9.18) и C9.19), вос-
пользовавп1ись алгебраической формулой
Для того чтобы короче записать результат, введем новые
обозначения. Положим k = (k^, ..., kj), \k\ = k^ + ... + k^, kl = k-^l ... kj,
й = (k^, ... , k^) называется мультииндексом.
В этих обозначениях формула Тейлора C9.18) с
остаточным членом в виде C9.19) перепигается в виде
/(х)= у №!!)(х - х@))* + у /<^>(х'«> + е(х - х@)))(^ _ ^@)),^
1*1 <т «' \k\-m «'
25S
Здесь, как всегда, х = (х^, ... , xj, х^^^ = (л:^^\ ... , х^^^) и
х@) + е(х - х@)) = (х^^^ + e(xi - х^^^),..., х^о) + е(^^ _ ^^о)))^
В этом виде формула Тейлора для функций любого числа
переменных выглядит так же, как и для функций одной
переменной.
Иногда, особенно в случае функций многих переменных,
для производных используют обозначение
Эх^! ... Эх^"
где k = (ftj, ... , й^) — мультииндекс. Если пользоваться этой
символикой, то формула Тейлора принимает вид
f(x)= У i-D^/(x@))(x - х@))^ +
+ у 12)^д^@) + е(^_^@)))(^_ ^@))^^ о<е<1.
Покажем единственность представления функции / в виде
/(х + Ах) = Р JAx) + о(р"^), р^О, C9.24)
где
PJAx)= £ а^Ах^ C9.25)
1^1-0
— многочлен степени не выпхе тот п переменных Ах^, ... , Ах^.
ЛЕММА. Если многочлен
т
PJx)= ^ a,x^
1^1-0
X = (*^1? ••• ? *^д/' *^ ^ *^1 ••• -^п ' ^ v^l? ••• ? ^д/'
тождественно равен нулю:
PJx) = о C9.26)
6 некоторой окрестности нуля, то все его коэффициенты
равны нулю.
Доказательство. Из C9.26) следует, что для любого
k = {k^,... ,kj) имеет место равенство Р^^\0) = 0. Но если О < |й| < т,
~289
то Р^\0) = Ы а^. Из двух последних равенств следует, что
для всех k таких, что О < |й| < т, выполняются равенства
а^ = 0. П
ТЕОРЕМА 2. Если функция f задана в окрестности точки х,
то ее представление в виде C9.24) единственно.
Доказательство. Пусть число 6 > О выбрано таким
образом, что для всех Ах, |Ах| < 6, у функции / наряду с
представлением C9.24) имеет место представление
т
/(х + Ах)= £ Ь^Ах^ + о(р"^), р^О. C9.27)
1^1-0
Тогда, положив
с^ = Ь^ - а^, \k\ = О, 1, ... , т, C9.28)
и вычтя из равенства C9.27) равенство C9.24), получим,
что
т
£ с^Ах^ + о(р"^) = 0, р ^ 0. C9.29)
1^1-0
Зафиксируем произвольно Ах, |Ах| < 6; тогда если О < f < 1,
то |f Ах| < 6 и в C9.29) можно вместо Ах подставить tAx.
Выполнив эту подстановку, будем иметь
£ c^fl%x^ + o(pf) = 0,
1^1-о
/ f; (Мх.J = tp^o при t -^ о
(так как Ах фиксировано, то и р также фиксировано), т. е. при
О < f < 1 имеем
т
£ ^^ ^ с^Ах^ + о(^"^) = о, t^O.
В силу теоремы 2 п. 13.2, отсюда следует, что ^ с^Ах^ = О,
причем это верно для всех таких Ах, что |Ах| < 6, т. е. стоягций
в левой части этого равенства многочлен относительно
переменных Axj, ... , Ах^ равен нулю в некоторой окрестности
нуля. Согласно лемме, отсюда следует, что все с^ = 0. Поэтому, в
силу C9.28), для всех k таких, что О < |й| < т, выполняется
равенство а^ = Ь^. П
^90
39.2. Формула конечных приращений
для функций многих переменных
Частный случай формулы Тейлора C9.18), в котором т = 1,
обычно называется формулой конечных прираш;ений Лагран-
жа для функций многих переменных. В силу сделанных в пре-
дыдуш;ем пункте замечаний к теореме 1 о предположениях,
при которых справедливы формулы C9.1) и C9.18), из
теоремы V получаем следуюпа;ее утверждение.
ТЕОРЕМА 3. Если функция f(x^, ... , х^) дифференцируема в
каждой точке некоторой выпуклой области G ^ R^, то для
каждой пары точек (х^, ... , х^) и (х^ + Ах^, ... , х^ + Ах^) из G
существует такое 9, О < 9 < 1, что
f(x^ + Axj, ... , х^ + Ах J - /(Xj, ... , xj =
М дх. ^'
или, короче,
/(х + Ах)-/(х)= f Э/(х + еАх)д^^^ C9.30)
i = 1 ^"^i
где X = (Xj, ... , xj, х + Ах = (х^ + Ах^, ... , х^ + Ах J и
X + 9Ах = (Xj + 9Axj, ... , х^ + 9AxJ.
Формула C9.30), как указывалось, и называется формулой
конечных приращений Лагранжа.
Эта формула, так же, как и вообпа;е формула Тейлора,
находит многочисленные и разнообразные применения в
различных вопросах математического анализа.
Обратим внимание на то, что теорема 3 не является частным
случаем теоремы 1, поскольку в ней требуется не непрерывная
дифференцируемость рассматриваемой функции в каждой
точке множества G, а лигаь ее дифференцируемость. Однако
доказательство теоремы 3 фактически содержится в доказательстве
теоремы 1. Действительно, как это отмечалось в замечаниях
к доказательству теоремы 1 и ее следствию (см. п. 39.1), при
т = \ приведенное выгае доказательство теоремы 1 сохраняет
силу и при предположениях теоремы 3, т. е. при
предположении лип1ь дифференцируемости (а не непрерывной дифферен-
цируемости) функции /.
в качестве примера применения формулы C9.30) докажем
следуюпа;ее утверждение.
ТЕОРЕМА 4. Если функция дифференцируема в каждой
точке выпуклой области G и имеет в G ограниченные частные
производные, то она равномерно непрерывна в этой области.
Доказательство. Если
|Э/(х)|
Эх,-
< с, / = 1, 2, ... , п, xeG
(с — постоянная), то для любых двух точек х' = (х{, ... , х^) и
х'' = (x'l, ... , х'^) из C9.30) следует, что
|/(х")-/(хО|< у \Ш1\\х;-х'^<спр(х\х'')
i = 1 I 3xj I
(здесь ^ — некоторая точка отрезка с концами в точках х' и х'').
Поэтому, если задано 8 > О, достаточно взять 6 = —, чтобы для
СП
любых точек х'е G и х''е G таких, что р(х\ х'') < 6, выполнялось
неравенство
|/(х") - f(x')\ < г, C9.31)
а это и означает равномерную непрерывность функции / в
области G. П
39.3. Оценка остаточного члена формулы Тейлора
во всей области определения функции
Остаточный член в формуле Тейлора, очевидно, зависит не
только от прирапа;ений аргументов, но и от самой точки, в
окрестности которой рассматривается разложение функции и
которую мы в п. 39.1 считали фиксированной. Теперь нас
будут интересовать поведение и оценка остаточного члена в
зависимости от изменения указанной точки. Чтобы
подчеркнуть эту зависимость, мы в этом пункте будем остаточный
член порядка т обозначать г^(х, Ах), где х = (х^, ... , х^) —
точка, в окрестности которой раскладывается данная
функция по формуле Тейлора. Как и раныае. Ах = (Ах^, ... , Ах^).
В формулах C9.21) и C9.22) будем вместо 8^ ^ (Ах) и
8(Ах) соответственно писать 8^ ^ (х. Ах) и 8(х, Ах). В даль-
нейгаем нам потребуется оценка остаточного члена формулы
Тейлора в форме Пеано сразу для всей области сугцествования
разложения по указанной формуле.
192
Введем сначала понятие непрерывности
частных производных в замыкании
открытого множества. Это требует специального
определения, так как в граничной точке
открытого множества G даже в случае, когда
функция определена на замыкании G
множества G, понятие частной производной, во-
обгце говоря, не определено (см., например, р «о
точку М границы области G на рис. 29).
Определение 1. Фг/^тсг^г/^ /, определенная на открытом
множестве G ^ R^, называется непрерывно продолжаемой на
его замыкание G, если существует такая непрерывная на
G функция F, что F = f на G.
Функция F называется непрерывным продолжением
функции f (на G) и для простоты будет также
обозначаться символом /.
Очевидно, в силу единственности предела функции, если у
функции, определенной на G, супа;ествует непрерывное
продолжение на G, то оно единственно.
Определение 2. Функция f называется непрерывно
дифференцируемой (соответственно т раз непрерывно
дифференцируемой) на замыкании G области G (т. е. на замкнутой
области), если функция f определена на G и все ее частные
производные первого порядка (соответственно частные
производные до порядка т включительно) непрерывно
продолжаемы с G на G,
УПРАЖНЕНИЯ. 1. Доказать, что если функция / определена на
открытом множестве G ^ R"^, имеет на нем непрерывно продолжаемую на его
замыкание G производную т-^ и в некоторой точке границы множества G су-
ществует (односторонняя) частная производная т-^, то она совпадает с не-
dXi
прерывным продолжением в эту точку частной производной г-^.
Указание. Воспользоваться следствием 3 из теоремы 3 в п. 11.2.
2. Доказать, что, для того чтобы непрерывная функция, определенная на
ограниченном открытом множестве G ^ R"-, была непрерывно продолжаемой
на его замыкание, необходимо и достаточно, чтобы она была равномерно
непрерывной на G. Показать, что в случае неограниченного открытого
множества условие равномерной непрерывности продолжаемой функции, являясь
достаточным для непрерывного продолжения, не является необходимым.
3. Построить пример непрерывной и ограниченной в области функции,
которую нельзя непрерывно продолжить на замыкание этой области.
^93
Вернемся теперь к формуле Тейлора. Пусть функция /
непрерывно дифференцируема т раз на замыкании G открытого
ограниченного множества G. Тогда, согласно результатам
п. 39.1, в каждой точке x&G для некоторой ее окрестности
имеет место разложение C9.20) функции / по формуле
Тейлора, причем стремление к нулю 8^ ^ (х. Ах) в формуле
C9.21) и 8(х, Ах) в формуле C9.22) при р -^ О равномерно на
множестве G (см. определение в п. 37.2), т. е. для любого 8 > О
супа;ествует такое 6 = 6(8) > О, что если
р = |Ах| = /£ Axf < 6, C9.32)
то |8^ ^ (х, Ах)| < 8 и |8(х, Ах)| < 8 ДЛЯ всех точек xg G.
Это в данном случае непосредственно следует из метода
получения функций 8^ ^ (х. Ах) и 8(х, Ах). Действительно, в
силу ограниченности и замкнутости замыкания G открытого
множества G, непрерывные продолжения на G частных
производных порядка т данной функции равномерно непрерывны
на G, поэтому (см. формулу C9.13) для случая п = 2; в обпа;ем
случае справедлива аналогичная формула), если выполнено
условие C9.32), то
К,... rni^^ М < со [5, ^^./'^_^^^.„> G], C9.33)
т = т^ + ... + т^.
Здесь правая часть (модуль непрерывности соответствуюпа;ей
производной) не зависит от точки множества G и стремится
к нулю при 6^0. Поэтому из C9.33) следует равномерное
стремление 8^ ^ к нулю на G при Ах -^ 0.
Теперь можно оценить бесконечно малую 8(Ах, Аг/) в
формуле C9.22). Для произвольного натурального п ее можно,
аналогично случаю п = 2 (см. C9.16)), представить в виде
/ А Ч ^.-^ /А ч/^AXi ^'^l f^.Xr
8(х, Ах) = у 8^^,,, ^ (х. Ах) —^'
р
Отсюда имеем
|8(х, Ах)| < ^ \г ... ^ (X, Ах)|. C9.34)
В правой части неравенства C9.34) стоит некоторое
фиксированное число слагаемых; обозначим его через N. В силу
уже доказанного равномерного в G стремления к нулю функ-
'294
ции 8^ ^ (х, Ах), для любого заданного 8 > О сугцествует
такое 6 = 6(8) > О, что если выполнено условие |Ах| < 6, то
Отсюда и из неравенства C9.34) следует, что |8(х, Ах)| < 8.
Отметим егце одну оценку в целом остаточного члена
формулы Тейлора, получаюгцуюся из записи его в форме Лагран-
жа C9.19).
Если функция / определена на открытом множестве G и
имеет на G ограниченные частные производные порядка т,
т. е. супа;ествует такая постоянная М > О, что
I ^"^^(•^) к с, mi + ... + m^ = m, x&G, C9.35)
|эх5^1... Эх'^"!
то при выполнении условия |Ах| < 6 для всех x^G справедливо
неравенство
Это сразу следует из формулы C9.19), если абсолютные
величины каждого слагаемого ее правой части оценить с помопа;ью
неравенства C9.35) и очевидного неравенства |Ах.| < 6.
39.4. Равномерная сходимость
по параметру семейства функций
В предыдупа;ем пункте мы встретились с понятием
равномерной сходимости на данном множестве семейства функций, за-
висяпа;их от некоторого параметра, когда этот параметр
стремится к определенным значениям. Такими функциями в на-
П1ем случае являлись 8^ ^ (х. Ах) и 8(х, Ах), где роль
параметра играло Ах. В простейгаем виде этот случай
встречался егце раныае в п. 37.2.
Сформулируем определение равномерной сходимости
семейства функций в обгцем случае.
Определение 3. Пусть X ^ й^, Y ^ R"^, у^^^ — точка
прикосновения множества Y, конечная или бесконечно удаленная
оо, +00, -оо (последние две бесконечности имеет смысл
рассматривать только при т = 1). Пусть, далее, функция ф(х)
определена для всех хеХ, а /(х, у) для всех хеХ и yeY,
^95
функцию f(x, у) называют равномерно стремящейся на
множестве X к функции ф(х) при у -^ у^^^ и пишут
/(х, г/)^ф(х), у^у^^К
X
если для любого 8 > О существует такая окрестность U(y^^^)
точки у^^\ что для всех хеХ и всех yeY П U(y^^^)
выполняется неравенство
|/(х, у) - ф(х)| < 8. C9.36)
Переменная у часто называется в этом случае
параметром, а функция f(x, у), yeY, — «семейством функций от х»
(б том смысле, что эта функция при различных
фиксированных значениях параметра уе Y задает функции переменной х).
Подобно случаю равномерной сходимости
последовательности функций (см. п. 32.1) условие равномерной сходимости
функций по параметру можно сформулировать, используя
понятие предела функции, следуюпа;им образом.
Функция f(x, у) равномерно стремится на множестве X
к функции ф(х) при у -^ у^^^ тогда и только тогда, когда
lim sup \f(x, у) - ф(х)| = 0. C9.37)
Таким образом, условие f(x, у) ^ ф(х), у -^ у^^\ равносильно
X
стремлению к нулю при у -^ у^^^ функции
F(y)^= sup |/(х, г/)-ф(х)|.
хе X
Доказательство этого утверждения совсем не сложно и
аналогично случаю равномерной сходимости последовательности
функций. Его проведение предоставляется читателю.
Справедлив в рассматриваемом случае и аналог критерия
Коп1и равномерной сходимости последовательностей.
ТЕОРЕМА 5 (критерий Кош]л). Для того чтобы функция f(x, у)
при у -^ у^^^ равномерно стремилась на множестве X к
некоторой функции, необходимо и достаточно, чтобы для
любого г > О нашлась такая окрестность U(y^^^) точки у^^\ что
для любых у'е U(y^^^) ПУ и у''е U(y^^^) п¥ и любого хеХ
выполнялось неравенство
\f(x, у'') - fix, у')\ < 8. C9.38)
Действительно, необходимость условия C9.38), как всегда
в подобных ситуациях, легко следует из условия C9.36). Для
доказательства же достаточности следует показать, что из ус-
ловия C9.38) вытекает, что для любого фиксированного хеХ
сугцествует lim /(х, у) и что стремление функции /(х, у) к
этому пределу при у -^ у^^^ происходит равномерно.
Все это также рекомендуется проделать читателю
самостоятельно.
УПРАЖНЕНИЕ 4. Доказать: для того чтобы функция f(x, у), хеХ, уеХ
равномерно на множестве X стремилась при у -^ у^^^ к функции ф(х), хеХ,
необходимо и достаточно, чтобы для любой последовательности y^^^eY,
п = 1, 2, ... , стремящейся к у^^\ последовательность /(х, г/^^^), п= 1, 2, ... ,
равномерно на множестве X сходилась к функции ф(х).
Примеры. 1. Рассмотрим семейство функций /(х, у) =
= е~^У, где 0<х<1,0<г/< +оо. Очевидно,
т .. . |0, еслих>0,
lim их, г/) = i 1 п
г^^+оо'"^ ' ^^ [1,еслих = 0
(переменная г/, если использовать указанную выгае
терминологию, является здесь параметром). Обозначим предельную
функцию через ф(х):
[ О, если X > О,
ф(^) = {1,еслих-0. C9-39)
Докажем, что стремление функции /(х, у) к ф(х) при у -^ +оо
происходит неравномерно. Для этого достаточно показать, что
супа;ествует такое 8q > О, что, какую бы окрестность С/(+оо) ни
взять, найдутся такие хе [О, 1] и уе U( +оо), что будет
выполнено неравенство \е~^У - ф(х)| > 8q. Возьмем 8q такое, что О < 8q < 1,
и произвольную окрестность С/(+оо). Тогда, какое бы уе С/(+оо)
ни взять, для него lim е~^У = 1, поэтому найдется такое
xg@, 1], что
{е-^'У - ф(х)| = {е-^'У - 0| > 8^.
Таким образом, в данном случае условия равномерной
сходимости не выполняются.
Однако при любом а, О < а < 1, семейство функций /(х, у) =
= е~^У при г/ ^ +00 равномерно стремится к нулю на отрезке [а, 1].
Проверим в этом случае выполнение условий равномерной
сходимости. Для любого 8 > О супа;ествует число Лг ^ О такое,
что е ^^ < 8 [достаточно взять любое Г| > LiLJ ] поэтому для
всех г/ > rig и всех хе [а, 1] будем иметь
\^-ху -0\ = е-^'У < е'""^^ < 8.
^97
Конечно, исследование равномерной сходимости
рассматриваемого семейства функций можно выполнить и применив
критерий C9.37). Действительно, использовав формулу C9.39),
получим
sup \е~^У - ф(х)| > sup е~^У = 1,
о < х< 1 0<х< 1
поэтому условие C9.31) заведомо не выполняется. Если же
О <а< 1, то
lim sup \е~^У - Ф(х)\ = lim sup е~^У = lim е~^У = 0.
Таким образом,
е-^у -tt ф(х), е-^'У ^0, 0<а<1, г/^+оо.
[0,1] [а, 1]
2. В том случае, когда Y является множеством
натуральных чисел Y = {1, 2, 3, ...}, а у^^^ = +оо, приведенное
определение равномерной сходимости по параметру преврагцается в
определение равномерной сходимости последовательности
функций /^(х) = f(x, п), п = 1, 2, ..., на множестве X.
3. Пусть функция /(х, у) непрерывна на прямоугольнике
Q = {(х, у): -оо < а< X < b < +оо, -оо < с < у < d< +00} и пусть
у^е[с,A].
Обозначим через соF, /) модуль непрерывности функции / в
прямоугольнике Q; тогда
|/(х, у) - fix, i/o)| < ш(|г/ - i/ol; /), (х, i/)e Q. C9.40)
Правая часть этого неравенства не зависит от х и, в силу
равномерной непрерывности функции / на прямоугольнике Q,
lim соF, /) = 0. Поэтому из неравенства C9.40) следует, что
при г/ ^ г/о функция /(х, у) равномерно на отрезке [а, Ь]
стремится к функции /(х, i/q).
УПРАЖНЕНИЕ 5. Доказать, что если семейство функций /(х, г/), хеХ ^
^ R^, yeYeR^ таково, что функции f(x, у) при любом фиксированном уеУ
непрерывны по х на множестве X и равномерно на этом множестве
стремятся к ф(х) при у -^ у^^\ то ф(х) также непрерывна на множестве X.
39.5. Замечания о рядах Тейлора
для функций многих переменных
Если функция /(х) определена и бесконечно дифференцируема
в некоторой 6-окрестности точки х^^^ = {х^^\ ... , х^^^)ей^, то для
этой функции формула Тейлора C9.20) будет, очевидно, спра-
~298
on
ведливой при любом натуральном я = 1, 2, ... и ^ Ах^^ < 6^. Ес-
i = 1
ЛИ при этом ряд
сходится к Ау = f(x) - f(x^^^) (см. п. 38.2), то получим формулу
Д, = т - /(х@)) = ^£^ ±[Ах,^^ + ... + Дх„5^- ) /(х@)),
где X = (Xj, ... , х^) и X. - х^^^^ = Ах., /=1,2, ... , п. Отсюда,
перенося /(х^^^) в правую часть, получим разложение функции в
степенной ряд, называемый р^Eож Тейлора функции /:
или, что то же,
оо 1
fix)= ^ i-D^/(x@))(x - х@))^
где k = (ftj, ... , й^) — мультииндекс.
УПРАЖНЕНИЕ 6. Разложить в ряд Тейлора функцию /(х, у) = е^^У.
§40
Экстремумы функций многих переменных
40.1. Необходимые условия экстремума
Изучаемые в настояпа;ем и некоторых следуюпа;их параграфах
вопросы носят аналитический характер, и их доказательства
не усложняются при увеличении числа переменных. Поэтому
мы проведем их рассмотрение сразу в обпа;ем я-мерном случае,
указывая при необходимости их специфические особенности
для случаев я = 2 и я = 3.
Определение 1. ili/cmb функция f(x) определена на
множестве X ^ R^, Точка x^^^gX называется точкой строгого
максимума, соответственно строгого минимума, если
существует такая окрестность U{x^^^) точки х^^\ что для всех
XG С/(х^^^) П X, X ^ х^^\ выполняется неравенство f(x) < f(x^^^),
соответственно неравенство f(x) > f(x^^^),
^99
Итак, точка строгого максимума (соответственно строгого
минимума) характеризуется тем, что А/ = f(x) - f(x^^^) < О
(соответственно А/ > 0) при всех хе U(x^^^) П X, х^ х^^^ (рис. 30).
Если же для точки х^^^ существует такая окрестность
U(x^^^), что при всех хе U(x^^^) П X выполняется условие f(x) <
< f(x^^^) (соответственно f(x) > fix^^^), то х^^^ называется
просто точкой максимума {соответственно минимума).
Определение 2. Точки {строгого) максимума и минимума
функции называются точками (строгого) экстремума,
ТЕОРЕМА 1. Пусть функция f(x), х = (х., )
определена в некоторой окрестности точки х^^^; если она является
точкой экстремума функции f(x) и если в ней существует
какая-то из производных ^ (у может принимать одно из
значении
и 1, 2, ... , n)j то она равна нулю: -!-^—^ = 0.
СЛЕДСТВИЕ. Если функция f(x) дифференцируема в точке
экстремума х^^\ то ее дифференциал равен нулю в этой
точке: df(x^^^) = 0.
Доказательство (теоремы и следствия). Пусть для
определенности j = 1. Если х^^^ = (х^^\ ... , x^j^^) является точкой
экстремума для функции f(x) = f(x^, ... , х^), то х^^^ является
точкой экстремума для функции f(x^, ^2^\ ••• ? ^д^^) одной
переменной Xj (рис. 31), причем так как точка х^^^ была
внутренней для области определения функции /(х^, ... , х^), то
х@)=(х@),х@))
Рис. 30
Рис. 31
300
точка х^^^ является внутренней для области определения
функции /(Xj, х^^\ ... , х^^^). Поэтому если в этой точке су-
па;ествует производная ^-^, то по теореме Ферма (см. п. 11.1)
она равна нулю, т. е.
Э/(х@))
dxi
df{Xi, X
@)
2 '
х@))
dx-i
0.
Аналогично обстоит дело в случае любой переменной х
и = 2,...,п).
Если функция f(x) дифференцируема в точке экстремума х^^\
1,2,
я, и.
то в этой точке сугцествуют все производные ^yi-
согласно доказанному, все они равны нулю, поэтому и
i = 1 ^"^i
Примеры. 1. Найдем точки экстремума функции z = х^ +
+ г/^. Точки экстремума, в силу доказанного, находятся среди
тех, для которых dz = 0. Так как dz = 2xdx + 2у dy, то условие
dz = О выполняется в единственной точке (О, 0). В этой точке
2 = О, во всех же других точках 2 = х^ + г/^ > 0. Поэтому точка
(О, 0) является точкой строгого минимума для функции z = х'^ +
+ г/2 (рис. 32).
2. Исследуем точки экстремума функции z = х'^ - у^'.
Поступая аналогично предыдупа;ему случаю, находим, что условие
dz = О снова выполняется в точке (О, 0) и в этой точке z = 0.
Однако здесь при г/ = О и любых х ^ О имеем 2 > О, а при х = О и
любом г/ ^ О имеем z <0. Поэтому точка (О, 0) не является
точкой экстремума, и, значит, функция z = х'^ — у^' вообпа;е не
имеет экстремальных точек (рис. 33).
Рис. 32
Рис. 33
301
40.2. Достаточные условия строгого экстремума
Напомним несколько определений из курса алгебры.
Определение3. Квадратичная форма А{х) = А{х^, ... , х^) =
п
= Y, ^ij^i^p ^ji ^ ^ip ^у J ^ 1' 2, ... , Пу называется положи-
i,i = 1
тельно {соответственно отрицательно) определенной, если
А(х) > О (соответственно А(х) < 0) для любой точки xeR^,
х^О.
Квадратичная форма, являющаяся положительно или
отрицательно определенной, называется также просто
определенной (или знакоопределенной) квадратичной формой.
Определение 4. Квадратичная форма, принимающая как
положительные, так и отрицательные значения, называется
неопределенной.
ЛЕММА 1. Пусть S — единичная сфера в R^:
S = {x: xf+ ... + х2 = 1},
и пусть А(х) — определенная квадратичная форма; тогда
inf \А(х)\ = ц > 0.
ХЕ S
Доказательство. Функция А(х) является многочленом
второй степени по переменным х-^, ... , х^, поэтому А(х),
следовательно, и \А(х)\ непрерывны во всем пространстве й^.
Отсюда вытекает, что функция \А(х)\ непрерывна на компакте S.
Согласно теореме Вейергатрасса, функция \А(х)\ достигает на S
своей нижней грани, т. е. сугцествует такая точка x^^^eS, что
[1^= inf \А(х)\ = \А(х^%
ХЕ S
По определению знакоопределенной квадратичной формы
\А(х)\ > О для всех точек xeS, следовательно, в частности, \х =
= |А(х@))| > 0. П
Определение 5. Пусть функция f дифференцируема в точке
xi^)eR^. Если df(x^^^) = О, то х^^^ называется стационарной
точкой функции /.
Очевидно, что точка х^^\ в которой функция /
дифференцируема, является стационарной в том и только в том случае, если
Щ^ = 0, 1=1,2, ..., п. D0.1)
^02
Согласно следствию из теоремы 1, точка экстремума, в
которой функция / дифференцируема, является стационарной;
обратное, конечно, вообш;е говоря, неверно: не всякая
стационарная точка, в которой функция дифференцируема,
является точкой экстремума (см. пример 2 в конце п. 40.1).
ТЕОРЕМА 2 (достаточные условия строгого экстремума).
Пусть функция f определена и имеет непрерывные
производные второго порядка в некоторой окрестности точки х^^\
Пусть х^^^ является стационарной точкой функции f; тогда
если квадратичная форма
Aidx^, ... , dxj = f ^!/(^ dx. dxj, D0.2)
ij^ 1 OX^OXj
m, e, второй дифференциал функции f в точке х^^\
положительно определенна {отрицательно определенна), то х^^^
является точкой строгого минимума {соответственно
строгого максимума); если же квадратичная форма D0.2)
неопределенна, то в точке х^^^ нет экстремума.
Доказательство. Пусть U{x^^\ Ъ^) — бд-окрестность
стационарной для функции / точки х^^\ в которой функция /
имеет непрерывные вторые производные. Пусть точка
х@) + dx = (х^^^ + dxi, ... , х^о) + dxJ
принадлежит этой окрестности.
По формуле Тейлора (см. C9.23)), учитывая условия
стационарности D0.1), получим
А/=/(х@) + dx) -/(х@)) = 1 у ^^U^dx.dx. + E(dx)p^,
2 . je 1 dXidXj J
где dx = (dx-^, ... , dx^), p^ = dxf + ... + dx^, и
lim 8 (dx) = 0, D0.3)
или
2L;j%i dXfdxj p p ' 'J
= ^^[A{^, ... , ^]+2e(dx)], p ^ 0. D0.4)
Точка f—-, ... , —^ 1 лежит на единичной сфере S (т. е. на сфе-
I р р J
ре с центром в начале координат и радиусом, равным 1), так
какГ^1Ч... + &Г-1.
303
Пусть квадратичная форма D0.2) знакоопределенна. Тогда,
согласно лемме, inf |А| = ц > 0. Выберем 6, О < 6 < 6q, так, чтобы
2|8((ix)| < ji при р < 6. Тогда при р < 6, т. е. при х^^^ + dxe Щх^^\ 6)
и dx ^ О, все выражение в квадратных скобках в правой части
формулы D0.4) будет иметь тот же знак, что и первое слагаемое
Sign А/= Sign А —i, ... , —^ .
I р р J
Поэтому если квадратичная форма D0.2) является
положительно определенной, то А/ > О, а если отрицательно опреде-
о
ленной, то А/ < О при х^^^ + dxeU (х^^\ 6). Значит, в первом
случае х^^^ является точкой строгого минимума, а во втором —
точкой строгого максимума.
Пусть теперь квадратичная форма D0.2) является
неопределенной; это означает, что существуют две такие точки dx' =
= (dx[, ... , dx'^) и dx''= (dx'(, ... , dx'^), что A (dx^, ... , dx^) > 0,
SiA(dx'{, ... , dx'j^) < 0. Мы не можем на основании этого сразу
сказать, что приращение функции А/ меняет знак в любой
окрестности точки х^^\ так как точки х^^^ + dx' = (х^^^ + dx[, ...
... х^^^ + dx^) и х^^^ + dx'' = (х^^^ + dxp ... , х^^^ + dx'^) могут,
вообще говоря, даже и не принадлежать области определения
функции /. Однако нужный нам результат будет следовать из
того, что квадратичная форма A(dx) сохраняет один и тот же
знак или равенство нулю на каждой прямой, проходящей
через точку х^^\ из которой удалена сама эта точка, а значение
А — , dx ^ О, вообще не зависит от выбора точки на этой прямой.
Рассмотрим точку dx = (dx^, ... , dx^), и пусть Р = / ^ dxl .
Проведем полупрямую, начинающуюся в точке х^^^ и
проходящую через точку х^^^ + dx\ Для
любой точки X = (Xj, ... , х^) этой
полупрямой положим dx- = Х- - х|^\
Рис. 34
cos а..
£ dxf. Тогда
i = 1
1,2, ...,/г, D0.5)
304
где cos а. суть направляюпа;ие косинусы рассматриваемой
полупрямой. Поэтому точка
—-, ... , —^ 1 = (cos а., ... , cos а„), D0.6)
р р J '^'^
лежапа;ая, очевидно, на единичной сфере"^ S с центром х^^\
будет одной и той же для всех точек х этой полупрямой, т. е.
точка D0.6) не зависит от расстояния р между х и х^^^ и
fdxi dx^\ _ fdx{ dx'^
I p p J I p p
Следовательно, и значение квадратичной формы D0.2) в
точке D0.6), т. е. А\—^, ... , —^ 1 не зависит от р. Отсюда для
I р р J
любой точки D0.6) имеем
rdx^ dx„\ .fdx\ dx' \ 1
p p J I p p J p
Af^,..., ^"bAf^,..., ^1 = :^A{dx[,..., dx;) > 0.
Пусть A{—i, ... , —- = ji" > 0. Выберем Po > 0 так, чтобы
II
при p < Ро имело место неравенство 2|8(йх)| < ц', что возможно в
силу D0.3). Тогда для любой точки х^^^ + dx, лежагцей на
полупрямой D0.5) и такой, что О < р = / ^ dxf < pg, в формуле
D0.4) выражение в квадратных скобках будет иметь знак
первого члена, и поэтому А/ > 0. Итак, в любой окрестности точки
х^^) имеются точки, для которых А/ > 0.
Аналогично, исходя из отрицательного значения
квадратичной формы D0.2) в точке (dx/')? доказывается, что в любой
окрестности точки х^^^ сугцествуют точки, для которых А/ < 0.
А это и означает, что в рассматриваемом случае х^^^ не
является точкой экстремума. П
При практическом применении этой теоремы возникает
вопрос: как установить, будет ли квадратичная форма D0.2)
положительно или отрицательно определенной. Для этой
цели может служить, например, так называемый критерий
Сильвестр а"^"^ положительной определенности квадратич-
* Напомним, что для направляющих косинусов справедливо
равенство cos^ а^ + ... + cos^ а^ = 1.
**Д. Д. Сильвестр A814—1897) — английский математик.
^05
ной формы, доказываемый в курсах алгебры. Он состоит в
следу югцем.
Для того чтобы квадратичная форма
Л\Х) Л\Х-^у ••• у ^л) 2^ ^ij'^V^p
D0.7)
у которой а.J = а-, i, у = 1, 2, ... , я, была положительно
определенной, необходимо и достаточно, чтобы
aii>0.
^11 ^12
^21 ^22
>о.
^11 ^12^13
^21 ^22^23
^31 ^32^33
>о.
^11 ^12-
^21 ^22*
.а
In
.а
2п
^п1 ^п2
>0.
Замечая, что квадратичная форма А(х) отрицательно
определена тогда и только тогда, когда квадратичная форма
п
-А(х) = Y, (~^ii)^i^i положительно определена, получаем,
пользуясь известными свойствами определителя, следуюпа;ий
критерий отрицательной определенности.
Для того чтобы квадратичная форма D0.7) была
отрицательно определенной, необходимо и достаточно, чтобы
а.. <0,
^11 ^12
^21 ^22
>0,
^11 ^12^13
^21 ^22^23
^31 ^32^33
<0,...,(-1)-
П1
ai2...a
In
^2\ "^22
аг,о»»»а
2п
а„о...а^
Ы1 ^п2
>0.
Сформулируем теперь теорему 2 для случая двух
переменных, выразив условия, накладываемые на квадратичную
форму D0.2), в явном виде через вторые частные производные.
ТЕОРЕМА 3. Пусть функция f(x, у) определена и имеет
непрерывные частные производные второго порядка в
некоторой окрестности точки (Xq, i/q), которая является
стационарной для f(x, у), т, е, в ней
4 = 4 = 0. D0.8)
Тогда если в точке (Xq, i/q) выполняется неравенство
f f
fly > 0,
D0.9)
306
то она является точкой строгого экстремума, а именно:
строгого максимума, если в ней f^^ < 0^, и строгого минимума, если
f^^ > 0. Если же в точке (Xq, у^) выполняется неравенство
f.Jyy-ny<0, D0.10)
то экстремума в ней нет.
Наконец, когда в точке (Xq, у^) выполняется равенство
f.Jyy-ny = 0, D0.11)
то может случиться, что экстремум в ней есть, и может
случиться, что экстремума нет.
Действительно, если /^^ ^ О в точке (Xq, у^), то
квадратичную форму D0.2) в нашем случае можно записать в виде
A(dx, dy) = f^^dx^ + 2f^y dx dy + f^^ dy^ =
= j-i(f.. dx + 4^ dyf + D/^^ - /IP dy^i D0.12)
' XX
Bee частные производные здесь и ниже взяты в точке (Xq, i/q).
Мы непосредственно видим, что при выполнении условия
D0.9) выражение в квадратных скобках в формуле D0.12)
положительно при dx^' + dy^' > О, т. е. A(dx, dy) является
определенной квадратичной формой, а именно
положительно-определенной при /^^ > О и отрицательно-определенной при /^^ < 0.
Это, конечно, следует и из приведенного вып1е критерия
Сильвестра. В первом случае, согласно теореме 2, точка (Xq, у^)
является точкой строгого минимума, а во втором — точкой
строгого максимума. Если же выполнено условие D0.10) и /^^ ^ О,
то при dy = О, dx ^ О, из D0.12) имеем sign А(йх, 0) = sign f^^,
а при dx = f^y, dy = -f^^ получим sign AD^, -/^J = -sign f^^,
откуда следует, что квадратичная форма А(йх, dy) при
выполнении условия D0.10) является неопределенной.
Итак, полностью разобран случай /^^ ^ О и f^Jyy - f^y ^ 0.
Случай f^^ = 0, fyy^Ou f^Jyy - fxy^^ исследуется аналогично.
Если же 4^ = fyy = О, но по-прежнему f^Jyy - fly ^ О, то,
очевидно, f;^y^O, следовательно, в этом случае выполняется условие
D0.10) vLA{dx, dy) = 2f^y dx dy. Отсюда сразу видно, что квадра-
' Очевидно, из условия D0.9) следует, что /^^ ^ О в точке (xq, z/q)-
307
тичная форма A(dx, dy) при сделанных предположениях
является неопределенной, так как sign А(йх, dy) = -signA(dx, - dy).
Поэтому достаточно взять сначала dx и dy одного знака, а затем
разных знаков, чтобы получить значения квадратичной формы
разных знаков. По теореме 2 точка (Xq, у^) не является в этом
случае точкой экстремума.
Наконец, случай /^^ = / ^ fxy^ ^ несовместим с
предположением f^^fyy - f^y ^ 0. Таким образом, разобраны все
возможные случаи при выполнении неравенства f^J^y - f^y ^ 0.
Для завершения доказательства теоремы достаточно
показать на примерах, что, когда имеет место соотногаение
D0.11), экстремум может быть, а может и не быть.
У функции 2 = х^ + 2ху + у^ точка (О, 0) является
стационарной, и в ней 2^^ = 2 = 2 = 2, и, значит, выполняется
условие D0.11). Замечая, что 2 = (х + у)^, видим, что всюду 2 > О,
причем 2 = Ohsl прямой х -\- у = 0; поэтому точка (О, 0) является
точкой экстремума, правда, нестрогого.
Для функции 2 = ху^ точка (О, 0) также является
стационарной, и в ней 2^^ = 2 = 2 = О, поэтому условие D0.11)
также выполняется. Однако в силу того, что в формулу, за-
даюгцую эту функцию, переменные х и г/ входят в нечетных
степенях, функция меняет знак в любой окрестности нуля,
значит, (О, 0) не является точкой экстремума. П
40.3. Замечания об экстремумах на множествах
Пусть функция / дифференцируема на открытом
ограниченном множестве G и непрерывна на его замыкании G. Пусть
требуется найти наибольп1ее и наименьпхее значения функции /
на множестве G (они супа;ествуют по теореме 3 п. 19.5). Для
этого можно, например, найти все стационарные точки
функции / в G, вычислить в них значения функции и выбрать, если,
конечно, это возможно (а теоретически возможно это,
например, когда число стационарных точек конечно), точки, в
которых функция принимает наибольпхее и наименьпхее значения
из всех значений в стационарных точках. После этого следует
сравнить эти значения со значениями, которые функция
принимает на границе открытого множества G, например найдя,
если это удается сделать, наибольп1ее и наименьп1ее значения
функции / на границе области G. Сравнив наиболыаее и на-
именыаее значения в стационарных точках с наиболыаим и
308
наименьшим значениями на границе множества G, мы можем,
очевидно, найти искомый максимум и минимум f uslG.
В том случае, когда G — плоская область и ее граница
является кривой, заданной некоторым представлением х = x(t),
у = y(t), а < f < Р, вопрос о нахождении экстремальных
значений функции /(х, у) на границе G сводится к исследованию на
экстремум функции одного переменного f(x(t), y(t)), что
делается уже известными методами.
Методы, которые можно применять в многомерном случае
для отыскания экстремальных точек на границе области,
будут рассмотрены в § 43.
§41
Неявные функции. Отображения
41.1. Неявные функции,
определяемые одним уравнением
Выясним условия, при которых одно уравнение с
несколькими переменными определяет однозначную функцию, т. е.
определяет одну из этих переменных как функцию остальных.
Начнем рассмотрение с изучения уравнения, содержапа;его два
неизвестных, F(x, у) = 0.
Если функция двух переменных F(x, у) задана на
некотором подмножестве А плоскости R^y, А ^ Rxy^ ^ супа;ествует
такая функция одной переменной у = f(x), определенная на
множестве В ^ R^, содержапа;емся в проекции множества А на ось
Ох, что для всех хеВ имеет место (х, f(x))eA и справедливо
равенство F(x, f(x)) = О, то f называется неявной функцией,
определяемой уравнением F(x, у) = 0.
Например, если задано уравнение х^ -\- у^ = 1, то функции
fi(x) = Jl - х^, /2(^) ^ "'^l ~ х^, -1 < X < 1, являются неявными
функциями, задаваемыми этим уравнением. Кроме них су-
па;ествует бесчисленное множество других неявных функций,
задаваемых этим уравнением. Например, для любого XqG[-1, 1]
функция
f( ) = \ ^1^^^' ^^"^^ ^ "^ ^0'
1 /зС^)' если X = Xq,
также представляет собой неявную функцию, определяемую
тем же уравнением.
309
Если потребовать, чтобы неявная функция удовлетворяла
некоторым дополнительным условиям, то может случиться,
что такая функция будет единственной. Так, если
потребовать, чтобы значения неявной функции, определяемой
уравнением х^ + г/^ = 1 на отрезке [-1, 1], были неотрицательны, то
имеется только одна такая неявная функция, а именно
/l(x) = Vl - X2, -1<Х<1.
Другой пример: если координаты точки (Xq, г/д), у^ ^ О,
удовлетворяют этому же уравнению х^ + г/^ = 1, и С/ = U(Xq, у^) —
какая-либо 8-окрестность точки (Xq, i/q), не пересекаюпа;аяся с
осью Ох (рис. 35), то снова супа;ествует единственная неявная
функция /, определенная уравнением х^ + г/^ = 1 на
ортогональной проекции окрестности U на ось Ох и такая, что ее
график содержится в окрестности U.
Сформулируем в виде леммы одно обгцее утверждение,
представляюгцее собой условие, при котором сугцествует
единственная неявная функция, определяемая заданным
уравнением.
ЛЕММА. Пусть функция F(x, у) непрерывна на некоторой
прямоугольной окрестности
Щ^у У о) = {(^у г/) : |х - XqI <Ь,,\у- у^) < цУ
точки (Xq, i/q) и при каждом фиксированном хе (Xq - ^, Xq + b)
строго монотонна по у на интервале (у-т\,Уо + Л)» Тогда, если
F(Xq, г/о) = О,
то существуют окрестности C/(Xq) = (Xq - 6, Xq + 6) точки Xq и
Щуо) = (у - ^, Уо + е) точки у^ такие, что для каждого хе C/(Xq)
имеется, и притом единственное, решение уе U{y^ уравнения
F(x, у) = 0. Это решение, являюш,ееся функцией от х и
обозначаемое у = /(х), непрерывно в точке Xq и /(Xq) = у^.
Таким образом, лемма, в частности, утверждает, что при
сделанных предположениях неявная функция у = /(х),
определяемая уравнением F(x, у) = О, сугцествует и обладает тем
свойством, что при условии хе C/(Xq), уе U(y^ равенства F{x, г/) = О и
У = f(x) равносильны.
* В соответствии с принятыми в курсе обозначениями окрестность
точки (xq, г/о) правильнее было бы обозначать через U((Xq, z/q)), а не через
U(Xq, г/о). Для простоты обозначений мы будем опускать вторые скобки.
у.
/^ Уо
\ ^
—7^ \
\(^о^Уо)\ 1
\ 1 \ /
V 1 Уу'
' 1 >
^0 1 X
i/0 + Л
i/o + e
Уо
Уо-^
Уо-^
О
А
f
f
f
w
1
F>0
1
1
L—^ U-^ 1
^
^^
F<0
Рис. 35
juq (^ juq о ju juq Xr\iO Xr\i(^
Рис. 36
Доказательство. По условиям леммы функция F(x, у)
при каждом фиксированном хе (Xq - ^, Xq + ^) строго монотонна
по переменной у на интервале (у^ - т\, у^ + т\), в частности, на
нем строго монотонна функция F(Xq, у). Пусть для
определенности она строго возрастает. Выберем произвольное 8 > О,
подчиненное лип1ь условию О < 8 < Г|. Поскольку функция F(Xq, у)
переменной у строго возрастает на отрезке [у^ - 8, i/q + 8] и по
условию F(Xq, г/о) = О, то
F(Xo, г/о - 8) < О, F(Xo, г/о + е) > 0.
Но функция двух переменных F(x, у) по предположению
непрерывна на открытом множестве U(Xq, у^) и (Хо, г/о - 8)g
gC/(Xo, г/о), (Хо, г/о + г)еи(х^, г/о), поэтому существует такое 6,
О < 6 < ^, что в 6-окрестности точки (Хо, г/о - 8) выполняется
неравенство F(x, г/) < О, а в 6-окрестности точки (Хо, г/о + 8) —
неравенство F(x, у) > О (см. лемму 1 в п. 15.3). В частности,
при всех хе (Xq - 6, Хо + 5) будут справедливыми неравенства
F(x, г/о - 8) < О, F(x, г/о + 8) > 0. D1.1)
Положим
def def
C/(Xo) = (Хо - 6, Хо + 6), [/(г/о) = (г/о - е, г/о + е)-
Поскольку при фиксированном хе С/(Хо) функция F(x, у)
переменной г/ непрерывна на отрезке [г/о - 8, г/о + 8], из условия
D1.1), согласно теореме Konin о промежуточных значениях
непрерывной функции (см. теорему 2 в п. 6.2), следует, что су-
гцествует такое у*е U(y^ (рис. 36), что F(x, у^) = 0. В силу
строгой монотонности функции F{Xj у) на отрезке [г/о - 8, г/о + 8] по
переменной г/, указанное у* единственно.
311
Таким образом, получено однозначное соответствие
(однозначная функция) X ^ г/"", xgC/(Xq), y'^eUiyo), которое будем
обозначать через /: у* = f(x).
По определению этого соответствия, для любого хе U(Xq) и
у* = f(x) имеем F(x, у*) = О, у*еи(уо), причем точка у'\ об-
ладаюгцая этим свойством, единственна. Тем самым нами
доказаны сугцествование и единственность искомой
функции /. Далее, по условию леммы, F(Xq, у^) = О и так как
XqG U(Xq), i/qG и(уо), то, в силу единственности функции /,
имеем г/о = /(Xq).
Наконец, заметим, что 8 > О было фиксировано
произвольным образом при условии, что 8 < Г|, и что для него было
найдено такое 6 > О, что из \х - Xq| < 6 (т. е. из условия хе U(Xq))
вытекало включение f(x)eU(yQ), т. е. неравенство \f(x) - /(Xq)! < 8.
Это и означает непрерывность функции / в точке Xq. □
Удобные для приложения достаточные условия
однозначной разреп1имости уравнения F(x, у) = О в некоторой
окрестности точки (Xq, г/о), для которой F(Xq, г/д) = О, даются следую-
гцей теоремой.
ТЕОРЕМА 1. Пусть функция F(x, у) непрерывна на
некоторой окрестности точки (Xq, г/д) и имеет в этой окрестности
частную производную Fy{x, г/), которая непрерывна в
точке (Xq, z/q). Тогда, если
F(Xq, г/о) = О, Fy (Xq, г/о) ^ О,
то найдутся такие окрестности U(Xq) и U(y^
соответственно точек Xq и г/д, что для каждого хе [/(Xq) существует,
и притом единственное, решение у = f{x)eU{y^ уравнения
F(x, у) = 0\ Это решение непрерывно всюду в C/(Xq) иу^ = /(Xq).
Если дополнительно предположить, что функция F имеет
в некоторой окрестности точки (Xq, z/q) частную производную
FJix, у), непрерывную в точке (Xq, z/q), то функция /(х) также
имеет в точке Xq производную и для нее справедлива формула
f^(^ \ _ _Fxi^o^ У о)
* В этом случае говорят также, что уравнение F(x, у) = 0 однозначно
разрешимо в окрестности U(Xq, i/q) = {(х, у): хе U(Xq), ye U(i/q)} точки (xq, z/q).
3i2
Доказательство. В силу непрерывности функции F{x, у)
в некоторой окрестности точки (Xq, г/д) и непрерывности
частной производной Fy{Xj у) в точке (Xq, i/q), супа;ествует
прямоугольная окрестность C/(Xq, у^) = {(х, у) :\х - Xq| < ^, |г/ - у^ < г\}
точки (Xq, г/о), в которой сама функция F(x, у) непрерывна, а
значения частной производной F (х, у) имеют тот же знак, что
и ее значение в точке (Xq, z/q). Поэтому при каждом фиксиро-
def
ванном xg(Xq - ^, Xq + ^) функция ф(г/) = F(x, г/)
дифференцируема на интервале (i/q - Л? ^о "^ Л)? ^ ®® производная ф'(г/) =
= ^„(л:, г/) сохраняет постоянный знак. Следовательно,
функция ф(г/) строго монотонна на указанном интервале.
Таким образом все условия леммы для функции F(x, у) в
построенной прямоугольной окрестности [/(Xq, г/д) выполнены.
Следовательно, сугцествуют окрестности [/(Xq) = (Xq - 6, Xq + 6),
C/(i/q) = (i/q - 8, i/q + 8) и единственная функция у = /(х),
определенная на [/(Xq), такие, что при каждом xeU(x) имеют место
включение f{x)&U{y^ и равенство F{x, /(х)) = О, причем
функция / непрерывна в точке Xq.
Поскольку для каждой точки (х, г/), для которой xgC/(Xo),
i/G С/(г/о), сугцествует ее прямоугольная окрестность С/(х, г/), со-
держагцаяся в прямоугольной окрестности
С/о(Хо, г/о) = {(х, г/) : |х - x^l < 6, |г/ - г/о| < 8}
(рис. 37), то для С/(х, г/) также выполняются все условия
леммы. Следовательно, в силу единственности регаения /(х)
уравнения F(x, у) = О в окрестности Uq{Xq, z/q), согласно той же
лемме, функция у = /(х) непрерывна в каждой точке хе C/(Xq).
Рис. 37
313
Докажем теперь последнее утверждение теоремы. В силу
непрерывности частных производных F^vi F в точке (Xq, i/q),
функция F дифференцируема в этой точке:
F{Xq + Ах, г/о + ^y) - F(Xo, у^) =
= F^(Xq, г/о)Ах + Fy(xQ, Уо)Ау + е^Ах + г^^у, D1.2)
где
lim 81 = lim 89 = О, р = JAx^ + Аг/^.
Возьмем в формуле D1.2)
Xq + AxG C/(Xq), Аг/ = /(Xq + Ах) - /(Xq).
Тогда, в силу условия F(x, f(x)) = О, получим
F(Xq + Ах, i/q + Ay) = F(Xq + Ах, /(Xq + Ах)) = О,
и так как F(Xq, i/q) = О, то из D1.2) имеем
Отсюда
А^ ^ _Fx(^0, у о) + £l .^^ дч
Ах F^(Xo, г/о) + 82*
Пусть теперь Ах -^ 0; тогда из непрерывности функции /
следует, что Аг/ ^ О, а значит, при Ах ^ О имеем р =
= л/Ах^ + Аг/^ ^ 0. В силу этого в формуле D1.3) lim 8. =
Ах^ о
= lim 82 = 0. Поэтому при Ах ^ О предел правой части ра-
Ах ^ о
венства D1.d) сугцествует и равен - —^ (напомним, что
Fy{xQ, у о)
F (Xq, z/q) ^ 0), следовательно, при Ах ^ О сугцествует и предел
левой части, т. е. сугцествует производная
Замечание. Если функции F^ и F непрерывны в
окрестности Uq(Xq, Уо) точки (Xq, i/q), то производная /'
непрерывна на интервале U(Xq). Действительно, применив формулу
D1.4) к произвольной точке xg C/(Xq), получим
^ ^ F/X, fix)) '
откуда по теореме о композиции непрерывных функций
вытекает непрерывность функции Г(х) на C/(Xq).
Jl4
Аналогичным образом вводится понятие неявной
функции, определяемой уравнением
F(Xi, ...,х^,г/) = 0, D1.5)
а также формулируется и доказывается теорема, аналогичная
теореме 1. Чтобы получить ее формулировку, достаточно в
формулировке теоремы 1 под х понимать точку я-мерного
пространства, X = (Xj, ... , xJeR^, в частности х^^^ = (х-^^^\ ... , х^^^).
ТЕОРЕМА 1'. Пусть функция F(x, у) = F(x^, ... , х^, у)
непрерывна в некоторой окрестности точки (х^^\ у^^^) и имеет
в этой окрестности частную производную Fy, непрерывную
в точке {х^^\ У^^^)-
Если F(x^^\ у^^^) = О, а Fy{x^^\ уЩ ^ О, то найдутся такие
окрестности U^ и Uy соответственно точек х^^^ и у^^\ что
для каждого xgC/(x) существует, и притом единственное,
решение у = f(x) = /(х^, ... , x^)g U уравнения F(x, у) = 0\
причем это решение у = f(x) непрерывно на U^ и у^^^ = f(x^^^).
Если, кроме того, в некоторой окрестности точки (х^^\ у^^^)
суш,ествуют все частные производные F^ , непрерывные в
точке (х^^\ У^^^), шо в точке х^^^ суш^ествуют и частные
производные /^ , /=1,2, ... , п, причем если частные
производные F^ , i= 1, 2, ... , п, и F непрерывны в окрестности
точки (х^^\ г/^^^), шо частные
производные /^ суш,ествуют и
непрерывны в некоторой окрестности
точки х^^К
При этом формулы для
частных производных неявной
функции у = /(х), определяемой
уравнением D1.5), имеют вид
Эг/ _
ЭХ;
дР
ЭХ;
дР'
Ьу
1,2,
Рис. 38
* На рис. 38 изображен случай, когда я = 2 и окрестность U^
прямоугольная.
315
УПРАЖНЕНИЯ. 1. Сформулировать условия, при которых функция f(x),
определяемая уравнением F(x, у) = О (теорема 1), имеет в точке (xq, у^)
непрерывные производные до п-то порядка включительно. Найти
формулы для f\xQ) и f'\x^.
2. С помощью теоремы 1 и ответа на предыдущие упражнения найти
достаточные условия существования функции х = ф(г/), обратной к у = f{x)
и имеющей в точке у^ непрерывные производные до п-то порядка
включительно. Доказать, что
[№)]
d^^ гупх)]^ - Пх)Г\х)
3' dy^ [№)]5
41.2. Произведения множеств
Прежде чем рассмотреть вопрос о разрешимости систем
уравнений, введем некоторые новые понятия.
Пусть R^ — я-мерное евклидово пространство, точки
которого будем обозначать х = (х^, ... , х^), R^ — m-мерное
евклидово пространство, точки которого будем обозначать у =
= (У1, ... , у^), а R^y^ ^ — (п -\- т)-мерное евклидово
пространство точек (х, у) = (Xj, ... , х^, i/j, ... , у^).
Определение 1. Пусть А ^ R^ и В ^ R^. Множество точек
(х, у) пространства R^^^ таких, что хеА и уеВ,
называется произведением* множеств А и В и обозначается А X В
(см. п. 1.2''). Таким образом.
АХ В = {(х, у) : хеА, уеВ}.
2 к
в
Примеры. 1. Если А = R^, В
R^, то
АХ В
R- X й-
ffn + m
^ху •
Рис. 39
2 . Пусть п = 2иА — круг; m = 1 и
В — отрезок. Тогда А X В — прямой
круговой цилиндр (рис. 39).
3. Пусть х@) = (х[^\ ... , х^^^)^Е^ и
A = P(x@);6i, ...,6J = {x:|x.
X
@I
<5,;
Применяется также термин декартово произведение.
316
i = 1, 2, ... , n} — прямоугольная окрестность точки х^^^; пусть
у@) = (у@), ... , у@))е й- и Б = Р(г/@); У],,..., л J = {у : \у^ - yf^ <
< Г| , У = 1, 2, ... , т} — прямоугольная окрестность точки у^^\
Тогда
АХ В = {(х, у) : \х. - х^^) < 6., / = 1, 2, ... , п;
\Уj-yf^<'^P у=1,2, ...,т} =
= Р((х@), у@)); 6,, ... , 6„ Л1, ... , Л J D1.6)
является прямоугольной окрестностью точки (х^^\ У^^^)»
Очевидно и обратное: поскольку всякая прямоугольная
окрестность точки (х^^\ у^^^) записывается формулой, стоягцей в
середине равенства D1.6), она всегда может быть представлена
как произведение прямоугольных окрестностей точек х^^^ и у^^К
УПРАЖНЕНИЕ 3. Доказать, что если множества А ^ R^ и Б ^ R^
являются открытыми множествами соответственно в пространствах R^ и R^,
то и их произведение А X В — открытое множество в пространстве R^J~ ^.
41.3. Неявные функции,
определяемые системой уравнений
Рассмотрим условия, при которых система уравнений
F.(x,y) = 0, i=l,2, ... ,т, хей^, уеК"^, D1.7)
или, подробнее,
Fi(xi, ... ,х^, i/i, ... ,yj = 0,
F^(x^, ... ,х^, i/i, ... ,yj = 0,
D1.8)
FJx^,...,x^,y^, ...,yj = 0
однозначно разреп1има относительно г/^, ... , г/^ в некоторой
окрестности точки (х^^\ У^^^), в которой функция F.(x^^\ у^^^) = О,
i= 1, 2, ... , т.
Определение2. Пусть задана система функций и. = u.(t-^,..., tj,
i = 1, 2, ... , т, имеющих в некоторой точке t^^^ все частные
производные первого порядка. Тогда матрица, составленная
из частных производных этих функций в точке t^^\
Гди^
'dtl
du2
dt^
dui
дГ^
du2
dt2
dt2
du^ л
к
du2
^tn
или, короче,
1, 2, ... ,m, j= 1, 2, ... , n.
называется матрицей Якоби* данной системы функций.
Если т = п,то определитель матрицы Якоби называется
определителем Якоби, или якобианом, системы функций и-^, ... , и^
^ ^^ d{u-i, ... , и„)
ПО переменным f.,..., f„ и обозначается : ^г— —.
Мы увидим в дальнейп1ем, что якобиан системы функций
естественным образом возникает в различных вопросах
теории функции многих переменных.
Прежде чем перейти к изложению основной теоремы,
кратко поясним на простом примере (не оговаривая все
детали) идею ее доказательства и покажем, каким образом в ее
условиях возникает якобиан рассматриваемой системы. Пусть в
какой-то окрестности точки (Xq, у^, Zq) заданы непрерывно
дифференцируемые функции F и Ф, причем F(Xq, у^, Zq) = О,
Ф(х0, i/q, Zq) = 0. Допустим, что необходимо регаить систему
уравнений: F(x, у, z) = О, Ф(х, у, z) = О в некоторой
окрестности указанной точки, найдя из нее переменные у = ф(х) и
Z = \|/(х), как такие непрерывные функции ф и \|/ переменной х,
что ф(Хо) = г/о, ^(Xq) = Zq. Разреп1ив для этого, например,
первое уравнение относительно z, получим z = f(x, у). Подставив
это выражение во второе уравнение и разрегаив его
относительно у, будем иметь у = ф(х). Полагая \|/(х) = f[x, ф(х)],
получим искомое регаение: у = ф(х), z = \|/(х).
К. Якоби A804—1851) — немецкий математик.
Применяется также обозначение
D{t^,...,tJ
318
Возникает, конечно, вопрос о том, при выполнении каких
условий возможно проделать указанные операции, или,
точнее, когда сугцествуют и однозначно определены все
упомянутые Bbinie функции. (Естественно, при этом надо выяснить,
где, т. е. для каких значений переменных х и г/, определены
эти функции. Этот вопрос мы сейчас не будем подробно
анализировать, чтобы не отвлекаться от основной идеи. Он будет
рассмотрен при доказательстве теоремы 2 этого пункта.)
Для того чтобы одно из данных уравнений, например первое,
было разреп1имым в некоторой окрестности точки (Xq, г/д, 2q)
относительно переменной 2, достаточно, чтобы (см. теорему V
в п. 41.1) ^' ^'—— ^ 0. Если 2 = f(x, у) — соответствуюгцее
регаение, то, для того чтобы уравнение, получаюгцееся в
результате подстановки этого репхения во второе уравнение,
Щ_х, г/, /(х, г/)] = О было разреп1имым относительно
переменной г/, достаточно, чтобы полная частная производная по у
левой части получивп1егося равенства не обрапа;алась в нуль в
точке (Xq, i/q), т. е. чтобы в этой точке
Но, согласно п. 41.1,
ЭФ ,
dz ду
дР
Эг
следовательно, подставляя это выражение в предыдупа;ее
неравенство, получим, что условие разреп1имости можно записать
в следуюпа;ем виде:
^(F, Ф) ^ Э^ЭФ _ Э^ЭФ ^^ (X и 2)
Из этого условия очевидно вытекает, что в точке (Xq, i/q, 2q)
либо тг- ^ О, либо тг- ^ О, т. е. одно из заданных уравнений разре-
дг OZ
П1ИМО относительно 2.
Таким образом, для заданной системы уравнений
неравенство нулю в точке (Xq, г/д, 2^) якобиана -^-^—^ обеспечивает су-
па;ествование в некоторой окрестности точки (Xq, i/q, 2q) penie-
ния вида у = ф(х), 2 = \|/(х).
з7^
Рассмотрим теперь обш;ий случай, т. е. решение системы
уравнений D1.8).
Сформулируем условия, достаточные для того, чтобы эту
систему можно было разрешить относительно переменных г/^, ... , г/^,
в результате чего получается система функций
задаюгцая отображение у = f(x) некоторой окрестности точки
xeR^ в т-мерном пространстве R^.
ТЕОРЕМА 2. Если функции F.(x-^, ... , х^, у^, ... , г/^), / =
= 1, 2, ... , т, непрерывно дифференцируемы в некоторой
окрестности точки (х^^\ у^^^) = (х^^\ ... , х^^\ y^i\ ••• ? Ут"^) и
F.(x@), г/@)) = о, /=1,2, ...,т,
d{F,,...,FJ\
Э(г/1, ... , у J
О,
(х@),1/@))
то существуют такие окрестности U^ и Uy точек х^^^ =
= (х^^\ ... , х^^^) и у^^^ = (у^^\ ... , г/^^) соответственно в
пространствах R^ и R^, что система уравнений D1.8)
однозначно разрешима в окрестности U^ X Uy точки (х^^\ у^^^)
относительно переменных у^, ... , у^. Иначе говоря, для
любого xeU^ суш^ествует, и притом единственное, y^Uy
такое, что (см, обозначение D1.7)) F.(x, у) = О, i= 1, 2, ... , т.
Если
У\ ^ /i(^i? ••• ? ^т)^
y = f{x)= \ лгеС/^,
[ Ут ~ ТтУ-^!^ ••• ' -^т)^
— указанное решение, то все функции /., /=1,2, ... , т,
непрерывно дифференцируемы на U^ и у^^^ = f{x^^^).
Таким образом, если выполняются предположения
теоремы, то условие
F,{x,y) = Q, i=l,2,...,m, ix,y)eU^X Uy
эквивалентно условию
у = fix), хе и^, уе Uy.
320
Доказательство. Прежде всего заметим, что
утверждение: решение у = f(x) системы уравнений D1.7) удовлетворяет
условию f(x^^^) = у^^\ очевидно, непосредственно следует из
утверждения о единственности решения у = f(x)e U при хе U^ и
условий F.(x@), у@)) = 0, / = 1, 2, ... , т, x@)g С/^, i/@)g U^.
Для доказательства теоремы применим метод
математической индукции. Для случая одного уравнения, т. е. когда т= 1,
теорема была установлена нами в п. 41.1. Пусть теперь она
верна для т — 1 уравнений (т > 1). Докажем, что тогда она имеет
место и для т уравнений.
Покажем сначала, что каждое из уравнений D1.8),
например F^(x-^, ... , х^, i/j, ... , у^) = О, можно разрешить в
окрестности точки (х^^\ у^^^) по крайней мере относительно одного
переменного. Действительно, по условию теоремы, в точке (х^^\ у^^^)
Э(г/1, ... , у J
^У\ '" ^Ут
^0,
поэтому в этой точке хотя бы один элемент последней строчки
определителя Якоби отличен от нуля. Пусть для
определенности это последний элемент:
Э^^х(О), 1/@)) ^ ^
^Ут
Отсюда, в силу теоремы V п. 41.1, следует, что уравнение
F^(x, у) = О может быть разрешено относительно у^ в
некоторой окрестности точки (Xq, i/q). Сформулируем это более точно.
Обозначим через U окрестность точки (х^^\ У^^^)у в которой
функции F., /=1,2, ... , т, непрерывно дифференцируемы, и
def
ПОЛОЖИМ ^ = (i/j, ... , Ут-i)' Тогда найдутся прямоугольная
окрестность U^ + n-i точки
(х@), ^@)) = (:^@), ... , ^@)^ у@)^ ... ^ yiO)_ ^) D1.9)
И окрестность U^ точки г/^^ такие, что U^ + ^"iXC/i^C/, и су-
ш;ествует единственная определенная на U^ + n-i функция
Ут = ^(^^ ••• ^^n^yv ••• '^m-l)' D1.10)
32i
удовлетворяюгцая следуюгцим условиям: если
(Х, Й = (^1. ••• у^пуУ1у ••• уУт-l)^ Jjm + n-l^
ТО
ф(х, ^) = Ф(Х1, ... ,х^, г/1, ... ,i/^_i)G С/Ч D1.11)
Fjxj, ... ,х^, i/i, ... ,г/^_1, ф(х, ^)) = 0. D1.12)
Кроме того, согласно той же теореме 1', функция ф(х, ^)
непрерывно дифференцируема на U^ + ^ " ^ и
ф(х@), ^@)) = у@). D1.13)
При этом если (х, §)eU^^^~^ и y^eU^, то система D1.8)
эквивалентна системе
^.(х,г/) = 0, у = 1,2, ...,т-1, D1.14)
г/^ = Ф(^' г/).
Подставим в первые т — 1 уравнения системы D1.14)
выражение D1.10). Тогда, введя обозначение
ФДХ1, ... ,Х^, l/i, ... ,i/^_i) =
= F.(x-^, ... , х^, i/j, ... , г/^_1, Ф(Х1, ... , х^, i/j, ... , i/^_i)),
/=1,2, ... ,m-l, D1.15)
получим следуюгцую систему т - 1 уравнений с т + п - 1
неизвестными:
Oi(Xi, ... ,х^, i/i, ... ,i/^_i) = 0,
D1.16)
0^_i(Xi, ... ,х^, i/i, ... ,i/^_i) = 0.
При этом для (х, ^)g С/"^ + я -1^ г^^е С/^ система уравнений
Ф.(х, ^) = 0, j= 1, 2, ... , m - 1,
г/^ = ф(:^,й D1.17)
эквивалентна системе D1.14).
Покажем, что система D1.16) удовлетворяет условиям, отли-
чаюгцимся от тех, которым удовлетворяет система D1.8), только
тем, что т - 1 заменено на т. Действительно, функции Ф^,
й = 1,2, ...,т-1, непрерывно дифференцируемы в
окрестности и^ + п - 1 j^g^j^ КОМПОЗИЦИИ непрерывно дифференцируемых
функций. Из условий F.(x^^\ у^^^) = О, / = 1, 2, ... , m и D1.15),
D1.13) следует, что Ф^(х@), ^^о)) = О, k = 1, 2, ... , т - 1.
322
Докажем, что в точке (х^^\ §^^^) (см. D1.9))
Э(Ф1,...,Ф^_1)
^0.
Э(г/1, ... , z/^_i)
Для этого предварительно заметим, что из D1.15) следует, что
ЭФ, ^ э^;, э^;. Эф ^ ;^ = i 2 т-1
а из D1.12) — что
^ + |^|Ф=0, й = 1,2,...,т-1.
^Ук ^Ут ^Ук
D1.18)
D1.19)
Теперь в определителе ^г—ИЛИ—^ к й-му столбцу прибавим
d(z/i, ... , у J
последний столбец, умноженный на .г-^-, й = 1, ...,т-1,от че-
^Ук
го, как известно, значение определителя не изменится.
Поэтому, использовав D1.18) и D1.19) и разложив получивгаийся
определитель по элементам последней строки, получим
dyi
=
d{F„
Э(г/1,
^Э^1 Эф
^Ут ^У1
1 ^ ^£т _Э(р
^Ут ^У\
ЭФ^
Эг/1
^Фт-1
Эг/1
0
•— ^J
- ^Ут)
(х@),
^^т - 1 ^^т
^^m- 1 ^^m
ЭФ1
^^m-1
^Фт-1
^Ут-l
0
j;@))
Эф Э^1
^Ут-\ ^Ут
Эф ^^
^^т-1 ^Ут
dF,
^Ут
^F^_
1
^Ут
^Ут
_Э^^(х@),1/@))Э(Ф1,... ,Ф^_1)
^^т
Э(г/1, ... , z/^_i)
(:^0П
(:^
0),^0)
(х@), !/(»))
323
и так как левая часть равенства отлична от нуля, то отлична
от нуля и правая, откуда
Э(Ф1,...,Ф^_1)|
Э(г/1, ... , Ут-i)
^0.
В силу выполнения для функций Ф., i= 1, 2, ... , т — 1,
условий, аналогичных условиям для функций F-, i = 1, 2, ... , m, и
согласно предположению индукции система уравнений D1.16)
однозначно разрегаима относительно переменных г/^, ... , г/^_ ^ в
некоторой окрестности точки {х^^\ ^^^^). Точнее, пусть [/"^ + ^-1 —
прямоугольная окрестность точки {х^^\ ^^^^), полученная при раз-
регаении уравнения F^ = О относительно переменной у^.
Разложим ее в произведение прямоугольных окрестностей С/^ и С/^
точек х^^^ = (х^^\ ... , х^^^) и ^^ = (у^^\ ... , у^^_ i) соответственно в
пространствах R^ и R^ ~ ^: U^ + n-i = С/^ X С/^. Тогда сугцеству-
ет окрестность U^ ^ С/^ точки х^^\ окрестность U^ ^ С/^ точки ^^^^
и единственная система функций
D1.20)
Ут-1^ fm-V<^) ^ /m-l(^l' ••• ' ^д)'
определенных на множестве С/^ и удовлетворяюгцих следую-
гцим условиям: если хе. U^, то
(/i(x), ...,/„_i(x))eC7^ D1.21)
И на С/^ функции D1.20) непрерывно дифференцируемы и
удовлетворяют системе уравнений D1.16):
Ф.(Х1, ... , х^, /i(x), ... , /^_i(x)) = 0, / = 1, 2, ... , m - 1. D1.22)
Важно заметить, что в силу единственности регаения D1.20)
системы D1.16) при хе U^, fie Uy и у^е U^, система уравнений
у, = 4(х), й = 1, 2, ... , m - 1, у^ = ф(х, й D1.23)
эквивалентна системе D1.17).
Подставив выражения D1.20) в D1.10), получим функцию
от X, определенную на U^; обозначим ее через /^:
Ут = ^(^1^ ••• ,Х^, /l(x), ... ,/^_i(x)) =
= fjx,,...,xj = fjx). D1.24)
324
Покажем, что система функций
Ук = 4(^1' ••• ' ^J' й = 1, 2, ... , т D1.25)
(см. D1.20) и D1.24)), и является искомой системой функций,
удовлетворяюпа;ей требованиям, сформулированным в теореме.
В самом деле, пусть U = U^ X U^; тогда если хе U^, то, в силу
D1.21) и D1.11), fix) = (/i(x), ... , fjx))e U^. Из D1.15), D1.22),
D1.24) и D1.12) следует, что F.(x, f(x)) = О, / = 1, 2, ... , т, для
всех хе U^. В силу теоремы 1' и предположения индукции,
функции D1.10) и D1.20), поэтому и функция D1.24)
непрерывно дифференцируемы.
Таким образом, доказано, что отображение /(х),
задаваемое функциями D1.25), является непрерывно
дифференцируемым регаением системы уравнений D1.8) на множестве С/^,
причем если xeU^, то у = f(x)eU . Отметим егце, что если
хе и^, то система D1.25) эквивалентна системе D1.23).
Остается доказать единственность регаения системы
уравнений D1.8). Для доказательства изобразим проделанные в
процессе доказательства переходы от одних систем уравнений
к другим, им эквивалентным, т. е. имеюгцим точно те же
регаения, системам в виде схемы следуюгцим образом:
Г.(х, у) = 0, i=l, 2, ... , т.
Fjix, у) = 0, ]= 1, 2, ... , m - 1,
Ут = Ф(^' ^)-
Ц Ф.(х, ^) = Fj(x, ^, ф(х, §)), j = 1, 2, ... , m - 1,
Ф.(х, §) = 0, j= 1, 2, ... , m - 1,
Ут = Ф(^' ^)-
y. = f.(x), j= 1, 2, ... , m- 1,
Ут = Ф(^' Й.
fjx) = ф(х, /i(x), ... , /^_i(x)),
y. = f.(x), i=l,2, ... , m.
325
Двойные стрелки обозначают эквивалентность
рассматриваемых систем уравнений, которая имеет место, во всяком
случае, для XG С/^, i/G и . Из этой эквивалентности и следует
единственность решения D1.25) системы D1.8) в рассматриваемых
окрестностях, откуда, как было отмечено выше, в силу
условия FJ^x^^\ у^^^) = О, i= 1, 2, ... , т, вытекает, что f(x^^^) = у^^\ П
Доказанная теорема о неявных функциях является одной
из основных теорем математического анализа и имеет много
разнообразных приложений в различных его разделах. С
некоторыми из них мы познакомимся в последуюгцих частях нагае-
го курса. Она является «чистой теоремой сугцествования»: ни
из ее формулировки, ни из приведенного ее доказательства не
следует, вообгце говоря, никакого конкретного метода для
решения системы D1.8). Например, если все F^^,ft = l,2,...,m,
в указанной системе уравнений являются элементарными
функциями, то, следуя схеме доказательства теоремы, вообш;е
говоря, не удастся «найти в явном виде» все те функции, суш;ест-
вование которых использовалось при проведении указанного
доказательства, и получить penienne системы так же в виде
элементарных функций. И в действительности в этом случае
решение системы уравнений D1.8), которое суш;ествует в силу
указанной теоремы, не является, вообш;е говоря, набором
элементарных функций (даже если эта система состоит из одного
уравнения).
Конечно, если функции Fj^ элементарные и, следовательно,
задаются некоторыми формулами, то решение системы D1.8)
может быть найдено с любой степенью точности, т. е.
принципиально с любой степенью точности можно составить таблицы
значений этих решений. Фактическая же точность, с которой
вычисляются регаения, определяется, конечно, конкретной
целью, для которой решается рассматриваемая система. Сама
теорема 2 в этом случае дает объективную уверенность, что,
проводя правильно соответствуюгцие вычисления, мы
действительно вычисляем искомое penienne системы. Мы не будем
останавливаться на численных методах решения систем
уравнений; лип1ь некоторые вопросы численного реп1ения уравнений
рассмотрены в «Дополнении» в конце третьего тома.
Сугцественным является также то обстоятельство, что
теорема 2, как и вообгце теоремы подобного типа, дает
качественные методы в данном случае для изучения свойств решений
системы уравнений.
^26
Интересно отметить, что частные производные репхения
системы D1.8) при выполнении условий теоремы 2 легко
выражаются в явном виде через частные производные
функций Fj^y й = 1, 2, ... , m. Действительно, чтобы найти
частную производную =г-^, надо продифференцировать равенства
D1. 8) по X., считая их тождествами по х^, ... , х^, т. е.
подставив в них их регаения г/у = г/Дх^, ... , х^), у = 1, ... , т. Тогда
получим
P^t'pT^-^^ k-l,2,...,rn.
гл « « Эг/;
«Зта система уравнении, линейных относительно т-^, в силу
того, что в рассматриваемой точке ее определитель не равен
нулю:
d{F,,...,FJ
^(г/l, ... , Ут)
^0,
имеет, и притом единственное, penienne, которое может быть
найдено, например, по правилу Крамера"^.
В случае если нужно найти все производные ^,i= 1, 2, ... , п,
дх^
j = 1, 2, ..., m, целесообразно вычислить дифференциалы
обеих частей указанных выгае тождеств D1.8). Использовав
инвариантность формы первого дифференциала относительно
выбора переменных, получим
п dFu ^ dFu
Эта система линейных относительно di/j, ... , dy^ уравнений, в
AF^,,„,FJ
силу того же условия ^г ^ О, имеет, и притом единст-
Э(г/1, ... , у^)
венное, penienne. Если его пайти, то коэффициент при dx- в
выражепии для dy^ и будет частной производной ^.
Оба эти метода применимы и для вычисления
производных ВЫС1ПИХ порядков функций z/(Xj, ... , х^), ЯВЛЯЮ1ЦИХСЯ ре-
1пениями системы уравнений D1.8) (например, в
предположении, что все функции F^, к = 1, 2, ... , т, имеют соответствую-
Г. Крамер A704—1752) — швейцарский математик.
327
из выражении для первых производных т-^, наиденных по
ох,-
па;их порядков непрерывные производные). Применяя метод
дифференциалов, следует, конечно, помнить, что
дифференциалы порядка вып1е первого в случае, когда они выражаются
через дифференциалы функций, имеют более сложный вид,
чем когда они выражаются только через дифференциалы
независимых переменных (см. п. 38.2).
Производные высгаих порядков функций г/Дх^, ... , х^)
можно получить последовательным дифференцированием и
формулам Крамера из указанной ранее системы уравнений
дх^ ^^1 dyj дх^
в виде отногаения двух определителей. Это отногаение можно
дифференцировать столько раз, сколько раз
дифференцируемы функции Ff^, k = 1, ... , т. При этом если все производные
функций Ff^, k = 1, ... , т, до порядка г включительно
непрерывны, то будут непрерывными и все частные производные
функций z/y(Xj, ... , х^), у = 1, ... , т, до того же порядка г.
Множество (называемое также часто классом) всех г раз
непрерывно дифференцируемых в области G функций
обозначается через C%G). Таким образом, если дополнительно к
условиям теоремы 2 Fj^eC^(U), й = 1, 2, ... , т, где U — некоторая
окрестность точки {х^^\ У^^^), шо решения у^ = г/Дх^, ... , х^
системы уравнений D1.7) также принадлежат классу C^(UJ
на некоторой окрестности U^ ^ U точки х^^К
АЛЛ. Векторные отображения
При изучении дифференцируемых отображений (их
определение будет дано ниже, в п. 41.6) пространство R^, в котором
лежит отображаемое множество, и пространство R^, в которое
происходит отображение, удобнее рассматривать как
векторные евклидовы пространства (см. п. 35.4). Для простоты
я-мерный вектор с координатами (х^, ..., х^) будем обозначать
тем же символом х, которым мы обозначали точку я-мерного
точечного пространства с теми же координатами. Это,
конечно, не приведет к недоразумениям, так как и точка я-мерного
пространства и я-мерный вектор представляют собой
упорядоченный набор п действительных чисел.
^28
Пусть X ^ R^ -и. f: X ^ R^, где теперь отображение / ставит
в соответствие каждому вектору хеХ некоторый вектор у =
= f(x)eR^. Такие отображения будем называть векторными.
Если е-^, ... , е^ — координатные векторы в пространстве R^
(см. п. 35.4), 8j, ... , 8^ — координатные векторы в пространст-
п т
ве Д™, X = (х^, ... , xj= ^ х^е^, у = (у^, ... , yj = ^ yfj и
i = 1 7 = 1
У = fix)y ТО каждая координата г/у, у = 1, 2, ... , т, вектора у
также является функцией от вектора хеХ и, следовательно,
функцией от его координат х^, ... , х^:
yj = fj(x) = fj(x^,...,xj, у=1,2, ...,m. D1.30)
Как и в случае точечного пространства (см. (п. 36.2)),
функции D1.30) называют координатными функциями
отображения f и пигаут f=(fi, ... , /^).
Интерпретация я-мерных точек (х^, ... , х^) как векторов не
препятствует, конечно, рассмотрению таких свойств
отображений, как их непрерывность и равномерная непрерывность.
Поэтому все сказанное о непрерывных отображениях точечных
множеств в п. 36.7 и 36.8 остается в силе при естественной
интерпретации и для векторных отображений. Напомним егце,
что для расстояния р(х, у) между векторами х и г/ справедлива
формула (см. формулу C5.53)) р(х, у) = \х - у\.
В качестве примера отметим, что длина |х| вектора x^R^
является непрерывной функцией в R^. Это следует из
неравенства C5.52): поскольку для любых x^&R^ и xeR^ справедливо
неравенство
то
о ^^ о у
lim |х|= lim |х|
^^•^0 \x-xJ^O
41.5. Линейные отображения
Рассмотрим специальный класс векторых отображений
пространства й^ в R^, называемых линейными.
Определение 3. Отображение f: R^ -^ R^ называется
линейным (или, более полно, линейным однородным), если для
любых двух векторов x'eR^, x''eR^ и любых двух чисел X'eR,
Х''е R выполняется равенство
f(k'x' + Х''х'') = Г fix') + Г fix'').
329
Из этого определения по индукции следует, что при
линейном отображении / любая конечная линейная комбинация
векторов х^^^е R^ отображается в такую же линейную
комбинацию образов f(x^^, j = 1, 2, ... , k, этих векторов
Обычно линейные однородные отображения называются
линейными операторами. О линейном операторе /: R^ -^ R^
говорят, что он действует из R^ в R^.
Из определения линейного оператора непосредственно
следует, что композиция g ^ f линейных операторов /: й^ -^ R^ и g:
Лт -^ Л8 также является линейным оператором g ^ f: R^ ^ R^.
Пусть /: R^ -^ R^ — линейный оператор. Образ каждого
координатного вектора e^eR^, j = 1, 2, ... , п, при отображении
/ является вектором пространства R^ и поэтому
раскладывается по координатным векторам E.eR^, i= 1, 2, ... , т.
Обозначим коэффициенты этого разложения через а-:
т
/(..) = у аф,.
]= 1
т
Пусть у = /(х), X = у х-е- и
y=t УгЧ' D1.31)
i = 1
Тогда, в силу линейности отображения /, получим
у = fix) = f(V xfj J = У xjfiej) = У xj X^ flye^
= ХДХ/У^/Ь- D1.32)
Сравнив коэффициенты разложения вектора у по
координатным векторам 8^, ..., 8^ в D1.31) и D1.32), получим
У1 = «1Л + ... + ^ы^п D1.33)
Ут ^ml^l + ••• + ^тп^п-
Наоборот, легко проверить, что всякое отображение /: R^ -^ R^,
координатные функции которого имеют вид D1.33), является
линейным оператором.
330
Матрица
f ^1
^\п л
D1.34)
называется матрицей линейного оператора f.
Очевидно, что если D1.34) является матрицей линейного
п
оператора /, то для любого х= Y, ^j^j имеет место (см. D1.32))
7-1
разложение
Пх)= ^[^ a,jXj)e,.
D1.35)
Пример. Пусть 71. — оператор проектирования на /-ю
координатную ось, т. е.
Чу) = Чу\^ '- ^Ут) = У1 D1.36)
(/ — фиксированное число среди чисел 1, 2, ... , т). Тогда тг-
является линейным оператором с квадратной матрицей
порядка т, состоягцей из одних лигаь нулей, кроме i-ro элемента
главной диагонали, равного единице:
О ... О О О ... 0^
0 0 0
0 10
0 0 0
[о ... О О О ... О
С помопа;ью операторов проектирования тт., / = 1, 2, ..., я,
легко устанавливается связь между произвольным векторным
отображением f: X ^ R^, X ^ й^ и его координатными
функциями /. (см. D1.30)):
fi = Tii4, D1.37)
Т. е. каждая координатная функция /., / = 1,2, ..., т, является
композицией отображения / с оператором проектирования тт..
Если m = 1, то линейный оператор f: R^ ^ R отображает
пространство R^ во множество всех действительных чисел и
называется обычно линейным функционалом.
В силу D1.33), всякий линейный функционал имеет вид
у = а^х^ + ... + а^х^, D1.38)
где а^, ... , а^ — некоторые действительные числа.
331
Обозначив через а вектор с координатами (а^, ... , а^),
получим, что всякий линейный функционал fiR^^R имеет вид
f(x) = (а, х), где через (а, х) обозначено скалярное
произведение векторов а и X. Очевидно и обратное: каждое отображение
вида X "-^ (а, х) является линейным функционалом /: й^ -^ R.
Напомним определения некоторых операций с матрицами
(известных из алгебры). Если А = {аф и В = {Ъф —
прямоугольные матрицы с одинаковым числом строк и столбцов
/ = 1, 2, ... , т, j = 1, 2, ... , я, то их сумма С =А-\- В
определяется как матрица, элемент с- которой является суммой соот-
ветствуюгцих элементов матриц А и Б, т. е.
def
C.J = a.j + b.j, / = 1,2, ... , m, j= 1, 2, ... , n.
Произведением С = XA матрицы A на число X называется
матрица, все элементы с- которой получаются из соответст-
вуюгцих элементов матрицы А умножением их на X:
def
C.J = Xa.j, /=1,2, ... , m, j= 1, 2, ... , п.
Если число столбцов матрицы А = (а-) равно числу строк
матрицы Б = (bjf), i= 1,2, ... ,m,j= 1, 2, ... ,n,k = \,2, ... , s, то
произведение С = АВ матриц А и Б определяется как матрица, со-
стоягцая из элементов с-^, которые определяются по формулам:
^ik = t ^ijbjk^ /=1,2, ... ,т, k=l,2, ... , s.
Отметим два нужных нам для дальнейгаего свойства
линейных оператора.
1^. Если fug — линейные операторы, f: R^ -^ R^, g: R^ -^
-^ R^, a X и [i — произвольные числа, то Xf + [ig также
линейный оператор, действующий из R^ в R^, причем если А и
В суть матрицы линейных операторов fug, то ХА + цБ
является матрицей оператора Xf + \xg.
Доказательство этого утверждения производится путем его
непосредственной проверки: если
У1= t ^ij^p i=l, 2, ... , т
j = 1
— координатные функции отображения /, а
^i= 11 Ьц^р /= 1, 2, ... , т
i= 1
— координатные функции отображения g, то для
координатных функций отображения Xf + \)ig будем иметь (при сложе-
332
НИИ и умножении на числа векторов их координаты
складываются и умножаются на те же числа)
7=1 7=1 7=1
Т. е., во-первых, координатные функции отображения Xf + \xg
являются линейными функциями, а во-вторых, элементами с-
матрицы С отображения Xf + [ig являются числа с- = Xa-j + цЬ-,
т. е. элементы матрицы С = ХА + цБ, где А = (а-), В = (Ь.). П
2^. Если fug — линейные операторы, f: R^ -^ R^, g: R^ -^
-^ R^, mo их композиция g ^ f (или, короче, gf) также
является линейным оператором R^ -^ R^, а ее матрица равна
произведению матриц отображений g и f.
Снова выполним непосредственную проверку
утверждения. Если
У1= Т. ^ii^i^ i= 1, 2, ... , m,
7=1
— координатные функции отображения /, а
т
2ft = Е ^kiUi^ к = 1,2, ...,s,
i = 1
— координатные функции отображения g, то
i = \ i = \ 7 = 1 7=li=l
T. е., во-первых, координатные функции композиции g о /суть
линейные функции, а во-вторых, элементы Cj^- ее матрицы С
получаются из элементов матриц а- и Ь^. операторов / и ^ по
правилу
т
ЧГ Е Ь^ц- D1.39)
i = 1
Как было сказано, такая матрица С = (с^ ) и называется
произведением матриц (Ь^.) и (а.). П
Заметим, что каждый линейный оператор /: R^ -^ R^
является непрерывным отображением пространства R^, ибо все его
координатные функции D1.33), будучи линейными, непрерывны.
Длина вектора xeR^, как это отмечалось в п. 41.4,
является непрерывной в пространстве R^ функцией. Поэтому если /:
R^ -^ R^ — линейный оператор, то функция |/(х)|, как
композиция двух непрерывных функций, будет также
непрерывной в й^.
333
Поскольку единичный niap Q^ = {xeR^: |x| < 1} является
компактом, для всякого линейного оператора /: R^ -^ R^
сужение непрерывной функции |/|: R^ ^ R usl niap Q^, т. е.
функция |/|: Q^ -^ R, ограничено:
sup |/(х)|<+оо. D1.40)
\х\<1
Определение 4. Дл^ линейного оператора (в частности, при
т = 1 — для линейного функционала) f: R^ -^ R^ число
sup \fix)\ называется его нормой* и обозначается через ||/||:
W<i
11/11 =' sup |/(х)|. D1.41)
\х\<1
в силу неравенства D1.40), норма любого линейного
оператора конечна.
Оценим длину образа вектора xeR^ через норму
оператора / и длину X самого вектора. Для любого х ^ О, xeR^, вектор
имеет длину 1 : |^|
|х| = 1. Поэтому, использовав
линейность оператора /, свойство C5.50) длины вектора и
определение D1.41), получим
\гы=\г(ы&л=Шш
= \х\
4ы
< Wsup|/(^)| = W
151 <1
т. е.
\fix)\ < 11/11 |х|. D1.42)
Из этого неравенства следует, что при |х| < 1 справедливо
неравенство |/(х)| < ||/||. Вспомним, что непрерывная на
компакте функция достигает на нем своего наибольп1его значения (см.
следствие теоремы 3 в п. 36.7). Поэтому функция |/| : Q^ ^ R,
будучи непрерывной на компакте Q^, достигает на нем своего
наиболыаего значения:
11/11 = sup |/(х)| = max |/(х)|,
\х\ < 1 к1 < 1
а поскольку при |х| < 1 имеет место неравенство |/(х)| < ||/||, то
указанный максимум достигается при |х| = 1, т. е. на
единичной сфере S^~^ = {х :\х\ = 1}. Таким образом,
ll/lh max |/(х)|. D1.43)
\х\ = 1
' Общее определение нормы будет дано в п. 58.2.
334
Отметим епа;е одно полезное выражение для нормы
линейного оператора
\\f\\= sup Щ. D1.44)
Докажем его. Используя снова свойство длины C5.50)
вектора, линейность отображения /и формулу D1.41), получим
sup \1^= sup
xeR^,x^O l-^l xeR^,x^O
Ля^)
sup
xe R^, x^O
/A
sup 1/(^I
151 = 1
Нетрудно оценить норму ||/|| линейного оператора / через
элементы его матрицы D1.34). Замечая, что квадрат длины
вектора равен сумме квадратов его координат, применяя
формулу D1.35) и неравенство Konin—Шварца C5.2), будем иметь
\fixf =
I = 1^ J = 1 '
2 т / п \2
<х х«§ х^;
Отсюда для каждого х ^ О, хей":
х,х,«^-
\f(x)
<
Х,Х,«о-
Поэтому, в силу D1.44),
sup
\f(x)
<
xe R^, XT^O 1^1
Тем самым «алгебраическим путем» доказано
неравенство, из которого епа;е раз следует неравенство D1.40).
41.6. Дифференцируемые отображения
Напомним определение символа «о малое» для отображений
(см. п. 36.3) в специальном, нужном нам случае.
Пусть X ^ й^ и XqG й^.
Отображение а: X ^ R^ называется бесконечно малым
(или, что то же самое, «о малым») при х ^ Xq по сравнению с
функцией \х - Xq\^ (\х - Xq\ — длина вектора х - Xq):
335
если супа;ествует такое отображение 8: X ^ R^, что для всех
точек хеХ, принадлежапа;их некоторой фиксированной
окрестности точки Xq, определены отображения а(х) и е(х) (в
частности, для х = Xq), имеет место равенство
а(х) = е(х) \х - XqI^
и
lim г(х) = О,
где О — нулевой элемент пространства R^,
Отображение а(х) определено в точке XqgX, поэтому
отображение е(х) также определено в этой точке, следовательно,
согласно определению предела, и непрерывно в ней: 8(Xq) = 0.
Элементы я-мерных пространств будем рассматривать
здесь как векторы. Для векторных выражений с символом
«о малое» сохраняются обычные правила действий с ними,
например о(х) + о(х) = о(х) при х ^ Xq и т. п.
Перейдем теперь к определению дифференцируемых
векторных отображений. Предварительно напомним, что функция п
переменных f: X ^ R, X ^ R"-*, определенная в окрестности
точки х = (х^, ... , xJgX, называется дифференцируемой в этой
точке, если сугцествуют такие постоянные а^, ... , а^\ они являются
частными производными функции / в этой точке: а- = -^^^ , что
/(Xi + ^1, ... , х^ + hj - /(Xi, ... , xj =
= a^h^ + ... + a^h^ + о(Л), Л ^ О, D1.46)
T^eh = (h^, ... , hj.
Линейное отображение (линейный функционал) (Л^, ... , Л^)"-^
"-^ a^h^ + ... + а^Л^ в формуле D1.46) называется
дифференциалом функции / в точке х. Обозначив его через Df = Df(x),
получим
Dfix)ih) = a^h^ + ... + a^h^. D1.47)
Таким образом, определение дифференцируемости D1.46)
можно представить в виде
/(х + Л) = /(х) + Df(x)(h) + 0(h), h^O.
Аналогично определяется и дифференцируемость
отображения в обгцем случае.
* Через R, как всегда, обозначается множество всех действительных
чисел.
336
Определение 5. Отображение f: X -^ R"^, X ^ й^,
определенное в некоторой окрестности точки xgX, называется
дифференцируемым в этой точке, если существует такое
линейное отображение {линейный оператор) I = 1{х): R^ -^ R^,
что
f(x + h) = f(x) + l(x)(h) + o(h), h^O, heR^. D1.48)
Линейный оператор 1(х) называется дифференциалом
отображения f в точке X и обозначается через Df(x), или, более
подробно, (Df)(x). Используя это обозначение, определение
дифференцируемости D1.48) можно переписать в виде
f(x + h) = f(x) + Df(x)(h) + o(h), h^O. D1.49)
Матрица дифференциала Df(x) (см. D1.34)) называется
производной отображения f в точке х и обозначается
через f\x).
Отметим, что из формулы D1.49) сразу следует, что
отображение, дифференцируемое в точке х, непрерывно в ней:
lim fix + h) = fix).
ТЕОРЕМА 3. Если отображение f: X ^ R"^, X ^ й^,
дифференцируемо в точке хеХ, то его дифференциал в этой точке
определяется однозначно.
СЛЕДСТВИЕ. Дифференциал линейного отображения
совпадает с самим отображением.
Доказательство теоремы. Пусть наряду с равенством
D1.48) (в котором для простоты записи вместо 1{х) будем
писать только I) выполняется также равенство
f{x + h) = f(x) + l^(h) + o(h), h^O, D1.50)
где l^: R^ ^ R^, l^ — линейный оператор. Вычитая одно из
этих равенств из другого, получим
1(Н) - l^ih) = oiji) при Л ^ О,
т. е. сугцествует такое отображение 8(Л) на некоторой
окрестности Vнуля пространства R^ в пространство R^, т. е. 8: F ^ R^, что
lim 8(Л) = О и для всех Ле V имеет место равенство
\Kh)-lM = Hh)\\h\. D1.51)
Возьмем теперь произвольное keR^; тогда для всех
достаточно малых чисел t будем иметь tkeV. Поэтому в D1.51) для
таких t можно взять h = tk:
\l(tk) - l^(tk)\ = \E(tk)\ \tk\.
Поскольку \tk\ = \t\ \k\ и отображения Z и /^ линейны, будем иметь
l(tk) - l^(tk) = t[l(k) - Zi(ft)],
поэтому
\l(k)-l^(k)\ = \e(tk)\\k\. D1.52)
Ho lim tk = 0, следовательно, в силу свойства функции 8, име-
ем также lim eitk) = 0. Переходя к пределу при t ^ Ов D1.52),
получим \l(k) - li(k)\ = о, т. е. для любого keR^ получим
l(k) = l^(k).
Это и означает, что I = 1-^.П\
Доказательство следствия. Пусть /: й^ -^ R"^ —
линейный оператор. Тогда в силу его линейности для любых
хей^иЛей^
fix + h) = fix) + /(Л),
т. е. равенство D1.48) выполняется при I = f л oih) = 0. В силу
единственности дифференциала Dfix) = f.U
ТЕОРЕМА 4 (линейность дифференциала относительно
отображений). Если отображения f: X ^ R"^ и g: X ^ R"^, X ^ й^
дифференцируемы в точке хеХ, то при любых числах X и [i
линейная комбинация Xf + \xg также дифференцируема в
точке X и
DiXf + Vig)ix) = XDfix) + ViDgix).
Доказательство. В силу дифференцируемости
отображений f л gB точке X, имеем (см. D1.49))
fix + h) = fix) + Dfix)ih) + oih), Л ^ 0,
gix + h) = gix) + Dgix)ih) + oih), h^O;
отсюда
Xfix + Л) + [igix + h) =
= \Xfix) + \igix)'\ + \XDfix) + \iDgix)Wi) + oih), h^O.
Так как XDfix) + [iDgix) является линейным
отображением (см. п. 41.5), то, в силу определения 5, оно является
дифференциалом отображения Xf -\- \xg.n
338
ТЕОРЕМА 5. Пусть X ^ R^^Y ^ R"^, f: X ^ Y, g: Y ^ ^г^
причем отображение f дифференцируемо в точке хеХ, а g —
в точке f(x). Тогда композиция g о f дифференцируема в
точке х и ее дифференциал в этой точке равен композиции
дифференциалов отображений fug:
D(g о f)(x) = Dg(f(x)) о Df(x). D1.53)
СЛЕДСТВИЕ. Если выполнены условия теоремы, то
производная композиции отображений равна произведению
производных:
(g- fY(x) = gy(x))nx). D1.54)
Как видно из приведенных формул, благодаря удачному
выбору определений и символики в формулировках теорем
имеет место полная аналогия с одномерным случаем.
Доказательство. В силу дифференцируемости
отображения /, имеем
(g о f)(x + h) = g(f(x + h)) =
= g(f(x) + Df(x)(h) + 0(h)), h^O. D1.55)
Таким образом, аргумент функции g в точке у = f(x) получил
прирагцение
k = Df(x)(h) + o(h). D1.56)
Поэтому из D1.55) в силу дифференцируемости функции g
имеем
(g о f)(x + h) = g(y + k) = g(y) + Dg(y)(k) + o(k), k^O. D1.57)
Поскольку (см. неравенство D1.42))
\Df(x)(h)\<\\Df(x)\\\hl D1.58)
где норма ||D/(x)|| линейного оператора Df(x) является
неотрицательным числом, то для функции k = k(h), определенной
равенством D1.56), получим
lim k = 0. D1.59)
Более того, справедлива оценка
\k\ < \\Df(x)\\ \h\ + \o(h)\, Л ^ О,
a так как при достаточно малых h имеет место неравенство
\o(h)\ < \h\, то для таких h справедлива и оценка
\k\ < (||D/(x)|| + l)\h\. D1.60)
339
Далее, из определения o(k) (см. D1.47) явствует, что супа;ест-
вует такая функция 8(й), что
lim E(k) = 0 D1.61)
и o(k) = E(k)\k\. Поэтому, в силу D1.60), для указанных
достаточно малых h выполняется неравенство
\о(к)\ = Hk)\ \k\ < eik)i\\Dfix)\\ + l)\h\. D1.62)
A поскольку из D1.59) и D1.61) вытекает, что lim E(k) = О и,
следовательно,
e(k)(\\Df(x)\\ + l)\h\ = o(h) при Л ^ О,
из D1.62) имеем
o(k) = o(h) при h ^ 0.
Это означает, что формулу D1.57) можно переписать в виде
(gof)(x + h) = g(y) + Dg(y)(k) + o(h), Л-О, D1.63)
где k задается по формуле D1.56).
Рассмотрим теперь среднее слагаемое в правой части
равенства D1.63). В силу линейности отображения Dg(y), имеем
Dg(y)(k) = Dg(y)(Df(x)(h)) + 0(h)) =
= Dg{y){Df{x){h)) + Dg{y)o{h), й-0. D1.64)
Вследствие неравенства D1.42) будем иметь \Dg(y)o(h)\ <
< ||-0^(г/)|| \oih)\, поэтому
Dgiy)oih) = oih), h^O;
следовательно, из D1.64) получим
Dg(y)(k) = Dgiy)(Df(x)ih)) + 0(h) =
= (Dg(y) о Df(x))(h) + 0(h), Л - 0.
Подставляя полученное для Dg(y) выражение в D1.63) и
принимая во внимание, что у = f(x), будем окончательно иметь
(g о f)(x + h) = g(f(x)) + (Dg(f(x)) о Df(x))(h) + 0(h), Л - 0.
Композиция линейных операторов является линейным
оператором, поэтому, в силу единственности дифференциала,
оператор Dg(f(x)) о Df(x) является дифференциалом
композиции / о ^, т. е. формула D1.53) доказана.
Формула D1.54) сразу следует из нее, поскольку при
композиции линейных операторов их матрицы перемножаются. П
340
ТЕОРЕМА 6. Отображение f = (f^, ... , /J: X ^ R"^, X ^ R^,
дифференцируемо в точке xeX в том и только в том случае,
когда все его координатные функции f.: X ^ R, i= 1, 2, ... , т,
дифференцируемы в этой точке, В этом случае элементы а-
матрицы дифференциала Df(x) являются
соответствующими частными производными координатных функций:
_ dflx)
""^j Эх, '
/= 1, 2, ... , m, j= 1, 2, ... , п.
Иначе говоря, производная f\x) является матрицей Якоби
системы функции /. (см. определение 2 п. 41.3)
Пх)
Э/хСх) 3/i(x)
дх„
D1.65)
и называется также матрицей Якоби отображения f в точке х.
Доказательство. 1. Координатные функции f. = 7Z. о /
(см. D1.37)) являются композицией двух дифференцируемых
отображений: отображения /, которое дифференцируемо в
точке X по условию, и проекции тг- (см. D1.36)), которая, как
всякий линейный оператор R^ -^ R, дифференцируема на
всем пространстве R^. Следовательно, согласно теореме 5,
функции /., /=1,2, ..., т, дифференцируемы в точке х.
2. Пусть все координатные функции f. = %. ^ f отображения
дифференцируемы в точке X. В силу D1.46), это означает, что су-
гцествуют такие постоянные а-, /=1,2, ... , т, j = 1, 2, ... , п, что
/.(X + h) = /.(х) + a-i^i + ... + а.^^ + о.(Л), Л - О, D1.66)
/ = 1, 2, ... , т.
Отсюда, как известно (см. C7.2)), следует, что
коэффициенты a-j при прирагцениях hj аргументов Xj являются соответ-
ствуюгцими частными производными функций /•:
^и
/=1,2, ...,т, j=l,2, ... ,п. D1.67)
341
Обозначим через I: R^ -^ R^ линейный оператор с
матрицей (a.j). Так как (о^(Л), ... , o(h)) = oJJi)Y, то равенства D1.66)
можно записать в виде
/(х + К) = fix) + lih) + о(Л), h^O.
Это и означает дифференцируемость отображения /, причем
из D1.67) следует справедливость формулы D1.65). П
Замечание 1. В силу формул D1.54) и D1.65),
следствие из теоремы 5 означает, что матрица Якоби композиции
отображений fug равна произведению матриц Якоби этих
отображений.
Это, впрочем, непосредственно следует и из формулы
дифференцирования сложной функции: если 2^ = euiVi^ ••• ? Ут)^
й = 1, 2, ... ,s, аг/. = /.(Xi, ... , xj, /= 1, 2, ... , m, то (см. C7.26))
ЧТО, согласно правилу умножения матриц (см. п. 41.6), и означает,
что матрица [ ^ ] является произведением матриц [ ^ ] и [ ^ ],
f^^k^_ f^^kY^yt
-.
\ dXj ) [ ду^ Л dXj )
fdflx)
Определение 6. В случае т = п определитель det -^—
матрицы Якоби D1.65) называется определителем Якоби или
якобианом отображения f: X ^ R^, X ^ R^ в точке хеХ и
обозначается (сш. п. 41.3)
Э(/1, ... , fn) ^^^ D{f,,...,fJ ^
Э(Х1, ... , xj D{x^, ... , xj'
Замечание 2. Из алгебры известно, что при
умножении квадратных матриц их определители перемножаются; по-
* Запись (o^(h), ... , Oj^(h)) = o(h) означает, что вектор, координаты
которого являются бесконечно малыми более высокого порядка, чем h, сам
является бесконечно малой более высокого порядка, чем h при h ^ 0.
Совпадение в данном случае обозначений вектора и его координат
связано с тем, что мы, чтобы не усложнять символики, выбрали для я-мерного
вектора обозначение х, в котором не отражена его размерность. Она
делается ясной, когда вектор записан с помощью координат: х = (х^, ... , х^).
342
этому при выполнении условий теоремы 5 в случае т = п = s
якобиан композиции отображений / и ^ равен произведению
якобианов отображений / и ^:
д{2^, ... , 2 J _ дB^, ... , 2 J ЭA/1, ... , у J
Э(Х1, ... , xj Э(г/1, ... , у J Э(Х1, ... , xj'
Действительно,
D1.68)
det ;^ Н det
1Эг/, Ас
Э(Х1, ... , х„) [dxj ) [dyj[dxj
= det r^O det r?^l = ^^'^' - ' '"^ ^^^^' - ' '^^
[dy^ ) [dxji Э(г/1, ... , у J Э(Х1, ... , xj'
Замечание 3. Пусть X ^ R^ л Id: X ^ X —
тождественное отображение множества X на себя. В координатной
форме оно записывается в виде условия равенства координат
точек образа и прообраза при этом отображении, т. е.
координатные функции имеют вид
f.(x) = х., i= 1, 2, ... , п, (Xj, ... , xJeX.
Если х^^^ — внутренняя точка множества X, то эти функции
можно дифференцировать в этой точке, и поскольку .г—' = О
dXj
Эх ■
при / ^ у и —' = 1, матрица Якоби тождественного
отображения является единичной матрицей
Г1 ... 0^
Е =
[о ... 1 J
Пусть теперь U ^ R^, V ^ R^ j^ f: U ^ V —
взаимно-однозначное (инъективное) отображение, а /"^: f(U) -^ U —
обратное ему. Тогда для любой точки хе U имеем f~^ (f(x)) = х, т. е.
композиция/"^ о /является тождественным отображением.
Пусть отображение / дифференцируемо в точке х^е U
(следовательно, Xq — внутренняя точка множества С/, ибо только
для таких точек определено понятие дифференцируемости), а
обратное отображение /"^ дифференцируемо в точке /(Xq).
Поскольку /"^ о / — тождественное отображение, то в силу
формулы D1.54) имеем
(Г^)Г = (Г^ ° /)' = (Id)' = Е. D1.69)
343
Перейдя от этого равенства матриц к их якобианам, получим
det(r^ydetf =1, D1.70)
так как det Е = 1.
Если отображение / задано координатными функциями
D1.30), то формулу D1.70) можно переписать в виде
Э(Х1, ... , xj ЭA/1, ... , у J _ ^ ^
Э(г/1, ... , у J Э(Х1, ... , xj '
Из этой формулы следует, что при сделанных
предположениях как якобиан отображения / в точке х, так и якобиан
обратного отображения /"^ в точке f(x) не обрагцаются в нуль и
0{,Xi, ... , X^j __ 1 . .^ 70\
Э(г/1, ... , г/„) ЭA/1, ... , yj'
o{Xi, ... , Xj^)
Эта формула является очевидным обобгцением формулы для
производной обратной функции одного переменного: -г^ ^ -г-»
dx
АЛЛ. Отображения с неравным нулю якобианом.
Принцип сохранения области
Прежде всего рассмотрим вопрос о сугцествовании
отображения, обратного данному. Как мы знаем, в случае п = \ для
непрерывно дифференцируемой на некотором отрезке функции
условие необрапа;ения в нуль ее производной (которое влечет
за собой ее строгую монотонность) является достаточным для
супа;ествования обратной ей однозначной непрерывно
дифференцируемой функции. В случае же произвольного п дело су-
па;ественно осложняется: соответствуюпа;ие точечные условия,
налагаемые на дифференциальные свойства отображения,
позволяют утверждать лип1ь, что локально, т. е. в окрестности
точки, супа;ествует обратное отображение.
Для простоты формулировок утверждений введем удобную
для этих целей терминологию.
Определение 7. Отображение f: X ^ R"^, Х^й^,
дифференцируемое в каждой точке хеХ, называется
дифференцируемым отображением множества X.
344
Очевидно, если отображение дифференцируемо на
множестве X, то, какова бы ни была точка хеХ, согласно
определению 8, отображение / определено в некоторой ее окрестности,
т. е. X — открытое множество.
Согласно теореме 6, отображение / = (/^, ... , /^)
дифференцируемо на множестве X тогда и только тогда, когда на этом
множестве дифференцируемы все его координатные функции
/j, ... , /^. Если все координатные функции непрерывно
дифференцируемы на X, т. е. все их первые частные производные
непрерывны на X, то отображение / называется непрерывно
дифференцируемым отображением множества X.
Ясно, что из дифференцируемости непрерывно
дифференцируемых функций (см. теорему 3 в п. 37.2) следует диф-
ференцируемость непрерывно дифференцируемых
отображений.
Напомним, что взаимно-однозначное непрерывное
отображение, у которого обратное отображение также непрерывно,
называется гомеоморфизмом (определение 5 в п. 36.7).
Определение 8. Гомеоморфное отображение f множества G
на множества D, где G и D — открытые множества
пространства R^, называется диффеоморфным отображением
или диффеоморфизмом, если как оно само, так и обратное
ему отображение f~^: D ^ G непрерывно дифференцируемы.
Определение 9. Отображение называется локально гомеоморф-
ным (локально диффеоморфным) в некоторой точке, если у
этой точки и у ее образа существуют окрестности гоме-
оморфно (диффеоморфно) отображающиеся друг на друга при
данном отображении.
ТЕОРЕМА 7. Если у непрерывно дифференцируемого
отображения его якобиан в некоторой точке не равен нулю, то
в этой точке отображение локально диффеоморфно.
СЛЕДСТВИЕ 1. Непрерывно дифференцируемое отображение
с якобианом, не равным нулю, отображает открытое
множество на открытое.
СЛЕДСТВИЕ 2 (принцип сохранения области). Образ области при
непрерывно дифференцируемом отображении с якобианом,
не равным нулю, является областью.
345
Доказательство. Пусть G — открытое множество в
пространстве R^, у = f(x) — непрерывно дифференцируемое
отображение множества G в пространство R^, х = (х^, Xg, ... , х^),
У = (Уг^ У2У ••• ' Уп)у пусть /• — координатные функции этого
отображения, /=1,2, ... , п:
У = f(x) =
У\ / IV^l? ^2'
У2 ^ /2V^1' *^2'
Уп 'д(*^1' *^2' ••• ' ^д)
И
Э(/1, /2, ... , /J
о(Х]^, Х2, ... , Х^)
^0, x@)gG.
D1.73)
D1.74)
Введем обозначения
F.(x, у) = /.(Xj, Х2, ... , xj - г/., /=1,2, ... , п, D1.75)
yi^) = f{x^^)), D1.76)
Функции F. определены на множестве G X й^ и
^—^^—^ ^ = ^—-!^—^ ^, при ЭТОМ ВЫПОЛНЯЮТСЯ сле-
дуюпа;ие условия:
D1.76)
3(^-1, ^2, ... , -FJ
дуХ-^, Х2-) ...» Л^д)
Э(/1, /2,
/J
D1.75) Э(Х1, Х2,
(x@),z/@)) D1.76) ^ ^
•^д)
^0. D1.77)
Рассмотрим систему уравнений
F.(x,i/) = 0, /=1,2, ...,я. D1.78)
В силу формул D1.75), эта система равносильна системе
/.(Xj, Х2, ... , xj - г/. = О, / = 1, 2, ... , я,
и, следовательно, уравнению
г/ = /(х). D1.79)
346
Из теоремы о неявных функциях (см. п. 41.3) следует, что
систему уравнений D1.78) или, что то же самое, уравнение
D1.79) можно разрешить относительно х = (х^, ^2, ... , х^) в
некоторой окрестности точки х^^^ (отметим, что в системе
D1.79) роли переменных х и г/ по сравнению с системой D1.8)
поменялись местами: там система разрепхалась относительно
г/, а здесь — относительно х). Это означает, что супа;ествуют
такие окрестности U и F соответственно точек х^^^ и у^^^:
x@)gC/, i/(%F, D1.80)
и для каждой точки г/е F уравнение D1.79) имеет в
окрестности и единственное penienne, которое обозначим х = g(y). Это
penienne непрерывно дифференцируемо.
Таким образом, для любой точки yeV супа;ествует, и при
этом единственная, точка хе U, sl именно, х = g(y) такая, что
f(g(y)) = y, D1.81)
И, следовательно, f(U) =^ V.
Рассмотрим отображение / только на открытом множестве С/,
иначе говоря, рассмотрим сужение /^ отображения / на
множество и. Обозначим через C/q прообраз множества V при этом
отображении:
U^=fuiV)- D1.82)
В силу формул D1.80) и D1.82),
fu(Uo) = V, х@)еС7о.
Поскольку / — непрерывно дифференцируемое на U
отображение, оно и непрерывно на U. Поэтому, согласно теореме 10
из п. 36.10, множество C/q, будучи прообразом открытого
множества и при отображении /, является также открытым и,
следовательно, окрестностью точки х^^К
Из того, что при отображении /^ для каждой точки i/eFcy-
гцествует единственная точка х = g(y)e U, отображаюгцаяся в
точку г/, следует, что отображение fjj , являюгцееся сужением
отображения /^ на множество C/q, взаимно-однозначно
отображает множество C/q на множество V и поэтому /^ = ^ на V.
347
Итак, отображение f^ , обратное отображению f^ ,
однозначно и дифференцируемо на множестве V. Это и означает, что
отображение /локально диффеоморфно в точке х^^\ П
Первое следствие из теоремы вытекает из того, что при
неравенстве нулю якобиана во всех точках открытого
множества каждая точка образа этого множества, согласно
доказанной теореме, имеет окрестность, на которую отображается
некоторая окрестность прообраза этой точки. Таким образом,
в этом случае каждая точка образа имеет окрестность, при-
надлежагцую образу отображаемого открытого множества.
Это и означает, что этот образ также является открытым
множеством.
Поскольку область есть линейно связное открытое
множество и непрерывный образ линейно связного множества также
является линейно связным множеством (теорема 8 в п. 36.9),
второе следствие вытекает из первого.
Замечания. 1. Условие того, что якобиан не равен
нулю в рассматриваемой точке открытого множества, супа;ествен-
но для справедливости утверждения доказанной теоремы.
Действительно, например, уже для случая п= \ функция /(х) = х^
отображает открытое множество (-1, 1) в неоткрытое [О, 1)
(здесь якобианом является производная и f\Qi) = 0).
2. Было доказано, что однозначное обратное отображение
для отображения с неравным нулю якобианом супа;ествует
только локально, т. е. в окрестности каждой точки. В целом
отображение с неравным нулю якобианом не имеет, вообпа;е
говоря, однозначного обратного отображения.
Покажем это на примере отображения w = 2^, zeC, weC,
единичного круга с выколотым центром: О < 1^1 < 1, которое
отображает это множество на себя. Такое отображение не
взаимно-однозначно, так как обратное отображение z = Jw
двузначно: для любого 1^, О < |i^| < 1, сугцествует два значения
корня 2 = Jw, О < 1^1 < 1. Покажем, что якобиан этого отображения
не равен нулю. Пусть z = х +iy,w = и +iv; тогда u + iv = {x + iy)^,
поэтому и = х^ - у^, V = 2ху. Отсюда
4(х2 + г/2) ^ О при z^O.
348
1 = Х^ - у
д{и, v) _
Э(х, у)
\v = 2
2х -2у
2у 2х
41.8. Неявные функции, определяемые уравнением,
в котором нарушаются условия единственности.
Особые точки плоских кривых
Мы уже знаем, что если координаты некоторой точки х^^^ =
= (х^^\ ... , x^j^^) удовлетворяют уравнению
F(x,,...,xj = 0 D1.83)
dF
и в этой точке производная =г— не равна нулю, то при соответ-
ствуюпа;их условиях, налагаемых на непрерывность самой
функции F и указанной производной, уравнение D1.83) раз-
peniHMO в некоторой окрестности точки х^^^ относительно х- и
penienne является непрерывно дифференцируемой функцией
остальных координат.
Естественно, возникает вопрос: что будет в случае, когда в
точке х^^^ частные производные по всем аргументам обрагцаются
в нуль — определяет в этом случае уравнение D1.83) какие-либо
функции или нет? Остановимся на этом вопросе. Ввиду его
сложности ограничимся рассмотрением двумерного случая.
Итак, будем рассматривать уравнение
Fix, у) = О, D1.84)
где функция F определена и непрерывно дифференцируема в
некоторой окрестности точки (Xq, у^) такой, что
F(x^,y^) = 0 D1.85)
F^ixo, г/о) = Fyixo, Уо) = «• D1.86)
Покажем, что и при выполнении этих условий уравнение D1.84)
иногда может быть разрепхено в окрестности точки (Xq, у^)
относительно одной из переменных, так что получится непрерывно
дифференцируемая функция; однако это можно сделать, вообпа;е
говоря, не единственным образом. Таким образом, условие
F|(Xo, г/о) + ^,'(^0'Уо) ^ о, D1.87)
которое в нап1ем случае (см. D1.76)) не выполняется и которое
позволяет применить теорему 1 о неявных функциях к
одному из переменных, естественно назвать условием однозначной
разреп1имости уравнения D1.84).
Определение 10. Точка (Xq, i/q), координаты которой
удовлетворяют условиям D1.85) и D1.86), называется особой точкой
уравнения D1.84).
^49
Особая точка называется изолированной у если
существует ее окрестность, в которой она является
единственной особой точкой.
Геометрически это означает, что если уравнение D1.84)
является неявным представлением какой-либо кривой, то в
окрестности особых точек уравнения кривая, вообгце говоря, не
является графиком некоторой гладкой однозначной функции (как это
имеет место при выполнении условия D1.87)); здесь возможны
разные особенности, которые мы сейчас и рассмотрим.
Введем для краткости записи обозначения
^хх(^0' Уо) = Кх^ ^ху(Ч^ Уо) = Ку^ ^уу(Ч^ Уо) = ^уг
ТЕОРЕМА 8. Пусть функция F(x, у) определена и дважды
непрерывно дифференцируема в некоторой окрестности
изолированной особой точки (Xq, z/q) уравнения D1.84) и пусть
ро ро _2го2 _^^
XX ху ху ^*
Тогда если
ПЛ-т>0, D1.88)
то (Xq, Уо) является изолированным решением уравнения
D1.84), т, е, существует окрестность точки (Xq, г/д),
никакая точка которой, кроме (Xq, i/q), не удовлетворяет
уравнению D1.84); если же
ПЛ-П1<0, D1.89)
то уравнение D1.84) разрешимо в некоторой окрестности
точки (Xq, Уо), но не однозначно: имеются две различные
непрерывно дифференцируемые функции, удовлетворяющие
уравнению D1.77). Точка (Xq, i/q) называется в этом случае
двойной точкой.
Например, если
F^yy^O, D1.90)
ТО сугцествуют две дифференцируемые функции /^(х) и /зС^)?
определенные в некоторой окрестности точки Xq и такие, что
в этой окрестности F{x, /^(х)) = О, F{x, /2(^)) ^ ^' причем
А(^о) ^ /2(^0) ^ ^0' ^ производные функций /^(х) и /2(^) в точке Xq
являются различными корнями уравнения
n. + ^'F%k + F^yyk^ = 0'' D1.91)
И, следовательно, непрерывны.
* Корни этого уравнения веш;ественны и различны в силу условий
D1.88) и D1.90).
35^
Д о ко 3 a тел b ств о. Пусть выполнено условие D1.88).
Вместе с D1.86) оно достаточно для наличия строгого
экстремума функции F{x, у) в точке (Xq, i/q) (см. теорему 3 в п. 40.2).
Поэтому сугцествует окрестность U точки (Xq, г/д) такая, что
при (х, i/)g и и (х, у) ^ (Xq, г/о) либо всегда F(x, г/) > F(Xo, i/q),
либо всегда F(x, у) < F{Xq, i/q), и так как F{Xq, у^) = О, то F(x, у)^ О
для всех (х, i/)g С/, (х, у) ^ (Xq, z/q)? т. е. (Xq, г/д) является
изолированным регаением уравнения D1.84).
Пусть теперь выполнено условие D1.89). Разложим
функцию F(x, у) по формуле Тейлора в окрестности точки (Xq, у^) до
слагаемых второго порядка; тогда, приняв во внимание
условия D1.85) и D1.86), получим
F(x, у) = 1[^о,(х - ХоJ + 2F%(x - Хо)(г/ - у^) +
+ ^о^(г/- г/оJ] + о(г2), D1.92)
где г = л/(^^^о)^^(^^^о)^ • Положим х - Xq = г cos <?, у - Уо =
= г sin ф. Очевидно, (г, ф) — полярные координаты точки
(х, г/), причем в качестве начала полярной системы координат
взята точка (Xq, г/д). В этих координатах
F(x, у) = ^(F^^cos^ ф + 2F^yCos ф sin ф + F^^^sin^ ф) + о(г^) =
= ^Р(Ф) + о(г2), D1.93)
где
Р(ф) = F^^cos^ ф + 2F^yCos ф sin ф + F^ySin^ ф. D1.94)
Предположим теперь, что выполнено также и условие D1.90).
Еслиф = ±^,тоР(ф) = ро
УУ
и
Р(х,у) = ^-ро^ + о(г^), г-0.
Следовательно, в некоторой окрестности точки (Xq, у^) при г ^ О
и ф = ± ^ имеем F(x, у) ^ 0"^. Поэтому при отыскании penie-
Li
НИИ уравнения Р(х, г/) = О в достаточно малой окрестности
В дальнейшем будем предполагать, что окрестность точки (Xq, z/q)
выбрана таким образом, что это условие выполняется.
точки (Xq, г/о) можно предположить, что ф ^ ^Bт + 1), т = О,
±1, ±2, ... . Тогда
Р(Ф) = cos2 ф(ро^ + po^tg ф + F0^tg2 ф). D1.95)
Пусть ftj и ^2 — корни уравнения D1.91) и пусть ф^ = arctg k-^
и Ф2 = arctg ^2» Тогда
Ф1^±7г/2, ф2^±7г/2, D1.96)
и из D1.95)следует, что
Р(ф) = cos2 ф(tg ф - tg Фl)(tg ф - tg Ф2). D1.97)
Из формулы D1.97) видно, что Р(ф) при ф ^ |Bт + 1),
m = О, ±1, ±2, ... , обрагцается в нуль только для ф = ф^ + тп и
ф = Ф2 + тп, т = О, ±1, ±2, ... , причем при переходе аргумента
через эти значения она меняет знак. Нам будет удобно
интерпретировать Р(ф) как функцию точки окружности С с центром в
точке (Xq, i/q) и радиуса, равного 1 (такой радиус выбирается для
простоты, чтобы длины дуг совпадали с углами ф).
Пусть 8 > 0. Обозначим через U^ = U^(e) открытый угол,
определяемый неравенством ф^ - 8 < ф < ф^ + 8, т. е.
C/i = {(г, ф) : ф1 - 8 < ф < ф1 + 8},
соответственно положим
и^ = {(г, ф) : ф2 - 8 < ф < ф2 + 8};
при этом выберем 8 > О столь малым, чтобы U^ и С/2 не
пересекались и не содержали в себе полуоси ординат, а значит, и во-
обпа;е вертикальных полупрямых (последнее всегда можно
выполнить вследствие условий D1.96)).
Пусть Ul и и2 — углы, центрально-симметричные с С/^ и
С/2 относительно точки (Xq, у^):
Ul = {(г, ф) : ф^ + 71 - 8 < ф < ф^ + 71 + 8},
С/з = {(г, ф) : ф2 + 71 - 8 < ф < ф2 + 71 + 8}.
В силу выбора числа 8 множества С/^, С/2, С/^ и и^ попарно
не пересекаются (рис. 40).
Рассмотрим теперь Р(ф) как функцию точки указанной
Bbinie окружности С. Точку окружности С, которой
соответствует полярный угол ф, будем для простоты также обозначать
через ф. Удалим из указанной окружности интервалы с цент-
352
Рис. 40
рами в точках ф^, фз, ф^ + тг и фз + тг длины 2е*; в силу выбора
8 > О, эти интервалы не имеют обш;их точек. Оставшееся
множество, которое обозначим через В, является ограниченным и
замкнутым, а следовательно, компактом. На В функция Р(ф)
непрерывна и не обрапа;ается в нуль, поэтому
inf |Р(ф)| = ц > 0.
фе В
D1.98)
Обозначим через К замкнутый круг с центром в точке (Xq, i/q)
и радиусом р: К = {(г, ф): О < г < р}, а через L обозначим
множество, которое получается вычитанием (в
теоретико-множественном смысле, см. п. 1.1) множеств С/^, U2, Ul и С/^ из круга К .
Функция Р(ф) не зависит от г, поэтому на множестве L , в силу
D1.98), имеем
inf |Р(ф)| = ц > 0.
Теперь, замечая, что из D1.93) следует
F(x, у) = ^- [Р(ф) + а(г, ф)].
D1.99)
где lim а(г, ф) = О, выберем р > О так, чтобы при г < р выпол-
г^ о
нялось неравенство
|а(г, ф)| < [I.
D1.100)
* Интегралом длины 28 на окружности с центром в точке, полярный
угол которой равен 9q, называется множество ее точек, полярные углы ф
которых удовлетворяют неравенству 9q - 8 < ф < фо + £.
353
Тогда из D1.99) следует, что для всех точек (г, (p)eL
выражение, стоягцее в правой части формулы D1.99), имеет тот же
знак, что и Р(ф).
Множество L состоит из четырех замкнутых секторов (см.
рис. 40), на каждом из которых, за вычетом их центра,
функция Р(ф), а значит, в силу выбора р, и функция F(x, у)
принимают значения одного и того же знака, а на соседних
секторах — разных знаков. Отметим, что функция F(x, у) в
силу своей непрерывности не меняет знак и при переходе
через прямую х = Xq, соответствуюгцую исключенным из
рассмотрения значениям ф = ± 7г/2, так как была выбрана
такая окрестность точки (Xq, i/q), что в этой окрестности на
прямой X = Xq функция F(x, у) не обрагцается в нуль.
Рассмотрим теперь угол U^ = U^(e). Пусть для
определенности О < ф^ < 7г/2. Пересечение замыкания U^ угла U^ с
вертикальной прямой X = X*, Xq< X* <: Xq-\- р cos (ф^ + 8),
представляет собой отрезок, на верхнем и нижнем концах которого
функция F(x\ у) принимает значения разного знака. Функция
F(x\ у), рассматриваемая как функция одного переменного
у при фиксированном х'\ будучи непрерывной на указанном
отрезке, обрапа;ается в некоторой его точке у* в нуль, т. е. для
каждого X*, где Xq < х* <: Xq -\- р cos (ф^ + 8), супа;ествует по
крайней мере одна точка у'^ такая, что
i^Cx*, г/*) = о, (x*,r/*)£C/i(8)nirp. D1.101)
Определим у = fi(x) как функцию, ставяпа;ую в
соответствие числу х'^ число у*:
fl(x*) = у*, Xq< X* < Xq-\- р cos (ф^ + 8).
Покажем, что при достаточно малых 8 и р функция Д
определена однозначно, т. е. супа;ествуют такие 8 > О и р > О, что при
заданном х* условия D1.101) однозначно определяют у'\
Допустим противное. Возьмем последовательности 8^ ^ О и р^ ^ О при
д ^ оо. Тогда сугцествуют две последовательности точек с
одинаковыми абсциссами х^ и разными ординатами г/^ и г/^ такие, что
(х^, y'Je C/i(8 J n К^^, P(x^, у'J = О,
(x^, y';)e C/i(8j n iiTp^, P(x^, y';) = 0.
Тогда, в силу теоремы Ролля, на отрезке [г/^, г/^] прямой х = х^
найдется точка у^ такая, что
Fy(x,,yj = 0, D1.102)
354
при этом, очевидно, (х^, г/^)еС/^(8^) П К ; по условию (см.
D1.86)) мы имели егце
Fyix^,y^) = 0. D1.103)
По формуле конечных прирагцений, примененной к
функции Fy(x, г/),
^у(^п^ Уп) - ^у(Ч^ У о) = ^ух(^п^ л я)(^я - ^о) + ^уу(^п^ л я)(г/я - г/о),
откуда, в силу D1.102) и D1.103),
F.y(^n^ л.) + Fyyi^n^ ^-)f^o ^ ^' (^1^104)
Пусть (х^, i/J = (г^, \|/J. Очевидно, |\|/^ - ф^ < 8^; поэтому
из условия 8^ ^ о следует, что \|/^ -^ ф^ при я ^ оо^ и так как
lim ^^"^o^tgф^ -fe.. D1.105)
Переходя к пределу в равенстве D1.104) при п ^ ^^, в силу
D1.105), имеем
подставляя это значение корня в уравнение D1.91), получим
XX уу ху ^'
что противоречит условию D1.89).
Итак, функция у = fi(x) действительно однозначно
определяется при достаточно малых 8 и р. В дальнейгаем будем
предполагать, что 8 и р выбраны именно таким образом.
Доопределим функцию /^ в точке Xq, положив у^ = /^(Xq).
Очевидно, по самому определению функции /^(х) имеем
F(x, fi(x)) = О, Xq < X < Xq + р cos (ф^ + 8).
Покажем, что в точке Xq у функции /^(х) сугцествует
правосторонняя производная и что она равна k-^. Пусть произвольно
фиксировано 8 > 0. Из изложенного выгае следует сугцествова-
ние такого р = р(8) > О, что соответствуюгцая часть графика
функции fi(x) целиком лежит в U^(e) П К :
(х, /i(x))g и^(г) П К^, Xq < X < Xq + р cos (ф^ + 8). D1.106)
Возьмем 6 = р cos (ф^ + 8), и пусть х таково, что О < х - Xq < 6,
у = fi(x) и (х, у) = (г, ф). В силу D1.106), имеем |ф - ф^| < 8. Это
355
означает, что lim ф = ф^ и поэтому lim tgф = tgф^.Пo-
ос 7 ОС г\ ~г и ОС 7 ОС г\ \ и
у ~ Уо
скольку tg ф = -, ИЗ доказанного следует, что
1. f^(^) ~ f^(^o) т У ~ Уо
hm li^—^—il^—^^ = hm -—— = tg фт,
x^Xq + 0 X - Xq x^Xq + Ox-Xq -^
T. e. у функции fi(x) сугцествует производная справа в точке Xq,
равная tg ф^ = ftj.
Подобным же образом из рассмотрения поведения
функции F(x, у) в угле Ul доказывается, что при некотором 6' > О
на отрезке [Xq - 6', Xq] сугцествует функция /^(х) такая, что
при Xq - 6' < X < Xq:
F(x, /i(x)) = О, (x, /i(x))g Ul и /i(Xq) = i/q, /^(Xq) = й^
(под производной, естественно, в данном случае понимается
левосторонняя производная).
Если число р взять столь малым, чтобы в круговой
окрестности радиуса р точки (Xq, i/q) не содержалось других особых
точек уравнения D1.84), кроме (Xq, i/q), то функция /^(х) будет
дифференцируемой и во всех точках х ^ Xq. Это сразу следует из
доказанной выгае теоремы о неявных функциях (см. теорему 1
в п. 41.1). В результате мы и получили функцию /^(х),
определенную в некоторой окрестности точки Xq и обладаюгцую всеми
требуемыми свойствами.
Аналогично доказывается сугцествование функции /зС^)'
также являюгцейся регаением уравнения D1.84) и удовлетво-
ряюгцей условиям теоремы, причем график этой функции
проходит в углах С/з ^ С/^ и через точку (Xq, i/q).
Если F^ = О, а F^^ ^ О, то все рассмотрения проводятся
аналогичным образом; следует только поменять местами роль
осей Ох и Ог/, так что в результате получим регаения
уравнения D1.77) в виде функций от переменной у: fi(y) и f2iy)'
Если, наконец, F^^ = F^y = О и, значит, F^y ^ О, то прогце
всего выполнить замену переменных: х = ^ + Г|,г/ = ^- Г| (повернуть
оси координат на угол 7г/4). Тогда (как легко убедиться
непосредственно дифференцированием) F$^ = -F^ = 2F^ ^ О, F9 = О,
т. е. в новой координатной системе получим уже изученный
случай. В частности, уравнение D1.31) для угловых коэффициентов
касательных в особой точке в координатной системе ^, Г| имеет
вид й^ - 1 = О, и, значит, k-^ 2 ^ — !• Иначе говоря, биссектрисы
координатных углов, являюгциеся координатными осями в ста-
356
рой системе координат х, у, суть касательные к графикам двух
функций, которые определяются уравнением D1.84) в некоторой
окрестности рассматриваемой особой точки. П
Если уравнение F(x, у) = О является неявным
представлением какой-либо кривой, то в особой точке (Xq, г/д) этого
уравнения кривая может (хотя и не обязана) иметь какие-либо
особенности, т. е. в окрестности особой точки этого уравнения кривая,
вообгце говоря, не является графиком некоторой гладкой
однозначной функции.
Следует напомнить также, что множество точек,
координаты которых удовлетворяют уравнению D1.84), вообпа;е
говоря, не является всегда кривой в смысле данного ранее
определения кривой (см. п. 16.2"^), задаваемой параметрически.
Примеры. 1. Пусть дано уравнение у\х^ + г/^ + 1) = 0.
Здесь F(x, у) = у^(х^ + г/^ + 1), поэтому F^ = 2ху^, Fy = 2х^у +
+ 4г/^ + 2г/. Условия наличия особой точки D1.85) и D1.86)
дают в этом случае
Xq = 0, г/о = 0.
Таким образом, особой точкой является (О, 0). Однако в
этой точке кривая, определяемая уравнением, не имеет
особенности, так как оно (множитель х^ + г/^ + 1 нигде не обрапа;а-
ется в нуль) равносильно уравнению г/ = О и рассматриваемая
кривая является графиком явной функции у = f(x) = 0.
Отметим, что, как легко убедиться, в этом случае в точке (О, 0)
Fx.Fyy-F'xy = 0. D1.107)
2. Для уравнения
(х2 + г/2)(х2 + г/2 - 1) = о D1.108)
условия D1.86) преврагцаются в следуюгцую систему уравнений:
2х^ + 2хг/2 -х = 0,
2г/3 + 2х^у -у = 0.
Сложив и вычтя эти уравнения, получим систему
(х + г/)Bх2 + 2г/2 - 1) = О,
(х - г/)Bх2 + 2г/2 - 1) = 0.
Отсюда либо х = у = 0, либо 2х^ + 2г/2 -1 = 0, однако точка (х, у),
координаты которой удовлетворяют последнему соотногаению,
не является корнем уравнения D1.108) [для нее х^ + г/2 = -, и,
значит, ни один из сомножителей левой части D1.108) не обра-
гцается в нуль
Таким образом, единственной особой точкой является (О, 0).
Легко проверить, что здесь выполняется условие D1.88), и,
357
значит, точка (О, 0) является изолированным корнем
уравнения D1.108). Геометрически, как это сразу видно:
уравнение D1.108) задает единичную окружность и ее центр (О, 0)
(это множество, очевидно, не является носителем никакой
кривой, заданной параметрически в смысле п. 16.2"^).
3. Для уравнения
х^ + у^-3аху = 0 D1.109)
условия D1.86) наличия особой точки приводят к системе
уравнений
х^ - ау = О,
у^ - ах = О,
откуда либо X = у = О и эта точка удовлетворяет уравнению
D1.109), либо X = а, у = а, но координаты этой точки не
являются реп1ением уравнения D1.109). Снова здесь (О, 0) —
единственная особая точка. Нетрудно убедиться, что при этом
выполняются условия D1.89), и, значит, (О, 0) является двойной точкой.
Геометрически для кривой, неявным представлением
которой является уравнение D1.109) (она называется «декартов
лист», и мы с ней уже встречались в п. 14.5); точка (О, 0)
является точкой самопересечения (см. рис. 73 в первом томе).
4. Для уравнения
у^-х^ = 0 D1.110)
(О, 0) является особой точкой; в ней выполняется уже условие
D1.107), и тем самым в этом случае не выполняются условия
теоремы 6. Геометрически кривая, выражаемая уравнением
D1.110) и называемая полукубической параболой у = ±х^^^,
имеет в точке (О, 0) касательную и расположена в окрестности
этой точки по одну сторону от нормали.
Точки такого типа называются точками возврата (рис. 41).
5. Для уравнения
у^-х^ = 0 D1.111)
(О, 0) также является особой точкой, и снова здесь
выполняется условие D1.107). Уравнение D1.111), очевидно,
распадается на два уравнения: у = х^ иу = -х^, которые задают две
параболы, имеюпа;ие в точке (О, 0) обпа;ую касательную.
Особые точки, в некоторой окрестности которых
уравнение D1.84) задает две непрерывно дифференцируемые
кривые, имеюпа;ие в точке (Xq, у^) обпа;ую касательную,
называются точками самоприкосновения (рис. 42) этих двух кривых.
Может случиться, что при выполнении условия D1.107)
особая точка окажется изолированным реп1ением уравнения
D1.84), или его двойной точкой.
358
Рис. 41
Рис. 42
В заключение дадим некоторые пояснения к уравнению
D1.91). Если (Xq, i/q) — особая точка уравнения D1.84), то
после параллельного переноса начала координат в точку (Xq, г/д)
уравнение D1.84) примет вид
F0,x2 + 2F%xy + F^y^ + о(х2 + у2) = о D1.112)
(здесь через х и г/ обозначены координаты точки в новой
системе координат, а индексом О наверху обозначены значения
частных производных в точке (О, 0) этой системы), откуда с
точностью до бесконечно малых более высокого порядка нагае
уравнение можно записать следуюгцим образом:
i^o^x^ + 2F%xy + F^yy^ = 0. D1.113)
В случае выполнения условия D1.89) левая часть уравнения
D1.113) распадается на два действительных множителя, каждый
из которых, приравненный нулю, и дает касательные к двум
ветвям кривой в точке (О, 0) (см. D1.91)). В случае же выполнения
условия D1.88) левая часть уравнения D1.113) распадается на
два комплексных множителя: «касательные мнимы». Это
естественно, так как здесь говорить о касательной не имеет смысла, ибо
в этом случае особая точка является изолированной.
Это замечание особенно удобно использовать для
определения характера особой точки в случае алгебраической кривой,
т. е. кривой, заданной уравнением
Р(х,у) = 0, D1.114)
где Р(х, у) — многочлен от двух переменных х и г/. Если (О, 0) —
особая точка этого уравнения, то из условий D1.85) и D1.86)
следует, что этот многочлен не содержит ни свободного члена,
ни членов первого порядка, т. е. уравнение D1.114) имеет вид
ах^ + 2Ьху + су^ + Q(x, у) = О,
где Q(x, у) — многочлен, все члены которого по крайней мере
третьего порядка. Характер поведения регаений этого уравне-
359
ния вблизи нуля определяется его главной частью, т. е.
уравнением
ах^ + 2Ьху + су^ = О,
которое является уравнением D1.113) для данного случая,
ибо, как легко видеть, здесь а = F^^, Ъ = F^ и с = F^ .
Если же точка (О, 0) удовлетворяет уравнению D1.114), но
не является особой, то D1.114) имеет вид
Ах + Ву + R(x, у) = 0, А^ + В^> О,
где R(x, у) — многочлен, все члены которого имеют порядок
не ниже второго. Из теоремы о неявных функциях (см.
теорему 1 в п. 41.1) следует, что уравнение Ах + By = О
является в этом случае уравнением касательной в точке (О, 0)
к графику единственного в некоторой окрестности этой точки
реп1ения уравнения D1.114).
41.9. Замена переменных
Часто в различных вопросах математического анализа и в его
приложениях при изучении той или иной формулы, содержа-
гцей какие-либо функции и их производные (обыкновенные или
частные), оказывается целесообразным перейти к другим
независимым переменным, а иногда и к другим функциям, которые
связаны с функциями, входягцими в рассматриваемую
формулу, определенными соотногаениями. Все эти преобразования
делаются на основании правил дифференцирования сложных и
неявных функций. Рассмотрим несколько примеров.
Пусть и = и(х, у). Преобразуем выражения \ ^] + (т^ | и
ft 7/ /f 7)
—^ + —^ К полярным координатам гиф. Первое из этих выра-
жений является квадратом длины градиента Vu функции г/,
т. е. равно |Vz/|^, а второе имеет специальное обозначение Аг/:
def 7J., 7J.,
Аи = У+ р- D1.116)
Символ А, указываюгций на применение к функции и
операции D1.116), называется оператором Лапласа"^.
Из формул, связываюгцих декартовы координаты с
полярными,
X = г cos ф, г/= г sin ф D1.117)
П. Лаплас A749—1827) — французский механик и математик.
360
находим
^ = со8ф, ^ = -rsin9, ^ = sin9, ^ = г cos ф. D1.118)
дг ^ Эф ^ дг ^ Эф ^
Применим к функции и(х, у) формулы дифференцирования
сложной функции
дг ах дг ду дг дх ду
т— = т—т— -\- т—т^ = —т—г sm (D -\- т—г cos ф.
Эф дх Эф ду Эф дх ду
Разреп1им эти равенства относительно т^ и т^
дх ду
^ = ^cos ф - ^?Н1Ф, ^ = ^sin ф + ^^^^^ D1.119)
Эх Эг ^ Эф г Эг/ Эг Эф г
И подставим получивп1иеся выражения в D1.115)
Уг/Р = ^cos ф - ^^^^ + ^sin ф + ^
\дг ^ д(р г ) \дг ^ Эф г
Эй у, UduV
дг I гНЭф J •
Теперь перейдем к вычислению выражения D1.116).
Продифференцируем формулы D1.117) сначала по х, затем по у
1 = cos ф|^ - г sin ф^, [о = cos ф^ - г sin ф|г,
О = sin ф^ + г cos ф^, 11 = sin ф^ + г cos ф^.
дх дх [ ^ду ду
Разрешим получивп1иеся системы относительно г-^, .-2, .-^ и .-2
дх дх ду ду
^ = С08ф, ^ = 8Шф, ^ = -?iEf, Эф^совф_ D1.120)
дх ду дх г ду г
Продифференцируем теперь формулы D1.119) по х и г/; тогда,
использовав D1.120), получим
Э% ^Af^cOSQ- — ^i^l— + Af^cOSQ- — ^i^l^ =
дx^^ дгкдг ^ Эф г Jdx Эф1Эг ^ Эф г )дх
= ^^^р(чо2 (п. _ 2COSфsinф д^и I sin^ф д^и , sin^ф ди , 2_cos(psin(p Эй.
дг^ г ЭгЭф г^ Эф^ г Эг г^ Эф'
^ = |.Г ^sin ф + $^ ^^^ 1^ + ^f^sin ф + ^ ^^^^ 1^ =
Эг/2 дгкдг ^ Эф г уЭг/ Эф1Эг ^ Эф г уЭг/
= Э% • 2 (г^ _L 2cosфsinф Э^1^ I cos^ф д^и , cos^ф Эй _ 2cosфsinф ди
Эг^ г ЭгЭф r^' Эф^ г Эг r^' Эф*
3^i
Подставив получивп1иеся выражения в D1.116), будем иметь
д ^ д^и I 1 д^и I 1ди
В случае, когда в преобразуемое выражение входит не одна,
а несколько производных данного порядка, удобно применять
метод вычисления не производных, а дифференциалов.
Например, считая независимыми переменными х и г/, найдем
выражения для дифференциалов dr и йф. Из формул D1.117) имеем
dx = cos (р dr- г sin ф йф, dy = sin ф dr + г cos ф йф,
отсюда
dr = cos ф dx + sin ф dy, d(p = -^^ dx + ^^^ dy D1.121)
(отметим, что из этих формул также сразу получаются
формулы D1.120)).
Для функции и = и(х, у) имеем
dr Эф
'gcos9-^^]dx + (^sin9 + ^^^^dy. D1.122)
В выражении для дифференциала du коэффициенты у dx и
dy являются производными .-^ и гг^, поэтому из D1.122) сразу
ох ду
получаются обе формулы D1.119). Найдем далее вторые
дифференциалы d^rn й^ф из D1.121)
d'^r = -sin ф йф dx + cos (р dip dy =
d^^ = -^^dx+'-^dy]di? + [^dx-^dy]dr =
^ 2со8ф81пфс^х^ - 2(со8^ф - sm^(p)dxdy - 2со8ф81пфс^1/^
Теперь из D1.122) для d^u получим
дr^^ ЭгЭф Эф2 ^ дг Эф
2 (п. ^^и _ 2со8ф81пф д^и , sin^ipd^u , зитЛрЭи ,
дr^' г ЭгЭф r^' Эф^ г дг
+ 2С08ф8ШфЭи^^^2 + 2(...) dx dr/ + (...) dy2.
362
ft ТI ft ТI ft TI
Отсюда и получаются выражения для —^, .^^^ и —— как соот-
дх^ дхду ду^
ветственно коэффициенты при dx^, 2dx dy и dy^'.
Аналогичные методы применимы, конечно, и в случае, когда
производится какая-либо другая замена переменных х = х(и, v),
у = у(и, v), когда имеются производные высгаих порядков, а
также когда речь идет о функциях болыаего числа переменных.
УПРАЖНЕНИЕ 6. Преобразовать выражение |Vwp, где и = и(х, у), к
ортогональным координатам ^, Г|, т. е. таким координатам, что
Эх Эх I Э^ Э^ ^ Q
Э^ дг\ Э^ дг\
Задача 9. в я-мерном пространстве преобразовать выражение |Vwp,
где и = w(x^, ... , х^), к ортогональным координатам ^^, ... , ^^, т. е. таким
координатам, что при i ^ k выполняется равенство
" Эг Эг
£ РР = 0, i,k=l,2,...,n.
§42
Зависимость функций
42.1. Понятие зависимости функций.
Необходимое условие зависимости функций
Определение 1. Пусть на открытом множестве G ^ R^
заданы непрерывно дифференцируемые функции
у. = (р.(х), i = l,2, ... ,т, х = (х^, ... ,xJeG. D2.1)
Если существуют открытое множество D в
пространстве R!^~'^ J. и непрерывно дифференцируемая на D функ-
ция Ф(У1, ... , г/^_ i) такие, что в любой точке хеО
выполняются условия (9i(x), ... , ф^ _ ^(x))eD и Ф(ф^(х), ... , ф^ _ ^(х)) =
= ф^(х), то функция ф^ называется зависимой на множестве G
от функций ф^, ... , Ф^_1.
Определение 2. Если среди функций системы D2.1) есть
функция, зависимая от остальных на множестве G, то эта
система называется зависимой на множестве G.
Если ни одна функция системы D2.1) не зависит от
остальных на множестве G, то эта система называется
независимой на G.
^63
Иногда для краткости вместо выражения «зависимая
(независимая) система функций» будем просто говорить
«зависимые (соответственно независимые) функции».
В вопросе зависимости системы функций D2.1)
фундаментальную роль играет матрица Якоби этой системы
^], i=l,2,...,m; j=l,2,...,n, D2.2)
где / — номер строки, у — номер столбца.
ТЕОРЕМА 1 (необходимое условие зависимости функций).
Пусть т <: п и система функций D2.1) зависима на
открытом множестве G, Тогда в любой точке этого множества
ранг матрицы Якоби D2.2)'' этой системы меньше т.
Доказательство. По условию, система функций D2.1)
зависима на G, т. е. по крайней мере одна из этих функций
зависит от остальных. Пусть для определенности ф^ зависит от
(?Jx) = Ф(ф1(х), ... , 9^_i(x)), xeG,
где Ф — непрерывно дифференцируемая функция от (т - 1)
аргументов у^, ... ,у^_^. Отсюда
4^= L^T^ длявсех у=1,2,...,я.
Эта формула показывает, что т-я строка матрицы Якоби
D2.2) в каждой точке хеО является линейной комбинацией
остальных строк этой матрицы, и, значит, ранг матрицы
Якоби D2.2) меньп1е т в каждой точке xeG. П
СЛЕДСТВИЕ 1. Пусть т = пи система функций D2.1)
зависима на открытом множестве G. Тогда ее якобиан ^^ ^''" '——^
d(Xi, ... , xj
равен нулю во всех точках множества G.
СЛЕДСТВИЕ 2 (достаточные условия независимости функций). Пусть
т <: п и пусть ранг матрицы Якоби D2.2) хоть в одной
точке открытого множества G равен т. Тогда система D2.1)
независима на множестве G.
* Напомним, что рангом матрицы называется максимальное число ее
линейно независимых строк. Это число совпадает с максимальным
порядком минора этой матрицы, не равного нулю.
364
Следствие 1 получается сразу из доказанной теоремы при
т = п.
Следствие 2 легко доказывается от противного.
Поскольку строки матрицы Якоби D2.2) являются
координатами градиентов функций D2.1), теорему 1 можно
перефразировать следуюгцим образом.
Если система функций D2.1) зависима в области G, то
градиенты V„ , ... , V„ этих функций линейно зависимы в
каждой точке G.
42.2. Достаточные условия зависимости функций
В этом пункте сохраним обозначения предыдугцего пункта и
будем, как и раныае, предполагать, что функции D2.1)
непрерывно дифференцируемы на открытом множестве G ^ й^.
ТЕОРЕМА 2 (достаточные условия зависимости функций).
Пусть ранг матрицы Якоби D2.2) системы функций D2.1) в
каждой точке открытого множества G не превышает чис-
ла г, г < т < п, а в некоторой точке х^^^еОравен г, иначе
говоря, существуют такие переменные х-, ... , х- и функции
Э(г/^^, ... , Vi)
Э(х^.^,...,х^О
0. D2.3)
Тогда все г функций, входящих в условие D2.3), независимы
на множестве G и существует окрестность точки х^^^
такая, что любая из оставшихся т - г функций зависит на
этой окрестности от указанных г функций.
Доказательство. Пусть для простоты записи условие
D2.3) имеет вид
Э(г/1, ... , у^)\
Э(Х1, ... , х^)
^0 D2.4)
ДО)
(этого всегда можно добиться, перенумеровав в случае
необходимости функции и аргументы системы D2.1) в нужном
порядке). Согласно следствию 2 из теоремы 1 п. 42.1, функции
у-^, ... , у^ независимы в G.
Покажем теперь, что каждая из остальных зависит от них
в некоторой окрестности точки х^^^ = (х^^\ ... , х^^^). Пусть
365
г/^^ = ф.(х^^^), / = 1, 2, ... , т. Рассмотрим систему первых г
функций системы D2.1):
i/i = 9i(xi, ... ,xj
D2.5)
г/, = фДх1, ... ,xj.
Прежде всего выберем такое tjq, чтобы всякая точка х =
= (Xj, ... , х^), принадлежапа;ая riQ-кубической окрестности
точки х^^\ т. е. всякая точка х, для которой \х- - xi^^\ < tjq,
i = 1, 2, ... , п, принадлежала множеству G: xeG. Это всегда
возможно в силу его открытости.
Далее, в силу условия D2.4) и теоремы о неявных
функциях (см. п. 41.3), система D2.5) разрегаима относительно
переменных Xj, ... , х^ в некоторой окрестности точки (х^^\ У^^^У»
^1 ^ /iv^i? ••• ? Уг^ ^г+1' ••• ' *^д)'
D2.6)
х^ — Тг\У\^ ••• ? Уг^ х^^ J, ... , х^).
При этом функции /j, ... , /^ определены и непрерывно
дифференцируемы в некоторой окрестности точки
Более подробно (если в качестве окрестностей брать
кубические окрестности) это означает следуюгцее: можно выбрать
такие числа 6 > О и Г| > О, причем для удобства взять их мень-
П1ИМИ tIqI 6 < TJQ, Г| < TJQ, что если через U обозначить
кубическую окрестность точки {у^^\ ... , у^^\ x^^l ^, ... , х^^^),
задаваемую неравенствами
\у^ - у[Ц < 6, / = 1, 2, ... , г, |х. - xf^ < 6, у = г + 1, ... , я,
то:
1) на окрестности U функции /^, й = 1, 2, ... , г, определены
и непрерывно дифференцируемы;
2) для всех точек (г/^, ... , г/^, х^+ ^, ... , x^)gC/ справедливы
неравенства
I4(i/i, ... ,1/^, х^+1, ... ,х^-х;^0)|<л, й = 1,2, ... ,г;
3) на окрестности С/ выполняются равенства
ф.(/1, ... ,/^, х^+1, ... ,xj = i/., / = 1,2, ... ,г,
где под /^, й = 1, ... , г, понимаются правые части равенств D2.6).
^66
Рассмотрим композицию функций D2.6) и (f^+iix-^, ... , х^),
т. е. функцию
yr + i = ^r + i(fv ••• '/г'^г+1' ••• '^J' D2.7)
где 4 = 4(г/1, ... , г/^, ^r + v ••• ' ^J' й = 1, ... , г. Эта сложная
функция заведомо определена и непрерывно
дифференцируема на указанной выпхе кубической окрестности U точки
«),...,г/@),х<0),,...,х@)).
Покажем, что на самом деле функция D2.7) в этой
окрестности и не зависит от переменных x^ +1, ... , х^, т. е. не меняется
при их изменении, и тем самым является фактически лип1ь
функцией переменных г/^, ... , г/^. Для этого достаточно показать,
что для функции D2.7) на окрестности U выполняется равенство
О, у = г+1,...,я D2.8)
(см. п. 37.4 или формулу конечных прирагцений Лагранжа
в п. 39.2, из которой сразу следует достаточность условия
D2.8) для независимости функции от переменных x^+1, ... , х^
в выпуклой области, а следовательно, и в кубической
окрестности).
Для доказательства равенства D2.8) зафиксируем одно из
значений у (у = г + 1, ... , я) и координаты х^ с индексами k,
принимаюгцими значения г + 1, ... , у - 1, у + 1, ... , я,
обозначив их через х^, причем выберем х'^ так, чтобы |х^ - х^^^| < 6,
й = г+ 1, ... ,у- 1,у+ 1, ... , п.
Рассмотрим отображение
г/1 = г/1.
D2.9)
У г = Угу
^г+ 1 ^ Фг+ IV/1' ••• ' 'г' *^г + 1' ••• ' *^у - 1' *^у' *^у + 1' ••• ' •^л)'>
vjxefl = fj,y^, ... ,г/^, х;+1, ... , xj_ ^ х-, xj+i, ... , х^), (r+1)-мер-
ной кубической окрестности С/^^) точки {у^^\ ... , г/^^\ х^^^),
задаваемой равенствами
\Уk-yf^<^^ k = l,2,...,r, \x.-xf>\<5.
Символически, чтобы подчеркнуть, какие именно
переменные меняются, изобразим отображение D2.9) в виде
367
(г/i, ... , г/^, Xj) ^ (г/i, ... , г/^, г/^+1). Это отображение непрерывно
дифференцируемо на U^^^; его матрица Якоби имеет вид
1
0
^Уг+1
Эг/1
ЭA/1,..
0
1
ду^_
Эг/2
. , Уг^
0
0
1 ^Уг+1
^Уг
Уг+l) _
0
0
^Уг+1
dXj
_ ^Уг+1
и поэтому
-^^^ -^ ^ ^^^^—, D2.10)
Э(г/1, ... , г/^, Xj) dxj
т. е. якобиан рассматриваемого отображения равен интере-
суюгцей нас производной.
На окрестности U^^^ это отображение можно представить в
виде композиции двух отображений: непрерывно
дифференцируемого отображения
окрестности С/^^^ и непрерывно дифференцируемого
отображения
/ ^ ^ ^ ^ \
^1 ФхЧ*^!? • • • ? *^г' *^г +1' • • • ' *^/ - 1' *^/' *^/ +1' • • • ' *^д/'
г/г ФД 1' • • • ' *^г' г +1' • • • ' i - 1' у' i +1' • • • ' д/'
/ ^ ^ ^ ^ \
^^+ 1 ~ ф^+ iV^l? ••• ? ^г' *^г + 1' ••• ' *^у - 1' *^у' *^у + 1' ••• ' *^д/
окрестности точки {х^^\ ... , х^^\ х^^^), задаваемой
неравенствами \х. - х[^^\ < Г|, / = 1, 2, ... , г, \Xj - х^^^\ < 6.
В силу выбора чисел 6 и Г|, композиция этих отображений,
которую для наглядности можно символически изобразить в
виде (г/1, ... , г/^, X.) -^ (Xi, ... , х^, X.) -^ (г/^, ... , г/^, г/^+1), определена
и непрерывно дифференцируема на окрестности U^\ Первое из
этих отображений непрерывно дифференцируемо в окрестности
[/(у) точки {у^^\ ... , у^^\ У^^^), а второе непрерывно
дифференцируемо в соответствуюгцей окрестности точки (х^^\ ... , х^^\ х^^^).
368
Поэтому из D2.10) и из свойств якобианов отображений (см.
п. 41.7) имеем
^Уг+1 _ ЭA/1, ... , у^, i/^+i) _ ЭA/1, ... , у^, г/^+ iK(xi, ... , х^, Xj)
dxj Э(г/1, ... , г/^, хр д(х^, ... , х^, Xj) д(у^, ... , у^, Xj)'
В силу условия теоремы, ранг матрицы Якоби на
множестве G меньше или равен г, следовательно,
ЭA/1, ... , Уг,Уг+1) _Q
ВСЮДУ на G. Поэтому из D2.11) сразу следует, что для любой
точки (i/j, ... , г/^, Xj)eU^i^ и, следовательно, для любой точки
(i/i, ... , г/^, х^+1, ... , xj_i, х^., xj+i, ... , x^)gC/ справедливо
равенство D2.8). Поскольку координаты х^ были
фиксированы произвольным образом, лип1ь бы \х1 — х^^| < 6; й = г + 1, ...
... , у - 1, у + 1, ... , я, то это означает справедливость равенства
D2.8) на окрестности U.
Таким образом, функция D2.7) зависит только от
переменных i/j, ... , г/^. Обозначив ее символом Ф, получим
9^+i(/i, ... ,/^, х^+1, ... ,х^ = Ф(г/1, ... ,у^).
Выберем теперь таким образом 6q, 6q < 6 и 6q < Г|, чтобы при
\х. - x^^l < 6q, / = 1, 2, ... , я, выполнялись неравенства
|r/,-r/W|<5, /=1,2, ...,г.
Это возможно в силу непрерывности функций г/ = Ф^лг^, ... х^),
у = 1, 2, ... , г, системы D2.5) в точке х^^\
В силу доказанного, для любой точки х из бд-кубической
окрестности точки х^^\ т. е. для любой такой точки х = (х^, ... , х^),
что |х. - x^^l < 6q, / = 1, 2, ... , я, справедливо тождество ф^+ ^(х) =
= Ф(ф^(х), ... , фДх)), т. е. в указанной окрестности точки х^^^
функции ф^, ... , ф^, ф^+j зависимы.
Подобным же образом доказывается зависимость каждой
из функций ф^+ 2' ••• ' Фт ^"^ Ф1' ••• ? Фг ^ некоторой окрестности
точки х^^^. П
Аналогично необходимому условию зависимости функций
достаточные условия также можно сформулировать в
терминах градиентов. Для простоты ограничимся случаем г=т—1.
369
Если во всех точках области G градиенты Уф^, ... , Уф^
линейно зависимы, то у каждой точки xeG существует ее
окрестность, в которой функции ф^, ... , ф^ зависимы. При
этом, если, например, градиенты Уф^, ... , Уф^_1 линейно
независимы в некоторой точке, и, следовательно, градиент
Уф^ 6 этой точке является их линейной комбинацией, то в
окрестности рассматриваемой точки функция ф^ зависит
от функций ф^, ... , Ф^_1.
Следует обратить внимание на то, что достаточные условия
зависимости функций, установленные в этом пункте, имеют
локальный характер в отличие от результатов предшествуюш;его
пункта, имеюпа;их глобальный характер. Это означает следую-
па;ее: если система т непрерывно дифференцируемых функций
D2.1) зависима на открытом множестве G ^ R^, то, согласно
теореме 1 п. 42.1,в каждой точке этого множества ранг
матрицы Якоби этой системы меныае т (соответственно если хотя
бы в одной точке множества G ранг рассматриваемой матрицы
равен т, то система независима на всем множестве G). Что
же касается теоремы 2 настоягцего пункта, то она утверждает
лип1ь, что если в какой-то точке x^^'^^G выполняются условия
этой теоремы, то только на некоторой окрестности
этой точки (а не на всем множестве G) данная система функций
является зависимой системой. Таким образом, действительно,
утверждение теоремы 2 имеет локальный характер.
Добавим егце, что если в каждой точке х^^^ открытого
множества G выполняются условия теоремы 2, то, конечно, в
этом случае в некоторой окрестности каждой точки
рассматриваемая система функций будет зависимой. Однако теорема 2 не
гарантирует, что эта зависимость будет одной и той же во всех
указанных окрестностях, т. е. из теоремы 2 не следует, что в
разных точках одни и те же функции будут зависимыми от
других и что функции Ф, «осупа;ествляюпа;ие» зависимости
одних и тех же функций, рассматриваемых на разных
окрестностях, будут совпадать в точках пересечения этих окрестностей.
Следовательно, из теоремы 2 не следует, что система функций,
удовлетворяюпа;ая условиям этой теоремы во всех точках х^^^
множества G, будет зависимой на всем множестве G в целом,
т. е. в смысле определения 1. Это и означает, что теорема 2 не
имеет глобального характера.
Заметим, что супа;ествует несколько более обпа;ий подход к
понятию зависимости функций, позволяюпа;ий построить
глобальную теорию этого вопроса, однако не будем на этом
останавливаться.
37^
Пример. Рассмотрим систему функций
и = sin (х + у),
D2.12)
V = cos (х + у).
Якобиан этой системы равен нулю на всей плоскости
о,
cos(x + у) cos(x + у)
-sin(x + у) -sin(x + у)
и, как легко видеть, ранг матрицы Якоби этой системы равен
единице во всех точках плоскости.
Согласно теореме 2, функции D2.12) зависимы в
окрестности каждой точки плоскости. В данном случае зависимость
функций легко находится в явном виде, например на
открытом множестве точек (х, г/), для которых cos (х -\- у) > О, она
может быть задана формулой v = Jl - и^.
УПРАЖНЕНИЯ. 1. Пусть и = х^ + у^ + 2^, v = ху + yz + zx, w = х + у + 2.
Доказать, что функции и, v, w зависимы, и найти уравнение, выражаю-
ш;ее их зависимость.
2. Исследовать вопрос о зависимости функций w = ^^ + Г|^ + ^^, i; = ^Г|^,
Задача 10. Функция и = и(х, у) называется гармонической в
плоской области, если во всех точках этой области она удовлетворяет
уравнению Аи = О (см. D1.109)). Доказать, что две гармонические функции
зависимы в плоской области тогда и только тогда, когда они линейно зависимы.
§43
Условный экстремум
43.1. Понятие условного экстремума
Пусть на открытом множестве G ^ R^ заданы функции
y, = f,ix), i=l,2,...,m, D3.1)
X = (Xj, ... , Xj^)eG. Обозначим через Е множество точек xeG, в
которых все функции /., /=1,2, ... , т, обраш;аются в нуль:
E = {x:f.ix) = 0, /=1, ...,m, хеО}. D3.2)
Уравнения
/.(х) = 0, /=1,2, ...,т, D3.3)
будем называть уравнениями связи.
371
Определение 1. Пусть на G задана функция у = f^ix).
Точка х^^^еЕ называется точкой условного экстремума*
функции /о(^) относительно (или при выполнении) уравнений
связи D3.3), если она является точкой обычного экстремума
этой функции, рассматриваемой только на множестве Е
(см. п. 40.1).
Иначе говоря, здесь значение функции f^ix) в точке х^^^
сравнивается не со всеми ее значениями в достаточно малой
окрестности этой точки, а только со значениями в точках, прина-
длежагцих одновременно указанной достаточно малой
окрестности и множеству Е. Как и в случае обычных экстремумов,
можно, естественно, рассматривать точки просто условного
экстремума и точки строгого условного экстремума. Точка
условного экстремума может быть либо точкой условного (строгого)
максимума, либо точкой условного (строгого) минимума.
Примеры. 1. Рассмотрим функцию
/(X, г/) = х2 + г/2 D3.4)
и уравнение связи
х + у-1 = 0. D3.5)
Найдем условный экстремум функции D3.4) при выполнении
уравнения связи D3.5). Из D3.5) имеем у = 1 - х, откуда
fix, 1 -х) = 2х2-2х+ 1.
Таким образом, при выполнении условия связи функция
D3.4) является функцией одного переменного. Ее экстремум
находится элементарно: приравнивая нулю ее производную
(необходимое условие экстремума), получим 2х - 1 = О,
откуда х = 1/2. В этой точке рассматриваемая функция, очевидно,
имеет минимум (она является многочленом второй степени
с положительным коэффициентом при стар гаем члене).
Значению X = 1/2, согласно уравнению связи D3.5), соответствует
г/= 1/2.
Следовательно, в точке A/2, 1/2) функция D3.4) достигает
минимума относительно уравнения связи D3.5).
Геометрически это означает, что точка параболоида 2 = х^ -\- у^, проекти-
руюгцаяся в точку A/2, 1/2), является самой низкой из всех
Принят также термин «относительный экстремум»
372
его точек, лежагцих над прямой D3.5) (рис. 43). Этот пример
показывает, что точка, в которой функция достигает
условного экстремума, не является, вообгце говоря, точкой
экстремума этой функции.
2. Рассмотрим функцию /(х, г/) = г/^ - х^ и уравнение связи
у = 2х. Имеем /(х, 2х) = Зх^, т. е. при выполнении уравнений
связи рассматриваемая функция также является функцией
одного переменного и, очевидно, достигает минимума при х = О
(рис. 44). Значению х = О, согласно уравнению связи,
соответствует значение г/ = О, а поэтому функция /(х, у) = у^ - х^
имеет в точке (О, 0) условный минимум относительно уравнения
связи у = 2х.
Следует заметить, что в этом случае сама функция /(х, у)
не имеет ни максимума, ни минимума ни в какой точке
плоскости. Таким образом, рассмотренный пример показывает,
что функция может не иметь экстремума, но при
определенных уравнениях связи может иметь условный экстремум.
В дальнейп1ем будем предполагать, что:
1) все функции /q, /j, ... , /^ непрерывно
дифференцируемы на открытом множестве G;
2) в рассматриваемой точке х^^^ векторы V/^, ... , V/^
линейно независимы, т. е. ранг матрицы Якоби
Эх,- )
^, у=1,2, ...,т, /=1,2, ...,я.
равен т — числу ее строк (строки матрицы Якоби являются
компонентами градиентов V/^, ... , V/^).
Рис. 43
2 = у^- Х^
Рис. 44
373
Согласно результатам предыдугцего параграфа, это
означает, что функции системы D3.1) независимы в некоторой
окрестности точки х^^\ Поскольку ранг матрицы не может быть
болыае числа столбцов, то из условия 2) следует, что т <: п.
Отметим, что в случае т = п, когда точка х^^^
удовлетворяет уравнениям связи D3.3), в некоторой окрестности этой
точки нет болыае точек, удовлетворяюгцих уравнениям связи.
Это следует из того, что отображение
f(x) = (/i(x), f^ix), ... , /Jx)), X = (Xi, ... , xJeG,
в силу неравенства нулю якобиана wi> ♦" > tjl ^ локаль-
Э(Х1, ... , xJl^^^o
но гомеоморфно (см. п. 41.7) в точке х^^\ Поэтому вопрос об
условном экстремуме в точке х^^^ сводится к вопросу об
экстремуме функции в изолированной точке ее множества
определения, т. е. вопросу, имеюпа;ему правильное penienne. Поэтому
в дальнейп1ем будем всегда предполагать, что т < п.
Согласно условию 2), в точке х^^^ хотя бы один из определи-
телей вида .г—^' '" ' "^ отличен от нуля. Пусть для определен-
Э(х, , ... , х^ )
1 т
ности в точке х^^^
d{f,,,„,fj
Э(Х1, ... , х^) '
Тогда при п> т,ио теореме о неявных функциях (см. п. 41.3),
систему уравнений D3.3) в некоторой окрестности точки
jr@) = (у.@) ^@L
МОЖНО разреп1ить относительно переменных х^, ... , х^\
D3.7)
Иначе говоря, супа;ествуют такие окрестности U = U(x^^^) nU =
= U(£^^^) точек х^^^ и £^^^ = (х^\ ^, х^\ 2' ••• ' ^^п^)
соответственно в пространствах R^ ий^""^, что точках = (х^, Хз, ... , х^) G U
удовлетворяет уравнениям связи D3.3) тогда и только
тогда, когда она имеет вид: х = (ф^(£), Ф2(£)? ... Ф^^С^)' ^)'
374
Подставив значения х^, ... , х^, заданные формулами D3.7) в
у = f^ix), т. е. рассмотрев композицию функции /q и ф^, ... , ф^,
получим функцию
def
"= g(x^+ „..., X J D3.8)
ОТ п - т переменных х^ + i, ... , х^, определенную и
непрерывно дифференцируемую в указанной выпхе окрестности U
точки £^^\
Поскольку, согласно теореме о неявных функциях,
условия D3.3) и D3.7) равносильны, справедливо следуюпа;ее
утверждение.
Точка х^^^ является точкой (строгого) условного
экстремума для функции /о(^) относительно уравнений связи
D3.3) 6 том и только в том случае, когда х^^"^ является
точкой обычного {строгого) экстремума функций D3.8).
Если х^^^ — точка обычного экстремума функции g, то она
является стационарной точкой этой функции (см. п. 40.1):
d^(£@)) = 0. D3.9)
Напомним, что дифференциал — линейная однородная
функция и его равенство нулю означает равенство нулю этой
функции при любых значениях ее аргументов, в данном случае —
при любых dx^ + 1, ... , dx^. Это возможно, очевидно, в том и
только в том случае, когда все коэффициенты при этих
аргументах, т. е. производные -—-—, й = 1, 2, ... , я - т, обрагца-
ются в нуль в точке х^^\ Условие D3.9) необходимо для
условного экстремума в точке х^^\
Таким образом, метод, основанный на репхении системы
уравнений D3.3), позволяет свести вопрос о нахождении
условного экстремума к уже изученному вопросу об обычном
экстремуме. Именно таким образом мы и поступали в
рассмотренных Bbinie примерах. Однако найти penienne системы
D3.3) в явном виде часто невозможно или весьма
затруднительно; поэтому желательно располагать методом, позволяю-
па;им находить условный экстремум, не репхая системы D3.3).
Этот способ изложен ниже.
^75
43.2. Метод множителей Лагранжа
для нахождения точек условного экстремума
В п. 43.2 предполагается, что все функции /q, /^, ... , /^
непрерывно дифференцируемы на открытом множестве G ^ й^,
п> т.
ТЕОРЕМА 1. Пусть х^^^ — точка условного экстремума
функции /q при выполнении уравнений связи D3.3). Тогда
в этой точке градиенты V/q, V/^, ... , V/^ линейно
зависимы, т, е, существуют такие, не все равные нулю, числа
Xq, \, ... , Х^, что
^oV/o + ^iV/i + ... + X^Vf^ = 0. D3.10)
СЛЕДСТВИЕ. Если в точке х^^^ условного экстремума
функции /q относительно уравнений связи D3.3) градиенты
V/j, ... , Vf^линейно независимы, т. е. ранг матрицы Якоби
^У j=l,2,..., т, i=l,2, ... ,п,
равен т, то существуют такие Х-^, ... , Х^, что в этой точке
т
V/o+E^Wy = 0, D3.11)
j -1
т. е. градиент V/q является линейной комбинацией
градиентов У f^, ... , V/^.
В координатной форме условие D3.11) имеет вид: для
любого i= 1, 2, ... , пв точке х^^^
функция
F(x)^=f^(x)+ f Xjfjix), D3.13)
где числа Х^, ... ,Х^ удовлетворяют условию D3.12),
называется функцией Лагранжа рассматриваемой задачи, а сами числа
Х-^, ... ,Х^ — множителями Лагранжа.
Условие D3.12) означает, что если х^^^ является точкой
условного экстремума функции /q относительно уравнений свя-
^76
зи D3.3), то она является стационарной точкой для функции
Лагранжа, т. е.
^^Х^ = 0, i = l,2,...,n. D3.14)
Иначе говоря,
dF(x@)) = 0.
Прежде чем доказать теорему, разъясним ее смысл и
покажем, как ее использовать для нахождения точек условного
экстремума. Прежде всего обратим внимание на то, что у
функции вида D3.13) при произвольных числах Я.^, ... , Х^
каждая точка ее условного экстремума является и точкой
условного экстремума исходной функции /q, и наоборот. Мы
выбираем такие значения Я.^, ... , Я^, чтобы выполнялись условия
D3.12), т. е. чтобы данная точка условного экстремума
оказалась и стационарной точкой функции D3.13).
Для отыскания точек условного экстремума следует
рассмотреть систему п -\- т уравнений D3.3) и D3.12)
относительно неизвестных х^^\ ... , x^^\ Я^, ... , Я^ и реп1ить ее (если это
окажется возможным), найдя х^^\ ... , х^^^ и по возможности
исключив \, ... , Я^. Сформулированная теорема утверждает,
что все точки условного экстремума будут находиться среди
найденных таким образом точек {х^^\ ... , х^О)). Вопрос о том,
какие же из них фактически будут точками условного
экстремума, требует дополнительного исследования; оно будет
проведено в пункте 43.5"^.
Доказательство теоремы. Докажем утверждение,
равносильное теореме: если в точке х^^^ = (х^^\ ... , х^^^), удовлетво-
ряюгцей уравнениям связи
4(х@)) = 0, й = 1,2, ...,т, D3.15)
градиенты V/q, V/^, ... , V/^ линейно независимы, то х^^^ не
является точкой условного экстремума.
Итак, пусть V/q, УД, ... , V/^ линейно независимы и,
следовательно, ранг матрицы Якоби [ ^ ], у = О, 1, ... , т, / = 1, 2, ... , п,
равен m + 1. Тогда в этой матрице сугцествует минор порядка
m + 1, не равный нулю. Для определенности будем считать,
что он образован первыми m + 1 столбцами, т. е.
Э(/о' /l' ••• ' fm)
377
^0. D3.16)
@)
Множество G — открыто, а поэтому супа;ествует такое бд > О, что
при всех 6, О < 6 < 6q, куб Qg = {х : \х. - х[^^| < 6, / = 1, 2, ... , п}
лежит в G, и, следовательно, на нем определены все
функции/q, Д, ...,/^.
Зафиксируем х^ + 2 ^ ^^ + 2' ••• ' ^п^ ^п^^ ^ введем следую-
па;ие обозначения:
X V^i? • • • ? ^^ + 1/'
Qm + i = {jc^: \х. - xW| < 6, / = 1, 2, ... , m + 1}.
Очевидно, функции/.(Xj,... , х^^^, х^^^ 2^... ,х^О)),у = 0, 1,... , т,
определены и непрерывно дифференцируемы всюду в Q^ + ^.
Рассмотрим отображение Ф: Q^ + 1 ^ Rm + 1^ задаваемое
формулами
^1 ^ /о(^1' ••• ' ^m + l' ^т + 2' ••• ' ^д )'
^2 ^ /IV^l? ••• ? ^т + 1' *^т + 2' ••• ' ^д )'
D3.17)
Ут + 1 'mV^l' ••• ' *^т +1' *^т + 2' ••• ' *^д )•
В силу D3.16), ДЛЯ ТОЧКИ х*^^^ = (х^^\ ... , х^\ ^) имеем
Э(г/1, ... , Ут+l)
d{Xi, ... , х^+ i)
Э(/о, /l, ... у fm)
^0.
X - х@)
Поскольку точка х^^^ является точкой условного экстремума,
она удовлетворяет уравнениям связи D3.3). Таким образом,
для точки х^^^ имеем Ф(х'^^^^) = (/о(л:^^^). О, ... , 0). Поэтому (см.
теорему 7 в п. 41.7 о локальной обратимости непрерывно
дифференцируемого отображения в точке, в которой его якобиан
не равен нулю) сугцествует такое 8 > О, что на окрестности
V={y = {y^,...,y^^^y.\y^-f^{x<^^))\<г^yj^<г,j = 2,г,...,ш + l)
(рис. 45, т = \, п = 2) определено обратное к Ф отображение,
и, следовательно, в любую точку этой окрестности
отображается какая-то точка из Q^ + ^.
В частности, поскольку при любом Г|, О < Г| < 8, имеет место
включение (/(х^^^) ± Г|, О, ... , 0)gF, то в кубе Qf^ ^ найдутся
точки х'* = (х[, ... , х^ + i) и х'''^ = (х'(, ... , х^ + 1)? отображаю-
гциеся при отображении Ф в указанные точки окрестности V:
378
У2
ei Y 1
I У I
\ • \
I I
J I
Рис. 45
Ф(х^') = (/(x@)) + л, 0, ... , 0), Ф(х^^') = (/(x@)) - л, О, ... , 0). Если
положим для краткости х' = (х[, ... , х^ + ^, л:^^+2, ... , л:^^^) и
х'' = (Хр ... , х^ + ^, х^^+ 2? ••• ? ^д^^)? то в координатной записи
(см. D3.17)) получим
4(х') = 0, k = l,2,...,m, x'eQg»
и
/о(х1 = /о(^^^>)-Л</(:^^'^),
4(х") = 0, й = 1,2, ... ,т, XGQf .
Поскольку число 6, о < 6 < 6q, может быть сколь угодно мало,
указанные выгае точки х' и х'' могут быть выбраны сколь
угодно близко от точки х^^\ и, таким образом, сколь угодно
близко от точки х^^^ имеются точки, удовлетворяюпа;ие
уравнениям связи, в которых функция /q принимает значения как
больп1ие, так и меньп1ие значения /q(x^^^). Это означает, что
точка х^^^ не является точкой условного экстремума.
Полученное противоречие доказывает теорему. П
Доказательство следствия. Если векторы УД, ... , V/^
линейно независимы, то в равенстве D3.10) имеем A.q ^ О, так
как в случае A.q = О указанные векторы, в силу D3.10),
оказались бы линейно зависимыми. Разделив обе части D3.10) на Xq,
получим равенство вида D3.11). П
ДЗ-З"". Геометрическая интерпретация метода Лагранжа
Дадим теперь некоторые геометрические пояснения к
теореме 1. Рассмотрим для простоты случай условного экстремума
функции двух переменных 2 = f(x, у) при выполнении
уравнения связи ф(х, у) = 0.
379
Пусть функции / и ф непрерывно дифференцируемы в ок-
рестности точки (х„ у,), ^<?(х„ у,) = {Щ^, ^-^1^] ^ О
И 9(Xq, i/q) = 0. в силу условия V9(Xq, i/q) ^ О, согласно теореме
о неявных функциях, уравнение ф(х, у) = О в окрестности
точки (Xq, i/q) задает некоторую гладкую кривую, обладаюгцую
явным представлением либо вида у = у(х), либо вида х = х(у).
Поскольку нас интересуют только достаточно близкие к (Xq, у^)
точки, то указанную кривую будем называть просто кривой
ф(х, у) = О (т. е., попросту говоря, всюду в дальнейгаем будем
рассматривать сужение функции / и ф на указанную
окрестность точки (Xq, i/q)).
Градиент Уф(Хо, г/д) является нормалью к кривой ф(х, у) = О
в точке (Xq, i/q) (п. 20.6). Обозначим через т единичный
касательный вектор к кривой ф(х, у) в точке (Xq, г/д). Пусть для
определенности рассматриваемая кривая задается уравнением у = у(х).
Если (Xq, i/q) — точка условного экстремума, то Xq является точкой
def
обычного экстремума для функции ^(х) = /(х, г/(х)) (см. п. 43.1),
и поэтому gXx) = О, т. е. производная функции / в точке (Xq, у^)
в направлении кривой ф(х, у) = О, или, что то же (см. п. 20.7),
в направлении вектора т равна нулю:
Щ^ = (VAxo, Уо), т) = 0.
Это означает ортогональность градиента V/(Xo, г/о) и
касательного вектора т, что равносильно коллинеарности
векторов V/(Xo, г/о) и Уф(Хо, г/о): V/(Xo, г/о) = ?^Vф(Xo, г/о), т. е.
выполняется условие D3.11). Выполнение этого условия в
точке условного экстремума можно пояснить и другим путем.
def
Пусть /(Хо, г/о) = с. Если в точке (Хо, г/о) не выполняется
условие D3.11), т. е. градиенты V/ и Уф не коллинеарны, то это
означает, что в этой точке V/ ^ О и линия уровня /(х, у) = с и
кривая ф(х, у) = О пересекаются в этой точке под некоторым
углом а, отличным от О и тг (рис. 46).
. ^ ^^ Поэтому в любой достаточно малой
""^^ "^ = ^ окрестности точки (Хо, г/о) часть
кривой ф(х, у) = О окажется
расположенной в области / < с (в «области мень-
П1ИХ значений»), а часть — в области
/ > с (в «области болыаих значений»).
380
О^
'<с
Рис.
Ф(:
\/(х,
46
^^у) =
= 0
У) = с
ф(х, у) = 0
fix, у) = с
Рис. 47
/(х, у) = с
f{x, у) = с
ф(х, I/) = о
Рис. 48
Это означает, что в точке (Xq, г/д) нет рассматриваемого
условного экстремума.
В случае же, когда векторы V/ и Уф коллинеарны, V/ = Я.Аф
часть кривой ф(х, у) = О может принадлежать некоторой
окрестности точки (Xq, i/q), целиком лежагцей в области меныаих
значений f < с (рис. 47) или в области больших значений f > с.
В этом случае в точке (Xq, i/q) достигается условный экстремум.
Однако в случае коллинеарности векторов V/ и Уф кривая
ф(х, у) = О также может оказаться расположенной в любой
достаточно малой окрестности точки (Xq, i/q) частично в области
меныаих, а частично в области болыаих значений функции /
(рис. 48) — тогда в точке (Xq, i/q) снова не будет условного
экстремума. Подобная ситуация возникает, например, когда
кривые /(х, у) = с и ф(х, у) = О имеют в точке (Xq, у^) обш;ую
касательную, причем кривая /(х, у) = с расположена в достаточно
малой окрестности точки (Xq, у^) по одну сторону от этой
касательной, а кривая ф(х, у) = О имеет в этой точке перегиб,
переходя с одной стороны касательной на другую.
Сказанное поясняет то обстоятельство, что D3.10) является
необходимым, но не достаточным условием
для условного экстремума.
Приведенные геометрические рассмотрения вопроса об
условном экстремуме распространяются и на многомерный случай.
ДЗ-Д"". Стационарные точки функции Лагранжа
В этом пункте будет дано описание стационарных точек
функции Лагранжа D3.13) посредством функции ^(х^ + ^, ... , х^),
введенной в п. 43.1 (см. D3.8)). Предварительно докажем
одну простую лемму из линейной алгебры.
Пусть задана система линейных однородных уравнений
a-iXi +
+ ^in^n
о,
1, 2, ... , т,
D3.18)
381
и егце одно линейное однородное уравнение
Ь^х^ + ... + Ь^х^ = 0. D3.19)
Систему уравнений, получаемую присоединением к системе
D3.18) уравнения D3.19), будем из^зыв^ть расширенной
системой D3.18)—D3.19).
ЛЕММА. Дл^ того чтобы расширенная система D3.18)—
D3.19) была равносильна основной системе D3.18),
необходимо и достаточно, чтобы уравнение D3.19) являлось
линейной комбинацией уравнений системы D3.18).
СЛЕДСТВИЕ. Для того чтобы уравнение D3.19) было линейной
комбинацией уравнений D3.18) или, что то же, чтобы вектор
b^=(b,,...,bj D3.20)
был линейной комбинацией векторов
а. = (a-i, ... , a.J, /=1,2, ... , m, D3.21)
необходимо и достаточно, чтобы каждое решение системы
D3.18) являлось решением уравнения D3.19).
Доказательство леммы. Пусть ранг матрицы (а.)
коэффициентов системы D3.18) равен т^. Очевидно, что т^ < т.
Если т^< т,то т - т^ уравнений системы D3.18) являются
линейными комбинациями остальных. Отбросив те m - т^
линейные уравнения, которые являются линейными комбинациями
оставп1ихся, получим систему из т^ линейно независимых
уравнений, равносильную системе D3.18), причем уравнение D3.19)
является линейной комбинацией уравнений системы D3.18)
тогда и только тогда, когда оно является линейной комбинацией
указанной системы из оставгаихся т^ уравнений. Поэтому будем
с самого начала считать, что m = ^q, т. е. что ранг матрицы (а-)
коэффициентов системы D3.18) равен т — числу уравнений
этой системы.
Пусть системы D3.18) и D3.18)—D3.19) равносильны. Это
означает, что пространства их регаений совпадают. Поскольку
все уравнения основной системы D3.18) входят в расгаиренную
систему D3.18)—D3.19), то каждое регаение расгаиренной
системы является и регаением основной системы, т. е.
пространство регаений расгаиренной системы содержится в пространстве
382
решений основной системы. Следовательно, совпадение этих
пространств равносильно равенству их размерностей.
Размерность s пространства репхений системы линейных
однородных уравнений равна, как известно, числу неизвестных п
этой системы, из которого вычтен ранг г матрицы
коэффициентов системы: s = п - г. Отсюда следует, что равносильность
систем D3.18) и D3.18)—D3.19) означает равенство рангов их
матриц. Ранг матрицы коэффициентов системы D3.18) по условию
равен т, т. е. векторы D3.21) линейно независимы.
Ранг матрицы коэффициентов расгаиренной системы
D3.18)—D3.19), согласно сказанному в naninx условиях,
также равен т. Поэтому векторы (см. D3.20) и D3.21))
Ь, ai, ...,а^ D3.22)
линейно зависимы. Это означает, что b является линейной
комбинацией векторов а^, ... , а^.
В самом деле, линейная зависимость векторов D3.22)
означает, что супа;ествуют такие числа jIq, ji^, ... , ji^, не все равные
нулю, что
ЦоЬ + ^1^1 + ... + [i^a^ = 0. D3.23)
Здесь заведомо jIq ^ О, так как в противном случае векторы
а^, ... , а^ оказались бы линейно зависимыми. Поделив
равенство D3.23) на jIq, получим, что b является линейной
комбинацией векторов а^, ... , а^.
Обратно, если b является линейной комбинацией векторов
D3.21), то в системах векторов D3.21) и D3.22) имеется в
точности по т линейно независимых векторов, т. е. ранги матриц
коэффициентов систем уравнений D3.18) и D3.18)—D3.19) равны.
Итак, условие, что вектор b является линейной
комбинацией векторов D3.21):
Ь = \а^ + ... + Х^а^,
эквивалентно равенству рангов матриц коэффициентов
рассматриваемых основной и расп1иренной системы уравнений,
следовательно, эквивалентно их равносильности. П
Утверждение следствия сразу следует из леммы,
поскольку системы D3.18) и D3.18)—D3.19), очевидно, равносильны
тогда и только тогда, когда каждое penienne системы D3.18)
является и реп1ением уравнения D3.19) — остальные
уравнения этих систем просто совпадают. П
383
Замечание 1. Доказанная лемма и ее следствия
имеют простую геометрическую интерпретацию в я-мерном е в-
клидовом векторном пространстве R^, т. е. в я-мерном
пространстве со скалярным произведением. Используя
обозначение скалярного произведения, систему D3.18) можно
записать в виде
(а.,х) = 0, /=1,2, ...,т, D3.24)
а уравнение D3.19) — в виде
(Ь, х) = О, D3.25)
где векторы а^, ... , а^ и Ь определены формулами D3.20) и
D3.21), ax = (Xi, ... , xj.
Множество всевозможных линейных комбинаций
векторов а^, ... , а^ образует подпространство пространства R^ и
называется подпространством, натянутым на эти векторы.
Обозначим его через L(a^, ... , а^).
Множество реп1ений системы D3.24) состоит из всех
векторов X, ортогональных подпространству L(a^, ... , а^).
Обозначим это множество репхений через Т. Оно также является
подпространством пространства R^.
def
ПодпространстваL = L(a^, ... , а^) и Т называются
ортогональными дополнениями друг к другу в пространстве R^.
Представимость вектора b в виде линейной комбинации
векторов а^, ... , а^ равносильна его принадлежности
подпространству L = L (а^, ... , а^) пространства R^: beL. Это
условие, в свою очередь, равносильно ортогональности вектора b
подпространству Т: b J- Т, которая означает, что для всех хе Т
имеет место равенство (Ь, х) = О, т. е. что любое penienne х
системы D3.24) является реп1ением уравнения D3.25). Это и
является утверждением следствия леммы.
Замечание 2. Напомним метод, которым можно
получить все реп1ения однородной системы линейных уравнений.
Пусть система D3.18) состоит из линейно независимых
уравнений. Тогда ранг матрицы его коэффициентов равен т. Это
означает, что сугцествует минор этой матрицы порядка т, не
равный нулю. Пусть для определенности
«11 ••• ^1т I
Ыо. D3.26)
^ml ••• ^тт \
384
в этом случае все репхения системы D3.18) можно получить,
задавая произвольно последние п—т координаты вектора
(Xj, ... , х^). Остальные координаты однозначно находятся из
системы уравнений D3.18). В самом деле, возьмем
произвольное penienne {х^^\ ... , х^^^) системы D3.18). После подстановки
^т + 1^ ^т\ 1' ••• ' ^п ^ ^д^^ ^ D3.18) получится система из т
линейных уравнений (с т неизвестными х^, ... , х^), матрица
коэффициентов которой, в силу условия D3.26), невырожденная.
Поэтому супа;ествуют единственные значения х^, ... , х^, удовлетво-
ряюпа;ие получивпхейся системе. Поскольку (х^^\ ... , х^^^) также
было реп1ением системы D3.18), то х^ = х^^\ ... , х^ = ^^^*
Перейдем теперь к анализу стационарных точек функции
Лагранжа.
ТЕОРЕМА 2. Пусть функции fo, fi, --- , fm непрерывно
дифференцируемы в области G ^ R^, x^^G, /^(х^^^) = О, / = 1, 2, ... , т,
и ранг матрицы Якоби функций Д, ... , /^ в точке х^^"^равен т.
Для того чтобы в точке х^^^ = (х^^\ ... , х^^^) градиент
V/qявлялся линейной комбинацией градиентов УД, ... , V/^, необходимо и
достаточно J чтобы точка х^^^ = (^^+ !'•••' ^1^^) была
стационарной точкой для функции g{x) = ^(х^ + j, ... , х^) (см. D3.8)).
Напомним, что если в точке х^^^ градиент V/q является
линейной комбинацией
^fo = K^fi + - + K^L D3.27)
градиентов V/^, ... , V/^, то это равносильно тому, что сугцест-
вует функция Лагранжа
F = fo-Kfi---KL' D3.28)
ДЛЯ которой точка х^^^ является стационарной:
Эх,-
О, i=l,2, ... ,п. D3.29)
Это просто координатная запись условия D3.27), так как, в
силу D3.28),
385
Доказательство. По условию ранг матрицы Якоби
системы функций /j, ... , /^ в точке х^^^ равен т. Будем считать
для определенности, как и в п. 43.1, что
Э(/1, ... , fj
d{Xi, ... , х^)
^0. D3.30)
ДО)
Подставим в уравнение связи D3.3) функции D3.7), являю-
па;иеся репхением этих уравнений, и продифференцируем полу-
чивп1иеся относительно переменных х^ + ^, ... , х^ тождества.
Получим для точки (£^^)) равенства й/^(£^^^) = О, i = 1, 2, ... , т,
справедливые для любых прирапа;ений dx^^ i? ... ? dx^
независимых переменных x^ + i, ... , х^ (напомним, что
дифференциал является линейной функцией, определенной на всем
пространстве). Использовав инвариантность формы первого
дифференциала относительно выбора переменных, получим, что в
точке х^^^ выполняются равенства
i= 1, 2, ... , т,
где dx^^ 1, ... , dx^ произвольны, а dx^, ... , dx^ находятся из
формул D3.7). Таким образом, вектор
dx = (dx^, ... , dx^, (ix^ + j, ... , dx^) D3.32)
является регаением линейной однородной системы D3.31).
Отметим, что в силу условия D3.30) значения
при заданных dx^ + j, ... , dx^ однозначно находятся и из
системы D3.31). Из замечания 2 следует также, что указанным
способом получаются все регаения системы D3.31).
Стационарность точки £^^) для функции g{ic) = g(x^ + ^, ... , xj
означает, что dg(£^^^) = 0. Это равенство, в силу
инвариантности формы первого дифференциала, можно более подробно
записать в виде
^ dx. + ... + 1^ dx^ + =^^^ rfx^ +1 + ... + ^dx= О, D3.33)
где dXjj^ + 1, ... , dXj^ можно задавать произвольно, а dx-^, ...
... , dXjj^ следует находить из формул D3.7) или, что дает тот
же результат, из формул D3.31). Иначе говоря, любое penie-
386
ние системы уравнений D3.31) является и регаением
уравнения D3.33). Согласно следствию из леммы, это возможно
тогда и только тогда, когда уравнение D3.33) является линейной
комбинацией уравнений системы D3.31), т. е. когда супа;ест-
вуют такие числа Х-^, ... , Х^, что
Замечание 3. Согласно замечанию 2, совокупность
всех реп1ений системы уравнений D3.31) образует
подпространство Т пространства R^, являюпа;ееся ортогональным
дополнением к подпространству L = L(Vf-^, ... , V/^). Любой
вектор уе Т ортогонален каждому градиенту V/., а поэтому его
естественно назвать касательным вектором в точке х^^^ к
гиперповерхности /Дх) = О, являюпа;ейся множеством уровня
(см. § 19) функции /., / = 1, ... , т.
Таким образом, пространство репхений Т системы D3.31)
состоит из векторов, касательных одновременно ко всем
гиперповерхностям /.(х) = О, / = 1, ... , т, и поэтому его
называют касательным пространством пересечения всех
гиперповерхностей /.(х) = О, / = 1, 2, ... , т. Напомним, что векторы
касательного пространства Т, т. е. регаения системы D3.31),
были обозначены через dx (см. D3.32)).
Поскольку в точке условного экстремума, согласно
теореме 2, имеет место включение
VfoeL = LiVf^,...,VfJ, то Vf^-LT.
Иначе говоря, градиент V/q одновременно ортогонален всем
касательным dx к гиперповерхностям /.(х) = 0,/=1,2,...,т:
(V/q, dx) = О
(это другая запись уравнения D3.33)), т. е. градиент V/q
перпендикулярен касательному пространству Т в точке х^^^. Но
множество всех векторов, ортогональных к V/q, образует (п - 1)-мерное
подпространство Tq, называемое касательным пространством
к гиперповерхности /q(x) = /q(x^^^). В силу сказанного выгае,
каждый вектор из Т, будучи ортогонален градиенту V/q,
принадлежит к Tq, т. е. Т ^ Tq.
Итак, если х^^^ — точка условного экстремума, то Т ^ Tq,
т, е, касательное пространство в точке х^^^ пересечения всех
гиперповерхностей, задаваемых уравнениями связи,
содержится в касательном пространстве в той же точке
гиперповерхности /q(x) = /q(x^^^).
^87
Замечание 4. Из теоремы 2 епа;е раз вытекает
следствие теоремы 1. В самом деле, если х^^^ является точкой
условного экстремума, то £^^^ является точкой обычного
экстремума для функции g (см. п. 43.1) и, следовательно, ее
стационарной точкой. Поэтому, согласно теореме 2, точка х^^^ является
стационарной точкой для функции Лагранжа, т. е.
выполняется условие D3.14) или, что то же самое, условие D3.11).
43.5*. Достаточные условия
для точек условного экстремума
В этом пункте также будем предполагать выполненными все
предположения, наложенные на функции /q и /., / = 1, 2, ... , т,
в п. 43.1. Пусть
т
i = 1
— функция Лагранжа (см. D3.13)) для функции /q и
уравнений связи D3.3). Пусть x^^^eG удовлетворяет уравнениям
связи D3.3) и является стационарной точкой функции
Лагранжа, т. е. точкой, координаты которой удовлетворяют системе
уравнений D3.12) и D3.3). Нагаей целью является получение
метода, с помогцью которого можно установить условия,
достаточные для того, чтобы х^^^ являлась точкой условного
экстремума рассматриваемой задачи.
Заметим прежде всего, что если точка xeG удовлетворяет
уравнениям связи D3.3), то
А/ = f(x) - /(х@)) = F(x) - F(x@)) = AF. D3.34)
Отсюда сразу видно, что если х^^^ является точкой обычного
экстремума для функции F, т. е. AF не меняет знака в некоторой
окрестности точки х^^\ то х^^^ является точкой условного
экстремума для функции /q. Действительно, из D3.34) следует в этом
случае, что прирагцение A/q для допустимых значений х, т. е.
удовлетворяюпа;их уравнениям связи, также не меняет знака.
Это достаточное условие, однако, накладывает слип1ком
сильное ограничение на поведение функции Лагранжа F(x) в
рассматриваемой точке — она должна иметь обычный экстремум, что
сильно сужает область возможного применения указанного
условия при регаении задач. Поэтому целесообразно получить более
обгций достаточный признак условного экстремума.
Пусть функции /о' Л' ••• ^ fm Дважды непрерывно
дифференцируемы в окрестности точки х^^^ и градиенты V/^, V/2, ... , V/^
линейно независимы в этой точке.
388
ТЕОРЕМА 3 (достаточные условия для условного
экстремума). Пусть точка х^^^ удовлетворяет уравнениям связи и
является стационарной точкой функции Лагранжа, т, е,
^-1^ = 0, i=h2,...,n. D3.35)
Если второй дифференциал
функции Лагранжа в точке х^^^ принимает только
положительные {отрицательные) значения при всех значениях dx^,
не равных одновременно нулю и
удовлетворяющих продифференцированным уравнениям связи D3.3), т. е.
уравнениям
й = 1, 2, ... ,п, D3.36)
то точка х^^^ является точкой строгого условного минимума
(максимума). Если при тех же ограничениях на значения
дифференциалов dx-^, dx2, ... , dx^ второй дифференциал функции
Лагранжа принимает как положительные, так и
отрицательные значения, то в точке х^^^ условного экстремума нет.
Доказательство. Из линейной независимости
градиентов V/j, V/2, ... , V/^ следует, что ранг матрицы Якоби ( ^ ]
равен т, т. е. у этой матрицы сугцествует не равный нулю минор
порядка т. Пусть для определенности
Э(/1, /2' ••• ' fm)
^0. D3.37)
@)
Тогда в некоторой окрестности точки х^^^ переменные х^, ^2, ...
... , х^, в силу уравнений связи
4 = 0, й = 1,2, ...,т, D3.38)
являются функциями переменных ^m + i^ ^т + 2^ *" •> ^п*
Ч = ^Мт + 1^^т + 2^ ••• '^J' Й= 1,2, ... ,т, D3.39)
т. е. являются регаениями системы уравнений D3.38).
Воспользуемся тем, что точка х^^^ = {^^i\ ^^2"^^ ••• ? л:^^^)
является точкой строгого условного экстремума функции при
выполнении уравнений связи D3.38) тогда и только тогда,
^89
когда точка £^^^ = (^т + i' ^m + 2' ••• ' ^i^^) является точкой
обычного строгого локального экстремума для функции
*^ ^ v^m +1' *^т +2' ••• ' *^д)' Dо.40)
ДЛЯ этого, согласно теореме 2 п. 40.2, достаточно, чтобы
d/o(^@)) = о, D3.41)
а второй дифференциал A^г^(£^^^) был знакоопределенной
квадратичной формой. Вычислим эти дифференциалы. Для удобства
функции /^, й = 1, 2, ... , т, в которых переменные х^, ^2, ... , х^
являются функциями D3.39) переменных х^ + ^, х^ + 2' ••• ' ^п^
будем обозначать /^:
/fe ^ 4 (9l(^)' (Ф2(^)' ••• 'Фт(^)'^т + 1' ••• '^J' Й=1, 2, ... ,т.
Пусть
^ = /о+ Е V. D3.42)
fe = 1
— функция Лагранжа для точки х^^\ т. е. координаты х^^\
х^ \ ... , х^^^ этой точки и числа Х-^, Я.2, ... , Я.^ являются penienn-
ем системы уравнений D3.3) и D3.12), и пусть F = г^+ У '^у^/у^»
fe = 1
Подставив D3.39) в D3.38), получим тождества /^ = О, й =
= 1, 2, ... , т, продифференцировав которые в точке £^^\ получим
(i/^ = 0, k = l,2, ... ,т, D3.43)
т. е., в силу независимости формы записи первого
дифференциала от выбора переменных,
f ^ dx. = О, k = l, 2, ... , т. D3.44)
Здесь dx^ + i, rfx^ + 2' ••• ' ^^д являются дифференциалами (при-
рапа;ениями) независимых переменных, а dx^ = йф^(£), ЙХ2 =
= йф2(£), ... , (ix^ = йф^(£) — дифференциалами функций.
Вычислим первый дифференциал функции /q в точке х^^^:
^^0 D3=43) ^^0 + J^ К dh = d(h + J^ Kh) D3=42) ^^ =
= и/-Ч4Гз5H- D3.45)
390
(В конце проведенной выкладки была снова использована
независимость формы записи первого дифференциала от выбора
переменных.)
Дифференцируя тождества D3.43), получим
^2/^ = 0, й = 1,2, ... ,т, D3.46)
где по-прежнему дифференциалы dx^, dx2, ... , dx^ связаны со-
отногаениями D3.44). Теперь для второго дифференциала
функции D3.40) имеем
^'^0D3=46) ^'^0 + t^ К d4u = d4h + i^ Kh) D3=42) ^'^ =
- d(d^) - it, I d\ - I ^ э^. <^-i d-> + X, I d'-^ D3Г35)
Итак,
dHoim= t ^-B^dx.dxj, D3.47)
где дифференциалы dx-^, dx2, ... , dx^^ удовлетворяют соотно-
гаениям D3.44).
Поэтому если дифференциалы dx-^, dx2, ... , dx^, не все
равные нулю, связаны соотногаениями D3.44) и для них
то, в силу D3.47), для дифференциалов dx^ + j, ^л:^ + 2? ••• ? dx^
будем иметь d^rQ(£^^^) > 0. При этом не все эти дифференциалы
равны нулю. В самом деле, условие D3.37) означает, что
определитель системы линейных относительно дифференциалов
dx-^, dx2, ... , dXj^ уравнений D3.44) не равен нулю, поэтому
указанная система однозначно разрегаима относительно
дифференциалов dx^, dx2j ... , dx^ и, следовательно, эти
дифференциалы являются линейными комбинациями дифференциалов
^^т +1' ^^т + 2' ••• ' ^^п* Отсюда И вытекает, что в случае
равенства нулю всех дифференциалов dx^ + ^, dx^ + 2' ••• ' ^^п были
бы равны нулю вообгце все дифференциалы dx^, dx2, ... , dx^.
Из сказанного следует, что точка £^^^ является точкой
строгого локального минимума для функции /q, поэтому точка
х@) — точка строгого условного минимума для функции / при
выполнении уравнений связи D3.38).
391
Аналогично с помош;ью той же теоремы 2 п. 40.2
получаются достаточные условия для точки строгого условного
максимума и для отсутствия условного экстремума. П
Таким образом, чтобы исследовать стационарную точку
функции Лагранжа D3.13) на условный экстремум, надо
исследовать на определенность квадратичную форму D3.39),
т.е. второй дифференциал функции Лагранжа в этой точке при
выполнении условий связи D3.3) (когда дифференциалы dx-,
/ = 1, 2, ... , я, связаны соотноп1ениями D3.31)). При этом
следует иметь в виду, что если второй дифференциал функции
Лагранжа в рассматриваемой точке окажется положительно
(отрицательно) определенным и без выполнения условий
связи, то он будет таковым, конечно, и при их выполнении.
Пусть, например, требуется найти точки экстремума
функции /(х, у) = ху, когда точка (х, у) лежит на прямой х - у = 0.
Функцией Лагранжа в данном случае является функция
F(x, у) = ху - Х(х - у), и так как — = у - X, — = х -\- X, то для
определения стационарных точек функции F(x, у), удовлетво-
ряюпа;их условиям связи, имеем систему уравнений
X - у = О, у -Х = О, X -\- Х = О,
из которых следует, что х = у = Х = 0.
Исследуем в точке (О, 0) второй дифференциал функции
F(x, у) при выполнении условий связи, т. е. когда dx - dy = 0.
Имеем
d^F=2dxdy, D3.48)
и, значит, при выполнении условий связи
d^F = 2dx^>0, D3.49)
т. е. второй дифференциал D3.48), являясь неопределенной
квадратичной формой, при выполнении условий связи пре-
врапа;ается в положительно определенную квадратичную
форму D3.49). Поэтому (О, 0) является точкой строго условного
минимума для рассмотренной задачи. Впрочем, в данном
случае это легко усмотреть и сразу: вдоль прямой х - у = О
функция /(х, у) = ху примет вид /(х, х) = х^, имея, очевидно, в
точке х = О строгий минимум.
392
5
Глава
Интегральное исчисление
функций многих переменных
§44
Кратные интегралы
44.1. Понятие объема в п-мерном пространстве
(мера Жордана). Измеримые множества
Напомним кратко основные понятия, связанные с
определением я-мерного объема (плопа;ади в случае я = 2), и дадим
новое определение понятия объема (меры) множества, которое
будет отличаться от введенного ранее (см. п. 27.1).
Пусть R^ — я-мерное евклидово пространство точек х =
= (Xj, ... , х^), где Х-, i = 1, 2, ... , п, — координаты точки х в
некоторой фиксированной системе координат (я = 1, 2, 3, ...).
Множество точек xeR^, координаты х-, i = 1, 2, ... , п,
которых удовлетворяют линейному уравнению вида
a^Xj + ... + а^х^ -\- а^ = О, af -\- ... -\- а^> О
(а-— фиксированные числа, i = 1, 2, ... , п), называется
гиперплоскостью в пространстве R^. При п = 3 понятие
гиперплоскости совпадает с понятием обычной плоскости в пространстве R^.
Семейство всевозможных гиперплоскостей
X. = ^, т = 0, ±1, ±2, ... , /=1,2, ...,я
(k — фиксировано, й = О, 1, 2, ...), «разбивает» пространство
R^ на я-мерные замкнутые кубы вида
Qn = \x:^^<x,< ^^, /=1,2,..., п\ D4.1)
I 10^ 10^ J
где т. при / = 1, 2, ... , я пробегают независимо друг от друга
множество всех целых чисел.
^93
Кубы D4.1) называются кубами ранга k, и их
совокупность обозначается через Т^, k = О, 1, ... .
Множество всех кубов ранга k, очевидно, покрывает все
пространство, т. е.
R^= и Q^.
Два куба одного ранга могут иметь в качестве обпа;их точек лип1ь
некоторые свои граничные точки. В случае п=1 куб D4.1)
является, очевидно, отрезком, а в случае п = 2 — квадратом.
1
Число
10^
называется я-мерным объемом (я-мерной
мерой) куба D4.1) и обозначается через jiQ^:
Для множества aS, представляюпа;его собой объединение
конечного или счетного числа различных кубов Qj^ данного ранга k,
У=1,2, ...:
его я-мерный объем (я-мерная мера) \xS определяется равенством
^iS'^'^^iQf.
D4.2)
Очевидно, [iS — неотрицательное число или +оо.
Мера \х пустого множества 0 по определению полагается
равной нулю: [10 = 0.
Пусть теперь Е — произвольное множество в й^. Обозначим
через s^ = ^k(^) множество точек всех
я-мерных кубов ранга k, целиком ле-
жагцих в ^, а через aS^ = 'S^(^) —
множество точек всех я-мерных
кубов ранга k, каждый из которых
пересекается с множеством Е по
непустому множеству (й = О, 1, 2, ...):
и Q^,
и
0\ Q-eT,.
D4.3)
Рис. 49
Таким образом, все кубы ранга k,
содержагциеся в s^, лежат во
множестве Е, а кубы ранга k,
содержагциеся в aS^, образуют покрытие
множества Е (рис. 49), т. е.
sJE) с £ с SJE).
394
При этом множество Е лежит «строго внутри»
многогранника aS^ = Sf^(E), т. е. не пересекается с его границей Эа8^.
Действительно, точка хеЕ П dSj^ не может суш;ествовать, так как,
будучи граничной для aS^, она принадлежала бы грани
некоторого куба ранга k. Поскольку рассматриваемые кубы
замкнуты, по определению многогранника aS^ к нему
принадлежали бы и все кубы ранга k, содержапа;ие указанную грань,
ибо она содержит точку хеЕ. Тем самым эта точка не была
бы граничной для aS^.
Очевидно,
s^c^s^c^ ...^s,^s,^^^ ..., aSo =^ Si =^ ... =. S, =^ aS, + 1=^ ...
и, следовательно, в силу определения D4.2),
[isq < lasi < ... < [iSf^ < las^ + 1 < ... ,
^aSo>^Si>...>^aS,>^aS, + i>....
Для дальнейгаего сугцественно, что, в силу включения s^ ^ aS^,
для всех й = О, 1, 2, ... выполняются неравенства jis^ < jIaS^.
Таким образом, получились две монотонные
последовательности, членами которых являются элементы расгаирен-
ного множества действительных чисел R (см. п. 2.5), а
именно, либо неотрицательные действительные числа, либо +оо.
Поэтому для любого множества Е ^ R^ всегда сугцествуют
конечные или бесконечные пределы
при этом, в силу неравенств jis^ < jIaS^, выполняется
неравенство
ОпреАеАеи]ле Л. Конечный или бесконечный предел lim \xSf^(E)
называется нижней или внутренней п-мерной мерой Жорда-
на множества Е и обозначается через \i^E:
ц.^^^'Дт^Ц8,(^), D4.4)
а предел lim \iSJ^E) называется верхней или внешней
п-мерной мерой Жордана множества Е и обозначается через \1*Е:
ц*£ =\lim^^S,(£). D4.5)
'395
Ясно, что
о < ц^^ < [i^'E.
Если нижняя [i^E и верхняя [i^E меры множества Е
конечны и совпадают, то оно называется измеримым по Жорда-
ну. Общее значение нижней и верхней меры Жордана
измеримого множества Е обозначается через \iE и называется
п-мерной мерой Жордана или п-мерным объемом множества Е:
[iE = [i^E = [i''E. D4.6)
Иногда вместо [lE будем писать [i^E, для того чтобы
подчеркнуть, что речь идет о мере множества Е,
рассматриваемого как подмножество именно я-мерного пространства.
В дальнейгаем для простоты меру Жордана будем часто
называть просто мерой, sl множество, измеримое по Жордану,
просто измеримым.
Под измеримым множеством, как это показывает сам
смысл слова «измеримый», в математике подразумевается
такое точечное множество в й^, которое можно каким-то
образом измерить, т. е. сопоставить ему, по определенным
правилам, некоторое неотрицательное число, являюгцееся
объемом в трехмерном случае, плогцадью в двумерном и длиной
в одномерном. Если размерность пространства п > 3, то
множество, измеримое по Жордану в этом пространстве,
называется также кубируемым, а в случае п = 2 — квадрируемым.
Термины «кубируемое и квадрируемое множество» отражают
тот факт, что указанное выгае измерение множества осу-
гцествляется посредством кубов, соответственно квадратов.
Простым вычислением нетрудно проверить, что если
множество Е представляет собой объединение конечного числа
различных я-мерных кубов (п = 1, 2, ...) данного ранга, то
оно измеримо и его мера Жордана совпадает с мерой,
определенной равенством D4.2).
Отметим епа;е, что легко также устанавливается
измеримость открытых и полуоткрытых я-мерных кубов с ребрами
длины Л, т. е. кубов, задаваемых при каждом i = 1, 2, ... , п
одним из неравенств вида х^^ < х- < х|^^ + Л, или х^^ < х- <
< х|^^ + h, или х|^^ < ^j ^ ^1^^ + Л и равенство \xQ = h^.
Для любого множества Е при каждом й = О, 1, 2, ... ,
очевидно,
[is^iE) > О, [iS^(E) > 0.
Перейдя к пределу при k ^ оо, получим \у.^Е > О, ц*£ > 0.
Отсюда вытекает следующее свойство меры Жордана.
^96
1^. Для всякого измеримого множества \iE > 0.
Далее заметим, что в силу определений D4.4) и D4.5) для
любого множества Е определена конечная или бесконечная
нижняя и верхняя меры Жордана, при этом
0<\1.,Е< ц^^.
Отсюда очевидным образом следует, что если верхняя мера
множества Е равна нулю, \i^E = О, то множество Е измеримо
vL\iE = 0.
Если у множества Е имеется внутренняя точка, то
найдется такой номер ^q, что множество s^ {Е) будет непустым;
следовательно, jis^ {Е) > О, откуда, в силу D4.3), D4.4) и D4.6),
будет следовать, что \i^E > 0. В самом деле, если х —
внутренняя точка множества Е, то сугцествует такое 8 > О, что
сферическая окрестность С/(х, 8) содержится в Е. Поэтому
достаточно взять такой ранг k^, чтобы длина диагонали куба"^
ранга ^Q была меныае 8:
10"^oV^ < 8.
Тогда куб Q^ ранга к, содержапа;ий точку х (такой куб, по
крайней мере один, всегда супа;ествует) будет целиком лежать
во множестве s^ {Е) (рис. 50). Поэтому jis^ {Е) > \iQ^ > 0.
Таким образом, если у множества Е имеется внутренняя
точка, то его нижняя мера положительна: \)i^E > jis^ {Е) > 0.
В частности, нижняя мера Жордана любого открытого
множества G всегда положительна: \хМ > 0.
Верно и обратное утверждение: если
[i^E > О, то у множества Е супа;ествуют
внутренние точки. В самом деле, в этом случае
lim \xsJE) = \x.j,E > 0; следовательно, су-
па;ествует такой номер k^, что jis^ (Е) > 0.
Это означает, в частности, что множество
s^ (Е) не пусто, а так как оно, состоя из
я-мерных кубов, имеет внутренние точки и
s^ (Е) ^ ^, то и множество Е имеет
внутренние точки. Рис. 50
Напомним, что диагональ я-мерного куба с ребром длины а равна
а J п.
397
Отметим, что определенный нами ранее в п. 27.1 объем
открытого множества совпадает с его нижней мерой Жорда-
на. Однако для построения достаточно обгцего аналога
интеграла Римана в случае функций многих переменных понятие
только нижней меры Жордана оказывается недостаточным.
Для этой цели очень удобно понятие измеримого по Жордану
множества.
Если множество Е ограничено, то [i^E и [i*E всегда
конечны. Действительно, из ограниченности множества Е следует,
что оно пересекается только с конечным множеством кубов
нулевого ранга и, следовательно, Sq(E) состоит из конечного
числа кубов. Поэтому, согласно D4.2), [18^(Е) < + оо. Но при
любом k = О, 1, ...
s,(E) ^ S,(E) ^ S^(E).
Поэтому
Отсюда, перейдя к пределу при й ^ + оо^ получим
О < М^) < [^ЧЕ) < [iS^iE) < + оо,
т. е. меры [i^E и [i*E конечны.
Если же множество Е неограничено, то для любого k =
= О, 1, 2, ... множество Sf^(E) состоит из бесконечного
количества кубов ранга k. Поэтому, в силу формулы D4.2), для
всех k имеем [iSf^(E) = + оо^ следовательно, и [i*E = + оо^ т. е.
множество Е заведомо не измеримо. Отсюда: если множество
измеримо по Жордану, то оно ограничено.
Как было отмечено выгае, в п. 27.1, при определении пло-
гцади плоских множеств мы ограничились лигаь внутренней
мерой открытых множеств. Для случая измеримых и,
следовательно, ограниченных множеств внутренняя мера
совпадает с мерой. Однако внутренняя мера может быть конечной и
для неограниченных множеств (это обстоятельство
использовалось при выяснении геометрического смысла
несобственных интегралов) и, конечно, в этом случае внутренняя мера
не является мерой Жордана.
Как нижняя, так и верхняя меры Жордана обладают так
называемым свойством монотонности.
Сформулируем его в виде леммы.
ЛЕММА 1. Если Е^ ^ ^2' ^^
398
Это вытекает непосредственно из того, что при всех k =
= О, 1, 2, ... справедливы включения
s,(E,)^s,(E,), S,(E,)^S,(E,), D4.8)
так как первое из них означает, что куб ранга k, лежагций в
Е-^, лежит и в ^2' ^ второе — что куб ранга k, пересекаюгцийся
со множеством Е-^, пересекается и с ^2» И то, и другое
утверждение следует из включения Е^ ^ ^2» Из D4.8), в силу D4.2),
вытекает справедливость неравенств
Ц8,(Е^) < [is.iE^), Ц8,(Е^) < [iS.iE^).
Устремив здесь й к + оо^ получим в пределе D4.7). П
СЛЕДСТВИЕ. ЕслиЕ^ ^ Е^и\уЕ^ = 0, mo[iE^ = 0.
Действительно, в силу леммы 1,
О < la^^i < |а^^2 = 1^^2 = 0.
Следовательно, [I'^E^ = О, откуда \хЕ^ = 0. П
Из леммы 1 для измеримых множеств вытекает следую-
гцее свойство.
2^ (монотонность меры). Если Е^ и Е2 — измеримые по
Жордану множества и Е^ ^ Е^, то
11^1 < 11^2- D4.9)
ЛЕММА 2 (полуаддитивность верхней меры). Для любой
конечной совокупности множеств Е-^, Е^, ... , Е^ имеет место
неравенство
\i\\J^E.< f^\i"E. D4.10)
Доказательство. Для любого ранга й = О, 1, 2, ...
справедливо равенство
В самом деле, каждый куб ранга к, который пересекается с мно-
т
жеством . У е., пересекается хотя бы с одним из множеств Е-, и
наоборот. Поэтому, в силу D4.2),
Перейдя здесь к пределу при k ^ + оо, получим D4.10). П
399
СЛЕДСТВИЕ. Объединение конечного числа множеств меры
нуль имеет меру нуль.
Действительно, если ц^. = О, j = 1, 2, ... , m, то в силу
D4.10),
т
Следовательно, множество U Е- измеримо и его верхняя ме-
ра, поэтому и мера равны нулю:
т
'^ j = 1 J
УПРАЖНЕНИЯ. 1. Показать, что объединение счетной совокупности
множеств жордановой меры нуль может не иметь меру нуль.
2. Доказать, что если Е-^^и Е2 — открытые множества, то
|а^ (Е^ и Е^) < 11*^1 + 11*^2-
(Указание. Полезно воспользоваться теоремой 5 из п. 35.3.)
Будет ли это неравенство всегда справедливым, т. е. без
предположения об открытости множеств Е-^ и ^2*^
3. Привести пример таких непересекаюпдихся множеств Е-^ и ^2> ^^о
^l" (Е^ и Е^) ^ ^"Е^ + ^Х-
Рассмотрим теперь связь между измеримостью множества
и мерой его границы. Предварительно сделаем несколько
замечаний.
Замечание 1. Любое объединение конечного или
бесконечного множества кубов данного ранга является
замкнутым множеством.
Действительно, пусть {Q.} — конечное или бесконечное
множество кубов данного ранга k,
E = IJQ, D4.11)
ji хеЕ (как всегда, Е обозначает замыкание множества Е).
Любая ограниченная окрестность точки х (как и вообпа;е
любой точки пространства й^) пересекается лип1ь с конечным
множеством кубов ранга k и, следовательно, с конечным
множеством слагаемых Q^ , у = 1, 2, ... , т, суммы U Q.. Поэтому
J
XG y^Q.. D4.12)
400
Поскольку кубы Q. являются замкнутыми множествами и
объединение конечного множества замкнутых множеств снова есть
замкнутое множество, то
V^Qi. = jy.Qi.- D4.13)
Таким образом,
т
Итак, из включения хеЕ следует, что хеЕ. Это означает,
что Е = Е, т. е. что Е — замкнутое множество. П
Для всякого множества Е (z R^ обозначим через а^ = ^k(^)
объединение кубов ранга k, содержагцихся в множестве aS^ =
= aS^ (Е), но не содержагцихся в множестве s^ = -s^C^)»
<^k = ^k(E)''= «U^^ Q. D4.14)
Из этого определения следует, что множество aS^ состоит из
кубов ранга k, каждый из которых принадлежит либо
множеству Sj^(E), либо множеству oJ,E):
S, = s,Ua„ D4.15)
причем никакой куб ранга k не принадлежит одновременно
множествам s^ и а^. Поэтому, согласно определению D4.2),
^Sk = ^4^ ^^^^ D4.16)
В силу определения D4.14), множество а^, так же как и
множества s^ и aS^, является объединением кубов одного
ранга, поэтому все эти множества являются замкнутыми
множествами (см. замечание 1):
h=4^ ^k = Sk, o^ = G^. D4.17)
Напомним, что для любого множества Е (Z R^ имеют место
(см. п. 35.2) равенства
Ё = Е^^^идЕ, Е^^^ПдЕ = 0, D4.18)
где Е^^^ — множество внутренних точек множества Е, SidE —
его граница.
* Меры \xSf^, \xSf^ и ixOf^ могут быть как конечными, так и
бесконечными, причем, как обычно, для любого действительного числа а считается,
что +00 + а = а + (+00) = +00 и (+оо) + (+^) = + оо.
401
Замечание 2. Для любого многогранника aS, состоя-
гцего из конечного или бесконечного множества кубов одного
и того же ранга к, его точка х имеет окрестность, содержа-
па;уюся в aS, тогда и только тогда, когда все кубы ранга к, со-
держагцие точку х, содержатся в многограннике S. Отсюда
следует, что точка пространства R^ принадлежит множеству
(s^)^j^^ тогда и только тогда, когда все кубы ранга к, к которым
она принадлежит, содержатся в множестве s^ = ^и^Щ*
Замечание 3. Наряду с равенством D4.15) имеет
место более точное равенство
S. = («^ntUa„ D4.19)
В котором слагаемые не пересекаются:
(s,X„,na, = 0. D4.20)
В самом деле, в силу формул D4.15) и D4.18), имеем
S. = (Sft)intUas,Ua,. D4.21)
Докажем, что
Эз.са,. D4.22)
Пусть xg3s^. Так как
ТО х^Е и, следовательно, любой куб ранга к, содержагций
точку X, содержится в множестве aS^. Согласно замечанию 2, хотя
бы один куб Q из этих кубов не содержится в s^ (в противном
случае точка х являлась бы внутренней точкой множества s^,
т. е. xg(s^).j^^, следовательно, не принадлежала бы его границе
3s^). Таким образом, xgQ с aS^ ^ s^.
В силу определения множества а^, куб Q, поэтому и точка
X, содержатся в а^, что и означает справедливость включения
D4.22). Из этого включения следует, что в равенстве D4.21)
можно отбросить слагаемое 3s^ (оно входит в другое
слагаемое), т. е. имеет место равенство D4.19).
Докажем теперь равенство D4.20). Если xg(s^).j^^, то,
согласно замечанию 2, любой куб Q ранга к, содержагций
точку х : Q Э х, содержится в s^ и, следовательно, не содержится
в а^ : Q ct а^. Это означает, что х^а^, т. е. имеет место
равенство D4.20). П
ЛЕММА 3. Для любого множества Е ^ R^ справедливы
включения
дЕ с а^ (Е) с aS^ (Э^). D4.23)
402
Доказательство. Сначала докажем включение
dEczCf^iE). D4.24)
Пусть X е дЕ. Заметив, что из включения Е ^ Sf^(E) следует
аналогичное включение для замыканий этих множеств:
получим
^^ ^^ D4Л8) ^ "" ^"^^^ D4=19) ^^^^)int ^ ^н(Е). D4.25)
Из включения Sf^(E) с ^ имеем
«.(£)intc£i,t. D4.26)
Из включения хедЕ следует, что точка х не является внутренней
точкой множества Е : х^ Е^^^ (так как Е^^^ ПдЕ = 0), Поэтому
^44^2в)^^(^)-• D4-2^>
Из D4.25) и D4.27) вытекает, что точка х принадлежит
множеству Of^(E), т. е. включение D4.24) доказано.
Покажем теперь справедливость включения
c,(E)<zS,(dE). D4.28)
Если xeaj^(E), то сугцествует куб Q ранга k, содержагцийся
в множестве а^(^) и содержагций точку х: Q Э х. Согласно
определению множества oJ^E), этот куб принадлежит
множеству SJ^E) и, следовательно, пересечение куба Q с множеством
Е не пусто. Поскольку этот куб, согласно тому же
определению, не содержится в множестве sJ^E), он содержит и точки,
не принадлежагцие множеству Е. Отсюда, согласно лемме 9
п. 44.2, вытекает, что куб Q, будучи выпуклым, а тем самым
и линейно связным множеством, содержит точки границы Э^
множества Е, поэтому, согласно определению множества
SJjdE), как объединения всех кубов ранга k пересекаюпа;ихся
с множеством Э^, куб Q содержится в этом множестве. Итак,
показано, что из условия x^oJ^E) следует, что xeSf^(dE), т. е.
включение D2.28) также доказано. П
Сформулируем теперь и докажем критерий измеримости
множества.
ТЕОРЕМА 1. Для того чтобы множество Е было
измеримым по Жордану, необходимо и достаточно, чтобы оно
было ограниченным и чтобы его граница дЕ имела меру Жорда-
на, равную нулю:
[1дЕ = 0. D4.29)
403
Доказательство теоремы. Необходимость. Пусть
Е — измеримое множество. Тогда, как доказано выгае, оно
ограничено. Далее, согласно определению измеримого множества,
нижняя и верхняя меры множества Е конечны и равны: [i^E =
^\im^lis,{E) = ^lun^^S,{E). D4.30)
Из определения многогранника о^(Е) следует (см. D4.16)),
что [iCj^(E) = [iSj^(E) - [iSj^(E), Поэтому из равенства D4.30)
имеем
^lim^liG,iE) = 0. D4.31)
В силу включения D4.24) и монотонности верхней меры
(см. D4.7)), при любом й = О, 1, 2, ... справедливо неравенство
ц^Э^ < ц%,(^) = [ic,(E).
Перейдя к пределу при k -^ +оо^ в силу D4.31), получим
\х*дЕ = 0. Следовательно, множество Э^ измеримо по Жорда-
ну, и [idE = 0.
Достаточность. Пусть Е — ограниченное множество и
\хдЕ = 0. Тогда, по определению меры,
lim^[iSf^idE) = 0. D4.32)
В силу включения D4.28) и определения D4.2), справедливо
неравенство |аа^(^) < [iSf^(dE) и, следовательно, неравенство
ц5,(£) - ViS,(E) ^^^g^ ViG,(E) < [iS.idE). D4.33)
Поскольку множество Е ограничено, его нижняя мера [i^E и
верхняя [1*Е конечны и поэтому (см. D4.4) и D4.5)) в
неравенстве D4.33) можно перейти к пределу при й ^ + оо. в силу
D4.32), получим
[i'^E - [i^E = О, т. е. [i'^E = [i^E.
Это и означает измеримость по Жордану множества Е. П
Замечание 4. Компакт, граница которого имеет меру
нуль, является измеримым множеством.
Это сразу следует из теоремы 1, так как всякий компакт
есть ограниченное множество.
Замечание 5. Граница измеримого множества, как
граница всякого ограниченного множества, является
ограниченным множеством, а так как граница всегда замкнутое мно-
404
жество, то в данном случае оно является компактом. Таким
образом, согласно теореме 1, граница измеримого множества
есть компакт меры нуль.
С помогцью теоремы 1 легко показать, что при
теоретико-множественных операциях объединения множеств,
пересечения и вычитания их измеримость не наругаается.
Предварительно докажем одну геометрическую лемму.
ЛЕММА Л. Для любых двух множеств А и В, лежащих в
пространстве R^, справедливы следующие включения (pj^c. 51):
Э (А и Б) ^ ЭА и ЭБ, D4.34)
Э (А П Б) ^ ЭА и ЭБ, D4.35)
Э(А\Б)^ЭАи ЭБ. D4.36)
Доказательство. 1) Докажем включение D4.34). Если
хед(А и Б), то в любой окрестности точки х содержатся как
точки, принадлежагцие множеству А U Б, так и точки, не при-
надлежагцие ему. Возможны два случая: либо в любой
окрестности точки X содержатся точки множества А, либо сугцеству-
ет окрестность C/q точки х, не содержагцая точек множества А.
В первом случае в любой окрестности точки х имеются точки
как принадлежагцие множеству А, так и не принадлежагцие
множеству А и Б и тем более не принадлежагцие множеству А.
Это означает, что хедЛ,
Во втором случае, какова бы ни была окрестность U точки х,
окрестность U П Uq этой точки, как и всякая ее окрестность,
содержит точки множества А U Б, причем в этом случае все
они принадлежат множеству Б (так как Uq не содержит точек
множества А) и содержат точки, не принадлежагцие
множеству А U Б, следовательно, не принадлежагцие и множеству Б.
Поскольку и П Uq ^ С/, в рассматриваемом случае в
произвольной окрестности U точки х имеются точки как
принадлежагцие, так и не принадлежагцие множеству Б. Это
означает, что хедВ.
Итак, имеет место по крайней мере одно из включений
хедА или хедВ, т. е. хедА U ЭБ.
2) Докажем включение D4.35). А^ ^ ^*^-<^
Если хед(А П Б), то в любой /^ /Ш^ ^\
окрестности точки х содержатся ( ^\^ Ш^Ш ^^ у
точки как принадлежагцие пере- Х,..^^^ .^^S^^C^ ^^^^^
сечению А П Б (и, следовательно, . ^ ^
точки множества А и Б), так и
точки, не принадлежагцие этому Рис. 51
10~5
пересечению. Возможны два случая: либо в любой
окрестности точки X имеются точки, не принадлежапа;ие множеству А,
тогда хеЭА, либо сугцествует окрестность C/q точки х, все
точки которой принадлежат множеству А. Тогда для любой
окрестности и точки X в ее окрестности U П C/q, как и во всякой
окрестности этой точки, имеются точки, принадлежагцие
пересечению А (Л В, следовательно, и множеству Б, и точки, не
принадлежагцие А ^ В, поэтому не принадлежагцие и
множеству В (ибо в C/q все точки принадлежат множеству А). Таким
образом, в окрестности U П C/q, и, следовательно, в любой
окрестности и точки X (так как С/ П C/q ^ U) имеются точки как
принадлежагцие множеству Б, так и не принадлежагцие ему.
Это означает, что хеЭБ.
Итак, если хеЭ(А П Б), то хеЭА U ЭБ.
3) Докажем включение D2.32). Если хеЭ(А\Б), то в любой
окрестности точки х содержатся как точки, принадлежагцие
разности А\В, так и не принадлежагцие ей. Возможны два
случая.
Первый случай: в любой окрестности точки х содержатся
точки, не принадлежагцие множеству А; тогда в любой
окрестности точки X имеются точки как принадлежагцие
множеству А (так как имеются точки из разности А\В), так и не
принадлежагцие А. Поэтому в этом случае xg ЭА.
Второй случай: у точки х сугцествует окрестность C/q, все
точки которой принадлежат множеству А. Тогда для любой
окрестности U точки х в окрестности С/ П C/q этой точки
имеются точки, принадлежагцие разности А\Б, а так как U ^ 17^^
^ А, то эти точки не принадлежат множеству Б. В
окрестности и П Uq сугцествуют также точки, не принадлежагцие
разности А\В, sl так как они принадлежат множеству А, то
они принадлежат и множеству Б (в противном случае они
принадлежали бы разности А\В). Поскольку С/ П C/q ^ С/, то в
окрестности U содержатся точки как принадлежагцие
множеству Б, так и не принадлежагцие ему. Это означает, что хедВ.
Таким образом, если хеЭ(А\Б), то хеЭА U ЭБ. П
Из включений D4.34) и D4.35) методом математической
индукции для любого конечного числа множеств легко
устанавливается справедливость включений
Э Пе.с иЭЕ., д.ПЕ.^ [JdE.. D4.37)
406
3^. Объединение и пересечение конечного числа
измеримых по Жордану множеств, а также разность двух
таких множеств являются измеримыми по Жордану
множествами,
В самом деле, если множества Е- измеримы, то, согласно
теореме 1, цЭ Е- = О, j = 1, 2, ... , т. Поэтому, в силу следст-
т
ВИЯ из леммы 2, jiU Э^ = О, тогда (см. следствие леммы 1)
из включений D4.37) следует соответственно, что
т т
[id UE. = 0, [id П^ =0.
m
Отсюда имеем, в силу той же теоремы 1, что множества . У^Е- и
т
■ Q-^E- также измеримы. Аналогично доказывается
измеримость разности измеримых множеств.
Теперь можно легко доказать, что для меры Жордана
справедливо неравенство, аналогичное неравенству D4.10) для
верхней меры. Сформулируем соответствуюпа;ее утверждение.
Для любой конечной совокупности измеримых
множеств Е-^, ^2' ••• ' ^т справедливо неравенство
т т
[iV^E^< ^ц£,. D4.38)
i= 1
Действительно, если множества Е- измеримы, то [i*E- =
т
= [iE., И, согласно доказанному выпхе, объединение . U Е. так-
. пг т
же измеримо, и, следовательно, [i . U^. = [i . U^.. Поэтому
формула D4.38) в рассматриваемом случае совпадает с
формулой D4.10).
4^ (аддитивность меры). Мера объединения конечного
числа попарно непересекающихся измеримых по Жордану
множеств равна сумме мер этих множеств.
Таким образом, если Е^ — измеримые множества, Е^ П Е- =
= 0, / ^у, /, j = 1, 2, ... , m, то
т пг
[^V^E,= l^[iE,. D4.39)
Докажем это. Поскольку для любого ранга k справедливо
включение sJ^E^ П sJ^E^ ^ Е.П Е-, из условия Е^ (Л Е- = 0 при
/ ^ j следует, что sJ,E) П sJ,E^ = 0, i ^ у; поэтому, согласно
D4.2),
^ ^^ т пг
1^\is^{,E;) = \iV^s^{E;). D4.40)
407
Если куб ранга k лежит в некотором множестве ^., то он ле-
т
жит и в объединении . U^^., следовательно,
Отсюда, в силу D4.40) и монотонности меры (в данном случае
даже из формулы D4.2)), вытекает, что
£ \У8^{Е^) = II ^ y^s,(E^) < 118,Ы Е,
Перейдя к пределу при й ^ + оо^ получим
т т
£ц£,<ц^у^£,. D4.41)
i= 1
с другой стороны, ДЛЯ любых измеримых множеств
справедливо обратное неравенство D4.38). Очевидно, что из
D4.38) и D4.41) следует равенство D4.39), т. е. аддитивность
меры.
Замечание 6. Из свойств 3^ и 4^ меры вытекает, что
если к измеримому множеству присоединить или вычесть из
него множество меры нуль, то полученное множество также
измеримо, и его мера будет равной мере исходного
множества. Действительно, если Е — измеримое множество, а [lE^ = О,
то по свойству 3^ меры, множества ^\^о и ^ U ^^ также
измеримы. Далее согласно свойству 4^ при Е^^ Е vi \1Е^ = О имеем
[lE = [1[(Е\Е^) и Е^] = [1(Е\Е^) + ц^о = [1(Е\Е^).
В силу же монотонности меры и неравенства D4.38), для
любого ^0' М^^о ^ ^' справедливы неравенства
[lE < [1(Е и Eq) <[iE + [iEq = [lE,
откуда [i(E и Eq) = [lE,
В свою очередь, из сказанного следует, что если к
измеримому множеству присоединить или вычесть из него какое-то
множество его граничных точек, то получится снова
измеримое множество с той же мерой, что и данное. Это вытекает из
того, что, в силу теоремы 1, граница измеримого множества,
а значит, и любое ее подмножество, имеют меру нуль. Таким
образом, в частности, если множество Е измеримо, то его
замыкание Е = Е и дЕ и внутренность Е^^^ также измеримы,
причем [lE = [lE = l^^int-
408
Обратное утверждение неверно: существуют
неизмеримые по Жордану множества, замыкания которых
измеримы. Простым примером подобного множества является
множество рациональных точек на некотором отрезке. Оно
неизмеримо (почему?), а его замыканием является отрезок, который
измерим.
Отметим егце, что замыкание измеримого множества, как
и всякого ограниченного множества, является компактом.
Таким образом, замыкание измеримого множества есть
измеримый компакт.
5^. Мера множества не меняется при параллельном
переносе.
Прежде чем доказывать это утверждение, докажем епа;е
одну лемму.
Л Е М М А 5. Если
А^, В^ — измеримые множества, т = 1, 2, ,,, , и
то множество Е также измеримо и
liE = lim iiA^= lim iiB^,
Щ ^ OO • "'- Щ ^ OO • "'-
Доказательство. Множества Б^, будучи измеримыми
множествами, ограничены. Из включения Е ^ Б^ следует, что
и множество Е ограничено, поэтому супа;ествуют конечные
пределы Jirn^s^(^), ^lirn^S^(^).
Зафиксируем произвольно 8 > 0. В силу условий леммы,
супа;ествует такой номер т^, что
Для номера т^ выберем такой номер k^, что для всех номеров
k > Uq выполняются неравенства
/ г^-ш I. 1^^.(Б^ ) < цБ^ +1
\^^Н^^ш.)>\^^ш.-Ъ^ \^^^<^ш.)<\^^шЛ1
Из включения
А^ (zE(zB^
имеем
4(AmJ<^sJE)czSJE)czSJB^)
409
и, следовательно.
Отсюда имеем, что для всех k> k^ выполняются неравенства
о < liS.iE
Это означает, что
о < iiS,iE) - iis.iE) < цБ„^ + I - цА^^ + I < 8.
Дгп^ (liS.iE) - lis.iE)) = 0.
Согласно доказанному выгае, сугцествуют конечные
пределы lim [iSf^(E) и lim [iSf^(E), поэтому
i™o ^^k(E) = }im^ [iS^iE) = [lE,
следовательно, множество E измеримо. Теперь из
включения А^ (Z Е (Z В^ получим \хА^ < \хЕ < \хВ^, откуда, положив
m ^ оо^ будем иметь
lim [iA^= lim [iB^ = [iE,
так как по условию леммы
Из леммы 5 следует, что для получения предельным
переходом меры множества Е его не обязательно
аппроксимировать изнутри многогранниками Sj^(E), а снаружи
многогранниками Sf^(E): можно вместо них брать любые измеримые
множества А^ и Б^, удовлетворяюпа;ие условиям Aj^(Z Е (Z Bj^,
k = l,2,...,\im^liiB,A,) = 0.
Докажем теперь свойство 5^ меры.
Пусть Е с R^, а е R^u
Е -\- а = {у е R"^ : у = X -\- а, X е Е},
В этом случае говорят, что множество Е -\- а получено из
множества Е параллельным переносом его на вектор а в
пространстве R^.
Если Q — я-мерный куб с ребрами длины Л,
параллельными осям координат, то множество Q -\- а также является
кубом того же вида, следовательно, как это отмечалось рань-
nie, — измеримым множеством и
ц (Q + а) = ц Q = Л^.
Для каждого натурального k множества А^ = s^ (Е) + а,
Б^ = Sj^(E) + а измеримы, так как являются объединением
конечного множества измеримых множеств вида Q -\- а, где
Q — куб ранга k и
так как меры множеств А^ и Б^ равны сумме мер (как в
формуле D4.2)) составляюгцих их кубов.
Пусть теперь Е — измеримое множество и, следовательно.
Поскольку
A,czE + aczB,
и
ii?L ^<^k \A) = iifL <^^k - i^A) = Д^о ^^^k(E) - i^s,(E)) = 0,
TO, согласно лемме 5, множество E + a измеримо и
\1{Е + а) = ^lirn^ \iA^ = ^lirn^ \is^ (E) = [lE. П
Замечание 7. Отметим, что как нижняя, так и
верхняя меры множеств не обладают свойствами аддитивности.
Это видно уже в одномерном случае. Например, если А —
множество рациональных, а Б — иррациональных чисел на
отрезке [О, 1], то
[i^A = [i^B = О, [i^(A и В) = |а^[0, 1] = 1 ^ О = [i^A + ц^Б,
ц'А = ц'Б = 1, [i\A иВ) = ц^О, 1] = 1 ^ 2 = ц'А + ц'Б.
Примеры измеримых множеств сколь угодно больпюй
размерности можно получить с помопа;ью построения
цилиндров, основаниями которых служат также измеримые
множества. Сформулируем определение цилиндра.
Определение 2. ili/cmb ^Q— множество, лежащее на
гиперплоскости Ш ~'^ = {х : Xj^ = 0} пространства R^, а и b —
действительные числа, а< Ь, Множество
Е = {х : (х-^, ^2, ... , х^_-^, 0) е Е^, а< х^< Ь}
называется цилиндром с основанием Е^ и образующей
(параллельной координатной оси х^) длины h = b - а.
Очевидно, что, используя понятие произведения
множеств (см. п. 1.2"^ или 41.2), можно сказать, что цилиндр Е
является произведением множеств ^q и отрезка [а, Щ : Е =
= Eq X [а, Ь], Если ^Q — ограниченное множество, то и
цилиндр с основанием ^q является ограниченным множеством.
In
Отсюда следует, что всякий цилиндр, в основании которого
лежит измеримое множество, ограничен, ибо измеримое
множество ограничено.
ТЕОРЕМА 2. Если Е^ — измеримое по Жордану множество
пространства R^ ~ ^, то всякий цилиндр Е с основанием Е^
является измеримым по Жордану множеством в
пространстве R^, и
^^E = h^^_,E^, D4.42)
где h — длина образующей цилиндра Е.
СА£АС1Ъ]Л£. Если основание цилиндра имеет (п - 1)-мер-
ную меру, равную нулю, то сам цилиндр имеет п-мерную
меру, также равную нулю.
Доказательство теоремы. Прежде всего заметим, что
проекция"^ каждого я-мерного куба Q^ ранга к является
{п - 1)-мерным кубом Q^~^ также ранга к и
|aQ^= lO-^liQ^-i.
Обозначим Qf ~ ^ ... , Q^~ ^ {п - 1)-мерные кубы ранга к, со-
ставляюш;ие множество SJ^E^, а gf ~^, ... , qf~^ — {п -1)-мер-
ные кубы ранга к, составляюш;ие множество sJ^E^. Пусть
Qf 1, ... , Qf„ суть те все я-мерные кубы ранга к, содержагцие-
ся в множестве SJ^E), которые проектируются в один и тот
же куб Qf~^ с SJ^E^. Поскольку множество Е — цилиндр,
число р^ таких кубов одно и то же для всех /=1,2, ... , т,
поэтому
^k Pk
Аналогично, если gf , ... , gf^ — кубы ранга к, содержа-
гциеся в множестве sJ^E) и проектируюгциеся в один и тот же
куб gf ~ ^ с sJ^Eq), то число г^ таких кубов одно и то же для
всех / = 1, 2, ... , /^ и, следовательно.
* Проекцией пр Е множества ^ С Д" на гиперплоскость R^ ^ =
п
= {х : х^ = 0} называется множество точек вида (х^, ... , x^_i, 0), для
каждой из которых существует такое х^, что (х^, ... , х^ _ i, х^)еЕ.
112
Проекции на координатную ось х^
множеств V^Qlj, i = 1, 2, ... , m^, и V^qlj. I
/ = 1, 2, ... , Z^, представляют собой отрезки
соответственно длин —^ и —^, при этом
(см. рис. 52) выполняются неравенства
^^<й+ 2 , Zk^h-JL. D4.43)
Поэтому
ц S, (£) = X X ^^^"i = X. ^. ^1^" " ' ^
' Pk_
D4.43)
D4.43I 10^ Jf^i '
h^^,]^S,(E,),
D4.44)
^ч(Е) = 1^1^т^, = 1^т^,мг'
i-l j-l
D4.43)
D4.43)V
Следовательно,
> > - ^. ] X ^^^f " ' = f^ - tIi >«. (^o). D4.45)
10^
i= 1
10^
^-l^.)^^^^^^o),,<,,,^^^.№)<^^S.(^) ,,<,,,
D^44I^+ ifO^^^(^o). D4.46)
В силу измеримости множества ^q, имеем
Поэтому, перейдя к пределу при й ^ оо в неравенствах D4.46),
получим, что супа;ествует предел
что означает измеримость цилиндра Е и справедливость
формулы D4.42). П
Задача 11. Построить пример неизмеримой по Жордану области.
Задача 12. Доказать, что мера Жордана не зависит от выбора
декартовой системы координат.
413
44.2. Множества меры нуль
В предыдуш;ем пункте было установлено, что множество
измеримо по Жордану тогда и только тогда, когда его граница
имеет меру нуль. Поэтому полезно иметь признаки, по которым
можно было бы установить, что множество имеет меру нуль.
Достаточно обгцим примером множеств меры нуль являются
цилиндры, в основании которых лежат множества меры нуль
(см. следствие из теоремы 2). Другой гаирокий класс
множеств меры нуль дается в следуюгцей ниже теореме.
ТЕОРЕМА 3. График всякой непрерывной на компакте
функции имеет меру нуль.
Доказательство. Пусть функция у = f(x) = f(x^, ... , х^)
непрерывна на компакте А ^ R^. Пусть Е — ее график, т. е.
множество таких точек (х, у) = (х^, ... , х^, у) в (я+1)-мерном
пространстве R^^ ^, что (х^, ... , х^^)еА, а г/ = /(х^, ... , х^):
Е = {(х, у) : (Xi, ... , xJeA, у = /(х^, ... , xj}.
Покажем, что (п + 1)-мерная мера Жордана множества Е
равна нулю. Множество А, будучи компактом, ограничено.
Поэтому супа;ествует такое натуральное число т, что я-мерный куб
Р^= {х :-т < х.< т, i= 1, 2, ,,, , п}
содержит множество А : Р^ =^ А. Тем более куб
Pjn + i ^ {^ • ~^ - 1 < X. < m + 1, / = 1, 2, ... , я}
также содержит А : Р^ + ^ =^ А, и, более того, каким бы ни был
куб Q некоторого ранга й = О, 1, 2, ... , пересекаюпа;ийся со
множеством А, т. е. Q ^ 'S^C^)? он также содержится в P^ + i :
Q ^ Pjn +1- Поэтому при любом k имеем aS^(A) ^ Р^ + ^. (Здесь и в
дальнейп1ем через aS^(A), Sf^(E), как и в п. 44.1, обозначаются
множества точек всех кубов ранга k соответствуюпа;их
пространств, пересекаюпа;ихся с множествами А ^ R^ и Е^ R^^ i.)
Обозначим Qp, / = 1, 2, ... , m^, я-мерные кубы ранга к,
составляюгцие множество aS^(A), т.е. SJ^A) = .U^Qf. Тогда
множество Sf^(E) распадается на конечное число «столбиков»
S^\ каждый из которых состоит из (п + 1)-мерных кубов
ранга k Qfi+^, ... , Qf ^ ^, имеюгцих одну и ту же проекцию
(см. сноску нас. 412), куб Qf в пространстве R^ (на рис. 53
изображен случай п = 1):
S,iE) = v\sll\ Sf=.\J^Ql^\ й = 0,1,2,.... D4.47)
ITi
Обозначим через соF)
модуль непрерывности функции
/ на компакте А. Замечая, что
диагональ (диаметр"^) я-мерно-
го куба с ребром длины 1/10^
равна л/п/10^, для высоты Л^^^
каждого столбика aS^^^ имеем
(см. рис. 53) оценку
+ ■
10^*
D4.48)
Действительно, для оценки
высоты Л^^^ к расстоянию coA0~^V^) между наибольп1им и на-
именьп1им значениями функции f(x) на кубе Q^^^ достаточно
добавить длины ребер самого нижнего и самого верхнего кубов
рассматриваемого столбика aS^^^ (эта оценка достигается, когда
точки графика, соответствуюгцие указанным экстремальным
значениям, окажутся на гранях кубов ранга k). Из D4.47) и
D4.48) получаем
ГУ, ^и ^и
<
Поскольку функция / непрерывна на компакте, она
равномерно непрерывна на нем, поэтому lim coA0~^V^) = О, и
k -^ +00
2
поскольку lim —^ = О, из D4.49) имеем lim \iSJ^E) = О, а
это и означает, что \i^E = О, следовательно, j^ [lE = 0. П
В силу теорем 2 и 3, всякое ограниченное множество,
границу которого можно представить как объединение конечного
числа множеств, каждое из которых представляет собой либо
часть графика непрерывной на ограниченном замкнутом
множестве функции, либо часть цилиндра с основанием меры
нуль, является измеримым множеством, так как, в силу
аддитивности меры, мера границы указанного множества равна
нулю, и, следовательно, согласно теореме 1, оно измеримо.
Таким образом, получено описание достаточно гаирокого
класса множеств, измеримых по Жордану и часто встречаю-
' Определение диаметра множества см. в п. 35.3.
415
ш;ихся в математическом анализе и его приложениях.
Например, плоские множества (криволинейные трапеции,
«секторы» кривых, заданных в полярных координатах, а также тела
врапа;ения, плопа;ади и соответственно объемы которых
вычислялись в § 28 т. 1 с помопа;ью одномерного интеграла Римана,
являются измеримыми по Жордану множествами, ибо, как
нетрудно убедиться, их границы имеют меру нуль).
Подобным же образом измеримы по Жордану
параллелепипеды и эллипсоиды, в частности — гаары, так как их
границы можно представить в виде объединения графиков
непрерывных на компактах функций.
Заметим, что в § 27 т. 1 было введено понятие меры mes G
для открытых множеств. Сравнивая ее определение с
определением, приведенным в п. 44.1, видим, что mes G = ji^G, т. е.
введенная в § 27 т. 1 мера, как это уже отмечалось, является
нижней мерой Жордана. Однако в силу сказанного выпхе все
рассмотренные в примерах § 28 т. 1 множества были
измеримыми по Жордану и, следовательно, для них мера mes G
являлась мерой Жордана, т. е. для них имело место mes G = \xG.
Представляет интерес обобпа;ить теорему 3 на случай
параметрически заданных множеств, в частности, на случай
параметрических кривых. Оказывается, что даже в этом случае
одной лип1ь непрерывности рассматриваемых кривых
недостаточно для того, чтобы они имели меру нуль. Супа;ествуют,
например, кривые Х- = x-(t), а <: t <: b, i = 1, 2, ... , п, (x-(t) —
непрерывные на некотором отрезке [а, Ь] функции), называемые
кривыми Пеано, которые проходят через каждую точку
некоторого я-мерного куба и, следовательно, не имеют меры нуль.
Задача 13. Построить пример кривой Пеано.
ТЕОРЕМА 4. Всякая плоская спрямляемая кривая имеет
меру нуль.
Доказательство. Пусть задана спрямляемая кривая Г,
длина которой равна S. Пусть далее г = г (t), а <: t <: b —
некоторое представление кривой Г. Разобьем ее последовательно,
т. е. в порядке возрастания параметра t точками r(t-), t-e[a, Ь],
/ = О, 1, ... , т, tQ = а, t^ = Ь, нат равных по длине частей, т. е.
возьмем такое разбиение т = {^Jf ^^ отрезка [а, Ь], чтобы
длина каждой части Г. (кривой Г), задаваемой представлением г =
S
= r(t), t-_^<: t <: t-, i= 1, 2, ... , m, имела длину —.
Обозначим через К- замкнутый круг с центром в точке
S S
r(t-_-^) и радиусом —. Дуга Г. имеет длину —, и ее начало явля-
Иб
Рис. 54
D4.50)
т
ется центром круга iiT.,
поэтому вся она лежит в этом круге
(рис. 54). Отсюда вытекает, что
вся кривая Г содержится в
объединении кругов К^\
т
Г<= .и ЛГ;.
г = 1 '■
Следовательно, в силу
монотонности и полуадцитивности
верхней меры (см. леммы 1 и 2 в
п. 44.1)
Но ^ ^^'
поэтому из D4.50) имеем \i^Y < nS^/m. Левая часть
неравенства не зависит от т, sl правая стремится к нулю при т -^ +оо^
вследствие чего цГ = 0. П
УПРАЖНЕНИЕ 4. Доказать, что всякая спрямляемая кривая в любом
я-мерном пространстве, п> 1, имеет меру нуль.
Из теорем 1 и 4 следует, что всякое ограниченное плоское
множество, граница которого является спрямляемой кривой,
измеримо.
Задача 14. Построить пример открытого на числовой оси
множества, граница которого не является множеством лебеговой меры нуль.
(Определение множества лебеговой меры нуль см. в п. 23.10 .)
44.3. Определение кратного интеграла
Сформулируем определение кратного интеграла Римана. Для
этого прежде всего введем понятие разбиения измеримого
множества и понятие мелкости этого разбиения.
Пусть Е — измеримое по Жордану множество, Е ^ R^.
Конечная система т = {Е^У^^ ^^ непустых измеримых по Жор-
* Действительно, окружность С, являющуюся границей круга К,
можно представить как объединение двух полуокружностей, каждая из
которых представляет собой график непрерывной на отрезке функции.
Поэтому, согласно теореме 3, \хС = 0; следовательно, всякий круг К
является измеримым множеством.
417
дану множеств Е., i = 1, 2, ... ,/^, называетсяра^бг/е^г/еж
множества Е, если:
1) попарные пересечения множеств Е. имеют меру нуль:
[i(E,nE.) = 0,i9^j;
2) и Е. = Е.
Число |т| = max diam Е., где diam Е. — диаметр
множества е., называется мелкостью разбиения т.
В силу аддитивности меры Жордана для всякого
разбиения т = {Е^У^^ ^^ множества Е, имеем
[iE=.y^[iE.. D4.51)
Действительно, пусть при фиксированном / Е* = V.(E- П Е-) и
Е* = .у^Е*. Тогда, в силу условия 1 определения разбиения
множества, [i(E. П Е^) = О, i^ у, поэтому [lE^ < ^ [i(E. П Е^) = О,
; 7^ i
Т. е. \iEl = 0. Отсюда \iE'' < ^ \iEl = О, следовательно, \iE'' = 0.
i- 1
Кроме того, множества^"^ и Е.\Е* = Е**, /=1,2,...,/^, попарно
не пересекаются, а в силу условия 2, . y^E'l'^ 1) Е* = . у Е. = Е.
Так как \хЕ. = \х(Е.\Е'') = [lE^'', то из всего сказанного, в
силу аддитивности меры, следует, что
ц£ = £ ц£Г + Ц£* = Е \iE^. П
Для простоты обозначений иногда вместо {Е^^}.^^ будем
писать {Е.},
Пусть т = {Е-} и х' ={E'i} — разбиения измеримого
множества Е, Разбиение т' называется вписанным в разбиение т, если
для каждого E'jEx' супа;ествует такой элемент Е-ех, что E'j ^ Е..
В этом случае пип1ут х > х' или х < х\
Отметим два свойства разбиений множества.
1^. Если X < х' и х' < х'\ то X < х'\
2^. Для любых двух разбиений х' = {Е\} и х'' = {EJ}
измеримого множества Е существует такое его разбиение т, что
X > Х' и X > Х'\
lis
Свойство 1^ очевидным образом следует из определения
вписанного разбиения. В качестве же указанного в свойстве 2^
разбиения т можно взять множество всевозможных непустых
пересечений ^'^ П EJ.
Л Е М М А 6. У всякого измеримого множества существуют
разбиения сколь угодно малой мелкости.
Пусть Е — измеримое множество, Е ^ R^. Обозначим
через Е^^\ j = 1, 2, ... , у^, всевозможные непустые пересечения
кубов ранга k с множеством Е. Таким образом, для каждого
у = 1, 2, ... , у^ сугцествует такой куб ранга к, обозначим его
Q^^\ что
^ E^^^ = Er\Q^^^^0.
Система множеств т^ = {^)^Ч/= [^ образует разбиение
множества Е. Действительно, множества Е^^"^ измеримы как
пересечение двух измеримых множеств Е и Q^^\ а. их
объединение составляет множество Е:
Е = (j Е^^\
Пересечения множеств Е^^"^ имеют меру нуль. В самом деле,
при / ^ у имеем
'- J '- J ^ У
и так как для любого куба мера его границы равна нулю, то
|1(^р) п Е{^^) < ц(Э(Эр^ п Э(Э)^^) < ц(Э)^^ = 0,i^ у.
Мелкость разбиения т^ стремится к нулю при й ^ оо:
lim |т^| = 0. Это следует из того, что диаметр я-мерного
куба ранга k равен ^, поэтому |т^| = max diam Е^^^ <
J » »•••» Jf^
< diam Q[^^ = JlL^ 0^ при k -^ oo.n
Определение 3. Пусть на измеримом по Жордану множестве
Е ^ R^задана функция у = f(x) = /(х^, ..., х^) и т ={E^y.Z^^ —
некоторое разбиение множества Е; выберем произвольным
образом точки Ь,-еЕ., i = 1, 2, ... , i^. Сумма вида
о, = G,(f; ^A), ... , f^^) = £ т^^Е^ D4.52)
i= 1
называется интегральной суммой Римана функции f.
ТТэ
Подобно случаю функции одного переменного,
определение кратного интеграла можно сформулировать, используя
понятие предела последовательности или «язык 8—6».
Определение 4. Число А называется интегралом Римана от
функции f по измеримому по Жордану множеству Е ^ R^,
если, какова бы ни была последовательность разбиений т^ =
= {E[^^\Zi'^\ т = 1, 2, ... , множества Е такая, что
мелкости разбиений т^ стремятся к нулю при т -^ +оо: Цщ |х^| =
= О, и каковы бы ни были точки ^^^' ^^еЕ^^^\ /=1,2, ... , i^^\
последовательность интегральных сумм о^ (/; £^^' ^\ ...
т
... , ^(^^"^^^ ^)) при т -^ +00 имеет своим пределом число А:
lim а, (/;^A'Ч...,^^^^"'^'"'^)=А. D4.53)
Интеграл от функции / по множеству Е обозначается через
\f{x)dE, \f(x)dx или
I I * * * I ТуХл, Хпу ... , Х^ jU/X-i (J/Xn ... (J/X^»
Е Е
Если сугцествует интеграл \f{x)dE, то функция /
называется интегрируемой по Риману на множестве Е.
Интегрируемые по Риману функции часто будем называть просто
интегрируемыми.
Равенство D4.53), т. е. определение интеграла, кратко
записывается в виде формулы
\f{x)dE= lim а, D4.54)
и говорят, что интеграл \f{x)dE является пределом
интегральных сумм а^ при |т| ^ 0.
В терминах 8 и 6 этот предел означает следуюпа;ее: для
любого 8 > О существует такое 6^ > О, что, каково бы ни было
разбиение т = {Е^У^^^^, множества Е мелкости |т| < Ъ^и
каковы бы ни были точки bj^^^eE-, / = 1, 2, ... , /^, выполняется
неравенство
|а,(/; ^A), ... , ^^'^^) - \f{x)dE\ < 8. D4.55)
Обычным путем доказывается, что определения D4.53) и D4.55)
предела интегральных сумм эквивалентны.
Отметим, что определение интеграла D4.54) в случае, когда
я = 1, а множеством, по которому производится
интегрирование, является отрезок, формально не совпадает с данным ранее
определением интеграла Римана от функции одной перемен-
120
ной, так как там рассматривались лип1ь разбиения отрезка на
отрезки, а теперь рассматриваются всевозможные разбиения
отрезка на измеримые по Жордану множества. Однако можно
показать (это будет сделано в п. 44.7"^), что при п = 1 оба
определения для случая, когда множество, по которому
производится интегрирование, является отрезком, равносильны, т. е.
приводят к одному и тому же понятию интегрируемости
функции и к одному и тому же значению интеграла.
При определении интеграла по множеству Е ^ й^ можно
для составления интегральных сумм использовать не все
элементы разбиений т множества Е, а отбрасывать те слагаемые,
которые соответствуют элементам разбиения, пересекаюпа;им-
ся с некоторым фиксированным множеством меры нуль.
Проанализируем это обстоятельство подробнее.
Пусть Е — измеримое множество, Е^^ Е и.х = {E^Y^Z ^^, —
разбиение множества Е. Обозначим через t(^q) совокупность
тех элементов разбиения т, которые не пересекаются с
множеством ^q; совокупность же оставп1ихся множеств Е-, т. е. тех,
которые пересекаются с множеством ^q, обозначим Tq(^q).
Таким образом,
т(^о) = {Ei^^ 'Е,ПЕ^ = 0}, D4.56)
То(^о) = {Ei^^ : Е,ПЕ^^0}. D4.57)
ЛЕММА 7. Пусть Е — измеримое по Жордану множество
пространства R^, Е^^ Е и \хЕ^ = 0. Тогда
lim ^ ^Е, = 0. D4.58)
Суммирование в формуле D4.58) происходит только по
тем индексам /, для которых Е. е Xq(Eq).
Доказательство. Пусть Е^^ Е л [lE^ = 0; тогда и [lE^ = О
(см. в п. 44.1 замечание 6 после доказательства аддитивности
меры). Поэтому для любого 8 > О супа;ествует такой ранг k, что
[iSf^iEo)<e. D4.59)
Здесь, как всегда, Sf^(Eo) обозначает совокупность точек всех
кубов ранга k, пересекаюпа;ихся со множеством ^о и,
следовательно, покрываюпа;их его:
^0 ^ Sf^(Eo)-
421
Множество Ео, как и всякое множество в R^, содержится в
множестве внутренних точек своего многогранника Sf^(Eo):
Ёо ^ Sf^ (^o)inf
Это следует из того, что для точки х, принадлежагцей
множеству ^0? все содержагцие ее кубы ранга k содержатся в
многограннике Sf^(Eo) и поэтому содержат некоторую
окрестность точки X. Таким образом, многогранник Sf^(Eo)
содержит окрестность точки хе Eq, что и означает принадлежность
этой точки к внутренности множества Sj^(Eo)' Следовательно,
множество ^0 не пересекается с дополнением й^\а8^(^о)ш1 ^
открытому множеству а8^(^о)ш1- ^^^ дополнение является
замкнутым множеством (см. лемму 6 в п. 35.2), не
пересекаю па;имся с компактом Ео, поэтому (см. там же лемму 7)
находится от него на положительном расстоянии:
6 =' р(£о, R^S.iEoU) > 0. D4.60)
Поэтому всякое множество D диаметра diam D, меньп1его чем 6,
пересекаюпа;ееся со множеством ^q ^ Eq, будет целиком
лежать в Sf^(Eo). Действительно, если diam D < 6 и супа;еству-
ет xgD П Eq, то (см. D4.50)) D ^ Щх, 6) ^ aS^(^o), где, как
обычно, U(x, 6) — п1аровая окрестность точки х радиуса 6
(рис. 55).
Пусть теперь т = {Е.} — разбиение множества Е
мелкости |т| < 6 и ^.gTq(^q), т. е. Е. П Eq ^ 0, Si так как диаметр
diam Е- < 6, то, в силу сказанного
выше, Е. ^ Sj^(Eo)- Поэтому
^ Е,^8,(Ёо).
Следовательно, в силу D4.59),
Введем епа;е одно обозначение.
Пусть Е — измеримое множество, т =
= {E^y.Z^^— некоторое его разбиение.
S
S,iEo)
Рис. 55
422
^0 ^ Е- Для всякой функции /, определенной на Е, положим
(см. D4.56) и D4.57))
с^х(Е,) = С7,(.)(/;^A),...,^^^^^)= Е f&'^)[iE,. D4.61)
Эта запись означает, что суммирование в правой части
равенства происходит только по тем индексам /, для которых
Е.ех(Ео). Как всегда bf^^^eE.. Для симметрии записи обычные
интегральные суммы Римана можно по аналогии записывать
в виде о^ = Y, f &^^) l^^i- Вместо символа суммирования ^
иногда для краткости будем писать ^.
ТЕОРЕМА 5. Пусть Е — измеримое по Жордану
множество пространства R^, т = {E^y.Z^^ — его разбиение, Е^^ Е и
[iEq = 0. Если функция f ограничена на множестве Е, то ри-
манов интеграл \f{x)dE существует тогда и только тогда,
когда существует конечный предел lim а^^^ у При этом
если последний предел существует, то он равен интегралу
\f(x)dE.
При выполнении условий теоремы сумма а^.^ л
называется неполной интегральной суммой для интеграла \f(x)dE.
Доказательство. Для всякого разбиения т = {^^} f _ ^^
множества Е каждый элемент Е. разбиения либо не пересекается с
множеством ^q, и тогда Е.ех(Ео) (см. D4.56)), либо
пересекается, тогда ^.GTq(^q) (см. D4.57)). Следовательно, т = t(^q) U Tq(^q),
причем t(^q) и Tq(^q) не имеют обпа;их элементов.
Положим
Здесь суммирование в правой части равенства происходит
только по тем индексам /, для которых Е.ех^(Ео). Очевидно,
что для любой интегральной суммы Римана а^ справедливо
равенство (см. D4.52) и D4.61))
В силу ограниченности на Е функции /, супа;ествует такая
постоянная М > О, что для всех хеЕ выполняется
неравенство |/(х)| < М. Поэтому
Е.ех^(Е^) Е.ех^(Е^)
723
A так как, согласно лемме 3, lim У iiE. = О, то lim а^ .г. ^ = 0.
В силу этого, из равенства D4.62) следует, что интегральные
суммы а^ и а^.^ ч одновременно имеют или нет пределы при |т| ^ О,
причем если эти пределы сугцествуют, то они равны. П
Из этой теоремы следует, что если функция определена и
ограничена на некотором измеримом множестве Е, то при
определении интеграла, как предела интегральных сумм, в них
можно отбрасывать все слагаемые, соответствуюпа;ие
элементам разбиения, которые содержат граничные точки, ибо
множество ^Q = Э^ имеет меру нуль (см. теорему 1 в п. 44.1).
Из теоремы 5 следует также, что если функция /
определена и ограничена на измеримом множестве Е, то изменение
ее значений на некотором множестве Eq ^ Е меры нуль, в
результате которого снова получается ограниченная на Е
функция, не влияет ни на интегрируемость функции, ни на
значение интеграла от функции, если он сугцествует. Это сразу
следует из того, что при указанном изменении функций
сумма а^(^^ ^ не меняется, а в силу теоремы 5, если ее предел при
|т| -^ О сугцествует, то он равен интегралу \f(x)dE:
Из этого замечания, в частности, следует, что функция /
является интегрируемой на измеримом множестве Е тогда и только
тогда, когда на этом множестве Е интегрируема всякая
функция, получаюгцаяся из / произвольным изменением ее
значений в граничных точках, т. е. на множестве Е П дЕ, таким, что
эти значения остаются, однако, ограниченными. При
указанной операции не меняется и значение интеграла \f(x)dE. Все
это следует из того, что граница измеримого множества, а
значит, и любая ее часть, имеют меру нуль.
Таким образом, интегрируемость и значение интеграла от
функции по множеству Е не зависят от значений функции в
граничных точках измеримого множества Е, если только эти
значения ограничены.
44.4. Существование интеграла
Простейп1им примером интегрируемой по Риману функции
является произвольная числовая функция /, определенная на
некотором множестве Е ^ R^, мера Жордана которого равна
нулю: \хЕ = 0. В этом случае для любого разбиения т = {E^y.Z^^
724
множества Е будем иметь [lE. = О для всех i = 1, 2, ... , i^,
поэтому при любом выборе точек bf^^^eE. получим f(b,^[iE. = О,
следовательно (см. D4.52)),
а, = G,if; ^A), ... , ^''^^) = i /(^«)ц£. = 0.
i= 1
Отсюда, согласно определению интеграла, он в этом случае
сугцествует и равен нулю:
\f(x)dE = lim а=0.
Поскольку функция / произвольна, в частности, она
может быть и неограниченной. Иначе говоря, условие
ограниченности функции не является необходимым для ее
интегрируемости по Риману на произвольном измеримом по
Жордану множестве. Вспомним, что для интегрируемости функции
по Риману на отрезке условие ограниченности функции было
необходимым (см. теорему 1 в п. 23.3). Однако с некоторым
видоизменением теорема об ограниченности интегрируемой
функции оказывается справедливой и для рассматриваемого
здесь интеграла.
Предварительно докажем лемму.
ЛЕММА 8. Пусть функция f определена на измеримом по
Жордану множестве Е, х = {E^y.Z^^— разбиение этого
множества и Е* — объединение всех элементов этого
разбиения, имеющих положительную меру: Е^ = U Е^.
Если функция f неограничена на множестве Е*, то,
каково бы ни было число М > О, можно так выбрать точки
tf^^^eE., что будет справедливо неравенство
^/(^(%^,|>М.
СЛЕДСТВИЕ. Пусть функция f определена на измеримом по
Жордану множестве Е. Если у множества Е существуют
сколь угодно мелкие разбиения, для которых функция f
неограничена на объединении всех их элементов положительной
меры, то функция f неинтегрируема на Е.
Доказательство леммы. По условию леммы
множество Е^ является объединением элементов Е^ положительной
меры разбиения т. Поскольку всякое разбиение состоит из ко-
125
нечного числа элементов, Е* является конечной суммой
указанных множеств Е.ет. Поэтому если функция /неограничена
на множестве Е*, то она неограничена и на некотором
множестве Е. положительной меры. Пусть для определенности это
множество Е^. В силу неограниченности функции / на ^^,
можно выбрать такую последовательность ^^^^g^^, п= 1, 2, ... , что
будет иметь место равенство lim /(^^^^) = '^. Зафиксируем ка-
КИМ-либо образом остальные точки ^^^^еЕ. при / = 2, 3, ... , /^.
Поскольку сумма ^ f(b,^\xE. — фиксированное число и
i- 2
[lE-^ > О, то в сумме f(b,^J-^)[iE-^ + ^ f(b,^[iE. при п ^ оо первое
i = 2
слагаемое стремится к бесконечности, а второе — постоянное.
Отсюда
lim
/(Ц1))ц£1+ £Д^(%£,
+ 00.
Поэтому для любого числа М > О можно подобрать такой
номер tIq = ^q(M), что будет справедливым неравенство
i = 2
>м. п
Доказательство следствия. Если функция /
интегрируема на множестве Е, т. е. супа;ествует предел
lim ^fi^(^^)^iE^ = lfix)dE,
|Т| ^0 ._ -^
ТО для любого 8 > о, например для 8=1, супа;ествует такое
6 > О, что для всех разбиений х = {Е^}.^ ^ множестваЕ
мелкости |т| < 6 при любом выборе точек Ь^^^^еЕ-ех выполняется
неравенство
l^m^%E,-lf(x)dE\<l
i= 1 I
И, следовательно, неравенство
\fix)dE - К i; f&^)[iE. < \fix)dE + 1, D4.63)
i- 1
Т. е. множество всех интегральных сумм а^ при |т| < 6
ограничено.
426
Если же функция / удовлетворяет условиям следствия, то
у множества Е сугцествует разбиение т мелкости |т| < 6, для
которого функция / неограничена на объединении всех
элементов положительной меры этого разбиения. Тогда, по лем-
ме 6, сумму Y, f&^)\^^i можно сделать сколь угодно болыаой
i = 1
по абсолютной величине за счет выбора точек Ь^^^^еЕ-ех,
Поэтому такая функция не может быть интегрируемой — для
нее не выполняется условие D4.63). П
Покажем теперь, что если пренебречь множеством меры
нуль, то всякая интегрируемая функция будет ограниченной.
ТЕОРЕМА 6. Если функция f интегрируема на множестве Е,
то существует такое множество Е^^ Е меры нуль: [iEq = О,
что функция f ограничена наЕ\Е^.
Доказательство. Пусть функция / интегрируема на ^ и
указанного в теореме множества ^q не супа;ествует. Возьмем
любое 6 > О и какое-либо разбиение т = {Е.} множества Е
мелкости |т| < 6. Обозначим через Е^ объединение всех элементов
разбиения т положительной меры. Тогда множество Е\Е^
является объединением конечного числа множеств Е.ет меры
нуль, и поэтому оно само имеет меру нуль: [i(E\E*) = 0.
Вследствие этого по сделанному предположению функция /
неограничена на множестве Е*. Отсюда, согласно следствию из
леммы 6, получаем, что функция / неинтегрируема. П
Покажем теперь, что для важного класса измеримых по
Жордану открытых множеств теорема об ограниченности
интегрируемой функции полностью сохраняется. Для
доказательства этого понадобится одна геометрическая лемма.
ЛЕММА 9. Непустое пересечение замкнутого п-мерного
куба с открытым множеством п-мерного пространства
имеет положительную нижнюю меру Жордана.
СЛЕ ДСТВИЕ. Дл^ любого открытого измеримого по
Жордану множества существуют сколь угодно мелкие разбиения,
все элементы которых имеют положительную меру.
Доказательство леммы. Пусть Q — замкнутый я-мер-
ный куб, G — открытое множество пространства R^j^Q HG^ 0.
Какова бы ни была точка xeQ П G, в силу открытости
множества G, сугцествует такая ее окрестность Щх), что
Uix)^G. D4.64)
427
Рис. 56
Нетрудно убедиться, что во
множестве U(x) всегда
имеется внутренняя точка у куба Q.
В самом деле может случиться,
что сама точка х является
внутренней для куба Q и тогда
можно взять у = X, Если же х —
граничная точка куба Q, то она
является граничной и для
множества его внутренних точек.
Поэтому ее окрестность U(x) заведомо содержит внутреннюю
точку у куба Q (рис. 56). В силу определения внутренней точки
(см. п. 35.2), сугцествует такая ее окрестность V(y), что
V(y)^Q. D4.65)
В силу D4.64) и D4.65), справедливы включения
Щх) П V(y) CZ Щх) ^ G, Щх) П V(y) CZ Q;
поэтому
Щх) П V(y) ^QnG. D4.66)
Так как yeU(x) и yeV(y), то пересечение U(x) П V(y) не пусто,
ибо содержит, во всяком случае, точку у. Далее, будучи
пересечением двух открытых множеств, оно также является
открытым, и поэтому (см. п. 44.1) [i^[U(x) П V(y)] > 0. В силу
свойства монотонности нижней меры (см. лемму 1 в п. 44.1),
из D4.66) имеем [1^[Щх) П V(y)] < MQ П G).
Из двух последних неравенств явствует, что [i^(Q П G) > 0. П
Доказательство следствия. Пусть G — измеримое
открытое в R^ множество. Зафиксируем разбиение пространства
R^ на кубы некоторого ранга k. Множество кубов Q этого
ранга, имеюпа;их непустое пересечение со множеством G,
является конечным, ибо множество G, в силу его измеримости,
ограничено. Перенумеруем все указанные кубы: Q., Q^, ... , Q, .
Множества^. = Q. П G ^ 0, / = 1, 2, ... , /^ измеримы и образуют
разбиение т = {Е^}.^ ^ множества G. Действительно, с одной
стороны, Е. = Q. П G ^ G, следовательно, U^^. ^ G, а с
другой — каждая точка хе G, как и всякая точка пространства
R^, принадлежит хотя бы одному кубу Q ранга k: xeQ П G.
Тогда Q П Geт, т. е. Q = Q- при некотором /, поэтому xeQ.nE =
= Е.^ и^^.. Таким образом, [JE. = G.
428
Далее, Е. П Е- ^ Q. П Q.. Если пересечение Q- П Q. непусто,
то оно представляет собой куб размерности, меныаей чем п,
и, следовательно, является графиком непрерывной (даже
линейной) функции на компакте. Поэтому его мера равна нулю:
\x(Q. П Qj) = О, откуда и \х(Е. П Е^) = О, i ^ у. Наконец, согласно
лемме 8, \хЕ. > О, i= 1, 2, ..., i^.
Очевидно, что сугцествуют сколь угодно мелкие разбиения т
указанного вида. Действительно, каково бы ни было 6 > О,
достаточно взять такой ранг k, чтобы ^^ < 6 (diam Q = 10~^л/п —
диаметр куба Q ранга k), тогда
diam Е. = diam(Q. nG)<: diam Q. = lO'^Jn < 6, / = 1, 2, ... , /^,
и поэтому |т| < 6. П
ТЕОРЕМА 7. Если функция интегрируема на открытом
множестве, то она ограничена.
Доказательство. Пусть функция / интегрируема на
открытом множестве G. Тогда, согласно определению
интеграла, множество G измеримо по Жордану, а на основании
следствия из леммы 10, сугцествуют сколь угодно мелкие его
разбиения, все элементы которых имеют положительную меру.
Если функция / была бы неограниченной на G, то, согласно
следствию из леммы 8, она была бы неинтегрируемой. П
Замечание. Как видно из приведенного
доказательства теоремы 7, открытость множества G потребовалась лигаь
для того, чтобы показать, что сугцествуют его разбиения
сколь угодно малой мелкости, все элементы которых имеют
положительную меру. Тем самым для всех множеств, обла-
даюгцих этим свойством, интегрируемость на них функций
влечет за собой их ограниченность.
Легко, например, можно убедиться в том, что замыкание
G любого измеримого открытого множества G также имеет
сколь угодно мелкие разбиения, мера всех элементов
которых положительна. Действительно, достаточно снова взять
все кубы Q. ранга к, имеюгцие с G непустое пересечение.
Тогда они будут и подавно иметь непустое пересечение с
замыканием G множества G : Q- П G ^ Q- П G ^ 0. При этом так как
aS^(G) — замкнутое множество и G ^ Sj^(G), то G ^ Sj^(G),
Следовательно, если положить Е. = Q. П G, где Q. П G ^ 0, то
429
т = {Е-} образует покрытие замыкания G множества G, ибо
многогранник aS^(G) состоит только из указанных кубов Q..
УПРАЖНЕНИЕ 5. Построить пример функции, неограниченной и
интегрируемой на множестве положительной меры.
Если функция / ограничена на измеримом множестве, то,
как и в одномерном случае, можно определить верхние и
нижние суммы Дарбу.
Определение 5. Пусть f — функция, ограниченная на
измеримом по Жордану множестве Е, х = {E^y.Z^^— разбиение
множества Е
inf /(х), М,= sup f(x), /=1,2,
хеЕ^ ^ хеЕ.
Тогда суммы
i= 1 i= 1
называются соответственно нижними и верхними
суммами Дарбу,
Аналогично одномерному случаю (см. определение 7 в
п. 23.1), для сумм Дарбу функций многих переменных
вводится понятие предела при |т| ^ 0.
Для сумм Дарбу и интегральных сумм Римана
справедливы очевидные неравенства s^ < а^ < aS^.
Как и для функций одной переменной, для любых двух
разбиений т^ и х^ справедливо неравенство s^ ^ Sx •
ТЕОРЕМА 8. Для того чтобы ограниченная на измеримом
по Жордану множестве Е ^ R^ функция f была
интегрируемой по Риману на этом множестве, необходимо и
достаточно, чтобы
lim (S -sj = 0. D4.67)
При выполнении этих условий
lim S = lim s=\f{x)dE. D4.68)
Условие D4.67) равносильно следуюгцему:
Ит^ ^ co(/; £,)ц£, = о, D4.69)
где со(/; Ej) — колебание функции / на множестве -Е^ех = {Е^.
Тзд
Доказательство этой теоремы проводится аналогично
одномерному случаю и рекомендуется проделать читателю в
случае внутренней потребности самостоятельно.
УПРАЖНЕНИЕ 6. Сформулировать определения пределов D4.67)—
D4.68) с помопдью последовательностей и используя «8—5-терминологию».
ТЕОРЕМА 9. Если функция непрерывна на измеримом по
Жордану компакте, то она интегрируема на нем.
Доказательство. Пусть Е — измеримый компакт, Е ^ R^,
Si f — непрерывная на нем функция. Всякая функция,
непрерывная на компакте, ограничена (см. п. 36.7) и равномерно
непрерывна (см. п. 36.8) на нем. Поэтому и здесь доказательство
протекает аналогично одномерному случаю (см. п. 23.5): легко
получается оценка
^ ш(/; Е,)^Е, < шF,; f)^E,
i= 1
где соF, /) — модуль непрерывности функции /. Из этой
оценки сразу следует выполнение условия D4.69), поэтому,
согласно теореме 8, и интегрируемость функции /. П
ДД-б"". Об интегрируемости разрывных функций
Непрерывность функции не является необходимым условием
интегрируемости: супа;ествуют и разрывные интегрируемые
функции. Достаточно п1ирокий класс разрывных
интегрируемых функций устанавливается следуюпа;ей теоремой.
ТЕОРЕМА 10. Если функция ограничена на измеримом по
Жордану компакте и множество ее точек разрыва имеет жор-
данову меру нуль, то эта функция интегрируема по Риману.
Доказательство. Пусть функция / определена и
ограничена на компакте, т. е. на ограниченном замкнутом
множестве ^ ^ R^. В силу ограниченности функции / на Е, супа;ествует
такая постоянная М > О, что для всех х^Е выполняется
неравенство
|/(х)|<М. D4.70)
Пусть ^Q — множество точек разрыва функции /. По
условию теоремы \1Е^ = О, поэтому для любого фиксированного
8 > О супа;ествует такой ранг k, что
^S,(E,)<^^. D4.71)
3М
731
Это следует из того, что в данном случае, согласно
определению меры, lim [iSf^iEo) = 0. Пусть многогранник aS^(^o) ^^"
к —^ +СХЭ
стоит ИЗ кубов Q^, Q2, ... , Qi- Обозначим через Pj куб, полу-
чаюгцийся из Q преобразованием подобия с центром в центре
куба Q и коэффициентом подобия, равным трем; тогда
[iP. = 3-[iQ., у=1,2, ...,Z. D4.72)
I
Положим Р = и р.. В силу неравенства D4.71) и
равенства D4.72), имеем
[iP = [i. у^ Pj < £ \iPj = t 3"^Qy = 3«ц5,(£о) < ^. D4.73)
Отметим, что множество Р получается из Sj^(Eq) окаймлением
последнего полосой кубов с ребрами длины 10~^, поэтому
всякое множество А с диаметром diam А, меньп1им чем 10~^, пере-
секаюпа;ееся с множеством Sj^(Eq), содержится в Р (рис. 57):
diam А < 10-^ А П S^(^o) ^ 0 ^ А ^ Р. D4.74)
Обозначим теперь через G множество внутренних точек
многогранника aS^(^q). Очевидно, G — открытое множество, а
поскольку по условиям теоремы Е замкнуто, то множество F =
= E\G также замкнуто, причем, в силу ограниченности Е,
множество F ограничено, поэтому F — компакт. Далее,
множество ^Q лежит внутри многогранника aS^(^q), т. е. Eq ^ G (как
отмечалось выпхе, см. п. 44.3, это справедливо вообпа;е для
любого множества Е и вытекает из
определения многогранника Sf^(E),
см. доказательство леммы 7).
Отсюда явствует, что функция /
непрерывна на компакте Р, а
поскольку, кроме того,
множество Р измеримо, как разность двух
измеримых множеств Р и G, то,
согласно теореме 9, функция /
интегрируема на Р. Поэтому для
выбранного Bbinie 8 > О сугцеству-
ет такое 6 > О, что для любого
разбиения Хр множества Р мелкости
|т^^| < 6 выполняется неравенство
S. -S. <■
Рис. 57
D4.75)
432
где aS^ и s^ — верхние и нижние суммы Дарбу функции /, со-
ответствуюпа;ие разбиению Хр множества F,
Пусть
6o = min{10-^6}, D4.76)
т = {^^}f_^^— какое-либо разбиение множества Е мелкости
def
|т| < 6q. Очевидно, что х^ = {Е. П F}, где Е.ПЕ ^^ 0, является
разбиением множества F мелкости |т^^| < |т| < 6q, и поэтому, в силу
D4.70), для т^^выполняется неравенство D4.75).
Положим
М. = sup f(x), т. = inf f(x),
M\= sup /(x), m\= inf /(x),
S,= I M;ii(E,nF), s = i: m]ii(E,nF).
E^nF^0 EpF^0
Каждое множество E.ex либо пересекается с G, либо нет.
В случае непересечения, т. е. если Е.ПС = 0,тоЕ.^Е,-и. для
таких индексов / имеем М. = М-, Е. П F = Е..
Заметив, что в написанных ниже суммах все слагаемые
неотрицательны, получим:
ЕрО=0 ЕрО=0
< ^ (Ml-m'^^(E,nF) = S -S <1. D4.77)
Если же ^. П G ^ 0, то, в силу D4.74) и D4.76), Е.^ Рл
поэтому для этих индексов / (см. егце D4.73))
Используя очевидные неравенства \т.\ < М, \М.\ < М, /=1,2,.../^,
непосредственно вытекаюгцие из D4.70), и применяя
неравенство D4.78), будем иметь
£ (М,-т,)ц£,< £ [|М,| + К|]ц£,<
<2М £ Ц-Е;<|. D4.79)
433
Из D4.77) и D4.79) вытекает, что
S, - S, = ^ (М, - т)\1Е^ =
i= 1
= £ (М,-т,)ц£,+ £ (М, - т,)ц£, < I + I = 8.
Отсюда, согласно теореме 8, следует интегрируемость
функции / на множестве Е. П
44.6. Свойства кратного интеграла
В этом пункте будут рассмотрены свойства кратного
интеграла, аналогичные свойствам интеграла от функции одного
переменного по отрезку. Напомним, что интегрируемость
какой-либо функции (по Риману) на некотором множестве
предполагает его измеримость по Жордану.
1^. Пусть Е — измеримое множество; тогда \dE = \iE.
Действительно, в данном случае подынтегральная функция
тождественно равна единице. Поэтому если х = {Е^}^^-^—
некоторое разбиение множества Еу то (см. D4.51))
\dE = lim У \iE- = \1Е,
2^. Пусть Е и Е* — измеримые множества, Е* ^ Е и
функция f ограничена и интегрируема на Е; тогда она
интегрируема и на Е\
В самом деле, множество Е** = Е\Е* так же измеримо, как
разность двух измеримых множеств. Пусть т"^ = {^П —
разбиение множества Е* мелкости It^^I и т"^"^ = {Е**} — разбиение
множества Е'^'^ мелкости It"^"^! < It^^I. Тогда т = {Е*, Е**} является
разбиением множества Е мелкости |т| = It^^I. Если
ш, = ^ш(/, Е^)^Е^ + ^ш(/, Ep^Ej'^
1* 1**
(О,* = £со(/, Ef)ViE*,
ТО, очевидно, О < со^^ < со^. Но lim со^ = О, поэтому
lim 00^^ = О,
откуда и следует интегрируемость функции / на множестве Е*
(см. D4.69)).
734
3^. Аддитивность интеграла по множествам. Если Е'
и Е'' — измеримые множества, Е = Е' 1) Е'\ Е' П Е'' = 0
и функция f ограничена и интегрируема на множестве Е,
то интегралы \f(x)dE' и \f(x)dE'' существуют и
\f(x)dE = \f(x)dE' + \f(x)dE'\ D4.80)
Сугцествование интегралов \f(x)dE' и \f(x)dE'' следует из
свойства 2^, поэтому нуждается в доказательстве лишь
формула D4.80). Пусть т' = {E'l} и т'' = {Е'-} — разбиения
соответственно множеств Е' и Е'\ Тогда т = {Е^, Е'-} является
разбиением множества Е и его мелкость равна наибольшей из мел-
костей разбиений т' и т'': |т| = max {|т'|, |т''|}.
Пусть ^^'^еЕ'., r{(J^eEJ,
о', = 1^тЩ[1Е\, а^ = 1тиУ)^Е';, а^ = а,^ + а,.. D4.81)
х' X
в силу интегрируемости функции / на множестве Е, Е' и Е'\
lim а^ = \f(x)dE, lim а^^ = \f(x)dE\ lim а^- = \f(x)dE'\
Поэтому, переходя к пределу в равенстве D4.81) при |т| -^ О,
получим D4.80).
Замечание 1. Если функция / интегрируема и
ограничена на множестве Е, то она интегрируема и на множестве
Е^^^ его внутренних точек, причем
lf(x)dE = lf(x)dE,^,.
Это следует из свойства 3^, так как
(см. замечание 6 в п. 44.1).
Замечание 2. Следует обратить внимание на следую-
гцее обстоятельство: может случиться, что функция /
определена на множестве Е = Е' U Е'\ где Е' и Е'' — измеримые
множества, Е' П Е'' = 0. Интегралы \f(x)dE' и \f(x)dE'' су-
гцествуют, а интеграл \f(x)dE не сугцествует.
Поясним сказанное на примере. Пусть (г, ф) — полярные
координаты точки на плоскости,
О, если г < 1,
/(^ Ф) I 1/ф^ если г = 1, О < ф < 271,
Е' = {(г, ф): г < 1} — открытый круг, Е'' = {(г, ф): г = 1} —
окружность. Очевидно, [lE'' = О, поэтому несмотря на то, что функ-
435
ция / неограничена на Е'\ она интегрируема и \f(r, (p)dE'' = 0.
Сугцествует и интеграл \f(r, (p)dE' = 0. Однако интеграл
\f(r, (p)dE по замкнутому кругу Е = Е' U Е'' не суш;ествует.
Действительно, множество представляет собой замыкание
области, поэтому у него супа;ествуют сколь угодно мелкие
разбиения, все элементы которых имеют положительную меру.
Следовательно (см. замечание к теореме 7), всякая
интегрируемая на Е функция ограничена, а заданная функция /
неограничена и поэтому не интегрируема.
Важно отметить, однако, что для ограниченных функций
подобной ситуации быть не может: если функция / ограничена и
интегрируема на измеримых множествах Е' и Е'\ Е' П Е'' = 0, то
она интегрируема и на множестве Е = Е' U Е'\ причем
справедлива формула D4.70). Это будет доказано в п. 44.7"^.
Заметим лигаь, что в случае, когда одно из множеств Е'
или Е'' имеет меру нуль, то интегрируемость ограниченной
функции / на их объединении, в предположении ее
интегрируемости на каждом из них, можно получить почти
дословным повторением рассуждений, проведенных при
доказательстве теоремы 10. В самом деле, пусть / интегрируема
и ограничена на измеримых множествах Е' и Е'\ [lE' = О,
Е = Е' D Е'\ Тогда если, как и в указанном доказательстве,
построить множество G ^ Е' (множество Е' играет здесь роль
множества ^q из теоремы 10) и положить F = E\G, то будем
иметь F ^ Е'' и, следовательно, в силу свойства 2^
интегралов, функция / окажется интегрируемой на множестве F,
откуда, как и Bbinie, вытекает ее интегрируемость на
множестве Е, а значит, в силу свойства 3^, и справедливость формулы
D4.70), T^e\f(x)dE' = 0.
Из доказанного следует, что, для того чтобы функция /,
ограниченная на замыкании Е измеримого множества Е,
была интегрируема на Е, необходимо и достаточно, чтобы она
была интегрируема на его замыкании Е, причем
^f(x)dx = I f(x)dx,
Е Ё
Действительно, если интеграл сугцествует по множеству Е, то
так как граница Э^ измеримого множества Е имеет меру, равную
нулю, то и \х(Е\Е) = О, так как ^\^ ^ Э^. Поэтому | f(x)dx = О,
Ё\Е
а так как Е = Е U (Е\Е), то, в силу сказанного выгае,
^f(x)dx = ^f(x)dx + I f(x)dx = ^f(x)dx.
Ё ^ Ё\Е ^
436
Наоборот, если существует интеграл по замыканию Е
измерительного множества Е, то, в силу свойства 2^, он сугцест-
вует и по самому множеству.
4^. Линейность интеграла. Если функции /^ и /2
интегрируемы на множестве Е, то для любых чисел Х^ и Х^ ^У~
ществует интеграл \\_\fi{x) + X2f2(x)]dE и справедливо
равенство
\[Xifiix) + XJ^^xWE = X^\f^(x)dE + Xjf2ix)dE.
5^. Если функции fug интегрируемы и ограничены на
некотором множестве, то и их произведение и отношение
f/g {при infill > 0) интегрируемы на этом множестве,
Е
6^. Интегрирование неравенств. Если функции fug
интегрируемы на множестве Е и для всех хеЕ выполняется
неравенство f(x) < g(x), то
\f(x)dE < \g(x)dE.
7^. Если функция f интегрируема и ограничена на
множестве Е, то и ее абсолютная величина \f\ интегрируема
на нем, причем
\lfix)dE\ < l\fix)\dE.
Доказательство свойств 4^—7^ проводится совергаенно
аналогично одномерному случаю (см. п. 24.1).
8^. Монотонность интеграла от неотрицательных
функций по множествам. Если Е и Е* — измеримые множества,
Е* ^ Е, функция f неотрицательна, ограничена и
интегрируема на Е, то
|/(x)d^' < \f(x)dE. D4.82)
Действительно, в силу свойств 2^ и 3^, интегралы \f(x)dE*
и \f(x)d(E\E*) сугцествуют и
\fix)dE = \fix)dE'' + \fix)diE\E'').
Поскольку f(x) > о, то, в силу свойства а
отсюда и следует неравенство D4.82).
9^. Пусть функция f интегрируема и неотрицательна
на измеримом открытом множестве G, x^^^eG, функция f
непрерывна в точке х^^^ и f(x^^^) > 0. Тогда
\fix)dG>0. D4.83)
Действительно, в силу непрерывности функции / в точке
х^^\ для любого 8 > о сугцествует такая окрестность U =
= U(x^^^) этой точки, что для всех хе U выполняется неравен-
437
ство f(x^^^) - 8 < f(x) < f(x^^^) + 8. При ЭТОМ, В силу открытости
множества G, окрестность U всегда можно выбрать так,
чтобы С/ с G.
Выбрав 8 = ^ \ получим для него такую окрестность U,
что для всех х, принадлежагцих этой окрестности, будем
иметь f(x) > '^^ К Отсюда, применяя последовательно свой-
ства 8^, 6^ и 1^, найдем, что
\f{x)dG > \f{x)dU > f-^\dU = f^[iU > О,
ибо [iU > О как мера всякого открытого множества. П
Отметим непосредственное следствие из свойства 9^.
СЛЕДСТВИЕ. Если функция f непрерывна, интегрируема и
неотрицательна на измеримом открытом множестве G и не
является тождественным нулем, то
10^. Полная аддитивность интеграла по открытым
множествам. Если G, G^ — измеримые открытые множества,
Gm'=Gm + i' т = 1,2,..., D4.84)
„У1^™ = ^' D4.85)
а функция f интегрирует на множестве G, то
lim \ f{x)dx= \f{x)dx. D4.86)
G^ G
т
Докажем сначала, что из выполнений условий D4.84) и
D4.85) следует, что
lim iiG^^iiG. D4.87)
Пусть задано 8 > О, тогда сугцествует такой ранг к, что
(см. D4.3), D4.5) и D4.6))
liG — 8<|as^(G). D4.88)
Множество G, будучи измеримым, ограничено. Поэтому
множество sjfi) представляет собой объединение конечного
множества замкнутых кубов и, следовательно, является
компактом. Поскольку этот компакт лежит в множестве G, в силу
равенства D4.85), система {G^} является его покрытием
открытыми множествами. Согласно теореме Гейне—Бореля (см.
теорему 4 в п. 35.3), из этого покрытия можно выделить конечное
покрытие. Ясно, что если т^ — наиболыаий номер множеств G^,
138
входяш;их в это конечное покрытие, то в силу включении
D4.84) имеет место включение
sJG) с G„
^0
Из неравенства D4.88) и включений
имеем при т> т^
jiG - 8 < [iSf^(G) < [iG^ < jiG.
Это и означает выполнение равенства D4.87).
Докажем теперь равенство D4.86). Функция /, будучи
интегрируемой на открытом множестве G, ограничена (см.
теорему 7 в п. 44.4). Ограниченность функции / на множестве G
означает сугцествование такой постоянной с > О, что для всех
точек xeG выполняется неравенство |/(х)| < с. Поэтому
I f(x)dx - I /(x)(ix| = I I /(x)(ix| < I |/(x)|(ix <
G\G^
70 J " ^ ^' 4050
G\Gm
Ло M ^^ P ciiiG\GJ = ciiiG - liGJ - 0
G\G^
при Й ^ oo^ т. e. равенство D4.86) доказано. П
Замечание 3. Отметим, что для любого измеримого
открытого множества G супа;ествует последовательность
измеримых открытых множеств G^, удовлетворяюпа;ая условиям
D4.84) и D4.85). Более того, эту последовательность можно
даже выбрать таким образом, что не только сами множества G^,
но и их замыкания G^ будут содержаться в множестве G:
G^<zGm<^G, m = l,2, .... D4.89)
При этом поскольку множества G^ измеримы, то они
ограничены. Следовательно, ограничены и их замыкания Gm,
которые являются поэтому компактами. В качестве таких
множеств G^ можно взять, например, множества
Gm=s„,iG\,t^ D4.90)
где, как обычно, множество s^(G) состоит из кубов ранга т,
содержапа;ихся в множестве G.
Проверим выполнение условий D4.84), D4.85) и D4.89)
для множеств D4.90). Свойство D4.84) в этом случае
выполняется очевидным образом:
^т ^ ^т (^)int ^ ^т + l(^)int ^ ^т +1*
439
Докажем свойство D4.85). Ясно, что из
следует, что
^yiG„<=G. D4.91)
С другой стороны, для любой точки X е G в силу открытости
множества G сугцествует ее 8-окрестность U(x; г), 8 > О, содер-
жагцаяся в G : С/ (х; 8) с G. Если ранг т^ кубов таков, что куб
этого ранга имеет диаметр меньше 8, т. е. ^^ < 8, то все кубы
ранга tUq, содержаш;ие точку х, лежат в окрестности U (х; 8)
точки X и, следовательно, в множестве G. Поэтому
Итак, если хеО, то суш;ествует такой ранг т^, что xeG^ и,
значит,
Gc^y^G^. D4.92)
Из включений D4.91) и D4.92) и следует равенство D4.85).
Наконец,
Т. е. условие D4.89) также выполнено.
Замечание 4. Поясним, почему свойство 10^
называется полной аддитивностью интеграла. Если
последовательность \ I f(x)dx [ заменить рядом
оо
J f(x)dx + ^ J fix)dx,
ДЛЯ которого эта последовательность является
последовательностью частичных сумм, то формулу D4.86) можно записать
в виде равенства
со
If{x)dx = jf{x)dx + £ j f{x)dx, G = G^\J{G^ + ^\GJ.
G Gi '^ - 1 G„ + i\G„
Свойство интеграла по сумме счетной совокупности непересе-
каюпа;ихся множеств быть равным сумме интегралов по этим
множествам называется полной аддитивностью интеграла.
11^ (Теорема о среднем), ^слг/ функции fug
интегрируемы на множестве Е с R^, т < f (х) < М, хеЕ, и
функция g(x) не меняет знак на Е, то существует такое
число \х, т < \х < М, что
I fix)g(x)dx = [i\g (x)dx. D4.93)
440
СЛЕДСТВИЕ. Если множество G — область, функции fug
интегрируемы, f непрерывна, а g не меняет знак на G, то в
области G существует такая точка ^, что
\ f(x)g (х) dx = /(^) I g (х) dx. D4.94)
G G
Свойство 11^ доказывается аналогично интегральной
теореме о среднем для интеграла по отрезку и не требует
предположения об ограниченности рассматриваемых функций, так как
основано лип1ь на интегрировании неравенств (см. п. 24.2).
В основе доказательства следствия лежит та же идея, что и в
одномерном случае, однако оно имеет некоторые особенности,
поэтому приведем его.
В силу интегрируемости функции / на открытом множестве
она ограничена (теорема 7), поэтому ее нижняя т = inf / (х) и
ХЕ G
верхняя М = sup / (х) грани конечны на области G:
X Е G
- оо <яг</(х)<М< +оо, xeG. D4.95)
Если число [1 в равенстве D4.93) удовлетворяет
неравенству m < ц < М, то, согласно определению нижней и верхней
граней, супа;ествуют такие точки x^^^eG и x^^^eG, что
/(хA))<|а</(хB)).
Отсюда, в силу линейной связности области G и
непрерывности на ней функции /, найдется такая точка ^ е G, что f (Ь,) = \х
(см. п. 36.7), и формула D4.94) в этом случае доказана.
Пусть \х = т или \х = М, например, \х = М, Тогда из
равенства D4.93) при \х = М следует, что
\ (M-f (х)) g (х) dx = 0. D4.96)
G
Если I g (х) dx = О, то на основании равенства D4.93)
G
имеем I f (х) g (х) dx = О и, следовательно, формула D4.94)
G
справедлива при любом выборе точки q в области G.
Пусть I g (х) dx Ф О, например,
\g{x)dx>Q. D4.97)
G
Функция g не меняет на G свой знак. Случай g (х) < О, х g G,
противоречит условию D4.97). Поэтому для всех точек х е G
выполняется неравенство
gix)>0. D4.98)
Согласно полной аддитивности интеграла по открытым
множествам (см. свойство 10^) и замечанию 3, из неравенства
D4.97) следует, что суш;ествует такое открытое измеримое
множество Gq, для которого Gq с Gq с G и выполняется
неравенство
I g(x)dx>0. D4.99)
Go
В силу измеримости области G, она ограничена, поэтому
ограничено и замыкание Gq множества Gq, следовательно,
оно является компактом. Если бы не сугцествовала точка
^G Gq , в которой /(^) = М, то для всех точек х е Gq
выполнялось неравенство М - f (х) > О, xgGq.
Согласно достижимости непрерывной на компакте
функцией своего наименыаего значения, имеем
т^= min (М-/(х))>0. D4.100)
X е G,
О
Поэтому
\ (M-f (х)) g(x)dx> \ (M-f (х)) g (х) dx >
G,
О
> тпг. [ g (х) dx > 0.
^^ i_ D4.99)
^0 D4.100)
Это противоречит равенству D4.96). Следовательно, сугцест-
вует такая точка ^g Gq ^ G, что / (^) = М,
Случай [1 = т рассматривается аналогично. П
44.7*. Критерии интегрируемости
функций Римана и Дарбу и их следствия
Пусть функция / определена и ограничена на измеримом по
Жордану множестве Е, т = {Е^У^^^^— его разбиение, т- =
= inf /, М. = sup f, s^= Y, ^i l^^j' '^x^ H^i ^^i ~ нижняя и
верхняя суммы Дарбу, соответствуюпа;ие разбиению т. Положим
/^ = sups,, r = infS,. D4.101)
/^ называется нижним, sl I* — верхним интегралом Дарбу
функции /. Оказывается, что нижний и верхний интегралы
Дарбу являются не только соответственно верхней и нижней
гранью интегральных сумм Дарбу, но и их пределом при
условии, что мелкость разбиений стремится к нулю.
142
ТЕОРЕМА 11. Если функция f ограничена на измеримом
по Жордану множестве Е, то
1^ = lim S-, Г = lim aS^.
|т|^0 ^ |х|^0 ^
Доказательство. Установим справедливость первой
формулы (вторая доказывается аналогично). Пусть |/(х)| < М,
XG^, а 8 > О задано. В силу определения D4.101), сугцествует
такое разбиение т"" = {Е^} множества Е, что
V>^--|- D4.102)
i
X
Здесь s^* = £ mfiiE*, т* = inf /, i = 1, 2, ... , i^*. Пусть E^ —
объединение границ Э^^" множеств Е^:
Е^=.у^дЕ^. D4.103)
Поскольку каждое множество Е* измеримо, \хдЕ* = 0; поэтому
[iEq = 0. Следовательно, сугцествует такой ранг k = k(E), что
^^S.(^o)<^- D4.104)
Покажем, что для любого разбиения т = {^^}f _ ^^
множества Е мелкости |т| < 10~^ выполняется неравенство
/.-8<s,</.. D4.105)
В силу произвольности 8 > о, это и означает, что lim s^ = I^,
|т| ^0
Неравенство s^ < /^ непосредственно вытекает из
определения нижнего интеграла /^ (см. D4.101)). Поэтому надо
доказать лип1ь неравенство
s,>/.-8 D4.106)
при условии |т| < 10~^.
Пусть aS^ = Sj^(Eq) состоит из кубов Q^, ... , Q^. Аналогично
тому, как это было сделано при доказательстве теоремы 10,
обозначим через Pj куб, получаюгцийся из Qj
преобразованием подобия с центром в центре куба Qj и коэффициентом
подобия, равным 3, у = 1, 2, ... , т. Положим
Р=.и^Р., G = E\P. D4.107)
Из определений множеств Р и G следует, что множество G
отделено от многогранника aS^(^o) «полосой» кубов с ребрами
443
длины 10 ^. Прежде всего оценим меру [iP. Из определения
множества Р (см. D4.107) и неравенства D4.104)) имеем (ср.
с D4.73))
т т т о
цР = ц ^у ^Р. < ^ цР. = 3" i: [iQj = 3«ц5,(£о) < ^- D4.108)
Далее заметим, что для любого множества А ^ Е с
диаметром diam(A) < 10~^, пересекаюгцимся со множеством G:
А П G ^ 0, сугцествует, и притом единственное, множество
Е^ех* такое, что
А^Е-. D4.109)
Действительно, выберем какую-либо точку хеА П G. Так как
А ^ ^, то хеЕ, и поэтому точка х содержится в некотором
элементе Е* разбиения т"^. Для этого элемента и выполняется
включение D4.109). В самом деле, если это включение не
имело места, то нагалась бы точка уеА\Е^, Так как хеА, уеА и
daim(A) < 10"^, то р(х, у) < 10"^. Следовательно, отрезок с
концами в точках хну, имея длину, меныаую чем 10~^, и один
конец X во множестве G, не пересекается со множеством
aS^(^o)' ^^^ ^^^ ^^^ отделено от G полосой гаирины 10~^.
Однако из того, что один конец отрезка принадлежит некоторому
множеству, в данном случае множеству Е*, а другой нет,
следует (см. лемму 9 в п. 35.2), что на этом отрезке сугцествует
точка zedE-. Но (см. D4.103)) Э^^ ^ ^о ^ ^^(^о)' т.е.
2GaS^(^q). Следовательно, указанный отрезок пересекается со
множеством aS^(^q). Полученное противоречие и доказывает
вложение D4.109).
Докажем единственность множества Е*, удовлетворяюгце-
го включению D4.109). Пусть сугцествует егце одно
множество Elex"" такое, что А ^ El, k ^ i. Тогда А ^ Е^ П El. Если
пересечение Е* П El содержало бы хоть одну точку, являю-
гцуюся одновременно внутренней для множеств Е* и El, то
эта точка была бы внутренней и для пересечения El П El, а
тогда имело бы место неравенство [1(Е* П Е^) > 0. Это
неравенство противоречит определению разбиения (см. п. 44.3), в
силу которого [i{E* П Е^) = О при i ^ к. Следовательно,
каждая точка пересечения Е^ П El, поэтому и каждая точка
множества А, является граничной точкой по крайней мере для
одного из множеств Е^, El. Но тогда А ^ U Э^^" = Е^ ^
444
^ aS^(^o)- Это невозможно, так как множество А пересекается
со множеством G, которое не пересекается с aS^(^q).
Противоречие получилось из предположения о супа;ествовании
второго элемента Е^ из т"^, содержагцего множество А.
Следовательно, такой элемент единствен.
Возьмем теперь произвольное разбиение т = {E-jiZ^^
множества Е мелкости |т| < 10~^. Нижнюю сумму Дарбу
^х= Ц ^j^^p ^j = }^l Ял:), j = 1, 2, ... , у,
разобьем на два слагаемых, соответствуюгцих тем Е-, которые
пересекаются со множеством G, и тем, которые с ним не
пересекаются, и, следовательно, целиком лежат в множестве Р
(см. D4.107)):
s^= ^ rnj[iEj+ ^ mj[iEj. D4.110)
EjnG^0 Е-сР
Использовав очевидное неравенство
|т.|<М, 7 = 1,2, ...,;;, D4.111)
где |/(х)| < М, хеЕ, и оценку D4.108), получим
I £ mjiiEjl < £ \mj\iiEj < М £ цЕ^ < МцР <М^ = 1.
^Е.сР \ Е.сР Е.сР
В частности, ^ ^j^-^j ^ ~§- Поэтому из D4.110) имеем
Ej^P
s,> £ mj[iEj-^. D4.112)
Теперь заметим, что diam Е- < |т| < 10~^, поэтому для
каждого Е-, пересекаюгцегося со множеством G, в силу D4.109),
сугцествует такое Е*ех'^, что Е- ^ Е*. Обозначим через G-
объединение всех тех Е-, которые пересекаются с G и
содержатся в Е*:
Gi= и ^ е..
E^nG^0
Группируя в сумме ^ ^j^-^j слагаемые, содержагциеся
EjO G ^ 0
В ОДНОМ и том же множестве G-, запигаем ее в виде
£ mJiiEj= £ £ mJ^iEj. D4.113)
Е-П G^0 i=lE.^G.
J J ^
445
Для оценки внутренней суммы заметим, что для любого
i = 1, 2, ... , i*, согласно очевидному равенству
Ef = (Е; П G,) и (£*\G,) = G, и (£*\G,)
(второе равенство следует из включения G- ^ Е*), имеем
т^^Е^ = mf^iG, + m^^(E^\G,) =
= т^^ ^ у^ Е. + mMEt\Gi) = < 1^ \iE. + ш1\х(Е^). D4.114)
Оценим второе слагаемое. Каждая точка xeE*\G.
принадлежит некоторому множеству Е-ет : хеЕ-. Это Е- не может
пересекаться с G, так как всякое Е^ех, пересекаюгцееся с G,
целиком содержится в некотором элементе разбиения т"^ (см.
D4.109)). Поскольку пересечение Ej П Е^ непусто: xeEj П Е^,
то в данном случае этим элементом может быть только
множество Е*, т. е. Е- ^ Е*. Но тогда, в силу определения
множества G., имело бы место включение Е- ^ G- и, следовательно,
xeG.. Это противоречит предположению, что xeE^\G.. Итак,
множество Е- не пересекается с G и поэтому Е- ^ Р. Отсюда, в
частности, вытекает, что хеР. Так как х — произвольная
точка множества E*\G., то E*\G. ^ Р, и поэтому E*\G. ^ Е* П Р.
Использовав это включение и неравенство D4.111), получим
m^[i(E^\G.) < M[i(E^ n Р). Подставив это неравенство в
D4.114), будем иметь
т^^Е^< l^ml\iE. + M\i{El^P).
Теперь заметив, что из включения Е- ^ G. ^ Е* следует
неравенство т* < m (нижняя грань подмножества не мень-
nie, чем нижняя грань самого множества), получим
^ m.\iE.>ml\iEl-M\i{El^P).
446
откуда
Просуммировав обе части по / от 1 до / ^, в силу D4.113),
будем иметь
^ * ^ *
^ nijiiEj > £ mfiiEj - М £ MEf П Р) =
i= 1
Поскольку, согласно D4.108),
i = 1
то
£ ц(£* П Р) = [lU^Ef п Р < ЦР < ^,
£ m^|i£^.>v-|- D4.115)
Применив теперь последовательно неравенства D4.112),
D4.115) и D4.102), получим
»х > L "^у+^^у - I > S,* - -| > /* - 8,
£. П G ^ 0
Т. е. неравенство D4.106), следовательно, и теорема 11,
доказаны. П
С ее помогцью можно установить два критерия
интегрируемости ограниченной функции.
ТЕОРЕМА 12 (критерий Дарбу). Ограниченная на
измеримом по Жордану множестве функция интегрируема по Ри-
ману тогда и только тогда, когда ее верхний и нижний
интегралы Дарбу равны.
Доказательство. Пусть 1^и.1* — соответственно нижний
и верхний интегралы Дарбу функции /, ограниченной на
измеримом множестве Е, Следовательно, для любого разбиения
т множества^ выполняются неравенства (см. D4.101))
s,</.<r<S,. D4.116)
Необходимость условия 1^ = 1*. Если функция /
интегрируема на множестве Е, то (см. D4.67))
Um^(S,-s,)-0,
И так как О < Г - 1^< S^- s^, то /^ = /''.
447
Достаточность условия 1^ = 1^. Если /^ = 1^у то,
в силу теоремы 11,
lim (aS^ - s^ = lim S^ - lim s^ = I.,- Г = 0,
И поэтому, согласно теореме 8 из п. 44.4, функция /
интегрируема. П
ТЕОРЕМА 13 (критерий Римана). Ограниченная на
измеримом по Жордану множестве Е функция f интегрируема по
Риману тогда и только тогда, когда для любого 8 > О
существует такое разбиение т множества Е, что
S,-s,<8, D4.117)
где s^ и S^ — нижняя и верхняя суммы Дарбу функции /,
соответствующие разбиению т.
Доказательство. Если функция / интегрируема на
множестве Е, то для нее выполняется условие D4.67) (см. теорему
8 в п. 44.4). Справедливость D4.117) следует из определения
предела при |т| ^ 0.
Если, наоборот, выполняется условие D4.117), то, в силу
D4.116), при любом 8 > О справедливо неравенство О <: I* - 1^ <
< 8, и поэтому /^ = Р. Отсюда, согласно теореме 12, и
вытекает, что функция / интегрируема на множестве Е, П
Вспоминая определение кратного интеграла (см. п. 44.3),
теорему 8 из п. 44.4 и теоремы 12 и 13, получим для
ограниченных функций эквивалентность следуюпа;их пяти
утверждений:
1) функция f интегрируема на множестве Е, т. е.
существует предел lim а^ = \f{x)dE\
2) lim (S, - зЛ = 0;
'^ i = i
3) lim Y, ^(fy ^i)^^i = 0, X = {E^}. _^— разбиение множе-
ства E;
4) для любого 8 > О существует такое разбиение т
множества Е, что S^ - s^ < 8;
5) /. = Г.
Таким образом, выполнение каждого из этих условий
равносильно супа;ествованию интеграла ]f(x)dE, причем
\f(x)dE = lim а^ = lim s^ = lim aS^.
448
Замечание 1. Доказанные теоремы позволяют теперь
без труда доказать аддитивность интеграла по измеримым
множествам для ограниченных функций (см. п. 44.6,
свойство 3^) в следуюгцем виде: если ограниченная функция f
интегрируема на непересекающихся множествах Е^ и Е2, то
она интегрируема и на множестве Е = Е-^ U Е^-
Действительно, если функция / ограничена и
интегрируема на множествах Е^ и ^2? ^о, в силу теоремы 13, для
любого 8 > О супа;ествуют разбиения т^ и х^ соответственно
множеств Е^ и Е^ такие, что
Поскольку т = т^ и Т2 является разбиением множества Е =
= ^^ и ^2 и соответствуюпа;ие ему верхняя aS^ и нижняя s^
суммы Дарбу выражаются через аналогичные суммы Дарбу, соот-
ветствуюпа;ие разбиениям т^ и Т2, по формулам aS^ = aS^ + 'S^ ,
s^ = s^ + ^x ' '^^' вычитая из первого из этих равенств второе,
получаем, в силу D4.107),
Из выполнения этого условия следует (снова согласно теореме
13), что функция / интегрируема на множестве Е.
Замечание 2. Как уже отмечалось в п. 44.3, для
функций одной переменной, определенных на отрезках, мы
располагаем двумя определениями интеграла, а именно,
определением, данным в п. 23.1 — с помогцью разбиений отрезков
только на отрезки, и определением из п. 44.3 — с помогцью
разбиений отрезков на любые измеримые по Жордану
множества. Эти два определения эквивалентны.
Докажем это. И при первом, и втором определении
необходимым условием интегрируемости является
ограниченность рассматриваемой функции: см. теорему 1 в п. 23.2 и
замечание к теореме 7 в п. 44.4 (отрезок является замыканием
интервала, т. е. замыканием открытого множества). Поэтому
рассмотрим ограниченную на некотором отрезке [а, Ь]
функцию /. Пусть для этой функции сугцествует интеграл
/ = lim У f{i,i)\^E-
в смысле п. 44.3, т. е. для всевозможных разбиений т = {Е^У^^ ^^
отрезка [а, Ь] на измеримые по Жордану множества Е^. Тогда
149
если ограничиться лигаь частью разбиений т, для которых все
множества^- являются отрезками, то при |т| -^ О предел интег-
ральных сумм ^ f(b^.)[iE. по указанной части разбиений также
i= 1
сугцествует и будет равен тому же числу /. Следовательно,
если сугцествует интеграл в смысле п. 44.3, то он сугцествует и в
смысле п. 23.1.
а
Пусть, наоборот, сугцествует интеграл / = ^f(x)dx в смысле
b
п. 23.1. Тогда, согласно теореме 2 из п. 23.4, lim (aS^ - s^) = О,
где т — разбиение отрезка [а, Ь] на отрезки. Следовательно,
для любого 8 > О сугцествует такое 6 > О, что для всякого
разбиения т отрезка [а, Ь] на отрезки длин, не превыгааюгцих 6,
справедливо неравенство aS^ - s^ < 8. Но уже из того, что
сугцествует по крайней мере одно разбиение т, для которого
выполняется неравенство aS^ - s^ < 8, следует, согласно теореме
13 этого пункта, что функция / интегрируема в смысле
определения п. 44.3. Итак, оба определения интеграла по отрезку
действительно эквивалентны.
Аналогично одномерному случаю для функций многих
переменных формулируется и доказывается критерий
интегрируемости функции в терминах описания множества точек
разрыва функции, называемый также критерием Лебега.
Сформулируем его.
Множество в я-мерном пространстве называется
множеством я-мерной лебеговой меры нуль, если для любого
заданного 8 > О это множество можно покрыть системой открытых
niapoB, сумма объемов которых меньгае 8.
Примеры. 1. Множество, жорданова мера которого
равна нулю, является и множеством лебеговой меры нуль.
2. Всякое счетное множество является множеством
лебеговой меры нуль.
3. Множество рациональных чисел на числовой прямой
является примером множества одномерной лебеговой меры нуль,
которое не является множеством меры нуль в смысле меры
Жордана.
ТЕОРЕМА 14 (критерий Лебега). Для того чтобы
ограниченная функция была интегрируема по Риману на измеримом
по Жордану множестве, необходимо и достаточно, чтобы
150
множество точек ее разрыва было множеством лебеговой
меры нуль.
Доказательства критерия Лебега приводятся по той же
схеме, что и в одномерном случае.
§45
Сведение кратного интеграла к повторному
Перейдем теперь к свойствам кратного интеграла,
связанными со специфическими чертами, отличаюпа;ими
многомерный случай от одномерного. Использование этих свойств
часто супа;ественно облегчает вычисление конкретных кратных
интегралов. Полные доказательства в этом параграфе будут
проведены лигаь для случая функций двух переменных. 06-
гций я-мерный случай в идейном отногаении не отличается от
плоского, однако рассуждения там принимают более
громоздкий и менее обозримый вид.
45.1. Сведение двойного интеграла к повторному
Покажем, что интегрирование функций многих переменных
может быть сведено к последовательному интегрированию
функций одной переменной. Начнем с того, что определим
понятие повторного интеграла.
Пусть на отрезке [а, Ь] заданы непрерывные функции ф(х)
и \|/(х) такие, что ф(х) < \|/(х), а < х < Ь, и пусть на множестве
(рис. 58)
Е = {(х, у) : а< X <Ь, ф(х) < г/ < \|/(х)} D5.1)
определена функция /(х, у).
Если для любого фиксированного хе[а, Ь] функция /(х, у),
как функция переменного г/, интегрируема на отрезке
[ф(х), \|/(х)], т.е. при любом хе[а, Ь] су-
гцествует интеграл | /(х, y)dy и функция
Ф(х)
\\fix)
F(x)= ]f(x,y)dy D5.2)
ф(х)
интегрируема на отрезке [а, Ь], то интеграл
][ ] f(x,y)dy]dx D5.3)
а ф(х)
а Ъ X
Рис. 58
451
называется повторным интегралом и обозначается
\dx I f(x,y)dy. D5.4)
а ф(х)
Функция F(x), задаваемая равенством D5.2), называется
интегралом, зависящим от параметра х. Таким образом,
повторный интеграл D5.4) является интегралом от
интеграла, зависягцего от параметра (см. также § 53 и § 54).
Заметим, что множество Е, задаваемое формулой D5.1),
измеримо в смысле плоской меры Жордана и замкнуто.
Действительно, из непрерывности функций ф и \|/ на отрезке
[а, Ь] следует их ограниченность, а поэтому множество Е
ограничено. Далее, его граница Э^ состоит из графиков указанных
функций ф и \|/, а также, быть может, отрезков прямых х = а
и X = Ь, Каждое из указанных множеств имеет меру нуль (см.
теорему 3 в п. 44.2), а поэтому и граница Э^ множества Е
также имеет меру нуль. Наконец множество Е задается с по-
мопа;ью нестрогих неравенств а < х < Ь, ф(х) < г/ < \|/(х), где
функции ф и \|/ непрерывны, следовательно, эти неравенства
сохраняются и при предельном переходе в
последовательностях (х^, у^)еЕ, п = 1, 2, ... , откуда и вытекает замкнутость
множества Е, Таким образом, Е — измеримый компакт.
Достаточные условия для возможности сведения
двукратного интеграла к повторному даются следуюгцей теоремой.
ТЕОРЕМА 1. Пусть функция f{x, у) непрерывна на
множестве Е, заданном формулой D5.1). Тогда
|/(х, y)dxdy = \dx I f(x, y)dy. D5.5)
E a ф(х)
Доказательству теоремы предпогалем следуюгцую лемму.
ЛЕММА 1. Б предположениях теоремы 1 функция D5,2)
непрерывна на отрезке [а, Ь].
Доказательство леммы. Прежде всего заметим, что
интеграл D5.2) сугцествует при любом хе[а, Ь], Действительно,
функция f(x, у), будучи непрерывной по совокупности
переменных X и г/, непрерывна по каждой из них. Поэтому указанный
интеграл сугцествует как интеграл от непрерывной по у
функции на отрезке [ф(х), \|/(х)].
Выполнив в этом интеграле замену переменной г/ на f по
формуле
у = ф(х) + (\|/(х) - (p(x))t, 0<t<l, D5.6)
452
получим
1
F(x) = I f(x, ф(х) + (\|/(x) - (p(x))t)(\\f(x) - (p(x))dt. D5.7)
Положим
g(x, t) = f(x, ф(х) + (\|/(x) - (p(x))t)(\\f(x) - ф(х)).
Поскольку функция g(x, t) получается с помопа;ью
арифметических операций и композиции из непрерывных функций
f(x, у), ф(х), \|/(х) и D5.6), в силу теоремы о непрерывных
функциях (см. п. 36.4 и 36.6), она непрерывна по
совокупности переменных х, t на прямоугольнике Р = {(х, f) : а < х < Ь,
О < f < 1}. Таким образом, для функции F(x) (см. D5.2)), в
силу D5.7), имеет место более простое представление F(x) =
1
^ \ §(^у t)dt (более простое в том смысле, что в нем постоянны
о
пределы интегрирования).
Пусть теперь хе[а, Ь], х + Ахе[а, Ь], Обозначим через
соF; g) модуль непрерывности (см. п. 19.6) функции g(x, t).
Тогда
|1 1 I
\F(x + Ах) - F(x)\ = I g(x + Ах, t)dt - \ g(x, t)dt\ <
'о о '
1
< I \g(x + Ах, t) - g(x, t)\dt < ш(|Ах|; g). D5.8)
о
Функция g(x, t), будучи непрерывной на прямоугольнике Р,
являюгцемся, очевидно, ограниченным замкнутым
множеством, равномерно непрерывна на нем, поэтому (см. п. 36.6)
lim соF; g) = 0. Отсюда, в силу неравенства D5.8), имеем
lim [F(x + Ax)-F(x)] = 0,
Ах ^ о
ЧТО и означает непрерывность функции F(x), определенной
формулой D5.2).П
Доказательство теоремы. Прежде всего заметим,
что интеграл, стояпа;ий в правой части равенства D5.5), т. е.
b Ъ ^{х)
I F{x)dx = ^dx ^ /(х, y)dy,
« « ф(х)
является интегралом от непрерывной функции (см. лемму) и
поэтому супа;ествует.
Для доказательства равенства D5.5) разобьем отрезок
[а, Ь] на k равных отрезков точками
х. = а + ^ /, / = О, 1, ... , k D5.9)
453
{k фиксировано) и рассмотрим функции
Фо(х) = ф(л:),
9i(x) = ф(х) + VW^,
ф/х) = ф(х) + Ш-l^j,
Ф^(х) = ф(х) + VWz_2Wft = 1^(х),
а<х<Ь, D5.10)
(рис. 59). Очевидно, из формул D5.10) следует, что
ф/х) = ф^._1(х) + ^Й^Ь-2^, j=l,2,...,k. D5.11)
Положим
^}f = {(х, г/) : X. _ 1 < X < X., ф. _ ^(х) < г/ < ф.(х)}, D5.12)
/, у = 1, 2, ... , й.
Множества Ei^^ образуют разбиение (обозначим его т^)
множества Е (рис. 59): т^ = {^if^}- Покажем, что
lim К| = 0.
D5.13)
Функции ф(х) и \|/(х), будучи непрерывными на отрезке
[а, Ь], ограничены на нем, т. е. сугцествует такая постоянная
с > О, что для всех точек хе[а, Ь] выполняются неравенства
|ф(х)| < с, |\|/(х)| < с, и, следовательно, из формул D5.11)
вытекает, что
|ф/х)-ф,._,(х)|<Й^^^^М^<|,
/■=1,2, ... ,k, а<х< &. D5.14)
г/-
0
i
с
\1/(х)
^//
Ф(х)
f
1
7 X
Пусть (X, y)sElf\ (х-, z/')G£lf.
Оценим расстояние
р((х\ г/0, (х, г/)) =
Рис. 59
= J(x' - х)^ + (у' -у)^. D4.15)
454
Имеем
W-x\ < ^, D5.16)
' ' D5.9) k
W -y\< W - Ф/^Ol + |ф/:^0 - ф/:^I + |ф/:^) - y\ ^^g< 2)
D5.14) ^
+ ш,(ф.), D5.17)
где со.(фу) — колебание функции ф^ на отрезке [х- _ ^, х-]
(см. п. 5.17). Для этого колебания имеет место оценка, не за-
висягцая от номера у = 1, 2, ... , й:
со.(ф.) = sup |ф/(л:0 - ф.(х)| <
'^^ X, х'е [X. _ р X.] '^^ ^^ D5.10)
< sup |ф(хО - Ф(х)| + |( sup |ф(л:0-
- ф(х)| + sup |\|/(xO - \|/(x)|) < 2со.(ф) + co.(\|/) D5.18)
[здесь 1^1? так как у = 1, 2, ... , й , где со.(ф) и со.(\|/) —
колебания функций ф и \|/ на отрезках [х-_^, х-], i = 1, 2, ... , k.
Колебания функций оцениваются через их модули
непрерывности и тем самым независимо от номера /: если соF, ф) и
соF, \|/) — модули непрерывности функций ф и \|/ (см. п. 6.4), то
ш,(ф) < ш(^; ф', ш,(ф) < ш(^; ф' D5.19)
Ь- а^
—г— у поэтому
h J
ш.(ф.) < 2o)f^; ф^ + 0)f^; \|/\ D5.20)
'^^•^445.18), D5.19) \ к ^) \ к ^ )
Из равенства D5.17) и D5.20) следует оценка
|у' - г/1 < f + 2со(^; ф^ + со(^; v) D5.21)
Теперь можно оценить расстояние D5.15)
р((л:', г/0, (х, г/)) = V(x' - хJ + {у' - г/J < \х' - х| + |г/' - г/1 < ^^
D5.16)
D5.21)
D5.16) ^ ^ I ^ ^ J I ^ ^ J
D5.21)
Отсюда
diam E^f^ = sup рЦх\ г/0, (x, г/)) <
<^ + f+ 2ш(^;фЧш(^;х^\/,у=1,2,...,й. D5.22)
Поскольку функции ф и \|/ непрерывны на отрезке [а, Ь],
они и равномерно непрерывны на нем, поэтому (см. теорему 6
в п. 6.4)
lim шГ^;ф^= lim шГ^;\|/^ = 0. D5.23)
Зададим теперь произвольно 8 > 0. Для него супа;ествует
такое натуральное число k^, что для всех номеров k > k^
выполняются неравенства
^<£, 4с ^8 2шГ^;фЧшГ^;х|/' < |, D5.24)
k 3' ^ 3' I ^ '^у I ^ '^УD5.23K' ^ ^
И, следовательно, из неравенств D5.22) и D5.24) следует, что
для всех номеров k> к^и всех /, у = 1, 2, ... , й имеет место
оценка: diam Е^^} < 8, а так как (см. п. 44.3) |т^,| = max diam Е^^},
^'•^ D5.22) ^ i,j ^'-^
D5.24)
ТО при всех указанных k имеют место неравенства |т^| < 8. Это и
означает выполнение условия D5.13). Теперь имеем
b ^(х) f^ х^ \\fix)
\dx \ f(x, y)dy = £ М^ I /(^' У)(^У =
а ф(х) ^ ^ 1 ^. 1 ф(х)
i = 1 х^ _ ^ 7 = 1 ф^ ^(^) i = 17 = 1 х^ _ ^ ф^ ^(^)
Положим
т.. = inf /(x,i/) и М.. = sup /(X, г/), /,у =1,2,..., й.
Заметив, что (см. п. 28.1)
Xj
[iE.j= \ [ф.(х)-ф._1(х)]йх,
получим
^^ %(х) х^ ф^(х)
I dx I /(х, y)dy < М.. \ dx I dy =
Хг-1 9^_i(x) ^.-1 9^_i(x)
= My J [ф(х) - ф^. _ ^(x)]dx = Муц£у D4.25)
45ё
и, аналогично,
/dx Y f{x,y)dy>m^j\yE,j. D4.26)
С помогцью неравенств D5.25) и D5.26) для повторного
интеграла D5.4) получаем следуюгцую оценку через нижние и
верхние суммы Дарбу s^ и aS^. функции /(х, у):
k k
^т, ^ L Ё ^Ф^а ^ И^ I Я:^, y)dy <
^=1/^1 a ф(х)
< У УМ,,ц^,, = Я. D5.27)
У УМ..\уЕ.. = 8^ .
Мелкости разбиений т^ при й ^ оо стремятся к нулю (см.
D5.13)), поэтому, в силу интегрируемости функции f(x,y) на Е
(см. п. 44.4),
lim s^ = lim aS^ = llf(x, y)dxdy.
G
Переходя теперь к пределу в неравенстве D5.27) при й ^ оо^
получаем формулу D5.5). П
Замечание. Воспользовавгаись теоремой 10 из п. 44.5"^,
доказательство теоремы 1 настоягцего параграфа можно
технически супа;ественно упростить. Достаточно выбрать
какой-нибудь прямоугольник Р = {(х, г/) : а < X < Ь, с < г/ < d},
содержапа;ий множество Е (см. формулу D5.1)), ^ ^ Р, и
продолжить функцию / нулем на дополнение Р\Е множества Е в
прямоугольнике Р. Полученная функция (обозначим ее тем
же символом /) интегрируема на прямоугольнике Р, так как
множество точек ее разрыва содержится в границе Э^
измеримого множества Е, которая, как известно, имеет меру нуль.
Разбив на k равных частей отрезок [а, Ь] на оси Ох и
отрезок [с, d] на оси Оу и проведя через точки деления прямые,
параллельные координатным осям, получим разбиение
прямоугольника Р на прямоугольники
^(;)={(х,^):(/-1)^<х</^,(у-1)^^<^<у^
i=l,2, ... ,k; j=l,2, ... ,k; k=l,2,...,
с длинами сторон, равными ^ и ^, и, следовательно, с
диагоналями (диаметрами) diam E.j = - л/(Ь-аУ^ + (й-ср.
457
Поэтому последовательность мелкостей |т^| разбиений т^ =
= {^^^^} стремится к нулю: lim |т^| = 0.
Далее, рассуждая так же, как и при доказательстве
теоремы 1, получим
b d
\\f{x, y)dxdy = I dx\ f(x, y)dy,
P a с
a так как функция / равна нулю вне множества Е, то, в силу
аддиативности интеграла по множествам, эта формула
равносильна формуле D5.5).
d
Заметим лип1ь, что все интегралы | /(х, y)dy сугцествуют,
с
так как при любом фиксированном хе[а, Ь] функция /(х, у)
как функция переменного у имеет не более двух точек
разрыва, а именно на пересечении отрезка, по которому
производится интегрирование с границей Э^. Сугцествование же
повторного интеграла следует, как и вып1е, из непрерывности
функции D5.2).
Если множество Е таково, что супа;ествуют такие
непрерывные функции а(у) и р(г/), а(у) < р(г/), с < у < d, что
Е = {(X, y):c<y<d, а(у) <х< Р(г/)}, D5.28)
а функция /(х, г/), как и раньпхе, непрерывна на Е, то, в
силу равноправия переменных х и г/, из теоремы 1 следует,
что
d Р(у)
\\f(x, y)dxdy = \dy \ /(х, y)dx. D5.29)
Е с а(у)
Если же для множества Е справедливо как равенство
D5.1), так и D5.28) (рис. 60), то, приравнивая правые части
равенств D5.5) и D5.29), для непрерывной на множестве Е
функции /(х, у) получим формулу
^1
d
KD.
. ч b Мх) d P(y)
f^^ I dx I /(X, y)dy=\ dy I /(X, y)dx, D5.30)
a ф(х) с a(y)
выражаюпа;ую собой правило
перемены порядка интегрирования в
повторных интегралах.
Отметим, что условия, при которых
были доказаны формулы D5.5), D5.29)
К Е 1 т
Ф(х)
а о :
Рис. 60 и D5.30), могут быть ослаблены.
458
1 y = ^
К
-1 0
■м.
1 X
Рис. 61
г/А
Рис. 62
Пример. Вычислим интеграл от функции z = х^у по
конечной области G, ограниченной частью параболы г/ = х^ и
прямой у = 1 (рис. 61). Имеем
j j x^ydxdy = I x^dx I z/dz/ = I ^
x2dx = ij(l
•/u I«/u хЛ/Л c\ Ч *
Если требуется вычислить двойной интеграл по множеству,
которое нельзя задать в виде D5.1) или D5.28), то для того,
чтобы использовать полученные формулы, надо попытаться
разбить данное множество на части, каждая из которых будет
уже иметь вид D5.1) или D5.28) (рис. 62). Если это удастся
сделать, то, в силу аддитивности интеграла по множествам (см.
п. 44.6), вычисление данного интеграла сведется к вычислению
интегралов по указанным частям, а последние с помопа;ью
формул D5.5) и D5.29) могут быть сведены к однократным.
УПРАЖНЕНИЕ. Доказать формулу Дирихле
Ъ X Ъ Ъ
I dx\ f(x, y)dy = \dy \ f(x, y)dx.
45.2. Обобщение на n-мерный случай
Рассмотрим сначала трехмерный случай. Пусть Е ^ R^ л
Е = {(х,у,2) : (х,у, 0)еЕ
9i(x, у)<2<: щ(х, г/)},
хг/'
где функции 9i(x, у) и \|/i(x, у)
непрерывны на множестве Е , которое в свою
очередь представимо, например, в виде D5. 1),
"^lix^y)
функция f(x, у, 2) определена на Е. Обозначим через Е^у
екцию множества Е на координатную
плоскость переменных х и г/ (рис. 63)
Е = {(х, у, 0): супа;ествует такое 2, что
(х, г/, 2)еЕ}.
Если множество Е имеет вид
про-
Рис. 63
459
a функция f(x, у, z) непрерывна на исходном множестве Еу то
справедлива формула, аналогичная формуле D5.5):
Ь Y(x) Yi(x, у)
\\\f{^y г/, z)dxdydz = ^ dx ^ dy J f(x, у, z)dz, D5.31)
E a ф(х) 9i(x, y)
Объединив в правой части два внеганих интеграла, можно
переписать D5.31) в виде
Yi(x, у)
\\\f(x, у, z)dxdydz = \ \dxdy | /(х, г/, z)dz. D5.32)
Е Е^у 9i(x, у)
Обозначим теперь через Е(х) сечения множества Е
плоскостями, перпендикулярными координатной оси Ох:
E(Xq) = Е П {(х, у, z) : X = Xq}.
Объединив в правой части формулы D5.31) два внутренних
интеграла, получим
b
\\\f(x, г/, z)dxdydz = ^dx^ J /(x, г/, z)dydz, D5.33)
E a Е(х)
Таким образом, формулы D5.32) и D5.33) показывают,
что в трехмерном случае сугцествует два способа сведения
трехмерного интеграла к повторному, содержагцему
интегралы меньп1ей кратности.
В частном случае, когда /(х, у, z) = 1, имеем (см. свойство 1^
кратных интегралов в п. 44.6) \\\dxdydz = [iE(x) ([lE — объем
множества Е), \ dydz = \хЕ(х) (\хЕ(х) — плопа;адь сечения ^(х)).
Таким образом,
D5.34)
[lE = j [iE(x)dx
— объем тела равен интегралу от переменной плопа;ади
сечений ^(х).
Пример. Найдем объем
эллиптического цилиндра высоты Л, в основании которого
лежит эллипс с полуосями а и Ь. Взяв за
координатную плоскость ху плоскость одного
из оснований цилиндра, а за ось Oz — его
ось симметрии, перпендикулярную
основаниям (рис. 64), получим, согласно формуле
h
D5.34), [iE = ^ [iE(z)dz, Но E(z) — эллипс с
о
полуосями а и Ь, поэтому (см. пример 4 в
п. 28.1) [iE(z) = nab, следовательно.
Рис. 64
\хЕ = 7гаЬ| dz = Tzabh,
460
Аналогично трехмерному случаю кратные интегралы от
функций любого числа переменных п > 3 можно свести к
повторным интегралам. Пусть R^ — я-мерное пространство,
Rn -1 — гиперплоскость х„ = о, Е ^ R^, Е^ ^ — проекция
а х^ ... х^ _ -^
множества Е на гиперплоскость переменных х^, ... , х^ _ ^, т. е.
Е^^... х^_^ = {(^1' ••• ' ^я -1' 0): Эх^, (Xi, ... , х^ _ 1, xJeE}.
Пусть имеются такие непрерывные на ^„ „ функции
ф(х^, ... , х^ _ ^) И \|/(х^, ... , л:^ _ i), что множество Е состоит из
точек X = (х^, ..., х^ _ ^, х^), для которых
(Xi, ... , Х^_1, 0)g^^^ _^^_ ^, ф(Х1, ..., X^_l) < Х^ < \|/(Xi, ..., X^_l).
Пусть множество Е^ ^ измеримо в смысле (п - 1)-мер-
ной меры Жордана и замкнуто. Тогда аналогично
двумерному случаю (см. п. 45.1) доказывается, что Е также измеримо,
но уже в смысле я-мерной меры, и замкнуто, потому
является компактом.
Если функция /(х) = /(х^, ... , х^) непрерывна на
компакте Е, то справедлива формула
п раз
I ••• I fix^, ... , xjdx^ ... dx^ =
Е
п - 1раз
= {•••I dxi ... (ix^_i I /(Xi, ..., xjdx^, D5.35)
E 9(xi,...,x^_l)
которая сводит интегрирование функции п переменных к
последовательному интегрированию функции одной переменной
и функции п - 1 переменных.
Если проекция Е^ ^ множества Е на гиперплоскость
й^ " 1 в свою очередь может быть представлена в виде,
аналогичном виду множества Е, то получивп1ийся в правой части
равенства D5.35) (п - 1)-кратный интеграл можно свести к
(п - 2)-кратному. Продолжая этот процесс, если, конечно, это
возможно, далыае придем к формуле вида
п раз
I ... I /(Xi, ... , xjdx^ ... dx^ =
Е
= I dx^ I dx^ I (ixg ... I /(x^, ... , xjdx^. D5.36)
« 9i(Xi) фзСх^, X2) 9„_i(xi, ... ,x„_i)
4^i
Таким образом, в рассматриваемом
случае интегрирование функции от п
переменных сводится к
последовательному интегрированию п раз функций
одной переменной.
Обозначим теперь через Е^ ^
проекцию множества Е в пространство
Rf ^ , а через Е{х^, ... , х )— сече-
1 *** т
ние множества Е гиперплоскостями
размерности п - т, проходягцими через
точку (х^, ... , х^, О, ... , 0) и
ортогональными подпространству R^ ^ . Объединив в формуле D5.36)
1 *** т
т первых и п - т последних интегрирований, будем иметь
п раз
I ... I /(х^, ... , xjdxi ... dx^ =
Е
п - т раз
dx^
Рис. 65
т раз
I •••! d^i-
Е^
I ... I /(Xi, ... ,xj(ix^ + i...dx^. D5.37)
Е{Х-^ ... Х^)
Если /(х^, ... , х^) = 1 на ^, то из этой формулы аналогично
D5.34) получим
\iE= {•••I цДх^, ... ,xj(ixi...dx^. D5.38)
Пример. Вычислим интеграл от функции /(х, г/, г) = хг/^2^
по конечной области Е, ограниченной поверхностями z = ху,
у = X, х= IvLZ = О (рис. 65). Применим формулу D5.36):
\ X ху
^^^xy^z^dxdydz = ^ xdx^y^dy J z^dz =
\\хЧх]уЧу = ^\х^Чх = -1-.
Ч г ^ 28^
45.3''. Обобщенное интегральное
неравенство Минковского
В качестве епа;е одного примера применения правила
перемены порядка интегрирования докажем одно часто применяемое
интегральное неравенство.
462
Пусть функция f(x, у) непрерывна на прямоугольнике А =
= {(х, у) : а < X < Ь, с < у < d}. Тогда она, очевидно, при
любом фиксированном уе[с, d] непрерывна по х на отрезке [а, Ь]
и при любом фиксированном хе[а, Ь] непрерывна по у на
отрезке [с, d].
Для любого р > 1 справедливо обобщенное неравенство
Минковского
d г b
U\\\f(x,y)\dx
Положим
^/р
dy\ <\dx\\\f(x,ytdy
^/р
F(y) = \\f(x,y)\dx.
D5.39)
D5.40)
Функция F непрерывна (см. лемму 1 в п. 45.1) и
неотрицательна на отрезке [с, d]. Поэтому ее р-я степень также
интегрируем
ема и неотрицательна на этом отрезке, и О < ^FP(y)dy < + оо.
с
d
Если ^FP(y)dy = О, то, в силу непрерывности функции F,
с
будем иметь (см. свойство 9^ п. 24.1): F(y) = О на [с, d].
Поэтому из формулы D5.40), в силу того же свойства, следует, что
при любом уе[с, d] имеет место / (х, г/) = О на [а, Ь], т. е.
f(x, г/) = О на А. В этом случае неравенство D5.39) очевидно
справедливо.
d
Пусть ^FP(y)dy > 0. Тогда, изменив порядок интегрирова-
с
ния и применив неравенство Гельдера B4.48), получим, в
силу D5.40),
\FP(y)dy = \FP - \у)\\ |/(х, y)\dx\ dy = I dx\\f(x, y)\FP ' \y)dy
<
л^/Prd
<
\\\\f{x,y)\Pdy\ \\F<i^-^)dy
i/g
dx, D5.41)
где \/p + 1/g = 1 И, следовательно, q{p - V) = p. Сократив обе
части неравенства D5.41) на множитель ^F^(y)dy ^ О,
будем иметь
\^/Р
Ъ rd
jF'(y)dyj <nj\f(x,y)\Pdy
nl/P
dx.
463
Подставляя в это неравенство D5.40), получаем
неравенство D5.39). Условие непрерывности функции / не является
сугцественным для справедливости неравенства D5.39) и
может быть ослаблено. Для простоты доказательства в качестве
области определения функции / был взят прямоугольник.
При более обгцих предположениях доказательство
неравенства Минковского, основанное на той же идее, можно найти в
монографии Харди Г. Г., Литтлъвуда Д. Е,, Полиа Г.
Неравенства. М., 1948. С. 179—180.
45.4. Объем п-мерного шара
Методом сведения кратного интеграла к повторному иногда
удается вычислить значение краткого интеграла. Поясним это
на примере получения формулы для величины объема я-мер-
ного niapa радиуса г. Пусть
V^= {х : xf -\- х^-\- ... -\- х^<: г^}
—я-мерный niap радиуса г с центром в начале координат.
В случае плоскости (п = 2) известно, что
^2^г = \ I dxdy = 2] Jr^-x4x = 7zr^. D5.42)
Отсюда можно найти объем трехмерного niapa следуюгцим
образом:
^гУ? D5=34) 21 ^2V'j;^^,d2 = 2п]^ (Г2 - 2^)dZ = |гЗ.
Применим этот метод для вычисления объема [i^ V^ niapa V^
при произвольном п = 1, 2, ... , предполагая, что
f 4 ^
где %^ _ 1 — некоторая константа %2 ^ ^' %з ^ о^ • Имеем
\^Уг = \ I '"\dx^dx^...dx^ =
X? + xf + ... + х2 < г2
1 Z П
г
= 2|dxJ 1 -ldx2dxs...dx„
О 4^ ^\ о
X-i = г COS t
%I2 %I2
= 2%^ _ 1 r^ I sin^ tdt = %^r^, Xn = 2x^-i\ sin^ tdt.
^0 0
464
X-, = r COS t
Получивп1ийся интеграл был вычислен раньпхе (см. пример 2
п. 26.2 в Т.1), откуда
/Сд
^^^-i^^lP^i "^^ учетном,
2%„ _ 1 ——77-^ при п нечетном.
^ я!!
Таким образом, для коэффициентов %^ получена
рекуррентная формула. Последовательно ее применяя, получим (при
п = 1 очевидно l^iF^ = 2г, поэтому %^ = 2)
X2. = S' 5^2..1 = (Й^. т = 1,2,.... D5.43)
45.5. Независимость меры
от выбора системы координат
При определении меры множества в п. 44.1 остался
невыясненным вопрос о независимости меры от выбора системы
координат. Мера множеств определяется посредством
многогранников, состоягцих из кубов, ребра которых параллельны
координатным осям. Поэтому вопрос о независимости меры
множеств от выбора системы координат сводится к
независимости объемов кубов от этого выбора. Отногаение (обозначим
его X) объемов одного и того же куба, вычисленных в разных
системах координат, не зависит от выбора конкретного куба,
так как любые два куба с ребрами, параллельными
координатным осям одной системы координат, могут быть получены
один из другого с помопа;ью параллельного переноса и
гомотетии с центром в совмепа;енных центрах симметрии кубов. Если
указанное отноп1ение равно единице, то мера множества не
зависит от выбора системы координат.
Пусть в пространстве R^ заданы две системы координат.
Меру множества, определенную с помопа;ью первой из них,
обозначим через ц, а с помопа;ью второй — через jit. Пусть
Q — я-мерный куб с ребрами, параллельными координатным
осям первой координатной системы, и пусть
^Q = X[iQ. D5.44)
Отсюда следует, что множества одновременно имеют меру
нуль в обеих системах координат, следовательно, множества
одновременно измеримы или нет, причем если множество X ^ R^
измеримо, то jitX = Х\хХ. Для доказательства равенства Я. = 1
465
заметим, что объем я-мерного niapa V^ радиуса г равен %^ г^
(см. п. 45.4), где %^ — определенное число. Величина длины
радиуса niapa, как и длина всякого отрезка, имеет одно и то
же значение при любом выборе системы координат. Таким
образом, объем я-мерного niapa V^ не зависит от выбора
системы координат:
^V^ = [iV^. D5.45)
Для многогранника Sf^(V^) (см. формулу D4.3)), состоягцего
из кубов ранга k в первой системе координат (следовательно,
с ребрами, параллельными ее координатным осям), будем
иметь
Поэтому
ЫУ?) D5=44) ^^^'(V-). D5.46)
hrn^ tEs,(F,") = ^Дт^ ^s,(F,") = X^V-,
НО (см. лемму 6 в п. 44.1 приА^ = s^ (Vr))
^^oo'^^^ r^ ^ r D5.45)'^ ^^
T. e. X\\V]!: = \\У^. Это означает, что Я. = 1.
Итак, действительно мера множества не зависит от выбора
системы координат. Поскольку переход от одного ортонорми-
рованного базиса к другому осуществляется с помощью
ортогональных матриц, мера является инвариантом при
линейных ортогональных отображениях, т. е. отображениях,
задаваемых формулами
п
У1= H^ij^p i= 1, 2, ... , п,
С ортогональными матрицами С = (с-у), /, у = 1, 2, ... , п (см.
п. 35.4).
45.6*. Формулы Ньютона—Лейбница и Тейлора
Приведем самый простой вывод формулы Тейлора: она может
быть получена последовательным применением формулы
Ньютона—Лейбница к получающимся подынтегральным
функциям. Остаточный член формулы Тейлора имеет вид повторного
интеграла, который с помощью формулы перемены порядка
интегрирования (см. формулу D5.35)), можно привести к уже
известному нам его виду в интегральной форме с однократным
интегрированием (см. теорему 6 в п. 33.5).
466
ТЕОРЕМА 2. Если функция f имеет на отрезке [а, Ь]
непрерывную производную порядка пи х^е [а, Ь], то для любого
X е [а, Ь] имеет место равенство
п-1 f^^HXr.) ^ *1 *" 1
Я^) = L -П^ ^^ " ^о)' + \dh \dh - I /^"Ни dt, D5.47)
k = о i^- Xq Xq Xq
(формула Тейлора с остаточным членом в форме
повторного интеграла).
Доказательство. Докажем формулу D5.47) по
индукции. При п= \ она является формулой Ньютона—Лейбница
f{x) = f{x^)+ ] r(t^)dt^.
Хо
Если при некотором т = 1, 2, ... , п - 1 имеет место формула
f(^)= L '-^^ (x-x^r+\dt,\dt,... I /(-)(О^^^Л45.48)
jl = Q rt . Xq Xq Xq
TO, применив формулу Ньютона—Лейбница к функции /("^^ (^^тг)'
т. е.
f(rn) ^tj = /(-) (Хо) + j /<'» +1) (*„ + i) dt
подставив получивгаееся выражение в интегральный член
равенства D5.48) и проинтегрировав первое слагаемое, получим
} dt, ] dt, ... Y (/(-) (Хо) + I /(- +1) (f„ + i) d^„ + i) df„ =
Xq Xq Xq Xq
= fM(x,)]dt,ldt,... Tdt^ +
Xq Xq Xq
+ ldt,l dt, ... j /<'" + i»(*„ + i)rf*„ + i= ^^;^ (x-Xo)'" +
Xq Xq Xq
+ ] dt/l dt.JX dtj f^'"^'4t^^i)dt^^,. D5.49)
Xq Xq Xq Xq
Из равенств D5.48) и D5.49) следует, что
f(x) = £ ^^^^ (X - Хо)^ +
+ ] dt,] dt.JX dim] f^'^^'Ht^ + r)dt^^v
Xq Xq Xq Xq
При m = n- 1 эта формула превращается в формулу D5.47). П
467
Покажем, что остаточный член
rjx)=\dt, \dt^... I n^4tn)dt.
D5.50)
в формуле Тейлора D5.50) может быть преобразован к уже
известной его интегральной форме с одним интегрированием.
Сначала заметим, что для любой непрерывной на отрезке
[а, Ь] функции ф имеет место формула
ъ у 1 ^
f dy \ (p(x)(y-xfdx= -^ \ (p(x)(b-xf + ^dx,k^-l. D5.51)
а а ^ + 1 а
Она получается с помогцью изменения порядка
интегрирования (см. рис. 66, интегрирование производится по загатрихо-
ванному треугольнику)
ъ у ъ ъ
I (ii/1 ф (х) (у - х)^ dx = I ф (х) dx I (у - х)^ dy =
а а ах
= -^ \ ф (х) (Ь - х)^ +1 dx.
Далее справедлива формула
I dt^ \ dt^... )\(t,)dt,= -^^ I (?it)ib-tr-^t,
a a a ^'^ ^' a
й = 1,2, .... D5.52)
Эта формула также доказывается по индукции: если
справедливо равенство D5.52), то, применив его к интегралу
получим
Ъ X
Рис. 66
I dt^... |ф(^^+1)й^^+1,
а а
\ dt^ \dt^... l<?it, + Odh + ^ =
а а а
DГ52) 0^ I ^*1 i Ф(*) (*1 - *)'"' ^* DГ51)
1 ^
D5.51) kl J ^
Т. е. формула D5.52) остается верной при
замене й на й + 1.
468
Остаточный член D5.50) формулы Тейлора, в силу
формулы D5.52), при ф(^) = /(^) (t), а = Xq, Ъ = X VL k = п имеет вид
т. е. получилась запись остаточного члена в интегральной
форме, полученной ранее в п. 33.5 (см. формулу C3.52)).
§46
Замена переменных в кратных интегралах
46.1. Линейные отображения измеримых множеств
В п. 41.5 изучались линейные однородные отображения
евклидовых пространств. Рассмотрим теперь обпа;ий случай
произвольных линейных, вообпа;е говоря, неоднородных
линейных отображений.
Линейное отображение L : R^ -^ R^ имеет вид
L{x)=A{x) + a, D6.1)
где А : R^ -^ R^ — однородное линейное отображение (будем
называть его соответствуюгцим отображению L),
X = (Xi, ... , xJeR^, у = (i/i, ... , у J е R^,a = (а^, ... , а J е R^.
Обозначим через Р параллельный перенос в т-мерном
пространстве на вектор а
Pi2) = 2 + a,2 = i2^,...,2je R^.
Тогда ясно, что
L = P-A,
или, как короче,
L = PA, D6.2)
т. е. линейное отображение L является композицией
однородного линейного отображения А и параллельного переноса Р.
Если (а.), i = 1, 2, ... , т, j = 1, 2, ... , п, — матрица
линейного однородного отображения А, то координатные
функции отображения L имеют вид
У1= 11 ^ij^j + ^i' ^= 1' 2, ... , т,
И ЯВЛЯЮТСЯ числовыми линейными функциями.
469
в дальнейгаем ограничимся рассмотрением линейных
отображений евклидова пространства в евклидово пространство
той же размерности, т. е. случаем т = п. Определитель
матрицы линейного однородного отображения при некоторой
системе координат будем называть и определителем самого
отображения. Из линейной алгебры известно, что этот
определитель не зависит от выбора в пространстве ортогональной
системы координат.
ЛЕММА Л.Если
Cq= max |а..|, D6.3)
i, j=l, 2, ..., п
то для любых точек х, x'eR^, выполняется неравенство
\L(x') - L(x)\ < jiCq \х' - х\, D6.4)
Доказательство. В п. 41.5 было доказано, что если А —
линейное однородное отображение А: R^ -^ R^, то для любого
вектора xGBj^ выполняется неравенство
^4(x)|<|^4|||x|, D6.5)
где ||А|| — норма оператора А, а также было доказано, что
1^11 < J Е Е «§' D6.6)
где (a-j) — матрица А.
Применив эти неравенства для рассматриваемого случая
т = п, получим
\Цх') - Цх)\, =,, \А(х') - А(х)\ = \А(х' - х)\ < ||А|| \х' - х\ <
D6.6) A/jf^l^r^l ■' D6.3) ^ ' '
Неравенство D6.4) доказано. П
ЛЕММА 2. Если J определитель матрицы однородного
линейного отображения А, то для любого измеримого
множества Е ^ R^ выполняется равенство
[iL(E) = \j\[iE, D6.7)
где L = РА (см. D6.2)).
Д о ка 3 а тел ь ст в о. Из линейной алгебры известно, что
всякое линейное однородное отображение А может быть
представлено в виде
А = ВС,
где В — неотрицательное самосопряженное линейное
отображение (неотрицательность линейного отображения В означа-
470
ет, что det Б > 0), а С — ортогональное отображение. Таким
образом,
L = PA = РВС.
При параллельном переносе Р и ортогональном
отображении С мера множества не меняется (см. п. 44.1 и п. 45.4).
Поэтому достаточно доказать, что для любого измеримого
множества Е выполняется равенство
[iB(E) = \j\[iE.
Из линейной алгебры известно также, что для
самосопряженного неотрицательного отображения супа;ествует система
координат, в которой его матрица диагональна:
Х^ О ... О
о х^... о
Х.>0, /=1,2, ...,я. D6.8)
О О ..Л,
Пусть Q — я-мерный куб, ребра которого параллельны осям
этой координатной системы и имеют длину h. Отображение В
сводится к «растяжениям» в направлениях координатных осей:
с коэффициентом Х- в направлении i-u оси, i = 1, 2, ... , п. При
таком растяжении объем всякого параллелепипеда с ребрами,
параллельными осям координат, изменяется с
коэффициентом Х-, а в результате коэффициент изменения объема куба Q
при отображении В будет равен Х^Х^ --- ^п- Таким образом,
\iB{Q) = Х^Х^... X^\iQ = det B\iQ.
Далее, из равенства А = ВС имеем det А = det В det С.
Определитель ортогонального отображения равен ±1, а det Б > О,
поэтому |J| = |det J\ = det Б. Следовательно, окончательно
HB(Q) = \j\viQ. D6.9)
Это равенство справедливо для всех кубов Q, ребра которых
параллельны координатным осям, в которых матрица
преобразования Б имеет диагональный вид D6.8).
Пусть Е — измеримое множество, ^ с i?J, а s^ (Е) и aS^ (Е) —
множества, состоягцие из кубов ранга k в указанной системе
координат и определяемые по формулам D4.3).
Из включений s^ (Е) с ^ с aS^ (Е) следует, что
В(8,(Е)) с В(Е) с В(8,(Е)). D6.10)
Отметим также включение
B(S,(E)) \ B(s,(E)) с B(S,(E) \ s,(E)).
471
Множества Sf^(E), Sf^(E) и aS^(^)\s^ представляют собой
объединение конечного множества кубов ранга k в выбранной
системе координат (часть этих кубов в множестве Sj^(E)\Sj^ (Е)
может быть открытыми или полуоткрытыми). Поэтому
множества Б(8^ (Е)), BiSf^iE)) и разность В(8^^(Е)) \ В(8^^(Е)) будут
объединением конечного множества образов этих кубов при
отображении В — «параллелепипедов» (замкнутых, открытых,
полуоткрытых) и поэтому являются измеримыми множествами.
Мера множества Sf^(E) \ Sf^(E) равна сумме мер составляю-
па;их его кубов, поэтому мера его образа B(Sf^(E) \ Sf^(E)) равна
сумме мер образов этих кубов, а для них справедливо
равенство D6.9). Следовательно,
ц (B(S,(E)) \ B(s,(E))) < liB(S,(E) \ s,(E)) = \j\ ц (S,(E) \ s,(E)).
Поскольку, в силу измеримости множества Е, имеет место
равенство lim [i (Sj^(E) \ Sj^(E)) = О, то
Дгп^ ц (B(S,(E)) \ B(s,(E))) = 0.
Отсюда и из включений D6.10), согласно лемме 6 п. 44.1,
явствует, что множество В(Е) измеримо, а из того, что
[iBis^iE)) = \j\[is^iE),
следует, что
[iB(E) = ^lirn^ [iB(s^(E)) = \J\ Jirn^ [is^(E) = \j\ [lE.
Лемма доказана. П
46.2. Метрические свойства
дифференцируемых отображений
Пусть G — открытое множество пространства R^, sl F —
отображение множества G в пространство R^ :
y = F(x), xeG. D6.11)
В координатной форме отображение F записывается в виде
у. = у.(х) = у.(х^, Х2, ... , xj, i=l,2, ... , п, хеО. D6.12)
Введем обозначения:
Ах = X - х^^^ = (Ах-^, Ах2, ... , Ах^), |Ах| = / £ Axf,
472
Напомним, что отображение F является
дифференцируемым в точке x^^'^^G (см. теорему 6 в п. 41.6), если его
координатные функции г/. = г/Дл:^, х^, ... , х^ дифференцируемы в
этой точке и, следовательно, их можно представить в виде
Vi = ^Г^ + L ^iMj - ^Г) + ^^^^'^ ^^) l^^l' ^ = 1, 2, ... , я, D6.13)
где
''^^•^^^' ^,7 = 1,2,..., я,
lim 8,.(x(^\ Ах) = О, /=1,2, ...,я.
Обозначим через L (О) линейное отображение, задаваемое
формулами
Уь = ^Г^ + t ^iji^j - ^Г)' ^ = 1, 2, ... , я.
Индекс х^^^ в обозначении L (О) показывает, что это линейное
отображение зависит от точки х^^\
Рассматривая элементы я-мерного пространства как
векторы и тем самым их отображение как я-мерную
вектор-функцию, дифференцируемое в точке х^^^ отображение F можно
записать (см. п. 41.6) в виде
F(x) = L @)(х) + 8|Ах|, lim 8 = 0, D6.14)
^ Ах ^ о
где 8 = е(х^^\ Ах) = (8^, 83, ... , 8^, 8- = Е.(х^^\ Ах), /=1,2, ... , п.
Отсюда, используя обозначение о(Ах) = г\Ах\, lim 8 = 0,
условие D6.14) можно записать в виде
F(x) - L^@)(^) = о(Ах), Ах^О. D6.15)
Это означает, что для дифференцируемого в точке х^^^
отображения F сугцествует такое линейное отображение L (О)? что в
окрестности точки х^^^ отображение F отличается от
линейного отображения L (О) на бесконечно малую более высокого
порядка, чем расстояние \х - х^^^\ = \Ах\ от точки х^^^ до точки х
при стремлении этого расстояния к нулю. В этом и состоит,
как мы знаем, смысл дифференцируемости отображения в
точке.
Напомним епа;е, что отображение D6.11) называется
непрерывно дифференцируемым и на открытом множестве G,
если все его координатные функции D6.12) непрерывно
дифференцируемы на этом множестве (см. п. 37.2).
473
ЛЕММА 3. Если отображение D6.8) непрерывно
дифференцируемо на открытом множестве G ^ R^, то
F(x) - L ^Q.^ (х) = е\Ах\, xeG, D6.16)
где на любом компакте Е ^ G функция 8 = е(х^^\ Ах)
равномерно стремится к нулю при х - х^^^ = Ах ^ О, х^^^еЕ,
Таким образом, новое, что привносит формула D6.16) по
сравнению с формулой D6.14), состоит в том, что в формуле
D6.14) точка х^^^ была фиксирована, а в формуле D6.16) эта
точка может меняться, оставаясь принадлежапа;ей
некоторому компакту Е. При этом стремление к нулю функции
г(х^^\ Ах) происходит равномерно на Е, Определение
равномерного стремления функции к нулю на множестве было
дано в п. 37.2.
Доказательство. Из непрерывной дифференцируемости
координатных функций D6.12) следует, что функции 8- =
= г.(х^^\ х), i = 1, 2, ,,, , п, в формулах D6.13) на любом
компакте Е ^ G при X -^ х^^^ равномерно стремятся к нулю (см.
теорему 4 в п. 37.2). Следовательно, на любом компакте Е ^ G
при X -^ х^^\ х^^^е Е, равномерно стремится к нулю и
вектор-функция 8 = (8^, 82, ... , 8j, так как |8| = Jef + 8| + ... + 8^. П
ЛЕММА 4. При непрерывно дифференцируемом отображении
открытого множества компакт меры нуль, лежащий в
этом множестве, отображается в компакт меры нуль.
Доказательство. Непрерывно дифференцируемое
отображение является, очевидно, и непрерывным, а известно,
что непрерывным образом компакта есть снова компакт (см.
теорему 2 в п. 36.7). Оценим верхнюю меру образа компакта.
Предварительно заметим, что всякое ограниченное
множество Е ^ R^ содержится в некотором я-мерном кубе Q^ с
ребром длины h = 2 diam Е (см. п. 36.8). В силу включения
Е ^ Q^, имеет место неравенство
ц*^ < [iQ^ = B diam^)^. D6.17)
Пусть теперь G — открытое множество в R^, Е — компакт,
Е ^ G. Тогда его расстояние до непересекаюгцегося с ним
замкнутого множества R^\G положительно (см. лемму 7 в п. 35.2):
5^= piE,R^\G)>0.
774
Выберем номер k^ так, чтобы диаметр куба ранга k^ (см.
п. 44.1) был меныае 6. Тогда всякий куб ранга k^, пересекаю-
гцийся с компактом Е, будет содержаться в множестве G.
Многогранник aS^ (Е), состоягций из всех таких кубов (см. D4.3)),
также является компактом. В самом деле, компакт Е есть
ограниченное множество, поэтому множество aS^ (Е)
представляет собой объединение конечного множества кубов ранга k^,
каждый из которых, очевидно, является компактом. Пусть
у = F(x) непрерывно дифференцируемое отображение
множества G в КГ;. Положим
max
i, j = 1, 2, ... , п
ду^х)
dxj
D6.18)
Пусть xeSf^ (Е), x'gaS^ (Е), и отрезок с концами в точках х и х'
содержится в многограннике aS^ (Е), F(x) = (yi(x), г/2(х), ... yj^x)),
F(x') = (z/i(xO, У2(^1^ ••• . Уп(^'))^ ^^i = ^\- ^i^^ = 1' 2, ... п.
Тогда, применив формулу конечных прирапа;ений Лагранжа для
функций многих переменных (см. теорему 3 в п. 39.2) и
неравенство Konin—Шварца, будем иметь
\Fix') - Fix)\ = lt^iylx')-y,ix))^ = Щ^^ЩШ^.
2
< яс / ^ /S.XJ = пс\х' - х\, D6.19)
Отсюда следует, что для любого выпуклого множества А ^ aS^ (Е)
(определение выпуклого множества см. в п. 35.2) выполняется
неравенство diam F(A) < en diam А. Действительно,
diamF(A)= sup \F(x') - F(x)\ <
x,x'eA D6.19)
^ cn suD \x'- x\ = cn disLiR A.
D6.19) ^,^.Гл
Если множество A является я-мерным кубом Q^ с ребром
длины Л, Q^ ^ aS^ (Е), то, заметив, что diam Q^ = hjn и что
\xQf^ = h^, имеем
diam F(Qf^) < cn diam Q^ = cn^^^h,
475
поэтому
D6.17)
< 2^ с''п^''/^h'' = 2^c^^3^/2 jiQ^. D6.20)
Заметим, что для любого ранга k > k^ справедливо
включение Sf^(E) ^ Sf^ (Е). Пусть
S,(E)=.y^Qf\ D6.21)
где Q^ — кубы ранга й, у = 1, 2, ... , у^. Нам понадобится егце
равенство (см. п. 1.2"^)
f(.UOW ^= .и F(qW). D6.22)
\J - ^ -I j 7-1 i
Из включения Е ^ Sf^(E) следует включение F(E) ^
^ F(Sj^(E)), следовательно,
D6722) ^^^Уx^(Q?^,<,o) |,^^*^^^?^4<^20)
<
\п h
2^c^^2 ^ ^Q(^ = 2^c^^3^/2|aSfe№). D6.23)
Если мера компакта ^ равна нулю, то lim [iSJE) = О, от-
куда, в силу неравенства D6.23), следует, что [i'F(E) = О,
поэтому и [iF(E) = 0. П
Обозначим якобиан непрерывно дифференцируемого
отображения D6.11) через J pi
j^=j^^^>^=^(yi^y2^"'^yn) D6.24)
ЛЕММА 5. Если F — непрерывно дифференцируемое
отображение с якобианом, не обращающимся в нуль, открытого
множества G ^ R^ в пространство R^, Е — компакт, Е ^ G,
Qf^ — п-мерный куб с ребром длины h, Q^^ ^ G, х^^^еЕ П Q^, то
имеет место неравенство
[i'^FiQf) < \Jp(x^^^)\ [iQ. + а(Л)Л^, lim a(h) = 0. D6.25)
476
Подчеркнем, что в этом неравенстве бесконечно малая а = а(Л)
не зависит ни от выбора точки х^^^еЕ, ни от выбора
конкретных кубов Q^, а зависит только от длин их ребер h (и,
конечно, от компакта Е). В этом случае говорят, что на компакте Е
имеет место равномерная оценка D6.25).
Заметив, что jiQ^ = Л^, эту оценку можно записать в виде
[1ЩЯ^) < |J^(x@)| ц(Э^ + o([iQ^), Л ^ 0. D6.26)
Доказательство. Для линейного отображения L (О) (см.
D6.13)), как и для всякого линейного отображения,
абсолютная величина определителя матрицы (а.р, согласно лемме 2,
равна коэффициенту изменения объемов тел при этом
отображении. Для отображения L (О) указанный определитель
совпадает с якобианом Jp(x^^^) отображения F в точке х^^\ и, таким
образом,
^^^x@)(Q/.)D^7)l^^(^'"VQ.. D6.27)
Используя связь D6.15) между отображениями F и L (О)?
докажем неравенство D6.25). Пусть Е — компакт, Е ^ G.
Тогда 6 = р(Е, R^\G) > 0. В дальнейпхем всегда будем
предполагать, что diam Q^ = hjn < 6. В этом случае всякий куб Q^^,
пересекаюпа;ийся с компактом Е, будет содержаться в
множестве G: Qf^ ^ G.
Согласно лемме 3 (см. D6.16)),
\F(x) - L @)(л:)| = |8(х(^\ Ах| |Ах|,
где функция е(х^^\ Ах) равномерно на компакте Е стремится к
нулю при X - х^^^ = Ах ^ О, х^^^еЕ. Поэтому если
8(Ах) = sup I г(х^^\ Ах\,
ТО
lim |8(Ах)| = 0 D6.28)
Ах ^ о
И справедливо неравенство
\F(x) - L^@)(^:)| < 8(Ах)|Ах|, х^^'^еЕ, х = х^^) + AxgG. D6.29)
Если точки х^^^ и X принадлежат одному и тому же кубу Q^^, то
|Ах| = \х - х^^^\ < hjn, х^^^ G Qf^, X G Qf^,
Поэтому, в силу неравенства D6.29), имеем
\F(x) - L @)(л:)| < г(Ах)кл/п,
477
Положим
а^ = а^{К) = Jn sup 8(Ах);
|Ajc| < h
тогда
\F{x) - (L^@)(^:)| < «оЛ, x@)g EnQ^, x = x^^) + Axg Q^^,
где
lim aJh)
D6.28)
D6.30)
0.
D6.30)
D6.31)
D6.32)
При линейном отображении L^^q^ образом P = L @)(Q/^)
куба Qf^ является невырожденный параллелепипед (якобиан
Jp (х^^^) ^ 0). Пусть и^ ^ = и (Р; а^К) является адЛ-окрестно-
стью параллелепипеда Р (определение окрестности
множества см. в п. 35.2, определение 23). Ясно, что
ПЯи)<^и^^,. D6.33)
Пусть Ррс /г — я-мерный параллелепипед, (п - 1)-мерные
грани которого параллельны соответствуюгцим (п - 1)-мер-
ным граням параллелепипеда Р и находятся от них на
расстоянии a^h, причем параллелепипед Р содержится внутри
параллелепипеда Р^ ^ (рис. 67). Тогда U^ ^ ^ Р^ ^ vi,
следовательно,
FiQH)<^Pa,h- D6.34)
Пусть а^, а2, ... , а^ — длины ребер параллелепипеда Р =
= L @) (Qh)- Оценим длины а- + Да- ребер параллелепипеда
Р^ j^j параллельных соответственно ребрам длин а-
параллелепипеда Р, /
У2^
0
р ^ ^
1 ^ - ^ а^+Аа^
'- "
1
1
1
У1
1, 2, ... , п. Пусть Н^ — расстояние между
двумя параллельными (п - 1)-мер-
ными гранями
параллелепипеда Р, содержапа;ими ребра длин
а^, ... , а._1, а. + 1, ... , а^.
Тогда расстояние между двумя
параллельными {п - 1)-мер-
ными гранями параллелепипеда
Р^ j^j содержапа;ими ребра длин
а,
+ Да,
Рис. 67
а^ + Да^, ..
«^ + 1+ А«^ + 1' ••• у «д + А«д' в си
лу определения этого паралле
лепипеда, равно Н^ + 2aQh. Ина
1'
478
че говоря, Н. Ji Н. -\- 2аоЛ являются длинами высот
соответственно параллелепипедов Р vi Р^ ^.
Обозначим ф., О < ф. < 7г/2, угол, образованный ребром
длины а. параллелепипеда Р с {п - 1)-мерной
гиперплоскостью, содержагцей его ребра длин а^, ... , <Xj _ i, <^j + i? ••• ? cin
(этот угол, очевидно, равен углу, образованному ребром длины
а. + Да. параллелепипеда Р^ j^ с соответствуюпа;ей {п - 1)-мер-
ной гиперплоскостью), т. е. угол между рассматриваемым
ребром и его проекцией на указанную гиперплоскость.
Длины ребер и высот параллелепипеда Р и Р^ ^^ связаны
ТТ М -\- 2A h
С углами ф соотногаениями а- = . ' , а- + Да, = —^. —. По-
этому
д i/, + 2аоЛ Н. 2аг.Н
Аа. = -^—. ^- - ^-^- = -г^- .
^ 81Пф^ 81Пф^ 81Пф^
Элементы матрицы ^—— , соответствуюгцеи линейному
отображению L (О) являются непрерывными функциями на
открытом множестве G, а углы ф. непрерывно зависят от этих
элементов и, следовательно, также являются непрерывными
функциями точки х^^^ на G: ф. = ф.(х^^^). В силу
невырожденности отображений L (О)? л:^^^ ^ G, т. е. не обрапа;ения в нуль
на G их якобианов, для всех точек х^^^ g G имеем ф.(х^^^) > О,
/= 1, 2, ... , я. Поэтому наименьп1ие значения непрерывных
на компакте Е функций ф. также положительны:
пипф^ (х) = е., О < с. < |, / = 1, 2, ... , я.
Пусть Сп = max j ^ , ... , — к Тогда
Да. < 2с^аок.
Разность замкнутого параллелепипеда Р^ ^^ и открытого
P^j^^ («рамка», окаймляюгцая параллелепипед Р) является
объединением параллелепипедов Р. ^ и Р. 2 с ребрами длин
ai +Да^, ... , а._1 +Да._1, a. + i +Да-^^, ... , а^ + Да д и
высотами длины адЛ. Поэтому
4''^^''*yi^biU.yi^<,2- D6.35)
179
Ребра длины а- параллелепипеда Р получаются при
отображении L @) из ребер куба Q^^, имеюпа;их длину h.
Следовательно, в силу леммы 1, имеет место неравенство
а. < cnh, с = max
^ i,j = 1,2,..
хеХ
dxj
< + оо.
Заметив, что объем любого я-мерного параллелепипеда не
превосходит объема прямоугольного праллелепипеда с ребрами
той же длины, т. е. произведения длин его ребер, имеюгцих об-
гцую верп1ину, имеем
|iP.. < (ai + Aai)... (а. _ 1 + Да. _ ^)(а. + ^ + Да- +1)... (а^ + Aaja^h <
< (cnh + 2с^а^к)'^~^а^к = (сп + 2с^ао)'^~'^ a^h"^ =
= (сп + 2с^аХ-^а^[1Я^^, i= 1, 2, ... , п, у =1,2. D6.36)
Bbinie было отмечено, что, согласно лемме 2, имеет место
равенство
цР = liL^^oiQk) = к^(^<"^I ^Qk- D6.37)
Оценим теперь верхнюю меру множества F(Qj):
Vi^'FiQr) < цР^ j^ < цР^ h^ У. V^Pii^f. \^Pi2 <
"^ D6.34) ^ ^О"^ D6.35) ^О'^ jt^o ^' ^ i^o D6.36)
D6.37)
D6^36I^^^^^'^^! ^^^ ^ ^''^'''' ^ 2соао(Л))--1ао (h) ^Q^. D6.38)
D6.37)
Положив
a(h) = 2п (сп + 2соао(Л))^-1 ^Л),
окончательно получим
^*T(Q,) ^^ <^g^ |J^(x@))| hQ, + а(Л) iiQ,, ^im «(Л) = 0. П
В левой части полученного неравенства стоит верхняя мера
образа F(Qj) куба Qj^ при отображении F, а не его мера, так как
осталось невыясненным, измеримо ли множество F(Qj^ при
сделанных вып1е предположениях. Для дальнейп1его нам
понадобится лип1ь случай взаимно-однозначных непрерывно
дифференцируемых отображений, якобиан которых не обра-
па;ается в нуль. Поэтому ограничимся доказательством
измеримости образа измеримого множества лип1ь в этом случае.
Если отображение F непрерывно дифференцируемо и его
якобиан не обрагцается в нуль на открытом множестве G про-
180
странства R^, то образ F(G) этого множества также является
открытым множеством и у точек xgG и F(x)eF(G) сугцествуют
сколь угодно малые окрестности, взаимно-однозначно отобра-
жаюгциеся друг на друга (см. п. 41.8). Если, кроме того,
отображение F взаимно-однозначно отображает все открытое
множество G на его образ F(G), то для любого множества Е ^ G его
внутренность Е^^^ отображается на внутренность F(E\^^ его образа:
F(E,J = F(EU, D6.39)
а если границы Э^ и dF(E) множеств Е и F(E) содержатся
соответственно в множествах G и F(G), то они также отображаются
друг на друга:
Е(дЕ) = дЕ(Е). D6.40)
В этом случае имеет место также равенство
F(E) = F(E). D6.41)
В самом деле.
Е = Е,^, и дЕ, F(E) = F(E\^, U dF(E),
поэтому
F(E) = F(E,^, и Э^) = F(E,J и F(dF) = F(E\^, U dF(E) = F{E).
ЛЕММА 6. Если отображение F открытого множества G ^
^ R^ в пространство R^ непрерывно дифференцируемо,
взаимно-однозначно и его якобиан не обращается в нуль на G, то
образ всякого измеримого множества, лежащего вместе со своим
замыканием в G, также является измеримым множеством.
Доказательство. Пусть Е — измеримое множество и его
замыкание Е лежит в G:
E^E^G. D6.42)
Замыкание Е множества Е, как замыкание каждого
измеримого множества, является компактом (см. замечание 3 в
п. 44.1), а отображение F непрерывно, поэтому образ F(E)
множества Е при этом отображении также является
компактом и, следовательно, ограниченным множеством. Но
поскольку F(E) ^ F(E), множество F(E) также ограничено.
Граница Э^ измеримого множества имеет меру нуль и
является компактом (см. замечание 2 в п. 44.1). Поэтому и образ
этой границы является компактом меры нуль (см. лемму 4):
[1Е(дЕ) = 0. D6.43)
481
Поскольку при отображении F граница образа множества
является образом его границы (см. D6.40)), граница dF(E)
образа F(E) множества Е имеет меру нуль:
^^З^(^) D6= 0) ^^(^^^ DГ43) О-
Таким образом, F(E) является ограниченным множеством
с границей меры нуль и поэтому измеримо. П
Так как я-мерный замкнутый куб является измеримым
множеством, в случае, когда этот куб лежит в открытом
множестве G, его образ при непрерывно дифференцируемом,
взаимно-однозначном отображении F с якобианом, не равным
нулю на G, является измеримым множеством. Поэтому для
таких отображений в неравенстве D6.26) (см. лемму 5) в его
левой части верхнюю меру можно заменить на просто меру,
т. е. в этом случае справедливо неравенство
ViFiQJ < \JpFix@))\ ViQu + aih)nQ,^, D6.44)
где
lima(/i) = 0. D6.45)
46.3. Формула замены переменных
в кратном интеграле
Пусть F — непрерывно дифференцируемое
взаимно-однозначное отображение открытого множества G ^ R^ в пространство
R^ и его якобиан Jp не обрапа;ается в нуль на множестве G.
ТЕОРЕМА 1. Если Е — измеримое множество,
содержащееся вместе со своим замыканием Е в открытом множестве G:
Е ^ Е ^ G, а функция f непрерывна на множестве F(E), то
j_ Ky)dy = [KF{x)) \Jp{x)\dx. D6.46)
F{E) E
Эта формула равносильна формуле
1 fiy)dy = \ f(F(x)) \J^x)\dx. D6.47)
F(E) E
Действительно, ограниченная функция одновременно
интегрируема или нет как на измеримом множестве, так и на
его замыкании, причем в случае интегрируемости интегралы
от функции по множеству и по его замыканию совпадают (см.
482
конец п. 44.3). В напхем случае функции /(г/) и f(F(x))\Jр(х)\
непрерывны соответственно на компактах F(E) и Е (являю-
па;ихся замыканием измеримых множеств F(E) и Е),
следовательно, ограничены и интегрируемы на них. Таким
образом, все входягцие в формулы D6.46) и D6.47) интегралы
сугцествуют, а сами эти формулы равносильны. Эти формулы
называются формулами замены переменных в кратном
интеграле.
Доказательство. Докажем формулу D6.46). Прежде
всего заметим, что ее достаточно доказать лигаь при
дополнительном предположении неотрицательности функции / на
множестве
ПЕ):
f(y)>0, yef(E). D6.48)
В самом деле, функция /, как это уже отмечалось выгае,
ограничена на компакте F(E). Поэтому сугцествует такая
постоянная с > О, что f(y) > -с, yeF(E),
Если теорема 1 справедлива для двух неотрицательных
функций fi(y) = f(y) + с и f2(y) = с, то она, в силу свойства
линейности интеграла, справедлива и для функции
Ау) = Ш) - f2iy)-
Обозначим через Е^.^\ j = 1, 2, ... , у^, всевозможные
непустые пересечения замыкания Е множества Е с кубами
ранга k. Таким образом, для каждого у = 1, 2, ... , у^ супа;ест-
вует такой куб ранга k, обозначим его Q^^\ что
Ef^ = Er\Qf^^0. D6.49)
Системы множеств
x, = {£f'};:;* D6.50)
образуют разбиения компакта Е, мелкости которых
стремятся к нулю:
lim |tJ = 0 D6.51)
(cm. лемму 7 в п. 44.3). Отсюда следует, что системы множеств
183
У2
Vi
Рис. 68
образуют разбиения замыкания F{E) множества F(^) (рис. 68),
мелкости которых также стремятся к нулю.
Действительно, элементы ^j^^ разбиения т^ являются
измеримыми компактами как пересечения двух измеримых
компактов Е и Q^^\ лежапа;их в открытом множестве G:
^(^) = Ё Г\ Q(^) ^ G,
поэтому, согласно лемме 6, их образы F(E^^'^) являются изме-
римыми множествами. Из Е = ,U Е\^^ следует, что
^(^) D6=41) ^(^) = 4i ^l^j'^ , = / y/(£j^)).
Наконец, в силу взаимной однозначности отображения F
пересечение образов множеств при этом отображении равно
образу их пересечения, поэтому
F(^p^) П F(^j^)) = FiEi^"» n Ef"»). D6.52)
Пересечения E\^^ П E^^\ i ^ y, имеют меру нуль и
являются компактами как пересечения двух компактов ^р^ет^^ и
E^^^eXf^. Следовательно, образы этих пересечений в свою
очередь оказываются множествами меры нуль, поэтому и меры
пересечений F(Ei^^) П F(E^^^) равны нулю:
ц(^(£р)) п F(£j*))) ^^g= 2) ^li^CBp) n £)*)) = 0, j ^ /.
Из выполнения условия D6.51) следует, что
liin|F(T,)hO.
D6.53)
Действительно, отображение F компакта Е, будучи
непрерывным, является и равномерно непрерывным (см. теорему 6 в
484
п. 36.8), и поэтому для любого 8 > о сугцествует такое 6 > О, что
для всех множеств А^ Е, diam А < 6, выполняется неравенство
diam ДА) < 8. D6.54)
Выбрав такой ранг k^, что 10 ^^ < 6, получим, что для всех
номеров k> Uq имеет место неравенство
\F (хЛ = max diam FiE^^"») < 8,
из которого непосредственно следует выполнение условия
D6.53).
Измеримый компакт Е лежит в открытом множестве G.
Его граница Э^ является компактом меры нуль, и ее образ
F(dE) при отображении F является границей образа F(E) =
= F{E) компакта Е (см. D6.41)), следовательно, согласно
лемме 4, также имеет меру нуль \idF{E) = 0.
Рассмотрим теперь неполные интегральные суммы (см.
п. 44.3) вида а (^wTe]) -^"^^ интеграла | f{y)dy и оценим их
^^k^ ¥{Ё)
С помопа;ью неполных интегральных сумм а .-.г^, для интег-
рала I f{F{x)) \Jp{x)\ dx.
(k)^
Отберем те из множеств F(E{^^), которые не пересекаются
с границей dF(E) множества F(E). В силу свойств
отображения F (см., в частности, D6.40)), это равносильно выбору тех
множеств Ei^\ которые не пересекаются с границей Э^
множества Е, Для таких множеств Е^^"^ имеем
^(^) =ЁП QW = Q(^) с Ё, D6.55)
т. е. множество Е^^"^ является в этом случае кубом ранга k.
Действительно, в силу условия D6.49), в кубе Q имеется
точка компакта Е. Если бы этот куб не содержался в ^, то в
нем нап1лась бы точка, не принадлежапа;ая Е, поэтому и
точка X, принадлежапа;ая его границе: хедЕ с Е (см. лемму 9 в
п. 35.2). Таким образом, хеЕ П Q(^^ = Е^^^ и хедЕ, что
противоречит выбору множества Е^.^^.
485
Выберем теперь произвольным образом по точке Г|^^' ^^ в каж-
дом из отобранных множеств F(E^.^^) разбиения i^(T^). В силу
включения Г|^^' ^^ g F(E^.^^), сугцествуют такие точки bj^' ^\ что
F(^0'^)) = r|0'^). D6.56)
Неполная интегральная сумма а^, л.л^ттт^л для интеграла
I f(y)dy при выбранных точках Г|(^' ^^ имеет вид
ПЁ)
D6=55) I W^'^))^^'(Qf'). D6.57)
Соответствуюгцая этой интегральной сумме неполная
интегральная сумма а^ .^^. для интеграла | / (Р(х)) \Jp (х)\ dx при
выборе D6.56) точек ^^^' ^^записывается следуюпа;им образом:
^х(ЭЁ)= L /(Д^^^''^))к^(^^^''^I^1е)'^ D6.58)
Заметив, что функция /, будучи непрерывной на
компакте f(E), ограничена на нем:
|/(г/)| < с <+00, yeF(E),
оценим сумму D6.57) с помопа;ью неравенства D6.44):
Первое слагаемое в правой части неравенства является
неполной интегральной суммой D6.58), а второе, в силу
выполнения условия D6.45), стремится к нулю при й ^ оо [здесь
h = Л':
lim са(—riiE = 0.
Мелкости разбиений т^ и i^(T^) стремятся к нулю при й ^ оо^
поэтому, согласно теореме 5 п. 44.3, рассматриваемые непол-
486
ные интегральные суммы стремятся при й ^ оо к соответст-
вуюгцим интегралам
F(E)
^ Е
Перейдя к пределу при й ^ оо в неравенстве D6.59), получим
неравенство
j_fiy)dy < I fiFix))\JAx)\dx. D6.60)
F(E) Е
Теперь заметим, что отображение F~^, обратное данному
отображению F, также непрерывно дифференцируемо,
взаимно-однозначно, а его якобиан Jp~\y) не обрагцается в нуль на
открытом множестве F(G), и для него имеет место формула
(см. п. 41.6 и 41.7):
Для отображений F и F~^ имеет место равенство
F(F-\y)) = y, ysF(G), D6.62)
так как отображение FF~^ является тождественным
отображением множества F(G) на себя.
Применим к интегралу, стояпа;ему в правой части
неравенства D6.60), само это неравенство для отображения F~^. Это
можно сделать, так как для обратного отображения F~^
выполняются все условия леммы 6. Заметив, что Е = F~^(F(E)),
получим
[fiFix))\JAx)\dx = _j_fiFix))\JAx)\dx <
D6^60) U^F^F~"^y))pFiF-\y)\\J,-Ay)\dy (,Oi) иШу.
X = F-\y) ^^^^ D6.62) F(E)
D6.63)
Из неравенств D6.60) и D6.63) следует формула D6.46). П
ТЕОРЕМА 2. Если отображение F : G ^ R^ открытого
измеримого множества G (z Щна открытое измеримое
множество G (z Щ взаимно-однозначно J непрерывно дифференцируемо,
его якобиан не обращается в нуль на G, если отображение F
187
и его якобиан непрерывно продолжаемы на замыкание G
множества G, а функция f непрерывна на множестве G и
непрерывно продолжаема на его замыкание G, то
I т dy=\f (F(x)) \J{x)dx, ё = FiG). D6.64)
G G
Таким образом, в условиях теоремы непрерывное
продолжение отображения F может и не быть взаимно-однозначным
на границе 3G области интегрирования G, а непрерывное
продолжение якобиана может на этой границе обрагцаться в нуль.
Доказательство. Замыкание G измеримого множества G
является измеримым компактом, на который по условию
теоремы непрерывно продолжаема функция /, поэтому это
продолжение интегрируемо на компакте G, следовательно, сама
функция / интегрируема на открытом множестве G. В силу же
непрерывной продолжаемости отображения F и его якобиана
на замыкание G множества G, рассуждая аналогичным
образом, получим, что функция f{F{x)) \Jp{x)\ интегрируема на
открытом множестве G. Таким образом, интегралы, стояпа;ие
как в левой, так и в правой части равенства D6.64), в
условиях теоремы супа;ествуют.
Множество G — открыто и измеримо, поэтому супа;ествует
последовательность таких измеримых открытых множеств
G^, й = 1, 2, ... , что (см. замечание 3 в п. 44.6)
G,cG, + i,ft= 1,2,...; D6.65)
со
,4pk = G, D6.66)
причем Gj^(z Gj^(zG, k= 1, 2, ... .
Ясно, что замыкание G^ множества G^ является
компактом. Применив теорему 1 к множествам G^, получим
I f{y)dy= \ f{F{x))\Jp{x)\ dx, й = 1, 2, ... . D6.67)
P^^k) G,
Теперь заметим, что множества F(Gf^), й = 1, 2, ... , также
открыты и для них, в силу условий D6.65) и D6.66),
выполняются условия
со |—
F(G,)cf(G, + i), k = l,2,..., ^U/{G,) = FiG) = e. D6.68)
488
Из D6.65) и D6.66), согласно полной аддитивности интеграла по
открытым множествам (см. свойство 10^ в п. 44.6), следует, что
lirn^ I f(F(x)) \Jp(x)\ dx = \ f(F(x)) \Jp (x)\ dx.
Аналогично из D6.68) имеем
lim^ I f{y)dy= I fiy)dy.
^ FiG,) FiG)
Поэтому, перейдя к пределу при й ^ оо в равенстве D4.67),
получим формулу D6.64). П
Замена переменных в кратном интеграле часто супа;ествен-
но упропа;ает его исследование и вычисление. При этом в
отличие от однократного интеграла нередко целью замены
переменного является не упропа;ение подынтегральной
функции, а переход к более простой области интегрирования даже
ценой некоторого усложнения подынтегральной функции.
В качестве примера применения формулы замены
переменных в кратном интеграле рассмотрим для двумерного
интеграла случай перехода от декартовых координат к полярным.
Рассмотрим плоскость, на которой декартовы координаты
обозначены г, ф и на ней открытый прямоугольник
G = {(г, ф):0<г<Д, 0<ф< 27г}.
При отображении
х = гсо8ф, г/ = Г8тф, О < ф < 27Г, О < г < R, D6.69)
прямоугольник G отображается на множество G плоскости с
декартовыми координатами х, г/, которое представляет собой
круг х^ -\- у^ < R^, из которого удален радиус 0<х<Е, у = 0
(рис. 69).
Отображение D6.69) и его якобиан
Э(х, у) _ I созф -гзшф
Э(Г, ф) 8Шф ГСОЗф
непрерывно продолжаемы на замкнутый прямоугольник
G = {(г, ф): О < г < i?, О < ф < 27г},
образом которого при
продолженном отображении является
замкнутый круг (j, на котором
отображение D6.69) уже не
является взаимно-однозначным:
взаимная однозначность нару-
гаается на границе прямоуголь-
271;
yk
G
R
G
\R
/1 X
Рис. 69
489
ника G — отрезки О < х < i? при ф = О и ф = 27Г отображаются в
один и тот же отрезок 0<x<i?, г/ = 0, а отрезок г = О, О < ф < 27Г
и вовсе отображается в точку (О, 0). Якобиан продолженного
отображения обрагцается в нуль при г=0.
Согласно теореме 2, для отображения D6.69) и
непрерывной на круге х^ + г/^ < i?^ функции /(х, у) имеет место формула
11 /(х, y)dxdy = ^^ f(r cos ф, г sin (p)rdr d(p,
х2 + у2 < ij2 О < ф < 2л;
0<r<R
Приведем конкретный пример вычисления интеграла по этой
формуле:
11 cos 71 Jx^ -\- y^dxdy = ^ ^ г cos тгг йгйф =
- у2 ^ 1 О < ф < 2л;
^ 0<г<1
riVL 1 р . I 1 1 1 ~\ Л
I йф I Г COS тгг dr = 271 Г^^^^^ - i| sinTirdr I = --.
о о
46.4. Геометрический смысл
абсолютной величины якобиана отображения
Пусть F — непрерывное дифференцируемое
взаимно-однозначное отображение открытого множества G с Щ на
открытое множество G с R^ : F(G) = G. Пусть якобиан Jp
отображения F не обрапа;ается в нуль на G и пусть как отображение F,
так и его якобиан, непрерывно продолжаемы на замыкание G
множества G. Как и раньпхе, будем эти продолжения
обозначать соответственно F и Jp, называя продолженную функцию
Jp по-прежнему якобианом отображения F.
Пусть D — измеримая область, т. е. измеримое линейно
связное открытое множество, содержапа;ееся в замыкании G
открытого множества G:
D(z G.
Таким образом, в некоторых точках области D якобиан
отображения может обрапа;аться в нуль. Это может
происходить в тех точках, которые принадлежат границе открытого
множества G. Примером такой точки является точка @,0)
для проколотого круга G = {(х^, Хз): xf + х| < 1} \ {@,0)} и
круга D = Нх^, Х2): ^:f + х| < -L
Пусть образ F(D) области D является измеримым
множеством. Будучи непрерывным образом области, множество F(D)
490
также является областью (см. п. 36.9). Для его меры имеет
место формула (см. свойство 1^ кратного интеграла в п. 44.6)
[iFiD)= I dy.
FiD)
Применив к интегралу в правой части этого равенства
формулу замены переменного в кратном интеграле (здесь
/ (у) = 1), получим [1 F(D) = I |Jj^(x)| dx,
D
По теореме о среднем (см. п. 44.6) имеем | \Jp(x)\dx = \Jp(b)\[iD,
t,eD, Таким образом, d
\^ = \j^i^)\, ^sD. D6.70)
Если {D} — семейство указанных областей, содержапа;ее
области сколь угодно малого диаметра, и если сугцествует
точка х^^\ принадлежагцая всем областям этого семейства, то
lim tiZ^) = |j (х@)|, x@)gD. D6.71)
Действительно, из неравенства |^ - х^^^\ < diam D, x^^^eD,
^eD, следует, что lim ^ = х^^\ Отсюда, в силу непрерыв-
diamD -^ О
ности якобиана Jp отображения F, имеем
lim Jpi^) = J^(x@)).
Поэтому, перейдя к пределу в равенстве D6.70), получим
формулу D6.71), которая и выражает геометрический смысл
абсолютной величины якобиана отображения. Короче говорят, что
абсолютная величина якобиана отображения в данной точке
равна коэффициенту изменения меры множества в этой точке.
46.5. Криволинейные координаты
Взаимно-однозначное отображение
у = Fix)
У2 У2(^1^ ^2' ••• ' ^д)' .д^ гг2\
Уп УпУ-^1^ *^2' ••• ' -^п)
множества G ^ R^ в пространство КГ; ставит в соответствие
каждой точке х = (х^, ^2, ... , х^) набор п чисел г/^, у2, ... , у^-
Эти числа можно рассматривать как другие координаты той
же точки X. Эти координаты называются, обычно,
криволинейными координатами, так как кривые, получаюгциеся из
уравнений у. = y^ix^, х^, ... , х^), /=1,2, ... , п, при фиксиро-
191
вании всех аргументов, кроме одного (эти кривые называются
координатными линиями), не являются, вообгце говоря,
прямыми, как в случае декартовых координат.
Таким образом, формулы D6.72) можно рассматривать не
только как формулы, задаюгцие отображение множества из
одного пространства в другое, в каждом из которых заданы
декартовы координаты, соответственно х^, х^, ... , х^ и г/^, г/2, ... , г/^,
но и как переход от координат х^, х^, ... , х^к новым
координатам г/^, г/2, ... , г/^ той же точки в том же самом пространстве.
В этом случае в формуле замены переменных в кратном
интеграле D6.64), т. е. при такой интерпретации cooTHonie-
ний D6.72), в обеих частях равенства следует писать одну и
ту же область интегрирования
|/(х, y)dy = \f{F{x))\Jp{x)\dx,
G G
так как интегрирование производится по одному и тому же
множеству, описываемому разными способами.
Обратный переход от г/^, г/2, ... , г/^ к х^, Х2, ... , х^ осу-
па;ествляется при помопа;и обратного отображения
*^1 ^ ^1\У1у У2^ ••• ' Ул)^
^2 ^ *^2v^l' У2^ ••• ' Уп)^
X = F-\y)
D6.73)
'п = ^ЛУ1^ г/2, ... , г/J.
Рассмотрим для наглядности более подробно двумерный
случай. Пусть задано взаимно-однозначное отображение
и = и(х, у), v = v(x,y) D6.74)
открытого множества G плоскости R^^ уВ плоскость й^ у. Будем
рассматривать пару (г/, v) как новые координаты точки (х, у).
Уравнения координатных линий в этом случае имеют вид
X = х(г/, Vq), у = у(и, Vq), Vq — const
и
X = x(Uq, v), у = у(и^у v)y Uq — const,
т. е. представляют собой параметрически заданные плоские
кривые.
Будем предполагать, что отображение D6.74)
удовлетворяет всем условиям, при которых была доказана формула
замены переменных в кратных интегралах (см. теорему 2 в
п. 46.3 при я = 2) и что отображение
x = x(u,v), y = y(u,v) D6.75)
является отображением, обратным к отображению D6.74).
192
Исследуем, какой смысл будет иметь в этом случае модуль
якобиана. Зафиксируем какие-либо значения Uq, Аи, Vq, Av.
Пусть Mq = (z/q, Vq), D — множество всех точек,
криволинейные координаты г/, v которых удовлетворяют неравенствам
Uq < и < Uq + Аг/, Vq< V < Vq + Av, и пусть: D ^ G. Множество
D называется координатным {криволинейным)
параллелограммом. Множество D открыто (почему?), и его граница
представляет собой кусочно-гладкий контур (он состоит из кривых
вида X = x(Uq, v), у = y(uQ, v), где Pq < i; < Pq + Ai; и т. п.),
поэтому D квадрируемая область. Вычислим ее плопа;адь (рис. 70).
Применив формулу замены переменного в интеграле и
интегральную теорему о среднем (см. п. 44.6), получим
|Э(х, у)\
[iD = ^^dxdy = I I
Ur.<u<Ur. + Аи
v^ < V < vX + Av
d{u, v)
dudv =
Э(х, у)
д{и, v)
Uq + Av Vq + Av
^ du ^ dv
Э(х, у)
д{и, v)
AuAVy Me D.
В силу непрерывной дифференцируемости функций D6.75),
Э(х, у)
д{и, v)
Э(х, у)
д{и, v)
+ 8, где lim 8 = 0. Таким образом.
Аи^ + Av^
[iD
Э(х, у)
д{и, v)
AuAv + zAuAv.
Эта формула показывает, что модуль якобиана в точке (z/q, v^
представляет собой коэффициент у произведения AuAv главной
части плопа;ади координатного параллелограмма с верп1иной в
точке (z/q, Pq) при Аи^ + Av^' -^ 0. Это замечание часто
используется на практике при вычислении якобиана преобразования
криволинейных координат в декартовы. Покажем это на
примере полярных координат г, ф. Зафиксируем какие-либо
значения г, г + Аг, ф и ф + Аф и рассмотрим координатный
параллелограмм D (рис. 71), образованный координатными линия-
У^
0
^ ""^-^^^— v = Vq^- Av
^^П<у^^^^^
Л u = Uq + Аи
1 \u = Uq
X
Рис. 70
Рис. 71
493
ми г, г + Аг, ф и ф + Аф. Длины двух его сторон равны
соответственно Аг и гАф. Вычислив плогцадь этого
параллелограмма так, как если бы он был обыкновенным
прямоугольником, будем иметь \iD ~ гАгАф.
Итак, коэффициент у произведения АгАф оказался
равным г, откуда естественно ожидать, что J"^' ^^ = г. В действи-
д{и, V)
тельности (см. пример в п. 46.4) так и есть. Это произогало
потому, что при нап1их неточных вычислениях плогцади D
допугцена огаибка более высокого порядка малости, чем
произведение АгАф при Аг^ + Аф^ ^ 0. В самом деле, вычислив
jiD как разность плогцадей двух секторов, получим
jiD = -(г + Аг)^ Аф - -г^Аф = гАг Аф + -Аг^Аф.
^ ^ ^
УПРАЖНЕНИЯ. Написать формулу замены переменной для следующих
преобразований координат.
1. X = г cos \\f cos (р, у = г cos \\f sin ф, г = г sin \(/;0<г< + оо, 0<ф< 2ж
(сферические координаты).
2. X = г cos ц>, у = г sin ф, 2 = z; О < г < + оо, О < ф < 2%, - оо < з: < + оо
(цилиндрические координаты).
§47
Криволинейные интегралы
47.1. Криволинейные интегралы первого рода
Пусть в трехмерном пространстве R^ задана кривая
Г = {r(t) a<t<b}
(см. § 16). Мы будем рассматривать однозначные функции F,
определенные на точках r(t) этой кривой: F = F(r(t)). Если
р(т), а < т < Р — какое-либо другое представление той же
кривой Г и f = ^(т), а < т < Р — отображение отрезка [а, Р] на
отрезок [а, Ь], осупа;ествляюпа;ее эквивалентность этих
представлений (т. е. t = t(T), а < т < Р — допустимое преобразование
параметра, см. п. 16.1), то, поскольку значение функции F
определяется лип1ь точкой кривой, будем иметь
F(p(x)) = F(r(t)), t = t(x), а<т<р.
Рассматриваемые функции F принимают, вообпа;е говоря,
различные значения в точках кривой, соответствуюгцих
различным значениям параметра, но совпадаюгцих как точки
494
пространства (см. кратные точки в п. 16.2). Такая точка
зрения соответствует физической интерпретации кривой Г,
например, как траектории движения материальной точки, а
функции F — как некоторой силы, действуюгцей на нее и за-
висягцей не только от положения точки в пространстве, но и
от момента, в котором эта точка находится в данном месте.
Кроме того, такой подход дает и определенные
математические преимугцества, которые будут видны в дальнейгаем.
Из сказанного следует, что указанные функции, заданные
на кривой, нельзя рассматривать как функции, определенные
на некотором множестве пространства R^, и поэтому, строго
говоря, их нельзя обозначать через F(x, г/, г), где х, у, 2 —
декартовы координаты пространственных точек. Однако в
рассматриваемых ниже вопросах такое обозначение является
традиционным, поэтому мы будем его употреблять. Если
всегда помнить, что в этих вопросах речь идет о функциях,
определенных на точках кривых, то его использование не
приведет к недоразумениям.
Пусть теперь задана спрямляемая ориентированная кривая
Г, причем r(s) = {x(s), y(s), 2(s), О < s < aS} — ее представление,
где в качестве параметра взята переменная длина дуги s, и
пусть А = г@) л В = r(S) — начальная и конечная точки этой
кривой.
В этом случае будем писать Г = АВ. Противоположно
ориентированную кривую обозначим ВА,
Определение 1. Пусть на точках r(s) кривой Г задана
некоторая функция F, Тогда интеграл \F{x, г/, z)ds определяется
по формуле ^ АВ
I F(x, у, 2)ds = I F(x(s), y(s), 2(s))ds D7.1)
АВ О
и называется криволинейным интегралом первого рода от
функции F по кривой АВ,
Этот интеграл обозначается также символами
^F{r{s))ds и |F(r(s))(is, или, короче, |F(is.
АБ г Г
Таким образом, хотя определение криволинейного
интеграла первого рода и связано с понятием кривой, т. е. с
геометрическим образом, оно сводится к обычному интегралу по
отрезку, и поэтому на криволинейный интеграл переносятся
все свойства обычного интеграла.
195
Отметим некоторые специфические свойства интеграла
D7.1).
10. \ ds = S.
АВ
Это свойство очевидно.
2^. Если функция F непрерывна в точках кривой Г как
функция параметра s, т. е. если непрерывная функция
F (r(s)), О < S < aS, то интеграл ^ Fds существует.
г
в самом деле, согласно определению D7.1), интеграл ^Fds
г
S
сводится к интегралу | F((x(s), y(s), 2(s))ds, от непрерывной
о
функции по отрезку, а этот интеграл, как известно, супа;ест-
вует.
3^. Криволинейный интеграл первого рода не зависит
от ориентации кривой:
I F(x, г/, z)ds = I F(x, г/, z)ds.
АВ ВА
Действительно, пусть М = r(s) — точка кривой АВ и s —
длина дуги AM. Если а = S - s, то а равняется длине дуги
ВМ (рис. 72). Функция г = г (S - а), О < а < S, является
представлением кривой ВА, поэтому, выполнив в интеграле
D7.1) замену переменного s = aS - а и заметив, что ds = -da,
получим
S
\F(x, у, 2)ds = I F(x(s), y(s), 2(s))ds =
AB 0
= -\ F(x(S - a), y(S - a), 2(S - a))da =
s
s
= I F(x(S - a), y(S - a), 2(S - c))dc = \ F(x, y, 2)dc.
0 BA
Это свойство криволинейного интеграла
первого рода связано с тем, что, согласно
r(S) определению, длина дуги кривой считает-
r(S) = r(S-b) ся положительной независимо от конца,
от которого она отсчитывается.
Прежде чем перейти к следуюгцему
свойству, заметим, что \ Fds, как и всякий
г
интеграл, является пределом соответству-
496
юпа;их интегральных сумм; специфика этого случая состоит
лип1ь в том, что эти суммы можно описать в геометрических
терминах, связанных с кривой Г, по которой ведется
интегрирование. Сформулируем это более точно.
4^. Пусть т = {SiV-Zq^ — разбиение отрезка [О, aS],
^•G [s. _ ^, s.]. As. = s. - s. _ ^ — длина дуги кривой Г от точки
r(s. _ i) до точки г (§•), /=1,2, ... , i^ и а^= ^ F(r(b,.))As. Тог-
i = 1
да если функция F(r(s)) интегрируема по Риману на
отрезке [О, aS], то
lim c=iFds. D7.2)
Действительно, а^, очевидно, является интегральной сум-
S
мой Римана интеграла ^ F(r(s))ds, и поэтому формула D7.2)
о
непосредственно следует из D7.1). Формула D7.1) очень
удобна для изучения свойства интеграла ^ Fds, однако она далеко
г
не всегда удобна для его вычисления, так как нередко бывает
очень сложно или даже практически невозможно найти
представление данной кривой, где за параметр взята переменная
длина дуги. Укажем поэтому формулу для интеграла ^ Fds
г
при любом параметрическом представлении кривой Г.
5^. Пусть Г — гладкая кривая (см. определение 16 в
п. 16.4), r(t) = {ф(^), \|/(^), X(t); а < t < b} — ее непрерывно
дифференцируемое представление, и, следовательно,
(?'4t) + ¥4t) + X'4t)>0, а<^<Ь').
Пусть функция F непрерывна на кривой Г (в том
смысле, что функция F\r(t)\ непрерывна на отрезке [а, Ь]). Тогда
IF{x, у, z)ds = ] F{^), x|/(f), X{t))j<^'\t) + X|/^2(^) + ^^2^t)dt. D7.3)
г «
в самом деле, при сделанных предположениях кривая Г
спрямляема, и переменную длину дуги s = s(t) можно
принять за параметр (см. следствие 2 из теоремы 2 в п. 16.5), и
поэтому интеграл ^ Fds имеет смысл. Выполнив замену пере-
* Напомним, что это условие означает отсутствие особых точек на
кривой (см. определение 15 в п. 16.4).
497
менного s = s(t) в правой части равенства D7.1) и вспомнив,
что (см. п. 16.5)
получим формулу D7.3).
Из D7.3) следует, что для данной кривой значение
интеграла, стояпа;его в правой части равенства D7.3), не зависит от
выбора параметра на кривой, так как при любом выборе
параметра этот интеграл равен интегралу, стояпа;ему в левой
части этого равенства.
47.2. Криволинейные интегралы второго рода
Ряд математических и прикладных задач приводит к
криволинейным интегралам другого типа. Например, если г = r(t)
является радиусом-вектором движугцейся материальной
точки, SiF = F(t) — сила, действуюгцая на эту точку, то
естественно определить работу силы F вдоль траектории Г
рассматриваемой точки как интеграл | Fdr или, если F = (Р, Q, i?), Sidr =
г
= (dx, dy, dz), в координатной записи как интеграл
I Pdx + Qdy + Rdz. D7 Л)
г
Вспоминая, что (см. п. 16.5)
^ = cosa, ^ = cosB, ^ = cosy, D7.5)
ds ds ds
где t = (cos a, cos P, cos y) — единичный касательный вектор,
интеграл D7.4) можно представить формально в виде
I (Pcos а + Qcos Р + i?cos y)ds.
г
Сформулируем теперь строгое определение интегралов
вида D7.4). Пусть Г = АВ — гладкая ориентированная кривая,
т. е. непрерывно дифференцируемая ориентированная
кривая без особых точек. Тогда сугцествует такое ее непрерывно
дифференцируемое представление
r(t) = {х = ф@, У = W)^ ^ = X(t), a<t<b},A = r(a), В = г(Ь),
что
ф^2(^) + Y^(t) + x'\t) > о, a<t<b.
Пусть S = s(t) — переменная длина дуги, О < s < aS,
S — длина всей кривой Г, отсчитываемой от точки А,
(cos а, cos Р, cos у) — единичный касательный вектор к
кривой, а = a(s), Р = P(s), у = y(s), О < s < aS, и пусть функция F,
498
как и в п.47.1, определена на множестве {r(t), а < f < Ь} всех
точек кривой Г.
Определение 2. if «теграл \ F(x, г/, 2)dx определяется по фор-
АВ
муле
^F(x,y, 2)dx= ^F(x, у, 2)cosa ds, D7.6)
АВ АВ
Аналогично, по определению полагается
\Fix,y,2)dy= \ Fix, у, 2) cos ^ds, D7.7)
АВ АВ
I F(x, у, 2)d2= I F{x, у, 2) COS у ds.
АВ АВ
Интегралы вида D7.6) г/ D7.7) называются
криволинейными интегралами второго рода от функции F по кривой АВ.
Естественность этих определений видна из формул D7.5).
Как в случае интеграла D7.1), так и в случаях интегралов
D7.6), D7.7) говорят, что функция F интегрируется по
кривой АВ.
Отметим некоторые свойства криволинейных интегралов
второго рода, ограничиваясь для краткости только случаем
интеграла D7.6).
1^. Если функция F непрерывна на кривой Г, т. е.
непрерывна функция F(r(t)), а < t < b, то интеграл D7.6)
существует.
Действительно, при сделанных относительно кривой Г
предположениях функция t = t(s) (t — параметр на кривой Г,
S — переменная длина дуги), непрерывно дифференцируема
на отрезке [О, aS], поэтому функция cos а = -^—- непрерывна
at as
на этом отрезке и, следовательно, функция F(r(t(s)))cosa(s)
непрерывна на [О, S] и, в силу криволинейных интегралов
первого рода, интеграл D7.6) сугцествует. П
В дальнейгаем в этом пункте для простоты будем
предполагать, что функция F непрерывна на кривой Г. В этом
случае все приведенные ниже интегралы заведомо сугцествуют.
2^. Криволинейный интеграл второго рода меняет знак
при изменении ориентации кривой, т. е.
I F(x, у, 2) dx = - ^ F(x, у, 2) dx.
АВ ВА
(Само собой разумеется, что в случае, когда
рассматриваемый интеграл равен нулю, никакого изменения знака не проис-
199
ходит, так как его просто нет.
Однако написанное равенство остает-
"^ ся верным.)
В самом деле, если а — угол,
образованный положительным
направлением касательной к кривой
р ггг. АВ с осью Ох, Si а' — угол,
образованный положительным
направлением касательной к кривой ВА с осью Ох, то для соответст-
вуюгцих точек имеем а' = а + тг (рис. 73) и, следовательно,
cos а' = -cos а.
Использовав теперь свойство независимости
криволинейного интеграла первого рода от ориентации кривой (см.
п. 47.1), получим
IF(x, у, z)dx = IF{x, у, 2)cos a'ds = - JF{x, у, 2)cos ads =
BA BA BA
= - \ F(x, y, 2)cos ads = - \ F(x, y, z)dx.
AB AB
Таким образом, это свойство криволинейного интеграла
второго рода вытекает из того факта, что криволинейные
интегралы
I F{x, у, z)dx и I F{x, у, z)dx
АВ ВА
равны соответствуюпа;им криволинейным интегралам первого
рода, подынтегральные выражения которых отличаются
только знаком. П
3^. Если F — непрерывная на кривой Г = АВ функция,
то для интеграла D7.6) справедлива формула
I F{x, у, 2)dx = I F((?(t), \\f(t), x(tW(t)dt. D7.8)
AB
Действительно, согласно определению D7.6),
s
\ F(x, у, z)dx = I F{x{s), yis), 2(s))cos a(s)ds.
AB 0
Выполнив в интеграле, стоягцем в правой части этого
равенства, замену переменного s = s(t), а < f < Ь, и замечая, что (см.
D7.5)) cos а = ^ = ^, получим
as Sf
I F{x{s), j/(s))cos ais)ds = ] Fiifit), \|/@, x{t))^s;dt =
0 a ^t
= 1Р(ф),л\1а),ха)ща)(И.п
a
500
Отметим, что мы доказали также, что интеграл, стояпа;ий
в правой части этой формулы, не зависит от выбора
параметра на кривой, сохраняюпа;его ее ориентацию.
В частном случае, когда за параметр t можно взять
переменную X, т. е. когда кривая Г обладает представлением у =
= у(х), 2 = 2(х), а < X < Ь, И, следовательно, не имеет кратных
точек, функция F является однозначной функцией не
только точек кривой, но и соответствуюгцих точек пространства
(в этом случае разным точкам кривой соответствуют разные
точки пространства, и наоборот). Формула D7.8) принимает в
этом случае вид
. b
J F(x, у, 2)dx = ^ F(x, у(х), 2(х)) dx, D7.9)
АВ «
Если на гладкой кривой
АВ = {r(t); a<t<b}, r(t) = (ф), \\f(t), %@),
заданы непрерывные функции P(r(t)), Q(r(t)), R(r(t)), то для
интегралов | Qdy и | Rd2 имеют место формулы, аналогичные
АВ АВ
формулам D7.8), и поэтому
I Pdx + Qdy + Rd2 =
АВ
= I [P(r(tW(t) + Q(r(tW(t) + R(r(t))x\t)]dt. D7.10)
a
Если вектор с координатами Р, Q, R, определенными на
кривой Г = АВ, обозначить через а, а вектор с координатами
dx, dy, d2 — через dr, то adr = Pdx + Qdy + Rd2 и для
интеграла D7.10) получится запись \adr, т. е.
\а dr = \Pdx + Qdy + Rd2.
Левая часть этого равенства называется векторной
записью криволинейного интеграла второго рода, а правая —
его координатной записью.
4^. Интеграл \ F(x, у, 2)dx является пределом соответ-
АВ
ствующих интегральных сумм, описываемых в терминах,
связанных с кривой Г, точнее: пусть т = {^J-Zq^ —разбиение
отрезка [а, Ь], |т| — его мелкость, ^^е[^. _ ^, ^.], i = \, 2, ... , i^u
a,= ^F(r(g)Ax„ D7.11)
i = 1
где Ах. = ф(^•) - ф(^• _ ^); тогда
lim G^= \F{x,y,2)dx. D7.12)
|т|^0 ^ Л
АВ
~501
Сумма д^ называется интегральной суммой
криволинейного интеграла второго рода D7.6).
В самом деле, по формуле конечных прирагцений Лагран-
жа. Ах. = (^\\)М-, где \^\t-_^, f.]. М- = t^-t^-iJ= 1, 2, ... , /,,
поэтому
а,= Х/(г(д)ф'(Лг)А*,.
Положим
i = 1
Сумма а^ является интегральной суммой Римана для
функции F(r(t))(f\t), поэтому
Ит^ а, = } FiritWit)dt. D7.13)
С другой стороны,
< coFJ ф')(& - а) sup \F(r(t))\,
а < t < b
где соF^; ф') — модуль непрерывности функции ф'. Так как из
непрерывности функции F(r(t)) на отрезке [а, Ь] следует, что
sup |F(r(f))| < оо^ а из непрерывности функции ф' на том же
отрезке следует, что lim соF ; ф') = О, то lim \а - а \ = 0. Поэто-
|т|^0 |т|^0
му, в силу D7.13), получим
lim a^ = \F(r(tW(t)dt.
Отсюда, согласно равенству D7.8), следует формула D7.12). П
Мы рассмотрели только те свойства криволинейных
интегралов, которые связаны со спецификой их определения,
с кривой, по которой производится интегрирование.
Естественно, что так как рассматриваемые интегралы сводятся к
обычным интегралам по отрезку, то нетрудно показать, что
для них справедливы свойства линейности, аддитивности по
дугам, по которым происходит интегрирование, возможность
интегрирования неравенств и т. п.
47.3. Расширение класса
допустимых преобразований параметра кривой
Непрерывно дифференцируемая ориентированная кривая без
особых точек определялась (см. п. 16.2—16.4) как кривая,
имеюгцая непрерывно дифференцируемые векторные пред-
102
ставления г (t), а < f < Ь, такие, что г' (t) ^ О на отрезке [а, Ь].
В качестве допустимых преобразований параметра при этом
рассматривались функции t = t(x), а < т < р, t(a) = а, t(^) = b,
которые были непрерывно дифференцируемыми и имели
положительную производную на отрезке [а, Ь]. Это требование,
однако, часто оказывается слигаком обременительным.
Например, для дуги Г единичной окружности с центром в начале
координат представления у = Jl - х^, 0<х<1,их = sin t,
у = cos t, О <: t <: 7г/2, оказываются неэквивалентными в этом
смысле. Да и само представление у = Jl - х^, О < х < 1, не
определяет в нагаем смысле непрерывно дифференцируемую
кривую, поскольку у него при х = 1 производная не сугцеству-
ет. Поэтому естественно расгаирить класс допустимых
преобразований параметров и допустимых представлений
непрерывно дифференцируемых кривых. Это можно сделать сле-
дуюгцим образом.
Рассмотрим совокупность векторных представлений г =
= r(t), а <: t <: b, непрерывных на отрезке [а, Ь] и непрерывно
дифференцируемых на интервале (а, Ь), Допустимым
преобразованием параметра будем называть всякую функцию t =
= t(T), а < т < р, t(a) = а, t(^) = b, непрерывную на отрезке
[а, Р], непрерывно дифференцируемую и имеюгцую
положительную производную на интервале (а, Р). Как всегда, два
представления называются эквивалентными, если можно
перейти от одного к другому с помогцью допустимого
преобразования параметра.
Определение 3. Класс эквивалентных представлений
указанного типа задает непрерывно дифференцируемую
кривую, если в этом классе существует по крайней мере одно
представление г = r(t), а < t < b, непрерывно
дифференцируемое на всем отрезке [а, Ь].
Определение 4. Непрерывно дифференцируемая кривая
называется кривой без особых точек, или, короче, гладкой
кривой, если при некотором ее представлении г (t), а< t < b,
выполняется условие r\t) ^ О, а <: t <: b.
В смысле этого определения для указанных выгае
представлений дуги окружности оказываются эквивалентны и
задают гладкую кривую.
Гладкие в смысле определения 4 кривые спрямляемы, так
как имеют непрерывно дифференцируемое на отрезке
представление. В качестве одного из параметров на такой кривой
может быть выбрана длина дуги.
1оз
Остаются в силе и все данные выгае определения
криволинейных интегралов и их свойства. Нужно только иметь в
виду, что при некоторых представлениях кривых в формуле
D7.10) могут получаться несобственные интегралы, так как
производные ф'(^), ^\t), x\t), стоягцие под знаком интеграла,
не являются, вообгце говоря, непрерывными вплоть до
концов промежутков интегрирования.
Следует подчеркнуть, что расп1ирение класса представлений
кривой позволяет вычислять криволинейный интеграл при
более разнообразных представлениях кривой. Например,
интеграл I Р(х, y)dy, где Г — рассматриваемая выпхе дуга единичной
г
окружности, а Р — непрерывная на кривой Г функция, можно
вычислить, используя оба указанных представления:
•Л/ \А/ *Л/
\Р{Х, y)dy = -\Р(Х, 71 - Х2)
Г о л/1 - Х^
к/2
\ Р(х, y)dy = - I P(sin t, cos t)sii[itdt.
г о
В первом случае может получиться несобственный интеграл.
Вместе с тем при доказательстве теорем можно
выбирать «xoponine представления», т. е. непрерывно
дифференцируемые вплоть до концов отрезка, а проведенные
рассмотрения окажутся справедливыми и для расгаиренного
понятия кривой.
УПРАЖНЕНИЕ 1. Доказать, что при новом определении непрерывно
дифференцируемой кривой Г = {x{t), y{t), z{t); а ^ t ^ b} ее длина выра-
b
жается формулой f Jx'^ + у'^ + z'^dt, где написанный интеграл, вообще
а
говоря, несобственный.
47.4. Криволинейные интегралы
по кусочно-гладким кривым
Определение 5. Если кривая Г — кусочно-гладкая, т, е, пред-
ставима в виде объединения конечного числа гладких
кривых Г^, Гз, ... , Г^, а функция F(x, у, z) по-прежнему
определена на точках кривой Г, то, по определению, положим
k
\ F(x, у, 2) dx= Y, IД^? У^ ^) dx.
Подчеркнем, что здесь гладкость кривых понимается в
обобпа;енном смысле, т. е. в смысле определения 4.
^04
Если Г — кусочно-гладкая кривая, sl х = x(t), у = y(t),
2 = 2(t), а <: t <: b, — ее кусочно-гладкое представление, то
также будем иметь
b
\Г(х, г/, 2)dx = \Fiixit), y(t), 2(t))x\t) dt
г a
(здесь производная x\t) может быть не определена в конечном
числе точек отрезка [а, Ь] и интеграл, стоягций в правой части
равенства, следует понимать, вообгце говоря, в несобственном
смысле).
Аналогичные определения имеют место и для интегралов
вида D7.7). В дальнейгаем придется иметь дело с суммами
интегралов вида D7.6) и D7.7), т. е. с интегралами вида
D7.4), где Р, Q и i? — некоторые функции, определенные на
точках кривой Г. Согласно определениям D7.6) и D7.7), для
кусочно-гладких кривых Г также справедлива формула
I Pdx + Qdy + Rd2 = \ Р cos а + Q cos Р + i? cos у ds,
г г
Замечание 1. Если Г — конечная совокупность
кусочно-гладких ориентированных кривых Г., / = 1, 2, ... , й, то,
по определению,
\F ds= Y, \F ds, \F dx= ^ jFdxHT. д.
г ^ ^ ^ г^ г ^ ^ ^ г^
Замечание 2. Мы дали определение криволинейных
интегралов для кривых, лежагцих в трехмерном
пространстве R^. Аналогично они определяются и для кривых,
лежагцих в любом я-мерном пространстве R^, я = 2, 3, 4, ... .
Криволинейные интегралы в я-мерном пространстве обладают
свойствами, аналогичными рассмотренным выгае в
трехмерном случае, причем доказательства их также совергаенно
аналогичны приведенным выгае. Поэтому не будем
останавливаться ни на формулировках, ни на доказательствах соот-
ветствуюгцих утверждений.
УПРАЖНЕНИЕ 2. Доказать, что данные в настоящем пункте
определения криволинейных интегралов по кусочно-гладким кривым не зависят
от способа разбиения этих кривых на гладкие дуги.
47.5. Интеграл Стилтьеса
Более обпа;ее понятие криволинейного интеграла второго рода,
независимое от понятия криволинейного интеграла первого
рода, можно получить с помогцью предела интегральных сумм а^
~505
(см. D7.11)), т. е. принять за определение равенство D7.12). При
этом нет необходимости делать предположения о какой-либо
гладкости кривой, по которой ведется интегрирование.
Такой подход к понятию криволинейного интеграла
второго рода приводит естественным образом к обобгцению
интеграла Римана, которое называется интегралом Стилтъеса.
Сформулируем его определение и опип1ем кратко его свойства.
Отметим, что интеграл Стилтьеса находит свое применение
не только в теории криволинейных интегралов, но, например,
и в теории вероятностей.
Пусть функции f{x) и g{x) заданы на отрезке [а, Ь], т =
^{^i}\Z^Q — разбиение этого отрезка, ^.g[x. _^, х-], А^(х.) =
= g(x.) - g(x. _ i), / = 1, 2, ... , /^, и
а,(/, g) = a^if, g; ^,, ... , ^, ) ^= ^ /(^,)А^(х,). D7.14)
'^ i = 1
Определение 6. Функция f называется интегрируемой по
функции g на отрезке [а, Ь], если для любой последователъ-
i = i^
ности разбиений т^ = {л:р^}. _ q этого отрезка такой, что
предел lim It I = О, и для любого выбора точек E(^^G[xf^\, х\^\
i = l,2, ... ,i^ , существует, и при этом один и тот же, предел
lim а^ (f,g) = \f(x)dg(x).
7, ^ ОО ^n J
П^ОО ^п
Этот предел называют интегралом Стилтъеса* функции f
по функции g и пишут
]f{x)dg{x)= lim o^{f,g). D7.15)
В случае g{x) = x интеграл Стилтьеса является, очевидно,
интегралом Римана. Если функция g{x) — постоянная, то
интеграл от любой функции по ней равен нулю.
Как обычно, можно сформулировать равносильное
определение интеграла Стилтьеса на «8—6»-языке. Сделаем это.
ъ
Число, обозначаемое ^f{x)dg{x), называется интегралом
а
Стилтъеса от функции / по функции g на отрезке [а, Ь], если
для любого 8 > О сугцествует такое 6 > О, что для всех разбие-
' Т. и. Стилтьес A856—1894) — нидерландский математик.
~506
НИИ т = {^iVi^ ^i отрезка [а, b] мелкости |т| < 6 и для всех
точек Ь,.е[х-_ ^, X.], / = 1, 2, ... , /^, выполняется неравенство
а,(/, ^;^1, ... , ^^)-\f(x)dg(x)
<8.
Интеграл Стилтьеса обладает свойством линейности как
относительно функций /, так и относительно функций g.
Более точно, справедливы следуюпа;ие теоремы.
ТЕОРЕМА 1. Если существуют интегралы Стилтъеса
ъ
I /.(х) dg (х), а X-eR, i= 1, 2, ... , п, то существует интеграл
а
Ь п
Стилтъеса \ {Y, ^ь ^Д^)) ^^ (^) ^
а i = 1
J (f V; (^)) ^^ (^) = Е ^J /; (^) ^^ (^)-
а i = 1 i = 1 а
ТЕОРЕМА 2. Если существуют интегралы | /(х) dg.(x), а Х-е R,
а
/=1,2,...,я, то существует и интеграл J /(х) (i ( ^ \gi (х)),
I /(х) rf ( f ^. ^. (х)) = £ ^J / (х) dg, (х).
а i = 1 i = 1 а
Эти теоремы доказываются аналогично случаю интеграла
Римана с помогцью предельного перехода в соответствуюгцих
равенствах для интегральных сумм.
47.6. Существование интеграла Стилтьеса
Отметим два класса функций, по которым у непрерывных
функций сугцествуют интегралы Стилтьеса.
Функция называется кусочно-постоянной на отрезке,
если она имеет на нем конечное число точек разрыва и
постоянна на каждом из промежутков, остаюгцихся на отрезке
после удаления из него точек разрыва функции.
ТЕОРЕМА 3. Непрерывная на отрезке [а, Ь] функция f
интегрируема по кусочно-постоянной на этом отрезке
функции g, и интеграл Стилтъеса равен сумме произведений
скачков с^ функции g во всех ее точках разрыва а^, а<. а^^<.Ъ,
й = 1, 2, ... , п, на значение функции f в этих точках:
] f(x)dg(x)= f с. Па,). D7.16)
507
Здесь, если а < а^ < Ь, то с^ = ^(а^ + 0) - ^(а^ - 0); если а^ = а, то
с^ = g(a + 0) - ^(а), а если а^ = Ь, то с^ = g(b) - g{b - 0).
Доказательство. Пусть сначала кусочно-постоянная
функция g имеет на отрезке [а, Ь] только одну точку разрыва
х = с. При х = а для любого разбиения 1 = {х{\\^ ^^ отрезка [а, Ь]
и точек ^. G [х-_^, X.], / = 1, 2, ... , /^, при i = 2, 3, ... , /^ имеем
А^(х.) = g(x.) - g(x._ ^) = О, и поэтому, в силу непрерывности
функции /,
b
I f(x) dg(x) = lim a, (/, g) = lim / (^^) (g(x^) - g(a)) =
= f(a) (g(a + 0) - g(a)),
так как в силу постоянства функции g на полуинтервале (а, Ь]
имеем g(a + 0) = g(x), хе (а, Ь].
Аналогично, если единственной точкой разрыва функции
g является точка х = Ь, то
I fix) dg (X) = fib) igib) - gib - 0)).
a
Пусть теперь единственная точка разрыва х = с функции g
лежит между точками а и Ь, т. е. а < с < Ь. Если т = {xJ[^q^ —
такое разбиение отрезка [а, Ь], что точка х = с в него не
входит, т. е. сугцествует такой номер /q, что
X; _1 <С<Х; , D7.17)
то, В силу кусочного постоянства функции g, для всех i^Iq имеем
Ag(x,) = g(x,) - ^(х._ i) = О, D7.18)
а при i = Iq, в силу неравенства D7.17),
^(^1^ -i) = ^(<^ - 0), ^(л:^^) = ^(с + 0)
и поэтому
А^(х^^) = gix^J - gix^^ _ i) = gic + 0) - ^(c - 0).
Если ^. G [x._ ^, X.], / = 1, 2, ... , /^, TO интегральные суммы
имеют вид
а, = Х^ mt) ^gi = f{%i^) ^g{x^^) = fi%^^) igic + 0) - gic - 0))
(остальные ее слагаемые при i ^ i^, в силу равенства D7.18),
обрапа;аются в нуль).
508
Обозначим через т"^ разбиение отрезка [а, Ь], получаюпа;ее-
ся из разбиения т добавлением к нему точки х = с, т. е. т"^ =
= т и {с}. Ясно, что It""! < |т|. Пусть Г|;^ е [х.^_ ^, с], Г|2 е [с, x-q] и
а,. = /(Лх) (^(с) - ^(с - 0)) + /(Л2) (^ (с + 0) - g(c)) D7.19)
— некоторая интегральная сумма, соответствуюпа;ая
разбиению т"^.
Рассмотрим епа;е частный случай интегральной суммы
D7.19), у которой T|i ^ Л2 ^ ^•
S, с = т (^(^) - ^(^ - 0)) + т (^(^ + 0) - ^(^)) =
= fie) (gic + 0) - gic - 0)).
Сравним суммы а^, а^^ и а^^ ^. В силу непрерывности функции /,
имеем
lim (о, - а,*,,) = lim (/(^. ) - /(c)) (^(с + 0) - ^(с - 0)) = О,
|т| ^ О hi ^ О О
lim (а,. - о,) = lim [(/(л2) - /(c)) (gic) - gic - 0)) +
|х| ^ о |т| ^ О
+ (Пщ) - /(c)) (^(с + 0) - ^(с - 0))] = о-
Из последних двух равенств следует, что интегральные суммы
а^, а^^ и а^^ ^ при |т| ^ О одновременно имеют пределы или нет,
причем если эти пределы сугцествуют, то они равны. Суммы
а^^ ^ — постоянные величины и, следовательно, очевидным обра-
b
зом имеют предел. Поэтому интеграл | f(x) dg (х) сугцествует и
а
I /(X) dg (X) = о,*^, = /(с) ig(c + 0) - gic - 0)). D7.20)
а
Если функция g — кусочно-постоянна, то она является
суммой кусочно-постоянных функций, имеюгцих только одну точку
разрыва. Применив к каждой из них формулу D7.20) и сложив
результаты, получим, в силу теоремы 2, формулу D7.16). П
Замечание. Одним из следствий доказанной теоремы
является возможность представить любую конечную сумму
п
^ и- как интеграл Стилтьеса. Действительно, кусочно-посто-
i = 1
янная функция
gix)
О, если X = О,
k
^ Uj^, если k - 1 < k, k = 1,2, ... , п,
i = 1
509
имеет при Uj^^ О точку разрыва Uj^ = k - 1, k = 1, 2, ... , п, со
скачком с^ = Uf^. Поэтому, в силу формулы D7.16), при f = 1
имеем
I dgix)= f г/..
о ^^1
Таким образом, понятие конечной суммы входит в понятие
интеграла Стилтьеса.
Обобгцением утверждения об интегрируемости по Рима-
ну непрерывной на отрезке функции является следуюгцая
теорема.
ТЕОРЕМА 4. Непрерывная на отрезке функция
интегрируема по монотонной на этом отрезке функции.
Доказательство. Пусть функция /(х) непрерывна на
отрезке [а, Ь], а функция g{x) монотонна на этом отрезке.
Достаточно рассмотреть случай только возрастаюгцих функций, так
как если функция g{x) убывает, то функция - g{x) возрастает и
ъ
из сугцествования интеграла Стилтьеса | f{x)d(-g{x)), согласно
а
теореме 2, следует и сугцествование интеграла Стилтьеса
]f{x)dg{x) = -]f{x)d{-g{x)).
а а
Таким образом, случай убываюпа;ей функции сводится к
случаю возрастаю па;ей.
Итак, пусть / — непрерывная, g — возрастаюпа;ая
функции.
ъ
Доказательство супа;ествования интеграла | f{x)dg{x) про-
а
ведем методом, аналогичным методу доказательства
интегрируемости по Риману непрерывной на отрезке функции.
Пусть X = {x}\Z^{ — разбиение отрезка [а, Ь], А^(х.) = g{x) -
- g{x^_^ > 0. Функция /, будучи непрерывной на отрезке [а, Ь],
принимает на отрезках А. = [х- _ ^, х-] в некоторых точках на-
ибольп1ие и наименьп1ие значения. Обозначим эти точки
соответственно Г|. и ^.:
т. = nun f{x) = яд, М. = max f{x) = /(л,), /=1,2, ... , /,. D7.21)
Положим
1^ т,А^(х,), S,= l^ M,Ag(x^). D7.22)
i = 1 i = 1
Лд
Очевидно,
s,<S^. D7.23)
Покажем, что
lim (S -s,) = 0. D7.24)
Имеем
О < S-s^ < У [/(л,) - Ш]А^(хЛ <
D7.23) ^ ^ D7.21) it-i '' ^* *
D7.22)
< ^ со(/; Ai)Agix) < со(/; |х|) ^ (^(х,) - ^(x,_i)] =
i = 1 i = 1
= ш(/;|т|)(^(Ь)-^(а)). D7.25)
Поскольку функция / непрерывна на отрезке [а, Ь], она
равномерно непрерывна на нем, поэтому ее модуль непрерывности
со(/; |т|) стремится к нулю при |т| ^ 0:
lim ш(/;|т|) = 0. D7.26)
Из неравенства D7.25) и равенства D7.26) следует
утверждение D7.24).
Покажем теперь, что для любых двух разбиений т^ и Тз
отрезка [а, Ь] выполняется неравенство
s,^<S,^. D7.27)
Пусть сначала разбиение т"" = {^/}, = i^* отрезка [а, Ь] вписано в
разбиение т. А'- = [х-_ ^, х-], Ag(x'j) = g(x'j) - g(x'j_ ^).
Обозначим через Af те отрезки разбиения т"", которые со-
держатся в отрезке А- разбиения т, / = 1, 2, ... , /^. Тогда
А, = уА;:, Ag, = l^Ag(xl) D7.28)
h
и, если mf = min f(x), Mf = max f(x), то
J J
m. < mUxf), M. > MUxf). D7.29)
Поэтому
s.
i^l ' ' D7.28) i^i ' ^ ^ -^/D7.29)
,,,% X^ "^Л ^(^I) - Z^jAgixJ) - V D7.30)
Аналогично доказывается, что
S^^S^. D7.31)
511
Поэтому для любых двух разбиений т^ и Тз отрезка [а, Ь],
взяв разбиение т этого отрезка, вписанное в разбиения т^ и Тз,
получим
S, < S, < S, < S, . D7.32)
-гт ^1D7.30) ^D7.23) ^D7.31) ^2
Положим
/. = sup s„ Г = inf S,. D7.33)
Из неравенства D7.32) следует, что
/.<Г. D7.34)
Покажем, что на самом деле
1., = Г. D7.35)
Из определения D7.33) и неравенства D7.34) следует, что
s,<r</,<S„ D7.36)
поэтому и неравенство
0<r-/.<S,-s,. D7.37)
Отсюда, в силу стремления правой части неравенства к нулю
при |т| -^ О (см. D7.24)), и следует равенство D7.35).
Если 1 = 1^ = Г\ то из D7.36) имеем s^ < / < aS^,
следовательно,
О < / - S, < S, - s„ О < S, - / < S, - S,. D7.38)
Из этих неравенств снова, в силу стремления к нулю их
правых частей при |т| -^ О, следует, что супа;ествуют пределы
lim s= lim S=I. D7.39)
Ixl^O ^ Ixl^O "
Для любой интегральной суммы Стилтьеса
^х = L /(QA^(x.), х._1 < С- < X., / = 1, 2, ... , /,,
i = 1
В силу очевидных неравенств /(Q ^^ <^^^ /(^.) ^^ <^^^ /(г|.), /=1,2,...
... , i^, имеем s^ < а^ < aS^. Отсюда и из равенства D7.39)
следует, что сугцествует конечный предел lim а^ = /, т. е. сугцеству-
|х| ^0
ет интеграл Стилтьеса от функции / по функции g. П
Укажем случай, когда интеграл Стилтьеса преврагцается
в интеграл Римана.
ТЕОРЕМА 4'. Если функция f непрерывна, а функция g
непрерывно дифференцируема на отрезке [а, Ь], то функция f
интегрируема на этом отрезке по функции g и
] f(x) dg(x) = I f(x)g\x) dx D7.40)
a a
(б левой части равенства — интеграл Стилтьеса,
справа — интеграл Римана).
Эта теорема равносильна доказанному выше свойству 4^
криволинейного интеграла второго рода (см. п. 47.2) при
т = Firit)), git) = 9(f).
Нам понадобится следуюгцая лемма.
b
ЛЕММА Л. Если существует интеграл Стилтъеса | /(х) dg{x) и
а
fix) = fia + b- х), g\x) = gia + b-x), a<.x<.b, D7.41)
то существует интеграл
]nx)dg4x) = -]fix)dgix). D7.42)
а а
Таким образом, при изменении ориентации отрезка [а, Ь], т. е.
при замене переменной х на f по формуле х = а-\- b - t, интеграл
Стилтьеса меняет знак. Это следует из того, что когда
переменная X изменяется в обратном направлении, т. е. от точки b к
точке а, прирапа;ения Ag(x-) функции g(x) меняют знак. Точнее,
Ag(x.) = g(x.) - g(x. _ i) = -(g(x. _ i) - g(x.)).
Поэтому интегральным суммам a^(/, g) будут соответствовать
интегральные суммы -а^(/, g), следовательно, и их пределы
будут отличаться знаком.
Левая часть формулы D7.42) обычно обозначается
а
^ f(x)dg(x). При такой записи эта формула принимает вид
b
а b
j fix) dgix) = -| fix) dgix).
b a
Доказательство. Если x = {x}]^-^ — разбиение отрезка
[a, Ь], ^;e[X;_i, X;], i = 1, 2, ... , i^,
xj = a + b-x^, i + j = i^, i = 0,l, ... ,ц, D7.43)
^; = a + b-^^ + i, i + / = i„ i = 0, l,...,i,-l, D7.44)
TO X* = {x*}'- '^ — также разбиение отрезка [a, b],
|x*| = |t|, ^/е[л:*_ 1, x*], / = 1, 2, ... , i^,
f'^P D7=41) ^(« + ^ - ^;) D7=44) f^^i + l)' ^ + / = h'
i=l,2,...,h, D7.45)
A^*(x;) = /(x/)-/(x;_ ,)^^ =^^^gia + b-x/)-gia + b-xj. ,)^^=^^^
D7=43) ^^^;) ~ ^^^l + l) = ~^^^^l + 1^'
j + / = j,, / = 0, 1, 2, ...,v D7.46)
Поэтому
MA ^*) = X/W)^^*^^;) D7=45)
^ D7.46)
D7.46)
D7.45) ^^,
Отсюда
/ = Г- 1 - ^Ш^ё^Ч) = -<^г(Г^ ё)- D7.47)
j Г(x)d^*(x) ^^ = ^^ I Ит^ а,.(Г, gl ,,,=,,,
D7=47) -|J|i^o ''^^^' ^^ D7=15) " J Я:^)^^^). П
b
Интеграл Стилтьеса | f(x)dg(x) обладает и рядом других свойств,
а
аналогичных свойствам интеграла Римана. Например,
свойством аддитивности по отрезкам интегрирования. Мы не будем
останавливаться ни на подробных формулировках этих свойств,
ни на их доказательствах, предоставляя это проделывать
читателю по мере внутренней потребности.
47.7. Обобщение понятия
криволинейного интеграла второго рода
Используя понятие интеграла Стилтьеса, дадим теперь более
обпа;ее, чем раньпхе, определение криволинейного интеграла
второго рода ^ Pdx + Qdy + Rdz по кривой Г.
г
Пусть Г — параметрически заданная кривая: Г = {r(t); а <
< t < Ь}, r(t) = (ф(^), Х|/@? %@)? и, следовательно, функции ф,
\|/, X непрерывны на отрезке [а, Ь], и пусть на множестве
точек этой кривой задана функция F, т. е. на отрезке [а, Ь]
задана функция Firit)) = Дф@, ¥@, %@).
Определение 2"". Криволинейным интегралом второго рода
^Fdx от функции F по кривой Г называется интеграл
г
Стилтьеса
]F(r(t))d(p(t). D7.48)
а
Если функция F непрерывна на кривой Г, т. е.
непрерывна функция F(r(t)) на отрезке [а, Ь], а кривая Г гладкая, и по-
Jl4
этому функция X = ф(^) имеет на отрезке [а, Ь] непрерывную
производную ф'@? то, согласно теореме 4 п. 47.6, имеем
J F(r(t))di?(t) = J F(r(tW(t) dt = IFdx, D7.49)
a a г
где, в силу формулы D7.10), в правой части равенства стоит
криволинейный интеграл второго рода в смысле определения 2
п. 47.2. Из равенства D7.49) следует, что для непрерывных на
гладкой кривой функций определения 2 и 2"^ криволинейных
интегралов второго рода равносильны.
Криволинейный интеграл второго рода в смысле
определения 2* можно брать и по кусочно-гладкой кривой, т. е. по
кривой, являюпа;ейся объединением конечного множества
гладких кривых. При этом указанный интеграл, в силу его
аддитивности, будет равен сумме интегралов по гладким частям
кривой, и тем самым он и в этом случае равен соответствую-
гцему интегралу второго рода в смысле определения 2 (см.
определение 5 в п. 47.4).
Сугцественное обобгцение понятия криволинейного
интеграла в определении 2* достигается прежде всего за счет того,
что интеграл B7.24) может сугцествовать и для «негладких»
кривых, т. е. в том случае, когда нельзя использовать
понятие касательных векторов, которое необходимо для того,
чтобы можно было применить определение 2.
Криволинейный интеграл D7.48), подобно
криволинейному интегралу D7.6) (см. определение 2), не зависит от выбора
представления ориентированной кривой. Действительно,
пусть t = f(u), а < г/ < р, — допустимое преобразование
параметра, т. е. непрерывное строго возрастаюгцее отображение
отрезка [а, Р] на отрезок [а, Ь] и пусть т = {и^У^^ ^^ —
разбиение отрезка [а, Р].
Положим
t, = f(u,), i = 0,1,..., i,. D7.50)
Тогда т"^ = i^i}i = 0^ является разбиением отрезка [а, Ь], и важно
заметить, что, в силу равномерной непрерывности функции
t = f(u) на отрезке [а, Р], из стремления к нулю мелкости
разбиения т следует стремление к нулю мелкости т"^, т. е.
lim И = 0. D7.51)
Если с^.е[и._ 1, г/.] и
Ц, = П^,), / = 1,2, ...,/,, D7.52)
Jl5
то для представлений r(t), а < f < Ь, и r(f(u)), а < г/ < р,
кривой Г, положив (см. D7.14))
а^ = а^ (F ° г ° /, ф ° /), а^., = а^., (F ° г, ф), имеем
^х D7Л4) X ^(тШМПЩ) - ф(/(^.- l))] D7750)
' ^ D7.52)
D7=50) Е/('-(Л.))[ф(*.) - Ф(*.- l)] D7=14) ^х-
D7.52) '
Поэтому ИЗ супа;ествования конечного предела lim SJ и вы-
полнения условия D7.51) следует сугцествование конечного
предела lim а,: и равенство
lim а,: = lim ст;.
Согласно определению интеграла Стилтьеса, это равенство
представляет собой равенство интегралов
} F(r(f(u)))di?(f(u)) = ] F(rit))dW),
а а
ЧТО, в силу определения 2* криволинейного интеграла,
означает равенство
\(F orof)d((pof) = \Fd(p.
г г
Это и означает независимость интеграла D7.48) от выбора
представления кривой.
Если под гладкой кривой понимать кривую, которая
имеет хотя бы одно представление, непрерывно
дифференцируемое вплоть до концов отрезка, на котором оно задано, и не
имеет особых точек внутри этого отрезка (см. определения 3
и 4 в п. 47.3), то для функций, непрерывных на такой
кривой, определения 2 и 2"^ криволинейных интегралов второго
рода эквивалентны, т. е. дают одно и то же значение
интеграла, какое бы представление этой кривой ни выбрать. В самом
деле, во-первых, для представления кривой непрерывно
дифференцируемого вплоть до концов отрезка, на котором оно
задано, эти определения, согласно доказанному выгае,
эквивалентны; во-вторых, оба эти определения не зависят от
выбора параметра на кривой.
Криволинейный интеграл D7.48), подобно интегралу D7.6),
меняет знак при изменении ориентации кривой, по которой
Лб
производится интегрирование. Это сразу следует из D7.42),
так как изменение ориентации кривой соответствует
преобразование параметра t = a + b-t\a<.t<.bj следовательно,
переход от функций F{r(t)), ф(^) к функциям F(r(a -\- b - t*)),
ф(а + Ь - f), a<f<b.
На криволинейный интеграл в смысле определения 2'^
переносятся и другие свойства интеграла D7.6) такие, как
линейность, аддитивность по дугам, интегрирование неравенств
и т. п.
Аналогично интегралу \F(x, г/, 2)dx обобпа;аются и поня-
г
тия криволинейных интегралов второго рода вида
\F{x,y,z)dy и \F{x,y,z)dz\
г г
ъ
они определяются как интегралы Стилтьеса ^ F{r{t))d\]f{t) и,
а
Ь
соответственно, ^F{r(t))d\]/(t).
а
Таким образом, можно рассматривать в этом смысле и ин-
ъ
теграл вида ^ Pdx + Qdy + Rdz, Этот интеграл, в силу его ад-
а
дитивности по дугам, совпадает с интегралом,
рассмотренным в п. 47.2, не только по гладким кривым (как это было
доказано выгае), но и но кусочно-гладким. Следовательно, в
данном случае остается справедливой формула
I Pdx + Qdy + Rdz = \ (Pcos а + Qcos р + i?cos i)ds, D7.53)
г г
где (cos а, cos Р, cos у) — единичный касательный вектор к
кривой в тех точках, в которых у нее сугцествует касательная.
Рассмотрим два примера криволинейного интеграла
второго рода в смысле определения D7.48).
Примеры. 1. Пусть кривая Г такова, что на ней можно
взять за параметр одну из координат, например координату х,
т. е. кривая Г имеет представление
у = у(х), z = z(x), а < X < Ь, D7.54)
а функция F непрерывна на этой кривой.
Тогда криволинейный интеграл \ Fdx в смысле опреде-
г
b
ления 2'" равен интегралу Стилтьеса |Р(х, у(х), z(x))dx,
а
Л?
который в этом случае является интегралом Римана от
непрерывной на отрезке [а, Ь] функции F(x, у(х), 2(х)) и поэтому
супа;ествует.
Итак, для криволинейного интеграла в смысле
определения 2'^ при сделанных предположениях, как и для
криволинейного интеграла в смысле определения 2, когда
интегрирование ведется по кусочно-гладкой кривой, имеет место
формула
b
\ F(x, у, 2)dx = \ F(x, у(х), 2(x))dx, D7.55)
г а
Отметим, что здесь эта формула в отличие от формулы
D7.9) получена для произвольной непрерывной кривой вида
D7.54), т. е. эта кривая может быть, в частности, неспрям-
ляемой, не иметь касательной ни в одной точке и т. п.
2. Если кривая Г лежит в плоскости, перпендикулярной
оси Ох, т. е. имеет представление
х = Xq, у = y(t), 2 = 2(t), а< t <b, D7.56)
то
\F(x,y,2)dx = 0. D7.57)
г
Это следует из того, что интеграл Стилтьеса (как это было
отмечено вып1е) от любой функции по постоянной равен нулю.
Криволинейный интеграл второго рода в новом pacninpen-
ном смысле встретится, во-первых, тогда, когда кривая Г =
= АВ является графиком непрерывной относительно одной
из координат функции, например функции у = f(x), а < х < Ь,
на плоскости переменных х, г/, а функция F(x, у) непрерывна
на этом графике. В этом случае
b
I Fix, у) dx = I Fix, fix)) dx
AB * «
И, следовательно,
b
I Fix, y)dx = -\ Fix, fix))dx; D7.58)
BA
во-вторых, тогда, когда кривая Г лежит в плоскости
переменных X, г/ и является отрезком, параллельным одной из
координатных осей, например оси Оу : х = Xq, с < г/ < d. В этом случае
lFix,y,2)dx^^=^^^0. D7.59)
57s
47.8. Формула Грина
В дальнейгаем для наглядности будем всегда предполагать,
что на плоскости и в пространстве заданы правые
прямоугольные системы координат (если, конечно, не оговорено что-то
другое).
Определение 7. Пусть простой замкнутый контур Г
является границей ограниченной плоскости области G. Если
ориентация контура выбрана таким образом, что при
движении по контуру соответственно выбранной ориентации
область G остается слева (такой обход обычно называется
обходом контура против направления движения часовой
стрелки), то эта ориентация называется положительной,
в противном же случае {т, е, когда обход контура
производится по направлению движения часовой стрелки) —
отрицательной (рис. 74).
Будем говорить также, что обход контура, соответствую-
па;ий положительной (отрицательной) ориентации,
происходит в положительном (отрицательном) направлении.
Положительно ориентированный контур будем обозначать
через Г+, а отрицательно ориентированный — через Г~. Эти
понятия определены не строго, не в точных математических
терминах («правая система координат», «слева», «справа» и т. п.).
В дальнейгаем во всяком отдельном случае рассматриваемая
ориентация всегда будет конкретно указываться. Тем самым
Hanie «обгцее» определение положительной и отрицательной
ориентации простого замкнутого контура послужит лигаь для
геометрической наглядности рассматриваемых ниже вопросов.
Конечно, понятие ориентации контура можно
сформулировать и в четкой математической форме. Сделаем это для
случая замкнутого гладкого контура. Пусть на плоскости задана
прямоугольная декартова система координат с
координатными ортами i, j. Пусть Г — гладкий замкнутый ориентирован-
Положительная Отрицательная
ориентация ориентация
Рис. 74
Jl9
ный контур, т — единичный
_J\ С^ касательный вектор, задаюпа;ий
d\^^ ^^ ^С ®^^ ориентацию (см. п. 16.4) и
\а{у) G P(i/)] V — единичная нормаль, направ-
^|\ Ф(-^) /^— ленная в сторону конечной об-
i~Ai В^~ I ласти, ограниченной контуром Г
I I (эта нормаль называется внут-
^ ^"^ ренней нормалью). Контур Г
называется положительно ориен-
Ри^- '^^ тированным относительно
заданной системы координат, если
упорядоченная пара векторов т, v имеет ту же ориентацию, что
и пара координатных ортов i, /. Это означает, что определитель
матрицы перехода от векторов т, v к базису i, / положителен.
В дальнейп1ем плоскую область G ^ R , замыкание
которой может быть представлено одновременно в виде D5.1) и
D5.28), т. е. область, граница которой может быть
представлена как в виде объединения графиков непрерывных функций от
переменной х, так и в виде объединения графиков
непрерывных функций от переменной у и, быть может, егце отрезков,
параллельных соответствуюгцим координатным осям, будем
для краткости называть элементарной областью (рис. 75).
Ясно, что элементарные области и объединения конечного
множества элементарных областей являются квадрируемыми
множествами, так как их границы имеют меру нуль.
Будем говорить, что квадрируемая плоская область G
разбита на конечное число квадрируемых областей G., / = 1, 2, ... , й,
если множество их замыканий {G{\\z\ является разбиением
замкнутой области G (см. п. 44.3).
ТЕОРЕМА 5. Пусть плоская область G может быть
разбита на конечное число элементарных областей и ее граница Г
является простым замкнутым контуром. Если на
замыкании G области G заданы функции Р(х, у) и Q(x, у),
непрерывные на G вместе со своими частными производными ^г-
и ^, то имеет место формула
* Непрерывность частных производных на G понимается как их
непрерывность на открытом множестве G и их непрерывная
продолжаемость на границу G (см. п. 39.3).
520
nf^-^^dxdy= [Pdx + Qdy, D7.60)
называемая формулой Грина''.
СЛЕ ДСТВИ E. ^слг/ в условиях теоремы контур Г,
являющийся границей области G, кусочно-гладкий и (cos а, sin а) —
единичный касательный к нему вектор (в тех точках, где
он существует), то
и(^Я- ^^dxdy = f (Pcos а + Q sin a)ds, D7.61)
J^J \дх dy ) J,
где s — переменная длина дуги на контуре Г.
Доказательство. Пусть сначала область G сама
элементарна и, следовательно, ее границу можно представить как
объединение графиков двух непрерывных функций ф(х) и
\|/(х), ф(х) < \|/(х), а < X < Ь, и, быть может, отрезков прямых
x = aux = b,Si также как объединение двух графиков
непрерывных функций а(у) и Р(г/), а(г/) < Р(г/), с < г/ < d и, быть
может, отрезков прямых у = с j^y = d.
В этом случае, применяя правило сведения двойного
интеграла к повторному, теорему Ньютона—Лейбница (п. 25.3)
и формулу D7.58), имеем
^^^dxdy=U I ^(ii/ dx = I Р X, \|/(х) - Р х, ф(х) dx =
ъ . л ^
= |Рх, \|/(х) dx - |Р[х, ф(х)]йх = ^P{x,y)dx- ^P{x,y)dx =
DC АВ
= - \P(x,y)dx- \P(x,y)dx. D7.62)
CD AB
Для кривых AB и CD ничего, кроме их непрерывности,
не предполагалось, поэтому естественно, что здесь все
криволинейные интегралы второго рода понимаются в смысле
определения 2* (см. п. 47.7).
Замечая, что для отрезков ВС и DA (см. D7.59))
\Pix,y)dx= \Pix,y)dx = 0, D7.63)
' Дж. Грин A793—1841) — английский математик.
^21
и сложив равенства D7.62) и D7.63), имеем
\\^dxdy = - \Pdx- \Pdx- \Pdx- \Pdx = -\Pdx. D7.64)
^ АВ ВС CD DA ^^
При этом получилась ориентация граничного контура Г, при
которой следуют последовательно одна за другой точки А, Б, С, D.
Эта ориентация является положительной (см. определение 6) и
обозначается через Г+.
Совергаенно аналогично, исходя из того, что область G
элементарна, выводится формула
G ^^ Г+
Вычитая из левой и правой частей этой формулы
соответственно левую и правую части формулы D7.64), получаем
формулу Грина D7.60).
Рассмотрим обпа;ий случай. Пусть область G разбита на
элементарные области G., / = 1, 2, ... , й, и Г. — ограничиваюпа;ие
их контуры. В силу доказанного, для каждого / = 1, 2, ... , й
Сложив эти равенства, получим
В силу аддитивности двойного интеграла по множествам (см.
п. 44.6), имеем
В сумме, стояпа;ей в правой части равенства D7.65),
криволинейные интегралы берутся дважды по всем внутренним
частям границ Г., областей G-, т. е. таким дугам кривых Г.,
которые являются частью границ двух областей G., / = 1, 2, ... , й,
и, следовательно, не входят в границу области G; при этом
ориентации этих дуг кривых Г. противоположны (рис. 76).
В силу изменения знака криволинейного интеграла второго
рода при изменении ориентации кривой, сумма двух
криволинейных интегралов по указанным частям кривых Г. равна
нулю. Поэтому в правой сумме формулы D7.65) останутся
522
Рис. 76
Рис. 77
только интегралы по положительно ориентированным частям
границы Г области G, даюгцие в сумме ^Pdx + Qdy. Таким
образом, г+
£ I Pdx + Qdy = \Pdx + Qdy.
J = 1 Г+ г+
D7.67)
Из D7.65), D7.66) и D7.67) следует формула D7.60) в обгцем
случае. П
Пусть G — ограниченная область на плоскости i?^ и пусть
ее граница состоит из конечного числа простых контуров,
которые будем называть граничными контурами. Если
граничный контур является одновременно и границей
неограниченной области, лежагцей в R^\G, то будем называть его
внешним, а если он является одновременно и границей
ограниченной области, лежагцей в R^\G, то внутренним. Так, на
рис. 77 контур Eg внеганий, а контуры Г. ^ и Г. 2 внутренние.
Если граница области G состоит из внеганего контура Г^ и
внутренних контуров Г. ^, Г. 2, ... , Г.^ и если область G может
быть разбита на конечное число элементарных областей, то
справедлива формула
dQ _дР^
\\(^-^'dxdy= \Pdx + Qdy+ f^ \Pdx + Qdy, D7.68)
в которой криволинейные интегралы берутся по отрицательно
ориентированным внутренним контурам и по положительно
ориентированному внеганему контуру.
Функции Р и Q, как и выгае, предполагаются
непрерывными вместе со своими производными — и -^ в замкнутой
области G.
Доказывается эта формула так же, как и D7.60), если
только заметить, что в сумме, стоягцей в правой части равен-
523
ства D7.65), останутся криволинейные интегралы по
положительно ориентированным частям внеп1него контура и по
отрицательно ориентированным частям внутренних контуров
(рис. 76).
Отметим епа;е, что в формуле D7.68) все контуры (как
внеп1ние, так и внутренние) ориентированы таким образом,
что при их обходе область интегрирования остается слева.
Определение 8. Пусть граница dG ограниченной плоской
области G состоит из конечного числа простых
кусочно-гладких контуров. Совокупность этих контуров,
ориентированных так, что при обходе по каждому из них область G
остается слева (справа), называется положительной
{отрицательной) ориентацией границы G и обозначается 3G+
{соответственно — 3G").
Формулу Грина можно распространить и на другой, чем
указанный в теореме 1, класс областей. Для этого заметим,
что, в силу этой теоремы, формула Грина справедлива для
треугольника, а значит, и для любого многоугольника.
Поэтому предельным переходом, аппроксимируя границу
области конечнозвенными ломаными, можно получить формулу
Грина для любой области (и даже просто открытого
множества), граница которой состоит из конечного числа кусочно-
гладких кривых. Мы не будем останавливаться на
доказательстве этого факта, а ограничимся лигаь его
формулировкой. При этом, используя определение 8, запигаем формулу
D7.68) в более компактном виде.
ТЕОРЕМА 5'. Пусть граница плоской ограниченной области
G состоит из конечного числа кусочно-гладких кривых. Тогда
если функции Р, Q, ^— и ^— непрерывны на замыкании G,
ду ох
области G, то
^ V ох оу ) ^^^
где 3G+ — положительно ориентированная граница области G.
Формула Грина является для кратных интегралов
аналогом формулы Ньютона—Лейбница для однократных
интегралов: и в той и в другой формуле интегралы от производных
по области интегрирования выражаются через значения
функции на границе указанной области (в случае формулы
Грина эти значения егце интегрируются).
'524
47.9. Вычисление площадей
с помощью криволинейных интегралов
Положив в формуле Грина Q = х, Р = О, получим \\dx dy =
G
= ^ xdy и, следовательно,
[iG=\xdy. D7.69)
г+
Аналогично, положив Р = -у, Q = О, получим
[iG = -\ydx. D7.70)
г+
Складывая формулы D7.69) и D7.70), имеем
[iG = l \xdy-ydx. D7.71)
Примеры. 1. Найдем с помогцью формулы D7.71) пло-
гцадь aS, ограниченную эллипсом ^ + ^ = 1. Используем его
параметрическое представление: х = а cos t, у = b sin t.
Применив формулу D7.71), получим искомую плогцадь:
1 -,27с
aS = - ^ xdy - ydx = -ab^ (cosH + sinH) dt = nab,
Г+ 0
Сравнивая этот метод вычисления плогцади,
ограниченной эллипсом, с приведенным раныае (см. пример 4 в
п. 28.1), легко убедиться, насколько здесь меныае объем
вычислений.
2. Найдем плогцадь, ограниченную астроидой (см. в т. 1
рис. 92) X = а cos^ t, у = b sin^ t, О < t < 2п, Замечая, что здесь
возрастание параметра t соответствует положительной
ориентации контура, имеем
S = ^\ xdy - ydx = ^\ (cos^ t sш^' t + sin^ t cos^ t) dt =
Г+ 0
.2k ^^,2n 3^^2
Q 2 Z7L Q 2 '^^
^ I sm^2t dt = ^\il- cos 4t)dt
8 i 16 ,
0 0
47.10. Геометрический смысл
знака якобиана отображения плоской области
Пусть F — взаимно-однозначное непрерывно дифференцируемое
отображение плоской области G ^ й^^ в плоскость R^y с
якобианом, всюду в G не равным нулю. Тогда, в силу принципа сохране-
^25
ния области, множество G* = F(G) также является областью (см.
следствие 2 теоремы 7 в п. 41.7), а якобиан, в силу его
непрерывности, сохраняет знак на G (см. следствие 2 теоремы 8 в п. 36.9),
т. е. либо всюду на G положителен, либо всюду отрицателен.
Пусть в координатной записи отображение F задается
формулами
x = x(u,v), у = у(и, v). D7.72)
ЛЕММА 2. Если Г — кусочно-гладкая кривая, лежащая в G,
то ее образ Г* = Г(Г) при отображении F также является
кусочно-гладкой кривой.
До ко 3 а тел ь ст в о. Пусть сначала Г— гладкая кривая,
т. е. непрерывно дифференцируемая кривая без особых точек
(см. определения 15 и 16 в п. 16.4), и пусть и = u(t), v = v(t),
а<: t <:b, — некоторое ее представление. Тогда на отрезке [а, Ь]
функции u(t) и v(t) непрерывно дифференцируемы и
Представлением кривой Г"^ = ^(Г) является пара функций
X = x(u(t), v(t)); у = y(u(t), v(t)); а < t < b, которые, в силу
свойств композиции непрерывно дифференцируемых
функций (см. п. 36.3 и 37.3), также непрерывно
дифференцируемы. Покажем, что кривая Г"^ также не имеет особых точек.
В самом деле, так как
djc ^ дх^ du , дх^ dv^ dy _ ду du , ду dv
dt ди dt dv dt^ dt du dt dv dt^
TO, рассматривая эти равенства как систему линейных
уравнений относительно -^ и -^, видим, что если в некоторой точке
dt dt
te [а, b] выполнялись бы равенства -f-^ -г- ^ ^у то, в силу необ-
CV L (J/ L
рагцения в нуль якобиана
Э(х, у)
д{и, v)
указанная система имела бы единственное регаение, которым
является нулевое регаение, т. е. в той же точке t были бы
справедливыми равенства -^ = -^ = О и тем самым соответствую-
CV L (J/ L
гцая точка кривой Г была бы особой, что, по предположению,
не имеет места.
Итак, если кривая Г — гладкая, то кривая Г"^ = ^(Г)
также гладкая. Отсюда сразу следует, что образ кусочно-гладкой
~526
Эх
ди
Ьу
ди
дх
dv
^У
dv
кривой при рассматриваемом отображении также является
кусочно-гладкой кривой, ибо кусочно-гладкая кривая (см.
определение 16 в п. 16.4) представляет собой объединение
конечного числа гладких кривых. П
Пусть теперь D ^ G, D — ограниченная область и ее
граница dD является простым кусочно-гладким контуром Г
(такие границы называются кусочно-гладкими). Пусть далее D* =
= F(D), Тогда, в силу принципа сохранения области,
множество D* также область и, кроме того, ее граница dD* есть
образ границы dD области D (см. D6.40) в п. 46.2), т. е. dD* =
= F(dD), Поэтому граница dD* также является простым (в силу
взаимной однозначности отображения F) кусочно-гладким
(согласно лемме 1 этого пункта) контуром Г"^. Следовательно, по
контурам Г = dD и Г"^ = dD* можно вычислять криволинейные
интегралы. Пусть области D л D* таковы, что к ним
применима формула Грина, например, они удовлетворяют условиям,
налагаемым на область в теореме 1 п. 47.8. (На самом деле,
как уже отмечалось, при сделанных предположениях формула
Грина всегда применима, однако это не было доказано.)
Обозначим через Г+, как обычно, положительно
ориентированный контур Г (см. п. 47.8). Пусть и = u(t), v = v(t),
а <: t <: b, — представление контура Г+ и, следовательно,
X = x[u(t), v(t)], у = y(u(t), v(t)); a<t<b, D7.73)
некоторое представление контура Г"^.
Будем предполагать егце, что сугцествуют смегаанные
производные -, ^ и -, ^ и что они непрерывны, следовательно, и
avau auav
равны друг другу во всех точках области G.
Согласно формуле D7.69),
[iD* = E\xdy, D7.74)
г*
где 8 = +1, если ориентация контура Г"^ положительна, и 8 = -1
в противоположном случае. Иначе говоря, 8 = +1
(соответственно 8 = -1), если положительному обходу данного контура Г
соответствует при отображении D7.72) положительный же
(отрицательный) обход контура Г"^ = ^(Г).
Преобразовав интеграл D7.74) по формуле D7.8) и
использовав представление D7.73) контура Г"^, имеем
^D* = 8 f Xy^dt = 8 f хГ^ ^ + ^ ^ ^dt =
{xp-du + x^dv. D7.75)
i du dv
~527
8
г
к получивп1емуся интегралу применим формулу Грина (см.
теорему 1 в п. 47.8). Положив Р = х^. О = х^^ и заметив, что в
ди dv
ЭТОМ случае
dQ ^дхду_^^ д^у дР_^дхду__^ ^ д^у
ди dudv dudv^ dv dv du dvdu
[здесь используется потребованное Bbinie супа;ествование вто-
рых частных производных ^ и ^ , получим
дО^ _ дР^ ^дх_ду^ _дх_ду_ ^ Э(х, у)
ди dv dudv dvdu d(u, vY
откуда
I^D" ,=,, 8 f Pdu + Qdv = E\\(^- ^^dudv = 8 W^i^dudv.
^ D7.75) ^^ ^ Jj^[du dv J ^j^d{u,v)
Левая часть этого равенства болыае нуля, значит, правая
часть также положительна, и так как якобиан отображения
D7.72) не меняет знака, то это возможно лигаь в том случае,
когда £-1^^-lM1 > о, т. е. когда число 8 имеет тот же знак, что и
д{и, v)
Э(х, у)
. Тем самым
якобиан J)^' ^1, а в этом случае 8_i^j_^
d{u, v) d{u, v) \д{и, v)\
знак 8 не зависит от выбора контура Г, а определяется знаком
якобиана, который один и тот же во всех точках области G.
Таким образом, доказана следуюгцая теорема.
ТЕОРЕМА 6. Если выполнены сделанные выше
предположения, то справедлива формула
^D^ = £rr^l^dz/di;. D7.76)
J^J d{u, V)
Следовательно у если .,, ' ^\ > О на D, то 8 = +1, иначе гово-
д(и, v)
ря, если якобиан отображения F положителен, то
положительному обходу всякого контура Г ^ G, являющегося
границей ограниченной области D ^ G, при отображении F
соответствует положительный обход контура Г"" = Р(Г).
Если же якобиан J"^' ^^ <0 наВ, то 8 = -1, т, е, положитель-
д{и, v)
ному обходу всякого контура Г указанного типа
соответствует при отображении F отрицательный обход контура
Г = Е(Г).
Таким образом, геометрический смысл знака якобиана
состоит в том, что в случае положительного якобиана
ориентация контура при отображении сохраняется, а при
отрицательном — меняется,
^28
47.11. Условия независимости
криволинейного интеграла от пути интегрирования
Все кривые (контуры), рассматриваемые в этом пункте, будут
всегда предполагаться кусочно-гладкими; для краткости это
каждый раз специально не оговаривается. Отметим егце, что
во всякой области G любые две ее точки всегда можно
соединить кусочно-гладкой кривой, например ломаной (см. лемму
1 в п.36.8), лежагцей целиком в G.
Пусть задана плоская область G и на ней определены
непрерывные функции Р = Р(х, г/) и Q = Qix, у). Рассмотрим
вопрос о том, при выполнении каких условий
криволинейный интеграл \ Pdx + Qdy при произвольно фиксированных
АВ
точках AeG и ВеО не зависит от выбора кривой АВ, их со-
единяюгцей и лежагцей в G.
ЛЕММА 3. Условие независимости рассматриваемого
криволинейного интеграла от указанного пути интегрирования
равносильно равенству нулю интеграла по любому
замкнутому контуру, лежащему в области G,
Доказательство 1. Действительно, пусть для любого
замкнутого контура Г ^ G имеет место равенство | Pdx + Qdy = О и
г
даны две кривые (АВ)^ и (АБJ, соединяюгцие в G точки А и В
(рис. 78). Обозначим через (ВАJ кривую, получаюгцуюся из
(АБJ заменой на ней ориентации на противоположную.
Объединение (АВ)^ и (БАJ кривых (АВ)^ и (БАJ является
замкнутым контуром, поэтому
I Pdx + Qdy = О, D7.77)
(AB)iU(EAJ
НО
I Pdx + Qdy = J
(AB)iUEAJ
(AB\
(J
= I Pdx + Qdy + I Pdx + Qdy =
= \ Pdx + Qdy- \ Pdx + Qdy. D7.78) ^^ (AB)
(^)i (^J Рис. 78
^29
Из D7.77) и D7.78) следует, что
I Pdx + Qdy = I Pdx + Qdy,
Т. е. криволинейный интеграл | Pdx + Qdy не зависит от пути
АВ
интегрирования АВ ^ G при фиксированных А^ G и Бе G.
2. Обратно: пусть интеграл \Р dx + Q dy не зависит от пути
интегрирования в указанном смысле и задан замкнутый
контур Г, лежагций в G. Выберем на нем две точки Ал В ^ А;
тогда Г = АБ U БА и
\Pdx + Qdy= \ + \ = \ - I =0,
г АВ ВА АВ {АВ\
где {АВ)^ обозначает кривую, получаюпа;уюся из кривой В А
заменой на ней ориентации на противоположную. П
Сформулируем критерий независимости интеграла от
пути интегрирования.
ТЕОРЕМА 7. Пусть функции Р{х, у) и Q{x, у) непрерывны в
плоской области G, Для того чтобы криволинейный
интеграл IPdx + Qdy при фиксированных точках АеG и BeG не
АВ
зависел от пути интегрирования АВ ^ G, необходимо и
достаточно, чтобы выражение Pdx + Qdy являлось полным
дифференциалом некоторой функции и = и(х, у),
определенной в области G:
du = Pdx + Qdy D7.79)
это равносильно тому, что ^ = Р, г^ = Q, (х, y)eG .
ох ду J
При выполнении этого условия для любых двух точек
А = (Xq, y^eG и В = (х-^, yi)eG и любой кривой АВ,
соединяющей эти точки в G : АВ ^ G, имеет место тождество
I Pdx + Qdy = и(х^, у^) - u(Xq, у^). D7.80)
АВ
Доказательство необходимости условия D7.79).
Допустим, что рассматриваемый интеграл не зависит от пути
интегрирования, лежапа;его в области G, а только от его
начальной и конечной точек. Пусть М^ = (Xq, yQ)eG л. М = (х, y)eG и
MqM — некоторая кусочно-гладкая кривая, соединяюгцая в G
1зд
точки Mq и М (такая кривая, даже ломаная, всегда суш;ест-
вует, см. лемму 1 в п. 36.8). Положим
def
и(М) = и(х, у) = \ Pdx + Qdy
Функция и(х, у) однозначна, так как значение и(М) = и(х, у)
не зависит от выбора кривой, соединяюш;ей в G точки М^ и М,
Покажем, что
^-^^^ = Р(х, у) и ^^^^ = Q(x, у).
Зафиксируем точку М = (х, у), sl точку М^ = (х -\- h, y)eG,
Л ^ О, выберем так, чтобы отрезок ММ^^, соединяюш;ий М и
М^ (который, очевидно, параллелен оси Ох и имеет длину |Л|),
содержался в G (рис. 79). Для всех достаточно малых чисел h
это всегда имеет место (почему?). Тогда
и(х -\- h, у) - и(х, у)= I Pdx + Qdy - J Pdx + Qdy =
= I Pdx + Qdy,
Вдоль отрезка MMj^ координата у постоянна, поэтому
I Qdy = О и, следовательно, и{х -\- h, у) - и(х, у) = | Pdx =
= I P(t, y)dt. Применив интегральную теорему о среднем,
X
получим
и(х -\- h, у) - и(х, у) = Р(х + dh,y) h, О < 9 < 1,
откуда
и{х + h, у) - и{х, у)
h
P(x + Qh,y).
Правая часть этого равенства, в силу У1^
непрерывности функции Р(х,у), имеет
предел при Л ^ О, следовательно, и
левая часть при h ^ О имеет предел.
Перейдя к пределу в D7.81), будем иметь
^fe^ = Р(х, у).
Совергаенно аналогично
доказывается и равенство ^^^' ^^ = Q(x, у).
оу
D7.81)
Рис. 79
531
Итак, супа;ествование функции и(х, у), для которой имеет
место cooTHonienne D7.79), доказано.
Пусть теперь AgG, BeG, АВ — некоторая кривая, соединяю-
па;ая в G точки А и Б, и пусть х = x(t), у = y(t), а < t < b — ее
представление и, следовательно, А =(х(а), у(а)), В = (х(Ь), уф)).
Тогда
\Pdx + Qdy = ] [P{x{t), yit))x\t) + Qixit), yit))y\t)yt =
AB
= u(x(b), y(b)) - u(x(a), y(a)) = u(B) - u(A),
T. e. формула D7.80) также доказана.
Доказательство достаточности условия D7.79) для
независимости криволинейного интеграла от пути
интегрирования непосредственно следует из формулы D7.80).
Действительно, начальная точка любого замкнутого контура Г совпадает с
конечной, а поэтому, в силу D7.80),
I Pdx + Qdy = и(А) - и(А) = 0.
г
Согласно лемме 3, это и означает независимость соответст-
вуюпа;его криволинейного интеграла от пути интегрирования. П
Теорема, аналогичная теореме 4, имеет место и в
пространственном случае для интегралов | Pdx + Qdy + Rdz, Ее доказа-
г
тельство проводится по той же схеме, что и в плоском случае.
Заметим, что, хотя доказанная теорема и дает
необходимые и достаточные условия независимости криволинейного
интеграла от пути интегрирования, эти условия трудно
проверяемы.
Если сузить класс рассматриваемых областей, то можно
получить сугцественно более простой и эффективный
критерий. Введем следуюгцее определение.
Определение 9. Плоская область G называется односвязной,
если, каков бы ни бы простой контур Г ^ G, ограниченная
область D, границей которой является Г, содержится в G.
Образно говоря, односвязность области означает, что
область не имеет «дыр». Круг является примером односвязной
области, круговое кольцо — неодносвязной (рис. 80).
~532
Прежде чем формулировать
другой критерий независимости
криволинейного интеграла от пути
интегрирования, докажем лемму, которая
понадобится при доказательстве
этого критерия. ^^'
ЛЕММА 4. Пусть функции Р(х, у) и Q(x, у) непрерывны в
области G,r — гладкая кривая, лежащая в G, х = x(t), у = y(t),
а< t < b, — ее представление, т = {^J-Zq^ —разбиение
отрезка [а, Ь], Л^— ломаная с вершинами в точках (х(^.), г/(^.)),
/ = О, 1, ... , \ ( см. п. 16.5). Тогда
lim fPdx + Qdy = \ Pdx + Qdy. D7.82)
\A^^i^ г
Заметим, что, в силу равномерной непрерывности на
отрезке [а, Ь] функций x{t) и y{t), длины звеньев ломаной Л^,
т. е. длины отрезков с вергаинами в точках (x(f. _ ^), y{t^_ ^)) и
(x(f.), yit-)), при |т| -^ О также стремятся к нулю.
Доказательство. Кривая Г является компактом; так как
этот компакт не пересекается с замкнутым множеством
R^y\G, то расстояние между ними болыае нуля (см. лемму 7
п. 35.2). Пусть Г| — какое-либо число такое, что р(Г, R^ \G) >
> Г| > 0. Обозначим через Г совокупность всех точек
плоскости, находягцихся от Г на расстоянии, не болыаем чем Г|.
Множество Г ограничено, замкнуто (см. в п. 35.3 лемму 11) и Г^ G.
В силу равномерной непрерывности функций x(t) и y(t) на
отрезке [а, Ь], сугцествует такое число 8 > О, что для любых
двух точек fe[a, b] и f'e[a, Ь], удовлетворяюгцих условию
\f — f'\ < 8, выполняется неравенство
р(М', М") = J[x(r) - х(Г)]^ + [у(П - у(Г)]^ < л,
где М' = (x(f), yif)), М'' = (х@? ^(О)- Все точки отрезка с
концами в точках М' и М'\ очевидно, также находятся от
точки М' на расстоянии, не больп1ем чем Г|, и поэтому лежат в
множестве Г и, следовательно, в G. Это означает, что если
мелкость |т| разбиения т отрезка [а, Ь] такова, что |т| < 8, то все
точки ломаной Л^ лежат в G и для таких разбиений т имеет
смысл интеграл ^ Pdx + Qdy,
533
Рассмотрим интегралы (Pdx и {Pdx. Положим
г л,
Xi = x(f;), г/j = y(t^), Р^ = P(X;, г/;), Ах^ = х^-х^_^, i = 1, 2, ... , i^,
i = 1
Как известно (см. и. 47.2, свойство 4^),
lim a={Pdx. D7.83)
Пусть далее М. = (х-, у-) — верп1ины ломаной Л^; тогда
\Pdx= Y, I Pdx. D7.84)
с другой стороны, заметим, что (используя обозначения из
п. 47.2)
^ dx = I cos а ds = \М. _ ^М.\ cos а = Ах-,
поэтому
о, = J Р,Ах, = ^ I P,dx. D7.85)
Обозначим через L^ длину ломаной Л^, через S — длину
кривой Г, а через соF; Р) — модуль непрерывности функции
Р(х, у) на компакте Г^ и положим 6^ = max \М. _ лМ\. В си-
^ ^ i= 1,2, ... , j ^ ^ ^
лу равномерной непрерывности функций x{t) и г/(^) на отрезке
[а, Ь], будем иметь lim 6^ = 0. Заметив, что, в силу определе-
|т| ^0
ПИЯ длины кривой, L^ < aS, из D7.84) и D7.85) получим
\\Pdx - aJ < ^ I I \Р- Pi\dx\ <
< @(|т|; Р) £ |AxJ < @(|х|; P)L^ < со(|т|; P)S.
i = 1
Отсюда, в силу равномерной непрерывности функции Р(х, у)
на множестве Г„, имеем lim (\ Pdx - оЛ= О и, значит, соглас-
1 |x|^0';J
НО D7.83),
lim \Pdx=\Pdx. D7.86)
Аналогично доказывается и равенство
lim \Qdy = \Qdy. D7.87)
N^OA, г
534
Из D7.86) и D7.87) непосредственно и следует
утверждение леммы, т. е. формула D7.82). П
Замечание. Утверждение, аналогичное лемме,
справедливо и для криволинейных интегралов в пространстве,
причем доказательство пространственного случая проводится
по той же схеме, что и для плоского.
ТЕОРЕМА 8. Пусть функции Р(х, у) и Q(x, у) непрерывны
вместе со своими частными производными г:— и ^ в
плоду ах
ской области G, Для того чтобы криволинейный интеграл
I Pdx + Qdy при произвольно фиксированных точках А& G и
АВ
Be G не зависел от пути интегрирования АВ ^ G,
необходимо, а если область G односвязна, то и достаточно, чтобы
во всех точках области G выполнялось равенство г:— = ^,
ду дх
Доказательство необходимости. Пусть
рассматриваемый интеграл не зависит от пути интегрирования, лежапа;е-
го в области G, а зависит только от его начальной и конечной
точек. Тогда супа;ествует функция и = и(х, у) такая, что du =
= Pdx + Qdy, т. е. такая, что ^ = Р, ^ = Q. Так как ^^ - ^^"
Эх ' Эг/ * ду Эг/Эх'
dQ д^и дР dQ
^ = т—г:— И, ПО условиям теоремы, производные т;— и ^, sl сле-
дх дхду ду дх
довательно, и смеп1анные производные .. ^ и .. ^ непрерыв-
дудх дхду
ны, то (см. п. 38.1) они равны, т. е. ^^ = тг^.
ду дх
Доказательство достаточности. Пусть сначала Г —
замкнутая ломаная без самопересечений, Г ^ G, и D —
ограниченная ею конечная часть плоскости, лежагцая в силу
односвязности области G в этой области: D^ G. Очевидно, функции PviQ
определены в замыкании D области Z), поскольку D = D U Г ^ G.
Многоугольник D можно разбить на треугольники, а каждый
треугольник является областью, элементарной относительно
обеих координатных осей. Поэтому для области D, согласно
теореме 1 п. 47.8, имеет место формула Грина, а так как г:— = г^,то
ду дх
\Pdx + Qdy = \\[^^-fyxdy = Q
~535
Отсюда следует, что и для любой замкнутой ломаной Г (быть
может, самопересекаюш;ейся), лежаш;ей в области G, также
имеет место равенство
\Pdx + Qdy = 0, D7.88)
г+
поскольку любая ломаная распадается на конечное число
замкнутых ломаных без самопересечений и отрезков, проходимых
и в одном, и в другом направлениях. И по первым, и по вторым
частям ломаной Г рассматриваемый интеграл равен нулю.
Наконец, если Г = {r(t); а < t < b} — произвольный
простой кусочно-гладкий контур Г ^ G, то при достаточно
мелких разбиениях т = {tiVi = Q^ отрезка [а, Ь] ломаные Л^ с вер-
П1инами в точках r(t-), / = О, 1, ... , /^, лежат в G. Поэтому, по
доказанному, ^ Pdx + Qdy = 0. Отсюда предельным перехо-
дом при |т| -^ о, согласно формуле D7.82), следует, что и
\Pdx + Qdy = 0.n
г
Иногда условие г:— = ^ называют критерием полного диф-
ау ах
ференциала в односвязной области, поскольку это условие
необходимо и достаточно для того, чтобы выражение Pdx + Qdy
в односвязной области G являлось дифференциалом некоторой
функции и{х, г/), (х, y)eG,
В заключение этого пункта отметим, что требование
односвязности рассматриваемой области при доказательстве
достаточности условий теоремы 7 для независимости
криволинейного интеграла от пути интегрирования является супа;ест-
венным и его нельзя отбросить. Подтвердим это примером.
Пример. Р{х,у) = -^У-- Q(x,y) = ^^
х^ + у^ х^ + у^
Легко проверить, что
Ш = ^Р D7.89)
ах ау
для всех точек плоскости, исключая начало координат (О, 0).
При X ^ О это следует, например, из того, что
dUvctgy' = -^±^, x2 + j/2>0; D7.90)
равенство D7.89) означает равенство смепханных вторых
производных функции arctg-.
X
~536
Таким образом, в этом случае за область G можно взять
всю плоскость с «выколотым» началом координат: G =
= R^\{@, 0)}. Область G, очевидно, не односвязна. В качестве
замкнутого контура возьмем единичную окружность Fq =
= {х = COS t, у = sin t, О < t < 2п}; тогда
I Pdx + Qdy= \ "^^f + ^/^ = ]dt = 271.
Следовательно, в этом случае условия D7.89) выполнены
и сугцествует замкнутый контур Fq, по которому интеграл не
равен нулю. Нетрудно убедиться, что вообгце по любой
окружности F радиуса г с центром в начале координат
\Pdx + Qdy = 27Z.
D7.91)
Далее, каков бы ни был простой кусочно-гладкий контур
F, являюпа;ийся границей ограниченной области D, содержа-
па;ей начало координат (в этом случае говорят, что контур F
содержит внутри себя начало координат), для него также
\ Pdx + Qdy = 2п. D7.92)
г
Для доказательства этого возьмем окружность F^ такого
радиуса г, что F^ ^ D; тогда F и F^ne пересекаются. Соединив
контуры F и F^ отрезками Л^ и Лз, как показано на рис. 81,
получим два замкнутых контура F^ и F2, не содержапа;их
внутри себя начала координат и состояпа;их из дуг F^ и F^',
окружности F^, частей F' и F'' контура F и отрезков Л^ и Лз.
В силу условия D7.89), для
этих контуров справедливы
равенства
I Pdx + Qdy = О, I Pdx + Qdy = 0.
Сложив эти равенства и опустив
для краткости подынтегральные
выражения, получим (рис. 81)
^=1+1=1+1+1+1+
г^ Гз г'+ л+ г; л+
+! +1+ !+!=
г"+ Лз г; л^
= ! + !-!- 1 = 1-!-
Г'+
Г"+
Г"+
Рис. 81
537
Рис. 82
Отсюда, в силу D7.91), и следует D7.92).
Более того, это равенство выполняется и в
случае, если контур Г, обходя «один раз»
вокруг начала координат, образует
конечное число «петель», не охватываюгцих
начало координат (рис. 82), поскольку
интеграл по этим петлям равен нулю.
Если Mq— фиксированная точка
рассматриваемой области G, MqgG, MeG,
MqM — какая-либо кривая, соединяюгцая
в G точки Mq и М, то и(М) = | Pdx + Qdy
является уже многозначной функцией,
значения которой определяются выбором различных путей, со-
единяюгцих точки Mq и М. Если Fq — какая-либо
фиксированная кривая, соединяюгцая Mq и М, то все значения функции и в
точке М задаются формулой
и(М) = I Pdx + Qdy + 2пп, п = 0, ±1, ±2, ...,
Го
И каждый обход вокруг начала координат изменяет значение
функции и(М) на величину ±2п в зависимости от направления
обхода.
В данном случае в этом легко убедиться и
непосредственно: из формулы D7.90) следует, что
lPdx + Qdy=\--M^§±^ = (Arctgy] ,
J J х2 + г/2 1, xJq
где fArctg ^1 — некоторое фиксированное значение Arctg ^;
поэтому и(М) = Arctg ^ — многозначная функция.
X
Вдумчивый читатель заметил, что многие рассуждения,
проведенные в этом примере, не зависят от конкретного вида
функции Р и Q и являются справедливыми всегда, когда мы
имеем дело с одной изолированной «особой точкой», т. е.
точкой, в которой наругаается условие D7.89). Конечно, при
однократном «обходе» такой особой точки будет получаться
не 271, а, вообгце говоря, какое-то другое число (может быть,
нуль).
Результат, аналогичный теореме 5, имеет место и когда
Г — пространственная кривая (см. п. 52.6).
538
УПРАЖНЕНИЕ 3. Доказать формулу
G G Г
где G — плоская область, для которой справедлива формула Грина, Г —
ограничивающий ее контур, v — единичная внешняя нормаль к
контуру Г, а А — оператор Лапласа (см. п. 41.10).
§48
Несобственные кратные интегралы
48.1. Основные определения
Как и ранее для однократных интегралов, введем понятие
несобственного кратного интеграла, т. е. кратного интеграла от
функций, которые могут быть неограниченными и
определенными на неограниченных областях. Определение кратного
несобственного интеграла сформулируем в таком виде, что оно
будет охватывать оба указанных случая (ср. с п. 29.1).
Определение 1. Пусть G — открытое множество
(ограниченное или неограниченное) в п-мерном пространстве R^,
Последовательность открытых множеств Gj^, й = 1, 2, ... ,
будем называть последовательностью, монотонно
исчерпывающей открытое множество G, если:
l)Gy^^G, + i, й = 1,2, ...;
Здесь G, как всегда, обозначает замыкание (см. п. 35.2)
множества G.
Замечание. Мы уже встречались с понятием
последовательности открытых измеримых по Жордану множеств
монотонно исчерпываюгцих измеримое же (и, следовательно,
ограниченное) открытое в R^ множество (см. замечание 3 в п. 44.6).
Докажем, что для любого открытого множества G ^ R^ сугцест-
вует монотонно исчерпываюгцая его последовательность
измеримых по Жордану открытых множеств.
Если Qj^ = {х \ \х\ <k) — niap радиуса йеЛ/', а s^ = sjfi П Q^) —
совокупность всех кубов ранга к, содержагцихся в множестве
~539
G П Q^, то сугцествует такая подпоследовательность k^
последовательности натуральных чисел, что последовательность
открытых множеств G^ = (Su ) , m = 1, 2, ... , состоягцих из
^'^^ ^^т int
внутренних точек многогранников s^ , монотонно исчерпы-
т
вает множество G. Выполнение условия Ощ ^ G^ + ^ при
выборе подпоследовательности k^ можно осугцествить, выбрав
для каждого номера т такой номер й^ + i, что Gm = s^^ ^
^ (s^ ). = G + ^. Номер k ^ ^ сугцествует, так как рас-
т + 1 int
стояние p(s^ , 3G) границы 3G открытого множества G до
компакта s^ положительно, а диаметры кубов, входягцих в
т
многогранники s^, стремятся к нулю при й ^ оо. Условие G =
со со
= и G^ следует из того, что G = U s^(G).
Определение 2. Пусть на открытом множестве G задана
функция f {ограниченная или неограниченная),
интегрируемая по Риману на любом измеримом по Жордану открытом
множестве D таком, что D ^ G, Функция f называется
интегрируемой в несобственном смысле на открытом
множестве G, если для любой последовательности открытых
измеримых по Жордану множеств G^, й = 1, 2, ... , монотонно
исчерпывающей множество G, существует предел lim \fdGj^,
не зависящий от выбора указанной последовательности G^,
й = 1,2, ... .
Этот предел называется несобственным интегралом
от функции f по открытому множеству G и обозначается
через \fdG, или, более подробно,
JJ***J J/(^l? ^2' ••• ' Х^ЩХ-^йХ^ ••• аХ^.
G
Таким образом,
\fdG= limJfdG^. D8.1)
Если интеграл \fdG существует, то говорят также,
что он сходится, а в противном случае — что он
расходится.
Следует заметить, что в случае п = \ данное здесь
определение несобственного интеграла не эквивалентно определению
несобственного интеграла от функции одного переменного,
данного в § 29. Это связано не только с терминами, в которых
~54д
формируются определения (там несобственным интегралом
называлась определенного вида функция), а прежде всего с
тем, что в указанном параграфе мы в качестве множеств G^
брали лип1ь интервалы, т. е. одномерные открытые
измеримые множества весьма специального вида. Поэтому введенное
в настояпа;ем параграфе понятие несобственного интеграла
D8.1) будем применять только в случае я > 2, сохранив для
случая п = \ прежнее понятие несобственного интеграла.
Если открытое множество G измеримо по Жордану и
функция / интегрируема на G, то несобственный интеграл от
функции / совпадает с обычным интегралом Римана; это
следует из полной аддитивности интеграла Римана (см. п. 44.6).
Определение D8.1) позволяет перенести на несобственные
интегралы ряд свойств собственных интегралов:
аддитивность интеграла по множествам, линейность интеграла,
интегрирование неравенств, сведение кратного интеграла к
повторному, формулу замены переменного и др.
Например, если х = F(u) — непрерывно
дифференцируемое взаимно-однозначное отображение открытого множества
D ^ R^ на открытое множество G ^ R^ и якобиан J(u) этого
отображения нигде не обрагцается в нуль на D, то для любой
непрерывной на G функции / справедлива формула замены
переменного в интеграле:
lfix)dG = lfi(Fiu))\J(u)\dD.
Доказать это можно точно так же, как доказана теорема 2
в п. 46.2; следует только вместо полной аддитивности
интеграла использовать определение D8.1).
Используя аддитивность несобственного кратного
интеграла по множествам интегрирования, определение D8.1) можно
переписать в другом эквивалентном виде. Замечая, что для
измеримого открытого множества Gq ^ G справедливо равенство
lfdG-lfdGo = lfd(G\Go),
МОЖНО сказать, что интеграл \fdG сходится тогда и только
тогда, когда для любой последовательности измеримых
открытых множеств G^, й = 1, 2, ... , монотонно исчерпываюгцей
множество G, сугцествуют интегралы \fd(G\Gk) и
lim^\fd(G\Gk) = 0. D8.2)
УПРАЖНЕНИЕ 1. Доказать формулу D8.2); в частности, показать, что
интегралы \fdG и \fd(G\Go) одновременно сходятся или расходятся.
^1
48.2. Несобственные интегралы
от неотрицательных функций
ТЕОРЕМА 1. Пусть функция f неотрицательна на
открытом множестве G ^ R^. Тогда, какова бы ни была
последовательность {Gf) открытых измеримых по Жордану
множеств Gj^, монотонно исчерпывающих множество G, предел
limJfix)dG, D8.3)
конечный или равный +оо^ всегда существует и не зависит
от выбора указанной последовательности {G^}.
Если он конечен, то интеграл \f{x)dG суш;ествует и,
следовательно, предел D8.3) равен этому интегралу, если же
предел D8.3) бесконечен, то интеграл ]f{x)dG не сугцествует.
В последнем случае пигаут \f{x)dG = +оо. Это
оправдывается тем, что, в силу сформулированной теоремы, для любой
другой последовательности {D^} открытых измеримых
множеств D^, монотонно исчерпываюгцих множеств G, также
имеем lim \f(x)dGj^ = +оо.
Д о ко 3 отельств о. Пусть G^, й = 1, 2, ... ,—
последовательность измеримых открытых множеств, монотонно исчер-
пываюгцая открытое множество G. Тогда, согласно
определению такой последовательности, G^ ^ G^ + ^, а так как / > О, то
+1? ^ — 1? 2, ... , И, следовательно, всегда супа;ест-
вует конечный или бесконечный предел lim \fdG^ = 1^,
Пусть теперь D^, k = 1, 2, ... • какая- либо другая
последовательность измеримых множеств, монотонно исчерпываю-
па;ая открытое множество G. В силу доказанного выпхе, су-
па;ествует конечный или бесконечный предел lim IfdD,. = lo.
Покажем, что
h = l2- D8.4)
Для любого фиксированного элемента G^ первой
последовательности супа;ествует номер k^ = к^(к) такой, что
Gk^D^^. D8.5)
В самом деле, G^ — измеримое и, следовательно,
ограниченное множество, поэтому его замыкание G^ также
ограничено, т. е. является компактом. В силу этого, сугцествование
такого номера k^, что имеет место включение D^ =^ G^,
вытекает из леммы Гейне—Бореля (см. п. 35.3), так как
542
система множеств {D^} образует открытое покрытие компакта
G^ и, следовательно, из него можно выделить конечное
покрытие {D^, 1J? ••• ? Dj^ }. Ясно, что, в силу включений D^ ^
^ 1J ^ ... ^ D^ , выполняется включение D8.5).
Теперь заметим, что, в силу условия / > О, из включения
D8.5) вытекает, что fdGj^ < fdD^ . Но, очевидно, fdD^ < 1^,
поэтому при любом й = 1, 2, ... , IfdGf^ < /2- Перейдя в этом
неравенстве к пределу при й ^ оо^ получим /^ < /2-
Подобным же образом доказывается и неравенство /^ > /2- 1^
Пример. Рассмотрим интеграл I = \ \ е~^ ~ ^ dxdy. Поло-
жим G^ = {(х, г/) : х^ + г/^ < й^}, й = 1, 2, ... . Эта
последовательность является последовательностью открытых квадрируе-
мых множеств (в данном случае просто кругов), монотонно ис-
черпываюгцей всю плоскость й^.
Пусть /^ = [|^^ ^ dxdy. Перейдем к полярным
координатам: Gj^
2% k ^
k
О
71A - е-П.
Ik = \\ е"- rdrdi^ = I йф| е-"- rdr = -27Г^
G, О О
Отсюда, согласно определению D8.1),
1= lim А = 71. D8.6)
Формула D8.6) позволяет найти величину интеграла
I е~^ dx,
—00
называемого интегралом Пуассона^ и часто встречаюпа;егося в
приложениях. Действительно, обозначая через D^ квадрат
{(х, у): \х\ < й, |г/| < й}, й = 1, 2, ... , и, применив к интегралу по D^
2 2
от функции е~^ ~ У формулу сведения кратного интеграла к
повторному (см. п. 45.1), получим
/ = J J е~^^' ~ y^'dxdy = lim J J e~^^' ~ y^dxdy =
p2 k^OO f,
lim \ dx^ e~^ у dxdy = lim J J e~^ dx J е~У dy
-k -k -k -k -k
f\ 2 Л^ f^T 2 Л^
= lim J e~^ dx \ =\ ^ e~^ dx .
' C. Пуассон A781 —1840) — французский физик и математик.
~543
Поэтому из D8.6) сразу следует, что
+9° 2 Г
J е~^ dx = Jn.
—со
ТЕОРЕМА 2 (признаксравнения). Пусть на открытом
множестве G выполняются неравенства О < f(x) < g(x), xeG,
Тогда из сходимости интеграла \g{x)dG следует
сходимость интеграла \f{x)dG, а из расходимости интеграла
\f{x)dG следует расходимость интеграла \g{x)dG,
Эта теорема доказывается аналогично подобной теореме в
одномерном случае (см. п. 29.3).
В качестве примеров и эталонов для сравнения с другими
интегралами рассмотрим интегралы
\---\ dx,...dx,_^ ^^gg^
X? + . . . + X? < 1
(Vxf+...+x2)
Первый интеграл берется по внеп1ности единичного niapa;
второй — по самому niapy.
Для исследования этих интегралов удобно ввести
сферические координаты р, ф^, ... , ф^ _ ^ в я-мерном пространстве.
Они вводятся по формулам
Х^ = рС08ф^ _^ С08ф^_2... С08ф2 С08ф^,
^2 = рС08ф^ _^ С08ф^_2... С08ф2 8тф^,
Xg = рС08ф^ _^ С08ф^_2... С08фз 8тф2, D8.9)
X. = РС08 ф^ _ 1 ... С08 ф. 8in ф. _ 1,
Р8тф^_1,
где
0<р< + оо, 0<ф1<27Г, -|<ф.<|, i = 2,3,...,n-l.
С помопа;ью этих формул декартовым координатам х^, ... , х^
точки пространства сопоставляются сферические координаты
р, ф^, ... , ф^ _ ^ и обратно. При этом следует иметь в виду, что,
подобно полярным координатам на плоскости, здесь не су-
па;ествует полного взаимно-однозначного соответствия между
544
множествами п чисел (х^, ... , х^) и (р, ф^, ... , ф^ _ ^). Отметим,
что р = ^х1 + ... + х^.
Элементарными, но несколько громоздкими
вычислениями, которые не будем здесь приводить, можно показать, что
якобиан этого преобразования имеет вид
=- ^ = р^ "^ С08фр СОЗ^фо ... С08^"^ф„ 1.
Положим для краткости
Ф(ф2, ... , ф^ _ i) = С08ф2 СОЗ^фз ... COS^- 2ф^ _ ^
Легко убедиться, что Ф(ф2? ••• , Ф^ _ i) ^ О и что
2к к/2 к/2
О -к/2 -к/2
Это сразу следует из следствия свойства 9^ кратных
интегралов в п. 44.6.
Исследуем теперь сходимость интеграла D8.7). В
качестве последовательности открытых измеримых множеств G^,
й = 1, 2, ... , монотонно исчерпываюгцей внеганость
единичного niapa Q, возьмем последовательность множеств
G^= х = (р,ф1, ... ,ф^_1): l + i<p<ft ,й = 1,2, ... .
Перейдя к сферическим координатам, получим
I-J
k 2k k/2 k/2
= I I I ... I Р^"^"'^Ф(ф2---Фя-1)Ф^Ф1---^Фя-1 =
1 + 1/fe 0 -K/2 -K/2
k
= c I р^-1-«ф.
1 + \/k
Таким образом, вопрос о сходимости интеграла D8.7) свел-
+ 00
ся к сходимости интеграла | р^ ~ ^ ~ ^dp, который, как извест-
1
но (см. п. 33.3), сходится при я - 1 - а < - 1, т. е. при а > п,
и расходится при а < я. Итак, доказана следуюпа;ая лемма.
ЛЕММА 1. Интеграл D8.7) сходится, если а больше
размерности пространства, и расходится в противном случае.
Рассмотрим теперь интеграл D8.8). Положив
Gy^ = V^ = (Р' Ф1' ••• ' Фя -1)- Z < Р < 1 - Z I ^ = 3, 4, ... ,
545
получим
Р р dX-^, ... ydX^
1 - \/k 2% Tz/2 Tz/2
= I I I ... I Р^"^"'^Ф(ф2---Фя-1)Ф^Ф1---^Фя-1 =
1/fe 0 -%/2 -%/2
Таким образом, вопрос о сходимости интеграла D8.8) свел-
1
ся к сходимости интеграла | р^ ~ ^ ~ ^dp. Этот интеграл, как из-
0
вестно, сходится, если я-1-а>-1, т. е. если а < я, и
расходится в противном случае. Полученный результат
сформулируем снова в виде леммы.
ЛЕММА 2. Интеграл D8.8) сходится, если а меньше
размерности пространства, и расходится в противном случае.
Подобно одномерному случаю (см. п. 29.3), с помогцью
интегралов D8.7) и D8.8) можно сформулировать критерии
сходимости несобственных кратных интегралов, однако мы не
будем на этом подробно останавливаться.
48.3. Несобственные интегралы от функций, меняющих знак
Определение 3. Несобственный интеграл \fdG называется
абсолютно сходящимся, если сходится интеграл \\f\dG.
Для изучения абсолютной сходимости интеграла от
функции f(x) будут полезны функции
f (^) = \f(x), если fix) > О, у.д^) = \-f(x), если f{x) < О,
[о, если/(х)<0; " 1 О, если/(х)>0.
Легко видеть, что
и = \Л±1, f_ = \fbl, D8.10)
о </+(х) < |/(х)|, 0<f_{x)<\f{x)\, D8.11)
f{x) = f4x)-f_{x), \f{x)\ = U{x) + f_{x). D8.12)
Из формул D8.10) следует, что если функция f
интегрируема по Риману на некоторой измеримой по Жордану области,
то и функции /^ и /_ интегрируемы по Риману на этой облас-
546
ти; из первой формулы D8.12) следует обратное
утверждение. Поэтому из D8.10)—D8.12) следует, что интеграл \fdG
абсолютно сходится тогда и только тогда, когда
сходятся интегралы \f+dG и \f_dG.
Как и в случае несобственных интегралов от функции
одного переменного, из абсолютной сходимости кратного
интеграла следует его сходимость (при этом, конечно,
рассматриваются только такие функции, которые интегрируемы на
каждом открытом измеримом множестве, содержапа;емся
вместе со своим замыканием в открытом множестве, по
которому производится интегрирование). Это сразу получается на
основании формул D8.11), первой формулы D8.12) и из
теоремы 2 настояпа;его параграфа (см. п. 48.2). Однако для
кратных несобственных интегралов справедлива и обратная
теорема.
ТЕОРЕМА 3. Если кратный интеграл \fdG (п > 2)
сходится, то он и абсолютно сходится.
Эта неожиданная на первый взгляд теорема связана с
отличием определения несобственных интегралов от функции
одного из п переменных (п > 1), указанных в начале этого
параграфа"^.
Доказательство теоремы. Пусть интеграл \fdG
абсолютно расходится, т.е. для некоторой (значит, и для всякой, см.
теорему 1 в п. 48.2) последовательности открытых измеримых
по Жордану множеств G^^, й = 1, 2, ... , монотонно исчерпываю-
гцей открытое множество G, имеем lim ||/|rfG^ = +оо. Без
ограничения обгцности (переходя, если надо, к
подпоследовательности) можно предполагать, что
\\f\dG, + ^>3\\f\dG, + 2k, /г = 1, 2, .... D8.13)
* Отметим, однако, что можно было бы и в я-мерном случае получить
ту же связь между сходимостью и абсолютной сходимостью интеграла,
что и в одномерном случае, если соответствуюш;им образом ввести
определение несобственного я-кратного интеграла. Например, в случае
интегралов по всему пространству для этого достаточно в определении
интеграла в качестве элементов монотонно исчерпываюпдей
последовательности брать только я-мерные пгары с центром в начале координат.
Впрочем, если применить к одномерному интегралу определение
несобственного интеграла, данное в п. 48.1, и понимать одномерный интеграл
Римана в смысле § 44, то теорема 3 вместе с ее доказательством будет
справедливой и при п = 1.
547
Пусть А^ = G^ ^ i\^fe' тогда А^ — открытое измеримое
множество, и так как Gf^'^ G^^ ^ -^^, то (см. рис. 221) G ^ _,. ;^ = А^^ U
и G^H
\\f\dG,^^ = \\f\dA, + \\f\dG,.
Отсюда, в силу неравенства D8.13), ||/|<iA^ > 2\\f\dG^ + 2k.
Используя вторую формулу D8.12), получим
\f^dA^ + \f_dA^>2\\f\dG, + 2k.
Пусть для определенности \f^dAf^ > \f_dAf^; тогда
2JMA, > \UdA, + \f_dA^ > 2\\f\dG^ + 2k
И, следовательно,
\f^dA^>\\f\dG^ + k. D8.14)
Нагаей целью является получение неравенства подобного
типа не для функции /+, а для функции /. Для этого,
казалось бы, можно просто отбросить точки, в которых функция
/+ обрагцается в нуль; тогда на оставгаемся множестве мы
имели бы / = /+. Однако получивгаееся множество может, во-
обгце говоря, оказаться неизмеримым, а поэтому мы будем
действовать обходным путем.
Из неравенства D8.14) следует, что при любом достаточно
мелком разбиении т = {Е^}\^ ^^ множества А^ (см. п. 44.3) для
любой интегральной суммы Римана имеем
^±f^{%;)\iE^>\\1\dG^ + k, %,^Е„ i = l,2,... , V
i = 1
Выберем указанное разбиение т открытого измеримого
множества А^ таким, чтобы все элементы Е^ этого разбиения,
имеюпа;ие положительную меру, также были открытыми
измеримыми по Жордану множествами. Обозначим через Е^ те
множества положительной меры Е-ех, для которых /+(^) > О
во всех точках t,eE., Пусть т"" = {Ei''}. Выбрав для тех Е.^х'',
у которых [lE. > О, точки ^i&E. так, что /(^.) = О, получим
£Y4^,)^£*>J|/|dG, + ft, D8.15)
i
где (а также и в дальнейпхем) знак «П1трих» у суммы означает,
что суммирование распространяется только на те индексы /,
548
для которых Е. = Е^. Положим Б^ = U'^J
^k + i
(см. рис. 83). Очевидно, что Б^ — открытое
измеримое множество, лежаш;ее в
множестве А^, Si т* = {Е*} является его
разбиением. На множестве Б^ имеем /+ > О и,
следовательно, /+ = /. Из неравенства D8.15)
следует, что для нижней суммы Дарбу s*
функции / на множестве Б^ справедливо
неравенство s\ > If^^^k "^ ^- Отсюда при |т| -
имеем, что
lfdB,>\\f\dG, + k.
Заметим, что / > -|/| и, следовательно,
lfdG,>-l\f\dG,.
Сложив неравенства D8.16) и D8.17), получим
\fdB, + lfdG,>k.
Пусть Dj^ = Bj^U Gj^, k = 1, 2, ,,, , Очевидно, D^ — открытое
измеримое множество и
Рис. 83
О, очевидно,
D8.16)
D8.17)
D8.18)
G, ^ D, ^ G
fe + 1'
й = 1,2.
D8.19)
В силу того что множества Б^ и Gj^ не пересекаются (так как не
пересекаются множества А^ и G^ из D8.18), имеем \fdD^ > k,
откуда
liin i/dD, = +oo.
D8.20)
Из включения D8.19) следует, что множества!)^, й = 1, 2, ... ,
образуют последовательность измеримых открытых
множеств, монотонно исчерпываюпа;ую открытое множество G,
так как таковой являлась заданная последовательность G^,
й = 1, 2, ... , поэтому равенство D8.20) означает, что интеграл
\fdG расходится. П
Итак, для кратных интегралов сходимость несобственного
интеграла \fdG эквивалентна его абсолютной сходимости.
УПРАЖНЕНИЕ 2. Заменив в определении кратного несобственного
интеграла всюду открытые множества областями (в частности,
рассматривая только монотонно исчерпывающие данную область
последовательности, состоящие только из измеримых областей), показать, что и при
таком «более узком» определении кратного несобственного интеграла
сохраняется аналог теоремы 3.
549
§49
Некоторые геометрические и физические
приложения кратных интегралов
49.1. Вычисление площадей и объемов
Пусть Е — измеримое множество в R^. Как известно (см.
п. 44.6),
[iE = \dE. D9.1)
Таким образом, с помопа;ью я-кратного интеграла можно
вычислять меру измеримых множеств в я-мерном пространстве (пло-
па;адь — в двухмерном, объем — в трехмерном). Если я-крат-
ный интеграл D9.1) можно свести к повторному (см. § 45), то
вычисление меры измеримого множества Е я-мерного
пространства сведется к вычислению (п - 1)-кратного интеграла.
Пусть, например, D — открытое измеримое множество
в (п - 1)-мерном пространстве и R^~}^,, х ^ ^п ^ /(^i? •••
... , х^ _ ^) — неотрицательная функция, определенная и
непрерывная на замыкании D множества D, а
G = {х = (х-^, ... , х^); (х-^, ... , х^_ i)gD, О < х^ < f(x-^, ,,, , х^_-^)}
(таким образом, G является я-мерным аналогом
криволинейной плоской трапеции, рассмотренной нами в п. 28.1). Тогда
[iG = \dG = \dD " I ^ 'dx^ = \f{x^, ... , x^_^)dD,
0
T. e.
n - 1раз
D
Меру произвольных (не обязательно измеримых по Жор-
дану), в частности неограниченных, открытых множеств
пространства R^y я > 2, если ее понимать в смысле определения
п. 27.1 и 27.2, т. е. как нижнюю меру Жордана ц^, можно
вычислить с помопа;ью несобственных интегралов.
Действительно, пусть G — произвольное открытое множество в й^ и G^,
й = 1, 2, ... , — последовательность открытых измеримых
множеств, монотонно исчерпываюпа;их множество G (см. п. 48.1).
Тогда, как известно (см. п. 27.2), lim uG^, = u^G. Но, в силу
D9.1), [iGf^ = \dG^y поэтому ji^G = lim \dG^.
~550
По определению же кратного несобственного интеграла,
lim \dGy = \dG. Таким образом,
/г ^ оо «
ji^G = \dG,
где интеграл в правой части равенства понимается, вообпа;е
говоря (а именно: если G не является измеримой областью), как
несобственный.
Напомним, что для вычисления объемов тел часто
оказывается удобным метод сечений (см. формулу D5.38)).
49.2. Физические приложения кратных интегралов
С помопа;ью кратных интегралов можно вычислить различные
физические величины: массу и заряд тела, центр тяжести,
момент инерции, поток жидкости.
Найдем в качестве примера центр тяжести плоской
фигуры. Пусть в некоторой квадрируемой области G,
расположенной в первом координатном квадрате, т. е. в множестве точек
(х, у), в которых X > О, г/ > О, распределена некоторая
масса, вообпа;е говоря, с переменной поверхностной плотностью
р (х, у), т. е. на замыкании G области G задана некоторая
неотрицательная и непрерывная функция р(х, у). Область G с
распределенной в ней массой будем называть фигурой S, sl
величину
М= \\pix,y)dxdy D9.2)
G
— ее массой. Если р(х, у) — не тождественный нуль, то М > 0.
Определим и найдем центр тяжести фигуры S. Возьмем
какое-либо разбиение т = {G.}, / = 1, 2, ... , k, области G (см.
п. 44.3). Множество G- с распределенной в нем массой
плотности р(х, у), (х, y)eG., назовем фигурой aS-. Выберем по
некоторой точке (^., Г|.)gG.. Величину т- = р(^., T\.)[iG- назовем
приближенным значением массы фигуры aS- (естественность
такого названия следует из формулы D9.2)). Величины же тД.
и т-Г\- назовем приближенными значениями статистических
моментов фигуры aS-, / = 1, 2, ... , k, соответственно
относительно координатных осей Оу и Ох (естественность этого
названия следует из того, что статическими моментами
материальной точки массы т с координатами (х, у) относительно
551
осей Ox и Оу называются величины ту и тх, см. п. 28.6).
Наконец величины
k k
D9.3)
i = 1 i = 1
назовем приближенными статическими т-моментами фигуры
S относительно осей Ох и Оу, sl их пределы при |т| -^ О
lim S(x) = S^, lim S(x) = S^
— статическими моментами фигуры S относительно осей
Ox и Оу. Эти пределы при сделанных предположениях су-
гцествуют. Действительно, из формул D9.3) видно, что S^(t) и
aS (т) являются интегральными суммами Римана для функций
ур(х, у) и хр(х, у), поэтому
^х = ЯМ^' y)dxdy, Sy = ||Xp(x, y)dxdy. D9.4)
G G
Определение 1. Точка (Xq, y^) называется центром тяжести
{центром масс, центром инерции) фигуры S, если
статические моменты относительно координатных осей
материальной точки массы М, равной массе всей фигуры S и
находящейся в точке (Xq, i/q), равны соответствующим
статическим моментам фигуры S, т, е, если Мх^ = Sy, Му^ = S^,
Из формул D9.2) и D9.4) получаем
||хр(х, y)dxdy Я^Р(*^' y)dxdy
Хп
у о
се 'ь'Огг *
J J р(х, y)dxdy J J p(x, y)dxdy
G G
УПРАЖНЕНИЕ. Доказать, что центр тяжести фигуры не зависит от
выбора системы координат.
В качестве примера рассмотрим «криволинейную
трапецию» G, порожденную графиками непрерывных
неотрицательных функций f{x) и g{x), О < g{x) < f(x), а < X < b:
G = {(х, у) : a<x<b, g(x) <у < f(x)}.
Пусть р(х, у) = 1, Так как ^^dxdy = \xG, то
G
^ ^ Ъ f(x) ъ
Xq = —- \\xdxdy = —- \ xdx \ dy = —-\ [f(x) - g(x)]xdx,
^ ^ Ь Kx) b
i^G^r ^^«i J/ 2nGJ
552
отсюда
b b
2пу^[1С = 7г| f\x)dx - 7г| g\x)dx,
а а
Здесь в правой части равенства стоит объем тела,
полученного врапа;ением криволинейной трапеции G вокруг оси Ох. Мы
прип1ли ко второй теореме Гульдина.
ТЕОРЕМА (теорема Гульдина). Объем тела, полученного
вращением плоской фигуры вокруг не пересекающей ее оси,
равен произведению площади этой фигуры на длину
окружности, описанной центром тяжести фигуры.
Пример. Вычислим с помогцью второй теоремы Гульдина
объем \iQ тора Q, полученного врагцением круга (х - а)^ + г/^ < г^,
О < г < а, вокруг оси О^: jiQ = 27га • тгг^ = 27Г^аг^.
§50
Элементы теории поверхностей
50.1. Векторные функции нескольких переменных
Пусть на плоскости й^ задана декартова прямоугольная
система координат и, V, множество X ^ й^ и каждой точке М =
= (и, v)eX поставлен в соответствие вектор г(М) = г(и, v)^ R^.
Такие функции называются векторными функциями двух
переменных и, V.
Аналогично случаю векторной функции одной переменной
(см. § 15) для них вводятся понятия предела, непрерывности,
дифференцируемости. Это было уже сделано раньпхе в § 36 и
§ 41 даже в более обпа;ем случае отображений f:E^ R^, Е ^ R^.
Напомним эти понятия в тех обозначениях, которые будут
здесь употребляться для случая функций г(и, v).
Вектор а называется пределом при (и, и) -^ (и^, Vq)
векторной функции г(и, v), заданной на множестве Е ^ R^, если для
любого 8 > О супа;ествует такое 6 > О, что для всех (и, v)eE,
для которых \и - Uq\ < 5, \v - Vq\ < 6, выполняется неравенство
\г(и, у) - а| < 8. в этом случае пип1ут
lim г(и, и) = а.
функция г(и, и) называется непрерывной в точке (и^, Vq),
если
lim г(и, V) = r(uQ, Vq).
{и, v)^{Uq, Vq)
553
Если функция г(и, v) определена в окрестности точки
дг
ди
дг
(uq, Vq), то ее частная производная г^ = — в этой точке опре
деляется равенством
dr(uQ, Vq) _ dr(u, Vq)
^Л^О^ ^o)
ди du
\U = Uq
Аналогично определяются и другие частные производные
первого и ВЫСП1ИХ порядков. При этом легко убедиться (см.
п. 15.1), что если в пространстве R^ введена декартова
прямоугольная система координат х, у, 2 и г (и, v) = (х(и, v), у(и, v),
2(и, и)), функции х(и, и), у(и, и), 2(и, v) называются
координатными функциями,то
д^г(и, у) _ Гд^х(и, у) д^у(и, у) d^zju, у) ^ k = Q I ^
Векторная функция г (и, v) называется
дифференцируемой в точке (z/q, Vq), если сугцествуют такие постоянные
векторы а Jib, что
Аг = г(и, v) - r(uQ, Vq) = aAu + bAv + г(Аи, Ai;)p,
lim e(Au, Av) = 0, Au = и - Uq, Av = v - Vq, p = VAz/^+Ai^.
Аналогично скалярному случаю легко убедиться, что в
dr(uQ, у о) dr(uQ, у о)
этом случае а = ^^—-, b = ^—— и, таким образом (опу-
ди ду
екаем обозначения аргумента),
Аг = ^du + ^dv + sp, E0.1)
ди дУ
lim 8 = 0, du = Аг/, dv = Av,
Функция
dr = ^du + ^dv E0.2)
au ay
называется дифференциалом дифференцируемой функции
r(u, v) в данной точке. Из формул E0.1) и E0.2) следует, что
Аг = dr -\- 8р, lim s = 0.
Подобно скалярному случаю для векторной функции г(и, v),
имеюпа;ей в окрестности точки (z/q, Vq) непрерывные частные
производные до порядка п включительно, имеет место формула
Тейлора
г(и, v)= t тА^г{и^^ ^о) + «(Р^)' Р ^ О' E0.3)
где
def
o(p^) = s(Au, Ai;)p^, lim s(Au, Av) = 0.
Формулу Тейлора для векторной функции можно
получить, использовав разложение по формуле Тейлора
координатных векторных функций или непосредственно, рассуждая
по аналогии со скалярным случаем.
Если вектор г(и, v)eR^ рассматривать как радиус-вектор,
то векторная функция г(и, и) задает отображение множества
Е, на котором она задана, в пространство R^: каждой точке
(и, v)eE она ставит в соответствие точку г(и, v) — конец
радиуса-вектора г(и, v).
50.2. Элементарные поверхности
Будем рассматривать отображения плоских областей и их
замыканий (напомним, что замыкание области называется
замкнутой областью) в пространство R^. Области будем
обозначать, как правило, буквой D*, sl их границу, как обычно, dD.
Определение 1. Элеже^тар^ой поверхностью называется
непрерывное отображение
f:D->R^ E0.4)
замыкания D плоской области D в пространство R^, а образ
f (D) множества D в пространстве R^ при рассматриваемом
отображении — носителем этой поверхности.
Таким образом, _
fiM)eR^, MeD^R^.
Подчеркнем, что при определении элементарной
поверхности не предполагается, что отображение E0.4) является
взаимно-однозначным. Точка носителя поверхности E0.4), в
которую отображаются по крайней мере две точки
замыкания D области D, называется кратной точкой поверхности
E0.4) или ее точкой самопересечения.
Таким образом, если точка Р является кратной точкой
поверхности E0.4), то сугцествуют по крайней мере две такие
точки M^eDi и M^eD, что f(M^) = f(M^) = P.
' От англ. domain — область.
555~
Если элементарная поверхность E0.4) не имеет кратных
точек, т. е. отображение E0.4) взаимно-однозначно
отображает замыкание D области D в пространство R^, то
элементарная поверхность называется простой.
В дальнейп1ем на плоскости R^^ всегда будет введена
прямоугольная система координат, например и, v. В этом случае
будем употреблять следуюгцие обозначения:
г(и,и)^= ПМ), M = iu,v). E0.5)
Тем самым отображение E0.4) будет записываться в виде
r(u,v)eR^, (u,v)eD, E0.6)
или в векторной форме
r(u,v)eR^, (u,v)eD, E0.7)
(г(г/, v) — конец радиуса-вектора г(и, v)). При такой записи
элементарной поверхности переменные и, v называются
координатами поверхности, или ее параметрами.
Если в пространстве R^ задана прямоугольная система
координат (иногда будем выбирать ее специальным образом,
исходя из целей, которые ставятся при изучении элементарной
поверхности), то отображение E0.4) можно записать в
координатном виде:
х = х(и, v), y = y(u,v), 2 = 2(u,v), (u,v)eD, E0.8)
где
Отображения E0.4), E0.6) и E0.8) называются
представлениями элементарной поверхности.
Если за параметры г/ и i; поверхности можно взять две
какие-либо координаты пространства R^, например х и г/, то
отображение E0.8) можно записать так: z = f(x, у), (х, y)eD;
здесь X = и, у = V, 2 = f(x, у). Такое задание элементарной
поверхности называется явным.
Ясно, что элементарная поверхность, имеюгцая явное
задание, является простой элементарной поверхностью.
В дальнейгаем будут изучаться прежде всего
дифференциальные свойства поверхностей определенных классов, состоя-
гцих из «достаточно гладких», т. е. достаточное число раз
непрерывно дифференцируемых поверхностей. Поэтому определим
понятие п раз непрерывно дифференцируемой элементарной
поверхности.
556
Элементарная поверхность E0.4) называется п раз
непрерывно дифференцируемой, если векторная функция E0.7)
или, что равносильно, координатные функции E0.8), задаю-
па;ие отображение E0.4), п раз непрерывно дифференцируемы
на замыкании D области D.
Напомним, что непрерывность частных производных в
замыкании D области D понимается в смысле супа;ествования
непрерывного продолжения этих производных с области D на
ее границу dD (см. п. 39.3). В случае если в некоторой точке
границы какая-либо частная производная, быть может,
односторонняя, сугцествует в обычном смысле, то ее значение
совпадает с указанным непрерывным продолжением (см. там же
упражнение 1).
Пример. Для элементарной бесконечно непрерывно
дифференцируемой поверхности, заданной отображением
X = R cos\|/ cos (f, у = R cos \|/ sin (f, z = R sin \|/,
0<ф<27Г, -|<х|/<|,
ее носителем является сфера с центром в начале координат и
радиусом R. Весь меридиан ф = О этой сферы состоит из
кратных точек.
Иногда термин «элементарная поверхность» (в случаях,
где это не может привести к недоразумению) употребляется и
в смысле «носитель элементарной поверхности».
50.3. Эквивалентные элементарные поверхности.
Параметрически заданные поверхности
Если вспомнить определение кривой (см. п. 16.1 и 16.2), то
понятие элементарной поверхности окажется аналогичным
понятию пути. Кривая определялась как класс в
определенном смысле эквивалентных путей. Подобным же образом
естественно считать некоторые элементарные поверхности
эквивалентными между собой и определить поверхность как класс
эквивалентных элементарных поверхностей.
Определение 2. Элементарная поверхность
f(M)eR^, MeD E0.9)
называется эквивалентной элементарной поверхности
f^iM)eR^, MeDi E0.10)
557
(здесь D и D^ — плоские области), если существует такое го-
меоморфное (см, определение 5 в п, 36.7) отображение F
замкнутой области D на замкнутую область Di, при котором
внутренние точки переходят во внутренние, а граничные —
6 граничные (т, е, D отображается на D^, а dD — на dD^), и
для каждой точки Me D выполняется равенство
f(M) = f^(F(M)), E0.11)
т. е. f = f-^° F,
В этом случае F называется отображением, осуш;ествляю-
ш;им эквивалентность элементарной поверхности E0.9) с
элементарной поверхностью E0.10) (или, что то же самое,
отображения / с отображением /^). Если / эквивалентно /^, то
пип1ут / ~ /i-
Схематически определение эквивалентных отображений
можно изобразить диаграммой, где стрелками изображены
рассматриваемые отображения и результат отображений не
зависит от выбора пути на диаграмме:
f/ \а
— F —
D ►Di
Очевидно, что:
1^. Всякое отображение эквивалентно самому себе: f - f
(здесь отображением, осугцествляюгцим эквивалентность,
является тождественное отображение) — свойство
рефлексивности.
2^. Если f ~ /^, то /i~/ — свойство
симметричности.
3^. Если f - fi и f^ - /2' ^^ f ^ fz — свойство
транзитивности.
Если / и /^ — эквивалентные непрерывные отображения
соответственно замкнутых областей D и Di, то из E0.11)
следует, что образы множеств D и Di при отображениях / и /^
совпадают: _ _
f(D) = f^(D), E0.12)
т. е. две эквивалентные элементарные поверхности имеют
одинаковый носитель.
Заметим егце, что условия, наложенные на эквивалентные
отображения в определении 2, независимы. Именно: из того,
что F является гомеоморфным отображением замкнутой
области D на замкнутую область Di, не следует, что оно перево-
558
дит внутренние точки во внутренние. Например, если D =
= {(и, V) :и^ -\- v^ <1} — круг, а Di = {(и, v) : О < и^ -\- v^ < 1} —
круг с «выколотым» центром, то тождественное отображение
(очевидно, являюгцееся гомеоморфным) D на Di переводит
внутреннюю точку (О, 0) области D в граничную точку (О, 0)
области D^.
Перейдем теперь к определению поверхности.
Определение 3. Всякий класс S эквивалентных
элементарных поверхностей называется поверхностью, или, более
подробно, непрерывной параметрически заданной поверхностью.
Каждая элементарная поверхность из этого класса, т. е.
отображение г (и, v), (и, v)eD, называется представлением
поверхности aS, тройка соответствуюгцих координатных
функций E0.6) — ее координатным представлением, а соот-
ветствуюгцая векторная функция E0.7) — ее векторным
представлением.
Очевидно, что поверхность S однозначно определяется
каждым из своих представлений, так как если имеется
какая-нибудь элементарная поверхность, то все эквивалентные
ей элементарные поверхности получаются с помогцью
всевозможных отображений, осугцествляюгцих эквивалентность.
Таким образом, чтобы задать поверхность, надо задать
некоторое ее представление.
Поверхность aS, заданную каким-либо своим
представлением, записанным в виде E0.4), E0.6), E0.7) или E0.8), будем
обозначать соответственно одним из следуюгцих способов:
S = {f(M);MeD},
S = {г(и, V); (и, v)e D}, E0.13)
S = {r(u, v); (и, v)eD},
S = {x(u, v); y(u, v), z{u, v); (u, v)eD},
Для того чтобы поверхность могла быть задана тремя
последними способами, на плоскости й^ должна быть задана
система координат, а для того чтобы четвертым — епа;е и
система координат в пространстве R^,
Поверхность однозначно определяется каждым из своих
представлений, поэтому это позволяет (что часто очень
удобно) правую часть каждого из равенств E0.13) понимать не
как совокупность всех представлений поверхности aS, а как
некоторое вполне определенное ее представление.
559
Если г (и, и); (и, v)eD и р(и^, v-^), (и-^ v-^)eDi —
представления одной и той же поверхности aS, то всякое отображение F,
осупа;ествляюпа;ее эквивалентность отображения г(и, v) с
отображением р(и^, v-^), в координатной записи имеет вид
и^ = (р(и, v), v^ = \\f(u, v), E0.14)
(г/, v)eD, (г/i, v^)eD^,
и называется допустимым преобразованием параметров и, v.
Как отмечалось вып1е, две эквивалентные поверхности
имеют один и тот же носитель, поэтому носители всех
элементарных поверхностей, составляюпа;их поверхность, т. е.
элементарных поверхностей, эквивалентных между собой,
совпадают. Это делает естественным следуюпа;ее определение.
Определение 4. Общий носитель всех элементарных
поверхностей, составляющих поверхность, называется
носителем этой поверхности.
Определим теперь, что называется точкой поверхности.
Точкой элементарной поверхности f : D ^ R^ назовем
пару (М, Р), где М е D, Р = f(M) е R^, т. е. точку М
замкнутой области D и ее образ Р при отображении /. Коротко
точка поверхности f: D ^ R^ обычно обозначается f{M),
соответственно г {и, v) или (х {и, v), у {и, v), z {и, v)), где
М = (и, V) е D.
Носителем точки f(M) элементарной поверхности
называется пространственная точка Р = f{M) е R^.
Определение 5. Пусть элементарные поверхности E0.9) и
E0.10) эквивалентны между собой и отображение F : D ^ Di
осуществляет их эквивалентность.
Точка f(M) элементарной поверхности E0.9)
называется эквивалентной точке /^(М^) элементарной поверхности
E0.10), если
M^ = F(M). E0.15)
В этом случае будем писать
Г(М) ~ /i(Mi).
Легко проверить, что это соотногаение эквивалентности
обладает свойством рефлексивности, симметричности и
транзитивности:
560
10. /(М) ~ /(М).
20. Если f(M) ~ /i(Mi), mo f^(M^) ~ /(М).
30. ^слг/ /(М) ~ /i(Mi) г/ /i(Mi) ~ /2(^2)' ^^ Я^) ~ /2(^2)-
Очевидно, что из выполнения условий E0.15) и E0.11)
следует, что две эквивалентные точки эквивалентных
элементарных поверхностей имеют в пространстве R^ один и тот
же носитель.
Определение 6. Каждый класс {/(М)} эквивалентных между
собой точек элементарных поверхностей, составляющих
некоторую поверхность, называется точкой этой
поверхности, а их общий носитель — носителем этой точки
поверхности.
Если М — внутренняя (граничная) точка области D, то
точка f(M) элементарной поверхности E0.9) называется ее
внутренней (соответственно краевой) точкой. Краевые точки
элементарной поверхности E0.9) — это те ее точки, которые
задаются сужением отображения / на границу dD области D.
Совокупность всех краевых точек элементарной поверхности
называется ее краем.
Если f(M) ~ /^(М^) и М — внутренняя (граничная) точка
замкнутой области D (см. E0.9) и E0.10)), то, согласно
определению 2, точка М^ также является внутренней
(соответственно граничной) точкой замкнутой области D^,
Точка {/(М)} поверхности S называется внутренней
(соответственно краевой) ее точкой, если каждая точка М (а для
этого достаточно, чтобы хотя бы одна из них) является
внутренней (соответственно граничной) точкой замкнутой области
D, на которой задано отображение /.
Совокупность всех краевых точек поверхности называется
ее краем. Ясно, что край поверхности представляет собой
совокупность всех краев ее представлений.
Каждая точка {/(М)} поверхности S однозначно
определяется каждой отдельной точкой f(M), входяпа;ей в нее, т. е. в
класс эквивалентных точек всевозможных представлений
поверхности aS, а каждая точка f(M) элементарной поверхности
E0.9) однозначно определяется точкой MeD, следовательно,
и ее координатами, если задана координатная система.
Таким образом, каждая точка поверхности S при выборе
какого-либо ее представления, например, вида г (и, v), (и, v)eD,
однозначно определяется значениями параметров и, v. Поэто-
561
му в этом случае точку поверхности S вместо {(и, v), г (и, v))}
будем просто обозначать г (и, и) (или, соответственно, (х (и, и),
у {и, V), г (и, v)) или /(М)).
Очевидно, что совокупность всех носителей точек
поверхности составляет ее носитель.
Точка носителя поверхности, являюгцаяся носителем по
крайней мере двух различных точек поверхности, называется
кратной точкой или точкой самопересечения поверхности.
Если поверхность имеет хотя бы одно представление /(М),
M^D, которое взаимно однозначно отображает плоскую
замкнутую область D в пространство R^, то и все другие ее
представления взаимно однозначно отображают соответствуюгцие
плоские замкнутые области, на которых они заданы, в
пространство. В этом случае поверхность не имеет кратных
точек и называется простой поверхностью.
Для простых поверхностей, как и для простых дуг, точка
носителя поверхности однозначно определяет точку
поверхности. Поэтому можно не делать между ними различия.
Отметим, что поверхность, имеюгцая хотя бы одно явное
представление, является простой поверхностью.
Понятие эквивалентных отображений замкнутых плоских
областей можно вводить не только для непрерывных
отображений, но и для других классов отображений, например для
непрерывно дифференцируемых. В применении к
параметрически заданным поверхностям это приводит к непрерывно
дифференцируемым поверхностям. Их определение
базируется на понятии отображений, эквивалентных относительно
непрерывно дифференцируемых преобразований.
Определим это понятие. Как и раньгае (см. п. 39.3), под
функцией, непрерывно дифференцируемой в замыкании
некоторой области, будем понимать такую функцию, которая
имеет непрерывные в самой области производные,
непрерывно продолжаемые на ее границу.
Отображение некоторой замкнутой области называется
непрерывно дифференцируемым, если каждая координатная
функция, задаюгцая это отображение (см. п. 36.2), является
непрерывно дифференцируемой функцией на
рассматриваемой замкнутой области. При этом продолженные функции в
этих случаях обозначаются теми же символами, что и
исходные продолжаемые функции.
Если некоторое отображение и^ = ф(г/, v), v^ = \|/(г/, v)
непрерывно дифференцируемо на замыкании D области D, то,
согласно сделанному соглагаению, это означает, в частности, что
~562
якобиан -У' ^; этого отображения непрерывно продолжаем с
д(и, V)
области D на ее замыкание D и его продолжение, обозначаемое
тем же символом J-^' ^ , также будет называться якобианом.
д{и, V)
Прежде всего сформулируем, что будем понимать под
эквивалентными непрерывно дифференцируемыми
отображениями. Для этого введем понятие регулярных отображений.
Определение 7. Гомеоморфное отображение F замыкания D
плоской области D на замыкание D^ плоской области D^,
переводящее внутренние точки во внутренние, а граничные — в
граничные, называется регулярным отображением
замкнутой области D на замкнутую область D^, если как само это
отображение F, так и обратное ему F~^ непрерывно
дифференцируемы соответственно на замкнутых областях D и D^.
Заметим, что всякое регулярное отображение F замкнутой
области D имеет во всех точках области D не равный нулю
якобиан. Действительно, согласно определению 7, при
отображении F образ каждой внутренней точки является
внутренней точкой. В этих точках прямое и соответственно
обратное отображения непрерывно дифференцируемы, поэтому их
якобианы не могут обратиться в нуль, ибо их произведение
равно единице (см. п. 41.6).
Отсюда следует, что якобиан регулярного отображения F
не равен нулю и на замкнутой области D. Действительно, в
силу непрерывной продолжаемости якобианов как прямого,
так и обратного отображений соответственно на замыкания D
и F{D) областей D и F(D), произведение этих якобианов равно
единице и для всех точек замкнутой области D,
Определение 8. Пусть f и f^ — непрерывные отображения
замыканий D и D^ плоских областей D и D^ в пространство R^
и пусть эти отображения непрерывно дифференцируемы в
замкнутых областях D и D^. Отображения f uf^ называются
эквивалентными относительно непрерывно
дифференцируемых преобразований, если существует такое регулярное
отображение F замкнутой области D на замкнутую область Di,
что для каждой точки MeD выполняется условие E0.11).
~563
Это соотношение эквивалентности обладает свойствами
рефлексивности, симметричности и транзитивности и,
следовательно, порождает разбиение множества всех
элементарных поверхностей, задаваемых непрерывно
дифференцируемыми представлениями, на классы эквивалентности.
Определение 9. Всякое множество элементарных
поверхностей, задаваемых непрерывно дифференцируемыми
отображениями
г=г(и, V), (и, v)eD, E0.16)
замыканий D плоских областей D в пространство R^ и
эквивалентных относительно непрерывно дифференцируемых
преобразований, называется непрерывно дифференцируемой
поверхностью, а каждое отображение (0.16) — ее
представлением.
Подчеркнем, что если поверхность S = {г(и, и); (и, v)eD}
непрерывно дифференцируема, то это, в частности, означает,
что каждое ее векторное представление г = г(и, v), (и, v)eD,
имеет частные производные г^ и г^, непрерывные в области D
и непрерывно продолжаемые на ее границу. Согласно
принятому соглагаению, продолженные функции обозначаются
теми же символами, что и продолжаемые"^, поэтому можно
считать, что функции г^ и г^ непрерывны на замкнутой
области D,
Аналогичным образом можно определить и другие классы
параметрически заданных поверхностей, например дважды
непрерывно дифференцируемые или вообгце п раз
непрерывно дифференцируемые параметрически заданные
поверхности, а также понятие их точки и носителя.
Подобно тому, как в п. 47.3 было обобгцено понятие
непрерывно дифференцируемой кривой, можно обобгцить и
понятие непрерывно дифференцируемой поверхности. Это
делается следуюгцим образом. Взаимно-однозначное отображение
замыкания одной плоской области на другую, переводягцее
внутренние точки во внутренние, граничные — в граничные,
называется регулярным в широком смысле, если как само
* Точнее, это соглапхение было принято (см. п. 39.3) для скалярных
функций и, следовательно, для координат векторных функций, поэтому
его естественно принять и для самих векторных функций.
~564
это отображение, так и ему обратное непрерывны на
замыканиях областей, на которых они заданы, и непрерывно
дифференцируемы в самих этих областях. Если в определении 8
регулярные отображения заменить на регулярные в гаироком
смысле, то получится определение отображений,
эквивалентных относительно непрерывно дифференцируемых
отображений в гаироком смысле.
Множество непрерывных отображений замыканий
плоских областей в трехмерное пространство, непрерывно
дифференцируемых в этих областях и эквивалентных в гаироком
смысле относительно непрерывно дифференцируемых
преобразований, называется параметрически заданной
непрерывно дифференцируемой поверхностью в широком смысле,
если среди рассматриваемых отображений сугцествует хотя бы
одно отображение, непрерывно дифференцируемое вплоть до
границы.
Примером непрерывно дифференцируемой поверхности в
гаироком смысле является полусфера х^ + г/^ + 2^ = 1, 2 > О,
заданная явным представлением z = J\ - х'^ - у^, х^ + г/^ < 1.
Это представление не непрерывно дифференцируемо вплоть до
границы х^ -\- у^ = 1 круга х^ + г/^ < 1. Однако если этот круг
спроектировать из точки (О, О, -1) на рассматриваемую
полусферу, то получится ее представление, непрерывно
дифференцируемое вплоть до границы указанного круга.
При этом можно рассматривать поверхности,
представления которых определены не на замыканиях плоских областей,
а только на самих областях и даже на произвольных открытых
множествах. Такие поверхности будем называть открытыми.
Их носители могут быть неограниченными множествами,
например гиперболоиды, параболоиды.
Окончательно можно сказать, что параметрически
заданной поверхностью какого-либо класса является некоторая
совокупность эквивалентных между собой в определенном
смысле отображений плоских областей или их замыканий
в пространство, называемых ее представлениями.
Понятие эквивалентности определяется в зависимости от
выбора класса.
Определение 10. Дреобра^ова^г/^ параметров,
осуществляющие переход от одного представления поверхности к
другому, ему эквивалентному, называются допустимыми,
~565
Таким образом, если г(и, и), (и, v)eD, и р(и-^, v-^),
(и-^, v-^)eD-^— два представления одной и той же
параметрически заданной поверхности некоторого класса, а
отображение и^ = ф(г/, v), v-^ = \\f(u, v) замкнутой области D на
замкнутую область D^ является допустимым преобразованием
параметров, то для всех точек (и, v)eD выполняется соотногаение
(см. E0.1)) г(и, v) = р(ф(г/, v), \\f(u, v)).
Параметрически заданная поверхность при заданном
классе допустимых преобразований параметров однозначно
определяется каждым своим представлением, поэтому, чтобы
задать такую поверхность, достаточно задать лигаь одно ее
представление.
Следовательно, для таких поверхностей, как и для
непрерывных поверхностей, имеет однозначный смысл их
обозначение с помогцью только одного их представления, т. е. только
одной из элементарных поверхностей, составляюгцих
заданную поверхность. Таким образом, при обозначении
поверхности S некоторого класса одним из способов E0.13) можно
считать, что в правой части каждого из равенств стоит не
совокупность всех представлений рассматриваемой поверхности, а
лип1ь одно из них. Так обычно мы и будем поступать.
Аналогично случаю элементарных поверхностей термин
«поверхность» иногда употребляется (если это не может
привести к недоразумению) и в смысле носителя поверхности.
Определим теперь понятие части поверхности.
Определение 11. ili/cmb S — поверхность некоторого класса
и f(M) — какое-либо ее представление, MeD, D — плоская
область.
Если и — область, содержащаяся в D, то поверхность,
представлением которой является сужение отображения f на
замыкании U области U, называется частью поверхности S,
Можно в качестве U брать и произвольное открытое
множество, лежапа;ее в D, и рассматривать сужение отображения
не на замыкании U множества U, sl на самом U; в этом случае
открытую поверхность, задаваемую сужением отображения /
на множестве U, будем называть открытой частью
поверхности S, а иногда и просто частью поверхности S, Эта
открытая поверхность называется окрестностью на
поверхность S всякой точки f(M) поверхности aS, где Me U.
566
50.4. Поверхности, заданные неявно
Отметим епа;е один подход к понятию поверхности. Если
F{x, г/, z) — непрерывная в некоторой трехмерной области
функция, то поверхность, координаты точек носителя
которой удовлетворяют уравнению
Дх,г/,2) = 0, E0.17)
называется поверхностью, заданной неявно. Не
останавливаясь подробно на анализе такого подхода к понятию
поверхности, отметим лип1ь, что в том случае, если функция F
удовлетворяет в некоторой точке (Xq, i/q, z^ условиям теоремы о
неявных функциях (см. п. 41.1), часть поверхности E0.17) в
некоторой окрестности указанной точки (т. е. пересечение
этой окрестности с данной поверхностью) допускает явное
представление, и можно сказать, что в этой ситуации часть
поверхности, заданной неявно, локально сводится к
поверхности, заданной явным представлением (см. п. 50.1). Только
такой случай поверхностей, заданных неявно, встретится в
дальнейп1ем, поэтому не будем специально останавливаться
на разъяснении тех или иных понятий для обпа;его случая
поверхностей, заданных неявно.
В качестве простейпхего примера поверхности, заданной
неявно, отметим уравнение х^ + г/^ + 2^ = 1. Точки,
координаты которых удовлетворяют этому уравнению, образуют
поверхность niapa единичного радиуса с центром в начале
координат.
50.5. Касательная плоскость и нормаль к поверхности
Пусть
S = {r{u,v); {u,v)^D) E0.18)
—непрерывно дифференцируемая поверхность, заданная ее
некоторым векторным представлением. Как и всякое ее
векторное представление, оно является непрерывно
дифференцируемой векторной функцией на замкнутой плоской области D.
Будем для простоты считать, что пересечение каждой
прямой и = Uq или V = Vq с замкнутой областью D состоит из
одного отрезка (быть может, вырождаюгцегося в точку) или пусто.
Пусть, например, пересечение D с прямой v = v^ue пусто;
тогда г = г(и, Vq), (и, i;q)gD, (Vq фиксировано) является представ-
567
лением некоторой непрерывно дифференцируемой кривой,
которая называется координатной линией (и-линией). Вектор
г^ = — = (х^, г/^, 2^) является касательным к ней вектором.
Аналогично определяются другие координатные линии (v-ли-
нии) с помогцью представления г = г(и^, v), (z/q, v)e D (Uq фик-
сировано) и касательные к ним векторы г^= — = (х^, г/^, 2^).
Определение 12. Точка г{и, v) поверхности E0.18), для
которой векторы г^ и г^ не коллинеарны {линейно независимы),
называется неособой при данном представлении этой
поверхности, В противном случае, т, е, когда векторы г^ и г^
коллинеарны в данной точке, она называется особой
точкой поверхности при данном ее представлении.
Если точка поверхности неособая, то в ней, в частности,
г^ ^ О, Гу ^ 0. Очевидно, что точка поверхности является
неособой при данном представлении поверхности в том и
только в том случае, когда в этой точке
г^Хг^^О. E0.19)
Если поверхность задана явным представлением
2 = fix, у), (x,y)eD, E0.20)
то она не имеет особых точек. В самом деле, в этом случае и = х,
V = у и, следовательно,
*^w^-*-' Уи^^^ ^и^'х^
х^ = 0, у^=1, 2^ = fy, E0.21)
поэтому г^ = A, о, f^), Гу = (О, 1, fy); отсюда явствует, что
\r.Xry\ = ^l + fl + fl>0.
Рассмотрим кривую на поверхности E0.18). Пусть эта
кривая задана непрерывно дифференцируемыми функциями
u = u(t), V = v(t), (u(t), v(t))eD, a<t<b,
т. е. непрерывно дифференцируемым векторным
представлением
г = r[uit), vit)], (uit), vit))eD, a<t<b, E0.22)
причем |r^p = u'^ + v'^(t) > 0 на [a, b].
Продифференцировав равенство E0.22), получим
dr = r^du + r^dv; E0.23)
здесь du = u(t)dt, dv = v\t)dt. Если точка поверхности, в
которой рассматривается равенство E0.23), неособая, то она
568
неособая и для кривой E0.22), поэтому вектор dr ^ О и
является касательным к кривой E0.22). Равенство E0.23)
показывает, что в данной точке г (z/q, Vq) поверхности E0.18)
касательная к любой кривой E0.22) на этой поверхности, прохо-
дяпа;ей через точку г (z/q, Vq), лежит в плоскости векторов
г^(г/о, Vq) и гДг/о, v^).
Определение 13. Плоскость, проходящая через точку г(и^, Vq)
поверхности E0.18), в которой лежат все касательные к
кривым E0.22), проходящим через эту точку, называется
касательной плоскостью к поверхности в данной точке
{называемой точкой касания).
Если данная точка поверхности E0.18) неособая, то в ней
всегда супа;ествует, и притом единственная, касательная
плоскость: именно, в силу E0.23), ею является плоскость, проходя-
па;ая через точку г{и^, v^ параллельно векторам rj^u^, Vq) и
гДг/Q, Vq). Отсюда легко написать ее уравнение в векторном
виде. Обозначив через Tq радиус-вектор точки касания, а через
г — текугций радиус-вектор точек на касательной плоскости,
получим (рис. 84) (г - Tq, г^, г^) = О (в левой части равенства
стоит смегаанное произведение указанных векторов).
Если г = (х, г/, 2), Го = (Xq, у^, 2^), г^ = (х^, г/^, 2j, г^ =
= (Ху, г/у, 2у), то уравнение касательной плоскости в
координатном виде принимает следуюгций вид:
X
X
о
У-Уо
Уи
yv
Z - Z,
г..
= 0.
В случае явного задания поверхности, т. е. в виде 2 =
= /(х, у) (см. E0.20)), в силу формул E0.21), уравнение
касательной плоскости имеет вид
откуда
2- 2п
= (х-х^)Г^+(у-у^)Гу,
где f^ -и. f — частные производные
4(х, у) и fy(x, у) в точке (х^, у^).
Рис. 84
569
Из этой формулы следует, что два определения
касательной плоскости для поверхности с явным представлением
E0.20), данные в настояпа;ем пункте и ранее в п. 37.5,
эквивалентны. В самом деле, оба определения приводят к одному
и тому же уравнению E0.24).
Определение 14. Прямая, проходящая через точку касания
поверхности с касательной плоскостью и
перпендикулярная этой плоскости, называется нормальной прямой к
поверхности в указанной точке.
Ее уравнение в обпа;ем случае в неособой точке
поверхности имеет вид
X — Xq _ у ~ Уо _ Z — Zq
у и ^и
Уи ^v
^и -^и
^v -^v
^и у и
^v Уи
в случае явного представления E0.20) эти уравнения
принимают вид
X Xq _ у г/о
/х
/.
= -B-2q).
E0.25)
Определение 15. Всякий ненулевой вектор, коллинеарный
нормальной прямой, проходящей через данную точку
поверхности, называется нормалью к этой поверхности в
указанной точке.
Примером нормали в неособой точке поверхности
является векторное произведение п = г^Х г^, взятое в этой точке.
Согласно данному определению, в каждой неособой (при
заданном представлении) точке г {и, v) рассматриваемой
поверхности при фиксированных значениях параметров г/ и i;
сугцествует, и притом единственная, нормальная прямая.
Следует иметь в виду, что если точка Р пространства
является кратной точкой поверхности, т. е. сугцествуют по крайней
мере две пары параметров (при заданном представлении)
(и^, v^ и (и^у V2) таких, что Р = г(и^, v-^) = г (и^, 1^2)' ^^ ^^"
жет, конечно, случиться, что этим парам параметров будут
соответствовать различные нормальные прямые, тем самым в
указанной точке Р нормальная прямая будет не единственна.
Для поверхности, заданной неявно уравнением F{x, у, z) = О,
где F(x, у, z) — непрерывно дифференцируемая в
окрестности точки (Xq, i/q, 2q) функция, F{Xq, i/q, 2q) = 0, и в этой
точке F| + F| + F| > О, уравнение касательной плоскости в
точке (Xq, г/о, z^ имеет вид
(X - Xo)F, + (г/ - г/о)^„ + (г - z^)F^ = О,
570
где F^, F и F^ обозначают значения соответствуюгцих частных
производных, взятых в точке (Xq, i/q, Zq).
Вспомнив, что вектор с координатами F^, F , F^, т. е.
вектор VF = (F^, F , F^), называется градиентом функции F (см.
п. 37.6), видим, что градиент функции в данной точке
поверхности F(x, у, 2) = О перпендикулярен касательной
плоскости в этой точке, т. е. коллинеарен нормальной прямой.
Поэтому уравнение нормальной прямой к поверхности
имеет вид
X — Xq ^ у — yQ ^ 2 — Zq
~F ~F ~F *
X у Z
Все эти формулы сразу следуют из E0.24) и E0.25).
Действительно, если, например, F^^ О j^ 2 = f(x, у) — функция,
определяемая уравнением F = О в окрестности точки (Xq, i/q, 2q), то
достаточно заметить, что / = ~~Е^у fn ^ ~~^ (^^- ^- 41.1).
^ Z ^ ^ Z
Если функция F(x, у, 2) задана и непрерывно
дифференцируема в области G, то для любой точки поверхности,
заданной неявно уравнением F{x, у, 2) = с (с — постоянная),
получим уравнение касательной плоскости и нормальной прямой
того же вида, что и в случае F = О, если только в этой точке
F^ -\- F^ -\- F^ > 0. Множество точек (х, г/, 2)eG, для которых
F = с, называется, как мы знаем, поверхностью уровня
функции F (см. п. 36.1).
Таким образом, градиент VF = (F^, F , F^) в точке (Xq, г/д, 2q)
поверхности уровня F(x, у, 2) = с направлен по нормальной
прямой к этой поверхности в точке (Xq, г/д, 2q). Иначе говоря,
градиент функции ортогонален к поверхности уровня (т. е.
перпендикулярен касательной плоскости к поверхности
уровня в рассматриваемой точке).
Мы доказали супа;ествование касательной плоскости в
неособой точке у непрерывно дифференцируемой поверхности
при фиксированном ее представлении. Возникает вопрос: что
будет, если перейти к другому представлению этой
поверхности? Прежде всего, останется ли неособая точка неособой, а
особая — особой? Оказывается, что да. Докажем это.
Пусть г(и, v), (и, v)eD и р(и^, v^), (и^, v^)eDi — суть два
представления одной и той же непрерывно
дифференцируемой поверхности. Переход от любого представления
непрерывно дифференцируемой поверхности к другому ее
представлению осупа;ествляется посредством регулярного
отображения, поэтому супа;ествует такое регулярное отображение
u^ = (p(u,v), v^ = \\f(u,v) E0.26)
J7I
замкнутой области D на замкнутую область Di, что для всех
точек (г/, v)& D справедливо равенство
г(г/, V) = р(ф(г/, у), \|/(г/, v)). E0.27)
При этом, как было доказано, якобиан отображения E0.26) не
равен нулю нигде в замкнутой области D\
Фи Ф^
Э(Ф, \|/)
д{и, v)
^0, (г/, i;)gD.
векторов г^, Гу с помогцью матрицы
Продифференцировав тождество E0.27), получим
ru = ^u^u, + '^u^v,^ ^. = Ф.Р.1 + ¥.Р.^. E0.28)
Следовательно, пара векторов р^ , р^ преобразуется в пару
Фи ¥и
.. ^- ^-..
Поэтому для данной точки (г/, v) векторы г^, г^ линейно
независимы тогда и только тогда, когда линейно независимы
векторы р^ , Ру в точке (г/^, у^), получаюгцейся из точки (г/, v)
с помогцью преобразования E0.26), причем в случае их
линейной независимости плоскость векторов r^j^r^j^ плоскость
векторов р^ и Ру совпадают.
Итак, неособая (особая) при данном представлении
точка непрерывно дифференцируемой поверхности будет
неособой {особой) и при любом другом представлении этой
поверхности, а плоскость, касательная к поверхности в
неособой точке при одном представлении поверхности, будет
касательной и при другом ее представлении.
Определение 16. Непрерывно дифференцируемая поверхность,
у которой нет особых точек, называется гладкой
поверхностью,
В силу доказанного выгае, чтобы проверить, что данная
поверхность является гладкой, достаточно убедиться, что у
нее имеется одно непрерывно дифференцируемое
представление и при этом представлении нет особых точек.
Следует обратить внимание на то, что у гладкой
поверхности S = {г(и, и), (и, v)eD} векторные функции г^ и г^ не
только непрерывны на замыкании D области D, но, согласно
определению, и не коллинеарны на этом замыкании. Иначе
говоря, у гладкой поверхности E0.18) всюду на замкнутой
области D выполняется неравенство (см. E0.19)) г^Х г^ ^ 0.
J72
Замечание. Из формул E0.28) следует, что
= ФЛ(Р„^ X р,^) + ф,^„(р,^ X р„^) = |J^(P„^ X р^^).
При допустимых преобразованиях параметров E0.26)
якобиан -У' ^; нигде в D не обрагцается в нуль, поэтому из полу-
д(и, V)
ченной формулы следует, что векторные произведения г^ X г^
и р^ ^ Ру ^ данной точке поверхности могут обрагцаться в
нуль только одновременно. Но было показано, что
необходимым и достаточным условием того, что данная точка
поверхности при данном представлении поверхности г(и, и)
неособая, является неравенство нулю в этой точке векторного
произведения г^ X г^. Тем самым егце раз доказано, что неособая
(особая) точка поверхности при одном представлении
поверхности будет такой же и при другом ее представлении.
Введем понятие гладкой поверхности в п1ироком смысле.
Представление поверхности называется гладким, если оно
непрерывно дифференцируемо на замкнутой области, на
которой оно задано, и не имеет на ней особых точек.
Допустимым преобразованием параметров гладкого
представления поверхности называется отображение, непрерывно
дифференцируемое на замкнутой области, на которой оно
определено. Непрерывная дифференцируемость обратного
отображения вплоть до границы не предполагается. Таким образом,
производные обратного отображения могут не иметь конечного
предела при приближении к границе отображаюгцейся области.
Этим допустимое преобразование параметров гладкого
представления поверхности отличается от регулярного
отображения. Поверхность называется гладкой в широком смысле, если
у нее сугцествует гладкое представление, а любое другое
представление получается гладким преобразованием параметров
некоторого ее гладкого представления.
Примером гладкой поверхности в гаироком смысле
является полусфера, заданная представлением
2 = Jl - Х^ -\- у , Х^ -\- у^ < 1,
которое не является гладким: на границе круга х^ + г/^ < 1
частные производные ^-^ и. ^^ бесконечны. Примером гладкого
ах ду
представления этой полусферы является проектирование на
J73
нее единичного круга х^ + г/^ < 1 координатной плоскости
переменных X и г/ из точки (О, О, -1). Это представление задается
формулами
2и 2у 1 + и^ + у^
1 + ^2 + ^2' у 1+^2 + у2' 1 + ^2 + у2-
Первые две из этих формул представляют собой допустимое
преобразование параметров (и, и) в параметры (х, у)
рассматриваемой полусферы.
50.6. Явные представления поверхности
Явное представление поверхности не является, как это может
показаться на первый взгляд, специальным способом ее
задания. Нетрудно показать, что локально во внутренней неособой
точке непрерывно дифференцируемая поверхность всегда
имеет явное представление. Это означает следуюгцее.
Пусть непрерывно дифференцируемая поверхность S
задана своим представлением
г(и, v) = (х(и, v), у(и, v), 2(и, v)), (и, v)eD E0.29)
и r(z/Q, Vq) — ее внутренняя неособая точка (uq, Vq)^D,
следовательно, в этой точке г^ X Гу ^ О, а так как
^и
^v
Уи
Уи
2
+
Уи
Уи
^и
^v
2
+
^и
^v
^и
^v
Г„ X г ,
то хотя бы один из определителей, стоягцих под знаком
радикала, отличен от нуля. Пусть, для определенности.
^0.
^и Уи
^v Уи
Тогда, согласно теореме о неявных функциях, для отображения
х = х(и, v), y = y(u,v) E0.30)
(см. E0.29)) супа;ествуют такие окрестности С/ и F
соответственно точек (z/q, Vq) и (Xq, г/о), где Xq = x(uq, Vq), у^ = у(и^, Vq),
что и отображается на V взаимно-однозначно и,
следовательно, система E0.30), рассматриваемая как система уравнений
относительно переменных и, v, может быть однозначно разре-
niena относительно их при (х, у)е V:
и = и(х, у), V = и(х, у).
574
Подставив эти формулы в выражение для z в E0.29),
получим
2 = f(x,y) = 2(u(x,y),v(x,y)), (x,y)eV. E0.31)
Таким образом, часть поверхности aS, соответствуюгцая
окрестности и точки (z/q, Vq), имеет явное представление E0.31).
Под частью поверхности S здесь понимается открытая
поверхность, задаваемая представлением г(и, v), (и, v)eU. Для
этой поверхности непрерывно дифференцируемое
взаимнооднозначное отображение E0.30) является допустимым
преобразованием параметров.
УПРАЖНЕНИЕ 1. Доказать, что в любой внутренней неособой точке
непрерывно дифференцируемой поверхности супдествует ее явное
локальное представление, заданное на замкнутой области.
Итак, при локальном изучении поверхности в неособой
внутренней точке можно ограничиться изучением
поверхностей, заданных явным представлением. Следует, однако,
иметь в виду, что формулы для вычисления тех или иных
величин, связанных с поверхностью, полезно получать и для
поверхностей, которые заданы обгцим параметрическим
представлением, так как при конкретном их использовании не
всегда бывает целесообразно переходить к явному
представлению поверхности, не говоря уже о том, что это бывает
практически неосугцествимо.
Иногда бывает полезным и более специальное явное
задание поверхности, чем E0.31). Для того чтобы установить его
возможность, докажем предварительно лемму.
ЛЕММА 1. Пусть функция г = f(x, у) непрерывно
дифференцируема в некоторой окрестности U точки (Xq, у^) и пусть Zq =
= КЧ^ Уо)- Тогда у точки (Xq, i/q, z^)
существует такая окрестность
V в пространстве R^ и такая
окрестность W на касательной
плоскости П к графику функции
f в этой точке, что пересечение
графика функции f с
окрестностью V взаимно-однозначно
проектируется на окрестность W
при проектировании в
направлении, перпендикулярном
плоскости П (рис. 85).
575
Доказательство. Введем следуюпа;ие обозначения:
Тх ^ ТхУ^оу Уо)у Ту ^ TyK^Qy Уо)-
Если f^ = fy = О, то координатная плоскость переменных
X, у параллельна касательной плоскости П и утверждение
леммы очевидно: W = U.
Пусть /f + /f > О и, для определенности,
/0^0. E0.32)
Напип1ем уравнение прямой, параллельной нормали в
точке (Xq, i/q, 2q). Вектор v = (/^, /^, - 1) параллелен этой
нормали (см. E0.25)), и уравнение указанной прямой в
векторной форме имеет вид
r = rQ + a + vt, -оо<^<+оо, E0.33)
где Tq = (Xq, i/q, 2q) и а — вектор, параллельный касательной
плоскости 71. Его можно записать в виде
а = (а, р, а/о + р/»), E0.34)
где а и Р — произвольные параметры (при любых а и р, имеет
место av = 0).
В координатной форме после исключения параметра t
уравнение прямой E0.33) принимает вид
(х-Хо-а)/0-(г/-г/о-Р)/о = 0,
X - Хо - а + B - Хо - (а/о + Р/^))/^ = 0. E0.35)
Подставив в эту систему уравнений 2 = /(х, г/), для
определения координат X, у точки пересечения прямой E0.35) с
графиком функции / получим систему уравнений
(х-Хо-а)/0-(г/-г/о-Р)/о = 0,
X - хо - а + (/(X, у)-2^- (а/о + ^fO))fO = о. E0.36)
Ее якобиан по переменным х, у не зависит от а и Р и имеет вид
J(x, г/) =
/О _fO
'у IX
{l + fj^ + fjpn. E0.37)
Левые части уравнений E0.36) являются непрерывно
дифференцируемыми функциями переменных х, г/, а и р, значения
X = Xq, г/ = i/q, а = Р = о удовлетворяют этим уравнениям и
^(^0'Уо) E0=37) (l + ^"' = ^f)^x°^0.
57ё
Поэтому, согласно теореме о неявных функциях, сугцествуют
такие окрестности C/q точки (Xq, i/q), C/q ^ С/, и окрестность Fq
точки (О, 0) на плоскости параметров а, Р, что система E0.36)
может быть единственным образом разрегаена относительно
переменных х и г/
X = X (а, р), у = у (а, р) E0.38)
таким образом, что отображение E0.38) отображает
окрестность Vq на окрестность C/q. При этом окрестность Vq всегда
можно выбрать круговой (уменыаив в случае необходимости
данную окрестность V^: любая плоская окрестность точки
содержит ее круговую окрестность), т. е. такой, что для
некоторого 8 > О будет иметь место равенство
Fq = {(а, Р) : а2 + р2 < ^2}^
Таким образом, для любого вектора а (см. E0.34)), для
которого
а2 + р2<82, E0.39)
прямая E0.33) имеет, и притом единственную, точку
пересечения с графиком сужения функции / на окрестность C/q
точки (Xq, г/о).
Координаты X, у этой точки находятся по формулам
E0.38), SiZ = fix, у).
Теперь заметим, что
\а\ = Ja^ + р2 + (а/о + р/О)^ > Ja^ + р2.
Поэтому если
\а\ < 8, E0.40)
то заведомо выполняется E0.39) и, следовательно, прямая
E0.33) пересекает график функции / в единственной точке.
Концы всевозможных радиусов-векторов Tq + а, где
вектор а удовлетворяет условию E0.40), образуют искомую
окрестность V точки (Xq, г/о, Zq) на касательной плоскости П, а
совокупность точек всех прямых E0.33), проходяпа;их через
точки окрестности V, образуют искомую пространственную
окрестность W той же точки (Xq, z/q, Zq). П
Из доказанной леммы следует, что при локальном
изучении поверхности, заданной явным представлением E0.31), в
окрестности U точки (Xq, i/q) можно за новую координатную
плоскость независимых переменных взять касательную плос-
J77
кость к данной поверхности в точке (Xq, г/д, 2q), Zq = fix^, у^).
При этом в некоторой окрестности точки (Xq, i/q, Zq) для
поверхности снова получится явное представление. Параметры
поверхности, конечно, изменятся, но новая область
изменения параметров получится проектированием параллельно оси
Oz на касательную плоскость некоторой окрестности точки
(^0' ^о) ^^ плоскости переменных х, г/. Это преобразование
взаимно-однозначно и взаимно бесконечно дифференцируемо
(оно линейно) и поэтому для некоторой окрестности точки
(^0' ^0' ^о) ^^ поверхности является допустимым
преобразованием старых параметров, декартовых координат х, г/, в
новые — декартовы координаты на касательной плоскости.
50.7. Первая квадратичная форма поверхности
Зафиксируем какое-либо векторное представление г = г(и, v),
(и, v)eD данной гладкой поверхности и рассмотрим
касательную к ней плоскость в некоторой ее точке. Как мы видели,
векторы г^ и Гу образуют в этой плоскости базис. Векторы, лежа-
па;ие в касательной плоскости, будем обозначать символом dr, sl
их координаты относительно базиса г^ и г^ — через du и dv*.
Таким образом,
dr = r^du + r^du.
Найдем квадрат длины вектора, лежапа;его в касательной
плоскости, выраженный через координаты естественного
базиса г^ и Гу (в линейной алгебре это выражение обычно
называется основной метрической формой рассматриваемого
пространства, в данном случае плоскости):
|(irp = dr^' = (r^du + r^dv)^ = r^du^ + 2 rj-^dudv + r^dv^.
Введем следуюгцие обозначения:
E = rlF = r^r^,G = r^; E0.41)
тогда
\dr\^ = Edu^ + 2Fdudv + Gdv^. E0.42)
* Это обозначение естественно, так как если вектор в касательной
плоскости является касательным к некоторой кривой E0.22) на
поверхности, то при соответствуюпдем выборе параметра вектор dr является
дифференциалом вектора E0.22) и, следовательно, для него
выполняется равенство E0.23).
J78
ОпреАеАеи]леМ. Квадратичная форма Edu^ + 2Fdudv + Gdv^
называется первой квадратичной формой поверхности.
Посмотрим, как она меняется или, что то же самое, как
меняется ее матрица
при переходе к другому
представлению поверхности (см. формулы E0.26)). Как известно
(см. E0.28)), при этом базисы в рассматриваемой плоскости
преобразуются с помопа;ью матрицы
Г Фи ¥и\
Следовательно, координаты векторов преобразуются с по-
мопа;ью транспонированной матрицы, т. е. матрицы Якоби
J_Гфu Ф.\
Если матрицу первой квадратичной формы E0.42) при
представлении поверхности г = г(и, v) обозначить через А,
а при представлении р = р(и^, v-^) — через А-^, т. е.
Е
F
F
G
Е
G
А
Г^1
F,
F^^
G,
^1
Pi
^1
9u^9v^^
G,
pI
TO, как известно из курса линейной алгебры, для первой
квадратичной формы поверхности, как и вообгце для всякой
квадратичной формы, А = J*A^J, где через J* обозначена матрица,
транспонированная с матрицей Якоби J,
Отсюда для соответствуюгцих определителей имеем
Е F
F G
_
Ег
Fi
Fi\
G,\
Ф»
^и
Ф.
¥^
ИЛИ
EG-F^ = (E^G^ - Ff)
Э(^1, i^i)
E0.43)
д{и, v)
Заметим, что по самому своему определению первая
квадратичная форма положительно определена (действительно,
если du^ + dv^ > О, т. е. dr ^ О, то \dr\^ > 0), поэтому по
критерию Сильвестра ее дискриминант положителен: EG -
- F^ > 0. В силу же отсутствия особых точек, выполняются
неравенства г^ ^ О, г^ ^ О, поэтому из определения
коэффициентов Е H.G E0.17) непосредственно следует, что ^ > О и G > 0.
579
Если известна первая квадратичная форма поверхности,
то можно, даже не располагая уравнением поверхности и не
зная ее формы, репхать ряд относяпа;ихся к ней задач,
например находить длины лежапа;их на ней кривых и углы между
ними, вычислять плогцадь частей поверхности. Совокупность
всех свойств поверхности, которые можно установить,
исходя из одной лип1ь первой квадратичной формы, называется
внутренней геометрией поверхности. К рассмотрению
подобных задач мы и перейдем.
50.8. Кривые на поверхности,
вычисление их длин и углов между ними
Рассмотрим непрерывно дифференцируемую кривую E0.22),
лежагцую на данной поверхности E0.18). Предположим, что
отсчет длины дуг s = s(t) на кривой производится в направле-
ds
НИИ возрастания параметра, т. е. что — > 0. Как известно, в
ds
этом случае (см. п. 16.5) —
, откуда ds = \dr\;
следовательно (см. E0.42)),
ds^ = \dr\^ = dr^ = Edu^ + 2Fdudv + Gdv^,
поэтому
dt ti \dt ) dtdt [dt
Таким образом, для длины L кривой E0.22) получаем формулу
Перейдем теперь к вычислению углов между кривыми на
поверхности.
Определение 18. Если две кривые пересекаются в некоторой
точке, то углом между ними в этой точке называется
угол, образованный их касательными в указанной точке
{если, конечно, эти касательные существуют).
Пусть две гладкие кривые, лежагцие на рассматриваемой
поверхности, пересекаются в некоторой точке. Обозначим
дифференциалы их представлений в этой точке
соответственно через dr и Ъг, а коэффициенты разложений по векторам г^
и Гу — через du, dv и Ъи, bv; тогда
dr = r^du + r^dv, Ъг = rj)u + r^bv.
~580
Поэтому если ф — искомый угол между кривыми, т. е. между
векторами dr и 6г, то
cos ф ■■
drbr
Edubu + Fjdubv + dvbu) + Gdvbv
1^И 1^И jEdu'^ + 2Fdudv + Gdv^jEbu^ + 2Fbubv + Gbv^
УПРАЖНЕНИЕ 2. Доказать, что, для того чтобы координатные и- и
у-линии на поверхности были ортогональными, необходимо и
достаточно, чтобы всюду на поверхности выполнялось равенство F = 0.
50.9. Площадь поверхности
Пусть непрерывно дифференцируемое векторное
представление г(и, v) рассматриваемой гладкой поверхности S определено
на замыкании D квадрируемой области D. Рассмотрим
разбиение Т^ плоскости переменных и и v на. квадраты некоторого
ранга k. Из квадрируемости области следует ее
ограниченность, поэтому замкнутая область D окажется покрытой
конечным числом квадратов Q. ранга k. Пронумеруем
каким-либо образом все непустые пересечения этих квадратов с
замкнутой областью D и обозначим их через Е., i= 1, 2, ,,, , i^. Тогда
T = {E,:E, = Q,nD^0, Q,e Т„ /=1,2, ... , /J
образует разбиение замкнутой области D (определение
разбиения см. в п. 44.3).
Рассмотрим множества Е., которые представляют собой
полные замкнутые квадрата, лежагцие в области D (при
достаточно малой мелкости разбиения т такие непустые
множества Е- всегда супа;ествуют; почему?). Совокупность всех
указанных множеств Е. обозначим через tCD) (ср. с п. 44.3).
Возьмем какой-либо квадрат Е.ет(дВ) (рис. 86). Пусть
длина его стороны равна h, а Р- — одна из его верп1ин. Тогда
при переходе от верп1ины Р- к соседним
верп1инам радиус-вектор г(и, v) с
точностью до бесконечно малых более высокого
порядка, чем Л, получит прирапа;ения,
равные по абсолютной величине
соответственно числам \r^h\ и \r^h\, так как
^1
г(и -\- h, и) - г(и, и) = rji + о(Л),
г(г/, V + К) - г(и, v) = r.h + o(h).
Pi
Et
h
\
'
1
Рис. 86
581
г I _ При определении плопа;ади
поверхности будем образы квадратов
Е.ет(дВ) заменять прямолинейными
параллелограммами, построенными
на векторах r^h и r^h (рис. 87). Най-
y-cons д^^ плогцадь такого параллелограм-
^ ма. Обозначив ее через Аа., получим
у
Аа^ = \rji X r^h\p_ = \r^ X r^h\ph^ =
P-- ^' = |r, X r^hlp^^E,
Функции r^ и Гу непрерывны на замкнутой квадрируемой
области D; поэтому
lim £ Aa-|||r„xrjdudi;, E0.44)
где |т|, как всегда, обозначает мелкость разбиения т. Очевидно,
условие, что мелкость разбиения |т| стремится к нулю,
равносильно тому, что ранги k квадрильяжей плоскости, из
которых мы исходили, стремятся к бесконечности.
Для доказательства справедливости равенства E0.44)
достаточно заметить, что при произвольном выборе точек
Р.е Е.ех, / = 1, 2, ... , справедливо равенство
lim ^ Аа, = lim ^ \г^ X r^h\p[iE, = \\\г^ X rjdudv. E0.44)
Действительно, во-первых, предел интегральных сумм
интегрируемой функции не зависит от выбора в данном случае
точек Р-еЕ-ех, sl, во-вторых, выбрасывание из интегральных
сумм слагаемых, соответствуюпа;их множествам Е.ех, не вхо-
дяпа;их в tCD), иначе говоря, элементам разбиения т, пересе-
каюпа;ихся с границей dD области D, т. е. пересекаюпа;ихся с
множеством меры нуль, не влияет, как известно (см. п. 44.3),
на величину предела интегральных сумм, в данном случае на
величину предела E0.44).
Определение 19. Предел E0.44) называется площадью или
мерой \xS поверхности S:
1^1^ о E.exidD)
Для вычисления плогцади поверхности из E0.44)
непосредственно получается формула
[iS= \\\r^XrJdudv. E0.45)
582
Запигаем ее в другом виде, выразив подынтегральное
выражение через коэффициенты первой квадратичной формы.
Прежде всего заметим, что для любых векторов а и Ь справедливы
формулы ^ ^
|а X Ь| = |a||b|sin аЪ, аЪ = |a||b|cos аЪ,
где аЪ — угол между векторами а и Ь. Возведем в квадрат и
сложим эти формулы: , ,„ „ „ „
|а X Ь|2 +(аЬ)^ = а^Ъ^
(это равенство называют тождеством Лагранжа). Отсюда
следует, что
К X '•J' = ^1^1 - (v.)' = EG- F\ E0.46)
поэтому формула E0.45) может быть записана также в виде
\}iS = \\jEG-F^'dudv, E0.47)
D
Иногда для краткости записи выражение dudv
обозначается символом dS:
dS = JeG - F^dudv E0.48)
и называется элементом площади поверхности. Применяя
это обозначение, формулу E0.47) можно переписать в виде
\18= \\dS.
D
Покажем, что величина плопа;ади поверхности не зависит
от выбора ее представления (при этом рассматриваются только
представления, заданные на замкнутых квадрируемых
областях). Перейдем к другому представлению р = р{щ, v^ данной
непрерывно дифференцируемой поверхности, которое задано
на замыкании Di квадрируемой области D^ и, следовательно,
для которого преобразование E0.26) параметров и, v в
параметры и^, v-^ является регулярным отображением D на Di.
В новой системе координат рассмотрим интеграл
Dl
Для сравнения его с интегралом E0.47) выполним замену
переменных E0.26), что возможно, так как все предпосылки
теоремы 2 п. 46.3 в данном случае выполнены. Использовав
E0.43), получим
|Э(Ф, \|/)|
D1 D1
liS^ = l\ JF^D,-Ffdu,dv, = \ \ JE^G,-Ff
Dl
\\ jEG-F^dudv = [iS.
д{и, v)
\dudv <
E0.43)
<
E0.43)
Dl
583~
Таким образом, действительно, величина плопа;ади
поверхности не зависит от выбора ее представления.
Найдем выражение для плопа;ади поверхности, имеюпа;ей
явное представление г = f(x, г/), (х, y)eD. В этом случае и =
= X, V = у, г = (х, у, f(x, у)) и, следовательно (см. формулы
E0.21)),
г„ = A,0,4), г, = @,1,4),
£ = г2 = 1 + /|, F = r^r^ = fjy, G = r2 = l + /2, E0.49)
EG-F^ = {\ + /2)A + ф - flfl = 1 + /2 + /2.
D
УПРАЖНЕНИЕ 3. Доказать, что площадь поверхности вращения,
определенная в п. 28.4, совпадает с площадью этой поверхности,
определенной в настоящем пункте.
50.10. Ориентация гладкой поверхности
В этом параграфе для наглядности будем считать, что в
пространстве выбрана правая система координат. Это означает
следуюгцее. Пусть i, j л k — единичные орты координатных
осей. Если смотреть из конца вектора k на плоскость хОу, то
вектор i надо повернуть на угол 7г/2 против часовой стрелки,
чтобы он совпал с вектором /. В этом случае говорят также,
что упорядоченная тройка векторов i, / и fe согласована по
«правилу niTonopa».
Аналитический аналог наглядного подхода к понятию
правой и левой системы координат можно сформулировать,
например, следуюпа;им образом: что в пространстве точек (х, г/, z)
рассматриваются только такие упорядоченные базисы е-^, е^, е^,
которые получаются из упорядоченного базиса i = A; 0; 0),
/ = @; 1; 0), k = @; 0; 1) (называемого по определению
«правым») с помопа;ью матриц, имеюпа;их положительный
определитель (точнее, равный 1). Таким образом, если
^т = ^т1^^^т21 ^^mS^^ m = 1, 2, 3
является базисом, задаюпа;им правую систему координат, то
^11 ^12 ^13
^21 ^22 ^23
^31 ^32 ^33
584
Пусть S — гладкая поверхность (см. определение 16). Это
означает, что всякое ее векторное представление г = г(и, и),
(и, v)eD, непрерывно дифференцируемо и г^ X г^ ^ О на
замкнутой области D. Следовательно, в каждой точке
поверхности S определен нормальный единичный вектор
'''''''' E0.50)
г„хг
являюгцийся непрерывной функцией на D. Кратко это
обстоятельство выражают, говоря, что на поверхности S сугцеству-
ет непрерывная единичная нормаль.
Определение 20. Всякая непрерывная единичная нормаль v =
= v(z/, v), (и, v)eD, гладкой поверхности S = {г(и, v); (и, v)eD}
называется ориентацией поверхности S,
Очевидно, что если вектор v является ориентацией
поверхности aS, то и вектор -V также является ориентацией той же
поверхности, и легко показать, что других ориентации нет.
УПРАЖНЕНИЕ 4. Доказать, что поверхность может иметь только две
ориентации.
Одна из двух ориентации v или -v (произвольно
выбранная) называется положительной, sl другая — отрицательной.
Таким образом, понятие положительности и
отрицательности ориентации в этом смысле не определяется однозначно
самой поверхностью. Положительная и отрицательная
ориентации поверхности называются противоположными ориента-
циями этой поверхности.
Для определенности в дальнейгаем для гладкой
поверхности, заданной фиксированным векторным представлением
г = г(и, v), (и, v)eD, за положительную ориентацию будем
принимать всегда вектор E0.50).
Подчеркнем, что непрерывность нормали v
рассматривается относительно переменных и, v, а не относительно
пространственных переменных х, у и 2, Если поверхность имеет
кратные точки, то может случиться, что в точке
пространства, являюпа;ейся носителем разных точек поверхности, может
оказаться несколько различных нормалей.
Чтобы при регулярном преобразовании параметров г/ и i;
у поверхности сохранялась ориентация, необходимо
дополнительно потребовать, чтобы якобиан этого преобразования был
положительным. Действительно, для преобразования пара-
585
метров и^ = ф(г/, v), v-^ = \|/(г/, v) из формул E0.28), как мы
видели (см. замечание в конце п. 50.5), следует, что
_ Э(ф, \|/)^
г Хг =
(Ри, XP.J.
и, следовательно, если якобиан ..у' ^:^ положителен, то векто-
д{и, v)
ры г^ХГуИр^ Хр^ направлены в одну и ту же сторону, а если
он отрицателен, то в противоположные.
Таким образом, для поверхностей, у которых выбрана
ориентация, допустимыми преобразованиями будем считать
такие непрерывно дифференцируемые преобразования, у
которых якобиан положителен.
Поверхность S с положительной ориентацией будем
обозначать aS+, а с отрицательной — S~.
Подчеркнем, что всякая гладкая параметрически
заданная поверхность всегда ориентируема, т. е. у нее всегда су-
гцествует ориентация.
Если гладкая поверхность S имеет явное представление
2 = f(x, у), (х, y)eD, D — область на плоскости переменных
X, г/, то
i i к
г. X г ,
1 О
О 1
-fx^-fyi ^^^
откуда, в силу формулы E0.50),
J^^IT
'у
Ji + fl + ff JiTJl
'у
E0.51)
и, следовательно (рис. 88),
/\ 1
cos vfe —
Д^
'у
>о.
т. е. ориентация v образует острый
угол с осью 2. Это означает, что
вектор V направлен вверх от
поверхности aS. Поэтому в этом случае
поверхность aS, ориентированная
единичной нормалью V, называется верхней
стороной поверхности S и обознача-
ется aS, а ориентированная противо-
586
положной нормалью - v (направленной вниз) — ее нижней
стороной J которая обозначается S.
Определение 21. iloeepxTiocmb, у которой фиксирована одна
из ее ориентации, называется ориентированной.
Данное выпхе определение ориентации, разумеется, не
переносится на негладкие поверхности. Примером
поверхности, не дифференцируемой в одной точке, на которой уже
нельзя выбрать непрерывную нормаль, является конус:
2 = л/л:2 + у2^ ^2 + ^2<^2^ E0.52)
в этом случае векторное представление имеет вид
г(х, у) = (х, г/, л/х2~Т^);
следовательно.
г = 1;0;—^, г = 0;1;
У
л/х2 + г/2 ^ ^ ^ л/х2 + г/2
Пределы lim ^ и lim ^ не супа;еству-
(X, I/) ^ (О, 0) 7x2 + ^2 (X, I/) ^ (О, 0) 7x2 + ^2
ЮТ (почему?), поэтому и единичная нормаль
kxX^z/l ^ 72(х2 + г/2)' 72(х2 + г/2)' 72^
не имеет предела при (х, г/) ^ (О, 0). Следовательно, на конусе
E0.52) нельзя выбрать нормаль, непрерывную на
^ = {(х, г/):х2 + г/2<а2}.
Простым примером негладкой поверхности aS, на которой
сугцествует целая линия, вдоль которой нормали при любом
их выборе терпят разрыв, является часть двугранного угла,
изображенная на рис. 89. Указанной линией на этой
поверхности является отрезок АВ.
Замечание 1. На первый взгляд может показаться,
что понятие ориентации поверхности не
является обобгцением понятия ориентации
плоской кривой. Это, однако, не так. Если
гладкая кривая Г = {r(s); О < s < aS}
ориентирована в направлении возрастания длин
ее дуг S, то в каждой ее точке определен
единичный касательный вектор t = -^, ко-
ds
587
торый, очевидно, является непрерывной на кривой Г векторной
функцией. Поставим в соответствие вектору t вектор п, полу-
чаюпа;ийся из вектора t поворотом против часовой стрелки на
прямой угол. Вектор п является единичным нормальным к
кривой Г вектором, непрерывно меняюпа;имся вдоль нее. Таким
образом, ориентация гладкой кривой порождает выбор
единичной непрерывной вдоль этой кривой нормали.
Верно и обратное: если на гладкой кривой задана
непрерывная единичная нормаль, то по этой нормали, в силу
указанного Bbinie соответствия, однозначным образом
определяется непрерывный на кривой единичный касательный к ней
вектор, который, в свою очередь, однозначно задает
направление возрастания параметра s, т. е. ориентацию кривой.
Замечание 2. Понятия «поворот против часовой
стрелки», «слева», «справа», «правило гатопора» и т. п. не являются,
конечно, математическими понятиями, но они очень удобны
при регаении конкретных задач.
Подобно ориентации кривой на плоскости (см. п. 16.4),
можно дать определение ориентации поверхности в
математических терминах, при условии, что в пространстве
фиксирована прямоугольная декартова система координат, т. е.
задан ортонормированный базис е-^, е^, е^ (тем самым, образно
говоря, в самом пространстве уже задана «ориентация»).
В этом случае положительной {отрицательной)
ориентацией гладкой поверхности S = {г(и, v); (и, v)eD} называется
всякая непрерывная на поверхности S упорядоченная тройка
вектор-функций а^, аз, а^, т. е. непрерывных на замкнутой
области D функций а^(и, v), a^iu, v), а^(и, v), (и, v)e D таких,
что векторы а^(и, и) и а2(и, и) являются
линейно-независимыми касательными к поверхности S в точке г(и, v), а не
нулевой вектор а^ (и, v) — ортогонален к ним, и определитель
матрицы перехода от векторов а^, а^, а^ к векторам базиса
положителен (отрицателен).
Например, тройка векторов г^, г^, г^ X г^ задает
положительную, а тройка векторов г^, г^, - (г^ X г^) —
отрицательную ориентацию гладкой поверхности S при заданной
системе координат в пространстве.
50.11. Склеивание поверхностей
Данное выпхе определение параметрически заданной
непрерывной поверхности не охватывает все то, что интуитивно
входит в понятие поверхности. Так, можно показать, что по-
~588
верхность шара не является носителем какой-либо
непрерывной параметрически заданной поверхности без кратных
точек. Считать же, что поверхность niapa имеет кратные точки,
представляется неоправданным усложнением. Супа;ествуют
различные пути для преодоления этого неудобства. Мы
выберем способ, основанный на склеивании конечного числа
поверхностей. Склеивание поверхностей естественным образом
возникает при рассмотрении самых простых задач.
Например, боковую поверхность цилиндра естественно
рассматривать как результат склеивания противоположных сторон
прямоугольника, полную поверхность цилиндра — как результат
склеивания его боковой поверхности и двух оснований,
полную поверхность конуса — как результат склеивания его
боковой поверхности с основанием и т. д.
Перейдем к точным определениям. Будем говорить, что у
поверхности S = {г = г(и, и); (и, v)eD} ее край (см. п. 50.2)
является кривой, если граница dD области D является кривой
(точнее, носителем кривой): dD = {u(t), v(t); а < t < b}, В этом
случае край Эа8 поверхности S можно также рассматривать
как кривую Эа8 = {r(u(t), v(t)); а < t < b}.
Определим операцию склеивания поверхностей для
поверхностей, края которых являются кривыми.
Пусть заданы поверхности aS- = {ri(u., v.); (и., v.)eDi}, края
Эа8. которых суть кривые, т. е. границы dD., областей D.,
являются кривыми:
u. = u.(t.), v. = v.(t.); a.<t.<b., /=1,2, ...,m.
Тогда края поверхностей Эа8. будут представлять собой
кривые Г. = {r.(u.(t.), v.(t.)); а. < t. < b.}. Пусть для некоторых
пар (/, у), /, у = 1, 2, ... , т, / ^ у, задано конечное число
отрезков [afj, bfj] ^ [а., Ь.], afj < bfj, и отрезков [af^, bfj ^ [а^., bj],
^fi ^ ^fi' ^ ^ 1? 2, ... , n.j= Tij., причем как отрезки [af, bfj],
так и отрезки [а^^, b^J попарно не имеют обпа;их внутренних
точек, а также гомеоморфизмы ф^ : [а^^, bf ] -^ [^ну ^fj'
называемые склеивающими гомеоморфизмами. При этом для
любого t-e [af, bfA имеет место «склеивание»:
г,{щЦ^), v,{t,)) = r.iu.m>fjit^)), i>/9,^(f,)). E0.53)
Обозначим через Tf- кривую с представлением
589
Кривые rfy называются кривыми склейки или кривыми,
по которым производится склеивание.
Очевидно, что, в силу E0.53), отображение
r = r.(u.(9'^'/*;))' t^^hH^
также является представлением кривой Г^, ибо
гомеоморфизмы ф^ представляют собой допустимое преобразование
параметра для кривой rf.
Будем предполагать, кроме того, что при у ^ у отрезки
[al, &f^] и [аК, &L], fe = 1, 2, ... , Пу, Z = 1, 2, ... , п^.,
также не имеют обгцих внутренних точек, следовательно,
каждый конец отрезка [а^^, Ъ^Л может принадлежать егце не
более чем одному отрезку Vdlyy ЬЬ]. Это условие означает, что
каждая кривая склейки Ff является частью только двух
кривых Г. и Г , образуюгцих края поверхностей aS- и aS .
Поверхности aS- и aS называются соседними, если они
склеиваются по крайней мере по одной кривой Г^^. Система
поверхностей aS^, ... , aS^ называется связной, если для
любых ее поверхностей aS и aS сугцествуют такие поверхности
aS,- , aS,-,... , aS,- , что aS,- = aS„, aS,- = aS^, и каждая поверхность aS,-
'^l '^2 r 1 ^ r ^ V
является соседней с aS, , т. е. склеена с ней по одной или
Ч +1
нескольким кривым, v = l, 2, ... ,г-1.
Определение 22. Связная система поверхностей aS^, S^j ... , S^
называется поверхностью, склеенной из поверхностей
S-^, ... , aS^, и обозначается S = {aSJ.
Это определение, несмотря на свою формальную
громоздкость, имеет, очевидно, простой геометрический смысл.
Образно говоря, склеенная поверхность S = {S.} представляет
собой поверхности aS^, ... , aS^, у некоторых пар которых aS-, aS
отождествлены (склеены) точки, лежапа;ие на кривых Г^ и
отображаюпа;иеся друг в друга при гомеоморфизмах ф^у, — в
этом и состоит условие склеивания E0.53). Безусловно, как
отмечалось, кроме того, предполагается, что от каждой
поверхности aS. можно через конечное число niaroB перейти к
любой другой поверхности aS^, переходя каждый раз с
некоторой поверхности на одну из соседних с ней.
^90
Если S = {S-} склеенная поверхность, то совокупность всех
дуг, являюгцихся такими частями кривых dS-, что никакие
точки этих частей, кроме, быть может, концевых, не
склеиваются ни с какими точками других кривых Эа8., называется
краем Эа8 склеенной поверхности S,
Можно показать, что, объединяя соответствуюгцим
образом указанные части кривых Эа8., принадлежагцие краю
поверхности S = {aS.}, можно получить конечное число
замкнутых кривых (контуров). Иначе говоря, край склеенной
поверхности состоит из конечного числа замкнутых
контуров.
Примером склеивания поверхностей служит склеивание
в сферу х^ -\- у^ -\- 2^ = 1 двух полусфер 2 = Jl - х^ - г/^ и
2 = -Jl - х^ - г/^, х^ + г/^ < 1, по их краю, т. е. по окружности
х^ -\- у^ = 1, 2 = 0. Задавая уравнение этой окружности в
параметрическом виде X = cos t, у = sin t, 2 = О, О < t < 2п, в
качестве склеиваюгцего гомеоморфизма ф : [О, 2%] -^ [О, 2%]
можно взять тождественное отображение отрезка [О, 2%] на
себя.
С помогцью склеивания гладких поверхностей можно
определить понятие кусочно-гладкой поверхности.
Определение 23. Поверхность S = {S.}, склеенная из гладких
поверхностей S-^, ... , aS^, называется кусочно-гладкой
поверхностью.
Поверхность кругового цилиндра, поверхность
параллелепипеда дают примеры кусочно-гладких поверхностей.
Прямой же круговой конус E0.27) нельзя разбить на конечное
число склеенных гладких частей, поэтому он не является
кусочно-гладкой поверхностью в смысле определения 23.
Можно обобпа;ить операцию склеивания поверхностей таким
образом, что при формальном сохранении определения
кусочно-гладких поверхностей для такой обобгценной операции
склеивания в класс кусочно-гладких поверхностей попадут
уже и конические поверхности. Мы не будем на этом
останавливаться и предоставим проделать это в случае
необходимости самому читателю.
Поверхность, склеенная из конечного множества гладких
поверхностей в гаироком смысле (см. п. 50.5), называется
кусочно-гладкой в широком смысле.
~591
50.12. Ориентируемые
и неориентируемые поверхности
Определим понятие ориентации для поверхностей, склеенных
из параметрически заданных поверхностей.
Определение ориентации с помопа;ью выбора непрерывной
единичной нормали на поверхности в случае поверхности,
склеенной из параметрически заданных поверхностей,
оказывается недостаточным даже при отсутствии кратных точек
и понимании непрерывности нормали как ее непрерывной
зависимости от точек пространства (а не параметров
склеиваемых поверхностей). Это связано с возможным нарупхением
гладкости поверхности на кривых, по которым происходит
склеивание.
Например, часть поверхности двугранного угла,
изображенную на рис. 89, можно рассматривать как результат
склеивания двух прямоугольников. Если стремиться по разным
граням к одной и той же точке на ребре этого угла, то
пределы соответствуюпа;их единичных нормалей получатся разные.
Другим примером кусочно-гладкой поверхности, не являю-
па;ейся гладкой, является поверхность куба, получаюпа;аяся,
очевидно, склейкой его граней (гладких поверхностей) по их
ребрам. Ясно, что на поверхности куба нет непрерывной
единичной нормали: в точках ребер она даже не супа;ествует.
Ниже будет дано такое определение ориентируемой
поверхности, при котором указанные поверхности являются
ориентируемыми.
Отметим, что при склеивании поверхностей даже «гладким
образом» (т. е. когда для любой кривой, по которой
произведено склеивание, в каждой ее точке можно так выбрать
единичную нормаль, что она будет пределом соответствуюгцим
образом выбранных в окрестности этой точки единичных нормалей
двух склеиваюгцихся поверхностей) у склеенных поверхностей
могут возникнуть качественно новые особенности: в отличие от
параметрически заданных поверхностей в этом случае не
всегда на всей поверхности можно выбрать непрерывную
единичную нормаль. Примером такой поверхности является так
называемый лист Мёбиуса"^.
Его можно получить, взяв прямоугольную полоску
бумаги ABCD, один раз перекрутив ее вокруг оси симметрии MN,
параллельной сторонам ВС и AD, и склеив ребро АВ с CD
' А. Ф. Мёбиус A790—1868) — немецкий математик и астроном.
^92
в
Е
М
-N
D
Рис. 90
(рис. 90). Правда, при таком способе образования лист
Мёбиуса получается в результате склеивания поверхности самой с
собой. Однако нетрудно получить его и склеиванием,
описанным в определении 22, двух прямоугольников AB^F и FECD.
Одной из характерных особенностей листа Мёбиуса
является то, что у него имеется лигаь одна «сторона»: его
невозможно, как, например, боковую поверхность цилиндра, покрасить,
скажем, с одной стороны красной, а с другой — синей
краской. Кроме того, на листе Мёбиуса нельзя выбрать единичную
нормаль, которая являлась бы непрерывной функцией точки
пространства.
Все приведенные соображения делают естественным
попытаться дать такое определение ориентации поверхности,
для которого поверхности, например, типа поверхности
параллелепипеда оказались бы ориентированными, а
поверхности типа листа Мёбиуса — неориентированными.
Обратим внимание на то, что лист Мёбиуса может
являться носителем параметрически заданной гладкой поверхности
с кратными точками, и эта поверхность, как всякая гладкая
параметрически заданная поверхность, будет
ориентированной, имея в кратных точках своего носителя по две нормали.
Это, конечно, не имеет никакого отногаения к
неориентируемости самого листа Мёбиуса.
50.13. Другой подход
к понятию ориентации поверхности
Опип1ем другой подход к понятию ориентации, основанный
на склеивании поверхностей, края которых суть кривые.
Пусть S = {г = г(и, v); (и, v)eD} — гладкая поверхность,
краем которой является кривая. Положительная ориентация
593
кривой dD = {u(t), v(t); a < f < Ь} (т. е. ориентация против
часовой стрелки на плоскости и, v с правой системой
координат), в силу отображения r(u(t), v(t)), а < t < b, порождает
вполне определенную ориентацию края Эа8 поверхности S,
Эта ориентация края Эа8 поверхности S называется
согласованной с ориентацией
\г,, X г„
(см. определение 20) поверхности S,
Естественность этого определения можно пояснить сле-
дуюгцим образом. Рассмотрим явно заданную поверхность
S : 2 = f(x, у), (х, у)е D. Для нее (см. E0.51))
V =
f. и
Ji + n + ff VI + f'y + f^' Ji + n + f^)
Следовательно, cos vfe = — > 0, т. e. вектор нормали v
ji+n + n
образует с осью Oz острый угол и поэтому согласован с
положительной ориентацией края Эа8 поверхности S по правилу
niTonopa: ориентация контура Эа8 соответствует направлению
врагцения ручки niTonopa, а направление нормали v —
движению самого niTonopa.
Очевидно, что если ориентация v рассматриваемой
гладкой поверхности S согласована с ориентацией ее края Эа8, то
ориентация -v согласована с противоположной ориентацией
кривой Эа8. Таким образом, задание ориентации v гладкой
поверхности равносильно заданию ориентации кривой Эа8, яв-
ляюпа;ейся ее краем. Поэтому ориентированный край Эа8
гладкой поверхности S будем, так же как и непрерывную
единичную нормаль V, называть ориентацией поверхности S.
Данное определение наглядно и удобно для конкретных
приложений. Его математическая супа;ность состоит в том,
что ориентация края гладкой поверхности является
согласованной с ее ориентацией, если тройка векторов: касательный
вектор к краю, который является кривой, нормальный к
нему вектор, направленный в сторону поверхности (это понятие
нетрудно определить), и вектор, задаюпа;ий ориентацию
поверхности (т. е. единичная непрерывная на поверхности
нормаль) в точках края ориентированы так же, как координат-
^94
ный репер в пространстве, т. е. преобразуются в него
матрицей с положительным определителем.
Для произвольной параметрически заданной поверхности,
т. е. без предположения о какой-либо ее гладкости, краем
которой является контур, его ориентацию примем за исходное
определение ориентации самой поверхности.
Пусть aS^ и aS2 — две поверхности, у которых края —
кривые, и пусть эти две поверхности склеены (в смысле
определения 22) по кривым у^, ... , у^, являюгцимся частями краев
поверхностей aS^ и аЗз- Ориентации Эа8^ и ЭаЗз поверхностей aS^
и aS2 называются согласованными, если каждая из них
порождает на склеиваюгцихся кривых у^, ... , у^,
противоположные ориентации.
Определение 24. Поверхность S, склеенная из поверхностей
aS^, ... , aS^, называется ориентируемой, если существуют
такие ориентации dS-^, ... , Эа8^ краев поверхностей S-^, ... , aS^,
что для любых соседних поверхностей S- и aS их ориентации
dS. и dS- согласованы,
^ J
Совокупность таких ориентации, если она сугцествует,
называется ориентацией поверхности S.
Если указанной совокупности ориентации краев Эа8.
поверхностей aS-, / = 1, 2, ... , т, не сугцествует, то
поверхность S называется неориентируемой.
Если ориентации краев Эа8^, ... , Эа8^ являются
ориентацией поверхности S = {S-}, то совокупность противоположных
их ориентации также является ориентацией поверхности aS,
называемой противоположной данной.
Можно показать, что если поверхность S ориентируема, то
никаких других ориентации, кроме двух указанных, у нее
нет. Одна из этих двух ориентации (произвольно какая)
обычно называется положительной, а другая — отрицательной.
Аналогично ранее рассмотренному в п. 50.10 случаю
ориентируемая поверхность, у которой фиксирована одна из ее
ориентации, называется ориентированной. При этом та из
ориентированных поверхностей, ориентация которой названа
положительной, обозначается aS+, а противоположно
ориентированная — S~,
Край ориентированной склеенной поверхности S = {S-},
как край всякой склеенной поверхности, состоит, согласно
^95
сказанному выше, из конечного числа замкнутых контуров.
Каждый из этих контуров, в свою очередь, представляет
собой объединение конечного числа кривых, каждая из
которых является частью одного из контуров dS-, а именно такой
частью, что все ее точки, кроме, быть может, концевых, не
склеиваются с точками других краев Эа8 . Поэтому заданная
согласованная ориентация склеенной ориентируемой
поверхности S = {S-} порождает определенные ориентации (т. е.
порядки точек) на указанных кривых. Можно показать, что эти
ориентации, вместе взятые, составляют ориентации всех
контуров, входягцих в край Эа8 склеенной поверхности S.
Совокупность этих ориентации контуров, составляюгцих край Эа8
поверхности aS, называется ориентацией этого края,
порожденной заданной ориентацией поверхности aS, или, что то же,
согласованной с ней.
Обратим внимание на то, что как в определении
склеивания поверхностей в п. 50.11, так и в определении 24
ориентации поверхности не предполагалось даже дифференцируемос-
ти склеиваемых поверхностей aS^, ... , aS^. Поэтому
определение 24 ориентируемости поверхности можно использовать и
для поверхностей, склеенных из поверхностей без
каких-либо предположений об их дифференциальных свойствах, если
только под их ориентацией понимать ориентации их краев,
являюпа;ихся кривыми.
Если поверхность S склеена из гладких поверхностей
aS^, ... , aS^, то для задания ее ориентации можно задать на
каждой поверхности aS^, ... , aS^ непрерывные единичные
нормали таким образом, чтобы согласованные с ними
ориентации Эа8. краев поверхностей aS- были согласованы между собой
в смысле определения 24, т. е. являлись ориентацией
поверхности S (рис. 91).
Для того чтобы при таком задании ориентации узнать,
совпадают или нет две ориентации кусочно-
гладкой поверхности, достаточно проверить
лип1ь в одной произвольной точке, в которой
супа;ествуют нормали, совпадают они или нет.
Если в ней нормали совпадают, то они
совпадают и всюду, а если они в этой точке не
совпадают, т. е. противоположны, то они и всюду
противоположны, поскольку, как выпхе
отмечалось, супа;ествуют только две ориентации за-
Рис. 91 данной поверхности.
~596
Однако в случае кусочно-гладкой поверхности уже
нельзя ввести понятие положительной ориентации, используя
заданные представления склеиваемых гладких
поверхностей и беря на них единичные нормали по формуле E0.50),
так как эти ориентации могут оказаться несогласованными.
Поэтому в случае кусочно-гладких поверхностей следует
всегда более обстоятельно оговаривать, что именно
подразумевается в данном случае под ориентациями поверхностей
aS-, / = 1, 2, ... , m, составляюпа;ими склеенную из них
поверхность S = {S-}.
Можно показать, что всякая кусочно-гладкая
поверхность, являюпа;аяся границей некоторой области трехмерного
пространства, ориентируема. При этом одна из ориентации
состоит из единичных нормалей, направленных от
поверхности в область — так называемых внутренних нормалей, а
другая состоит из единичных нормалей, направленных от
поверхности наружу от области — так называемых внешних
нормалей. Примером такой поверхности является сфера.
В качестве ее ориентации можно взять, например, единичные
нормали, направленные по радиусу от точки сферы к центру
(рис. 92).
Примером неориентируемой поверхности (в смысле
определения 24) является лист Мёбиуса.
Иногда ориентируемые кусочно-гладкие поверхности
называют также двусторонними поверхностями: они имеют
две «стороны», соответствуюпа;ие двум выборам единичных
нормалей, задаюпа;им две ее ориентации. Соответственно нео-
риентируемые поверхности называются односторонними.
Оправдание этого термина было пояснено в п. 50.12 на
примере листа Мёбиуса.
Мы не будем останавливаться на математизации всех
описанных наглядных соображений и доказательстве
высказанных утверждений. Это потребовало бы
использование методов, изучение которых
выходит за рамки настоягцего курса.
Упомянутые Bbinie без доказательства обгцие
утверждения, по сугцеству, не
используются в дальнейгаем изложении. В каждом
конкретном случае, о котором будет идти
речь, можно будет всегда непосредственно
указать, какая именно ориентация
рассматривается в данном случае. Рис. 92
~597
УПРАЖНЕНИЕ 5. Пусть заданы вектор т и кривая Г = {p(w), а < и < b}.
Цилиндрической поверхностью S с образующей Г и направляющей,
параллельной вектору т, называется поверхность, заданная представлением вида
def
г = г(и, v) = р(и) + ут, а< и< Ь, с < V < d.
Доказать, что если кривая Г — кусочно-гладкая, то и поверхность
S — кусочно-гладкая.
50.14. Кривизна кривых, лежащих на поверхности.
Вторая квадратичная форма поверхности
С помопа;ью первой квадратичной формы были получены
формулы для вычисления длин кривых на поверхности, углов
между кривыми и плопа;ади поверхности. Однако знание всех
этих величин епа;е не определяет поверхность. Например,
прямоугольник можно изогнуть так, что он будет образовывать
половину боковой поверхности цилиндра. Эта цилиндрическая
поверхность и исходный прямоугольник — разные
поверхности, однако при указанном изгибании длины кривых углы
между ними и плогцади частей поверхности сохраняются
неизменными. Вместе с тем кривизна кривых на поверхности при
таком изгибании, вообпа;е говоря, меняется: прямолинейный
отрезок может перейти, например, в полуокружность.
Дальнейп1ие локальные исследования поверхности в
окрестности заданной ее точки будем проводить, изучая всевозможные
кривые, лежагцие на поверхности и проходяпа;ие через
рассматриваемую точку, в частности, изучая кривизны этих кривых.
Пусть _
S = {г(и, V); (и, v)e D} E0.54)
— дважды непрерывно дифференцируемая поверхность и
r(uQ Vq) — ее внутренняя неособая точка. Рассмотрим кривую
на поверхности aS, заданную представлением
r(s) = riuis), vis)), О < s < S, E0.55)
где функции u(s) и v(s) дважды дифференцируемы на отрезке
[О, aS], s — переменная длина дуги кривой E0.55), u(Sq) = Uq,
v(Sq) = Vq, о <: Sq <: aS, И, следовательно, KSq) = г(и^, Vq). Будем
предполагать, что точка Ksq) является неособой для кривой
E0.55). Вспомним, что вдоль кривой выполняется равенство
dh-
ds
где п — главная нормаль кривой, а й — ее кривизна. Будем
предполагать, что k ^ 0; тогда главная нормаль п определена
однозначно.
^98
2 kn, E0.56)
Обозначим через v единичную нормаль к
поверхности E0.54) в ее точке г(и^, Vq) и
через 9 угол между вектором v и главной
нормалью п кривой E0.55) в ее точке Ksq)
(рис. 93). Тогда, умножив скалярно обе части
равенства E0.56) на вектор v, получим
ds
Заметив, что
^v = ftcose. E0.57)
Рис. 93
d^r ^ А.(—^ = —(г — -\- г —^ = г (—^ + 2г ^^ + г (—^ =
ds^ ds[ds) ds[ ""ds ''ds] ""Usj ''''dsds ''Ads]
,^du^ + 2r^^dudv + r^^dv^
E0.58)
ds^
из E0.57) получим
k cose ^5 =5,^ r,,vd.^ + ''•";;f ^^^ ^ '-'"'"'. E0.59)
E0.58)
Введя обозначения
L(u,v)^=r^^v, M(u,v)^=r^^v, N(u,v) = r^^v E0.60)
и вспомнив, что ds^ = Edu^ + 2Fdudv + Gdv^ (см. E0.44)), за-
пигаем равенство E0.59) в виде
й cos е = Ldu^ +^Mdudv + Ndv^ ^ E0.61)
Определение 25. Квадратичная форма
Ldu^ + 2Mdudv + Ndv^
называется второй квадратичной формой поверхности.
Ее коэффициенты L, М и Л/', согласно определению
E0.60), однозначно определяются в каждой точке
поверхности при заданном ее представлении и выборе к ней
единичной нормали в рассматриваемой точке (от этого выбора
зависит лип1ь знак коэффициентов L, М, N), Коэффициенты
первой квадратичной формы также однозначно определяются в
каждой точке поверхности при заданном ее представлении,
поэтому в этом случае дробь, стоягцая в правой части
формулы E0.61), зависит в данной точке поверхности только от от-
ногаения du : dv (в чем легко убедиться, разделив числитель
и знаменатель дроби на du или dv).
Для кривой E0.55) dr = r^du + r^dv, поэтому отнопхение
du : dv задает положение касательной к кривой E0.55) в точке
г (z/q, Vq), Таким образом, правая часть равенства E0.61) имеет
^99
одно и то же значение для всех кривых E0.55), проходяпа;их
через точку г(и^, Vq) и имеюпа;их одну и ту же касательную.
В левой части формулы E0.61) угол 9 между векторами п
и V зависит для данной точки поверхности от вектора
главной нормали кривой E0.55). Главная нормаль лежит в со-
прикасаюгцейся плоскости, поэтому если задана не только
касательная к кривой, но и ее соприкасаюгцаяся плоскость,
то с точностью до знака определен и cos 9 (главная нормаль
может иметь одно из двух взаимно противоположных
направлений, перпендикулярных касательной к кривой). Знак
cos 9, а следовательно, и одно из двух указанных возможных
направлений нормали определяются из формулы E0.61),
поскольку кривизна всегда положительна.
Итак, если задана касательная и соприкасаюгцаяся
плоскость кривой, лежагцей на поверхности и проходягцей через
заданную точку поверхности, то ее кривизна k однозначно
определяется из формулы E0.61):
г ^ 1 Ldu^ + 2Mdudv + Ndv^ /^q ao)
COS0 Edu^ + 2Fdudv + Gdv^ ' У - )
Иначе говоря, доказана теорема.
ТЕОРЕМА 1. Две кривые на дважды непрерывно
дифференцируемой поверхности с одними и теми же касательными и
главными нормалями во внутренней неособой точке
поверхности имеют в этой точке одинаковую кривизну, для
которой имеет место формула E0.62).
Две такие кривые имеют одну и ту же соприкасаюгцуюся
плоскость, пересечение которой с касательной плоскостью к
поверхности является касательной к кривой.
Но одну и ту же касательную и соприкасаюгцуюся
плоскость могут иметь много различных кривых, лежагцих на
поверхности. В каком-то смысле наиболее простой из них
является плоская кривая, лежагцая в соприкасаюгцейся
плоскости. Таким образом, изучение кривизны кривых, лежагцих на
поверхности, сводится к изучению кривизны плоских
кривых — сечений данной поверхности плоскостями. Напомним,
что плоская кривая полностью, с точностью до положения в
пространстве, задается своей кривизной (см. п. 17.6).
Обратим внимание на то, что мы изучаем поверхность в
окрестности неособой точки. Поэтому в замыкании некоторой
окрестности этой точки поверхность допускает явное
представление (см. п. 50.6) и, следовательно, является простой
поверхностью (см. п. 50.2). Подобным образом часть кривой в
600
замыкании некоторой окрестности неособой точки является
простой дугой (см. п. 16.2). Простые поверхности и простые
дуги однозначно определяются своими носителями, поэтому
мы здесь вместо «носитель поверхности» или «носитель
кривой» говорим просто «поверхность или кривая».
Сечения поверхности плоскостями будут рассмотрены чуть
позже, а сейчас вернемся ко второй квадратичной форме.
50.15. Свойства второй квадратичной
формы поверхности
Знание первой и второй квадратичных форм на поверхности
дает возможность вычислять кривизны кривых, лежагцих на
этой поверхности. Поэтому важно иметь удобные формулы
для вычисления коэффициентов второй квадратичной формы
поверхности: S = {г(и, v); (и, v)eD},
Если за единичную нормаль v к поверхности S в
рассматриваемой ее неособой точке взять, как обычно, вектор
г„хг„
и вспомнить (см. E0.46)), что \г^ X г J = JeG - F^, то из
формул E0.60) получим
L(u.v) = ^-L^}il^Jil^. М(ш1Л = ^'^^'''^''''''\ М(ш1Л=^-^''^''''''\ E0.63)
JeG - F^
JeG - F^ '
Л
JEG - F
где в числителе дробей стоят смегаанные произведения
векторов. Нетрудно записать эти формулы и в координатной форме.
Сделаем это для случая, когда поверхность S задается явным
представлением:
2 = f(x,y), (x,y)eU. E0.64)
Здесь и — открытое плоское множество. В этом случае (см.
E0.49)) EG - F^ = 1 + /| + /|, а так как радиус-вектор г точек
поверхности имеет вид г = (х, г/, /(х, г/)), то
V XX' ^Х'
^)-
0 0 f,.
1 0 f,
0 1 /,
'хх' ''*хг/' '*х' ^yf
('*!/!/' ^Х' '*!/) ^
0 0 f^.
1 0 f.
0 1 fy
= f .
' yy
0 0 f:cy
0 1 /,
/X!/'
601
Таким образом, в этом случае, в силу формулы E0.63),
имеем
L = ^-^ , М = ^-^ , N = tm . E0.65)
j^+n + п vi + п + п ji+n + п
Для дальнейп1его анализа второй квадратичной формы
выберем более специальную систему координат: перенесем
начало координат в рассматриваемую точку поверхности и за
плоскость переменных х, у выберем касательную плоскость к
поверхности (см. п. 50.6).
Пусть для поверхности
2 = f(x,y), (x,y)eU, E0.66)
координатная плоскость переменных х, у является
касательной плоскостью к поверхности в точке @,0) и, следовательно,
/(О, 0) = 4@, 0) = /^@, 0) = 0. E0.67)
Вторая квадратичная форма в точке (О, 0) в этом случае
принимает вид (см. E0.65))
/,/х2 + 2f,ydxdy + fyydy^ E0.68)
Т. е. совпадает со вторым дифференциалом функции / в этой
точке.
Разложим функцию / по формуле Тейлора в окрестности
точки (О, 0). В силу E0.67), получим
^ = ^(/хх@' 0)^' + 24,@, 0)ху + 4^@, 0)г/2) + о(х^ + у^),
(х,г/)-@,0), E0.69)
т. е. вторая квадратичная форма поверхности в точке (О, 0)
fxx ^^ + ^fxy^y + fyy г/^
с ТОЧНОСТЬЮ ДО ПОСТОЯННОГО множителя 1/2 равна главной
части отклонения поверхности от ее касательной плоскости при
стремлении точки поверхности к точке касания.
Формулы E0.61) и E0.69) раскрывают геометрический
смысл второй квадратичной формы.
50.16. Плоские сечения поверхности
Как мы видели, изучение кривизны кривых на поверхности
сводится к изучению кривизны сечений поверхности
плоскостями. Прежде всего покажем, что, вообгце говоря, при
сечении поверхности плоскостями действительно получаются
кривые. Выражение «вообгце говоря» добавлено, так как ука-
602
занное явление не всегда имеет место; например, при сечении
плоскости совпадаюпа;ей с ней плоскостью получается целая
плоскость, а не кривая; при сечении поверхности z = х'^ - у^'
плоскостью 2 = 0 получается пара пересекаюпа;ихся прямых:
X + у = 0, X — у = 0.
При изучении сечений поверхности ограничимся
рассмотрением только ее неособых точек и будем предполагать, что
поверхность задана явно и что плоскость переменных х, у
является касательной плоскостью к поверхности. Это не
ограничивает обгцности рассмотрений, так как локально поверхность
в неособой точке всегда имеет указанное представление (см.
лемму 1 в п. 50.6), а кривизна кривых на поверхности,
которая нас будет интересовать, является локальным свойством.
Л Е М М А 2. Если
2 = f(x,y), (x,y)eD, E0.70)
—дважды непрерывно дифференцируемая на открытом
множестве D функция, (О, 0)gD,
/(О, 0) = 4@, 0) = 4@, 0) = О E0.71)
(т, е, координатная плоскость переменных х и у является
касательной плоскостью к графику функции /) и П —
плоскость, проходящая через точку (О, О, 0) и не касающаяся в
этой точке графика S функции /, то существует такая
окрестность и точки (О, О, 0), что пересечение поверхности S
с плоскостью П, содержащееся в замыкании U окрестности U,
является дважды непрерывно дифференцируемой простой
дугой, для которой точка (О, О, 0) является внутренней точкой.
Доказательство. Уравнение плоскости П, проходягцей
через начало координат, имеет вид
Ах + Ву + С2 = 0, E0.72)
причем если эта плоскость не является касательной
плоскостью в точке (О, О, 0) к поверхности aS, т. е. не совпадает с
координатной плоскостью переменных х, у (см. E0.71)), то
коэффициенты А и Б не могут одновременно обратиться в нуль:
А2 + Б2>0. E0.73)
Подставив в формулу E0.72) выражение E0.70) для 2,
получим
F(x, у) ^=Ах + Ву + Cf(x, у) = О, E0.74)
откуда
603
Согласно условию E0.73), хотя бы одна из этих частных
производных не равна нулю. Пусть, для определенности,
F (О, 0) ^ 0. Так как, кроме того, F@, 0) .^^rr-,. О, то из
теоремы о неявных функциях, примененной к уравнению E0.74),
следует, что сугцествует такая окрестность
Uq = {(х, у) : а < X < Ь, с < у < d}
точки (О, 0) на плоскости переменных х, г/, в которой
уравнение E0.74), а следовательно, и система уравнений E0.70),
E0.72) имеют единственное регаение:
г/ = ф(х), хе(а, Р), E0.75)
где (а, Р) — некоторый интервал, содержагций точку х = О и
лежагций в интервале (а, Ь). Это означает, что в окрестности
точки (О, О, 0) пересечение поверхности E0.70) с плоскостью
E0.72) является кривой, задаваемой представлением х = х,
у = ф(х), 2 = f(x, ф(х)), а < X < р.
Если теперь а < а^ < О < Ь^ < ^, то кривая
г/= ф(х), 2 =/(х, ф(х)), aQ < X < ^Q, E0.76)
является простой дугой (отображение E0.76)
взаимно-однозначно), имеюгцей точку (О, О, 0) своей внутренней точкой.
Выберем теперь числа Cq и d^ так, чтобы с < Cq < О < d^ < d, и
пусть
и = {х,у,2):а^<х< Ь^, с^<у < d^,-оо < z < +00}
— бесконечный открытый параллелепипед, являюгцийся,
очевидно, окрестностью точки (О, О, 0). Часть кривой E0.76),
лежагцая в замыкании U окрестности U точки (О, О, 0),
является простой дугой (частью простой дуги E0.76)), для которой
точка (О, О, 0) также является внутренней точкой.
Функция /, по условию, дважды непрерывно
дифференцируема, поэтому по теореме о неявных функциях функция ф
(см. E0.75)) также дважды непрерывно дифференцируема, а
следовательно, и простая дуга E0.76) дважды непрерывно
дифференцируема. П
В дальнейп1ем нас будет интересовать структура
поверхности лип1ь вблизи данной точки, и мы всегда будем
предполагать, что на поверхности выбрана такая окрестность этой
точки, что пересечение каждой рассматриваемой плоскости с
поверхностью (в нап1их рассмотрениях всегда участвует
лип1ь конечное множество таких плоскостей), лежапа;ее в
замыкании указанной окрестности, будет всегда представлять
собой кривую (даже простую дугу), что, согласно лемме 2,
всегда имеет место для достаточно малой окрестности.
604
50.17. Нормальные сечения поверхности
Среди всех сечений поверхности плоскостями, проходягцими
через некоторую ее точку, особую роль играют так
называемые нормальные сечения, т. е. сечения поверхности,
образованные плоскостями, содержагцими нормаль к поверхности в
рассматриваемой ее точке. Такие плоскости называются
нормальными плоскостями.
Нормальных сечений, проходягцих через данную точку
поверхности, бесконечно много. Однако если заранее задать
прямую, которая должна быть касательной к нормальному
сечению (эта прямая, очевидно, должна лежать в
касательной плоскости к поверхности, где лежат касательные ко всем
кривым на поверхности (см. п. 50.5)), то нормальное сечение
определяется однозначно. В самом деле, это нормальное
сечение должно лежать в плоскости, проходяпа;ей через нормаль
к поверхности, и через заданную касательную, так как
касательная плоской кривой лежит в той же плоскости, где и
кривая. Плоскость же, проходяпа;ая через две пересекаюпа;ие-
ся перпендикулярные прямые, определяется однозначно.
Пересечением этой плоскости с касательной плоскостью к
поверхности является заданная прямая, так как она лежит в
обеих плоскостях. Получивпхееся нормальное сечение будет
иметь своей касательной заданную прямую, так как его
касательная должна, с одной стороны, лежать в его плоскости, а
с другой — в касательной плоскости к поверхности.
Начнем изучение кривизны плоских кривых на
поверхности с изучения кривизн кривых, имеюпа;их одну и ту же
касательную.
Пусть г (z/q, Pq) — неособая внутренняя точка дважды
непрерывно дифференцируемой поверхности S. Рассмотрим
кривые на поверхности, проходяпа;ие через эту точку и имеюпа;ие
обпа;ую касательную. Если через эту касательную и нормаль к
поверхности S провести плоскость, то получим нормальное
сечение Fq, кривизну которого обозначим k^. Рассмотрим случай,
когда ^Q ^ 0. Главная нормаль нормального сечения Fq лежит,
очевидно, в плоскости сечения и поэтому, будучи
перпендикулярной касательной, направлена по нормали к поверхности.
Выберем за нормаль v к поверхности S в точке г (z/q, v^
главную нормаль нормального сечения Fq; тогда угол между ними
равен нулю и, следовательно, из формулы E0.61) имеем
г ^ Ldu^' + 2Mdudv + Ndv^' /^q rjrj\
605
Для кривизны любой другой кривой г, лежащей на
поверхности aS, которая проходит через точку г(и^, Vq) и имеет
ту же касательную в этой точке, что и нормальное сечение Fq,
справедлива формула E0.61)
ftcos9 =
Ldu^ + 2Mdudv + Ndv^
E0.78)
Edu^ + 2Fdudv + Gdv^ '
где 9 — угол между нормалью v к поверхности S и главной
нормалью п кривой.
Правые части формул E0.77) и E0.78) равны, так как
зависят только от отногаения du : dv, т. е. от касательной,
которая у них обгцая. Из равенства правых частей этих формул
следует и равенство левых их частей:
fto = ftcos9. E0.79)
Итак, мы прип1ли к следуюгцей теореме.
ТЕОРЕМА 2 (теорема Менье''). Если во внутренней неособой
точке дважды непрерывно дифференцируемой поверхности у
некоторого ее нормального сечения радиус кривизны Rq
конечен, то радиус кривизны R любой другой кривой, имеющей
ту же касательную, что и указанное нормальное сечение,
равен Rq, умноженному на косинус угла 9 между нормалью к
поверхности и главной нормалью к кривой:
R = RqCosQ. E0.80)
Эта формула сразу следует из формулы E0.79), так как
k = 1/R, k^ = 1/Rq.
Дадим геометрическую
интерпретацию формулы E0.80). Рассмотрим
сечение поверхности S плоскостью, про-
ходягцей через точку Mq = г (uq, Vq)
и перпендикулярной обгцей
касательной рассматриваемых кривых (рис. 94).
В этой плоскости лежат нормаль v к
поверхности S и главная нормаль п
кривой Г (они обе перпендикулярны
обгцей касательной к кривым),
следовательно, и центры кривизн Cq и С
соответственно кривых Fq и г. Соотно-
Поверхностъ
' Ж. Менье A754—1793) — французский математик.
606
nienne E0.80) показывает, что центры кривизн С составляют
окружность, для которой отрезок MqCq длины Rq является
диаметром.
Если рассмотреть только плоские сечения поверхности,
имеюгцие обгцую касательную с нормальным сечением Fq,
т. е. образованные плоскостями, проходягцими через эту
касательную, то на рис. 94 прямая MqCq является следом на
плоскости чертежа нормального сечения, прямая М^С —
следом секугцей плоскости, а 9 — углом между этими
плоскостями. Формула E0.80) показывает, что центр кривизны С
любого плоского сечения является основанием перпендикуляра,
опугценного на секугцую плоскость из центра кривизны Cq
нормального сечения, имеюпа;его ту же касательную, что и
рассматриваемое плоское сечение.
При врапа;ении секупа;ей плоскости от совпадения ее с
нормальным сечением до совпадения с касательной плоскостью
(это соответствует изменению угла 9 от О до 7г/2) радиус
кривизны сечения изменяется от Rq до О, в частности, когда се-
купа;ая плоскость стремится к касательной плоскости, т. е.
9 -^ 7г/2, радиус кривизн плоских сечений будет стремиться к
нулю, а следовательно, их кривизны — к бесконечности.
Конечно, согласно теореме 1 п. 50.14, таким же будет и
закон изменения кривизн кривых, которые имеют обпа;ую
касательную с нормальным сечением Fq и для которых
указанные секупа;ие плоскости являются соприкасаюпа;имися
плоскостями.
50.18. Главные кривизны. Формула Эйлера
В том случае, когда рассматривается нормальное сечение
поверхности S в данной ее точке, для его кривизны k имеет
место формула (см. E0.59)—E0.61))
-f ^ _ Ldu^ + 2Mdudv + Ndv^ _ Ldu^ + 2Mdudv + Ndv^ Г50 81)
так как угол 9 между нормалью v к поверхности S и главной
нормалью п нормального сечения равен О или тг, а
следовательно, cos 9 = ±1.
Рассмотрим теперь, как изменяются кривизны
нормальных сечений в зависимости от положения нормального
сечения в неособой внутренней точке поверхности. Как известно,
в окрестности такой точки поверхность всегда можно задать
607
явным представлением, в котором плоскость независимых
переменных является касательной плоскостью в
рассматриваемой точке поверхности (см. п. 50.6). Мы и будем
рассматривать поверхность, заданную таким представлением.
Пусть поверхность S задана дважды непрерывно
дифференцируемой функцией /(х, у) в окрестности U точки (О, 0):
2 = f(x,y), (x,y)eU, E0.82)
причем координатная плоскость переменных х, у является
касательной плоскостью к поверхности aS в ее точке /(О, 0) и,
следовательно,
/(О, 0) = 4@, 0) = 4@, 0) = 0. E0.83)
Введем следупа;ие обозначения:
/S/= иО,0), /о/=/,,@,0), fo/^'fJO,0)
и зафиксируем какую-либо единичную нормаль v к
поверхности S в точке (О, О, 0), например v = (О, О, 1).
Формула для кривизн нормальных сечений поверхности S
в точке (О, О, 0) имеет вид (см. E0.81), E0.65) и E0.83))
Касательная к нормальному сечению лежит в плоскости
переменных х, г/, поэтому -^ = cos ф? 77^ ^ sin ф, где (см.
as as
A6.19) и A6.22)) ф — угол между касательной к
нормальному сечению и осью Ох. Поэтому формула E0.84) для
нормальных сечений поверхности S имеет вид
±^ = /xxcos^ ф + /o^cos ф sin ф + /^^sin2ф.
Для простоты записи отнесем здесь знак минус к кривизне й,
т. е. будем считать кривизну нормального сечения
положительной, если направления нормали к поверхности S и
главной нормали нормального сечения совпадают, и
отрицательной, если они имеют противоположное направление. При этом
соглагаении имеем
k = /J^cos^ ф + 2/5^cos ф sin ф + /^i^sin^ ф. E0.85)
Повернем теперь координатные оси Ох и Оу в их
координатной плоскости так, чтобы член с произведением косинуса
и синуса в формуле E0.85) обратился в нуль. Это всегда
можно сделать, согласно обпа;ей теории приведения квадратичных
'608
форм к каноническому виду. Впрочем, в данном случае в
этом легко убедиться непосредственно.
В самом деле, координаты точки х, у выражаются через
ее координаты х^, у* в системе координат, полученной
поворотом координатных осей на угол \|/, по формулам
X = X* COS ^ - у* sin \|/,
у = X* sin ^ -\- у* cos \|/.
Подберем угол \|/ так, чтобы для функции
Пх"", у"") = fix"" cos\|/ - у"" sin \|/, х"" sin \|/ + г/"" cos \|/)
имело место равенство
/V,,*@,0) = 0. E0.86)
Так как /*^* = /^ cos \|/ + fySin \|/, то
f*x*y* = ~4xCos V sin V + /xz/(cos^ ¥ - sin^ ¥) + 4^^^"^ X|/ COS \|/ =
= !((/,, - 4x) sin 2v + 24^cos 2x|/\
следовательно, для того чтобы выполнялось условие E0.86),
следует выбрать угол \|/ так, чтобы
fO _ fO
ctg2x|/=^^^|-/M.
После поворота на этот угол \|/ формула E0.85) принимает
вид
k = ft^cos^ ф + k2sш^• ф. E0.87)
Здесь k^ = f''^ *@, 0), ^2 = /\ *@, 0), а ф — угол между
касательной к нормальному сечению и новой координатной осью
Ох*. Для простоты новые координаты будем обозначать
по-прежнему через х и г/ без звездочек.
Из формулы E0.87) следует, что й^ является кривизной
нормального сечения, произведенного нормальной
плоскостью, проходяпа;ей через ось Ох, а ^2 — кривизной
нормального сечения, произведенного нормальной плоскостью, прохо-
дяпа;ей через ось Оу.
Из формулы E0.87) следует также, что кривизны k^ и ^2
являются экстремальными значениями нормальных
кривизн. Действительно, если k^ = k^y то из формулы E0.87)
получим, что для всех углов ф выполняется равенство k = k^ =
= ^2, Т. е. что кривизна не зависит от угла ф.
609
Если же k^ ^ ^2 и, например, k^ > ^2, то, записав формулу
E0.87) в виде
k = (k^- Й2)С08^ ф + Й2(С08^ ф + Sin^ ф) = (k^ - Й2)С08^ ф + ^2,
получим, ЧТО Й > ^2 И Й = (k-^ - Й2)С08^ ф + ^2 < (k-^ - ^2) + ^2 ^ ^1'
Т. е. что ^2 < й < й^.
Определение 26. Экстремальные значения k^ и ^2 кривизн
нормальных сечений в данной точке поверхности
называются главными кривизнами, соответствующие им
нормальные сечения — главными нормальными сечениями, а их
касательные — главными направлениями.
Кривая на поверхности, которая в каждой своей точке
имеет главное направление, называется линией кривизны.
Полученный Bbinie результат можно в терминах главных
направлений сформулировать в виде следуюгцей теоремы.
ТЕОРЕМА 3. Кривизна k любого нормального сечения во
всякой внутренней неособой точке дважды непрерывно
дифференцируемой поверхности выражается через кривизны k-^ и
^2 двух взаимно-перпендикулярных главных нормальных
сечений по формуле
k = k^cos^ ф + ^^2 ^^^^ Ф'
где ф — угол, образованный плоскостью нормального сечения
с плоскостью главного нормального сечения с кривизной k^.
Формула E0.87) называется формулой Эйлера.
В случае k^ ^ ^2 для любой кривизны к, не равной ни
одной из главных кривизн, сугцествует четыре значения угла ф,
для которых выполняется соотногаение E0.87): ф, ф + 7г/2,
ф + 71 и ф + 37Г/2. Углы, отличаюгциеся друг от друга на тг,
определяют одно и то же нормальное сечение, поэтому для
каждой указанной кривизны к супа;ествует точно два различных
нормальных сечения, имеюпа;их данную кривизну.
Если же к = к^ или к = к2, то из формулы E0.87) следует,
что супа;ествует только одно нормальное сечение, имеюпа;ее
своей кривизной данную главную кривизну.
Отметим, в частности, что при к-^ ^ ^2 значение к = О
(которое было исключено из рассмотрения при доказательстве
теоремы Менье) может либо совсем отсутствовать в данной
точке поверхности, когда главные кривизны одного знака,
либо получаться при одном значении ф, когда одна из главных
кривизн равна нулю, либо при двух, когда главные кривизны
имеют разные знаки. Направления, которым соответствуют
нормальные сечения нулевой кривизны, называются
асимптотическими направлениями на поверхности. В каждой
точке поверхности, в которой й^ ^ ^2, в силу сказанного выгае,
имеется не более двух асимптотических направлений. Кривая
на поверхности, которая в каждой своей точке имеет
асимптотическое направление, называется асимптотической линией.
Экстремальное свойство главных кривизн, очевидно, не
зависит от выбора представления поверхности: оно
определяется свойствами кривизн кривых, лежагцих на поверхности,
и, таким образом, главные кривизны являются
характеристиками самой поверхности. Замечательным фактом является
то обстоятельство, доказанное выгае, что главные
направления, т. е. направления, отвечаюгцие экстремальным
значениям кривизн нормальных сечений, ортогональны.
Подведем некоторые итоги. Из полученных результатов
следует, что изучение кривизн кривых на поверхности в данной ее
точке сводится к кривизнам плоских сечений (теорема 1),
кривизны плоских сечений — к кривизнам нормальных сечений
(теорема 2), а кривизны нормальных сечений выражаются
через главные кривизны по формуле Эйлера (теорема 3).
50.19. Вычисление главных кривизн
Перепигаем формулу E0.77) для определения нормальной
кривизны в виде
(L - kE)du'^ + 2(М - kF)dudv + (N - kG)dv^ = 0.
Разделив это уравнение на dv^' и введя вспомогательную
переменную t = -^ (значение t определяет нормальное
сечение), получим
(L - kE)t^ + 2(М - kF)t + (N- kG) = 0. E0.88)
Корни квадратного уравнения E0.88) определяют положение
нормального сечения, отвечаюгцего кривизне k. Для главных
кривизн, и только для них, такое положение единственно,
поэтому для них корни квадратного уравнения E0.86) должны
слиться, т. е. его дискриминант должен обратиться в нуль:
(М - kFf - (L - kE)(N -kG) = 0 E0.89)
или в виде, более удобном для запоминания,
L-kF _M-kF
M-kF N-kG'
Это и есть уравнение для определения главных кривизн.
'бП
E0.90)
Если главные кривизны k^ и ^2 найдены, то, подставив их
значения в уравнение E0.88), найдем значение главного
направления t.
Определение 27. Произведение главных кривизн поверхности
в данной ее точке называется полной или гауссовой^
кривизной поверхности
K = k^k^, E0.91)
а их полусумма
H = \{k^ + k^) E0.92)
— средней кривизной поверхности.
Очевидно, что знание главных кривизн в точке
поверхности равносильно знанию ее полной и средней кривизн в этой
точке. Однако в некоторых вопросах, в чем мы скоро
убедимся, удобнее иметь дело с полной и средней кривизной, чем с
главными кривизнами.
Для получения формул для полной и средней кривизн запи-
П1ем уравнение E0.89) для главных кривизн в следуюгцем виде:
{EG - F^)k^ - (EN - 2FM + GL)k + LN-M^ = 0.
Отсюда по теореме Виета получим
^ E0791) ^A-f^^ E0.93)
Н = ^(k +к )-EN-2FM + GL E0 94)
^ E0.92) 2^^1^^2>> 2{EG-F^) ' (^и.У4)
Главные кривизны в данной точке поверхности не зависят
от представления поверхности, поэтому не зависят от
представления поверхности полная и средняя кривизны. Так как
первая квадратичная форма поверхности положительно
определенная (она равна ds^), и, следовательно, ее дискриминант
болыае нуля: EG - F^ > О, то из формулы E0.93) для полной
кривизны следует, что и сигнатура дискриминанта LN - М^
второй квадратичной формы поверхности не зависит от
представления поверхности: если полная кривизна равна нулю,
то и этот дискриминант равен нулю, а если полная кривизна
отлична от нуля, то его знак совпадает со знаком полной
кривизны.
Пример. Вычислим полную и среднюю кривизны для
гиперболического параболоида 2 = х^ - у^.
К. Ф. Гаусс A777—1855) — немецкий математик.
'612
Согласно формулам E0.49) и E0.65), в этом случае
Е = 1 + 4x2, р = _4хг/, G = 1 + 4г/2, EG - F^ = 1 + 4х^ + 4г/2,
L = 2, М = О, N = -2, LN - М^ = -4,
поэтому
?г - 4 _ 4(j/2-x2)
-IV .^^—^.. —-—■—:—т;—.—:—о, г1 ^^—^,
E0.91) 1 + 4x2 + 4г/2' E0.92) 1 + 4x2 + 4г/2*
50.20. Классификация точек поверхности
С помогцью полной кривизны поверхности оказывается
удобным классифицировать точки поверхности.
Определение 28. Точки поверхности, в которых полная
кривизна положительная, называются эллиптическими
точками поверхности, в которых она отрицательная —
гиперболическими, а в которых она равна нулю, но одна из
главных кривизн отлична от нуля, — параболическими.
Точки, в которых обе главные кривизны равны нулю, а
следовательно, равна нулю и полная кривизна, называются
точками уплощения поверхности.
В эллиптической точке поверхности К = k-Ji^ > 0. Будем
считать, что й^ > О и ^2 > О, так как этого всегда можно
добиться, изменив в случае необходимости направление
нормали к поверхности, в результате чего знаки главных кривизн
изменятся на противоположные. В этом случае все кривизны
нормальных сечений положительные и, следовательно, все
главные нормали нормальных сечений направлены в одну и
ту же сторону — в сторону нормали v к поверхности, —
поэтому все нормальные сечения загибаются в сторону
вектора V (см. п. 17.3). Иначе говоря, поверхность в некоторой
окрестности рассматриваемой точки располагается по одну
сторону от своей касательной плоскости (рис. 95).
Рис. 95
613
Асимптотических направлений в эллиптической точке
нет: если й^ > О и ^2 > О, то из формулы Эйлера E0.87)
следует, что для любого нормального сечения его кривизна
k = й^соз^ф + ^ззш^ф > 0.
Так как знак полной кривизны К совпадает со знаком
дискриминанта LN - М^ второй квадратичной формы
поверхности (см. п. 50.19), то в эллиптической точке
ЬЛГ-М2>0. E0.95)
В гиперболической точке поверхности гауссова кривизна
отрицательна: К = k^k2 < 0. Следовательно, главные
кривизны имеют противоположные знаки, поэтому главные
нормали главных нормальных сечений направлены в
противоположные стороны. Это означает, что одно главное нормальное
сечение загибается от касательной плоскости в сторону
нормали V к поверхности, а другое — в противоположную.
Когда нормальное сечение непрерывно врагцается от
одного главного сечения до другого, его кривизна непрерывно
меняется от отрицательного до положительного значения или
наоборот и, следовательно, для некоторого нормального
сечения обрагцается в нуль. Направление касательной этого
сечения (а именно угол ф, который она образует с одним из
главных направлений) находится из формулы Эйлера: k^cos^ ф +
+ ^ззш^ Ф = О, откуда
tgф = ±J-k^/k2.
(Так как k^ и ^2 имеют разные знаки, то под знаком корня
стоит положительная величина.) Итак, в случае
гиперболической точки сугцествует два асимптотических направления:
одно — под углом ф = arctg J--k^~/k~2, другое — под углом ф =
= -arctg J-k'^/k2, и, следовательно, симметрично первому
относительно главных направлений.
Из двух пар вертикальных углов, образованных
асимптотическими направлениями, в одной паре кривизны
нормальных сечений положительны, в другой — отрицательны.
Поэтому нормальные сечения в одной из указанных пар
вертикальных углов отклоняются от касательной плоскости к
поверхности в противоположную сторону по сравнению с
отклонением от этой плоскости нормальных сечений в другой
паре вертикальных углов (рис. 96).
'614
Рис. 96
Из совпадения знаков полной кривизны и дискриминанта
LN - М^ следует, что в гиперболических точках поверхности
выполняется неравенство
ЬЛГ-М2<0. E0.96)
В параболической точке К = k^k2 = О и одна из главных
кривизн отлична от нуля, например й^ > 0. В этом случае главное
нормальное сечение с кривизной k^ загибается в сторону
нормали V к поверхности, а другое имеет в этой точке кривизну,
равную нулю, например имеет эту точку своей точкой перегиба,
т. е. соответствует асимптотическому направлению (рис. 97).
В этом случае из формулы Эйлера k = ft^cos^ ф следует, что
других асимптотических направлений в параболической точке нет.
Из равенства нулю полной кривизны следует, что в
параболической точке поверхности (см. E0.93))
LN —М^ = 0. E0.97)
Если в точке поверхности й^ = ^2 и, следовательно,
кривизны всех нормальных сечений равны между собой, то такая
точка поверхности называется точкой закругления или
омбилической точкой; ее частным случаем является точка уплопа;ения.
Рис. 97
615
т. е. точка, в которой й^ = ^2 = 0. В омбилической точке все
направления главные. Это означает, что уравнение E0.88) при
k = k-^ = k2 должно удовлетворяться при любом t, что возможно
лип1ь в случае, когда все его коэффициенты равны нулю:
L - kE = М - kF = N - kG = 0.
Отсюда следует, что для точек уплогцения, т. е. когда k = О,
выполняются равенства L = M = N = OySi для точек
закругления, не являюпа;ихся точками уплопа;ения, условие
Е F G'
каждое из этих отноп1ений равно кривизне k.
В заключение выясним, как характеризуются различные
виды точек на поверхности, если в окрестности этих точек
выбрать явные представления поверхности, при которых
плоскость независимых переменных х, у параллельна
касательной плоскости к поверхности в рассматриваемой точке.
Пусть 2 = f(x, у) — дважды непрерывно
дифференцируемая в окрестности U точки (Xq, z/q) функция, Zq = fix^, у^) и в
точке (Xq, г/о, 2q) касательная плоскость к графику функции /
параллельна плоскости переменных х, у. Тогда
иХо,Уо) = Гу(Хо,Уо) = ^- E0.98)
Введем, как и выпхе, следуюпа;ие обозначения:
Согласно формулам E0.65), условие E0.95)
эллиптичности точки (Xq, i/q, 2q) графика функции / имеет вид
LN-M^ = nJly-ffy>0. E0.99)
Условия E0.98) и E0.99) являются достаточными условиями
строгого экстремума функции / в точке (Xq, i/q). Таким образом,
если точка (Xq, i/q, 2q) графика функции / является
эллиптической, то функция / имеет в точке (Xq, i/q) строгий экстремум и,
следовательно, в некоторой окрестности точки (Xq, i/q, 2q)
график функции / (поверхность) расположена либо над
касательной плоскостью, либо под ней, исключая, конечно, саму точку
(Xq, г/о, ^о)' ^^оторая лежит на касательной плоскости.
Условие E0.96) гиперболичности точки (Xq, г/д, z^ имеет вид
nJty-ffy<^- E0.100)
Выполнение соотногаений E0.98) и E0.100) является
достаточным условием того, чтобы в точке (Xq, z/q) функция / не име-
'бТб
ла экстремума. Поэтому в любой окрестности гиперболической
точки имеются точки по обе стороны от касательной плоскости.
Таким образом, мы егце раз подтвердили некоторые
результаты предыдугцего анализа структуры поверхности
вблизи эллиптических и гиперболических точек.
Наконец, условие параболичности имеет вид
f о f о - fO^ = о
'XX'уу Iху ^
и В ЭТОМ случае ничего сказать об экстремуме функции / в
точке (Xq, i/q) нельзя.
Мы убедились, что с помогцью первой и второй
квадратичных форм можно достаточно детально изучить структуру
поверхности в окрестности ее неособой внутренней точки.
Оказывается, что первая и вторая квадратичные формы поверхности
в известном смысле полностью описывают поверхность
подобно тому, как кривизна и кручение пространственной кривой
определяют ее с точностью до положения в пространстве.
Например, можно доказать, что если две простые поверхности
имеют такие представления, параметры которых меняются в
одной и той же области, что в точках поверхностей, соответст-
вуюгцих одним и тем же значениям параметров, у
поверхностей совпадают их первая и вторая квадратичные формы (т. е.
совпадают их коэффициенты), то эти поверхности
конгруэнтны (см.: Погорелое А. В. Лекции по дифференциальной
геометрии. — Харьков: Изд-во ХГУ, 1961).
§51
Поверхностные интегралы
в этом и следуюгцих параграфах будут рассматриваться
гладкие поверхности, задаваемые параметрическими
представлениями (см. определение 16 в § 50) и склеенные из них
кусочно-гладкие (см. определение 23 в § 50).
51.1. Определение и свойства
поверхностных интегралов
Пусть задана гладкая поверхность aS, причем
г = г(и, v) = {х = х(и, v), у = у(и, v), 2 = 2(и, v); (и, v)eD} E1.1)
— ее представление, т. е. непрерывно дифференцируемое
отображение без особых точек, D — квадрируемая плоская
область и, как обычно, Е, G и F — коэффициенты первой
^17
квадратичной формы поверхности S. Пусть, далее, на
множестве точек г(и, и) поверхности S задана функция Ф, т. е.
функция Ф(г(г/, и)) = Ф(х(и, и), у(и, и), z(Uy v)). Иногда функцию Ф
будем обозначать также через Ф(х, г/, z) (ср. с п. 47.1).
Определение 1. Интеграл ||Ф(х, г/, z)dS определяется равен-
S
ством (см. формулу E0.48))
\\ Ф(х, г/, z)dS = ||Ф(х(г/, у), г/(г/, у), z{u, v))JeG - F^dudv. E1.2)
S D
Этот интеграл называется поверхностным интегралом
первого рода.
Таким образом, в поверхностном интеграле ^^ Ф(х, г/, z)dS
S
под dS понимается элемент площади E0.48).
При определенных ограничениях, налагаемых на
функцию Ф, интеграл E1.2) существует. Так, например, он
существует для всякой непрерывной на гладкой поверхности S
функции Ф, т. е. для непрерывной на замкнутой квадрируе-
мой области D функции Ф(г(г/, v)). В самом деле, в этом
случае, согласно определению 1, интеграл ||Ф(х, г/, z)dS сводится
к интегралу И(г(и, v)) JeG - F^dudv от непрерывной на D
D
функции, который, как известно (см. п. 44.4), существует.
Более общие условия существования поверхностного интеграла
первого рода могут быть получены из соответствующих условий
существования кратных интегралов (см. п. 44.4), примененных
к интегралу, стоящему в правой части равенства E1.2).
Пусть для простоты функция Ф непрерывна на гладкой
поверхности S и пусть
р = р(г/1, v^) = (ф(г/1, v^), \|/(г/1, v^), % (и^, v^))
— другое представление этой поверхности, которое задано на
замыкании Di квадрируемой области D^ и для которого
преобразование E0.14) параметров и, v в и-^, v-^ взаимно-однозначно и
непрерывно дифференцируемо на D и имеет на D не равный
нулю якобиан. Если Е^, F^n G^ суть коэффициенты первой
квадратичной формы, соответствующие этому представлению, то
||Ф(х(г/, у), г/(г/, v), z(u, v))JeG - F^dudv =
D
= 11 Ф(ф(г/1, ^i), \|/(z/i, ^i), %(г/, v))Je^G^ - Ffdu^dv^. E1.3)
618
Чтобы в этом убедиться, достаточно в интеграле, стоягцем в
правой части этого равенства, выполнить замену переменных
E0.14) и воспользоваться формулой E0.43). Таким образом,
поверхностный интеграл первого рода не зависит от выбора
представления поверхности. Поверхностные интегралы
первого рода встречаются в различных вопросах математики и ее
приложений. Например, плопа;адь поверхности (см. п. 50.7)
выражается с помопа;ью поверхностного интеграла первого
рода: если функция Ф(х, г/, z) тождественно равна единице на
поверхности aS, то формула E1.2) преврапа;ается в формулу
для плопа;ади \xS поверхности S (см. E0.47)):
[iS = \\JEG-F4udv = \\dS,
D S
Если Ф(х, г/, z) — плотность некоторой массы,
распределенной по поверхности aS, то интеграл E1.2) дает величину
массы всей поверхности.
Пусть теперь i, j и fe, как обычно, единичные
координатные векторы.
п
г Хг ■■
и V
J
Уи
Vv
1^. ^ 1^ . ^ д{^. E1.4)
д{и, V) д(и, v) д{и, V)
И
E1.5)
причем, согласно предположению о гладкости поверхности,
нормаль V непрерывно продолжаема на границу области D.
Поверхность aS, на которой выбрана единичная нормаль v,
обозначим, как и раньпхе, через aS+, а ту же поверхность, на
которой выбрана нормаль -v, — через S~ (очевидно, v и -v
суть две ориентации поверхности aS). Подчеркнем, что aS+ и S~
определяются самой поверхностью «с точностью до
ориентации» и поэтому зависят от выбора представления поверхности.
Через а, Р, у обозначим углы, образованные единичной
нормалью V с координатными осями Ох, Ог/, Oz, т. е.
V = (cos а, cos р, cos у). E1.6)
Пусть на поверхности S задана векторная функция
а = а(г(и, V)) = (Р, Q, R),
Р = Р(х(и, V), у(и, V), z(u, v)), Q = Q(x(u, v), y(u, v), z(u, v)),
R = R(x(u, v), y(u, v), z(u, v)). E1.7)
619
Определение2. Поверхностным интегралом ^ ^adS второго
S+
рода по ориентированной поверхности S^ называется
интеграл IJavdiS, т, е.
\\adS^= \\avdS.
S+ S
E1.8)
Обозначение 11 adS называется векторной записью ин-
S+
теграла второго рода. Его координатной записью
называется выражение
11 Pdydz + Qdzdx + Rdxdy.
Таким образом,
11 adS = \\ Pdydz + Qdzdx + Rdxdy, E1.9)
так как, по определению, левая и правая части этого
равенства являются разными записями одной и той же величины.
Согласно определению E1.8),
11 Pdydz + Qdzdx + i?dxd^ = 11 adS j^3 \\ avdS =
(бГб) Я (P^^^ ^ + Qcos P + ^cos y)^^' E1.10)
E1.7) ^
в частности, беря поочередно две из функций Р, Q и R
тождественно равными нулю, будем иметь
\\Pdydz = \\PcosadS, \\Qdzdx = JJQcospdS,
s+ s s+ s
11 Rdxdy = ^^ Rcos ydS.
E1.11)
Интуитивный смысл этих формул
состоит в том, что элемент плогцади
(см. E0.48)) данной поверхности,
умноженный на косинус угла, который
он «составляет» с некоторой
координатной плоскостью, «приближенно»
равен элементу плогцади его проекции
на рассматриваемую координатную
плоскость, как если бы речь гала о
плогцади плоской фигуры и ее
проекции. На рис. 98 изображен случай,
когда указанное проектирование
производится на плоскость
переменных X и г/. В этом случае dxdy ~
620
~ dScos у, где dS — элемент плогцади поверхности aS, а dxdy —
элемент плогцади проекции этой поверхности на плоскость
переменных х, г/, а у — угол между dS и указанной
плоскостью, очевидно, равный углу между нормалью v к
поверхности и единичным ортом k оси Oz.
Ориентируемая поверхность имеет две ориентации v и -v.
Поверхность с ориентацией v обозначена aS+, поверхность с
ориентацией -v, как обычно, S~. Имеем
11 adS '^' Я a(-v)dS - -Ц avdS = - 11 adS;
S- S S S+
таким образом, при изменении ориентации поверхности
интеграл второго рода меняет только знак.
Если векторная функция а непрерывна на поверхности aS,
то интеграл ^ ^ adS сугцествует, так как, в силу сказанного
S+
выгае о поверхностных интегралах первого рода, сугцествует
интеграл, стоягций в правой части равенства E1.8).
51.2. Формула для представления
поверхностного интеграла второго рода
в виде двойного интеграла
Пусть S — гладкая поверхность, заданная своим векторным
представлением S= {г(и, и); (и, v)eD} и, как обычно, aS+—
поверхность aS, ориентированная посредством нормали
Вспомнив, что (см. E0.46) и E0.48)) dS = \г^ X г^\ dudv,
получим
\\adS = ЯavdS = ЯаГ±^ |г, X rj dudv =
= \\ia,r^,rjdudv, E1.12)
G
где (a, r^, Гу) — смегаенное произведение векторов а, г^, г^.
Если а = (Р, Q, R), г(и, v) = (х(и, v), у(и, v) z{u, v)), r^ =
= (x^, г/^, 2J, r^ = (x^, i/^, 2^), TO формула E1.12) в
координатной форме имеет вид
Р Q R
-^и Уи ^и
-^v Уи ^v
где Р = Р(х(и, V), у(и, V) 2(и, v)), Q = Я(х(и, v), у(и, v) z(u, i;)),
R = R(x(u, v), y(u, v) 2(u, v)).
'621
\\adS = \\
S+ G
dudv, E1.13)
Формула E1.13) справедлива и для гладких
представлений гладких поверхностей в п1ироком смысле этого термина
(см. п. 50.5). Для других представлений этих поверхностей
она получается заменой переменных в интеграле в правой
части равенства E1.13) с помопа;ью гладкого преобразования
параметров в гладком представлении поверхности.
В частном случае, когда на замкнутой области D всюду
Р = Q = О, т. е. а = (О, О, R), имеем
d{u,v)'
\ О О R
(«' ^и^ ^v) = \^и у и ^и
•^v Уи ^v
Формула E1.13) в этом случае принимает вид
И Rdxdy = Ц R{x{u, v), у{и, v), 2{и, v)) ^^^Ьу1 dudv.
Если поверхность S имеет явное представление z = f(x, у),
(х, y)eD, то
' 1 О
^и Уи
^v Уи
о 1
(здесь X = и, у = и) Ji для интеграла по верхней стороне S
поверхности S (см. пример в п. 50.10) в случае, когда Р = Q = О,
на S имеем
\\Rdxdy = \\R{x, г/, /(х, y))dxdy,
E1.14)
а для интеграла по нижней стороне S поверхности S получим
^^Rdxdy = -^^R(x, у, f(x, y))dxdy.
s
Вместо iiRdxdy иногда пигаут просто ii Rdxdy, sl вместо
s '
И Rdxdy — соответственно iiRdydx, т.е. в случае нижней
s '
S/'
стороны S поверхности S дифференциалы dx и dy пигаут в
обратном порядке.
Если функция R непрерывна на поверхности aS, то
формула E1.14) справедлива и тогда, когда явно заданная
поверхность S гладкая в гаироком смысле (см. п. 50.5), т. е. тогда,
когда функция /, будучи непрерывной на замыкании D об-
622
ласти D, непрерывно дифференцируема лигаь в самой
области D; однако наряду с этим предполагается, что у
поверхности S имеется представление
г(и, и) = (х(и, и), у(и, и), 2(и, и)), (и, v)eDi,
непрерывно дифференцируемое вплоть до границы
квадрируемой области D^, на замыкании которой оно задано, и,
следовательно, для этого представления справедлива формула E1.13).
Действительно, достаточно, как это отмечалось выгае, в
интеграле
\\Щх, у, f(x,y))dxdy
D
сделать замену переменных х = х(и, и), у = у(и, и), (и, v)eD^.
Это возможно, так как функция R(x, у, f(x, у))
непрерывна на замыкании D квадрируемой области D, а якобиан
J"^' ^' непрерывен вплоть до границы области Z). (по предпо-
д(и, v)
ложению частные производные г-^, г-^, ^г^, .-^ непрерывны
ди ди av av
вплоть до границы области D^, т. е. на ее замыкании) и не
обрапа;ается в нуль в самой области D^.
Итак, имеем
\\Щх, у, f(x, y))dxdy =
I \R(x(u, у), г/(г/, у), f(x(u, v), у{и, v)))
Э(х, у)
д{и, v)
dudv.
Из доказанного следует, что формула E1.14) справедлива,
например, для поверхностных интегралов от непрерывных
функций по полусфере, заданной явным представлением z =
= Jl - х^ - г/^, х^ + г/^ < 1 (оно не является непрерывно
дифференцируемым вплоть до границы х^ + у^ = 1 круга х^ + г/^ < 1,
на котором оно задано).
51.3. Поверхностные интегралы
кок пределы интегральных сумм
Поверхностные интегралы могут быть получены также и как
пределы соответствуюгцих поверхностных интегральных сумм.
Пусть S — гладкая поверхность и г = г(и, v), (и, v)eD, — ее
представление, D — квадрируемая область.
^23
Рассмотрим разбиение Xj^ замкнутой области Z), состоя-
па;ее из всевозможных непустых ее пересечений с квадратами
ранга k (ср. с п. 50.9). Пусть т^ (dD) = {A^^^}j_(^ —
совокупность можеств, входягцих в разбиение т^ и являюгцихся
квадратами ранга k, т. е. квадратами ранга k, целиком лежагци-
ми в замкнутой области D. Иными словами, Xj^ (dD) состоит
из элементов разбиения т^, не пересекаюгцихся с границей dD
области D.
Пусть
Множество В^^^ содержится в объединении у^ всех
элементов разбиения т^, пересекаюгцихся с границей dD области D,
т. е. с множеством меры нуль. Поэтому (см. лемму 4 в п. 44.3)
lim иБ(^) = 0. E1.15)
Сужение отображения г(и, и), (и, v)eD, на замкнутый
квадрат А^^^ является представлением некоторой
поверхности, которую обозначим S^^, j = 1, 2, ... , у^. Очевидно, все
эти поверхности также гладкие.
Пусть функция Ф (г(и, и)) непрерывна на замкнутой
области D, пусть также (и^^\ v^f^)eA^f^^ и Ф^ • = Ф (r(u^f\ y^f^)).
J J J 'J J J
Положим
И назовем ее поверхностной (неполной) интегральной суммой
для интеграла \\ ФйЗ и докажем, что
S
lim аA) = [[ Фаз. E1.16)
S
Прежде всего заметим, что
\\Фа8 = \\Ф^ЕС-Т'^ dudv =
S D
||Фл/^0-^2 (iudv+ ||Фл/^0-^2 ^^^y^
lim ff Ф JeG-F^ dudv = 0.
/j ^ OO J J
где
Б(*)
Это следует из ограниченности подынтегральной функции
И равенства E1.15). Поэтому
lirn^ \\ Ф JeG - F^ dudv = \\ Фс18. E1.17)
^ А(*) S
Обозначим через со F, Ф) модуль непрерывности функции
Ф на замкнутой области D. В силу равномерной
непрерывности функции Ф на D, имеем
lim со F, Ф) = 0.
Далее, ^
аA) - f f Ф JeG - F^ dudvl
*<3^' Am
h
f; Ф^ ^. |iS(*' - JJ Ф JEG - F^ dudvl
£ Фй,у Я JEG - F^ dudv - Y, II Ф JEG - F^ dudvl
<
< E Я
\Фь ■ - Ф\
^ k,] '
JeG - F^ dudv <
^ ^ iU' ^] я ^^(^ - P' d^dv < Ш (^^; Ф] US ^ 0 E1.18)
при Й ^ oo. Из E1.17) и E1.18) непосредственно следует
равенство E1.16).
Рассмотрим теперь интеграл второго рода
^^ Фdxdy = \\ ^ cos (v, fe) dS,
s s
Если обозначить через cos^ у (v, k) косинус угла между
нормалью V к поверхности S и координатным ортом k в точке
(и^^\ v^^h и положить
/г 7=1
ТО, аналогично равенству E1.16), доказывается формула
.1™оо <1иг Я *(^' У' '^^^^у- E1.19)
Подобные утверждения справедливы и для интегралов
второго рода других типов E1.11), следовательно, и для
интеграла ^^ adS.
УПРАЖНЕНИЕ. Доказать формулу E1.19).
625
51.4. Поверхностные интегралы
по кусочно-гладким поверхностям
Определим поверхностные интегралы по кусочно-гладким
поверхностям.
Определение 3. Пусть S = {S^}iz^ — кусочно-гладкая
поверхность (см. определение 23 в п. 50.11) и Ф(х, у, z) — функция,
определенная на множестве точек поверхности S, Тогда, по
определению,
S ^~ S^
Определение 4. Если кусочно-гладкая поверхность S =
^ {>Si}iZi ориентируема и S^ = {S^}lz^ — одна из
соответствующих ей ориентированных поверхностей
(обозначения см. в п. 50.13) с помощью нормалей \^ на S-, i = 1, 2, ... , k,
то, по определению,
\\adS= f; \\av.dS.
Конечно, это определение содержательно только в том
случае, когда интегралы, стояпа;ие в правых частях равенств,
супа;ествуют. Для этого, прежде всего, представления
поверхностей aS. должны быть заданы на квадрируемых областях.
Аналогично в рассматриваемом случае определяются и
интегралы по поверхности S~ = {а8^~}^^^.
Мы остановились только на тех свойствах поверхностных
интегралов, которые связаны со спецификой их определения
и с поверхностью, по которой производится интегрирование.
Естественно, что, поскольку они сводятся к обычным
кратным интегралам, на них переносятся и различные их
свойства (линейность, интегральная теорема о среднем и т. п.).
51.5. Обобщение понятия
поверхностного интеграла второго рода
Подобно тому как в п. 47.5 было обобгцено понятие
криволинейного интеграла второго рода, может быть обобгцено и
понятие поверхностного интеграла второго рода на более гаирокий
класс поверхностей, по которым производится интегрирование.
Для функций многих переменных, как и для функций
одной переменной, сугцествует понятие интеграла Стилтьеса, с
помогцью которого можно обобгцить понятие поверхностного
интеграла второго рода. Но чтобы не вводить новых понятий,
проделаем непосредственно нужное нам для дальнейгаего
обобгцение.
Пусть S — элементарная поверхность, т. е. непрерывное
отображение г(и, v), (и, v)eD, замкнутой плоской области в
пространство, г(и, и) = (ф(г/, v), \|/ (и, и), %(г/, и)) (см. п. 50.2),
D — квадрируемая область, функция Ф задана на множестве
точек поверхности S и отображение
X = ф(г/, у), у = \|/(г/, у), (и, v) е D, E1.20)
является гомеоморфизмом и отображает множества меры нуль
также в множества меры нуль.
Если т = {Х^У^^^^— разбиение замкнутой области D (см.
п. 44.3), то образы D* и X* соответственно множеств D и X.,
/ = 1, 2, ... , /^, при отображении E2.20) также измеримы и
система множеств т"^ = {Х*}.^-^ является разбиением
множества D*.
Пусть (г/., v.)eX., i = 1, 2, ... , i^. Положим
@. = @.(Ф; ф; \|/; (г/^, у^), ... , (г/^^, v^)) ^=
= ^Ф(г(щ,и))цХ*. E1.21)
i = 1
К числу элементарных поверхностей, удовлетворяюгцих
указанным выгае условиям, относятся полусфера 2 =
= Jl - х^ - у^, х^ + г/^ < 1, цилиндрическая поверхность 2 =
= Jl - х^, - 1 < X < 1, О < г/ < 1, и т. п.
Определение 2\ Если существует конечный предел lim @ ^
сумм E1.21), то он называется поверхностным интегралом
второго рода от функции Ф по элементарной поверхности S
и обозначается ^^ Ф((х, г/, 2)dxdy.
S
Таким образом,
ИФЦх,у,2)с1хс1у^= lim @.. E1.22)
у hi ^ о ^
В этом определении не предполагается какой-либо
гладкости элементарной поверхности aS, поэтому в целом к
такому классу поверхностей неприменимо ранее
сформулированное определение 2 поверхностных интегралов второго рода.
Правомерность же использования в определении E1.22)
термина «поверхностный интеграл второго рода» оправдывается
627
тем, что если элементарная поверхность S — гладкая,
отображение E1.20) — регулярное (см. определение 7 в п. 50.3),
а функция Ф — непрерывна на aS, то на поверхности S можно
так выбрать ориентацию, что определения 2 и 2' будут
эквивалентны. Это доказывается аналогично доказательству
равенства E1.16) в п. 51.3. Действительно, используем
обозначения, введенные в п. 51.3. Пусть т^ = {Хр^}^.^^^^, Х''^^ —
образ множества Х^^^ при отображении E1.20), у = 1, 2, ... , у* ,
т1 = {Х""!^^}. -^^. В силу равномерной непрерывности
отображения E1.20), имеем lim |т^| = 0.
Обозначим через Aj^^^ образ множества А^^^ = X^^^gt^CD),
у = 1,2, ... , у^ (см. п. 51.3) при отображении E1.20) и снова
рассмотрим соответствуюгцую неполную интегральную сумму
Э(х,1/)
d{u,v)
dudv E1.23)
^ 7 = 1 7=1 J^ik)
(мы воспользовались теоремой 2 п. 46.3 о замене переменных
в двойных интегралах). Нетрудно убедиться, что в
предположении сугцествования предела E1.22) справедливы равенства
lim с0^,-.^^,= lim ё^^ ^^ = ^il Ф dxdy. E1.24)
fe^oo -Cf^idD ) 1^1 ^Q т E1.22) J J ^ "^ ^
D
С другой стороны, если поверхность S — гладкая и А^^^ =
= .G A(f), то (см. п. 51.3)
lim \\ф^iЩdudv= \\Ф^iЩdudv= ff Ф cos (Cfe) dS, E1.25)
где поверхностный интеграл в правой части равенства
понимается в смысле определения 2 п. 51.1.
Далее, выбрав ориентацию плоскости переменных и, v
так, чтобы выполнялось неравенство ^f^'^^ > О, легко пока-
d{u,v)
зать, что разность
|с0.^ . - \\ф^ЛЩdudv\ < у \\\ф^.-ф\^ЛЩdudv
I ^^(^^ ) jJ) д(и,и) I E1.23) ^-^-ijJJ ^'^ |ЭA^,1;)
стремится к нулю при й ^ оо и, следовательно,
lim @.,,^. = lim \\ Ф^^Щ, dudv ^=^^i\ ФсоБ(ук) dS,
fe^oo Т^^(Э1) ) fe^oo JJ d{u,V) E1.25)JJ "^ ^
Отсюда, в силу равенства E1.24), следует, что в случае
гладких поверхностей S новое определение 2' равносильно
определению 2 в п. 51.1.
628
Рассмотрим примеры, на которых хороню видны преиму-
гцества расгаиренного понятия поверхностного интеграла
второго рода.
Пусть элементарная поверхность S имеет явное
представление 2 = f(x, у), (х, y)eD, D — измеримая по Жордану
область и функция Ф (непрерывна на aS, т. е. непрерывна
функция Ф(х, г/, /(х, г/)), (х, г/) gD. В этом случае отображение
E1.20) является тождественным, и поэтому применимо
определение E1.22). Сумма @* имеет здесь вид
ё\. = ^ Ф(х., г/., /(х., y.))[i X., (х., z/.)gX.,
i = 1
Т. е. является обычной интегральной суммой Римана а^
функции, непрерывной на замкнутой квадрируемой области D.
Поэтому
lim сЕ. = \\ Ф(х, г/, /(х, y))dxdy. E1.26)
|т| ^ о ^ •'^•^
Следовательно, в этом случае поверхностный интеграл
второго рода E1.22) равен интегралу Римана, стояпа;ему в
правой части равенства E1.26):
\\ Ф(х, г/, 2)dxdy = ||Ф(х, г/, /(х, y))dxdy. E1.27)
S D
По аналогии со случаем гладких поверхностей интеграл
E1.27) будем называть «интегралом по верхней стороне
поверхности» и обозначать ||Ф(х, г/, 2)dxdy, sl тот же интеграл
/\
S
со знаком минус, т. е. -||Ф(х, г/, /(х, y))dxdy, будем называть
D
«интегралом по нижней стороне поверхности» и обозначать
||Ф(х, г/, 2)dxdy или ||Ф(х, г/, 2)dydx. Следовательно,
S '
^^ Ф(х, г/, 2)dxdy = ||Ф(х, г/, 2)dxdy =
^ S
= ||Ф(х, г/, /(х, y))dxdy, E1.28)
D
\\ Ф(х, г/, 2)dydx = ||Ф(л:, г/, 2)dxdy = -||Ф(х, г/, /(х, y))dxdy.
S -
Таким образом, для поверхностного интеграла E1.22)
получены те же самые формулы E1.26), что и для поверхностного
интеграла в смысле определения 2 (см. E1.14) и E1.15)).
Однако на этот раз эти формулы доказаны без предположения о
какой-либо гладкости элементарной поверхности, кроме ее не-
629
прерывности, тогда как раныае, в силу самого определения 2,
предполагалось, что рассматривается поверхность непрерывно
дифференцируемая.
Опигаем егце один случай поверхностного интеграла E1.22),
который встретится в дальнейгаем. Пусть представление г (и, v),
(и, v)eD, поверхности S таково, что образ множества D при
отображении E1.20) имеет меру Жордана, равную нулю, а Ф —
произвольная функция, заданная на поверхности S. Тогда
\\ Ф(х, г/, 2)dxdy = 0. E1.29)
S
В самом деле, в этом случае для любого разбиения т =
= {X^}f_^^ замкнутой области D мера всех множеств X* на
плоскости переменных х, у равна нулю. Поэтому все суммы
@* равны нулю, а следовательно, их предел при |т| -^ О, т. е.
интеграл E1.22) также равен нулю. В этом случае бывает
удобно для единообразия терминологии говорить об
интеграле по той или иной стороне поверхности, в зависимости от
задачи она может называться верхней, нижней, внутренней
или внеп1ней. Будем по определению считать, что в
рассматриваемом случае все термины «поверхностный интеграл по
той или иной стороне поверхности aS» равносильны, и писать
^^ Ф(х, г/, z)dxdy = ^^ Ф(х, г/, z)dydx = 0. E1.30)
S S
в частности, если S является ориентируемой
кусочно-гладкой цилиндрической поверхностью с образуюпа;ей,
параллельной оси OZy то отмеченная вып1е эквивалентность определений 2
и 2' поверхностных интегралов легко проверяется
непосредственно. Действительно, образ на плоскости хОу замкнутой
области D при отображении E1.20) совпадает с проекцией на эту
плоскость самой поверхности S. Поэтому поверхность в данном
случае является частью цилиндра, основанием которого
является указанная проекция меры нуль, а образуюгцая —
параллельна оси Oz. Таким образом, если v = (cos а, cos Р, cos у) —
какая-либо ориентация поверхности aS, то нормаль v
ортогональна оси Oz, поэтому cos у = О, откуда явствует, что
интеграл ||Ф(х, г/, z) cos ydS = О, и тем самым в этом случае
S
справедлива формула
^^ Ф(х, г/, z)dxdy = ^^ Ф(х, г/, z) cos ydS,
s s
так как обе части этого равенства равны нулю.
Так же как и в частных случаях E1.26) и E1.29), можно и
для обгцего понятия интеграла второго рода E1.22) ввести по-
^30
нятие интеграла по той или иной стороне поверхности.
Именно, по аналогии со случаем гладких поверхностей, интегралы
^^Ф(х, у, 2)dxdy и -^^Ф(х, у, 2)dxdy
S S
называются интегралами по разным сторонам поверхности S,
При этом следует обратить внимание на то, что термин
«та или иная сторона поверхности» как самостоятельный
термин не определяется, а определяется только в целом
термин «поверхностный интеграл второго рода по той или иной
стороне поверхности».
Аналогично тому, как вып1е было введено обобпа;ение
понятия поверхностного интеграла второго рода E1.22) вида
ii Ф(х, г/, 2)dxdy, вводятся и обобгцения понятий поверхност-
S
ных интегралов второго рода вида ||Ф(х, г/, 2)dyd2 и
S
||Ф(х, г/, 2)d2dXy следовательно, и вида ^^Pdyd2 + Qd2dx +
s s
+ Rdxdy no заданной стороне поверхности.
§52
Скалярные и векторные поля
52.1. Определения
Вместо терминов «числовая функция точки», «векторная
функция точки» употребляются и равнозначные им:
«скалярное поле», «векторное поле». Эта терминология подчеркивает,
что значения рассматриваемых функций зависят именно от
точек пространства (в которых эти функции определены), а не от
их координат, при выборе той или иной системы координат.
Используя эту терминологию, можно сказать, например,
что всякое скалярное поле и = и(М), определенное и
дифференцируемое в некоторой области G, порождает векторное
поле его градиентов (см. п. 37.6 и п. 50.5): а(М) = grad и(М).
Определение 1. ili/cmb в области G* задано векторное поле
а = а(М) и существует определенная в G функция и = и(М)
такая, что а(М) = grad и(М). Тогда функция и(М) называет-
* В этом параграфе для простоты рассматриваются только плоские
или трехмерные области G.
^3i
ся потенциальной функцией или потенциалом данного
векторного поля*.
Вводя символический вектор набла, V = i.:— + ].:— + fe.^
(см. п. 37.7), можно написать grad и = Vz/, где в правой части
равенства стоит «произведение» символического вектора
набла на числовую функцию и.
Пусть, например, Е{М) — напряженность электрического
поля, созданного единичным отрицательным зарядом,
который помегцен в начале координат. Тогда в точке М(х, г/, г)
вектор Е(М) имеет, как это известно из физики, длину —, где
г = л/л:^ + 1/^ + 2^, и направлен от точки М к началу
координат. Отсюда получаем, что
£(М) = (-^з,-^.-^
Электрический потенциал рассматриваемого поля, т. е.
функция и(М) = -, является и потенциалом в указанном вы-
г
Hie смысле, поскольку grad и(М) = Е(М).
Рассмотрим снова векторное поле а = а(М), определенное
в некоторой области G. Зафиксируем систему координат, в
этом случае векторную функцию а(М) можно рассматривать
как функцию трех переменных — координат х, г/, z точки М:
а = а(х, у у z).
Пусть точка М^ = (Xq, i/q, ZQ)eG и задан единичный вектор
е = (cos а, cos Р, cos у). Проведем через точку Mq прямую в
направлении е:
X = Xq-\- tcos а, у = Уо + tcos р, z = Zq-\- tcos у,
-оо <t< +00.
Определение 2. Производная векторной функции
а = (Xq + f cos а, у^ + f cos р, Zq + f cos у)
no t при t = 0 (если она существует) называется
производной векторной функции а{М) по направлению е в точке М^ и
обозначается через т^:
де
Эа(Мо) _ da
дё dt
* Иногда в приложениях потенциал и определяется формулой а
-grad и.
^32
По правилу дифференцирования сложной функции,
опуская для простоты обозначения аргумента, получим
^ = ^cos а + ^cos р + ^cos у. E2.1)
де дх ду dz
Полагая eV = cos а.^ + cos В.^ + cos у^:— («скалярное произве-
дх ду az
дение» вектора е и символического вектора V), перепигаем
формулу E2.1) в виде .г^ = (eV)a.
ое
Определение 3. Если Ь = (Ь^, Ь^, Ъ^ — произвольный {не
обязательно единичный) фиксированный вектор, то вектор
(bV)a = Ъ^^ + h^ + b,^
^дх Уду ^dz
называется градиентом вектора а по вектору Ъ.
Если Ъ = ЪЪ^у где ^^ = 1, то «формальными
преобразованиями» получим
(bV) а = (ЬЬо V)a = b{b^V)a = b^.
Переходя к координатной записи, легко непосредственно
убедиться в справедливости полученной формулы и показать, что
с символом V можно обрагцаться при вычислениях, как с на-
стоягцим вектором, не забывая, конечно, при этом, что, кроме
этого, V означает также и определенную операцию
дифференцирования. Мы не будем останавливаться на обосновании
законности таких «формальных преобразований с символом V».
Любая формула, полученная подобным образом, может быть,
конечно, получена и без применения символа V обычными
обоснованными рассуждениями в координатах. Следует иметь
в виду, однако, что применение символа V часто весьма супа;е-
ственно сокрапа;ает выкладки.
Вернемся снова к исходному векторному полю а = (а^, а , а^)
в области G.
Определение 4. Пусть поле а = (а^, а^, а^) дифференцируемо в
некоторой точке. Число ^ + ^ + ^ называется диверген-
дх ду dz
цией поля в этой точке и обозначается через div а, т, е,
diva = ^- + ^^^. E2.2)
дх ду dz
Символически diva может быть записана как скалярное
произведение символического вектора V и вектора а:
div а = Va.
^33
Геометрический и физический смысл div а будет выяснен
в дальнейшем.
Определение 5. Вектор с координатами
да,_дау да^_да, да^ _да^ E2 3)
ду дг ' дг Эх' Эх ду
называется вихрем, или ротором, векторного поля а =
= а(М) и обозначается rot а.
С помогцью символического вектора V ротор можно
записать в виде следуюпа;его векторного произведения:
rot a = V X а-
i j
э э
Эх ду
«X %
к
Э
dz
^z
E2.4)
Термин «ротор» происходит от слова «ротация» (врапа;е-
ние). Это объясняется следуюпа;ими обстоятельствами.
Рассмотрим движение твердого тела. Зафиксируем в нем точку и
обозначим ее Mq. Из механики известно, что скорость v =
= v(M) любой точки М этого тела выражается по формуле
i; = i;q + со X г,
где i;o — скорость точки Mq, g> — мгновенная угловая скорость
врагцения всего твердого тела относительно точки Mq, а г —
радиус-вектор с началом в точке Mq и концом в точке М.
Векторы i;q и (D не зависят от точки тела М (при фиксированной
точке Mq), а радиус является, очевидно, функцией точки
тела: г = г(М).
Зафиксируем в пространстве систему координат х, у, г, и
пусть V = (V^, Vy, V^), (D = (Ш^, Ш^, Ш^), г = (Х, у, 2), Vq =
= (^ох' %' ^0.); тогда
^х = ^Ох + %^ - ^гУ^ ^у = ^Оу + ^2^ - ^х^' ^2 = ^02 + ^хУ - %^'
Отсюда
dv^ dv^ Эу,, Эу,, Эу™ Эу™
ду ^^' dz ^У Эх ^^' dz ^^' Эх ^У ду ^^•
Выясним теперь, как меняется в рассматриваемом
твердом теле ротор скоростей его точек. Для этого воспользуемся
формулами E2.3):
Эу™ dv,, dv^ dv^ dv,, dv^
— ^ = 9m — = 9m —^ = 9m
ду dz ^^^' dz Эх ^%' Эх ду ^^^-
^34
Таким образом, rot v = 2g). Иначе говоря, с точностью до
числового множителя ротор скоростей v точек тела совпадает
с мгновенной угловой скоростью врагцения твердого тела.
Отсюда и происходит название «ротор».
Приведем пример формальных преобразований с
символом V. Если за символом V следует несколько членов, на
один из которых он действует как оператор
дифференцирования, а на другие нет, то для ясности будем обозначать этот
член вертикальной стрелкой. Поясним это на примере.
Пусть / — скалярное, а — векторное поле; тогда
i i
rot /а = V X /а = V X /а + V X /а = /(V X а) + (V/ X а) =
= f rot а + grad / X а.
Введем некоторые определения, связанные с векторным
полем а = (а^, а„, aj в области G.
^ л у Z'
Определение 6. Пусть Г — замкнутая кусочно-гладкая
кривая в области G. Интеграл
^ adr = ^ a^dx + aydy + a^dz
г г
называется циркуляцией векторного поля а = (а^, а^, а^ по
кривой Г. Здесь dr = (dx, dy, dz).
Если Г — ориентированная гладкая кривая, s —
переменная длина дуги, t = (cos а, cos Р, cos у) — ее единичный
касательный вектор, а пр^ а — величина проекции вектора а на
касательную, то
^ adr = |пр^ ads.
г г
Действительно,
I adr = I a^dx + a^dy + a^dz = J (a^cos a + a^cos P + a^cos y)ds =
г г г
= I atds = I np^ ads.
г г
Определение 7. Поле, циркуляция которого по любой
замкнутой кусочно-гладкой кривой, лежащей в области G, равна
нулю, называется потенциальным.
Напомним, что в п. 47.8 было показано (см. лемму 2), что
условие равенства нулю интеграла ^ Pdx + Qdy по любому
г
замкнутому контуру Г ^ G равносильно тому, что интеграл
I dx + Qdy не зависит от пути интегрирования между точка-
635
ми A и Б. При доказательстве этого утверждения нигде не
использовался тот факт, что кривая Г лежит в плоской области.
Поэтому доказательство леммы 2, приведенное в п. 47.8,
сохраняет силу и для криволинейных интегралов по
пространственным кривым. Таким образом,
циркуляция ^adr = \ a^dx + а dy + a^dz равна нулю по
г г
любому замкнутому кусочно-гладкому контуру Г ^ G
тогда и только тогда, когда интеграл \ a^dx + aydy + a^dz не
АВ
зависит от пути интегрирования, т, е, от кривой с
началом в точке А, концом в точке В и целиком лежащей в
области G,
Рассмотрим в качестве примера плоское векторное поле,
т. е. поле а = (Р, Q), заданное на плоской области G : Р =
= Р(х, у), Q = Q(x, у). Вихрь этого поля имеет вид
rot а
i j k
_э_ _э_ _э_
Эх ду dz
Р Q О
\ ах ду
Теорема 4 п. 47.11 во вновь введенных терминах может
быть перефразирована следуюгцим образом. Для односвязной
плоской области G потенциальность поля, существование
потенциальной функции и условие, что вихрь поля во всех
точках равен нулю, эквивалентны.
Определение 8. Пусть S — некоторая кусочно-гладкая
ориентированная поверхность, лежащая в области G, v —
единичный вектор нормали к поверхности, задающей ее
ориентацию, и S^ — поверхность S с указанной ориентацией.
Интеграл \\cidS = ^^avdS называется потоком векторного
поля через поверхность.
Очевидно, что av = пр^а, поэтому
\\adS = \\up^adS.
s+ s
В дальнейп1их пунктах этого параграфа будут рассмотрены
некоторые свойства векторных полей, в частности, установлены
в трехмерном случае необходимые и достаточные условия
потенциальности поля. Предварительно докажем теоремы о
кратных и поверхностных интегралах, тесно связанные с понятия-
ми, введенными в этом пункте. Начнем с доказательства
инвариантности этих понятий.
УПРАЖНЕНИЕ 1. Доказать следующие формулы:
а) rot grad w = 0;
б) div rot a = 0;
в) div grad I. = Ai., где Ai. = |i| + |if + |!f;
dx^ dy^ 62'^
r) rot rot a = grad div a - Aa, где Aa = (Aa^, Aa^, Aa^), a = (a^, a^, a^);
д) div (fa) = /diva + grad/a;
е) div аХЪ = Ъ rot a — a rot Ъ.
52.2. Об инвариантности понятий
градиента, дивергенции и вихря
Прежде всего заметим, что при ортогональном
преобразовании декартовых координат символический вектор V
преобразуется по правилам преобразования обычных векторов.
Действительно, пусть задано ортогональное преобразование
координат
х' = а^^х + а^2У + ^13^'
у = а^^х + а^^у + азз^,
2' = agiX + а^^У + «33^- E2.5)
Для таких преобразований матрица обратного
преобразования совпадает с транспонированной матрицей, поэтому
X = а^^х' + а21у' + a^i2\
у = а^^х'+ а^^у + а^22\
2 = а^^х + а^^у + а^^2. E2.6)
При этом, как хороню известно, по формулам E2.5) и E2.6)
преобразуются как координаты точек, так и координаты
векторов.
Используя формулы E2.5) и правило дифференцирования
сложной функции, получим
дх Эх'Эх ду'дх dz'дх ^^дх' ^^^у' ^^dz'^
^-^'^ + ^¥ + ^^'-«12^ + «22^ + «32^, E2.7)
ду дх'ду ду'ду dz' ду ^^Эх' Эг/' "^^Эг
Э ^ Э Эх^ , Э ду^ -[- ^ ^L. = п ^ -\- п ^ -\- п ^
Эг Эх^Эг 'dy^dz 'd7dz ^^Эх^ ^^Э^ ^^^
^37
Обратные формулы, выражаюгцие производные по
переменным х\ у\ z' через производные по х, г/, 2, имеют вид
э ^^ э ^ э ^ э
э ^^ э ^ э ^ э
47, = <^2i4- + a'+a' E2.8)
Формулы E2.5)—E2.8) показывают, что координаты
обычных векторов и «координаты» символического вектора V при
ортогональных преобразованиях декартовых координат
преобразуются по одному и тому же правилу. В частности, из E2.8)
следует, что градиент функции и в системе координат х, г/, 2,
т. е. вектор с координатами ^, ^, ^, в системе х\ у\ г' будет
иметь координаты .г-^, .Д, =г^, т. е. являться градиентом и в этой
ох оу OZ
системе координат. Тем самым егце раз доказано (см. п. 20.7),
что градиент функции не зависит от выбора декартовой системы
координат. Так как вектор V преобразуется подобно обычным
векторам, то естественно ожидать, что и скалярное
произведение Va не зависит от выбора указанной системы координат.
Пусть вектор а в системе х, г/, z имеет координаты а^, а , а^,
а в системе х\ у\ г' — координаты а^,, а^^,, а^,. В силу формул
E2.7) имеем
Эх Ъу Ъг ^^Ъх ^^Ъу "^^Ъг
dUy dUy dUy да^ да^ да^ ^
= Э^С^П^х + «21^^ + «31«.) + Э7(^21«х + «22^^ + «23«.) +
_Э_
Применяя формулы E2.5) к вектору а = (а^, а^, а^) (т. е.
заменяя в этих формулах х, г/, 2 на а^, а , а^, а х', г/', z' на а^,
а' а'^), получим, что выражения в круглых скобках в правой
части равенства E2.9) равны последовательно а^., а^^., а^. и,
следовательно,
Эа„ , да., , Эа„ Эа„' , да,' , Эа„'
Эх Эг/ Эг Эх' ду' dz''
Это равенство и показывает, что дивергенция векторного
поля в каждой точке однозначно определяется самим вектор-
638
+ ^(«31«х + «32«z/ + «зз«.)- E2.9)
ным полем, а не зависит от выбора системы координат, как
это могло бы показаться сначала из формулы E2.2).
Векторное произведение обычных векторов в силу своего
геометрического смысла не зависит от выбора декартовых
систем координат с одинаковой ориентацией (например,
векторное произведение двух векторов не изменится, если от
одной правой декартовой системы координат (см. п. 50.8)
перейти к такой же другой). Поэтому естественно ожидать, что
тем же свойством обладает и «символическое векторное
произведение» rot а = V X а.
В самом деле, если обозначить единичные координатные
векторы системы координат х\ у\ г' соответственно через
i\ ]\ k\ то, как известно, единичные координатные векторы
1, /, k системы координат х, г/, z выражаются через i\ j\ k'
посредством матрицы, транспонированной к матрице
преобразования E2.5), т. е. посредством матрицы преобразования
E2.6):
i = a^^i + a^i f + (i^ik\
j = a^^i + a22 f + a^Jt\
k = а^зГ + «23/' + CL^s^'. E2.10)
Используя формулы E2.6), E2.7) и E2.10), получим
k
Э
rot a = V X а
1 /
_э_ _э_ _
Эх ду дг
а.
а..
а.
aiiV + a2iJ' + a^^k' ai2i' + a22/' + «32^' «1з^' + «2з/' + «зз^'
'^^Э? ''12Э7^''22Э7^''''Э7 '"'^d^^'^'W^''''^'
*'Z\^z'
а^с,а
12"'х'
-а
22^1/' + ^32^г'
^ХЗ'^х'
^23^1/'^^ЗЗ^г'
^11 ^12 ^13
^21 ^22 ^23
^31 ^32 ^33
I
_э_
Эх'
aw
_э_ _э_
ду' дг'
E2.11)
Последнее равенство доказывается так же, как для
обычных числовых матриц доказывается тот факт, что
определитель произведения двух квадратных матриц одного и того же
порядка равен произведению их определителей. Для
доказательства этого равенства достаточно убедиться, что в обеих
его частях стоят одинаковые алгебраические суммы одних и
тех же слагаемых.
639
Определитель ортогонального преобразования равен +1
или -1, причем если это преобразование сохраняет
ориентацию, то +1. Поэтому если в рассматриваемом случае выбрать
системы координат х, г/, 2 и х\ у\ 2\ ориентированные
одинаково, то будем иметь
^\\ ^12 ^13
^22 "^23
= 1
^31 ^^32 ^^33
И, следовательно, из E2.11) получим
i j k
_э_ _э_ _э_
Эх ду дг
а^ а„
а.
V
_э_
Эх'
а.'
У
э
Э^/^
«,/
к'
Э
dz'
а,'
Это равенство и означает, что вихрь векторного поля не
зависит от выбора декартовой системы координат, имеюгцей ту же
ориентацию, что и заданная. Заметим, однако, что если от
одной системы координат перейти к системе с другой
ориентацией, например от правой системы координат — к левой, то
каждый вихрь (как и обычное векторное произведение)
заменится противоположным вектором. Это следует из формулы
E2.11), поскольку определитель ортогонального
преобразования, меняюпа;его ориентацию, равен -1.
Таким образом, вихрь векторного поля однозначно «с
точностью до знака» определяется самим векторным полем, а
если ограничиться только одинаково ориентированными
декартовыми системами координат, то не зависит от их выбора.
52.3. Формула Гаусса — Остроградского.
Геометрическое определение дивергенции
Пусть G — область в пространстве й^^^* Предположим,
что на плоскости R'^y супа;ествует такая квадрируемая область
D, что граница 3G области G состоит из двух поверхностей aS^
и aS2, задаваемых явными представлениями, соответственно
2 = ф (х, г/) и 2 = \|/ (х, г/), где функции ф и \|/ непрерывны на
замкнутой области D, ф (х, г/) < \|/ (х, г/), (х, г/) g D, и, быть
может, из поверхности aSq, являюпа;ейся частью цилиндра,
основанием которого является граница 3D области D, а обра-
зуюгцая параллельна оси 02 (см. п. 44.1),
aG = SiUS2USo. E2.12)
640
в этом случае область G называется элементарной
относительно оси Oz. Она имеет вид
G = {(х, г/, z) : (х, у) е D, ф(х, у) < z < \|/(х, у)}. E2.13)
Области такого типа уже встречались при изучении вопроса
о сведении кратного интеграла к повторному. Обозначим для
краткости границу dG области G через S: тогда (см. E2.12))
S=SiUS2USo. E2.14)
Пусть на S задана функция Ф = Ф (х, у, z). Поверхностные
интегралы второго рада [|Ф(х, у, z) dxdy от функции Ф по
верхней стороне поверхности aS^, ||Ф(л:, г/, z) dxdy по нижней
\^
стороне поверхности 182 и ^^ Ф(х, г/, z) dxdy по поверхности aSq
-So
(см. п. 51.4) называются «поверхностными интегралами
второго рода по внеп1ним сторонам этих поверхностей», а их
сумма — «интегралом по внешней стороне поверхности aS» и
обозначается ||Ф(л:, г/, z) dxdy, т. е.
||Ф(х, г/, z) dxdy = ||Ф(х, г/, z) dxdy + ||Ф(х, г/, z) dxdy +
+ \\ Ф(х, г/, z) dxdy. E2.15)
So
Аналогично определяется «поверхностный интеграл
||Ф(х, г/, z)dxdy по внутренней стороне поверхности S»:
S-
11 Ф(х, г/, z)dxdy = ||Ф(х, г/, z)dxdy + ||Ф(х, г/, z)dxdy +
+ \\Ф(x,y,z)dxdy. E2.16)
-So
Напомним (см. п. 51.5), что ||Ф(х, г/, z)dxdy = О и, следо-
вательно, это слагаемое можно было бы и не писать. Его пи-
П1ут для того, чтобы формулы E2.15) формально
соответствовали формуле E2.14). Как следует из дальнейгаего, это
оказывается очень удобным.
Если поверхности aS^, S2 и aSq кусочно-гладкие, то
интеграл ||Ф(х, г/, z)dxdy представляет собой поверхностный ин-
641
теграл по поверхности aS, ориентированной с помогцью внега-
ней единичной нормали v. В этом случае если
V = (cos а, cos р, cosy), E2.17)
то
||Ф(х, г/, z)dxdy = ^^ Ф(х, г/, z) cos ydS. E2.18)
s+ s
Здесь термин «кусочно-гладкая поверхность» понимается
в п1ироком смысле (см. п. 50.11). Например, поверхность S
(см. E2.14)) является кусочно-гладкой, если у замкнутой
области D сугцествует такое ее разбиение т = {Dj}/ = i^, где D- —
области, границы которых состоят из кусочно-гладких
кривых, что функции ф и \|/ непрерывны на замыканиях Z).
областей Z)., непрерывно дифференцируемы в самих Z). и у
поверхностей, задаваемых представлениями ф(х, г/), (х, y)&D. и
\|/ (х, г/), (х, y)eD., /=1,2, ... , i^, супа;ествуют представления,
непрерывно дифференцируемые вплоть до границ областей,
на которых они заданы. Отсюда следует, что поверхности aS^
и aS2 кусочно-гладкие в п1ироком смысле. Кусочная гладкость
поверхности aSq следует из того, что граница области D
состоит из частей границ областей Z)., т. е. является
объединением конечного множества кусочно-гладких кривых.
Поэтому цилиндр, основанием которого является граница области
D, а образуюгцая параллельна оси Oz, так же как и всякая
поверхность, являюгцаяся его частью, представляет собой
кусочно-гладкую поверхность.
Аналогично областям, элементарным относительно оси
Oz, определяются области, элементарные относительно
осей Ох, Ог/, и интегралы
^^Фdydz, ^^Фdydz, ^^Фdzdx, ^^Фdzdx,
S+ S- S+ S-
а следовательно, для областей, одновременно элементарных
относительно всех координатных осей, и интегралы
11 Pdydz + Qdzdx + Rdxdy, \ \ Pdydz + Qdzdx + Rdxdy E2.19)
s+ s-
ПО внеп1ней и внутренней сторонам границ этих областей.
Области, элементарные одновременно относительно всех
координатных осей, называются элементарными областями.
Примерами элементарных областей являются тетраэдры,
кубы (вообгце любые выпуклые многогранники), гаары,
эллипсоиды и т. п. (рис. 99).
642
При рассмотрении
поверхностных интегралов
^^ Pdydz + Qdzdx + Rdxdy
К
v/i:
к.
^1
^0
Y
Рис. 99
по поверхностям, являюгцимся
границами элементарных
областей, становится ясной
целесообразность включения третьего
нулевого слагаемого в правых
частях формул типа E2.15) и E2.16).
Действительно, поверхность, яв-
ляюпа;аяся частью цилиндра с
образу юпа;ей, параллельной одной из
осей координат, не является,
кроме случая, когда она вырождается в точку, частью цилиндра с
образуюпа;ей, параллельной другой оси координат. Поэтому если
бы не включать в интеграл E2.19) по всей границе области
указанные нулевые слагаемые, то интегралы \\Pdydz, \{Qdzdx и
S S
и Rdxdy следовало бы понимать как интегралы по различным,
S
вообгце говоря, частям границы рассматриваемой области.
ТЕОРЕМА 1. Пусть G — элементарная область и на ее
замыкании G заданы функции Р(х, у, z), Q(x, у, z) и R(x, у, z),
непрерывные вместе со своими частными производными^
—, -^ г/ —. Тогда имеет место формула
дР ,dQ , dR
+
+
Эх ду dz ) '
Adxdydz = \\Pdydz + Qdzdx + Rdxdy, E2.20)
ш
где интеграл в правой части равенства берется во внешней
стороне границы S области G.
Формула E2.20) называется формулой
Гаусса—Остроградского,
СЛЕДСТВИЕ. Если при выполнении условий теоремы
граница области G кусочно-гладкая, то
^^^ Г|^ + ^ + ^Xlxdydz = II(Pcosa + QcosP + Rcosy)dS,
^ Удх ду dz ) ^ E2.21)
где cos a, cos p, cos у — направляющие косинусы единичной
внешней нормали v (см. E2.17)) к поверхности S.
* Непрерывность частных производных на границе понимается как
их непрерывная продолжаемость на границу области.
643
Положив
a^=(P,Q,R), E2.22)
формулу E2.21) Гаусса—Остроградского можно переписать в
виде
\\\ div а dxdydz = \\avdS. E2.23)
G S
Доказательство. Рассмотрим, например, интеграл
\\\ Т~ ^^^У^^' Использовав обозначения, введенные в начале
G
ЭТОГО пункта, получим
G D ф(х, у)
= \\{R[x, г/, \|/(х, г/)] - R[x, г/, ф(х, y)]}dxdy =
D
EГ27) Я^^^' ^' z)dxdy + \\Щх, г/, z)dxdy. E2.24)
Заметим далее (см. E1.27)), что ||i?(x, г/, z)dxdy = О, так
как проекция на плоскость хОу поверхности S содержится в
границе квадрируемой области D и поэтому имеет плоскую
меру Жордана, равную нулю. Таким образом, формулу
E2.24) можно переписать в виде
Я1 Тг ^^^^^^ = llRdxdy + Я Rdxdy + llRdxdy =
^ S2 S, «о
,b2-u,ll^dxdy. E2.25)
CoBepnieHHO аналогично доказываются формулы
\\\ ^ dxdydz = \\Pdydz, \\\ ^dxdydz = \\ Qdzdx. E2.26)
Складывая E2.25) и E2.26), получим формулу E2.20). П
Подчеркнем, что формула E2.20) доказана без
предположения о какой-либо дифференцируемости поверхности, огра-
ничиваюпа;ей область G (поверхностные интегралы второго
рода берутся здесь в смысле определений п. 51.5).
Формула Гаусса—Остроградского E2.12) может быть
доказана и в случае областей G более обпа;его вида, чем было
указано, а именно для таких, для которых супа;ествует конечное
разбиение на элементарные области G., / = 1, 2, ... , /q. Для
этого достаточно написать формулу Гаусса — Остроградского
644
для каждой области G-, и полученные результаты сложить;
в результате получается искомая формула для области G.
Действительно, в левой части равенства, в силу аддитивности
интеграла, получится соответствуюгций интеграл по области G, а
в правой части равенства сумма всех поверхностных
интегралов по частям границ, которые принадлежат границам двух
областей, равна нулю. В самом деле, если некоторая
поверхность представляет собой часть границ двух областей, то
интеграл по внеп1ней стороне поверхности относительно одной
из этих областей является интегралом по внутренней стороне
поверхности относительно другой области, т. е. первый
интеграл отличается от второго только знаком и поэтому они
взаимно уничтожаются. В результате останутся только
интегралы по частям границ G., составляюгцим в совокупности
границу области G (ср. с п. 47.5). Указанные разбиения области G
часто бывает удобно производить плоскостями,
параллельными координатным плоскостям.
Заметим, что среди областей такого типа есть и области,
граница которых состоит из нескольких «кусков», т.е.
может быть представлена как сумма конечного числа
кусочно-гладких непересекаюгцихся поверхностей (ср. с соответст-
вуюгцими обобгцениями формулы Грина в п. 47.8).
Можно показать, что формула Гаусса—Остроградского
справедлива для любой ограниченной области, граница которой
состоит из конечного числа кусочно-гладких поверхностей.
Однако это довольно громоздко, и мы не будем на этом
останавливаться, а ограничимся лигаь формулировкой теоремы.
ТЕОРЕМА 1^ (теорема Гаусса—Остроградского). Пусть
граница до ограниченной области G состоит из конечного
числа кусочно-гладких поверхностей, а вектор-функция а =
= (Р, Q, R) и частные производные —, -^ и — непрерывны на
замыкании G области; тогда
^^^ diY adxdydz = ^ ^ adS.
G dG
В качестве ориентации на гладких частях границы дО
области G здесь выбрана внеганяя нормаль.
Например, если G = {х, у, z) : О < а < Jx^ -\- у^ -\- z^ < b} —
niapoBoe кольцо и, следовательно, его граница состоит из
двух сфер S^ = {(х, г/, z) : х^ -\- у^ -\- z^ = а^} и S2 = {(х, у, z) :
х^ + г/^ + 2^ = Ь^}, то на внутренней сфере aS^ надо взять нормаль,
направленную к центру niapa G, а на внеганей сфере 182 — от
центра niapa.
'645
Формула Гаусса—Остроградского позволяет найти
выражение для объема области через соответствуюгций
поверхностный интеграл. В самом деле, полагая в E2.20) Р(х, у, z) =
= X, Q(x, у, z) = г/, i?(x, у, z) = z VL заметив, что ^^^ dxdydz =
G
= \xG, получим
\xG = -\\ xdydz + ydzdx + zdxdy,
или в случае E2.21)
[iG = -^Wix cos a-\- у cos P + 2 cos y)dS.
Формула Гаусса—Остроградского дает также возможность
установить геометрический подход к понятию дивергенции.
ТЕОРЕМА 2. Пусть в трехмерной области G"" определено
непрерывно дифференцируемое векторное поле а = а(М),
Пусть MqgG и D — область с кусочно-гладкой границей S
такая, что M^eD, D ^ G и, следовательно, для области D
справедлива формула Гаусса—Остроградского**.
Обозначим через S^ поверхность S, ориентированную с
помощью выбора внешней нормали, а через diamD —
диаметр области D, Тогда
\\ adS
div а(Мп)= lim ^^ ^ . E2.27)
Доказательство. По формуле E2.23) имеем
\\\ div а dxdydz = \\ adS. E2.28)
D S+
Но по интегральной теореме о среднем (п. 44.6)
\\\ div а dxdydz = div a(M)[iD, MeD. E2.29)
D
Подставив E9.29) в E2.28), получим
\\ adS
div а(М) = ^^-^. E2.30)
* Здесь на структуру области G не накладывается никаких
ограничений.
**К таким областям D, например, относятся все шары достаточно
малого радиуса с центром в точке Mq и кубы достаточно малого размера с
центром в точке Mq.
646
Переходя к пределу в формуле E2.30) при diamD ^ О, в силу
непрерывности в точке М^ функции div а(М), получим
формулу E2.27). П
Можно показать, что величины, входягцие в правую часть
равенства E2.27), не зависят от выбора системы координат
(в правую часть входит двойной интеграл от скалярного
произведения векторов и объем области), поэтому отсюда егце
раз следует, что дивергенция векторного поля не зависит от
выбора системы координат.
Из равенства E2.27) следует также, что правая часть
этого равенства может быть принята за определение
дивергенции данного поля.
Точки векторного поля а, в которых div а ^ О,
называются источниками векторного поля. Интуитивно
естественность этого термина объясняется тем обстоятельством, что
если точка является «источником», то, как видно из формулы
E2.27), для всех достаточно малых по диаметру областей D,
содержапа;их точку Mq, будем иметь ii adS ^ О, т. е. поток
S
векторного поля а через любую достаточно малую
поверхность, окружаюгцую источник, не равен нулю.
52.4. Формула Стокса.
Геометрическое определение вихря
Пусть S — дважды непрерывно дифференцируемая
поверхность без особых точек в пространстве R^y^ и г = г(и, и) =
= (х(и, v), у{и, v), z{u, v)), (и, v)eD, — ее представление, D —
плоская ограниченная область, для которой справедлива
формула Грина. Допустим, что граница области D состоит из
одного простого кусочно-гладкого контура. Обозначим через Fq
положительно ориентированный контур, ограничиваюгций
область D, и через и = u(t), v = v(t), а< t <b, — его представле-
V X у
ние. Пусть V = 7-^ — ориентация на поверхности S (см. оп-
ределение 20 в п. 50.10), v = (cos а, cos р, cos у). При
сделанных предположениях нормаль v непрерывна на D.
Обозначим через aS+ поверхность S с выбранной на ней
нормалью V. Пусть Г — контур с представлением г = г (u(t), v(t)),
а <: t <: b, т. е. Г является краем поверхности S. Будем
говорить также, что поверхность S натянута на контур Г.
647
Пусть, наконец, G — область в пространстве R^y^ ^ S ^ G.
При выполнении этих предположений справедлива следую-
па;ая теорема.
ТЕОРЕМА 3 (теорема Стокса''). Пусть функции Р, Q и R
непрерывны вместе со своими первыми частными
производными в области G и пусть а = (Р, Q, R). Тогда
I adr=\\ rot adS, E2.31)
г s+
т, е, циркуляция векторного поля по контуру Г,
являющемуся краем поверхности S, равна потоку вихря этого поля
через эту поверхность, В координатной форме формула
E2.31) имеет вид
cos а cos р cos у
I Pdx + Qdy + Rdz = \\
д
Эх
Р
э
Эг/
Q
Э
дг
R
dS,
или
I Pdx + Qdy + Rdz =
Доказательство. Рассмотрим, например, интеграл | Pdx.
г
Заметив, что вдоль кривых Fq и Г переменные и и v являются
функциями от ty и употребив обозначения, введенные в начале
этого пункта, получим
\ Р(х, у, z)dx =
г
= |Р(х(г/@, v{t)), y(u(t), v(t)), z(u(t), v(t)))x\(u(t)), v(t))dt =
a
= I P{x{u, V), y{u, V), z{u, V)) {^-^^ du + ^£^ dv)
Мы здесь воспользовались формулой
x'(u(t) v(t)) = ^-^(^(O^ v(t))du _^ dx{u(t), v(t))dv^
^ ' du dv dv dt'
' Дж. Стоке A819—1903) — английский механик и математик.
648
Применив формулу Грина к получивпхемуся интегралу
f P^du + P^dv, будем иметь
•! ди av
ii[i
ЭР Эх ЭР Э^ ЭР Э£^Эх д^х _
дх ди ду ди dz ди idv ди dv
ГдРдх дРду дРдгЛдх p^^^l^ ^ _
[ дх dv ду dv dz dv )ди dv du\
= J|f|fcos|3-|^cosy]dS. E2.33)
(Здесь использовано соотногаение E1.13).) Аналогично
доказывается, что
|Qdz/=||fg cosy-g cos a]dS, E2.34)
I Rdz = \\ [y c^s ^ " ^ c^s P V'S. E2.35)
Складывая формулы E2.33), E2.34) и E2.35), получим
формулу E2.32), которая называется формулой Стокса. П
Используя координатную запись поверхностного
интеграла второго рода (см. формулу E1.10)), формулу Стокса
E2.32) можно записать в следуюгцем виде:
[[{^ - ^Уу^^ ^Ц- э! V^^^+f э? - ^У^'^у=
= I Pdx + Qdy + Rdz.
г
Чтобы наглядней представить себе связь выбора нормали v
на поверхности S с ориентацией ограничиваюпа;его ее контура
Г, рассмотрим поверхность aS, имеюпа;ую явное представление
2 = f(x, у), (х, y)eD.
Пусть Fq — положительно ориентированный на
плоскости хОу контур, являюпа;ийся границей D, и х = x(t), у = y(t),
а <: t <: b, — его представление. Как и выпхе, ориентацию
кривой Г зададим представлением
x = x(t), y = yit), 2 = f(x(t), y(t)), a<:t<:b. E2.36)
649
Рис. 100
В рассматриваемом случае контур Fq
является проекцией кривой Г. Нормаль
же V, как это было показано, при явном
представлении поверхности образует
острый угол с осью Oz (см. п. 50.10),
поэтому если смотреть на поверхность S с
положительного направления оси Oz, то
контур Г будет ориентирован против
часовой стрелки, т. е. ориентация кривой
Г согласована с нормалью v «по правилу
niTonopa» (рис. 100). Это равносильно
тому, что наблюдатель, обходягций
поверхность S по ориентированному контуру Г и смотрягций на
нее из конца нормали v, видит поверхность S слева. Такая
наглядная интерпретация согласованности ориентации
нормали V и контура имеет то преимугцество, что она не связана
с выбором системы координат и остается справедливой для
любой поверхности S рассматриваемой в теореме Стокса, а
не только для явно заданной поверхности. Конечно, все
подобные рассуждения не являются математическими
доказательствами, а служат лигаь для наглядного пояснения формулы
Стокса.
Следует заметить, что формула Стокса остается
справедливой, если в ней взять противоположную ориентацию
контура и противоположные нормали -v, в этом случае обе
части равенства E2.31) изменят знаки на противоположные.
Формула Стокса может быть доказана и для ориентируе-
{«а;:
а именно
мых кусочно-гладких поверхностей S
таких, для которых поверхности S-, i = 1, 2, ... , i^,
удовлетворяют условиям доказанной теоремы 3. При этом край
поверхности Эа8 (см. п. 50.11) состоит из конечного числа
замкнутых контуров Г., j = 1, 2, ... , /q.
Для доказательства этого достаточно написать формулы
Стокса для каждой поверхности aS-, / = 1, 2, ... , /q, и сложить
их (ср. с обобпа;ениями формулы Грина в п. 47.5 и теоремы
Гаусса—Остроградского в п. 52.3).
Отметим также, что в теореме 3 условие дважды
непрерывной дифференцируемости поверхности S было
наложено только для простоты доказательства (оно в этом случае
супа;ественно упропа;ается, вторые производные
появились в процессе доказательства и затем исчезли). Формула
Стокса E2.31) справедлива и при предположении лип1ь глад-
650
кости поверхности S (при сохранении прочих условий
теоремы 3). Доказательство этого факта выходит за рамки нагаего
курса.
Из всего сказанного следует, что формула Стокса остается
справедливой и для просто ориентированных кусочно-гладких
поверхностей aS = {aS^}^ _ ^^ (т. е. без предположения о дважды
непрерывной дифференцируемости поверхностей aS-).
Сформулируем теорему для этого случая.
ТЕОРЕМА 3' (теоремаСтокса). Пусть векторная функция а
непрерывно дифференцируема в области G и пусть S^ =
= {S^y.Z^^ — ориентированная кусочно-гладкая поверхность
(S- — гладкие поверхности), лежащая в G, udS — ее край с
ориентацией, порожденной заданной ориентацией
поверхности S+ (см. п. 50.13). Тогда
I adr = IIrot adS.
ds s+
Наглядно согласование ориентации контуров Г, из
которых состоит край Эа8 поверхности aS, с ориентацией этой
поверхности и, следовательно, с ориентациями v поверхностей
aS., означает, что наблюдатель, движупа;ийся по контуру Г^,
у = 1, 2, ... , /q, и смотряпа;ий на поверхность S из конца
нормали V, видят поверхность S слева.
Теорема Стокса дает возможность установить
геометрический подход к понятию вихря векторного поля.
ТЕОРЕМА 4. Пусть в трехмерной области G определено
непрерывно дифференцируемое векторное поле а = а(М);
Mq — фиксированная точка, М^е G; v — произвольный
постоянный единичный вектор, П — плоскость,
перпендикулярная вектору V и проходящая через точку Mq, S —
ограниченная область в плоскости П,
границей которой является кусочно-
гладкий контур Г; diam S —
диаметр области S; пусть контур Г
согласованно ориентирован с
нормалью v^ MqG SuS^G"' (рис. 101). Рис. 101
' Как и в теореме 3 (по «правилу niTonopa»).
'^Указанные области aS, очевидно, всегда существуют (почему?).
651
Тогда"^
\adr
rot a(Mr,)= lim ^—. E2.37)
Доказательство. По формуле Стокса,
^adr = llrot^adiS,
г s
но по интегральной теореме о среднем
IJrot^adS = rot^a(M)[iS, MeS.
s
Следовательно,
\adr
Tot^a(M) = ^—. E2.38)
Заметим, что при diam aS ^ О и М ^ Mq. В силу
непрерывности в точке Mq функции rot^а(М), переходя к пределу
в E2.38) при diam aS ^ О, получим формулу E2.37). П
Из формулы E2.37) следует, что ее правая часть может
быть принята за определение проекции вихря данного поля
на произвольный, но фиксированный единичный вектор v.
Это приводит и к новому определению самого вихря, так как
достаточно, например, взять три произвольных
ортогональных единичных вектора v^, V2, V3, проекциями на которые,
как это xoponio известно, однозначно определяется всякий
вектор.
Можно показать, что величины, входягцие в правую часть
равенства E2.37), не зависят от выбора системы координат,
однако согласованность ориентации вектора v и контура Г
зависит от ориентации системы координат: при переходе от
правой системы координат к левой согласованность
ориентации V и Г по правилу niTonopa заменяется согласованностью
по правилу «антип1топора», т. е. при фиксированной
ориентации вектора v ориентация контура Г изменяется на
противоположную. Тем самым интеграл \adr при изменении ори-
г
ентации системы координат изменяет знак, так же как и
векторное произведение, каковым в данном случае является
rot а.
* Через rot^a обозначена проекция вектора rot а на вектор v, т. е. rot^
а = пр rot а.
652
Из сказанного следует, что формула Стокса E2.32)
справедлива как в правой, так и в левой системе координат, так
как при изменении ориентации системы координат и левая,
и правая части равенства E2.32) меняют знак.
52.5. Соленоидальные векторные поля
В этом пункте ограниченную область, для которой
справедлива формула Гаусса—Остроградского E2.23), будем называть
допустимой.
Bbinie отмечалось (см. п. 52.3), что теорема
Гаусса—Остроградского справедлива для любой ограниченной области,
граница которой состоит из конечного числа
кусочно-гладких поверхностей. Поэтому всякая такая область допустима.
Читатель, предпочитаюпа;ий пользоваться только
доказанными фактами, может под допустимыми областями понимать
именно те, для которых в настояпа;ем курсе была доказана
теорема Гаусса—Остроградского.
Определение 9. Непрерывно дифференцируемое в области G
векторное поле а = а(х, у, z) называется соленоидалъным в
этой области, если его поток через ориентированную
границу любой допустимой области D, замыкание D которой
лежит в G : D ^ G, равен нулю:
\adS = 0. E2.39)
ds
Если рассматриваемое векторное поле является,
например, полем скоростей текупа;ей жидкости, то его соленоидаль-
ность означает, что в каждую область, содержагцуюся внутри
текугцей жидкости, сколько жидкости втекает в каждый
момент времени, столько же ее и вытекает.
Граница dD допустимой области D имеет две ориентации,
порожденные соответственно внутренней и внеганей
нормалями. Очевидно, если условие E2.39) выполняется при одной
ориентации, то оно выполняется и при другой, так как соот-
ветствуюпа;ие интегралы могут отличаться только знаками.
Поясним определение соленоидальности поля на примере.
Пусть G — niapoBoe кольцо: часть пространства, заключенная
между двумя сферами S^j^ Sj^c обгцим центром О и радиусами г
и i?, г < i?, а векторное поле а соленоидально в G. Тогда его
поток будет равен нулю, например, через любую сферу aS, лежа-
гцую в G и ограничиваюгцую niap, также лежагций в G.
653
Однако поток векторного
поля а через сферу aS с центром в
точке О и радиусом р, г < р < i?,
не обязан быть равным нулю, так
как niap, ограниченный этой
сферой, не содержится в области G
(рис. 102).
Вместе с тем сумма потоков
векторного поля а будет равна
нулю через две сферы iSp и iSp
с тем же центром и радиусами р^
Рис. 102 и р2, г < р^ < р2 < i?, если одну из
них ориентировать, выбрав
нормаль, идугцую к центру, а другую — от центра.
Действительно, указанные сферы ограничивают niapoBoe кольцо,
целиком лежагцее в области G, а выбранная их ориентация
является ориентацией границы, соответствуюгцей внеганей или
внутренней нормали. Поэтому, по определению соленоидаль-
ности поля, его поток через рассматриваемую
ориентированную границу будет равен нулю.
ТЕОРЕМА 5. Для того чтобы непрерывно
дифференцируемое в области G векторное поле было соленоидалъным в ней,
необходимо и достаточно, чтобы его дивергенция равнялась
нулю во всех точках области G:
diva(Mo) = 0, MeG.
Доказательство необходимости. Пусть а — соле-
ноидальное в области G векторное поле и M^eG. Обозначим
через Q^ открытый niap радиуса г > О с центром в точке Mq, а
через aS^ — ограничиваюпа;ую его сферу. Поскольку все точки
Me G, в том числе и точка Mq, являются внутренними для G, то
супа;ествует такое Tq > О, что при г < Tq все пхары радиуса г
вместе с ограничиваюпа;ими их сферами aS^ будут содержаться в G.
Заметим теперь, что предел E2.27), равный значению
дивергенции векторного поля а в точке Mq, супа;ествует для
произвольных допустимых областей D, D ^ D ^ G, диаметры
которых стремятся к нулю. Поэтому он супа;ествует и при
специальном выборе D
Qr^ г < Tq:
\\adS
div a(MQ) = lim
о [iQr
654
в силу определения соленоидальности поля, для всех г < г^
имеет место равенство
\\adS = 0,
поэтому div а(Мо) = 0.
Доказательство достаточности. Пусть а —
непрерывно дифференцируемое в области G векторное поле с
дивергенцией, равной нулю во всех точках области G. Если D —
произвольная допустимая область такая, что D ^ D ^ G, то, в
силу теоремы Гаусса—Остроградского,
11 adS = ^^^ div adxdydz = О,
dD D
Т. е. поле а соленоидально. П
Типичным примером соленоидального поля является
векторное поле, представляюгцее собой в некоторой области поле
роторов дважды непрерывно дифференцируемого в этой
области векторного поля.
Действительно, если а — дважды непрерывно
дифференцируемое в области G поле, то rot а является соленоидаль-
ным в G полем, так как div rot а = 0.
Нетрудно провести правдоподобное рассуждение, убеж-
даюгцее в справедливости этого соотногаения. Для этого
достаточно перейти к символическому вектору V; тогда
рассматриваемое равенство примет вид V(V X а) = 0. Смеп1анное
произведение обычных векторов в случае, когда два сомножителя
совпадают, равно нулю, ибо в этом случае параллелепипед,
натянутый на эти векторы, вырождается в параллелограмм,
и, следовательно, его объем равен нулю. Поэтому естественно
ожидать, что указанное равенство справедливо и для
вектора V. Это правдоподобное рассуждение можно превратить в
математически обоснованное и тем самым имеюпа;ее
доказательную силу, если доказать, что символический вектор V на
самом деле обладает использованными нами свойствами,
аналогичными соответствуюпа;им свойствам обычных векторов.
Это можно сделать простой проверкой, переходя, например, к
координатной записи (см. формулы E2.2) и E2.4)).
52.6. Потенциальные векторные поля
В этом пункте поверхность aS, для которой справедлива
теорема Стокса, будем называть допустимой.
Определение 10. Трехмерная область G называется одно-
связной, если, какова бы ни была замкнутая ломаная Л, ле-
'655
жащая в G, существует допустимая поверхность S, также
лежащая в G и натянутая на ломаную Л (см. п. 52.4).
Если рассматриваемая область G выпуклая, то супа;ествует
очень простой способ натягивания поверхностей на контур.
Искомую поверхность всегда можно взять в этом случае в
виде конуса с верп1иной в произвольно фиксированной точке
MqgG, направляюгцей которого служит заданная кривая Г.
Если р = р(и), О < г/ < 271, — представление этой кривой и
Tq — радиус-вектор точки Mq, то искомый конус aS,
натянутый на данный контур, задается представлением
г = Го + 1;[р(г/) - rj, О < г/< 27Г, О < i; < 1. E2.40)
Рассматривая и и v как полярные координаты, видим, что
«представление» конуса задано на единичном круге, причем
единичная окружность Fq = {(и, v) : v = 1} переходит в
заданный контур Г, ее центр — в вергаину конуса (рис. 103).
Слово «представление» взято в кавычки, так как понятие
представления поверхности было введено выгае лигаь для
случая, когда параметры и и v являлись декартовыми
координатами. Конус E2.40) в обгцем случае будет иметь кратные
точки и не будет кусочно-гладкой поверхностью даже в
случае, когда Г достаточно гладкая кривая, т. е. если Г
достаточное число раз непрерывно дифференцируемая кривая без
особых точек. При этом на конусе E2.40) будут иметься, вообпа;е
говоря, особые точки, отличные от верп1ины. Чтобы
устранить это затруднение наиболее простым образом, мы и
ограничились при определении односвязной области
рассмотрением лип1ь контуров, являюпа;ихся замкнутыми ломаными.
В этом случае верп1ину конуса Mq всегда можно выбрать
таким образом, что указанный конус будет кусочно-гладкой
поверхностью. Действительно, при
любом выборе верп1ины конуса в случае,
когда его направляюпа;ей является
некоторая ломаная Л, конус распадается на
конечное число треугольников aS^, / =
= 1, 2, ... , k, правда, быть может,
вырожденных, т. е. превративп1ихся в
отрезок или точку. Одной из верп1ин этих
треугольников будет вергаина конуса
Mq, а противоположной стороной —
одно из звеньев ломаной Л. Каждый такой
треугольник можно рассматривать как
Рис. 103 непрерывно дифференцируемую любое
656
число раз поверхность и задавать его представлением, осу-
гцествляемым линейными функциями (см. п. 16.5 и E2.40)).
Если треугольник вырожденный, то все его точки будут
особыми. Однако сколь угодно малым смепа;ением верп1ины
конуса можно добиться того, что она окажется в обпа;ем
положении со всеми звеньями ломаной Л, т. е. не будет лежать ни на
одной прямой, проходяпа;ей через какое-либо звено ломаной Л.
В результате все треугольники S-, i = 1, 2, ... , k, станут
невырожденными и, следовательно, могут рассматриваться как
гладкие поверхности без особых точек. Сам же конус S
окажется, таким образом, кусочно-гладкой поверхностью S =
= {S^yjZi» При этом поскольку при всех достаточно малых
смепа;ениях каждой точки области она остается внутри
области, верп1ину Mq конуса S всегда можно выбрать в области, и
поэтому, в силу ее выпуклости, весь конус S будет лежать в
этой области. К получивгаемуся кусочно-гладкому конусу S
можно применить теорему Стокса, иначе говоря, этот конус
является допустимой в этом пункте поверхностью. Итак, мы
доказали, что всякая выпуклая область односвязна.
Примером неодносвязной области является тор, т. е.
область, образуемая врагцением круга вокруг не пересекаюгцей
его оси (рис. 104).
Напомним, что поле называется потенциальным, когда
его циркуляция ^adr равна нулю по любому замкнутому кон-
г
туру г ^ G, или, что то же, когда интеграл ^adr не зависит
АВ
ОТ пути интегрирования, соединяюгцего в области G точки
А VI В. Подробнее об этом см. п. 52.1.
В п. 47.11 (теорема 6) для произвольной плоской области
было доказано, что непрерывное в ней векторное поле
является потенциальным тогда и только тогда, когда у него су-
гцествует потенциальная функция. В приведенном там
доказательстве не было сугцественным, что рассматриваемая
область была именно плоской. Подобным же рассуждением и
для пространственной области
устанавливается аналогичный факт.
Для того чтобы непрерывное в
трехмерной области векторное поле а было
потенциальным, необходимо и
достаточно, чтобы оно имело в этой области
потенциальную функцию и:
а = grad и.
657
При этом потенциальную функцию и можно получить из
векторного поля а по формуле
и{М) = I adr,
где кусочно-гладкая кривая М^М лежит в рассматриваемой
области, а М^ — ее произвольно фиксированная точка.
Как и в плоском случае, в пространстве для односвяз-
ных областей имеется егце один критерий потенциальности
векторного поля, очень удобный, в частности, для
приложений.
Оказывается, что в односвязной области векторное поле
потенциально тогда и только тогда, когда оно безвихревое.
Это утверждение содержится в нижеформулируемой и
доказываемой теореме 6.
ТЕОРЕМА 6. Пусть в односвязной области G задано
непрерывно дифференцируемое векторное поле а = (Р, Q, R). Тогда
эквивалентны следующие три свойства:
1^. Векторное поле а = а{М) является в области G
потенциальным,
2^. Существует потенциальная в G функция и = и(М),
т, е, такая функция и(М), что а = grad и. В этом случае
для любых двух точек А& G и BeG и любой кусочно-гладкой
кривой АВ, соединяющей в G эти точки,
\adr = и(В)-и(А).
АВ
3^. Векторное поле а = а(М) является безвихревым:
rot а = О в области G, т, е,
dP^dQ dQ^dR дК^дР E2 41)
ду дх' Эг Эг/' Эх Эг *
Доказательство. Применим следуюпа;ую схему. уг1 \
Первый niar: 1^2. Это утверждение, т. е. ( \
супа;ествование потенциальной функции, как это з 2
уже отмечалось выпхе, доказывается соверпхенно ^^^—^
аналогично рассмотренному раньп1е случаю
плоской области (см. теорему 4 в п. 47.11), и поэтому не будем
приводить его доказательство.
Второй niar: 2^3. Утверждение 2^3 также
доказывается аналогично плоскому случаю: оно означает
просто-напросто равенство соответствуюпа;их вторых смеп1анных
производных потенциальной функции.
658
Утверждения 1 ^ 2 и 2 ^ 3 справедливы и без
предположения односвязности области.
Третий niar: 3^1. Пусть rot а = О в G. Допустим
сначала, что Г — кусочно дважды непрерывно
дифференцируемая замкнутая кривая, лежапа;ая в G. Если супа;ествует
допустимая поверхность aS, содержапа;аяся в G и ограниченная
контуром Г, то из теоремы Стокса сразу получаем
I adr = ^^ rot adS = 0.
г S
в силу односвязности области G (см. определение 10), это
верно, в частности, для любой конечнозвенной ломаной.
Поэтому, если Г — любая кусочно-гладкая замкнутая кривая,
лежагцая в G, то, выбирая последовательность ломаных Л^,
вписанных в Г со звеньями, стремягцимися к нулю при
п -^ оо^ по лемме 4 п. 47.10 получим
f adr = lim f adr = 0. П
J Д ^ OO J
л л„
Замечание 1. Условие потенциальности а = grad и
непрерывного векторного поля а = (Р, Q, R) в некоторой
области равносильно тому, что функция Pdx + Qdy + Rdz
является полным дифференциалом потенциальной функции и =
= и(х, у у z) в указанной области. Действительно, условие а =
= grad и означает, что Р = т^, Q = т^, R= ч^, и, следователь-
дх ду 02
НО, du = Pdx + Qdy + Rdx. Поэтому теорема 6 может быть
перефразирована следуюгцим образом.
Если функции Р = Р(х, у, z), Q = Q(x, у, z), R = R(x, у, z)
непрерывно дифференцируемы в односвязной области G, то
для того чтобы в области G функция Pdx + Qdy + Rdz
была бы полным дифференциалом некоторой функции,
необходимо и достаточно, чтобы в области G выполнялись
условия E2Л1).
Замечание 2. Если функции Р, Q, R непрерывно
дифференцируемы в некоторой окрестности точки (Xq, у^, Zq), то
теорема 6 дает ответ на вопрос, когда сугцествует окрестность
точки (Xq, i/q, Zq), в которой функция Pdx + Qdy + Rdz
является полным дифференциалом некоторой функции и = и(х, у, z).
Действительно, поскольку открытый niap является
односвязной областью, согласно теореме 6, ответ на поставленный
вопрос гласит: тогда и только тогда, когда у точки (Xq, у^, Zq)
супа;ествует окрестность, в которой выполняются условия
E2.41), так как если супа;ествует какая-то окрестность, обла-
659
даюгцая этим свойством, то сугцествует и гааровая
окрестность с тем же свойством.
Примеры. Пусть г = (х, у, z), r=\r\ = Jx^ + г/^ + 2^.
1. Векторное поле а = г потенциальное, так как
функция и = -г^ является, очевидно, его потенциалом:
V fi г2^ = i V (х2 + г/2 + ^2) = (х, у, z) = Г.
Рассматриваемое поле не солиноидально, так как div г = 3.
2. Рассмотрим поле а = - = (-, ^, - 1, г ^ 0. Заметив, что
г \г г г)
т:— = -, т— = ^, т— = -, ВИДИМ, ЧТО Vr = -, т. е. поле а = - потен-
дх г ду г 02 г г г
циальное и функция и = г является его потенциалом.
Найдем его дивергенцию. Имеем
г-х—
д f х^ _ Эх _ г^ - х^
Эх \ г) г^ г^
и аналогично
Э fy^ г^-у^ Э -(^]- r^'-z^'
ду \г) г^ ' Эг V ГУ ^3 *
Следовательно,
г г^ г
и поэтому поле а = - не соленоидальное.
3. Рассмотрим поле а = ^ = [ 4? -^? 4 ? ^ ^ 0. Для выясне-
j^A \ уЛ уЛ уЛ \
НИЯ его потенциальности найдем его ротор. Вычислим первую
координату ротора:
_Э__^__Э_х_^_2^Эг,2хЭг^ -2ух + 2ху ^ ^
Эх г^ Ъу г^ г^ Эх г^ Эг/ г^
Аналогичным образом показывается, что и две другие
координаты ротора равны нулю. Поскольку пространство с
выколотым началом координат является односвязной областью,
векторное поле а = —- потенциальное. Нетрудно найти и его
потенциал и = и {х, у, z). Например, заметив, что
,,^-(t^ + a^) ^,^^,
видим, что ц = - In {x^■ + у^ + z^):
\ Y%^ у*^ у*^ i у*^
'660
Заметим, что векторное поле а = ^, рассматриваемое,
например, на плоскости переменных х и г/, т. е. при г = (х, г/),
х^ + г/^ > О, также будет потенциальным с потенциалом и =
= - In (x^^ + г/^). При этом плоскость с выколотым началом ко-
ординат уже не будет односвязной. Вообпа;е любое
потенциальное поле является безвихревым, т. е. его ротор равен нулю
во всех точках области определения поля — это доказывается
без предположения об ее односвязности (см. доказательство
теоремы 6).
Для выяснения вопроса о соленоидальности поля а = г 1г^
найдем его дивергенцию. Имеем
2-9 ^L
Ъ (хЛ дх г^ - 2х^
Аналогично
Поэтому
Эх \г^ J г^
г^
_Э_ Гу_~^ _ г2 - 2у^ д_ r^^ _ г2 - 22^
у^ 1^4 у^
т. е. поле а = ^ не соленоид альное.
4. Рассмотрим поле а = — = —, -^, — . Заметив, что .— - =
J.3 \у.з J.3 J.3 J дх\г)
= - - — = --, — - = - % ^\- = --.у видим, что функция
г^ дх г^ ду\г J г^ dz\r) г^
и = - - является потенциалом рассматриваемого векторного
поля, т. е. V г/ = г/г^ и, значит, поле а = г/г^ является
потенциальным.
Найдем дивергенцию этого поля. Имеем
Аналогично
Отсюда
Эх
дуУг^
г^
Эх г^
т^б
-3J/2
dzKr^J
-3
г5
^
X2
-322
г^ axKr^J ду\г^ J azKr^j
т. е. поле а = г/г^ является соленоидальным в пространстве с
выколотым началом координат. Напомним, что в этом случае
661
его поток через любую кусочно-гладкую поверхность, ограни-
чиваюгцую область, не содержагцую начало координат, равен
нулю.
Таким образом, векторное поле а = г/г^ является
потенциальным и соленоидальным. С физической точки зрения оно
представляет собой поле напряженностей единичного заряда.
Его дивергенция в любой точке, отличной от начала
координат, равна нулю, а его поток через любую кусочно-гладкую
поверхность, ограничиваюпа;ую область, не содержапа;ую
начало координат, равен нулю. Последнее неверно для
поверхностей, ограничиваюпа;их области, содержапа;ие начало
координат. Поток векторного поля а = г/г^ через сферу х^ + г/^ +
-\- 2^ = г^' равен 47Г/3. Действительно, заметив, что в этом
случае единичная нормаль v = г/г, имеем
Я «vds- я ^-/^-^ Я ^^-|^-
х^ + у^ + z^ = г^ х^ + у^ + z^ = г^ х^ + у^ + z^ = г^
в заключение заметим, что хотя потенциальные и солено-
идальные векторные поля не исчерпывают совокупности всех
возможных векторных полей, однако они позволяют описать
п1ирокий класс векторных полей. Именно: при достаточно
обпа;их предположениях любое векторное поле а представляет
собой сумму потенциального и соленоидального векторного
поля. Более точно, супа;ествуют такие скалярная функция и и
векторное поле Ь, что а = Vu -\- rot Ъ. Так как rot Vz/ = О и
div rot Ь = О, то первое слагаемое является потенциальным
полем, а второе — соленоидальным.
Это предложение называется теоремой Гельмгольца"^ (ее
доказательство можно найти в кн.: Шилов Г. Е.
Математический анализ. Функции нескольких переменных. — М.:
Наука, 1972).
УПРАЖНЕНИЯ. 2. Доказать, что поток ротора непрерывно
дифференцируемого в некоторой области векторного поля через любую сферу,
лежащую в указанной области, равен нулю.
3. Доказать, что
{{{ grad фго1 adxdydz = \\{(^^ grad ф) dS.
G S
Здесь предполагается, что для области G, ограниченной
поверхностью aS, применима теорема Гаусса—Остроградского.
Г. Гельмгольц A821 —1894) — немецкий физик и физиолог.
662
§53
Собственные интегралы, зависящие от параметра
53.1. Определение интегралов, зависящих от параметра;
их непрерывность и интегрируемость по параметру
Пусть Y — некоторое множество действительных чисел, ф(г/) и
\|/(г/) — две функции, определенные на Y, ф(г/) < \|/(г/), и
функция /(х, у) определена на множестве
{(х, у): y^Y, хе[ф(г/), \|/(г/)]}. E3.1)
Интегралы вида
Ф(г/)= |/(x,z/)dx E3.2)
ф(г/)
называют интегралами, зависящими от параметра, а
переменную у называют обычно параметром.
Часто встречается тот частный случай такого типа
интегралов, когда функции ф и \|/ постоянны, т. е. интегралы вида
Ф{у) = ]Кх,у)ах, E3.3)
а
Если Y является множеством всех натуральных чисел Y =
= N = {1, 2, ... , п, ...}, то, полагая fj^x) = f(x, п), п = 1, 2, ... ,
интеграл E3.3) можно переписать в виде
b
\f^ix)dx, я = 1, 2, ... .
а
Тем самым получилась числовая последовательность,
образованная интегралами от функций некоторой функциональной
последовательности.
Рассмотрим случай, когда множество Y представляет
собой отрезок [а, Р], функции ф(г/) и \|/(г/) непрерывны на этом
отрезке и ф(г/) < \|/(г/), г/е[а, Р]. Пусть графики функций ф(г/) и
\|/(г/) и, быть может, отрезки прямых у = а и у = ^
образуют границу ограниченной области G
(рис. 105). Она, очевидно, квадриру- ^1
ема (см. п. 44.1). В этом случае мно- а[
жество E3.1), на котором определена
функция /(х, у), является
замыканием G указанной области G:
G = {(х, г/); а < г/ < Р,
ф(г/)<х<Х|/(г/)}. E3.4)
Рис. 105
663
в дальнейп1ем мы изучим свойства функции Ф(г/) (ее
непрерывность, правила ее дифференцирования и
интегрирования) в зависимости от свойств функций /(х, у), ф(г/), \|/(г/).
Некоторые из этих свойств были получены раньпхе при
изучении кратного интеграла. Так, например, лемма, доказанная в
п. 45.1, дает условия, при которых интеграл, зависягций от
параметра, является непрерывной функцией этого
параметра. Сформулируем эту лемму в обозначениях настоягцего
параграфа в виде теоремы.
ТЕОРЕМА 1. Если функция f(x, у) непрерывна на
замыкании G области G (см. E3.4)), то функция Ф(г/), задаваемая
формулой E3.2), непрерывна на отрезке [а, Р].
Утверждению этой теоремы можно придать следуюгций вид:
lim \\f(y)
\\fiy) У^Уо
lim \ f(x, у) dx= f lim f(x,y)dx. E3.5)
^^^^ у^Уо
Действительно, из теоремы 1 следует, что предел, стоягций
в левой части равенства E3.5), равен Ф(г/о), а, в силу
непрерывности функций ф, \|/ и /, правая часть равенства также равна
¥(г/о)
I fix, г/о) dx = Ф(г/о).
В частности, для интеграла E3.3) имеем
b Ъ
lim [ fix, y)dx = f lim /(x, уМх,
T. e. в этом случае возможен предельный переход под знаком
интеграла.
В теореме о предельном переходе под знаком интеграла
можно ослабить требования, накладываемые на функцию /(х, г/),
потребовав вместо ее непрерывности по совокупности переменных
лип1ь непрерывность по одной переменной и равномерное
стремление к пределу по другой.
ТЕОРЕМА 2. Пусть функция f(x, у) определена для всех
хе[а, Ь], yeY и непрерывна по х на [а, Ь] при любом
фиксированном уе Y. Тогда если при у ^ у^ функция f(x, у)
равномерно на отрезке [а, Ь] стремится к ф(х) (см. п. 39.4), то
ъ ъ
lim I /(х, y)dx = I (p(x)dx.
У Уо а а
* Здесь Y — произвольное числовое множество: Y ^ i2, а z/q — число
или одна из бесконечностей оо, +оо или -оо.
664
Доказательство. Рассмотрим какую-либо
последовательность yji^Y, п = 1, 2, ... , такую, что lim у^ = у^. Тогда
(см. упражнение 5 в п. 39.4) последовательность ф^(х) =
= fi^j Уп) будет равномерно на отрезке [а, Ь] стремиться к
функции ф(х). Отсюда следует (см. п. 32.4), во-первых, что
ф(х) непрерывна и, следовательно, интегрируема на отрезке
[а, Ь], а во-вторых, что
b Ъ Ъ
lim I /(х, yj)dx = lim J (^J^x)dx = J ф(х)йх,
a a a
И так как это верно для любой указанной последовательности
{г/^}, то теорема доказана. П
Перейдем к вопросу об интегрировании интегралов E3.2),
зависягцих от параметра.
ТЕОРЕМА 3. Пусть область G элементарна относительно
обеих осей координат, т. е.
G = {(х, г/) : а < г/ < Р, ф(г/) <х< \|/(г/)} =
= {(х, у):а<х<Ь, (?^(х) <у< щ(х)},
где функции ф г/ \|/ непрерывны на отрезке [а, Р], а функции
ф^ г/ \|/^ — на отрезке [а, Ь]. Тогда если функция /(х, у)
непрерывна на замыкании G области G, то
I Ф(г/)йг/ = 11 /(л:, г/)йх \dy = \\ \ /(х, г/)йг/
Ф(г/)
dx
- 9i(x)
= ||/(x,i/)dxdi/. E3.6)
G
Очевидно, теорема 3 является перефразировкой соответст-
вуюгцей теоремы о сведении кратного интеграла к
повторному (см. п. 45.1).
53.2. Дифференцирование интегралов,
зависящих от параметра
При изучении дифференциальных свойств интегралов, завися-
па;их от параметра, рассмотрим сначала интегралы вида E3.3).
ТЕОРЕМА 4 (правило Лейбница). Если функция /(х, у) и ее
частная производная '^^'У^ непрерывны в замкнутом
прямоугольнике А = {(х, г/): а < X < Ь, а < г/ < р, то функция Ф(г/) =
ъ
= I /(х, y)dx дифференцируема на отрезке [а, Р] и
AФ{у) _ г M^L^)dx.
dy [ Эг/
'665
Таким образом, чтобы при сделанных предположениях
продифференцировать интеграл, зависягций от параметра,
достаточно продифференцировать подынтегральное выражение,
оставляя пределы интегрирования неизменными.
Доказательство. Пусть г/е[а, Р] и г/ + Аг/е[а, Р]; тогда
Ф(у + Ау) - Ф(у) ^ 1 I ^^(^^ ^ + ду) _ ^(^^ ^)^^^ ^ I Щх,у + еду) ^^^
о<е<1.
Здесь применена формула конечных прирагцений Лагранжа.
Обозначив теперь через со[6; tJ- модуль непрерывности
V ду J
функции г/, получим
оу
Ф(у + Ау) - Ф(у) _ г Э/(х, у)^\ ^ г
^У I ^У I I
ъ
^ 'df(x,y + QAy) _ df(x, у)\
dx <
ду dy
] ш[|Аг/|; |]dx < ш[|Аг/|; |](Ь - а). E3.7)
В силу равномерной непрерывности функции ./ на замкнутом
^У
прямоугольнике А, имеем lim со[|Аг/|; ^^ ^ 0; поэтому из
Ai/ ^ о V оу )
E3.7) получим
liin Ф{у + Ау)-Ф{у) = f дЩ^ ^^^ ц
У^О Ау а ^У
Теорема 4 легко обобпа;ается и на случай зависяпа;его от
параметра интеграла обпа;его вида E3.2).
ТЕОРЕМА А\ Пусть: 1) функция f(x, у) и ее частная
производная '^^' ^^ непрерывны на замкнутом прямоугольнике
А = {(х, г/): а < X < Ь, а < г/ < р};
2) G ^ А (см. E3.4));
3) пусть функции ф(г/) и \|/(г/) имеют непрерывные на
отрезке [а, Р] производные.
Тогда интеграл E3.2), зависящий от параметра,
также имеет производную на отрезке [а, Р], причем
fy = Т^-^ ^^ - ^(^^^)' ^> ^ + ^(^(^>' ^> ^- ^^^-«^
Доказательство. Рассмотрим функцию
V
F{y, u,v) = ^ /(х, y)dx, а< u<by а< v Kb, а<г/<р.
666
Нетрудно непосредственно проверить, что частные
производные ТГ-, ТГ-, тг- функции F супа;ествуют и непрерывны по сово-
ду ои OV
купности переменных г/, и, v. Проверим сначала супа;ествова-
ние и непрерывность частной производной ^г-. Ее супа;ествова-
оу
ние непосредственно следует из теоремы 4, причем
^^ = ]Ш^с1х. E3.9)
^у i ^у
Докажем ее непрерывность. Пусть а<г/<Ь, a<i;<b, а<г/<
< Р, а < г/ + Аг/ < Ь, а < L? < Ау < Ь, а < г/ < Аг/ < Р; положив
jidFiy, и, у) ^ dF{y + Ay, и + Аи, v + Av) _ dFjy, и, v)
ду ду ду
получим
/s^dFjy, и, у)\ _ г Y"" Э/(х,1/ + Ai/)^^^ _ f df(x, у)^^
ду
ду
<
<
? [df(x,y + Ay) _ df(x, y)l^J , I )
L дд ^^ri^lJ
+
dy
V + Av
dy
df{x,y + Ay) ^^^
dy
[ Э/(х, у + Ai/)^^
C^Z/
+
E3.10)
Э/
Поскольку функция =г^ определена на прямоугольнике А,
ду
в силу выгаеуказанного выбора значений аргументов, все
написанные интегралы имеют смысл и
\v-u\<b-a, E3.11)
Далее, из непрерывности функции ^ на прямоугольнике А
следует, что она ограничена на нем, т. е. сугцествует такая
постоянная М > О, что для всех точек (х, г/)еА выполняется
неравенство
Э/(х, у)
dy
<М.
E3.12)
Обозначив, как и выгае, через со[6; ^ модуль
непрерывности функции tJ- на прямоугольнике А и использовав нера-
ду
венства E3.11) и E3.12), из E3.10) получим
^тм^\,,,[М;%)
jdx
+ М\
I '^А
+ м\
J dx
<
< (& - a)(S)[\^y\^, ^ ) + М\Аи\ + M\Av\.
667
Отсюда следует, что lim А—(^> ^> ^) = о. Это и
VAi/2 + Аи^ + Ai;2 ^ О ^
означает непрерывность частной производной тг- на множест-
ве {(г/, г/, у) : с < г/ < d, а < г/ < Ь, а < L? < Ь}. Непрерывность
на этом множестве частных производных
^£ = -Аи,у), ^£ = fiv,y) E2.13)
очевидна.
Связь между функциями Ф и F устанавливается формулой
Ф(у) = Fiy, ф(г/), Х|/(г/)).
В силу доказанного выгае, функцию Ф можно
дифференцировать по правилу дифференцирования сложных функций:
ЭФ _ ар _^ dFdu _^ dFdv
ду ду диду диду'
Подставляя сюда выражения для частных производных т^, ^^
ду ди
dF
И — (см. E3.9) и E3.13)) и полагая и = ф(г/) nv = \|/(г/), получим
формулу E3.8). П
§54
Несобственные интегралы,
зависящие от параметра
54.1. Основные определения. Равномерная сходимость
интегралов, зависящих от параметра
Мы будем рассматривать интегралы вида
Ф(у) = ]пх,тх, E4.1)
а
где -оо < а < Ь < +оо^ переменная у принадлежит некоторому
множеству Y и интеграл E4.1), быть может, при некоторых
(в частности, при всех) значениях у является несобственным.
Определение 1. Если для каждого уqeY интеграл
ъ
Ф(г/о) = 1Я^'г/о)йх
а
сходится, то интеграл E4.1) называется сходящимся на
множестве Y.
В дальнейгаем, если не оговорено что-либо другое, будем
рассматривать только случай, когда выполняются условия:
'668
1) -oo < a < b < +00;
2) при любом yeY функция f(x, у) по переменной х
интегрируема, по Риману, на каждом отрезке [а, Г|], где Г| таково,
что а < Г| < Ь.
В этом случае сходимость интеграла E4.1) на множестве
Y означает, что при любом yeY сугцествует предел
л b
lim f /(х, y)dx = f /(x, y)dx
(если b = +00^ TO Ь - 0 = +oo). Отсюда, в силу равенства
b Ц b
I /(x, y)dx - I /(x, y)dx = |/(x, y)dx,
a a Ц
при каждом фиксированном ye Y имеем
b
lim f/(x, y)dx = 0.
Таким образом, если интеграл E4.1) сходится на
множестве Y, то при каждом фиксированном yeY для
любого числа 8 > О существует такое г\^ = r\J^y) < b, что если
Г[^< Г[ < Ь, то
< п < h тп
'<8. E4.2)
М/(х, y)dx
Условия, при которых для несобственных интегралов, за-
висягцих от параметра, справедливы теоремы, аналогичные
доказанным в предыдугцем параграфе для собственных
интегралов, основаны на понятии так называемой равномерной
сходимости интеграла.
Будем предполагать, как было отмечено, что интеграл
E4.1) удовлетворяет выпхеуказанным условиям 1) и 2).
Определение 2. Сходящийся на множестве Y интеграл
b
I /(х, y)dx называется равномерно сходящимся на этом мно-
а
жестве, если для любого 8 > О существует такое г\^ < Ь, что
для всех yeY и всех г\ таких, что rj^ < Г| < Ь, выполняется не-
\Ь I
равенство М /(х, y)dx\ < 8.
1л I
Напомним, что в рассматриваемом нами случае b может
быть как конечным, т. е. числом, так и бесконечным, т. е.
равным +00, Таким образом, в приведенном виде определение
равномерной сходимости годится одновременно как для
случая, когда интегрирование производится по конечному отрез-
'669
ку [а, Ь], а несобственный интеграл может возникнуть за счет
неограниченности подынтегральной функции, так и для
случая, когда несобственный интеграл получается за счет
неограниченности промежутка интегрирования [а, +оо).
Приведенные определения сходимости и равномерной
сходимости интеграла напоминают соответствуюпа;ие
определения для рядов (см. п. 32.1 и 32.3). Между ними действительно
имеется связь.
Пусть {г|^} — некоторая последовательность такая, что
r\i = a, Г|^е[а, Ь), я=1,2, ..., и ^lim^ Г|^ = Ь.
Наряду с интегралом E4.1) рассмотрим ряд
оо ^k + 1
^ I f(x,y)dx. E4.3)
Пусть
^п(У) = L I Ял:, y)dx = \f(x, y)dx
— его частичная сумма. Тогда, если интеграл E4.1) сходится
(соответственно равномерно сходится) на множестве Y, то,
очевидно, сходится (соответственно равномерно сходится) на
множестве Y и ряд E4.3); при этом
ь л„
I /(х, y)dx = \im^ I /(х, y)dx = ^lirn^ SJ,y),
т. е. рассматриваемый интеграл равен сумме ряда E4.3).
Определение равномерной сходимости интеграла можно
перефразировать епа;е следуюпа;им образом.
Определение 2^ Сходящийся на множестве Y интеграл E4.1)
называется равномерно сходящимся на этом множестве,
если
\\f{x,y)dx\ = Q. E4.4)
Действительно, если интеграл E4.1) равномерно сходится
на множестве Y в смысле определения 2, то для любого 8 > О
сугцествует такое ц^ < Ь, что выполняется неравенство E4.2)
при i/gY и r|g < Г| < Ь и, следовательно.
lim sup
ц^Ъ- Оуе Y
sup
yeY
b
|/(х, y)dx
<8, Г|^<Г|<Ь,
"л
откуда и следует E4.4). Обратно, если рассматриваемый
интеграл равномерно сходится на множестве Y в смысле
определения 2\ то из условия E4.4) для любого 8 > О следует сугцест-
^70
вование такого числа rj^, что при всех г/е Y и rj^ < Г| < Ь
выполняется неравенство E4.2). П
Если рассмотреть интеграл
Р(у,Г[)^= \f(x,y)dx,
л
то очевидно, что условие E4.4) означает, что этот интеграл
равномерно на Y стремится к нулю при Г| ^ Ь - О (здесь в
терминологии п. 39.4 параметром является не г/, как это было
там, а переменная Г|).
Равномерная сходимость на множестве Y интеграла E4.1)
означает также равномерное стремление на множестве Y
функции
def
Ф(г/,Л) = \f{x,y)dx
E4.5)
при Г| ^ Ь — О к функции E4.1).
Действительно, последнее означает (см. п. 39.4), что для
любого 8 > О супа;ествует такое rj^ < Ь, что для каждого Г|,
удовлетворяюпа;его условию rj^ < Г| < Ь, и всех г/е Y
выполняется неравенство |Ф(г/) - Ф(г/, Г|)| < 8. Но
ь л ь
Ф(г/) - Ф(г/, Г|) = I Кх, y)dx - \ fix, y)dx = |/(х, y)dx.
Поэтому
I /(х, y)dx\
<8.
Таким образом, условие Ф(х, Г|) ^ Ф(г/) при Г| ^ Ь - О
равносильно выполнению условий определения 2, т. е.
равномерной сходимости на множестве Y интеграла E4.1).
+ 00
Примеры. 1. Рассмотрим интеграл Ф(г/) = | ye'^^dx. В ка-
0
честве множества Y возьмем полуось г/ > О (при любом г/ < О этот
интеграл расходится). Легко убедиться, что рассматриваемый
интеграл сходится на Y. Он даже вычисляется: при у = О он
равен нулю, а при у > О имеем
+ 00 +00 I + 00
I уе~^^ dx = ^ е~^У dxy = -е~^У = 1.
0 0 1о
Для любого а > о он сходится равномерно на промежутке
[а, +оо). Действительно, в этом случае легко проверяется,
например, выполнение условия E4.4)
lim sup
rj^+oo j^ > a
\ ye ^ydx\
= lim sup e "^y = lim e ^^ = 0.
671
lim sup
= lim sup e "^y = 1.
Ha всей же полуоси Y равномерной сходимости нет. В
самом деле,
I+00 I
I ye~^ydx\
ц I
т. е. на множестве Y условие E4.4) не выполняется.
2. Рассмотрим более обгций пример. Если функция / неот-
+ 00
рицательна при х > О, а интеграл | f(x) dx сходится, то при
о
+ 00
а > о интеграл | f(y^x) dx не сходится равномерно на полу-
0
оси г/ > о, но при любом z/q > О сходится равномерно на
полуоси у > у^.
Действительно, для любого Г| > О имеем
+ 00 1 +00
sup 1 f{y"-x)dx = sup - J f{t)dt >
-I +00 1 +00
> sup ^ I fit)dt> sup ^ I fit)dt = +oo^
поэтому
+ 00
lim sup \ f(y^x)dx =-\-oo^
T. e. условие E4.4) не выполняется, это и означает, что
рассматриваемый интеграл не сходится равномерно для г/ > 0.
Если же г/ > i/q > О, то
+ 00 1 +00 1 +00
sup lf(y^x)dx _= sup i- lf(t)dt<\ \f{t)dt.
+ 00 +00
Так как по условию f f(t)dt сходится, то lim [ f(t) dt = О,
0 ' у^ц
и поэтому из полученного неравенства следует, что
+ 00
lim sup f f(y^x)dx = О,
т. е. выполняется условие E4.4), а это и означает
равномерную сходимость рассматриваемого интеграла при у > у^.
В частности, интеграл J е~У^ dx является интегралом ука-
л
занного вида при f(t) = е~^ и а = 1/2. Поэтому этот интеграл
не сходится равномерно для г/ > О, но при любом г/д > О он
сходится равномерно на полуоси у > у^.
Замечание. Отметим, что равномерная сходимость не
сохраняется, вообпа;е говоря, при замене переменной, по кото-
^72
рой производится интегрирование, если в формулу замены
входит параметр. Так, в примере 2 сходягцийся интеграл
+ 00
I f(t)dt сходится равномерно, так как не зависит от парамет-
0
+ 00
ра, а интеграл | f(y'^x)dx, получаюгцийся из него заменой пе-
0
ременной t = у^х, не сходится равномерно на множестве г/ > 0.
ТЕОРЕМА 1 (признак Вейерштрасса). ^слг/ существует
неотрицательная функция ф(х), определенная на промежутке
[а, Ъ) и интегрируемая по Риману на каждом отрезке [а, Г|],
где а <г\<Ь, и такая, что:
1) |/(х, у)\ < ф(х), где а < х < Ь, yeY;
ъ
2) интеграл | (^{x)dx сходится,
а
то интеграл (ЪАЛ) равномерно сходится на множестве Y.
Доказательство. Прежде всего, в силу признака
сравнения (см. п. 33.3), интеграл E4.1) абсолютно, а значит, и
просто сходится при любом y^Y. Далее, в силу сходимости интег-
ъ
рала I ф(х)йх, для любого числа 8 > О супа;ествует такое ц^ < Ь,
а
Ь
ЧТО если r|g < Г| < Ь, то |ф(х)йх < 8. Тогда, в силу условия 1 тео-
л
ремы,
М /(х, y)dx\ < ||/(х, y)\dx < I ф(х)йх < 8, rj^ < Г| <Ь, г/е Y,
\ц I л Л
ъ
а это и означает равномерную сходимость интеграла | /(х, г/)йх
а
на множестве Y. П
С помопа;ью признака Вейерп1трасса, например, сразу ус-
танавливается, что интеграл | ^ 2 Равномерно сходит-
-оо 1 + X + у
ся на всей вепа;ественной оси -оо < у < +оо. Действительно,
интеграл | —^ = тг сходится и при любых х и г/ выполняет-
-оо1 + X
ся неравенство ^ 1 ^ г
1 + X + у 1 + X
Из критерия Коп1и равномерной сходимости функции по
параметру (см. п. 39.4) непосредственно получаются
необходимые и достаточные условия (также называемые критерием
Коп1и) для равномерной сходимости интегралов.
'673
ТЕОРЕМА 2 (критерий Коши равномерной сходимости
интегралов). Дл^ того чтобы интеграл {ЪАЛ) равномерно
сходился на множестве Y, необходимо и достаточно, чтобы для
любого 8 > О существовало такое г| < Ь, что для всех г( и г(\
удовлетворяющих условиям Г| < Г|' < Ь, Г| < Г|'' < Ь, и всех yeY
выполнялось неравенство
л" I
I fix,y)dx\<E. E4.6)
In' I
Действительно, как было отмечено, равномерная
сходимость интеграла E4.1) равносильна равномерному
стремлению к пределу функции Ф(г/, Г|) (см. E4.5)), а неравенство
E4.6) в обозначениях E4.5) можно записать в виде
|Ф(г/, л") - Ф(г/, Л0| < е.
Поэтому теорема 2 является просто перефразировкой
теоремы 4 из п. 39.4 для рассматриваемого здесь случая.
бД-г"". Признак равномерной сходимости интегралов
В этом пункте будет доказан признак равномерной
сходимости интегралов, аналогичный соответствуюгцему признаку для
равномерной сходимости рядов (см. п. 32.3).
ТЕОРЕМА 3. Пусть функции f(x, у) и g(x, у) определены
для хе[а, +оо), aeR и yeY ^ R, причем функция f(x, у)
непрерывна по переменной х, а функция g(x, у) имеет
непрерывную по X производную. Если:
1) функция g(x, у) при каждом yeY монотонно убывает
по X и равномерно стремится к нулю на множестве Y при
X -^ +оо;
X
2) интегралы |/(f, у) dt ограничены в совокупности на
а
множестве [а, +оо) х Y, то интеграл
+ 00
\f{x,y)g{x,y)dx E4.7)
а
равномерно сходится на множестве Y.
Доказательство. Из условия 1) теоремы следует, что
gix,y)>Q E4.8)
И что ^\ ' ^^ < о, поэтому
дх
Э^(х, у)
дх
= -Мр^. E4.9)
дх
674
Условие 2) теоремы означает, что супа;ествует такая
постоянная с > О, что для всех хе[а, +оо) и г/е Y выполняется
неравенство
\f(t,y)dt
<€.
E4.10)
Интегрируя по частям на отрезке [а, Ь], получаем
b Ъ X
I /(х, y)g{x, y)dx = I g(x, y)d \f{t, y)dt =
a a a
= g{b,y)]f{t,y)dt-] Пf(t,y)dt^Щ^dx. E4.11)
a a ^ a J OX
Согласно условию E4.10), имеем
g(b,y)\f(t,y)dt
< cgib, у)
и, следовательно, в силу условия 1) теоремы, первое слагаемое
правой части равенства E4.11) равномерно стремится к нулю
на множестве Y при b -^ +оо.
Для того чтобы оценить поведение второго слагаемого при
Ъ -^ +00, докажем, что интеграл | | f(t, y)dt -^Щ^-^dx абсо-
а^ а J ОХ
лютно и равномерно сходится на множестве Y, т. е.
равномерно сходится интеграл
\\\m,y)dt\
Э^(х, у)
дх
dx.
Проверим для этого интеграла выполнение критерия Ко-
П1И равномерной сходимости. Зададим 8 > 0. В силу 1)
теоремы найдется такое ^q > а, что для всех ^ > ^q и всех г/е Y будет
с
выполняться неравенство ^(^, г/) < - и, следовательно, при
Г| > ^ неравенство
л I X
\\\f{t,y)dt
Э^(х, у)
дх
dx < -c\Щ^dx
E4.9) J Эх
E4.10) ^
= С(^(^, у) - g(j\, у)) < С^(^, у) < 8.
E4.8)
Итак, оба слагаемых правой части неравенства E4.11)
при b -^ +00 равномерно стремятся к конечным пределам на
множестве Y и, таким образом, интеграл E4.7) равномерно
сходится. П
Замечание. Предположение о супа;ествовании у
функции g{Xj у) непрерывной по х производной т^ не является супа;е-
ох
ственным: оно сделано лип1ь для упропа;ения доказательства.
675
I sin ty dt
+00
Пример. Интеграл f ^^^^^^dx равномерно сходится при
^ 1 + x^
d.6f X
у > у^> 0. Действительно, функция g(x) = убывает при
X > О и lim g(x) = О, причем, поскольку g(x) не зависит от г/,
X -^ +00
стремление g(x) к нулю при х -^ +оо происходит равномерно
относительно у; кроме того,
^ 1 - cosxy <- 2
У ^ Уо'
Таким образом, оба условия теоремы 3 выполнены.
Задача 15. Доказать, что если функции f(x, у) и g(x, у) определе-
+ 00
ны при -оо <а < X < +00 и yeY, причем [ /(х, y)dx равномерно сходится
а
на Y, а функция g(x, у) монотонна по х и ограничена на множестве
+ 00
[а, +00) X Y, то интеграл | g(x, y)f(x, y)dx сходится равномерно на Y.
а
УПРАЖНЕНИЕ 1. Пусть функции /(х) и g{x, у) непрерывны по х,
функция g{x, у) монотонно и равномерно относительно г/е Y стремится к нулю
и six I/)
при X -^ +00 и имеет непрерывную производную * ^ , х > а, z/eY,
ох
+ 00 +00
а интеграл [ f{x)dx сходится. Доказать, что интеграл [ /(x)g'(x, y)dx
а а
равномерно сходится на множестве Y.
54.3. Свойства несобственных интегралов,
зависящих от параметра
При изучении свойств несобственных интегралов, зависяпа;их
от параметра, очень часто придется иметь дело с перестановкой
предельных переходов по различным переменным. Поэтому
прежде всего докажем лемму, относягцуюся к этому вопросу.
ЛЕММА Л. Пусть X и Y — два числовых множества;
функция f{x, у) определена на их произведении X X Y : xgX, г/е Y;
Xq иу^— числа или какие-то из бесконечностей оо^ +оо^ -оо
и существуют конечные пределы
ф(х)= lim /(х, г/), xgX, и \\f(y)= lim f(x, у), yeY.
Если стремление функции f хотя бы к одному из
указанных пределов происходит равномерно, то существуют
и равны оба повторных предела:
lim lim fix, у) = lim lim fix, у).
x^x^y^yQ y^yQX^XQ
Доказательство. Пусть, например, функция /(х, у)
равномерно на X стремится к ф(х) при у -^ у^. Тогда для любого
фиксированного 8 > О сугцествует окрестность C/(z/q) такая,
что, каковы бы ни были уе и(уо) П Y и xgX, выполняется
неравенство
|/(х,г/)-ф(х)|<|. E4.12)
Если j/iG Щуо) П У и j/2G Щу) П Y, то
\f{x, j/i) - fix, г/з)! < \fix, г/i) - ф(х) |+| ф(х) - f{x, г/з)! < е.
Переходя здесь к пределу при х -^ Xq, получим
Мг/1)-¥(г/2I<е- E4.13)
Согласно критерию Konin для сугцествования предела
функции (см. п. 4.11), из E4.13) следует сугцествование
конечного предела lim \|/(г/) =А. Итак, доказано сугцествование
у ^Уо
повторного предела
lim lim fix, у) = А.
y^y^x^XQ
Зафиксируем теперь у-^е и(у^) П Y. Тогда из E4.12) при у = y^vi
из E4.13) при у2 -^ г/о соответственно получим
|/(х,г/1)-ф(х)|<|, |х|/(г/1)-А|<8. E4.14)
Для всех y&Y сугцествует предел lim /(х, у) = \|/(г/).
Поэтому при фиксированном г/^е C/(z/q) П Y для заданного 8 > О
найдется такая окрестность C/(Xq), что для всех xgC/(Xq) П X
будем иметь
|/(x,z/i)-v|/(z/i)|<8. E4.15)
Из неравенств E4.14) и E4.15) для всех xg C/(Xq) П X имеем
|ф(х) - А| < |ф(х) - /(х, у^)\ + |/(х, i/i) - \|/(i/i)| + |\|/(i/i) - А| < 38,
что и означает сугцествование повторного предела
А = lim ф(х) = lim lim /(х, г/)
X —> Xq X —> Xq I/ —> 1/q
И равенства его повторному пределу
lim lim fix, у). П
у^у^х^х^
ТЕОРЕМА 4. Пусть -оо < а < Ь < +оо г/ функция /(х, г/) оя-
ределена для всех хе[а, Ь), yeY и при любом yeY непрерывна
по X на [а, Ь). Тогда если при любом г\е[а, Ъ) функция /(х, у)
'677
равномерно на отрезке [а, Г|] стремится к функции ф(х) при
у -^ у^^ и интеграл
]fix,y)dx E4.16)
а
равномерно сходится на множестве Y, то
ъ ъ ъ
lim |/(х, i/)(ix = I lim f{x,y)dx = ^ (^{x)dx. E4.17)
Доказательство. Если а < г| < Ь, то, в силу теоремы 2
п. 53.1, имеем
л л л
lim I f(x, y)dx = I lim f(x, y)dx = J (p(x)dx. E4.18)
" "O a a 0 a
Поэтому, согласно определению несобственного интеграла,
равенство E4.17) можно переписать в виде
л л
lim lim \ f(x,i})dx= lim lim \ f(x,i})dx. E4.19)
Таким образом, остается доказать возможность перестановки
порядка предельных переходов для функции
л
Ф(г/, л) = |(^. г/)йх.
а
Это следует из доказанной выгае леммы. В самом деле,
согласно E4.18), сугцествует предел lim Ф(г/, Г|). С другой сто-
у^Уо
роны, сугцествует и предел
л ь
lim Ф(г/, Г|) = lim ^ [ /(х, y)dx = \ fix, y)dx,
причем здесь, согласно условию теоремы, стремление к
пределу происходит равномерно на множестве Y. Следовательно,
справедливость равенства E4.19) непосредственно вытекает
из утверждения леммы. П
ТЕОРЕМА 5. Пусть функция f(x, у) определена и
непрерывна {как функция двух переменных) на полуоткрытом
«прямоугольнике» {(х, у) : а < X <Ъ, с < у < d), -оо < а < Ь < +оо,
-оо < с < d< +00. Тогда, если интеграл
ъ
Ф(г/) = I /(х, y)dx
а
сходится равномерно на [с, d], то он является непрерывной
функцией на этом отрезке.
' Здесь z/q — число или одна из бесконечностей оо, +оо, -оо.
^78
Доказательство. Каково бы ни было у^е[с, d], функция
f(x, у) при у ^ Уо равномерно на любом отрезке [а, Г|], а < Г| < Ь,
стремится к функции f(x, у^) (см. C9.4). Поэтому, согласно
предыдупа;ей теореме (см. E4.17)),
b Ъ
lim Ф(г/) = I lim /(х, y)dx = \ /(х, г/о)йх = Ф(Уо). □
" "о а " "о а
ТЕОРЕМА 6. Если выполнены предположения теоремы 5, то
d d Ь Ь d
\Ф{у)с1у = \dy\ fix, y)dx = J dx\f{x, y)dy. E4.20)
С с a ас
Доказательство. Если а < г| < Ь, то по теореме 3 п. 53.1
имеем
d Ц Ли
\dy\f{x, y)dx = \dx\f(x, y)dy. E4.21)
с a ас
Л
Функция Ф(г/, Г|) = |/(х, y)dx непрерывна по г/ и при Г| ^ Ь - О
а
стремится к своему пределу Ф(г/) равномерно на отрезке [с, d].
Поэтому, согласно теореме 2 п. 53.1, в левой части равенства
E4.21) можно перейти к пределу под знаком интеграла при
d Ц d
lim \dy\f(x, y)dx = lim |Ф(г/, r{)dy =
d d d b
= I lim Ф(у, ц)dy = lФ(y)dy = ^dy^ fix, y)dx;
^Tj^OU ^ с a
при ЭТОМ полученный предел конечен. Следовательно, при
Г| ^ Ь - О сугцествует тот же предел и у правой части равенства
E4.21), который, в силу определения несобственного интегра-
b d
ла, равен | dx^f(x, y)dy. П
а с
Докажем одну теорему о перестановке порядка
интегрирования для случая, когда оба интеграла несобственные.
ТЕОРЕМА 7. Пусть функция f(x, у) определена и
непрерывна на полуоткрытом прямоугольнике
{(х, у) : а < X < Ь, с < у < d},
-оо < а<Ь < +00, -оо < с < d<: +00.
Если интеграл
]fix,y)dx E4.22)
679
равномерно сходится на любом отрезке [с, Г|], с <г\< d, а
интеграл
]fix,y)dy E4.23)
С
равномерно сходится на любом отрезке [а, ^], а < ^ < Ь, г/
существует один из двух повторных интегралов
d Ъ Ъ d
\dy\ |/(х, y)\dx, I dx\\f{x, y)\dy,
с a ас
то существуют и равны между собой оба повторных
интеграла
d Ъ Ъ d
\dy\ /(х, y)dx и I dx\f{x, y)dy,
с а ас
т. е.
d Ь Ь d
\dy\ f(x, y)dx = I dx\f(x, y)dy. E4.24)
с a a с
Доказательство. Пусть, например, сугцествует интеграл
] dxjlfix, y)\dy E4.25)
а с
И пусть с < Г| < d. в силу равномерной сходимости на отрезке
[с, Г|] интеграла E4.22), согласно теореме 6, имеем
Ц b b Ц
\dy\ f(x, y)dx = I dx\f(x, y)dy. E4.26)
с a a с
Предел левой части этого равенства при Г| ^ d - О, очевидно,
d b
равен интегралу ^dy^ f(x, y)dx. Покажем, что предел правой
с а
b d
части равенства E4.26) равен интегралу | dx^f(x, y)dy, т. е. что
а с
В ЭТОМ случае возможен предельный переход при Г| ^ d - О под
знаком интеграла. Проверим выполнение предпосылок теоре-
л
мы 4 этого пункта. Функция Ф(х, Г|) = |/(х, y)dy непрерывна
с
по X (см. теорему 1 п. 53.1) и, согласно условию теоремы, на
любом отрезке [а, ^], а < ^ < Ь, при Г| ^ d - О равномерно
стресс
мится к интегралу E4.23), т. е. к функции F(x) = |/(х, y)dy.
с
Наконец, интеграл
b b Ц
I Ф(х, r[)dx = I dx^f{x, y)dy
680
сходится равномерно относительно Г|, с < Г| < d, так как
d
|Ф(х, л)| < \\f{x, y)\dy,
с
а интеграл E4.25), по предположению, сходится.
Следовательно, условия теоремы 4 для правой части
равенства E4.26) выполнены, поэтому
b Ъ Ъ d
lim I Ф(х, rOdx = I lim Ф(х, Г|)йх = J йх|Ф(х, y)dy.
Итак, доказываемое равенство E4.24) получается из E4.26)
предельным переходом при Г| ^ d - 0. П
Перейдем теперь к рассмотрению дифференцируемости
несобственных интегралов, зависягцих от параметра.
ТЕОРЕМА 8. Пусть функции /(х, у) и '^^' ^^ определены и
непрерывны на полуоткрытом прямоугольнике
А = {а< X <Ь, с < у < d},
-оо < а <Ь < +00, -оо < с <d < +00.
Если интеграл |/(х, y)dx сходится, а интеграл | '^^' ^^ dx
равномерно сходится на отрезке [с, d], то функция Ф(г/) =
ъ
= I /(х, y)dx непрерывно дифференцируема на этом отрезке и
а
^Ь(x,y)dx = ]Ш|^dx.
(^У{ ' i ^У
ъ
Доказательство. Представим функцию Ф(г/) = |/(х, y)dx
а
В виде сходягцегося на отрезке [с, d] ряда
Ф{y) = ]f{x,y)dx= £ ^ff(x,y)dx, E4.27)
а д = 1 п„
где Г|^, я = 1, 2, ... , — фиксированная последовательность
такая, что Г|^е[а, Ь), Г|^ = а и lim Г|^ = Ь, а функцию
г _мф_Ш(^х — в виде равномерно сходящегося на отрезке [с, d]
ряда
]Щ_У)ах= У^ТЩ-yldx. E4.28)
681
Согласно теореме 4 п. 53.2, каждый член ряда E4.28)
является производной по переменной у от соответствуюгцего
члена ряда E4.27), а поэтому, в силу теоремы о
дифференцировании рядов (см. п. 32.4), сумма ряда E4.28) является
производной суммы ряда E4.27). П
Как уже отмечалось, все предыдугцие формулировки и
доказательства относятся к несобственным интегралам, завися-
гцим от параметра, которые удовлетворяют условиям 1) и 2),
сформулированным в начале п. 54.1. Совергаенно аналогично
рассматриваются и другие случаи, например когда:
1') -оо < а < Ь < +оо;
2') при любом уе Y функция /(х, у) на переменной х
интегрируема по Риману на каждом отрезке [^, Г|], где а < ^ < Г| < Ь.
Построенная теория интегралов, зависяпа;их от параметра,
естественным образом переносится и на случай, когда
интеграл зависит от двух или вообпа;е от некоторого конечного
числа параметров г/^, ... , г/^. При этом многие формулировки
определений и теорем, а также доказательства формально
остаются прежними, если только вкладывать новый смысл в
применяемые обозначения. Это относится, например, к
определению равномерной сходимости и теореме о предельном
переходе под знаком интеграла, следует только считать, что у =
= (У1, ... , у^)— конечная точка я-мерного евклидова
пространства, i/q — конечная или бесконечно удаленная точка
того же пространства, а г/ ^ i/q понимать в смысле предела в
этом пространстве.
54.4. Применение теории интегралов,
зависящих от параметра,
к вычислению определенных интегралов
До сих пор в нагаем распоряжении было два способа
вычисления определенных интегралов. Первый из них исходит из
определения интеграла как предела интегральных сумм и ninpo-
ко используется в численных методах (с ними мы более
подробно ознакомимся в п. 62.4). Второй способ, которым мы уже
постоянно пользовались, основан на нахождении
первообразной подынтегральной функции и применении формулы
Ньютона—Лейбница. Оказывается, что иногда удается получать
точные значения определенных интегралов, используя
теорию интегралов, зависягцих от параметра. При этом ценность
этого метода состоит в том, что с его помогцью в ряде случаев
вычисляются интегралы от функций, первообразные которых
682
не являются элементарными функциями, и тем самым
обычный способ использования формулы Ньютона—Лейбница
оказывается неприменимым.
Примеры. 1. Пусть требуется вычислить интеграл
J = \^Ip^dx. E4.29)
Q X aJ Л. X
Приведем способы вычисления этого интеграла, основанные
на его замене некоторым интегралом, зависяпа;им от
параметра, для которого E4.29) является частным значением.
Рассмотрим функцию /(х, у) = ^^^ ^ ^^ и интеграл
X aJ А. X
J(y) = I fix, y)dx = J arctg xy^^^ E4.30)
0 Q X /\J л. X
Очевидно, что интеграл E4.29) получается отсюда при у = 1.
Так как ^1£*£^ = О A)при х - О и ^1Щ^ = о(-^=] при
xjl - х^ xjl - х^ ^ л/Г-х^ ^
X ^ 1 и любом фиксированном г/, то интеграл E4.30) сходится
при любом у.
|Э/(х, у)\
Из неравенства
^У
A + х2г/2)л/1 - х2
< , и схо-
Vl-X2
г Эх тс
димости интеграла | ^ = ^ следует, что интеграл
Jfe^dx E4.31)
равномерно сходится на всей вегцественнои оси и, согласно
теореме 8 п. 54.3, равен J\y).
Выполнив последовательно замены переменного
интегрирования X = cos ф и ф = arctg t, получим
1 т к/2 -, +00 т ,
J\y) = Г ^ = Г ^ = Г ^ =
i A + х2г/2OП^ i 1 + y4os\ i l+y^ + t^
: arctg- ^
ж
2УГТ
У^
Ji + y^ Ji + y'
Отсюда, согласно определению неопределенного интеграла,
вытекает, что
Лу) = lj\y)dy = fI^i^, = fin (у + Vl + J/2) + с.
2 7ГТ72 2
683
Но из E4.30) следует, что J@) = О, поэтому С = О и
Лу) = I In (г/ + 71 +г/2).
Подставляя сюда у = 1, получаем значение искомого
интеграла E4.29) J = J(l) = 5ln A + л/2).
Интеграл E4.29) можно вычислить и используя
интегрирование по параметру. Заметив, что ^^^ ^ ^ = f ^:г^? полу-
X о ■'■ ^ "^ ^
чим для J выражение
Интеграл же f ^ сходится равномерно по г/, так
как ^ < ^ а интеграл [ ^ "^ сходится.
A + х2г/2)л/1-х2 Jl-x^ Ь Jl-x^
Поэтому в E4.32) можно переменить порядок
интегрирования (см. теорему 6 п. 54.3). Тогда (используя
непосредственно найденное выпхе значение получаюпа;егося интеграла по х)
находим
J = ]dy ] ^ = ^} -^^- = ^1п A + V2).
i 'iil + x^y^)Jl^^ HJTTV^ 2 ^ ^ ^
2. Вычислим значение интеграла
+ 00 .
/(а)= EiH^^dx. E4.33)
о ^
Можно показать, что соответствуюпа;ий неопределенный
интеграл при а ^ О не выражается через элементарные функции,
и тем самым данный интеграл нельзя вычислить обычным
приемом с помогцью формулы Ньютона—Лейбница.
Интеграл E4.33) сходится при всех значениях а.
Действительно, если а = О, то, очевидно, /@) = 0. Если же а ^ О,
то, производя замену переменного t = ах при а > О и t = -ах
при а < О, получим
sin^
Г Ei£Idf = /A), если а > О,
J f.
Да) = <
о '
+ 00
sin^.
- I E^dt = -1A), если а < 0.
i о ^
Интеграл же /A) сходится (см. т. 1, п. 29.5), поэтому и
интеграл 1(a) сходится.
684
Для того чтобы вычислить интеграл E4.33), рассмотрим
-Рх,
smax
dx, сходягцийся
более обгций интеграл /(а, Р) = \ е
о ■"'
при Р > 0.
Продифференцировав формально по а под знаком интеграла,
+ 00
получим интеграл | е~^^ cos dxdx, который при любом фикси-
0
рованном р > О равномерно сходится относительно параметра а,
-оо < а < +00. Следовательно, при Р > О (см. т. 1, п. 22.4)
- Р
Э/(а, р)
Эа
откуда
+ 00
о
Р^ COS axdx = ^-Hocsinax-pcosax)
а^
Р2
2 , о2'
а + р
^(^' Р) = ] -^2 + С(Р) = arctg I + С(Р).
Р
Но /(О, Р) = О, следовательно, С(Р) = 0. Итак,
Да, Р) = arctg ^, р>0.
Нас, однако, интересует значение интеграла /(а, Р) при
Р = 0. Прогце всего попытаться обосновать возможность
предельного перехода под знаком интеграла /(а, Р), при Р -^ +0.
Зафиксируем число Ь > О и покажем, что интеграл /(а, Р) при
любом фиксированном а ^ О равномерно сходится по
параметру Р на отрезке [О, Ь]. Действительно, интегрируя по
частям (см. там же, п. 22.4), получим
|g-Px
л
_1 -рх ОС COS ах + р sin ах
^ а' + р'
smax
dx =
+ 00
л
.^х acosax + psinax dx
a + p X
Зададим произвольно 8 > 0. Выберем r\^ так, чтобы при Г| ^ Лг
выполнялись неравенства
acosarj + Psinarj 1 i^p
а + р П
^г° 3-у а cos ах + psinax dx
J 2 , о2 2
л а + р X
<
<
ос
2 л 2'
а- П
|а|+ьТс^х
а^
г ох ^ е
J 2 9*
л X "^
Тогда при Г| > r|g получим
T^_p,sinocx^^
J X
< 8, что и доказывает
равномерную сходимость интеграла /(а, Р) по параметру Р на
любом отрезке [О, Ь]. Теперь, в силу теоремы 4 п. 54.3,
Да) = Да, 0) = lim Да, Р) = lim arctg ^ = ?sign а;
Р^О р^+О Р 2
685
итак,
+00 f V2, если a > О,
/(a) = I 5Hi^^ dx = 0, если a = 0,
0 ^ |-7г/2, если a < 0.
Следует обратить внимание на то, что дифференцирование по
со
а в E4.33) привело бы к расходягцемуся интегралу Jcos axdx.
о
Оно стало возможным в /(а, Р), благодаря наличию
множителя е"Р^, Р > О, называемого множителем сходимости. Вычис-
со со
ление интеграла вида ^f{x)dx путем перехода к |е"Р^ f(x)dx,
о о
дифференцирования по Р, нахождения полученного интеграла
и перехода к пределу при Р ^ О называется методом введения
множителя сходимости.
Знание значения 1(a) позволяет легко находить и
значение многих подобных интегралов. Например, легко можно
показать (и это мы используем в дальнейпхем), что
Ji^lS^dx = \a\Tt. E4.34)
Действительно, интегрируя по частям, найдем
Tl - cosax^^ ^ ^ T^ia^^dx = 2а 7^^^dx = \а\п.
о ^
54.5. Эйлеровы интегралы
Рассмотрим интегралы
В(р, q) = ]xP-1A - х)^ - Чх, E4.35)
о
+ СО
T{s)= I x^-V^dx, E4.36)
о
называемые эйлеровыми интегралами соответственно первого
и второго рода. Интеграл E4.35) называется также бета-
функцией, а E4.36) — гамма-функцией.
Выясним прежде всего, для каких значений параметров
р, q и S имеют смысл правые части формул E4.35) и E4.36).
Рассмотрим сначала интеграл E4.35). Подынтегральная
функция имеет, вообгце говоря, две особенности: при х = О и при
X = 1, поэтому представим его в виде
1/2 1
В(р, q)= \хР-1A - х)^ -Чх+ \ хР-1A - х)^ - Чх.
о 1/2
686
Сравнивая первый интеграл в правой части с интегралом
1/2 1
\ хР ~ ^dx, а второй — с | A ~ х)^ ~ ^dx, которые сходятся соот-
0 1/2
ветственно при р>0ид>0и соответственно расходятся при
выполнении неравенств р < О и g < О (см. п. 29.3), получим,
что областью определения бета-функции E4.35) в плоскости
р, q является прямой утолр > О, g > 0. Далее, интеграл В (р, q)
равномерно сходится в каждом прямом угле р ^ Pq, q ^ q^,
каковы бы ни были Pq > О и ^Q > 0. Действительно, это следует,
согласно признаку Вейерп1трасса (см. п. 54.1), из неравенства
хР -1A - х)^ - 1 < х^о " \l - х)^о " \ о < X < 1,
и доказанной вып1е сходимости интеграла
В(Ро' ^о) = I ^^' " ^A -xf^~ ^dx, ро > О, go > 0.
о
Поскольку всякая точка (р, д), р > О, g > О, принадлежит
некоторому углу: р >Ро? g > go? при соответствуюпа;ем выборе чисел
Pq > О и gQ > О, в силу теоремы 5 п. 54.3, функция В (р, д)
непрерывна по всей своей области определения.
Для отыскания области определения гамма-функции
E4.36) представим ее в виде
1 +00
r(s) = I х^ -1 e-'^dx + I х^ -1 e-^'dx. E4.37)
о 1
Сравнивая первое слагаемое в правой части равенства с интегра-
1
лом I х^" i(ix, который сходится при S > о и расходится при s < О,
о
1
получим, что I х^ ~ 1 e~^dx сходится и расходится при тех же зна-
0
чениях параметра s. Что же касается второго интеграла в правой
части равенства E4.37), то он сходится при всех значениях s.
Это, например, следует из справедливости при любом s
асимптотического равенства х^ ~ ^ е~^ = о(е~^^^) для х ^ +оо и из сходи-
+ 00
мости интеграла | e~^^^dx = 2е~^^^. Таким образом, интеграл
1
E4.36) сходится для всех s > О и расходится при s < 0.
Покажем теперь, что интеграл E4.36) равномерно
сходится на всяком отрезке [s^, §2]? где О < s^ < S2 < +^.
Действительно, пусть s^ < S < §2? тогда если О < х < 1, то
yS 1/3 X ^ у 1 /3 X
687
a если X > 1, то
х^ ^е ^ < X ^ е
1 ^ +00
и так как интегралы Jx^^ е ^dx и | х^^ е ^dx сходятся, то
о 1
из формулы E4.37), в силу признака Вейергатрасса
равномерной сходимости интегралов (см. п. 54.1), вытекает
равномерная сходимость интеграла Y{s) на отрезке [s^, 82]. Отсюда, в
силу теоремы 5 п. 54.3, следует, что функция Y{s) непрерывна во
всей своей области определения.
УПРАЖНЕНИЕ 2. Доказать, что функции В(р, q) и Y{s) бесконечно
дифференцируемы .
Задача 16. Доказать, что В(р, q) и Y{s) являются аналитическими
функциями.
Установим некоторые свойства интегралов r(s) и В(р, д).
Прежде всего из формулы E4.36) непосредственно получаем
r(s)>0 (s>0), E4.38)
в частности, гамма-функция не имеет нулей. Далее,
проинтегрировав по частям, получим
+ 00 . , ^ +00
r(s + 1) = I x'e-^dx = -х^е--^|о + S I х^ - ^e'^dx = sY (s). E4.39)
о о
Таким образом, если s > п (п = 1, 2, ...), то
r(s) = (s - 1) (s - 2) ... (s - я) Г (s - п). E4.40)
При любом S > О можно выбрать целое неотрицательное
число п так, чтобы О < s - я < 1 (я = О, 1, 2, ...), и тогда Y(s)
с помопа;ью формулы E4.40) будет выражаться через
значение гамма-функции в некоторой точке промежутка (О, 1].
Иначе говоря, зная значения гамма-функции на промежутке
(О, 1], можно найти ее значение в любой точке.
Заметим егце, что ГA) = 1, и, следовательно, в силу
формулы E4.40), Y (п -\- 1) = п1. Отсюда видно, что
гамма-функция Y(s + 1) является продолжением функции si,
определенной только для целых s = 0, 1, 2, ... ,на всю полуось s > -1
действительных чисел.
Из свойств бета-функции В(р, q) докажем следуюпа;ие.
1^. Для любых р > О и q > О
B(p,q) = B(q,p). E4.41)
Чтобы в этом убедиться, достаточно в интеграле E4.35)
выполнить замену переменного t = 1 - х.
688
2". Для любых р > О и q > 1
Bip,q) = ^l-^\Bip,q-l). E4.42)
Аналогично, в силу симметрии (см. E4.41)), для любых
g > О ир > 1
В(Р. Q) = JT^^(P - 1' ^)- E4.43)
Действительно, проинтегрировав по частям E4.35) и
заметив, что хРA - х)^ ~ ^ = хР ~ \1 - х)^ ~ ^ - хР ~ \1 - х)^ ~ ^,
получим
В(р, q) = f A - х)<?-1 d^ = ££ii^l£)ilif + 1^\хРA - x)i - Чх =
о Р Р
Р
о ^0
= ^В(р, g - 1) - ^В(р, g),
откуда следует E4.42), a в силу симметрии, и E4.43).
3^. Дл^ любых р > О
B(p,n)^B(n,;,)^^-^^^lA:^_(^, п^1,2,....
Эта формула получается последовательным применением соотно-
1
гаения E4.42), если только заметить, что В(р, 1) = ^ хР ~ ^dx =
о
= -. Если же и р = т — натуральное число, то В(т, п) =
_ (П- 1IG71- 1)!
G71 + 71-1)!
Между функциями В(р, q) и r(s) сугцествует связь,
которая устанавливается формулой Эйлера
В(р,д)=^^|™, р>0, q>0. E4.44)
Докажем ее, следуя методу Дирихле. Сделаем в формуле
E4.36) замену переменного х = A + t)y, t > 0:
r(s)
I у'-'^е-^^ + ^Ыу
{1 + tr
и положим s = р + q, р > о, q > 0; тогда
^^ + ^) = 7уР + ^ - 1 е-A + ^ЗДг/.
A + 0^ + ^ у ^
689
Умножим обе части этого равенства на ^^ ^ и проинтегрируем
по f от О до +оо:
+ 00 J. П - 1 +00 +00
Г(р + д) ^—L^-——dt= \tP-4t \yP + ^-^e-^^ + ^'^ydy. E4.45)
^ A + t)P ^ о о
В интервале, стоягцем в левой части этого равенства,
выполним замену переменного t — ^ *
J 7TT7^FT-,dt = 1хР-Ч1- х)<1 - Чх = В(р, q). E4.46)
О ^ ^^ о
Для вычисления правой части равенства заметим, что
1-х
1
\ tP-^ dt \ уР^^~^ е-^^ + ^^ydy
о о
+ 00 +00
= lim ltP-4t Jz/^' + 5-ie-(i + *)J'dy. E4.47)
+ 00
Действительно, обозначая Ф(^, ^) = \ уР^^~^ e~^^^^^ydy, из оце-
нок
о < Ф(^ 0) - Ф(^ ^)<\уР^^-^ e-ydy,
о
+ 00 +00
\tP-^ Ф(t, b,)dt < \tP-^ Ф(t, 0)dt
о о
заключаем, что при ^ ^ +0 функция Ф(^, ^) стремится к
Ф(^, 0) равномерно относительно ^е@, +оо) и что интеграл
+ 00
I fр - 1 ф(^, ^)dt равномерно сходится относительно ^, так как
о
сходится интеграл E4.45). Следовательно, в правой части
E4.47) можно перейти к пределу под знаком внеп1него
интеграла. Далее,
+ 00 +00
\tP-^ dt I г/^ + ^ " 1 е-A + ^^ydy =
о ^
+ 00 +00
= \ yP + ^-'^e-ydy \ tP-'^e-^ydt, t,> О,р > 1, q> 1. E4.48)
^ о
Перестановка порядка интегрирования здесь возможна в силу
+ 00
того, что, во-первых, интеграл tP~^ \ У^^ ^~^ ^"^^ ^ ^^ydy равно-
мерно сходится по t на любом отрезке [О, а], что следует из
равномерной оценки подынтегральной функции
tp-^yp + ч- 1е-A + % ^аР-'^уР^^- Ч-У, Q<t<a,
и сходимости интеграла \ уР ^ ^ ^е ^dy, во-вторых, интеграл
+ 00
уР + q-1 ^-у [ tP~ ^e~^ydt равномерно сходится по у на любом от-
0
резке [^, Ь], ^ > О, что следует из равномерной оценки
подынтегральной функции уР ^ ^ ~ ^е~У fP ~ '^е~^У <: bP ^ ^ ~ Нр ~ ^е~^^ и
+ 00
сходимости интеграла \ tP~^ e~^^dt; в-третьих, интеграл, стоя-
0
гций в правой части равенства E4.48), сугцествует. Таким
образом, законность перестановки порядка интегрирования в
E4.48) следует из теоремы 7 п. 54.3 (отметим, что здесь
подынтегральная функция неотрицательна).
Выполнив замену переменного ty = и, получим
+ 00 +00 +00
^yP + Q-'^e-ydy \tP-'^e-4t = r(p) \y^-^e-ydy. E4.49)
^ о ^
Наконец,
+ 00
lim \y^-4-y = Y{q). E4.50)
Из E4.45) — E4.50) получаем формулу E4.44) дляр > 1, g > 1.
Если теперь р > О и g > О, то, по доказанному,
В(р+1,д+1)=П£±Ж(£±1).
Применяя соотноп1ения E4.39), E4.42) и E4.43), получим
формулу E4.44) в предположениир > О, g > 0. П
54.6. Комплекснозначные функции
действительного аргумента
Мы будем в дальнейп1ем систематически рассматривать
комплекснозначные функции w{t) = u(t) + iv(t) действительного
аргумента t (функции u(t) и v(t) принимают действительные
значения). Мы уже встречались с понятием предела и непрерывности
подобных функций. Производная функции w(t) определяется по
формуле
w\t) ^= uit) + iv\t).
Покажем, например, что, согласно этому правилу, (е^^О' ^
= ia е^^К Действительно,
= ia (cos at + / sin at) = iae^^K
691
Исходя из определения производной w\ легко
доказывается и правило дифференцирования сложной функции: если t =
= t(T) — дифференцируемая функция действительного
аргумента т, то iu[ = w\f^.
Аналогично определяется и интеграл (собственный или
несобственный) от функции w = и + iv:
ъ . . ъ ъ
I w(t)dt = I uit)dt + i\ v(t)dt, -oo < a < Ь < +00.
a a a
b
Интеграл J (u(t) + iv(t))dt называется несобственным, если
a
b b
ХОТЯ бы один из интегралов | u(t)dt и | v(t)dt несобственный.
а а
b
При этом несобственный интеграл | (u(t) + iv(t))dt называет-
а
b b
ся сходящимся, если сходятся оба интеграла | u(t)dt и | v(t)dt.
а а
В этом случае
I {u{t) + ш@)^^ ^= I г/@<^^ + i I i^@<^^-
а а а
При этом функция W называется абсолютно интегрируемой,
если абсолютно интегрируемы обе функции г/ и у. Это
равносильно тому, что абсолютно интегрируема абсолютная
величина \w\ самой функции w^, что сразу следует (в силу
признака сравнения для сходимости интегралов), из неравенств
V2 2 I I I I / 2 2 I I I I / 2 2 II II
и + V = \w\, \v\ < л/г/ + i; = |i^|, |i^| = л/г/ + i; < |г/| + |i;|
(последнее неравенство получается возведением в квадрат
обеих его частей).
Очевидно, что ряд свойств интегралов от действительных
функций (линейность интеграла, аддитивность его по
множествам и т. п.) автоматически переносится и на комплексно-
значные функции. Отметим, например, что если w(t) = u(t) +
+ iv(t), где u(t) и v(t) — интегрируемые по Риману на отрез-
b
ке [а, Ь] действительные функции, то интеграл | w(t)dt так-
а
k
же является пределом интегральных сумм ^^ = Y, ^(^j) ^^j'
* Здесь и везде предполагается выполнение условий, при которых
имеют смысл несобственные интегралы от функций и тл v (см. т. 1,
п. 29.1).
'692
т = {ti}i = 0^ — разбиение отрезка [а, Ь], t- _ ^ <: Ь,- <: t-. At- = t- -
~ ^j - 1' J — 1? ^j ... J J^i
I
b
f w(t)dt = lim a^,
где |t| — мелкость разбиения т. Отсюда, как и для
действительных функций, следует, что в этом случае функция \w{x)\ также
интегрируема по Риману и что выполняется неравенство
ъ I ъ
I w(t)dt\ < I \w(t)\dt.
а I а
Предельным переходом справедливость этого неравенства
устанавливается и для абсолютно интегрируемых в
несобственном смысле комплекснозначных функций.
Из того, что формула Ньютона—Лейбница, формула
замены переменной в интеграле и формула интегрирования по
частям справедливы для действительной и мнимой частей комп-
лекснозначной функции действительного аргумента, следует,
что эти формулы имеют место и для самой этой функции.
Вместе с тем в случае функций, принимаюпа;их
комплексные значения, следует быть осторожным при использовании
аналогов теорем, доказанных для действительных функций.
Далеко не все утверждения, справедливые для функций
действительного аргумента, принимаюпа;их только действительные
значения, переносятся на комплекснозначные функции. С
подобной ситуацией мы уже встречались при изучении
векторных функций (см. п. 15.2 и п. 33.9"^). Например, утверждения,
подобные теореме Ролля, а следовательно, и теореме Лагранжа
о средних значениях, не имеют места для комплекснозначных
функций. Это показывает пример, приведенный в п. 15.2, если
его записать в терминах комплексных чисел.
Именно: рассмотрим функцию f(t) = cos t + /sin f, О < f <
< 27г; тогда ДО) = fBn) = 1, f(t) = -sin t + i cos t. Так как \f(t)\ =
2 2
sin t + COS t = 1, TO ue сугцествует такой точки ^g[0, 27г],
что f(b) = 0. Следовательно, аналог теоремы Ролля в этом
случае не имеет места.
Неверным оказывается и правило Лопиталя,
доказательство которого было основано на теоремах о среднем.
Подтвердим это примером"^.
^
* Этот пример заимствован из книги: Рудин У. Основы
математического анализа. — М., 1966.
'693
Пусть f(t) = t, g(t) = t + t4'/^^, 0 < t < 1. Поскольку,
согласно формуле Эйлера, е^/^^ = cos — + / sin —, то
I 7/f2| / 2 1 , . 2 1 1
Поэтому lim f(t) = lim ^(f) = 0 и
lim Щ = lim A + fe^/^V = 1. E4.51)
Заметив, что
получим
g'{t) = l + [2t-^y/*\
|/@| > \2(^- - t^e^/t^ -l\>2\i-t\-l
\t J t
_ 2л/1 + ^4 _ -|^ ^ 2_ -|^ _ 2 - t
t ^ t t '
Следовательно,
nt)
< , вследствие чего
^^(^)| 1^X^I 2 - t ^
lim Щ = 0. E4.52)
Сравнивая E4.51) и E4.52), убеждаемся, что в данном случае
правило Лопиталя не применимо.
54.7* Асимптотическое поведение гамма-функции
Покажем, что асимптотическое поведение гамма-функции
+ 00
r(s + l)= \ e-^'x'dx, s>-l, E4.53)
о
при болыаих значениях независимой переменной s может
быть описано довольно простой формулой, содержагцей
только элементарные функции.
Подынтегральная функция в интеграле E4.53)
принимает, как легко видеть, наиболыаее значение при х = s.
Выполним в этом интеграле замену переменной интегрирования,
перенеся точку х = s в новое начало координат: х = s + у,
а затем произведя преобразование подобия с коэффициентом,
равным s: у = sty т. е. положим х = s(l -\- t). Получим
+ 00
r(s + l) = e-«s« + i \(e-*(l + t)ydt. E4.54)
Рассмотрим функцию
<pit)'^=e-til + t), -cxD<f<+cxD. E4.55)
694
Поскольку ф'(^) = -te~^, то при t > О функция ф убывает, при
t < О — возрастает, а в точке t = О достигает наиболыаего
значения ф@) = 1. Далее, положив
получим
где при 1^1 < 1
и поэтому
hit)^=-t + lnil + t), -1<^<+оо,
ф) = е^^^\ -1<^<+оо,
+2 +г +4
hit)
-f+ o(f2), t
0.
E4.56)
E4.57)
E4.58)
Итак, гамма-функция представима в виде (см. E4.54), E4.55)
и E4.57))
r(s + l) = e-«s« + iJe«Wdf, E4.59)
+ 00
где поведение функции | h(t) при t ^ О описывается соотно-
-1
гаением E4.58).
Прежде чем переходить к выводу асимптотической
формулы для r(s + 1) при S -^ +оо^ поясним метод ее получения
с помогцью нестрогих, но правдоподобных рассуждений.
График функции ф(^) имеет вид, изображенный на рис. 106. При
возрастании параметра s график функции [ф(^)]^ будет
«прижиматься» к оси переменной f и к единичному отрезку оси
ординат. Поэтому ясно, что интеграл
I е'^^^Ыг,
E4.60)
стояпа;ий в правой части формулы E4.59), при больп1их
значениях S будет xoponio приближаться интегралом
Je^^d^ E4.61)
-6
(где 6 > О произвольно, но фиксировано), причем с тем боль-
П1ей точностью, чем больп1е значение параметра s. Иными
словами, если S достаточно велико, то
как при -1 < t < -6, так и при t > 5
значения функции е^^(^) столь малы,
6
что каждым из интегралов | е^^^^^ dt и
-1
со
г ^shit) d-f- можно С ВЫСОКОЙ ТОЧНОСТЬЮ
6
пренебречь. Естественно ожидать,
что при фиксированном 6 > О и отно-
Рис. 106
695
сительная погреганость приближения интеграла E4.60) с по-
могцью интегралов вида E4.61) может быть сделана сколь
угодно малой за счет выбора достаточно больпюго значения
параметра s.
В силу E4.58), взяв достаточно малое 6 > О, можно
интеграл E4.61) xoponio приблизить интегралом
I e-''^/4t = /^ I е"" du. E4.62)
Если 6 > О, то интеграл В правой части этого равенства при
S -^ +00 стремится к интегралу Пуассона (см. п. 48.2)
^\e-^^du = J%. E4.63)
—со
в результате интеграл E4.60) при больп1их значениях s
оказывается в каком-то смысле xoponio приближенным
выражением 7B7i)/s (см. E4.62) и E4.63)). Поэтому естественно
попытаться доказать асимптотическое равенство
'2%
S
Покажем, что оно действительно имеет место. Зададим
произвольно 8, О < 8 < 1/2. В силу E4.58), супа;ествует такое 6,
О < 6 < 1, что для всех ^е[-6, 6] выполняется неравенство
\h{t) + ^2/2| < 8^^ т. е. -A/2 + 8)^2 < щ>^ < _A/2 - 8)^^^
Следовательно, в силу монотонности функции е^, при всех
S > О имеет место неравенство
A + 28)S^^ A - 28)S^^
е 2 <gsMO<g 2 ^ E4.64)
Заготовим егце одно соотногаение, которое нам
понадобится: выполнив замену переменной интегрирования t =
= и 72/A ± 2e)s, получим
Нужная оценка сверху интеграла
+ 00
j e"^mt E4.66)
-1
696
получается легко:
\е'ЧЩ^ < \е 2 dt< \е ^ dt ^=,,^
Д E4.64) Д _4, E4.65)
^^ E4.67)
E4.65) А/A -28)S
Снизу интеграл E4.66) оценивается сложнее.
Предварительно докажем одно вспомогательное неравенство:
g A + 28)8^2 ^^ A + 28)8^2 g A + 28)8^2
A + 28)S _Jg E4.65) _J^ _J^
_g A + 28)8^2 ^^ A + 28)8^2
= I e 2 df + I e 2 ^^ ^
-oo g
, A + 28)[(s - 1) + 1]^^ A + 28)[(s - 1) + 1]^^
—о +00
= \ e 2 dt+ \ e 2 ^^_
-oo g
A + 28)(8- l)t^ A + 28)^^ A + 28)(8 - l)t^ A + 28)^^
~0 (^ (^ +00 n ел
|e e (if+|e e dt<
-oo g
(l + 28)(8-lM2 , _g A + 28)^2 A + 28)^2
< e 2 I g 2 ^^ + I g 2 ^^
<
g > ^ = uV2/(l + 28)
^ / Z ( f 7/2
^ e
t = uj2/il + 28)
A + 28)(8- 1M^
,2.
^. ^ /гТ2-е 1 -"^^" +
-^ j a/1 + 28_-L E4.63)
VCl +28)/2
A + 28)85^ A + 28M^
..Гао.е 2 e 2 /-^ < ce-""' E4.68)
E4.63) Vl + 281 + 28>1 ^ ^
(no ходу вычислений мы воспользовались здесь тем, что функ-
-A + 28)(8-1)^^/2 ^ / ^ s:n
ция е на бесконечных промежутках (-оо, 5] и
[6, +оо) принимает наиболыаие значения в точках f = ± 6), где
а = A + 28N2/2 > О, с = еA + 28N2/2^^
Таким образом, а и с зависят от 8, но не зависят от s
(напомним, что 6 также зависит от 8).
'697
Теперь можно оценить интеграл E4.66) снизу:
J E4.64) J J E4.68)
-1 -1 -О
E4.68) V A + 28)S
Итак,
> I 27Г
-ce-«^ E4.69)
^— - ce-""' < f e'^^^^t < ' ^^
41 + 28)S E4.69) Д E4.67) V A - 28)S
Поделим полученное неравенство на J27z/s:
л 27Г //о^л /о J
л/1 + 28 A/ 27C VB7c)/s 4 Vl -28
Перейдя в этом неравенстве к пределу при s -^ +оо^ получим,
что для любого 8 > О имеет место неравенство
< lim -^ fe«Wdf<
л/1 + 28 S^+oo ^B7C)/S Д VI -28
Устремив здесь 8 к нулю, получим
1 +00
lim -^ е^ад^^ = 1,
или, что то же (см. E4.55) — E4.59)), искомое
асимптотическое равенство
+00 ПГ~.
\\_e-\\^t)fdt- ^, s^+oo.
-1 ^ ^
Умножив обе части этого равенства на е~^ s^ + ^, в силу E4.54),
получим асимптотическую формулу
Г(8+1)-7271^-^8^ + 1/2^ S^+oo, E4.70)
называемую формулой Стирлинга для гамма-функции. Эта
формула является, очевидно, обобгцением формулы Стирлинга для
факториала натуральных чисел (см. п. 33.8), которая получается
из E4.70), если положить s = п, ибо Г(п -\- 1) = п1 (см. п. 54.5).
54.8*. Асимптотические ряды
В п. 37.10"^ изучались разложения функций в
асимптотические степенные ряды при х -^ +оо. Напомним, что ряд
называется асимптотическим разложением функции f при
X -^ +оо^ если частичные суммы
S„(x) = ao + ^... + ^
" " X Х"
'698
удовлетворяют условию
f(x)-S,(x) = o(\\ х-+00.
Понятие асимптотического разложения функции
естественным образом обобгцается на ряды по системам функций,
образуюгцих так называемые асимптотические
последовательности.
ОпреАеАеи]леЗ. Последовательность функций Ф^(х), п = 0,1,
2, ..., определенных в некоторой проколотой окрестности
точки а (конечной или бесконечно удаленной), называется
асимптотической последовательностью при х ^ а, если
для всех п = 0,1, 2, ... имеет место соотношение
Фд + 1(^) = ^(фд(^))' л:^а. E4.71)
Примерами асимптотических последовательностей при
X ^ а являются 9^(x) = (х - а)^, если а — конечная точка, и
ф^(х) = х~^, если а = +оо или а = -оо, п = О, 1, 2, ... .
Определение4. Пусть Ф^(х), п = О, 1, 2, ... , является
асимптотической последовательностью при х ^ а. Ряд
аофо(х) + ai9i(x) + ... + а^Ф^(х) + ... E4.72)
называется асимптотическим рядом (или
асимптотическим разложением) при х ^ а заданной функции f,
определенной в некоторой проколотой окрестности точки а, если
его частичные суммы
S^(x) = аофо(х) + а1ф1(х) + ... + а^Ф^(х) E4.73)
удовлетворяют условию: для любого п = О, 1, 2, ... имеет
место асимптотическое равенство
f(x)-S^(x) = o(i^^(x)), х^а. E4.74)
ЛЕММА 2. Пусть ф^(х), п = 0,1, 2, ... , — асимптотическая
при X ^ а последовательность. Для того чтобы ряд E4.72)
являлся асимптотическим разложением функции f при х ^ а,
необходимо и достаточно, чтобы
f(x)-S^(x) = 0((?^^^(x)), х^а, п = 0,1,2,.... E4.75)
Иначе говоря, ряд E4.72) является асимптотическим
разложением функции / при X ^ а тогда и только тогда, когда
его частичная сумма aS^(x) служит приближенным значением
функции f(x) с точностью до 0(ф^ + ^(х)) при X ^ а, т. е. оп1иб-
ка имеет порядок первого отбрасываемого члена.
699
Доказательство необходимости условия E4.75).
Соотношение E4.74) при п = 1, 2, ... можно переписать в виде
f{x) -S^_ i(x) - а^Ф^(х) = о(ф^(х)), X ^ а,
откуда
f(x) -S^_ i(x) = а^Ф^(х) + о(ф^(х)) = 0(ф^(х)), X ^ а, я = 1, 2, ... ,
т. е. выполняется условие E4.75). П
Доказательство достаточности условия E4.75). В
силу E5.75) и E4.71), имеем
fix) - S^(x) = 0(ф^ + i(x)) = 0(о(ф^(х))) = о(ф^(х)),
X ^ а, п = О, 1, 2, ... ,
что совпадает с E4.74). П
Отметим егце, что если для любого п = О, 1, 2, ...
выполняется условие
/(х) - S^ + i(x) = 0(ф^ + i(x)), х-а, E4.76)
более слабое, чем E4.74), то из него, в силу E4.71), следует
E4.74). Иначе говоря, выполнение условия E4.76) для всех
п = О, 1, 2, ... означает, что ряд E4.72) является
асимптотическим разложением функции / при х ^ а.
Если асимптотическая последовательность ф^(х), п = О, 1,
2, ... , такова, что сугцествует проколотая окрестность
точки а, в которой при всех п = О, 1, 2, ... имеет место
неравенство ф^(х) ^ О, то аналогично случаю степенных
асимптотических рядов функций получаем:
если функция f раскладывается при х ^ а в
асимптотический ряд E4.72), то такое разложение единственно и его
коэффициенты последовательно определяются по формулам
х^а -^^^ФД-^Л k = 0 J
Однако для практического нахождения асимптотических
разложений заданных функций эта формула оказывается не
всегда удобной. Часто пропа;е получить нужное разложение
другим путем, например в случае интегралов при помопа;и
интегрирования по частям. При этом обычно заранее не
задаются асимптотической последовательностью {ф^(х)}, а строят ее,
исходя из свойств данной функции в окрестности точки а.
Пример. Разложим в асимптотический ряд при х -^ +оо
функцию ^^ .^
F(x,a)= \^dt, х>0, E4.77)
X ^
(а > о — параметр), подобрав соответствуюпа;ую
асимптотическую последовательность. В силу равенства
F(x, а) = J^dt + i J^dt,
X ^ X ^
700
согласно признаку Дирихле (см. п. 33.6), мнимая и
действительная части функции F(x, а) представляют собой при х > О
сходягциеся интегралы. Поэтому сходится и интеграл E4.77).
Отметим что действительной и мнимой частью интеграла
-F(x^, - являются неполные интегралы Френеля (см. § 29)
+ 00 +00
jcose^de, jsine^de.
X X
Чтобы в этом убедиться, достаточно в интеграле -Fix^, -
сделать замену переменной интегрирования t = Q^.
Интегрируя по частям E4.77), получим
F х,а = { —dt =t^-ia f -^dt = t^ - iaFix, a + 1).
Применяя последовательно эту формулу к значениям
функции F, получаюпа;имся в правой части, будем иметь
F{x, а)
le^-
iaF(x, а + 1)
^а + 1
га+ 2
_^ (-1)^а(а+ 1) ... {а + п- l)r^ + ig^^ _^
у-а + п
+ (-/)^ + 1а(а + 1)... (а + n)F( х, а + я + 1)
le
а(а + 1) ... (а + ^ - 1) , а(а + 1) ... (а + п)
(ix)^
+
in+l
Ряд
ie^ ^ а(а+ 1) ... (a + fe- 1)
F{x,a + n+ 1).
E4.78)
E4.79)
является асимптотическим разложением функции F(x, а) при
Действительно, последовательность функций фДх) = е^^х~^ ~ ^,
п = О, 1, ... , является, как легко проверить, асимптотической, а
для частичных сумм SJ^x, а) ряда E4.79), в силу E4.78), имеем
|а(а + 1) ... (а + п)
\F{x, а) - S^(x, а)| =
-F(x, а + я + 1)
= а(а + 1)... (а + я)
^ а(а + 1) ... (а + я - 1)
"°° it I +00 т ,
—^-—М < «(« + 1) - (а + «) Г\,
i +а + п + \ ^ ^ ^ ^ i +а + п + \
о\
X ^ ОО
701
т. е. выполняется условие E4.76), и, следовательно, ряд E4.79)
действительно является асимптотическим разложением
функции F(x, а) при X ^ оо.
54.9* Асимптотическое разложение
неполной гамма-функции
При любом X > О для гамма-функции r(s) имеем
+00 X +00
r(s) = \ t'- ^e-4t = \t'- ^e-4t + \t'- ^'^dt.
0 0 X
Функция
IP +00
r(s,x) = \t'-4-4t, x>0, E4.80)
X
называется неполной гамма-функцией. Она определена при всех
действительных значениях параметра s. Найдем ее
асимптотическое разложение при х ^ + оо. Выполняя в правой части
E4.80) интегрирование по частям, получим
+ 00 +00
r(s, х)= \t'- ^e-4t = X'- ^е-^ + (s-l) \ t'' 4-4t =
X X
= х^-V^ + (s- l)r(s- 1, x).
Применяя последовательно эту формулу к значениям неполной
гамма-функции, получаюгцимся в правой части, будем иметь
r(s, х) = х^~ ^е~^ + (s - V)x^~ ^е"^ + ...
... + (s - l)(s - 2) ...(s -n + l)x^-^e-^ +
+ (s - l)(s - 2) ... (s - n)Y{s -n,x) =
= ^-x^s у {s-l){s-2) ...js-k + l) _^
+ (s - l)(s - 2) ... (s - n)r(s - n, x).
Отсюда при n> s - 1 имеем
ns, X) - e-^x^ У (^-l)(^-2):-(^-fe+l)
(s - l)(s - 2)... (s - nWis - n, x)\ = \{s - 1)... (s - n)\ \ -^,dt <
X ^
1 +00
<\is-l)is-2)...{s-n)\-^^lj-*dt =
^\is-l)...(s-n)\-^^-0[-^^], x^+oo,
702
т. е. для частичных сумм ряда
е-^х^ У (s-l)is-2)...is-n + l) E4.81)
и для последовательности ф^(х) = х~^ + ^ ~ ^е~^, которая
является, как это легко проверить, асимптотической, при х -^ +оо
выполняется условие E4.75). Таким образом, ряд E4.81)
является асимптотическим разложением неполной
гамма-функции r(s, Х) при X -^ +00.
В п. 54.7"^ был найден первый член асимптотического
разложения гамма-функции r(s + 1) при s -^ +оо. Можно найти
и следуюгцие члены, т. е. разложить гамма-функцию в
асимптотический ряд. Он выглядит следуюпа;им образом:
r(s+l)~ 7271^-^8^+A/2)
^4l2^s ^2!2'V.. J
E4.82)
Здесь {c^} — последовательность коэффициентов разложения
в степенной ряд (в окрестности нуля) функции t = tB),
определяемой равенством -2^ = ~h(t), где h(t) задана формулой
E4.56).
Можно получить и асимптотическое разложение для
натурального логарифма гамма-функции. Оно имеет вид
lnr(s)~fs-illnS-S + iln27r+ f ^^^^- -, S^+oo,
E4.83)
и называется рядом Стирлинга, Здесь Бз^ — так называемые
числа Бернулли, определяемые равенством
т - 1 „ 1 ^ . W .
(все нечетные числа Бернулли, кроме В^ = -1/2, равны нулю).
Из формулы E4.83) с помопа;ью потенцирования можно
найти асимптотическое разложение для гамма-функции, в
котором коэффициенты выражены в явном виде. Оно имеет вид
Г(8) ~ B71I/2^-^5^ - A/2) jl + 1 + ^_ - ^^ + .
^ ^ ^ ^ [12s 288s2 51840s3
S -^ +00.
Доказательство формул E4.82) и E4.83) не входит в
задачу настоягцего курса. Описание методов, с помогцью которых
случаются подобные разложения, можно найти в книге:
Федорюк М. В. Метод перевала. М., 1977.
703
54.10. Замечания о кратных интегралах,
зависящих от параметра
Мы рассмотрели выше «одномерные» интегралы, зависяш;ие
от параметра, т. е. случай, когда и переменная
интегрирования и параметр являлись числовыми переменными. Эта
теория обобгцается на случай кратных интегралов, зависягцих
от «многомерного» параметра, т. е. на интегралы вида
F(y) = jf(x,y)dG. E4.84)
Здесь функция /(х, у) определена по переменной х на
открытом множестве G ^ й^ и интегрируема по Риману на любом
открытом измеримом по Жордану множестве Г таком, что его
замыкание содержится в G: Г ^ G. Параметр у пробегает
некоторое множество Y, которое может быть, например,
подмножеством т-мерного пространства R^, а интеграл E4.84)
понимается, вообпа;е говоря, в несобственном смысле.
Интеграл E4.84) называется сходящимся на множестве Y,
если при каждом фиксированном Уо^Т интеграл |/(х, y^dG
сходится. В случае п> 2 это, как известно (см. п. 48.3),
эквивалентно условию сходимости интеграла ||/(х, y^\dG. Сходя-
гцемуся интегралу E4.84) и любой последовательности
открытых измеримых по Жордану множеств G^, й = 1, 2, ... ,
монотонно исчерпываюгцей множество G, естественным
образом сопоставляется ряд, суммой которого он является:
\Кх, y)dG = \Кх, y)dG^ + £ \Кх, y)d(G, + i\Ga). E4.85)
k = l
Подобно одномерному случаю определяется и равномерно
сходягцийся интеграл.
Определение 5. Сходящийся интеграл E4.84) называется
равномерно сходящимся на можестве Y, если для любого г> О
существует такой компакт А ^ G, что для каждого открытого
измеримого по Жордану множества Г, для которого А ^ Г ^ Г ^
^ G,u всех yeYвыполняется неравенство \\f(x, y)d(G\r)\ < 8.
Это определение равносильно следуюгцему.
Определение 5'. Сходящийся интеграл E4.84) называется
равномерно сходящимся на можестве Y, если, какова бы ни
была монотонно исчерпывающая открытое множество G
последовательность открытых измеримых по Жордану
704
множеств G^, й = 1, 2, ... , г/ каково бы ни было число 8 > О,
существует номер k^, зависящий от данной
последовательности и числа 8, такой, что для каждого номера k > k^u
всех ye Y справедливо неравенство
\\f(x, y)d(G\G, )| < 8.
Если интеграл E4.84) равномерно сходится на множестве G
относительно параметра г/е Y, то ряд E4.85) также
равномерно сходится на G.
Для кратных интегралов, зависягцих от параметра,
остаются в силе теоремы об их непрерывности, дифференцируемости,
интегрируемости, аналогичные доказанным выгае. В этом
легко убедиться, и мы не будем на этом останавливаться.
Встречаются интегралы, зависягцие от параметра и более
сложным образом: в них не только подынтегральная
функция /, но и множество G, по которому происходит
интегрирование, зависит от параметра, т. е. G = G(y):
F(y) = lf(x,y)dG(y). E4.86)
Примером такого интеграла в одномерном случае
является интеграл
Здесь G(y) состоит из двух (кроме случая у = aviy = Ъ)
интервалов (а, у) и (г/, Ь), меняюпа;ихся с изменением параметра г/.
Рассмотрим аналогичный пример в я-мерном
пространстве. Пусть G — открытое множество в R^, функция ц = |а(х)
непрерывна в G, |х - г/| — расстояние между точками х и г/,
xeG, yeR^ и а — некоторое число. Интегралы вида
0?f. E4.87,
называются потенциалами и относятся к типу E4.86), так
как в них множеством, по которому производится
интегрирование, является множество G\{y}, зависяпа;ее от у (в формуле
E4.87), мы обозначили, как это делается обычно, область
интегрирования просто через G). Если а=1ия = 3, то функция
E4.87) называется ньютоновым потенциалом.
Задача 16. Доказать, что если G — измеримое по Жордану
открытое множество и функция \х = \х(х) непрерывна на его замыкании G, то
интеграл E4.87) при а < п непрерывен во всем пространстве.
705
и(у) = \
Предметно-именной указатель
Абсолютно интегрируемая комп-
лекснозначная функция
действительного аргумента 692
— сходящееся бесконечное
произведение 62
— сходяпдийся несобственный
кратный интеграл 546
ряд 30, 69, 159
Аддитивность интеграла 435
— меры 407
Аналитическая функция 110
Асимптотическая линия 661
— последовательность 699
Асимптотический ряд 145, 699
Асимптотическое направление на
поверхности 611
— разложение 145, 699
Базис пространства 205, 203
Безвихревое поле 658
Бесконечно убывающая
геометрическая прогрессия 8
Бесконечное произведение 53
Бесконечный предел 155, 177
Бета-функция 686
Биекция 227
Билинейная форма 227
Вектор 203
Векторная функция 209
двух переменных 553
Векторное отображение 328
— представление поверхности 556
Верхний интеграл Дарбу 442
Верхняя я-мерная мера Жор-
дана 395
— сторона поверхности 586
— сумма Дарбу 430
Взаимно-однозначное
отображение 227
Вихрь 634, 651
Внешний контур 523
Внешняя нормаль 597
— я-мерная мера Жордана 395
Внутренний контур 523
Внутренность множества 178
Внутренняя нормаль 597
— я-мерная мера Жордана 359
— точка 178, 561
поверхности 561
Возрастающая последовательность
68
Вписанное разбиение 418
Вторая квадратичная форма
поверхности 599, 601
Выпуклое множество 193
Гамильтон У. 268
Гамма-функция 686, 694
Гармоническая функция 371
Гармонический ряд 12, 49
Гаусс К. 612
Гауссова кривизна поверхности 612
Гелъмголъц Г. 662
Гиперболическая точка
поверхности 613
Гиперболические функции в
комплексной области 126
Гиперплоскость 393
Гиперповерхность уровня 211
Главная ветвь логарифма 130
Главные кривизны 610
— направления 610
— нормальные сечения 610
Гладкая кривая 503
— поверхность 573
Гомеоморфизм 227
Гомеоморфное множество 227
— отображение 227
Гомеоморфный образ множества
227
Градиент 265, 267, 572, 631, 633
Граница множества 189
График функции 210
Грин Дж. 521
Даламбер Ж. 20
Двойная последовательность 154
— точка 350
Двойной ряд 154
Двусторонняя поверхность 597
Декартово произведение 316
Дзета-функция Римана 65
Диаметр множества 199
Дивергенция 633, 646
Дини У. 93
Диффеоморфизм 345
Диффеоморфное отображение 345
Дифференциал векторной функции
двух переменных 554
706
— отображения 337
— функции многих переменных
245
— высшего порядка 227
Дифференцируемость векторной
функции двух переменных 554
— функции многих переменных
245
Дифференцируемое отображение
337, 344
Длина вектора 205
— кривой на поверхности 580
Дополнение множества 185
Допустимая область 653
— поверхность 655
Допустимое преобразование
параметра 503, 565, 586
Евклидово пространство 168, 205
8-окрестность бесконечно
удаленной точки 211
множества 187
точки 169
Жордан К. 193
Зависимая система функции 363
Замкнутая область 193
Замкнутое множество 183
Замыкание множества 182
Знакоопределенная квадратичная
форма 302
Знакопеременный ряд 27
Знакочередующийся ряд 27
Значение бесконечного
произведения 54
Измеримое множество 396
— по Жордану множество 396
Изолированная особая точка
уравнения 350
Инвариантность формы
дифференциала 256
Интеграл, зависяпдий от
параметра 663, 668
— от комплекснозначной функции
действительного аргумента 692
— Пуассона 543
— Римана 420
— Стилтьеса 506
— Эйлера второго рода 686
первого рода 686
Интегральная сумма 419, 423, 624
Интегральный признак
сходимости ряда 23
Интегрирование неравенств 437
Интегрируемая в несобственном
смысле функция 540
— по Риману функция 420
Интервал сходимости степенного
ряда 114
Инъекция 227
Источник 647
Касательная плоскость к
поверхности 264, 569
Касательное пространство 387
Касательный вектор 387
Квадратичная форма 302
Квадрируемое множество 396
Колебание функции
на множестве 230
Компакт 193
Композиция отображений 224, 333
— функций 225
Конечное покрытие 196
Координатная ось 168
Координатное представление
поверхности 559
Координатные векторы 205
Координатные линии 492, 568
— функции отображения 213
Координатный параллелограмм 493
Координаты вектора 203
— поверхности 556
— точки 166
Коэффициенты степенного ряда
101
Краевая точка поверхности 561
Край поверхности 561
Крамер Г. 327
Кратная последовательность 154
— точка поверхности 562
Кратный интеграл 419
, геометрические приложения
550
, зависящий от параметра 704
несобственный 540
, основные свойства 434—442
, сведение к повторному 452,
461
, физические приложения
551—553
, формулы замены
переменных 482, 487
— ряд 153, 162
707
Кривая в пространстве R^ 190
— Неано 416
— склейки 590
Криволинейные координаты 492
Криволинейный интеграл второго
рода 499, 514
первого рода 495
Критерий Дарбу 447
— измеримости множества 403
— независимости криволинейного
интеграла от пути
интегрирования 530, 535, 658
— КопЕи равномерной сходимости
интеграла 674
последовательности 77
ряда 83
Критерий Коши равномерной
сходимости семейства функций 296
сходимости бесконечного
произведения 57
ряда 11
— Лебега 450
— полного дифференциала в од-
носвязной области 659
— потенциальности поля 657, 658
— Римана 448
— Сильвестра 305—306
— соленоидальности поля 654
Круг сходимости степенного ряда
102
Куб ранга k 394
Кубируемое множество 396
Кубическая окрестность 171
Кусочно-гладкая граница 527
— поверхность 591
Лаплас П. 360
Лемма Гейне—Бореля 196
— Коши—Шварца 167
Линейно-связное множество 191
Линейное отображение 329, 469
Линейность интеграла 437
Линейный оператор 330
— функционал 331
Линия кривизны 610
— уровня 211
Лист Мёбиуса 592
Логарифмическая функция в
комплексной области 129
Локально взаимно-однозначное
отображение 348
— гомеоморфное отображение 345
— диффеоморфное отображение
345
Локальный гомеоморфизм 345
Луч 266
Мажорирующий ряд 81
Масса фигуры 551
Матрица линейного оператора
331
— Якоби 318, 341
системы функций 318
Мелкость разбиения 418
Менъе Ж. 606
Мера 396
— поверхности 582
Метод введения множителя
сходимости 686
— выделения главной части 19, 37
— множителей Лагранжа 376
— суммирования рядов 52
средними
арифметическими 52
Мёбиус А. Ф 592
Многочлен Тейлора 282
Множество лебеговой меры нуль
450
Множители Лагранжа 376
Множитель сходимости 686
Модуль непрерывности 231
Монотонность меры 399
Мультииндекс 288
Набла 268, 632
Направляющие косинусы вектора
208
Начало координат 168
Независимая система функций 363
Неопределенная квадратичная
форма 302
Неориентируемая поверхность 592,
595
Неособая точка поверхности 568
Неполная гамма-функция 702
— интегральная сумма 423
Непрерывно дифференцируемая
кривая 503
поверхность 564
в широком смысле 565
функция 249, 293
— дифференцируемое
отображение 345, 562
— продолжаемая функция 293
708
Непрерывное продолжение функ- Омбилическая точка 615
ции 293 Оператор Лапласа 360
Непрерывность векторной функ- Определенная квадратичная форма
ции двух переменных 553 302
— отображения в точке 218 Определитель Якоби 342
— — на множестве 226 Ориентация контура 519
Неравенство Абеля 44 — края поверхности 594, 595, 596
— Гёльдера 25 — поверхности 585, 594, 595
— Коши—Шварца 167, 207 Ориентированная поверхность 587,
— Минковского 25 594, 595
обобщенное 462 Ориентируемая поверхность 585,
— треугольника 166, 205 595
Несобственный интеграл, завися- Ортогональное дополнение 384
щий от параметра 668 Ортогональные векторы 208
от комплекснозначной — матрицы 209
функции действительного Ортонормированные базисы 208
аргумента 692 Основная метрическая форма по-
— кратный интеграл 540 верхности 578
Неявная функция 309, 317, 349 Особая точка поверхности 568
Неявное задание поверхности 567 уравнения 349
Нижний интеграл Дарбу 442 Остаток ряда 6, 10
Нижняя я-мерная мера Жордана Остаточное произведение 56
395 Остаточный член формулы Тейло-
— сторона поверхности 587 ра 284, 292
— сумма Дарбу 430 в интегральной форме
я-мерная мера Жордана 396 119, 467, 469
я-мерный объем куба 394 форме Коши 119
множества 396 Лагранжа 119, 282
Норма линейного оператора 334 Неано 142, 285
Нормаль к поверхности 570 Открытая поверхность 566
Нормальная плоскость 605 — часть поверхности 566
— прямая к поверхности 570 Открытое множество 178
Нормальное сечение поверхности Отрицательная ориентация грани-
605 цы 524
Носитель поверхности 555, 560 контура 519
— точки поверхности 561 поверхности 585, 595
элементарной поверхности Отрицательно определенная квад-
560 ратичная форма 302
— элементарной поверхности 555 тт ^
т-г ^ %rf.^ Параболическая точка поверхности
Ньютонов потенциал 705 ^^^ ^
Область 192, 233 Параметр 296
Образ кривой 234 Параметры поверхности 556
Объем тела 394, 396, 550 Первая квадратичная форма по-
Ограниченная последовательность верхности 579
68, 176 Период 126
Ограниченное множество 175 Периодическая функция 126
Односвязная область 532, 656 Площадь плоской фигуры 396,
Односторонняя поверхность 597 416, 525, 550
Окрестность на поверхности 566 — поверхности 582
Окрестность множества 187 Поверхностный интеграл второго
— точки 169, 171, 180 рода 620, 627
бесконечно удаленной 211 первого рода 618
709
Поверхность 555, 559, 565
— уровня 211
Повторный интеграл 452
— предел 221
Подпространство 205
— натянутое на данные векторы
384
Показательная форма
комплексного числа 124
— функция в комплексной области
131
Покрытие множества 195
Полная аддитивность интеграла
438
— кривизна поверхности 612
Полный дифференциал 245
Положительная ориентация
границы 524
контура 519
поверхности 585, 595
Положительно определенная
квадратичная форма 302
Последовательность, монотонно
исчерпывающая открытое
множество 539
— точек пространства 173
, стремящаяся к
бесконечности 177
Постоянная Эйлера 49
Потенциал 632
Потенциальная функция 632
Потенциальное поле 635
Поток векторного поля 636
Правая система координат 584
Правило Лейбница 665
— «штопора» 584
Предел векторной функции двух
переменных 553
Предел двойной
последовательности 154, 217
— отображения 213
— последовательности 173
— функции 214
по множеству 215
Представление поверхности 556,
559
Преобразование Абеля 44
Признак Абеля 46
— Вейерштрасса равномерной
сходимости интеграла 673
ряда 81
— Даламбера 20, 38
— Дедекинда 53
— Дирихле 44
— Дюбуа—Реймона 53
— Коши 22, 38
— сравнения для несобственных
кратных интегралов 544
рядов 16
Принцип сохранения области 345
Проекция множества на
гиперплоскость 413
Произведение матриц 332
— матрицы на число 332
— множеств 316
— ряда на число 9
— рядов 33
Производная векторной функции
по направлению 632
— комплекснозначной функции
действительного аргумента 691
— отображения 337, 341
— по направлению 266, 270
— частная 240
Проколотая окрестность 181
Простая поверхность 556, 562
— элементарная поверхность 556
Пространство точечное 166
— векторное 204
Противоположная ориентация
поверхности 585
Прямая в пространстве 190, 209
Прямоугольная окрестность 170,
171
Прямоугольная сумма 156
Пуанкаре А. 145
Пуассон С. 543
Путь 190
Равенство Эйлера 61
Равномерно непрерывная
функция 230, 292
Равномерно непрерывное
отображение 229
— ограниченная
последовательность 68
— сходящаяся функциональная
последовательность 71
— сходящееся семейство
функций 295
— сходящийся интеграл 669, 704
функциональный ряд 79
Равномерное стремление
функции к нулю 250
710
Радиус сходимости степенного
ряда 102, 108
Разбиение множества 418
Разложение основных
элементарных функций в ряд Тейлора
121—131
Ранг матрицы 364
Расстояние 165, 166
— между множествами 187
множеством и точкой 187
точками 165, 166
Расходящееся бесконечное
произведение 54
Расходяпдийся интеграл
— ряд 6
Регулярное в широком смысле
отображение 564
— отображение 563
Регулярный метод 52
Ротор 634, 652
Ряд 5, 153
— Лейбница 132
— Маклорена 116
— Стирлинга 703
— Тейлора 116, 142, 298
Связная система поверхностей 590
Семейство функций 296
Сильвестр Д. Д. 305
Символический вектор
Гамильтона 268
Скалярное произведение 205
Склеенная поверхность 590
Склеиваюш;ий гомеоморфизм 589
Смешанная частная производная
273
Согласованные ориентации
поверхностей 595
Соленоидальное поле 653
Соседние поверхности 590
Средняя кривизна поверхности 612
Стандартный базис 205
Статический момент фигуры 552
Стационарная точка 302
Степенной ряд 100
Степень с комплексным
показателем 131
Стилтъес Т. И. 506
Стирлинг Дж. 138
Стоке Дж. 648
Сумма матриц 332
— ряда 6
— рядов 9
Суммирование рядов 52
Сферическая окрестность 169
— сумма 156
Сферические координаты 494
Сходяш;аяся последовательность
68, 174
Сходяш;ееся бесконечное
произведение 54
Сходяш;ийся интеграл 668
— ряд 6, 68, 155
Теорема Абеля вторая 104
первая 101
— Гаусса—Остроградского 645
— Гельмгольца 662
— Гульдина вторая 553
— Дини 93
— Лейбница 27
— Менье 606
— о геометрическом смысле
вихря 651
дивергенции 646
Теорема о единственности
разложения аналитической функции в
степенной ряд 111, 116
круге сходимости
степенного ряда 102
необходимом условии
сходимости ряда 8
почленном
дифференцировании ряда 97
сведении двойного
интеграла к повторному 452
среднем для кратного
интеграла 440
— об интегрировании ряда 95
— Римана о перестановке членов
условно сходяш;егося ряда 41
— Стокса 648, 651
Теоремы о бесконечных
произведениях 59, 60
геометрическом смысле
модуля и знака якобиана 491, 528
двойных рядах 157—162
дифференцируемых
отображениях 345
зависимости функций 364,
365
замене переменных в
кратных интегралах 482, 487
кривизне кривых на
поверхности 600, 606
711
множествах меры нуль 414,
416
непрерывных отображениях
замкнутых множеств 238
компактов 226, 228, 230
линейка связных
множеств 234
открытых множеств
236
несобственных интегралах,
зависящих от параметра 677—
682
кратных интегралах 542—
549
неявных функциях 312, 315,
320
равномерно сходящихся
последовательностях и рядах 74,
78, 80, 81, 87, 89, 90, 93, 94,
97, 100
рядах Тейлора 118—121
сведении двойного
интеграла к повторному 452
собственных интегралах,
зависящих от параметра 664—
668
сходящихся рядах 9—10
— об интегрируемых функциях
427, 429, 430, 431, 443, 447,
448, 450
многих переменных
423, 427, 429, 430, 431
условных экстремумах 376,
385, 389
экстремумах функций
многих переменных 300, 303, 306
Тождественное отображение 227,
343
Тождество Лагранжа 583
Тор 657
Точка возврата 358
— граничная 189
— закругления 615
— изолированная 181
— касания 569
— предельная 181
— прикосновения 180, 212
— максимума 300
— минимума 300
— самопересечения 358, 555, 563
— самоприкосновения 358
— строгого максимума 299
минимума 299
экстремума 299, 300, 303
— поверхности 561
— уплощения поверхности 613
— условного экстремума 372, 375
— экстремума 300
— элементарной поверхности 560
Треугольная сумма 156
Тригонометрические функции в
комплексной области 124
Убывающая последовательность
68
Угол между векторами 207
кривыми 580
Уравнение связи 371
Условно сходящийся ряд 39
Фигура 551
Формула Грина 521
— Дирихле 459
— конечных приращений
Лагранжа для функций многих
переменных 291
— Коши—Адамара 108
— Гаусса—Остроградского 643
— Стирлинга для гамма-функции
698
факториала 138
— Стокса 649
— Тейлора 118, 141, 282, 287, 467
— Эйлера для гамма- и бета-
функций 689
кривизны нормального
сечения поверхности 610
показательной функции в
комплексной области 124
Функциональная
последовательность 61
Функциональный ряд 61
Функция Лагранжа 376
Харди Г. 87
Центр тяжести фигуры 552
Цилиндр 411
Цилиндрическая поверхность 598
Цилиндрические координаты 494
Циркуляция 635
Частичная сумма ряда 6
Частичное произведение 54
Частная производная 240, 554
высшего порядка 273
712
Частный дифференциал 241
Часть поверхности 566
Числа Бернулли 703
Число е 51, 125
— i 125
— % 125
Числовой ряд 5
Член ряда 5
Шаровая окрестность 169
Шварц Г. 167
Эйлер Л. 66
Эквивалентные отображения 503,
558, 563
— представления кривой 503
— точки элементарных
поверхностей 555
— элементарные поверхности 557
Элемент плопдади поверхности 583
Элементарная область 520, 642
— поверхность 555
Элементарная функция многих
переменных 225
Эллиптическая точка поверхности
613
Явное задание поверхности 556,
574
Якоби К. 318
Якобиан отображения 342
— системы функций 318
Указатель основных обозначений
£ и^— ряд
п ^ 1
со
ГТ а^— бесконечное произведение
п = 1
fji ^ f — последовательность {/^} сходится к функции / на множестве X
f^^f — последовательность {fj равномерно сходится к функции f на
множестве X
Ln 2 — логарифмическая функция в комплексной области
\п 2 — главная ветвь логарифма
C,(s) — дзета-функция Римана
°° а °° а
/ ~ ^ -^ при X -^ +00 — асимптотический ряд ^ -^ соответствует
функции / при X -^ +00
2^ ^п^ ... п^
кратный ряд
k = (^^, ..., k^y k^— целое неотрицательное число, г = 1, 2, ..., п
мультииндекс
-, k = {k^, ... , k^ — частная производная ^-го порядка
Эх^ ... Эх^"
/(х, у) =^ f{x) при у -^ у^^^ — семейство функций /(х, у) (у — параметр) рав
номерно по X стремится к функции f(x) на множестве X при у -^ г/^^^
^ «11 ... ^1п ]
; (а^р, i = 1, ... , т; j = 1, ... , п
""ml ••• ""щд
«11 ••• «1д
Ы1
.. а„
матрица
, det(a^p, j=l, ... ,я;у=1, ... ,я — определитель матрицы (а^р
713
^—!^ ^, ——!^ Y — якобиан системы функции u^, ... , u^uo nepe-
менным ^^, ... , ^^
11/11 — норма линейного оператора /
Id : X ^ X — тождественное отображение множества X на себя
\х*Е — верхняя мера множества Е
\х^Е — нижняя мера множества Е
\хЕ, \х^Е — я-мерная мера множества Е
\f(x)dE, ]]•••] /(х^, ... , xj dx^ ... dx^ — я-кратный интеграл от функции /
Е
ПО множеству Е; несобственный я-кратный интеграл от функции /
по множеству Е
\ \ /(л:, y)dx dy — двойной интеграл от функции / по множеству Е
Е
I (ix I f(x,y)dy, \dy \ f(x,y)dx — повторные интегралы
« Ф(х) с а(у)
АВ — кривая с начальной точкой А и конечной точкой В
Г+ — положительно ориентированный контур
Г~ — отрицательно ориентированный контур
I F(x, у, z)ds, I F(r(s))ds — криволинейный интеграл первого рода от
АВ АВ
функции F по кривой АВ
[ adr = [ Pdx + Qdy + Rdz — криволинейный интеграл второго рода
АВ АВ
ОТ векторной функции а = (Р, Q, R) по кривой АВ; циркуляция
векторного поля а по кривой АВ
S = {/(М); MeD}, S = {г(и, v); (и, v) е D},
S = {х(и, v); у(и, v); z{u, v); {и, у) е D) — поверхность
aS+ — положительно ориентированная поверхность
S~ — отрицательно ориентированная поверхность
||ф(х, г/, z)dS — поверхностный интеграл первого рода от функции Ф
S
по поверхности S
\\adS = \\avdS = | \Pdydz + Qdzdx + Rdxdy — поверхностный ин-
S S S+
теграл второго рода от векторной функции а = (Р, Q, R) по
поверхности aS; поток векторного поля через ориентированную
поверхность aS+
А — оператор Лапласа
div а, Va — дивергенция вектора а
rot а, V X а — ротор вектора а
В = В(р, q) — бета-функция
Г = r(s) — гамма-функция
V = r— + /г— + кт- «набла оператор»
grad /, V/ — градиент функции
714
Оглавление
Предисловие
Глава 3
Ряды
§ 30. Числовые ряды 5
30.1. Определение ряда и его сходимость 5
30.2. Свойства сходящихся рядов 9
30.3. Критерий КопЕи сходимости ряда 11
30.4. Ряды с неотрицательными членами 13
30.5. Признак сравнения для рядов
с неотрицательными членами.
Метод выделения главной части члена ряда 16
30.6. Признаки Даламбера и Коши для рядов
с неотрицательными членами 20
30.7. Интегральный признак сходимости рядов
с неотрицательными членами 23
30.8*. Неравенства Гёльдера и Минковского для конечных
и бесконечных сумм 25
30.9. Знакопеременные ряды 27
30.10. Абсолютно сходящиеся ряды. Применение абсолютно
сходящихся рядов к исследованию сходимости
произвольных рядов 30
30.11. Признаки Даламбера и Копей для произвольных
числовых рядов 38
30.12. Сходящиеся ряды, не сходящиеся абсолютно.
Теорема Римана 39
30.13. Преобразование Абеля. Признаки сходимости
Дирихле и Абеля 43
30.14*. Асимптотическое поведение остатков сходящихся
рядов и частичных сумм расходящихся рядов 48
30.15. О суммируемости рядов методом
средних арифметических 52
§ 31. Бесконечные произведения 53
31.1. Основные определения. Простейшие свойства
бесконечных произведений 53
31.2. Критерий КопЕи сходимости бесконечных
произведений 57
31.3. Бесконечные произведения с действительными
сомножителями 58
31.4. Абсолютно сходящиеся бесконечные произведения ... 62
31.5*. Дзета-функция Римана и простые числа 65
§ 32. Функциональные последовательности и ряды 67
32.1. Сходимость функциональных последовательностей
и рядов 67
715
32.2. Равномерная сходимость функциональных
последовательностей 71
32.3. Равномерно сходящиеся функциональные ряды 79
32.4. Свойства равномерно сходящихся рядов
и последовательностей 90
33. Степенные ряды 100
33.1. Радиус сходимости и круг сходимости степенного ряда 100
33.2^. Формула Коши—Адамара для радиуса сходимости
степенного ряда 108
33.3. Аналитические функции 110
33.4. Аналитические функции в действительной области ... 112
33.5. Разложение функций в степенные ряды. Различные
способы записи остаточного члена формулы Тейлора . . 116
33.6. Разложение элементарных функций в ряд Тейлора ... 121
33.7. Методы разложения функций в степенные ряды 131
33.8. Формула Стирлинга 138
33.9^. Формула и ряд Тейлора для векторных функций 141
33.10*. Асимптотические степенные ряды 143
33.11*. Свойства асимптотических степенных рядов 149
34*. Кратные ряды 153
34.1. Кратные числовые ряды 153
34.2. Кратные функциональные ряды 162
Глава 4
Дифференциальное исчисление
функций многих переменных
35. Многомерные пространства 165
35.1. Окрестности точек. Пределы последовательностей
точек 165
35.2. Различные типы множеств 178
35.3. Компакты 193
35.4. Многомерные векторные пространства 203
36. Предел и непрерывность функций многих переменных
и отображений 210
36.1. Функции многих переменных 210
36.2. Отображения. Предел отображений 212
36.3. Непрерывность отображений в точке 218
36.4. Свойства пределов отображений 220
36.5. Повторные пределы 221
36.6. Предел и непрерывность композиции отображений . . . 223
36.7. Непрерывные отображения компактов 226
36.8. Равномерная непрерывность 229
36.9. Непрерывные отображения линейно-связных
множеств 233
36.10. Свойства непрерывных отображений 235
П6
37. Частные производные. Дифференцируемость функций
многих переменных 240
37.1. Частные производные и частные дифференциалы .... 240
37.2. Дифференцируемость функций в точке 244
37.3. Дифференцирование сложной функции 253
37.4. Инвариантность формы первого дифференциала
относительно выбора переменных. Правила
вычисления дифференциалов 256
37.5. Геометрический смысл частных производных
и полного дифференциала 262
37.6. Градиент функции 265
37.7. Производная по направлению 265
37.8. Пример исследования функций двух переменных .... 271
38. Частные производные и дифференциалы выспеих
порядков 273
38.1. Частные производные высших порядков 273
38.2. Дифференциалы высших порядков 277
39. Формула Тейлора и ряд Тейлора для функций многих
переменных 281
39.1. Формула Тейлора для функций многих переменных . . 281
39.2. Формула конечных прирапдений для функций многих
переменных 291
39.3. Оценка остаточного члена формулы Тейлора
во всей области определения функции 292
39.4. Равномерная сходимость по параметру семейства
функций 295
39.5. Замечания о рядах Тейлора для функций многих
переменных 298
40. Экстремумы функций многих переменных 299
40.1. Необходимые условия экстремума 299
40.2. Достаточные условия строгого экстремума 302
40.3. Замечания об экстремумах на множествах 308
41. Неявные функции. Отображения 309
41.1. Неявные функции, определяемые одним уравнением. . 309
41.2. Произведения множеств 316
41.3. Неявные функции, определяемые системой уравнений 317
41.4. Векторные отображения 328
41.5. Линейные отображения 329
41.6. Дифференцируемые отображения 335
41.7. Отображения с неравным нулю якобианом.
Принцип сохранения области 344
41.8. Неявные функции, определяемые уравнением,
в котором нарушаются условия единственности.
Особые точки плоских кривых 349
41.9. Замена переменных 360
42. Зависимость функций 363
42.1. Понятие зависимости функций. Необходимое условие
зависимости функций 363
42.2. Достаточные условия зависимости функций 365
43. Условный экстремум 371
43.1. Понятие условного экстремума 371
43.2. Метод множителей Лагранжа для нахождения точек
условного экстремума 376
43.3*. Геометрическая интерпретация метода Лагранжа ... . 379
43.4*. Стационарные точки функции Лагранжа 381
43.5*. Достаточные условия для точек условного экстремума 388
Глава 5
Интегральное исчисление
функций многих переменных
44. Кратные интегралы 393
44.1. Понятие объема в я-мерном пространстве
(мера Жордана). Измеримые множества 393
44.2. Множества меры нуль 414
44.3. Определение кратного интеграла 417
44.4. Существование интеграла 424
44.5*. Об интегрируемости разрывных функций 431
44.6. Свойства кратного интеграла 434
44.7*. Критерии интегрируемости функций Римана и Дарбу
и их следствия 442
45. Сведение кратного интеграла к повторному 451
45.1. Сведение двойного интеграла к повторному 451
45.2. Обобщение на я-мерный случай 459
45.3*. Обобщенное интегральное неравенство Минковского . . 462
45.4. Объем я-мерного шара 464
45.5. Независимость меры от выбора системы координат . . . 465
45.6*. Формулы Ньютона—Лейбница и Тейлора 466
46. Замена переменных в кратных интегралах 469
46.1. Линейные отображения измеримых множеств 469
46.2. Метрические свойства дифференцируемых
отображений 472
46.3. Формула замены переменных в кратном интеграле . . . 482
46.4. Геометрический смысл абсолютной величины
якобиана отображения 490
46.5. Криволинейные координаты 491
47. Криволинейные интегралы 494
47.1. Криволинейные интегралы первого рода 494
47.2. Криволинейные интегралы второго рода 498
47.3. Расширение класса допустимых преобразований
параметра кривой 502
VTs
4:7л. Криволинейные интегралы по кусочно-гладким
кривым 504
47.5. Интеграл Стилтьеса 505
47.6*. Супдествование интеграла Стилтьеса 507
47.7. Обобщение понятия криволинейного интеграла
второго рода 514
47.8. Формула Грина 519
47.9. Вычисление плопдадей с помопдью криволинейных
интегралов 525
47.10. Геометрический смысл знака якобиана отображения
плоской области 525
47.11. Условия независимости криволинейного интеграла
от пути интегрирования 529
48. Несобственные кратные интегралы 539
48.1. Основные определения 539
48.2. Несобственные интегралы от неотрицательных
функций 542
48.3. Несобственные интегралы от функций,
меняющих знак 546
49. Некоторые геометрические и физические приложения
кратных интегралов 550
49.1. Вычисление площадей и объемов 550
49.2. Физические приложения кратных интегралов 551
50. Элементы теории поверхностей 553
50.1. Векторные функции нескольких переменных 553
50.2. Элементарные поверхности 555
50.3. Эквивалентные элементарные поверхности.
Параметрически заданные поверхности 557
50.4. Поверхности, заданные неявно 567
50.5. Касательная плоскость и нормаль к поверхности 567
50.6. Явные представления поверхности 574
50.7. Первая квадратичная форма поверхности 578
50.8. Кривые на поверхности, вычисление их длин
и углов между ними 580
50.9. Площадь поверхности 581
50.10. Ориентация гладкой поверхности 584
50.11. Склеивание поверхностей 588
50.12. Ориентируемые и неориентируемые поверхности 592
50.13. Другой подход к понятию ориентации поверхности . . . 593
50.14. Кривизна кривых, лежащих на поверхности.
Вторая квадратичная форма поверхности 598
50.15. Свойства второй квадратичной формы поверхности . . . 601
50.16. Плоские сечения поверхности 602
50.17. Нормальные сечения поверхности 605
50.18. Главные кривизны. Формула Эйлера 607
50.19. Вычисление главных кривизн 611
50.20. Классификация точек поверхности 613
719
51. Поверхностные интегралы 617
51.1. Определение и свойства поверхностных интегралов ... 617
51.2. Формула для представления поверхностного интеграла
второго рода в виде двойного интеграла 621
51.3. Поверхностные интегралы как пределы интегральных
сумм 623
51.4. Поверхностные интегралы по кусочно-гладким
поверхностям 626
51.5. Обобпдение понятия поверхностного интеграла
второго рода 626
52. Скалярные и векторные поля 631
52.1. Определения 631
52.2. Об инвариантности понятий градиента, дивергенции
и вихря 637
52.3. Формула Гаусса—Остроградского. Геометрическое
определение дивергенции 640
52.4. Формула Стокса. Геометрическое определение вихря. . 647
52.5. Соленоидальные векторные поля 653
52.6. Потенциальные векторные поля 655
53. Собственные интегралы, зависящие от параметра 663
53.1. Определение интегралов, зависящих от параметра;
их непрерывность и интегрируемость по параметру . . . 663
53.2. Дифференцирование интегралов, зависящих
от параметра 665
54. Несобственные интегралы, зависящие от параметра 668
54.1. Основные определения. Равномерная сходимость
интегралов, зависящих от параметра 668
54.2*. Признак равномерной сходимости интегралов 674
54.3. Свойства несобственных интегралов, зависящих
от параметра 676
54.4. Применение теории интегралов, зависящих
от параметра, к вычислению определенных интегралов 682
54.5. Эйлеровы интегралы 686
54.6. Комплекснозначные функции действительного
аргумента 691
54.7*. Асимптотическое поведение гамма-функции 694
54.8*. Асимптотические ряды 698
54.9*. Асимптотическое разложение неполной
гамма-функции 702
54.10. Замечания о кратных интегралах, зависящих
от параметра 704
Предметно-именной указатель 706
Указатель основных обозначений 713
720