Н.Е.КОЧИН,И.А.КИБЕЛЬ,Н.В.РОЗЕ
ТЕОРЕТИЧЕСКАЯ
ГИДРОМЕХАНИКА
ЧАСТЬ-Н
и

II. Е. КОЧИН, И. А. КИБЕЛЬ, Н. В. РОЗЕ
ТЕОРЕТИЧЕСКАЯ
ГИДРОМЕХАНИКА
ПОД РЕДАКЦИЕЙ
И. А. КИБЕЛЯ
ЧАСТЬ ВТОРАЯ
ИЗДАНИЕ ЧЕТВЁРТОЕ,
ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего специального образования РСФСР
в качестве учебника для университетов
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1963

532
К 75

ОГЛАВЛЕНИЕ
Предисловие к четвёртому изданию	 7
Глава первая. Теоретические основы газовой динамики (И. А. Ки-
бель)	 9
А. Уравнения газовой динамики
§ 1. Введение		9
§ 2. Уравнения гидродинамики в форме интегралов. Сильные раз-
разрывы 		11
§ 3. Уравнения газовой динамики в дифференциальной форме ...	18
§ 4. Слабые разрывы. Характеристики уравнений газовой дина-
динамики 		21
§ 5. Распространение сильных разрывов. Теорема Цемплена ...	29
Б. Установившиеся движения. Плоская задача
§ 6. Плоская задача. Функции 9 и/,	 32
§ 7. Поверхности разрыва в плоской задаче	 35
§ 8. Критическая скорость. Трубки тока в сжимаемой жидкости ... 40
§ 9. Плоские вихревые движения со сверхзвуковыми скоростями.
Характеристики. Угол Маха	 t4
§ 10. Плоские безвихревые движения при v > аА	 50
§ 11 Использование характеристик для решения плоской безвихре-
безвихревой задачи при v > а^	 56
§ 12. Движение газа вне выпуклой поверхности. Обтекание угла,
большего чем т.. Выход из отверстия. Движение внутри трубы.
Сопло Лаваля	¦ . . 69
§ 13. Движение газа около вогнутой поверхности. Образование силь-
сильного разрыва. Движение внутри угла, меньшего чем т.. Обте-
Обтекание профиля с острой передней частью	 76
§ 14. Крыло в плоскопараллельном сверхзвуковом потоке. Прибли-
Приближённые формулы Аккерета, Буземана, Донова. Гиперзвуко-
Гиперзвуковые движения	 87
§ 15. Функция у. Примеры. Точные решения	 &6
§ 16. Дозвуковые скорости. Теория Чаплыгина. Примеры	114
§ 17. Дозвуковые скорости. Метод Христиановича	130
§ 18. Приближённый метод Христиановича для решения плоских
безвихревых задач. Сверхзвуковые скорости 	146
§ 19. Переход через скорость звука. Предельные линии. Примеры
точных решений	156
§ 20. Классификация сверхзвуковых течений по Христиановичу . . . 165
1»

4	ОГЛАВЛЕНИЕ
§ 21 Построение <безударного» сопла Лаваля Истечение raja
из отверстия, сопровождаемое переходом через скорость
звука ...	. .				174
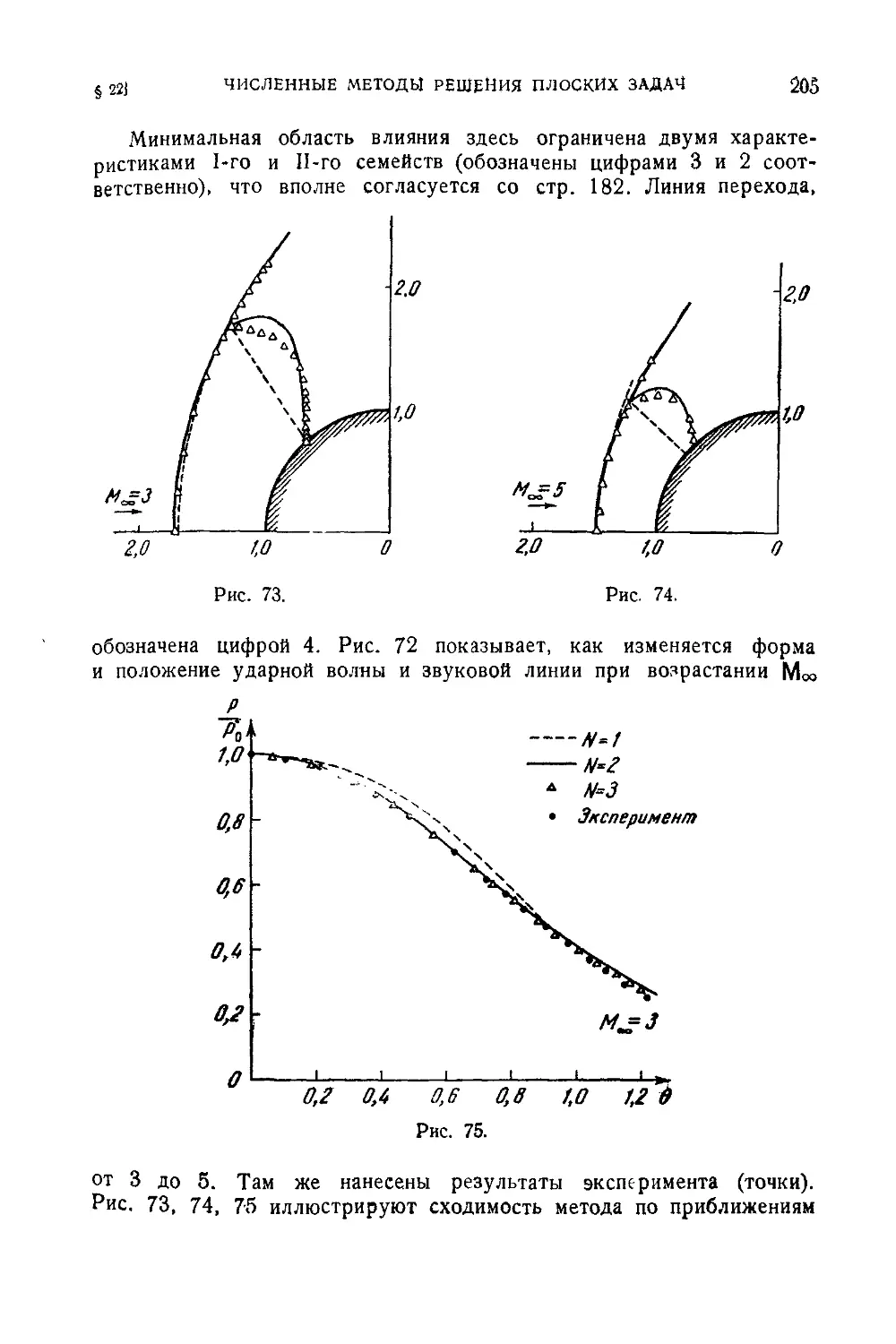
§ 22 Численные методы решения плоских задач газовой динамики
Расчет сверхзвукового обтекания кругового цилиндра . . 190
§ 23 Движение с очень большими сверхзвуковыми скоростями Ги-
Гиперзвуковые течения и обтекание тонких тел	. . . 206
§ 24 Случай реальною газа, «Идеально-диссоциирующийся» газ . 213
В. Установившиеся движения Пространственная
задача
§ 25 Движения с осевой симметрией		. . . 221
§ 26. Безвихревое осесимметрическое движение при v > а. Метод
Франкля			... .	225
§ 27. Осеснмметрнческое обтекание круглого конуса Конические
течения Обтекание осесимметричных тел	229
§ 28. Пространственная задача. Линеаризация уравнении. Снаряд,
движущийся под углом к оси симметрии		. . 245
§ 29 Потенциал ускорения Теорема Прандтля-Глауэрта Крыло
конечного размаха в сверхзвуковом потоке . . .... 262
§ 30 Сверхзвуковое обтекание тонкого крыла конечного размаха
произвольной формы в плане. Концевой эффект и вихревая
пелена			273
§ 31 Сверхзвуковые конические течения Некоторые точные (не-
(нелинейные) решения	301
§ 32 Осесимметричное обтекание с отошедшей ударной волной . . 320
Г Неустановившиеся движения
§ 33. Одноразмерные движения Общие уравнения Характе-
Характеристики 	 325
§ 34 Сильные разрывы в одномерной нестационарной задаче . . 329
§ 35. Случай постоянной энтропии. Движение поршня в неограни-
неограниченной трубе. Точные решения Наличие отражающей
стенки	331
§ 36 Возникновение и перемещение сильного разрыва	341
§ 37 Односторонний взрыв. Плоский, цилиндрический и сфери-
сферический взрыв без противодавления. Сферический взрыв
с противодавлением	344
Глава в 1 о р а я. Движение вязкой жидкости (//. Е. Кочин)') • ¦ • 369
А. Основные уравнения движения вязкой жидкости
§ 1. Понятие вязкой жидкости ...	.	369
§ 2. Тензор скоростей деформации ...	.	. .	373
§ 3. Тензор напряжений		377
§ 4. Уравнения движения вязкой жидкости		385
§ 5 Различные формы уравнений движения вязкой несжимаемой
жидкости		388
') § 10, § 19, § 20, часть § 34, § 35 н § 36 написаны И. А. Кибелем.

ОГЛАВЛЕНИЕ	5
§ 6. Начальные и граничные условия		397
§ 7. Диссипация энергии		400
§ 8. Обобщение уравнений Гельмгольца	 ...	403
§ 9. Закон подобия. Число Рейнольдса		406
§ 10. Уравнение притока тепла для вязкой сжимаемой жидкости . .	415
Б. Точные решения уравнений движения вязкой
жидкости
§ 11. Одномерное течение между двумя параллельными плоскими
стенками		420
§ 12. Течение Пуазейля		427
§ 13. Общий случай стационарного одномерного течения		432
§ 14. Нестационарное одномерное течение		437
§ 15. Стационарное течение жидкости между двумя цилиндрами . .	447
§ 16. Диффузия вихря	 ....	450
§ 17. Течение в диффузоре		460
§ 18. Решение Гамеля и его обобщения		475
§ 19. Одномерное движение вязкой сжимаемой жидкости		481
§ 20. Задача об обтекании полубесконечной пластинки несжимаемой
жидкостью		485
В. Приближённые решения уравнений движения
вязкой жидкости в случае малых чисел
Рейнольдса
§ 21. Плоское течение между двумя пластинками .... . .	498
§ 22. Медленное вращение сферы .... .	502
§ 23. Медленное движение сферы	 .	504
§ 24. Парадокс Стокса	 . .	511
§ 25. Уточненное решение задачи о движении сферы . . .	516
§ 26. Движение цилиндра	 .	528
§ 27. Гидродинамическая теория смазки		534
Г. Приближённые решения уравнений движения
вязкой жидкости в случае больших чисел
Рейнольдса
§ 28. Общая характеристика течений при больших числах Рей-
Рейнольдса. Вывод основных уравнений теории пограничного
слоя		542
§ 29. Вывод Мизеса. Уравнение Мизеса		549
§ 30. Интегральное соотношение Кармана и его обобщения ....	556
§ 31. Уравнения теории пограничного слоя для сжимаемой
жидкости		566
§ 32. Пограничный слой в несжимаемой жидкости вдоль плоской
пластинки		569
§ 33. Пограничный слой в диффузоре. Ламинарная струя		578
§ 34. Приближённые методы теории пограничного слоя. Отрыв
слоя. Метод Кочина—Лойцянского		588
§ 35. Пограничный слой в сжимаемой жидкости. Обтекание пла-
пластинки. Метод Дородницына		608
§ 36. Сжимаемая жидкость. Пограничный слой для произвольного
профиля 		627
§ 37. Основные уравнения теории исчезающей вязкости		632
§ 38. Реакция потока на тело		641
§ 39. Обтекание цилиндра	 . . ¦	644
§ 40. Обтекание плоской пластинки	 . 		652

6	ОГЛАВЛЕНИЕ
Глава третья. Элементы теории турбулентности (И. А. Ки-
бель)	658
А. Турбулентность и неустойчивость
§ 1. Введение 	658
§ 2. Устойчивость движения между двумя коаксиальными цилиндрами 659
§ 3. Устойчивость течения между пластинками и устойчивость в по-
пограничном слое	666
Б. Развитая турбулентность
§ 4. Сглаживание	686
§ 5. Основные уравнения Рейнольдса	691
§ 6. Характеристики турбулентности	698
В. Добавочные напряжения и средние значения
гидродинамических элементов
§ 7. Путь перемешивания и метод подобия	706
§ 8. Примеры 	709
Литература	718
Именной указатель	721
Предметный указатель . . . . •	•	724

ПРЕДИСЛОВИЕ К ЧЕТВЁРТОМУ ИЗДАНИЮ
В новом издании книги наиболее значительной переработке под-
подверглась первая глава — теоретические основы газовой динамики.
В неё введено пять новых параграфов, в которых приводятся ре-
результаты, полученные с помощью электронных быстродействующих
машин для задач на сверхзвуковое обтекание как в плоском,
так и в пространственном случаях, изложены теория гнперзву-
ковых движений, теория диссоциирующего газа, линейная простран-
пространственная задача обтекания крыла. Ряд параграфов значительно рас-
расширен. Так, в параграфе, посвященном взрыву, даётся теория точеч-
точечного взрыва без учёта противодатления, а также детально излагается
способ решения на электронной быстродействующей машине задачи
о взрыве с учётом противодавления; в параграфе, посвященном
крылу в плоско-параллельном потоке, расширено изложение, касаю-
касающееся обтекания пластинки; даны новые примеры точных решений
в осесимметричном случае. Уточнён ряд отдельных результатов
н методов. Так, например, для метода характеристик указываются
новые варианты и, в частности, излагается применение его к расчё-
расчётам, проводимым с помощью электронных вычислительных машин.
В главе о вязкой жидкости вставлен параграф, посвященный точ-
точному решению задачи обтекания пластинки, и дано сравнение этого
решения с известным решением, относящимся к пограничному слою.
При подготовке нового издания исправлены опечатки, допущенные
в предыдущем издании. Как и в прежних изданиях, мы старались
не только познакомить читателя с теми или иными основными идеями,
но и изложить, по мере возможности, технику решения гидродина-
гидродинамических задач.
И. Кабель

ГЛАВА ПЕРВАЯ
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
А. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ
§ 1. Введение. Газовая динамика — это гидродинамика больших
скоростей и малой пространственной протяжённости. Области её
применения суть: конструирование скоростных самолётов, внутрен-
внутренняя и внешняя баллистика, теория паровых турбин, теория ракет
и т. п. Малая пространственная протяжённость изучаемого явления
позволяет отбросить в уравнениях газовой динамики внешние силы
(совершенно так же, как это делается в обычной теории крыла
аэроплана). Действительно, абсолютное значение изменения давле-
давления |Др|, происходящего благодаря наличию силы тяжести, при
перемещении по вертикали на Дг будет:
отсюда
9 8
9 8
р ~ё RT ~~ ' 287- Т '
и если принять Т за 273, то для изменения давления на 1 % пона-
понадобится перемещение по вертикали примерно на 80 м. Этот вывод
подтверждается также и принципом подобия, согласно которому
действие внешних сил будет тем меньше, чем меньше будет масштаб
явления.
Вторая особенность газовой динамики — наличие больших ско-
скоростей — заставляет отказаться здесь от рассмотрения несжимаемой
жидкости. Действительно, несжимаемая жидкость, имеющая давле-
давление pv плотность pj и движущаяся со скоростью vv приобретает,
набегая на препятствие (v = 0), давление

10	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Напротив, сжимаемая, движущаяся адиабатически жидкость приобре-
приобретает давление
2\'
, ?1
Отсюда видим, чго лишь когда plv2l/4v.p1 < 1/100, т. е. при •/. =
= 1,405, Г=273, fj < 70 м/сек, давления для случаев сжимаемой
и несжимаемой жидкости будут разниться меньше чем на 1 %. Га-
Газовая динамика имеет, однако, зачастую дело со скоростями, значи-
значительно большими. На необходимость учёта сжимаемости при боль-
больших скоростях указывает (качественно) также принцип подобия.
Как будет выяснено в следующей главе, при больших скоростях
вязкость играет меньшую роль (большие значения числа Рейнольдса)
и область влияния её ограничивается ничтожным пограничным слоем.
В гаких вопросах, как сопротивление трения, наличие погранич-
пограничною слоя будет, конечно, при всей малости слоя, иметь принци-
принципиальное значение. Однако, как мы увидим, при больших скоростях
возникают, вообще говоря, другие виды сопротивлений, отодвигаю-
отодвигающие на задний план сопротивление трения. Наконец, при больших
скоростях обмен теплом с внешним пространством не успевает, как
правило, совершиться — отсюда вытекает возможность ограничиться
рассмотрением движений адиабатических. Таким образом уравнения
газовой динамики суть, вообще говоря, уравнения движения идеаль-
идеальной сжимаемой жидкости, не подверженной действию внешних сил.
В дальнейшем мы увидим, что наличие больших скоростей по-
порождает совершенно специфическое явление, резко отличающее
i азовую динамику от иных областей применения механики сжимаемой
жидкости (динамическая метеорология и акустика): мы имеем в виду
образование поверхностей, при переходе через которые давление,
а также и другие гидродинамические элементы претерпевают разрыв
непрерывности. Наличие таких поверхностей («волны», «поверхности
разрыва», «скачки уплотнения») заставляет осторожнее подойти
к выводу уравнений гидродинамики в дифференциальной форме,
выводу, обычно делаемому в предположении, что гидродинамические
элементы непрерывны. Мы начнём поэтому с уравнений в форме
интегралов.
Сделаем ещё одно замечание. При весьма больших скоростях,
таких, например, с какими приходится иметь дело в случае искус-
искусственных спутников Земли, в газе за скачком уплотнения могут
образоваться огромные температуры. В реальной атмосфере, состоя-
состоящей в основном из молекул кислорода и азота, возникает при этом
ряд процессов, связанных с диссоциацией молекул на атомы, а при

§ 21	УРАВНЕНИЯ П1ДР0ДИНАМИКИ В ФОРМЕ ИНТЕГРАЛОВ	И
еще больших температурах — с их ионизацией. Поэтому мы должны
быгь подготовлены к необходимости использования более общих
законов термодинамики, чем те, с которыми приходится иметь дело
в акустике, динамической метеорологии и в классической механике
сжимаемой жидкости.
§ 2. Уравнения гидродинамики в форме интегралов. Сильные
разрывы. Уравнения движения могут быть записаны, в нашем слу-
случае, в виде (приращение количества движения равно импульсу силы):
h
=- J(ffpnds)dt B.1)
М	//=/, \ <т>	/<=',	«, \ (S)	/
[(")—произвольный объём жидкости, ограниченный поверхностью (S),
п — единичный вектор внешней нормали к (S), tx и t2 — два каких-то
момента времени]. Уравнение неразрывности естественнее всего при
этом записать в виде:
Уравнение энергии [приращение живой силы частицы (т), сложенное
с приращением внутренней энергии I I I pU dx, где U — внутрен-
внутренняя энергия единицы массы, равно работе внешних сил, приложен-
приложенных к частице] имеет вид:
-Miff»
(т)	/t = t,	\ (т)
Все три уравнения [B.1), B.2), B.3)] могут быть записаны сле-
следующим образом:
(г)
причём в первом случае
a = pV, cn = — pn,	B.5)
во втором
с = Р, ся = 0,	B.6)

12	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
в третьем
Х; с„=— pV-n.	B.7)
Если функции а и сп и их производные существуют и непре-
непрерывны в интервале от ti до t2 и во всех точках обьёмов, занимае-
занимаемых жидкой частицей (т) при движении её от tx до t2, то мы можем
вывести из B.4) обычные дифференциальные уравнения гидродина-
гидродинамики. Производные от наших функций могут при этом претерпевать
разрыв при переходе через отдельные поверхности.
Предположим, однако, что всегда существует одна поверхность ')i2:
F(x, у, z, 0 = 0,	B.8)
проходящая через точки (t) и перемещающаяся в пространстве [вхо-
[вхождение t в уравнение B.8)], такая, что сами функции а и сп пре-
претерпевают при переходе через эту поверхность разрыв. Часть про-
пространства, прилегающая к поверхности Е, делится этой последней
на две области: с одной стороны от поверхности
F(x, у, z, t) <0,
с другой:
F(x. у, z, *)>0.
Первую область назовём отрицательной и условимся обозначать зна-
значения, к которым стремится некая функция Ь(х, у, z, t), если при-
приближаться к Е, оставаясь в отрицательной области, через bL; вто-
вторую область назовём положительной, а соответствующие ей значения b
на X назовём Ь+. Разность Ь+ — Ь_ обозначим через [Ь]:
и назовем разрывом или скачком функции b на поверхности 2. Сама
поверхность Е называется при этом поверхностью разрыва функ-
функции Ь.
Предполагая, что [а] и [сп\ отличны от нуля, посмотрим, какие
условия налагает на эти разрывы наличие уравнения B.4). Предва-
Предварительно введём некоторые термины. Поверхность B.8) в разные
моменты времени будет занимать в пространстве различные положе-
положения. Рассчитаем скорость N, с которой поверхность эта будет в не-
некоторой своей точке удаляться по нормали от своего положения.
Возьмём некую точку М(х, у, z) на поверхности S в момент t и
проведём нормаль к Е в М, направляя эту нормаль в положитель-
положительную область. Пусть эта нормаль пересекается с той поверхностью,
') Мы ограничиваемся случаем существования единственной поверх-
поверхности; никакого труда не представит перенести наши рассуждения на сли-
сличай любого конечного числа поверхностей.

§ 2]	УРАВНЕНИЯ ГИДРОДИНАМИКИ В ФОРМЕ ИНТЕГРАЛОВ	13
в которую переходит 2 к моменту t-\~t', в точке М*(х*, у*, z*).
Тогда
.. ММ*
lim —тг-
1
и будет искомой скоростью. Но
*_	MM* dF
jC —- JC —	^— > , , , ,
1	g dx
где
g = _j_- ]/"^2~1)_ /?2	_j_ pi (p^^-fML, \
у	\ ox i
и
F{x\ y\ z-,
= F (x, y, z.
Здесь и далее символ О(/'2) означает: «величина порядка //2».
Далее, Fix, у, z, t) = 0, так как точка М(х, у, z) лежит в мо-
момент t на поверхности S, и потому
.. MM*	F,
140 *	8
Получаем важную формулу
л^-- F^~ ,	'		i?.	B.9)
У \дх) ~т~\ду) ^\дг)
Величина N носит название скорости перемещения поверхности
разрыва. Она имеет чисто геометрический характер и никак не
связана с существующим движением жидкости. Однако, поскольку
речь идёт о перемещении поверхности S в движущейся, в свою
очередь, жидкости, представляет интерес ещё и другая величина —
именно скорость, с которой поверхность разрыва S перемещается
от одной жидкой частицы к другой (скорость эта была бы равна N
в случае, если бы жидкость покоилась). Чтобы найти эту скорость
в каждой точке М поверхности S, достаточно, очевидно, вычесть
из скорости N величину Vп проекции на нормаль п к поверхности S
скорости V движения жидкости в этой точке М поверхности. Полу-
Полученная величина
% = N — Vn	B.10)
носит название скорости распространения поверхности разрыва.
Заметим, что если Vп будет претерпевать разрыв, то то же будет
происходить и с 0.

14
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГЧЗОВОП ДИНАМИКИ
[IЛ I
Пользуясь понятием скорости распространения поверхности раз-
разрыва, мы без труда можем вывести соотношения, связывающие
вследствие уравнений гидродинамики скачки (разрывы) различных
гидродинамических элементов. Для этого обратимся сперва к мо-
моменту tx и обозначим через ?<( положение поверхности разрыва в этот
момент, а через Е/2—положение в момент tx тех точек жидкости,
которые в момент /2 (бесконечно близкий к t{) окажутся на поверх-
поверхности разрыва.
На поверхности ?<, отметим точку М и построим малый цилин-
цилиндрик (рис. 1) с осью, совпадающей с нормалью к 2/( в точке М и
Рис. 1.
Рис. 2
до пересечения с поверхностью ?<а>); объём этого цилиндрика и
примем за объём интегрирования (т) (к моменту tx) в выражении
B.4). Посмотрим теперь, что произойдёт к моменту t2. Вследствие
движения жидкости, точка М перейдёт в какую-то точку М'\ по-
поверхность T,ti, переместившись и деформировавшись, займёт некоторое
положение ?^; наконец, точки поверхности ?<„ перейдут в точки по-
поверхности разрыва Е<2, отвечающей моменту t2. Цилиндрик наш де-
деформируется, причём в то время как в момент tx он находился
целиком в положительной области, в момент t2 он ляжет в отрица-
отрицательной, отвечающей этому моменту области (рис. 2).
Обращаясь сперва к левой части уравнения B.4), оценим вели-
величины объёмов интегрирования (t)<t и (х)/,. Очевидно, что первый
будет:
^2
') Пусть нормаль эта пересекает 2jo в точке Р. Считая, что нормаль
направлена в сторону положительной области (не представит труда про-
провести все рассуждения для противоположного случая), будем, очевидно,
иметь для малых t2 — tx:

2]
УРАВНЕНИЯ ГИДРОДИНАМИКИ В ФОРМЕ ИНТЕГРАЛОВ
15
где г — бесконечно малый радиус.цилиндрика, а е, — величина беско-
бесконечно малая; второй же:
где е2 бесконечно мала. При этом как в том, так и в другом
случаях мы разумеем под 6 значения скорости распространения
в одной и той же точке Жив один и тот же момент времени tx —
значения, вычисленные при приближении с разных сторон к поверх-
поверхности ?(, ')¦
Теперь мы можем написать:
П f fadx\ = а
\ (-)	)и
a dx\ = а_
— tx) + V2 (t2 — tx)
(s( — всюду в дальнейшем бесконечно малые величины), и следо-
следовательно,
Я/»*) -
= — кг2 (t2 — tx) [аЦ -f- е5;
(а+ и а_—значения а в точке М в момент
к правой части B.4). Поверхность {S)
складывается из трёх частей (рис. 3):
боковой поверхности цилиндра, на
которой, очевидно,
). Перейдём теперь
f f
= O(\)r(t2 —
и двух оснований AS и AS'. Наш
цилиндрик деформируется и пере-
перемещается так, что поверхность раз-
разрыва в момент tx является его одним
основанием, в момент t2 — его дру-
i им основанием, а в моменты t, лежа-
лежащие между tx и t2, занимает проме-
промежуточные положения, располагаясь
где-то между «нижним» и «верхним» основаниями (рис. 3).
Отсюда получается, что AS находится за весь промежуток времени
Рис. 3
') Вообще говоря, [G]
рыва не терпит.
0, ибо [Vn\ Ф 0, величина же N из B.10) раз-

раз16	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
от tx до t2 в одной области, a AS'— в другой. Предположим, что
AS находится в области отрицательной, a AS' — в положительной.
Тогда в выражении Г \сп ds величина с„, как легко показать, отли-
(S)
чается от значения сп, взятого в точке Жив момент tv на величину,
исчезающею вместе с (t2— tx) ncr. Замечая, что вследствие B.5),
B.7) всегда можно написать:
сп = сх cos (п, х) -f- су cos (п, у) + cz cos (я, г),
где »— внешняя по отношению к области (т) нормаль, и сохраняя
для нормали к AS (вернее, для нормали МР) обозначение п, мы
должны, очевидно, написать для AS [нормаль, идущая в сторону
положительной области, направлена здесь внутрь (т)]:
J J
cnds = — cn_u/-2 + e6r2.
DS)
Совершенно аналогично этому
(нормаль, идущая в положительную область, направлена здесь во
внешнюю часть пространства). Теперь мы можем написать, очевидно:
= Cn+~r>(t2~ tx)- с„_*г2(t2-/,) + e8r2(t2-tx) +
Собирая вместе полученные оценки, будем иметь
/\ J J J	I	J \ J *7	I
Переходя к пределу, полагая (t2 — ^) —>0, а затем и	г—>0, получим
основное соотношение
[ав]-\-[сп] = 0.	B.11)
Остаётся только вспомнить значения а и сп из B.5), B.6) и B.7);
полечим:
= [р]п,	B.12)
= 0,	B.13)
BЛ4)

§ 2]	УРАВНЕНИЯ ГИДРОДИНАМИКИ В ФОРМЕ ИНТЕГРАЛОВ	17
Так как по B.13) произведение р9 не терпит разрыва, то мы можем
это произведение вынести всюду за знаки разрыва и написать:
?HV] = \p]n,	B.15)
[рб] = О,	B.16)
-	BЛ7)
До сих пор мы не говорили о виде внутренней энергии нашего
газа. Мы обратимся теперь к классической газовой динамике, газовой
динамике так называемого идеального (в термодинамическом смысле),
или совершенного газа. В этом случае внутренняя энергия U еди-
единицы массы имеет вид
U=cJ,	B.18)
где cv — теплоёмкость газа при постоянном объёме (величина по-
постоянная), а Т—температура.
Мы вернемся в § 24 к случаю реального газа, а пока будем рас-
рассматривать только идеальный газ. Для него условие B.17) должно
быть заменено соотношением
VLi_mi/ 1	B.19)
Соотношения B.15), B.16) и B.19), коими связаны величины 9,
р, V, р, Т по обе стороны поверхности разрыва, носят название
условий динамической совместности. Здесь имеется в виду совме-
совместность двух движений: с элементами V+, p+, ... и с элементами
V_, р_, ... Весьма существенным является наше предположение
о том, что существует всегда одна и только одна поверхность разрыва.
В этом смысле условия динамической совместности необходимы, и
если бы оказалось, что в некоторый момент в жидкости образовалась
поверхность разрыва, такая, что гидродинамические элементы с обеих
сторон от неё различны, но не связаны соотношениями B.15), B.16)
и B.19), то такая поверхность разрыва существовать в дальнейшем
одна не смогла бы; здесь возникает взрыв (см. далее § 37 этой главы).
В тех точках пространства, через которые поверхность разрыва
в данный момент не проходит, мы должны удовлетворить обычным
уравнениям гидродинамики.
Если
6 = 0,
то поверхность разрыва не распространяется по частицам, отделяя
всегда одну массу газа от другой. Такая поверхность разрыва назы-
называется стационарной. Здесь по B.15) [/?] = 0, а по B.19) [У„] = 0;
напротив, [о] и скачок касательных к S составляющих скорости
совершенно произвольны. Примерами такой поверхности могут
2 Теоретическая гидромеханика, ч, II

18	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
служить: волнующаяся поверхность реки (отделяющая воздух о г воды),
поверхность тёплого или холодного фронта (в метеорологии), по-
поверхность газовой струи.
Значительно больший интерес для газовой динамики представляют
случаи, когда
Здесь обязательно будет
[р] Ф 0, [Vn] Ф О
(если при вфО [р]=0, то по B.15) [V] = 0, затем по B.19) [Т] = 0
и, значит, [р] = 0 '), т. е. разрыва вообще нет). Пример — «балли-
«баллистическая волна», бегущая перед носом снаряда. Полезно отметить,
что при б Ф О скачок касательной к S составляющей скорости равен
нулю (в этом убеждаемся, умножая скалярно обе части B.15) на
любой единичный вектор, расположенный перпендикулярно к п).
Поверхности ?, на которых сами гидродинамические элементы
претерпевают разрыв, носят название поверхностей сильного раз-
разрыва. В том случае, если сами гидродинамические элементы непре-
непрерывны, но среди их первых производных по координатам или по
времени найдётся хотя бы одна, меняющаяся скачком при переходе
через поверхность; последняя называется поверхностью разрыва пер-
первого порядка. Вообще говоря, если при переходе через поверх-
поверхность ? функция b непрерывна, но производная по координате или
по времени, начиная с некоторого порядка, терпит разрыв, то S
называется поверхностью слабого разрыва для функции Ь. Употре-
Употребительны также термины просто «разрыв» или «волна». Поверхности
сильного разрыва, представляющие разрыв давления, называются ещё
скачками уплотнения или ударами сжатия.
§ 3. Уравнения газовой динамики в дифференциальной форме.
Для той части жидкости, в которой гидродинамические элементы
и их первые производные остаются непрерывными, мы можем на-
написать уравнения в дифференциальной форме.
Уравнения движения уже были подробно выведены в ч. 1 из на-
начала Даламбера. Чтобы получить эти уравнения из B.1), поделим
сначала обе части B.1) на разность t2 — tx и перейдём затем к пре-
пределу, полагая, что t2-^-t1^=t. Получим, очевидно:
?fff?™=-ffp*<°- (ЗЛ)
Мы не можем внести слева дифференцирование под знак инте-
интеграла, ибо объём (х) сам зависит от времени, но мы можем написать,
') Последнее заключаем из уравнения состояния:

§ 3] УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ 19
вводя лагранжевы координаты:
f f f ?Vdt = f f fpVdxdydz= С f fpVDdadbdc,
CO	W	(-о)
где (^о)—положение объёма (-:) в некоторый закреплённый момент
;0, а, Ь, с — лагранжевы координаты, D — функциональный опреде-
определитель
п_ Р{х, у, г)
~~ D (а, Ъ, с) •
С другой стороны, из уравнения неразрывности следует, что
PD = Ро.
где
Ро = р(а> Ъ, с, /о) = Ро(й, Ь, с).
Таким образом
Г J CpVdx = J J Г V(a, Ь, с, t)po(a, b, c)dadbdc.
(-¦)
Отметив, что (т0) и р0 от времени, по самому их определению, не
зависят, мы можем написать:
dt
Возвращаясь к старым переменным и к C.1), получим окончательно
М
Далее, преобразуем правый интеграл по формуле Грина к объём-
объёмному интегралу и перенесём всё под знак объёмного интеграла.
Получим, вследствие произвольности объёма (х) и предполагаемой
непрерывности подынтегральной функции:
dV
что совпадает с уравнением D.3) гл. II части первой, если там от-
отбросить объемные силы F.
Уравнение неразрывности подробно было выведено в первой части.
Это будет для сжимаемой жидкости
¦||-Н-р div V = 0.	C.3)

20	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Наконец, уравнение энергии, если разделить обе его части на f2~~^i
и перейти к пределу, полагая, что t2—>-t1~t, даст после собирания
членов:
(S)
Применяя к левой части этого уравнения преобразования, анало-
аналогичные тем, что были применены при выводе уравнения, получим:
)
(")	E)
Преобразуя левую часть к объёмному интегралу по формуле Грина,
перенося всё в одну сторону и собирая под один знак интеграла,
напишем:
и вследствие произвольности объёма (т) и непрерывности подынте-
подынтегрального выражения
Умножим теперь обе части равенства C.2) скалярно на V и
вычтем из C.4). Так как
V — d V' V
dt ~~ dt 2
и так как
V ¦ grad p — div (pV) — p div V,
мы получим:
Деля обе части этого равенства на р, заменяя div V по формуле C.3)
и вспоминая, что по уравнению состояния
р — R?T,	C.5)
мы получим:
1 cv dT I do
AR T dt p dt ~u>
Это можно записать ещё, используя снова C.5), в виде
1 f d\np d\n$\ d\no
~AR Cv \di	W) 5Г""~ '

§ 4]	СЛАБЫЕ РАЗРЫВЫ ХАРАКТЕРИСТИКИ	21
Собирая члены с производными, замечая, что
и производя простые преобразования, получим окончательно:
at p*
где v. есть отношение теплоёмкостей. Так будет выглядеть «уравнение
притока тепла» — условие адиабатичности в дифференциальной форме.
Отметим, что % всегда будет больше единицы. Для одноатомного
Газа "'¦=5/з. для двухатомного газа "/-= 7/s (ПРИ обычных температу-
температурах). Для воздуха мы будем принимать чаще всего •/. = 7/5= 1.41).
При выводе уравнений этого параграфа мы предполагали гидро-
гидродинамические элементы и их производные непрерывными. Пусть теперь
есть поверхность Е, являющаяся поверхностью слабого разрыва, так
что сами функции непрерывны всюду, но уже первые их производные
по координатам и времени претерпевают при переходе через ? разрыв.
Такого рода слабые разрывы возможны, как мы в дальнейшем увидим,
дтя нестационарного движения и для широкого класса стационарных
движений. Остановимся на этом вопросе детальнее.
§ 4. Слабые разрывы. Характеристики уравнений газовой ди-
динамики. Наличие поверхности сильного разрыва не накладывало,
само по себе, никаких ограничений на скачки гидродинамических
элементов, и только необходимость удовлетворить уравнениям B.1),
B.2) и B.3) привела к установлению соотношений B.15), B.16)
и B.19). Напротив, в случае слабых разрывов уже самый факт
существования разрыва производных, имеющего место вдоль много-
многообразия деформирующегося и перемещающегося, но всегда остающе-
остающегося единственной поверхностью, заставляет связать скачки названных
производных некоторыми условиями. Последние являются следствиями
1еометрической или, вернее, кинематической картины движения и выво-
выводятся совершенно независимо от уравнений гидродинамики. Условия
эти носят название «условий тождественности» и «кинематической
совместности». Чтобы их получить, предположим, что функция
Ф(х, у, z, f) непрерывна во всём пространстве, занимаемом жидкостью,
но что её первые производные претерпевают разрыв на некоторой
поверхности S, имеющей уравнение2)
/(х, у, г, t) = 0.	D.1)
') Употребительны ещё числа %=1,41, а также значение х = 4/з' По-
Последнее получается, по Лайтхиллу, в пределе, если, рассматривая реальный,
по так называемый идеально-диссоциирующийся газ (в котором у, зависит
от Т и от числа диссоциированных молекул), устремлять число диссоцииро-
диссоциированных молекул к нулю (см. § 24 этой главы).
2) Под функцией Ф (х, у, г, t) мы можем подразумевать какой-нибудь
1 идродинамический элемент непосредственно или же какую-либо его произ-
производную по координатам или по времени.

22	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Мы можем говорить о четырёхмерном пространстве (дг, у, z, t) и в нём
изображать уже неподвижную гиперповерхность D.1). Пусть теперь
имеется непрерывная вместе с производными функция ф от четырёх
наших независимых переменных и такая, что на гиперповерхности D.1)
ty(x, у, z, *) = const.
Torja вдоль гиперповерхности
? + $*зЧ-$Л + 1</Л	D.2)
причём дифференциалы берутся вдоль этой поверхности; но здесь,
вследствие уравнения D.1),
^ + f<fy + ?<te + ?* = O.	D.3)
это есть единственное условие, которое следует наложить на диффе-
дифференциалы наших координат вдоль поверхности. Сопоставляя D.2)
и D.3), заключаем, что во всех точках поверхности разрыва и для
любого момента времени должно быть:
дх ' дх ~~ ду " ду ~ dz " dz ~~ dt ' dt ~[j?'	( '
где р,ф — некоторая функция от координат и времени, определенная
на D.1).
Рассмотрим теперь функцию Ф (х, у, z, t), непрерывную во всём
нашем гиперпространстве и имеющую непрерывные же первые
производные по координатам и времени. Пусть эта функция тожде-
тождественно равна функции Ф, но только в положительной области;
тогда на поверхности S
•=•¦; ?-(?).¦••¦
Рассмотрим ещё функцию Ф, непрерывную вместе со своими
первыми производными во всём гиперпространстве и такую, что в отри-
отрицательной области Ф==Ф; тогда на S:
дх \дх
Функция Ф — Ф непрерывна со своими производными во всём гипер-
гиперпространстве и, так как [Ф] = 0, — обращается в нуль на S. Но тогда
мы можем принять функцию Ф — Ф за функцию ф предыдущей теоремы,
и, если заметить, что на S, по определению Ф и Ф, будет:

§ 4]	СЛАБЫЕ РАЗРЫВЫ ХАРАКТЕРИСТИКИ	23
мы можем написать:
дФ] Г_дФ1.["дФ] Г дф 1 __ <?/ . df df . df
что можно записать ещё так:
[VO] = ^V/; [?] = P.f •	D.5)
Условия D.5) и суть условия совместности, о которых мы говорили-
Они показывают, что достаточно задать одну лишь функцию ц.ф, чтобы
определить затем разрывы всех производных Ф. Достаточно знать
также разрывы одной какой-нибудь производной. Так, например, если
разрыв одной из производных первого порядка равен нулю, то и все
производные первого порядка будут на D.1) непрерывны.
Формулы D.5) могут быть ещё представлены путем деления и
лмножения на ^Щ+ (jL^ Щ в виде
D.6)
не п — единичный вектор нормали, а /V, по B.9), — скорость пере-
перемещения поверхности слабого разрыва.
Кроме кинематических условий D.5), нам следует подчинить раз-
разрывы производных от различных гидродинамических элементов усло-
условиям динамическим, проистекающим оттого, что элементы эти должны,
в положительной и отрицательной областях отдельно, удовлетворять
уравнениям гидродинамики. Считая, что vx, vy, vz, p, p непрерывны,
можем написать:
D.7)
Уравнения наши не содержат производных более высокого порядка,
чем первый. Приписывая один раз всем производным знак плюс,
а другой раз знак минус и вычитая получаемые уравнения друг из друга
соответственно, придём к соотношениям:
Щ -%p Ш+?v ¦[Vp] -ypV ¦[Vp]=

24	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
Используя D.6), получим тогда:
pyV - - ;.p\N — рУяХ„ + vpVnkf == 0
(/v есть вектор с компонентами Xj, , \v , Xt, V Собирая члены с ),
будем иметь:
|
Xp(/V — Уя) = рХу • «,	D.8)
PXp (W- у-„) - xp (ЛГ - Vn) Xp = 0.	)
Пять величин Х удовлетворяют пяти однородным уравнениям. Для того
чтобы существовали X, отличные от нуля, необходимо, чтобы был
равен нулю определитель системы; проще всего получить это усло-
условие, умножая скалярно первое уравнение из D.8) на п и вставляя
вместо р(Ху • п) выражение из левой части второго из уравнений D.8).
Получим тогда:
что в соответствии с последним из D.8) даст либо
N-Vn = 0.
либо
(N — Vny = *? = a'.	D.9)
Первое из этих равенств отвечает случаю стационарного разрыва @ = 0).
Второе равенство показывает, что скорость распространения нестацио-
нестационарной (О Ф 0) поверхности разрыва первых производных всегда равна
Величина эта носит название скорости звука.
Мы говорили о скорости распространения поверхности слабого
разрыва для производных первого порядка. Можно показать, что
скорость S распространения любого слабого разрыва (т. е. разрыва
производных любого порядка) будет либо 6 = 0, либо | 0[ = а. На-
Напротив, как мы вскоре увидим, скорость 0 для сильного разрыва
со скоростью звука никак не связана.
Покажем теперь, как слабый разрыв связан с характеристиками
системы уравнений газовой динамики. Последняя есть система пяти
уравнений в частных производных первого порядка по четырём неза-
независимым переменным, содержащих пять неизвестных функций. Известно,
что к рассмотрению характеристик приводит задача Коши, каковая

СЛАБЫЕ РАЗРЫВЫ ХАРАКТЕРИСТИКИ
25
в нашем случае формулируется следующим образом. На некоторой
шперповерхности S с уравнением
f(x, у, z, 0 = 0	D.10)
заданы значения всех функций: vx, vy, vz, p, p. Требуется найти
в области, окружающей S, непрерывные и однозначные функции
vr, ..., р, удовлетворяющие уравнениям D.7) и обращающиеся на 5
и систему заданных значений. Напомним, что доказательство теорем
существования однозначного решения задачи Коши находится в связи
с возможностью определения на многообразии S значений всех произ-
производных от всех искомых функций. Чтобы лучше уяснить себе процесс
определения этих производных применительно к нашей системе D.7),
сделаем замену независимых переменных, переходя от х, у, г, t
к х, у, z, t, так что
х — х;
= f(x, у, z, t); t = t.
В этих новых переменных уравнение гиперповерхности S примет
простой вид:
и если обозначить
vx(x, у, z, t) = vx(x, у, z, t); ...,
io, по условию задачи, нам будут даны функции:
{vx(x, у, z, t)}f=o = vx(x, у, 0, 7); ...	D.11)
С другой стороны, для любой функции а будем иметь
D.12)
D-13)
di
da
dz
так что
да
dx
da
dz
1
i
df
dz
da
dJ
df .
dx'
da
dy
da
dt
da
dy
da
dt
+
+
da
dz~
da
dz
df
dy '
df
dt '
dx /r „
-=0 \ dx
Но если
(a)/=o = a(jr, y, 0, t)
известно, то, так как (da(x, у, z, ~i)jdx)-=Q будет просто равно
fa (x, у, 0, Т)/дх, производная (да/дх)-^0 может считаться также из-
известной; то же можно сказать и про (da/dy)-=0 и (da./dt)-=G. Таким
образом, если бы нам удалось ещё найти {dajdz)-^Q, то мы, зная (а)/_0,

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
сумели бы по D.13) рассчитать (da/dx)f=0, ... У нас имеется пять
функций: vx, vy, vz, p, p, так что нам надо найти пягь производных
д!
dl
)-=0' \dl)-
Чтобы найти их, обращаемся к пяти уравнениям D.7) и записываем
их в новых переменных, пользуясь D.12). Имеем (мы выписываем
лишь те члены, которые содержат дифференцирование по z):
dz
dvy
d~z
dz
- df_
Vr~dx
~d~x~
dy
- V_
V> dy
v ?L
y dy
dz	dt ]	?	dx dz
Vz dz	dt i	p	dy dz
- df	| df\	, 1	df dp
V*~dz	~dt)	7	^T^F~"
()г (9-v dz	dy dz
i 1	<?P '— df
p	dz \ A dx
" d/ . -	df . -i
dz
dt
(->t)\d7
D.14)
Пять наших производных можно найти из этой системы алгебраиче-
алгебраических уравнений лишь в том случае, если её определитель отличен
от нуля. Определитель этот, если обозначить
df _ „
будет:
А
0
0
df
dx
0
0
А
0
df
dy
0
0
0
А
dz
0
1
Р
1
Р
1
Р
"дИ
df
dy
~dz
0
А
df
dx
—
+
0
0
0
1
p
7
Г df , -
у ду ~r Vz
A
- A
11 {
dl^
dz
D.15)

§ 4]	СЛАБЫЕ РАЗРЫВЫ ХАРАКТЕРИСТИКИ	27
Если гиперповерхность D.10) и заданные на ней функции vx, vy, ...
таковы, что D.15) обращается в нуль, система D.14) может допускать
лишь неопределённые решения. Чтобы эти решения оставались ко-
конечными, необходимо при этом потребовать обращения в нуль всех
определителей, составленных путём последовательного введения пра-
правых частей D.14) в столбцы определителя системы. В таком случае
многообразие D.10) называется характеристическим многообра-
многообразием (характеристической гиперповерхностью) или просто харак-
характеристикой. Заметим, что при вычислении старших производных
нам придётся иметь дело вновь только с определителем D.15). Таким
образом, если <3 в задаче Коши есть характеристическая поверхность,
то, если и существует решение задачи Коши, оно может не быть
единственным. Это значит, что могут найтись два различных реше-
решения, принимающих на S одни и те же значения, у которых, однако, уже
первые производные на <5 различны; таким образом может оказаться,
что с разных сторон от © движение представляется разными зако-
законами, а на самой © гидродинамические элементы обоих движений
(но не их производные) совпадают. Но в таком случае мы назвали
бы <3 перемещающейся поверхностью слабого разрыва. В самом деле,
не представляет никакого труда убедиться, что условие равенства
нулю D.15) будет совпадать с одним из условий D.9). Для этого
стоит лишь ввести «скорость распространения» S характеристики:
1	I' df . - df . - df . - df\
и заметить, что
Тогда равенство определителя D.15) нулю будет означать, что
03/б2 — ^t-\=0,	D.16)
и мы вернёмся к D.9).
Мы видим, таким образом, что перемещающиеся поверхности
слабого разрыва и характеристические многообразия системы D.7) —
это одно и то же.
Всегда ли можно говорить о характеристических многообразиях?
Всегда ли они будут действительными? Отбрасывая случай, когда
9 = 0, мы должны иметь на характеристике
или
df . Of , df , df , , ГI df
2
а
D.17)

28	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
(мы отбрасываем черту над гидродинамическими элементами), где а,
как прежде, — скорость звука. В нестационарных случаях уравне-
уравнение D.17) позволит, очевидно, при любых i>v., vy, vz, а найти дей-
действительную функцию f(x, у, z, I), и существование последней
никаких ограничений на гидродинамические элементы, вообще говоря,
не накладывает.
Предположим, однако, что мы имеем дело с установившимся
движением. Естественно считать здесь, что и поверхность разрыва
будет неподвижна в пространстве, т. е. что её скорость перемещения
(но не скорость распространения) равна нулю:
/V = 0 или 8 = — Vn.	D.18)
Тогда на поверхности разрыва имеем
-—±а	D.19)
у I Jz
у ~ ~ду ' **~~1
или ещё
\Vn\ = a.	D.20)
Пусть теперь установившееся движение жидкости таково, что
скорость везде меньше местной скорости звука:
В таком случае, какую бы поверхность S мы ни провели через
некую точку М, всегда проекция Vп скорости жидкости V в Ж на
нормаль п к поверхности ® будет меньше, чем а, и равенство D.20)
нигде не будет иметь места. Напротив, если жидкость движется так,
что
\V\>a,
то найдутся поверхности 3, проходящие через М, такие, что проек-
проекция Vп скорости V в М на нормаль к этим поверхностям будет
в точности равна а. Отсюда вытекает весьма важное следствие.
Если жидкость движется стационарно (установившееся движение) и
притом повсюду с дозвуковой скоростью, то действительные харак-
характеристические многообразия существовать не могут. Напротив, если
движение жидкости совершается со сверхзвуковыми скоростями, то
всегда могут быть построены действительные характеристики. Мы
видим, что переход через скорость звука играет в установившемся
движении весьма существенную роль, меняя тип дифференциальных
уравнений движения (эллиптический при дозвуковых скоростях на
гиперболический при сверхзвуковых).

$ 5] РАСПРОСТРАНЕНИЕ СИЛЬНЫХ РАЗРЫВОВ. ТЕОРЕМА ЦЕМПЛЕНЛ	29
Наличие действительных характеристик при сверхзвуковых ско-
скоростях значительно облегчает решение задачи о движении. Здесь
могуг быть развиты эффективные графические методы решения,
с каковыми мы и познакомимся в соответствующем месте.
Мы вернёмся сейчас к случаю существования сильных разрывов,
чтобы доказать несколько общих теорем, сюда относящихся.
§ 5. Распространение сильных разрывов. Теорема Цемплена.
Чтобы найти величину скорости распространения сильного разрыва,
прибегнем сначала к соотношениям B.15), B.16) Умножая B.15)
скалярно на я, получим:
р9 [Vn] = [p],	E.1)
и замечая, что вследствие формулы B — N—Vn
[Vn\ = — [91,	E.2)
E.3)
E.4)
напишем вместо E.
Но по B.16)
поэтому мы можем
р 92 р 92 -
откуда по E.4):
и мы можем найти
1)
Р9(бт — е_) =
р 0 —
написать E.3)
- р_ — р или
о2 д2 / Р_ — Р +
Р~ " \ Р-Р +
в виде
Р+е +
р
J — P-
6_ из соотношения
62 _ Р+ Р+-
Р_ Pj.-
¦р_ Р-
рУ
pie2.
р_
р^
[р]
[р] *
E.5)
Особенно явной станет разница между величиной скорости рас-
распространения слабого разрыва, всегда равной а, и выражением,
получающимся из E.5), если мы преобразуем E.5), использовав для
этого одно важное следствие соотношения B.19). Заметив, что
T~p/Rp и что ср — cv=AR, придадим сначала B.19) вид
Умножим теперь обе части B.15) скалярно на V+-f-V_:
р9 (V., 4- V_) • (V+ - V_) = Р9 [ V ¦ V] = [р] п ¦ (V+ + V.)
и вставим p8[V-V] в E.6); получим:

30	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. !
Раскроем знаки разрывов и перенесём все члены в одну сторону;
получим:
или после сокращений:
-(P+ + P-)lVg+^[f] = 0.	E.8)
Но по E.2) и B.16) можно написать
и мы можем переписать E.8):
Раскрывая, далее, знаки разрыва и отыскивая отношение р /р_,
мы придем к следующей важной формуле, заменяющей условие B.19):
р, (* + l)Pi—(*—1) Р
f-±- = - ^ +_(х_1)р •	E.10)
Пользуясь E.10), преобразуем теперь выражение E.5). Вычтем для
этого из обеих частей E.10) по единице:
Р	\р] (*- Ч- 1) Гр1 Ч- (*- "•— 1) Гр 1	2т, Гр]
Следовательно,
[p]	2t.p_		....
и по E.5)
62_=x—	—P+		.	E.12)
Наряду с формулой E.5) отметим выражение
получающееся умножением E.5) на р2_ и сравнением с р!92+. а также
8+ = *— 7—Пх—^=
+ Р+ (* + 1)р+ —
получающееся из B.16), E.12) и E.10).
+ = *— 7—Пх—^=7	г;—¦	E-14)
+ Р+ (* + 1)р+ — (* — 1)р_

§ 5] РАСПРОСТРАНЕНИЕ СИЛЬНЫХ РАЗРЫВОВ. ТЕОРЕМА ЦЕМПЛЕНА	31
Формулы E.12) и E.14) показывают, что скорость распростране-
распространения сильного разрыва всегда отлична от местной скорости звука.
В самом деле, по этим формулам равенство
или равенство
Р_
одинаково влекут за собой условие р+=р_; но тогда по E.10)
р+ = Р-, а по B.15) [VJ = 0, и нет никакого сильного разрыва.
Нетрудно далее убедиться, что если |6+|<а+, то | 9_ | > а_ и
наоборот: если | 9_ | < а_, то ) 6+ | > а+.
Если обратиться к стационарным движениям, для которых ЛГ = О,
т. е. 6 = — Vп, то мы получим очень важное следствие: скорость
V,, по крайней мере с одной стороны от поверхности разрыва пре-
превосходит местную скорость звука. Значит, неподвижные поверхности
сильного разрыва, так же как и неподвижные характеристики, могут
существовать лишь при наличии сверхзвуковых скоростей.
Докажем ещё теорему Цемплена: возможны лишь такие
сильные разрывы, при которых
[Vn}<0.
Для доказательства этого положения приходится привлекать второй
закон термодинамики, согласно которому энтропия при физических
процессах не убывает. Энтропия S может быть представлена в виде
5 = -Т1п?'	EЛ5)
и, таким образом, вопрос о возрастании энтропии эквивалентен
вопросу о возрастании величины pjf. Итак, величина р/р' не убывает.
Пусть имеется у нас нестационарный сильный разрыв. Некая масса,
находящаяся с одной стороны от разрыва, попадает затем на другую
сторону. Могут представиться два случая: 0+<О и 6^ > 0. Если
0+ > 0, то массы, лежавшие с положительной стороны поверхности
разрыва, попадут на отрицательную, и энтропия положительной
области заменится на энтропию области отрицательной; так как
энтропия не убывает, будет
т. е,
СО.

32	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
Напротив, если 8+ < 0, то массы отрицательной области будут
заменены массами положительной стороны, так что окажется
[?]>»¦
Покажем, что в обоих случаях будет [Vn] < 0. В самом деле, вслед-
вследствие E.10j можно написать:
Р- \р_
_ р_
~"рЛ
t-
Нетрудно убедиться, что выражение, стоящее здесь в фигурных
скобках, будет положительно при р /р_ > 1 и отрицательно при
р /р_<1. Так как р и р положительны, заключаем, что если
[Р1р*\ > 0> т0 1р] > 0; если [pjf] < 0, то 1р] < 0. Таким образом,
если 6+ > 0, то [р] <0, и если 8+ < 0, то [р] > 0, но
р_ р+ '^ + р+р_
и, значит, при 8+ > 0, [р] < О будет [Vn] < О и при 8+ < О, [р] > О
также [Vn]<0. Теорема Цемплена доказана.
Б. УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ. ПЛОСКАЯ ЗАДАЧА
§ 6. Плоская задача. Функции в1 и /0. Рассмотрим стационар-
стационарное движение газа, происходящее одинаково во всех плоскостях,
параллельных плоскости (х, у), и притом так, 4TOfz = 0. Уравнения
Эйлера представим в форме Лэмба:
р дх ~~ Ш 2 ~гМ&е ду)'
1 др	д I-2
Alz^rJ	F-2)
Уравнение неразрывности даёт
f^i^-O	F.3)
дх ^ ду ~и>	к '

§6]	ПЛОСКАЯ ЗАДАЧ4 ФУНКЦИИ & II h	33
а условие адиаоатичности:
Vx^?.-\-Vy^.A==Q,	F.4)
Уравнение F.3) позволяет заключить о существовании функции
тока <\>(х, у) такой, что
_ (Эф г _ _ _#_	6 .
С другой стороны, вдоль линии тока имеем:
dx 	 dy
вставляя в это равенство vx и vy из F.5), получим без труда
й , , д'Ь , „
дх ' ду '
так что уравнения
ф (л:, у) = const.
суть уравнения линий тока (последние, вследствие стационарности,
совпадают с траекториями жидких частиц и остаются во время всего
движения неизменными).
Умножая первое из F.5) на vy, второе на vx и вычитая, получим:
V I	ТА	/ f\ C\\
х дх ' У ду ' '	'
Но если v ф 0, соотношения F.4) и F.6) заставляют нас считать,
чго
D {х, у)
Отсюда заключаем, что
^г = Эх(ф),	F.7)
где
зависит от ф.
Легко выразить ft через энтропию 5. В самом деле, по E.15)
предыдущего раздела имеем:
^ln»1).	F.8)
') Кроме того, 0 есть, с точностью до постоянного множителя, потен-
потенциальная температура. Под последней разумеется та температура -, которая
получится, если газ адиабатически привести к нормальному давлению Ро.
Это будет
t = -~- » = const. Ь.
3 Теоретичеикая i идроме1- аника, ч II

34	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. J
Умножим теперь F.1) на vx, a F.2) на vy и сложим получен-
полученные уравнения, заменив предварительно р по формуле F.7). Так как
и так как вследствие F.7) и F.6)
х дх ~" У ду	'
мы получим после простых преобразований:
д I % ——о , v2
Это означает, что вследствие F.6)
v2	•/	—
_—|	-ySjf * =^о(Ф)'	(С.9)
где /0—функция одного только ф.
Чтобы уяснить физический смысл /0, заметим, что <у2/2 есть кине-
кинетическая энергия единицы массы, а
х	х-1	*.	о	С„	С„
	 „
у и у		 -	т~		 _	г	А
X	 1	У,	 1 р	Сп ' -~ Су	J\
есть «теплосодержание» (принято обозначение срТ/А = i)'); таким
образом, /0 есть теплосодержание при отсутствии скорости (t> = 0).
Величина /0 определяется, коль скоро известна температура То той
точки, в которой скорость равна нулю
I/0 = -4-
Уравнение F.9) представляет собою не что иное, как уравнение
Бернулли.
Из уравнений F.1) и F.2) мы получили одно лишь соотноше-
соотношение F.9). Второе соотношение позволит нам выразить вихрь и пока-
показать, что если Ь и /0 будут постоянными величинами (не завися-
зависящими от ф), то движение будет безвихревым, и обратно — если дви-
движение безвихревое, то, вообще говоря, & и /0 постоянны. В самом
') Величина i ыожег быть определена как сумма внутренней энергии
и отношения р/р:
. _ 1 _j_ P cvT p cv + ART _ cpT
t = ~A ' ~У ~ А ~^~р~= А ~~А~'
Кроме термина теплосодержание для обозначения i употребляются ещё
названия: leii.iouasi функция единицы массы и энтальпия.

7]	ПОВЕРХНОСТИ РАЗРЫВА В ПЛОСКОЙ ЗАДАЧЕ	35
деле, возьмём, например, F.2) и вставим в него v2 из уравнения
Бернулли. Произведя сокращение, получим:
dvу dvx	1 / di0	х -izi д§ \
дх ду	vx \ ~ду~ х— 1 Р ду J
или, так как & и 10 зависят от у через посредство ф:
ду '
наконец, вследствие F.5) можем написать:
—— db\	,„ ...
)	FЛ1)
Формула F.11) показывает, что если & и iQ постоянны, то 2^=0.
Обратно, пусть 2 = 0. Тогда по F.11)
dt0	% ^ db
и если dbjd'^ ф 0, то р, а значит, по F.9) и v, будут функциями
одного ф:
——	 ?¦ — 1 di0
d\i
Случай этот не представляет интереса; ему отвечают движения с ли-
линиями тока — либо концентрическими кругами, либо параллельными
прямыми (см. ниже § 15). Таким образом, вообще говоря, если 2 = 0,
то должно быть
а по F.12) и
Заметим, что может оказаться, что dio/d<b Ф 0 a dbfd^ = 0 или же
dio/d'b = O, а й?&/й?ф =? 0; при этом, разумеется, 2=^0. Мы увидим,
что случай постоянного /0 и переменной энтропии & представляет
для газовой динамики наибольший интерес.
§ 7. Поверхности разрыва в плоской задаче. Покажем прежде
всего, что в плоской стационарной задаче /0 не претерпевает скачка
при переходе через поверхность сильного разрыва. Для этого обра-
обратимся к уравнению E.6) и перепишем его, заметив, что, вследствие
стационарности, Vп = — 6, так:

36	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОП ДИНАМИКИ	[ГЛ. I
или, что очевидно,
откуда, перенося всё влево и собирая члены под знаками разрыва
а это и означает, что если 6 Ф 0, то вследствие F.9) и F.7)
[/01 = 0.	G.1)
В приложениях газовой динамики речь идёт обычно о незавихрен-
ных потоках газа, обтекающих какое-либо препятствие (крыло,
например) или вытекающих из отверстия (сопло и т. п.). Так как
в незавихренном потоке 1й — const, и так как по G.1) даже наличие
сильного разрыва не изменяет величины /0, то, оставляя в стороне
влияние пограничного слоя, мы можем считать в практически важных
и интересных случаях просто
/0 = const.
Обратимся ко второй величине, характеризующей завихренность
потока,— 9. Покажем, что если в набегающем потоке и было Ь = const.,
то после прохождения потока сквозь поверхность сильного разрыва
обязательно, вообще говоря, станет db\d§ Ф 0, т. е. если поток до
прохождения скачка уплотнения и был потенциальным, то после он
становится вихревым. Для доказательства обратимся к формуле E.10)
и умножим обе её части на (р_/р+)х. Можем написать тогда:
у. + 1 — (х —
рл р! ' - ч-	v
f-t Р- \Р+/ (х+1)-^-(/-1)
или, по определению 9 из F.7):
-л + 1 — С'- — 1) —
Формула G.2) показывает, что &^/9_ = 1, т. е. [9] —0, лишь в том
случае, когда р_ /р == 1, т. е. [р] — 0, т. е. когда скачка уплотнения
просто нет. Как мы увидим дальше, [р] будет, вообще говоря, раз-
различен в разных точках поверхности разрыва, но тогда и [Щ будет
меняться от одной линии тока к другой, так что если & «слева» от
поверхности разрыва и было постоянно, то, претерпев в разных

§7]	ПОВЕРХНОСТИ РАЗРЫВА В ПЛОСКОЙ ЗАДАЧЕ	37
точках этой поверхности разные скачки, оно станет функцией от ф.
Движение, бывшее перед скачком уплотнения безвихревым, станет
затем, вообще говоря, вихревым.
Восемь гидродинамических элементов: р + , р+, vx+, vy + , p_, p_,
t'r_, ¦wy_ — связаны вдоль поверхности разрыва четырьмя соотноше-
соотношениями [формулы B.12), B.13) и E.10)]:
pf)[vx] — [p]cos(n, х),	G.3)
pQ[vy] = [p]cos(n, у),	G.4)
[p6j = 0,	G.5)
Р+ _<»+1)Р+-(*-1)р_	fi
содержащими, кроме упомянутых элементов, ещё девятую вели-
величину— угол между нормалью п к поверхности разрыва и осью Ох
или Оу. О, вследствие стационарности движения, выражается через Vп:
6 = -У„.	G.7)
Таким образом, мы можем, зная все гидродинамические элементы
с одной стороны от поверхности разрыва, найти связи между любой
парой элементов по другую сторону от поверхности или между
каким-либо из этих элементов и углом наклона поверхности. Наи-
Наибольший интерес представляет установление соотношения между
обеими компонентами скоростей, а также выражение плотности через
угол наклона поверхности разрыва.
Рассмотрим произвольную точку М поверхности разрыва. Пусть
нам известны величины р_, р_, vx_, v _. Повернём ось Ох так,
чтобы она пошла параллельно направлению скорости V_ в точке М,
и обозначим
Пусть ещё угол наклона (я, х) нормали п в точке М поверхности
разрыва будет ср. Тогда, так как v —0, имеем прежде всего
—	S+ = Vn+ = vxcoscp-\-vv sin cp,	G.8)
—	6_=:Vn_='&1cosep,	G.9)
а используя E.12), получим:
1 T Pi (* + l)Pi— (*— 1)P
откуда без всякого труда найдём p/pj через tgcp:
-L =	^	,	G.10)
Pi	of
14	^

38	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
где, как всегда, буквой а обозначена скорость звука
Формула G 10) показывает, что если <р меняется от точки к точке
вдоль поверхности разрыва, то p/pj будет разным в разных точках
поверхности, и по G.2), если даже и было 8^ = const., то Ь станет
в разных точках разное, и возникнут вихри. Так, например, если V_
сохраняет всюду постоянное направление, то при кривой линии раз-
разрыва вихри образуются неизбежно; лишь если поверхность разрыва
есть плоскость, движение останется безвихревым.
Чтобы найти зависимость между vx и vy, разделим сперва G.4)
на G.3); получим:
VlG.11)
tgp
vx — vl
С другой стороны, по G.3), после сокращения на cos (и, x) = coscp,
х — «i) = /> — Pv	G-12)
а вследствие G.6)
	^	 .	G.13)
f
+()f
Pi
Сравнивая два выражения для р—рг (G 12) и G.13)), вставляя
вместо p/pj правую часть G.10) и заменяя tgcp через посред-
посредство G.11), приходим после простых преобразований к следующей
формуле, связывающей vx и vy:
2 (	а\
'- + 1 «1
Остановимся на формулах G.10) и G.14).
Формула G.10) выряжает р/р, через ср. Представляют интерес
также формулы, выражающие через ср отношение р/рх, а также
величины vx и vy. Внося G.10) в G.6), получим после элементар-
элементарных преобразований
G.15)
/?( у -\-1 aj	' у. -\-1
Вставляя это отношение в формулу G.12), получим:
G.16)

§71
ПОВЕРХНОСТИ РАЗРЫВА В ПЛОСКОЙ ЗАДАЧЕ
Наконец, внося vx из G.16) в G.11) и решая полученное уравне-
уравнение относительно vy, получим:
2
V..
-1
G.17)
Формула G.14) имеет многочисленные приложения.
В плоскости (их, vy) при данных значениях ах ч vl уравне-
уравнение G.14) представляет кривую, симметричную относительно оси vx,
пересекающую её в точках
(двойная точка) и
у^ 	 1
и имеющую в качестве асимптоты пря-
прямую (рис. 4)
2 а\
Рис. 4.
Эта кривая может быть получена путём инверсии гиперболы в её
вершине и называется гипоциссоидоп (обычная циссоида Диоклеса
может быть получена путём инверсии параболы в её вершине). Если
скорость в точке Ж_ отрицательной области имеет величину vl
(при этом скорость звука ах получится, если i0 известно, из урав-
уравнения Бернуллн), то конец вектора V+ скорости в точке М+ будет
лежать где-то на упомянутой гипоциссоиде. Если бы нам было
известно направление V+, мы могли бы, воспользовавшись гипоцис-
соидой, найги и величину вектора Vj_; совершенно аналогично, зная
величину V+, мы нашли бы без труда и направление (вернее, абсо-
абсолютную величину угла, составляемого вектором V+ с направлением vx).
Наконец, при помощи нашей гипоциссоиды можно найти напра-
направление поверхности разрыва в точке М, если известно направление
скорости после прохождения поверхности разрыва. В самом деле,
так как вследствие G.3) и G.4)
(t — касательная к линии разрыва в тоскости х, у), то, если обозна-
обозначить через Vz проекцию скорости на касательную к линии раз-
разрыва,— будет [VT] = 0. Отсюда следует, что направление поверх-
поверхности разрыва должно быть таково, что если на него спроектировать
скорость тп м после разрыва, то эти цве проекции будут одинаковы

40	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
(Vz+ = Vx_). Имея гипоциссоиду (рис. 5) и зная направ!ение ON,
а значит, и величину ON скорости V+ после прохождения разрыва,
соединим двойную точку Р гипоциссоиды (ОР = V_) с точкой N
и опустим на продолжение прямой PN перпендикуляр из точки О
но пересечения с PN в точке Q. Очевидно теперь, что направле-
направление OQ таково, что проекции на него V+ и V_ одинаковы. Нам
остается ютько перенести это направление на плоскость (х, у),
чтобы полечить нужное направление кривой разрыва.
Заметим, что всякий луч, выходящий из точки О, пересечет
1ипоциссоиду, вообще говоря, в трех точках (рис 5). Однако, в силу
теоремы Цемплена, точки N', расположенные на уходящих в беско-
бесконечность ветвях гипоциссоиды рас-
рассматривать не следует В самом деле,
желая получить при помощи точки N'
направление касательной к поверхности
разрыва, мы должны опустить перпен-
перпендикуляр OQ', но тогда Q'N' есть нор-
нормаль к этой поверхности и
q7p = v^, Q7W' = vn+1
так что, вопреки теореме Цемплена
(§ 5), имеем.
V ^> V
Рис 5	Точки N и N" обе допустимы с точки
зрения теоремы Цемплена
Ветвь гипоциссоиды, содержащая точки типа Л'', также может
быть использована. Для этого достаточно поменять местами знаки
плюс и минус при выводе формулы G.14), положив ОР = V+>
а векторы типа ON' принять за V_. Теперь шпоциссоида будет
совокупностью точек, изображающих концы векторов тех скоростей,
которые после прохождения разрыва могут совпасть с ОР. При
таком толковании гипоциссоиды точки типа N не могут быть допу-
допущены по теореме Цечплена.
Сказанным здесь относительно сильных разрывов мы пока огра-
ограничимся, мы вернёмся к ним уже непосредственно в припоЖениях
к конкретным случаям движений.
§ 8. Критическая скорость. Трубки тока в сжимаемой жидко-
жидкости. Мы знаем из предыдущих параграфов, а также из недавнего
рассмотрения разрывов, как важно отличать стучач, когда движение
происходлт со скоростью меньшей, чем скорость зт ка от случаев
сверхзвуковых скоростей. Введем теперь важное поняше «крпги-

§ g]	КРИТИЧЕСКАЯ СКОРОСТЬ ТРУБКИ ТОКА	41
ческой скорости». Напишем для этого уравнение Бернулли F.9) в виде:
Т+7^Т = /о	(8-1)
(здесь и в дальнейшем мы считаем, на основании сказанного в на-
начале предыдущего пункта, что io = const.) и предположим, что в не-
которой точке М скорость движения v оказалась в точности равной
существующей в этой точке скорости а распространения звука:
v = a.	(8.2)
Соотношения(8.1), (8.2) представляют собой систему алгебраических
уравнений, из которой мы можем определить непосредственно в чис-
числах величину скорости v в точке М. Это будет vr:
ттт'°1	(8-3)
Скорость эта и носит название «критической скорости». Соответ-
Соответственно этому имеем и критическую скорость звука а^.
+Т 'о-	(8-4>
Мы видим, что величина v* не зависит от рода движения и поло-
положения точки. Для всех движений, обладающих одним и тем же i0,
будем иметь всегда одно и то же vi. Нетрудно убедиться, вслед-
вследствие (8.1), что если в какой-то точке оказалось v > at, то будет
также ия>а (скорость газа будет больше местной скорости звука),
и если v < at, то будет также и v < а. Обратно — наличие нера-
неравенств v^a повлечёт за собой, соответственно, наличие неравенств
Привлекая ещё скорость звука а0 в тех точках, где скорость
газа v — 0,	2
-5т = /о>	(8'5)
мы можем дать для ак выражение
при -/. = 1,405. Таким образом, критическая скорость всегда меньше
той скорости звука, которая возникает в покоящемся газе, обладаю-
щем данным значением i0.
Уравнение Бернулли, если выразить в нём /0 через посредство as,
примет вид:
±L.
-л— 1 -~ -/.— 1 2 '
Г87)
') Это можно непосредственно установить из (8.9) (см. ниже).

42	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Формула (8.1) показывает, что максимальное возможное значение v
получится, когда второе слагаемое левой части обращается в нуль,
т. е. это будет
По (8.7) мы можем написать
"?=!" я'да 2,437а,.	(8.8)
Дальнейшее увеличение скорости газа привело бы к отрицательным
давлениям и к явлениям кавитации. Таким образом, величина ги\ал
заключается всегда в сравнительно тесных пределах:
При расчётах удобно пользоваться безразмерными скоростями
vxla*> vyla*- Отношение M=f/a называется числом Маха.
Деля (8.7) на v2, мы можем затем найти связь между vja и vja.t
в виде:
а)
—!—
у. +1 /Пг'
х — 1 \а, /
Видим, что число М может изменяться в пределах от 0 до оо.
Отметим ещё три употребительные формы уравнения Бернулли.
Введём po(ty) — давление, которое возникло бы в некоторой точке
линии тока ф = const., если бы в этой точке скорость обратилась
в нуль. Очевидно, что вследствие F.9) и (8.6)
так что
Заменяя а2 в уравнении (8.7) этим значением, получим
х-1
(?.y = 1 __*_-.	(8.10)
Аналогичным образом, вводя ро(ф) (плотность при г> = 0) и имея
в виду, что

§ 6)	КРИТИЧЕСКАЯ СКОРОСТЬ. ТРУБКИ ТОКА	43
мы получим
' Ро /	*-М „2
Наконец, вводя температуру То при v = 0 и замечая, что
~~~~Х И х—1 =у.— IT"'
можем написать
^.= 1	-——-.	(8.12)
х— 1 *
Величина Го зависит лишь от ах и поэтому не зависит от ф; на-
напротив, /?0 и р0 будут постоянны лишь в случае безвихревого дви-
движения; так как р0 и р0 просто связаны с 9-, то легко найги скачки
этих величин при переходе через поверхность разрыва. Очевидно,
будем иметь
л	1
Ро+ _ / 9- V"-1 и Р°+ ( Э Х
причём 9-_/9+ можно найти по G.2) и G.10) через наклон поверх-
поверхности разрыва.
Формула (8.11) позволяет доказать очень важную теорему, отно-
относящуюся к трубкам тока в стационарном движении сжимаемой жидко-
жидкости. Рассмотрим бесконечно тонкую трубку тока, и пусть скорость
в элементарном сечении её Д/} (ортогональном к линии тока) будет vv
а плотность рх; пусть какое-либо другое сечение Д/2 характеризуется
скоростью v2 и плотностью р2. Так как масса между этими двумя
сечениями исчезнуть не может, мы должны написать
Таким образом, площадь Д/ любого ортогонального сечения нашей
трубки будет
, ,	 const.
^	pi)
В несжимаемой жидкости (р = const.) площадь, таким образом, обратно
пропорциональна скорости (чем больше скорости, тем уже трубки
тока, и наоборот). Для сжимаемой жидкости мы можем, пользуясь
(8.11), написать:
, ,		const.

44	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Постоянная, стоящая справа, сохраняет своё значение вдоль всей
трубки. Но такая функция будет иметь минимум, и притом един-
единственный, при v = at. В самом деле:
d If	const.	( .	Уг	2v2
n(dkf/dv)v=a = 0, а, как легко видеть, {d2 t\fjdv2)v^a > 0. Мы получа-
получаем следующий замечательный результат: при дозвуковых скоростях, так
же как и в несжимаемой жидкости, трубки тока будут тем уже,
чем больше скорости; наоборот, при сверхзвуковых скоростях трубки
тока будут тем шире, чем больше скорости.
§ 9. Плоские вихревые движения со сверхзвуковыми ско-
скоростями. Характеристики. Угол Маха. Продолжим изучение диф-
дифференциальных уравнений движения, предполагая, что /0 = const. Мы
имеем два конечных соотношения: уравнение Бернулли
vl + v)
и условие адиабатичности:
а2
и два соотношения дифференциальных: выражение для вихря
дуу дух _ хр-г db
дх	ду ~~ %—\ 'Р аГф	К Л
и уравнение неразрывности
дх ' ду
Исключим из уравнения неразрывности плотность. Заметим, что
по определению Ь и а:
Можно теперь написать уравнение неразрывности, введя In p, в виде
д'пр , <?lnp | dvx dv^ _
~~дх~ Vjc ^~ ~~ду~ Vy ~^~ ~дх~ "т~ ~~ду~ ~~
а потом, выражая р через Ь и а2 и замечая, что
дЬ . дЬ „

§ 9]	ПЛОСКИЕ ВИХРЕВЫЕ ДВИЖЕНИЯ	45
(см. F.4) и F.7)), привести после простых преобразований к форме:
dvx dvv \	1 / да2	да2
а
Выражая далее а2 по формуле Бернулли через v2 и собирая члены
при различных производных, получим:
dvx	dv,-	dvv	dvv
Отметим, что (9.2) имеет один и тот же вид как для вихревого,
так и для безвихревого движения. В самом деле, заменив в (9.2) а2
по формуле (8.7), приведём (9.2) к виду:
ду ' д.
гак что % совершенно выпадает из уравнения (в (9.2) & могло вхо-
входить через а). Уравнение (9.1), напротив, указывает на наличие
вихря (^&/й?ф=^О).
В большинстве задач газовой динамики функцию & приходится
рассматривать как известную функцию от ф. Если линии тока ухо-
уходят на бесконечность (например, в случае обтекания контура безгра-
безграничным потоком), задание &(ф) входит как своеобразное условие на
бесконечности. Если мы имеем стационарное движение, в котором
вихрь на бесконечности равен нулю, в таком потоке везде будет
& — const., если на пути несущихся в этом движении жидких частиц
не встречается поверхность сильного разрыва. Если же частицы
проходят сквозь поверхность сильного разрыва, то % в них изме-
изменится скачком, причём, как мы видели, скачок этот будет, вообще
говоря, для разных точек разным. Это и заставляет нас в общей
теории брать уравнение (9.1) с правой частью, отличной от нуля.
Введём обозначение
тогда (9.1) напишется в виде
dvv dv,
= S,	(9.4)
жг-^-й-	(9-5>
Нам надо научиться решать совместно дифференциальные уравне-
уравнения (9.3), (9.5). В них входят две неизвестные скорости vx и v и,
кроме того, неизвестная функция ф.
Функция ф входит, однако, только в (9.5), и притом нг под зна-
знаками дифференциалов. Для определения ф необходимо ещё прибавить

46
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
одно из двух соотношений [см. F.5)]'):
vx = у^1 Ъ~* (а2)' -^ : vy = -*=i Ъ~' (*2)" -Ц- • (9-6)
Мы начнём с теории наиболее простого случая. Именно, предпо-
предположим, чго движение таково, что скорость во всех точках плоскости
(х, у) превышает скорость звука, т. е. во всех точках плоскости
v > at. Наличие действительных характеристик позволяет здесь раз-
развить эффективные методы решения системы (9.2), (9.5).
Чтобы построить характеристики, которые в случае плоской ста-
стационарной задачи будут, очевидно, линиями пересечения с плоско-
плоскостью (х, у) цилиндрических поверхностей, предположим, что неко-
некоторая кривая L с уравнением
У = У (*)
есть характеристика для данного движения. Обозначая производную
, d ( д , dy д \	,
по х, взятую вдоль линии L, через -т—= 1-=	\Г"Х~) и прибавляя
к системе (9.2), (9.5) соотношения, выполняющиеся вдоль L:
(9.7)
(9 8)
дх
dy
dx
dy
dy
dvx
dy
dv
dvx
dx
dvy
dx
напишем условие того, что L есть характеристика [т. е. условие
невозможности однозначного определения четырёх производных dvxjdx,
dvjdy, dvyjdx, dvy[dy из нашей системы четырёх уравнений (9.2),
(9.5), (9.7) и (9.8)]. Выражая dvjdx и dvy/dx из (9.7) и (9.8) и
вставляя их в (9.2), (9.5), получим:
[y'(a*-vl
1UX/ *-	г/
ду
,_dy_
dvx , dvy _ dvy Q
ду ' У ду dx "u'
dx ~vxvy dx '
где у' = —г- ¦ Следовательно, вдоль L должно быть
' dx
v' (а2 — v2 \ -4~ v v — v'v v — а
У \	х) I х у	' х у
1	у'
= 0
(9.9)
') Каждое из этих двух соотношений есть следствие другого, что вы-
вытекает из (9.2).

§ 9]
ПЛОСКИЕ ВИХРЕВЫЕ ДВИЖЕНИЯ
47
у' (а2
1
xvy(a2-vl) -jf-vxVy
dvy
~~~dx~
dx
Q
= 0*). (9.10)
Обращаясь сперва к (9.9), попучим, раскрывая определитель,
следующее соотношение, связывающее у', vx и vy:
у'2 {vx — а2) — 2т>xv у' + v] — а2 = 0.
(9.11)
Заметим попутно, что это соотношение было уже получено нами
в другом виде в общей теории слабых разрывов. В самом деле, мы
видели, что проекция Vп скорости газа на нормаль п к характери-
характеристической поверхности должна равняться местной скорости звука
В нашем случае
Vn — vx cos (it,
\Vn\=a.
vy cos (n, y) = —
и потому условие V2n = а2 примет вид:
что, как нетрудно убедиться, совпадает с (9.11). Таким образом, тан-
тангенс угла наклона у' характеристики может принимать два значения,
определяемые как корни квадратного уравнения (9.11):
(9.12)
Соответственно этому через каждую точку плоскости (л:, у) можно
провести два элемента характеристик, а вся плоскость (х, у) (в пред-
предположении всюду сверхзвуковой скорости) может быть покрыта двумя
семействами характеристик. Если движение уже известно, т. е. vx
и vy известны как функции координат, уравнения (9.12) представят
два дифференциальных уравнения, каждое из которых, будучи про-
проинтегрировано, даст одну систему характеристик в плоскости (х, у).
В дальнейшем мы всегда будем называть ту характеристику, которая
отвечает знаку плюс перед корнем в (9.12), характеристикой первого
семейства, а ту, что даёт у' со знаком минус перед корнем,—второго
*) Равенство нулю определителя с заменённым первым столбцом полу-
получается как следствие (9.9) и (9.10).

vxvy + aVv\
9
vx-
¦"xvy~aVt
v2-
vx
¦ H- v2y
a2
-a2
48	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОП ДИНАМИКИ	[ГЛ. Т
семейства. Будем писать соответственно \>i(x) или у2(лг), так что
y\ = ^^a\v*t.v2y~~—'	(9ЛЗ)
(9.14)
Обратимся, однако, к уравнению (9.10), которое должно вы-
выполняться вдоль характеристик наравне с уравнением (9.9). Раскрывая
его и группируя члены, получим сперва
[ '/ 2_^2\ I о	\^L. — ( 2_ 2\d^? _
= [у' /а2 _ уТу^у^ 1 Qj (9. 1 5)
или вследствие (9.11)
откуда, деля на у ,— и заменяя члены в квадратной скобке правой
части по формуле (9.12):
dx	uj — a1 dx	Vy — a*
где справа знак минус отвечает первому семейству, и тогда вместо у'
должно стоять у'{, а знак плюс отвечает значению у1' = у'г
Мы можем представить произведение корней уравнения (9.11)
в виде:
и потому вдоль характеристик первого семейства будет
~f-y\dx, (9.18)
а вдоль второго
i 1 , r-.^]/"ti2 — а2 ,,	/П1пч
dv Ч—rdvr=Q——=.	s— \Ldx.	(9.19)
У ' v' x	„2	л
У\	иу и
Соотношениям (9.12) и (9.17) можно придать более обозримый
вид, если ввести вместо проекций vx и vy скорости величину ско-

§9!
ПЛОСКИЕ ВИХРЕВЫЬ ДВИЖЕНИЯ
44.
рости v и угол J3, образуемый вектором скорости с осью Ох (рис. 6):
vx = t>cosfS; fy == ^ sin p.	(9.20)
Заметим, прежде всего, что скорость V в точке М(х, у) будет
ксегда направлена по биссектрисе между касательными к обеим
характеристикам, проходящим через М. В этом можно убедиться
из рассмотрения (9.12), проще же это можно получить из равенства
В самом деле, тот факт, что проекция Vп на нормаль к обеим харак-
характеристикам скорости V точки М равна по абсолютной величине
одному и тому же числу, указывает,
что скорость составляет один и тот у
же угол с обеими касательными,
проведёнными в М к нашим харак-
характеристикам. Угол этот называется
углом Маха. Обозначим его бук-
буквой а; тогда по определению а
будет (рис. 6):
sin а. = — .
v
(9.21)
0
Следует подчеркнуть, что величина	рис g
угла Маха а зависит исключительно
от отношения vja, но не зависит от угла р. В самом деле, по (8.9)
мы можем написать:
sin а — —2~ \-jr)	2 '	*- ;
Теперь мы можем представить (9.12) в виде:
у' = tg ф ± а).	(9.23)
Прежде чем преобразовать (9.18) и (9.19), найдём, как изменяется Ь
при перемещении вдоль характеристики. Вдоль последней будет
так что
или, по F.5),
dx dty \дх ' ду
= — р (Vy — Vxy>) —
Но тогда можно представить 2, стоящее в (9.18) и (9.19), в виде
v-l
Q =
V.	^	1
1
«у — vxy' dx
-А— 1 Vy — Vxy' dx '
4 Теоретическая шдромеханика, ч II

50	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
Вставим это значение 2 в (9 18) и (9.19) и заменим еще vx и vy
по (9.20), а у' по (9.23). Получим:
d(t>sinB)+ctg(p т. a) d (v cos В) =
ьг _ аг tg (з ±
+
~~ х—1 v {sin p — tgO + а) cos 3} (у2ып2? — а2) '
Наконец, собирая члены с dv и rfB, деля на коэффициент при d$ и
применяя (9 21), получим посае простых преобразований:
dpT^ii.dw=±iI?iL?2ifdln&.	(9.24)
Мы вернемся к вихревой задаче в § 13, а сейчас приступим
к решению отдельных конкретных задач в безвихревом случае. Здесь
мы будем иметь значительное упрощение формул (9.18), (9.19) и
сможем значительно дальше продвинуться в общей теории.
§ 10. Плоские безвихревые движения при v > at. Если вихри
отсутствуют, т. е.
2 = 0,
уравнения (9 18) и (9.19) могут быть записаны в виде: вдоль харак-
характеристик первого семейства:
dvy	1
dvx	У1
вдоль характеристик второго семейства:
dv.,	1
A0.1)
dvx	У\
Рассмотрим, кроме плоскости (л:, у), которая вся покрыта линиями
характеристик у —^(х) и у =-у<2,{х), плоскость компонентов ско-
скоростей (vx, vy). Мы имеем дело со сверхзвуковыми скоростями,
значит, в этой плоскости мы должны рассмотреть точки, лежащие
вне круга v-=at. С другой стороны, мы знаем (§ 8), что скорость
движения газа
Таким образом, интересующие нас точки плоскости (vl, vy) все рас-
положены в кольце между окружностями v = at и v = 1/ ——у at.
Предположим, чго мы перемещаемся вдоль характеристики у —у,(х)
в плоскости (х, у). В плоскости {vx, Vy) мы будем перемещаться

§ 10]	ПЛОСКИЕ БЕЗВИХРЕВЫЕ ДВИЖЕНИЯ ПРИ »>«ф	51
при этом, вообще говоря, вдоль некоторой линии. Эту линию на-
назовём характеристикой первого семейства в плоскости (vx, v ). На
этой линии должно быть выполнено всюду соотношение A0.1).
Аналогичное построение повторим для характеристик второго семей-
семейства. Через точку М плоскости (л:, у) проведём элементы характе-
характеристик первого и второго семейства. Пусть точке М отвечает точка М'
плоскости (vx, vy) (координаты точки М' суть компоненты скорости
в точке М). Равенство A0.2) показывает тогда, что касательная
к характеристике первого семейства, проходящей в плоскости (л:, у)
через М, будет нормальна к характеристике второго семейства,
проходящей через соответствующую точку М' в плоскости {vx, vy)
(ось Ох параллельна оси vx)\ также, по A0.1), касательная к харак-
характеристике второго семейства в (л:, у) будет параллельна нормали
к характеристике первого семейства в (vx, vy).
Характеристики в плоскости (л:, у) будут иметь в различных
задачах газовой динамики различную форму. Напротив, характе-
характеристики в плоскости (vx, vy) будут для всех безвихревых задач
иметь всегда один и тот же вид, так что мы можем их рассчитать
раз и навсегда. Действительно, из уравнения (ЮЛ), например,
вследствие (9.14), следует, что
dv.,	v\ — а2
у
dvx	vxvy — а yv* — a2
т. е., так как а1 выражается только через vx-\-v2 и правая часть,
таким образом, зависит только от vx, v , но не зависит явно от х,
у, то мы имеем для определения характеристики первого семейства
в плоскости (vx, vy) обыкновенное дифференциальное уравнение.
Для интеграции этого уравнения удобно обратиться в плоскости
(vx, vy) к полярным координатам v, C, уже введённым нами по
формулам (9.20). Именно, (9.24) даст нам для безвихревого случая
(& = const.) просто
^v = 0,	A0.3)
и так как cfga зависит исключительно от г» (вернее, от отношения v/aj,
то переменные разделены, и достаточно выполнить квадратуру.
Вследствие (9.22), имеем:
иг)

52
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
так что
Р=±
(—У
• 1 d —
a»
— 1 / у
—(-const.
Квадратура легко выполняется, и мы получим
V	T—rarct§ 1/ ТТЛ/ 	z-Л-
V	x-1	^|/ x+1 у al-^v
/т^—i
1—^i^
+ const. A0.5)
Уравнения A0.5) представляют два (соответственно двум знакам
правой части) семейства линий, зависящих каждое от одного пара-
параметра. Все эти линии располагаются в кольце
Нетрудно убедиться, что это—эпициклоиды, которые можно получить,
следя за движением точек окружности радиуса
катящейся по кругу v = at. Мы приходим к важному результату:
характеристики в плоскости (vx, vy) представляются в случае без-
безвихревой задачи всегда в виде эпициклоид.
Равенство A0.5) может быть ещё записано, если ввести вместо v
угол а по A0.4), так:
агс^
const-
Для удобства дальнейших вычислений мы будем писать для харак-
характеристики первого семейства
а для второго'
A0.7)

§ Ю]	ПЛОСКИЕ БЕЗВИХРЕВЫЕ ДВИЖЕНИЯ ПРИ v > af	53
где X и и. — постоянные, а
о/а*
¦ (л_\- [л/ (д*)
J г '-щи
V
Через каждую точку М' плоскости (vx, vy) (в кольце a^
^ 1/ _. a^j проходит одна эпициклоида первого семейства и одна
второго семейства. При этом, по A0.7), разность соответствующих
значений постоянных [х — X будет в точности равна полярному углу В
точки (vx, vy):
т. е. будет сохраняться на всём радиусе-векторе, проходящем через М'\
а сумма значений \ и ц будет
т. е. сохраняется на всём круге с центром в начале (проходящем
через М').
На прилагаемой таблице I мы даём значения числа S{vla^) =
= 1000—180/тс-С, начиная от 1000 вниз через 1, и рядом соответ-
соответствующие значения а в градусах и значения величин pjpu, via, vja^
и ?Ф*?*-
В плоскости (х, у) направление обеих характеристик, проходя-
проходящих через точку М, можно узнать по формулам (9.13), (9.14), если
известны vx и vy в этой точке М. Если, однако, наши эпициклоиды
уже заготовлены, то, зная vx, vy, можно найти направления у[, у'2,
не производя вычислений по формулам (9.13) и (9.14). В самом
деле, достаточно вспомнить, что элементы эпициклоид, проходящих
через М' (с данными vx и vy), нормальны к элементам характери-
характеристик противоположных номеров, проходящих через М; таким образом,
чтобы построить, например, направление характеристики первого се-
семейства в точке М, надо провести через М линию, перпендикулярную

54
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. t
S
1000
999
998
997
996
995
994
993
992
991
990
989
988
987
986
985
984
983
982
981
980
979
978
977
976
975
974
973
а
90,00
67,28
61,96
58,18
55,12
52,66
50,58
48,70
47,07
45,54
44,16
42,84
41,62
40,51
39,48
38,47
37,53
36,67
35,82
35,02
34,26
33,51
32,80
32,10
31,45
30,80
30,19
29,58
р
Ро
0,527
0,477
0,449
0,424
0,401
0,381
0,363
0,345
0,329
0,313
0,298
0,284
0,270
0,257
0,245
0,233
0,221
0,210
0,199
0,189
0,179
0,170
0,161
0,153
0,145
0,137
0,130
0,123
via
1,000
1,084
1,133
1,178
1,220
1,258
1,295
1,332
1,366
1,401
1,435
1,470
1,505
1,539
1,572
1,608
1,641
1,675
1,710
1,744
1,779
1,815
1,850
1,884
1,918
1,954
1,989
2,025
v/a
1,000
1,068
1,107
1,141
1,173
1,201
1,227
1,253
1,276
1,299
1,322
1,344
1,666
1,387
1,407
1,428
1,448
1,467
1,486
1,504
1,523
1,541
1,559
1,576
1,592
1,609
1,625
1,641
1,000
0,994
0,986
0,976
0,965
0,953
0,940
0,926
0,912
0,897
0,882
0,865
0,849
0,832
0,815
0,797
0,779
0,762
0,743
0,725
0,707
0,689
0,670
0,653
0,635
0,617
0,600
0,582
5
972
971
970
969
968
967
966
965
964
963
962
961
960
959
958
957
956
955
954
953
952
951
950
949
948
947
946
870,68
28,98
28,42
27,88
27,34
26,82
26,32
25,80
25,33
24,87
24,42
23,98
23,54
23,12
22,70
22,29
21,89
21,49
21,11
20,73
20,37
20,00
19,64
19,29
18,93
18,59
18,26
17,97
0,00
р
Рч
0,116
0,110
0,104
0,097
0,092
0,086
0,080
0,075
0,071
0,066
0,062
0,058
0,054
0,051
0,047
0,044
0,041
0,038
0,036
0,033
0,031
0,029
0,027
0,025
0,023
0,021
0,019
0,000
via
2,062
2,098
2,135
2,174
2,214
2,251
2,296
2,339
2,378
2,422
2,466
2,508
2,550
2,595
2,640
2,689
2,734
2,778
2,826
2,873
2,920
2,968
3,021
3,074
3,131
3,188
3,350
со
Таб л
14 а
1,657
1,673
1,688
1,704
1,720
1,735
1,752
1,767
1,781
1,795
1,810
1,824
1,837
1,851
1,864
1,878
1,891
1,903
1,917
1,928
1,939
1,951
1,963
1,975
1,987
1,999
2,012
2,437
и ца ]
0,564
0,547
0,530
0,512
0,494
0,477
0,459
0,442
0,426
0,410
0,394
0,379
0,364
0,349
0,335
0,320
0,306
0,294
0,281
0,269
0,257
0,246
0,234
0,222
0,211
0,200
0,188
0,000
к касательной к проходящей через М' эпициклоиде второго се-
семейства (оси х и vr всегда параллельны).
На рис. 7 изображен кусок плоскости (vx, vy) (сектор в 70°
круга радиуса у —Ц- а с центром в начале координат), на кото-
ром нанесены попадающие туда части эпициклоид первого и второго
семейств и некоторые круги 5 = const. Если в A0.7) ввести вместо С
число 5, мы получим
= 1000— Мх =
ЮО),
5 — р° = 1000 — ^f- [х = 2 (tj — 100)
ф° — в градусах), где ? и tj — новые постоянные, заменяющие 1и ц,
На рис. 7 эпициклоиде первого семейства, проходящей через точку
v = at E=1000), [Зо = 0 (на рисунке надписаны значения tj— ?,

10]
ПЛОСКИЕ БЕЗВИХРЕВЫЕ ДВИЖЕНИЯ ПРИ v > a
55
а не C), соответствует ij = 400, эпициклоиде второго семейства, про-
проходящей через ту же точку, отвечает tj=600. Эпициклоиды прове-
проведены для ? = 400; 401; 402;...; для ? = 399; 398;..., для
Рис 7.
у — 600; 601; . . .; ^
5^=1000, 990, 980 .
599; 598; . . . Круги 5= const, проведены для
.. Заметим, что в каждой точке
= 6 + 1). р° = ? —т)+200.

56
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ I
Покажем теперь, как при помощи характеристик можно числен-
численным образом определить поле скоростей и давление во всех точках
плоскости (л:, у) в отдельных задачах газовой динамики.
§ 11. Использование характеристик для решения плоской
безвихревой задачи при w>at. Мы увидим, что любой случай
движения газа со сверхзвуковой скоростью и при отсутствии
Рис 8.
Рис 9.
сильного разрыва мы сможем изучить, если научимся решать следую-
следующие четыре задачи:
Задача 1. Поле скоростей [т. е. vx(x, у) и v (х, у)] задано
в плоскости (х, у) на дуге АВ некоторой линии L (рис. 8), не являю-
являющейся характеристикой. Определить vx и vv во всех точках обла-
сти, ограниченной дугой АВ и двумя
характеристиками (разных семейств), вы-
выходящими из точек А и В (рис. 8) (в не-
некотором криволинейном треугольнике).
Задача 2. Поле скоростей известно
на дугах АВ и АС двух характеристик
разных семейств, выходящих из точки А.
Найти vx и vy в области, ограниченной
этими дугами и дугами BD и CD ха-
характеристик разных семейств, выходящих
из В и С (рис. 9).
Задача 3. Поле скоростей задано на дуге АВ характеристики
какого-либо семейства, причём известно, что точка А лежит на твёр-
дой стенке'). Найти vx и v в области, ограниченной АВ, твёрдой
стенкой АС и характеристикой ВС другого семейства, выходящей
из точки В (рис. 10).
Рис. 10.
') Направление последней в А таково, что вторая характеристика, про-
проходящая через А, пойдет «внутри» стенки.

Ill
ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК ПРИ v > a
57
О
Задача 4. То же, чго и в 3, но вместо стенки АС речь идет
о свободной поверхности АС, форма которой заранее, конечно, не-
неизвестна (рис. 11).
Заметим, что в задаче 1 нам за-
дана линия АВ, отрезки же характе-
характеристик DC и ВС заранее неизвестны.
Напротив, в задаче 2 характеристики
АВ и АС считаются заранее известными
(неизвестны АВ и CD), в задаче 3 ха-
характеристика АВ и контур считаются
заданными, наконец, в задаче 4 дана дуга АВ характеристики,
а свободная поверхность неизвестна, так же как и ВС.
Чтобы приближённо решить задачу 1, поместим на дуге АВ густой
ряд точек Мх, М2	Мп (рис. 12). Так как значения (vx, vy)
на АВ известны, то в каждой из точек A, v
Mv M2, . . ., Мп, В мы можем построить у
отрезки прямых по направлениям касагель-
Рис. 13.
ных к обеим характеристикам по формулам (9.13) и (9.14). Прове-
Проведенные нами отрезки прямых приближённо примем за элементы самих
характеристик, выходящих из А, Мх	В; в точке А нам доста-
достаточно построить лишь элемент характеристики АС (пусть это
будет характеристика второго семейства), а в точке В — элемент ВС
(первого семейства). Пусть элементы характеристик разных семейств,
проведенные из соседних точек дуги АВ, пересекаю 1ся в точках Nv

58	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
N2, . • • (например, N2 есть пересечение элемента характеристики
второго семейства, выходящей из Mv и характеристики первого
семейства, выходящей из М2). Чтобы найти vx, vy в точках Nv N2
рассуждаем так. Отметим скорости vx и vy точек А, Мх, ..., В
в плоскости (г»л, vy); пусть это будут точки А'', м[, .. ., В' (рис. 13).
Перемещаясь и плоскости (л;, у) по характеристике второго семей-
семейства из точки А, мы будем в плоскости (vx, vy) двигаться по эпи-
эпициклоиде второго семейства, проходящей через А'; перемещаясь же
вдоль характеристики первого семейства из Ж,, мы пойдём по пло-
плоскости (vx, vy) вдоль эпициклоиды первого семейства, выходящей
из Мь Обе нужные нам эпициклоиды могут быть заранее нарисо-
ьаны, поэтому точка их пересечения N\ (рис. 13) может быть сразу
найдена хотя бы графически. Совершенно очевидно, что коорди-
координаты vx и vy точки Ni и дадут скорости vx и vy в точке Nv Ана-
Аналогичным образом мы найдём скорости точек N2 и т. д. Ниже мы
укажем на очень удобный прием графического определения скоро-
скоростей vx, vy в этих точках.
Теперь мы можем взять за отправную сеть ряд точек Nv N2, ¦. .
и рассуждать по отношению к ним так же, как мы рассуждали
о точках A, Mv ..., Мп, В. Именно в Nv N2, ... скорости уже
известны; значит, можно во всех этих точках построить характери-
характеристики обоих семейств [по формулам (9.13), (9.14) или как нормали
к эпициклоидам плоскости (vv, vy)\ до пересечения их в точках Рх,
Р2, Р3> • • •'< скорости же в этих точках найдутся как координаты
точек пересечения эпициклоид, проходящих через точки N\, N2, ¦ ¦ .
соответственно. Так постепенно мы заполним весь криволинейный
треугольник, о котором идёт речь в задаче 1. Линии АС и ВС,
неизвестные вначале, построятся при этом сами собой (приближённо,
как ломаные, а не как плавные кривые; это же относится ко всем
характеристикам). Таким образом, в густой сетке точек (густота эта
будет зависеть от густоты точек Мь М2	Мп на АВ) нашего
«треугольника» мы будем знать скорости. Линии тока определить
теперь легко, если вспомнить, что скорости направлены по биссек-
биссектрисам углов между характеристиками, а последние по самому по-
построению нам везде известны. Давление находится по уравнению
Бернулли. Задача 1 решена.
Решение задачи 2 принципиально не отличается от решения
задачи 1. Поместим на характеристике АВ густой ряд точек
Мх, М2, . . ., Мп, а на характеристике АС густой ряд точек Nv
N2, ¦¦¦, Nn- Во всех этих точках скорости vx, vy нам заданы.
Через точки Mv М2, . . . проведём затем элементы характеристик

§ II]
ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК ПРИ v > а
59
второго семейства (считаем, что АВ— характеристика первого семей-
семейства), а через точки Nv N2, ... — отрезки характеристик первого
семейства (рис. 14). Пусть пересечением характеристики первого
семейства, вышедшей из N{, и характеристики второго семейства,
вышедшей из Мх, будет точка Р1. Чтобы найти скорость в Pv
замечаем, что перемещение вдоль характеристики A/,Pj означает
передвижение в плоскости (vx, vy) вдоль некоторой эпициклоиды
первого семейства, выходящей из
точки N\ с координатами, равными
компонентам скорости в точке Nl,
а перемещение вдоль М1Р1 означает
передвижение по эпициклоиде
второго семейства от точки М.'х с
Рис. 14.
Рис. 15.
координатами — компонентами скорости в точке Му Точка пересече-
пересечения Р[ (рис. 15) упомянутых эпициклоид и даст компоненты ско-
скорости в Pj. Зная скорости в точке Рх, можем провести через эту
точку обе характеристики до пересечения с элементами характери-
характеристик первого и второго семейства, выходящих из N2 и из М2
соответственно. Получим точки Р2 и Р3. Чтобы найти скорость в Р2,
рассуждаем совершенно так же, как это делали при рассмотрении
точки Pj, только роль прежней точки А будет теперь играть точка Nv
роль точки Мх будет играть Pv а на место точки Nx придётся
ставить N2. Аналогично можно сказать про точку Р3. Продолжая
построение далее, покроем постепенно весь криволинейный четырёх-
четырёхугольник, о котором идёт речь в задаче 2, сеткой характеристик;
на пересечениях последних мы будем знать всюду vx и vy. Линии
тока поведутся затем как биссектрисы между касательными к харак-
характеристикам, а давление найдётся из уравнения Бернулли. Задача будет
решена. Отметим, что все заданные точки А , N\, N2, ¦ ¦ ¦ располо-
расположатся на одной и той же эпициклоиде второго семейства, точки же
А , Мг, М2, . . . лягут на одну и ту же эпициклоиду первого семей-
семейства. Обе эти эпициклоиды выходят из А'.

60
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Переходим к решению задачи 3. Пусть дуга АВ есть дуга задан-
заданной характеристики первого семейства. Нанесём на ней ряд точек
Мх, М2, ¦ . ¦ (рис. 16). Так как скорости везде на АВ нам известны,
мы можем в каждой из точек Mv М2, ¦ ¦. построить элементы
характеристик второго семейства [хотя бы по формуле (9.14)]. Про-
Проделаем это построение. Характеристику второго семейства, прохо-
проходящую через vWj, доведём до пересечения в точке N: с заданной
нам стенкой. Теперь мы можем опреде-
определить скорость в точке Nv В самом деле,
направление скорости там известно — это
направление стенки. Проведём в пло-
плоскости (vx, vy) радиус-вектор под углом,
Рис. 16.
Рис. 17.
равным углу между направлением касательной в Nx к контуру и
осью Ох. Где-то на этом радиусе-векторе нам надо будет искать
точку, координаты которой vx, vy дадут скорости в точке Л^.
С другой стороны, точка N1 лежит на характеристике второго се-
семейства, выходящей из точки Mt. Пусть точке Мх отвечает в пло-
плоскости (vx, vy) точка М{ (рис. 17). Проводя через М[ эпициклоиду
второго семейства до пересечения с упомянутым выше радиусом-
вектором, мы встретим последний в точке Ni, которая, очевидно,
и будет иметь в качестве координат скорости vx, vy в точке Л^,.
Зная скорости в Nv построим в плоскости (х, у) характеристику
первого семейства NXN2 до пересечения N2 с характеристикой вто-
второго семейства M2N2, выходящей из М2. Скорости в N2 найдутся
как координаты точки vx, vy пересечения эпициклоиды первого
семейства, проходящей через N\, и эпициклоиды второго семейства,
идущей через М2. Проведём из N2 обе характеристики, причём
характеристику первого семейства доведём до пересечения /V3 с харак-

§11]	ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК ПРИ и > а^	61
теристикой второго семейства, выходящей из vW3, а характеристику
второго семейства, выходящую из N2, проведём до пересечения
с контуром (пусть это будет точка Рх). Скорость в /V3 находится
аналогично тому, как находилась скорость в N2; чтобы найти ско-
скорость в Р1? замечаем, что направление скорости там известно (так же
как было известно направление скорости в NJ, и построим радиус-
вектор с этим направлением в плоскости {vK, vy)\ пересечение Р\
этого радиуса-вектора с эпициклоидой второго семейства, проходя-
проходящей через A^2> и даст нам искомую скорость в Pv Зная скорость
в Р, и в Л/g, проводим там характеристики и т. д. Задача наша
будет решена.
Обратим внимание на один очень важный частный случай за-
задачи 3. Предположим, что нам известно, что вдоль характеристики
АВ скорости имеют всюду одну и ту же постоянную величину и
направление. Случай этот представится, например, в задаче обте-
обтекания профиля безграничным потоком, имеющим постоянную вели-
величину и направление скорости. В самом деле, пусть профиль этот
начинается от точки А (рис. 16), причём безграничный поток набе-
набегает на него слева со скоростью, параллельной оси Ох. Тогда вдоль
характеристики АВ (точка В может быть взята на бесконечности)
совершается переход от режима прямолинейного набегания на контур
к режиму обтекания контура. Вдоль характеристики АВ происходит
«склеивание» двух различных движений {АВ как характеристика мо-
может быть такой линией слабого разрыва), и на всей АВ скорость
постоянна по величине и направлению и равна скорости набегаю-
набегающего потока. Отметим попутно, что в таком случае линия АВ будет
прямая. Действительно, тангенс наклона у'х вдоль этой кривой, вы-
выражающийся при помощи формулы (9.13), будет всюду один
и тот же, так как правая часть (9.13) состоит лишь из компонентов
скоростей, а они считаются постоянными вдоль АВ.
Итак, пусть вдоль АВ всюду $ = $v a v = vv Обратим внима-
внимание на характеристики второго семейства M1N1 и др. Вдоль них
будет, согласно формуле A0.7),
где р. — различные постоянные, характеризующие отдельные харак-
характеристики семейства. Найдём jx для характеристики MXNV Послед-
Последняя пересекается с АВ в точке Мг; здесь P = Pi и v^=vlt

62	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
следовательно, должно быть
и уравнение, связывающее о и р вдоль MlN1, будет иметь вид:
Но вдоль М2Рг будет выполняться в точности то же соотношение,
ибо М2 лежит на АВ, а там г> = г>1 и C=Pi, так что и для этой
линии должно быть выполнено A1.1). Таким образом, в нашем слу-
случае скорость v и угол р во всех точках, лежащих между контуром
и характеристикой АВ, будут связаны соотношением A1.1) с одной
и той же константой \х, в то время как в общем случае постоянная
будет меняться от характеристики к характеристике.
Соотношение A1.1) играет здесь роль дополнительного конечного
соотношения, связывающего компоненты скоростей (vx и г/у могут
быть выражены через v и {)). Пользуясь этим соотношением, мы
можем привести задачу к решению лишь одного уравнения в част-
частных производных первого порядка с одной искомой функцией (на-
(напомним, что в общем случае мы имеем систему двух уравнений
с двумя функциями), т. е., в конечном счёте, к обыкновенным диф-
дифференциальным уравнениям. Чтобы получить это единственное урав-
уравнение, напишем, например, условие отсутствия вихря, выражая vx
и vy через v и [3:
dv sin р	dv cos р __ 0	П121
дх	ду	'	' '
Помня, что теперь v и р! связаны соотношением A1.1), мы можем,
далее, выполнить дифференцирование и написать
или, так как по A0.3)
dy
-^=
(мы имеем дело с характеристикой второго семейства), где а — угол
Маха, мы можем написать, после простых преобразований:
-gr + tg(P+a)-|-=:O	(Ц.З)
[здесь a — функция v по (9.22), а v — функция от pi по A1.1)].
Это уравнение в частных производных первого порядка интегри-
интегрируется и даёт:
$ F(y tg(pH-a)x),	(П.4)
где F — произвольная функция своего аргумента, каковая может

§ II]
ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК ПРИ и > а
63
быть определена, если задан контур АС; достаточно написать, что
на данной линии АС ф есть данная функция от координат х и у.
Итак, если отрезок АВ характеристики в задаче 3 есть прямая
линия, то движение внутри треугольника ABC может быть найдено
совершенно точно. Стоит только после того, как F из (П.4) известна,
решить (П.4) относительно C; мы по-
получим р, а затем по A1.1) и v в функ-
функциях от х и у.
Мы еще не раз вернёмся к этому
вопросу.
<
Mi
N.
^-—
*%
\
-C
"Pi
В
Рис. 18.
Рис. 19.
Перейдем к решению задачи 4. Пусть скорости заданы вдоль некото-
некоторой дуги АВ характеристики, например второго семейства, и пусть из-
известно, что А лежит на свободной границе потока. Надо найти
форму свободной поверхности АС и движение между АС, АВ и
отрезком ВС характеристики первого семейства, проходящей через В
(рис. 18). Нанесём на АВ ряд точек Мх, М2, . .. Проведём через
точку А элемент прямой, направленной вдоль известной в точке А
скорости; этот элемент примем за элемент свободной поверхности,
проходящей через А. Проведём затем через М1 характеристику
первого семейства до пересечения с этим элементом в точке Nv На
свободной поверхности величина давления р будет всюду одна
и та же (это определение свободной поверхности), значит, величина v
скорости всех точек свободной поверхности, по уравнению Бернулли,
будет всюду одинакова. Построим поэтому в плоскости (vx, vy)
круг радиуса v = vv где vx — именно это постоянное значение.
Чтобы определить направление скорости точки Nv достаточно будет
теперь, так как N1 лежит на свободной поверхности, найти в пло-
плоскости {vx, vy) точку пересечения N[ эпициклоиды первого семейства,
идущей из точки M'v координаты которой суть известные компо-
компоненты скорости точки Mv с окружностью v = vt (рис. 19). Определив

64	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
скорость в точке Nv построим продолжение свободной поверхности
как отрезок прямой, направленной вдоль этой скорости, затем из Л^
проведём элемент характеристики второго семейства до пересечения
в точке N2 с элементом характеристики первого семейства, идущей
из М2. Скорость N2 найдётся как точка пересечения эпициклоиды
первого семейства, проходящей через М'2 (изображение М2 в пло-
плоскости {vx, Vy)\, и эпициклоиды второго семейства, идущей через Nj,
Зная скорость в N2, проводим характеристику первого семейства
до пересечения с элементом свободной поверхности в точке Р1
и т. д. Задача будет решена.
Прежде чем приступить к приложениям к конкретным задачам
газовой динамики, скажем несколько слов об оценке погрешности
излагаемого здесь метода. Нетрудно убедиться, что решение всех
наших четырёх задач основано на умении пользоваться следующими
двумя операциями,—назовём их А и Б.
Операция А. Даны скорости vx и vy в двух соседних точках М1
и М2 плоскости (х, у). Найги скорость в точке N пересечения ха-
характеристик разных семейств, выходящих из Мх и М2 соответ-
соответственно. Чтобы проделать эту операцию, достаточно найти точку
пересечения эпициклоид разных семейств, выходящих из М[ и М'2
[точки плоскости (vx, vy), координаты коих сугь заданные компо-
компоненты скоростей точек Мх и М2 соответственно].
Операция Б. Скорость в точке М плоскости (х, у) известна.
Дана линия L, не являющаяся характеристикой (точка М лежит
вблизи неё) и такая, что на ней мы знаем направление (или вели-
величину) скорости. Найти величину (или направление) скорости в точке N
встречи характеристики MN, идущей из М, с линией L. Здесь до-
достаточно в плоскости (vx, v ) разыскать точку М' с координатами,
равными данным в точке М значениям vx и vy, и провести через М'
эпициклоиду до пересечения с радиусом-вектором, параллельным
направлению скорости в N' (или до пересечения с кругом, отве-
отвечающим известной величине скорости в N').
Для примера рассмотрим подробнее операцию А. Точно мы можем
провести лишь половину этой операции: мы можем найги точку N'',
т. е. скорость в точке N; положение последней точки нам, однако,
неизвестно, ибо вид характеристик в плоскости (х, у) заранее неиз-
неизвестен. Мы можем, однако, построить отрезки касательных к ха-
характеристикам в точках М1 и М2 [по формулам (9.13) и (9.14)]. Эти
отрезки мы и принимаем приближённо за характеристики MlN
и M2N (рис. 20). Пересечение этих отрезков даст точку N*, а не N,
но мы можем в случае одно-однозначной зависимости между vx, vy
и х, у заключить каждую из кирволинейных дуг характеристик
в некий угол и таким образом оценить погрешность, получающуюся
оттого, что вместо N мы взяли N'. Для этого, пользуясь упомяну-

11J
ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК. ПРИ v :
65
той однозначной зависимостью, надо лишь доказать, что делается
без особого труда (см. уравнения эпициклоид), что наклон каса-
касательной к характеристике монотонно меняется вдоль соответствую-
соответствующего участка характеристики; если это так, то, провгдя чергз Мх
отрезок прямой MXN \ параллельный направлению касательной
к одной аз характеристик в N [это направление мы можем вы-
вычислить заранее, хотя положение точки N в плоскости (х, у) неиз-
неизвестно, совершенно точно, используя (9.13) или (9.14) и найденную
точно точку N'], а через М2—	у
отрезок A\2N \ параллельный
Рис. 20.
Рис. 21.
касательной к другой характеристике в N, мы можем утверждать, что
криволинейная дуга M1N характеристики лежит вся внутри угла
/_ N'MXM'*, а дуга M2N— внутри угла /_N"M2N''*\
Таким образом, точность вычисления зависит лишь от близости
точек Мх и М2.
Решение всех приведённых здесь задач производится при помощи по-
построения в плоское 1 и (х, у) характеристик обоих семейств, проходящих
через точки, в коих скорости известны. Мы ссылались при этом всё время
на формулы (9.13) и (9.14), позволяющие всегда проделать расчёт направле-
направлении ух или у2- Хотя этот расчёт и элементарен, он требует всё же непри-
неприятных выкладок — извлечения корней и т. п. Буземан дал графический
приём быстрого определения направления характеристик в плоскости (х, у)
(в тех точках, где скорости уже известны). Пусть скорость точки
М (х, у) плоскости {х, у) будет V (vx, v y). Отметим в плоскости точку
м (vx< vy) с соответствующими координатами и проведём через М' эллипс
с центром в начале и с полуосями, равными о, и V ^4 а* соответ-
ственно. Легко видеть, что таких эллипсов будет, вообще говоря, два
(рис. 21). Покажем, что большие оси этих эллипсов окажутся как раз па-
параллельными характеристикам, проходящим в плоскости (х, у) через точку М
(оси Ох и vx всегда параллельны). Чтобы доказать это, представим себе,
что вектор скорости V точки М разложен на две составляющие: VT по ка-
касательной к характеристике (например, первого семейства), проходящей
в плоскости (х, у) через М, и Vn — no нормали к этой характеристике
5 Теоретическая гидромеханике, ч. II

66	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
в плоскости (х, у). Мы знаем, что
I Vn I = a.
Обратимся к уравнению Бернулли (8.7) и заменим в нём а2 на V\ , a v2
на V2n + V2.. Тогда, собирая члены при v\ и V2n и деля на -У". . ,
I (х — 1)
получим соотношение
V2	V2
7ТО + ^=Й-	(И.5)
±1
— 1
Спроектируем теперь радиус-вектор ОМ' = | V \ на большую ось одного из
проведённых нами эллипсов и на перпендикуляр к ней. Пусть первая про-
проекция будет vv а вторая vn. Тогда по самому построению эллипсов будет
= 1.
Так как, с другой стороны, для точки М' имеем V2 = v2n + v\, то ве-
2	2
личины vn и vx удовлетворяют тем же двум линейным уравнениям, что
и величины Vп и Vx, и поэтому можно положить
vx=,Vv vn=Vn.
Следовательно, направление большой оси нашего эллипса будет совпадать
с направлением характеристики, идущей через М, а направление малой
оси — с направлением нормали к этой характеристике.
Изложенный здесь способ построения характеристик в плоскости (х, у)
годится, естественным образом, не только для безвихревого, но и для ви-
вихревого случая, ибо он основывается на равенстве | Vn \ = а, одинаково
справедливом в обоих этих случаях.
Эллипс, о котором здесь идёт речь (назовём его эллипсом Буземана),
может быть заготовлен раз навсегда на прозрачной бумаге (или на целлу-
целлулоиде); совместив его центр с началом координат, будем поворачивать его
вокруг начала до тех пор, пока точка М', дающая в плоскости (vx, vy)
скорости точки М, не окажется на эллипсе; нам останется тогда лишь
снести направление большой оси эллипса в этом его положении на пло-
плоскость (х, у) — направление характеристики, проходящей через М, будет
найдено. Направление второй характеристики найдётся как направление
большой оси второго возможного положения эллипса.
Эллипс Буземана позволяет построить также и характеристики в пло-
плоскости (vx, vy), т. е. эпициклоиды. В самом деле, мы видели [формулы A0.1),
A0.2)], что характеристики плоскости (vx, vy) (эпициклоиды) будут ортого-
ортогональны к характеристикам (другого номера) плоскости (х, у). Направление
большой оси эллипса Буземана совпадает с направлением характеристики
в плоскости (х, у) — значит, направление малой его оси (ортогональной
к большой оси) будет совпадать с направлением эпициклоиды (другого се-
семейства). Поэтому, чтобы построить элемент эпициклоиды, проходящей
через М', нам достаточно провести через М' эллипс Буземана и затем по-
построить элементарный отрезок, выходящий из М' и параллельный малой
оси эллипса (рис. 22). Вторая эпициклоида найдётся при построении вто-

ш
ИСПОЛЬЗОВАНИЕ ХАРАКТЕРИСТИК ПРИ и > а
67
рого возможного положения эллипса. Отсюда получаем способ построения
всех эпициклоид плоскости (vx, vy) при помощи эллипса Буземана. Поме-
Поместим на эллипсе Буземана, находящемся в произвольном положении, ряд
точек и проведём через эти точки отрезки, параллельные малой оси эл-
эллипса (рис. 22); повернём затем эллипс на малый угол и, отметив точки
пересечения его с малыми отрезками, построим в этих точках новые эле-
элементарные отрезки, параллельные новому положению малой оси эллипса.
Продолжая построение дальше (причём вращать эллипс придётся как по,
так и против часовой стрелки), заполним всё кольцо
—=• аф эпициклоидами.
Способ использования характеристик для
приближённого решения плоских безвихревых
задач при v > а„, изложенный в этом па-
параграфе, был приспособлен для ручного счета
и широко применялся до появления быстро-
быстродействующих электронных вычислительных
машин.
Для вычислений с помощью электронных
машин способ этот неудобен тем, что в расчёт
входят тригонометрические функции (это за-
заставляет обращаться к большому числу под-
подпрограмм и требует много машинного времени).
В самом деле, рассмотрим, например, вновь
операцию А. Вдоль характеристик выполняются соотношения (9.23)
и A0.3). Это значит, что мы можем написать в точке М2 (рис. 20)
для характеристики 1-го семейства:
Рис. 22.
где постановка индекса 2 означает, что соответствующая функция
взята в точке М2. С другой стороны, в Мх имеем для характери-
характеристики 2-го семейства:
(индекс 1 относится к значениям в точке Мх). Заменяя производные
конечными разностями (это фактически мы все время и делали), мы
найдём координаты (х*, /) точки пересечения наших характеристик
из соотношений:
A1.7)
A1.8)
A1.9)
В то же время по A0.3) имеем:
5*

68	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
где Р", т>1 — значения этих функций в точке М*. Таким образом, х*,
у*, р\ v* определяются из системы линейных уравнений (П.6) —
A1 9), а коэффициенты этой системы содержат тригонометрические
функции.
Элсрсх) предложил приспособить расчёты с помощью характе-
характеристик для электронных вычислительных машин следующим обра-
образом В качестве искомых величин следует принять не а и C (г;, C),
а две новые величины
T = ctga, 8=tgp.	A1.10)
В этих новых величинах соотношения на характеристиках (9.23)
примут вид:
dy = ^dx.	A1.11)
В то же время по (9.22)
ai х — 1	2 1
v2 x -f 1 у- + 1 1 + T2 '
так что, после элементарных выкладок, мы получим
dv 1 ,, / ах \2
— = ~ Т rf 1п ПГ ) =
1
и й?р =v-y-pu?o. Поэтому A0.3) запишется в следующем виде:
1	у2 dy
Коэффициенты в A1.11), A1.12) — алгебраические функции. Сам
расчет следует проводить итерациями. Именно, если для сокращения
письма ввести обозначения:
iB -L 1	76-1-1	,
7-5
то мы можем написать (рассматриваем операцию А) в первом при-
приближении
У* — у2 — Ч (х* — х2); у' - у, — Ьх (х' — л-,),
(о* — 32) Е2 = (-{*— 72)^2' (^ — Ь\)Е\~ G —1\}Р\
!) Е h i e r s, The method of characteristics tor iboenergetic supersonic
flows adapted for high-speed digital computers, J. Soc. Ind. a. Appl. Math.
7, 1959.

§ 12]
ДВИЖЕНИЕ ГАЗА ВНЕ ВЫПУКЛОЙ ПОВЕРХНОСТИ
69
или, решая эти уравнения относительно х\ у*, 5*, f*:
Л (Ь2Е2 -
ExF,
т == ¦
F,
A1.14)
После того как первое приближение построено, надо перейти ко
второму приближению, вычислив значения a*, b*, E*, F* (по пер-
первому приближению) и вставив в формулы A1.13), A1.14) вместо
а2, bv
F —U F*
?2> Z7!, /^2 величины
аг-\-а*
F -4—
—2	• —о	 соответственно. Таким образом, получим новые
значения х, у, о, -[ — второе приближение. Этот процесс нужно
повторять до тех пор, пока не будет достигнута требуемая точность.
На протяжении этого параграфа мы говорили несколько раз
относительно ограничений, при которых наши рассуждения были
справедливы. Так, например, мы считали, что в участках, нас инте-
интересующих, не возникало поверхности сильного разрыва, мы предпо-
предполагали одно-однозначное отображение плоскости (х, у) на плоскость
(vx, vy) (что существенно было при оценке погрешности приближён-
приближённого метода). В § 20, где мы будем говорить о движениях, про-
происходящих в одной части плоскости с дозвуковыми скоростями,
в другой — со сверхзвуковыми скоростями, мы вернёмся, следуя
Христиановичу, к детальному и строгому обследованию всех случаев,
которые могут представиться в сверхзвуковом поле; а сейчас
перейдём к конкретному рассмотрению отдельных простых примеров.
§ 12. Движение газа вне выпуклой поверхности. Обтекание
угла, большего чем я. Выход из отверстия. Движение внутри
трубы. Сопло Лаваля. Рассмотрим некоторые движения со сверх-
сверхзвуковыми скоростями.Предпола-
скоростями.Предполагаем, как в предыдущем пункте,
отсутствие сильных разрывов.
Начнём с задачи о движении газа
вокруг искривлённого контура,
выпуклость которого всегда на-
направлена в сторону газа. Пред- \^\\\\\\\\\-л
положим, что контур предста-
представляется при х < 0 в виде отрица-
отрицательной оси Ох, а при х > 0 — в
виде кривой, лежащей «под» осью
положительных х-ов и так, что
касательная к этой кривой меняется непрерывно и в точке О совпа-
совпадает с осью Ох (рис. 23). Вдоль оси Оу поток безграничен. Считаем,
что поток, бегущий над прямолинейной частью контура, постоянен
но величине и направлению и имеет скорость, по величине большую
Рис. 23.

70	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. X
скорости звука. Пусть в этой области vx — vx > а#; vy = 0. Прове-
Проведём характеристику первого семейства через точку О. Характери-
Характеристика первого семейства ОА, проходящая в плоскости (х, у) через
точку О, будет, как мы уже знаем, прямой линией [всем её точкам
будет отвечать в плоскости (vx, vy) одна и только одна точка
М'(v1, 0)], значит, во всех её точках у'х будет иметь одно и то же
значение. Чтобы найти движение «вправо» от характеристики ОА,
напомним, что вследствие постоянства скорости на ОА, по ска-
сказанному в предыдущем параграфе (задача 3), мы будем здесь иметь
не только
вдоль каждой характеристики второго семейства, но и вообще
во всей части плоскости, ограниченной контуром и характеристикой О А.
Это значит, что скорости этой части плоскости все расположатся
на одной и той же эпициклоиде второго семейства, проходящей
через М''. Проведём эту эпициклоиду. Чтобы найти теперь скорость
в какой-либо точке Мх контура, достаточно провести в плоскости
(vx, vv) радиус-вектор, параллельный касательной к контуру
в точке Мх; пересечение Мх этого радиуса-вектора с проведённой
эпициклоидой и даст искомую скорость. Зная М\, мы можем найти
направление элемента характеристики первого семейства, выходящей
из Мх, в плоскости (х, у). Однако легко видеть, что вся характе-
характеристика первого семейства, выходящая из Мх, будет прямой линией,
так же как и характеристика ОА. В самом деле, перемещаясь
в (х, у) вдоль характеристики 'МХАХ, мы будем пересекать различ-
различные характеристики второго семейства (не обозначены на рисунке),
но в плоскости {vx, vy) всем этим различным характеристикам
отвечает, как мы знаем, одна-единственная эпициклоида второго
семейства, проведённая нами через М', скорости вдоль МХАХ най-
найдутся поэтому как пересечение эпициклоиды первого семейства,
проходящей через Мх, и всегда одной эпициклоиды второго се-
семейства, идущей через М', т. е. все скорости вдоль МХАХ
будут равны по величине и направлению скорости точки Mv
а отсюда и заключаем, что МХАХ есть прямая линия. Таким образом,
все характеристики первого семейства в нашей задаче будут прямые
лир и i (характеристики второго семейства будут, конечно, криволи-
криволинейны). Отметим, что, как в этом легко убедиться из рассмотрения
эпициклоиды, выпуклость контура ведёт к тому, что, по мере про-
продвижения вдоль контура «вправо», мы будем встречать всё большие

5 12]	ДВИЖЕНИЕ ГАЗА ВНЕ ВЫПУКЛОЙ ПОВЕРХНОСТИ	71
и большие значения скорости, причём характеристики первого
семейства будут становиться всё менее и менее наклонными к оси Ох.
Рассмотрим теперь задачу об обтекании угла.
Предположим, что контур при х < 0 совпадает с отрицательной
ветвью оси Ох, а при х > 0 имеет уравнение у =— ^ё$ох (Рис- 24);
по-прежнему над горизонтальной стенкой
и мы можем провести характеристику первого семейства О А, построив
предварительно точку М' {vx, 0) в плоскости (vx, v). Далее,
начинается обтекание угла, причём поток должен в конечном счёте
пойти вдоль стенки ОВ (рис. 24);
чтобы найти величину скорости этого
нового потока, достаточно найти пере-
пересечение N' характеристики второго
семейства, проходящей через М', с ра-
радиусом-вектором в плоскости (vx, vy),
параллельным направлению ОВ. Опреде-
Определив N', проведём характеристику перво-
первого семейства ОС. Мы можем сказать, что	Рис- 24.
в угле СОВ поток будет обладать всюду
постоянной скоростью, параллельной линии ОВ. Поворот потока со-
совершается, таким образом, внутри угла АОС. Пучок прямых, выходящих
из О (в том числе ОА и ОС), представит там характеристики первого
семейства, причём во всех точках каждой такой прямой, выходящей
из О, скорость будет иметь одно и то же значение, легко опреде-
определяемое из рассмотрения эпициклоиды второго семейства, проходящей
через М'.
Движение внутри угла АОС легко построить при помощи (П-4);
именно, для обтекания точки будем иметь просто
у — xtg$ + a) = 0.	A2.l)
С другой стороны, по A0.6), в нашем примере будет
^ctga,, A2.2)
где а, — угол Маха, отвечающий скорости г/, (когда C равно нулю),
т. е. угол между прямой ОА и осью Ох, причём на основании (9.22):

72	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Но A2.1) можно записать так:
_a) = -^- = tg6 или р -f- a = б,	A2.3)
где t) — полярный угол в плоскости (х, у), отсчитываемый от оси Ох
против часовой стрелки. Введём еще угол 9:, отсчитываемый по часо-
часовой стрелке от некоторой новой полярной оси из условия:
01 = «1 + ]/~йт агс ^ V^\ ctS «i — О-
Тогда A2.2) и A2.3) дадут:
у ^-i~r arc tg 1/ —j—j- ctg a =9,	A2.4)
или
По этой формуле, вспоминая выражение для ctg a A0.4), можем
найти величину скорости на каждом
Q -.Q	/	радиусе-векторе, проходящем через иа-
А
чало.
\ .-'"" / ^^^^^	Уравнения линий тока в полярных
координатах будут:
dr rdu,
к'	(г — радиус-вектор, vT — проекция ско-
скорости на радиус-вектор; v9 — проек-
проекция скорости на перпендикуляр к радиусу-вектору); при этом, так
как радиус-вектор есть в то же время характеристика, а угол
между скоростью и характеристикой есть а, то
и мы можем написать.
откуда для линий тока окончательно получим:
f
где г0—радиус-вектор точки, в которой 9]—0.
На рис. 25 сплошными линиями изображены две такие линии
тока. Полярная ось расположена в области, в которой происходит

§ 12]
ДВИЖЕНИЕ ГАЗА ВНЕ ВЫПУКЛОЙ ПОВЕРХНОСТИ
73
еще прямолинейное движение (Все продолжения линий тока образуют
угол тс/2 с осью 6j = 0, ибо при бх = 0 будет по A2 5) а = тс/2.)
Найдем еще крайнюю характеристику, после которой начинается
обтекание стенки у = — tg
уравнению
ox Ее угол Маха а2 будет удовлетворять
tg
а соответствующее 6 найдется по формуле
6 = а2 — р0.
В том случае, если стенка у = — ig%x отсутствует и газ выры-
вырывается под давлением pv связанным с vl уравнением Бернулли, в среду
с давлением р2, причем р2<Срх, поток газа будет поворачиваться
и скорость его будет расти до тех пор, пока не станет равной вели-
величине %>2, получающейся из уравнения Бернулли при данных & и i0.
Тогда для последней характеристики получим значение а = а2
из соотношения (9 21) (а2 — скорость звука при v~v2);
sin а„ =
v2
При этом угол 01 наклона струи газа после поворота вокруг
обтекаемого угла найдется по формуле A2.4) в виде:
Наибольшее значение получим, когда газ вырывается в пустоту;
здесь а2 = р2 = а2 — 0.
°1 — у ^ZT\ ~2
Если р2 > рх или если после
угла О (рис. 24) газ должен дви-
двигаться вдоль стенки _у ^ tg- $Qx, где
тс/2 > C0 > 0, наступает явление
сильного разрыва (см. § 13).
Рассмотрим задачу об истече-
истечении газа из отверстия.
Пусть газ вырывается из отверстия (две параллельные прямые),
причем скорость движения у места выхода АВ (рис. 26) имеет ком-
компоненты
Рис 26
vl > ах > 0 (а1 — местная скорость звука). Построив точку М' {vx, 0)
в плоскости (vx, Vy) (рис. 27), проведём через А характеристику

74
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. Г
первого семейства в плоскости (х, у), а через точку В — характери-
характеристику второго семейства (рис. 26). В угле ВС А имеем по-прежнему
поток с vx = vv vy — 0. Пусть давление в пространстве, в которое
выходит газ, будет р2. Построим в плоскости (vx, vy) круг ради-
радиуса v2, определяемого из уравнения Бернулли при р = р2. Двигаясь
по эпициклоиде второго семейства, проведённой через М!, дойдём
до этого круга в точке N' и таким образом узнаем направление
скорости после обтекания точки А. Аналогичным образом, привлекая
эпициклоиду первого семейства, проходящую через М', найдём
скорость Р' около точки В (вообще мы, оче-
очевидно, будем иметь симметрию по отношению
к оси отверстия). Зная N' и Р', проведём харак-
характеристики AD и BE и заполним углы CAD и СВЕ
, р'\	пучками характеристик (см. предыдущую задачу).
Пусть CD и СЕ будут криволинейные отрезки
характеристик второго и первого семейства соот-
соответственно, выходящие из С. Из рассмотрения
движения в углах мы будем знать эти линии,
а также будем знать скорости вдоль них. Поль-
Пользуясь способом, изложенным в задаче 2 преды-
предыдущего пункта, мы найдём теперь движение в кри-
криволинейном четырёхугольнике ECDF [точке F от-
отвечает точка Q' плоскости (vx, vy)] (см. рис. 27).
Уменье решать задачу 4 нам даст затем возможность найти движение
в области ADO (и ВЕН), где DO (и ЕН) — характеристика второго
(первого) семейства, проведённая через D (Е), причём попутно мы
сможем найти форму свободной поверхности АО (ВН)г). Определив
скорости на DO и DF {ЕН и EF), можем, решая задачу 2, найти
движение в четырёхугольнике DGKF (FЕНГ), где FK(FJ) — характе-
характеристика второго (первого) семейства, выходящая из F, а 0К(Н1) —
характеристика первого (второго) семейства, идущая из О (Н). Затем
решаем задачу 4 для области GKL{HIM), причём попутно определяем
и свободную поверхность (на этот раз криволинейную) и т. д. Мы
предоставляем читателю разбор деталей этой задачи. Мы получим
здесь, по-видимому, картину периодического сужения и расшире-
расширения струи, причём максимальная скорость достигается внутри
струи. Картина эта в общем хорошо согласуется с данными экспе-
эксперимента.
Рассмотрим теперь задачу о движении внутри трубы. Предположим,
что в некотором, может быть, криволинейном, сечении трубы АВ поле
Рис. 27.
') Легко убедиться, что это будут отрезки прямых, а всё движение —
плоскопараллельным потоком со скоростями, равными по величине v2.

12]
ДВИЖЕНИЕ ГАЗА ВНЕ ВЫПУКЛОЙ ПОВЕРХНОСТИ
75
Рис. 28
скоростей нам известно (рис. 28). Решаем сначала задачу 1, строя
последовательно и поле скоростей и все характеристики (в том числе
и крайние характеристики АС и ВС), выходящие из точек отрезка АВ.
Между характеристикой АС (ВС) и стенкой решаем задачу 3, в ре-
результате чего находим поле скоростей и характеристики (в том
числе крайнюю — СЕ (CD)) области АСЕ (BCD).
Решаем далее задачу 2 для области ECDF
(DF — характеристика первого семейства, иду-
идущая через D, EF — характеристика второго
семейства, проходящая через Е) и т. д.
Большой практический интерес предста-
представляет построение так называемого сопла Ла-
валя. Здесь речь идёт о получении в трубе,
в лабораторной обстановке, сверхзвукового по-
потока, который был бы в некоторой области
трубы постоянным по величине (заданной зара-
заранее) и направлению. Задача эта распадается на две части: во-первых,
требуется получить сверхзвуковой поток, во-вторых, надо сделать
этот поток равномерным. Получение сверхзвукового потока основы-
основывается на том факте, что если мы находимся за пределами крити-
критической скорости, то при увеличении скорости трубки тока будут
расширяться (в то время как при дозвуковых скоростях трубка тока
тем уже, чем больше скорость) (см. § 8 этой главы). Если поэтому нам
удастся, всё увеличивая скорость вдоль трубы (путём сужения трубы),
достигнуть в некотором сечении трубы критической скорости и если
затем мы заставим нашу трубу в направлении потока расширяться,
то мы и окажемся в области сверхзвуковых скоростей. Как практи-
практически это достигается, мы разберём позже (§ 21), тогда же мы
увидим, какого рода трудности
здесь встречаются. Сейчас же
предполагаем, что, например, А0В0
(рис. 29) есть сечение трубы (ось
трубы совпадает с осью Ох),
в котором скорости равны крити- о
ческой. Плавным расширением
добьёмся того, что на оси трубы
(последнюю мы считаем симметричной относительно оси Ох) получится
нужная нам величина скорости. Предположим при этом, что в нашей
трубе не возникло никаких поверхностей сильного разрыва (см. § 21).
Пусть нужная нам величина vx скорости получилась в точке А на
оси Ох. Теперь попробуем сделать так, чтобы, начиная от некоторого
сечения трубы, скорости всех точек были далее направлены вдоль
оси трубы и равны в точности vv Нам придётся для этого подо-
подобрать форму контура трубы, начиная от некоторой точки. Именно
Рис. 29.

76
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
(ГЛ Г
обратим внимание на точку В контура трубы, находящуюся на харак-
характеристике второго семейства, проходящей через ту точку А оси
трубы, в которой мы уже получили нужную нам скорость vv
Пусть Mv М2, ¦ ¦ . суть точки пересечения этой характеристики
с густой сеткой характеристик первого семейства. В плоскости
(vx, vy) точкам В, Mv М2, . . ., А пусть отвечают лежащие на одной
и той же эпициклоиде второго семейства точки в!, М\, Л1'2, ..., А'
(рис. 30).
Мы желаем получить «справа» от А поток, параллельный оси Ох
и имеющий повсюду скорость v1. Но тогда характеристика первого
семейства, проходящая через А, должна
оказаться строго прямолинейной, и направле-
направление её известно. Тогда в соответствии с тем,
что мы уже говорили при решении задачи 3,
и все характеристики первого семейства,
выходящие из Мх, М2, ..., также будут
строго прямолинейны. Это означает, что
скорости всех точек, лежащих на характе-
характеристике, идущей из Mv например, будут
равны по величине и направлению скорости
точки Mv Достаточно поэтому проделать
следующее построение: в точке В продол-
продолжаем стенку по касательной до пересечения
в точке С с характеристикой МХС (прямой).
Рис 30.	От точки С мы должны затем направить
стенку параллельно скорости в Ж, (т. е.
параллельно лучу ОМ\,рис. 30) и идти так до пересечения в D
с характеристикой M2D; начиная от D, направляем стенку парал-
параллельно лучу ОМ<ь и т. д. Так мы дойдём, наконец, до точки Е
(рис. 29), после чего контур следует взять паряллельным оси Ох.
Заметим, что отношение ширины рабочего сечения трубы к ши-
ширине критического сечения мы могли бы получить заранее из условия
равенства количества движения в этих обоих сечениях:
(F*—ширина критического сечения; р* — критическая плотность;
F — ширина сечения с потоком vx; pj — плотность при скорости vj.
В таблице на стр. 54 нами были даны значения p^Jp^a^ в функциях
от числа давления, или, если угодно, от vja.%.
§ 13. Движение газа около вогнутой поверхности. Образова-
Образование сильного разрыва. Движение внутри угла, меньшего чем я.
Обтекание профиля с острой передней частью. Пусть газ движется
вдоль контура, который при х < 0 совпадает с осью Ох, а при х > 0

13]
ДВИЖЕНИЕ ГАЗА ОКОЛО ВОГНУТОЙ ПОВЕРХНОСТИ
77
Рис. 31.
представляется в виде кривой, угол наклона касательной к которой
есть, по крайней мере, в некоторой области около О непрерывная,
монотонно возрастающая функция х. Касательная к контуру в точке О
совпадает с осью Ох. Поток, бегущий над прямолинейной частью
контура, имеет постоянную по величине и направлению сверхзвуковую
скорость: vx = vx > a*, vy — 0. Скс-
рость эту отметим в плоскости (vv,
vy) в виде точки М' оси vx и прове-
проведём затем характеристику первого се-
семейства через точку О (рис. 31). Эта
характеристика будет прямой линией.
Прямыми будут также и все остальные
характеристики первого семейства, вы-
выходящие из различных точек Mv
М2, ¦ ¦ ¦ контура. Различие по сравне-
сравнению с задачей обтекания выпуклого
контура заключается, однако, в том, что чем дальше мы бу-
будем подвигаться по контуру от точки О, тем круче по отно-
отношению к оси Ох будут становиться характеристики. В самом деле,
перемещаясь по контуру, мы в плоскости (vx, vy) будем двигаться
по эпициклоиде второго семейства, проходящей через М' (см. первый
из разобранных в предыдущем параграфе случаев), причём точки
М\, М2	изображающие на эпициклоиде скорости точек О, Mv
М2, . .., получаются путём пересечения эпициклоиды с радиусами-
векторами, параллельными касательным в О, Mv M2, ... к рас-
рассматриваемому контуру; но тогда, по мере того как мы будем пере-
перемещаться от Ж] к М<ь и т. д., эти радиусы-векторы будут повора-
поворачиваться против часовой стрелки (вследствие вогнутости контура), сле-
следовательно, характеристика первого семейства, проведённая через Мх,
будет наклонена к оси Ох под углом ббльшим, чем характеристика,
идущая через О, и т. д. Но если это так, то обязательно найдутся
точки, в которых две характеристики одного и того же (первого)
семейства будут между собой пересекаться. Так как вдоль харак-
характеристики скорость имеет своё постоянное значение, то в месте
встречи двух таких характеристик мы получим, грубо говоря,
два разных значения скорости. Здесь наступает явление сильного
разрыва.
Чтобы найти точку А разрыва, нужно определить предел, к кото-
которому стремится точка пересечения характеристики, проходящей через О,
и характеристики, идущей _через Mv когда Мх приближается к О.
Уравнение характеристики ОА будет
= У[@. 0)х,
A3.1)

78	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
где у уО, 0) обозначает у[ в точке х — у = §{0)\ уравнение харак-
характеристики М{А будет
У — ДУо = У[ (д*о. дУо) (х — Дх0),	A3.2)
где ^xo, Ду0 — координаты точки М{ контура. Выразим координаты
вдоль контура - х0, у0 — параметрически через угол р наклона кривой
к оси Ох; тогда у1 вдоль контура будет функцией одного р; опре-
определим хл (абсциссу А) из системы уравнений A3.1), A3.2) (ищется
точка пересечения):
i @, О)-у,'(длсо.
наменатель на Д
х	к пределу, пол
Дх0—>0 и Ду0—>0, получим (—^-\ =0 :
1\ "Р /р=о J
Деля справа числитель и знаменатель на Др (угол наклона контура
в точке Мх) и переходя к пределу, полагая Др —> 0, а с ним и
Чтобы найти у'х в функции р, вспомним, что
где а — угол между характеристикой МХА и линией тока; но наш
контур является в то же время и линией тока, поэтому, вспоминая
определение а (9.22), а также принимая в расчёт, что «справа» от
прямолинейной характеристики первого семейства ОА будет выпол-
выполняться A0.3) с нижним знаком, получим без труда:
	/ dxa \ 2 ып а0 cos3 а0 _		/ dx0 \ 2 ып2 а0 cos2 a0
где
sin а0 = -^-.
Прежде чем решать нашу задачу дальше, посмотрим, что будет,
ко1Да на контуре имеется угловая точка. Сперва рассмотрим случай,
*) Формула эта справедлива только в том случае, когда кривизна обте-
обтекаемого контура будет отлична от нуля в точке О. С. Валландер показал,
что если I -—) = 0, то разрыв образуется впервые не на характеристике
\ах0) i о
A3.1), а на одной из следующих характеристик. В некоторых случаях разрыв
также может образоваться и не на первой характеристике даже при

§ 13]
ДВИЖЕНИЕ ГАЗА ОКОЛО ВОГНУТОЙ ПОВЕРХНОСТИ
79
когда вдоль контура (рис. 32):
у = 0 при х<0; y = ig
при х > 0 @ < % < т),
где гп — некоторая положительная величина, связанная с г^, о которой
будет сказано ниже. Поверхность разрыва начнётся здесь непосред-
ивенно у точки О.
Пусть слева набегает поток
По прохождении поверхности разрыва поток получит новую
скорость и станет параллельным наклонной стенке. Найдём величину
этой скорости, а также направление линии разрыва (последняя будет
прямой, ибо после её прохождения ско-
скорость опять будет всюду постоянной).
Обратимся к плоскости (vx, vy) и в ней
проведем гипоциссоиду G.14), отвечающую
7777777777777777777/ п'
Рис 32
Рис 33
скорости vv Построим радиус-вектор MOi под углом J3O к оси vx:
точка М\ его встречи с гипоциссоидой даст величину скорости по-
потока наклонной стенки (рис. 33), а описанный в § 7 приём по-
позволит найти направление ON, параллельное направлению разрыва
в Ох). Существенно при этом отметить, что наша задача допускает
решение, о котором мы здесь говорим лишь в том случае, если
угол р0 не будет слишком велик. Именно должно быть C0 < р+,
где р* — полярный угол в точке пересечения круга v = a+ с гипо-
гипоциссоидой, отвечающей нашему vx 2).
') Из двух точек пересечения прямой ОМ[ с гипоциссоидой одна всегда
находится в дозвуковой области (внутри круга радиуса яД другая — в сверх-
сверхзвуковой. Мы выбрали сверхзвуковой режим (точка М[). Эксперимент по-
показывает, что из двух возможных режимов осуществляется именно выбранный
нами. Строгого математического доказательства необходимости выбора
сверхзвукового режима ещё не имеется.
2) Если угол Ро бУДет больше, чем р*, но меньше, чем угол ртах, обра-
образуемый осью vx с тем радиусом-вектором плоскости (vx, vy), который
касается гипоциссоиды, то можно говорить по-прежнему о движении рас-

80
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Чтобы иметь возможность решать задачи обтекания угла при
различных значениях vx, следует изобразить заранее [в плоскости
(vx, vy)] семейстьо гипоциссоид, зависящих от параметра vl. Вводя
Рис. 34.
величины vja*, vja*, vyla* и заменяя в G.14) а\ через v\ посред-
посредством уравнения Бернулли, получим для этого семейства линий
уравнения	Vy ^
A3.3)
На рис. 34 изображено это семейство линий для различных vja^
(сплошные кривые) *).
сматриваемого типа, только теперь скорость после прохождения разрыва
станет дозвуковой.
Если jb > Pmaxi то решения рассматриваемого типа не будет — поверх-
поверхность разрыва отскакивает от точки О (см. ниже).
') Здесь же нанесены пунктиром кривые постоянных значений Ро+/ро_
(стр. 43).

13)
ДВИЖЕНИЕ ГАЗА ОКОЛО ВОГНУТОЙ ПОВЕРХНОСТИ
81
В рассмотренном нами случае угла простота заключается в том,
что после прохождения разрыва поток становится снова прямолиней-
прямолинейным, что линия разрыва есть прямая и что скачок энтропии всюду
постоянен [формула G.10) и т. п.], а потому движение остаётся
безвихревым. Обратимся теперь
к тому случаю, когда стенка
совпадает с отрицательной осью
Ох при х < 0, а начиная от
точки О переходит в криволи-
криволинейный контур, составляющий
в точке О с осью Ох угол ро,
малый, но отличный от нуля ').
Мы предположим для большей
иллюстративности, что стенка
от передней кромки до некото-
некоторой точки М является прямо-
прямолинейной (её уравнение: у = 77777777777
== t? Ро-*О и только потом на-
начинает плавно переходить в
кривую (рис. 35). Строим ги-
поциссоиду, отвечающую скорости vx набегающего параллельно
оси Ох потока, и находим направление разрыва О А около точки О,
так же как и в разобранном уже случае угла. Из точки М прово-
проводим характеристику первого семейства до пересечения А с по-
построенным элементом кривой разрыва. Вследствие прямолинейности
Рис. 35.
Рис. 36
отрезка ОМ, отрезок ОА линии разрыва будет строго прямолиней-
прямолинейным, скорости во всех точках области ОАМ будут постоянны по
величине и направлению и изобразятся одной точкой А' плоскости
(vx, vy) (рис. 36); движение будет здесь безвихревым, и характери-
характеристика МА будет строго прямой линией. Решим задачу 3 для области,
') Достаточно взять р0 < %, где Э„ есть угол, о котором речь шла выше,
6 Теоретическая гидромеханика, ч. II

82	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ 1
ограниченной характеристикой /ИЛ, контуром MNn и характеристикой
второго семейства (криволинейной) ANn, проходящей через Л. В этой
области задача может быть решена точно, ибо вдоль МА скорости
всюду одинаковы, так что здесь будет выполняться соотношение
{си. § 11, а также § 15). Далее начинаем приближённое графическое
решение.
Нанесём на характеристике ANn густой ряд точек Nv N2, ...;
им отвечают известные нам точки N'v N'r . . . эпициклоиды второго
семейства, проходящей через А'. Проведём через точку /V-, элемент
характеристики первого семейства ]Ч{В до пересечения в точке В
с продолжением прямой разрыва ОА. Скорость В' в точке В най-
найдётся на пересечении с нашей гипоциссоидой эпициклоиды первого
семейства, проходящей через Л/"^ Зная В' и N'2, построим с помощью
их элементы характеристик /V2P, первого семейства и SP, второго
семейства. Было бы ошибочно думать, что скорость в точке Р1 мо-
может быть найдена простым пересечением эпициклоиды второго се-
семейства, проходящей через В', и эпициклоиды первого семейства,
проведённой через N'2. Такое построение справедливо лишь для
безвихревого движения, а движение, происходящее справа от поверх-
поверхности разрыва и характеристики ANn, обязательно будет вихревым.
В самом деле, наклон линии разрыва в точке В найдётся как
направление перпендикуляра, опущенного из точки. О в плоскости
(ух, vy) на продолжение прямой Е'В', и так как В' не совпадает
с А', то наклон в точке В будет отличен от наклона в О или в А,
строго говоря, уже начиная от точки А, наша линия разрыва стано-
становится кривой, и только неточность графического метода заставила
нас заменить прямой линией ОАВ кривую линию разрыва, в то время
как на самом деле лишь касательная в точке А к линии разрыва
совпадает с прямой АВ. В соответствии с формулами G.2) и G.10),
&+ будет вдоль линии разрыва теперь меняться от одной линии тока
к другой, начиная от точки А, а тогда в формулах (9.18), (9.19)
нельзя положить Q = 0. Чтобы найти скорость в Рх, обратимся
к уравнениям (9.18) и (9.19). Перемещению от В до Р-, вдоль харак-
характеристики второго семейства, выходящей из В, отвечают изменения
скоростей, связанные соотношением (9.19). Заменяя, как всегда, диф-
дифференциалы конечными разностями, пишем:
Д*„ = (v у)Л — (vy)B; bvx = (vx)Pi — (vx)B; Ax=^xPi~xB.

§ 13]	ДВИЖЕНИЕ ГАЗА ОКОЛО ВОГНУТОЙ ПОВЕРХНОСТИ	83
Вследствие (9.19), точка Р[ плоскости {vx, vy) с координатами (vx)p,
(vy)Pi найдётся поэтому где-то на элементе прямой
V V +	(VV)
При Q = 0 мы должны были бы искать vx и vy на элементе прямой,
проходящей через В' и параллельной элементу эпициклоиды второго
семейства; если й =? О, мы должны по A3.4) искать (vx)p^ и (vy)pl на
прямой, параллельной той же эпициклоиде второго семейства, не
проходящей через точку В'. Чтобы построить эту прямую, мы дол-
должны знать правую часть A3.4). Туда входят известные в точке В
величины v, a, y'2, v и хр — хв. Таким образом, нам надо только
узнать
о_ а2 р rf&
ч. — 1 9 d<\> '
Заменим снова db на Д& и d^ на Дф, причём для определения 9
в точке В напишем:
Так как «слева» от поверхности разрыва vx — v{ = const., vy = 0,
то, очевидно, там будет
(pi =
но линии тока не претерпевают разрыва, а только изламываются при
переходе через поверхность разрыва, поэтому можно положить
Переходя к определению ЬА и Ьв, заметим, что здесь, очевидно,
идёт речь о Ь+, так что надо применить формулы G.2) и G.10):
9,
2а?
где уА и <рв — углы наклона нормали к линии разрыва в точках А
и В соответственно.
Точка Рх (хР|, ypj лежит на пересечении характеристики ВРХ
и характеристики первого семейства N2PV Перемещаясь по BPV мы
6»

84	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
будем двигаться в плоскости (vx,vy) по прямой A3.4); перемещаясь
по N2PV мы будем, очевидно, двигаться в плоскости {vx,vy) по
прямой
. 1 ,	.	/ aQ.
Vy — VyN, + , ,, (VX — VXN2) = —
A3.6)
Ho (Q)N = 0, ибо N2 лежит ещё в безвихревой области. Таким об-
образом, перемещение по A3.6) есть перемещение по элементу эпицик-
эпициклоиды первого семейства, проходящей через Л^, и мы найдём точку
Р'х на пересечении этой последней эпициклоиды с элементом прямой
A3.4). Зная Р'{, проведём обе характеристики РгР2 и РгС, где
Р2 — точка, лежащая на характеристике первого семейства, выходя-
выходящей из N3, а С — точка линии разрыва. Скорость в С найдётся как
точка С пересечения прямой (9.18) [типа A3.6)] с гипоциссоидой,
скорость же в Р2 — как точка Р'2 пересечения прямой (9.19) [типа
A3.4)] с эпициклоидой первого семейства, идущей из N'3. Нам при-
придётся в обоих случаях знать Q в точке Рх; чтобы определить {d^jdif)p t
заметим, что изменение dty, происшедшее благодаря перемещению
от В к Pv будет
или
ДФ = - ?в (vyB - y'iBVxB) {xPi - хв),
причём
р. х — 1	2а?
+	(! +1?2 <?У
г + ТТ7ГТ (+? ?вУ
что же касается Д&, то оно может быть получено интерполированием,
ибо, например, изменение 9S — ЬА известно. Нужно помнить только,
что если окажется фр < фл, то надо просто положить QPi = 0.
Определив скорости в С и Р2, мы можем по указанным выше ре-
рецептам найти в этих точках Q, а также построить характеристики
CQ{ и /^Qi- Скорость в Qj (не обозначена на рисунке) найдётся
затем как пересечение в плоскости (vx, vy) элементов линий (9.18)
и (9.19), отвечающих точкам С и Р2 и т- Д- Наша задача, таким
образом, будет решена.
Формулы (9.18) и (9.19) представляют то неудобство, что в пра-
правые части их входит dx; таким образом, мы как бы отдаём предпо-
предпочтение координате х перед координатой у, в то время как они равно-
равноправны. Вспомним, однако, что направление прямой (9.18) или (9.19)

131
ДВИЖЕНИЕ ГАЗА ОКОЛО ВОГНУТОЙ ПОВЕРХНОСТИ
85
[где вместо dvx и dvy стоит vx — (vx)M, и vy — {vy)M,] легко опре-
определяется; чтобы провести эту прямую, нам, таким образом, доста-
достаточно узнать, на каком расстоянии 8 от точки М' плоскости (vx, v )
она проходит. Согласно известному правилу аналитической геометрии,
чтобы найти 8, приведём (9.18) и (9.19) к нормальному виду, умно-
жая их на
соответственно. Замечая, что эле-
мент дуги ds вдоль характеристики первого семейства будет
dst = Ydx2-{- dy2 =\dx\
а вдоль второго
ds2 = | dx
мы получим величину о в виде:
Но
8
V
=
а\ ¦
v2
У\
1 + уГ \
г
У2
-У[2У~1+У2
У\Уч
1 + у\ +У2 + У\ Уг
и вследствие свойств корней Квадратного уравнения (9.11):
УхУг	vl-a2
Таким образом,
A3.7)
Остаётся только определить, в какую сторону следует отложить 8,
для чего достаточно найти, например, знак проекции о на ось Ох.

86	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Рассматривая (9.13) и (9.14), легко убеждаемся, что, так как
Sign tip,.S = Sign |(yj — y'2)~ rfjfj ') .
Для практических вычислений удобно, как всегда, ввести безразмер-
безразмерные величины: v, а, &, <|>, 8, s, связанные с v, a, ... соотноше-
соотношениями
v = atv; а — а^а; 9 = &,&, Ф = р1с^ф, 8 = сД s — ls,
где / — произвольная величина. Замечая, что ai = x9Jpi~', и заменяя
в A3.7) а2 по уравнению Бернулли, мы придем к следующему выраже-
выражению для 8:
8 =
Зх-1
*+l
4x
'1, 2
где v, = -
x—1
2x
x—1
— COS f
1/*
x + 1 v[
Изложенная здесь вихревая задача была впервые решена Ф. Фран-
клем.
Несколько слов о решении задачи, о которой мы говорили в на-
начале этого пункта. Пусть точка А есть первая точка характеристики
первого семейства, выходящей из О, в кото-
которой образовался сильный разрыв (рис. 37).
В области между прямой ОА, контуром и
характеристикой АВ второго семейства, про-
проходящей через А, мы имеем, вообще говоря,
течение с прямолинейными характеристиками
первого семейства. Но дальнейшее решение
_л задачи ничем не будет отличаться от реше-
решения уже разобранной задачи об обтекании
углового контура, причём линия АВ будет
играть роль линии ANn (рис. 35).
Рассмотрим теперь пример. Пусть на неподвижную пластинку АВ,
наклонённую под углом Ро(<Р*) к оси ®х' набегает поток, обла-
') Для характеристик 2-го семейства. Для 1-го семейства знак будет
обратным.
У/////Щ
У/////////"'
Рис. 37.

§ И)
КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ
дающий сверхзвуковой скоростью vx > аг, параллельной оси Ох,
Посмотрим сначала, что происходит вблизи пластинки. Над пластин-
пластинкой, начиная от точки А (рис. 38), поток будет непрерывно пово-
поворачиваться до тех пор, пока не станет параллельным направлению
пластинки (см. предыдущий пункт: обтекание угла, большего чем я);
далее, от точки В пойдёт линия сильного разрыва; пройдя сквозь
неё, поток снова станет параллельным оси Ох (см. начало этого пункта:
движение внутри угла, меньшего чем тс). Под пластинкой в точке А нач-
начнётся разрыв, и поток станет параллельным к направлению пластинки;
около же точки В вдоль характеристики
поток начнёт плавно поворачиваться (об-
(обтекание угла, большего чем те) до тех
пор, пока, пройдя последнюю выходя-
выходящую из В характеристику, не станет вновь
параллельным оси Ох. Отметим теперь
точки Е и D, в которых линии прямо-
прямолинейных разрывов пересекаются с край-
крайними характеристиками BE и AD, про-
проходящими через В и А соответственно.
Характеристика EF, идущая через Е,
будет, очевидно, играть роль характери-
стики ANn на рис. 35. Таким образом,
от точки Е начнётся искривление линии
разрыва, образование вихрей и искривле-
искривление характеристик; аналогичную роль
играет характеристика CD. Таким обра-
образом, на больших расстояниях от пластинки
движение будет носить весьма сложный
характер. Так, по Ландау, там должны возникнуть дополнительные
поверхности разрыва. Мы можем ожидать, что только в области
Ур < У < Уп
мы будем иметь сзади пластинки скорости, постоянные по величине
и направлению. Заметим при этом, что скорости будут различны
сверху и снизу от линии, проходящей через В параллельно оси Ох;
в этом легко можно убедиться из рассмотрения эпициклоид плоско-
плоскости (ух, fу) и гипоциссоид.
§ 14. Крыло в плоскопараллельном сверхзвуковом потоке.
Приближённые формулы Аккерета, Буземана, Донова. Гиперзву-
Гиперзвуковые движения. Парадокс Эйлера-Даламбера справедлив не только
для несжимаемой, но и для сжимаемой жидкости, но лишь для случая
дозвуковых скоростей. Крыло, двигающееся со сверхзвуковой ско-
скоростью, обязательно подвергается действию сопротивления (так назы-
называемого, волнового) и подъёмной силы, причем эти силы, вообще
Рис 38.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. Г
говоря, значительно превышают обычные силы, происходящие за счёт
образования вихрей в пограничном слое крыла.
Пусть крыло помещено в поток сжимаемой жидкости, бегущей
параллельно оси Ох со скоростью vx > at. Предположим, что крыло
имеет острую переднюю кромку (поместим на ней начало коорди-
координат О) (рис. 39) и острую заднюю кромку (точка Р). Проекции на
оси Ох и Оу сил, действующих на крыло, делённые на величину дТ,
где q = p^zfi/2, а Т—«хорда» крыла, т. е. длина ОР, обозначим
через
Сг и С
Тогда,
у.
очевидно, будет
х~1т\ .1
A4.1)
A4.2)
где s — длина дуги вдоль контура крыла, \i — угол касательной
к контуру с осью Ох, знак «в» означает, что величина вычисляется
в точках верхней части контура, а «н» — в точках нижней части кон-
контура. Угол р положителен, если он откладывается против часовой
стрелки от оси Ох и отри-
отрицателен, если он отклады-
откладывается по часовой стрелке.
Касательная к контуру на-
направлена в сторону возра-
возрастания дуги s. Дуга s от-
считывается как для нижней,
так и для верхней ветви
контура от точки О.
Чтобы найти рв, мы
должны отдельно решить
задачу обтекания контура,
состоящего из отрицатель-
Рис. 39.	ной части оси Ох, верхней
части крыла и прямой, па-
параллельной оси Ох и выходящей из Р (жидкость расположить «над»
этим контуром). Аналогичным образом рк получится, как давление
на крыле, образующееся в результате обтекания контура, составлен-
составленного из отрицательной оси Ох, нижней части крыла и прямой (парал-
(параллельной оси Ох), выходящей из Р.
Заметим, что если бы оказалось, например, что для всех точек
верхней части контура

4 14]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	89
(крыло лежит «под» осью Ох), то характеристика первого семей-
семейства, выходящая из О, была бы прямолинейна (так же как и все
характеристики первого семейства, начинающиеся в разных точках
верха крыла), и мы могли бы найти рв в функции от [Зв, т. е.
в функции от места на крыле, совершенно точно. Для этого доста-
достаточно было бы написать
(считаем, что рв@) —0), а загем, решив это равенство относительно
vB, вставить полученное значение vB в уравнение Бернулли [напри-
[например, в (8.10)], и разрешить последнее относительно рв. Аналогично
можно было бы найти рп, если бы оказалось
Р„>0.
В случае, если фвH > 0 и фнH < 0, перед крылом образуется
поверхность разрыва (рис. 35); предположим, что |(Рв)о1<Р*
и I (Рн)о I ^ Р*> Tor^a после прохождения разрыва скорости останутся
сверхзвуковыми. Наличие кривых линий разрыва, исходящих в обе
стороны от О, усложняет задачу, порождая, с одной стороны, искри-
искривление характеристик обоих семейств, с другой стороны, — вихри.
Графический метод, изложенный в предыдущем пункте, позволяет
и здесь решить задачу до конца. Однако, он не даёт готовых окон-
окончательных формул расчёта (для Сх и Су, например), а заставляет
решать задачу для каждого случая отдельно, так сказать, арифме-
арифметически; кроме того, графический метод может здесь привести
к большим неточностям, так как характеристики МА, МгВ и др.
(рис. 35) будут практически почти параллельны линии разрыва АО.
Однако для случая тонких и мало наклонённых к оси крыльев
(малые абсолютные значения углов [Зв и рн) можно провести проме-
промежуточные операции в общем виде и дать готовые формулы, по
которым, зная форму контура крыла, можно найти непосредственно
давление в каждой точке крыла, а также Сх и Су. Это было сде-
сделано впервые Аккеретом A925 г.) для случая, когда углы ||3|
настолько малы, что членами, содержащими их квадраты, можно
пренебречь по сравнению с единицей (линеаризация уравнений);
Буземан и Вальхнер A933 г.) дали формулы, учитывающие квад-
квадраты углов |р|, наконец, Донов A937 г.) учёл третьи и четвёртые
степени углов | ф |. Мы изложим ход рассуждений и окончательные
результаты Донова; попутно мы получим, как частный случай, резуль-
результаты предыдущих авторов.
Рассмотрим произвольную точку N на нашей кривой линии раз-
разрыва OQ (рис. 39). В этой точке гидродинамические элементы
меняются скачком от значений V_ (vx, 0), pv p{, &x до значений
V+ {vx, vy), p, p, 9-. Любая пара значений элементов «справа» от

90	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
разрыва может быть связана одним соотношением. Уравнение гипо-
циссоиды G.14), в частности, связывает между собою vx и vy,
и значит, г» и р. Замечая, что скорость после прохождения разрыва
в точке N образует с осью Ох угол $N, который будет иметь тот
же порядок малости, что и углы рв контура крыла, решим уравне-
уравнение гипоциссоиды (написанное в координатах v и [3) относительно v,
представляя v в виде ряда по восходящим степеням [3. Простые
вычисления дадут нам (так как мы ищем четвёртое приближение, то
мы ограничиваемся здесь и далее членами с [З4):
где
ft, = —(M2—l)~v\
b2 = - (М2 - I) [\
= - (М2 — \)''ы [j + ~ М2 + j (х — 1) М4 +
Э*»-12*
24
M
16	IVI	4g
3*« М10] .
IVI j ,
С другой стороны, формула G.2) позволит вместе с G.10) найти
отношение &/B-J в функции от tgcp, a tgcp по G.11) выразится через
vx и г> и, следовательно, по A4.3) в виде ряда по $N. Производя
выкладки, получим :):
^L = l+Z3^+^+....	A4.4)
где
/ ^^М6(М2-1 Г''1;
*з~ 12 "'
/4 = ^=i М6 (М2 — 1)"а [4 + 2 (х - 2) М2 — (я — 1) М4].
То замечательное обстоятельство, что ряд A4.4) не содержит первых
и вторых степеней C^, позволяет заключить, что если мы пожелаем
') При разложении в ряд здесь удобно ввести сначала Др = р/р, — 1
и разложить отношение J)/d, по степеням Др (величина того же порядка ма-
малости, что и Р), используя лишь G.2) и G.10); уже в этом разложении будут
отсутствовать члены с Д в первой и второй степени.

5 lfl	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	91
учесть лишь первые и вторые степени C, отбрасывая члены с [З3
и далее, как малые (приближения Аккерета и Буземана), то мы
в праве будем считать bN/%1= 1; это значит, что в первом и во вто-
втором приближениях вихреобразование можно не учитывать и считать
всюду & = &х = const.
Остановимся несколько подробнее на первом и втором прибли-
приближениях. Так как с точностью до малых второго порядка включительно
вихрей не будет, характеристики будут здесь снова эпициклоидами
Рассмотрим на нашей линии разрыва OQ какие-нибудь точки
Nv N2, ¦.. (не изображены на рисунке) и через каждую из них
проведём по характеристике второго семейства до пересечения с кон-
контуром в точках Mv М2, . .. соответственно. Точкам Nlt Л/2, ...
отвечают в плоскости (vx, v ) точки гипоциссоиды N\, N%, . . . Так
it
как углы Рдг малы, то все точки N\, N2, ... будут располагаться
поблизости от двойной точки гипоциссоиды ф = 0, ¦# = !»[). Обра-
Обратим теперь внимание на то новое обстоятельство, что с точностью
до малых второго порядка включительно уравнения гипоциссоиды
и эпициклоид, выходящих из точки (vx = vx, vy = 0), совпадают.
В самом деле, для эпициклоиды будет по A0.3) и (9.22):
d2v \ 	(\	Vi (da
так что
I dv\	. 1 / d2v
что и доказывает наше утверждение. Но тогда все точки N[, N2, ...
можно считать, с точностью до малых второго порядка, расположен-
расположенными на эпициклоиде
а если это так, то, выходя из точек Mv М2, ... и двигаясь по ха-
характеристикам второго семейства N^MV N^vl2,. . ., мы будем в пло-
(кости скоростей выходить из N\, Nv .. . и перемещаться прибли-
приближённо всегда по одной эпициклоиде A4.5), проходящей через (v = v{,
Р = 0) (ибо все точки Nb N2, ... на этой одной эпициклоиде при-

92	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
ближённо лежат). Это значит, что с нашей точностью для всей
«верхней» области скорости связаны уравнением одной эпициклоиды
A4.5), совершенно аналогично тому, как это было в случае отсут-
отсутствия поверхности разрыва. В частности, имеем для точек контура
крыла:
&)?)	<»¦«
Решая это уравнение относительно vB (в виде ряда, расположенного
по степеням [Зв), получим:
Нам остаётся вставить это vB в уравнение Бернулли, чтобы найти
давление рв в функции от (Зв, т. е. в функции места на контуре.
Уравнение Бернулли
х-1
*»р	v\
2 ' V. — 1	~ 2 |" •/. — 1
v2 -*»р * v\
удобно заранее решить относительно р, взяв его в виде:
(для второго приближения надо затем положить &/&х?«1).
Вернёмся к третьему и четвёртому приближениям. Здесь нам
придётся считать 0 переменным по A4.4), а тогда, вместо уравнения
эпициклоид, на основании (9.24) мы должны написать вдоль характе-
характеристики NM, например:
Прибавим и отнимем в правой части A4.8) член	°'_ а' rflnft.
Получим:
jfn I г ! v М	sinct.cosct, ,. о sin a COS a — sin a, COS a.	-
d P + C —)| =	!—j—'dlnO-—	;—:—	-dlab. A4.9)
L	V^s/J	x i	xl
Проинтегрируем теперь A4.9), двигаясь по характеристике от
точки N до М. Получим:
Sin a, COS *! ,f_ .m
Л?
м
С sin a cos а — sin ax COS a, db
J	^—j -	-,

§ 14]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	93
что мы можем записать ещё, если применить к стоящему справа
интегралу теорему о среднем значении в виде:
sinaicosai &	»
[Q	О.	1
~	sin a COS а — sin а, COS а,
где Я—значение разности 	-.—	 для некоторой сред-
ней точки кривой MN.
При помощи A4.10) найдём теперь vM в функции от $м; для
этого нам надо выразить входящие в правую часть A4.10) величины
через элементы в точке М.
Прежде всего замечаем, что
где %0 — значение & на передней кромке (в верхней области), ибо &
сохраняется после прохождения разрыва вдоль линии тока, каковой
является линия контура крыла ОМ. Теперь вследствие A4.4) мы
можем написать
A4.11)
(как всегда, не выписываем члены, содержащие J3 в пятой степени и
выше); таким образом, наша разность логарифмов выражается через
известные величины (/3. 1$, ^о) и чеРез угол $N. Выразим теперь
Рдг-f-С(vN/at) также через угол $N. Мы уже знаем, что с точностью
до малых второго порядка включительно изображение скорости
точки N лежит не только на гипоциссоиде в плоскости (vx, vy), но
и на эпициклоиде, проходящей через точку vx = v{, J3 = 0. Значит,
мы можем ожидать, что p^-f l(vN/aJ — (.(vja)-^- б. м. третьего и
четвёртого порядка. Чтобы найти эти малые третьего и четвёртого
порядка, удобно ввести в рассмотрение величину v, определяемую
равенством
(J
Разлагая v в ряд по степеням [Зд,, получим:

94	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
где
2х2-52х +
м6],
м8__ 3-8* + 7»»-2х» ч
-f	32	m	96	М j*
Мы можем написать теперь:
~t~\dv2)v=vt	2	-f-
(J) (	)	- М> 5'г0 поРядка> A4.12)
причём
\й»/	\dv)v=v,
Г" fil\ = /^
Итак, мы можем выразить правую часть уравнения A4.10) через $N,
через Н и через известные величины; при этом $N входит в степенях
не ниже, чем в третьей. Тщательный анализ, на котором мы не мо-
можем здесь останавливаться, позволил затем Донову выразить $N через
координату хм точки М и через величины, характеризующие наклон
и кривизну контура в точке О (на передней кромке). Именно, при-
привлекая характеристику первого семейства NS, а также исследуя вид
линии разрыва и обеих характеристик, Донов показывает, что
$N=$o+-7^xM$o(-Jz)Q-i- б- м. третьего порядка, A4.13)
где
a d$/dx — производная' по х от угла [Зв, вычисленного как функция
одного х для верхней части крыла:

§ И]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	95
Но теперь ясно, что член, содержащий Н, может быть отброшен
как имеющий пятый порядок малости. В самом деле, Н имеет сама,
как разность двух функций, вычисленных при бесконечно близких
значениях аргумента, первый порядок малости, величина же |3о — ^дт
имеет по A4 13) четвертый порядок малости [(d$jdxH—мало].
Вставляя A4 13) в правые части A4 11) и A4 12), внося эти
выражения в сьою очередь в правую часть A4 10), полечим, соби-
собирая члены.
3s, (bo — br>	sin a, cos a, \	/ fl!3 \
~ 24 \ b, ~i" x-1 W хм?о \ dx Jo +" •'
Решая это уравнение относительно vM и выписывая члены до четвер-
четвертого порядка малости включительно, получим
^ = ^{1+6^4- ЬЛ -Ь ьТм + KVm + Fз ~ К) Р30 +
Ъ< - Ь\ - f- (ft, - Ц)]} р' + ^ (ft, - ftj) рзрж +
ii
Нам остается сделать последний шаг. вставит^ это vM в правую
часть выражения A4 7) для давления, и мы полечим давление в ка-
каждой точке М обтекаемого контура в функции от (Зж и от хм Вы-
Выражение Эд^/Эр входящее в A4.7), есть Ьо/Ь1 и по A4 4) будет
После элементарных преобразований получим окончательную формулу
Р, = Pi + Ч [аА + а?\ -}- a?l + aft + ajl @) + ам^в @) +
где |3В — значение угла наклона касательной в точке контура верхней
части крыла, в которой ищется рв, х — абсцисса этой точки,

96	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
рв@) — угол наклона касательной к контуру (верх крыла) в точке О,
коэффициенты имеют следующие значения:
2
-^- М4);
аъ = (М2 - \Гк [4 - 2М2-f |- (/ + 1) W
15 + 20х — 8у.2 +J№_ Мз _
^	12
__ 21 4- 20х Зх2	2х3 ju|10 , 3 -f- 2x y.2 f. l2
48	IVI "т"	48	lVI
' \ T ~i A	¦" l <TA "¦ I'
(М2 - 1) (-
¦
_1
_
	 Qv 	 fiv 2 I v 3	Q __ 7-y	7- 2
u" u^ ~| ^ fcЛ4 i	—	—
24	'" r	96
^ =-Ц^ М8 (М2 - 1Г 5 (- 1 + ^=^ М2 +-3-^=^ М4) •
Совершенно аналогичным путём для точек нижней части крыла
найдём:
Ы	МР2 @) +
вмР2 (°) Рн + aJl @) (^)о х] + б. м. 5-го порядка.

I 14] КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	97
Остановимся на характере различных членов, входящих в наши
формулы. Если бы мы пожелали ограничиться вторыми степенями [3,
то нам надо было бы сохранить лишь члены с а: и а2. Мы полу-
получили бы приближения Аккерета и Буземана. Далее, члены с av a2,
аъ, а4 — это как раз те члены, которые получились бы, если бы мы
из уравнения эпициклоиды A4.6) нашли v в виде ряда по степеням [3
и, вставив это выражение v в уравнение Бернулли A4.7) (при & = &j),
ограничились бы затем четвёртыми степенями [3. Так, если [Зв -^ О,
то, как мы уже говорили в начале этого пункта, линии разрыва OQ
не будет, и тогда членов с аы, аи, a3d, aid не надо брать вовсе
при вычислении рв. Наличие разрыва фв0 > 0, [Зн0 < 0) порождает
члены с аы	аы в рв и рн. Это — члены третьего и четвёртого
порядка малости. Интересно отметить, что влияние кривизны контура
в точке О (и следовательно, влияние вихреобразования, ибо если
контур прямолинеен около О, то по крайней мере на некотором
участке, прилегающем к О, вихрей не будет) появляется лишь
в четвёртом приближении — это член, стоящий при ам.
Переходя к вычислению Сх и Су по формулам A4.1), A4.2),
введём вместо углов [3 углы, отсчитываемые от хорды ОР крыла;
именно, обозначим
где [3 — угол наклона хорды ОР к оси Ох (на рис. 39 — отрица-
отрицательный). В качестве переменной интегрирования в интегралах A4.1),
A4.2) удобно взять длину t, отсчитываемую по хорде ОР от точки О.
При этом
что же касается хв и хш, входящих в давление, то их следует рас-
рассчитать по формулам
Y — f rnc й 	cin I
,l — sin
Тригонометрические функции углов C, которые входят в формулы
A4.1) и A4.2), надо, конечно, разложить в ряды, ограничиваясь
членами четвёртого порядка. Производя элементарные выкладки, по-
получим окончательно
х> -\- CXf -J- б. м. 5-го порядка,
7 Теоретическая гидромеханика, ч. II

98	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
где
о
с*. = Щ- f (К2 - РД dt+¦*- /(р;3 - р;3) л,
о	о
*i — \ ^az	ч~ ) г г" а\ъУ I Г "Г Рв (U)j ~Г й1нР 1 " Н" Рн (у)|
\	О J
+ тDаз —"
о	о
и
Су = Су -\- Су -\- Су -\- Су -j-б. м. 5-го порядка,
где
(в1 - 2«з)?3 - «1в [Р + Рв (О)]3 - а1и [f + р; (О)]3
Су4 = ~ Й2в [ р + Рв (О)]4 + Й2„ [ р + (Зн (О)]4 - ЙЗвр [Р + Рв @)f +
+ «з„ Р [ Р + Рн (О)]3 - -f а4в [1 + pi (О)]3
о
г
о
В этих формулах надо положить

§ 14]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	99
если р—j— рв @) > 0 (если линия разрыва сверху), и
«1В = Й2в = «Зв = «4в = °.
если р + Рв@)<0 (нет линии разрыва вверху); аналогично,
anH = and(n=l, 2. 3, 4), если р + р'н@)<0
и
аяв = 0(»=1, 2, 3, 4), если р +р|, @) >0.
Коэффициенты а,	а4, аи, ..., аы вычисляются по-прежнему.
Что же касается вычисления интегралов, то оно в отдельных кон-
конкретных случаях сильно упрощается. Так, например, если контур
крыла симметричен по отношению к прямой, перпендикулярной к ОР
и проходящей через середину ОР (например, если контур есть дуга
круга), то будет
т	г
о	о
Отметим, что если р = 0 и [Зн = 0, мы должны ожидать отрицатель-
отрицательной подъёмной силы, ибо здесь будет Су1 = 0, С 2 < 0.
Выбрав контур конкретной формы, мы можем заранее подсчитать
все коэффициенты, стоящие в Сх и Су при разных степенях [3; мы
получим тогда как для Сх, так и для Су выражения в виде полино-
полиномов четвёртой степени относительно р. Исключая C, получим Сх
в функциях от Су.
Остановимся более подробно на расчёте сил, действующих на
пластинку (рис. 38).
Здесь мы имеем точные формулы как для верхней, так и для
нижней частей профиля. Для верхней части пластинки имеем
по A4.5) и A2.2)
, A4.14)
где aj —угол Маха набегающего потока (sin<Xj= 1/M). С другой
стороны, для коэффициента давления Ср имеем здесь:
ръ ~ ~\ г ~ ч.
1*

100	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. J
В то же время
Pi
или, используя (9.22):
:__ /_f_\"«ri"	(HLJL Vl \"*~'"	/ sin2a v2 \"JTf
\al)	\ v t>i «i /	\ sln2aj v\ )
2 sin2 a
Отсюда, сопоставляя последнее равенство с равенством A4.15), по-
получим
-^-_*-1 A4.17)
Вставляя выражение для а из A4.17) в соотношение A4.14), полу-
получим явную зависимость C0 от Ср .
Над пластинкой имеем течение разрежения: так как v > vv то
a < ar Если при заданном М увеличивать наклон пластинки (|ро|
растёт), то а будет падать (движение по эпициклоиде, рис. 7 «вниз»),
пока при некотором предельном значении (|30 = Рпред) не обратится
в нуль; это будет по A4.14) для
Рпред
При этом рв = 0 образуется вакуум. При дальнейшем увеличе-
увеличении |poj будет всё время рв = 0.
Остановимся подробнее на случае так называемых гиперзвуковых
движений. Посмотрим, как ведёт себя число давления над пластин-
пластинкой при весьма больших значениях числа М> т. е. когда
В формуле A4.14) разложим правую часть в ряд по степеням a
и aj (если aj<^l, то и подавно будет a<s^ 1). Имеем
_ 2	2 х+1 з	2	2 *+1 з i
или, если ограничиться первыми степенями а и о^:

и по A4.16):
a = 0,4-^-^0	A4.18)

§ 14]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ	101
2 1	/
ЕСЛИ Р <	ЦТТп» Т° Р* НаД° СЧИТаТЬ Равным НУЛЮ (Рпред^
_2	Д
Отметим теперь два весьма важных обстоятельства. Во-первых,
формула A4.19) получена линеаризацией по отношению к 1/М, а не
по отношению к %. Структура её такова, что линеаризация её по
отношению к [30 даёт неточные результаты. Поэтому формула A4.19)
более точна при больших М, чем линейная формула. Во-вторых,
формула A4.19) содержит комбинацию
Эта комбинация характерна для гиперзвуковых течений, в чём мы
убедимся в дальнейшем при рассмотрении общей теории таких те-
течений (см. § 23).
По A4.15) и A4.19) мы получим
].	A4.20)
Закрепим значение К. Тогда, по A4.19), рв/рг будет закреплено,
а по A4.20) коэффициент давления окажется пропорциональным ква-
квадрату угла наклона пластинки.
Для нижней части пластинки имеем ещё более простые формулы.
Именно, аналогично A4.15) пишем:
Ср =-|_ (?» _ А.	A4.21)
Ри *М2 \Pi	/	К	'
Но теперь для определения отношения pjpx используем формулу G.15),
по которой
где v=rit/2 — tp — угол наклона поверхности разрыва к оси х. Те-
Теперь мы имеем по A4.22) и A4.21)
A4-23)
С другой стороны, деля G.17) на G.16), получим
A4.24)
Внося v из A4.23) в формулу A4.24), получим явную зависимость tgВо
от С .
Остановимся опять на гиперзвуковых движениях. Здесь угол v
будет мало отличаться от ро (см., например, построение v по рис. 4

102	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
и 5). Между пластинкой и скачком образуется очень тонкий слой
весьма уплотнённого газа. Картина течения напоминает ту, что отве-
отвечает теории Ньютона; согласно последней, частицы воздуха ударяют
о тело и затем продолжают двигаться уже по поверхности тела.
Надо отметить, что для М ^> 1 сходство с теорией Ньютона оказы-
оказывается не только качественным, но и количественным. В самом деле,
легко можно убедиться в том, что при очень больших М и неболь-
небольших Во коэффициент давления будет пропорционален В2, как это сле-
следует из теории Ньютона. В самом деле, сначала заметим, что
по A4.24) при малых |v| (а значит, и малых |В0|) величина
sin2v— 1/М2 будет малой более высокого порядка, так что при-
приближенно можно записать
2 cos /	1
Заменяя здесь sin v на v, cosv на 1, tgB0 на Во, получим
„ ^ * + 1 о
•~ 4 ™
или для очень больших М:
v^^±^-B0.	A4.26)
С другой стороны, по A4.23) имеем
Сря**ТТт(*-Мг)	(U-27)
или для М^>1 Ср ^^-j-v2, т. е. по A4.26) Ср «(-/+1)^.
По Ньютону мы должны иметь Ср = 23о. Обе величины будут со-
совпадать при ч=1. Любопытно отметить, что выражение для скорости
звука ]Лс/?Г будет совпадать с выражением ньютоновской ско-
скорости У RT также, если 4=1.
Формулы A4.25) и A4.27) для М ^> 1 ближе к точным форму-
формулам, связывающим С и Во, нежели аналогичные линейные формулы.
н
Действительно, по линейной теорш- мы имели бы просто (стр. 98)
На рис. 40 нанесены значения С для величин М = 3, 5 и 10 соот-
ветственно по точным формулам A4.23), A4.24), по линейному за-
закону и по формулам A4.25), A4.27). Из рисунка видно, что при
М = 5 формулы A4.25), A4.27) дают почти точные, а при ЬЛ= Ю —
весьма точные результаты.

14]
КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ
103
Так же, как и для верхней части пластинки, характерной вели-
величиной будет произведение К=М$0- Именно, комбинируя A4.27) и
A4.25), можно написать:
При значениях |Р@)|, близких к $* (определённому в § 13,
стр. 79), но меньших, нежели р„, можно пользоваться приближён-
приближённым метоюм, указанным в предыдущем параграфе. Еслир*< |[30|<[Зтах,
^s	 гиперзбук
	линейная теория
точные значения
четбертое приближение
2 4	6 8 Ю
Рис. 40.
причём (d$BldxH = (d$nldx)Q — 0 (кривизны равны нулю), можно
ожидать ещё, что поверхность разрыва будет «прилипать» к точке О,
хотя после прохождения поверхности разрыва около О возникнут
дозвуковые скорости. К анализу движения нужно теперь подходить
с большой осторожностью; так как движение после прохождения
разрыва будет происходить (во всяком случае близ точки О) с до-
дозвуковыми скоростями, уравнения движения будут теперь эллипти-

104	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
ческого типа; даже если обтекаемый контур будет обладать конеч-
конечным прямолинейным участком (как это было на рис. 35, или же,
если рассматривается, например, обтекание пластинки, поставленной
под углом | р | > р,,.), поверхность разрыва, образовавшаяся перед
ним, станет криволинейной, возникнут вихри, и задача окажется
весьма сложной. Более того, Крокко (Сгоссо) показал, что наличие
кривизны контура ускоряет «отскакивание» поверхности разрыва,
так что здесь прилипание может осуществляться лишь, если
I P [< Ркр- ™е P* < Ркр < Ртах-
Но, пожалуй, самой большой трудностью явится то, что мы выну-
вынуждены будем обратиться здесь к исследованию движений, происхо-
происходящих в одной части плоскости с дозвуковыми, а в другой со сверх-
сверхзвуковыми скоростями. В самом деле, если обтекаемый контур
ограничен в направлении оси Оу [например, если речь идёт об обте-
обтекании пластинки (рис. 38)], то можно ожидать, что его возмущаю-
возмущающее влияние на больших расстояниях пропадает и после прохождения
разрыва скорость на некотором расстоянии от контура останется
сверхзвуковой. В §§ 19, 20, 21 мы изложим некоторые работы,
относящиеся сюда.
Особняком стоят здесь результаты Релея, который дал точную
формулу для подсчёта давления за поверхностью разрыва.
Речь идёт об обтекании газом, имеющим сверхзвуковую скорость,
тупого (встречающего под прямым углом ось) профиля, симметрич-
симметричного относительно оси потока. Сосредоточим внимание на частице,
движущейся по оси симметрии. На некотором расстоянии от профиля
она пройдёт, как показывает опыт, сквозь поверхность сильного
разрыва, а затем добежит прямолинейно до профиля в точке Мо его
пересечения с осью симметрии с тем, чтобы после этого начать дви-
двигаться по криволинейной траектории, огибая профиль. Найдём давление
в точке Мо. Если не учесть появления перед стенкой сильного раз-
разрыва, то давление в Мо следовало бы рассчитать просто по уравнению
Бернулли, полагая в нём v = 0. Релей первый обратил внимание на
появление поверхности разрыва и на связанное с ним изменение
давления в Мо. Чтобы дать формулу Релея, предположим, что газ
движется с постоянным давлением pv постоянной плотностью pj и
постоянной скоростью vx>. При этом
1	*-1
а	i ni/i. Д2— * ~~ 1 7,2 | о . х	ft я *
Пусть
vXl > о*.
Образуется поверхность разрыва, причём

§ н]	КРЫЛО В ПЛОСКОПАРАЛЛЕЛЬНОМ СВЕРХЗВУКОВОМ ПОТОКЕ
105
Найдём сперва р+; полагая в G.15) coscp=l, получим
Р+ = v\ 2* y—1
рх	«J х+1
По уравнению Бернулли (8.10) можно написать:
х-1
A4.29)
р2
где р%— давление в Мо при наличии сильного разрыва, но по (8.9)
1 —
—1
так что
х-1
A4.30)
Но по E.10) и E.14):
Ъ.
Pi
р+"
и мы можем переписать A4.19) следующим образом:
^С— +<¦+¦>,*;]}•
Комбинируя A4.29) и A4.31), мы можем составить отношение
для различных величин vxjav
Здесь приведены для сравнения две таблицы: таблица А даёт р^Р\
в предположении, что существует поверхность разрыва, таблица Б
даёт р2/р1 по уравнению Бернулли, т. е. так, как если бы поверхность
разрыва отсутствовала. Рядом с vxjai мы помещаем всюду более
показательную величину vxja^.
Таблица А	Таблица Б
а,
а*
Рг
Pi
1
1
1,19
2
1,63
5,82
3
1,96
12,4
4
2,13
21,7
а,
Pi
Pi
1
1
1,89
2
1,63
7,80
3
1,96
36,4
4
2,13
149,1

106
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
На рис. 41 изображены две кривые (I по закону Релея, II по урав-
уравнению Бернулли) в функциях от числа Маха vxjal набегающего по-
потока. Для больших значений vxjal мы можем воспользоваться при-
приближённой формулой, полагая вместо
A4.19)
Ра. .
30
а,
и принимая вместо A4.20)
Р\
4х
2 3 4
Рис. 41.
4*
Формулы A4.30) и A4.31) суть
формулы Релея.
Значительно больше изучены
движения, происходящие со всюду
дозвуковыми скоростями. Прежде
всего нужно упомянуть здесь точную
теорию струй сжимаемой жидкости,
принадлежащую Чаплыгину; дока-
доказаны также теоремы существования
(Франкль и Келдыш, Христианович);
разработаны эффективные методы приближённых расчётов (Христиа-
(Христианович, Некрасов и др.) и даны приближённые оценки влияния сжи-
сжимаемости (например, теорема Прандтля — Глауэрта (см. § 29)). Прежде
чем переходить к изучению движения при дозвуковых скоростях,
остановимся ещё несколько на исследовании вихревого движения
и дадим приём построения различных классов вихревых движений
как с до, так и со сверхзвуковыми скоростями.
§ 16. Функция х- Примеры. Точные решения. Если движение
безвихревое, то система двух уравнений в частных производ-
производных (9.5), (9.3) первого порядка с двумя функциями vx и vy может
быть заменена одним уравнением второго порядка с одной функцией.
В самом деле, при 2 — 0 существует потенциал скоростей Ф, так
что
	 дФ		 дФ
v*—~5x' vy—~dy"-
Вставляя его в (9.3), мы получим наше уравнение:
{а\ - Фх)
»] Фхх -
= 0. A5.1)

§ 15]	ФУНКЦИЯ / . ПРИМЕРЫ. ТОЧНЫЕ РЕШЕНИЯ	107
заменяющее, в случае сжимаемого газа, уравнение
имеющее место для несжимаемой жидкости,
Рассмотрим, однако, общий случай, когда движение вихревое,
т. е. 2 Ф 0. Функция Ф здесь не существует, однако мы можем
ввести некоторую новую функцию и построить для неё единственное
уравнение в частных производных 2-го порядка, линейное по отно-
отношению ко вторым производным и решающее вихревую задачу. Чтобы
построить эту функцию, перейдём сперва от независимых перемен-
переменных х и у к переменным \ и ф, где ф(х, у) есть введённая выше
функция тока [ф(лг, у) = const.—уравнение линии тока], а \ —х.
Мы имеем, кроме уравнения Бернулли:
A5.2)
и условия адиабатичности
р = &х(ф)р\	A5.3)
одно из уравнений
dvx ¦ dvx 	 1 _д?	.. _ ..
dvy	dvy	I dp
и определение ф:
Замену переменных очень легко сделать, если написать сперва
по A5.6):
iy	A5.7)
и затем, заменив х на 5:
dx = dl,	A5.8)
решить A5.7) относительно dy:
dy== — d?-|	rfi]).	A5.9)
Мы можем теперь написать:
4-=-?-.	05.10)

108	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	(ГЛ. I
Удобно затем перейти к переменным ? и ф в A5.5). Получим:
dvy dvy дф \	dvy <Эф	1 др йф
"dT + ~5f 5*7 + ^"Эф" 7 = ~ 7 ф"7' A5Л2>
Заменяя vx и vy (не входящие под знаки дифференциалов) по A5.6)
и производя сокращения, получим окончательно простую формулу
duu	dp
A5ЛЗ)
Теперь мы можем легко построить то единственное уравнение,
о котором мы говорили. Из A5.13) заключаем о существовании
функици х(?> Ф) такой, что
Уравнение A5.10) может быть теперь написано, если принять в ра-
расчет, что г»? -f- v2 — v2, в виде:
4?- =	'	-Й-,	A5.15)
где w2 следует выразить по уравнению Бернулли и на основании
A5.14), в виде:
Уравнение A5.11) можно представить, используя A5.3) и A5.14),
в виде:
'	'('')""	A5.17)
Правая часть уравнений A5.15) и A5.17) не содержит функции у;
перекрёстным дифференцированием мы исключим таким образом у
и получим одно уравнение для определения функции х> уравнение,
о котором мы упоминали выше:
05.18)
Мы считаем всегда & и /0 заданными функциями ф. Определив из
уравнения A5.18) функцию х(?> Ф). мы можем затем, путём простых
квадратур, найти у(|, ф) из уравнений A5.15), A5.17). Линии тока
в плоскости (х, у) будут таким образом найдены: достаточно положить

g 15]	ФУНКЦИЯ 1- ПРИМЕРЫ. ТОЧНЫЕ РЕШЕНИЯ	109
в функции у = у (?, ф), ф = const. Компоненты скоростей г^ и г>у
и давление р найдутся из A5.16) и A5.14) как функции ? и ф и,
поскольку нам известны линии тока, легко могут быть получены как
функции от х и у. Задача о дгижении будет решена.
В качестве примера на применение функции х найдём все движения,
при которых давление сохраняется вдоль линии тока (см. § 6). Здесь
Р=РШ
т. е. по A5.14)
и, значит,
где q (ф) — неизвестная, так же, впрочем, как р (ф), функция ф. Теперь A5.15)
и A5.17) примут вид:
ду ^	9р-№
где р' = dpjd^, q' = dqjdty, a i>2 на основании A5.16), зависит лишь от ф.
Предположим сперва, что
т. е. что давление различно на разных линиях тока. Первое из уравне-
уравнений A5.19) интегрируется и даёт:
+5(ф),	A5.20)
где s{Y) — произвольная функция от ф. Дифференцируя A5.20) по ф и срав-
сравнивая полученное выражение со вторым из A5.19), получим:
лГ v* (а л. Ч'
У v~v+y
L dif р'2
р'2 \ р' j Щ р'
Но переменная 5 входит сюда явным образом; очевидно, что написанное
равенство будет иметь место лишь, если
^- = 0- -^--21 = 0
d'\i	di> p'
т. е. s = const., q'lp' = const., при этом четыре функции ф: v (ф), />(ф),
'о (Ф)> Э (ф) будут связаны двумя соотношениями: уравнением Бернулли
и формулой

110	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	(ГЛ. t
линии же тока, согласно A5.20), будут иметь вид E = х):
V2
(у + COnSt.J + (X + COnst.J = —jj .
Это — семейство кругов с общим центром.
Если р' = 0, то давление одинаково во всём пространстве. Вследствие
первого из уравнений A5.19):
а'% , /тч	ду	. d	a'	ds
Но по второму из A5.19):
ду __
(Эф ~
поэтому должно быть
= 0, т. е.	q — = const.,
V2
и семейство линий тока будет семейством параллельных прямых:
у = const, х 4- s (ф).
В качестве второго примера рассмотрим безвихревое движение с
$ = const., /0 = const.
Здесь величина скорости к выражается по уравнению Бернулли через
одно р:
»-1
v* = 2lt — 2~jp * .	A5.21)
Попытаемся найти все те движения, в которых также и направление ско-
скорости Eггол наклона её Р) зависит лишь от давления: [i = р (р), так что
vx = v cos p = ^ (р); t/j, = wy (/р). Тогда
dp	dvy	dvy dp
'^7==~Г= ~df~di'
и мы получаем, интегрируя это уравнение:
d'b d\	dvv
f	г ^
dp
где /, (р) — неизвестная функция от р. Удобно далее ввести в качестве
переменных вместо 5 и ф величины р и ф = ф. Тогда
5 = * = -^Ч +/,(/>): Ф = ф.	05.23)
и мы можем написать
dy dy rffy dy ду ду ( d2vy _

§ 15)	ФУНКЦИЯ у. ПРИМЕРЫ. ТОЧНЫЕ РЕШЕНИЯ	\\\
Вставим сюда ду/дх — ду/д1 из A5.15), а ду/д]> из A5.17); так как из A5.14):
то получим:
ду	fv dvv	Ър~1/Х	d лг—2	j	dv*
V —u2 dp '
ду
Первое из этих уравнений иитегрируется и даёт
У = --^4+/*(/>).	A5-24)
где /2 — произвольная функция р. Вставляя это у во второе уравнение,
видим, что для возможности движения выбранного нами типа должно быть
d4x	d2vv
dp vx dp
A5.26)
Уравнение A5.25) показывает, что связь между (J и р не может быть про-
произвольной; уравнение A5.26) мы используем при установлении краевых
условий. Обращаясь к A5.25), замечаем, что
" \	" 1 \( 2V' г / 2\	'2	'2
х х > У У 2 1-^ ^' ^ У' \ X	у
— IT (vi)" — ("' cos р — w sin ffi'J — (f' sin p + v cos JJ?'J = vv" — v2$'2.
Но тогда A5.25) даёт:
— = P'2.	A5.27)
С другой стороны, вследствие A5.21),
a*~ }'
dp2	%v	va	v3
где а — по-прежнему скорость звука. Таким образом, A5.27) примет вид:
/ dp \2 Ь2р~2/Х I v2 \
\~dj) =~Т* \~aY~1)'
Для возможности движений рассматриваемого здесь типа необходимо,
чтобы выражение в скобке в правой части было положительно, т. е. чтобы

112	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
было v > а Таким образом, отыскиваемое нами движение возможно только
при сверхзвуковых скоростях Далее,
dp dv dp	dv v
Поэтому, извлекая из обеих частей квадратный корень, получим
_
dv ~ аи
Но эта формула в точности совпадает с формулой A0.3), дающей связь
между риг» вдоль характеристик Следовательно, отыскиваемые нами дви-
движения будут такими, что одно из соотношений
С (—) т S = const.
выполняется не только вдоль характеристики, но и во всей области дви-
движений
Мы уже упоминали [ § 11 A14)], что здесь могут быть даны решения
в замкнутом виде. Эти решения мы сейчас и получили Обращаясь к опре-
определению /] н /2, привлечем контурные условия Предположим, что речь идет
об обтекании контура
y = F(x),	A529)
где F— заданная функция от х Заметим, что A5 23) и A5 24) при ф = const,
представляют параметрические (с параметром р) уравнения линий тока.
Пусть на обтекаемом контуре ф = 0 Тогда, вследствие A5 29), должно быть
05.30)
Но по A5.26)
dp
Л
dF df}
dfx dp
(/>>)
sP
dp
следовательно,
-|^- = tgp.	A531)
Уравнение A5 31), решенное относительно /,, и даст /, в функции JJ, т. е.
через />, уравнение A5.30) даст затем /2(/>) Задача будет решена. Отметим,
что по A5 21) и A5 28)
dvx dv cos В dv	. rfB
- — — - = —г- cos В — v sin я r —
rf/>	dp	dp v	^ dp
cos
т. e.
x-l
sinB&p-1/* /" t<2 ,
= *> 	„I	У р—1.
—	__	—	—
dp	f.vp sin a
и аналогично
dvv
sin (i;P) = - Psma sin (a q: p)	A5.32)

§ 15]	ФУНКЦИЯ у ПРИМЕРЫ ТОЧНЫЕ РЕШЕНИЯ	113
причём по A0.5)
arc fS (Vt~\- 1&а) +const-
Таким образом можно записать A5.23) и A5.24) в виде:
X = X 	COS (а х В)
A5 34)
V Sin а	. г
——— Sin (ax ft) <],+/,(/>).
При практическом использовании формул A5.34) надо вспомнить, что v и
sin а связаны соотношением (9.22) (уравнение Бернулли)
= ^±| 	*		A5.35)
х-1	2 sm2c(
' х— 1
и что р и sin а связаны, вследствие (8.10) и A5.35), соотношением
Тогда A5.34) примут вид:
cos
<¦
Так, например, при обтекании угла (задача, решенная в § 12) мы должны
положить
Тогда будет
т. е.
далее будет
Ч^
и, вследствие A5.33), вводя 6, по формуле A2.4), получим сразу
где
8 Теоретическая гидромеханика, ч. II

114
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. Г
§ 16. Дозвуковые скорости. Теория Чаплыгина. Примеры.
Переходя к движениям, происходящим со всюду дозвуковыми ско-
скоростями, мы начнём с точных решений, получаемых в явном виде.
Эти решения были даны в замечательных работах Чаплыгина, содер-
содержащих обобщения теории струй Кирхгофа — Жуковского на случай
безвихревого движения сжимаемой жидкости.
Имеем безвихревое движение и берём уравнение Бернулли в виде:
A6Л)
где р0 = const, вследствие отсутствия вихрей. В формуле F.5) пишем
роф вместо ф (иная нумерация линии тока)
Введём потенциал скоростей ср:
dx
	 ду
A6.3)
Оставим 9 и ф в качестве искомых функций, но введём в качестве
независимых переменных вместо координат х и у величину ско-
скорости v и угол наклона C скорости по отношению к оси Ох. В этом
и заключается преобразование Чаплыгина.
Прежде всего имеем:
vy = v sin J
По A6.4), A6.3), A6.2) будем иметь:
Решая эти уравнения относительно dx и dy, получим:
A6.4)
A6.5)
A6.6)
Это значит, что
дх_
dv
дх
— cos
dtp
-^ sin В -^_
pi> r dv
1	п Of
_Po.
pi/
sin
d?
d^
dv
dy 	 1 . q dy
~d$ v ' dp
A6.7)

161
ДОЗВУКОВЫЕ СКОРОСТИ ТЕОРИЯ ЧАПЛЫГИНА ПРИМЕРЫ
115
Нам остаётся только исключить хну путем перекрестного диффе-
дифференцирования уравнений, входящих в A6 7) соответственно. Мы по-
получим сперва (ро/р по A6 1) зависит лишь от v):
— sin ft df ро о dty 	 cos Э dtp	.pdji	d ( ?o \
v dv pu	l ov z^2 dp	r d^	rf^ \ ?v)
cos S d» pn	n d>V sin 3 дц>	, л di>	rf / Pn \
	^__ T . _± Z— Sltl D 	' 	 	¦—~	^"^ С О S О .' , 	 I * \
v dv pu	' dv v2 d$	' г dp	rfi/ \ pv /'
Умножая первое из	этих уравнений на —sin p, второе на cosj3 и
складывая, получим:
±JtL — JL(A. 1L	(\б r)
v dv ~ dv \"pTJ d? '	lU)'SJ
Умножая первое из наших уравнений на cos^, второе на sinp	и скла-
складывая, получим:
Представляя ро/р по уравнению Бернулли A6.1), будем иметь:
V2
d
а ро
dv p« dv
или, так как по (8.9)
Ро
— 1
1-
-/.—1 v2 а2
v	?v< ! *-l *
— 1 =М2— I,
¦*.+ ! а%
где М = г>/а, мы можем написать вместо A6.8)
ду	 М2 — 1 р0 <Эф
A6.10)
Наконец, введем вместе с С. А. Чаплыгиным вместо v величину т:
A6.11)
Мы получим окончательно:
1 —
У,—1
A6.12)

116	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	1ГЛ. 1
или одно уравнение для ф:
f 1 хГ"^^] 1
у. 4-1
~x1
\l ТГ	пб 134
Уравнения A6.12) и A6.13) решают вопрос о движении газа, если
известна область переменных т, [3, отвечающая этому движению, если
дано ф на границах этой области, если везде внутри области -с, C.
функция ф со своими первыми производными конечна, однозначна и
непрерывна, наконец, если всегда будет
0<т<-^=1, т.е. 0<v<a^,	A6.14)
и только в отдельных точках контура области может быть т = 0 или
х	j
i= . 1 • Остановимся на доказательстве определённости вида функ-
функции ф, удовлетворяющей указанным условиям. Применим доказатель-
доказательство от противного: пусть есть две функции <\)х и ф2> удовлетворяю-
удовлетворяющие нашим требованиям; покажем, что ф,—'-|>2 — 0- Функция ф3 = ф,—ф2
в данной области (т, р) конечна, непрерывна, удовлетворяет уравне-
уравнениям A6.13) и обращается в нуль на контуре. Умножим A6.13)
на фзйкйф и проинтегрируем по всей нашей области (х, [3). Обозначая
результат интегрирования через /, получим без труда
где двойной интеграл распространён на всю площадь (т, Р), одно-
однократный— на её контур. Но на контуре будет ф3 —0, значит, равен-
равенство / = 0 может иметь место лишь при условии равенства нулю
двойного интеграла, а при высказанных выше условиях подынтеграль-
подынтегральная функция в этом интеграле не может быть отрицательной. Ясно,
что надо принять эту подынтегральную функцию равной нулю, так
что внутри области будет везде
т. е. фз =
В работе С. А. Чаплыгина доказывается, на основании A6.14).
что и ср и ф, рассматриваемые как функции координат х, у, не имеют

§ 16]	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	Ц7
в области течения ни максимума, ни минимума; далее доказывается
с помощью A6.10) и A6.11), что р как функция от 9 и f не имеет
ни максимума, ни минимума, а х не имеет максимума (минимум т = 0).
Отсюда следует, что в области ср и ф не может существовать зам-
замкнутых кривых, вдоль которых х, у, г, р сохраняли бы постоянное
значение. Наконец, из A6.12) заключаем о невозможности существо-
существования максимума или минимума функций ср и ф от т и C.
После того как функция ф, а за ней ср определены, остается ещё
показать, что эти функции действительно представляют функцию
тока и потенциал скоростей, т. е. надо показать, что формулы для
ср и ф определяют х и C в зависимости от л; и у однозначно. Для
этого достаточно показать, что якобиан D(x, y)/D(x, [¦}) не обра-
обращается в нуль внутри области (х, C); рассчитаем этот определитель:
D (х, у) _ D (х, у) D (у, ф)
D (т, р) ~ D (Ь ф) ' D (т, р) •
Но на основании A6.6), A6.7) и A6.1):
D (х, у) __ A — х) *~' х—1
?>(?. ф) ~ а^т	х+1 '
и на основании A6.12)
> ZEL\
D(t.P)— 2т A-х) ^ х'
х4- 1
Отсюда видно, что если всюду будет 1	^-рх^-0, т. е. v-^a^, то
равенство
О(^.У) _п
возможно лишь при обращении в нуль обеих производных д§/д$
и d'ifjdx одновременно. Это может быть лишь в исключительных
случаях.
Обратимся к задаче о струях. Будем рассматривать течения газа,
преграждённые плоскими стенками, с краёв которых газ срывается,
обтекая затем области постоянного давления. Будем искать частное
решение уравнения A6.13) в виде:
где zn (x) — функция одного т, а п и а„ — постоянные.
Для определения 2„ получаем уравнение
\—1±±
т

118	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
ИЛИ
, 2 — v.
Положим теперь:
мы получим для определения уп уравнение:
y-=ft <16Л6>
Это есть известное уравнение для гипергеометрического ряда. Со-
Составляя характеристическое уравнение для показателя р в области
точки т = 0, имеем:
р(р — 1) + Bд+1)Р = 0,
т. е.
Pi = 0; р2 = - 2/i.
Сохраняя то решение для ф, которое остаётся конечным при х = 0
(т. е. беря р, = 0), мы будем иметь, пользуясь обозначением Гаусса:
\-e),	A6.17)
где
Посмотрим теперь, какие из задач указанного выше типа могут быть
решены при помощи функции
<(* = A -f В$ + 2 5««в (") sin Bяр + «„).
где я пробегает счётную последовательность возрастающих положи-
положительных значений, А, В, Вп, ап — постоянные.
Так как газовая струя ограничена линиями тока, то вдоль кон-
контура области (х, |3) функция ф должна принимать те или иные по-
постоянные значения. При этом, если рассматриваемая часть контура
отвечает плоской стенке, то вдоль неё [3 = const.; если же речь идёт
о свободной поверхности, то там будет Pi~ const., и по уравне-
уравнению Бернулли v~vx = const., а значит, и
= т, = const.
¦ 1
Сравним теперь нашу задачу с задачей о течении несжимаемой жид-
жидкости при тех же граничных условиях, т. е. при том же располо-

§ 16]	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	Ц9
жении стенок, при тех же скоростях в бесконечности и при тех же
скоростях на границе струй. Задача о струйном течении несжимае-
несжимаемой жидкости была решена по методу Жуковского в части 1. Сле-
Следуя этому методу, найдём связь между переменными
1п-^- + Ф = In]/ -^--f-/p
и
¦о/ = Ф -(- *ЧГ,
где Ф и I — потенциал скоростей и функция тока в соответствую-
соответствующей задаче о несжимаемой жидкости. Пусть мы получили
A6.18)
предположим, что / может быть разложена в ряд вида:
(где К, В, Кп — постоянные), так что
f	*п),	A6-19)
где А, Вп— некие постоянные. Наша задача о течении газа разре-
разрешится тогда формулой:
^(?)П^ап), A6.20)
где уп(~) есть гипергеометрический ряд A6.17), уп х = уп (ij), I —
постоянные, а А, В, Вп имеют как раз те значения, которые входят
в A6.19). В самом деле, при т = tL правые части A6.19) и A6.20)
совпадают, — значит, если было W — const, при -1 = 1^, то будет
ф^= const, при 1 = ^. Далее, если при каком-нибудь значении C .= [30
функция, определяемая A6.19), не зависит от т, то это будет лишь,
если sin BяC0 -f- ал) = 0 при всяком п, участвующем в сумме. Но
тогда и правая часть A6.20) будет постоянна при том же C. Таким
образом, ф из A6.20) будет удовлетворять граничным условиям за-
задачи. Формально A6.20) удовлетворяет уравнению A6.13). Таким
образом, если ряд A6.20) будет сходиться при всяком т < т^ а при
т = т1 будет стремиться к тому же пределу, что и ряд A6.19),
причём не только ряд A6.20), но и ряды, составленные формально
из A6.20) путём его почленного дифференцирования по х и C,
будут сходиться абсолютно и равномерно, то мы вправе считать, что
частные производные дф/ck и дф/<?C находятся путём дифференциро-
дифференцирования ряда A6.20) и что ф будет действительно искомой функцией
тока; тогда, используя A6.12) и A6.6), мы сможем по известному ф

120	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
найти <р, х и z. Задача будет решена. В частности, по A6.12) имеем
для d<f.
X— 1
— Я-
2т A-х)
2,(l-x)
Заменяя члены, стоящие при dx под знаком S, при помощи A6.15)
и выполняя интегрирование, получим без труда:
1
, A6.21)
—"	\  / /Л. 1
где
х = 1 4- — —
" ^ п Уп
Доказательства сходимости даны у Чаплыгина.
В качестве первого примера на применение метода Чаплыгина
рассмотрим удар струи газа в пластинку, перпендикулярную началь-
начальному направлению струи; предположим, что струя симметрично
делится пластинкой на две части, причём дана длина пластинки 11
и толщина струи на бесконечности — 2Ь, а также задана скорость
на границе струи.
В случае соответствующего движения несжимаемой жидкости
потенциал Ф и функция тока W связаны с In vjv и f) формулой
A6.22)
где Q/2 и —Q/2 суть значения W на верхней и нижней внешних
границах струи соответственно, а от — угол, под которым каждая
из двух частей струи наклонена к оси X на бесконечности [см.
часть 1, глава шестая, формула A7.10)].

§ 16]	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	121
Чтобы решить задачу о струе газа, разложим A6.22) в ряд и
отделим его действительную и мнимую части. Имеем сначала:
Щ- w = 2 In sin (В — i In -?-) — In [sin2 (б — Лп ^j — sin2 m] =
= 2 In sin U — i In ^A — In [cos 2m — cos 2 (В — / In -^j-\j -(- In 2 =
= 2 In Sin 	:	In Sin	:	In Sin
:In Sin:In Sin:.
Вводя вместо тригонометрических функций показательные, получим:
— In LI — e
. [e-2n(p-m)( ! t
In!T
~~22J~—n— t1 ~cos 2nm^ ^cos 2n$ ~l sin 2n^~
Наконец, для W получаем, вставляя 2 In vjv = In ijs:
sin
Таким образом, для газовой струи можно написать
Вследствие A6.21) мы можем затем написать E = 0):
(мы взяли С = 0, что означает, что при т = В == 0 мы берём не только
ф = 0, но и <р = 0). Остаётся только определить значение чисел Q
И т.; воспользуемся для этого известными нам величинами I и Ь.
Для определения Q представим поток жидкости через прямую,

122	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ t
перпендикулярную к оси Ох и находящуюся на бесконечности «слева»,
двумя способами: во-первых,
+ь \	+ь
j vp dy I	= J ulPl dy = 2bvlPl,
-ь
где
Pi = Ро | 1 —
во-вторых:
fvpdy] =*[fpo$-dy\ =PoQ;
\-г>	/jt=-oo \~ь
таким образом,
A6'25)
Чтобы найти от, запишем, что длина пластинки есть 21. Так так при
перемещении вдоль пластинки будет ф = const., т. е. й?ф —0, то
вдоль пластинки
кроме того, на пластинке
P^const. „ rf9 = -
Таким образом, вдоль пластинки
но, вследствие A6.6),
ду 	 sin 3 	 sin
Так что вдоль верхней части пластинки будет (f) =

§ 16]	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	123
и, следовательно,
Воспользовавшись второй из формул A6.12) для выражения dy/dz
и вспоминая уравнение A6.15), которому удовлетворяет zn = *nyn,
получим для /, вследствие A6.23):
В этом уравнении I нам задано, a Q определяется по A6.25). Та-
Таким образом, мы можем из A6.26) найти т. Остановимся ещё на
выражении сопротивления R пластинки. Очевидно, что
f	^
где р1 — давление, отвечающее скорости vl, т. е. давление позади
пластинки. Но по уравнению Бернулли [формула (8.10)]:
X	X
где р0 = J" а|р0. Таким образом, будем иметь для R:
со
D_ Q а %-4-1 V С")" 1 —cos2wm
"¦	Р 2 	^
у 	 ]
ч	_-
Интегралы, входящие в A6.26) и A6.27), легко вычисляются.
В самом деле, обозначая неопределённый интеграл A6.26) через

124	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
/л(т), имеем:
	1_	I
г-	*"' , A- ~s~ x~l
1-х) "-1 dx.
Но вследствие A6.15) последний член справа даёт 1/4/г2 /я (-с). Та-
Таким образом:
4л2
Что же касается неопределённого интеграла из A6.27), то его можно
представить в виде:
J A _ х)т=г dIn = A _ ху=т 1п + _^_ J A _ т)т^- /л (х) dx =
= A - '=)^Г'« + 1^Т-^Т V^V	A6.29)
Замечая ещё, что вследствие A6.28)
/я@) = 0 (ггл = хлул)(
напишем A6.26) в виде
а A6.27) даст вместе с A6.30):

Э 161	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	125
Первый и третий члены правой части сокращаются (см. выражение
для р{). Что же касается суммы, то она вычисляется в виде
V1 / 1\п+1 1 — cos 2nm те .,	.	,,,...
2/—*>	4я»-1 ==TA~COSm)-	A6.31)
1
Заменяя l/ _ 1 д« ^Ti — v\ и вставляя Q из A6.25), получаем:
A6.32)
Запишем ещё, используя A6.28) и A6.31), I из A6.30) в виде
1 =	S—	1-|A — cosot) +
-T1)-^r. A6.33)
1"	т у	т
Легко видеть, чтохл=1+-^ = Я
A6.31) на A6.33), получим окончательно
1
л+^ Я7ЛГ + ^^] ДбЛЯ
V (_ i)«+i ^«М A _ cos2«m)
, A6.34)
1 1 — cos m
1
где р1 — по-прежнему плотность позади пластинки.
Напомним, что т приходится определять из A6.33) после того,
как Q известно. В случае, когда b — со, т. е. на пластинку набе-
набегает поток бесконечной ширины, мы получим, очевидно,
от —0.
В качестве второго примера рассмотрим истечение газа из беско-
бесконечно широкого сосуда. Пусть давление во внешнем пространстве
есть pv давление внутри сосуда, на бесконечности, там, где ско-
скорость и=0, есть р0. Пусть р0 > pv Обозначим ширину отверстия

126
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
1ГЛ I
ВВ' (рис. 42) через 2Ь, а угол, который составляют стенки с осью
Ох, — через qn/2 (при q = 1 получим истечение из сосуда, у ко-
которого стенки служат одна продолжением другой). Для соответствую-
соответствующей задачи в несжимаемой жидкости мы будем иметь (lm. ч. 1,
стр. 321 и далее; мы применяем рассмотренную там нумерацию ли-
У	ний тока):
A!	w = Ф -f iW =
"	Q
— _Л ]n /Sin I
It
A6 35)
При этом, когда E = 0, мы имеем
справа действительную величину, т. е.
W = 0 (ось Ох— середина струи).
Если р = Tzq/2 (прямая АВ), получим
Рис 42.	W=—Q/2; то же значение W будет
на нижней границе ВС струи {vjv= 1,
> 0). Если же р = — тг^/2, то 47 = Q/2 (стенка Л'Л'), и если р < О,
= ©! (верхняя часть fi'C' струи), то тоже будет 5;
Мы можем представить w в виде:
к \ q ' q v
Разлагая в ряд In, получим:
¦ In 1 _е-2(Э-< In *,/?)« |. A6.36)
так чго, если vjvi=^(rzjxl)^, то
f!=l
Q ^ ~ q LL1
2n
Ряд этот — абсолютно сходящийся, и, применяя формулу A6.20),
получим для функции тока <j\ определяющей истечение сжимаемой
жидкости из того же сосуда и при той же скорости на струе:
n=l
Уп/q
A6.37)

§ 16]	ДОЗВУКОВЫЕ СКОРОСТИ. ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	127
Потенциал скоростей по A6.21) запишется в виде (В = — 1/<7):

__i
1 Г A-т) '-1
wj
Остаётся только определить Q. Чтобы сделать это, найдём, как
меняется у вдоль струи. Определим сперва вообще у как функцию
от т до р. Для этого напишем выражение для ду/дф. Имеем:
ду 	 ду ду . ду дф
Но
ду 	 1 йф.	 р v sin р (?у 	 1 69 	 v cos C
^ ~ ^ ТУ 1Г ~" "р7 "~Z5 ' lH}~~D!)x~ D~'
где
Таким образом,
Воспользовавшись A6.37) и A6.38), мы получим:
y
ft — 1
Интегрируя по (З, получим:
<-w — — (i — v Z^i^r) "^—г ° / T" l
3	1	1
cos ^ cos p dp — -sinp(l — x) x-',

128
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ [
где С(х) — произвольная функция от т. Так как при
должны получить у — 0, то следует считать
С(т)==0.
Вдоль линии тока т = xt (граница струи) имеем '):
= 0 мы
osMdp -^ -1 sinP.
О	и=1	J
Второй из интегралов, стоящих справа, легко вычисляется. В самом
деле, так как по известной теореме тригонометрии
т
2-
sin Bm + 1L
sin —
q
иы можем написать:
J
cos
cos
Ho
2az3 »r. .. 1 Г n
—!- яр = hm -к- I cos p
4	m-*co ^ J
/* sin \
sin-
'
sin —
причём знак плюс надо брать, когда у>0, и знак минус, — когда
У<0.
Итак,
Таким образом, вдоль границы струи
		1
я ,/ * + 1 2 ,,	чТ—Г	2
sin p 2j *«. sin -^
причём — it/2 будет для нижней границы ф > 0) и тс/2 — для верх-
верхней ф < 0).
') Подробности о сходимости рядов см. в работе С. А. Чаплыгина.

§ Кч	ДОЗВУКОВЫЕ СКОРОСТИ ТЕОРИЯ ЧАПЛЫГИНА. ПРИМЕРЫ	129
В точке В будет
в точке В':
Таким образом, мы получим связь между Q и Ь в виде:
j CO
n-l
со
0
2
1
sii
nBs
An
Мы вернёмся к несжимаемой жидкости, полагая 1/ -' а -с =
= vx, хп->\, 1—Xj —> 1. Так как
4	2 sin -1--
то
со	p
7 I sin В sin -^- rf8 —
/ sin Bm +1)^	! /
= 4-111X1 j sinp	—^-rfP-j-^ I sin0ctg--d3 =
•-'	z sin —	J
9	о	;i
= ±9| + 1 j sinpctg^-rf3,
0
причём верхний знак надо броть при 3>0 и нижний при 3 < 0.
Теперь получим
s^ctgl.3,
о
что совпадает с формулой A7.6) ч. 1, гл. VI; надо лишь, в согла-
согласии с принятым там обозначением, заменить vx на с, а щB на а.
9 Теоретическая гидромеханика, ч. II

130	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Определим ещё «сжатие струи» в сжимаемой жидкости.
Так же как и в жидкости несжимаемой, максимальное сжатие
будет иметь место в бесконечно удалённой части струи (иначе ско-
скорость получила бы максимальное значение где-нибудь внутри струи).
Если ширина бесконечно удалённой части струи будет Ь', то
и мы будем иметь
Нужно помнить, что движения, о которых мы говорили в этом пара-
параграфе, совершаются с дозвуковыми скоростями, в частности, в нашей
задаче о струе, максимальные скорости не должны превосходить
скорость звука, т. е. должно быть
«1 < «*.
что эквивалентно условию
?l <r Ь. —
Ро ^ Ро
в одном из следующих параграфов мы рассмотрим обратный случай:
1 ъ pi
§ 17. Дозвуковые скорости. Метод Христиаиовича. В настоя-
настоящее время существует значительное число работ, посвященных при-
приближённому решению задачи о движении газа с дозвуковыми скоростями.
Работы эти можно разбить на две группы: в первой группе работ
решение даётся последовательными приближениями, во второй авторы
ограничиваются той или иной линеаризацией задачи.
Мы изложим основные идеи метода последовательных приближе-
приближений, предложенные Христиановичем, отсылая за деталями непосред-
непосредственно к его статье !).
По-прежнему считаем движение безвихревым и скорости всюду
дозвуковыми. Введём прежде всего безразмерную скорость v — vjat
')Христиановнч С. А., Обтекание тел газом при больших дозву-
дозвуковых скоростях, Труды ЦАГИ, вып. 481, 1940.

§ 17]	ДОЗВУКОВЫЕ СКОРОСТИ МЕТОД ХРИСТИАНОВИЧА	131
и новую искомую функцию S(v), определяемую из равенства
V 1-Й- *
dS=l/ 	^Т1	A7.1)
W
где
« — ^	1 ¦
Уравнения A6.12) примут теперь, после простых преобразований, вид
где
A7.3)
Введём в рассмотрение комплексную величину S — $ и обозначим
через [)--|-^v некую совершенно произвольную аналитическую функ-
функцию от этого аргумента
= /(S — ф).	A7.4)
Связь между S, В, [л, v определится с помощью условий Коши—Римана;
в частности, будет:
dS	 д$_, dS_	 d$_	.._ ..
Так как
d<o ду dfi i d<p dS
dp d$ dp ^^ dS dp
то no A7.5) и A7.2) будет
Таким образом, если перейти в уравнениях A7.2) от S и В к [х и v,
то получим:
Наконец, л; и у можно связать с [х и v следующим образом. Согласно
формулам A6.6) предыдущего параграфа, можем написать:
dx _ cos p . dx	 po sin [
d<t	v	dty	P "v
dy 	 sinp #	_dy_	^ cos p
d<o	v	db P v
A7.7)

132
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Зная S (а значит, и ti), р, ср и ф в функциях от ia и v, мы сможем,
таким образом, найти х и у по формулам A7.7).
Обратим теперь внимание на то замечатетьное обстоятельств,
что если v^aO, то dS ^advjv, так что Ss: In f —j— const., a yKzal.
Но тогда при малых v уравнения A7.5) и A7.6) будут в точности
совпадать с уравнениями, описывающими в плоскости ([л, v) движе-
движение жидкости, имеющей комплексную скорость ese~li и комплексный
потенциат (р-|-/ф. При этом, как
нетрудно убедиться, будет х ?5й |л,
у ~ v.
Обозначим вообще
1,0
0,9
0,7
0.6
ui
Off
0,3
02
01
О
/
/
/
/
1
/
ПК'ФФ,
/
7(v)
У
\
\
О 0.1 в? 0,3 0,4 0,5 0.6 0,7 0,8 0,9 1,0
Рис 43
S = lnV.
Квадратурами можно найти из
A7.1) выражение для V в функ-
функциях от v. Именно, производя
подстановку
-i=4" = «2. A7-8)
пол\чим
4,(l7.9)
(h — uf 1 + и
где с — произвольная постоянная. Эту последнюю выберем так, чтобы
lim V/v—1. Так как вследствие A7.8) мы имеем
v~>o
Х= hm
h
(h-u)h~\l+uf
TO ПО 1УЧИМ
(A—1)'
ft-1
1h
; 0,7579.
A7.10)
На рис. 43 изображены значения V и ]/ЛГ в функциях от v. Эти
же величины даны в таблице II 1). Мы видим, что расхождение
между V и v становится заметным лишь в промежутке 0,6<;г»<;1,
а У К близко к единице в интервале О <С v -^0,5. Отметив это,
пойдём дальше.
До сих пор функция / в A7.4), связывающая S — ij3 с \l-\-1>,
бьпа произвольной аналитической функцией. Попробуем теперь,
') Рисунок и таблица заимствованы из статьи С. А. Христиановича.

17]	ДОЗВУКОВЫЕ СКОРОСТИ. МЕТОД ХРИСТИАНОВИЧА	133
Таблица II
V
0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,625
0,650
V
0
0,0500
0,0998
0,1493
0,1983
0,2467
0,2943
0,3410
0,3862
0,4307
0,4734
0,5144
0,5535
0,5722
0,5904
1
0,9995
0,9980
0,9954
0,9917
0,9870
0,9811
0,9742
0,9655
0,9571
0,9467
0,9353
0,9224
0,9156
0,9083
Ук
1
1
1
0,9999
0,9996
0,9991
0,9982
0,9965
0,9940
0,9899
0,9840
0,9754
0,9632
0,9553
0,9461
V
0,675
0,700
0,725
0,750
0,775
0,800
0,825
0,850
0,875
0,900
0,925
0,950
0,975
1
V
0,6080
0,6251
0,6413
0,6568
0,6717
0,6857
0,6988
0,7110
0,7223
0,7324
0,7413
0,7483
0,7546
0,7577
viv
0,9007
0,8930
0,8845
0,8758
0,8667
0,8571
0,8471
0,8365
0,8255
0,8138
0,8015
0,7882
0,7739
0,7577
0,9350
0,9221
0,9068
0,8925
0,8672
0,8416
0,8156
0,7740
0,7271
0,6788
0,6015
0,5092
0,3728
0
ориентируясь на указанное сходство с уравнениями обтекания в не-
несжимаемой жидкости, поставить краевые условия для дифференциаль-
дифференциальных уравнений A7.5) и A7.6) следующим образом. Рассмотрим в пло-
плоскости ([л, v) некий замкнутый контур С (например, профиль крыла
с задней кромкой — остриём — в точке А) и поставим следующие
условия:
1) на контуре С [3 совпадает с углом наклона касательной к оси [х:
2)	на бесконечности Voo^=e °°— заданная величина и (Зоо —0;
3)	если С имеет острую кромку Л, то в Л V имеет конечное
значение. Если тело острой кромки не имеет, то дано значение цир-
куляции Г вектора Ve вдоль замкнутого контура, охватываю-
охватывающего С в плоскости (jj., v).
Эта группа условий позволит полностью найти из A7.5) функ-
функции «S(|i, v) и J3 ([л, v). Следующие условия позволят определить
v) и (
4)	на С ф = 0;
5)	на бесконечности
6) наконец, потребуем, чтобы х = х(р, v) у=у([А, v), полу-
получаемые при посредстве уравнений A7.5), A7.6), A7.7), давали взаимно
однозначные отображения в соответствующих областях (t)., v) и (х, у).

134	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Прежде чем начать интегрировать систему A7.5), A7.6), A7.7)
при краевых условиях 1) — б), выясним, отвечает ли это какой-либо
гидродинамической задаче вообще и если да, то какой.
Вследствие условия б), контур С будет в плоскости (х, у) пере-
переходить также в замкнутый контур с (так как уравнения A7.7) опре-
определяют л; и у с точностью до произвольных постоянных, то можно
добиться того, что точке А будет отвечать какая-то заранее выбран-
выбранная точка а контура с). Вследствие 4) на с будет ф — 0; отсюда
на с будет
. дх _,— , ду —
ах = —— rfcp, ay = —~- dy
ду	ду
и по A7.7) вдоль контура имеем
Далее, бесконечно удалённая точка плоскости (jji.v) отвечает беско-
бесконечно удалённой точке плоскости (х,у); при этом в плоскости (х, у)
на сю будет вследствие 2):
где Vqo — то значение v, которому по формуле A7.9) отвечает
К —Коо. Наконец, используя A7.7), получим без труда вследствие 5)
на со в плоскости (х, у):
<fy 	_Ро__дф_	- ду_	 Po<ty_A
Если, например, мы сопоставим эти, полученные для плоскости
(х, у), условия с уравнениями A6.1)-—A6.3), то придём к важному
следствию. Всякий раз, когда мы решаем в плоскости ([л, v) систему
A7.5) —A7.7) при условиях 1)—6), мы тем самым решаем в пло-
плоскости (х, у) задачу обтекания некоторого контура сжимаемой жидко-
жидкостью, имеющей определённую скорость на с». Система A7.5)—A7.7)
может быть, однако, исследована гораздо проще, чем система урав-
уравнений для сжимаемой жидкости. Более того, для A7.5)—A7.7) могут
быть легко получены приближённые решения.
Именно — задача интегрирования A7.5) при краевых условиях 1),
2), 3) 1) замечательным образом совпадает с задачей определения
логарифма и угла наклона скорости в несжимаемой жидкости, обте-
обтекающей контур С при циркуляции Г и имеющей на бесконечности
скорость Усо. Христианович называет это движение фиктивным пото-
') Конечно, должно быть Уто < 0,7579, чтобы было vm < 1; см. уравнения
A7.8) —A7.10).

§ i/j	дозвуковые Скорости метод христианович^	135
ком. Таким образом, как только мы сможем найти обтекание нашего
контура С несжимаемой жидкостью — сразу же мы найдём V (а зна-
значит, по A7.9) и v) и р в функциях от |л и v. Если мы теперь сумеем
установить, какая точка плоскости (\х, v) отвечает той или иной точке
плоскости (х, у), то мы узнаем распределение скоростей (v, C)
в точках (х, у), а затем по уравнению Бернулли давление, и тем будет
решена задача обтекания с некоторой скоростью на оо какого-то
контура плоскости (х, у).
Соответствие между точками ([л, v) и (х, у) устанавливается
с помощью уравнений A7.6), A7.7) и условий 4), 5), 6). Именно,
будет:
= Г
м
s 3
А	К	A7.11)
Г I sin 3 г i Ро cos 8 ,т\ i
J \ V	р V	}
МА
(лгд, уА—координаты той точки плоскости (х, у), в которую мы
переводим точку А плоскости ([л, v)).
В частности, вдоль контура с будет (tf> = 0):
/cos 3 ,— ,	/* sin В _,— ,	... ,„.
-z^rftp+хд; у=/ -JLdy + yA. A7.12)
V	'J	V
х =
о	о
Чтобы нагляднее представить степень отличия контуров С и с, по-
построим функцию тока Ф и потенциал скоростей W для введенного
выше фиктивного потока несжимаемой жидкости, обтекающей кон-
контур С в плоскости ([л, v) с циркуляцией Г и со скоростью Voo на
бесконечности. В частности, будет
ф 	 cos В . дч sin В
дФ	V ' дФ	V '
так что (Ф =: 0) по A7.12)
}
+ хА\ у= I -^-^rrfv-f-yA. A7.13)
^	v, v аФ
Отсюда видим^ что для ^малых скоростей, когда Vjv близко
к единице_(и_ ср близко к Ф), контур С будет близок к контуру с.
Так как Vjv < 1, то контур с будет искажен по сравнению с С.

136	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
Для точного определения величин х и у по формулам A7.11) или
A7.13) надо выразить ср и ф через ц и v из уравнений A7.6) при
условиях 4), 5), 6). Чтобы это сделать, Христианович разбивает
каждое из ср и ф на два слагаемых:
ср0 и ф0 удовлетворяют уравнениям
С^ро 	л/ is "Yo • ^?о 	 л Ггу~ ^Yo	/1*7 1 А\
где Коо = К (vM), и краевым условиям:
A7.15)
При этом <р* и ф* должны удовлетворять уравнениям:
дч ~
при условиях
ф* = 0 на С и ср* и ф* ограничены на со.
Интеграция A7.14) при условиях A7.15) совершается элементарно.
Так как У^Ксо—постоянная величина, уравнение A7.14) означает,
что ср0-j-/ УКаэ% есть аналитическая функция от ji-f-jv, и краевые
условия A7.15) позволяют эту функцию определить. ср0 и y~K~Z%
совпадают с потенциалом скоростей и функцией тока в соответствую-
соответствующей задаче для несжимаемой жидкости. Однако при нахождении ср0
и У~Коо% не следует торопиться с определением «циркуляции» из
условия регулярности в остриё А контура С (как это надлежало бы
сделать в задаче обтекания).. Не надо забывать, что гидромехани-
гидромеханический смысл имеют не ср0 и ф0, а суммы cpo-f-cp* и фо-4-ф*, поэтому
надлежит оставить циркуляцию, входящую при определении ср0 и ф0,
назовём её Г*, неопределённой с тем, чтобы после нахождения <р*
и ф* найти Г* из условия 6) для ср и ф (т. е. требуя, чтобы обрати-
обратились в нуль интегралы типа A7.11) по замкнутому контуру, обходя-
обходящему вокруг С).
Для определения <р* и ф* Христианович пишет
-Ф,	A7.16)

§ 17]	ДОЗВУКОВЫЕ СКОРОСТИ. МЕТОД ХРИСТИАНОВИЧА	137
где срп(л=1, 2) удовлетворяют уравнениям:
A7.17)
а Ф и W:
причём ф! —ф2 = ч7 = 0 на С и все шесть функций ограничены на
бесконечности.
Уравнения A7.17) сводятся к уравнениям Пуассона. Путём остро-
остроумного и тщательного анализа, на котором мы здесь не останавли-
останавливаемся, Христианович не только даёт в эксплицитном виде (квадра-
(квадратуры) решения системы A7.17), но и находит точные выражения
главных членов функций ср„ и ф„ (п = 0, 1, 2) на бесконечности.
Затем он показывает, что Ф и ЧГ на бесконечности регулярны. Но
тогда известны главные члены функций ср и ф, и мы можем подо-
подобрать Г* так, чтобы выполнилось для ср и ф условие 6).
Далее Христианович получает:
Г
где
М9, = (^9 =Л
а Г—полное значение «циркуляции» в задаче о движении сжимае-
сжимаемой жидкости.
Мы уже упомянули о том, что при малых скоростях искаже-
искажение с по сравнению с С незначительно. При малых скоростях для
определения контура с можно ограничиться «первым приближением»,
полагая сря=;<р0, фяь;ф0. Остановимся на первом приближении
подробнее.
Обозначим
/^о = Ф*+^*1)-	A7.19)
') Разница по сравнению с Ф + i4f та, что здесь циркуляция будет Г,
а не Г. В случае отсутствия циркуляции Ф* +/ЧГ* = Ф-f-if'*'.

138	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
В работе Христиановича и Юрьева') дан анализ первого прибли-
приближения как для циркуляционного, так и для бесциркуляционного
обтекания. В первом приближении есть возможность выполнить
квадратуры типа A7.13) в общем виде и оценить сразу же то иска-
искажение контура, которое мы получаем в методе Христиановича.
Чтобы сделать это, заметим, что если мы ограничиваемся первым
приближением, т. е. принимаем
^р>сро = Ф*. ф« «[>„ = _* ЦТ-.
V /v»
то пользоваться точными формулами A7.11) и A7.12), дающими х
и у через ц и v, — нет смысла. Более того, если мы в этих точных
формулах используем наши приближённые решения, то выражения
? \ \	A7.20)
, sin в ,- , On cos В ,— I
dy = —^- dm + — —=±- йф
V	р	t/	j
не будут полными дифференциалами. Чтобы сохранить в правых
частях полные дифференциалы, мы должны дать новые, уже при-
приближённые, представления величин \(v и po/pf как функций от S.
Обозначим
~ = P(S), -^r = Q{S)	A7.21)
V
и исключим ср при помощи A7.2). Мы получим
- [VK cos рР^| + Q sin p Щ dS,
Напишем условие того, что dx есть полный дифференциал. Это
будет:
!) Христианович С. А. и Юрьев И. М., Обтекание профиля при
докритической скорости потока, ПММ, т. XI, вып. 1, 1947.

? 17]	ДОЗВУКОВЫЕ СКОРОСТИ. МЕТОД ХРИСТИАНОВИЧА	139
Выполняя дифференцирование и исключая старшие производные от ф
при помощи A7.2), мы получим следующие два равенства:
L	^	0.	A7.22)
Эти равенства выполняются совершенно точно, если P=l/f,
Q = po/pu, a YK имеет точное значение A7.3). Посмотрим теперь,
чем нам надо заменить Р и Q, если YK мы заменим на Y^co
(в этом заключается первое приближение). Наши уравнения нам
дадут сразу:
P = Cle-s+Cte+s; Q = VKZ^eS — c2e+s), A7.23)
где сх и с2 — произвольные постоянные интегрирования. Эти постоян-
постоянные мы подберём так, чтобы Р и Q равнялись их точным значениям
при v = Vca. Так как S = lnV и так как по A7.3) и (8.9)
= ^-VT^W. где M = -J-.
. A7.24)
Итак, в первом приближении мы должны заменить A7.11) на
мв
х= f H = + c2F\cosp^*— (= — c2v\sm§dW*-\ + xA,
МА
м
в
A7.25)
где tj и с2 определяются по A7.24), а функции Ф* и W* как функ-
функции от (а и v находятся из задачи обтекания в несжимаемой жидкости.
Нужно отчётливо помнить, что в то время, как V и р суть
скорость и угол соответственно в потоке несжимаемой жидкости,
обтекающей данный контур со скоростью на бесконечности V^> и
с циркуляцией Г, функции Ф* и W представляют обтекание того
же контура и с той же скоростью на бесконечности, но с другой
циркуляцией — Г*. Как найти эту циркуляцию? Она получается, как

140	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
и для точного решения, из условий однолистности плоскости (х, у),
отвечающей нашему решению. Подробный и простой вывод имеется
в упомянутой статье Христиановича и Юрьева. Оказывается, что
надо взять, как и в точном решении
A7.26)
Если обозначить комплексный потенциал нашего потока с цирку-
циркуляцией Г* через F*, комплексный потенциал Ф-|-/ч7 через F, нако-
наконец, [л. —J- /v = г, то мы сможем написать, в частности:
Уе~1* = §	A7.27)
и привести подынтегральное выражение A7.25) к более компактному
виду:
) = Cl-^rff+Cjig.rfF*.	A7.28)
15"
где dF* — комплексная сопряжённая с dF* : dF'— AФ* — i dW*.
Приведём пример. Пусть в несжимаемой жидкости в плоскости (jx, v)
имеет место бесциркуляционное обтекание круга радиуса 1 со ско-
скоростью Vco на со. Тогда
( у)	A7.29)
и A7.28) примет вид:
так что
x 4- ty = cxz -+- c2V% (J+ { —
Искажение может быть теперь легко подсчитано.
В случае обтекания эллипса, уравнение которого имеет вид
A+r2J "+~ A— r2J ~1( °<''<1'
достаточно перейти от плоскости z (— jx -J- iv) к плоскости С по
формуле
Область |С| > 1 отображается в плоскости (z) на область, внешнюю

§ 17]
ДОЗВУКОВЫЕ СКОРОСТИ МЕТОД ХР11СТИАНОВИЧА
141
по отношению к нашему эллипсу. Равенство A7.28) мы запишем
теперь в виде:
1 ""	 ^ ^1*р\аг~. A7.30)
При отсутствии циркуляции F* = F. Тогда, производя несложные
выкладки, получим:
Если эллипс сильно вытянут так, что rttl и 1
малая величина, то можно приближённо написать
г = е, где е —
= Сх /С
— 2е
—
=
\
Этот последний профиль будет весьма близок к нашему эллипсу.
В общем случае циркуляционного потока уравнение A7.28) или
A7.30) позволит сразу выяснить особенности, которые возникают
из-за обращения в нуль	„
функций dF"/d^ и dFjdb.
За подробностями мы отсы-
отсылаем к цитированной работе
Христиановича и Юрьева,
в которой показано, что
если контур в плоскости
([j., v) гладкий, то на контуре
в плоскости (х, у) возник-
возникнут в местах, отвечающих
упомянутым особенностям,
угловые точки. Христиано-
вич и Юрьев показывают,
как можно избежать по-
появления этих угловых точек
в плоскости (х, у) подбором
специального профиля в пло-
плоскости ([л, v). На рис. 44
дан пример появления осо-
-OJB-
¦0,6-
-QA
0,2
0,8 -0,6 -0,4 -0,2 О
-0,2
-0,4-
-0,6-
-0,8-
\
0,2 0,4 0,6 0,8
Рис 44.
причём обтекается
бенностей в контуре на пло-
плоскости (х, у); здесь Мл =0,333 и Г'/'
в плоскости ([л, v) круг радиуса 1.
На рис. 45 дан в плоскости (х, у) гладкий контур, обтеканию
которого отвечает в несжимаемой жидкости (в плоскости (a, v))

142
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ I
движение вокруг контура, изображённого на рис. 46. Этот последний
контур есть круг- радиуса 1, к которому присоединён отрезок дуги
круга ббльшего радиуса (как и
в предыдущем примере Мю =
= 0,333, r/Vuo = l).
1,2
-0,8-
-0,4
-0,8 -0,4- О
-0,4
-0,8
<1г2_
Рис. 45.
0,4
Рис. 46.
При больших скоростях нельзя ограничиваться первым приближением.
Вычисление функций ер,, ф, бывает громоздко, но можно воспользоваться
следующим рассуждением. Для dep вдоль контура С имеем:
,— бер , , дер ,
d® = ^J- dp. 4- -51- dt,
причём rfv, например, можно найти через dy. при помощи формулы
Таким образом, вдоль С
дч
С другой стороны, мы можем написать приближённо:
дер	dep0 depj	depg
A7.31)
A7.32)
пренебрегая членом дФ/др. Пренебрежение функцией Ф (или XV) означает,
вследствие A7.18), что мы можем пренебречь в формулах A7.17) (для п = 2)
членами д^2/дч и дф2/др-, но тогда

§ 17]	ДОЗВУКОВЫЕ СКОРОСТИ МЕТОД ХРИСТИАНОВИЧА	143
а если вставить дЬ^дч из первого из A7.17) для п = 1, получим.
Вспомним еще, что j/"/f,x> <tyo/dv = ^о/^'х' мы п°лучим теперь
Аналогичным образом найдем, что
Вставляя это выражение в A7.32), используя еще раз A7.14) и пренебрегая
членами, содержащими tp1( по сравнению с членами, содержащими ср0, полу-
получим окончательно
где V—скорость в несжимаемой жидкости (отличная от V, ибо за цирку-
циркуляцию мы берем Г*, а не Г). Таким образом, вдоль контура с будет на осно-
основании A7.11):
А
Остановимся еще на следующих весьма простых соображениях.
Предположим, что мы изучаем в плоскости (р, -i) обтекание круга
(хотя бы бесциркуляционное); в плоскости (х, у) мы имеем сплю-
сплющенный круг. Пусть скорость фиктивного потока I/,» =0,35;
ей отвечает скорость сжимаемой жидкости г>оо=0,36 (близкая к V;»).
Но максимальная скорость г>тзх, получающаяся в сжимаемой жи ко-
кости, будет близка к скорости звука. Действительно, г>тах получится
там же, где V достигнет максимума. Но VtMX — 2Voa=0,70, а этой
скорости отвечает по таблице г> —0,825. Скорость звука будет
достигнута, когда будет v—1, т. е. при 17=0,7577; значит, в на-
нашем примере сплющенного круга при 1/00—0,7577/2 = 0,3789, т. е.
1Ко?« 0,354, мы обязательно получим звуковые скорости на контуре.
Очевидно, что это явление еще раньше возникнет, если контур с
в плоскости (х, у) будет точным кругом. Таким образом, можно
с уверенностью сказать, что при vx > 0,36 при обтекании круга
возникнут сверхзвуковые зоны.

144	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[1Л I
Можно ожидать, что при обтекании вытянутого контура, напри-
например профиля Жуковского или профиля крыла современного само-
самолета, искажение будет получаться гораздо менее значительным, чем
в случае круга. Но если грубо считать, что профили с к С тожде-
тождественны, то метод Христиановича дает замечательное средство быстро
рассчитывать распределение скоростей и давлений вдоль профиля
крыла с учетом сжимаемости при любых дозвуковых скоростях,
если известно обтекание крыла при малых скоростях. Действительно,
п^сть мы получили, хотя бы путем продувки крыла в аэродинами-
аэродинамической трубе при малых скоростях vx на бесконечности, распределе-
распределение давления вдоль крыла С. Пусть vx настолько мало, что эффек-
эффектом сжимаемости можно пренебречь: критерием этого может служить,
например, то, что величина vjat будет почти совпадать с соответ-
соответствующей величиной V и с таблицей.
По уравнению Бернулли для несжимаемой жидкости
1 __ /' v \'г _
Ui ) ~<?несж'
где
РР
Мы считаем, что q в каждой точке профиля известно, значит, мы
можем найти Vjvx для каждой точки профиля. Теперь спросим себя,
каково будет распределение скоростей и давлений вокруг крыла С,
если скорость на бесконечности будет v2, причем v2~J^>vl? Рас-
Рассчитаем сперва v2/a),~ v2, обратимся затем к табтице или к фор-
формуле A7.9) и найдем соответствующую скорость фиктивного потока
несжимаемой жидкости; пусть эго будет V2', для этого фиктивного
потока несжимаемой жидкости конечно снова будет
1де ^несж принимает прежние значения в соответствующих точках
контура. Так как V2 известно, эта формула позволит найти V
для каждой дайной точки нашего контура С. Тогда по табпице мы
можем найти безразмерную скорость v для каждой точки контура с,
близкого к С (а грубо говоря, тождественного с С) и обтекаемого
со скоростью v2 на бесконечности.
Распределение давления найдется затем по формуле
-л + 1 •/¦ — 1

§ 17]	ДОЗВУКОВЫЕ СКОРОСТИ МЕТОД ХРИСТИАНОВИЧА	145
В начале этого параграфа мы уже упомянули о том, что сейчас
имеется много работ, посвященных приближённому решению задачи
о движении газа с дозвуковыми скоростями. Из этих работ значи-
значительное число отправляется от уравнений Чаплыгина. Сам Чапльпин
предлагает перейти от переменных C, т к переменным р, о, где
а = — f 4~A — ^ГГГ^~ + const. = — /-^--^-f const. A7.34)
Уравнения A6.12) примут тогда вид
ду __ д\, d<f _krd\i
д$	дз да	б?	v	'
где
х1	1"'A7.36)
— ранее упомянутая функция, использованная Христиановичем. Если
положить теперь приближённо
мы получим для ср и ф в переменных р и о уравнение Лапласа.
Чаплыгин произвёл это построение для приближённого решения задачи
о струях в сжимаемой жидкости. Слёзкин *) первый указал на воз-
возможность применения этих уравнений к решению задач о бесцирку-
бесциркуляционном обтекании криволинейных профилей. Карман 2) и Сюэ-сэнь
цянь3) исследовали также бесциркуляционную задачу при помощи
A7,35) и приняли К постоянным, но равным Коэ4)-
Преимущество метода Христиановича заключается в том, что
Христиаиович, не ограничиваясь первым приближением, рассмотрел
') Слёзкин Н. А., К вопросу о плоском движении газа, Труды МГУ,
1935.
2)	К а г m a n Th., Compressibility Effects in Aerodynamics., Journ. Aer.,
Sci. 8, 1941.
3)	T s i e n H. S., Two-dimensional Subsonic F[ow of Compressible Fluids ,
Journ. Aer. Sci. 6, 1939.
4)	Равенство К = Лло выполнялось бы точно, если бы мы приняли
вместо формулы
(д = const., так как движение безвихревое) линейный закон
р = А — В 1/о,
связывающий давление и удельный объем, причем А и В подобрали бы так
чтобы наша прямая в плоскости (/>, 1/р) была бы касательной к кривой
р = Г(\/?у
в точке р^, A/;>)м- В самом деле, при нашем линейном законе Пуассона
10 Теоретичен )я ги фсше^.ишкч, ч II

146	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
общий случай обтекания при наличии циркуляции и что уже в пер-
первом приближении он получил большую точность ценой введения,
вместо а, величины S.
§ 18. Приближённый метод Христиановича для решения
плоских безвихревых задач. Сверхзвуковые скорости. В пре-
предыдущем параграфе мы рассказали о приближённых методах решения
дозвуковых задач. Эти методы опирались на использование ф и ф
в качестве искомых функций, а плоскости скоростей — в качестве
плоскости независимого переменного. В сверхзвуковом случае такого
рода искомые функции и независимые переменные также могут
помочь решению многих задач.
Христиановичу ') удалось, используя <р и ф в качестве искомых
функций от C и v, дать новый приближённый способ решения всех
основных плоских безвихревых задач в сверхзвуковом случае.
Идея решения заключается в следующем.
До сих пор, рассматривая движения со сверхзвуковой скоростью,
мы строили характеристики в плоскости (х, у) или в плоскости
(vx, vy). Вместе с Христиановичем будем теперь строить характе-
уравнеиие Бернулли запишется в виде
v2 В ( 1 \2	vl В
Но тогда в уравнении A6.8) мы будем иметь:
d p0	ppot> d	Poo р?„
dv pt>	2 dv	Bv2	v2	В
так что на месте К будет стоять постоянная величина
^ооРоо Л РО
1
в
С другой стороны,
Мы получим одно и то же значение Кх при В = x/^/p^, но это как раз
и означает, что прямая
p = A-B-l/i
будет параллельна касательной к кривой
в точке (pw, 1/рю).
') X р и с т и а н о в и ч С. А., Приближённое интегрирование уравнений
сверхзвуковых течений газа, ПММ, т. XI, вып. 2, 1947.

§ 18]	ПРИБЛИЖЁННЫЙ МЕТОД ХРИСТИАНОВИЧА	147
ристики в плоскости (ср, ф) (речь идёт о безвихревом движении).
Чтобы связать ср и ф при перемещении вдоль характеристики, удоб-
удобнее всего обратиться к соотношениям A6.6) § 16. Вдоль характе-
характеристик мы имеем (см. 9.23):
A8.1)
где верхний знак отвечает характеристикам первого семейства, ниж-
нижний— второго. Значит, по A6.6) вдоль характеристик будет:
¦i-[cosptg(p±a)-slnp]dtp—fl[sinptg(p±a) + cosp]tfj. = 0. A8.2)
или, после сокращения и приведения членов:
d<? = ±-^ ctgadip.	A8.3)
Величина (po/p)ciga зависит только лишь от v = v[at: [см., напри-
например, (9.22) и A6.1)]:
'	о
2 t>2	2
^- 08.4)
A »-1
V * + i
Обозначим вместе с Христиановичем
¦)¦	A8.5)
_
Легко видеть, что y^{v) есть монотонно растущая функция от v,
не отрицательная при v^> 1, обращающаяся в нуль при г>=1 и
в бесконечность при v=—:?-т . Итак, вдоль характеристик первого
семейства будет
di( = ~=d9.	A8.6)
а вдоль второго:
<*!> = —-7==-</<р.	A8.7)
') 7. (и) = —^(г'). где K(f) —ф)гнкция, введенная в § 17, только AC (v)
^ определено для и<1, а у_ (р), напротив, мы рассматриваем лишь
для v > 1.
10*

148	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Вспомним теперь, что характеристики в плоскости скоростей
связаны соотношением
р + С (?) = const.,
где
v	_
Г / V2— 1	du
1 г	% +1
r	x +1
—arctg
A8.8)
Обозначая
С (о) — р = 2Х, СЙ + Р=2^.	A8.9)
и переходя к независимым переменным X и [л, мы должны из A8.6)
и A8.7) получить:
°
При этом, вследствие A8.9),
Х + ^	A8.11)
т. е. 1/Vx(fl) есть функция от X-)-ia.
Как выглядит эта функция? Не представляет труда изобразить
Х в функции от С: и ту, и другую величину можно считать пара-
параметрически представленной через v [формулы A8.5), A8.8) соответ-
соответственно]. Так, например, легко убедиться, что в области Ся^О
(t»wl, причём v~^>'\) Л[х имеет вид
Далее, кривая имеет точку перегиба при
При дальнейшем росте С знак кривизны у ]// не меняется, и она
асимптотически уходит на бесконечность при

§181
ПРИБЛИЖЁННЫЙ МЕТОД ХРИСТИАНОВИЧА
149
Кривая Ух в Функции от С представлена на рис. 47.
Христианович замечает, что для значений С, не слишком близких
к нулю, можно с большой точностью аппроксимировать нашу кривую
как куски парабол; так в интервале
0,015 <С< 0,57, A8.12)
в котором v меняется в пределах
1,06 <Ъ< 1,74,
можно написать
A8.13)
В интервале
0,57 < С < 1.02 A,74 <©< 2.07)
A8.14)
можно написать
— 1,30)
-2
A8.15)
и т. п. Обычно в безвихревых зада-
задачах мы заранее знаем, в каких преде-
пределах меняется поле скоростей v (см.
§ 11) и поэтому мы можем выбрать
представление для Ух в виде наибо-
наиболее подходящей параболы.
Но, если
А? + с)*\ A8.16)
raeA.cnk — постоянные (причём k— целое число), то система
может быть решена в общем виде. Именно, исключая из A8.
используя A8.11) и A8.16), мы получим для ф уравнение
Рис. 47.
A8.10)
10) tp и
Исключая же ф, мы получим для
д2ч	k
X + V- + с \д1
A8.18)
Если k положительно, удобно использовать A8.17), если k < 0,
— возьмём A8.18). В обоих случаях мы получим уравнение Дарбу,
причём тот тип, который в общем виде решается до конца. Так,
если к = -\-1, как это будет по Христиановнчу в интервале A8.12),

150	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
мы просто будем иметь в качестве общего решения:
где \Fj и W2—две совершенно произвольные функции, каждая от
одного аргумента; вид этих функций определится аналогично тому,
как это делается в классической задаче о струне — из краевых
условий. После того как ф известно, <р найдётся из A8.10) путём
простых квадратур. Это будет
Аналогичным образом в интервале A8.14) мы имеем A8.15), т. е.
й = —1, и по A8.18) можем написать
ig±M,	A8.20)
где Фг и Ф2 — произвольные функции.
Прежде чем начать ставить краевые условия, построим ещё,
как определяется связь между л:, у и <р, <|>.
Как прежде (см. § 16), мы имеем равенства:
1
Слева в этих равенствах стоят полные дифференциалы, и это
в конечном итоге обеспечивалось тем, что ср и <|>, v, В были связаны
уравнениями A6.9), A6.10). Теперь, когда ср и ф мы представляем
приближённо, как функции X и |л (т. е. как функции В и v), мы
должны позаботиться о том, чтобы A8.21) оставались полными диф-
дифференциалами. Величины \[v и pjpv зависят только от v, т. е. от С.
Поэтому запишем A8.21) в виде:
dx = p (С) cos В rfcp — q (С) sin В dty, \
|». J	A8.22)
и посмотрим, как надо представить р и q, чтобы A8.22) были
полными дифференциалами. Мы можем прежде всего записать,

§ 18]	ПРИБЛИЖЁННЫЙ МЕТОД ХРИСТИАНОВИЧА
используя A8.10):-
dx = — \р У/ cos В -t- q sin 8| ~- rfX -4-
I^ZC0SP — 9sinP]-57
151
A8.23)
Напишем условие того, что rfx есть полный дифференциал. Имеем:
или если выполнить дифференцирование и вспомнить, что С = (*-f-
Р =r= jjl — X, и собрать члены с одинаковыми производными от ф:
= 0.
Наконец, замечая, что вследствие A8.10) должно быть
2
мы получим окончательно два соотношения
A8.24)
Те же соотношения получаются из условий, что dy есть полный
дифференциал 1).
До сих пор наши выкладки были совершенно строгими. Под-
Подставим теперь вместо Ух наши приближённые выражения. В случае,
когда
•2.	A8.25)
') Легко проверить, что если мы вставим q = po/pt>, p — \\v, Y~/. =
*= У (у2 — 1)/A — у2/Л2)Аа, то A8.24) будут тождественно удовлетворяться.

152	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
мы получим вследствие A8.24):
Исключая^, придём к уравнению
dQ ^ Z + c dr. -т-Р — и-
Общим интегралом этого уравнения будет
Р = J^J fCl Sin К + С) + С2 C0S & + С)Ь
Для функции q мы получим при этом
q = A\cx sin(C + c)+C2cos(^ + c) —
—	$. + c)[clco
В случае, когда
V7-—4—
^ Х ~ (С + СJ ¦
получим для q уравнение
d2q . 2 dq ,	„
т. е. теперь будет
q = j-^-r [Cj sin (С + с) + с2 cos G+ с)]
и
/? = — -^ {c!sm((;+cL-c2cos(C + c) —
—	(С + с) [«1 cos (С + с) — с2 sin (С + с)]}.
Для функций р и q, отвечающих параболе A8.13), Христианович
выбирает постоянные сх и с2 так, чтобы при С = 0,2 было р = IJv,
q = ро/р-у, тогда
Cj = 0,553, с2 = 0,082.
Христианович даёт решение всех четырёх основных задач, о которых
говорилось в § 11. При этом оказывается, что задачи I, II и IV
решаются сразу же в конечном виде, или при помощи квадратур;
задача же III приводится к решению одного обыкновенного диф-
дифференциального уравнения первого порядка. Начнём с задачи I.
Задача I. Движение известно на некоторой кривой, не являю-
являющейся характеристикой (кривая АВ на рис. 12). Пусть А'В' есть
линия, проставляющая кривую АВ в плоскости скоростей (А'В' изо-

§ 18]	ПРИБЛИЖЕННЫЙ МЕТОД ХРИСТИАНОВИЧА	153
браженз на рис. 13). Пусть уравнение этой последней линии в пло-
плоскости (л, |л) нам известно:
X = Л (|л) или jx = M(X).	A8.26)
Вдоль этой линии заданы <р и А. Пусть будет здесь, в частности:
A8.27)
В общее решение для 4
входят две функции Ч^ и Ч?2. Определим их. Умножим обе части
последнего равенства на X —[— (х —j— с и продифференцируем по X и [х;
Эти равенства, справедливые всюду, запишем для нашей заданной
линии. Здесь можно написать:
- [х —)— с] (-3-М
Члены, стоящие в правой части этих уравнений, известны все, за
исключением (<?4/<?Х) и (д4/<Э|х). Найдём эти выражения. Очевидно,
что если двигаться вдоль нашей кривой A8.26), будем иметь
С другой стороны,
или, если воспользоваться A8.10) и A8.25),
<ty	д'Ь	ф, (X)
1М/(Ц?
Из A8.30) и A8.31) мы получим:
о8-32)

154	TEOPETII4FCK1IE ОСНОВЫ ГАЗОВОП ДИНАМИКИ	[ГЛ. 1
Остаётся подставить A8.32) и A8.33) в правые части A8.29) и про-
провести квадратуры. Постоянные интегрирования найдутся из условия
совпадения ср и ф с заданными значениями из начальной кривой.
Мы приняли приближение A8.25). Аналогичным образом решается
задача при Yx = -^/(C-j- сJ.
Задача II. Если в задаче I пришлось брать ещё квадратуры,
то задача II решается совершенно элементарно. Имеем две характе-
характеристики: X = Хо и \х = |х0> выходящие из одной точки (рис. 14 и 15).
На этих характеристиках движения известны. Пусть будет
при 1 = \0 ф = ф1((х),
при (л = ;л0 ф = ф2(Х),
причём <h Ы = Ы\>)-
Тогда, полагая в A8.28) Х = Х0, мы получим:
а полагая ;а —|л0, получим:
._ *¦(*) + '
A8-35)
Кроме того, первое из этих соотношений даст нам:
Из A8.34)
Из A8.35) имеем:
ЧГ, (X) = — ?2 (jx0) + (X + jx0 + с) ф2 (к).
Поэтому окончательно мы получим:
С) ф2 (X) — (Хо + t^o + С) ф,
A8.36)
Задача III. Движение задано вдоль одной из (заданных) характе-
характеристик. Пусть, например, при Х = Х0 будет ф = ф2(|л), где Ф2—из-
Ф2—известная функция. Движение происходит между этой характеристикой
и стенкой, причём уравнение последней мы напишем в виде х — Хф),
у=Кф) и на стенке примем ф = 0. Ищем вновь решение в виде
A8.28). Полагая сперва там Х = Х0, получим:
отсюда сразу найдём W2(\x) с точностью до постоянной ^(Xq);
остаётся определить Wi (к). Чтобы это сделать, заметим, что если

§ 18]	ПРИБЛИЖЕННЫЙ МЕТОД ХРИСТИАНОВИЧА	155
идти вдоль стенки, где ф=0 и йф=О, получим по A8.22):
dX
последнее равенство можно написать, вследствие A8.10), в виде:
«[-*f-l-|].	08.38)
С другой стороны, вдоль линии стенки (ф = 0) будет:
ЦГ1(ХL-Чг2(|а) = 0	A8.39)
и ещё
Таким образом, комбинация, входящая в A8.38), будет
По A8.39) выражение в квадратной скобке, стоящее здесь справа,
будет просто
Итак, мы можем дать формуле A8.38) вид
+%.]. A8.41)
Наконец, мы можем сюда подставить Ч?2 из A8.37) по формуле
Мы получим обыкновенное дифференциальное уравнение первого
порядка для определения вдоль стенки С в функциях от р. Дальше
решение сводится к квадратурам.
Задача IV. Эта задача решается значительно проще, чем пре-
предыдущая. Вдоль свободной поверхности, которая есть линия тока,
пусть будет ф = 0. Кроме того, на свободной поверхности давление
и, значит, скорость известны; пусть будет там C = Cj. Тогда:
^100+ ^2(^ = 0. если X+li = C1.
Далее, вдоль характеристики (см. рис. 18), пусть это будет Х = Х0,
имеем ф = ф2 ([>¦)< гДе ^2 — заданная функция. Тогда

156	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Итак,
% (Хо)
\Рг (X) = - (Хо + с + d - X) ф2 (Cj -).) - Ц\ (Хо).
Постоянная Ч\ (Хо) определится из условия совпадения значения ср
с заданными её значениями на характеристике.
§ 19. Переход через скорость звука. Предельные линии.
Примеры точных решений. Представим себе несжимаемую жидкость,
обтекающую с определённой по величине и направлению скоростью
на бесконечности, замкнутый контур. Если, не меняя направление
скорости, мы увеличим величину её, то конфигурация линий тока
останется неизменной — только нумерация функций тока изменится.
Существует лишь одно семейство кривых, которые могут служить
линиями тока при обтекании (под данным углом атаки) заданного
контура несжимаемой жидкостью. Совсем иначе будет обстоять дело
в сжимаемой жидкости. Если в несжимаемой жидкости мы могли
написать
~ 	 бф 	 ду ~ 	 d'\i 	 ду
Vjc~~dy~~!hc' Vy~~~~dI"Ty~'
где
так что для ф мы имели просто уравнение Лапласа, то в сжимаемой
жидкости мы должны положить
р0 х ду ' р0 У ~~ дх ' х дх ' У ду '
причем
Ро (
\	х—1 - /
так что уравнение, получающееся для ф, будет содержать в качестве
коэффициента г>оо/я* — число Маха на бесконечности. Сама конфигура-
конфигурация линии тока будет меняться с изменением числа Маха и, таким
образом, одному профилю будет отвечать бесконечное множество
линий тока, представляющих обтекание этого профиля при различных
по величине скоростях на бесконечности').
S2
1
со
а2
1
Г1
') Несжимаемая жидкость получается как предельный случай, когда
1>оо/я* <СС 1> так что в выражении для р/р0 можно пренебречь членом, со-
содержащим (vco/a^Y; это приводит к приближённому условию p/po«sl. Дру-
Другой предельный случай получится, если скорость «со будет сверхзвуковой и

§ 19]	ПЕРЕХОД ЧЕРЕЗ СКОРОСТЬ ЗВУКА. ПРЕДЕЛЬНЫЕ ЛИНИИ	157
Особенно резко проявляется изменение формы линий тока, когда
в плоскости течения (обладающего ещё дозвуковой скоростью на
бесконечности) возникают сверхзвуковые зоны. Мы уже видели
в одном из предыдущих параграфов, на примере обтекания контура,
близкого к кругу, что уже при Va,^ 0,36 на профиле появляется
точка, где v > ая; при дальнейшем росте скоростей следует ожидать
появления сверхзвуковой области. Но здесь возникает новая специ-
специфическая трудность. Дело в том, что течения сжимаемой жидкости
обладают двумя особенностями по сравнению с движениями жидкости
несжимаемой. Во-первых, в сжимаемой жидкости невосможны беско-
бесконечно большие скорости (максимальная возможная скорость есть
1/ — i-j-д ), во-вторых, в сверхзвуковом потоке газа, в проти-
воположность жидкости несжимаемой, трубки тока расширяются
с увеличением скорости (см. § 8). Последнее обстоятельство приводит
к тому, что в сверхзвуковой зоне линии тока будут, расширяясь,
расходиться по отношению к обтекаемой границе; в дозвуковой
зоне, напротив, линии тока будут сужаться и как бы сходиться
с приближением к сверхзвуковой зоне. Можно ожидать, что при
заданном контуре будут существовать скорости на бесконечности,
при которых невозможно будет удовлетворить этим обоим законам.
Конечность скорости, с другой стороны, приводит к тому, что там,
где решение для несжимаемой жидкости даёт бесконечные скорости,
например, при обтекании острия, там решение для жидкости сжи-
сжимаемой либо не существует, либо соответствующие линии тока не
образуют острого угла.
Математически дело сводится к тому, что в сверхзвуковой зоне
могут появиться точки и целые линии, на которых производные от
скоростей будут обращаться в бесконечность. Это так называемые
«предельные линии». Такие решения уравнений газовой динамики,
формально существующие, физического смысла не имеют и реали-
реализоваться не могут. В этих случаях движение перестраивается так,
что возникает линия сильного разрыва (не совпадающая, конечно,
с предельной линией), и решение с самого начала следует искать
очень большой, т. е. если М<х> = Vm/cka ~2>> 1. В этом последнем случае, так
как по (9.22)
«.—1	1
мы получим, пренебрегая членом, содержащим l/М^, р/роякA — «2IЛ* !)-
Таким образом, в этом предельном случае поток вновь не зависит от числа
Маха на бесконечности.

158	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
не в виде непрерывного безвихревого обтекания, а в виде движения,
в котором имеется поверхность разрыва, форма и местоположение
которой заранее неизвестны и после перехода через которую течение
становится вихревым.
Опыт показывает, что скачки, как правило, «садятся» на крыло
в сверхзвуковой зоне (крыло движется с дозвуковой скоростью).
Такие же скачки образуются в сопле Лаваля, даже при нужном пере-
перепаде давления, сразу после того, как совершился переход через
звуковую скорость, если только профиль сопла не удовлетворяет
специальным условиям (см. следующий параграф).
Условие наличия предельных линий в том или ином решении
уравнений газовой динамики, т. е. условие, при котором появляются
бесконечные ускорения (производные от скоростей), нетрудно написать.
В самом деле, это условие очевидно равносильно обращению в нуль
якобиана D (x, y)jD(v, C); но последний можно записать так:
D {х, у) _ D (х, у) D (у, ф)
D (v, р) D (9, ф) D (v, р) '
что вследствие A6.8), A6.9) и A6.10) даст:
D(v, p) — v» Lip ) (М 1)\д$) \д? ) J-
Мы видим, что если М2 •< 1, наш определитель не может обратиться
в 0; значит, предельные линии невозможны в дозвуковом потоке.
Предельные линии образуются там, где
Любопытно, что первые примеры точных решений, в которых осу-
осуществлялся переход через скорость звука, обладали все предельными
линиями:). Татаренчик2) первый показал, как можно найти ряд
точных частных решений уравнений газовой динамики, в которых
осуществляется переход через скорость звука, причём движения
имеют физический смысл (предельная линия не успевает образоваться).
Чтобы получить примеры таких решений, вернёмся к уравнениям
Чаплыгина и обратим внимание на то, что каждый член ряда (стр. 118)
ф = А Ч- ?C + 2 Bnzn (т) sin B»p + а„)
будет формально удовлетворять уравнениям газовой динамики. Тата-
Татаренчик рассматривает решения вида:
A9.2)
') Toll mien W., ZAMM 17, стр. 117—136A937).
2) Татаренчик В. В., О частных решениях уравнений газовой дина-
динамики, ПММ, т. VIII, вып. V, 1944.

§ 19]	ПЕРЕХОД ЧЕРЕЗ СКОРОСТЬ ЗВУКА ПРЕДЕЛЬНЫЕ ЛИНИИ	159
где А и В — постоянные, a zn по-прежнему будет
и v, удовлетворяет уравнению гипергеометрического ряда A6.16):
Здесь /г — любое число. Вместе с Татаренчиком положим:
тогда для уп получим:
1	> dx* "т" х—1 rfx ~
Это уравнение интегрируется и даёт:
где Cj и с2 — произвольные постоянные. Итак, мы можем принять
в качестве решения:
A9.3)
ф=-^[с,A—x)+
V ^
При этом для ср получается [см., например, A6.21)]:
BcosP). A9.4)
р
Рассмотрим частные случаи. Положим сперва
сх = А = 0; — с2б |/ =
t = —	7Г = v2
V.+ 1 Й2 x+l
-i- = ^ = -lsinp. -*-=9 = i —cosB.	A9.5)
Найдём сперва, как выглядят в плоскости (х, у) линии г> = const.
Так как вдоль этих линий
и так как, по A6.7) и по A9-.5)
й?	w2 p	6,3 pt>2
то
; dy = -4?- cos 28 <ffl.
p^2

160	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
Интегрируя по 3 в пределах от тс/2 до р, получим:
отсюда
[ГЛ I
Остается найти лишь xo(v) и yo(v). Это суть значения, которые при-
принимают х и у ъ функциях от v на линии ^ = тс/2. Но вдоль линии
Р = тс/2 = const, будет
, дх .— . ду .—
dx=—=rdv, dy = —b-dv,
dv	dv
причем (dxjdvH_j;2 = pjpv3, a(dy/dv),_n2 = 0. Таким образом, линия
C = тс/2 в плоскости (х, у) переходит в прямую, параллельную
оси Ох, и можно считать
что же касается х0, то оно найдется квадратурой1)
xQ(v)- /Л—
Таким образом, линиями v— const, будет семейство кругов с цен-
центрами вдоль осп Ох и различных радиусов (см. рис. 48, на котором
Рис
изображена «верхняя» часть течения). Так как на линии у = 0 будет
Р = тс/2 — все линии тока под прямым углом пересекают ось Ох.
Рассмотрим линию тока ф=с. По A9.5) там, где эта линия тока
пересекает ось Ох, будет v= \jc. Перемещаясь вдоль линии тока,
') Квадратура выполнится, если положить ¦*¦ == 1,40.

4 19!
ПЕРЕХОД ЧЕРЕЗ СКОРОСТЬ ЗВУКА ПРЕДЕЛЬНЫЕ ЛИНИИ
161
мы будем встречать различные значения v. Попадём ли мы на пре-
предельную линию? Вдоль предельной линии A9.1) имеем по A9.5):
Если двигаться вдоль линии тока ф = с, то будет по A9.5) sinp =
= cv, cos2p= 1 —с2-у2, и на месте встречи нашей линии тока с пре-
предельной линией будет по (8.9):
2 -,	1
X— 1
._ 1\A— с2 г»2)— cV =
или, если собрать члены и произвести упрощения,
_1 -> , *4-1 1
с'
V	С\	-7
2 с2
У этого уравнения будут действительные корни только при
с2 "-" х + 1 '
Но, как мы видели, 1/с равно значению скорости в точке пересече-
пересечения нашей линии гока с осью Ох. Значит, на всех тех линиях тока,
для которых скорость v на оси Ох будет меньше, чем
+ 1 '
бесконечные ускорения не возникают, и соответствующие течения
имеют физический смысл. На рис. 48 изображены эти линии тока, вплоть
до крайней возможной
/
у
8
t I
Круги постоянной
В-55.
?«5°
Рис 49
скорости сгущаются по мере при-
приближения к линиям тока, на которых
возможны бесконечные ускорения.
Любая из линий тока, изображенных
на рис. 48, можег быть принята за
границу обтекаемо; о контура. На
рис. 49 изображена одна из таких линий тока и нарисованы харак-
характеристики первою и второго семейства, которые возникают в нашем
движении в сверхзв)ковой зоне.
Второй частный случай решения A9.3), A9.4) получим, полагая
Со — А. ^= \
Тогда
р0
11 Теоретическая гидромеханика, ч II

162	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
Вдоль линии v = const.
[ГЛ. I
X-f-1
dy=(-i-XiLcos2p	-'
\	f2	7.
Так что можно написать:
1
sin 2?
где х0("У), yu(v)—значения х и у в тех точках, где р = л/2. Как
и в предыдущем примере, определим х0 и у0, перемещаясь по линии
^ = тс/2. Получим без труда:
14-
dv,
= 0,
так что
а-0 -= const. — — + In г», >'о -= 0.
Вновь можно найти связь между ^ и г> на предельной линии, а также
выяснить, на к.гких линиях ф^= const, мы не встретим предельной
Рис. 50.
линии. Картина течения (в области, имеющей физический смысл)
дана \\а ,'ис. 50. На рис. 51 изображена крайняя линия тока и характе-
характеристики.

ПЕРЕХОД ЧЕРЕЗ СКОРОСТЬ ЗВУКА. ПРЕДЕЛЬНЫЕ ЛИНИИ
163
Другие примеры точных решений для движений с до- и сверх-
сверхзвуковыми скоростями можем найти в статье Ринглеба') и Крафта
и Диббла2). Эти авторы отправляются также от решений Чаплыгина.
Полезно отметить, что решения вида A9.2) переходят в несжимаемой
жидкости в решения типа
A9.6)
где
Рис. 51
z — х -f- iy.
В самом деле, для несжи-
несжимаемой жидкости мы имели
бы вместо A9.2) просто (см.
стр. 119):
w = ф _|_ iw =
Но тогда
	.. - Т/p~~ip	const
dz
Отсюда и получится A9,6). Так решениям Татаренчика отвечает
Bя = - 1)
ф _j_ № — k Yz.
Здесь линии тока — семейство парабол с общей осью — осью Ох,
а линии равных скоростей суть концентрические окружности (с цен-
центром в начале). На рис. 50 видно, как искажаются эти линии из-за
сжимаемости. Крафт и Диббл рассмотрели детально случаи, когда
п=±114, ± 3/4, ± 1. На рисунке 52 изображены некоторые линии
тока и линии v — const, для случая п = — 3/4 3). Отдельно показано
в увеличенном виде поле, обведённое квадратом. Здесь как раз по-
появляются предельные точки. Лишь вне некоторой линии тока воз-
возможно физически осуществимое обтекание, сходное с тем, что разобрал
Татаренчик. В несжимаемой жидкости этому движению отвечает об-
обтекание угла в 60э.
В приведённых примерах вопрос о возникновении или невозник-
невозникновении предельных линий решается задним числом — после того,
как решение получено, применяется критерий A9.1). Нельзя ли,
') R i n g I e b F., Exakte Losungen des Differenzialgleichungen einer adiaba-
ti?her Qasstromung, ZAMM 20, 1940.
2)	Kratt and Dibble, Dimensional Adiabatic Compressible Flow Pat-
Patterns. Journal of the Aeronaut. Sci. 11, № 4, 1914.
3)	Постоянные, входящие в zn, подобраны здесь гак, чтобы максималь-
максимальная скорость была v— 1,8.
11*

164
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ 1АЗОВОЙ ДИНАМИКИ
|ГЛ. I

§ 20}
КЛАССИФИКАЦИЯ СВЕРХЗВУКОВЫХ ТЕЧЕНИЙ ПО ХРИСТИАНОВИЧ5 165
однако, выяснить заранее, получатся ли безразрывные, имеющие
физический смысл, решения при обтекании данного контура, при
данной скорости на бесконечности и при условии возникновения
[.верхзвуковой зоны. Этот вопрос тем более важен, что очень редко
удается получить точное решение задачи обтекания. Почти всегда при-
приходится довольствоваться решением приближённым, а благодаря неточ-
неточности тою или иного приближённого метода мы можем пропустить по-
появление опасных областей. Так, например, при неудачном подборе вход-
входной части сопла Лаваля может оказаться, что непрерывное движение не
осуществимо, и в сверхзвуковой зоне возникает поверхность сильного
разрыва (см § 21). Некоторый свет на условие отсутствия или
возникновения разрывов проливают работы Христиановича, а также
Никольского и Таганова. Мы изложим в общих чертах содержание
этих исследований.
§ 20. Классификация сверхзвуковых течений по Христиано-
вичу. Рассмотрим некоторую область течения газа, ограниченную
четырьмя характеристиками. Пусть криволинейный четырехугольник
MiM2MsM4 (составленный из дуг эпициклоид) изображает рассма-
рассматриваемую область течения в плоскости (vx, v ) (рис. 53). Пусть
'-5Г
м:
Рис 53.
дуги М'3М'2, М'^М[ принадлежат к эпициклоидам 1-го семейства,
а дуги М'4М'3, М[М'2 — к эпициклоидам 2-го семейства.
Как в плоскости (ср, ф) расположатся точки Mv M2, М3, М4,
являющиеся изображениями точек М\, М2, А1з, NU соответственно?
Минимальное значение ср может оказаться в одной из четырех
точек Мх, М2, М3, М4. Мы не рассматриваем здесь вырождаю-
вырождающихся с 1}чаев, когда в плоскости (vx, vy) мы будем иметь, вместо

166	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
четырёхугольника, дугу характеристик 1-го или 2-го семейства.
Эти случаи полностью были разобраны раньше (см. § 12).
Рассмотрим все четыре возможных случая.
I. Минимальное значение <р оказалось в точке М3. Двигаясь
от М3 по характеристике 1-го семейства М3М2, мы будем попадать
в область с большим у; следовательно, по A8.6) ф в точке М2
должно быть больше, чем в Мг. Аналогично этому, чтобы попасть
в Л14, надо двигаться по характеристике 2-го семейства М3М4< и
значение ф в точке Л14 должно быть по A8.7) меньше, чем в М3. Таким
образом, в этом случае взаимное расположение точек М2, Ж3, Ж4 будет
таким, как показано на рис. 54. Далее, двигаясь от Ж3 к Л14 по
характеристике 2-го семейства, мы будем получать по A8.6) для
тангенса наклона dty/dy касательных к характеристикам 1-го семейства
всё меньшие и меньшие (по модулю) значения, ибо при передвижении
по эпициклоиде от Л13 к Мц v растёт и значение (Ух) убывает.
Аналогично, двигаясь по характеристике М3М2 от М3 к М2, мы по
A8.7) будем встречать всё
меньшие и меньшие значения
М2	| dfy/dy | для характеристик 2-го
семейства.
Таким образом, можно уста-
установить характер выпуклости
характеристик обоих семейств.
Схематическое изображение на-
нашей области в плоскости (9, <|0
дано на рис. 54. Христиано-
вич 1) называет движения такого
типа «течениями расширения».
9 Криволинейные характеристики
рис 54	как 1"го> так и 2-го семейства
ведут себя здесь, если пере-
перемещаться в направлении течения (т. е. по линиям ф = const, от мень-
меньших 9 к большим) так же, как ведут себя прямолинейные характеристики
1-го семейства в задаче о движении газа вне выпуклой поверхности
(§ 12, рис. 23). Возникновение предельной линии (пересечение ха-
характеристик) здесь невозможно.
П. Минимальное значение 9 пришлось на точку Му Передвижение
от точки /Mt к точке М2 позволит теперь заключить, благодаря
предположенной минимальности 9 в точке М1 и на основании A8.7),
что ф в точке М2 должно быть меньше, чем в Мх; аналогично —1|»
') Хрисщанович С. А., О сверхзвуковых 1ечения.ч газа, Труды
ЦАГИ, вып. 543, 1941.

20] КЛАССИФИКАЦИЯ СВЕРХЗВУКОВЫХ ТЕЧЕНИЙ ПО ХРИСТИАНОВИЧУ 167
в М4 будет больше, чем в Мх. Таким образом, точки М{, М2, М4
расположатся так, как показано на рис. 55. Если теперь мы будем
перемещаться по характеристике 2-го семейства Ж3Л14 от точки М3
к точке М4, то мы будем
в плоскости (vr, vy) дви- <f>
гаться в сторону увеличе-
ния v и, значит, по A8.7)
будем получать всё меньший
и меньший (по модулю) на-
наклон характеристик 1-го се-
семейства (см. рис. 55). Ана-
Аналогичным образом при пе-
перемещении
от М, к Мо
Рис. 55.
будем получать все меньший
и меньший наклон характе-
характеристик 1-го семейства. Такие
движения Христианович на-
называет «течениями сжатия».
Двигаясь по течению (слева
направо по линиям ф =
— const.), мы будем встречать характеристики обоих семейств, веду-
ведущие себ [ так же, как вели себя характеристики (прямолинейные)
в задаче о движении около вогнутой поверхности (§ 13). Характери-
Характеристики сближаются по направлению течения. Предельная линия может
здесь возникнуть как оги-
огибающая каждого из семейств
характеристик. Христиано-
Христианович говорит в таких случаях,
что течение стремится к раз-
разрушению. В случае И тече-
течение стремится к разрушению
в трёх направлениях: в на-
направлении возрастающих ф,
в направлении убывающих ф,
в направлении движения.
III. Минимальное значе-
значение 9 принадлежит точке Л12.
Рис 56
Движение по характеристике от М2 к М, приведёт теперь, вследствие
A8.6), к росту ф; движение от М2 к Мх, по A8.7), - к уменьшению ф
(см. рис. 56). .При движении от м'2 к М'г мы будем попадать в область
меньших v, значит, характеристики 2-го семейства, встречающие ЩМЪ,
будут подходить [вследствие A8.7)] всё круче и круче по мере пе-
перемещения от М2 к М3. Напротив, если двигаться от М2 к Mv мы

168
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
будем встречать всё менее и менее наклонённые характеристики
1-го семейства. Наконец, как и в предыдущих случаях, при переме-
перемещении по любой характеристике мы будем иметь монотонное изме-
изменение тангенса наклона этой же характеристики (неизменность знака
кривизны). Такое решение стремится к разрушению в направлении
убывающих ф, но в направлении течения оно может не претерпевать
разрушения — разрыв может и не возникнуть, ввиду того, что ха-
характеристики разных семейств ведут себя здесь по-разному. Этот тип
можно назвать «смешанным».
IV. 9 достигает минимума в точке Ж4. Теперь рост ф получим,
двигаясь от Л14 к Ж,, и убывание —двигаясь от Ж4 к Ж3. При
передвижении от Л14 к Л13 будем попадать в область с меньшими v
и, значит, по A8.6) характеристики 1-го семейства, пересекающие
Ч	'
Ж4Л13, будут становиться всё круче по мере перемещения от Ж4
к Ж3. Напротив, двигаясь от Ж4 к Ж1? будем встречать всё менее
и менее наклонённые характе-
характеристики 1-го семейства. Движе-
Движение стремится к разрушению
в направлении растущих ф
(рис. 57). Как и в предыдущем
случае, вопрос о возникнове-
возникновении линии разрывов останется
открытым. Течения такого типа
Христианович также называет
смешанными, объединяя их
с предыдущими.
Мы имеем таким образом
	 ф три типа течений.
'	Можно было бы провести
Рис 57.	классификацию и по поведению
характеристик в плоскости
(лг, у) непосредственно, но здесь число классов пришлось бы удвоить.
В самом деле, рассмотрим направление вогнутости характеристик
в плоскости (лг, у). Имеем:
Так что
dx
d2y
dx2
tg(P±
1
cos2C
a).
-1- at
d
dv
) dv
dx.
Но вдоль характеристик [см., например, A0.3)]
dv

, ,Oj КЛАССИФИКАЦИЯ СВЕРХЗВУКОВЫХ ТЕЧЕНИЙ ПО ХРИСТИАНОВИЧУ 169
а по (9.22)
da	<	/ * — 1	о \ 2
2 sin ос cos ос — = — (/-f 1)^г = — [—g- + sin2aj-.
Таким образом,
i-i-= ± 	5-?s	г-з	\ cos2 a	s	sin^oc >.
dx2	COS2 C ± a) rfx t» sin a COS a ^	2	)
Кривизна обратится в нуль при значении a = a0, где
¦ о	3 — у.
sm2 осо = —J— .
При у =1,4 sin a0 = 0,6325, соответствующее число Маха будет
2
M
а «0=/2-
Такие точки перегиба на характеристиках отчётливо видны, на-
например, на рис. 49 и рис. 51 там, где наши характеристики пере-
пересекаются с линиями v== \ 2.
Таким образом, классифицировать пришлось бы отдельно для М<Мо
и М > Мо-
Посмотрим теперь, к какому классу движений принадлежит дви-
движение, получающееся сразу же за «переходной линией» (так мы
будем называть линию, где v = at) в сверхзвуковой области. Отпра-
Отправляемся на этот раз от уравнений (9.2):
/ 9	9\ dvv
+ D - а2) -? = о
и условия отсутствия вихрей
dv,. dvr
дх ду ~""
Вводя величину скорости v и угол C, так что
мы можем переписать наши уравнения в виде
или, если ввести v = v[at и обозначить М = v/a:
B0.2)

170
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Чтобы выяснить, что будет происходить около линии v~\, рас-
рассмотрим сперва произвольную линию v = const. Пусть Р— точка на
этой линии. Обозначим длину, отсчитанную по дуге от точки Р вдоль
линии v = const., через s. Нормаль в Р к линии v = const, обозначим
буквой п. Направив ось Ох по касательной, а ось Оу по нормали
к линии v — const, в точке Р, мы можем переписать уравнения B0.1)
в виде:
(М2
dv
Здесь 8 — угол, составляемый вектором скорости с касательной
к линии v = const, (см. рис. 58). Исключив из этих уравнений dbjdn,
мы получили следующее равенство, свя-
связывающее dbjds и dv/dn:
Особенно простой вид получит формула
B0.3), когда наша линия v — const, есть
линия перехода, т. е. если v=\. Тогда:
dv
—
= СО52Ь—.	B0.4)
Заметим, что если нормаль направлена
в сторону сверхзвуковой зоны, то будет
dv/dn > 0, и таким образом дЪ/ds > 0.
Рис. 58.	Отсюда мы получаем важное следствие:
если перемещаться по линии v= 1, то угол
между направлением скорости и направлением касательной к линии г>=1
будет меняться монотонно и именно так, что если при нашем пере-
перемещении сверхзвуковая скорость остаётся слева, то вектор скорости
будет вращаться против часовой стрелки.
Может ли получиться бесконечное ускорение уже на самой линии
v= 1? Согласно B0.4): dv/dn = (\/cos2b)dbjds. Может представиться
два случая: 1) 8 = тт/2, 2) S Ф л/2. Если 8 = тт/2, то вектор скорости
ортогонален в точке Р к переходной линии. Так как при v~\ sina=l,
т. е. а = тс/2, то в точке ©=1 вектор скорости должен быть орто-
ортогонален к характеристикам Значит, когда S = ти/2, то характеристики
будут касаться в Р переходной линии (рис. 59). Пусть
значения угла р на линии v=\ в функциях от длины дуги s,

I 20] КЛАССИФИКАЦИЯ СВЕРХЗВУКОВЫХ ТЕЧЕНИЙ ПО ХРИСТИАНОВИЧУ 171
отсчитываемой от точки Р. Дифференцируя это соотношение вдоль
дуги, получим
(как и прежде, 8— текущий угол, составляемый вектором скорости
с направлением касательной к линии v—\, так что |3 — 8 — угол
наклона касательной к линии v—\ к оси х). Кроме того, дифферен-
дифференцируя вдоль кривой <и=\, имеем:
К этим двум уравнениям мы можем
присоединить ещё два уравнения, *.
которые получатся из B0.2) при
М=1. v=\:
sin В -g- - cos В -g- = 0,
п dv	n dv .
sin В -,	cos 3 -,	\-
" дх	' ду '
,Q	,c	Рис 59.
Решая наши уравнения относительно производных, получим
dv^ _ cos О — S) rfp* di7 	 sin (P — 8) rfg*
йу	cos2 S rfs"' их	cos2 S ds
d} 	 sut ,3 d'f d$ _ cost°> d^
N
ччч>
/
V
7Г

«^	"_
„/'
	vt=1
ду cos S ds ' cb: " cos
Мы предположили, что в точке P(s = 0) S = тт/2. Около точки Р
мы можем написать
поэтому cos2 8 = (db*jdsJ s2 -f- O (s3), где O(s3) обозначает член по-
порядка не ниже s3. С другой стороны, для d$*jds имеем
так что для dvjdy, например, имеем

172	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ 1
Для ограниченности производной необходимо выполнение равенств
Таким образом, для возможности непрерывного перехода от дозвуко-
дозвуковой скорости к сверхзвуковой в том случае, когда в некоторой
точке линия перехода ортогональна к вектору скорости (например,
на оси симметрии сопла Лаваля), необходимо выполнение специаль-
специальных условий B0.6) относительно равномерности потока около этой
точки.
Если линия v=\ сама является характеристикой (или во всех
точках касается характеристик), то для непрерывности движения усло-
условие B0.6) лолжио выполняться во всех точках этой линии, т. е. должно
быть
и линия перехода должна быть простой прямой. В противном случае
на всей линии перехода мы будем иметь бесконечные значения на-
наших производных, т. е. бесконечные ускорения, и тогда движение
нельзя продолжить за линию перехода (сама линия перехода будет пре-
предельной линией) и всё решение не будет иметь физического смысла.
Простейшим примером такого решения может служить аналог источ-
источника или стока в несжимаемой жидкости. Именно, если в цилиндри-
цилиндрических координатах
Vr = Vr </)>	^9 = 0
{vr — функция одного только г), то, так как по уравнению Бернулли
_j
-L— (\ •/~1 7д\»-'
Ро~"\ *+1 i
(z> = | vjaj), а вследствие уравнения неразрывности,
dr
мы можем написать:
const.
Если г, — радиус того круга, на котором v обращается в единицу,
то постоянная интегрирования будет г А . j ', так что
г =	—-^	г- •	B0-7)
-/»+! »-1-,\7Т
^2	2 )

20]
КЛАССИФИКАЦИЯ СВЕРХЗВУКОВЫХ ТЕЧЕНИИ ПО ХРИС1 ИАНОВИЧ\ 173
Мы можем, казалось бы, представить себе движение таким' на бес-
бесконечности v — 0, всюду vr < 0 — жидкость устремляется по радиусам
h иентр>; скорость движения монотонно растет по закону B0.7) и
на окружности г = гх достигает критического значения. Однако вдоль
окружности /¦ = /"» будет dbjds=\/rt, так что B0 6) не выпол-
выполняется. С другой же стороны, как нетрудно убедиться, написав
уравнения характеристик в цилиндрических координатах, все характе-
характеристики должны касаться окружности г = г„ (где ctga = O). Движение
наше не может быть продолжено внутрь круга радиуса r = rt. В са-
самом деле, знаменатель B0 7) имеет максимум, и следовательно,
г имеет минимум в точности при v = 1 Этот пример может служить
иллюстрацией к сказанному в начале предыдущего параграфа о невоз-
невозможности в сжимаемой жидкости осуществления таких течений, кото-
которые в жидкости несжимаемой давали бы бесконечные скорости. Вместо
источника, или стока в начале координат, которые получаются в не-
несжимаемой жидкости, мы имеем здесь ядро в виде круга радиуса
г — гх, внутрь которого течение нельзя продолжить.
Вернемся теперь к общему случаю, когда 8 Ф к/2 (см. рис 60)
Нетрудно убедиться, что движение, возникающее в сверхзвуковой
области сразу за линией перехода, будет принадлежать к типу
смешанных течений по Христиановичу. Действительно, найдем
изменение ср при перемещении по характеристике. Полная
производная по х при перемещении по характеристике будет
= v [cos
Таким образом,
sin p tg (p + а)].
Ha
dx
линии
U=1
Рис 60
cos(P ± а) Ф K^v.o)
перехода а = rJ2,
Продифференцируем B0 8) ещё
раз по л: и определим эту производ-
производную на линии перехода Получим:
/ rf2?\ _ + _«!L_ da^
\ dx* J* - sin Э dx -
Знак плюс следует взять при перемещении вдоль характеристик
1-го семейства, знак минус —для 2-го семейства. Таким образом,
рсли по мере передвижения от какой-либо точки Р переходной линии
по характеристике 1-го семейства ср будет расти, то при перемеще-
перемещении от Р по характеристике 2-го семейства ср будет убывать и на-
наоборот. Ясно, что это может быть лишь в случае смешанного тече-
течения (рис. 56 и 57). Итак, за переходной линией действительно может

174
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
возникнуть предельная линия, в чём мы и имели случай убедиться
на конкретных примерах § 19.
§ 21. Построение «безударного» сопла Лаваля. Истечение
газа из отверстия, сопровождаемое переходом через скорость
звука. В § 12 мы видели, как можно путём подбора профиля сте-
стенок получить равномерную сверхзвуковую скорость в сопле Лаваля,
после того как уже получено сверхзвуковое течение в некотором
сечении сопла. Подбор стенок производится в сверхзвуковой области.
На первый взгляд может показаться, что форма стенок в дозвуковой
части сопла — так называемой входной части — может быть произ-
произвольна, лишь бы можно было достигнуть перехода через скорость
звука. Однако это не так. Затруднения с отысканием решения,
о которых мы говорили в предыдущем параграфе, здесь проявляются
особенно отчётливо. Если профиль входного отверстия будет произ-
произвольным, может оказаться, что переход через скорость звука будет
сопровождаться появлением бесконечных ускорений. Физически это
будет означать, что движение перестроится, так что сразу течение
будет «испорчено». На рис. 61, заимствованном из статьи Астрова,
Р_
Ро
0,75
U.50
0,25
О
L
а
о
v
а
о (
о
о
и
\
*>.
эсос
ч
соа
а&
оса
ахх
pax
ах*
со
100
200
300
Рис. 61.
400
500 хмм 600 х
Левина, Павлова и Христиановича'), даны результаты эксперимен-
экспериментальных измерений распределения давления р/рп вдоль оси одного
сопла Лаваля. Сопло это было рассчитано без учета возможности
') Астров В., Левин Е., Павлов Л., Христианович С,
О расчёте сопел Лаваля, ПММ, т. VII, 1943.

§ 21]	ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ	175
возникновения разрыва. Как видно на рисунке, недалеко от линии
перехода (на ней р/ро = 0,528) в сверхзвуковой области возник раз-
разрыв; он породил возмущение, отражающееся от стенок сопла и
распространяющееся по всей длине сопла. Равномерность потока
оказалась испорченной.
Как же следует построить входное отверстие, чтобы скачок не
образовался? Как построить безударное сопло Лаваля?
В качестве простейшего приёма можно, казалось бы, предложить
следующий1). На оси симметрии сопла, каковую мы примем за
ось Ох, с началом координат в точке линии перехода, зададим ско-
скорость vx как некую аналитическую функцию от х. Пусть разложе-
разложение этой функции в ряд около точки х = 0 имеет вид:
B1.1)
Уравнения газовой динамики [см. A5.1)]:
*-IK]-^- = 0, B1.2)
где Ф — безразмерный потенциал скоростей, так что
дФ	дФ	,о1 о.
^ = -3—. v „ = -з—,	B1.3)
¦* d*	v dy	v '
вместе с условиями симметрии и условием B1.1), позволят тогда
последовательно определить в точке О @, 0) любую производную от
Ф_по х к у. Так, например, из условия B1.1) имеем для точки О:
дФ/дх — 1, а из условия симметрии: дФ/ду = 0 (vy = 0). Затем из того
же условия B1.1) д2Ф/дх2^=А, из условия симметрии д2Ф/дхду =0,
из_ уравнения B1.2) получим д2Ф/ду2 = 0. Далее, дЧ/дх3 = 2В,
д3Ф/дх2ду = 0; производные же д3Ф/дх ду2, дэФ/ду3 определим путём
дифференцирования B1.2) по х и из условия симметрии и т. д.
Производя эти совершенно элементарные выкладки, получим:
'^М,?^ег Т' Ueber zweidimenslonale Bewegungsgleichung in elnem Gas.
mlt Ueberschallgeschwindlgkelt stromt, Forschungheft 72, 1908.

176	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Теперь мы можем написать разложения для vx и vy:
—I \*- —1 1 / -** 	q	 A_y —j— . . . y? 1 ,O)
x —— 1 j j\	pr	дг v ——
+ J^±g^iilly3 _)_... B1.6)
и путём простых квадратур определить функцию тока Ч":
4=fj;(i>xdy-vydx),
где
Одну из линий тока Ф = const, можно принять за стенки сопла. Схо-
Сходимость участвующих здесь рядов обеспечивается теоремой Коши —
Ковалевской, благодаря аналитичности функции vx(x, 0). Однако
радиус сходимости по оси Оу заранее неизвестен, и это сразу же
заставляет отбросить изложенный здесь метод построения сопла.
Действительно, так как неизвестно, на каком расстоянии мы ещё
можем пользоваться нашими рядами, то заранее мы не знаем, не встре-
встретимся ли мы с тем же затруднением, о котором говорили в преды-
предыдущем параграфе: наше решение может оказаться не имеющим смысла
за некоторым у.
Изложенные здесь подсчёты дают, однако, совершенно строгие
значения производных в точке О от Ф и W и полезны для ориенти-
ориентировки. Они показывают, как ведёт себя движение недалеко от линии
перехода в случае аналитического решения на оси. Так, например,
они позволяют дать уравнение линии перехода около самой точки О.
Именно, если искать это уравнение в виде
х = я2;у2 + а4/ + •••¦	_	B1-7)
то, вставляя B1.7) в B1.5) и B1.6) и написав условие vx -f- vy = 1,
получим без труда:
х =	^— Ау2 — v ^ ' АВу* + ...
Далее, для характеристик обоих семейств, выходящих из О, будем
иметь:

211
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ
и если искать их уравнение в виде
х = ту2 -(- .. .,
то для 1-го семейства (знак плюс) получим:
для 2-го:
B1.8)
х== — 1±±Ау*+ ...	B1.9)
На рис. 62 дана схема расположения линии перехода и обеих харак-
характеристик.
Чтобы избежать затруднения, связанного с необходимостью знать
радиус сходимости, Христианович, Астров, Левин и Павлов предло-
предложили способ построения всего течения в эксплицитном виде, а не при
Характеристика
Тсемейства
Линия
перехода
•Характеристика
Лсемейстеа
Рис 62.
Рис. 63.
помощи рядов. В основу они положили построение входного отвер-
отверстия по методу Христиановича (§ 17). Именно они приняли в качестве
фиктивного потока течение через так называемый насадок Борда.
Уравнение этого течения имеет вид
VM(p. -f-h)	\
Линии тока схематически даны на рис. 63. Стенки насадка полу-
получаются при Ч = ± тт (у — + /V)
стенку насадка.
О
а рис. 63. Стенки насадка полу
) — линия тока дважды повторяет
ну насадка.
Отделяя действительную и мнимую часть, получим:
= -=-[Ф —e-*cos4T],
00
v
Линии тока, для которых f=i тг/2, могут быть приняты за «стенку» С
фиктивного потока. Уравнения этих стенок будут
У
12 Теоретическая гидромеханика, ч. II

178	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
Потребуем теперь, чтобы V^ было в точности равно тому значению,
при котором соответствующая скорость vM в потоке сжимаемой
жидкости равна единице:
2А л/ (h~l)"h++, ~ 0,7579.
Как показал расчёт упомянутых авторов, контуры в плоскости (х, у)
укорачиваются, так что линия г»=1 оказывается на конечном рас-
расстоянии !). Далее, весьма существенно то, что линия перехода оказы-
оказывается отрезком прямой, перпендикулярной к оси Ох, и вдоль линии
перехода скорость всюду имеет одно и то же направление, парал-
параллельное оси Ох (в несжимаемой жидкости поток стремится к этому
направлению на бесконечности). Мы уже видели в предыдущем
параграфе, что прямая линия перехода обладает преимуществом по
сравнению с другими. Тот факт, что линия перехода прямая, позво-
позволяет считать, что разрывов в сверхзвуковой зоне не образуется.
Практически ход построения входной части следующий. Пересечение
прямой перехода с осью сопла принимается за начало координат
в плоскости (х, у) (положительная ось Ох направлена по оси сопла
в сторону сверхзвуковых скоростей, отрицательная — в сторону
дозвуковых скоростей). Начиная от линии перехода (в сторону дозву-
дозвуковых скоростей), расчёт стенок ведётся вплоть до тех мест, где
vя» 0,8 по формулам типа A7.2), упрощённых за счёт того, что здесь
VKwO, v^\; начиная от того места, где г»я^0,8, расчёт ведётся
по формулам A7.23). В сверхзвуковой части следует сперва отойти
от прямой линии v=\ путём разложения v и р в ряды, но не по
степеням х и у, как это делалось в начале этого параграфа, а по
степеням ф и ф. С этой целью можно использовать, например, урав-
уравнения Чаплыгина A6.9), A6.10), которые можно записать сперва
в виде
df ~~ Ро d<\> <^9 М2—1 ро <5ф
д$	р dv dv	Dp dp
затем принять за независимые переменные ф и ф, а за искомые функ-
функции v и р и, наконец, принять за неизвестную функцию t = v2—1.
Написав разложение t и р по степеням (риф (практически можно
ограничиться членами с пятыми степенями), можно при помощи этих
рядов отойти немного от линии v=\ в сторону сверхзвуковых
скоростей. Определив вдоль линии ф = const, (упомянутые выше
авторы брали ф = 0,44721) скорости в нескольких точках, можно
') Это связано с наличием множителя УК под интегралом выражений
для х через у.. Ср. приближённые формулы стр. 143.

§ 2П
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ
179
затем уже строить сверхзвуковую часть по методу, изложенному
в § lz-
На рис. 64, заимствованном из упомянутой работы, изображён
профиль сопла, рассчитанного так, чтобы на конце его было v= 1,7;
тут же дано распределение давления вдоль оси этого сопла, найден-
найденное экспериментально. Сравнение с рис. 61 подтверждает, что здесь
удалось избежать появления скачка и связанного с ним искажения
потока.
*	1	Ось сопла
см
Ро
1,0
0,5
О
1
\
_¦¦•¦
-——г~
' 1
Т*—JOO—^37 и	263	*+*	200	-Н
Входная часть\ Профилированный участок Рабочая часть
сопла \ сопла
Цилиндр.участок
•'п
О,
п
'о
ю
Г©1
о,
гпз
IYY1
YYY1
ч
о	/оо гоо ?пп 400
Рис, 64.
500 Кмм 600
Наличие плоской поверхности перехода обеспечило «безударность»
сопла. Однако условие, что линия перехода — прямая, является доста-
достаточным, но не необходимым для возможности непрерывности движе-
движения. Как показал Франкль1), можно использовать непосредственно
уравнения Чаплыгина для построения входной части безударного
сопла. При этом линия перехода будет, вообще говоря, криволиней-
криволинейной. Франкль показывает, как можно продолжить ряды типа рядов
Чаплыгина (§ 16) в сверхзвуковую зону, и находит условия, доста-
достаточные для того, чтобы решение оказалось безударным. Главная
трудность заключается в том, что функция тока ф, которая по Чаплы-
Чаплыгину отыскивается как функция Виг», оказывается неоднозначной
функцией этих переменных в сверхзвуковой области, прилегающей
мат '* %Р ?qH к л ь ф' И- К теории сопел Лаваля, Изв. АН СССР, серия
12*

180	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ J
к линии перехода. Остановимся несколько на выяснении этого обстоя-
обстоятельства. Способ изложения, более простой, чем у Франкля, был дан
позже Фальковичем'). Мы будем придерживаться именно этого
способа.
Уравнения Чаплыгина берём в виде
д$	р dv ' dv	v p d[i
Примем за независимые переменные ср и ф, а за искомые функции v
и р. Получим
_L±i^ = _^l Ро 1 -М2 dv _ __ dl
р0 v d'\i df ' p v d<f	db	У ¦ )
Вместе с Франклем введем теперь вместо v величину -q = ~q(x)) из
равенства
Величина эта будет действительной как при М < 1, так и при М > 1,
причём при v < 1 7j > 0 и при v > 1 tj < 0.
Совершенно элементарные преобразования дадут нам тогда
З #
и, если обозначим
ftft^iLjAlzJ!!.,	B1.14)
получим окончательно
0==^|l__j_f-.	B1.16)
Такая форма уравнений удобна при анализе перехода через скорость
звука. Функция Ь(-ф может быть представлена около т; = 0 (т. е.
около v=\) в виде ряда по степеням -q:
') Ф а л ь к о в и ч С. В., К теории сопла Лаваля, ПАШ, 1946.

„21|	ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ	181
[]о B1.14) при 7] = 0 мы имеем неопределённость, которая легко
раскрывается. Действительно, подсчитаем, например,
Так как по (8.9)
и по B1.11)
Нт —-—=—— =	(х + 1) ''т V 1 — М2
: ^ 1	dv	2	- . ,
Нт -Lffk = — Jim l(|/"l_M2),
ТО
'"'"'(y.+ l)''3.	B1.17)
Чтобы выяснить поведение решения около линии перехода (т; = 0),
заменим в уравнениях B1.15), B1.16) член Ь(-ф на д@). Мы получим
при этом главные члены ряда, представляющего точное решение1).
Теперь B1.15) и B1.16) примут вид:
b @)
B1.18)
Пусть ось симметрии сопла есть линия ф = 0. Тогда C(ср, 0) = 0.
Кроме того, 7j(cp, ф) = т;(ср, —ф); р (ср, ф) = — р (ср, —ф). Таким обра-
образом, р содержит лишь нечётные степени ф, a i] — лишь чётные.
Частные, точные решения системы уравнений B1.18) будут поли-
полиномы (а не ряды):
где А — произвольная постоянная. Смысл этой последней легко уста-
установить. Действительно, из B1.19)
п \	А
с другой стороны,
d-q д-ц dv дх	Y 1 — М2 dv cos |
так что, полагая ф = ср=О (точка пересечения линии перехода с осью
сопла), получим
''dvK
') Строго это следует из упомянутой работы Франкля.

182
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ.
(мы совмещаем начало координат в плоскости (х, у) с точкой ср=ф=
Итак,
B1.20)
Ось Ох направлена в сторону сверхзвуковых скоростей, так что
/
А<0.
Полиномы B1.19) годятся, конечно, лишь в небольшом удаления от
линии перехода т; = 0, но зато для всей области движения. Посмотрим,
как в плоскости (ср, ф) представятся переходная линия и характе-
характеристики. На переходной линии по B1.19) будет (т] = 0):
ср = тф2.
Вдоль характеристик, проходящих через точку [3 = 0, г>=1,
имеем A0.6):
где
= / ^-dv.
1		,
Но так как sina=^- и ctga=|/M2—1, то, привлекая B1.11),
М
Характеристика Характеристика
[семейства ^	^-Л семейства
найдём без труда:
B1.21)
(т) < 0 при г/> 1). Таким образом,
вдоль характеристик, проходящих
через точку х — у — 0, будет
Р=±|(-^)!/2 B1.22)
Рис. 65.
(в плоскости C, у\ характеристики —
полукубические параболы).
Вставляя в B1.22) C и т; из B1.19), получим для характеристик
1-го семейства:
ср = 4ф2	B1.23)
и для характеристик 2-го семейства
B1.24)
На рис. 65 схематически даны в плоскости (ср, ф) стенки сопла, линия
перехода и обе характеристики.

21]
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ	183
Линия перехода и обе характеристики, выходящие из точки О,
делят всю полосу плоскости (ср, ф), отвечающую решению, на шесть
областей. Области эти пронумерованы на рисунке римскими циф-
ами I —VI, так что, например, во всей области VI мы имеем дозву-
дозвуковые скорости.
Посмотрим теперь, будет ли ф всюду однозначной функцией от C
и т]. С этой целью исключим ср из уравнения B1.19). Получим:
A3f -4- ЪА№ @) 7ji[> — ЪЬЪ @) р = 0.	B1.25)
Относительно ф это — кубическое уравнение. Оно будет иметь
только один вещественный корень, если
•|р2 + ?13>0.	B1.26)
Таким образом, в дозвуковой области, в области VI, где -ц > 0,
однозначность функции ф, а значит и ср, обеспечена. Далее, B1.26)
сохраняется и при ~q < 0 до тех пор, пока не будет
_9g2 3==0
4
Следовательно, однозначность будет иметь место ещё и в областях IV
и V. Итак, в областях IV, V, VI мы можем написать
В частности, на переходной линии, где т; =
причём -^_^=Т1_.	B1.28)
Ьф) дп ^зр
УЩ, прч
6@)	v	Ьф)
Отметим, что аналитическое решение, которое мы приводили в начале
этого параграфа, давало при т; = 0, как показывает простой подсчёт,
те же ф и дф/дг>, что получаются по B1.28). Решение в областях I, II, III
изобразится в виде складчатой поверхности. Интересно отметить, что
мы можем расширить наше решение, предполагая, что в области IV
(а значит, и V и VI) мы имеем B1.19), в которых А — Ах, а в об-
области III имеем B1.19), но с А = А2 Ф Ах (скачок производной dvjdx
скорости в точке О). Оба эти решения могут быть «склеены» при
помощи переходных областей I, II следующим образом. В областях I. II
ищем решение B1.18) в виде
Тогда первое из уравнений B1.18) даст

184	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ
где t = ср/ф2, а второе приведёт к соотношению
Исключая отсюда F, мы придем к одному уравнению
02f + 4/2) /" + b*f'2 - 2 (if - /) = 0.
Уравнение это можно записать в виде
d
dt 2tf'—f ~u'
Таким образом, мы можем написать
f 2с,/
f
где Cj — произвольная постоянная. Это уравнение сразу интегрируется
и даёт:
V @) / = 4Cj/ - 8с2 + с2 /Г^ё;,
где с2—вторая произвольная постоянная. Постоянные сх и с2 мы
должны теперь подобрать так, чтобы при t = AJ4 (характеристика,
отделяющая область I от области IV) было / = — А\/4 и при
t = — A^2 (характеристика, отделяющая I от III) было / = — А%.
Итак, мы исследовали поведение главной части частных реше-
решений B1.19) системы B1.15), B1.16) в сверхзвуковой области, примы-
примыкающей к линии перехода. Эти частные решения будут аналитическими
(величина ф и производная dty/dv, если их получить из B1.28),
в точности совпадут со значениями ф и dty/dv, построенными из анали-
аналитического решения Мейера, данного в начале этого параграфа.
Опасность появления скачков может возникнуть в случае склеивания
решений, отвечающих А = А{ и А — А2, но здесь могут быть даны
неравенства, связывающие Ах и А2, выполнение которых достаточно
для безударности решения'). Чтобы построить входную (дозвуковую)
часть сопла, Франкль предлагает теперь использовать ряды типа
рядов Чаплыгина, следующего вида:
^> Jgjgg	B1.29)
где А и с — постоянные.
Детальный анализ, за которым мы отсылаем к статье Франкля,
показывает, что на окружности х = х* будет:
l) См. упомянутые выше работы Франкля и Фальковича.

§ 21]
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ
185
где постоянная k определяется через с и А. Сравнивая это с B1 28),
замечаем, что главные члены ф и д^/дч] совпадают с главными членами
нашего частного решения, построенного для сверхзвуковой области.
Франкль устанавливает, что ряд B1.29) годится для сколь угодно
далекого расстояния от критического сечения в глубь дозвуковой
области. Мы можем теперь построить сопло следующим образом
В дозвуковой части использовать ряд типа B1.29), вблизи линии
перехода использовать решение вида B1.19); начиная с некоторого
расстояния от линии перехода, в сверхзвуковой области, применить
графический метод, изложенный в § 12. Параметры А, с, а также
наклон стенок в дозвуковой области на большом расстоянии от линии
перехода могут быть использованы для приспособления к заданным
техническим условиям
Как показал Франкль в другой работе'), ряды Чаплыгина можно
использовать при решении задачи о струе, вытекающей в пространство,
в котором давление будет меньше кри-
критического.
В § 16 мы видели, как происходит
истечение струи, если
j
(Pj—давление во внешнем простран-
пространстве, ра—давление внутри сосуда там,
где газ покоится). Посмотрим теперь,
что будет в том случае, когда
Ро
V
i I
/(*-i>
Рис 66
Имеем сосуд с симметрично расположенными стенками, угол между
которыми равен q-к (при q= 1 стенки будут служить одна продолже-
продолжением другой) (рис. 66) Через отверстие сосуда АХА2 газ вырывается
во внешнее пространство Следуя Чаплыгину, будем искать функцию
тока и потенциал скоростей в зависимости от величины и направле-
направления скорости. Вместо уравнений A6 12) теперь удобнее будет взять
уравнение A7 35):
где о и К зависят то1ы<о от v
1
j/ Ро v
ly-
1 —
') Франкль Ф. И, О задачах Чаплыгина для смешанных до- и сверх-
сверхзвуковых течении, Изв АН СССР, серия матем , 9 1945.

186
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Исключая из этих уравнений ср, получим для
= 0.
да*
B1.32)
Уравнение будет эллиптического типа, когда о>0 (г/< 1, К > 0),
и гиперболического при о < 0 (г/ > 1, К < 0).
Посмотрим теперь, для каких границ и при каких граничных
условиях мы должны решать уравнение B1.32) нашей задачи. Обра-
Обратимся к плоскости скоростей и отметим в этой плоскости направле-
направления скоростей, отвечающие стенкам сосуда (рис. 67). Эти направле-
направления продолжим до пересечения с кругом критической скорости.
Рис. 67.
Назовём точки пересечения Л] и А2. Проведём теперь из точки А2
эпициклоиду 2-го семейства, из точки С (vx — at, vy ~ 0) — обе
эпициклоиды (изображены пунктиром) и из точки А\—эпициклоиду
1-го семейства. Пусть эпициклоиды пересекутся в точках В\ и B'2.
Вследствие предположенного симметричного расположения стенок
точки В[ и В2 лягут симметрично относительно оси Ох на одну
окружность.
Исследуем сперва частный случай. Именно, пусть давление р1 во
внешнем пространстве в точности равно тому давлению, которое
по уравнению Бернулли отвечает кругу В'2В[. Такое давление, мы
назовём его рв< есть функция одного только q.
По Франклю, картина движения теперь будет следующей. Точка Ах
плоскости (х, у) отвечает точке Ах в плоскости (vx, v ); точка А2
отвечает точке А2. Таким образом линия перехода проходит через
края выходного отверстия (пунктир на рис. 66). Далее, отрезку
эпициклоиды AiB\ отвечает в плоскости {х, у) одна точка Av отре-

§21)
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ
187
зок эпициклоиды а'чВ'2 стягивается в одну точку А2. Эпициклоидам
второго семейства в криволинейном треугольнике С А1В1 отвечает
пучок характеристик, выходящих из Av а характеристики первого
семейства в С'А2В2 изображаются пучком характеристик, идущих
из А2. Так как радиусу-вектору ОА\ отвечает вся верхняя стенка
сосуда, а радиусу-вектору ОС — ось симметрии сосуда, то четырех-
четырехугольник ОА\В\с' отобразится на верхнюю
часть области дозвуковых скоростей и на
область, заключённую между верхней частью
АС переходной линии и характеристикой АХС
(двуугольник АХС переходит в треугольник
А[в\с'\ Таким образом в четырехугольнике
ОА\В\с' мы должны решить уравнение
B1.32), удовлетворяя краевым условиям1):
ф=4г на ОА\в\, )
2	[	B1.33)
ф = 0 на ОС.
Рис 68
Анатогичным образом область ОА^В^С отобразится на нижнюю
часть дозвуковой области и на двуугольник СА2, причем мы должны
решить здесь B1.32) при краевых условиях
= — -^ на ОА2В'Ъ
= 0 на ОС.
B1.34)
') Значение ф на характеристике С'В\ мы найдем при этом в конце
решения задачи Задавать эти значения заранее мы не можем Дело в том,
что мы имеем здесь дело с обобщенной задачей Трикоми Последняя заклю-
заключается в следующем Имеем дифференциальное уравнение второго порядка
d2z . d2z n
ду
дх*
где г = г {х, у),
которое меняет тип из эллиптического на гиперболический, когда мы попа-
попадаем из верхней полуплоскости (х, у) в нижнюю Рассмотрим область D,
ограниченную кривой L, лежащей в эллиптической области (с концами на
оси ОХ) и характеристиками /., и L2 разных семейств, исходящими из кон-
концов L (рис 68) Пусть заданы значения z на кривых L и /., (но не на L2)
Грикоми доказал существование и единственность решения этой задачи
паше уравнение B1 32) является обобщением уравнения Трикоми (вместо а
мы имеем /< (а) положительное при а > 0 и отрицательное при а < 0) Зада-
Задание \f на прямых ОА\ и ОС' будет отвечать заданию г на ?, а задание ф
на А{В{ отвечает заданию z на Lx Доказательство однозначности решений
B1 32) имеется > Франкля

188
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ.
Предположим, что нам удалось найти решения поставленных здесь
задач. Это значит, в частности, что нам удалось найти движение и
на характеристиках Afi и А2С. Но тогда мы будем знать скорости
иа характеристике АХС (и А2С), а нам, кроме того, известно, что
Ах (А2) лежит на свободной поверхности, и мы можем, поскольку
мы находимся уже в сверхзвуковой области, применить хотя бы метод,
изложенный в § 12 (задача 4), и найти вид свободной поверхности
AiDl (A2D2) и движение внутри треугольника AXCDX (Л2СО2), где
CD\(CD2)— вторая характеристика, выходящая из С (рис. 66).
Заметим, чго линии CDl{CD2) отвечает в плоскости (vx, vy) харак-
характеристика С'В'2(с'В]). Мы можем теперь решить задачу 2 (§ 12),
ибо на характеристиках CDX и CD2 скорости будут известны, и найти
движение внутри криволинейного четырёхугольника CDjfDj (точке Е
будет отвечать точка Е' плоскости (vx, vy), лежащая на пересечении
крайних эпициклоид). Далее, определим (задача IV) свободные поверх-
поверхности, идущие от точек Ог, D2 и т. д. Задача будет решена.
Прежде чем сказать о том, как же конкретно решается уравне-
уравнение B1.32) при условиях B1.33) и B1.34), посмотрим, что полу-
получится, когда /?! Ф рв.
Пусть сперва
Р\ < Рв-
Проведём в плоскости (vx,vy) дугу круга с центром в начале координат
и с радиусом, отвечающим давлению Р\« Рв) (Рис- 69), а также
эпициклоиды второго (первого) семейства, выходящие из Л2(л|),
и обе эпициклоиды, выходящие из С Отметим пересечение всех наших
четырех эпициклоид с кругом, отвечающим давлению рх (точки D2,
Fu F2, Di). Треугольнику AXCD: теперь будет в плоскости (vx, vy)

§ 21]
ПОСТРОЕНИЕ «БЕЗУДАРНОГО» СОПЛА ЛАВАЛЯ
189
отвечать четырёхугольник BiF\D\C . Аналогично этому, треуголь-
треугольнику A2CD2 отвечает в плоскости (vx, vy) четырёхугольник ВчРъРгС .
Далее, криволинейный четырёхугольник С D'xED\ плоскости (vx, vy)
(р'\Е и D^E —дуги эпициклоид) отвечает в плоскости (х, у) фи-
фигуре, образованной характеристиками CDV DXE, D2E, CD2 и т. д.
Таким образом и здесь всё сводится к решению B1.32) при
условиях B1.33), B1.34) для областей ОА^С' и ОА\в\С'. Отме-
Отметим, что эти последние области будут в точности теми же, что и
области в случае, когда Р\ = рв- Таким образом, течение внутри
сосуда полностью определяется решением B1.32) и не зависит от
величины давления во внешнем пространстве, если только рх «^ рв.
Наконец, в том случае, когда р0 > рг > рв, мы должны рассмо-
рассмотреть в плоскости (vx, vy) картину, представленную на рис. 70.
Рис. 70.
Здесь мы должны решить уравнение B1.32) для области OAiD\E\C
при краевых условиях
ф = ~2- вдоль OA'\D[E\,
4> = 0 вдоль ОС.
Также надо решить B1.32) для области OA'2DiE2C' при краевых
условиях
ф = — -?- вдоль OA'iD'iE^
ф = 0 вдоль ОС.
Коль скоро решения эти получены и мы выходим в сверхзвуко-
сверхзвуковую область, мы можем далее вновь применить методы, изложенные

190	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. ]
Нам остаётся только сказать, как конкретно ищется решение
уравнения B1.32) в смешанных (до- и сверхзвуковых) областях,
участвующих в наших задачах. Как мы уже упомянули, Франкль
предлагает искать эти решения в виде рядов типа рядов Чаплыгина.
Рассмотрим для конкретности решение B1.32) для области ОА\В\С
(рис. 67 и рис. 69). Будем искать ф в виде
Ф—у—+2^а«тлоГ Т"'	( }
где
С» = *„(*)•
ап — постоянные коэффициенты, пока неопределённые, но такие, что
со
ряд 2 fln сходится. Краевые условия на прямых ОС и ОЛ[ удо-
и = 1
влетворятся при этом сами собой. Сходимость ряда в дозвуковой области
(треугольник OAiC ) обеспечивается на основании результатов Чап-
Чаплыгина. Франкль показывает'), что при непрерывном изменении дан-
данных Коши на переходной линии решение задачи типа нашей, в соот-
соответствующем характеристическом треугольнике, меняется непрерывно.
Отсюда можно заключить, что B1.35) может представлять решение
не только внутри круга г)=1, но и внутри характеристического
треугольника. Неопределённые до этого коэффициенты ап надо найти,
удовлетворяя краевому условию на характеристике AiB\. Именно,
должно быть
где а ф) есть результат представления о через fl из уравнения эпи-
эпициклоиды А\В\. Путём переразложения наших функций от ji в ряды
и сравнения коэффициентов мы получим теперь бесконечную систему
линейных алгебраических уравнений для определения ап. Практически
достаточно будет сохранить конечное число членов ряда для ап,
требуя выполнения равенства B1.36) для конечного числа заранее
выбранных значений jj.
§ 22. Численные методы решения плоских задач газовой
динамики. Расчёт сверхзвукового обтекания кругового цилиндра.
С появлением электронных быстродействующих вычислительных
') Франкль Ф И., loc. cit См также Франкль Ф. И., О задачах
Коши д.1я уравнений смешанного эллиптико-гиперболического типа с на-
начальными условиями на переходной линии. Изв. АН СССР, серия матем.,
8, 1944.

«, 221
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ
191
машин стало практически возможным получение, с нужной степенью
точности, решения наиболее трудных задач газовой динамики. В ка-
качестве примера применения соответствующих численных методов рас-
рассмотрим расчёт обтекания сверхзвуковым потоком (со скоростью Vm)
кругового цилиндра S (рис. 71). От цилиндра отходит ударная
волна ?, после прохождения которой поток становится вихревым и
смешанным. Требуется найти форму ударной волны, её положение
и движение между ударной волной
и цилиндром вплоть до не известной
заранее линии перехода через ско-
скорость звука и далее. Изложим здесь
схему численного решения этой за-
задачи, разработанную (и применённую
к расчётам) О. М. Белоцерковским
на основании метода А. А. Дород-
Дородницына '). Этот последний метод
сводит задачу интегрирования си-
системы нелинейных дифференциаль-
дифференциальных уравнений в частных производ-
производных к решению некоторой аппро- " ,
ксимирующей системы обыкновенных
дифференциальных уравнений.
Прежде чем излагать схему чи-
численного решения, запишем урав-
уравнения плоской вихревой стационарной задачи в полярных координа-
координатах (г, 6); такая система естественна для рассматриваемой задачи
обтехания круга.
Уравнения движения примут вид
dvr
dvr
1 dp
dr
B2.1)
B2.2)
(vr, vf> — составляющие скорости по осям гиб соответственно).
Уравнение неразрывности запишем в виде:
B2.3)
') Дородницын А. А., Об одном методе численного решения неко-
некоторых задач аэродинамики, Труды III Всесоюзного матем. съезда, Изд.
АН СССР 2 A956), 3 A958).
Ьелоцерковский О. М., Обтекание произвольного профиля с ото-
отошедшей ударной волной, ПММ, т. XXII, вып. 2, 1958; Расчёт обтекания кру-
кругового цилиндра с отошедшей ударной волной, Вычислит, математика, № 3,

192	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	|1Л. I
Может быть введена функция тока ф(г, б) такая, что
nv _ _ 0*L ov — Й-	/02 4^
rPvr~ дв ' 9V"~ dr '	{2.2.Л)
Условие адиабатичности запишется в виде:
„iii^ii_O	Г225)
где, как и прежде, & = р1/*р~1. Комбинируя B2.4) и B2.5), заклю-
заключаем, что Ь зависит только от ty:
jPl" = *W-	B2.6)
Уравнение Бернулли, получающееся путем комбинации B2.1), B2.2)
и B2.4), запишется, как в любом плоском случае, в виде:
где, как и прежде (§ 8, стр. 42) ^ах=0Н-1)/(«— l)fil (о, — кри-
критическая скорость, не меняющаяся при переходе через поверхность
разрыва и потому постоянная как для вихревого, так и для безви-
безвихревого движения).
Умножая B2.1) на рг и используя уравнение неразрывности B2.3),
получим без труда
^ (г р^+рг)*-^ =<*+,.	B2.8)
Определяя из уравнения Бернулли B2.7) плотность через ви 8и
вводя её в уравнение неразрывности B2.3), получим
где
max
Наконец, используя B2.4), почучим для изменения ф вдоль какой-то
линии' г = /? (8) соотношение
B2Л0)
Неизвестными функциями являются здесь vr, щ, ф и Ь. Давление р
и плотность р находятся из соотношений B2.6) и B2.7) через <иг
vit Ь. Вводя давление рй и плотность р0 адиабатического затормо-

,22]
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ	193
жйнного (в невозмущенной среде) потока и потенциальную темпера-
температуру ^о д0 скачка- можем написать
	i—-Ьг-Ч Ч-) *• B2-u>
Pa
( ]	A	Sr-M =( — I	^ B2.12)
Po
Запишем теперь краевые условия задачи на поверхности разрыва S
и на обтекаемом цилиндре 5.
Выразим vr, Vtj, ф и Ь сразу после прохождения поверхности
разрыва через угол наклона ср нормали к поверхности разрыва
к оси X. Из уравнений G.16) и G.17) имеем для vx и vy (соста-
(составляющие скорости по оси Л" и ей перпендикулярной)
B2.13)
"Г
tgcplff — cos^l,	B2.14)
где До, — скорость звука, связанная со скоростью набегающего по
тока ¦Уо, и максимальной скоростью г>шах соотношением
2	2	1
со |	оо	* 2
~~о "т" ~Z Т~ == "о" ^тах>
так что
2
Сочетая B2.13), B2.14) с очевидными соотношениями
vr = г)у sin б —
г»9 = vx sin б -j-
„	 и„сО5б, \
л \	B2.15)
uvcos9, J	v '
получим выражение через <f значений vr и v$ сразу же после пере-
перехода через поверхность разрыва.
Функция ф не претерпевает скачка после прохождения разрыва.
До прохождения разрыва мы имеем
= pmvoo sin 9 = р0 (\	^- ] г»оо sin 9.
13 Теоретическая гидромеханика, ч. II

194	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
Следовательно, на поверхности разрыва
1
tfoorsine.	B2.16)
При этом, если поверхность ? имеет уравнение
г = го-Н(в),	B2.17)
где г0—радиус обтекаемого цилиндра S, то г и	9 на поверх-
поверхности 2 будут связаны очевидным геометрическим	соотношением
Id \
B2.18)
Наконец, для определения значений 0 после прохождения разрыва
получим, воспользовавшись формулой G.10):
МУ = —f—Y=—
hj	Ро\ Р /	Роо
2* i?	*—1\/	<& 1 -f- tg2
B2.19)
Остаётся записать краевые условия на обтекаемом цилиндре. Здесь
имеем, очевидно,
при r = r0 vr = 0 ф—0.	B2.20)
При этом, так как 5 является линией тока, то вдоль г — га вели-
величина 0 должна сохранять постоянное значение, которое можно
получить из B2.19), полагая там <р = 0. Таким образом,
'* — 1\ж/ 2* v2^ %—1\ /	2
при r—t
B2.21)
Теперь, когда записаны дифференциальные уравнения и краевые
условия задачи, перейдём к описанию аппроксимирующей системы,
разработанной и применённой к расчётам О. М. Белоцерковским на
основе метода интегральных соотношений, развитого А. А. Дородни-
Дородницыным.
Разобьём всю область между цилиндром 5 и поверхностью раз-
разрыва S на N полосок, проводя N— 1 кривую с уравнениями:
/• = r,(9) = ro + ^e(9), /-1.2	N-1. B2.22)

225	ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ	195
Линии эти отстоят друг от друга на равные расстояния е
(имеется в виду расстояние по г при закрепленном 9). Индекс i — N
отвечает линии разрыва 2; индекс /=1 отвечает первой, наиболее
близкой к цилиндру S, линии и т. д.
В дальнейшем будем обозначать все величины на г-й промежу-
промежуточной линии индексом i, на ударной волне — индексом S (или N),
на поверхности цилиндра — индексом S.
Обратимся теперь к уравнению B2.8) и проинтегрируем обе его
части по г вдоль произвольного луча б = const, от поверхности тела
г = г0 до границы каждой из полученных нами полос. Получим N
соотношений (по числу полос) вида
Г; (8)	Г^Щ
\ - (r?vl 4- pr)s + / ^f± dr = / Wp + p) dr.
далее, вынося дифференцирование по 9 за знак интеграла (слева) и
принимая во внимание определение B2.22) функции гг(9), запишем:
Г; (в)
(pv%vr) dr — jj (pv,pr\ -щ- -f (rpv2r + pr)i — (pr)s —
rt (в)
= / (vlp + p)dr, i=l, 2	N. B2.23)
Аналогичным образом получим из уравнения B2.9):
~-Jj(^)i^ + (rvr<)l = 0, /=1,2	N. B2.24)
Уравнения B2.23), B2.24) содержат интегралы вида
Г; (9)
/ /(Л В)dr.
Го
Аппроксимируем теперь любую подынтегральную функцию интер-
интерполяционным полиномом по г степени N, принимая за узлы интер-
интерполяций границы полос:
в[т^Г•	B2-25)
13*

196	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Коэффициенты ат(Ъ) определим так, чтобы значения /?F) = /[гг@), 8]
нашей функции / на линиях гг(9) точно представлялись с помощью
нашей интерполяционной формулы. Иначе говоря, определим ах,
а2, . • ¦, uN из следующей системы N уравнений
N
Sn Г Г' Г° У" — f i — 19	АГ
т	~о	 	•* ^*			• ' ¦ » Jv
т-0
или же
N
2jam\4j) —fl<	/=1. 2	Л^.
т=0
Кроме того, заметим, что ао = /о (значение / при г = г0). Пусть
мы получим
N
Яо = /о. flm = *yw/o4-2*/w/y (i«=l. 2	ЛО- B2.26)
Коэффициенты bjm, bQm могут быть рассчитаны заранее. Так, для
Л^= 1 имеем
Для N =2 имеем
fo — о fo —	4 b ~— 2*
для N=3:
_ 9 .
32	—  '
_ . _9
33	— -г 2 •
Ч
Ориентируясь на B2.25), мы можем теперь вычислить Г f dr. Вве-
Введем обозначение:
11 .
	2' Ь
= 9, b.
9
— ~2"' *i
Q
18 = -
27
з— о
0
45 .
2 ' °
• "
_ 9
21 2 '
22=18.
_ 27
23 ~~" о '
/,(в)= /(г. 6)rfr.	B2.27)
Го
Используя представление B2.25) функции /, мы получим
=1. 2	ЛГ>

. 221	ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ	197
иЛИ, по B2.22):
N
пг~О
i=l, 2	N.
Достаточно будет вставить сюда вместо ат их выражения из B2.26),
и мы получим /; (для каждого i) через линейные комбинации от зна-
значений /у с/ = о, 1	ло
Pw/o+2Py*/J (/" = /*). B2-29)
j=l, 2	N.
Для N=1
Poi=2-. Pii = -
Для N = 2
5	1	1
Poi = "Si"'	™~T' га —~-24"'
1	2 R 1
Для N=3
о _ 1	R— 19 R— 5	R — -L
Poi —¦ "§" > Рп — 72" ' l —' 2"' 1 — 72 '
14	1
Q 	 1	Q .	 3	fi 	 3	д 	 J_
Роз — ~g~ - Pi3 — ^"' P23 — "8" *¦	Рзз — 8 '
Наконец, удобно будет иметь ещё формулу, позволяющую выразить
/i>	fN через Jv f2, .... fN, f0. Чтобы получить эту формулу,
достаточно решить систему уравнений B2.29) (записанную для /= 1,
2	N) относительно /;-.
Получим выражения типа
N
Приведём коэффициенты а,, для Л^= 1, 2 и 3.
Для JV= I	;
) Формула B2.30) особеиио полезна в случаях, когда

198	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
Для N— 2
«01 — ~~2' «ц —A	«2i =2"'
«02= Ь	«12 = — 8' «22 = 4-
Для ЛГ=3
_ 1	_ 3	_ 3	1
«01 — —""з1 «п—~2< «21 —у-	a3i = —g" >
1	с	q	2
«02 = у-	а12= — "> a22=d>	«32 = "J'
27 _	27	13
а13 —~2~' «23 =	g~' азз=у-
и т. д.
Вернёмся теперь к формулам B2.23), B2.24) и запишем их сперва
в виде:
где для сокращения записи обозначено:
*( = (р«в«Л. 'j = (^)i-	B2.32)
С другой стороны, в силу B2.30), мы можем записать dsj/db в виде
N
dsj	d 1
1 vi rfs;	I de
rf6 rf6 e (I
или, выполняя дифференцирование:
N
^ Тг С/=1, 2	Л0-
B2.33)
Аналогично, для dt.jdb имеем
dtj	dt0	I vj> rf^j	1 de vji —
B2.34)
Но теперь мы можем внести в эти два последних соотношения выра-
выражения ds-Jdft, dl-Jdb из B2.31). Мы получим, выражая еще st, tt,
г>2р -f p. с помощью B2.29), систему уравнений, в которых слева
будут стоять производные dSj/dft и dtj/dQ, а справа — комбинации

^ 22]	Численные методы решения плоских задач	igg
всех искомых функций (г>9M, {vh\	{vh)N; (vr)v (vrJ	(vr)N;
$., &j, . . ., bN; e (при этом правые части будут содержать про-
производные de/dQ и ещё dto/dd).
Получим систему 2Л/(у'=1, .... N) обыкновенных дифферен-
дифференциальных уравнений 1-го порядка, линейную относительно производ-
производных. Система эта будет содержать 2N-\- 1 скорости (wr),, (vrJ, ...
	(vr)N; (v,)s, (o9)[, .... (t>e)^ (причём (о,.)^ = (©,.)., (vH)N = (vh)r),
функцию bs, bv ..., bN, а также функцию еF) — итого
i функции. Чтобы замкнуть систему, сперва обратимся к крае-
краевым условиям. Заметим, что (fr)v, ('Vii)z связаны с углом ср соот-
соотношениями B2.13), B2.14), B2.15). Мы можем, поэтому, ввести
вместо двух неизвестных функций (fr)s и (г>9J одну искомую функ-
функцию <р (угол наклона). При этом производные, входящиь
в наши уравнения, будут содержать как саму функцию <р, так и
Именно, для d(vH)Jdti и d(vr)z/dQ будем иметь
где
dvv	dvx	I dvx	dvy
+i69	li6 +
m{ и ftj, вычисляемые посредством формул B2.13), B2.14) суть
известные функции от ср и 9.
Далее, мы имеем ещё соотношение B2.18), связывающее функ>
ции е(б) и срF). Недостающие Л/-)-1 уравнения составим, используя
уравнение для дЬ/дЬ. Так как & зависит лишь от ф, то можно считать
0(. = &(. (ф.). Поэтому dbjdb = dbljd^l • dtyjdft. С другой стороны,
ясно, что в/(«Ь,)=а(»1(ф1)) , так что dbJd^mjd^X . На-
конец, напишем dbz/dtyz — dbz/dy ¦ d<fldQ • db/dtyz и заметим, чго
в этом выражении rf&j/rfcp может быть вычислено (через <р) непосред-
непосредственно по формуле B2.19), a dbjd^ может быть рассчитано по
формулам B2.16), B2.17).
Если мы запишем теперь dtyJdQ с помощью соотношения B2.10),
в котором под R(B) будем подразумевать ri (9) из B2.22), то по-
получим окончательно
rf9
Это соотношение надо записать для i=l, 2, . .., Л^— 1. Для t = N(L)
имеем непосредственно равенство B2.19); на поверхности цилиндра
будем иметь постоянное значение bs по формуле B2.21).

200	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
Таким образом мы замкнули задачу: число уравнений будет равно
числу искомых функций. При этом краевые условия на теле и удар-
ударной волне удовлетворяются автоматически при любом N.
Полученная таким путем система обыкновенных дифференциаль-
дифференциальных уравнений 1-го порядка (так называемая аппроксимирующая си-
система) решается численно шагами по 6. При этом будем отправляться
от некоторых начальных значений, отвечающих 0 = 0. Здесь, однако,
мы встретимся с тем затруднением, что не все искомые функции
задаются при 6 = 0. Именно на оси 6 = 0:
2x »„ х _ 1
Таким образом мы имеем 3N—1 условия, в то время как искомых
функций 4N—1 (vr и V-t — выражаются на ? через <р). Неизвест-
Неизвестными оказываются (vr\, (vrJ ¦ • ¦ (vr)N_v e@) (N параметров задачи).
Обратим внимание на то, что наши дифференциальные уравнения
будут содержать подвижные особые точки. Разрешим нашу систему
относительно производных от искомых функций. Мы привели си-
систему к виду, решённому относительно производных dsjdb, dtj/db,
где Sj и tj определяются из B2.32) через (vr)j и (<уа);-. Используя
эти связи, получим для J = 0, 1, 2	N:
B2.38)
где аЯ = х~ (Рдах —р' — f>f) — местная скорость звука. На обте-
обтекаемом цилиндре (У = 0) надо учесть, что (vr)s = 0 (тогда s5 = 0).
На поверхности разрыва, где j = N (L), справедливо B2.35) и dtjdb,
dsz/d6 выражаются через dyjdb. Теперь без труда из B2.38) и B2.37)
получим выражение для d(vr)j/dd (у=1, 2, .... N—1) и rf(t;,);/rf9
j — 0, 1	N—l) через dtjdb, dt\dh и ds/jdQ (j = 1, 2	N),

22]	ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ	201
9 = Uj. где
1 Г 1 / »,-\ */(*-« ds,	dt,	x	rf!n9/l
B2.39)
?/	аЗ d</	d(vr)j
^ 44^7 ^^7^ыЧ^г B2-40)
Выражение B2.37) или B2.38) при j= N(E) используется для опре-
определения rfcp/d9. После этого аппроксимирующую систему в нормаль-
нормальной форме можно записать так:
dr,
d(va)s __ Eo	d{v,)] _	Ej
7=1, 2	W—1.
Входящие в правые части dSj/db и <#;/d0 определяются по B2.33) и
B2.34). Неизвестными функциями здесь являются е, fy, bj, <р, (fr)y,
Из аппроксимирующей системы видно, что правые части всех
уравнений, кроме уравнения для dvj/db (J=s, I, 2, .... ./V—1),
являются голоморфными в области определения функциями от 9 и
искомых величин.
В уравнениях же для d{v^)jjdb (j = s, I, ..., N— 1) при
(v$)j=^aj знаменатель обращается в нуль. Если мы не потребуем,
чтобы и числитель Е, в этих точках обращался в нуль, то мы будем
иметь бесконечные значения производных
db ' dt)
т. е. бесконечные ускорения. Тогда движение не может быть про-
продолжено за соответствующие точки — мы получим особую предель-
предельную линию (ср. решение на стр. 164) и всё решение не будет иметь
физического смысла. Таким образом, /V уравнений нашей аппрокси-
аппроксимирующей системы в окрестности звуковой линии будут иметь по-

202	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	(ГЛ. I
движные особые точки и для возможности непрерывного перехода
через эти точки необходимо выполнение в них N условий: при
—cij должно быть
?\=0 O'=s. 1, 2	N—l).	B2.41)
Для удовлетворения этих условий в нашем распоряжении имеется
N параметров при 9 = 0. Теперь задача полностью замыкается. От-
Отметим, что при 6 > 0, как следует из B2.39), уравнения для d (vr)j/db
особенностей не имеют, а при 6 = 0 d(vr)j/db = 0.
Проведённый О. М. Белоцерковским анализ особых точек по-
показывает, что в уравнениях B2.40) особенности будут типа «седла»,
причём во всей рассматриваемой области интегрирования существует
единственное решение, голоморфное всюду и удовлетворяющее усло-
условиям как при 9 = 0, так и при (v^)j = aj. Техническая трудность
построения такого решения заключается в том, что в особых точках
в правых частях уравнений B2.40) будут неопределенности типа 0/0.
Заранее раскрыть эти неопределенности нельзя, так так положение
самих особенностей и значения многих искомых величин в них не-
неизвестны. Для возможности счёта в окрестности таких точек можно
поступить, например, так: решение в окрестности регулярной точки
9 = 9,, близкой к особой, разлагается по степеням F — 90) в ряды,
по которым оно достраивается вплоть до особой точки 6 = дк
(/г=1, 2, ..., N—1); затем в окрестности Qk строятся ряды по
(9 — 9ft), которые дают возможность «выйти» из особой точки. В случае
необходимости значения Ьк и других величин в этой точке могут
быть уточнены методом итераций по условиям склейки при 9 = 90
рядов, отправляющихся от Ьк с решением, полученным обычным
путём. Как правило, это делать не приходится, а для возможности
«выхода» из особых точек достаточно бывает знать 2—3 члена раз-
разложения.
Продемонстрируем теперь более детальный ход решения на
простейшем случае, когда N=1 («первое приближение»).
Промежуточных линий здесь нет и все подынтегральные функ-
функции аппроксимируются линейно по их значениям на цилиндре и на
волне. Искомых функций будет три: е(9), <р(9) и (V(,)s. Функции
(vr)s и (х/9)? на поверхности разрыва (т. е. (vr\ и (v9\) найдутся
сразу же из B2.13) — B2.15) после того, как <р(9) известно. Одним
из трёх дифференциальных уравнений, служащих для определения
е> ?> (vti)s> будет уравнение B2.18), а два других получатся из инте-
интегральных соотношений B2.23) и B2.24). При N= 1 каждое из этих
соотношений записывается только один раз — для rt = rt = r0 -4- e F).
Соотношение B2.23) приведёт нас к равенству:
B2.42)

| 2Я	ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ	203
Соошошение B2.24) записывается в виде:
dtc , dt, I f	, ^ de _, ,
"Ж + -5Г = 7 L^1 - ^ Ж - 2ri 0^
Здесь (/ = 5, 1):
E^ = 0, так как (i»r),s0),
причём /7, и р, определяются через (vb\ и (vr\ с помощью B2.11),
B2.12), B2.19) и B2.21).
С другой стороны:
Pl
Здесь
B2.44)
где rfln&j/dtp находится по B2.19). Подставив из B2.35) выражения
d(vr\/dd и d(v9ydB через rf<p/d9 в B2.44) и B2.43), получим окон-
окончательно
где
B2.45)
причем ntj и пх по B2.13), B2.14) и B2.35) — известные функции
<р и 6.
Аналогично,
dtx d	dv
где
0=- ^ »i - ^- («2 - «S)i «i- B2-46>
Учитывая, что на поверхности цилиндра (vr)s = 0, получим также:

204
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ.
Теперь из B2.45) и B2.47) мы получим оставшиеся два уравнения
аппроксимирующей системы при Л/=1:
d(v{
р
"*
Входящие в правые части dsJdQ и dtjdb находятся по B2.42) и
B2.43), a dtjdb определяется из B2.46).
Итак, мы можем выразить de/db, dvjdQ, d(v%)Jdb через 9, е, ср,
(vb)s. Интегрирование системы проводится шагами по 6 от 6 = 0 (на-
(направление набегающего потока), где <р = 0, (г^^О, ео=е(О) —
неизвестный параметр, кото-
\^'/ V /У	Рый определяется из усло-
&~/ »V/ л^	вия B2.41) конечности
должно быть
Во втором приближении
(N=2) вводится одна про-
f,0 межуточная линия (ква-
(квадратичная аппроксимация),
в третьем (N=3) — две и
т. д. В каждом приближе-
приближении (N^-2) добавляется по
одному неизвестному пара-
параметру (vr)j при 0 = 0 и по
одному условию B2.41)
конечности производной
d(vt)jldb. Совпадение ре-
результатов с требуемой точ-
точностью в двух последних
приближениях свидетельствует о практической сходимости расчёта.
Следует заметить, что метод интегральных соотношений весьма
быстро сходится.
Приведём некоторые результаты расчётов обтекания кругового
цилиндра (го=1, х=1,40), взятые из работы О. М. Белоцерков-
ского1). Расчёты проводились на быстродействующей электронной
вычислительной машине БЭСМ-1 АН СССР. Уже приведённый выше
рис. 71 отвечает случаю Moo = tW^co — %.
2,0 1,703\1А81 /,0
Рис. 72.
') См. сноску на стр. 191.

, 22J
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ПЛОСКИХ ЗАДАЧ
203
Минимальная область влияния здесь ограничена двумя характе-
характеристиками 1-го и Н-го семейств (обозначены цифрами 3 и 2 соот-
соответственно), что вполне согласуется со стр. 182. Линия перехода,
2,0
t,o
Рис. 74.
обозначена цифрой 4. Рис. 72 показывает, как изменяется форма
и положение ударной волны и звуковой линии при возрастании Моо
Р
ТА
1,0
0,8
0,6
0,2 0,4 0,6 0,8 1,0 1,2 ё
Рис. 75.
от 3 до 5. Там же нанесены результаты эксперимента (точки).
Рис. 73, 74, 75 иллюстрируют сходимость метода по приближениям

206	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
для Моо= 3 и 5: пунктиром нанесены результаты расчётов при N=1,
сплошной линией — при N=2, треугольниками — при N=3 и точ-
точками — эксперимент (Г. М. Рябинков).
Как видим, уже расчёт по первому приближению даёт в основном
правильное положение и форму ударной волны, распределение давле-
давления на теле, на волне. Для определения величин в поле при Моо^СЗ
надо считать по крайней мере три приближения, в то время как при
Моо > 3 достаточно двух.
§ 23. Движение с очень большими сверхзвуковыми скоро-
скоростями. Гиперзвуковые течения и обтекание тонких тел. В совре-
современной газовой динамике, имеющей дело со скоростями порядка
нескольких километров в секунду, возникает много теоретических и
практических вопросов, требующих изучения движения газа при очень
больших значениях числа Моо- Обтекания с очень большими сверх-
сверхзвуковыми скоростями обладают рядом специфических особенностей.
В § 14, а также в § 19 мы уже обратили внимание на некоторые
характерные свойства движений, в которых Мсо]^> 1. В настоящем
параграфе мы остановимся на некоторых общих законах таких
движений.
С. В. Валландер доказал A949) наличие предельного, не зависящего
от Me» состояния течения, возникающего при очень больших Мсо J).
Покажем, как это получается для плоского случая.
Пусть обтекаемое тело помещено в поток газа, обладающий ско-
скоростью vx. Образуется поверхность сильного разрыва, после про-
прохождения которой начинается вихревое обтекание тела. Движение
описывается уравнением Бернулли
B3.1)
уравнением неразрывности, которое можно взять в форме (9.2):
и уравнением для вихря скорости (§ 6):
~х-1р
dx ду)~х-1р ду —*-i ду
') Результаты Валландера были получены также Осватичем (К. Oswa-
titsch) в работе Ahnlichkeitsgesetze fur HyperschallstrOmung, Zs. f. angew. Math,
u. Phys., 1951.

23) ДВИЖЕНИЕ С ОЧЕНЬ БОЛЬШИМИ СВЕРХЗВУКОВЫМИ СКОРОСТЯМИ 207
Вводя а2 из B3.1) в уравнения B3.2) и B3.3) и переходя к безраз-
безразмерным скоростям vx/vco = vx, vy/Vjo = vr получим два уравнения:
x , dv
2 W^^~°' B3'4)
. B3.5)
Уравнения B3.4), B3.5) содержат три безразмерных функции: vx,
v , !п Ь и, если не считать х, один безразмерный параметр Моо.
Последний входит таким образом, что при М»3> 1 членом, его содер-
содержащим, можно пренебречь. Отсюда, однако, было бы поспешно
сделать вывод о независимости нашего движения от М» при весьма
больших Моо- Дело в том, что мы еще не знаем поведения функ-
функции !п Ь и не учли краевые условия.
Определение !п Ь тесно связано, как известно, с видом поверх-
поверхности разрыва. Краевые условия надо будет как всегда записывать
на поверхности тела и на поверхности разрыва. На поверхности тела:
«у = «ИеР.	B3.6)
где р—угол наклона касательной к поверхности тела к оси X. На
поверхности разрыва можем написать (см., например, B2.19)):
2х 2 1 х —1\/х—1 ,2	1 \х /о_ 7Ч
Кроме того, по G.16) и G.17)
2	/ 1	\
v = —-~cos<p sincp —	г — 1
у % +1	\ М^ cos2? / •
Отметим теперь, и это является важным обстоятельством, что, в силу
сверхзвукового характера потока, форма поверхности вдали от тела
не влияет на течение вблизи головной части тела. Поток вблизи тела
находится под влиянием лишь ограниченной, наиболее интенсивной
части ударной волны. На этой части cos9 будет отличен от нуля. При
оотекании тупого профиля cos ср будет близок к единице; при симме-
симметричном обтекании клина coscp будет близок к косинусу угла раствора
клина и т, д. Поэтому, на некотором участке будет всегда достигаться

208	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	t™ .
такое течение, при котором не только Мс»^> 1, но и MooCOS(p^> 1-
Но тогда и в краевых условиях B3.7), B3.8) мы можем отбросить член,
содержащий 1/ML- Теперь параметр Mm остаётся в одном лишь
выражении для \пЬ:
причём член, содержащий Мсо, входит в 1п & аддитивно. Но 1п & вхо-
входит в формулу B3.3) лишь под знаком производной по координате
поэтому в окончательной задаче Мсо полностью исчезнет, и мы полу-
получим доказательство утверждения Валландера '). Закон независимости
от Мсо при больших Мсо хорошо подтверждается экспериментально.
Обратимся теперь к специальному рассмотрению обтекания тонких
тел при больших сверхзвуковых скоростях. На примере обтекания
пластинки (§ 14) мы уже видели, что простая линеаризация уравне-
уравнений по отношению к основному потоку в случае, когда Мсо^>1. не
даёт удовлетворительных результатов. Мы видели, что характерным
параметром задачи является, в случае пластинки, величина Mooi Pol-
Для общего случая обтекания тонких тел при Моо^§> 1 были открыты
специальные законы подобия. Это было сделано Цзянем для безвих-
безвихревых движений и обобщено Хэйсом на случай движений выхре-
вык 2).
Следуя Г. Г. Чёрному 3), попробуем сперва дать оценки порядка
различных гидродинамических величин нашей задачи.
Пусть, в общем случае, мы имеем установившееся обтекание со
скоростью Vx, на бесконечности тонкого заостренного впереди тела,
расположенного так, что углы между касательными к поверхности
тела и основным потоком близки к нулю. Направив ось X вдоль
основного потока, имеем
О (cos (я, х)) = х,	B3.9)
где п — нормаль к телу, х— малый безразмерный параметр (напри-
(например, относительная толщина тела, наибольшее значение угла, обра-
образованного поверхностью тела с направлением потока, наибольшее
значение cos(n, x) и т. п.), буква О, как обычно, означает порядок
величины.
Из краевого условия обтекания следует тогда, что на контуре
B3.10)
') В случае безвихревого движения, т. е. в случае отсутствия поверх-
поверхности разрыва, доказательство независимости движения от М^ при M^^l
было нами приведено выше. См. сноску на стр. 156.
2)	Tslen H. S., Similarity laws of hypersonic flows. Journal Math. Phys.
3 A946), 25; Hayes W. D., On hypersonic similitude. Quart. Appl. Math. 5
A947).
3)	Чёрный Г. Г., Течение газа с большой сверхзвуковой- скоростью,
Физматгиз, 1959.

s 23] ДВИЖЕНИЕ С ОЧЕНЬ БОЛЬШИМИ СВЕРХЗВУКОВЫМИ СКОРОСТЯМИ 209
где, как и раньше, vx = vjvjo, г/у = иу/г;л. Это соотношение есте-
естественно распространить и на всю область течения между поверхно-
поверхностью разрыва и контуром. Но на поверхности разрыва мы имеем
соотношения G.12), G.15), из которых следует, что
— Pcofл (vx — v^^p — p^^-^j (MLcos2cp — l) B3.11)
(Рос. P&>—значения р и р до прохождения поверхности разрыва).
С другой стороны, так как касательные к поверхности разрыва,
составляющие скорости, непрерывны, то
B3.12)
где V=V(vx—г'СоJ~Ьг;2- Внося это выражение в B3.11), получим
квадратное уравнение относительно cos<p, из которого без труда
найдём
где V=v(vx—lJ4-f2,. так что
O(cos?) = V+~.	B3.13)
"'оо
Далее, по G.11) и B3.12) имеем
Zy = (vx—l)tg<f = —Van<f.	B3.14)
Но sincpsbl. Значит,
O(V) = O(vy)
или, по B3.10),
О A0 = т.	B3.15)
Возвращаясь теперь к B3.12) и учитывая B3.13), B3.14) и B3.15),
имеем окончательно для скоростей:
O(vx — voa) = vm(x*+-?-),	B3.16)
O(vy) = vjt.	B3.17)
Наконец, найдём ещё порядок величин р — рт и р — роо. По B3.11)
имеем сперва
Poo	МС° «о
так что, используя B3.16), получим
0
J4 Теоретическая (идромеханика, ч, II

210	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
р — р
Что же до 	, то по G.10) можем написать
Роо
и тогда, на основании полученных выше оценок для Mr,cos<p. имеем
М'^	B3.19)
- М^х + Г
Проанализируем теперь полученные нами оценки.
Пусть сперва мы имеем дело с умеренными сверхзвуковыми ско-
скоростями, так что Moo^l- Наши оценки показывают, что тогда при
обтекании очень тонких тел (х<^1) возмущения всех гидродинами-
гидродинамических элементов малы и имеют один и тот же порядок малости:
~ — l~_L х ~Ъ яйх Р~Ро° тМ х Р~~Рсо ~'М
VjC	"^Ма)Х'	У Х'	Рм	JO'C>	Poo ~ ЛХ'
В то же время по B3.13), B3.15) имеем
1
cos ср ~-т«— >
со
т. е. наша поверхность разрыва будет иметь наклон того же порядка,
как и наклон характеристики (большой по сравнению с наклоном
обтекаемой поверхности). Мы можем поэтому при исследовании
сверхзвукового обтекания тонких тел, если Мсо~1, линеаризовать
уравнения движения по отношению к основному потоку, обладающему
скоростями vx = vco, Wy = 0, давлением р^ и плотностью роо-
Иначе будет обстоять дело при исследовании обтекания тонких
тел, когда Мсо^= 1 или же Мс»х^> 1. Здесь наши формулы приведут
к новым соотношениям:
Vx	l~t, Vy 	X,
y	,	|Vloo
r'co	rco
«Малость» возмущений скорости сохраняется, но характер этой мало-
малости будет различным для продольных (vx) и поперечных (уу) соста-
составляющих. Возмущения давления и плотности не будут уже малыми;
более того, возмущение давления может иметь тот же порядок, что
и самодавление и даже превышать его во много раз; отметим, что при
этом коэффициент давления
п	2	.	.	2	Р— Ра=
будет весьма мал — он будет иметь порядок т2. Наконец, cos? по
B3.13) и B3.15) будет мал и будет иметь порядок тот же, что и косинус

§ 23J ДВИЖЕНИЕ С ОЧЕНЬ БОЛЬШИМИ СВЕРХЗВУКОВЫМИ СКОРОСТЯМИ 211
нормали к поверхности обтекаемого контура — поверхность разрыва
будет как бы прилипать к поверхности тела.
Мы видим, таким образом, что метод линеаризации, по отношению
к потоку на со, не применим в нашем случае больших сверхзвуко-
сверхзвуковых скоростей.
Движение с очень большими сверхзвуковыми скоростями около
тонких тел называют в современной литературе гиперзвуковыми.
Выведем теперь, используя наши оценки, важный принцип подо-
подобия, касающийся гиперзвуковых движений. Обратимся вновь к общим
уравнениям движения, неразрывности и притока тепла для плоского
стационарного случая.
Выделим основное движение по формуле
и перейдём к безразмерным координатам из соотношений:
х = *i. У = ^Уг
Теперь уравнения движения примут вид:
к ^ ' дх, ^ йу,^р, ду,
Уравнение неразрывности запишется в виде
JLP A+т2И)+4^- = о,
dxt rl v ' ' ' dy,
и условие адиабатичности даст:
р	р
В согласии с приведенными выше оценками, мы можем считать, что
все наши безразмерные функции имеют теперь порядок 1. Считая,
что х мало и отбрасывая член, содержащий х2 (это единственное упро-
упрощение, которое здесь делается), мы придём к уравнениям
B3.22)
B3.24)
14*

212	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Пусть уравнение обтекаемого контура в новых координатах имеет вид
Тогда краевое условие на контуре запишется
¦ ч иг , иг
или, если отбросить член х2,
?+*wr°-	<23-25)
Далее, на больших расстояниях от тела возмущения пропадают, и мы
должны там написать
„ = * = 0. Pl=l, Pl = -^-^-.	B3.26)
Наконец, выпишем еще условия на поверхности разрыва.
Пусть уравнение этой последней (в новых координатах) имеет вид
/(*,. у,)=<).
Тогда по G.5) имеем
или, в нашем приближении:
,^v dyj
Аналогичным образом вместо уравнений G.3), G.4) получим теперь
„ = Л—-^	B3.28)
дхг
.	B3.29)
а вместо G.6) будем иметь:
х+1_(х_1)р
B3.30)
Из двух параметров задачи (т и Моо) ни один не входит в уравне-
уравнения B3.21) — B3.24) и краевое условие B3.25). Краевые условия на
бесконечности B3.26) содержат лишь комбинацию этих параметров
(результат Цзяня). Условия на поверхности разрыва B3.28) — B3.30)
также содержат лишь комбинацию этих параметров (результат Хэйса).
Отсюда принцип подобия, который может быть сформулирован так:

g 24] СЛУЧАЙ РЕАЛЬНОГО ГАЗА. «ИДЕАЛЬНО-ДИССОЦИИРУЮЩИЙСЯ» ГАЗ 213
движения около двух тел, аффинно преобразуемых друг в друга,
имеющих относительные толщины т' и т", будут подобны, если числа
Маха М' и М^ этих движений таковы, что
Уравнения наши распадаются на две группы: уравнения B3.22) —
B3.24) содержат искомые функции v, pv рг и не содержат и; крае-
краевое условие B3.25) и условия на поверхности разрыва B3.27), B3.29),
B3.30) также содержат лишь v, pv pv Таким образом, задача сильно
упрощается. После того как v, pv p, определены, для нахождения и
может служить уравнение B3.21) и краевое условие B3.28). Проще
определить и из уравнения Бернулли.
Хэйс обратил внимание на то, что уравнения B3.22) — B3.24)
совпадут с уравнениями для одноразмерного нестационарного дви-
движения газа вдоль оси Yv если заменить хх через некое фиктивное
время. При этом краевое условие B3.25) представит аналог краевого
условия на поршне, движущемся по закону F (xv у^ = 0 (х1 — время),
а условия B3.27), B3.29), B3.30), как легко видеть, отвечают в точ-
точности условиям на поверхности разрыва в нестационарном случае.
§ 24. Случай реального газа. «Идеально-диссоциирующийся»
газ. При прохождении поверхности сильного разрыва, если сверх-
сверхзвуковые скорости движения очень велики, температура может увеличи-
увеличиваться до весьма больших значений.
В самом деле, комбинируя формулы G.10) и G.15), мы получим
для отношения температур 7у7\ на скачке формулу:
Если ср — 0 (прямой скачок), то при Mi = 5 будем иметь для х = 1,4
7У7\?«5,8, а при Mi =10 Т/Т1^20,8; это значит, что если
7\ = 280° К, мы получим увеличение температуры в первом случае
примерно до 1642° К, а во втором — примерно до 5712° К- При таких
высоких температурах отдельные молекулы кислорода, входящего
в состав воздуха, начнут диссоциироваться.
Соответствующий пересчёт, основанный на рассмотрении стати-
статистической физики процесса, был проведён, применительно к газовой
динамике, рядом авторов. Остановимся более подробно на теории
Лайтхилла ') «идеально-диссоциирующегося» газа. Рассмотрим газ,
состоящий из двухатомных молекул. Пусть в нём начинается диссо-
диссоциация: часть молекул начинает делиться на свободные атомы. Обо-
Обозначим через а процентное отношение (по массе) числа свободных
') L i g h t h 111 M. J., Dynamics of dissociating gas, I Journal of fluid mecha-
mechanics, 2 A957).

214	ТЁбРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
(возникших за счет диссоциации) атомов
[ГЛ. 1
А
где пА — число диссоциированных атомов (в единице массы газа),
п2А — число недиссоциированных молекул (в единице массы газа). По
Лайтхиллу имеем соотношение
1 —а
B4.2)
где Td и pd—некоторые параметры. Именно, величина Td = D/k,
где D — энергия диссоциации, k — постоянная Больцмана (й=1,38Х
Х10~16 эрг/град); величина же pd представляется более сложно: она
выражается через температуру и некоторые функции распределения;
приближенно pd может считаться постоянным. В этом смысле Лайт-
хилл говорит об «идеально-диссоциирующемся» газе.
Для кислорода 7^ = 59 000° К, pd=150 г/см3;
для азота	Td = 113 000° К, pd = 130 г/см3.
На рис. 76 (заимствованном из статьи Лайтхилла), где по оси
ординат отложено а, а по оси абсцисс — TjTd, даны три кривые —
зависимости а от T/Td, отвечающие ]g pdjp — 7, 6 и 5 соответственно.
0,036 0,0371>0А 0,04S О,Р5 0,06 0,070,060,09 0,120,1k ОМ
Рис. 76.
Из рисунка видно, что если при Тяь 1600°К (случай МХ~Ь, см.
выше), когда TjTdi^i0,027, практически ещё нет диссоциации, то
при Т =5700°К (случай с Ж1=10), когда TjTd^0,097, мы имеем
при ^р/р^^б почти полную диссоциацию (для нижних слоев атмо-
атмосферы p?tilO г/см3, поэтому рй/ря»1,3- 105 и lgpd/p~5).

§24] СЛУЧАЙ РЕАЛЬНОГО ГАЗА. «ИДЕАЛЬНО-ДИССОЦИИРУЮЩИЙСЯ» ГАЗ 215
Для частично диссоциированного газа уравнения движения и урав-
уравнения неразрывности остаются прежними. Изменяется прежде всего
уравнение состояния, которое может быть записано теперь в виде
а).	B4.3)
где R, как и прежде,—газовая постоянная. Для воздуха /? = 2,87Х
Х106 см2/сек2 ¦ град; для кислорода Я = 2,59-106 см2\сек2 ¦ град,
для азота /? = 2,97 ¦ 10 см2\сек2 ¦ град.
Изменится и уравнение энергии; при выводе последнего уравнения
для внутренней энергии и\и==~д< см- СТР- 17) теперь придётся
написать:
-=?? + «.	B4.4)
где ud — RTd (в механических единицах). Для кислорода ad = 1.53Х
Х1011 см2(сек2, для азота ud — 3,35 ¦ 10й см2\сек2. При а=0 мы полу-
получим при этом U = 3RT. Для идеального газа мы имели (стр. 17)
и — CjLr- —	т , так что если х = 1,4, то и = 2,5 RT. Формула B4.4)
4
отвечает случаю, когда х —-^-.
Уравнение энергии (аналог уравнения C.4)) будет теперь иметь вид
И 1/1/	И,,
pS^ + pS+
или же (см. стр. 20):
p-g- + Pdiv V=0,	B4.5')
при этом и выражается через B4.4).
Теперь, кроме функций V, р, р, Т, в качестве искомых величин
входит еще а, которая связана с р и Т конечным соотношением B4.2).
Как и прежде, уравнение B4.5) описывает факт сохранения
Энтропии 5 частицы, ибо по определению энтропии:
du-\- pd —
так что, в силу уравнения неразрывности и, по B4.5) имеем
dS 0
B4.6)
Используя B4.3) и B4.4), мы получим для dS из B4.6) выражение
3ud dT . ud
= yj- -y—f- -f

216	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ.
Но по B4.2) имеем
запишем ещё
Р
далее получим
A—a)ln(l — a) + aB — 2 1na)\
J
Для сравнения напомним, что в случае идеального газа мы имели
(см. F.8), стр. 33):
d ~ = —Ц- d In 0х == —Ц- d In GV-*) = d (—Ц- In Г — In pV
что согласуется (для х = 4/3) с формулой B4.7), если в ней поло-
положить а = 0.
Посмотрим теперь, как изменятся, в случае диссоциирующегося
газа, условия на поверхности сильного разрыва.
Условия B.12), B.13) останутся без изменения. Условие B.17)
мы должны записать, вводя вместо U/A его выражение по B4.4I).
Ограничимся только рассмотрением стационарного случая, когда
6 = -К„ и [РУя1 = 0. Записывая \pVn\ = [^?Vn] =Р^Я[^]. мы
можем представить B.17) в виде
Р.
Введя вновь теплосодержание (стр. 34) /, мы получим
-О,	B4.7)
') Мы можем получить взамен B.16), повторяя рассуждения, приведен-
приведенные на стр. 29, также и аналог формулы E.9). Это будет

§24] СЛУЧАЙ РЕАЛЬНОГО ГАЗА. «ИДЕАЛЬНО-ДИССОЦИИРУЮЩИЙСЯ» ГАЗ 217
причём теперь, в отличие от того, что отвечает совершенному газу,
мы имеем
^	+«(/ai).	B4.8)
Обратимся к плоскому случаю и будем обозначать значение наших
элементов до прохождения разрыва значком «1», после прохожде-
ния—значком «2». Умножая B.12) скалярно на п и замечая, что
б = — Vn, получим
+ <	+ <-	B4-9)
Умножая обе части B.12) скалярно на единичный вектор т, каса-
касательный к поверхности разрыва, получим, как и раньше,
«t, = wv	B4.10)
где г>, — составляющая скорости, касательная к поверхности разрыва.
Условие B.13) перепишем в виде
hvn^?2vrh-	B4.11)
а условие B4.7) даёт нам, в соответствии с B4.10):
v2	v2
-|l + /1 = -|i+j2.	B4.12)
Аналогично тому, что было в случае идеального газа, соотноше-
соотношения B4.9) — B4.12) связывают пять величин р2, р2> vX2, fy2. T2 че-
четырьмя уравнениями. К ним надо прибавить B4.2), записанное для р2
и Т2; в качестве шестой величины будет фигурировать <х2.
Анализ формул B4.9) — B4.12) несколько облегчается тем обстоя-
обстоятельством, что в интересующих нас сейчас случаях—случаях возникно-
возникновения диссоциации — величины 1Х и рх всегда могут считаться пре-
пренебрежимо малыми по сравнению с кЧ2 и р^2п соответственно2).
Для того чтобы это показать, обратимся вновь к рис. 76.
Даже для ничтожно малой диссоциации, когда а = 0,05, мы должны
считать T2/Td> 0,0475. Но тогда по B4.8) 7yMd= 7/7^D +а)+ а=
= 0,05 + 0,0475D+0,05)^:0,25. Таким образом, по B4.12) мы
') Аналогом формулы E.14) будет теперь более громоздкое соотношение,
Если а_ = 0, а — а, ТО МЫ получим
7_-L=-
2Td_
Т
Р
при a = 0 получим вновь E.14) с k — *lz.
2) Упрощённые условия на скачках, получающиеся путём отбрасыва-
иия рх н «,, называются «приближениями для очень сильных разрывов».

218	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
должны иметь—---\—=	2~">0,25. С другой стороны, при обыч-
««*'!	2«^„,
ных температурах 7^ порядка ЗОО'К, при отсутствии диссоциации
мы имеем TjTd < 0,005 и, следовательно, \judix = 4T/Td < 0,02.
Таким образом, даже при ничтожных а величина '/г^я должна зна-
значительно превышать /,. Ещё в большей степени это относится
к раг>2 и ру Итак, приближенно имеем
Исключаем х>„2 с помощью равенства B4.11):
vn, = ^-vni.	B4.14)
Второе равенство из B4.13) дает нам P2 = Piv2n ( 1	"—y~ ). или.
по B4.14):
1	г,
Наконец, третье из B4.13) даёт нам /2 = — г>М 1	^-), т. е.
Используя B4.8), можем, по B4.16) и B4.15), написать
^2D + a)+a«d = I<(,-i
Или, исключая р2 с помощью B4.3):
Отсюда выразим р2/ра через Г2 и а:
&-= *т* + аТ* +1,	B4.17)
Pl ^2(l+a)
или если использовать ещб B4.2):
— = 7+ т-Г-Aп(— -^Г-)— з).	B4.18)
Может быть построено одно трансцендентное уравнение для опре-
определения T2jTd (или а) через vni и pj/p,;. Уравнение это громоздко

§24] СЛУЧАЙ РЕАЛЬНОГО ГАЗА. «ИДЕАЛЬНО-ДИССОЦИИРУЮЩИЙСЯ» ГАЗ 219
и трудно обозримо!). Лайтхилл предлагает анализировать поведение
функций после скачка последовательными приближениями. Именно,
возьмём сначала какое-либо грубое значение р21Р\< например Р2/Рг = Ю,
и найдбм с его помощью по B4,16) i2; но по B4.8), используя B4.15),
можно получить
(	)f —•	B4.19)
Из этого равенства, внося сюда выбранное нами р2/рх и найденное
нами 12, получим величину а. Вставив это а в правую часть B4.18)
(вместе с выбранным рг/Pi). мы получим новое, уточненное отноше-
отношение р2/Рг Отправляясь от этого значения проведём расчёт снова и т. д.
Приведём пример. Пусть v2n /ad=l,44 (г»л як 4,68 км/сек), pj/pd =
= 2 ¦ 10~?(р1^0,26 • 10~3 г/сл*3). Тогда по B4.16) имеем (пренебре-
(пренебрегая членом с (pj/paJ) /2/Bd«0,72. При р2/р1= 12 HMeeMp2/pd=2,4 • 10~6;
при этих значениях t2 и p2/pt получим по B4.19) (отбрасывая р,/р2
в скобках) а =0,42 и тогда по B4.18) мы сможем найти исправлен-
исправленное p2/pi- Эт0 будет p2/Pi == 13,2. Теперь p2/pd = 2,64 • 10~G; если это
новое значение внести в наши формулы, величины а и p2/pj оста-
останутся практически теми же. Итак, мы получим T2/Td=z 1/13,2якО,075
') Уравнение для T%jTd можно получить, исключив сперва а из соот-
соотношений -=--A+а) = —— (l — —) (следствие B4.15) и B4.3)) и
' d	"ij Рг \ Рг /
Т v2n I p, \
_ D -f «) + а = 77^- И	-) (следствие B4.16) и B4.8)). По отношению
-* d	^d ^	?2'
к р,/р2 получим при этом квадратное уравнение:
Л Р,\2	2rd Л р,\	ц^C7-2-^)Г2 _0,
\ <W r2 - '	о ..„.„.„ .
при этом
Решив указанное квадратное уравнение, найдём р,/р2 через 7, а затем а
через Г2. Останется вставить эти выражения в B4.2), и мы получим одно
трансцендентное уравнение, связывающее T2\Td с pd/pj и v2njud. Это урав-
/	7*
мение будет аналогом соотношения B4.1) (вернее, соотношения ~ =
2-а(х—1) 2 2
= / , ^2- IVIj cos <f, получающегося из B4.1) для очень больших М,, т. е.
для рассматриваемого нами сейчас случая «очень сильных разрывов»).

220	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
(Г2яй4400°К), в то время как при отсутствии диссоциации мы полу-
получили бы по B4.1):
Т2 2х(» —1) Г, 2 2 2(»-1) v\
т. е. при принятых в этом примере величинах
-^«^§^¦«0,176 (Г2^ 10 000° К).
Любопытной особенностью движений с диссоциацией является то,
что величина p2/Pi имеет определенный экстремум, при котором
а дй0,6-г-0,7; этот экстремум отвечает примерно значениям pj/pj^a
я» 13 -г— 15. Заметим, что для идеального газа р2/рх монотонно растёт
с ростом М! и достигает предельного значения только при М1 = оо
(ср. G.10)),
И^Ц т. е. при х = 1, it
v	3
И^^Ц-, т. е. при х = 1, it^7.
Pi * —1	v	3 р,
Остановимся теперь на выражении для энтропии; посмотрим, что
можно сказать об изэнтропических движениях диссоциирующегося газа.
Аналогично случаю идеального газа мы можем и здесь ввести
скорость звука как скорость распространения малого возмущения.
Заметим сперва, что энтропию 5 вновь можно сштагь функцией
только р и р, ибо хотя по определению S зависит от Т, р и а, мы
можем считать, что с помощью уравнений B4.2), B4.3) Г и а выра-
выражены через р и р.
Возвращаясь к системе уравнений D.14), мы должны заменить
лишь последнее из уравнений этой системы соотношением
дх у ду^ г дг dt ) \ др дг ^ д? дг
Повторяя рассуждения § 4, мы получим теперь для квадрата ско-
скорости звука а2 выражение:
2_____^L ¦ dS
dp ' dp
Если обозначить
то f> аналог отношения теплоемкостей, будет зависеть от р и р.
Мы можем представить f в виде:
	 d\np

j 25]	ДВИЖЕНИЯ С ОСЕВОЙ СИММЕТРИЕЙ	221
(дифференциалы берутся при dS = 0) и получим, после простых
выкладок:	277X1 - а») + B + За» - »') 71	2
7	~Г|аA-а2)+3B-а)A+а)Г2 "
Для крайних значений а = О и а = 1 получим соответственно
-г = 4/3 и f = s/31). Интересно отметить, что, подобно p2jpv вели-
величина т имеет экстремум (для отношений TjTd, 1 ежащих между 0,04
и 0,10) Для каких-то промежуточных значений а; в этом убеждаемся
из анализа формулы B4.20).
Мы ограничимся сказанным здесь относительно особенностей
диссоциирующегося газа. Вопрос о движении в пограничном слое,
влиянии вязкости, а также диффузии рассмотрен в ряде работ,
из которых упомянем работу В. В. Щенникова2).
В. УСТАНОВИВШИЕСЯ ДВИЖЕНИЯ. ПРОСТРАНСТВЕННАЯ ЗАДАЧА
§ 25. Движения с осевой симметрией. Из пространственных
движений рассмотрим сперва обладающие симметрией по отношению
к некоторой оси. Последнюю примем на ось Oz цилиндрической
системы координат; расстояние от оси будем обозначать через г,
полярный угол через 6, проекции скоростей — через vz, vr, v^ соот-
соответственно. Условие осесимметричности запишется тогда в виде:
dp _ dvr _
Кроме того, движение предположим стационарным, так что ни один
из его элементов не зависит от времени. Так как движение про-
происходит одинаково во всех меридиональных плоскостях (полуплоско-
(полуплоскостях), проходящих через ось Oz, мы можем рассмотреть одну такую
полуплоскость (z, г). Уравнения движения примут вид:
1 др _ д v*	(dvr dvz\
J_ dp 	 д v2	(dvr dvz
J~5F~~~dF~2 v*\~dz dF
Уравнение неразрывности примет вид:
Т + Т = °=
условие адиабатичности даст:
4
дг р"
) Последнее значение совпадает с тем, которое приводится обычно
Для идеального одноатомного газа: % = 5/з (стр. 21).
) Щенннков В. В., Расчёт ламинарного пограничного слоя у субли-
сублимирующей поверхности, Сб. выч. матем. н мат. фнзикн, 1 A961), № 5,

222	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. i
Мы видим, что все уравнения, кроме уравнения неразрывности, отли-
отличаются от уравнений плоской задачи (§ 6) лишь заменой х на z
и у на г. Поэтому мы можем повторить все те выводы, которые
мы получили, не употребляя уравнения неразрывности, в плос-
плоской задаче.
Введём функцию тока фB, г). Из уравнения неразрывности имеем:
и F.11) заменится на
х-1
-?.	B5.3)
oz or
Снова вихри будут отсутствовать, если diQ/dty = d%ldty = O; обратно,
если Q = О, будет, вообще говоря, diJdty — db/dty — O.
Обращаемся к условиям на поверхности сильного разрыва (в пло-
плоской задаче это были цилиндрические поверхности, сейчас — это
поверхности, получающиеся вращением около оси Oz; их пересече-
пересечение с плоскостью меридиана назовём линией разрыва); получим,
очевидно, вновь G.1) и G.2), а также формулы
р9 [vz] = [р] cos (n, z); p9 [vr] = [р] cos (n, г)
вместо G.3), G.4), причём по-прежнему имеют место G.5), G.6),
G.7). Но тогда справедливо и G.10), где <р есть угол между нор-
нормалью к линии разрыва и осью Oz, a vl есть скорость до разрыва.
Далее, G.14) запишется в виде:
т. е. нам придётся иметь дело с прежней гипоциссоидой. Наконец,
всё, что мы говорили о критической скорости и об уравнении Бер-
нулли (§ 8), останется в силе, если только заменить там, где они
входят, буквы х и у на z и г соответственно.
Обратимся к изучению движений со сверхзвуковыми скоростями
и привлечём уравнение неразрывности. Примем, что
tQ= const.; Q = г 	. рр * —j-r-,
причём
^l _ !**_ _ о	/95 5)
дг дг —Шш	^ '

§ 25]
ДВИЖЕНИЯ С ОСЕВОЙ СИММЕТРИЕЙ
223
Уравнение неразрывности (второе из дифференциальных уравнений
задачи) запишется так:
, dlnp , dvr . dvz __ ar .
выражая р через а, получим после простых преобразований:
d%)	dv	dl'r ./о	2 &v	a2V
=	-Г- B56)
Уравнение B5.6) отличается от уравнения (9.2) наличием свобод-
свободного от производных члена — a2vr\r.
Предположим, что v > a^, и введём характеристики
г = r (z).
Вдоль них мы имеем:
dvz , dvz dr 	 dvz , dvr , dvr dr __ dvr
dz ' dr dz dz ' dz ' dr dz dz
Находя отсюда dvjdz и dvrjdz и внося в B5.5) и B5.6), приведем
последние уравнения к виду:
SF № + r (fl - ^)J - -w ir\vz + о? - vl) =
dr ' dr dz
Чтобы линия r = r(z) была характеристикой, должно быть:
г' (а2 — v2)-]- v v —r'vv, — (а2 — vl\
\	ZJ '	Г Z	Г Z	\	Т)
a2vr
1
r' (a2 _
= 0,
= 0.
Первый из этих определителей даст нам, очевидно, аналогично пло-
плоскому случаю:
г'2 (у\ — а2) — 2vrvzr' -+ v\ — а? = 0	B5.7)
rfr
vrvz ± a
— а2
B5.8)
где значку 1 отвечает знак плюс, значку 2—знак минус перед корнем.
Мы видим таким образом, что в плоскости (z, r) характеристики
г = г (z) строятся из скоростей vz, vr совершенно так же, как в

224	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ.
плоскости (х, у) характеристики y==y(x) строятся из vx и vy. Обра-
Обратимся теперь ко второму определителю. После простых преобразо-
преобразований получим:
Замечая, что вследствие B5.7) коэффициент при v' будет равен
(v2 — a2\Jr'', деля на него и заменяя члены в квадратной скобке
правой части по формуле B5.8), получим:
dvr / v\ — a2 dvz _ аи Yv2 — аг / аЧгг'
Вспоминая затем, что
„2 „2
получим окончательно:
вдоль характеристики первого семейства:
a2v. , .
f;1^ B5.9)
вдоль характеристики второго семейства:
+ аЯ Vv2 — а2г'2	а\
r[vi — <
B5.10)
Так же, как и в плоском случае, можно придать формулам более
обозримый вид, если ввести величину скорости v и угол наклона р
к оси z:
B5.11)
Мы получим тогда вместо B5.8)
в>-	B5Л2)
где, как и прежде, sin a = ajv.
Формулы B5.9) и B5.10) перейдут при этом в соотношения
B5.13)
^AL. B5.14)

5 261	БЕЗВИХРЕВОЕ ОСЕСИММЕТРИЧЕСКОЕ ДВИЖЕНИЕ ПРИ V>a 225
Формулы B5.9), B5.10) существенно отличаются от формул (9.13),
(9.Н) плоской задачи наличием вторых членов фигурной скобки
справа. Формулы B5.13), B5.14) отличаются от (9.24) наличием
члена, содержащего drjr. Это будет особенно явно в безвихревом
случае, к которому и переходим.
§ 26. Безвихревое осесимметрическое движение при v > a.
Метод Франкля. Если вихри отсутствуют, т. е. 2 = 0, будет: вдоль
характеристики первого семейства:
B6.1)
вдоль характеристики второго семейства:
Л,г + ^л,, = _*к__,;л.	B6.2)
Задача об исследовании такого движения была решена впервые
Франклем.
Наряду с плоскостью (г, г) рассмотрим плоскость (vz, vr). Совер-
Совершенно аналогично тому, как это было в плоской задаче, нашему
движению отвечают точки плоскости (vz, vr), лежащие между кру-
кругом v2 = v2z -f- v2 = а2 и кругом #2=—i-y а2№; это объясняется тем,
что уравнение Бернулли
vl + v*	a2 _ х + 1 а\
пишется здесь так же, как и в плоской задаче. Однако характеристики
в плоскости (vz, vr) не будут теперь эпициклоидами и даже более
того, они аналогично характеристикам в плоскости (z, r) не могут
быть найдены до тех пор, пока движение не определено. Происхо-
Происходит это вследствие наличия в B6.1) и B6.2) правых частей. Легко
видеть, что наша задача представляет формальную аналогию с рас-
рассмотренным нами в § 8 случаем плоского вихревого движения.
В самом деле, соотношения вдоль характеристик в плоскости (vx, vy)
в вихревой задаче представлялись в виде неинтегрируемых комбина-
комбинаций (9.18) и (9.19), заменяемых при практических расчётах урав-
уравнениями типа A3.4), A3.6). Но B6.1), B6.2) отличаются от (9.18),
(9.19), кроме того, что вместо л; и у в них стоят z и г, только
видом коэффициента при dz; при этом коэффициент при dz в B6.1)
и B6.2) даже проще, чем коэффициент при dx в плоской задаче
(последний содержит подлежащую сложному определению величину Q).
Что же касается до характеристик плоскости (z, r), то они опре-
определяются по формулам B5.8), т. е. совершенно так же, как
15 Теоретическая гидромеханика, ч, II

226	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
характеристики в плоскости (х, у); уравнения B5.8) по-прежнему
эквивалентны соотношению
(п — нормаль к характеристике); уравнение Бернулли справедливо
в прежней форме; можем легко провести характеристики в плос-
плоскости (г, г).
Обращаясь к задачам типа 1, 2, 3 и 4, рассмотренным в § 11,
заметим, что для приближенного (графического) решения их здесь,
как и там, достаточно научиться следующим трём операциям:
1) находить скорость в точке пересечения характеристик разных
семейств, выходящих из двух различных, близко расположенных
точек, в которых скорости уже известны;
2)	находить скорость в точке пересечения с заданным элементом
стенки характеристики, выходящей из близкой к стенке точки, в кото-
которой скорость известна;
3)	находить скорость в точке пересечения характеристики, выхо-
выходящей из точки, близкой к некоторой свободной поверхности,
с заданным элементом этой свободной поверхности.
Научимся сперва операции 1.
Операция 1. Пусть в близких точках М1 и М2 плоскости (z, r)
(рис. 77) известны скорости; отметим в плоскости (vz, vr) точки М\
и М.% координаты которых суть компоненты скоростей в точках Мх
и М2 соответственно. Через точки М1 и М2
проведём элементы характеристик разных се-
семейств до их пересечения в N} (пусть для
конкретности MlMi— элемент дуги характе-
характеристики первого семейства, a M2NX — второго
	z семейства). Это построение можно выполнить,
вычисляя r\ 2 по B5.8). При этом, как и в пло-
Рис. 77.	ской задаче, элементы характеристик следует
заменять элементами касательных к характе-
характеристикам. Чтобы найти скорость в точке Л^г, рассуждаем так. Пере-
Перемещаясь по элементу MlNi в плоскости (z, r), мы будем, вслед-
вследствие B6.1), перемещаться в плоскости (vz, vr) по элементу прямой
B6-3)
где постановка значка М1 при скобке означает, что выражение
в скобке вычисляется в точке Мх. С другой стороны, перемещаясь

§ 26]	БЕЗВИХРЕВОЕ ОСЕСИММЕТРИЧЕСКОЕ ДВИЖЕНИЕ ПРИ V>a 227
по ЩМр будем двигаться по прямой
Точка N{ плоскости (vz, vr), лежащая на пересечении прямых B6.3)
и B6.4), даст компоненты скорости точки Nx.
Операция 2. Известна скорость в точке Мь и дан элемент твёр-
твёрдой стенки, близкий к Мх, но не проходящий через Мх (рис. 78).
Через Ж, проведём характеристику, например, первого семейства
4
Рис. 78.
Рис. 79.
до пересечения со стенкой в точке Nv Скорость точки Nl находится
в плоскости {vv vr) на пересечении прямой B6.3) с радиусом-векто-
радиусом-вектором, параллельным направлению касательной к стенке в точке Nx
(рис. 79).
Операция 3. Известна скорость в точке М1 и дан элемент сво-
свободной поверхности, близкий к Mlt но не проходящий через Mv
Проведём через М1 характеристику, например, первого семейства
до пересечения со свободной поверхностью в точке Nv Скорость
в Nx найдётся в плоскости (vz, vr) на пересечении прямой B6.3)
с кругом v — v^, где v1 есть скорость, отвечающая, по уравнению
Бернулли, давлению, имеющемуся на свободной поверхности.
В практических приложениях построение прямых B6.3) и B6.4)
можно проводить графически, используя то их свойство, что каждая
из них ортогональна соответствующей характеристике другого номера,
проведённой в плоскости (z, r) (тангенсы наклона наших прямых
суть—l/(Vo) и 1/(/-,') V Но если мы знаем направление элемен-
тов B6.3), B6.4), то, чтобы уметь их провести, достаточно найти
ещё, например, их расстояние от точек М\ и Жг соответственно.
Приводя уравнения наших прямых к нормальной форме, получим
Для этих расстояний 8 следующие выражения:
dz
rtf-J) Vl+r*
¦dz
15*

228
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
Заменяя в случае первой характеристики \dz\ на \dz\
[ГЛ. I
dst
--.-
где dsx — длина дуги вдоль характеристики (например, отрезок
рис. 77), а для §2 '• \^z\ = - 5г ,¦ и замечая, что
(см. вывод для плоской вихревой задачи § 13), получим:
rv*
\dsx\\ o2 =
rv2
\ds2\.
B6.5)
Остается только найти, с какой стороны от той или иной точки
плоскости (vz, vr) надо проводить на расстоянии Ъх или 82 наши
характеристики, иначе говоря, надо знать знак проекции \ и 82 на
какую-либо ось, например, на ось Oz. Из элементарных геометри-
геометрических соображений получим, что
V, -2^2" dZ ) = Sig" [Vr {Vl — a2) dZ\ ¦ B6-6)
В качестве примера рассмотрим движение внутри трубы заданной
формы, обладающей осевой симметрией по отношению к оси Oz.
Предположим, что в некотором произвольном сечении трубы
АВ (рис. 80, рассматриваем одну только полуплоскость) скорость
движения превышает звуковую и
нам известна. Нанесём на отрезке
АВ ряд точек А, Мх, М2, ... и
через все эти точки проведем эле-
элементы характеристик первого се-
семейства. Характеристику, выходя-
выходящую из Mv доведём до пересе-
пересечения с контуром в точке Nx и,
пользуясь операцией 2, найдём
g	q	скорость в Nx; проводя затем
из Nx элемент характеристики
второго семейства до пересечения
в точке N2 с характеристикой первого семейства, идущей из Ж2, найдём
с помощью операции 1 скорость в точке N2 и т. д. Заметим, что ско-
скорости точек, лежащих на оси Oz, должны находиться из условия
vr = 0 (скорость направлена там вдоль оси Oz); при этом, желая
найти о для точек оси Oz, мы должны будем вычислять там выра-
выражение vr/r = 0/0. Последнее надо заменить на dvrjdr, так что при

,7J	ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА	229
вычислении 8 в точках оси трубы придётся брать значение vrjr для
соседних точек, которые не лежат на оси, и в которых скорости
уже известны.
Решим задачу о получении плавного потока (сопло Лаваля). Пусть
в точке С мы имеем нужную нам сверхзвуковую скорость, и CD
(рис. 80) есть характеристика второго семейства, проходящая через С.
Так как в осесимметрических задачах нет интегрируемых комбина-
комбинаций характеристик, то здесь не будет, вообще говоря, и прямоли-
прямолинейных характеристик, а потому применить метод, данный в § 12,
нам здесь не удастся. Но всё же одна прямолинейная характеристика
(след в меридиональной плоскости характеристического конуса с осью,
совпадающей с осью Oz) может существовать и здесь, а именно,
она получится для потока, параллельного оси Oz и обладающего
всюду постоянной скоростью. Как раз такой поток мы и хотим по-
получить «вправо» от точки С; проведём же через С заранее прямолинейную
характеристику первого семейства. Чтобы подобрать вид стенки,
начиная от точки D «вправо», нанесем на прямолинейной характе-
характеристике (так же, как и на кривой CD) ряд точек и, пользуясь опе-
операцией 1, начнём узнавать скорости в криволинейном четырёхуголь-
четырёхугольнике, рассмотренном в задаче 2 (§ 11). Если мы возьмём крайнюю
точку на прямолинейной характеристике достаточно далеко, нам надо
будет затем лишь построить (путём интерполяции) линию тока, про-
проходящую через D. Её мы и можем принять за искомую стенку.
Переходим к внешним задачам и прежде всего к вопросу об
обтекании конического острия. Случай этот не поддаётся нашему
методу, ибо на таком острие г — 0, a vr Ф 0 и 8 обращается в оо.
§ 27. Осесимметрическое обтекание круглого конуса. Кони-
Конические течения. Обтекание осесимметричных тел. Пусть поток,
обладающий постоянной сверхзвуковой
скоростью fj > alF набегает на круго-
круговой конус с вершиной в точке Р и
с осью вдоль оси Oz. Перед конусом
образуется коническая поверхность раз-
разрыва (рис. 81) с вершиной в Р; на
этой поверхности линии тока претер-
претерпят, как всегда, излом, а затем нач-
начнётся обтекание конуса. В противопо-
противоположность тому, что мы имели в плоской	Р
задаче при обтекании угла (§ 13 и	Рис. 81.
рис. 32), линии тока, после прохожде-
прохождения разрыва, станут здесь кривыми. Простота задачи обтекания конуса
заключается, однако, в том, что скорости будут иметь одну и ту же
величину и направление во всех точках какого-либо конуса с осью Oz
и с вершиной в Р. Таким образом, наш поток не только не будет

230	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
зависеть от полярного угла б плоскости, перпендикулярной к оси Oz,
но также не будет зависеть от расстояния s от точки Р. Вводя в мери-
меридиональной плоскости (z, г) (плоскости, проходящей через ось Oz)
полярные координаты (с полюсом в Р) s и ср. будем таким образом
считать, что скорости vr и vz зависят лишь от ср:
«* = *,(?): «V = «»¦(?)•	B7Л)
В плоскости {t)z, vr) мы получим, исключая ср из B7.1), неко-
некоторую кривую
отвечающую обтеканию нашего конуса. Построим эту кривую. Для
этого обратимся к уравнениям B5.5) и B5.6) B=0) и, перейдя в них
к переменным s и ср. положим dvrjds = dvjds = 0. Получим вместо
B5.5) после простых преобразований:
vr
или
W
	,	уг
Отсюда заключаем, что направление
Рис. 82.	нормали в некоторой точке М' нашей
кривой f(vz) в плоскости (г/г, vr) будет
совпадать с направлением того радиуса-вектора в плоскости (z, r)
(угол ср). скорость точек которого изображается точкой М' в пло-
плоскости {уг, vr) (оси Oz и Ovz совпадают; рис. 82).
Обратимся теперь к уравнению B5.6). Оно примет в полярных
координатах вид:
[(а2 — vl) sin2 <р + vrvz sin cp cos <p] -^- —
— [VrVz S'n2 T ~f" (fl2 — VV) s'n f cos ?] ~7Г~ — a^vr'
и если заменить dvrjdy на dvr/dvz-dvz/dy — f dvjdy, то можно найти
выражение для dyldvz:
^„ (я2 — f2) sin2 9 + vTvг sin if cos if — vT vz sin2?/' — (a2 — v2) sin 9 cos 9/'
dvz	a2vr
Наконец, заменяя /' по B7.2), мы получим:
df 	а2 — (vz sin f — vr cos ^J
dvz	a2vr
Вставляя сюда ср, выраженное по B7.2) через /, беря vr = f(vz)
и а2 по уравнению Бернулли, получим дифференциальное уравнение

. ,71	ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА	231
второго порядка для определения f(vx). Найдём теперь радиус кри-
кривизны R кривой vr = f(vz) в точке М'. Очевидно, что
A+/)= 1	1_=:—±
°	/"	sin3 9 d , sin3
/"	sin3 9 d ,, sin3 9 dy d „
dvz	dvz dy
sin3 9 a2 — (vz sin 9 — vr cos 9J
или
B7.3)
	 sin2 9
1
smtp / vz sin 9 —1>,. cos 9
Выпишем еще дифференциальное уравнение второго порядка,
которому удовлетворяет / (vz) Это будет
/^==1+(^' "	^~'	B7'4)
где
Предположим теперь, что в какой-то точке М' нашей кривой
нам известно ср, т. е. предположим, что мы знаем для нашего дви-
движения величину и направление скорости на каком-нибудь определён-
определённом конусе с вершиной в Р. На основании B7 2) и B7.3) мы можем
тогда дать графический способ приближенного построения кривой
vr = f(vz) для нашего движения. Зная ср, vz, vr можем вычислить R
по B7 3), откладывая это R по нормали в М' (направление ее из-
известно, ибо ср известно), найдем центр кривизны N для М' и про-
проведем малую дугу круга радиуса R с центром в N. Взяв точку М\
этой дуги, близкую к ЛГ, найдем угол наклона cpi B точке М\ ра-
Диуса проведенного нами круга и снимем vTl и vZl как координаты
точки Mt. Мы можем теперь, вновь обратившись к B7.3), найти
R\ — радиус кривизны в точке Mi, построить центр кривизны Ыг
и т. д.
Рассмотрим теперь вопрос об обтекании конуса с углом рас-
раствора 2j30. Пусть нам заранее известно, что угол раствора конуса
') В пространстве (vx, vy, vz) уравнение vr—f(vz) представляет собой
поверхность вращения вокруг оси vz. А. А Никольский исследовал также
Движрния, в которых пространство годографа вырождается в любую по-
поверхность или же, наконец, в линию. В последнем случае получается обоб-
обобщение тех случаев плоских течений, в которых годографом служили эпи-
эпициклоиды (см ниже § 31)
Аналогичные результаты получили С В Валландер и Жермен (Jermain)

232	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ 1
сильного разрыва, расположенного перед нашим конусом, будет 2v0.
Построим гипоциссоиду, отвечающую скорости набегания vz = vx,
<иг = 0, и при помощи угла v0 найдем величину скорости (vz, vr)
(опуская перпендикуляр из точки (vx, 0) на прямую, наклоненную
под углом v0 к оси vz и отыскивая пересечение этого перпендикуляра
с гипоциссоидой) после прохождения разрыва. Примем теперь наше v0
за отправной угол ср (рис. 82), а нашу скорость отметим в плоскости
(vz, vr), и будем строить линию vr = f(vz) до той ее точки Q, где
направление нормали к нашей кривой пойдет в точности по напра-
направлению радиуса-вектора OQ этой точки; точка Q даст величину
скорости в том месте, где скорость будет направлена вдоль конуса,
на котором она измеряется, т. е. даст скорость на поверхности
v	. обтекаемого твердого конуса (угол OQ
v	с осью z равен ро).
При построении, на основании B7.3),
кривой / (vz) полезно заметить, что B7.3)
может быть записано в виде
1--К
рис 83	где RU = BM' (рис. 83) есть отрезок нор-
нормали от точки М' до пересечения с осью
vz, a U есть проекция скорости V в точке М' на направление каса-
касательной к кривой vr = f (vz) в этой точке.
Совершенно очевидно, что, зная кривую vr = f(vz), мы будем
знать все движение, ибо, чтобы найти скорость на радиусе-векторе
полярного угла <р (конус с углом раствора 2ср) достаточно будет
найти на нашей кривой такую точку, чтобы нормаль в ней пошла
под углом ср к оси z. Трудность состоит только в том, что в за-
задачах на обтекание острия бывает задан угол острия, а не угол по-
поверхности разрыва.
В работе Хантше и Вендта') даются кривые, связывающие при
различных значениях vxjat величины [Jo и v0. Эти авторы взяли сперва
ряд значений vxjat(vxjat = 1,17; 1,25; 1,37 и т. д.), построили для
каждого из них гипоциссоиду, взяли на каждой такой гипоциссоиде
по нескольку точек (8 или 9) и построили линии / (vz), выходящие
из этих точек. Пример такого построения дан на рис. 84. Здесь
Oj/a, = 1,6582 {vxjax — 2,0636). «Концы» наших линий (т. е. те места,
где нормаль к этим линиям совпадает с продолжением радиуса-вектора)
соединены в свою очередь кривой (авторы упомянутой работы наз-
назвали эту кривую «яблоковидной»), числа, стоящие у концов линии / (vz),
') HantscheW.WendtH, Mit Ueberschallgeachwindigkeit angebla-
sene Kegelspitzen. Jahrbuch deutschen Luftfahrtforschung, 1942.

§27]
ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА
233
означают отношение ро+/ро_, отвечающее тому или иному случаю.
На рис. 85 изображено семейство яблоковидных кривых (верхняя
полуплоскость) вместе с соответствующим семейством гипоциссоид
(нижняя полуплоскость). На рис. 86 по горизонтальной оси отложены
углы v0> по вертикали — углы [Jo и дано семейство кривых, завися-
зависящих от параметра vja^. Тут же дан рис. 87, где по оси абсцисс
отложены Mx = vxjav по оси ординат отложены v0, а кривые зависят
от параметра [30. Наконец, рис. 88 даёт величину (р—/^/'/гР^. гДе
р — давление на конусе, в функциях от угла ро для разных vja^!).
"у.
\0,в6 0,92
0,80
0,969
0,996
?=1,6582 ,
Рис. 84.
j- =2,0636
В решении рассмотренного типа «концы» линий vr = / (vz) лежат
на яблоковидной кривой, а «начинаются» эти линии на гипоциссоиде.
Другой тип движения, описываемого уравнениями B7.2), B7.3),
может быть получен в виде конического течения сжатия в сопле
специального вида, в котором прямолинейный поток vz = vv vr = 0,
начиная от некоторого конуса ВРВ (рис. 89), плавно переходит в ко-
коническое течение, а затем, после прохождения конической поверх-
поверхности сильного разрыва АРА, опять становится прямолинейным, но
уже с новой скоростью vz = v2, vr — О (Буземан).
Чтобы найти это движение (а заодно и форму стенки), можно
задать скорость г/2(<а„) после прохождения разрыва и угол ср0
конуса разрыва. Тем самым мы можем определить значения v'z, v'r
скоростей перед прохождением разрыва, а затем, используя B7.3),
построить соответствующую кривую vr = / (vz) (Z,), подобно тому
как мы это делали в случае обтекания конуса.
) «Левые» ветви кривых на рис. 86 и 88 отвечают режиму обтекания
со сверхзвуковыми скоростями на поверхности конуса, «правые» — с дозву-
дозвуковыми (две точки пересечения гипоциссоид с радиусом-вектором).

234
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
60'
So
50е
40°
SO0
20°
10°
Рис. 85.
fff" гО' 30° 40° 50' 60° 70' 80"v030°
Рис. 86.

§271
ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА
235

236
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
(ГЛ. 1
Для удобства можно вновь обратиться к гипоциссоиде G.14), но
теперь вместо vx следует подставить в эту формулу v2 — скорость,
возникающую после прохождения разрывах). Уравнение для 0о'г, v'\
примет вид (аналог A3.3)):
B7.5)
Так как теперь v2 < a^, то гипоциссоида B7.5) будет иметь иной
вид, чем рассматривавшиеся до сих пор. Именно, кривая B7.5)
состоит из изолированной точки vz = v2, vr = 0 и из линии, распо-
располагающейся в полосе 2v2/(*-{-l)-\-a4v2 > vz~^> a2jv2 (см. рис. 90),
д	пересекающей ось <ог в точке
,	a2/vz и имеющей асимптоту
С и -
Кривая L будет теперь
«начинаться» на гипоцис-
гипоциссоиде, а «заканчиваться» на
оси z (в точке В), где и
определится скорость vv
Оба типа течений, рас-
рассмотренных нами, реали-
реализуются только при наличии
конической поверхности
сильного разрыва и являются
течениями сжатия. Следующим образом доказывается, что движение
2-го типа не может существовать без поверхности сильного разрыва.
Пусть наша кривая L может быть продолжена до пересечения с осью
симметрии (пунктир на рис. 90) в точке D. Дифференцируя урав-
уравнение B7.4) по vz и полагая / = 0, получим
Рис. 89.
ГГ =
B7.6)
Равенство это показывает, что /'/" должно быть положительным.
С другой стороны, из рисунка видно, что /' < 0 около точки D,
что же до /", то, в силу B7.2), мы можем написать /"== — d(tg<f>)/dvz.
Так как (см. рис. 89) ctg<p по мере продвижения слева направо все
время растёт, переходя от отрицательных значений через нуль к по-
положительным, a vz уменьшается (течение сжатия), мы имеем /" > 0;
но тогда /'/" < 0, и мы получим противоречие с B7.6). Это про-
') См. аналогичное рассуждение в § 7,

, 27]
ОСЕСИММЕТРИЧЕСК.ОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА
237
тиворечие не имеет места в случае, отвечающем точке В, где /' > 0.
Третий тип движений, удовлетворяющих B7.2), B7.3), был найден
д. А. Никольским A949). Это
осесимметрическое коническое
течение, при котором невозму-
невозмущённый поток со скоростью vv
начиная с некоторого характери-
характеристического конуса (с вершиной
на оси симметрии), непрерывно
разряжается. Течение это можно
рассматривать как внешнее обте-
обтекание невозмущённым сверхзвуко-
сверхзвуковым потоком некоего тела враще-
вращения—полубесконечного цилиндра,
который после некоторого сечения
начинает постепенно сужаться
(см. рис. 89). Возможность су-
существования такого течения видна
из следующего рассуждения.
Возьмём в плоскости годо-
годографа скорости (рис. 91) неко-
некоторую точку Bi (y'z, v'\. Через эту
точку проходит бесконечное мно-
множество интегральных кривых	Рис. 90.
уравнения B7.4). Среди этих кри-
кривых найдутся такие, которые будут обращены выпуклостью к оси v2.
В самом деле, по B7.3), если проекция U на касательную к нашей
кривой скорости в точке Вх
будет меньше чем а, то
радиус/? будет отрицатель-
отрицательным (vr <; 0), что и означает
выпуклость соответствую-
соответствующей кривой L. Между тем
всегда можно выделить та-
такой угол с вершиной в точ-
точке Bv что проекция ско-
скорости на любую прямую,
проходящую через Вх внутри
этого угла, окажется меньше Рис. 91.
чем а. Итак, через Вх про-
проходит бесконечное множество интегральных кривых L, выпуклых по
отношению к оси vz. Если мы будем двигаться по одной из таких
кривых по направлению к оси vz, то, как легко видеть, выпуклость
нарушаться не будет (точки перегиба не встретятся), и мы сможем

238
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
пройти по нашей линии L до оси vz. Пусть мы попадём при этом
в точку Ах (vx, 0). Наклон нормали к линии L в точке Л, легко
определить. Для этого достаточно положить в уравнении B7.4) vr***0,
Получим
B7.7)
где
1.2
¦«?•
Рис. 92.
Соответствующий (в смысле равенства B7.2)) конус Я\ (рис. 92)
будет иметь наклон <рх, опре-
определяемый равенством
1
S1H Ф, = гт- .
м,
Следовательно, конус /Cj будет
характеристическим конусом.
Таким образом, движение, опре-
определяемое нашей линией L,
можно представить в виде
прямолинейного потока со ско-
скоростью vx, который после прохождения характеристического конуса Кх
начинает плавно поворачиваться, расширяясь.
Точка Вх нашей кривой не может быть расположена сколь угодно
далеко от оси vz. Двигаясь по L, начиная от Ах, мы рано или поздно
дойдём до точки перегиба (/"=0) этой кривой, после чего кривая L
станет обращаться вогнутостью к оси vz. При движении от Ах по L
нормаль к L вращается по часовой стрелке; после прохождения точки
перегиба нормаль начнёт вращаться против часовой стрелки, т. е. мы
вынуждены будем возвращаться в область течения, уже описанную
кривой АХВХ, и это решение не имеет смысла. Поэтому движение
наше может быть доведено только до точки перегиба кривой L.
Приравнивая нулю /" в уравнении B7.4), мы можем найти значение/^
на месте точки перегиба:
vrvz
.,
Наклон f'o отвечает некоторому конусу Ко (рис. 92) (он также есть
конус характеристик). Раствор продольного конуса Ко будет различен
для различных интегральных кривых (различных точек Вх). Течение
этого типа можно построить (и параллельно построить соответствующую
обтекаемую поверхность), отправляясь от оси ог=г0и задавая скорость
t/j. Затруднением, однако, является то, что линия vr = 0 является особой
линией для уравнения B7.4) и такой, что через каждую точку Аг оси
vr=0 проходит бесконечное множество интегральных линий L и кривизны

§ 27)	ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА	239
всех «тих линий будут одни и те же1). Окончательно можно оста-
остановиться н* следующем способе построения течений Никольского.
Задаёмся *начением г>г; по этому значению определим Mi и построим f'x
по формуле B7.5)
Отойдем теперь в плоскости годографа от оси vz на небольшое рас-
расстояние /2тзз0,01ая. по нормали (/г = '*>,•)¦ Соответствующее значе-
значение (vzJ находится по приближённой формуле (замена производной
конечной разностью):
(vzJ ~v1^-r /2.
f\
Мы получили точку А2 ((vгJ, /2), в которой можем найти а2 по
уравнению Бернулли:
В точке А2 зададим теперь значение f'r Так как, по определению
нашей кривой L, проекция скорости на касательную к L должна
быть меньше скорости звука (U < а), и так как проекция на харак-
характеристическое направление будет всегда в точности равна скорости
звука, мы должны выбрать /2 так, чтобы наклон L оказался боль-
большим, чем наклон, отвечающий B7.2). В остальнЬм f'2 может быть
произвольной, и от выбора этой величины зависит, какую именно
интегральную кривую мы получим в конце расчёта.
') Действительно, по формуле B7.4) мы получим для (f")i неопределён-
неопределённость типа 0/0, которую надо раскрыть по правилу Лопиталя:
^1^,2 (Vz+f/У
lim /" = lim	д2 _
Отсюда, принимая во внимание B7.7) найдём
/" = 1+1 Mi
1 й /fZ

240	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
После того как /'2 известно, мы можем найти /? по формуле B7.4):
¦ = -^1
[Ы2+/2/2Г
4
г
Дальнейшее построение можно проводить шаг за шагом, задавшись
близкими друг к другу значениями (vz)z, (fzL, ..., (vz)n величины vz.
Если fn_v f'n_y f'n-\ известны, то величины fn, f'n найдутся по
формуле
/„=/._!+/;.! [(va\ -(Vj)e_j; /; -rn_x+/:_x [(«,)„ -(«,),_,].
величина а„ найдётся затем из уравнения Бернулли:
из соотношения
J п /|
'2
Вычисление надо вести до тех пор, пока /" не станет нулём. Рас-
Расчёты ведутся практически, конечно, в безразмерных величинах
(vJa*< vrla* и т> Л-)- На рис. 93 даны примеры, взятые из работы
-0,5 \
Никольского, двух профилей рассматриваемого типа, отвечающих
одному и тому же значению Mi =1,7. Здесь же показано распре-
распределение давления вдоль профиля Никольского.
Задача обтекания произвольного тела вращения, имеющего впе-
впереди остриё, и с осью вращения, расположенной вдоль потока, была

§27]
ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА
241
исследована впервые Ф. Франклем. Угол острия должен быть, как и
в плоском случае, не слишком велик, чтобы не образовалось до-
дозвуковых скоростей. Если это условие выполнено, то задача обтека-
обтекания решается без труда. В меридиональной плоскости имеем контур
с остриём в Р (рис. 94). Пусть обтекаемое тело представляется
близ Р в виде конуса, а затем контур его начинает плавно перехо-
переходить в криволинейный. Перед конической частью (отрезок контура РА)
образуется коническая поверхность разрыва (линия РВ), и мы можем
найти движение в области между РА и РВ по методу, изложенному
выше; проведём при этом через Л характеристику АВ
первого семейства, отметим на ней ряд
точек: Мг, М2, .. . (рис. 94) и построим
элементы характеристик второго се-
семейства, проходящие через эти точки.
Пусть Мг — самая близкая к А точка,
МуС — проведённый через неё элемент
характеристики второго семейства,
С — точка контура. При помощи опе-
операции 2 (§ 26) найдём скорости
в точке С и проведём через С характе-
характеристику первого семейства до пересе-
пересечения в точке Nx с характеристикой
второго семейства, идущей из М2. Ско- pt
рости в Nx найдутся при помощи опе-
операции 1 (§ 26) и т. д. Так мы заполним
всю область между линией АВ, конту-
контуром АЕ и характеристикой второго семейства BE, выходящей из В.
Из близкой к В точки. Nn характеристики BE проведём элемент ха-
характеристики первого семейства до пересечения D с продолжением
прямой РВ. Точка D лежит на поверхности разрыва; чтобы найти
скорость в D, мы должны поступить так же, как в операциях 2 и 3,
только вместо пересечения соответствующего отрезка характеристики
плоскости {vz, vr) с радиусом-вектором (или с кругом) нам придётся
искать пересечение с гипоциссоидой. Определив в D скорость (при
помощи гипоциссоиды) и направление поверхности разрыва, прове-
проведём из D характеристику второго семейства до пересечения Q
с характеристикой PnQ первого семейства (Рп — точка, близкая к Nn
и лежащая на BE).
Ход решения дальше был бы ясен (определение скорости в Q,
проведение характеристики QF до пересечения с отрезком DF ли-
линии разрыва и. т. д.), если бы не пришлось учесть появления вихрей.
Последние не появлялись при обтекании конуса, ибо поверхность
16 Теоретическая гидромеханика, ч, II
Рис. 94.

242	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[Гл I
разрыва там пересекала меридиональную плоскость по прямой; но
теперь линия разрыва есть кривая, после прохождения возникнут
вихри, и придётся воспользоваться формулами B5.9), B5.10). «Рас-
«Расстояние» 8 из § 26 найдётся теперь по более сложной, чем B6.5),
формуле, содержащей Ь и dbjdty. Впрочем, вычисления db/dty и &
совершенно аналогичны вычислениям этих величин для плоской за-
задачи (§ 13).
Изложенный здесь графический приём решения задачи на обте-
обтекание при всей его простоте отличается громоздкостью. Могут быть
предложены другие методы использования соотношения на характе-
характеристиках (даже если по-прежнему говорить о ручном счёте).
А. А. Дородницын предлагает использовать формулы B5.13) и
B5.14) (при движении вдоль характеристик), выполняя в них инте-
интегрирование (вдоль той или иной характеристики) с попутной аппрок-
аппроксимацией самих характеристик в виде кривых второго порядка по г;
при этом подынтегральные функции там, где они остаются, также
аппроксимируются тем или иным способом.
Применение этого приёма иллюстрируем на случае наличия при обте-
обтекании криволинейного скачка уплотнения.
Пусть обтекаемое тело вращения имеет с самого начала кривизну,
отличную от нуля (рис. 95). Надо определить форму скачка уплотнения и
течение позади него.
Возьмем на поверхности обтекаемого тела вращения вблизи носика Р
точку А. Пусть через эту точку проходит характеристика 2-го семейства АС
и характеристика первого семей-
семейства АВ; точки С, В лежат на
поверхности разрыва. Форма этих
обеих характеристик, так же, как
и форма поверхности разрыва, не-
неизвестна. Мы будем их аппрокси-
аппроксимировать с помощью трех па-
парабол.
Для поверхности разрыва
примем
z = Clr + ctr», B7.8)
где с,, с2 подлежат определению.
Для характеристики 1-го се-
семейства АВ напишем
Рис. 95.	г = Za + в, (г - га) + 6, (г - га)\
B7.9)
где (га, га) — координаты (известные) точки А, а{ и а2 — постоянные, под-
подлежащие определению.
Наконец, для характеристики 2-го семейства АС напишем
г = га-\-а2(г-Га) + Ьг(г-гаУ,	B7.10)
где аг и b2 заранее неизвестны.
Обозначим через ч угол касательной к поверхности разрыва с осью г.
Дифференцируя B7.8), получим

27j	ОСЕСИММЕТРИЧЕСКОЕ ОБТЕКАНИЕ КРУГЛОГО КОНУСА	243
где v , v_ — углы наклона поверхности разрыва в точках Р и В соответ-
соответственно, о, —ордината (неизвестная) точки В. Таким образом, вместо B7.8)
мОжем написать
Ctg-yn —Ctgv
г = ctg ,pr + & в2гь	?- Л	B7.11)
В частности, в точке В
Угол чр можно считать известным и равным углу скачка для конуса, каса-
касательного к телу в точке Р. Три известных величины: -у^, гь, гь связаны
одним соотношением B7.12). Далее, дифференцируя уравнение B7.9) и учи-
учитывая B7.12), мы можем написать
Cfg (К ~ «А) = Я1. С[ё (Рд + ав) = d8 <?Л + ал) + 2*1 (Гь - Га),
так что для точки В по B7.9) имеем
Г^	+ «a)j.	B7.13)
В этом соотношении $А — угол касательной к контуру в точке А — известен,
но неизвестны величины аА, рд, ав, гь, rft. Так как точка В лежит на по-
поверхности разрыва, то значения $в и а^ могут быть выражены через чв.
Именно, из условия непрерывности скорости, касательной к поверхности
разрыва, имеем
vb = vlcos4Bstc{4B-^B).	B7.14)
Здесь и, — скорость набегающего потока, скорость vb выражается через
угол Маха ад как всегда с помощью соотношения (9.22). Кроме того,
деля G.17) на G.16), можем получить
= ctg vfi
Таким образом, в качестве неизвестных остаются четыре величины: ч , а.
гь< гь.
Воспользуемся теперь соотношением B5.13). Проинтегрируем его вдоль
линии АВ
в
В VA	_
В
Г sin ft sin a dr
-J sin(p_a)— <27Л6>
л
(Функция С определена по формуле A0.8)).
Вклад первого интеграла правой части B7.16) незначителен, приближённо
можно принять, в качестве подынтегрального выражения этого интеграла,
16*

244	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. \
значение его в одной какой-то точке, например до прохождения поверхности
разрыва. Выражение, входящее во второй интеграл, можно аппроксимиро-
аппроксимировать в виде
sin 3 sina	N
sin (8 —а) ~/и+ г '
определяя М и N так, чтобы соотношение это выполнялось в точках А и В:
sin 3, sina.	N sin 3D sin a	N
-^Л	A — AH	, .	L^	S = AH	•
sin (\i ~—~ ol л	f	sin (A — ct _ i	f,
Тогда соотношение B7.16) примет вид
sin 8 л sin а . /	г	г.\ sin р _ sin a /	rb
Ф4 (i+^'" е)+^4('+
B7.17)
Здесь рд, ra известны, рд и rft выражаются через 9^, 9fi найдётся по vfi
с помощью G.2), G.10); что же до 9 , то оно известно и определяется че-
через чр, ибо вдоль линии тока (обтекаемой поверхности) 9 не меняется.
Неизвестными являются по-прежнему -у^, гь, гь, а^.
Таким образом, мы имеем три соотношения B7.12), B7.13) и B7.17),
содержащие четыре неизвестных. Чтобы замкнуть задачу, используем соот-
соотношение вдоль характеристики АС. Точка С находится на поверхности раз-
разрыва B7.11); значит, во-первых, можно написать
гс =
н, во-вторых (как результат дифференцирования),
ctg чс = ctg vp + CtgVg~°tgV r,	B7.19)
В последних двух равенствах содержатся новые три неизвестные вели-
величины: гс, гс, чс.
Запишем, наконец, условия на характеристике B7.10)
и соотношение B5.14), проинтегрированное вдоль АС
V«\ r(VA S'n a, COS a,	bc
B7.21)
В равенстве B7.20) величины 3e, vc и Ьс находятся через чс, а остальные
величины введены были выше. Таким образом, мы имеем семь трансцендент-

§ 28)	ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	245
ных уравнений: B7.12), B7.13), B7.17) —B7.21) с семью неизвестными гь
гь> гс< гс ад> v?> V Практически решение этих уравнений облегчается тем,
что гс будет значительно меньше, чем гь, так что чс очень близко к чр.
Положив в первом приближении чс — чр, мы получим
Подставляя эти величины в B7.20), определим гс и гс через известные ве-
величины га, га, |5Л, р^, а^ и неизвестную величину а^. Затем, вставляя най-
найденные г с гс в B7.21), найдём и а^. После того как а^ получено, сразу
можно найти из системы B7.12), B7.13) величины гь, гь через чв и затем
из уравнения B7.17) найти vfl. Теперь подставим найденные значения чв
и гь в B7.18), B7.19). При этом мы получим новые значения гс и чс в функ-
функциях от г с а используя B7.20), B7.21), определим исправленное значение а^,
Переходя снова к системе B7.12), B7.13), B7.17), найдём исправленные зна-
значения -у^ и гь и т. д.
Наконец заметим, что при решении осесимметрических задач на
электронных быстродействующих машинах удобно использовать пе-
переменные, аналогичные тем, что были введены в § 11 (по Элерсу).
Этот вопрос подробно рассмотрен в упомянутой выше статье Элерса
(стр. 68), а также в работе П. И. Пушкина1).
§ 28. Пространственная задача. Линеаризация уравнений.
Снаряд, движущийся под углом к оси симметрии. Обращаясь
к общему пространственному случаю установившегося движения,
напишем уравнения движения:
|^	gradp	B8.1)
(Q — вектор вихря), уравнение неразрывности:
gradlnp- V+divV = 0	B8.2)
и уравнение притока энергии:
V . grad ^- =. 0.	B8.3)
Уравнение B8.3) равносильно тому условию, что величина
сохраняется в частице, т. е., вследствие стационарности движения,
на каждой линии тока. Умножая B8.1) скалярно на V, получим,
так как
— grad;» —ft;?-1^	*
') Ч у ш к и н П. И., Затупленные тела простой формы в сверхзвуковом
потоке газа, ПММ, т. XXIV, в. 5, 1960.

'246	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
для величины /0:
^Г~+Т=ТЬР * ='о	B8.4)
сохраняется на каждой линии тока. Мы примем, как и раньше, что
вообще
/0 = const.
Тогда B8.2) после преобразований, аналогичных тем, что были сде-
сделаны в § 9, даст:
к-
+ f
где,
а*
*V
как
0Vr
\ х |
) cU '
\ ду '
раньше,
-С г»2
V У
dvy
дх
а
)+
;2 =
) ду
VXVz (¦
^ _
Р
- + (*?-
х-1
¦жЪр х
-а>)
dvz\
дх )
дг
-И
>у-
+
-1
(¦
dvy
дг
+
<^у j
B8
0,
• 5)
Предположим, что поле скоростей в нашем движении может быть
представлено в виде:
где v', v , vr — бесконечно малые, зависящие от х, v, z функции,
ао, — постоянная величина. Такое движение получится, например,
если поток скорости vl3 параллельный оси х, набегает на бесконечно
тонкое, наклонённое под бесконечно малым углом атаки к оси х
крыло, или же на бесконечно тонкий и бесконечно мало отклонен-
отклоненный от своей оси симметрии снаряд и т. п.
В свою очередь, давление р и плотность р будем искать в виде:
где рх и pj — постоянные; при этом
B8-6)
tf?
По аналогии с тем, что было в подобных случаях в плоской
задаче (приближение Аккерета и Буземана для тонких крыльев), мы
и здесь вправе считать, что, с точностью до малых второго порядка,

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	247
вихри будут отсутствовать, если на бесконечности поток был потен-
потенциальным. Будем же считать, что существует потенциал скоростей Ф:
B8.8)
причём
ф^ф^Ф',	B8.9)
где
Ф, =-»!*.
а ф' — бесконечно малая функция от х, у, z такая, что
дФ'	дФ'	дФ'
v' — ow • v' — " . ¦ р' — gw	(8 101
* дд:	у ду ' г dz	\ • /
Теперь уравнения B8.1) могут быть заменены одним уравнением
Бернулли B8.4) и уравнением B8.5), причём будет
&=^&j = const.
Уравнение Бернулли даст, если ограничиваться малыми первого по-
порядка:
"~1	"'.-I P'
2	' *,—1 "LyL
или вследствие B8.7) и B8.6):
^^4- — — о.	B8.11)
Вводя потенциал скоростей, напишем ещё
Wli*l + :?l = 0.	B8.12)
Уравнение B8.5) примет вид, если ограничиться малыми первого
порядка:
\ i i) дх	1 ду	1 &г	'
где a2i = xpl/pl или, если разделить на а^ и ввести Ф':
v2 \ дЧ' д2ф' сРф'
v\ \ дЧ дЧ дЧ
Прежде чем идти дальше, заметим, что линеаризация, которую
мы только что произвели, не будет точной в двух случаях: когда
^i^uj (околозвуковые течения) и когда •D1^>a1 (гиперзвуковые
случаи). В обоих случаях мы можем провести частичную линеариза-
линеаризацию. В первом случае мы можем построить уравнение, заменяющее

248	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
уравнение B8.13), следующим образом. Пусть для простоты v{ = av
Тогда обе эти величины равны а* и мы можем написать
где ~—, -~—, -J— малы по сравнению с а*. Запишем теперь
уравнение B8.5) в виде:
= 0 B8.15)
(это аналог уравнения A5.1)) и оставим лишь главные члены
в квадратных скобках. Именно, в первой скобке мы получим, пре-
пренебрегая cp2-f-'?2> 2(у.+ 1)ад^.; во второй и третьей квадратных
скобках оставим только 2а?, заменим в остальных членах ух на а*
и отбросим член, содержащий произведение трёх малых величин:
cpVcp' Мы получим вместо B8.13):
Заметим далее, что если О(у'\ = е, то порядок v' будет s*'».
Действительно, пусть порядок v' будет еа; сопоставляя 1-й и 2-й
члены уравнения B8.16), замечаем, что O(f'у) — О (-^—1 = е2, зна-
значит дифференцирование по у имеет порядок е2-"; но тогда по B8.14),
так как О (<р') = О (J^) = е, имеем О (г>у) = О (J^-} = ?3"я. Итак,
s3~a = е2, т. е. а = 3/2. Аналогичным путём докажем, что О Ы'Л = в8/!.
Но тогда О (tp'tp' )= О((р^ср^.г) = б3 и мы можем пренебречь двумя
последними членами уравнения B8.16). Получим окончательно вза-
взамен B8.13)
Во втором случае — в случае гиперзвуковых движений — мы по-
получим уравнения, совершенно аналогичные уравнениям B3.21) — B3.23)
плоского случая. Вывод их очевиден и мы на нём не останавливаемся.
Вернёмся к детальному исследованию случаев, описываемых
уравнением B8.13).
Решение нашей задачи сводится к определению функции Ф' из
линейного уравнения B8.13) с постоянными коэффициентами; при

s 2g]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	249
этом давление определится из уравнения B8.12). В качестве краевых
условий надо принять:
>	*№ + »') д 0	B8.18)
на обтекаемых твёрдых стенках, или
pl-{- р' = const.
на свободной поверхности.
Можно указать сразу же ряд замечательных частных решений
уравнения B8.13). Именно, если формально перейти от переменных
х, у, z к переменным х, у, z, так чго
* = *; у=|/ 1—^-У; * = |/ 1—-г*. B8.19)
го уравнение B8.13) перейдёт в уравнение Лапласа, и мы можем
в качестве решения взять, например, потенциал источника, находя-
находящегося в точке @, 0, 0):
const.
Ф' =
Возвращаясь к старым переменным, получим в качестве решения
уравнения B8.13):
Ф' =—-	const- ¦¦¦	B8.20)
У
V
Если v1<^av то приближённо B8.19) будет иметь тот же вид,
что и потенциал, в несжимаемой жидкости источника, помещённого
в точке @, 0, 0). Мы можем, таким образом, считать, что потенциал
вида
С, у, ) = VlX-[	==.	=
; - x'f + М - -1 ) [(у - у'J + (г - г'J]
представляет в сжимаемой жидкости результат наложения потока г»,,
параллельного оси х, на источник бесконечно малой интенсивности,
помещенный в точке (х', у', z'). Так как уравнение B8.13) линейно,
то сумма выражений вида
/-
B8.21)

250	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
для разных (х', у', г') и с будет также решением B8.13). Кроме
того, решениями будут функции, получающиеся путём дифференци-
дифференцирования правой части B8.21).
Потенциалы вида Фд мы можем теперь использовать для краевой
задачи газовой динамики. Пусть для конкретности речь идёт об
обтекании крыла конечного размаха, бесконечно тонкого и беско-
бесконечно мало отклонённого к оси х. Поместим во всех точках
М' (х', у', z') поверхности крыла источники с потенциалами Ф^
вида B8.21), считая, что с есть функция от х', у', z', а затем возьмём Ф'
в виде интеграла от Ф^, распространённого по поверхности крыла:
Ф'(х, у, z) =
= f f	c(M')d°	B8.22)
Г	( v^
Вид функции с останется определить из краевого условия B8.18),
которое, если ограничиться малыми первого порядка, может быть
записано в виде
дФ'
vxcos(n, x)-\—-5— = 0 на поверхности крыла B8.23)
(так как cos (я, х) —б. м., cos (я, у) — б. м., cos (я, z)= 1+6. м.),
и, таким образом, даст интегральное уравнение для с. Если vx < ах,
то подкоренное выражение в Фд положительно во всём пространстве,
и мы можем действительно распространить интеграл B8.22) на все
точки поверхности крыла. Качественно движение будет происходить
здесь так же, как в несжимаемой жидкости.
Принципиально иначе будет обстоять дело при vx > ах. Теперь Фд
будет иметь смысл лишь до тех пор, пока
(х — x'f> (-L- 1 )[{у — у'? + (z — z'?\.
\«i /
Это значит, во-первых, что если мы имеем единственный источник,
помещённый в точке М'(х', у', z'), то он будет поставлять потен-
потенциал Ф' лишь в точки М(х, у, z), расположенные внутри прямого
круглого конуса, вершина которого находится в М', ось параллельна
оси х, а котангенс половины угла раствора равен yi^/a*—1, ибо
уравнение такого конуса в пространстве (х, у, z) будет
Во-вторых, это значит, что если мы имеем ряд источников, поме-
помещённых в различных точках М' (х'> у', z'), то в какой-нибудь точке

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	251
М (х, у, z) пространства (х, у, z) будут проявляться лишь те источ-
источники М' (х', у', z'), которые попадут внутрь конуса
(*' - х? = (^—\\ [(у' - y?+(z' — z)\	B8.25)
вершина которого находится в М, ось параллельна оси х, а котан-
котангенс половины угла раствора равен yvya* — 1 . Но если это так, то
при вычислении потенциала Ф' в точке М'(х, у, z) мы должны, при
выполнении интегрирования B8.22), распространять интеграл лишь
на ту часть поверхности крыла, которая отсекается конусом B8.25)
и лежит внутри этого конуса.
Легко видеть, что угол раствора нашего конуса есть в точности
двойной угол Маха, отвечающий невозмущенному потоку: если
= a,/f1, то
/4->-/-}--¦-
У а\	У пп\
ctga,
Конусы B8.24) — это характеристики наших линеаризированных диф-
дифференциальных уравнений гиперболического типа.
Прежде чем переходить к конкретным случаям, отметим ещё, что
с точки зрения нашего первого приближения безразлично, интегри-
интегрировать ли в B8.22) по поверхности крыла, или же по площадке,
получающейся как проекция нашего крыла на плоскость (х, у).
Это происходит от того, что с само бесконечно мало и, заменяя
интегрирование B8.22) на интегрирование по бесконечно близкой
поверхности z' = 0, мы совершаем ошибку второго порядка ма-
малости. То же относится и к условию B8.23), каковое можно на-
написать при z' = 0.
Итак, чтобы найти потенциал Ф', вызываемый в точке М(х, у, z)
заданными источниками, расположенными на поверхности бесконечно
тонкого и бесконечно мало наклонённого крыла, бегущего со сверх-
сверхзвуковой скоростью, надо: 1) построить проекцию (F) крыла на
плоскость (х, у), 2) построить конус, вершина которого находится
в точке М, ось параллельна оси х, угол раствора равен 2ах, 3) рас-
рассчитать интеграл B8.22), распространяя его на ту часть площади (F),
назовем её (F'), которая находится внутри построенного конуса.
В качестве примера рассмотрим сперва уже разобранное нами
выше крыло бесконечного размаха. Пусть передняя кромка его совпа-
совпадает с осью у, а «глубина» его равна Т (рис. 96). Очевидно, что Ф'
не будет зависеть от у, и можно искать Ф', например, в точках
М (х, 0, z); естественно, далее, считать, что с также не зависит
ОТ у';

252	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
Тогда имеем (z' =¦ 0):
Ф' (х, 0. z)=f [ -^ШШМ^^
[ГЛ. I
B8.26)
где k2 = cXg2a.v
Желая выбрать (F'), мы должны рассмотреть отдельно три случая,
в зависимости от того, как расположена точка М. Конус характе-
характеристик, выходящий из М, всегда пересекает плоскость (х, у) по
гиперболе1), ибо плоскость (х, у)
параллельна оси конуса; однако
эта гипербола либо:
1)	целиком лежит вне полосы
0 < х < Т, z ~ 0,
занимаемой крылом (кривая / на
рис. 96), либо
2)	пересекает наше крыло так,
что вершина гиперболы лежит
внутри этой полосы (кривая //),
либо
3)	гипербола пересекает крыло,
но вершина её лежит вне нашей
полосы.
В первом случае крыло не попадает внутрь конуса вовсе, и мы
должны положить там
Ф' = 0.
Так как уравнение нашей ветви гиперболы будет
Рис. 96.
*' — *=— А У/2+ 22
(х' и у' — текущие координаты), то первый случай мы получим,
когда
x<k\z\, т. е. | -г| > tg-агдт,
результат, уже известный нам по плоской задаче.
Во втором случае мы должны принять за (F') сегмент, отсекае-
отсекаемый от нашей гиперболы отрезком АВ (рис. 96), т. е. написать
¦-7'
/
с(х')
dx'.
') Мы берём лишь ту ветвь гиперболы, которая уходи г на —со.

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	253
Выполняя интегрирование по у', получим:
х'=х-к\г\
Ф'= XJO С(Х ' \Т aKSm V(x-x')*~k*z2 >ky^-V<x-x')*-k*z>dX ~~
х-к\ г\
= ~ f c(x')dx'.	B8.27)
ft J
о
Наконец, в третьем случае имеем:
х'=Г
Ф'
Л = 1
'= / с(х')
дг'=О
х'=Г
— ~	с (х') dx' = const.
х'=0
Этот последний потенциал будет существовать везде, где
х — k\z\>7, т.е. \z\<tgal(x — T).
Краевое условие B8.23) позволит определить вид функции с (х')
в B8.27), если известен вид сечения нашего бесконечного крыла.
Так как в B8.27) входит |г|, то удобно отдельно произвести вы-
выкладки для верхней (z > 0) и для нижней (z < 0) части пространства.
Пусть уравнение верхней части крыла будет
Тогда по B8.23) должны написать
( х'=0	Jz=O
Итак,
Аналогично получим для ся(х'):
Итак, для z > 0:
Фв(х, 0, z) = — -^- Св (х — kz),
для z < 0:

254	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
По уравнению Бернулли мы получим при этом
Так, для пластинки бесконечного размаха, бегущей под углом "р
к плоскости (х, у), получим:
так что будет
что совпадает с первым приближением Аккерета (см. § 14). При
этом получится
В областях 1 и 3 мы имеем
В качестве второго примера рассмотрим уже изученный в § 27
случай обтекания снаряда, ось симметрии которого параллельна на
этот раз оси х. Предположим, чтобы можно было применить наш
метод линеаризации, что снаряд сильно вытянут, так что его мери-
меридиональное сечение имеет вид:
г = /?(*).
где R вместе с dRfdx — бесконечно малы (г — расстояние от оси х).
Здесь удобно воспользоваться уравнением B8.13), записанным в ци-
цилиндрических координатах:
2ЛдЧ' 1 дФ' дЧ' 1 дЧ'
ь2
Потенциал Ф', не зависящий от G (осевая симметрия) и удослетво-
ряющий этому уравнению, возьмём в виде
(источники расположены на оси снаряда).
Мы можем теперь написать потенциал Ф' в точке (х, г) мери-
меридиональной плоскости в виде
х' -x-kr
ф' =
У ( у 	 у'\2
,,=0	V (X	X) — ,

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	255
Вычисления с этим потенциалом удобно делать после замены пере-
переменных, перейдя от х' к и по формуле
кг
Тогда
х — х .
= ch и.
ы-0
Ф' = — J с (х — kr ch и) du	B8.29)
u = ar chx/kr
[ar ch a — In (a -(- yV—l)], и если предположить, что с @) = 0, то
г<^ = ^— = — / -з—с (х — krchinau —
х дх	J дх v	y
и =
х' =х-
-1
и = аг chx/kr
х' -x-kr
dx'
x'=o
u=0
= dx'.
v'r = -g— = / k ch и -5— с (х — kr ch и) du =
'J = ar chx/kr
dc (xr)
x'=0
Для определения с будем иметь интегральное уравнение
x'=x-kr
Зная с, можем найти р' по уравнению Бернулли, а затем и силу W,
действующую на снаряд. Последняя будет, очевидно,
х^Г
W = 1- f ( '\
J {P'r=,
где Г—длина снаряда.
Если обтекаемое тело есть конус, т. е.
dx> V(x-x')	J
B8.31)

256	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. Г
то можно считать, что
^-р- = vyK = const.
При этом уравнение B8.30) действительно удовлетворится, и надо
будет лишь найти К из условия
К=	tg2^° - ян — R2	B8.32)
Сопротивление такого конуса, рассчитанное по B8.31), деленное на
pjfj/2 и на площадь те tg2 р0Г2 основания конуса, будет
с j
V"l
В случае снаряда произвольной формы рассмотрим на линии его
меридионального сечения густой ряд точек О @, 0), Мх (х}, Rx), ...
..., MN(xN, RN). Равенство B8.30) должно быть справедливо для
любого х; запишем же его N раз, вставляя вместо х последова-
последовательно значения xv х2	xN. Буи ем теперь считать все дуги OMV
М1М2, ..., ^iN_lMN за отрезки прямых линий, т. е. представим
себе, что снаряд построен из отрезков конусов, имеющих каждый
свой угол раствора; тогда в пределах каждой из упомянутых дуг
величина dcjdx' будет сохранять постоянное значение (на дуге ОРАХ
это будет vxKv .... а на дуге MN_1MN будет vxKN). Теперь для
какой-нибудь точки хп, Rn мы можем написать вместо B8.30):
xa-xf
Л V{xn-xJ
f
n_]-kRn_] * \xn x )
что даст после выполнения квадратур и простых преобразований
(хо=/?о=О):
B8.33)

§28]
ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ
257
Придавая п последовательный ряд значений я=1, 2	N, мы
получим систему N линейных уравнений для определения N вели-
величин К1г К2, ..., KN. Заметим, что система наша такова, что в пер-
первое (при й=1) уравнение входит только Кх, во второе — только Кх
и К2, в й-е — Кх, K<i, .... К„. Таким образом мы можем сперва
найти Кх из уравнения первой степени {п = 1), затем вставить Кх
в уравнение при п — 2 и найти К2 из этого уравнения и т. д. После
того как Kt найдены, давление р'п в точке (хп, R\ найдётся в виде
-arch
. ),
«=1
а поделённое на PjfJ/2 и на площадь основания я/?^ сопротивле-
сопротивление Сх снаряда может быть вычислено по формуле B8.31):
B8.34)
— arch
хп — xi-\
Отметим, что наши формулы пригодны лишь до тех пор, пока
vja (а значит, и k) не слишком велико. Так, например, фор-
формула B8.32) теряет смысл, если, несмотря на малость C0, ktgfy0
будет близко к единице.
В качестве третьего
примера рассмотрим слу-
случай вытянутого симмет-
симметричного снаряда, поме- О*
щённого в поток со ско-
скоростью vv направление
которого составляет ма-
малый угол | рГ| с осью сим-
симметрии снаряда (рис. 97).
Разложим скорость
потока vl на две состав-
составляющие: « — параллель-
параллельную оси симметрии снаряда и w — перпендикулярную к этой оси;
тогда
причём и будет величиной конечной, a w — в силу малости угла $ —
бесконечно мало. Поместим начало координат по-прежнему в вершине
17 Теоретическая гидромеханика, ч, II
Рис. 97.

258	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
снаряда и направим ось х цилиндрической системы коорди-
координат г, 6, х вдоль оси симметрии (рис. 97). Будем теперь искать
потенциал Ф' в виде суммы трёх потенциалов Ф^, Ф'2 и Ф^:
?	B8.35)
из коих
ф[ = — wr cos 6 я&! v$r cos 6,
и представляет плоско-параллельный поток скорости (бесконечно
малой величины w), бегущий параллельно плоскости, проходящей
через направление 1>1 и через ось снаряда; Ф^ представляет уже
разобранный нами потенциал осесимметрического обтекания, полу-
получающегося от того, что снаряд помещён в поток скорости и (она же
приближённо равна V\), а Ф3 — не обладающий осевой симметрией
потенциал, получающийся из-за наличия, кроме скорости и, ещё
и боковой скорости w. В силу линейности задачи, такую суперпо-
суперпозицию трёх решений строить совершенно законно.
Чтобы найти Ф2 достаточно, как мы это уже и делали, отпра-
отправляться от обладающего осевой симметрией решения уравнения B8.28)
(a«i)i), т. е. искать Фг не зависящим от б. Чтобы найти Ф3, нам
надо обратиться к полному уравнению B8.28).
Феррари и Цзянь предлагают искать Ф3 в виде
г).	B8.36)
Тогда B8.28) даст
/ v\\d2F I dF d*F F
1-4 ттН	Г- + ТТ- — = °- B8-37)
Но теперь легко видеть, что в качестве F можно принять
F = ^~.	B8.38)
где Ф' — выражение вида B8.29). Действительно, продифференци-
продифференцировав по г уравнение
v\\d4 1дФ д_
получим
д2 дФ' 1 д дФ' д2 дФ' 1 <ЭФ'_
что совпадает с B8.37), если заменить дФ'/дг на F.

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	259
Используя подстановку, употреблённую в B8.29), мы можем
таким образом окончательно написать:
Ф3(х, г, 6) = ft cos 6 / с2(х — ftr ch и) ch и du =
и = ar ch x/kr
x' =x-kr
	 cos В Г	,	x — x'
—	^Г~ J C2(x >Y{3T—x'y~
dxr.
где c2(x') — функция, подлежащая определению.
Что же касается Фг(х, г), то его мы ищем по-прежнему в виде
г(х, /-) = — / сх(х — krchtt)du =
н
х' =х
= С
н = аг сЪх/кт
х' =х—кг
где сх (х') — функция, определяемая, как это уже было проделано
выше, из интегрального уравнения B8.30), где вместо с стоит сх.
Краевое условие задачи B8.18) напишется теперь так:
cos (п. *)^.(	?
при г — R (х) (уравнение контура снаряда). Но
cos(«, л:) = б. м.; cos (га, г)=1-|-б.м., cos(«, б) = 0,
так что, оставляя малые первого порядка, получим:
(дФ'Л	(дФ'
cos(n, x)^ + ^cos8+^Jr=i?+^
или, если разделить члены, содержащие б и свободные от 9:
, (дФ'	<
cos(ra, x)Vl + {w
Первое из этих уравнений даст
RmVl+\x 7 х-х
dx	U
dx	U=o V(x-x'Y-k*r* dx'
17*

260	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
что в точности совпадает с уравнением B8.30) уже решённой нами
задачи (надо только заменить с на Cj). Второе уравнение даст
(И = 0	ч
-Q-k I с2(х—kr ch и) ch и du I —
u = arch*/ftr	/r=R
g
f gcVada) =
x'=x-kr
dx' Пх-
Это интегральное уравнение и следует решить, чтобы найти с2
и, значит, Ф'г Избыток давления р' определится по уравнению Бор-
нулли [см. B8.12)]
дФ~ дФ'Л
(а=0
/ с[(х — kr ch и) du —
u=ar chx/kr
u=0	\
— 6 cos 9 J c'2(x — kr<±u)daudu\ — p\-{-cosbp'r B8.40)
I
u=ar chx/kr
\
Сила А, действующая на снаряд перпендикулярно оси х, будет
теперь
х=т e=ic
Л = 2 J J (/>;
8
J
*=0 8=0
Х=Т
д:=0
"=0	1
J c'2(x — krchu)chudu\	dx. B8.41)
)r=R(x),

§ 28]	ПРОСТРАНСТВЕННАЯ ЗАДАЧА. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ	261
Сила W, действующая вдоль оси х, будет:
х=0 9=0
х=0
= 2itp!«, / Л^| / «л; — krchu)du\ dx, B8.42)
т. е. имеет в точности тот же вид, что и для осевой симметрии.
Можно ещё подсчитать момент М относительно вершины О
снаряда:
= 2 J J (p; + p2cos6)r
Х=0 9=0
jr=T	/	u = 0	\
= — ftp^ic Г д;/?(д;)( Г c^chudu) dx. B8.43)
J
\u = ar chx/kr	^
Для конуса
R(x) = ig$ox; с'г = §-= const. =«, pL.
причём по B8.39)
?. = —	2	, где C = ——. B8.44)
k2 Cy^^T + ch!:	fttgp
По B8.41) мы получим для конуса силу А, делённую на pjt^/2 и на
площадь основания, в виде
— 1 +ar
B8.45)
Коэффициент момента См будет:
С,	У.	2 г -	4С/^=Л?	„ 4fi
л" ?~ тС'—ww=tt^>- <28-46)
Мы видим, что Сг и См оба пропорциональны углу |, который ось
симметрии конуса составляет с направлением скорости.
Для снаряда произвольной формы, как и в случае осевой сим-
симметрии, нанесём на поверхности снаряда ряд точек О@, 0),

262	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
/И, (xv RJ	MN (xN, RN) (xN — T) и будем считать, что дуги
OMV МХМ2, • • ¦ могут быть заменены отрезками прямых. Теперь
в пределах каждой из упомянутых дуг величины dc2ldx' будут
сохранять постоянные значения, и нам надо будет лишь найти N
неизвестных Lv L2, ..., LN из N раз написанного (для точек Мх,
М2, . .., MN соответственно) уравнения B8.39):
2 = 1
— ln> i-г V^n.i-i — 4' B8.47)
где
t , _ ХП — Xl + kRj , x 	 D __ Q
Определив Lv L2, . .., LN последовательно из N уравнений первой
степени B8.47) с одним неизвестным каждое, мы можем затем
написать р2 в точке Мп в виде:
_	п
так что Сг и См могут быть записаны в виде:
N
Как Cr, так и См пропорциональны углу р.
§ 29. Потенциал ускорения. Теорема Прандтля—Глауэрта.
Крыло конечного размаха в сверхзвуковом потоке. В предыдущем
параграфе отправным пунктом является проведение для получения
решения уравнения B8.13) операции вида B8.22) над потенциалом
вида B8.21). Однако функция с (Ж'), участвующая в этом методе,
не имеет наглядного аэродинамического смысла. Прандтль предлагает
подвергнуть B8.21), с целью получения решения, операциям, отлич-
отличным от B8.22); он отправляется при этом от понятия потенциала

3 29]	ПОТЕНЦИАЛ УСКОРЕНИЯ. ТЕОРЕМА ПРАНДТЛЯ - ГЛАУЭРТА	263
ускорения. Последний существует всегда, коль скоро существует
потенциал скорости, ибо тогда
и мы можем назвать величину
потенциалом ускорения.
При линеаризации, проводимой как в предыдущем пункте, полу-
получим (в стационарном случае):
причём по уравнению Бернулли B8.11):
,, = ?..	B9.2)
Уравнение B9.1) показывает, что ср удовлетворяет уравнению B8.13)
так же, как и Ф'. Если крыло обладает подъемной силой, то давле-
давления р'в в какой-либо верхней точке М' крыла и р'н— в нижней
точке с теми же координатами х, у будут различны. Это значит, что,
с принятой нами точностью, мы можем сказать, что р' терпит скачок
при переходе через горизонтальную площадку (F), на которую проек-
проектируется крыло. Но тогда по B9.2) ср терпит скачок при переходе
через (F). В несжимаемой жидкости ср удовлетворяло бы уравнению
Лапласа (так же как и Ф'), и мы могли бы искать ср в виде потен-
потенциала двойного слоя:
(П
,1 J 4по, dz r	* dz ,1 J 4лр, г
(F)	(F)
где срн и срв — значения ср в точках М' площадки (F), а
г = V (х - x'f + (у — уУ + (г — z'f.
В сжимаемой жидкости ср удовлетворяет уравнению B8.13), а его
решением, имеющим характер потенциала источника, будет, как мы
знаем, не l/r, a B8.21). Прандтль предлагает по аналогии с несжи-

264	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
маемой жидкостью, искать <р для сжимаемой жидкости в виде
9(х, у, *) =
4.Р, /
Так как разность р'а — р'в представляет подъёмную силу, отнесённую
к единице площади крыла, то удобно её обозначить, ориентируясь
на теорему Жуковского, так:
К — Р'в = ?№(*'. У)	B9.3)
и назвать f «циркуляцией». Тогда ср запишется в виде:
<?(х, у, z) =
_v{ д Г Г , ,,	dx' df
— fcWJ J Т(*-У)-у=	, v2
{П	]/ {х - х')* +(l—±) [(у - у у + ж»]
Зная ср, найдём Ф' путём квадратур по B9.1):
B9.4)
B9.5)
а скорости будем иметь в виде:
— со
X
— оэ	—со
B9.6)
Запишем ещё краевые условия задачи определения ср. На поверх-
поверхности крыла Vn = 0, т. е.
cos(re, x)vl + (v'z) = 0 на (F).	B9.7)
Это последнее уравнение и должно служить для определения цирку-
циркуляции 1 (х', у').
Для дозвуковых скоростей уравнение B9.4) позволяет сделать
одно важное заключение. Замена переменных
х, у = у. z =

§ 29)	ПОТЕНЦИАЛ УСКОРЕНИЯ ТЕОРЕМА ПРАНДТЛЯ — ГЛАУЭРТА	265
приведёт B9.4) к виду:
.	;	г», д Г Г	T(x\y')d?dy
ф(Х, V, Z) =	т1 -д— / / у	_i_L___=
но это в точности совпадает с потенциалом ср для жидкости несжи-
несжимаемой. Отсюда выводится следствие: подъёмная сила тонкого
крыла, помещенного в поток сжимаемой жидкости, имеющей на бес-
бесконечности скорость v, и плотность р., будет в ¦		 раз
У1 — (f]/a,J
больше подъёмной силы того же крыла, помещенного в поток
несжимаемой жидкости плотности р, и скорости vx на бесконечности.
Эта теорема была доказана Прандтлем и Глауэртом.
Обратимся к сверхзвуковым скоростям и напишем B9.4) в виде 1):
причем, как и прежде, будем считать
если (л; — д;'J<^2[(У — УJ-г-^2]. так чт<> площадь (F') будет
выбираться, как в предыдущем пункте.
Рассмотрим в качестве примера случай, когда крыло есть трапе-
трапециевидная пластинка, наклонённая под углом {5 к плоскости (л;, у);
пусть в проекции на плоскость (х, у) крыло даёт трапецию ABDC
(рис. 98), так что передняя кромка расположена по стороне АВ (она
лежит на оси у), и крыло имеет размах АВ = Ь, а ширину OE = t.
Пусть
Начало координат — в середине передней кромки.
Из точек А, В, С, D проведём конусы характеристик, т. е.
прямые круглые конусы с вершинами в этих точках, с осями, парал-
параллельными оси х, и с углами раствора 2ар где
sin а, =—-.
Линии пересечения этих конусов с плоскостью (х, у) изображены
на рис 982). Чтобы найти поля скоростей и давления, вызываемые
наличием этого крыла в некоторой точке М(х, у, z) пространства
') <р берется удвоенным против B6.3), чтобы сохранить за i смысл цир-
циркуляции (см ниже)
2) Предполагается, что «j > 89 > О,

266
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ I
(х, у, г), нам надо (аналогично тому, как мы это делали в преды-
предыдущем параграфе) при пользовании формулой B9.8) выбрать за
площадку (Ff) часть трапеции ABDC, попадающую внутрь конуса
характеристик, вершина которого находится в точке М. Ветвь гипер-
гиперболы, по которой этот последний конус пересекает плоскость (ху),
*¦/
Рис. 98.
будет в зависимости от расположения М отсекать разные части тра-
трапеции ABDC. Так, например, для точек М, расположенных «над»
плоскостью
Z = tg «j*
или «под» плоскостью
эта гипербола вовсе не встретит прямоугольника ABDC, и для этих
точек надо считать
Число всех возможных случаев равно здесь 15, в то время как для
крыла бесконечного разь;аха их было только 3 (см. предыдущий
параграф).
Метод Прандтля позволяет найти скорости и давления в любой
из этих областей. Мы остановимся подробно лишь на отыскании f
и на вычислении сил, действующих на наше крыло; для этого необ«
ходимо найти скорость v'z и давление р' в точках крыла. Если
вспомнить, что в краевое условие B9.7), служащее для нахождения -у,
входят только точки крыла, станет ясно, что из всех пятнадцати
областей нам достаточно теперь рассмотреть лишь те, пересечения

§ 29]	ПОТЕНЦИАЛ УСКОРЕНИЯ, ТЕОРЕМА ПРАНДТЛЯ - ГЛАУЭРТА	267
которых с плоскостью (х, у) не выходят за пределы трапеции ABDC,
Области эти, пересекающиеся с ABDC по площадкам: AFGB (обозна-
(обозначена цифрой 2), ACF (цифра 5) и BGD (цифра 4), назовём
областями //, ///, IV соответственно.
Начнём с области //. Область, отсекаемая от крыла нашей гипер-
гиперболой, будет здесь совершенно такая же, как если бы мы решили
задачу о крыле бесконечного размаха. Если бы речь шла о движе-
движении трапеции ABGF, то силы, на неё действующие, были бы поэтому
в точности те же, что и в случае крыла бесконечного размаха.
Желая подсчитать -у для области 2, мы можем заранее считать
его постоянным, и условие
«Lo=^	B9-9)
при постоянном y удовлетворится. Действительно, здесь будет (для
верха):
x'=x-kz y'=y+A
	 dy'dx'
,__м1 С f
2к dz J	J
vfl д x—kz	 Vif
~ т aF l ~~2~'
где A = -r Y(x — x'f — k2z2. Для области 1 (лежащей над пло-
ft
скостью z = xjk или под плоскостью z = — x/k) имеем просто
<р= 0.
Поэтому в выражении
нам достаточно распространить интегрирование от ? = kz (или от
? =— kz при z < 0) до ? = х. Итак:
так что

268	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
мы действительно можем удовлетворить B9.9), если положим1)
Т = —п?-	B9.11)
Обратимся к области IV (для области /// вычисление можно
будет провести по аналогии). Здесь мы имеем переменное ~[ = •]¦ (х', у'),
причём, так как возмущение, происходящее в углу GBD, обусло-
обусловлено наличием точки В, можно искать 7 как функцию от комбинации
т. е. считать -у одинаковым во всех точках одного луча, выходящего
из В, и меняющимся от луча к лучу. Можно считать, что f обра-
обращается в нуль на луче BD и обращается в fQ:
<29Л2>
на луче ВО. Но тогда в интеграле B9.8) удобно перейти к цилин-
цилиндрическим координатам z, r', 6' по формулам:
х' = г' cos 6'; у' — ~ b — г' sin в';
и для области IV получим:
С У. *) =	"
в'=тс/2 r'=ri
1 Г	Г
r'=o
< (х — г' cos G
7 (в
'J-й2|
')г'
.+rsinG
B9.
13)
') Мы видим, что -jf действительно похоже на циркуляцию, ибо
ft '
так что Сг будет
Cz~"" *„.„2 ~ ~ft~'
2
что отвечает формуле Аккерета.

§ 29]	ПОТЕНЦИАЛ УСКОРЕНИЯ. ТЕОРЕМА ПРАНДТЛЯ - ГЛАУЭРТА	269
Здесь rj — наименьшее из тех двух значений г1 и г2, которые обра-
обращают подкоренное выражение в формуле B9.13) в нуль. Эти зна-
значения суть
х cos 0' — к2 (у — -|А sin 8'
ri'2 =	cos* 6' — ?2sm20;	+
k у \х sin 8' — I'A — у) cos 8' 1* + г2 (cos2 6' — ft2 sin2 6')
--	>V-ft» sin» 6^	' B9Л4)
причём верхний знак отвечает случаю rv а нижний — случаю г2.
Для того чтобы выполнить дифференцирование по z в B9.13), удобно
перейти к новому переменному \ из соотношения
Мы получим сперва:
<flv(x, у, г) =
9
Теперь мы можем выполнить дифференцирование по z; используя
B9.14) и выполняя квадратуры по ?, получим:
у, z) =
г
Заметим, далее, что
вшб' —it — y\ cos G'T+22(cos26' — ft2 sin2 0')
B9.15)
_
\х sin 6' — {^ — у j cos 6' J + г-2 (cos2 6' — ft2 sin* 8')
(^2-^2)tg8'-x(|—у)
=		tfarctg		w ^
') Это преобразование было дано Фальковичем. Первое применение
теории Прандтля принадлежало Шлихтингу, но его рассуждения оказались
неточными. Дальнейший подсчет ведётся здесь по Фальковичу.

270
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Вставляя это выражение в B9.15) и производя интегрирование по
частям, получим:
;F')arctg-
*» (А _
6'=!t/2
{Х
2 _
Нам надо положить -j F0) = 0. Кроме того, во всём интервале от
S'^ctj до 6' = тс/2 мы должны принять -f == const. = To- Таким
образом мы получим:
<?JV(x, у, г) =
2%
v-2
- ft*** - ft* (д -
B9.16)
Чтобы найти f, нам достаточно теперь использовать краевое усло-
условие B9.9). Предварительно заметим, что согласно B9.6) мы должны
иметь:
^ 1-^.	B9.17)
Vi dz	K	>
дх
Но дифференцируя B9.9) по х, мы получим (р=const.)
г=0
и, значит, вследствие B9.17),
Таким образом, нам достаточно продифференцировать B9.16) по Z,
подставить 2 = 0 и приравнять полученное выражение нулю. Произ-
Производя эти несложные выкладки, получим после сокращения:
*tg6'— k —

§ 29]	ПОТЕНЦИАЛ УСКОРЕНИЯ. ТЕОРЕМА ПРАНДТЛЯ — ГЛАУЭРТА	271
Это однородное интегральное уравнение для определения
примет особенно простой вид, если ввести в качестве переменной
интегрирования величину
& = *tg9'	B9.18)
и обозначить
X x ' =-4-	B9.19)
Мы получим тогда
8 = 1
/ TIT^rf& = 0'	<29-2°)
где т' означает дифференцирование по аргументу &, а &0 = k ig 60.
Это уравнение имеет решение1)
с'		B9.21)
где сх — произвольная постоянная.
Производя интегрирование, получим:
Т (Щ = d arc sin 2ft TA + %o) + ga,	B9.22)
где c2 — новая постоянная интегрирования. Для определения с{ и с2
вспомним ещё раз, что
Тогда получим окончательно:
^+^^У	B9.23)
Зная 1, мы можем без труда подсчитать силы, действующие на наше
крыло. Подъёмная сила Z складывается из трёх частей: Z2 (в об-
области 2), Z3 и Z4 (ZS=Z4); при этом
Z2 = РЛТо X площадь АВОг = p<i)<tcf)t A	гг I,
в'=Я| Г'=</СОЗб'

272	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Если обозначить
— Г f(&)rf& = /C,	B9.24)
То *f
то
Если вспомнить определение B9.12) для т0. поделить Z на p,i^/2 и
на площадь t (b — ttg 90) крыла, получим для коэффициента Cz:
1 —A —/С)^
Сг = -|р	—-.	B9.25)
4
Остаётся только определить К. Вставляя B9.23) в B9.24), можно
написать по B9.18):
Т
±±=аъ.
1 — w0
9=90
Этот интеграл сразу же вычисляется и даёт:
К = ! ~ а° ¦	B9.26)
Таким образом, окончательно мы получаем Cz в виде:
B9.27)
Что же касается сопротивления X, то его можно рассчитать, как
интеграл, распространённый на всю площадь крыла от выраже-
выражения p^ifP. т. е. это будет:
так что
1 — A — /С) '
1б
Связь между Сх и Сг получится при этом в виде
t
/~>	1	Ь	->2
С^— 4tg«, l-(l-
где К по-прежнему даётся при помощи B9.16),

СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
273
Поляры, отвечающие 60 = 0 (прямоугольная пластинка) при зна-
значениях t/b = O; lj5 и У2 для г»1/а1 = 1,2; 2,0; 3,0, нанесены на рис. 99.
В этом и предыдущем параграфах мы рассмотрели лишь простей-
простейшие случаи решения линеаризованной задачи.
о
0,50	0,75
Рис. 99.
f,0 Cx f,25
В следующем параграфе мы изложим общий метод получения
решения для произвольного тонкого крыла.
§ 30. Сверхзвуковое обтекание тонкого крыла конечного
размаха произвольной формы в плане. Концевой эффект и вихре-
вихревая пелена. Обратимся теперь к общему случаю сверхзвукового
обтекания тонкого крыла с острыми кромками. Как и в предыдущих
параграфах, считаем крыло мало наклонённым к основному сверх-
сверхзвуковому потоку и рассматриваем линейную задачу. Исследование
этой задачи для случая произвольной формы крыла в плане дано
в работах Е. А. Красилыциковой, а также в работах К. И. Бабенко,
Уорда (Ward) и др. Дадим изложение, следуя Крэсилыциковой.
18 Теоретическая гидромеханика, ч. II

274
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Для простоты изложения остановимся на случае, когда угол
наклона касательной к контуру крыла меняется монотонно как для
передней, так и для задней кромки крыла (рис. 100). Пусть урав-
уравнение передней кромки крыла (снесённого на плоскость г==0)
будет x=W(y) (уравнение дуги BOD, рис. 100). Уравнение задней
кромки пусть имеет вид д; = W (у). Перемещаясь вдоль передней
кромки от 0 к В (или от 0 к D), мы будем встречать все значе-
значения
dy
от 0 до со, Пусть в точке А (С) окажется
О
— ctga,.
А'
Проведём касательные к передней кромке в точках А к С. Обо-
Обозначим через Е область плоскости (я, у), занятую крылом; обозна-
обозначим через Т область «вихревой пелены» сзади крыла, т. е. область,
ограниченную задней кромкой крыла и параллельными оси х полу-
полупрямыми, выходящими из точек В и D соответственно (см. рис. 100).
Обозначим ещё через R(Q) область «концевого эффекта» крыла,
т. е. часть плоскости, расположенную между касательными в точ-
точках Л и В (С и D) (рис. 100).
Так же как в § 28, ищем решение для потенциала Ф'(лг, у, z).
Представим его в виде:
= Г Г	c{x',y')dX'dy'
J J Y(x-x'f-^{(y-y'f
V '
причём интегрирование распространяется на ту часть плоскости (л;', у'),
для которой подкоренное выражение в C0.1) положительно (рис. 101).
Так же как и в § 28, нам придётся, таким образом, иметь дело
с областями, отсекаемыми ветвями гиперболы
{х — x'f — & (у — y'f =

§ 30]	СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА	275
как и в § 28, мы берём лишь ту ветвь гиперболы, для которой
Заметим теперь, что с(х', у') в C0.1) имеет простой гидро-
гидродинамический смысл:
C0.2)
Чтобы убедиться в этом, запишем сперва C0.1) в виде
Ф(х,у,г)-.
Т f
с (х\ у') dx' dy
ДГ'=-со
1 ¦./-,
у' -У--Г- У {x-x'p-k
C0.3)
и введём вместо у' независимую переменную 6 из равенства
/ = У — i V(x — x'f — ktz2 cos 6.
Так как
1 ,/•—¦
dy' — j у (х — x'f — k4i sin 9 rf8
и
(x — x'f — k2 [(y — у'J + 22] = sin2 9 [(x — *'J —
получим:
'тл с (x't y—lyix — x'y — kW cos 6
Ф'(х,у,г)= j j
6 = 0
C0.4)
18*

276
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. t
Дифференцируя C0.4) по параметру г и полагая затем z — Q, при-
придём к соотношению C0.2).
Можно отметить четыре характерных положения ветви гиперболы,
составляющей границу области интегрирования в выражении C0.1):
1)	ветвь гиперболы лежит целиком вне крыла (кривая I, рис. 102);
2)	ветвь гиперболы пересекает крыло, но так, что точки А и С
остаются вне области интегрирования (кривая 1); 3) ветвь гиперболы
пересекает крыло, и точка А (или С) находится внутри области
1
Рис. 102
интегрирования, но точка В (и D) находится вне области интегриро-
интегрирования (кривая III); 4) ветвь гиперболы расположена так, что А и В
(С и D) попадают внутрь области интегрирования.
В случае 1) точки области интегрирования потоком не возму-
возмущаются. Мы имеем здесь
Ф'(х, у, г)==0.
В случае 2) подынтегральная функция из C0.1) будет известна
всюду, и точки области интегрирования все лежат на крыле; если
уравнение поверхности крыла
г = С(*. у),
то по B8.23) и C0.2)
«С.Й —i??U.	C0.5)
В случае 3) область интегрирования будет частично выходить за
пределы крыла (часть плоскости между линией АА' и контуром
крыла); здесь принято говорить о влиянии «концевого эффекта».

§ 30]	СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛ\	277
Функция с (л;, у) будет и здесь определяться с помощью C0.2),
однако теперь с будет заранее неизвестна в тех точках области
интегрирования, которые лежат вне поверхности крыла. В случае 4)
область интегрирования заходит за пределы крыла ещё и в вихревую
пелену; здесь говорят о влиянии «вихревой системы за крылом».
Как и в 3), функция с будет заранее неизвестна в точках области
интегрирования, находящихся вне крыла.
Чтобы решить задачу в случаях влияния концевого эффекта и
вихревой системы, поставим краевые условия. Но прежде чем это
делать, обратимся к описанию формы поверхности крыла.
До сих пор мы не определяли вид поверхности крыла. Пред-
Предположим, что поверхность верхней (z > 0) части крыла представлена
уравнением
*	= CB(*, у),	C0.6)
а поверхность нижней части крыла имеет вид:
*	= СН(*, У).	C0.7)
Рассмотрим два типовых случая: а) случай крыла, симметричного по
отношению к плоскости г = 0; здесь Св(лг, у) = — Сн(лг, у) и
6) случай крыла нулевой толщины; здесь Св(*, у) — Сн (х, у). Легко
видеть, что общий случай может быть сведён к рассмотрению этих
типовых случаев. Действительно, пусть крыло задано уравнением C0.6)
и C0.7). Составим комбинации
Нх. У)=[С.(*. У)—Ся(*. у)]~; 7j = [Cb(a:, у) + С„(х, у)]1 C0.8)
и решим задачу обтекания, симметричного по отношению к пло-
плоскости г = 0 крыла с уравнением поверхности
*„ = ?(*, у), гя = ~-Цх,у),	C0.9)
а также задачу обтекания крыла нулевой толщины с уравнениями
поверхности
*в = Ч(*. У). *н = Ч(*. У)-	C0.10)
Так как Е-|-7):=Св, у\ — Е = СН и так как наша задача линейна, то,
складывая решения, отвечающие крыльям C0.9) и C0.10), мы полу-
получим решение, отвечающее задаче обтекания произвольного профиля
C0.6), C0.7).
Перейдём теперь к формулировке краевых условий задачи.
В случае крыла, симметричного относительно плоскости z = 0,
естественно считать, что скорости вдоль оси г антисимметричны по
отношению к плоскости 2 = 0. Тогда для всех точек плоскости
г = 0 вне поверхности крыла мы должны будем считать
о	<30и)

278
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Таким образом, в формуле C0.1) надо просто положить с = 0
во всех точках вне крыла и определить с по формуле C0.5) в точ-
точках, отсекаемых на крыле гиперболами типа III или IV.
Гораздо сложнее обстоит дело в случае профиля нулевой тол-
толщины. Здесь дФ'/dz будет симметрично относительно плоскости 2 = 0.
Поверхности R, Q, Т являются поверхностями разрыва функции Ф';
на этих поверхностях должны выполняться условия непрерывности
нормальной составляющей скорости и давления. Это означает, что
вне крыла, при переходе через плоскость 2 = 0, производные дФ'/dz
и дФг/дх по B8.12) будут непрерывны. Но так как теперь дФ /dz
симметрично относитель-
относительно плоскости 2 = 0, то
дФ'/дх должно быть анти-
антисимметрично, или, так
как дФ'/дх непрерывно
при переходе через пло-
плоскость 2=0, то мы
должны потребовать,
чтобы было
-дх~ = 0 при 2 = 0
C0.12)
на вихревой пелене Т,
а также в областях R
Рис. 103.	и Q. Заметим ещё, что
на линии АА' (СС)
(рис. 103) должно быть Ф' = 0, и тогда, по C0.12), во всей об-
области R (Q) будет Ф' = 0. Таким образом, в случае крыла нуле-
нулевой толщины мы должны решить следующую краевую задачу. Опре-
Определить Ф' так, чтобы было при 2 = 0
дФ' - К - ------ -	C0.13)
X
дг
дх
дх
¦' = 0
' = 0
в области Е,
в области
в области Т.
C0.14)
C0.15)
Покажем, как можно решить эту задачу.
Начнём со случая влияния одного концевого эффекта. Итак,
пусть положение гиперболы, отделяющей область интеграции в выра-
выражении C0.1), отвечает на рис. 102 кривой III. В области R функ-
функция с (х, у) неизвестна. Построим интегральное уравнение для её
определения. Для этого обратимся к той части области R, которая
расположена между характеристикой А А' (рис. 103) и характеристи-
характеристикой ВВ" (точка А — по-прежнему точка, в которой характеристика

§ 30]	СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА	279
касается контура, точка В— крайняя справа точка контура). Выразим
по формуле C0.1) потенциал скорости Ф' какой-либо точки N(x, у, 0)
этой области. По C0.14) этот потенциал равен нулю. Область
интегрирования разобьём на две части (как показано на рис. 103) —
область S(x, у) и а (х, у). Область 5 — это часть крыла, находя-
находящаяся внутри характеристического конуса с вершиной в N(x, у, 0).
В области S, согласно C0.2) и C0.13), функция задана. Область о —
часть области /?, находящаяся внутри нашего конуса. В этой об-
области с является неизвестной величиной. Таким образом, мы прихо-
приходим к интегральному уравнению
0= Г Г	с (л', у')	-dx'dyf-\-f(x. у). C0.16)
где f(x, у) — известная функция:
C0.17)
Интегральное уравнение C0.16) существенно упрощается и может
быть легко решено, если ввести вместо х а у характеристические
координаты xv у, из равенств:
хх = х~ х0 — k(y — у0); у^х — xo-\-k{y — y0);
Здесь х0, у0 — любые числа, например, координаты точки О, пересече-
пересечения характеристик, проходящих через А и С соответственно (рис. 103).
Так как по известному правилу
1, 1
— k, ft
то мы получим вместо C0.17):
=Fdx'1dy[=: — 2k f.	C0.19)
г г _ф;. уо
J J л/1\- j\t<.
В новых координатах переменные интегрирования в области а будут
меняться в пределах
0 <*;<•*„ Нхг)<У1<Уъ
где уг = tyj (x{) — уравнение в новых координатах боковой кромки
крыла — дуги АВ (рис. 104), в области 5 переменная д;' меняется

280	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
в тех же пределах, а переменная yj меняется в пределах
где у1 = >1{(х1) — уравнение передней кромки крыла — дуги С А.
О,
Рис. 104.
Таким образом, наше интегральное уравнение C0.19) будет
иметь вид
с(х[,у[)
—/ /
/ Jt) /(*-*',)(*-*)
= dy[dx'lt C0.20)
где
C0.21)
(известная величина). Решение уравнения C0.20) равносильно ре-
решению двух уравнений Абеля. Собирая оба интеграла из C0.20),
получим
/* 1 \ Г С{Х'\'У\) , Г ' a(x'v У?) , ,
•' Y^x 	х	Vy 	v'	i/"v 	 ' ^i I i
C0.22)
Это — уравнение Абеля с переменным пределом и с правой частью,
тожаественно равной нулю. Следовательно, квадратная скобка

i 30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
281
в C0.22) должна быть нулем при х'х = х и, таким образом,
У. . ,.	ФО*.) .	,ч
Ух — У1
C0.23,
Это вновь уравнение Абеля, но с правой частью.
Чтобы решить его, умножим сперва обе его части на l/yt —
и проинтегрируем по уг от уг — ф: (х^ до у1 = t. Получим
Или, меняя порядок интегрирования справа и слева:
t
ф|(^1)
= — f а(х.,у'л
dJl
Но
и мы придём к формуле:
t
\dy' C0.25)
arc sin I — 2
У1-У1
V	*-У1
Дифференцируя обе части этого равенства по t и заменяя затем t
на j>i. получим окончательно:
C0.26)

282
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Заметим, что по C0.26) скорости возмущённого потока v' обра-
обращаются в бесконечность при приближении к дуге АВ (к линии у^ —
= ф1(х1)) извне как 1/R, где R — расстояние от точки N(xlt yv 0)
до дуги.
Значение функции с в области Q найдётся аналогичным образом
заменой функций ф и фг на соответствующие функции, представляю-
представляющие форму кромки «левой сто-
стороны».
Зная с в области R, мы можем
найти теперь потенциал Ф' в любой
точке М, для которой область
интегрирования в C0.1) распро-
распространена на поверхность крыла
и область R (случай III, рис. 102);
пусть эта область интегрирова-
У, ния отсекается гиперболой Г
(рис. 105). Для нахождения по-
потенциала перейдём к координа-
координатам Xv Ур Zy
Xj = х — х0 — k (у — у0),
У: = х — х0 + k (у — у0),
zx = kz,
где х0, у0 — координаты точки О1
пересечения касательных, прохо-
проходящих через А и С (рис. 105).
В новых координатах C0.1) запишется в виде:
a(x'v У[)
2*1 ' ' —"
Рис. 105.
2k\s\s
[*у'Х C0.27)
Js
Область интегрирования разбита в этой формуле на три части
^0 + ^1 + ^2 (Рис- 10^)- Здесь S2 — часть области интегрирования,
расположенная в R; So — часть крыла, расположенная между гипер-
гиперболой Г и прямой, параллельной оси Kj и проходящей через точку Е
пересечения гиперболы Г с контуром крыла; Sl — остальная часть
крыла.
Пользуясь формулой C0.26), вычислим интеграл по площадке 52
в формуле C0.27). В пределах площадки S2 переменная х\ меняется
от 0 до хЕ, где хЕ—абсцисса упомянутой точки Е: 0-^х^-^хя;

§30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
так как уравнение ветви Г будет (х1 — х'Л(у1 — у[)~-2^
г2
у' ут, то у[ на площадке 52 лежит в пределах
283
:0, ИЛИ
х\ х\
Таким образом, мы можем написать по C0.26):
у,—
У=
c(x'vy[)dx[dy[
sa
—if f
О ф,'(дг,)
или, меняя интегрирование по у* и yj:
А) (У: -*)-
1 /*	/*	/7 I У
71 (/	,/
X
о
У| —
К х1 jr j
X
/
Внутренняя квадратура выполняется и даёт
Интеграл
fvu-am-MS,-* с помощью замены ^-)(р-^)'
= (у^ — At приводится к виду
со
2[	*L
J H L »y^2	 " /

284
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
и таким образом мы получаем
ХЕ ф, (х,)
ф,
--/ f
(г
dxx
C0.28)
о ф,"
Обращая внимание на пределы интегрирования в C0.28), заметим,
что последнее распространяется на площадку S^ По C0.27) можем
теперь написать:
__L Г Г
~2k .1 J
r (*i--«i) (У1-У1) -
__± Г Г а{х>1'у
' 2k J J уг -г:
5, Г К.Х X )
Но тогда интегралы по площадке
нимает вид:
сокращаются так, что Ф' при-
приC0.29)
Мы получили, таким образом, интересный результат: для вычисле-
вычисления Ф' приходится интегрировать по поверхности крыла, причём
только по той его части, которая находится между гиперболой Г
и прямой, параллельной
характеристике и выходя-
выходящей из точки Е пересечения
гиперболы Г с контуром
крыла (заштрихована на
рис. 105).
В рассматривавшемся
нами случае, отвечающем
рис. 105, приходилось
учитывать концевой эффект
только одного края крыла
(АЕ). На рис. 106 пред-
представлен такой случай пере-
пересечения гиперболы Г с пло-
плоскостью крыла, при котором
приходится учитывать кон-
концевой эффект обоих краев.
Повторяя рассуждения, при-
приведённые выше, убедимся, что достаточно будет распространить инте-
интегрирование на площадь 501-|-502 (заштрихована), причём интеграл,
распространённый на область S02, надо взять с обратным знаком.
Простота этого случая заключается в том, что части R(Q), кото-
которые здесь приходится рассматривать (области 5г, 5г), находятся
Рис

г 30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
285
X,
У,
каждая под влиянием концевого эффекта лишь своего края: влияние
«левого» концевого эффекта не распространяется на область S2,
влияние «правого» края крыла не распространяется на S2. В общем
случае может оказаться так, что для некоторых точек поверхности
крыла и области R(Q) будут интерферировать влияния обоих концов.
Это может произойти в случае, когда крыло мало распространено
вдоль оси Y и вытянуто вдоль оси X. Такое
крыло называется крылом «малого удлинения»
(рис. 107).
Пусть Ах (Cj) точки контура крыла, в кото-
которых касательные к контуру параллельны ха-
характеристикам. Введем, как и прежде, систему
осей Xv Kj (аналогично случаю, изображённому
на рис. 105). Через точку Л, проведём харак-
характеристику (параллельную оси Хх) до пересече-
пересечения с контуром в точке С2. Из точки Сх прове-
проведём характеристику (прямую, параллельную
оси Kj) до пересечения с контуром в точке А2.
Из точки А2 проведём характеристику до пере-
пересечения с левой частью контура (С3); из
точки С2 проведём прямую до пересечения с пра-
правой частью крыла в Л3 и т. д. Полоски об-
области R (Q), лежащие между проведёнными
характеристиками, обозначим через °i(°i),
°2(°'2\ ••• (см. рис. 107). Пусть ещё уравнение
правой концевой кромки крыла (линия АХА2 ...В)
записывается как и прежде в виде уг = фх (хх),
а уравнение левой концевой кромки (линия
СгС2 ... D) имеет вид уг = ф2(Xj). Запишем	рИс. 107.
теперь условие, что потенциал Ф' в любой
точке N(xv yj) полоски ak равен нулю. Аналогично тому, как это
имело место в случае рис. 104, мы получим вновь уравнение Абеля
типа C0.20), откуда последует равенство типа C0.21). Это будет
Ум-У i
4-Х
k-1
=0. C0.30)

286
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Здесь ck = —
в точках полоски ak, yk— ордината точки
k
пересечения через точку y=\/N и прямой, параллельной оси хх и
проходящей через точку ck_v Что же касается до функций с|(х1( ух),
c'2(xv уЛ	c'k_l(xv у:), то это значения величин —1/пд<?'/дг
в полосках о|, а'2, .. ., а'к_г соответственно (член, содержащий 2,
появляется только при k^-Ъ).
Если известны с[, с'у .... c'k_v то функция ск найдётся путём
решения уравнения Абеля C0.30). Совершенно так же, как и в слу-
случае C0.21), мы получим
ск(х
м-
1 \ 1
I
xn) ,
C0.31)
другой стороны, можем написать аналогичную формулу для
)	б	М(	)
'к(хм,
р
уж), где хм и ум — координаты любой точки М(х
м,
)	)
области о'к. Именно, если записать уравнение правой концевой кромки
в виде, решённом относительно xl : •^i=:Xi(yi)> а левой — xl = )
то мы будем иметь:
I
VxM-x[
[-dx[+
1 \ /I
/
k-i(x
i=k-2 t-
,
F
dx[
C0.32)
Формулы C0.31), C0.32) позволят последовательно определить все
функции с?, с\. В самом деле, функции су с\ уже определены выще
(формулы типа C0.26)). Зная cv c'v
значения с2 и с'2 и т. д.
найдём по C0.31) и C0.32)
На деталях расчёта мы не будем останавливаться. Перейдём
теперь к рассмотрению влияния вихревой системы за крылом (рис. 102,

§ 30]	СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА	287
гипербола IV). Будем отправляться вновь от основной формулы потен-
потенциала (ЗОЛ). Вновь введём характеристические координаты xv yv
Влияние вихревой системы за крылом будет распространяться на
точки области Т (рис. 105), а также на точки области R(Q), рас-
расположенные внутри конуса характеристик, выходящего из точки B(D).
В области Т должно выполняться условие C0.15), которое в пере-
переменных xv уг имеет вид:
|^+^ = 0.	C0.33,
Во всех точках области R выполняется условие C0.14): ср'==О.
Следовательно, и в этих точках будет выполняться условие C0.33).
Потенциал ср' в точках N интересующей нас области имеет вид
{f	<3034)
причём интегрирование распространяется на три площадки: 1) пло-
площадку SQ -f- S[, отсекаемую на крыле характеристикой, проходящей
через N параллельно оси Уг (рис. 108), 2) площадку S2 — полоску
области R (вне крыла), расположенную между Yl и линией, парал-
параллельной Kj и проходящей через точку В, 3) площадку о — область
вне крыла, лежащую внутри конусов характеристик с вершинами
в точках В а N.
Заметим теперь, что значение с на поверхности крыла нам из-
известно; мы обозначили его через а(хг, у,). Значение с в области 52
мы уже умеем находить (формула C0.26)), причём мы знаем, что
интеграл C0.34), взятый по области S2, должен сократиться в силу
C0.28) с интегралом, взятым по части S1 (рис. 108) крыла, отсекае-
отсекаемой продолжением характеристики, проходящей через В параллельно
оси Yv В области о функция неизвестна.
Для определения с области з воспользуемся условием C0.33).
Прежде чем начать производить выкладки, связанные с дифферен-
дифференцированием под знаком интеграла, поставим условие непрерывности
функции с на задней кромке крыла (линия bWD), т. е. поставим
условие
c(xv f («,))== о (jclt «|/(*,)),	C0.35)
где у1 = ф'(лг1) —уравнение задней кромки. Это требование анало-
аналогично условию Жуковского для обтекания крыла несжимаемой
жидкостью.

28В
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Если уравнение передней части кромки (дуга АА'С) будет yt
= ф(х1), то мы можем записать C0.33) в виде:
c(xvy1)dy1dx1

/ \ " '"
Jfi	У,
Г Г с{хуУ1) У\*х\ _0> C0зб)
ду,
где хв—абсцисса точки В (рис. 108). Прежде чем дифференцировать,
С.
преобразуем наши интегралы путём интегрирования по частям.
Именно, интегрируя по х'у получим
"' c(x\,y\)dy\dx[ _
/ /
хв Ф|
Г cj^y^dy
— 2 |/ *i ^в /
4(^в)
' с(а:в, у;)^;
—У\
rf<-
-2 f У7?=**®-РЩ«-
/	dxx V *- + (*!)

§ 301
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
289
Аналогично условию C0.35) примем ещё непрерывность с при пере-
переходе через линию А'В (рис. 108). Тогда первый интеграл правой
части равенства C0.37) будет равен нулю (см. C0.23)), и мы полу-
получим, дифференцируя обе части C0.37) по параметру хх:
с{х', y')dy[ dx\
д Г Г с(х', у )dyxdxx	Г Г
-dx-,.1 J уШ^х'Ж-у'^и
f
[. C0.38)
Второй интеграл в правой части C0.38) берётся вдоль линии А'С
передней части кромки крыла.
Запишем ещё раз наш интеграл, выполняя на этот раз частное
интегрирование по у'у
II,
хв ф(*;
c(xl,yl)dy1dx1
1
хх—хх
1Л1
2 /v4-H*;)-^dy;W C0-39)
v '/	J
Дифференцируя C0.39) по параметру у,, получим:
ду
т/f
<ь Ух)
a{s/ У{Х1-Х1){У1-УХ
dc
¦dx\dy[ +
dx'i
19 Теоретическая гидромеханика, ч. II

290
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Складывая C0.38) и C0.40) и заменяя с(х', yf) там, где оно из-
известно, на а(х', у'), придём по C0.36) к соотношению:
dy[ dx\ =
да(х[,у[) да(х[,у[)'
дх.
¦л \
~ J ТА
dx.
\dy[dx[~
C0-41)
Второй интеграл справа следует брать вдоль линии дуги СА' (ее
уравнение: у1 = ^{х1)) передней части контура крыла. Дважды решая
уравнение Абеля C0.41), мы сможем найти ^	(- л—> после чего,
решая уравнение первого порядка в частных производных, найдём
c(xv yj.
Собирая в C0.41) интегрирование по у'( и приравнивая подынте-
подынтегральное выражение нулю (см. наши рассуждения для уравнения
C0.22)), сразу же решим одно уравнение Абеля и получим:
C0-42)
Это уравнение легко решается (см. аналогичное уравнение C0.23)
и его решение с помощью формул C0.24) и далее). Мы придём
к равенству:
?
дс . дс 	 1
дх, д\,	к
— + ¦
. C0.43)

30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
291
Уравнение C0.43) проинтегрируем вдоль прямой, параллельной набе-
набегающему потоку. При этом удобнее перейти к переменным ?, т) из
равенств
так что
дс
де
дс
¦ = -^-, а линия
= const, представляет линию
по C0.18), линию у = const., являющуюся
х 	У\ = const., т. е.,
прямой, параллельной основному потоку.
Нам остаётся выполнить одну квадратуру по \ (заменив в пра-
правых частях C0.43) переменную хх на \, ух— на \ — tj). Если точка
N(xlt у{), для которой ведётся расчёт, находится в полосе Т, то
интегрировать по \ надо будет от \ до \, где \ найдётся из уравне-
ния \—^' (|) = jtj — ух (точка контура находится на пересечении
с прямой ^ = *1 — У\, выходя-
выходящей из N).
Таким образом, функция
c(xv y{) будет определена внутри
вихревой полосы Т.
Остановимся ещё на определе-
определении давления р (х,
верхности
По B8.
р'
крыла.
12)
У.
дФ'
~дх
0)
на
C0
по-
.44)
х,
/
/
/
/
В случае крыла, симметричного
относительно плоскости z = 0,
функция дФ'/дх будет антисим-
антисимметрична (см. стр. 278) и мы
можем написать, например:
А'
Рис. 109.
Таким образом, как для определения давления, так и для определе-
определения разности давлений достаточно будет уметь определить производ-
производную дФ'/дх на поверхности крыла (иначе говоря —определить потен-
потенциальное ускорение <f~v1d<&'ldx; см. предыдущий параграф).
Остановимся на этом подробнее.
Рассмотрим конкретный, но достаточно общий случай, отвечающий
рис. 109. Пусть передняя кромка АС крыла имеет в характеристи-
характеристических координатах уравнение y1 = l|,(Xi)i a в решенном относи-
относительно хх виде х1=х(У\У, пусть концевая кромка крыла задана
в виде уг = фп (хг) (дуга А В), или хг = Хп (У1) и ^ = ^л{хх) (дуга CD),
19*

292
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ 1
или *! —Хл^); задняя кромка дана в виде yt = y (х^), или хх =
= yf(yx). Найдем давление потока на поверхность крыла.
Пусть характеристики, выходящие из точек Л и С, пересекаются
между собой на крыле в точке Е (рис. 109) и пересекают заднюю
кромку крыла в точках А' и С соответственно.
Пусть ещё характеристики, выходящие из В и D, пересекаются
между собой на поверхности крыла в точке Е' и встречают кромку
крыла в точках В' и D'
соответственно.
Всю поверхность крыла
естественно разбить на 9 об-
областей (см. рис. 109). В об-
области / концевой эффект не
сказывается. В области 2 C)
сказывается концевой эф-
эффект правой (левой) части,
но не сказывается концевой
эффект левой (правой)
кромки; в области 4 сказы-
сказываются оба концевых эф-
эффекта; в области 5 F) ска-
сказывается влияние вихревой
пелены, сбегающей с правой
(левой) части крыла. В области 7 (8) сказывается эффект вихревой
пелены, сбегающей с правой (левой) части кромки и еще концевой эф-
эффект, отвечающий левой (правой) кромке. Наконец, в области 9 сказы-
сказываются вихревые полосы, сбегающие как с правой, так и с левой стороны.
В дальнейшем будем пользоваться следующими обозначениями.
a(xv У1)—	д—	[д^-Гд^I
Рис
d(x'v yj; xv Ух)=у	»,=тт I ^
В характеристических координатах
<Ji
'+¦
ду\
Обратимся к области / (рис. ПО). Здесь имеем по C0.29):
¦*¦¦ у.
)'— 1 f f h( ' '¦	' '
C0.45)
C0.46)
C0.47)

§ 30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
293
Выполним здесь частное интегрирование по х'х и продифференцируем
полученное выражение по хх (при этом мы воспользуемся преобра-
преобразованием на стр. 278 и далее); выполним затем частное интегриро-
интегрирование по у[ и продифференцируем результат по yv Складывая оба
выражения, получим для области 1
So
x'\ C0-48)
где /,— дуга М'М" передней кромки крыла (при интегрировании
перемещаемся от М' к М").
В области 2 (рис. 111) отправляемся от выражения C0.29):
ф:=тгг
У\
C0.49)
Выполняем дифференцирование аналогично тому, как это было сде-
сделано выше'). Мы получим для области 2:
So
>) При дифференцировании по yL удобно будет начать с дифференци-
дифференцирования по нижнему пределу.
1 д
дФ2 1 д г	1
"ау7 ~~ ~2k ay, •/. г/";, _ ;_
Хп(У,)
2k
¦I VZ Т
Хп(
dx.

294
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
где 50 — заштрихованная на рис. 111 площадь, L — дуга М"Мт
передней части контура, ?,— прямая линия М"Мг (направление
интегрирования по L и Lx указано стрелками).
Рис, Ш.
Рис. 112.
Совершенно аналогично для области 3 получим:
ffd(xv y'v *v Уда<аУ[ +
f 4x'v ЬЫ* xv y^'
C0.51)
где площадь So, дуга L и прямая L2 даны на рис. 112.
при этом для вычисления квадратной скобки удобно записать
У.
_д_ Г a(Xvy\)dy\ =
— 2

I 30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
295
В области 4 при вычислении Ф' нам придётся вести интегриро-
интегрирование по двум площадкам (см. рис. 113): S0l и 502 или же по одной
Рис. 113.
Рис. 114.
площадке So (рис. 114) в зависимости от того, пересекаются ли
характеристики MfMiV и М"'М'" на крыле или вне крыла.
В первом случае будет
Ф4= / {b(x'v »i> xv y,)dx[dy[-$ §b(x'v y'{, xv yl)dx\dy[
Sol	S02
и тогда, после преобразований, аналогичных тем, что были сделаны
выше, мы получим
/
о
f fd(x'i- -Vi; *i'
J
+1 —
Ux^ xv
C0.52)
где L есть дуга М'"М™, Lx — прямая M1VM', L2 — прямая М'"М";
направление интегрирования указано на рисунке.

29S
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
В случае, изображенном на рис. 114, имеем:
d(x'v y'v *v Ух)ах'М
Li
где Z.j, L2, L изображены на рис. 114.
Распределение для области 5 (аналогично лля 6) вычисляется проще.
Для случая 5 интегрирование для Ф' мы должны распространить на
область So-j- Sj -f- S2 (S2 находится вне крыла в области R), или же,
Рис. 115.
Рис. 116.
по аналогии с C0.28), на область So (рис. 115). Здесь вновь мы по-
получим простую формулу, аналогичную формуле, отвечающей области /:
']' C°-54)
где L — дуга М2М3 (рис. 115).
Аналогичным образом для области 6 имеем:
(W —n'v — ii-L / d(x',, у',; х„ yAdx'.dy
I- s.
[см. рис. 116).

30]
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
297
Для областей 7 и 8 получим, комбинируя наши соотношения:
-^пг! Г fd(x'v * хг *№№-
1 So
- / f' d(x[, y[; xv yi)dx[dy[-
-fb{x'v Hx[); xv yJl -!^Шах\ +
L	1 J
(см. рис. 117; линия L — это дуга Ж4/И3; линия L2 — прямая Ж4/И2),
- J J d{x\, y'{, x
Si
(площадки So и Sv линии L и L, даны на рис. 118).
чЯ
Рис. 117.
Рис. 118.
Мы не останавливаемся отдельно на случае, когда точка пере-
пересечения МхМц и М2М3 находится вне крыла.

298
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
Наконец, в области 9, где сказывается влияние вихревой пелены,
сбегающей с обеих задних кромок, имеем (см. рис. 119)
[ fd(x'v
s,
ffd(x[.
'i\- C0-58>
В заключение заметим, что для вычисления подъёмной силы или
момента, действующего на крыло, не обязательно вычислять пред-
предварительно р'к—р'в; так как //—p'B=2p]v1-^—, то для вычисления,
например, подъёмной силы Р
имеем
P=2PlvlJ J ^r
\
\
в
н
У,
или,
по х'\
Я =
выполняя
ув
УО
интегрирование
{X{y'),y')dyr,
C0.59)
где х = X (у) — уравнение задней
кромки крыла (в старых коорди-
координатах), решённое относительно х,
У в и Уо — ординаты точек В и D
соответственно, а интегрирование
Рис. 119.	распространяется на линию задней
кромки.
Переходя к примерам применения формул этого параграфа,
отметим ряд упрощений, которые будут иметь место в отдельных
случаях.
1.	Если концевые кромки АВ и CD суть прямые, параллельные
набегающему потоку, то в формулах C0.52), C0.53) d^Jdx1 и
dXn/dy\ будут тождественно равны единице и последние два члена
в правых частях пропадут.
и —•
2.	Если поверхность крыла плоская, т. е. а =	;гр— const.
(р — угол атаки крыла), то
d(x'v y[; ху ^) = 0	C0.60)

i 30)
СВЕРХЗВУКОВОЕ ОБТЕКАНИЕ ТОНКОГО КРЫЛА
299
и тогда поверхностные интегралы всюду пропадают, остаются только
контурные интегралы и интегралы, распространённые на прямо-
прямолинейные отрезки Lv L2.
Равенство C0.60) будет также иметь место, когда поверхность
крыла есть линейчатая поверхность, с образующими, лежащими
в плоскостях, параллельных плоскости XZ (в старых координатах).
3. Если выполняется C0.60) и, кроме того, концевые кромки
являются прямыми, параллельными основному потоку, разность
давлений представляется в любой области в виде:
k
(знак плюс надо брать, если прямые М'МУ* и М"М'" пересекаются
на крыле, и знак минус в противоположном случае).
4. Если форма крыла такова, что /очка А совпадает с В, а точка С сов-
совпадает с D, то будут отсутст-
отсутствовать области 2, 3, 4, 7, 8.
Это, в частности, будет
иметь место для случая
трапецевидного крыла, рас-
рассмотренного нами в преды-
предыдущем параграфе.
В качестве примера рас-
рассмотрим вновь случай тра-
трапецевидного крыла, накло-
наклонённого под углом р к пло- '
скости X, Y, размаха b и
ширины t (рис, 120). В этом	Рис 120
случае концевые кромки вы-
вырождаются в точки, а задняя кромка состоит из трех частей: пря-
прямой, параллельной передней кромке (находящейся на расстоянии f),
и двух прямых, расположенных под углами ± 80 к направлению
основного потока. Считаем, что 80<а1.
Уравнение передней кромки имеет вид:
х\ + У1 = kb
(в характеристических координатах); это значит, что
Уравнение задней кромки даётся в трёх видах:
У — -о Ь — tg еолг или у, = т-
1 = / или
= xt -\- 2kt 23
или Л = ¦
*,-А* в^
C0.61)
C0.62)

300	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
Существуют лишь области типа 1, 5 н 6 (рис. 120). Всюду
а =	—р. Так как по C0.61) имеем -^iiA==—1, то по C0.48)
dxx
имеем
?
где хм, хм — абсЦИссы (в характеристических координатах) точек
Мх и М2 соответственно (рис. 120). Ясно, что л: == kb— ур xM = xv
Так как
2х, 4- у, — х, ¦— kb
arcsin-1 ' ' , C0.63)
Г
мы получим
что совпадает с равенствами B9.12), B9.3).
Для области 5 получим по C0.54) (см. рис. 120)
хм
^ 5	1
вM
причём ^^ !_^|б! (У1~~^> JfAf.==j:1 (абсцисса точки Ж4
будет та же, что и абсцисса точки Ж3; последняя находится на пря-
прямой C0.62) и имеет, так же как и М, ординату у^. По C0.63) мы
получим теперь
fa |2
¦
arcsin
или, если вернуться к обычным координатам х, у (по формулам
xl=x-\—2	ky, ух = х-\—2—\-kyj, ввести 6', как и в § 29,
то из равенства -~ — х = у tg б' найдём
агс cos
что находится в полном согласии с B9.23).

i 31]
СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	301
§ 31. Сверхзвуковые конические течения. Некоторые точные
(нелинейные) решения. Обтекание прямого круглого конуса так же,
как и обтекание края плоского прямоугольного крыла, являются
частными случаями более общей задачи обтекания произвольного кони-
конического тела. Представим себе, что тело конической формы с вер-
вершиной в начале координат и с произвольной направляющей обте-
обтекается сверхзвуковым потоком сжимаемой жидкости. Пусть ещё наше
тело расположено по отношению к потоку таким образом и имеет та-
такую форму, что скорость обтекания получится в виде:
Vx = V'x' VV = V'r Vz = Vl + <-
где v', v', v'z малы по сравнению с vv и их квадратами можно
пренебречь, аналогично тому, как это было сделано в предыдущих
параграфах. Задача о таких движениях была исследована Буземаном *).
Как и прежде, мы можем написать для потенциала скорости:
д*Ф' , д2Ф' /..2 ,ч д*Ф'
(где M1=^i/fli) и совершенно такие же уравнения для v', v', v'\
х у z
в частности,
;
дх2 ~ дуг v ' ' дг2 —	( '
Простота решения задачи в случае, когда обтекаемое тело	имеет
коническую форму, заключается в том, что здесь все решения	будут
зависеть от
. 		X		 У
а не от л:, у, z. Компоненты скорости возмущения v', v', v'	вдоль
каждого луча, выходящего из О, будут постоянными, меняясь
от луча к лучу.
Вводя в качестве переменных 5. -ц и z = z н считая, что v' не
зависит от z, придём, после совершенно элементарных преобразо-
преобразований, к уравнению
	 ^ dvT	dv
где, как и прежде,
г+^)- C1-3)
k =
• = ctg a,.
C1.4)
0 В u s e m a n n A., Infinlteslmale kegelige Ueberschallstromung. Schriftea
Deut. Akad. d. Luftfahrtforschung, 1943.

302
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
Плоскости (?, rj) можно дать простой геометрический смысл: это —
плоскость, параллельная плоскости (х, у) и находящаяся на рас-
расстоянии 2=1 от последней [2=1 в C1.2)].
Нетрудно убедиться в том, что уравнение C1.3) будет смешан-
смешанного типа: в одной части плоскости ($, rj) эллиптического, в дру-
другой— гиперболического. В самом деле, вдоль характеристик, если
искать уравнения последних в форме ч\ — "ц (|), будет:
— ет ±
1
Значит, внутри круга радиуса l/k наше уравнение C1.3) будет
эллиптического типа; напротив, при ^2-f-^2 > l/k2— вне круга ра-
радиуса l/k— будут существовать действительные характеристики.
Последние представляются в виде всевозможных прямых линий,
касательных к кругу радиуса l/k1). На рис. 121 даны некоторые
из этих характеристик (одно се-
семейство сплошными линиями, дру-
другое— пунктиром). Окружность ра-
радиуса l/k в плоскости ($, т;) является,
вследствие C1.4), местом пересече-
пересечения с плоскостью 2=1 конуса ха-
характеристик в пространстве (л:, у, z).
Обтекаемое тело пересечёт плоскость
(I, ij) по некоторой кривой, которая
может лежать или целиком внутри
круга радиуса \jk или целиком вне
этого круга, или, наконец, частично
внутри, частично вне круга. Написав
краевые условия, мы должны при-
приступить к решению C1.3).
Путём геометрических преобра-
преобразований переменных, заимствован-
заимствованных из одной работы Чаплыгина, Буземан приводит C1.3) к двумер-
двумерному уравнению Лапласа2). Это сведение к уравнению Лапласа можно
Рис. 121.
') Проще всего убедиться в этом, если перейти в (?, ij) к полярным
координатам г, <р. Уравнение C1.5) после интеграции примет тогда вид:
Г COS (<(> — <(>„):= 1/А,
где ф0 — постоянная интегрирования.
*) Значительно раньше, чем это было сделано Буземаном, решение
рассматриваемого здесь типа было получено, в связи с другой физической
задачей, в работе С. Л. Соболева и В. И. Смирнова. См., например, допол-
дополнения С. Л. Соболева в книге Франк Р. и Мизес Р., Дифференциальные и
интегральные уравнения математической физики, ч. II, ОНТИ, 1937.

§ 31]	СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	303
проделать и другим пут&м. Мы остановимся на выведе, данном в ра-
работе Гуревича'). Чтобы это сделать, удобно вернуться к уравнению
в форме C1.1) и перейти сперва формально к переменным х, у, z:
Мы получим в переменных х, у, z трёхмерное уравнение Лапласа,
и, если ввести «сферические координаты» г, о, ft из равенств
х = г cos о sin ft, у = г sin о sin Ь, z = r cos ft,
то можно написать:
Вспомним теперь, что v'z зависит лишь от \ и % это значит, что
в переменных г, о, ft, v'z не зависит от г: v'z=v'z(a, ft). Тогда будет
<?Ч	д I dv',
"г
1h*~
Мы легко избавимся от мнимости	преобразования, положив ft = /9
Итак, если
f	 cos a th 8		 sin а th 8	.о, с-.
k	к
то C1.3) примет вид:
сг1>г	д I dv \
-, ,—I— sh 6 -nr7r I sh 9 ,. = 0	C1.7)
да2 '	дЧ \	дЧ 1
Остается сделат, последнюю замену переменных, вводя вместо 6
величину s так, чтобы было
dt d%
с sh I
т. е.
C1.8)
и мы окончательно получим для v'z уравнение Лапласа в плоскости
полярных координат е (радиус-вектор) и о (полярный угол):
Л« .-*•-"•• «	C1.9)
')Гуревич М И, Подъёмная сила стреловидного крыла в сверх-
сверхзвуковом потоке, ПММ., том 10, вып. 4, 1946.

301	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Таким образом, можно рассматривать i/ как действительную часть
некоторой функции комплексного переменного
i = sel\	C1.10)
Обозначим мнимую часть этой функции буквой 5 и напишем
«;м*/со	Cili)
Легко видеть, что внутренность круга радиуса \\k плоскости (?,
переходит на плоскости (т) во внутренность круга радиуса 1 (г=
В самом деле,
C1.12)
так что при в, меняющемся от 0 до 1, R будет меняться от 0 до l/k.
Так как 7j/l- = tga, — полярные углы при нашем преобразовании
не меняются.
Прежде чем переходить к выяснению краевых условий в пло-
плоскости (т), посмотрим, как выражаются скорости v'x, v' в функциях
новых переменных в и о. Найдём полный дифференциал от
при движении по радиусу-вектору (т. е. при о = const.). Имеем
да	да	, да .	1 /. да ,	да \
~ттт = ~з?- cos a 4- -^— sin a — — I i; -д1- + "Ч -s— I.
dR di	' Й1)	R \ dZ ' • д-q j
С другой стороны, мы можем вспомнить, что в переменных %, tj, z:
1 /. да	да \
z \ д?
da
d~i
Таким
p.
образом,
da
dR
da
dz
z
R
dm д?,
d? дг
da
dz
da
a,
'(
R \
d-ц
dz
К
dz
д?
_ dv'y
Вследствие отсутствия вихрей мы имеем:
dvx dv2 1 dv'z dv'y dvz 1 dvz
dz dx z di ' дг dy z d-q
так что
da l/d,.
/си 1оч
C1ЛЗ)

, 31]
СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	305
Далее, нетрудно выразить правую часть этого равенства через функ-
функции /и / (сопряжённая с /). Если ввести С:
7 = Ле'в; Z==Re~1',	C1.14)
ю, очевидно, можно написать:
A-f-f —=2-iL.	C1.15)
dt дц	дИ
Наконец, можно связать дифференцирование по С с дифференцирова-
дифференцированием по тит. В самом деле, по C1.10), C1.14) и C1.12) имеем:
t R 2 1	2 1
x	e	k 1 + Е2 А 1 +т
так что
. __ 2 т	у	 2 х
C1.16)
k 1-frt
дХ,	1 — т2т2 \ дх дх)	\ — 12\дхдх
Принимая во внимание, что
можно написать теперь
dR	4 1 — е2
Если теперь двигаться по радиусу-вектору а = const., то будет:
dR=?- ,^&; di = edz, <h = ede,
так что окончательно изменение м при передвижении по радиусу-
вектору будет:
и мы получим для ш следующую формулу:
Произвольная постоянная интегрирования должна содержать о, но,
как показывает более подробный расчёт, может быть приравнена
нулю.
При помощи функций ш и / мы можем записать краевые условия.
В общем случае конуса произвольного сечения условия эти будут
20 Теоретическая гидромеханика, ч. П

306
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
1ГЛ.
иметь сложный вид. Просто они будут выглядеть в случае, когда
обтекаемая поверхность состоит из отрезков плоскостей (или из про»
должений плоскостей), пересекающих плоскость (С) по прямым (или
по продолжениям прямых), проходящим бесконечно близко от начала
координат. Не останавливаясь более на общих рассуждениях, перейдём
к рассмотрению примеров.
В качестве первого примера рассмотрим обтекание прямого круг-
круглого бесконечно тонкого конуса с углом раствора 2^0, ось которого
расположена вдоль оси z. Слу-
Случай этот уже был изучен нами
точно в § 27 и § 28 при-
приближённо. На рис. 122 схе-
схематически дано расположение
обтекаемого конуса, а также
конуса характеристик(пунктир)
и плоскости 2=1. Обте-
Обтекаемый конус пересекает пло-
плоскость (С) внутри круга ра-
радиуса l/k по кругу бесконечно
/"	малого радиуса tgC0«C0. На
Рис. 122.	круге радиуса 1 в плоскости
(т) v'z должно быть равно нулю.
В начале координат должна быть особенность. Нетрудно проверить,
что решение для / имеет вид:
= с 1пх,
C1.19)
где с надо подобрать так, чтобы были выполнены краевые условия.
Именно, так как нормали к нашему конусу с точностью до малых
величин будут совпадать с радиусами-векторами нашего бесконечно
малого круга в плоскости (С), то:
v'x cos о -f- v sin о -j- v$Q = 0.
Это условие можно записать ещё так:
Re (u>e-h)-+-v$o = O при s = s0, причём ¦	^-у = ро.
С другой стороны, по C1.18) и C1.19) имеем:
ш =	с (х — — 1 =	с (е	\ еи,
2 \ т/	2 \ г)
Итак,

, 31]
СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ
307
Так как радиус е0 нашего круга в плоскости (х) будет
мы получим для с:
с = —
так что будет:
— к
,2О2
< = Re-/(x) = —-
*
¦ Ins;
вспомнив, как выражается е через величину R = У %2 -f- rj2 =
= Ух2-f- у2/2 [формула C1.12)], мы придём в точности к резуль-
результатам, полученным в § 28').
В качестве второго примера рассмотрим обтекание края прямо-
прямоугольной пластинки, наклонённой под бесконечно малым углом атаки В
(передняя кромка совпадает с отрицательной осью х). Пересечение
крыла с плоскостью (?, ^)даст
отрицательную ось х (см.
рис. 123). Край крыла дейст-
действует лишь внутри конуса ха-
характеристик. За пределами
этого конуса, т. е. в пло-
плоскости (?, if) за пределами
круга радиуса l/k, крыло будет
действовать либо как беско-
бесконечная полоса [в левой части
плоскости (!-, tj) вне круга ра-
радиуса Ijk], либо не будет
совсем вызывать скоростей
[правая часть плоскости (?, if)
вне круга радиуса l/k]. Таким
образом, на круге радиуса l/k мы будем иметь v'z — -\-v$/k (фор-
(формула Аккерета) для левого верхнего квадранта, v'z =—v$/k — для
левого нижнего квадранта и v'z — 0 на всей правой полуокружности.
Эти же условия надо написать на круге е = 1 в плоскости (х).
Посмотрим теперь, какое краевое условие получится внутри круга
s=l из-за наличия там крыла. В том случае, когда крыло рассе-
рассекает плоскость (;, rj) по любому радиусу-вектору (или по продолже-
продолжению радиуса-вектора), мы должны в качестве краевого условия (Vtt = 0)
записать:
— v'x sin о -j- v' cos о — v§ = 0.
Рис. 123.
') Мы должны лишь изменить название осей.
20*

308	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
Это означает, что здесь будет
[ГЛ. J
т. е., как легко видеть из C1.18) и C1.11), на нашем радиусе-век-
радиусе-векторе ds = 0.
Итак, мы должны найти аналитическую функцию /(х), удовлет-
удовлетворяющую следующим условиям: 1) на дуге АВ (рис. 124) круга
радиуса, равного единице, Re/ = — vfi; 2) на дуге АС круга
Re/ =-\-v§; 3) на полуокружности BDC Re/ = 0; 4) на отрезке ОА
действительной оси Im / = const. = 0.
Таким образом мы имеем разрез вдоль действительной оси и
особенности в точках В и С. Преобразуя плоскость т в плоскость
v = "|/\, мы получим 4 особенности —
в точках:
i —	_ • JL
V, = е 4, v9 = е 4.
v, = e
ч 	 а 4
 ь
и по этим особенностям легко построим
решение для /. Оно будет иметь вид:
In
C1.20)
Легко проверить, что C1.20) действительно удовлетворяет всем
нашим краевым условиям.
Подсчитаем ещё значение v'z на крыле (сверху и снизу), чтобы за-
затем, применив уравнение Бернулли, найти подъёмную силу. По C1.20)
1 + х — V%
•in
/2т
arg
так что
1
^ = tRe/=.
•arg-
На верхней части крыла (а = тс) имеем:
H^=-r-arg
14- ееь — 1

, 311
СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ
309
для нижней части крыла
= -я) имеем:
1 — е- V2ti
г'
Наконец,
?н — P'B = РЛК ~^ )= 2-^-^-argf-—-—^rl-
Таким образом,
2P.W?!"	2A — e)V2T	2p
arc cos-
Остаётся перейти от s к Д по формуле B7.12), и мы получим
окончательно
»' — »'=¦
"н "в
arc cos (I— 2&/?I).
C1.21)
В качестве третьего примера на применение этого метода рас-
рассмотрим сверхзвуковое движение стреловидного крыла, симметрично
расположенного по отношению к оси z. Задача о таком движении
была решена М. И. Гуревичем
в цитированной выше работе.
Обозначим через 8 угол стрело-
стреловидности (рис. 125) и через C
угол атаки. Рассмотрим сперва
тот случай, когда угол стрело-
стреловидности будет больше чем ар
так что наше крыло выходит
из конуса характеристик.
Крыло пересекает плоскость
(S. f\) по отрезку (АВ) оси \
(рис. 126). Выступающие части
будут действовать лишь внутри
соответствующих треугольни-
треугольников характеристик, вне круга радиуса Ijk. В каждой из областей
АСО, AGE, DBH, ВНР (см. рис. 126) скорости г/ и давле-
давления р' будут сохранять постоянные значения, причём при переходе
через крыло будут менять знак. Таким образом, на дуге СО и на
дуге HD мы имеем v'z = wv На дуге QE и на дуге HF имеем
v'z = — w0; на дугах CD и EF v'z = 0; при этом wQ мы должны
определить через заданные величины: р, 3 и vv Обозначим угол
Рис. 125.
') Эта формула отвечает частному случаю формулы B9.23) при 60 = 0.

310
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. t
дуги DH через <з0. Так как при переходе от плоскости (?) к пло-
плоскости (т) углы сохраняются, нам надо решить следующую задачу.
Определить аналитическую функцию /(т) так, чтобы
{Re/ = kw0, если 0 < <j < <з0 и те — <з0 < <з < те,
Re/ = — kw0, если 0>а>а0 и —те-)-ао><з>.—iz.
Далее, на круге е= 1:
Re/ = 0, если те — а0 > а > о0 и —я + ао < Q < ~~ ао-
Наконец, на отрезке действительной оси от е = —1 до e = -f-l:
Im/=0.
Функцию / можно построить по особенностям. Это будет:
C1.22)
По рис. 125 и 126 заключаем, что OB— OA=igb и что, таким
образом, угол о0 будет определён равенством
C123)
Величину wu найдём из краевого условия на крыле (мы использовали
Рис. 126.
это условие лишь частично, записав, что 1т/ = 0). Именно, на крыле
мы имеем:

§ 31]	СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	311
а из C1.18), интегрируя по мнимой оси от / до 0 и замечая, что
на мнимой оси х = — х, dj/dx = — df/dx, получим:
Im//T + ЦЦ
о
0
= —— sin cin Im
%
In
Таким образом, по C1.24)
jfw,
: sin o0
Найдбм ещё коэффициент подъёмной силы Су.
Так как для крыла будет
то подъёмная сила Y, действующая на крыло высоты L и основа-
основания 2Z,tg3, будет:
L zigi	tgb
off'
О -ztgS
Если S — площадь крыла (S = L2 tg 8), то
2 Г v,dh
1Y	-fsrS
Так как вдоль частей крыла, выступающих из конуса характеристик,
будет vz — const. = ± w0, то получим:
+i
-'

312	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Интеграл, стоящий справа в числителе, можно взять по частям,
записав (S = 0 на действительной оси):
2	8wn Г т2	sin 2а„
= -^Wn
— I
_ _.ЁЕ° С -Jl
А;" Ада_,7 1 -|_ Т2 (Т2_ е-2«0)(т2 _ е
Интеграл в правой части легко вычисляется и даёт:
Г т2	dx	 к I 1	\
J 1 + Т2 (Х2 _ в-И<*) (Х2 _ е2^„) — 4 \ COS а0	§" a°j '
Собираем теперь члены в Су и принимаем в расчёт C1.23) и C1.25);
получим окончательно простое соотношение:
каковое в точности совпадает с формулой Аккерета для пластинки
бесконечного размаха').
Иначе будет обстоять дело, если стреловидное крыло всё целиком
лежит внутри конуса характеристик (8 < а). Теперь мы должны будем
искать аналитическую функцию, действительная часть которой обра-
обращается в нуль на круге радиуса е=1 и мнимая часть которой равна
нулю на отрезке действительной оси длины 2Ь. Ясно, что
*е8 = ттт^'	CL27)
где 8 — по-прежнему угол стреловидности.
М. И. Гуревич продолжает функцию I/ft/(т) навею плоскость (т)
с разрезами от — со до—\jb, от — b до -(— 6 и от \\Ь до со и даёт
решение в виде
t2+1	C1.28)
у w-Mj*-
где В есть действительная постоянная, которую мы должны найти
из краевого условия на пластинке (v'z — $v\ Решение легко прове-
проверить непосредственно. Чтобы найти В, используем вновь C1.18) и
произведём, как и в предыдущем случае, интеграцию по мнимому
') Пластинка есть частный случай стреловидного крыла E = те/2).

31]	СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	313
радиусу. Получим, как и прежде,
2	)
Таким образом,
Подстановкой s = 6tg<p приведём это выражение к виду
где
Раскрывая числитель подынтегрального выражения, напишем:
^° ~ 2Ь J [ 1 — A — й4) sin2 <f]'h /Г—*
f
2Ь J [ 1 — A — й4) sin2 <f]'h /Г—A—
-f /l—A—64)sin2cf>| dep.
Правая часть может быть выражена через эллиптические интегралы
1-го и 2-го рода и через элементарные функции1). В самом деле, если
л	л
В{х. к) = / УТ^ХЧ^-Х dx, Fix.k) = f-fT=i
dx,
о
то
х
Г	dx	 Е (х, k)	k2	sin x cos x
>' (l/^T	h2 < ,n2 v\&	1	i>2	1 	 Ь2 l/~] 	 hi от2 у
\l I —~ К ЬШ XI	1 ~~~ К	1	К f к 	 К sin Л
о
так что
= -^Ч?<
') См., например, Журавский А. М., Справочник по эллиптическим
Функциям, стр. 37, формула 126.

314	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. !
Таким образом, постоянная В найдётся по формуле:
к\Е
Коэффициент подъёмной силы Су запишется по C1.26) в виде:
+ь
4
Чтобы вычислить этот интеграл, заменим его контурным интегралом,
взятым вокруг крыла:
/
F2_t2)/j__x2\
Деформируя контур в круг единичного радиуса с обходом вокруг
обоих полюсов т= ± / по бесконечно малым окружностям и применяя
теорию вычетов, получим:
г — 2яВ
Используя C1.30), получим окончательно
с =_i?яй
?
26s/7 (?1, /1— 6
Таким образом, в противоположность тому, что имело место в пре-
предыдущем случае, отношение Су/-г- здесь не является постоянным,
а будет зависеть от b и ер, т. е. по C1.27) и C1.29) от произведе-
произведения ktgb. На рис. 127, заимствованном из статьи Гуревича, по гори-
горизонтальной оси откладывается величина fttgS, по вертикальной оси
величина — Су/-?-. До значения fttg§=l используем C1.31), при
k tg Ь > 1 получим постоянную, равную единице (формула Аккерета
справедлива для стреловидного крыла, выходящего за конус харак-
характеристик).
Вернёмся к общей пространственной задаче и покажем, как можно
найти некоторые новые классы точных (нелинейных) решений.
В случае осесимметрического обтекания конуса (?) концы вектора
скорости располагались на кривых vr—f(vz). Это значит, что в про-
пространстве (vx, Vy, vz) концы вектора скорости располагались в этом

, 31]
СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ
315
случае на поверхности вращения. Возникает вопрос, нельзя ли по-
построить другие виды движений, более общие в том смысле, что в них
концы вектора скорости хотя и лежат на некоторой поверхности Е,
но последняя не обязательно является поверхностью вращения.
0,8
0,6
DA
0,2
n
J
/
/
/
О 0,2 0,4 0,6
Рис. 127.
Задача эта была исследована впервые А. А. Никольским 1) A949 г.).
Изложим некоторые результаты этих исследований.
Пусть уравнение поверхности 2 в пространстве скоростей запи-
записывается в виде
vz = F(vx, vy).	C1.32)
Построим дифференциальное уравнение в частных производных, ко-
которому удовлетворяет функция F,
Мы рассматриваем безвихревое движение, так что выполняются
соотношения:
dvv
dv.
dv.
dvr
	 rfv '	Л, 	 Л„ '	Ay	Л, 4	C1.33)
dz
dz
') Никольский А. А., О классе адиабатических течений газа, кото-
которые в пространстве годографа скорости изображаются поверхностями, ЦАГИ,
Сборник теоретических работ по аэродинамике, Оборонгиз, 1957.
Никольский А. А., Об одном классе точных решений простраи-
?Тме<5?,ых УРавнений газовой динамики, АН СССР, Инженерный журнал,
1 A9Ы), в. 4.

316	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Кроме того, должно выполняться уравнение B8.5), которое,
используя C1.33), мы можем записать в виде:
dvx	dvv	dv.
Вставим теперь vz из C1.32) в уравнение C1.34), используем еще
раз C1.33) и перегруппируем члены. Получим
dy
Перейдём теперь от переменных л:, у,	z к переменным к, f, С из
соотношений:
и = vx, v = vy,	С = z.
Легко видеть, что
dvx dy	dvr	дх	dvv дх
^Д	*—	.Д 	*- =	Д
dv	ду ди
	^_=_Д 	-	.Д	=
дх dv	dy	dv	ду ди
где ^ =
dvx dvv I dvx \2
^1)
сано в виде:
I dvx \2
	1-з—) • Но тогда C1.35) может быть перепи-
перепи' L	ди '	dv ' к	' du dv J dv '
В этом уравнении коэффициенты, стоящие при ду/dv, dx/dv, дх/ди,
зависят только от и, v, сами же величины х, у зависят как от и, v,
так и от С. Покажем теперь, что в нашем движении х а у суть ли-
линейные функции от С с коэффициентами, зависящими от и и г». Для
этого введём в рассмотрение функцию х из равенства:
1 = их -\-vy-\- F (и, v) • С — <f(x, у, С),
где ср — потенциал скоростей, так, что и — drf/dx, v = d<?ldy,
р = df/d(.. Легко видеть, что ^ зависит лишь от и и г>, но не зави-

§ 31)	СВЕРХЗВУКОВЫЕ	КОНИЧЕСКИЕ	ТЕЧЕНИЯ	317
сит от С Действительно:
dx	dy |^ p dj dx	df dy dy
^	<?C	dC	dx dC	dy dC, d?
dx , dy i o	<?jc	dy _
oC	ОС	ОС	ос
Да lee,
dx . dy , r dF
- - Л —t— (*¦ —7	Г С -i ~~1— >» -i
^и	~т~ ди ' d« '^ d« дх ди ду ди
Таким образом,
~du~'
- = -?— C-g.	C1.37)
Аналогично
y==_jL_C.|'L.	C1.38)
Таким образом, л; и у являются линейными функциями от С с коэф-
коэффициентами, зависящими от и и г».
Мы можем теперь написать
ду 	 d2i ., d2F dx 	 d\
_ <?2Х 	г
du dv
dv dv2	dv2 ' dv du dv	du dv '
dL _ d\ , d2F
du ~ du*	du2 '
Вставляя эти выражения в C1.36) и приравнивая нулю члены с С,
почучим уравнение для определения функции F:
+F)
Г
du dv
Одновременно с этим, приравнивая нулю члены, свободные от С,
получим \равнение для у.
иг» + г»/7 -5	Ь «^ -^	т (F — а) т	т—' -з—з—г
Обратим прежде всего внимание на одну замечательную особен-
особенность нашего движения Рассмотрим какую-либо точку поверхности
(dl 32) г»Л = и0, г»у = г»0, г»г = w0 = F (и0, г»0). В силу C1.37), C1.38)

318	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ.
этой точке в пространстве (х, у, z) будет отвечать целая прямая
Таким образом, в нашем движении сущеС1вуют целые прямые, вдоль
которых значение скоростей сохраняется (меняясь от прямой к прямой).
Расположение этих прямых в пространстве (х, у, z) зависит от вида
функций х и F- Задание поверхности F уже определяет направление
этих прямых: каждая из прямых C1.41) параллельна нормали к Е,
проведённой в точке и0, vQ.
Размещение этих прямых в пространстве регулируется функцией
у (и, v). В частности, если y^ = cons\. (это значение тождественно
удовлетворяет уравнению C1.40)), имеем
\ ди J '	V 0v I
и тогда все прямые постоянного вектора скорости проходят через
одну точку х = у = z = 0.
Если взять
Х = cxti-\- C2V-\-czF(u, v)-\-C,
где cv c2, c3, С — произвольные постоянные (такая х> как легко
видеть, вновь удовлетворяет уравнению C1.40), если F удовлетво-
удовлетворяет уравнению C1.39)), получим:
' 'Ио. оо
Теперь мы будем иметь в пространстве (л:, у, z) пучок прямых,
проходящих через точку лг = с,, у = с2, z = c3. Это — своего рода
конические течения (не осесимметрические), вид которых остаётся
в значительной степени произволен, пока не задана F.
На конкретных примерах различных F мы не останавливаемся.
Рассмотрим теперь пространственные течения газа, в которых концы
вектора скорости располагаются на некоторой линии. Такие течения
были рассмотрены А. А. Никольским A950) в том виде, как это
излагается ниже.
Пусть в пространстве vx, vy, vz области течения соответствует
кривая /, имеющая уравнение
vx—u, v =v(u), vz = w(u).	C1.42)
Рассмотрим в нашем течении, в пространстве (х, у, z), поверхность
р{х, у, z) = pQ = const.	C1.43)

g 31]	СВЕРХЗВУКОВЫЕ КОНИЧЕСКИЕ ТЕЧЕНИЯ	319
По уравнению Бернулли и в силу C1.42) мы будем иметь во всех
точках этой поверхности одни и те же значения vx, vy, vz\ пусть
это будут vx = u0, Vy = vQ, vz = w0. Таким образом, в пространстве
(v , v , vz) всей нашей поверхности будет отвечать одна точка
А(и0, v0, w0) кривой /. Докажем теперь, что поверхность C1.43)
есть плоскость в пространстве координат. Действительно, по урав-
уравнению движения
dV	1
— ^---gradp.
Это равенство означает, что при бесконечно малом удалении вдоль
линии тока от поверхности р = const, приращение d\! вектора ско-
скорости будет всегда нормально к поверхности р = const. Но построен-
построенные таким образом приращения d\! во всех точках поверхности
р = const, имеют одно и то же направление — они параллельны ка-
касательной к кривой / в одной-единственной точке А (и0, v0, w0). Зна-
Значит, любая поверхность р = const, является плоскостью, нормали
к которой параллельны касательной, проведённой через соответствую-
соответствующую точку кривой.
Воспользуемся теперь уравнением C1.33) и C1.34). По C1.33)
имеем:
dvy
dy
dvx
dy
dv
du
dvy
дх
dvx I
ду \
dvz
dz
dv du
du dx '
dv \2 du
du) dx '
dw dvx
du dz
dvx
dz
dz
(
dw
du
dvz
dx ~~
dv dv.,
du dz
\2 du
I dx '
dw
du
du
dx
dv
du
dw
du
du
dx
Подставим полученные выражения в уравнение C1.34) и сократим
его на величину dujdx; получим следующее соотношение между диф-
дифференциалами du, dv, dw вдоль кривой Z:
(а2 — ф) (duf + (а2 — г»2) (dvJ -f (а2 — да2) (dwf —
— 2uv du dv — 2uw du dw — 2vw dv dw = 0. C1.44)
Это соотношение можно записать в виде:
C1.45)
где дифференциалы берутся вдоль кривой 2, причём У2= и2 -f- v2 -f- w2.
Прежде всего отсюда следует, что движение рассматриваемого типа
будет обязательно сверхзвуковым. Действительно, соотношение C1.45)
инвариантно по отношению к направлению осей и, v, w {vx, vy, vz).
Возьмём какую-либо точку М кривой / и направим ось и по каса-
касательной к I в точке М; тогда в этой точке dv = dw — 0 и мы будем
иметь (а2—«2)^и2 = 0 и, так как da Ф 0, то «2 = а2, т. е. величина

320	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. t
проекции скорости на направление / равна скорости звука. Отсюда
следует, что рассматриваемое движение может быть только сверх-
сверхзвуковым.
Плоские безвихревые движения, которые мы изучали ранее,
являются частным случаем рассматриваемых сейчас движений: они
получатся в случае, когда кривая / — плоская кривая. При этом,
как мы знаем, годографом скорости будут те или иные эпициклоиды.
Уравнения этих эпициклоид найдутся сразу же из уравнения C1.44),
если положить там dvo = 0.
Уравнение C1.45) можно будет ещё записать в виде
ds2 = (~-dV)\	C1.46)
где ds — элемент дуги вдоль линии / в пространстве (и, v, w). Так
как скорость звука а есть функция одного только модуля V, это
уравнение интегрируется в квадратурах; оно даёт ту же зависимость
длины дуги s от V, какая связывала в случае эпициклоид соответ-
соответствующие величины на плоскости.
Если провести прямолинейные лучи через некоторую точку кри-
кривой I и через начало О системы (и, v, w), мы получим коническую
развёртывающуюся поверхность. Развернув её в плоскость, увидим,
чго кривая / обратится в эпициклоиду. В самом деле, расстояния V
точек кривой / от точки О, а также элементы длины дуги при этом
не изменятся и поэтому уравнение C1.46) будет удовлетворяться и
для плоскости; но на плоскости уравнение C1.46) есть уравнение
эпициклоид.
Это соображение позволяет найти все интегральные кривые урав-
уравнения C1.44). Для их получения достаточно взять любую коническую
поверхность, развернуть ей на плоскость, нанести на ней два семей-
семейства эпициклоид и затем снова восстановить исходную поверхность.
Нанесённые нами эпициклоиды перейдут в систему /.
Более подробно вопросы геометрии движений, отвечающих случаю
наличия /, были рассмотрены в работах А. А. Никольского, С. В. Ва-
ландера и П. Жермен.
§ 32. Осесимметричное обтекание с отошедшей ударной
волной. При обтекании тупого осесимметричного тела сверхзвуковым
потоком (скорость по бесконечности направлена вдоль оси симметрии
тела) образуется осесимметричная ударная волна, отходящая от по-
поверхности тела. Задача определения формы ударной волны и вихре-
вихревого движения между поверхностью разрыва и поверхностью тела
решается численно. Схема решения была дана О. М. Белоцерковским
и реализована на электронной быстродействующей вычислительной
машине. Так же как и в аналогичном плоском случае (§ 22), здесь
был применён метод Дородницына, позволяющий решить задачу в точ-

§ 32] ОСЕСИММЕТРИЧНОЕ ОБТЕКАНИЕ С ОТОШЕДШЕЙ УДАРНОЙ ВОЛНОЙ 321
ной постановке и с нужной степенью точности. Путь решения заклю-
заключается в следующем.
Вводятся сферические координаты (г, 0, X) (ось 6 — вдоль потока).
В силу осевой симметрии движение не зависит от X и составляю-
составляющая vk скорости равна нулю. Уравнения движения примут вид:
dvr vb dvr vb __ I dp
vrv9 __ 1 dp	_ „
г дг ' г dr ' г	?r dr '
Используя уравнение неразрывности
~р (r2pvr sin 9) + -щ (rpvH sin 6) = 0,	C2.3)
введём функцию тока W такую, что
r2ov sin 0 ^=		rov sin В •	^32 4^
При этом
77Г~ -~—- *vP Sill t/ I Tfy ^7Г	* fX'Vf 1 ,	(O^.D)
если дифференцирование проводится вдоль некоторой линии г — R (9),
Уравнение C2.5) есть аналог уравнения B2.10) плоского случая.
Комбинируя C2.2) и C2.3), получим аналог уравнения B2.8):
Соотношения, выражающие р и р через V2 = vj-j-v2r, будут иметь
тот же вид, что и в плоском случае (см. B2.11) и B2.12)). Неиз-
Неизвестными функциями являются vb, vn W и S. В качестве краевых
условий имеем на теле:
причём значение &@) дайтся формулой B2.21). На ударной волне
г== го4~еF), где е(б)—функция от б, подлежащая определению,
имеем вновь соотношения B2.13) — B2.15), связывающие vH, vr и ср
V? угол наклона нормали к поверхности разрыва к оси симметрии);
кроме того, имеем очевидное соотношение
аналог соотношения B2.18). Наконец, по C2,4) должны иметь на
Ударной волне:
^	(^^^0. C2.9)
21 Теоретическая сидроме\аника, ч. II

322	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ \
Процесс решения задачи, как и в плоском случае, заключается в раз-
разбиении области интегрирования между телом и поверхностью разрыва
на N областей путём проведения линий
/¦; = го(б) + ^(б), где k = jf (L 2, .... N)
с последующим интегрированием уравнений C2.3) и C2.6) вдоль
тиний 8 = const, от контура тела до границы каждой из полос и
с заменой подынтегральных функций интерполяционными полиномами.
Искомыми функциями будут значения функций на границах полос.
Граничные условия выполняются точно. Задача сводится к численному
интегрированию системы обыкновенных дифференциальных уравнений
по б, причём часть краевых условий задается на оси симметрии:
при 0 = 0
а остальные на особой линии. Небольшое отличие от плоского слу-
случая заключается в том, что теперь, кроме N подвижных особых точек,
мы будем каждый раз иметь для некоторых уравнений системы
особенности вдоль оси симметрии. Эти последние особые точки будут,
однако, фиксированными регулярными особыми точками; как и в пло-
плоском случае, и здесь придётся иметь дело с рядами по степеням 9.
Здесь (как и в плоском случае на стр. 191) предполагалось, что
граница тела представляет собой гладкий контур. По рассмотренной
методике можно проводить расчёт тел, образующая которых в обла-
области влияния имеет излом (в этом случае один из параметров опре-
определяется из условия того, что в точке излома должна быть звуковая
vKopocTb), а также расчёт «комбинированных» тел (сфера — конус
и др.). Метод может быть обобщён на случай сверхзвукового обте-
обтекания затупленных тел потоком реального газа (с учётом диссоциации
и ионизации). Если задаться целью создать единую программу для
быстродействующих электронных счётных машин, пригодную для рас-
расчётов как плоских, так и осесимметричных тел разнообразной формы
(гладких, сильно затупленных, с изломом образующей, «комбиниро-
«комбинированных») при различных значениях показателя адиабаты k и чисел
Маха набегающего потока A < Мсо < со), то весьма удобно за не-
независимые переменные взять s и п (s — длина дуги вдоль тела, от-
отсчитываемая от критической точки, п — нормаль к телу).
Приведём некоторые результаты расчётов осесимметрических тел,
полученные О. М. Белоцерковским J).
На рис. 128, 129, 130 представлены картины обтекания эллип-
эллипсоидов вращения (8 = 0,5; 1,5) и сферы (8=1,0) при различных
значениях М» (8 —отношение вертикальной оси эллипсоида к гори-
') Белоцерковский О. М., О расчёте обтекания осесимметриче-
осесимметрических тел с отошедшей ударной волной на электронной счетной машине,
ПММ, т. XXIV, вып. 3, 1960.

,о1 ОСЕСИММЕТРИЧНОЕ ОБТЕКАНИЕ С ОТОШЕДШЕЙ УДАРНОЙ ВОЛНОЙ 323
i 32]
ш ibs io	as
да т
Рис. 128.
аи шш	us
щам
Рис. 129.
0,5
185 W
IJ58 tJW
Рис. 130.
21*

324
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. 1
0,4	0.6
Рис. 131.
о,*
о,з
0,2
0,1
о
у \
?=1.5
Усеченный цилиндр
Эллипсоид
2	4	S	8
Ряс. 132.
о,а
M-t,0;S-i,0
/,0	#Д	О
Рис. 133.
^?<?
ОЛ
-
	i
f
0
i
'X
\
, „1
4
\
4
1
N=t
N-2
4^
1
I

7Г
д,4	0,8	t,2
Рис. 134.

33]
ОДНОРАЗМЕРНЫЕ ДВИЖЕНИЯ ОБЩИЕ УРАВНЕНИЯ	325
зонтальной). На рис. 131 дано распределение давления р/ро =
= Р (го« ®УР ^го- 0) вдоль поверхности эллипсоида с 8 = 0,5. На
рис. 132 показано, как меняется расстояние от тела до поверхности
разрыва вдоль оси симметрии.
Рис. 133 и 134 иллюстрируют сходимость метода при N=1,2,
^1^=4; на рис. 133 приведена ударная волна, звуковая линия и
характеристики I и /I семейств; на рис. 134 даны распределения
давления вдоль тела и поверхности разрыва.
В заключение следует отметить, что метод интегральных соот-
соотношений с успехом применялся и для решения других задач газовой
динамики и прикладкой математики. Так, П. И. Пушкиным1) было
рассмотрено обтекание произвольного тела в дозвуковом и звуковом
потоке газа, а также дозвуковое обтекание эллипсов с циркуляцией.
Г. НЕУСТАНОВИВШИЕСЯ ДВИЖЕНИЯ
§ 33. Одноразмерные движения. Общие уравнения. Характе-
Характеристики, Пусть газ движется вдоль оси х так, что все элементы
движения vx, p, p являются функциями одного только х и времени t.
Таким образом,
vy = vz = 0; vx = vx(x, t); p = p(x, t); p = p(x, t).
Предполагая, что внешних сил и сил вязкости нет, мы можем напи-
написать уравнение движения в виде
1 dp 	 dvx	dvx
~^~дх"~ Ш v* дх -
Уравнение же неразрывности даст:
dp . d$vx _
ж+-дГ^°-
Прибавим ещё условие адиабатичности движения
dt вх ' х дх f-
Мы имеем таким образом три уравнения для определения трёх функ-
функций: vx, p, р. Как и прежде, введем величину Ь, просто связанную
с энтропией, из условия
р = ЬЦх, t)p\	C3.1)
') Чушкин П. И., Обтекание эллипсов и эллипсоидов дозвуковым
потоком газа, Выч. мат., 2 A957); Расчёт некоторых звуковых течений газа,
НММ, т. XXI, в. 3, 1957; Расчет обтекания произвольного профиля и тела
вращения в дозвуковом потоке газа, Выч. маг., 3 A958); Дозвуковое обтека-
обтекание эллипсов с циркуляцией, ДАН СССР, 125 A959), № 4.

326	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
Тогда	дЪ . дЬ .
Уравнение C3.2) показывает, что в случае непрерывности движе-
движения 0 сохраняется в частице. Вместо функций vx, p, p удобно бу-
будет ввести vx, а (скорость звука) и Ъ. Так как
vx,
V 1
2 1
сР~-*.?-—%Ъ*р-'1 — ъ%р ''¦ , то 1пр =	г\па	Ц-1п(х&*).
Таким образом, уравнение неразрывности даст после простых пре-
преобразований:
2 (д\п а , д\па\	1 / д , Ov . й. „\ , dvx л
у.— 1 \ dt ' х дх ) t.— \\dt	' х дх	I ' дх
что, вследствие C3.2), может быть записано в виде:
х—1 dvx . да , да _	._„ ..
а^+ + ^ °	C33)
Уравнение движения даст
dvx , dvx 	 р д\пр 	 а2 I 2х д\па	у. сМпх9\
dt	х дх ~~ р дх	х \ х — 1 дх	х — 1 дх )'
что может быть представлено в следующем виде:
dt ' х дх ' т. —¦ 1 дх "х — 1 дх
Мы уже упомянули о том, что 0 сохраняется в частице; распре-
распределение % от частицы к частице следует считать поэтому в задачах
газовой динамики как бы начальным условием и данной функцией
[наподобие того, как в плоской стационарной задаче мы считали
известной функцию 0 = 9(ф)] от лагранжевой координаты (мы будем
обозначать её в этой главе буквой {):
© = »(?).
Аналогично тому, как в плоском случае мы вводили вспомогательную
функцию ф от х и у, введём теперь вспомогательную величину % —
лагранжеву координату — функцию от х и t:
5 = 5(л;, t).
Функцию эту мы получим, если решим уравнение
Л 	 A, ^q, i J
относительно 5.
С другой стороны, уравнение неразрывности позволяет заключить
о существовании функции А (х, t), такой, что
дА	дА

§ 33]
ОДНОРАЗМЕРНЫЕ ДВИЖЕНИЯ ОБЩИЕ УРАВНЕНИЯ	327
Уравнение C3.2) заставляет нас считать, что А зависит лишь от ?.
Бо iee того, вводя плотность р1 в некий исходный момент как функ-
функцию Ь Ро (?)• мы можем найти связь между А и ?. В самом деле,
напишем тождество
« = &(*(?, t). t)
и продифференцируем его обе части по \\ получим
j ^ dj (х, 0 (?д: (?, t)
~~ дх	&¦ '
но вследствие уравнения неразрывности, написанного в форме Ла-
гранжа, для нашего одноразмерного движения имеем:
дх _ Ро (') .
значит,
так что
Таким образом, <;(х, f) должна удовлетворять одному из двух урав-
уравнений
di 	 р _ di 	 pt/x	„„ _.
дх р0 ' dt	ро
Заметим, что, задав ft (?) и ро(?), мы можем определить и /70 (S) и
йи(?) (давление и скорость звука в исходный момент). В самом деле:
( г,* х-1\"»	о* »
йо = \,у-" Ро ,/ "; Рй = " Ро-
Мы можем теперь записать C3 4) в виде
Eих . Eг/ж . 2 Eа 	 а2 р d\nb
х дх ' dt ' х — 1 дх х — 1
где
C3 6)
р — л ""' (у6х) *~!.	C3 7)
Таким образом мы должны определить две функции: vx{x, t),
а(х, t) удовлетворяющие дифференциальным уравнениям C3.3) и
C3 6), причем в последнее уравнение входит ещё третья функция
s(x t) но уже не под знаками дифференциаюв; эта функция \ должна
>дсолетворять одному из уравнений C3.5) Задача наша представляет
анаю1ию с плоской вихревой задачей, рассмотренной выше (§ 9):
Tav' речь шла об определении функций vx, vy из уравнений (9.1),
С-* 2), причем формула (9.1) содержала еще функцию vj>, каковая

328
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ. I
должна была удовлетворять одному из дифференциальных уравне-
уравнений (9.6).
Обращаясь к системе C3.3), C3.6), будем иска1ь для неё харак-
терципческие многообразия в виде
Вдоль этих линий
dvx 	 dvx j dv
~~ ~ ~dt
dt
~дх~
-V;
da	да . да ,_ dl
dt
dx
dt
i
dt
дх
1 dv,
Находя отсюда dvxjdt и da/df и вставляя их в уравнения C3.3),
C3.6), получим:
,. да 	 da
' дх	dt '
2а да 	 р0 din9 2 dvx
'. — 1 dx " -л — 1 di	dt
Условие невозможности определения dvxjdx и да/дх из этой системы
уравнений заключается в равенстве нулю определителей
x '
¦a v r — х
1а
da_
dt
= 0
х' —v.
?
у. — 1 d%
Из первого равенства находим
dx
Tit
Из второго:
dt
х—1
C3.8)
a
7.— 1 dt
dt
Г
*/[_¦*¦—1
dt
= 0
или, если применить C3.8), после простых преобразований:
dvx j_ 2 da 	 р0 d 1 п 9
: —1
¦1 rfi
а-1.
C3.9)
Уравнение C3.8) показывает, что при любом нестационарном
одноразмерном движении 1аза через каждую точку плоское in (x, t)

<j 34] ШИЬНЫЕ РАЗРЫВЫ В ОДНОМЕРНОЙ НЕСТАЦИОНАРНОЙ ЗАДАЧЕ 324
проходят две характеристики. Назовем характеристикой перво! о
семейства ту, что отвечает знаку плюс, а характеристикой второго
семейства — ту, что отвечает знаку минус. Те линии, вдоль которых
мы перемещаемся в плоскости (vx, а), когда в плоскости (х, t) мы
идем по характеристикам, назовем характеристиками (первого или
второго семейства) плоскости (vx, а). Заметим, наконец, что вдоль
характеристик, вследствие C3.8) и C3.5):
dt dt ^^ дх	ро	х^^ 1	ро	v • • I
Итак, вдоль характеристик первого семейства
dx___
dt ~Vx ' a'
C3.11)
dvx , 2 da 	 a rflnft	dz 	 "TIT T^T
~dT + ~^\ 4t = T^T ~~dT~' Ж~ао a ' j
вдоль характеристик второго семейства:
dx 		_ dvx	2 da 		a d\x\.b
~d7~~Vx~~a' ~di V^T IF= ~ T^l dT~
1
\ C3.12)
§ 34. Сильные разрывы в одномерной нестационарной за-
задаче. Поверхность разрыва в одномерной задаче будет плоскостью,
перпендикулярной к оси, вдоль которой происходит движение. Если
мы условимся считать отрицательной областью ту, что лежит от
поверхности разрыва в направлении отрицательной оси х, а поло-
положительной областью — ту, что лежит «справа» (в направлении по-
положительной оси х), то у нас будет просто
(п направлено всегда в сторону положительной области). Таким об-
образом,
9 = yV— Vn=N— vx.	C4.1)
Уравнения B.15) и B.16) § 2 этой главы примут вид:
o6(wx+— vx_) = p+— p_.	C4.2)
Р+6+ = р_6_.	C4.3)
Кроме того, как всегда, имеет место формула E.10) § 5. Таким
образом, семь вечичин: N, p + , p_, p+, p_, i>xf, vx_ связаны тремя
соотношениями, и мы можем, считая три величины (например, vr + ,
Р и о ,_) известными, выразить любую из оставшихся величин через
из этих постедних величин. В предыдущем параграфе мы заме-

330	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
нили, однако, отыскание величин р и р отысканием а и f>; поэтому
и здесь мы выразим р и р через а и 0. Будем искать связь между
а_ и vx_ и между &_ и N. Попутно найдём также зависимость vx_
от N.
Мы ограничимся для простоты дальнейших выкладок тем слу-
случаем, когда vx+ = О, т. е. разрыв распространяется в покоящейся
среде. При этом будем считать, что а+ = а0 = const., p+=pQ =
= const., p+=p0= const, («исходная» плотность). Назовём затем
vx_=v, p_=p, р_ = р, а_=а.
Формула E.14), решённая относительно р + /р_, даст:
р, х—1	2 а2,
— =-—тЧ	-7Tf:	C4.4)
Р_ * + 1 х+1 0^+
заменяя здесь р+/р_ по C4.3) через 9_/9+ и замечая, что по C4.1)
Q_ = N—vx, B+ = N, получим из C4.4) зависимость между N и vx
в виде:
N2 — ^~^Nvx — al^=0.	C4.5)
С другой стороны, формула C4.4) даст нам
У^^ТГ + ^ТТЙ'	C4.6)
что в соединении с формулой
Ро + Ро р	,_, _ч
— — ТГТ =	р—	C4.7)
Р
даст возможность написать Ь_ через посредство N (и конечно, &+,
р0, а0). Наконец, чтобы найти зависимость между а и г^, восполь-
воспользуемся сперва формулой, аналогичной формуле C4.4),
Р_ т.—1	2 а2_
	 	 | 	 I
Р+ х -|- 1 х -\- 1 В_
т. е.
_^ _ х—1 _J>	a2
что, вследствие C4.3), напишем ещё так:
х—1 , 2	а2	N
¦Х. + 1 ' х + 1 (TV—w,-J TV —% '
Остаётся только исключить из C4.5) и из этого уравнения N. Для
этого запишем сперва последнее уравнение в виде

,351
СЛУЧАЙ ПОСТОЯННОЙ ЭНТРОПИИ ДВИЖЕНИЕ ПОРШНЯ
331
и вычтем из него почленно C4.5); получим после простых преобра-
преобразований
" ~" \	C4.8)
	2 ' х—1 vx •
Нзконец, вставляя это N в C4.5), получим искомую зависимость
между а и vx:
2 г 2	л / 2	2\2
,, 2	L_%2	1	Л- = 0-	C4.9)
* I	X	А	X (х— IJ
Уравнение C4.9) представляет в плоскости (a, vx) некую кривую
четвертого порядка. В интересующей нас области значений а {а > 0)
она имеет двойную точку: а ~ а0, vk—0 (рис. 135) и симметрична
по отношению к оси vx, а также по отношению к оси а; её асим-
н юты имеют уравнение
-= ±у ¦
*(%-!)
Кроме того, оказывается, что достаточно рассмотреть только ту часть
кривой, на которой а > а0.
Уравнения C4.6) и C4.7)
показывают, что если ir'+ =
= const., но jV меняется
(зависит от времени), то ft_
С1анет переменной величи-
ной, т. е. если в среде,
покоящейся и обладающей
постоянной энтропией, пере-
перемещается с переменной ско-
скоростью поверхность силь-
сильного разрыва, то после прохождения её среда получит в разных
точках разную энтропию.
§ 35. Случай постоянной энтропии. Движение поршня в неог-
неограниченной трубе. Точные решения. Наличие отражающей стенки.
Предположим сперва, что
0E) = const.
Уравнения для характеристик (§ 32) примут тогда особенно простой
вид: здесь df)/d$ = O, и мы можем проинтегрировать уравнение C2.9).
Получим вдоль характеристик:
2
Х
¦ а = const.
Таким образом, в плоскости (vx, а) характеристиками являются два
семейства параллельных прямых, наклонённых к оси vx под углом,

332
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ 1
ташенс которого есть ±(х—1)/2 (рис. 136). Будем писать для ха-
характеристик первого семейства
а для второго
C5.1)
C5 2)
(наше семейство прямых является аналогом семейства эпициклоид
пюской безвихревой задачи). Аналогично тому, как это было в § 11
мы можем и здесь намеш1Ь
две основные операции, назо-
назовем их а и pi.
Операция а. В дв>х распо-
расположенных близко друг 01
др\га точках Мх и М2 пло-
плоскости (х, t) даны значения г\
и а. Найти vx и а в точке Р
пересечения характеристик p. i-
ных семейств, выходящих in
Ml и М2 соответственно. Эта операция выполняется сразу, если
отметим точки /И| и М'2 плоскости (vx, а) с координа!ачи, равными
скоростям в точках М1 и М2 соответственно; действитетьно, заме-
заметим, что, перемещаясь в плоскости по характеристике МгР, — пунь
для конкретности это будет характеристика первого семейства, мы
будем двигаться в плоскости (vx, а) по известной прямолинейной
характеристике первого семейства,
проходящей через М\.
vx — (i>jMi + 	, {а — ам) = 0;
двигаясь же вдоль М2Р, мы пойдем
в (vx, а) вдоль известной прямой
2
vx — (vx)m2	г (а — ам2) =~ О
О
Рис 137
Точка Р' пересечения этих прямых
и даст скорость vx и а в Р.
Операция р. На некоторой кривой L, не являющейся характе-
характеристикой и лежащей в плоскости (jc, t), даны значения vx В точке М,
расположенной близ кривой, но вне ее, известны vx и а. Надо
найти обе скорости в точке Р пересечения с кривой L характери-
характеристики, проходящей через М (рис. 137). Чтобы это сделать, обра-
обратимся к плоскости (vx, а) и, отметив в ней точку М', координаты
ко юрой cyib скорости в точке М, проведем через М' прямолиней-

§ 351	СЛУЧАЙ ПОСТОЯННОЙ ЭНТРОПИИ ДВИЖЕНИЕ ПОРШНЯ	333
ц\ ю характеристику (того же семейства, что и МР) и на ней оты-
отыщем точку Р', в которой vx равно известному значению величины vx
в Р Ордината точки Р' (vx, а) и даст нам скорость звука в Р'.
Практически мы сможем провести наши операции точно лишь
наполовину (так же как это было в § 11) именно, мы можем точно
найти величины vx и а в точке Р' характеристики в плоскости
(<yv я), но не сможем определить точно местонахождение точки Р,
ибо вид характеристик плоскости (х, t) неизвестен. Можно, однако,
по формуле C3 8) найти углы касательных к характеристикам в точ-
точках М{ и М2 (ити М), провести эти касательные, найти пересече-
пересечение Р этих отрезков прямых и считать, что точке Р как раз и oi-
вечте! найденная точка Р' плоскости (ух, а) Ошибка при этом тем
мен ше, чем бтиже точки Мх, М2 друг к другу ити Чем ближе
к кривой L точка М Мы можем, гак же как и в § 11, дап> оценку
noi решноии, заключая неизвестные нам дуги характеристик в из-
известные угльс мы сможем, в случае однозначной зависимости между
точками плоскости (vx, а) и (jc, t), опираясь на легко доказываемую
монотонность изменения при перемещении вдоль характеристики
}па наклона касательной к характеристике, заключить, что харак-
характеристика МХР, например (операция а), лежит внутри угла между
огр<.эком М{Р* касательной к характеристике в М1 [находящейся
по форму те C3 8)] и отрезком МХР**, параллельным касательной
к харткгерисшке МХР в точке Р [наклон отрезка МХР найдется
по C3 8), так как скорости в неизвестной точке Р нам точно из-
весшы — это координаты Р']
Два стова об определении величины Ё Если нам известно ?
в точках Мх и М2, то чтобы найти % в Р, надо обратиться к фор-
м^там C3 11), C3 12).
2 т. + 1
Зная ? в точке Мх или М2, можем найги там ао(?) и таким образом
найги dljdt Остается написать приращение.
2	7 + 1 '
двшаться по МХР или Д? = — \а0 X+I a y~l )м2 ht, если дви-
двигаться по М2Р, причем первый раз M = tp — Ьщ, а во второй раз
Переходя к конкретным задачам, остановимся сперва на одном
важном частном случае, сразу же допускающем сведение задачи
h обыкновенным дифференциатьным уравнениям. Пусть движение

334	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
наше таково, что в плоскости (х, t) существует одна характе-
характеристика Л, во всех точках которой как vx, так и а сохраняют по-
постоянное значение. Эга характеристика Л будет тогда прямой линией
[вследствие C3.8) вдоль неё будет dxjdt = const.]; пусть для кон-
конкретности Л есть характеристика первого семейства. Рассмотрим
теперь характеристики второго семейства: Lb L2, ... Пусть они пе-
пересекают Л в точках Ж], М2, . . . соответственно:
вдоль линии Z-j будет, по C5.2),
2
vx x_ j a — 2ia,;
вдоль L2:
vx — ^гу а, ¦= 2u2
и т. д. Очевидно, что \>.1 можно найти из условия, что Lx проходит
через My
2
также \х2 найдётся по формуле
(vx)m2 — -^—j (а)м2 = 2;а2
и т. д. Но, вследствие предположенного, (vx)m, = (vx)m2 = • • ¦; (а)м1==
^=(а)м2= ..., значит, будет ^ = \х2 =..., т. е. не только вдоль
каждой характеристики, но и во всей плоскости будет выполняться
соотношение
vx — ^ТГГ а = const = w*. — Т=ГТ fll>	C5-3)
где vXi и ах суть постоянные значения vx и а на Л. Но тогда урав-
уравнение C3.4) в соединении с C0.3) даст:
dvx . Гх-f-l /	4 1	I I dvx
- = 0.	C5.4)
Таким образом, задача сводится к одному уравнению в частных про-
производных первого порядка, т. е. к системе обыкновенных диффе-
дифференциальных уравнений.
Заметим ещё, что в этом случае не только характеристика Л,
но и вообще все характеристики первого семейства будут прямыми.
В самом деле вдоль каждой такой характеристики будет vx-\~
—|— [2/(-х.— 1)]д = 2Х(на каждой своё к), но, кроме того, повсюду вы-
выполняется C5.3); таким образом, вдоль каждой характеристики пер-
первого семейства vx и а будут связаны двумя алгебраическими соот-
соотношениями, т. е. будут постоянны. Отсюда, вследствие C3.8), сле-
следует прямолинейность характеристик первого семейства. Разумеется,
что vx и а будут, сохраняясь на каждой характеристике первого се-

§ 35]	СЛУЧАЙ ПОСТОЯННОЙ ЭНТРОПИИ ДВИЖЕНИЕ ПОРШНЯ	335
мейсгва, меняться с переходом от одной характеристики первого
семейства к другой, так что характеристики второго семейства бу-
д\ т кривыми [в плоскости (х, ()].
Подобного рода картина будет всегда иметь место при распро-
распространении движения в покоящейся и обладающей постоянным давле-
давлением и температурой среде, заключенной в неограниченный цилиндр
(прямолинейность движений). В самом деле, постоянство давления и
температуры означает постоянство ft и скорости звука (обозначим
последнюю через а0); условие покоя даст 1^ = 0, таким образом,
dxjdt = ±ао = const., лг— +aot-\- const., и мы имеем прямолиней-
прямолинейные характеристики в плоскости (х, t). Если вдоль одной из них
движение начнёт переходить в другую форму, то мы сможем заклю-
заключить, чго в эгом новом движении все характеристики одного кс-
кого-то семейства будут прямыми.
Пусть в неограниченном цилиндре движется по заданному закону
поршень. Предположим, что газ в момент ? = 0 был в покое и
обладал всюду одной и той же энтропией 0 и скоростью звука aQ.
Пусть в начальный момент скорость поршня равна
а затем монотонно убывает. Найдём движение, которое возникнет
при этом в газе «вправо» (т. е. в направлении положительной
оси х) от поршня. Пусть х0 = ОА (рис. 138) есть расстояние поршня
от начала координат в начальный момент.
Все точки оси х, лежащие вправо от А
(точки, лежащие влево от А, нас совер-
совершенно не интересуют — мы изучаем лишь
движение газа вправо от А), имеют одно
и то же значение скорости:
и одно и то же а:
(как точки при ? —0). Возьмём какую угодно точку В вправо от А
на оси х и представим себе, что мы провели из А характеристику
первого семейства, а из В — характеристику второго семейства и
что эти характеристики встретились в точке С. Но тогда, применяя
оперщию з, убеждаемся в том, что скорости в С совпадают со ско-
скоростями в А (или в В); в самом деле, и А и В представляются в пло-
плоскости (vit а) одной и той же точкой А' (рис. 139),—значит, и
характеристики типа м[р' и М'2Р' из операции а пересекутся в этой

336	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОП ДИНАМИКИ	[ГЛ I
самой точке А' (это будут просто характеристики, выходящие из
этой точки). Так как В (и, значит, С) произвольны, то на всей ха-
характеристике, выходящей из А, будем иметь одни и те же значе-
значения скоростей. г»х = 0, а — а0, т. е. мы имеем целую прямолиней-
прямолинейную характеристику первого семейства:
х — х0 — aot.
Это есть та характеристика, вдоль которой покой будет перехо-
переходить в движение. Мы уже знаем, что в плоскости (vx, а) мы будем
при этом находиться на одной и той же
прямой
-а=— -	гай. C5.5)
Х	f. 	 1	X 	 1
Нанесем в плоскости (х, t) закон дви-
движения поршня —пусть это будет линия L.
Возьмем произвольную точку А этой ли-
139	нии и постараемся найти в ней vK и а.
Значение vx находится сразу — скорость
частиц газа, прилегающих к поршню, равна скорости поршня — нам
надо только найти в точке Ах тангенс наклона нашей кривой к оси t:
dfjdt. Чтобы найти а в точке Ах, вспомним, что vx и а должны
быть связаны соотношением C5.5). Достаточно на прямолинейной
характеристике второго семейства, идущей через А', найги орди-
ординату той точки А'у абсцисса которой равна скорости поршня в Ах.
Определив vx и а в Ах, можем построить не только направление
характеристики первого семейства, идущей через А{, но и всю ха-
характеристику (ибо мы знаем, что она прямолинейна) по формуле
х — xAl = [(vx)Al + a Al ](t — tA,).
Вдоль всей этой прямой будет vx = (vx)a, и а = ад1. Заметим, что,
вследствие предпотожения о неположительности производной /', число
(•и-гК+Дд, будет меньше, чем (vx)A -\~ аА = 0 -f- a0 (aAl < а0 вслед-
вследствие наклона характеристики второго семейства, идущей через А');
следовательно, характеристика первого семейства, проходящая че-
через Л,, нигде не пересечется с характеристикой первого семейства,
идущей из А. Подобные рассуждения можно применить ко всем
точкам линии L и можно построить расходящийся веер прямых ха-
характеристик первого семейства с известными на них скоростями. Так
мы узнаем скорости во свех точках плоскости (х, t), т, е. скорости
в любой точке вдоль цилиндра и в любой момент времени Мы мо-
можем изобразить затем в плоскости (х, t) законы движения всех
частиц, т е. провести линии ? = ?(х, t) = const В самом деле, на
оси х достаточно положить 1. = х (начальные координаты), то же

5 35]	СЛУЧАЙ ПОСТОЯННОЙ ЭНТРОПИИ ДВИЖЕНИЕ ПОРШНЯ	337
самое можно сделать на характеристике первого семейства, выхо-
выходящей из А. Затем, пользуясь формулами
2 х + 1
мы можем найти \ во всех точках плоскости. Останется только
соединить линиями точки, в которых \ одинаковы. Задача о движе-
движении будет решена
Несколько слов об аналитическом решении задачи. Для интегри-
интегрирования C5.4) мы должны написать в нашем случае:
dt 		dx
—g— vx + fl0
значит,
\(^tL	^]	C5.6)
где F — совершенно произвольная функция своего аргумента. Мы
должны подобрать эту функцию так, чтобы на поршне, движущемся
по закону x — f(t), имелись данные скорости vx = dfjdt. Это зна-
значит, что надо положить для определения F:
Рассмотрим пример. Пусть поршень движется равномерно замедленно
так, что
Тогда должно быть
обозначая —-^—|- 7" "Г nt2 — aot = r), получим:
И гак,
F A) = — 7
т. е.
Решая это уравнение относительно vx, найдем окончательно:
22 Теоретическая гидромеханика, ч. II

338
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ I
Последняя формула годится лишь до тех пор, пока скорости поршня не
станут слишком велики. Именно, по C5.5) а станет отрицательно, если
*\<0 и К| >
Частицы, прилегающие к поверхности поршня, имеют скорость поршня;
r.t2
значит, если принять для поршня закон х—	^-, то для момен-
моментов t
аа
формула будет неприменима. Позади поршня обра-
зуется вакуум.
Обратимся теперь к более трудному случаю. Попробуем изучить
движение, в которое приходит газ, находящийся между перемещаю-
перемещающимся по заданному закону поршнем и стенкой. Пусть в начальный
момент газ находился в покое (vx = 0) и имел постоянное а = а0,
а поршень движется по закону х = f (t), причем в начальный момент
/'= 0, f@)=x0. Пусть стенка имеет абсциссу xv В плоскости
(х, t) изобразим закон движения поршня L и проведем «линию стен-
стенки» Z.J, уравнением которой будет х = хх. Проведём через точку
A(x = xQ. t = 0) прямую характеристику первого семейства АВХ
до пересечения со стенкой в
точке Вх\ получим
X 	 Xq 	 Cl^t.
Треугольник АВ{АХ будет отве-
отвечать покою. В области между L,
1
L,
д
с,
Рис. 140
прямой АВХ и характеристикой (криволинейной) второго семейства,
проходящей через Вх, будет движение уже разобранного типа с пря-
прямолинейными характеристиками первого семейства. Нанесём на харак-
характеристике ВХВ густой ряд точек Вх, Мх, М2, ..., В (рис. 140).
В плоскости (vx, а) этим точкам буаут отвечать точки В\, М\, /Иг, . ••
прямолинейной характеристики второго семейства, проходящей через
точку @, а0) (в точке Вх еще будет vx=0, а = а0) (рис. 141).
Чтобы найти скорости в точке Сх пересечения с Lx характеристики
первого семейства, проходящей через Мх, обращаемся к операции р.

ij я5]	СЛУЧАЙ ПОСТОЯННОЙ ЭНТРОПИИ ДВИЖЕНИЕ ПОРШНЯ	339
На Lx всюду vx = Q, значит, в плоскости (vx, а) нам придётся
от Мх перемещаться по прямой характеристике первого семейства
до встречи в С] с осью а. Определив таким образом скорость
в точке Ср применим теперь к точкам М2 и Сх операцию а и опре-
определим скорости Р[ на пересечении Р, характеристик М2Рг и С1Р1
[ючкп Р\ найдется в плоскости (vx, а) на пересечении харак1еристнк,
ид)Ш.их из M<z и Сг соответственно]. Дойдя до точки Рп (рис. 140),
применим к Рп и к линии L операцию р и найдём скорость в точке С
я т. д. Легко видеть, что теперь оба семейства характеристик
в (х, t) будут криволинейными.
Изложенный здесь метод графического решения задачи очень
прост и позволяет произвести вычисления с любой точностью. Он
аналогичен тому способу решения плоской стационарной задачи при
помощи характеристик, который мы подробно излагали в разделе Б
этой главы. Однако, в то время как в главе о плоских движениях
мы не имели общих решений, кроме как в случае наличия прямо-
прямолинейных характеристик, здесь в одноразмерной стационарной задаче
можно написать точные решения и в общем случае. Правда, эго
относится лишь к таким газам, для которых х удовлетворяет опре-
определенному соотношению (см. ниже), но, в частности, это отностся
к сл\чаю, когда х=1,4. На это обратил внимание еще Адамар').
Чтобы показать это, возьмём уравнения C3.6) (при & = const.) и
C3.3) и примем в качестве независимых переменных, вместо х и i,
величины vx и а. Используя наши характеристики, мы можем очень
легко выполнить это преобразование следующим образом. Для удоб-
удобства письма обозначим vx через и:
Обозначим, затем, как и прежде,
C5.7)
2
X— 1	Г J
и введём в качестве независимых переменных X и \х. Очевидно, что
6}дрт л — const, вдоль характеристик первого семейства и р. = const.
вдоть характеристик второго семейства.
-Мы можем всегда вернуться к переменным а и а по формулам
') Н a d a m a r d J., Lemons sur la propagation des ondes, 1903.

340	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
Так как вдоль характеристик первого семейства
dx — (a -f- a) dt,
то мы можем написать:
.|? = (и-j-о) .|L.	C5.9)
Вдоль второго семейства характеристик
dx = (и — a) dt,
и мы можем написать
Ж = («-«)"Ж-	C5Л0>
Остаётся вставить в C5.9) и C5.10) значения и и а из C5.8),
и мы получим систему уравнений для определения х и / в функциях
от л и р.:
дх _/*+1 , , 3-% ,д dt
3
9	' 2
' "	C5,11)
2	2
Исключая дг, придём к уравнению
4 ~ 01. д'х ' 2 7. — 1
Если
1 7.+ 1
где m — целое число, то мы получим уравнение Дарбу, которое
интегрируется в общем виде. В частности, при у. = 1,4 мы будем
иметь т = 3, так что наше уравнение примет вид:
Уравнение это имеет общим решением
После того как t определено, х может быть сразу найдено по C5.11).
Эш будет
Произвольные функции А и М, входящие в C5.12), должны опре-
определяться из краевых условий, аналогично тому, как это делается
в классической задаче о струне.

§ %\
ВОЗНИКНОВЕНИЕ И ПЕРЕМЕЩЕНИЕ СИЛЬНОГО РАЗРЫВА
341
§ 36. Возникновение и перемещение сильного разрыва. Пред-
поюжим теперь, что в покоящейся среде, обладающей всюду по-
постоянной энтропией ft и постоянной скоростью звука а0 и заполняю-
заполняюдвижется поршень по закону х — f (t).
щей бесконечный цилиндр,
Пусть, как и прежде,
но в то время, как раньше мы считали, что /' — монотонно убы-
убывающая функция t, предположим теперь, что /" (/) может оказаться
положительной. Для большей ясности предположим просто, что
всегда будет /"(^)>0 (рис. 142). В этой задаче, так же как и
в соответствующей задаче предыдущего параграфа, характеристики
первого семейства будут прямые, и движение может быть определено
и iрафически и аналитически. Однако в то время как характеристики
первою семейства при /" < О станови-
становились, по мере продвижения вдоль линии L,
начиная от точки хо = /(О), всё круче по
отношению к оси х, здесь характеристики
будут становиться всё положе. В самом
деле, точка Ль например, будет иметь
vх > 0 и а > а0, значит,
что и доказывает наше утверждение. Но	Рис. 142.
тогда прямолинейные характеристики пер-
первого семейства, исходящие из разных точек L, начнут, рано или
поздно, пересекаться. Наступит явление сильного разрыва.
Нетрудно подсчитать расстояние от начального положения поршня
До «первой» точки поверхности разрыва и момент возникновения
такового. Для этого достаточно найти предел, к которому будет
стремиться место пересечения характеристики, идущей из А (рис. 142),
и характеристики, идущей из Av когда Л, стремится к А,
Для первой из этих характеристик имеем:
= aot.
Для второй
где Ах0 есть разность абсцисс Л, и Л, а М— разность ординат
в этих точках. Отсюда найде'м для точки пересечения этих прямых:
t ~ Z^1xq +• [д (л'о + Лл"°' Af) -1- vx ixo + Ьх0, AQ] А^ х __ х _|_ а ^
iij. -|- а (jf0 + A.v0, \t) — аа	'	о i о ¦

342
Но
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
1ГЛ. t
1+1
vi	2	2
и мы получим в пределе для момента Т возникновения разрыва
2а0 ь
а для положения X:
Т =
Х-
t
М,
Появившийся таким образом разрыв усложняет картину явления
в двух направлениях. Во-первых, он заставляет искривляться все
характеристики первого семейства [после того, как они пересекут
характеристику второго семейства, идущую через точку {X, Т)],
во-вторых, и это существеннее, бла-
благодаря тому, что скорость N пере-
перемещения поверхности разрыва бу-
будет, вообще говоря, переменной,
Lt поверхность будет оставлять позади
себя область переменной энтропии.
Поэтому формулы § 35 и прямо-
прямолинейные характеристики в плоско-
плоскости (vx, а) неприменимы, и нам надо
обратиться непосредственно к фор-
~х мулам C3.11) C3.12), C3.13) из
§ 33.
Покажем, как решается графи-
графически задача о движении разрыва,
если разрыв возникает уже при < = 0 и у самого поршня. Это будет
в случае, если поршень в начальный момент получает сразу ско-
скорость vx, отличную от нуля. Пусть некоторое время поршень дви-
движется с этой постоянной скоростью, а затем скорость поршня на-
начинает непрерывным образом меняться по произвольному закону.
Изобразим, как всегда, закон движения поршня L в плоскости (х, f)
(рис. 143). Обращаясь к плоскости (vx, а), найдем на кривой
четвертого порядка C4.9) значение а = а1, отвечающее значению
vx = v1 (С на рис. 144). По формуле C4.8) мы можем найти теперь
Рис 143.
'1 Мы предполагали при выводе, что «первая» точка разрыва лежит на
«первой» характеристике. Условие это может и не выполняться. В общем
случае первую точку надо искать на огибающей системы прямолинейных
характеристик.

al aO
x—1
§ Зо]	ВОЗНИКНОВЕНИЕ И ПЕРЕМЕЩЕНИЕ СИЛЬНОГО РАЗРЫВА	343
JV—скорость перемещения поверхности разрыва:
Отрезок АС прямой
будет представлять отрезок линии Lx, изображающей перемещение
поверхности разрыва около точки А. Пусть В есть точка L, после кото-
которой L начинает искривляться; проведем прямую характеристику первого
семейства ВС до пересечения с проведённым уже отрезком АС.
В прямолинейном треугольнике ABC движение происходит со ско-
скоростью vx=^v1 = const. В области, ограниченной прямой ВС, криво-
криволинейным отрезком BD линии L и криволинейной характеристикой CD
Рис 144
второго семейства, движение найдется так же, как это было сделано
в предыдущем параграфе (прямолинейные характеристики первого
семейства и т д.). На линии CD нам будут, таким образом, известны vx,
а и с. Нанесем на CD густой ряд точек: Mv М2, . ..; из точки Мх
проведем характеристику первого семейства (элемент ее) МХЕ, исполь-
3Уя формулу
dx	,
io пересечения с продолжением СЕ прямой АС. Чтобы найти
скорость в точке Е, проведём из точки М\ (рис. 144) [в плоско-
плоскости (г\, а)], отвечающей точке Ж, плоскости (х, /), прямую ха-
характеристику первого семейства до пересечения в Е' с нашей кри-
кривой четвертого порядка. Определив координаты Е', т. е. найдя зна-
ч кия vх и а в точке Е, можем затем построить новую скорост>
поверхности разрыва в Е по формуле C4.8) и провести из точки Е
"°счй, не яв-пгощийся продотжечием прямой СЕ элемент линии раз-
Рнча Построим теперь элемент характеристики второго семейства,

344	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
идущий из М2 по формуле
и элемент характеристики второго семейства, выходящий из Е, по
формуле
Было бы ошибочно искать скорости в точке Р1 пересечения этих
характеристик как координаты точки пересечения в плоскости (vx, a)
прямых:
vx — (vK)E= -_т (а — пе)> vx — («\)ж, = ~ тиу (а — aMl);
в самом деле, уже начиная от точки С, линия разрыва начнет искри-
в тяться, т. е. /V начнет меняться со временем, а это, как мы знаем,
приведет к гому, что разные точки получат разную энтропию; нельзя
будет больше считать dbjd% = О, а следовательно, нельзя пользо-
пользоваться соотношениями C5 1), C5.2). Мы должны обратиться к общим
формулам C3.11), C3.12) и искать Р\ на пересечении прямых
2 аР Ьп
vx — (ух)р	-р {а — aF) =	— 1п -~-.
Значение %Е находится по формулам C4.6), C4,7), ибо TV в ? мы
уже знаем. Значение $м2 будет тем же, что и постоянное для всего
криволинейного треугольника ACD значение ft. Чтобы найти $рг
найдем сперва, чему будет равно \ в точке Рх; по C3.12)
/	!_ i±l\
Д? = Ь - \Е = - \а0 "-1 а <-> )в (tPl -~ tB),
причем в качестве «исходной» скорости а0 в точке Е можно при-
принять просто значение аЕ, что же касается ЧЕ> то это будет просто
координата хЕ (закон движения представляется для всех точек между
линией ALX и осью АХ прямыми, параллельными оси t; линии
закона движения разрыва не терпят, а лишь изламываются при
переходе через ALX). Зная ?р( и вспоминая, что & зависит лишь
от ?, мы можем затем найти ftp, простым интерполированиеч (по &я
и Вж,).
§ 37. Односторонний взрыв. Плоский, цилиндрический и
сферический взрыв без противодавления. Сферический взрыв
с противодавлением. Мы уже упомянули в § 2 этой главы, что если
\иювия B 15), B.16) и B.17) не выполнены, то возникает взрыв.

§ 37]	ОДНОСТОРОННИЙ ВЗРЫВ	345
На примере одноразмерных движений покажем, как это явление
будет протекать. Пусть в начальный момент (Y —0) по обе стороны
от плоскости х =0 заданы значения гидродинамических элемен-
элементов vx, р, р; для простоты предположим, что для х < 0 в началь-
начальный момент всюду:
vx — const. = vx; p = const. = pp р = const. = px,
и для х > 0:
vx — const. = v2, P = const. = рг\ р = const. = р2,
и эта шестерка чисел совершенно произвольна (р и р лишь поло-
положительны), т. е. их значения не удовлетворяют уравнениям B.15),
1,2.16) и B.17) ни при каком /V [например, пусть vl = v2 = 0,
а р2фрг — тогда B.15) не выполняется]. Сразу же от того места
(х = 0), где был в начальный момент разрыв, побегут три поверх-
поверхности разрыва, одна из них — крайняя «слева»—будет распростра-
распространяться по среде имевшей в начальный момент vx = vv . . ., другая —
крайняя «справа»—будет распространяться по среде, имевшей при
t — 0 vr = v2, ... Наконец, средняя будет поверхностью стационар-
стационарною разрыва и она, перемещаясь в пространстве, не будет распро-
распространяться по частицам, отделяя всегда газ, обладавший значениями
элементов v2, р2, р2 от газа, имевшего значения элементов vl, p{, р1.
В момент времени, бесконечно близкий к начальному, рассмотрим
все четыре области, таким образом образовавшиеся. Назовем через
v'{, р'у pj значения i идродинамических элементов между крайней
«слева» и средней поверхностью разрыва; пусть v'2, p'y р'2 — значе-
значения элемешов между средней поверхностью разрыва и крайним
справа разрывом Тогда, вследствие стационарности средней по-
поверхности разрыва, давление р' на этой поверхносш разрыва не
lepniir, так чю
Р\~Р2 = Р'\
при лом будет
(епи / одинаково в обеих средах). Кроме того, так как 6 — 0, то
v'2 — v'^, пусть это б)дег v'.
v' = v[ = v'2.
H E Кочни показал, что могут быть четыре случая: 1) обе край-
крайние поверхиосщ суть поверхности сильного разрыва (разрыв давле-
нч'), 2) обе крайние поверхности разрыва суть поверхности слабого
разрыва (характеристики); 3) правая крайняя поверхность есть ха-
характеристика, левая крайняя — сильный разрыв; 4) левая крайняя
"o	характеристика, правая крайняя — сильный разрыв.

346
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ I
В качестве примера рассмотрим подробнее, чго произойдет, если:
v1 — v2— О,
причем
Pi > Ръ
будем искать решение задачи, как в случае 4.
Крайняя справа (рис. 145) поверхность разрыва будет переме-
перемещаться в среде с величинами р2, р2, fJ с постоянной, подлежаще]
определению скоростью N (рис. 146, линия О А); средняя поверх-
поверхность будет перемещаться с постоянной скоростью v', также за-
заранее неизвестной (линия 05); наконец, слабый разрыв будет бежать
/ У V
справа налево с заранее известной скоростью а, — 1/ — (линия ОС).
Между этой последней поверхностью и поверхностью стационарного
разрыва (средней) будет осуществляться непрерывный переход ско-
скорости vK движения жидкости от
значения 0 до значения v', при-
причем, так как крайняя характери-
характеристика прямолинейна, то и все
характеристики, выходящие из
точки О, будут прямолинейны
(пучок прямых, обозначенных
пунктиром). Нам остается только
связать семью соотношениями
¦<* семь постоянных величин:
Рис 146	р2, &2, Л', р', V, pj, Ь[.
Прежде всего, так как при переходе через поверхность слабого раз-
разрыва величина Ь измениться не может, можно считать, что
>;=»..
тогда по C7.1) имеем:
C7.2)
C7.3)

§ 37]	ОДНОСТОРОННИЙ ВЗРЫВ	347
Далее, так как характеристика второго семейства ОС прямолинейна
и {>; = const., то мы можем считать, что соотношение
2
vr -4	г о- ~ const.
х	У. — 1
выполняется не только на каждой характеристике первого семей-
семейства в углу СОВ, но и во всем этом углу. В частности, для ли-
линии ОВ плоскости (х, t):
где
п'2 — v Р'	Л2 — v Р^
Pi	Pi
причем, по определению Ь,
р' = $\?'\-	C7.5)
Наконец, мы имеем условия на линии разрыва (ОА). Здесь
v = 0, р ~ р р = рг В =N — v = N,
и по C4.2)
= Р2~р',	C7 6)
= p'2(N—v').	C7.7)
/ (х+1)р2-(х-1)р2
Уравнения C7.2), C7.3), ..., C7.8) и позволят нам определить
семь неизвестных величин. Чтобы найти движение внутри угла СОВ
плоскости (х, t), нам надо написать вместо C3.4), по аналогии
с уравнением C5.4):
dvx , /-/.+ 1 .. . \ dv,
и искать решение этого уравнения, зависящее от отношения x/t.
Это будет
	 2а, , 2 х_
Изменение скорости от 0 до ¦»' происходит в ?_COD. Именно, на
линии ОС имеем x\t = — av т. е. vx = 0, что же касается наклона
линии OD, то он найдется из условия

348	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
после того как v' уже известно. Внутри /_ DOB имеем постоянную
скорость v', посюянное давление р' и постоянную плотность р'.
Дтя того чтобы найти v', p' и р', заметим прежде всего, что
все эти величины в отрицательной области MoiyT быть выражены
через р2, Рг и 1>2 и через N. Действигельно, по C4.5) имеем
2	/	а2,
тогда по C7.6) и C7.9) имеем
а по C7.7) и C7.9) можем написать
х + 1 /	2 4\~1
Таким образом, остаётся только найти N. Для того чтобы это сде-
сделать, вспомним сперва, что v' и а'х связаны соотношением C7.4).
С другой стороны,
так что мы можем написать по C7.4):
х-1
Остается только вставить в это равенство выражения для v' и р'
из C7.9) и C7.10), и мы получим уравнение для определения не-
неизвестной величины N:
Г а, х-1 N ( а20 \12 Я, Г 2х / N \2
. C7.12)
Отметим еще формулу, по которой можно вычислить Ь'о. Комбинируя
C7.10) и C7.11), получим
N2 х-Г
¦1
C7 13)
Поверхность сильного разрыва бежит со скоростью N, оставляя за
собой область со значениями потенциальной температуры %'2 постоян-
постоянной, но отличной от Ь2. Позади поверхности сильного разрыва дви-
движется со скоростью v' поверхность стационарного разрыва, после
прохождения которой & вновь меняется скачком от значения \>'2 до

§ 37)
ОДНОСТОРОННИЙ ВЗРЫВ
349
значения 9,. Простота задачи, только что нами рассмотренной, происте-
проистекает из того, что среду мы считали безграничной. Рассмотрим ещё
с.пчай, когда в начальный момент будет p = pv р —р(, v = 0 не для
реей бесконечной полупрямой (х < 0), а только на отрезке:
	/ <- v <¦ 1
На всей остальной прямой пусть будет вначале p = ph р = р2, г» —0,
причём, как и прежде, рх > р2.
Возникают две поверхности сильного разрыва, бегущие одна
вправо, другая влево (рис. 147, линии ОХА, О-^А ; сзади них дви-
движутся поверхности стационарного разрыва (ОХВ, О\В'). Характери-
Характеристики 2-го семейства A-го се-
семейства), выходящие из О, (OJ), —
это пучок прямых. На характе-
характеристиках ОгС и О'ХС ("так же, как
и во всём треугольнике О\СОХ),
всюду будет а = av v = 0. Внутри
криволинейного треугольника
СВОХ, сторонами которого будут
криволинейная характеристика
1-го семейства СВ, прямолиней-
прямолинейная характеристика 2-го семей-
семейства OjC и закон движения ста-
стационарного разрыва (прямая) 0,5,
движение будет происходить
в точности по законам, оплсанным выше для случая бесконечной
среды. Аналогичное можно сказать про треугольник СВ'о[.
Зная движение на криволинейных отрезках СВ, СВ' характе-
характеристик обоих семейств, выходящих из С, мы можем теперь найти
Движение в криволинейном четырёхугольнике СВЕВ'. Движение на
СВ и С В' может быть точно найдено (с помощью формул этого
параграфа). В частности, легко получается, что:
*—-
на дуге СВ характеристики 1-го семейства имеем
, L (\ x—1 (x\-
2 x-1
X— 1
= const.,
на дуге СВг характеристики 2-го семейства будет
¦ 1 X \ 2 х-1	а,	,
— —)	, М-=	Ц-= const.,
л,/	г	х—1
пРичём /. и A определены по C5.7).

350	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ IАЗОВОИ ДИНАМИКИ	[ГЛ I
Предположим далее, что х=1,4. Тогда мы можем использовать
формулы C5.12), чтобы найти А (к) и М(\ь) по двум условиям, за-
записанным нами на дугах характеристик СВ, СВ'. Тем самым мы
опредечим движение внутри всего криволинейного четырехуголь-
четырехугольника СВЕВ', а значит, в частности, и на характеристиках BE и В'Е.
Теперь мы должны перейти к определению движения в четырех*
угольнике ABEF (A'B'EF'). Здесь нам приде'тся сопрягать решения
вдоль заранее неизвестной линии BF (B'Fr), определяющей закон
движения стационарного разрыва. Так как в каждой из областей ВАЕ
(В'А'Е), BFA (B'F'A1) величины % ещё остаются постоянными, то
мы можем вновь воспользоваться формулами типа C5.12) для каждой
из этих трехугольных областей. Начиная от точек А (Л'), линия,
представляющая закон движения ударной волны, начинает искри-
искривляться; $2 становится переменным и точных решений, вообще говоря,
не будет. Решение можно вести дальше аналогично тому, как это
описано в § 36
Если устремить L к нулю, мы придем к задаче о плоском взрыве.
Замечательное точное решение этой задачи (с меняющейся энтропией)
удается получить, если краевые условия C7.9), C7.10), C7.11) взять
в приближенном, применительно к «сильному взрыву», виде :).
Именно, при «сильном взрыве» можно пренебречь давлением перед
ударной волной по сравнению с давлением за ударной волной. Это
исследование взрыва «без противодавления». Пренебрежение это экви-
эквивалентно пренебрежению величиной a2jN по сравнению с единицей.
При этом пренебрежении C7.9), C7.10), C7.11) примут вид
v'^^-N,	C7.14)
C7.15)
C7.16)
Конечно, формулы C7.14)—C7.16) годятся лишь для начальной ста-
стадии возникновения взрыва; на больших расстояниях от начального
положения давления за и перед ударной волной выравниваются; кроме
того, формула C7.16) не очень точна, так как она получена путём
пренебрежения в C2.11) членом _ . (—- \ = 5 [—-Г (если -/=1,4)
по сравнению с единицей.
Однако для первых моментов после начала взрыва можно говорить
о большой точности выполнения условия C7.14)—C7.16). Аналитиче-
') Ср аналогичные приближения в стационарном случае, которые были
нами приняты в § 24 при рассмотрении диссоциирующегося газа.

ГЛ
ОДНОСТОРОННИЙ ВЗРЫВ
351
ское решение задачи о взрыве без противодавления было дано впер-
впервые Л. И. Седовым A946) !). Изложим решение Седова.
Будем искать автомодельное решение уравнений C3.2), C3.3),
C3.4):
_2
()'в(H. а=уД(Х).	C7.17)
где X — безразмерный параметр
C7.18)
C7Л9)
?t~2
ык что b — постоянная с размерностью L?t~2. Мы увидим впослед-
авии, как эта постоянная выражается через начальную энергию Ео
взрыва и через плотность р2.
Задача сводится к решению системы обыкновенных дифферен-
дифференциальных уравнений. Именно, уравнение C3.2) приведёт к равенству
-	C7.20)
= 0. C7.21)
Уравнение C3.3) приведёт к соотношению
Наконец, уравнение C3.4) даёт нам равенство
6 ХА™—***
¦i- — 1	dX у. — 1 0
1
6
C7.22)
или, если исключить 6 с помощью C7.20):
dV 2 ЛОГ, ,
4
3
C7.23)
Нам надо решить систему обыкновенных дифференциальных уравне-
уравнений C7.21) — C7.23) содержащую две искомые функции А и V.
По отношению к dV/dX и dAjd'k уравнения наши представляют си-
иему двух линейных алгебраических уравнений. Решая эту систему,
') Постановка задачи и численное решение полученной системы уравне-
й независимо от Седова дано Тейлором A941, 1947).

352	TF0PETH4FCKME ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. I
'¦аПдём
3/. ^ =	±	Йг"^	'—.	C7.24)
(V-*) -Л»
C7.25)
Если принять в качестве независимой переменной вместо X функ-
функцию К, мы получим без труда уравнение
dA
~dV"
V--
C7.26)
не содержащее \. После того как А в функциях от V будет из
этого уравнения определено, останется выполнить квадратуру в урав-
уравнении C7.24), чтобы найти X в функциях от V, а затем найти 6 из
уравнения C7.20), которое можно записать в виде:
rflne 2 V—\	\ »,	C7 27)
dV ' 3	2^

Наша система содержит три дифференцирования. Три краевых усло-
условия мы получим, привлекая равенства C7.14), C7.15), C7.16), кото-
которые должны выполняться на поверхности сильного разрыва. Равен-
Равенства эти согласуются с нашим решением C7.17), C7.18), если счи-
считать, что поверхность разрыва перемещается так, что на ней всегда
>.==: const. He нарушая общности, мы можем положить на поверх-
поверхности разрыва	\—\	C7 28)
(при этом параметр Ь остаётся подлежащим определению). Поверх-
Поверхность разрыва перемещается, таким образом, по закону х — х* {t),
где
_1 1	C7.29)
x*(t) = b 'Ч'6
вторая поверхность разрыва движется по закону х* = —Ь 3
При этом N найдётся в виде Ш~ —~)
N = ~b H з=44--	C7.30)
О	О t

<S Ч7|	ОДНОСТОРОНННП ВЗРЫВ	353
Посмотрим теперь, как можно согласовать наше решение с усло-
условиями C7.14) — C7.16) при Х=1 (на поверхности разрыва). Сопо-
2 2 х1
ставление с C7.14) нам даёт x*jtV(l) =—-т-у у-г-1 значит, нам
достаточно положить
Комбинируя C7.15) и C7.16), найдём затем L.K-=aA (~\2А2(\)
2A) 4 ( \2
2v.(y.—1) 4 ( х\2
irqn^-9l—) ¦ откуда
A) = -
Наконец, из равенства Э- —^/"р получим
Таким образом, мы должны лишь при отыскании наших решений
удовлетворить краевым условиям C7.31)—C7.33) и сопряжение будет
достигнуто.
Остаётся ещё найти значение параметра Ь. Потребуем, чтобы
полная (кинетическая и внутренняя) энергия оставалась постоянной,
равной начальной энергии Ео, выделяющейся при взрыве. Это зна-
значит, что
2
2 f ^fdx + i f Ci>?TR dx = E0= const. C7.34)
о	u
1	2	/.
Так как р = (у)*'1 о711"»"^", Т=-~а2, то, используя C7.17),
C7.18) и переходя к независимой переменной ^ по C7.19), получим
/
6 "-1
1	J	w
C7.35)
Равенство C7.35) позволит определить b по заданному ?"„, после
того как V, A, G известны.
Заметим, что в то время как V и А не зависят ни от каких
параметров [как это следует из уравнений C7.21), C7.26) и их
кРаеаых условий C7.31), C7.32)], функция б зависит от р2. По C7.33),
есл» принять в расчёт уравнение C7.27), функция 6 будет пропор-
23 Те,
оретическая гидромеханика, ч, II

354	TrOPFTHMECKHE ОСНОВЫ lAJOBon ДИНАМИКИ	1ГЛ, 1
циональна величине р2 ж . Поэтому интегралы из C7.35) будут
пропорциональны первой степени р2, и мы можем написать
6 = а — ,	C7.36)
где у — число, зависящее только от /..
ОсI,к гея тотько решить уравнение C7.26).
Особыми точками уравнения C7.26) в плоскости (V, Л) будут
точки с координатами: @, 0), B/3, 0), A, 0), B/Зх, оо), B/3, со). По
Счову надо выбрать ту ветвь решения, которая проходит через
точку B/Зх, со), как единственную, с помощью которой можно со-
сопрячь движение и покой (с переходом через подвижную поверхность
разрыва).
Седов нашел замечательное решение уравнений C7.26) - C7.28),
отвечающее этой ветви и удовлетворяющее краевым условиям
C7.31)-C7.33). Оно имеет вид:
¦~"?")(^г"~ 0 - C7-37')
_3 '-'	5/-4
C7.38)
у.	2-3U
-f)'-2. C7.39)
Подставляя C7.37)—C7.39) в формулу C7.35), получим при /. = 1,4
для а величину порядка 0,6. Уравнения C7.37)—C7.39) вместе
с формулами C7.18), C7.19), C7.36) полностью решают задачу
о плоском взрыве без противодавления.
Аналогичным образом Седов построил решение для цилиндриче-
цилиндрического и сферического взрывов. Покажем, как эти решения строятся.
В том случае, когда движение зависит лишь от расстояния г от
оси z цилиндрической системы координат и от времени, условия
¦адиабатичности, уравнение непрерывности и уравнение движения при-
примут вид:
_
dt г vf IF "+" T^T п Tr ~~ Ч^Т ~ЬТ

§ 37]
ОДНОСТОРОННИЙ ВЗРЫВ
355
В случае же, когда движение зависит лишь ог времени и от рас-
1.ЮЯНИЯ R от центра сферической системы координат, мы получим:
db_
"dt
Vr dR ~
•л - 1
Ov
а
R
dR
dt
da
da
~dR
da
2a v
К — I
a2 d\nb
Оба эти случая можно объединить с плоским случаем и уравнение
адиабатичности записывать всегда в виде
—г-4- и
дЬ
— О,
C7.40)
[где и — скорость (vK, vr или vR), а х — координата (х, г или R)],
а уравнение неразрывности — в виде:
du . 2 / да , да
t ' дх
а

дх ' у. —
аи
—
a:
/о 7 ...
C7.41)
(ч — 1 для ппоского случая, ч — 2 для цилиндрической и v=-3 для
сферической симметрии); уравнение движения запишется в пиде:
ди . ди
~3/ I	А 77 "
Движение ищем всегда в форме:
да
din»
C7.42)
C7.4,3)
Решения этой формы действительно удовлетворяют системе C7.40)
C7.42); аналогом уравнению C7.24) будет теперь уравнение
— v] A2
-. C7.44)
сто уравнения C7.26) теперь будет иметь место соотношение:
=- л
__!_) |к^-
C7 45)
23*

_ 2 7—1	\V~ ч + 2
dV	'-IT-	"	ЛТ I^T	1\ (I?
356	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	(ГЛ. I
Вместо уравнения C7.27) получим
О
C7.46)
Заметим теперь, что в формуле C7.9), дающей условие на поверх-
поверхности разрыва, v' имеет смысл нормальной к поверхности разрыва
скорости (см. § 2 этой главы). Поэтому при отсутствии противо-
противодавления мы опять можем применить краевые условия C7.14)—C7.16),
причём под v' можем разуметь во всех случаях величину и после
скачка. Вновь считаем, что на скачке Х=1, так что закон движе-
движения x*(t) поверхности скачка будет иметь вид:
Тогда
9 rv
дг — __?	_
v + 2 t '
и мы получим
О /v 	 1 \ .,	ч
C7.47)
Р2
Параметр Ь определяется вновь из условия сохранения полной энер-
энергии (формула типа C7.34)), которое в цилиндрическом случае при-
приведёт к соотношению
х*	х*
I" tg-2nxdx-\- f T^rT2^x2dx = ?0 = const., C7.48)
о	о
а в сферическом случае —
X*	X*
f ^- 4тсд;2dx + У ~Т 4тсд;2 dx = ?0 = const. C7.49)
о	о
Точное решение C7.45), удовлетворяющее C7.47), имеет вид
у г 1——Z	у |
A2==lL=±_Sl±2 	1.	C7.50)
x(v+2)

§37]	ОДНОСТОРОННИЙ ВЗРЫВ	357
Внося А2 из C7.50) в уравнение C7.44), легко приведём последнее
к виду
d\n>. _ 2 (х,— l)(v+2)
~~~dV V	+2( 1)
Наконец, комбинируя C7.46) и C7.50), будем иметь
2 2(%

dV ~ V „+2(«.— 1)	2 ~г~~^Г7 2
*B + >) *(+2)
—^C-у2 —8v+4)+4v(v —2)
C7.52)
Элементарные квадратуры завершают решение задачи. Постоянная Ь,
как и прежде, может быть представлена в виде Ъ = аЕ0/р2, причём
a?siO,8 для цилиндрического случая и а яь 1,175 для случая сфе-
сферического.
Особенностью всех приведённых здесь точных решений является
то, что они дают в центре (х = 0) значения р = 0, Г=оо (рфО),
что следует непосредственно из вида соответствующих формул
(особая точка V — —/ _±-2\ ' ^ == °°) •
Решение Седова хорошо согласуется с экспериментом. В случае,
когда противодавлением нельзя пренебречь и- приходится пользо-
пользоваться точными формулами C7.9) — C7.11), автомодельного реше-
решения больше не существует. Случай этот можно рассчитать численно,
построив соответствующие конечно-разностные уравнения и выбрав
расчётную схему. В качестве примера приведём путь решения
полной задачи для случая сферической симметрии, предложенный
в работе Д. Е. Охоцимского, И. Л. Кондрашевой, 3. П. Власовой и
Р. К. Казаковой1).
В качестве независимых переменных введём лагранжевы коорди-
координаты: х — время и % — расстояние от начальной точки взрыва.
Уравнение C7.40) примет теперь простой вид
¦д^= 0 или й = &(?)-	C7.53)
')Охоцимский Д. Е., Кондрашева И. Л., Власова 3. П.,
^ а з а к о в а Р. К., Расчёт точечного взрыва с учётом противодавления,
•РУДЫ Матем. нн-та им. В. А. Стеклова, 1957.

358	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ Г43ОВОЙ ДИНАМИКИ	[ГЛ I
Вид функции 8 (X) надлежит опредечить. Вместо уравнения C7 41)
имеем уравнение неразрывности в чаграпжевых координатах.
дх _ ? р2
д- ~ х2 р '
где, как и прежде, р2 — начатьная пчогность среды, предполагаемая
постоянной. Выразив р через а и Ь, поучим
При этом
г) у
¦^¦г = «	C7 55)
Наконец, уравнение C7.42) можег быть приведено к виду
—Y^ = 0 C7 56)
В качестве искомых функций фигурируют «(?, т), а ($, т), л* (^, т)г
Ъ (?) Движение должно сопрягаться с покоем путем перехода через
поверхность разрыва, при этом должны выполняться условия C7 9),
C7.10), C7.11). С помощью и, а, Ь мы представим эти устовия
в виде:
и	2 N	4
C758)
4 ,
2 * C7.59)
1 х—1 Л
Выберем теперь начальные данные Мы примем что д ш малого
промежутка времени от начала взрыва до некоторого момента т0
процесс можно считать автомодельным, т е. можно пренебречь
противодавлением. Решение дтя такого движения нами уже изчожено.
Тогда нам предстоит решить следующую задачу Найти гидродина-
гидродинамические элементы в части плоскости (с, t), ограниченной неизвестной,
подлежащей опредетению, линией ВС (см рис 148) изображающей
закон движения ударной волны (на этой линии должны удовтетво-
ряться условия C7 57) — C7 59)), отрезком прямой АВ (~ = -0~)
(здесь все искомые функции нам известны) и осью симметрии с = О
(здесь и = О = л;). Прежде чем приступить к изложению схемы

8 57]
ОДНОСТОРОННИП ВЗРЫВ
359
решения задачи, рассмотрим поведение искомых функций на «началь-
«начальном» отрезке АВ. Для этого обратимся к формулам C7.50), C7.51),
C7.52) при V —3. При х = 0 (т. е. ? = 0) авгомолетьные решения
«. 1Я а и 0 обладают особенностью. Последняя отвечает значению
9	2
у ——
т. е. при
члсги V и /. будут связаны соотно-
соотношением
2
= 3 V =-=—. В силу C7.51) главные
0\
_2_
Ъ'1-
j 1-2)
5G-1)
пли, по C
7A3X0(V-^) = x
2/. + I
х-1
закреплённом т). Но тогда,
по C7.50), имеем
2ч_1
О (Л2)
и, по
5х-2 1
Рис. 148.
C7.52), 0(S)=0(l/-
5у-2
	 у /- — 1 /.
¦ Обращаясь теперь
к C7.54) и C7.55), мы можем определить характер зависимости 9-
от ? па отрезке АВ. Именно, привлекая C7.42), имеем сперва
ос:.	о	q	9-/4-1	Я
7.-1
Таким образом, по C7.54),
О (а2) = х
2--
z-1
X
U -
-2
Z+L
где С — некоторая постоянная. Отсюда получим
л; = const. S " .
Определив, таким образом, асимптотическую зависимость х от I
л ш точек, прилегающих к центру (отрезок АВ), мы найдём, далее,
'¦го вблизи центра
= const.?
а2 = const.?
« — const.
C7.60)
Подготовим теперь нашу систему уравнений для расчёта.
Заметим сперва, что уравнение C7.55), если его продифферен-
продифференцировать по ? и привлечь C7.54), приведёт к соотношению:
/	2
2 да	ди хг (Ьг\х-х / а х~7=\ 2аи	m r]

360	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ. \
Будем теперь искать линейные комбинации 9 и f от наших функ-
функций а и а по формулам:
Введем ещё безразмерную координату ?' = ?Д2 и безразмерное время
г/т2 —т', причём примем
что же до выбора ?2< т0 е^ мы определим из рассмотрения полных
энергий — формулы C7.49). Можно положить
= Е. т. е. Ъ = Е
где Е = аЕ0, а а — параметр, введённый выше (а = 1,175 при ж = 1,4).
Складывая уравнения C7.56) и C7.61), получим после простых
преобразований
&	?	1|(?H.	C7-63)
где
C7.65)
C7.66)
Вычитая из C7.61) уравнение C7.56), получим аналогичным образом
?-^Ж+А+У?Й = 0'	C7-67)
Наконец, уравнение C7.54) примет вид
Теперь искомыми функциями будут ср. ^, &, Jf и для их определе-
определения служат четыре уравнения: C7.63), C7.67), C7.68) и C7.53).
Краевые условия C7.53), C7.57) запишутся теперь в виде:
Третье условие, C7.59), остается без изменения.

37]
ОДНОСТОРОННИЙ ВЗРЫВ
361
Опишем схему численного интегрирования, составленную упо-
упомянутыми выше авторами применительно к счёту на электронной
вычислительной машине. Предварительно сделаем ещё одно замечание.
Определяя функции ср и 47, мы имели дело с безразмерными функ-
функциями а/а2, и\а2, $/Ь2> сами функции ср, 47 тоже безразмерны.
В качестве X и х' входят безразмерные величины. Поэтому все
наши уравнения и краевые условия будут носить универсальный
характер.
Приступая к численному интегрированию, рассмотрим плоскость
(;', т') (рис. 149). Разделим отрезок на равные интервалы Ь?, и про-
проведём через точки деления прямые %' = const. Шаг по времени будем
выбирать так, чтобы было
Дт —Д|—р C7.71)
где N—скорость переме-
перемещения ударной волны.
Таким образом, шаг по
времени будет меняться,
в то время как шаг по %'
остаётся одним и тем же.
Перенумеруем горизонталь-
горизонтальные линии т' = const., на-
начиная с прямой АВ; пере-
перенумеруем вертикальные ли-
линии ?'= const., начиная с линии ?' = 0. Будем обозначать значе-
значения какой-то функции, например ср, в узлах нашей сетки путем
постановки номеров прямых, проходящих через эту точку. Так,
»? означает, что ср берётся на пересечении 1-й вертикальной линии
и я-й горизонтальной.
Предполагаем, что нам известны значения всех функций (в том
числе и N/a2) вплоть до я-й горизонтальной линии. Как найти
значения наших величин на я-}-1-й горизонтальной линии?
Заменим сперва в уравнениях C7.68), C7.67) частные производ-
производные конечными разностями по формулам:
Рис. 149.
d<f\n+l
4
I
C7.72)
._1Ц?±2_}.
C7.73)
Аналогично запишем dW/dlr, dWjdx', Производные эти записаны,
как видно, в центре соответствующей клетки. Тогда мы получим

362	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ 1АЗОВОИ ДИНАПИКИ	[ГЛ 1
следующие разностные уравнения:
„Я-Ч I ,„« + 1	,„Я	,„Я	nj-L „П	| „«4 1	„Я	,.«-1
2
^
V( .
4 2 (AH- n" i=0, C7.74)
Дх	, I	Л;	'
2
1
+ 2 (А +К') ^=0, C7.75)
где V— V-~т (-„-1 (причем, в силу C7.53), дй/d;' зависш 1ишь
от номера I, но не зависит от п).
Уравнение C7.75) решим относительно Ч'« г 1; получим
W?+i = AX"l + Bt,	C7.76)
где
жм1+й (ж,Д~-?т	C7-77)
/ я -	Л "!	и -
5i = ^H, — ЛД'/— 2 /ж" 1+41) (A+V')"iA=. C7 78)
V м	/	м-2
Будем считать пока известными ветчины (/И, А, V) ~, а ыкже
'¦¦7
значение величины Дт (Д| — стандартно). Тогда Л() Вг будут из-
известны. Пусть последняя «справа» точка га-й горизонтальной линии
(т. е. точка, отвечающая поверхности разрыва) имеет номер «й». Ясно,
что Лг, Bv будут иметь смысл лишь до тех пор, пока /+1 к. Это
же относится и к формуле C7.76). Применяя формулу C7.76) сперва
для i-\-\=k, потом для i~\-l=k — 1 и т. д., получим
или
т. д.

Г]	ОДНОСТОРОННИМ ВЗРЫВ	363
образом, п\ гем рекуррентных соотношений мы можем вы-
1 ikhm
рази 1Ь
41.pei посреаство xl t ' (m твесшая ветчина).
Именно,
Ч, —A,4/, -j- bt,
i le
al = Alal + v	C7.79)
*« = ЧГ?Т1 — Л, («f — A, + 1) - c«.	C7.80)
1 /	I	V -1
с , br ct все последовательно определяются, причем ak + l=l, bk + i = 0.
Так как по определению C7 77) величина At всегда будет меньше
единицы, то коэффициенты а1 будут по C7.80) убывать к центру
(к осп т') и при достаточно большом числе расчетных точек мы
можем считать ао^О. Но тогда в центре будет ^'+1<гай0, причем,
TiK как па оси ¦:'(?'= 0) имеем а = 0, то по C7.62) мы можем
<?^ = bQ.	C7.82)
Но теперь мы можем обратиться к уравнению C7.74) для определе-
определения значений ср^-1' во всех остальных точках соответствующей гори-
зонгаш. Получим сперва
чП\ = $-А№+1-Я+1)-с,-	C7-83)
Из этого равенства без труда получим значения <р^+1 во всех точках
п -|- 1-й горизонтали, за исключением точек, лежащих на линии
скачка (i. e. за исключением ср?+{) Итак, мы можем найти пока все
значения cp" + 1, Wn + i, за исключением Wn^\, Wnk+\ уЦ]. Для того
чтобы найти эти последние величины, запишем условие на ударной
волне. При этом мы представим производные в виде односторонних
конечных разностей:
Ч
Записывая в развернутом виде разностные уравнения C7 63) и C7.67)
на поверхности разрыва, заметим, что теперь производную дЬ/д'^

364	ТЕОРЕТИЧЕСКИЕ «GHQBW ГАЗОВОЙ ДИНАМИКИ	[ГЛ. 1
нельзя считать известной, так как значение её в граничной точке
га-]-1-й горизонтали нам неизвестно. Мы должны будем написать
(в коэффициентах уравнения) в виде:
2»

&2). Теперь разностные уравнения записываются для строки
и столбца ft. Уравнение C7.63) примет вид
1	1 п. _
4- &l+1 + -j*- ¦ &*+2'д7 &* ~ °- C7-84)
Вместо C7.67) имеем
1 ,	v	1	n+I
1 fVF"H ! __ VB"?^ .	1_ M 2 /VFn + 1	Wn + l _i_ VF"
"? i *
В уравнении C7.84) неизвестными являются <pj+} и &ft+1; в уравне-
уравнении C7.85)—4TJ+1, WjJtJ и С11Ова d*+i-
Присоединим к нашим уравнениям три условия на ударной
волне — условия C7.59), C7.69), C7.70), записанные для л—1-го
ряда и й-)- 1-го столбца, и мы получим пять уравнений для определе-
определения пяти неизвестных
Уравнения эти следует решать методом итераций. Именно, зада-
зададим в качестве первых приближённых значений jV значения, отве-
отвечающие предыдущей горизонтальной строчке, т. е. N1- Тогда C7.59)
/ о \ Л+1
позволит найти (-»-) ", подставив это значение в уравнение C7.84),
найдём cpJJ+J. Зная (в, N, Ь)Ц\, найдем с помощью C7.69) значе-
значение !"?+}, после чего из уравнения C7.70) получим новое значе-
значение jVfc + 5- Это новое значение N сравним с Л^*; если эти величины
не совпадут с желаемой точностью, то в качестве следующего при-
приближения возьмем среднее арифметическое из них, снова проделаем
выкладки, пока не получим с заданной точностью все четыре вели-
величины N, &, ср, W на ударной волне. Теперь из уравнения C7.85) най-
найдем *Fj+1 и тем самым завершим задачу определения функций ср, ч?, 0

» 37]
ОДНОСТОРОННИЙ ВЗРЫВ
365
Таблица III
Радиус ударной волны, скорость ударной волны, давление на фронте
в зависимости от времени
1 5
t е^рГ*
0,00037119261
0,00042703441
0,00048762427
0,00059950718
0,00072549370
0,00086611344
0,0010218613
0,0011932119
0,0013806457
0,0015846036
0,0018055170
0,0021440497
0,0026888478
0,0033083766
0,0040053246
0,0047821258
0,0056408701
0,0065835082
0,0076119879
0,0087278918
0,0099326948
0,011770857
0,014707855
0,018014821
0,021693103
0,025740906
0,030154165
0,034926422
0,040049353
0,045513409
0,051307927
0,059953460
0,073321085
0,087792738
0,10326763
0,11964943
0,15478498
0,17338380
0,19257978
0,24075188
0,28279541
0,32624714
0,37087547
0,41649606
0,46296120
1 1
. з ~Т
х L р2
0,042446289
0,044882500
0,047327794
0,051398404
0,055473749
0,059544816
0,063621568
0,067691539
0,071766942
0,075838074
0,079912387
0,085610903
0,093763569
0,10190901
0,11006138
0,11820625
0,12635901
0,13450470
0,14265665
0,15080230
0,15895343
0,17035588
0,18666876
0,20296826
0,21928414
0,23558771
0,25190755
0,26821567
0,28453352
0,30084347
0,31716492
0,33999960
0,37266609
0,40539768
0,43807059
0,47077027
0,53615332
0,56881836
0,60154095
0,68006497
0,74537449
0,81084344
0,87613419
0,94159634
0,0068640
' .=2
45,740446
42,072805
38,858086
34,337009
30,632996
27,554225
24,964868
22,759084
20,861669
19,217523
17,780127
16,051502
14,030664
12,407207
11,082088
9,9845968
9,0655001
8,2843368
7,6144750
7,0358149
6,5316905
5,9289607
5,2296777
4,6739525
4,2254576
3,8581134
3,5536611
3,2986924
3,0831432
2,8991640
2,7411281
2,5546710
2,3430052
2,1783594
2,0480066
1,9430553
1,7863459
1,7269304
1,6766648
1,5833527
1,5262107
1,4817491
1,4463630
1,4176835
1,3940443
Р = Рг
1743,3237
1474,9341
1258,1257
982,35847
781,81703
632,52942
519,20386
431,47993
362,50770
307,59432
263,27742
214,54226
163,88294
128,11566
102,17722
82,910144
68,319410
57,025197
48,150192
41,085577
35,385817
29,127146
22,624607
18,038194
14,712077
12,237532
10,357089
8,9011431
7,7548102
6,8376267
6,0948195
5,2719535
4,4080611
3,7877080
3,3286093
2,9795533
2,4925263
2,3185739
2,1760040
1,9225047
1,7744325
1,6629836
1,5766384
1,5081888
1,4527996

366
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ
[ГЛ 1
Продолжение
1 5
, и 3 6
0,54835908
0,65517718
0,72426297
0,82415753
0,92521260
1,0272174
1,1300115
1,3374959
1,4420092
1,6914759
1,9062747
2,1190714
2,5469597
2,7618034
3,1928620
3,4089552
4,1458222
4,5804748
5,4517159
5,8880975
6,7620252
7,8123402
9,5656357
11,321325
13,078688
14,837283
17,828865
I 1
Г-.3 3
х :Е р,
1,1375785
1,2682835
1,3596500
1,4902189
1,6207801
1,7513436
1,8819135
2,1430754
2,2736583
2,5870953
2,8483764
3,1096352
3,6320036
3,8931742
4,4155604
4,6767533
5,5650727
6,0876013
7,1325834
7,6550605
8,6996139
9,9534905
12,043741
14,133640
16,223401
18,312821
21,865845
1,3607171
1,3309649
1,3163134
1,2994275
1,2860387
1,2751971
1,2662619
1,2524510
1,2470215
1,2367219
1,2302327
1,2250545
1,2173414
1,2144031
1,2097478
1,2078762
1,2030347
1,2009411
1,1977943
1,1965853
1,1946576
1,1929425
1,1909554
1,1896108
1,1886454
1,1879209
1,1871626
P = Pi
1,3692012
1,3095501
1,2772341
1,240426b
1,2115796
1,1884397
1,1695159
1,1402280
1,1292188
1,1079008
1,0945604
1,0839654
1,0682668
1,0623125
1,0529082
1,0491373
1,0394105
1,0352162
1,0289260
1,0265136
1,0226724
1,0192598
1,0153124
1,0126449
1,0107315
1,0092968
1,0077958
для всей горизонтальной га-f-1-й поносы. Остается ещё найти эйле-
эйлерову координату х'. Для этого воспользуемся уравнением C7.68),
в силу которого
Расчет этого интеграла проводится по формуле трапеций; при вы-
вычислении в первом интервале (примыкающем к точке %' = 0) нам
придётся при этом использовать асимптотические представления C7.60).
П+1г
До сих пор мы предполагали коэффициенты (Л, М, V) ,
в разностных уравнениях известными. На самом деле счег прихо-
приходится проводить в два этапа. На первом счете коэффициенты, упо-

§ il
односторонний взрыв
367
мянутые выше, записываются в серединах соответствующих ищерва-
юв л-m ряда. После нахождения всех функций W, ср, ft в п -|- 1-м
ряду вычисляются значения коэффициентов Л, М, V в центрах
С00ГВР1СГВ) ющих ячеек, после чего производится пересчет значений
ф\нкцнй в /г —(— 1-м ряду. Наконец, Дх в первом счете определяется
по значениям N в га-м ряду, а при пересчете — по среднему ариф-
арифметическому из решений на л-й и л-}-1-й горизонтали.
/00000
60000
40000
20000
/0000
БООО
4000
2000
1000
д,ооь
0,002
0,00/
0,0006
0,060,080,1 0,2 0,4 0,6 0,81 2
Рис 150.
Не ос:аиав шваясь на дальнейших подробностях вычислений
уменьшение числа интервалов с увеличением времени, контроль
счета н т. п ), приведем некоторые результаты расчетов, заимство-
заимствованные из упомян} гой выше работы (см. сноску на стр. 357, таб-
|ица III) В табчице даны значения расстояния поверхности взрывной
отны от центра, а также скорости волны и давление на волне —
1! функциях от времени (все в безразмерных величинах). Расчет на-
1 инался от автомодельного решения при х' = 0,00037119; при этом
' —т'* •= 0,042448. Первоначальный шаг по пространству был
взят Д;' — 0,0026530. На первом этапе область задания начальных
значений была разбита на 16 интервалов,

368	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ГАЗОВОЙ ДИНАМИКИ	[ГЛ I
На рис. 150 даны в логарифмической шкале давление, скорость,
плотность и температура за фронтом волны и время в функциях от
положения фронта Тут же пунктиром изэбраже ы значения соответ-
соответствующих величин для автомодельного решения. Для конкретности
на рисунке взяты в качестве начальных данных />2=10 321 кг/м2,
р, .= 0,125 кг сек2/м? (стандартное давление и плотность на уровне
моря),
?0=8,54- 1011 кг. м, Е = Е0-а- а= 1,175
(как мы видели, решение определяется полностью заданием трех
величин: р2, р2 и Е).
Мы не затрагивали в этой книге явлений горения и детонации,
при которых наша постановка задачи будет неверна. С теорией этих
явлений читатель может познакомиться, например, по книге: Лан-
Ландау Л Д. и Лифшиц Е. М., «Механика сплошных сред», 1944.

ГЛАВА ВТОРАЯ
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
А. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
§ 1. Понятие вязкой жидкости. До сих пор мы рассматривали
исключительно движения идеальной жидкости, т. е. мы предполагали,
что поверхностные силы, приложенные к элементам поверхности dS
любого объема жидкости, представляют собой нормальные давления,
направленные внутрь объёма.
Однако все действительные
жидкости являются в той или
иной степени вязкими; иначе
говоря, они обладают свойст-
свойством внутреннего трения.
Для выяснения сущности
этого свойства рассмотрим
следующий типичный пример.
Имеются две параллельные
пластинки (рис. 151), между
которыми находится жидкость.
Нижняя пластинка удержи-
удерживается неподвижной, в то время
как верхнюю заставляют дви-
1аться в одном и том же направлении в своей плоскости с постоянной
скоростью U. Обозначим расстояние между пластинками через h.
Тогда, в конце концов, получим следующую картину движения жидко-
сти. Слой жидкости, непосредственно примыкающий к нижней пла-
спшке, будет находиться в покое; слой жидкости, непосредственно
примыкающий к верхней пластинке, будет обладать той же самой ско-
скоростью U, что и эта пластинка. Наконец, любой промежуточный
слой будет двигаться со скоростью v, пропорциональной расстоя-
расстоянию у от неподвижной пластинки;
V^U^r-.	A.1)
0
У
	*
и
7
У/////////////////////////////////////////////
Рис. 151.
2 ]¦ 1 сор ел i чесьая г идрочечаника, ч. II

370	ДВПЖ.ЕНИЕ ВЯЗКОЙ ЖПДКОС Ш	1Л II
При эюм как к верхней, так и к нижней пластинке необходимо
приложить силы, а именно: к верхней пластинке необходимо прило-
приложить силу, лежащую в её плоскости и имеющую то же направле-
направление, чго и направление движения пластинки. К нижней же пластинке
необходимо приложить такую же силу, тоже лежащую в ее плоско-
плоскости, но имеющую прямо противоположное направление. Величина
как той, гак и другой силы, отнесённая к единице плошади, равна
<J2)
Коэффициент [j. в этой формуле имеет для каждой жидкости при
заданной температуре своё значение и называется коэффициентом
внутреннего трения или коэффициентом вязкости.
Формулу A.2) можно в только что рассмотренном случае напи-
написать и так:
^=^-	A.3)
Мы примем, как опытный факт, справедливость формулы A.3) и
в гом случае, когда два соседних слоя, перпендикулярных оси Оу
и находящихся на расстоянии dy друг от друга, двигаются парал-
параллельно оси Ох со скоростями, соответственно, v и v-\-dv. При
этом т означает касательное напряжение, т. е. силу, отнесённую
к единице площади.
Отсюда видно, чю в случае движения вязкой жидкости мы не
можем ограничиваться при рассмотрении поверхностных сил одними
только нормальными давлениями, а должны вводить в рассмотрение
также и касательные напряжения.
Можно поэтому дать такое определение: жидкость называется
вязкой, если поверхностные силы, приложенные к элементам
поверхности любого объёма жидкости, имеют, вообще говоря,
кроме нормальных, ещё и касательные составляющие.
Происхождение сил вязкости следует искать в молекулярной
природе строения материи. Отдельные молекулы жидкости при своих
собственных движениях переносят вместе с собой из одного места
пространства в другое определенные количества Maiepmi, энергии,
количества движения. Те величины, с которыми мы имеем дело
в гидродинамике, представляют собой средние величины, получаю-
получающиеся в результате суммарного учёта, относящегося к весьма боль-
большому количеству молекул. Собственное движение молекул способ-
способствует выравниванию в соседних слоях значений этих средних
величин. Так, например, при наличии двух соседних слоев одной и
той же жидкости, но разной плотности, перенос молекул будет
способствовать выравниванию этих плотностей: получается процесс
диффузии. Точно так же, если имеем неравномерное распределение

§ I]	ПОНЯТИЕ ВЯЗКОП ЖИДКОСТИ	,371
темпера!}ры, то перенос молекул будет способствовать выравнива-
выравниванию температур: в этом находит свое объяснение процесс тепло-
теплопроводности. Наконец, в нашем случае наличия вязкости мы имеем
дело с процессом переноса молекулами своего собственного коли-
количества движения; этот процесс приводит к выравниванию скороеюй
соседних слоев жидкости. В соответствии с этим можно дать вывен
основных уравнений движения вязкой жидкости, основанный на пр^ i,-
став.чииях молекулярной теории материи.
Мы, однако, ограничимся выводом основных уравнений движения
вязкой жидкости из нескольких простых предпосылок. Для этою
нам нужно будет вернуться еще раз к разобранному уже в главе I
части первой этой книги вопросу о деформации жидкой частицы,
рассмотреть затем подробно вопрос о тензоре напряжений и уста-
установить, наконец, связь между напряжениями и деформациями.
Для того чюбы слепагь читателю более ясной структуру эгоп
главы, скажем 1еперь несколько слов о современном состоянии ieo-
рии движения вязкой жидкости.
Уравнения движения вязкой жидкости, которые мы гопчич,
имеют довольно сложный вид; поэтому их полное nnieip фоваиие
удается произвести в сравнительно небольшом количестве с 1}чаев;
некоторые из этих случаев будут разобраны во втором разделе этой
главы.
Теория движения вязкой жидкости пошла, гл?внгм of разом, по
линии развития приближенных методов интегрирования уравнений
движения вязкой жидкости.
Уравнения движения вязкой жидкости являются математическим
выражением равновесия нескольких сил; нас сейчас не интересует
точное выражение каждой из этих сил по отдельности; для нас
достаточно только перечислить, каковы эти силы: 1) внешние силы,
приложенные к жидкости (например, сила тяжести), 2) силы инер-
инерции, 3) силы давления и 4) силы внутреннего трения.
Ясно, что при невозможности учесть все эти силы, т. е. при не-
невозможности полностью проинтегрировать уравнения движения вязкой
жидкости, можно попытаться одну из этих сил, наименее важную,
отбросить. Но мы не можем отбрасывать внешние силы, так как,
конечно, мы их вводим только тогда, когда считаем их важными.
С другой стороны, мы не можем отбрасывать силы давления, так
ьак эти силы суть силы вн\треиние, через посредство которых
осуществляется равновесие всех остальных сил.
Если мы отбросим теперь силы внутреннего трения, оставив
тотько силы инерции, то мы получим, очевидно, гидродинамику
идеатыюй жидкости. Напротив, отбросив силы инерции и оставив
<¦" 1Ы трепня, мы получаем возможность приближенного решения ряда
задач о движениях вязкой жидкости. Целый ряд примеров такого
Р° ia разбирается нами в третьем разделе этой главы.

372	/№h>rfhiif вячкоп жидкости	[гл п
Однако полное пренебрежение ситами внутреннего трения или
силами инерции не всегда дает достаточно iочные результаты.
Заметим при этом, что когда силы внутреннего трения малы по
сравнению с остальными силами, мы можем говорить о маловязкой
жидкостг. Напротив, когда мы пренебрегаем силами инерции в виду
их малости сравните шно с силами вязкости, мы можем говорить
о снльновязкой жидкости Таким образом первым приближением для
теории маловязкой жидкости явтяегся теория идеальной жидкости,
первым же приближением для теории сичьновязкой жидкости является
теория, в которой полностью выброшены силы инерции.
Как было указано выше, и та и другая приближенные теории
имеют ограниченный круг применений Гораздо лучшие результаты
дают 6oiee точные теории, принадлежащие шведскому ученому О с е-
е н у (С W. Oseen) и немецкому ученому Прандтлю (L. Prandtl).
Основная мысль Осеена состоит в том, что при изучении движе-
движений сильновязкой жидкости не нужно полностью выбрасывать из
рассмотрения силы инерции, а следует оставить в уравнениях, кроме
сил вязкос1и, также и главную часть сил инерции Оказывается, что
и при эюм допущении уравнения движения во многих случаях могут
быть проинтегрированы. Примеры такой трактовки движений сильно-
сильновязкой жидкости будут нами приведены в том же третьем разделе
этой главы.
Точно так же заслуга Прандтля состоит в том, что он обратил
внимание на невозможность пренебрегать силами вязкости вблизи
твёрдых стенок даже в случае маловязких жидкостей. Вблизи твер-
твердых стенок образуется тонкий пограничный слой, внутри которого
необходимо учитывать влияние сил вязкости; вне этого тонкого
слоя влиянием вязкости можно пренебрегать. В результате развития
этих мыслей получается очень плодотворная теория пограничного
слоя, позволяющая разъяснить ряд вопросов, не поддающихся реше-
решению в рамках теории идеальной жидкости, как, например, вопрос
о зарождении вихрей.
Изложению теории Прандтля посвящен последний раздел настоя-
настоящей главы. Вторая половина этого раздела посвящена другой теории,
тоже относящейся к движениям маловязкой жидкости и принадлежа-
принадлежащей Осеену. Сущность этой теории Осеена в двух словах такова:
найти то движение жидкости, которое поаучается в пределе из
движения вязкой жидкости, если после интегрирования уравнений
движения вязкой жидкости мы совершим предельный переход, устре-
устремив коэффициент вязкости и. к нулю. Оказывается, что это предель-
предельное движение будет отлично от того движения, которое мы могли бы
ожидать на основании обычной гидродинамики идеальной жидкости.
Можно думать, что движение маловязкой жидкости будет мало отли-
отличаться от предельного движения Осеена Нужно, однако, отметить,
что Осеену не удалось совершить предельный переход, исходя из точ-

i 2]
ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ
373
ных уравнений движения вязкой жидкости. В основу рассуждений
им были положены упрощённые уравнения вязкой жидкости, и это
до некоторой степени умаляет ценность полученных Осееном резуль-
результатов.
Наконец, в заключение этого параграфа заметим, что даже точ-
точные уравнения движения вязкой жидкости не могут непосредственно
описать целую группу движений жидкости, движений, являющихся
для практики, пожалуй, наиболее интересными и
важными. Мы говорим о так называемых турбулент-
турбулентных движениях жидкости, отличительным признаком
которых является крайне беспорядочный характер
перемещений отдельных частиц жидкости. Теории
турбулентных движений будет посвящена следующая
глава, в настоящей же главе вопросы турбулентных
движений жидкости будут затрагиваться лишь по-
попутно.
§ 2. Тензор скоростей деформации. В главе I,
части первой, в §§ 5—9, был уже подробно разо-
разобран вопрос о деформации жидкой частицы. В целях
большей ясности дальнейшего изложения мы вспом-
вспомним введённые нами обозначения и сделаем несколько
дальнейших замечаний, относящихся к этому вопросу.
Рассмотрим какую-либо точку О движущейся
среды; скорость этой точки обозначим через v0.
Пусть далее А — бесконечно близкая к О точка
(рис. 152); обозначим через р радиус-вектор О А и через ?, f\,
С — проекции этого вектора на прямолинейные прямоугольные оси
координат. Как в § 1 главы I части первой, введём обозначения:
О
Рис. 152.
dvx	dvy	dvz
~~dz
dvx
2 1
dvz
' dvz
\ dy
dx
dVy
dVy\
dz -
ft
Ш1>
1
2
dvx
dz
ldvx
[dz
dvz
' dx
to*)
dx j
= ?,
dvy
~dx~
dvv
dvx
B.1)
причём все эти величины вычисляются для точки О; ясно, что u>v
<«2. шз являются составляющими вектора
о) = ~ rot v.	B.2)
Как было выяснено в главе I части первой, скорость точки А
может быть представлена в следующем виде:

374
ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ
1ГЛ И
1дс л, = и х р есть скорость вращательною движения точки А
вокруг мгновенной оси, проходящей через точку О, причем пек юр
угловой скорости равен to, а вектор ©2 есть скорость чисти дефор-
деформации Составляющие этой последней скорости имеют ник
" 1 *"
4'
) V
B.4)
Таблица девяти величин
ф =
?, тт Oi it
U
^
B.5)
носит название тензора скоростей деформации. Если этот тензор
обращается в пуль, т. е. если все девять составляющих выше}казан-
пой таблицы равняются нулю, то по формулам B.4) и скорость
деформации обратится в нуль. Это означает, что распределение ско-
скоростей частиц жидкости в окрестности точки О дается юй же
формулой
что и распределение скоростей точек твердого тела, т. е. что дефор-
деформация частицы в окрестности точки О отсутствует.
Рассмотрим кроме системы осей х, у, z еще другую прямоли-
прямолинейную прямоугольную систему осей х, у, г. В этой новой системе
осей составляющие введенных нами векторов и тензора Ф примут
какие-то другие значения; условимся отмечать эти новые значения
путём постановки черточки над соответствующими буквами. Поста-
Поставим себе задачу вывести соотношения, связывающие новые и старые
составляющие тензора Ф.
Для краткости письма введем следующие обозначения для коси-
косинусов углов между старыми и новыми осями координат
cos(x, x^
cos(y, x"
COS (Z, X,
) rrz: ^Ui COS (X, y) = ^^2'
) = cx21. cos(>7 y) = a?2,
) = 231, cos (z, y) — a.z2,
cos(x,
cos (y,
cos {z,
«) = «,„ j
2) = a25> j
B
.6)

% >}	ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ	375
Составим теперь скалярное произведение векторов v,2 и р. Не-
Несложное вычисление показывает, что
»2 ¦ Р = v2xl + v2vti + viz\ = ?l« + e2f + гр + 0^; + 02"J- + ^-
Но очевидно, чю эго выражепиг не может зависеть от того, в какой
системе коор шнат мы ею вычисляем. Мы имеем поэтому равенство:
+ б1?: + 62Й + 03^. B.7)
С другой стороны, вследствие формул B.6), между старыми и но-
новыми составляющим» вектора р существуют соотношения
, х) -f- 7j cos (у, x) + CcosB, лг) = =ocu -f- ^аз! -j- Са3
-f- Са32,
а33.
Подставляя эти выражения в правую часть формулы B.7). про-
производя вычисления и сравнивая затем коэффициенты при ?2, т,2, ...
б обеих частях тождества B.7), мы придём к искомым формулам,
из которых приведем только две:
1 -	1	1
+ ^ б2я23а31 + у 62а21аЗЗ + 9За21а32 +У °За31а22-
Если бы мы ввели обозначения
1 " 1 Л \	1 } B.8)
ю. как легко убедиться, предыдущие формулы приняли бы гораздо
более компактный вид:
_	3 3
^*"=^j 2 Ф^гА^ ('- k~\, 2, 3).	B.9)
Формулы преобразования B.9) являются характерными для пре-
преобразования составляющих какого-либо тензора. Именно, если мы для
каждой системы координат имеем девять величин р1к, причем значе-
"чя р1к, соогве!ствующие какой-либо системе координат х, у, z,

376	движение вязкой жидкости	[гл. и
связаны со значениями pik, соответствующими системе координат х,
у, z равенствами
_	зз
Рт= 2 2 Prs*ir4s'	B.10)
т-Л «•= 1
то говорят, что величины plk образуют тензор (точнее говоря, афин-
ный ортогональный тензор второго ранга, но мы никаких других
тензоров рассматривать не будем). Формулы B.9) показывают, что Ф
действительно есть тензор, так что данное нами выше название
«тгнзор скоростей деформаций» вполне оправдано.
Рассмотрим поверхность второго порядка:
^ = С;
направим теперь новые оси координат х', у', z' по осям симметрии
этой поверхности. Тогда уравнение поверхности примет вид:
Мы в 1дим, что в системе координат х', у', г' составляющие тензора
скоростей деформаций имеют особенно простой вид, ибо, как выте-
вытекает из предыдущего уравнения:
/	/	/
Ot . \j<y ~~~~ Ут '.ту- (J,
Положим ещё
Направления осей х', у', z' носят название главных осей тензора
скоростей деформаций, величины ev e2, ег называются главными
значениями тензора скоростей деформаций или главными ско-
скоростями удлинений.
В системе осей х', у', г' тензор скоростей деформаций прини-
принимает особенно простой вид:
ех О О
B.11)
кз
Величины ev е2, е3 были уже введены в § 3 главы I части первой,
где было приведено и уравнение третьей степени, которому эти
величины удовлетворяют.
Напомним ещё непосредственно вытекающую из обозначений B.1)
формулу:
dv? dvv dv,
х ' v ' ± = div г>.	B.12)
ех
0
0
0
е2
0
0
0
е
Эта формула имеет место в любой системе координат, так что,
в частности, мы имеем

§ 3]	1ТП30Р НАПРЯЖЕНИЙ	377
В § 4 главы I части первой было показано, что эта величина пред-
представляет собой кубическое расширение жидкости, отнесённое к еди-
единице времени.
§ 3. Тензор напряжений. Перейдём теперь к рассмотрению по-
поверхностных сил, появляющихся при движении вязкой жидкости.
Вырежем внутри жидкости объём т при помощи замкнутой поверх-
поверхности 5; рассмотрим элемент dS этой поверхности. Обозначим
через п направление внешней нормали к этому элементу поверхности.
Тогда действие частиц жидкости, расположенных с внешней стороны
элемента dS, на частицы жидкости, прилегающие к этому элементу
с внутренней стороны, может быть приведено к действию поверх-
поверхностной силы pndS.
Если обозначить через рх, ру, р2 напряжения поверхностных сил
для площадок, внешние нормали которых параллельны и одинаково
направлены, соответственно, с осями х, у, z, то, как было выяснено
в § 3 главы II части первой, имеет место соотношение
pn=pxcos(n, x)-\-pycos(n, y)-±-pzcos(n, z).	C.1)
Введём теперь следующие обозначения для проекций на оси коорди-
координат векторов рх, ру и рг:
Ддя вектора рх,
»	» Ру
»	1> Pz-
»	» Pn>
при этом рхх носит название нормального напряжения, действую-
действующего на площадку, перпендикулярную к оси Ох, а рху и pxz на-
называются касательными напряжениями.
Тогда, проектируя C.1) на оси координат, будем иметь:
y)-\-pzxCOS(n, Z),
y	y	C,2;
X)-\-pyiCOS(n, y)-\-pzzCOs(n, Z),
Введём теперь в рассмотрение ещё произвольное направление т и
обозначим через рпт проекцию вектора рп на это направление.
Так как
Pnm = Pnxcos(m- x) + pnycos(m, y)-\-pnzcos(m, z),
то предыдущие равенства приводят к следующей формуле;
Pnm = Pxxcos(n' x)cos(m, x)+ Pyxcos(n, y)cos(m, x)-\-
-{-pzxcos(n, z)cos(m, x) -f- pxy cos in, x)cos(m, y)-{-
-{-pyycos(n, y)cos(m, y) + pzycos(n, z)cos(m,
-\-pxicos(n, x)cos(m, z)-\-pyzcos(«, y)cos(m,
z)cos(m, z). C.3)
Рхх>
Pyx'
Ргх.
Рпх-
Рху
Руу
Pzy
Рпу
Pxz
Pyz
Pzz
Pnz
) + pyycos(n, y)-\-pzycos(n, z),

378
ДВПЖЕНЬЬ ВЯЖОИ ЖИДКОСТЬ
[ГЛ 11
Эта общая формула содержит в себе, как частный случай, дев я п.
формул B.10), если мы условимся обозначав рхх чере* ри, р
через р12 и т д и аналогично будем обозначав р-х черсз pfj,
р	через Pj-j и т. д.
Но теперь мы можем утверждать, что табтица jujplii bi шчин
Pu Piy Pi.
Л x Руу Руг	C 4)
Pzx Pzs Pzz
определяет тензор, который называется тензором напряжении.
Можно доказать, опираясь на общие законы механики, симме-
симметричность тензора П, выражающуюся форму тачн1):
Рх
ху
Ру>
C 5)
В нашем случае напряжений в вчзкой жидкости симметричность
тензора II полечится как следствие тех предпосьнок которые мы
ПО1ОЖИМ в основу вычисления эюго тензора
Относительно тензора II можно повторить все то, что было
сказано о тензоре деформаций Ф Существ>ют три взаимно перпен-
перпендикулярные главные оси тензора напряжений и соответствующие им
главные напряжения рх, р2, рА- Будучи отнесен к г 'авным осям,
тензор напряжений принимает особенно простой вид.
C 6)
Pi
0
0
0
Pi
0
0
0
;;
При этом, анатогично равенств}
-1-Г--2-
+ е,,
имеет место равенство
¦+ Pzz = А + РгЛ- Ръ>
C 7)
т. е. сумма нормальных напряжений на три взаимно перпенди-
перпендикулярные площадки не зависит от ориентации этих площадок
Перейдем теперь к установлению связи между тензором скоростей
деформаций и тензором напряжений в вязкой жидкости В основу
наших рассуждений мы положим два допущения.
I. Составляющие тензора напряжений при отсутствии вяз-
вязкости должны приводиться к соответствующим составляющим
') См, например, Кочин Н Е, Векторное исчисление и начала тен-
тензорного исчисления, 1938, стр 363.

§ 3]	ТЕНЗОР НАПРЯЖЕНИЙ	379
тензора напряжений в идеальной жидкости. Иными словами, мы
должны иметь
г ie величины -„, туу, тгг, хлу, ... могут быгь отличны от нуля
юлько в случае вязкой жидкости.
П. Величины ххх, ~уу, ¦ ¦ . являются линейными однородными
функциями от составляющих тензора скоростей деформаций,
причём коэффициенты этих функций не зависят, от выбора
прямолинейной прямоугольной системы, координат.
Линейный характер рассматриваемой нами зависимости вполне
естественно допустить, ибо такой тип зависимое! и является простейшим.
Независимость же коэффициентов рассматриваемых линейных функций
от выбора координатной системы выражает, очевидно, свойство
изотропности вязкой жидкости, т. е. свойство однородности по
отношению к различным направлениям. Выводимые нами уравнения
справедливы только для таких изотропных вязких жидкостей.
Пусть теперь оси координат х', у', z' направлены по главным
осям тензора скоростей деформаций, так что бх ^^ б2 = б3 =^ 0, и
пусть ех, ez, c3 суть соответствующие главные скорости удлинений,
так что тензор скоростей деформаций имеет в рассматриваемой
системе координа1 вид B.11). Нетрудно определить общий вид
неличин т в эгой системе координат. Пусть, например, мы имеем:
где ах, а2, аг—некоторые, не зависящие ог выбора осей координат,
коэффициенты. Ясно тогда, что т , , и tz,z, должны определяться
фврмулами:
\y = aie2+a2e3+a3ev Vz'=V3 + a2ei + <y2, (ЗЛО)
ибо достаточно переименовать в соотношении C.9) ось х' в ось у',
ось у1 в ось z' и, наконец, ось z' в ось х', чтобы получить первое*
из соотношений C.10). Аначогично получается второе из соотно-
соотношений C.10).
Покажем теперь, что а2= а3. Произведём для этого преобразо-
преобразование координат
х' — х', у' — z', ? =г _ /;
ясно, что новые оси координат опять являются главными осями
тензора скоростей деформаций. Очевидно, далее, что в новой системе

380	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
координат мы имеем следующие формулы:
dv-
X
дх'
dv
X
дх'
dv
di
С—
V'
d
i
i
' X"
dv-
У
д?
dv
Z
dz
Соотношение C.9) можно применить, согласно допущению П,
и к системе координат х\ у', г':
откуда, на основании вышеупомянутых формул, выводим:
Сравнение с формулой C.9) приводит нас к искомому соотно-
соотношению а2 —аз- Вводя теперь обозначения
мы можем переписать формулы C.9) и C.10) в следующем виде:
C.LI)
Докажем теперь, что в системе координат л/, у', z' все каса-
касательные напряжения хх, ,, тл,4, и т. д. обращаются в нуль. Доста-
Достаточно обнаружить, что т , , = 0.
х у
Согласно допущению II, мы должны иметь:
где а4, аь, а6 — некоторые постоянные коэффициенты. Но произведём
преобразование координат
х' = х', / = — у', г' = — z'.

i i]	ТЕНЗОР НАПРЯЖЕНИЙ	381
Новые оси координат опять будут главными осями тензора ско-
скоростей деформаций, причем имеют место формулы:
vv = vx> vy -=~vy v? = — «,-.
dv— dv	dv— dv
Г ?L	7	^
дх'	дх'	ду'	ду'
_ dv— dv
v
Последняя формула вытекает из следующих соображений: -zx, ,
есть проекция на ось у' напряжения, действующего на площадку,
внешняя нормаль к которой имеет направление оси х'\ ^-; есть
проекция на ось у' напряжения, действующего на ту же самую
площадку, ибо оси х' и х' одинаково направлены. И так как оси у'
и у' имеют прямо противоположное направление, то ясно, что
V У ~~	х'у"
Вследствие допущения II, мы должны иметь формулу:
На основании предыдущих равенств мы выводим отсюда, что
но тогда сравнение с формулой C.12) показывает, что
а4 — а5 — ав = О'
иными словами, что
Итак, мы показали, что
Собирая вместе формулы C.8), C.11) и C.13) и припоминая, что
приходим к следующим выражениям для составляющих тензора
напряжений в системе осей х', у', z', служащих главными осями
тензора скоростей деформаций:
Рх'х' = — Р +l div " + Vi •
Ру'Г = — Р + > div v + 2ае2,
У = Рх-,' = Рух- = Руг> = /V,.
C.14)

382
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. II
Из этих формул следует, что главные оси тензора напряжений
совпадают с главными осями тензора скоростей деформации:
Выведем теперь выражения для составляющих тензора напряже-
напряжений в произвольной прямолинейной прямоугольной системе координат.
Предварительно остановимся на нескольких элементарных поня-
понятиях из теории тензоров.
Легко прежде всего убедиться, что таблица девяти величин,
заданных в любой системе координат следующим образом:
т __
1 О О
О 1 О
О 0 1
C.15)
определяет тензор; этот тензор называется единичным тензором.
Пусть, далее, мы имеем два тензора:
А =
'21
'23
В=.
'зз
Ь,
22
Z31 Й32 аЪ
тогда под суммой этих тензоров A -f- В и под произведением
kA = Ak тензора А на постоянное число k понимаются следующие
тензоры:
A -f- В =
kA — Ak =
a2l -\~ b2l а22
«31
ka
ka2l ka22 ka
«33
a2l
23
C.16)
При этих обозначениях девять равенств C.14) могут быть сле-
следующим образом записаны в тензорной форме:
10 0 1
I
0 10 1
0 0 1
Рх
Ру
Pz
' X'
'X'
' X'
Рх-
Ру
Pz'
у'
у'
у'
Рх
Ру
Pz
'z'
' z'
' z'
*! 0 0
0
0
\
или, вследствие C.4), C.15) и B.11):
II = (— р -j-). div v) I + 2аФ.
I
0 0
Ч
C.17)
Но если соответствующие составляющие двух тензоров равны
в какой-либо системе координат, то они будут равны и в любой

S 3|
ГГНЗОР НАПРЯЖЕНИИ
383
jipvгой uicieMe координак Поэюму предыдущее равенство в системе
осей л", у, z принимает вид:
Рх х Рху Рхг
Pyx Piy Руг
Pzx Ргу Pzz
1 О О
= ( p-+ldlvv)\ 0 1 О
О 0 1
огк}да вытекают следующие равенства:
Рхх=-Р+ } divt>+-2(j.e1, j
2.x
|о3 io2
1 б -
" з -2
Т°2
01
C.18)
Из этих выражений ясно видна симметричность тензора напря-
напряжений.
Складывая первые три формулы C.18) и вспоминая, что
е1 + ?2 +" Ч — div <0>
легко потучим равенство
вгг+ р л- р = — 3p+-C), + 2j)divn,	C 19)
В несжимаемой жидкости, где	div© = 0, коэффициент л сам
собой выпадает в выражениях для	напряжений, и послед1!,i прини-
принимают вид:
dvx	j дох
1 \ ду
"Г
-I* ду '
dv,
Ptz
Pzx — lJ-{ J7~
~SJ
C.20)
В частном случае, когда мы имеем течение, параллельное оси Ох,
так что vy~vz = 0, причем скорость течения vx = v есть функция
одного тотько у, мы пол} чаем из формул C.20) для касательно! о
напряжения выражение
dv
Рху — Рух — Р-ау
совпадающее с формулой A.3), с рассмотрения которой мы начали
эту глав\.

384	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	(ГЛ И
Мы уже упоминали, что постоянная (j. называется коэффициентом
внутреннего трения или коэффициентом вязкости. Нетрудно
установить размерность этого коэффициента Если А\ есть символ
единицы массы, L — единицы длины и Т—единицы времени, то
симьотом единицы ускорения будет LT и единицы силы — MLT~2,
поэтому символом единицы напряжения рх яв чающеюся силой,
отнесенной к единице тощали, будег AlLi2, с другой стороны,
размерностью величины dvjdy служит, очевидно, Т~\ Так как
Pxv
dvx dv
|
у
ду ^ дх
то для размерности ц получаем выражение ML~XT~X. Так, например,
в системе CGS ja будет измеряться в г/см сек. Например, коэффи-
коэффициент вязкости для воды при температуре О С равняется 0,018 г/см- сек,
а при температуре 20JC этот коэффициент имее! значение
0,010 г/см • сек; для воздуха при температуре 0°С и давлении 760 мм
ртутного столба коэффициент вязкости равняется 0,00017 г/см сек.
Часто для характерисгики вязкости употребляют вместо а друг)ю
величину, а именно
эта величина носит название кинематического коэффициента вяз-
вязкости. Так как размерность р есть AIL 3, то размерностью v
является L Т ; в системе CGS значения v измеряются в см2/сек, на-
например, при температуре 0°С кинематический коэффициент вязкости
для воды равняется 0,018 см^/сек, а для воздуха при вышеуказан-
вышеуказанных условиях 0,133 см2/сек.
В общем случае сжимаемой жидкости коэффициент X остается
наряду с у., так что формулы дчя напряжений принимают вид:
dvx	I dvx dvv
C 21)
dvz	j dvy dvz
; pP^^
Чтобы определить коэффициент \, можем сделать следующее допу-
допущение: примем, что давление в вязкой жидкости всегда равно взя-
взятому с обратным знаком среднему арифметическому из трех напря-
напряжений, приложенным к трем взаимно перпендикулярным площадкам.
Формулы C.19) показывают, что это само собой выполнится для

5 41	УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ	385
несжимаемой жидкости. Чтобы это допущение выполнялось и в общем
случае, надо, очевидно, положить
Х=-|ц1).	C.22)
§ 4. Уравнения движения вязкой жидкости. В главе II, § 2
части первой было выведено общее уравнение движения сптошной
среды;
f (F~w)odx + JpndS^Q.	D 1)
т	S
Здесь х означает произвольный объем, вырезаемый внутри
жидкости поверхностью 5, р—плотность частицы жидкости, F— вектор
массовой силы, отнесенной к единице массы, ио — ускорение частицы
жидкости, п — направление внешней нормали к поверхности S,
рп — вектор напряжения поверхностной силы. Мы имеем при этом
равенство
рп =рх cos(п, х) + ру cos (n, y)-{-pzcos(n, z).	D.2)
Преобразуем теперь поверхностный интеграл, входящий в фор-
формулу D.1), в обьемный. Для этого заметим, что имеет место сле-
следующая формула:
f a cos (n, x)dS= f |j dx,	D.3)
где а есть произвольный вектор, непрерывный вместе со своей про-
производной по х в объеме т.
В самом деле, если составляющие вектора а суть ах, ау, аг,
так что
где i, j, k — координатные орты, то мы имеем, применяя формулу
Гаусса, следующие три формулы:
/ aAcos(n, x) dS = / -~~dt,
'-.
Г	f
/ aycos(n, x)dS= /
azcos(n, x)dS —
да
-j— dx,
s
daz
') Некоторые физики склонны вводить понятие второго коэффициента вяз-
H или «второй вязкости» и не пользоваться допущением, приводящим
к формуле C.22), см., например, Ландау Л Д и Л и ф ш и ц Е. М.,
Механика сплошной среды, Гостехиздат, 1944
25 Теоретическая гндромочтннка ч II

386	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
Умножая первое из этих равенств на i, второе на J, третье на k
и складывая три полученные формулы, мы докажем равенство D.3).
Но тогда ясно, что на основании равенства D.3) и аналогичных
ему равенств, мы имеем:
— j [pxcos(n, x)-\-pycos(n, у)-\-ргcos(n,
^ др^ др
1flXl
дх ^ ду ^ dz
Потому равенство D.1) принимает вид:
Мы, конечно, предполагаем при этом, что все те функции и их
производные, которые мы рассматриваем, являются непрерывными
функциями от своих независимых переменных. Но при этом условии
предыдущее равенство, в котором t есть произвольный объём жидко-
жидкости, может иметь место только в том случае, если в каждой
жидкости в любой момент движения подынтегральная функция будет
равна нулю.
Мы приходим таким образом к следующему уравнению движения:
Его можно записать также в форме
w = F+ - div П,	D.5)
если условиться называть расхождением тензора	П и обозначать
через div II вектор
-т	\- -s-^ + -т— = div П.	D.6)
дх ду ' dz	K
Проекциями этого вектора на оси координат, очевидно, являются:
1
дх -i ду
1
-j-
D.7)
1>г— дх ' ду ' dz ''
ибо проекциями вектора рх являются рхх, рх , /?^ и т. д.

4]	УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ	387
Обозначая проекции массовой силы Fm оси координат через X, Y, Z
и вспоминая, что проекциями ускорения w являются величины dvjdt,
dv /dt, dvjdt, найдём из D.5) уравнения движения в следующей
форме:
dvx у . 1 ( дРхх . друх дргх \
dt ~ ' p \ dx ' dy r
dvy _ у , l (dp*y | dPyy | a^y \
? (
dt ~ *- "Г" р V дх
D.8)
Воспользуемся теперь формулами C.21), C.22) и предположим,
что ^ = const. Тогда без труда получим, что, например:
,,. „ч дрхх , <Э/>у* , дргх	dp 2 й div о , „ d2vx .
d2vx
г r dy2 ] r dxdy Г ' йг2 "т- V дх dz
dp 2 a div v	I d^v x d^v x d2v*
dx 3 " dx	^ \ dx2 dy2	dz2
d ldvK dVy dvz\	dp 1 д div
Поэтому, выписывая ещё в полном виде проекции ускорения,
получим из D.8) следующие окончательные уравнения движения
вязкой жидкости:
°vx ,
dt {
dvy
dt '
dvz
dt '
<o dVjc 4-
V*dx +
at»y
Vjc dx '
&vx
Vy dy
dvy
dvz
Vy dy
+ v
dvx
dz
dvy
dvz
dz
X l
P
1
1
p
dp
dx
dp
dp
v a div v , Airi
3 dx ' '0-lr'
v a div г»
v a div г» .
3 dz ' ; 2'
D.9)
К этим уравнениям нужно присоединить ещё уравнение неразрыв-
неразрывности
do d (oVy) d (ovv) д (оуЛ
Уравнения D.9) называются уравнениями Навье-Стокса. Они
были опубликованы французскими учёными Навье (Navier), рассмат-
рассматривавшим только случай несжимаемой жидкости, в 1827 г., и
Пуассоном (Poisson), рассматривавшим случай сжимаемой жидкости,

388	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
в 1831 г.1). И тот и другой исходили из гипотетических предста-
представлений о молекулярных силах. В 1843 г. Сен-Венан (Saint-Venani)
и в 1845 г. Стоке2) (Stokes) дали новые выводы уравнений D.9),
по образцу которых построено и наше рассуждение.
Уравнения D.9) имеют очень сложный вид, поэтому их точное
интегрирование удаётся лишь в редких случаях. Однако в ряде
случаев получается хорошее совпадение результатов экспериментов
с результатами вычислений, основанных на использовании их. Это
показывает, что уравнения D.9) с большой степенью точности
описывают движения действительных жидкостей. Можно поэтому
сказать, что построение теории движения вязких жидкостей сводится
к всестороннему исследованию этих уравнений.
§ 5. Различные формы уравнений движения вязкой несжи-
несжимаемой жидкости. Если мы имеем дело с движением вязкой несжи-
несжимаемой жидкости, то четырёх уравнений D.9) и D.10) недостаточно
для определения пяти неизвестных функций р, р, vx, vy, vz. В этом
случае необходимо учитывать также и термодинамические свойства
изучаемых процессов.
В § 10 этой главы мы дадим подробный вывод дополнительного
соотношения — «уравнения притока тепла» для вязкой сжимаемой
жидкости, а пока обратимся к жидкости несжимаемой.
Уравнениям движения вязкой несжимаемой жидкости можно при-
придать различную форму; в одних случаях выгодно пользоваться
одной формой уравнений, в других — другой.
Прежде всего, уравнения D.9) и D.10) для случая несжимаемой
жидкости упрощаются следующим образом:
dvx . dvx . dvx , dvx	 ,, I dp . .
E.1)
dvy	dvy	dvy	dvy	1 dp
vy	dvy	dvy
dv, . dv, , dv, , dv, .-, 1 dp
f + vf + v + v=Z
dvx
~~dx
') N a v! e г С. L., M. H. Memoire sur les Lois du Mouvement des Fluides,
Mem. de l'Acad. des Sciences 6 A872), Poisson, S. D., Memoire sur les
Equations generates de l'equifibre et du Mouvement des Corps solides elasti-
ques et des Fluides. Journal de l'Ecole Polytechnique 13 A831).
2) Saint-Venant, Note a joindre au memoire sur la dynamique des
fluides, Comptes Rendus de l'Acad. a Paris 17 A843), 240; Stokes CO.,
On the Theories of the Jnternal Friction of Fluids in Motion, Math, and Phys.
Papers 1, 75.

Б]	РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ	389
В векторной форме эти уравнения имеют вид:
-^ = F	grad р -f- ч До; divo = 0.	E.2)
При v = 0 эти уравнения приводятся к уравнениям движения идеаль-
идеальной жидкости.
Последние уравнения были записаны нами в § 6 — 7 второй
главы части первой, в так называемой форме Ламба. Дадим обоб-
обобщение этой формы на случай вязкой жидкости. Для этого заметим,
что мы имеем для любого вектора а следующее тождество:
Да = grad diva — rot rot a.	E.3)
Применим теперь это тождество к вектору скорости несжимаемой
жидкости v, причем воспользуемся последним равенством E.2) и
обозначением
Q = rot v,
тогда получим
До = — rot Q.
Вспоминая уравнение F.4) 1лавы II части первой, можем поэтому
переписать первое уравнение в следующем виде:
d'D	v^	1
~at Ч" gfaci ~o~ + ** X v = F	grad р — v rot Q.
Ot	?	р
Предположим еще, что массовая сила F имеет потенциал V:
и введем обозначение
^^у + ^ + у.
тогда уравнения гидромеханики вязкой несжимаемой жидкости при-
н}т следующий виа
-0j- -j- Q X v — — grad H — v rot Si,
dlV'r'==0'	I	E.4)
i! = rot©.
Во многих сл}чаях, как, например, при изучении вопроса об
обтекании цилиндра и!и сферы, бывает удобно пользоваться, вместо
прямолинейных прямоугольных координат х, у, z, криволинейными
координатами, чаше всего ортогональными, например, цилиндриче-
цилиндрическими или сферическими. Представляет поэтому интерес иметь

390	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
уравнения гидромеханики вязкой несжимаемой жидкости в криво-
криволинейных ортогональных координатах.
Пусть qv q2, q3 суть криволинейные координаты, так что в не-
некоторой области изменения этих координат имеются зависимости
(для краткости мы обозначаем х через xv у через х2 и z через х^):
решая эти три уравнения относительно qv q2, 9з> получим обратные
зависимости:
qi = Ft(xv х2. х3) (/=1, 2, 3).
Мы будем рассматривать только ортогональные криволинейные
координаты; условием для этого является тождественное выполнение
следующих трёх равенств:
«=1
Вводим далее в рассмотрение коэффициенты Ламэ:
i=i
Тогда, как было показано в § 20 главы I части первой, мы имеем
следующие выражения для основных операций векторного анализа —
градиента, расхождения и вихря:
(gradcp)J=7L-||- (/=1, 2, 3),	E.5)
. д{а2Н3Н,) ,
1	W	•-
(rot a)! —
(rot aJ -
E.7)
Исходя из этих формул и пользуясь тождеством E.3), нетрудно
найти выражения для проекций на оси криволинейных координат век-
вектора Дс. Обозначая через (Да^ проекцию этого вектора на напра-

с1	РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ	391
§ 5J
вленне касательной к координатной линии qi% будем, очевидно, иметь,
ито:
1 д ( 1 Гд(а,НгН%) 0(а,Я,Я,) . dja^H,)]]
(Д^^яГЖ"! я,я2я3 L дЧ1 "*" <??, ~*~ <ty3 Jf
1 ( а г я3 а (я2д2> 1	д г я3 а(я,д,I
Я2Я3 ( <ty2 L Я,Я2 <??, J <ty2 L Я,Я2 dq2 J
Н2 д(Н,а,)Л . а Г Я2 а(Я3д3)
JIx dq3 J^ dqt[HaHl dqx
Для (ДсJ и (Ас3) имеем две аналогичные формулы. Если рас-
раскрыть предыдущее выражение, то после длинных, но совершенно
элементарных вычислений получим следующую окончательную фор-
формулу:
да,	\ Hj ) . да,	\ Я2 ' . да,
dq,	dq, ~*~ dq2 dq2 dq3
. 2 дН{ да2	2 (?Я2 да2	, 2 дНх да3
Н\Н<2 dq2 dq^	H^H2 dqx dq2 H^H3 dq3 dq^
2 дН3 да3	. I 1 д Г 1 д (Н2Н3) 1 .
\Hd dq} dq3 | Нх dqx [ НХН2Н3 dqx j
1 д
"
Я2Я3 ^2 [ Я,Я2 dq2 J" Я2Я3 dq3 L Я,Я3 dy,
я3
j i ^ r
( Я, dgr, L Я,
J Я2Я3 dq2 [ Н,Н2 dq
, 2Я3 о^з J Я2Я3 о^з L Я3Я|
Точно так же, применяя для вычисления проекций ускорения w на
оси криволинейных координат формулу
dv dv , , „. _ dv
и пользуясь формулами E.5) и E.7), после несложных вычислений
получим:
v\ dvx . v, dv, . v2 dv, , v3 dvt . v,v2 dH, .
dqx ( ' >
и лве аналогичные формулы для w2 и w3.

392	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	|ГЛ II
Теперь мы могли бы уже написать уравнения движения в проек-
проекциях на криволинейные оси координат, но предварительно мы хотим
еще показать, как вычисляются в криволинейных координатах со-
составляющие тензора скоростей деформаций и тензора напряжений
Пусть М{ и М2— две бесконечно близкие частицы жидкости, и
пусть Mi и М2— положения этих частиц через бесконечно малый
промежуток времени dt. Обозначим криволинейные координаты
точки Л1, через qv q2, q3, а точки М2 — через qi~\-<>q\, <?s4~"<72>
<7з~1~'^з Криволинейные координаты точки М\ б) ч) г (точка над
буквой означает дифференцирование по времени).
-,dt>
но так как мы имеем равенства
то будем иметь:
Точно так же, обозначая координаты точки м'2 через q'i-\-bq',, бу-
будем иметь:
а'4-So' — a +bq I ^(g'+'g» g« + »?2, ?з + »gs, 0 dt
Я, ^г Щ, —q,-t *qt -h Hi (?i + bqu g2 + Чг> ?з + Цз) at.
Сравнивая это равенство с предыдущим, находим:
Но ясно, что lq't означает значение 8^, в момент t-\-dt, можно
поэтому, с другой стороны, написать, что
bq'i = bqi-irdoqi.
Поэтому мы имеем следующее равенство:
t (i=l, 2, 3).
Рассмотрим теперь бесконечно малый жидкий отрезок MiM2 = $s
и его удлинение dos = М\М2 — М1М2 Для квадрата бесконечно
малого элемента длины ls—MxM2 мы имеем в криволинейных коор-
координатах выражение
з
Is1 = ^H\ (qv q2, <73) Ц]-
Дифференцирование даёт:
з	з
85 • d Is = 2 И, dHt bq] + 2 Н\ ?< d ?q,.
4-1	1-Х

РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИИ ДВИЖЕНИЯ
393
Мы имеем далее очевидные формулы:
;	V^ &Hi
k h **J dqk '
3 дШ
-V
dqk Hk
поэтому предыдущая формула может быть приведена к виду:
з з (
5s ¦ d bs	VI	V^ { vk4i dHt 2 _i_
' di ~" Ju	Zj, [ Hk Ли ^« '
e=i	ft=i
Обозначим теперь через bst = Ht bqt элементарные перемещения
в направлении координатных линий, тогда можем написать:
05 ¦ d bs
dHl g
E.10)
В случае прямоугольных координат х, у, z мы имеем Я, = Я2=
легко убедиться, что предыдущее выражение принимает вид:
5s • rf 8s dvx ч	dt/y	dvz
= ех 8д;2+
; By. E.11)
Но теперь, сравнивая выражение E.10) с E.11) и обозначая
в случае криволинейных координат составляющие тензора скоростей
деформаций
1 A l t
у 6з Ч -2^
Ф —
'J

394
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. II
теми же буквами, что и в случае прямолинейных координат, легко
найдём искомые выражения, например:
,=?
к-\
ддк
Я,Я
,Я2
Я,Я3
_1_ dt;2 , 1
Н dq Я
Я2
dv3
v2 дН2
дН3
dq3 H2 dq2 H2H3 dq3 H2H3 dq2
E.12)
Выражения для е2, е3, 02, 93 получаются из предыдущих цикли-
циклической перестановкой.
Так как тензор напряжений
П =
Pll
fti Рз2 Рт
связан с тензором скоростей деформаций для случая несжимаемой
жидкости соотношением
П = —р/+2цф,
то для составляющих тензора напряжений получим формулы сле-
следующего типа:
1 dvt , 1 dv2
v2
<?Я,
dq2
dq,
E.13)
Напишем теперь уравнения движения вязкой несжимаемой жидко-
жидкости в цилиндрических и сферических координатах.
Рассмотрим сначала цилиндрические координаты г, 6, z, связан-
связанные с декартовыми координатами формулами:
х = г cos 6, г = У х2~\- у2,
у = г sin 9, б = arc tg -^-,
z — z,
= z.
В этой системе координат коэффициенты Ламэ имеют следую-
следующие значения:
Нт = 1, Н§ = г, Hz = 1.
Обозначим через Fr, F$, Fz проекции массовой силы F на оси
цилиндрических координат. Тогда, производя вычисление всех чле-

§5]
РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИЙ ДВИЖЕНИЯ
395
нов уравнений E.2) по формулам E.9), E.5), E.8) и E.6), найдем
окончательно уравнения движения вязкой несжимаемой жидкости
в цилиндрических координатах:
dvr ,
dv,
dr r
F l
Г Р
dvT
dp ,
dr '
dvz
VZ(dtr
v ( dr'
Щ
r
1
1 r2
' r
d>vr
dvr
dr
d2vr
r2 56
1
1
VT \
r* '
1 dp
г2 дЬ
dv.
dv,
E.14)
_P i_^_j_ /^2^г , 1 d4z d*vz , 1 Jpt\
—"r* p дг "^ \ dr* "^ r2 cN2 "•" аг2 "•" r dr )'
dvz
Формулы E.13) позволяют составить составляющие тензора на-
напряжений в цилиндрических координатах
dr
г }'
E.15)
Сферические координаты г, 6, X связаны с декартовыми коорди-
координатами следующими соотношениями:
л; =/-sin 9 cosX, г = Ух2-\- у2 + z2,
— г sin 6 sin X, 9 = arc tg
= г cos i
= arc tg -^-.
Коэффициенты Ламэ имеют следующие значения:
Нг=\, Нь = г, Hx = rsmQ.

396
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[гл. и
Поэтому уравнения движения вязкой несжимаемой жидкости
в сферических координатах имеют следующий вид:
dv.
dv.
dv.
dvr
-dT-rvr дг -г
, ctg 9 dvr
r sin 9 ax

" r2 sin2 9
1	2 dvr
"T~7~a7
2	ctfif 0
r2 sin
-Щ\
^ctgO
ctg 9
r sm 9 ax
¦ i а2Уй
" '~7r аи2
2 cos 9 di/>
1
r2 sm2 e ax2
2 aVr
r dr ' r2 a9 r2 sin2 9 aX
at/j , i/n at;v , f, dv-,
ae
a^x at/^ t/g dV) . fj of) |^ tv^v i
"a/ f~ ^ ar ' ~~F ~W ' r sm e ax ~"~ r >
^ i dp . / a2*/, , l a2vi , l
ctg 0
* pr sin 9
2 ai>> , ctg 9
? + ¦
r2 a92 "T" r2sui2 5
, 2 cos 0 dva
r2 sin 0
r2 sm2 о ax
•9
	 n
E.16)
dr ' r ao ' r sm 9 ax ~ л ' л
причем для составляющих тензора напряжений получаются формулы:
E.17)
В этом параграфе мы рассматривали переменные Эйлера. Для некото-
некоторых задач представляет интерес использование переменных Лагранжа.
Чтобы записать уравнение E.1) в переменных Лагранжа, представим
сперва в этих переменных величины kvx, kVy, hvz.
Заметим сперва, что для любой функции f (х, у, z, t) мы можем напи-
написать
а/ _ D U, У, г)	df _Р {х, /, z)
дх D (х, у, г) ' ду D (х, у, г) '
К.
дг
D (х, у, /)
D (х, у, z)

6]
НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯ	397
или, если ввести переменные Лагранжа а, Ь, с,
df _ D (/, у, z) D (а, Ь, с) df D (х, /, z) D (а, Ь, с)
дх ~~ D (а, Ъ, с) D (х, у, г)' ду ~ D (а, Ь, с) D (х, у, z) '
М. = D (х< у' Я D (д' Ь' с)
dz ~~ D (а, Ь, с) D (х, у, г)'
D {а, Ь,с) , „
В несжимаемой жидкости ~±—	~ = 1. Для сокращения письма введём
бзначение
обозначение
D(a,b, с)
Тогда
+ -fc \х< У' Л = f [/> У' *]• У> г] + Iх- Iх' /• гЬ Л + Iх' У Iх. У. Л ]¦
Поэтому взамен уравнения E.1) мы получим в переменных Лагранжа
#-*-¦>,. .! + -{[[?•'¦•]¦'•'] +
х, -?:, г |, z
У,
§ 6. Начальные и граничные условия. Начальные условия для
задачи о движении вязкой несжимаемой жидкости не отличаются от
таковых же условий для случая идеальной жидкости. И в том и
в другом случае должно быть задано в начальный момент ? = 0
распределение скорости во всей рассматриваемой области, т. е.
должны быть заданы три следующие функции:
vx{x. у, z, 0) = /!(*. у, z), vy(x, у, г, 0) = /2(*. у, г), \
vAx, у, z, 0) = /g(*. у, г).	1 ' }
') См. М о н и н А. С, О лагранжевых уравнениях гидродинамики не-
несжимаемой жидкости, ПММ, 1962.

398	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
Впрочем, в очень многих задачах приходится рассматривать дви-
движение или стационарное, или сводящееся к стационарному, и тогда
вопроса о начальных условиях вовсе не возникает.
Напротив, граничные условия в случае вязкой жидкости будут
иными, чем в случае идеальной жидкости. Это обстоятельство имеет
1ромадное принципиальное значение. Нужно особенно подчеркнуть,
что с математической точки зрения исследование движений вязкой
жидкости отличается не только усложнённостью уравнений движения
по сравнению со случаем идеальной жидкости, но и своеобразием
по1раничных условий.
Переходим теперь к формулировке пограничных условий в слу-
случае вязкой жидкости. Мы рассмотрим три случая, которые в даль-
дальнейшем нам понадобятся: 1) жидкость примыкает к неподвижной
стенке, 2) жидкость примыкает к подвижной стенке и 3) жидкость
ограничена свободной поверхностью.
Мы будем считать, что в точках, где вязкая жидкость при-
примыкает к твёрдой неподвижной стенке, скорость жидкости
обращается в нуль. Иными словами, в точках соприкосновения вяз-
вязкой жидкости с твёрдой неподвижной стенкой не только нормальная
составляющая скорости обращается в нуль, как это имеет место и
для случая идеальной жидкости, но и касательная составляющая ско-
скорости тоже равна нулю. Таким образом, вязкая жидкость прилипает
к твёрдым стенкам. В настоящее время считается, что это допуще-
допущение достаточно хорошо подтверждается опытом.
В точках, в которых вязкая жидкость примыкает к подвижной
стенке, мы потребуем выполнения следующего условия: в этих
точках скорость жидкости должна по величине и направлению
совпадать со скоростью соответствующей точки стенки.
Рассмотрим теперь случай свободной поверхности жидкости,
граничащей с пустотой, где давление рй принимается равным нулю,
или с воздухом, где давление принимается имеющим постоянное
значение р0. На такой поверхности должно выполняться, во-первых,
кинематическое условие: нормальная к свободной поверхности
составляющая скорости должна совпадать со скоростью пере-
перемещения поверхности разрыва, и во-вторых, динамическое условие:
вектор напряжения рп для площадок, касательных к свободной
поверхности, должен быть направлен по нормали к этим пло-
площадкам внутрь и по численной величине должен быть равен р0,
так что мы должны иметь Рпп — — JV Pns—®< если 5 есть
любое направление, касательное к поверхности в рассматриваемой
точке.
Приведём теперь несколько соображений, показывающих, какое
большое значение имеет правильный учёт граничных условий. Рас-
Рассмотрим уравнения вязкой несжимаемой жидкости E.4). Эти урав-
уравнения отличаются от уравнений идеальной жидкости только членом

. 6]
НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯ	399
vrotQ. Если вектор Q = roti> есть потенциальный вектор, т. е.
если
rot v = grad x,
то rotQ = 0, и уравнения вязкой жидкости совпадут с уравнениями
идеальной жидкости. В частности, это имеет место для безвихревого
движения, когда rot о = 0, т. е. когда
© = grad(p,	F.2)
причём, вследствие уравнения неразрывности, <р есть гармоническая
функция, т. е. удовлетворяет уравнению Лапласа
Дер = 0.	F.3)
Итак, мы имеем довольно общее решение уравнений движения
несжимаемой жидкости, как вязкой, так и идеальной. Однако это
решение, в случае идеальной жидкости позволяющее рассмотреть
целый ряд задач, в случае вязкой жидкости оказывается почти со-
совершенно бесполезным. Допустим, например, что мы рассматриваем
задачу о прямолинейном и равномерном движении твёрдого тела
в жидкости со скоростью О параллельно оси х. Тогда в случае
идеальной жидкости мы имеем всего лишь одно граничное условие,
которое должно выполняться во всех точках поверхности S, огра-
ограничивающей тело, а именно
vn — U cos (л, л;) или -^- — U cos(n, х),	F.4)
где п есть направление нормали к поверхности 5. Как известно,
условие F.4) определяет гармоническую вне поверхности 5 функ-
функцию ср единственным образом, если отвлечься от постоянного слагае-
слагаемого, которое, по F.2), не играет никакой роли при определении <о.
В случае вязкой жидкости мы имеем, вместо F.4), во всех точ-
точках поверхности 5 три граничных условия:
дх
F.5)
и легко видеть, что не существует решения уравнения F.3), удо-
удовлетворяющего всем условиям F.5).
Этот пример показывает нам, что трудность решения задач гид-
гидромеханики вязкой жидкости кроется не только в усложненном виде
уравнений движения, но и в большем, по сравнению со случаем
идеальной жидкости, количестве пограничных условий.
Мы видим далее, что безвихревые движения не дают решений
задач гидромеханики вязкой жидкости не потому, что они не удо-
удовлетворяют основным уравнениям движения, а потому, что они не
выполняют пограничных условий. А это означает, что завихренность
Движений вязкой жидкости обусловливается наличием граничных
условий, т. е. существованием прилипания жид! ости к стенкам.

400	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	|ГЛ II
Поэтому в движениях вязкой жидкости следует, вообще говоря,
ожидать наличия большой завихренности в областях вблизи стенок,
в то время как в областях, далеких от стенок, движение может
приближаться к потенциальному.
Особенно большое значение приобретают эти рассуждения в слу-
случае жидкостей с очень малыми коэффициентами вязкости. В самом
деле, в этом случае уравнения движения всюду очень мало отлича-
отличаются от уравнений движения идеальной жидкости и поэтому каза-
казалось бы, что соответствующие решения уравнений идеальной жидко-
жидкости должны давать движения жидкости, очень мало отличающиеся от
истинных движений вязкой жидкости. Но вся беда в том, что ука-
указанные решения уравнений идеальной жидкости не могут, вообще
говоря, удовлетворить пограничным условиям, имеющим место для
вязкой жидкости. Это приводит к тому, что движение даже мало-
маловязкой жидкости может очень сильно отличаться от движения идеаль-
идеальной жидкости и притом, главным образом, вблизи стенок.
§ 7. Диссипация энергии. В этом и двух следующих парагра-
параграфах мы рассмотрим ряд общих свойств движений вязкой жидкости, при-
причём будем исходить из выведенных выше общих уравнений движения.
Вглядываясь внимательным образом в уравнения E.1), мы можем
прежде всего подметить необратимость процессов, описываемых этими
уравнениями. Это означает следующее: рассмотрим некоторое дви-
движение вязкой жидкости, происходящее под действием сил, не зави-
зависящих от времени, и в некоторый момент времени / — 0 определим
поле скоростей; переменим теперь направления всех скоростей на
обратные и примем это распределение скоростей за начальное; тогда
жидкость будет совершать некоторое движение. Если бы жидкость
была идеальной, то каждая частица жидкости проходила бы
в обратном порядке ту траекторию, по которой она двигалась до
момента t = 0 и притом с теми же самыми скоростями, но только
прямо противоположно направленными; в случае вязкой жидкости
этого обстоятельства существовать не будет—новое движение не
будет уже иметь такой непосредственной связи с первоначальным.
С математической точки зрения это последнее утверждение сводится
к тому, что если мы имеем решения v(x, у, z, t) и р{х, у, z, t)
уравнений E,1), то функции
i^C*. у, z, f) = — v(x, у, г, —t), 1
px(x,y,z,t) = p(x,y,z,—t) )
не будут уже давать решения уравнений E.1). В самом деле, со-
соотношения G.1) приводят к равенствам типа:
dt ~~ЬТ' Vl* dx ~V*~W V» ду ~~УУ ду '
«, ^li— „, ^jl dp,	dp
Vl* dz ~ * dz ' dx ~~ dx '

3 7]	ДИССИПАЦИЯ ЭНЕРГИИ	401
причём в левых частях этих равенств аргументами являются х, у, z, t,
а в правых х, у, z, —t. С другой стороны, мы, очевидно, имеем
равенства:
Дг>! к = — &vx, До1у = —Дг>у, Д^1г= — Avz,
а тогда ясно, что функции vl и рг не удовлетворяют системе E.1),
что и доказывает необратимость движения вязкой жидкости.
С этим обстоятельством тесно связано наличие так называемой
диссипации энергии, которая состоит в том, что при движениях
вязкой жидкости некоторая часть механической энергии переходит
в энергию тепловую. Исходя из уравнений движения, мы можем,
конечно, обнаружить только потерю механической энергии, причем
можем подсчитать количество теряемой энергии. О гом, что эта
энергия переходит в тепловую, мы судим уже на основании общего
принципа сохранения энергии, по которому при потере энергии
в одном каком-либо виде должно появиться эквивалентное коли-
количество энергии в других формах.
Рассмотрим внутри жидкости произвольный объем т, ограничен-
ограниченный поверхностью 5 Как выше, обозначим через F массовую силу.
Элемент d~ имеет массу pd*, поэтому массовая сила, приложенная
к элементу dx, будет равна Fpdt, а работа этой силы за время dt
будет равна F-vpdtdt, ибо перемещение элемента жидкости d~
равно v dt. Работа всех массовых сил, приложенных ко всем эле-
элементам объема т, будет равна:
Ах = j F ¦ vp di dt.	G.2)
Далее, к элементу dS поверхности S приложена сипа pndS, работа
которой за время dt будет равна рп ¦ vdSdt, а работа поверхност-
поверхностных сил, приложенных ко всем элементам поверхности 5, будет равна:
А2= j pn-vdSdt.	G.3)
5
Пользуясь формулой C.1) и формулой Гаусса, мы можем пре-
преобразовать выражение Л2:
А2= [рх ¦ «cos (и, х)-{-ру • г» cos (и, у)-\-р2 • г» cos (я, z)} dS dt =
= J {
= J { dx +~Ту
z
мы имеем далее:
dtdz<
J°)_ , d(Py-v) . д(рг-у) _/дрх дру дрЛ
дх ~Г ду -+- ^2 — ^ дх -Г" ^ + ^2 j ¦ V -t
i	dv .	dv ,	d© .. тт
1 ГХ dX l ry	Ay I fz ()z
26 Теоретическая гидромеханика, ч II

402	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. П
причем мы пользуемся следующим обозначением:
дъ ,	dv .	dv
dvx
Px* dx
или, что то
Итак,
+ P
же,
= л
А-
<^у
^ ^ ' J
ГЖ?1 + Рууе
°xz
;2 +
Pzzh
«р+
1 -Ггж ^ 1
div П • v -I- E] d-
dvy
ду ' Ру-
р ^4
^^У ^ ^
!+РуЛ-
idt.
¦ dy i"
G.4)
Воспользуемся теперь уравнениями движения D.5), тогда получим
Ах -f Л2 = Г [w ¦ vp -j- E] di dt.
Но если обозначить через Т кинетическую энергию рассматри-
рассматриваемого объема:
то будем, очевидно, иметь:
и так как
d (-^-) = -к d (v • v) = v • dv = v • w dt,
то
dT— \ pv • w dxdt.
X
Поэтому окончательно получаем:
d-.dt.	G.6)
Это равенство говорит, что производимая массовыми и поверх-
поверхностными силами работа только частью идет на увеличение кинети-
кинетической энергии Т. Другая часть этой работы, которая, будучи огне-
сена к единице объема и единице времени, численно равняется Е,
в случае несжимаемой жидкости пропадает, как механическая работа.

% g)	ОБОБЩЕНИЕ УРАВНЕНИЙ ГЕЛЬМГОЛЬНА	403
Таким образом, в случае несжимаемой жидкости количество диссипи-
р)ющейся энергии, т. е. количество механической энергии, превра-
превращающейся в тепловую, будучи отнесено к единице времени и еди-
единице объема, определяется выражением G.4).
Если воспользоваться формулами типа
ii условием несжимаемости
divw = 0,
то легко получим другое выражение для
Е = v. [2г\ -f 2г\ + 2е23 + 6? + b\ + в§] =
<">
Эта формула показывает, что диссипация энергии отсутствует только
в таких движениях жидкости, когда все составляющие тензора ско-
скоростей деформаций приводятся к нулю, т. е., когда движение сво-
сводится к комбинации поступательного и вращательного движений,
иначе говоря, сводится к движению твердого тела.
§ 8. Обобщение уравнений Гельмгольца. В главе V части
первой при рассмотрении вихревых движений в идеальной жидкости
были выведены уравнения Гельмгольца. Смысл этих уравнений за-
заключается в том, что они дают возможность количественного учета
изменений, происходящих с вихрями. Выше было отмечено, чго
громадное большинство движений вязкой жидкости является движе-
движениями вихревыми. Понятно поэтому то большое значение, которое
должны иметь в случае вязкой жидкости уравнения, аналогичные
уравнениям Гельмгольца. К выводу этих уравнений, протекающему
совершенно аналогично случаю идеальной жидкости, мы теперь и
приступим, причем мы предположим для определенности, что имеем
дело с вязкой несжимаемой жидкостью, находящейся под действием
массовых сил, имеющих потенциал. Тогда основные уравнения гидро-
гидромеханики даются форм)лани E.4), первая из которых имеет вид:
^ + SXo = - grad H — v rot Q.
Возьмем от обеих частей этого равенства операцию rot, тогда
получим:
rot-д^-4-rot [Q х v) — — v rot rot Q,	(8.1)
2Ь*

404	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
ибо rotgrad/f = 0. Заметим теперь, что, с одной стороны,
div г» — 0,
с другой стороны,
div Q = div rot v = 0.
Поэтому формула векторного анализа
roi (а ХЬ) — a divb ~ b div a-ir (Ь • V)a —(a ¦ V)&
сразу даёт нам, что
rot (S X я) = 0» • V) S — (Q • V) ч?.
Тогда так же формула E.3) сразу показывает, что
Дй = — rot rot Q.
Замечая, наконец, что
dv 	 д rot v 	 dQ
Ж ~~~ dt = ~dt '
мы можем записать уравнение (8.1) в виде:
-^ + (i>- V)Q —(Q- V)w = vAQ
или короче:
^	AG.	(8.2)
Это уравнение, равносильно трём скалярным уравнениям, первое
из которых мы выписываем:
дг ~
?. + 2 ^L + Sz-^ + vAQr, (8.3)
и представляет собою обобщение уравнения Гельмгольца. Полагая
v = 0, мы получим уравнения, установленные Гельмгольцем для слу-
случая идеальной несжимаемой жидкости. В главе V части первой было
подробно исследовано физическое значение этих последних уравнений.
Из сказанного там вытекает, что уравнение (8.2) при v = 0 является
математическим выражением следующего факта: вихри с течением
времени изменяются таким образом, что вихревая линия все время
совпадает с той жидкой линией, с которой она совпадала в начальный
момент времени, причём интенсивность любой вихревой трубки с те-
течением времени не изменяется. Иными словами, вихри перемещаются
вместе с частицами. Таким образом, те члены уравнения (8.2), кото-
которые не зависят от вязкости, определяют такое изменение вихрей,
которое можно коротко охарактеризовать как перенос вихрей вместе
с частицами жидкости.

. „,	ОБОБЩЕНИЕ УРАВНЕНИЙ ГЕЛЬМГОЛЬЦА	405
Остается выяснить какое значение имеет последний член в урав-
уравнении (8.2) или в уравнениях (8.3). Рассмотрим, например, уравне-
уравнение (8.3) и заметим, что, как показывается в векторном анализе J),
(Дер) и =lim ~sp (.<?M —
в->0	s
dS,
где М есть переменная точка сферы S с центром в точке Мо, ра-
радиус которой равен е. Отсюда вытекает, что если (Дф)уц0 > 0, то
среднее значение функции ср на бесконечно малой сфере с центром
в точке Мо больше значения функции tp в центре Мо этой сферы;
ести же (Дф)уи0 < 0, то среднее значение функции ср на сфере меньше
значения этой функции в центре сферы. Вглядываясь теперь в урав-
уравнение (8.3), мы замечаем, что если Дй^. > 0, то от члена с вязкостью
вечичина dQJdt получает положительную слагаемую, т. е. в этом
случае влияние вязкости сказывается в уравнении Qx. Но, как мы
точько что указывали, в этом случае среднее значение Qx на беско-
бесконечно малой сфере больше значения Qx в центре этой сферы. Та-
Таким образом вязкость стремится сравнять значение Я.х в какой-либо
точке со значениями Qx в окружающих точках. Аналогичные обстоя-
обстоятельства имеют место и в случае Д2^ < 0. Отсюда мы можем вы-
вывести заключение, что дрйствие вязкости сводится к выравниванию
значений вихрей внутри жидкости. Коротко этот процесс выравни-
выравнивания величин вихрей можно назвать диффузией вихрей. Итак, член
) ДЙ в уравнении (8.2), зависящий от вязкости, определяет измене-
изменение вихрей, сводящееся к их диффузии. В дальнейшем мы будем
иметь несколько конкретных примеров диффузии вихрей.
Особенно простой и важный вид получает уравнение Гельмгольца
в случае плоского движения. В этом случае v2 = 0, a vx и v не
зависит от z. Уравнение неразрывности принимает вид:
dvx dvv
vv
i	L __
' ду
	i_
дх ' ду
и показывает, что существует функция тока ^(х, у, t), через ко-
которую проекции скорости выражаются формулами:
^ = -а7- *у = --зт-	(8-4)
Из трёх составляющих вихря только одна Qz может быть отлична
от нуля. А именно, мы имеем:
^^ -^W.	(8.5)
дх ду
') См., например, Кочин Н. Е„ Векторное исчисление, ГОНТИ, 1938,
р. 197.

406 ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ П
Обобщенное уравнение Гельмгольца сводится к	одному уравне-
уравнению, аналогичному уравнению (8.3), имеющему вид:
t+Vd + vf = '>^	(8.6)
Подставляя сюда значения vx, vy и &2, окончательно находим
стедующее уравнение для функции тока 47:
д AW д^" д AW д^ д АЧ?
¦	1	 =¦ v ДДЧГ.	С8 7)
at	ду дх	дх ду	\ • J
Это уравнение, играющее фундаментальную роль при изучении
плоских движений вязкой жидкости, является, таким образом, мате-
математическим выражением тех изменений, которые происходят с вих-
вихрями в этом движении.
§ 9. Закон подобия. Число Рейнольдса. В предыдущих пара-
параграфах мы уже вывели, опираясь на общие уравнения движения вяз-
вязкой жидкости, целый ряд свойств этих движений, например, что эти
движения должны быть вихревыми движениями, что с течением вре-
времени происходит диффузия вихрей, что кинетическая энергия дви-
движения частью переходит в тепловую и т. д.
В настоящем параграфе мы, также исходя из общих уравнений
гидромеханики вязкой жидкости, рассмотрим очень важный вопрос
о законах подобия в гидромеханике, а также приведем ряд связан-
связанных с этим вопросом соображений.
Вопрос о подобии в гидромеханике особенно важен потому, что
экспериментальные исследования могут быть произведены зачастую
только над моделями тел и по этим экспериментальным данным
необходимо бывает выяснить, как будут вести себя в соответствую-
соответствующем потоке сами тела.
Положим, для определенности, в основу наших рассуждений
уравнение 1идромеханики вязкой несжимаемой жидкости. Выпишем
одно из этих уравнений:
dvz , dvz	dvz , dv2 	у	1_ др_ , .	,„ ..
dt	x дх ' у ду z dz	p dz ' "' v • /
Рассмотрим теперь какое-нибудь движение жидкости, например
обтекание сферы радиуса а потоком, имеющим на бесконечности
скорость U, или течение жидкости внутри цилиндрической трубы
радиуса а со средней скоростью U и т. п.
Производя соответствующие экспериментальные исследования, мы
будем иметь дело с различными размерами обтекаемых тел, с раз-
различными скоростями движения и с жидкостями различной вязкости.
В соответствии с этим, в результате опытов получается зависимость
формы течения и других интересующих нас величин, как, например,
численного значения сопротивления, испытываемого телом при его
движении в жидкости, от целого ряда параметров. Оказывается,

§9]
ЗАКОН ПОДОБИЯ. ЧИСЛО РЕЙНОЛЬДСА	407
однако, что, изучая движения жидкости около или внутри геометри-
геометрически подобных тел, мы при определенных соотношениях параметров
получаем геометрически подобные течения. А это имеет своим след-
следствием, что интересующие нас величины, как, например, величина
сопротивления, испытываемого телом, могут зависеть только от
определенных комбинаций упомянутых выше параметров. Для целей
обработки экспериментальных данных это обстоятельство имеет гро-
громаднейшее значение, так как оно позволяет в большом числе случаев
сводить результаты экспериментов к выявлению функциональной
зависимости от одного или двух независимых переменных.
Переходим теперь к более подробному рассмотрению всего этого
комплекса вопросов.
Установим прежде всего достаточные условия механического
подобия двух течений жидкости около или внутри двух геометри-
геометрически подобных тел.
Обозначим через tx, xx, yx, zx, vx, Xx, Yv Zx, px, px, vx величины,
относящиеся к первому течению, а через t2, x2, y2, z2, v2, X2, Y2,
Z2, p2, p2, v2— величины, относящиеся ко второму течению. Если
рассматриваемые течения механически подобны, то после надлежа-
надлежащего выбора начала координат и начала отсчёта мы будем иметь
соотношения:
j- = c(> :!г=^г==т-=='г==с1'	(9>2)
где tx и t2 — соответствующие моменты времени, хх, ух, zx и х2, у2,
z2 — координаты соответствующих точек, 1Х и 12 — соответствующие
размеры; Ct и С1 суть постоянные. При этих обозначениях мы имеем
далее, в силу самого понятия механического подобия:
V2(x2, y2, z2, t2,) = Cvvx{xi, yx, zv tx),	(9.3)
где Cv есть новая постоянная, равная	при этом C{ICt, ибо, на-
например,
	 dx2 	 Ci dxt	Ci
dt2 С i dt i	С i
Допустим далее, что для соответствующих точек мы имеем соот-
соотношения:
"^2 \-^2» 3^2» ^2» *2) 	 '2 	 ^2 	/*>	|
(9.4)
где Ср, Ср, Cv — тоже постоянные величины.
Составляя уравнение (9.1) для второго течения, мы на основании
только что выписанных равенств (9.2), (9,3), (9.4) легко перепишем

408	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
его в виде:
dt ^ Ct \V^ дх, ~^Vly дУ[ ^Vl* дг1
Но если первое течение действительно имеет место, то должно
удовлетворяться равенство
Щг — У - 1 df>i
4l>, ^ + V ^- + V	У
(9.6)
Отсюда мы заключаем, что если
Г Г
" v
Рг=: с~ Р\>	(9-8)
то уравнение (9.5) и ему аналогичные будут удовлетворены и, сле-
следовательно, второе течение, по условию подобное первому, тоже
может иметь место в действительности.
Равенства (9.7) позволяют выразить все постоянные С через две
из них, за которые мы примем Cv и Сг. А именно, мы имеем:
С,С	СиС,	С	,
Подставляя сюда значения постоянных С из равенств (9.2), (9.3)
и (9.4), мы легко придем к следующим соотношениям:
^_	Q Q
i "~~ . '	2 	 2 '	. 	 f '	9 		9 ' V'-^)
h	h	4	V\	V2l2	v\h	bv2	hvl
Следовательно, достаточными условиями механического подобия
является выполнение соотношений (9.9) для любых двух соответ-
соответствующих точек рассматриваемых течений. Первое из этих соотно-
соотношений является, собственно говоря, условием кинематического подо-
подобия, последнее же из соотношений (9.9) определяет р2 и, следова-
следовательно, всегда может быть выполнено. Таким образом, по существу
говоря, мы получаем в рассматриваемом случае два условия
механического подобия:
(9.11)

^ 9]	ЗАКОН ПОДОБИЯ ЧИСЛО РЕЙНОЛЬДСЛ	409
Обозначим через I характерный для данного движения размер,
например, в случае задачи об обтекании сферы эго будет радиус
сферы; точно так же обозначим через V характерную для данного
движения скорость, например скорость на бесконечности в случае
задачи об обтекании сферы. Положим, наконец, что внешний мас-
массовой силой является сила тяжести, так что Z — — g.
Введем в рассмотрение два числа:
R=-V-	(9-12)
называемое числом Рейнольдса, и
1/2
F = -|p	(9.13)
называемое числом Фруда.
Мы видим, таким образом, что для вязкой несжимаемой жидко-
жидкости, находящейся под действием силы тяжести, два течения,
обладающие одинаковыми числами Рейнольдса и Фруда, являются
подобными. Конечно здесь, как и в дальнейшей части этого пара-
параграфа, всегда предполагается, что речь идёт о течениях около или
внутри геометрически подобных тел. Примером, где закон подобия
должен был бы применяться в только что полученной форме,
является испытание моделей кораблей. В самом деле, сопротивление
корабля слагается как из сопротивления трения, так и из волнового
сопротивления, обязанного своим происхождением волнам, образую-
образующимся на свободной поверхности жидкости под действием силы
тяжести. Однако на практике мы встречаемся со следующим затруд-
затруднением: пусть величина модели в 100 раз меньше величины судна
в натуре; по уравнению (9.13), для того чтобы число Фруда F
осталось неизменным, нужно взять скорость V в 10 раз меньше
скорости судна в натуре. Чтобы число Рейнольдса R тоже осталось
неизменным, коэффициент вязкости v нужно взять в 1000 раз меньше
коэффициента вязкости воды; практически этого осуществить нельзя.
Поэтому при испытаниях применяют тоже воду и сопротивление
трения определяют по особым опытным формулам. Остаточное же
сопротивление — волновое — пересчитывается по закону подобия для
идеальной несжимаемой жидкости, находящейся под действием силы
тяжести, но этому закону
два течения с одинаковыми числами Фруда будут подобными
(закон подобия Фруда).
Таким образом, при испытаниях моделей судов линейные размеры
модели цолжны быть пропорциональны квадрату скорости движе-
движения модели.
Если жидкость находится под действием силы тяжести, но сво-
свободных поверхностей в рассматриваемом течении нет, то закон

410	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
подобия сильно упрощается. В самом деле, в этом случае в уравне-
уравнения движения можно ввести вместо давления р новую величину
? = Р + Р?-2,	(9.14)
если считать ось Oz направленной вертикально вверх. Тогда урав-
уравнения движения принимают вид:
grad7f-vAt>,	(9.15)
т. е. сила тяжести является исключённой. В случае наличия свобод-
свободной поверхности этот искусств&нный приём не дал бы результата,
так как на свободной поверхности имеется граничное условие, в ко-
которое входит величина р, а не q.
Но раз внешняя сила оказалась исключённой, то условия (9.10)
уже более не получается, и мы приходим к следующему закону по-
подобия, открытому Осборном Рейнольдсом:
для вязкой несжимаемой жидкости при отсутствии внеш-
внешних сил или при действии силы тяжести, но при отсутствии
свободных поверхностей, два течения, обладающие одинако-
одинаковыми числами Рейнольдса, являются подобными.
Отсюда вытекает, что при рассмотрении течений вязкой жидкости
число Рейнольдса должно играть колоссальную роль. Так, например,
мы указывали в самом начале этой главы, что кроме правильных,
так называемых ламинарных течений жидкости, существуют течения
беспорядочные, так называемые турбулентные. Когда мы рассмат-
рассматриваем различные течения жидкости около или внутри геометриче-
геометрически подобных тел, то оказывается, что при малых числах Рейнольдса
эти течения ламинарны, при больших же числах Рейнольдса они
становятся турбулентными. Таким образом, число Рейпольдса опреде-
определяет даже самый характер течения.
Подойдем теперь к вопросу о подобии с несколько другой точки
зрения. Рассматривая какое-либо течение жидкости, введем, как выше
было указано, характерную для данного течения скорость V и ха-
характерную длину /. Так как можно принять, что характерная ско-
скорость V равна отношению характерной длины I к характерному для
данного течения промежутку времени Т, то характерным промежут-
промежутком времени будет T=ljV. Наконец, характерным ускорением бу-
будет VjT или V2/l.
Введём в рассмотрение безразмерные величины, а именно, по-
положим:
= Pp.

- 9]	ЗАКОН ПОДОБИЯ. ЧИСЛО РЕЙНОЛЬДСА	411
Преобразуем теперь уравнения движения, например, уравнение
(9.1), к введённым безразмерным величинам, причём для определён-
определённости будем считать, что массовая сила есть сила тяжести. Так, на-
например, мы имеем:
dt
V I дги2 d*uz , d>uz \ V
Простые вычисления показывают тогда, что уравнение (9.1) после
указанного преобразования и умножения на 1/V2 принимает следую-
следующий вид:
duz , duz . duz |^ duz 	 IZ P dp ,	•¦/_ .
Мы положим:
P = PV2,
и введём, как выше, числа Рейнольдса и Фруда:
QlV FV2-
тогда уравнение принимает вид:
-бГ + ^-бГ+йу-^- + ^^Г— — ^-— бГ+ r-^«z- (9.17)
Из этого уравнения ясно видно, что характер течения зависит от
значений чисел F и R. Обратно, если для двух течений около гео-
геометрически подобных тел числа Рейнольдса и Фруда одинаковы, то
уравнения движения в безразмерных величинах для обоих течений
будут одинаковы, так же как и граничные условия и, следовательно,
их, иу, uz будут для обоих течений одинаковыми функциями от \, т\,
С, г. Но тогда из уравнений (9.16) ясно видно, что
¦?*- — IX. — ii. _ А *г — ^Vi „. _ Ут.
хх у, г, — /, ' tx— 1XV2 ' 2~ V, "!•
а это и означает, что два рассматриваемых течения подобны между
собою. Итак, при совпадении для двух движений чисел Рейнольдса
и Фруда эти движения подобны между собою.
Наконец, третий способ вывода условий подобия основан на
соображениях теории размерностей'). Возьмём определённое течение
жидкости, характеризуемое в некоторой системе единиц величинами
') В книге Бриджмэн П. В., Анализ размерностей, ГТТИ, 1934, со-
содержится подробное изложение теории размерностей, см. также:
р едов Л. И., Методы теории размерностей и теории подобия в механике,
Гостехиздат, 1944.	г г у	г

412	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
х, у, z, t, vx, vy, vz, p, p, v, g. Пусть мы имеем дело с физической
системой единиц, так что основными единицами являются: единица
длины, единица времени и единица массы. Изменим теперь эти еди-
единицы, положив старую единицу равной L новым единицам длины,
старую единицу времени — Т новым единицам времени и старую
единицу массы — М новым единицам массы. Принимая во внимание
размерности всех вышеперечисленных величин, а именно
[х] = [у] = [г] = L, [t] = Т.	[vj = [vy] = [vz] = А,
[о\=МГ\	[р)=МГ1Т-\ [v]==i2r-1. [g] = LT~\
и обозначая численные значения всех вышеприведенных величин
в новой системе единиц теми же буквами с чертой наверху, будем
иметь:
x = Lx,	у = Ly,	2 = Lz, J= Tt,
		т			т		т
M	М	L2
P	P v
(9Л8)
Обратим внимание на то, что в новой системе численные значе-
значения всех рассматриваемых величин изменились, но так как нами
рассматривается одно и то же движение жидкости, то уравнения дви-
движения все равно будут удовлетворяться.
Итак, величины vx, vy, vz, p, p удовлетворяют уравнениям дви-
движения, в которых вместо g стоит g и вместо v стоит v. Но тогда
никто не может нам помешать вернуться к старым единицам и рас-
рассматривать такое новое движение новой жидкое!и (коэффициент вяз-
вязкости которой в старых единицах равен v) и находящейся под
действием силы тяжести, ускорение которой равно g, в котором
численные значения составляющих скорости, плотности и давления,
измеренные в старых единицах, равны как раз vx, vy, vz, p, p.
Из первых двух строк равенств (9.18) сразу видно, что старое
и новое движения будут подобны между собою. Последние два
равенства (9.18), определяющие значения, которые должны иметь
для нового движения величины v и g, дают нам искомые условия
механического подобия. Обозначая опять через I и V я соответ-
соответственно через I я V характерные длину и скорость, мы будем иметь:
._! l _V_ ^1_JZ. L _X!l
~Т' y~~V ~f lv' Y*~Tv*'

, 9j	ЗАКОН ПОДОБИЯ. ЧИСЛО РЕЙНОЛЬДСА	413
и поэтому два последних условия (9.18) принимают вид:
V W 1 V4	iv iv v2 ___ V2
v IV ' g IV2	v	v	lg lg
Короче говоря, должно быть:
R = R, F = F.
т. е. в двух рассматриваемых нами подобных движениях числа Рей-
нольдса и Фруда совпадают.
Этот вывод, может быть, не столь простой, как предыдущие,
замечателен тем, что нам совершенно не понадобилось использовать
вид уравнений движения вязкой жидкости: нам достаточно было знать
только, какие величины входя г в эти уравнения. С другой стороны,
эют вывод уясняет нам до некоторой степени связь, которая суще-
ciisyei между законами подобия и теорией размерности.
К уяснению этой связи можно подойти еще иным способом.
Допустим, что нами рассматривается вопрос о сопротивлении Q,
испытываемом телом определенной геометрической формы, двужущимся
в вязкой несжимаемой жидкости прямолинейно и равномерно со
скоростью V. Обозначим характерный размер тела через /, плотность
жидкости через р, коэффициент вязкости через v. Если свободных
границ нет, то действие силы тяжести скажется только в гидро-
гидростатической подъемной силе, т. е на сопротивлении Q никак i e
отразится. Нам нет теперь надобности знать точный вид уравнений
движения, а достаточно только точно перечислить все величины, от
которых может зависеть сопротивление Q. В данном случае мы будем
иметь:
/, V, р, /).	(9.19)
Применим теперь соображения теории размерностей. Формула
(9.19) должна иметь место, какой бы системой единиц мы ни поль-
пользовались. Пусть, как выше, мы пользуемся физической системой
единиц и пусть мы вводим новые единицы длины, времени и массы,
соответственно в L, Т и М раз меньшие старых единиц Обозначая,
как выше, численные значения всех рассматриваемых величин в новой
системе единиц теми же буквами с чертой наверху, будем иметь
7"_ ц V — —V 7 = — 7 — — v О — ^- О
Поэтому равенство (9.19), которое должно иметь место и в новой
системе единиц, принимает вид:
ML „

414	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. П
Сравнивая (9.19) и (9.20), мы приходим к выводу, что должно
существовать следующее тождество:
(и. ±V. ??. %-.)=*?<!><!. V. р. *).	(9.21)
ф
Положим теперь в этом тождестве:
L — — Т-— Ж——
тогда получим равенство:
Ф(/, V, р, v) — рУ*Рф(\, 1,1, -^Л.	(9.22)
Чтобы подойти к обычной форме для сопротивления, обозначим
через 5 величину площади проекции тела на плоскость, перпенди-
перпендикулярную к направлению движения. Ясно, что 5 = а/2, где з есть
безразмерная величина. Пусть, далее,
есть число Рейнольдса. Если ввести теперь обозначение
2ф
а
то формула (9.22) принимает вид:
Итак, при сделанных допущениях мы получаем следующее выражение
для испытываемого телом сопротивления:
^	(9.23)
Таким образом, чтобы уметь вычислить сопротивление, испыты-
испытываемое телом данной геометрической формы при его равномерном
движении во всех жидкостях, при всевозможных скоростях и раз-
размерах тела, достаточно знать функцию /(R) одного только аргу-
аргумента R. Эта функция в некоторых случаях может быть найдена
теоретически, в громадном же большинстве случаев её можно полу-
получить только экспериментально. Заметим ещё раз, что для каждой
формы тела и даже для одной и той же формы тела, но в различ-
различных его положениях (например, для эллипсоида, движущегося в на-
направлении наибольшей оси и для того же эллипсоида, движущегося
в направлении наименьшей оси) функции /(R) будут различными.
Если мы имеем дело с движением тела в вязкой несжимаемой
жидкости при наличии свободной поверхности, то формула для

^ ,0]	УРАВНЕНИЕ ПРИТОКА ТЕПЛА	415
сопротивления усложняется. А именно, вместо (9.19) мы имеем
в этом случае формулу:
Q = 3>(/, V, p, v, g).
Те же самые рассуждения, что и выше, приводят в этом случае
к формуле:
*?, F),	(9.24)
где р = V2/lg есть число Фруда.
До сих пор мы всюду предполагали, что имеем дело с несжи-
несжимаемой жидкостью. В случае сжимаемой жидкости все наши выводы
усложняются. Как известно, в случае сжимаемой жидкости фунда-
фундаментальное значение имеет скорость а распространения звука. В связи
с этим для сжимаемой жидкости появляется, кроме чисел Фруда и
Рейкольдса, еще число Маха
М = -?.	(9.25)
При одновременном действии сил тяжести и вязкости в случае
сжимаемой жидкости два течения около или внутри геометрически
подобных тел с одинаковыми числами Фруда, Рейнольдса и Маха
будут подобными.
Точно так же закон сопротивления (9.24) усложняется и прини-
принимает следующий вид:
Q = S&Lf(R. F, М).	(9.26)
Если число Маха М невелико, то /(R, F, M)~/(R. F, 0) и коэф-
коэффициент Маха пропадает из закона сопротивления. Таким образом,
влияние сжимаемости начинает сказываться только тогда, когда харак-
характерная скорость достигает значений, сравнимых со скоростью звука.
§ 10. Уравнение притока тепла для вязкой сжимаемой жидко-
жидкости. Начиная с § 5 и далее, мы занимались лишь несжимаемой
вязкой жидкостью. Уже было указано, что в случае вязкой сжи-
сжимаемой жидкости четырёх уравнений D.9), D.10) недостаточно для
определения пяти функций р, р, vx, vy, vz. С подобным обстоятель-
обстоятельством мы столкнулись ещё в главе по газовой динамике. Там нам
пришлось прибавить пятое, заимствованное из термодинамики соот-
соотношение, и лишь тогда мы сумели замкнуть систему дифференциаль-
дифференциальных уравнений. Однако то уравнение, которое мы называли в пре-
предыдущей главе уравнением притока тепла, носило частный характер —
N'bi рассматривали там движение с большими скоростями и считали,
L'i') частицы не успевают обмениваться теплом с окружающим про-
пространством. Сейчас мы рассмотрим общий случай. Имея в виду кон-
кРетные приложения, мы, как и прежде, ограничимся рассмотрением
Свершенных газов.

416	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Уравнение притока тепла мы выведем из принципа сохранения
энергии. Рассмотрим произвольный обьём (т) конечный или беско-
бесконечно малый, вырезанный внутри жидкости замкнутой поверх-
поверхностью (S). Этот объём обладает массой:
где dt — элемент объёма (х). Так же как и в случае газовой дина-
динамики, этот объем обладает двумя видами энергии: кинетической К и
так называемой внутренней. Первая может быть представлена в виде
вторая, для совершенных газов, имеет вид:
cvTp dt,
/¦
где cv—теплоёмкость при постоянном объёме, Т — температура.
Изменение энергии частицы (т) происходит теперь, в отличие от
того, что было в газовой динамике, не только за счёт работы
объёмных и поверхностных сил, приложенных к частице, но и за счёт
притока тепла к этой частице извне. Основным видом притока тепла
к частице является приток, происходящий при помощи теплопровод-
теплопроводности. Если обозначим коэффициент теплопроводности через k, то
количество тепла, прошедшего благодаря теплопроводности через по-
поверхность частицы внутрь её за промежуток времени от tx до t2 будет:
/
//*?«*•
E)
где п — внешняя нормаль к элементу dS нашей частицы.
Пусть, кроме того, е будет происходящей за счёт других причин
приток тепла за единицу времени и в единице объёма частицы.
Это может быть, например, притоком тепла от излучения. Тогда
к предыдущему интегралу мы должны прибавить величину
е dt dt.
j
t, w
Работа объёмных и поверхностных сил за тот же промежуток
времени будет:
и	t,
j j pF -vdzdt-{- j jpn-vdSdt,
где F — вектор силы, отнесенной к единице объёма.

10]	УРАВНЕНИЕ ПРИТОКА ТЕПЛА	417
Итак, мы можем записать:
I (т)	(X)	>t = t,	I	(Т)	(I)
и
= fl f*dx + f k^-dS + Af pF-vd-. + A f pn.vds\dt,
t\ {(t)	E)	it)	E)	i
(ЮЛ)
где интегралы в левой части берутся, как показывают значки, один
раз в момент t2, другой раз в момент ?,, а А — термический экви-
эквивалент работы.
Деля обе части нашего равенства на t% — tv устремляя t2 к ^
и переходя к пределу, получим:
f k~dS + A f F-vpdT-*rA fpn-vdS. A0.2)
i
1-)
is»	W	(i)
По самому смыслу составления уравнения A0.1) мы следим за дви-
движением одной и той же частицы, так что в уравнении A0.2) мы
слева имеем индивидуальные производные по времени.
Так как масса частицы сохраняется, мы можем заменить выра-
выражение вида
(т)
f Ф? dx.
где Ф — какая-то функция координат и времени, на
С другой стороны, по теореме Грина,
f k-^dS= f div(kgrad T)dx
(S)	W
') Подробно это доказано было в первой главе при выводе уравнения
притока гепла в § 3.
27 Теоретическая гидромеханика, ч, II

418	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
А I рп ¦ vdS= A I [рх -vcos(n, х)+ру ¦ vcos(n,
-\-pz • v cos (п, z)\ dS ¦=
Таким образом мы можем записать A0.2) в виде:
A -kl
Собирая все члены в обеих сторонах под один знак интеграла, вспо-
вспоминая, что объем (~) совершенно произволен и предполагая непре-
непрерывность подынтегральных функций, получим уравнение притока
тепла в виде
2" р W v ' v "I" cfP Ж — s + div
Соотношение это и является тем пятым уравнением, которое следует
прибавить к четырем уравнениям § 4 в случае сжимаемой жидкости.
Температура Т связана с давлением р и плотностью р соотношением
(для совершенного газа) Клапейрона:
р = R?T.
Вид s следует, конечно, уточнить при решении той или иной задачи.
В приложениях этого уравнения, которые будут иметь место в этой
главе, мы будем считать е = 0.
Уравнение A0.3) может быть преобразовано к более простой
форме, если использовать уравнения движения D.8). Действительно,
умножая скалярно обе части D.4) на v, получим
„	, дрг	дру	dpz	ln ..
pF-v—pw v+v--^-+V- -fif + v- -gj- = O. A0.4)
Ho w = dv/dt, так чю
dv ? d

§ 10]	УРАВНЕНИЕ ПРИТОКА ТЕПЛА	419
и мы можем написать по A0.4):
1 d	дрх	дру	dpz
Вставляя это значение -^p-^rV ¦ v в A0.3) и производя сокращения,
получим
dT	. ,.
e+di
Вспоминая, наконец, как выражаются компоненты векторов рх, ру, рг
[формулы C.21)], получим, после простого приведения членов,
уравнение притока энергии в виде:
cvP ^L = s + div (k grad T) — Ap div v -\- A | X (div г»J +
Кйи„
Так же как это мы делали при выводе уравнения притока тепла
в идеальной жидкости, преобразуем в A0.5) divt» на основании
уравнения неразрывности и соотношения Клапейрона. Тогда получим
...	. \ dp .dp . р dT л dp . _ dT
AP^v = AP=A-A	= AARP
Вставляя это в A0.5), собирая члены и вспоминая, что
получим окончательно
ср — cv=
Уравнение A0.6) отчётливо показывает, за счет чего происходит
изменение температуры движущейся частицы и является существен-
существенным дополнением к рассуждениям § 7.
При X=[j.=:/i> = 0 мы получим вновь уравнение притока тепла
Для идеальной сжимаемой жидкости, которое в случае, когда г = 0,
даст условие адиабатичности.
27*

420	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Отметим еще форму, которую примет A0.5) для несжимаемой
жидкости при е = 0. Здесь
cv? -я = div (A grad T) + A* {2 [(-?) + (^j + (^) J +
Так как температура не входит в уравнения движения вязкой несжи-
несжимаемой жидкости, уравнение A0.7) можно решать отдельно, после
того как поле скоростей определено. Это—обобщение на случай
жидкости классического уравнения теплопроводности для твёрдого
тела:
~= div (a2grad T),	A0.8)
где а2 — так называемый «коэффициент температуропроводности».
Новые краевые и новые начальные условия, которые следует вво-
вводить при решении нового уравнения A0.5), мы будем давать в каждом
конкретном случае приложений этого уравнения в различных раз-
разделах этой главы.
Заметим ещё, что в сжимаемой жидкости часто нельзя будет
считать коэффициенты вязкости постоянными. Это же относится и
к коэффициенту теплопроводности k. Дело в том, что и вязкость
и теплопроводность могут зависеть от температуры Т. Зависимость
эта определяется в физике, и мы используем её в отдельных кон-
конкретных приложениях (см. ниже). Здесь отметим только, что отно-
отношение [хср/& A0.9) будет уже, для данного газа, постоянным. В этом
отношении ср — теплоёмкость при постоянном давлении, которая, как
мы отмечали в главе по газовой динамике, связана с cv формулой
Безразмерная величина pcjk носит название числа Прандтля и обо-
обозначается буквой Р. Эта величина вместе с отношением
должна быть прибавлена в случае сжимаемой жидкости к числам
Рейнольдса, Фруда и Маха в рассуждениях о подобии.
Б. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ
ВЯЗКОЙ ЖИДКОСТИ
§ 11. Одномерное течение между двумя параллельными
плоскими стенками. В предыдущем разделе мы вывели основные
уравнения гидромеханики вязкой жидкости в различных формах и
установили ряд свойств, присущих либо всем движениям вязкой

, ш ТЕЧЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКИМИ СТЕНКАМИ 421
жидкости, либо большим классам таких движений. Теперь же мы
переходим к исследованию отдельных конкретных движений вязкой
жидкости и, в первую очередь, к исследованию важнейших из тех
с,п чаев, когда можно точно проинтегрировать уравнения движения
вязкой жидкости. При этом мы будем иметь дело, как правило,
г несжимаемой жидкостью.
В качестве первого примера мы рассмотрим течение несжимаемой
жидкости между двумя параллельными плоскими стенками. Пусть
уравнения этих плоскостей будут сооизегственно
z — —h, z = h;
допусшм еще, что внешних сил нет, что движение стационарно
и происходит параллельно оси Ох, так что
X=Y—Z = Q, г»у = Уг=0, vx — v(x, у, z).
Основные уравнения гидромеханики E.1) при сделанных допущениях
сильно упрощаются:
дх 1 \ду2 ' дг2 ) ду	дг	дх	v '
Последнее из этих уравнений показывает, что v может зависеть
только от у и z: средние же уравнения показывают, что р может
зависеть только от х; но то1да первое уравнение A1.1), в левой
част которого стоит функция от одного только х, а в правой
части функция от у и z, может выполняться только в том случае,
если левая и правая части этого уравнения являются постоянными
величинами. Итак, должно быть:
др
-у-= const.
Для определения v имеем уравнение:
ду2 1 dz2 ~~ |J- дх	A1-^)
и граничные условия
1) = 0 при z=i.h,	A1-3)
вытекающие из требования прилипания жидкости к ограничивающим
неподвижным стенкам. Легко найти частное решение уравнений A1.2)
и A1-3), зависящее только от z; в самом деле, в этом случае мы
имеем:
d2v __ 1 dp
dz2 |л дх '
11 интегрирование этого уравнения даёт нам:

422
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[гл. и
где А и В— две произвольные постоянные, для определения которых
служат два уравнения A1.3). Из этих последних уравнений мы вы-
выводим, что
1 др ,„,,,,„ „ 1 йв ..
откуда
и, следовательно:
= 0,
—
2ц
Легко доказать, что полученное нами решение и есть то решение
уравнений A1.2) и A1.3), которое нам нужно. В самом деле, по-
положим:
тогда ясно, что функция и (у, z)
должна удовлетворять уравнению
Лапласа
\
h
э-
и двум граничным условиям
и— О или г = ±h. A1.5)
Рис. 153.	Но если потребовать, чтобы, v,
а, следовательно, и и оставались
ограниченными в рассматриваемой нами области, то единствен-
единственным решением уравнений A1.4) и A1.5) будет иэеО1).
Итак, при сделанных допущениях, течение жидкости определяется
следующей зависимостью:
дх
A1.6)
На рис. 153 графически изображено полученное распределение
скорости по закону параболы.
Вычислим количество жидкости Q, протекающее в единицу вре-
времени в призме, ограниченной стенками и двумя плоскостями у = 0
и у = Ъ. Так как
дх,
-h
') В противном случае функция и, будучи ограниченной при указанных
граничных условиях, достигала бы максимума или минимуме.

ц] TE4EHHF МЕЖДУ ДВ1 МЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКИМИ СТЕНКАМИ 423
Деля это выражение на попергчног сечение 2hb вышеупомянутой
призмы, получаем для средней скорости жидкости v выражение:
Если взять на оси Ох две точки Мо и Мх на расстоянии / друг
от друга и обозначить давления в этих точках соответственно через
р0 и pt, то, замечая, что
др __Р\—Ра
дх	I
получим из A1.7) для падения давления формулу:
ра — pt 	 За О
A1.9)
Таким образом, в рассматриваемом случае падение давления на
единицу длины прямо пропорционально коэффициенту вязкости
и протекающему количеству жидкости и обратно пропорцио-
пропорционально кубу расстояния между стенками.
Рассмотрим теперь другой частный подслучай. А именно, допу-
допустим, что жидкость ограничена двумя параллельными стенками, одна
из которых z=Q остается все время неподвижной, в то время
как другая z — h перемещается в своей собственной плоскости парал-
параллельно оси Ох со скоростью U. При тех же допущениях, чк> и
выше, мы найдём, что
др	,
—!— = const.
дх
Для простоты примем, что
Тогда те же рассуждения, что и выше, покажут нам, что v должно
опрецеляться дифференциальным уравнением
только теперь граничные условия будут
v= 0 при z = 0, )
, ,	A1.12)
ибо частицы жидкости, пршегающие к нижней стенке, должны ос-
оставаться неподвижными вместе со стенкой, частицы же, прилегающие

424	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. 11
к верхней стенке, должны перемещаться с той же скоростью, что
и эта стенка.
Интегрирование уравнения A1.11) даёт:
V— Аг 4- В,
где А а В — произвольные р.ос гоянные. определяющиеся из уравне-
уравнений A1.12):
Итак, в рассматриваемом случае течение определяется формулой
Как раз с рассмотрения этого течения мы начали нашу главу и уже
представили графим ски полученный лик йный закон распределения
скорости на рис 151 Просты вычисления дают для протекающего
количества жидкости и для ср шей скорости выражения
Q = 4^-, «=*?.	A1.14)
Вычислим ещё силу трепня, действующую на каждую единицу
площади стенки. Мы имеем формулу
dv
и, следовательно, для искомой силы тргния получаем выражение
Наконец, чтобы показать пример того, как надо учитывать гра-
граничные условия на свободной нов.р^нопп, риберёч ещё один частный
подслучай. Пусть на жидкость дейс1вует сила тяжести, и пусть
жидкость ограничена сверху свободной поверхностью снизу же непо-
неподвижной плоскостью Оху, наклонённой к горизонту noi углом а,
причём ось Оу горизонтальна, а ось Oz направлена перпеидикулярно
к плоскости вверх, так что
X=zgs\ni, K = 0, Z= -g-cosa.	A1.16)
Будем опять считать движение происходящим параллельно оси Ох
и стационарным. Рассмотрение основных уравнений гидромеханики
снова приводит к выводу, что
др
¦—- = const.
дх
Примем для простоты, что
¦^¦ = 0.	A1.17)

6 И) ТЕЧЕНИЕ МЕЖДУ ДВУМЯ ПАРАЛЛЕЛЬНЫМИ ПЛОСКИМИ СТЕНКАМИ 425
Уравнения E.1) приведутся тогда к виду:
А_о op Js3 = y	A1Л8>
так что
р = С — ogz cos a,
1де С некоторая постоянная ве шчина
Граничные \сювия, согласно § Ь, имеют следующий вид. На
неподвижной плоскости
v — 0 при z ¦= 0;
на свободной же поверхности z-—h аотжны выполняться условия:
Pzz	А> Ргх ' Piv	•
Но так как г»у = г»г = 0 и vK~b есть функция только от у
и z, то
.. , г. OV,	_	..	/ W,	6»U. \	(Jt/
следовательно, мы прихоаич к следующим граничным условиям:
Р=Р<), -^-=° при г = й.	A1.19)
Первое из этих условий определяет постоянную С:
так что
p = Po + ?g(h—z)cosa.	A1.20)
Отыскиваем теперь частное решение уравнения A1.18), зависящее
тотько от z, гак что
i	d2v	n
pg-sina-f [1-^^ = 0.
Общее решение этого уравнения есть
t/=-J^—z
постоянные Л и 5 определяются из граничных условий
г» = 0 при z = Q,
dv r,	.

426
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[гл п
которые дают
Итак,
= 0, Л - ?gh Sln a ,
, — Р8г B!г — *)sln <*
2[А
A1.21)
Легко теперь убедиться, что это и есть то решение рассматри-
рассматриваемой задачи, которое нам нужно. В самом деле, если положить
р== (.^Bй-г)Япв + я(у|г)>
то для функции и (у, z) получится уравнение Лапласа
при граничных условиях
и == 0 при z = О,
¦^- = 0 при z = h;
если потребовать еще ограниченности и во всей рассматриваемой
нами области, то непременно должно быть и^О, что и доказывает
высказанное утверждение.
Распределение скоростей получается по параболическому закону
(рис 154). Для протекающего количества жидкости Q и для сред-
средней скорости легко получаем
формулы.
pgbh3 sin а
= —а:—
A1.22)
так что протекающее коли-
х чество жидкости обратно
пропорционально коэффи-
коэффициенту вязкости жидкости
Рис 154	и прямо пропорционально
кубу глубины жидкости.
Осветим еще на этом последнем примере вопрос о диссипации
энергии.
Рассмотрим то кочичество жидкости, которое находится над пря-
прямоугольной площадью основания, одно ребро которой, параллельное
оси Ох, имеет дтану I, а другое, паралтечьное оси Оу, имеет
4 iiiii\ b. Ста тяжести, действуя на отдельные частицы этого объёма

. l2]	ТЕЧЕНИЕ ПУАЗЕПЛЯ	427
жидкости, производит некоторую работу. А именно, частицы объёма
Ibdz и массы plbdz, для которых координата z лежит между z и
z-\-dz, за единицу времени опустятся на г» sin а, так что работа
силы тяжести будет
plb dz ¦ vg sin a.
Интегрируя это выражение по z от 0 до h, мы найдём работу
силы тяжести, производимую за единицу времени:
Г ,. . ,	,, .
А= olbgv sin а dz = pg7? sin
ра2е2№1Ь sin2
Но так как никакого увеличения кинетической энергии жидкости
не получается, то, очевидно, вся энергия, получаемая за счёт силы
тяжести, диссипируется. Действительно, если мы вычислим по фор-
формуле G.7) дисснпирующуюся энергию Е, отнесённую к единице
времени и единице объёма
и проинтегрируем это выражение по рассматриваемому объёму, то
получим:
л
lbfg2sm2a f	,	ibhYg2 sin2 a
\f{h-z?dz='-
т. е. величину, равную как раз А.
В заключение отметим, что при больших числах Рейнольдса
рассматриваемое течение становится турбулентным, следовательно,
полученные нами формулы применимы только к случаю очень малых
глубин и сравнительно малых скоростей и неприменимы, например,
к случаю течений воды в реке, имеющих уже турбулентный ха-
характер.
§ 12. Течение Пуазейля. Мы займёмся теперь теорией ламинарного
течения в цилиндрических трубах. Исследование течений в трубах
имеет, как это вполне очевидно, громадное практическое значение;
понятно поэтому, что этому вопросу посвящены были многочислен-
многочисленные работы, приведшие к открытию важных закономерностей. Так,
например, Гаген (Hagen) на опытах с трубами изучал как ламинар-
ламинарную, так и турбулентную формы течений, а также переход от одной
формы течения к другой. Осборн Рейнольде установил известное
уловие перехода от ламинарной формы течения к турбулентной,
заключающееся в том, что число Рейнольдса переходит через неко-
некоторое критическое значение, также на основании своих опытов
с течениями в трубах.

428	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ U
Задача о течении в трубе имеет, как мы сейчас увидим, вполне
точное и строгое решение. О л ако это относится только к случаю
ламирарро" формы кчьння ri тя t\р^уленгний формы течения мы
такого iipircio pan i ия пока аце fk имеем. Одьако преобладающее
бо и шинство Tt4iibfl в тр}6а\, с которыми приходится името дело
на практике,- течения i\p6\ Ti нтиые. Наибо iee ватным сл\чаем
ламинарных 1ечишй ЯВ1ЯЮ1СЯ течения в тонких; трубках, так назы-
называемых каш 1 is pax
Het'oipH i а зЮ обстоятели ibo, теория лампнарпою 1ечения
в ip\6a\ ими i веема чмшое оШлние Дело в шм '.ю поскольку
мы имеем в iiсм сл}Чс'с lt pci oe решение уравнений гидромеханики
ьязкой жидкосш, пол\чается возможность сравнить результаты тео-
теории с результатами опыта Оказалось, что опьп с шегяще подтвер-
подтверждает выводы теории а это показывает, чю основные предпосылки
теории сравнения I авье — Слоксл и приняты3 нами граничные усло-
условия (при 'ипаниь жижосп! к с гонкам сосуда) являются оправданными.
С	ря! приборов атя опрс ie пения вязкости
капи.1 ippn\io гр\бк\, через koiodjio
i, ык чю теории эп!х приборов Осно-
ч ' |'ц жихкпеш ч^рез 1р\бы
т иы ttrtCiBtruio поюлить основные
'й iii с кича^мой жткостп в цилиндри-
цилиндриС дрмой i
имее г i мв,
пронеАО in i
вача ьг i
В oinii
\ past eldi i I
ЧеСКИХ ku'H
-lip МЫ,
Of ebO.'t
ИЧ till
.¦• i a N4
\ 1 d all '
и po\ie\<
) II 4dld4
Ц(г 1ЫИ
* »de Г1 К
ЖР .КОС
i <<t) I'! 0
* ))dee\ i
'ШЛИ bii
.5 14 и
Сформ} nip ei основные тогппиппя. П}сть мы имеем цптшири-
ческ\ю 1 р\ох крмовою сеч ния рали\с которою рати а Ось
этой гр)бм примем "d o> I ()z цн iniupii4t ской сисгьмь1 координат.
П}сть HtOMiva мая / hikoi-Тг, тьчет вдоть этой гр^бы, причем внеш-
внешние сты отс\1ств)ют. 'оп\сп1М наконец, что течение стационарно
и что в каждой точке скороеd направлена параллельно оси трубы,
так что
vr=zvj = Q, vz~v(r, Q, z).
При этих допущениях уравнения E.14) принимают, как легко
видеть, следующий простой вид.
др „ др 	„ dp	I d2v	. 1 d'v , 1 dv \ )
~дг	~Ш	~dz~ == ^ \ дгг	' 7* (№ ~*~ 7 "dF) ' I
dv	} A2Л')
"дг~ '	)
Первые т.ва из этих уравнений показывают, что р может зависеть
тол'ко or z, посл^дч^е же \равнение по, азыва т что v есть функ-
функция только г и 6 Но так как правая част, ip тьего уравнения
A2.1) не зависит or z, то и левая часть не може! зависеть от z и,

§ 12]	ТЕЧЕНИЕ ПУАЗЕЙЛЯ	429
dp
следовательно, -?- есть постоянная величина
др
-f- = const.
дг
Если давления в двух точках Мх и М2 на оси Oz, отстоящих
одна от другой на расстоянии /, обозначить соответственно через рх
и р2. то будем, очевидно, иметь:
дР — ElZZlx — — Pi—Рг	/i о ол
дг ~ I ~~	I ''	{ ¦ >
Hiai<, функция г» (г, 8) удовлетворяет уравнению
f_v_ ,J_a«w ,i^;_li?.	п9оч
йг2 ^~л2 ао2 гг*~ |л дг	U^-V
и очевидно граничному условию па стенке
v = 0 при г = а.	A2.4)
Мы можем легко найти решение уравнения A2.3), зависящее
только от г и удовлетворяющее условию A2.4). В самом деле, если
v — v(r), то A2.3) может быть переписано так:
dr V dr j ~ [л дг '
интегрируя, получаем:
dr ~ 2a <te • '
деля на г и ещё раз интегрируя по г, находим:
v = J-^r-r2-}- A\nr + B.	A2.5)
Произвольные постоянные А к В нужно определить из гранич-
граничного условия A2.4) и добавочного условия, что скорость v остаётся
ограниченной во всей рассматриваемой области. Но если АфО, то,
как показывает формула A2.5), скорость v становится бесконечной
при г = 0, т. е. на оси трубы; поэтому надо непременно положить
Л = 0.
Условие A2.4) даёт теперь:
откуда
В— — — ^
75 ~~ 4;;. дг

430	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. tl
Итак, мы нашли решение уравнений A2.3) и A2.4):
v = — -.—-f- (а2 — г2).
Никакого другого решения задачи не существует. В самом деле,
положим
^ B 2)* и (г, б),
тогда ясно, что функция и (г, 6) должна удовлетворять уравнению
\„— дЧ л_ х <52« , 1 ди __п
т. е. должна быть гармонической функцией и, кроме того, должна
удовлетворять условию
и = 0 при г —а.
Но известно, что гармоническая функция достигает своего максимума
и минимума на контуре, следовательно, должно быть и == 0, откуда
и вытекает наше утверждение.
Заменяя, наконец, dpjdz его значением по A2.2), окончательно
находим:
Распределение скорости подчиняется, очевидно, параболическому
закону. Наибольшая скорость, равная
vo= ^f2^.	A2.7)
имеет место на оси трубы. Объём жидкости, протекающей в еди-
единицу времени через поперечное сечение трубы, определяется, оче-
очевидно, по формуле
^?±^-.	A2.8)
о
Деля это выражение на тм2, найдбм среднюю скорость течения
Определим, наконец, силу трения т0, действующую на стенки
трубки. Для этого вычислим по формуле E.15) значение величины
dvz dvr\	 dv __ KP\—Pi)r
21

12]
ТЕЧЕНИЕ ПУАЗЕИЛЯ	431
прИ г = а и изменим знак (prz даёт силу, действующую на	элементы
жидкости; на стенку же будет действовать та же сила, но в прямо
противоположном направлении); в результате получим:
__ (р, —Pi) а- __ W	г1о 1Оч
о— ^fl — а '	A4.ш)
В опытах обычно определяется величина р{ — р2 = \р.	Поэтому
решим уравнения A2.8) и A2.9) относительно ^p:
Мы получаем, таким образом, закон Гагена — Пуазейля:
При ламинарном течении падение давления пропорционально
секундному объёму протекающей жидкости и длине трубы и
обратно пропорционально четвёртой степени радиуса трубы.
Или иначе: падение давления пропорционально средней скорости
течения и длине трубы и обратно пропорционально квадрату
радиуса трубы.
Только что выведенные соотношения были экспериментально
найдены независимо друг от друга Г. Гагеном в 1839 г. и Пуазей-
лем (Poiseuille) в 1840—1841 гг. Мы имеем, таким образом, в этом
случае блестящее совпадение результатов опыта с выводами теории.
В заключение настоящего параграфа остановимся ещё на вопросе
о пределах применимости полученного нами теоретически течения
Пуазейля. Мы уже несколько раз упоминали, что существуют две
формы течений жидкости: ламинарная и турбулентная. Ламинарная
форма течения характеризуется правильным движением частиц жидко-
жидкости, как, например, это имеет место в течении Пуазейля. Напротив,
в турбулентном движении частицы двигаются весьма беспорядочным
образом, так что при турбулентном движении в трубе на главное
движение в направлении оси трубы налагаются беспорядочные пуль-
пульсации движения как в направлении оси трубы, так и перпендику-
перпендикулярно к этому направлению. Наглядно можно показать различие
этих двух форм течений, если ввести в некотором месте оси трубы
небольшое количество окрашивающей субстанции; тогда при лами-
ламинарной форме течения мы увидим одну резко окрашенную струйку
жидкости, в то время как при турбулентной форме течения вся
жидкость окажется окрашенной, что показывает на сильное переме-
перемешивание частиц жидкости.
Мы уже упоминали выше, что закон Гагена — Пуазейля, выражаю-
выражающийся формулами A2.11), для турбулентной формы течения перестаёт
иметь силу. Таким образом, закон сопротивления при переходе от лами-
ламинарной формы течения к турбулентной резко меняется. Это измене-
изменение закона сопротивления является, пожалуй, наиболее важным кри-
критерием для различения ламинарной формы течения от турбулентной.

432	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Осборн Рейнольде показал, что при движении воды в трубе
ламинарный или турбулентный характер течения зависит от значения
соответствующего числа Рейнольдса
R=~.	A2.12)
Если число Рейнольдса меньше некоторого критического значе-
значения Rft, то течение будет ламинарным, в противном случае оно
будет турбулентным. Позднейшие исследования внесли в это поло-
положение целый ряд уточнений, о которых будет идти речь в главе
0	турбулентности, но сейчас для нас только что приведённая грубая
формулировка условий перехода ламинарного течения в турбулентное
будет вполне достаточна.
Итак, движение жидкости будет ламинарным, если или скорости
течения достаточно малы, или диаметр трубы достаточно мал, или
жидкость достаточно вязка.
Опыты показывают, что для течений в цилиндрических трубах
критическое число Рейнольдса равняется приблизительно 1000—1100.
В качестве примера рассмотрим течение воды в трубе диаметра
1	см. Так как v = 0,018 см2/сек, а = 0,5 см, то, принимая Rft = 1000,
найдём, что движение будет ламинарным при v < 36 см\сек. При
диаметре трубы в 1 мм движение остаётся ламинарным при скорости
v < 3,6 м/сек.
§ 13. Общий случай стационарного одномерного течения.
В двух предыдущих параграфах мы рассмотрели наиболее важные
случаи стационарных одномерных течений. Рассмотрим теперь общий
случай стационарного течения.
Допустим, что движение стационарно и происходит вдоль оси Oz,
так что
vx = vy = 0, vz=v(x, у, z).
Считая внешние силы отсутствующими и повторяя рассуждения
начала § 11, мы легко придём к выводу, что
-?- ¦= const.
дг
и что функция v зависит только от х и у и удовлетворяет уравнению
*V~ дх* ^ ду2 — (х дг •	A6Л)
Мы различим теперь два случая, смотря по тому, обращается ли
dpjdz в нуль или нет.
I. др/dz — O. В этом случае скорость v удовлетворяет уравнению
Лапласа

общий случаи стационарного одномерного течения
433
рассмотрим теперь вопрос о граничных условиях. Ясно, что
в данном случае границами жидкости могут служить только цилиндры
с образующими, параллельными оси Ог, которые могут оставаться
неподвижными или перемещаться параллельно оси Oz с постоянной
скоростью.
Пусть, например, рассматривается движение жидкости между двумя
цилиндрами, сечения которых плоскостью Оху суть кривые С1 и С2,
охватывающие одна другую (рис. 155). Пусть первый цилиндр пере-
перемещается параллельно оси Oz со скоростью vv а второй со ско-
скоростью v2. В этом случае граничные усло-
условия, которым должна удовлетворять гар-
гармоническая функция v, будут:
на Сг,
» С2.
A3.3)
Рис. 155.
Но тогда ясно, что рассматриваемая
задача сразу может быть сведена к экви-
эквивалентной задаче о плоском безвихревом
движении несжимаемой жидкости. В са-
самом деле, рассмотрим такое плоское
течение жидкости в области S, расположенной между контурами Cj
и С2, причём потребуем, чтобы сами контуры Сх и С2 были бы
линиями тока этого течения и чтобы на контуре Сх значение функ-
функции тока равнялось бы vv а на контуре С2 равнялось бы v2. Если
комплексный потенциал этого вспомогательного течения обозначить
через
w = <
то ясно, что i]> тоже должна удовлетворять как уравнению Лапласа
так и тем же граничным условиям, что и функция v:
> = г>, на
С2.
Но ясно, что при этих условиях функции ф(лг, у) и v(x, у)
должны совпадать. Таким образом, рассматриваемый случай стацио-
стационарного одномерного движения вязкой жидкости полностью свёлся
к хорошо изученной ранее задаче о безвихревом движении несжи-
несжимаемой жидкости.
Эту аналогию можно продолжить ещё дальше. Известно, что
Д-тя плоских движений несжимаемой жидкости важную роль играет
понятие циркуляции скорости. Посмотрим, что является аналогом
Icopein'ietha» nv
d, ч, II

434	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ Ц
циркуляции скорости для рассматриваемого случая движения вязкой
жидкости.
Подсчитаем дтя этого силу трения, которая действует на один
из ограничивающих цилиндров, например второй, со стороны жидко-
жидкости. Достаточно рассмотреть часть поверхности этого цилиндра,
заключённую между плоскостью Оху и параллельной плоскостью,
отстоящей от плоскости Оху на расстоянии, равном единице длины.
Рассмотрим элемент ds контура С2 и обозначим через п направле-
направление внутренней (т. е. направленной внутрь области S) нормали.
Тогда на элемент ds рассматриваемой части поверхности будет дей-
действовать сила трения, равная
а на всю рассматриваемую часть цилиндра будет действовать сила
трения
j&	A3.4)
Переходя к соответствующему плоскому течению, получим для
силы трения выражение
Но, как известно:
дп ds	^ ds
с
где Г есть циркуляция скорости по контуру С. Следовательно, мы
находим, что
Г=цГ2,	A3.5)
где Г2 есть циркуляция скорости по контуру С2.
Итак, сила трения, испытываемая каким-либо ограничиваю-
ограничивающим цилиндром и отнесённая к единице длины этого цилиндра,
равняется произведению коэффициента трения \i на цирку-
циркуляцию скорости по контуру поперечного сечения цилиндра в соот-
соответствующем плоском течении, причём контур пробегается в по-
положительном направлении, т. е. так, что область при обходе
этого контура остаётся слева.
Теперь остановимся на примерах1). В качестве первого возьмём
следующий пример. Пусть Сх и С2 — окружности радиусов гх и г2
с общим центром в начале координат, и пусть i>j = U, v2 = 0, так
') См. также Brillouin М, Lemons sur la viscosite des liquides et
des gaz, 1 A907), стр. 61—73, Paris,

. l3]	ОБЩИЙ СЛУЧАЙ СТАЦИОНАРНОГО ОДНОМЕРНОГО ТЕЧЕНИЯ	435
что имеем дело со скольжением внутреннего цилиндра внутри дру-
другого неподвижного цилиндра. Известно, что безвихревое течение между
двумя окружностями определяется комплексным потенциалом
Г
1Ю — -kzt In Z -f- const.,
где мы вводим, как обычно это делается в теории плоского тече-
течения, комплексную координату
Z = х -j- iy,
причём Г есть циркуляции скорости как по окружности Cv так и
по окружности С2. Вводя полярные координаты г и 6, будем иметь:
Граничные
определяют
условия
нам Г
г
JL -
Следовательно, мы
Z = reib; ф =
ф = ?/
и С: '
2т.и
1п/-2 — In/1!
= —
при
получаем, что
v ?/
1п/-2
¦йг1пл+
С/In
In / —
i — 1ПГ
— 1п/-[
С.
г2
In /-,
и что сила трения со стороны жидкости на подвижный цилиндр,
отнесённая к единице длины, равна
Г=— , 2"^—•	A3.7)
Знак минус берётся потому, что циркуляция скорости по контуру Cv
пробегаемому по часовой стрелке, равна —Г. Из формулы A3.7)
видно, что при заданном диаметре внеш-
внешнего цилиндра сила трения будет тем
больше, чем уже зазор между цилинд-
цилиндрами.
В качестве второго примера возьмём
Движение пластинки шириной 2с — С'С
внутри эллиптического цилиндра АВА'В',
полуосями которого являются а и Ь,
а фокусы лежат как раз в точках С и С
(рис. 156). Таким образом, здесь Сх есть
Дважды пробегаемый отрезок СС, а С2
есть эллипс АВА'В'. При этом эллиптический цилиндр мы считаем
неподвижным, а пластинку СС предполагаем перемещающейся парал-
параллельно оси Oz со скоростью U.

436	движение вязкой жидкости	ил и
Конформное отображение области 5 на кольцо 1 < |i| < R пло-
плоскости С даётся в данном случае, как известно, формулой
причем
так что
о _ а + ь _
с	j/V _ й2	а —
Мы можем теперь применить формулы A3 6) и A3 7), в кото-
которых надо принять r1=\, r2 = R, л=|С|. В результате дтя ско-
скорости вязкой жидкости получаем общее выраженцр
v ]n	A38)
а для силы трения, испытываемой пластинкой СС (с обеих ее сто-
сторон) и отнесенной к единице эгой пластинки:
1* -~
II. -—-- -fc О В этом случае скорость v удовлетворяет уравнению
Пу ассона
Дг,_^+^-=-А.	A3Л0)
дл2 ' дуг
если для краткости ввести обозначение
k - L^JL— p±zz?i	из in
где pj — р2 есть падение давления на отрезке длины I, расположен-
расположенном параллельно оси Oz.
Наиболее важным случаем этого типа является вопрос о движе-
движении вязкой жидкости в неподвижной цилиндрической трубе с обра-
образующими, параллельными оси Oz Если поперечное сечение этой трубы
есть кривая С, то граничным условием для искомой функции v будет
служить
v = 0 на С.	A3.12)
Мы имеем в этом случае обобщение течения Пуазейля на случай
трубы произвольного сечения.
К задаче решения уравнения A3 10) при граничном условии
A3.12) приводится также задача теории упругости о кручении
призмы, а также задача о плоском движении идеальной несжимаемой

5 14]	НЕСТАЦИОНАРНОЕ ОДНОМЕРНОЕ ТЕЧЕНИЕ	437
жидкости в области 5, контур которой С вращается с постоянной
ji повой скоростью и, наконец, задача о прогибе мембраны под дей-
действием равномерной нагрузки В связи с этим задача интегрирования
уравнения A3.10) при граничном условии A3.12) решена для весьма
большого числа контуров1)
Мы 01 раннчнмся одним простым примером. А именно, легко
най1И решение уравнения A3 10) в виде полинома второй степени
v (х, у) = Ах2 + By2 -r- D.
Достаточно для этого принять
А + В = — ^.	A3.13)
Условие A3.12) показывает, что уравнением контура С является
Теперь ле1ко добиться юго, чтобы контур С оказался контуром
э пипса
¦^+^~1=-0.	A3.14)
Дтя этого достаточно принять
чтобы удовлетворить также и условию A2.13), нужно принять
2 (а' 4- Ьг) 2;л/ (а2 + Ь2)
и спедовательно,
V КХ< У) == о,,;
Итак, функция A3 15) решает задачу о ламинарном течении вяз-
вязкой жидкости через тр)бу эллиптическою сечения. Полагая а — Ь,
мы вновь восстановим решение задачи о течении Пуазейля Простое
вычисление дает для объема протекающей в единицу времени через
трубу жидкости выражение:
д=	_J	A3.16)
§ 14. Нестационарное одномерное течение. Рассмотрим теперь
случай движения вязкой жидкости более общий, чем тот, с которым
мы имечи дело в предыдущем параграфе, а именно отбросим усло-
R'ie стационарности.
') См., напоимер, об1орч>ю статью Pose hi Th, Bishenge Losungen
des Torsionsproblerns, Zs f angew Math u. Mech, 1 A921), ctp 312—328.

438	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. IT
Итак, допустим, что движение вязкой несжимаемой жидкости
при отсутствии внешних сил происходит параллельно оси Ох
v = v = 0.
Уравнение неразрывности показывает, что vr не зависит от х, т. е.
vx — г>(у, z, t).
Уравнения гидромеханики поэтому сильно упрощаются:
Из последних уравнений видно, что р зависит только от х и t.
Но тогда в первом уравнении левая часть не зависит от у и г,
а правая часть не зависит от х; следовательно, как левая, так и
правая части являются функциями одного только t:
7-Й-= /(')•	A4-2)
Если /(/) —0, уравнение для v принимает вид:
dt ~ *'\~ду* ~т~ ~§z* ) '	A4-d)
Если же / (t) ф 0, то введём вместо v новую функцию v, положив
t
v = v-\-ff(t)dt;	A4.4)
о
тогда
dv dv
и, следовательно, v будет удовлетворять тому же уравнению A4.3);
правда, граничные условия при этом несколько изменяются.
Итак, во всех случаях нестационарного одномерного течения дело
сводится к интегрированию уравнения A4.3). Это уравнение есть
основное уравнение теории теплопроводности; известно решение
большого числа частных задач, связанных с этим уравнением, что
дае'т возможность определить большое число соответствующих тече-
течений вязкой жидкости. Конечно, при решении уравнения A4.3) необ-
необходимо также учитывать соответствующие граничные и начальные
условия; последние сводятся к заданию функции v для начального
момента времени ? — 0. Если и граничные и начальные условия не
зависят от координаты у, то и решение v уравнения A4.3) не будет
зависеть от у, а тогда функция v(z, f) будет удовлетворять уравне-
уравнению теплопроводности для линейного случая
dv	d2v	,. . сч

§ I4j	НЕСТАЦИОНАРНОЕ ОДНОМЕРНОЕ ТЕЧЕНИЕ	439
Мы рассмотрим задачу о движении вязкой жидкости, занимающей
все пространство, причём будем считать распределение скорости
Б начальный момент известным и заданным формулой
v(z, Q) — F(z).	A4.6)
Для интегрирования уравнения A4.5) можно было бы применить
метод Фурье; мы применим другой метод — метод источников.
Допустим сначала, что функция F(z) отлична от нуля только
в окрестности точки z = 0 и что
(z)dz = Q.	A4.7)
Ясно, что в этом случае скорость v(z, f) в какой-либо точке будет
функцией следующих четырёх величин:
v{z, t)— Ф(г, t, v, Q),
причём очевидно также, что v будет прямо пропорционально Q,
так что
v (z, t) = QW(z, t, v).
Применим теперь соображения теории размерностей. Мы имеем,
очевидно, следующие размерности отдельных величин:
Но тогда, применяя те же соображения, что в § 9, мы легко при-
придем к тождеству
i W (г. t. v) = W [Lz, Tt, ~ v) .
Полагая здесь Г= —, L =	, легко получим:
*	у it
V(z, t, v) = —Lr 4F /-^=r , 1, l) или <FB, Л 4) = ^^=-/
Итак,
Ф	/^ y \it}~~ У^
где положено
it

440	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Но функция v(z, t) должна удовлетворять уравнению A4.5). Соста-
Составляя dvjdt, dv/dz, d2v(dz2, находим:
-=	W/E) — -^=./'(y-i_ =	!< [/(y_|_2;/'($)],
Поэтому уравнение A4.5) даёт нам равенство
— у [/ @ + 2;/' (?)] == 2 [/' E) + 2;/" (Е)];
поделив обе части этого равенства на |/"?, получим:
^У / (?) + /Г /' (?) + 4 [-^ /' (?) + У\ г (?)J = о,
или
откуда
Но при I = 0 левая часть этого равенства обращается в нуль (если
считать /@) и /'@) ограниченными) и, следовательно, С — О. Итак,
Интегрирование этого уравнения даёт нам
где Л есть некоторая численная постоянная. Итак,
Чтобы найти значение постоянной Л, составим
СО	OD	>
fv(z, t)dz = ~L f e'^
— OO
L
OO	—CO
Но известно, что
со
f e-x>dx=Vn.	A4.8)

,4]	НЬСТАЦИОН\РНОЕ ОДНОМЕРНОЕ ТЕЧЕНИЕ	441
Полагаясь здесь
получим, что
\ е м (Iz = Vk.	A4.9)
Таким образом, имеем:
в частности,
со
Urn {v{z, t)dz =
<->о *"
— _о
ио по условию A4.7) левая часть должна равняться Q, поэтому необ-
необходимо взять
и мы окончательно находим следующее выражение для г»:
г; (г, 0 = —^=-* 4v< •	A4.10)
Нетрудно теперь разобрать и общий случай начального зада-
задания A4.6). В самом деле, уравнение A4.5) линейно, поэтому сумма
частных его решений тоже будет решением этого уравнения. Разо-
Разобьем !еперь всю ось Oz на малые участки и, рассматривая участок
а <С z < a -)- da., положим:
v (z, 0) = 0 вне участка а < z < а -f- da.,
v(z, 0) = F(a) на участке a<2<a-f-rfa.
Ясно, что для величины Q мы получаем в этом случае значение
a + da
j F (Z) dz = F (a) da..
Поэтому рассматриваемый элемент rfx даёт, согласно формуле
.10), в которой надо, очевидно, заменить z на 2 — а, для функции

442	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
v (z, f) следующее выражение:
,	(г-а)'
v (z, () = --^е ** F(a)da.
2 у t
Интегрируя полученное выражение по всем элементам dz, мы и
найдём требуемое выражение для функции v (z, t), удовлетворяющей
уравнению A4.5) и начальному условию A4.6):
со
v(.z,t)=—±=fe~~bi~F(a.)d*.	A4.11)
2 У it-it J
'	-л
Можно, впрочем, если не считать предыдущий вывод достаточно
строгим, непосредственной проверкой показать, что функция A4.11)
удовлетворяет как уравнению A4 5), так и начальному условию A4.6).
Покажем, например, последнее. Для этого сделаем в интеграле A4.11)
замену переменной, положив
тогда интеграл примет вид:
v(z,t)=-^ f e-VF(z + 2(.V^)dL	A4.12)
Положив теперь ? = 0, увидим, что вследствие равенства A4.8)
со
vО, 0) = ~ f e-"
что и требовалось доказать.
Рассмотрим теперь два простых примера применения полученной
формулы. Пусть в начальный момент распределение скорости имеет
следующий вид:
( vn, если z > 0,
«(*. 0)=	°	-\„	(Н.13)
\ — v0, » z < 0,
так что плоскость Оху является в начальный момент поверхностью
разрыва скорости. Можно сказать, что в начальный момент вдоль
плоскости Оху расположен вихревой слой. Посмотрим, что будет
происходить с этим вихревым слоем с течением времени. Применяя
формулу A4.12) к данному случаю, получим:
v(z,t) = -^L-f e-"<r,+ 2L
21
*-"•• л = -^

н]	НЕСТАЦИОНАРНОЕ ОДНОМЕРНОЕ ТЕЧЕНИЕ	443
ибо
—q	со
Точно так же
-д	о
поэтому получаем окончательную формулу:
z
2У7?
е-^сК..	A4.14)
о
Функция
X
Ф(х)=~ fe-^dC,	A4.15)
/	1
играющая большую роль в теории вероятностей, носит название
функции Крампа или интеграла вероятности. Для этой функции
имеются таблицы. Из формулы A4.8) следует, что Ф(со)=1,
с другой стороны, ясно, что Ф@) = 0.
Итак,
v(z, t) = v0o{-^=-).	A4.16)
При ?>0 функция v(z, f) будет уже непрерывной функцией
от z, так что при t > 0 скачка скорости уже нет. Можно сказать,
что он рассеялся по всей жидкости. Рассматриваемое движение целе-
целесообразно поэтому назвать диффузией вихревого слоя. Из формулы
A4.14) видно, что при z > 0 значение скорости непрестанно падает
от величины vQ при ? = 0 до нуля при ^->со. Простое вычисление
по таблице функций Крампа показывает, что скорость уменьшится
г2
вдвое через промежуток времени ?=1,1—.
Составим ещё выражение для вихря скорости
dv ^ fo_?-^7t	A4.17)
йг УтЫ
Мы видим, что в каждый данный момент максимальное значение
вихря будет при 2 = 0, т. е. на месте бывшего разрыва скорости.
Далее, простое исследование функции A4.17) показывает, что в дан-
данном месте величина вихря сначала нарастает, достигает максимума

444	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
в момент t = z2/2v и затем падает до нуля; при этом значении ма-
максимума равно, очевидно,
р0 	 щ_
y"jiWe \г\
В качестве второго примера рассмотрим движение жидкости,
расположенной выше плоскости Оху и находящейся в начальный
момент в состоянии покоя, так что
v (z, 0) = 0 при z> 0,	A4.18)
и допустим, что ограничивающая жидкость бесконечная плоскость
Оху внезапно получает в момент t = 0 скорость v0 в направлении
оси Ох, которую затем сохраняет. Решение этой задачи легко полу-
получается на основании предыдущего. В самом деле, функция A4.16)
обращается при z = 0 в 0; поэтому, если образовать функцию
A4.19)
то ясно, что при ^ = 0 эта функция обратится в нуль, а при Z — 0
в v0, т. е. удовлетворит всем поставленным требованиям.
При любом z > 0 функция v(z, t) стремится при t->oo к значе-
значению v0. Это означает, что в вязкой жидкости, ограниченной с одной
стороны твёрдой стенкой, последняя при своём движении увлекает
за собой всю жидкость.
Заметим ещё, что вследствие соотношения Ф(оо)=1 мы имеем:
1 — Ф (*) = Ф (оо ) — Ф (х) =
OJ	X	СО
уи J	уи. J	v* J
г о	' о	^
и, следовательно, формулу A4.19) можно заменить такой:
оо
,t) = ^- [е-'-1 Я..	A4.21)
У тс </
Полученные выше результаты можно применить к решению ещё
одной частной задачи.
Пусть жидкость занимает полупространство ниже плоскости Оху
и находится в начальный момент в состоянии покоя, так что, считая
ось Oz направленной вертикально вниз, будем иметь:
v(z, 0) = 0 при 2>0.	A4.22)
Положим, далее, что на свободную границу жидкости действует,
помимо нормального давления pQ, ещё касательное напряжение Т по»

, ..,	НЕСТАЦИОНАРНОЕ ОДНОМЕРНОЕ ТЕЧЕНИЕ	445
§ J4J
стоянной величины и направленное по положительной осп Ох. Опре-
Определим возникающее движение жидкости.
К такой постановке задачи сводится, очевидно, в первом при-
приближении вопрос о возникновении морских течений под действием
ветра.
Вспоминая выражение для касательных составляющих напряже-
напряжения, запишем граничное условие, которое должно выполняться на сио-
бодной поверхности, в виде
]х~ = — Т при 2 = 0.	A4.23)
Итак, нам нужно решить уравнение
при начальном условии A4.22) и граничном условии A4.23).
Покажем, как решение поставленной задачи можно сразу выве-
вывести из только что полученных результатов.
Для этого заметим, что функция
dv
тоже удовлетворяет уравнению A4.24) и, кроме того, начальному
условию
w(z, 0) = 0 при г > 0.
На свободной же поверхности граничное условие, вследствие
A4.23), имеет, очевидно, вид
w =— Т при 2 = 0.
Но легко видеть теперь, что если заменить v0 на — Т, то функ-
функция v (z, t), построенная нами во втором из рассмотренных выше
примеров, будет полностью удовлетворять всем условиям для функ-
функции w (z, t). Поэтому, применяя формулу A4.21), находим, что
в нашей задаче
уъ J
——
дг
Дифференцируя это выражение по г, определим pd^vjdz2, а тогда
уравнения A4.24) найдем:

446
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. Ц
Интегрируя полученную функцию по t и замечая, что при t~
v обращается, вследствие A4.22), в нуль, находим:
t
Т Г
v — 	 / i
У тми. •'
<ы
dt
A4.25)
Для численных подсчётов удобнее преобразовать эту формулу.
Введём вместо t новую переменную С, положив
j.г	~rj*	dt	zdQ
'	~ г; У7' Y7 ~
Так как при ? — 0 имеем С = оо, то получим:
v(z, t)~-
Тг
2 V;t
J е V-
Простое вычисление показывает, что
*
Л
*
В результате получаем для функции к B, f) выражение:
(
2 V -.t
или, что то же, по A4.20):
v (z, t) = -
При бесконечном возрастании /* последний член в скобках стре-
стремится к нулю; второй остаётся конечным, а первый бесконечно растёт,
так что мы имеем приближённое равенство
A4.27)
A4.28)
v{z, 1O^2—у — при t->co;
[А г	7Z
при z—0 мы имеем совершенно точно:

s -5] СТАЦИОНАР ТЕЧЕНИЕ ЖИДКОСТИ МЕЖДУ ДВУМЯ ЦИЛИНДРАМИ 447
Мы видим, таким образом, что течение всюду стремится принять
ту скорость, которая имеет место на свободной границе. При этом
на какой-либо глубине z скорость v достигает половины значения
скорости на свободной границе в тот момент t, когда
A4.29)
в_С + СФ(С) = —1=.
\ л	I у it
где
с-5тт-	<1430)
Решая уравнение A4.29), находим С = 0,35, так что глубина г,
на которой скорость v равна половине скорости на свободной гра-
границе, определяется уравнением z = 0,7Y"y[.
Так, например, для воды v = 0,018 см1\сек\ примем, далее,
z =^100 .м = 104 см, тогда
^1	сек. ==359 лет.
Отсюда видно, что указанным образом морские течения объяснить
нельзя, так как в движение приводятся только поверхностные массы
воды; следует, по-видимому, думать, что движение воды будет не
ламинарным, а турбулентным; грубо можно учесть турбулентный
характер движения таким образом, что вместо коэффициента вязкости v
нужно взять значительно больший коэффициент турбулентной
вязкости V; тогда время, в течение которого внутренние массы
жидкости придут в движение, значительно уменьшится. Кроме того,
в задаче о морских течениях очень существенную роль играет откло-
отклоняющая сила вращения земли, которой мы в нашем примере прене-
пренебрегали. Мы заметим только, что при учёте отклоняющей силы вра-
вращения Земли течение жидкости не будет уже одномерным и что
скорость не будет с течением времени возрастать до бесконечности,
как в нашем примере, а будет оставаться ограниченной.
§ 15. Стационарное течение жидкости между двумя цилин-
цилиндрами. Переходя к рассмотрению плоских течений вязкой несжи-
несжимаемой жидкости, начнём с простейшего примера движения жидкости
между двумя концентрическими цилиндрами. Пусть жидкость заклю-
заключена между двумя круговыми соосными цилиндрами радиусов гх и г2
(рис. 157), вращающимися около общей оси с постоянными угловыми
скоростями ш, и ш2. Определим движение жидкости, считая его ста-
стационарным, а внешние силы отсутствующими. Вводя цилиндрические
координаты г, 6, г, можем, очевидно, считать, что движение проис-
происходит по окружностям с центрами на оси Oz, так что
vz = vr = 0, v, = v (r), р = р (г).
Очевидно, проще всего использовать уравнения движения вязкой
жидкости в цилиндрических координатах E.14), которые в данном

ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[гл.
случае сильно упрощаются:
1 dp __ v*
р dr r
d2v . 1 dv
dr2 ^ г dr
— — О
A5.1)
Уравнение для v есть уравнение типа Эйлера, поэтому два его
частных решения должны иметь вид:
v = г\
подстановка этого значения v
в уравнение A5.1) дает
•—1=0,
Рис. 157
откуда получаем следующие значе-
значения k:
и следующие частные решения:
=	— —
^	г
Итак, общее решение уравнения
A5.1) есть
v = Ar+—. A5.2)
Произвольные постоянные А и В нужно определить из граничных
условий, которые, очевидно, имеют вид:
v = i
J2'2
При Г = Гц
» /¦ = г2,
так как имеет место прилипание жидкости к поверхности цилиндров.
Простое вычисление определяет Л и В и дает окончательное выра-
выражение для v:
__
- "г) ЛЛ
A5.3)
Вычислим, какая сила трения действует на элементы внутреннего
и внешнего цилиндров. Применяя формулы E.15), находим:
/ dt; w \	2|xB
2ц. (о), — о>,) г\г\
V2 г0
A5.4)
Рассмотрим, например, часть цилиндра Cv высота которой
в направлении оси Oz равна единице. На элемент rx dQ этой части
поверхности действует в направлении, касательном к цилиндру, сила
Ь, момент которой относительно оси цилиндра равен Рт/\^'

s ,5] ГТ ЩИОНАР TE4FHHE ЖИДКОСТИ ЧИЖДУ ДВ1, \1Я ЦИЛИНДРАМИ 449
Поэтому полный момент сил трения, приложенных к элементам рас-
рассматриваемой части цилиндра Cv равен
Г2 — 7
A5.5)
Точно так же полный момент относительно оси Oz сил трения,
приложенных к части цилиндра С2, отнесенный к единице длины
этого цилиндра, равен:
М2 =	^Ц	li-L?-.	A5.6)
г2 /-,
Таким образом, чтобы заставить цилиндры вращаться с пред-
предписанными угловыми скоростями, нужно приложить к цилиндру Сх
на каждую единицу длины этого цилиндра вращающий момент — Мх,
а к цичиндру С2— вращающий момент —М2. По известному правилу
вычистения работы необходимо при этом затрачивать в каждую еди-
единиц} времени количество работы, равное
Ц	Ц-±*-.	A5 7)
Все это количество энергии, очевидно, диссипируется. Диссипация
энергии отсутствует, если ioj = u>2, но в этом случае v ~ <яхг, и дви-
движение жидкос1и состоит в чистом вращении около оси Oz, тожде-
тождественном с вращением твердого тела. В этом и только в этом слу-
случае оба момента N\x и М2 тоже обращаются в нуль.
В частном случае, когда г2 —сю, ш0 = 0, получаем движение
жидкости вне цилиндра, вращающегося с заданной угловой скоростью
о),Г2
v=-~.	A5.8)
Как известно, в таком движении жидкости вихри отсутствуют. Для
вращающего момента получаем выражение:
М = 47Г[ш1/-2,	A5.9)
пропорциональное коэффициенту вязкости, угловой скорости враще-
вращения цилиндра и квадрату радиуса цилиндра.
Опыты показывают для рассматриваемого случая удовлетвори-
удовлетворительное согласие величин, получаемых экспериментально, с величи-
величинами, вычисленными на основании вышеприведенных формул. Конечно,
это имеет место только в случае ламинарных течений, т. е. пока
>1.,овые скорости вращения цилиндров остаются достаточно малыми
11 не переходят критических значений, после чего наступает турбу-
турбулентный режим.
2е) Теоретическая тдроч»\аника " II

450	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
§ 16. Диффузия вихря. В качестве важнейшего примера неста-
нестационарного плоского движения вязкой жидкости рассмотрим вопрос
о диффузии прямолинейной вихревой нити.
Пусть в начальный момент времени имеется распределение ско-
скоростей, соответствующее прямолинейной вихревой нити, расположен-
расположенной по оси Oz и имеющей интенсивность Г.
Таким образом, в момент времени ? = 0 проекции скорости на
оси цилиндрических координат г, 0, z имеют следующие значения:
Г
vr = Q, vh = -н—, vz=Q.	A6.1)
Требуется определить движение жидкости в любой следующий
момент времени. Совершенно ясно, что в этом движении vr и vz
все время равны нулю, a v^ зависит только от г и г1:
vr = vz= 0, vn = v (r, t), p = p (г, t).
Уравнения E.14) показывают нам, что
dv 	 / d2v . 1 dv v\
Введем еще в рассмотрение вихрь скорости
2 = 1^>.	A6.3)
В § 8 мы вывели уравнение (8.6), определяющее изменение вихря
с течением времени. В цилиндрических координатах это уравнение
имеет вид:
dQ , dQ . vh dQ	ДГ1 / d2Q . 1 dQ , 1 д'
В нашем случае, когда ^ = 0 и Q не зависит от 8, это уравне-
уравнение сильно упрощается:
/ dQ\
v V дг)	164
AЬ4)
dQ V/^Q ¦ 1
164
Л	) Т д?'	AЬ-4)
Впрочем ясно, что A6.4) вытекает из A6.2) вследствие A6.3).
При рассматриваемых начальных условиях мы без всякого труда
проинтегрируем уравнение A6.2) или A6.4), если воспользуемся
соображениями теории размерностей. Рассмотрим, например, уравне-
уравнение A6.4). Функция 2, кроме переменных rut, может зависеть
только от двух параметров ¦< и Г, причем ясно, что Q прямо про-
пропорционально Г; итак,
2 = ГФ(/-, t, v).	A6.5)
Выписываем теперь размерности всех входящих в эту формулу величин:

16]
ДИФФУЗИЯ ВИХРЯ	451
Если мы произведем изменение единиц длины и времени, умень-
уменьшив единицу длины в L раз, а единицу времени в Т раз, то числен-
численное значение г увеличится в L раз, численное значение t — в Г раз,
численное значение 2 — в 1/Т раз и т. д. Поэтому в новых единицах
мы будем иметь
О	/2
Заменяя здесь Q его выражением A6.5), получаем следующее
тождество:
ф(г, t, v) = L2<$>(rL, tT, v-
Положим теперь 7'= —, L — — , тогда будем иметь:
t	у 4t
Итак,
Q - Г f(r* \
Полагая
вычисляем:
Составляя теперь уравнениь A6.4), легко находим уравнение для
функции /(?):
/ @ + V E) + 4 [/' (Ё) +«/" «)] = 0.
Его можно переписать также в форме
/ (?) 4- 4/' (Е) + Е -J [/ @ + 4/' (S)] - О,
откуда видно, что
U/(E) +4/'EI = С.
Но если считать, что / (:) и /'(?) при S = 0 остаются конечными,
то следует принять С = 0, как это видно из предыдущего равенства,

452	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
если в нем положить ? — 0. Итак,
/(!¦)+ 4/'E) = О.
Интегрируя это уравнение, получим:
с
/© = Л<>Ч
где Л — постоянная, подлежащая определению. Итак,
•it
Вычислим циркуляцию Гл по окружности радиуса R, с ценiром
в начале координат. По формуле Стокса мы имеем.
R	r г
Гл = f jQdS= f Q ¦ 2Krdr = ?^ f e~^rdr =
о
r=R	i	jj,
г=0=4ЯЛг11-в"^).
A6.6)
Если устремить I к 0, то { 4vil тоже будет стремиться к нулю,
поэтому
Но, по условию, в начальный момент времени ГД = Г, следова-
следовательно, должно быть
Л = ~.	A6.7)
Итак, мы окончательно получаем следующее решение нашей
задачи:
Мы имеем далее, из равенств A6.6) и A6 7), след>ющее выра-
выражение для циркуляции скорости по окружности радиуса г с центром
в начале координат:
ГГ=^Г\1 — е ы) .	A6.9)
Но так как Гг = 2r.rv, то
v^±-\l-e «j.	A6.10)

i It,]	ДИФФУЗИЯ ВИХРЯ	453
Легко, впрочем, проверить и непосредственной подстановкой,
чго функция A6.10) удовлетворяет уравнению A6.2). Очевидно
id.iee, что при t—>0 мы имеем предельное равенство
ык что удовлетворены и начальные условия A6.1).
Исследуем полученное нами решение задачи о диффузии вихря.
Формула A6.8) показывает, что вихрь, сосредоточенный в начальный
момент времени в начале координат, с течением времени все' более
я более расплывается. При эюм видно, однако, что наибольшая
завихренность будет в том месте, где первоначально находился
вихрь; по мере удаления от этого места завихренность очень быстро
падает. Чтобы численно охарактеризовато расплывание вихря, найдём,
как изменяется с течением времени радиус той окружности с цен-
центром в начале координат, которая содержит внутри себя половину
всех вихрей, иными словами, радиус г той окружности, циркуляция
но которой равна 112Т. Формула A6.9) показывает, что г должно
определяться равенством
-И 1
е — 2 ,
<ик уда
Простое исследование Q показывает, что завихренность в дан-
пом месте возрастает с течением времени от нуля до максимума,
равного
н затем опять падает до нуля.
Рассматриваемый пример является чрезвычайно характерным для
ишамики вихревого движения в вязкой жидкости. Он показывает.
что основной тенденцией внутри вязкой жидкости является вырав-
выравнивание завихренностей различных частиц жидкости. Наоборот, мы
\ видим датее, что в соседстве с ограничивающими жидкость стенками
вязкая жидкость обладает, по сравнению с идеальной жидкостью,
резко выраженной вихреобразующей способностью.
Рассмотренную нами задачу можно значительно обобщить.
А именно, вместо того частного распределения скорости в началь-
начальный момент времени, которое дается формулами A6.1) и соответ-
соответствует случаю сконцентрированного вихря, рассмотрим произвольное
распределение скорости v в начальный момент времени
v{r, O) = vo{r).	A6.16)

454	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Начальное распределение вихря даётся в этом случае формулой:
2 (г, 0) = Q0(r)=I-^g^.	A6.14)
Но, как мы видели выше, искомая нами функция Q(r, t) удовле-
удовлетворяет линейному дифференциальному уравнению
dQ	ло (д*9. , д29.\
dt	\дх2 ' ду2 I
Поэтому сумма отдельных частных решений этого уравнения
тоже будет его решением. Но заданное начальное распределение
вихря можно заменить бесчисленным множеством отдельных сосре-
сосредоточенных вихрей; для этого введём на плоскости цилиндрические
координаты R, \ и положим, что на элементе RdRd\ плоскости
находится сосредоточенный вихрь интенсивности
Qu(R)RdRd\.	A6.15)
Обозначим через и расстояние между точками (R, X) и (г, 0),
так что
Тогда по формуле A6.8) получим, что от вихря A6.15) в точке (г, 0)
в момент t получится завихренность:
4-ntt
Интегрируя это выражение по всем R и всем X, мы и получим
требуемое выражение вихря:
Р р	/У-4 i^-2/?rcosX
Q(r' Ъ = Ъы] J Qo(R->e	Ы RdRdl. A6.16)
f
о о
Но, как известно из теории бесселевых функций, мы имеем 1):
e
о
Поэтому
') См., например, Смирнов В. И., Курс высшей математики, 3 A939),
стр. 679 и 688.

§ i6]	диффузия вихря	455
Так как v{r, t) связано с Q (r, t) формулой
т
(r, t) = у f Q (r, t)rdr.
то для определения скорости v отдельных жидких частиц находим
равенство:
T
dR. A6.18)
Формулы A6.17) и A6.18) полностью решают поставленную нами
задачу о плоском движении вязкой жидкости, в котором все частицы
двигаются по концентрическим окружностям.
Рассмотрим теперь два конкретных примера.
Примем сначала, что в начальный момент времени завихренность
равна нулю всюду, кроме круга радиуса а с центром в начале ко-
координат, в точках которого завихренность имеет постоянное значе-
значение 20. Мы должны, таким образом, принять:
20(Я) = const. = Qn для 0</?<а, )
Ясно, что мы получили задачу о диффузии вихря конечных размеров,
интенсивность эгого вихря равна, очевидно,
Г = ™220.	A6.20)
Применяя формулу A6.17), мы найдём распределение вихрей
в любой следующий момент времени:
9(Л t) = l±e-i* f e'&Io^RdR.	A6.21)
о
Преобразуем эту формулу к другому виду, более удобному для
численных вычислений.
Введем прежде всего безразмерные переменные, полагая
.?l_a iL — n J^—r
4 4	' A-d ' ' 4-4 '
тогда будем иметь
а
2 (г, t) = Qoe-( f e-40{2VVOdL	A6.22)
о

456	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ ц
Воспользуемся теперь первой из следующих основных формул в тео-
теории бесселевых функций '):
J (z\-— fe"~b*L
Jo<z>— ъи J e	и '
/о
(
I
1де 10 есть окружность произвольного радиуса с центром в начале
координат, и интеграл берется по контуру этой окружности в поло-
положительном направлении.
Так как
/0B VJ) = JuBtV^),
то, применяя предыдущую формулу, найдём:
и, следовательно,
О	I	\0
Внутренний интеграл сразу берется
и
J
1 ?
——	'1	С-	/ j
и — ;
:=о
и поэтому
... F*
' —р
о	/,	/»
Радиус окружности /0 можно брагь по произволу. Мы воспользуемся
этим произволом для того, чтобы получить дтя Q две формулы,
одной из которых удобнее будет пользоваться для малых значе-
значений rja, другой для больших. А именно, выберем сначала радиус
окружности 10 меньшим, чем р. В этом случае
A6.24)
u — o
') См., например, Смирнов В. И., Курс высшей математики, 3 A939),
стр 677.

§ 16]	диффузия вихря	457
так как подынтегральная функция голоморфна внутри окружности /0.
Мы имеем, далее, на окружности /0 разложение
GO	,, ,
1 	1 1 = 1	±_*а_ ___ v и"-1
и — {	Р 1 _ ?	Р Р2 Р3 "'
Р
и поэтому
U — р	м
Но по той же основной формуле теории бесселевых функций мы
имеем
ш fuk'h'H " du = ^
^0
Вводя, далее, функции Бесселя с мнимым аргументом
i
легко найдем, что
L
Пгак,
/о
Теперь по формулам A6.23) и A6.24) легко получим первую нуж-
нужную нам формулу:
сю	_*_
Q (г, t) = Вов-»- 2 (уJ /* B /^)-	A6.25)
Возьмем теперь в формуле A6.23) радиус окружности 10 превос-
превосходящим р. Тогда по известной теореме о вычетах будем иметь:
Г?^ = <Л	A6.26)
2т J и —р
/о
Да iee, на окружности /0, вследствие того, что | и \ > р, будем иметь
Разложение
1	11	1 . р , о2 ,	_ °°
" "т ¦ • •
• р и , р и и' и*

458	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
и поэтому
h	ft = 0 L
со	k
B /^ = - S (тO
Вследствие формул A6.23), A6.26) и A6.27), находим:
к
2 (г, 0=^о- So«-a-p2(^^B УоГр).	A6.28)
Возвращаясь к прежним независимым переменным, получим оконча-
окончательные формулы:
г*+а2 °°
(r, i) — iiQ — ыое	т.
A6.29)
Совершенно ясно, что первой из этих формул следует пользоваться
при r^-а, а второй при г < а. Пользуясь таблицами бесселевых
функций, нетрудно теперь вычислить значения Q (г, г1) для различных
значений rut. Рис. 158 даёт зависимость 2/S0 от rja для значений
2vt „ 1 1 . „
— = 0, -j, -~-, 1. Ясно видно, как вихрь расплывается по всему
пространству.
Чтобы иметь количественную характеристику быстроты расплы-
вания вихря, найдём, через какой промежуток времени г значение
завихренности в центре вихря будет равно 20/2. Последняя из фор-
формул A6.29) показывает, что
A6.30)
и, следовательно, т должно определяться из формулы
Для воды при v = 0,01 см2/сек имеем т = 36а2, например при
а = 1 см будет х = 36 сек. Для воздуха при v = 0,133 см2/сек имеем

16]
ДИФФУЗИЯ ВИХРЯ
459
^^-2,7а2, т. е. при а—1 см будет т = 2,7 сек. Но уже при
а=1 м окажется т = 450 мин. Отсюда ясно видно, что на вихрях
малых размеров диффузия проявляется гораздо сильнее, чем на боль-
больших. С этой точки зрения при рассмотрении атмосферных движений
больших масштабов (циклона, антициклона) мы могли бы совсем
пренебрегать вязкостью, считая воздух идеальной жидкостью. Однако
нужно иметь в виду, что движения атмосферы, особенно в нижних
её слоях, носят часто турбулентный характер; турбулентность же
действует на вихри таким
же образом, как вязкость.
Иногда грубо оценивают 1,0
диффузию вихрей, происхо- ду-
дудящую под действием турбу- 08 Г"
1ентности, формулами, ана- '
логичными вышеприведён-
вышеприведённым, только коэффициент v
берут гораздо большим
(в 100 000—1000 000 раз). 04
В качестве второго при- oj
мера рассмотрим цилиндри-
цилиндрический вихревой слой. При-
Примем, что в начальный момент
вихри всюду равны нулю,
кроме окружности радиуса а,
ча которой мы имеем равно-
равномерное распределение вих-
вихрей, причём полная интенсивность этих вихрей равна Г. Математи-
Математически это означает, что функция 20(/?) равна нулю всюду, кроме
бесконечно малой окрестности точки а, причём
0,6 -
A6.32)
Но тогда ясно, что формула A6.17), в которой все подынтеграль-
подынтегральные элементы равны нулю, кроме элементов, соответствующих зна-
значению fi = a и бесконечно близким значениям, даст нам
t) =
Г —
4-xyt
/п
Ы
A6.33)
Рис. 159 даёт вычисленную по этой формуле зависимость Q/Г
от г/а для значений 2-4ja2=ll5, 1/4, 1/2, 1. Совершенно отчётливо
видно, как вихрь, сконцентрированный в начальный момент времени
кдоль окружности радиуса а, начинает расплываться в обе стороны,

460
ДВИЖЕНИЕ ВЯЗКОР1 ЖИДКОСТИ
[ГЛ II
быстро заполняет всю внутренность круга радиуса а, после чего
происходит процесс расплывания вихря по всей плоскости.
Распределение скорости в этом
случае определяется формулой, вы-
вытекающей из A6.18) на основании
сделанных предположений:
V (Г, t) .=
1,0
0,9
0,8
0,7
0,6
0,5
0,4
пз
QZ
0,1
0
/LA
Г'ггЛ
0,6 1,0 1,5
Рис. 159.
\
, г
' Anvrt
ilt
A6.34)
Но выражение в правой части с точ-
точностью до перемены обозначений
B0 = Г/2т:г, а= г, г — а) совпадает
с правой частью формулы A6.21).
А тогда ясно, что, производя ту же
самую перемену обозначений в фор-
формулах A6.29), мы получим для рас-
рассматриваемого нами случая цилиндрического вихревого слоя следую-
следующие результаты:
Г
ar
A6.35)
§ 17. Течение в диффузоре. Очень важным для понимания
механизма течения вязкой жидкости вблизи стенок является подроб-
подробное изучение точного решения уравнений гидромеханики, определяю-
определяющего течение в диффузоре, т. е. в расширяющейся трубе.
Мы будем разбирать, следуя в основном Гамелю '), только пло-
плоскую задачу, т. е. будем изучать движение вязкой жидкости между
двумя плоскими стенками, наклонёнными друг к другу под углом а.
Естественно предположить, что движение будет чисто радиальным
(рис. 160). В соответствии с этим возьмём уравнения гинромеханики
в цилиндрических координатах E.14) и поставим себе задачей найти
точное решение этих уравнений следующего вида:
') Harael Q., Spiralformige Bewegungen zaher Flussigkeiten, Jahres-
bericht der deutschen Mathematiker Vereinigung, 25 A916), стр. 34—60.

ТЕЧЕНИЕ В ДИФФУЗОРЕ
461
Уравнения E.14) дают при этих условиях следующие равенства:
v дг ~~ ~~ У дг ~*~ v \дг2 ~*~ Д Ж2 ~т~ г дг г2)
г2)'
= 0.
A7Л>
Последнее из этих уравнений показывает, что
rv(r, 8) = и (8).	A7.2)
Очевидно, н(8) даёт нам распределение скоростей в единичном рас-
расстоянии от начала координат.
Среднее из равенств A7.1) приводит теперь к равенству
dp	2fA du
Ж ~ >т d 8 '
откуда следует, что
/*
Наконец, подставляя это выражение для р в первое уравнение
A7.1), легко найдём следующее дифференциальное уравнение для
определения функции и F):
А2,,	,,1	ft 1~\ гЗ	" ,
откуда видно, что как левая, так и пра-
правая части являются постоянной вели-
величиной. Итак,
откуда
/ (г) — 2^2"' 1
и окончательно
Р(г, 9) = ^
-Cv A7.3)
С другой стороны, и F) должно удов-
удовлетворять уравнению
m"-j-4k_j_^ — C^O, A7.4)
Рис. 160.
которое легко интегрируется в квадратурах. А именно, умножив
предыдущее уравнение на а', мы можем после этого просто его

462	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
проинтегрировать; в результате получим:
Решаем это уравнение относительно и':
Ж и + 3vC2),
разделяем переменные и интегрируем:
Если воспользоваться эллиптическими функциями, то можно дать
явное выражение зависимости и от 6. А именно, переписываем пре-
предыдущее равенство в виде:
и полагаем
в@) = — 2>-f «j (8).
Тогда
— 12vCm— 12vC2 = 4m3 —g-^j —§-3.
где g2 и ё'г — новые произвольные постоянные.
Если значение 6 при а = со есть 60 (конечно, 60 может оказаться
комплексным числом), то, как следует из A7.6):
/F-в0) _ , Г	dux
±f.
Таким образом, 6 является известной функцией от и1 и, обратно,
«1 будет известной функцией от 0. Эта последняя хорошо исследо-
исследована, а именно, она непосредственно выражается через эллиптическую
функцию f Вейерштрасса. Итак,
и, значит,
A7.7)

§ 17]	ТЕЧЕНИЕ В ДИФФУЗОРЕ	463
Остаётся исследовать полученное решение, представленное фор-
формулами A7.5) и A7.7). Последняя из этих формул содержит три
произвольных постоянных: б0, g2 и g3, для определения которых
мы имеем как раз три условия. Прежде всего на стенках диффузора,
уравнения которых пусть будут 6 = ±<х/2, должно выполняться усло-
условие прилипания жидкости к стенкам:
0.	A7.8)
Кроме того, мы должны выразить ещё условие, что через любое
поперечное сечение диффузора в каждую единицу времени проходит
определённый объём жидкости. Этот объём выражается, очевидно,
формулой:
ее	а
2	~2
v{r, 6)- г dB= | и@)<*6.	A7.9)
Величину Q мы будем называть обильностью источника и будем
считать ее' заданной. Если Q положительно, мы имеем дело с источ-
источником, т. е. с расходящимся течением в диффузоре; если же Q
отрицательно, то мы имеем дело со стоком, т. е. со сходящимся
течением.
Итак, для определения трёх произвольных постоянных 60, g2
и g3 мы получили три уравнения A7.8) и A7.9). Кроме того ясно,
что искомая функция и F) не должна обращаться внутри промежутка
(—а/2, а/2) в бесконечность. Мы не будем в полном объёме решать
вопрос о том, имеет ли поставленная нами задача решения и, если
имеет, то сколько будет этих решений и каков будет их характер.
Нашей главной задачей будет показать, что сходящиеся и расходя-
расходящиеся течения в диффузоре имеют при некоторых условиях совер-
совершенно различный характер.
Целесообразно при этом сразу же ввести в рассмотрение безраз-
безразмерные величины. Основной безразмерной величиной является, как
VI
мы знаем, число Рейнольдса R= —, где V — характерная ско-
Рость, а / — характерная длина. Формула A7.9) показывает, что
в нашем случае величина Q имеет как раз размерность, равную
произведению размерности скорости на размерность длины. Поэтому,
обозначая через | Q абсолютное значение величины Q, удобно будет
определить число Рейнольдса формулой
R-J^-.	A7.10)

464	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ Ц
Вместо величины к F) мы введём в рассмотрение безразмерную вели-
величину U (8), полагая
«F)=|Q|t/(e).	A7.11)
Ясно теперь, что уравнение A7.4) перейдёт в
?/"_(_ 4t/-)-Rt/2 — D = 0,	A7.12)
а формула A7.5) превратится в
где D, Dv D2— новые произвольные постоянные.
Наконец, формулы A7.8) и A7.9) перейдут в
A7.14)
причём в последней формуле имеет место знак плюс для источника
и знак минус для стока.
Разложим теперь полином, стоящий под знаком корня в фор-
формуле A7.13), на простые множители:
1
D2 -- (U - ех) (U - е2) (U - е3).
Сравнение коэффициентов при U2 в двух частях этого равенства
показывает, что
3 = -^.	A7.15)
Формула A7.13) принимает теперь вид:.
3	,/ Y(e,-U)(U-et)(U-e3)
Полином третьей степени с вещественными коэффициентами, стоящий
в правой части равенства, имеет три корня, один из которых всегда
вещественный, два же других корня могут оказаться или веществен-
вещественными, или же комплексно сопряжёнными.
Разберём сначала случай, когда имеется один вещественный
корень ех и два комплексно сопряжённых е2 и е3. Тогда для всех
вещественных U имеет место неравенство
(U-e2)(U-e3)>Q

§ 17!	ТЕЧЕНИЕ В ДИФФУЗОРЕ	465
н, следовательно, для вещественности корня, входящего в интеграл
A7.16), необходимо считать
ех — U > О,
так что U ограничено сверху числом ех. Но мы знаем, что на стен-
стенках U обращается в нуль, следовательно, U меняется в пределах
от 0 до е{:
О <?/<>!,
причём ег должно быть положительным. Ясно, что мы имеем дело
с источником.
Пусть теперь все три корня вещественны. Расположим их
и порядке убывания
Ясно вследствие равенства A7.15), что е3 отрицательно и что
Очевидно теперь, что
(е1 — U) (U—e2) (U ~ <?3) > 0, если — со < U < е3 или е2 < U < ev
(в, — U) A1—е2) {11 — е3) < 0, если е3 < U < е2 или ^ < ?/ < со.
Так как выражение, входящее под знаком корня в формулу A7.16),
пе может быть отрицательно, то ясно, что U должно изменяться
либо в пределах от — со до е3> либо в пределах от е2 до ех. Но
первый случай должен быть исключён, так как U должно принимать
на стенках значение 0. Итак, мы во всяком случае должны иметь:
Различим теперь случаи источника и стока. При этом как в том,
так и в другом случаях мы ограничимся рассмотрением только наи-
наиболее интересного случая, когда во всём диффузоре имеет место
течение одного направления, т. е. вытекание в случае источника,
втекание в случае стока. Ясно тогда, что в случае источника U поло-
положительно, причём на стенках обращается в нуль. Это может быть
только, если е1 > 0, е2 -^ 0, причём U лежит в промежутке
Напротив, в случае стока U отрицательно, поэтому должно быть
е2 < 0, ех > 0 и
е2 < U < 0.
Резюмируя сказанное, получаем: в случае стока все корни веще-
вещественны, причём
во < U < 0 е > 0 е <¦	— i	A7.17)
30 Теоретическая гидромеханика, ч. II

466
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ
в случае же источника есть один вещественный положительный
корень ех и два корня е2 и е3 либо отрицательных, либо комплексно
сопряжённых, причём
0<L'<e1.	A7.18)
Рассмотрим теперь подробнее случай источника. Из симметрии
ясно, что максимальное значение функции U, равное ех, достигается
на оси диффузора, т. е. при 6 = 0. При увеличении S значение U
уменьшается, следовательно, в формуле A7.16) нужно взять знак
минус и за нижний предел нужно взять ev Итак, в случае источ-
источника:
Г 3	.
dU
(о<е<°). A7.19)
Значению U = 0 соответствует 6=-у. Это даёт нам равенство:
/{=/'= dU
У Ь J Y(e,-U)(
Так как:
=		_
(e,-U)(U~e2)(U-e3)
A7.20)
последнее равейство A7.14), эквивалентное в случае источника
равенству
2 '
даёт нам условие
Три равенства A7.15), A7.20) и A7.21) служат для определе-
определения трёх величин ev e2 и е3 ПРИ заданных R и а. Однако эта
система не всегда имеет решение; мы это покажем при помощи про-
простых оценок.
Мы имеем вследствие A7.15):
(U —

§ 17]	ТЕЧЕНИЕ В ДИФФУЗОРЕ	467
и так как для случая источника е<1еъ > 0 (ибо е2 и еъ либо ком-
комплексно сопряжённые, либо е3 -^ е2 -^ 0), то
A/-е2)(?/-«а» («
Поэтому из равенства A7.20) находим:
и так как
С	dU	С dx
•/ у U (е, — U) ¦' у х A — х)
О	О
то получаем оценку
-	„ли а< ^JL— .	A7.22)
Мы видим, таким образом, что угол а во всяком случае должен
быть меньше л.
Пусть теперь угол а задан. Из условий A7.18), A7.20) и A7.21)
мы сразу можем вывести неравенство:
,/"R" . Г	dU	,/"R"
' 6 ^ ; ,/ /(е, — U){U— e2){U — es)	r 6
о
откуда следует, что
С другой стороны, из A7.22) вытекает, что
6 ^ •- —- .
т. е. вследствие предыдущего неравенства:
R<Hu2~a2) ¦	A7.23)
Итак, расходящееся течение в диффузоре рассматриваемого типа
не может иметь места при больших числах Рейнольдса. Следова-
Следовательно, при больших числах Рейнольдса вытекание жидкости из
Диффузора может происходить только таким образом, что внутри
диффузора области вытекания жидкости будут сменяться областями
втекания.
30 *

4Й8	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Таким образом, для случая расходящегося течения в диффу-
диффузоре заданного угла раствора а < т. мы имеем следующую картину;
при малых числах Рейиольдса имеет место симметричное течение
рассматриваемого типа; при увеличении числа Рейнольдса на-
наступит момент, когда на стенке не только U, но и U1 обратятся
в нуль.
При дальнейшем увеличении числа Рейнольдса будут существовать
только такие решения, в которых области вытекания жидкости будут
сопровождаться областями втекания. А именно, мы будем иметь выте-
вытекание в некоторой области —C < 6 < р, где C < а/2, и втекание
около стенок в областях р < 6 < а/2 и —а/2 < 6 <—р. Будут
существовать также и более сложные картины течения, в которых
имеет место вытекание около одной стенки (в некотором интервале
— а/2 < S < ~() и втекание около другой (¦[ < 6 < а/2). Число таких
чередующихся областей втекания и вытекания может быть сколь
угодно большим, причём при увеличении числа Рейнольдса растёт и
минимальное число чередующихся областей вытекания и втекания
жидкости.
Если бы вязкость отсутствовала, то течение жидкости предста-
представлялось бы простыми формулами *):
1/=1, р = Ро-Ж..	A7.24)
т. е. жидкость вытекала бы во всех направлениях с одинаковой
скоростью.
Мы видим, что расходящееся течение в диффузоре при больших
числах Рейнольдса резко отличается от соответствующего потенциаль-
потенциального течения. Обратим ещё внимание на то, что расходящееся
течение в диффузоре есть течение против градиента давления, так
как в потенциальном потоке давление быстро убывает при г— >0.
В случае стока мы имеем совсем другую картину. Напишем для
этого случая основные формулы. Мы знаем, что в случае стока
<?2<{У<0, ех>0. *,< —-R--	A7-25)
Считая течение симметричным относительно оси дуффузора, мы
должны принять, что минимальное значение функции U, равное е2,
получается при 6 = 0. При увеличении 6 увеличивается и U, следо-
следовательно, в формуле A7.16) надо взять знак плюс и за нижний пре-
предел надо взять е2. Итак, в случае стока
A7.26)
Y{e,-U)(U-e2)(U-e3)
') Эти формулы легко получить, интегрируя A7 1) при v = 0 и применяя
формулу A7.9).

]7]	ТЕЧЕНИЕ В ДИФФУЗОРЕ	469
Условие U (а/2) = 0 даёт равенство
A727)
аУ  = J Y(e,~
последнее условие A7.14) — равенство:
/	UdU	A7.28)
A7.29)
Наконец, мы имеем основное соотношение A7.15):
Покажем, что для случая стока симметричное решение рассматри-
рассматриваемого типа имеет место как для случая очень малых, так и для
случая очень больших чисел Рейнольдса.
Случай малых чисел Рейнольдса мы разберём сразу и для случая
стока и для случая источника. Проще всего при этом исходить из
установленного нами выше уравнения A7.12):
где D есть произвольная постоянная. Так как R считается малым,
то в предыдущей формуле можно пренебречь членом R?/2; в резуль-
результате получим уравнение
U" -\-W=D,	A7.30)
которое непосредственно интегрируется,
U = j + A cos 26 -f- В sin 29,
причём А, В и D суть произвольные постоянные, подлежащие опре-
определению из трёх условий:
я/2
= о, f
-я/2
Эти условия дают нам следующие равенства:
D ,
-r-\- A cos a — В sin a = 0,
^ a -j- A sin a = ± 1.

470	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. Ц
Считая, что угол а меньше тс, сразу получим, что
В 0А	D
sin a — a COS a	sin a — a COS a
причём верхний знак всегда относится к случаю источника, ниж-
нижний—к случаю стока.
Итак, искомое решение имеет следующий вид:
± СО8 26-СО8С
v '	Sin a — a COS a	4	'
Вспоминая формулы A7.2) и A7.11), получим для радиальной ско-
скорости течения выражение:
Q(cos2B-cos^)
v '	Г (sin а — a COS а)	ч	>
пригодное одновременно и для случая источника и для случая стока
(см. рис. 160, вычерченный для случая источника при a = 90°).
Как видим, распределение скорости в случае малых чисел Рей-
нольдса получилось по косинусоиде как для случая расходящегося,
так и для случая сходящегося течения.
Остановимся ещё на частном случае малого угла раствора диф-
диффузора. В этом случае результат значительно упростится, если функ-
функции, входящие в формулу A7.32), разложить в ряды по возрастаю-
возрастающим степеням 6 и а и ограничиться главными членами полученных
разложений:
v(r, 6) = 4^- ~34°2.	A7.33)
Как видим, получилось распределение скорости по параболе,
чего и следовало ожидать, ибо, в силу малости угла а, мы прибли-
приблизились к случаю течения между двумя параллельными стенками, при-
причём, вследствие малости R, влиянием сил инерции можно пренебречь.
Рассмотрим теперь случай очень больших чисел Рейнольдса R.
Как мы знаем уже, в этом случае симметричное течение рассматри-
рассматриваемого типа невозможно, если течение расходящееся. Остаётся ис-
исследовать случай стока. В основу рассуждений мы положим урав-
уравнения A7.27), A7.28) и A7.29). Угол а мы считаем заданной
величиной, не превосходящей 2тс, величину же R будем считать
очень большой.
Введём теперь в интегралы A7.27) и A7.28) вместо U новую
переменную ф, положив
U = е2 + (ех — е2) cos2 >\=ех — {ех — е2) sin2 <]>, A7.34)
и введём еще параметр k <. 1, положив
ft2^ g'—gA,	A7.35)

§ 17]	ТЕЧЕНИЕ В ДИФФУЗОРЕ	471
Тогда будем иметь:
gl — и = (е1 — е2) sin2 ф,	U — е2 — {ех — е2) cos2 ф,
U — е3 = (е, — е3) A — k2 sin2 ф),	dl/ == —2 (et—e2) sin ф cos ф йф,
при этом значению U = е2 соответствует значение ф = тс/2, а значе-
значению U==0 значение ф = ф0, где ф0 есть решение уравнения
A7.36)
Простое вычисление показывает теперь, что равенство A7.27)
заменится через
г/2
nApf	A7'37)
равенство же A7.28) примет вид:
_	я/2
R.= _ 2	/" [gi - (gi - ga) sin2 ф] ^ф =
6	/<?, — e3 •/	/1 — A2 sin2 ф
т/2
2g3	/"
,—e,J Vl —
e3 ¦' /1 — k2 sin2 ф
T,4
~2Ye{ — e3 J Yl—k2sin^d<\>. A7.38)
Фо
Полученные равенства показывают, что k должно быть очень
близко к 1, так как в противном случае эллиптические интегралы
имеют конечное значение, и правые части формул A7.37) и A7.38)
были бы конечными, в то время как левые части этих формул, по
предположению, очень велики. Итак, к мало отличается от 1; по
формуле A7.35) это означает, что е3 мало отличается от е2:
Но тогда формула A7.29)
в которой можно пренебречь правой частью, показывает, что при-
приближённо

472	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ П
В соответствии с этим упрощаются и формулы A7.37) и A7.38);
первая из них принимает вид:
я/2
V — 3e2 f У~1 — k2 sin2 ф '
во второй же формуле можно отбросить в правой части второй
интеграл, как имеющий конечное значение; в результате получим:
		г/2
4
	~ е.
3	,/ у\ _ ?2 5Ш2 ф
Сравнение двух полученных соотношений показывает, что должно
быть
я/2
= _± и Г	*»
2 = _± и Г	»	- = 1^--
2	«	,/ /1_?251П2ф	F 8
Для определения угла ф0 мы имеем формулы A7.36), которые дают
нам:
= ]/r-i-, %=54Э44'. A7.40)
Остаётся отыскать fe; для этого заметим, что
т/2	л/2
«/ У 1 — k2 sm2 4* -' V\—k?sm2ty J yi — k2 sin2 ф
и что при kt близких к единице, мы имеем приближённые равенства:
«.in # 4	.).
n2 Ф /1 *2
у 1 —
ГУ
+,=0
Поэтому равенство A7.39) даёт нам, что
4
1п
') См. напр., У и т т е к е р—В а т с о н, Курс соврем, анализа, ГТТИ, 1934
стр. 371—372.

3 17]	ТЕЧЕНИЕ В ДИФФУЗОРЕ	473
от куда
Но по формуле A7.35) мы имеем:
н приближённо ех — е3~—Зе2> поэтому
- е, = - 48 (УТ -
Итак, при больших числах Рейнольдса R симметричное течение
рассматриваемого типа для случая сходящегося течения в диффузоре
существует и определяется следующими приближёнными значениями
параметров:
e^[l+48(YdY2fv^\, A7.41)
Остаётся найти распределение скоростей. Из равенства A7.26)
после простых вычислений получим:
л/2
61/ — =
JL_ f
V
Рассуждая, как выше, получим:
г 2
4
й In	— — In i
6 Ye, — <?з ;' /1 — k2 sin2 <Ь '
¦\4 27 ~
™	3
Iак как ещё ех — е3^^ — , то легко находим, что
(!). A7.42)
Но по основной формуле A7.34):
U =-- е2 -f (^ — е2) cos2 ф = — - + - cos2 <]>.	A7.43)
a ' o.

474
Так как
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. И
и так как
v(r, 6) = —
+ (/3-
QU
то мы находим окончательное выражение для распределения скорости:
v (г, Ь)~
О f	12	^
=— > 1
[(VI + V2) еу <*> <*/2-е> + (КЗ - /2)
|/___ /2_В|2 ¦ A7.44)
Легко теперь видеть, что почти во всём секторе 0 < 6 < а/2, за
исключением непосредственной близости стенки, значение скорости
v(r, б) очень мало отличается от значения Q/ra (см. рис. 161, вычер-
вычерченный для a = 60°, R = 100). Только при значениях 0, близких
к а/2, значение показательной функции ev R/2a М-6) будет невелико,
и второй член в фигурных скобках
предыдущей формулы сильно повлияет
на величину v(r, 6).
Итак, для случая сходящегося тече-
течения в диффузоре течение при больших
числах Рейнольдса очень мало отли-
отличается от потенциального течения
идеальной жидкости. Только вблизи
стенок происходит очень быстрое изме-
изменение скорости от значений, соот-
соответствующих потенциальному потоку
идеальной жидкости, до нулевых зна-
значений, требуемых условиями прилипа-
прилипания вязкой жидкости к стенкам. Обра-
Обратим внимание на то, что сходящееся
течение в диффузоре происходит в на-
направлении падения давления. В то время,
как при малых числах Рейнольдса схо-
сходящееся и расходящееся течения в диффузоре имеют одинаковый
характер, при больших числах Рейнольдса течения носят совершенно
различный характер, а именно, сходящееся течение всюду, кроме
непосредственной близости стенок, мало отличается от потенциаль-
потенциального течения, расходящееся же течение резко отличается от потен-
потенциального течения.
Рис. 161.

§ 18]	РЕШЕНИЕ ГАМЕЛЯ И ЕГО ОБОБЩЕНИЯ	475
§ 18. Решение Гамеля и его обобщения. Течение в диффузоре,
рассмотренное нами в предыдущем параграфе, является частным
случаем гораздо более общего точного решения уравнений гидро-
гидромеханики вязкой несжимаемой жидкости, которое мы сейчас и рас-
рассмотрим. Движение жидкости мы будем предполагать плоским,
стационарным и происходящим под действием сил, имеющих потенциал.
В § 8 было показано, что в этом случае проекции скорости
могут быть выражены через функцию тока *Р(х, у):
которая удовлетворяет уравнению
ду дх дх ду	v '
Введём теперь вместо х и у криволинейные координаты <р и у,
которые мы выберем таким образом, чтобы выражение
т=ср(х, y)-\-ix(x, у)
было аналитической функцией от
г = x-\-iy.
Итак,
<Р + 'Х = *(*).	A8-3)
так что <р(х, у) и х(х, у) удовлетворяют уравнению Лапласа
Дср = ДХ= 0.	A8.4)
Смысл этого преобразования состоит в следующем: составив
уравнение для W в переменных <р и у< мы можем затем отыскивать
решение этого уравнения, зависящее, например, только ог ср. Ясно
тогда, что линии тока нашего движения вязкой жидкости будут
совпадать с линиями ср = const., т. е. линиями тока некоторого
потенциального движения, хотя само движение не будет потенциаль-
потенциальным, если вихрь 2 = — ДЧ?" будет отличным от нуля.
Прежде всего преобразуем к новым переменным выражение
"	дх* ^ ду2 ¦
При этом мы будем для отчётливости пользоваться временно
следующим обозначением:
Составим теперь производную
^1 — д-1
dz~~ дх ду ~ ду ~>~ дх

476	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ и
и обозначим через Q квадрат ее модуля:
Q —
dz
2
дх) ^\ду) ~\дх)
— ?iHi__HiHi _.
?> (л:, }') '	UO.oj
Простое вычисление показывает, что
ДФ' = <ЗД(р?.	A8.6)
Левая часть уравнения A8.2) можег быть представлена в виде
якобиана:
Р(АЧ, t)
_ 	^	_
(?у (?х dx ду	D (х, у) '
но, как известно, для якобианов имеет место правило дифференциро-
дифференцирования сложных функций.
D (ДТ, Ч") D (ДЧ , ЧГ) D (^>, у)	D (Д?, U )	D (Q Д9*-, Ч )
A87)
(лг, у)	D (<?,/) О(лг, у)" "* D(9, 7) ~^ О
Поэтому уравнение A8.2) принимает следующий вид:
Поскольку теперь мы будем рассматривать все функции зависящими
от ср и х< не будем больше писать значок <р при обозначении лапла-
лапласиана Д.
Производя дифференцирование всех членов уравнения A8 7) и
деля все члены его на Q, мы придем к равенству:
/dlnQ дЧ' d\nQ дЧх^
д<?
+-^ДФ). A8 8)
Функция ]n(dxjdz) есть аналитическая функция от z и, следова-
следовательно, от т. Вещественной частью этой функции является, как
известно,
Отсюда мы заключаем, что, во-первых, In Q есть гармоническая
функция, т. е. удов!етворяет уравнению Лапласа
Д1п<2 = 0	A8.9)
и, во-вторых, имеем равенство
d . d~
d~ dz	д-р	д i

§ 18]	РЕШЕНИЕ ГАМЕЛЯ И FTO ОБОБЩЕНИЯ	477
Введем теперь обозначения
??Ua. -^ = Ь,	08.10)
jorna мы будем иметь
2^-\n~ = a-\-tb.	A8.11)
dx dz	'	v	'
Заметим ещё, чго
Поэтому равенство A8.9) даёт нам, если принять во внимание ещё
A8.10), что
A8.12)
Итак, уравнение A8.8) принимает следующий окончательный вид:
\ ду_ ' dtp J ' до ду	ду д®	'
Достаточно решить это уравнение для каких-либо гармонических
сопряжённых функций с(ср, у) и Ь(с?, у), чтобы получить некоторое
точное решение уравнений движения вязкой жидкости.
Мы примем, что а и Ъ суть постоянные величины. Интегрирова-
Интегрирование уравнения A8.11) даёт нам в этом случае, что
откуда
Разделяя переменные и ещё раз интегрируя, найдём:
2 -?±f» х
С(г-г0) = —5Тйв ^ ,
inn, наконец,
x = f-!-/-/=- ^jIn (г-г0).	A8.14)

4178
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. И
Здесь положено для простоты С =	лТЬ' что нисколько не вре-
вредит общности рассуждений.
Вводя полярные координаты
z — zo = relH	A8.15)
и разделяя в A8.14) вещественную и мнимую части, получим:
,„_ 2(а1пг + 68) „= 2(Япг-д9) ^	A8Л
Очевидно, что кривые <р== const, и / = const, образуют два семей-
семейства логарифмических спиралей, ортогонально пересекающих друг
друга (рис. 162).
Рис. 162.
Мы можем теперь отыскивать частные решения уравнения A8.13).
Так, например, Гамель нашёл решение этого уравнения, зависящее
только от <р:
A8.17)
A8.18)
Осеен !) рассмотрел решения уравнения A8.13) вида:
') О seen С. W., Exakte Losungen der hydrodynamischen Differentialglei-
chungen, Arkiv for Matematik, Astr. und Fysik, Ms 14, 22 A927).

$ 18]	РЕШЕНИЕ ГАМЕЛЯ И ЕГО ОБОБЩЕНИЯ	479
где с — постоянное число; Розенблатт !) же изучил более общие
решения уравнения A8.13), имеющие вид:
^ = /(?) +Xя1/, (?).	A8.19)
где т — положительное число.
Рассмотрим, например, случай Гамеля, т. е. положим, что
Т = /(?);	A8.20)
тогда уравнение A8.13) приводит к уравнению четвёртого порядка
для определения функции /:
/iv + 2a f" + (с2 + b2) f" — ~ /'/" — 0,
которое сразу интегрируется
/'" + 2аf" + («2 + *2) f'-~f = С,
где С есть произвольная постоянная. Положим теперь, вместе с Гаме-
лем,
/'==«.	A8.21)
тогда и удовлетворяет уравнению второго порядка
а" ¦+ 2аи' + (с2 + Ь2) и — ~и2 = С.	A8.22)
Проекции скорости в цилиндрических координатах просто выра-
выражаются через и; в самом деле, аналогично формулам A8.1), мы
можем написать:
Поэтому на основании A8.20) и A8.16) мы имеем, например:
Vr ~ г дй ~~ г J W дЬ ~~~ a2 + b2 r '
Итак, мы получаем формулы:
		26 и,	__ 2а и	ПЯ91\
vr~ аг + Ь2 г- v>— а? + Ь2 г'	AЙ./4)
Заметим, что при 6 = 0 мы получаем vr = 0, т. е. получаем
движение по концентрическим окружностям, разобранное нами в § 15;
напротив, при а —0 мы получаем и9 = 0, т. е. мы имеем дело
с чисто радиальным течением, случай, рассмотренный нами в преды-
предыдущем параграфе.
') Rosenblatt A., Solutions exactes des equations du mouvement des
liquides visqueux, Memorial des Sciences Mathematiques, fasc. 72 A935).
Эта работа содержит обзор точных решений уравнений двнжения вяз-
вязкой жидкости.

480	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	(ГЛ It
Если же как а, так и b отличны от нуля, то уравнением линий
тока будет служить
W = const.,
так как W зависит только от ср. то линиями тока будут кривые
ср = const., т. е. a In r -f-?8 = const.	A8.25)
.Мы уже упоминали, что эти кривые образуют семейство логарифми-
логарифмических спиралей. Итак, решение Гамеля определяет движение по
логарифмическим спиралям.
В качестве второго примера отыщем частное решение уравне-
уравнения A8.13), имеющее вид:
Сх.	A8.26)
Вводя прежнее обозначение
/'(?)=«.	A8.27)
будем, очевидно, иметь:
dtp2 ' ду2	d-~f	д/
поэтому уравнение A8.13) приведётся к такому:
v [и'" + 2fl«" + (fl2 -f b2) и'] = aCu' + buu' + Си".
После простого интегрирования получаем:
^^	A8.28)
где С] — новая постоянная. Полученное уравнение легко интегри-
интегрируется до конца в том частном случае, когда постоянная С имеет
такое значение, что из уравнения выпадают члены, содержащие и',
т. е. когда
C=2vfl,
так что
b2vflX.	A8.29)
В самом деле, умножая вытекающее из A8.28) уравнение:
на и', мы сможем проинтегрировать его ещё один раз, в результате
чего получим:
U'2 = JL «3 _|_ (в2 _ ?2) „2 + 2CtH + С3,
где С2—новая постоянная. Если теперь подставить
,	 du

$ 14]	OflllOMEPIfOF ДВИЖННИГ ВЯЗКО''1 СЖИМАЕМОЙ ЖИДКОСТИ 481
ю переменные мсмут быть разделены, и мы получаем искомое реше-
решение в виде:
Полученное уравнение определяет ср как некоторую функцию от и;
обратная функция я(<р) является, как известно, эллиптической
функцией.
§ 19. Одномерное движение вязкой сжимаемой жидкости.
В качестве примера точного решения для вязкой сжимаемой жидкости
рассмотрим одномерное стационарное движение, в котором все
гидродинамические элементы зависят лишь от одной координаты,
например, от х:
vx~u(x), vy = vz--=0, р = р(х), р = р(л:).
Здесь
,.	da
div v -= —г—,
dx
и мы можем написать
Рх г = — Р + (>• + 2»*) ~~, Рху = Рух = Pxz = pz v = руг ~ ргу = О,
, , du	. ^ du
P	P+'	P	P+'
Если внешних сил нет, первое из уравненчй движения D.8) дасг
du I a
it- ,		i
dx p d.
остальные два выполняются сами собой. Уравнение неразрывности дасг
4? = 0.	A9.2)
Наконец, уравнение притока тепла A0.5) в нашем движении при-
приведётся к виду
причем, как и прежде, мы считаем, что
Т^^.	A9.4)
Уравнение A9.2) интегрируется и даёт
ом = а = const.	A9.5)
]\ Теоретическая ги tpove\ <ы<кЛ ч И

482 ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	!ГЛ II
Умножая обе части A9.1) на р и используя A9.5),	получим, путём
интегрирования:
4? + Ь.	A9.6)
где b— вторая произвольная постоянная интегрирования.
Обратимся к уравнению A9.3). Из уравнения A9.6) мы можем
найти (X -)- 2[а) du\dx и вставить это в правую часть A9.3); кроме
того, мы можем заменить ри по A9.5). Мы получим:
dT . , d \ d I. dT\ . , da ,
v dt ' ^ dx p dx \ dx I ' dx '
>
но теперь легко видеть, что члены, содержащие р в этом уравне-
уравнении, сокращаются; в самом деле, по A9.5):
d 1 	 d a 	 da
dx p dx p dx
Мы можем теперь выполнить и здесь квадратуры и тогда получим
и т	л
cvaT=k^-+aj-u* — bAu + c,	A9.7)
1де с — третья постоянная интегрирования.
Итак, задача сводится к определению четырёх функций u, T, р, рг
из двух дифференциальных уравнений первого порядка A9.6), A9.7)
и двух конечных уравнений A9.4), A9.5). Умножая обе части A9.6)
на и и, замечая, что up = upRT = aRT, получим:
|	— bu.	A9.8)
Как только мы найдём и и Т из двух дифференциальных уравне-
уравнений A9.7) и A9.8), мы определим давление из соотношения A9.6),
а плотность из A9.5).
И и и Т являются функциями одного только х, значит, мы можем
считать, что Т есть функция одного и, например. Беккеру удалось
найти решение этих уравнений, имеющее совершенно ясный физи-
физический смысл. Именно, Беккер ищет Т в виде полинома второй
степени от и:
+ ти2	A9.9)
с коэффициентами, которые надлежит далее подобрать. Вставляя
это Т в A9.7), получим, после приведения подобных членов
VT — а 4)  + (ас$ И" аА)и + acva — с-
4
Уравнение же A9.8) даст:
(). + 2и.) и -|j = {a -\- Ratf и2 -f- (Ra$ — b) и + Ran. A9.10)

§ 19]	ОДНОМЕРНОЕ ДВИЖЕНИЕ ВЯЗКОЙ СЖИМАЕМОЙ ЖИДКОСТИ 483
Сравнение этих двух уравнений заставляет нас считать, что
S_0
Для определения двух коэффициентов а и f мы имеем три уравне-
уравнения A9.11). Решая эти уравнения, мы получим без труда
но при этом обязательно должно выполняться следующее соотноше-
соотношение, связывающее между собой оба коэффициента X и \х, коэффи-
коэффициент теплопроводности k и величину ср:
Соотношение это выполняется для воздуха с большой точностью;
так, если Х = — -д-ц, то получается -~-=0,75; для воздуха:
Предположим поэтому вместе с Беккером, что A9.13) имеет место.
Так как ср — cv~AR, то теперь
«=4г- т=-^-	A9Л4)
Уравнение A9.10) примет вид:
da	с„ + с-	RC
^ = а-^-ц2-^ + _.	A9.15)
Уравнение это легко интегрируется. Прежде всего, его можно пред-
представить в виде
du	с„ 4- с„
('•Н-2|*)и-2- = в-Л-—(и — их){и — и2),	A9.16)
'де постоянные и1 и и2 связаны с Ъ/а и с/а соотношениями:
2ср Ъ	2R с
cp-\-cv ~a и\~Ги2> Cp + cv~a Ux 2'
¦Мы можем теперь записать интеграл A9.16) в виде:
¦/. 4- 1	U,	. U, — U	U«	, U — Ко	/щ 1-т,
с\[ ,- .—л—г* 1*Л —'— —^—~—-—— in	— ——~— 1|j ——^^—— , ^ 1 с? . 1 ( у
—"/. ^Л -j~ ^[^)	Wj — W2	^1 — '^2	^1 — ^2	^1 — ^2
rJ.e произвольная постоянная интегрирования, входящая вместе с х
лхаитивно, положена равной нулю (что, конечно, не нарушав i
61*

484	движение вязкой жидкости	[гл п
общности). Выражение для температуры Т примет при этом вид:
Физический смысл A9.17) очень прост. При х — — оо мы имеем
и — uv, при х = -\- оо и = и2 (нетрудно убедиться, что мы всегда
можем считать их > и2). Назовём ещё через pj, p{, Тх плотность,
давление и температуру при х = — оо. а через р2, р2> Т2 — те же
величины при лг = -}-оо. Равенство A9.5) даст тогда:
A9.19)
Так как вследствие A9.16) du/dx обращается на	бесконечности
в нуль, равенство A9.6) даст:
Pi«i + P1=P2«2 + ^2-	A9.20)
Наконец, исключим b из A9.6) и A9.7) и заметим, что на беско-
бесконечности не только du/dx, но и dTjdx обращаются в нуль. Получим
после простых преобразований
(^L)	<'2/?2- A9.21,
Но уравнения A9.19) — A9.21) в точности совпадают с теми соотно-
соотношениями, которые получаются из условий существования сильных раз-
разрывов в идеальной жидкости [глава первая, формулы B.15) — B.17)]
для случая одномерного стационарного движения (8 = — Vп =. — и).
В идеальной жидкости мы имели бы движение с постоянной ско-
скоростью их, плотностью pj, давлением рх, вплоть до поверхности раз-
разрыва; затем движение скачком приняло бы скорость и„ плотность р2,
давление р2. В вязкой жидкости мы имеем непрерывный переход
от их к и2 при помощи A9.17); но A9.5) мы можем найти о,
по A9.6) — р. Мы имеем как бы «размывание» поверхности разрыва.
Какова же будет толщина переходного слоя, заменяющего поверх-
поверхность разрыва? Подсчитаем по A9.17), чему будет равно расстоя-
расстояние Ах, на протяжении которого и изменится от 0,9 их до 1,1 и2.
Это будет
.	Ъ. X -j- 2jj. (	п , 0,1л . 1 . 0,9л — 1 }
V. + 1	О,	(.	П — 1	П— 1,1	Л — 1	0,1	|
где п = uju2.
Пусть
Х = — -|jx, /=1,40; -^ = 0,133 смЦсек, л=2;
ах = 4 ¦ 10* см/сек,
тогда будет
10~° см.

<i 2П]
ЗАДАЧА ОБ ОБТЕКАНИИ П0ЛУБЕСК0НЕЧНОИ ПЛАСТИНКИ
485
Величина эта имеет порядок длины пробега молекул; такое расстоя-
расстояние пренебрежимо с точки зрения механики сплошной среды. Это
является до некоторой степе-ни подтверждением правильности тех
исследований разрывов, которое мы проводили в главе по газовой
чинамике. Некоторым предостережением является то, что при рас-
рассмотрении расстояний порядка длины пробега молекулы мы едва ли
можем пользоваться уравнениями механики сплошной среды.
§ 20. Задача об обтекании полубесконечной пластинки не-
несжимаемой жидкостью. Пусть плоская полубесконечная пластинка
движется параллельно самой себе с постоянной скоростью v вдоль
отрицательной оси X. Нам удобно будет обратить движение и рас-
рассматривать обтекание пластинки, расположенной вдоль оси ОХ (л;>0).
равномерным потоком, имеющим постоянную скорость U (рис. 163) *).
Рассмотрим случай несжимаемой жидкости.
Вводим функцию тока ф из равенств
х ду '
и приходим вновь к уравнению
д±
дх
ду дх дх ду
B0.1)
B0.2)
Это уравнение будем решать при следующих краевых условиях.
Вдоль пластинки мы должны записать условие прилипания
(vx — vy = 0), и это значит, что
ф=^- = 0 при
= 0.
B0.3)
') Исследование задачи излагается по работе Кочина Н. Е., выполненной
и 1944 г. и опубликованной впервые в Собр. соч. Кочина Н. Е., т. II; 1948.

486	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
На бесконечности имеем условие
~ду~~ '
[Г Л II
B0.4)
Для удобства решения задачи перейдем от координат х, у> к пара-
параболическим координатам хх, ух с помощью соотношения
z = v>,	B0.5)
где z= х -\-iy, Z — xl-\-iyx, так что х — х\-—у\, y = 2x1yr Коор-
Координатные линии хх = const. = С представляют собой параболы
У	 Г2	L_ ,.2
X — Ь	4С2 У •
причем линия лех = 0 вырождается в дважды проходимый отрезок
вещественной оси л; от — со до 0.
Линии У[ = const. = С являются также параболами
причем линия ух = 0 вырождается в дважды проходимый отрезок
вещественной оси от х = 0 до х = -\-оэ.
Чтобы перейти в уравнении B0.2) к новым переменным, мы можем
воспользоваться преобразованием, приведенным в предыдущем пара-
параграфе; достаточно положить в A8.3):
ср(л\ y) = xv х(х, у) = У1-
При этом будет по A8.5)
dV~z
dx
dz
dz
4\г\
и уравнение B0.2) по A8.7) может быть записано в виде
д<\> д Дф	<Эф д Дф	Д,ф
'	I	Т_ 	 	Т	 	„ ,. Д 	' »
дух дхх х\ + у\ дх: дух
¦Л'
B0.6)
причем
Установим теперь краевые условия для ф. Пластинка соответ-
соответствует линии ух = 0. Таким образом, по B0.3) имеем
при ух = 0: ф == 0, -5-^- = 0.	B0.7)
При удалении от пластинки скорость должна стремиться к U.

§ ?, 1	ЗАДАЧА ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ	487
Удаление о г пластинки отвечает стремлению У] к со. Так как
с)ф йф dxt . d']i dyt 		1
то мы имеем
Разделим это равенство на у1 и устремим у! к с>о, принимая во вни-
внимание, что при у1—»• оо vx-^>U, г>у—>0. Получим:
у,->оо аЛ
Будем искать решение уравнения B0.6) в виде ряда
Ряд этот можно рассматривать лишь для больших значений xv
сходимость его сомнительна, но можно считать его асимптотическим
рядом.
После подстановки B0.9) в B0.6) получим, собирая члены при
одинаковых степенях х{, рекуррентную систему обыкновенных диф-
дифференциальных уравнений для определения функций /0, fx, /2, . . .:
^	;' = О;	B0.10)
¦'/г+/«/г+з/;/;'+/о /; - /;"/, -»(зэду+^/«о
+ У?/о/о' + ЧГоП + 2У1/о/о-. B0.11)
^2V + /O/2' + 5/;/2-3/o72 =
= v (y?/iV + 4У1/;" - 12/; - 4yf/|v- SyJ/J') -
- (yj/o/o" - 5yf/о/о + 4У? /о /о) +
+у! (/о /Г + 5/; /0' +- з/; /; - /; д)+2У, (/„/;' - /ovo) -
- 2 (/0/; + 5/;д + /,/f - з/;/;"), B0.12)
и вообще
B0.13)
причем правая часть содержит независимую переменную у; и функ-
функции /0, fx	fn-i с их производными до 4-го порядка.

488	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ 11
Ход решения будет теперь следующим. Из нелинейною уравне-
уравнения B0.10) надо определить /0. После того, как /0 известно, мы
можем перейти к определению Д из линейного (по отьошению к Д)
уравнения с коэффициентами и правой частью, зависящими от /0.
Далее, определим /2 из линейного (по отношению к /2) уравнения
с коэффициентами, зависящими от /0 и с правой частью, содержа-
содержащей /0, Д и т. д.
Граничные условия для функций /0, Д, ... будут счедуюшие
/я@) = /;@) = 0. я = 0, 1, 2, 3, ...	B0.14)
lim A==2U, lim ^- = 0, «=1,2,3,... B0.15)
Применяя правило Лопигаля, запишем условия B0.15) в виде
f'Q(oo) = 2U. fa(oo)=0.	B0.16)
Обратимся к решению уравнения B0.10).
Заметим, прежде всего, что оно может быть записано в виде:
Zy7« + /o^o)=0	<20-17)
и, следовательно, допускает одно интегрирование; после проведения
этого интегрирования полечим
*/о" + /е/о=°	<20Л8>
(постоянная интегрирования выбрана равной нулю, что обеспечивает
затухание f и f," no со).
Уравнение B0.18) известно в гидродинамической литературе под
именем уравнения Блази}са. Оно впервые было исследовано в 1908 г
при решении задачи о пограничном слое (см. ниже § 32), с теми же
краевыми условиями, что и в нашей задаче1).
Для исследования этого уравнения перейдём к безразмерной
функции С и безразмерчой координате % из условий:
При этом мы полечим уравнение
•27" 4-",(," — 0	B0 20)
и ьраевое условие
;@) = С @) = 0, С'(оо)=1.	B0 21)
') В I a s i u s Н , Gren/schlchten in Fliibsigke ten nut kleiner Reibung. Zs.
1 Mafli и Ph\b 156 A408), ctv. 1—37

s. 20)	ЗА/ПЧЛ ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧНОП ПЛАСТИНКИ	489
Ищем решение уравнения B0.20) в виде ряда, расположенного по
возрастающим степеням 5. Обозначим ещё
С"@) = а.	B0.22)
Тогда последовательно дифференцируя уравнение B0.20) и исполь-
з\я условия B0.21), легко найдём
?'"@) = 0; CIV@) = 0; Cv@)= —^a2.
Применяя к равенству B0.20) формулу Лейбница, легко обнару-
обнаружить, что вообще
;№@) =:(ЗМ1)@) = 0 (А = 0, 1, 2, ...)• B0.23)
Положим, лалее,
( ^\*ta*+» (ft=0, 1, 2. ...) B0.24)
и найдём рекуррентные соотношения для коэффициентов ck; мы
имеем прежде всего е0—1. Применим теперь формулу Лейбница
к B0.20), взяв от обеих частей этого равенства производную
порядка 3ft—1; тогда получим:
1дс ( п )= —тт—	гг означает биноминальный коэффициент.
\ m) от! (и—от)!	^^
Пользуясь формулами B0.23) для начальных значений производ-
производных, получим равенство:
;<3*+2> @) = -1 [С3*' @) С" @) -f CV{) r-i3k~2) (°)с'"
@)] - -12
полставляя, наконец, сюда значения B0.24) и сокращая всё равенство
/ 1N*
на (—=¦) a* + 1, получим искомую рекуррентную формулу:
41
Теперь мы без труда можем написать ряд Тейлора для функции С:
B0-26)
ft = O

490	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
При заданном а этот ряд сходится для достаточно малых по модулю
значений \. При а=1 мы получаем функцию
со
4>W — 2и\ 2} C* + 2)!4 '	Uw.^O
fc = 0
дающую решение уравнения B0.20), определяющееся начальными
условиями
Со@) = 0, С0@) = 0, Со @) = 1.	B0.28)
Сравнивая выражения B0.26) и B0.27), легко убедиться, что
»).	B0.29)
При больших значениях 5 мы не можем воспользоваться рядом
B0.27) для вычисления функции Со© и должны прибегнуть к ана-
аналитическому продолжению, чтобы получить значения функции Со0О
для всех положительных значений %. В рассматриваемом случае прак-
практически проще всего произвести численное интегрирование уравне-
уравнения B0.20). В самом деле, мы сейчас покажем, опираясь на элемен-
элементарные соображения, что кривая Со(?) имеет очень плавный характер.
Вследствие начальных условий B0.28) функция Со(?) и её две
первые производные Со (?) и Со @ при малых положительных зна-
значениях % положительны, а так как при всяком %
Со' = — -g-W?.	B0.30)
то Со'(?) будет при тех же условиях отрицательна. Покажем, что
при всех положительных X функция С0@ и её производные Co(S)
и Со E) будут положительны, а производная Со (?) будет отрицательна.
Рассмотрим прежде всего Со E) и допустим, что эта функция обра-
обращается в нуль в некоторой точке \ > 0, оставаясь положительной
для \ < ?j. Тогда в этой точке и Со обратится в нуль, согласно
уравнению B0.30). Но дифференцирование этого уравнения даёт нам
riv	1 .I.» 1
откуда следовало бы, что и
и т. д. В результате получилось бы, что в точке %х все производные
функции Со(<;)> начиная со второй, обращаются в нуль, т. е. что
функция Со(?) есть линейная функция, а это противоречит начальным
условиям B0.28).

§ 20]	ЗАДАЧА ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ	491
Итак, при всех положительных ? функция Со О;) положительна,
но тогда ясно, что
о
так же как	Е
тоже положительны, а следовательно, по уравнению B0.30) функ-
функция Со' (?) отрицательна.
Теперь ясно, что при изменении $ от 0 до оо функция Со (?) все
время убывает, функции же Со (?) и Со© все время возрастают.
Докажем, наконец, что при ?->со значение Со (?) стремится
к определенному конечному положительному значению к. Возьмём
какое-нибудь определенное значение \, например 1=1, и вычислим
СоA) и СоA). Вследствие сказанного ясно, что при ?> 1
0>(Е) >to(l)-f-C0(l)(? — 1)	B0.31)
и следовательно, Со(?) неограниченно возрастает вместе с %. Из ра-
равенства B0.30) мы можем вывести, что
fill	.
интегрируя это соотношение по \ в пределах от 0 до ^ и принимая
во внимание начальные условия B0 28), получим:
\	_±JCo<?)dE
ЛЪ\й\ или Со(^ = е °
о
Ещё раз интегрируя это соотношение и пользуясь B0.28), найдём-
?
2o	ai	B0.32)
о
При ^—> со этот интеграл сходится, так как подынтегральная функ-
s
цня очень быстро стремится к нулю, ибо fco(?)d? при больших %
о
по неравенству B0.31) имеет порядок ?2. Итак, мы доказали наличие
предельного равенства
htn C.Q(&)=*.

492	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
Произведя численное интегрирование уравнения B0.30), получаем:
k = 2,0854.
Подберём теперь з. так, чтобы удовлетворить граничному усло-
условию B0.22). Соотношение B0.29) показывает, что
и, следовательно, при ;—>оз
Но по условию левая часть этого равенства должна равняться еди-
единице, поэтому величина з дотжна иметь следующее значение:
2
<* = k'^ = 0,332 >)•
Нам понадобятся ещё ассимптотические выражения для функции С и
её производных при больших значениях Е. Прежде всего, аналогично
B0.32), имеем
i
l" = oe ° .	B0.33)
Проинтегрируем обе части этого равенства по \ от 0 до "х. и уч1ём
условие B0.21). Получим
Г'= 1 4- Jae ° di.	B0.34)
Выполним ещё одно интегрирование по 5, от оо до ?. Будем иметь
С —с, — X-f I «e ° didl	BC.35)
где >. — постоянная интегрирования, или, зыполияя интегрирование
по частям,
4/.
B0.36)
') Более точное значение a =- 0,33206-

§ 20]	ЗАДАЧА ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧИОП ПЛАСТИНКИ	493
Постоянная X может быть определена, когда решение известно, по
формуле
— Х = lim (С — ?).
? -> со
Производя численное интегрирование, получим
Х= 1,72077.
Мы можем, таким образом, представить С в виде
С-=5 — Х-КE),	B0.37)
где 11 (Е) обращается в нуль при с-*оо.
Возвращаясь к B0.33), представим теперь входящий туда инте-
i рал в виде
а
с © rfe =
о	о
О	оо
так что
— -т-($ — М2 2 J
Iw " J
ей
B0.38)
где
Численное значение для С будет:
С = 0,23378.
Теперь по B0.34) инеем
С'= 1+С Je~?<e~"XJe 2o rfs,	B0.39)
со
а по B0.36) и B0.37)
— ?j)e	^ dt\.	B0.40;

494
Так как
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ II
1 , , J
= 4
12A — 1
(=-X)*
со
то, no B0.40), имеем для больших к:
ч ='
(?->.)'
и мы можем написать окончательно для больших
» = 1 + С / Г? ^ХИ^ + О
. = ?-). + С /E
Е-?'JE - X)-4).
О
B0.41)
Обращаясь к определению функций fv /2, заметим, что уравне-
уравнение B0.13) может быть представлено в виде:
d m	n	i i	и
Введём, наряду с B0.19), безразмерную функцию С„ из равенства
Выполняя квадратуру, получим теперь (левая часть обращается
в нуль при ?—>оо, так что справа следует взять интеграл от со
до 5):
„rf?. B0.42)
В частности, для функции С; в правой части B0.11) заменим v/Jv
и v/y" no B0.17) и B0.16); получим после простых преобразований
Ш -

§ 201	ЗАДАЧА ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧНОИ ПЛАСТИНКИ	495
так что, выполняя квадратуру в правой части и замечая, что
по B0.41) (&' — С); —X, получим окончательно
Как обычно, решение ищем в виде суммы общего решения одно-
однородного уравнения B0.44) и частного решения неоднородного урав-
уравнения. Однородное уравнение имеет в качестве одного из решений
Гн = С', в чём убеждаемся простой подстановкой с учётом уравне-
уравнения B0.20). Остальные два решения однородного уравнения ищем
в виде е„ = ч'и. Обозначим ещё v = -rr. Тогда для v имеем диф-
ференциальное уравнение второго порядка
Назовём его независимые решения буквами vi и f2.
Три решения однородного уравнения — мы назовем их К,, К2,
Кл — мы можем тогда представить в виде:
СО	чз
К, = С, К2 == С J t», d5. K3 = С' J
Поведение функций vv v2 (и К2, К3) при больших % можно опреде-
определить из следующих соображений. Заметим, что по асимптотическим
выражениям B0.41) коэффициенты С/С и {.'"/(.' в B0.45) стремятся
к нулю при больших ?(С—>1, С-*^—-X); поэтому решения vl и v2
при больших \ окажутся близкими к решениям уравнений
2v" -И? — Ц v'2 + 2от> = 0.
Оба независимых решения этого последнего уравнения известны. Мы
можем положить
rf2"-'
: ,г2П- 1
где Я2л_1 — полином Эрмита степени 2и—1.
Имея это в виду, можем считать, что при больших ? наши ре-
решения ведут себя как

496
ДВИЖЕНИЕ ВЯЗКО» ЖИДКОСТИ
[П U
Как обычно записываем теперь общее решение уравнения B0.42)
в виде
J
B0.46)
где W — де1ерминант Вронского системы, коюрый можно взять
в виде W = C", a / —правая часть B0 42)
Асимптотическое представление подынтегральных выражений будет
соответственно
const./(?), в-Т«->>*E
При и = 1 имеем, по B0.41),
' —СJ —>
fc-f-CS f е *1п }>=tfvj —
Ё-f-X
¦С
/E-1)'
./.2	фСг 4<: >);
Теперь мы видим, что (для п=1) все члены правой части B0 46),
за исключением члена, содержащего Cv таковы, что соответствую-
щее Ci—>е 4 . Мы должны, поэтом}, положить С3 = 0. Чго же
до С1 и С2 то их надо определить из краевых условий.
Аналогичные соображения можно высказать относительно функ-
функций с любым значком п. На рис. 164 нанесены значения функций
С(?) и С](?). На рис. 165 нанесены величины vJU и \0vyIU в функ-
W
циях от безразмерного расстояния К = — у. Подсчёт произведен по
формуле B0.9) (/2, /3 и далее считаются нулями) для безразмер-
W
ного значения X — — л: = 100; величина vJU с увеличением К
стремится к 1, величина vy/U—к нулю.

§ 1»)	ЗАДАЧА ОБ ОБТЕКАНИИ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНКИ	497
ш~' гоо ~ зоо w
Рис. 165.
ЯЮ 600 700
32 Теоретическая 1идромеханика, ч, II

498	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. П
В. ПРИБЛИЖЁННЫЕ РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ
ВЯЗКОЙ ЖИДКОСТИ В СЛУЧАЕ МАЛЫХ ЧИСЕЛ РЕЙНОЛЬДСА
§ 21. Плоское течение между двумя пластинками. В преды-
предыдущих параграфах было дано в точном виде решение нескольких
задач гидромеханики вязкой жидкости. Как уже указывалось, инте-
интегрирование уравнений гидромеханики вязкой жидкости в точном виде
удаётся сравнительно редко; нужно, помимо того, отметить, что
многие точные решения уравнений гидромеханики вязкой жидкости
имею г мало гидродинамического интереса, так как они могут быть
осуществлены только при наличии граничных условий необычного
в практике вида. С другой стороны большинство важных с точки
зрения возможности эксперимента или наблюдения в природе дви-
движений вязкой жидкости не поддаётся точному гидромеханическому
анализу. В качестве примера можно указать на задачу о движении
сферы в вязкой жидкости с постоянной по величине и направлению
скоростью.
Совершенно естественно, что при невозможности точного реше-
решения какой-либо проблемы мысли учёных обращаются на изыскание
приближенных методов решения этой проблемы. Такими приближён-
приближёнными методами гидромеханики вязкой жидкости мы теперь и зай-
займёмся.
Все приближённые методы гидромеханики характеризуются одним
общим признаком: в этих методах либо в основных уравнениях,
либо в граничных условиях часть членов или совсем отбрасывается,
или учитывается не в полной мере.
В тех случаях движений вязкой жидкости, которые будут нас
преимущественно интересовать, входят в рассмотрение три категории
сил: силы инерции, силы вязкости и силы давления. Последние силы
являются внутренними силами, и порядок их величины определяется
порядком величины первых двух категорий сил.
Что касается сравнительной величины сил инерции и сил вяз-
вязкости, то некоторую ориентацию в этом направлении даёт нам число
Рейнольдса R = /V/v, равное, как мы знаем, отношению произве-
произведения характерной скорости V на характерную длину / к кинема-
кинематическому коэффициенту вязкости v.
В соответствии с этим мы можем говорить о двух типах при-
приближённых решений уравнений механики вязкой жидкости.
К первому типу принадлежат те случаи движений, в которых
силы инерции малы по сравнению с силами вязкости и для которых,
следовательно, является малым число Рейнольдса, содержащее коэф-
коэффициент кинематической вязкости в знаменателе. Но число Рей-
Рейнольдса будет малым в трёх случаях: 1) когда характерая длина /
очень мала, либо 2) когда характерная скорость V очень мала,
либо, наконец, 3) когда коэффициент кинематической вязкости v

§ 211	ПЛОСКОЕ ТЕЧЕНИЕ МЕЖДУ ДВУМЯ ПЛАСТИНКАМИ	499
очень велик. Таким образом, к рассматриваемому типу относятся,
например, случаи медленных движений очень малых частиц в сравни-
сравнительно вязких жидкостях. Приближённая трактовка движений пер-
bojo типа состоит либо в полном отбрасывании из уравнений гидро-
гидромеханики членов, дающих силы инерции, либо же в упрощении вида
этих членов.
Другой, противоположный тип движений охватывает те случаи,
когда силы вязкости малы по сравнению с силами инерции и когда
стедовательно, число Рейнольдса является очень большим. Для этого
нужно, чтобы либо характерная длина, либо характерная скорость
били очень большими, либо же чтобы вязкость жидкости была очень
малой. Таким образом, ко второму типу движений относятся случаи
быстрых движений тел большого размера в маловязких жидкостях.
Ести мы полностью отбрасываем, при приближённом рассмотрении
дпилений второго типа, силы вязкости, то мы приходим, очевидно,
к уравнениям движения идеальной жидкости. Нам остается поэтому
рассмотреть только ту трактовку движений второго типа, когда мы
лишь отчасти учитываем силы вязкости, оставляя в уравнениях из
членов, дающих силы вязкости, лишь главнейшие.
Мы начнём теперь рассмотрение ряда конкретных случаев дви-
движений первого типа, т. е. движений, обладающих малыми числами
Ррпнольдса.
Рассмотрим течение очень вязкой жидкости между двумя парал-
тельными пластинками, расстояние А между которыми мы будем
считать очень малым. Если мы будем считать значения средних ско-
скоростей жидкости тоже малыми, то число Рейнольдса R = VA/v будет
очень мало. Будем далее считать внешние сичы отсутствующими.
При этих условиях мы можем в основных уравнениях гидроме-
гидромеханики E.1) пренебречь находящимися в левых частях этих уравне-
уравнений ситами инерции; тогда получим уравнения:
dp	(d2vy t d2vy t d2vy
B1.1)
ду ~~ ' V дх2 ~г ду2 ' дг2
dz ' \ дх2 ~~^ ду2 dz2 )
дх ~^ ду ~^ dz
Вудем теперь считать, что оси Ох и Оу лежат в одной из гранич-
граничных плоскостей, а ось Oz направлена по перпендикуляру к этим
плоскостям, так что уравнения граничных плоскостей суть
z — О и z = А.
32*

500	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Примем далее, что скорость каждой частицы направлена парал-
параллельно граничным плоскостям, так что
Заметим, наконец, что ввиду малости h изменение скоростей vv
и Vy по направлению оси Oz будет происходить гораздо быстрее
изменения этих величин в направлении осей Ох и Оу; это означает,
что порядок производной dvjdz велик по сравнению с порядками
производных dvjdx и dvjdy; точно так же порядок производ-
производной d2vjdz2 велик по сравнению с порядками производных д2юх/дх2
и d2vjdy2. При этих условиях уравнения B1.1') принимают вид:
др	дЧ\- dp	d2vv dp	dvr dvv
dx l dz2 dy l дгг dz	dx ' dy	^ '
Третье из полученных уравнений показывает, что р зависит
только от х и у; но тогда первое уравнение легко может быть
проинтегрировано:
^ = ? Ш + zA {х • у) + В (л' ¦ уг'
функции А и В могут быть определены из граничных условий
1^ = 0 при z~0 и 2=/г;
этл условия сразу дают нам
В(у, х) = 0, А(х,у)=-±§?
и, следовательно,
vx = ~±-l-P-zih-z).	B1.3)
Точно так же легко получим, что
Наконец, последнее уравнение системы B1.2) сразу даёт, после
подстановки значений B1.3) и B1.4), уравнение для определения
функции р(х, у):
&0
Заметим, что из формул B1.3), B1.4) и B1.5) сразу следует,
что
vy дЧ'у
dvy дЧ'у
= 0>	+
~дх^ + Iff = 0> ~Щг + Ту* ~ °"
Но тогда ясно, что найденное нами решение строго удовлетворяет
уравнениям B1.1\ ибо те члены, которыми мы пренебрегли в этих
уравнениях, тождественно обращаются в нуль.

, 211	ПЛОСКОГ TF4FHHF МЕЖПУ ДВУМЯ ПЛАСТИНКА-МП	501
Введем вместо vv и vy средние скорости по высоте:
ft	A
—	\ Г	—	] Г
vr(x, у)—- -г- I vx{x, у, z)djz; vy(x, y)~-^j vy{x, y, z)dz. B1.6)
о	о
Так как	''	2
I у ( h 	 у\ г}у —
~~ТГ f V	/ — ~л^ '
о
го для средних скоростей vx и vy получаем формулы:
- х	_Л^ др^ - ,х	V др
Введём iеперь вместо р(х, у) функцию
91*. У)— - T2JT-	(^-7)
топа ясно видно, что cp(jr, у.) еоь потенциал средних скоростей
причём функция ср, отличающаяся от гармонической функции р лишь
постоянным множителем сама является гармонической функцией
Формулы B1.8) и B1.9) показывают, что в рассматриваемом
случае среднее движение жидкости происходит так же, как безвих-
безвихревое движение идеальной несжимаемой жидкости, для которого по-
leHHHaJiov: скорости является функция о(х, у). Конечно, в этих
двух движениях давление р определяется по совершенно различ-
различным формулам.
Рассмотрим теперь следующий конкретный пример движения вяз-
вязкой жидкости: пусть между пластинками вставлен цилиндр с обра-
образующими, параллельными оси Oz, сечение которого плоскостью Оху
есть некоторая кривая С. Пусть далее поток набегает на этот ци-
цилиндр со скоростью U на бесконечности, направленной пс поло-
положительной оси Ох. Допустим, что обтеканию цилиндра С потоком
идеальной жидкости соответствует потенциал <р(х, у), тогда фор-
формула B1.7) определит соответствующее давление в вязкой жидкости,
а формулы B1.3) и B1.4) определят соответствующие скорости
течения.
Однако полученное движение вязкой жидкости, помимо того, что
для него основные уравнения гидромеханики выполняются лишь при-
<">.1чженно, обладает ещё тем недостатком, что для него условие при-

502	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	1Г,1 II
шпания к стенкам выполняется только на ограничивающих пластинах,
по не выполняется на боковой поверхности цилиндра С, потому что
в соответствующем движении идеальной жидкости обращается в нуль
юлько нормальная к поверхности С составляющая скорости, в то
время как для вязкой жидкости должна обращаться в нуль также
и касательная составляющая.
Можно поэтому ожидать, что среднее течение вязкой жидкости
будет очень мало отличаться от соответствующего движения идеаль-
идеальной жидкости только в некотором отдалении от контура С
Действительно, экспериментальные работы показали, что при
обтекании очень вязкой жидкостью цилиндрического препятствия,
помещенного между двумя очень близкими пластинками, получается
картина тиний гока, очень близко напоминающая ту, которая дается
ieopnefl безвихревого потока идеальной жидкости.
§ 22. Медленное вращение сферы. Рассмотрим теперь движе-
движение вязкой жидкости, вызываемое медленным вращением погружен-
погруженной в жидкость сферы радиуса а около своего диаметра, причем
угловая скорость вращения равна <и Так как за характерную ско-
скорость в этом случае мы можем принять линейную скорость ша
точек экватора сферы, то за число Рейнольдса можно взять
R _=	 — —. Мы будем считать это число малым, т. е. будем
считать вращение сферы происходящим достаточно медленно.
Применим уравнения движения в сферических координатах E.16);
при этом вследствие малости числа Рейнольдса мы можем отбросить
в первых трех из эгнх уравнений левые части Получившимся урав-
уравнениям мы можем удовлетворить, приняв, что vr и г>0 тождественно
равны нулю, р есть постоянная величина, г^ зависит только от г и
6, глк что
vx = v(r, 6),
причем функция v должна удовлетворять уравнению
o2v . 1 <Pv_ . 2 &v_ . ?tg 6 ду
На поверхности сферы частицы жидкости должны двигаться
с той же линейной скоростью <i)asin6, что и точки поверхности
сферы, поэтом} мы получаем следующее^ пограничное условие:
v {а, Ь) — ш a sin 6.	B2.2)
Вид этого условия наводит на мысль искать решение уравнения
B2.1) в форме
v(r, 6) = Л (г) sin 6.	B2.3)

§ 22)	МЕДЛЕННОЕ ВРАЩЕНИЕ СФЕРЫ	503
Подстановка згого значения v приводит нас к обыкновенному диф-
дифференциальному уравнению Эйлера
d*A 2 dA	2А- — П
dr2 ~> r dr ~r*~ ~U>
коюрое легко интегрируется и даёт нам, что
Л(г) = С,г + -^-.	B2.4)
Постоянные Сг и С2 должны определяться из граничных условий
В случае бесконечной жидкости нужно, очевидно, принять ?^ = 0,
чтобы скорость жидкости на бесконечности стремилась к нулю;
итак, в этом случае
граничное условие B2.2) даёт нам, что С = ша2, так что мы полу-
получаем окончательную формулу.
г,(л,6)=юа3Д1пе .	B2.5)
Для поддержания вращения сферы необходимо к ней приклады-
прикладывать вращающий момент М. Величину этого момента мы можем
рассчитать по формулам E.17), которые дают в рассмагриваемом
случае:
(^	)	B2.6)
такое напряжение действует на каждую единицу площади зоны
сферы, расположенной между двумя параллелями сферы; так как
площадь этой зоны равна 2яа sin Ьа dd и так как плечом этих сил
напряжения служит, очевидно, a sin б, то для искомого вращающего
момента мы получаем выражение:
М
— Г 3A.@ sin б • a sin 0 • 2к a2 sin б dd —
Г sin3 bdb — 8itjj. а3ш . B2.7)
Если бы рассматривалось движение вязкой жидкости между
Двумя сферами радиусов а^ и а2, вращающимися с угловыми ско-
скоростями u)j и ш2 около общего диаметра, то, исходя из того же
решения B2.4) и определяя произвольные постоянные Сх и С2 из
граничных условий
А (г,) = шх av A (r2) ~ ш2 а2,

504	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	1ГЛ П
мы пришли бы к следующему решению задачи:
v(r, 6) = ^l
Для вращающего момента в этом случае получаем выражение
B2.9)
§ 23. Медленное движение сферы. Рассмотрим теперь задачу
о течении вязкой жидкости, вызываемом движением сферы радиуса
а, перемещающейся прямолинейно и равномерно со скоростью U.
Сразу же отметим, что задача, очевидно, эквивалентна задаче об
обтекании сферы радиуса а потоком вязкой жидкости, имеющим
па бесконечности постоянную по величине и направлению ско-
скорость U.
За число Рейнольдса в рассматриваемом случае можно, очевидно,
взять
R = ^.	B3.1)
Если число Рейнольдса R достаточно мало, т. е. для заданной
жидкости либо скорость движения сферы достаточно мала, либо
рлдиус сферы очень мал, то можно опять применить приближенный
метод решения задачи, использованный нами в предыдущих пара-
параграфах, а именно при интегрировании уравнений движения отбросить
в них инерционные члены.
Так именно и поступил Стоке1), впервые решивший в 1851 г.
задачу о движении сферы в вязкой жидкости. Отбрасывая в основ-
основных уравнениях движения E.1) инерционные члены и полагая, что
внешние силы отсутствуют, мы получим систему уравнений:
dvx
дх ду	dz	'	J
Рассматривая, для определённости, задачу об обтекании покоя-
покоящейся сферы, центр которой находится в начале координат, пото-
потоком вязкой жидкости, будем, очевидно, иметь следующие граничные
условия:
vx = vy = v2 — 0 при г = а,	B3.3)
где г = у х2-f-у2-f- z2; кроме того, считая, что на бесконечности
поток имеет направление, параллельное положительной оси Ох, будем
•) Stokes G. G., 1. с. § 4 и On the effect of the internal friction oi
fluids on the motion of pendulums, Math, and Phys. Papers, 3, стр. 1.

МГДЛЕННОЕ ДВИЖЬНИЕ СФЕРЫ
505
"меть следующие условия на бесконечности:
U, vy~>0,
при
oo.
B3.4)
Среди различных методов решения поставленной задачи одним
из наиболее естественных, хотя, может быть, и несколько громоздким,
является метод использования сферических координат, который мы
н применим. Совершенно очевидно, что, вводя сферические коорди-
координаты г, 6, X, вследствие симметрии движения относительно осп Ох,
от которой мы будем отсчитывать углы 6, мы будем иметь:
vr = vr(r,Q), г»в = г»й(л 6), vx = 0, р~р(г,д).
Поэтому основные уравнения движения E.16), после отбрасывания
в них инерционных членов, примут вид:
др
7 он
dzvr
т
г2
or2
1 d:
6 dvr
C8
- ьг2 -
'62
2
r2
d(J
')
+
дг '
2wr
r2
2 du8 ,
r fir "^
2 ctg fl
дщ
¦<)¦
\ B3.5)
' r2 dfl г2 ып2 b) '
dvr
~дГ
T1W
Граничные jciobhh B3.3) заменятся счедующими:
vr(a, 8) = 0, г>„(а, 8) = 0.
B3.6)
Что же касается условий на бесконечности, то, как видно из
рис. 166, они примут, очевидно, такой
вид:
vr-> U cos 6, vb-> — ?/sin 6
при
л~>со	B3.7)
Вид граничных условий наводит на
мъ'счь попробовать отыскать решения
основных уравнений B3.5> в форм-4:
vr(r, 6) = f(r) cos 6,
yfl(/\ б) .= ~g(r) sin 0,
p(r, 6) -а
166
В самом деле, простое вычисление показывает, что для трех функ-
функций /О), g(r) и А (г) получаются из B3.5) )ри обыкновенных

506	ДВИЖЕШП* ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
дифференциальных уравнения:
A —g 2 г' 1
B3.8)
причем из B3.6) и B3.7) вытекают следующие граничные условия:
/(а) = 0, g(a)~0, f(oo)=U, g(oo)--=U.	B3.9)
Решение системы B3.8) не представляет никакого груда; третье
уравнение определяет нам g:
g = \fr + f,	B3.10)
после чего из второго уравнения B3.8) после простых дифферен-
дифференцирований находим h:
h = ~ f" r2 -+- 3/7" + 2/'	B3.11)
и, наконец, первое уравнение B3.8) доставляет дифференциальное
уравнение для определения /:
/•3/lv + 8л2/'" -f 8л/" — 8/' — 0.	B3.12)
Но это последнее уравнение есть уравнение типа Эйлера и потому
легко интегрируется; среди его частных решений всегда существуют
решения вида
/ = г»;
уравнение будет удовлетворяться, если к есть решение уравнения
четвёртой степени
k(k — l)(k — 2) (As — 3)-|-8/г(/г— 1) (k — 2) +8ft {к— 1)— 8/г = 0
или
k(k — 2) (A + 1)(/г + 3) = 0,
т. е. ft должно принимать одно из следующих четырёх значений:
/г = 2, k = 0, k = —L k = — 3.
Таким образом, частными интегралами уравнения B3.12) являются
fi = r~' /г==^> /з —т^ f^'=z~j^>
я общим его интегралом будет

§ 23)	МЕДЛЕННОЕ ДВИЖЕНИЕ СФЕРЫ	507
Уравнения B3.10) и B3.11) дают теперь соответствующие значения
g и А:
Постоянные А, В, С и D определяются из граничных условий
B3.9), которые дают:
D==0, C=t/, Я = —-|t/a. Л=-1Gа3.
Собирая все полученные результаты, приходим к следующему
решению задачи:
} B3.13)
Вычислим ещё силу, с которой поток воздействует на сферу-
Для этого вычислим по формулам E.17) напряжения, действующие
на элементы сферы:
dVr
a-^ о — u ( l dVr -4- дщ Щ
На поверхности сферы г>г —г>9 = 0, а следовательно, и dvrjdb ==0,
dv!t/d8 = 0; наконец, из последнего из уравнений B3.5) ясно, чго
dvjdr на поверхности сферы тоже обращается в нуль, поэюму
предыдущие формулы сильно упрощаются и дают для точек сферы
следующие соотношения:
Лг = _ р = _JL_ cose, р,, = ^ -^ = - ^- srn 0.
Направления этих сил показаны на рис. 166. Ясно, что направление
равнодействующей всех сил, приложенных к элементам сферы, совпа-
совпадает с направлением потока на бесконечности. Поэтому величина
этой равнодействующей определится формулой
W = f j(prr cos 6 — рг, sin 6) dS —
s
= j(prr cos 6 — PrH sin 6) 2^a2 sin 9 db = 3ru,t/a Jsin 9 ^9
о	о
или
B3.14)

508
ДВИ/КЬНПЬ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ II
Полученная формула для силы сопрогив тения, испытываемой
сферой в вязкой жидкости, носит название формулы Стокса.
Интересно попутно отметить, что та часть силы сопротивления,
которая происходит за счет сил давления, равна
prr cos
-ix Ua B3.15)
и составляет, таким образом, только третью часть полной силы со-
сопротивления, испытываемого сферой при её движении в вязкой
жидкости, остальные две трети проис-
происходят за счет сил вязкости.
На рис. 167 построены линии тока
полученного движения. Аналитически
эти линии тока можно получить сле-
следующим образом. Проведём через
точку М с координатами {г, 8) окруж-
окружность с центром на оси Ох, располо-
расположенную в плоскости, перпендикуляр-
перпендикулярной к этой оси, и подсчитаем коли-
количество жидкости, протекающей через
Рис. 167.	сегмент сферы радиуса г с центром
в начале координат, ограниченной этой
окр)жнос1ью; это количество можно определить формулой
F (г, 6) = jvr (/-, 6) 2-г2 sin 8 db.
B3.16)
В нашем случае для функции тока W получается выражение
? (г, Ь) = kU sin2 8 (г2 — §- аг +• у ^-\.	B3.17)
Приведем еще выражение функции тока для того случая, когда
рассматриваегся движение сферы в неограниченной жидкости, покоя-
покоящейся на бесконечности. Это движение получается из предыдущего
наложением добавочного потока со скоростью U, направленной по
отрицательной оси Ох. Аналитически это наложение сводится к вы-
вычитанию из выражения B3.13) для vr величины Gcos6 и соответ-
соответственно из выражения для г»о величины — U sin 8; поэтому для рас-
рассматриваемого случая получим:
1 ... , / а'6
4- u sin J \Т>
а
3 7
B3.18)

23]
МЕДЛЕННОЕ ДВИЖЬНИЕ СФЕРЫ
509
м, следовав,1ьно, функция тока будет выражаться уравнением:
—3^).	B3.19)
Соответствующие линии тока абсолютного движения сферы пока-
показаны на рис. 168. Как эти линии тока, так и линии тока относи-
относительного движения (рис. 167) лежат совершенно симметрично отно-
относительно плоскости, перпендикулярной к направлению движения
сферы и проходящей через центр сферы.
Чтобы получить решение в декартовых координатах, совершим
преобразование по известным формулам:
B3.20)
у = г sin 6 cos X, vy = vr sin 6 cos X -f- vi, cos 6 cos X—V\ sin X,
z — г sin 6 sin X, vz = vr sin 6 sin X -f- vlt cos 6 sin X -\- vx cos A;
в результате получим для случая обтекания сферы:
3 Uax%{\ a2 )
г3
I	9 I *
B3.21)
Поставим теперь вопрос о юм, в каких случаях полученное
решение может считаться достаточным приближением к точному
решению задачи. Для этого нужно по-
посмотреть, как велики те члены, которыми
мы пренебрегли. Обращаясь для такой
оценки к уравнениям E.16) и рассматри-
рассматривая для простоты только точки, лежащие
на оси Ох, для которых 9 = 0, легко
получим следующее выражение для про-
проекции ускорения на направление оси г:
I dv\	: dvr\
6 = 0
_ 3 U4 I,
~ 2 г* \
)
За
1	а3
2	г*
Рис. 168.
1 др
Для величины же ——- и для равной этой величине соответствую-
соответствующей составляющей сил вязкости мы получим, согласно последней
формуле B3.13), выражение
\	з [Х Ua 3'/Ua
У
в=0

510	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Отношение двух полученных величин имеет значение
которое для больших по сравнению с а значений г приближенно
равняется i/r/2v. Отсюда мы видим, что наше решение пригодно
только в той области, в которой число Ur/v достаточно мало, во всяком
случае меньше единицы. Чтобы решение годилось в сфере, радиус
которой в несколько раз превышал бы а, необходимо, чтобы вели-
величина R = t/a/v была бы в соответствующее число раз меньше единицы.
При выполнении этого условия то обстоятельство, что вне упомянутой
большой сферы члены, которыми мы при решении пренебрегли, ста-
становятся большими в сравнении с оставленными членами, не имеет уже
значения, так как на больших (по сравнению с а) расстояниях как
оставленные, так и выкинутые члены будут очень малы (опять-таки
по сравнению со значениями этих величин вблизи сферы радиуса а)
и не смогут повлиять на течение вблизи ограничивающей жидкость
сферы.
Конечно, все эти рассуждения носят общий характер, и только
опыт может подтвердить правильность полученного решения и указать
пределы его применимости. В результате многочисленных экспери-
экспериментальных исследований над падением шариков в вязких жидкостях
была установлена справедливость формулы сопротивления Стокса
B3.14) и формул, её уточняющих (об одной из которых мы будем
юворить ниже, при изложении теории Осеена), для достаточно малых
чисел Рейнольлса, а именно для значений R < 1/2. Не останавливаясь
на численных данных, доставляемых опытом, мы отметим только то
обстоятельство, что формула Стокса была использована как для
измерения коэффициента вязкости жидкости, так и в других иссле-
исследованиях, как, например, в исследовании Милликена об измерении
заряда электрона.
В заключение этого параграфа рассмотрим следующий харак-
характерный для рассматриваемого круга вопросов пример. Пусть капля
воды сферической формы падает в воздухе. Кроме силы тяжести
на нее будет действовать сила сопротивления воздуха; допустим,
что последнюю можно вычислить по формуле Стокса и что указан-
указанные две силы взаимно уравновешиваются, так что капля падает
равномерно со скоростью U. Если плотность воды есть р', а плот-
плотность воздуха р, и если радиус сферы обозначим через а, то на
каплю будет действовать сила тяжести 4l^a3^'g (подъемной силой
Архимеда 4/^a3pg можно, очевидно, пренебречь); приравнивая эту
силу силе сопротивления Стокса GnpUa, получим равенство

$ ?41	ПАРАДОКС СТОКСА	511
ИЛИ
// _ 2 8й2 ?'
и — -д-ГТ'
С другой стороны,
к— v >
поэтому легко находим, что
a^l^jrR, (/3 = |^R2^,	B3.22,
Подставляя численные значения v2 = 0,133 см^/сек, §г = 981 см/сек2,
р'/р = 770, легко находим
а = 0,0047 1^"R ел, ?/ = 28
Если R < 1/2, то а < 0,0037 ел, ?/ < 18 см/сек. Как видно, раз-
размеры тех капель, к которым применима предыдущая теория, равно
как и их скорости, очень малы.
§ 24. Парадокс Стокса. Как было выше отмечено, решение
Стокса задачи о движении сферы, изложенное в предыдущем пара-
параграфе, представляется неудовлетворительным, потому что в этом
решении отбрасываются члены, которые на достаточно больших рас-
расстояниях становятся сколь угодно большими по сравнению с оставлен-
оставленными членами.
В случае плоской задачи с решением дело обстоит гораздо хуже.
А именно, оказывается, что задача об обтекании плоским потоком
вязкой жидкости кругового цилиндра совсем не имеет решения,
если в основных уравнениях отбросить полностью инерционные члены.
Форма цилиндра не имеет при этом никакого значения. Высказанное
утверждение, как будет сейчас доказано, справедливо для цилиндра
произвольной формы.
Пусть С есть кривая, содержащая внутри себя начало координат,
по которой плоскость Оху пересекает наш цилиндр (образующие
которого предполагаются параллельными оси Oz), и пусть рассма-
рассматривается обтекание цилиндра потоком, имеющим на бесконечности
скорость U, направленную параллельно оси Ох. Тогда, пренебрегая
в основных уравнениях движения E.1) инерционными членами и
внешними силами, мы приходим к системе:
dp	dp	dvx dvv
?	&	+
¦их = vy — 0 на С,
при граничных условиях
¦
vx->U, vy ->0 при /"--> о, (,24.2)

512	ДВИЖЕНИЕ ВЯЗК0Г1 ЖИДКОСТИ	[ГЛ. II
где г —= У х'2 4- у*. Обозначим через 5 область плоскости, ограни-
ограниченную кривой С и окружностью Г большого радкуса /? с центром
в начале координат, и составим двойной интеграл
m/dvr
Ы1+Ьш
дх	' dy J
sbVjc + VybvJdxdy. B4.3)
По формуле Гаусса, замечая, что vx и vy обращаются на кри-
кривой С в нуль, и обозначая через п направление внешней нормали
к контуру Г, получим:
dv.
().t
dx dv _
Й, , . , dvx ,
dx COS (Wl x) + if COS (?l'
¦^cos(«. x)-+^cos(«, y)J)ds=J ^,^- + ^,
Далее, вследствие уравнений B4.1) и вследствие той же формулы
Гаусса, имеем:
f f {vx kvx ¦+ vy kvy) dxdy = ±f f (vx -g + vy d?) dx dy =
' s	s
1 с г Г dp	dp	ldvx dvv\~\
s
;'- J J I Ox ' dy J -"
1 /*
^5 = — J /Jfs rf
^ ; Lpvx cos (я, x)~j~pvy cos (п, ,,,... {j
Итак:

(j 241	ПАРАДОКС СТОКСА	513
Обратимся теперь к уравнениям B4.1). Вследс!вие последнего
из этих уравнений мы можем написать, что
_ <?ЧГ _ dV
vx— ду • vy	-gj.
где ч7 есть функция тока. Тогда	предыдущие два уравнения прини-
принимают вид:
др _ ф. ДУ	др __ #ДУ
дх	ду '	ду	дх
и показывают, что р-(-/[* ДЧГ есть аналитическая функция от z=x-{-ly.
Заметим при этом, что ДЧ?" совпадает, с точностью до знака, с выра-
выражением вихря скорости, ибо
дх ду
и есть, следовательно, так же как и р, однозначная функция от х
н у. Итак, функция
есть однозначная аналитическая функция вне контура С. Производная
от этой функции имеет выражение
~ к ' дх ду
Поэтому, на основании уравнений B4.1), можем написать:
i(z) = ^{vx — tvy).	B4.5)
Пусть теперь г — х — 1у означает число, комплексно сопряжён-
сопряжённое с z = x-\-iy, тогда
	 z -\- z		z — г
Возьмём в какой-нибудь функции А(х, у) вместо х и у за неза-
независимые переменные z и z, т. е. положим
А(х, у) =
тогда простое вычисление показывает, что
да __ 1 дА 1 дА
дг ~~ 2 дх~*~ 21 ду '
да__Ъ_дА_	1 дА
д~г ~ 2 дх % ду *
_д2а _ 1 (д*А . д*А\_ 1
33 Теоретическая гидромеханика, ч. II

514	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Поэтому уравнение B4.5) может быть переписано в виде
дг&х—шу)
ф (г) = 4ц.	=—,
дгдг
после чего оно очень легко интегрируется
_	д (vx —
*) 4
B4.6)
где XiC2) есть> очевидно, однозначная аналитическая функция от z.
Интеграл от этой функции
может быть, не будет уже однозначной аналитической функцией,
но получающуюся многозначность очень легко выделить. В самом
деле, мы имеем дело с двухсвязной областью, лежащей вне контура С.
Пусть контур Сх охватывает контур С один раз в отрицательном
направлении, и обозначим через К значение интеграла
Ясно, что функция
K\nz
при обходе контура Сх в отрицательном направлении увеличивается
на 2щК. Поэтому функция
будет уже однозначной аналитической функцией от z вне контура С.
Теперь мы можем проинтегрировать уравнение B4.6) последний раз:
4ц (vx - ivy) =1<р (г) -4- х (z) + Kin I+ *i ^).
Если мы представим аналитическую функцию \(z) в виде суммы
то получим окончательное равенство
4^ {vx - ivy) == гср (z) + х (г) + ^ (z) + /С1п («). B4.7)
В этом последнем равенстве все члены, кроме Х(г), по доказанному,
являются однозначными функциями от х и у, следовательно, и Х(г)
будет однозначной функцией от z.
Используем теперь заданное нам условие, что при г->со функ-
функция vx — iVy стремится к предельному значению U. Если бы vx — lvy
было бы аналитической функцией от х -j- iy, то, как показывается

§ 24]	ПАРАДОКС СТОКСА	515
в теории аналитических функций, из только что указанного условия
сразу вытекало бы разложение
аз
п= 1
В рассматриваемом нами случае имеет место аналогичный же
результат. А именно, напишем разложения в ряды Лорана одно-
однозначных аналитических функций <р(г), хB)> Mz):
пусть, далее, Сг есть окружность большого радиуса г с центром
в начале координат. В точках этой окружности
и, следовательно, на Ст мы имеем следующее равенство:
Умножим обе части этого равенства на etS9 и проинтегрируем
по 6 в пределах от 0 до 2тс. Замечая, что
2л
fe^dB — O при гфО,
о
легко придём к следующим соотношениям:
2л
f\vx-ivy)e^db^2^(^+^_krk H-JS-j (*=±1, ±2,...),
о
По предположению, vx — ivy равномерно стремится к U при
г—•=> со, следовательно, в первом равенстве левая часть стремится
к нулю, а во втором к 8тг(х О. Это возможно только в том случае,
если
<xo-f-p"_1 = O, 04 = 0, p"_ft = 0 (A>2), aft = 0 (й<—2),
Ts-0 (ft< —1). a_,^0,
33*

516	движение вязкой жидкости	[гл. и
Но тогда формула B4.7) показывает, что функция vx-—ivy должна
иметь следующий вид:
л=1	и=1
Дифференцируя это равенство по г и принимая во внимание равен-
равенство B4.6), найдём, что
я-2
Но теперь ясно, что при возрастании г давление р убывает
как 1/г2, так же убывают производные dvJdr и dvy/dr (мы могли бы
к р, а следовательно, и к tp(z) прибавить ещё произвольную постоян-
постоянную р0, но мы можем, не нарушая общности, считать последнюю
равной нулю). Но тогда подынтегральная функция в выражении B4.4)
будет порядка I//?2, а сам интеграл / будет порядка 1/R. Мы дока-
доказали, таким образом, что
lim/ = 0.
Но так как подынтегральная функция в двойном интеграле / неотри-
неотрицательна, то непременно должно быть во всякой точке
dvx dvx dvy dvy
дх ду дх ду	'
т. е.
vx= const., г>у = const.,
и вследствие первых двух граничных условий B4.2):
что противоречит условиям на бесконечности B4.2).
Парадокс Стокса показывает нам, что мы не можем получить
приближённого решения плоской задачи даже для малых чисел Рей-
нольдса путём полного отбрасывания инерционных членов.
§ 25. Уточнённое решение задачи о движении сферы. Осеен
(Oseen) показал в 1910 г. на примере движения сферы в вязкой
жидкости3), что мы получим гораздо лучшие результаты, если
в уравнениях движения оставим только важнейшие из инерционных
членов, отбросив остальные инерционные члены.
А именно, будем рассматривать задачу об обтекании сферы потоком,
имеющим на бесконечности скорость, параллельную оси Ох и рав-
1) О s е е п С. W., Ueber die Stokessche Formel und iiber eine verwandte
Aufgabe in der Hydrodynamik, Arkiv fur Mat., Astr. och Fysik, 6 A910), № 29;
7 A911), № 1.

§25]
УТОЧНЕННОЕ РЕШЬНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ
517
ную U. Как было отмечено выше, неудовлетворительность решения
Стокса проявляется на далеких от сферы расстояниях. Но в дале-
далеких от сферы точках
:?/-
-V , V =¦
B5.1)
где v'x, v' v'z суть малые величины. Рассматривая теперь инерцион-
инерционные члены, стоящие в левых частях первых трех из уравнений E.1),
мы увидим, что они отличаются от
U
дх
дх
U
дх
B5 2)
малыми членами второго порядка, если считать vx, v , vz и инер-
инерционные члены за малые члены первого порядка. Поэтому мы по-
полечим гораздо лучшее приближение в далеких от сферы областях,
если заменим уравнения E.1) следующими обобщенными уравне-
уравнениями Стокса:
.. dvx 	 1 dp . .
и*'
дх
1 dp
Р ду '
U-^ = — —
1 др
дх
dv
dvy
ЧУ
B5.3)
которые имеют очень простой вид, если их записать в векторной
форме:
дх	р ь
Av, diviJ==0.
B5 4)
Нужно отметить, что для области жидкости, непосредственно при-
примыкающей к сфере, замена инерционных членов величинами B5 2)
ничуть не лучше замены этих членов нулями, так как в этой обла-
области vx, Vy, vz малы (на самой поверхности сферы vx, vy, vz обра-
обращаются в нуль), и мы не можем использовать факта малости v'x по
сравнению с U. Однако, поскольку мы рассматриваем движения
с малыми числами Рейнольдса, го как полные инерционные члены,
так и заменяющие их в наших уравнениях выражения B5 2) буд>т
*(алы по сравнению с членами, происходящими от сил вязкости
Следовательно, в области, примыкающей к сфере, уравнения B5 3)
и сравнения Стокса являются в одинаковой мере хорошими прибли-
приближениями к полной системе дифференциальных уравнений E.1).

518	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Граничные условия, которым должно удовлетворять решение
системы B5.3), остаются прежними:
vx = vy = г)г = 0 при r = a, \
vx~>U, vy~>0, vz~>0 » r->oo. /
Для решения поставленной задачи мы применим метод Ламба').
Образуем расхождение и вихрь от обеих частей первого из уравне-
уравнений B5.4); принимая ещё во внимание второе из этих уравнений,
придём к формулам:
Д/> = 0,	B5.6)
U^-^vAQ,	B5.7)
где
Q == rot v.
Используем теперь симметрию движения относительно оси Ох.
Ясно, что вихревые линии должны быть окружностями с центрами
на оси Ох, так что во всяком случае
2, = 0.	B5.8)
Но тогда условие
dQr dQv dQz
dx ' dy ' dz
приводит к равенству
ay ' dz
откуда следует, что
о	^L о —- fy
Vjy — —W ^~~ду~'
Итак, мы имеем формулы:
dvy	dvx dvz	d^ dvy dvx
vy
y
dz	'
dy dz	' dz dx	dz ' dx d~y~ ~dy~'
Сразу видно, что частным решением этой системы является
•о* = — Ъ *>у = 0, кг = 0,
общим же решением будет
• -,-f. »,=§¦ да.
') L a m b H., On the Uniform Motion of a Sphere through a Viscous
Fluid, Phil, Mag., 21 A911), стр. 120.

§25]	УТОЧНЁННОЕ РЕШЕНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ	519
Подстановка значений B5 9) в уравнение B5.7) приводит к ра-
равенствам, которые будут удовлетворены, если
и дх —v ДХ-
С другой стороны, подставляя значения B5.10) в уравнение не-
неразрывности, находим:
и, на основании предыдущего равенства,
откуда видно, что следует принять
где tp удовлетворяет уравнению Лапласа
Д<р=О.	B5.11)
Введем для краткости обозначение
? = *;	B5.12)
тогда выражения для составляющих скорости примут следующий
окончательный вид:
v — А.4- —-&- —v v —-^--4- l dt
vx — дх ^ 2k дх '-' vy ~ ду "+" 2k ду '
причём tp удовлетворяет уравнению Лапласа B5.11), а / — уравне-
уравнению
ДХ-2й|^ = 0.	B5.14)
Подставляя значения B5.13) в уравнения B5.3), можем ргшить эти
последние уравнения относительно р, в результате чего получим:
B5.15)
Уравнению Лапласа B5.11) удовлетворяет функция
1	1

520	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	(ГЛ. 11
очевидно далее, что функции дуо/дх, д2у0/дх2 и т. д. тоже являются
решениями уравнения Лапласа B5.11). Мы положим поэтому
где постоянные коэффициенты Ай, Ах, А2 должны быть определены
из граничных условий.
Перейдем теперь к решению уравнения B5.14). Сделаем под-
подстановку, положив
тогда, после простых вычислений, найдём для определения функ-
функции (J) уравнение
Ц — ?2<j> = 0,	B5. 17)
которое в сферических координатах г. О, X имеет вид:
<?Ч> 2 *|; 1 д^ ctgO д*	1 д^ ku—n
дг2 "• г дг ~^~ г2 дО2 ~i rJ дЬ "• г2 sin !9I! « у — и.
Отыщем те решения этого уравнения, которые зависят только от г;
в этом случае мы можем переписать уравнение следующим обра-
образом:
откуда следует, что
л<|> = Вхект -(- В2е~кт.
Так как нас интересуют решения, обращающиеся на бесконеч-
бесконечности в нуль, то мы примем за основное решение уравнения B5.17)
следующее:
%{х, у, z) = ——.
Ясно, что dtyQ/dx, d2ty0/dx2 и т. д. тоже являются решениями урав-
уравнения B5.17), а екх%, екх dtyjdx и т. д. — решениями уравнения B5.14).
Кроме того, последнему уравнению удовлетворяет также ^ = const.
Мы примем поэтому
B5.18)
тогда граничные условия на бесконечности будут удовлетворены;
остаётся определить постоянные AQ, Av ... Со, Сг, ... так, чтобы
удовлетворялись граничные условия на поверхности сферы. Для
этого удобно будет перейти к сферическим координатам г, 6, X. Этот
переход очень легко совершить на основании формул B5.13), если

§251	УТОЧНЁННОЕ РЕШЕНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ	521
вспомнить, что проекции вектора grad ср на оси сферических коор-
координат равняются соответственно dyjdr, l/rdy/dO и 1/r sin 0 <Эср/дХ.
Поэтому вследствие формул B5.13), B5.16) и B5.18) для соста-
составляющих вектора скорости в сферических координатах получаем
следующие выражения:
л — 0.
B5.19)
Мы не будем строго решать поставленную нами задачу, а огра-
ограничимся приближённым её решением. Именно, мы возьмем в разло-
разложениях B5.16) B5.18) только несколько первых членов и опре-
определим их коэффициенты так, чтобы значения на поверхности сферы
отношений vTjU и v^U были малыми величинами второго порядка
относительно считаемого малым числа Рейнольдса R — 2ka.
Чтобы решить вопрос о том, сколько членов взять в разложениях
B5.16) и B5.18), обратимся к решению Стокса.
Сравнивая выражение B5.15) для р с выражением B3.13), мы
видим, что в решении Стокса
~д~х~ =
т. е.
чах
г3
3
2
д
' дх
ча
~р~ ¦
если мы выразим v через k по формуле B5.12) для того, чтобы ср
было пропорционально U, то найдем:
	3 U а
А — - 3 Ua — 3 Ua2
°~ 4 k ~ 2 R '
Мы видим, таким образом, что Ао содержит множителем R;
можно поэтому сделать предположение, что в разложении B5.16)
Ло будет порядка 1/R, Ах — порядка 1, А2—порядка R и т. д.
Обращая, далее, внимание на формулы B5.19), мы видим, что в %
главный член должен быть порядка 1, так как тогда выражения
Ij2kdxjdr и \j2krdyjdft будут порядка 1/R и смогут сократиться
с членами этого же самого порядка, происходящими от слагаемого А0/г
функции ср. Итак, мы можем ожидать, что Со будет порядка 1,
С, — порядка R, С2 — порядка R2 и т. д. Конечно, сделанные нами
предположения о порядке малости различных коэффициентов должны
быть проверены после вычисления.

522	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	(ГЛ. II
Считая теперь число Рейнольдса малым, разложим функции <р и )(
по степеням R, причём в разложении для ср мы должны взять члены
до первого порядка относительно R включительно, т. е. члены, со-
содержащие коэффициенты Ло, Л, и А2\ в разложении же для i мы
должны учесть также и члены второго порядка относительно R,
так как в формулах B5.19) производные от % входят с множи-
множителем l/k.
Помня, что x = rcos6, без труда находим:
/J_\_	х _
\Т) ~~ 73~~
cos 0 д2 /1\	1 . Зх2 3 cos2 6 — 1
дх \г) ~~ г3 ~ г2 ' дх2\г)	г3 ' г5 ~ г3
и, следовательно, для ср получается следующее приближённое выра-
выражение:
^ Л Л cos 6 A,Ccos20 — I) ^	B5 20)
Составим теперь приближённое выражение для yj, мы имеем,
прежде всего, с точностью до членов второго порядка включительно:
g-k (г-х) g-kr A-cosB)
— cos0J+ ...;
далее, с точностью до членов первого порядка включительно,
dx\ j
COS 6	ft COS2 6
pk
e
kx	 |f	] — pkr cos bp-
\ j~e	e
(	!	A\-? —
\ r* r) r ~
и, наконец,
'e~kr\ 3 cos2 6 — 1
|
~Г • • •
Г ]	Г"
Поэтому приближенное выражение для % имеет вид:
X = — U + со [у — k A — cos 6) + -^- A — cos 0J] —
—. B5.21)
Составляем теперь равенства vr(a, 6)^=0, v,(a, 0) = O, причём
в выражениях — ^ cos 9 и )(sin9 малые величины второго порядка

§25]	УТОЧНЁННОЕ РЕШЕНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ	§23
относительно R отбрасываем; в результате получаем:
Ао ,2Al cos 6 	 ЗА2 C cos2 6 — 1)
cos 6
Приравнивая в первом равенстве коэффициенты при 1, cos 0 и
3 cos2 6—1, а во втором коэффициенты при 1 и cos 0, получаем
пять уравнений для определения шести коэффициентов Ао, Av A2,
Со. С, и С2:
2A
l-C(fl*(l
^L) + -iL =
С,^ ЗС2 _
	2	i~~2ft~~~ '
ал	Ьрк" , о^2 	л
ОЛ2	2 "I ft —
Исключая из второго и четвёртого равенств Ах и Cj, получаем:
B5.22)
z 2—
исключая же из третьего и пятого уравнений А2 и С2, находим:
a* — Сга2 = 0.
откуда
1 ТПМГ'	(
2
после этого первое и второе уравнения определяют Ло и Аг:
—3fta) '
3
4—зла*

524	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Наконец, А2 и С2 определяются только в комбинации
Л +	B5.26)
так как при принятой степени приближения невозможно отделить Л2
от С2. Мы видим, что сделанные нами допущения о порядке коэф-
коэффициентов А и С действительно имеют место.
Перейдём теперь к исследованию полученного решения. При этом
мы будем ограничиваться в разложениях для ср и )( только первыми
двумя членами и соответственно этому упростим найденные выраже-
выражения для коэффициентов Ао, Ах, Со и Сх, отбросив в Ай и Ах члены
порядка k, а в Со и Сх — члены порядка k2. Тогда можно принять
Х	'	B5.27)
Составляем теперь по формулам B5.19) выражения для проекций
скоростей vr и Vf), причём будем пренебрегать членами, содержащими
k множителем:
. С, cos Qetracos)
н	^	1"u cos е>
"»— /-3 ^ 2/-
+ 1	л —ЙГ A —COS 8) 	 //ctnfl	/О f-\ OQ4
о. з "	7 	 tV bin 0, ^/O.^Coj
Для давления, на основании B5.i5) и B5.20), мы имеем формулу:
, ,, . cos В ,, , 3cos20— 1
Р = Ро+?иAo-fS~ ~
+^)^ -!^Cco*fl-l). B5.29)
Для точек вблизи сферы, разлагая в формулах B5.28) показа-
показательные функции по степеням kr и ограничиваясь той же степенью
цриближения, получим:
п ¦ й/, З	«
= _?/Яп9{1—?т_т_|,

§ 2Ы
УТОЧНЁННОЕ РЕШЕНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ
525
т. е. восстанавливаем формулы Стокса B3.13). Следовательно, вблизи
сферы течение имеет, по-прежнему, вид, изображённый на рис. 167
(относительное движение) и на рис. 168 (абсолютное движение).
На далёких от сферы расстояниях дело обстоит совсем иначе.
В этом случае мы можем отбросить в формулах B5.28) члены,
содержащие коэффициенты Ах и С{, как малые, по сравнению
с членами, содержащими Ао и Со. Мы будем, далее, рассматривать
для определённости абсолютное движение сферы в жидкости, покоя-
покоящейся на бесконечности; тогда в выражениях B5.28) нужно отбро-
cirib также и члены ?/cos6 и — t/ sin 9. В результате мы приходим
к следующим простым выражениям:
[l+ftr(l+cos9)].
^ ^osina c_ftf(i_cos(
B5.31)
причём нужно помнить, что сфера двигается вдоль оси Ох в отрица-
отрицательном направлении со скоростью U.
Рассмотрим теперь отдельно движения жидкости перед телом и
позади тела. Рассмотрим сначала ту область, где kr{\ —cos 6) имеет
значительную величину, т. е. где kr
велико, а 0 достаточно отличается
от нуля; в этой области мы можем
пренебречь значением показательной
функции, в результате чего полу-
получим:
Ша /, |^ ЗАй\ 1
~Г 4 } г2 *
B5.32)
—
Но к упомянутой области не при-
принадлежит только узкий хвост позади
тела. Поэтому полученная формула
показывает, что на далёких расстоя-	Рис. 169.
ниях всюду, кроме узкого хвоста па-
раболоидального вида позади тела, течение мало отличается от
течения, вызванного источником, находящимся в центре сферы и имею-
имеющим интенсивность
Q = —J~[1^—^j=6'rav\1H—гI	B5.33)
Только что высказанное положение наглядно подтверждается рис. 169,
i'a котором даны линии тока для абсолютного движения сферы.
Напротив, рассмотрим область далеко позади тела, в которой
угол 0 мало отличается от 0, a kr велико, причём величина

526	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. И
/fer A—cos9) близка к нулю. Тогда выражение 1 + kr A -f cos б)
мало отличается от 2kr, значение g-йг a- cos в, мал0 отличается от
единицы, и мы получаем приближённое выражение для vr следую-
следующего вида:
2М*?(+.^).	B5.34)
Мы видим, что в узком хвосте далеко позади тела жидкость дви-
движется в том же направлении, что и тело, причём на больших рас-
расстояниях скорость изменяется обратно пропорционально первой сте-
степени расстояния. На рис. 169 видно резкое различие течений впереди
и позади тела.
Сущность этого различия легко выяснить, если найти распреде-
распределение вихрей в рассматриваемом течении. Для вычисления вихрей
проще всего воспользоваться формулами B5.8) и B5.9), в которых
мы, согласно рассматриваемому приближению, должны взять
В результате находим:
откуда
Q = Coe-*'-(I-<:ose>-i:i^-sin0.	B5.35)
Для больших значений kr(l—cosG), т. е. далеко впереди тела
(точнее говоря, вне узкого хвоста позади тела), значение 2 очень
мало, следовательно, далеко перед телом движение носит почти потен-
потенциальный характер. Напротив, в узком хвосте позади тела, где вели-
величина kr (I —cos 6) очень мала, движение носит завихренный характер.
Правда, при 0 = 0 мы получаем й —0, но при b=\(\fkr> где kr—
очень большое число, т. е. на поверхности параболоидального вида,
мы получаем:
2 —<
так что вихри в области позади тела затухают обратно пропорцио-
пропорционально полуторной степени расстояния.
Чтобы вычислить функцию тока W(r, 6), мы можем применить
формулу B3.16). При этом мы воспользуемся формулой B5.31),
чтобы получить функцию тока для движения сферы в жидкости,
покоящейся на бесконечности, в соответствии с рис. 169 вычерчен-

§25]	УТОЧНЁННОЕ РЕШЕНИЕ ЗАДАЧИ О ДВИЖЕНИИ СФЕРЫ	527
ным при этих же предположениях. В результате простого вычисле-
вычисления находим:
2^()—e-*'d-eose>]. B5.37)
Покажем, наконец, как вычислить силу воздействия потока
на тело. Мы уже имели в § 23 общую формулу для рассматривае-
рассматриваемого случая
W = / /(Р
s
причём на поверхности сферы

Ртт — ~~
Проще всего вычислить значение dv^jdr, если воспользоваться выра-
выражениями E.7) для проекций вихря в сферических координатах г, б
и X:
д (sin ®У\)
~ /-sm8 L
_ 1 Г dvr
) — ТШТГ31
dvr д (r sin
дг
dvr И	 dv$ . 1 	 ]_ dvr ш
в нашем случае 2r = Qr) = 0; что же касается значений их, то на
поверхности сферы v$ = О, ©,. = 0, а следовательно, и dvrjdb = 0.
Итак, на поверхности сферы
g — Цщ_
1 дг
С другой стороны, мы имеем для составляющих вихря выражения:
следовательно, по формулам B3.20) перехода от декартовых коор-
координат к сферическим
Qr = — 2„ sinX-4-^rcosX = -^- cos X-|~-^sinX.
Помня, что р = р0 — pUdy[dx, находим для подынтегральной функ-
функции в формуле B5.38) выражение
ртг cos 9 — ртП sin 0 =
= — {рп — р?/-Д-| cos 0 — и -Д- cos X sin 0 — а -Д- sin X sin 0 =
\ и ' ох •	1 оу	иг

528	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
конечно, это равенство справедливо только на поверхности сферы.
Но ведь на поверхности сферы vx = vy = ©г = 0; поэтому по фор-
формулам B5.13)
^JL — — Oh дЧ	д1 — 9h д<?
ду	ду oz	oz
Замечая, наконец, что по тем же формулам преобразования B3.20)
да	0	да	-v . я | дер . •, . п	дер (Г, 6)
-J-cos 8-4--ri-cos X sin 6 Н--г-sin X sin 8 = \ ,
дх	' ду	' йг	дг
приходим к следующей простой формуле:
dS.	B5.39)
ибо интеграл от p0cos6, очевидно, равен нулю. Но для со мы имели
общее выражение B5.16). Все члены этого выражения, кроме первого,
при интегрировании ду/дг по всей поверхности сферы дадут нуль;
первый же член даёт, очевидно, значение
S	S
Итак, мы получаем следующую формулу:
W = — 4TzpUAu.	B5.40)
Воспользовавшись теперь выражением B5.27), найдём:
B5.41)
Эта последняя формула, данная Осееном, представляет уточнение
формулы Стокса.
Аналогичные предыдущим вычисления были произведены и для
более сложных случаев, как, например, для случая движения сферы
в полупространстве, ограниченном плоской стенкой, или для случая
движения сферы по оси цилиндра. Полученные для этих случаев фор-
формулы сопротивления, обобщающие формулу Стокса, могли быть прове-
проверены на опыте. Не останавливаясь на цифровых данных, мы отметим
только, что получилось удовлетворительное совпадение результатов
опыта и теории для малых чисел Рейнольдса, не превышающих еди-
единицы.
§ 26. Движение цилиндра. Решение задачи об обтекании цилиндра
потоком вязкой жидкости в предположении, что за исходные урав-

§ 26]	ДВИЖЕНИЕ	ЦИЛИНДРА	529
нения можно взять
1 т dvx	I dp . .
дх	р дх '	*'
B6.1)
протекает совершенно аналогично решению задачи об обтекании сферы,
так что при изложении этого решения можно быть очень кратким.
Мы имеем опять формулы:
причём <р удовлетворяет уравнению Лапласа
Дер ' — -гг— —1-- —-—— z^z \).	B, и. о)
Ох	Оу
а х — уравнению
д^—2А-^- = 0.	B6.4)
Тогда все уравнения B6.1) будут удовлетворены, если взять
Р—Ро—Р^ ~а—•	B6.5)
Уравнению B6.3) удовлетворяет функция In г, а также —-з—, . 2
н т. д. Поэтому мы принимаем
tp — ^40 In г —f- Al—-з	Ь^2—л~г	Ь ••"•	B6.6)
В уравнении B6.4) делаем подстановку
тогда получаем для определения ф уравнение
имеющее в полярных координатах (г, 8) вид:
^ + ^ + ^^-^ = 0.	Рв.7,
Отыскиваем то решение этого уравнения, которое зависит только
от г и, следовательно, удовлетворяет обыкновенному дифференциаль-
дифференциальному уравнению
34 Теоретическая гидромеханика, ч. IJ

530	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Решениями этого последнего уравнения являются бесселевы функции
с чисто мнимым аргументом г):
Однако 10(кг) безгранично возрастает вместе с г, в то время
как K0(kr) стремится к нулю при г —>со ; поэтому единственно прием-
приемлемым для нас решением уравнения B6.8) является K0(kr).
Функции
дК0 (kr) д*К0 (kr)
дх '	дх1 ' * *"
также будут решениями уравнения B6.7). Мы можем поэтому принять:
Так как
д In г 	 х 	 cos 6 б2 In г 	 cos 26	. . *
~~дх~~7*~~~Г~' дх* ~ W	 И>.Ш)
то для <р находим следующее разложение:
. . , . cos 6 . cos 26 .	.__ <..
«pr^olnr + ^j—	Л2—72	г----	B6.11)
С другой стороны, мы имеем при малых кг разложения:
где f— постоянная Маскерони G = 1,7811; In 7 = 0,57722). Огра-
Ограничиваясь самым первым приближением, мы можем принять, что
дКа (kr) ^ 1 х _ cos 6
дх ~ г г	г '
поэтому вблизи цилиндра, считая ka малым, будем иметь приближённо
С,-^-, B6.12)
Теперь мы можем вычислить по формулам
dtp , 1 дХ	с	1 д® . 1
') См., например, Смирнов В. И., Курс высшей математики, т. Ш,
1939, стр. 687 или Кузьмин Р. О., Бесселевы функции, ГТТИ, 1935.

ДВИЖЕНИЕ ЦИЛИНДРА
531
приближенные выражения для проекций скорости вблизи цилиндра;
Ао А{ cos 8
"г- ~
vt = — —
cos9 —
A, sin I
¦ — (у sin e — с,
sin О
\п{~
2kr2
С, sin 6
B6.14)
при вычислениях мы отбрасываем некоторые члены, малые в сра-
сравнении с оставляемыми, а именно, вычисляя xcos^ и 5<. sin 0, мы
пользуемся ещё более упрощенным выражением для у:
кроме того, в выражении для <р берутся только два первых члена.
Полагая в полученных формулах г—а, составляя равенства
vr(a, b) = v$(a, 6) = 0 и приравнивая нулю коэффициенты при 1,
cos 6 и sin 6, приходим к трем уравнениям для определения четырёх
коэффициентов: Ло, Av Со, С^.
2ka
J
откуда легко находим:
= 0>
Ао = -
2U
4v
k м	2 In ( 4г '
	W
1—2 In
2k ~~"
B6.15)
При принятой степени приближения коэффициенты Ах и С1 по отдель-
отдельности определены быть не могут. Подставляя найденные значения
коэффициентов в формулы B6.14), находим выражения для проекций
скоростей, пригодные в области вблизи цилиндра:
B6 16)
1-21П (-д-
34*

532	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	ГГЛ. Ц
На больших расстояниях от цилиндра, беря только Ч1ены, содер-
содержащие Ао и Со, и рассматривая абсолютное движение цилиндра
в жидкости, покоящейся на бесконечности, будем иметь:
vr = A + -2 Coe*r cos e f/Co (&O — cos QK0 (kr)],
B6.17)
Из теории бесселевых функций известно, что для больших значений
аргумента имеют место асимптотические формулы
Отсюда вытекают заключения, совершенно аналогичные тем, которые
мы делали, рассматривая движение сферы. А именно, рассмотрим
семейство парабол, зависящих от параметра а:
АгA—cos6) = a.	B6.18)
Если а достаточно велико, то vr мало отличается от А0/г, т. е.
в области вне некоторой из парабол B6.18) движение мало отли-
отличается от движения, соответствующего источнику с интенсивностью
B6.19)
Напротив, если a — порядка 1, но kr велико, то cos 6 будет близко
к 1, и мы будем иметь следующую приближённую формулу:
Г1	B6.20)
показывающую, что за цилиндром жидкость увлекается вместе
с цилиндром.
Для вихря мы легко находим по формулам B6.2) выражение
dvv dvx д-/	и i	v
дх ду ду	° п ' г
B6.21)
на больших расстояниях от цилиндра мы будем иметь:
B6.22)
Как рассмотрение скоростей течения, так и рассмотрение вихрей
приводят к одинаковому заключению об асимметрии течения; перед
цилиндром течение носит потенциальный характер, за цилиндром —
вихревой.

.26]
ДВИЖЕНИЕ ЦИЛИНДРА	533
Приведём теперь формулу для давления; вследствие	B6.5) и
B6.6) имеем:
cos 6 , ... cos 20 ,	,ос „„.
{pUA—2	)-...	B6.23)
Вычислим, наконец, сопротивление, испытываемое цилиндром;
общая формула
W = I (prr cos 9 — prfl sin 6) ds
с
в данном случае упрощается:
2х
W = a f( — pcos6 — [A-^-sin6)rf9.	B6.24)
о
Так как в полярных координатах вихрь выражается формулой
о	 1 д (rv$) 1 dvr 	 диъ . v^	 1 dvr
"" г дг	г дв	дг ' г г дЬ '
dvr n
и так как на контуре цилиндра v,, = vr— .. = U, то на контуре
цилиндра будем иметь формулу
—- = 2 = _.
Теперь нетрудно найти значение подынтегральной функции в выра-
выражении B6.24):
ду
Так как на поверхности цилиндра t> = 0, то вторая из фор-
формул B6.2) показывает, что
Ik ду	ду '
и так как ещё
ду	дг
2%
о
то мы приходим к следующему общему выражению для сопротивле-
сопротивления цилиндра:
2*
p-dB.	B6.25)

534	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Но по формуле B6.6) мы имеем на поверхности цилиндра:
дер 	_Ло_	A cos 6 . 2А2 cos 20
дг	а	а2 '	а3
И ЯСНО, ЧТО
Г = 21ф?/Л0.	B6.26)
Подставляя найденное выше значение Ло, получаем формулу Ламба
для величины сопротивления, испытываемого цилиндром при его
движении в вязкой жидкости, причём эта сила отнесена к единице
длины цилиндра:
8^Д	B6.27)
	Д	¦
l-2ln(TT*fl)
Конечно, следует ожидать справедливости этой формулы только
при малых значениях числа Рейнольдса R, как это и подтверждается
опытами.
§ 27. Гидродинамическая теория смазки. Одним из наиболее
важных для техники случаев ламинарного движения вязкой жидко-
жидкости является движение смазочной жидкости между цапфой и под-
подшипником. Более того, в этом случае числа Рейнольдса бывают
обычно очень малы, так что мы имеем право применять приближен-
приближенные методы решения.
Законы трения, имеющие место при наличии смазки, резко отли-
отличаются от обычных законов сухого трения. В первом приближении
сухое трение определяется законом Кулона, по которому на единицу
поверхности трущихся тел при их скольжении друг по другу дей-
действует касательная сила Т, определяемая формулой
T=kN,	B7.1)
причём коэффициент трения k принимается не зависящим от вели-
величины нормального давления N, величины трущихся поверхностей
и их относительной скорости.
Обозначим для случая трения в подшипнике через Р нагрузку,
приходящуюся на цапфу, через г — радиус цапфы и через М —
момент сил трения относительно оси цапфы. Если бы для этого слу-
случая можно было применить закон сухого трения, то сила трения
была бы равна kP, плечо этой силы относительно оси цапфы рав-
равняется г, и следовательно, момент сил трения определялся бы фор-
формулой
M = kPr.	B7.2)
В 1883 г. Н. П. Петров высказал положение, что в трении под-
подшипников основную роль играет внутреннее трение смазочного слоя,
и установил соответствующий закон трения для простейшего случая.
Он исходил из рассмотренного нами в § 15 движения вязкой жидко-

27]
ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ	535
СТи в области между двумя цилиндрами. Он предполагал, правда,
что жидкость может скользить по поверхности этих цилиндров, при-
причем развивается внешнее трение, пропорциональное относительной
скорости скольжения жидкости вдоль поверхности цилиндра. Если
принять, как это всегда теперь делается, условие прилипания жидко-
жидкости к ограничивающим стенкам, то решение Н. П. Петрова совпа-
совпадает с решением, изложенным в § 15.
Для теории смазки имеет значение случай, когда внутренний
цилиндр радиуса гг = а вращается с угловой скоростью ш и, следо-
следовательно, с окружной линейной скоростью U = toa, а наружный
цилиндр радиуса г2= о-}-§(§— толщина смазочного слоя) остается
неподвижным. Для момента сил трения мы получим в этом случае
формулу A5.5)
М= I У ,	B7.3)
величина 8 всегда очень мала; поэтому мы имеем приближенно:
rl — r\ = (r2 -f- rj (r2 — rx)
отсюда
Так как мы рассматриваем момент, отнесённый к единице длины
цапфы, то площадь смоченной смазкой поверхности F = 2%a; введем
далее вместо ш линейную скорость U, тогда предыдущая формула
примет вид:
M = ^aF~;	B7'.4)
эта формула и должна заменять формулу B7.2) для случая трения
смазанного подшипника. Из нее видно, в противоположность фор-
формуле B7.2), что момент сил трения не зависит от нагрузки на
цапфу, но зато растет вместе со скоростью U.
Однако все это справедливо только в первом приближении.
В самом деле, основное допущение Н. П. Петрова о том, что цапфу
и подшипник можно рассматривать, как соосные цилиндры, не может
соответствовать действительности, ибо при этом допущении силы
трения будут распределены симметрично относительно оси цилиндра
и очевидно, что главный вектор этих сил трения сведется к нулю;
эго означает, что цапфа не может нести никакой нагрузки. Решение
Н П. Петрова соответствует, таким образом, случаю очень малой
нагрузки.
Более общее решение мы получим, если примем, что цапфа
расположена относительно подшипника эксцентрически, причем смазка
может запотнять или все пространство между цапфой и подшипни-
i ом, или же часть этого пространства,

336	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Мы рассмотрим, следуя А. Зоммерфельду, приближенное решение
плоской задачи о смазке для случая, когда жидкость заполняет всё
пространство между цапфой и подшипником, длину которых будем
считать очень большой. В соответствии с этим под цапфой и под-
подшипником будем понимать их сечения, нормальные к оси.
Пусть О обозначает центр цапфы С, О' — центр подшипника С
(рис. 170). Расстояние 00' обозначим через е и примем прямую 00'
за ось полярных координат г, 6, а точку
О—за центр этих полярных координат.
Радиус цапфы С обозначим через а,
внутренний радиус подшипника — через
a -f-8. Уравнение окружности С можно
написать в виде
r = a-\-h,
причем с достаточной степенью точности
можно принять, что
6,
Рис 170	как показывает простое геометрическое
вычисление.
Обозначая, наконец, окружную скорость точек цапфы через U,
легко можем написать следующие граничные условия:
vr = О, Vb — U при г = а, }
„, = 0. „ = 0 » г=а + Н.)	<27-5)
Примем теперь во внимание, что величина Ь/а очень мала, отсюда
следует, что величина дщ(дг будет очень велика в сравнении с вели-
величиной Ijrdv^jdb. В самом деле, щ изменяется от 0 до У на очень
малом расстоянии h, имеющем порядок 8, поэтому производ-
производная дщ/дг имеет порядок ?//&, в то время как производная dv^/db
имеет порядок U, и следовательно, l/rdv^/db имеет порядок Ufa.
Точно так же порядок производной d2v^jdr2 равен ?//§2.
Рассмотрим теперь второе уравнение E.14). В этом уравнении
мы пренебрегаем, прежде всего, левой частью, определяющей инер-
инерционные члены; мы полагаем далее /79 = 0, так как считаем внешние
силы отсутствующими или пренебрежимыми; наконец, из членов,
содержащих множителем v, мы сохраняем только первый, так как
только он один будет иметь порядок ?//82, все же остальные члены
будут иметь меньшие порядки. При этих допущениях рассматри-
рассматриваемое уравнение примет вид:

§ 27]	ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ	537
Мы можем, наконец, заменить в левой части г на а; югда полу-
получим окончательно следующее простое уравнение:
Мы будем считать левую часть не зависящей от г; тогда преды-
предыдущее уравнение легко может быть проинтегрировано по г. Удоб-
Удобнее, однако, ввести вместо г новую независимую переменную С,
положив
в результате интегрирования уравнения B7.6), получим:
где А и В — постоянные, не зависящие от С, но могущие зависеть
от 6 и определяющиеся из граничных условий B7.5):
Vo — U при С = 0, Vu = 0 при С = А.
Таким образом мы получаем:
	•	B7)
Через всякое сечение между цапфой и подшипником протекает
одно и то же количество жидкости, которое мы обозначим через Uh0j2:
a+h	li
d — f d' — — l dp —4- — — Uh°
Отсюда находим равенства:
dp 	 6a
h3
B7.8)
Но в случае замкнутого слоя смазки давление р должно быть
непрерывной периодической функцией от угла 9, т. е. должно иметь
место условие
рBи) = р@),	B7.9)
- е.
2я	2я

538	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
откуда находим й0, после чего мы полностью будем знать t»e и давле-
давление р, последнее, впрочем, с точностью до произвольного постоян-
постоянного р @).
Введём обозначение
a = -J-(l <a<co);	B7.11)
тогда
/z = e(a + cos9).	B7.12)
Положив ещё
2л	it
'ft
о
будем иметь:
(а + COS 6)*	J (а -)- cos °)* '
Так как
0 + cos6
TO
e
Г db	2 /Г a—i
/ —	— =	, arc tg /1/ 	tg
«/ a 4- COS 6	VV — 1 l Г a + 1
— 1
Дифференцирование под знаком интеграла показывает, что
j 	 dlx 		2:та	_		 1 dl2 __ ~Bя2 + 1)
da	У (а2 — IK	°	2 da
Из B7.13) найдём теперь, что
_ 2га («з _ ;
П0	Оу2 J_ 1
В точках цапфы, характеризуемых углом б0, где давление имеет
максимум или минимум, производная др/д$ обращается в нуль,
следовательно, по уравнению B7.8) Л = /г0, т. е.
г I	оч 2еа(а2— 1)
e(a-fcos80)= 2^а + 1 >-,
откуда
Таким образом, места наибольшего и наименьшего давления лежат
на той половине цапфы, которая ближе к подшипнику.
Чтобы получить силу трения, применим формулу E.15)

§ 27)	ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ	539
но на поверхности цапфы vb =¦ U, vr = 0, поэтому формула упро-
упрощается:
отбрасывая здесь последний член, малый по сравнению с предыду-
предыдущим, и подставляя значение
dp 	 Qa\xU(h—ha) __
~Ж~	W
_6ацУГ	1	2а(а2-1)	1	I
е2 L(a + cos6J	2а2+ 1 (a + COs6KJ' ^'•lu-'
получим:
2,xE/
COS
За (а2-!)	1	1
2а2+ 1 (a + COS0JJ'
Чтобы получить нормальное давление ргг на цапфе, воспользуемся
первой из формул E.15):
Р = Р+2Р'
но из уравнения неразрывности (последнее из уравнений E.14))
dvr . 1 дун , vT _»
следует, что на поверхности цапфы, где vr = 0, v$=U, будет
и поэтому нормальное давление на цапфе определяется величиной р.
Подсчитаем теперь, каковы будут силы гидродинамического воз-
воздействия на цапфу, причём будем все силы относить к единице
длины цапфы. Из вышесказанного ясно, что на элемент add будет
действовать нормальная сила, направленная к центру цапфы и рав-
равная ap(d)dB, и касательная сила, направленная в сторону возраста-
возрастания угла 6 и равная aprH(B)dB. Главный момент этих сил относи-
относительно центра цапфы, считаемый положительным в направлении,
противоположном направлению вращения цапфы, будет, очевидно,
равен
За (а2 — 1)
е Bа2 + 1) /а2—1

540
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. И
Легко видеть, что для двух точек, симметричных относительно
оси 00', касательные силы имеют составляющие вдоль этой оси,
одинаковые по величине, но противоположные
по знаку; то же самое относится к переменной
части нормальных сил
[p(b)~p@))add
(рис. 171). Следовательно, главный вектор
приложенных к поверхности цапфы сил, кото-
который мы обозначим через Р, имеет направле-
направление, перпендикулярное к прямой 00'. Счи-
Рис. 171.	тая Р положительным, когда направление
главного вектора получается из направле-
направления 00' поворотом навстречу вращению цапфы, мы будем иметь:
2л	2т
р = Г pa sin 6 dO — Г prfla cos 0 db.
о	о
Но
2л	2п
/ р sin S dfi = — / pd cos 6 =
2т
2л
2т.
= — р cos О
Поэтому
Здесь можно пренебречь величиной pr-t по сравнению с dp/dB, ибо
последняя величина содержит, как показывает формула B7.16),
малую величину е в знаменателе во второй степени, в то время
как prft содержит эту величину только в первой степени.
Итак:
2к
=а f -^cos6d6 = a f ~? (a
о
Ы2\хЦ
2а (a2 —
2|—
cos 6) dd =
\2т.}ха?и
Исследуем полученные формулы
о2 {2-J.2 +
— 1
B7.18)

§ 27]	I ИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ	541
Видно, что как Р, так и М прямо пропорциональны как коэф-
коэффициенту вязкости \х, так и окружной линейной скорости U. Счи-
Считая известными jx, U, а, 3 и Р, мы по второй из предыдущих фор-
форму! определим а, а следовательно, и эксцентриситет е — Ь/а,, после
чего первая формула определит /И. Введём безразмерную величину
f —
J ~
Pa
яв шющуюся для закона сухого трения коэффициентом этого трения.
В нашем случае
/=* ±-*+1.	B7.19)
J Pa а За.	v	'
При значениях а, близких к единице, коэффициент / имеет значение,
близкое к
f 	 _^_
Jo a "
Но из B7.18) ясно, что значениям а, близким к единице, соогве!-
сгв)ют малые значения скорости U, точнее, величины
1^?-	B7.20)
Таким образом, в случае малых скоростей гидродинамическая тео-
теория смазки приводит к формуле
B7.21)
аналогичной закону сухого трения B7.2).
Напротив, в случае очень больших значений а значения вели-
величины B7.20) должны быть велики; в то же время из B7.18) простым
предельным переходом получим для момента сил трения выражение
М = ^,	B7.22)
совпадающее с формулой B7.4) Н. П. Петрова.
Минимальное значение / получится, как это легко установить
из формулы B7.19), при а = У 2, тогда
f , _
/mln—¦
соответствующие же значения U и Р связаны соотношением
РР— 25Г — °'0663-
Более строгое решение рассмотренной задачи было дано в ра-
работе Н. Е. Жуковского и С. А. Чаплыгина, рассмотревших плоскую
задачу о движении вязкой жидкости в области между двумя эксцен-

542	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
трически расположенными окружностями при единственном пред-
предположении о том, что в уравнениях гидромеханики можно пренебречь
инерционными членами. Для случая, когда радиусы окружностей
отличаются друг от друга на весьма малую величину, их решение
переходит в только что рассмотренное приближенное решение.
Нужно отметить, что разобранный выше простейший случай пол-
полного заполнения жидкостью области между цапфой и подшипником
представляет простейшую схему явления и не позволяет полностью
осветить его, тем более, что мы ограничились только плоской задачей.
Г. ПРИБЛИЖЁННЫЕ РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ ВЯЗКОЙ
ЖИДКОСТИ В СЛУЧАЕ БОЛЬШИХ ЧИСЕЛ РЕЙНОЛЬДСА
§ 28. Общая характеристика течений при больших числах
Рейнольдса. Вывод основных уравнений теории пограничного
слоя. Нами было уже указано, что приближённые методы решения
уравнений движения вязкой жидкости были развиты только в двух
случаях, а именно, в случае очень малых чисел Рейнольдса и, наобо-
наоборот, в случае очень больших чисел Рейнольдса. В предыдущем раз-
разделе этой главы мы рассмотрели подробно методы, относящиеся
к случаю движений с малыми числами Рейнольдса. Обратимся теперь
к изучению методов исследования движений с большими числами
Рейнольдса. Большие числа Рейнольдса получаются, когда характер-
характерная длина / велика, или когда характерная скорость V велика, или же
когда кинематическая вязкость v мала.
Казалось бы, в этом случае мы должны получить очень хорошее
приближение, целиком отбрасывая силы вязкости, пропорциональ-
пропорциональные коэффициенту кинематической вязкости v. Однако так делать
нельзя, потому что при этом получаются уравнения Эйлера движе-
движения идеальной жидкости, решения которых не могут, вообще говоря,
удовлетворить тем граничным условиям прилипания к стенкам, кото-
которые мы имеем для случая вязкой жидкости, движущейся хотя бы
и при очень больших числах Рейнольдса.
Отсюда можно сделать вывод, что при больших числах Рейнольдса
главное воздействие сил вязкости будет проявляться около стенок,
ограничивающих жидкость; понятно, что частицы жидкости, побывав-
побывавшие около стенок, попадая при дальнейшем своём движении внутрь
жидкости, могут распространить эти воздействия сил вязкости
на внутренние области жидкости. Мы можем, однако, ожидать, что
во всей той области внутри жидкости, в которую не попадают ча-
частицы жидкости, побывавшие около стенок, движение жидкости
будет мало отличаться от движения идеальной жидкости и с очень
большим приближением может быть принято за движение идеальной
жидкости. Остаётся определить характер течения жидкости в непо-

, 281
ОБЩАЯ ХАРАКТЕРИСТИКА ТЕЧЕНИИ ПРИ БОЛЬШИХ R
543
средегвенной близости стенок и в той области, которая заполнена
частицами, побывавшими у стенок. К сожалению, мы не имеем пока
полной теории этого вопроса.
Одна из первых работ на эту тему относится к 1904 г. и при-
принадлежит Л. Прандтлю'). В результате развития идей Прандтля воз-
возникла теория, носящая название теории пограничного слоя, изложе-
изложению основ которой и будет посвящен этот раздел.
Иначе подошёл к той же самой проблеме движений вязкой жид-
жидкости при больших числах Рейнольдса Осеен2). Он поставил вопрос
о том, во что переходит движение вязкой жидкости, если число
Рейнольдса R устремить к бесконечности. Однако Осеен смог дать
ответ на этот вопрос только для того случая, когда исходные урав-
уравнения Навье — Стокса берутся в упрощённом виде, и в этом состоит
недостаток его теории, носящей название теории исчезающей вяз-
вязкости. Полное изложение теории Осеена потребовало бы много
места; поэтому мы ограничимся несколько упрощённой трактовкой
этой теории (см. § 37 и далее).
Прежде чем переходить к выводу дифференциальных уравнений
теории пограничного слоя, мы остановимся несколько на выяснении
общего характера течений вязкой
жидкости при больших числах Рей-
Рейнольдса. Для определенности будем
рассматривать задачу об обтекании
цилиндрического твердого тела по-
потоком, имеющим на бесконечности
заданную скорость V (рис. 172).
Если бы мы могли совсем пре-
пренебречь силами вязкости, то мы
получили бы потенциальное обтека-
обтекание тела потоком идеальной жидко-
жидкости. В точках контура С нормальная составляющая скорости этого
потока обращается в нуль, касательная же составляющая отлична
от нуля. Но в течении вязкой жидкости как касательная, так н
нормальная составляющие скорости должны в точках контура С обра-
обращаться в нуль. Принимая ещё во внимание, что при больших числах
Рейнольдса в некотором отдалении от контура С течение жидкости
мало отличается от течения идеальной жидкости, мы приходим к за-
заключению, что распределение касательной составляющей скорости
вдоль нормали к контуру С должно иметь вид (см. рис. 172)
кривой, относящейся к точке Мх. Эта кривая показывает, что каса-
1	N
Рис. 172.
') Prandtl L., Ueber Flussigkeitsbewegung bei sehr kleiner Reibung.
Verhandlungen der dritten Internat. Math. Kongr. in Heidelberg 1904, Leipzig,
1905; имеется русский перевод.
2) О s e e n C. W., Neuere Methoden und Ergebnisse in der Hydrody-
namik, Leipzig, 1927.

544	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
1ельная скорость, равная нулю в точке Mv для точек, рчсноаожен-
ных на нормали к контуру, постепенно увеличивается и, наконец,
на некотором расстоянии от контура принимает значение, очень мало
отличающееся от значения, соответствующего потенциальному тече-
течению идеальной жидкости. Как мы увидим далее, при больших чис-
числах Рейнольдса, переход от нулевой скорости на контуре С к ско-
скорости, мало отличающейся от скорости потенциального течения
идеальной жидкости, совершается в очень тонком слое жидкости, ко-
который и носит наименование пограничного слоя.
Как мы знаем, силы вязкости тем больше, чем больше соответ-
соответствующие изменения скорости. Так как в пограничном слое происхо-
происходит быстрое изменение касательной составляющей скорости от нуля
до величины порядка V, то силы вязкости в пограничном с we могут
получать значшельную величину. Таким образом, главное воздействие
сил вязкости будет иметь место около стенок: на далеких же от
стенок расстояниях силы вязкости будут очень малы.
Мы можем поэтому представить себе схематически картину тече-
течения вязкой жидкости при больших числах Рейнольдса следующим
образом. Всю область течения мы разбиваем на две части, а именно
на тонкий пограничный слой вблизи тела и на остающуюся область
течения, в которой течение можно считать совпадающим с потенциаль-
потенциальным течением идеальной жидкости. В пограничном же слое мы будем
учитывать также и силы вязкости, однако, то обстоятельство, что
толщина по1раничного слоя очень мала, позволяет сильно упростить
уравнения Навье — Стокса, в результате такого упрощения мы полу-
получим уравнения Прандтля, решения которых тем менее будут отли-
отличаться от точных решений уравнений движения вязкой жидкости,
чем больше будет число Рейнольдса и чем, следовательно, меньше
будет толщина пограничного слоя.
Необходимо, однако, обратить внимание на то, что частицы,
побывавшие у стенок тела, могут в дальнейшем попасть внутрь
жидкости, так как внутри пограничного слоя мы имеем сильно
завихренное движение жидкости, то при этом внутрь жидкости
попадают вихри, образовавшиеся в пограничном слое; происходит,
как говорят, отрыв вихрей.
Причины такого отрыва вихрей лежат в следующем. Пусть для
определенности выпуклый контур С имеет симметричную форму
относительно прямой АВ, имеющей направление скорости на беско-
бесконечности, и пусть циркуляция потока отсутствует. Тогда в потен-
потенциальном течении идеальной жидкости касательная скорость будет
возрастать от нуля в точке А до максимальной скорости в точке К
и затем будет убывать до нулевой скорости в точке В. В соответ-
соответствии с этим, согласно уравнению Бернулли, р-\- ptJ/2 = const.,
давление будет убывать от точки А до точки К и затем возрастать
01 точки К до точки U. Как jвидим в дальнейшем, распределение

q 28]	ОБЩАЯ ХАРАКТЕРИСТИКА ТЕЧГНПП ПРИ БОЛЬШИХ R	545
давления в псмранпчном слое очень мало отличается от распределе-
распределения давления по контуру С в потенциальном течении идеальной
жидкости. Иначе будет обстоять дело с распределением скоростей.
Ясно, чго силы вязкости приводят к некоторому затормаживанию
частиц жидкости в пограничном слое. Поэтому, попадая в область
задней части тела, где давление возрастает, частицы начинают полу-
получать ускорение в направлении от точки В к точке /Сив результате
касательная скорость этих частиц обращается в нуль где-то на ли-
линии МЛМ, проходящей между точками К и В. В области BM3N
касательная скорость частиц получает обратный знак, т. е. возни-
возникает возвратное движение жидкости, результатом которого является
срыв завихренных частиц с поверхности тела и унос их внутрь
жидкости. Теория пограничного слоя не дает возможности просле-
проследить, как меняется в этом случае характер течения в области BMZN,
прилегающей к задней части тела.
Следует, таким образом, различать два случая.
Если мы имеем дело с телом, имеющим очень плавные очерта-
очертания контура, то возможно, что срыва вихрей происходить не будет.
В этом случае мы можем сказать, что вне тела имеет место потен-
потенциальное течение идеальной жидкости, и действие сил вязкости ска-
сказывается только в пограничном слое.
Если же условия обтекания таковы, что с тела срываются вихри,
то за телом образуется вихревая зона; что касается пограничного
слоя, то мы можем теоретически рассмотреть только ту часть его,
которая простирается до места отрыва вихрей.
Сделаем ещё одно общее замечание. Течение жидкости внутри
пограничного слоя может быть или ламинарным или турбулентным,
в зависимости от значений числа Рейнольдса и от условий обтека-
обтекания тела, например, от степени гладкости или шероховатости кон-
контура и т. п. Мы будем рассматривать только ламинарные течения;
некоторые соображения о турбулентном пограничном слое будут
изложены в следующей главе, посвященной турбулентности.
Перейдём теперь к выводу дифференциальных уравнений Пранд-
тля, определяющих течение в пограничном слое, причём рассмотрим
для определённости случай течения вязкой жидкости вдоль пластинки.
Мы будем, таким образом, иметь дело с плоско-параллельным
течением жидкости; предположим, что внешние силы отсутствуют.
Тогда основные уравнения гидромеханики E.1) принимают вид:
dvx . „, Ovx __ 1 dp , „ / d2vx , <9%
tfw	owv	duv	1 dp
f,,
\, дх2 ~т~ ду2 }'
-j ( Vy -i- Уу ),
\ дх2 "г dy2 /
с!.' ~ "-f Ea; "T" > dy ~~ ~~ p ^T \ d*2 ^ dy2
dx ' ()y
Теоретическая гидромеччника, ч. II
B8.1)

546	ДВИЖЕНИГ ВЯЗКОП ЖИДКОСТИ	[ГЛ Ц
Дифференциальные уравнения Прандтля получаются в результате
надлежащего упрощения предыдущих уравнений. В основе этого
упрощения лежит сравнение различных членов уравнений B8.1) по
их относительной величине. Как мы уже указывали, толщина погра-
пограничного слоя, которую мы будем обозначать буквой S, очень мала
(см. рис. 173); это выражение нужно, конечно, понимать так, что
чало отношение 8:1, где I есть характерный размер для рассматри-
рассматриваемой задачи. Отметим попутно, что толщина о в разных точках
контура и в разные моменты времени мои-ег быть различна, так
чго о есть функция от х и t. Кроме
у	того, нужно отметить, что самое поня-
понятие толщины пограничною слоя имеет
несколько неопределенный характер,
поскольку в действительности нет ни-
никакой резкой границы, отделяющей
'Ш?ШШШ~ "" область пограничного слоя от внешней
области, в которой силы вязкости
Рис 173	совсем не учитываются. Однако мы
увидим, что эта неопределенность по-
понятия толщины пограничного слоя не повлияет на окончательный вид
уравнений Прандтля. В следующем параграфе мы дадим иной вывод
этих уравнений, свободный от только что указанного недостатка,
сейчас же мы будем следовать Прандтлю.
Составляющая vx может иметь на внешней границе пограничного
l чоя различные значения, но все Э1И значения будут иметь один и
ют же порядок, а именно V, где V есть характерная скорость
рассматриваемого течения. На стенке эта составляющая обращается
в нуль. Рассматривая изменение vx в зависимости от координаты у,
мы видим, что прл изменении у от 0 до 8 значение vx изменяется
от нуля до величины порядка V. Но отсюда следует, что среднее
гчачение dvjdy в точках внутри пограничного слоя имеет поря-
порядок Vjb. Точно так же придем к заключению, что d2vx/dy2 имеет
внутри пограничного стоя порядок Vjb2. Порядок производных по
координате х мы можем оценить, учитывая, что составляющая ско-
скорости vx при перемещении точки параллельно контуру С на отре-
отрезок порядка характерной длины I может испытать изменение порядка V;
поэтому величина dvKjdx имеет порядок Vjl, а величина d2vxjdx2— по-
порядок Vji2.
Но тогда из последнего уравнения системы B8.1)
dvy,	dvx
ду	дх
следует, что dvy/dy тоже имеет порядок Vjl. А таьг как при у —О
значение vy вследствие условия прилипания равно нулю, то из ра-

. 28]	ОБЩАЯ ХАРАКТЕРИСТИКА ТЕЧЕНИИ ПРИ БОЛЬШИХ R	547
венства
у
найдём, что vy внутри пограничного слоя будет иметь порядок Vbjl.
Далее, для величины dvjdx находим порядок Vbjl2, для d2v jdx2
порядок Vb/l3 и, наконец, для d2vyjdy2 порядок V//8.
Ясно теперь, что в первом из уравнений B8.1) мы можем огбро-
сигь член d2vjdx2 порядка Vjl2 как малый по сравнению с чле-
членом d2vxjdy2, имеющим порядок Vjb2, ибо отношение -^ : -р- — (—V
есть квадрат малой величины.
II i а к, первое уравнение системы B8.1) принимает следующий
вид:
i^?_U7i !^_l_7i дя)* — 1 др I -j д2%>х	С98 94
dt ^v*'dx ~^^у dy ~ р дх "Г" <9у2 '	<- 0< j
Второй и третий члены слева имеют, как показывает простой
подсчет, один и тот же порядок V2jl, второй же член справа имеет
порядок vV/S2. Отношение сил вязкости к силам инерции имеет,
таким образом, порядок:
Ь2 ' I	Vb2 IV \Ь ) ~ '
Прандгль принимает, что внутри пограничного слоя силы вязкости
и силы инерции имеют одинаковый порядок: но тогда величина
R \-j) ——гг должна иметь порядок единицы; иными словами, вели-
величина о// должна иметь порядок l/]/"R- Мы получаем, таким обра-
образом, первый результат теории пограничного слоя: образующийся
при течениях с большими числами Рейнольдса R пограничный
слои имеет толщину 8, порядок которой равен i/VR< t- е-
Е
v ¦
Приведем простой численный пример: возьмём Z— 1 м— 100 см,
V—1 м/сек =100 см/сек, v = 0,01 см2/сек (вода при 20° С),
то1да у -^- = 0,1 см=1 мм. Как видно, толщина образующегося
пограничного слоя очень мала.
В уравнение B8.2) входят ещё члены dvjdt и (l/p)dpjdx; мы
''Удем предполагать, что изменение течения со временем, если оно
происходит, совершается столь плавно, что порядок dvjdt не пре-
превосходит порядка V2jl, тогда член (\jp)dp/dx сам собою должен
6} 1ет иметь тот же порядок V2/l.
35-

548	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ U
Переходим теперь к рассмотрению второго из уравнений B8.1).
Мы без всякого труда найдём, что порядок левой части этого урав-
уравнения равен V4/12. Точно так же для порядка сил вязкости, входя-
входящих в правую часть этого уравнения, найдем, по вышесказанному,
выражение yVjlb, имеющее, по сделанному выше допущению Прандтля,
тот же порядок, что и выражение V4jl2.
Мы видим теперь из второго уравнения B8.1), что О1р)др/ду
имеет порядок V2bjl2 в то время, как A/р)др/дх имеет порядок V2/l.
Но это означает, что градиент давления в направлении нормали
к контуру очень мал в сравнении с обычными значениями градиента
давления. Поэтому можно с большой степенью точности заменить
второе уравнение системы B8.1) простым уравнением
-|- = 0.	B8.3)
Мы получаем таким образом второй результат теории погранич-
пограничного слоя: давление внутри пограничного слоя не меняется вдоль
нормали к контуру тела и равняется, следовательно, тому
давлению, которое имеет место на внешней границе погранич-
пограничного слоя в рассматриваемом месте. В предыдущем параграфе
мы уже воспользовались этим результатом при рассмотрении каче-
качественного характера течений вязкой жидкости при больших числах
Рейнольдса.
Итак, задача определения течения вязкой жидкости в погранич-
пограничном слое свелась к решению следующей системы:
~Ш г^ дж -г-'Уу ду ~ р дх -г" ' ду2 ' \
dvx dvy	'
Здесь vx и х>у суть неизвестные функции от х, у at, ар есть
заданная функция от х и t.
Если можно принять, что вне пограничного слоя течение жидкости
есть потенциальное течение идеальной жидкости, то р(х, t) совпа-
совпадает со значениями давления этого течения на внешней границе по-
пограничного слоя, а так как толщина пограничною слоя очень мата,
то за р(х, t) можно взять просто значения давления этого течения
в точках самого контура С. Если же с тела срываются вихри и
последние сильно видоизменяют картину течения пограничного слоя,
то приходится р брать на основе экспериментальных данных.
Функции vx и Vy должны удовлетворять след) ющим граничным
условиям: во-первых, на стенке должно выполняться \словие при-
прилипания
vx==vy=^0 при у = 0.	B8.5)

§ 20]	ВЫВОД МИЗЕСА УРАВНЕНИЕ МИЗЕСА	549
н, во-вюрых, на внешней границе пограничного слоя, т. е. при
v .= 8, составляющая vx должна переходить в соответствующую
^оставляющую vx скорости течения вне пограничного слоя. Как выше
в случае давления, можно за vx принять составляющую скорости
в точках самого контура С: для краткости мы обозначим эту со-
составляющую через U (x) = (vx)c. Кроме того, ввиду неизвестности 8,
мы можем потребовать выполнения граничного условия при у = со
вместо у = 8, т. е. потребовать, чтобы vx асимптотически прибли-
приближалось к U. Тогда при у = 8 величина vx будет очень мало отли-
отличайся от vx^U, и мы получаем такое граничное условие:
vl = U при у—>со.	B8.6)
Наконец, в случае неустановившегося движения нужно принимать
еще во внимание начальные условия: при ? = 0 vx должно приво-
приводиться к заданной функции от х и у.
§ 29. Вывод Мизеса. Уравнение Мизеса. Дадим теперь вывод
основных уравнений Прандтля, основная идея которого принадлежит
.Мизесу '). Этот вывод носит более формальный, но в то же время
более строгий характер. Из него ясно вытекает, что уравнения
Прандтля являются предельной формой уравнений гидромеханики
вязкой жидкости, получающейся при определённых условиях при
устремлении числа Рейнольдса R к бесконечности.
При этом выводе нет никакой необходимости ограничиваться
случаем прямолинейного контура. Итак, положим, что мы имеем
дело с обтеканием криволинейного контура С.
Мы будем исходить из тех же основных уравнений гидромеха-
гидромеханики E.1), что и в предыдущем параграфе, только напишем их
в безразмерном виде. А именно, если I есть характерная длина,
а V — характерная скорость, то мы введём новые безразмерные
величины формулами:
IV
После подстановки этих значений в формулы E.1) и сокращения
обеих частей дв)Х первых уравнений этой системы на V2jl, а по-
') Mis,es R., Bemerkungen zur Hydrodynamik, Zeitschr. fur angew
. und Mech., 7 A927), стр. 425—431 и чисьуссия по поводу этой статьи
{-) Прандтлем и Мпзесом в том же жу риале, 8 A928), стр. 249—252.

550
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. II
следнего уравнения — на Vjl, легко получим уравнения:
у ду
v ^
dv,.
	 	 иУ i *
~ ~дх ' ~R~
¦ = 0,
_
-)¦
B9.2)
отбросив, для простоты, чёрточки над буквами.
Итак, уравнения гидромеханики, написанные в безразмерном виде,
сохраняют свой вид, только плотность р заменяется при этом на 1,
а кинематический коэффициент вязкости v — на 1/R, где R — число
Рейнольдса.
Пусть теперь ql и q2 — криволинейные ортогональные коорди-
координаты, а Н1 и Н2—соответствующие коэффициенты Ламэ. Напишем
уравнения B9.2) в криволинейных координатах ^i и д2, для чего
воспользуемся общими формулами § 5. В результате мы получим
систему из трёх уравнений, первым из которых будет
dt. 'Я, 5ffi Я,
V2
^i т—
R I Я2 dq\ ^ H\
¦ + ¦
'(t)
df,
dq2 dq2
ЙЯ,
Я, <?^, \ Я,Я2 dq
— JL
H\ dc[\
1
дН,
а вторым и третьим —
I "i " *^2 i	2 ^^2
H1 dqt Нг dq2
dq2 dqx
1 d
1 б
<ЭЯ,
;^2 i
1 6Я,
1 6Я,
^2\
dqx )
B9.30
Я2
H\ dq\
i%)
дН,
НХЩ dq2 dq2 H\H2 dq2 dqx
+ ¦
dq, dq1
дН, dv,
0q2

1 д
"Я, dqx
2
ВЫВОД МИЗЕС4 УРАВНЕНИЕ ЧИЗЕСА
! 1 дИ,
551
ддг
B9.3'")
Выберем теперь следующую систему криво тинейных ортогональ-
ортогональных координат (рис. 174). Проведем в точках контура С нормали
к С, и пусть нормаль через произвольную
точку М, лежащую вблизи контура С, пере-
пересекает этот контур в точке N. Выбрав на
контуре С определенную точку О за начало
отсчета дуг, будем определять положение
точки М координатами qx = s и q2~ п, где
s и п суть взятые с надлежащими знаками
длины дуги кривой ON и отрезка нор-
нормали NM. Возьмем соседнюю с М точку М'
и вычислим расстояние da между точками М
и М'. Бесконечно близкие нормали MN и
M'N' пересекаются в центре кривизны К
кривой С, соответствующем точке N. Обо-
Обозначим радиу кривизны кривой С в точке N через r(s) и пред-
предположим, что г(s) есть непрерывная функция or s вместе со своей
первой производной.
Так как, с точностью до бесконечно малых высшего порядка,
мы имеем.
Рис 174.
^= ML2 + LM'\
ML=
ds,
ГО
и следовательно,
= Г1 + -^f
L ^ r (s) J
ds2
Я, -- 1.
B9.4)
Сделаем, наконец, последнее преобразование. Положим, чтобы
не вводить новые буквы
У
<7j s х,
= 1 +
q2 = n--
V* '
" /R
¦ , Ho—1.
B9

552	ДВИЖЕНИЕ ВЯЧКОП ЖИДКОСТИ	1ГЛ 11
Таким образом, теперь уже х означает расстояние между точ-
точками О и Л/, измеренное по кривой линии С (следует помнить, что
за единицу расстояния принята длина /), у же означает расстояние
точки М от контура С, увеличенное в у R раз; точно так же г>
есть проекция скорости на нормаль, увеличенная в V^R раз.
Вставим теперь значения B9.5) в уравнения B9.3), обе части
среднего из которых мы поделим на V^R и найдем, какую предель-
предельную форму они получат, если мы устремим R к бесконечности,
считая при этом величины vx, vy, p и их первые и вторые про-
производные по t, х и у конечными. Легко видеть, что большинство
членов уравнений B9.3) будет содержать множителями некоторые
целые положительные степени 1/J/R- В пределе все эти члены об-
обратятся в нуль, и мы получим уравнения:
B9.6)
Мы будем считать, что вне по1раничиого слоя происходит обте-
обтекание контура С потенциальным потоком. Но при R-> со весь по-
! раничный слой прижимается к контуру С; это видно из того, что
по формулам B9.5) всякому конечному у соответствует значение п,
сколь угодно малое при достаточно большом R.
Пусть в точках контура С для потенциального потока давление
имеет значение р(х, t), а скорость—значение U (x, t). Тогда мы
можем считать, что при у—> зо решение уравнений B9.6) должно
удовлетворять граничным условиям:
lim p--—p{x, t\ lirn vA — U(x, t),
по по среднему из уравнений B9.6) p не зависит от у; следова-
следовательно, во всём пограничном слое р имеет значение р(х, t).
Итак, мы приходим к следующей системе для определения vx
dt "i"
dvx
dvr
dr
, dvx
'у dy
0 -
dvv
г)лг
dp
~ dy '
A
d2u
dy2
Of + - a- >
Ox ' dv
	' !	B9.7)
- -" U.	i

29j
ВЫВОД АШЗЕСА. УРАВНЕНИЕ МИЗЕСА	553
lie p(x, t) берётся из потенциального потока, обтекающего кон-
ivp С; кроме того, должны выполняться пограничные условия
vx = Vy — Q при у = 0, 1
vx=U(x, t) » у>оо )	B9'8)
и, если речь идёт о неустановившемся движении, — также ещё и
начальные условия.
Вернёмся теперь к первоначальным размерным координатам B9.1),
•г. е. заменим х на xjU у на yVRJl, t на Vtjl, vx на vx/V, vy на
vy VR/V, p на p/pV2 и R на /V/v.
Тогда вмесю системы B9.7) мы получим систему уравнений:
4 JrVx дх 4rVy ду
dvx dvy
дх ~ ду
B9.9)
вполне тождественную с уравнениями Прандтля. Напомним ещё раз,
что в этой системе у означает расстояние какой-либо точки погра-
пограничного слоя от контура С, измеряемое по нормали к С, а х есть
расстояние от основания этой нормали до начальной точки контура С,
измеряемое вдоль этой кривой.
Приведённый в этом параграфе вывод показывает вполне чётко,
что )равнения Прандтля являются предельной формой уравнений
Навье — Стокса при R ~> со. Необходимо, однако, отметить следующее
обстоятельство. При очень больших числах Рейнольдса движение
вязкой жидкости имеет обычно турбулентный характер. С этой точки
зрения может показаться, что предельный переход R—>оо не может
иметь физического смысла. На самом деле это не так, а именно:
пусть число Рейнольдса R/;, характеризующее переход ламинарной
формы течения в турбулентную, очень велико, тогда для больших
чисел Рейнольдса R, не превосходящих Rk, мы с очень большим
приближением можем считать верными уравнения Прандтля, так как
эти уравнения отличаются от точных уравнений членами порядка
ЧУ R, малыми при больших R.
Для чисел же Рейнольдса R, превосходящих Rft, пограничный
слой становится турбулентным, и к нему уже нельзя применять
уравнения B9.9); теория турбулентного пограничного слоя будет
затронута в главе о турбулентности.
Для стучая установившегося движения Мизес свёл систему урав-
уравнений B9.9) к одному нелинейному уравнению в частных производ-
производных второго порядка типа уравнения теплопроводности. В основе
вывода уравнения Мпзеса лежит введение новых независимых пере-
переменных и новой функции.

554	движение вязкой жидкости	;гл и
Последнее из >равнений B9 9) показывает, что можно принять
¦71 —	ti — "у	/nq (л-,
¦* ду	У	дх	'
где ф(х, у) есть функция тока, причем можно считать, что на кон-
контуре С ф обращается в нуль Возьмем теперь за новые независимые
переменные х и ф и преобразуем уравнение
« J^ + « .*^ = _li?_|_,4^	B9 11)
х дх ' У ду	р dx ' ду2	v	y
к этим новым независимым переменным Функции vx и vy, выражен-
выраженные в новых переменных х и ф, обозначим для ясности через vx
и vy, так что
г'х(х' y) = t'v(x' ^); 'y)i(x. У) ='Иу О^. Ф)
Теперь ясно, что, рассматривая vx и г^у как сложные функции от х
и у, мы будем иметь.
дх дх у
бил dvx d\i	dv
ду	d\i dy	x d\
d I- dv \ - d2
2
Подставляя эти значения в уравнение B9 11), получим:
_ dvx	I dp - d2 I v2x
По условию, нам дочжна быть известна функция р(х) Эта функция
связана с U (х) интегралом Бернулли:
Jo4-^=const.,	B9.12)
имеющим место в потенциальном течении вне пограничного слоя.
Мы имеем таким образом уравнение
dU2 _ дЧ\
dx dx ' x бф2
Поэтому, если мы введем новую неизвестную функцию
B9.13)
z(x, ф)={72— vx,	B9 14)
так что

^ ,q]	ВЫВОД МИЗЕСА. Ъ РАВНЕНИЕ Л1ИЗЕСА	555
го уравнение примет очень простой вид:
^'W'	B9Л5)
Это и есть уравнение Мизеса. Найдём ещё, каким пограничным
условиям должно удовлетворять решение этого уравнения. На кон-
контуре, т. е. при ф = 0, составляющая скорости vx обращается в нуль,
счедовательно, вследствие B9.14) имеем
z = U2(x) при ф = 0.
На внешней границе пограничного слоя, т. е. в наших новых
независимых переменных при ф = со, составляющая vx должна пере-
переходить в U (х); поэтому получаем второе пограничное условие:
Z —> 0 при ф—>оо.
Наконец, если мы знаем распределение составляющей vx(x, у) при
х = 0, т. е. знаем функцию vx@, у), то нетрудно будет вычислить
и значение функции 2@, ф). В самом деле, первое из уравнений
^29.10) определяет ф через у равенством
решив это уравнение, мы найдём зависимость у от ф, после чего
по формуле B9.14) получим:
2@, ф)=^2@) — ^@, у).
Таким образом решение уравнения B9.15) должно удовлетворять
таким трём пограничным условиям:
B9.16)
при ф = 0,
z = 0	» ф = со
г =2@, ф) » х — 0.
Найдя z(x, ф), мы определим vx(x, ф) из уравнения B9.14)
ггДх, ф)==/^2 — «,	B9.17)
после чего из первого уравнения B9.10) можем определить у(х, ф):
B9.18)
Решая это последнее уравнение относительно ф, мы получим
Функцию тока t^(x, у), т. е. окончательно решим задачу.

556	движение вязкой жидкости	[гл. ц
§ 30. Интегральное соотношение Кармана и его обобщения.
При детальном изучении какого-либо движения жидкости прихо-
приходится всегда исходить из дифференциальных уравнений движения
жидкости. Но если мы хотим рассматривать движение только в общих
чертах, то тут часто большую помощь оказывают общие теоремы
гидромеханики, а именно закон количеств движения, закон моментов
количеств движения и закон энергии.
Настоящий параграф будет посвящен применению закона коли-
количеств движения к теории пограничного слоя.
Для ясности мы будем исходить сначала из основных уравнений
теории пограничного слоя B9.9). При этом мы введём в рассмотре-
рассмотрение толщину пограничного слоя о. Мы знаем
уже, что понятие толщины пограничного слоя
есть несколько неопределённая величина, так
как в пограничном слое скорость vx изменяется
от нуля па контуре С до скорости U, имею-
имеющей место в потенциальном потоке, асимпто-
асимптотически приближаясь к этой последней вели-
величине (рис. 175). Можно было бы, например,
определять о как то расстояние от контура С,
на котором величина vx отличается от U
на 1 %. Для нас будет несущественно то или
Рис. 175.	иное определение величины о, лишь бы при
этом соблюдались следующие два условия:
во-первых, скорость vx при у = о должна мало отличаться от ско-
скорости U (т. е. разность vx — U должна быть мала в сравнении
с характерной скоростью V), и, во-вторых, значение производной
dvx/dy должно быть мало (опять-таки в сравнении с V/1). Наиболее
точным с математической стороны представляется введение так на-
называемой толщины вытеснения 5*, определяемой условием:
U — vx)dy = b*U.	(ЗОЛ)
Если прямая АВ на рис. 175 пересекает кривую распределения
скоростей OKL так, что площадь OAK равна площади KBL, то ясно,
что Ь*=ОА. Ясно, что в общем случае 3* будет функцией от х и t.
Проинтегрируем теперь обе части первого из уравнений B9.9)
по у в пределах от 0 до 5 и рассмотрим по отдельности все полу-
получающиеся при этом члены. Мы имеем прежде всего по правилу
дифференцирования интегралов с переменными пределами:
Ж f "*«* = f Чг** + **(*'ъ-'^-	C0.2)

5 чо] ИНТЕГРАЛЬНОЕ	СООТНОШЕНИЕ КАРМАНА II FIO ОБОБЩЕНИЯ 557
сле'лова!ельно,
о	8
f!f	f ?• C0.3)
Мы
имеем
0
6
далее:
_ д
fit I
0
Й
x У x \ * »
v=.: С
У —	tJ
= «y(*. S, t)vx(x. b, t) — fvx
0
ибо ^ = ^ = 0 при у = 0. Но из второго уравнения B9.9) имеем:
б
dvy __ _ dvx	^ /> dvx
6
заметим, что
5	5
		dvx
дх
о	о
поэтому
v*dy = J
о	6
6
vy (х, b.t) = -^-f vx dy + vx (x, Ь, t) -g-	C0.4)
о
и, значит,
о	о
о	о	о
Вычислим интеграл
Г dvx	1 Г dv\	1 д } n	1	дЬ
J v'-Wdy = Sj ~dTdy=2H7J ^dy-^vlix, b, o-gj.
о	о	о
Собирая все полученные результаты, придём к выводу, что
A
и
д
Ж
о
о	С	8
/ vxdy + ^ J v\ dy-vx (x, b, t) -^ J vx dy-vx{x, I,

558	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ II
Вычислим теперь интеграл от правой части уравнения B9.9}. Здесь
мы имеем:
дх >	дх '
о
так как р не зависит от у. Далее,
I dv
^.dv (-^-\ —(
ду* а>—\ ду )у^ \ ду
поэтому
A
В итоге, первое уравнение системы B9.9) даёт нам следующее
равенство:
о
1 dp 5.
? дх
5. . / dvx \	I dvx \	/Qn _
8 + ^ \-^rL-1 —v l-r^ •	C0.5)
Это равенство справедливо при любом значении Ь; примем теперь,
что 8 есть как раз толщина пограничного слоя, тогда, как было
выше указано, мы можем принять vx(x, 8, t) равным U (x, t),
a (dvx/dy) ^a можем заменить нулём. В результате получается инте-
интегральное соотношение Кармана
C0.6)
р ду	\ дх y
которое в частном случае установившегося движения имеет вид:
U- C0-7)
Подчеркнём ещё раз приближённый характер этих соотношений,
вывод которых основывался на отбрасывании некоторых малых ве-
величин.

30]
ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ КАРМАНА И ЕГО ОБОБЩЕНИЯ
559
Сам Карман получил уравнение C0.6) путём применения закона
количеств движения1). Выведем этим методом уравнение C0.6). Пусть
кривая КК, уравнение которой есть
y = S(Xi t),	C0.8)
ограничивает область пограничного слоя от области внешнего потен-
потенциального течения (рис. 176). Рассмотрим объем жидкости, вырезае-
вырезаемый из пограничного слоя ординатами АВ и А1В1 (как всегда, тол-
толщину жидкого слоя в направлении, перпендикулярном плоскости
чертежа, принимаем равной единице). Пусть ААХ — dx. Количество
движения вырезанного слоя (в направлении оси Ох), очевидно, равно
К = j pvxdy dx.
C0.9)
dx
А,
х'
Рис 176.
По закону количества движения, измене-
пне количества движения какой-либо си-
аемы точек равняется импульсу всех
внешних сил, действовавших на точки
системы. Изменение за время dt количества
движения системы частиц, заполнявших в начале этого промежутка
времени объем АВВХАХ, складывается из двух частей. Прежде всего,
в случае нестационарного течения, происходит изменение скорости
в каждой точке пространства; в силу этого обстоятельства мы полу-
получаем за время dt приращение количества движения рассматриваемого
объема жидкости на величину
dxK
= dx f
Р
dt
¦ dt dy.
Но, кроме того, нужно иметь в виду, что за время dt некоторые
частицы, составляющие наш объем в начале этого промежутка вре-
времени, уйдут из пределов области АВВ^А^; количество движения
этих частиц нужно причислить к dxK. Наоборот, количество дви-
движения тех частиц, которые вошли внутрь области АВВХАХ за время dt,
надо вычесть из dxK или, что то же самое, считая количества вхо-
входящей в область жидкости отрицательными, нужно за d2K принять
количество движения, выносимое через контур АВВ1А1. Через ААХ
протекания жидкости нет совсем, через А1В1 выносится
I
x+dx
') К а г m a n, Ueber laminare und turbulente Reibung, Zeit fur ang. Math.
Mech, т. I, 1921, стр. 233—252.

560	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
через АВ:
— / У°х ¦ vx dy dt.
о
Итого через АВ и АгВг выносится количество движения жидкости
-^ fpvldydtdx.
о
Ясно, далее, что через А1В1 и АВ вытекает количество жидкости
д
дх
I pvx dy dt dx;
следовательно, такое же количество жидкости должно втекать через
контур BBV Но на контуре ВВХ мы имеем равенство vx = U, ибо
на границе пограничного слоя КК скорость vx переходит в скорость U
внешнего потенциального потока. Итак, через ВВХ выносится коли-
количество движения
и, значит,
d2K— j^
о
~~U~dx~J
I pv2xdydtdx—U -j^ j pvxdyd(dx.
Итак, полное изменение количества движения рассматриваемой
системы точек равно:
dK= d.K+d^dx dt\ J9^fdy + -^ f ?v\ dy-U-^f pvx dy }.
10	6	0	)
Подсчитаем теперь импульс внешних сил. Прежде всего, на
отрезке ААХ действует сила трения, величина которой, отнесённая
к единице площади, равна
причём знак минус берётся потому, что т0 есть напряжение на стенке,
а нас интересует сейчас обратная по направлению сила воздействия
на чзстицы жидкости. Умножая предыдущее выражение на величину

HHTFTP^bHOE СООТНОШЕНИЕ КАРМАНА И FTO ОБОБЩЕНИЯ 561
1 • dx и на промежуток времени dt, получим выражение
импульса силы трения
— xodxdt = — (A f —;ри dx dt.
.Мы имеем, далее, силы давления, причоженные к АВ, ВВХ и А1В1
(соответствующими силами вязкости можно пренебречь). Проекции
этих сил на ось Ох равны соответственно
(рЬ)л, pds-~ = pdb, -(pb)x Jx = ~(рЪ)х — d(pb), C0.11)
где ds = BBx и dljds есть синус угла который ВВХ составляет
с осью Ох. Сумма этих проекций равна
(рЬ) г + р db — (РЪ)Х - d (pb) = - 8 dp = - 3 -g- rfx,
импульс же этих сил будет равен
Приравнивая dK полному импульсу всех сил
— x.dxdt — l^-
0	дх
приходим к требуемому равенству
^-^/р^»-^-»!?. C0Л2)
0	0	0
Если теперь воспользоваться формулами C0.10) и C0.3), то по-
получим соотношение
dt ,
о
ж f К dy - и
о
gJ^\ , C0.13)
дх
т. е. мы вновь докажем формулу C0.6).
Придадим полученному интегральному соотношению еще иную
форму, а именно такую, в которую входят интегралы по у, взятые
по всему бесконечному интервалу от 0 до со. В этом случае, чтобы
обеспечить сходимость интегралов, надо рассматривать вместо vx
его отклонение от предельного значения U, а именно пусть будет
U — vx = q,	C0.14)
36 Теоретическая гидромеханика, ч II

562	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
то!да будем, очевидно, иметь:
0
— 2U f q dy + §q2dy,
поэтому равенство C0.13) принимает, после простых вычислений,
форму:
«д(/ д Г , , »,, dU ,, д Г , о dU Г , , д
0	0	0	0
__ 6 др
р дх	\ ду
Но для потенциального течения мы имеем соотношение
Л ^ йж ~ f дх'	(ЫЛЬ)
являющееся следствием первого из уравнений гидромеханики идеаль-
идеальной жидкости.
Поэтому в предыдущем уравнении члены, содержащие множите-
множителем 8, взаимно сокращаются. В оставшихся членах мы можем поло-
положить 8 = оо, тогда получим точное равенство:
дУ
=Ло_ C0.16)
Р
В стационарном случае пропадает первый член левой части равен-
равенства C0.16), и уравнение это принимает вид:
dy = f. C0.17)
Введём вновь толщину вытеснения по формуле C0.1), а также неко-
некоторую длину 8**, которую называют «толщиной потери импульса»:
J vx{U -v_K)dy.

4, --,0]	ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ КАРМАНА И ЕГО ОБОБЩЕНИЯ 563
То!да, гак как
со	со	оо
f qdy= f (U -vx)dy = U f [\ —?jf)dy=W
об	о
оо	оо
= U J' qdy-U* J'
мы найдем, после простых вычислений:
^ + ^.B8«-Ь8*)=^.	C0.18)
Эта форма соотношения Кармана была предложена Прандтлем. Мы
воспользуемся ею в приближенной теории пограничного слоя.
Л. С. Лейбензон указал, что можно получить интегральное соот-
соотношение, аналогичное соотношению Кармана, исходя из закона энер-
энергии >). Приведем вывод интегрального соотношения Лейбензона для
случая установившегося движения. Вырезая, как выше, из погранич-
пограничного слоя объем жидкости, ограниченный ординатами АВ и АХВХ
(рис. 176), для живой силы этого слоя будем иметь выражение:
Т
= ) Щ-йУЛх'	C0.19)
ибо составляющая vy очень мала по сравнению с vx. Изменение
м время dt живой силы частиц, составляющих вырезанный объем,
<- 1агается из живой силы
хл их
выносимой через AXBV живой силы
„2
Г vx
— J ?-i-vxdydt.
') Лейбензон Л. С, Энергетическая форма интегрального условия
leopnit пограничного слоя, Груды ЦАГИ, вып. 240, 1935.

564	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. Л
выносимой через АВ, и живой силы
U2 d Г
'~2~~dx ]
выносимой через BBV Поэтому полное изменение живой силы рас-
рассматриваемой системы точек равно:
v%	U2 d с	\
I о	о	J
Подсчитаем теперь работу внешних сил на контуре ААХВХВ.
Работа сил вязкости на отрезке АА± равна нулю, так как скорость
жидкости на АА{ обращается в нуль; на прочих частях контура
работой сил вязкости можно пренебречь. Работа сил давления на
контуре АА-^Вф выражается интегралом
— I pvn ds dt,
где п есть внешняя нормаль к контуру. Но по формуле Гаусса
Гpvnds= ( \ div(pv)dxdy,
с	s
где 5 есть площадь, ограниченная контуром С; далее
div (pv) = р div v -j- grad p • v,
и в нашем случае div v — 0, a p зависит только от х, так что
giadp-v = -?vx.
Поэтому искомая работа сил давления равна
о
dA — — f pvndsdt=: — dx-^ f vxdydt.
аа\в
Как мы знаем, работа приложенных к частицам вязкой жидкости
сил расходуется не только на увеличение кинетической энергии этих
частиц, но частью диссипируется. Функция диссипации ?(см. § 7)
в нашем случае упрощается на основании G.7), принимая следую-
следующий вид:

3 -.Oj	ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ КАРМАНА И ГГО ОБОБЩЕНИЯ 565
ибо остальные слагаемые, входящие в Е, малы по сравнению с напи-
написанным. За время dt в рассматриваемом объёме жидкости рассеи-
иаегся количество энергии, равное
0
Состав тяя равенстпо
dT = dA — dB,
приходим к интегральному соотношению Лейбензона:
d Г" {'v\ U2 d f dp Г	Г ( да
—— I — =— d\)	п—-г- / ovу d\ =	-т— / Vydy — u / I -3-
о	о	00'
C0.20)
Это соотношение может быть выведено также непосредственно
из основных уравнений Прандтля B9.9). В. В. Голубев указал, что
из этих уравнений можно получить даже ещё более общую форму
интегрального соотношения.
В самом деле, умножая обе части уравнения
., dv*_ 1 .. dvx _ I dp d4x
х дх ~г у ду ~ р dx ~r дуг
на vkx и интегрируя после этого по у в пределах от 0 до о, получим:
о	о
Простые преобразования дают:
J vyvX
к + 1 J	ду
о
A,.

566	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ. II
вследствие C0.4) и того, что можно принять vx(x, 6)= {/(я),
k -\~\ L dx dx J	x * J ' * +1 J i
о	о
Но ясно, что
! dvx	1 Г ^^ж4"	rf Г иж	^
Далее, интегрирование по частям даёт, вследствие того что
(f^)y=o = 0, (—Нн =0, следующее соотношение:
о	о
Поэтому окончательно при любом положительном А получаем:
При й -= 1 получаем, в частности, интегральное соотношение Лей-
бензона.
§ 31. Уравнения теории пограничного слоя для сжимаемой
жидкости. Рассуждения Прандтля мы можем легко обобщить на
случай сжимаемой жидкости. Как и раньше, рассмотрим для простоты
С1>чай плоско-параллельного течения и предположим отсутствие
внешних сил. Уравнения движения D.8) примут вид:

5,31] УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ ДЛЯ СЖИМАЕМОЙ ЖИДКОСТИ 567
причем по C.4)
dv
dvv
dvy
C1.3)
Уравнение неразрывности даст:
Введём вновь в рассмотрение 8 и / как в § 28. Если в уравнении
C1.4) все члены—одного порядка и если V есть характерная ско-
скорость рассматриваемого течения (vx), то снова мы должны считать,
что внутри пограничного слоя vy имеет порядок Vb/l. Но тогда
четыре члена правой части C1.1), содержащие производные от ско-
скоростей по координатам
д /. dv,, \ д I dvr \ д / di\
д \а
1х~[(
Л
дх Г дх \Л ду )' ~ЬТVх ду }' ду [^ дх
имеют соответственно порядок (к и ;х имеют один и тот же порядок):
Ы
V	1 КЗ
и мы должны оставить из
вместо первого уравнения:
V
Vb
них лишь один — третий — и записать
д
Так же как и в несжимаемой жидкости, все члены левой части C1.5)
имеют один и тот же порядок рК2// и опять, по Прандтлю, мы при-
примем, что pV2jl и (J.K/82 имеют один и тот же порядок. Тот же по-
порядок имеет член др/дх.
Обратимся теперь к уравнению C1.2). Порядок членов, содержа-
содержащих коэффициент вязкости и стоящих здесь справа, т. е. членов
д I dv, \ д I dv,, \ д Г	dvrldf. dvv
будет
Vb
V
_
/в '
it
соответственно. Максимальная из них |xV/Z8, а это, по принятому
Уже нами допущению Прандтля, всё равно, что pV2b/P. Таков же

568
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
порядок членов, стоящих слева. Итак, др/ду имеет порядок pF28//2,
а др/дх— порядок pV2/l. Отсюда заключаем, как и в случае не-
несжимаемой жидкости, что второе уравнение движения заменяется
соотношением
f = 0.	C1.6)
Уравнение неразрывности остаётся без изменения:
Посмотрим теперь, как видоизменится в пограничном слое уравнение
притока тепла A0.6).
В случае плоско-параллельного движения и при е = 0 уравнение
A0.6) перепишется в виде:
дТ
дТ
дТ
.(др . др , др\
Из двух членов, содержащих коэффициент теплопроводности, мы
должны в пограничном слое сохранить один:
ду Г ду Г
Очевидно, далее, что из всех членов, содержащих коэффициенты
вязкости, останется лишь
Принимая, наконец, во внимание C1.6), мы получим уравнение при-
притока тепла в теории пограничного слоя в виде:
Уравнению этому мы можем дать еще другую форму. Ваавим др/дх
из C1.5). Производя совершенно элементарные преобразования, по-

1Q]	П01РАННЧНЫП СЛОЙ ВДОЛЬ ПЛОСКОП ПЛАСТИНКИ	569
лучим окончательно:
dt ~ ду
!де Е ¦= -г — механический эквивалент тепла.
В заключение этого параграфа получим ещё интегральное соот-
соотношение Кармана для сжимаемой жидкости. Для этого запишем
сперва C1.5), привлекая уравнение неразрывности в виде
dov v dov v duvju.,	dp д I dvr \
dt ' dx "¦ dy	дх ' ду у ду ) '
и проинтегрируем по у от 0 до 8:
о	о
Но из уравнения неразрывности следует, что
у = 0 = 0.	C1.12)
о	о
Обозначая, как и прежде,
вставляя (pvy) o из C1.12) в C1.11), вынося дифференцирование
из-под знаков интегралов и производя сокращения, получим:
от f :«
= 8^(!Х^ . (з1.13)
дх V ду /у=о	v
и есть интегральное соотношение Кармана для сжимаемой
жидкости. При о = const., ц = const, оно автоматически перейдет
в C0.13).
§ 32. Пограничный слой в несжимаемой жидкости вдоль
плоской пластинки. Переходим теперь к исследованию конкретных
счучаев движений в пограничном слое.
Пусть плоская пластинка, бесконечно длинная в направлении, пер-
перпендикулярном к плоскости чертежа (рис. 173), движется с постоянной

570	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ П
скоростью U в направлении отрицательной оси Ох. Нам удобнее
будет обратить движение и рассматривать обтекание пластинки,
расположенной вдоль оси Ох, равномерным потоком, имеющим
постоянную скорость U. Очевидно, в основном потоке мы имеем
отсутствие градиента давления
и поэтому, предполагая, что мы имеем дело с несжимаемой
жидкостью и со стационарным ламинарным пограничным слоем, можем
написать основные уравнения в виде:
dvx	dvx	d2vx	dvx dvv
H	^	± + / °	С321
x
' у dy
x дх ' у dy	dy2	dx ' dy	v '
Вчодя функцию тока ф (х, у), будем иметь:
v x = fL, Wv = -#,	C2.2)
х ду	У	дх	'
и первое уравнение C2.1) даёт тогда
^	Ч9
йу дхду dx ду* ~v t)y3""	(,о-.о;
Но ясно теперь, что ф, кроме л: и у, может зависеть только ог
U к у.
Следуя Блазиусу1), мы введём вместо <|) безразмерную величину С
по формуле
ф^г/>Т73сС,	C2.4)
а также безразмерную величину
- .	C2.5)
Предположим теперь, что С зависит только от Ъ
Простые вычисления показывают, что если мы условимся штрихами
обозначать производные по ;, то
It
ду
V, = ¦
C2.6)
') Blasius H., Orenzschlchten In Flusslgkeiten mit Kleiner Reibimg,
Zeit. fur Math, und Phys., 56 A908), стр. 1—37.

< i2]	пограничный слой вдоль плоской пластинки	571
Подставляя эти значения в уравнение C2.3), после сравнительно
простых вычислений найдём обыкновенное дифференциальное урав-
уравнение для определения С:
= 0.	C2.7)
Граничные условия vx = vy = 0 при у —0 дают нам вследствие
соотношений C2.6), что
С = 0, С = 0 при е = 0,	C2.8)
граничное же условие vx = U при у = со показывает, что
С=1 при Е = оо.	C2.9)
Й1ак, надо интегрировать уравнение C2.7) третьего порядка при
трех граничных условиях C2.8) и C2.9). Решение этой задачи мы
уже привели выше (см. § 20). Этим решением сейчас и восполь-
воспользуемся.
Напомним теперь ещё раз наши обозначения. По первому из
уравнений C2.6):
С'E) = -^-,	C2.10)
по уравнению же C2.5)
/-	C2.11)
Заметим, что в рассматриваемой задаче мы не имеем в нашем
распоряжении характерной длины; рассматривая пограничный слой
в месте пластины, соответствующем координате х, мы можем при-
принять число Рейнольдса равным
R = ^,	C2.12)
и тогда
Таким образом X пропорционально координате у.
Приведём теперь таблицу (см. таблицу IV), составленную Пранд-
тлем на основе вычислений Тёпфера, и дадим (рис. 177), распреде-
распределение скорости в пограничном слое. Так как в основе теории по-
пограничного слоя лежит предположение о том, что число Рейнольдса R
очень велико, то из формулы C2.12) явствует, что мы не можем
применять полученные результаты к самому краю пластинки, где х
имеет малые значения.
Прежде чем идти дальше, сопоставим решение, полученное здесь,
<- решением в точной постановке (§ 20). В качестве независимой

572
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. и
Таблица IV
0
0,2
0,4
0,6
0,8
1,0
0,0000
0,0664
0,1328
0,1990
0,2647
0,3298
1,2
1,4
1,6
1,8
2,0
2,2
0,3938
0,4563
0,5168
0,5747
0,6298
0,6813
2,4
2,6
2,8
3,0
3,2
3,4
С (У
0,7290
0,7725
0,8115
0,8461
0,8761
0,9018
3,6
3,8
4,0
4,2
4,4
4,6
"(У
0,9233
0,9411
0,9555
0,9670
0,9759
0,9827
1
4,8
5,0
5,2
5,4
5,6
5,8
6,0
С (?)
0,9878
0,9916
0,9943
0,9962
0,9975
0,9984
0,9990
переменной в § 20 фигурировала величина
где Х =— х,
К > 0), то k=
Ш
у (см. B0.5) и B0.19)). Если К<Аг(А'>0,
_ = у л/ JL .
X У * чх
2	2VX - ' чх
Таким образом, если только Y <^Х, аргумент, введённый в § 20,
будет совпадать с независимым переменным теории пограничного
слоя.
V-
Кроме того, так как хх=-к- t rr r	о
К <^ X имеем x^^i-^\/ -^1^^= \^х. Таким образом, для К
то для

j 32]	ПОГРАНИЧНЫЙ СЛОЙ ВДОЛЬ ПЛОСКОЙ ПЛАСТИНКИ	573
имеем по B0.9) (если ограничиться первым членом) <b=Vxf (у у —)>
пли по B0.19) & — V "'Ux''-,\y у — ). и мы придём к формуле C2.4).
Отметим, что по Блазиусу lim —- — Wm-^jj у —(^'—С), или,
у ->• со U	^и	х
на основании B0.41),	hm ——=—1/ —x=—^=r-^—W,
11 v
в ю время как в точной постановке hm -.-—> 0. Различие в рас-
У -> со '-'
пределении значений vy видно из сравнения рис. 165 и 177.
Чтобы вычислить сопротивление, испытываемое пластиной, най-
найдем сначала
dvx\
но вследствие предыдущих формул
*!.=.«. да
поэтому
''о=^}/Г-~^"(О) = У^^у^-	C2-13)
Если пластинка имеет ширину Ъ и длину Z, то суммарное сопро-
сопротивление, испытываемое как верхней, так и нижней сторонами пла-
пластинки, будет равно:
W — 2b VW^ f Y^ ==
о
т. е.
C2.14)
Вводя коэффициент сопротивления по формуле
t/2	C2.15)
где F — 2bl, получим:
/"^=-^.	C2.16)
r le R =/t//v есть число Рейнольдса. Полученное значение коэффи-
коэффициента сопротивления хорошо согласуется с коэффициентами, нак-
^енными из экспериментов над гладкими пластинками для чисел
рейнольдса, не превосходящих 3 • 105.

574	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ И
Определим еще толщину пограничного слоя. Вычислим величину Ь*,
определённую формулой C0.1):
о
По формулам C2.21) и C2.22)
о
произведя вычисления, получим:
S*= 1,72 уГ^--	C2 17)
Толщину пограничного слоя можно принять равной, например, 3§*,
как рекомендует Прандтль; тогда будем иметь:
Хт.	C2 18)
Такому 8 соответствует ?=5,2, т. е. по вышеприведенной табличке
отклонение скорости от скорости внешнего потока на 1/2%-
Применим теперь к рассматриваемой задаче метод использования
интегрального соотношения Кармана. Так как мы имеем дело с уста-
установившимся движением, в котором
дх '
то основное уравнение теории Кармана C0 7) напишется так:
Если бы нам было известно, что распределение скорости внутри
пограничного слоя определяется формулой
где
то мы имели бы
Г	6	1
) г	т т I	j	/ ТО"* t г ri
v^dy — U | vxdy — U2(j j [f2 (
о

j. 32)	пограничный слой вдоль плоской пластинки	575
где для краткости введено обозначение
Т = /(/ — P)dv\.	C2.20)
о
Далее,
поэтому уравнение C2.19) принимает вид:
откуда
Интегрируя это уравнение и считая, что 8 = 0 при х = 0, по-
получим:
Так как вследствие формул C2.32) и C2.33):
2* '
то для сопротивления, испытываемого с обеих сторон пластинкой
ширины b и длины /, мы получим формулу
W = 2b f У wf fl U^ dx = ЪЪУЧщГ @) Uzil: C2.23)
о
в иной форме это соотношение принимает вид:
Ш.	C2.24)
Наконец, для определения величины 8* мы имеем, согласно формуле
C0.1):
i
8* =8 J[l— /G))]d7i.	C2.25)
о
Основная идея метода Кармана состоит в том, что вместо того
чтобы отыскивать точный вид функции /(¦»]), можно задать вид этой
функции. Если мы правильно схватим общий характер распределе-
распределения скоростей в пограничном слое, то получим хорошее приближение
как для зависимости 8 от х, так и л л я численной величины коэф-
коэффициента сопротивления.

576	ДВИЖГНИГ ВЯТКОЙ ЖИДКОСТИ	ГГЛ II
Отсюда видны и положительные и отрицательные стороны метода
Кармана. Этот метод хорош тем, что он требует гораздо мень-
меньших вычислений по сравнению с точными методами интегрирова-
интегрирования дифференциальных уравнений теории пограничного слоя. Пло-
Плохая же сторона метода Кармана состоит в том, что он приме-
применим, в сущности говоря, только к тем случаям, когда мы имеем
плавное распределение скорости в пограничном слое, так как
только в этих случаях мы можем ожидать, что задаваемая с до-
довольно большим произволом функция f(rj) отразит общий характер
1ечения в пограничном слое. Поэтому, в сущности говоря, мы
должны довольно много знать о характере течения в пограничном
слое, чтобы иметь возможность применять метод Кармана.
В нашей задаче мы имеем дело с очень плавным распределением
скоростей, и потому мы должны ожидать, что метод Кармана даст
хорошие результаты. В самом деле, примем, например, что
/(¦/)).= т);	C2.26)
это обеспечивает нам при у = 0 vx~Q, а при у = о vx~U, как
и должно быть. Мы будем тогда иметь:
1
7) ( 1 — Vj) llT{ — -1 , /' @) — I ,
о
поэтому формула C2.33) даёт:
j/--^,	C2.27)
а по формулам C2.34) и C2.35)
Y	=;±jE-.	C2.28)
У R
Наконец аля о* имеем формулу:
1
)^j-,	C2.29)
о
почти совпадающую (конечно, случайно) с формулой C2.28).
Возьмём теперь распределение скоростей по параболе третьей
степени
причём выберем следующие граничные условия:
^ = 0, ^=0 при у = 0; vx = U,^ = 0 при у = 8, C2.30)
последнее из которых выражает, что на внешней границе погра-
пограничного слоя не только vx, но н dvxj0x плавно переходят в соот-

ПОГРАНИЧНЫЙ ПОП ВТ.ОЛЬ ГПОСКОП ПЛАСТИНКИ
577
Beii-iB\ ющне значения внешнего потенциального течения. Второе
iu взя1ых 1'ами пограничных условий сразу вытекает из первого }рав-
}равнения (.32 1), если заметить, что при у = 0 как vx, так и vy должны
обращайся в пуль. Просюг вычисление показывает, что наао взято
/(^-§^—1^	C2.31)
и ia-ке
1
следовательно,
2Ы)	2 J
о
. _ /~80vx ___ . г.. лГ~ч±
±,
70к
C2.32)
Примем еще, чтобы показать пример применения уравнения C0.16),
следующий закон распределения скорости:
C2.33)
тогда
U J q dy — J q2 dy = U4 J A — th tj) th
Введём новую переменную
и заметим, что
ch2 r{
ch2 ^— sh2
поэтому
J (l-thTj)th 7, </¦/,= /"A -0:^-5
0	S	'
37 Теоретическая гидромеханика, ч II

578	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ. И
Далее
dvr	U 1
поэтому уравнение C0.16) даёт нам
« do 		[л
откуда
s
dx p(/(l —1п2)
и, следовательно, после интегрирования
§ = /"G(Г=12)~2'553/т'	C2-34>
Вычисляем теперь сопротивление
0 5 V	2х
и следовательно,
W=2bV2(\ — ln2)|j.pt/3Z^l,567 6Vup/t/3, cw^^L. C2.35)
Т R
Наконец,
1	rs ^
"-	C2-36)
Мы видим, что величина о* во всех случаях получается очень
близкой к той, которую даёт точное решение; ошибка в определе-
определении cw доходит до 20%, хотя в частном случае, когда за f (rf) выби-
выбирается полином третьей степени, эта ошибка не превышает 4%.
Еще раз подчеркнём, что при применении метода интегральных
соотношений мы имеем очень большой произвол в выборе распре-
распределения скорости. Кроме того, остаётся также произвол в выборе
интегрального соотношения, которым мы можем воспользоваться.
§ 33. Пограничный слой в диффузоре. Ламинарная струя.
В качестве второго примера применения теории пограничного слоя
в несжимаемой жидкости рассмотрим течение в плоском диффузоре1).
') Р о h I h a u s e n К., Zur naherungwelsen Integration der Dlfferentialglei-
chung der laminaren Grenzshlcht, Zeltschr. fur angew. Math, und Mech., 1 A921),
стр. 252—268.

§ 33]	ПОГРАНИЧНЫЙ СЛОЙ В ДИФФУЗОРЕ. ЛАМИНАРНАЯ СТРУЯ	579
Пусть мы имеем плоское течение жидкости между двумя плоскими
стенками ОАВ и OCD, наклонёнными друг к другу под углом а
(рис. 160, стр. 461). Мы будем стараться придерживаться тех же
обозначений, что и в § 17, в котором вопрос о течении в диф-
диффузоре был рассмотрен вполне строго. В соответствии с этим обо-
обозначим через Q обильность источника, считаемую положительной,
если мы имеем дело с расходящимся течением в диффузоре, и отри-
отрицательной—для случая сходящегося течения.
Мы будем рассматривать пограничный слой, образующийся вдоль,
стороны ОАВ угла, и будем отсчитывать координату х вдоль этой
стороны от точки О. Тогда для скорости течения идеальной жид-
жидкости мы будем иметь выражение
Мы можем теперь из уравнения Бернулли определить градиент
давления
1 1L— пп>— Q2
р dx ~ ии — -^з •
Введя функцию тока ty(x, у), из основного уравнения теории погра-
пограничного слоя, получим:
	91_ i!l
ду дхду дх ду2	а*хг ' дуг '
Положим
	91_ i
а*хг ' ду
C3.3)
простые вычисления показывают тогда, что
дЧ 	 1 ., 5 .„ д2ф 1
ду3 х3 ч ¦	J
Поэтому уравнение C3.2) сильно упрощается:
	(Г'J __ _ .51 _|_ уг///_
Введём для простоты обозначение:
С' (?) = — и (?,),	C3.5)
тогда будем иметь уравнение
¦^-«"=1— и2	C3.6)

580	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	|ГЛ. и
и граничные условия
м@)=0, и(со)=1,	C3.7)
вытекающие из C3.4), вследствие того, что при у = 0 (т. е. ? = 0)
vx должно обращаться в нуль, а при у = оо (т. е. ? = со) vx должно
обращаться в U = Qjax.
Умножая обе части уравнения C3.6) на и' и интегрируя, получим:
	и' 	С —1_ it —	/qq q\
Q/-J w ¦	 *-* I w	о )	\UO,OJ
где С есть произвольная постоянная. При ?->со величина и по усло-
условию C3.7) стремится к единице, но тогда из предыдущего уравнения
ясно, что и' тоже стремится к определённому пределу, и ясно, что
этим пределом может быть только нуль. Итак, C-j- 1	5- = 0, откуда
Q	±_
Но
и значит, уравнение C2.8) принимает вид:
-g-«/2=-|(«-lJ(« + 2).	C3.9)
Так как правая часть всегда отрицательна в интервале 0<«<М,
то Q непременно должно быть отрицательно. Таким образом,
пограничный слой рассматриваемого вида может образоваться только
для случая сходящегося течения в диффузоре; для случая расходящегося
течения такого правильного пограничного слоя не получается. Эти
результаты находятся в полном согласии с тем, что мы нашли в § 16.
Для случая сходящегося течения мы можем продолжить вычисле-
вычисления дальше. Введём, как в § 17, число Рейнольдса
R—а-
Заметим теперь, что вследствие граничных условий C3.7) и должно
возрастать вместе с %\ поэтому, разрешая уравнение C3.9) относи-
относительно и', найдем:
da
C3.10)

I]	ПОГРАНИЧНЫЙ СЛОЙ В ДИФФУЗОРЕ ЛАМИНАРНАЯ СТРУЯ	581
Чтобы взять интеграл, совершим подстановку:
= 3<72 — 2,
du = 6qdq; 1 — и = 3A — ^г2
du
Г
J A _и)jjq^
У
()q
У ~5
Положим далее
4
'	ch2 и 1 — ^2
и заметим, что если y = l/ -^-, то г» = In (УЗ —|—1/ )= 1,146. Pa-
BenciBo C3.10) даёт теперь
2а — " '
Возвращаясь к переменной и, найдем:
и = 3th2 [in (/3 + /2) + 6 j/"-|- ] - 2,
и наконец по формулам C9.4), C9.5) и C9.3)
"|]-2}. C3.11)
Преобразуем несколько эту формулу; мы имеем:
lLi	4
поэтому предыдущая формула может быть записана и так:
J
C3.12)
Эта формула является совершенно тождественной с формулой
A7.44) § 17; в самом деле, для пограничного слоя yjx есть малая
величина, которая с точностью до бесконечно малых высшего порядка
опредетяет угол, составляемый ОАВ с радиусом, проведённым из
точки О в рассматриваемую точку пограничного слоя. Но в § 17
этот угол выражался как раз величиной а/2 — б. Заменяя в формуле
< 17.44) а/2 — й на у/х, мы опять получаем формулу C3.12).
Применим теперь к рассматриваемой задаче способ Мизеса, изло-
изложенный в § 29. В этом способе за независимые переменные берутся
х и 6, а за функцию берётся
z = U2 — v2.	C3.13)

582	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Уравнение B9.15) для определения функции z в нашем случае
принимает вид:
~дх"~	W
причем, чтобы vx получилось положительным, мы принимаем ОАВ
за отрицательную ось Ох, так что в рассматриваемой нами области х
всюду отрицательно. Граничные условия будут иметь вид:
z — 0	» ф — сю.
Будем искать решение уравнения C3.14), имеющее вид:
* = ^да(Ф);	C3.15)
тогда функция w должна удовлетворять уравнению (мы опять вводим
число Рейиольдса R = — Q/v):
2w	™W»	C3.16)
У 1— w	a
и граничным условиям
¦да(О)—1; да(оо) = 0.	C3.17)
Умножая уравнение C3.16) на w', интегрируя и принимая во
внимание граничные условия, получим:
w
v2R ,2	 Г 2ю й»
о
Полагая
YT^w = q,
после простых вычислений получим:
2а
1
При возрастании ф от 0 до оо изменение q происходит от нуля до
единицы, поэтому из предыдущего уравнения находим:
а
JET_ С
3R —./ п—
(\-д)У2 + д
Сделаем теперь, как выше, подстановку

^ 35]	ПОГРАНИЧНЫЙ СЛОИ В ДИФФУЗОРЕ. ЛАМИНАРНАЯ СТРУЯ	583
тогда простые вычисления покажут, что
v
~ / C th2 v — 2) dv =
3R
V
-4, f
In (Г 3+1 2)
По формуле C3.13) мы определим v/.
Чтобы выяснить геометрическое значение введённого нами пара-
параметра v, найдём у из уравнения B9.18):
J ~?	J
Итак, в нашем движении
2)
фг=-,|/ -~ {^ — 3 th -у — 1 пA/ + 1/)-f/О}, C3.19)
где
г» = InA/3+1/2) — -j^y ~ .	C3.20)
Для определения vK имеем формулу C3.18), дающую:
— 2J C3.21)
li совершенно тождественную с C3.11), если учесть перемену обо-
обозначений (х заменено у нас на — х, a vx на — vx).
В задаче о диффузоре для скорости течения на внешней границе
пограничного слоя мы имели выражение
х
Более общий случай, когда
U=kxm,	C3.22)

58-1	4BII/KFIIIIE ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
допускает совершенно аналогичную трактовку вопроса *). А именно,
вмесю C3.2) мы будем иметь:
it i!iit i!t
it _i!i	it i!t дая^ v i!i
ду дх ду дх ду2 ~~т	^ ду3 •
Полагая
т-\	т + \
1 = ух~*~; ^=^х~г(,&,	C3.23)
мы получим для определения С (?) обыкновенное дифференциальное
уравнение
яЛ'2 — ^±^- СС" — vCw — т&2 = о	C3.24)
np.i граничных условиях
Не останавливаясь на дальнейшем рассмотрении получающегося
течения, заметим только, что два частных случая, в которых урав-
уравнение C3.24) сильно упрощается, а именно, случаи /я. = 0 (плоская
пластинка) и т — — 1 (диффузор), нами уже изучены.
Рассмотрим теперь задачу о плоском установившемся движении
вязкой жидкости в виде струи, исходящей из узкого отверстия2).
Пусть в покоящейся жидкости, расположенной справа от оси Оу,
распространяется струя жидкости, исходящая из узкою отверстия,
находящеюся в начале координат, и имеющая ось Ох осью симметрии.
Так как поперечные размеры струи весьма малы по сравнению
с продольными, то мы можем применить уравнения теории погра-
пограничного слоя. Конечно, как и в случае пластинки, полученные
результаты будут пригодны, только начиная с некоторого удаления
or начала координат.
В виду того что в покоящейся жидкости мы имеем постоянное
давление и, следовательно, отсутствие градиента давления, то для
функции гока <1>(х, у) мы получаем то же уравнение
ду дхду дх ду2 ~ ду* '	{oo.zo>
как и в случае обтекания пластинки равномерным потоком. Однако
граничные условия будут теперь другими. А именно, на оси Ох мы
имеем условия:
~i = 0, ©у = 0 при у = 0,	C3.26)
') F alkner V. М. и Skan Sylvia W., Some approximate solutions
of the boundary layer equations, Aeronautical Research Committee, Reports
and Memoranda, № 1314, 1930.
21 Schlichting H, Laminare Strahlausbreitung, Zeitschr. fur angew.
Math und Mech., 13 A933), стр. 260—263 и Bike ley W. O., The plane jet,
Phil. Mag., 23 A937), № 156, стр. 727—731.

5 3j]	ПОГРАНИЧНЫЙ СЛОИ В ДИФФУЗОРЕ. ЛАМИНАРНАЯ СТРУЯ	585
выIекающие из симметрии движения относительно оси Ох. Условие
па бесконечности в данном случае принимает вид:
vx->0 при у->со,	C3.27)
ик как основной поток отсутствует и, следовательно, (У — 0.
Докажем теперь, что количество движения жидкости, проходящее
через каждую прямую х = хп, будет постоянной величиной, не зави-
зависящей от х0. В самом деле, через элемент dy прямой х = х0 прохо-
проходит масса жидкости pvxdy, несущая количество движения pvxvdy,
проекция которого на ось Ох равна ^vxdy. Вследствие симметрии,
нам достаточно найти проекцию количества движения жидкости на
ось Ох; эта проекция имеет величину
СП	о--
М= J рг? dy — 2 J [jv\ dy.	C3.28)
-се	О
Но из уравнения C0.16), в котором надо положить U = 0,
(—f-Ц =0, g = —vx, следует, что
ибо первый член в левой части уравнения C0.16) пропадает вслед-
вследствие стационарности движения. Итак,
vldy = const.,	C3.29)
X
о
т. е. количество движения жидкости М имеет действительно постоян-
постоянное значение.
Чтобы решить уравнение C3.25), положим, обобщая прием Бла-
зиуса, упомянутый в § 32,
\ = х«у; ф =
Обозначая штрихами производные по 5, легко найдём, что
vx = дЛ Xa+rv,	vy = - g =
(зз.зо)

586	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Поэтому уравнение C3.25) принимает вид:
А.2аЬ2р-1[(а + 3)С/2 —рСС"]-= чхА^К'".	C3.31)
Мы получим обыкновенное дифференциальное уравнение для опре-
определения С, если примем, что
2а+ 2^ — 1 =3а + р,
откуда
Р = а+1.
С другой стороны, условие
со
2 J рг»2 dy = М
о
приводит к равенству
со
2?х*+*<> fv2dt = M,	C3.32)
о
и так как М не зависит от х, то необходимо положить
а -f- 2р = 0.
Решая два полученных уравнения для а и р, находим
а = -д-; р = т.
Итак, если мы примем, что
1=,ух-\ ^=хЧ(\),	C3.33)
то для определения С(?) мы будем иметь вытекающее из C3.31)
уравнение
C'2 + Ct:"+3vC"/ = 0.	C3.34)
Из C3.26), C3.27) и C3.30) вытекают граничные условия, которым
должна удовлетворять функция С(?)'-
= 0 при i = 0, )
>	C3-35)
s—>-СО. J
С —>0	»
Уравнение C3.34) очень легко интегрируется
CC' + 3vC" = C1.
Из условий C3.35) следует, что надо принять С1 = 0, так что
с;' -f- з-/," = о.

ПОГРАНИЧНЫЙ СЛОП В ДИФФУЗОРЕ ЛАМИНАРНАЯ СТРУЯ	587
\равнение опять-таки сразу интегрируется
-| -+¦ 3vV = С2.
Так как I'—»-0 при %—.>со, то значение С2 неотрицательно, положим
поэтому
Итак,
6vC = b2 — С2, или -уз—^ = ^г1;
интегрируя это уравнение, находим:
* + :_ us
Так как ^ = 0 при 5 = 0, то С3=0. Поэтому
Для сокращения письма положим:
тогда находим окончательный результат
C(^):=6vathai	C3.36)
Величина а легко выражается через М п>тём использования фор-
формулы C3.32):
но
(:' = -^^ = 6vc2—-1-С2; С'Л = Л; С@) = 0;
поэтому
J (	yC=-48pv2a3.	C3.37)
о
Итак,

588
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. И
Пользуясь выражениями C3.36) и C3.33) для С(?), получаем:
C3.39)
Для проекций скорости легко находим выражения
vy = 2-т
2аух~
ch2 {ayx~2'3)
C3.40)
Рис. 178 даёт построенные на основе этих выражений линии тока
и зависимость составляющей скорости vx от у в трёх сечениях
струи. Из неё ясно видно, как струя постепенно захватывает всё
большее и большее количество жидкости. Легко проверить эго и
аналитически. Количество жидкости, протекающей через прямую,
параллельную оси Оу и от-
отстоящую от неё на расстоя-
расстоянии х, очевидно, равно
Q = Р
= 2p f v, dy =
6
= 2рх'/° J С d\ = 2ох'/< (со);
но
С(оо)= 6va,
Рис. 178.
и, следовательно,
Q— 12рчах'1\ C3.41)
Этот процесс связан с подтеканием жидкости к оси Ох, и дей-
действительно, легко видеть, что
lim Vy = — 2vax-2^; lim vy = 2vax/';
у -> -f со	у ~> — оэ
это подтекание наиболее интенсивно в непосредственной близости
от оси Оу и убывает по мере возрастания х.
§ 34. Приближённые методы теории пограничного слоя. Отрыв
слоя. Метод Кочина — Лойцянского. Мы уже упоминали выше,
при общем описании теории пограничного слоя, что следствием этой
теории является возможность срыва вихрей с поверхности обтекае-
обтекаемого тела. Этот факт имеет кардинальную важность: в самом деле,
в предыдущих главах, при изучении движений идеальной жидкости,
рассматривались такие теории, в которых необходимым элементом
является наличие вихрей или, вообще, циркуляции, отличных от нуля,

. ,4)	ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРХНИЧНОГО СЛОЯ	589
как, например, теория вихревых цепочек Кармана или теория обте-
обтекания контура плоским потенциальным циркуляционным потоком
несжимаемой жидкости. В рамках самих этих теорий наличие таких
циркуляции, отличных от нуля, не может быть обосновано, ибо, как
мы знаем, в рассматриваемых условиях, т. е. когда жидкость иде-
aibna и несжимаема, а силы консервативны, вихреобразование
невозможно.
Таким образом, с рассматриваемой точки зрения, значение теории
пограничного слоя состоит в том, что она объясняет появление вих-
вихрей в жидкости и тем делает более обоснованными некоторые схемы
движений идеальной жидкости, вроде вышеупомянутых.
Нетрудно теперь установить условия для отрыва слоя. Обозначим
через х0 координату точки отрыва; рассматривая кривые распреде-
распределения скорости (рис. 172, стр. 543) в различных точках обтекаемого
контура, мы видим, что отрыв слоя происходит в той точке Мъ,
в коюрой происходит смена прямого течения на возвратное. Но на
самом контуре vx= 0, вблизи же контура vx > 0 для х < х0 и vx < О
для х > х0 (предполагаем, что основное течение происходит в напра-
направлении возрастающих значений х). Поэтому
-^~\ > 0 для х < х0 и (~^-} < 0 для х > х0.
"У /у=о	\ °У /у=о
Ясно, что место отрыва слоя должно определяться формулой:
Установим ещё одно условие, которое должно выполняться для
того, чтобы отрыв слоя был возможен. В самом деле, в той точке
кожура М3, в которой происходит отрыв, во всяком случае должно
быть
^>0,	C4.1)
ибо профиль скоростей обращен в этой точке своей вогнутостью
в направлении течения. Во внешней части пограничного слоя знак
кривизны меняется, и следовательно, в какой-то из точек профиля
скоростей мы должны иметь точку перегиба. Условие C4.1), отно-
относящееся к точке Мъ, имеет простое динамическое истолкование.
В самом деле, в точках контура vx = v = О, поэтому основное.
Уравнение теории пограничного слоя для случая установившегося
Движения B9.9) дает нам, что в точке Мъ
дх ^
Итак, для возможности отрыва слоя необходимо, чтобы на неко-
ором участке контура давление возрастало, а так как во внешнем

590	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ. II
потенциальном потоке давление р и скорость U связаны формулой
p-r-J-7p = const,
то предыдущее условие равносильно тому, чтобы на некотором
участке контура происходило замедление основного движения.
Отметим ещё то обстоятельство, что при заданном распределении
давления место отрыва слоя определяется однозначно и, следовательно,
не зависит от числа Рейнольдса, если только последнее не скажется
на распределении давления в окружающем потоке. Напротив, угол,
под которым линия отрыва слоя M3N (рис. 172) наклонена к контуру
АКВ, будет тем меньше, чем больше число Рейнольдса. В самом деле,
мы знаем, что при увеличении числа Рейнольдса R толщина погра-
пограничного слоя изменяется обратно пропорционально корню квадратному
из числа Рейнольдса; также будет изменяться и угол NM3B. В пре-
пределе при безграничном увеличении числа Рейнольдса толщина погра-
пограничного слоя обратится в нуль, место отрыва слоя останется без
изменения, и срыв вихрей будет происходить по линии, касательной
к контуру.
Для нахождения течения в пограничном слое и для определения
точки отрыва имеется ряд приближенных методов. Мы остановимся
только на некоторых из них.
В способе Блазиуса предполагается, что мы имеем дело с обте-
обтеканием симметричного контура бесциркуляционным установившимся
потоком, имеющим на бесконечности скорость, параллельную оси
симметрии. При этих условиях, обозначая через х длину дуги кон-
контура от точки разветвления потока, будем иметь, что U есть нечёт-
нечётная функция от х, разложение которой в ряд Тейлора есть
U = ахх + а3х3 -f- a5x5 -f • • •	C4.2)
Простое вычисление позволяет теперь определить
Вводя функцию тока W(x, у), так что
напишем основное уравнение Прандтля в следующем виде:
ду дх ду дх ду2
^	5-г- ... C4.4)
Ищем формально решение этого уравнения в виде
W = *ф, (у) + хЦг (у) + х% {у)+ ....	C4.5)

§ 34]
ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
591
где r]v Ф2> Фз> • • • СУТЬ Функции одного только у. Слово «формально»
мы прибавляем потому, что на самом деле неизвестно даже, можно ли
разложить lF в ряд вида C4.5).
Подставляя разложение C4.5) в уравнение и сравнивая коэффи-
коэффициенты при одинаковых степенях х, получаем ряд равенств, из кото-
которых мы выпишем только первые три:
C4.6)
Граничные условия
v,. = v., = 0 при у = 0, v r = U при у = со
х у г j х г s
дают для tyj, фз и Фб следующие граничные значения:
Введем теперь безразмерные величины, полагая
C4.7)
34.8)
тогда уравнения C4.6) примут вид:
/1-/17,=/;"+1.
б/;л; - bf\nb - fxh\ = j + С - s (/1 - /3/;>
а граничные условия C4.7) обратятся в
/,@) = /;@) = 0; /;(оо) = 1; /3@)=/3'@) = 0;
C4.9)
C4-10)
За1авая /j'@), можно численно проинтегрировать первое из урав-
уравнений C4.9); путём проб можно определить то значение f'[ @), при
котором окажется выполненным граничное условие /|(оо)=1,

592
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. II
Совершенно так же можно поступить с остальными уравнениями C4.9).
В результате получается следующая таблица значений /J (tj), /'3(г[),
Таблица V
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
0,0000
0,2266
0,4144
0,5662
0,6859
0,7778
0,8467
0,8968
0,000
0,125
0,213
0,269
0,300
0,313
0,313
0,307
4<1>
0,00
0,11
0,18
0,22
0,24
0,24
0,24
0,23
0,00
0,01
0,01
0,00
—0,02
—0,03
—0,05
—0,05
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
1\ ТО
0,9324
0,9569
0,9732
0,9841
0,9905
0,9946
0,9971
0,9985
/j (Т,
0,298
0,288
0,278
0,269
0,263
0,258
0,256
0,253
Ч (V
0,21
0,20
0,19
0,18
0,18
0,18
0,17
0,17
—0,05
—0,05
—0,04
—0,03
—0,03
—0,02
0,00
0,00
Совершенно аналогично определяются следующие члены разло-
разложения C4.5).
Тот же самый метод может быть применен и к более общему
случаю, когда распределение скорости на внешней границе погра-
пограничного слоя даётся вместо C4.2) формулой
U = ахх -f- а2х2 -\- аях3 -f- ...
Конечно, в этом случае вместо C4.5) надо полагать:
C4.11)
3(ЫУ)-Ь •••	C4.12)
Возвращаемся к рассматриваемому нами случаю. Распределение
скоростей в пограничном слое выражается, если мы ограничимся
только тремя членами в C4.5), формулой
Условие для отрыва слоя
= 0
у=0
-~- хЧ'ъ(г1). C4.13)
C4.14)
приводит к соотношению
axxf[ @) + 4а3х*/; @) + 6а3х% @) + 6 -^ х% @) = 0,

§31]	ПРПБЛНЖГЛШЫЕ МЕТОДЫ TfOPHIl IIOI РЛПИЧИО1 О СЛОЯ	593
н0 /'{@)^=1,23264, /з'@) = 0,7246, ^'@) = 0,637, ^'@) =
.-^0,12, следователю, для определения места отрыва получается
биквадратное уравнение
9
1,23264 flj -4- 2,8984 а^х- -+¦ C.S22 а- + 0,72 ~\ х1 ¦= 0. C4.15)
Применим этот результат к круговому цилиндру.
Хименц1) нашел эксперимент тьным пук-ч распределение давле-
давления вдоль контура цилиндра диаметром 9,75 см при обтекании ею
водяным потоком, имеющим скорость 19,2 см/сек. Исходя из этого
распределения давления, Хименц получил следующее распределение
скорости:
?/ = 7,151 х — 0,04497 х3 — 0,00033 х5,	C4.16)
1дс U дается в см/сек, х есть длина дуги цилиндра от точки раз-
разветвления, измеренная в сантиметрах. Применяя уравнение C4.15),
находим для точки отрыва хо = 6,97 см, что дает в угловой мере
0 = 82°, в согласии со значением, получающимся из опыта.
Другой приближенный метод, который мы изложим, основан на
применении интегрального соотношения Кармана и его обобщений и
был уже использован в § 32 при рассмотрении пограничного слоя
вдоль плоской пластинки. Сущность метода в применении к этому
последнему случаю заключалась в том, что распределение скорости
внутри пограничного слоя задавалось формулой
и затем из интегрального соотношения Кармана получалось уравнение
для определения функции Ь(х). Таким образом, в этом примере
профили скорости в различных точках контура предполагались
подобными между собой, и менялся только масштаб.
В общем случае такое предположение недостаточно, и необхо-
необходимо рассматривать более общий класс профилей.
Из основных уравнений теории пограничного слоя
dvx _ 1 dp , >t d2vx __у dU , _ ч] d2vx
дх ~1~ "у ду — р дх -Г ' ду2 —^ dx -Г ду
dv
дх
-==0
') Hiemenz К, Die Qrenzschicht an einem in den gleichformigen Flus-
^ekeiNstrom eingetauchten geraden Kreis^vlinder, Dinglers Poivtechnlsches
Journal, 328, 1911
Impc 1ИЧО1 k.i! 1ндроме\аника ч II

594	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ П
и из того, что на контуре vx = vy — 0, без труда получим, что на
контуре имеют место соотношения:
d*v	U dUdvy __
у	;
ду2	~ dx ' Ту
продифференцировав же первое из уравнений C4.17) по у, найдём,
что на контуре будет также
Итак, должны выполняться условия
"<=0. ^ = -^: -^ = 0 при у = 0. C4.18)
Обозначая толщину пограничного слоя через о, условия плавного
перехода скорости пограничного слоя в скорость внешнего потен-
потенциального течения можно записать в виде ряда равенств:
v* = u- тг = °- ^г = 0' ¦¦¦' р 5 C4Л9)
Положив
примем, следуя Польгаузену, чго vx представляется полиномом чет-
четвертой степени от tj:
v^U(AQ + Al'n+Art + A^-f Arf).
Для определения пяти коэффициентов этого полинома восполь-
воспользуемся двумя первыми условиями C4.18) и тремя первыми усло-
условиями C4.19), гогда получим:
Л 0 Л 2+А	^
4	6 v
Введем обозначение
тогда, после простых вычислений, найдём:
^)	C4.20)
Остается определить 8(jc) или, что то же, Х(х), для чего восполь-
воспользуемся интегральным соотношением Кармана C0.7)
1о • C4l21)

§ 311
ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ	595
Произведя соответствующие вычисления, получим для определения
функции
г(х)=»®- = Р&	C4.22)
следующее дифференциальное уравнение первого порядка:
Г = T + lJ
7гГ UT liJ	C4.23)
где
°>8 [—}-3 — 47'4Х" + 1670.4Х — 9072]
— 213,12	'
JD— 213,12 — 5.76А — к" '
причём \ надо заменить на zU'.
Интегрируя полученное уравнение, для чего надо знать начальное
значение 8@), найдём Ь(х) и, следовательно, Х(х), после чего можем
определить все элементы движения. Затруднение возникает в том
случае, если в начальной точке пограничного слоя мы имеем крити-
критическую точку, т. е. если ?/@)=0. Чтобы правая часть в уравнении
C4.23) оставалась конечной, необходимо, чтобы Ц0) было корнем
уравнения g(k) — 0. Корнями последнего уравнения являются 7,052;
17,75 и 70. Последний корень не годится, если ?/'@)>0 и нужно
принять
= 7,052. §@) =
чтобы между критической точкой и точкой минимума давления,
в которой ?/' — 0, и следовательно, X —0, не лежала точка ^=12,
в которой правая часть C4.23) обращается в бесконечность. Условие
для отрыва потока
—^=0 при у = 0
ду	v y
приводится к обращению в нуль коэффициента Аь что будет при
>•=— 12.
Вычислим ещё толщину вытеснения
Только что изложенный метод, применённый к круговому цилин-
цилиндру, даёт для рассмотренного Хименцем случая почти то же положе-
положение точки отрыва, какое получилось у Хименца. Однако распределе-
ние скоростей получается менее удовлетворительным, особенно
в области за точкой минимума давления.
38*

596	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ и
Можно думать, что только что рассмотренный метод дает более
или менее приемлемые результаты только в области ускоренного
движения, где давление падает. Дело в том, что профиль скоростей
должен удовлетворять при у = 0 бесчисленному множеству условий,
первыми из которых являются три условия C4.18). Принятое же
распределение скоростей удовлетворяет только двум первым из этих
условий. Получается сравнительно малое разнообразие профилей ско-
скоростей, что сильно ограничивает область применения метода.
Конечно, метод можно различными способами видоизменять.
Можно, например, взягь три условия C4.18) и два первых усло-
условия C4.19).
Можно, определяя распределение скоростей полиномом четвертой
сюпени, взять два условия C4.18) и два условия C4.19), тогда
наряду с л появится еще один параметр и можно использовать вместе
с mireipa 1Ы1ым соотношением Кармана C0.7) шпшральпое соотно-
соотношение Лейбензона C0.18). Можно ыкже использовать вместо поли-
полиномов другие функции п т. д.
В частности, мы должны ожидать юраздо тучшнх результатов,
если возьмем набор профилей, получающихся при решении какой-
либо частной задачи из теории пограничного слоя. В самом деле,
в этом случае автоматически удовлетворяются три условия C4.18)
и, кроме юго, все условия C4.19). В этом состоит, по существу,
идея метода, предложенною Хауэрсом1). Сначала решается некоторая
частная задача, относящаяся к тому случаю, когда скорость внеш-
внешнего потока определяется линейной функцией
U = bo — b1x, Ь0>0, ft, > 0.
После введения функции тока W(x, у) первое из уравнений C4.17)
примет в рассматриваемом случае вид:
дЧ/ дЧ' дЧГ дЧ-	дЧ' ... , ,
C4.25)
Положим теперь
и будем искать функцию тока в виде ряда
...), C4.27)
так что
^ = 47 = T*o{/i(i)-8«/;(i) +(8^/2A)-...} C4.28)
') Howarth, On the solution of the laminar boundary layer equations,
Proc Roy. Soc. London, Ser. A., 164 A938), № 919, стр. 547—579.

q :н]	ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ	59?
Подставляя это разложение в уравнение C4.25) и сравнивая коэф-
коэффициенты при одинаковых степенях S, получаем ряд равенств, из
которых первые три имеют вид:
Г-Ь/оЛ-2/^ + з/;/^-!,
/'" + fJl - W + 5/072 = ~ 4 + 2/i2 - Wi •
Граничные условия
прнвопяг к следующим пограничным условиям для функции fk:
f'(c^) = 2 /'@0) = — /'(со) = 0 (й -— 2 3 ...)
Для функции /0A4) получилось то же самое уравнение и те же
граничные условия, что и для функции CBij) в § 32; следовательно,
эти две функции совпадают. Для остальных функций fv /2, ...
получились линейные неоднородные уравнения, которые могут быть
численно проинтегрированы. Главная трудность заключается в оты-
отыскании таких значений вторых производных этих функций при т] = 0,
чтобы получились требуемые значения первых производных при
rj=cv. Этими значениями являются
/о = 1,32324, /;' = 1,02054, f2 =- 0,06926,
/з = 0,0560, /;'=-0,0372, /5 = 0,0272,
/„ = — 0,0212, /1' = 0,0174, /'' = — 0,0147.
•'О	•* I	¦'о
Для определения места отрыва из условия
—т~ = 0 при v = 0
оу
получается равенство
fl @) — 8?/;' @) + $%ffi @) —... = о,
однако полученные ряды не обеспечивают достаточной точности
вблизи места отрыва. В результате дополнительных вычислений Хауэрс
нашёл для места отрыва значение $ = 0,120.
Давая q все значения от 0 до 0,120 и определяя
*х 1 К E, Ъ)
U ~~ 2 1-

598
ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ
[ГЛ. It
по формуле C4.28), мы получаем набор профилей скоростей, зави-
зависящих от одного параметра. Дадим таблицу, определяющую один-
одиннадцать таких профилей.
Таблица VI
¦") \
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
0
0
133
265
394
517
630
729
812
876
923
956
976
988
994
998
999
999
1000

.

—
0,0123
0
125
251
377
498
611
711
796
864
914
949
972
985
993
997
998
999
1000



—
Значения величины -=j- ¦
0,0250
0
117
237
358
477
590
692
779
850
904
942
967
983
991
996
998
999
1000

.

—
0,0375
0
108
222
338
455
567
670
760
834
891
934
962
979
990
995
998
999
1000


—
—
0,0500
0
99
205
317
430
541
645
738
815
877
923
954
975
987
994
997
999
1000


—
—
0,0625
0
89
188
293
403
513
617
712
794
860
910
946
969
984
992
996
999
1000



—
0,0750
0
78
168
267
372
480
585
682
769
839
894
934
961
979
989
995
998
999
1000

—
—
100
0,0875
0
66
146
237
337
442
546
646
736
812
872
918
951
972
985
992
997
999
1000


—
0,1000
0
52
120
202
294
394
498
598
692
776
844
897
936
962
978
989
994
998
999
1000

—
0,1125
0
34
85
152
234
325
426
527
625
716
794
858
908
943
967
982
991
995
998
999
1000
—
0,1200
0
10
38
85
149
227
318
416
517
616
708
787
853
903
940
965
981
990
995
998
999
1000
Для применения полученного набора профилей необходимо соста-
составить характеристики этих профилей. А именно, нам понадобятся
прежде всего величины
выражая Ьо и Ьх через скорость U и её производную W, получим:
поэтому величина

§ 34]	ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПО1РАНИЧНОГО СЛОЯ	599
зависит только от \. Составим затем выражение для толщины вытес-
вытеснения
о
таким образом, величина
D^b = O® C4'30)
6
тоже зависит только от \. Составим также толщину потери им-
импульса 8**:
^П f 1^[2-Щ-]*щ = г® C4.31)
эю также будет функция одного ?.
Вставляя выражения
C4.32)
в уравнение Кармана, взятое в форме Прандтля C0.16), и вспоми-
вспоминая, что в нашем случае
U = bQ(\—%), U' = -bv x = ~t,	C3.34)
получим следующее соотношение
A - Е)Х' Ю— 2х(&) — G(l) = FE).	C4.35)
Интегрируя это уравнение при начальном условии '/(О)—0> выте-
вытекающем из C4.31), найдём:

600
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ
При малых \ главной частью подынтегральной функции будет
как следует из C4.29) и C4.30):
1
—ГьФ)-
C4.37)
4VT '°'
поэтому при малых % первым членом разложения в ряд функции
z(?) = a|'T, a = 0,664...	C4.38)
Нижеследующая таблица даёт для ряда значений ? функции
F. °' /.- 1' " 7./Х'-
Т а б л и ц а VII
0,0000
0,0125
0,0250
0,0375
0,0500
0,0625
0,0750
0,0875
0,1000
0,1125
0,1200
У -U'U\dyU
со
2,773
1,817
1,360
1,064
0,843
0,663
0,503
0,345
0,184
0,000
Q.\f-w »
U У v
0,0000
0,199
0,292
0,371
0,447
0,523
0,603
0,691
0,794
0,931
1,110
у
0,000
0,076
0,110
0,137
0,162
0,186
0,209
0,231
0,254
0,276
0,290
со
3,16
2,39
2,08
1,93
1,85
1,82
1,81
1,83
1,88
1,92
г/г'
0,000
0,024
0,046
0,066
0,084
0,100
0,115
0,128
0,139
0,147
0,151
Мы можем теперь применить полученный набор профилей для
определения движения в произвольном пограничном слое в той обла-
области последнего, в которой давление возрастает. Скорость внешнего
потока U (х) предполагается, таким образом, убывающей функцией
от х. Решение основывается на предположении, что профиль ско-
скорости, соответствующий некоторой точке контура, полностью опре-
определяется значениями U, U' и 8** в этой точке и совпадает с соот-
соответствующим профилем нашего набора, т. е. с тем профилем, для
которого U, U' и 8'* имеют заданные значения. Этот последний
профиль определяется следующим образом. По U' и 8** находим:
X
= У -
¦ и1
8**,
после чего по вышеприведённой таблице определяем \.
Параметры b0, b1 и х определяются очевидными формулами:
bl=-U';
U
X ^^ —
т

, jt]	ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ	601
nocie чего нетрудно установить связь между у и ч\:
jf-y-	C4-39)
п по таблице стр. 598 найти vK в функции у. Наконец, по преды-
предыдущей табтнце найдем толщину вытеснения сл и поверхностное
трепне па сгенке
ду /о'
Как видим, дтя определения всех элементов движения достаточно
знать значение \, соответствующее каждой точке контура. Если мы
будем знать значение ; в одной точке контура, то во всех других
точках контура его можно определить, используя интегральное соот-
соотношение Кармана в форме C0.17).
Вспоминая опять соотношения C4.32), получаем из C0.17) для
опрсде тения ф}шаиш 1'уХ) следующее уравнение:
UU'
^иУ^Ш7 f,
или
Воспо (ьзовавшись C4.35), можем также написать:
di 1 7 U" W ,,
Так как функцию //у/ мы знаем, а функция U(x) предпола1аегся
заданной, то из этого уравнения мы сможем найти к в функции х,
если только известно начальное значение I. Тот набор профилей,
который мы пол}чили выше, относится только к случаю возрастания
Давления, поэтому по1раничный слой до того места, откуда мы начи-
начинаем примени1ь только что рассмснренный метод, надо исследовать
каким-либо др\шм способом, который и даст нам профиль скорости
в начальной точке, определив для этого профиля о**, мы найдем x,(t),
а тем самым и Е, которое и нужно принять за начальное значение. В част-
'"-•сти, если мы берем за начальную точку точку минимума давления,
в которой U' = 0, то / обращается в нуль, и следовательно, началь-
начальным значением % будет тоже 0. Но тогда уравнение C4.40) будет
име1ь в начальной точке особую точку. Чтобы найти направление

602	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	ГГЛ II
интегральной кривой в этой точке, достаточно заметить, что по
правилу Лопиталя
%* = lim /"III z (?) = lim
и следовательно,
U"n ..,.2	2,269
C4.42)
Точно так же из уравнения C4.39) получим, что в этом случае
ul (dx\	y 0,332y
(	^ЧЛ	C4.43)
Дальнейшее интегрирование уравнения C4.40) может быть произве-
произведено либо численным путём, либо методом графического интегриро-
интегрирования. То значение координаты х, при котором достигается значение
?=---0,120, определяет место отрыва пограничного слоя.
Шубауер1) измерил распределение давления па эллиптическом
цилиндре, обтекаемом в направлении большой оси, превосходящей
малую ось в 2,96 раза. Беря за единицу длины величину малой полу-
полуоси, он нашёл, что минимум давления находится на расстоянии
х -1,30 от передней критической точки, а срыв нронехочиг при
х~= 1,99.
Хауэрс, определив графически U' и U" по экспериментальным
значениям U и применив до точки минимума давления метод Поль-
гаузена, а после неё свой метод, получил отрыв в точке лг—1,925,
в то время как по способу Полыаузена отрыва не получается
вовсе.
Выше было уже отмечено, что профили скоростей, употребляе-
употребляемые в только что рассмотренном способе, лучше соответствуют
граничным условиям, чем профили способа Полыаузена, и в этом
состоит преимущество метода Хауэрса. Но зато в последнем ме-
методе мы не имеем для профилей таких простых аналитических
выражений, как в способе Полыаузена. Очевидно, что метод
Хауэрса можно сделать применимым ко всему пограничному слою;
для этого надо решить сначала задачу о пограничном слое для
случая, когда скорость внешнего потока U (х) есть какая-либо
функция, сначала возрастающая от нуля, а затем убывающая.
Мы уже упоминали, что удача Хауэрса состоит в том, что он
берёт набор профилей, получающихся при решении частной задачи
') Schubauer, NACA, Rep. № 527, 1935.

34]
ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
603
пограничного слоя, именно — того случая, когда скорость U
линейная функция от х. Однако, к сожалению, решение для
такого U получается само в виде рядов, и расчет оказывается, как
мы видели, довольно громоздким. Если бы удалось подобрать такое U,
ля которого задача о пограничном слое допускала бы замкнутое
решение (подобно случаю Блазиуса), мы могли бы надеяться, при-
применяя идею Хауэрса, притти к менее громоздким выкладкам. Случай
Бтазиуса не подходит, ибо мы здесь не имеем ни одного параметра
типа bv которым мы смогли бы распорядиться. Как мы уже знаем,
ещё один случай точного решения в виде одночлена получается по
Фалькнеру (Falkner) и Сильвии Скан (Sylvia Skan)!), если взять
и = схт.	C4.44)
Уравнение для пограничного слоя примет здесь вид:
1де 6 —ф(х, у)— функция тока. Полагая
мы получим:
Ф-
C4.46)
C4.47)
Перейдем от переменных х, у к переменным х = х и X, югда
~' ^ ° ^ ^) D &
ду дх ду ду ду2 ~~ D (х, у)
D (x, S) D (х, у)
х
х
С др^юй стороны,
и мы получим, после приведения подобных членов и сокращений,
Уравнение
Ф'" -4- ФФ" = р (ф'2—l),	C4.48)
i ле
Р = ^г.	C4.49)
') C\t. сноску ') на cip- 584.

604	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ II
Таким образом, как и в случае Блазиуса, задача сводится к опреде-
определению одной функции из обыкновенного дифференциального уравне-
уравнения. Случай Блазиуса мы вновь получим, полагая т = 0, т. е. В = 0').
Краевые условия задачи: г^ —г>у = 0 при у — 0, vx — U при
у =со дадут сразу же:
Ф @) = Ф'@) = 0, Ф'(оо)=1.	C4.50)
Решение уравнения C4.48) при краевых условиях C4.50) будет за-
зависеть от \ и от параметра 8; будем его записывать так:
Ф = ФE, 3).	C4.51)
Хартри2) дал численное решение уравнения C4.48) при различных 8
и при краевых условиях C4.50).
Кочин и Лойцянский3) использовали функцию Харчри для по-
построения приближённого решения задачи о пограничном слое совер-
совершенно так же, как Хауэрс использовал решение, отвечающее
U = Ьо — Ьхх. Именно, заметив сперва, что у Хартри U'~mcxm~l
и что поэтому
попробуем искать приближённые решения, отвечающие любой функ-
функции U \х) в виде
Г~г; в],	C4.52)
где ФЕ (?; Р) есть производная по аргументу ? от функции ф(§, Р)
из C4.51). Однако будем теперь считать, что р будет не постоян-
постоянной величиной, а функцией от х, причём функцию эту подберём так,
чтобы при помощи C4.52) можно было бы удовлетворить интеграль-
интегральному соотношению Кармана в форме Прандтля C0.16). В соотно-
соотношение Прандтля входят три величины §*, 8*\ х0. Подсчитаем их.
Прежде всего имеем
Определенный интеграл, входящий справа, будет зависеть лишь от
второго аргумента, входящего в ф', т. е. от В. Обозначим его бук-
') Блазиус не вводит двойки под корень в подстановку для С и 5; отсюда
разница в множителе при Ф'" в C4.48) и при К!" в C2.7).
z) Hartree D. R., Ргос. Cambridge Phil. Soc, 33 A937).
3) Кочин Н. Е. и Лойцянский Л. Г., Об одном приближённом
методе расчёта ламинарного пограничного слоя, ДАН СССР, 35 A942), № 9.

§ 34]	ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ	605
вой Аф). Вид функции Л(Р) будет, конечно, определяться полностью
и.ч решения Хартри. Ниже мы приводим табличные значения этой
функции. Итак,
/~|	C4.53)
причём Фс взято из решения Хартри.
Далее
и	о	о
т. е.
&** = у |^-5 ф),	C4.54)
где
причем 5(Р) так же, как и Лф), находится из решения Хартри и
может быть табулировано (см. ниже).
Наконец,
C4.55)
где Фс;@, Р) есть вторая производная от функции Харгри по I, вы-
вычисленная при | = 0; это — функция от р и таблица для неё приве-
приведена ниже.
Теперь соотношение Прапдтля примет вид:
d
~dV
^г Я (Р)] -Ь ? /|f B5 + Л) = /^ Ф^ @; Р).
Сократив на у v, продифференцировав первый член и умножив всё
н» УТР, получим:

606
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. II
Умножим обе части нашего равенства на 2 Ур В и обозначим
—4/
Мы получим тогда
+ 2ВФц @; р) == />.
C4.56)
C4.57)
и, так как f к F зависят (и притом известным образом) лишь от р,
мы получим дифференциальное уравнение для определения р в функ-
функциях от х. В таблице VIII приведены значения функций Ф^@, Р),
А, В, f и F. Для практических расчётов удобно выразить F через /.
Таблица VIII
—0,1988
—0,19
—0,18
—0,16
—0,14
—0,10
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,80
1,00
1,20
1,60
2,00
Фс: @)
0,0000
0,086
0,1285
0,1905
0,2395
0,3191
0,4696
0,5870
0,6869
0,7748
0,8542
0,9277
0,996
1,120
1,2326
1,336
1,521
1,687
2,359
2,007
1,871
1,708
1,597
1,444
1,217
1,080
0,984
0,911
0,853
0,804
0,764
0,699
0,648
0,607
0,544
0,498
0,585
0,577
0,568
0,552
0,539
0,515
0,470
0,435
0,408
0,386
0,367
0,350
0,336
0,312
0,292
0,276
0,250
0,231
/
—0,0681
—0,0632
—0,0580
—0,0488
—0,0406
—0,0266
0,0000
0,0190
0,0333
0,0446
0,0538
0,0613
0,0677
0,0778
0,0854
0,0914
0,1002
0,1069
F
0,821
0,792
0,760
0,708
0,661
0,584
0,441
0,341
0,266
0,208
0,161
0,123
0,090
0,039
0,000
—0,030
—0,075
—0,107
Зависимость F от / оказывается близкой к линейной. Мы её пред-
представим поэтому в виде
так что уравнение C4.58) примет вид:
Уравнение это будем решать методом последовательных прибли-
приближений. В первом приближении можно отбросить е(/) и проинтегри-
проинтегрировать наше уравнение относительно /, как линейное. Мы получим:
U'
и»
;f>
C4.59)

I 34]
ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
607
1де с — произвольная постоянная интегрирования, определённая из
условия, что / принимает заданное значение при х — 0. Так, напри-
например, если при х — 0 пограничный слой только начинает развиваться,
следует положить с = 0. В качестве второго приближения можно
примять:
Выберем
= 0,45, &—5,35;
нужном нам интервале значений /
Таблица IX
тогда, как показывает таблица IX, в
будет иметь место неравенство
|е(/)| < 0,03а,
а это показывает, что в боль-
большинстве случаев практически до-
достаточно пользоваться формулой
C4.59).
Как только найдено / в функ-
функции от х, мы сейчас же, по пре-
предыдущей таблице VIII, определим р
в функции от х и по той же таб-
таблице Фц@; Р)> л(Р). 5(Р) И. зна-
значит, по C4.55), C4.54), C4.53)—
напряжение трения, толщину вы-
вытеснения и толщину потери им-
импульса. В частности, можем найти
и точку отрыва — точку, в кото-
которой то=фц(О, Р) = 0, т. е. /=
= — 0,0681 (см. таблицу VIII).
В качестве примера рассмотрим
случай Хауэрса. Пусть
и потребуем, чтобы пограничный слой начинался при jc = O (т. е.
при х=:0, / = 0). Тогда
/
—0,0681
—0,06
—0,05
—0,04
—0,03
—0,02
—0,01
—0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
F
0,821
0,772
0,715
0,658
0,602
0,548
0,495
0,441
0,388
0,336
0,283
0,232
0,180
0,130
0,078
0,028
—0,023
—0,074
0,007
0,001
—0,003
—0,006
—0,008
—0,009
—0,009
—0,009
—0,008
—0,007
—0,006
—0,004
—0,002
0,001
0,003
0,006
0,009
0,011
Для точки отрыва xs имеем:
— 0,0681 = — 0,0841 [A — л,)"8'35 — II,

608
ДВИ>ЬГН11Е ВЯЧКОИ ЖИДКОСТИ
(ГЛ. Tt
откуда полечим
0,105
вместо точного значения xs = 0,120.
Второе приближение (/) дало бы хч= 0,106, и это же значение
получилось бы при интеграции точного уравнения C4.58).
Мы видим, чю практически достаточно потьзоваться простой
формулой C4.59).
§ 35. Пограничный слой в сжимаемой жидкости. Обтекание
пластинки. Метод Дородницына. Обратимся теперь к пограничному
слою в сжимаемой жидкости. Как и в несжимаемой жидкости, огра-
ограничимся рассмотрением стационарного случая.
В качестве отправных уравнений мы имеем (см. § 31):
дх
ду
ду \ ду /
4-
ду
ду
C5.2)
C5.3)
В эти уравнения входят кроме величин vx, vy еще р и Т. Величину/)
мы должны считать известной. Именно, по уравнению Бернулли
C5-4)
где U (х) — скорость на внешней границе пограничного слоя, р0 —
давление в той точке адиабатического потока, где скорость обра-
обращается в нуль, at — критическая скорость в адиабатическом потоке.
По закону Клапейрона, р, р и Т связаны соотношением p — RpT.
Таким образом,
C5.5)
о — температура и плотность «адиабатически заторможён-
заторможённого» потока. Заметим, что
где То и о

«45] 11О1РАНИЧЯЫЙ СЛОИ В СЖИ vtArwoiI ЖИДКОСТИ	R09
Наконец, р следует считать известной функцией or T,	в обычных
приложениях принимают закон
($	<35-7>
где (х0 — постоянная, п = 0,5, или « = 0,76, или п=\.
Таким образом, задача сводится к определению vx, v и Т из
системы уравнений C5.1), C5.2), C5.3), причём р задано по C5.4),
а р и [х определяются из C5.5), C5.7) соответственно. Краевые
условия для скоростей остаются те же, что и в несжимаемой жидкости:
vx = vy = 0 при у = 0,	C5.8)
vx—U	при у = оо.	C5.9)
Краевые условия, содержащие температуру, будут разчичными
в разных задачах; так, например, если мы решаем задачу в предпо-
предположении, что температура стенки Tw искусственно поддерживается
постоянной (вопросы теплоотдачи), мы должны просто написать:
при у = 0 T=TW.	C5.10)
Кроме того,
при у = оо Т—Тм,	C5.11)
где Та есть также заданная величина. В задаче обтекания самолыа
или снаряда естественно считать, что поверхность у = 0 предоста-
предоставлена сама себе и что задано лишь Т^, a Tw есть величина неиз-
неизвестная, определяемая попутно вместе с решением задачи. Здесь
можно принять, что отсутствует теплоотдача обтекаемой поверхности,
1. е. что
при у = 0 if = °-	C5-12)
Это предположение обычно и делается при решении задач на обте-
обтекание в вязкой сжимаемой жидкости, хотя точнее было бы принять
условие «теплового баланса», приравняв то тепло, которое поверх-
поверхность получает, к тому теплу, которое она отдаёт. Так, если k"
есть теплопроводность, а Т* — температура обтекаемого предмета и
если принять ещё в расчёт, что обтекаемая поверхность может из-
излучать как абсолютно чёрное тело и что к ней подходит поток ра-
радиации 5 со стороны жидкости, мы должны написать:
_ fc?i._f-fc*EL- = S — oT\	C5.13)
rie
0 = 0,817 • 10~10 г1к<*л см2 мин град4
есть постоянная Стефана—Больцмана.
Кроме того,
Т
Л9 Теоретическая тдриыехаиика,

610	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	(ГЛ II
Пренебрегая притоком тепла, идущим от обтекаемой поверхности,
и считая, что S^aT4, мы вновь придем к условию C5.12).
Переходя к решению нашей системы дифференциальных уравне-
уравнений, преобразуем сперва уравнение C5.3), вводя вместо неизвестной
температуры Т величину 6 из соотношения
Путём элементарных преобразований получим:
<Э6 . C0 \ 1 д I C0 \ . /, 1\ д
^^)' C5Л5)
где Р — число Прандтля, определяемое равенс1вом
и не зависящее от Т.
Величина 0 носит название температуры торможения; она равна
температуре там, где скорость жидкости равна нулю.
Решению уравнений C5.1), C5.2), C5.15) посвящено большое
количество работ, из которых наиболее значительными являются
исследования Буземана, Кармана и Цяня и Дородницына. Наиболь-
Наибольшими преимуществами обладает метод Дородницына. Путем остро-
остроумной подстановки Дородницын приводит систему уравнений к виду,
сходному с тем, что имеет место для жидкости несжимаемой, и полу-
получает широко обозримые результаты. Подстановка Дородницына
заключается во введении вместо координаты х величины \:
X
?_ j P_V±dx<	C5.17)
о
а вместо координаты у — величины г\:
У У
rf, — / г V > // л,. — Р \ ) I 	о^ л,.	{^^ 1 ЯЧ
о	о
Так как
д 	 д р (х) . д dq	д 	 р д
дл di ра "' дт} дх ' ду р0 дг\
то уравнение C5 1) принимает теперь вид:
р dvx	drj dvx	p dvx	dp , p i

§ 35]	ПОГРАНИЧНЫЙ СЛОИ В СЖИМАЕМОЙ ЖИДКОСТИ	611
С другой стороны, по уравнению Бернулли
dx Ро	*+1л2	dx Ро	х + 1 2	di р0
поэтому, деля обе части C5.19) на р —, мы получим, вставляя о
"о
по C5.5):
di V x p dx ' T У] d-q
1	T ,, dl
,
Преобразуем теперь уравнение неразрывности. Вводя функцию тока Ф,
получим:
pvr = -~ — — -X, т. е. vx = —-^-.	C5.21)
х Оу	ро 0ч\	Ро Or)	'
С другой стороны,
дЬ	д<\> dtj d'i p 		dv) p til
так что
р0 dl Т У ~т~ х р дх '
Поэтому, если мы обозначим
т^ + ^7^ = ^	C5-22)
то получим
fr=	т—, и,. =^ — ¦—-лт-.	C5.^3)
х Ро dr)	У	р0 d;	v	;
Теперь уравнение неразрывности можно записать в виде:
а уравнение C5.20) даст
I—Г
¦i9*

612	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. Ц
Мы видим, что в переменных 5 и т; уравнения для vx и V будут
отличаться от уравнений B9.9), имеющих место для жидкости не-
несжимаемой, лишь наличием множителя 7/70 в C5.25).
Преобразуем теперь уравнение притока тепла C5.15). Вводя $
и У] и заменяя Ее по C5.6), получим:
I р C8 , <3i) дЪ\,	р дЬ
х \Ра di дх дт) / '	ро dij
'	Х ' ' '	*	' "	х Х ¦ . C5.26)
1 \ р д / р д vl\
	1 — — f р.Г0	1 )
Деля на р р//?0 и принимая в расчёт C5.22), придём к уравнению
JLJL i 1/ ^ _L —
Если
P=l.	C5.27)
уравнение C5.26) сильно упрощается и принимает вид:
дО . .. дЬ	д Г/ Т \"~l C8
Мы перейдём к подробному изучению этого случая.
Начнём с конкретной задачи обтекания пластинки, расположен-
расположенной вдоль оси Ох. Здесь U = const., так что
U' = 0,
и уравнение C5.25) примет вид:
>г , ,, dvr	д \[ Т \п dvу~\	,„,_ orv4
# + Vv -г5 — vn т- Ьг- I -х^ •	C5.29)
'; ' У dnj ° (Зт) LV ^о / ^ J
¦71
V* д.
Если обозначить
?¦,	C5.30)
Ро
то уравнения C5.23) примут вид:
__ <ЗИ" „ 	 ffi'
Вводя C5.31) в C5.29), получим окончательно:
C5.31)
C5.32)

ПОГРАНИЧНЫЙ СЛОП В СЖИМАЕМОЙ ЖИДКОСТИ	613
в качестве краевых условий мы должны написать:
дЧ~
при т] = оо -j-=?/!).
Наконец, вследствие C5.14), C5.31) получим:
C5.33)
В качестве первого примера решим задачу об обтекании пластинки
без теплоотдачи, т. е. при краевых условиях:
при у)=0 -г—= 0; при у)=оо 7=7^,
или, на основании C5.34) и условия прилипания:
,п	C5.35)
При 7]=ОО	0=70,,+
2Еср
Заметим теперь, что уравнение C5.28) имеет тривиальное решение
6 = const. Если выбрать эту постоянную равной Тт-\-^—, то мы
удовлетворим и краевым условиям l-^—=0). Используя C5.34), по-
получим теперь:
В частности, на поверхности пластинки, где dW/dri = O, будем иметь
температуру
Tw^T^-\-~ .	C5.37)
Замечательно, что мы, не решая уравнения C5.32), можем при по-
помощи C5.37) найти температуру пластинки по температуре набегаю-
набегающей жидкости (Too) и по числу Маха набегающего потока (?//Доо)-
В самом деле, так как
alo = *.RTm = у.Е (ср —¦ cv) Too = срЕ (% — 1) 7ОО,
') Любопытно отметить, что при п — \Т выпадает из уравнения C5.29)
и последнее обращается в точности в уравнение C2.3), если заменить Ч.'
на 'у, < на х, ч\ на у. Так как краевые условия будут и здесь и там одина-
одинаковы, то мы можем здесь прямо заимствовать готовое для несжимаемой
жидкости решение Блазиуса. Нужно только, конечно, установить затем
связь между плоскостью (х, у) и плоскостью (?, г[).

614	ДВИЖЕНИЕ ВЯЗКОП ЖИДКОСТИ	[ГЛ II
мы получим из C5.37):
C5.38)
Если U/aco<dl > температура Tw будет незначительно превосходить 7^.
Но при скоростях жидкости, превосходящих скорость звука или
приближающихся к таковой, пластинка будет нагреваться сильно. Так,
при ?//асо = 0,1 будем иметь Tw— 1,002Гоо. так что, если 7^ — 273,
7^=273,005; если ?//<*=„= 1, Tw= 1,2Тм (при 730=273° 7Щ=327°,6),
если Ujax=\O, Tw = 21 Tm (при 7^=273° 7К, = 5733"). Конечно,
при таких больших температурах едва ли можно пренебречь излу-
излучением пластинки и краевые условия надо, повидимому, взять
в форме C5.13), а не в виде C5.12). К этому вопросу мы ещё
вернёмся, а сейчас обратимся к анализу уравнения C5.32).
Заметим, что в этой задаче температура на стенке Tw будет со-
совпадать с температурой 70 адиабатически заторможённого потока.
В самом деле, по уравнению Бернулли:
сопоставляя с этим равенством C5.36) и C5.37), получим, что
'w = 'о-
Отметим ещё, что давление на стенке будет, как и везде,
Г'^Рс
плотность же на стенке pw будет
Уравнение C5.32), если принять в расчёт C5.36) и C5.37), может
быть записано в виде:
Совершенно аналогично тому, как мы поступали в случае Блазиуса,
введём вместо W величину С по формуле
Ф=2]Л^71С,	C5.41)

q 35]	ПОГРАНИЧНЫЙ СЛОЙ В СЖИМАЕМОЙ ЖИДКОСТИ	615
а также безразмерную величину
t = .1j/"J^.	C5.42)
Предположим, что С зависит только от -с:
С = С (х);
тогда
vx = ~=2V *0Щ 7~ у ^~ = ?/С (х),	C5.43)
и если ввести еще \ = \\
	 г т ^ VS , ^ Г "pi". V l^ (?, *) 	 	 т j2
D (?, п)	D E, х)	D («, г))	2=
Вставим еще в C5.39) , 2 = . г С", перенесем все члены в одну
сторону, произведем сокращения и прив течём C5.6). Получим окон-
окончательно
а]
C5.44)
Уравнение это по виду отличается от уравнения Блазиуса C2.7) лишь
наличием при С" выражения в скобке, возведенного в степень «—1.
Краевые условия для С те же, что и в случае Блазиуса. По C5.41)
и C5.43)
при т = 0 С = 0, С' = 0;
при т = оо С = 1.
В отличие от того, что имеет место в несжимаемой жидкости, ско-
скорость U на бесконечности входит в уравнение для С, но, как мы
увидим далее, вхождение это будет слабым. Однако величина Uja^
будет весьма существенным образом входить в представления X и tj
через х и у.
Для решения обыкновенного дифференциального уравнения C5 44)
Дородницын вводит новую независимую переменную z и искомую
Функцию Z из условий
C5.45)
C5.46)

616	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. II
Уравнение C5.44) даст нам по C5.46):
dZ dz
~dz~4z~
так что по C5.45) получим, сокращая на С":
1
Дифференцируя обе части этого равенства по г и замечая, что
dl
-.— 1 i
получим окончательно
Z-ff = —~A-^I-я •	C5-48>
Граничные условия для функции Z будут
при z = 0 4f =0,	C5.49)
-~ Z = 0.	C5.50)
Решение уравнения C5.48) при граничных условиях C5.49) и
C5.51) проще всего получить, задавая сперва произвольное значе-
значение функции Z при г = 0, назовём его Zo, удовлетворяя условию
C5.49) (задача Коши) и подбирая затем Zo так, чтобы выполнялось
условие C5.50).
После того, как Z(z) известно, легко найти все интересующие
нас величины. Именно, по C5.46) имеем:
Ч/^ТТ ?]	C5.51)
По C6.45)
^ = j/"^|^z-	C5.52)
Так как, далее, С" =="^i" —^ *•' =^' "^~ и ПРИ ^ = 0 z = 0 (ибо
С'@) = 0), то
C5'53)

§ 35)	ПОГРАНИЧНЫЙ СЛОЙ В СЖИМАЕМОЙ ЖИДКОСТИ	617
Наконец, так как С = -^- — у % 4l- z, то
z = \y !Lj-LJLj J ___iiiL_—.	C5.54)
о
Таким образом, все нужные нам величины параметрически находятся
через z.
Чтобы построить профили скоростей и температур, нам остаётся
только научиться переходить от переменных \ и х к переменным х
и у. В нашем случае обтекания пластинки, когда р(х) = const,,
формула C5.17) даёт прямо
где, по C5.4)
-?— =11—	s"	•	C5.55)
Далее, по C5.18), C5.36), C5.39) имеем:
у
	 *, ,Г2— d*	C5.56)
так что

= ?lL f (I -Z2)d'q=2yr^- Р± f A - z*)dx, C5.57)
р J	тир
о	о
и мы можем написать:
			 1 z
У
C5.58)
Найдём ещё сопротивление, испытываемое пластинкой. Напряже-
Напряжение трения на пластинке х0 будет:
ду
1ак что по C5.5) и C5.55) имеем:
1 г.
то=|- /1 -*-1--^-^

618	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. п
Для пластинки ширины b и длины L суммарное сопротивление,
испытываемое как верхней, так и нижней сторонами, будет:
1	X
Введём коэффициент сопротивления cw по формуле
где F—2bL — площадь обеих поверхностей пластинки. Так как
по C5.5)
а по C5.38)
то мы получим после простых преобразований
Наконец, введём ещё число Рейнольдса Rx из равенства
ГЧоо 	 '	,
•от
причём будем помнить, что по C5.7)
Т„\п
получим окончательно
„ _ 2 /. , х-1 ,,2\-5-
На рис. 179 нанесены значения С"@) в функции от величины
U2
— единственного параметра, от которого зависело решение
.4-1 ,
V,— 1
для С. Кривая начинается от значений С" = 0,664, что отвечает числу
Блазиуса BС" @)= 1,328).

ПОГРАНИЧНЫЙ СЛОЙ В СЖИМАЕМОЙ ЖИДКОСТИ
619
На рис 180, заимствованном из работы Дородницына, по верти-
vx г,
кальной оси отложено -^ = (,, по горизонтальной оси отложено
v /~ТГ
\ = —~= 1/ — , причем кривая / дает профиль скоростей для не-
у х ' v0
О 0,1 0,2 02 ОА 0,6 0,6 0,7 0,8 0.9 1,0 Щ а*
Рис 179
сжимаемой жидкости (случай Блазиуса, ср. рис. 177), кривая 2 дает
профиль скоростей при М = 3,05, когда в качестве абсцисс стоят не
у	/ JJ~	у.	I JJ~
—т=-1/ — , а 2т — —~1/ — . Зависимость vJU от т остается
Vх f v0	П У ч0
почти неизменной при изме-
изменении числа Маха, даже
в сравнительно широких
пределах, этого и следовало
ожидать, ибо, как мы уже
отмечали, вид уравнения
C5 44) в переменных т
близок к виду уравнения
Блазиуса в переменных
2/7 0
На рис. 181 по вер-
вертикальной оси отложено
vxlU, по горизонтальной
У /~~~
^7
1,0 15
Рис 180
2,6
У /~~Ц~
^ 1/ 	•
Кривые дают резко различные профили скоростей для
разтичных значений числа Маха.
На рис. 182 по одной оси отложено Т/Т^, по другой снова
У Г~ТГ
~~~— 1/ — ; эго — кривые распределения температур в жидкости.
г х У v „

620
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ.
Для построения их достаточно было воспользоваться формулой, полу-
получающейся сразу же из C5.36):
и уже готовым графиком скоростей. Так решается задача обтекания
пластинки, когда Р=1 и когда теплоотдача отсутствует.
0 4 8 12 16 20 24 28 32 36 40'
Рис. 181.
В качестве второго конкретного примера рассмотрим случай
обтекания пластинки, когда по-лрежнему Р=1, но в качестве крае-
краевого условия на пластинке мы имеем
) = О Т— Т
где Tw—заданное число. Мы будем вновь иметь уравнение C5.32)
и должны решать его при прежних краевых условиях C5.33). Но
ir'VS
О U 8 12 16 Z0 24 28 32 36 40
Рис. 182.
теперь отношение TjT0 будет выражаться иначе. Краевые условия
для 8 будут теперь иметь вид:
при т) = О G = Tw,	|
А Г _L U*	Т )	^35-6°)
При Tj=OO Q = 7 от -|- -=р— ¦=: /0, I

§ 35] ПОГРАНИЧНЫ)"! СЛОЙ В СЖИМАЕМОЙ ЖИДКОСТИ	021
причем 0 должно удовле1ворять по-прежнему уравнению	C5.28).
Леп<о видеть, что это последнее уравнение имеет следующий инте-
интеграл:
е = а4 "?vx,	C5.61)
где а и р— постоянные. В самом деле, подставляя C5.61) в	C5.28).
мы получим:
что после сокращения на р совпадёт с C5.29).
Постоянные аир мы подберём так, чтобы удовлетворялись
краевые условия, и получим:
Теперь вместо C5.36) мы будем иметь:
T-Tw + iTo-TJ+r^L-^™)'.	C5.62)
так что уравнение C5.39) надо заменить на уравнение:
DE, tj) — ° dij Ц 7"o ' V ^о / U д-ц 2ЕсрТа \
Вводя, как и прежде, С и t по C5.41) и C5.42), мы получим
для определения С обыкновенное дифференциальное уравнение
Вводим
Получим теперь вместо уравнения C5.48) уравнение
Краевые условия будут иметь прежний вид: C5.49) и C5.50). Все
величины: С", »', С. т. y/Y'x> легк0 найдутся параметрически через z.

622
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. П
Например, для yjYx получим:
dz.
Наконец, для cw будем иметь:
я-1
причём, по-прежнему
Rco —-
C5.67)
C5.68)
C5.69)
где L — длина пластинки. Заметим, что С"@) зависит теперь от двух
параметров: от числа Маха
ttn.	Ц
М =•— и от отношения Т /То,
1,0\	ут—у	—>-- |	„ а*
где lw — заданная температура
пластинки, а То — заданная
температура в адиабатически
заторможённом потоке. Второе
из этих отношений входит
в дифференциальное уравнение
JTF для Z. Краевые условия содер-
~°-? жат лишь М-
На рис. 183 изображены
распределения скоростей vx/U
г 4 б в ю a it ю
Рис. 183.
V ^
= 4 и для разных
в функциях от —==¦ 1/ — для значений
чисел М-
На рис. 184 даны распределения Т/Тх, которые получаются, по
нижеприводимой формуле, после того как скорости станут известны:
U
^-)\ C5.70)
Поток тепла через единицу площади пластинки будет:
(к дТ\
(к-ду)у=0=1
причём т0 находится по C5.59J.
-1 — i
и
C5.71)

3--.1
ПОГРАНИЧНЫЙ СЛОГ! В СЖИМАЕМО!! ЖИДКОСТИ
623
В качестве третьего примера рассмотрим обтекание пластинки,
предоставленной самой себе, но излучающей. По-прежнему будем
считать, что Р=1. Здесь температура пластинки, так же, как и в
первом примере, будет неизвестна и в качестве краевого условия
для температуры мы примем
C5.13), в котором
причём будем считать его
удовлетворяющимся в среднем,
так что
L
при
T4)dx, C5.72)
Рис. 184.
где L — длина пластинки. Температуру пластинки мы будем считать
постоянной, подлежащей определению х)\ обозначим её через Tw.
Решение для температуры торможения ищем по-прежнему в виде
C5.61) и записываем его в виде C5.62), так что будет опять
Вновь задача сводится к уравнению C5.65), и опять в него будет
входить неизвестное заранее отношение Tw/T0, и решение С будет зави-
зависеть от одного данного параметра М и от одного неизвестного: Tw/T0.
Предположим, что нам удалось найти это решение в общем виде,
для любого значения Tw/T0 2). Тогда условие C5.72) даст нам транс-
трансцендентное уравнение для определения Tw/T0. В самом деле вслед-
вследствие C5.73) имеем:
—T\k(i Tw) 1
=O °t \	Tj U
0у/у=о~"°1Т П/ U ду
или, так как число Прандтля равно	единице,
__		Jo
ду
у=0
U
') Решение задачи будет приближённым в том смысле, что мы берём
в условии C5.72) конечную длину L, а пластинка до сих пор считалась
бесконечной в направлении оси х.
2) Технически это удаётся сделать, отыскивая решение в виде рядов
по " около т = 0 и в виде асимптотических разложений для больших т.

624
движение вязкоп жидкости
[гл
где т0, как и прежде, есть напряжение трения на пластинке; но по
C5.69) имеем:
О	г ¦--» \ '0 /	\ О
поэтому C5.72) примет после простых преобразований вид:
1 + л
C5.74)
в этом равенстве ?"@) есть функция от ?//я» и от TJTQ. Таким
образом, из C5.74) мы можем
найти Tw/T0 в функциях от без-
-18 ¦
Г!
/г
в
г
о
1 ' ' '
^ /
/
/
г
размерного параметра
аГ3„
Vic
с р
Ц1
В/3 0,4 0,5 о,в oj Dfi 0,9
Рис. 185.
и от Ujar. На рис. 185 по оси абс-
цисс отложена величина 2- 104е2М,
по оси ординат — значения Tw/Tm
для различных М- Мы получим
значение TJT^, отвечающее
C5.38), теоретически говоря, лишь
для 1 = 0. При любом конечном L TJTO будет значительно ниже. При
L—>oo мы получим для всех М -=^-—>1.
со
До сих пор мы рассматривали примеры в предположении, что
Р=1. Если РФ1, то приходится обратиться к уравнениям C5.25)
и C5.26). В качестве примера рассмотрим обтекание пластинки, т. е.
случай, когда U' — Q. По-прежнему, вводим функцию Ч' так, что
Уравнение движения примет вид:
а уравнение притока энергии запишется в следующем виде:
д- То di д-ц То

j 34]	ПОГРАНИЧНЫЙ СЛОИ В СЖИМАЕМОЙ ЖИДКОСТИ	625
причём
Уравнение C5 76) не допускает тривиального инте>рала, поэтому
приходится искать решение системы C5.75) — C5 77) в виде
где
То1да C5.75) примет вид:
2СС" + -|г [(Ф — -§r^'2)" *•" } ~ 0> C5.78)
а C5 76) даст после простых преобразований
Таким образом задача сводится к совместному определению двух
функций Ф и С от х из системы обыкновенных дифференциальных
уравнений 5-го порядка C5.78), C5 79) В качестве краевых усло-
Ш1Й мы примем прежде всего три условия для С:
По определению Й C5 77) мы имеем далее:
Ф(оо)=1.
Остается поставить последнее, пятое, краевое условие. Оно, как и
при Р= 1 будет иметь различный вид в зависимости oi того, какую
задачу мы изучаем.
Еали
(?-) - о.
то мы должны написать
ф'@) = 0.
Если
/'тч 	 'р
\ /у = 0	w
где Tw — заданная величина, то
ф@) = ^-
и т. д.
40 Теоретическая гидромеханика, ч II

626	ДВИЖГНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. I]
Для решения системы C5.78), C5.79) удобно принять, как мы
это уже делали раньше при Р=1, в качестве независимого пере-
переменного не t, а переменную:
s U г,
Мы не будем останавливаться на этом общем случае подробнее.
Чтобы выяснить влияние числа Прандтля, положим для простоты
га=1. Это значение близко к действительному значению п для воз-
воздуха (ге»0,8). Тогда Ф выпадает из C5.78) и последнее просто
перейдёт в уравнение Блазиуса
решение которого нам уже известно, уравнение же C5.79) даст
Задача сводится к двум квадратурам. Мы получим, принимая в расчёт,
что Ф(со)= 1:
C5.80)
где с — произвольная постоянная, подлежащая определению из вто-
второго краевого условия для Ф.
Так как
где С" @) = 0,664, то, если (^-) =0, имеем Ф'@) = 0 и с~0.
\ оу /у=о
Мы получим тогда температуру пластинки Tw по формуле:
^==ф@)=1--^1в|
где
со	т
а==A-Р)/(С'0-Р/(СТР^/2^т.	C5.81)
о	о
Таким образом вместо прежней формулы C5.38) мы получим теперь,
|^-1 -f-^(l ~a)M2.
i со	4

а6]	сжимаемая жидкость	627
так как
^М2—Ц	.	C5.82)
о;
2г°
Если Р=1, то а = 0 и мы вернёмся к C5.38). Для воздуха
р^ 0,75 (точное значение: Р — 14/19). Принимая в C5.81) Р = 0,75,
получим путём численного интегрирования а ^0,132').
Таким образом температуры на пластинке при Р = 0,75 будут
несколько ниже, чем «температуры торможения» в C5.38), отвечаю-
отвечающие числу Р = 1.
§ 36. Сжимаемая жидкость. Пограничный слой для произ-
произвольного профиля. В случае криволинейного профиля мы должны
обратиться к уравнениям C5.25) и C5.28). Если ограничиться слу-
случаем, когда теплопередача отсутствует, т. е. когда
^-\ =0, следовательно, (~) ~0,	C6.1)
ду )у=0	Wy/y=o	^ '
то мы можем вновь взять в качестве 8 тривиальный интеграл
6 = С = const. Чтобы найти значение этой постоянной С, обратимся
к условию на бесконечности. Теперь U = U (х), но также и Г^ будет
зависеть от х, следовательно, Г^ = Гсо(х). Эти величины связаны
уравнением Бериулли [глава I, (8.1)], которое, если учесть (8.5) из
главы I, мы можем написать в виде:
х/?Г0
где То — постоянная (температура в том месте, где скорость равна
нулю), R — газовая постоянная. Но по определению G C5.14), мы
имеем:
или, так как
% — 1
') Подсчёт был произведён А. С. Мониным, который, использовав урав-
уравнение Блазиуса, преобразовал предварительно C5.81) к виду:
40»

628	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. It
эта величина должна быть постоянной и равной С. На бесконечности
правая часть C6.3), вследствие C6.2), обратится в То, поэтому
С = То. Определив б полностью, мы можем найти TjT0 в виде:
Вместо уравнения C5.29) мы будем теперь иметь C5.25):
дхъ dvx_ т ии-	___|7___
^1	дг> L\7"o

7.+ 1 ai
где Т/То определяется по C6.4), a Vy — по-прежнему находится из
C5.22) и удовлетворяет уравнению:
dvx дУу __ п
Следуя Дородницыну, дадим приближённый метод решения задачи,
основанный на идее работы Кочина и Лойцянского (см. § 34).
Построим сперва интегральное соотношение, аналогичное соотно-
соотношению Прандтля C0.18). Для этого уравнение C6.5) запишем, вслед-
вследствие C6.6), в виде
dvl . *^__Г ^'__+*о__МГ'^. C6.7)
и уравнение C6.6) (умножив его обе части на U) приведём к виду:
dUvx dVvU	dU
sr + nfr-^^-w	CO)
Вычтем из уравнения C6.8) уравнение C6.7) и проинтегрируем обе
части по т) от 0 до оо. Получим:
По аналогии со введёнными в несжимаемой жидкости толщиной
потери импульса и толщиной вытеснения введём величины:
- C6.10)

j 36]	СЖИМАЕМАЯ ЖИДКОСТЬ
Привлекая C6.4), мы можем написать:
629
U
1 —-
* + Г
-/. 4- 1 а2
*
•л—1 U2
vx—U
1 —
т.—1
1 —
—1
U
х+1 а\
Принимая ещё во внимание, что (Vy)y=0 = 0 по C5.22) и
-) ->0, мы получим из C6.9):
.(?/28-)-|-.
1 —
1 —-
- v0
п=о
inn после деления на
М"* U'
2 +
ML
2/о
1 —
U2
2/„
8-
1_Д!.
3fU C611)
Эго уравнение является обобщением соотношения Прандтля C0.18).
При L/2/2i0—>0 и, заменяя ч\ на у, ? на х, мы вернёмся к несжимае-
несжимаемой жидкости и C6.11) перейдёт в точности в C0.18).
Вместе с Дородницыным будем искать приближённое решение,
предполагая, что безразмерная скорость vJU (x) есть функция от т)/8**
и некоторого параметра E, зависящего от %. Именно, положим, что
^ = ?/(*)Ф/(^
C6.12)
Здесь Ф' означает дифференцирование по первому аргументу, а в ка-
качестве функции Ф от двух аргументов мы примем вновь как раз ту
функцию Хартри, которую Кочин и Лойцянский использовали при
построении приближённого решения для несжимаемой жидкости
[см. стр. 604, формулу C4.51) и др.]; под функцией 5(8) по-преж-
по-прежнему разумеем
СО
\d\,	C6.13)

630
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. It
а Ь** есть функция, входящая в уравнение C6.11). Параметр р ц
функцию Ь** подберём так, чтобы выполнялось соотношение C6. Ц)
и чтобы, кроме того (на обтекаемом профиле т]=:0) выполнено
было дифференциальное уравнение C6.7). Последнее условие, вслед-
вследствие C6.4), даст
ии'	(д^л	C6Л4)
1 —
т Г2
ч
т. е. по C6.12)
V
C6.15)
— ?2ф"'@, Р) =
Таким образом §**, р и $ связаны соотношением
где Ф'" означает третью производную от Ф по первому аргументу.
Обозначим, как и в § 34 C4.56)').
C6.16)
C6.17)
f	1^)]^ = ^-А, C6.18)
о	о
где под А разумеется, как и в § 34, известная функция одного р
где /—известная функция от р. Далее,
Наконец,
Теперь уравнение C6.11) запишется в виде:
и2
2i0
2/„	2L
C6.19)
') Так как Ф удовлетворяет уравнению C4.48) и так как Ф @, (i):
. Ф'@, Э) = 0, то Фда@, р) = — р и C6.16) совпадает с C4.56).

- 36]
СЖИМАЕМАЯ ЖИДКОСТЬ
631
11Ли после умножения на 5**, по C6.19):
После простых преобразований получим:
df.
w
или, если вспомнить обозначение C4.57)]:
df _\U" . 2UU'
U'
/+
C6.20)
Уравнение C6.20) перейдёт в C4.58), если 10—>со.
Используем вновь тот факт, что F(f)tta — bf (см. таблицу на
стр. 607), где а = 0,45, ? = 5,35. Мы получим тогда
¦ U" , 2UW	bW
Отсюда путём простых квадратур (полагая попутно /@) = 0) получим:
Наконец, так как
о	о
то мы можем избавиться от I и написать:
Ь 3*-2
2х-1
Ub~ldx. C6.21)
Эта формула была получена Лойцянским и Дородницыным1). Урав-
Уравнение это позволит, зная U = U (х), найти для всякого х значе-
значение f (х). Так как таблица на стр. 607 даёт нам C и В в функциях
от /, то мы будем знать теперь C и В в функциях от х. Формула
C6.17) даст нам &**. Таким образом может быть построен весь
') Лойцянский Л. Г. и Дородницын А. А., К теории перехода ламинар-
ламинарного слоя в турбулентный, ПММ, т. IX, вып. 4, 1945.

632	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. ц
профиль скоростей. Точка отрыва на профиле получится для того
значения х, при котором f (х), вычисленное по C6.21), даст значе-
значение / = — 0,0681.
§ 37. Основные уравнения теории исчезающей вязкости.
Теория пограничного слоя показала нам, что при движении твёрдого
тела в вязкой жидкости при больших числах Рейнольдса возможен
при известных условиях отрыв от тела вихрей. Мы уже указывали
на большое значение этого обстоятельства для обоснования тех схем
движения тела в идеальной жидкости, в которых существенное зна-
значение имеет наличие вихрей или вихревых слоев (как, например,
схема вихревых дорожек Кармана). Однако во всех таких схемах
имеется известная доля произвола. Чтобы избавиться от этого про-
произвола, следовало бы, рассматривая движение какого-либо тела
в жидкости, решить такую задачу: проинтегрировать точные уравне-
уравнения гидромеханики вязкой жидкости, а затем в полученных интегра-
интегралах перейти к пределу, устремив ^ к нулю. Ничто не заставляет
нас ожидать, что при этом получится как раз движение тела в идеаль-
идеальной жидкости, так как мы многократно уже указывали на то, что
различный характер движений в вязкой и идеальной жидкостях опре-
определяется не только и не столько различием вида уравнений, сколько
различием граничных условий. Задача в таком виде была поставлена
Осееном, который в своих исследованиях сделал и первые шаги
к её разрешению, совершив предельный переход для упрощённой
системы уравнений движения вязкой жидкости.
Не имея возможности, за недостатком места, изложить ориги-
оригинальные методы Осеена '), мы дадим эвристический вывод тех урав-
уравнений, к которым он приходит; основные идеи этого вывода при-
принадлежат Бюргерсу2).
Мы будем исходить из уравнений движения вязкой жидкости E.4)
в форме Ламба, причём сразу же предположим, что внешние силы
отсутствуют, так что эти уравнения принимают вид
dv	1
-т	© У rot © =	grad a A- v Дф; divs = 0,	C7.1)
at	р ъ ^ '	х
где
Я — Р -\-~f ¦	C7.2)
Предположим теперь, что в вязкой безграничной жидкости дви-
движется с постоянной по величине и направлению скоростью U твёрдое
тело, ограниченное поверхностью 6\ Для определённости примем, что
') О seen С, W., Hydrodynamik, Leipzig, 1927. См. также изложение
теории Осеена в книге Н. V i I I a t, Lecons sur rhydrodynamique, Paris, 1929.
2) Burgers J. M., On Oseen's theory for the approximate determination
of the flow of a fluid with very small friction along a body, Proced. of
the Kon. Akad, von Wetenschappen Amsterdam, 31 A928), № 4 и 5.

§ 37]	ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ИСЧЕЗАЮЩЕЙ ВЯЗКОСТИ 633
5 есть выпуклая поверхность. Свяжем с телом систему осей х, у, г,
причем ось Ох выберем так, чтобы тело двигалось как раз в на-
направлении положительной оси Ох. Введём ещё на время систему
осей х, у, z, неподвижных в пространстве и совпадающих в момент
времени i = 0 с системой осей х, у, г. Ясно, что между координа-
координатами х, у, z и х, у, z имеют место зависимости
x=--x — Ut, y = }>, z=H.	C7.3)
Будем под v понимать вектор абсолютной скорости частиц жидкости,
т. е. вектор скорости частиц жидкости относительно системы
осей х, у, z. С другой стороны, мы будем считать движение ста-
стационарным относительно системы осей х, у, г. Но тогда ясно, что
вектор V есть функция только от х, у, г, а так как для всякой
функции f (х, у, z) = f(x— Ut, у, z) = fl(x, у, z, /), мы имеем
тождество
Т) равенство C7.1) в системе осей х, у, z принимает вид:
— U-— — я X rot я = — — grad^-f-vAo.	C7.5)
Наибольшие трудности интегрирования этого уравнения связаны
с присутствием квадратичного члена fXrottf. Мы допустим, что
можно этим членом пренебречь. Тогда мы получаем систему урав-
уравнений:
цДф + р?/^ —grad? = 0; divtf = 0,	C7.6)
причём д имеет значение C7.2). Так как на поверхности тела 5
абсолютная скорость частиц жидкости v должна совпадать со ско-
скоростью точек самой поверхности тела, то мы легко можем написать
граничные условия в следующем виде:
vx = U, fy = 0, vz = 0 на 5.	C7.7)
Система уравнений C7.6) и послужила предметом исследований
Осеена. Как мы видели, эта система получается из точных урав-
уравнений гидромеханики вязкой жидкости, если в последних пренебречь
квадратичным членом ©Xroti», содержащим вихрь скорости, иными
словами, если пренебречь вихрями. Если бы в результате перехода
к пределу ^->-0 в интегралах точных уравнений движения вязкой
жидкости мы получили теорию идеальной жидкости, а в частности
отсутствие вихрей, то при очень малых значениях (л вихри были бы
очень малы, т. е. наше допущение о пренебрежимости вихрями было
бы оправдано, и мы, исходя из решений уравнений C7.6), должны

634	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ ц
были бы в пределе при «j. —> 0 тоже получить теорию идеальной
жидкости. Как показал Осеен, это не имеет места, а следовательно,
теория исчезающей вязкости должна отличаться от теории идеальной
жидкости.
Установим теперь некоторые общие свойства движений, опреде-
определяемых системой уравнений C7.6). Беря вихрь от обеих частей пер.
вою из уравнений этой системы и вводя обычное обозначение
rot v — й,
мы получим уравнение
Рг/^ + |*да = о,	C7.8)
заменяющее для рассматриваемого случая обобщённое уравнение
Гельмгольца (8.2).
Чтобы истолковать это уравнение, вернёмся к координатам х,
у, z относительно неподвижных в пространстве осей координат.
Применяя тождество C7.4), можем переписать предыдущее уравне-
уравнение в виде
pg-цДЙ.	C7.9)
Если в этом уравнении положить ц — О, то получится равенство
dt ~v'
из которого следует, что в каждой точке пространства вихрь сохра-
сохраняет неизменное значение. Полное же уравнение C7.9) выражает,
как мы знаем, процесс диффузии вихрей. Но равенства C7.3) показы-
показывают нам, что неизменной точке пространства соответствует в си-
системе осей х, у, г точка, перемещающаяся в отрицательном напра-
направлении оси Ох с постоянной скоростью U. Следовательно, смысл
уравнения C7.8) состоит в следующем: вихри перемещаются в отрица-
отрицательном направлении оси Ох с постоянной скоростью U, при этом
несколько рассеиваясь. В пределе, при \х—>0, процесс диффузии
вихрей исчезнет и, следовательно, вихри будут, сохраняя постоянное
значение по величине и направлению, перемещаться вдоль отрица-
отрицательной оси Ох с постоянной скоростью О. В частности, мы будем
иметь равенство
?=0.	C7.10)
Но так как мы имеем дело не с безграничной жидкостью,
а с жидкостью, в которой движется твёрдое тело, то нужно учесть
ещё то вихреобразование, которое происходит на поверхности этого
тела, и о котором уже была речь выше при изложении теории по-
пограничного слоя.

37)
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ИСЧЕЗАЮЩЕЙ ВЯЗКОСТИ	635
Во всяком случае, из этих общих рассуждений совершенно ясно,
какую картину распределения вихрей мы должны ожидать для того
движения, которое получается в результате предельного перехода
а—>0 из движения, удовлетворяющего уравнениям C7.6).
Остановимся для определённости на случае плоского движения.
По предположению, контур С, двигающийся параллельно оси Ох,
есть выпуклый контур (рис. 186). Проведём крайние прямые KXL{
и K2L2, параллельные оси Ох и имеющие с контуром С всего но
одной общей точке, соответственно Кх и К?. Эти точки разобьют
контур С на две части: перед-
переднюю Сх и заднюю С2. Тогда,
как показано на рисунке, полу-
полупрямые KXLX и K2L2 ограничат
область D2\ всю же остальную
область течения обозначим че-	lj~	•"* 0 '	*~~х
рез Dv
Мы утверждаем теперь, что
во всей области Dx вихрь Si
для предельного течения обра-
обратится в нуль. В самом деле,
из предыдущего рассуждения совершенно ясно, что те вихри, кото-
которые сходят с поверхности тела, могут попасть только в область D2.
Поэтому, если принять ещё, что на бесконечно далёких расстояниях
перед телом жидкость покоится, то вихри во всей области Dl будут
отсутствовать, в области же D2 эти вихри должны удовлетворять
условию C7.10).
Совершенно аналогично в случае пространственного течения мы
должны около поверхности тела 5 описать цилиндр, образующие
которого параллельны оси Ох; пусть этот цилиндр касается поверх-
поверхности 5 по линии /.; последняя разобьёт поверхность 5 на две
части: переднюю Sx и заднюю 52. Часть S2 поверхности 5 вместе
с той частью поверхности цилиндра, которая тянется в направлении
отрицательной оси Ох, являются границами для вихревой области D2
предельного течения, во всей же остальной области течения, которую
мы обозначим через Dx, вихри будут уже отсутствовать.
Возвратимся теперь к плоскому течению. Вихрь Q имеет в этом
случае всего одну составляющую по оси г, которую мы обозначим
через С
^~ дх ду •
По условию C7.10) С не зависит от х и является функцией только
°т у, притом отличной от нуля только в области D2.
Как мы видели, равенство C7.8) переходит в пределе при [х-»0
в равенство C7.10), имеющее место как внутри области Dv так п

636	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[гл ц
внутри области D2. Точно так же первое из равенств C7.6) обра-
тится в пределе при ц—>0 в равенство
pU ~
которое даст нам соотношения
Мы видим, что -~ и —vy суть гармонические сопряжённые функ-
функции, так что
где z — x-\-ty. Вводя обозначение
w(z) = f f(z)dz = <f(x, y)-\-ity(x, у),
будем, очевидно, иметь
/(z) = |?_,?,
J х ' дх ду
т. е. во всей области течения имеем формулы:
причём функция <р(х, у) есть решение уравнения Лапласа
Что касается составляющей vx, то в части Dx области течения,
в которой вихри отсутствуют, мы можем, очевидно, принять, что
*, = ?.	C7.13)
в области же D2 мы имеем из первого уравнения C7.11):
^=^Г + *(У). т- е- <>х = ^ + л(У)-
Рассмотрим теперь, какому граничному условию должна удовле-
удовлетворять функция ср на передней части контура С1. Для вывода этого
условия удобнее рассматривать относительное движение жидкости
относительно тела, которое получается, если на абсолютное движе-
движение наложить прямолинейное равномерное движение вдоль отрица-
отрицательной оси Ох со скоростью U, т. е. движение с составляющими
скорости—U, 0; в результате проекции относительной скорости

: 37]
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ИСЧЕЗАЮЩЕЙ ВЯЗКОСТИ	637
получатся равными vx— U, vy. Заметим теперь, что при малых
значениях ц, т. е. при больших числах Рейнольдса, вдоль Сх обра-
образуется пограничный слой, толщина которого при R —> со стремится
к нулю. Внутри этого пограничного слоя будет происходить посте-
постепенный переход касательной к контуру составляющей относительной
скорости от нуля до тех значений, которые эта составляющая имеет
в потенциальном потоке; что же касается нормальной составляющей
относительной скорости, то она при R—>оо стремится к нулю.
Можно поэтому ожидать, что при [л->0 мы будем иметь на части
контура С, следующее граничное условие:
vn0 = 0 на Cv
где 1>п0 есть нормальная составляющая скорости относительного
движения, т. е.
vn0=z(vx—U)cos(n, *)H- fycos(«, у).
Пользуясь формулами C7.12) и C7.13), найдём:
17, COS (ft, x)-\-VyCOS(tl, у) = |^ COS (ft, X) + ^ COS (ft, у) = ^
и, следовательно, граничное условие на Ct мы можем написать сле-
следующим образом:
-?- = и cos (ft, x) на С,.
В дальнейшем мы будем под ft понимать направление внешней
нормали к контуру С. Таким образом для части контура Сх полу-
получилось то же самое граничное условие, которое имеет место для
идеальной жидкости.
На первый взгляд может показаться непонятным, что, исходя из
условия прилипания
vx=U, vy = 0 на Cv	C7.14)
мы, после предельного перехода ц—>0, получили лишь одно гра-
граничное условие
vxcos(n, x)-\-vycos(n, у) = U cos (ft, x) на Cv C7.15)
Здесь все" дело заключается в том, что интегралы системы урав-
уравнений C7.6) при jj. —> 0 стремятся к своим пределам неравномерно.
Но, как известно, при неравномерной сходимости пределом последо-
последовательности непрерывных функций может оказаться разрывная функ-
Ция. Приведём этому простой пример. Пусть имеем функцию

638	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ I,
зависящую от параметра р.. При всяком положительном р. эта функ-
функция есть непрерывная функция от х, причём при х — 6 мы имеем
равенство
/О*. 0) = 0.	C7.16)
Устремим теперь \ь к нулю. Если х ф О, то ясно, что при [j.->q
мы будем иметь предельное равенство
lim
С другой стороны, из C7.16) ясно, чго
*, 0)=0.
Поэтому, вводя обозначение
lim /((i, x)=F(x),
мы будем иметь
/=¦ @) = 0, /="(л;)=1 при хфО.
Тлким образом предельная функция F(х) имеет при л; = 0 разрыв.
Совершенно такие же обстоятельства имеют место и в рассматри-
рассматриваемом нами случае. Интегралы системы уравнений C7 6) удовле-
удовлетворяют на контуре С1 условиям C7.14). Но когда мы совершим
предельный переход jj. —> 0, то в пределе получатся такие функции,
которые будут в точках контура С1 терпеть разрыв. Для этих пре-
предельных функций в точках самого контура С1 будут выполняться
граничные условия C7.14), но в бесконечно близких к контуру С\
точках области Dj будет уже выполняться граничное условие C7.15),
подобно тому как для функции F(x) при положительном, но сколь
угодно малом х мы получаем значение 1, а не 0.
Рассмотрим теперь граничные условия на задней части контура Сг
vx = U, vy = 0 на С2.	C7.17)
Так как в D2 мы имеем формулы:
то условия C7.17) приводятся, во-первых, к условию для опреде-
определения ср
J?=0 „a С2,
ду	2
а, во-вторых, к условию для определения а (у):

ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ИСЧЕЗАЮЩЕЙ ВЯЗКОСТИ	639
где {ду1дх)мг озиачает значение функции dcp/дл; в точке М2 кон-
контура С2 имеющей заданную ординату у (рис. 186).
Собирая все полученные результаты, мы приходим к следующим
формулам, определяющим течение рассматриваемого нами типа:
dy B
— -^- в
Здесь М2 есть та точка конгура С2, которая имеет ту же орди-
ординату у> что и точка Ж области ZJ, в которой определяется <ох
(рис. 186). Функция <?(х, у) есть решение уравнения Лапласа
удовлетворяющее граничным условиям:
^ = Ucos(n, х) на Сх, р- = 0 на С2.	C7.20)
Кроме того, должно выполняться еще очевидное условие на беско-
бесконечности
g-0, g^O при V^+72^oo.	C7.21)
Функция q определяется формулой:
и следовательно, давление р определяется формулами
Г
На линиях ATjZ-! и ЛГ2^-2' отделяющих область Dj от области D2,
составляющая скорости vx и давление р терпят разрыв. Это обстоя-
обстоятельство сильно уменьшает значение полученного решения. Нужно
обратить внимание также на то, что в основу вывода было положено
Допущение о пренебрежимости вихрями, в то время как в полученном
решении вся область D2 оказалась заполненной вихрями.
Переходя к пространственным течениям, мы рассмотрим только
частный случай осесимметричного течения, причем будем пользоваться
Цилиндрическими координатами х, г, 6. Система уравнений C7.6)
Переходит в пределе при ja —> 0 в систему
pL/ ^ — grad q — 0;

640	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ ц
Так как мы считаем движение осесимметричным, то г/й = 0, a vx, v
и q могут зависеть только от х и г, поэтому предыдущие уравне-
ния принимают вид:
дх
fjt/^ —™ =0,
dvx 1 д (rvr) _ n
дх ' r dr
C7.23)
Кроме того, мы должны записать ещё условие отсутствия вихрей
в области Dy
дг дх
Поэтому среднее из уравнений C7.23) даёт нам, что
да ,, dvx „
~i- = pU —-i В Д.
Соединяя это равенство с первым из равенств C7.23) и замечая,
что q определяется только с точностью до постоянной, легко выве-
выведем, что
q = pUv_, в Dv	C7.24)
Но второе из уравнений системы C7.23) показывает, что во всей
области течения существует функция ср(л\ г), такая, что
На основании первого из уравнений системы C7.23) во всей
области течения
^S^fl.	C7.26)
дх дх2
а тогда последнее из уравнений системы C7.23) даёт нам, что
д»ч , 1 д
т. е. что ср удовлетворяет уравнению Лапласа
Дер = 0.
В области Dv вследствие равенств C7.24) и C7.25), мы имеем:
дх
В области же D2 на основании равенства C7.24) получим:
»Лх.г) = &?4- + о(г) в D,

i 38]
РЕАКЦИЯ ПОТОКА НА ТЕЛО
641
Установим теперь граничные условия. На передней части тела Sl
мы, аналогично условию C7.20) плоской задачи, получим условие:
^ = U cos(n, х) на Sv
На задней же части S2 поверхности тела мы потребуем выполнения
условий прилипания; в результате получим, во-первых, условие для
определения функции <р:
Jf == 0 на 52,
и, во-вторых, формулу для определения функции а (г):
где М2 есть точка поверхности S2, имеющая заданную координату г.
В окончательном итоге для случая осесимметричного течения мы
приходим к следующим формулам:
dtc	д<? „
:^ ,	v. = т^ в и,,
ox	r or	l
C7.27)
"ох 2 [До.*/ \дг ] J
Здесь tp(x, г) есть решение уравнения Лапласа:
. д2<о , 1 д
Удовлетворяющее следующим граничным условиям:
• = t/cos(/i, х) на Sv ^=0 на S2,
дп
¦ оо.
C7.28)
C7.29)
Осеен получил в результате предельного перехода [х->0 уравне-
уравнения для более общего случая, чем тот, который рассмотрен нами.
Для частного случая прямолинейного равномерного движения тела
его уравнения совпадают с полученными только что нашим нестро-
нестрогим методом уравнениями.
§ 38. Реакция потока на тело. Вычислим теперь силы воз-
Действия потока на тело для рассматриваемых течений, причём
ограничимся только случаем плоской задачи. Если К и Y суть
41 Теоретическая гидромеханика, ч. II

642
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ.
проекции на оси координат силы воздействия потока на контур с,
то очевидно:
X — — j p cos (n, x)ds, К — — Г р cos (п, у) ds.
с	с
На основании формул
их — — ds cos (п, у), dy = ds cos («, х),
можем написать
= — fpdy, Y=
. C8.1)
Применяя к точкам контура С формулы C7.22) и замечая, что
на С2 имеем ду/ду — 0, получим:
у — ^ дх 2\\дх) г \ ду
Введя в рассмотрение функцию
будем иметь:
p = Pl на
и следовательно:
на Сь
C8.2)
^f] на С2
¦ C8-3)
Положим теперь
C8.4)

§ 38]	РЕАКЦИЯ ПОТОКА НА ТЕЛО	643
тогда
где щ> = ср-j-Д!>. а ф есть функция, гармонически сопряжённая с ср.
Но dwjdz есть однозначная аналитическая функция от z вне кон-
контура С, обращающаяся в нуль на бесконечности; следовательно,
вблизи бесконечно далёкой точки мы имеем разложение
dw 	 д<р , д<? 	 й| |^ й2 .^	.„Q ,..
И у	rt v	rt\t ' ¦? ' -?2 I • • •	V, °- У
Поэтому
' / dw \*
Ы
с
так как вместо С за контур интегрирования можно взять окружность
сколь угодно большого радиуса, на которой подынтегральная функ-
функция имеет порядок 1/|г|2.
Итак,
A ~\-tB = О, А=—1В.	C8.6)
Далее
/ (? ? Й	^ ] * =-
что вследствие граничных условий даёт:
с,
)
С»
Но формулы C8.3), C8.4) и C8.6) показывают, что
41»
С	Са

644
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ.
Подставляя сюда значение В и отделяя вещественную и мнимую части,
легко найдём после простых вычислений:
х-%!{%-
C8-7>
с
с,
где Г = — 2тг Im ax есть циркуляция для течения с потенциалом
w = «р —|— /ф. Заметим, что значение А" всегда получится отрицатель-
отрицательным, так как при положительном обходе контура С значения dy
на С2 отрицательны.
§ 39. Обтекание цилиндра. Как первый пример применения
предыдущих уравнений разберём задачу об обтекании цилиндра
радиуса а. Нам нужно прежде всего определить гармоническую
функцию ср по условиям
-Д
= U cos (га, х) на Cv
-|^->0 при
-Х
= 0 на С2,
Функция ср—(Ух удовлетворяет первым двум условиям, но не удовле-
удовлетворяет условиям на бесконечности. Положим
?=l/jt + Ti;	C9-1)
обозначим через ф} функцию, гармонически сопряжённую с <pi> и
введём ещё комплексную функцию
заметим, что wx очень удобно рассматривать как комплексный потен-
потенциал некоторого вспомогательного течения.
Для функции срх мы будем иметь такие граничные условия:
4?
да
= o на
ду
= 0 на
Положим, наконец,
при
ду
C9.2)
Ясно, что ю (г) есть аналитическая функция от z\ легко выяснить
механическое значение вещественной и мнимой частей этой функции.
А именно, обозначим через V абсолютную величину скорости вспомо-

§39]
ОБТЕКАНИЕ ЦИЛИНДРА
645
гательного течения, а через & — угол, составляемый этой скоростью
с осью Ох. Тогда мы будем иметь:	„
OlL=V cos 0-,
дх
ду
C9.3)
и, следовательно,
откуда видно, что
C9.4)
Рис. 187.
Но вследствие граничных условий C9.2) векторы скорости во вспомо-
вспомогательном течении имеют направления, указанные на рис. 187. Таким
образом мы имеем следующие граничные условия для функции Ь:
ДЛЯ 	ТС
для
для
я
2"'
-~ <е<о,
для
| < е < iz.
C9.5)
При 9 = 0 функция 8-j терпит конечный разрыв.
Применим теперь формулу Шварца, определяющую аналитическую
функцию / (z) = к-f-ш, которая регулярна вне единичного круга и
вещественная часть которой принимает на контуре окружности
радиуса а заданные непрерывные значения иДб):
в этой формуле а есть произвольная вещественная постоянная.
Формула Шварца годится и для интересующего нас случая, когда
Функция «г (Э) в нескольких точках терпит конечный разрыв: а именно
в этом случае граничное значение вещественной части функции f (z)
будет равно их(Ъ) во всякой точке контура единичного круга, в кото-
Рой «j F) непрерывна.

646	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[Гл
Итак,
»*» + /1пГ—^ f^)j^dB + iz. C9.7)
— ТС
Подставляя в эту формулу z — со, найдем:
Но по формулам C9.5):
Следовательно,
(о (оо) = тс -f ':a, ('-^-) = е
С другой стороны, вследствие граничного условия на бесконеч-
бесконечности C9.2) должно быть
еначит мы должны принять
a = ln U.
Теперь формулы C9.7) и C9.5) позволяют написать:
т	О
1
2 ' / в*«в-г
2«J U
о ^
НО	it
/ 	!—dv = — 2ic, если 2 > a,
2
J
о

39,	О5ТЕКАНИЕ ЦИЛИНДРА	647
«этому получаем следующее окончательное выражение для
причём берётся то значение логарифма, которое при z = oa обра-
обращается в 0.
Исследуем прежде всего характер течения на бесконечности. Мы
имеем при \z\ > 1 разложение:
но
2"
J
о
ЛЯ	ЛЯ	ПТ.
= 2/-
2
Je — j
поэтому
2	^	ПЯ	ля
S111 ~т^ *~~~ ^— COS
~2
Далее
значит при \z\ > 1
C9.10)
Отсюда

648
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. J,
и окончательно, обозначая через w=^-\-iif комплексный потенциал
абсолютного движения в области Dv будем иметь:
dw
dw,
к — 2 а
C9.11)
Эта формула показывает, что далеко перед телом течение имеет
такой же характер, как если бы оно происходило от источника
находящегося в начале координат и имеющего мощность
= 2aU(iz — 2)= 2,283а".
C9.12)
Теперь найдём распределение скорости вдоль цилиндра. Для этого
нам нужно найти мнимую часть функции ia(z) при z — aet9°. Мы имеем:
а-п0 _ о-в0
«—6„
• = — / ctg ¦
-I-
е —в
Чтобы иметь дело только со сходящимися интегралами, сделаем еле-
дующее преобразование:
	2	2
Г д ае'8 + z .й д Г аел + г fl , Г ,fl fl ae'« + г ..
/ 6 —^т— ^е = бо / —^Г— d®+ / F — V —г11—- ^9 =
J аел — г	J ае'н—г	J	аел—г
ТС
-I—+7
причём мы воспользовались двумя последними формулами C9.8)
Положим теперь в формуле C9.9) z — aelbi> и отделим мнимые части
замечая, что при z = ael% мы имеем
— аеы\ — 2а
sin-
и что, следовательно,
Rein
- = ln

5 39]
ОБТЕКАНИЕ ЦИЛИНДРА
649
мы легко получим следующее выражение логарифма абсолютной вели-
величины скорости вспомогательного течения при z = aeibK
i / се —
^-^e. C9.13)
Если ввести нечётную функцию
то будем иметь:
1
1
F —
Jt	во_
4 2
= -?- f
C9.14)
х Во
Jt Во
2+Т
о	6
Поэтому получаем следующую формулу:
X
ипт||яп(т~т)|
C9.15)
Нас интересуют значения 90 в промежутке (— к, тс); из преды-
формулы следует, что для вычисления V1 необходимо знать
значения функции /F) в интервале @, Зтс/4); эти значения даны
в таблице IX (см. стр. 607). Отметим попутно, что /(тс/2) = In 2.
После этого мы можем вычислить значения Vx\ в частности, при
9о=тс/2 мы имеем V1 = t/V~2-
Принимая, далее, в расчёт формулы C9.1), C9.3) и C9,5), мы
найдём следующие выражения для значений <?<?/<?# и <?<р/<Эу на

650	движение вязкой жидкости
контуре цилиндра:
1ГЛ.
и y
', -g_ = —VlCos8 для —-J<Q<0,
. = — V, sin в -|- С/. -^- = V,
для
C9.16)
По формулам C7.22) мы можем затем определить распределение
давления на конгуре С:
==±(U2-V\) для 0<e<-J, |
= -|AЛ —21%) для |<9<и. |
C9.17)
Что касается распределения скоростей внутри области течения,
то, определив по формуле C9.9) & и V, мы будем, на основании
C9.1), C9.3) и C7.18), иметь
Таблица X следующие формулы:
0°
0
9
18
27
36
45
54
63
/(8)
0,000
0,100
0,198
0,293
0,382
0,465
0,539
0,601
72
81
90
99
108
117
126
135
/(8)
0,650
0,682
0,693
0,680
0,636
0,554
0,424
0,228
¦Vv
C9.18)
¦у = V sin & в D2,
vx — V cos » +¦ и ¦
Vy = V Sin г) В ?>,,
причем берётся значение Vx в той
точке контура С2, которая имеет
ту же ординату у, что и точка М
области D2 в которой опреде»
ляется vx.
При переходе из области Dx
в область Ь, составляющая ско-
рости vx терпит разрыв, величина которого равна
Это значит, что вдоль прямых линий, отделяющих область D\ oT
области D2, имеются вихревые слои.
Точно также из формул C9.17) ясно видно, что на тех же линиях
и давление терпит разрыв, величина которого в точках К\ и ^2

39]	ОБТЕКАНИЕ ЦИЛИНДРА
оТдешющих С1 or C2, равна:
651
) «
2
— l) = _ 0,414pt/2.	C9.19)
Если бы мы определили давление в задней части течения D2
формулой
+ {V2—\)pU2, C9.20)
отличающейся от формулы C9.17) только постоянным слагаемым,
то давление на всём контуре С менялось бы непрерывно, но всё-таки
на линиях KlLl и K2L2 (рис. 186) давление продолжало бы терпеть
разрыв.
Приведём теперь таблицу XI, дающую значения VJU и р ¦
в точках контура С:
Таблица XI
8°
0
9
18
27
36
45
54
63
72
81
90
и
0,000
0,280
0,552
0,807
1,038
1,236
1,395
1,507
1,563
1,551
1,414
р
hu
1,000
0,922
0,696
0,349
0,076
—0,528
—0,946
—1,270
—1,443
—1,405
—1,000
6°
90
99
108
117
126
135
144
153
162
171
180
и
1,414
1,274
1,217
1,183
1,160
1,144
1,133
1,125
1,120
1,117
1,116
р
hu'
—1,828
—1,548
—1,434
—1,366
—1,320
—1,288
—1,266
—1,251
—1,240
—1,235
—1,233
Наконец, применяя формулу C8.7), мы можем вычислить сопро-
сопротивление, испытываемое цилиндром при его движении, в виде
C9.21)
Чт° после численного интегрирования даёт нам сопротивление
C9.22)

652
ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
[ГЛ. „
Это значение слишком велико по сравнению с экспериментальными
данными и объясняется тем, что в то время, как распределение
давления на передней части цилиндра довольно хорошо соответ-
соответствует опытным данным, давление на задней части цилиндра, вычислен-
вычисленное по формуле C9.17), оказывается чересчур низким. Производя
вычисление давления по исправленной формуле C9.20), мы должны
во всех точках задней части цилиндра увеличить давление
на 0,414рG2. В результате получается уменьшение сопротивления
на 0,414pf/2 • 2а — 0,83р(У2а и, следовательно, в этом случае мы
будем иметь
W = 0,48pU2a,	C9.23)
что гораздо лучше соответствует опытным данным.
§ 40. Обтекание плоской пластинки. В качестве второго при-
примера применения уравнений теории исчезающей вязкости рассмотрим
обтекание прямолинейной пластинки. Пусть пластинка К\К% длины 21,
Рис. 188.
Рис. 189.
наклонённая к оси Ох под углом а, движется параллельно оси Ох
со скоростью U (рис. 188).
Отобразим внешность контура КХК2 на внешность единичного
круга в плоскости Z так, чтобы точка Кх перешла в точку /,
а точка z —со перешла в точку Z = co. Для этого надо взять
при этом точка К2 переходит в точку Z = — /(рис. 189). Построим
теперь вспомогательное течение wt — cpx -(- /^ по условиям C9.2).
Полагая по-прежнему
-gi-=:e-'ffl^. U)Br) = & + /!nV	D0.2)

40]
ОБТЕКАНИЕ ПЛОСКОЙ ПЛАСТИНКИ
653
я рассматривая ш как функцию от Z, легко найдём значения 9-
в точках окружности единичного радиуса. В самом деле, векторы
скорости вспомогательного течения имеют, очевидно, направления,
указанные на рис. 188. При этом точка разветвления потока С нам
пока неизвестна.
Итак, граничные условия для функции 0 таковы:
D0.3)
где т—аргумент точки С, соответствующей в плоскости Z точке С.
Применение формулы C9.7) сразу определяет нам функцию ш:
т
для
для
для
-f<9<
— -J и
•
с-г.
ш (z
= — -о— / я —-11-— с?0 — s— / к	~— db —
где р — вещественная произвольная постоянная. Но
причём берётся то значение логарифма, которое при Z = co при-
приводится к нулю. Поэтому после простых вычислений получим:
Подставляя сюда z — co, Z = oo, получим
г=со
|| так как вследствие граничного условия на бесконечности C9.2)
Должно быть

654	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ. Ц
а с другой стороны f должна лежать в интервале (—я/2, я/2), то
необходимо взять
Итак, мы получаем следующее окончательное выражение для функ-
функции ш (г):
ш(г) = тс-f- /In t/ -f— iIn—~	.	l-^-ln ~'. . D0.4)
Для комплексной скорости вспомогательного течения мы находим:
D0.5)
Введём еще одну переменную С, положив
Z—i
: = /¦
Z + i
при этом внешность единичного круга в плоскости Z переходит
в верхнюю полуплоскость С, точка О' в 1, точка К[ — в О, точка О'
в — 1. Между z и С существуют простые соотношения
z = lel -ТТ1-,' =1/ —rr1-	D0-6)
Окончательно для комплексной скорости абсолютного движения
в области Dj мы найдём после простых вычислений следующее
выражение:
dz ~ ^ dz
о. I
1-
= t/ 1-е-* cos^- ^^p_sin^ f^-Г ' ¦ D0-7)
Чтобы выяснить характер течения на бесконечности, лучше ис-
исходить из формулы D0,5); замечая, что
а	а
легко найдём, что
dw	Ui /, _,•<* 2з
и вследствие формулы преобразования D0.1)
dw	U
Г .- =^5+ .... D0.8,

§ 40]	ОБТЕКАНИЕ ПЛОСКОЙ ПЛАСТИНКИ	655
где
А = Ц.{\— cosa+~cosa), B^^-fl — ^) sina. D0.9)
Полученная формула показывает, что далеко перед телом тече-
течение имеет такой характер, как если бы оно происходило от сово-
совокупности источника и вихря, находящихся в начале координат, причём
мощность источника равна
Q = 2~ А — Ю [- — я cos a -f- 2а cos а],	D0.10)
а интенсивность вихря равна
Г = 2пВ = II) (тг — 2а) sin а.	D0.11)
При малых значениях а циркуляция получается равной rdUa, в то
время как по теории Жуковского циркуляция должна равняться
2rdUv.. Значение циркуляции, имеющее место в действительности,
лежит между этими двумя значениями.
Течение в области D± определяется формулой D0.7). Чтобы опре-
определить течение области D2, необходимо вычислить значения функ-
функции D0.7) в точках задней стороны пластинки. Для этих точек С
лежит в промежутке (—со, 0), a z имеет значение х -\- yi = у ctg a -j-
-j-/y = ——е1"; поэтому из формулы D0.6) следует, что
: Sin а — у
'¦ Sin а -(- У
Мы имеем далее:
_— 	 la / I Sin а—У \2тс	f"i=~' 		/а / / Sin а— у \ 2тс
' \ / sin а + у ) '	"	\ / Sin а + У /	'
и поэтому по формуле D0.7) находим:
df 	. /у I I	jx_{ I sina — у \2*	 . а / / sin а — у \ гТ~ Т I
¦р- = 0 на С2;	D0.12)
применяя после этого формулы C7.18), найдём течение в области О2.
Вычислим, наконец, сопротивление, испытываемое пластинкой,
Для чего применим формулу:
-г sin я
2 ./ \ дх	) 7 2 ,/ \ дх	) *
Подставим сюда предыдущее выражение для ду/дх и воспользуемся
подстановкой
у = 1ц sin a;

656	ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ	[ГЛ
тогда получим
а 1
Но если положить
то будем иметь
-1	О
Теперь без труда после ряда тригонометрических преобразований
получим:
Х = -№Гк_{к_2а)со*2*_1	D0.13)
2L	' COS a J	v	'
Аналогичным образом, пользуясь второй из формул C8 7) и зна-
значением Г из формулы D0 11), мы могли бы вычислить Y. Но в дан-
данном случае достаточно заметить, что все элементарные силы давле-
давления направлены по нормали к пластинке. Поэтому результирующая
сила должна быть перпендикулярна к пластинке. А отсюда сразу
следует, что
^[^] D0.14)
При угле а = т:/2 составляющая Y обращается в нуль, как и должно
быть, для X же получается выражение
X _* = — v у' "*" ' — — 2,57pU4,	D0.15)
"~ 2
в то время как опыты дают коэффициент 1,56. Как видим, сопро-
сопротивление получается чрезмерно большим. Причиной этого является
то же обстоятельство, которое имело место и в случае обтекания
цилиндра в то время как распределение давления на передней сто-
стороне пластинки хорошо соответствует действительному, на задней
стороне пластинки получаются чересчур низкие давления.
Можно получить лучшие результаты, видоизменяя несколько
основные предпосылки теории, как это сделал в ряде работ Цейлон
(ZeilonI).
') См , например, О s e e n С. W., Hydrodynamlk, приложение, содержащее
две работы Цейлона.

§ 401	ОБТЕКАНИЕ ПЛОСКОЙ ПЛАСТИНКИ	657
Рассмотрим, например, стационарное	плоское движение и до-
допустим, что вектор полной скорости v	может быть разложен на
две части
г» = г»04-г»',	D0 16)
где 1>0 есть вектор скорое i и основного движения, a v' — вектор
дополнительной скорости Для определённости примем, что vQ есть
безвихревой потенциальный вектор
« — —A	V —it	ДА— ^L^-O
Примем теперь, что в выражении vy^rotv, входящем в основ-
основные уравнения C7.1), мы можем пренебречь квадратичным членом
v'y,totv', так что эти уравнения можно записать так:
О	Ч |	Л •	СЛ	Ч I	Л I	f Л Г\ 1 *7\
где
Q— Vy	-L,
dx dy
Из предыдущих уравнений после перекрёстного дифференциро-
дифференцирования легко найдем, что
dQ	dQ _ Q-
в пределе при [х->0 получаем уравнение
dQ .	dQ п	д&) dQ- dii dQ п ,.л 1О.
vnr-^	\-vn., ^— = 0 или -тг-т	з1-^— = 0. D0.18)
ох dy	°У dy	dy dx dx dy	'
Это последнее уравнение показывает, что 2 = /((]»), т. е. что вихрь
имеет постоянное значение на линиях тока основного движения.
Принимая (]»= —Uу, мы получаем прежний результат, что за
телом вихри перемещаются по прямым, параллельным оси Ох.
Выбирая иную функцию <]», мы получаем другие траектории для вих-
вихрей и, следовательно, другое решение задачи.
Ещё одно видоизменение теории касается граничных условий.
В основной теории исчезающей вязкости мы имеем резкое разграни-
разграничение передней стороны, на которой происходит обтекание потоком
тела, от задней, на которой происходит прилипание жидкости
к телу. Можно ввести некоторые переходные участки, на которых
один режим обтекания будет сменяться другим. Ясно, что путем
надлежащего подбора этих участков можно значительно улучшить
совпадение получающихся теоретических результатов с эксперимен-
экспериментальными данными, особенно, если использовать также и произвол
в выборе функции тока основного течения <Ji.
42 Теоретическая гидромеханика, ч- Ц

ГЛАВА ТРЕТЬЯ
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
А.ТУРБУЛЕНТНОСТЬ И НЕУСТОЙЧИВОСТЬ
§ I. Введение. По-видимому, Га ген (Hagen) первый, произ-
производя опыты с водой, движущейся в цилиндрических трубках, заметил,
что характер движения внезапно меняется, если, увеличивая посте-
постепенно скорость течения, мы перейдём через некоторый предел.
Именно, при движениях со скоростями, меньшими, чем этот предел,
струи имеют вид твердых стержней, но, как только этот предел
перейден, движение сразу становится неравномерным, и струи начи-
начинают разбиваться и пульсировать. Г а г е н обратил внимание также
и на то, что переход потока из одного типа в другой может быть
ещё получен путем изменения коэффициента вязкости (температуры)
или радиуса трубки. Однако, Гагену не удалось подметить здесь
общего принципа. Это сделал Осборн Рейнольде, показав,
что переход одного типа движения в другой совершается, когда без-
безразмерная величина Иг\ч (U — средняя скорость, г — радиус трубки,
v — кинематический коэффициент вязкости) переходит через некоторую
границу. Новый, беспорядочный тип движения, который при этом
возникает, получил название турбулентного1), число t/r/v было
названо впоследствии числом Рейнольдса (см. гл. II) и стало
обозначаться буквой R, а то значение R, начиная с которого воз-
возникает турбулентное движение, — критическим значением Rk. При
этом плавное движение с R < R^, получило название ламинарного.
Многочисленными экспериментами было установлено, что Rft
меняется в зависимости от того, как эксперимент обставлен. Именно,
если в начальном потоке было очень мало возмущений, то, увеличи-
увеличивая постепенно число Рейнольдса, мы придем к турбулентному дви-
движению нескоро, так что Rk будет велико, напротив, если основной
поток сильно возмущен, Rft имеет малое значение. Заметим ещё,
что в то время, как, по-видимому, нет оснований считать, что суще-
существует верхняя граница для Rk (используя всё более и более спокой-
') Термин «турбулентность» был предложен Кельвином.

$ о]	УСТОЙЧИВОСТЬ ДВИЖЕНИЯ МЕЖДУ ДВУМЯ ЦИЛИНДРАМИ	659
ный начальный поток, будем отодвигать Rk всё далее и далее),
можно утверждать, что есть граница нижняя. Это значит, что каково бы
ни было начальное возмущение, оно потухнет, не переходя в тур-
турбулентное движение, если R меньше некоторого числа.
Мы говорили о турбулентном движении в трубах (так называемая
внутренняя задача); не меньший интерес представляет изучение тур-
турбулентности при обтекании (внешняя задача); наконец, в отличие от
турбулентности механического происхождения, можно говорить
о турбулентности происхождения термического (например, о турбу-
турбулентности, возникающей в воздухе близ поверхности земли при
отсутствии ветра, но при неравномерном нагревании почвы), или
о турбулентности смешанного, термическо-механического происхожде-
происхождения (теплотехнические задачи, общая атмосферная турбулентность).
С точки зрения теоретической гидромеханики (так же как и
с точки зрения эксперимента) проблема турбулентности распадается
на две части: 1) изучить, при каких условиях и как возникает тур-
турбулентность (например, при каких условиях ламинарное движение
в трубе переходит в турбулентное или как образуются турбулентные
струйки в неравномерно нагреваемом воздухе), 2) изучить уже раз-
развитый турбулентный поток.
Первый из этих вопросов совершенно естественно связать с про-
проблемой устойчивости, отождествляя возникновение турбулентности
с потерей устойчивости.
Мы рассмотрим в следующих параграфах некоторые относящиеся
сюда работы.
§ 2. Устойчивость движения между двумя коаксиальными
цилиндрами. Чтобы установить устойчивость или неустойчивость
движения, прибегнем к методу малых колебаний, накладывая на
движение («основной поток») бесконечно малые нестационарные
возмущения; если эти возмущения будут иметь характер малых
периодических колебаний (или затухающих со временем), будем счи-
считать основной поток устойчивым; напротив, если возмущения будут
расти со временем — можем считать основной поток неустойчивым.
Тейлор первый дал пример такого ламинарного течения, кото-
которое может при известных условиях стать неустойчивым '). Он рас-
рассматривал колебания, обладающие осевой симметрией и наложенные
"а движение, происходящее между двумя коаксиальными вращаю-
вращающимися цилиндрами.
В качестве основного потока возьмём движение со скоростями
vr, — vZj = 0; vfj A +
') Taylor О., Stability of a Viscous Liquid contained between two ro-
rotating Cyliders, Proc. Roy. Soc. (A), 223 A923), стр 289, далее, Proc. Int. Cong.
Appl. Mech. Delft A924) и Z A. M. M., 5 A925), пр. 250.
42*

660	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	1ГЛ щ
B — ось цилиндров, г — расстояние от оси, v —скорость, касатель-
касательная к окружности радиуса г с центром на оси), причём подберём
А и В так, чтобы описать движение между двумя коаксиальными
цилиндрами радиусов гх и г2, вращающимися с угловыми скоро-
скоростями coj и со2 соответственно. Тогда должно быть (см. главу II, § 15):
D	D
/-jcoj = Arx -f- —; г2ш2 = Ar2-\-—-,
откуда
я
Рассмотрим теперь движение со скоростями
где v'r, v'z, v' — бесконечно малые величины, квадратами которых
можно пренебречь. Напишем уравнения Навье — Стокса в цилиндри-
цилиндрических координатах и вставим введённые значения скоростей, отбра-
отбрасывая малые второго порядка. Получим уравнения движения:
дх>'ж
=-^-т-]	-г- , р' — возмущение давления), и уравнение не-
неразрывности
drv'T drvz
При этом граничные условия будут иметь	вид:
v'r = v' =v'g = 0 при /¦ = г1	и при г —
Примем:
v'T — их cos lzer?t; v' — и2 cos \ze?t; v'g — н3 sin

§ 2]	УСТОЙЧИВОСТЬ ДВИЖЕНИЯ МЕЖДУ ДВУМЯ ЦИЛИНДРАМИ	661
где uv и2> нз — функции одного только г, и исключим р' из наших
уравнений. Получим:
J,_X'2)«1, B 1)
где
Эту систему уравнений надо проинтегрировать, принимая во внима-
внимание краевые условия:
Hj = и2 = и3 = 0 при г = гг и при г = г2.
Будем искать решения для их{г) в виде ряда Фурье-Бесселя,
расположенного по бесселевым функциям Zx(kmr) = cxJx(kmr)-{-
-j-c2Ni(kmr), где сг и с2 подобраны так, чтобы Z1(kmr1)—Z1(kmr2)=Q\
последнее, очевидно, означает, что kv k2	km, ... суть корни
уравнения
т	т = 0.
Тогда
со
причём коэффициенты ат неизвестны и подлежат определению; они
должны иметь вид:
а
"~'т
г,
ат=щ
Гг	Гг
-] rui (r) Zx (kmr) dr; Hm = j rZ\ {kmr) dr.
Теперь для н2 мы получим уравнение:
m-l
и, так как
2 . 1 d 1 ,
+
решение его можно получить как сумму общего решения однород-
однородного уравнения

662	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ III
(с3 и с4 — произвольные постоянные) и ряда
со
2 bmzx (kmr),
т = \
где
*,„ = - AЛат12<-	B.3)
Условия и2 (г{) = и2 (г2) = 0 дадут затем
с3 = с4 = 0.
Чтобы определить «3, обратимся ко второму из уравнений B.1) и
рассмотрим сперва решение однородного уравнения. Так как по
известному свойству функций Бесселя
мы. очевидно, удовлетворим уравнению
положив
«з = Zo (ik'r) -\- const.
Таким образом нам, очевидно, надо искать выражение для и3(г)
и виде:
со
«з (г) = с5 -+- c6J0 (iX'r) + c7yV0 (Л'г) + 2 dmZ0 (kmr), B.4)
где съ, с6, с7 — произвольные постоянные, а для определения rfm
получим уравнение:
()
т = 1	m = 1
Таким образом в качестве неизвестных коэффициентов у нас фигу-
фигурируют пока с5, с6, с7> «!> а2, .... am	dj, d2	dm, ...
Вместо того чтобы определять dv d2, ... из уравнения B.5) через
av a2, ..., удовлетворим сперва последнему из оставшихся уравне-
уравнений— уравнению неразрывности [третьему из уравнений B.1I. Член
,	со
—+ —р- дает, очевидно, ^k,namZ0(kmr)*), и уравнение иераз-
7 (х\
*) Вследствие известного соотношения, Z[ (х) = Zq(x)	'¦¦-¦ ¦ -.

§ 2]	УСТОЙЧИВОСТЬ ДВИЖЕНИЯ МЕЖДУ ДВУМЯ ЦИЛИНДРАМИ	663
рывности можно будет заменить на основании B.4) следующим
соотношением:
со
2 (kn am -\-~kdrn) Zu(kmr) -f- X }c5-f- c6Jo@Sr)-{-c7No(ik'r)} =0> B.6)
m = l
Этим уравнением мы и воспользуемся для определения dm через
посредство av a2, ... и через с5, с6, с7. Чтобы возможно было это
сделать, надо, однако, предварительно переразложить J0(lk'r) и
N0(&'r) в ряды Фурье-Бесселя, но уже не по Zl(kmr), а по функ-
функциям ZQ(kmr) (Л ф km). Мы можем написать
где
dr\
r,
c'. — постоянная, содержащая в качестве слагаемого с5. Для опреде-
и
ления ат замечаем, что интегралы типа Г rJu(kmr)Ju(ik'r)dr легко
вычисляются. Действительно, по общей формуле:
'г
frJn(ksr)Jn(ktr)dr =
следовательно:
„ ^6 <	-j- [t'A Zo (kmr) Jq (iK r) — kmJo (ih'r
1
Ho Z'o(kmr) = — Zi(Amr) и потому z'0(kmri)~ Z'0(kmr2) = 0. Вводя
•6 и с-, проиЕ
с7Л^о(й'г2)},
ещё вместо произвольных постоянных с6 и с-, произвольные постоян
ные с' и с':
с?
? = — il'n [cgJo (ik'ri) -j- c-,No (Л'п)} ,

664	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ III
получим:
а.„ —
-j- [c'6Z0 (kmr2) + c'i
Уравнение B.6) позволяет теперь заключить, что
и позволяет найти все dm через посредство с6, с1 и atll при помощи
соотношений
т~ ^Ж^)" »ж^'2) 7 l m' ( }
Нам остается теперь воспользоваться B.5) и вставить туда эти dm.
В B.5), однако, имеются члены вида const. -prZ1(kmr). Эти члены
нам надлежит сперва разложить в ряды по функциям Zx (kmr).
Только когда это будет сделано, возможно будет, вставив dm
в B.5), произвести сравнение коэффициентов при Zx (kmr) с одина-
одинаковым т. Имеем:
^TJlZiM.	B.8)
s=l
где коэффициенты
г,	г,
могут быть вычислены, если известны ks. Мы можем теперь вста-
вставить B.7) и B.8) в B.5) и приравнять коэффициенты при одина-
одинаковых Z, (kmr). Получим после простых преобразований:
Ш
т
o (kmr2) c's + Zo {kmrx) c'7\ + ~ (k2m + \' ) (k2m + X2) a
4A
> = 0. B.9)
Придавая т разные значения, получим систему бесконечно боль-
большого числа однородных линейных алгебраических уравнений для
определения с'6< с'7, av ay ... Прибавим еще сюда неиспользованные
условия обращения н3 ПРИ г~г\ и г — гч в нуль. Для этого заме-
заметим, что по уравнению неразрывности, обращение н3 в нуль экви-
эквивалентно равенству: —--\—-^- = 0, т. е. (см. выше)
т=\

§2]
УСТОЙЧИВОСТЬ ДВИЖЕНИЯ МЕЖДУ ДВУМЯ ЦИЛИНДРАМИ
665
Итак, имеем ещё два условия:
...=0. J
... =0. I
B.10)
Бесконечная система B.9) и B.10) и должна служить для опреде-
определения Cg, c'7, flr a2, ... Приравнивая её определитель нулю, мы
получим то, что мы ставили себе целью получить — вековое уравне-
уравнео2, гх и г2 величины
ние, связывающее при данных со1
(вернее X и I' = V\* + P/v)-
Тейлор дал детальный анализ этого векового уравнения, причём,
ввиду чрезвычайных вычислительных трудностей, ограничился слу-
+
чаем, когда г2 — гх мало по сравнению с
Отсылая за дета-
лями к цитированным выше работам Тейлора, в которых имеются
также и результаты экспериментальной проверки, укажем на глав-
главнейшие выводы. Анализ показывает, что если цилиндры вращаются
в одну и ту же сторону, то при Wj^ < со^ всегда будет иметься
устойчивость. Элементарный критерий этот неприменим, если вра-
вращение происходит в противоположных направлениях. На рис. 190
ч
200
Нвус
iff/}
СП
Устои
чюйча
/
/
чиво
у
/ и,
/'
//
//
//
/
/
Т
//
'/
-250 -Ж -!5О -100 -50 О 50 100 150 ZO0
Рис. 190.
дана кривая, представляющая по Тейлору границу устойчивости.
По горизонтальной оси отложены здесь значения co2/v, по вертикаль-
вертикальной o)j/v, причём взято гх — Ъ,ЬЬ см, г2= 4,035 см, так что
(r2//-jJ= 1,292 (ниже прямой a)j/u>2= 1,292 —всегда имеет место
устойчивость). Интересно отметить, что в случае, когда вращение
происходит в разных направлениях (со2 < 0), значение и^, начиная
от которого будет иметь место неустойчивость, должно быть больше,
чем то, после которого будет неустойчивость при со2 = О.
На рис. 191 приведено сравнение данных теории и эксперимента

666
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ. Ill
Если оба цилиндра вращаются одинаковым образом, потеря
устойчивости проявится в возникновении рядов вихрей в плоскости
меридиана, имеющих чередующиеся противоположные вращения и
занимающих всё пространство между цилиндрами (рис. 191). Экспери-
Экспериментально можно обнаружить возникновение этих вихрей, помещая
вдоль внутреннего цилиндра тонкий слой окрашенной жидкости;
краска эта, когда возникают вихри, располагается по кольцам,
окружающим вихревые области (рис. 191).
Если цилиндры вращаются в противоположные стороны, обра-
образуются два ряда вихрей; из них один соприкасается с внешним,
Риг. 191.
Рис. 192.
а другой с внутренним цилиндром (рис. 192). При этом краска
распределяется как показано на рисунке.
Как качественно, так и количественно теория Тейлора даёт пора-
поразительное совпадение с опытом.
Сайндж (SyngeI) в 1938 г. привёл задачу Тейлора к уравнениям
значительно более простого вида и показал, что критерий устойчи-
устойчивости ш^ < (о,/1 (при o)j и ш2 одинакового знака) будет справедлив
не только, когда г2 — гг мало по сравнению с ^ * ¦ н0 и
в общем случае.
§ 3. Устойчивость течения между пластинками и устойчи-
устойчивость в пограничном слое. Перейдём теперь к исследованию
устойчивости других движений. Мы остановимся на движениях
') Synge J., On the Stability of a Viscous Liquid between rotating coa-
coaxial Cylinders, Proc. Roy. Soc. (A), London, 167 A938), № 929, стр 250—256.

§ 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	667
между двумя неподвижными параллельными стенками1) и на движениях
в пограничном слое. Будем рассматривать эти задачи параллельно;
первую из этих задач будем называть сокращённо случай I, вто-
вторую—случай П. Во всех случаях мы будем считать как движение,
так и возмущение плоскими2).
Функция тока ф плоского движения вязкой несжимаемой жидкости
удовлетворяет, как мы знаем, уравнению (см. гл. II, § 8);
д , , д<1> д Дф , д'Ь д Дф ... „	.„ ,
Дф	~ , тгт^ — vДДф = O,	C.1)
dt ~ дх ду ' ду dx	T	v ;
где v — кинематический коэффициент вязкости. Наше движение мы,
как и в случае, рассмотренном Тейлором, считаем разбитым на два:
основное, стационарное с функцией тока 47 и бесконечное малое
возмущение с функцией тока ф'
ф(х, у, t) = W(x, yL-f (*. У. t).	C.2)
Таким образом скорости vx и vy представятся в виде:
	 дЧ' ,	_ (ЭФ1 , ,
Vjc ~ ~ду~ ~т~V*' V? ~ дх~ "т" Vr
где
vx ~~ ду '	Vv~ дх '
Функция 47 должна сама удовлетворять уравнению
(?л: ду ' <?у <?л:
Заметив это, мы получим, подставляя C.2) в C.1), сохраняя линей-
линейные члены и отбрасывая члены второго порядка малости:
дЬ.у дУ dty' 	 ду d&W , dW д Аф' ду д ДЧ' лл,/_п
~di ~дх~~ду~ дх ду ~~^ ду дх ~+~ йу F ^ЛФ~°-
В случае движения между двумя параллельными стенками W не
зависит от х (ось л; направлена параллельно стенкам), а в случае
пограничного слоя можно считать, как всегда, что производные
от W по х малы в сравнении с производными по у (ось х напра-
направлена вдоль границы). Напротив, производные от возмущений ф' по
хну, конечно, будут иметь одинаковый порядок малости. Таким
образом мы можем написать вместо предыдущего уравнения:
C.3)
') Движения между параллельными стенками, из которых одна непо-
неподвижна, а другая движется, исследуются аналогичным образом.
2) Squire J. L. (Proc. Roy. Soc, London A, 142 A933)), показал, что
трёхмерные возмущения того типа, который мы будем рассматривать, более
устойчивы чем двухмерные, поэтому наиболее важные черты в проблеме
потери устойчивости можно уловить, изучая двухмерную задачу.

668	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ III
где U (у) — скорость основного потока, отвечающая тому значе-
значению х (пусть это будет х = х0), в области которого мы изучаем
устойчивость потока:
a U" (у)— вторая производная от U по у.
Решение уравнения C.3) будем искать в виде:
Для / получим, очевидно:
U -1)(/" - а2/) - U"f = ~ Т V™ ~ 2a*f" + fl4/)- C-4)
Т
Величину а всегда будем считать действительной (рассматриваем
волны длины 2-к/а вдоль оси х); величина Ь может быть комп-
комплексной:
Если будет 6г < 0, ф' будет затухать во времени, и движение будет
устойчиво; при Ъ{ > О движение неустойчиво; bt = 0 даёт нейтраль-
нейтральный случай. Наше уравнение C.4) — четвёртого порядка и мы
должны решать его при четырёх краевых условиях. В случае I,
когда движение происходит между плоскостями у = 0, y = 2h, нам
надо поставить условия прилипания к стенкам, т. е. (V = v' = 0);
/@) = /'@) = /BА)==/'BА) = 0.	C.5)
В случае II, когда изучается устойчивость пограничного слоя, будем
брать кроме условия прилипания к стенке
/@) = /'(<)) = 0	C.6)
ещё условие обращения решения вне пограничного слоя в решение
для идеальной жидкости. В идеальной жидкости v = 0 и U" = 0
и C.4) переходит в уравнение
/" _ а2/ = 0,
имеющее решением / = const. е±а*. Решение типа const. eay мы
должны отбросить как неограниченное на бесконечности: значит,
должно быть / = const. e~ay. Итак, если границей пограничного
слоя будет у =/7, мы должны потребовать выполнения условия
/'(*) + а/(*) = 0.	C.7)
Кроме того, мы должны потребовать ограниченности / на бесконеч-
бесконечности.
Для удобства решения задачи введём безразмерные величины х,
у, t, U при помощи равенств
x — hx, y~hy, t = ~l, U = UJJ.	C.8)

§ 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	669
Здесь h — характерная длина — половина расстояния между пла-
пластинками в случае I и толщина пограничного слоя в случае II;
Uт — характерная скорость основного движения, за которую мы
примем максимальную скорость в случае I и скорость на границе
пограничного слоя в случае II.
Обозначим
ah = «> i = c' ~=R-	C-9)
Тогда <]/ мы можем взять в виде
ф' = /(у) «¦'«<*-«<),	C.10)
и уравнение C.4) примет вид:
;Uy2	/ Луг	aR \dy*	dy*^ Jj
C.11)
Краевыми условиями задачи будут:
в случае I
/@) = /'@) = /B) = /'B) = 0.	C.12)
в случае II
= 0, /(оо)<оо. C.13)
Ход решения нашей задачи об устойчивости можно представить
далее следующим образом.
Уравнение C.11) содержит кроме заданной функции (/(у) ещё
три параметра с, a, R; два из них: а и R характеризуют длину
волны возмущения и число Рейнольдса основного потока соответ-
соответственно и суть величины действительные; третий — с — может быть,
вообще говоря, комплексной величиной. Четыре линейно независи-
независимые решения уравнения C.11) в случае I должны быть связаны
однородными соотношениями C.12); три конечных на бесконечности
линейно независимых решения того же уравнения в случае II связаны
тремя однородными условиями C.13). Вековое уравнение, получаю-
получающееся в том и другом случае, будет связывать три параметра a, R
и с соотношением вида
F(c, a, R) = 0.
Решая это уравнение относительно с, мы получим 1)
с = с(а, R).
') Возможность решения относительно с векового уравнения получается
пак следствие того факта, что функция F будет целой функцией от своих
трох переменных. В самом деле, будем в уравнении C.11) считать у ком-
комплексной величиной, так же как и все три параметра a, R, с. Примем
для и (у), которая определена лишь для действительных значений у, для
Других значений — аналитическое продолжение. Тогда уравнение C.11), для

670	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ, Щ
Отделив действительную и мнимую часть с (= сг -}- ic^), получим
далее cr = cr(a, R) и сг = сДа, R). Кривая
с, (a, R) = 0	C.14)
будет отделять область устойчивости от области неустойчивости.
Задача определения характеристических чисел, связанная с реше-
решением уравнения C.11), была предметом исследования ряда авторов.
Одними из первых были Орр 1) и Зоммерфельд2), которые исследовали
устойчивость движения между двумя пластинками и не нашли потери
устойчивости. К тому же выводу приходили и такие авторы как: Мизес,
Хопф (Hopf), Гольдштейн (Goldstein), Пекерис (Pekeris) и многие
другие. Если не считать теории Гейзенберга3), которая считалась
неполной и неточной и не была поэтому общепризнана, все теорети-
теоретические работы до сравнительно недавнего времени давали отсутствие
возможности потери устойчивости движения между двумя пластин-
пластинками. Первое строгое доказательство того, что движение между парал-
параллельными пластинками может оказаться неустойчивым при некоторых
значениях R, было дано в работе Линя4). В этой же работе даётся
попутно анализ ошибок, или неточностей, из-за которых ни один
из предыдущих авторов не мог добиться верного результата.
Прандтль5) в 1921 г. и Титьенс6) в 1925 г. впервые рассмотрели
вопрос об устойчивости пограничного слоя; при этом они предполо-
предположили, что профиль скорости основного потока может быть соста-
составлен из нескольких, различным образом наклонённых прямолинейных
кусков 7). Авторы эти пришли к парадоксальному выводу: пограничный
слой везде неустойчив. Позднее Толлмиен8) показал, что вывод
получился благодаря предположению, что кривизна профиля скоростей
основного потока всюду равна нулю. Принимая, что кривизна профиля
скоростей хотя бы в отдельных частях этого профиля отлична от нуля,
которого все точки в любой конечной области регулярны и коэффициенты
которого суть целые функции от параметров а, с и aR, будет, по известной
теореме теории дифференциальных уравнений, иметь систему четырёх неза-
независимых решений, являющихся аналитическими функциями у и парамет-
параметров с, a, aR и целыь и функциями этих параметров.
') О г г, Ргос. Roy. Irish Acad., 27, 1906, 1907.
2)	Som merfel ii, Proc. 4th. Int. Congress Main., Rome, 1908.
3)	Heisenberp, Ann. d. Physik. 74 A924).
4)	Lin C, On the Stability of Two — Dimensional Parallel Flows. Quart-
Quarterly Appl. Mathematics, т III, № 2, № 3, № 4, 1945, 1946.
5)	P г a n d t 1 L., Bemerkungen fiber die Entstehung der Turbulenz,
ZaMM, 1921.
6)	T i e t j e n s O., Beitrag zur Entstehung der Turbulenz, ZaMM, 1925.
7)	Предположение это было связано - желанием описать тот факт, что
в местах, находящихся около « очки отрыв .> ламинарного слоя, профиль
скоростей имеет на некотором расстоянии от стенки точку перегиба.
3) Toll mi en, Ueber die Entstehung der Turbulenz, Gdtttngen Nachrich-
ten, 1929, стр. 24.

§ 3J	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	671
Толлмиен получил, что коль скоро числа Рейнольдса не превосходят
некоторой величины, изучаемое движение устойчиво.
Толлмиен рассмотрел конкретно лишь профиля U, состоящие
из кусков прямых и парабол. В более поздней работе1) Толлмиен
вернулся к случаю произвольного профиля в пограничном слое.
Розембрук2) применил метод Толлмиена к исслелованию движения
в диффузоре, аппроксимируя профиль скоростей в виде полинома
шестой степени.
В упомянутой работе Линя дается также и решение задач об устой-
устойчивости в пограничном слое для произвольного распределения скоро-
скоростей U. Мы расскажем в общих чертах о работе Линя, отправляясь
от изложенной выше постановки задачи, параллельно проводя рас-
рассуждения для случая I и случая II.
Путь построения решения, принятого Линем, заключается в сле-
следующем. Уравнение C.11) содержит три параметра: а, с, 1/aR.
Параметр 1/aR можно считать малым, ибо устойчивость теряется при
больших числах Рейнольдса. Поэтому для целей подсчетов удобно
искать четыре независимых решения нашего уравнения четвертого
порядка в виде рядов по малому параметру 1/aR. Однако при построе-
построении этих рядов встретится принципиальное затруднение. Дело в том,
чю параметр 1/aR входит в наше уравнение при старшей производной.
Если просто отбросить член с 1/aR в C.11), то мы придем к урав-
уравнению второго порядка, имеющему особеннос1ь в гой точке, где
и = с.	C.15)
Пусть это будет точка
Для точного уравнения четвертого порядка у = ус не будет особой
точкой. При построении наших асимптотических рядов надо тща-
тщательно проследить за проявлением этой особенности, вводимой лишь
математическим методом интегрирования. Это можно будет сделать,
если мы получим возможность сравнения наших асимптотических
разложений по 1/aR, удобных для практических расчетов, с точными
решениями уравнения четвертого порядка C.11).
Начнем с построения решения C.11) в виде:
/О0=/(О)О0-т-/шО0^ + /12)(у)Щ + ••• C-16)
Подставляя это в C.11) и сравнивая члены при одинаковых
степенях 1/aR, получим следующую систему дифференциальных
') Toll mien W., Ein allgemeines Kriterium der Instabilitat laminarer
Geschwindigkeitsvertellungen Qottingen Nachrichten, 1935.
2) Rosenbrook, Instabilitat der Grenzschicht im schwach divergenten
'vanal, ZS ang. Math. u. Mech., 17 A937), вып. 1, стр. 8—24.

672	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
уравнений:
([/_ с) (/i°>" — а2/<°>) — G@) = О,
(у — с) (/<*>" — а2/<*>) — U"fW ~
[ГЛ. III
C.17)
Уравнение C.17) это просто уравнение, отвечающее колебаниям
в идеальной жидкости. Его можно решить при помощи рядов по
степеням а2. При этом мы получим два независимых решения:
где
f?(y) = (U-c)[ho(y)
/<°) (у) = A7 —с)!*!(у)
Л0(у)=1,
2(у) + а4/г4(у)+ ...],
з(у) + а4А5(У)+ ¦••].
C.19)
у	Г у
= f(U-cf \j{U~cfh2n(y),
О	Lo
(U- су
й2я+з(У) =
C.20)
Определив два независимых решения для /(°>, получим дальше
любое fW при помощи квадратур.
При конкретных расчётах достаточно бывает ограничиться функ-
функциями /W.
Уравнение C.11) можно рассматривать в комплексной плоскости у
(см. сноску на стр. 669) и считать, что aR, a — комплексные числа,
а U (у)— аналитическое продолжение функции U, определённой лишь
для действительных у. Тогда / будет целой функцией от aR и aR = оо
будет особой точкой (если / зависит от aR). Поэтому ряды C.16) суть
асимптотические ряды (или полиномы) по 1/aR. Далее, решения C.17)
будут целыми функциями от а2 и ряды C.19) равномерно сходятся
для любой конечной области комплексной плоскости а2, для закре-
закреплённого у, за исключением того случая, когда у = ус. В точке у = ус
уравнение C.17) имеет логарифмическую особенность, и это затруд-
затрудняет выбор пути интегрирования от 0 до у в C.20) (при интегри-
интегрировании приходится переходить через точку, где U — с). Выбор этот

§ 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	673
получается путём сравнения, с асимптотическими представлениями для
больших ocR точных решений полного уравнения C.11). К этому мы
вернёмся ниже, а сейчас построим другую пару решений уравнения
четвёртого порядка C.11) непосредственно для больших 1/aR.
На этот раз будем искать / в виде
/ = «****.	C.21)
Тогда для g мы получим следующее нелинейное уравнение:
(Z7— C)(g2 + ?' —a*)—f/" =
Представим g в виде следующего ряда
y	^	••¦ C-23)
Мы получим тогда уравнения:
Ф - с) {g'Q
с)(g\ + g\+ 2gog2 -a*)- U" =
C.24)
Последовательно, без интеграции, мы можем определить отсюда все
наши функции. Выпишем первые две:
go=±Yi(U-c), gl = --^-,...	C.25)
Два разных знака перед корнем отвечают двум независимым ре-
решениям. Для C.17) точка у —ус была логарифмической; теперь
это — алгебраическая точка ветвления. Мы можем положить для кон-
конкретности argj — Y и считать для ?/>carg(?/ — с) > с; будет ли
затем arg(?/—с) = -|-г или arg(t/ — с)= — л для отрицательных
V - с, мы сможем сказать лишь после рассмотрения полного ре-
решения C.11), о котором мы уже упоминали выше.
Используя функции g, мы можем, таким образом, написать и вторую
пару независимых решений уравнения C.11); назовём эти решения /3
и /4. Если ограничиться лишь первыми двумя членами в разложе-
43 Теоретическая гидроме\аника, ч. II

674	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
нии C.23), можно написать:
5 - J Vi*R [U-<
f3 = (Z7 — с)~те ус
[ГЛ. Ш
C.26)
Как же построить теперь то полное решение C.11), о котором
мы уже несколько раз упоминали и которое мы дотжны знать, чтобы
найти поведение функций / около точки у = ус и решить вопрос
о путях интегрирования в C.20) и C.26)?
Чтобы установить поведение C.11) около точкч у — ус, введём
сперва новое независимое переменное т] из соотношения
у — ус = 67], где s = (aR)
C.27)
Если обозначить
то уравнение C.11) перейдет в следующее:
/ /ту
. C-28)
причём функции U — сн U", участвующие в качестве коэффициентов,
будут представляться рядами:
C.29)
C.30)
/ г IV
77'
где Uс =
dU
и т. п.
с
Теперь можно искать решение в виде ряда, расположенного по
степеням е:
C.32)
C.33)
/ G) = х A) = х@)
Уравнения для у}°1, ха\ ... будут:

$ 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	675
1де Ln_l(x)—линейная комбинация из х{0)	Х1"'- ^ и их про-
производных; в частности,
Уравнение C.32) имеет следующие четыре независимых решения:
v@) — -n v@)	 1	("Ч Ч/1\
C.35)
= Jd-n
3
где
з
а Н(\ и Я 1 —функции Бесселя порядка '/з-
"з	J
Следующее приближение мы получим в виде
xi"»= i f *ч f dri {40)* / xf" ^„-1W rf^ - 40)" / xf" in
Сходимость рядов C.31) будет обеспечена коль скоро будут
сходиться ряды C.29), C.30). Заметим теперь, что аргумент функций
Бесселя может быть записан, если вернуться к старому независимому
переменному, по C.27) и C.36), в виде
о	о
1 V
так что при больших значениях ocR аргумент этот будет по модулю
велик. Поэтому, желая обследовать поведение функции ^ при боль-
больших ocR, мы можем использовать асимптотические разложения функ-
функций Бесселя.
Производя несложные выкладки, Линь показывает, что первые
члены этих разложений для ул, /2. Хз- Х4 как Раз совпадают с теми
функциями Д, /2, /3, /4 соответственно, которые даны были в ра-
равенствах C.19), C.26), и попутно получает возможность уточнить
путь интегрирования в квадратурах, участвующих в этих формулах.
Отсылая за подробностями к цитированной статье Линя, укажем лишь,
что путь интегрирования должен, по Линю, удовлетворять условию:
Х*))<^-	C-37)
43*

676
)ЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
!ГП
Обратимся теперь к собственно краевой задаче Сличай I движе-
движения межд> двумя параллельными пластинками удобно подразделить
на два подслучая Дело в том, что возмещение всегда можно раз-
разбить встедствие линейности, на две независимые части — симме-
симметричную по отношению к линии у — 1 (середина расстояния между
тастинками) и антисимметричную
В случае I удобнее записать краевые условия не для у~0 и
у = 2 а лпя у = 0 и у=\ При этом в случае, назовем его I',
копа /(у) симметрично мы должны написать
В с л} чае 1' когда / антисимметрично, — мы должны записать:
Наконец для случая II движения в пограничном счое мы, как и
выше, напишем
= /'@)=0
= 0 для
/(оо)<оо.
В качестве четырех линейно независимых решений мы примем
наши функции fv /2, /3, /4 определенные выше
Тогда вековое уравнение для случая I' будет иметь вид
д
д
д
д
Для случая I" мы
/,
/;
f
@)
@)
(о
(i)
f2
/2
/2
/2
должны
@)
@)
(О
(О
@)
@)
A)
'A)
будем
/2@)
/2
/2
/'
@)
A)
A)
/з@)
/з(°)
/з(])
/Г (О
д
д
/4
¦'4
написать
/з@)
/з@)
ДО)
/з'A)
Д
/4
/4
/4
@)
@)
A)
A)
@)
@)
A)
A)
= 0
C 38)
= 0
C 39)
Наконец, в сч^чае II мы должны отбросить /4 как решение, не
ограниченное на бесконечности и написать
Д@)	/2@)	/3@)
Д@)	Д@)	/з@)
ДA) + «ДО) ДA)+«/2A) о
= 0.
C 40)

I il
ОСТОЙЧИВОСТЬ ТЕЧЕНИЯ .МЕЖДУ ПЛАСТИНКА НИ
677
Соотношения C.38), C.39), C.40) значительно упрощаются для
больших значений aR. Используя выражения C.26) для (\ и /4, мы
можем записать: Д— A(y)e~v и fi^zB(y)ev, где А а В — вели-
величины порядка единицы, а
у
В определителе C.38) удобно поделить все члены третьего столбца
на /3@), а все члены четвертого столбца на /4(,0). Мы можем за-
записать затем:
/>)	лГ-
где
/з
/;
/з
п
А
А
@)
A)
@)
f
@)
@)
@)
/1A)
Л
/"
@)
'A)
о-Р
5@)
C.41)
— c)dy.
Пренебрегая теперь в определителе C.38) членами порядка е~р
или 1/aR по сравнению с единицей, приведем уравнение C.38)
к виду:
Л> (а, с) = Л @)
¦Ма><) /з@)
i де
i@) /2@)
42)
/\j(a, с):
C.43)
причём F<i и ^ не зависят от R, ибо мы принимаем за fl и /2
представления с помощью C.19), C.20) (Д0-1 и /*).
44 иоретнчесьая гидромеханика, ч II

678
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[Г Л II!
Аналогичным образом, преобразуя определитель C.39) (для чего
/зA) Ad) /зA) /U
надо будет сперва записать ещё
придём к равенству.
Л (а, с)
_
/з @) ' /4 @) ' /3 @) ' Л @)
где
(а. с) =
мы
C.44)
C.45)
а /^ имеет прежнее значение.
Наконец, обращаясь к случаю II, мы должны преобразовать
C.40). Мы получим после простых выкладок:
где
/з @)
/з@)
F2, F4 имеют значения, приведенные выше, а
F3(a, c) =
C.46)
C.47)
Правые части равенств C.42), C.44), C.46) одинаковы и зависят
от a, R и с. Левые части — все различны, но зависят лишь от а
и с, но не от R (по самому смыслу построения функций /1( /2,
F F F /)
участвующих в Flt F2. F3, /\j).
Преобразуем сперва левые части наших равенств. Вследствие
C.19), C.20):
/х@) = —с, /2@) = 0, ]
где. ?/о
?/о = | ——)
с ' j
. Поэтому мы можем написать:
(а, С) = —
¦ J
C.49)

§ 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ	679
Величины /Д1), /20)> /j(О» /<H) Должны быть вычислены с по-
помощью интегралов C.20). Именно:
1 		1 		1
f (U -cfdy + z* f (U-c)n2(y)dy+ ... U
...]¦
1 —с
U'(l)
/«О)-
Дальнейшие преобразования удобно делать для тех или иных кон-
конкретных видов U (у), а не в общем виде. Правая часть может быть
преобразована к удобной форме для всех случаев сразу. Мы могли бы
грубо представить, по C.41), выражение /3@)//3@) для больших aR
в виде	2HL
/з@) _ *4
/з @)	V^RT '
Однако величина с оказывается иногда малой, и тогда даже при
больших aR, пользоваться этой формулой нельзя. Следует обратиться
непосредственно к точным решениям C.35). Мы получим теперь:
Г
/з @) ^ со
/з@)
со	3
или, если ввести вместо i\ аргумент С по формуле
будем иметь:
-z	I !
Л
+со	3
—z
¦ Z
I
СО
44*

680
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ III
где
C.51)
В приводимой здесь таблице XII даны значения Fr и Ft в функ-
функциях от z по Линю.
Таблица XII
г
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
0,89161
0,78969
0,71970
0,66931
0,63143
0,60144
0,57599
0,55230
0,52773
0,49052
—0,35025
—0,27310
—0,21213
—0,16009
—0,11274
—0,0Ь741
—0,02226
-0,02395
—0,07203
0,12220
г
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
0,46456
0,41947
0,36110
0,28802
0,20352
0,11800
0,04698
0,00240
0,02160
0,01477
F
0,17391
0,22520
0,27193
0,30705
0,32130
0,30721
0,26559
0,20811
0,14475
0,09875
Итак, мы приходим к решению уравнений типа
Е(с. a)=Fr + lFt,
причём для случая I':
/2 A)
Е(с. а) =
Ус
для случая I":
для случая II:
Е(с. а
Е(с. а)=~
о \Л 0) + «/2 AI + у \/{ A) + =/, A)]
C.52)
C.53)
C.54)
	. C.55)
Уравнение типа C 55) было получено еще Толлмиеноч в упомя-
упомянутой выше работе об устойчивости пограничного слоя. Если пред-
представить левую часть этого уравнения в виде '):
Е(с, л) — Ег(с, a)-\-tEt(c, я)
(при этом мы берем ct = 0, т. е. занимаемся лишь нейтральной
линией), то задача определения нейтральной линии сводится к исклю-
'•) Левая часть бз'дег комплексной благодаря интегрированиям, имею-
имеющимся ч форм_. их C 20).

«3]
УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖДУ ПЛАСТИНКАМИ
681
чению с из двух уравнений
Е,(с, а) = /
?\(с, a) =
В плоскости (a, R) мы получим тогда линию, отделяющую об-
область устойчивости от области неустойчивости. Чтобы исключить с,
Толлмиец изображает в
некоторой плоскости кри-
кривую, абсциссы и орди-
ординаты которой суть Fт (z)
и Ff (z) соответственно
(z рассматривается при
этом, как действительный
параметр); затем в той же
плоскости изображается
семейство кривых, полу-
получающихся при разных с,
если Ег(с, а) и Et(c, а.) изо-
изображать как абсциссы и
ординаты (переменный па-
параметр на каждой кривой
а). Точки пересечения этих кривых дадут «совместные» значения z n у,
а так как с при этом известно, то по C.51) может быть найдено R.
Толлмиен рассматривает профиль U (у), состоящий из')
Рис. 193.
прямой ?/=1,687)
параболы ?/ = 1—A,015 —
прямой ?/=1
от т) = 0	до т) = 0,175,
ottj = 0,175 дот; =1,015.
при т; > 1,015 7j = y/8.
На рис. 193 изображены кривые Е(с, а) для этого случая.
Там же дана кривая F (zJ)
(по Толлмиену).
ah
4
На рис. 194 изображена
линия, отделяющая область не-
неустойчивости (внутри) от об-
области устойчивости; здесь по
оси абсцисс отложены ?/m8*/v>
а по оси ординат аЬ*, причем
Ь* = 0,3418, где 8 —толщина
по!раничного слоя, введённого
0Л
0,3
0,2
0,1
О,
{
N
\
к
ч
ч
! |
!
Юг 103
Ю! Ws Ю7 № /О'
Рис. 194.
') Этот профиль подправляется около стенки, а также при рассмотрении
критического места tj = -q при этом принимаются в расчёт формулы Б л а-
з и у с а.
2) Данные рисунка и таблицы для F несколько расходятся. Таблицы —
точнее.

ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ. III
as
выше. Кривая зависимости между а и R показывает, что при
R < 420 возмущение будет затухать.
Линь вместо громоздкого графического способа решения разви-
развивает метод, годящийся для любого профиля скоростей и основанный
нг. представлении левых частей C.52) при помощи рядов C.19),
C.20). Попутно Линю удается дать ряд общих теорем, касающихся
^	поведения нейтральной
Щ—|—|—|—|—|—|—|—|—\—|—|—|	кривой при очень боль-
больших значениях R. Так,
например, Линь показы-
показывает, что нейтральная кри-
кривая ct (a, R) = 0 имеет две
асимптоты при R ->¦ со,
причём эти две асимптоты
сливаются в одну (а = 0),
когда основной профиль
скоростей не имеет точки
перегиба, но эти две
асимптоты различны (одна
из них отвечает а = 0,
другая — a = as Ф 0), когда профиль основного потока имеет точку
перегиба.
Линь дает также приближенные правила подсчета минимальных
вначений критического числа R. Отсылая за подробностями к статье
Линя, дадим без вывода эти последние правила.
Прежде всего надо найти значение ус из уравнения
>,
иг
\
\
ч
— —
——
'о ю го зо ьо so so ?o во so too no
Рис 195.
.77'@) | 3 - 2 Е
(оно
ЕША. = о,58
U (уе) \	U'{y3f
решается графически). Надо затем вспомнить, что по опреде-
определению ус и с:
и найти по ус соответствующие значения с. Минимальное критиче-
критическое число Rm!n найдется по Линю в виде:
для случая I
Rraln '
для случая II
тиг @)
Rmln ;
25U' @)
На рис. 195, заимствованном из статьи Линя, дана кривая ней-
нейтральной устойчивости для случая движения между двумя неподвиж-

% 3]	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ .МЕЖДУ ПЛ^СГИНКЛЧИ
ными плоскостями. Здесь
683
Две ветви этой кривой при больших R даются уравнениями
RT=8,44(a2) * и R3 = 5,96(а2)""е.
На рис. 196, также взятом у Линя, мы даём кривую нейтраль-
нейтральной устойчивости для случая Блазиуса (обтекание пластинки). Линь
выбирает профиль U в виде:
а толщину пограничного слоя определяет по формуле !)
Здесь Линь получает Rmin = 420 и асимптотические ветви кривой
в виде:
= 0,0622a.
= 2,2- 1(Г5а"~10,
Путём очень тонких измерений удалось получить количествен-
количественное сравнение теории с экспериментом. При помощи специальных
J 0,6
0,5
ОА
0,3
0,2
о воо 1600 лоо згоо то
R
Рис. 196.
термопар Шубауэр и Скрэмсчэд 2) измерили пульсации скоростей в са-
самом пограничном слое. На рис. 196 наряду с теоретической кривой
—1
\°
о
——
о
о—,
¦——
-
\
"—
') Ср. стр. 574, где принято 8 = 5,2 |/ -^-.
S	i
2)Schubauer and Skramstad, Laminar Boundary Layer Ostilla-
ions and Stability of Laminar Flow, J. Aeronautical Sc , 14, 1947, № 2.

684	ЭЛ1.Л1ЕНТЫ ТЕОРИИ ТЛ'БУЛЬНШиСТ!,	[i.i III
Линя нанесены (точками) некоторые значения R и а для «нейтраль-
«нейтральных» точек, полученные экспериментально. Совпадение следует при-
признать хорошим.
Потерю устойчивости пограничного слоя в неоднородной (хотя
несжимаемой; жидкости исследовал Шлихтинг.
Написав уравнение движения в виде
*-dt =~vP-rV-^'+?F,
уравнение неразрывности и условие несжимаемости в виде
,.	„ do до , _
Шлихтинг обращается к плоской задаче и предполагает что на
основное движение
vy--=0, р=-р{)(у), р = ро(у>.
накладываются малые колебания типа vXl(y)el<-ax~bt), Vy1(y)el^aic~bt),...
р, (у) е'«"-*". В качестве ро(у) Шлихтинг берёт затем функцию
ро(у) — Ро1е~ГУ- где 0 < 7 = const, и принимает v = —= const.
Если ввести затем, как это мы уже сделали при рассмотрении
пограничною слоя в несжимаемой жидкости, безразмерные величины
U,,
а также
то для определения функции / (множитель при el(ax~bt) в уравнении
функции тока Ь' = fei{ax"bt) накладываемых колебаний) получится
следующее уравнение, являющееся непосредственным обобщением
уравнения C.11):
(U - с? (/" — а2/) — (U -с) U"f ¦+ Kf-L(t/-с) \(U-с) f' — U'f] =
= _ !1~-С1 [/!V — 2aV" ¦+- a4/ — L (f" — a"/')]-
Шлихтhhi дает приближенный анализ этого уравнения, отыскивая
решение его в виде
и ограничиваясь первыми степенями К \\ L (К » L значительно меньше
единицы); здесь /", представляет решение Тол.тмпена. Анализ устой-
устойчивости проводится совершенно аналогично тому, как это делается

§ 3)	УСТОЙЧИВОСТЬ ТЕЧЕНИЯ МЕЖД5 ПЛАСТИНКАМИ	685
в случае несжимаемой жидкости (отыскание решения при
исследование особенности U — с и т. д.); однако теперь надо оты-
отыскать целых два семейства кривых, отделяющих области устойчи-
устойчивости и неустойчивости (дающих связь между а и R) в зависимости
от значений, которые мы дадим двум параметрам К и ?. Заметим,
что в то время как кривые, изображённые на рис. 196, уходят на
бесконечность, здесь могут оказаться случаи, когда область неустой-
неустойчивости будет ограничена замкнутой, находящейся на конечном рас-
расстоянии кривой. За подробностями отсылаем к цитированной работе
Шлихтинга.
В качестве примера на определение неустойчивости сжи\а\мой
жидкости покажем как получается потеря устойчивости в находя-
находящейся в равновесии атмосфере. Пусть воздух, рассматриваемый как
идеальная жидкость, находится в равновесии под действием силы
тяжести и при наличии линейного падения температуры с высотой
Т=Та—~[Z (Го= const., О < у = const.)
(начало координат — на поверхности земли, ось z смотрит верти-
вертикально вверх). Пусть в этой среде поднимается частичка воздуха
(адиабатически) и притом так, что давление ее (р) в каждый момент
поднятия равно давлению р окружающей среды. Последнее зависит
от закона падения температуры с высотой, ибо, встедствие равно-
равновесия, мы имеем
*Р_ — _ео — _ IE.
dz	s'	RT '
так что
у — „	Та
где А = const.
Обозначим температуру нашей частицы через Т. Тогда, на осно-
основании адиабатичности ее движения,
х-1
т f ( р
1 = 'о —
V Ра .
где То и р0 — исходные температура и давление частицы; таким
образом, как только частица достигнет высоты г, она получит тем-
температуру
х-1
Изменение температуры при подъеме будет поэтому таково, что
7 — 1 р <lz • — !	.; ,'
d\\\ T= —	d\np — —
7< 7	v. R-J Т '

686	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ. Ш
Величина —	„- называется в метеорологии адиабатическим гра-
градиентом и обозначается буквой -{а:
10	х R '
Таким образом мы получим:
Та
7*0 \Та)
Установив это, предположим теперь, что частица имела в исход-
исходном положении ту же температуру 7=Г0, что и соседние, но по-
получила вертикальный сдвиг. Частица начнёт двигаться, причём ей
уравнения движения будут иметь вид (лагранжевы координаты):
dt2	7 dz"
Но, по предположению, -~- — ~ == — g[>\ поэтому
Р	Р	Т
или, вследствие установленного для Т выражения (Та=Т0):
Предположим сперва, что у < уа. Пусть тогда масса получает
сдвиг вверх; при этом она попадает в область таких значений г, для
которых Т{z) < Го, и так как будет iJ-\— 1 > 0, то tfizfdt2 < О,
и масса будет стремиться опуститься. Если же масса получит сдвиг
вниз (Г>Г0), то d2zjdt2^>0, и масса будет стремиться подняться.
Воздух будет находиться в устойчивом равновесии. Напротив, если
будет у > 7а («сверхадиабатический градиент»), то при подъёме
(Г<70) будет d2z/dt2>0, при опускании (Г> To)d2z/dt2 < 0, т. е.
частица будет продолжать двигаться вверх или вниз. Равновесие
неустойчиво и может начать развиваться турбулентность1).
Б. РАЗВИТАЯ ТУРБУЛЕНТНОСТЬ
§ 4. Сглаживание. Три основных признака характеризуют так
называемое турбулентное движение: во-первых, большая пестрота и
быстрая изменяемость поля скоростей, во-вторых, неупорядоченность
') Более точные исследования можно найти в книге. Кочин Н. Е. и
Извеков Б. И., Динамическая метеорология, ч. 1, 1935.

» 4]	СГЛАЖИВАНИЕ	687
в смене скоростей и, в-третьих, сопровождающее эту смену пере-
перемешивание жидких частичек.
Структура развитого турбулентного потока весьма сложна, и
траектории его жидких частичек чрезвычайно запутаны; если движе-
движение частиц турбулентного потока и удовлетворяет уравнению Навье -
Стокса или Эйлера, то для описания этих движений потребовались
бы, очевидно, интегралы уравнений, настолько сложные, что отыска-
отыскание их было бы по безнадежности равносильно отысканию траекто-
траекторий каждой отдельной молекулы, движущейся среди других молекул1).
Сказанное здесь заставляет, на первых порах, отказаться от воз-
возможности получить точную математическую картину того, что про-
происходит в каждый момент времени и в каждой точке пространства
в турбулентном движении. Вместо этого приходится обратиться
к суммарно статистическому описанию явления. Нужно построить
сглаженную картину того что происходит в турбулентном про-
процессе,— построить уравнения для сглаженного, осредненного поля
скоростей, для средних давлений, для средних траекторий.
Чтобы «сгладить» какую-либо функцию f(x) одного аргумента2),
выбирают обычно сглаживающую функцию ш (?), которая удовлет-
удовлетворяла бы условию
l = 1.
J
— <JO
Сраженная функция /(х) получается затем по форм}ле
+ -*>
Дх)= J /фш(* —с)Я.
1)	Здесь может возникнуть сомнение можно ли вообще представчять
скорость в турбулентном движении как некоторую непрерывную функцию
координат и времени?
«Обладает ли ветер скоростью?» задает вопрос один из создателей тео-
оии турбулентности Ричардсон (Richardson) Можно ли представлять ско-
скорость частицы турбулентного движения как предел отношения элемента Дл:
траектории частицы к элементу времени Ш Может быть, стилизовать тра-
траекторию в турбулентном движении мы должны будем, беря в качестве закона
движения непрерывную функцию, ни в одной точке не имеющую производной
io времени, вроде известной функции Вейерштрасса-
x-^kt + У^ (±-\" cos (Ь'-тЛ).
2)	Не представляет никакого труда обобщить операцию сглаживания
ча сл}чай функций любого числа аргументов.

688
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ Ш
или, что то же,
/(*)= / /(* —
D.1)
Обычно в качестве со(?) берут чётную, неотрицательную функцию,
не возрастающую с ростом модуля аргумента. Заметим, что операция
сглаживания линейна по отношению к сглаживаемым функциям, так
что результат сглаживания суммы двух функций fx(x) и f^{x) ра-
равен сумме результатов сглаживания этих функций:
— со	—со
При повторном сглаживании некоторой функции / при помощи
какой-либо другой сглаживающей функции «j(?) получим, очевидно.
+ СоГ	-4-ОГ	
/Г
J	'
— со I	со	J
-t-CO	+X>
/г
J
— со	—со
что равносильно одному сглаживанию со сглаживающей функцией
ш, (т;):
+ со
— СО
При этом
о>2 ("ф =± to
Одним из наиболее распространённых видов сглаживания является
«осреднение» в некотором интервале /. Здесь в качестве и>(?) при-
принимается:
1
ш (:) = — при
w (?) = 0 »
L
2 '
L \
2 '
D.3)

§ 4]	СГЛАЖИВАНИЕ	689
При этом
/ „
1
~~2
4.
: — t)d% = \- f f(i)d*	D 4)
(среднее значение функции / в интервале /)!).
Прежде чем обратиться к уравнениям гидромеханики, обозначим
разность / — /(/—какой-либо гидродинамический элемент) через /',
гак что
и предпоюжич, что сглаживаемые функции и сглаживание таковы,
что выпотняются равенства:
\\IL — EL IL — ^L K—^L K — ^L
' dt dt ' dx ~~ dx ' ду ~~ ду ' dz ~ dz '
3) /, = /„ 7i/2 = o, JJ2= /J2.
Условия 1 и 2 можно считать выполняющимися вполне точно
Условия 3 будут, вообще говоря, иметь место лишь приближенно
Чтобы установить характер этих последних условий заметим, что
по самому смыслу описания турб)лентных процессов функция /
должна быть представлена в виде
') Повторное «осреднение» приводит по D 2), как нетрудно убедиться,
к сглаживанию с функцией ш2
o>o (?) —¦ -пг (I — ' -1). когда ? < /, о>„ (?) —¦ 0, когда I ? [ !s» /
/2	'	'
Как правило, повторное осреднение не будет простым осреднением Нетрудно
) бедиться, что, повторяя простое осреднение, в интервале / п раз, пол) чим
составную операцию сглаживания, функция о„ (с) которой будет асимптоти-
1ески подходить к закону
м fa ^ I i/"X e'^2
Тип сглаживающей ф}нкции
со (с) =	=r- e 2*2	(а)
встретится нам в теории перемешивания Сглаживание с этой функцией
"азывагот иногда спажнванием по Гаусс) [ю \i) и\ист вит га)ссовои кривой
ihh6okj

690	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ Ш
где F(x)— cia6o меняющаяся функция своего api} мента, а <?(х),
напротив, —функция, представляющая очень быструю изменяемость
и неупорядоченность гидродинамического элемента / в турбулентном
процессе; иначе говоря, tp изображает пульсацию нашего элемента
около его значения F и очень часто переходит через нуль. Тогда
Пусть для конкретности мы имеем дело с простым осреднением,
так как F(x) слабо меняется, то, беря интервал осреднения I не
слишком большим, можем приближённо написать:
F~\ f F(x — k)fttt-j f F{x)d% = F{x)\	D.5)
2	2
если все же / будет настолько велико, что внутри интервала /
функция tp много раз будет обращаться в нуль, то приближенно
будет:
1
Таким образом приближенно получим
f^F;	D.6)
но тогда, осредняя ещё раз, получим:
или, на основании D 5)
7«л
т. е. по D.6)
и мы получим первое из условий 3. Из этого условия, в частности,
следует, что
7^0,
ибо
/' = /-/ и 7 = /-7-7-7-0-
Также можно разъяснить требование /1/2 = 0- В самом деле,
2 = /2—/2, т. е. /г имеет характер tp, а Д имеет характер F, но

§ 51	ОСНОВНЫЕ УРАВНЕНИЯ РЕИНОЛЬДСА	69.
ф>нкция вида F. tp будет в интервале очень часто переходить через
нуль и ^срдзО Аналогичным образом >становим, что fx /2 е»/1 /2 *)
В заключение этого раздела заметим, что если под / разумеется
ел)чайная функция в том смысле, как это понимается в теории
вероятностей, и если под знаком / разумеется математическое ожи-
ожидание, то наши «постулаты» выполнятся совершенно строго сами
собой.
§ 5. Основные уравнения Рейнольдса. Обращаясь к }равнениям
гидродинамики, рассмотрим сперва случай ьесжимаемой жидкосш
(р = const.). Напишем уравнение неразрывности и уравнения Навье —
Стокса и произведем сглаживание над правыми и левыми частями этих
уравнений, пользуясь всегда одной и той же сглаживающей функ-
функцией (например, произведем осреднение в одном и том же интер-
интервалеJ), удовлетворяющее перечисленным выше условиям.
Уравнение неразрывности даст вследствие условий 2 и 1:
dvx dvv dvz
дх ' ду
') Вместо трех постулатов 3 мы можем формально принять один по-
постулат
/if2 = /l fit
понимая здесь под /, и f2 любые величины, например, постоянные. Действи-
Действительно, при /2 = 1 получим, вследствие этого равенства, fx = f{, далее, /,/2 =
7=fif2~fif2 Наконец, условие fxf'i = ^ следует из того, что Д/2 =
= /i(/2 — /2) =/1/2—f\fi=f\h—/1/2, так что по нашему постулату и по
лсловию fxf2 = f\f2' 6yfleT/j/2 = 0 Вопрос о возможности точного, а не
приближенного выполнения условии 3 при разных формах сглаживания,
гак же как и вопрос о независимости наших постулатов, разобран в статье
Изаксона А «К определению турбулентности» Ж Р Ф — X. О , 61
A929), 3
2) Мы говорили о сглаживании функции f(x) одного аргумента Если
есть функция f(x, у, z, t), можно определить соответствующую сглаживаю-
сглаживающую функцию ш (S, т], С, т), так что
7= f J f f/(X-B, >-!;,*-:,*--)»(«, т„:, z)dUrtd:dz.
Рейнольде осредняет уравнения, гидродинамики по одном} лишь,
аргументу— по времени.

692	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ. Щ
Уравнения Навье — Стокса дадут:
dv	г	dvr	/ dv Y	ov v , dvv\
~ r 	 or 	 0	— 	 D I 1) 	*	\— 1) 	 -	V~ 1} 	— 1 -4—
-|	^ -j	^L _|- -
dp	dvy	/ dvy	dvy	OVy
dy r У ' dt ^ \ x dx У dy	z dz
_4_ ^!L __ ^L
dx ~r dy ~r dz '
(считаем, что FX = FX и т. д.). Преобразуем входящие в ускорение
нелинейные по отношению к скоростям члены; заметим, что вообще
/i/2 = (Л + /0 (/1 + h) - hh + /1/2 4- /i /14- /'1/2.
а потому /j/: может быть записано, на основании свойств 2 и 3
в виде
Таким образом, например:
dvx , dvx , _. dv,
— di\	dv,	dv f	ovx
д	I ^'i dv'y dv'z \
uz ^ > a \ dx	dy ' dz )
но
dvr	av,	(
v' —r^-4-v' —-4-t/ -
¦« dA ' у dy	¦*
_ t/ ,2 r'
~ d.v Ui T uy У'г
С' ,2	У , ,	О /
= 	1) -4	1) 1) -г 	 V
dx ' dy l v d^
ибо вследствие линейности уравнения неразрывности будет
0У ~1~ OZ ~~

5]
ОСНОВНЫЕ УРАВНЕНИЯ РЕЙНОЛЬДСА
693
Мы можем, таким образом, переписать уравнения Навье — Стокса
в виде
дх
др
dp_
dz
дх
д ,—
— dvv
* дх У Vх ' х у}~ ду V уу i ^у / г^ дг \
у
dv, . — Й1»г . — dv, , —
E.1)
Мы видим, что уравнения для средних скоростей и для среднего
давления имеют тот же вид, что и уравнения Навье — Стокса, с той
лишь разницей, что к компонентам тензора напряжений прибавлены
величины — pv , —
г>
соответственно. Шесть величин
P = — i
E.2)
носят название добавочных напряжений. Так как ххх, .. . суть линей-
линейные функции от производных vx, vy, vz по координатам, то ххх, . . .
так же выразятся через средние скорости, как ixx, .. . выражаются
через точные скорости, и мы получаем следующий замечательный
результат: если ввести в уравнения гидромеханики вместо истинных
скоростей их средние значения, то одновременно с этим надлежит
ввести новые поверхностные силы, изображающиеся в виде тензора
с компонентами Р,
ху
Pzz. Добавочные напряжения пред-
представляют как бы суммарный эффект всех беспорядочных отклонений
скоростей от их среднего значения.
Смысл величин Рхх, ..., Ргг станет особенно выпуклым, если
вспомним, как в кинетической теории газов получаются уравнения
Навье — Стокса. Мы знаем, что ряд свойств газа, такие, как вязкость,
диффузия, теплопроводность, обязан своим происхождением суммар-
суммарному эффекту молекулярных движений, каковые в деталях мы описать
не можем. Более того, в кинетической теории газов показывается,
что компоненты тензора напряжений в уравнениях Навье — Стокса

694	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ щ
получаются из величин сх— сх, су — су, сг—сг(сх' су сг—скорости
движения молекул, сх, су, сг—средние значения скоростей —скорости
всего потока) совершенно так же, как наши Рхх, Рху	Ргг по-
получались из v'x, v' v'z. И там и здесь мы суммарно описываем
эффект беспорядочных движений.
Отметим, что при формальном введении величин Р хк, ... вяз-
вязкость (а никакой роли не играет: уравнения для средних элементов
турбулентного движения идеальной жидкости отличаются от построен-
построенных нами уравнений для вязкой жидкости отсутствием членов zKX,
члены же, дающие добавочные напряжения, имеют в обоих случаях
одинаковый вид.
Кинетическая энергия турбулентного движения будет для единицы
объёма:
= -§- {vl + v2y -f- vl) 4- р (vxv'x Н-оуоу 4- Vzv'z) 4- y {y'l + V* 4- v'*).
Рассмотрим некоторый конечный объём (т) нашей жидкости и
найдём скорость изменения средней кинетической энергии этого
объёма, т. е. величину
А.
dt
(т)
Для простоты рассуждений предположим сперва, что объем наш
ограничен твёрдыми стенками и что внешние силы отсутствуют (F=0).
Умножая уравнения Навье-Стокса на vx, vy, vz соответственно и
складывая их, получим:
vl + v]
	=
dp	dp	dp	(dzxx дхху дх
Беря интеграл от обеих частей по всему нашему закреплённому
объёму, внося vx, ... под знаки производных, применяя формулу
Грина и замечая, что на стенках всюду г> = 0, мы получим, после

§51
ОСНОВНЫЕ УРАЗНЕНИЯ РЕЙНОЛЬДСА
695
простых преобразований:
J р J*_J_!i,_
J L xx dx ~> *y by ' 'r"xz dz
dt
i"
dvz , duz	dvz
Введём обозначения:
'2 , '2 i '*
E.4)
тогда для скорости изменения средней кинетической энергии Т
нашего объёма получим, очевидно:
dT _dT0 dT' _
dt dt "i dt
5.5)
где \'хх = т^ — -c^, ... С другой стороны, нетрудно найти другое
выражение для dTojd( = dTQjdt. В самом деле, умножая E.1) на
г»,, оу, vz соответственно, и складывая, получим:
d . — d . — d —-
— dp
= — V
dx
Интегрируя по объёму (t) обе части этого равенства и применяя
формулу Грина, получим, на основании того, что на стенках
						"\ Гр

695	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ щ
Сравнивая E.6) с E.5), получаем для скорости изменения со вре-
временем средней кинетической энергии Т турбулентных пульсаций
выражение
Наконец, вставим в E.6) и E.7) выражения Tfr> . .. через произ-
производные от скоростей по координатам
dvv	dv\
ду	дх
Ъ'х	dvy
ду	' дх
получим окончательно:
dt
где
'г = — J Ф'di— j'wdn,	E.9)
Знак в правой части выражения E.9) скорости изменения энергии
пульсаций может быть положителен или отрицателен в зависимости
от знака члена | Тйт, первый член— Г Ф' dx зависит от коэффи-
коэффициента вязкости (а и всегда отрицателен.

§ 5]	ОСНОВНЫЕ УРАВНЕНИЯ РЕПНОЛЬДСл	Су7
Если надо принять в расчёт внешние силы F\., F.,, Fг и если
объём (Ч) не ограничен твёрдыми стенками, так что на границах
г>фО, в уравнении E.8) придётся добавить члены, представляющие:
1)	поток кинетической энергии осредненного движения через 1раницы,
2)	работу внешних сил, 3) работу, совершённую на границе сред-
средними напряжениями ziX, ... и средним давлением, а также доба-
добавочными напряжениями.
Напротив, в уравнении E.9) надо будет добавить лишь члены,
зависящие от конвекции энергии турбулентного движения через гра-
границы области (т).
Обращаясь к случаю сжимаемой жидкости, запишем уравнения
движения, вводя вектор количества движения (с компонентами
mx=<jvx, my = [)Vv, niz = pvz) и принимая во внимание уравнение
неразрывности
dp . дтх . &ту . дтг	-
Ж ~т~ ~дх~ + ~ду~ "т" ~~dz ~ '
в виде:
, д ,	, dm у
ду- = ?РУ + Jx (Т* «• - v*my) + ду- (туу - "у
~
Произведём теперь над правыми и левыми частями всех четы-
четырёх уравнений сглаживание с одной и той же сглаживающей функ-
функцией (например, осреднение в одном и том же интервале), удов ie-
творяющее трём перечисленным выше условиям. Уравнение неразрыв-
неразрывное in даст, на основании условий 1 и 2:
dt^~ дх "+" бу "+ дг ~
Выпишем первое из уравнений движения:
"= ?Fx +- ^ (^.« - ^~А) + Ту (^v ~ V*
45 Теоретчс^кал гид[>омечаника, ч II

698	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	1ГЛ. Ill
Обратим внимание на выражения типа ъхтх. Имеем:
vtmx = (v_ -f <)(«*+
пли, вследствие свойств 3:
Если пульсациями плотности можно пренебречь (р' = О)р = р
(это, по-видимому, имеет место в атмосферных движениях), то для
добавочных напряжений мы получим те же выражения, что и в слу-
случае несжимаемой жидкости; в самом деле, здесь
V'xm'x = V'x К —<) = V'j? К - <) ¦= ?<*¦
Построив уравнения для средних величин, мы сталкиваемся с ди-
дилеммой, либо поставить шесть новых величин — добавочные напря-
напряжения — в зависимость о? старых величии vx, vy, vz, р, p, либо,
считая эти шесть величин за независимые новые функции (новый
симметрический тензор), построить какие-то новые уравнения, ибо
теперь осреднённых уравнений движения и неразрывности, очевидно,
будет недостаточно.
§ 6. Характеристики турбулентности. Богатейший эмпириче-
эмпирический материал последних лет явился основой развития полуэмпири-
полуэмпирических, полутеоретических методов нахождения добавочных напряже-
напряжений через средние значения скоростей. С некоторыми изысканиями,
сюда относящимися,- мы познакомимся в следующем параграфе. Что
касается присоединения новых уравнений к системе осреднённых
уравнений гидродинамики, то здесь наиболее совершенная постановка
вопроса принадлежала Келлеру и Фридману '). Идея заключалась
в присоединении к величинам vx, vy, vz, p, p (для общего случая
сжимаемой жидкости) в качестве искомых функций 15 дальнейших
«характеристик» турбулентности, вводимых под названием «момен-
«моментов связи» и являющихся обобщением рейнольдсовских добавочных
напряжений. Моменты связи строятся после того, как введены «кор-
«корреляционные моменты». Под последними понимают выражения вида
R(fv /2) = /1/2 — /1/2 (поскольку равенство /i/2 = /i/2 выпол-
выполняется лишь приближённо, R(f\f<i) лишь приближённо будет равно
/1/2). где /j и /2 — какие-либо гидродинамические элементы; задав
теперь произвольные приращения ± ?, + rt, ± С координат х, у, z,
') См. работу Келлер Л., Ueber die Aufstellung eines Systems von Cha-
rakterlsiiken der a'mospliarischen Tmbulenz, Иза. гл. Физ. Обсерватории, 1925.

§6]	ХАРАКТЕРИСТИКИ ТУРБУЛЕНТНОСТИ	699
определим момент связи (fv /2) для дв}х каких-либо функций Д
и /2 в виде
Ч\> fti = R\hi.x — \, y — % z — C; t), f2(
Таким образом, моменты связи суть функции времени, координат
и трех добавочных переменных 1) Легко видеть, что придется рас-
рассмотреть пятнадцать моментов связи для случая сжимаемой жидкости,
или десять для несжимаемой жидкости
В работе Кармана, а затем в работе Кармана и Хауэрса 2) и
одновременно в работах Миллионщикова и Лойцянского 3) решение
получаемой таким образом системы уравнений доведено до конца
в одном весьма частном случае турбулентного движения — в случае
гак называемой однородной и изотропной турбулентности. Послед-
Последнее понятие было расширено Колмогоровым, который ввел в рас-
рассмотрение «локально однородную» и «локально изотропную» турбу-
турбулентность Изложение первых результатов, касающихся этих частных
видов турбулентности так же, как и соответствующего аппарата
исследования турбулентности, можно найти в монографии Обу-
Обухова А. М «Приложение методов статистического описания непре-
непрерывных процессов и полей к теории атмосферной турбулентности»,
Диссертация, Москва, 1947 г
Ричардсон и Тейлор4) пришли совсем из других соображений
к рассмотрению моментов связи для различных гидродинамических
элементов Мы еще вернемся к этим работам, а сейчас остановимся
на вопросе о сопровождающем турбулентность перемешивании
Рейнольде ввел в качестве «характеристик» турбулентности
шесть компонентов тензора добавочных напряжений, Ричардсон,
Шмидт и Тейлор вводят в рассмотрение лагранжевы переменные
Это дает возможность следить за конечным перемещением индиви-
') При построении дополнительных уравнении приходится воспользо-
воспользоваться новой гипотезой касающейся осреднений, примегытелоно < необходи-
необходимости осреднять произведения уже не двух, а трех функций Эта новая гипо-
гипотеза сводится к приближенному соотношению f[f2f'3 = 0, где, как и прежде,
/j = f1 — f1 и т д После того, как система уравнении построена, надлежит
еще проверить независимость отдельных уравнений системы
2)	К а г m a n and H о w а г t h On the statistical Theory of Isotropic Turbu-
Turbulence Proc Roy Soc 164, A938) № 917, стр 192—215
3)	Миллионщиков М Д, Вырождение однородной изотропной тур-
турбулентности в вязкой несжимаемой жидкости ДАН СССР, 26 A939), № 5,
стр 236—240, Л Г Лоицянский Некоторые основные закономерности
изотропного турбулентного потока, Труды ЦАГИ № 440, 1939
См также Седов Л И, Методы подобия и размерностей в механике,
Гостехиздат, 1957
4)	Richardson, Atmospheric diffusion on a distance neighbour graph,
Proc Roy Soc London (A), 110 A926) стр 729—757 Taylor O, Diffusion
by continuous mouvements, Proc Lond Math Soc B), 20, 1921
45*

700	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ ш
дуальных частичек и, таким образом, позволяет ближе подойти
к изображению процесса «перемешивания» (Austausch, Conductivity).
Выведем уравнение перемешивания какой-либо субстанции, располо-
расположенной в среде, находящейся в турбулентном движении. Вместе
с Тейлором и Шмидтом ограничимся рассмотрением перемешивания
только в одном направлении (назовём его z). Относительно субстан-
субстанции, подверженной перемешиванию, предположим, что она: 1) не-
уничтожима, т. е. сохраняется в некотором элементарном объёме
жидкости, пока тот движется, не смешиваясь с другими; 2) сохра-
сохраняется при смешении двух масс. Обозначим количество субстанции
в единице массы жидкости через s. Под самой субстанцией можем
разуметь либо какую-нибудь примесь к жидкости (пыль, например),
либо какую-нибудь физическую характеристику самой жидкости (на-
(например, её количество движения в направлении, перпендикулярном
к оси z, запас её тепловой энергии). Предположим ещё, что субстан-
субстанция распределена приблизительно равномерно в направлении оси,
перпендикулярной к оси z (например, х и у), но равномерность эта
имеет статистический характер: именно, выбрав достаточно большую
площадь, перпендикулярную к оси z, и осреднив s по этой площади,
получим уже величину, не зависящую от положения центра выбран-
выбранной площади (не зависящую от х и у):
s (х, у, z, t) = s(z, t).
Введём затем плотность субстанции о = ps (p — плотность жидко-
жидкости)— количество субстанции в единице объёма. Естественно теперь
принять, что средний поток субстанции через плоскость z — const,
будет пропорционален проекции градиента о на ось z; пусть это
будет
dz
где к — некоторый положительный коэффициент пропорциональности
(если бы было k < 0, то мы имели бы дело не с рассеиванием,
а с концентрацией субстанции). Сравнивая поток субстанции на уров-
уровнях z и z-\-dz, находим прирост субстанции за единицу времени:
dt~ д
Мы видим, таким образом, что плотность субстанции удовлетво-
удовлетворяет, независимо от механизма турбулентного перемешивания, днф-
') На основании второго постулата а не теряется и не появляется
и элементе dz само по себе.

§ 6]	ХЛРАКГЬРИСТИКИ ТУРБУЛЕНТНОСТИ	701
ференциальному уравнению F.1). Тр}?днос1ь заключается в опреае-
лении коэффициента k ').
Желая определить k, заметим прежде всего, что если субстанция
переносится жидкостью пассивно и своим присутствием на движение
существенно не влияет, то величину k естественно считать не зави-
зависящей ни от рода субстанции, ни от её мгновенного распределения; k
определяется исключительно состоянием неупорядоченного турбу-
турбулентного движения жидкости. При данном движении рассеяние любой
субстанции описывается одним и тем же уравнением F.1).
Предположим, что k не меняется ни в пространстве, ни во вре-
времени (это - статистическая характеристика некоторого состояния дви-
движения). Рассмотрим также еще случай, когда р = const. Тогда F.1)
обращается в простое уравнение теплопроводности, и мы можем
написать решение его в виде:
_	1	Р (г-гоJ
2 У r.k (t — t0) J
— со
где a(z, t0) представляет среднее распределение плотности субстан-
субстанции на уровне z в момент времени t — tQ. Мы видим, что турбулент-
турбулентность действует на начальное распределение о (z0, t0) по высоте z0
как сглаживание со сглаживающей функцией
Мы уже говорили выше о сглаживающей функции такою типа
(формула (а), § 4).
Возьмем теперь некоторый уровень z0 и посмотрим, какая судьба
постигнет в момент t частицы жидкости, лежавшие в момент tQ на
уровне z0. Обозначая через (,(х, у, t) значение z для разных точек
нашего уровня в момент t, мы, очевидно, должны иметь, на осно-
основании самого определения турбулентности,
С(х, у, t) — zo = O.
Рассчитаем, однако, величину
f	F.3)
') Уравнение F.1) по своему обоснованию тесно примыкает к аналогич-
аналогичному уравнению, построенному Фикком (F i с k, Ann. Phys. Chem., 1885, т 49)
для молекулярной диффузии; поэтому в английской литературе по тур-
турбулентности оно называется уравнением Фикка. Вывод его, так же как спо-
способ нахождения (см ниже), мы заимствуем из главы Келлера по атмосфер-
атмосферной турбулентности в книге «Динамическая метеорология» под редакцией
Извекова и Кочина, ч. II, 1936.

702	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ 1П
где интеграл взят по элементу df площади /, достаточно большой
и расположенной в плоскости (х, у).
Величину эту можно выразить через k. Чтобы это сделать, за-
заметим сперва, что, рассматривая частицы, лежащие в момент t0 на
уровне z0 или, точнее, в слое от z0 до zo-{-dzo, как примесь, и
предполагая, что они к моменту времени t разбросаются по раз-
различным уровням z от—со до со, можно применить интеграл F 2)
(вернее один элемент этого интеграла, ибо a (z0, t0) сосредоточено
у нас на элементе dz0) к определению тою количества наших ча-
частиц которое попадает в момент t на уровень z; на единицу пло-
площади их будет
(Z-Zp)»
а на единицу массы пг — — (очевидно, след}ет положить о (z0, to) = pQ).
Но теперь, вместо того, чтобы вычислять интеграл B.18) интегри-
интегрированием величины (С—z0J по площади, мы можем разбить вычи-
вычисление F.3), беря сперва для каждого z л-г(С— z0J, умноженное
на соответствующую площадь, а затем, интегрируя это по z от-—со
до-|-оо (частицы распределятся, по предположению, во всем про-
промежутке от — со до -j- со). Но тогда получим:
		1	7 (z-Zq)»
(С — zof = ——- х	/ е <*«-** (z —zQfdz.
Интеграл в правой части вычисляется и дает 2k (t —10). Отсюда
Таким образом, нами найден гидродинамический смысл величины k.
Имея в виду этот смысл, величину k называют мерой рассеяния.
Одновременно с k часто вводят еще величину А — pk, где под р
разумеется средняя плотность; величина эта носит название мери
обмена
Размерность А совпадает с размерностью коэффициента вязкости и.,
размерность же k будет L2/T, что совпадает с размерностью кинема-
кинематического коэффициента вязкости v.
Покажем еще, как можно иначе выразить величину k. Пусть
по-прежнему перемешивание происходит лишь в направтении z, сосре-
сосредоточим внимание на одной какой-либо частице и будем обозначать
значения ее скорости в моменты времени t через vz(t) Следуя Тей-
Тейлору (loc cit.), привлечем к рассмотрению коэффициент корреляции
(или момент связи) между значениями vz(t) и v,(t-\-r:), где х рас-

§6]	ХАРАКТЕРИСТИКИ ТУРБУЛЕНТНОСТИ	703
сматривается как произвольный постоянный параметр, и выразим k
через этот коэффициент. Строгий вывод был дан Л. Келлером '). Мы
укажем лишь путь получения строгого вывода, отсылая за подроб-
подробностями к статье Келлера.
Вместе с Келлером подчиним vz следующим четырём требованиям.
Предположим: 1) что существует предел для среднего значения vz(t)
при увеличении интервала осреднения до бесконечности, и этот пре-
предел равен нулю (мы считаем, что у нас нет среднего переноса, а есть
лишь турбулентное движение, так что vz = Q); 2) что существует пре-
предел при увеличении до бесконечности интервала осреднения, для сред-
среднего значения vz{tJ и, более обще, для среднего значения выражения
vz(t)vz(t -j-т); эти пределы будем обозначать v'z{tf av'z(t)v'z(,t-\-x)
соответственно (на основании свойства 1 можно положить vz = vz);
3) что по мере того, как мы будем увеличивать интервал изменений
t до со величина Р[о. <vz(t) < 3], равная вероятности того, что vz(t)
заключается во взятом интервале изменения t между а и В, стре-
стремится к какому-то определённому пределу; 4) что если через R(i)
обозначить коэффициент корреляции между vz(t) и vi{t-\-T.)\
v' (t) v' (t
R(x) = 	--—
интеграл I R{x)dx имеет определенное конечное значение (мы харак-
о
теризуем турбулентное движение как неупорядоченное, а в таком
случае естественно потребовать, чтобы корреляция между v2(t) и
vz(t-\-x) при возрастании х дальше некоторого предела быстро стре-
стремилась к нулю).
Рассмотрим затем некий, конечной длины /, интервал оси t и
обозначим среднее значение от vz(t) в этом интервале через vz(t, I);
vz(t, 1) = y / vz(i,)d\. Величина vz(t,l) будет, вообще говоря,
отлична от нуля. Можно теперь доказать следующую теорему2): вероят-
вероятность P{i < vz(t, I) < 3) существования неравенства а < vz(t, I) <3
') Келлер Л., Распространение предельных теорем теории вероятности
на интегралы и средние значения функции сплошного аргумента, Труды
Главной географической обсерватории, вып 4, 1935 Далее, статья Келлера
по теории турбулентности, из книги «Динамическая метеорология».
2) К е л л е р Л , loc. cit. Теорема эта является обобщением на случай функ-
функций сплошного аргумента известной предельной теоремы теории вероятности,
применяющейся обычно к дискретной последовательности случайных величин.

704	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ. Ill
при увеличении I к со стремится к выражению:
с
1
/ е 2 df\,
а V I
с
где
l/ 2г/~2
о
i
Рассмотрим, в частности, осреднение вида у / vz(l)dt. Имеем:
о
в
(I	ч	fl'T
Г	\	1	Г	-- Г'
а если перейти под знаком интеграла справа от переменного -ц к пере-
переменному и — г\су I, то получим
/^	,	в
г
Примем теперь / = ^ — tQ. Тогда Г г;г (?)cf? = С — z0 представит вер-
о
тикалыюе уклонение частицы от её первоначального положения
в некоторый момент t, и мы придём к статистическому закону рас-
распределения уклонений С — zu:
(С-гоJ
ф(С, t)= ,	L=— e 2tJ('-'°)
Непосредственным дифференцированием убеждаемся, что 9 удовле-
удовлетворяет уравнению
Заметим, что величина с будет, вообще говоря, разной для разных
частиц. Предполагая турбулентность однородной, можем, однако,
считать, что с для всех частиц одинаково. При этом условии осред-
осреднение по большому промежутку времени, применённое к смене соста-
составляющих скорости одной частицы, может быть заменено осреднением

§ 61	ХАРАКТЕРИСТИКИ ТУРБУЛЕНТНОСТИ	705
уже не по времени, а по массе — для всей совокупности частиц,
содержащихся в рассматриваемой массе. Можно тогда сравнить
с'
наше уравнение для ср с уравнением Фикка F.2) и написать & = —,
Мы придем таким образом к формуле:
со
k = v'l j R D) dx,
о
а это и есть выражение, предложенное Тейлором для меры рассеяния.
Мы уже говорили, что приведённое здесь рассуждение можно
отнести лишь к тому случаю, когда турбулентные процессы проис-
происходят достаточно однородно внутри достаточно протяжённой во всех
направлениях массы, т. е. когда речь идёт об однородной турбулент-
турбулентности. В том случае, когда имеется турбулентность, так сказать,
разных масштабов (как, например, это имеет место в земной атмо-
атмосфере), процесс турбулентного рассеяния будет существенным обра-
образом зависеть от размеров области, занимаемой рассматриваемой при-
примесью. Чтобы пояснить эту мысль, посмотрим, как будет рассеи-
рассеиваться дым в свободной атмосфере. Представим себе две молекулы
ацетилена, находящиеся на расстоянии 10 ° см друг от друга; по
истечении одной секунды они, подвергнувшись действию молекуляр-
молекулярной диффузии, разойдутся, но всё ещё будут друг от друга на рас-
расстоянии порядка 101 см. Совсем иная судьба постигнет две молекулы
ацетилена, находящиеся на расстоянии 105 см = 103 м друг от друга;
здесь появляется диффузия турбулентная (порывистость ветра), наши
частицы могут быть подхвачены разными порывами ветра, так что
через секунду расстояние между ними может измениться на несколько
метров, а не на величину порядка 101 см—10 см яй 101 см, как
это и было в первом случае. Иначе говоря, такая существенная вели-
величина, как скорость расширения «диффундирующего» в турбулентной
среде облака, будет меняться по мере того, как облако будет «жить»,
ибо «живя», облако всё время увеличивается в размерах и, следова-
следовательно, попадает в сферу влияния всё новых и новых вихрей.
Ричардсон предложил учитывать этот эффект, полагая k функ-
функцией диаметра области, и получил на основании эмпирических данных
следующую зависимость:
k (d) == ссСы,
где d — диаметр области, с — постоянная. Эта зависимость была
теоретически обоснована А. М. Обуховым в работе: «О распределе-
распределении энергии в спектре турбулентного потока» !).
') Изв. АН СССР, Серия геогр. и геофиз, 1941, 4—5.

706	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	'ГЛ. III
Мы рассматривали случай перемешивания, происходящего в одном
направлении. В общем случае вместо величины k из F.4) нам при-
придётся ввести «тензор рассеивания». Именно, вводя «исходные» коор-
координаты а, Ь, с частиц (координаты в момент ^0) и координаты х,
у, z этих же частиц в момент t, можем построить шесть величин:
— (х—а){х— а)	_ (х—а)(у—Ъ)
~ 2 (*-*„) '• ^У~~Т(Г=^Г~'
_ (г—с) (г—С)
Kzz—
"«— 2(t-t0)
(с этой точки зрения наше k равно kzz); аналогично этому можно
получить:
л	(х—а)(х— а)	.	(z — с)
Тензор с компонентами Ахх, .. . , Azz представляет обобщение вве-
введённого Рейнольдсом тензора добавочных напряжений и впервые
введён Келлером ').
В. ДОБАВОЧНЫЕ НАПРЯЖЕНИЯ И СРЕДНИЕ ЗНАЧЕНИЯ
ГИДРОДИНАМИЧЕСКИХ ЭЛЕМЕНТОВ
§ 7. Путь перемешивания и метод подобия. В этом разделе
мы приведём вывод нескольких наиболее важных формул, связываю-
связывающих добавочные напряжения со средними значениями гидродинами-
гидродинамических элементов, а также дадим некоторые приложения этих фор-
формул. Мы начнём при этом с введённого Прандтлем понятия «пути
перемешивания».
Представим себе плоское турбулентное движение, которое прои-
происходит в среднем в направлении оси л: и в котором средняя ско-
скорость vx существенным образом зависит лишь от координаты у. Наи-
Наиболее существенным из добавочных напряжений является здесь
Р = — pv'xv', Чтобы представить его выражение иначе, Прандтль
вводит некую характерную длину— «путь перемешивания», играющую
ту же роль, что и путь пробега молекулы в кинетической теории
газов. Если обозначить через V различные пути перемешивания, т. е.
различные расстояния от той точки М, где мы вычисляем величины
v'xv' до тех точек, из которых приходят в точку М различные
частицы жидкости (например, если говорить об осреднении по вре-
времени), то частицы, приходящие со скоростями v', будут иметь ско-
') См. об этом Келлер Л., Joe. cit.

§ 7]	ПУТЬ ПЕРЕМЕШИВАНИЯ И МРТОД ПОДОБИЯ	707
рости vx, равные vx-\-V -^. Но тогда
¦*	ду '
и добавочное напряжение Р = — P^'xv'y будет
= P^xvy
Введем затем среднее значение абсолютных величин |/'| и назовем
его /.
Предположим вместе с Карманом, что внутренний механизм тур-
турбулентности во всех местах жидкости имеет один и тот же характер
и может отличаться только масштабами длины и времени. Иначе
говоря, мы предположим, и это — основная гипотеза Кармана, что
турбулентные движения в различных частях жидкости между собой
подобны. Если нам было бы известно, от каких гидродинамических
элементов зависит величина I, мы могли бы теперь, пользуясь сооб-
соображениями, изложенными в главе второй, пытаться найти вид зави-
зависимости I от этих элементов. Предположим же, и в этом заключается
вторая гипотеза Кармана, что в выражение для / не входят третьи
производные от vK по у, так что / может зависеть от р, dvxjdy, d2vx/dyz
(мы исключаем возможность зависимости от vK, ибо, прибавляя к vK
всюду постоянное число, мы, очевидно, не изменим картины явле-
явления). Итак, пусть
l=Z(p, vx, vv),
где
f dy ' x~~ dy* '
Введем новые единицы длины, времени и массы соответственно в L,
Т, М раз ббльшие старых единиц. Тогда, обозначая численные зна-
значения всех рассматриваемых величин в новой системе единиц через
l\> Pi' vx\' • ¦ • соответственно, будем иметь:
/// о	о
11 Н—-?3Hi> dy ~~ Г dyx ' dy2 ~ TL a
Поэтому наша предполагаемая зависимость примет вид:
II	7 / М
1== [U
М	1 dvxl I dlvx
Т dyx ' TL dy\
') Выражение — yv'V имеет размерность ци аналогично этому коэффи-
коэффициенту. Ср. также с мерой обмена, введенной в предыдущем параграфе.

708	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ	[ГЛ III
С другой стороны, должно быть в новой системе единиц:
—Z (о
так что (мы отбросим значок «1»)
(М 1 - 1-
В этом тождестве положим у^ — — , T=-rx-, LT~vr; тогда полу-
Z.3 p	ay	x	J
чим равенство
2(Р. vx, vx) = TZ{\, I, l) = -^/-5-3iE.const.
Таким образом,
i — kdVx I d*Vx	G 2x
где А есть постоянная, каковую надлежит определить из эмпириче-
эмпирических данных.
Зная выражение для /, без всякого труда найдём выражение
для Рху. Считаем, что последнее может быть функцией от /, р, vx, vx:
Pxy = F(p, I, vx, vx).
Тогда введём
(d2vr\
так что
М ,п , „ /М
С другой стороны,
(Pxy)l = F(?V lV «jrl. ^l)
и, следовательно (отбрасываем значки):
Наконец, полагая
М 1
мы придём к соотношению
Г? /	I —.	\

§ 8А	ПРИМЕРЫ	709
Но вследствие G.2)
/ ¦х?-= const.,
vx
и ми приходим к важной формуле
Р„„ = р,
Формула G.3) была установлена впервые Прандтлем, который,
исходя из выражения C.1), нашел
dy
Пользуясь G.2), можем переписать G.3) в виде:
Pxy = k^~-.	G.4)
ЧУ
§ 8. Примеры. Формулу G.4) применим к изучению турбулентного
движения между двумя гладкими параллельными стенками (у = 0,
y — 2d). Напишем теперь уравнения E.1) для осредненного движе-
движения, считая, что средние напряжения, так же как и vx, зависят лишь
от у и что сила отсутствует, a vy = 0. Получим, очевидно:
др~ дРху
дх	ду '
откуда заключаем, что в нашем движении Рху есть линейная функ-
функция от у. Вместе с Карманом положим, что при 0^ у
считая, что Рху обращается в нуль на середине расстояния Id между
ненками, а при d^y^l2d
Р — _т (\ _iL\
где т0—добавочное напряжение около самой стенки (точнее на гра-
границе ламинарного пограничного слоя, имеющегося внутри нашего
турбулентного слоя). Но тогда G.4) даст нам дифференциальное
уравнение второго порядка, из коего можно найти vx (у):
VX
') Мы положили F(\, 1, 1, *)= 1; это можно сделать, выбирая / долж-
должным образом.

710
или
откуда
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
k
[ГЛ. Ill
-4- + Y ¦
?
-х-= ± Л/ -- Ш\/~1 —~ут -f-const.
Vx	'	-о	'	«
/ 		.
Полагая const. = 2kd j/ -—¦- (при у = 0, i>x = oo), получим:
1 —
(выбираем знак минус, чтобы vx убывало с возрастанием у), инте-
25х	,	, грируя ещё раз, придём, в предположении, что
"vx{d) = vxma, к формуле Кармана:
(8.1)
Формула (8.1) Кармана даёт, как мы уже
отмечали, хорошее совпадение с данными экспе-
эксперимента. На рис. 197 изображена кривая (8.1).
Граница между областью, где эта формула
применима, и пограничной областью, где даёт
себя знать вязкость («ламинарный подслой»),
определяется значением у — yv при котором
vx = vxl = — ух (внутри ламинарного слоя ско-
скорость считаем меняющейся по линейному за-
закону, причём там т0 = jj. dvjdy). Если бы мы знали величину т0,
то, вставляя значение vx=vxl в левую часть (8.1) и значение у = у\
в правую часть, мы нашли бы, при данном vxma%, уг, т. е. толщину
ламинарного пограничного слоя, погружённого в наш турбулентный
слой, при этом (8.1), поскольку речь идёт о точках, лежащих
очень близко от стенки (уя^О), можно заменить приближённым
равенством
~":max vx\_^_, 1 (\„'^_	\\	'8.2)
У1

§ 8i	ПРИМЕРЫ	711
Наша формула связывает три величины vxmax, x0 и у,. Прандтль1)
предлагает далее принять, что так как слои жидкости, в которых
проявляется трение, должны быть одинаковы, то vx, должно быть
кратным 1/ — , т. е.
где р есть уже некоторая постоянная, каковую надо найти раз на-
навсегда из эксперимента. Но тогда C.6) даст:
«.-.~/?{м4«-')}- о.»
причём здесь y. = ^-vxl = y — Bv.
Введём теперь вместо "охты и х0 «коэффициент сопротивления» \т,
отнесённый к максимальной скорости vxmix,
т	2 '
и число Рейнольдса Rm, отвечающее г>х
	. vx max ^
in	v
Мы получим тогда, вместо (8.2), после простых преобразований:
X —	4*2
m~~(lnRmJ/^ + cJ'
где
C = k$~- 1 — In p.
Сравнение этой формулы с опытами Никурадзе, Шиллера и др.
дало очень хорошие результаты для значений Rm, доходящих до
1,8- 106. При этом оказалось, что ? — 0,44 (по Карману 0,36),
С = 2,83. На рис. 198 по горизонтальной оси отложены значения
]g"j/XmRm, а по вертикальной оси — значения 1/]//^. Точками изо-
изображены данные эксперимента.
Желая учесть шероховатость стенки, обратим сперва внимание
на величину / из формулы G.3). Пользуясь формулой G.3) и выра-
выражая vx по закону Кармана, мы получим:
<=»"[/¦-*-(>-$)]
') См., например, Прандтль и Титьенс, Гидро- и аэродинамика,
т. II, 1935, стр. 93.

712	ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
н, следовательно, при больших d и малых у:
[ГЛ. Ш
Так будет обстоять дело при отсутствии шероховатости. Шерохо-
ваюсть действует в том смысле, что / оказывается отличным от
нуля на поверхности у = О (так же как и средняя скорость).
Чтобы это описать, поместим начало координат не на поверхности
стенки, а под стенкой на уровне у =— е(е — размеры шерохова-
шероховатости), и для новых вертикальных координат у, напишем
(y1==y-j-e). Очевидно, будет по-прежнему:
и мы напишем вместе с Прандтлем
(8-4)
здесь у0, как это установлено из наблюдений над некоторыми шерохо-
шероховатыми поверхностями, будет
г
Формулу эту мы применим к построению турбулентного погранич-
пограничного слоя, получающегося при движении вдоль пластинки (здесь пер-
первая пластинка остается при у = 0, а вторая отодвигается очень
далеко). Над пластинкой образуется турбулентный слой неизвестной

ПРИМЕРЫ
71 j
нам высоты о (не смешивать с ламинарным пограничным слоем).
Над этим пограничным слоем пусть скорость имеет постоянное зна-
значение V (8). Тогда по (8.4) можно написать у самой пластинки
Уо
причём значение т0 добавочного напряжения у самой пластинки будет
^о=Р*2-^.	(8.6)
1п2~
Уо
Обратимся к общим уравнениям E.1) для осреднённого движения
и, пренебрегая влиянием вязкости, напишем первое из уравнений
для нашего случая плоской задачи со стационарным средним потоком:
/- dvx . — dvx\
\ х дх ' ду /
1).
:х дх ^ " ду ) ~ ду
Проинтегрируем обе части нашего уравнения по у от у0 до гра-
границы 3 турбулентного слоя. Вследствие уравнения неразрывности
ду
имеем:
,/ ^-37^ = V* у,- ,/ ^-с^Г^^
Уо
причем
Уо
(8.7)
У)
Таким образом, получаем (Рху(Ь) = 0, так как Рху на границе тур-
турбулентного слоя равно нулю):
f%-dy = -±iPJty)» = —* • (8.8)
Уо	Уо
Чтобы выполнить интегрирование, заметим, что мы ищем скорости vx
в виде (8.5), причём vx может зависеть от х через посредство 8
') Добавочное напряжение Рхх включается обычно в давление р; гра-
градиент выражения —рЛ-Рхх вдоль оси х считается, как всегда в подобных
задачах, отсутствующим.
46 Теоретическая (идромеханика, ч. Ц

714
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ III
(нарастание пограничного слоя вдоль пластинки). Мы поместим
начало координат у самого края пластинки (8 = 0) и ось х напра-
направим вдоль пластинки. Как мы сказали уже, вне пограничного слоя
всюду существует поток с постоянной скоростью V, параллельной
оси х, так что vx (8) = V = const. Тогда
Уо
In
Уо
Уравнение (8.8) даст нам возможность найти 5(х). Замечая, что
в	а	s
Уо
Уо
Уо
и заменяя т0 по (8.6), получим, производя дифференцирование
4
принято равным 0,4):
Уо
0,161п-
Уо
Уо	Уо V Уо 8 )	у0
Чтобы найти Ь = Ь(х), остаётся проинтегрировать это уравнение-
Вводя в качестве вспомогательного переменного In —, получим:
5
40
30
20
10
О
Уо
.—-~
?-¦)('¦¦?-«)
= 0,16—.
Уо
100 200 300 Ш 500 ' Уо
Рис 1Э9	Кривая о = 3 (х) изобра-
изображена на рис. 199.
В качестве второго примера на применение соотношения G.3)
рассмотрим задачу о смешении широкого однородного потока воз-

ПРИМЕРЫ
715
духа, бегущею со скоростью vx = v = const , г>у = 0, с окружающим
его спокойным воздухом. Так как здесь речь идет о свободной тур-
турбулентности и стенки отсутствуют, то нам нельзя будет ориентиро-
ориентироваться на Рху как на известную величину. Напротив, величина /,
о которой мы уже имели случай говорить, может считаться здесь
Рис 200
пропорциональной ширине той зоны, в которой существует турбу-
турбулентность '). Зону эту примем ограниченной лучами, исходящими из
начала координат (рис. 200), в соответствии с чем и будем считать:
W = vxF (-J) = vxF (т,) (ч = -jr) -
(8.9)
(8.10)
где qr — функция тока, а с — постоянная, подлежащая определе-
определению. Теперь осредненное уравнение турбулентного движения (рассма-
(рассматривается идеальная несжимаемая жидкость) принимает, вследствие
G.3) и (8.9), вид:
- dv:
ду
0 Г 2
ду [рС
ду
(8.11)
а по (8 10), так как (Fr означает — \
v*~~dy = v ' vv~ дх
после простых преобразований
FF"-\ 2c2F"Fl" — 0.
Ц Tollraien W, Berechnung turbulenter Ausbreitungsvorgange Zeitschr.
i. angew. Math und Mech , 6 A92b), стр. 468.
м Т
f. angew
46*

716
ЭЛЕМЕНТЫ ТЕОРИИ ТУРБУЛЕНТНОСТИ
[ГЛ III
Уравнение это может быть удовлетворено, либо если
(vx — const., v == О или г»х = 0, v = const.), либо
если
тогда
Р==Ав
2 у 2с*
На «верхнем» крае турбулентного луча
(8.12)
МЫ ДОЛЖНЫ ПОЛОЖИТЬ
т. е. должны считать
f"=l, F" = 0, /7 = a1 при 71 = 0!.
На «нижнем» крае
у = — а2х
мы должны положить
—	dv
vx=0, -g-i = 0, т. е. принять, что F' = F" = 0 при ?) = — а2.
Эти пять условий позволяют не только определить гри произволь-
произвольные постоянные cv c2, с3, участвующие в решении уравнения (8.12),
1,0
-2 -1,5 -1,0 -0,5 О 0,5	10
Рис. 201,
но также и найти неизвестные величины	ах и я2- Величину с
следует определить из экспериментальных	данных. На рис. 201

ПРИМЕРЫ
717
изображена функция vx, причём по оси ординат отложены vx/v,
по оси абсцисс — значения ^	Рис. 202, где нанесены
Рис 202.
результаты, экспериментальные и теоретические, показывает,
сколько велико совпадение теории с данными опытов.
на-

ЛИТЕРАТУРА
К ГЛАВЕ I
Б е р с Л , Математические вопросы дозвуковой и околозвуковой газовой ди-
динамики, перев с англ, ИЛ, Москва, 1961
Гудерлеи К, Теория околозвуковых течении, пер с нем, ИЛ, Москва,
1960
Донов А., Второе приближение для уравнении одноразмерной акустики, Изв
Акад наук СССР, 1938
Донов А, Плоское крыло с острыми кромками в сверхзвуковом потоке,
Изв Акад наук СССР, 1939, серия матем , стр 603—626
Зауэр Р, Введение в газовую динамику, пер с нем, Гостехиздат, 1947
К и бель И А, К вопросу о сопротивлении при скоростях, близких к ско
рости звука, Труды конференции по изучению стратосферы, Акад наук
СССР, 1934
Кочин Н Е, Sur !a theone des ondes de choc dans un fluide Rendie del
Circolo Mat di Palermo, т 50, 1926 (см также К очи и Н Е, Собрание
трэдов)
Красилыцикова Е А, Влияние вихревой пелены при установившемся
движении крыла, ДАН СССР, 58 A947), № 6
Красилыцикова Е А, Влияние концевых кромок при движении крыла
с вибрациями со сверхзвуковой скоростью, ДАН СССР, 58 A947), № 5
Красильщикова Е А, Влияние концевых кромок при движении крыла
со сверхзвуковой скоростью, ДАН СССР, 58 A947), № 4
Красильщикова Е А, Возмущенное движение воздуха при вибрациях
крыла, движущегося со сверхзвуковой скоростью, ДАН СССР, 16 A947),
№ 6
Курант Р и Фридрихе К, Сверхзвуковые течения и ударные волны,
перев с англ , ИЛ, Москва, 1950
Ландау Л Д иЛифшицЕ М, Механика сплошных сред, 1953
Пойцянский Л Г, Механика жидкости v газа, Гостехиздат, Москва,
1957
Овсянников Л В, Об одном газовом течении с прямой линией перехода,
ПММ, т XII1, вып 5, 1949
РыжовО С, О газовых течениях в соплах Лаваля, ПММ, т XXII, вып 3,
1958.
Седов Л И, Методы подобия и размерности в механике, Гостехиздат,
Москва, 1957.
Станюкович К П, Теория неустановившихся движений газа, Гостехиздат,
1948
Фалькович С В, Околозвуковые плоские течения газа с особыми точ-
точками на звуковой линии, ПММ, т XXV, вып 2, 1961
Ферри А, Аэродинамика сверхзвуковых течений, пер с англ, Гостехиздат,
Москва, 1952,

ЛИТЕРАТУРА	719
ФранкльФ И, Вихревое движение и обтекание тел в плоскопараллельном
течении сверхзвуковой скорости. «Реактивное движение» 1935,
стр 82—92.
ФранкльФ И, Исследования в области окочозвуковых течений Инже-
Инженерный журнал, вып 1, 1961.
Франк ль Ф И, Сверхзвуковые течения осевой симметрии, Известия Ар-
тилл академии, Ленинград, № 1, 1934
ФранкльФ И, Карпович Е А., Газодинамика тонких тел, Гостехич-
дат, Москва, 1948
Хейз У Д и Пробстин Р Ф, Теория гиперзвуковых течений, пер с
англ , ИЛ, Москва, 1962
Хильтон У., Аэродинамика больших скоростей, ИЛ, Москва, 1955
X о у а р т Л , Современное состояние аэродинамики больших скоростей, пер
с англ , ИЛ, Москва, 1955.
ХристиановичС А, Обтекание тел газом при больших дозвуковых ско-
скоростях, Труды ЦАГИ, вып 481, 1940
Чаплыгин С А, О газовых струях Собрание сочинений, т II, Гостехнз-
дат, Москва, 1948
Черный Г. Г, Течения газ? с большой сверхзвуковой скоростью, Гостех-
издат, Москва, 1959
Busemann A, Aerodynamischer Auftneb bei Ueberschallgeschwindigkeit
Luftfahrtforschung, 12 A935), стр 210—220
Busemann A, Drucke auf kegelformige Spitzen bei Bewegung mit Ueber-
Ueberschallgeschwindigkeit, Z. angew Math Mech , 9 A929)
Busemann A, Walchner O, Profileigenschaften bei Ueberschallgeschwin-
Ueberschallgeschwindigkeit, Forsch -Arb Ing -Wes , № 4, 1933
С г о с с о L, Singolarita, della corrente gassosa iperacustica nell'interno di una
prora a diedro. L'aerotechnica, 17 A937), № 6, стр. 518—534
Goldstein H, Neumann J, Blast Wave Calculations, Commun Pure and
Appl Math, 3 A955)
Meyer Th, Ueber zweidimensionale Bewegungsvorgange in einem Gas das
mit Ueberschallgescbwmdigkeit stromt Forsch -Arb Ing -Wes, N° 62,
1908
Sears W (редактор). General theory of high speed aerodynamics, т 6,
1955
Taylor G, The formation of a blast wave by a very intensive explosion, Proc
Roy Soc, 1950
Taylor, Maccool, Air pressure on a cone moving at high speeds Proc Roy.
Soc, (A), London, 139 A933), стр 278—297.
Ward G, Linearized theory of steady high-speed flow, 1955.
К ГЛАВЕ II
Гидродинамическая теория смазки, сборник статей под ред Л С Лейбензона
ГТТИ, Москва, 1934
Голубев В В, Теория крыла аэроплана конечного размаха, гл 2 Труды
ЦАГИ, вып 108, 1931
Гольдштейн С, Современное состояние гидродинамики, вязкой жидкости,
пер с англ, ИЛ, Москва, 1948
ДюрэндВ Ф, Аэродинамика, т III, перев с англ, Оборонгиз, Москва,
1939, статья Л Праидтля «Механика вязких жидкостей»
Ламб Г, Гидродинамика, пер с англ, Гостехиздат, Москва, 1947
Ландау Л Д иЛнфшицЕ. М, Механика сплошных сред, Гостехиздат,
Москва, 1953.

720	ЛИТЕРАТУРА
Л о ft ц я н с к и ft Л Г , Механика жидкости и газа, изд 2, Физматгиз, Москва,
1957 и 1959
Лоицянский Л Г, Ламинарный пограничный слой, Физматгиз, Москва,
1962
Прандтль Л, Гидроаэромеханика, перев с нем, ИЛ, Москва, 1949
Шлихтннг Г, Теория пограничного слоя, пер с нем, ИЛ, Москва, 1960
Brillossin M, Zecons sur la viscosite des liquides et des gaz. Pans, 1907,
Gortler H (издатель), Grenzschichtforschung-Springer, 1958
Hopf Z, Zahe Flussigkeiten, Handbuch der Physik, 7 A927), стр 91—172
О seen С W, Neuere Methoden und Ergebnisse in der Hydrodynamik, Leipzig,
1927.
T о 11 m i e n W , Grenzschichttheone, Handbuch der Expenmentalphysik, т. 4,
ч 1, стр 239—289
V 111 a t H , Lecons sur l'hydrodynamik, Leipzig, 1927
К ГЛАВЕ III
Бэчелор Дж, Теория однородной турбулентности, перев с англ, ИЛ,
Москва, 1955
Гольдштейн С, Современное состояние гидродинамики вязкой жидкости,
пер. с англ , ИЛ, Москва, 1948
Колмогоров А Н, Локальная структ>ра турбулентности в несжимаемой
вязкой жидкости, ДАН СССР, 1941.
Колмогоров А Н, Рассеяние энергии при локально изотропной турбу-
турбулентности, ДАН СССР, 1941
ЛандауЛ Д иЛифшицЕ М, Механика сплошных сред Гостехиздат,
1953
Линь Цзя-цзю, Теория гидродинамической > стойчивостп, пер с англ, ИЛ,
Москва, 1958
Лоицянский Л Г, Механика жидкости н газа, Гостехиздат, Москва,
1957
Лоицянский Л Г, Перенос тепла в турбулентном движении, ПММ,
т XXIV, вып 4, 1960
Прандтль Л, Гидро-аэромеханнка, пер с нем, ИЛ, Москва, 1951.
Седов Л И, Методы подобия и размерности в механике, Гостехиздат, Мо-
Москва, 1957.
Таунсенд А, Структура турбулентного потока с поперечным сдвигом, пе-
перев с англ, ИЛ, Москва, 1959.
L e 11 a u, Atmosphansche Turbulenz, 1939
Richardson, Weather prediction by numerical process, 1922
Шлихтинг Г, Возникновение турбулентности, пер с нем, ИЛ, Москва,
1962

ИМЕННОЙ УКАЗАТЕЛЬ
Адамар (Hadamard J) 339
Аккерет (Ackeiet J) 89
Астров В. 174, 177
Бабенко К И 273
Беккер (Becker R ) 482
Белоцерковскии О М 191,204,320,322
Берс (Bers L ) 717
Блазиус (Blasius H) 488, 570, 604
Бриджмэн (Bndgman P W) 411
Бриллуен (Bnllouin M) 434, 719
Буземан (Busemann A) 65, 89, 233,
301, 302, 610, 718
Бэчелор (Batchelor J) 720
Бюргере (Burgers J M) 632
Валландер С В 78, 206, 231, 320
Вальхнер (Walchner) 89, 718
Ватсон (Watson J N) 472
Вендт (Wendt H) 232
Вилла (Villat H) 632, 720
Власова 3 П 357
Гаген (Hagen G) 427, 431, 658
Гамель (Hamel G ) 460, 478
Гертлер (Gertler H ) 720
Голубев В В 565, 719
Гольдштейн (Goldstein S ) 670, 719,
720
Го>лдстайн (Goldstine H) 719
Глауэрт (Glauert H.) 265
Гудерлей (Guderley К) 717
Гуревич М И 303, 309, 314
Диббп (Dibble С G) 163
Донов А 89, 717
Дородницын А А 191, 242, 320, 610,
615, 619, 628, 631
Дюренд (Durand) 719
Жермен (Jermam P) 231, 320
Жуковский Н Е 541
Журавский Н Е 313
Зауэр (Sauer R) 717
Зоммерфельд (Sommerfekl A ) 536, 670
Изаксон А А 691
Извеков Б И 686
Казакова Р К 357
Карман (Karman Ih) 145, 559, 610,
699
Карпович Е А 718
Келдыш М В 106
Келлер Л В 698, 701, 703, 706
Кельвин (Kehin) 658
Кибель И А 717, 718
Колмогоров А Н 699, 720
Кондрашева И Л 357
Кочин Н Е 345, 378, 485, 604, 628,
686, 717
Красплыцикова Е А 273, 717
Крафт (Kraft) 163
Крокко (Crocco L ) 104, 718
Кузьмин Р О 530
K>pam P 717

722
ИМЕННОЙ УКАЗАТЕЛЬ
Лайтхилл (Lighthill H J) 21, 213,
219
Ламб (Lamb H) 518, 719
Ландау Л Д 87, 368, 385, 717, 719.
720
Левин В. 174, 177
Лейбензон Л С 563
Леттау (Lettau) 720
Линь (Lin С С) 671, 675, 680, 682,
720
Лифшиц Е М 368, 385, 717, 719,720
Лойцянский Л. Г 604, Ь28, 631, 699,
717, 719, 720
Мейер (Meyer T) 175, 719
Мизес (Mises R) 302, 549, 553, 670
Милликен (Millikan R. А) 510
Миллионщиков М Д 699
Монин А С 397, 627
Навье (Navier С L) 387, 388
Нейман (Neumann J) 719
Некрасов А И 106
Никольский А А 165, 231, 237, 315,
318, 320
Никурадзе И 711
Обухов А М 699, 705
Овсянников Л В 717
Opp (Orr W. M F.) 670
Осватич (Oswatitsch К) 206
Осеен (Oseen С W ) 372, 478, 516, 528,
543, 632, 633, 634, 641, 656, 720
Охоцимский Д Е 357
Павлов Е 174, 177
Пекерис (Pekens) 670
Петров Н. П 534
Пёшль (Poschl Th ) 437
Польгаузен (Pohlhausen К) 578,594
Прандтль (Prandtl L) 262, 263, 265,
372, 543, 565, 571, 670, 706, 709,
711, 719, 720
Пробстин (Probstien R. F) 718
Пуазейль (Poiseuille) 431
Пуассон (Poisson S D) 387, 388
Рейнольде (Reynolds О.) 410, 427,
432, 658, 691, 699
Релей (Reyleigh) 104
Ринглеб (Ringleb F.) 163
Ричардсон (Richardson E G) 687,
699, 705, 720
Розенблатт (Rosenblatt A) 479
Розенбрук (Rosenbrook G ) 671
Рыжов О С 718
Рябииков Г М. 206
Седов Л И 351, 354, 411, 718,
720
Сен-Венан (Saint-Venant В) 388
Синг (Synge) 666
Сире (Sears W) 719
Скан Сильвиа (Sylvia Skan W) 584,
603
Сквайр (Squire J L) 667
Скрэмстэд (Skramstad) 683
Слезкин НА 145
Смирнов В И 302, 454, 456, 530
Соболев СП 302
Станюкович К П 718
Стоке (Stokes G G) 388, 521, 504
Таганов Г. И 165
Татаренчик В В 158
Таунсенд (Townsand A) 720
Тейлор (Taylor G.) 351, 659, 665,
699, 705, 719
Тепфер (Topfer) 571
Титьенс (Tietjens О) 670, 711
Толмин (Tollmien W) 158, 670, 671,
680, 681, 715, 720
Уиттекер 472
Уорд (Ward G. N.) 273, 719
Фалькович С В 180, 184, 269, 718
Феррари (Ferrari С) 258
Ферри (Fern A) 718
Фикк (Fick) 701
Фокнер (Falkner V М) 584, 603
Франк (Frank P.) 302

ИМЕННОЙ VRA3ATE.Tb
723
Франкль Ф И 86, 106, 179, 181 184,
185, 187, 190, 241, 718
Фридман \ А 698
Хантше (Hantsche W) 323
Хартри (Hartree D R) 604
Хауэрс (Howarth L) 596, 699, 718
Хильтон (Hilton W) 718
Хименц (Hiemenz К) 593, 595
Хопф (Hopf L) 670, 720
Христианович С А 69, 106, 130, 134,
138, 141 146, 165, 177, 718
Хэйз (Hayes W D) 208, 213, 718
Цейлон (Zeilon) 656
Цянь Сюэ сеиь 145, 258, 656
Чаплыгин С А 106, 114, 116, 120,
128, 145, 302, 341, 718
Черный Г Г 208, 718
Чушкин П И 245, 325
Шиллер (Schiller L ) 711
Шлихтинг (Schlichting H) 269, 584,
684, 719, 720
Шмидт (Schmidt) 699
Шубауер (Schubauer) 602, 683
Щенников В В 221
Элерс (Ehlers) 68
Юрьев И М 138, 14'

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Взрыв 17
—	без противодавления 350
—	односторонний 345
—	плоский 350
—	с противодавлением 357
—	сферический 354
—	цилиндрический 354
Волна 10, 18
—	баллистическая 18
—	ударная 191
Вязкость 369
Газ идеальный 17
—	идеально-диссоциирующийся 21,
213
—	совершенный 17
Гиперповерхность характеристиче-
характеристическая 27
Гипотеза Кармана 707
Гипоциссоида 39, 222
Градиент адиабатический 686
—	сверхадиабатический 686
Движение см. Течение
—	атмосферы 459
—	безвихревое осесимметрическое
при сверхзвуковой скорости 225
	плоское со сверхзвуковой ско-
скоростью 50, 147
¦	сжимаемой жидкости 114
—	вихревое плоское со сверхзвуко-
сверхзвуковой скоростью 44
—	в пограничном слое 667
—	внутри трубы 228
—	— угла, меньшего чем л 77
—	вязкой жидкости 369
—	в цилиндрической трубе
436
—	газа вне выпуклой поверхности
69
	 внутри трубы 74
	 вокруг искривленного конту-
контура 69
Движение атмосферы с дозвуковой
скоростью 130
—	гиперзвуковое 100, 211
—	жидкости перед телом 525
—	— позади тела 525
—	— при исчезающей вязкости
632
—	ламинарное 658
—	между двумя коаксиальными ци
линдрами 660
—	неустановившееся 325
	 одномерное 325
—	одномерное вязкой сжимаемой
жидкости 481
—	около вогнутой поверхности 77
—	пластинки внутри эллиптического
цилиндра 435
—	поршня в неограниченной среде
338
	в неограниченном цилиндре
335
—	с дозвуковой скоростью 114
—	с осевой симметрией неустано-
неустановившееся 221
—	с очень большой сверхзвуковой
скоростью 206
—	снаряда под углом к оси симме-
симметрии 257
—	стреловидного крыла 309
—	сферы в вязкой жидкости 516
—	турбулентное 373, 658
	между двумя гладкими па-
параллельными стенками 709
—	установившееся плоское 32
	 пространственное 245
—	цилиндра 528
—	— внутри другого неподвижного
цилиндра 435
Динамика газовая 9
Диссипация энергии 401
Диссоциация 213
Диффузия вихревого слоя 443
—	вихря 405, 450

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
725
Жидкость вязкая 370
—	идеальная 372
—	маловязкая 372
—	сжимаемая 627
—	сильновязкая 372
Задача Коши 24
—	плоская, численные методы ре-
решения 190
—	пространственная 245
—	Трикоми 187
Закон Гагена—Пуазейля 431
—	Кулона 534
—	подобия 406
—	— Рейнольдса 410
	Фруда 409
—	Релея 106
Изотропность вязкой жидкости 379
Истечение газа из бесконечно широ-
широкого сосуда 125
	отверстия 73
	.сопровождаемое пере-
переходом через скорость звука 174
Источник 463
—	в диффузоре 465
Коэффициент внутреннего трения
370, 384
—	вязкости 370, 384
— — кинематический 384
	 турбулентный 447
—	корреляции 702
—	Ламэ 390, 395
—	температуропроводности 420
Кривая «яблоковидная» 232
Крыло в плоскопараллельиом сверх-
сверхзвуковом потоке 87
—	конечного размаха в сверхзвуко
вом потоке 262
Линеаризация уравнений 247
Линия переходная 169
—	предельная 157
Мера обмена 702
—	рассеяния 702, 705
Метод Дородницына 191, 610
—	источников 439
—	Кармана 575
—	Ламба 518
—	Польгаузена 602
—	Прандтля 266
—	Франкля 225
—	Хауэрса 602
—	Христиановича 130, 144. 146
Моменты корреляционные 698
—	связи 698
Напряжения добавочные 693, 706
—• — рейнольдсовские 698
—	касательные 377
•— нормальные 377
Насадок Борда 177
Неустойчивость 658
Обильность источника 463
Обтекание излучающей пластинки
623
—	конического острия 229
—	криволинейного контура 549
—	круглого конуса осесимметриче-
ское 229
—	— цилиндра со сверхзвуковой
скоростью 191
—	крыла бесконечного размаха 251
—	— конечного размаха 250
—	осесимметричное с отошедшей
ударной волной 320
—	осесимметричных тел 229
—	пластинки без теплоотдачи 613
—	— со сверхзвуковой скоростью 87
—	плоской пласгинки 652
—	полубесконечной пластинки не-
несжимаемой жидкостью 485
—	профиля с острой передней кром-
кромкой 86
—	сверхзвуковое конуса 306
—¦ — крыла «малого удлинения» 285
—	снаряда 254
—	тонкого крыла с острыми кром-
кромками сверхзвуковое 273
-	— тела со сверхзвуковой ско-
скоростью 208
-	тупого профиля со сверхзвуко-
сверхзвуковой скоростью 104
-	угла, большего чем л 71
—	цилиндра 524, 644
Отрыв вихрей 544
—	слоя 589
«Отскакивание» поверхности раз-
разрыва 104
Парадокс Стокса 511
—	Эйлера—Даламбера 87
Пелена вихревая 274
Переход через скорость звука 156
Поверхность разрыва 10, 12
	 в плоской задаче 35
	, ее размазывание 484
—	— сильная 18
—	— слабая 18

726
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Поверхность разрыва стационарная
17
Подслой ламинарный 710
Постоянная Маскерони 530
¦— Стефана—Больцмана 609
Потенциал источника 263
—	скорости 263
—	ускорения 263
Поток фиктивный 134, 135
Процесс диффузии 370
—	перемешивания 700
—	теплопроводности 371
Путь перемешивания 706
Разрушение течения 167
Разрыв 18
—	сильный 77, 341
	 в одномерной нестационарной
задаче 329
—	слабый 21
Реакция потока на тело 641
Решение Гамеля 475, 478
Ряды Чаплыгина 184
Семейство гипоциссоид 233
Сжатие струи 130
Скачок уплотнения 10, 18
Скорости удлинений главные 376
Скорость звука 24
—	критическая 41
—	максимальная в сжимаемой жид-
жидкости 157
—	перемещения поверхности разры-
разрыва 19
—	распространения поверхности раз-
разрыва 13
—	— — сильного разрыва 29
	слабого разрыва 24
—	— характеристики 27
Слой вихревой цилиндрический 459
—	пограничный 544
	в диффузоре 578
	в несжимаемой жидкости
вдоль плоской пластинки 569
¦	в сжимаемой жидкости 608
	 на произвольном профиле
627
Смешение потока воздуха с окру-
окружающим его спокойным воздухом
714
Соотношение Кармана интегральное
558, 561, 563
—	Лейбензона 565, 566
—	Прандтля, его обобщение 629
Сопло Л аваля 75, 158, 229
¦— — безударное 174, 179
Сопло Лаваля, его построение
75
Сопротивление волновое 87
Сток 463
—	в диффузоре 465
Струя ламинарная 584
Температура торможения 610
Тензор добавочных напряжений 699
—	единичный 382
—	напряжений 378
—	рассеивания 706
—	скоростей деформации 374
—	, его главные значения 376
—	,	оси 376
Теорема Прандтля—Глауэрта 106,
262
—	Цемплена 31
Теория Гейзенберга 670
—	исчезающей вязкости 543
—	пограничного слоя 372, 543
	, приближенные методы 588
—	смазки, гидродинамическая 534
—	струй Кирхгофа—Жуковского 114
—	турбулентности 658
—	Чаплыгина 106
Теплосодержание 34
Течение см. Движение
—	в диффузоре 460, 474, 475
—	в плоском диффузоре 578
—	вязкой жидкости вдоль пластин-
пластинки 545
—	газа, прегражденное плоскими
стенками 117
—	жидкости внутри цилиндрической
трубы 406
—	—, вызываемое вращением сферы
502, 504
	между двумя цилиндрами 433
¦	концентрическими ци-
цилиндрами 447
—	коническое 229
	 сверхзвуковое 301
—	ламинарное 410, 431
—	— в цилиндрической трубе 427
—	морское, его возникновение под
действием ветра 445
—	нестационарное одномерное 437
—	плоское между двумя параллель-
параллельными пластинками 499
—	при больших числах Рейнольдса
542
	малых числах Рейнольдса 499
—	Пуазейля 431
—	расширения 166
—	сжатия 167, 236

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
727
Течение сжимаемой жидкости ме-
между двумя параллельными пло-
плоскими стенками 421
—	смешанное 168
—	стационарное одномерное 432
—	струйное 117
—	турбулентное 410, 431
—	—, внешняя задача 659
	, внутренняя задача 659
—	через насадок Борда 177
Толщина вытеснения 556
—	пограничного слоя 556
—	потери импульса 562
Турбулентность 658
—	изотропная 699
—	«-локально однородная» 699
—	«локально изотропная» 699
—	однородная 699
—	развитая 686
Угол Маха 49
Удар сжатия 18
—	струи в пластинку 120
Уравнение Бернуллп 34, 41, 42
—	Блазиуса 488
—	вековое 665
—	Дарбу 149
—	для функции тока г|э 405
—	Мизеса 555
—	неразрывности 19, 32
—	притока тепла для вязкой сжи-
сжимаемой жидкости 416, 418
—	теории теплопроводности 438
—	Фикка 701
Уравнения газовой динамики 18
—	Гельмгольца обобщенные 404,
634
—	движения вязкой жидкости 387,
388
	в форме Ламба 389
	— — при больших числах
Рейнольдса 542
—	— — — при малых числах Рей-
Рейнольдса 498
	несжимаемой жидкости в
переменных Лагранжа 397
	•	в сферических коор-
координатах 396
—	— —	-в	цилиндрических
координатах 395
—	Ламба 32
-— Навье —Стокса 387, 693
—	пограничного слоя для сжимае-
сжимаемой жидкости 566
Уравнения Прандтля 545
—	Стокса, обобщенные 517
—	Рейнольдса 691
Условие адиабатичности 33
Условия граничные для движения
несжимаемой жидкости 398
Условия динамической совместности
17
—	кинематической совместности 21
—	начальные для движения несжи-
несжимаемой жидкости 397
—	совместности 23
—	тождественности 21
Устойчивость пограничного слоя 671
—	течения между пластинками 666
Формула Аккерета 263, 307
—	Ламба 534
—	Стокса 508
—	Шварца 645
Формулы приближенные Аккерета 89
	Буземана 89
—	— Вальхнера 89
¦	Донова 89
Функция Крампа 443
—	тепловая единицы массы 34
—	Хартри 604
Характеристики 27, 329
—	безвихревою движгния 56
—	вихревого движения со сверхзву-
сверхзвуковой скоростью 47
—	второго семейства 47, 51
—	одномерного движения 329
—	первого семейства 47, 51
—	системы уравнений газовой дина-
динамики 24
—	турбулентности 699
Циркуляция 264, 268
—• для сжимаемой жидкости 137, 139
Циссоида Диоклеса 39
Число Маха 42, 415
—	Прандтля 420, 610
—	Рейнольдса 409, 658
—	— критическое 658
—	Фруда 409
Эллипс Буземана 66
Энтальпия 34
Энтропия 33, 220
Эпициклоида 52
Эффект концевой 274

Кочан Николаи Евграфояич,
Кабель Илья Афанасьевич
Розе Николаи Владимирович
Теоретическая гидромеханика, ч Ц.
М., Физматгиз, 1963 г , 728 стр с илл.
Редактор Н И Розальская
Техн редактор Е А Ермакова
Корректор Г С Плетнева
Сдано в набор I2'X I962 г Подписано к пе-
печати 26 III I963 г Бумага 60x90/16 Физ
печ л 45,5 Х'сювн печ л 45,5 Уч-изд
л 42.8J	Тираж 12 000 чкз	Т 0-1906
Цена книги 1 р 39 к Заказ 787
Государственное издательство
физико-математической литературы
Москва, В 71 Ленинский проспект 15
Типография № 2 им Евг Соколовой
УЦБ и ПП Ленсовнархоза
Ленинград Измайловский пр 29