Автор: Клумов А.С.
Теги: авиация и космонавтика летательные аппараты ракетная техника космическая техника воздушный транспорт авиация и воздушные соединения воздушные линии и аэропорты авиация пилотирование самолеты
ISBN: 5-217-00113-5
Год: 1988
А.С.Клумов
ПРОДОЛЬНАЯ
УСТОЙЧИВОСТЬ
И УПРАВЛЯЕМОСТЬ
МАНЕВРЕННОГО Л
САМОЛЕТА ..«М
Машиностроение
АС.Клумов
ПРОДОЛЬНАЯ
УСТОЙЧИВОСТЬ
И УПРАВЛЯЕМОСТЬ
МАНЕВРЕННОГО
САМОЛЕТА
Москва
Машиностроение
1988
ББК 39.52
К51
УДК 629.7.0.001.2.015.017.2
Рецензент д-р техн, наук В.К. Святодух
Клумов. А. С.
К51 Продольная устойчивость и управляемость маневренно-
го самолета. — М.: Машиностроение, 1988. - 200 с.: ил.
ISBN-5-217-00113-5
Изложены инженерные методы расчета основных характеристик
продольной устойчивости и управляемости маневренного самолета. Даны в
аналитическом виде приближенные оценки динамических характеристик
управляемого короткопериодического движения самолета.
Рассмотрены типовые характеристики систем управления и проана-
лизированы особенности динамики замкнутого контура самолет - звено
управления. Полученные результаты пригодны для практических расчетов
на этапах проектирования маневренных самолетов и их систем управления.
Для инженерно-технических работников авиационной промышлен-
ности и гражданской авиации.
3606030000 - 105
1)38(01) -88
105 - 88
ББК 3952
ISBN 5-217-00113-5
©Издательство ’’Машиностроение”, 1988.
ПРЕДИСЛОВИЕ
Расширение эксплуатационного диапазона скоростей и высот поле-
та современных маневренных самолетов потребовало внедрения авто-
матизации систем ручного управления для обеспечения безопасности
полетов и повышения их эффективности.
При проектировании автоматизированных систем управления воз-
никают задачи взаимодействия системы управления с самолетом как
с динамической системой в замкнутом контуре управления. Решение
таких задач производится, как правило, на пилотажных стендах или спе-
циальных моделирующих установках. Уравнения движения самолета
решаются на ЭВМ, а реальная система управления при этом может быть
заменена математической моделью, полунатурным макетом и т. п.
в зависимости от постановки задачи. Однако полунатурное и натурное
моделирование динамики самолета проводится обычно на завершаю-
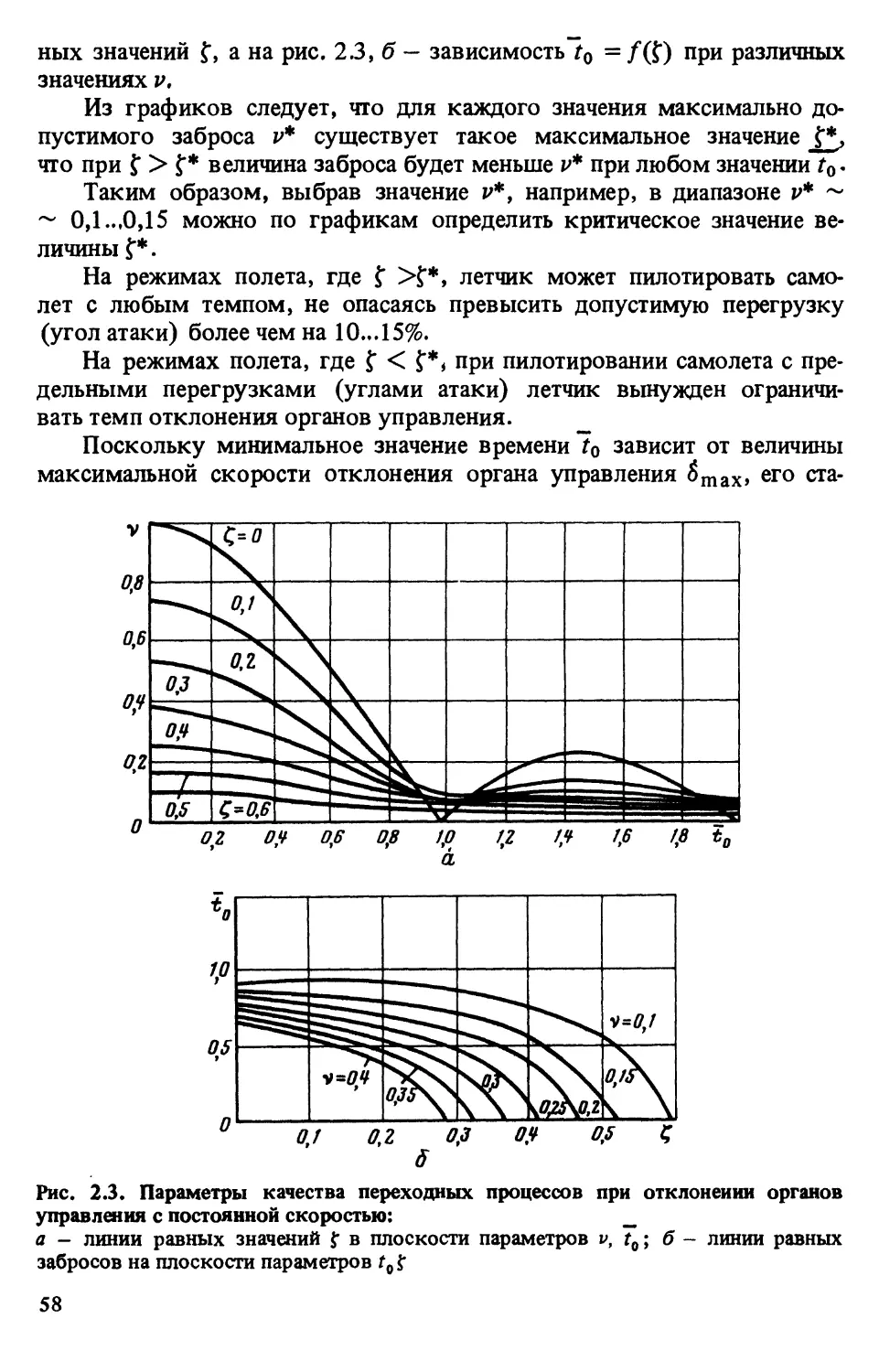
щей стадии проектирования системы управления. На ранних этапах
проектирования при определении принципиальной структуры системы
управления, алгоритмов ее работы для оперативности удобнее поль-
зоваться приближенными аналитическими оценками, позволяющими
определить основные динамические характеристики замкнутого кон-
тура, выявить расчетные случаи, диапазоны изменения передаточных
чисел и др. При этом не требуется высокая точность расчетов, так как
исходные данные известны лишь приближенно.
В книге сделана попытка обобщить инженерные методы расчетов
управляемого продольного движения маневренного самолета и про-
анализировать влияние наиболее характерных параметров на динами-
ческие характеристики движения самолета.
Несмотря на обширную литературу по динамике полета, большин-
ство вопросов, затронутых в данной книге, в настоящее время осве-
щено недостаточно полно и широко. Поэтому в ряде случаев автор
стремился выявить физическую сущность особенностей поведения само-
лета и получить качественные опенки.
Для количественных оценок полученных результатов и исполь-
зования их в практических расчетах приводятся приближенные ана-
литические выражения в безразмерной форме. Такой подход позволя-
ет свести к минимуму число независимых параметров, определяющих
общие свойства описываемого являения, наглядно выделить из них
доминирующие и построить в виде номограмм основные зависимости,
3
характеризующие данный процесс (например, безразмерные критичес-
кие коэффициенты усиления при потере устойчивости замкнутым кон-
туром, безразмерные частоты колебаний при этом, безразмерные вели-
чины амплитуд и частот автоколебаний и т. п.).
Использование таких приближенных зависимостей может оказать-
ся полезным при проектировании самолета и его системы управления
для предварительных расчетных оценок, когда основные характеристи-
ки самолета известны недостаточно точно.
Автор выражает глубокую благодарность д-ру техн, наук В.К. Свя-
тодуху за ценные замечания по содержанию и методике изложения при-
веденного в книге материала.
4
ВВЕДЕНИЕ
Современная маневренная авиация, продолжая непрерывно разви-
ваться, осваивает новые диапазоны скоростей, высот и углов атаки
полета. Интенсивное развитие современных маневренных самолетов
происходит в основном по пути расширения маневренных характерис-
тик, повышения эффективности и безопасности полетов, дальнейшей
автоматизации систей управления.
Однако несмотря на резкое повышение степени автоматизации,
характерной особенностью современного маневренного самолета оста-
ется присутствие летчика как основного управляющего объекта, от-
ветственного за выполнение целевых задач.
В связи с расширением диапазона режимов полета, функциональ-
ных обязанностей летчика и дефицитом времени для принятия им ре-
шения возникают весьма сложные проблемы обеспечения особо жест-
ких требований к безопасности полета, характеристикам устойчивости и
управляемости самолета, созданию комфортных условий летчику.
Эти обстоятельства существенно расширяют круг задач классической
динамики полета, требуют применения современного математического
аппарата и создания мощной экспериментальной базы в виде пилотаж-
ных стендов и моделирующих установок.
Представляет интерес проследить, как в течение длительного пери-
ода развития менялись основные характеристики маневренных самоле-
тов, пути и способы их обеспечения, как расширялся круг актуальных
задач динамики полета.
На заре развития авиации, в начале века, полеты даже на одномест-
ных легких самолетах совершались без маневров — по прямой. Разво-
роты рекомендовалось выполнять без крена — ’’блинчиком”. Летчики
того времени не умели выполнять фигурные полеты.
Одним из первых инициаторов и энтузиастов выполнения фигурных
полетов был выдающийся русский летчик штабс-капитан Петр Никола-
евич Нестеров. 27 августа 1913 г. на серийном самолете ’’Ньюпор-ГУ”
[10, 19] с двигателем мощностью 51,5 кВт (70 л. с.) ПЛ. Нестеров
впервые в мире совершил маневр в вертикальной плоскости с пово-
ротом вектора скорости на 360° (’’мертвую петлю”). Этот маневр,
названный в честь автора ’’петля Нестерова”, был выполнен с нисходя-
щей траектории со скоростью 100 км/ч на высоте порядка 600 м. Ра-
диус маневра составлял 15 ... 20 м. Выдающийся полет ПЛ. Нестерова
5
вызвал широкий отклик в мировой прессе и вскоре был повторен
французом Пегу, а затем и другими летчиками. Началась эпоха манев-
ренной авиации. Без преувеличения можно сказать, что первый маневр
П.Н. Нестерова явился мощным стимулом к развитию маневренной
авиации во всем мире.
Одновременно с освоением летчиками маневренных возможностей
существующих самолетов зарождались теоретические и практические
основы будущей аэродинамики и динамики полета, проектировались,
строились и испытывались новые самолеты, совершенствовались их
аэродинамические формы.
Маневренные самолеты времен первой мировой войны имели мак-
симальные скорости 90... 150 км/ч и высоту полета 2000...4000 м при
нагрузке на крыло 200...300 Па (20...30 кгс/м2) и массе самолета
700... 1000 кг.
Дальнейшее развитие маневренной авиации характеризуется рас-
ширением диапазона скоростей и высот полета, увеличением мощ-
ности двигателей, массы самолета и удельной нагрузки на крыло. Все
это потребовало создания специальной экспериментальной базы и раз-
работки основ теории динамики полета.
Экспериментальные исследования на моделях в аэродинамических
трубах позволили достаточно точно определить аэродинамические силы
и моменты, действующие на самолет, до проведения летных исследова-
ний. Расчетные методы, созданные на основе уравнений Ньютона и Эйле-
ра, использовались для предварительных оценок основных аэродинами-
ческих характеристик самолетов на этапе их проектирования.
В 1918 г. по инициативе Н.Е. Жуковского и его учеников создан
Центральный аэрогидродинамический институт (ЦАГИ), и к концу
30-х годов проектирование отечественных маневренных самолетов
было обеспечено прочной научной и экспериментальной базой.
В течение 30—40-х годов были тщательно отработаны и подтверж-
дены опытом массовой эксплуатации основные требования к пило-
тажным и маневренным характеристикам, ставшие традиционными
для самолетов-истребителей.
Эти требования, выраженные наиболее четко в количественных
показателях маневренности и управляемости, актуальны и в настоя-
щее время. Однако выработанные в процессе эксплуатации и теоре-
тически обоснованные требования касались в основном статических,
установившихся характеристик самолета. Динамические свойства са-
молета как, объекта управления почти не проявились в эксплуатаци-
онном диапазоне режимов полета в силу ограниченности этого диапа-
зона и специфики аэродинамической и массово-инерционной компо-
новки самолетов того времени (за исключением критических режимов
полета).
Тем не менее широко разрабатывались теоретические методы рас-
6
четов динамических свойств самолета. Итогом этих работ явилась книга
В.С. Ведрова ’’Динамическая устойчивость самолета” (1938 г.) — одна
из первых отечественных монографий по динамике полета.
Период конца 40-х — начала 50-х годов ознаменовался успешным
штурмом ’’звукового барьера”, однако прежде чем это произошло,
потребовалось принципиальное изменение аэродинамической компо-
новки и внешнего облика маневренного самолета. Поршневые дви-
гатели были заменены турбореактивными, расположенными в хвосто-
вой части фюзеляжа, вместо прямого крыла нашло применение стрело-
видное с малой относительной толщиной. Увеличились моменты инер-
ции, и возникла необходимость учета динамических характеристик са-
молета.
Обеспечение безопасности полетов на околозвуковых и сверхзву-
ковых скоростях полета потребовало создания принципиально новых
систем управления с применением цельноповоротных поверхностей
органов продольного управления и необратимых гидроусилителей в
качестве силовых приводов, что привело к необходимости частичной
автоматизации системы ручного управления самолетов.
Применение стреловидных крыльев и реактивных двигателей поз-
волило перейти к освоению значительных сверхзвуковых скоростей
и больших высот полета, в связи с чем возникла необходимость авто-
матического демпфирования колебаний самолета для обеспечения
удовлетворительных динамических характеристик.
Характерная особенность реактивных двигателей на сверхзву-
ковых маневренных самолетах — увеличение тяги с возрастанием ско-
рости полета — привела к возможности превышения установленных
ограничений по скорости полета, поэтому для обеспечения безопасности
полетов на режимах, близких к предельным, потребовалась разработка
и внедрение специальных автоматических устройств — ограничителей
предельных режимов полета. Накопленный опыт свидетельствует, что
дальнейшее расширение диапазона скоростей и высот полета без серьез-
ной автоматизации системы ручного управления самолетом становит-
ся небезопасным.
Одновременно разрабатываются теоретические методы расчетов
динамических характеристик самолета, создается методика летных ис-
следований с целью определения основных характеристик самолета
при летных испытаниях. В 50-е годы выходят монографии В.С. Ведрова
и М.А. Тайца ’’Летные испытания самолетов”, И.В. Остославского и
Г.С. Калачева ’’Продольная устойчивость и управляемость самолета”,
В.Н. Матвеева ’’Расчет возмущенного движения самолета”, учебник
И.В. Остославского ’’Аэродинамика самолета”. Расчетные методы дина-
мики полета прочно входят в практику проектирования маневренных
самолетов не только в ЦАГИ, но и в опытных конструкторских бюро.
В начале 50-х годов темпы роста скоростей полета маневренных
7
самолетов несколько снизились, однако фундаментальные достижения
отечественной авиационной науки и техники, накопленные за это
время, привели к тому, что уже конец 50-х годов и последующее
десятилетие ознаменовались серией авиационных мировых рекордов
и прочным освоением режимов длительных полетов на больших высо-
тах с большими числами М в сочетании с энергичным маневрирова-
нием на этих режимах. В 1959 г. Г .К. Мосолов установил абсолютный
мировой рекорд скорости полета на базе 15 ... 25 км — 2388 км/ч, В
1960 г. К.К. Коккинаки установил абсолютный мировой рекорд скорос-
ти полета по замкнутому маршруту протяженностью 100 км, равный
2149 км/ч. В 1961—1962 гг. А.В. Федотов установил новый абсолютный
мировой рекорд на замкнутом маршруте: 2401 км/ч. Г,К. Мосолов
перекрыл свое достижение на базе 15 ... 25 км — 2681 км/ч. ILM. Ос-
тапенко установил абсолютный мировой рекорд высоты полета при
установившейся скорости горизонтального полета на базе 15 ... 25 км -
22 670 м*.
В середине 60-х — начале 70-х годов советскими летчиками А.В, Фе-
дотовым, П.М. Остапенко, Б.А. Орловым, М.М, Комаровым и другими
был установлен целый ряд мировых рекордов скороподъемности,
скорости и высоты полета. Часть из этих рекордов, в том числе абсо-
лютных, не превышена до настоящего времени, несмотря на то, что
период интенсивного освоения больших сверхзвуковых скоростей
и высот полета, расширения маневренных возможностей самолета про-
должается.
С проникновением маневренной авиации в область больших ско-
ростей и высот полета разрабатываются новые методы анализа дина-
мики полета, закладывается теоретическая и экспериментальная ба-
зы для моделирования и стендовых исследований, создается принци-
пиально новый математический аппарат в теории управления, вариа-
ционном исчислении, качественной теориии нелинейных дифференци-
альных уравнений.
В 1967 г. выходит монография Г.С. Бюшгенса и Р,В. Студнева
’’Динамика пространственного движения самолета”, в которой мето-
дами качественной теории нелинейных дифференциальных уравнений
были получены результаты исключительной важности для решения
прикладных задач динамики полета, возникающих при анализе харак-
теристик устойчивости маневренного самолета при больших сверх-
звуковых скоростях полета,
В конце 50-х — начале 60-х годов группой советских математи-
ков во главе с Л.С. Понтрягиным разрабатывается теория оптимального
управления динамическими системами на основе принципа максимума
Л.С. Понтрягина,
* Авиация и космонавтика. 1964, № 12. С. 18-23.
8
В середине 60-х годов А.Я. Дубовицким и А.А, Милютиным бы-
ли получены фундаментальные результаты, существенно расширяющие
область применения теории оптимального управления в прикладных
задачах динамики полета. С выходом в свет в 1972 г. монографии ’’Ме-
ханика оптимального пространственного движения летательных аппа-
ратов в атмосфере” [22] теория оптимального управления динамичес-
кими системами прочно вошла в рабочий аппарат динамики полета
и в расчетные методики самолетных ОКБ.
В 1979 г. опубликована классическая монография Г,С. Бюшгенса
и Р.В. Студнева [4], в которой подведен итог многолетних теоретических
и экспериментальных исследований по общим вопросам динамики
бокового и продольного движения самолета. В этой книге исследованы
динамические характеристики маневренных самолетов в боковом и
продольном движениях, причем основное внимание уделено анализу
стендовых испытаний и качественных оценок летчиком поведения
самолета.
С начала 80-х годов в динамике полета начинают применяться но-
вые методы качественной теории дифференциальных уравнений, раз-
рабатываемой школой советского математика В.И. Арнольда, полу-
чившей за рубежом название теории катастроф. Современный матема-
тический айпарат, лежащий в основе этой теории, позволяет существенно
упростить анализ ’’поведения” решений сложных нелинейных уравне-
ний при изменении отдельных параметров, определяющих движение
динамической системы.
В 1983 г. вышла новая монография Г.С. Бюшгенса и Р.В. Студне-
ва ’’Динамика самолета. Пространственное движение” [5], которая
посвящена исследованию нелинейных уравнений динамики, описыва-
ющих энергичное маневрирование самолета с учетом работы автома-
тической системы управления. Анализ динамических характеристик
самолета проводился фактически методами теории катастроф.
Как показали М.Г. Гоман и Г.И. Загайнов в дальнейших иссле-
дованиях, эти методы могут быть успешно использованы в расчетах
устойчивости движения самолета при энергичном пространственном
маневрировании.
Таким образом, современная динамика полета базируется на мощ-
ном «математическом аппарате, что при наличии быстродействующих
ЭВМ позволяет ставить и решать широкий круг прикладных задач,
возникающих в процессе проектирования, испытаний и доводки сов-
ременного маневренного самолета.
В соответствии с расширением возможностей теоретических и рас-
четных методов динамики полета, возросшими быстродействием и
объемом памяти современных ЭВМ существенно расширились требо-
вания к современным маневренным самолетам. Общие требования
диктуются широким комплексом противоречивых проблем, вклю-
9
чающих в себя назначение самолета, эффективность выполнения целе-
вых задач, обеспечение безопасности полета, стоимость и технологич-
ность конструкции, приемлемые для серийного производства само-
летами т.п.
Рациональное решение комплекса перечисленных проблем, опреде-
ляющее облик самолета (его аэродинамическую схему, степень авто-
матизации системы управления, область допустимых режимов полета,
условия базирования, состав оборудования и т. п.), становится невоз-
можным без решения широкого круга задач динамики полета.
Обеспечение указанных требований к характеристикам самолета
и безопасности пилотирования в таком широком диапазоне режимов
полета становится практически невозможным без существенной авто-
матизации системы управления.
Необходимая z рациональная степень автоматизации системы управ-
ления зависит от целого ряда факторов, важнейшими из которых яв-
ляются надежность и отказобезопасность работы системы управления,
В связи с этим все более широкое применение получает вероятностный
подход к потребным характеристикам устойчивости и управляемости
самолета.
При таком подходе существенную роль играет среднее время воз-
можного пребывания самолета на данном режиме полета. Чем боль-
ше это время, тем жестче должны быть требования к характеристикам
устойчивости, управляемости, безопасности полета и наоборот. Для
редко встречающихся в процессе эксплуатации режимов полета требо-
вания к характеристикам устойчивости и управляемости могут быть
снижены.
Для определения алгоритмов работы системы автоматического
управления (САУ) с целью удовлетворения основным требованиям,
предъявляемым к современному маневренному самолету, необходимо
на ранних стадиях проектирования проанализировать результаты реше-
ния различных классов задач динамики полета.
Удовлетворение требования энергичного маневрирования само-
лета на больших углах атаки приводит к необходимости решения клас-
са задач, связанных с проблемами декомпозиции движений многосвяз-
ной динамической системы. С практической точки зрения решение
задачи сводится к отысканию перекрестных алгоритмов работы САУ,
обеспечивающих летчику раздельное, поканальное управление боко-
вым и продольным движением самолета при энергичном пространствен-
ном маневрировании.
Аналогичные задачи возникают также при полетах на больших
высотах с большими числами М. Анализ решения уравнений, описы-
вающих пространственное движение маневренного самолета, нашел
достаточно полное отражение в перечисленных монографиях.
10
Длительное маневрирование с высокими значениями нормальной
перегрузки пу, полеты со сверхзвуковыми скоростями на бесфорсаж-
ных режимах работы двигателей, увеличение максимального числа
М полета — все это требует помимо увеличения энергетических воз-
можностей силовой установки повышения аэродинамического качес-
тва самолета.
Одним из возможных путей повышения аэродинамического качес-
тва является применение аэродинамических компоновок, статически
неустойчивых или близких к нейтральным (в продольном движении)
при околозвуковых скоростях полета. Необходимость обеспечения
возможности длительных полетов на этих режимах выдвигает повышен-
ные требования к характеристикам управляемости самолета и удоб-
ству пилотирования, что достигается автоматизацией системы управ-
ления путем выбора рациональных алгоритмов работы САУ.
11
ГЛАВА 1. СИЛЫ И МОМЕНТЫ, ОПРЕДЕЛЯЮЩИЕ
ДВИЖЕНИЕ САМОЛЕТА В АТМОСФЕРЕ
1.1. ПРИНЯТЫЕ СИСТЕМЫ КООРДИНАТ
И УРАВНЕНИЯ ДВИЖЕНИЯ САМОЛЕТА
КАК ТВЕРДОГО ТЕЛА
Движение самолета как твердого тела происходит под действи-
ем аэродинамических и гравитационных внешних сил и моментов.
При движении самолета относительно воздушной среды на самолет
действуют аэродинамические силы и моменты, зависящие от парамет-
ров его движения и физических свойств среды. Движение самолета
как твердого тела относительно инерциальной системы координат,
связанной с неподвижной плоской Землей, определяется шестью урав-
нениями второго порядка. Шесть независимых переменных, характе-
ризующих в каждый момент времени положение самолета относительно
земной системы координат, представляют шесть степеней свободы: три
координаты центра масс самолета и три угла (или эквивалентных па-
раметра), характеризующих взаимное положение связанной и земной
системы координат.
Аэродинамическое воздействие среды на самолет определяется его
конфигурацией, положением связанной системы координат относитель-
но вектора скорости центра масс самолета и вектора угловой ско-
рости самолета как твердого тела. Свойства неподвижной среды
задаются условной стандартной атмосферой, основные параметры ко-
торой подчиняются уравнению статики атмосферы
и уравнению состояния идеального газа рн = РцВТн для заданной
высоты полета.
Целенаправленное изменение конфигурации самолета, например,
отклонение органов управления, сброс баков и т. п., рассматривается
как управление.
Отклонения параметров среды от принятых стандартных значе-
ний рассматриваются как возмущения. Такими возмущениями могут
быть, например, флуктуации плотности или температуры, турбулент-
ность атмосферы, ветровые порывы и т. п.
Связанная система координат OXYZ с началом в центре масс са-
молета (рис. 1.1) представляет собой три правые взаимноперпендику-
лярные оси и располагается относительно самолета следующим образом:
плоскость OXY совпадает с плоскостью симметрии самолета. Положи-
тельное направление оси ОХ, совпадающей с условной строительной
горизонталью самолета ,т.е. средней аэродинамической хордой крыла
(САХ),— по направлению полета.
12
Проекции на связанные оси сил и моментов, действующих на ле-
тательный аппарат в полете, зависят от параметров стандартной атмос-
феры (т. е. от координат центра масс самолета в земной системе коор-
динат), положения связанной системы координат относительно земной
и положения вектора скорости центра масс самолета относительно
связанной системы координат.
Пространственное положение связанной системы координат отно-
сительно земной можно задать различными способами, например, при
помощи девяти направляющих косинусов, четырех параметров Родри-
га, трех углов Эйлера — Крылова, В любом случае количество незави-
симых переменных равно трем, и ’’лишние” параметры исключаются
дополнительными уравнениями связи. Ниже будут использованы тра-
диционно принятые в динамике полета углы Эйлера — Крылова — уг-
лы тангажа, крена и рыскания:
угол тангажа & — угол между горизонтальной плоскостью и свя-
занной осью ОХ;
угол крена у — угол между вертикальной плоскостью, проходящей
через связанную ось ОХ,и связанной осью OY;
угол рыскания ф — угол между проекцией связанной оси на гори-
зонтальную плоскость и земной осью OXg,
Из геометрических соображений очевидно, что углы крена и рыс-
кания не определены при значениях угла тангажа & = ± я/2, так как
связанная ось ОХ в этих случаях перпендикулярна горизонтальной
плоскости.
Условно принятое в динамике полета правило знаков таково, что
положительные значения проекций вектора угловой скорости самолета
на связанные оси совпадают с положительными направлениями свя-
занных осей и обозначаются соответственно ссх, coy, (см. рис. 1.1,
б). Положительные направления углов 0, 7, 0 и скоростей их измене-
ния 7, 0 приведены на рис. 1.1, а. Из рисунка следует, что проекция
мгновенного вектора угловой скорости самолета Й на связанные оси
Рис. 1.1. Связанная и земная системы координат:
а - относительные положения связанной и земной систем координат; б - поло-
жение вектора угловой скорости самолета в связанной системе координат
13
координат ссх, coy, coz связана с угловыми скоростями у, ф кине-
матическими соотношениями:
со* = у + 0 sin # ;
(л}у = 0cos#cos 7 + $sin 7 ; (Ы)
goz = #cos 7 — 0cos # sin 7.
Скорость центра масс самолета измеряется относительно непод-
вижной, инерциальной, земной систем координат. Положение вектора
скорости центра масс самолета относительно связанных осей коор-
динат однозначно определяется тремя проекциями вектора скорости
на связанные оси: Vx, Vy, Kz.
Величина модуля вектора скорости определяется из соотношения
г=|г| + +
Положение вектора скорости относительно земной системы коорди-
нат однозначно определяется его проекциями VXg, Vyg, Vz . Как сле-
дует из рис. 1.2 и 13, эти проекции связаны с проекциями vх, Vy, Vz
и углами тангажа, крена и рыскания следующими соотношениями:
Kxcosi>cos0 - Vy (cos7sin#cos0 - sin7sini//) +
+ Kz(cos7sini//+ sin7sini>cosi//);
Vyg = = Vxsin& + K-yCOS7cos#- Kzsin7cos$; (1.2)
Vz = Kxcos#sini//+ Ky(cos7sin#sini// + sin7COsi//) +
о dt
+ Kz(cos7cos0 — sin7sin#sin0).
«У lUlK \ ft r< Рис. 1^. Положение вектора скорости в земной системе координат У Г \ / Рис. 1.3. Положение вектора скорости в связанной системе координат
14
Наличие мощной силовой установки на современных маневренных
самолетах приводит к необходимости на ряде режимов полета учи-
тывать дополнительные моменты, вызванные гироскопическими эф-
фектами из-за вращения роторов двигателей.
Вектор кинетического момента вращающихся частей двигателей
= М «/дв <^дв >
где /дв - момент инерции вращающихся частей двигателей; о>дв —
угловая скорость их вращения; п — количество двигателей.
В соответствии с принятым правилом знаков моментов и направ-
лением вращения вращающихся частей двигателей (по ГОСТу против
часовой стрелки, если смотреть со стороны соплового аппарата), проек-
ция К на связанную ось ОХ(Кх) всегда положительна. Проекции век-
тора К на связанные оси OY и OZ могут иметь произвольные знаки в
зависимости от углов установки двигателей на самолете.
Полученные из геометрических соображений шесть уравнений
(1.1) и (1.2) связывают параметры движения самолета и их производ-
ные по времени. Эти уравнения описывают кинематику поступательно-
го и вращательного движений самолета.
Уравнения движения самолета как твердого тела постоянной массы
в связанной системе координат (в предположении совпадения связанной
системы координат с главными осями инерции самолета), как извест-
но [4], имеют вид
т ( + wyVz - wz7y) = РХ — X - ragsind;
+ wzYx—ajxVz) = Py + У-rag cos £ cos 7;
+ wxVy — wyVx)=Pz + Z + ragcos#sin7;
(1.3)
^x + ^z~ = Mx\
J у + ~ ~ My + Kxcoz ;
J2 ——Mz— Kx(jJy ,
Системы уравнений (1.1) — (13) содержат двенадцать дифферен-
циальных уравнений первого порядка, связывающих между собой
двенадцать независимых параметров движения самолета в простран-
стве. Эти параметры называются фазовыми координатами. Для запи-
15
санных выше уравнений фазовыми координатами являются естествен-
ные геометрические координаты, определяющие движение самолета:
три линейные координаты центра масс самолета, три угловые коорди-
наты, характеризующие пространственное положение самолета, и шесть
скоростей (три угловые и три линейные) их изменения.
В качестве обобщенных фазовых координат можно выбрать две-
надцать произвольных независимых переменных, однозначно выра-
жаемых через двенадцать естественных фазовых координат. Рациональ-
ный выбор обобщенных фазовых координат зависит как от общей
постановки решаемой задачи, так и от конкретных значений силовых
и моментных характеристик, определяющих движение самолета в задан-
ном диапазоне режимов полета.
Поэтому, прежде чем переходить к анализу особенностей уравне-
ний движения самолета, следует оговорить класс рассматриваемых
задач и режимов полета. Одной из актуальных задач динамики полета
маневренного самолета является исследование движения самолета
при воздействии на него целенаправленных управляющих возмущений.
Уравнения пространственного движения самолета, записанные
в общем виде, существенно нелинейны, поэтому для их решения при-
менимы только численные методы. Однако численные методы позво-
ляют получить лишь конкретные, труднообозримые результаты, мало-
пригодные для общего качественного анализа движения самолета. Ка-
чественный анализ возмущенного движения самолета удобно прово-
дить аналитическими методами в обобщенном безразмерном виде.
С этой целью следует упростить систему уравнений, описывающих
движение самолета. Упрощение уравнений целесообразно проводить
по двум основным направлениям: снижение порядка системы диф-
ференциальных уравнений и их линеаризация.
В качестве первого шага к упрощению системы уравнений следу-
ет выделить плоское движение самолета. Плоское движение твердо-
го тела, как известно, имеет три степени свободы: одно угловое пе-
ремещение и два линейных. Таким образом, количество фазовых ко-
ординат снижается до шести, и порядок системы дифференциальных
уравнений понижается.
Для симметричного самолета, имеющего плоскость симметрии,
представляет интерес рассмотреть класс маневров, при которых плос-
кость симметрии тождественно совпадает с вертикальной плоскостью
земной системы координат в течение всего времени маневра. Такой
класс движений называют изолированным продольным движением
самолета.
Из приведенных выше определений принятых параметров движе-
ния самолета видно, что в этом случае должны тождественно выпол-
няться условия
7=Шл = ^=0, (1.4)
откуда следует 7 = 0; 1^ = 0.
16
Не нарушая общности рассуждений, можно положить = О, выб-
рав оси земной системы координат таким образом, чтобы плоскость
симметрии самолета тождественно совпадала с плоскостью OXgYg.
Тогда система уравнений примет вид
= Ку sin#;
K^ = Kxsin# + Kjcos#;
m ~b}zvy-Px- rngsinti', (1.5)
m d-^ + a>zVx —Py+ Y- rngxos#;
Независящие от параметров бокового движения уравнения (1.5)
описывают широкий класс маневров, часто встречающихся в практике
летной эксплуатации маневренных самолетов. К ним относятся все
плоские маневры без крена: наборы высоты, снижения, прямолиней-
ные полеты с разгоном или торможением и криволинейные маневры
самолета в вертикальной плоскости.
Строгое выполнение условий (1.4) возможно лишь при выпол-
нении самолетом прямолинейных полетов (со2 = 0), так как наличие
угловой скорости тангажа со2 всегда вызывает возмущенное боковое
движение самолета из-за гироскопического момента вращающихся
роторов двигателей. Однако в реальном полете возможны случаи, ког-
да условия (1.4) выполнены лишь приближенно, но параметры боко-
вого движения настолько малы, что ими можно пренебречь. При этом
уравнения изолированного продольного движения описывают реаль-
ное движение самолета с некоторым приближением.
Корректность приближенной математической модели изолирован-
ного продольного движения самолета зависит от потребной степени
точности, необходимой для конечных результатов расчетов, постанов-
ки задачи, режимов полета и т. п. Если летчик или автоматическая
система управления своевременно парируют возмущения бокового
движения, то, как показывает опыт эксплуатации маневренных само-
летов, в широком диапазоне режимов полета продольное движение
самолета также можно считать изолированным с достаточной для прак-
тических расчетов степенью точности.
Таким образом, для решения уравнений, описывающих изолиро-
ванное продольное движение, необходимо найти шесть фазовых коор-
динат, четыре из которых определяют движение центра масс (напри-
17
мер xgt yg, dxgldt, dyg/dt, а две - вращательное движение самолета
(например, #, dtydf).
Несмотря на кажущуюся простоту оставшейся системы нелиней-
ных уравнений (1.5), решение в общем виде возможно только числен-
ными методами. Для получения аналитических решений системы (1.5)
необходимо дальнейшее упрощение уравнений. Такое упрощение мож-
но получить, наложив ограничения на отдельные фазовые координаты
или их совокупность, характерные для типовых режимов полета.
Как показывает статистический анализ опыта эксплуатации ма-
невренных самолетов, наиболее часто встречающимися режимами полета
являются режимы, близкие к горизонтальному прямолинейному полету.
В условиях, близких к горизонтальному полету, можно считать угол
тангажа малым, а изменение плотности воздуха — незначительным:
# « 0, р = const. В этом случае в (1.5) следует положить cos# » 1,0;
sin# #.
Дальнейший анализ возможности линеаризации уравнений движе-
ния требует определения правых частей уравнений (1.5) и их зависи-
мостей от параметров движения самолета.
Поскольку правые части уравнений определяются в основном аэро-
динамическими характеристиками самолета, то целесообразно выявить
зависимости аэродинамических сил и моментов, действующих на са-
молет, от режима полета и параметров воздушной среды.
12. АЭРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ,
ДЕЙСТВУЮЩИЕ НА САМОЛЕТ В ПОЛЕТЕ
На самолет в полете действуют силы трех типов: гравитационные,
аэродинамические и тяга силовой установки.
Гравитационная сила всегда приложена в центре масс самолета
и момента не создает. В пределах эксплуатационного диапазона высот
полета современных маневренных самолетов эта сила не зависит от
положения центра масс самолета в земной системе координат. Аэро-
динамическая сила приложена в центре давления самолета и зависит
от всех фазовых координат, определяющих движение самолета, кон-
фигурации самолета, его аэродинамической компоновки, аэродина-
мических критериев подобия и т. п.
Тяга обычно применяемых на маневренных самолетах воздуш-
но-реактивных двигателей имеет газодинамическую природу и зависит
от характеристик как внешнего обтекания самолета, так и внутреннего
тракта (канал—двигатель—сопло).
В этом смысле указанное разделение сил, действующих на само-
лет, носит несколько условный характер, однако такое разделение
удобно, так как тяга обычно задается в виде полуэмпирических гра-
18
фических зависимостей от параметров режима полета и режима работы
двигателей.
Тягу можно определить как суммарную силу, создаваемую сило-
вой установкой (включая воздухозаборники, двигатель, сопловой
аппарат), пропорциональную векторной разности входного и выход-
ного импульсов, проходящих через двигатель газов, с учетом внутрен-
них и внешних потерь.
Тяга зависит от режима работы двигателей и параметров внеш-
ней среды. В дальнейшем рассматриваются проекции тяги Рх и Ру на
связанные оси ОХ и OY.
Чтобы оценить соотношения сил и моментов, действующих на са-
молет в полете, необходимо выявить физические причины образова-
ния аэродинамических сил и моментов и проанализировать их качест-
венные зависимости от режима полета и параметров воздушной среды.
Анализ таких зависимостей проводится на основе применения фунда-
ментального принципа относительности, согласно которому физические
законы имеют одинаковую форму во всех инерциальных системах
отсчета. В силу этого принципа воздействие неподвижной (относительно
инерциальной системы координат) воздушной среды на движущийся
самолет идентично воздействию движущейся среды на неподвижный
самолет, т. е. относительные движения самолета и воздушной среды
обратимы в произвольной инерциальной системе координат. Причем
под скоростью воздушной среды понимается скорость в бесконечно
удаленной точке, а под скоростью самолета — скорость его центра масс.
Таким образом, причины возникновения аэродинамических сил
и моментов, действующих на самолет в полете, объясняются законами
обтекания неподвижного тела движущимся потоком воздуха, и для
анализа этих сил и моментов следует пользоваться уравнениями, опи-
сывающими движение сплошной среды.
Как известно, движение сплошной среды описывается системой
дифференциальных уравнений в частных производных, полученных
из общих законов сохранения механики и термодинамики. Наиболее
простой моделью движения сплошной среды является плоское движе-
ние несжимаемой жидкости.
Несжимаемость жидкости означает постоянство плотности в любой
точке потока и бесконечную скорость распространения малых возму-
щений потока в любом направлении.
При расчетах сил и моментов, возникающих при обтекании тела
равномерным потоком несжимаемой жидкости, уравнения движения
жидкости обычно записываются в безразмерной форме и определяются
характеристики распределения безразмерного коэффициента давления
р по поверхности тела, где р в данной точке тела определяется отношени-
ем величины местного давления р к величине скоростного напора
рИ^э/2 набегающего потока, измеряемого также в единицах давления
(Иоо — скорость потока в бесконечноудаленной точке).
Расчеты показывают, что при одинаковых форме тела и относитель-
ном положении вектора скорости V распределение безразмерных коэф-
фициентов давления по поверхности тела не зависит от скорости потока,
плотности и температуры среды и определяется геометрическими па-
раметрами тела и положением вектора скорости в связанной с телом
системе координат. Зная распределение безразмерных коэффициентов
давления по поверхности тела, нетрудно подсчитать безразмерные коэф-
фициенты, пропорциональные аэродинамическим силам и моментам,
действующим на тело. Очевидно, что зависимость между распределени-
ем давлений, силами и моментами зависит от формы тела. Таким обра-
зом, в случае установившегося продольного движения самолета в идеаль-
ной (несжимаемой и невязкой) атмосфере аэродинамические коэффи-
циенты сх, су, mz зависят от конфигурации самолета и угла атаки:
сх = сх (°0’> су = су (а); mz = mz (а) • По теореме Жуковского коэффи-
циент подъемной силы для плоской пластинки
Су = 27rsina.
Учитывая требование плавности обтекания профиля (небольшие
углы атаки), можно написать су ~ 2тга для а, измеряемого в радианах,
или Су « 0,11а для а, выражаемого в градусах.
Нарушение плавности обтекания, как показывает опыт, не проис-
ходит при углах атаки менее а = 15...200, поэтому соотношение sina «
~ а выполняется с высокой степенью точности.
В конце прошлого века Гельмгольц построил математическую
модель разрывного обтекания плоской пластинки установившимся
потоком идеальной жидкости при малых углах атаки, предположив,
что на верхней поверхности пластинки и в следе за ней жидкость поко-
ится. Границей раздела между покоящейся и движущейся жидкостью
являются линии тока, отходящие от передней и задней кромок плас-
тинки. При таких предположениях коэффициент подъемной силы ока-
зался равным Су % а (для а в радианах), т. е. в четыре раза мень-
ше, чем по формуле Жуковского.
Сравнивая выражения, полученные Гельмгольцем и Жуковским,
можно сделать качественно верный вывод о том, что нарушение плав-
ности обтекания профиля снижает его несущие свойства. Этот вывод
хорошо согласуется с опытными данными.
Для того чтобы получить величину индуктивного сопротивления
в скоростных осях координат, вызванного образованием подъемной
силы, следует спроектировать подъемную силу на направление скорос-
ти: сх » 2тга sina = 27га2, т. е. величина дополнительного сопротивле-
ния пропорциональна квадрату угла атаки.
Таким образом, теоретические исследования обтекания тонких
профилей плоским потоком идеальной несжимаемой жидкости поз-
20
воляют получить приближенные аналитические выражения для рас-
чета подъемной силы, хорошо согласующиеся с результатами экспе-
римента.
Зная положение точки приложения подъемной силы, можно по-
лучить величину коэффициента момента, действующего на профиль.
Расчеты показывают, что точка приложения подъемной силы находит-
ся на расстоянии 1/4 хорды от носка профиля.
Полученные таким образом коэффициенты сх, су, тп2 не зависят
от скорости полета в силу предположения о несжимаемости воздушной
среды.
В связи с влиянием сжимаемости воздуха на аэродинамические
коэффициенты необходимо ввести понятие скорости звука, или ско-
рости распространения слабых возмущений в воздушной среде. При
этом оказывается небезразличным, при каких условиях определять
эту скорость. Опыт показывает, что в диапазоне звуковых частот воз-
мущений скорость звука характеризуется относительным изменением
давления и плотности при постоянной энтропии газа:
= (^ )S = const > где 5 ~ энтропия.
Свойства потоков определяются безразмерным параметром —
числом М (равным отношению скорости невозмущенного потока к
скорости звука в покоящемся газе) - основным критерием подобия
сжимаемых потоков.
При обтекании тела со скоростями, меньшими скорости звука,
возмущения потока, вызванные телом, передаются во все стороны
со скоростью звука (в этом смысле определяется скорость невозму-
щенного потока в бесконечно удаленной точке). При достаточно боль-
шой скорости потока плотность воздуха уже нельзя считать всюду
одинаковой, так как плотность в каждой точке потока зависит от мест-
ной скорости в этой точке. Изменение плотности Др удобно оценивать
относительной величиной ApIpq, где р0 — плотность покоющегося воз-
духа. Нетрудно показать, что эта величина имеет порядок 1/2 (v2/a2),
где v — местная скорость потока. Таким образом, увеличение плотности,
например,на 10% происходит при v » 0,45а.
Поскольку аэродинамические коэффициенты отнесены к величине
условного скоростного напора pVooll, определяемого для плотности
покоящегося газа, то очевидно, что в силу увеличения плотности с
ростом скорости потока реальные значения скоростного напора бу-
дут больше условной величины. Поэтому при дозвуковых скоростях
величины аэродинамических коэффициентов увеличиваются с ростом
скорости полета.
В области околозвуковых и трансзвуковых скоростей полета струк-
тура обтекания самолета может характеризоваться наличием местных
21
сверхзвуковых зон, что не позволяет качественно оценить изменение
аэродинамических коэффициентов.
Результаты экспериментов показывают, что в этой области чисел
М аэродинамические коэффициенты сил и моментов достигают своих
максимальных значений и существенно зависят от числа М из-за перес-
тройки структуры обтекания самолета и появления ударных волн. Фо-
кус самолета резко смещается назад.
При больших сверхзвуковых скоростях полета устанавливается
чистое сверхзвуковое обтекание самолета, возмущения вперед по по-
току не передаются, и полет происходит в невозмущенной атмосфере.
Несущие свойства самолета постепенно снижаются с ростом числа М про-
порционально величине 1/ \/М2 — 1', положение аэродинамического
фокуса самолета практически не зависит от числа М.
Поскольку скорость звука в атмосфере определяется температу-
рой воздуха, то в стандартной атмосфере скорость звука уменьшается
с ростом высоты полета в диапазоне высот от 0 до 11 км. Далее с рос-
том высоты полета скорость звука остается постоянной, принимая
значение а = 299 м/с. В связи с этим свойством атмосферы полеты
с равными числами М на различных высотах ниже 11 км происходят
при различных значениях истинной скорости.
Другим аэродинамическим критерием подобия является число
Рейнольдса Re = pVb/p = Vbfv, где b — характерный линейный размер;
у, ц — коэффициенты кинематической и динамической вязкости; р —
плотность; V — скорость полета. Этот параметр, характеризующий со-
отношение инерционных сил и сил трения, определяет структуру вих-
ревого обтекания самолета. Поскольку вязкость характеризует явле-
ния переноса в газах, то число Рейнольдса зависит от температуры.
В стандартной атмосфере температура изменяется с ростом высоты
полета (для Н < 11 км), вместе с температурой изменяется и число
Рейнольдса. Относительная величина Re = Re (O)/Re(//) для постоян-
ной скорости полета приведена на рис. 1.4. Изменение числа Рейнольд-
са влияет на величину коэффициента нулевого сопротивления самоле-
та, так как часть лобового соп-
22
ки. Принципиально иная картина возникает с ростом угла атаки. Об-
разование вихревой пелены, область распространения срывных зон и
структура обтекания самолета на больших углах атаки существенно
зависят от числа Рейнольдса и определяют силовые и моментные ха-
рактеристики самолета. С ростом угла атаки несущие свойства крыла
падают, и характеристики изменения безразмерных аэродинамических
коэффициентов по углу атаки становятся существенно нелинейными.
Таким образом, аэродинамические коэффициенты самолета мо-
гут зависеть от двух критериев аэродинамического подобия — числа
М и числа Рейнольдса — и угла атаки.
Полученный вывод справедлив при условии прямолинейного по-
лета самолета с постоянной скоростью на постоянном угле атаки. При
этом аэродинамические силы и моменты, действующие на самолет в
полете, являются установившимися, т. е. не зависят от времени. При
выполнении самолетом каких-либо эволюций движение будет неуста-
новившимся, и могут появиться дополнительные аэродинамические
силы и моменты, вызванные неустановившимся, нестационарным дви-
жением самолета.
В теории сплошных сред влияние нестационарное™ потока приня-
то определять числом Струхаля - безразмерным соотношением ЪКУТ) =
= Sh, где b — характерный линейный размер; V — характерная скорость,
&Т — характерное время изменения параметров потока.
Вместо характерного времени можно взять, например, характерную
величину угловой скорости или частоты колебаний/.
Тогда число Струхаля запишется в виде
Sh= A-о? или Sh=-A-/.
Очевидно, что при прочих равных условиях картины обтекания
будут подобны при равенстве чисел Струхаля.
Поскольку в силу принципа обратимости скорость центра масс
самолета соответствует скорости потока в бесконечно удаленной точ-
ке, то неинерциальность движения самолета эквивалентна нестационар-
ности потока в обратимом движении. Поэтому аэродинамические коэф-
фициенты самолета должны зависеть еще от одного безразмерного
параметра — числа Струхаля. В продольном движении самолета в ка-
честве характерных угловых скоростей можно принять два параметра:
и dajdt. _
^гЬд da da Ьд
Безразмерные величины и — = — в продольном
движении самолета являются аналогами чисел Струхаля в теории сплош-
ной среды.
Таким образом, аэродинамические силы и моменты, действующие
на самолет в полете, определяются величиной скоростного напора и
23
аэродинамическими коэффициентами, которые являются функциями
трех критериев подобия, X = сх
s ;Y = сур^ S; Мг = mzP-^ Sb;
2
сх = Fi (М, Re, Sh); су = F2 (М, Re, Sh); mz = F3 (M, Re,Sh).
С математической точки зрения критерии подобия представляют
собой безразмерные коэффициенты в системе дифференциальных урав-
нений, описывающих движение сплошной среды в безразмерной форме.
Величины этих коэффициентов характеризуют тот или иной физический
процесс и определяют вклад этого процесса в общее движение потока.
С физической точки зрения эти величины определяют доминирующее
влияние соответственно вязкости, сжимаемости и нестационарности
потока на изменение аэродинамических коэффициентов сил и моментов.
Аэродинамические коэффициенты, характеризующие продольное
движение самолета, можно разложить в ряд Тейлора. Ограничиваясь
рассмотрением малых приращений аргументов, можно линеаризовать
зависимости сх = Fx (а, М, Re, Sh); су = F2 (а, М, Re, Sh); mz = F3 (а,
M, Re, Sh), оставив члены не выше первого порядка малости:
сх = схо + Аа +—^- ДМ + ARe +-^ ASh + ...;
х да ЭМ 3Re Э Sh
С =С о+^Да+ Э££дм+-^- ARe+4^- 4Sh + ...;
у у да ЭМ dRe 9Sh
. А , dmz А1. . dmz А„ , dmz ACU ,
wz = ntz0 + ~ Aa + -тс-- ДМ + -г—ARe + ASh + ...
Эа ЭМ 9Re 9Sh
Такая линеаризация справедлива лишь для малых углов атаки
самолета. На больших углах атаки пренебрегать членами выше перво-
го порядка некорректно, так как характеристики аэродинамичес-
ких коэффициентов становятся существенно нелинейными. Начиная
с некоторого значения угла атаки вихревая система становится неус-
тойчивой, появляются местные зоны отрыва потока, распространя-
ющиеся на все большую поверхность самолета при дальнейшем увели-
чении угла атаки.
При полете на малых и средних высотах в околозвуковом диа-
пазоне чисел М аэродинамические коэффициенты су и mz из-за нежест-
кости конструкции самолета могут зависеть также от величины ско-
ростного напора.
Как показывает опыт эксплуатации маневренных самолетов, не-
сущие свойства крыла вследствие упругости конструкции несколь-
ко снижаются по сравнению с ’’жестким” самолетом, сопротивление
самолета практически не изменяется. При полетах с большими чис-
лами М на больших высотах влияние упругости конструкции на аэро-
динамические характеристики продольного движения самолета прак-
тически не проявляется.
24
Изменение моментных характеристик упругого самолета и поло-
жение аэродинамического фокуса в продольном движении существен-
но зависят от аэродинамической компоновки и силовой схемы конст-
рукции планера, поэтому типовых зависимостей не существует.
1.3. УПРАВЛЯЮЩИЕ МОМЕНТЫ В ПРОДОЛЬНОМ ДВИЖЕНИИ САМОЛЕТА
Управляющие моменты в продольном движении создаются различ-
ными органами управления в зависимости от аэродинамической схемы
самолета. У маневренных самолетов нормальной аэродинамической
схемы в качестве органа продольного управления применяется цели-
ком подвижное горизонтальное оперение, расположенное в
хвостовой части фюзеляжа. Его эффективность, как и всякой несу-
щей поверхности, зависит от местного угла атаки и числа М полета.
Продольный момент пропорционален коэффициенту статического
момента: Аг о = 5г,о^г.о/(^л)» где ^г.о - расстояние от фокуса ста-
билизатора до центра масс самолета. Поскольку стабилизатор распо-
ложен в скошенном потоке за крылом, то его эффективность сохраня-
ется до больших углов отклонения при создании кабрирующих момен-
тов. На больших углах атаки эффективность стабилизатора может ока-
заться недостаточной для создания необходимых пикирующих момен-
тов из-за больших значений местного угла атаки на дозвуковых ско-
ростях полета.
При больших числах М эффективность стабилизатора незначительно
снижается вследствие общего для всех несущих поверхностей свойства
снижения несущих способностей с ростом числа М.
У самолетов бесхвостой схемы органы управления расположены
на задней кромке крыла. Такие органы управления теряют значитель-
ную часть своей эффективности при полете самолета со сверхзвуко-
выми скоростями из-за уменьшения ’’обслуживаемой” площади крыла
и падения собственных несущих свойств отклоняемой поверхности с
ростом числа М. Величина статического момента элевонов также значи-
тельно меньше, чем у самолетов нормальной схемы, в силу геометри-
ческих особенностей бесхвостой схемы.
Самолеты, скомпонованные по схеме ’’утка”, имеют эффективность
органов продольного управления, близкую к самолетам нормальной
схемы. Характеристики продольных моментов самолетов с горизон-
тальным оперением, расположенным перед крылом, и эффективность
таких органов управления существенно зависят от их взаимного рас-
положения относительно крыла, особенно при больших углах отклоне-
ния органов управления.
Кроме традиционных в качестве органов продольного управления
могут использоваться также отклоняемые носки крыла, закрылки,
25
различного рода щитки, отклонение вектора тяги двигателей и др.
Для оценки направления действия силы, потребной для баланси-
ровки самолета в прямолинейном полете, удобно воспользоваться
понятием фокуса органа управления — точкой приложения приращения
силы, возникающей при отклонении органа управления хр2. Фокус
органа продольного управления может находиться впереди или сза-
ди центра масс самолета. В случае, если положение фокуса Хр2 совпа-
дает с центром масс самолета, реализуется безмоментное, непосредст-
венное управление подъемной силой.
Полагая несущие свойства каждого органа управления пропорци-
ональными коэффициенту можно определить его эффективность:
mbzl = cby\(xF2i- хм).
Из данного выражения следует, что, комбинируя кинематические
связи углов отклонения различных органов управления, можно полу-
чить потребные соотношения балансировочных сил (в том числе, на-
пример, безмоментное управление подъемной силой самолета). При
этом естественно стремление получить выигрыш в величине суммар-
ной подъемной силы, действующей на сбалансированный по продоль-
ным моментам самолет.
Сравнительное соотношение действия сил в простейших случаях
для самолетов различных аэродинамических
рис. 1.5.
Как следует из рисунка, принципиальное
схем иллюстрируется на
значение, определяющее
чпд
д
Рис. 13. Соотношение действия балансировочных сил на самолетах различных
аэродинамических схем:
а — схема ’’утка”; б — схема ’’бесхвостка”; в - нормальная аэродинамическая
схема; I - заднее положение аэродинамического фокуса хр^ вихревой системы
крыло - фюзеляж; II - переднее положение аэродинамического фокуса хр^
26
направление балансировочной силы органа продольного управления,
имеет взаимное расположение центра масс самолета (х/^) и аэроди-
намического фокуса вихревой системы крыло—фюзеляж.
При заднем расположении фокуса относительно центра масс (хм —
- XFX < 0) на самолетах бесхвостой и нормальной схем для создания
балансировочного кабрирующего момента требуются дополнительные
силы, снижающие суммарную подъемную силу самолета (см. рис. 1.5,
I, а I, Ь). Такое положение аэродинамического фокуса характерно для
сверхзвуковых скоростей полета. На схеме ’’утка” в этом случае балан-
сировочная сила повышает суммарную аэродинамическую силу само-
лета (см. рис. 1.5,1, а).
При расположении фокуса хр j впереди центра масс самолета/типич-
ном для дозвуковых скоростей полета, балансировочные силы орга-
нов управления на самолетах нормальной и бесхвостой схем увели-
чивают суммарную подъемную силу самолета, а на схеме ’’утка” —
снижают (см. рис. 1.5, II).
Следует заметить, что для самолетов бесхвостой схемы положе-
ние фокуса вихревой системы крыло—фюзеляж (х/^ = хр) опреде-
ляет устойчивость по перегрузке собственного продольного движения
самолета: т2сУ = хм- хр. Поэтому аэродинамически устойчивый само-
лет бесхвостой схемы должен всегда иметь заднее положение фокуса
(хр{ = хр). Еще более заднее положение фокуса вихревой системы
крыло—фюзеляж должно быть у аэродинамически устойчивого само-
лета схемы ’’утка”. Для самолетов нормальной аэродинамической схемы
это условие может не выполняться, особенно на дозвуковых скоростях
полета.
Из рассмотрения рис. 1.5 также следует, что комбинированное от-
клонение органов управления с передним и задним положением фоку-
са повышает суммарную подъемную силу самолета независимо от поло-
жения фокуса вихревой системы крыло—фюзеляж. Поэтому в схеме
’’утка” может оказаться выгодным, например, управление вектором
тяги.
У самолетов бесхвостой и нормальной аэродинамической схем
увеличение суммарной подъемной силы из-за отклонения органов управ-
ления происходит лишь при переднем положении фокуса вихревой
системы крыло—фюзеляж, что заведомо обеспечивается на статичес-
ки неустойчивом самолете. При этом также может оказаться выгод-
ным управление вектором тяги,
Таким образом, отклонение органов продольного управления (или
их комбинации) вызывает появление силы и момента в продольном
движении самолета. Если время отклонения органа управления много
меньше характерной постоянной времени, определяющей рассматрива-
емое движение самолета, то можно считать управляющее возмущение
мгновенным. В таком случае можно записать и = 6, где |w| < const —
безынерционный параметр управления.
Если время отклонения органов управления соизмеримо с вели-
чиной постоянной времени, характеризующей рассматриваемое дви-
жение самолета, то следует учитывать скорость отклонения органов
управления. В простейшем случае отклонения органов управления с
постоянной скоростью можно записать 5 = и.
Максимальные углы и скорости отклонения органов управления
зависят от величины и знака действующих на них аэродинамических
шарнирных моментов и располагаемой мощности силовых приводов.
Поэтому следует рассмотреть зависимости аэродинамических шар-
нирных моментов органов продольного управления от параметров
движения самолета и геометрических характеристик органов управ-
ления.
Аэродинамическим шарнирным моментом органа управления, как извест-
но [45],называется момент относительно оси вращения этого органа, вызванный
аэродинамическими силами и моментами, действующими на орган управления
в полете.
Аэродинамические шарнирные моменты органов продольного управления
зависят от целого ряда параметров: геометрических параметров органа управления
(площади, хорды, положения оси вращения органа, его профилировки, формы
в плане и т. п.) ; величины и знака балансировочной силы и параметров движения
самолета (высоты и скорости полета, перегрузок, углов атаки и скольжения,
углов отклонения органов управления, угловых скоростей самолета и т. п, ),
а также от конфигурации самолета (наличие внешних подвесок, выпущенной
или убранной механизации, тормозных щитков, шасси и т. п.)
Аэродинамический шарнирный момент управляемого стабилизатора опре-
деляется величиной и точкой приложения равнодействующей аэродинамической
силы и величиной и знаком пары сил, вызванной асимметричным обтеканием
стабилизатора. Знак шарнирного момента считается положительным, если шар-
нирный момент стремится повернуть стабилизатор носком вверх.
Линеаризуя аэродинамические сиды и моменты, действующие на орган про-
дольного управления, можно записать выражение для определения аэродинами-
ческого шарнирного момента, действующего на отклоняемую поверхность:
= ^шо + ^ш + ^ш а + ^ш Z ^z + Мщ d,
где МШо - момент пары сил, действующих на орган продольного управления
в плоскости, перпендикулярной оси вращения при нулевых значениях параметров
G 6 — ~ й ” 0.
Следует заметить, что угол отклонения 6, характеризующий изменение мест-
ного угла атаки органа управления, измеряется в плоскости симметрии самоле-
та, тогда как угол отклонения 6^, определяющий шарнирный момент, преодоле-
ваемый бустером, - в плоскости, перпендикулярной оси вращения органа управ-
ления.
Зависимость между этими углами выражается соотношением
61 = arctg (
tg6
cosxq.b
где Хо.в — уг°л стреловидности оси вращения органа продольного управления,
Откуда
1 - cos2 6 sin2 хо.в
28
или при малых углах отклонения 6, cos2 6 « 1
6 « COSXo ^i .
Для установившихся режимов полета Мш = МШо + Уг, где г - расстояние
от точки приложения балансировочной силы У до оси вращения органа управ-
ления.
Если на самолете реализовано дифференциальное управление органами
продольного управления, то на каждой поверхности появляется дополнительная
сила ±УН, пропорциональная углу "ножниц” <рн дифференциального отклонения
органов управления.
В этом случае аэродинамические шарнирные моменты правого и левого ор-
гана управления будут различными. Причем разность между ними
^шлр — ^ш.лев «ри ,
где <^н = (бдр - 5лев) /2 - угол дифференциального отклонения органов управления.
Зная максимальную величину произведения 6л^тах, определяемую маневрен-
ными и прочностными характеристиками самолета, нетрудно определить макси-
мальную величину балансировочной силы, действующей на орган продольного
управления.
Из рис. 15 видно, что эта сила
« GMy--------- .
z *м - xFr
Таким образом, из приближенного соотношения следует, что если считать рав-
ной нулю величину нулевого шарнирного момента МШо, то максимальный пот-
ребный шарнирный момент зависит от геометрических характеристик органа
управления, максимальной величины Gny, а также от числа М полета и не зависит
от величины скоростного напора.
1.4 ТИПОВЫЕ АТМОСФЕРНЫЕ ВОЗМУЩЕНИЯ
Под атмосферными возмущениями понимаются отклонения пара-
метров состояния реальной атмосферы от принятых характеристик
стандарной атмосферы. Эти возмущения могут воздействовать на само-
лет либо длительное время (например, в течение отдельных установив-
шихся режимов или всего полета), либо кратковременно. В зависи-
мости от длительности действия возмущений и их физической при-
роды могут изменяться различные параметры движения самолета.
Длительность воздействия атмосферных возмущений на самолет
зависит от скорости полета и пространственных размеров области ат-
мосферы, в которой проявляется отклонение параметров от стандар-
тных значений.
В стандартной атмосфере, неподвижной относительно земной сис-
темы координат, основные параметры — плотность, давление и темпе-
ратура воздуха — однозначно определяются высотой, измеряемой от
условного уровня моря, и принятыми начальными значениями для
нулевой высоты: tQ = + 15°С; р0 = 125; р0 = 760 мм рт.ст. (для
29
географической широты ^45°). Остальные параметры, характеризу-
ющие свойства воздушной среды (например, вязкость, скорость зву-
ка и др.), рассчитываются по известным зависимостям р(Н), t(H),
р (Н) и также являются однозначными функциями высоты Я, где Н —
геопотенциальная высота над условным уровнем моря.
В реальных условиях статические параметры атмосферы могут
изменяться в зависимости от времени года, суток, географических
координат и т. д. Фактические значения этих параметров периодически
замеряются при зондировании атмосферы на метеостанциях в конкрет-
ных географических районах и должны быть учтены в расчетах летно-
технических характеристик самолета для нестандартных условий поле-
та. Максимальные отклонения основных параметров атмосферы от
стандартных значений, полученные в результате статистической обра-
ботки многолетних фактических замеров, обычно приводятся в от-
раслевых стандартах.
Кроме отклонений статических параметров атмосферы от стандарт-
ных значений в реальной атмосфере практически всегда существует
движение воздушных масс, которое может воздействовать на самолет
в виде кинематических возмущений вектора скорости различной дли-
тельности, интенсивности и направления.
Движение воздуха с постоянной скоростью относительно земли
на большой протяженности (ветер) обычно учитывается в навига-
ционных задачах динамики полета, при определении стационарных
характеристик управляемости самолета и т. п.
Однократное изменение вектора скорости воздушной среды от-
носительно самолета по величине или направлению рассматривается
в динамике полета как воздушный порыв. Простейшей моделью воз-
душного порыва является мгновенное изменение вектора скорости
воздушного потока относительно самолета, которое согласно гипотезе
обратимости эквивалентно мгновенному изменению вектора скорости
центра масс самолета (по величине или по направлению) относительно
неподвижной среды. При этом на самолет действуют возмущения удар-
ного типа, при которых ускорения и скорости (угловые и линейные)
изменяются скачкообразно. Угловая ориентация самолета и положение
его центра масс в земной системе координат в момент удара не изменя-
ются. Положения вектора скорости и вектора угловой скорости са-
молета относительно земной системы координат в момент воздуш-
ного порыва ударного типа могут изменяться скачкообразно.
Возмущенное движение самолета от воздействия воздушного по-
рыва ударного типа корректно оценивать лишь тогда, когда время од-
нократного изменения скорости порыва много меньше постоянных
времени, характеризующих рассматриваемое движение самолета. В
противном случае следует задаться профилем порыва, т. е. зависимо-
30
стью изменения скорости порыва от времени либо от расстояния, про-
летаемого самолетом.
Помимо однократных воздушных порывов, которые действуют
на самолет, например при попадании в восходящий или нисходящий
поток воздуха при выполнении горизонтального полета, в атмосфере
встречаются воздушные порывы со знакопеременным профилем ско-
рости.
На малых и средних высотах полета, особенно в условиях кучевой
облачности, часто образуется хаотическое (турбулентное) движение
воздушных масс в атмосфере, вызванное в основном конвекционными
потоками воздуха с различными скоростями и температурами. Распре-
деление скоростей движения воздушных масс в пространстве, интен-
сивность и частота воздушных порывов характеризуются при этом
случайными величинами. Вероятностные характеристики трубулентной
атмосферы для различных географических регионов приводятся в
соответствующих стандартах.
При воздействии воздушных порывов на продольное движение
самолета изменение аэродинамических сил и моментов может быть
обусловлено в основном следующими причинами:
изменением угла атаки самолета и безразмерных аэродинамических
коэффициентов, зависящих от угла атаки (вертикальный порыв);
изменением величины скоростного напора вследствие изменения
модуля вектора скорости при неизменных значениях аэродинамических
коэффициентов и угла атаки (горизонтальный порыв);
изменением безразмерных аэродинамических коэффициентов в
результате изменения числа М при горизонтальном порыве.
Безразмерные аэродинамические коэффициенты сил и моментов
зависят также от безразмерных критериев подобия — чисел М — и кон-
фигурации самолета. Критерии подобия, в свою очередь, зависят от
параметров атмосферы (температуры, плотности и вязкости воздуха)
и скорости центра масс самолета относительно воздушной среды. По-
этому возмущения, вызванные изменением параметров неподвижной
атмосферы, например температуры, плотности, скорости звука, так-
же могут изменять величины аэродинамических сил и моментов, дей-
ствующих на самолет в полете.
В связи с этим следует оценить соотношения аэродинамических
сил и моментов, возникающих от воздействия типовых атмосферных
возмущений, имеющих различную физическую природу.
Для оценки порядков величин соотношений аэродинамических
сил и моментов можно ограничиться рассмотрением лишь простей-
шего вида типовых атмосферных возмущений — ступенчатым (мгно-
венным) отклонением характерных параметров воздушной среды
от исходных. Таким параметрами в продольном движении могут быть
порыв ветра (изменение скорости полета, угла атаки), мгновенное
31
изменение температуры (изменение скорости звука, числа М) и мгно-
венное изменение плотности воздуха (изменение величины скорост-
ного напора).
Влияние атмосферных возмущений на аэродинамические силы и
моменты и характеристики движения самолета зависит от величины
частных прозводных аэродинамических сил и моментов соответствен-
но по температуре, плотности и составляющим скорости ветра:
А (X, Y, Р, Mz); 4- (X, Y, Р, Mz);
от ор
-L (х у, р, м2у А = (х y, р, м2у
и W х О W у
Записав величину подъемной силы (нормальной к вектору ско-
ч УК2 wv „ wv
рости) в виде - = -у Су и считая малой и —а, легко по-
лучить:
Э (У/S') _ 1 Э(У/5) = pV а.
bWy ~ v Эа 2 у'
d(X/S) ~ 1 3(X/S) _ pV а
bWy V да 2 у ’
d(MzISbA) ~ 1 d(Mz/SbA) ^pvma .
dWy ~ v ba 2 2 ’
3(P/S) ~ 1 d(P/S) _ pV a
dWy V ba 2 CP’
где Wx, Wy — соответственно тангенциальные и нормальные к вектору
скорости составляющие порыва ветра. Здесь предполагается, что из-
менение величины модуля скорости, равное V - \/ V2 + Wy\ пренеб-
режимо мало.
Аналогичным образом нетрудно получить значения частных произ-
водных по величине тангенциального порыва ветра Wx, считая
(К+ Нх)2*72 (1+ ф).
Однако в этом случае к величинам частных производных сил и
моментов, характеризующих их изменение вследствие изменения ве-
личины скоростного напора, необходимо добавить частные производ-
ные аэродинамических коэффициентов по числу М, так как прираще-
ние АИ\/а = AM может повлиять на их величину.
Полагая зависимости сх и су от числа М для сверхзвуковых ско-
32
ростей полета пропорциональными величине 1/ \/ М2 — 1, значения
частных производных выразим соотношениями
М _ 2М
Сх ~Схксх (М2-1)3/2
И М _ 2М
Су ~Су™ (М2 ’
где ехисх и Су исх — соответственно коэффициенты лобового сопро-
тивления и подъемной силы для исходного режима полета. Величина
2М/(М2 — I)3 72 для достаточно больших значений числа М ведет себя
как 1/М, поэтому на больших сверхзвуковых числах М полета част-
ными производными с^и в первом приближении можно пренебречь,
При околозвуковых скоростях полета, где аэродинамические коэф-
фициенты претерпевают резкие изменения (при переходе самолета
через скорость звука), частные производные г? и с^как правило, оп-
ределяют поведение самолета.
Изменение тяговых характеристик силовой установки, характе-
рузующееся условной величиной Ср1, существенно зависит от режима
работы двигателей, угла атаки, числа Мит. п., поэтому в каждом кон-
кретном случае требуется отдельное рассмотрение необходимости уче-
та величины
Величина at?!1 может быть значительной на дозвуковых и особенно
на трансзвуковых скоростях полета. На больших сверхзвуковых ско-
ростях полета обычно близка к нулю.
Легко видеть, что при отсутствии влияния числа М отношение при-
ращений подъемной силы самолета, вызванных тангенциальной и нор-
мальной составляющими порыва ветра одинаковой величины (Wx =
= Wy), имеет порядок угла атаки исходного режима полета:
ЭУ , ЭУ _
---- / Ч-
ЭИ\ dWy
Поэтому в ряде случаев влиянием тангенциальной составляющей поры-
ва ветра можно пренебречь по сравнению с нормальной. При этом сле-
дует иметь в виду, что вероятностное распределение вертикальных
и горизонтальных порывов ветра по высотам нормируется в земной
(геопотенциальной) системе координат, поэтому в расчетах влияние
ветровых порывов необходимо оценивать с учетом угла наклона тра-
ектории исходного режима полета.
Изменение температуры наружного воздуха приводит к изменению
скорости звука и, как следствие этого, к изменению числа М полета
при неизменной истинной скорости. При постоянном давлении с изме-
нением температуры изменяется и плотность воздуха в соответствии
с уравнением состояния газа р = pRT. Поэтому полное изменение, на-
33
пример, подъемной силы при изменении температуры характеризует-
ся суммой частных производных:
ЭГ ЭУ др + ЭУ ЭМ
Эт ” Эр” Эт7 ~Эм ~Эт ’
Эр
где
дТ
определяется из уравнения состояния газа
Эр _ Р
Ьт 7”
ЭМ ЭМ да
а величина---=--------
дТ да дТ
М
2Т
ЭУ ,ЭУ р ЭУ М ч ЭУ 1 ,dY dY М ч
откуда-=-(— г + — - _).
Очевидно, что с ростом числа М влияние температурных возмуще-
ний возрастает. Особенно чувствительны к изменению температуры на
больших сверхзвуковых скоростях полета тяговые характеристики
турбореактивных двигателей. Поэтому при полетах с большими чис-
лами М температурными возмущениями пренебрегать нельзя. Опыт
измерения профиля температур по высотам показывает, что на боль-
ших высотах полета могут возникать значительные области с резкими
градиентами температур.
Возмущения, возникающие от температурных градиентов, следу-
ет также учитывать на околозвуковых скоростях полета, где могут
быть значительными величины частных производных аэродинамичес-
ких коэффициентов по числу М. В частности, на этих режимах полета
температурные градиенты могут оказывать влияние на моментные
характеристики самолета из-за отличной от нуля величины При
маневрах с интенсивным изменением высоты полета это влияние может
оказаться весьма существенным, особенно при наличии инверсных об-
ластей изменения температуры на малых и средних высотах полета.
(Под инверсией понимается возрастание температуры при увеличении
высоты полета). Такие явления в средних широтах довольно часто
наблюдаются в холодное время года.
Влияние изменения плотности воздуха необходимо учитывать на
больших скоростях полета и больших высотах. Например, длительный
прямолинейный полет самолета на больших высотах вследствие сферич-
ности земли и зависимости плотности атмосферы от геопотенциаль-
ной высоты полета не может быть реализован с постоянными углом
атаки и числом М. Эту особенность полетов на больших высотах необ-
ходимо учитывать при анализе характеристик фугоидного движения и
расчетах практических потолков сверхзвуковых самолетов.
34
13 УПРОЩЕНИЕ УРАВНЕНИЙ ПРОДОЛЬНОГО ДВИЖЕНИЯ САМОЛЕТА
Для оценки возможности понижения порядка системы уравнений,
описывающих продольное движение, следует выявить характерные
параметры, определяющие поступательное и вращательное движение
самолета.
Движение центра масс самолета определяется аэродинамически-
ми и гравитационными силами, равнодействующие которых лежат
в вертикальной плоскости земной системы координат. Для прибли-
женного анализа характерных параметров траекторного движения
удобнее действующие силы спроектировать на нормаль и касательную
к траектории центра масс самолета. Предварительно следует определить
положения равновесия системы уравнений продольного движения.
Для определения особых точек, характеризующих положения рав-
новесия системы уравнений (1.5) или установившиеся режимы полета,
следует все правые части в (1.5) приравнять нулю,заменив & = а +
+ в. Очевидно, что равенства выполняются либо при условии V = О,
либо при условии sin0 = 0. Таким образом, единственным положением
равновесия в продольном движении является установившийся режим
горизонтального прямолинейного полета. Обычно такой режим полета
принимается за исходное, невозмущенное движение самолета.
Для качественной оценки возмущенного траекторного движения
центра масс самолета в качестве первого приближения можно сделать
дополнительные упрощающие предположения о независимости аэро-
динамических коэффициентов сх, су, тп2 от скорости и высоты полета.
Полагая в исходном горизонтальном полете V = Ко, 0О = 0, можно
записать уравнения движения центра масс в приращениях ДК = V
иД0 = 0:
т(К0 + К + ДУ- G + Ру+ ЫРу\
dV
*РХ + ЛРх-(Х + ДГ)-^0,
ТаккаКДУ = р^!Го^21_^1 ~ 2mgV ,
У 2 2 Ко
то первое уравнение можно записать, полагая ДРу ~ 0, в виде
v dO 2gV
° dt ~ Ко '
Можно также считать, что определяющим членом в правой части
n dV л
второго уравнения является проекция веса mgv, т. е. — ~ — g0.
35
Исключая дифференцированием из полученных приближенных
уравнений 0 или V, легко получить уравнения второго порядка:
dt2 Vl dt2 V20
Аналогичное уравнение описывает, малые незатухающие коле-
2 К А
бания маятника с постоянной времени Тм = -------и периодом ко-
лебаний (в секундах) Т = я V 2 ~ О,45Ко, Приведенная длина I =
= gT1 /47г2 математического маятника с таким периодом колебаний
равна I = V о/2g.
Характерные масштабы времени и длины, определяющие траек-
торные параметры возмущенного движения самолета, сбалансированно-
го по моментам, дают возможность выявить доминирующие члены
в уравнениях продольного движения самолета.
При изменении модуля вектора скорости или угла наклона траек-
тории дальнейшее движение центра масс самолета представляет собой
колебания высоты и скорости полета. Период этих колебаний зави-
сит от скорости полета и величины ускорения свободного падения.
Чем больше скорость исходного режима полета, тем больше период
колебаний, тем меньше влияние изменения скорости на фиксирован-
ном интервале времени. Например, при скорости полета Ко = 1000 м/с
величина постоянной времени Гм = 70 с, а приведенная длина /= 50 км.
Таким образом, величину постоянной времени, характеризующая
траекторное движение самолета, зависит от ускорения свободного
падения g и скорости невозмущенного исходного режима полета Ко
и не зависит от геометрических параметров самолетов, аэродинами-
ческих коэффициентов и т. п. Этот факт имеет простое физическое
объяснение: при упрощении поставленной задачи движение самолета
заменено движением материальной точки в гравитационном потенци-
альном поле сил. Поэтому приведенная длина математического маят-
ника оказалась равной ’’энергетической высоте” Н = Vl /2g, характери-
зующей равенство кинетической и потенциальной энергий.
Следует заметить, что учет изменения разности сил сопротивления
и тяги двигателей в зависимости от скорости полета не изменяет ве-
личину постоянной времени Тм, так как в уравнении движения появ-
ляется лишь дополнительный член, пропорциональный dVIdt, а коэф-
фициент при V не изменяется.
Аналогичным образом можно оценить величину постоянной вре-
мени, характерной' для вращательного движения самолета. Если пред-
положить, что моментные аэродинамические характеристики самоле-
36
та не зависят от угловых скоростей, то восстанавливающий момент
в возмущенном движении пропорционален разности хм — xF и подъем-
ной силе:
ДМг »(хм -Х/г)ДУ
или
- М? « (хм - xF)c$ qSbA ,
а величина постоянной времени вращательного движения выразится
соотношением:
7^2
° Q
(xF - xM)cymg
Это соотношение легко преобразовать к виду
~ 1 аГ.П „ 2
у0 ~ — ---------rz ,
6 XF-xM
где аг п — угол атаки исходного горизонтального полета (в радианной
мере); = Jz/m — квадрат радиуса инерции самолета.
Величина постоянной времени То существенно зависит от линей-
ных размеров самолета и относительного расположения аэродинами-
ческого фокуса и центра масс. В явном виде от скорости полета То
не зависит.
Грубые оценки показывают, что для современных маневренных
самолетов, аэродинамически устойчивых в продольном движении (хр-
- хм) > 0, величина постоянной времени может иметь порядок от
10“1 до 1,0 с.
Сравнивая порядки величин постоянных времени, характеризующих
поступательное и вращательное движение самолета, можно сделать важ-
ный вывод: при оценке вращательного движения самолета скорость
полета и плотность воздуха можно считать неизменными.
Таким образом, ’’медленное” движение самолета с постоянной
времени Гм, пропорциональной истинной скорости полета, соответству-
ет изменению модуля вектора скорости, а ’’быстрое” движение с пос-
тоянной времени Го, не зависящей от скорости, соответствует изменению
направления вектора скорости при практически неизменном значении
модуля. Полученные результаты основаны на предположениях о неза-
висимости аэродинамических сил и моментов от числа М и высоты
полета. Эти предположения достаточно строго выполняются при полетах
с малыми скоростями на малых и средних высотах при умеренных уг-
лах атаки.
Медленное движение на этих режимах полета, связанное с измене-
нием модуля вектора скорости, близко к периодическому колебатель-
ному движению, характерному для самолетов ранних поколений. Такое
37
Рис. 1.6. Типовая область высот и ско-
ростей полета маневренного самолета:
1 - возможны установившиеся поле-
ты при Пу > 1,0; 2 - возможны поле-
ты с торможением при пу = 1,0;
3 - возможны полеты с торможе-
нием при пу < 1,0.
движение получило название
длиннопериодического в отличие
от короткопериодического дви-
жения, связанного с вращением
самолета относительно центра
масс.
У современных маневренных
самолетов, для которых харак-
терен типовой диапазон скоростей и высот полета, приведенный на рис.
1.6, медленное движение не является периодическим практически во
всем диапазоне скоростей и высот.
Этот факт объясняется следующими обстоятельствами. Полеты со
скоростями, близкими к минимальным, из-за высоких значений удель-
ной нагрузки на крыло происходят на больших углах атаки, где су-
щественным становится влияние скорости и числа М на аэродинами-
ческие коэффициенты и характеристики силовой установки самолета.
При полетах с малыми углами атаки на больших скоростях и умеренных
высотах становится существенным влияние числа М на силовые и момен-
тные характеристики самолета.
При полетах с большими числами М на больших высотах, где про-
изводными аэродинамических коэффициентов по числу М можно пре-
небречь, становится существенным влияние изменения плотности с
высотой полета на аэродинамические силы и моменты и характеристики
силовой установки самолета.
Современные маневренные самолеты вследствие запасов кинети-
ческой энергии при полетах с большими числами М могут существенно
превышать высоту статического потолка.
На рис. 1.6. показана типовая область возможных динамических
траекторий полета с торможением. Там же приведена граница области,
где возможны горизонтальные полеты с торможением. Эта граница
определяется максимальными несущими свойствами самолета при
больших числах М, сбалансированного по моментам предельными уг-
лами отклонения органов продольного управления. Выше этой границы
возможны полеты только с перегрузками пу, меньшими единицы.
Из рисунка следует, что понятие статического потолка как пара-
метра, характеризующего предельную высоту полета самолета, для
38
современных маневренных самолетов утратило свой смысл, так как
появилась возможность маневрировать на высотах, существенно пре-
вышающих статический потолок.
Следует также заметить, что определение в полете статического
потолка самолета на больших числах М представляет значительные
трудности, так как длительное выдерживание режима стабилизации
числа М и высоты полета при ручном пилотировании практически не-
возможно. При полете с большими числами М повышается точность
выдерживания угла наклона траектории, так как при скорости полета,
например, 1 км/с ошибка в один градус приводит к появлению вер-
тикальной скорости приблизительно 15 м/с. В то же время при полете
на постоянной (геопотенциальной) высоте угол наклона траектории
самолета должен непрерывно изменяться с угловой скоростью О »
» - V/R3 (приблизительно равной одной сотой градуса в секунду)
вследствие сферичности земли и изменения местной вертикали в про-
цессе полета. При характерном времени медленного движения 400...
500 с накапливается ошибка в угле наклона траектории 4...5°. В слу-
чае прямолинейного полета над сферической землей изменение геопо-
тенциальной высоты при тех же условиях составит ДН ~ (F7)2/2/?3
« 1,3 ...2 км, что приведет к значительному изменению плотности воз-
духа. В связи с этим для больших чисел М характерны неустановив-
шиеся режимы, сопровождающиеся плавным изменением высоты и
скорости полета.
Изменения плотности воздуха и скорости полета по времени харак-
теризуются величинами производных dp/dt и dV/dt, и при малых зна-
чениях этих величин (при полете на больших числах М и высотах) мож-
но пренебречь влиянием скорости и плотности воздуха на параметры
быстрого (вращательного) движения самолета.
В области околозвуковых скоростей полета, характеризующейся
большими значениями величин производных аэродинамических коэф-
фициентов по числу М, даже относительно малые изменения скорости
и параметров атмосферы могут приводить к существенным изменениям
сил и особенно моментов, действующих на самолет.
Следует также учитывать, что на современных маневренных са-
молетах, как правило, устанавливаются специальные автоматические
устройства, которые могут изменять конфигурацию самолета или его
силовой установки по сигналам так называемых М-реле, настроенных
на дискретные значения числа М. Естественно, что при этом могут изме-
няться аэродинамические характеристики самолета.
Таким образом, в широком диапазоне скоростей и высот полета
быстрое вращательное движение самолета с достаточной для практичес-
ких расчетов степенью точности можно рассматривать при постоянной
скорости и плотности воздуха.
39
Для оценки характеристик короткопериодического движения
самолета уравнения удобно записать в виде
mV = = cyqS- GcosO;
Jz = qSbA (mZQ + m& a + m^d + mffz + 6);
da dO
—— — — J— >
dt dt
~ = Ksin0.
dt
Полагая малыми исходные значения угла атаки и угла наклона
траектории, эти уравнения можно записать в приращениях от исход-
ного режима полета, выразив правые части через размерные аэродина-
мические коэффициенты:
^=ГЯа+ ?Д5;
М?Д.а + М% Да + Л^гДшг + Д8;
dr
dAa А dA0
—- = Acoz —т~;
dr dr
Jz
-^=КА0,
dr
где а
Ya = Су •
т V ’
v5 - СУ 4s . л7“ - mi(isbA .
mV ’ z Jz
= m^qSbA .
Z Jz
3 2
= mz qSbA
Z J_zV ’
= m<?\4sbA
JZV
Переходя к безразмерному времени т = tlTQ и безразмерному па-
раметру р = d/dr, характеристическое уравнение, соответствующее
40
уравнениям короткопериодического движения самолета, можно запи-
сать в виде
р2 + 2ip + 1 =0,
где
П = —_-1 _ ;
_ м “ _ у ам
у/- м<* - YaMza>z
Таким образом, в пространстве безразмерного времени т = t/TQ
один безразмерный коэффициент f определяет динамические свойства
свободного движения самолета. Это уравнение имеет корни
Р1,2 = “Г V 1 ~f2>
т. е. при f < 1,0 свободное движение самолета имеет колебательный
характер. Масштаб времени при этом определяется величиной постоян-
ной времени 7’0, а степень затухания колебаний в безразмерном времени
— величиной действительной части корней (параметром f).
Простые выражения, определяющие динамические характеристики
продольного короткопериодического движения самолета, позволяют
в аналитическом виде решить ряд важных прикладных задач, возника-
ющих при проектировании самолета и его системы управления, обес-
печить необходимые пилотажные характеристики самолета, определить
оптимальную степень автоматизации системы управления на различ-
ных режимах полета и т. п.
Для того чтобы определить динамические характеристики управ-
ляемого движения, необходимо знать законы управления и передаточ-
ные функции управляемой системы по различным параметрам коротко-
периодического движения самолета. Эти вопросы рассматриваются
в следующей главе.
41
ГЛАВА 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ
ПРОДОЛЬНОГО ДВИЖЕНИЯ САМОЛЕТА
2.1. ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ ПОЛЕТА
Уравнения, описывающие изолированное продольное движение,
используются для решения широкого круга задач динамики полета,
возникающих в процессе создания самолета начиная с самых ранних
этапов предварительного проектирования и кончая этапами доводки
самолета и его серийного производства. Сюда относятся, например,
все задачи аэродинамического расчета, связанные с определением ос-
новных летно-технических характеристик самолета — дальности, скоро-
подъемности, взлетно-посадочных характеристик и т. п. Методы решения
большинства упомянутых задач достаточно подробно изложены в су-
ществующей литературе [6], где имеется также обширная библиография.
Вместе с тем детальный анализ короткопериодического движения
и его влияния на траекторные параметры движения самолета не нашел
широкого освещения в литературе. Большое количество материала,
имеющееся по этому вопросу, изложено в виде статей, и недоступно
широкому кругу читателей из-за малого тиража подобных изданий.
Поскольку характеристики продольного короткопериодического движе-
ния самолета определяют выбор многих важных параметров самолета
и его системы управления, то в настоящей главе сделана попытка вос-
полнить существующий пробел, проанализировав влияние переходных
процессов короткопериодического движения на траекторные парамет-
ры полета.
2.2.КРАТКИЙ АНАЛИЗ ОБЩИХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Систему дифференциальных уравнений, описывающих свободное
движение твердого тела, как известно [1, 2, 7], можно записать в век-
торной форме:
X = F(x,0,
где X — вектор состояния; t — время; F(x, f) — известная векторная
функция фазовых координат и времени.
Если время в явном виде не входит в векторную функцию, то
такая система уравнений называется автономной и записывается в виде
* = F(x). (2.1)
Размерность вектора X определяет порядок системы и зависит от
рассматриваемой задачи.
42
Если функция F(x) является линейной относительно фазовых
координат, то система дифференциальных уравнений называется ли-
нейной. Общим решением системы линейных дифференциальных урав-
нений является сумма экспонент вида Cki^kt, где Рк — корни харак-
теристического уравнения исходной системы дифференциальных урав-
нений и к = 1 п (п — порядок системы).
Так как алгебраическое характеристическое уравнение имеет
тот же порядок, что и система дифференциальных уравнений, то коли-
чество корней совпадает с порядком уравнения. Считая, что все корни
различны, можно записать общее решение дифференциального уравне-
ния, например, для третьего порядка в виде
xf = CnePif + C2,ep2f + C3fep3^ L Л, -/) (2.2)
где z=l,2,3. z С
Произвольные постоянные Q/ для каждой фазовой координаты
определяются из трех начальных условий, которым должны удовлет-
ворять значениях1}х2,хз в начальный момент времени t = 0. Корни
характеристического уравнения рк являются решениями алгебраическо-
го уравнения вида
р3 + а2р2 + агр + а0 = 0, (2.3)
где коэффициенты ак определяются матрицей исходной системы диф-
ференциальных уравнений. Если исходное дифференциальное урав-
нение задано в виде одного уравнения
d3x d2x , dx
—Г + «2 —г + «1-77 + «о* = 0,
dt3 dt2 dt
то коэффициенты дифференциального уравнения ак являются коэф-
фициентами алгебраического характеристического уравнения. Для
того чтобы решение (2.2) было устойчивым, необходимо и достаточно,
чтобы все корни Рк имели отрицательную действительную часть.
В соответствии с формулой Эйлера для комплексного числа вида
р = X + /со можно записать
epf = e^ + = e^f(cosutf+ /sin со t),
откуда ясно, что если в (2.2) действительная часть хотя бы одного
корня положительна, то переменная х неограниченно возрастает с рос-
том времени, и движение устойчивым назвать нельзя, так как даже
самое малое возмущение приведет к неограниченному отклонению сис-
темы от начального положения.
Если все действительные части корней характеристического урав-
нения отрицательны, то с течением времени все слагаемые в (2.2) стре-
мятся к нулю,и возмущение затухает. Очевидно, что чем больше по аб-
солютной величине отрицательная часть корня, тем быстрее затухает
движение.
43
Таким образом, задача обеспечения устойчивости движения системы,
описываемой линейными дифференциальными уравнениями с постоян-
ными коэффициентами, сводится к обеспечению отрицательной дей-
ствительной части корней алгебраического характеристического урав-
нения.
Если ввести в рассмотрение комплексную плоскость, то требо-
вание к устойчивости сводится к обеспечению расположения всех кор-
ней характеристического уравнения слева от мнимой оси. Несмотря на
то, что общего решения алгебраического уравнения степени выше чет-
вертой не существует, необходимые и достаточные условия располо-
жения всех корней в левой полуплоскости получены для произвольного
порядка алгебраического уравнения, например критерий устойчивости
Рауса—Гурвица, который для уравнения (2.3) имеет вид
а0 >0; ava2 — aQ >0.
Таким образом, задача обеспечения устойчивости движения системы
сводится к удовлетворению системы неравенств из известных ком-
бинаций постоянных коэффициентов характеристического уравнения,
что позволяет, не решая уравнений, судить об устойчивости движения.
Зависимость (2.2) определяет собственное движение системы,
или собственные колебания системы, которые в случае устойчивости
системы с течением времени затухают.
Если возмущение остается постоянным с течением времени, то
после затухания собственных колебаний (с принятой степенью точности)
реализуется установившееся движение системы, вызванное постоянным
возмущением. Если возмущение не постоянно, а изменяется с течением
времени, то движение не будет установившимся. Однако в частном слу-
чае периодического возмущения после затухания собственного движения
реализуется периодическое установившееся движение, называемое
вынужденными колебаниями.
Очевидно, что качественные и количественные характеристики дви-
жения системы существенно зависят от вида возмущающих воздействий.
Реакция линейной системы на каждый из трех типов возмущений —
ступенчатое, импульсное и гармоническое — позволяет получить исчер-
пывающие сведения о поведении системы при произвольных возмуще-
ниях. Поэтому целесообразно выписать зависимости, характеризующие
движение системы при воздействии указанных типовых возмущений.
Процессу перехода системы от одного установившегося состояния
к другому можно поставить в соответствие некоторую условную вели-
чину времени. Теоретически, как следует из (2.2), это время равно бес-
конечности для линейных систем дифференциальных уравнений с пос-
тоянными коэффициентами. Поэтому в практических расчетах под
временем затухания свободных колебаний при воздействии ступенчатого
возмущения понимается обычно время, начиная с которого амплитуда
44
Рис. 2.1. Параметры качества переходных процессов:
а - апериодический и колебательный переходные процессы при ступенчатом от-
клонении органа управления; б - типовой колебательный переходный процесс
при ступенчатом отклонении органа управления
колебаний не превышает 5% установившейся постоянной величины е
Переходный процесс может быть колебательным или апериоди-
ческим. Для сравнения эти два переходных процесса для уравнений
первого и второго порядка приведены на рис. 2.1. Основные характе-
ристики этих двух процессов видны из рисунка. Колебательный про-
цесс обычно характеризуется четырьмя параметрами — временем сра-
батывания, временем затухания, величиной заброса и частотой (перио-
дом) колебаний. В апериодическом процессе время затухания и время
срабатывания совпадают и определяются временем достижения перемен-
ной величиной 95% ее установившегося значения. Для сравнения вре-
мени срабатывания апериодического и колебательного процессов иног-
да вводится величина времени достижения 70% установившегося зна-
чения.
Переходные процессы, приведенные на рис. 2.1, характеризуют
движение систем в безразмерном времени, описываемых уравнениями
второго и первого порядков при воздействии постоянного по времени
ступенчатого возмущения.
При этом все перечисленные характеристики качества переходного
процесса остаются неизменными. Эти характеристики для линейных
систем с постоянными коэффициентами не зависят от величины воз-
мущений и определяются однозначно корнями характеристического
уравнения.
Характеристические уравнения линейных систем дифференциаль-
ных уравнений с постоянными коэффициентами первого и второго
порядков принято записывать в виде
Тр + 1 = 0; Р = - -L ;
45
rgp2 + 2J7oP + 1 = 0; P1>2 = -I ±4 /1-fX
70 7 0
где T, To — характерные постоянные времени.
Характеристики качества переходных процессов, изображенных
на рис. 2.1, и решения уравнений при нулевых начальных условиях
соответственно выражаются соотношениями:
для систем первого порядка
х(0 = (1 - е- f/r),
^зат = ^сраб ЗТ;
для систем второго порядка
-4>
х (г) = 1 — А е 1 ° cos (йЯ +
где w = 1. >/1 - f2'; гСраб » Т’о (0,25 + tg<p);
1 о
21
То
+ Vl-f2 .
</» = arctg-I—J; Гзат
Величина заброса р = е“ _ ,
Зависимости величины заброса и времени срабатывания от пара-
метров f, Tq приведены на рис. 2.2, а, б.
Из ^приведенных соотношений следует, что, вводя безразмерное
время t = t(T и t = Z^/T’o, можно исключить один параметр. Характе-
ристические уравнения в этом случае будут иметь вид
р + 1 =0;
Р2 + 2fp + 1 = 0,
и уравнение второго порядка определяется лишь одним параметром -
f — коэффициентом относительного демпфирования.
Гармоническое возмущение, изменяющееся по закону sin wt или
Рис, 2.2. Время срабатывания (а) и заброс в колебательном переходном процео
с (б)
46
cosccf, выводит линейную систему на режим установившихся коле-
баний. В этом случае определяется переходный процесс и установив-
шаяся реакция системы (после затухания переходного процесса). Оче-
видно, что установившиеся колебания системы будут происходить
с той же частотой, но могут быть сдвинуты по фазе по сравнению с
возмущающим воздействием. Зависимость амплитуды и фазы вынуж-
денных установившихся колебаний системы от частоты возмущающе-
го единичного гармонического воздействия определяет частотную ха-
рактеристику системы.
Таким образом, для определения характеристик движения объек-
тов, описываемых системой линейных дифференциальных уравнений
с постоянными коэффициентами (порядка не выше четвертого), соот-
ношения могут быть получены в аналитическом виде. Так как воз-
мущение произвольного типа может быть получено суммированием
рассмотренных стандартных возмущений, то в силу принципа супер-
позиции можно определить переходный процесс системы от воздей-
ствия любого возмущения. По этому же принципу проводятся рас-
четы на ЭВМ.
Возмущения, действующие на систему, могут иметь принципиаль-
но различную природу: целенаправленные, управляющие воздействия
и случайные возмущения, характеризующие непредсказуемое влияние
внешней среды. Систему с целенаправленными возмущающими воз-
действиями принято называть управляемой динамической системой.
Безынерционный параметр управления, обозначаемый обычно и, до-
пускает разрывы первого рода.
Векторная запись уравнений, описывающих движение управля-
емой системы, имеет вид
х = F (х, u, t).
Для управляемых динамических систем возможна постановка
двух основных принципиально различных классов задач:
определение поведения системы при известных законах управления;
определение законов управления при выполнении определенных
условий, накладываемых на поведение системы.
Если управляющий параметр не зависит от фазовых координат
динамической системы, то такая система является разомкнутой.
Задачи первого класса в этом случае сводятся к определению пе-
реходных процессов по различным фазовым координатам при различ-
ных (как правило, типовых) законах управления.
Если параметр управления является функцией одной или несколь-
ких фазовых координат, то система становится замкнутой. Поведение
замкнутых динамических систем рассматривается в гл. 4.
Ко второму классу задач относятся, например, вариационные зада-
чи отыскания оптимальных траекторий движения системы. Актуальной
47
является, в частности, задача перевода системы из одного состояния
в другое за минимальное время. (Такие переходные процессы и соот-
ветствующие им законы управления называются оптимальными по
быстродействию). Для ее решения задания только начальных условий
оказывается недостаточным. Следует ввести дополнительные условия
для определения значений фазовых координат в конечной точке управ-
ления, определяемой неизвестным заранее моментом времени Г.
Таким образом, для системы дифференциальных уравнений при-
ходится решать краевую задачу на конечном интервале времени [0 — Т].
В отличие от времени затухания переходного процесса в линейной
системе (теоретически бесконечного) интервал времени в задачах на
быстродействие всегда конечен, и условия на конце интервала в момент
времени t = Г должны быть выполнены абсолютно строго.
Использование динамических систем, описываемых линейными
дифференциальными уравнениями с постоянными коэффициентами,
в качестве математической модели реального процесса позволяет ста-
вить и решать широкий круг задач, имеющих важное практическое
значение в динамике полета. В то же время совершенно ясно, что та-
ких динамических систем в природе не существует, так как практи-
чески все физические процессы описываются нелинейными дифферен-
циальными уравнениями. Однако если нелинейности представляют со-
бой произвольные, но непрерывные и дифференцируемые функции,
то такие функции можно линеаризовать, разложив в ряд Тейлора в
окрестности исследуемой точки и оставив лишь члены первого поряд-
ка малости.
Заранее не ясно, как оценить поведение динамической системы,
описываемой нелинейными дифференциальными уравнениями. Однако
существуют известные теоремы Ляпунова, позволяющие судить о по-
ведении нелинейной системы по ее линейному приближению при ма-
лых отклонениях движения системы от рассматриваемого исходного
движения. Так, например, на основании теорем Ляпунова можно су-
дить об устойчивости в малом динамических систем с нелинейными
характеристиками по устойчивости линеаризованных систем (их ли-
нейных моделей).
Таким образом, теоремы Ляпунова позволяют, решив характе-
ристическое уравнение линеаризованной системы, сделать вывод об
устойчивости в малом исходной нелинейной системы.
Если все корни характеристического уравнения имеют отрицатель-
ные действительные части, то исходная нелинейная система асимпто-
тически устойчива в малом. Если хотя бы один корень характеристи-
ческого уравнения имеет положительную действительную часть, то
движение исходной нелинейной системы неустойчиво в малом. Если
хо/Тя бы один корень имеет нулевую действительную часть, то линеа-
ризация исходной нелинейной системы некорректна, и об ее устойчи-
вости нельзя судить по линейному приближению.
48
Физический смысл теорем Ляпунова ясен из следующих сообра-
жений, Для устойчивой линеаризованной динамической системы при
малых отклонениях от исходного движения возмущения со време-
нем затухают, и система возвращается к исходному невозмущенному
движению. В случае неустойчивости линеаризованной системы урав-
нений малые возмущения неограниченно возрастают, движение откло-
няется от исходного и начиная с некоторого момента времени линеа-
ризация становится некорректной.
Если линеаризованная система ’’нейтральна”, т. е. линейное прибли-
жение хотя бы одной из фазовых координат не изменяется с течением
времени, то при разложении в ряд Тейлора данной фазовой координаты
отброшенными нелинейными членами пренебречь нельзя. В этом слу-
чае линеаризация системы уравнений не позволяет решить вопрос об
устойчивости в малом, и устойчивость исходной системы уравнений
определяется членами более высокого порядка (так как малыми от-
клонениями фазовых координат от исходных значений являются такие
отклонения, когда линейные члены разложения в ряд Тейлора значи-
тельно превышают сумму членов высших порядков и играют домини-
рующую роль в изменениях фазовых координат). При больших откло-
нениях от исходного движения доминирующими могут стать члены
высших порядков и принятые при линеаризации допущения станут
неправомочными.
В связи с этим при использовании линейных математических мо-
делей, описывающих реальное движение самолета, не следует забывать
о пределах допустимости и степени корректности линеаризации системы
уравнений. Динамическая система, устойчивая в малом, может быть,
например, неустойчивой ”в большом”.
2.3. КРАТКИЙ АНАЛИЗ ХАРАКТЕРИСТИК
КОРОТКОПЕРИОДИЧЕСКОГО ДВИЖЕНИЯ САМОЛЕТА
ПОД ВОЗДЕЙСТВИЕМ УПРАВЛЯЮЩИХ МОМЕНТОВ
Уравнения продольного короткопериодического движения в со-
ответствии с общепринятой в динамике полета терминологией опре-
деляют математическую модель движения самолета в вертикальной
плоскости при условии постоянства скорости полета, плотности воз-
духа и массы самолета. Эти уравнения, описывающие свойства быст-
рого вращательного движения самолета, являются определяющими
при оценке летчиком пилотажных характеристик самолета, маневренных
качеств и т. п. Динамические свойства самолета как управляемого
объекта оцениваются летчиком с точки зрения удобства управления
основными параметрами движения: угловой ориентацией самолета
(углом тангажа) и кривизной траектории (величиной нормальной
перегрузки).
49
Передаточные функции самолета в короткопериодическом движении,
управляемом отклонением органов продольного управления
Таблица 2.1
Обозначение У6 = 0
ад) - Tof®p + 7^ (Wf У5 + Y^M^) T0M«— L_ p 2 + 2fp + 1
Р 2 + 2fp + 1
и^ф) LT*MS—1 g 1 9MZ _ S p2 + 2fp+l
g P2 + 2fp 2 + 1
ад) T2(M®- Увм“)р+Т^(У“м£-У8м“) _ p+TeYa T2MSZ L - °. _ P(P2 + 2fp+ 1)
P (p 2 + 2?p + 1)
T„ Y 6 p 2 - To (Й“+ M^z)p + T2 (У “wf - У SAf “ ) T* YaMSz i P(P2 + 2fp+ 1)
p(p2 +2JP + D
f5p2 +T0(MS2+Y6m“z)p T*MSZ p + 2Jp + 1
p2 +2Jp+ 1
wz Tt(^-YS^+Tl(YttMSz- Y6M^ P + 2$P + 1
p 2 + 2?p + 1
^,(p) wz (M^- FSM°)p2 4- Ta (YaMz — YSM^)p p2 + 2Jp + 1
5 р(р + Г0У“)
Z -
P2 +2ГР+1
v T„ YSp2 + Т2У* *(М^ +m“z)p + T* (YaMz - YbM%)
p2 (p2 + 2fp + 1)
VT*YaMz --------------
P2(^2 + 2fp+ 1)
У-М“- Y°m“z' 2-J-M^-YaM^z
F“ = CyqS YS = CyqS
mV mV
mzqSbA mSzqSbA
JYlZ---------- M- = ---------
JZ 1.
* T TZ
Динамические характеристики самолета в управляемом движении
можно определить переходными процессами при типовых законах
управляющих сил и моментов.
Принимая за исходный режим установившийся прямолинейный
горизонтальный полет самолета и пользуясь обозначениями разд. 1.5,
можно записать
= qS[cy а + Су w(f)];
Л ^~-=Q^bA (т?а+m?d + m¥zGjz +
dO л da (2.1)
dF+^=^'
(Здесь опущены знаки приращений: Д0 = 0; ... и т. п.).
Для уравнений (2.1) следует выписать передаточные функции
для приращений параметров короткопериодического движения при
отклонении органов управления. Эти передаточные функции приведе-
ны в табл. 2.1.
Из рассмотрения передаточных функций для различных парамет-
ров короткопериодического движения следует, что характеристичес-
кое уравнение в зависимости от управляемого параметра может иметь
четвертый, третий или второй порядок.
При управлении высотой полета* характеристическое уравнение
имеет кратный нулевой корень, так как в короткопериодическом дви-
жении под высотой понимается вертикальное перемещение центра масс
самолета (в земной системе координат) при постоянной плотности воз-
духа. Поэтому аэродинамические силы и моменты от высоты не за-
висят, и самолет ’’нейтрален” по высоте.
Точно так же не влияют на аэродинамические силы и моменты
углы тангажа и наклона траектории: самолет ’’нейтрален” по этим па-
раметрам движения, и характеристическое уравнение имеет нулевой
корень.
Однако если управляющий момент непосредственно изменяет ско-
рость фазовых координат # и 0, т. е. первую производную dOfdt и d'&jdty
то в случае управления высотой, как следует из уравнений (2.1), из-
меняется ’’ускорение”, т. е. вторая производная d2Hldt29 поэтому в
характеристическом уравнении появляется кратный нулевой корень.
Таким образом, при отклонении органа продольного управления
на постоянную величину такие параметры движения самолета, как
угол наклона траектории, угол тангажа и высота в короткопериоди-
ческом движении, не имеют установившихся значений.
52
Чтобы определить установившиеся значения остальных парамет-
ров движения самолета, необходимо рассмотреть числители передаточ-
ных функций, приведенных в табл. 2.1. Как следует из таблицы, выра-
жение для числителя зависит от силы, действующей на самолет при
отклонении органа продольного управления, которая характеризует-
ся величиной i. _
Для того чтобы оценить влияние величины на установившееся
значение, например, перегрузки, следует рассмотреть свободный член
в числителе передаточной функции по перегрузке:
пФ F“d - /«а _ zg.
/И 2 * mZ Су
Это выражение можно переписать в виде
П ф Г <* (1 - *м ~ у ), (2.2)
*М %р2
откуда легко видеть, что для самолетов с малыми запасами устойчи-
вости, когда аэродинамический фокус близко расположен к центру
масс, можно считать » 0 с достаточной для практики степенью точ-
ности.
Для самолетов с близкорасположенными к центру масс органами
управления (например, на задней кромке крыла у самолетов бесхвос-
той схемы) отношением (хм - х/?)/(хм — х/?2) по сравнению с едини-
цей пренебрегать нельзя, особенно на сверхзвуковых скоростях полета,
при заднем положении фокуса самолета.
Выражение, стоящее в скобках в (2.2), можно записать в виде
х/7 - х^2/хм - х/?2, откуда следует, что влияние величины У® на уста-
новившееся значение перегрузки пропорционально расстоянию от аэро-
динамического фокуса самолета до точки приложения силы, действу-
ющей на орган продольного управления (до второго фокуса органа
управления). Поэтому для органов управления, расположенных сзади
центра масс самолета, величина установившейся перегрузки снижа-
ется при смещении фокуса самолета назад, При переднем расположении
органов управления установившаяся перегрузка увеличивается при сме-
щении фокуса самолета назад.
Из выражения (2.2) следует, что для нейтрального по углу атаки
самолета (когда фокус по углу атаки совпадает с центром масс) сила,
действующая на орган продольного управления, не влияет на величину
установившейся перегрузки, так как приращение подъемной силы
совпадает с центром масс и момента не создает.
При этом из уравнения моментов определяется установившаяся
величина угловой скорости тангажа coz, а установившиеся угол атаки
и перегрузка определяются из уравнения сил.
53
Влияние величины У® на динамические характеристики переход-
ного процесса можно оценить приближенно, рассмотрев выражение
у 5 -2 5 2
jz у су _ rz___________
bA mb bA(xM-xFi)'
Для самолетов нормальной схемы величина хм - хр2 с достаточ-
ной для практических расчетов точностью определяется расстоянием
от центра масс самолета до четверти (или половины в зависимости от
числа М) средней аэродинамической хорды горизонтального опере-
ния. Эта величина обычно имеет порядок средней аэродинамической
хорды крыла Ьд. В таком случае можно записать приближенное ра-
венство
У5 г
4 ЬА
щих па-
выраже-
Из приближенных оценок следует, что в практических расчетах
можно пользоваться упрощенными уравнениями, полагая У^ = О для
большинства режимов полета. В этом случае переходные процессы по
углу атаки и перегрузке совпадают с точностью до постоянного мно-
жителя Пу\
Пуа = Пу, где Пу = Су1сугЛ1. (2.3)
Для более точных оценок влияния величины У® на параметры пе-
реходных процессов по перегрузке следует выписать аналитические
выражения ny(t) при различных законах управления 6 (t).
При ступенчатом отклонении органа продольного управления пере-
ходные процессы, характеризующие изменение соответствуь
раметров движения в безразмерном времени определяются
ниями:
для приращения угла атаки Да:
Да = Т% (м« + F5 м"0[1 - е~ - • Sin(x/TT27 + </>)-
VFF
-То У5 ,е sinx/1-f2?];
для приращения величины нормальной перегрузки пу:
е- & /-----—
1----7= sin( у 1 - f2r + </?) +
ч/TF
е- е- )----- 1
+ В ----sinyl — £2Г- Л —------sin(x/l-f2f - <р) J ;
(2.4)
Ди =1 TlR
(2.5)
54
для приращения угла наклона траектории Д0:
г - $7 1_
Д0 = t—2f + sin(\A-f21 + 2«p) + ВГ1 -
e" I--e~ & i-------------------
- .., . sin(\A-f2? +<р)] + Л --sin\A — $~2f ; (2.6)
x/TF x/TF
для приращения высоты:
Г 72 - е— & I-------'
ДЯ = К St + 4f2 - 1-Д= sin(V1 - f2 + 3<p) +
I2 _ x/17?
e- f f ,----5_
+ B[t — 2f + —sin(y 1 — f21 + 2<p) +
xA-f2
+ A[1---12, , sin(\/l - f27+ tp) I •
xA-F J
При отклонении ^органа продольного управления с постоянной
скоростью за время t0 закон отклонения органа управления в безраз-
мерном времени имеет вид:
5 =§о^о при t < 70 и 6 = 1 при t > tQ.
Поэтому переходные процессы определяются ^различными выра-
жениями на разных участках управления при t < tQ и t > FQ.
Выражения для приращения величины нормальной перегрузки
Длу имеют вид _
= Г Г° Т"Г “ *—Л vsin(x/l - 2^) -
® L \/1 — f2
_ в[ -12 sinCVl^Fr + р) - 1 ] + А[-1 .sinVFp?]}
Vi - f2 J
при 0 < t < t0 ;
= ~ ToR f1 ~ у j [sin(\/l-f27 + 2</>) -
g I f° xA - f2
- e sin(\A-f27 - >/l - f270 + 2</>) + A sin>/l-f27 -
-Ae^o sinVl-f2 (7- 70)- 5sin(x/l-f2V+^) + Bsin(Vl -f2'7 -
- Vl-f2 70 + </>)] l при 7 > 70.
55
Для приращения угла наклона траектории Д0 можно получить
аналогичные выражения при вычислении интеграла от &пу:
приО<7<Го Д0 = j ^nvdi\
v О
при7 > 70 Д0 = s°^nydi + S &nydi.
V О V to
Значения сдвига по фазе <р и постоянных R, Л, В в переходных про-
цессах определяются по формулам:
= arccos f = arcsin \/1 - f2 ;
R = YSM%;
yb -X
A =—- ,B= — + M?)Y5IRTo.
RT$
Поскольку величина нормальной перегрузки является важней-
шим параметром управляемого движения маневренного самолета,
представляет практический интерес оценить величины забросов по
перегрузке в переходном процессе при различных законах ^управления
и выявить влияние величины Y& на характер зависимости пу (t).
Для определения величины заброса по перегрузке v необходимо
определить первый максимум в зависимости ny(t). Для определения
времени достижения первого максимума 7тах достаточно продиффе-
ренцировать по времени зависимость пу (7) для значений t > tQ и поло-
жить dny /dt = 0.
Поскольку
_ п г е- ^0
d7 пУУст—
sin (\/1 - f2r + ф)
то-^2- = 0, когда sin(\/l -f2? + i//) = 0,
dt
и величина относительного заброса
V = — е~ frmax , (2.7)
гДе tm ах ~ минимальный положительный корень уравнения
sin(x/l - f27max + Ф) = 0. (2.8)
56
Так как величина г выражается через А соотношением
г = У(1 - А)2 + А? (2 - A) Ve2 ?f° - 2eFf° cosx/1 - f270"+T (2.9)
и параметр А пропорционален У®} то случаю у$ = О соответствует А =
= 0 в выражении (2.9). _
Для оценки влияния на величину rmax следует выписать соот-
ношения, определяющие cos 0.
Учитывая, что В/А = - (M^z + 7И^)Т0, А = Y^ITq, можно считать
с достаточной для практики степенью точности В % А$.
Тогда приближенное соотношение для cos 0 имеет вид
2cos0~f(l - е^°cos\/l -f2^o) - (1 - Л)>/1 -f^e^° sin\/1 — f 210.
(2.10)
Расчеты показывают, что на величину заброса по перегрузке с уче-
том А Ф 0 влияет в основном выражение (2.9), а величина cos 0 в (2.10)
практически не изменяется при варьировании параметра А в пределах
его реальных значений.
Таким образом, можно записать, что влияние У® на отношение
забросов по перегрузке определяется отношением значений пара-
метра г.
^И±2.^у/(1-А)2 +ЛГ2(2-Л)2’ (2.11)
VA = о ГА = О
или для малых Л:
(2.12)
vA=0
Из сравнения (2.7), (2.9) и (2.10) следует, что при У® =_0 (А = 0)
величина заброса является функцией двух параметров f и t0, опреде-
ляющих соответственно характеристики самолета и закона управле-
ния в безразмерном времени. Зависимость р = /(f, tQ) можно вы-
числить и построить, например, в координатах р, t0 при фиксированных
значениях f. Зная зависимость р = /(f, t0) и величину Л, можно из
(2.11) или (2.12) определить величину заброса с учетом У®.
Зависимость v = t0) при А = 0 имеет вид
v = 2-е^°cos^o + 1 ё~ (2.13)
f0
где Гтах - минимальный положительный корень уравнения (2.8).
На рис. 2.3, а приведена сетка кривых v = Д70) Для фикси'рован-
57
ных значений f, а на рис. 2.3, б - зависимость tQ = /(f) при различных
значениях р.
Из графиков следует, что для каждого значения максимально до-
пустимого заброса р* существует такое максимальное значение f*^
что при f > f* величина заброса будет меньше р* при любом значении t0*
Таким образом, выбрав значение р*, например, в диапазоне р* ~
~ 0,1..,0,15 можно по графикам определить критическое значение ве-
личины f*.
На режимах полета, где f >f*, летчик может пилотировать само-
лет с любым темпом, не опасаясь превысить допустимую перегрузку
(угол атаки) более чем на 10... 15%.
На режимах полета, где f < f*, при пилотировании самолета с пре-
дельными перегрузками (углами атаки) летчик вынужден ограничи-
вать темп отклонения органов управления.
Поскольку минимальное значение времени tQ зависит от величины
максимальной скорости отклонения органа управления 6тах, его ста-
Рис. 2.3. Параметры качества переходных процессов при отклонении органов
управления с постоянной скоростью: _
а - линии равных значений £ в плоскости параметров v, t0; б - линии равных
забросов на плоскости параметров
58
тической эффективности ЬпУ и допустимого заброса, то можно, задав-
шись величиной допустимого заброса р, получить ограничение на ве-
личину 5 тах в зависимости от режима полета и безразмерных пара-
метров короткопериодического движения самолета из условия
7 — пУ тах
Го , >
^тах
где v = определяется по кривым рис. 2.3. _
Из рисунка следует, например, что при f = 0,1 и t0 = 0,9 и 0,.
Следует заметить, что приведенные рассуждения справедливы лишь
при рассмотренном выше монотонном законе пилотирования. В случае
отклонения органа управления, например, по закону, приведенному
на рис. 2.4, б, т. е. со знакопеременной скоростью отклонения в про-
цессе выхода самолета на установившуюся перегрузку, величины заб-
росов могут быть значительно меньше. Однако техника пилотирования
при этом существенно усложняется.
Уравнения короткопериодического движения самолета были полу-
чены в предположении малости углов наклона траектории при исход-
ном горизонтальном прямолинейном установившемся полете самоле-
та. Однако рассмотренные переходные процессы предполагают выход
самолета на предельно допустимую перегрузку, что может приводить
к значительному искривлению траектории и изменению высоты полета.
Для оценки корректности полученных соотношений можно опреде-
лить изменение высоты и угла наклона траектории за время переходно-
го процесса при выходе самолета на максимальную перегрузку.
Полагая, что изменение угла наклона траектории 0 за время пере-
ходного процесса находится в пределах корректности линеаризации
тригонометрических функций sin0 «
простые приближенные выражения для
расчета изменения высоты и угла
наклона траектории.
Анализ полученных выше соот-
ношений показывает, что если подоб-
рать величину Го таким образом, чтобы
заброс перегрузки не превышал 10...
Рис. 24. Качественный характер переходных
процессов при различных законах отклоне-
ния органов управления:
1 - монотонное отклонение с постоянной
скоростью; 2 - знакопеременная скорость
отклонения
0, cos0 1, можно получить
59
15% установившегося значения, то выражение 0 (г) при t > tQ сущест-
венно упрощается, и можно записать
в * Ф 'Ь'устк -2f].
В земной системе координат Н = Yg и изменение высоты опреде-
ляется выражением
Я(Г) = КТО J 0 dt.
О
Если обозначить гзад время выхода на заданную перегрузку, то
при t >^зад имеют место приближенные равенства:в =
— 2f) в случае мгновенного отклонения рулей и 0 = —-
пууст О’ “
пууст (t ~
— 2f- ^?) в случае ограниченной скорости перекладки.
t
При этих условиях легко вычислить J Qdt и получить приближен-
0
ную зависимость H(t) в явном виде.
Для критической величины относительного времени перекладки
органа управления f0* можно получить нижнюю оценку, задавшись
максимальной величиной заброса по перегрузке. Считая максималь-
но допустимую величину заброса по перегрузке равной v = 15%, нет-
рудно получить при f < 0,5
7$ > 5,5
Таким образом, если относительное время перекладки будет мень-
ше, то заброс по перегрузке превысит принятую условно предельно
допустимую величину v = 15%.
При f > 0,5 Го*= т. е* Даже при ступенчатом отклонении органов
управления величина заброса для значений f > 0,5 не превышает 15%.
Если в процессе пилотирования не превышаются ограничения по
допустимой перегрузке (или углу атаки), то темп отклонения органа
управления от летчика может быть произвольным и ограничивается
энергетикой силового привода. Такому случаю соответствует переход-
ный процесс при вводе самолета в маневр с установившейся перегруз-
кой или углом атаки, например не более 50% допустимых значений.
При выполнении маневра с установившимися перегрузками (углами
атаки), близкими к предельно допустимым, большие величины забро-
сов могут стать небезопасными. Однако маневры с предельными пере-
60
грузками или углами атаки в силу естественных ограничений управ-
ляемости возможны в ограниченных областях режимов полета,
С этой точки зрения эксплуатационную область скоростей и вы-
сот полета современного маневренного самолета можно условно раз-
делить на три подобласти, зная зависимости допустимых углов атаки
и перегрузок от режима полета.
Типовые эксплуатационные ограничения адоп = Л(М) и л^доп =
= f2 (М) приведены на рис. 2.5, где числа М = М* скачкообразного из-
менения допустимых значений угла атаки и перегрузки на графике для
простоты приняты одинаковыми, хотя имеют различную физическую
природу.
Снижение допустимого значения угла атаки на околозвуковых
числах М полета вызвано ухудшением характеристик боковой устой-
чивости и управляемости на больших углах атаки в этом диапазоне
чисел М, что может приводить к более раннему сваливанию самолета,
Снижение допустимой величины нормальной перегрузки обуслов-
лено требованиями равнопрочности конструкции планера на дозвуко-
вых и сверхзвуковых скоростях полета, так как в диапазоне около-
звуковых и трансзвуковых скоростей полета аэродинамические наг-
рузки, действующие на крыло и органы продольного управления, воз-
растают,
Учитывая зависимости адоп = A (М); л^доп = f2 (М) и статические
характеристики продольной управляемости самолета, можно во всей
YZZZZZZZZ
^ZZZZZZZ
I
j_________>
Рис. 2.5. Типовые эксплуатационные ограничения маневренного самолета:
а - типовые зависимости адоп == (М); ИуДОП « Д (М); б - типовая зависимость
допустимой приборной скорости от высоты полета; I - область возможного пре-
вышения адоп (вертикальная штриховка); II - область возможного превышения
Лудоп (горизонтальная штриховка); III - область допустимого пилотирования
предельными отклонениями органов управления
61
эксплуатационной области скоростей и высот полета выделить три
дополнительные различные области с точки зрения предельных воз-
можностей системы продольного управления самолетом, т. е. при пол-
ностью отклоненной на себя ручке управления.
Границы этих областей можно определить, построив балансировоч-
ные зависимости а(5тах, Д ^пр) ; пу Фтах, Н, vпр) •
Положив в этих зависимостях
а(^тах, Н, Vпр) = Лдоп» пу (^тах, ^пр) ~ пудоп,
можно получить в координатах Н, Ипр границу, отделяющую на рис.2.5
область III от областей I и II. Границу, разделяющую между собой облас-
ти I и II, легко получить из условия су (аДОп) А>г.п == и^доп-
На этой границе одновременно достигаются допустимые значения
угла атаки и перегрузки.
На рис. 2.5. приведены типовые ограничения современного манев-
ренного самолета на плоскости Ипр,77. Там же нанесена линия предельно
допустимого числа М полета.
Область I, одной из границ которой является ограничение по ми-
нимальной приборной скорости полета, характеризуется ’’избыточной”
управляемостью самолета по углу атаки. В силу малых величин ско-
ростного напора в этой области максимально допустимая перегруз-
ка самолетом не достигается. Линия М* = const, на которой меняются
скачком величины допустимых значений перегрузки и угла атаки, нане-
сена штрихпунктиром. Две подобласти А и Б различаются лишь величи-
нами адоп-
В этой области справедливы неравенства пу <и^дОп’>а > адоп,
т. е. статические характеристики продольной управляемости самоле-
та позволяют превышать допустимые значения угла атаки, не превы-
шая максимальной перегрузки.
Поэтому при пилотировании в области I требуется ограничивать
угол атаки, величину и скорость отклонения органов продольного уп-
равления из условий безопасности самолета от сваливания, Забросов
по перегрузке летчик может не опасаться.
Область II характеризуется возможностью превышения допусти-
мой величины нормальной перегрузки пу, т. е. ’’избыточной” управля-
емостью самолета по перегрузке.
В этой области из-за больших величин скоростного напора невоз-
можно достичь допустимых углов атаки, не превысив при этом установ-
ленную величину максимальной перегрузки. Аналогично предыдущему
случаю подобласти А и Б различаются значениями допустимых углов
атаки и перегрузок.
Поэтому в области II требуется ограничивать величину и скорость
отклонения органов продольного управления из условий прочности
62
самолета. При энергичном маневрировании самолета забросы по пе-
регрузке не должны превышать 10... 15%.
В области III статические характеристики продольной управля-
емости самолета недостаточны для достижения установленных огра-
ничений допустимых углов атаки и перегрузки.
Дополнительных ограничений на величины и скорости отклонения
органов продольного управления в области III режимов полета не тре-
буется. В этой области возможно энергичное пилотирование при полном
отклонении органов продольного управления на себя.
Рассмотренная градация эксплуатационной области режимов по-
лета получена для типовых ограничений положительных значений до-
пустимых углов атаки и перегрузок самолета.
Ограничения допустимых отрицательных перегрузок и углов ата-
ки маневренных самолетов назначаются в основном из условий надеж-
ной работы силовой установки в зависимости от числа М полета.
Характеристики продольной управляемости самолета при предель-
ных отклонениях ручки управления от себя существенно зависят от
характера изменения по числам М и высотам балансировочных зависи-
мостей 6 и хр в горизонтальном полете, Поэтому типовую градацию
режимов полета для отрицательных значений перегрузок и углов ата-
ки привести затруднительно.
Таким образом, оценка величины заброса по перегрузке наиболь-
ший практический интерес представляет во второй области режимов
полета, характерной большими значениями приборной скорости и
скоростного напора.
Следует заметить, что выполнение установившегося горизонталь-
ного полета самолета возможно не во всей области из-за скачкообраз-
ного изменения тяги силовой установки при изменении режима рабо-
ты двигателя от максимального до форсажного. В отличие от отме-
ченной в предыдущих разделах области полетов на высотах, превы-
шающих статический потолок самолета, где возможен горизонтальный
полет только с торможением из-за недостатка тяги силовой установки,
в рассматриваемой области режимов полета при одной и той же высоте
и скорости полета возможен полет как с торможением, так и с раз-
гоном в зависимости от режима работы двигателей на ’’максимале”
или на ’’форсаже”.
Однако учитывая разницу в энерговооруженности самолета при
максимальных режимах работы силовой установки и режимах мини-
мального форсажа (Дих не более 0,2), нетрудно оценить время изме-
нения, например, числа М на величину 0,1. Это время, считая скорость
звука а ~ 350 м/с, ускорение ~ 2 м/с, составляет примерно 17 с, что
значительно превышает характерное время короткопериодического
движения самолета на режимах полета в рассматриваемой области.
Воспользовавшись полученными выше приближенными соотно-
63
шениями для изменения высоты полета и угла наклона траектории в
переходном процессе, можно оценить количественные величины Н
и 0 рдя конкретных значений скорости полета из рассматриваемой
области.
Полагая V = 300 м/с, n^max = 8,0, ГТ0 = 1,0 с, нетрудно оценить
0Гзад ~ 10...120, что свидетельствует о корректности использования
уравнений короткопериодического движения для оценки переходных
процессов при энергичном маневрировании,
При точном пилотировании на малых высотах полета оценка лет-
чиком динамических свойств самолета в значительной мере базирует-
ся на характеристиках переходного процесса при импульсном управ-
лении.
Для оценки характеристик переходного процесса в этом случае в
качестве управляющего импульса удобно принять полуволну сину-
соиды. Таким образом, следует оценить реакцию самолета на отклс>
нение ^органа управления по синусоидальному закону: 6 = 6 0 sin со t
при со t <7г, 5=0 при со t >п.
Полагая для простоты Р® = 0, для значений безразмерного време-
ни t < я/co можно записать
дПу (t) = . ПЦС* - . [ е“ Sin(\/1 - f27 +</>) +
Vd-w2)2 +4f2w2 71-f2
+ sin(a>? - </>i)], (2.14)
где уст — установившееся значение перегрузки при отклонении орга-
на управления на величину 6 0,
tg^i =-----, .
l-w2
Для определения первого максимума в зависимости Диу (?) необ-
ходимо решить уравнение = 0.
Это трансцендентное уравнение приводится к виду
е“ ^sin(\ZT- f27 + 0) = \fl - f2 cos(co7- <pi),
W ! _ VTTT? (2.15)
tg0 = -----Z ----------
1 + CO2 S
Разрешив уравнение (2.15) относительно t и подставив полученное
решение в (2.14), можно определить искомую величину заброса при
различных значениях J и w. Такие зависимости приведены на рис. 2.6.
Из графиков, приведенных на рисунке, следует что при f < 0,6
существует некоторая ’’резонансная” область частот в безразмерном
64
Рис. 2.6. Характеристики забросов в переходном процессе при ’’импульсном”
отклонении органа управления по синусоидальному закону:
а - ддя значений параметра <0,8; б - для значений параметра > 0,8
65
времени, в которой забросы достаточно велики» В этой области час-
тот самолет обладает повышенной чувствительностью по перегрузке
к импульсному отклонению органов управления,
Как показывает многолетний опыт эксплуатации маневренных
самолетов, ’’рабочий диапазон” частот летчика находится в пределах
f = 0,8...1,5 Гц. Поэтому при проектировании маневренных самолетов
не следует допускать совпадения рабочего диапазона частот летчика
с резонансной областью при импульсном управлении.
Таким образом, управляемое короткопериодическое продольное
движение самолета определяется параметрами f и То, характеризующи-
ми собственное движение самолета, относительными герметрическими
параметрами, характеризующими силовую и моментную эффективность
органов продольного управления, и безразмерными параметрами, харак-
теризующими закон управления. Указанные параметры могут служить
критериями динамического подобия управляемого продольного дви-
жения, например при сравнении самолетов различных компоновок,
различных режимов полета и т. п.
Динамические характеристики переходных процессов в реальном
времени зависят не только от режима полета и аэродинамической схемы,
но и от размерности самолета.
Величину квадрата собственной частоты колебаний самолета мож-
но выразить через безразмерные параметры в виде
Wo2 = (хР- хы - ), (2.16)
'•zOr.II д
где аг,п — угол атаки самолета в горизонтальном полете; хр- хм —
расстояние между центром масс самолета и положением аэродинами-
ческого фокуса; д = р$Ьд — относительная плотность самолета.
Из приведенного выражения следует, что с ростом размерности
самолета частота собственных колебаний падает. С ростом скорости на
постоянной высоте полета угол атаки горизонтального полета умень-
шается и частота растет. На сверхзвуковых Скоростях полета фокус
самолета смещается назад и частота увеличивается. С ростом высоты
полета (или массы самолета) при фиксированном числе М угол атаки
горизонтального полета растет и собственная частота уменьшается.
Поэтому собственная частота достигает максимальных значений при
сочетании предельных скоростных напоров со сверхзвуковыми ско-
ростями полета.
На дозвуковых скоростях полета аэродинамический фокус рас-
положен относительно близко к центру масс самолета, и демпфиру-
ющий член может внести существенный вклад в величину
частоты короткопериодических колебаний. Так как величина 1/д про-
порциональна плотности ря> то очевидно, что с ростом высоты вклад
демпфирующего чЬена падает.
66
Влияние демпфирующего члена на частоту колебаний обратно про-
порционально удельной нагрузке на крыло G/S, т, е. увеличение удель-
ной нагрузки на крыло уменьшает влияние демпфирующего члена.
При переходе к сверхзвуковым скоростям полета фокус само-
лета смещается назад, и влиянием демпфирующего члена можно
пренебречь.
Характеристики затухания переходного процесса определяются
величиной коэффициента относительного демпфирования f, который
зависит от аэродинамических коэффициентов: dy, т^2, Безразмер-
ные коэффициенты моментов определяются демпфирующими свойства-
ми самолета при его вращении относительно центра масс в неустановив-
шемся движении. Безразмерный коэффициент производной подъем-
ной силы по углу атаки (при фиксированном положении органов про-
дольного управления) демпфирует вертикальные колебания центра
масс самолета.
Коэффициент Су вносит существенный вклад в суммарное демпфи-
рование продольных колебаний, поэтому для самолетов с крыльями
большой стреловидности по передней кромке и малыми несущими
свойствами требуется применять искусственные средства демпфирования
продольных колебаний самолета даже на малых высотах полета. По
этой причине для самолетов с крыльями изменяемой в полете стрело-
видности характерно слабое затухание продольных колебаний при по-
летах с максимальными углами стреловидности крыла.
Так как величина демпфирующих сил и моментов пропорциональна
произведению РцУ, то при постоянной скорости полета колебательность
переходного процесса увеличивается с ростом высоты полета, и на
больших высотах полет на самолете с выключенными демпферами ко-
лебаний становится неприятен для летчика.
В последнее время за рубежом получили распространение аэродина-
мические компоновки маневренных самолетов с переменной по разма-
ху стреловидностью крыла. В корневой части крыла применяются боль-
шие стреловидности (более 70°) передней кромки, которые иногда
называют наплывами. Такая аэродинамическая компоновка крыла
имеет очевидные конструктивные преимущества, так как позволяет
обеспечить необходимые строительные высоты конструкции крыла
при малой относительной толщине корневой части и существенно по-
высить полезные объемы крыла. Базовое крыло при этом имеет уме-
ренный угол стреловидности по передней кромке - порядка х 40°.
Таким образом, аэродинамическим компоновкам свойственны особен-
ности обтекания, присущие крыльям малого удлинения на дозвуковых
скоростях полета. Эти особенности проявляются в нелинейных зави-
симостях подъемной силы и продольного момента от угла атаки на-
чиная с относительно небольших углов атаки.
67
Передняя кромка большой стреловидности образует мощную вих-
ревую систему, расположенную над верхней поверхностью крыла уже
на умеренных углах атаки . Этот эффект приводит к тому, что разре-
жение на верхней поверхности крыла, вызванное вихревым жгутом,
распределяется равномерно по хорде и становится аналогичным сверх-
звуковому распределению давлений. Фокус при этом сдвигается назад,
зависимость т2 = /(а) становится нелинейной, и характеристики про-
дольного короткопериодического движения самолетов таких компо-
новок определяются рассматриваемым диапазоном углов атаки. Можно
выделить три основных диапазона углов атаки на дозвуковых скоростях
полета.
Диапазон околонулевых и отрицательных углов атаки характери-
зуется наиболее передним положением аэродинамического фокуса са-
молета.
Диапазон умеренных углов атаки характеризуется наиболее зад-
ним расположением фокуса,
Диапазон углов атаки примерно более 15° характеризуется нелиней-
ной зависимостью mz — f (а).
Динамические характеристики управляемого короткопериодичес-
кого движения могут в значительной мере повлиять на маневренные
характеристики самолета. Для анализа изменения маневренных характе-
ристик самолета следует оценить влияние переходного процесса в ко-
роткопериодическом движении на траекторные параметры полета
самолета.
2.4. ВЛИЯНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
КОРОТКОПЕРИОДИЧЕСКОГО ДВИЖЕНИЯ САМОЛЕТА
НА ИЗМЕНЕНИЕ ТРАЕКТОРНЫХ ПАРАМЕТРОВ ПОЛЕТА
В последние годы широкое распространение получила концепция
сверхманевренности, т. е. самолета с максимально допустимыми манев-
ренными возможностями.
Создание самолета такого типа неизбежно связано с решением ши-
рокого класса экстремальных задач, причем одно из центральных мест
занимает задача оптимального по быстродействию управления вектором
скорости самолета. Эта задача, как правило, решалась в упрощенной
постановке [22].
Обычно при рассмотрении задач, связанных с траекторным движе-
нием самолета и определением его маневренных характеристик, исполь-
зуется упрощенная система уравнений: уравнение моментов не учиты-
вается, и движение самолета оценивается движением его центра масс
как материальной точки. Считается, что самолет сбалансирован по мо-
ментам в каждый момент времени, а величины углов атаки и перегруз-
68
ки могут изменяться скачкообразно. Такой подход позволяет опреде-
лять установившиеся (или близкие к установившимся) траектории
полета, не рассматривая начальную фазу маневра. В этом случае при
переходе самолета с одного установившегося значения перегрузки на
другое (например, из прямолинейного горизонтального полета в вер-
тикальный маневр) кривизна траектории и величина перегрузки в
идеализированном случае изменяются скачком: траектория из прямо-
линейной переходит в окружность.
В реальном маневре перегрузка изменяется плавно. За время на-
растания перегрузки в переходном процессе плавно возрастает кривиз-
на траектории, и самолет пролетает некоторое дополнительное рассто-
яние. Поэтому недооценка роли переходного процесса в ряде случаев
может привести к серьезным ошибкам при расчете маневренных ха-
рактеристик самолета.
Для того чтобы построить реальную траекторию самолета на на-
чальной фазе маневра, следует определить изменение угла наклона
траектории в переходном процессе короткопериодического движе-
ния самолета. Качественное сравнение идеализированной и реальной
траектории приведено на рис. 2.7.
Сравнивая реальную траекторию центра масс самолета с идеали-
зированной, можно определить, в каких случаях необходимо учиты-
вать влияние переходного процесса в короткопериодическом движе-
нии самолета на его траекторию. Для сравнительных оценок удобно
ввести следующие обозначения: Ro — радиус идеализированного ма-
невра; RM — радиус-вектор маневра, соединяющий точки начала и кон-
ца маневра: LM — дистанции маневра, определяемая как проекция
радиус-вектора RM маневра на направление скорости в точке начала
маневра (см. рис. 2.7).
Из рисунка видно, что величина дистанции маневра LM зависит
от угла поворота вектора скорости за время маневра и достигает сво-
его максимального значения при
повороте вектора скорости на
90°. Поэтому в качестве ха-
рактерного типового маневра
следует рассмотреть маневр с
поворотом вектора скорости на
90°.
Очевидно, что чем больше
величина нормальной перегруз-
Рис. 2.7. Идеализированная и реаль-
ная типовые траектории при верти-
кальном маневре самолета
69
ки, используемой при маневре, тем меньше величина дистанции маневра.
Таким образом, величина min {maxZM} определяет минимальные
размеры пространства при выполнении вертикального маневра и яв-
ляется одним из основных критериев, определяющих маневренные
характеристики самолета.
Для идеализированного маневра с постоянной перегрузкой и ско-
ростью уравнение траектории центра масс самолета представляет собой
окружность радиуса RQ, который зависит от величины перегрузки
и скорости полета. Очевидно, что в принятых обозначениях для идеа-
лизированного маневра
у2 Г
Ro = = ^°’ ' । = •
уст
Для решения поставленной задачи следует выписать уравнения дви-
жения самолета в вертикальной плоскости в безразмерном времени
и удобной для дальнейших расчетов форме, используя результаты,
полученные в разд. 2.3.
д0 = ^1ди?,уст[7-А _2f].
В земной системе координат Н = Yg ; L = Xg и характеристики
плоского вертикального маневра в каждый момент времени опреде-
ляются выражениями:
7 _
ДЯ(7) = VT0 J Mdt;
0
L(t) = VTot.
Если обозначить Гзад - время выхода на заданную перегрузку,
то при 7>7зад имеют место приближенные равенства: Д0 = Дпууст
(t _ 2f) в случае мгновенного отклонения рулей и Д0 = ДиууСт
(t - 2f —в случае ограниченной скорости перекладки органа уп-
равления. _
7
При этих условиях легко вычислить J* ^Bdt, откуда
0
Ям Rq
% О [ 1 + уст (-g- ^0 + ) J.
(2.17)
70
Как следует из (2.17), величина дистанции реального маневра боль-
ше дистанции идеализированного маневра, характеризуемого величи-
ной Rq. При определении предельных маневренных возможностей са-
молета (min {maxZM} ) естественно рассматривать траектории с мак-
симально возможными значениями нормальных перегрузок и^тах,
При этом становятся недопустимыми забросы более 10...15% устано-
вившейся величины nymSLX.
Отсюда следуют условия на ограничение величины максимальной
скорости перекладки органа управления при энергичном пилотировании
самолета или на время tQ, которое определяется из условий 70 =
= ^пУпугпахТо/8щах*
3 -
Величина— tQ + 2f, как было показано выше, является функцией
8
величины относительного демпфирования f, и при изменении f от 0 до
1/2 изменяется от 2,4 до 1,0. _
Следовательно, при постоянном значении t0 минимальное влияние
переходного процесса на величину дистанции маневра может быть реа-
лизовано при значении коэффициента относительного демпфирования
f> 0,5, так как при этом величина tQ может быть сколь угодно малой
(отсутствует ограничение на величину скорости перекладки органа
управления). При увеличении коэффициента относительного демп-
фирования f более 0,51 ограничения на скорость отклонения органов
управления отсутствуют, однако величина дистанции маневра возрас-
тает с ростом величины f, так как переходные процессы становятся
затянутыми по времени.
Приближенную оценку изменения дистанции маневра с учетом
переходного процесса можно получить, введя понятие эквивалентной
перегрузки и^экв. Обозначив время выхода самолета на установив-
шуюся перегрузку и^тах через Т, можно записать
LM=RQ+AR = VT- Rq sin0 (7).
Величину эквивалентной перегрузки и^экв удобно определить из
соотношения
L - V2
5"УЭКВ
Тогда зависимость между реальным значением максимальной перег-
рузки и^тах и эквивалентной перегрузкой и^экв можно определить
из простого выражения:
V
ПУЭКЯ = Путлх ——_^П0(Г)) • <2-18)
71
Рис. 2.8. Зависимость и-^экв ~ f(nymax) ПРИ
скорости полета V = 250 м/с
Из рис. 2.8 видно, что величина и^экв
стремится к некоторому пределу при
неограниченном возрастании максималь-
ной перегрузки:
lim и^экв--——(пуэкв)шах •
nymax->°° Si
(2.19)
Считая малой величину угла наклона траектории О (Г) при дости-
жении самолетом значения максимальной перегрузки Иутах, можно
упростить выражение (2.18), положив sin0 (Т) » 0,
_ пу m ах
Луэкв
1 + -j^Hjmax
Безразмерный коэффициент Tg/V = Т представляет собой безраз-
мерное время выхода самолета на максимальную перегрузку и^тах
(отнесенное к масштабной единице времени V/g). При малых значениях
Т (2.19) можно записать в виде
Иуэкв wymax(l ~ ^\утах).
Очевидно, что физический смысл величины эквивалентной пере-
грузки состоит в замене реальной траектории самолета с максимальной
перегрузкой иутах некоторой условной траекторией, которая представ-
V2
ляет собой окружность радиуса R =------. При этом начальные точки
#луэкв
маневра совпадают.
Из полученных приближенных соотношений следует, что харак-
теристики переходного процесса короткопериодического движения
могут оказывать существенное влияние на траекторию центра масс
самолета. Так, например, при скорости полета V = 250 м/с, максималь-
ной перегрузке Иушах = 8 и времени достижения самолетом величины
wymax Т= 1,5 с эквивалентная перегрузка равна и^экв = 5,4.
Таким образом, учет влияния переходного процесса по перегруз-
ке на траекторию полета приводит к запаздыванию в выполнении ма-
невра по сравнению с идеализированным случаем. При этом реальную
траекторию можно аппроксимировать окружностью радиуса Яо =
= V2 /gnymSLX, сдвинутой относительно начала маневра (в координатах
Н, Xg) на величину Xg = ДЯ, которая зависит от темпа нарастания и
абсолютной величины перегрузки, т. е. реальная траектория при такой
аппроксимации заменяется прямолинейным участком ДЯ, который
72
представляет собой как бы ’’холостой” пролет, и окружностью ради-
уса Rq.
Очевидно, что чем меньше время достижения самолетом максималь-
ной перегрузки, тем меньше величина ’’холостого” пролета и тем мень-
ше пространство, потребное для выполнения маневра.
При обычном пилотировании, когда орган управления отклоняет-
ся с максимальной скоростью на потребную величину, соответствующую
максимальному значению перегрузки, существуют ограничения на ми-
нимальное время перекладки органа управления, вызванные ограничен-
ностью допустимого заброса по перегрузке (условно не более 0,15), что
снижает маневренные возможности самолета. Для расширения манев-
ренных возможностей следует минимизировать время достижения
самолетом величины максимально допустимой перегрузки пут2Л, не
превышая при этом допустимого заброса. Это можно сделать, реализо-
вав оптимальный по быстродействию закон отклонения органов управле-
ния. Краткий анализ таких законов управления проводится в следующем
разделе.
Помимо параметров траектории, характеризующих маневр разво-
рота вектора скорости на 90е, для ряда режимов полета бывает необхо-
димо оценить влияние переходного процесса на изменение траектории
самолета в начальной фазе маневра, например, оценить так называемую
”просадку”самолета при отклонении органов продольного управления.
Как указывалось ранее, сила, действующая на орган продольного
управления, может изменить переходный процесс самолета по пере-
грузке. Для оценки влияния величины Y& на изменение траекторных па-
раметров следует записать выражение для переходного процесса по
углу наклона траектории с учетом Y$:
О = gT0/Vnyус&- 2f + В + ety>/l - f2sin(Vl - f2r + ад -
— Be ?- f2'sin(x/l - f2 ? + <p) + Ae tyy/1 - f2 sin(Vl - f2?)], (2.20)
где
A = To !(CyM^ - cyM?) =cJnl(xF2 (xM- xFi)I(xf2 - xFi)
В = ( - + M?)l(TorfM^ - c$M?) «= f A.
Очевидно, что при 7=0
0 = 0; 6=gTonyyclA/V; 'e = gTonyycJ (В - 2$A)IV • (2.21)
Выражение (2.20) описывает затухающие периодические колеба-
ния угла в относительно наклонной асимптоты. Уравнение асимптоты
в координатах 7,0 = OV/g TQ пУуСТ9 как следует из (2.21), запишется
в виде
0oo=7+B-2f.
73
о
Рис. 2.9. Типовой переходный процесс по
углу наклона траектории
/у Таким образом, на плоскости t\ О
Л/ асимптота представляет собой прямую с
/ углом наклона 45°, сдвинутую по оси t
/у на величину ta = 2f - В (рис. 2.9).
ta=2C-fiу/ Из рисунка следует, что при от-
----------Т клонении органа управления для соз-
дания нормальной перегрузки пу на
начальном этапе переходного процесса центр масс самолета начинает
перемещаться в сторону действия силы на органе управления, т. е. на-
чальное приращение перегрузки в центре масс совпадает с направлением
действия силы на органе управления.
Для самолетов нормальной и бесхвостой схемы при создании поло-
жительной перегрузки из режима прямолинейного горизонтального
полета пу сила, действующая на орган продольного управления, направ-
лена вниз. Поэтому при создании положительной перегрузки самолет на
начальном этапе маневра теряет высоту, а исходная величина перегрузки
в центре масс начинает уменьшаться. Явление потери высоты при взя-
тии ручки на себя на таких самолетах получило у летчиков название
’’просадки” самолета, а период времени, в течение которого высота
остается меньше исходной, - временем обратной реакции самолета.
Следует отметить, что при этом летчик физически не ощущает об-
ратного действия перегрузки в центре масс самолета, так как кабина
расположена впереди мгновенного центра ускорения при движении
самолета, вызванного отклонением органов продольного управления.
Приращение перегрузки, ощущаемое летчиком в кабине, как ука-
зывалось выше, можно оценить из соотношения
= ^уц.м +-~-
Так как при резких отклонениях органов продольного управления
м£д§ . У5Д5
можно считать, что « —-— , а величина , то при-
Jz * G
ращение перегрузки в кабине летчика
у5Д5 (L L G
—т;— \ьльг.о 7—
1),
G
г-°75
так как безразмерная величина LnL
^л^г.о
rZ
больше единицы
для современных самолетов, то знак приращения перегрузки в каби-
74
не определяется знаком произведения У$Д5. Отсюда следует, что у са-
молетов нормальной и бесхвостой аэродинамической схемы приращение
перегрузки в кабдае на начальном этапе маневра положительно при
взятии ручки на себя и отрицательно при обратном движении, что сов-
падает с привычными ощущениями летчика.
Поэтому при совершении резкого маневра кратковременное изме-
нение высоты, не соответствующее нормальной перегрузке, ощущае-
мой летчиком в кабине, воспринимется им как ’’обратная реакция”
и ’’просадка”.
Для оценки влияния ’’просадки” самолета на траекторные пара-
метры начальной стадии маневра следует ввести еще одну величину -
безразмерное время £обр, в течение которого угол наклона траекто-
рии остается отрицательным. Это время, очевидно, является корнем
уравнения в (t) = 0, и его несложно оценить. _
Расчеты показывают, что время обратной реакции Гобр, приближенно
равное Гобр % - 6Л, не играет практически никакой роли в харак-
теристиках маневра, в частности в величине дистанции маневра. Дей-
ствительно^чем больше величина Л, т. е. больше отрицательный наклон
кривой 0 (t) в точке t = 0, тем больше вторая производная (положи-
тельная) 0 > 0.
Таким образом , влияние величины на траекторию маневра
сказывается лишь в сдвиге асимптоты 0о© (t) на величину -В ~
-£Л. Следовательно, этим влиянием можно пренебречь, если — В <
< 2f или \А | <2. Если же величиной В по сравнению с 2f или величи-
ной А по сравнению с 2,0 нельзя пренебречь, то, пользуясь изложенным
выше методом для определения LM, можно написать для дистанции
маневра
= Дуст + (%- В) « Дуст + КТ0 f (2 - А).
Нетрудно видеть, что для ступенчатого отклонения органов про-
дольного управления увеличение идеализированной дистанции манев-
ра вследствие влияния переходного процесса составляет величину Д£м,
равную Д£м = 2fT0K при У® = 0 и (2 - А)£TQV при У5 Ф 0.
Выразив 2fT0K и параметр Л через аэродинамические коэффициен-
ты и конструктивные параметры самолета, можно получить
2W=bAk-----------------------
Это выражение не зависит в явном виде от скорости полета и явля-
ется функцией геометрических и массовых параметров самолета.
75
Параметр А определяется выражением
Очевидно, что наиболее неблагоприятное влияние на дистанцию
маневра оказывают органы управления, фокус которых расположен
на небольшом расстоянии сзади фокуса самолета.
Для оценки изменения высоты в начальной фазе маневра следует
разложить в ряд решение уравнения для приращения высоты полета
в окрестности малых значений ДЯ. Произведя необходимые выклад-
ки и отбросив члены высшего порядка малости, можно получить приб-
лиженные соотношения, необходимые для построения траектории центра
масс самолета на начальной стадии маневра.
Нежелательное для летчика изменение высоты ДЯ, вызванное от-
клонением органов продольного управления на самолетах нормаль-
ной и бесхвостой схемы, можно оценить по приближенным формулам
ДЯ«-1,5ЛЭДД^ ;
tH «V- 12Л,
где — время действия просадки.
Зависимость tH от А приведена на рис. 2.10. Величина ’’просадки”
ДЯ, как правило, невелика по сравнению с радиусом маневра, однако
при необходимости точного пилотирования может оказать существенное
влияние на безопасность выполнения маневра (например, при выводе
самолета из пикирования на малой высоте, при посадке, при групповом
пилотировании и т. п.).
Реакция летчика на изменение высоты полета проявляется обычно
визуально при наличии ориентиров или вблизи земли, так как показа-
ния приборов в кабине, фиксирующих барометрическую высоту полета,
практически не изменяются на начальной стадии маневра.
Таким образом, влияние короткопериодического движения са-
молета на его траекторию при маневре эквивалентно некоторому запаз-
дыванию выполнения идеализированного маневра и увеличению необ-
ходимого для маневра пространства. Для
некоторых аэродинамических компоно-
вок разница между идеализированным и
реальным маневром может оказаться зна-
Рис. 2.10. Зависимость времени "просадки”
самолета от параметра относительной эффек-
тивности органа управления
76
чительной. Поэтому влияние характеристик короткопериодического
движения самолета на траекторные параметры полета следует учитывать
при сравнении предельных маневренных возможностей различных
аэродинамических компоновок.
2Л. НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ МАНЕВРЫ САМОЛЕТА
Проектирование современного маневренного самолета немыслимо без ре-
шения целого ряда задач динамики полета, которые можно классифицировать
как вариационные. При этом ищется наилучшее, оптимальное решение, удовлет-
воряющее заранее поставленным условиям. Такие задачи, как правило, легко
формулируются в словесной форме, например определить максимально возмож-
ную дальность или продолжительность полета, минимальное время набора заданной
высоты, потолок самолета при выполнении определенных условий, накладывае-
мых на аэродинамические, массовые характеристики самолета, режимы полета
и т. п. Однако очевидно, что словесная формулировка задачи не дает возможности
даже наметить пути ее решения. Для решения таких задач необходимо создать
математическую модель и выработать строгие критерии, позволяющие сформу-
лировать в математической форме требования к неизвестным параметрам, опреде-
ляющим решение задачи.
С математической точки зрения трудность решения экстремальных задач,
особенно нахождения оптимальных законов управления, состоит в нахождении
неизвестных заранее функций, которые, вообще говоря, не обязаны удовлетво-
рять классическим требованиям непрерывности и дифференцируемости. Это естест-
венно и понятно, так как реальные возможности всегда связаны с наличием раз-
личного рода ограничений, физически или искусственно налагаемых на неизвестные
параметры и функции.
Наличие ограниченных и разрывных функций делает неприменимыми методы
решения экстремальных задач, хорошо разработанные в классическом вариацион-
ном исчислении.
Потребовалось создание нового математического аппарата, которое началось
в середине 50-х годов в основном советской математической школой,и, быстро
развиваясь, новое направление выделилось в самостоятельную научную дисцип-
лину - теорию оптимального управления.
Применение общей теории оптимального управления к задачам динамики
полета позволило сформулировать и получить целый ряд практически важных
результатов и по-новому подойти к решению многих проблем, возникающих на
этапе проектирования летательных аппаратов. Одной из таких проблем в динамике
полета является определение оптимальных траекторий, частным случаем которой
является задача о развороте вектора скорости самолета на заданный угол за мини-
мальное время. Практический интерес к решению подобной задачи очевиден.
Минимальное время разворота характеризует предельные маневренные возмож-
ности самолета. Задачи отыскания законов управления, обеспечивающих перевод
динамической системы из одного фазового состояния в другое за минимальное
время, получили название задач на быстродействие.
В динамике полета большое количество работ, посвященное решению задач
на быстродействие [22], в основном касается траекторной динамики полета. В
этих задачах такие параметры короткопериодического движения самолета, как
перегрузка или угол атаки, считаются безынерционными управляющими пара-
метрами, т. е. могут изменяться скачкообразно. Естественно, что короткоперио-
дическое движение самолета при этом не рассматривается.
77
В разд. 2.4 было показано, что в ряде случаев при определении траектор-
ных параметров движения необходимо учитывать влияние переходных процессов
короткопериодического движения самолета. Однако законы отклонения орга-
нов управления, рассматриваемые при этом, были явно неопгимальными с точки
зрения быстродействия перевода самолета из одного состояния в другое.
Представляет практический интерес рассмотреть оптимальное по быстродей-
ствию управление самолетом в короткопериодическом движении и оценить его
влияние на параметры траектории. Полученные таким образом результаты дадут
возможность определить предельные маневренные возможности самолета, обес-
печиваемые его системой управления и соответствующими аэродинамическими и
прочностными характеристиками конструкции планера. Для решения такой задачи
следует задать начальные и конечные условия маневра. За начальный (исходный)
режим полета целесообразно принять прямолинейный установившийся горизон-
тальный полет самолета при заданных скорости и высоте. Конечные или граничные
условия зависят от постановки задачи.
Можно рассмотреть, например, задачу о быстрейшем развороте вектора ско-
рости самолета в вертикальной плоскости на заданный угол, потребовав при этом,
чтобы в конце маневра угловая скорость поворота вектора скорости равнялась
нулю. Ясно, что при этом величина заданного угла поворота существенным образом
влияет на искомый закон управления.
При достаточно большой заданной величине угла разворота необходимо ис-
пользовать предельные маневренные возможности самолета, т. е. совершить ввод
самолета в маневр с предельной для данного режима полета нормальной пере-
грузкой.
Если заданный угол разворота вектора скорости мал, то маневр с пр сдельной
нормальной перегрузкой может и не потребоваться: самолет ”не. успеет”на нее
выйти. Если заданный угол разворота велик, то разворот будет сопровождать-
ся изменением величины скорости полета. Очевидно, что существует класс манев-
ров самолета с выходом на предельные значения нормальной перегрузки, при кото-
рых величину скорости полета можно считать неизменной.
Учитывая высокую энерговооруженность современных маневренных само-
летов, можно считать вертикальный маневр самолета с постоянной скоростью по-
лета одним из типовых маневров целевого назначения самолета. В дальнейшем
будет рассматриваться начальная фаза маневра: быстрейший ввод самолета в
маневр с предельно допустимой для исходного режима полета величиной нормаль-
ной перегрузки Пу или угла атаки а.
Таким образом, задача сводится к отысканию законов отклонения органов
продольного управления, обеспечивающих изменение угла атаки самолета на
заданную величину за минимальное время. При этом углы отклонения органов
управления органичены конструктивными возможностями системы управления.
Ясно также, что и максимальная скорость отклонения органов управления
ограничена мощностью силовых приводов системы управления и зависит от уров-
ня действующих на органы управления аэродинамических шарнирных моментов.
Таким образом, имеется три вида ограничений: на величину и скорость угла от-
клонения органа управления и на величину угла атаки или нормальной перегрузки.
Чтобы упростить решение задачи, характеристики продольного коротко перио-
дического движения самолета рассматриваются для случая У6 * 0, поэтому в
дальнейшем для краткости будет рассматриваться угол атаки, однако все рассуж-
дения остаются справедливыми в отношении величины нормальной перегрузки,
так как они однозначно связаны между собой соотношением Any * пу Да.
Первые два ограничения являются физическими ограничениями и могут
быть математически заданы в виде системы неравенств. Ограничение угла атаки
или перегрузки - искусственное ограничение. Оно не вытекает непосредственно
из уравнений, так как при достаточной эффективности органов продольного уп-
78
равления уравнения движения допускают полет самолета на углах атаки, превы-
шающих заданный. Отсюда следует, что достижение предельного значения задан-
ного угла атаки в процессе движения может быть реализовано только при условии
равенства нулю угловой скорости изменения угла атаки в этот момент времени
dot
— / _
dt а — азад
0. В противном случае ограничение будет нарушено.
Общие методы решения такого типа задач (определение законов быстродей-
ствия) основаны на применении принципа максимума Понтрягина [1], который
дает необходимые условия оптимальности. При решении прикладных задач на-
иболее важным с практической точки зрения являются грамотное и корректное
использование основных теорем и положений, рассматриваемых в общей теории,
В ряде случаев результаты общей теории можно сформулировать в виде конкрет-
ных практических рекомендаций, позволяющих правильно поставить и решить
экстремальную задачу.
При наличии ограничения в виде неравенств, определяемых из физического
смысла задачи, задача на быстродействие сводится к нахождению закона управ-
ления и времени Т при заданных начальных и конечных значениях параметров
движения системы с учетом дополнительных условий выполнения заданных огра-
ничений.
Условия принципа максимума, необходимые для нахождения оптимального
по быстродействию закона управления, в основном сводятся к следующему:
вводится безынерционный параметр управления из области допустимых
управлений, который может изменяться скачкообразно (рис. 2.11) ;
Рис. 2.11. Область допустимых управлений и типовые оптимальные зависимости
ИО:
а - изменение параметра управления и (f); б - типовая зависимость 6_(0 в оп-
тимальном законе управления с фиксированными граничными условиями 6 (7) = 0;
в — типовая зависимость 6(0 при свободных условиях на конце оптимальной тра-
ектории
79
уравнения движения рассматриваемой системы записываются в канонической
форме:
х, = Л «);
xt =/а(Х|,и);
хп xfn(Xi,u);
выписываются граничные условия задачи:
х/(0) = x„i; Х{(Т)=$ ;
х/(0) = х<>Г, Xi(T) = £[;
вводятся сопряженные переменные, определяемые системой дифференци-
альных уравнений при произвольных начальных условиях, исходя из уравнений
движения заданной системы:
_ Э/, (xj, и)
dt Эх,
dtn _ Э/Л(х;,и)
dt дхп ’
вводится функция Понтрягина Я, составляемая по закону
н = ф! (ОД (х/, И) +... + V/ц (ОЛ (х/, и) + и) ,
и произвольная неотрицательная константа а0 > 0.
Принцип максимума Понтрягина для рассматриваемого случая формулирует-
ся в следующем виде: при оптимальном по быстродействию законе управления
сумма Н + а0 равна нулю.
Принцип максимума дает необходимые и достаточные условия оптимальнос-
ти управления для динамических систем, описываемых линейными дифференци-
альными уравнениями. В этом случае, если решение существует, то оно единствен-
но и обладает Свойствами оптимальности. Для нелинейных систем решение может
быть неединственным. Поэтому если в результате решения найдено несколько
законов управления, то оптимальный выявляется непосредственной проверкой
при сравнении переходных процессов, определенных по этим законам управления.
Может показаться на первый взгляд, что применение принципа максимума
приводит к усложнению задачи, так как существенно увеличивается порядок
системы дифференциальных уравнений, причем начальные условия для сопряжен-
ных переменных заранее неизвестны. Ценность принципа максимума для приклад-
ных задач состоит в том, что выявлен строгий алгоритм, позволяющий определить
необходимые признаки оптимального управления.
В ряде простых случаев, имеющих практическое приложение, можно, испол^
зуя принцип максимума, определить качественную структуру оптимального уп-
равления и не решать систему уравнений для сопряженных переменных. Зная
закон оптимального управления, можно по уравнениями движения заданной сис-
темы определить искомые переходные процессы,
В качестве иллюстрации такого подхода удобно рассмотреть оптимальное по
быстродействию управление углом атаки самолета, нейтрального по перегрузке
(ал « 0). Уравнения короткопериодического движения самолета в этом случае
сводятся к виду
а + а = и (Г ),
а Т1 .
где а=---------_ >
«max м«
80
smax’ ° y“-MzWz-M“
Для определения оптимальных законов управления и(Т) следует учитывать
ограничения на величину и скорость перекладки органов управления, вызванные
реальными характеристиками силовых приводов, используемых в системе уп-
равления. Как указывалось выше, характеристики силовых приводов, применя-
емых на современных маневренных самолетах, с достаточной для практических
расчетов точностью могут быть аппроксимированы квадратичной зависимостью
между величиной преодолеваемой нагрузки и скоростью движения штока.
Зная соотношения между располагаемым ходом штока силового привода
и углом отклонения органа управления, можно получить зависимость между
скоростью его отклонения и величиной аэродинамического шарнирного момента.
Это влияние (для простоты) можно оценить на примере самолетов бесхвостой
схемы, на которых в качестве органов продольного управления используются
элевоны. Может оказаться, что мощность силового привода недостаточна для
преодоления аэродинамического шарнирного момента, действующего на элевон
при максимальном угле его отклонения. В этом случае угол отклонения элевона
будет ограничен величиной максимального шарнирного момента, развиваемого
силовым приводом. Полагая, что аэродинамический шарнирный момент элевона
линейно зависит от угла его отклонения и нулевой шарнирный момент отсутству-
ет, можно записать уравнение границы допустимых скоростей перекладки элевонов:
5*тах < б о ± “7“ * (2.22)
°шах
еде знак минус (5 max “* мшшах), если аэродинамический момент препятствует
отклонению элевона и знак плюс, если аэродинамический шарнирный момент
направлен в сторону движения штока силового привода. Типовая зависимость
б/бшах = Лбшах) приведена на рис. 2.11.
Проинтегрировав уравнение (2.22) при нулевых начальных условиях, полу-
чим зависимость при отклонении элевона в направлении, например, против дей-
ствующего аэродинамического шарнирного момента:
---Г2 t
6 (f) = _ + 2 — .
т» т0
Время отклонения элевона на максимальный угол
т0 =26/60.
Наличие ограничений на величину максимальной скорости отклонения орга-
на управления, выраженное системой неравенств, не позволяет применить принцип
максимума Понтрягина в рассмотренном виде к решению задачи оптимального
управления. Для решения такого рода задач требуется воспользоваться матема-
тическим аппаратом общего принципа максимума разработанным Дубовицким и
Милютиным [9].
С этой целью необходимо сформулировать задачу с учетом общепринятых
обозначений и ограничений, выраженных системой неравенств (2.22), введя новую
фазовую переменную 7Г и считая параметром управления величину скорости откло-
нения органа управления: и ~ б"
Тогда задача может быть сформулирована следующим образом:
y = -y-z; (2.23)
z= и.
81
Ограничения удобно записать в виде
1 2
Ф1 (z, и) = - и2------(1 —z) < 0, и >0; (2.24)
2 т2
1 2
Ф2 (z, и) = и2--------(1 + z) < 0, и < 0; (2.25)
2 т2
Gj (z) = z - < О, ОС 6Х < 1; G2(z)=62-z < 0- 1< 62 < 0. (2.26)
Ограничения такого вида называются смешанными фазовыми ограничениями.
Можно показать, что в зависимости от величины | ~lmax возможны четыре раз-
личных типа оптимального управления:
-l<z<l;-l<z<l;-l<z<l;-l<z<l.
Аналогичная картина возникает при изменении граничного условия z(T) на
правом конце траектории. Если потребовать z (Т) = 0, то, очевидно, появляется
вторая точка переключения управления. При этом исчезает тип оптимального уп-
равления -1 < z < 1, так как в этом случае не может быть удовлетворено гра-
ничное условие
х (Т) = - а (а > 0).
Качественный характер оптимальных законов управления трех различных
типов для граничных условий z (7) = 0 приведен на рис. 2.12.
Введение дополнительных фазовых ограничений вида -82 < z < <5Х не вносит
ничего принципиально нового и не меняет качественную структуру оптимального
управления.
Появление фазовых ограничений вида | У| < const изменяет структуру опти-
мальных законов управления и приводит к увеличению точек переключения
управления на единицу. Структуру оптимального управления в этом случае мож-
но определить из следующих соображений. Чтобы не превысить ограничения | У| <
П в момент достижения ограничений Т*, необходимо выполнение условия
Y (7*) ss 0 (так как ограничение | У| СП наложено искусственно и не вытекает
из уравнений движения).
Но из уравнений движения следует, что в этот момент времени выполняется
равенство
_ y(7*) = z(7*)= П
и при Г > Г * у (г) = const; z (t) = const.
Рис. 2.12. Структура оптимального управления:
в-|8(г)|<1; б-6(7)= 1,[Г(7а)|< 1; 6-8(7,)=!
5(7,) = - 1
82
Определив качественную структуру законов оптимального управления, не-
трудно вычислить оптимальные переходные процессы. Для этого нет необходи-
мости интегрировать систему уравнений сопряженных переменных: достаточно
выписать решения уравнений движения в аналитическом виде и потребовать удов-
летворения граничных условий.
В зависимости от типа режимов оптимального управления и вида граничных
условий может быть от двух до шести участков с различными решениями, кото-
рые необходимо ’’сшить” по стыкам. В результате может быть получена система
трансцендентных уравнений в аналитическом виде, решение которой не представ-
ляет трудностей и дает искомые моменты переключений управления.
Возможен иной подход к решению задачи, основанной на численном реше-
нии краевой задачи. Выбирая в качестве первого приближения параметры релей-
ного управления, методом последовательных приближений можно получить реше-
ние задачи с реальным управлением.
Таким образом, законы оптимального по быстродействию управления углом
атаки самолета при наличии нерегулярных смешанных ограничений полностью
определяются безразмерными величинами времени переключения в пространстве
Т
безразмерных параметров 70Ухзад, Т. Из соотношения хзад = / "8 (7)dr следует,
О
что величина определяется разностью площадей оптимального закона управления
Г(0.
Поэтому зависимости Ц,Т = являются однозначными функциями
параметра 70, определяющего характеристику силового привода и максимального
угла отклонения органа управления, в силу чего задача становится автомодельной.
Эти зависимости можно раз и навсегда вычислить и построить в координатах
tjr[, в Л^зад/’Ъ) в виде номограмм (рис. 2.13, 2.14). Таким образом,
установлена единственность оптимального закона управления: если оптимальный
по быстродействию закон управления существует, то решение единственное, и
принцип максимума дает в рассмотренных случаях необходимые и достаточные
условия оптимального управления. _ __
Из рассмотрения зависимостей Т/т0 = /(хзад/т^) в частности, следует, что
полное время оптимального по быстродействию переходного процесса при пово-
роте самолета на одинаковый заданный угол атаки меньше, если не фиксировать
величину б (Л в конце процесса. Физически этот факт легко объясним: не тратится
дополнительное время на возврат органа управления в нейтральное положение.
Отсюда становится ясной и физическая причина отражения оптимальной траекто-
рии, от фазового ограничения | х| < а при выполнении разворота. Это же обстоя-
тельство позволяет построить оптимальный по быстродействию закон перевода
самолета с одного угла атаки на другой при заданном перерегулировании. Очевид-
но, что в этом случае можно получить выигрыши во времени ’’срабатывания”.
Проведенный качественный анализ законов оптимального управления фак-
тически представляет собой синтез оптимального по быстродействию управления
самолетом, так как рассмотрены основные виды начальных условий и фазовых
ограничений, имеющих практический смысл для прикладных задач динамики по-
лета.
Аналогичный анализ можно провести, считая орган управления перекомпен-
сированным по аэродинамическому шарнирному моменту. Очевидно, что струк-
тура оптимальных законов управления не изменится, однако соотношения времен
переключений будут иными.
Поскольку анализ проводился для безразмерного времени и безразмерной
формы уравнений движения самолета, то полученные результаты оптимального
по быстродействию управления имеют достаточно общий характер.
83
Рис. 2.14. Зависимость бремени переключения в оптимальном процессе от парамет-
ров управления
84
Следует отметить, что конкретный вид ограничений для рассмотренной зада-
чи не является принципиальным и может повлиять лишь на количественные резуль-
таты. Общие выводы (непрерывность сопряженных функций, качественная струк-
тура оптимальных режимов управления и т. п.) остаются справедливыми практи-
чески для любых выпуклых кусочногладких ограничений типа Ф/(х^ и) = О,
частным случаем которых являются ограничения, например типа (и - их )(и - на) <
< 01 (*а - 5t)(xa “ 5 j) <0, характерные для ряда электрических силовых при-
водов. Картина также не изменится принципиально, если в уравнения движения
добавить статический член и рассмотреть движение статически устойчивого по
перегрузке (или неустойчивого) самолета. При этом следует провести перенорми-
ровку безразмерных параметров, так как их количество увеличивается на единицу,
и рассмотренные выше безразмерные комбинации становятся неудобными для
анализа.
В заключение следует отметить, что динамические характеристики силовых
приводов, неучтенные в рассмотренной математической модели, могут повлиять
на корректность принятых допущений в случаях, когда времена переключений
соизмеримы по порядку с величинами постоянных времени силовых приводов.
Для современных силовых приводов эти величины достаточно малы., а анализ
оптимальных по быстродействию законов управления на коротких промежут-
ках времени вряд ли имеет практический смысл.
Поэтому полученные результаты представляют практический интерес в ин-
тервалах времени, соизмеримых с собственными частотами продольных корот-
копериодических колебаний самолета. Эти интервалы, как известно [4, 6], имеют
порядок секунд. Полное время перекладки органов продольного управления име-
ет практически тот же порядок.
Таким образом, полученные времена оптимальных по быстродействию пере-
ходных процессов в продольном короткопериодическом движении самолета
могут в ряде случаев определять некоторую минимальную реализуемую величи-
ну дистанции маневра и использоваться в качестве критериев при сравнении пре-
дельных маневренных характеристик самолетов различных схем. Использование
такого рода маневров может представлять практический интерес, например в
случае автоматического приведения самолета к режиму горизонтального полета
при потере летчиком пространственной ориентации, при выводе самолета из пики-
рования и т. п.
В рассмотренных маневрах конечными условиями определялась криволи-
нейная траектория самолета с постоянной величиной нормальной перегрузки.
Аналогичным образом можно рассчитать оптимальный по быстродействию ма-
невр вывода самолета с криволинейной траектории в прямолинейный полет. При-
менив последовательно дважды изложенный выше метод расчета, нетрудно опре-
делить минимальное время ввода самолета, например, в заданную ’’горку” или
минимальное время перевода самолета с одной высоты полета на другую.
Таким образом, оптимальное по быстродействию управление углом атаки
самолета может быть использовано для расчетов достаточно широкого класса
типовых маневров самолета в вертикальной плоскости.
85
ГЛАВА 3. СИСТЕМЫ ПРОДОЛЬНОГО УПРАВЛЕНИЯ
И УПРАВЛЯЕМОСТЬ САМОЛЕТА
3.1. ОБЩИЕ ТРЕБОВАНИЯ К РУЧНОМУ УПРАВЛЕНИЮ
Влияние системы управления на аэродинамическую компоновку
современного маневренного самолета столь велико, что облик само-
лета, его аэродинамическая компоновка в значительной мере опреде-
ляются функциональными возможностями системы управления.
Развитие бортовой вычислительной техники позволило существен-
но повысить надежность и расширить функции автоматических систем
управления, применяемых на современных самолетах. В настоящее
время системы управления используются даже для снижения массы
конструкции и действующих на самолет в полете аэродинамических
нагрузок. Все это приводит к необходимости выбора характеристик
системы управления и степени ее автоматизации на самых ранних
этапах проектирования самолета.
Вместе с тем главным действующим лицом в самолете, несмотря
на высокую степень автоматизации системы управления, по-прежне-
му остается летчик. Поэтому уже на этапах предварительного проек-
тирования самолета перед конструкторами возникает сложная задача -
обеспечение комфортных условий работы летчика, а проблема реали-
зации приемлемых характеристик управляемости в ручном режиме
пилотирования становится одной из самых актуальных задач динами-
ки полета.
Ощущения летчика в полете при пилотировании самолета долгое
время являлись единственным и непреложным критерием оценки при-
годности к эксплуатации самолета и его системы управления. Естествен-
но, что при этом роль элемента субъективизма была весьма значитель-
ной, так как физические и эмоциональные различия индивидуальных
особенностей летчика порождали разнобой в требованиях к прием-
лемым характеристикам загрузок и перемещений рычагов управления,
размерам кабины, расположению приборов в кабине и т. п.
Очевидно, что даже такие физиологические данные, как рост, фи-
зическая сила, размеры корпуса, длина рук и т. п., которые могут су-
щественно различаться, приводят к различным требованиям удобства
и комфорта рабочего места.
В настоящее время в результате опыта эксплуатации маневренных
самолетов всего мира накоплен огромный статистический материал,
на основании которого выработаны основные требования к характе-
ристикам управляемости маневренных самолетов. Примечательно, что по
основным нормируемым параметрам эти требования практически совпа-
дают в нормах летной годности различных стран. По-видимому, сов-
ременный мировой опыт летной эксплуатации маневренных самолетов,
86
накопленный за время существования маневренной авиации, выражен-
ный в часах налета, имеет порядок 1О9...1О1 °.
Если сформулировать кратко, то современные требования к ха-
рактеристикам управляемости самолета содержат рекомендации по
обеспечению приемлемых перемещений рычагов управления и усилий
на них. На первый взгляд может показаться, что проблемы обеспечения
необходимых характеристик системы управления современных манев-
ренных самолетов значительно упростились (по сравнению с самолетами
старых поколений), так как применение необратимого бустерного
управления почти на всех современных маневренных самолетах позво-
ляет обеспечить независимую от режима полета загрузку рычагов уп-
равления. Однако ясно, что многорежимность современного манев-
ренного самолета существенно усложняет требования к обеспечению
необходимых характеристик управляемости самолета в широком
эксплуатационном диапазоне углов атаки, скоростей и высот полета
и требует применения высокой степени автоматизации систем управ-
ления в ручном режиме пилотирования.
Пилотирование маневренного самолета на различных этапах полета
существенно зависит от целевой задачи, поставленной перед летчиком.
Такими задачами могут быть, например, выполнение полета на даль-
ность, исполнение фигур пилотажа, группового полета и т. п. Естествен-
но, что требования к характеристикам управляемости самолета у лет-
чика могут при этом изменяться в зависимости от поставленной перед
ним задачи. Поэтому целесообразно последовательно рассмотреть основ-
ные характеристики управляемости самолета на различных этапах полета
и попытаться выявить при этом влияние системы управления на пове-
дение самолета и ощущения летчика.
При пилотировании самолета по тангажу в установившемся режи-
ме полета положением ручки управления и усилием на ней определя-
ются статические, или балансировочные характеристики системы
управления. Эти два фактора (положение ручки и усилие, прикладывае-
мое летчиком) зависят от режима полета, конфигурации самолета,
величины нормальной перегрузки самолета и характеристик системы
управления. Задача конструктора состоит в обеспечении приемлемых
усилий на ручке управления и по возможности удобных ее положений
при выполнении длительных или часто встречающихся в летной эксплу-
атации режимов полета.
Кроме того, летчику небезразлично, какими усилиями и переме-
щениями ручки вблизи ее балансировочного положения парируются
внешние возмущения. Эти отклонения обычно характеризуются вели-
чинами производных dxpldny и dP^dny, которые определяются, как
правило, для исходного режима прямолинейного горизонтального по-
лета и балансировочного положения ручки управления. Традиционно
принято определять величины производных dx^dny и dP^driy как
87
соответствующие приращения отклонений ручки и усилий на ней, по-
требные для создания единицы приращения установившегося значения
перегрузки (т. е. при переводе самолета из установившегося прямо-
линейного горизонтального полета при стриммированной по усилиям
ручке в установившийся полет с перегрузкой пу = 2,0). Однако следует
заметить, что общепринятой точки зрения на этот счет не существует,
так как характеристики Рр (пу) и хр (пу) могут быть существенно не-
линейными. Так, например, при предварительной затяжке пружины
загрузочного механизма усилие на ручке неопределено при ее нейтраль-
ном положении, и величина отношения приращений усилия ДРр к пе-
ремещению Дхр существенно изменяется при небольших изменениях
приращений отклонения ручки. Наличие трения в проводке управления
усугубляет неопределенность малых приращений усилий.
Использование в качестве критерия продольной управляемости
традиционной величины dxpldny для современных маневренных само-
летов также приводит к неоднозначности в силу нелинейности зависи-
мостей mz = /(а). При малых запасах продольной статической устой-
чивости самолета величина dxpldny близка к нулю, а для нейтрального
по перегрузке самолета — равна нулю, что создает неверное представ-
ление о пилотажных характеристиках нейтрального самолета.
Следует отметить, что выбор в качестве критериев продольной
управляемости традиционных параметров dxp/dny и dP^!dny был сде-
лан на основании опыта эксплуатации самолетов ранних поколений с
безбустерным управлением, у которых характеристики Рр = f(ny) и
хр = f(ny) сохраняли линейность в эксплуатационном диапазоне перег-
рузок и режимов полета, а динамические свойства самолета как объек-
та управления практически не проявлялись. Естественно, что такой вы-
бор был вполне оправдан.
Пилотажные свойства современных маневренных самолетов по-
мимо статических параметров dxpldny и dPpldny зависят также от
динамических характеристик продольного короткопериодического дви-
жения, определяющих поведение самолета при достаточно малых крат-
ковременных отклонениях ручки от исходного положения.
Время и амплитуды малых отклонений ручки в установившемся
режиме полета зависят от индивидуальных особенностей летчика, его
манеры пилотирования и определяются величиной рабочей частоты
летчика, которая обычно лежит в пределах/= 1,0...2,0 Гц.
Для оценки динамических пилотажных свойств самолета удобно
кратковременные отклонения ручки управления аппроксимировать
синусоидальным законом и определять величину (dxJdny)mn, рав-
ную отношению максимальных значений x(t) к ny(t). Зависимость
безразмерной величины (^хр/б?и^)дин, равной отношению {^хр/б?и^)дин =
= (dxpldny)wnl (dXpldny}CT2i^ от безразмерной длительности импуль-
са т = я/(соТ0) приведена на рис. 3.1. Из рисунка следует, что для зна-
88
Рис. 3.1. Относительная эффек-
тивность по перегрузке при им-
пульсном управлении по сину-
соидальному закону
чений длительности им-
пульса в диапазоне т & 2... 10
при значениях f <Z 0,75
величина дии су-
щественно меньше стати-
ческой величины, т. е. ди-
намическая эффективность
органов продольного управ-
ления повышается. При зна-
чениях безразмерной ве-
личины длительности им-
пульса более т 15 ди-
намические свойства само-
лета практически не прояв-
ляются для всех значений f.
При т 3...5 величины
(бгхр/^)дин больше (dxp/dny)c^, (dxp/dny)дин > 1. Динамическая
эффективность органов продольного управления снижается.
Описанные эффекты имеют простой физический смысл. При рез-
ком импульсном пилотировании самолет в силу своей инерционности
”не пропускает” высокие частоты, т. е. не успевает реагировать на зна-
копеременные отклонения органов управления. При плавном пилоти-
ровании движение самолета мало отличается от установившихся режи-
мов полета. При совпадении частоты импульса с диапазоном частот
максимальных забросов (при значениях 0 < f < 0,75) кажущаяся эффек-
тивность органов управления повышается: самолет энергичнее реаги-
рует на отклонения ручки управления.
Введение в качестве характерного параметра величины (сГхр/б^)дин
позволяет также оценивать характеристики управляемости нейтраль-
ного по перегрузке самолета, при этом величина (dx^ldny)дин не обра-
щается в нуль.
Определяя последовательно забросы по перегрузке при синусоидаль-
ном знакопеременном отклонении органов управления, можно на плос-
кости параметров f, о>0 рассчитать и построить линии равных отношений
забросов перегрузки, например первого заброса по второму, третьему
и т. п. В пределе легко получить отношение величины первого заброса
к амплитуде частотной характеристики ”свободного”самолета для
каждой возмущающей частоты. Задаваясь диапазоном ’’рабочих” час-
89
тот летчика, можно выделить замкнутую область на плоскости пара-
метров f, сс0, на границе которой отношение забросов постоянно. Если
это отношение меньше единицы, то в первом приближении можно счи-
тать, что самолет с такими характеристиками склонен к раскачке, так
как при синусоидальном отклонении органа управления с постоянной
амплитудой последующий заброс перегрузки больше предыдущего.
Если эффективность продольного управления на таких режимах
полета избыточна, то продольная раскачка самолета может стать опас-
ной. Избыточная эффективность продольного управления может также
привести к потере колебательной устойчивости замкнутого контура
самолет — летчик. Эти вопросы рассматриваются в гл. 4.
Величина dx^driy не всегда является основным критерием продоль-
ной управляемости самолета, так как летчик рефлекторно реагирует
на изменение нормальной перегрузки самолета лишь при превышении
некоторого порогового значения. При этом для летчика немаловажную
роль играет величина изменения угла тангажа или угла атаки, соответ-
ствующая приращению перегрузки. Поэтому одним из важных парамет-
ров, характеризующих управляемость самолета в продольном движе-
нии, является соотношение между углом атаки самолета и величиной
действующей на самолет нормальной перегрузки пу. Этот параметр
определяется в приращениях и численно равен величине производной
da/dny апУ = da/driy = G/gScfy. Физический смысл этого параметра оче-
виден. Это — величина угла атаки, потребная для изменения на едини-
цу величины нормальной перегрузки. Если при нулевом угле атаки
на сбалансированный по моментам самолет не действует подъемная
сила, то величина с/1 У определяет угол атаки в горизонтальном полете.
При пилотировании на малых высотах и умеренных углах атаки
летчик помимо перегрузки одновременно визуально ощущает угол
тангажа. Так как # = а + 0, то при возрастании величины с^У выше
некоторого значения летчик начинает уделять внимание изменению
угла тангажа и следить за ориентацией самолета в пространстве. При
этом изменение перегрузки пу становится для летчика второстепен-
ным фактором.
Очевидно, что при малых значениях величины о?У основное вни-
мание летчик уделяет изменению перегрузки. Самолет с точки зрения
летчика становится ’’строгим” по перегрузке. Таким образом, в за-
висимости от величины параметра апУ летчик, пилотируя самолет,
рефлекторно следит либо за углом тангажа, либо за перегрузкой.
Условно принято считать [4, 6, 8], что таким граничным значением
параметра о?У является величина, приблизительно равная четырем
(градусам угла атаки, потребным для приращения перегрузки на еди-
ницу). При значениях параметра о?У, больших четырех, летчик при пи-
лотировании следит за углом тангажа, при меньших значениях - пило-
тирует по перегрузке.
90
Однако существует ряд режимов пилотирования, при которых
летчику приходится осуществлять точное управление самолетом по
совокупности значений угла тангажа и перегрузки.
К таким задачам приводит, например, слежение за целью, дозап-
равка топливом в полете, выполнение группового полета и т. п. В этих
случаях необходимо одновременно строго выдерживать как величину
угла тангажа, так и величину нормальной перегрузки самолета, поэтому
они могут являться расчетными при определении характеристик систем
управления, обеспечивающих устойчивость замкнутого контура управле-
ния самолет - летчик.
Таким образом, для исходного прямолинейного горизонтального
полета выбор системы управления в продольном движении определяют
четыре параметра: балансировочные - усилие на ручке Рр, положение
ручки Хп и характеристики управляемости — dP^dny и dXpfdriy или
(^Хр/б?и-/)дин и (dPpIdny)]^. Причем значения dx^fdny и dP^driy
являются критериями лишь при значениях параметра с? У < 4.
Балансировочные характеристики определяются потребным от-
клонением органов продольного управления самолета и реализован-
ной в системе управления зависимостью между перемещением ручки
управления хр, усилием на ней Рр и углом отклонения органов про-
дольного управления. Для режимов горизонтального полета статические
(балансировочные) характеристики управляемости зависят от угла ата-
ки и эффективности органа продольного управления самолета. По из-
вестным зависимостям mz =fr (а, М, Н) и = /2 (а, М, Н) можно по-
строить балансировочные значения углов отклонения как функции
высоты и числа М полета.
Функциональная зависимость потребных балансировочных углив
отклонения от числа М и высоты полета может быть различной в зави-
симости от степени статической устойчивости самолета по углу атаки,
и задача конструктора состоит в том, чтобы обеспечить комфортные
условия летчику для наиболее часто встречающихся длительных уста-
новившихся полетов, реализовав удобные балансировочные положения
ручки управления.
На сверхзвуковых скоростях полета самолет обычно обладает
достаточным запасом продольной статической устойчивости по углу
атаки, поэтому балансировочные значения углов отклонения органов
продольного управления, как правило, отрицательного знака. При
фиксированном числе М полета и умеренных скоростных напорах с рос-
том высоты полета балансировочные значения углов отклонения ор-
гана продольного управления увеличиваются по абсолютной величине
вместе с увеличением угла атаки, потребного для выполнения горизон-
тального полета. При увеличении числа М полета на заданной высоте
полета величины балансировочных значений 8ГЛ1, как правило, практи-
чески не изменяются, так как падение эффективности органа управле-
91
ния и снижение несущих свойств самолета с ростом числа М полета
компенсируются увеличением скоростного напора.
При полете с большими скоростными напорами, что характерно
для малых высот полета, вследствие малости углов атаки величины
балансировочных значений углов отклонения органов продольного уп-
равления определяются главным образом зависимостью mZQ =/(М, q, И),
характеристиками аэроупругости и режимом работы силовой установки,
поэтому типовые зависимости 5ГД1 = /(М, q, Н) в этой области режи-
мов полета приводить нецелесообразно.
Изложенное выше относится к органам продольного управления,
расположенным сзади центра масс самолета, широко применяемым на
самолетах нормальной и бесхвостой схемы.
Органы продольного управления, расположенные впереди центра
масс самолета, как, например, в схеме ’’утка”, имеют противополож-
ные по знаку углы отклонения по сравнению с отмеченными выше.
Принципиальные особенности режимов полета при этом остаются анало-
гичными нормальной схеме.
Традиционная, сложившаяся в результате многолетнего опыта
эксплуатации маневренных самолетов величина максимального пере-
мещения центрально расположенной ручки управления в продольном
канале управления составляет приблизительно хртах 250...300 мм.
Принимая во внимание полный диапазон углов отклонения органов
продольного управления на современных маневренных самолетах,
который колеблется в пределах 45..,50°, нетрудно определить величину
передаточного числа от перемещения ручки к углу отклонения орга-
на управления. Эта величина х& составляет 4..,5 мм хода ручки на гра-
дус угла отклонения органа управления. Очевидно, что при неизменном
значении передаточного числа невозможно обеспечить приемлемые ха-
рактеристики продольной управляемости в эксплуатационной области
режимов полета: с этой целью применяются специальные устройства
автоматического изменения в зависимости от режима полета.
Максимальная величина усилий на ручке управления при созда-
нии предельной установившейся перегрузки полным отклонением
ручки на себя должна х составлять приблизительно 200...250 Н. В то же
время на режимах взлета и посадки, на малых скоростях полета та-
кая величина усилий на ручке управления утомительна для летчика.
Величина приращения усилия на ручке, потребная для увеличе-
ния нормальной перегрузки самолета на единицу dP^dny, составляет
приблизительно — dP^driy « 30...35 Н.
Таким образом, приемлемые для летчика величины усилий на руч-
ке также должны быть обеспечены средствами автоматизации системы
управления.
Зависимость балансировочных усилий на ручке управления от
скорости полета, обычная для самолетов ранних поколений, не может
92
быть обеспечена на современных маневренных самолетах ввиду широ-
кого эксплуатационного диапазона режимов полета.
Из-за малого диапазона углов отклонения органов управления,
используемого в САУ, которые применяются в системах управления
с механической проводкой, автоматическое обеспечение потребных
зависимостей становится затруднительным.
32. СИСТЕМЫ РУЧНОГО УПРАВЛЕНИЯ
Система ручного управления маневренного самолета помимо обес-
печения комфортных условий летчику должна отвечать высоким требо-
ваниям к надежности ее работы и отказобезопасности. В связи с этим
на современных маневренных самолетах широко практикуется в качест-
ве исполнительных механизмов, отклоняющих органы управления,
применение двухкамерных силовых гидравлических приводов, рабо-
тающих от двух независимых друг от друга гидравлических систем.
В случае отказа одной из гидросистем (давление в гидросмеси стано-
вится ниже некоторого допустимого значения) вторая гидросистема
продолжает нормально функционировать. При этом величины усилий,
преодолеваемых бустерами, снижаются пропорционально снижению
давления в отказавшей гидросистеме, но не более чем вдвое (в случае
падения давления в отказавшей гидросистеме до нуля). Максимальные
скорости перекладки органов управления (при Мш = 0) остаются при
этом неизменными.
Особенности систем ручного управления в продольном канале
удобно рассмотреть на примере системы управления с механической
проводкой, так как по эксплуатации таких систем управления нако-
плен огромный опыт, а функциональные возможности таких систем в
силу очевидных конструктивных ограничений существенно ниже, чем
у дистанционных.
В системе продольного управления маневренного самолета уста-
навливаются, как правило, два силовых привода, отклоняющих два
органа продольного управления (элевоны, стабилизатор, переднее гори-
зонтальное оперение). Золотники бустеров жестко связаны механиче-
ской проводкой с ручкой управления самолетом.
В системе управления на участке проводки до силового привода
могут быть установлены автоматические подсистемы для механичес-
кого изменения передаточного числа от ручки управления до силового
привода, для регулирования загрузки ручки управления, для ограниче-
ния опасных режимов полета, а также короткоходовая автоматическая
рулевая машинка в виде раздвижной тяги, пружинный загружатель
ручки управления и нелинейный механизм обеспечения потребной
зависимости 6 = /(хр). Принципиальная схема такой системы управ-
ления приведена на рис. 3.2.
93
Рис. 3.2. Принципиальная схема системы продольного управления маневренного
самолета с механической проводкой:
1 - орган управления; 2 - силовой привод; 3 - автомат АРУ; 4 - раздвижная
тяга; 5 — автомат АРУ (АРЗ); 6 — загрузочный механизм ручки управления;
7 - механизм триммерного эффекта; 8 - ручка управления; I - принципиальная
схема дифференциального отклонения органа управления
Автоматическое регулирование передаточного числа от ручки уп-
равления к углу отклонения органа управления, как отмечено в пре-
дыдущем разделе, необходимо реализовать для получения приемле-
мых значений характеристик dxpjdny и dP^dny.
Величину dxpjdriy можно представить в виде dx^driy —dx^jdbdbldny,
где 6 — угол отклонения органа продольного управления, а величина
dxpldb характеризует искомую зависимость между перемещением
ручки и углом отклонения органов управления.
Как указывалось выше, наиболее предпочтительный диапазон из-
менения величины dxpldny = 20..30 мм/ед., откуда следут, что произ-
ведение dx^jdb dbjdny должно незначительно меняться с изменением
режима полета. Поскольку величина dbldny, определяемая из условий
d^ldny = onCyTnlm%, существенно зависит от режима полета, то условие
dx^db dbfdny const практически невыполнимо и значения dbfdny
возрастают с высотой полета.
Аналогичное выражение можно записать для усилий на ручке управ-
ления: dPpIdny ~ dPpldXpdXpldny.
В этом случае появляется второй параметр dP^[dx^ изменением
которого принципиально можно компенсировать влияние режима
полета на величину dP^ldny, однако при этом следует иметь в виду,
что максимальные усилия на ручке управления должны оставаться
в пределах нормы.
Полеты с большими скоростями на больших высотах обычно произ-
водятся с меньшими величинами допустимых скоростных напоров
по сравнению с полетами на малых высотах. Это обстоятельство объяс-
няется влиянием сжимаемости воздуха на аэродинамические нагрузки,
действующие на самолет в полете. При полете с большими числами
94
М плотность потока за скачком уплотнения значительно выше плотности
покоящегося газа, и на конструкцию канала силовой установки действу-
ют повышенные давления. Так как одним из естественных требований,
предъявляемых к конструкции планера, является требование равно-
прочности, то обычно величина допустимого скоростного напора при
полете с большими числами М на больших высотах ниже, чем на малых
высотах.
В силу этого обстоятельства, а также из-за снижения несущих свойств
самолета с ростом числа М для выполнения горизонтальных полетов
с большими числами М требуются умеренные углы атаки. Соответствен-
но с ростом высоты полета снижаются величины максимальных, рас-
полагаемых по условиям продольной управляемости,нормальных перег-
рузок самолета.
Время выполнения криволинейного маневра самолета, например
разворота на 180°, пропорционально скорости полета и обратно пропор-
ционально величине нормальной перегрузки. Это время существенно
возрастает при полетах с большими числами М, что приводит к утомля-
емости летчика при выполнении маневров.
Например, при скорости 300 км/ч, близкой к диапазону взлетно-
посадочных скоростей полета современных маневренных самолетов,
и на скорости полета 3000 км/ч при равных перегрузках время раз-
ворота вектора скорости на один и тот же угол различается в 10 раз.
Ясно, что даже небольшие усилия на ручке управления, возникающие
при маневре, летчику утомительно выдерживать в течение длительного
времени.
Для снижения балансировочных усилий на ручке управления по
желанию летчика, в проводке управления устанавливается механизм
триммерного эффекта, представляющий собой раздвижную телескопи-
ческую тягу, обжимающую пружины загрузочного механизма и тем
самым изменяющую усилия на ручке управления (см. рис. 3.2),
В качестве силового привода механизма триммерного эффекта
обычно используются электромоторы с относительно небольшой ско-
ростью перемещения штока. Поскольку механизм триммерного эффек-
та и загрузочные механизмы располагаются в непосредственной близо-
сти к ручке управления, то размеры напряженной части проводки уп-
равления невелики, что позволяет получить удовлетворительные час-
тотные характеристики проводки управления в целом (в диапазоне
рабочих частот летчика), так как часть проводки управления от за-
грузочного механизма до золотников бустеров практически не нагру-
жена при нормальном пилотировании самолета.
Для того чтобы перемещения ручки и усилия на ней были одноз-
начно связаны с режимом полета и положением механизма триммер-
ного эффекта, механическая проводка управления должна быть сба-
лансирована в весовом отношении по усилиям, приведенным к репер-
95
ной точке на ручке управления, так как весовая несбалансированность
проводки управления может приводить к дополнительным усилиям
на ручке управления при маневрировании самолета. Эти усилия зависят
от распределения несбалансированных масс по длине проводки управле-
ния и распределения местных перегрузок, возникающих при маневре.
Если местоположение несбалансированной части проводки известно,
то можно подсчитать изменение усилий, приведенных к ручке управ-
ления, зная значения местной перегрузки при различных маневрах
самолета. В частности, в дистанционных системах управления нетруд-
но обеспечить постоянное, не зависящее от режима полета, значение
dPyldny при помощи весового балансира. В системах управления с меха-
нической проводкой применение весового балансира не всегда обес-
печивает постоянство dPpfdny, так как весовая несбалансированность
может быть рассредоточена по всей длине проводки управления, В
этом случае изменение усилий на ручке будет зависеть от распределения
местных значений перегрузок по всей длине проводки. Причем возмож-
ны случаи, когда в наземных условиях величину весовой несбаланси-
рованности проводки управления экспериментально определить не пред-
ставляется возможным. В таких случаях следует определять несбалан-
сированность расчетным путем.
Небольшая весовая несбалансированность проводки управления
порядка сотен граммов усилий, приведенных к ручке управления,
вполне допустима, так как при высоких значениях нормальной пере-
грузки ручка управления в отклоненном положении разгружается в
результате увеличения веса руки летчика и вследствие собственного
отклонения на себя от связанной с самолетом оси OY. Эта разгрузка
может быть значительной. Если считать, что вес части руки летчика от
локтя до кисти составляет 20...30 Н, то при местной перегрузке в каби-
не, равной восьми, инерционная сила, действующая на эту часть руки,
составляет 160...240Н.
Разгрузка ручки управления от воздействия нормальной перегруз-
ки зависит, как видно из рис. 33, от угла отклонения ручки и дости-
гает своего максимального значения на режимах полета, при которых
максимальная эксплуатационная перегрузка обеспечивается максималь-
ным отклонением ручки. При сохранении истинной скорости полета с
увеличением высоты располагаемая перегрузка уменьшается, и усилия
разгрузки ручки падают вместе с падением располагаемой перегрузки.
Если при этом автомат, регулирующий загрузку ручки, не изменяет
передаточного числа, то суммарное усилие при фиксированном поло-
жении ручки будет возрастать с ростом высоты полета, и управление
с точки зрения летчика будет становиться более ’’тяжелым”.
Таким образом, расчетными режимами для обеспечения приемле-
мых усилий на ручке в ее крайних положениях при больших скоростях
полета являются режимы полета в диапазоне умеренных высот, где
96
располагаемая величина нормальной перегрузки меньше ее эксплуата-
ционного значения. В практике эксплуатации маневренных самолетов
известны случаи, когда летчики жаловались на ’’затяжеление управ-
ления” с ростом высоты полета при неизменных характеристиках пру-
жинного загружателя.
Силовые приводы располагаются, как правило, в непосредствен-
ной близости от оси вращения органа управления с целью повышения
жесткости силовой части проводки управления.
Все автоматические подсистемы расположены, как следует из
рис. 3.2, в несиловой части проводки управления. Таким образом, лет-
чик, перемещая ручку управления, преодолевает усилия загружателя и
и трение в подшипниках проводки управления и золотниках силовых
приводов. Величины трения, приведенные к реперной точке ручки уп-
равления, не превышают, как правило, одного килограмма.
Статические усилия на ручке управления могут быть значительно
ниже усилий, возникающих на ручке при резких ее перемещениях.
Эти дополнительные усилия могут возникать по двум причинам: во-
первых, механическая проводка обладает инерционностью, которая
характеризуется величиной приведенной массы проводки; во-вторых,
скорость движения золотника ограничена максимальной скоростью
штока бустера, которая определяется величиной аэродинамического
шарнирного момента, действующего на орган управления.
Типовая характеристика двухкамерного силового привода приве-
дена на рис. 3.4, где изображена зависимость скорости перемещения
штока бустера от величины шарнирного момента, действующего на
орган управления.
Динамические характеристики силовых приводов обычно выби-
Рис. 3.3. Схема действия сил на ручку
управления в продольном канале при
выполнении маневра с нормальной
перегрузкой
Рис. 3.4. Типовая статическая харак-
теристика бустера:
1 - работают две гидросистемы:
2 - работает одна гидросистема
97
раются из условий безопасности самолета от флаттера и обеспечения
устойчивости высокочастотных колебаний самолета с САУ.
Эти характеристики в первом приближении можно охарактеризо-
вать математической моделью, описываемой одним уравнением
К
первого порядка с передаточной функцией W(p) =--------, Величина
Тр +1
постоянной времени Т исчисляется сотыми долями секунды. Учитывая
величины максимальных скоростей перемещения ручки управления от
летчика и диапазон передаточных чисел от ручки до золотника бустера,
можно пренебречь собственной динамикой бустера при рассмотрении
задач, связанных с ручным пилотированием.
Таким образом, влияние бустера на характеристики пилотирования
в ручном режиме определяет один параметр - максимальная скорость
перекладки бустера 50. Как указывалось в гл. 2, величина 60 зависит от
уровня аэродинамического шарнирного момента, действующего на ор-
ган управления по закону, который можно аппроксимировать зависи-
мостью:
против нагрузки §тах ~ V --------;
max
/----------(3.1)
в сторону нагрузки 5max = V1 + — •
max
Из соотношения (3.1) следует, что при достаточно высоких зна-
чениях действующего на орган управления аэродинамического шар-
нирного момента Мш, близкого по величине к максимальному, рас-
полагаемая скорость перекладки органа управления может существен-
но снижаться.
Применение в механической проводке управления в качестве теле-
скопической раздвижной тяги рулевой машинки, управляемой по сиг-
налам САУ и отклоняющей органы управления на относительно не-
большие углы, позволяет на ряде режимов полета существенно улуч-
шить характеристики устойчивости и управляемости самолета.
Исторически сложилось так, что основной функцией раздвижной
тяги являлась задача демпфирования колебаний, так как при исполь-
зовании демпфера тангажа, отклоняющего органы продольного управ-
ления пропорционально величине угловой скорости тангажа сэ2, не
требуются большие углы отклонения в силу высокой эффективности
органов продольного управления и относительно малых моментов,
необходимых для демпфирования колебаний.
Это традиционное направление получило широкое распространение
и применяется сейчас практически на всех маневренных самолетах.
Однако естественно, что это не единственно возможное использование
98
раздвижной тяги. Возможны и другие варианты ее применения с целью
улучшения характеристик устойчивости и управляемости самолета.
Например, использование раздвижной тяги для компенсации нелиней-
ностей в протекании балансировочных зависимостей 6 = /(а, М), когда
для этого требуются незначительные углы отклонения органов продоль-
ного управления для компенсации по специальным сигналам САУ раз-
личного рода внешних возмущений и т. п.
Основным преимуществом использования короткоходовых руле-
вых машинок в системах автоматического управления в силу малости
используемых углов отклонения органов управления является их отка-
зобезопасность и, как следствие этого, отсутствие резервирования,
что значительно упрощает конструкцию системы управления. Очевидно,
что при этом существенно ограничиваются функциональные возмож-
ности САУ.
Применение дистанционных систем управления требует много-
кратного резервирования жизненно важных подсистем САУ, вплоть
до источников питания и датчиков, регистрирующих параметры полета.
Поэтому довольно широкое распространение получили компромиссные
решения идеологического подхода к проектированию автоматических
систем управления маневренных самолетов [5, 6].
Одним из таких компромиссных решений является система улуч-
шения устойчивости и управляемости самолета (СУУ) . В таких системах
управления в целях безопасности полета сохраняется механическая
проводка управления, а автоматическая система управления использу-
ет значительные, но неполные диапазоны углов отклонения органов
управления. Механическая проводка управления в случае отказа СУУ
обеспечивает безопасное пилотирование. При этом возможны различные,
идеологические подходы к вопросу о необходимой степени резерви-
рования автоматической части системы управления. Сохранение ме-
ханической проводки управления в сочетании с достаточно больши-
ми углами отклонения органов управления, используемыми в СУУ,
вносит ряд специфических особенностей в конструкцию таких систем
управления.
Для обеспечения быстродействия отклонения органов управления
в качестве силовых приводов в таких системах управления обычно
используются электрогидравлические рулевые машинки, которые
закольцовываются в случае отказа СУУ. При этом на ручке управления
могут появляться недопустимые по величине усилия трения. Чтобы
избежать появления больших усилий трения на ручке в тракт механичес-
кой проводки иногда устанавливается дополнительный вспомогатель-
ный бустер небольшой мощности, называемый предбустером, и таким
образом, летчик управляет только перемещением золотника предбус-
тера, который перемещает остальную проводку управления и управляет
золотниками силовых приводов.
99
Бескомпромиссным решением является применение дистанцион-
ной системы управления без механической проводки. Естественно,
что такая система управления должна быть не менее надежной, чем при-
вычная система управления с механической проводкой, время эксплуата-
ции которой составляет практически весь опыт эксплуатации маневрен-
ной авиации. Дистанционная система управления должна не уступать
механической также и по количеству отказов в единицу времени ее
эксплуатации.
Таким образом создание дистанционной системы управления без
механической проводки является сложной задачей. Однако уровень
современной вычислительной техники позволяет ее решить. В настоя-
щее время за рубежом созданы и эксплуатируются дистанционные
системы управления с использованием цифровой элементной базы в
вычислительной части автоматической системы. Функциональные воз-
можности таких систем ограничены только эффективностью органов
управления, установленных на самолете.
3.3. ОСОБЕННОСТИ СИСТЕМ УПРАВЛЕНИЯ
С ДИФФЕРЕНЦИАЛЬНЫМ ОТКЛОНЕНИЕМ ОРГАНОВ
ПРОДОЛЬНОГО УПРАВЛЕНИЯ
На современных маневренных самолетах органы продольного уп-
равления, как и на самолетах бесхвостой схемы, используются в ка-
честве органов поперечного управления. Применение таких комбини-
рованных систем управления, которые прочно вошли в практику проек-
тирования современных маневренных самолетов, позволяет обеспечить
потребные характеристики поперечной управляемости самолета на боль-
ших скоростях полета относительно простыми конструктивными спо-
собами, без существенных усложнений и утяжелений конструкции
планера.
Однако реализация дифференциального управления органами про-
дольного управления может вносить принципиальные особенности
в характеристики управляемости самолета при высоких значениях аэро-
динамических шарнирных моментов органов управления, соизмеримых
с располагаемыми моментами силовых приводов.
Физические причины возникновения этих особенностей удобно
рассмотреть на примере систем управления с дифференциально откло-
няемым стабилизатором, в которых помимо симметричного откло-
нения органов управления, обеспечиваемого перемещением управления
в направлении от себя — на себя, реализуется асимметричное (диф-
ференциальное) их отклонение при перемещении ручки в поперечном
канале управления. Например, для самолетов с изменяемой в полете
стреловидностью крыла это практически единственный способ обес-
100
печить необходимую поперечную управляемость самолета на режимах
полета с использованием больших углов стреловидности крыла, при
которых органы поперечного управаления, расположенные на крыле,
становятся малоэффективными.
При дифференциальном отклонении консолей стабилизатора мест-
ные углы атаки, под которыми обтекаются правая и левая консоли,
будут различными, а следовательно, будут различными и аэродинами-
ческие шарнирные моменты, действующие на консоли.
Из соотношения, связывающего максимальную скорость откло-
нения консоли с действующим на нее аэродинамическим шарнирным
моментом, следует, что при этом максимальные располагаемые ско-
рости отклонения консолей, также будут различны. Обозначив аэро-
динамические шарнирные моменты, действующие соответственно на
правую и левую консоли Мщ, соответствующие максимальные
скорости отклонения 5qp, 5q, легко получить их отношение
$5Р = ^/^штах ~^щР 2)
^штах —
где знак плюс или минус берется в зависимости от направления дви-
жения каждой консоли по отношению к действующему на нее шар-
нирному моменту. Из (3.2) легко видеть, что при достаточно больших
величинах аэродинамических шарнирных моментов скорости правой
и левой консолей могут существенно различаться. Ясно, что при су-
щественном различии в скоростях перекладки правой и левой кон-
солей в случае резкого пилотирования самолета, например по танга-
жу, отставание одной консоли от другой приводит к появлению до-
полнительных ’’ножниц”, и создается непредусмотренный летчиком
кренящий момент. Аналогичная картина может возникать при резком
пилотировании по крену. Вследствие различных располагаемых скорос-
тей правой и левой консолей появляется дополнительный также непре-
дусмотренный летчиком продольный момент из-за нарушения симмет-
рии ’’ножниц” консолей, так как балансировочное положение стаби-ш
лизатора исходного режима полета в продольном канале определяется
полусуммой углов отклонения правой и левой консолей:
§бал = SV5jl •
Эти дополнительные моменты могут приводить к неуправляемому
с точки зрения летчика движению самолета по крену при резком от-
клонении ручки в направлении от себя - на себя и к неуправляемому
изменению угла атаки самолета при резком отклонении ручки в по-
перечном канале.
Такое явление получило название смешения каналов управления,
когда пилотирование по тангажу вызывает непреднамеренное движение
101
самолета по крену, пилотирование по крену вызывает непреднамеренное
движение самолета по тангажу.
На самолетах с механической проводкой в системе управления
статические зависимости между положениями ручки по тангажу и крену
и соответствующими углами отклонения консолей обеспечиваются
механической связью золотников силовых приводов правой и левой
консолей с перемещениями ручки управления, реализованной через
дифференциальный механизм. Однако механическая связь, обеспе-
чивающая указанные статические характеристики системы управления,
не является абсолютно жесткой. Наличие дифференциального меха-
низма, расположенного в несиловой части проводки управления, сни-
жает суммарную эффективную жесткость проводки на участке от руч-
ки до золотников бустеров. Поэтому при резком пилотировании само-
лета по тангажу или по крену из-за деформаций несиловой части про-
водки управления от ручки до золотников бустеров заданные стати-
ческие зависимости между положениями ручки и отклонениями кон-
солей стабилизатора могут кратковременно нарушаться, что вызы-
вает смешение каналов управления.
В дистанционных системах управления, не содержащих механичес-
кой проводки, силовые приводы правой и левой консолей механически
не связаны между собой, статические характеристики системы управ-
ления, связывающие между собой положения ручки и отклонения орга-
нов управления, обеспечиваются при помощи электрических сигналов,
поэтому отклонению консолей с разными скоростями ничто не пре-
пятствует.
Случаи существенного проявления эффекта смешения каналов
управления встречались в летной практике маневренных самолетов
и достаточно подробно описаны в работе [12].
Отмеченные особенности принципиально присущи всем комбини-
рованным системам управления, использующим дифференциальное
управление органов продольного управления. Однако не следует за-
бывать, что неблагоприятные эффекты смешения каналов управления
проявляются кратковременно при движении органов управления с мак-
симальной скоростью отклонения, обеспечиваемой силовым приво-
дом при действии на него аэродинамического шарнирного момента.
В связи с этим представляет практический интерес оценить рас-
четные случаи для выбора энергетики силовых приводов и вырабо-
тать требования к допустимым рассогласованиям максимальных ско-
ростей отклонения органов продольного управления.
। нт
Очевидно, что при малых отношениях | ——। различия в мак-
^штах г
симальных скоростях отклонения правого и левого силовых приво-
дов также будут малыми. Соотношение (3.2) в этом случае можно
записать в виде
102
$Р ~ 1 ± епр/2
S3 ~ 1 ± ел/2
где е"Р = |_£1_|; е” = |Л“_ |,
мmax Мтах
м ш м ш
ИЛИ
~ « (1 ± (1 + ~ « 1 ± y (епр ± ел).
°0
(33)
(3.4)
Таким образом, выбор необходимых мощностей силовых при-
водов необходимо производить, учитывая описанные выше эффекты.
Поскольку при работающей одной гидросистеме величина располагае-
мого шарнирного момента снижается вдвое, то этот случай и являет-
ся расчетным для выбора потребной мощности силовых приводов
в продольном канале управления.
Из (3.3) следует, что если действующие на правую и левую кон-
соли аэродинамические шарнирные моменты составляют не более 10%
располагаемых по мощности бустеров (е < 0,1), то и располагаемые
скорости отклонений правой и левой консолей могут отличаться не
более чем на 10%, что практически не ощущается летчиком и вполне
допустимо для нормального пилотирования. Максимальное различие в
скоростях консолей будет в случае, когда одна консоль движется в
сторону действующего аэродинамического шарнирного момента, а
другая - в сторону, противоположную действию шарнирного момента.
Наличие перекомпенсации шарнирного момента консоли по углу
ее отклонения (положительные значения может увеличить время
рассогласования скоростей отклонения консолей, а в ряде случаев при-
вести к заклинению одной из консолей. Поэтому расчетными режимами
полета для выбора мощности силовых приводов в продольном канале
управления следует считать дозвуковые скорости полета у земли и на
малых высотах, где возможна перекомпенсация шарнирных моментов,
а эффективность органов управления максимальна.
3.4. ТИПОВЫЕ НЕЛИНЕЙНОСТИ В СИСТЕМАХ РУЧНОГО УПРАВЛЕНИЯ
Требования к ограничению максимальных усилий на ручке управле-
ния в сочетании с обеспечением необходимого диапазона градиентов
усилий по перемещениям ручки управления приводят к необходимости
применения загрузочных механизмов с существенно нелинейными
характеристиками. Типовая характеристика усилий на ручке управ-
ления в зависимости от ее положения приведена на рис. 3.5 Д На графи-
ке видно несколько характерных точек излома, обеспечиваемых под-
103
бором жесткостных характеристик пружин загрузочного механизма.
Предварительная затяжка пружины при нейтральном положении
ручки управления реализуется с целью смягчить ’’отдачу” на ручку
усилий, развиваемых в проводке управления раздвижной тягой.
При работе телескопической раздвижной тяги в автоматическом
режиме, например при демпфировании колебаний самолета усилия,
развиваемые тягой, могут передаваться на ручку управления и созда-
вать неприятные ощущения у летчика. При этом располагаемый
диапазон углов отклонения органов управления от раздвижной тяги
реализуется неполностью.
Для устранения этих эффектов нейтральное положение ручки уп-
равления центрируется пердварительным натяжением двух пружин,
которые создают усилие предварительной затяжки ручки управления
и тем самым препятствуют перемещению части проводки управления
от ручки до раздвижной тяги. Величина этого усилия в продольном
канале управления зависит от положения штока АРУ, регулирующего
усилия на ручке управления. Обычно максимальная величина этого
усилия не превышает 15...20Н.
Необходимость обеспечения высоких градиентов усилий по ходу
ручки управления вблизи нейтрального положения ручки требует изло-
ма в зависимости Рр = /(хр), так как постоянство градиента в полном
диапазоне перемещения ручки приводит к недопустимо большим вели-
чинам усилий при ее крайних положениях.
Рис. 35. Принципиальная схема работы автомата АРУ:
а - регулирование передаточного числа от ручки до бустера; б - регулирование
передаточного числа загрузочного механизма ручки управления
104
Величина диапазона перемещений ручки управления, в котором
обеспечены высокие значения градиентов усилий, обычно выбирается
из условий, определяющих балансировочные положения ручки при
различных конфигурациях самолета в горизонтальном полете в диапа-
зоне дозвуковых скоростей полета на малых и средних высотах. Из
этих же соображений выбирается также диапазон существенной нелиней-
ности в зависимости изменения передаточного числа Кш от ручки до
органа управления по ходу ручки в продольном канале.
Для снижения вероятности попадания самолета на опасные режимы
полета или для предотвращения подобных случаев создается система пре-
дупреждения и ограничительных устройств предельных режимов полета.
Одним из таких режимов является, например, предельнодопустимый
угол атаки самолета, определяемый из условий обеспечения безопас-
ности самолета от сваливания. Величина допустимого для эксплуата-
ции угла атаки самолета устанавливается с некоторым запасом отно-
сительно угла начала сваливания самолета. Этот запас обычно состав-
ляет 2...3°.
Принципы работы предупредительных устройств обычно осно-
ваны на световой, звуковой или тактильной сигнализации. Одним из
возможных путей создания ограничительных устройств для маневренных
самолетов с механической проводкой управления является автома-
тическая система, обеспечивающая резкое изменение усилий на ручке
управления при достижении самолетом допустимого угла атаки. При
этом учитывается темп нарастания угла атаки, характеризуемый вели-
чиной производной da/dt.
Величину угла атаки аср, при которой появляется дополнительное
усилие на ручке, можно представить в виде
аср = азад ~ 9 гДе К >
Очевидно, что чем больше темп нарастания угла атаки, тем при
меньших значениях угла атаки должна срабатывать система ограни-
чений.
Величина дополнительного усилия, проявляющегося на ручке уп-
равления, может находиться в пределах 100...200 Н, чтобы при необ-
ходимости (например, в случае ложного срабатывания) летчик смог его
пересилить. Такие системы применяются на ряде зарубежных самолетов,
Однако на практике положение осложняется тем, что величина
угла сваливания самолета является функцией многих переменных
и создание ограничительных устройств, надежно защищающих само-
лет и летчика от превышения допустимых углов атаки, представляется
весьма сложной задачей. В то же время снижение величины допусти-
мого эксплуатационного значения угла атаки вследствие увеличения
запаса по отношению к минимальным значениям угла сваливания приво-
дит к снижению маневренных возможностей самолета.
105
В дистанционных системах управления конструктивные решения
являются более простыми, так как в таких системах появляется воз-
можность ограничивать величину электрического сигнала, а не меха-
нические перемещения ручки управления, однако полностью предот-
вратить возможность сваливания самолета при грубых ошибках пило-
тирования средствами автоматизации, по-видимому, не удастся.
Поскольку современные маневренные самолеты обладают, как
правило, высокой энерговооруженностью, то появляется возможность
превышения установленных из условий прочности и аэроупругости
ограничений по максимально допустимой скорости полета. Вместе с
тем маневренные возможности самолета позволяют выполнять ма-
невры в вертикальной плоскости с произвольными значениями углов
тангажа и наклона траектории. При торможениях самолета на верти-
кальных маневрах возможны случаи превышения ограничений по мини-
мальной скорости полета. Такие маневры могут сопровождаться ма-
лыми углами атаки, например при выполнении горки.
Поскольку в вычислительной части системы автоматического уп-
равления содержится информация о траекторных параметрах полета,
то функциональной задачей САУ является предупреждение летчика
о приближении самолета к предельным режимам полета. Обычно такое
предупреждение выдается в виде речевой информации и световой сиг-
нализации в кабине летчика без механического вмешательства в управ-
ление самолетом.
В силу технологического несовершенства и износа в процессе
эксплуатации в системе управления могут появляться естественные
для любой конструкции со многими степенями свободы люфты по
перемещениям. Следует различать люфты в заделках органов управле-
ния при их креплении к силовой части проводки и силовым приводам,
люфты в несиловой части проводки от ручки до золотников бустеров
и зоны нечувствительности в электрических сигналах. Обычно люфты
в проводке управления, приведенные к реперной точке на ручке управ-
ления, не превышают нескольких миллиметров и практически не ока-
зывают влияния на характеристики пилотирования самолета.
Наличие люфтов других типов может приводить к автоколебаниям
системы управления малой амплитуды, которые, как правило,не переда-
ются на ручку управления. Появление дополнительных люфтов в про-
цессе эксплуатации самолета вследствие естественного износа конструк-
ции оговаривается специальными нормативами, нарушение которых
недопустимо, особенно при наличии участков с тросовой проводкой
управления.
Суммарное время запаздывания в механической проводке управ-
ления не превышает 0,1 с, что при рабочей частоте летчика, например,
/ ~ 2,0 Гц может приводить к фазовому сдвигу между перемещением
ручки и отклонением органа управления не более чем на 50°, что впол-
106
не допустимо для ручного пилотирования. Но фазовый сдвиг между
усилием на ручке и отклонением органа управления при резком пило-
тировании может быть значительно больше вследствие инерционности
механической проводки управления.
В современной литературе по динамике полета [4, 8, 21] принято
считать, что время запаздывания летчика тл при нормальном пилоти-
ровании характеризуется величиной тл 0,2...0,3 с,и поэтому запаз-
дывание в системе управления практически не оказывает влияния на пи-
лотажные характеристики самолета.
Однако при рефлекторных действиях летчика время запаздыва-
ния, по-видимому, может быть значительно меньше, так как предель-
ные физиологические возможности человека характеризуются време-
нем запаздывания реакции на внешние раздражители, исчисляемым
сотыми долями секунды. Уменьшение времени запаздывания требу-
ет от летчика повышенной эмоциональной и физической нагрузки, что
проявляется лишь в экстремальных ситуациях. В таких случаях время
запаздывания в системе управления может стать соизмеримым со вре-
менем запаздывания летчика и оказать существенное влияние на харак-
теристики устойчивости замкнутого контура.
Нормальная работа автоматических и полуавтоматических под-
систем в системе управления существенным образом зависит от дос-
товерности информации о параметрах полета. У современных маневрен-
ных самолетов возможность энергичного маневрирования допускает
быстрые изменения высоты и скорости полета в процессе маневра, что
может приводить к существенным запаздываниям в показаниях от-
дельных приборов и датчиков. Применяемые на современных само-
летах датчики высоты и скорости полета замеряют величины статичес-
ких и динамических давлений приемниками воздушного давления
(ПВД). Барометрическая высота и скорость полета в силу естественных
физических свойств воздушного тракта в системе ПВД имеют макси-
мальное время запаздывания. Поэтому при маневрах, связанных с
энергичным изменением высоты или скорости полета, положение што-
ка исполнительного механизма АРУ вследствие запаздывания датчи-
ков высоты или скорости полета может не соответствовать истинным
значениям этих параметров, связанных с энергичным изменением высо-
ты или скорости полета.
35. СИСТЕМЫ ПОЛУАВТОМАТИЧЕСКОГО И АКТИВНОГО УПРАВЛЕНИЯ
Наиболее широко применяемой системой полуавтоматического
управления на самолетах с механической проводкой является авто-
мат регулирования управления (АРУ). Принцип работы АРУ доста-
точно прост: он изменяет передаточные числа от ручки до загрузочного
107
механизма и от ручки до золотника бустера путем изменения соот-
ветствующего плеча в проводке управления.
Величины передаточных чисел являются функциями высоты и ско-
рости полета. На режимах избыточной эффективности органов продоль-
ного управления, что характерно для полетов на малых высотах с боль-
шими скоростями, следует уменьшить располагаемые углы отклонения
органов продольного управления и увеличить усилия на ручке управле-
ния. На режимах взлета и посадки, при полетах с малыми скоростя-
ми и на больших высотах следует снизить усилия и восстановить рас-
полагаемые углы отклонения органов управления, обеспечиваемые
конструктивными возможностями системы управления.
Диапазон изменения передаточных чисел при действии АРУ должен
быть выбран из условий обеспечения возврата на аэродром вылета
и посадки самолета при отказе АРУ в любом из возможных положений.
Первая конструкция АРУ относится к середине 50-х годов, когда
на самолете МиГ-19 был установлен в качестве органа продольного
управления цельноповоротный стабилизатор. Избыточная эффективность
стабилизатора на больших дозвуковых скоростях полета проявилась
в неизвестном ранее явлении: в раскачке устойчивого в продольном
движении самолета летчиком при попытке парировать собственные
колебания самолета.
Таким образом, устойчивый в свободном продольном движении
самолет в случае раскачки становится неустойчивым при попытке лет-
чика парировать возмущения, откуда следует, что неустойчивым ста-
новится замкнутый контур управления летчик — система управления —
самолет. Проблема создания, математической модели, которая позво-
лила бы описать поведение замкнутого контура и проанализировать
процесс возникновения раскачки самолета летчиком в аналитическом
виде, является, вероятно, одной из наиболее сложных в динамике поле-
та. Однако из общих соображений очевидно, что снижение передаточного
числа от ручки до органа управления компенсирует избыточную эф-
фективность органа управления. Очевидно также, что затяжеление руч-
ки управления затрудняет ее перемещения с большой частотой и ампли-
тудой.
Опыт летной эксплуатации показал, что увеличением градиента
усилий и снижением передаточного числа в системе управления само-
летом можно обеспечить устойчивость замкнутого контура управления
для статически устойчивого по перегрузке самолета в продольном
движении.
Повышение усилий на ручке управления в продольном канале
в зависимости от скорости и высоты полета может быть достигнуто при
помощи автоматического программного механизма, изменяющего
расстояние от точки крепления загрузочного механизма, до оси вра-
щения ручки управления по заранее заданной программе. Типовые за-
108
Рис. 3.6. Типовой закон нелинеИйон
зависимости 6 = /(*р) в продольном
канале управления
От себя На себя
X. *7
висимости изменения передаточ- \
ных коэффициентов от высоты и \
скорости полета и принципиальная \
схема работы такого устройства
ясны из рис. 3.5. Такой механизм (АРУ) широко применяется на всех
современных маневренных самолетах.
Возможны и другие пути снижения передаточного числа в системе
продольного управления самолетом. Одним из таких путей является
применение нелинейного механизма в проводке продольного управ-
ления (рис. 3.6), обеспечивающего заданную зависимость угла откло-
нения органа управления от перемещения ручки: 8 = /(хр).
В связи с тем, что на режимах полета, где возможно появление
раскачки самолета летчиком углы отклонения органов продольного уп-
равления, потребные для балансировки самолета в горизонтальном поле-
те, обычно малы и незначительно изменяются при изменении конфи-
гурации самолета, то в этом диапазоне углов можно ’’положить” за-
висимость 8 = /(хр), как это ясно из рисунка, и тем самым снизить
коэффициент Кш.
При этом на режимах полета, где не проявляется избыточная эф-
фективность органов продольного управления, балансировочные зна-
чения углов лежат, как правило, в диапазоне больших значений переда-
точного числа Кш, однако это практически не ухудшает характеристи-
ки управляемости самолета.
Естественным путем обеспечения устойчивости замкнутого кон-
тура управления является также. применение средств автоматизации
с различного рода законами управления, направленными на улучшение
динамических характеристик свободного самолета. Принципы работы
таких автоматических систем и применяемые в них алгоритмы управ-
ления достаточно подробно рассмотрены в работе [6].
На маневренных самолетах широкого целевого назначения внеш-
ние возмущения, связанные с изменением конфигурации самолета,
на ряде режимов полета могут вызывать значительные забросы по перег-
рузкам и углам атаки. Такие возмущения могут возникать при сбросе
внешних подвесок самолета, например подвесных топливных баков,
при выпуске тормозных щитков. Парирование возмущений такого
типа при помощи традиционных автоматических систем с обратными
связями при достаточно большой величине возмущающих моментов
весьма затруднительно, так как такие системы реагируют на параметры
развившегося движения самолета. Поэтому получение приемлемых
109
забросов по перегрузкам, возникающих^Ьри рассматриваемых резких
возмущениях, требует значительного увеличения коэффициентов уси-
ления в цепи обратной связи, что не всегда можно реализовать в систе-
мах управления с механической проводкой вследствие потери устой-
чивости замкнутого контура самолет — САУ.
С целью парирования возмущений такого рода могут применять-
ся автоматические программные устройства без обратной связи. Прин-
цип работы таких устройств достаточно прост, и они имеют ряд преи-
муществ по сравнению с традиционными автоматическими системами,
использующими обратные связи. Зная заранее величину возмущения
и потребную для его парирования величину угла отклонения органа
управления, можно практически одновременно с действием возмущения
подать сигнал на управляющее устройство рулевой машинки, которая
с максимальной скоростью отклонит орган управления на заданную
величину. Поскольку возмущения такого типа возникают обычно по
команде летчика, то момент воздействия возмущения на самолет из-
вестен.
В результате можно получить необходимую реакцию самолета
от воздействия разности возмущающих моментов.
Программные автоматические системы управления целесообраз-
но применять также в тех случаях, когда маневр и реализация его вы-
полнения заранее известны. К маневрам такого вида можно отнести
маневры оптимального по быстродействию управления углом атаки
или перегрузкой самолета, которые требуют резкого знакоперемен-
ного отклонения органов продольного управления.
Зависимости от времени углов отклонения органов управления,
обеспечивающие оптимальное по быстродействию управление углом
атаки самолета, можно определить заранее и запрограммировать в
вычислительном устройстве автоматической системы управления как
функции режимов полета и потребных углов атаки. При необходимости
летчик, подав соответствующую команду, может реализовать такой
маневр, например при приведении самолета к режиму горизонтально-
го полета в случае потери пространственной ориентировки при выво-
де самолета из пикирования и т. п.
Перспективы и направления дальнейшего развития систем управле-
ния маневренных самолетов тесно связаны с общими требованиями
к устойчивости и управляемости маневренных самолетов, с их целе-
выми назначениями. Чтобы яснее представить возможные пути даль-
нейшего совершенствования современной маневренной авиации, по-
лезно кратко проследить изменения общих требований к устойчивос-
ти и управляемости маневренных самолетов на примере их историчес-
кого развития.
Если исключить из рассмотрения самые ранние этапы зарождения
маневренной авиации, когда такие требования отсутствовали вооб-
110
ще, то первым требованием, определяющим устойчивость самолета,
было ограничение на изменение центровки самолета, т. е. требование
к положению центра масс самолета, обеспечивающего продольную
статическую устойчивость самолета при всех вариантах его загрузки.
По мере расширения диапазона скоростей и высот полета манев-
ренных самолетов появились требования к статическим характерис-
тикам устойчивости и управляемости самолета, а затем к динамическим
характеристикам устойчивости свободного самолета.
Так как принятая математическая модель движения самолета опи-
сывается системой линейных дифференциальных уравнений с постоян-
ными коэффициентами (на заданном исходном режиме полета), то
динамические характеристики самолета однозначно определяются,
например, параметрами переходного процесса от воздействия единич-
ного ступенчатого возмущения.
Исторически сложилось так, что в качестве нормируемых парамет-
ров продольного короткопериодического движения самолета были
выбраны величины времени срабатывания, относительного заброса по
перегрузке и времени затухания переходного процесса при ступенча-
том воздействии продольного момента. С дальнейшим расширением
эксплуатационного диапазона скоростей и высот полета маневренных
самолетов стало невозможным обеспечение нормируемых параметров
без применения средств автоматизации системы управления, которые
начали широко применяться с начала 60-х годов.
По мере развития автоматизации системы управления самолетом
и расширения диапазона высот и скоростей применения САУ в руч-
ных режимах пилотирования динамические характеристики собствен-
ного движения самолета (без САУ) стали играть второстепенную роль.
Поскольку окончательная оценка приемлемости характеристик
устойчивости и управляемости самолета остается за летчиком, то ос-
новным критерием становятся характеристики замкнутого контура
управления летчик — САУ — самолет, и перед конструктором ставится
задача обеспечения удовлетворительных характеристик замкнутого
контура путем выбора необходимых алгоритмов работы САУ в руч-
ных режимах пилотирования.
ГЛАВА 4. АНАЛИЗ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
САМОЛЕТА С МОДЕЛЬЮ ЛЕТЧИКА ИЛИ АВТОПИЛОТА
4.1. ОСНОВНЫЕ ЗАДАЧИ ИССЛЕДОВАНИЯ ЗАМКНУТОГО КОНТУРА
Расширение диапазона скоростей и высот полета и повышение тре-
бований к точности пилотирования привело к увеличению степени авто-
матизации систем ручного управления и значительному расширению
функций таких систем. Повышение надежности автоматических уст-
ройств позволило ’’доверить” автоматике полные диапазоны углов от-
111
клонения органов управления самолетом, обеспечиваемые конструк-
цией системы управления, не снижая при этом безопасности полета.
Таким образом, возникла необходимость традиционные динамичес-
кие характеристики ’’свободного” самолета, которые определялись
ранее только аэродинамическими характеристиками, рассчитывать с
учетом работы САУ.
Широкий класс функциональных алгоритмов, используемых в САУ,
работает по принципу систем регулирования с обратными связями,
и ’’свободный” с точки зрения летчика самолет на самом деле являет-
ся замкнутым контуром самолет — автопилот. Поэтому еще на этапе
предварительного проектирования маневренного самолета и его сис-
тем управления необходимо в первом приближении определить дина-
мические характеристики замкнутого контура самолет — САУ (рис. 4.1).
С другой стороны, летчик сам является динамическим звеном в
контуре управления самолетом. Зная математическую модель пове-
дения летчика при пилотировании самолета, можно (в простейших
случаях) определить динамические характеристики замкнутого конту-
ра самолет — летчик.
Большое количество теоретических и экспериментальных работ,
посвященных исследованию динамических характеристик замкнутого
контура самолет — летчик [4, 6, 8, 11, 21], свидетельствует о сложности
проблемы. Если динамические характеристики САУ заранее известны
а б
Рис. 4.1. Структурная схема замкнутого контура управления Самолетом и типо-
вые зависимости качества переходного процесса в замкнутом контуре управления
от коэффициента усиления:
а - без запаздывания; б - при наличии запаздывания; в - зависимостью =/(АЭ;
г - зависимость ==
112
и математическую модель САУ можно записать с достаточной степенью
точности, то в отношении летчика как динамического звена в контуре
управления дело обстоит совсем иначе.
Во-первых, индивидуальные особенности, свойственные каждому
летчику, характеризующие его ’’технику пилотирования”, могут при-
водить к существенным различиям в поведении летчика, в оценке об-
становки, принятии решения и т. п. Эти особенности объясняются раз-
личиями в степени натренированности, а также физическими, физиоло-
гическими и психологическими различиями людей, их характером,
темпераментом, типом нервной системы и т.п.
Во-вторых, летчик как управляющее звено является исключитель-
но сложной системой, не имеющей, по-видимому, однозначного матема-
тического описания вида Хвых = ^(Хвх)? гДе ^вых> например, переме-
щение рычага управления, а Хзх — один из параметров полета, вос-
принимаемых летчиком. Поэтому одним из кардинальных направлений
в изучении динамических характеристик замкнутого контура самолет —
летчик являются экспериментальные методы стендовых исследований.
Исчерпывающие обобщающие материалы по стендовым исследованиям
динамики полета самолета с летчиком изложены в монографии Г.С. Бю-
шгенса и Р.В. Студнева [4].
Тем не менее в ряде случаев поведение летчика удается аппрок-
симмировать достаточно простой математической моделью, доступ-
ной для аналитических исследований. Например, при внезапном нару-
шении режима полета представляется естественным рассматривать
рефлекторные действия летчика, направленные на скорейшее париро-
вание нежелательного возмущения. Ситуации такого рода могут воз-
никнуть при групповом полете, при полете в турбулентной атмосфере
на малых высотах и т л.
Рефлекторное поведение летчика можно аппроксимировать, в част-
ности, упрощенной релейной математической моделью с учетом не-
которого запаздывания его реакции. Помимо рефлекторного пилоти-
рования летчику часто приходится решать задачи стабилизации угло-
вого положения самолета, точного выдерживания заданного режима
и т. п. Поведение летчика в этих случаях можно аппроксимировать
линейной математической моделью с запаздыванием. Упрощенные
математические модели летчика как динамического звена в системе
управления самолетом позволяют приближенно оценить основные харак-
теристики замкнутого контура и провести параметрический анализ
в аналитическом виде применительно к ряду практически важных задач.
Алгоритмы управления, применяемые в реальных системах авто-
матического регулирования, также можно аппроксимировать упрощен-
ной математической моделью релейного или линейного типа. С этой
точки зрения безразлично, что понимается под управляющим звеном:
модель летчика или модель автопилота.
113
Разница между моделью летчика и автопилота может заключать-
ся в параметрах движения самолета, на которые они реагируют, и в ко-
личественных характеристиках принятой модели. Например, летчик,
находясь в кабине, непосредственно ощущает только местные значения
перегрузок. Так как кабина на современных маневренных самолетах
расположена далеко перед центром масс самолета, то величины перегру-
зок, ощущаемые летчиком, не совпадают с перегрузками центра масс
самолета, особенно при энергичном маневрировании. Автопилот мо-
жет реагировать практически на произвольную комбинацию параметров
полета, реализованную в его вычислительном устройстве.
Поэтому представляет практический интерес проанализировать
в безразмерном виде динамические характеристики замкнутого кон-
тура с различными типовыми алгоритмами управления в цепи обратной
связи и оценить влияние величины времени запаздывания на устойчи-
вость контура и качество переходных процессов для отдельных управля-
ющих параметров и некоторых их комбинаций.
Поскольку оценки динамических характеристик замкнутого кон-
тура проводятся по единой методике для различных алгоритмов уп-
равления, то описание общих методов расчета и основных обозначе-
ний, применяемых в дальнейшем в настоящей главе, выделено в разд. 4.2.
4.2. ОБЩИЕ МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ЗАМКНУТОГО КОНТУРА
С ЛИНЕЙНЫМ АЛГОРИТМОМ УПРАВЛЕНИЯ
Если управляющий параметр и зависит от какой-либо фазовой
координаты, то динамическая система становится замкнутой. Простей-
шим алгоритмом управления в замкнутой системе является линейное
управление одной фазовой координатой по закону: и = Кх^
Передаточная функция замкнутой системы, управляемой по тако-
му закону (см. рис. 4. 1, а), выражается соотношением
w(p)------
и зависит от параметра К — коэффициента усиления обратной связи.
Здесь И7! (р) — передаточная функция разомкнутой системы по уп-
равляемой фазовой координате х/.
Характеристическое уравнение замкнутой системы имеет вид
1+7СИ/1(р) = 0. (4.1)
Корни этого уравнения называются полюсами передаточной фун-
кции замкнутой системы (в дальнейшем для краткости - полюсами).
Корни уравнения W(p) = 0 называются нулями передаточной функ-
ции замкнутой системы (в дальнейшем для краткости — нулями).
114
Зная корни уравнения (4.1), можно сразу записать решения системы
линейных дифференциальных уравнений для замкнутой системы, и оп-
ределить ее динамические характеристики методами, изложенными
в гл. 2.
Таким образом, основной задачей, возникающей при определении
динамических характеристик замкнутой системы, является исследова-
ние поведения корней алгебраического уравнения (4.1) в зависимости
от передаточного числа К. Решение этой задачи сводится к построению
траекторий корней характеристического уравнения замкнутой системы
(или корневых годографов) при изменении коэффициента К от 0 до
бесконечности. Очевидно, что при К = 0 система становится разомкну-
той, и поведение ее определяется распределением корней собственного
характеристического уравнения. Эти корни являются полюсами разом-
кнутой системы и одновременно являются начальными точками кор-
невых годографов замкнутой системы.
В силу того, что корни алгебраического уравнения — непрерывные
функции его коэффициентов, можно считать, что при малых изменениях
величины коэффициента усиления К корни замкнутой системы (4.1)
будут незначительно отличаться от корней, определяемых характеристи-
ческим уравнением разомкнутой системы. Малые изменения корней
удобно охарактеризовать величинами производных в точках полюсов
на комплексной плоскости:
dx . du
Ик ** = о илГ'*=0’
где х и со — соответственно действительная и мнимая части исследуе-
мого комплексного корня. Так как эти производные определяются"
в точке К = 0, то определить их обычно бывает не сложно,
~ dG) . dx du w
Отношение производных — /— = — | к = 0 представляет собой
угол наклона касательной к корневой траектории на комплексной плос-
кости в точке рассматриваемого полюса.
г» । - ,
Величина — | & _ 0 имеет ясный физическии смысл: ее знак опреде-
ляет тенденцию к изменению времени затухания колебательной состав-
ляющей замкнутой системы по сравнению с разомкнутой, свободной
системой.
Аналогично знак величины производной | к _ Q характеризует
изменение собственной частоты замкнутой системы при изменении пере-
„ п dx . dec ,
даточного числа л. Величины—— I г Л и \ л являются важными
dK а — и dK Л — о
параметрами, позволяющими выделить различные типы корневых
годографов замкнутой системы.
115
Влияние передаточного числа удобно анализировать при помощи
зависимости х(К)9 характеризующей изменение действительных частей
комплексных корней замкнутой системы при изменении передаточного
числа К. Важно также уметь оценить отношение t2
х(0)
= 77^ ’ 0ПРеДеля"
х (Л)
ющее время уменьшения амплитуды колебаний вдвое.
Ясно, что может существовать передаточное число, при котором
х(А0 достигает максимального значения. Такое значение передаточного
числа целесообразно назвать оптимальным. Значение К Ф 0, при котором
х(К) = х(0), удобно назвать эффективным значением передаточного
числа А"эф, так как при К = КЗф время затухания колебательной состав-
ляющей замкнутой системы равно времени затухания разомкнутой,
свободной системы. Если дальнейшее увеличение передаточного числа
приводит к увеличению времени затухания (уменьшению |х(£)|), то
значение передаточного числа, при котором действительная часть ком-
плексного корня обращается в нуль, является критическим А^кр, так как
замкнутая система при этом находится на границе колебательной устой-
чивости.
Величину А^опт, можно оценить, например, непосредственно диффе-
ренцируя зависимость х(К ) = f(K)9 приравняв нулю производную
df(K)jdK = 0 либо при грубых оценках положив А^опт ~ М;Эф.
Выявление характерных точек Х’опт, А^Эф иА^кр зависимости х (К)
позволяет построить качественный вид функции х (К) и дает наглядную
возможность судить об устойчивости замкнутой системы при изменении
передаточного числа К, Простота определения характерных точек поз-
воляет получить в аналитическом виде приближенные оценки значений
АГОПТ, ^эф, *кР (если они существуют) и приближенную количествен-
ную картину изменения поведения замкнутой системы с изменением
передаточного числа для каждой корневой траектории.
Для проведения параметрического анализа характеристик замкну-
той системы необходимо уметь находить качественный вид зависи-
мостей f(K) и корневых траекторий при изменении характеристик
разомкнутой системы, т. е. при изменении коэффициентов характерис-
тического уравнения разомкнутой системы.
При этом важную роль для качественного анализа играют точки
ветвления годографа, или бифуркационные точки, соответствующие
появлению кратных корней характеристического уравнения.
Для уравнений не выше третьего порядка (с действительными
коэффициентами) точки ветвления могут находиться только на дей-
ствительной оси комплексной плоскости, так как кратными корнями
могут быть только' действительные числа, Поэтому для качественной
оценки поведения корневой траектории в точке ветвления достаточно
116
ограничиться рассмотрением квадратного уравнения вида j^2 + ру +
+ q = 0, корни которого х ± /со выражаются через коэффициенты pnq'.
х = —?~ ; G) = \/D ,
2
W г. Р2
D = q-L.
Так как
Эх _ _ 1 а Эсо _ 1 ЭР •
Эр- 2 ’ Эр 2у/г>" <>Р ’
dco _ л
то-^—-*°° при £>-* О,
откуда следует, что касательная к корневой траектории в точке вет-
вления (D = 0) перпендикулярна действительной оси.
В этой точке пара сопряженных комплексных корней превращает-
ся в пару кратных действительных корней, и корневые траектории
терпят излом. Условие существования действительных корней можно
получить, положив в характеристическом уравнении р = — х д.
Легко видеть, что в координатах К, хд кратные корни должны
удовлетворять уравнению dKjdx^ = 0.
Если порядок характеристического уравнения выше второго, то
могут появиться корни тройной кратности или выше, В координатах
К, хд точка трехкратных корней является точкой перегиба, и опреде-
ляется из системы двух уравнений:
dKfdx^ = 0;
c?Kldx* = 0.
Таким образом, для заданного алгоритма управления в продоль-
ном короткопериодическом движении можно построить качественный
вид корневого годографа на комплексной плоскости и оценить харак-
терные параметры, определяющие поведение замкнутой системы.
Анализ типовых алгоритмов управления продольным короткоперио-
дическим движением самолета проводится ниже по единой методике в
безразмерной форме.
Подстановкой р = — х + ш в характеристическое уравнение замкну-
той системы _1_+ KWf(p) = 0 выделяются действительная U(x, со, К)
и мнимая V (х, со, К) части:
U(x, й,£)=0;
К(х, сЗ,Г)=0.
Определяются четыре параметра полюса (при К = 0): х| % _ 0;
^1? = о>
117
dx , dco .
~~=~ I К = 0’ I к = о
dK dK
Из системы уравнений
^^ф^ф) == О»
и(£,^эф;*эф) = о.
определяются эффективные параметры системы соЭф, ^Эф, соответ-
ствующие х = — f, а из системы уравнений
^кр) = 0;
(0, ^кр) = О-
определяются критические параметры, соответствующие границе ус-
тойчивости системы (х = 0).
Проверяются условия существования кратных корней (со = 0)
t/(^,0,^) = 0;
Г(^,0Л)=0
и координаты нулей системы
Таким образом, при исследовании динамических характеристик
замкнутой ^системы в простейших случаях появляется дополнительный
параметр К, характеризующий эффективность управления и опреде-
ляющий динамические свойства замкнутой системы.
При усложнении алгоритмов управления или при увеличении числа
регулируемых параметров увеличивается также количество безразмер-
ных коэффициентов, определяющих поведение замкнутой системы.
Анализ линейных алгоритмов управления двумя фазовыми коорди-
натами типа и = KtXi + К2х2 удобно проводить, приняв один из коэф-
фициентов Kj равным единице, и рассматривать закон управления,
например, в виде и = К(хг + vx2), где К = Klf v = К21КХ. При такой
форме записи управление одной фазовой координатой является част-
ным случаем. Например, и = Кхх соотвествует v = 0, а и —Кх2 соответст-
вует v = 00.
Естественно, что введение дополнительного коэффициента сущест-
венно усложняет анализ поведения замкнутой системы из-за увели-
чения размерности пространства независимых параметров, определя-
ющих динамические характеристики системы.
118
4.3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ЗАМКНУТОГО КОНТУРА
ПРИ НАЛИЧИИ ЗАПАЗДЫВАНИЯ
Учет запаздывания в цепи обратной связи, всегда присутствующего
в реальных системах управления, в аналитическом выражении пред-
ставляет собой введение дополнительной передаточной функции W(p) =
= е“ рТ, где т — время запаздывания.
Амплитудная характеристика такой передаточной функции тож-
дественно равна единице при любых частотах (амплитудные искажения
отсутствуют), а сдвиг по фазе пропорционален произведению частоты
на время запазывания.
Для анализа динамических характеристик управляемых систем
с учетом запаздывания необходимо предварительно выяснить основные
свойства таких систем, вытекающие из общей теории дифференциальных
уравнений с запаздывающим аргументом.
Дифференциальные уравнения с запаздыванием (или уравнения с
отклоняющимся аргументом, дифференциально-разностные уравнения)
отличаются от обычных дифференциальных уравнений тем, что при
наличии запаздывания неизвестные функции и их производные входят
в уравнения при различных значениях времени.
Наличие запаздывания в системах автоматического регулирования
вносит принципиальные трудности в исследование динамических харак-
теристик таких систем в аналитическом виде (даже для систем, опи-
сываемых линейными дифференциальными уравнениями невысокого
порядка с постоянными коэффициентами). Эти возникающие трудности
с математической точки зрения связаны в основном с неразрешимостью
трансцендентных уравнений в аналитическом виде.
В настоящее время достаточно полно разработана теория уравне-
ний такого типа, сформулирован и доказан ряд общих теорем существо-
вания и единственности решений, исследованы важные для практических
применений частные случаи. Однако количественный анализ систем ре-
гулирования с запаздыванием возможен только приближенными мето-
дами.
Для упрощения дальнейшего изложения необходимо отметить
ряд общих аналитических результатов, характеризующих поведение
и свойства решений дифференциальных уравнений с запаздыванием.
Поскольку короткопериодическое движение самолета описывается
линейным дифференциальным уравнением с постоянными коэффициен-
тами не выше третьего порядка, а передаточная функция замкнутой
системы имеет вид W(p) =-----------, то при наличии запаздывания
1 + KW!e~pT
в цепи обратной связи достаточно ограничиться рассмотрением урав-
нений не выше третьего порядка двух типов:
119
^£1 +2f^I)+ К[А^-^.^ в ^L22 +
dt3 dt2 dt dp dt
+ Cz(t- r)] = 0;
+ 2f + z(0+ К[А
dt2 dt dt2 dt
+ Cz(t- r)] = 0.
В соответствии с принятой терминологией [18, 23] первое уравнение
называется уравнением запаздывающего типа, второе — уравнением
нейтрального типа.
Для такого рода уравнений известно, что при заданных начальных
условиях существует единственное решение в виде бесконечной суммы
№«>
экспонент S где Рк — некратные попарно-различные корни
№0
характеристического уравнения, называемого квазиполиномом*.
Этот принципиальный строго установленный факт позволяет пере-
нести хорошо известные методы исследования линейных дифференциа-
льных уравнений с постоянными коэффициентами на системы с запаз-
дыванием.
В связи с этим решение прикладных задач с учетом запаздывания
сводится фактически к определению корней характеристических урав-
нений, которые становятся трансцендентными.
Для рассматриваемых дифференциальных уравнений квазиполи-
номы соответственно имеют вид
р3 +2£р2 +р+К(Ар2 +Вр + С)е рт = 0;
р2 + 2£р + 1+Х’(Лр2 + Вр + С)ё~рт =0,
т. е. к обычному характеристическому уравнению добавляется произ-
ведение К (Ар2 + Вр + С)е~рт. Различие между характеристическими
квазиполиномами состоит в том, что показатель степени старшего чле-
на первого уравнения выше показателя степени в скобках, а во втором
уравнении показатели степени старших членов совпадают.
В цитированных работах показано, что устойчивость движения сис-
тем, описываемых уравнениями с запаздыванием определяется, так
же как и для обычных линейных дифференциальных уравнений с пос-
тоянными коэффициентами, знаками действительных частей корней
* Строгие доказательства этого факта приводятся в работах [18, 23]. Там
же приведена подробная библиография по теории дифференциальных уравнений
с запаздыванием.
120
характеристического уравнения. Однако простых критериев устой-
чивости (типа критериев Рауса - Гурвица), накладывающих ограни-
чения на коэффициенты характеристического уравнения, для общего
вида квазиполиномов пока не получено из-за возникающих трудностей в
оценке поведения корней при изменении коэффициентов уравнений.
Трудности обращения с квазиполиномами состоят в том, что в
комплексной области такие характеристические уравнения имеют бес-
численное множество корней. В этом легко убедиться, положив z = х +
+ /о? и разделив действительные и мнимые части по известной формуле
Эйлера:
е2 -= е?+ = e*(cos (у + 2ктг) + i sin (у + 2ктг)),
где х, у — действительные числа.
Разделив уравнения для мнимой и действительной частей друг на
друга, легко получить одно уравнение вида
tgGJT =
Pi(x, GO)
Р2(х, GO)
гдеРх (х, о?) иР2 (х, о?) - обычные алгебраические многочлены.
Поскольку tgccr - периодическая функция с периодом я, то полу-
ченное уравнение имеет бесконечное множество корней, причем раз-
ность соседних частот go^ - gok _ 1 не больше отношения тг/т gok —
- GOk- i < я/т, при этом бесконечные ’’цепочки” корней не пересекают-
ся между собой.
Можно показать [23], что траектории корней квазиполиномов
на комплексной плоскости представляют собой бесконечный набор
не пересекающихся дискретных кривых, уходящих в бесконечность
слева от мнимой оси. Это утверждение позволяет выделить доминиру-
ющие корни характеристического уравнения, которые при К -* 0 стре-
мятся к полюсам разомкнутой системы, и следить только за траектория-
ми доминирующих корней, имея в виду, что корни из оставшейся бес-
конечной цепочки заведомо устойчивы.
Однако интуитивно ясно, что при очень малых значениях т беско-
нечная цепь корней практически не оказывает влияния на решение,
и доминирующие корни уравнения в этом случае близки к исходным
значениям без запаздывания.
Аналогичным образом можно считать, что при очень малых К корни
уравнения замкнутой системы близки к копиям уравнения разомкну-
той системы.
Исследование траекторий корней при изменении передаточного
числа К удобно и в этом случае проводить методами, изложенными
в разд. 4.2. При этом практический интерес представляет поведение до-
минирующих корней при изменении передаточного числа К.
121
Таким образом, учет влияния запаздывания в цепи обратной связи
на динамические характеристики замкнутого контура сводится к ана-
лизу изменения характерных параметров системы, рассмотренных в
(А^оптэ *эф и т. п.), и их зависимостей от величины запаздывания.
Вследствие громоздкости выражений, необходимых для прове-
дения анализа в целях краткости изложения основные исходные урав-
нения для различных типовых законов управления сведены в табли-
цы, приведенные в разд 4.4.
44. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОГО КОНТУРА
ПРИ ТИПОВЫХ ЗАКОНАХ РАЗДЕЛЬНОГО УПРАВЛЕНИЯ
ПАРАМЕТРАМИ ДВИЖЕНИЯ САМОЛЕТА
В настоящем разделе рассматриваются типовые законы управ-
ления отдельными параметрами короткопериодического движения
самолета.
В качестве типовых законов анализируется управление углом атаки
или перегрузкой (с точностью до постоянного множителя пу =
= п°у а) , углами тангажа # и наклона траектории 0, угловой скоростью
и угловым ускорением goz тангажа.
Исходное управление продольного короткопериодического движе-
ния самолета записывается в предположении = 0. ___
Величина времени запаздывания т ограничена неравенством сот <
< я, т. е. не превышает полупериода собственных колебаний замкну-
того контура.
Анализ проводится в безразмерной форме методами, изложенны-
ми в предыдущих разделах настоящей главы с использованием основ-
ных соотношений, сведенных в табл. 4.1 — 4.3.
Для получения приближенных оценок в ряде случаев предпола-
гается выполнение приближенного равенства параметров В и f:
так как 5= , a 2f = Т^01-М?),
то 5 - f (Mz°z + м“) « 0,
Хх е. такое предположение вполне допустимо вследствие малой разности
В — f, при условии, что В или f не являются бифуркационными парамет-
рами (корнями уравнений, определяющих кратные корни характерис-
тического уравнения). _
В приводимых ниже результатах такая замена В = f будет исполь-
зована при необходимости без дополнительных разъяснений.
Управление углом атаки (перегрузкой) 6 = Кор1(КПуПу). Из табл.4.2
следует что в этом случае корневой годограф и качество переходного
процесса имеют вид, изображенный на рис. 4.2; на тех же рисунках при-
122
Основные параметры корневых годографов и качества переходных процессов
замкнутой системы при различных законах управления (т3 = О, В = F°T0)
Таблица 4.1
Параметр управле- 6 = Каа,К = 6 =K^,K = 6 = кве,к = S - К шгК~ 8 ~ Kuj7wzK -
НИЯ z z
= = - KqT^Y01!^ ^-KWT„M6Z = -K,.MS, z
Характеристичес - Р2 + 2?р +1 + р3 +2ip2 +р+ р3 + 2fp2 +р + p2 +2fp+ 1 + P2 + 2?p + 1 +
кое уравнение + К = 0 + К(р+В) = 0 + К = 0 + f(p+B)=0 + fp(p+B)=0
1 - 1 __
Система уравне- х = f КВ= 2(Г - K=2(i-x)(w2 + X = ?+ 2 x=^+-KB)/(l+K)
ний для о пределе- u> = \/^+l-f2 -x)(cJ2 + х2) + Я2) со2 = йг=-х2 +2BX+ 1 u>2 = -x2 + (2x -
ния комплексных й2 = = 3£2-4^+1 -B)/(2?-B)
2(х-{) + В
+В(3х2 -4dc+ 1)
корней + 1
dx dw dx 1 - dx _ 1 dx _ 1 dx В - 2?
Параметры корне- — = 0; — = dK dK Тк = -2В’_ ~dk “ ~F’ dK~ 2’ - - ZX -i » dK 2
= 1 da) __ 1 — В$ dw _ B-g dco 2£2-1-Д?
вого годографа 2ч/1-?2' dK 2x/T-f’’ dK 2Vl-f2' dK 2^/1-^ dK 2-Jl-i2'
при К = 0 в точке
с координатами
х= ftwVl-f2
Координаты ну- лей корневого годографа х — В, со = 0 х = В, со = 0 хх = В, сох= 0, х2 = 0, со2=0
Система уравне- ний для определе- ния параметров ^кр» ^эф *эф = К при любом К Не имеет решений Не имеет решений Не имеет решений Не имеет решений
Система уравне- ния для опреде- ления парамет- ров Ккр, о>кр Не имеет решений То же ^кр = 2fco2Kp соКр = 1 То же То же
Уравнения для определения дей- ствительных корней То же К = (В-х) = х(х2- - 2ix + 1) -К=х(х2- -2fx"+l) К = (В-х) = х- -2?Г+1) Кх(В-х)=-(хг - -2J-X+1)
Система уравне- ний для опреде- ления кратных корней Не имеет решений Не имеет решений К(В-х) = х2 + 2$х+ + 1 X — 2Вх — -1 = 0 Кх (В -х)= -(х2 - - 2?х + 1) К(2х-В)= 2(£-х)
Основные параметры годографов доминирующих корней и качества переходных процессов
замкнутой системы при различных законах управления с запаздыванием
к
Таблица 4.2
Параметры управления 5 = Каа,К=КаТ1^ Б = К#0,К=-К$Т1М% Б = квв,к=-квт>мЬ
Характеристическое урав- нение p + 2fp+l + Ke рт = 0 р3+2?р’ + р + £ф+В)е рт=0 p3+2fpJ+p + fe“PT=0
Система уравнений для определения комплек- сных корней К eXrcos co7 = co2 + 2$x — - xj_= 1 КeXT$inut = 2co(f — x ) KeXT[(B — x) cos co 7 + co sin got J= = 2(co2 -x2)(X-x)-xX X (co2 + x2 - 1) К qXt[gj cos (луг — (В — x)sinco7] = = 4xco(f-x)+(3(co2 + x2 -1) ^eXTcosw7 = 2(co2 -x2)(f- -x)-x(co2 +a2 - 1). XeXrsinco7= -4xco(? - - x) -co(co2 +a2 - 1)
dx dK
Параметры комп- лексного полюса К = 0 х= ы = ^Tsinx/1 - f2 т 2х/1-Г2 2ч/1-Р X cosVl-f2r+(l - Bi) X X sin\/l—f2r] ——^Tts/i-e x 271-Г2 X sinx/1- f2 7 + ?COS\/1 -f27]
duj ~dK —--—-4e^Tcosy/1 - f2 т 2>/l^? —к_е^[(1-ВПХ 2<Vi _ >2 X cos^1 - f2 7 - B\/1 - f2 X X sin>/l-f27]
=Vi-г
126
Продолжение табл. 4.2.
Параметры нуля ~ Х = В й = 0 ~
Система уравнений для определения параметров ^эф» ^эф ^эф=(“’эф+?а-1)е ?Г ^эФ=и^ф->-?а-1)Х ? X (.в-Га)1Х X е~^т ^эф * f2 - 1) X X ч/£|ф + /]е-?г
tgu^T= 0 ^шэфт = - ^эф/^эф + -ВО tga>^T= CJ^/f
Система уравнений для ^кр = ^^кр" 2 + ^кр~ WKp^WKp- + /кр = “крх/£<р-1)а +
определения параметров + 4fa^p + 4?’шкр/^кр+®2) ^’"’кр)
^эф» ^Кр tg^Kp2 = 2ft*4cp/(wKp' -1) tgwKp?=(2fG^p+S(l- «4<рг= (1-
-“кр)]/[“кр(“кр-1 + 2?£)] - “кр)/(2?Ч<р)
Уравнение для опреде- К еХт = -(*’ - 2ix +1) К(Х-В)еХт = -(х2 - 2$х+ 1)* КеХт =х(х2 - 2}х+ 1)
ления действительных корней
Система уравнений
для определения крат-
ных корней
Действительных корней К (х - В)ъХт - (х2 - 2£х + 1) х
не существует К(хт - Вт+ 1) еХт = - (Зх2 -
-4^+1)
КеХт_ = х(х — 2$х+1)
КтеХт= Зх2 -4J-I+1
Система уравнений
для определения кор-
ней тройной кратности
То же
Кратных корней не существует КеХт=х (х2 - 2fx + 1)
КтеХт= Зх2 -4fx + l
КтеХт= Ьх - 4f
Таблица 4.3
Основные параметры годографов доминирующих корней и качества переходных процессов
замкнутой системы при различных законах управления с запаздыванием
Параметры управления Ь => к =-кштм^ 6=K^ziK=-K^2MSz
Характеристическое уравнение р2 + 2?р + 1 + К (р+В)е рт = О
р2 +2$р + 1+Кр(р+В)е ?т = О
Продолжение табл. 4.3.
128
Система уравнений для определе- ния комплексных корней КеХт[(В — х) cos сот + со sincor ] = = со2 + 2£х - х2 - 1 Хе*7 [go cos сот - (В - x)sincoT] = = — 2co(f -х) КеХт[(х2 — uj2Bx ) со scot — со(2х — - Я) sin сот] = со2 + 2fx - х2 - 1 Хе*7 [со(2х-B)coscot + (х2 - со2 - - 5x)sincor]= 2co(f - х)
dx —,е^т [x/l-f2 cos\/l- £ т- - че^т[(2£ - Вх/1 - £2 со9>/1 - f2'т +
dk 2х/1-Га 2х/1 — <*2
- (В -f)sinVl-faT + (2f’ - 1 -Bf)sinVl- f’r]
Параметры комплексного
/ dco х = г, w = v 1 - ? — —Д==,е?г[(Я - f)cos\/l - Ит + —^=,eiTl(,2i2 -1 -Bf)cosx/1 - f’r +
dK 2Vl-f’
+ х/1 - £2 COS\/1 - Г2 7 ] + (2f - S)V 1 - f’sinV1 - f’7]
Параметры нуля {К -► °°) х = В, со = 0 Xj = B9 cox = 0,x2 = 0, coa = 0
Система уравнений для оп- *эф= [(йэф+f’-D/ ^эф = -К“Й> + ?’ - !>/
ределения параметров (В-f)2 ]е?т ^-^эф#)3 + Йф(2?-Я)2]е“!'т
*эф> соэф tgU^T = со эф/ (В- f) *ёсоэфт= (2Г-В)соэф/(со£ф-£2+Я£)
*кр, ^кр ^кр — V(wKp - I)2 +4£2 о?кр/ Ккр — [хА^кр 1 )2 + 4f2 и>кр J/
х/и>кр + Я2 tgtJKpT~ (и>3кри>кр + о?Кр5)/ (5 <*>2кр — 2fu?Kp) [и>кр\/и>кр + ^2 1 tg^Kp7^ ^(wKp~ 1)~2fu?Kp]/ [u>Kp(u>Kp+1 +
Уравнение для определения действительных корней К (В - х)ехт = - (? - 2?х +1) Кх(х - В)еХт = -(х2 - 2fx+1)
Система уравнений для определения кратных корней К(В-х)ехГ= -(х2 - 2fx+ 1) К(хт — Вт+1)ехт = 2(x-f) Кх (х - В)еХт = ~(х2 -2fx + 1) К(2х - В) + х2 т - В х 7)ехт= - 2(х - f)
Система уравнений для определения корней трой- ной кратности К (В - х)еХт = - (х2 - 2ix+1) К(хт-Вт+1) еХт = 2(х-0 К(хт2 -Вт+2т)еХт = 2 Кх(х -В)ехГ= - (х2 - 2ix + 1) К (2х - В + х2 т - Вх т - ДМ еХт= - 2(х - ?) К(2 + 4хт -2Вт + х2т2 -Вхт2)еХт= -2
129
ведены кривые, отражающие деформацию годографа и качества переход-
ного процесса вследствие влияния запаздывания т.
Как следует из табл. 4.1, эффективных значений частот и переда-
точных чисел в случае управления углом атаки не существует, и не-
равенство х < f выполняется при любом К.
Преобразовав систему уравнений для определения критических
значений частот и передаточных чисел (х = 0) к виду
tg^KPT = 4vK-P-
WKp - 1
^кр — v(w кр ~ I)2 + 4f2c*^p,
для малых значений сокр можно получить приближенные оценки крити-
ческих частот и передаточных чисел:
Рис. 4.2. Типы корневых годографов и параметры качества при управлении перег-
рузкой или углом атаки: _
а - без запаздывания; б - при наличии запаздывания; в - зависимость х = f(K)'
г - зависимость ~ f(K)
130
Для определения действительных и мнимых частей х и аз домини-
рующих корней замкнутой системы при значениях параметра К из ди-
апазона 0 < К < ASKp из системы
4 -- 2сЗ (f- х)
tgaiT = _ -----;
w 2 + 2f х - х2 - 1
К = x/(w2 + 2fx - х 2 - I)2 + [2w(f - x)]2e~xT
можно получить, учитывая малость хит, путем разложения tgccr в ряд
Маклорена приближенные оценки:
- ~ 2f - Кт
х ;
2 + Кт2
- 2+ Кт2
--
\/1 + А-
При управлении углом тангажа # в случае отсутствия запаздывания,
как следует из табл. 4.1, действительная часть корня х < f, и асимптота
корневого годографа определяется уравнением х = f —На рис. 4.3
приведен годограф комплексного корня, полюсом которого является
точка с координатами (f, - f2), и годограф действительного корня,
который начинается в начале координат и стремится к точке с коорди-
натами (В, 0). Величину действительного корня легко оценить для
. - КВ
малых Г^д=-р-т-7-
А т 1
Для комплексного корня, используя малость х, также можно полу-
чить простое соотношение:
х = ---------?— ; о?2 *К + 1.
К+ 1
При наличии запаздывания т Ф 0 для реальных величин В и J* в широ-
ком диапазоне значений времени запаздывания т кратных корней и
эффективных значений передаточного числа/Сэф не существует.
Рис. 43. Типы корневых го-
дографов при управлении уг-
лом тангажа:
а - без запаздывания; б -
с учетом запаздывания
131
При выполнении условий неравенства хдт < 1 действительный
корень практически не зависит от величины т и
хп =----Влияние
д 1 + К
запаздывания т заключается в том, что величинахд несколько медленнее
стремится к своему пределу В при неограниченном возрастании пара-
метра/^.
Для определения критических значений передаточного числа и час-
тоты колебаний следует рассмотреть систему уравнений в виде
. _ 2fr? + 5(1-а>2)
tg^Kp^ = ;
w(w2 -1+ 2ffi)
К = ш
/(1-а>2)2 + 4{~2g?
cj2 + в1
Эта система в общем виде решения не имеет. Однако для ряда
частных случаев, представляющих практический интерес, можно полу-
чить приближенные оценки с достаточной для практических расчетов
степенью точности.
Система имеет решение при а?кр1т = —Для c5Kpi = 1 - 2f2? при
- я - -
т = — ----- ЧВ этом случае Л?кр1 = 2fu?Kpi,
2 Vi - f* '
Очевидно, что для всех значений со > сЗкр1; сЗГ < я/2; т < я/2,
а для всех значений со < сЗкр; сЗт > я/2; т > я/2.
При достаточно малых значениях величины сот и со2 > 1 уравнение*
для тангажа можно разрешить относительно со, заменив в левой части
уравнения тангенс малого угла его значением:
— 2fco2 + В(1-с32)
сот « ;
со(со2 -l+2f5)
-2 2$-В _ 2?-В
^кр 1 + —z— ~ ———
откуда следует приближенная оценка для величины критического пере-
даточного числа, при котором происходит потеря устойчивости:
jF ~Т,2 — В
Лкр ~ ^кр ~ ’
Полученные простые соотношения позволяют оценить параметры
границ колебательной устойчивости в зависимости от режима полета,
характеристик свободного самолета и величины запаздывания.
132
Сравнивая полученные результаты с результатами, полученными
при т = 0, можно сделать вывод, что наличие запаздывания в цепи обрат-
ной связи может привести к потере устойчивости замкнутого контура
при управлении углом тангажа.
Оценку качества переходного процесса в замкнутом контуре уп-
равления можно получить, воспользовавшись малостью значений сот и f.
Приближенная оценка величины корней и времени затухания пе-
реходного процесса имеет вид
2$-Кт-ВК/(1+К)
2 +Кт2
1 +К ;
—_,-+5_г2 _
2^ — Кт — ВК/(1+К')
Полученные приближенные соотношения хорошо согласуются с
точными решениями.
Управление углом наклона траектории 6 = Кд6. При управлении
углом наклона траектории, как следует из табл. 4.1, 4.2 характерис-
тическое уравнение со старшим членом третьего порядка имеет три
доминирующих корня.
Анализ показывает, что при т < -=1. - arctg—. и малых
К частота колебаний и действительная часть комплексных
корней характеристического уравнения по абсолютной величине умень-
dx 1 - d(jJ 1 - п
шаются с ростом параметра К, так как —— | к = q < 0 и —-1 к = 0 < 0.
dK dK
Качественный вид зависимости К(х) при фиксированных f и т
приведен на рис. 4.4. Из рисунка следует,что при различных значениях
параметра К характеристическое уравнение может иметь либо два дей-
ствительных корня, либо вообще не иметь действительных корней.
Рис. 4.4. Типы корневых годографов при управлении углом наклона траектории:
а - без запаздывания; б - с учетом запаздывания; в - К = /(хд)
133
Анализ показывает, что существует некоторое максимальное зна-
чение параметра
~ ~ 135
Лтах ~ ZT" >
у
при котором уравнению удовлетворяет действительный корень двой-
ной кратности. При увеличении параметра К > А^тах характеристи-
ческое уравнение действительных корней не имеет.
При малых значениях параметра К
Pi = -хд^К.
Для рассмотрения доминирующих комплексных корней систему
уравнений, определяющих критические значения частоты и параметра
К, следует записать в виде
— 1 -о?
tgwr = —=— ;
К = w V(1 -w2)2 + 4f2w2 .
Из табл. 4.2 следует, что в приведенных соотношениях для величины
относительной частоты и времени запаздывания должньд выполняться
неравенства: со < 1; сот < я/2. _ __
При стремлении величины со к единице величина сот стремится к
нулю и величина параметра К стремится к значению 2f. При стремлении
частоты со к нулю величина параметра К стремится к нулю, при этом
допустимая величина запаздывания неограниченно возрастает.
Можно показать, что на границе устойчивости значение частоты
колебаний близко к единице. Разложив полученные выражения в окрест-
ности точки со = 1 в ряд по сЗ, можно получить приближенные соотно-
шения для оценки критических значений параметров А и со:
,-т ~1
WKP * ------ >
l+fr+ f tg т
„ 2t .
1+JT+ ftgr
Полагая величину запаздывания малой и заменяя tgr ~ т, эти соот-
ношения можно преобразовать к более простому виду:
^кр ~ 1-------ZT" ’
1 + 2?Т
*кр ~ 2s71 ч 2fr
134
Поскольку в интервале значений 0 < К < А^кр величина частоты
лежит в пределах \/1 - f2 < о? < 1 — $т, то можно получить приближен-
ные соотношения для оценки времени затухания переходного процесса:
2(1 - КТ)
„ - _ f ~ 2f(l - КТ)
И I2---=“ ~ -~— •
х 2f-/C(l + 2$Т)
Эти соотношения при т < 1 дают хорошую аппроксимацию точного
решения системы трансцендентных уравнений.
Управление скоростью изменения угла тангажа 6 = K^z gjz. Домини-
рующими корнями характеристического уравнения при К = 0 является
пара сопряженных комплексных корней свободного самолета.^
Из табл. 43 следует, что при малом значении параметра т величина
производной -3-1 к — q >0, частота увеличивается с ростом параметра
К при малых К при условии В = 0.
Если величина В Ф 0, то при В > f так же, как и при малых значениях
f, частота растет с ростом параметра К | = о > 0) практически
при всех значениях величины запаздывания т.
При больших значениях коэффициента относительного демпфиро-
«. - ~ do? . _
вания s, близких к единице, знак производной—3-1 ^ = о определяется
dK
знаком разности (В - f). Таким образом, возможны два различных
. dco
типа корневого годографа, в зависимости от знака производной —3
dK
в окрестности К = 0 (рис. 4.5).
Для малых значений относительного времени запаздывания т воз-
можно существование действительных корней характеристического
уравнения. _ _
Зависимость параметра К от величины хд и от величины запазды-
вания т представлена на рис. 4.5. _
Так как при f < 1 выражение (хд — 2£хд + 1) > (хд — I)2 > 0,
то из выражений, приведенные в табл. 4.3, следует, что действительные
корни всегда существуют и по абсолютной величине больше параметра В.
Из рис. 45, б видно, что в зависимости от величины запаздывания
т число действительных корней может быть различным. Для фикси-
рованного значения К возможны следующие варианты: один, либо два,
либо три действительных корня. При наличии трех корней возможны
135
корни двойной и тройной кратности, при малых значениях запаздывания
т, разложив в ряд е « 1 + хт, несложно получить х -=----,
Это выражение дает хорошую оценку действительного корня при
больших и малых значениях параметра К. _ _ _
При значениях параметра л, лежащих в диапазоне <к<ка1,
существует пара кратных корней. _ _
Для оценки значений параметра в АГД1 и АГД2, как это следует из
табл. 4.3, следует определить значения хд1 и хд2 в зависимости от 7
из условия
- . х2 -1 + 2В(^-х)
Т = -----—---------—---- .
(7 - В)(х* - 2f“ + 1)
Эта зависимость при постоянном значении f имеет вид, изобра-
женный на рис. 4.5, б. _
Для малых т при В « f решениями этого уравнения являются
Рис. 4.5. Типы корневых годографов при управлении угловой скоростью тангажа:
а - без запаздывания; б — типовые зависимости К ~ f (хд); в - области реали-
зации различных типов годографов при наличии запаздывания; г - тб52; д -
т G S2; е — т 6
136
Из рисунка следует, что при т больше некоторого значения т3 кор-
невой годограф не пересекает действительной оси. Этому значению
т3 соответствует корень кратности 3.
Из табл. 4.3 можно получить условие для определения т3:
-х4 + 4Вх3 + (4 - 8В$ - 2В3) х2 + (- + 85f2 + 4В£)х +
+ (1 + 2В5 -4В2Г2) = 0.
При т = т3 несложно получить значение параметра К, при кото-
ром действительный корень имеет кратность 3:
при? = 0,5 = Ох «2,06, т3 «0,зЛ= 1,37;
При ? = 1,5 = 0 X = 1, Т3 = °°, ТС = 0 .
При В = ? это уравнение решается точно.
п - -П+блЛ”’ 0,3
В этом случае т =----удя-Л-- « —
о /1 ^2 * /1 >*2
0,3 (f + 2ч/1 - f2)
х = Г + 2л/1-£2’;£«2,5\/1 -f2'e v1 - f2
Таким образом, пространство параметров ?, т разбивается на три
области Si, S2, 53, в которых поведение годографа доминирующего
корня имеет качественные различия.
Эти области приведены на рис. 4.5, в.
Область Si ограничена снизу:
1 + В - ?
т = arctg —===; •
области
области
Из рисунка следует, что действительная часть доминирующего
комплексного корня монотонно уменьшается до 0. _
Область S3 характеризуется неравенствам т < т3. В эт.ой области
существует оптимальное значение параметра А\>пт.
Годограф доминирующего корня, определяющего переходный
процесс,_имеет вид, изображенный на рис. 4.5, е. Очевидно, что KQTVl =
= ^Д1 ИХ0ПТ =ХД1 • _ _
Область S2 ограничена снизу зависимостью 7 = В этой
также существует_ оптимальное значение параметра ЛГ0ПТ. В
S2 зависимость х (К) может быть аппроксимирована параболой:
- _ х'(Кэф) - —=-1^=0 _
__ dx I ам fr- , dK тгН
х (К) = ? + —~ l/f = о % + ----------=-----------% ’
dK
2ЛГэф
137
где х'(£эф)= .
^кр - ^эф
Тогда Х^опт --------------------
*'<Жэф) - ~^1£ = о
[~= 1к=°]2 *эф _ f
ИХ опт f " L.----> ^2ОПТ ------ •
2^'^эф)- -^НК=О]
Управление угловым ускорением тангажа 6 = KuzuZ' Анализ реше-
ний системы уравнений,приведенных в табл. 4.3, с целью упрощения
проводится в предположении В » £.
Положив в этих уравнениях В = f и обозначив R2 = х2 + о?, можно
получить
KeXTR2[R2 - f(2x - f)]sinL7 =L[- R2{ + (27- f)] ;
KexTR2[R2 -f(2x-f)]cosL7 = -/?4 + /?2(3f7 + l-2f2) -
- x(2x - f).
Заметим, что
R2 -f(27-f>72 -2fr+ f2 + Z? >0,
следовательно,
R2£ <2x-f
Из табл. 4.3 следует, что
и —=• | £ — q < 0 для всех значений рассматриваемых параметров.
dK
Таким образом, возможны два различных типа корневых годо-
графов. Качественный вид этих годографов изображен на рис. 4.6.
138
На плоскости параметров г, f на рис. 4.6, б отмечены области и
S2, где корневые годографы имеют различный вид.
Для оценки значения кратного действительного корня хд и соответ-
ствующего ему значения параметра Кд преобразуем систему уравнений
из табл. 4.3 к виду
~ — 2*д ~ + О________
*д(£ ~ *д) (ХД - 2£ХД +
-д = х£ - 2&д + 1 е-хдт
*д(?- *д)
Из анализа приведенных выражений следует, что величина хд удов-
летворяет неравенству 0 < хд < f, а для определения значений кратных
корней можно получить достаточно точные аппроксимации:
кл.
1 -fr2
-4
4
¥
которые хорошо согласуются с точными расчетами.
Таким образом, при К <КD доминирующие корни — комплексные.
При К > KD имеется два действительных корня, один из которых с рос-
том параметра/^ стремится к нулю, а другой — к значению В « f.
Рис. 4.6. Типы корневых годографов и параметры качества при управлении уг-
ловым ускорением:
а - без запаздывания; б - область реализации различных типов годографов;
в - tGSj; г - те S2; д - параметры качества переходного процесса с учетом
запаздывания
139
Прй К = KD — корни становятся кратными, причем корней крат-
ности три не существует.
Для оценки нижней и верхней границ действительной части домини-
рующего комплексного корня хд воспользуемся неравенством R2$ <
< 2х - £, справедливым, в частности, и при а5 = 0.
Из x2f < 2х - f можно получить, что
1 - V1 - Г2 / г / 1 + х/1 - f2
Г f ’
_ откуда следует, что для всех значений величины запаздывания
т и параметра К замкнутая система устойчива при f ¥= 0.
Эффективные значения параметра А^Эф и частоты колебаний при
этом соЭф можно получить, воспользовавшись очевидными неравенствами
й2эф + f2 - 1 <0;
<ЬэфТ<7Г/2
и выражением
<^эф
откуда несложно вывести приближенную оценку для искомых парамет-
ровАГэфИШЭф:
Лэф ~ .
Качественный характер зависимости х (К) имеет вид, изображенный
на рис. 4.6, д.
В качестве примера можно привести одно из наиболее простых
выражений, удобных при приближенных оценках оптимальных значе-
ний параметра К и действительной части корня х:
^опт % ’
хопт ~ S 4 1^ = о •
* аК
Таким образом, получены основные динамические характеристи-
ки замкнутого контура самолет - звено управления при управлении
отдельными параметрами продольного короткопериодического дви-
жения.
140
Полученными результатами удобно пользоваться при выполнении
прикидочных инженерных расчетов, на ранних этапах проектирования
самолета и его системы управления и т. п. (в тех случаях, когда не
требуется высокая точность конечных результатов и можно ограничить-
ся качественными результатами). Удобство использования прибли-
женных аналитических оценок в безразмерной форме состоит в ос-
новном в возможности оперативного проведения расчетов без исполь-
зования ЭВМ.
При этом в ряде случаев в приближенных формулах наглядно вы-
является физическая сущность явления, что особенно важно знать при
анализе границ устойчивости замкнутого контура.
На основе приведенных формул, учитывая безразмерность выраже-
ний, можно провести также точные расчеты на ЭВМ для диапазона реаль-
ных значений параметров самолета с учетом режимов полета и т. п.
Результаты расчетов можно построить в виде номограмм, которыми
удобно пользоваться при выполнении оперативных прикидочных оце-
нок. Однако при этом не следует забывать, что результаты получены
для приближенных уравнений короткопериодического движения само-
лета при упрощающих предположениях.
43. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОГО КОНТУРА
ПРИ ТИПОВЫХ ЗАКОНАХ СОВМЕСТНОГО УПРАВЛЕНИЯ
ПАРАМЕТРАМИ ДВИЖЕНИЯ САМОЛЕТА
Выше было рассмотрено раздельное управление основными пара-
метрами продольного короткопериодического движения самолета.
В настоящем разделе анализируется динамические характеристики зам-
кнутого контура при совместном управлении комбинацией двух па-
раметров. При этом появляется дополнительный безразмерный пара-
метр р, характеризующий отношение передаточных чисел совместного
управления, что значительно усложняет исследование поведение системы.
Поэтому все приближенные оценки, приводимые ниже, получены в пред-
положении В = f, Су = 0.
В связи с тем, что современные маневренные самолета практически
все режимы полета выполняют с включенным демпфером тангажа,
представляется целесообразным рассмотреть динамические характерис-
тики замкнутого контура при управлении углами атаки (перегрузкой)
тангажа и наклона траектории в сочетании с угловой скоростью тан-
гажа coz.
Поскольку летчик в кабине ощущает нормальную перегрузку пу
как сумму углового и линейного ускорения, то для анализа динами-
ческих характеристик замкнутого контура самолет — летчик полезно
рассмотреть комбинированный закон управления вида
141
8 =К(пу + VG>Z).
Величина v = L/g (L — вынос кабины) для современных маневрен-
ных самолетов находится в пределах р = 0,3...0,6.
Для удобства характеристические уравнения и основные параметры
замкнутого контура при различных законах управления сведены в
табл. 4.4 — 4.7.
Управление перегрузкой и угловой скоростью тангажа 6 = К (пу +
+ vuz). Как следует из табл. 4,6, при значении параметра р = 1 харак-
теристическое уравнение совпадает с рассмотренным выше уравнением
для раздельного управления углом тангажа. Отличие от рассмотренного
случая заключается лишь в том, что константа В заменяется на констан-
ту 1 + В. Учитывая, что при значениях v => 0 и р -> °° законы управления
переходят в рассмотренные случаи раздельного управления соответствен-
но перегрузкой и угловой скоростью тангажа, достаточно ограничить-
ся рассмотрением значений параметра р, лежащих в диапазоне 0 < р <
< 1. Тогда
1 <1 + рВ< 3.
Из анализа выражений, приведенных в табл. 4.7, можно сделать
следующие выводы относительно поведения корневого годографа при
малых значениях параметра К:
частота колебаний возрастает в широком диапазоне изменения
параметров: т, f, р;
в пространстве т, f, v существуют области, отличающиеся знаком
- dx । _
Производной-^хг I к = Q.
dK
Эти области, приведенные на рис. 4.7, определяются неравенствами
dx . . Л v гл п > \ t&vl - f2r
lxr=o<OnPH'V —7^=4,-—
dK T y/i -
или
При 1 v<tgr ;
При? = 0 v< ----*1.
1 - Bt+ t
Нетрудно оценить значения параметра К, при которых изменяется
характер переходного процесса: движение из колебательного становится
апериодическим или наоборот.
142
Таблица 4.4
Основные параметры корневых годографов и качества переходных процессов
замкнутой системы при различных законах управления
Параметры управления <5 — КпуПу + K^z^z $— Kyv + K^z^z — KqQ^K^z^z ^K^KKnyV^T, p=^Wz/(^T(,),K= К=-КПу ^YaTl,M6z К=-К-еГ“7*М®
Характеристическо е уравнение p2 + 2£p+l+K(yp + vB + 1) = 0 p3 + 2$p + p + K(p + B)(yp +1) =0 p3 + 2$p + p+K(yp2 +vBp+l) = = 0
Система уравнений для определения комплекс- ных корней K(Bv+ 1- px)= u>2 -x2 + K( -- p)=2(f-x) K(vx-vB +—^-—) = X2+CJ2 GJ2 +x2 + 2fx - 1 K(l+Bv-vx ) = = x2 - 2fx+ 1-u>2 g32 + x2 Kv=2(x-i) =w’-x’+2fx-l К (V - i—= 2(x-f) u?2 + X2
Параметры комп- лексного полюса (К = 0) х= f,<J= V1 - г’ dx dK V V - В V - 1 2 2 2
duj dK Bv + 1 - vx 1 + vB + B$ - - vB + f 2^1-$2 1 ' 2V1 -f2
143
Продолжение табл. 4.4
144
Параметры нуля я--» х । II + * 1 - Sr II о %! = В, а>х =0,х2 = = 0 x i II K>| tfc( E i II 1 *1*'
Система уравнения для определения параметров /Сэф, <*>эф (В f) •^эф ~~ ^эф + ?2 ~ 1 Хэфр = 0 ^эф^эф = (<*>эф + ^М^эф + + Г - 1) Аэф(£ - р?2 - ^эф) = 0 Кэф? эф ?2 )(и,эф + + ?’ - 1) ^эф(р -2 •• ) 0 <*>эф + f
Система уравнений для определения па- раметров ^кр’ WKp *К₽=(^р- 1)/ (Sv+1) Ккр»= - 2? KKp(l+Bv)=Z2Kp- 1 *кр(*- Ра,кр)= 2fwjcp ^KpP^ = UKp — 1 ^Kp(PU>Kp~l) = —2fu>Kp
Уравнение для определе- ния действительных корней К(уВ + 1 - vx} = - (х2 - 2fx +1) К(х - В)(ух - 1) = х3 - 2fx2 + х K(yx2 - vBx + 1) =x3 - 2fxa + + X
Система уравнений для определения кратных корней К (у В + 1 - vx) = - (х2 - 2$х + 1) Kv = 2(х -?) К(х —В)(ух - 1) = х3 - 2fx2 + х K(2vx - 1-Bv) = 3x2 -4fx +1 K{vx2 - vBx + 1) = x3 - 2fx2 +x K{2vx- vB)= 3x2 - 4£x + 1
Система уравнений для определения корней тройной кратности Трехкратных корней не существует K(x - B)(yx - 1) =x3 - 2fx2 + x K(2vx -1 - Bv) = 3x2 - 4fx + 1 К • 2v = 6x - 4f K(yx2 - vBx +1) = x3 - 2fx2 +x K(2vx - vB} = 3x2 - 4fx + 1 K2v= 6x-4f
Таблица 4.5
Основные параметры корневых годографов и качества переходных процессов
замкнутой системы при различных законах управления
Параметры управления 5 — КПуПу + К^ь^ ^^/(Кп^Т2,^ = ~KnyVYaTiMSz/g 5 — + K-C^z^z V = К^гИ.Кы1гТ9 ),K=-
Характеристическое уравнение P 2 +2fr> + l + K(yp2 + wBp +1) =0 p2+2(p + l+K[i>p2+ (l + vB)p+B]=0
Система уравнений для определе- K(2vx - vB) = 2(f - x) K(vx2 - pco 2 - x — vBx + B)~
ния комплексных корней K(vx - pco 2 - vBx + 1) = = co2 - x 2 + 2$x - 1
= co2 - x2 + 2fx - 1 K(l + vB-2vx)~2(x - П
dx K2^-B) 1 +vB- 2pf
Параметры комплексного полюса dK~ 2 2
(f=0) <7 со 1 + 2itf2 - vB£ - v 2p? 2 -v-^-vB^ + B
dK 2^1 -f2 ’
X = f' СО =x/l-f2
Параметры нуля (К -► °°) x = В /2 w = x/(l/p) - (B2 /4) Xj = 1/p coj = 0 x2 = В co2 = 0
(p> 0)
Продолжение табл. 4.5
146
Система уравнений для определе- ния параметров Лэф, и>эф ^эф(^2 " ^эф “ ^+1) = = ^эф+^ -_1 Аэф (2^ - уВ) = 0 ^эф("?2 - Ри>экв - i-vBi + B) = = <^|ф + ?2 - 1 Кэф (1 + кВ - 2itf) = 0
Система уравнений для определе- ния параметров ккр, шкр АкрС^^кр — 1) — ~ (^кр — 1) Акр VB ~ KKp(B- ywKp) = икр ~ 1 KKp(l+vB)=-2?
Уравнение для определения действи- тельных корней К(»х2 - vBx + 1) = - (х2 - 2fx +1) K[vx2 - (1 + vB)x + B. ] = - (x2 - 2fx +1)
Система уравнений для определе- ния кратных корней K(vx2 - vBx + 1) = - (х2 - 2fx + 1) K(2vx- vB) = -2(x- f) К[vx2 -(1 + vB)x + B]= - (x2 - 2?x + 1) K[2vx- (1 + pB)] = - 2(x - »
Система уравнений для определе- ния корней тройной кратности -vBx+1) = -(x2 - 2fx + 1) K(2vx-vB)=-2(x-t) K-2v=-2 K[vx2 -(.l + vB)x + B]=-(x2 -2fx + 1) K[2vx - (1 + vB)J = - 2(x- f) К 2v = - 2
Таблица 4.6
Основные параметры годографов доминирующих корней и качества
переходных процессов замкнутой системы при различных законах управления с запаздыванием
Параметры управления 5 — КпуПу + » = K^gKKnyV^ll y,K=- KnyV^T.M6zg
Характеристическое уравнение p2 + 2fp+l + K(vp2 + vBp + 1)е~рт = о
Система уравнений для опре- деления комплексных корней KeXT[vx2 - w 2 - vBx + 1) coscot - (2^xco - vBuj) sin cor ] = co2 - x2 + 2fx - 1 KeXT[(2vxw - coscor + (yx2 - pco2 - vBx + 1) sin сот] = 2co( f - x)
Система уравнений для опре- деления действительных корней K(vx* - vBx + l)e* = - (x2 - 2fx + 1) K[2vx — vB + (ma? - vBx + 1) 7]exr = - 2(x - f) K[2v+2(2vx-vB)t + (vx2 -vBx+ 1) ?‘]eXr = -2
Параметры комплексного полю- са (К = 0) X f ; ш = л/1 - f2 dx dK - e?T/2[v(2f - fi)cos Vl - i2r + (1 + 2«2 - vBf - v)sinx/l - f2'r/Vl - f’ J
dw dK e?T/2[(l + 2f2 v - vBi - «OcosVl - f’r/х/l - f2’ - »(2f - B)sinVl -f2?]
Продолжение табл. 4.6.
Параметры нуля (К -► °°) х = В/2; о> = У(1/р) - (В2 /4); (р > 0)
Система уравнений для опреде- *эфе?Т[<«*’ +1)С08мэфТ-(2?-В)ммэф8тмэфй=^’ф + ?2-1
ления эффективных параметров *эфе?Т[(2? - ^)р^эфСО8и,эфт+ ("?’ - ‘'Чф “ + 5‘Пи,эфг = 0
^эф» ^эф
Система уравнений для опреде- *кр1(1 -«'w^pc°swKpT+>'BwKpsina>KpTj= u£p- 1
ления критических параметров ^KPlp^u,KPcoswKp’’ - (1 - ^’кр) sin wKpr) = - 2wKpf
^кр» ^Кр
Параметры управления 5 — Kgoz^z + V = К^(КШ2ТйУ, K = -
Характеристическое уравнение p2 +2ip+ 1+K(vp2 + (1 + vB)p + B]e~ PT = 0
Система уравнений для опре- деления комплексных корней KeXT[(yx2 — vu1 - x — vBx — jB)coscjt + (u> + vBw — 2puzx) sinwT]=w2 -x2 + + 2£x - 1 KeXT[(uj + vBw — 2vX(jj}cosgjt — (vx2 — vw2 —5c— vBx — B) sin cor ] = 2gj(x — f)
Система уравнений для опре- деления действительных корней K{vx2 - (1+ vB)x + B]eXT = - (x2 - 2{x + 1) K[2vx - 1 - vB + (vx2 — x - vBx + B)r ]eXr= - 2(x - t) K(2v+2(2vx — 1 — vB)r+(vx2 - x - vBx + B)r2 ]eXT = - 2
Параметры комплексного полюса (К = 0) jc=f;u, = Vl-f2 dx dK e?T/2((-2pf + 1 + mB)cosx/1 - f’r- (2vi2 -v-t-vBt + B)sins/1 “f2!
duj dK e?T/2[(2pf2 - v-f-vBf + B)cosx/l-fJr/Vl-f2 + (-2p? .+ 1 + MB)sinVT^p71
Параметры нуля (К -► °°) = 0; x2 = u?2 = 0
Система уравнений для опреде- ления эффективных параметров ^эф» ^эф *эфе?Т[ f - "Я? - В)созшэфг +(1 - 2р?)мэф8ШМэфТ] = ^эфе^ГИ1 + vB - 2pf)w^coiW^T - (у? - ки’ф- i-vBi -В)япмэф7]=0
Система уравнений для опреде- ления критических параметров ^кр; ^кр *кр[(* + Pu>Kpcosu>KpT — ^кр (1 + p^)sinu>KpT] = 1 — <*>кр ^кр[<*>кр (1 + ^)cosu>KpT + (В + ^kpSincjKpF] = - 2u>Kpf
149
Таблица 4.7
Основные параметры годографов доминирующих корней и качества
переходных процессов замкнутой системы при различных законах управления
с запаздыванием
Параметры управления 5 ~ КПупу + К V= Кш^ККпу VYaT<iy,K=-Kny V/g^T^
Характеристическое уравнение p + 2ip + 1 (yp + vB + 1) е~рт = 0
Система уравнений для определения комплекс- ных корней Kex1\(Bv + 1 — wr)cosu>T + pa>smo>T]= oj2 — - 5 + 2fx - 1 KeXT[v<2 coswt -(Bv+1- ia)sinwrl = = - 2<J(f - x)
Система уравнений для определения действи- тельных корней K(yB + 1 *- vx)eXT = - (x2 - 2fx + 1) [- v + (yB + 1 - их)?]еХт = - 2(x - f) K{- 2p? + (vB + 1 - px)t2 ]eXT = - 2
Параметры комплексно- го полюса (К — 0) х — f ; cj = \/1- f2 dx dK e^T/2 [pcosx/F- Pr - (Bv + 1 - - pfsin\/l - f2r/\/l - f2 J
dw dK е^т/2[(5р+ 1 - pf)cos\/l - ?2т/\Л - f2 + + psin\/l - f2r]
Параметры нуля (К -► °°) о II 1 3 1 a + •oq II i к
Система уравнений для определения эффектив- ных параметров ^эф> ^эф Ф ~ £) 150 *эф = [(“эф + f2 - 1)/У1 + "2 “1ф)е-?Т tg и>эфт - Ри>эф
Продолжение табл. 4.7.
Система уравнений для определения критичес- ких параметров ^Кр’ ^кр *кр = х4“кр - 1) ’ + 4f’с4р] / [(1 + ‘'2<^кр) — — ^KplK^Kp — 1 2fB)+2f) tg^xpT- _ _ (1 + мВ)(и£р - 1) - 2^и£р
Параметры управления v = Kt IUW k^-KqT^
Характеристическое уравнение p3 +2ti>2+P + K& + B)(up + 1) e-pr = 0
Система уравнений для определения комплекс- ных корней КeXT[( 1 + Bv - их - Вх/(й2 + x2)) cos L7 + + (pu> - x2)) sin u?t] = cj2 — x2 + 2fx- 1 KeXT[(va) — Ba)/(a)2 + x2) cos u>r — (1 +Bv — Bxf /о?2 +x2))sinu?T]= 2u?(x - f)
Система уравнений для определения действи- тельных корней K(x - B)(vx - 1 )eXT = (x3 - 2}x2 + x) K[2vx-l -Bv+(x-B)(yx-l)i-]eXr= 3x2 - -4?x+l _ K{2v + 2(2vx- 1 -Bv)t+ (x-B)fvx- 1)t2 ]eXr= = 6x - 4?
Параметры комплексно- го полюса (К = 0) x=f;u> = \/l-f2 dx dK e^T/2[(v - ZOcosVl - ?2T + (y? - 1 - vB - -Bf)sinVl ~f2r/Vl-f2l
duj dK - efT/2[(vf - 1 - vB - fif)cosx/l-f27/ /У1 -f2'- (p- 5)sinx/l -f2r]
Параметры нуля (К -» °°) x, — В ; cjj = 0 ; x2 = 1/p; u>2 = 0
151
Продолжение табл. 4.7.
Система уравнений для
определения эффектив-
ных параметров
^эф» ^эф = £)'
Система уравнений для
определения критичес-
ких параметров
*кр> ^кр
*эф= -1)У^ф + г]/
/ I мэф х/ 1 -fp)2 + и4ф J е“?т
tg МэфТ = [И^эф + fs)- f )/^эф
*кр = 7[(^кр- 1)’ + 4f2w’:p]/(51 +
+ WKp)(p2 + l/^Kp]
tg(u^pT - X) = 2^р/(^р - 1)
Ри>2Кр ~
tgx= —-—~--------—
<^кр(1 + vB)
Параметры управления 6 — KqQ + v = КШгККвГ“Т0 ) К=-Кв
Характеристическо е уравнение р3 +2$р+р + K(vp2 + vBp + 1) е-рт = 0
Система уравнений для определения комплекс- ных корней КеХт[ух - vB + х/(о>2 + х2 )) cos сот - (рсо - - со/(со2 + x2))sincor] = х2 - 2fx + 1 - со2 КеХт[(уи> — со/(со2 +x2))coscjt + (ух — vB + + х/(й? +x2))sinu>T] = 2uj(x - f)
Система уравнений для определения действи- тельных корней K(vx2 - vBx + 1) eXr = (x3 - 2fx2 + x) K[2vx — vB + (vx2 — vBx + 1) т]е*т = = Зх2 - 4fx + 1 K{2v+2 (2vx - vB)t + (px2 - v.Bx + 1 )? ]eXr= = 6x - 4f
152
Продолжение табл. 4.7.
Параметры комплексно- го полюса (К = 0) х= ? ; о> = х/1 - ?2 dx dK е^т/2[(р - l)cos\/l ~ £2т + fsin\/l ~f2T / /Vi -fsj‘
div dK - e^T/2[?cos\/l - - f2 - (y - - l)sinx/l -
Параметры нуля (К -► <») _ _ /1 в2 x = B/2 — v 4
Система уравнений для
определения эффектив-
ных параметров
/Сэф, <*>эф = О
Система уравнений для
определения критичес-
ких параметров
^кр» ^кр
^эф ~ (^эф"* *" f2 ~ ОхМ^эф^^2 /
/ 7(1 - "<^эф)2 + ’ шэф е~
tgu>3<j,T= w/f(l - + f2)J
/—---------------- . . . -->.
*кр=У1(<^р-1)’+4?3с^р]/[р2В’ +
+ <УШкр - 1/^кр)г)
- - ("“кр - 1)(^кр - 1) +
tg ^кр7 — ~Z~= ~ Z7
^^кр(^кр - 1) ~ 2(^£р - 1)
С этой целью следует преобразовать системы уравнения для оп-
ределения кратных корней:
- их 2 + 2 (1 + Bv) х + (2f + 2VB$ - Р)
т =------——----—-------—------—-----
(х 2 - 2fx + 1) (Рх - 1 - VB)
К = х 2^Х + 1 е-ЛЛ
р[х - (В + 1/р]
Первое уравнение представляет собой полином третьей степени
относительно х, который приближенно можно записать в виде
vrx3 - (т + р)х2 + 2х + (р - 2f - т) = 0.
153
Очевидно, во-первых, что один из действительных корней хд при
К -* ©о стремится к значению х“Д1 = В + i, а во-вторых, что все действи-
тельные корни удовлетворяют неравенству хд > В +
Чтобы получить качественный характер зависимости действительных
корней характеристического- уравнения от параметра К9 полезно рас-
смотреть график функции ДХд). Этот график имеет вид, изображенный
на рис. 4.7, б. Из рисунка следует, что возможны два решения системы.
Корней тройной кратности не существует.
Подробный анализ показывает, что может быть реализовано четыре
различных типа корневых годографов В, A, С, D, изображенных на
рис. 4.7. Для типов А и D качественный характер годографа доминиру-
Рис. 4.7. Типы корневых годографов и параметры качества при комбинированном
управлении по закону 6 = КПу Пу + K^z
а — без запаздывания; б - зависимость К(хд, т); в - области реализации различ-
р tg х/1 — т р
ных типов корневых годографов при т =£ 0; г — > 6; д------------- < - < 6 ;
т
е-
1 1
1 <-< ---г- ;
Т
154
ющего комплексного корня совпадает с аналогичным годографом при
управлении параметрами со2 и пу,
У годографа типа В время затухания переходного процесса замкну-
той системы в широком диапазоне параметров меньше, чем у свобод-
ного самолета. __
У годографа типа С имеется диапазон значений параметра К, в кото-
ром качество переходного процесса хуже, чем у свободного самолета,
и возможна потеря устойчивости замкнутым контуром. При этом го-
дограф типа С переходит в годограф типа D. На графиках видно, что
годографы А иВ отличаются от годографов CnD производной-^-| £ = 0.
dK
Годографы типа А и В различаются количеством действительных
корней характеристического уравнения. Удобным критерием для этого
может служить величина отношения р/т. Используя известные методы,
можно получить оценки значения параметра р/т, при которых куби-
ческое уравнение имеет один либо три действительных корня.
Для грубых оценок можно считать, что при р/т > 6 движение дина-
мической системы характеризуется годографом типа А; при значениях
параметра р/т, лежащих в диапазоне, определяемом неравенствами
tg vl — С2 т р
—<— < 6, — годографом типа В.
хЛ-£2т т
Чтобы получить аналогичные критерии для сравнения годографов
типа С и D, следует оценить приближенные решения уравнения, опреде-
ляющего границы устойчивости замкнутой системы. Оценим сначала
кратные корни.
Учитывая приведенное выше неравенство, можно записать
ртх 2 - (р + т)х + 2 = 0, откуда
_ Р+ Т ±\fv2 + Т2 - 6РТ
ХД1,2 — ———-
2рт
Отсюда, например, при т < р хД1 « 3/(2р), хД2 « 1/т. Соответству-
ющие значения параметра/^ при этом равны:
Зт
К 2,25 2Р. г 1
лД1 ~ — ------—— е , лД2 = *
Р2(0,5 -ДР)
При значении-^ < 6 зависимость К(х) становится монотонной, и
т
единственный действительный корень при малых значениях параметра
К может быть оценен простым приближенным равенством
155
Хд «
1 , Крт
— —In ------
T 2
При больших значениях параметра К приближенная оценка име-
ет вид
- х (i+i)2-2f(S+±)+ 1
хд ~ (В + — ) + ----=------—-------•
р РКе(В + 2/Р
Для определения критических значений параметра А^кр и частоты
колебаний сокр систему уравнений следует привести к виду
t - г - ^кр~ 1 + 2&)+ 2$___________________ .
tg^Kp т — ^кр —---------z----Z------Z------ >
^U?U?Kp — В — 2fcJKp + (и?кр — 1)
^кр = V^[(^Kp ~ I)2 + 4f2и>кр]/[( 1 +Вр)2 +^2<^кр) ]'
При р = 0, т. е. в случае управления перегрузкой пу,
tg^KP~r= ,
О>кр - 1
При р = 00, т. е. в случае управления угловой скоростью со2?
tgWKpT ____^Кр— >
^^кр —
т.е.
2^-В
7Г/2
^кр ^кр
Для значения р = 1 первое уравнение имеет вид
tg^Kp7’- ^кр
<^кр - 1 + ~
(В + 1)<^кр “ 2fu?Kp — В
______^кр______
(В + 1 ) СОкр - 2f
156
Расчеты показывают, что в этом случае
~ 7Г 2? - В - 1
I « —г + -----------
кр 2т
Х^кр ~ ^кр ,
т. е. при v > 1 корни уравнения критических частот находятся в
малой окрестности^ сЗкр т » я/2.
Зависимости Хкр = F(v) можно аппроксимировать кусочно-линей-
ной функцией:
при 1 Ккр » + v
т т
F 1*57
при v >1 АГкр .
Аналогичным образом можно определить эффективные значения
параметра К и частоты колебаний из соответствующей системы урав-
нений, приведенной к виду
^эф
1+ (В - №
- -
Эф \/(l+Bv - fr>)2 + »>2«эф
е"^
При v = 0 эта система не имеет решений. При р = 1 уравнение для
нахождения частоты запишется в виде
гёЧэф? = «эф/ (1 - Д - О •
_ _ - - я
Решение этого уравнения близко к о?Эф т « —, что совпадает с реше-
нием для управления угловой скоростью
Переписав первое уравнение
х - - - - р
-=---=--------- ,
* Ф 7(1 + BP - fP)
можно показать, что при о>ЭфТ < я/2 решение существует только при
выполнении неравенства
р/т > 1 + Bp - fp
или приближенно при р/т > 1.
Таким образом, это неравенство может служить приближенным
критерием, по которому различаются типы корневых годографов СиР.
В плоскости параметров р/т, т можно построить области реализа-
157
ции различных типов корневых годографов. Эти области приведены
на рис. 4.7.
В случае годографа типа С следует оценить также эффективные
значения передаточного числа, так как в интервале передаточных чисел
О < К < АГэф переходные процессы замкнутого контура хуже процессов
р
свободного самолета. Для этого величину —------=------- в правой
т(1 + Bv - fr>)
части уравнения удобно представить в виде 1 + 5, где
5 < tg>6..~ ------1.
VTT’F
Раскладывая tg озэф т в ряд, можно получить
^Эф7 +Ц- L^r3 ^эфт5 «<Зэф7 + 5шэфт ,
откуда для малых значений запаздывания
^>эфт =
+ ”
4 V 16 2
Точность полученного решения удовлетворительна лишь при ссЭфТ <
V 4
< 1, при этом величина 6 < 1/3. Так как =-=-- =1+6 <—,
р 4 7(1 + BV - $V) 3
то отношение.
т 3
Таким образом,
/ v ‘
,----- л/3 (--—=-----------1)
V35 т(1+ Bv -&) \
оэф ----------------------------------- < -=- ;
*ЭФ
е-^т .
В интервале 0 < К < А^Эф зависимость х (К) можно аппроксимиро-
вать квадратичной параболой. В этом случае
хтах = х(—’
и эта величина легко вычисляется из уравнения
Г = ? + (-^Lljf=o )К- J- (Л 1к=0Й2.
dK /Сэф dK
158
откуда _
*max = f + т *эф ( ~=• I К = о) ’
* dK
и потеря устойчивости может произойти при значениях параметра К, оп-
ределяемого из уравнения
— dx — “
f + (1-К/Кэф) |х=0 )Х' = 0,
dK
Р . 4
если =- < — .
т 3
Управление углом и угловой скоростью тангажа. При управлении
комбинацией параметров естественно возникает вопрос, каким образом
трансформируются корневые годографы, соответствующие разделенному
управлению с изменением параметра р.
Очевидно, что случай v = 0 соответствует управлению углом тан-
гажа, р = о© - управлению угловой скоростью тангажа. Корневые годо-
графы этих предельных случаев рассмотрены выше.
Условия существования действительных корней, условия ^появ-
ления кратных корней следует рассмотреть_в первую очередь для т = 0.
На рис. 4.8 приведена зависимость А^(хд^,из рассмотрения которой
следует, что для любого значения параметра к > 0 при v<\jB существу-
ет действительный корень хД1 < f, величину которого нетрудно оценить:
КВ
ХД1 ------—---------
1 + К + KBv
Очевидно, что если существуют еще действительные корни хД2
и хдз, то они больше, чем 1/р : хД23 > 1/р. Тогда приближенно можно
записать
р2 + (2Г + Kvp + (1 +£) =0;
pm=- (г+-^) ±Уа+-^)2-(1 + ^) •
Следовательно,значение параметра К, при котором возникают боль-
шие по величине действительные корни, можно оценить как Кх « 4/р2,
— — _ 2
а соответствующую Кх величину xr — kbkxj «f +~[Г' Таким образом,
при К < Ki решениями характеристического уравнения являются один
действительный и пара комплексных корней, а при К > - три дей-
ствительных корня. При К = — три действительных корня и два из
них кратны.
Корневой годограф может иметь вид, изображенный на рис. 4.8.
Из рисунка следует, что возможны три различных типа корневого
годографа А, В и С.
159
Годографы типа С и А аналогичны годографам при управлении
углом и угловой скоростью тангажа соответственно. Годограф типа
В требует исследования.
Очевидно, что годографы типа А и В будут отличаться только зна-
~ dx . п
ками производной—= | ^ = q, а типы В и С — возможностью возник-
dK
новения потери устойчивости. _
Таким образом, при отсутствии запаздывания при и (В - f) + 1 > О
(т. е._в широком диапазоне значений р) частота колебаний в окрест-
ности К =_0 с ростом возрастает. _
При т #= 0, v < В^при малых К действительная часть комплексного
корня по абсолютной величине с ростом К уменьшается, и приведенное
выше неравенство можно принять как отличительный признак случая
А от случая В.
Легко видеть, что при т Ф 0^-| £ = 0 < О* ^ри {у - В) cos \/1~-
dK
- f 2 т + (pf — 1 - vB - В£) sin —- < 0 или приближенно для
в ж
Рис. 43. Типы корневых годографов и параметры качества при комбинированном
управлении по закону 6 = K$v + K^z :
Oj, б, в - реализация различных^типов корневых годографов без з&газдывания
(т = 0); г_~ зависимость К = f(x%, т); д, е, ж - различные типы корневых годог-
рафов при т Ф 0
160
малых т при р < В + т зависимость Х(хд) для т Ф 0 построена на
рис. 4.8, г. Величина меньшего по абсолютной величине действительного
корня характеристического уравнения оценивается той же формулой,
что и при г = 0. Из рисунка следует, что минимальное количество дей-
ствительных корней при любом значении параметра К равно двум, а
максимальное-четырем. _ _
Характерные_величины ХД1 и ХД2 разделяют на графике значе-
ния параметра К, которым соответствует разное число действитель-
ных корней.
Из условий существования действительных и кратных корней сле-
дует неравенство (vx - 1X1 > 0 и приближенная оценка
х
~ 2* + + 3$ - V
(vx- 1)(1 - t/x)(x2 - 2fx + 1) ’
Так как числитель этого выражения должен быть положительным, то
х > 1 + + \/1 ~ 4& + 2р2 > 1 +
v v
Приближенно для малых значений f и v можно получить
т(рх-1)х2 ^vx2-2х(1 + v$)^vx2-2xz
откуда
Д1,2
Т + V ± \/(Т + V)2 - 8TV
2TV
- _ 2 2 111
а для т < v хЛ1 ~ -=- ~ ; хП2 - + — «-=
Д1 т + v » Д2 т » т
и
^2 р 2 , 1
Хд« ~ —т- е ~ , ХД2 ~ — е
Д1 р2 р2 Д2 TV
В пространстве параметров f, т, v можно выделить области, соот-
ветствующие различным типам корневых годографов. Для этого необ-
ходимо оценить возможность существования эффективных и критичес-
ких значений параметра К.
Из системы уравнений для нахождения эффективных значений
параметра К и частоты колебаний (при В = f) можно показать, что
v(f +w2)-f>0,
тогда при Тот < со2 + f2 > 1 и сЗ > >/1 - f2 .
При сот > со2 + f2 < 1 и со < 1 - f2 .
161
Уравнение частот имеет вид
t - - _ ^эф) - £
tgo?3d)T --------=----*----
“>эф
Если при малых о?Эф т < 0,2 решение существует, то оно равно
- ~ J- 1 - Г ~ ^Эфе ~ Z. 1 - pf ‘ fт
^эф « S-T—-г> КЭф « —^=.— =е <
V"Т 71+ "2 - ^эф v ~т
Несложно получить нижнюю границу значений р, удовлетворяю-
щую условиям существования этого решения. Очевидно, что v/т > 1,
Из системы уравнений для нахождения_критических значений пере-
даточного числа и частоты колебаний при В = f можно сделать вывод,
что при v < 0,2 возможен выход замкнутого контура на границу устой-
чивости при малых значениях сокр т.
Тогда
tew т «w - _ (1 - <ЗкР) (»£>кр - ?) ~ д.
(^кр _ f) + ^кр (1 _ ^кр)
^кр + ~ ^1ср + f
^кр (^кр ~ 1)
откуда следует о^р « 1 + $!(т — v).
Эта формула дает хорошую оценку для критической частоты ко-
лебаний в случае малых значений v.
Далее, при всех значениях р > 1 граница устойчивости характеризу-
ется частотой колебаний, близкой к я/2т.
Годограф типа А характеризуется значениями коэффициентов
р > т + s, при этом критическая частота равна сокр т =- — е, где е - ма-
, - 1 - 2 - - тг
лая величина, т. е. tgwKp т = ctge = - « ро>кр. Поэтому сокр т «— -
1 - л 2т
, откуда wKp « п=- —
г 2т
^кр
и
! ~~ ^кр
Кр —Т-- -*===; -----=г
у1 + Р2о>кр 2РТ
Годограф типа С характеризуется малыми значениями коэффици-
ента р < т. При этом критическая частота
^Кр № 1 + —*=-- и Ккр » U>KP — 1 » .
Т-Р Т-Р
162
Годографы типа В являются промежуточными. Для них харак-
терно наличие эффективных значений_параметра_К и частоты колебаний.
В диапазоне значений параметра К 0 < К < АГэф движение замкнуто-
го контура имеет худшие показатели качества переходного процесса по
сравнению с движением свободного самолета.
В случае и < 0 движение замкнутой системы осуществляется по
типу С и полученные формулы дают хорошее совпадение с точными
решениями. Сравнение корневых годографов различных типов при-
ведено на рис. 4.8 д, е, ж.
Управление угловой скоростью и ускорением тангажа. Анализ ди-
намических характеристик замкнутого контура для закона управле-
ния 6 = goz + К^2 проводится для случая В = f. При т = 0 не-
трудно определить корни характеристического уравнения:
- _ 2f+ 1(1 + Р0 . >/[2f + 1(1 + Pf)]2 - 4(1 + lf)(l + ДР)
Pl ,2---------=----- “ ------------------=-------------------
2(1 + Kv) 2(1 + Kv)
Отсюда следует, что значение параметра /Сд, при котором ста-
новятся кратными действительными корнями, равно
£д = * -2pf+ 1].
Очевидно, что величина К % положительна при всех значениях па-
раметра V.
тт г х 1 - f2+ хЛ2 - + 1)2
Легко видеть также, что Кп + - = -------------------г-----
Д v р(1-р02
иприр<0 ХдС--.
Соответствующий величине Кд корень характеристического урав-
нения
1 - fr
1+£др
Поэтому при всех значениях параметра v должны выполняться не-
. 1
равенства v <
хд > f, и на плоскости гддографа бифуркационная
точка перехода комплексного корня на действительную ось — един-
ственная.
Из соотношения нулей на плоскости годографа следует, что воз-
можны три случая, которые определяются величиной и знаком пара-
метра v \ v < 0, 0 < v < 1/f, v> \ Три диапазона значений параметра
v характеризуют три типа корневого годографа (рис. 4.9). Аналогич-
ная картина имеет место при наличии запаздывания-? Ф 0. Однако, при
163
Рис. 4.9. Типы корневых годографов
и параметры качества при комбиниро-
ванном управлении по закону 6 =
= + &Cjz
а - без запаздывания для различных
значений р; б - зависимость К (хд, т)
и корневой годограф_при_т =#= 0; и < 0;
в - зависимость К(х%, т) и корневой
годограф при т Ф 0, v > 0
этом появляется принципиальная
возможность существования корня
тройной кратности (при v < 0).
В диапазоне 0 <v < 1/f корне-
вой годограф имеет тип, аналогич-
ный рассмотренному выше при уп-
равлении только a v > 1/f при
управлении только 6>z.
В диапазоне 0 < v < 1/f можно определить отличия в переходных
процессах замкнутого контура, вносимые параметром р, по сравнению
с идеальным демпфером тангажа.
Для различных значений v можно построить зависимости К (хд),
которые могут иметь вид, изображенный на рис. 4.9.
Из анализа соотношений в табл. 4.6 можно заключить, что в широ-
— dx , Л
ком диапазоне значении запаздывания т -=- I = q > 0. Приближенно
dK
164
du , -
можно оценить также интервалы знакопостоянства -^-| £ = 0, которые
зависят от величины р. Для малых т можно показать, что если v < т,
£ = 0>0,аесли,'>”’то5=-1 к = о<°-
аК аК
На плоскости годографа можно определить бифуркационные точки
ветвления траекторий доминирующих корней при переходе их на дей-
ствительную ось.
Для этого следует преобразовать условия существования кратных
корней к виду
- = _ Р (1 - р?) + 2рр - {•) - (1+ р£- 2f2)
(х - 1)(х2 - 2f7+ 1)
(уравнение 4-й степени относительно х) ;
X" = — х ~ 1 е — хт
(рГ-1)(7-£)
Тогда должны выполняться неравенства:
> х > f при v > О,
х > f при v < О,
либо X < 1 при V < Ос >
Поскольку х2 (1 - pf) + 2х(р - f - (1 + pf - 2f2) >0, то для малых
значений f и и можно получить приближенную оценку x>l+f-p^l.
Можно показать также, что в случае р > 0 имеется только одна
пара кратных корней, т. е. если годограф попадает на действительную
ось, то он с нее не сходит._
Если произведения pf, pt, rf малы и_можно пренебречь их величи-
ной по сравнению с единицей, то ртх4 - тх2 + х2 (2£ + т - 2р)х - 1=0
и большие по абсолютной величине корни, если они существуют, мож-
но оценить
- т ±\/т2 - 4vf~'
При малых р< тхД1 » 1/р;хД2 « 1/т. _ __
Два малых корня имеют порядок хдз,4 ~ ± l+f-p+уТ. Из
цих наименьший положительный корень будет близок к единице:
Хдз ~ 1.
165
Соответствующее значение передаточного числа
- 2 - 2v+ т
—
(1 - р)(1 - р+ т/2)
Тогда при К < Кдз х = £ (1 - f - е“ е2тК2 + е^тК + f и
й = -1 у/1-?'етК + х/1-Г2'.
Из системы уравнений, определяющих границу устойчивости, мож-
но получить
1 4- - 2$2
1 -W
<^кр
> 1.
_ ZL2 (1 - pf) - (1 + pf - 2f2)
и tgO7KpT — GJKp ------£74--------7-------- --«---
- ^Kp + (^ - f " 2Pf2)GJ2 p - f
При p = 0 уравнение вырождается:
— <x)Kp
tg^KpT =------,
что соответствует условию потери устойчивости демпфера тангажа.
При малых значениях параметров р и f
, — — ““ ^кр — 1
tgWKP Т ~ 63 К Р--=4----=~2 ----7“--—
- ^кр + “>кр (^ - 0 - f
Так как выход на границу устойчивости при управлении угловой
скоростью тангажа осуществляется при достаточно больших значениях
параметра К, а при управлении goz система__устойчива всюду, то опти-
мальным значением можно считать величину А'д 3.
Управление углом наклона траектории и угловой скоростью тангажа.
Зависимость действительного корня от параметра К при т = 0 определя-
ется решениями уравнения 3-й степени (В = f):
к=7а 4---^д+- •
vx%- фсд + 1
Для различных значений параметра v при т = 0 качественный вид
корневого годографа представлен на рис. 4.10, а, б. _
Из графиков видно, что во всех случаях с ростом параметра К
действительный корень возрастает по абсолютной величине, а действи-
тельная часть комплексных корней уменьшается, поэтому возможна
потеря колебательной устойчивости.
При наличии запаздывания т Ф 0 можно оценить действительный
корень характеристического уравнения из соотношения
166
К
Рис. 4.10. Типы корневых годографов и
параметры качества при комбинирован-
ном управлении по закону 6 = Л# 0 +
+ _________________
а - зависимость К (хд) и корневой годог-
раф при т = 0, v < 0; б - зависимость
К (хд) и корневой годограф_ при т = 0,
v < 0; в - зависимость К (хд) и корне-
вой годограф при т Ф 0, v < 0; г - зави-
симость К(хц) и типы корневых годог-
рафов при т ¥= 0, v < 0; д - область реали-
зации различных типов годографов
167
к = *Д<*Д ~ 2^*Д * е"хдтв
- р?Хд + 1
Качественная зависимость К (Хд) представлена на рис. 4.10, в, г.
Из графиков видно, что при К < Кд и р > 0 существуют большой и
малый по абсолютной величине действительные корни характеристичес-
кого уравнения, которые в точке К = Кд переходят в пару комплексно-
сопряженных корней. Малый корень, как нетрудно видеть, приближенно
равен К.
_ Оценка величин хд и соответствующего Кд дает значения хд » 1/т;
Кд » 0,3/ (рт) , что хорошо совпадает с точными расчетами при малых
величинах запаздывания. Соответствующие типы годографов приведены
на рис. 4.10.
Из анализа выражений, приведенных в табл. 4.7 следует также,
что в диапазоне значений параметра р, определяемого неравенством
. 8 - 9f2 п
р< ------г— % 2, комплексные корни не пересекают действительную
4(1 - f2)
ось годографа.
При \/1 - f2 г < я/2 и малых К действительная составляющая с
ростом передаточного числа растет по абсолютной величине, если па-
раметр р удовлетворяет неравенству
(р- 1)cos\/1-?2t+ f —> 0
x/l^F
откуда
tgx/l - f2 T.
В этом случае | % _ 0 < 0, если соблюдается соотношение
dK
----7=^=—-, cos у/1 - f2 т + (р — 1) sin — f2 т ,
>/l^F
т.е. р< 1 + -Д,—, ctg >/1 — f2т .
Зависимость /(£, т) = 1 +
рис. 4.10, д.
Таким образом, для малых значений величины запаздывания имеет-
ctg \/1 - F т представлена на
ся три типа годографа, приведенные на рис. 4.10 в, г.
168
Для определения критических значений передаточных чисел сле-
дует преобразовать систему характеристических уравнений к виду
- - Р<34кр - (у + 1- 2^Р)^р + 1 .
tg^Kp т — -----\г=-- -2--------—-->
- f«KP(^KP + V- 2 )
К _..Л-“кр)2+4№р -
Акр - V -—— ^кр •
(р<4р - 1)2 + ^f2w2Kp
Эта система при v = 0 вырождается в рассмотренный выше случай
управления углом наклона траектории:
<Лр ~ 1 -М1 + 2?Т);
АКр ~ -------в-- .
1 + 2fT
При значении параметра i> = 1
tg й крт = ^кр- 2(1-?2)^2кР + 1
fWKP (WKP - 1)
fWKP
и решение этого уравнения дает значения, близкие к о> ^р 1 тт/2т;
1 « ш/v = оГ
КР —
Точные расчеты показывают, что зависимость /Скр = f(y) близка к
линейной, поэтому линейная аппроксимация по закону
^кр = ^кр + К-^^Кр! ~ ^кр)
дает достаточную для практических оценок точность. Однако начиная
с некоторого значения параметра р0 = 1 — tg \/1 — f2 гра-
ница устойчивости совпадает с границей устойчивости для демпфера тан-
7Г “ 7Г ___ w
лкр ~ Поэтому линеинои аппроксимацией зави-
2т 2tv
кр = /(О следует пользоваться лишь при значениях пара-
гажа сокр ~
симости К*
метра v<vQ.
Совместное управление нормальной перегрузкой и угловым ус-
корением тангажа. Полагая для простоты в дальнейшем В = f, легко
получить при О 1
1 + — /СР г-
> 2 4. V25
Р1,2----f -----=----- ±-----=~ 1
где 1+KV l+Kv
D = - [(1 +ХХ1 + Kv) -^(1 + 2. Kuf].
169
Анализ удобно проводить раздельно для положительных и отри-
цательных значений параметра р.
В случае v_> О, D < 0 действительная часть комплексных корней
Pi ,2 с ростом К монотонно убывает от f до f/2, а мнимая - монотонно
/ » >2 '
изменяется от у 1 — f2 до у------ . В случае v < 0 для анализа следует
р 4
выделить характерные точки:
при£ = 0 Л = -(1-Г2) <0, x = f,w =x/l-f2' ;
при£=-1 D = If2 >0, Г1Д= 1 (1 - 1)Г2Д =оо.
В малой окрестности точки К = — - слева (К = — - — е, е > 0) D = 0,
. 1 - ер
и имеются кратные корни Pi 2 = $-----
’ 2ер
В окрестности справа (К = — l + e)D> 0. Один корень меняется скач-
ком от минус бесконечности до плюс бесконечности, затем уменьшается
при дальнейшем росте параметра К, оставаясь положительным. Дру-
гой корень, отрицательный, уменьшается по абсолютной величине, т. е.
= 1 f +у/1 f2 + 1 >0;хП2 = - f -\Z- f2 + - <0.
Д1 2 v 4 V д2 2 V 4 V
Корневые годографы имеют вид, изображенный на рис. 4.11, а, б.
Действительные части корней характеристического уравнения в зави-
симости от параметра К приведены на рис. 4.11.
Из рассмотрения графиков следует, что при К = — 1/р > 0 имеет
место потеря устойчивости: действительная часть терпит разрыв от
— 00 до + °°. Поэтому не следует выбирать величину параметра К, близ-
кую к значению К — —
Для оценки влияния величины запаздывания следует оценить об-
ласть существования действительных корней характеристического ква-
зиполинома:
к = - 2^1- е-ЛТ-
Vx 2 - + 1
Очевидно, что при v > 0 и К > 0 действительных корней не
существует.
При отрицательных значениях параметра v < 0 возможны положи-
тельные и отрицательные действительные корни:
1 ~ ln<- Kv} Л
для К < - - х ъ - --- > 0;
т
170
X с с/z
г
Рис. 4.11. Типы корневых годографов
и параметры качества при комбиниро-
ванном управлении по закону 6 =
55 КПуПУ &Z-
а - •качество переходного процесса и
корневой годограф при т = 0, v < 0;
б - качество переходного процесса
и корневой годограф при т — 0, и > 0,
В < в - область возможной потери
устойчивости в пространстве параметров
р, т; г - корневой годограф при
т Ф 0, р < 0^ м = -р; д - корневой
годограф при т Ф 0, р > 0
171
1 - ln(— Kv)
для/7>---x^- ---------=-- <0.
v т
Для положительных значений параметра р > 0:
при VI -f т <- 1^=0 <0;
z dK
- dai . . ,
при малых т «г- I к — Q > (
dK
а для отрицательных значений v < 0:
- dx
при малых т —=- I г — п > (
dK
Л 77- . Я dGJ . . А
при VI — f < < у 7= I К = 0 > °-
z аК
Для определения критических параметров на границе устойчивости
следует преобразовать систему уравнений к виду
- - . - ^ко - 2
tgwKFr = f^KP ;
^кр - (1 + V -2РГ)+ 1
А^кр — \J[(^кр - 1) 2 + 4£о)кр]/[(1 ^кр)2 + ^2f ^кр]
Для малых значений коэффициента относительно демпфирования
ж “ ~ ~ ~^кр + 2 . р 60 кр - 1 !
tg^KpT —-----------=---—------ , ^кр ~ I ----— I •
(С^КР - 1) (1 - ^кр) 1 - ^КР
Для положительных значений параметра К и для малых т можно
записать (с учетом малости величины f)
<^кр?< tf/2 ; 1 <^кр < 1/^ •
Если сокр т невелико, то
WKpT ~ fwKp —=-----------V—zr------ ,
(^кр ~ 1) (1 “ ^^кр)
откуда следует v
2$* -=
^кр « Ki + ^+ f 4 Ж1 -p-f -------------------)].
172
Из системы уравнений для определения комплексных корней сле-
дуют очевидные соотношения:
-i^(a>2 + х2) + J-(2-«0-2x (1 -v) > 0;
pf(co2 + х2) + 2х(1 - р)<f(2 - v) .
При v > 0
v$x2 + 2х (1 - v) <.1$(ы2 + х2) + 2х (1 — p)<f(2 - р),
откуда
Так как при
"К" -Г «“Г >
Очевидно также, что для 0 < у < 1
ро? <р(о>2 + х2)< 2 - р - 2 (1-р)<2 -у< 2,
т. е. частота колебаний о? ограничена всюду. ___
Таким образом, в предположении малости т, f и величины сст не-
трудно выписать неравенства, определяющие границу устойчивости
замкнутой системы:
4fr/r <1 m К 1 + ~^1 + 3^2 ~ d * $7d2 1
(l-p-fr/T)2 (1+f/T)2
_ Ргр-
_Эта граница приведена на рис. 4.11, в в плоскости параметров у,
£/т. Величина критического значения параметра К определяется приб-
лиженным соотношением
f/r - 1 ,
^кр ~ I . - I •
pf/T - 1
Можно показать, что при отрицательных значениях параметра у
из диапазона — 1 < у < 0 граница устойчивости существует и при всех
173
значениях параметров величина критического передаточного числа
определяется неравенством
Ккр < I 1/Н .
Для определения^ корней квазиполинома при значении передаточ-
ного числа, равного Л^Эф, можно записать характеристическое уравнение
в виде
- 1)
^<^эф — — -
(1 - vul<b ) (<4ф - 1) 1 ~
откуда следует, что при положительных значениях параметра v уравнение
не имеет решений. Для отрицательных р решение можно оценить, поло-
жив д = — р > 0:
шэф ~ = - -д > Аэф
t/т - 1/Д + Г2-1
м£2/т + gf2 - fr
Очевидно, что решение существует в диапазоне параметров, для
которых выполняется неравенство
& cos V 1 - f27 - (1 - ц- 2 ) ,
V i-f
или откуда для малых т можно записать т <
-----. Таким образом,
* + м
корневые годографы имеют вид, приведенный на рис. 4.11 г, д.
Рассмотренные выше динамические характеристики замкнутого
контура с запаздыванием при раздельном управлении параметрами
продольного короткопериодического движения и некоторыми их
комбинациям в основном получены приближенными методами реше-
ния систем трансцендентных уравнений. Поскольку все соотношения
получены в безразмерной форме, то в рамках линейности характерис-
тик самолета и управляющего звена при условии корректности приб-
лиженных оценок полученные соотношения могут являться критериями
подобия. Такими критериями могут служить, например, основные па-
раметры, определяющие динамические свойства замкнутого контура.
В рассмотренных выше простейших случаях линейных алгоритмов
управления не учитывались динамические характеристики системы уп-
равления, силовых приводов и т. п. Такая упрощенная постановка за-
дачи продиктована в основном возможностью получения простых приб-
лиженных оценок в аналитическом виде, позволяющих выявить качест-
венно верные, легко обозримые результаты.
Естественно, что при детальных расчетах с использованием ЭВМ
можно значительно усложнить передаточную функцию управляющего
звена, учесть типовые нелинейности и т. п.
174
Однако на этапе предварительного проектирования самолета и
системы управления вряд ли имеет смысл усложнять задачу. Опыт
показывает, что на начальных стадиях проектирования, когда исходные
данные известны недостаточно точно, можно вполне обойтись прики-
дочными расчетами идеализированных моделей, которые в целом дают
правильную качественную картину явления.
Поведение управляемых динамических систем, описываемых ли-
нейными дифференциальными уравнениями, однозначно определяется
расположением корней характеристического уравнения. Движения
таких систем могут быть устойчивыми либо неустойчивыми. Наличие
нелинейных функций в уравнениях, описывающих движение систем, мо-
жет привести к качественно новому виду движения, несвойственного
линейным системам — к незатухающим автоколебаниям. Автоколебания
характеризуются обычно величинами амплитуд и частот колебаний.
Существуют различные приближенные методы определения параметров
автоколебательных систем, из которых наиболее распространенным
является метод гармонического баланса [18].
Для анализа автоколебаний замкнутого контура управляемой
динамической системы, описываемой линейными дифференциальными
уравнениями, можно ограничиться рассмотрением релейного звена в
цепи обратной связи, закон управления которого определяется урав-
нением
хвых = & ЗДэ11 Хвх •
С математической точки зрения решения уравнений движения ди-
намической системы в режиме автоколебаний описываются периоди-
ческими функциями времени. Разрывность релейной функции в точке
хвх = 0 и постоянство формы входного сигнала управляющего эле-
мента в случае существования автоколебаний в системе позволяют
применить простой и наглядный метод определения параметров авто-
колебаний. Сущность этого метода состоит в следующем. Предположив,
что автоколебания существуют, можно разложить в ряд Фурье после-
довательно повторяющиеся с неизвестным периодом заранее известные
по форме И амплитуде импульсы управляющего сигнала релейного
элемента.
Поскольку такое разложение в ряд Фурье представляет собой бес-
конечную сумму гармонических колебаний различных частот, то оп-
ределить установившуюся реакцию линейной части замкнутой системы
(зная ее частотную характеристику) на бесконечную сумму гармони-
ческих воздействий не представляет особого труда в силу принципа
суперпозиции линейных систем.
Так как высокочастотные гармонические воздействия не вносят
существенного вклада в общее установившееся движение системы, то
для практических расчетов достаточно ограничиться несколькими пер-
175
выми гармониками разложения в ряд Фурье. При этом остается опре-
делить время переключения релейного элемента из условий периодич-
ности повторения импульсов.
Из условия переключения вытекает уравнение для определения
периода автоколебаний замкнутой системы. Зная величину периода,
можно определить амплитуду автоколебаний по частотной характерис-
тике линейной части замкнутой системы.
Очевидно, что форма импульса не играет принципиального значения
при использовании изложенного метода: важны лишь условия постоян-
ства формы и периодичности движения. Таким методом можно опреде-
лять, например, параметры автоколебаний систем с ограничением ско-
рости изменения управляющего воздействия и его величины, оценивать
устойчивость системы ”в большом”.
Таким образом, если автоколебания в замкнутой системе с линей-
ной частью и релейным управляющим звеном существуют, то опреде-
ление амплитуд и частот этих автоколебаний производится достаточно
просто. Остается открытым вопрос об устойчивости автоколебаний и о
том, как они возникают.
4Л. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОГО КОНТУРА
ПРИ НАЛИЧИИ РЕЛЕЙНОГО УПРАВЛЯЮЩЕГО ЭЛЕМЕНТА
При рассмотрении линейных задач считается, что фазовое пространст-
во не ограничено, возмущения произвольны и реакция линейной систе-
мы прямо пропорциональна величине возмущений. Ясно, что на самом
деле это не так. Углы отклонения органов управления ограничены пре-
дельно возможными конструктивными значениями, скорости их откло-
нения ограничены мощностью исполнительных механизмов, параметры
движения самолета ограничены прочностью конструкции и т. п.
Таким образом, реальное фазовое пространство является замкну-
тым и ограниченным, и это принципиальное обстоятельство следует учи-
тывать при решении практических задач, так как линейная математичес-
кая модель может неверно отражать рассматриваемый процесс. Поэтому
следует оценить влияние возможных ограничений параметров движения
самолета на его характеристики.
Известно, что ограничения на фазовые координаты могут приводить
к появлению новых типов движения — устойчивых циклов замкнутых
траекторий на фазовой плоскости, называемых автоколебаниями. Воз-
можность существования автоколебаний в замкнутом контуре может
быть вызвана наличием управляющего звена с существенно нелинейными
характеристиками. Общие методы приближенного анализа таких систем
хорошо разработаны [18, 23] и в настоящее время широко использу-
ются в практических расчетах. В настоящем разделе рассматривается
176
задача управления продольным короткопериодическим движением са-
молета нелинейным управляющим звеном, отклоняющим орган управ-
ления по релейному закону с ограничением на величину и скорость от-
клонения органа управления.
Решение такой задачи может представлять практический интерес
при анализе некоторых критических ситуаций, которые могут возник-
нуть в полете (например, при исследовании различного рода отказов
САУ, когда в качестве исполнительного органа используется элемент
с ограниченным диапазоном углов отклонения органа управления).
При этом принципиально возможно возникновение автоколебаний
с амплитудой движения исполнительного ограна управляющего звена
”от упора до упора”. Если время перекладки органа управления из
одного крайнего положения в другое много меньше периода собствен-
ных колебаний самолета на данном режиме полета, то для первого
приближения такое управляющее звено можно заменить релейным эле-
ментом и не учитывать ограничения скорости перекладки органа уп-
равления.
Если время перекладки с ргана управления соизмеримо с периодом
колебаний самолета, то следует учесть ограничение величины макси-
мальной скорости перекладки органов управления.
При ручном пилотировании в ряде случаев математическую модель
летчика можно аппроксимировать релейной характеристикой. Извест-
ные из летной практики случаи продольной раскачки самолета летчи-
ком позволяют предположить, что рефлекторные действия летчика
базируются в основном на предыдущем личном опыте и накопленных
навыках, и первые его реакции на непредвиденные возмущения непро-
порциональны величине возмущений. (По-видимому, при возникновении
возмущений, например, по перегрузке выше некоторого порогового
значения, определяемого летчиком в каждой конкретной ситуации,
летчик реагирует определенной ’’порцией” отклонения рычага управ-
ления либо усилия, не коррелируя величину ’’порции” с величиной
возмущения).
Косвенным подтверждением такого предположения могут служить
общепринятые рекомендации летчикам не пытаться парировать воз-
мущения и при возникновении раскачки бросить ручку управления,
что эквивалентно размыканию контура самолет — летчик.
В защиту такой ’’релейной” точки зрения на действия летчика можно
высказать также следующие соображения. Если считать, что появив-
шееся нежелательное внешнее возмущение летчик стремится убрать как
можно быстрее, то правомочным становится постановка вопроса об
оптимальном по быстродействию законе управления самолетом, от-
куда немедленно следует релейность управления.
Как было показано в разд. 2.4, такое управление имеет как мини-
мум два переключения. В связи с этим приближенный математический
177
Рис. 4.12. Структурная схема замкнутого контура управления самолетом с ре-
лейным управляющим звеном:
а — с запаздыванием; б — типовые характеристики управляющего звена
анализ возмущенного движения замкнутого контура самолет - управ-
ляющее звено с релейной характеристикой закона управления может
представлять определенный практический интерес.
Структурная схема такого замкнутого контура приведена на
рис. 4.12, а. Математическая модель самолета описывается традицион-
ными уравнениями короткопериодического движения, W(p) — пере-
даточная функция свободного самолета. Входными сигналами управ-
ляющего звена могут быть параметры короткопериодического движе-
ния самолета, рассмотренные в разд. 4.5.
Характеристики управляющего звена могут быть, вообще говоря,
достаточно произвольными. Важно только, чтобы форма импульса
не менялась со временем. При рассмотрении релейного звена (с гис-
терезисом или без него) форма импульса — прямоугольная. При анализе
звена с характеристикой, изображенной на рис. 4.12, б, форму импульса
можно варьировать от прямоугольной до треугольной.
Постановка задачи состоит в следующем: ищутся периодические
установившиеся режимы колебаний в замкнутом контуре управления
при отсутствии периодических воздействий (рис. 4.13). Идея решения
этой задачи заключается в разложении в ряде Фурье постоянных по
форме периодических импульсов управляющего звена и нахождения
реакции линейной части системы (по ее частотной характеристике)
на сумму гармонических воздействий.
Зависимость регулируемого параметра от времени является непре-
рывной дифференцируемой периодической функцией времени F(t)
периода 2Т. В принятых обозначениях, как это ясно из рис 4.13, для
возникновения автоколебаний необходимо и достаточно [23] выпол-
нение трех условий:
ЛП = Ко; (4.1)
^1?=т>о; (4.2)
F(t) >- к0 при0<7< Т. (4.3)
178
О
б
Рис. 4.13. Качественная зависи-
мость параметров автоколебаний
) от времени:
а - при наличии гистерезиса в
управляющем звене; б - при на-
личии запаздывания в управляю-
щем звене; в - при наличии ог-
раничений на скорость переклад-
ки органа управления
Как следует из рис. 4.13, первое условие обеспечивает надлежа-
щий момент переключения релейного элемента. Второе условие обес-
печивает отрицательную обратную связь управляющего звена (т. е.
необходимый знак управляющего сигнала). Третье условие обеспе-
чивает отсутствие переключений релейного элемента внутри полупе-
риода. Выполнение этого условия отбрасывает класс возможных авто-
колебаний с переключениями внутри полупериода. Автоколебания
такого вида имеют более сложную форму и требуют применения приб-
лиженных методов расчета.
Если функция F(t) получена, то из уравнения (4.1) определяют-
ся периоды автоколебаний при соблюдении неравенства (4.2). Условие
(4.3) проверяется при расчете.
Для определения функции F(t) следует воспользоваться частотным
методом. По определению автоколебаний функция F(t) представляет
собой установившуюся реакцию линейной части системы с передаточ-
ной функцией И'О?) на последовательность прямоугольных импульсов,
являющуюся выходным сигналом управляющего звена.
Так как движение разомкнутой системы описывается линейными
дифференциальными уравнениями, то справедлив принцип суперпозиции
колебаний. Поэтому, разложив последовательность прямоугольных
импульсов в ряд Фурье и зная передаточную функцию W(p), можно
получить функцию F(t) как реакцию линейной системы на сумму гар-
179
моник разложения в ряд Фурье последовательности прямоугольных им-
пульсов.
Ряд Фурье для последовательности прямоугольных импульсов
имеет вид
4tfp ~ sin(2w + l)cor
’ Ло ----------------
где со = я IT.
Для рассматриваемых регулируемых параметров линейной систе-
мы передаточные функции представлены в табл. 2.1.
Если передаточной функции соответствует амплитудно-фа-
зовая характеристика
^(z со) = iz(co) + zv(co) ; со = со/соо,
то установившаяся реакция линейной части на сумму гармоник опреде-
лится соотношением
F(7)-----—Р S — Jм[А7со]sinncof + v|Xco]cosncor
7 И =1,3,5... п I
Для рассматриваемых параметров короткопериодического движе-
ния самолета амплитудно-фазовую характеристику можно предста-
вить в виде
W(p) = _А? 2 + с .
р (р 2 + 2fr + 1)
5(1 -Ш2) - 2£(С-ЛО>2) . (С-ЛО>2)(1 - W2) + 2Bfw2
lT\ZCO) = -----—--------—----------I —~------—---------—------
(1 - co2)2 + 4f2co2 co[(l - co2)2 +4f2co2]
тогда
f(7) = -^p s
я A: =1,3,5
В (1 - и2со2) - 2f (С - Ли2со2) .
------------=----------------sm nut -
и[(1 - w2co2)2 +4f2w2co2]
(C - An2a>2)(l - w2co2)+2Bf«2co2 --
--------------— ---------------- cos и co Г .
и2со[(1 - мео2)2 +4f2w2co2
(4.4)
Разложив каждое слагаемое под знаком суммы (4.4) на простей-
шие дроби, можно получить
F(t) = ((5 - 2fC) S + е" 'V----1=^-, X
Я I п =1,3,5 " 2/хЛ - £2
180
X (5 - A e - Ce" ifP) S ” s.in_^2_ + e ZV----------------------------------------* - -, X
n= 1,3,5... n2+J_e2V’ 2z\/l-f2
,-,2
~ n sin n Got
« = 1,3,5... n2+— e~ 2i<f
1 00
—^[C S
ш «=1,3,5
cos ncor
n2
Aei'/> + Ce~ - В
S
COS nliJt
n- 1,3,5...„2 +J_e 2,V
U>2
-Ae‘* - Ceilf>+ В ~
+ у III r — , 2/
2/Vl-t2 n= 1,3,5... n2+ ——e
a>2
cos «cor
- 2r</>
(4-5)
Для упрощения правой части (4.5) следует применить известные
соотношения:
___ I при 0 < t < Т
~ sin nut _ I 4
n = 1,3,5 п I 0 при7=0, Т -
~ cos п о7 я2 , Т ~
S -------ь(— -t) при 0 < t < Т ;
«=1,3,5... " 4Г 2
Г сЦе^у-Т)]
__ ____=—=------при 0 < t < Т
~ п sin nut J 4 r ±jyT
2 ----------- =/ ch[e —J
«= 1,3,5... „2+J_ e*2'*’ 2
оз2 0 при t = О, T
shle^-L -7)1
S ------ при 0 <7< T.
«=1,3,5...„2+_1_ e±2'^ 4Г chl-Ie^l
O2 2
Подставив их в выражение (4.5) и преобразовав его, несложно полу-
чить функцию F(t) в виде
F(i) = Кр |с(7- I) + (В - 2fC) Y^Tt )+ (А - С)У2(Г, Т,7) |
приО<7<Т. (4.6).
181
Здесь _ _______ ________________
У1 (£, т,7) = 1 - е- & 1 - Г2~+ V» ~ sin[x/1- ?2(Г- 7)-<р] .
V 1 - f2 (chfТ + cos \/1 - f2 Т)
(4.7)
y2(f т 7) = JZiILZiIL = е- e^TsinX^F7~ sin5/^r<J~7>
dt VI - f2’(chjf + cosa/ 1 -f2 T)
откуда
-^1 =kAa- (A - 07^)45- 2U)r2(f, T.t) j-
dt I '
при 0<7<T.
_ На рис. 4.14 а, б представлены типовые зависимости функции У1 (f,
T, 7) и K2 (f5 Tt t) от времени при различных значениях параметров f иТ.
Из выражений (4.7) следуют основные свойства этих функций:
Ki(f, Г, 0) = - KiCf, ff ту y2«, Т, 0) = - r2(f, Т9 Т) ,
откуда следует, что на интервале [0, 71 функция Yx имеет один экстре-
мум и один нуль, а функция У2 один раз обращается в нуль, и при
значениях f < 0,5, Т< 2 является монотонной функцией времени.
Чтобы получить значение dF/dt в точке t = Г, следует продифферен-
цировать выражение (4.6) и положить t = Т, Проведя необходимые
преобразования, можно записать
1?= Т =*р{- (А - ОК,(г, Т, Т)+ (В- 2M)y2(f, Т, Т)Л
dt I J
Таким образом, условия для нахождения периодов (4.1) и (4.2)
записываются в явном виде:
кр |с I + {В - 2?С)П (J-, Т, Т) + (А- с)у2«7, Т)}=-Ко;
- (А - С) Yi (tf, 7) + (В- 2М) y2(f, Т, Т) < 0. (4.8)
Из (4.8) следует, что период автоколебаний определяется значения-
ми функций Л и Г2 на концах_ интервала 0 7^ На рис. 4.14 в,г
представлены функции Yl (f, Tt t = T) и Y2(^t Tf t = T) в зависимости
от периода Т при различных значениях величины относительного демп-
фирования f. На рисунке видно, что с ростом f кривые сглаживаются
и приближаются к оси абсцисс. В некоторых случаях по виду этих кри-
вых можно судить о существовании автоколебательных режимов. Напри-
182
мер, в случае управления углом атаки (А = О, С = О, В < 0), при нали-
чии гистерезиса существуют автоколебательные режимы для всех реаль-
ных значений f, а при к0 = 0 такого режима нет. Из рис. 4.14, в сле-
дует также, что для каждого значения f существует максимальное зна-
чение величины гистерезиса к0,при котором реализуется автоколебатель-
ный режим. На рис. 4.14, д показаны максимальные значения гистере-
зиса kq и соответствующие им амплитуда и период колебаний. Из ри-
сунка следует, что при релейном управлении максимально возможный
период автоколебаний приближается к периоду собственных колеба-
ний задемпфированного самолета^ а соответствующая ему амплитуда
совпадает с предельным значением к0.
Рис. 4.14. Производящие функции
Л (Г, Г -4) У2 <*> в простран-
Т J
стве параметров T,tjT\______
а - зависимость (£, 7^ t/T); б -
зависимость Y2 (f, Т,~ t/T)\ в -
зависимость Yx (Г, Т, t = Т); г -
^зависимость У3 (£, Т, t — Т);д -
предельное значение параметров авто-
колебаний при управлении углом
атаки
183
Для нахождения амплитуд автоколебаний_необходимо решить урав-
нение dF/dt = 0 относительно t при известном Та. _ _
Как было отмечено выше, на интервале 0 < t < Т функция dF/dt
имеет один корень. _ _
Легко видеть, что если fmax — корень уравнения dF/dt = 0, то ам-
плитуда автоколебаний есть значение функции F(t) в точке t = rmax.
Условие для нахождения Гтах и выражение для амплитуды автоко-
лебаний запишутся в виде
А - (А - С) У, (ffjmax ) + (В -2£4) Y2 (f Та 7тах) = 0; (4.9)
^max = Кр {C(7max - Z2-) + (5 - 2fQ У, (ГТв7тах) +
+ (Л-С)У2(?Тв7тах)}. (4.10)
Таким образом, соотношения (4.9) и (4.10) определяют пара-
метры автоколебаний через известные функции Л (L Г, г) и Y2 (f,
Г, 7) и параметры движения свободного самолета. Функции Ki (£, Г,
f) и_ Y2 (f, Г, t) могут быть затабулированы для различных значений
?иТ.
При наличии запаздывания в релейном элементе качественная кар-
тина изменения параметров движения по времени приведена на
рис. 4.13, _
Для оценки влияния запаздывания т = т/Tq на характеристики
автоколебаний следует использовать условия (4.1) и (4.2).
Очевидно, что условия возникновения автоколебаний с учетом
запаздывания имеют следующий вид (при отсутствии гистерезиса):
1)F(T-t) = 0;
t = Т - т
<0.
Функция F(t) при этом имеет тот же вид, что и при отсутствии
запаздывания. Изменяются лишь значения функций Kj (f, Т, t) и Y2 (f,
Tt t) в момент переключения. Эти функции можно записать в виде
У1 (?, т, т -”) = 1 - sin^1 -J2 ncos(i-Vi-j:2T) + _
>/1 -f2’(ch J-T+ cosx/l-^ r )
+ (e f T+ cos\/1 -f2'rising - x/1 -f2T)
5
Y2(S,T T ~)~sin(\/l-S~2r)cos(x/1-^2t)- .
\/l-f2(chjT + cos\/l-f2f)
-(е~$Т+ cos\/l-f2,r)sin(Vl-f27)
(4.И)
184
Рис. 4.15. Влияние запаздывания на вид
производящих функций Yx и У2
Запаздывание не меняет ка-
чественного характера протекания
кривых Ki ji Y2 в зависимости от
периода Т, как следует из
рис. 4.15.
При необходимости учитывать
ограничение на скорость перек-
ладки управляющего органа сле-
дует изменить форму импульса
входного сигнала (см. рис. 4.12,
6). Такая необходимость может
возникнуть либо в случае воз-
никновения автоколебаний дос-
таточно большой амплитуды, ког-
да время перекладки органа уп-
равления из одного крайнего по-
ложения в другое соизмеримо с
периодом собственных колебаний
самолета, либо в случаях, когда величина аэродинамического шарнир-
ного момента органа управления соизмерима с располагаемым мо-
ментом силового привода.
В первом случае, пренебрегая влиянием аэродинамического шар-
нирного момента на величину скорости перекладки органа управления,
можно считать скорость отклонения постоянной, а импульсы - трапе-
циевидной формы. Во втором случае величина скорости отклонения
является функцией величины и знака угла отклонения, а импульсы по
форме аналогичны приведенным на рис. 2.11.
Ниже приводится оценка влияния формы импульса на параметры
автоколебаний на примере рассмотрения первого случая. Качественная
зависимость параметров автоколебаний от времени изображена на
рис. 4.13, в. Для получения количественных оценок следует опреде-
лить реакцию линейной части системы с передаточной функцией W(p)
на последовательность трапециевидных импульсов.
Ряд Фурье такой последовательности имеет вид
5(0 = -^^ 2
7ГТ! Л =1,3,5
sin sin нам
где сс=7г/Т. (4.12)
Установившаяся реакция линейной части системы на сумму гар-
моник (4.12) определяется соотношением
185
— 4А'пГ 00 sinwGjTi | _ __ — __
F(t) = —2— S -------------- Ju(nco)sinna)t + v(nu))cosflcof ►
7Г2 T i n = 1,3,5 „2
(4.13)
и = Re И7(z co); v = JmW(zco); t = t/TQ T! = T\/Tq; T = T/TQ>
Просуммировав ряд Фурье (4.12), нетрудно получить искомую
функцию F(t).
Используя приведенный выше метод, можно получить выраже-
ния для реакции линейной части системы на серию трапециевидных
импульсов:
ОС 7 С f i ;
F(7) = Кр [(В - 2$С)7/Т\ -C(T-72/Tl-T1)+(-B + 2f C)(Y2 а,
Т,7+ Т1) + Y2 (L Т.Т + 7- Т\У)127\ + [А - 2$В + (4J-2 - 1)С] X
Х(У1(£, Т, 7+ 7\)+ У2(£, Т, Т+ 7- Л))/2Л]
О < 7 < л;
dF/d7=Кр[с7/Тг + (в- 2ГСХК!а,Т7 + Л) + у2(Г,т, т +
+ 7-т1))/2Г1 + (A -c\y2^,T,7+ 7\)+ y2(S,t,t+7-
-Т2))/2Т2] ;
Т\ <7 <7 - Л;
F(t) = Kp[(B-2$C)+ O(7-7/2)-(B-2fCXr2(f,r,7+ 71)-
- У2(Г, т, 7- Т2)}12Т2 + [А - 2W + (4f2 - 1)С](Г!(Г, 7.7+Л)-
-У1(?,77-Т1))/271];
(4.14)
Т2 <7 <Т - ;
dF/dt=tfp[С + (В-2ГСХУ1 (f,7,7+ Л)- У1 (f, 7,7- 71 ))/27, +
+ (А- СХУ2(Г, 7,7 + Л) - y2(f, 7,7- 71))/2Т1 ];
7-71 < 7 < 7;
F(t)=кр[(в - 2fC)(7 -7)/71 - с/2[(7-7)2/71 - 7+ 7J + (в -
- 2fсху2 (Г, т, 7- 71) + у2 (Г, 7,7- Л) + у2 (f, т, 7+ т2 - т))/2Г1
186
- [A - 2Г5 + (4f2 - 1)C КЛ (Г, Т, 1 - Л ) + Y. (Г, Т, t + 7\ - T))l2T\ ];
Т - Л < 7 < Т;
dF/di=к? [с(Г - 7)1 т\ - (в - 2ГСХГ1 (Г т, 7 - т\) + у, (f, г, 7+
+ Л - Т))12ТХ - (А - cxr2(t, г.7-тх) + У2(Г, Т.7+ Л - П)/2Л ].
Соотношения (4.14) получены при условии, что линейной части
разомкнутой системы соответствует передаточная функция достаточ-
но общего вида
р(р 2 + 2?р + 1)
которая, как следует из предыдущих разделов, характеризует продоль-
ное движение самолета (в безразмерной форме) при управлении ос-
новными параметрами. Форма симметричного трапециевидного импуль-
са зависит от величины Л и при изменении Т\ от нуля до Т\ -’Т/2
трансформируется из прямоугольной в треугольную.
Таким образом, параметры автоколебаний для достаточно широ-
кого класса формы импульсов и регулируемых параметров движения
с учетом и без учета запаздывания и гистерезиса зависят от однотип-
Рис. 4.16. Параметры автоколебаний при управлении перегрузкой и углом атаки:
а - зависимости т)Лутах G*, т); б - зависимости Та($, к0),
187
Рис. 4.17. Расчетные методы пара-
метров автоколебаний:
-------точный метод; О - метод
гармонического баланса
ных производящих функций
Yi (f, Т, t\ r2(f, T, 7): по-
ведение этих функции на ин-
тервале [0, т] во всех рас-
смотренных случаях определяет
амплитуду и период автоко-
лебаний.
На рис. 4.16 приведены
результаты параметрических
расчетов на примере управ-
ления перегрузкой пу и углом
атаки самолета. Из анализа
полученных результатов сле-
дует, что период и амплитуда
автоколебаний монотонно
уменьшаются с ростом f и
монотонно увеличиваются с
ростом величины запаздывания Г. Амплитуда автоколебаний наиболее
резко уменьшается в интервале изменения величины f от 0 до 0,5 и при
f > 0,5 асимптотически приближается к оси абсцисс. Период колебаний
с ростом величины f уменьшается плавно, переходя в прямую с углом
наклона dT/d.^ ~ - 0,6.
Влияние гистерезиса на алплитуду и период автоколебаний при
малых значениях величины к0 аналогично влиянию запаздывания. Одна-
ко при увеличении параметра К возможно возрастание периода автоко-
лебаний при изменении f от 0,2 до 1. Амплитуда при этом изменяется
слабо.
Изменение формы импульса от прямоугольной до треугольной
вызывает незначительное изменение периода и амплитуды автоколе-
баний независимо от величины f.
На рис. 4.17 приведены частоты и амплитуды колебаний при управ-
лении углом атаки самолета для двух значений величины f. Для срав-
нения нанесены точки, полученные расчетом по методу гармонического
баланса. Из рисунка видно хорошее совпадение обоих методов.
Следует заметить, что условие возникновения автоколебаний в
методе гармонического баланса определяется уравнением
1 = 0,
где /(Л)_— комплексный коэффициент усиления нелинейного элемен-
та, a W(ko) характеризует передаточную функцию разомкнутой линей-
ной системы.
188
Ф (A sina?t)sina? t dt;
Это условие формально совпадает с условиями на границе устой-
чивости замкнутого контура, рассмотренными в разд. 4.5, если рассмат-
ривать параметр К как комплексное число.
Комплексный коэффициент усиления нелинейного элемента 1(A)
записывается обычно в виде 1(A) = g(A) + ib(A) [27], где действитель-
ная и мнимая части#(А) и Ь(А) вычисляются из соотношений
о 2 7Г/J
ТТЛ q
1 2п/ш __________ _________
Ь(А) = ----- J Ф(А sin со Г) с? (Я sin cor) = —- .
It А 2 о 7Г А 2
Зцесъ Ф (A sin со7) — статическая характеристика релейного элемента.
$
Отсюда следует, что Ь(А) можно записать в виде -----, где S —
ТТА
площадь петли, образованной статической характеристикой релейного
элемента за период.
Легко видеть, что для симметричных релейных элементов с одно-
значными (без гистерезиса) статическими характеристиками величина
S = 0 и комплексный коэффициент усиления вырождается в действи-
тельное число: 1(A) = g(A) Так, например, для релейного элемента
с гистерезисом к0 комплексный коэффициент усиления 7 (Л) равен:
1(A) = ( ^/а2 -к%- ik0)
ттА
и при отсутствии гистерезиса (к0 = 0) становится действительным
числом:
1(А) = _^Р .
ттА
В этом случае условия возникновения автоколебаний в точности
совпадают с условиями потери устойчивости замкнутой системы, рас-
смотренными в разд. 4.5. Частота автоколебаний при этом определяется
полученными в разд. 4.5 соотношениями для значений частоты на грани-
це устойчивости.
Это обстоятельство дает возможность использовать результаты ана-
лиза динамических характеристик замкнутого контура линейных уп-
равляемых систем для оценки параметров автоколебаний в методе
гармонического баланса при условии вырождения комплексного переда-
точного числа нелинейного элемента. Эти условия охватывают, вообще
говоря, широкий класс нелинейных характеристик управляющего звена.
Рассмотренные методы определения параметров автоколебаний по-
189
зволяют находить в безразмерной форме установившиеся режимы дви-
жений, так называемые предельные циклы на фазовой плоскости. При
этом остается открытым вопрос об устойчивости таких режимов. Неус-
тойчивый предельный цикл характерен тем, что может исчезать при
малых изменениях параметров, характеризующих поведение системы
(передаточные числа, коэффициенты характеристического уравнения
и т. п.), однако при проведении предварительных оценок вопросы, свя-
занные с устойчивостью автоколебательных режимов, могут не рассмат-
риваться. Расчетным анализом выявляется лишь возможность появ-
ления автоколебательных режимов. Выявленные таким образом ’’подоз-
рительные” режимы должны исследоваться на более сложной математи-
ческой модели явления: с учетом динамических характеристик системы
управления,силовых приводов и т. п.
Дальнейшего анализа требуют также автоколебания с частотами,
лежащими в диапазоне рабочих частот летчика.
Детальные исследования таких режимов следует проводить в эк-
спериментах на пилотажных стендах и летающих лабораториях.
Следует отметить, что исследование явления раскачки на пило-
тажных стендах является сложной задачей, так как связано с особеннос-
тями поведения летчика в различных ситуациях, которые трудно вос-
создать или сымитировать в наземных условиях при моделировании про-
цесса на пилотажных стендах.
Особенности поведения человека в различных эмоциональных сос-
тояниях, по-видимому, зависят от принадлежности человека к тому или
иному психологическому типу. Изменение поведения летчика в различ-
ных ситуациях косвенно подтверждается известными из летной практи-
ки случаями. Один и тот же летчик может ’’раскачать” самолет в не-
обычной ситуации, в то время как при нормальном пилотировании на
том же режиме полета поведение самолета у него замечаний не вызывает.
При математическом описании явления раскачки можно считать ос-
новными два параметра летчика: коэффициент усиления К и время
запаздывания т. Если считать, что при изменении состояния летчика
каждый параметр может оставаться неизменным, увеличиваться или
уменьшаться, по сравнению с его нормальными значениями, то прин-
ципиально возможны девять различных комбинаций изменения этих
параметров при изменении эмоционального состояния.
Оставив лишь комбинации, в которых изменяются оба параметра,
ясные из приведенной ниже таблицы, можно классифицировать людей
по типам, основываясь на изменении поведения человека при изменении
его эмоционального состояния (в таблице знак плюс соответствует уве-
личению, а минус — уменьшению соответствующего параметра). При
таком подходе можно выделить два принципиально отличающихся типа
людей: второй и четвертый типы.
Второй тип людей под влиянием эмоциональных воздействий ста-
190
новится более собранным, активным, действует энергично, без промед-
ления (увеличивается коэффициент усиления и уменьшается время за-
паздывания) .
Четвертый тип людей в аналогичных ситуациях ’’теряется”, ведет
себя более пассивно, чем в нормальном состоянии (уменьшается коэф-
фициент усиления и увеличивается время запаздывания). Такое разде-
ление не противоречит нашим обычным представлениям: одни люди те-
ряются в критических ситуациях, другие наоборот, становятся более
активными.
Тип | Дт Тип Г ! Ат
1 + + 3
2 + - 4 - +
Таким образом, зная качественные характеристики изменения па-
раметров передаточной функции летчика, можно было бы учесть это
в расчетах, так как среднестатистические величины параметров пе-
редаточной функции летчика при нормальных условиях его работы
достаточно хорошо известны в простейших случаях.
Нетрудно было бы также и искусственно ввести аналогичные изме-
нения в коэффициент усиления летчика и время его запаздывания при
моделировании подобных явлений на пилотажных стендах с летчиками
или операторами.
Любопытно, что психологи ставили подобные эксперименты по
определению влияния эмоциональных воздействий на характеристики
человека-оператора, выполняющего простейшие тесты [И]. Различные
ситуации создавались под влиянием гипноза, испытаниям подвергались
23 человека (мужчины в возрасте 18...20 лет, не имеющие отклонений
в состоянии здоровья), в которых каждый испытуемый подвергался
120 тестам двух категорий сложности. После статистической обработ-
ки было выявлено три различных типа операторов, названных в работе
[11] устойчивым, менее устойчивым и неустойчивым. У операторов пер-
вого типа (по классификации авторов) под влиянием стресса снижа-
лась величина времени запаздывания в зависимости от сложности
предъявляемого теста от 25 до 55% по сравнению с их нормальным
состоянием. В то же время снижалось относительное количество не-
правильных действий - ошибок оператора соответственно от 16 до 7%.
У операторов второго типа время запаздывания увеличилось от 26
до 37%, однако количество ошибок соответственно снизилось на 19%
в наиболее простом случае и увеличилось на 22% в более сложном.
Операторы третьего типа (неустойчивые к эмоциональным воз-
действиям) характеризуются увеличением времени запаздывания на 17
и 18% и увеличением количества ошибок на 18 и 132% соответственно.
191
Результаты экспериментов подтверждают предположение о том,
что поведение человека при эмоциональных воздействиях может су-
щественно изменяться по сравнению с нормальными условиями рабо-
ты, хотя для получения количественных результатов, которые можно
было бы использовать при моделировании и расчетах замкнутого конту-
ра самолет — летчик, проведенных экспериментов пока еще недостаточно.
Все это свидетельствует о том, что следует с осторожностью отно-
ситься к результатам экспериментов, полученных на пилотажных стен-
дах без учета возможного влияния эмоциональных воздействий на
поведение оператора. Так, например, отсутствие раскачки на стенде,
по-видимому, не гарантирует ее отсутствия в полете.
192
СПИСОК ЛИТЕРА ТУРЫ
1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление.
М.: Наука, 1979.429 с.
2. Арнольд В.И., Варченко А.Н., Гусейн-Заде С.М. Особенности дифферен-
циальных отображений. М.: Цаука, 1984. 336 с.
3. Байдаков В.Б., Клумов А.С. Аэродинамика и динамика полета летатель-
ных аппаратов. М.: Машиностроение, 1979. 344 с.
4. Бюшгенс Г,С., Студнев Р.В. Аэродинамика самолета. Динамика продоль-
ного и бокового движения. М.: Машиностроение, 1979. 350 с.
5. Бюшгенс Г.С., Студнев Р.В. Динамика самолета. Пространственное движе-
ние. М.: Машиностроение, 1983. 244 с.
6. Гуськов ЮЛ.9 Загайнов Г.И. Управление полетом самолетов. М.: Маши-
ностроение, 1980. 214 с.
7. Гилмор Р. Прикладная теория катастроф. М.: Мир. 1984. TI. 350 с.
8. Доброленский Ю.П. и др. Методы инженерно-психологических исследований
в авиации. М.: Машиностроение, 1975. 280 с.
9. Дубовицкий АЛ., Милютин АЛ. Теория принципа максимума // Методы
теории экстремальных задач в экономике. М.: Наука, 1981,45 с.
10. Дузь ПД. История воздухоплавания и авиация в России М.: Машиностро-
ение, 1981, 271 с.
11. Епишкин АЖ., Шилова ВЛ. Исследование психофизиологических характе-
ристик оператора в состоянии эмоционального стресса // Методические и техничес-
кие вопроссы экспериментальной психофизиологии. М.: Наука, 1980. 95 с.
12. Калачев Г.С. Самолет, летчик и безопасность полета. М.: Машиностроение,
1979. 222 с.
13. Клумов А.С., Меркулов А.Е.// Автоматика и телемеханика, 1984. №12.
С. 13-21.
193
14. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978. 736 с.
15. Микаладзе В.Г., Титов В.М. Основные геометрические и аэродинамические
характеристики самолетов и ракет. М.: Машиностроение, 1982. 150 с.
16. Постников М»М. Устойчивые многочлены. М.: Наука, 1981. 172 с.
17. Пышнов В.С. Основные этапы развития самолета. М.: Машиностроение,
1984.91 с.
18. Удерман Э.Г. Метод корневого годографа в теории автоматических систем.
М.: Наука, 1972.448 с.
19. Шавров В.Б. История конструкций самолетов в СССР до 1938 г. М.: Ма-
шиностроение, 1978.576 с.
20. Шавров В.Б. История конструкций самолетов в СССР 1938-1950 гг. М.:
Машиностроение, 1978.440 с.
21. Шеридан Т.Б., Феррелл У.Р. Системы человек - машина. М.: Машиностро-
ение, 1980. 399 с.
22. Шкадов Л.М. и др. Механика оптимального пространственного движения
летательных аппаратов ватмосфере. М.: Машиностроение. 1972. 240.
23. Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных урав-
нений с отклоняющимся аргументом. М.: Наука, 1971. 296 с.
194
ОГЛАВЛЕНИЕ
Предисловие.....................................................3
Введение . ....................................................5
Глава 1. Силы и моменты, определяющие движение самолета в атмос-
фере ............................................................12
1.1. Принятые системы координат и уравнения движения самолета
как твердого тела...........................................12
1.2. Аэродинамические силы и моменты, действующие на самолет
в полете....................................................18
1.3. Управляющие моменты в продольном движении самолета.....25
1.4. Типовые атмосферные возмущения.........................29
1.5. У прощение уравнений продольного движения самолета.....35
Глава 2. Исследование уравнений продольного движения самолета...42
2.1. Основные задачи динамики полета........................42
2.2. Краткий анализ общих методов решения систем дифференци-
альных уравнений............................................42
2.3. Краткий анализ характеристик коротко периодического движе-
ния самолета под воздействием управляющих моментов..........49
2.4. Влияние динамических характеристик коротко периодического
движения самолета на изменение траекторных параметров полета.... 68
2.5. Некоторые оптимальные маневры самолета.................77
Глава 3. Системы продольного управления и управляемость самолета . ... 86
3.1. Общие требования к ручному управлению..................86
3.2. Системы ручного управления.............................93
3.3. Особенности систем управления с дифференциальным отклоне-
нием органов продольного управления.........................100
3.4. Типовые нелинейности в системах ручного управления.....103
3.5. Системы полуавтоматического и активного управления.....107
Глава 4. Анализ динамических характеристик самолета с моделью лет-
чика или автопилота.................................................111
4.1. Основные задачи исследования замкнутого контура............111
4.2. Общие методы расчета динамических характеристик замкнутого
контура с линейным алгоритмом управления........................114
4.3. Методы расчета динамических характеристик замкнутого конту-
ра при наличии запаздывания.....................................119
4.4. Динамические характеристики замкнутого контура при типовых
законах раздельного управления параметрами движения самолета. ... 122
195
43. Динамические характеристики замкнутого контура при типовых
законах совместного управления параметрами движения самолета ... 141
4.6. Динамические характеристики замкнутого контура при наличии
репейного управляющего элемента...............................176
Список литературы..................................................193
196
Производственное издание
Клумов Александр Сергеевич
ПРОДОЛЬНАЯ УСТОЙЧИВОСТЬ
И УПРАВЛЯЕМОСТЬ МАНЕВРЕННОГО САМОЛЕТА
Редактор Н.В. Корженевская
Художественный редактор BJB. Лебедев
Обложка художника Е.Н. Волкова
Технический редактор Н.В. Павлова
Корректор А.Л. Георгиевская
Оператор Н.Б. Жилина
ИБ № 4920
Сдано в набор 13.03.87. Подписано в печать 4.03.88. Т-05154.
Формат 60Х 84 1/16 Бумага офсетная №1 Гарнитура Пресс Роман
Печать офсетная Усл.печл. 11,63. Усл. кр-отт. 11,86. Уч.-изд. л. 12,53.
Тираж 2600 экз. Заказ 1173 Цена 65 к.
Ордена Трудового Красного Знамени издательство ’’Машиностроение”,
107076, Москва, Стромынский пер., 4
Отпечатано в Московской типографии № 9 НПО
’’Всесоюзная книжная палата” Госкомиздата,
109033, Москва, Волочаевская ул., 40, с оригинала-макета,
изготовленного в издательстве ’’Машиностроение”
на наборно-пишущих машинах
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Издательство ’’Машиностроение” ежегодно выпускает
книги по специальным вопросам машиностроения, тиражи
которых определяются на основании предварительных
заказов покупателей.
Своевременный предварительный заказ экономит время
и гарантирует приобретение нужной книги.
Издательство ’’Машиностроение” просит отдельных по-
купателей, научные учреждения, предприятия, учебные
заведения, библиотеки и другие организации сделать за-
казы на специальную литературу по машиностроению в ма-
газинах, торгующих технической книгой.
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
ЛИНИЯ ОТРЕЗА
С целью получения информации о качестве наших изда-
ний просим в предлагаемой анкете подчеркнуть позиции,
соответствующие оценке книги ’’Продольная устойчивость
и управляемость маневренного самолета” А.С. Клумова.
1. В книге существует: острая необходимость, значитель-
ная потребность, незначительная потребность.
2. Эффективность книги с точки зрения практического
вклада в отрасль: весьма высокая, высокая, сомнительная,
незначительная.
3. Эффективность книги с точки зрения теоретического
вклада в отрасль: весьма высокая, высокая, сомнительная,
незначительная.
4. Материал книги соответствует достижениям мировой
науки и техники в данной отрасли: в полной мере, частично,
слабо.
5. Книга сохранит свою актуальность: один-два года, до
пяти лет, длительное время.
6. Название книги соответствует содержанию: в полной
мере,частично, слабо.
Просьба по линии отреза отрезать страницу и выслать в
издательство ’’Машиностроение” по адресу 107076, Москва
Стромынский пер., д. 4, сообщив о себе следующие сведения:
фамилия, имя, отчество ----------------------------------
образование ----------, ученое звание--------------------,
специальность и стаж работы по специальности-------------
--------------------------------, должность и место работы
домашний адрес
ЛИНИЯ ОТРЕЗА