Текст
THE JOUKOVSKT
CENTRAL INSTITUTE FOR AEROHYDRODYNAMICS
COMMISSION FOR PUBLICATION OF THE WORKS OF Prof. N. E. JOUKOVSKY
Prof. N. E. JOUKOVSKY
COLLECTED PAPERS
VOLUME IX
MATHEMATICS • ASTRONOMY • REPORTS • LECTURES
CHARACTERISTICS AND BIOGRAPHIES
Edited by Prof. A. P. KOTELNIKOV
PEOPLE’S COMMISSARIAT OF HEAVY INDUSTRY OF THE USSR
ONT1
(UNITED SCIENTIFIC TECHNICAL PUBLISHING HOUSE)
EDITORIAL OFFICE FOR AVIATION LITERATURE
%
MOSCOW 1 93 7 LENINGRAD
ЦЕНТРАЛЬНЫЙ АЭРОГИДРОДИНАМИЧЕСКИЙ ИНСТИТУТ qtii
нм. проф. В. Е. ЖУКОВСКОГО С
КОМИССИЯ ПО ИЗДАНИЮ ТРУДОВ проф. Н. Е. ЖУКОВСКОГО
Проф. Н. Е. ЖУКОВСКИЙ
ПОЛНОЕ
СОБРАНИЕ СОЧИНЕНИЙ
ТОМ IX
МАТЕМАТИКА • АСТРОНОМИЯ • РЕЧИ • ДОКЛАДЫ
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Под редакцией проф. А. П. КОТЕЛЬНИКОВА
ОНТИ НКТП СССР
ГЛАВНАЯ РЕДАКЦИЯ АВИАЦИОННОЙ ЛИТЕРАТУРЫ
МОСКВА
19 3 7
ЛЕНИНГРАД
+ №
+ 3 6 • bf//
|ЮШГАНТБ
(1916 г.)
ОТ РЕДАКЦИИ
Том IX распадается на три отдела: в первом помещены
статьи математического характера, во втором—по астрономии
и математической физике, в третьем — публичные речи и
характеристики работ русских и иностранных ученых, био-
графия и некрологи.
В статьях „Геометрическое разъяснение некоторых вопросов
теории уравнений с частными производными", „Геометрическое
доказательство теорем С. А. Чаплыгина о диференциальных
неравенствах", „Заметка по вариационному исчислению", на-
писанных в характерной для Н. Е. Жуковского манере, теоремы
и вопросы теории диференциальных уравнений и вариацион-
ного исчисления облекаются в простую геометрическую форму.
Две последние работы были напечатаны уже после смерти
Н. Е. Жуковского. Работа по вариационному исчислению была
проредактирована по рукописи Н. Г. Ченцовым. Доказательство
теорем С. А. Чаплыгина было записано Н. Г. Ченцовым по
лекции Н. Е. Жуковского в ЦАГИ и затем отредактировано
для печати В. П. Ветчинкиным.
В статьях по теоретической астрономии Н. Е. Жуковский
останавливается на теории кометных хвостов, на способе
Гаусса по определению элементов планетных орбит по трем
наблюдениям и на доказательстве теоремы Ламберта,' причем
и в этих работах он широко пользуется для упрощения задач
геометрическим методом.
Астрономические статьи, опубликованные в свое время на
французском языке, даны в настоящем издании также и
в русском переводе, сделанном проф. А. П. Котельниковым.
К статьям по математической физике относятся две работы:
„К вопросу о давлении диэлектрического газа в электрическом
поле" и речь „Старая механика в новой физике"; последняя
6
ОТ РЕДАКЦИИ
предназначалась для университетского акта 12 января 1918 г.,
но не была прочитана, так как акт не состоялся. Речь эта
в несколько расширенном изложении была прочитана затем
Н. Е. Жуковским на заседании математического общества
3 марта 1918 г. В печати она появляется впервые в настоящем
издании. Обе указанные физические работы были просмотрены
для настоящего издания проф. Н. П. Кастериным.
Публикуемые в настоящем томе статьи и речи отражают
физико-механические и натур-философские взгляды Н. Е. Жу-
ковского. Бесконечно-далекий по всему складу своей личности
и по своему миросозерцанию от позиции „жреца чистой на-
уки", не устававший подчеркивать неразрывную связь между
теорией и практикой, гордившийся своими личными связями
с практической инженерией, Н. Е. все же был сыном своего
века, и в его высказываниях советский читатель иногда ощу-
тит налет идеализма.
Часть публикуемого материала имеет официально-юбилей-
ное назначение, которое не могло не оставить отпечатка на
манере изложения и на характеристике юбиляров. Редакция
публикует эти статьи как ценный историко-документальный
материал к биографии Н. Е. (помещенной в I томе настоящего
издания), характеризующий научные взгляды Н- Е. и их
эволюцию, и как материал, не утративший и по сию пору
научного интереса.
Некоторые из характеристик научных работ, биографи-
ческих очерков и некрологов, написанных Н. Е. Жуковским
и напечатанных в разное время в различных изданиях, были
даны с портретами лиц, которым эти статьи посвящались
(С. В. Ковалевская, Ф. А. Слудский, М. В. Остроградский,
А. И. Пермяков, О. Лилиенталь, Г. Гельмгольц); эти портреты
воспроизводятся и в настоящем издании.
В соответствии с пожеланием редакционной комиссии по-
мещены также портреты Д. И. Менделеева, А. Ю. Давидова,
Ньютона, А. Г. Столетова, Н. А. Умова, Ф. Е. Орлова,
В. Я. Цингера, В. Г. Ишменецкого, характеристики работ ко-
торых или биографии, принадлежащие перу Н. Е. Жуков-
ского, вошли в настоящий том. К сожалению, портрета
Л. И. Ливенцова разыскать не удалось.
РАЗДЕЛ ПЕРВЫЙ
МАТЕМАТИКА
ГЕОМЕТРИЧЕСКОЕ РАЗЪЯСНЕНИЕ НЕКОТОРЫХ ВОПРОСОВ
ТЕОРИИ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
(1885 г.)
Для разъяснения учащимся главных приемов интегриро-
вания уравнений с частными производными первого порядка,
мы излагаем здесь эти приемы в виде решения некоторых
геометрических задач.
Задача 1. Даны направления касательных семейства
кривых линий; провести через данную точку пространства
поверхность, перпендикулярную этому семейству.
Вообразим прямоугольные оси координат и предположим,
что косинусы углов, которые касательная,
проведенная через
точку (х, у, z), образует с этими осями,
находятся в отношении
P-.Q-.R,
где Р, Q и R— функции х, у и z.
Прежде чем приступить к решению
задачи, определим условие ее возмож-
ности.
Начертим (фиг. 1) на плоскости ху
бесконечно малый прямоугольник ZZET'Tj,
стороны которого параллельны осям
Ох и Оу и равны dx и dy. На этом
прямоугольнике, как на основании, по-
строим прямоугольную призму и про-
ведем по ее сторонам непрерывную
линию NMLKH, ортогональную дан-
ному семейству линий. Понятно, что
условие возможности
нашей задачи состоит в том, чтобы эта линия замыкалась,
т. е. чтобы было NH=O.
10
МАТЕМАТИКА
Для определения NH обозначаем через dz, lz, d'z, %'z
бесконечно малые изменения z при переходах: от L к М, от
L к К, от К к Н и от М к N. Получим:
NH= d'z — dz — (8'z — 8z).
Но p
dz —----dx,
d'z — dz —
Uy dz R I \dff dz RJ , ,
-----------------pa—:--------------dx dW>
g'z — t>z =
/ dQ dQ \ dx dz R J | R— | [dx dz R J
R2
dxdy,
поэтому
NH=-^ [ pl U Q ( )
R2 L \ dz dy ) \ dx dz J
+ R
(dP_dQ
\ dy dx
Отсюда следует, что искомое условие будет:
pldQ dR\ IdR dP\ (dP dQ
\ dz dy)‘^\dx dz)~‘K\dy dx
)=0. (1)
Положим, что это условие удовлетворено, и оси координат
взяты так, что точка А, через которую надо провести поверх-
ность, лежит на оси Oz. Проведем сначала через эту точку
кривую АВ по плоскости xz ортогонально данному семейству
линий. Для этого интегрируем диференциальное уравнение
& _Р
dx R’
положив в нем у = 0. Произвольное постоянное определяем
под условием, что при х = 0, z = О А. Пусть найденный
йнтеграл по замене в нем z на с будет:
/(лг, с) = 0. (2)
ГЕОМЕТРИЧЕСКОЕ РАЗЪЯСНЕНИЕ ТЕОРИИ УРАВНЕНИЙ 11
Через произвольную точку В найденной кривой проведем
плоскость параллельно yz и на ней построим кривую BN,
ортогональную данному семейству линий. Чтобы найти урав-
нение этой кривой, интегрируем диференциальное уравнение:
dz Q
dy~ R’ •
считая х постоянным, и определяем произвольное постоянное,
полагая при J/ = 0, z = c. Найдем интеграл:
ф(х, у, z, с) = 0. (3)
Если теперь исключим с из уравнений (2) и (З),1 то, оче-
видно, найдем уравнение искомой поверхности.
Называя через dx, dy, dz диференциалы координат при
переходе от одной точки этой поверхности к другой беско-
нечно близкой и замечая, что элемент дуги, соединяющий эти
две точки, должен быть перпендикулярен к касательной дан-
ного семейства кривых, найдем уравнение с полными дифе-
ренциалами:
Pdx-\-Qdy-\-Rdz = G, (4
которому должна удовлетворять наша поверхность. Поэтому
решенная нами задача заключает в себе способ интегрирования
этого уравнения.
Задача 2. Даны направления касательных семейства
кривых линий', провести поверхность, образованную линиями
этою семейства, проходящими через точки данной кривой.
Пусть касательные даны отношением косинусов
P-.Q-.R.
Прежде всего определяем уравнения линий данного се-
мейства, интегрируя совместные диференциальные уравнения:
dx dy dz
~P—~Q—~R’
Пусть
f (x, у, z) = a, I
/i (*> y, z) = b I
12
МАТЕМАТИКА
будут их интегралы. После этого обращаемся к кривой, через
которую должна проходить искомая поверхность. Положим,
что уравнения кривой суть:
« (х, у, z) = 0,)
<?i(x, у, z) = Oj '
Исключив из уравнений (5) и (6) х, у, z, найдем связь
между параметрами а и Ь:
a = Q(b), (7)
которая должна иметь место для всех линий данного семейства,
пересекающих кривую (6). Заменяя в уравнении (7) а и Ь их
величинами из уравнений (5), найдем уравнение искомой по-
верхности.
Если теперь предположим, что это уравнение решено от-
носительно z и назовем через р и q частные производные z
по х и у, то направление нормалей поверхности будет опре-
деляться отношением косинусов углов:
р-я- — 1,
и так как эти нормали должны быть перпендикулярны каса-
тельным семейства линий, то искомая поверхность должна
удовлетворять линейному уравнению с частными производными
Pp+Qq = R. (8)
Найденный способ решения задачи дает нам способ инте-
грирования этого уравнения.
Задача 3. В каждой точке пространства построен конус’,
провести через данную кривую поверхность, нормали которой
направлены по образующим этих конусов.
Предположим, что косинусы углов образующих конуса на-
ходятся в отношении
р:<7: —1,
где р и q связаны уравнением
Я, х, у, z) = 0. (9)
Ьоо5р ажаем в каждой точке пространства другие конусы:
? (Р, 9, х, у) = 0 (10)
ГЕОМЕТРИЧЕСКОЕ РАЗЪЯСНЕНИЕ ТЕОРИИ УРАВНЕНИИ 13
и выбираем их так, чтобы образующие, по которым они пере-
секаются с конусами (9), давали направления касательных се-
мейства линий, к которому можно провести ортогональную
поверхность.
Это требует по формуле (1), чтобы величины р и q, опре-
деленные из уравнений (9) и (10), удовлетворяли условию:
Р dz dz ду ' дх
(И)
Подставляем сюда по формулам (9) и (10):
dq 1/ dF ду ду dF \
дх А \ дх др дх др / ’
др___1 /ду dF dFду \
dy~b\dydq ду dq ) ’
др 1 dF ду
dz A dz dq ’
dq 1 dF ду
dz A dz dp ’
где
д__dF ду__dF dy
dp dq dq dp '
Находим
dy dF dy dF , dy / dF , dF \
dx dp dy c/q ' dp \ dx p dz )
dy / dF . dF\ п
dq \ dy dz /
(12)
Это уравнение, из которого z может быть исключено с по-
мощью формулы (9), представляет линейное уравнение с част-
ными производными, из которого можно определить функцию у.
Для этого надо обратиться к совместным диференциальным
уравнениям:
dy _ dp _ dq
~dF~ ~dF~~dF. dF dF dF’
dp dq dx'Pdz dy'Pdz
14
МАТЕМАТИКА
причем достаточно будет определить только два интеграла
этих уравнений
/ (х, У, Р, Ч) = а, |
fi(x, у, р, q) = b.\
(14)
Получив эти интегралы, обращаемся к уравнению кривой
Х = ^ (z), I
^==%(z)J
(15)
через которую должна проходить наша поверхность. Понятно
что на этой кривой направление нормали нашей поверхности,
вполне определено, так как она должна не только быть напра-
влена по образующей конуса (9), но и должна быть перпен-
дикулярна этой кривой. Таким образом на данной кривой р
и q удовлетворяют условию
Р'¥ (?) + Я'\\ (z) — 1 = 0. (16)
Определяя из уравнений (9), (15) и (16) х, у, р и д, как
функции z, и подставляя в уравнения (14), найдем два урав-
нения, из которых можем исключить z и получить;
О (а, Ь) = 0. (17)
Подставляя сюда аргументы а и b из формул (14), найдем
искомую нами связь:
<? (р, Я, х, у) = О,
которая вместе с данным уравнением (9) позволит определить
для каждой точки направление касательной семейства линий,
к которому можно провести ортогональную поверхность. После
этого остается только через какую-нибудь точку заданной
кривой (15) провести такую ортогональную поверхность, кото-
рая и будет искомая.
Если бы мы решили уравнение искомой поверхности отно-
сительно z и положили бы
ГЕОМЕТРИЧЕСКОЕ РАЗЪЯСНЕНИЕ ТЕОРИИ УРАВНЕНИЙ 15
то нашли бы, что она должна удовлетворять нелинейному
уравнению с частными производными
F(p, q, х, у, z) = 0.
Поэтому найденное нами решение задачи дает способ
интегрирования этого уравнения.
28 марта 1884 г. в заседании физико-математической комиссии Отделе-
ния физических наук Общества любителей естествознания Н. Е. Жуковский
сделал сообщение на тему „Разъяснение некоторых вопросов интегрирования
уравнений с частными производными посредством геометрии". Работа
„Геометрическое разъяснение некоторых вопросов теории уравнений с част-
ными производными* впервые была напечатана в 1885 г. в „Отчете о дея-
тельности Московского технического училища за 1882—1883 гг.“ Вторично
работа была напечатана в юбилейном издании Сочинений Н. Е. Жуковского,
т. 1, 1912. Прим. ред.
geometrical elucidation of some questions on the
THEORY OF PARTIAL DIFFERENTIAL EQUA TIONS
In this note the fundamental methods of integration of
partial differential equations of the first order are being stated
in a geometrical form and elucidated in the solution of the
following three problems.
Problem I. Knowing the directions of the tangents to
a certain curves family in space, it is required to draw through
a given point of the space a surface orthogonal to that curves
family.
The solution of this problem results from the integration of the
equation (4) with perfect differentials.
Problem II. Knowing the directions of the tangents to the
curves family, it is required to draw a surface formed by lines
of that family passing through the points of the given curve.
The solution of this problem gives the solution of differential
equation (8).
Problem III. At every point of the space is constructed
a cone. It is required to draw through a given curve a surface,
whose normals are directed along the generating lines of those
cones.
Let us assume that the cones are given by equation (9).
For the solution of the problem other cones (10) are being sought
for in such a way that the generating lines, along which they
intersect with cones (9) might give the directions of the tan-
gents to the family of lines to which it were possible to draw
an orthogonal surface. The solution of the problem leads to the
solution of the partial differential equations.
ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
(145—1923 г.)
V)
1. В 1879 г. была напечатана мною в „Математическом
сборнике" статья „О начале наименьшего действия" 1, в кото-
рой доказывается, что интегралы, выражающие действие
в форме Лагранжа
г
f2 Tdt
о
и в форме Гамильтона
t
|(7 + (/)Л,
о
имеют между двумя неизменными конфигурациями системы
при действительном движении сильный минимум сравнительно
со всякими движениями, которые для первого случая должны
удовлетворять теореме живых сил, а для второго должны
быть одновременными. Прием доказательства, которым я тогда
пользовался, может быть распространен на различные виды
подинтегральных функций и с большой простотой дает ре-
зультаты, полученные при современном развитии вариацион-
ного исчисления, опирающемся на методы Вейерштрасса и
Гильберта 2.
Я вывожу здесь моим способом эти результаты, останав-
ливаясь на случае, когда подинтегральная функция зависит
только от одной неизвестной функции и ее первой произ-
водной.
1 „Математический сборник", т. IX, а также Сочинения Н. Е. Жуков-
ского, М. 1912, т- I, стр. 171—178.
2 См. сочинение Н. П. Г ер нет,) Об основной простейшей задаче
вариационного исчисления, С. Петербург 1913.
Зак. 2430. Н. Е. Жуковсадпй. Том IX.
2
МАТЕМАТИКА
18
2. Вариация интеграла
V
(1)
при слабом варьировании выражается формулой:
ndF d (dF\U , . Г„, „ , ,
di UJJ)-л й5/]“>+
Я70
dF
дУх
- Г dF'
7 Й<Л — Г (Уо)—У о J Ч>
dF _
дуо
(2)
где члены вне знака интеграла зависят от вариаций Sxj,
охо, йг/0 концов рассматриваемой линии, а у/ и у0' — тангенсы
углов наклонения этих концов к оси Ох.
Интегрируя диференциальное уравнение
dF_ J (dF\= n
dy dx \ dy' / 1
(3)
мы получим линии, называемые экстремалями, которые зави-
сят от двух произвольных параметров, а, устанавливая между
этими параметрами связь, найдем однопараметренное семей-
ство экстремальных линий. Каждому такому семейству экстре-
малей соответствует семейство эквидистантных линий, ко-
торые удовлетворяют диференциальному уравнению:
г д/П , , dF ,
F-p-^\ х+^р у= '
(4)
причем вместо у' в функцию F формулы (4) подставлена
функция р, представляющая тангенс угла касательной с осью
Ох рассматриваемого семейства экстремалей, выраженный
в функции х, у. Легко усмотреть, что левая часть формулы
(4) является всегда полным диференциалом. Действительно,
условие
,дГ1_ d (dF\
dy L P dp dx \ dp )
§ 2
ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
19
приводит нас к уравнению:
dF dF др dp dF (FF______ d2Fdp d2F .d2f dp
dy' dp dy dy dp p dp dy p dp2 dy dxdp' dp2 dx ’
или:
dF d2F d2F ,^Fdp ,^Fdp_^d_(dF\
dy dx dp ' dp dyP dp2 dy p dp2 dx dx\ dpj’
которое удовлетворяется на основании уравнения (3).
Интеграл уравнения (4) с одной произвольной постоян-
ной и дает нам семейство эквидистантных линий.
Предполагая, что в формуле (1) сравниваются экстремали
некоторого семейства, начала которых (xq, у0) лежат на од-
ной эквидистантной линии, и заменяя у' на р, найдем, что
8У =
г/ 1 ^1
(5)
В частности, когда все экстремали выходят из одного
полюса, мы будем принимать эту точку за начало сравнивае-
мых экстремалей и полагать 8х0 = 8</0 = 0.
Если концы рассматриваемых экстремалей лежат тоже
на эквидистантной линии, то
г/ \
Г(р'>-р>^]
8^4-
dF
dpi
8^ = 0
(6)
и
8 У=0.
Уравнение эквидистантных линий представится при этом
в виде
V = const, (7)
так что сами эти линии можно рассматривать как линии рав-
ного значения интеграла V (в моем вышеупомянутом сочине-
нии эти линии называются линиями равного действия).
Если бы конец экстремали переместился по эквидистант-
ной кривой, а координаты ее начала имели бы вариации
s*o, 8</о> то
(Г dFl dF. 1
oV = -([Hpo)-Po^J Ч + (Г)
2*
20
математика
Предполагаем, что все начала экстремалей прикасаются
к одной и той же линии, которая является огибающей рас-
сматриваемого семейства экстремалей и называется погра-
ничной кривой. Тогда, так как для пограничной кривой
= Uq — р0, формула (7') принимает вид:
ох0
8V=-F(j/0')8x0. (7")
3. Условившись обозначать через
Vг— (а, Ь)
интеграл, данный формулой (1), взятый по кривой (ab), до-
кажем следующую основную теорему нашего изложения
(фиг. 1).
Теорема I. Для двух бесконечно близких экстремалей
ab и ас, выходящих из полюса а, концы которых соединены
элементом дуги Ьс, имеет место равенство-.
(Ьс) + (аЬ) — (ас) = F(y') — F(p)
^1^)1^. (8)
°Р J
Здесь у' есть тангенс угла наклонения касательной к эле-
менту Ьс с осью Ох, а р — тангенс угла наклонения к оси Ох
экстремали в точке Ь. Вторая часть равенства представляет
помноженную на dxi известную функцию Вейерштрасса:
Е = F(y') —F(p) — (у' - р). (9)
Для доказательства проведем через точку Ь эквидистант-
ную линию be и отнесем к ее элементу (be) уравнение (4).
Согласно фиг. 1 мы можем подставить в это уравнение
</х - </х( — </х2,
Получим:
Г г/ ч
dy=y'dxl — pdx2.
(dXi — </x2) 4
dP
(y'dx{ ~pdx^) — 0,
или
Г rdFl
(p) + (y' — p) — F(p) dx% = 0.
(10)
§ 3 ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
21
С другой стороны, из чертежа видно, что
(Ьс) = F(y')dX1, (11)
(ас) — (ab) = (ес) = F(p) dx2,
вследствие чего
(М + (ab) — (ас) = F(y') dxx — F (р) dx2. (12)
Вычитая из второй части формулы (12) первую часть фор-
мулы (10), получаем формулу (8). Желаемое, таким образом,
доказано.
Данная теорема имела бы место и в том случае, если бы
начала рассмотренных экстремалей не находились бы в од-
ном полюсе, а лежали бы на одной и той же эквидистантной
линии. Если же начала экстремалей лежат на пограничной
линии ag, то, принимая во внимание (фиг. 2), что на основа-
нии уравнения (7")
(Яс) — (hb) = (ес) — (hg),
нужно вторую формулу (11) заменить нижеследующей:
(gc) ~ (W 4- (hg) = (ес) = F(p) dx2.
Вследствие этого равенство (8) видоизменилось бы в такое:
(bc) — (gc)-\-(hb) — (hg) = EdXi. (13)
22
МАТЕМАТИКА
Для исследования функции Вейерштрасса Е строится для
каждой точки рассматриваемого поля линия, называемая
характеристической кривой. Ее уравнение есть:
^ = F{x, у, у'),
причем £ представляет ординату, у'-—абсциссу, а х, у — па-
раметры. Если припишем (фиг. 3) абсциссе значение ОА = р,
соответствующее рассматриваемой экстремали, и, построив
ординату АВ — F(p), про-
ведем к характеристиче-
ской кривой касательную
BD, то для направления
элемента Ьс на фиг. 1,
выраженного тангенсом уг-
ла у’, найдем, при ОН = у',
ординату HC=F(y'), отре-
зок которой
dF
CD = F(y')-F(p)-^(y'-p)
и будет величиной Е.
Для значений у', близких к р, знак функции Е одинаков
&>F(p)
со знаком второй производной о -.
При положительности этой производной характеристическая
кривая в точке В обращена выпуклостью к оси абсцисс, и
знак Е положителен; при отрицательности наоборот. Если
характеристическая кривая не пересекает касательную BD,
то Е имеет постоянный знак для всякого наклона эле-
мента Ьс.
На фиг. 4 представлен случай, в котором характеристиче-
ская кривая прикасается к касательной BD еще в точке В,.
Этот случай играет важную роль для минимальных и макси-
мальных линий с угловыми точками. Называя через р и р(
абсциссы точек касания В и В„ найдем из чертежа:
dF(p)dF(P1)
др др, ’
§ 4
ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
23
OK=F(p)-p^- = F(p,)-p,^f. (М)
Эти равенства называются условиями Эрдмана.
4. Переходим теперь к разбору минимальных и максималь-
ных свойств различных экстремалей.
Теорема II. Если на части экстремали aef (фиг. 5),
на которой нет точек соприкосновения с пограничной кривой,
yip
-,—5- имеет постоянный знак -Т или —,
др-
то (aef) будет иметь в первом случае
минимум, а во втором максимум срав-
нительно со всеми величинами (abcf), взя-
тыми по весьма близким кривым, прохо-
дящим через точки а и f.
Воображаем семейство экстремалей
выходящих из полюса а, и срав-
Фиг. 5.
af, ас, аЬ,
отстоять на конечное расстояние от af, но во всех точках
которой Е имеет постоянный знак, положим, положительный.
Тогда, на основании теоремы I, для всякого элемента кривой
abcf-.
(be) > (ас) — (ab).
Суммируя это неравенство на все элементы Ьс сравнивае-
мого пути, найдем
(abf) > (aef).
Воображая, что соседняя кривая abf весьма близка aef,
&F(p) ,
заключим из постоянства знака —£ на экстремали aef о по-
24
МАТЕМАТИКА
стоянстве знака Е на кривой abf и о том, что (abf) более
или менее (aef). Таким образом доказывается существование
минимума или максимума (aef). Для того, чтобы было допу-
стимо сильное вариирование, т. е., чтобы кривая abf при бес-
конечной ’близости к aef могла представлять предел зубчатки,
нужно, чтобы характеристическая кривая, построенная дли
всех точек экстремали aef, была обращена к оси абсцисс
на всем своем протяжении выпуклой или вогнутой стороной.
При отсутствии этого условия ВОЗМОЖНО
только ограниченное вариирование, т. е.
в соседней кривой разность у' — р должна
Фиг. 6.
не выходить из пределов, указываемых фиг. 3. Если на каком-
й ч г ^F(p)
нибудь элементе кривой aj --— равно нулю или имеет
знак, обратный с остальными точками кривой aef, то (aef) не
дает минимума или максимума. Действительно, если например
на всей кривой aef кроме места тп вторая производная поло-
жительна, а на элементе тп она отрицательна, то всегда
можно выбрать соседний путь amenf (фиг. 5а), в котором
элемент тп прежней экстремали заменен зубчиком теп,
и доказать по предыдущему, что (amenf) < (amnf).
Данное доказательство теоремы II не будет иметь места,
если на экстремали agf есть точка g, прикасающаяся к по-
граничной кривой для семейства экстремалей, выходящих
из полюса а. Действительно, прилагая (фиг. 6) к соседней
кривой aef вышеупомянутые рассуждения, мы докажем в слу-
чае Е положительного, что (aef) > (aqf). Что же касается
ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ 25
до (agf), то, проводя через разные точки отрезка gf экстре-
мали, выходящие из полюса а (что становится возможным,
когда точка g попадает на пограничную кривую), докажем, что
(gf)> (aqf) — (ag),
(ag) (gf) > (aqf),
или
(agf) > (aqf).
Таким образом экстремаль
когда на нее попадает точка
кривой.
Теорема III. Отрезок ghk
&F
тором g имеет постоянный
перестает давать минимум,
прикосновения к граничной
пограничной кривой, на ко-
знак, дает для (ghk) мини-
мум или максимум сравнитель-
но со всеми величинами (glbck),
взятыми по весьма близким
контурам, проведенным через
точки g и к и лежащим вну-
три поля рассматриваемого
семейства экстремалей.
Пусть (фиг. 7) ghk — отре-
зок линии, огибающей экстре-
мали, выходящие из точки О.
Проведем через точки g
и k некоторую кривую glbck,
лежащую в поле экстремалей настолько
&F
во всех ее точках, согласно условию
Тогда:
(М > (gh) 4- (he) — (gb).
близко к ghk, что
> 0, имеем Е > 0.
Суммируя эти неравенства на все элементы Ъс кривой
bek, найдем:
(bek) > (ghk) — (gb) или (ghk) < (bck)-{-(gb).
Но
(gb)<(glb),
поэтому
(ghk) < (glbck).
26
МАТЕМАТИКА
Теорема IV. Если на экстремали имеется точка с тан-
генсом угла касательной р, удовлетворяющая условию Эрд-
мана, и мы через эту точку проведем другую экстремаль
с тангенсом угла касательной в рассматриваемой точке
равными р„ то построенная ломаная линия будет мини-
мальной или максимальной кривой, смотря по тому, будем
d2F л d2F
ли в ее точках иметь -3 г- > 0 или о < 0.
др- др2
Положим, что от ломаной экстремали аЬс мы переходим
к соседней ломаной линии akflc, во всех точках которой
Е > 0 (фиг. 8).
Проведем весьма малый элемент еЬ, перпендикулярный
к оси Ох, и другой весьма малый элемент ef, направленный
по эквидистантной линии
лагранжева пучка с полю-
сом а..
По формулам (6) и (8),
так как 8х = 0, имеем:
(ае) — (аЬ) = Ъу,
(ес)-(Ьс) = -д-^ iy,
UP\
где 8</ = —eb. Но по пер-
Фиг. 8. вому условию Эрдмана
[формула (14)]
dF(p) _dF(Pl)
др др,
поэтому
(ае) — (аЪ) -|- (ес) — (Ьс) — 0,
или
(ае) 4- (ес) = (ab) -f- (6с).
Далее легко усмотреть, что элемент ef эквидистанты, по-
строенный для пучка лагранжевых кривых с полюсом а,
будет одновременно и элементом эквидистанты, построен-
ным для пучка лагранжевых кривых с полюсом с, так как
§ 4
ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
27
тангенсы угла наклонения того и другого элемента выра-
жаются согласно формуле (4) так:
_ д^(р) m n dF(Pi) г/_ \
p_jp—F(p) = ,15)
dF(p) dF(pt)
др дР1
но
а эти величины по первому и второму условию Эрдмана между
собой равны.
Таким образом
(об) + (6с) = (af) + (/с),
(аб/) < (akf) и (fnc) < (flc),
(ab) + (bc)<(akf) + (flc).
поэтому
Место угловых точек в лагранжевом пучке, выходящем
из а, называется кривой Каратеодори, а семейство экстре-
малей (6с), выходящих из точек кривой Каратеодори в напра-
влениях называется семейством, сопряженным данному
лагранжеву пучку. Если на сопряженном семействе линий
отметим точки, удовлетворяющие условию Эрдмана, то полу-
чим вторую кривую Каратеодори, для точек которой можно
построить второе семейство сопряженных линий и т. д.
Идя по лагранжевой кривой до линии Каратеодори, повер-
нув от точки пересечения по сопряженной экстремали, пройдя
по ней до второй кривой Каратеодори и повернув от нее по
экстремали второго сопряженного семейства и т. д., мы полу-
чим ломаную экстремаль, которая при постоянстве знака
&F
2 • и отсутствии на ней точек прикосновения к соответ-
ствующим огибающим кривым будет обладать максимальными
или минимальными свойствами.
Теорема V. Если на пучке лагранжевых кривых (фиг. 9),
•выходящих из полюса О, отметить место лр точек, для
которых то всякая эстремалъ Оа, идущая от
полюса до этого места, при постоянстве на ней знака
&F(p) „
“^2-^, будет иметь минимум или максимум сравнительно
28
МАТЕМАТИКА
Ofb
Если
со всеми соседними кривыми, выходящими из О и оканчи-
вающимися на параллели оси Оу, проведенной через а.
Возьмем соседнюю кривую
конец b лагранжеву кривую 0b.
и проведем через ее
d2F(p)
—т-г-положительно, то
др1
(Ofb)>(Oeb).
С другой стороны
по формуле (5)
dF
(Oeb) — (Oa) = ~ab.
* Так как отрезок ab>
лежит влево от Хи. и,
вследствие положитель-
d2F(p)
ности —^5— , произ-
дГ(р)
водная —□---- должна
др
возрастать при подходе
к Xjjl? то она будет по-
ложительна, и
(ОеЬ) > (Оа).*
оканчивалась за кривой Xijl
бы отрицательно, но зато
Если бы соседняя кривая
dF
в нижней точке с, то -т— было
др
вместо ab надо было бы взять — (са); таким образом опять*
получили бы
(Ос)>(Оа).
На основании двух написанных неравенств находим
(Ofb)>(Oa).
Как только мы перейдем за точку h в некоторую точку п,
то (On) перестает быть минимум, и мы получаем (Оа) < (On).
Если во всех точках одной из лагранжевых линий, напри-
мер Oh, имеем = 0, > 0, то любой отрезок От
этой линии вплоть до отрезка Oh, конец которого лежит на
кривой Хи., будем иметь минимум сравнительно с соседними
§ 5 ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ 29
кривыми, выходящими из О и имеющими в конце абсциссу
От. Доказательство будет такое же, как вышеприведенное.
Теорема V, которая, насколько мне известно, не приво-
дится в курсах вариационного исчисления, играет весьма
важную роль в теории устойчивости упру-
гих систем1.
5. Окончим нашу заметку рассмотрением
задачи об устойчивости вертикальных колонн.
Определим потенциальную энергию
-стержня OB = I, защемленного в точке О,
который постепенно сгибается действием
вертикального груза Р, приложенного к его
концу В (фиг. 10). При сгибании каждого
элемента ds от прямолинейного вида в про-
db
гнутое состояние при кривизне мы запа-
саем в каждом элементе С стержня работу
1 Гр (db \а
2 JE Us ) ds’
Фиг. 10.
1 Поставленная между звездочками часть доказательства теоремы, при-
водимая нами по рукописи Н. Е. Жуковского, не совсем ясна, и самую
теорему, в приведенной выше формулировке, мы не считали бы доказан-
ной.
Знак разности
(Oeb) — (Оа) = — ab =
<7р Ор
имеющий решающее значение для доказательства теоремы, может быть
определен следующим образом.
а
Раскладывая в ряд около точки а, мы получаем:
dF ~(dF\ , , d2F . , daF _
др ~ \дР )a + др2 °P' + -дрду °4-
Так как точка ex лежит на кривой Ар, а точка Ь имеет одинаковую абс-
циссу с точкой «, то
= 0, = 0,
а потому для точки Ь
MF др , d3F
до2 ду дрду
30
МАТЕМАТИКА
где 6 есть угол касательной с осью Оу. Кроме того, пово-
рот на угол
начала О на
всякого элемента С стержня, отстоящего от
расстоянии s, заставляет груз опуститься на
(I— s)sin6c/0 = (Z—s)sin6-j— ds.
as
Это дает потерю потенциальной энергии, равную:
— Р(1— s) sin 6-у- ds — d\P(l— s)cos 6] Feos 0 ds.
Вся потенциальная энергия прута в каком-нибудь его со-
гнутом состоянии выразится интегралом:
i^-\2ds — | P(l - s) Sin f) ds =
\ds / J ds
0
где
ds /
+ Pcos ft
8
ds P (I — s) cos
0
Вставляя это значение в формулу разности (ОеЬ) — (Ос), находим
(ОеЬ) — (Оа) = s
д'-F др d-F ] . .,
. др2 д3 дрду J °S1 ’
0
<1.
8
v==S^jE
о
0
Таким образом, знак разности будет одинаков со знаком выражения
др
др2 др
d2F _ \
дрду d у\др )'
Лишь в частном случае, когда
d-F
дрду
0 и ^->0,
d^F
знак разности (ОеЬ) — (Ос) будет всецело определяться знаком -тг. (Этот
ф-
случаи имеет место в разбираемой ниже задаче об устойчивости колони).
В общем же случае теорему следовало бы, п о нашему мнению, форму-
лировать так:
Если на пучке лагранжевых кривых,
тить место Хр точек, для которых
выходящих из полюса О, отме-
= 0, то всякая экстремаль аО,
- ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ 31
Предполагая, что длина прута остается неизменной и рав-
ной I, получим:
ds — Pl =
I
= Р [ Г(^)2+ cos 6 Id's-Pl.
J \_ 2 г \ as / J
о
Для того, чтобы изогнутое состояние удерживалось в рав-
новесии грузом Р, необходимо и достаточно, чтобы неизвест-
ная функция 6 от 4 была такова, чтобы вариация интег-
рала
IZ C\lJEldb\> J,
+cos6fs
0
идущая от полюса до этого места, при постоянстве и одинаковости на
и ей знаков выражений
&F J_(dF\d2Fdp &F
др- ” dy \др ) др2 ду дрду
будем иметь минимум или макси-
мум сравнительно со всеми кри-
выми, выходящими из О и оканчи-
вающимися на параллели Оу, про-
веденной через а.
Геометрически ясно, что знак
d (dF\ * т
-г- — I для точек, близких к Лр-,
dy \др ) д
зависит от распределения положи-
тельных и отрицательных значе-
. 6F , ,
нии —т— на плоскости (х, и).
др ' ’у'
Если, двигаясь в сторону возра-
если от положительных значений к отри-
стания ординат, мы переходим
(фиг. 9 и фиг. 9а) от отрицательных значений к положительным,
, ‘ d (dF
то будем иметь —г- ( -г-
dy \др
d (dF
цательным, то — I -т—
dy \др
0. Прим. ред.
32
МАТЕМАТИКА
при постоянном значении верхнего предела s — l была ну
лем, т. е. ?
О J* 0'2 -j- COS 6 j</s = 0.
о
Отсюда согласно уравнению (3) получаем диференциаль
ное уравнение экстремалей в виде:
JE d
|£(^)+Sin6=o,
или
JF
fi'dO' 4- sin 6 <76 = 0,
которое по интегрировании дает:
~6'2 = 2 cos 6 4- С.
Произвольное постоянное определим под условием, что 6' == 0,
при 6 = 60; тогда
JF
-р 6'2 = 2 (cos 6 — cos 60).
Отсюда
г____ в
= 1 f I Г
* Р J 12 (cos 6 — cos60) *’
причем новое постоянное С\ определяем условием 6 = 0 при
s —0, так что
___ в
f db /1<л
I ? J ]/2 (cos 6-----cos 60)
Эта формула аналогична известной формуле качания маят-
ника. Мы выражаем в ней вторую часть помощью эллиптиче-
ского интеграла первого вида, сделав подстановку:
6 6„
sin = sin sin ф, (18)
тогда:
cos 6 = 1—2 sin2-?r = 1 — 2 sin2 4г- sin2Ф,
§ 5 ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ 33
6
COs~2
cos 60= 1 — 2 sin2 ,
cos 6 — cos 60 = 2 sin2-b- cos2'},
• 60 ,
-g- = sin cos v
6
2 sin cos ф dty
— sin2—- sin2'}'
Так как при 6 = 0 ^ = 0, то
Ф
J0 =
s =
о
cty
— sin2 sin2 ф
Будем откладывать по оси абсцисс величину а
Ф
(17')
а =
Р
EJ ’s’
о
1 —sin2 sin2'}'
а по оси ординат угол 6 [угол 6 по формуле (18) выражается
через '}, а ф по формуле (17') выражается эллиптической
Функцией ’от s] и построим (фиг. 11) лагранжево семейство
экстремалей. Каждая экстремаль будет иметь параметром 60,
Зак. 2430 Н. Е. Жуковский. Том IX
3
34
МАТЕМАТИКА
Когда угол 6 получает значение %, при котором 6' = О,
тогда согласно формуле (16) получается ф=-^-. Длина /.ко-
торую должен иметь стержень
по формуле (17) представится
в сделанном предположении,
полным эллиптическим инте-
гралом первого вида
К
2
(19)
который развертывается в известный ряд
- (20)
Уравнение (20) дает нам кривую Хи., точки пересечения
dF
которой с лагранжевыми кривыми дают 6' — 0 или = 0.
е
Фиг. 12.
Что касается уравнения характе-
ристической кривой, то оно на осно-
вании уравнения (16) будет:
/ 1 JF
C=f-i-Te/2_bcOs6
причем 6' надо откладывать по оси
абцисс, а 6 считать параметром.
Характеристические кривые бу-
дут параболами, обращенными вы-
пуклостью вниз (фиг. 12); поэтому
во всех точках поля функция Вейер-
штрасса Е > 0.
Интеграл формулы (16), взятый
по каждой лагранжевой кривой от О
до кривой Хр., будет иметь минимум
сравнительно со значением этого ин-
теграла, взятого по соседним кривым
при том же /, т. е. потенциальная энергия изогнутого прута,
углы которого 6 следуют закону линии Оа, будет менее энер-
гии прута той же длины I при всяком другом изгибе его. Это
§ 5 ЗАМЕТКА ПО ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ 35
показывает, что при данной длине мы получим устойчивое
положение прута, причем выполнены два условия: в точке О—
условие 6 = 0, и в точке а — условие f)' = 0, которое ука-
зывает, что на конце прута нет вращающей пары. Лангран-
жева линия, направленная по оси Os, как было сказано в тео-
реме V, при всякой длине ее отрезка вплоть до Ок является
минимальной кривой, но, как только длина пути перейдет
длину отрезка Ок, то полная энергия перестает иметь мини-
мум, и положение прута делается неустойчивым, причем он
из положения Ое будет- стремиться к устойчивому положению.
На основании сказанного, по формуле (20) заключаем, что
вертикальная колонна, несущая нагрузку Р, имеет устойчивое
положение, пока длина колонны стеснена условием
/ Т-
2
Эта работа была сообщена автором 31 марта 1915 г. в заседании Мо-
сковского математического общества. Напечатана впервые после смерти
Н. Е. Жуковского в редакционной обработке Н. Г. Ченцова Комитетом по
увековечению памяти Н. Е. Жуковского, Москва 1923. Прим. ред.
3*
NOTE ON CALCULUS OF VARIATION
ac-
of
In this note N. E. Joukovsky proves some theorems of the
calculus of variation with regard to the necessary and suffi-
cient conditions of the existence of maximum or minimum of in-
tegral whose expression under the sign of integration contains
an unknown funktion у and its first derivative y'. His demon-
stration method presents an extension on an arbitrary form of
the function under the sign of integration of the method which
he made use of in his work: “On the principle of the least
tion“. His fundamental theorem I which serves for the proof
all others consists in the following:
Theorem I. For two infinitely close extremals ab and ac
(Fig. 1) issuing from the pole a whose ends are connected by
the element be there is the equality (8).
In this equality by (ab), (be), (ac) are denoted the values of
the integral (1) taken over the curves ab, be, ac; by p and y'—the
angular coefficients of the extremals at the point b and of the ele-
ment be; by dxv the difference of abscissae of the point b and c.
As to the function (of Weierstrass) E (9), it is seen with the help
of its geometrical representation that for values y' approximate
to p its sign will coincide with the sign of —
Op-
The method of application of this theorem to the proof of
other theorems is being made clear in the most simple way by
the demonsratrion of the theorem II.
If at the portion of the extremals aef, at which there are no
points of contact with the bordering curve, the curve enve-
. . ^F
ioping the family of extremals, has a constant sign-]-or—,
(aef) will have then in the first case minimum, and in the second —
SUMMARY
37
maximum, as compared with all the values of (abcf) taken along
the adjacent curves passing through a and f.
We conceive a family of extremals af, ac, ab, issuing from the
pole a and a curve abcf, compared with extremals aef at all
d2/
points of which - has a constant sign, for instance positive.
Then on the ground of the theorem I for every element of the
curve abcf
(6c) > (ac) — (ab).
Summing up similar inequalities for all elements of the curve
abcf we find (abf) > (aef).
In the same manner other theorems are also being proved.
At the end of the paper is set forth the application of the
calculus of variation to the discovery of the condition of stabi-
lity of equilibrium of a compressed rod.
dy
dx
ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ПЕРВОЙ И ВТОРОЙ
ТЕОРЕМ С. А. ЧАПЛЫГИНА О ДИФЕРЕНЦИАЛЬНЫХ
НЕРАВЕНСТВАХ1
(1919—1932 и.)
§ 1. Еще 20 лет тому назад, на юбилее Политехнического
общества, при обсуждении доклада о связи науки и техники
С. А. Чаплыгин рассказал мне о своих идеях приближенного
интегрирования.
Задача интегрирования диференциального уравнения 1-го
порядка, решенного относительно производной:
= /(*>
с геометрической стороны сводится к задаче о проведении
на плоскости ху через точку (х0, уо) такой кривой, у которой
тангенс угла наклона касательной к оси х выражается в ка-
ждой точке плоскости функцией f(x, у).
Для практики будет иметь второстепенное значение, бу-
дем ли мы знать самое течение кривой на плоскости ху точно,
или будем знать только достаточно узкую полоску плоско-
сти ху, из которой искомая кривая не будет выходить.
Во втором случае вместо искомой интегральной кривой
будем знать две линии, близко лежащие друг от друга и за-
ключающие между собой искомую кривую.
Последнее решение задачи будет вполне достаточно для
нужд техники.
Законченное выражение своим идеям С. А. Чаплыгин при-
дал только в нынешнем году при своих работах в Экспери-
1 Лекция Н. Е. Жуковского в Центральном Авро-Гндродинамическом
институте 18 декабря 1919 г., записанная Н. Г. Ченцовым. Прим. ред.
§ 2 ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ ЧАПЛЫГИНА 39
ментальном институте Комиссариата путей сообщения ’. Он
применил свою методу интегрирования к решению уравнения
Риккати, к которому привелась поставленная им задача о дви-
жении поезда 1 2.
Идеям Чаплыгина я придал геометрическую интерпре-
тацию.
Проф. Н. Н. Лузину принадлежит мысль изображать дифе-
ренциальное уравнение геометрически в виде особой поверх-
ности, принимая координатную плоскость ху за область изме-
нения независимого переменного х и функции у, и отклады-
вая по вертикальной оси z (или т) значения производной
f (х> у)- С. А. Чаплыгин предложил способ находить первое
приближение, заменяя данное диференциальное уравнение, не
интегрирующееся в квадратурах, видоизмененными — интег- '
рирующимися, близкими к заданному. Например, интегрируя
уравнение Риккати, Чаплыгин отбрасывает член с у2 или за-
меняет его постоянной величиной.
Найдя таким образом две функции, между которыми дол-
жна заключаться искомая, дальше можно сближать эти
пределы.
1-я теорема Чаплыгина указывает признак, достаточ-
ный для того, чтобы выбранную функцию можно было рас-
сматривать или как верхний, или как нижний предел искомой
функции.
2-я теорема Чаплыгина относится к предложенному
им способу сближать эти пределы при помощи точного ин-
тегрирования линейных диференциальных уравнений.
§ 2. 1-я теорема С. А. Чаплыгина. Пусть требуется найти
частный интеграл диференциального уравнения 1-го порядка,
решенного относительно производной:
Е = (1)
удовлетворяющий некоторым начальным данным.
1 С. А. Чаплыгин. Основания нового способа приближенного ин-
тегрирования диференциальных уравнений, „Бюллетень Научно-Экспери-
ментального института путей сообщения", № 13, Москва 1919.
2 Основные начала механики железнодорожного транспорта, гл. XIV,
стр 308—334, „Бюллетень* № 9 НЭИПС, Москва 1919.
40
МАТЕМАТИКА
С геометрической точки зрения нахождение общего инте-
грала сводится к проведению на плоскости ху кривых, таких,
чтобы они в каждой точке плоскости имели заданное напра-
вление касательных.
Ограничивая нашу задачу разысканием частного инте-
грала, мы должны найти только одну из указанных кривых,
проходящую через некоторую определяемую из условий за-
дачи точку, которую мы вправе всегда принимать за начало
координат.
Если удалось найти какую-нибудь функцию
f = <p(x)
такую, что для интервала х0 < х < Л,
/к, ?(*)], (2)
то вся кривая t — (х) лежит в том же интервале наверное
выше интегральной кривой у.
Функция же z=<p(x), удовлетворяющая в интервале
х0 < х < X неравенству
</[х, ВДЪ (3)
дает кривую, всеми своими точками лежащую ниже интегральной.
Способы нахождения функций <р(х) и ф (х) могут быть
весьма различны.1
1 Например, иногда наперед известен приблизительный ход искомой
кривой у; тогда мы можем, примиряясь с довольно большой ошибкой, про-
сто задать
/ = <р(х)>^; z=<p(x)<^. (а>
Более тонким и чаще всего применяемым способом является замена
данного диференциального уравнения (1) другими, несколько измененными,
которые интегрируются в конечной форме, например:
~ = (6)
dz
fa (x’ Z) <f (•*• z), (c)
интегралами которых и являются функции
*=4>(х)>5, г = ф(х)<^.
Прим. ред.
dx
g 2 ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ ЧАПЛЫГИНА 41
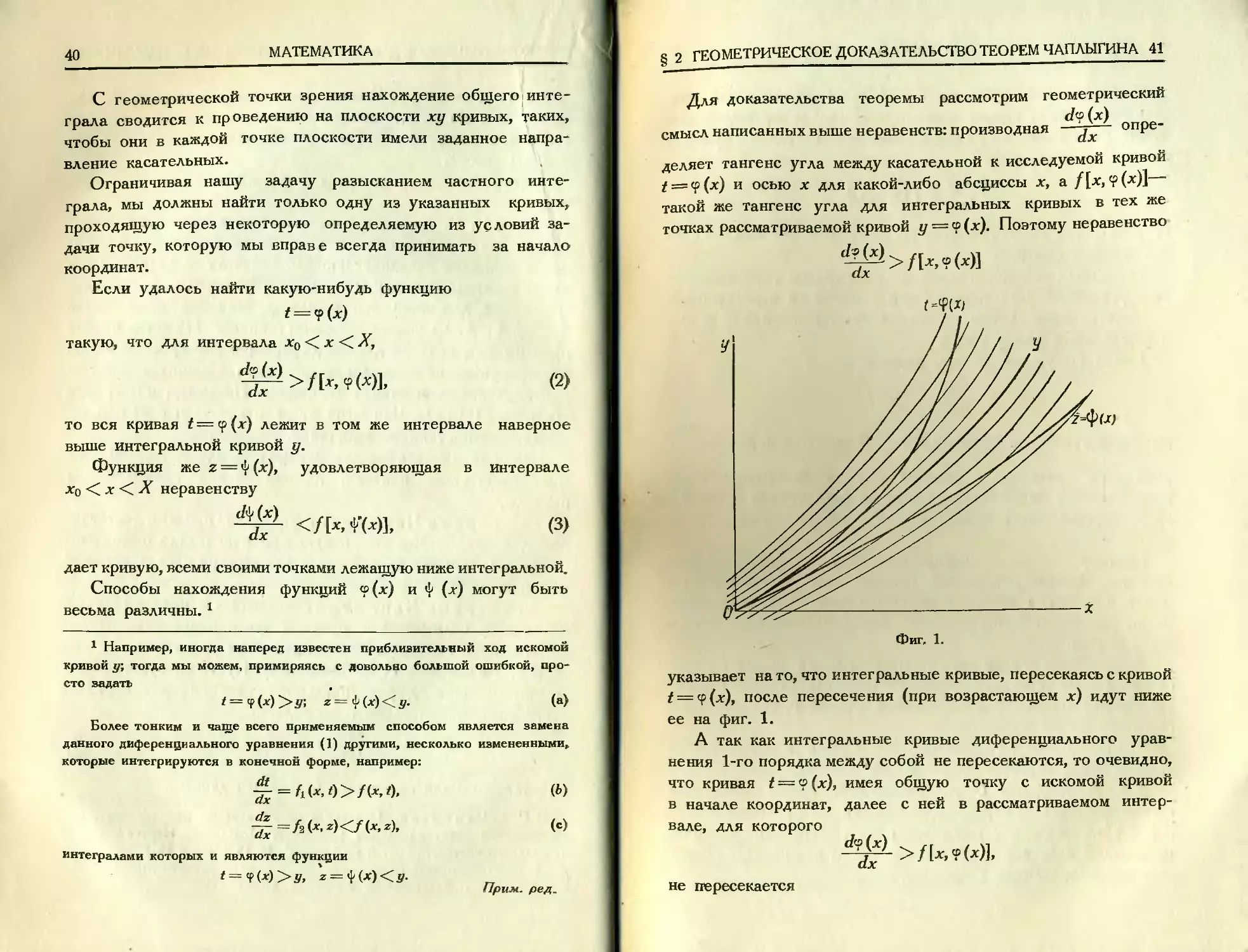
Для доказательства теоремы рассмотрим геометрический
d<?(x)
смысл написанных выше неравенств: производная —- опре-
деляет тангенс угла между касательной к исследуемой кривой
t = (f(x) и осью х для какой-либо абсциссы х, а /[х, ?(х)]
такой же тангенс угла для интегральных кривых в тех же
точках рассматриваемой кривой у — ® (х). Поэтому неравенство
указывает на то, что интегральные кривые, пересекаясь с кривой
/ = <р(х), после пересечения (при возрастающем х) идут ниже
ее на фиг. 1.
А так как интегральные кривые диференциального урав-
нения 1-го порядка между собой не пересекаются, то очевидно,
что кривая t ~«(х), имея общую точку с искомой кривой
в начале координат, далее с ней в рассматриваемом интер-
вале, для которого
>/[х,?(х)],
не пересекается
42
МАТЕМАТИКА
Следовательно, функцию /=’?(х) мы можем рассматри-
вать как верхний предел искомой интегральной функции. По-
вторяя подобные же рассуждения относительно функции
z = ^(x), для которой
dx
</[х, ф(х)],
убедимся, что z — (х) можно рассматривать как нижний пре-
дел искомой функции.
Выше было указано, что интегральные кривые диференциаль-
ных уравнений 1-го порядка между собой не пересекаются.
Интегральные кривые уравнений высших порядков могут
и пересекаться между собой.
Например, уравнение 2-го порядка
d\
dx2
выражает уравнение колебательного движения с периодом -j-.
„Соседние" кривые, т. е. бесконечно мало отличающиеся от
данной своими начальными условиями (амплитудой и фазой),
будут пересекаться с основной кривой вблизи точек, где у"
меняет знак.
Поэтому теорема о диференциальных неравенствах дает
верхнюю кривую t наверное больше искомой кривой у и
нижнюю кривую z наверное меньше у лишь в области изме-
нения независимого переменного, где соседние кривые еще
не пересекаются.
В противном случае верхняя приближенная кривая t, пере-
секая одну из „соседних" кривых и направляясь выше ее, все-
таки может оказаться ниже искомой кривой у, так как сама
соседняя кривая идет ниже у.
Так же и нижняя приближенная кривая z может пойти
выше у после пересечения „соседних" кривых.
§ 3. 2-я теорема С. А. Чаплыгина. Найдя каким-либо
способом в качестве первого приближения две функции t = (х)
и z = (х), между которыми заключается искомая функция,
производим дальнейшее сближение границ при помощи линей-
ных диференциальных уравнений.
§ 3 ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ ЧАПЛЫГИНА 43
Возможность такого сближения основывается на 2-й тео-
реме Чаплыгина.
Здесь мы дадим геометрическое доказательство ее, идея
которого принадлежит проф. Н. Н. Лузину.
Дано диференциальное уравнение
<4>
Фнг. 2.
Возьмем (фиг. 2) оси координат х, у, т с началом коорди-
нат в точке, через которую проходит искомая кривая, и по-
строим поверхность Лузина:
т =/(*>#)•
Проведя через искомую кривую и кривые ОА и ОВ (най-
денные, как первое приближение и удовлетворяющие теореме
о диференциальных неравенствах) цилиндрические поверхно-
44
МАТЕМАТИКА
сти с образующими, параллельными оси т, получим в пересе-
чении с поверхностью Лузина кривые О А' и О'В'.
В свою очередь плоскости, перпендикулярные оси х, будут
пересекать поверхность Лузина по некоторым плоским кри-
вым, лежащим в плоскостях, параллельных плоскости у<
Проводим через различные точки т кривой О’В' касатель-
ные mt к этим плоским кривым и стягивающие их хорды тп,
последние так, что их концы п лежат на кривой О'А'. Тогда
получим две линейчатые поверхности, проходящие через О'В',
с образующими, параллельными плоскости у~, причем отрезок
поверхности Лузина будет лежать между ними независимо от
того, куда кривая тп обращена выпуклостью, кверху или
книзу. На нашем чертеже (фиг. 2) кривая обращена выпук-
лостью кверху.
Диференциальное уравнение, заданное поверхностью Лу-
зина т=/(х, у), не интегрируется в квадратурах. Уравнения
же, изображенные линейчатыми поверхностями, будут линей-
ными и интегрируются точно.
Линейные диференциальные уравнения функций и, и и2,
соответствующих линейчатым поверхностям, будут:
/) + £(« — t), (5)
или
z) + Z/(u —z), (5')
i
где k угловой коэфициент образующих этих поверхностей,
параллельных плоскости yt.
Для поверхности, касательной к поверхности Лузина, вели-
чина углового коэфициента будет:
к . df (х, t) df[x, ф (x)J
dt Эф
или (6)
k, = df(x, z) = d/[x,<p(x)]
dz dtp
Для поверхности, образованной хордами, имеем
А- __ f(x,z) f(x,t) =’/[х, ф (х)] — f[x, <? (х)]
z —/ <Р(х) —ф(х) •
£ 3 ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ ЧАПЛЫГИНА 45
Вставляя в диференциальные уравнения линейчатых поверх-
ностей значения функций £ = <?(х) и z — ^(x), а также ука-
занные значения угловых коэфициентов, получим для каса-
тельных поверхностей:
g = /[X,« WJ + [и - ? , <8>
или
=f[x, «р (х)] + [и -ф (х)] -Z-[*|*-x)] (8')
и для секущей поверхности:
s=/[x,?WJ + [U-?W]------------------------- <’>
Все три уравнения могут быть представлены в виде:
5^ + Pz + Q = 0, (10)
ах
где Р и Q — функции одного х и интегрируются в квадра-
турах
Покажем, что интегральные кривые для указанных линей-
ных уравнений будут лежать между кривыми t и z, получен-
ными как первое приближение (при чем / > у >z).
Рассмотрим сначала линейчатую поверхность, образованную
хордами тп.
Так как кривые О'А' и О'В' являются пересечениями
поверхностей, характеризующих данное диференциальное
уравнение и рассматриваемое приближенное диференциальное
уравнение, то, вставляя функцию t в линейное диференциаль-
ное уравнение (9), будем получать в обеих частях его те же
величины, что и при подстановке в данное диференциальное
уравнение. А потому, если функция t оставалась всегда больше
искомой функции у, то она будет больше интегральной функ-
1 Например, для уравнения (8) имеем:
р_ d/t*. ?(*)]
д <р (х)
и аналогично для уравнений (8') и (9). Прим. ред.
46
МАТЕМАТИКА
ции Uj линейного уравнения, характеризуемого линейчатой
поверхностью 1.
Наоборот, функция z, меньшая искомой, будет меньше
интегральной для линейчатой поверхности 2.
Итак, функция ии являющаяся интегралом линейного ди-
ференциального уравнения, будет лежать между кривыми
t и z.
С другой стороны, согласно теореме о диференциальных
неравенствах, функция tq будет меньше искомой, так как
соответствующая ей поверхность Лузина проходит ниже по-
верхности Лузина для заданного уравнения.
Обращаемся к рассмотрению линейчатых поверхностей,
касательных к поверхности Лузина.
Если кривые обращены вогнутостью книзу, то линейчатгя
поверхность, касающаяся к поверхности по нижней граничной
кривой О'В', даст интегральную кривую п2, лежащую между
кривыми I и z, полученными как первое приближение.
В самом деле, кривая z, как общая обеим поверхностям
Лузина, удовлетворяет одному и тому же признаку Чаплы-
гина, а потому, будучи меньше искомой функции, будет
меньше интеграла касательной линейчатой поверхности.
Что касается функции t, то будучи подставлена в линейное
уравнение
шую, чем
(8'), она даст в правой части его величину боль-
в левой
Nt > Nn >
а потому будет больше
du \
dx /’
интеграла диференциального уравнения.
Итак, в случае выпуклости, обращенной кверху, интеграль-
ная кривая и2 линейчатой поверхности будет итти между t и z.
С другой стороны, кривая п2 будет больше искомой, так как
соответствующая линейному уравнению поверхность Лузина
проходит выше поверхности Лузина для заданного уравнения.
1 Это ясно из того, что данная уравнениями (8) и (9) величина и ближе
к искомому интегралу у данного диференциального уравнения, нежели
первоначальные функции t у и z у. Если кривые и и у не пересекаются
(а это как раз имеет место для кривых/ и z), то ни в одной точке разность
d и) не может быть ни больше разности t — z, ни равна ей, а также не
может обратиться в нуль. Прим. ред'.
“ Такие же рассуждения справедливы для разности и — z. Прим. ред.
§ 3 ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ ЧАПЛЫГИНА 47
Взяв другую линейчатую поверхность, касающуюся к по-
верхности Лузина по верхней граничной кривой О'А', мы
получили бы другую интегральную кривую н2', которая
также лежит между t и z и вместе с тем больше искомой
кривой у.
Таким образом, функции иг и п2 (или Щ и и2') ограничи-
вают искомую функцию сверху и снизу, и притом более тесно,
чем функции t и z, найденные как первое приближение.
Вместе с тем обе функции щ и н2 удовлетворяют теореме
С. А. Чаплыгина о диференциальных неравенствах.
В предыдущем доказательстве мы предполагали, что кри-
вая Лузина в промежутке тп обращена выпуклостью кверху.
В противном же случае линейчатая поверхность, соприкасаю-
щаяся с поверхностью Лузина, дала бы не верхний, а ниж-
ний предел для второго приближения.
Найдя вторые приближения, мы тем же путем можем искать
третьи, четвертые и т. д.
Эта работа была напечатана в обработке проф. В. П. Ветчинкина
в книге „Методы приближенного и численного интегрирования обыкновен-
ных диференциальных уравнений", вып. I, стр. 42—48, 1932. Прим. ред.
GEOMETRICAL PROOF OF S. A. CHAPLYGIN’S THEOREMS ON
DIFFERENTIAL INEQUALITIES
In this note, drawn up by V. P. Vetchinkin and N. G. Chent-
-zov from lectures of N. E. Joukovsky, is given a geometrical
proof of two theorems of S. A. Chaplygin.
T h e о r e m I: If t = « (x) satisfies within the interval
x0 < x < X the condition ~— f[x, ® (x)] > 0, then t within the
than the function y, which is
dy -
same interval will be greater
being determined by the differential equation Ц— = /(x, y) and
dx
taking the value y0 for x = x0.
The proof is based on the fact that, owing to the condition
>f[x, ® (x)], the integral curves drawn through the points of
the curve t = ® (x) intersect it passing with the increase of x
from above downwards. The curve t = <p(x) should therefore
be situated within the boundaries indicated above the curve y.
The orem II: Having found as a first approximation by
any method whatever two functions / = ®(x) and z = ty(x) be-
tween which is comprised the integral of the given differential
equation =f(x, y), it is possible to effect a further bringing
closer the boundaries by means of integration the linear diffe-
rential equations.
For the geometrical proof of the theorem Prof. N. E. Jou-
kovsky makes us of the idea of N. N. Lusin and represents
the given differential equation as a surface t=f(x,y) (Fig. 2).
Drawing through curves OA an.d OB cylindrical surfaces with
the generating lines parallel to the axis t, we obtain in the
SUMMARY
49
intersection with the surface the curves O' A' and O'B'.
Planes non-perpendicular to the axis x intersect the surface
along the plane curves mn. Through the points m of the
curve O’B' are being traced tangents mt to these plane
sections and chords mn.
In this way are obtained two surfaces which represent
linear differential equations (9) and (8') as well as the surface
t=f(x,y) represents the given differential equation. Since the
surface, formed by chords, intersects with the surface т =f (x, y)
along the curves O' A' and O'B', then, due to the first theorem,
the integral curve и, of the first equation (9) will be comprised
between the curves OA, t = <p(x) and OB, z = <p(x). Between
the same curves will also be situated the integral curve u2 of
the second equation (8'). But on the other hand since the sur-
face z—f(x,y) in the interspace between the lines OA and
OB is comprised between the surfaces formed by chords and
tangents, then iq > u > ut. Thus и2 and iq will represent new
more adjacent limits of the function y.
Зак. 2430. H. E. Жуковекж>. Том Е2Г
4
РАЗДЕЛ ВТОРОЙ
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ
ФИЗИКА
LA DEDUCTION DES FORMULES EXACTES DU MOUVEMENT
PRODUIT PAR LA FORCE REPULSIVE DU SOLEIL
(1879)
Soient x et у les coordonn6es de I’hyperbole rapportees
au centre de la courbe et posons:
e6 —e"6
2
alors
x2 У2 Гев-(-е_612 Ге6 — e~6 T2
Я2 ~ — [ 2 — 2 J ~L
Pour la branche convexe vers le soleil, qui se trouve au
foyer de 1’autre branche, on aura:
R cos V = AE 4~ x,
R sin V = y,
tfc9sr=Z-^----------------l-AE, (1)
/Э& , , f} 6
/г-sin V=B ~* , (2)
(3^ - 43 6
dR cos V—R • sin V • dV=Ae—^—-db, (3)
dtf sin И +A* cos V-dV=B?-±^— - db. (4)
En composant 1’expression (1) • (4) — (2) (3), on obtient:
R2-dV=AB
p6 —I— f» 6
1+E^~ dO = Cdt,
dt = ^
db
54
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
et
АВ
С
La division de (2) par (1) nous donne:
(5)
ee_i_e-e ‘ (6)
E + -~-
En eliminant В et C:
b=Vap-, c=K]/p- ^=}^,oilK=kV^
V/ /\
et on obtient finalement:
з
(=47=r
kV?- L
(I)
et
-----e6 — p-fi
te v =---------------
s F , e8 + e-"
E ~2^
(П)
Quand
rejeter
on a:
les
I’anomaiie hyperbolique n’est pas grande,
membres avec ia quartrieme puissance de 0
on
et
pent
alors
6 + £
е'1 — е 8 '
2
e6 — e 6'
2
- e~e
2
63
6 5
e8 — e 6
2
2 ’
ce qui
fait:
з
A 2 Г fis
t
et
lg и-У£3~Ч
g (1 + O!
i(2-£)]b
ou
2
t Л2
L Lk
62’
6
= w z,
LES FORMULES DU MOUVEMENT DES PARTICULES COMETAIRES 55
et
tg v _ Ve*~ i
D DUA-EJ2
6’2 1
ой
On
Et pour avoir
tgH
D
arc tg — ,
(HI)
il faut que
ZU —------------------------=
D(l + E)‘2
---—— et D =VE— 1.
(1+^P
Mais
Л2
LkV^
et par consequent
i 1
A2 (l+£)2
№
L expression (III) est la formule du Prof. Norton, mentionnee
plus haut.
Эта небольшая заметка была включена Ф- А. Бредихиным в его статью
„Remarques generates sur les cometes", напечатанную в Melanges mathema-
tiques et astronomiques, tires du „Bull, de 1’Academie Imperlale des sciences
de St.-Petersbourg“, t. V
56 АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
В этой статье Ф. А. Бредихин пишет о своем докладе, сделанном
28(16) декабря 1878 г. в Московском математическом обществе, и добавляет:
„Г. Жуковский, профессор механики в Московском техническом училище,
присутствовал на этом заседании нашего общества и живо заинтересовался’
вопросом. Через несколько дней он мне принес вывод точных формул
движения по ветви гиперболы, обращенной выпуклостью к солнцу, т. е.
движения, произведенного отталкивающей силой этого светила. . . Г. Жу-
ковский решает задачу при помощи гиперболических синуса и косинуса
следующим образом". Далее напечатана заметка Н. Е. Жуковского. После
этой заметки Ф. А. Бредихин пишет: „Возможно, что прием г. Жуковского
(вывод формулы (III)] подобен приему Г. Нортона, который нам неиввестен".
Прим. ред.
ВЫВОД ТОЧНЫХ ФОРМУЛ ДВИЖЕНИЯ, ПРОИЗВЕ-
ДЕННОГО ОТТАЛКИВАЮЩЕЙ СИЛОЙ СОЛНЦА 1
(1879 г.)
Пусть х и у координаты гиперболы, отнесенные к центру
кривой, и положим:
.e6-l-e-B „ е6— е~6
2~> J, = S——;
тогда
х2 у'2 Гее--}-е~вТ2 Ге'1—е-еТ2_______
2 J ~L 2 J —1'
Для ветви, обращенной выпуклостью к солнцу, которое
находится в фокусе другой ветви, получим:
R cos V = АЕ-\-х,
R • sin V — у,
/?-со8Г=Ле-у -YAE, (1)
е6_₽-в
R sin V— В--—, (2)
dR cos V— R • sin V• dV= A dh, (3)
dR • sin V'-j- R • cos V• dV= В6 ~^e- JO. (4)
Составляя выражение (1) • (4) — (2) • (3), получаем:
/?2 • dV= АВ
dV = Cdt,
AB Г . „ее + е e1
dt = 1 -j- E------- JO,
1 В заметке приняты следующие обозначения: А и В — полуоси гипер-
болы, С—удвоенная секториальная скорость, Р — параметр гиперболы.
V— истинная аномалия частицы, Е — эксцентриситет. Прим. вед.
58
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
и
АВ
еб— 8
2
Деление (2) на (1) нам дает:
-------------------- „ , л В л — б
V£2-l
^6
tg J/ =
2
Исключая В и С:
В= V АР; С = КУ Р
, где К — k\/ у.,
(5)
(6)
окончательно получаем:
з
А2
t=^
ее — е~9
2
И
tg
г------------ рВ----л в
__ р(} —1— р — 6
(И)
Е + ~^-
Когда гиперболическая аномалия невелика, можно
сить члены, содержащие четвертую степень 6; тогда
—-е-ч r i (j3
б"5
2
-в
62
2 ’
2
откуда
получаем:
отбро-
имеем:
з
,=-4L[
kV н
63J
т
и
tg V =
62
(i+m
6
или
3
t __
L LkV~^
6 = ги • z
ФОРМУЛЫ ДВИЖЕНИЯ КОМЕТНЫХ ЧАСТИЦ
59
и
tg V _
D
l/E2 — !
b2
l+£_ —(2-£)
6,
где
A2
w = —- —__
Lk p.
Имеем:
t w3z®
arc tg y- = w • z---y-
= w b
Для того, чтобы
tg V
-гГ = arc tg
t
L ’
(Ш)
нужно положить
V £2 — 1
w“D(l + £)2
и d = Ve~ 1.
1
з
Но
A2
Lk K7
и, следовательно,
3 3
Л2(1+£)2
kV у-
Выражение (III) есть вышеупомянутая формула проф.
Нортон.
Эта статья представляет собой русский перевод предыдущей статьи,
выполненный для настоящего издания проф. А. П. Котельниковым.
Прим. ред.
DEDUCTION OF PRECISE FORMULAE OF THE MOTION PRODUCED
BY THE REPULSIVE FORCE OF THE SUN
In this note N. E. Joukovsky deduces formulae (I) and (II)
representing the equations of the hyherbolic motion of the
particle of the cometary tail in a parametrical form, in formu-
lae A, В denote the semi-axes of the hyperbola (A is a real
semi-axis), C—a doubled sectorial velocity, P—the parameter
of the hyperbola, К — k\/ jx —the coefficient of the repulsive
force, I — the time counted from the instant of the passing of
the particle through the perihelion, V—its real anomaly at
time t.
Representing t and tg V by means of power series of the
argument 6 and restricting himself to the terms of the third
order N. E. Joukovsky obtains the approximate formulae of
Norton (III).
This brief note was inserted by Bredikhin in his paper
“General remarks on the comets”.
In this paper Bredikhin writes about his reports delivered
on the 28th (16) Dec. 1878 at the Moscow Math. Soc. and he
adds: “Mr. Joukovsky professor of Mechanics at the Moscow
Tech. Sch., attended this conference of our society and took a
great interest in the question. After some days he brought me
the deduction of precise formulae of the motion along the branch
of a hyperbola exposed with its convexity to the sun, i. e. of
the motion produced by the repulsive force of this celestial
body. . . Mr. Joukovsky solves that problem by means of hyper-
bolic functions in the following manner”. Further is cited
the note of N. E. Joukovsky. Below that note Bredikhin writes:
“It is possible that the method of deducing the formula (III)
used by Mr. Joukovsky is similar to that of Mr. Norton unknown
by us”. *
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
ОПРЕДЕЛЕНИЯ ПЛАНЕТНЫХ ОРБИТ
(1883 г.)
Вопрос об определении планетных орбит был решен во
всей полноте Гауссом в его „Theoria motus“, но сочинение это,
ввиду обширности содержания и сжатости выводов, не мо-
жет служить руководством учащимся. Этой цели, на наш
взгляд, еще менее удовлетворяет изложение Ганзена, наполнен-
ное многими вспомогательными величинами, геометрическое
значение которых не указано. Ввиду этого мы предлагаем
здесь краткое изложение теории Гаусса на основании новых
геометрических соображений, значительно упрощающих дело.
В первых двух параграфах помещено определение элемен-
тов орбиты по двум радиусам-векторам, углу между ними и
времени, в которое планета проходит этот угол; в остальных
же трех излагается определение элементов орбиты по трем
наблюдением с помощью составления последовательных
приближений для гауссовых величин Р и Q.
В нашем изложении везде сохранены обозначения, приня-
тые в „Theoria motus“.
§ 1. Пусть будут: а и Ь—большая и малая полуоси орбиты;
2р—параметр; е — эксцентриситет; ©— эксцентрический угол;
так что 6 = a cos'?; г и /-радиусы-векторы; 2/—угол между
ними; t— время, в которое планета описывает этот угол;
р — хорда, соединяющая положения планеты в начале и в
конце времени f; к2 — коэфициент притяжения; 0—-величина,
равная kt', Е и Е' — эксцентрические аномалии при первом и
втором положениях планеты; 2G и 2 g— величины, равные
сумме и разности эксцентрических аномалий; — отношение
площади эллиптического сектора, заключенного между радиу-
сами г и г, к площади соответствующего треугольника.
62
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Т е о р е м а. Если с изменением орбиты величины а, р
и г / не изменяются, то и величины g, е cos G, t и tj
тоже не изменяются.
Выражаем г -4- г' и р с помощью эксцентрических аномалий.
Мы имеем:
г = а (1 — е cos £),
г — а (1 — е cos Е'),
откуда
г г' = 2а(1 — е cosg cos С).
Далее
р2 = а2 (COs £' C<JS ££ _l_ £2 (sin £' s;n
ИЛИ
p2 — 4a2sjnS^ ---e2 cqs2 Q
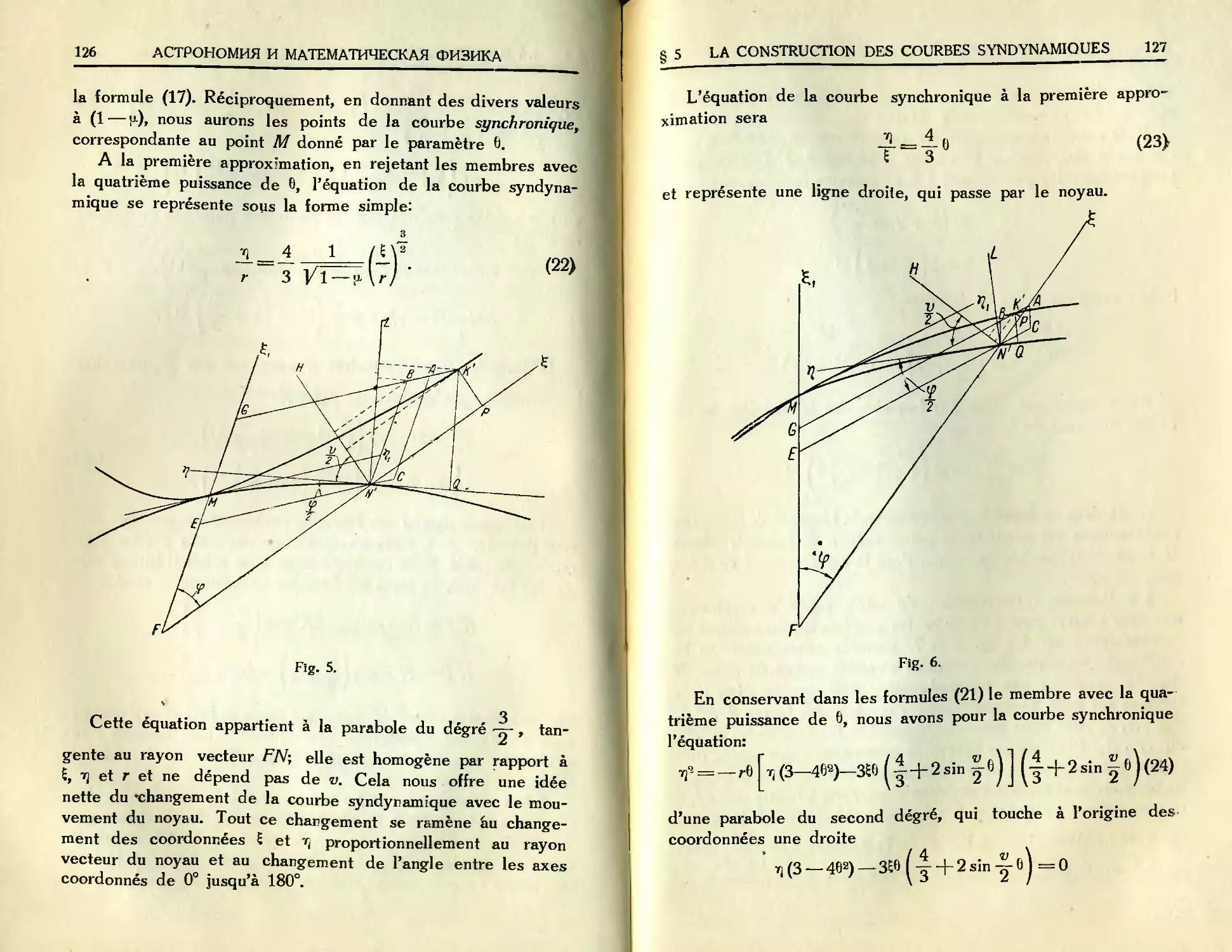
Выведенные формулы показывают, что при постоянных
а, г-\-г' и р величины g
Фиг. 1.
и е cos G будут тоже постоянны.
Пусть (фиг. 1) точки А и В со-
ответствуют первому и второму по-
ложениям планеты. Опуская из них
перпендикуляры на большую ось и
продолжая их до пересечения с опи-
санным кругом, получим точки
С и D, определяющие эксцентриче-
ские аномалии; соединяя же эти
точки с центром эллипса О, най-
дем, что угол COD = 2g. Про-
водим линию ОМ, делящую угол
COD пополам, и замечаем, что угол
MOF = G. Описываем из центра О
круг радиусом ОН, равным ае cos G *, и назовем его внутрен-
ним кругом. Проводим к внутреннему кругу из фокуса F,
в котором находится солнце, касательную FH, и замечаем,
что точка прикосновения Н будет лежать на линии ОМ,
потому что
cos HOF — ае cos G: ае = cos G.
* Мы предполагаем, что угол G острый. Если бы он был тупой, то
надо бы в этом выражении, а равно и в формуле (9) поставить перед cos G
знак минус. При этом на фнг. 1 касательную из точки F к внутреннему
кругу надо провести снизу, а на, фиг. 2 хорду CD надо взять с левой
етороны.
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
63
Отсюда следует, что FH\\ CD, а потому площадь треуголь-
ника FDC равна площади треугольника HDC. Так как при
постоянных a, g и ecosG отношение площади фигуры HDMC
к площади треугольника HDC есть постоянная величина, то
и отношение площади фигуры FDMC к площади треугольника
FDC тоже постоянно.
Замечая теперь, что площадь эллиптического сектора
FBLA и площадь треугольника FBA являются проекциями
под углом ® площадей фигуры FDMC и треугольника FDC,
убеждаемся в постоянстве 7].
Остается обнаружить постоянство t. Для этого припомним,
что к У р есть двойная скорость изменения площади, так
что
^_2 пл. FBLA_2 пл. HDMCcos9
откуда
2 пл. HDMC
1= у .
ка2
§ 2. Обращаемся к опреде-
лению элементов орбиты по дан-
ным г, г', c2f и t. Решение этой
задачи начинается с определения
т] и g. Так как эти величины не
изменяются с изменением орбиты,
при котором а, r-р г и р остаются
постоянными, то предположим, что
Фиг. 2.
подобное изменение произведено
так, что хорда р приняла (фиг. 2) положение АВ, перпенди-
кулярное большой оси. Это будет в том случае, когда фокусное
расстояние сделается равно aecosG, потому что тогда каса-
тельная к внутреннему кругу будет перпендикулярна большой
оси.
Мы получим:
^DOH=g,
FB =
r+r'
2 ’
64
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
В№ = (F + г'2 — 2 rr' cos 2/),
FN — ]/BF* — BN-= У rr' cos f.
Условимся обозначать элементы преобразованной орбиты
теми же буквами, как данной, только с прибавлением значка
„прим".
Найдем, что
BN = b' sing,
вследствие чего площадь треугольника FBA будет равна
Ь' sin gV rr cos f.
Что касается площади эллиптического сектора FBMA fgro
она будет:
7 W
2 VP 2У а'
Приравнивая отношение второй площади к первой величине
т] и определяя из найденного уравнения а, получим:
4 т)3 rr cos2/sin2 g ’
Составляем другую формулу для а. Так как
ON = a cos g,
то
r + r' ,
—о— = а — ае cos g;
но
, acosg—У rr cosf V rr'
e ---------------= cos g------cos /,
о a
следовательно,
__ r 4~ / — 21/ rr' cos/cos g
2sin2g
Сравниваем эту величину а с вышенайденной’ и опреде-
ляем Т(2:
7]2 -------------------------------------- ф
2rr'cos’2/(r-|-г' — 2 V rr cosfcosg)
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА 65
Чтобы представить эту формулу в более простом виде, пола-
гаем, что1
6
(2 Уrr cos/)2
гЦ-г'______1
4 Vrr' cos / 2
Это дает нам:
Z + sin2
(2)
(3)
Остается отыскать еще другое уравнение, связывающее
т] и g. Назовем площадь эллиптического сегмента ВМА
через ни и напишем, что
'<1=1 + —------
о sin g V г г cos /
Так как абсциссы и ординаты нашего эллипса с помощью
эксцентрической аномалии я представляются через a cos а и
Ь' sin а, то
s
w — 2ab' J sin2 а da.
О
д
sin2 at/я,
Подставляя в вышенаписанную формулу и исключая а
с помощью формулы (1), найдем:
4тп2
V2sin3g
о
или
, ш2 2g— sin 2g
tq2 sin3g
(4)
С помощью уравнений (3) и (4) определяются искомые
величины т] и g. Гаусс рассматривает здесь два случая:
у гол g— большая величина, и элементы орбиты приблизительно
известны; угол g — малая величина, и орбита совершенно
неизвестна.
1 Мы останавливаемся только на случае 2/ 180°, поэтому т у нас
величина действительная.
Зак. 2430. Н. Е. Жуковский. Том IX.
5
66
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
В первом случае определяем сначала приближенную ве-
личину g, которая при нашем изложении получается с по-
мощью рассматривания отношения площадей треугольников
в данной и преобразованной орбите. Мы имеем:
rr sin 2 У ____ cos
2 Угг' Ь' sin g cos f c°s У ’
поэтому
b sin g — Уrr' sin /. (5)
Зная приблизительную величину Ъ, найдем из этого урав-
нения g\ подставляя его в уравнение (4), определим »); под-
ставляя же найденное значение Л в уравнение (3), опять
определим g и т. д. После ряда таких действий найдем, на-
конец, величины т; и g, весьма точно удовлетворяющие урав-
нениям (3) и (4).
Во втором случае, полагая
sin3g ’
напишем по сказанному выше, что
о
4 Г
X — -г-s— I sin2 а (/а.
s,n « J
о
Вводим новое переменное р, полагая:
sin а = р sin g;
найдем, что
1
г 1
X = 4 | (1 — р2 sin2 g) 2 р2 </р.
о
Разлагаем подинтегральную функцию по биному и интегри-
руем:
у 4 । 2 • о । 3 . . .
Л з -у sin-g sin'g - • • •
Здесь вторая часть может быть легко выражена через
sin2 ~, подставляя
sin2 g = 4 sin- — 4 sin4 .
§ 2
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
67
Сделав это и возведя обе части полученного равенства
в степень — 1, найдем:
Производим возведение в степень и обозначаем
9 f
через уд с
получаемые при этом члены четвертого и высших
потом определяем X’.
Х= 3 9 / J. sin2-^
4 io'
порядков*;
Гаусс дает в «Theoria motus“ табл. Ill, в которой по аргументу
Я Г ГТ
sin2 можно найти с. Подставляем полученную величину X
в формулу (4):
4
тп2
sin2 — Е)
Подставляем сюда на основании формулы (3)
. g т2 .
и совершаем некоторые преобразования:
л _ (л zzlb?2.
(6)
(7)
здесь
. ™2
А- 5
6
Так как из формул (2) видно,
порядка, то с точностью до
жить, что
(8)
что т есть величина первого
шестого порядка можно поло-
тп2
ь
h =
1
9
г 6 и g принимаем ва малые величины первого порядка.
68
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Определив при этом значении h величину т; из формулы (7),
можно будет по найденному т; из формулы (6) определить
™’-2 ’ “
по этому аргументу из табл. III взять 5. Внося эту
величину в (8), найдем из уравнений (7) и (6) "более точные
величины и g.
Для облегчения решения уравнения (7) Гаусс дает табл. II,
в которой по аргументу h определяется Ig q.
Когда т] и g найдены, то сейчас же определяются а и Ь по
уравнениям (1) й (5), а следовательно, становятся известны
о и е. Далее, так как в нашей преобразованной орбите фо-
кус F лежит на внутреннем круге, то
ае cos G = a cos g— ]/ rr cos /;
(9)
отсюда определяем G. После того находим, что
E — G—g,
и определяем истинную аномалию v в первом положении и
время Т перехода планеты от перигелия до этого положения
по известным формулам:
(10)
3
Т = ~~Jr~ (Е— е sin Е).
§ 3. Говоря о трех положениях планеты, условимся все
величины, относящиеся к первому положению, обозначать
буквами без штриха и приписывать один и два штриха вели-
чинам, относящимся ко второму и третьему положениям; ве-
личинам же, относящимся к двум 'положениям, будем припи-
сывать индекс третьего положения.
Таким образом последовательные радиусы-векторы будут
г, г', г", а угол между гиг' будет 2/".
Определение абсолютных положений планеты в простран-
стве по трем ее видимым положениям мы начнем с того про-
стейшего случая, при котором С и t суть величины беско-
нечно малые, так как метод Гаусса, на наш взгляд, состоит
§ 3
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
69
в приспособлении для случая конечных промежутков времени
способа решения, непосредственно получающегося в этом
предельном случае. Пусть (фиг. 3)5будет солнце, а С, С',’С"
— три последовательные бесконечно близкие положения
планеты на орбите. Проведя радиусы-векторы г, г', г" и хор-
ду СС", которая пересечет радиус г в точке М, займемся опре-
делением отношения СМ к С"М и длины
стрелки МС'.
Для этого заметим, что, пренебрегая
бесконечно малыми величинами третьего
и высших порядков, можем предположить
что планета в продолжении времени I' дви-
жется под действием постоянной силы
t2:r/2, направленной по радиусу С'S.
Вследствие этого, проведя линии СА
и С'В параллельно скорости v' во втором
положении планеты, найдем:
Фиг. 3.
CA=v'f, C"B=v't,
откуда, обращая внимание на подобие треугольников MCA
и МС"В,
поэтому
СМ-^- (12)
Зная (фиг. 4) положения земли А, А', А!' в моменты на-
блюдений и направления луча, идущего от планеты к земле,
мы имеем положение в пространстве трех линий ВС, В'С
В"С", на которых должны выбрать три точки С, СУ, С" так,
чтобы все ^они лежали в одной плоскости с солнцем 5 и
удовлетворяли уравнениям (11) и (12).
70
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Для решения этой задачи сначала определим прямую, на
которой должна лежать точка М. Делим кратчайшее расстоя-
ние между ВС и В" С" в отношении 6"-’6 и проводим через
точку деления плоскость N, параллельную прямым ВС и В"С".
Эта плоскость разделит lb упомянутом отношении всякую
хорду, соединяющую) точку прямой ВС с точкой прямой В"С",
поэтому на ней должна лежать и искомая нами точка М.
Кроме того, точка М
должна лежать на
плоскости, проходя-
щей через солнце и
прямую В'С'-, следо-
вательно, она будет
находиться на линии
СМ, по которой эти
две плоскости пере-
секаются.
Теперь остается
удовлетворить урав-
нению (12). Для этого
строим в плоскости SB'C' кривую линию В'А’С, выражае-
мую уравнением (12), и определяем точки пересечения этой
кривой с прямой В'С'. Таких точек пересечения, как увидим
ниже, будет три. Одна из них, например, точка А', соответ-
ствует положению земли, которое удовлетворяет всем усло-
виям решаемой нами задачи; одна же из двух других, напри-
мер, С', будет соответствовать положению планеты во втором
наблюдении.
Точка пересечения радиуса SC' с прямой GM будет точка М.
Проведя через нее и линию В"С плоскость, найдем в пере-
сечении этой плоскости с прямой ВС точку С, соответствую-
щую первому положению планеты; соединив же эту точку с
М и продолжив хорду СМ до пересечения с прямой В"С",
найдем точку С", соответствующую третьему положению пла-
неты. Вопрос таким образом будет решен.
Займемся теперь составлением уравнения кривой В' А’С',
принимая линию GM за ось абсцисс, а перпендикуляр, опу-
щенный на нее из солнца, за ось ординат (фиг. 5).
§ з УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА 71
Пренебрегая бесконечно малыми величинами третьего и
высших порядков, можем уравнение (12) написать в таком
виде:
2/3ёг=,ял (12'}
Но, называя через Л расстояние точки S от оси абсцисс,
имеем:
/2 = (Л+у)2 + х2,
С'М_у_
SM h :
поэтому
Г I3 /66"\2
<q(A+«/)2+*a]
или, отбрасывая малую величину у перед h,
/66"Is
№+%2)3 = Л2.
Это уравнение показывает, что кривая симметрично рас-
положена относительно осей координат и состоит из двух
ветвей, асимптотически расстилающихся по оси Ох. Каждая
из ветвей имеет две точки перегиба на расстояниях
Из этого следует, что прямая линия может пересекать
нашу кривую только в двух или четырех действительных
Точках; при этом в последнем случае три точки пересечения
лежат на одной ветви кривой.
Так как в нашей задаче планета и земля дают две точки
пересечения ветви В'А’С с прямой В'С, то на той же ветви
должна лежать еще третья точка пересечения этой прямой.
Если земля занимает среднее положение А', то не может
быть сомнения относительно того, где находится планета,
потому что по направлению, в котором она видна, мы всегда
отличим точку С' от В'; если же земля занимает одно из
крайних положений, например, В', то мы не можем по трем
данным наблюдениям решить, находится ли планета в С или А'.
72
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
§ 4. Уравнения (11) и (12') перестают удовлетворяться,
как скоро 6", 6 суть конечные величины. Для решения вопроса
в этом случае Гаусс заменяет в них величины и 6" • 6
величинами Р и Q:
^•^=<2: (И)
потом, считая Р и Q известными, определяет с помощью их
и данных наблюдения величины: г, г', г", f", f и При этом
будут иметь место геометрические соображения предыдущего
параграфа с той только разницей, что положение земли А' не
попадет на кривую линию, служащую для определения точки С',
и точка L, в которой плоскость N пересекает радиус-вектор
земли A'S, не будет лежать на хорде А А'.
Прежде всего определим (фиг. 5) угол SC'A', который
обозначим через z. Пусть будут:
SA' — R', ^SA'B' =5', zlA'DG = c, ^LDS = ^.
Мы получаем из треугольников CMD и MDS, что
С'М sin a sin (z— с— со)
SM ~ sin z sin oi
а из треугольника SA'C находим:
, R sin о
r =------;-----.
sin z
(15)
Подставляя эти величины в уравнение (14), найдем для опре-
деления z следующее уравнение:
cQ sin со sin4 z = sin (z — о— co), (16)
где
2R'3 sin 3o' sin о (17)
Здесь ° не изменяется с изменением Р, так как при этом
плоскость N перемещается, оставаясь сама себе параллельной;
что же касается угла «о, то он при таком перемещении пло-
§ 4 УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА 73
скости N изменяется. Определим его по Р и величинам, не
зависящим от Р. Мы имеем из треугольников A'DL и LDS".
SL sin о> sin о'
~IV ~ sin (o' — о) sin (w + с) ‘
Для определения входящей сюда величины SL опускаем
(фиг. 6) из солнца 5 на плоскость N перпендикуляр SH и
определяем его длину. Если назовем радиусы земли через
R, R', R", а углы, которые они образуют с плоскостью Л,
через л, Ct', Cl", то найдем, что
„ R sin а + PR" sin а"
ЭЛ— , i 5 >
откуда
Rsina | RR'sin а"
SL= (1 + РЫг,— ’• (18)
Подставляем и определяем tgw:
где
cos з
R sin Л
R"sin а"
R' sin 8' sin а'
R" sin (S' — a) sin Cl" ’
(20)
Теперь следует определить по данным наблюдениям не-
зависимые от Р величины о, а и Ь. Для этого обращаемся
к фиг. 7, начертанной на внутренней стороне небесной сферы.
Пусть А, А' А’ будут гелиоцентрические положения земли,
В, В’ и В" — геоцентрические положения планеты. Проводим
дуги больших кругов В'В", В"В, ВВ' и А А'А", из которых,
последняя будет эклиптика. Соединяем дугами больших кру-
гов соответственные гелиоцентрические положения земли и
геоцентрические положения планеты и продолжаем эти дуги
до пересечения так, чтобы получился сферический треуголь-
ник DD'D".
74
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Относительно отсчитываний дуг и углов принимаем сле-
дующие условия Гаусса: направления эклиптики и гелиоцентри-
ческого пути планеты считаем положительными в сторону
гелиоцентрического движения земли и планеты; дуги АВ,
А'В', А"В" считаем положительными от гелиоцентрического
положения земли к геоцентрическому положению планеты;
углы в точках пересечения двух дуг берем между частями дуг,
идущими в положительном направлении; треугольник DD'D"
строим так, чтобы, идя в положительном направлении АВ, мы
имели бы в D" и D' положительные направления дуг А'В' и
п А" В" направо, а идя
в положительную сторону
.А’В' , имели бы в D поло-
жительное направление ду-
ги В" А" тоже направо.
Обозначаем через 8, 8', 8"
величины дуг АВ, А'В',
А"В", а через у, у', у"
углы их наклонения к эк-
липтике и определяем эти
величины по долготам
л а, а', °-" и широтам [3, р', р"
точек В, В', В" и по долго-
там I, I', Г точек А, А', А"
с помощью формул вида:
in («— I)’
СПК Г
Далее решаем по стороне и двум прилежащим углам сфери-
ческие Треугольники A'DA", A"D'A и AD"А', пользуясь фор-
мулами вида:
sin г sin (A'D - A"D) = sin (I" — Г) sin ^(f" + l'),
sin -1 « cos 4 (A 'D + A"D) = oos 4- (Г - О sin 4 G" - Y).
z, z z
§ 4 УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА 75
cos | е sin | (A'D - Л"Я) - sin | (Г - Г) cos | (/' + /) ,
cos ye cos -i (A'D — A"D) = cos у (I" — Г) cos у (/' — V),
где e, s', e" суть углы при вершинах D, D', D".
После этого можно будет перейти к определению искомых
величин: а, а и Ь.
Сравнивая фиг. 4 с фиг. 7, замечаем, что плоскость SA'C'
пересекает небесную сферу по дуге А'В', плоскость же, про-
веденная через центр сферы параллельно плоскости 7V, пере-
секает ее по дуге ВВ'. Отсюда следует, что радиус, парал-
лельный прямой GM, пересекает небесную сферу в точке М,
так что искомый угол с выражается дугой МВ'. Обозначим
через т и п долготу и широту точки М и выразим, что три
точки В, М и В" лежат на дуге одного большого круга. Вообра-
зим прямоугольные оси координат, имеющие начало в солнце S,
плоскость ху которых совпадает с плоскостью эклиптики,
а ось X направлена в точку весеннего равноденствия. Опишем
около небесной сферы, радиус которой примем за единицу,
цилиндр, прикасающийся к ней по эклиптике, и определим
координаты точек пересечения этого цилиндра с радиусами
SB, SM и SB". Они будут:
cos a, sin a, tgp,
cos т, sin ти, tgTi,
cos a", sin о-'', tg P'.
Условие, что три вышеупомянутые точки лежат в плоскости,
проходящей через начало координат, состоит в том, что опре-
делитель, составленный из девяти вышенаписанных координат,
равен нулю.
Отсюда искомое нами условие будет:
tg Р sin (я" — ти) — tg и sin (а" — я) -J- tg ?" sin (ти — а) = 0.
Подставляем в это уравнение
tg 71 = sin (т — I') tg ч'
76
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
и даем ему следующий вид:
cos (т — Г) [tg 0 sin (а" — Г) — tg 0" sin (а — I’) =
= sin (т — Г) [tg 0 cos (а" — Г) — tg 0" cos (а — Г) -{-
+ tg/ sin (а" —а)].
Но, так как
tg (т — I') — cos у' tg (o' — с),
то
tg(8'— =
______________tg 0 sin (а" — Г) — tg 0" sin (а — /')
~ cos f' [tg 0 cos (a" — Г) — tg 0" cos (a — /')] -f- sin 7' sin («"—a)
Гаусс упрощает эту формулу с помощью подстановок
tg 0 sin (a"— Г) — tg 0" sin (a — /') = 5, )
tg 0 cos (a" — I') — tg 0" cos (a—I') = T sin t, (21)
sin (a" — a)=Tcost J
и получает:
tg (8' — =) = т £ , , . . (22)
/ sin (Z -f- у ) ' '
Для определения а и b заметим, что углы, которые мы
назвали выше через Д, д', Д', выражают на фиг. 7 расстояния
точек А, А', А’ от дуги ВВ". Если обозначим через Ь, Ь', Ь,у
расстояния от той же дуги точек D, D', D", то найдем:
sin Д _ sin 8
sin b' sin {AD' — 6) ’
sin fl" sin 8"
sin b' sin (Л"О'— 8") ’
sin a' sin (8' — o)
sinb sin{A'D — 8' -J- 0) ’
sin fl" sin 8"
sin b sin (A"D — 6") ’
откуда
sin Д _ sin 8 sin (A"Dr — 8")
sin d" sin 6" sin (AD' — 8) ’
sin «' _ sin (o' — o) sin (A"D — 8")
sin fl" sin (A'D — 8'+ c) sin 8"
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
77
Подставляя эти величины в уравнения (20), найдем:
__ R sin 2 sin (A"D' — 8")
R" sin 8" sin (AD' — 8)
_ R' sin 8' sin (A"D — 8")
R" sin 8" sin (A'D — 8' -J- a) *
Таким образом найдены все величины, необходимые для
определения z по уравнению .(16), которое решается по спо-
собу ложных положений.
Определив z, получаем по формуле (15) расстояние /; по-
том, отложив на круге В'А' дугу В'С, равную z, получаем
на основании фиг. 4 гелиоцентрическое положение С' нашей
планеты во втором наблюдении.
Переходим к определению гелиоцентрических положений
С и С" в первом и третьем наблюдениях и расстояний г и г".
Для этого назовем через п, п, п" двойные площади тре-
угольников, заключенных между радиусами-векторами планеты,
м определим сначала величины дробей
п' г
п г
--- и
п
Мы имеем по фиг. 4:
/Г
П
П
— = (р+1)-у-.
п г
Но так как по фиг. 5
5Л/=Я-/М8'---й,
sin (z — с}
то
г'п ID I 5Lsin(8'—о)
— =(Л+1)
Подставляя сюда величину SL из уравнения (18) и обращая
внимание на уравнение (20), получаем:
г п __(Р~\-а) R' sin o'
TsiT(z"-^y ’ (23)
г'п 1 г'п
п" ~7> п -
78 АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Назовем через X и С" дуги D'C и D'C", определяющие на
фиг. 7 гелиоцентрические положения планеты С и С", и за-
метим, что отношение синусов дуг С"С и С'С или, что все
равно, отношение синусов расстояний точек С и С' от
окружности AD’ должно быть равно отношению п г к пг"',
следовательно,
sin X" sin s': sin {A' D" — 8' z) sin e" = nr' : n"r".
Прибавляя сюда еще уравнение, аналогичное (15), будем иметь-
для определения г" sin X" и г" cos X" два уравнения:
zz . rn П r Sin s . , । лггм
г sin, =—т,---г—7sin(z4-A D —o'),
п sin е "
/'sin (X" — A"D' + 8") = R" sin 8".
Также найдем для определения г sin С и г cos С уравнения:
. « п г sine
г sin <• = ------—- sin (z -4- A D — о ),
п sine
г sin (С — AD' 8) = R sin 8.
(24')
Таким образом определяются X, г и г".
Построив точки С и С, соответствующие гелиоцентриче-
ским положениям планеты в первом и третьем наблюдениях,
можно будет перейти к определению углов /, /', /".
Назовем через и и и" углы прн вершинах С и С" и ре-
шим сферический треугольник CD'C" по формулам:
sin/'sin (u"-j-u) = sin — e'sin-jy (Х-|-Х"),
sin /' cos -i- (и" 4- u) = cos -y s' sin Sy (X — X")
cos /' sin (u" — u) = sin s' cos'7y (- 4~
cos /' cos -y (u" — u) — cos — s' cos (X — X").
(25)
Отсюда определим /' и и. Что же касается / и /", то их
Удобнее определить, пользуясь отношением площадей тре-
угольников, по формулам:
§ 5 УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА 79
sin 2/ = г sin 2/' >
п г
sin 2f" = г" sin 2f П, , .
п г
(26)
§ 5. Задавшись наперед величинами Р и Q, мы нашли
величины г, г', г", /, f,f ", которые вполне определяют иско-
мую орбиту. Чтобы решить, верно ли взяты Р и Q,
нужно посмотреть, проходит ли планета в случае найденной
орбиты углы 2/" и 2/ во времена t" и t? Это всего удобнее
сделать, определяя по данным г, г', f", 6" и г', г", /, 6 отно-
шения f" и т] по способу, указанному в § 2, и составляя
потом с помощью этих отношений Р и Q.
Мы имеем:
п?) = О,
откуда
п" _
п 6т/' ’
Величина Р получается сразу:
(27)
Для составления Q напишем по уравнению (14), что
п' 4 ’ 11 11 п6"6 11’ ~j 11 п'
Q~2r'3 — ' Ч------— = 2r'3 Az--------—------- •
п 7) 11П 11
Чтобы определить р, берем:
Р 1 ।
— = 1 -4- е cos v,
г
Р ! f
— = 1 е cos v ,
Р Ч I гг
-~ = 1 4- е cos v т
80 АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
где v, v', v"—истинные аномалии в моменты наблюдений.
Умножаем эти уравнения на sin 2/, — sin 2/, sin 2/" и скла-
дываем, обращая внимание на тождества:
cos v sin 2/— cos v' sin 2/' + cos v" sin 2/" = 0,
sin 2/+ sin 2/" — sin 2/' = 4 sin / sin /' sin f;
получим:
p(n--nf . . . ,, .
----- , „-----= 4 sin f sin f sin / .
rr r
Умножим это уравнение на 2 (rr'r")2cos/cos/' cos/":
Ip cos/cos f cos f" rr'r" (n" — n n) = nnn".
Определяем отсюда p и подставляем его в формулу для Q:
г'2 6"6
Q = — ~r,------7---т,----рГ- (28)
rr 7] 7] COS J COS J COS f
Если P и Q, вычисленные по уравнениям (27) и (28), совпа-
дают с теми величинами, которыми мы задались, то орбита
вычислена верно. Отсюда видно, что наша задача может быть
решена рядом последовательных приближений.
Мы показали в § 3, что при бесконечно малых Ь" и 6 вели-
6"
чины Р и Q обращаются в -j— и 66"; то же следует и из урав-
нений (27) и (28).
Вследствие этого при небольших величинах Р и t за
первые приближенные значения Р и Q можно принять
и 66". В случае же, если орбита приближенно известна, то
выгодно брать большие промежутки времени Р и t и вычис-
лять первые приблизительные величины Р и Q по формулам
(27) и (28), пользуясь данными приближенной орбиты.
По первым приближенным величинам Р и Q определяем,
как было показано в § 4 и 2, величины г, г', г", /, f, f", 7]", т]
и составляем с помощью их по уравнениям (27) и (28) опять
Р и Q; по этим последним снова определяем г, г', г", f, f,’ f,
rl", т; и составляем новые значения для Р и Q и т. д. После
ряда подобных действий придем к значениям Р и Q, которые
не изменяются от повторения, над ними указанной операции
и потому соответствуют истинной орбите.
§ 5
УПРОЩЕННОЕ ИЗЛОЖЕНИЕ ГАУССОВА СПОСОБА
81
Вычисление элементов а, Ь, о, v, Т может быть сделано
с помощью г, г', f, т" или с помощью г', г", /, "»] и совер-
шается, как было показано в конце в § 2. При этом удобнее
пользоваться теми и другими данными, чтобы иметь поверку.
Остается только определить наклонение орбиты к эклип-
тике i и долготу восходящего узла Q. Это делается (фиг. 7),
решая сферический треугольник ACQ по формулам
sin у i sin у (g 4- Л) = sin у (AD' — C) sin у (l + «),
у г sin у cosy (AD' — С) sin у (?—u),
cos у i sin -у (g — h) = sin у (AD' — C) cos у ft + u).
cos у i cos у (g — h) = cos у (AD' — Q cos у (y — u),
(29)
где
CQ=g,
AQ = h.
Определив из формул (29) i и h, найдем S по формуле
Q — l — h.
4 февраля 1883 г. в заседании физико-математической комиссии От-
деления физических наук Общества любителей естествознания Н. Е. Жу-
ковск сделал сообщение на тему „Определение кометных и планетных
орбит” и 15 февраля 1883 г. в заседании Московского математического
общества —• на тему „Вычисление кометных и планетных орбит”. Работа
была впервые напечатана в „Математическом сборнике”, т. XI, 1883, вто-
рично — в Сочинениях Н. Е. Жуковского, т. 1> 1912. Прим ред.
За.к. 2430. Н. Е. Жуковский. Том IX.
6
SIMPLIFIED EXPOSITION OF GAUSS’METHOD OF DETERMINATION
THE PLANET ORBITS
In this work N. E. Joukovsky gives a concise exposition of
Gauss’method based on geometrical considerations appreciably
simplifying the theory.
In the first two paragraphs is stated the determination of
the orbit by means of two radii-vectors, of the angle between
them and of the time t, in which the planet passes that angle;
the last three paragraphs contain the determinations of the orbit
elements by three observations with the help of drawing up
successive approximations for Gauss’ values P and Q.
In the solution of the first problem the notations given by
Gauss are being retained: a and b are the major and the mi-
nor semi-axes of the orbit; Ip is the parameter; e — the eccen-
tricity, <p— the eccentric angle, so that b = a cos'?; r and r'
are radii-vectors; 2/—the angle between them; t — the time,
in which the planet describes that angle, ® is the chord, con-
necting the positions of the planet at the beginning and at the
end of the time /; № — the coefficient of the attraction; в — the
value kt\ E and E' eccentric anomalies in the first and second
positions of the planet; 2G and 1g— values equal to the sum
and difference of the eccentric anomalies; tq is the ratio of the
area of the elliptic sector comprised between the radii-vectors
r and r' to the area of the corresponding triangle.
In the first problem r, r', If, ft —kt are considered as
given ones and in the first place rj and g are being determi-
ned from the equations (3) and (4), in which I and m are being
obtained from formula (2); the deduction of those equations
are simplified by N. E. Joukovsky by means of a transformation
of the unknown orbit into another (Fig. 2) based on the follo-
wing theorem: If with the transformations of the orbit the va-
SUMMARY
83
lues g, P and r-j-r do not change the values g, ecosG, t and
7] do not change too.
When Ц and g are found from the equations (3) and (4) by
the method of successive approximations, a and b will be de*
termined by formulae (1) and (5), G and the time of passing the
perihelion — by the formulae (9) and (10).
In the diagrams 4, 5, 6, which refer to the second problem,
the letters С, O', C denote three positions of the planet in
the space; A, A', A' — are the corresponding positions of the
earth; 5 denotes the sun; M—the point of intersection of
the straight lines SC', C'C"; N—the plane perpendicular to
the line of the shortest distance BB" between the straight li-
nes A"C" and A'C' and the straight line BB" passing through
the point which gives the distance BB" in the ratio CM'.C"M—P;
GLM denotes the line of intersection of the planes N
and SA'C'-, L — the point of intersection of the line SA' with
the plane /V; r, r, r"— the radii-vectors of the planet;
a, cd, az/ — the angles formed by them with the plane
TV, SH—the perpendicular fallen from 5 on the plane TV.
In Fig. 7 drawn on the internal surface of the celestial
sphere the letters A, A', A" denote the heliocentric positions
of the earth; С, С', C" — the heliocentric, В, В', B"—
the geocentric positions of the planet; 8, 8', 8" — the arcs
AB, A'B', A"B"', 7, /, t" — the angles of their inclination to the
ecliptic A, A', A"; W, 1И,0" — the distance of the points D, D',D"
from the axis BB". The meanings of the angles z, ш, a, e, e',
e" are shown in Fig. 5.
The second problem is to determine the radii-vectors
r, r', r" of the planet and the angles 2/, 2Г, 2f' between them
by means of the given longitudes a, a', and latitudes P, P', pz/
of the points В, В', B" and of the longitudes l, Г, I" of the
points A, A', A" (Fig. 7) and also of the radii-vectors R, R', R"
of earth.
The idea of Gauss’ method for the solution of this prob-
lem consists in the opinion of N. E Joukovsky in the follo-
wing.
If the intervals t', t between the observations are small, we
may then reckon that during the time t between the first
6®
84
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
and second observations the motion of the planet proceeds
under the action of a constant force k2: r'2 directed along
the radius C'S (Fig. 3) with which the planet is being attracted
by the sun in its mean position C. Then
6"
P= CM-. CM= -y- (11)
and
Q = 2/>^=66" (12)
will be known. The equation (12) in the plane SA'C (Figs. 4, 5)
represents the equation of the curve of the 8th order, and by
the point of intersection of it with the ray A'C going from
the earth to the planet is being determined in the second ob-
servation the position of the planet C and then the points M.
The plane passing through the ray A"C" and the point M
intersecting with the ray AC will determine the point C, and
the point C" will be determined by the intersection of the
straight lines CM and A"C".
Thus, knowing the position of the earth and knowing by
three observations the direction of the rays connecting the
earth with the planet as well as the intervals between the
observations it will be possible to determine three positions of
the planet in space.
According to N. E. Joukovsky Gauss’ method consists in the
adaptation of the method of solution just outlined for the case
of finite spaces of time.
With finite 6, Ь" the values P and Q will no more be equal
6"
to у and 66" and will not be known beforehand. Gauss’ method
implies the determination of the values P, Q and by the way
the determination of the unknowns r, r', r", f, f, f".
The solution of the problem starts with the determination
of the values r, r', r", f, f, /" on the assumption that P and Q
are known.
By means of the formulae of spherical trigonometry are
being determined first the angles y, f", arcs 8, 8', 8", angles
e, e', e" and the arcs A’D, A"D, AD', A"D', A'D". AD'. Next,
SUMMARY
85
by the formula (22), which is being obtained if we express
that three points В, В", M are lying on the arc of a great
circle, we find the angle a and by formula (20') — are obtained
the values a and b (not the semi-axes); by formula (19) — the
angle <o, by formula (16) — z and lastly by formula (15) the
radius-vector r' of the mean position of the planet.
Knowing r' it will be possible by formula (23) to determine
the ratios n’.nr:n" of the area of triangles comprised between
r, r, r" and then by formula (24) С', C", where C = D'C, C—D'C'
are being determined by z, z" and from the spheric triangle
CD'C the angle f and by formula (26) the angles f and f'.
In this way with P and <2 prescribed it will be possible
to calculate r, r, r", /, f, f", which just determine the orbit
sought for.
To ascertain that P and Q are taken correctly we have to
see whether the planet passes, when the orbit is found, the
angles If' and 2/ at times t" and t'.
For this purpose by means of the method above stated are
being determined the values 'Л and if and by them P and Q
(from. 27 and 28). If the obtained values of P and Q coincide
with those prescribed, the orbit is then calculated correctly,
otherwise we have to determine once more r, r , r",
by the values of P and Q and new the values of P and Q are
thus drawn up, and so on. Performing a number of these ope-
rations we shall arrive at values of P and Q, that will not change
under the repeated operations just mentioned and therefore
they will correspond to the real orbit.
The inclination of the orbit to the ecliptic, i, and the longi-
tude of the angle are obtained from the spheric triangle ACQ-
О ГРАФИЧЕСКОМ РЕШЕНИИ ОСНОВНОГО УРАВНЕНИЯ
ПРИ ВЫЧИСЛЕНИИ ПЛАНЕТНЫХ ОРБИТ
(1883 г.)
При вычислении планетной орбиты по трем наблюдениям
мы встречаемся с разрешением уравнения восьмой степени,
дающего угол z между радиусом-вектором планеты во вто-
ром наблюдении и линией, соединяющей планету и землю
в момент этого наблюдения.
Мы предлагаем здесь весьма простой графический способ,
служащий для приближенного определения z в случае, если
промежутки времени t" и t между наблюдениями малы.
Возьмем (фиг. 1) линию АВ, соединяющую планету и
Землю в момент второго наблюдения, и соединим положение
планеты А во втором наблюдении с солнцем 5. Отметим на
радиусе-векторе 71.S точку D, в которой он пересекается
хордой, соединяющей первое и третье положения планеты.
О ГРАФИЧЕСКОМ РЕШЕНИИ УРАВНЕНИЯ ОРБИТ
87
Через точку D проведем плоскость N, параллельную пря-
мым, соединяющим положения планеты и Земли в моменты
первого и третьего наблюдений, и построим линию ОВ, по
которой плоскость /V пересекает плоскость SAB.
Угол z, который на нашем чертеже есть угол SAC, нахо-
дится в способе Гаусса с помощью уравнения, которому
можно дать следующий вид:
Д Г)
2ASds=Q;
здесь Q в первом приближении выражается произведением
ft на коэфициент притяжения к2.
Принимаем линию ОВ за ось абсцисс, а перпендикуляр,
опущенный на нее из S, —за ось ординат, и выражаем урав-
нение (1) с помощью координат х и у точки А:
+ + = (2)
где h есть расстояние 5 от ОВ.
Таким образом положение планеты А, определяющее не-
известный угол z, является точкой пересечения кривой, имею-
щей уравнение (2), с прямой АВ; но так как эта кривая
зависит от двух параметров А и Q, то сю неудобно поль-
зоваться для графического решения задачи, ибо для каждого
отдельного случая пришлось бы вычерчивать новую кривую.
Чтобы свести вопрос к пересечению прямой с постоянной
кривой, мы воспользуемся двумя замечаниями: во-первых, по
малости у мы можем в первой части уравнения (2) написать h
вместо h-\-y; во-вторых, при малых f и t одна из точек пересече-
ния кривой, имеющей уравнение (2), с прямой АВ весьма близко
подходит к положению Земли в момент второго наблюдения.
Пусть это будет точка С, имеющая координаты х0, у* *.
Мы получаем для определения координат точки А уравнения:
О'2
(3)
(4)
л хо ______________________
* Всех действительных точек пересечения будет четыре, из которых
три лежат на верхней ветви кривой, а одна на нижней; эта последняя не
соответствует ии положению планеты9ни положению Земли.
88
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
где
а = £ ABD.
Делаем теперь подстановку
x — h ctg С;
найдем по уравнению (3)
*=2^SIn&”
(5)
(6)
Подставляем х и у из уравнений (5) и (6) в уравнение (4):
sin3C0— sin3-. 2А3
(7)
Здесь вторая часть может быть выражена приближенно
с помощью гауссовой величины с, так как, обозначая угол
OBS через <о, имеем:
с~
2Л3
sin (oj-4-0) -
-----;------ Sin
•Sin ш J
что по малости о можно написать так:
1
2Л3 tg с'
С другой стороны, нетрудно заметить на фиг. 1, что наш
угол С с тем же приближением может быть заменен на z.
Вследствие этого уравнение (7)
можно написать так:
sin3 8 — sins(z__1 . .
tg z — tg 8 Qc ’
где 8 есть угол z0, т. e. угол между
линией АВ и радиусом-вектором
Земли во втором наблюдении.
Теперь вопрос об определении z приведен к отысканию
точек пересечения прямой с постоянной кривой и может
быть решен с помощью линейки, представленной на фиг. 2.
Приняв, что ось ординат проходит через середину линейки,
а ось абсцисс совпадает с ее краем HG, даем в формулах
X — ctg Z,
у = sin8z
(9)
О ГРАФИЧЕСКОМ РЕШЕНИИ УРАВНЕНИЯ ОРБИТ
89
всевозможные значения аргументу z от 90° до 0° и от 90° до
180°. Полученные точки образуют кривую ЕСА, которую вы-
черчиваем на линейке, отмечая величины [аргумента z по
стороне линейки RF.
Ширину линейки HR берем равной единице, а на стороне
ее HG откладываем величины ? по аргументу р, положив
Е = 10% причем значения аргумента р отмечаем на краю ли-
нейки HG.
С помощью этой линейки задача решается таким образом:
отмечаем по данному аргументу z = 8 точку М, а по ней на
кривой точку С; по аргументу
Р = Q + 1g с
находим точку L и соединяем ее с точкой R линией RL',
проводим через точку С линию С А || RL, и определяем точки
пересечения линии СА с кривой ЕСА.
Одна из точек пересечения Е или А дает нам искомую
величину z. При этом имеют место известные два случая.
Когда аргументу z = 8 соответствует точка С, то по напра-
влению, в котором видка планета, мы всегда сделаем надле-
жащий выбор между точками А и Е; если же аргументу о
соответствует точка А или Е, то нельзя решить, которой из
двух остальных точек соответствует положение планеты.
Эта работа была доложена автором на VII Съезде русских естество-
испытателей и врачей в Одессе 26 августа 1883 г, и напечатана впервые
в „Трудах*1 названного съезда. Вторично работа была напечатана в Сочи-
нениях Н. Е. Жуковского, т. I, 1912. Прим. ред.
ON A GRAPHICAL SOLUTION OF THE FUNDAMENTAL EQUATION IN
THE DETERMINATION OF PLANETARY ORBITS
This note deals with to the determination of the points of
intersection of a curve (2), depending on two parameters
h = OS (Fig. 1) and Q, with the straight line AE (4) traced
through the given point A (x0, y0) of the curve and determining
with the axis x the angle o. By the substitution of
x = hctgz, у = ~^sin2z, x0 = Actg8, y0 = -^-sin28
the equation (2) is being transformed into equation (8) contai-
ning a parameter Qc. The question on the determination of
the value of the angle z corresponding to the point of interse-
ction may be solved by means of one and the same curve for
all values of two parameters h and Q, shown in Fig. 2. Admit-
ting that the axis of coordinates passes through the middle
of the ruler HRFG and the axis of abscissae coincides with
Its edge HG, we construct a curve by the parametric equa-
tion (9) marking off the values z along the edge RF.
The breadth HR of the ruler we take = 1, and along the
side HG we lay off the values $ of the argument putting
£ — IO1'; marking the value of the argument p- at the edge of
the ruler HG.
By the formula — 1g Q -f- 1g c we find the point L and con-
nect it with R. Then we construct the point C corresponding
to the value 8, through it we draw CA || RL and determine
the intersection of the line CA with the curve.
The point of intersection will just determine the corres-
ponding value of the argument z.
SUR UNE DEMONSTRATION NOUVELLE DU THEOREME
DE LAMBERT
(1884)
§ 1. Nous proposons ici une demonstration nouvelle du
theoreme de Lambert, fondee sur la formule de la variation
d’action
8 I v ds = щ28з2 cos (v2, cos (»j, SsJ, (1)
oil vt et v2 sont les vitesses d’un point materiel a 1’origine et
a la fin de la trajectoire AB; 8at et 8з2 sont les deplacements
AA' et BB' des points A et B, quand la trajectoire AB se
change en une trajectoire infiniment voisine A'B'.
§ 2. La formule (1), donnant la variation de Paction, peut
servir aussi a la determination de la variation du temps du
mouvement des planetes a cause du lemme suivart: Le temps
dans lequel la planete, sollicitee par le soleil F, parcourt Гаге
elliptique AB, est egal a la fraction , multipliee par Faction,
du mouvement de la planete sur le meme arc elliptique AB, le
soleil etant transmis du foyer F dans un autre foyer d’ellipse Fit
P- est le coefficient de 1’attraction, et 2a est le grand axe
de 1’orbite elliptique.
Le temps t, dans lequel la planete parcourt 1’arc AB, est
t = f —, (2)
oil la ' vitesse v peut etre definie comme une fonction d un
rayon vecteur r par rapport au soleil F
92
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
mais, si le rayon
est n,
vecteur de la planete par rapport au foyer
(3)
d’oii
<4)
Le soleil 6tant
planete se change
transmis dans le foyer la vitesse de la
en
En у substituant cette valeur de dans la formule (4),
nous recevons
/ = -J-[^ds. (6)
Le lemme est done demontrG.
§ 3. Revenons a la demonstration du th6oreme de Lambert.
Le temps, dans lequel la planete parcourt Гаге elliptique AB,
est une fonction seulement de la corde 2c de Гаге parcouru, de
Fig. 1.
la somme 2« des rayons
vecteurs des points A et В
par rapport au soleil,
et du grand axe 2a.
Les points A et B,
6tant pris pour les foyers,
construisons (fig. 1) sur
la corde 2c deux ellip-
ses confocales, dont les
grands axes sont
CD = 2a,
EC — 4a — 2a.
La premiere de ces ellipses passera par le soleil, parce
que
EA+FB = 2a,
(7)
§ 3 LA DEMONSTRATION DU THEOREME DE LAMBERT
93
et la seconde passera par un autre foyer Ft de I’orbite, parce
que, en soustrayant de la somme des deux relations
FxA + FA = 2a,
FxB + FB = 2a (8)
la formule (7), nous recevrons
FxA-[-FXB — 4a — 2a. (9)
Supposons, que a et c restant constants, le soleil est trans-
pos6 du point F dans un point infiniment voisin F' de la meme
ellipse CD, et cherchons la variation du temps t de passage
de la planete du point A au point B. A cause du lemme
etabli, cette variation est egale a la fraction -—multipliee par
la variation de I’action dans le mouvement de la planete du
point* A jusqu’au point B, subie par la transposition du soleil
du point Fx dans un point infiniment voisin Fx de la meme
ellipse EG.
Cela pose, nous recevons par la formule (1)
= — I t)28a2 cos (t»2, 8a2) — cos (vx, 8a,)); (10)
oil 8a, et 8a2 sont les deplacements des points A et В dans le
mouvement de translation du triangle AFXB, par lequel le point
Fx est amene au point F/, c’est-a-dire
8a, # 8g2 # F,F,'.
Soient AH et BH les tangentes de 1’orbite elliptique aux
points A et B. A cause d’un theoreme de geometric la ligne
FXH est la bissectrice de Tangle AFXB, c’est-a-dire elle est
normale a 1’ellipse EG, d’oii
cos (o, ,6s,) = sin (AHFX),
cos (гмЛ’-г) = sin (EHF,).
Menons du point Fx deux perpendiculaires FXK et FXL sur
les lignes AH et BH et ecrivons a cause du principe des
aires
vxFiK = v.3F1L-,
94
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
d’autre part, on а
FtK = FtH sin (AHF() = FXHcos (ор Soj),
FyL — FyH sin (BHFy) = F{H cos (o2,
et par suite
Oj COS (WpSoJ — OgCOS
d’oii il vient par la formule (10)
8/—0.
Ainsi, a, c, « restant constants, le temps t ne change pas,
c’est-a-dire qu’il depend seulement de ces variables. Ce qu’il
s’agissait d’etablir.
§ L Le thfioreme etant demontre, il est facile de reduire la
determination du temps du mouvement de la planete a la deter-
mination du temps dans le mouvement rectiligne.
En у soustrayant les formules (8), nous recevons
FA — FB — FB — FA-
Cette equation montre que les foyers F et Fy de 1’orbite
elliptique se trouvent sur la meme hyperbole confocale aux
ellipses CD et EG.
Ainsi (fig. 2) a la position donnee du soleil F et de la
corde AB correspondent deux orbites elliptiques FyF et FF<,.
§4
la demonstration du theoreme de lambert
95
A la limite, pour a=oo, les points Fr et s’eloigneront a
1’infini, et les ellipses se changeront en des paraboles, ayant
les axes paralleles aux asymptotes de 1’hyperbole.
Par le th6oreme de Lambert nous pouvons transposer le
soleil du point F dans un point D de 1’ellipse CD, en у con-
servant le temps t.
Cela pose, les branches de 1’hyperbole doivent se confondre
avec les lignes droites BX' et AX, et les orbites elliptiques
FFy et FF.2 avec la ligne droite DE, parce que
DE — 2a — a -J- a = 2a.
Le temps t peut etre determine par la formule (4) en у
posant
ds—dr
et en prenant
___________________________a+c
a—c
pour 1’агс AMB, et
a—c _________ a-f-e
f J/(12)
о 0
pour 1’arc ANB.
De ces formules nous recevons, en integrant, la formule de
Lambert:
з .
I/ a — a — c . a — a — c \
£ = arc cos-----------------sin arc cos-------—
Vv-\\ a a J
( a — a-}-c . (a — « + <0 \1
— arc cos-------------sin arc cos ------ _ If •
\ a ° /J
Dans le cas oil I’orbite est parabolique
et les egalites (11) et (12) donnent la formule d’Euler:
6/h
96
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Le signe (—) doit etre pris dans cette formule, si le soleil
est au dehors du contour forme par Pare et la corde AB, et le
signe ( + )» s’il est a I’interieur de ce contour.
§ 5. La meme methode de raisonnement peut etre admise
pour la determination du temps dans le mouvement hyperbo-
lique; seulement, en у transportant le soleil dans le J.emme du
§ 2, il faudra changer sa force attractive en replusive.
21 сентября 1882 г. H. E. Жуковский сделал сообщение в Московском
математическом обществе на тему: „Новый вывод формулы Ламберта".
Работа была впервые напечатана в „Bulletins de la Soclete Imperiale des
Naturalistes de Moscou“, 1884. Вторично работа была напечатана в Сочи-
нениях Н. Е. Жуковского, т. I, 1912. Прим. ред.
О НОВОМ ДОКАЗАТЕЛЬСТВЕ ТЕОРЕМЫ ЛАМБЕРТА
(1884 г.)
§ 1. Мы предлагаем здесь новое доказательство теоремы
Ламберта, основанное на формуле вариации действия
8 fv ds = vs оа2 cos (v.2,8а2) — v1 Ssj cos (vlf 8а,), (1)
где Oj и f-2 — скорости материальной точки в начале и в конце
траектории АВ, 8з( и 8а2—перемещения АА' и В В' точек
А и В, когда траектория АВ изменяется в траекторию, бес-
конечно близкую А'В'.
§ 2. Формула (1), дающая вариацию действия, может слу-
жить так же для определения вариации времени движения
планет на основании следующей леммы: время, в течение
которого планета, находящаяся под действием солнца F,
проходит дугу АВ, равняется дроби умноженной на дей-
ствие в движении планеты по той же эллиптической дуге АВ,
если предположить, что солнце перемещено из фокуса F
в другой фокус эллипса Fr. у— коэфициент притяжения
и 2а — большая ось эллиптической орбиты.
Время t, в течение которого проходит планета дугу АВ,
равно
где скорость v может быть определена как функция радиуса-
вектора г, проведенного из солнца F:
= /2~
а ’
Зак. 2430. Н. Е. Жуковский. Том IX.
7
98
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
если радиус-вектор планеты относительно другого фокуса Fx
есть г1г то
v
(3)
откуда
/ =
ds.
(4)
Если солнце переместить в другой фокус Т7], то скорость
планеты изменится в
(5)
Подставляя эту величину V, в формулу (4), мы получим
ds.
(6)
Итак, лемма доказана.
§ 3. Обратимся к доказательству теоремы Ламберта.
Время, в течение которого планета проходит эллипти-
ческую дугу АВ, зависит только от длины хорды 2с прой-
денной дуги, от суммы 2а радиусов-векторов точек А и В,
Фиг. 1.
проведенных из солнца,
и большой оси 2а.
Взяв точки А и В
за фокусы, построим
(фиг. 1) на хорде 2с
два софокусных эллип-
са, большие оси кото-
рых равны
CD = 2а,
£G = 4a —2а.
Первый из этих эл-
липсов пройдет через
• солнце, ибо
£44-££ = 2а, (7)
§ 3 о НОВОМ ДОКАЗАТЕЛЬСТВЕ ТЕОРЕМЫ ЛАМБЕРТА 99
а второй пройдет через другой фокус /4 орбиты, ибо вычи-
тая из суммы двух равенств
F1A + FA = 1a, |
FtB+FB = 1a I ' '
формулу (7), мы получим:
FaA 4- F\B — 4а — 2а. (9)
Предположим, что при а и с, остающихся постоянными,
солнце переместилось из точки Р в бесконечно близкую
точку F' того же эллипса CD, и найдем вариацию времени t
прохождения планеты из точки А в точку В. На основании
„ - а
доказанной леммы эта вариация равна дроби —, умножен-
Р
ной на вариацию действия в движении планеты от точки А
до точки В, происходящую вследствие перемещения солнца
из точки Fi в бесконечно близкую точку F^ того же
эллипса EG.
Поэтому мы получим по формуле (1)
8/ = — ш 8а2 cos (v2, 8с2) — vi ^°icos (ui, ®3i) ); (10)
где Ssj и 6a2 — перемещения точек А и В при поступательном
перемещении треугольника AFJ3, при котором точка Fs пе-
решла в точку F-J, т. е.
Пусть АН и ВН касательные к эллиптической орбите
в точках А и В. На основании теоремы геометрии линия
есть биссектриса угла AFrB, т. е. она нормальна к
эллипсу EG, вследствие чего
cos (и„ ScJ = sin (AHF^,
cos (v2, йз2) = sin (BHFj).
Проведем из точки FT два перпендикуляра F\К и FrL к ли-
ниям АН и ВН и напишем по закону площадей
w1F1A' = v2F
7*
100
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
I не
с другой стороны мы имеем
FtK — FXHsin (AHF{) = F^Hcos (vlt SaJ,
FtL = РЛН sin (BHF^) = F^H cos (w.2, S°2),
и следовательно
Vi cos (vu 8а J = V.2 cos (v2, 8a2),
откуда по формуле (10) выходит
8/ = 0.
Таким образом, когда а, с, а остаются постоянными, время
меняется, т. е. оно зависит только от этих переменных,
что и требовалось до-
казать.
§ 4. После того как
теорема доказана, легко
свести определение вре-
мени движения планеты
к нахождению времени
в прямолинейном дви-
жении.
Вычитая формулы (8)
одну из другой, мы по-
лучаем
FA — FB = FiB — FiA.
Это уравнение по-
казывает, что фокусы
эллиптической орбиты находятся на одной и той же
F и
гиперболе, софокусной с эллипсами CD и £G.
Таким образом заданному положению солнца Т7и хорды АВ
(фиг. 2) соответствуют две эллиптические орбиты F{F и
FF2. В пределе, при а = оо, точки Ft и F2 удалятся в бес-
конечность, и эллипсы обратятся в параболы с осями, парал-
лельными асимптотам гиперболы.
По теореме Ламберта мы можем переместить солнце из
точки F в точку D эллипса CD, не изменяя времени t. Тогда
ветви гиперболы сольются с прямыми ВХ' и АХ, а эллипти-
ческие орбиты с прямой линией DE, ибо
DE = 2а — а а = 2а.
§5 О НОВОМ ДОКАЗАТЕЛЬСТВЕ ТЕОРЕМЫ ЛАМБЕРТА 101
Время t может быть определено по формуле (4), полагая
в ней
ds — dr.
Для дуги АМВ
Г/йБ* <п>
а—С
и для дуги ANB
'=/f I//Я <12>
о о
Из этих формул, интегрируя, получаем формулу Ламберта:
Г/ а — « — с . а — а — с \
, f =—;= I arc cos---------sinarccos------j zt
у/ р L \ а а /
. / Л — а~Ьс . а — а 4~ с \ ] . .
zt I arc cos------sin arc cos------ . (13)
\ a a / J
В случае параболической орбиты
liml/ — 1/ =1/
У р У 2а — г У 2р
«
и равенства (И) и (12) дают формулу Эйлера:
/ = -^=[(2аД-2сГ.±(2а-2с)Ч (14)
бур
В этой формуле должен быть взят знак (—), если солнце
находится вне замкнутого контура, образованного дугой и
хордой АВ, и знак ( + ), если оно — внутри этого контура.
§ 5- Такой же метод рассуждения может быть применен и
Для определения времени в гиперболическом движении; но.
только при перемещении солнца в лемме § 2 надо изменить
силу притягательную на отталкивательную.
Настоящая статья представляет собой русский перевод предыдущей
статьи, выполненный для настоящего издания проф. А. П. Котельниковым.
Прим. ред.
ON A NEW PROOF OF LAMBERT’S THEOREM
Lambert’s theorem put down as follows: “the time during
which the planet describes an elliptic arc AB depends only
on the chord 2c of the arc, the sum 2« of radii-vectors of
points A and B, drawn from the sun, and the major axis 2a“ is
proved by N. E. Joukovsky in the following way:
Let us construct according to the prescribed value of the
chord 2c —AB two ellipses EG and CD (Fig. 1), having as
focii the points A and В and the major semi-axes being
equal to CD —2a, EG — 4a— 2a respectively. The problem
to consctruct an elliptic orbit of the planet by the given
2c, 2a, 2a is not defined.
From the equalities FA-\-FlA — 2a, FB-\~FlB=2a,
A-f- FB = 2a is seen that one focus F of the unknown
ellipse lies on the ellipse CD and the other, Fr lies on the
ellipse EG, in which case if we prescribe the position of the
focus F on the curve CD, in which lies the sun, then the se-
cond focus will be situated at the point of intersection of the
ellipse EG with the hyperbola co-focal with the ellipses CD
and EG passing through the focus F (Fig. 2).
For the second focus it will be possible, with the given
position of F to have two positions, and F2, and to the
given positiqn of F will correspond two ellipses.
N. E. Joukovsky demonstrates further on, that wherever
on the ellipse CD be the sun F, the time of passing the агсЛВ
will be the same. Here he makes use of the lemma given
at the beginning of his note: “The time during which the pla-
net attracted by the sun F passes the elliptic arc AB is equal
to the fraction -, multiplied by the action
, a C ,
t — — I v,ds
P- J
SUMMARY
103
in the motion of the planet along the arc AB, when the sun
is in the other focus F} of the ellipse".
e case, when the sun F is situated at the point D, the
two corresponding orbits will be converted into rectilinear seg-
ment ED, the arc AB into the segment AB or ACB, the pla-
net motion into a rectilinear motion and the time t of the pas-
sing of the arc AB will be determined for the arc AMB — from
the formula (11) and for the arc ANB from the formula (12).
РЕШЕНИЕ ОДНОЙ ЗАДАЧИ ИЗ ТЕОРИИ КОМЕТ
(1884 г.)
§ 1. Мы предлагаем здесь решение следующей задачи:
Вычислено для данного времени М геоцентрическое поло-
жение частицы хвоста, вышедшей из ядра во время Мх под
действием отталкивательной силы 1 — р; определить измене-
ние этого положения, если сила изменяется на d (1 — р).
При постоянном Mt и изменяющемся р частица хвоста
передвигается по синхроне, поэтому для решения задачи надо
знать направление на своде небесном элемента синхроны ds
и отношение
<1-р)
ds
Воспользуемся для определения этих величин уравнением
траектории частицы хвоста, отнесенной к осям и из ко-
торых ось Ej направлена от Солнца по радиусу-вектору ядра
во время Ми а ось — по касательной к параболе, прохо-
дящей через это положение ядра. Это уравнение, как мы по-
казали *, можно написать так:
1А>2 —1 2^ cos ,8
/1^Р I1
(1)
где — радиус-вектор ядра во время Mlt р — угол касатель-
ной к этому радиусу, а
D=i_2az^> к
1 Annales de 1’observatoire de Moscou, 1884.
См. ниже стр. 135, „О построении синдииамических и синхронических
кривых". Прим. ред.
§ 1
РЕШЕНИЕ ОДНОЙ ЗАДАЧИ ИЗ ТЕОРИИ КОМЕТ
105
Проведем (фиг. 1) через положение А частицы хвоста ор-
динату AQ и определим площадь о гиперболического отрезка
AOQ. Мы имеем по формуле (1):
Et2cos Р
и
(2)
где верхний знак соответствует гиперболе, обращенной к Солнцу
выпуклой стороной, а
к Солнцу вогнутой сто-
роной. Когда 1 — р изме-
няется на d (1 — р), то ча-
стица хвоста перемещает-
ся по синхроне из Л в бес-
конечно близкое положе-
ние В, причем дуга гипер-
болы ОА изменяется в
ОВ. По теореме площадей
площадь бесконечно тон-
кого треугольника SAB
должна быть при этом
равна бесконечно тонкой
криволинейной площади
О АВ, которая при отбра-
сывании бесконечно малых
нижний — гиперболе, обращенной
величин второго порядка Фиг. 1.
может быть заменена на
OAD. Эта последняя площадь есть не что иное, какЧ^®
при постоянном Ej; определяем ее из формулы (2):
da
sin 3
r 2—2+h_
Г1 £
4(1 - p)2
V
Гг»2 — 1 dv -f-
(1 — p) P
VV2 1 Sj2 COS p \
r' 1 ." J
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Преобразуем эту формулу с помощью формул (1) и (2):
, __ 2Ч~Н /__________ а ' , Vcos р \ .
~ "sin Р L 2 (1 — р) р- \ sin р р / "Г
। 2 Е/2 cos Р Et2 cos р 1 ,.
ф(1— р)р (1 —р)р2-|~ и2 J u
Здесь по сказанному выше
=jz2Ja=/?2J<p.
где R = SA, а = /_CSA. Кроме того, называя через Н ско-
рость ядра в момент времени Mt, имеем по теореме площадей:
± О = -| sin р [(п + Q Ч1 - Hr, (М—Л/,)].
Подставляя и делая некоторые преобразования, найдем иско-
мую производную
d (1 — р) _
dty
=--------п-----...____________________________________.(3)
sinp^l+~jri [Н(М— М,)—-/liJ + ^1—^2cosP^
Обращаемся к определению угла /, который касательная
синхроны образует с радиусом-вектором R. Для этого под-
ставляем в формулу (1) вместо и
t R sin (а + Р) R sin а
ч Q • Q f
Ч Sin р sin р
где а = ^_ASO, и диференцируем ее по независимому пере-
менному <Ь, замечая что da — —d'\. Найденный при этом ре-
зультат можно будет представить так:
П<^(1--и) , / I COS“
—R-^-----Fmcos(a + P)------Q-
33 -
Rd^~
m sin (a p)
sin a
2
§ 2
РЕШЕНИЕ ОДНОЙ ЗАДАЧИ ИЗ ТЕОРИИ КОМЕТ
107
где
sin Р • п =
4(1 —Р-)2
Уч______
р2 Vv2—1 у 1—р.
Ej COS ₽
р.2
Так как из бесконечно малого прямоугольного треугольника
АВЕ имеем:
gZ dR ’
• / I sin ct
тп sin (a + P)--—
/„ i ox । ^(1—!x) cos a
m cos (a + ₽) -r n —----------—
§ 2. Переходим теперь к изменению положения частицы
хвоста на небесном своде. Пусть (фиг. 2) 5 и С будут гео-
центрические положения Солнца и
кометы во время М, а А — подобное
положение частицы хвоста. Соеди-
нив точки С и А с S дугами боль-
ших кругов, продолжаем эти дуги до
пересечения в точках К и L с ду-
гой КР, по которой видимый не-
бесный свод пересекается плоско-
стью, проходящей через центр Земли
параллельной плоскости кометной
орбиты. Дуги SC и SA представ-
ляют сферические изображения ра-
диусов-векторов ядра и частицы хво-
ста в момент времени М; если из
центра Земли проведем прямые,
параллельные этим радиусам, то
точки их пересечения с небесным Фиг. 2.
сводом должны лежать с одной
стороны на дугах SK и SL, а с другой на дуге КР; по-
этому эти точки пересечения будут К и L, а дуга KL есть
108
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
}• (5)
J
наша дуга 4- Предположив, что с изменением 1—р на
d (1 — р.) видимое положение частицы хвоста перемещается из
точки А в бесконечно близкую точку В, найдем, что дуга
АВР представляет сферическое изображение касательной син-
хроны и, подобно предыдущему, убедимся, что дуга LP из-
меряет наш угол у. Из сферического треугольника ALP, в
котором угол ALP = i и стороны LP и LA известны, опре-
деляем угол LAP=j по формулам:
cos {АР) = cos (/IL) cos у -j- sin (AL) sin у cos i,
. . sin i sin у
Sin;_ sin(AP) ’
Потом, проведя дугу большого круга SB и заметив, что
LT—dty, определяем АВ = ds из бесконечно тонких сфери-
ческих треугольников SLT и SAB'.
, dty sin i sin G4S)
as —------; . A- . (6)
sin j sin (SL)
Теперь вся задача решена, так как формулы (4) и (5) дают
нам направление элемента дуги синхроны на своде небесном,
а формулы (3) и (6) позволяют определить
ds
§ 3. Если бы мы желали вместо точных формул (3) и (4)
воспользоваться приблизительными формулами, то могли бы
прибегнуть к данным формулам, выражающим координаты
частицы хвоста с точностью до членов четвертого порядка
относительно М—Мх. Мы бы нашли с помощью этих фор-
мул
Что касается направления касательной синхроны, то для его
определения пришлось бы увеличить степень точности на-
ших формул до членов пятого порядка, как это делает
РЕШЕНИЕ ОДНОЙ ЗАДАЧИ ИЗ ТЕОРИИ КОМЕТ
109
Гепергер, и тогда бы получилось следующее простое выраже-
ние для дуги QP, заключенной между дугами АВР и CAQ:
(8)
4 января 1884 г. в заседании физико-математической комиссии Отде-
ления физических наук Общества любителей естествознания Н. Е. Жуковский
сделал сообщение на тему „О построении некоторых кривых в теории ко-
метных хвостов" и 27 января 1884 г. в заседании той же комиссии — доклад
на тему „О кометных кривых". Работа была впервые напечатана в „Bul-
letins de la Societe Imperiale des Naturalistes de Moscou", 1884. Вторично
работа была напечатана в Сочинениях Н. Е. Жуковского, т. I, 1912.
Прим. ред.
SOLUTION OF A PROBLEM OF COMET THEORY
In this paper is given the solution of the following problem:
it is calculated for a given time M the geocentric position of
tail particle issuing from nucleus at time under the action of
the repulsive force of the sun; it is required to establish the
alteration of that position if 1 —• p- alters by J(1—p), p being
the coefficient of the force.
In the case of a constant and a variable p the particle of
the tail moves along a synchronal line and therefore for the
solution of the problem it will be necessary to know the direc-
tion of the element of the synchronal line ds on the celestial
d (1 — p')
vault and the ratio ------v—-—.
as
For the determination of these values N. E. Joukovsky makes
use of the equation (1) that was deduced by him in his paper:
“On construction of syndynamical and synchronical curves” (for-
mulae (10) and (11)) for the trajectory of the tail particles referr-
ed to the axes and the axis is directed from the sun
along the radius-vector SO of the nucleus at time and the
axis г;, — along the tangent at point О to the parabolic orbit
of the nucleus. In those equations г}=50, — is the angle
between I4 and
In order to find the angle /, which is formed by the tangent
to the synchronal curve with the radius-vector of the particle R,
the equation (1) are being expressed in polar coordinates R, a,
where ot — / ASO and are being differentiated on the as-
sumption that R, a and у alter.
On the other hand the expression of the area of the
hyperbolic segment a is being differentiated (form 2) and
by means of the theorem of the areas is being determined
. From the comparison of the two
d(l —p) _ d(l—p)
da d<b
SUMMARY 111
— " ” — . I. И II. .
obtained formulae the formula (4) for tg/ is being ob-
tained.
In Fig. 2 is represented the celestial sphere and on it the
geocentric position of the sun, S, of the cometary nucleus, C,
and two infinitely adjacent positions of the particle, A and B,
so that AB — ds. The great circle К T represents the intersection
of the plane drawn through the centre of the earth and a
parallel cometic orbit; the arc KL ==ф, LP = y^ the arc ABP
is the spherical representation of the tangent to the synchronal.
From the consideration of the spherical triangles are being ob-
tained formulae (5) and (6) for the angle j and element ds.
SUR LA CONSTRUCTION DES COURBES SYNDYNAMIQUES
ET SYNCHRONIES
(1884)
§ 1. Nous proposons ici des formules nouvelles pour la con-
struction des lignes, nominees par M. Bredichin „courbes
syndynamiques" et „courbes synchroniques". Ces formules
representent les coordonnees £ et de la particule de la ma-
Fig. 1.
tiere caudale par rapport aux axes, diriges suivant le rayon
vecteur et la tangente a la parabole du noyau de la comete,
en fonction de 1’angle о entre les rayons vecteurs du noyau
et du point de depart de la particule caudale du noyau. L’ap-
proximation de nos formules est la meme que celle de la for-
mule de M. Norton, parce que nous rejetons les membres
§2 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 113
avec la cinquieme puissance de ®, A la fin de noire article
nous donnons une construction graphique des lignes nominees
ci-dessus, fondee sur les formules exactes.
§ 2. Soit M le point de 1’orbite parabolique, ou la particule
de la queue abandonne le noyau sans vitesse initiale relative-
ment a ce dernier, sous Paction de la force repulsive ou Pat-
traction newtonienne affaiblie. Cette particule decrira une hy-
perbole, ayant avec la parabole une tangente commune au point M.
Dans le premier cas (fig. 1) 1’hyperbole sera convexe vers le
soleil et dans le second (fig. 2) — elle sera concave. L’un des
foyers de cette hyperbole se trouve dans le soleil et Pautre est
situe sur la perpendiculaire MQ, abaissee du point M sur la
directrice de la parabole. Le lieu de ce foyer F' se trouvera
en prenant sur la perpendiculaire Л/Q une longueur QF', egale
a Paxe reelle 2A de 1’hyperbole a droite de la directrice dans
le premier cas et a gauche dans le second cas. Le demi-axe A
est donne par la formule 1
dans laquelle, comme dans toutes les autres qu’on trouve plus
bas, le signe superieur se rapporte a la force repulsive et le
1 „Annates de 1’observatoire de Moscou“, vol. V, liv. 2, p. 34.
Зак. £430. Н. E. Жуковский. Том IX.
8
114
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
signe inferieur a la force attractive, est le rayon vecteur
FM et
2
m = —,
oil [J- est la valeur absolue du coefficient de la force. Ce co-
efficient etant pris avec le signe-}-pour la force attractive et
avec le signe—pour la force repulsive, la formule devient:
A-~ И-Ч-.
(1)
Cela pose, nous trouvons pour le rayon vecteur MF' = r i
rl' = ri^‘lA = -^-.
1 —
(2)
Le milieu О du segment FF' est le centre de 1’hyperbole;
menant par ce point la droite OM et la droite OP parallele
a la tangente ML, nous aurons les diametres conjugues de
1’hyperbole. Prenons-les pour axes des coordonnees x, y.
L’equation de 1’hyperbole, rapportee a ces axes, devient
x2 y2
A* ~K
(3)
Imaginons encore les axes des coordonnees '/jj ayant pour
origine le point M et diriges: Mv^ suivant la tangente ML
dans la direction du mouvement de la comete et Mix — sur le
prolongement du rayon vecteur FM.
Exprimons les nouvelles coordonnees en fonction des ancien-
nes. La tangente ML etant bissectrice de 1’angle FMF', les
segments LF et LF' sont proportionnels aux rayons vecteurs
rx et d’oii on obtient:
LF—
FF'r,
ri + n'
FF\ = FF'^ — r,') = A-FF
2 / ~ 2 Gi -f- r/) rt + r/ *
LO _ A
LF ri •
§2 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 115
Mais a cause de ML || OP
LO _MP
LF rx ’
c’est-a-dire
MP=A.
En prenant maintenant sur 1’hyperbole un point K, nous
trouverons pour lui les coordonnees
OH^X, KH-y, MG = ±lx, KG=^.
A cause des triangles semblables OMP et GMH
x _ MG+ MP
MO MP ’
et comme on a
MO = AX, MP—A,
Passons a la determination du segment HG. Abaissons des
points F et F' les perpendiculaires FR et F'S sur la tangente
ML. A cause des triangles semblables FLR et F'LS
LR FL _ r,
LS~FL~ r/’
d’oii
ML MS-rx+MR-r'
ri + n'
En rempla^ant MS et MR par rx cos P et rx cos P, on a
ML = 2 nr/ cosP
П + *7
oil P est 1’angle FML.
Mais a cause des triangles semblables FML et FPO'.
OP— rx cos p.
Puis a cause des triangles semblables MGH et OMP on a
GH___rx cos P
GM A ’
8*
116
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
d’oti
r/ COS P El
A '
Ayant determ^ HG, nous trouvons
_______________________ ___ r/ cos
А
ou d’apres la formule (3)
41 =
Е1П'cos p
~A
En у substituant
B = ——-^1
P 2 2 ’
ou V; est 1’anomalie vraie du point M, on obtient:
• »i
Sin
41
X2
Л7
"" 2
A
5i.
Posons maitenant
et rempla^ons les formules (4) et (6) par
9 / •
u2 — rx sin
u-.
(5)
(6)
(7)
(8)
(9)
-^i
Divisons les equations (7) et (9) par et eliminons A etr/
a 1’aide des equations (1) et (2):
E,
W-.r (10>
• в
A = _ s,n~2 “ .
ri 11 — н 1— p-
§2 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 117
Revenons aux coordonnees x, у et determinons 1’aire s du
demi-segment hyperbolique MKH en fonciion de x. Nous avons
AA sin а Г x
A
A2
2
oil a represente I’angle MOP.
En soustrayant de I’aire s 1’aire du triangle MKH, egale a
Afisina/ x_____1\1/' x2
2 \A )V А2
nous obtiendrons I’aire = du segment hyperbolique KM
A^i sin a
2
ou, en ay ant egard aux formules (5), (8) et a la formule
. __A sin 3
/11----: >
sin a
obtenue du triangle OPM,
o = ^sinM^r/ ( u ^2^_ 1g (1 + U2 + u/2-
Designons par 8 le quotient de la division de a par
1 • 4
-y Tj Sin 3
et ёспуопз a 1’aide des formules (1) et (2)
= +"--------3( uy2+^-lg(l + u2 + uV^^). (12)
2(1—h)2'
Le quotient 3 a ici une signification suivante: imaginons sur
la base MP un triangle equivalent au segment hyperbolique
MK et menons par son sommet une droite parallele a la tan-
gente ML jusqu’a 1’intersection avec la base MF-, la longueur
de cette droite sera 3.
118
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Supposons maintenant, que le noyau de la comete passe de
M a N en meme temps, que la particule caudale passe de
M a K, et designons par h le quotient de la division de 1’aire
du secteur parabolique FMN par
-y ri sin ₽.
Ce quotient represente aussi la longueur de la ligne droite,
menee parallelement a ML par le sommet du triangle jusqu’a
1’intersection avec sa base FM, le triangle etant equivalent au
secteur parabolique MFN.
D’apres le theoreme des aires, 1’aire FMK, decrite par le
rayon vecteur de 1’hyperbole, est egale a I’aire FMN, decrite
par le rayon vecteur de la parabole; par suite
ou
= — _L
(13)
h
Passons a la determination de—. L’aire du secteur pa-
rabolique FMN est egale au tiers de la somme du triangle
MFN et du trapeze MQJN:
1
““ 6
rtr sin (oj — v) -f- (/-j -f- r) (rj sin — r sin v)
ou r et v sont le rayon vecteur et 1’anomalie vraie du point N,
Or, 2p etant le parametre de la parabole,
p P
r =-------- -----, r. =-----------;
O « V O 2
2 cos- -y 2 cos?
par suite
P2 sin -y f 3 cos2 + 3 cos2 ---------si:
0) = ----------------------------------------
24 cos8 -y cos8 -y
§2 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES
119
Mais, en remarquant, que
, Q 8<u cos3
h ___ 2<d __ 2
/"i rf2 sin P p'2
il vient
. ® /о | о О®
sin — I 3 COS' -f 3 cos“-g
о 3 V
3 cos3 -g-
Posons ici vt = v -j~ ®:
Sin -g- Sin -g- Sin -g- Sin « OCOS^-g----z
— =------------------------------------------------sin3 (14)
rl V 2 V Q 3 ® 2 ' '
COS -g- COS2 -X- 3 COS3 -g-
£ £ £
Nous pouvons maintenant obtenir une ёquation entre les
variables и et ®. En effet, tenant compte des equations
(13), (11), (12) et (14), nous avons
2 .
-----sin
V
cosT
V Z 2 ® О
sin-g- o 6 cos2 y —2 ю
--------sin -jy sin <?----------------sin3 -~
о v 2 1 3 V 2
COS' -g- 3 COS3 -g-
uV24-u2 u“ . v <? U' v . <? .
—7——-----;----sin -s' cos -s-;-cos 77 sin — -f-
1/1— и, 1—В 2 2 1 —p. 2 2
H----(u V2 + U‘2 - 1g (1 + и2 + и V2 4- u2)). (15)
(1-P)2
Quand и est determine de cette equation, et se trou-
vent par les formules (10) et (11).
Pour obtenir I’equation (15) nous avons suppose, que la
comete s’approche du soleil; si elle s’eloigne du soleil, 1’angle
120 АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
entre les axes positives et r(1 sera obtus, et au-lieu des
points К et N (fig. 1, 2) nous devons prendre K' et N'; ce qui
conduit au changement du signe dans le second membre de la
seconde partie de la formule (11) et au changement du signe
dans le second membre de la seconde partie dans la formule (14).
La formule (15) sera dans ce cas:
. v 2 . 9 , S’nT 6 cos2 2 • _ . ® 2 . „ 9
. < I . у z . „ о
sm -5- -f- '-------- sin 9 sin -75--------------------- sin3 -77 =
V Z , V cos COS' 2 Q 4 V * э cosd ~
и ]/ 2 + и2 . u2 . v u2 v . 9 ,
iI . SIH _ COS /1— 1 — H 2 2 L“’ COS ~ Sill -7; 1 — И 2 2
H-------—s’ [u У2 h u2 — ig (1 + u2 -f- и /2 + W“)].
(1-P-)2
Cette formule sera identique a la formule (15), si 1’on change
v en (— v). Cela remarque, nous nous occuperons seulement
de la formule (15), en changeant dans le resultat final v en
(— v), quand la comete s’eloigne du soleil.
§ 3. Passons maintenant aux developpements des fonctions,
qui entrent dans la formule (15), en termes ordonnes suivant
les puissances entieres de u et sin en s’arretant aux ter-
mes avec la quatrieme puissance. Nous avons
и /24- u2 —lg(l + H2 + u/2-|-ua) = ^u8.
En substituant ces valeurs dans la formule (15), on a
§ 3
LA CONSTRUCTION DES COURBES SYNDYNAMIQUES
121
2
v
COS 2
v -2 v a
» 6е°«2Т-2
Sin 2--------- Sin2^.------:-------
2 2 V . 2 _ „ w
COS2 -y 3 COS3 -y
£ £
s'?
sin 2
g__El7u+1/2A+('+4„,
(1 —h)2 12(1 —H)8
ug
1 — [X
. v 9
Sin "2“ cos ~~
u2
V о
En у posant
Sin-x-
—— = 6.
V
COST
(17)
on trouverait une expression plus simple
a 2 u о • v
6 cos-2----2 .<2 sin2"
26 —2sin y-6g-----------f------6;i= * u — —— u2 +
Z Э . — 1 !-Ь
(1 — h)3
9 V
+ 1'2 2+O + h) -------e„, (18)
12(1-^ 11
Maintenant nous pouvons developper и d’apres la formule
du д 1 d2u 62 . dsu 63
U = dU № L2 “Г 263 ~f23 ‘
Pour obtenir les coefficients de cette formule, prenons les
derivees successives par rapport a 6 de la formule (18) et po-
sons dans les resultats obtenus 6 = 0. Nous trouvons ainsi:
^ = /2(1-^.
gs=-/2(l-,0- (1 + 1*).
122
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
П resulte de ceci
u = ]/2 ((i—р-)~ о—os).
(19)
La formule (19), contenant
seulement cos
peut etre
egalement appliquee
<}ui s’eloigne de lui.
a la comete qui s’approche du soleil ou
nt
Fig. 3.
§ 4. Prenons maintenant (fig. 3, 4) pour axe E le prolonge-
ment du rayon vecteur FN du noyau et pour axe rj la tangente
de la parabole, dirigee inversement au mouvement de la co-
mete. Pour determiner les coordonnees E et tq de la particule
caudale, construisons auparavant les coordonnees
KG=r^ MG = ±\
et menons par le point N deux lignes droites NB et NE pa-
LA CONSTRUCTION DES COURBES SYNDYMINAQUES 123
ralleles aux axes Mil et 2l7rit. Du point E dans la direction
de la droite EN prenons une longueur EC~h, et par le point
C menons une droite CA parallele a 1’axe Le segment
KA aura ici la longueur 8, donnee par la formule (12); quant aux
longueurs CN et ME, elles aurons les valeurs, qui re^oivent
8 et—4 dans les formules (12) et (10), quand on suppose
jj,==1; nommons ces valeurs 8' et —
Fig. 4.
D’apres les formules (10), (12), (16) et (19), en rejetant les
membres avec la cinquieme puissance de G, on a
124
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
d’oii
(6* \
6* -т(2 + и)1 ги
ВК=АВ±АК= — (1 — {1) 03л.
Determinons maintenant les longueurs des perpendiculaires
KQ et KP, abaissees du point К sur les axes coordonn6s TVc
et N'ft. Nous obtenons ces longueurs, prenant les projections
du contour NBK sur les droites NL et NH perpendiculaires
a TVvj et TVS:
KP = NB sin ®— BK cos ----------—
\ £ Л
KQ = NB cos ® j -j- BKsin ~,
ou d’apres les formules preccdentes
KP= (1 — jx) ^02- 04) rt sin ® -
—|(1-r)68cos
KQ=(1 - u) (e* - (-^±^ 0*) Г1 cos + <?) +
+ 4 (1— !л) 6s sin-y-
J X
Substituons dans ces expressions
sin® = 2cos 0
. ® V
sin-7j- = cos
§ 5 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES
125
en rejetant les membres avec la cinquieme puissance de 6, nous
obtenons
KP=(\- ji)rcos-^-(4 63 + 2sin ~ 04
z \ э 2.
KQ=(i — ^rcos-^-fe2 — (1+4) H
£ \ \ 3 / /
Divisant les perpendiculaires trouvees
les coordonnees cherchees du point К
v
par cos , on trouve
+=(1-н)(4 6s+2sin+-e4
' \ z /
(21)
Nous avons obtenu ces formules fondamentales en nous ser-
vant des fig. 3, 4, correspondantes au cas oil la comete s’ap-
proche du soleil. Si la comete s’eloigne du soleil, il faut se ser-
vir des fig. 5, 6, et alors les formules (20) s’ecriront ainsi:
(7> О \
K'Q = N'B cos ( + — ®) + BK' sin -i-.
\ z / *
Cesformules seront identiques aux formules (20), si on у change
v en (— v); par consequent les equations (21) peuvent etre
appliqudes aussi a la comete s’eloignant du soleil, v etant
change en (—v).
§ 5. Les equations (21) nous servent a la construction des
courbes syndynamiques et synchroniques. En donnant dans ces
equations des diverses valeurs a 6, nous aurons les points de
la courbe syndynamique de la force donnee 1—p-, et le lieu
ou chacun de ces points a quitte le noyau se trouve d’apres
126
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
la formule (17). Reciproquement, en donnant des divers valeurs
a (1 — p), nous aurons les points de la courbe synchronique,
correspondante au point M donne par le parametre 6.
A la premiere approximation, en rejetant les membres avec
la quatrieme puissance de 6, I’equation de la courbe syndyna-
mique se represente sous la forme simple:
(22)
Fig. 5.
3
Cette equation appartient a la parabole du degre -g- > tan-
gente au rayon vecteur /TV; elle est homogene par rapport a
Tj et r et ne depend pas de v. Cela nous offre une idee
nette du 'changement de la courbe syndynamique avec le mou-
vement du noyau. Tout ce changement se ramene au change-
ment des coordonnees 5 et v; proportionnellement au rayon
vecteur du noyau et au changement de I’angle entre les axes
coordonnes de 0° jusqu’a 180°.
§ 5 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 127
L’equation de la courbe synchronique a la premiere appro-
ximation sera
y = yO (23}
et represente une ligne droite, qui passe par le noyau.
En conservant dans les formules (21) le membre avec la qua-
trieme puissance de 6, nous avons pour la courbe synchronique
l’equation:
=—rd
(4
J+ 2 sin
J6)l(| + 2sin|6)(24)
£ / J \ J £ j
d’une parabole du second degre, qui touche a I’origine des-
coordonnees une droite
(3 — 462) — (y + 2 sin ~ 0 I = 0
128
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
et a un diametre parallele au rayon vecteur du noyau. Cette
parabole est convexe vers le soleil.
Pour achever ce paragraphe demontrons un iheoreme con-
cernant la tangente de la courbe syndynamique. Differencions
Jes formules (21) par rapport a 6 et prenons leur rapport
, 26(l+2sin-^o)
ctv] _ \________z /
1—2^ + 1) 02
Puis a cause de la fig. 3 ecrivons
NE'___ sin ® ___20
AT7
cost—-]-®) 1—zsm-^-0
\ z / £
En se contentant dans ces formules des termes avec la se-
conde puissance de 6, on a
dy NE' . v
tfc ~ NF 2e^ + 2sin2e]-
Ainsi, dans ce degre d’approx'mation la tangente de la courbe
•syndynamique est parallele au rayon vecteur du point de depart
de la particule caudate du noyau. Pour le cas 1—'J- = l ce theo-
reme est exact.
§ 6. Passons a 1’explication de notre methode graphique,
-qui nous a servi pour construire les courbes syndynamiques et
synchroniques sur les fig. 8 et 7. Pour la construction de la
courbe synchronique des particules caudales sorties du point M
(fig. 7), abaissons une perpendiculaire MQ sur la directrice.
Prenons sur cette perpendiculaire une serie des foyers F't Ft',
F2', F7, qui nous servent a construire les hyperboles A, Alt
A2, ...,A7. Pour cheque hyperbole construisons une courbe cor-
respondante a, alf a.2t ..., a„ d’une maniere suivante. Du point b
de 1’hyperbole A menons une droite Z>3 parallele a la tangente
•et prenons sur cette droite une longueui 63 egale a 5, la valeur
2®
de 8 etant determin6e a I’aide de la formule 8 = —;. Le
rsin p
point 3 ainsi obtenu se trouvera sur la courbe correspondante a.
§6 LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 129
Fig- 7.
L’ne courbe correspondarte peut etre aussi construue pour
la parabole As, en faisant dans les formules (12) ^ = 1. Il vient
dans ce cas
9 1
(25)
3 V n
Cette courbe sur notre figure est a8.
Зак. 2430. H. E. Жуковский. Том IX.
9
130
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Les courbes correspondantes etant construites, la courbe
synchronique du parametre h peut etre construite par le pro-
cede suivant. Portons sur la tangente AZtQj une longueur MO=h
et menons par le point О une droite BD parallele а Гахе Mtx.
Par les points de 1’intersection de cette droite avec les courbes
correspondantes p, pj, p2, • ••,^7, Pb menons les droites paralleles
a la tangente jusqu’aux points de 1’intersection avec les hyper-
boles. Ces points b, 6j 62, • • - , 67, N seront situes sur la courbe
synchronique cherchee.
Cette courbe passant par le noyau N s’approche de la droite
BD, la coupe au point О et s’eloigne d’elle, en s’approchant
de 1’asymptote AC, qui passe par le point E eloigne du M
a la distance 2A. Pour demontrer cette derniere propriete de la
courbe synchronique, introduisons dans les formules (12) et (13)
u'2
--------T = s
(1-pH
et ecrivons
En у posant 1 — jjl = 00, и = 00 1’on trouve
d’oii il resulte, que pour ^ = 00, o = A. Ce qu’il s’agissait
d’etablir.
Pour construire la courbe syndynamique (le noyau etant
en N, f’g. 8) d’une force donnee, prenons sur la parabole des
points M, Mu M.2, ..., Л/Г); abaissons de ces points les perpen-
diculaires MQ, MXQX, M.2Qn, ..., MhQ- sur la directrice et divi-
sons les en rapport
MQ : MF' = MXQX: MXFX = ... = 1 —и
§6
LA CONSTRUCTION DES COURBES SYNDYNAMIQUES 131
A
/
Fig- 8.
(pour notre figure 1 — p = 5). Prenant les points P, Ft', F2,.Fb'
pour les foyers, construisons les hyperboles A, Alr A%, .
pour cheque hyperbole construisons une courbe' correspondante
a, alf a.,, ...,a6 par la methode donnSe; pour la parabole A6
construisons aussi une courbe correspondante afi. Par les points
9*
132
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
М Л/1, М.2, ..-,МЪ menons les droites paralleles a la tangente
de la parabole au point N jusqu’aux points de 1’intersection
m, mv m.y, • avec courbe a6. Ces points seront les som-
mets des triangles construits sur la base FN et dquivalents aux
secteurs paraboliques FNM, FNMX, FNM.2, .FNMR. Abaissons
de points m, mlt m,, ..m- les perpendiculaires p, plt p2,.. .,p5
sur le rayon vecteur NF et posons
, NFp NFPi
MF ’ 1 MtF ’ ’' ’
Menons les droites BD, BtDlt B J).^ ..B5Db parallelement
aux rayons vecteurs MF, MYF, M<F, ..M?F, eloignees de ces
rayons aux distances I, llf l2, l&. Les points (3, (32, ..(3r>
de 1’intersection de ces droites aves les lignes correspondantes
etant trouvcs, menons par ces points les droites pi, P161,
P262, .. paralleles aux tangentes de la parabole dans les
points M, Mlt M2, ..Mr,. Les points b, b}, b2, ..Ьъ de 1’inter-
section de ces droites avec les hyperboles seront siiu£s sur la
courbe syndynamique cherchee.
Эта работа была впервые напечатана в „Annates de t’Observatoire de
Moscou“, publ. par Th. Bredichin, vol. X, liv. 2, 1884. Вторично работа была
напечатана в Сочинениях Н. Е. Жуковского, т. 1, 1912. Прим. оед.
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ И СИНХРОНИ
ЧЕСКИХ КРИВЫХ
(1884 г.)
§ 1. Мы предлагаем здесь новые формулы для построения
линий, названных Бредихиным „кривыми синдинамическими“
и „кривыми синхроническими“. Эти формулы представляют
собой координаты £ и т] частицы хвоста относительно осей,
направленных по радиусу-вектору и касательной к параболи-
ческой орбите ядра, в функции угла ® между радиусами-векто-
рами ядра и той точки, в которой частица отделилась от ядра.
Точность наших формул такова же как и точность формулы
Нортона, так как мы отбрасываем члены, содержащие пятую
степень ®. В конце нашей статьи мы даем графическое по-
строение вышеупомянутых линий, основанное на точных фор-
мулах.
§ 2. Пусть М есть точка параболической орбиты, в кото-
рой частица хвоста отделяется от ядра без начальной ско-
рости относительно ядра под действием отталкивательной
силы или ослабленного ньютонианского притяжения. Эта
частица будет описывать гиперболу, имеющую в точке М
общую касательную с параболой. В первом случае (фиг. 1)
гипербола будет обращена выпуклостью к солнцу, а во вто-
ром (фиг. 2) — вогнутостью. Один из фокусов этой гиперболы
будет находиться в солнце, а другой на перпендикуляре MQ,
опущенном из точки М на директрису параболы. Положение
этого фокуса F' найдем, отложив на перпендикуляре MQ
длину QF', равную действительной оси 2А гиперболы, вправо
от директрисы в первом случае и влево-—во втором. Полу-
ось А определяется формулой
134
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
в которой, так же как и во всех нижеследующих, верхний
знак относится к отталкивательной, а нижний — к притягатель-
ной силел Г1 есть радиус вектор FM и
2
т = — ,
р
где р— абсолютная величина коэфициента силы. Этот коэфи-
для отталкивательной силы, и формула обращается
щую:
2(1—р.)
вследую-
(1)
А = +
Таким образом для радиуса-вектора MF' ~гх' мы^ находим
г1' = г1^2А = Т^
(2)
Середина О отрезка FF' есть центр гиперболы; проведя
через эту точку прямую ОМ и прямую ОР, параллельную
касательной ML, мы будем иметь сопряженные диаметры
§2 О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ 135
гиперболы. Примем их за оси координат х, У- Уравнение
гиперболы, отнесенной к этим осям, будет:
т-2 „2
4---------— = 1 (3)
А* В* к v '
Вообразим еще координатные оси имеющие начало
в точке М и направленные: Мтп по касательной ML по на-
правлению движения кометы и М^{—по продолжению радиуса-
вектора FM.
Выразим новые координаты в функции старых. Так как
касательная ML служит биссектрисой угла FMF', то отрезки
LF и LF' пропорциональны радиусам-векторам Л и г/, и мы
получаем
LF =
FF'rx
rl + Гу ’
FF' \ = FF'(rx — r/) A • FF'
2 / “ + n + n' ’
LF rt •
Но вследствие того, что ML || OP,
LO _MI>
ft ’
LF
136
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
и следовательно МР= А.
Взяв теперь на гиперболе точку К, мы находим для нее
координаты
ОН=Х, КН—у, MG = ±^, КС = ^.
Вследствие подобия треугольников ОМР и GMH
X MG+MP МО МР
и так как МО=Аи МР=А,
ТО АГ^1- (4)
Перейдем к определению отрезка HG. Опустим из точек
Fn F' перпендикуляры FR viF'S на касательную ML. Вслед-.
ствие подобия треугольников FLR и F’LS
LR FL г, LS F'L ~~ г/’
откуда ML — MS- ty-^MR- g' g+g'
Заменяя MS и MR через r/cosp и rjCosp, имеем = 2 r^/cos 3 G + G’
где р— угол FML.
Но вследствие подобия треугольников FML и FPO: OP— г/cos р.
Потом вследствие подобия треугольников MGH и ОМР-. GH г/cos Р GM А ’
откуда GH=± r*'c°s^ Et
Определив HG, находим
„ r/cosP £
§ 2
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
131
или, по формуле (3),
41=#
Подставляя сюда
Ejr/cos р
А
в_ ~
‘ 2 2 ’
где vt — истинная аномалия точки М, получаем:
/ .
G sm -х-
А
(5)
41 =
Положим теперь
(6)
(7)
и заменим формулы (4) и (6) следующими
А
'fli=Vr1rl' и V2+u2 —r/sin^-u2.
Разделим уравнения (7) и (9) на г\ и исключим
при помощи уравнений (1) и (2):
(8)
(9)
А и г/
—— =-----'---
К 2(1-ч) ’
. Vi о
п/2+^ sinT“"
(Ю)
и.
1 —и
(И)
Вернемся к координатам х,
гиперболического полусегмента
дем иметь
/l.B.sin а
s =—*—5--------
X2
А2
площадь
у и определим
МКН в функции х. Мы бу-
2
1 —
где а представляет угол МОР.
Вычитая из площади s площадь треугольника МКН, рав-
ную _____
Л] Asin а/ х -I \ 1 __1
2 1а Ж А2 ’
138 АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
мы получим площадь гиперболического сегмента КМ
AxBxs\n а
а~
или принимая во внимание формулы (5), (8) и формулу
. A sin Р
Ах = ——- ,
sm а
полученную из треугольника ОРМ,
° = 4sinP Vr.7-/(ul/2+Vs_lg(1 „2н/2+^j).
Обозначим через о частное от деления з на
1 • ч
-yT-jSinp
и напишем при помощи формул (1) и (2)
g „ _____ _____________________
— - =й 2(11и)з/2(и^2 + и2-lg(i + и2 + и/2-Ьu2)).(12)
Частное 8 имеет такое значение: вообразим на основа-
нии MF треугольник, равновеликий с гиперболическим сег-
ментом МК, и проведем через его вершину прямую, парал-
лельную касательной ML, до пересечения с основанием MF',
длина этой прямой и будет о.
Предположим теперь, что ядро кометы переходит из М в /V
в то же время, как частица хвоста переходит из М в К,
и обозначим через h частное от деления площади параболи-
ческого сектора FMN на
4-rjsin ₽.
Это частное так же представит длину прямой линии, про-
веденной параллельно ML через вершину треугольника, равно-
великого с параболическим сектором MFN, до пересечения
с его основанием FM.
По теореме площадей площадь FMK, описанная радиусом-
вектором гиперболы, равняется площади FMN, описанной
радиусом-вектором параболы; следовательно
А = 8
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
139
или
(13)
Г1 П г\
Перейдем к определению . Площадь ш параболического
сектора FMN равняется одной трети суммы площадей тре-
угольника MFN и трапеции MQJN-.
1
6
т-jr/sin (о1 — v) + (f\ + г) (л-jsin — г sin v)
где г и v — радиус-вектор и истинная аномалия точки /V
Но обозначая через 2р параметр параболы, имеем
0 2® О 9
2cos* 2-g- 2 cos2 —
следовательно
2’ • ? / Q 9 ®1 1 о о V
р2 Sin -g -1 J COS- — -f- 3 COS- -g-
<ij =----------------------------------
n. a я V
24 cos8 — cos3 * * -g-
Принимая во внимание, что
e ч ®1
2w 8<»cos3-g-
r^sin P p'2
получаем
h
h
ri
3 cos2
3 cos3 -g-
Положим здесь = <u -j-
_ . о r 2 v о
2 sin— Sin 77 sinSin» О COS -K z
----f------------------------------sin8 . (14)
W „ V 0 4®
COS cos- -g- 3 COS -g-
140
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Мы можем теперь получить уравнение между перемен-
ными и и <р. В самом деле, принимая во внимание уравне-
ния (13), (11), (12) и (14), мы имеем:
sin v;
2 . ® 2
----- sin 77-----------
v 2 о и
cos -g cos2 2
6 cos2 77 — 2
. <р . 2 . ,
Sin 77 Sin <Р------------• sm377 =
3 cosd g-
uV2H“U2 U2 . V U2 v • V I
= , r ---,--- Sin 77 COS 77-7-COS 77 sin 77 H-
yi—p, 1 — p 2 2 1—p 2 2
H-----L * * *—i(«/2 + u2-lg (1-Нп2 + пГ2 + «2)). (15)
(1-H)2
Когда из этого уравнения и будет определено, то и
найдутся по формулам (10) и (11).
При выводе уравнения (15) мы предполагали, что комета
приближается к солнцу; если бы она удалялась от солнца, то
угол между положительными направлениями осей и ifo был
бы тупой, и вместо точек К и N (фиг. 1 и 2) мы должны
взять точки К' и N', что приводит к изменению знака во вто-
ром члене второй части формулы (11) и к изменению знака
во втором члене второй части в формуле (14). Формула (15)
будет в этом случае:
2 . ®
®sm 2
cos 2
v c. <zv ъ
Sin 77 0 COS2 77 2
2 . . ф 2
------sin ф sin
2 V
cos 2
Q 3 V
3 cos6 —
• 3 .
sm 2
u/2^u2
u2
1 —
. v '}
sm -% cos
и2
V . V
COS 77 sin 77
1 — p 2 2
2
1- (n’/2 + u2 - 1g(1 4- H2 + u/2 + u2)).
Эта формула сделается тождественной с формулой (15),
если мы заменим v на (— v). Заметив это, мы будем зани-
маться только формулой (15), изменяя в окончательных ре-
зультатах v на (— v), когда комета удаляется о г солнца.
§ з
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
141
§ 3. Перейдем теперь к разложению функций, которые
входят в формулу (15) по целым степеням и и sin-|~, оста-
навливаясь на членах четвертой степени. Мы будем иметь
ср
COST
sin ® sin = 2 sin2
— sin2-^- — 2 sin2 -~
© 1 ©
sin2T = l~TSin2T’
U3
т
— из.
3
и
(16)
п}2 и
Подставляя эти величины в формулу (15), мы имеем
2 . <?
rsin 2
cos 2
sin -у
2--------sin'3 —
2 и 2
cos 2
6 cos2— 2
sin3 =
3 cos3
~(1-P)V’U
1/у2Ч-(1 +н)
1/2 12(1— :л)%“
„ И2 . V ф
~lZ^sin 2"COS 2
И2 V
— COS у sin т.
Полагая здесь
sin
----— =6,
v
cos 2"
(17)
мы найдем более
простое выражение:
6 cos2-?---2
26 — 2 sin у 62-------у------63 =
_ и ц* + Г2 (1--Ь> и3 _ ^116 (18)
(l-|x)l-U 1-PU 212(1-^U 1-Р
2
©
142
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКл
Теперь мы можем разложить и по формуле
du. , d2u О’2 . d3u О3
u — db 1-2 1-2-3'
Ч~обы получить коэфициенты этой формулы, возьмем
последовательные производные по 0 от формулы (18) и по-
ложим в полученных результатах 9 = 0. Таким образом мы
найдем
^ = /2(1-И)Ч
^=-V2(l-^(l + H).
Отсюда следует
и =J/2 (fl — ^6 - -1 —63 I , (19)
Формула (19) как содержащая только cos может быть
одинаково применена как к комете, которая приближается
к солнцу, так и к комете, которая от него удаляется.
§ 4. Поймем" ^теперь /фиг. 3, 4) за ось Е продолжение ра-
диуса-вектора FN ядра и за ось — касательную к параболе,
направленную в сторону, обратную движению кометы. Чтобы
определить координаты с и 7] частицы хвоста, построим сна-
чала координаты
, KG= ril, MG = ±l}
и проведем через точку N две прямые 7V5 и NE, парал-
лельные осям и Мт^. От точки Е по направлению пря-
мой EN отложим отрезок ЕС = h и через точку С проведем
прямую С А параллельную оси М^. Отрезок КА будет дли-
ной 8, данной формулой (12); что же касается длин CN и
ME, то они будут равны величинам о и—в формулах (12)
И (10), когда мы положим и. = 1; обозначим эти величины
через 6' и — Е/.
§ 4
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
1’43
Фиг. 3.
По формулам (10), (12), (16) и (19), отбрасывая члены
с пятой степенью 6, имеем
144
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
откуда
NB = ME MG = - Е,' 4- Е = (1 - и) (б2 — у (2 + и)
2
BK = АВ ± АК = ~ (1 — и) 8%
Фиг. 4.
Определим теперь длины перпендикуляров KQ и КР,
опущенных из точки К на оси координат № и Кц. Мы по-
лучим эти длины, взяв проекции контура NBK на прямые NL
и NH, перпендикулярные к Л/?| и 7VE:
KP— NB sin о — В К cos I -х-К I,
KQ — КВ cos (-J- 9 j 4~ BKsin ,
(20)
§ 4
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
145
или по предыдущим формулам
КР= (1—р)^62-----fi^rjsin? —
----т(1-н)езс°8
KQ = (1 - в) (о2 - 6^riCOS (^ + <?) +
+ 4"(1 — р) О3 sin
Подставим в эти выражения
Sin<?= ZCOS-^- О,
отбрасывая члены с пятой степенью 6, получим
КР= (1 - и) г cos ( 4-63 + 2 sin4 Н >
KQ — (1— (j.) г cos ( в2—)•
Л \ \ / /
Разделив найденные величины перпендикуляров на cos най-
дем искомые координаты точки К’.
2L=
-|-= (1-в) (б2- (i + yb4).
’Зак. 2430. Н. Е. Жуковский. Том IX.
(21)
10
146
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Мы получили эти основные формулы, пользуясь фиг. 5 и 6,
соответствующими тому случаю, когда комета приближается
к солнцу. Если комета удаляется от солнца, то формулы (20),
напишутся таким образом:
К'Р= N'B
K'Q — N'B cos (— ° ) ~Ь BK'sin .
Фиг. 5.
Эти формулы будут тождественны с формулами (20), если
в них заме'ним v на (— v); следовательно уравнения (21)
могут быть также применены к комете, удаляющейся от
солнца, если изменим v на (— v).
§ 5. Уравнения (21) служат нам для построения синдина-
мических и синхронических кривых. Давая в этих уравнениях &
различные значения, мы будем получать точки синдинами-
ческой кривой, соответствующей данной силе 1 — р-, и место,
где каждая из этих точек покинула ядро, определится фор-
мулой (17). Обратно, давая 1—р- (различные значения, мы
§ 5
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
147
будем получать точки синхронической кривой, соответствую-
щей точке М, заданной параметром 6.
В первом приближении, если отбросить члены с четвертой
степенью 6, уравнение синдинамической кривой представится
в простом виде:
т] = 4 1 /
Г з г ) '
(22)
Фиг. 6.
Это уравнение принадлежит параболе порядка у/о, каса-
тельной к радиусу-вектору FN; уравнение однородно по
отношению к 5, 1] и г и не зависит от v. < о обстоятельство
дает нам ясное представление о том, как меняется синдина-
мическая кривая при движении ядра. Все изменение сво-
дится к изменению координат £ и пропорционально радиусу-
вектору ядра и к изменению угла между осями координат
от 0° до 180°.
10*
148
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Уравнение синхронической кривой в первом приближении
будет
Е 3
(23)
и представит прямую линию, которая проходит через
ядро.
Если сохраним в формулах (21) члены с четвертой сте-
пенью 6, то для синхронической кривой будем иметь урав-
нение
ч (з-4 е2)_з + 2 sin е) ] ч- 2 sin ь) (24)
параболы второго порядка, которая касается в начале коор-
динат прямой
7](3 —4 62) —2siny б)=0
и имеет диаметр, параллельный радиусу-вектору ядра. Эта
парабола обращена выпуклостью к солнцу.
Заканчивая этот параграф, докажем одну теорему отно-
сительно касательной к синдинамической кривой. Продифе-
ренцируем формулы (21) по 6 и возьмем их отношение
Потом на основании фиг. 3 напишем
Сохраняя в этих формулах члены второй степени от 6,
имеем
d-r\ _ NE1 _ / . V . \ ,
JE “* NF p + 2sin 2 fj.
Таким образом
к синдинамической
при такой степени точности касательная
кривой параллельна радиусу-вектору той
§ 6
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
149
точки, из которой частица хвоста отделилась от ядра. В слу-
чае 1 —= 1 эта теорема точная.
Фиг. 7.
§ 6. Перейдем к изложению нашего графического метода,
который служит для построения синдинамических и синхро-
нических кривых на фиг. 7 и 8. Для построения синхрони-
ческой кривой частиц хвоста, вышедших из точки М (фиг. 7),
150
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
опустим перпендикуляр MQ на директрису. Возьмем на этом
перпендикуляре ряд фокусов F', F, F2'. . ,F7', которые нам
послужат для построения гипербол A, Alt Д2,...,Л7. Для
каждой гиперболы построим соответствующую кривую
а, аи а.,,.. ., а7 таким образом. Из точки Ь гиперболы А проведем
прямую 6р, параллельную касательной М\, и на этой прямой
возьмем отрезок &Р, равный 8, причем величина 8 опреде-
ляется при помощи формулы 8 = —_ Таким образом
построенная точка Р будет лежать на соответствующей кри-
вой а.
Соответствующая кривая для параболы А8 может быть
так же построена, если в формуле (12) сделаем ;* = 1. В этом
случае будет
o = (25)
Зу 7-1
Эта кривая на пашем чертеже обозначена через а8.
Когда соответствующие кривые построены, то синхрони-
ческая кривая для параметра h может быть построена сле-
дующим образом. Отложим на касательной М'г^ отрезок
МО = h и проведем через точку О прямую BD, параллель-
ную оси М^. Через точки пересечения этой прямой с соот-
ветствующими кривыми Р, ₽!, Р2,-.., Р7, Р8 проведем пря-
мые, параллельные к касательной, до пересечения с гипер-
болами.
Точки пересечения b, blf N будут расположены
на искомой синхронической кривой.
Эта кривая, проходящая через ядро N, приближается к пря-
мой BD, пересекает ее в точке О и удаляется от нее, при-
ближаясь к асимптоте АС, которая проходит через точку Е,
удаленную от М на расстояние 2Л. Чтобы доказать это пос-
леднее свойство синхронической кривой, введем в формулы
(12) и (±3) обозначение
и2
§ 6
О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ
151
и напишем
Полагая здесь 1 — р = оо, и — оо, найдем
е _ 8 h
2 /-j г/
откуда следует, что для — оо S = h, что и требовалось
доказать.
Чтобы построить синдинамическую кривую (ядро нахо-
дится в точке N, фиг. 8) при заданной силе, возьмем на
параболе точки М, Mlt М2, - -., МГ), опустим из этих точек пер-
пендикуляры MQ, MrQlt M2Q.на директрису и раз-
делим их в отношении
MQ : MF' = M1Q1 : М^' = ... = 1 — а
(для нашей фигуры 1 — р = 5). Принимая F', F/, F2,...,Fb'
за фокусы, построим гиперболы А, А1г У12,..., ; для всех
гипербол построим соответствующие кривые а, а2,..., а5
указанным выше способом; для параболы А6 построим также
соответствующую кривую а6. Через точки М, Мх, М2,-..,М-
проведем прямые, параллельные касательной к параболе
в точке N, до пересечения в точках т, mlf т.2,..., тъ с кри-
вой «6. Эти точки будут вершинами треугольников, построен-
ных на основании A7V и равновеликих с параболическими
секторами FNM, FNMX, FNM:,,..., FNI\F. Опустим из точек
т, гтц, т2,. тъ перпендикуляры р, Pj, р2,..., рв на радиус-
вектор NF и положим
152
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
NFp ,__
~ MF> M.F
Фиг. 8.
Проведем прямые BD, B{D{, BJD.2,..., B:Dr> параллельно
радиусам-векторам MF, MtF, M.F,..M-tF, отстоящие от этих
радиусов-векторов на расстояниях I, 1и 12, —, 1&.
§6 О ПОСТРОЕНИИ СИНДИНАМИЧЕСКИХ КРИВЫХ 153
Найдя точки р, Рр р5 пересечения прямых с соот-
ветствующими кривыми, проведем через эти точки прямые
рб, Pj6j, параллельные касательным к параболе
в точках М, Mit М2,..., М?,. Точки Ь, Ь19 Ь2,..., Ь& пересечения
прямых с гиперболами будут расположены на искомой син-
динамической кривой.
Эта работа представляет собой русский перевод предыдущей статьи
„Sur la construction des courbes syndynamiques et synchroniques", выполнен-
ный для настоящего издания проф. А. П. Котельниковым. Прим. оед.
ON THE CONSTRUCTION OF SYNDYNAMICAL AND SYNCHRONICAL
CURVES
In this paper N. E. Joukovsky deduces formulae for the
construction of curves playing in the theory of comet tails
an appreciable part, and being called by Bredikhin syndyna-
mical and synchronical curves. Those formulae express the
coordinates E, (Figs. 3 and 4) of the particle A* of the comet
with respect to the axes, one of which being set along the
radius-vector of cometary nucleus N, and the other in the
direction of the tangent to the parabolic orbit of the nucleus
in the function of the angle о between the radii-vectors of the
nucleus /V and the point M of its orbit at which the particle
got detached from the nucleus. These formulae (21) are being
obtained by means of a successive transition from one system
of coordinates to another: First (Figs. 1 and 2) are being taken
as axes Ox and Oy conjugated diameters OM and OL of the
hyperbola which describes the particle under the action of the
repulsive force of the sun or of the relaxed Newtonian attrac-
tion, then as axes is being taken the radius-vector traced
from the sun to the point M and the tangent to the para-
bolic orbit of the nucleus at the point M and lastly are being
taken the axes, above referred to. The coordinates $ and are
being expressed as a power series of the argument 6, determi-
ned by equation (7), where v is the real anomaly of the point
N, and the forth powers of 0 are being retained in the expan-
sions. These formulae involve the coefficient of the force p.
If we change p leaving to be constant-/ the equation (21) will
represent the equations of the synchronical curve in a para-
metric form, i. e. they will establish the geometrical place of
all particles, flying out simultaneously of the nucleus and being
subjected to forces characterized by different coefficients p. It
SUMMARY
155
will be the parabola (24). Should we regard p- as a constant
and change but 6, the same equations will be then equations
of the syndynamical curve, i. e. the geometrical place of the
particles being under the action of the force with the same
coefficient p, but got detached at different times from the
nucleus. It establishes the form of the comet tail correspon-
ding to a definite value of p.. In the first approximation it
will be a semi-cubic parabola (22).
At the end of the paper is being expounded the method of
graphical construction of synchronical and syndynamical curves,
based on prec'se formulae.
К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА
В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
(1893 г.)
§ 1. В этой заметке мы имеем в виду доказать, что из
общепринятых формул для электрической энергии системы
диэлектриков и проводников получается заключение о незави-
симости от силы электрического поля характеристической
формулы, выражающей давление диэлектрического газа п о
его плотности и температуре. Если же в электрическом поле
имеется соединение насыщенного жидкостью, то сила
Р ,
электрического поля не имеет влияния на величину р-р ,
где р и р — давление и плотность пара, а р и р' суть давле-
ние и плотность жидкости.
Мы будем рассматривать диэлектрики, заключенные между
двумя листами конденсатора и соприкасающиеся между собой
или по поверхностям силовых линий, или по эквипотенциаль-
ным поверхностям.
Первое расположение, кажется, было мало спекулируемо
математическими физиками. Между тем оно заслуживает осо-
бого внимания, так как позволяет делать весьма разнообраз-
ные изменения диэлектриков, не нарушая однородности элек-
трического поля.
§ 2. Вообразим (фиг. 1) два весьма широких параллельных
листа конденсатора А и В, отстоящие друг от друга на
постоянное расстояние h и заряженные количествами элек-
тричества -]-е и —е. Между этими листами заключен ряд
диэлектриков, имеющих формы прямых цилиндров с произ-
вольными основаниями, лежащими на том и другом листе
конденсатора. Все остальное пространство представляет так
называемую пустоту, диэлектрическое постоянное которой
r
3 2 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 157
пусть будет £0. Назовем через к, к', к",... диэлектрические
постоянные рассматриваемых диэлектриков и через °, о",...
площади, которыми они опираются на листы конденсатора.
Легко усмотреть, что в рассматриваемом случае мы получим
равновесие электричества при однородном поле,
зованном некоторой постоянной силой R, напра-
вленной перпендикулярно листам от А к В.
При этом свободное электричество будет ле-
жать на листах однородными слоями плотности
R
4*
, сообщенное же извне электричество будет
иметь большую плотность на площадях основа-
ний диэлектриков ^и тем большую, чем диэлек-
трическое постоянное более. Это произойдет
от того, что диэлектрик с постоянным к выдви-
нет к листам А и В электричество с плот-
ностью — kR и 4- kR, которое нейтрализует часть
сообщенного электричества. На фиг. 1 предста-
охарактери
Фиг. 1.
влены схематически плотности сообщенного электричества
в предположении А-о < к < к' < к"...
Называя площадь листа конденсатора через ас, выразим
все количество ® находящегося на нем сообщенного элек-
тричества формулой *:
е = (°о —3 — 3’ — • • •) 4-
, 1 4- Adk . 1 -4- Акк' , .
° + -„
или
Е = 7?[с-Ь(/с —Л0)о-Ь (^-Ло)с/4-...],
где с — некоторое постоянное.
Отсюда находим, что
е
с-\-(к—к0)^-\~ (к'—к^о'.
(1)
1 Чтобы устранить всякое сомнение относительно краев конденсатора,
можно воображать бесконечно широкий конденсатор, разбитый на квад-
раты, в которых симметрично повторяются расположения диэлектриков
k, к."..., и рассматривать один такой квадрат.
158
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Z Л,
и
J
и
Фиг. 2.
Разность потенциалов Н при переходе от листа В к листу
А и электрическая энергия w всей рассматриваемой системы
выражаются формулами:
Н= Rh,
w = — ~2
Подставляя сюда величину R, получим:
„_____________ s/i
~ с + ’ (2)
е2Л
W-2[c-[-(k-k0)a~h(k'-k0)^+-..] (3>
Вообразим теперь, что плоскость листа конденсатора А
совпадает с плоскостью чертежа и что рассматриваемые
диэлектрики суть газы, заключенные (фиг. 2)
в прямоугольной коробке ZMN, образованной
стеклянными стенками, перпендикулярными ли-
стам конденсатора, и самими этими листами.
Газы отделяются от пустоты и разделяются ме-
жду собой некоторыми стеклянными поршнями,
могущими свободно скользить по стенкам ко-
робки. Все члены, стоящие в знаменателях фор-
мул (2) и (3) и относящиеся к стенкам сосуда
и поршням, будем считать включенными в по-
стоянное с, так что к, к', к",..., о, а', а",...
будут величины, относящиеся только к одним
рассматриваемым газам. Назовем через р, р', р",... давление
этих газов и предположим, что на упомянутые поршни дей-
ствуют еще некоторые внешние силы, которые, отнесенные
к единице площади поршней, пусть будут: Р, Р', Р',...
Будем считать эти силы положительными, когда они напра-
влены вниз.
Если закрепим все поршни и сделаем свободным один
из них, например, второй, то по принципу сохранения е и
началу возможных перемещений найдем, что
(Р' + р — р') hds—(~ — =
\ Q'J GO /
§2 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 159
откуда:
, div / div \
~Р ~Td<d~\P~ Г
На основании таких рассуждений все внешние силы, дей-
ствующие на поршни, выразятся формулами:
n div
P-p~~hd^’
ry - div
P p hdd'
div \
h dz )
div \
lids' J ’
(4
Когда на поршень, разделяющий два диэлектрические газа,
не действует никакой внешней силы, то из формул (4) мы
сейчас же найдем разность давлений этих газов.
Положив /у = 0 и обратив внимание на формулы (3) и (1)
получим:
(5)
Здесь положено, что
dk ___________________ dk ___ dk _______ g
Ja — f/lgp~ ’
где p — плотность газа; такое же значение имеет и коэфи-
циент 6'.
Коэфициенты 6, как показывает опыт, суть весьма незна-
чительные величины сравнительно с к~, поэтому при к’ > к
будем иметь из формулы (5) р > р'г т. е. два смежные ди-
электрические газа могут быть в равновесии только в том
случае, когда давление менее совершенного диэлектрика из
них (у которого диэлектрическое постоянное более) будет
меньше давления более совершенного. Если давления обоих
газов равны, то диэлектрик менее совершенный будет расши-
ряться и сжимать более совершенный до тех пор, пока раз-
ность давлений не достигнет указанной величины.
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
g 3. Обращаемся к определению изменения давлений
р, Р , Р г • • • с изменением е. Этот вопрос разрешается по прин-
ципу свободной энергии, установленному Гельмгольцем1).
Свободная энергия выражается формулой
F=U—ITE,
где U—полная энергия рассматриваемой системы, Е—ее
энтропия, а Т—одинаковая для всех частей систем абсо-
лютная температура. В нашем случае как U, так и Е суть
функции от е, Т, о, о', о", так что при постоянной тем-
пературе свободная энергия является функцией только гео-
метрических размеров системы и количества сообщенного
электричества на листах конденсатора.
Пусть наша система совершает обратимый изотермиче-
ский процесс вследствие того, что силы Р, Р , Р', ... и коли-
чество электричества е непрерывно изменяются.
Отрицательное приращение свободной энергии будет равно
работе, потраченной на преодоление внешних сил, а также и
работе, выделяемой системой при переходе электричества от
более высокого потенциала к более низкому. Вследствие этого
— dF=P + + ...) h-\-
+ Р' ..) А+ ...— Hds.
Подставляя сюда величины Р, Р, ... из формул (4) и за-
мечая, что на основании формул (3) и (2)
я=^,
de
получаем: «
— dF=(ph^^-\da+(p'h — ^\d='+...— -^-de. (6)
\ do ) у do' ) 1 de
Вторая часть этого равенства должна быть полным ди-
ференциалом функции переменных: е, а, а', а", ...; поэтому
dp _ dp’ _ dp"
de de de ’ ’ ‘ ~U- V?
Мы видим, что давления р, р', р", ... рассматриваемых ди-
-электрических газов не зависят от е и имеют те же вели-
1 Helmholtz, Wissenschaftllche Abhandlungen, Bd. II, S. 958.
§4 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 161
чины, какие имелись бы при данных Т, а, а', ... в случае е = 0.
Таким образом давление диэлектрического газа в рассмотрен-
ном электрическом поле определяется по его плотности и
температуре обыкновенной формулой Мариотта-Гей-Люссака.
§ 4. Вследствие сказанного изменение объемов рассма-
триваемых диэлектриков с изменением е должно объясняться
только изменением скачка в гидростатическом давлении, со-
вершающегося на поверхности соприкосновения диэлектри-
ков. Эти скачки подобны тем, которые рассматриваются в
теории капиллярных явлений, причем поверхность соприкос-
новения аналогична капиллярной по-
верхности, обращенной вогнутостью
в сторону более совершенного ди-
электрика.
В известном опыте Quincke
(фиг. 3) воздушный пузырь D, за-
Фиг. 3.
ключенный между листами конденсатора А и В, заполнен-
ного терпентином, сжимается, уступая место менее совер-
шенному диэлектрику — терпентину. При этом давление воз-
духа в пузыре возрастает до тех пор, пока разность давлений
воздуха и терпентина не достигает вели-
чины, даваемой формулой (5).
Если вообразим (фиг. 4) между двумя
конденсаторными листами стеклянные стен-
ки ZMN, наполненные воздухом, а внутри
барометр D, ограниченный стеклом и на-
полненный терпентинсм, причем плоскость
чертежа совпадает с плоскостью листа кон-
денсатора А и все стеклянные стенки рас-
положены, как объяснено в § 2, то при-
дем к заключению, что с увеличением си-
лы поля барометр будет подниматься.
Это оттого, что (менее совершенный диэлектрик) воздух бу-
дет расширяться на счет (более совершенного диэлектрика)
барометрической пустоты.
Не принимая во внимание скачка в гидростатических да-
влениях и желая объяснить оба упомянутых явления изме-
нением характеристической формулы воздуха в электрическом
Зак 2430. И. Е. Жуковский. Том IX.
11
162
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
поле, мы бы должны были допустить из первого опыта, что
с увеличением силы поля давление воздуха уменьшается,
а из второго, что оно увеличивается от той же причины.
Скажем еще несколько слов о диэлектрике переменной
плотности. Если предположим (фиг. 1), что диэлектрики
k, к', к", • расположены весьма узкими слоями, причем постоян-
ное к изменяется постепенно, то перейдем в пределе к не-
однородному диэлектрику. Вообразим некоторую ортогональ-
ную линию к поверхностям равного к и назовем ее длину
через s. По формуле (5) напишем:
dp , R2 dk d /
ds"2 | dsA
ds =
/ dk\
f ds\dp /
R2 dk dk dp
2 L ds dp ds
или
dp___R2 d (dk\
ds 2 Г ds \ dp / '
Разделяя на p и интегрируя, находим:
f dp R2 6 . .
I -- = -77---h const. (6 )
J P 2 P
По этой формуле определяется разность давлений в двух
точках неоднородного диэлектрика, причем при разсмотрении
более общей задачи обнаруживается, что эта формула остается
справедливой и в переменном электрическом поле ].
Воображая конденсатор с открытыми краями, окруженный
воздухом, найдем по данной формуле и закону Мариотта
следующее соотношение между давлением наружного воздуха
Ро и воздуха внутри конденсатора р:
Ро 2 р
откуда приближенно
р-Ро = у«- (7Л)
1 Helmholtz, Wissenschaftliche Abhandlungen, Bd. I, S. 817.
§5 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 163
Таким образом в открытом конденсаторе увеличение силы
поля производит сгущение воздуха.
§ 5. Переходим к вопросу об изменении в зависимости
от е упругости р насыщенного пара и упругости р' его
жидкости. Пусть (фиг. 5) между вертикальными листами на-
шего конденсатора посредством стеклянных стенок устроен
прямоугольный вертикальный сосуд, при-
крытый сверху стеклянным поршнем, могу- °п
щим свободно скользить в сосуде и нахо- 1 5
дящимся под действием внешней силы, ве- \
личина которой на единицу площади порш-
ня есть Р. В этом сосуде заключена жид- \р
кость с диэлектрическим постоянным к'
и ее пар с диэлектрическим постоянным к.
Жидкость и пар соединены еще трубкой С, С
проходящей сквозь конденсаторный лист В
и выходящей таким образом из электриче- ;
ского поля (легко показать, что при пере- +
мещении по трубке сила поля быстро за-
тухает). Если при переходе в конденсатор |
через поверхность раздела пара и жидкости
мы будем получать скачком понижение да-
вления от р до р', то жидкость в трубке С
будет стоять ниже, нежели в конденсаторе Фиг. 5.
(волосность не принимаем в соображение),
как это изображено на фиг. 5. Определим величину упомя-
нутого скачка. Предположим, что поршень закреплен. Испа-
рение жидкости или конденсация пара делаются невозмож-
ными, так как сумма объемов жидкости и пара неизменны.
Возможным перемещением остается перемещение жидкости
из конденсатора в трубку С или наоборот. Пусть это переме-
щение охарактеризовано изменением площадей с/з = —d^'.
По началу возможных перемещений находим, что 1
/ '\lj [(dw\ — n
(p p )hd° — j — d-> — 0,
1 Первый член этой формулы можно рассматривать как работу веса
жидкости, опустившейся в конденсаторе и поднявшейся в трубке.
164
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
откуда получим:
, 1 / dw \ 1 / dw'
Р Р h \ do J h \ do' / ‘
(8)
Здесь производные в скобках показывают, что не надо изменять
к и к'. На основании формул (3) и (2) формула (8) обра-
щается в
- Д>2
р-р' = ^(к'-к). (9)
Так как к' > к, то давление жидкости будет менее давле-
ния ее пара.
Обращаемся к определению Р. Для этого делаем поршень
подвижным и сообщаем ему бесконечно малое перемещение
вверх, испаряя воду в трубке С. Пусть при этом о возрастет
на аа, а <з убудет на do, где р — плотность пара, ар —-
плотность воды. По началу возможных перемещений будем
иметь:
(— P-f- р) (1--т ) А - (р — р')~ hdo —
\ о / о
Подставляя сюда р — р' из формулы (8) и делая сокращения,
находим:
<10>
или по формулам (3) и (2)
P^p+^(k-k0). (11)
Теперь остается еще рассмотреть изменение величин р и р’
с изменением е. По принципу свободной энергии будем
иметь:
— dF= Р (do + do') — Hde.
Подставляем сюда величину Р из формулы (10) и при-
бавляем ко второй части величину, тождественно равную
нулю по формуле (8):
, 1 / dw \
р ~T\dJ)
(dw\
do /
do=0.
р
h
§ 5 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 165
Получаем:
l ( dw\~\ , . / dw\ dw ,
— dr = ph — —- cfa-j- р'Л----------Г7 -------d&.
' / J \ “° / a£
Допускаем с некоторым приближением, что отношение dz
и d<d постоянно и выражается через
dz _
Jo' р ’
где р и р' — плотность воды и пара при s = 0.
Получаем:
Здесь д выражает изменение по о, считая а' функцией а.
Так как вторая часть должна быть полным диференциалом от
s и о, то
(13)
Мы видим, что величина, стоящая в скобках, не изменяется
и имеет при всяком е то же значение, какое она имеет при
е=0. Назовем через р0 давление, даваемое при рассматри-
ваемой температуре таблицами упругости насыщенного
пара.
Получаем:
Р — у р' = (1 — у)ро- (14)
Решая уравнения (9) и (14), найдем искомые давления:
Р — /ZZ? (k' — Л) ’
г г
р' & (I/ м
р =po-y^2'(k
Эти формулы показывают, что с возрастанием силы поля
уменьшается давление насыщенного пара и соприкасающейся
с ним жидкости, но первое уменьшение гораздо менее, нежели
второе.
166
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Мы предположили для простоты при выводе формул (10)
и (12), что испарение совершается в трубке С. Но легко
усмотреть, что вывод этих формул не изменится, если пред-
положим, что входы в трубку С закрыты и испарение совер-
шается в конденсаторе.
§ 6. Будем теперь рассматривать диэлектрики, поверхности
раздела которых направляются по эквипотенциальным поверх-
ностям. Воображаем опять
- Е
—-—В
Z
Z'
А
te
Фиг. 6.
весьма широкие листы конденса-
тора А и В (фиг. 6), на которых
лежит сообщенное электричество,
и назовем здесьчерез-|-еи — sко-
личества электричества на единице
площади этих листов. Между ли-
стами поместим ряд диэлектриков,
соприкасающихся по плоскостям,
параллельным конденсаторным листам, и предположим, что
остальное пространство между листами представляет пустоту.
На весьма большом расстоянии от рассматризаемого места
диэлектрики ограничены некоторыми стеклянными стенками,
перпендикулярными к листам конденсатора. Пусть h будет
постоянное расстояние между листами конденсатора, а
z, z , 2", . .. пусть будут толщины диэлектриков. Обозначаем
через к, к', к", ... диэлектрические коэфициенты рассматри-
ваемых диэлектриков и через ка— диэлектрическое постоян-
ное эфира и полагаем для сокращения письма:
1+4^о = Ко, 1-Н^ = К. 1+4^' = ^', ... 1(16)
Электрическая сила рассматриваемого поля будет напра-
влена от листа А к листу В и будет изменять свою вели-
чину скачком при
деляющую два диэлектрика. Назовем величину этой силы
в пустоте через Rq, в первом диэлектрике — через R, во вто-
ром— через R' и т. д.
Будем иметь на основании известной связи между плот-
ностью электричества и силой:
переходе через граничную плоскость, pas-
^о —-р-
$6 к ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 167
При переходе через первую граничную плоскость Ro
изменяется в R, причем должно быть удовлетворено соотно-
шение:
K0Ro — KR = 0,
из которого следует, что
р__Ко р ___
R~ к R°~ к •
Продолжая рассуждать подобным образом, находим:
Если назовем через и, р", - • • плотности свободного
электричества (мы предполагаем, что внутри конденсатора
нет сообщенного электричества) первой, второй и т. д. гра-
ничным плоскостям, то увидим, что эти плотности будут иметь
величины:
Сумма этих плотностей для всех граничных плоскостей равна
нулю.
Составим теперь разность потенциалов // на наших кон-
денсаторных листах. Эта разность будет:
Н— Ro (h — z — z' —z!'— . •.) + Rz + Rrz
Подставляем сюда величины сил из формул (17):
[с~ (к~ 2- 6Ы') г'~ • ] (18)
где с = h : Ко.
168
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Мы будем теперь предполагать, что наши диэлектриче-
ские слои состоят из газообразных тел и разделяющих их
стеклянных поршней, причем вся система ограничена снизу
стеклянным дном, а сверху прикрыта стеклянным поршнем.
Все части формулы (18), относящиеся к дну и стеклянным
поршням, отнесем к постоянному с, так что z, z', zw, ...,
К, К', К", • будут величины, соответствующие диэлектри-
ческим газам.
Зная Н, находим величину w электрической энергии, от-
несенную к единице площади конденсатора:
w = 2r^ с— ------i^)z—(11-----К") z'—” ‘
Называем через р, р', р", .. силы упругости рассматривае-
мых газов и предполагаем, что на поршни действуют внешние
силы, величины которых, отнесенные к единице поверхности
поршней, обозначим через Р, Р, Р'. Будем считать эти вели-
чины положительными, когда силы направлены вниз.
Если закрепим все поршни и сделаем свободным один из
них, например, второй, то по началу возможных перемещений
найдем, что
(Рг +p — p')dz — № — ~\ dz = Q,
\ dz dz /
откуда
р-р'
dw
dz'
dw \
На основании таких же рассуждений все внешние силы, дей-
ствующие на поршни, выразятся формулами
dw
dz ’
Р=р
(20)
Когда на поршень, разделяющий два диэлектрических газа,
не действует никакой внешней силы, то из формул (20) мы
сейчас же найдем разность давлений этих газов.
§ 7 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 169-
Положив 7у = 0 и обратив внимание на формулу (19),
получим:
где 6 и 6' суть коэфициенты, указанные в § 2. Так как эти
коэфициенты малы сравнительно с диэлектрическими постоян-
ными и оказывают незначительное влияние на разность
р — р', то можно сказать, что эта разность будет положи-
тельна при К' > К. Таким образом и здесь два смежных
диэлектрических газа могут быть в равновесии только в том
случае, когда давление менее совершенного диэлектрика из
них будет меньше давления более совершенного. Если давле-
ния обоих газов равны, то диэлектрик менее совершенный
будет расширяться и сжимать более совершенный до тех пор,
пока разность давлений не достигнет указанной величины.
§ 7. Обращаясь к исследованию изменения давлений
р, р', р", ... с изменением е, мы доказываем совершенно так
же, как в § 3, что эти давления от е не зависят и должны
определиться по обыкновенной формуле Мариотта-Гей-
Люссака.
Действительно, отрицательное приращение свободной энер-
гии, отнесенной к единице площади, будет:
— dF ~ Р (dz dz' dz" + .. Р' (dz' dz" dz". . .)-f-
+ ...— Hde.
Подставляя сюда Р, Р', ... из формул (20) и величину Н
из формулы (18), видим, что
— dF=^P— ^)dz+(p'— dz' + •••"Г j£’ (21)
откуда получаем:
dP 4pL == . = о. (22)
de de de
§ 8. Переходим к вопросу об изменении в зависимости от
е давлений р и р' в насыщенном паре и его жидкости, пред-
полагая здесь, что поверхность раздела пара и жидкости
есть эквипотенциальная поверхность.
170
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Пусть (фиг. 7) весьма широкий сосуд, рассматриваемый
в § 6, заключает в себе жидкость и ее насыщенный пар и
имеет только один верхний горизонтальный поршень. Кроме
соприкосновения в поле конденсатора, пар и жидкость соеди-
няются еще трубкой С, выходящей из поля конденсатора,
как это представлено на фигуре. Эта трубка будет отчасти
& разрушать однородность поля,
---------------р-------------------- но мы вообразим ее, так же
:_________________________t-как края сосуда и конденсато-
~ ра, весьма удаленной от иссле-
А дуемого места. Мы сейчас уви-
дим, что в рассматриваемом
Фиг. 7. случае, как и в прежнем, жид-
кость в трубке С будет стоять
ниже, чем в конденсаторе. Предположим, что поршень закре-
плен. Испарение жидкости или конденсация пара делаются
невозможными, и единственным возможным перемещением
остается перемещение жидкости из конденсатора в трубку С
или наоборот. Пусть это перемещение охарактеризовано из-
менением dz— —dz'. По началу возможных перемещений
имеем:
(p — p')dz— ( <7z = 0,
\ az j \dz)
откуда
. I dw \ ( dw \
p-r
(23)
Здесь производная в скобках показывает, что не надо изме-
нять К и К'. На-основании формулы (19) полученная разность
давлений представляется в виде:
, Q J 1 1 \
р-р =2,.-^-^.
(24)
Так как К' > К, то давление жидкости будет менее давле-
ния ее пара.
Обращаемся к определению Р. Для этого делаем поршень
подвижным и сообщаем ему бесконечно-малое перемещение
§8 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 171
вверх, испаряя воду в трубке С. Пусть при этом z возра-
стает на dz, а z' убывает на — dz, где р и р' выражают
плотность пара в жидкости. По началу возможных переме-
щений будем иметь:
( —Р + — у) dz 4- (р — p')y-dz —
(dw \ / dw \ Р 1 ,
-г-—I )“/ az —О.
dz / \dz / р
Подставляя сюда р—р' из формулы (23) и делая сокра-
щения, находим:
P=p~(4z) (25)
\ az /
или по формуле (19)
+ (26)
Далее по принципу свободной энергии пишем:
— dF = P(dz dz') —Н ds.
Подставляем сюда Р из формулы (25) и прибавляем
ко второй части величину, тождественно равную нулю по
Получаем:
_dF=[p-(-^)]jz+rp'-(^-)l dz' — ^-ds. (27)
' \ dz ) \ L \dz ) \ ds '
Здесь, так же как в § 5, берем с некоторым приближением
dz =------— dz',
Р
где величины плотностей определяем при е = 0.
Принимая это во внимание, находим, что
— dF— (р—ур'^
dw
dz
dz
dw
ds
ds.
(28)
172
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Здесь д выражает изменение по z, считая z' функцией z.
Так как вторая часть формулы (28) должна быть полным
диференциалом, то
й (»>
Таким образом величина,
стоящая в скобках не изме-
няется и имеет при всяком е то же значение, какое при
е = 0.
Назовем через pQ давление пара и жидкости при е = О
и напишем, что
Р~^Р = 1-4U- (30)
I \ г /
Решая уравнения (30) и (24), получаем:
Мы видим, что здесь, так же как в § 5, давление насы-
щенного пара и соприкасающейся с ним жидкости с увели-
чением силы поля уменьшается, но главное уменьшение па-
дает на жидкость.
Мы предполагали при выводе формул (25) и (28), что
испарение совершается в трубке С; но те же результаты
будут иметь место, когда предположим входы в трубку С
закрытыми.
Чтобы сравнить формулы (31) с формулами (15), преобра-
зуем первые на основании формул (16) и (17):
Р = Р0-у~ ^-к),
, р/ RR' (к' к) I (32)
р ^Po-yzzy— (* -*)’ ]
Так как R' <Z R, то при той же силе поля в паре фор-
мула (32) дает для р большую величину, нежели формула (15).
Таким образом нельзя трактовать о изменении упругости насы-
щенного пара в электрическом поле независимо от напра-
§9 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 173
вления силовых линий к поверхности раздела пара и жид-
кости. Собственно говоря, весь эффект электрического поля
состоит в том, что оно способствует конденсации и испаре-
нию при находящемся над жидкостью паре, который для
е=0 есть пар ненасыщенный- Вследствие этого становится
понятным, \то эффект этот будет изменяться с изменением
направления уровня жидкости.
В давлении же самого пара при данной плотности, так же
как и в давлении газа, изменение поля никаких изменений,
по нашему мнению, не производит. Если бы мы заперли входы
в трубку С, потом испарили всю воду в конденсаторном со-
суде (фиг. 7) и разрядили конденсаторные листы, то полу-
чился бы в сосуде ненасыщенный пар.
§ 9. Предположим, что поверхность жидкости внутри кон-
денсатора в сосуде фиг. 7 прикрыта поршнем, на который
действует некоторая сила Р', и напишем вместо формулы (8)
следующую:
(33)
Формулу же (25) при этом надо будет сохранить, так как
при неподвижном нижнем поршне и при подвижном верхнем
будем иметь по началу возможных перемещений:
(-Р+р) dz-^dz-O.
Поступая далее, как при выводе формулы (21), получим
формулу (27) для совершенно произвольных перемещений
dz и dz'.
Отсюда следует, что
dp — W — о
Л ~
(34)
Таким образом если в электрическом поле нет свободной
поверхности жидкости, то р и р' имеют то же значение,
какое они имеют при данном расположении системы, когда
е = 0.
То же самое можно сказать и о сосуде, изображенном
на фиг. 5.
174
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Вообразим теперь, что конденсатор разряжен, и поднимем
нижний поршень над уровнем жидкости в трубке С на вы-
соту 8, соответствующую высоте всасывания при заряде sA
Обыденные соображения по аэростатике приведут нас
к заключению, что насыщенный пар будет лежать только
над поверхностью жидкости в трубке. Поднимаясь1 же от этой
поверхности вверх, мы будем получать пар, при данной тем-
пературе ненасыщенный, давление которого будет убывать.
Над поверхностью нижнего поршня будет лежать пар
с давлением:
р = р0—ро.
Подставляя сюда по формуле (24)
8 —-2-'2 L1 —
р' —р V/С К')’
получим:
(35)
(36)
Сообщим теперь конденсатору заряд е, от которого ри р'
не изменяются по сказанному, и потом отнимем нижний пор-
шень [который вообразим столь тонким, что его влияние
на w в формуле (19) бесконечно мало]. Получим равновесие
системы, так как жидкость не будет всасываться в конден-
сатор вследствие выбора 8, а конденсация или испарение,
как заметил Блондло (Blondlot), не будут иметь места.
Это рассуждение доказывает высказанное нами мнение,
что пар над поверхностью жидкости в конденсаторе имеет
плотность ненасыщенного пара.
§ 10. Доказанной нами теореме о независимости характе-
ристической формулы, выражающей давление диэлектрического
газа по его плотности и температуре, от силы электрического
поля противоречат результаты, найденные Б. Б. Голицыным
в сочинении „Общие свойства диэлектриков с точки зрения
механической теории теплоты11
1 „Ученые записки Московского университета, отдел физико-матема-
тический", вып. 10.
g 10 К ВОПРОСУ О ДАВЛЕНИИ ДИЭЛЕКТРИЧЕСКОГО ГАЗА 175
В этом сочинении автор дает для давления газа формулу h
№
Р = Ро---(37)
где Ру есть давление, определяемое по закону Мариотта-Гей-
Люссака; вследствие чего, по его мнению, изменение силы
поля изменяет самую характеристическую формулу газа.
Но мы думаем, что вывод Б. Б. Голицына неверен и яв-
ляется следствием ошибочного способа определения силы
электрического действия на поршни.
Он не пользуется для этого выражением электрической
энергии и началом возможных перемещений, а определяет
силу прямо как взаимодействие электрических масс.
Такой способ вообще сомнителен и, будучи приложен
к поршням, изображенным на фиг. 2, ведет к очевидному про-
тиворечию с началом возможных перемещений.
Б. Б. Голицын рассматривает случай конденсатора (фиг. 6),
в котором сам лист В служит поршнем и имеется только
один газ. В нашей формуле (19) для этого случая надо взять
h = z, z = z — ... = С.
Получим:
2~г‘2
вследствие чего первая формула (20) дает:
в dw
Р=р-^-р-^
К* )'
Голицын же пишет неправильно, что
Р=р
2те1 2
Вследствие этого наша формула (21) у него принимает
вид:
, „ I dw , 8яге20 \ . dw ,
= (р - s+~ *•
1 Это есть в сочинении Голицына формула (Iх) в § 2, которую мы
пишем при своих обозначениях.
176
АСТРОНОМИЯ И МАТЕМАТИЧЕСКАЯ ФИЗИКА
Это приводит к условию:
d / , 8т2е26 \ п
и дает на основании формулы (17) выражение (37).
Эта работа была доложена автором 29 октября 1893 г. в заседании
-физико-математической комиссии Отделения физических наук Общества
любителей естествознания. Напечатана работа впервые в „Трудах Огделе-
яия физических иаук Общества любителей естествознания", т. VI, вып. 2,
1893. Для настоящего издания работа просмотрена проф. Н. П. Кастери-
чым. Прим. ред.
TO THE QUESTION ON THE PRESSURE OF A DIELECTRIC GAS
IN AN ELECTRIC FIELD
In this note N. E. Joukovsky intends to prove that from
formulae, universally adopted for the electric energy of dielectric
and conductor system, a deduction may be obtained as to the
absence of dependence of the characteristic formula, expressing
the pressure of the dielectric gas in terms of its density and
temperature, from the force of the electric field. But if in the
electric field there is a combination of saturated steam with
liquid, the force of the electric field will have no effect on the
magnitude p-----p', where p and p are respectively the pres-
sure and density of the steam and p' and p' the pressure and
density of the liquid.
Зак. 2430. H. E. Жуковский. Том IX.
12
РАЗДЕЛ ТРЕТИЙ
РЕЧИ И ДОКЛАДЫ
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
12-т
О ЗНАЧЕНИИ ГЕОМЕТРИЧЕСКОГО ИСТОЛКОВАНИЯ
В ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
(РЕЧЬ)
(1894 г.)
На мою долю выпала честь сказать несколько слов в этом
торжественном заседании. Я посвящу их вопросу, о котором
так много думал и который особенно близок мне, как учено-
му,— вопросу о значении геометрического толкования в теоре-
тической механике.
Я рассмотрю этот вопрос сначала с точки зрения чистой
науки, потом с педагогической стороны.
Механика при своем первоначальном развитии опиралась
исключительно на геометрический метод. Механические ис-
следования Архимеда, Галилея и Гюйгенса — геометрического
характера. Весь строй изложения в „Принципах натуральной
философии" Ньютона — чисто геометрический. В том же на-
правлении шли работы последующих авторов: Бернулли,
Айвори, Маклорена и др. Но после того, как Декарт дал
способ выражать движение в пространстве по трем движе-
ниям на осях координат, и анализ бесконечно-малых, откры-
тый Ньютоном и Лейбницем, вошел во всеобщее употребле-
ние, в исследованиях по теоретической механике стал все
более и более преобладать аналитический метод, который
в творениях Лагранжа и его последователей достиг своей
высшей точки.
Геометрическая постановка задачи заменилась составле-
нием возможной работы, реакции связей1—неопределенными
множителями, изыскание движения отождествилось с задачей
об интегрировании диференциальных уравнений.
Поощренные успехом, выразившимся рядом блестящих
теорем в общей теории интегрирования уравнений динамики,
182
РЕЧИ И ДОКЛАДЫ
представители аналитического метода стремились возможно
шире ставить рассматриваемые вопросы, почти совершенно
игнорируя их геометрическую и механическую сторону.
Вследствие этого возникли аналитические трудности, иногда
нисколько не вызываемые сущностью дела. Данная механи-
ческая задача запутывалась и усложнялась вследствие отне-
сения ее к произвольной системе координат и упущения из виду
той, которая всего ближе к ней подходит.
Вращаясь в недоступной области общих интегралов ди-
фференциальных уравнений данной задачи, авторы иногда
упускали из виду ее пограничные условия и то обстоятельство,
что при этих условиях решение доступно, потому что является
частной формой искомого общего решения.
Так, задача о движении твердого тела по инерции, хотя
и разрешенная аналитически Эйлером, представлялась труд-
ной и запутанной, а задачи гидродинамики, хотя и сведенные
Эйлером и Лагранжем к уравнениям с частными производ-
ными, оставались без решения, так как последнее неразрыв-
но связывалось с отысканием общих интегралов этих ура-
внений.
Здесь на помощь анализу снова явилось забытое на время
геометрическое толкование. В своем изящном мемуаре „Theorie
nouvelle de la rotation des corps" Пуансо поставил себе зада-
чей „изучать вещи сами в себе" и, следуя этому девизу,
давал геометрическую интерпретацию рассматриваемого дви-
жения до той степени наглядности, при которой оно со всеми
подробностями рисуется перед глазами читателя.
По пути, указанному Пуансо, пошли позднейшие авторы—
Мак-Куллах, Максвелл, Сильвестр и др. Дарбу обнаружил,
что теорема Якоби разложения движения гироскопа на два
движения вида Пуансо, полученная Якоби из рассмотрения
интегралов этой задачи, может быть доказана геометрически
на основании ее диференциальных уравнений, и дал нагляд-
ную интерпретацию движения гироскопа.
Подобным же образом геометрическое толкование сослу-
жило важную роль в исследованиях по гидродинамике. В своем
замечательном сочинении „Uber Integrate der hydrodynami-
schen Gleichungen" Гельмгольц дает геометрическую интер-
О ГЕОМЕТРИЧЕСКОМ ИСТОЛКОВАНИИ В МЕХАНИКЕ
183
претацию интегралов гидродинамики, которые 20 лет раньше
были найдены Коши и оставались без применения. Он раз-
вивает эту интерпретацию в учение о движении вихрей, ко-
торое легло в основание современной гидродинамики.
Выяснилось весьма важное разделение движения жидкости
на невихревое и вихревое. Выяснились совершенно непра-
вильная погоня за общими интегралами уравнений гидроди-
намики и выдающаяся роль, которую в этой задаче играют
границы жидкости: стенки сосуда и свободная поверхность.
Здесь геометрическое толкование направило на верный
путь анализ, указывая, что соответственно пограничным
условиям должны быть подобраны и изучены функции, кото-
рые послужат для решения данной задачи.
Таким образом, конец нашего столетия ознаменовался
возвращением к геометрическому толкованию и соединением
аналитического метода исследования с геометрическим. Ме-
ханика сознательно пошла по тому пути, которого при своем
возникновении держалась по необходимости. При этом сбы-
лось желание, высказанное Ампером, и изучение движения
независимо от сил, его производящих, развилось в самостоя-
тельную—кинематическую часть механики, образуя звено,
соединяющее эту науку с геометрией.
Что в кинематике первое место принадлежит геометрии,
что в решении вопросов динамики геометрическое толкование
играет важную роль для удачной постановки задачи и разъ-
яснения смысла решения, найденного аналитическим путем- те-
перь признается всеми.
Но может ли геометрический метод служить к разрешению
новых — недоступных до сих пор задач динамики?
Я побоюсь дать решительный ответ на этот вопрос, но
укажу на данные, которые вселяют надежду на утвердительный
ответ.
Мы имеем много случаев, в которых геометрический метод
давал полное решение задач, диференциальное уравнение
которых удавалось свести к квадратурам и аналитическим
методам. Таковы: решение Ньютона о движении материальной
точки под действием центральной силы; решение Пуансо
° движении твердого тела по инерции; интерпретации Дарбу
184
РЕЧИ И ДОКЛАДЫ
для движения гироскопа и найденная Делоне интерпретация’
движения в задаче С. В. Ковалевской, в случае, когда чет-
вертый найденный ею интеграл распадается на два. К тому
же типу принадлежит и изящная интерпретация движения,
твердого те/а в жидкости, изложенная в сочинении Чаплыгина,
увенчанном в этом году премией Брашмана. Эта интерпретация
относится к так называемому случаю Вебера, при котором
существует четвертый алгебраический интеграл, и два остаю-
щихся интеграла находятся по принципу последнего множителя.
Но можно указать на случай, в котором получается полное
геометрическое решение задачи, хотя ее и не удалось свести
к квадратурам.
Таково движение тела, указанное Гессом, в котором
с аналитической стороны вопрос приводится к необинтегри-
рованному уравнению первого порядка.
Если присоединить к этому попытки некоторых ученых:
Софуса Ли, Дюбуа-Реймона и др. ввести геометрические
интерпретации в самую теорию интегрирования диферен-
циальных уравнений, то мысль о будущей самостоятельной
роли геометрии в решении недоступных до сих пор вопросов
динамики не будет казаться слишком смелой.
Как приближение к этой цели я могу указать на изыска-
ния частных решений недоступной задачи, в которых геомет-
рический метод особенно силен. Если бы нам удалось, напри-
мер, к немногим частным решениям задачи о трех телах
прибавить новые, то это познакомило бы нас ближе со свой-
ствами неизвестного движения, а может быть, и раскрыло бы
пути к его полному определению.
Отстаивая достоинства геометрического метода исследо-
вания, я далек от мысли об его исключительности. Механика
должна равноправно опираться на анализ и геометрию,
заимствуя от них то, что наиболее подходит к существу
задачи. Своими новыми методами: исследованием интегралов
по диференциальным уравнениям, изысканием признаков,
при которых«существуют алгебраические интегралы, и т. д.
анализ дает нам могущественное орудие для разрешения
задач динамики. Но последняя обработка решений задачи
всегда будет принадлежать геометрии.
О ГЕОМЕТРИЧЕСКОМ ИСТОЛКОВАНИИ В МЕХАНИКЕ 185
Геометр всегда будет являться художником, создающим
окончательный образ построенного здания.
Я перехожу к значению геометрического толкования при
преподавание механики. Если могут быть споры о самостоя-
тельной роли геометрии при решении недоступных до сих
пор задач динамики, то ее высокое значение в преподавании
механики не подлежит сомнению.
Ум изучающих весьма часто склонен к формальному по-
ниманию. Я из своего педагогического опыта знаю, как часто
запоминаются формулы без усвоения стоящих за ними обра-
зов. Как это ни кажется странным, но одним из затрудняющих
вопросов является иногда вопрос о значении той или другой
буквы в бойко написанной формуле.
В этом отношении геометрическое толкование, предпочте-
ние геометрического доказательства аналитическому всегда
приносит пользу.
Если формулы и подстановки некоторыми из изучающих
легко запоминаются, то так же скоро они исчезают бесследно
из памяти; но раз усвоенные геометрические образы, рисую-
щие картину рассматриваемого явления, надолго западают
в голову и живут в воображении изучающего.
Сравните, например, способы изложения теории притяже-
ния эллипсоидов, данные Шалем и Дирихле. Оба способа
одинаково прекрасны: один в области геометрии, другой
в области анализа. Который из них ближе ознакомит изучаю-
щего с рассматриваемой задачей?
Из способа Дирихле он узнает остроумный искусствен-
ный прием брать многократные интегралы, ничего общего
с притяжением эллипсоидов не имеющий; способ же Шаля
проведет его через теоремы Айвори, Маклорена и Лапла-
са, выясняющие существенные свойства рассматриваемого
явления.
Говоря о высоком значении геометрического толкования
для преподавания теоретической механики, не скрою, что не-
которые авторы геометрией злоупотребляют. Нагромождение
кинематических теорем, так же как и нагромождение формул,
только запутывает дело преподавания.
Геометрическое толкование должно быть ясно и просто и
186
РЕЧИ И ДОКЛАДЫ
должно всегда близко прилегать к рассматриваемой задаче,
стремясь к изучению вещей самих в себе.
Можно говорить, что математическая истина только тогда
должна считаться вполне обработанной, когдр она может
быть объяснена всякому из публики, желающему ее усвоить.
Я думаю, что если возможно приближение к этому идеалу,
то только со стороны геометрического толкования или моде-
лирования.
Моделирование стоит рядом с геометрическим толкованием
и представляет еще высшую степень наглядности.
Прежде думали, что прибегать к моделям следует только
при элементарном преподавании и что высшие науки, пред-
лагаемые изучающим высшего развития, не нуждаются
в [Этой степени наглядности. Но эта мысль едва ли спра-
ведлива, так как высшие науки часто являются очень слож-
ными и с накоплением научного метериала год от году
усложняются. Модель, удачно построенная, является хорошим
подспорьем даже и для разъяснения теоретического вопроса.
Томсон сказал, что явление только тогда может считаться
вполне понятным, когда мы можем представить его на мо-
дели. Согласно этому английские и германские профессора
все более и более начинают пользоваться при препода-
вании механики и математики моделями. Прошлой осенью
Соединенное немецкое математическое общество устроило
в Мюнхене выставку математических и механических мо-
делей.
По его примеру Московский университет устроил при
настоящем съезде русских естествоиспытателей выставку
своих механических моделей, которая была предложена вашему
благосклонному вниманию.
Московский университет всегда содействовал расширению
своих механических и геометрических коллекций, а Московское
математическое общество со вниманием рассматривало ; новые
приобретения механического кабинета, которые обыкновенно
демонстрируются в его заседаниях.
Я окончу мою речь приветствием этому Обществу, кото-
рое никогда не являлось односторонним и равномерно поощряло
аналитические и геометрические исследования, и выражением
О ГЕОМЕТРИЧЕСКОМ ИСТОЛКОВАНИИ В МЕХАНИКЕ
187
моего уважения перед Московским университетом, который
считаю главным рассадником геометрического знания в нашем
дорогом отечестве.
Эта речь была произнесена проф. Н. Е. Жуковским 9 января 1894 г.
на торжественном объединенном заседании Московского математического
•общества и IX Съезда русских естествоиспытателей и врачей, посвященном
двадцатипятилетию Московского математического общества. Речь была
-напечатана в „Математическом сборнике", т. 18. Прим. ред.
О ВОЗДУХОПЛАВАНИИ
(РЕЧЬ)
(1898,.)
Горячий защитник авиации 1 Д’Амекур (D Amecourt) в со-
чинении „Победа над воздухом с помощью винта" выставляет
следующий исходный пункт своих рассуждений: „Птица ле-
тает. Неужели мы не можем подражать ей?"
Действительно, глядя на летающие вокруг нас живые
существа: на стрижей и ласточек, которые со своим ничтож-
ным запасом энергии носятся в продолжение нескольких часов
в воздухе с быстротой, достигающей 50 м, и могут переле-
тать целые моря, на орлов, ястребов, которые описывают
в синем небе свои красивые круги с неподвижно распростер-
тыми крыльями, на неуклюжую летучую мышь, которая, не
стесняясь ветром, бесшумно переносится во всевозможных
направлениях, мы невольно задаемся вопросом: неужели для
нас нет возможности подражать этим существам?
Правда, человек не имеет крыльев и по отношению веса
своего тела к весу мускулов он в 72 раза слабее птицы;,
правда, он почти в 800 раз тяжелее воздуха, тогда как птица
тяжелее воздуха только в 200 раз. Но, я думаю, что он по-
летит, опираясь не на силу своих мускулов, а на силу своего
разума. Посмотрим же, что дала нам до сих пор эта надеж-
ная сила.
Я не имею времени изложить здесь весь обширный мате-
риал, представляющий постепенные завоевания в трудной
задаче воздухоплавания, и потому оставлю в стороне вопрос
о летании на,баллонах, тем более, что между моими слуша-
телями находятся известные русские исследователи в этой.
1 Динамический способ летания.
О ВОЗДУХОПЛАВАНИИ
189
области, которые с помощью обстоятельного изучения воз-
душных течений и умелого управления балластом сулят нам
возможность на надежном сферическом аэростате с громадной
скоростью ветра лететь в желаемом направлении.
Я оставлю также в стороне и вопрос об управляемых
удлиненных аэростатах. Скажу здесь только, что, по моему
мнению, вся трудность в их устройстве сравнительно с устрой-
ством морских судов заключается в громадной скорости ветров
сравнительно со скоростью водных течений. Я помню, как
мне казалось странным видеть в Интерлакене пароход, иду-
щий против течения клокочущего Ара, а ведь скорость этого
течения была не более 2 лг, в верхних же слоях атмосферы
ветры дуют со средней скоростью 10 м.
Если вообразим судно, вместимость которого равна объему
управляемого аэростата, то найдем, что на него можно по-
ставить двигатель в 770 раз тяжелее, а следовательно, и
в 770 раз сильнее, нежели на управляемый аэростат. Но зато
управляемый аэростат преодолевает сопротивление воздуха,
которое при той же скорости в 770 раз менее сопротивления
воды. В результате получаются равные условия.
Но в том то и дело, что от управляемого аэростата
требуется гораздо большая скорость, нежели от морского судна,
так как для возможности полета в любом направлении нужно
иметь скорость, превосходящую скорость ветра.
Направляемый аэростат, который построил Жиффар (Gif-
fard), имел скорость 2,5 м и не мог сопротивляться силе
ветра, дующего при его полете; то же случилось с аэроста-
тами, которые построили Дюпюи де Лом иТиссандье (Dupuy
de Lome, Tissandier), хотя они имели скорость около 3 м.
Только Ренар и Крэбс (Renard, Krebs), которые довели
скорость своего аэростата „La France" до 6 м, могли при
небольшом ветре совершить свой знаменитый полет с полным
возвращением на место отправления. Но при среднем ветре
эта скорость оказалась уже недостаточной.
Уменьшение веса двигателей, которое год от года все
более прогрессируется, позволяет надеяться на еще большее
Увеличение скорости управляемых аэростатов, и есть слухи,
что стены Медонского воздухоплавательного парка хранят
190
РЕЧИ И ДОКЛАДЫ
секрет аэростата со скоростью, значительно превосходящей
скорость аэростата „La France". Таким образом в этом на-
правлении мы приближаемся, хотя и медленно, к одному из
способов решения вековой задачи.
Но не это решение рисуется в нашем воображении, когда
мы следим за полетами окружающих нас живых существ. Нам
представляется летательная машина „тяжелее воздуха", кото-
рая не стесняется воздушными течениями, а несется в любом
направлении, утилизируя эти течения наподобие больших
птиц.
Об этой-то стороне воздухоплавательной задачи, которая
уже много лет живо интересует меня как механика, я и буду
иметь честь побеседовать с вами.
За последние десять лет разработка вопроса о динами-
ческом способе летания значительно подвинулась вперед:
были построены многие летательные машины и произведены
точные исследования над сопротивлением воздуха и полетом
птиц; основались многочисленные воздухоплавательные обще-
ства, из которых некоторые, как, например, Гамбургское
общество „Dadalos", посвятили свою деятельность исключи-
тельно авиации; появились многочисленные воздухоплаватель-
ные журналы, переполненные статьями по авиации. Вот какие
слова сказал проф. Больцман (Boltzman) в речи о воздухопла-
вании, произнесенной на съезде естествоиспытателей в Вене
в 1894 г.: „Несостоятельность прежних формул теперь ясно
обнаружена, и можно дать доказательство, что решение авиа-
ционной задачи не только возможно, но не заставит себя
долго ждать".
Посмотрим же,'как получается это доказательство на осно-
вании наблюдений над построенными летательными машинами.
Я позволю себе обратить ваше благосклонное внимание на
одну теоретическую мысль. Существуют два числа, характе-
ризующие достоинство летательной машины. Первое число
проф. Вельнер (Wellner) называет фиктивной скоростью паде-
ния. Оно дает нам количество килограммометров работы,
потребное на поддержание в продолжение 1 сек. каждого
килограмма летящего тела. При этом так как работа лошади
75 кгм, а вес среднего человека около 75 кг, то фиктивная
О ВОЗДУХОПЛАВАНИИ
191
скорость дает нам число лошадиных сил, потребных на под-
держание веса каждого аэронавта (при этом вес самой машины-
должен быть приравнен весу нескольких аэронавтов).
Если человек спускается с постоянной скоростью на пара-
шюте, то фиктивная скорость парашюта есть его действи-
тельная скорость падения.
Если же машина висит в воздухе, удерживаясь вращаю-
щимся винтом, то легко доказать, что фиктивная скорость
летательной машины равна половине скорости воздуха, отбра-
сываемого ею вниз Так как произведение нз массы бросае-
мого вниз воздуха на его вертикальную скорость равно весу
машины, то с уменьшением фиктивной скорости будет воз--
растать вес отбрасываемого вниз воздуха. Совершенная лета-
тельная машина бросает вниз возможно большее количество
воздуха с возможно меньшей скоростью. Затруднение состоит
в том, что эти два условия, говоря вообще, противоречивы.
Вращая, например, быстро винт с вертикальной осью, мы
бросаем им вниз большое количество воздуха, но и сообщаем
воздуху при .этом большую скорость. Надо или увеличивать
поверхность пропеллеров, или употреблять какие-нибудь
искусственные приспособления.
Один из существенных факторов, служащих к уменьшению
фиктивной скорости, заключается в сообщении воздухоплава-
тельной машине большой поступательной скорости. Это есть
знаменитый „принцип наклонной плоскости". Двигаясь под
малым углом к горизонту с большой горизонтальной ско-
ростью, наклонная плоскость сообщает громадному количе-
ству последовательно прилегающего к ней воздуха малую
скорость вниз и тем развивает большую подъемную силу
вверх при незначительной затрате работы на горизонтальное
перемещение.
Другое число, характеризующее достоинство воздухопла-
вательной машины, дает нам количество килограммометров
работы, которое надо затрачивать в 1 сек. на каждый кило-
грамм летящего груза и на каждый метр его горизонтальной
1 Для этого надо разделить работу, равную живой силе, иа подъемную
силу, равную количеству движения.
192
РЕЧИ И ДОКЛАДЫ
скорости. Это число получается через разделение фиктивной
скорости на горизонтальную скорость машины и есть, соб-
ственно говоря, число отвлеченное. Я буду называть его
коэфгщиентпом транспорта.
Для наклонной плоскости оба коэфициента уменьшаются
с уменьшением угла наклонения плоскости к горизонту и
с увеличением ее горизонтальной скорости. Но это справед-
ливо только до некоторого наивыгоднейшего угла. Ланглей
(Langley) нашел, что при испытуемых им моделях наклон-
ных плоскостей с заостренными краями наивыгоднейший угол
наклонения плоскости равен 2°, что дает коэфициент транс-
порта 0,03. Но если сделать большие планы из прутьев и
обтянуть их материей, то наивыгоднейший угол наклонения
плоскости увеличивается до 15°, а с ним увеличивается и
коэфициент транспорта до 0,26. Здесь на помощь воздухо-
плавательному делу является эффект вогнутости поддерживаю-
щих планов, который открыл Отто Лилиенталь (Otto Lilienthal).
Если план, имеющий небольшую вогнутость, обращенную
вниз, движется по горизонтальному направлению перпендику-
лярно к образующим плана, то он получает подвешивающую
силу даже и в том случае, когда стягивающая его хорда
горизонтальна или слегка наклонена навстречу движению.
Коэфициент транспорта при этом близок к нулю. Венский
профессор Max (Mach), открывший способ фотографирования
воздушных струй, сделал ряд интересных фотографий с пря-
мыми и изогнутыми пластинками, помещенными в потоке
воздуха.
Из этих фотографий видной что воздух образует в вогну-
той части пластинки вихрь, который сверху прикрыт пластин-
кой и отбрасывает действием центробежной силы частицы
воздуха книзу, что и дает подъемную силу вверх. Известный
строитель змеев Хэргрэв (Hargrav), обращая внимание на то,
что в вихре всегда находится разреженный воздух, сравни-
вает подъемную силу потока на вогнутую пластинку с дей-
ствием маленького баллона с разреженным газом, подложен-
ного под пластинку. Вероятно, значительная экономия работы
при летании птицы имеет одной из причин эффект вогнутости
ее крыльев.
О ВОЗДУХОПЛАВАНИИ
193
Рассмотрим теперь различные построенные летательные
машины. Еще акад. Бабине (Babinet) разделил летательные
машины на три класса: геликоптеры, ортоптеры и аэропланы.
Первые получают свою подвешивающую силу действием винта,
вторые — ударами крыл, а третьи — от несущейся по гори-
зонтальному направлению наклонной плоскости.
Физиолог Рони (Rauny) и механик Бьенвеню (Bienvenu)
построили впервые маленький геликоптер, в котором два
винта, сделанные из перьев и пробки, приводились в движение
лучком наподобие доели. Эту игрушку впоследствии усовер-
шенствовал Пэно (Penaud), заменив винты из перьев двухло-
пастными винтами из шелковой материи, а лучок—скрученной
резиной. Оба упомянутых геликоптера имели устойчивый
полет и поднимались на значительную высоту.
Геликоптер, приводимый в движение маленькой паровой
машиной, устроил Форланини (Forlanini). Он летал, унося
с собой машину и котелок, но печки при этом котле не было,
и он действовал запасом пара, который получал, будучи по-
мещен прежде в жаровню.
Горячие защитники геликоптера: Надар, д’Амекур, Бабине
и Ландель (Nadar, d’Amecourt, Babinet, Landelle), не могли
построить проектируемый ими воздушный корабль, и проект
их послужил только как материал для известного рассказа
Жюль Верна. Маленькая же модель, которую построил д’Аме-
кур, дала при испытании удовлетворительные результаты.
Над всеми упомянутыми аппаратами, насколько мне известно,
не производилось точных измерений. Такие измерения недавно
произвел над большими винтами с вертикальной осью про-
фессор Вельнер в Бруне с целью построения геликоптера,
могущего поднимать воздухоплавателя. Проф. Вельнер поль-
зовался винтами, которые имели в диаметре 6 м и в площади
13 м2. Они приводились в движение паровой машиной в 4 л. с.
со скоростью 160 об/мин. Получалась наибольшая подъемная
сила 65 кг при скорости на окружности винта 40 м. Разделяя
работу 300 кгм на подъемную силу 65 кг, находим для рас-
сматриваемого случая фиктивную скорость 4,6 м. Этот резуль-
тат объясняет нам неуспех с так называемым „воздушным
велосипедом" Дельпра. Для того чтобы поднять свой вес,
Зак. 2430. Н. Е. Жуковский. Том IX
13
194
РЕЧИ И ДОКЛАДЫ
не считая веса аппарата, Дельпра должен бы работать с силой
4 6 лошади, что далеко превосходит ресурсы человека.
Надо полагать, что найденный коэфициент подвешивающей
силы геликоптера уменьшится при поступательном горизон-
тальном движении его, как это доказывает Карос (Karos)
в одном из последних номеров журнала „Luftschiffahrt"; Но
вопрос этот, к сожалению, не исследован с опытной стороны;
также не определен и коэфициент транспорта геликоптеров.
Эти исследования заслуживают внимания, так как за геликоп-
тером всегда будет оставаться преимущество безопасного
подъема и спуска.
Я думаю, что к геликоптерам должно быть отнесено и воз-
душное колесо с горизонтальной осью, которое построил
проф. Вельнер. Оно получает поступательное движение вдоль
оси от действия винтовых выступов на своих лопатках, а под-
вешивающую силу вследствие малых поворотов лопаток при
вращении колеса от действия эксцентрика, что вызывает поток
воздуха вниз.
Проф. Вельнер пека еще не мог осуществить проекта
летательной машины с воздушными колесами, но сделанная им
модель колеса дала при испытании удовлетворительные ре-
зультаты. Модель приводилась в движение машиной в 1,33 л. с-
Шесть лопаток ее имели площадь 12 л/2 и при скорости вра-
щения 15 м давали подъемную силу 43 кг.
Отсюда получается фиктивная скорость 2,32. Таким обра-
зом воздушное колесо действует совершеннее обыкновенного
винта. Но выполнение этого воздушного колеса в больших
размерах имеет конструктивные трудности, что и заставило
его изобретателя сосредоточить теперь свое внимание на обык-
новенных геликоптерах.
Переходим к классу ортопгерных машин.
Маленькие механические птицы были построены Пэно,
Гюро де Вильнев (Hureau de Villeneve) и Пишанкуром (Pi-
chancourt). Они приводились в движение скрученной резиной
и имели шелковые крылья, способные прогибаться с задней
стороны. Птицы эти летали горизонтально при сообщении им
небольшой поступательной скорости рукой или при падении
с руки вниз. При опущении крыло выгибалось с задней своей
О ВОЗДУХОПЛАВАНИИ
195
стороны и давало птице подвешивающую силу и силу для
горизонтального перемещения, а при подъеме оно сохраняло
под собой сжатый воздух вследствие горизонтальной скорости
и давало птице только подвешивающую силу.
Наиболее совершенной по конструкции является птица,
которую устроил Пишанкур и в которой имеется остроумный
механизм для поднятия обоих крыл под одинаковыми углами.
Довольно большая модель этой птицы находится в механи-
ческом кабинете Московского университета.
Труве (Trouve) построил стальную птицу, которая приво-
дилась в движение пороховыми взрывами, направляемыми осо-
бым револьверным барабаном в трубку Бурдона. От действия
взрывов трубка Бурдона раскрывается и дает энергичные
удары крыл. Эта птица делала 12 энергичных ударов
крыл и пролетала по горизонту 80 м. По числам, кото-
рые дает Труве, находим для его летательной машины фик-
тивную скорость 1,5.
Большая ортоптерная машина, которую сделал Хэргрэв,
весила 2 кг и имела площадь 2,3j л/2. Она приводилась
в движение машиной, работающей сжатым воздухом и разви-
вающей секундную работу 4,4 кгм. Эта птица имела непо-
движную парусность и веслообразные крылья, к концам кото-
рых были приделаны иглицы из китового уса, так что крылья
с своей задней стороны могли прогибаться. Аппарат при при-
ведении крыл в движение снимался с своей подстановки
и пролетал по прямой линии пространство 103 м в 23 сек.,
т. е. имел среднюю скорость 4,5 м. По указанным данным
находим фиктивную скорость 1 и коэфициент транспорта 0,22.
Самую большую механическую птицу построил Штенцель
(Stenzelt) в Гамбурге. Она имела стальной каркас, покрытый
батистом, пропитанным каучуком. Расстояние между кон-
цами раскрытых крыл было 6,3 м при ширине крыл 1,5 м.
Вместе с двигателем, действующим сжатой угольной кислотой,
птица весила 34 кг. В ней, так же как в птице Пишанкура,
широкие эластические крылья прогибались с своей задней
стороны. При надлежащем числе ударов крыл (3 удара
в 2 сек.) птица, подвешенная к проволоке, теряла весь свой
вес и двигалась вдоль проволоки со скоростью 6 м. При этом
13'
196
РЕЧИ И ДОКЛАДЫ
двигатель развивал секундную работу 120 кгм. Это дает нам
фиктивную скорость 3,5 м и коэфициент транспорта 0,58.
Насколько мне известно, Штенцель еще не достиг полной
устойчивости своей летательной машины в воздухе, и она не
делала свободных полетов.
Все вышеописанные ортоптерные аппараты были построены
по образцу птиц; но недавно майор Мур (Moore) построил
ортоптер по образцу летучей мыши. Мур много занимался
изучением полета больших индийских летучих мышей и нашел,
что они принадлежат к хорошим летателям и достойны под-
ражания. Он устроил модель, которая имела длину крыл
0,6 м и уносила с собой электромотор, сообщающий прямо-
колебательные движения, и питающую его батарею. Эта
машина имеет наименьшую достигнутую фиктивную скорость
0,74 и является таким образом значительно совершеннее птицы
Штенцеля. Другая летательная машина Мура имела длину
крыл 1,3 м и дала фиктивную скорость 1 м. Это обстоя-
тельство показывает, что с увеличением размеров машины
фиктивная скорость возрастает.
Нам остается еще рассмотреть третий класс летательных
машин.
Существует древний миф о человеке, летающем на стреле
по воздуху. Я думаю, что этот миф очень близко подходит
к основной идее аэроплана. Аэроплан есть та же стрела,
быстро несущаяся по воздуху под малым углом наклонения
к направлению своего движения.
Прежде рассмотрим аэропланы без двигателя, которые те-
перь принято называть скользящие летательные машины.
Уже с давних времен делались различными аэронавтами
попытки опускаться с помощью планов с высоты против ветра
по наклонной линии к горизонту. Но все эти попытки пред-
ставлялись одиночными случаями, оканчивавшимися по боль-
шей части катастрофами. Человек, разработавший с теорети-
ческой и практической стороны вопрос о скользящих лета-
тельных машинах, был знаменитый немецкий воздухоплаватель
Отто Лилиенталь. В продолжение трех лет сделал он около
1000 полетов, летая иногда на высоте 20 м и пролетая по
горизонтальному направлению 250 м. Он пал жертвой своего
О ВОЗДУХОПЛАВАНИИ
197
неудержимого рвения к разрешению воздухоплавательной за-
дачи. Лилиенталь изучил на практике способы регулирования
аппарата на ветре и стремился к практическому усвоению
приемов парения по воздуху наподобие орлов. Если бы ран-
няя смерть не похитила этого борца за науку, то он еще
более приблизил бы нас гк решению вековой задачи в одной
из ее существенных сторон: полета по воздуху за счет работы,
скрытой в неравномерности ветров. Ланглей исследовал с по-
мощью чувствительного анемометра пульсации в скорости
ветра и разъяснил, каким образом, пользуясь этими пульса-
циями, можно двигаться против ветра, приобретая высоту. Для
этого надо на скользящей летательной машине опускаться
вниз, когда ветер ослабевает, и подниматься вверх, когда он
усиливается. Пульсации ветра удалось недавно прямо наблю-
дать исследователю авиации Ляпуант (Lapointe). Он пишет,
что видел сноп электрического света, проникающий ночью
через мелкий дождь, несомый ветром, и мог ясно заметить
волнообразное движение дождя с амплитудой около 2 м и со
скоростью волны около 5 м. По всей вероятности, такие пуль-
сации ветра позволяют морской чайке, качаясь на воздухе
с распростертыми крыльями, двигаться против ветра без вся-
кой потери энергии, как это прекрасно описывает Шанют
(Chanute). К тому же, согласно теоретическим исследованиям
Гельмгольца, над морской волной должна непременно бежать
воздушная волна.
Еще при жизни Лилиенталя у него были усердные подра-
жатели в Америке: Хэринг и Пилчер (Herring, Pilcher). Фа-
тальная смерть изобретателя скользящей летательной машины
не устрашила американских исследователей воздуха, и к ним
присоединились еще Эвери (Avery) и Шанют. В выдающемся
аэромеханике Шанюте заветы покойного Лилиенталя нашли
достойного преемника. Он построил ряд скользящих лета-
тельных машин, отличающихся устойчивостью и компактной
конструкцией.
Полеты, которые он делал в соучастии с Хэрингом и Эвери,
тщательно исследовались, и все нужные величины измерялись.
Оказалось, что на новых аппаратах можно скользить под
углом 8° к горизонту со скоростью, достигающей 7,5 м по
198
РЕЧИ И ДОКЛАДЫ
горизонтальному направлению и 0,76 м пэ вертикальному. Эта
последняя скорость 0,76 м и будет фиктивной скоростью,
а коэфициент транспорта будет 0,05, принимая скорость ветра
равной 7 м.
Проф. Вельнер указывает, что птица имеет фиктивную ско-
рость 0,75; мы видим, что такова же фиктивная скорость сколь-
зящей машины.
Херинг занят теперь присоединением к скользящей лета-
тельной машине легкого двигателя. Я думаю, что путь иссле-
дования задачи воздухоплавания с помощью скользящей лета*
тельной машины является одним из самых надежных. Проще
прибавить двигатель к хорошо изученной" скользящей лета-
тельной машине, нежели сесть на машину, которая никогда не
летала с человеком.
Я не стану утомлять вас, излагая в историческом порядке
различные конструкции аэропланов, так как маленький аэро-
план Брэри (Breury), приводимый в движение гребным винтом
с помощью скрученной резины, был, пожалуй, единственным,
имевшим хороший прямолинейный полет. Многие другие аэро-
планы, построенные в прежние времена, или не летали совсем,
или не имели надлежащей устойчивости, как аэроплан Татэн
(Tatin).
Большие аэропланы удалось осуществить только в послед-
ние годы благодаря открытию средств, служащих для увели-
чения подъемной силы аэроплана и его устойчивости. Увели-
чение подъемной силы без увеличения размеров летательной
машины достигается устройством многоэтажных аэропланов,
как это предложил Стрингфлоу (Stringfflow), и посредством
сообщения подъемным планам вогнутости вниз по системе
Лилиенталя. Устойчивость получается через присоединение
к аэроплану хвоста на длинном стержне и через расположе-
ние в одном горизонте двух или четырех планов, так чтобы
получился незанятый планами промежуток, пересекающий ось
аппарата, как это впервые сделал Броун (Brown).
Инж. Кресс (Kress), пользуясь принципами,"которые уста-
новили Броун и Лилиенталь, построил ^небольшой аэроплан
весом в 0,6 кг, приводимый в движение двумя гребными вин-
тами от действия скрученной резины. Этот аппарат, названный
О ВОЗДУХОПЛАВАНИИ
199
аэровелос, имел большую устойчивость и летел прямо со стола
по прямой линии. Он был демонстрирован в 1894 г. в Вене
во время речи проф. Больцмана и пролетел чрез всю залу.
По цифрам, которые дает Кресс, его прибору следует при-
писать фиктивную скорость 1,6 и коэфициент транспорта 0,05.
Весной этого года в Венском воздухоплавательном обществе
образовалась подписка в 12000 fl. для образования капитала
на построение аэровелоса, могущего поднять двух аэронавтов.
Другая модель аэроплана, давшая хорошие результаты, при-
водилась в движение реакцией струи угольной кислоты, испа-
ряющейся в аппарате. Ее построил Гофман (Hofmann) в Бер-
лине. Она имела два боковых плана по 0,5 м ширины и со-
храняла устойчивость благодаря присоединению к ней, кроме
хвоста, еще переднего руля. По расчету, который делает
Гофман, коэфициент транспорта его летательной машины дол-
жен бы быть 1/1Б.
Обращаемся к описанию больших аэропланов, приводимых
в движение паровыми машинами.
Летательная машина, которую сделал Филиппе (Philipps),
поддерживается в воздухе целой системой тонких планов, рас-
положенных наподобие жалюзи. Она имеет вес 148 кг и по-
лучает начальную скорость от неподвижной паровой машины,
которая катает аппарат по круговым рельсам. Когда желае-
мая скорость достигнута, то аппарат делается свободным
и летит, поддерживая свое движение гребным винтом, вращае-
мым паровой машиной, поставленной на летательном аппарате.
Аэроплан этот не имел достаточной устойчивости и летал
на небольшое расстояние.
Самый тяжелый аэроплан построил Максим (Maxim). Аппа-
рат вместе с тремя аэронавтами весил 3600 кг и приводился
в движение двумя гребными винтами, вращаемыми легким
двигателем в 300 л. с. Вес машины и трубчатого котла, на-
полненного водой, на каждую лошадиную силу составлял
2,25 кг (но сюда надо прибавить питательную воду вследствие
неудачи проектируемой конденсации воздушным потоком).
Подвешивающая сила машины развивалась планами, располо-
женными в 4 этажа и имеющими общую площадь 360 лр,
а устойчивость удерживалась посредством перестановок хвоста
200
РЕЧИ И ДОКЛАДЫ
и двух боковых рулей, которыми должны управлять три
аэронавта.
Так как эта сторона дела была мало обеспечена, то Ма-
ксим не рискнул предоставить своей машине свободный полет,
а пускал ее только по рельсам, причем каждое колесо было
помещено между двумя рельсами и могло катиться или по
нижнему, или по верхнему рельсу.
При скорости 15 м, которая развивалась при действии
300 л. с-, летательная машина теряла весь свой вес. Отсюда
следует, что для фиктивной скорости ее надо взять 6,2 м,
а для коэфициента транспорта 0,4. Числа эти невыгодны.
К аэропланам больших размеров следует также отнести
аэроплан, который начал строить Адер (Ader) еще в 1891 г.
и который он теперь усовершенствовал. Есть слухи, что при-
бор этот дает хорошие результаты.
Первым большим аэропланом, давшим свободный полет
с полным сохранением устойчивости, является аэродром, ко-
торый построил Ланглей. Он весил 13 кг и имел 4 шелковых
крыла на стальном каркасе, по 2 м каждое. Его гребные двух-
лопастные винты были поставлены между планами и приво-
дились во вращение паровой машиной в 1 л. с., при которой
имелся маленький запас воды и топлива на 5 мин. Прибор,
пробежав по рельсам, установленным на крыше пловучего
домика, приобретал надлежащую скорость и пролетал по пря-
мому направлению против слабого ветра в 1 мин. 46 сек.
пространство 1600 м, т. е. он имел среднюю скорость 15 м.
К этой скорости надо прибавить скорость ветра, которую
примем равной 5 м. Тогда по имеющимся данным найдем для
аэродрома Ланглея фиктивную скорость 5,8 м и коэфициент
транспорта 0,3 (этому коэфициенту соответствует угол накло-
нения планов к горизонту около 16°).
Правда, эти числа не дают желаемой экономии в работе,
так как из них следует, что перемещение по горизонтальному
направлению требует столько же работы, сколько нужно для
поднятия ’/з всего веса по вертикальному направлению.
Но при первых шагах в решении задачи экономия стоит
на втором плане. Нам нужно только иметь устойчивый полет
со скоростью, превосходящей скорость ветров, а этому аэро-
О ВОЗДУХОПЛАВАНИИ
201
дром Ланглея вполне удовлетворяет. Защитник управляемых
аэростатов, инж. Соро (Soreau), высказал в своей недавно
появившейся книге сожаление, что знаменитый Ланглей посвя-
тил себя решению авиационной задачи. Я не могу здесь не
высказать моего удовольствия по тому же поводу. Глубокие
исследования Ланглея по сопротивлению воздуха и по авиа-
ции дают нам ту опорную силу человеческого разума, о кото-
рой я упомянул в начале речи. Ланглей разрешил практи-
чески вопрос об устойчивости больших аэропланов; Максим же
показал, какую значительную подъемную силу может нам дать
летательная машина. Соединение этих двух результатов утвер-
ждает нас в справедливости слов, сказанных в речи проф-
Больцмана.
Но в какой форме осуществится летательный аппарат, на:
котором в первый раз полетит человек? Будет ли он подо-
бие аэродрома Ланглея или аэровелоса Кресса? Будет ли это
геликоптер или-ортоптерная машина? Выгода ортоптерной ма-
шины намечается малыми величинами коэфициентов в машинах
Труве, Хэргрэва, Мура. Может быть, изучение действия крыл
в связи с эластичностью воздуха, о чем писали Якоб и Жи-
рардвиль (Jacob, Girardville), а также и я имел честь сделать
доклад в Русском техническом обществе, откроет нам новый
принцип, облегчающий летание. Может быть, скользящая ле-
тательная машина, которая, как мы видели, при хорошем
устройстве дает фиктивную скорость, почти равную фиктив-
ной скорости птиц, из машины, медленно опускающейся вниз,
разовьется при прибавлении двигателя в машину, летающую
в любом направлении, причем двигатель будет служить для
нее только в известные моменты времени, а главный источник
работы будет заимствоваться из силы ветра. Кому суждено
знать будущее! Но внимательный наблюдатель прогресса авиа-
ции не может не заметить, что мы приближаемся с разных
сторон к решению великой задачи, и, может быть, новый век
увидит человека, свободно летающего по воздуху.
Впрочем, по имеющимся теперь данным нельзя ожидать
осуществления мечты Лендаля о большом воздушном корабле,
несущемся с массой пассажиров. Вы заметили, что фиктивная
скорость у машин больших размеров более, а это требует
202 РЕЧИ И ДОКЛАДЫ
для них уменьшения веса двигателя на каждую лошадиную
силу. Согласно теории подобия Гельмгольца увеличение ма-
шины в 4 раза, не изменяя коэфициент транспорта, увеличи-
вает ее фиктивную и действительную скорость в 2 раза.
Для управляемого аэростата фиктивная’скорость не имеет
значения, а коэфициент транспорта для аэростата „La France",
например, был около !/16. С увеличением размеров управляе-
мого аэростата будет при сохранении коэфициента транспорта
увеличиваться горизонтальная скорость, и потому такая ма-
шина, может быть, будет служить в будущем для транспорта
пассажиров. Машина же более тяжелая, нежели воздух, даст
нам, по моему мнению, средство для быстрого полета одного
или двух человек в любом направлении и заставит нас пе-
рестать завидовать птице.
Эта речь была произнесена проф. Н. Е. Жуковским 25 августа 1898 г.
на общем собрании X Съезда естествоиспытателей н врачей в Киеве; речь
была впервые напечатана в „Трудах Отделения физических наук Общества
любителей естествознания”, т. IX, вып. 2, 1898, н вторично в „Бюллетене
Московского общества воздухоплавания", № 1—2, 1910. Прим. ред.
МЕХАНИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ
ЗА ПОСЛЕДНЕЕ ПЯТИДЕСЯТИЛЕТИЕ
(РЕЧЬ)
(1911 г.)
Когда человек прошел уже большую часть своего жизнен-
ного пути, тогда перед его умственным взором невольно
встает то, что составляло главное содержание его жизни.
Для меня главный жизненный интерес сосредоточен на излю-
бленной мною науке — механике, поэтому я и назвал свою
сегодняшнюю речь „Механика в Московском университете за
последнее пятидесятилетие". Я хочу воскресить перед вами
образуя моих незабвенных учителей и поговорить с вами об
ученых трудах моих дорогих товарищей и учеников. Я посту-
пил в Московский университет в 1864 г. Этот год совпал
с годом оставления профессорской службы Николаем Дмит-
риевичем Брашманом. Мне не пришлось его слушать, но
от моего покойного товарища Федора Евпловича Орлова я
очень много слышал о Брашмане. Н. Д. Брашман был человек
большой эрудиции, с живым интересом следивший за разви-
тием математики. К своим ученикам, особенно к даровитым,
он относился с чрезвычайным вниманием. Он приглашал
их к себе для бесед по математике и механике. Из этих
собраний в 1864 г. под руководством Н. Д. образовался мате-
матический кружок, который явился зерном Московского мате-
матического общества. Брашман занимал кафедру механики
в Московском университете в продолжение 30 лет и им зало-
жены первые научные основы преподавания этого предмета. Он
написал несколько ученых трудов: „О молекулярных силах ,
„Определение давления реки на берег", „О начале наимень-
шего действия". Первая из этих работ была им доложена на
заседании британской ассоциации, причем ему пришлось делать
204
РЕЧИ И ДОКЛАДЫ
доклад вместе с геометром Якоби и получить от астронома
Гершеля одобрение. При этом знаменитый астроном сказал:
„незадолго еще мы считали бы математический реферат на
русском языке явлением необыкновенным, но науки подви-
гаются вперед, и успехи России изумительны".
Работа Брашмана „О начале наименьшего действия" на-
писана под влиянием Остроградского и Лагранжа. Творениями
Лагранжа Н. Д. весьма увлекался, но тогда воззрения Лагранжа
еще не представлялись столь простыми. Надо согласиться,
что Остроградский, который ввел в представление о пере-
мещениях идею времени, затруднил изложение метода Ла-
гранжа. Я слышал от учеников Брашмана, что понимание метода
при его изложении было трудно. Существует известный рас-
сказ, что Брашман, говоря о начале наименьшего действия,
признавался, что когда он размышляет об этом вопросе утром,
то ему кажется, что Лагранж прав, а когда размышляет вече-
ром— что Остроградский прав.
Во время моего пребывания в университете лекции по
механике параллельно вели Ф. А. Слудский и В. Я. Цингер,
причем последний дочитывал механику старшему курсу, и
потом уже все чтение перешло к Ф. А. Слудскому. Мы все
время слушали лекции Ф. А. Слудского. В сжатом и ясном
изложении он охватил методом Лагранжа всю теоретиче-
скую механику. Ему обязаны мы легким усвоением этого
метода. Он разъяснил все сомнения, высказываемые Браш-
маном.
В первых томах „Математического сборника" помещен ряд
статей русских ученых: Остроградского, Сомова, Соколова и
Слудского о начале наименьшего действия, и Ф. А. Слудскому
принадлежит полное разъяснение вопроса. Он показал, что
начала в форме Лагранжа и в форме Остроградского пред-
ставляют две различные теоремы, причем начало Остроград-
ского есть теорема Гамильтона. Мне иногда приходилось
посещать и лекции по механике В. Я. Цингера. В них высту-
пал на первый план геометрический элемент. Я помню его
прекрасное изложение теоремы Давидова о 12 положениях
равновесия трехгранной призмы и теории притяжения эллип-
соидов по способу Гаусса.
МЕХАНИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ ЗА 50 ЛЕТ 205
Мое пребывание в университете совпало со временем
защиты диссертаций наших учителей, и большинство этих дис-
сертаций относилось к гидромеханике. Еще раньше А. Ю. Дави-
дов написал две прекрасные работы по равновесию плавающих
тел и по капиллярности. Ф. А. Слудский защищал при нас
свою докторскую диссертацию „Движение жидкости при взаимо-
действии частиц", а В. Я. Цингер свою докторскую диссер-
тацию „Вращательное движение жидкого эллипсоида с измене-
нием вида". На меня особое впечатление произвела последняя
работа. Стремление ученого дать детальный образ рассматри-
ваемого движения, указать, как видоизменяется каждая частица
движущейся жидкости, мне очень понравилось, и, можеть быть,
эта работа натолкнула меня на мое первое сочинение „Кине-
матика жидкого тела". Я с благодарностью вспоминаю теперь
двух моих учителей, из которых один разъяснил^нам широкое
значение общих аналитических метод, а другой — указал силу
геометрических толкований рассматриваемых явлений. Но,
несмотря на то, что Ф. А. Слудский был по характеру ана-
литиком, его главной задачей в научных исследованиях всегда
являлось решение определенных задач механики, что сказа-
лось во многих из его сочинений: „О равновесии трехгранной
призмы", задача „О многих телах", '„О колебании центра
тяжести тяжелого тела" и т. д., а также и в его капитальных
работах по высшей геодезии. Мне кажется, что этот девиз —
решение определенных реальных задач механики — явился
руководящим для большинства учеников московской школы
теоретической механики. Учениками Ф. А. Слудского, посвя-
тившими себя исследованиям в области теоретической меха-
ники, были мои покойные товарищи Владимир Васильевич
Преображенский, Ипполит Степанович Громека и я, и все мы,
по примеру наших учителей, начали заниматься гидромехани-
кой. В. В. Преображенский напечатал в „Математическом сбор-
нике" статью „О движении жидкой площади и, вернувшись
из заграничной командировки, сделал на Казанском съезде
естествоиспытателей и врачей доклад „Об определенности за-
дач гидродинамики". Этот доклад по тогдашнему времени
пролил много света на решение гидродинамических задач.
Из него стало ясным, что движение жидкой массы управляется
206
РЕЧИ И ДОКЛАДЫ
свободной поверхностью и что силы, действующие на капель-
ную жидкость в замкнутом сосуде, никакого влияния на ее
движение не имеют. Теперь все это так просто, но тогда
вопрос о том, что уравнения гидродинамики при данных
начальных и граничных данных вполне определяют движение
жидкости, подлежал сомнению, и А. Ю. Давидов при защите
своей диссертации даже поставил тезис: „Уравнения гидро-
динамики недостаточны". В. В. Преображенский получил место
профессора математики в Одессе и написал магистерскую
диссертацию по чистой математике, но его докторская дис-
сертация „О логарифмическом потенциале" имеет тесную
связь с вопросами о плоскопараллельном движении жид-
кости.
Работы профессора Казанского университета Ипполита
Степановича Громеки, к сожалению, мало известны, а между
тем в них разрешаются многие вопросы гидромеханики. Он
дал оригинальное изложение теории капиллярных явлений,
исследовал движение вихрей на сфере, исследовал движение
жидких капель, движение вязкой жидкости в трубках, причем
нашел интересный тип движения жидкости, который он назвал
винтовым. Некоторые из теорем об установившемся движении
жидкости, обыкновенно приписываемые Ламбу, раньше най-
дены проф. Громекой. Сраженный тяжким недугом, он перед
самой смертью прислал в „Математический сборник" статью
о распространении звуковой волны в неравномерно нагретой
жидкости.
Мои главные работы по гидромеханике представляют три
статьи: „Кинематика жидкого тела", „Движение твердого тела
с целостями, наполненными жидкостью" и „Видоизменение
метода Кирхгоффа". Во всех своих работах я стремился нари-
совать картину движения — дать его отчетливый геометриче-
ский образ. Многие из разрешенных мной вопросов были
впоследствии развиты Вольтерра, Гринхилем и Митчелем. Но
в мое время дело не представлялось столь простым, и я могу
ставить себе в заслугу: исследование критических точек нуле-
вой скорости, разъяснение динамических эффектов жидкости,
наполняющей полости движущегося тела, и установление
способа, позволяющего в струйной теории Кирхгоффа при-
МЕХАНИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ ЗА 50 ЛЕТ 207
способляться к заданному числу струй и критических
точек.
Мой покойный учитель Ф. А. Слудский был особенно дово-
лен установленной мной теоремой о том, что жидкость
с трением, заполняющая полость движущегося твердого тела,
заставляет мгновенную ось его вращения приближаться
к главной оси инерции всей движущейся массы.
Мне приятно теперь отметить мои совместные работы
с профессорами Московского университета, в число которых я
имел честь вступить в 1887 г. Ф. А. Бредихин охотно вводил
меня в различные интересующие его в то время вопросы.
По его указанию мной были написаны статьи: о колебании
штатива оборотного маятника, об очертании кометных хво-
стов, о движении атмосферы на Юпитере. В Математическом
обществе я имел удовольствие делать сообщение вместе
с Б. К. Млодзеевским по вопросу об огибающих траекторий
планет. Б. К. Млодзеевский всегда живо интересовался задачами
механики и напечатал на эту тему статьи: „О перманентных
осях в задаче Штекеля", „Об определении орбит двойных
звезд". Он являлся вместе со мной постоянным оппонентом
при защите диссертаций по механике. Вместе с П. А. Некра-
совым я имел удовольствие разрабатывать задачу о движении
тяжелого твердого тела в случае Гесса. На заседаниях Мате-
матического общества анализ переплетался с геометрическими
исследованиями, и в результате получалась отчетливая кар-
тина рассматриваемого сложного явления. Упомянув здесь
о динамике твердого тела, я не могу не вспомнить жену про-
фессора Московского университета — знаменитую С. В. Кова-
левскую. Я имел удовольствие впервые познакомиться с ней
на Одесском съезде естествоиспытателей и врачей, где она
делала доклад о волне Френеля. О ней сохранилось у меня
самое отрадное воспоминание. Живая и жизнерадостная, она
с одинаковой охотой говорила и о математике и о прогулках
по морю. Впоследствии ей удалссь разрешить одну из недо-
ступных до нее задач механики и присоединить свое имя
к именам великих геометров Пуансо и Лагранжа. Ею найден
был так называемый третий случай в задаче о движении
тяжелого твердого тела около неподвижной точки, в кото-
208
РЕЧИ И ДОКЛАДЫ
ром интегрирование уравнений движения является воз-
можным.
За детальную разработку задачи Ковалевской взялись меха-
ники московской школы. Н. Б. Делоне указал на интересный
случай, в котором движение получает простой вид. Этот случай
был подробно исследован Г. Г. Аппельротом, которому удалось
в прошлом году найти еще второй случай в задаче Ковалевской,
допускающий решение в простых трансцендентных. Мне
удалось дать геометрическую картину общего вида рассматри-
ваемого движения и указать значение одной системы криво-
линейных координат, которая им управляет. Мой способ иссле-
дования был впоследствии несколько упрощен тулузским про-
фессором Таненбергом. Таким образом новый случай в задаче
о движении тяжелого твердого тела почти всецело исследован
русскими учеными, и мы можем теперь с некоторым правом
повторить слова Гершеля, сказанные Брашману: „Науки бы-
стро подвигаются вперед, и успехи России изумительны". Я
уже начал говорить о работах по механике моих дорогих
учеников. Буду продолжать об этом.
Рядом с задачей о движении тяжелого твердого тела при
произвольном толчке стоит задача о частных видах движения,
при которых начальный толчок стеснен некоторым условием
и форма тела Определенная. К таким задачам принадлежит
упомянутый мной случай Гесса. Д. Н. Горячеву вместе
с С. А. Чаплыгиным удалось найти интересный по своей про-
стоте новый случай упомянутого движения, который вместе
со случаями, найденными Д. К. Бобылевым, В. А. Стекловым
и Г. В. Колосовым, пополняет богатый материал по динамике
твердого тела. Этот материал еще расширяется работами
С. А. Чаплыгина по движению катящегося по плоскости
тяжелого твердого тела и работой Е. А. Болотова об ударе
тел с трением. В последнем сочинении дается геометрическое
разъяснение различных парадоксов, указанных Пенлеве, Ле-
корню и др.
Я перейду теперь к задаче о движении по инерции твердого
тела внутри несжимаемой жидкости. Эта задача ввиду богатства
форм допускаемых движений живо заинтересовала меня, когда
я в качестве приват-доцента начал свои лекции в Московском
МЕХАНИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ ЗА 50 ЛЕТ 209
университете чтением специального курса гидродинамики.
При напечатании этого курса я высказал некоторые сообра-
жения о постановке этой задачи с геометрической точки зре-
ния. За разрешение этой задачи взялся тогда еще начинавший
свою ученую деятельность С. А. Чаплыгин и в двух своих
прекрасных работах показал, какой силой могут обладать
остроумно поставленные геометрические методы исследова-
ния. Ему удалось в случаях Клебша и Кирхгоффа дать такие
же простые геометрические интерпретации, какие дал Пуансо
для движения по инерции в пустоте. Если прибавить к этому
результаты, полученные впоследствии в рассматриваемой за-
даче В. А. Стекловым, А. М. Ляпуновым и Г. В. Колосовым,
то можно сказать, что и в разработке вопроса о движении по
инерции твердого тела в жидкости русские ученые занимают
видное место. Мой дорогой товарищ С. А. Чаплыгин пополнил
исследования своего учителя еще другой работой. Ему удалось
метод исследования струй распространить на газовые струи.
При современных успехах воздухоплавания исследования
С. А. Чаплыгина получают выдающееся значение.
Но прежде нежели говорить о приложении гидродинамики
к воздухоплаванию и о аэродинамических лабораториях, я вер-
нусь назад и отмечу, какое влияние имела на мою ученую
деятельность прикладная механика.
Проф. Д. К. Бобылев сказал мне однажды, что я счастлив
тем, что начал свою педагогическую деятельность в Техниче-
ском училище и что соприкосновение с технической практикой
да от мне обильный материал для научных исследований. И
он был в этом отношении совершенно прав. Я с удоволь-
ствием вспоминаю беседы с моими дорогими товарищами по
Техническому училищу, в котором с 1870 г. протекает моя
педагогическая деятельность. Они указывали мне на различные
тонкие вопросы техники, требующие точного разрешения. От
них научился я сближению научного исследования с наблюда-
емой действительностью и уменью пользоваться прибли-
жением.
Я благодарен им за многие мои сочинения прикладного хара-
ктера. Я всегда буду сохранять добрую память о Н. П. Зимине,
который пригласил меня быть руководителем работ, поставлен-
Зак. 2430. Н. Е. Жуковский. Том IX.
14
210
РЕЧИ И ДОКЛАДЫ
ных при Алексеевской водокачке для исследования гидравли-
ческого удара в водопроводных трубах. В этих работах тео-
ретическое исследование задачи о распространении и отражении
ударных волн нашло свое полное подтверждение в действи-
тельности. Московские исследования были одобрены американ-
скими учеными и недавно получили благоприятный отзыв от
французского инженера Гупиль, который напечатал о них под-
робный доклад.
В Московском университете за смертью моего дорогого
товарища проф. Ф. Е. Орлова заведывание собранным им
богатым кабинетом прикладной механики было поручено мне.
Я присоединил к деятельности кабинета лабораторную дея-
тельность, и уже в продолжение 8 лет кабинет располагает
некоторыми аппаратами для аэродинамических исследований,
которые теперь составили аэродинамическую лабораторию.
Кроме этого, около Москвы был построен аэродинамический
институт Д. П. Рябушинским, и в прошлом году возникла
аэродинамическая лаборатория при Техническом учи-
лище.
Сколько интересных вопросов аэродинамики подлежат раз-
решению. Удобство исследования над воздухом позволит про-
никнуть в сокровенные законы распределения струй и теснее
сблизить две науки — гидродинамику и гидравлику. Теперь
все более и более оправдываются слова Гельмгольца, что
уравнения гидродинамики выражают реальное движение жид-
кости. Силы сопротивления, развивающиеся при потоках, обте-
кающих тела, кроме Кирхгоффской теории срывающихся струй,
находят себе объяснение в новом факторе, указанном мной
и Ланчестером, — в циркуляции скорости. Прекрасные теоре-
тические исследования профессоров Кутта и Чаплыгина под-
тверждаются в лабораторных опытах Московского универси-
тета и Технического училища. Уже намечается тот анализ,
который всю теорию сопротивления жидкости двинет вперед
от приближенных исследований Понселе, Сен-Венана и Буси-
неска и даст новые данные для рациональной конструкции
летательных машин.
Но когда человек прошел уже большую часть своего
жизненного пути, он с грустью задает себе вопрос: суждено-
МЕХАНИКА В МОСКОВСКОМ УНИВЕРСИТЕТЕ ЗА 50 ЛЕТ 211
ли ему увидать те манящие горизонты, которые расстилаются
там впереди. Утешением ему является то, что там впереди
идут молодые, сильные, что старость и юность сливаются в
непрерывной работе для познания истины.
Эта речь, произнесенная проф. Н. Е. Жуковским 16 января 1911 г. на
торжественном заседании в Политехническом музее, посвященном сорока-
летнему юбилею научной деятельности Н. Е. Жуковского, была напечатана
в „Трудах Отделения физических наук Общества любителей естествознания”,
т. XV, вып. 1. Прим. ред.
14*
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ МОСКОВСКОГО
УНИВЕРСИТЕТА И МОСКОВСКОГО ТЕХНИЧЕСКОГО
УЧИЛИЩА
(РЕЧЬ)
(1910-1911 гг.)
Я счастлив тем, что в этом торжественном заседании
Общества, основанного незабвенным Христофором Семено-
вичем Леденцовым, могу почтить его память указанием тех
результатов, которые достигнуты в этом году аэродинами-
ческими лабораториями Московского университета и Техни-
ческого училища при поддержке нашего Общества.
В настоящее время, при блестящем развитии воздухопла-
вания, научные исследования по сопротивлению воздуха ста-
новятся на первую очередь- К прежним аэродинамическим
институтам: Римскому, институту проф. Цама в Америке,
институту Д. П. Рябушинского, присоединяются новые, пре-
красно оборудованные аэродинамические учреждения: лабо-
ратория Эйфеля и Рато в Париже, лаборатория проф. Прандтля
в Геттингене и институт для испытания винтов в Линдесмите.
Скоро заканчивается постройка в Сен-Сире большого аэро-
динамического института, построенного на средства Дейча
с испытаниями на рельсовом пути, и уже действует в Англии
громадная ротативная машина Викерса для испытания винтов
на открытом воздухе.
С начала наступающего года открывается аэродина-
мическая лаборатория Петербургского политехнического
института, построенная на правительственные средства, с ее
большой для искусственного потока воздуха вентиляционной
трубой.
Наша аэродинамическая лаборатория при Московском
университете уже давно занималась исследованиями по со-
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
213
противлению воздуха, пользуясь маленькими средствами, от-
пускаемыми университетом на механический кабинет.
На фиг. 1 изображен ряд летающих игрушек и змеев,
которые исследовались в механическом кабинете Московского
университета при зарождении проблемы о полете тел, более
тяжелых, нежели воздух.
Фиг. 1.
На фиг. 2 представлена машина Атвуда, которая слу-
жила В. В. Кузнецову в бытность его студентом для про-
изводства интересных опытов над сопротивлением конусов.
Изображенный на фиг. 2 аппарат ставился в нижнем по-
мещении университетской лестницы и такая же доска с фрик-
ционными колесами — в верхнем ее помещении. Модель при-
креплялась к одной ветви бесконечного шнура, охватывающего
нижний и верхний блоки, времена каждого оборота блока
записывались на хронографе Марея, изображенном на фиг. 3.
При этом изображались рядом отметки сотой доли секунды
и одного оборота колеса (фиг. 4).
214
РЕЧИ И ДОКЛАДЫ
На фиг. 5 дано
изображение вести-
бюля университета
и установки рас-
сматриваемого аппа-
рата.
В 1902 г. была по-
строена наша малень-
кая галлерея для ис-
кусственного потока
воздуха с квадратным
сечением 75X75 см2,
которая является од-
ной из первых вса-
сывающих труб, по-
строенных в Европе
(фиг. 6).
В этой галлерее
производились мно-
гочисленные испыта-
ния, из которых за-
служивают особенно-
го внимания: иссле-
дование- удара ветра
на решетки, произ-
веденное студентами
Эйгес и Загордином,
исследования о цен-
тре парусности, сде-
ланные Соколовым,
Шебуевым и Крюко-
вым, и исследования,
сделанные Лукьяно-
вым над изменением
коэфициента сопро-
тивления воздуха с
возрастанием скоро-
сти.
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
215
На фиг. 7 изображе-
на диаграмма, данная
Лукьяновым для изме-
нения коэфициента со-
противления шара (ми-
делевое сечение 0,022л/2)
при изменении скоро-
сти потока в трубе от
2 до 9 jnjceK.
Из нее видно, что
коэфициент в рассма-
триваемом промежутке
падает. Такое же паде-
ние коэфициента было
наблюдено при опытах
на вышеописанной ма-
шине Атвуда. Это яв-
ление имеет важное зна-
чение в вопросе о пу-
скании шаров-зондов.
Прошлым летом в
университетской квад-
ратной галлерее были
произведены интерес-
ные исследования А. И.
Морошкина над трением
воздуха о твердые стен-
ки. Внутри галлереи
подвешивалась длинная
картонная труба, и опыт
располагался так, что
воздух протекал только
внутри этой трубки. На-
блюдения дали резуль-
таты, близкие к тем, ко-
Фиг. 5.
торые были получены американским ученым проф. Цамом.
Оказалось, что трение пропорционально скорости в степени
1,85 и коэфициент трения равен 0,0002.
216
РЕЧИ И ДОКЛАДЫ
Одновременно с квадратной галлереей в механическом
кабинете Московского университета был по моему проекту
построен прибор для испытания винтов без поступательной
скорости, изображенный на фиг. 8.
Фиг. 6.
На фиг. 9 дана схема этого прибора. Рамка а имеет воз-
можность поворачиваться около двух взаимно перпендикуляр-
ных осей хх и уу. Винт Н приводится во вращение круглым
коэфициент сопрошФФения к
ремнем ЬЬ, бегущим по
роликам с, с' и с" и еще
по двум, помещенным в
рамке.
Ролики в рамке распо-
ложены так, что ремень не
дает пары сил, стремящей-
ся вращать рамку. Когда
винт будет вращаться, то-
гда он потянет рамку вниз
или вверх—в зависимости
от того, куда будет со-
вершаться вращение. Эту
силу тяги измеряют из-
менением груза у. Одновременно с этим рамка, в силу
действия горизонтальных составляющих сил давления воз-
духа, будет вращаться около оси уу в сторону, обратную
вращению винта. Измеряя момент пары, вызывающей это
вращение, грузом р, умноженным на плечо длиной во всю
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
217
I
Фиг. 8.
фнг. 9.
218
РЕЧИ И ДОКЛАДЫ
рамку, и помножая этот момент на угловую скорость винта
определяем работу, потраченную на вращение винта; пр!
этом все вредные сопротивления в счет не идут и из отсчета
исключаются.
Фиг. 10.
Кроме этого прибора для испытания геликоптерных вин
тов был еще построен второй маленький
}енара, изображенный на фиг. 10.
На фиг. 11 изображен умформер с пятисильным двигате
прибор по типу
лем,
ный.
преобразующий переменный городской
Этим постоянным током приводятся
ток в постоян
в действие
все
.вышеописанные аппараты.
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
219
Благодаря поддержке Леденцовского общества в Аэроди-
намической лаборатории Московского университета вскоре
-будет поставлен построенный механиком Кирхгоффом большой
прибор для испытания винтов типа, указанного на фиг. 8,
в котором рамка а заменяется стальной трубой, внутри ко-
торой вращается вал, передающий с помощью зубчатых колес
свое вращение горизонтальному винту и получающий это
Фиг. 11.
вращение от неподвижного мотора с помощью шарнира Гука,
причем этот шарнир не мешает трубе с валом вращаться
около осей хх и уу. На этом новом аппарате можно будет
испытывать винты диаметром до 5 м.
Поддержка Общества позволила Аэродинамической лабо-
ратории университета закончить также две большие установки:
новой большой трубы и компрессора с котлом.
Большая круглая труба (фиг. 12), поставлена в вестибюле
университета под его стеклянной крышей; ее внутренний
диаметр равен 1,6 л«, а длина 10 м. Воздух сосется вентиля-
220
РЕЧИ И ДОКЛАДЫ
Фиг. 12.
тором „Сирокко", приводимым во вращение мотором пере-
менного тока в 20 л. с. Вся труба выполнена из картона за
исключением своей средней
деревянной части.
На фиг. 13 изображен
счетчик числа оборотов тру-
бы, который подает звонки
через каждые 100 оборотов,
а на фиг. 14 — динамометр
с горизонтальным плечом,
позволяющий измерять го-
ризонтальную и вертикаль-
ную составляющие силы со-
противления воздуха на мо-
дель, поставленную в трубу.
В настоящее время поле
трубы обстоятельно иссле-
фиг довачо. На фиг. 15 изобра-
жены диаграммы скоростей
в трубе в 'различных точках вертикального диаметра сред-
него сечения при изменении скорости от 6 до 14 м.
аэродинамические лаборатории
221
Фиг. 14.
Первые работы, которые прошли в нашей новой трубе,
были работы об ударе ветра на цилиндры, ось которых перпен-
дикулярна потоку, и ра-
бота по сравнению под-
держивающей силы кры-
ла аиста и изогнутого
плана по типу Блерио.
Последняя работа была
сделана М. М. Иконни-
ковым по поручению
Леденцовского общест-
ва по поводу изобрете-
ния Н. В. Спасова.
Отчет об этой ра-
боте будет напечатан
в следующем выпуске
„Временника". Работа
об определении силы да-
вления ветра на цилин-
дры была сделана сту-
222
РЕЧИ И ДОКЛАДЫ
дентами Никольским и Шифальда. Она привела к заключе-
нию, что для цилиндров, так же как для шара, коэфициент
Фиг. 16.
Фиг. 17.
сопротивления в проме-
жутке скоростей от 6 до
12 м уменьшается.
На фиг. 16 изобра-
жен компрессор, приводи-
мый в движение пятисиль-
ным электромотором; этот
компрессор нагнетает воз-
дух в котел в 3*/2 л«а
(фиг. 17). Из котла будет
выпускаться тонкая струя
воздуха из-под давления
до 10 ат для определе-
ния скорости истечения и
силы удара на маленькие
тела.
Опыты этого рода по-
зволят решить спорный
вопрос, называемый пара-
доксом Сен-Венана и за-
ключающийся в том, что
независимо от давления
скорость истечения не мо-
жет быть более скорости
звука (330 м1сек). С дру-
гой стороны, они разъяс-
нят законы сопротивления
воздуха на артиллерийские
снаряды.
Оканчивая описание
Аэродинамической лабора-
тории Московского уни-
верситета, я укажу еще
три исследования, которые
производятся в ней в последнее время. Первое и второе от-
носятся к разъяснению коренного вопроса аэродинамики —
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
223
о трении двух слоев воздуха на границе раздела соприкасаю-
щихся потоков, текущих с различными скоростями. К средине
ыалой (фиг. 6) трубы присоединялся прямоугольный колпак,
как представлено на фиг. 18; на той же фигуре в отдельности
представлен боковой поперечный разрез колпака.
Фиг. 18.
Ток воздуха в трубе приводил массу, заключенную в кол-
паке,” в движение по замкнутым траекториям, как это видно
из фотографии флажков, расположенных на стенке колпака,
идущей по потоку (фиг. 19). По этой фотографии можно вы-
чертить линии токов, ко-
торые позволят по ско-
ростям, определенным
на средней вертикали
колпака, найти все ско-
рости потока. Опреде-
ление же давлений на
передней и задней стен-
ках колпака, перпенди-
кулярных оси трубы, по-
зволит определить всю
силу взаимодействия
скользящих потоков.
Для решения вопроса
о распространении тре-
ния вдоль жидкой массы
была сделана установка,
изображенная на фиг. 20.
Воздух всасывался вентилятором из пространства, заклю-
ченного между двумя параллельными дисками, причем труба
Л V 1 Л -S. '•;> у»
1 \ ’К Ж.
I Ч
%. V- jr- — у
Фиг. 19.
224
РЕЧИ И ДОКЛАДЫ
вентилятора примыкает к центральному отверстию нижнего
диска, и воздух входит по периферии между дисками.
Против центрального отверстия между дисками устанав-
ливалась крылатка, приводимая во вращение отдельным эле-
ктромотором. Вращение, сообщаемое крылаткой, распростра-
нялось по воздуху между дисками, причем образовывалась
некоторая поверхность раздела, за которую вращение диска
Фиг. 20.
не распространялось. По месту этой поверхности можно су-
длть о быстроте распространения вращательного движения
по воздушной массе.
Я закончу описание аппаратов аэродинамической лабора-
тории Московского университета указанием на установку,
с помощью которой в последние дни удалось опытно оправ-
дать замечательную теорему проф. С. А. Чаплыгина. Резуль-
таты этих наблюдений лаборатория Университета приносит
в дар Обществу незабвенного X. С. Леденцова к этому тор-
жественному дню.
На основании теоретических соображений проф. С. А. Чап-
лыгин вывел, что горизонтальный поток при одной и той же
скорости должен оказывать на вогнутые планы различных
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
225
ту же подъемную силу. На фиг.
30см
20см
1Бсм
!2см
182г ПЗг
Фиг. 21.
Ч65г
77= 7,5м
h ’/, 1см
Фиг, 22.
глубин (ширина по направлению потока) и одной и той же
стрелки прогиба одну и
изображены четыре мо-
дели, которые все имели
стрелку прогиба 1,1 см
и размах 70 см, глубина
которых была в 12, 16,
20 и 30 см.
Все они при скорости
потока в трубе 7,5 м{сек
дали почти одинако-
вые подъемные силы,
указанные на фигуре.
На фиг. 22- изображена модель и приподнятая крышка
трубы, помещенная в средней части университетской квадратной
трубы. При наблюдении
крышка опускается вниз
и закрывает окно трубы,
а весы, показанные на
фиг. 22, позволяют изме-
рять силу, с которой поток
воздуха отклоняет модель
по направлению, перпен-
дикулярному оси трубы.
Опытно оправданная
теорема С. А. Чаплыгина,
которая против ожидания
обнаруживает, что подъем-
ная сила не зависит от
глубины поддерживающих
планов, а только от стрелки
прогиба, имеет большую
практическую важность,
так как показывает, что
нет нужды употреблять
планы с очень большой
шириной, а выгоднее увеличивать стрелку прогиба. Разумеется,
теорема остается справедливой до тех пор, пока поток воздуха
Зак. 2430. И. Е. Жуковский. Том IX.
15
226
РЕЧИ И ДОКЛАДЫ
обтекает планы без образования разрывов. При увеличении
отношения стрелки прогиба к глубине произойдет схождение
струй в выпуклой части планов и образование вихрей, причем
подъемная сила будет уже увелчииваться с увеличением глу-
бины планов.
Я перехожу к аэродинамической лаборатории Технического
училища. Она основалась только прошлой весной благодаря
Фиг. 23.
энергичной работе Воздухоплавательного кружка при Техни-
ческом училище, который на маленькие средства от устроенной
им выставки начал постройку основных аппаратов лаборатории.
При поддержке Леденцовского общества эта лаборатория раз-
растается и скоро станет в ряд лучших русских аэродинами-
ческих институтов. На фиг. 23 изображена плоская’труба этой
лаборатории. Между стенками, сделанными из зеркального
стекла, движется воздух, всасываемый вентилятором „Сирокко",
приводимым в движение электромотором постоянного тока
в 23 л. с. Сечение трубы представляет прямоугольник 150X30 сл«2,
причем широкая сторона горизонтальна. В этой трубе удобно
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
227
приспособления, пред-
определять силу действия потока воздуха на часть аэроплана,
вырезанную двумя параллельными плоскостями, перпендику-
лярными планам и параллельными оси аэроплана. Теоретически
говоря, плоская труба позволяет исследовать действие потока
воздуха на бесконечно длинные цилиндры. Величина силы
сопротивления воздуха и точки приложения этой силы опре-
деляются весьма просто с помощью
ставленного на фиг. 24. Рамочка
DFE, в которую вставлено зер-
кальное стекло, катается на трех
шариках по горизонтальному зер-
кальному стеклу плоской трубы.
К рамочке приделана ручка Н, под-
держивающая с помощью стерж-
ня В, проходящего чрез отвер-
стие в трубе, модель ААСС.
Высота модели АА = 29,5 см; она
почти заполняет все простран-
ство между верхней и нижней
стенками трубы. Модель и рамочка
составляют одно твердое тело, ко- * ...
Фиг. 24.
торсе может перемещаться только
горизонтально. При испытании укрепляют рамочку последова-
тельно в центрах D, F и Е и определяют моменты силы
сопротивления воздуха относительно этих трех центров,
пользуясь разновесками, положенными на чашки весов М и
/V. Эти чашки подвешены на нитях, перекинутых через непо-
движные блоки и прикрепленных к ручке Н. Зная моменты
силы сопротивления воздуха относительно трех центров мо-
ментов, мы легко определяем ее величину, направление и
точку ее приложения.
Построенная труба дала чрезвычайно равномерное поле.
На фиг. 25 изображена величина скорости потока в различных
точках среднего сечения трубы. Верхняя диаграмма соответ-
ствует скорости для точек, взятых в горизонтальном напра-
влении, а нижняя диаграмма — для точек, взятых в вертикальном
направлении. Исследования в описанной трубе производятся,
меняя скорость потока от 16 до 20 м.
15::
228
РЕЧИ И ДОКЛАДЫ
На фиг. 26 изображена круглая труба аэродинамической
лаборатории Технического училища. Эта труба приводится
в движение тем же мотором, который приводит в движение
плоскую трубу, при-
чем на шкив мотора
надевается новый ре-
мень. Труба имеет в
диаметре 1,2 м. Воз-
дух всасывается в нее
от действия крыльча-
того вентилятора и
может получить ско-
рость до 30 м/сек.
В той же зале, где
помещены две выше-
описанные трубы, по-
мещается ротативная
машина, изображен-
ная на фиг. 27.
Фиг. 26.
Вертикальная ферма, опирающаяся шариковыми подшип-
никами в пол и потолок и несущая на горизонтальном плече
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
229
испытуемые аппараты, вращается около вертикальной оси
с помощью горизонтального ступенчатого колеса, надетого
на ферму. Бесконечный ремень, охватывающий горизонтальное
ступенчатое колесо, переходит на вертикальный ступенчатый
шкив меньшего радиуса. Этот шкив соединен с помощью
другого ремня с горизонтальным шкивом мотора в 2 л. с. Гори-
Фиг. 27.
зонтальное плечо ротативной машины имеет длину 3 м. С по-
мощью указанного приспособления концу плеча можно сообщать
скорость от 3 до 20 м1сек. Описанная машина послужила нам
для проверки анемометров на большие скорости. При этом
оказалось, что при больших скоростях имеющиеся в продаже
анемометры обыкновенно показывают большую скорость против
настоящей и ошибка достигает до 2 м1сек. Для испытания
маленьких пропеллеров при перемещении их оси вращения,
в середину вертикальной фермы описанной ротативной машины
230
РЕЧИ И ДОКЛАДЫ
поставлен маленький мотор в 1/4 л. с., который с помощью беско-
нечного круглого ремня приводит во вращение ось гребного
винта, который устанавливается в конце горизонтального плеча
фермы. Приготовляются динамометры, которые будут изме-
рять силу тяги винта и его крутящий момент. Число оборотов
винта будет регистрироваться через каждые 100 оборотов элек-
трическими звонками. Предполагается производить параллельно
опыты с маленькими винтами на ротативной машине и в выше-
описанной круглой трубе. Для испытаний над большими вин-
Фил 28.
тами будет устроено при
аэродинамической лабора-
тории Технического учили-
ща два приспособления.
В отдельной комнате
будет поставлен аппарат
для испытания винтов с
неподвижной осью враще-
ния, того же самого типа
(фиг. 8), который делает
Кирхгофф для универси-
тетской аэродинамической
лаборатории.
С другой стороны вдоль коридора, примыкающего к боль-
шой зале лаборатории Технического училища, будет устроена
воздуходувная галлерея нового типа с помощью бесконечных
вентиляционных полотен, которые я называю „вентилятор
Нория“. На фиг. 28 изображена фотография модели этого
вентилятора. Он дает очень сильный поток воздуха и пред-
ставляет то удобство, что в нем нет больших вращающихся
масс и соединенных с ними сотрясений подшипников.
На фиг. 29 изображена модель той воздушной галлереи,
с помощью которой можно установить дутье в коридоре.
Полотна типа „Нория" висят вертикально и, подсасывая
воздух, бросают его в задний кожух. Воздух, пробегая по
трубе, помещенной в верхней части коридора, возвращается
в передний его конец.
Расположение помещений аэродинамической лаборатории,
которое указано на плане (фиг. 30), позволит в будущем
АЭРОДИНАМИЧЕСКИЕ ЛАБОРАТОРИИ
231
присоединить к ней штольню, которая расположится в башне,
пристроенной со стороны здания. [На фиг. 31 показан внешний
Фиг. 29.
вид здания, в котором помещается лаборатория.] Все описанные
мной приспособления сделали бы из аэродинамической лабо-
Фиг. 30.
ратории Технического училища выдающееся учреждение, даю-
щее возможность производить научные исследования разнооб-
разных вопросов воздухоплавания и достойное той энергии,
232
РЕЧИ И ДОКЛАДЫ
которую проявили студенты училища в аэродинамической
работе. Я думаю, что проблема авиации и сопротивления
воздуха, несмотря на блестящие достигнутые успехи в ее
разрешении, заключает в себе еще много неизведанного, и
что счастлива та страна, которая имеет средства для открытия
этого неизведанного. У нас в России есть теоретические силы,
Фиг. 31.
есть молодые люди, готовые беззаветно предаться спортивным
и научным изучениям способов летания. Но для этих изучений
нужны материальные средства. Поэтому всегда будет с глу-
бокой благодарностью сохраняться память основателя нашего
Общества Христофора Семеновича Леденцова, завещавшего
свое обширное состояние на поощрение научных исследований
и изобретений.
Эта речь была произнесена проф. Н. Е. Жуковским 5 декабря 1910 г.
на торжественном заседании, посвященном памяти X. С. Леденцова. Речь
была напечатана в Журнале „Временник** Общества содействия успехам
опытных наук им. X. С. Леденцова, вып. 2, 1911. Прим. ред.
НОВЫЕ НАУЧНЫЕ ЗАВОЕВАНИЯ В ТЕОРИИ СОПРОТИ-
ВЛЕНИЯ ЖИДКОСТЕЙ
(РЕЧЬ)
(1413- 1914 г.)
Покойный Д. И. Менделеев указал путь, по которому дол-
жна совершаться разработка трудного вопроса о сопротивле-
нии жидкостей. Необходим, — писал он, — разумный и твердый
опыт, за которым пойдет теоретическая мысль, которая, на-
правленная по верному пути, сама поведет [за собой разра-
ботку вопроса. Теоретическая мысль в первоначальной раз-
работке вопроса о сопротивлении давала результаты, несо-
гласные с действительностью. Струйная теория Эйлера и
учение о неразрывном невихревом потоке Кирхгоффа и Гельм-
гольца приводили к парадоксальным выводам об отсутствии
силы сопротивления жидкости движущемуся в ней телу и
о невозможности для тела, погруженного в жидкость, переме-
щаться посредством воздействия на жидкость. Приходилось
для объяснения явлений сопротивления жидкости придержи-
ваться ударной теории Ньютона и Лоссля, в которой остава-
лось без рассмотрения, что делается с частицами жидкости
после удара их о тело. Эта же теория лежала в основании
расчета винтов по Ранкину, Буслею, Рузскому и др.|
Обширный опытный материал, даваемый судостроением,
показал недостаточность ударной теории, причем совершенно
неверным оказался закон квадратов синусов, из нее вытекаю-
щий. Выяснилось, что для судов с хорошими обводами, с ко-
торых струи в относительном движении не срываются, глав-
ным фактором сопротивления является трение жидкости о
стенки тела. Были произведены лабораторные наблюдения
Бофуа и Фруда над трением жидкости о движущиеся в ней
Доски и на основании этих опытов возникла так называемая
234
РЕЧИ И ДОКЛАДЫ
фрикционная теория сопротивления, главным представите-
лем которой явился Ранкин. Он принимает, что движущееся
в жидкости тело окружено невихревым потоком, о котором
писали Кирхгофф и Гельмгольц, а к самой поверхности тела
прилегает тонкий завихренный слой жидкости, развивающий
силу трения, приблизительно пропорциональную квадрату
скорости. Для тел с резко изменяющимися обводами теория
Ранкина неприложима, и здесь для определения сопротивле-
ния возникли две теории: одна, опирающаяся на теорему
Борда, и другая с обстоятельной гидродинамической обра-
боткой. Первая, называемая теорией каналов, была предло-
жена Понселе и Сен-Венаном. По ней тело рассматривается
как бы перемещающимся в некотором идеальном канале,
стенки которого отделяют возмущенную жидкость от покоя-
щейся, причем потеря энергии струй, обтекающих в относи-
тельном движении тело и вступающих в медленно движу-
щуюся жидкость за телом, определяется по теореме Борда.
Вторая теория была предложена Кирхгоффэм и называется
теорией струй', она со всей строгостью относится к так на-
зываемому плоскопараллельному потоку жидкости, т.
кости, протекающей между двумя параллельными стенками
(как это имеет место в плоской аэродинамической галлерее
Московского технического училища) и обтекающей призмати-
ческие тела, образующие которых перпендикулярны потоку.
Теория струй была разработана по отношению к плоским
пластинкам и к клину в сочинениях Рэлея, Митчеля, Бобы-
лева, Мещерскаго, в моей большой работе и в сочинениях
проф. Чаплыгина, посвященных сопротивлению газов. Но
теория струй заключала в себе невыполнимое требование
затраты громадной энергии для того, чтобы образовалась
спутная масса жидкости, следующая за плывущим телом.
Предполагалось, что в действительности Кирхгоффские струи
будут иметь место только вблизи тела, а на некотором рас-
стоянии от него относительный поток жидкости получит вслед-
ствие вязкости равномерное поступательное движение, обрат-
ное движению тела.
Сила сопротивления на наклонные пластинки, определяе-
мая по методу Кирхгоффа, оказалась менее действительной.
е. к жид-
НОВОЕ В ТЕОРИИ СОПРОТИВЛЕНИЯ ЖИДКОСТЕЙ
235
Таково было состояние теории сопротивления до 1906 г.,
когда братья Райт и Сантос-Дюмон впервые поднялись на
воздух на аппаратах, более тяжелых, нежели воздух. Начиная
с этого времени, воздухоплавание пошло по своему победо-
носному пути и достигло за семь истекших лет блестящих
результатов.
Искусные летчики поднимаются теперь на аэропланах на
высоты до 5 км и пролетают по безостановочному 12-часо-
вому пути пространство, достигающее 1000 км. Практика
значительно опередила теорию. Потребность в рациональной
конструкции летательных машин и расчета их безопасного
полета заставила построить многочисленные аэродинамиче-
ские лаборатории и производить в них тщательное исследова-
ние влияния воздушного потока на различные формы моде-
лей и изучение действия воздушных пропеллеров. Франция,
Германия, Италия и Россия конкурируют друг перед другом
результатом своих аэродинамических наблюдений и накопляют
тот твердый опыт, который позволит теории, по словам Д. И.
Менделеева, принять на себя руководящую роль в разреше-
нии вопросов по сопротивлению жидкостей. Это время те-
перь приближается. Протекшие семь лет блестящего развития
воздухоплавания ознаменовались новыми завоеваниями в тео-
рии сопротивления жидкостей, указание на которые состав-
ляет предмет моей речи.- Они, по моему мнению, заключаются
в следующих трех пунктах:
1. Теоретическое объяснение поддерживающей силы пла-
нов аэроплана с помощью циркуляции скорости.
2. Объяснение лобового сопротивления тел и пластинок
образованием за кормой убегающих вихрей, расположенных
в шахматном порядке.
3. Разработка вихревой теории гребного винта.
Во всех этих трех пунктах выдающуюся роль играет ги-
дродинамическая величина, названная Томсоном циркуляцией
скорости по замкнутому контуру.
Эта величина аналогична работе, которую бы совершила
на заданном контуре сила, равная скорости жидкости в соот-
ветствующей точке контура. Прямолинейный вихревои шнур,
как известно, вращает жидкость со скоростью, убывающей
236
РЕЧИ И ДОКЛАДЫ
в обратном отношении расстоянию рассматриваемой точки от
оси шнура, поэтому циркуляция скорости по окружностям,
описываемым частицами жидкости, одинакова. Половиной этой
циркуляции измеряется так называемое напряжение вихревого
шнура. Существуют теоремы Стокса и Томсона о циркуляции;
по первой теореме циркуляция равна двойной сумме напря-
жений всех вихревых шнуров, проходящих через рассматри-
ваемый контур, а по второй циркуляция скорости по замкну-
тому контуру, проходящему через одни и те же частицы
жидкости без трения, не изменяется при движении этих ча-
стиц. На эти теоремы опирается Гельмгольцев принцип со-
хранения вихрей, по которому в жидкости без трения не
могут зарождаться вихри, а имеющиеся в ней вихри должны
сохраняться. Когда жидкость в относительном движении под-
текает к движущемуся телу, тогда подплывающие к ним за-
мкнутые контуры имеют циркуляцию нуль, так как она в от-
далении от тела была нулем, и весь поток жидкости будет
невихревой, причем циркуляция скорости по всяким замкну-
тым контурам будет нуль. Но если тело цилиндрической
формы движется, опираясь основаниями на две параллельные
стенки, между которыми заключена жидкость, то для замкну-
тых контуров, не охватывающих цилиндр, циркуляция скоро-
сти относительного движения будет, на основании приведен-
ного выше рассуждения, попрежнему равна нулю; циркуляция
же скорости по контурам, охватывающим цилиндр, может и
не равняться нулю, так как такие контуры могут сделаться
замкнутыми, после того как их концы проскользили по по-
верхности цилиндра, а вдали от цилиндра они были разомк-
нутыми. Полученное при этом плоскопараллельное движение
жидкости не будет иметь вихрей внутри жидкости, но она
будет управляться прямолинейными вихревыми шнурами, за-
ключенными в цилиндре. Такое движение называется невих-
ревым движением с циркуляцией. Оно возникает тогда, когда
вихревое движение без циркуляции сопровождалось бы гро-
мадными скоростями на острых краях цилиндрического тела,
например, когда последнее имеет вид поддерживающих пла-
нов аэроплана. Легко усмотреть, что при невихревом движе-
нии с циркуляцией развивается подъемная сила, перпендику-
НОВОЕ В ТЕОРИИ СОПРОТИВЛЕНИЯ ЖИДКОСТЕЙ
237
лярная к относительному потоку жидкости. В отдалении от
тела придется слагать поступательную скорость относитель-
ного потока жидкости со скоростью, сообщаемой вихревым
пшуром, заключенным в теле. Принимая поток горизонталь-
ным, набегающим на тело справа налево, а вращение вихря
против стрелки часов, мы увидим, что скорости набегающей
жидкости будут приподняты немного вверх, а скорости убе-
гающей— будут опущены немного вниз. От обеих причин на
тело будет действовать сила снизу вверх. Я показал в своем
сочинении „О присоединенных вихрях", что эта сила будет
равна произведению из плотности тела, циркуляции и скоро-
сти поступательного движения тела. Эта теорема одинаково
имеет место и в том случае, когда поддерживающие планы
представляют некоторую цилиндрическую поверхность. Для
случая, когда планы дают в сечении дугу круга, подъемная
сила была определена проф. Кутта и независимо от него
проф. С. А. Чаплыгиным. Способ определения подъемной
силы и точки ее приложения для различных однопланных и
многопланных контуров получил широкую математическую
разработку в дальнейших трудах Чаплыгина, Кутта, моих,
Блазиуса, Больтце, Блюменталя и др. Результаты этих работ
дают хорошее согласие с лабораторными исследованиями.
Таким образом вполне оправдалось на опыте заключение
проф. Чаплыгина, что подъемная сила вогнутых планов зави-
сит не от ширины планов, а от стрелки их прогиба, что ука-
зывает на рациональность узких планов на аэроплане Сикор-
ского. Но до сих пор мы говорили о плоскопараллельном
потоке жидкости, который непосредственно исследуется в аэро-
динамической лаборатории Московского технического учили-
ща. Для того чтобы указанные результаты распространить
на планы, имеющие открытые концы, следует воображаемый
внутри планов вихрь выпустить из этих концов в виде двух
шнуров, направляющихся по струям сбегающей жидкости.
Циркуляция скорости около таких вихревых шнуров будет
равна циркуляции скорости по контурам, охватывающим под-
держивающий план. Теоретическое указание на такие спут-
ные вихревые шнуры было дано Ланчестером, Финстерваль-
дером, Чаплыгиным и Прандтлем. Опыты в Круглой аэродина-
238
РЕЧИ И ДОКЛАДЫ
мической трубе Технического училища с двумя вертушками,
поставленными на пути струй, сбегающих с концов планов,
показали, что эти вертушки вращаются в сторону плана для
наблюдателя, глядящего на его выпуклую сторону. Таким
образом разъяснилась теоретически подъемная сила поддер-
живающих планов аэроплана. Но указанный принцип невихре-
вого движения с циркуляцией не дает нам лобового сопро-
тивления планов, т. е., не дает силы сопротивления, направ-
ленной по относительному ветру. , ‘
Над моделями дирижаблей, которые должны быть отнесены
к телам с хорошими обводами, были произведены многочис-
ленные наблюдения в Геттингенской аэродинамической лабо-
ратории профессорами Прандтлем и Фурманом. Кроме опре-
деления общей силы сопротивления с помощью динамометра,
определялись еще манометром давления воздуха в каждой
точке модели, которая делалась пустотелой с дырками в
стенках, причем все дырки, кроме одной, заклеивались
бумажками.
Г рафика давлений показала, что при хороших обводах давле-
ния, начиная от носа модели до кормы, совпадают с теоре-
тическими величинами, даваемыми теорией невихревого потока,
на корме же давления меньше теоретических. Вычитая из
силы сопротивления, определенной динамометром, силу, опре-
деленную по манометру, авторы нашли силу сопротивления,
близко совпадающую с силой, определенной по фрикционной
теории Ранкина. Такие же наблюдения в целях определения
коэфициента трения воздуха производились в Москве Сороко-
умовским и Морошкиным. Коэфициент трения получался
близким к тому, который определил Цам: около 0,0002, т. е.
почти в 800 раз менее коэфициента трения воды. Это пока-
зывает, что трение жидкостей о стенки при больших скоро-
стях зависит от их плотностей, а не от их вязкости, так как
отношение приведенных к единице массы коэфициентов вяз-
кости воды и воздуха есть 1:14. По всей вероятности, трение
жидкости о стенки при больших скоростях имеет своим источ-
ником образование мелких вихрей, сбегающих при хороших
обводах тонким слоем за корму. Для тел с дурными обводами,
дающими срыв струй со стенок тела, образуются вихри за
НОВОЕ В ТЕОРИИ СОПРОТИВЛЕНИЯ ЖИДКОСТЕЙ 239
кормой, столь отчетливо представленные на фотографиях
Альборна и Д. П. Рябушинского.
Проникнуть в механизм лобового сопротивления при
образовании вихрей удалось аахенскому профессору Карману.
Работая еще в звании [лаборанта вместе с проф. Прандтлем
в Геттингенской лаборатории над вихрями на поверхности
воды, образующимися за вертикальным движущимся цилиндром,
Карман заметил, что эти вихри располагаются всегда в шах-
матном порядке. Упомянутые вертикальные вихревые шнуры
плывут согласно закону движения вихрей вдогонку за убегаю-
щим от них цилиндром и уменьшают в относительном потоке
жидкости скорость струй за кормой. Вследствие этого обра-
зуется потеря количества движения, по которой можно опре-
делить лобовое сопротивление. Изучая вопрос с помощью
математического анализа, Карман доказал, что только шах-
матный порядок убегающих в относительном движении вихрей
дает устойчивое расположение их, причем между расстояниями
вихрей и их напряжением должно существовать некоторое
простое соотношение. Это позволило ему дать формулу
лобового сопротивления цилиндра, которая с точностью не
соответствовала закону квадратов, но давала хорошее совпа-
дение с опытом. Здесь следует указать, что устойчивость
шахматного порядка вихрей с опытной стороны еще раньше
Кармана указывалась Д. П. Рябушинским при его опытах
с самоподдерживающим качанием маятников, помещенных в по-
токе воды так, чтобы плоскость качания была перпендику-
лярна движению воды, и маятник представил пластинку,
лежащую в этой плоскости. Сбегание образовавшихся за кор-
мой вихрей в таком случае понятно. Но почему отбегают они
от неподвижного тела в потоке жидкости? В своем выше
упомянутом сочинении „О присоединенных вихрях' я указывал
на невихревой, плоскопараллельный поток жидкости, обегаю-
щий пластинку, поставленную перпендикулярно к потоку,
с образованием за ней двух вихрей, вращающихся в противо-
положные стороны. Струи жидкости, срываясь с краев пла-
стинки, смыкаются иа оси симметрии потока и охватывают
вихри. Эти вихри, вообще говоря, будут двигаться, изменяя
весь поток жидкости; когда они отбегут на некоторое рас-
240
РЕЧИ И ДОКЛАДЫ
стояние от пластинки, то струи жидкости, сбегающие с краев,
могут сомкнуться в новом месте и образовать между собой
и пластинкой новое замкнутое пространство, в котором
разовьются новые вихри, и т. д. К сожалению, последова-
тельный способ образования вихрей еще мало изучен. Работы
Прандтля и Блазиуса, которые стремились получить это обра-
зование из последовательного завихрения жидкости, приле-
гающей к стенкам тела, не дали результатов, согласных
с опытом, и я думаю, что источник образования вихрей за
телом с дурными обводами связан с образованием замкнутых
пространств за кормой. Что касается стационарных вихрей,
прилегающих к обтекаемым пластинкам, которые обстоятельно
исследованы проф. Чаплыгиным, то они, изменяя подъемную
силу, не дают лобового сопротивления. Последнее получается
только от движущихся вихрей. В своем сочинении „Поддер-
живающие планы типа Антуанетт" я определяю действие
убегающих вихрей, образующихся в той точке планов, где
вследствие громадной скорости должно образоваться схожде-
ние струй, и получаю формулу, тождественную с формулой
лобового сопротивления, данной Кутта.
Так как формула Кармана для лобового сопротивления
цилиндров не согласна с законом квадратов скоростей, то
можно ждать от распространения теории убегающих вихрей
на сопротивление шара (в этом случае надо рассматривать
убегающие вихревые кольца) объяснения парадоксальных на
первый взгляд явлений, получаемых при изучении изменения
силы сопротивления шара со скоростью. На I Всероссийском
воздухоплавательном съезде Г. И. Лукьянов доложил свои
опыты над уменьшением коэфициента сопротивления шара
с возрастанием скорости в пределах от 6 до 12 м. В этом
году Эйфель подтвердил опыты Лукьянова и обнаружил, что
для шаров небольших диаметров не только коэфициент, но
и самая величина лобового сопротивления уменьшается с
увеличением скорости. Это имеет место для шарика в 16 см
при изменении скорости от 12 до 16 м)сек. Напомню здесь,
что подобный результат был найден В. А. Слесаревым для
стоек аэроплана и доложен им на 1 Всероссийском воздухо-
плавательном съезде.
НОВОЕ В ТЕОРИИ СОПРОТИВЛЕНИЯ ЖИДКОСТЕЙ 241
Переходим к третьему пункту отмеченных нами завоеваний
в теории сопротивления жидкостей.
С точки зрения кирхгоффского невихревого потока, вращаю-
щийся в жидкости винт, представляющий тело, обладающее
винтовой симметрией, на которую указывает Ламб, переме-
щался бы в жидкости, сохраняя, так называемую, импульсив-
ную силу и пару. Если на массу такого тела по направлению
оси винтовой симметрии подействует некоторая сила в сторону,
обратную перемещению, то оно получит добавочное равно-
мерно-ускоренное движение в направлении силы, как это было
указано акад. Стекловым, и по прошествии некоторого
времени начнет двигаться в сторону силы, как бы она ни
была мала.
Получается теоретический вывод, совершенно несогласный
с действительностью. По этой причине теоретические иссле-
дования над гребным винтом в прежнее время имели свою
опору почти исключительно в ударной теории. За последнее
время ввиду накопившегося опытного материала в лабора-
ториях Эйфеля, Доранда, Рябушинского, Бендемана, Крокко
и Прандтля, явились попытки поставить теорию винта на более
рациональном основании.
Расширилась теория элементарного винта, построенная
нашим соотечественником С. К. Джевецким. Он рассматривает
движение вырезки лопасти винта в потоке жидкости между
двумя соосными цилиндрами, причем силу действия воздуха
на такой элементарный винт определяет с помощью наблюде-
ний над поддерживающими планами. К этой теории примкнули
теории Рато, Тейлора, Сабинина и др.
С теоретической точки зрения задача об элементарном винте
в потоке между двумя соосными цилиндрами есть задача
о действии плоскопараллельного потока на бесконечно длинную
решетку. С точки зрения кирхгоффских струй эта задача раз-
решена в моем сочинении „Видоизменение метода Кирхгоффа“,
а с точки зрения теории Кутта она разрешена проф. С. А. Ча-
плыгиным и доложена этой весной в заседании Математиче-
ского общества.
В случае движения пропеллера с большой поступательной
скоростью радиальная скорость частиц жидкости незначительна
Зак. 2430. Н. Е. Жуковскгй. Том IX.
16
242
РЕЧИ И ДОКЛАДЫ
сравнительно со скоростью поступательного движения, и пред-
положение о движении жидкости в соосных цилиндрах при-
ближенно удовлетворяется; но рассматриваема^ теория делается
неприменимой для геликоптерного винта. Наблюдения пока-
зали, что за винтом и над винтом жидкость движется по
радиусу к оси винта, как будто бы она вытекала через от-
верстие кружка, ометаемого лопастями винтов. Отсюда воз-
никала теория винта, основанная на рассмотрении струи,
отбрасываемой винтом, и применении к ней общих формул
динамики. Такова элементарная теория винта, данная Фин-
стервальдером и Бендеманом.
Доктор Кюммель построил линии токов невихревого тече-
ния жидкости, текущей в бесконечности с постоянной скоро-
стью и образующей струю, опирающуюся на плоскость упомя-
нутого кружка. Эти линии тока близки к тем, которые даны
Крокко в его исследованиях над потоком воздуха, окружаю-
щего вращающийся пропеллер. Но в таком потоке не принято
во внимание вращение жидкости в струе винта.
Наибольшее значение, на мой взгляд, для построения
рациональной теории винта имеют фотографии Фламма над
расположением воздушных пузырьков в струе, отбрасываемой
винтом. Эти пузырьки располагаются внутри винтообразных
вихревых шнуров, сбегающих с краев лопастей пропеллера, при-
близительно в направлении последних и по осевому вихревому
шнуру, причем винтообразные вихревые шнуры вращаются со
скоростью вращения винта. Наблюдения Фламма дали осно-
вания для моей статьи „Вихревая теория гребного винта“.
К этой теории примыкают работы Д. П. Рябушинского и
В. П. Ветчинкина, и, поскольку мне известно, тем же вопросом
в настоящее время занимается и проф. Прандтль. Откуда
берутся вихри, которые появляются за винтом? Было бы
ошибочно думать, что источником их является только трение
жидкости о стенки лопастей. По моему мнению, здесь мы
имеем дело с тем простым образованием вихрей, на которое
указывает творец теории вихрей — знаменитый Гельмгольц.
Если погрузить ложку в чашку кофе и, немного продвинув
ее горизонтально, вынуть вверх, то в чашке зарождается
вихревое полукольцо, отмечаемое двумя воронками на поверх-
НОВОЕ В ТЕОРИИ СОПРОТИВЛЕНИЯ ЖИДКОСТЕЙ
243
ности кофе. Конец лопасти является такой ложечкой; на задней
нерабочей стороне ее образуются замкнутые контуры, по
которым циркуляция скорости не равна нулю. Эти контуры,
смываясь сбегающей жидкостью, питают завихренной жид-
костью вихревые винтовые шнуры. Точно так же, лопасти
винта сообщают жидкости циркуляцию по замкнутым контурам,
охватывающим ось винта, вследствие чего образуется осевой
вихревой столб. Эти замкнутые контуры не могут образо-
ваться из частиц, которые подошли к винту в виде замкнутых
контуров, так как, разрезаясь лопастями винта, они более не
смыкаются в замкнутые контуры.
Согласно теореме Стокса, циркуляция скорости по конту-
рам, охватывающим винтовые шнуры, равна циркуляциям по
контурам, охватывающим соответственные лопасти, а суммы
этих циркуляций для всех лопастей равны по абсолютной
величине циркуляции осевого столба. Получается такая же
картина, какая была указана для поддерживающих планов:
как будто внутри лопастей проходят вихревые шнуры, кото-
рые, выходя из их концов, образуют винтовые вихри и осевой
вихревой столб. Но для того, чтобы поток, создаваемый винтом,
управлялся указанными вихрями, лопасти винта должны иметь
определенную конструкцию, представляющую форму, сужи-
вающуюся к концам. Такой винт дает на некотором расстоянии
от себя постоянную осевую скорость и является весьма
выгодным как в качестве геликоптерного винта, так и в
качестве гребного. Мой ученик В. П. Ветчинкин дал удобный
способ построения такого винта, и мы имеем в виду привести
с помощью его в движение воздух в строящейся теперь боль-
шой галлерее Московского технического училища (2,5X2,5 м2).
Но когда винт отступает от указанной формы, то, кроме
упомянутых вихревых шнуров, развивается в струе, отбрасы-
ваемой винтом, бесконечное множество вихрей, которые
должны лежать в поверхностях тока относительного движения,
являющихся продолжением поверхностей винтовых лопастей,
так как только при этом условии не может получиться замкну-
тых контуров, охватывающих вихри, которые притекли из
бесконечности и не разрезались полостями винта. В. П. Вет-
чинкин исследовал этот более общий случай и показал воз-
165
244
РЕЧИ И ДОКЛАДЫ
можность постановки вихревой теории для винтов произволь-
ной формы.
На основании всего сказанного можно надеяться, что при-
ближается то время, когда направляемая твердым опытом
теоретическая мысль сделается хозяином в решении вопросов
о сопротивлении жидкостей, когда аэропланы и дирижабли
будут строиться с таким же верным расчетом, с каким теперь
строятся пароходы и автомобили.
Заканчивая свою речь, я хочу отметить, что в разработку
вопросов о сопротивлении жидкостей как с теоретической,
так и с практической стороны внесли свою лепту и русские
ученые, несмотря на то, что им приходится работать сравни-
тельно в невыгодных условиях: наши аэродинамические лабо-
ратории только возникают и обставлены сравнительно с запад-
ными бедно как со стороны оборудования, так и со стороны
наблюдателей; тогда как Франция, Германия и Италия имеют
теперь специальные органы по научному воздухоплаванию,
работы наших лабораторий и ученых или не печатаются, или
же печатаются в специальных математических журналах,
вследствие чего остаются неизвестными заинтересованным
лицам в Европе.
Позвольте высказать пожелание, чтобы у нас возник орган
по научному воздухоплаванию, который было бы лучше
издавать на иностранном языке, и чтобы средства наших
аэродинамических лабораторий стали в соответствие с могу-
ществом и творческими силами нашей родины.
Эга речь была произнесена Н. Е. Жуковским 20 июня 1913 г. на
XIII Съезде русских естествоиспытателей и врачей в Тифлисе. Напечатана
в „Дневнике ХП1 Съезда русских естествоиспытателей и врачей", № 10,
нфлис 1914. Прим. ред.
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
(РЕЧЬ)
(1918—1937 и.)
Я назвал свою актовую речь „Старая механика в новой
физике". Эта тема меня, преклоняющегося перед великими
началами Галилея и Ньютона, живо затрагивает.
К концу прошлого века механика, идущая по своему по-
бедоносному пути в разрешении различных проблем по есте-
ствознанию, достигает своего апогея. Блестящие успехи астро-
номии и небесной механики, многочисленные приложения
в области физики и химии, установление всеобъемлющего
принципа сохранения энергии и успехи колебательной теории
света утверждают ту мысль, что всякое физическое явление
может считаться только тогда вполне объясненным, когда оно
получает полное механическое толкование. Взгляд на могу-
щество механики отмечен у Лапласа, который, воображая
разум, знающий начальное положение всех элементов все-
ленной, говорит, что для такого разума ничего бы не было
неизвестно, и прошедшее и будущее было бы для него
открыто. Но, развиваясь в беспредельную ширь, физика на-
копляла все новые и новые опытные факты, и ученые оста-
новились перед объяснением некоторых из них. Возникла
мысль, что может быть они и не могут быть объяснены с по-
мощью начал классической механики, и что для объяснения
тонких физических явлений нужны некоторые видоизменения
этих начал, причем эти начала стали уже прилагать не к про-
стейшим элементам механики—силе и массе, а к различным
физическим элементам: магнитному полюсу, элементу тока,
наэлектризованному шарику, электрону, квантам и т. д. За-
кон действия и противодействия, отнесенный к элементу
тока и магнитному полюсу, представлялся вообще верным
246
РЕЧИ И ДОКЛАДЫ
только в его первой части, что силы действия и противо-
действия равны и противоположны, но его вторая часть о на-
правлении сил по одной прямой, по мнению некоторых уче-
ных, должна бы быть отброшена, так как по закону Био и
Савара элемент тока и магнитный полюс выталкиваются из
общей плоскости. Световое давление как будто не удовле-
творяло принципу’сохранения импульса, а излучение радия —
принципу сохранения энергии. Когда открыли электроны и
стали изучать движение р-частиц, то нарушилось основное
начало о постоянстве массы, которое заменилось понятием
о постоянстве заряда электрона.
Но ни одно из этих видоизменений основных положений
механики не сулило ей такой ломки, как распространение на
все физические явления второго основного закона механики—-
так называемого Галилеева принципа относительности. По
этому .принципу никакими механическими явлениями, наблю-
даемыми на движущейся системе, нельзя обнаружить ее дви-
жения, и никакими наблюдениями над механическими явле-
ниями между двумя движущимися равномерно и поступательно
системами нельзя обнаружить их абсолютного поступатель-
ного движения, а только их относительное движение. Дей-
ствуя какой-нибудь силой на шарик, лежащий на палубе плы-
вущего равномерно и поступательно корабля, мы сообщаем
шарику движение, как будто бы корабль был неподвижен,
а бросая 'тело с одного плывущего корабля в другой, мы
наносим ему такой ^удар, как будто бы второй корабль был
неподвижен, а первый двигался со скоростью, геометрически
равной его относительной скорости относительно второго
корабля.
То, что говорится в Галилеевом принципе о механических
явлениях, современные физики распространяют на всякие
физические явления, т. е. на световые и электромагнитные
волны. Многочисленные попытки обнаружить поступательное
движение земли около солнца с помощью физических наблю-
дений на ее поверхности привели к отрицательным резуль-
татам. Сначала делались более грубые наблюдения, в кото-
- V
рых должно бы проявиться отношение — скорости земли
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
247
к скорости света в первой степени, потом прибегли к гораздо
более тонким расположениям, но зато в них уже определялось
/ V \2 v" g.
1 — I . Классическим наблюдением этого рода является сде-
\ с /
данное в 1881 г. наблюдение Майкельсона, которое по-
том в 1905 г. со всей точностью было повторено Морлеем
и Миллером. Сильный луч света падал под углом в 45°
на посеребренное стекло и, отражаясь от него по направле-
нию движения земли, попадал под прямым углом на зеркало,
отразившись от которого проходил опять через посеребрен-
ное стекло и попадал в зрительную трубу. Другая часть
первоначального луча проходила сквозь посеребренное стекло
по направлению, перпендикулярному к движению земли, и,
отражаясь от зеркала, отбрасывалась обратно — к посеребрен-
ному стеклу, отражаясь от которого, также попадала в трубу.
Оба луча проходили частью по одинаковым путям, частью
по различным, причем по этим последним, равным по длине,
один луч шел в ту и другую сторону по направлению дви-
жения земли, а другой — перпендикулярно этому направлению.
Простое геометрическое соображение показывает, что число
N смещенных полос в интерферометре должно быть
21 v
(1)
где I—расстояние отражающих зеркал от посеребренного
стекла, а 1— длина волны данного луча света. В установке
Морлея и Миллера число N должно бы равняться 0,37. Между
тем, никакого показания не получалось, несмотря на то, что
прибор по своей точности мог бы обнаружить ’/200 этой
величины.
Точно так же не удалось обнаружить движение земли и
никакими электромагнитными наблюдениями.
Трутон и Нобль подвешивали на унифилярном под-
весе стержень под углом в 45° к направлению поступатель-
ного движения земли, на концах которого помещали два оди-
наково заряженных конденсатора. От движения земли, со-
гласно исследованиям Роланда и проф. Эйхенвальда, мы
должны бы иметь расположение, аналогичное двум па-
248
РЕЧИ И ДОКЛАДЫ
раллельным токам, идущим в одну сторону, и стержень дол-
жен бы приблизиться к направлению движения земли, повер-
нувшись около нити подвеса. На самом деле движения стержня
не получается.
Таким образом опытно доказана первая часть принципа
относительности физических явлений. Что касается явлений
между двумя телами, то здесь мы должны обратиться к астро-
номии: к явлению передачи сигналов, аберрации и к прин-
ципу Допплера. Согласно с воззрением о неподвижном эфире
явление сигналов зависит от относительной скорости и от
скорости наблюдателя, явление аберрации только от скоро-
сти наблюдателя и только одно явление Допплера зависит
только от относительной скорости обоих небесных тел.
В одном из своих популярных сочинений Фламмарион
рисует перед читателем следующую картину. Неподвижный
наблюдатель Люмен смотрит на землю, приближающуюся к нему
со скоростью, превосходящей скорость света (300 000 км/сек).
Вследствие этого сигналы, подаваемые на земле раньше,
приходят к Люмену позже тех, которые были поданы после.
Если бы он, например, наблюдал битву при Ватерлоо, то
увидал бы, как убитые воины встают, сражаются и потом
собираются в поход. Если же предположить, что земля не-
подвижна, а сам Люмен приближается к ней, то ни при ка-
кой скорости обращения событий не произойдет, но чем
быстрее бы двигался Люмен, тем более быстро протекали
бы для него события, происходящие на земле.
Если назовем через т промежуток времени между двумя
подаваемыми сигналами, то промежуток времени между двумя
наблюденными сигналами будет:
где v — скорость наблюдателя, a v'— скорость источника
света.
Известный способ Рёмера для определения скорости света
с помощью наблюдения затмений спутников Юпитера осно-
ван на методе сигналов. Явление аберрации света состоит
в том, что луч немного отклоняется навстречу движущейся
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
249
земле, причем малый угол (в наибольшем случае 20") зависит
только от отношения скорости земли к скорости света.
Что касается явления Допплера, то оно заключается
в смещении спектральных линий, происходящем от движения
земли и от движения небесного тела. Так как на изменение
длины волн оказывает совершенно одинаковое влияние как
перемещение источника света, так и перемещение наблюда-
теля, то это смещение зависит только от относительной
скорости тел.
Разумеется, никакими прямыми наблюдениями не могла
быть доказана зависимость всех трех упомянутых явлений
только от относительной скорости, так как нельзя перенести
наблюдателя с земли на планету. Между тем, принцип отно-
сительности был принят во всей его полноте. Приняли, что фи-
зические явления на двух поступательно движущихся систе-
мах протекают совершенно одинаково, т. е. наблюдатели той и
другой системы видят явление совершающимся по закону
распространения волн с одной и той же скоростью, равной
скорости света. Пытаясь объяснить этот принцип, Эйн-
штейн в 1905 г. стал на метафизическую точку зрения, ко-
торая решение прилегающий к рассматриваемому вопросу
идеальной математической проблемы возвела в физическую
реальность. По воззрению Эйнштейна абсолютного покоя
нет и самостоятельного понятия о времени без пространства
не существует. Время всегда связано с положением точки
в пространстве и является четвертой координатой, опреде-
ляющей мировое положение точки. Понятия об одновремен-
ных событиях не существуют.
„Требуется не мало усилий и продолжительная работа
над самим собой, — пишет проф. Хвольсон чтобы освоиться
с представлениями Эйнштейна о времени, но еще несравненно
труднее принять те многочисленные следствия, которые от-
носятся ко всем без исключения отделам физики. Многие из
этих следствий явно противоречат тому, что принято назы-
вать с далеко не всегда достаточной мотивировкой здравым
смыслом".
Я бы выпустил в этой цитате слова „с далеко не всегда
достаточной мотивировкой".
1250
РЕЧИ И ДОКЛАДЫ
Почему я не могу себе представить неподвижного тела?
Бур пишет в своем прекрасном курсе механики: „Хотя мы
нигде не имеем неподвижного тела, но идея абсолютно не-
подвижного тела для нас совершенно ясна“. Если мы нахо-
димся на ускоренно движущемся теле, то посредством сейс-
мографа, которым определяются ускорения железнодорожных
поездов, мы сейчас же подсчитываем изменение его скорости.
Но, если скорость тела может изменяться, то почему же она
не может быть равна нулю? Почему, когда мы здесь с Вами
разговариваем, нельзя сделать представления о других собы-
тиях, происходящих в тот же момент? Мы не можем устано-
вить эту одновременность, и это установление практически
связано со скоростью распространения света и скоростью
движения земли, но неужели одновременности не сущест-
вует?
Учение Эйнштейна вызвало громадную литературу, бле-
щущую именами знаменитых геометров и физиков. В ней
приняли участие: Пуанкаре, Клейн, Минковский, Планк, Кон,
Вин, Хвольсон, Умов, Лауэ, Кармихель, Брилль и др. Боль-
шинство торжественных речей на заседаниях естественно-
исторических обществ за последнее время произносилось на
тему об относительности. В основании всех этих речей разъ-
яснялось, что тот способ, который мы бы употребили» нахо-
дясь на движущейся системе, для определения времени и про-
странства в предположении, что эфир этой системы движется
вместе с ней, и есть верный способ определения простран-
ства и времени для этой системы. Я приведу здесь коротко
рассуждение Кона.
Синхронность часов в двух пунктах А и В земной по-
верхности, расположенных по направлению движения земли,
мы определяем так: посылаем в момент времени t световой
или электромагнитный сигнал из А. Замечаем момент t' его
появления в В по часам в пункте В и сейчас же отражаем
сигнал назад в А, куда он приходит по часам в пункте А
в момент времени t"; если
2 ’
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
251
то часы А и В синхронны. Для неподвижного наблюдателя
Люмена, который считает неподвижным окружающий его
эфир, часы в пункте В будут отставать против часов в пункте
А и тем более, чем дальше В отстоит от А. Если теперь из
пункта А пошлем сигнал в пункт С по направлению АС
перпендикулярному к движению земли, и отразим его из С
назад в А, то приняв время пробега сигнала за
t 2AC
. с ’
мы установим масштаб часов, который будем считать верным
для всех пунктов земли. Люмен же будет считать, что наш
масштаб часов увеличен, потому что по неподвижному
относительно его эфиру луч проходит не путь АС, но боль-
ший путь.
Наконец, если бы мы хотели сравнить свой эталон длины
с эталоном длины Люмена и для этого расположили свой
метр по направлению движения земли и нанесли бы из его
концов одновременно по нашему местному времени отметки
на неподвижную линейку Люмена, то последний на своей
линейке получил бы длину большую метра и думал бы, что
наш масштаб длины в направлении движения земли увеличен.
Этого не было бы при расположении метра по направлению,
перпендикулярному движению земли.
Итак, поставленные нами с верным ходом в различных
пунктах земли синхронные часы будут с точки зрения Лю-
мена замедлены в своем ходе, и начала их счета будут ото-
двигаться все более назад по мере их удаления в направле-
нии движения земли. Точно так же все длины в напра-
влении движения будут казаться Люмену увеличенными,
а длины в направлении, перпендикулярном движению, неиз-
менными.
Если полагать, что без движения земли верен счет вре-
мени и пространства у Люмена, а при ее движении стал
верен 'счет времени и пространства у земного наблюдателя,
то можно сказать, что от движения земля сжалась в напра-
влении 'движения, все времена сократились, а начала всех
времен продвинулись вперед тем более, чем далее место рас-
252
РЕЧИ И ДОКЛАДЫ
положено в направлении движения земли. Величина сжатия
земли будет ничтожна и представляется числом 5 10\
На мой взгляд наиболее ясно отмечен математический
характер проблемы относительности в изложении Минков-
ского и Умова. Она ставится так. Имеются две находя-,
щиеся в относительном движении системы 3" и S', в которых
совершается некоторое физическое явление. Какое соответ-
ствие между х, у, z, t и х’, у', z', t', т. е. между координа-
тами и временами в обеих системах надо установить, чтобы
физическое явление в той и другой системе протекало по
закону распространения волн с одной и той же скоростью,
равной скорости света с. Минковский решает эту задачу
в предположении, что соответствие линейно, Умов же в об-
щем виде. Тот и другой для удобства вычисления заменяют
время некоторой мнимой переменной, — рассматривают мни-
мое время.
В последнем заседании Московского математического об-
щества я указал новый способ решения задачи при линейном
соответствии, не прибегая к мнимому времени. Способ осно-
ван на теореме аналитической геометрии о том, что един-
ственная точка, расстояние которой от точки эллипса вы-
ражается линейной функцией координат, есть фокус эллипса.
Я изложу здесь коротко этот способ. Воображая, что си-
стема 5 неподвижна, a S' движется относительно нее со ско-
ростью v, предположим, что в некоторой точке F произошло
возмущение, которое в системе S' согласно условию, распро-
странилось во время Т' на сферу радиуса сТ', центр которой
отошел от F на расстояние FO =vT, где Т и Г — соответ-
ственные времена.
Наблюдатель в системе S будет видеть это возмущение
распространяющимся по прямым линиям из неподвижной
точки F. Вследствие линейности соответствия точки, распо-
ложенные в системе S' на упомянутой сфере, будут пред-
ставляться ему расположенными на растянутом эллипсоиде
вращения, описанном около этой сферы, причем соответствен-
ные точки будут лежать на прямых, параллельных V. На
основании вышеуказанной теоремы аналитической геометрии
линейность соответствия требует, чтобы точка F была фо-
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
253
хусом эллипсоида. Легко показать, что отношение полуосей
эллипса , выражающее удлинение системы о , видимое на-
блюдателем системы S, будет:
(3)
а эксцентриситет эллипса будет
v
е = —.
с
Времена t' =Т в системе S' получаются, деля на с радиус
сферы, а времена, t в системе S, деля на с радиусы-векторы
* В самом деле на основании чертежа (фиг. 1) можем написать:
а = FA = сТ,
— = FO = vT,
Ь=ОА= УFA2~FCP = eV.
Отсюда:
V а2 — Ь2 v
е =--------== —
а с
Далее имеем:
x=fn=fo+~
где х' = ON' — координата точки М' сферы.
Так как во всех точках сферы время f одинаково и равно Т', то можно
писать:
х = ~(x' + vf').
Из теоремы о радиусе-векторе эллипса следует:
х' ctr . v х'
FM — ci = a-f е (x — FO) — а + ----.
откуда
254
РЕЧИ И ДОКЛАДЫ
эллипсоида, считая от фокуса. В этом способе изложения
рисуется ясная картина соотношения времен и пространств
в системах S и S'. Выражая эту картину формулами, мы
сейчас же получаем уравнения преобразования Лоренца
(см. сноску на стр. 253):
= (4)
(5)
Если обернуть эти формулы, т. е. разрешить их относи-
тельно t' и х', то получатся такие же уравнения, только
v будет заменено на—v. Этого и следовало ожидать, так
как системы S и S' [играют в задаче совершенно одинако-
вую роль.
Но не надо думать, что полученное решение является
единственным решением [предложенной задачи. Мы нашли
его при условии линейности преобразования. Проф. Умов
указал, какими уравнениями будут определяться преобразо-
вания для более сложных предположений. То обстоятельство,
что преобразований, удовлетворяющих принципу относитель-
ности, может быть много, подрывает на мой взгляд то особое
физическое значение, которое приписывается преобразованию
Лоренца. Раз возможно придумать много соответствий, при
которых физическое явление в обеих системах протекает по
волновому закону со скоростью света, то, почему же при-
рода должна следовать только преобразованию Лоренца? На
самом деле нельзя без искажения понятия о времени полу-
чить волновой закон в двух системах, перемещающихся одна
относительно другой.
Из формулы преобразования Лоренца сейчас же развер"
тывается вся новая механика. Диференцирование формул
(4) и (5):
dx = -р- (dx' -J- vdt'),
dt = ~(dt'-\--^
р \ с2 /
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
255
дает правило сложения скоростей:
dx' .
dt 1 i 1 dx' ’
1+-?v-dF
(6)
по которому скорость сложного движения не просто равняется
сумме слагаемых скоростей, а равна этой сумме, разделен-
ной на единицу плюс произведение слагаемых скоростей,
поделенное на квадрат скорости света. По этой теореме,
когда одна из слагаемых скоростей приближается к скорости
света, то и результирующая скорость приближается к ско-
рости света. Сколько бы мы ни слагали скоростей, мень-
ших скорости света, результирующая скорость будет всегда
меньше скорости света.
„Эта теорема подавала иногда повод к ложным толкова-
ниям", пишет Лауэ. По его мнению, могут существовать
беспредельные скорости, но с ними будет двигаться „немате-
риальная точка". Лауэ указывает, что, вращая линейку,,
образующую малый угол а с другой неподвижной линейкой,
мы можем получить громадную скорость точки пересечения
при приближении угла а к нулю. Замечу здесь, что много
лет тому назад на том же принципе я построил прибор,
в котором подвижной конус катался внутри неподвижного
конуса почти равного диаметра, причем вращение оси под-
вижного конуса около оси неподвижного воспринималось
особым механизмом, приводившим в движение вполне мате-
риальные тела — прядильные веретена.
Будучи приложена к опыту Френеля над прохождением
луча света вдоль текущей воды, теорема сложения скоростей
по принципу относительности дает для результирующей ско-
рости величину:
I С
v-\---
п
1 + —
СП
хорошо согласную с опытом (и есть показатель преломления
жидкости).
1------
СП
п-
I
256
РЕЧИ И ДОКЛАДЫ
Диференцирование формулы (6) дает нам при
dx'
dt'
= 0:
d?x____r 3 d2x'
dfi ~di^>
а двойное диференцирование равенств
У=у', z= z
при обращении внимания на формулу (3)
</х'
= 0 дает нам:
&У = R2
dfi Р dt'2 ’
dt2 Р dt'2 ’
положении
(7)
(8)
и положении
Эти формулы определяют тангенциальное ускорение и уско-
рение, нормальное к скорости материальной точки в системе
S, в предположении, что точка начинает свое движение
в системе S', движущейся относительно системы 5 поступа-
тельным движением со скоростью, которую в данный момент
имеет материальная точка.
Зная ускорения, мы от кинематики переходим к динамике.
Если напишем уравнения движения в системе S', в которой
в данный момент точка покоится, и перейдем от них к урав-
нениям в системе S, то, в предположении, что сила осталась
та же, что в системе S', получим:
т‘ d2x у, т' d2y у, т' d2z
~F~d? ’ ^di2^ ’
где т' — масса неподвижной точки при ® = 0.
Для того, чтобы уравнения сохранили свой вид, надо
допустить, что в новой системе масса точки изменилась
и для продольного и поперечного направления получились
< массы:
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
257
где то есть масса точки на покоющейся системе S'. Таким
образом преобразование Лоренца, выражая принцип относи-
тельности для волнового движения, уничтожает его для
обыкновенной механики. Сила, действующая на тело, движу-
щееся по инерции, уже не сообщает ему такого же ускоре-
ния, как сила, действующая на покоющееся тело.
Действуя некоторой силой на шарик, лежащий на палубе
корабля, движущегося прямолинейно и равномерно, мы уже
не сообщаем ему того же движения, какое сообщили бы при
покоющемся корабле. Инерция шарика будет возрастать
со скоростью корабля, и она будет более в направлении
движения, нежели в направлении, к нему перпендикулярном.
В возрастании массы со скоростью лежит причина того,
что с точки зрения принципа относительности конечная сила
не может сообщить телу скорости более световой. С воз-
растанием скорости и с приближением ее к с величина
3 приближается к нулю, и, следовательно, масса тела растет
до бесконечности.
Применительно к задаче о движении электронов находят
удобным умножить второе и третье уравнения (9) на Р
и отнести этот множитель к составляющим силам. Тогда
в первых частях уравнений мы будем иметь, как нетрудно
проверить, обращая внимание на формулу (3), в которой
•следующие величины:
d / тп0 dx\ d / mG dy \ d I m0 dz
dt\^~dt)' jFy'p'jF/’ P dt
Это будут производные по времени от количества движе-
Иия электрона, предполагая, что его масса равна
|Л =
Р •
(И)
Вводя в формулу (9) зависимость массы от скорости,
принцип относительности разрушает большинство обыденных
ТеоРем динамики.
Зак. 2430. Н. Е. Жуковский. Том ТУ
17
258
РЕЧИ И ДОКЛАДЫ
Работа, совершенная движущей силой, уже не будет
равна приращению живой силы. Она представляется иной
величиной.
Согласно указанному (формула 9) выражению тангенци-
альной движущей силы X, совершенная ею элементарная
работа будет:
Сумма этих работ при изменении v от нуля до некоторого
значения v есть
с2™() 0-----1
Если будем определять массу электрона по формуле (11),
то увидим, что ее изменение при изменении v от нуля до
значения v есть
/ 1 i
I1 —'J0 = I -q---1
\ Р
Таким образом работа движущей силы равна
С2(Н —Но)-
Она пошла на живую силу прибавившейся массы, движущейся
со скоростью света. При этом ничтожное прибавление массы
поглощает громадную работу. Результат этот имеет большой
интерес для радиологии; но я думаю, что его можно получить
и в обыкновенной механике, составляя уравнения движения
электронов с помощью уравнений Максвелла, как это делает
Абрагам.
Из сказанного мною видно, что принцип относительности
с качественной стороны совершенно разрушает классическую
механику; что касается до количественной стороны, то фактор
Р, который производит это разрушение, отличается на нич-
тожно малую величину от единицы. Так при v, равном ско-
рости земли1, I — I = 10 8. Для техники и даже для астро-
1
v — 30 км)сек\ с = 300 000 км!сек.
СТАРАЯ МЕХАНИКА В НОВОЙ ФИЗИКЕ
259
номии эта точность была бы совершенно достаточна, но
с отведением старой механике такой скромной роли я не
могу согласиться. Я убежден, что проблемы громадных
световых скоростей, основные проблемы электромагнитной
теории разрешатся с помощью старой механики Галилея
и Ньютона.
Покойный профессор Столетов, оканчивая свою бле-
стящую речь „Эфир и электричество" на VIII съезде
естествоиспытателей и врачей, сказал: „Механика электри-
чества со включением лучей света и тепла есть механика
эфира. Эта механика опирается на уравнения Максвелла,
которые обыкновенно выводят из закона Био и Савара
и закона индукции. Но не вывод этих уравнений, против
которого можно сделать возражение, а согласие их со всеми
прежними и новыми физическими опытами ставят их во главе
всей теоретической физики".
„Нельзя изучать, — пишет Герц, — эту удивительную те-
орию, не испытывая по временам такого чувства, как будто в
математических формулах есть самостоятельная жизнь, как
будто они умнее нас, умнее даже своего автора, и дают больше,
чем в свое время в них было вложено".
Эти уравнения охватили все световые явления, электро-
магнитные волны Герца и в тонком анализе Абрагама дали
полную теорию движения электронов. Мне сомнительна
важность работ Эйнштейна в этой области, которая обстоя-
тельно была исследована Абрагамэм на основании уравнений
Максвелла и классической механики.
Проф. Н. П. Кастерин в своем докладе в Петроград-
скую Академию наук об анализе опытов Бехерера над
полетом Р-частиц, выделяющихся из радия, указывает на
несогласие этих опытов с формулой Эйнштейна.
Чтобы построить механику эфира, надо, по моему мнению,
постигнуть механическую конструкцию уравнений Максвелла,
не уклоняясь от того классического приема, которому сле-
довали Томсон и Гельмгольц. Всякую физическую систему,
полная энергия которой выражается с помощью некоторых
параметров и их производных, можно трактовать с помощью
уравнений Лагранжа и начала Гамильтона, хотя подробности
17*
260
РЕЧИ И ДОКЛАДЫ
конструкции системы нам могут быть неизвестны. В ней
могут совершаться некоторые скрытые от нас циклические
процессы, которые на первый взгляд затемняют явление.
Взявши в руки шар с вращающимися внутри гироскопами,
мы на первый взгляд можем подумать, что его движение
отступает от механических законов, но оказывается, что для
изучения этого движения нам не нужно знать, что вращается
внутри шара, но нужно только иметь момент количества
движения вращающегося.
Вывод уравнений Максвелла в указанной классической
форме сделан проф. Н. П. Кастериным. С разрешения автора
я закончу свею речь указанием на идею этого вывода. Первая
группа уравнений Максвелла, оказывается, выражает неиз-
менность трубок Фарадея, вполне аналогичную закону
сохранения вихрей в гидродинамике несжимаемой жидкости,
причем роль вихревых линий играют линии электрических
сил, роль напряжения вихря — элементарный заряд электри-
чества и роль скорости — скорости смещения эфира. Если
рассматривать систему трубок Фарадея и составить ее полную
энергию по известней формуле энергии электромагнитного
поля, то начало Гамильтона дает вторую группу уравнений
Максвелла, выражающую производную по времени магнитных
сил, с некоторым обобщением, приводящим к обыкновенным
уравнениям Максвелла при перпендикулярности смещений
к направлению электрических сил.
Не является ли аналогия трубок Фарадея с вихрями
несжимаемой жидкости указанием того пути, следуя которому
можно построить механику эфира, и действительно ли утра-
тилась роль старой механики в новой физике?
Эта речь была приготовлена проф. Н. Е. Жуковским к акту 12 января
1918 г. в Московском университете. Речь была произнесена 3 марта 1918 г.
в Мос ковском математическом обществе. Печатается речь впервые. Для
настоящего издания рукопись была просмотрена проф. Н. П. Кастериным;
им же был выполнен чертеж по наброску Н. Е. Жуковского в рукописи.
Прим. ред.
НЬЮТОН КАК ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОЙ
МЕХАНИКИ
ИСААК НЬЮТОН
(1643—1727)
НЬЮТОН КАК ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
(РЕЧЬ )
(1887—1888 и.)
На мою долю выпало указать то высокое значение, кото-
рое имело творение Ньютона j,Philosophiae Naturalis Principia
Mathematica" для развития теоретической механики. Чтобы
рельефнее выставить это значение, я начну с краткого очерка
истории механики до Ньютона.
Как известно, до начала XVII столетия все исследования
в этой области относились только к статике. Таковы откры-
тия Архимеда по теории рычага и по гидростатике, исследо-
вания Паппуса и Гульдена о центре тяжести и знаменитая
теорема Стевина о равновесии сил на наклонной плоскости,
основанная на постулате о невозможности вечного движения
и заключающая в себе правило параллелограма сил. Осно-
вателем динамики был Галилей, который, по словам Лагранжа,
„сумел выделить из обыденных явлений основные законы
природы, столь долго ускользавшие от внимания философов".
Эти обыденные явления были: падение тяжелых тел, их
движение по наклонной плоскости, движение маятника
и движение тел, брошенных под углом к горизонту. Описание
этих явлений и их глубокое математическое исследование
Галилей поместил в своем сочинении „Разговоры и матема-
тические доказательства, относящиеся к двум новым уче-
ниям" (1638 г.), представленном в виде разговора между
тремя лицами. В этом сочинении Галилей устанавливает два
основные механические закона: закон инерции и закон неза-
висимости силы от движения тела. Я не приведу здесь
первого закона, так как упомяну о нем, когда буду говорить
о Ньютоне; что же касается второго закона Галилея, то
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
в несколько расширенной форме его выражают теперь так:
Если на тело, движущееся по инерции или от действия
других сил, будет действовать сила, то движение его сло-
жится из прежнего движения и из того движения, которое бы
сила сообщила покоющэмуся телу“.
Из этих двух законов сейчас же вытекает, что постоянная
сила сообщает телу, не имеющему начальной скорости, по
своему направлению равномерно-ускоренное движение. Но
это заключение не было сделано Галилеем, который смотрел
на равномерно-ускоренное падение тел на землю как на их
свойство и не указывал, что оно происходит от постоянней
силы тяжести. Эго заключение было сделано последователем
Галилея, Гюйгенсом (Huygens) в его сочинении „Horologium os-
cillator ium“ (1673 г.). Он разбирает в этом сочинении результаты,
добытые Галилеем, и прибавляет к ним многие новые важные
открытия, относящиеся преимущественно к несвободному
движению: определение центробежной силы, изохронизм
циклоидального маятника, решение задачи Мерсена о сложном
маятнике, исследование удара тел и т. д.
„После открытия Галилея, — говорит Дюринг в своей
„Истории механики",—расширение старых взглядов и форму-
лировка принципов совершается, главным образом, в двух
направлениях: для одного из них указующим типом служит
учение Галилея о движении по наклонной плоскости, для
другого — его же исследования о параболической траектории
брошенного тела. Главным представителем первого напра-
вления является Гюйгенс, второго — Ньютон". Я позволю себе
по поводу этих слов забежать несколько вперед и заметить,
что сравнительно небольшая статья в „Principia" о несвобод-
ном движении вносит весьма важное упрощение в исследо-
вание этого вопроса, заключающееся в пользовании парал-
лелограмом сил. Дело в том, что, несмотря на теорему
Стевина, которая заключала в себе правило параллелограма,
ни Галилей, ни Гюйгенс нигде не пользуются им. Так, для
того, чтобы доказать, что тяжелые тела сбегают со всех
наклонных плоскостей одинаковой высоты с одинаковой ско-
ростью, Галилей прибегает к опыту, а Гюйгенс пользуется
установленным им принципом, что центр тяжести может под-
НЬЮТОН —ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ 265
няться только на ту высоту, с которой он упал. Гюйгенс
воображает две наклонные плоскости одной высоты, стоящие
на горизонтальной плоскости — одна против другой. Если бы
тело приобретало большую скорость, сбегая с правой
плоскости, то, уменьшая высоту подъема, мы получили бы
при падении скорость, с которой оно могло бы подняться на
левую плоскость, а это противоречит вышеупомянутому прин-
ципу. Разумеется, здесь доказательство желаемого могло бы
быть легко получено через разложение силы тяжести.
Скажем еще несколько слов о Декарте. Он первый
установил понятие о количестве движения, но, как кажется,
не приписывал ему знака, потому что утверждал, что при
ударе легким шаром по покоющемуся тяжелому шару последний
остается в покое, а первый отскакивает. Декарт, а за ним
Гюйгенс указали, что движение центра тяжести соударяющихся
тел не изменяется ударом. Но, как увидим ниже, первое
доказательство так называемого начала сохранения центра
тяжести принадлежит Ньютону.
Указав таким образом в кратких словах, что было сде-
лано по теоретической механике до Ньютона, я перехожу
к изложению содержания его знаменитого творения, в кото-
ром весь вышеупомянутый разбросанный материал получил
строго систематическое распределение и пополнился массой
новых исследований и открытий.
„Principia" Ньютона разделяются на три части, из которых
первые две посвящены теоретической механике, а третья —
небесной. Первая часть начинается установлением основных
определений (definitiones). Мы приведем здесь важнейшие из
них, пользуясь современной терминологией. Масса опреде-
ляется как количество материи, практически измеряемое весом;
количество движения — как произведение массы на скорость;
сила — как причина, сообщающая телу количество движения,
причем величина силы есть количество движения, сообщаемое
в единицу времени. Заметим, что количеству движения, так
же как и силе, надо приписывать направление, которое есть
направление скорости.
Затем следуют основные законы движения (axiomata, sive
leges motus), которые я приведу здесь в подстрочном переводе:;
2б6 ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Закон 1. Всякое тело пребывает в состоянии покоя или
равномерного и прямолинейного движения, пока сообщенные
ему силы не заставят его изменить это состояние.
Закон 2. Изменение движения (т. е. количества движе-
ния) пропорционально сообщенной движущей силе и происхо-
дит по той прямой, по которой действует сила.
Закон 3. Всякому действию соответствует противодей-
ствие равное и противоположное, т. е. действия двух тел
одного на другое всегда равны и направлены в противопо-
ложные стороны.
Здесь первый закон есть закон инерции Галилея. Второй
закон, — вместе с добавлением, которое делает Ньютон при
выводе правила параллелограма сил и по которому одно-
временно приложенные силы производят то же изменение
в количестве движения, как силы действующие порознь,—
эквивалентен приведенному выше закону независимости
силы от движения тела. Что же касается третьего закона,
то хотя сам Ньютон и упоминает, что он был известен Гюй-
генсу, но в ясно определенной форме он встречается впервые
в „Principia" и всеми авторами приписывается Ньютону.
Я позволю себе здесь несколько остановиться, чтобы ука-
зать, каким образом отнеслись к основным началам механики
ученые последующего времени и как к ним относятся теперь.
Сначала явилось стремление уменьшить число этих начал
через математическое доказательство некоторых из них. Эйлер
считает математически необходимым принцип независимости
силы от движения. Лаплас доказывает правило параллелогра-
ма сил, но считает за опытное начало пропорциональность
силы и ускорения. Пуассон принимает закон инерции, но до-
казывает правило параллелограма и пропорциональность
силы ускорению. Остроградский доказывает закон инерции
и т. д. Но эта попытка уменьшить число основных законов
механики не имела успеха, и доказательства, даваемые од-
ними авторами, встречали по большей части возражения со
стороны других. В настоящее время установилась мысль о
необходимости положить в основание механики некоторые
законы, которые для большей ясности относят не к телу,
•а к материальной точке. При этом существуют два способа
НЬЮТОН —ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОМ МЕХАНИКИ 267
изложения. Одни авторы (Бур, Понселе, Резаль, Лоран, Жиль-
бер) принимают за основные механические величины: про-
странство, время и силу, массу же определяют по ускорению
и силе. За основные законы механики они принимают: закон
инерции, закон независимости силы от движения и третий закон
Ньютона. Другие же авторы (Томсон и Тет, Риттер, Бобылев)
берут за основные механические величины: пространство, время
и,массу; силу же определяют по количеству движения, сооб-
щаемого ею в единицу времени покоющейся материальной
точке. Тогда основные законы механики представляются
в форме Ньютона, с тем дабавлением ко второму закону,
о котором было упомянуто выше. Кроме стремления дать
математическое доказательство некоторым из основных начал
механики, следует еще упмоянуть о попытках изменить опре-
деление механических величин и совместно с этим по-новому
формулировать основные законы механики.
Нельзя не согласиться с Томсоном и Тетом, что „всякая
такая попытка оканчивалась полной неудачей". Так, напри-
мер, в недавно вышедшей критике механических принципов
Маха1, автор находит рациональным сделать следующее из-
менение в изложении Ньютона. Третий закон он относит к
определению массы, говоря, что отношение масс двух вза-
имодействующих тел равно обратному отношению получае-
мых ими ускорений; так что от закона остается только ут-
верждение, что ускорения взаимодействующих тел противо-
положны и что отношение масс двух тел не зависит от их
физического состояния и от того, определено ли оно непо-
средственно, или с помощью промежуточного тела. Первый
и второй законы Ньютона он опускает, так как они, по его
мнению, заключены в определении силы, величину которой
Мах определяет приращением (геометрическим) количества
движения тела движущегося. После этого к остатку от третье-
го закона он прибавляет принцип независимости действия
силы от действия другой силы. По нашему мнению, в таком
изложении, прежде всего, представляется неправильной мысль
считать силу и массу понятиями производными. Если опре-
1 М а с h, Die Mechanik in ihrer Entwickelung hlstorisch-kritisch darge-
stellt, 1883.
268
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
делять массу тел, взаимодействуя на них телом единицы
массы, то остается неизвестным, будет ли масса тела, состо-
ящего из двух одинаковых тел, вдвое более массы каждого
из них; а между тем это несомненно имеет место. Так что
к началам Маха придется еще прибавить такое начало: масса
сложного тела равна сумме масс слагаемых. Что касается
определения величины и направления силы, то, на наш взгляд,
они должны быть даваемы по действию силы на покоющееся
тело, и тогда второй закон Ньютона выразит независимость
действия силы от скорости, а сделанное им добавление вы-
разит независимость действия силы от другой силы. Что ка-
сается закона инерции, то его следует ставить отдельно для
того, чтобы указать, что причина изменения количества дви-
жения не заключается в самой материальной точке. Я окончу
сделанное мною отступление тем, что в настоящее время,
когда общепринятыми являются единицы: пространства, вре-
мени и массы, — изложение механики в форме, предложен-
ной Ньютоном, получает особую цену.
Переходим теперь к указанию тех замечательных выводов,
которые сделал Ньютон из ясно установленных им начал ме-
ханики.
Первым таким выводом является теорема о сохранении
центра тяжести многих свободных, взаимодействующих друг
на друга илн соударяющихся тел. Ньютон доказывает с по-
мощью своего третьего закона, что центр тяжести этих тел
будет или покоиться, или двигаться прямолинейно и равно-
мерно. Потом следует глубокий анализ движения тела или,
как мы теперь скажем, материальной точки, под действием
центральной силы, т. е. такой, направление которой посто-
янно проходит через один центр. Ньютон доказывает мето-
дом, который вошел в большинство элементарных учебников
механики, что путь материальной точки будет при этом пло-
ский, и что площади, описываемые радиусом, соединяющим
материальную точку с центром силы, будут пропорциональны
протекшим временам; он показывает также, что это свойство
движения служит доказательством, что точка движется под.
действием центральной силы. Затем является вопрос об оп-
ределении величины движущей силы. Ньютон делает это во
НЬЮТОН — ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ 269
всех разбираемых им случаях однообразным приемом, поль-
зуясь выражением силы с помощью бесконечно малой линии,
называемой им стрелкой. Обратим внимание на приложенную
здесь фиг. 1. Здесь BFA есть весьма малая дуга, пробегае-
мая материальной точкой по ее пути; Е — средина хорды ВА\
FE— стрелка, проводимая параллельно действующей силе.
Движение материальной точки по пути FA сложится из дви-
жения по пути FE от действия силы и из движения по пу-
ти ЕА от инерции. Величина Р движущей силы найдется, разде-
ляя двойной путь FE на квадрат протекшего времени и умно-
жая полученную дробь на массу материальной точки; но вре-
мя равно пути ЕА (или */2 ЕА), раз-
деленному на скорость точки (эту ско-
рость назовем v). Таким образом, по-
лучается формула:
FE
Р-^ВА,-
предельное значение
представлять величину
триваемом месте пути.
Ньютон прилагает
определения величины
силы при движении
которой будет Д
силы
в рассма-
эту
Фиг. 1.
формулу
централь-
на окружности с произволь-
для
ной
ным центром силы, по коническим сечениям с центром силы
в центре кривей и, наконец, по коническому сечению с цен-
тром силы в его фокусе. Последний случай, который имеет,
разумеется, капитальную роль для третьей части „Principia ,
дает притягательную силу, обратно пропорциональную квад-
ратам расстояния точки от центра силы. Если сюда прибавить
дальнейшее исследование Ньютона о построении конического
сечения, дающего путь материальной точки при данной при-
тягательной центральной силе, обратно пропорциональной
квадратам расстояния, и при данной начальной скорости, то
будет ясно, что при упомянутой силе путь материальной точ
ки есть всегда коническое сечение. Задачу о движении по
коническим сечениям Ньютон решает во всей полноте: он
устанавливает даже связь между временем и положением точ-
270
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ки, преодолевая трудность задачи остроумными геометриче-
скими построениями.
За исследованием движения под действием центральной
силы следуют еще статьи: о движении по движущемуся пути,
о несвободном движении, о движении многих притягивающихся
тел, о притяжении сфер и тел иной формы. Я не стану
подробнее останавливаться на обширном материале, заклю-
ченном в этих статьях, но позволю себе здесь сказать не-
сколько слов вообще о методе математиче-
<ского исследования, употребляемом великим
ученым в разбираемом нами сочинении. Это есть
метод геометрии бесконечно малых, употребляе-
мый Гюйгенсом, но проведенный Ньютоном в
строго систематическом порядке. Замечательно,
что он никогда не выражает рассматриваемых
величин (силы, массы, скорости) формулами,
а рассматривает только отношения их, выра-
жаемые отношением конечных или беско-
нечно малых линий. Написав при рассмотрении
фиг. 1 формулу для силы Р, мы отступили не-
сколько от способа изложения Ньютона. Для
и указания этого способа я приведу здесь нью-
Фиг. 2. тоново доказательство начала сохранения
энергии при действии центральной силы. На
фиг. 2 О есть центр силы, FEG и FBA — прямолинейный и
криволинейный пути двух материальных точек с одинаковой
массой, которые обе вышли из F с одинаковой скоростью:
одна по направлению радиуса, другая — как-нибудь. Требу-
ется доказать, что во всех точках того и другого пути,- равно
отстоящих от центра О, скорости будут равны. Для этого
проведем из центра О две бесконечно близкие окружности
ЕВ и GA и опустим из D перпендикуляр DC на АВ. Допу-
стив, что скорости в точках В и Е равны, доке жем, что они
будут равны в точках А и G. Приращения скоростей на пу-
тях ВА и EG будут, с одной стороны, в зависимости от от-
ношения времен прохождения этих путей, т. е. от АВ: BD;
с другой—-от отношения сил, действующих на этих путях,
т. е. от BC-.BD.
НЬЮТОН — ОСНОВАТЕЛЬ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ 271
Таким образом, отношение приращений скоростей выра-
зится через
АВ ВС=АВу.ВС
BD Х BD BD2
и равно, по известному свойству прямоугольного треуголь-
ника, единице.
Подобными геометрическими приемами Ньютон справлялся
с самыми трудными задачами теоретической механики, и
некоторые авторы (Клеро, Араго, Боссю), приходя в недоу-
мение над геометрическим решением особенно трудных во-
просов, предполагают даже, что они были найдены Ньюто-
ном методом флюксий (которым он уже владел при издании
„Prine.pia“) и потом приведены к геометрической форме. Но
нам думается, что объяснение заключается в синтетическом
складе ума великого геометра, который в самый метод флюк-
сий ввел идеи о пространстве и времени.
«Не надо забывать, — говорит Шаль, — что, приписывая
анализу открытия Ньютона, мы будем обязаны допустить,
что этот геометр пользовался также и вариационным исчис-
лением, открытие которого принадлежит великому Лагранжу_
Наконец, приписывая анализу открытия Ньютона, мы должны
будем, чтобы быть последовательными, сказать то же о рабо-
тах Маклорена и Савара».
Вторая часть „Principia" заключает^ себе учение о сопро-
тивлении среды и развита Ньютоном в видах опровержения
вихревой теории планет Декарта. В ней Ньютон рассматри-
вает сначала движение свободного тела в среде, сопротивле-
ние которой пропорционально первой или второй степени
скорости, под действием силы тяжести и центральной силы,
потом дает теоретическое и опытное исследование сопроти-
вления среды и заканчивает рассмотрением движения вращаю-
щегося жидкого цилиндра. Так как в этой части трактуются
вопросы, которые и до сих пор не получили своего полного
решения, то, несмотря на все остроумие ее автора, она не
отличается богатством результатов. Что же касается опытных,
исследований Ньютона над сопротивлением среды, то следует
указать, что найденный им результат о пропорциональности
272
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
силы сопротивления кведрату скорости и плотности среды
вполне согласен с современными гидродинамическими иссле-
дованиями Кирхгоффа, Рэлея и др.
Затем следует третья и последняя часть „Principle". Эта
часть носит заглавие „О системе мира" и содержит в себе не-
бесную механику Ньютона; ей будет посвящен следующий
реферат. Это та часть книги, которая всего более прослави-
ла Ньютона; но уже в первой части своего труда он так да-
леко двинул вперед теоретическую механику, настолько при-
вел в порядок излсжение ее начал, что одной этой части
было бы достаточно, чтобы обессмертить его имя. Читатель на-
шего времени — а между ним и Ньютоном стоит целый ряд ве-
ликих ученых — преклоняется перед гением Ньютона, встречая
в „Principia" полное и всегда верное решение вопросов, кото-
рые, повидимому, могли бы быть решены, только опираясь
на результаты позднейших открытий. Невольно приходишь
в изумление, читая, например, ньютоново исследование о дви-
жении по вращающемуся пути, в котором великий геометр
принял во внимание все обстоятельства, проистекающие от
сил относительного движения, указанных только Кориолисом.
Книга Ньютона, по ясному и систематическому изложению
основных механических понятий, еще и теперь может служить
и служит для глубокого изучения механики. „Быть может,
никогда и ни в одной науке, — замечают Томсон и Тет,—
столь простые и, в то же время, столь широкие начала не
были положены в основу системы", и „два столетия, протек-
шие с тех пор, как Ньютон дал свои законы движения, не
указали надобности что-либо в них изменить или дополнить".
Эта речь была произнесена проф. Н. Е. Жуковским на собрании От-
деления физических наук Общества любителей естествознания, посвящен-
ном памяти Ньютона, и напечатана в сборнике „Двухсотлетие памяти Нью-
тона (1687—1887 г.)“, Москва 1888. Прим. ред.
ТРУДЫ А. Ю. ДАВИДОВА ПО АНАЛИТИЧЕСКОМ
МЕХАНИКЕ
Зак. 2430 Н. Е. Жуковский Том IX.
18
А. Ю. ДАВИДОВ
(1823-1885
ТРУДЫ А. Ю. ДАВИДОВА ПО АНАЛИТИЧЕСКОМ
МЕХАНИКЕ
(1890 г.)
Первые ученые работы А. Ю. Давидова относятся к ме-
ханике, несмотря на то, что по складу своего ума он более
имел расположения к чистой математике. Вероятно в этом
сказалось, с одной стороны, влияние его учителя Н. Д. Браш-
мана, и с другой — увлечение аналитическими приемами
исследования, которые в то время господствовали в теорети-
ческой механике. В начале своего сочинения „Теория равно-
весия тел, погруженных в жидкость" А. Ю. Давидов выразил
свой взгляд на современную ему механику следующими сло-
вами: „Достоинство новой механики заключается в ее боль-
шой аналитической общности, превосходный образец которой
дает механика Лагранжа", — и во всех своих работах по ме-
ханике, он действительно, являлся достойным последователем
Лагранжа.
Вот перечень напечатанных трудов А. Ю. Давидова по ана-
литической механике:
1. Теория равновесия тел, погруженных в жидкость (Рас-
суждение, написанное для получения степени магистра), Мо-
сква 1848.
2. Uber die Gleichgewichts-Lagen eines mit seiner ganzen
Grundflache in eine Fliissigkeit getauchten geraden dreiseitigen
Prisma’s („Journal von Crelle", Bd. 38,1849).
3. Sur le maximum du nombre des positions d equilibre d un
prisme triangulaire, homogene, plonge dans une fluide („Bulletin
physico-mathematique de I’Academie de St-Petersbourg , t. XIII,
1854).
4. Теория капиллярных явлений (Рассуждение, написанное
на степень доктора), Москва 1851.
18*
276
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
5. La theorie de phenomenes capillaires („Bulletin de la So-
ciele imperiale des naturalistes de Moscou", № 2, 1885).
Магистерская диссертация А. Ю. Давидова „Теория рав-
новесия тел, погруженных в жидкость" представляет и по сие
время самый полный трактат на эту тему.
Рассматривая вариации определенных интегралов, выра-
жающих объем, отсеченный от тела некоторой плоскостью,
и центр тяжести этого объема, А. Ю. Давидов составил
диференциальные уравнения, служащие для определения по-
верхности центров (место центров тяжести постоянного
отсеченного объема), и показал, как с помощью этой поверх-
ности находятся положения равновесия плавающего тела.
Поясним здесь метод исследования А. Ю. Давидова на слу-
чае равновесия прямых 'цилиндров, плавающих при горизон-
тальных образующих, рассмотрением которого начинается
его сочинение. Это есть случай равновесия площади. Если
y=f(x),
у = ах-\-b
будут уравнения контура площади и прямой сечения, то пло-
щадь и отсеченной части и координаты 5, т] ее центра тя-
жести определяются при помощи уравнений:
' а-2
u = f (ax+b—f(x))dx,
а?,
а?.
= J (ах 4- 6 —/(%)) xdx,
а?,
а-2
«4==-^- J (ax-f-6 — f(x))~dx,
X,
I
где х, и х2 суть два действительные корня уравнения
/(x) = ax-J-fe
(Давидов останавливается на предположении, что линия сече-
ния пересекает контур площади только в двух действитель-
ных точках). Так как для всякого положения линии сечения
и должно быть постоянно, то вариация первого интеграла
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
277
должна быть равна нулю. Это дает нам, вследствие обраще-
ния в нуль подинтегральной части, уравнение:
а?,
| (х da -f- db) dx = -X2 - - da -f- (x2 — xj db — O
a;,
ИЛИ
^^da + db = 0. (1)
Складывая это уравнение с уравнением
Уй+gi __п *->4~Xi , L
2 “ 2 ’
находим, что
= (а + da) 4- ь + db,
т. е. две бесконечно близкие прямые сечения пересекаются
в ^середине отсекаемой хорды. Называя линией сечения
огибающую прямых сечения, А. Ю. Давидов получает отсюда
теорему: линия сечений прикасается к прямым сечения
в срединах отсекаемых хорд.
Берем вариации от второго и третьего интеграла, заме-
чая, что и в них подинтегральная функция обращается при
пределах в нуль. Получаем:
uJE ( (xda db) xdx = _ - 1 - da 4-~ db,
J 3 £
a?i
а?2
uJt) = [(ах2 4- bx) da 4~ (ах 4~ Ь) db] dx =
ат
(у 8__ у 3 у 2____у 2 \
-Х1 а 4- 2 о — И da +
(у 2__у 2 \ ,,
——— а 4- (х2 — Х1) ь j db.
Так как последняя формула на основании уравнения (1) при-
нимает вид:
I ( хъ —х13 д I (хь
udr\ = а[---5---da 4~‘ о ао I,
\ J /
278
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
то
Л “°'
(2)
Из этого уравнения следует, что касательная к линии
центров параллельна соответственной линии сечения.
Исключая из выражения для величину db с помощью
формулы (1), находим:
12 и
(3)
С помощью формул (2) и (3) А. Ю. Давидов выводит весьма
простое выражение для радиуса кривизны R кривой центров
Из формулы (2) имеем:
d2rri da
~d&~~dt’
что вследствие формулы (3) приводит к
d2rj _ 12u
Л2 ~ (х2 —Xj)8’
Но если предположить, что линия сечения параллельна оси
Ох, то а = 0 и
р 1 xt):i
d2n 12 и
При а — 0 имеем: х2 — х{ = d, где d отсекаемая хорда,
так что
n d3
12u ‘
(4)
ds
Так как есть момент инерции хорды относительно ее
центра, то заключаем, что радиус кривизны линии центров
равен центральному моменту инерции отсекаемой хорды,
разделенному на отсекаемую площадь.
Уравнения (1), (2), (3) служат для определения линии цен-
тров. Выразив х2 и %] в функции а и Ь, интегрируем уравне-
ние (1) и устанавливаем связь между а и Ь; потом исключаем
с помощью этой связи b из уравнения (3) и, интегрируя его,
ТРУДЫ А. ю. ДАВИДОВА ПО МЕХАНИКЕ
279
определяем ? в функции а; далее подставляем вместо di его
значение через а и da в уравнение (2) и, интегрируя его,
определяем nq в функции а. После этого для получения урав-
нения линии центров остается только исключить а из двух
найденных уравнений Ч
Но для отыскания положений равновесия плавающего
тела в этом исключении собственно нет нужды. На основании
второй из доказанных теорем следует, что все положения
равновесия найдутся, опуская из центра тяжести тела
нормали на линию центров и проводя соответствующие
этим нормалям линии плавания.
Называя через х, у координаты центра тяжести тела, бу-
дем иметь вследствие этой теоремы для определения поло-
жения равновесия формулу:
Ь^о + 1 = 0. (5)
х — с
Подставляя сюда i) и £ в функции а, получим уравнение,
из которого определяем значения а, соответствующие равно-
весию (причем надо будет взять только те значения, при
которых прямая сечения пересекает рассматриваемую ветвь
кривой в двух точках, лежащих на контуре). Совершенно
таким же способом исследует А. Ю. Давидов задачу о рав-
новесии плавающего тела в трех измерениях, при этом роль
1 В 1860 г. Н. Д. Брашман в брошюре: „Определение положения равно-
весия плавающих тел“ показал, что для всех тех случаев, в которых центр
тяжести отсеченной площади лежит на средине хорды параллельной пря-
мой сечеиия, диференциальное уравнение линии центров может быть полу-
чено сразу.
Определив
xi + х2 .
-i-2--= ?(«, Ъ\
Брашман замечает, что в случае сказанного при вамене'-Ц^-1 иа 5 следует
заменить Ь на т] — о£, что дает
£ = <р (а, ц — а£).
Подставляя сюда величину а из уравнения (2), получим диференциальное
уравнение линии центров.
280
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
линии сечения и центров играет поверхность сечений и
поверхность центров. А. Ю. Давидов находит, что секущая
плоскость прикасается к поверхности сечений в центре
тяжести площади, отсекаемой на этой плоскости поверх-
ностью тела, и что касательная плоскость к поверхности
центров параллельна соответственной секущей плоскости.
Это приводит задачу к опусканию нормалей из центра тяже-
сти тела на поверхность центров. Рассматривая затем глав-
ные радиусы кривизны поверхности центров А. Ю. Давидов
получает для них формулы:
D _ П __
к1— 1/ > ---т7
(6)
где и Д/2 суть наибольший и наименьший момент инерции
площади, отсекаемой на секущей плоскости поверхностью тела,
относительно осей, проведенных по секущрй плоскости через
центр тяжести упомянутой площади, а V— объем, отсеченный
от тела. Упомянутые свойства поверхностей сечений и цен-
тров и основанное на них построение положений равновесия
плавающего тела были найдены А. Ю. Давидовым самостоя-
тельно, хотя они раньше были открыты геометрическим путем
Дюпеном Но несомненная заслуга, которая принадлежит
А. Ю. Давидову заключается в составлении диференциальных
уравнений для определения линии и поверхности центров.
На первый взгляд кажется, что для определения линии цен-
тров будет проще взять вышенаписанные многократные инте-
гралы и, исключив из них а и Ь, получить сразу конечное
соотношение между $ и 1]. Но такой путь гораздо труднее, и
часто при невозможности получить с помощью его связь
между £ и т] (если квадратуры нельзя выполнить) мы нахо-
дили такую связь весьма просто с помощью диференциальных
соотношений. Это объясняется тем, что уравнение рассматри-
ваемой ветви кривой центров зависит только от тех ближай-
ших частей контура плавающей площади, которые пересе-
1 В мемуаре, представленном Парижской академии наук в 1814 г. Гео-
метрический вывод теорем Дюпена см. еще в следующих сочинениях:
J u 111 е и, Problemes de mecanique rationnelle, p. 402; В e s a n t, A Treatise
on Hydromechanics, par. I, Chap. IV.
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
281
каются с прямой сечения, и, если эти части контура суть,
например, прямые линии, то ветвь линии центров будет
непременно гиперболой или параболой, несмотря на слож-
ность остальных частей контура отсеченной площади. Вероятно
то обстоятельство, что вывод уравнения поверхности центров
казался затруднительным, и было причиной того, что теоремы
Дюпена до А. Ю. Давидова почти не прилагались к решению
задач о равновесии плавающих тел.
В сочинении А. Ю. Давидова мы встречаем обширное
применение его общей теории к решению частных задач-
Он исследует цилиндры второго порядка и призматические
тела и показывает, что для первых линии центров будут
подобные кривые второго порядка, а для вторых они будут
состоять из поочередно выпуклых и вогнутых ветвей гипер-
бол или парабол ’.
Переходя к задачам в трех измерениях, он разбирает
равновесие плавающих тел, ограниченных поверхностями
второго порядка, и равновесие трехгранной призмы, погру-
женной в жидкость при негоризонтальных образующих.
Последняя глава сочинения посвящается вопросу об устой-
ч вости равновесия плавающих тел. Здесь, как и везде
А. Ю. Давидов отдает предпочтение общему аналитическому
способу исследования. Он говорит: „Решение этого вопроса
можно основывать на частных соображениях, извлекаемых из
свойств самой задачи; правда, что предмет сделается от этого
очевиднее, но предпочтительнее, кажется, связать его с общей
теорией прочности равновесия и из нее вывести его как след-
ствие. Тут та выгода, что объясняются в подробности все
обстоятельства явления". Пусть начало координат в центре
тяжести площади отсеченной на свободной поверхности
жидкости поверхностью тела, ось Oz направлена по вер-
тикальной линии вниз, а оси Ох и Оу по главным осям
1 Для треугольника н квадрата А. Ю. Давидов находит, что линия
центров будет состоять из б и 8 ветвей, для остальных же многоугольников
он указывает только верхний предел числа ветвей. Но легко показать
из теорем, установленных А. Ю- Давидовым, что для всякого выпуклого
n-угольника получатся линии центров с 2п ветвями, соприкасающимися
в вершинах.
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
282
инерции упомянутой площади. Силовая функция веса тела и
сила давления жидкости йа его погруженную часть будет:
где трикратный интеграл распространяется на все элементы
dm массы тела, а двукратный на всю площадь сечения,
р есть плотность жидкости. Для суждения о максимуме и ми-
нимуме этой функции А. Ю. Давидов составляет ее вторую
вариацию при бесконечно малом перемещении тела и находит
для нее выражение
где z есть координата центра тяжести тела, С — координата
центра тяжести вытесненного объема, 8<pj и 8ф2— бесконечно
малые угловые перемещения тела около осей Ох и Оу,
а 87—бесконечно малое tпоступательное перемещение его
по оси Oz. Из этого выражения следует, что силовая функ-
ция будет иметь максимум при z < С, т. е. что достаточным
условием устойчивости является то обстоятельство, что центр
тяжести тела ниже центра тяжести вытесненной жидкости.
Чтобы получить необходимый и достаточный признак устой-
чивости, назовем через 8ф угловое перемещение, слагающееся
из 8<pt и 8<р2, и через ® угол оси этого углового перемещения
с осью Ох. Обращая внимание на формулы (6), представим
вторую вариацию от силовой функции так:
— НI cos2 ф + R2 sin2 ? — (С — z)] 8<l<2 + -р- 8Т2 } , (7)
где р вес тела. Для того чтобы это выражение было отри-
цательно при произвольных ф, 8<р и 8у необходимо, чтобы
С — z было менее наименьшего радиуса кривизны. Таким
образом необходимым и достаточный условием прочности
является требование, чтобы центр тяжести тела лежал
ближе к центру тяжести вытесненного объема нежели блиЖ'
ний из главных центров кривизны поверхности центров-
Сочинение оканчивается приложением общей теории проч-
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
283
ности плавания к исследованию прочности плавающего шара,
эллипсоида и многих цилиндрических и призматических тел.
Особый интерес в русской и иностранной литературе воз-
будили исследования А. Ю. Давидова о равновесии плавания
тригранной призмы. Эти исследования он развил еще в двух
небольших статьях: „Uber die Gleichgewichts-Lagen eines
mit seiner ganzen Grundflache in eine Fliissigkeit getauch-
ten geraden dreiseitigen Prisma’s" и „Sur le maximum du
nombre des positions d’equilibre d’un prisme triangulaire,
homogene, plonge dans une fluide". В первой А. Ю. Давидов
излагает случай равновесия призмы, погруженной в жидкость
своим основанием, и приходит к весьма интересному резуль-
тату, что при равностороннем основании поверхность центров
есть параболоид вращения, так что, если для такой призмы
возможно одно наклонное положение равновесия, то возможно
их бесконечное множество. Во втором сочинении А. Ю. Да-
видов разрешил вопрос о наибольшем числе положений рав-
новесия прямой тригранной призмы, плавающей при гори-
зонтальной образующей. По прежним исследованиям В. Я.
Буняковского это число считалось не более 15 *. А. Ю. Давидов
показал, что это число не может быть более 12, и обнаружил,
что равносторонняя призма при плотности, заключенной
между 7/16 и 9/16, будет иметь все 12 положений равновесия.
Это исследование А. Ю. Давидова послужило поводом для
дальнейших работ русских ученых о равновесии призмы 1 2.
Докторская диссертация А. Ю. Давидова „Теория капил-
лярных явлений" и французская статья „La theorie de pheno-
menes capillaires" представляют одну и ту же работу, причем
последняя является несколько сжатым и упрощенным изло-
жением общей теоретической части первой работы. Обра-
титься к подробному исследованию капиллярных явлений
1 „Bulletin de I’Academle de St-Petersbourg“ т. I, p- 346, 1852.
2 Ф. А. Слудский, О числе положений равновесия плавающей
прямой трехгранной призмы, «Математический сборник”, т. VII, стр. 490;
Ф. С. Сигов, К вопросу о числе положений равновесия прямой
трехгранной призмы, „Математический сборник”, т. VIII, стр. 392;
Н. В. Та т а р и и о в, О числе положений равновесия горизонтально
плавающей прямой многогранной призмы, „Математический сборник”,
т. XIII, стр. 544.
284
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
А. Ю. Давидов имел в виду еще при составлении своей
магистерской диссертации, в которой он писал: „Три главы
этого рассуждения далеко не исчерпывают всей теории пла-
вающих тел, потому что полная теория должна бы содержать
исследование малых качаний около положения прочного равно-
весия, также и влияние капиллярности".
Теория капиллярных явлений, над которой трудились
такие выдающиеся математики как Лаплас, Пуассон и Гаусс,
представляла для А. Ю. Давидова весьма привлекательную
тему. Цель, которую он себе поставил при новой математи-
ческой обработке вопроса, заключалась в применении к его
решению метода возможных перемещений по примеру Гаусса,
но с принятием во внимание изменения плотности на грани-
цах жидкости, на чем особенно настаивал Пуассон 1. А. Ю-
Давидов пишет во вступлении к математической части своего
труда: „Исследования Пуассона исчерпали почти всю теорию
капиллярных явлений, оставалось одно только после его
изысканий — связать эту теорию с общей теорией равновесия
жидкостей и обратить ее в отрасль аналитической механики,
чего и хотел достигнуть Гаусс с помощью своей теории. Но
он не обратил внимания на изменение плотности ни около
свободной поверхности, ни около поверхности сосуда; по-
этому теорию его нельзя считать ни совершенно общей, ни
вполне строгой. Для получения совершенно строгой и общей
теории капиллярности должно руководиться общими прави-
лами механики, не опуская из виду ни одного физического
обстоятельства, существенно до вопроса относящегося. Вот
цель, которую я имел в виду при исследованиях, предлагае-
мых в этом рассуждении". Эта цель была А. Ю. Давидовым
вполне достигнута. Он показал, что допущение в изменении
плотности влияет только на выражения постоянных коэфи-
циентов капиллярности (п и aj через молекулярные силы, и
так как эти коэфициенты прямо определяются опытом, то
и не оказывает никакого влияния на окончательные резуль-
таты. Исходным пунктом вычислений А. Ю. Давидова яв-
ляется составление функций Фиф-]-представляющих
1 Nouvelle theorie de Faction capillaire, 1831.
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
285
потенциальные функции для действия на единицу массы жид-
кости стенок сосуда и массы всей жидкости. Если dM<fi (г)
есть потенциал молекулярного притяжения единицы массы
жидкости массой dM частицы сосуда, то
ф=^ С f dM^(r),
где трикратный интеграл распространяется на все элементы
массы стенок сосуда. В виду того, что часть поверхности
стенок, заключенная внутри сферы, проведенной из рассма-
триваемой точки радиусом молекулярного действия, может
быть принята за плоскость, А. Ю. Давидов определяет Ф
в предположении, что трикратный интеграл распространяется
на бесконечное пространство, ограниченное касательной пло-
скостью к стенке сосуда, проведенной через подошву нормали п,
опущенной из рассматриваемой точки на стенку сосуда-
Совершая интеграцию вдоль элементарных конусов и полагая
R
где R—расстояние от рассматриваемой точки до плоскости
в направлении конуса, найдем, что Ф представит силу притя-
жения нашей точки касательной плоскостью, поверхностная
плотность которой выражается тем же числом D, каким
объемная плотность вещества сосуда, при законе притяжения
F(R)
R2 ’
Легко увидеть, что это дает нам:
Ф=2~Пп
п
(8)
При составлении потенциала
т,
где (rjdm есть потенциал молекулярного притяжения еди-
ницы массы жидкости элементом dm жидкости, а интеграция
распространяется на всю жидкость, А. Ю. Давидов опускает
286
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
из притягиваемой точки на поверхность жидкости нормаль п
и проводит из ее подошвы к этой поверхности касательную
плоскость. Замечая, что вследствие малости радиуса молеку-
лярного действия можно интеграцию распространять на беско-
нечную массу жидкости, ограниченную этой плоскостью, он
пишет:
СО СО
ф-\-ф1 = ^ni J *Р (r) udu,
о о
где п, — расстояние какой-нибудь точки жидкости от касатель-
ной плоскости, и — расстояние подошвы перпендикуляра пх
от подошвы перпендикуляра п, А— плотность жидкости, кото-
рую вследствие малости радиуса молекулярного действия можно
считать функцией пх и координат подошвы нормали п. Так как
г2 = u2 (и, — л)2, и du = rd г,
то, положив
со
J* ? (r)rdr = F(x), A = 41 (х),
X
где х — расстояние от плоскости, найдем:
П со
ф-\-фг — 2* J F(n — л,)ф (л,) d^-j-2^ Jf(h,— ^^(njdn^
О п
Вводим в первом интеграле переменное е = п — л, и во вто-
ром e = zi, — п. Получаем:
П ОО
ф + ф, = 2~ j F(e)ty(n—е) de-j-2^J F(e) (л 4- е) de. (9)
о о
Функция 41 (s) изменяется только при очень малом значении
переменного и обращается при заметных его значениях
в постоянную величину, посему при заметных значениях п
вторая часть формулы (9) обращается тоже в постоянную вели-
чину, которую А. Ю. Давидов ц обозначает буквой ф:
ОО
0 = 4ttaJ" F(e)de. (10)
о
Таким образом ф, есть переменная часть определяемой по-
тенциальной функции, которая обращается в нуль при замет-
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
287
ном удалении притягиваемой точки от границ жидкости; для
точек же весьма близких к этим границам фх есть функция
нормали п и координат подошвы этой нормали.
С помощью найденных функций полный момент сил дей-
ствия стенок сосуда на жидкую массу будет:
JJ [dm8&=8j f jtfdm — J J J ФЗ (Л dv) dm,
гДе интеграция распространяется на всю жидкость и dv есть
элемент объема жидкости. Момент же сил действия жидкости
самой на себя будет:
8'.s dm —
=И J Р™ [! If ~f J P(4 A,) im ]=
= f J (!тЗф1 — J(^ + 0j)8(A dv)dm~
=Цз j j jfadm —
Замечая, что функции Ф и ф1 быстро приближаются к нулю
при удалении от границ жидкости, полагаем:
где двойной интеграл распространяется на все элементы ds
граничной поверхности жидкости, а
/= ^(ф^Ф)^
о
(11)
есть, вообще говоря, некоторая функция координат точки по-
верхности. Кроме того вводим еще обозначение *:
|(ф + 2^ + 2)С0 = х (12)
1 Вместо букв f и у Давидов пишет 0 и <р, но эти буквы у него имеют
раньше другое значение, н потому мы их заменили другими.
288
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
и составляем полный момент молекулярных сил, силы тяжести
(ось z направлена по вертикальной линии вверх) и сил внеш-
него давления для перемещений, удовлетворяющих условию
несжимаемости и условию при стенках сосуда. Приравнивая
этот момент нулю, А. Ю. Давидов получает следующее усло-
вие равновесия:
- J/х8(д<М+/ J JwW+8J J/Js+
-4- j J" p (cosa 8x -|- cos? 8г/ cosy 8z) ds = 0. (13)
Здесь тройная интеграция распространяется на весь объем
жидкости, первый двукратный интеграл — на всю поверхность
жидкости, второй двукратный интеграл — на свободную по-
верхность ее, ограниченную стенками сосуда; Р, Q, R суть
отнесенные к единице площади компоненты силы, действующей
на свободную поверхность жидкости; 1 и р суть множители,
соответствующие давлению жидкости и реакции стенок сосуда
а, ₽, I суть углы нормали граничной поверхности, направлен-
ной внутрь жидкости. При освобождении во втором и третьем
трикратном интеграле вариаций 8%, 8 у, 8z из-под знаков
диференциалов производные от Д по х, у, z сокращаются, и мы
получаем, приравнивая нулю коэфициенты вариаций под три-
кратным интегралом:
dK dy d\ . dy d'K dy . .. ..
— =Д-,--, -г- —-г = Д~г—Яд- (14)
dx dx dy dy dz dz
Для точек, не находящихся весьма близко от границ жид-
кости, Д есть постоянная, ф; = 0и Ф= 0, посему у постоянно,
и уравнения (14) обращаются в обыкновенные уравнения
равновесия тяжелой однородной жидкости. Вообразим весьма
тонкий слой, ограниченный поверхностью жидкости и некоторой
внутренней поверхностью, на которой можно принять Д по-
стоянной величиной. При передвижении по нормали этого слоя
от его внутренней поверхности к внешней Д быстро изме-
няется, являясь функцией расстояния от внешней поверхности
и координат подошвы перпендикуляра, опущенного из точки
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
289
на внешнюю поверхность. Умножим уравнения (14) соответ-
ственно на dx, dy, dz и сложим:
d X = Д d/ — Д gdz.
Интегрируя это уравнение по направлению толщины слоя
от его внутренней поверхности до какой-нибудь точки внутри
слоя, будем иметь:
\ = Ja d/_ — b'g (z — Zj),
где Xt и zt суть значения на внутренней поверхности слоя,
а Д' есть среднее значение плотности на пути интеграции.
Для точки, лежащей на внутренней границе слоя, как для
точки, принадлежащей внутренней массе жидкости, можно по-
ложить:
\ =
или, по малости разности z — z},
Xt= —kgz-\-C.
По той же причине можно положить, что
A'^(z —Zj) = 0.
Так что для всякой точки внутри слоя найдем:
4" A^z=J* Д cfy-f-С. (15)
Это равенство требует, чтобы у было функцией Д:
у = 6(Д).
Давидов показывает, что следствием этого условия и фор-
мул (9) и (8) является то обстоятельство, что у и Д суть
функции одного расстояния п точки от внешней поверхности
упомянутого слоя.
Рассмотрим только точки, прилегающие к свободной по"
верхности жидкости. Ограничиваясь величинами е в первой
степени, напишем:
Ф(л+«) = Д+«^.
Зак. 2430. Н. Е. Жуковский.- Том IX.
19
290
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Положим, что
2-jF(e)</e+2^jF(e)<Ze
о о
= 7V,
и представим уравнение (12) в виде:
0(Д) = /УД_|-Л^
ап
Интегрируя
это уравнение, найдем:
/(Д,п) = А
где А — постоянное относительно п, которое может зависеть
от координат подошвы нормали п. Но это последнее предпо-
ложение в нашем случае не будет иметь места, так как при
приметном значении п величина А делается постоянной.
Таким образом А должно быть функцией одного п. Приняв
это, положим:
)l<l7,dn=h
(16>
Далее возьмем в формуле (15) для верхнего предела
интеграла п = 0, а для нижнего вместо п, равного толщине
упомянутого слоя, возьмем п = ос. Получим:
0 со
со 0
Отсюда для свободной поверхности жидкости будем иметь
соотношение:
-/A — = — b — С. (17)
Затем следует обратиться к поверхностным интегралам
формулы (13). От изменения плотности вследствие вариаций
свободной поверхности второй интеграл формулы (13) дает:
х cos а 3 у cos Р + 3 z cos т) dv,
ТРУДЫ А. ю. ДАВИДОВА ПО МЕХАНИКЕ 291
где 8 х, %у, 8 z, а. р, суть значения на свободной поверхно-
сти для подошвы перпендикуляра п рассматриваемой точки.
Пользуясь формулой (16), представляем этот объемный
интеграл интегралом, распространенным на свободную поверх-
ность: г г
Ъ I I (8 х cos ct-f-8 у cos р + 8 z cos f) ds.
Кроме этого от интеграции по частям во втором и третьем
трикратном интеграле получим распространенный на'свободную
поверхность интеграл:
J" (/А — X) (8 х cos а 8 у cos Р -f- 8 z cos у) ds.
Сумма этих интегралов по формуле (17) обращается в
J f(^£z — Q(8 х cos а-|-8 у cos р-]-8 z cos 7) ds.
Вследствие того,‘что фх и Д зависят только от и, функция f
данная формулой (12), есть постоянная величина, которая
для свободной поверхности будет:
1^УФ1Д£/п’ (18)
о
а для стенок сосуда:
со
| = |[(ф1 + 2Ф)Д^п. (19)
О
При составлении вариации интеграла
позволим себе отступить от несколько длинного изложения
А. Ю. Давидова и получить его
Вся вариация граничной по-
верхности, как видно на фиг. 1,
произойдет от того, что сво-
бодная поверхность АВ пере-
ходит в А'В'. Построив на
каждом элементе площади ds
прямой цилиндрик, вырежем на
измененной свободной поверх-
ности элемент площади ds'-
19*
292
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Называя через 8 п высоту цилиндрика, будем иметь известную
формулу:
ds' — ds 8 ds___1 1
dsdn ds tin R Rt
где R и Rt — главные радиусы кривизны поверхности, счи-
таемые положительными, если они направлены вне жидкой
массы. Таким образом
г*=(1+А)*г„=-(1+А)(г^с°5».+
+ 8 у cos р -f- 8 z cos у) ds.
Проведя через все точки контура свободной поверхности
АВ (фиг. 1) элементы нормалей 8п, мы определим точками
их пересечения с поверхностью А'В' некоторый контур,
площадь которого будет разниться от площади свободной
поверхности А'В' на сумму элементарных площадей A'DEC'.
Кроме этого смачиваемая площадь сосуда при новом положе-
нии жидкости будет разниться от смачиваемой площади при
старом на сумму элементарных площадей АА'С'С. Называя
элемент длины АС контура свободной поверхности через dl
и угол этой поверхности со стеною сосуда через I, найдем:
пл. A'DEC' = dl%ncigi, пл. АА'С'С = dlc>n ——. ,
sin i
где
8 n = CE — — (8 x cos a -j- ^у cos p -j- 8 z cos 7).
На основании всего сказанного и формул (18) и (19) получаем:
8 f f fds= — J ( jF X C°S & C°S Z C°S —
cq——. I (8 x cos a 4- 8 у cos p -f- 8 z cos 7) dl,
где двукратный'интеграл распространяется на свободную по-
верхность, а однократный — на ее контур.
Соединив все двукратные интегралы, относящиеся к сво-
бодной поверхности, и приравняв в них нулю коэфициенты
при 6 х, 8 у, 8 z, найдем, что
P-.Q‘R== cos a: cos p: cos y,
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
293
а равнодействующая этих сил есть
Р =
Таким образом давление на свободную поверхность жидкости
должно быть нормально к этой поверхности. Если это дав-
ление р постоянно, то уравнение свободной поверхности есть:
/1.1
Z = а I “Г
(20)
const,
где
а
(21)
Для стенок сосуда двойные интегралы рассматривать нет
нужды, так как они поведут к определению множителя v, не
играющего роли при решении задачи. Рассмотрение одно-
кратного интеграла приводит к заключению о постоянстве
угла i:
«1
cos i==------
а
(22)
А. Ю. Давидов прилагает установленную им теорию к реше-
нию следующих вопросов: о равновесии тел, погруженных
в жидкость, о возвышении и понижении жидкости в узких
трубках, о поверхности жидкости, заключенной между парал-
лельными вертикальными плоскостями, о виде поверхности
капель, о сцеплении и прилипании жидкостей. Все эти вопросы
он подвергает тщательному исследованию получая как прежде
известные результаты, так и многие новые и сравнивая их
с опытными данными, изложенными в первой части сочинения.
Эта часть разбираемой работы представляла в свое время
самое полное изложение наблюдений различных ученых над
капиллярными явлениями.
Из ненапечатанных сочинений покойного А. Ю. Давидова
сохранились неоконченная рукопись „Теория прочности рав-
новесия" и студенческое сочинение, удостоенное золотой
медали: „Теория бесконечно малых качаний". Первое имеет
дату 3 сентября 1848 г. и надпись: „рассуждение магистра
294
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Давидова", откуда следует заключить, что оно было начато
тотчас же после защиты магистерской диссертации и предна-
значалось для докторской. Замечая, что в методе Лагранжа
при исследовании бесконечно малых колебаний системы урав-
нения ее движения преобразуются в линейные через отбрасы-
вание бесконечно малых членов выше первого порядка, А. Ю.
Давидов пишет: „Этот способ рассматривания предмета может
нам казаться неудовлетворительным. Лагранж предполагает
расстояния масс от места их покоя весьма малыми и, прене-
брегая в уравнениях движения вторыми и высшими степенями
малых величин, выводит из этих уравнений заключения, кото-
рые, может быть, суть только следствия предположенного."
Этот недостаток способа исследования Лагранжа А. Ю. Да-
видов задумал устранить, пользуясь выражением интегралов
уравнений движения посредством теоремы Фурье, в которой
под знаки многократных интегралов он вводит неизвестные
функции времени, представляющие все члены уравнений, обык-
новенно отбрасываемые. К сожалению, сохранившаяся часть
рукописи не выясняет вполне мысли автора, и мы не нашли
возможности восстановить эту работу. Сочинение на золотую
медаль составлено главным образом по Коши, но оно заклю-
чает в своем начале оригинальное изложение обыкновенной
теории прочности равновесия. Этим изложением воспользо-
вался Н. Д. Брашман в своем курсе механики 1 Мы воспро-
изведем здесь коротко его существенную часть.
Пусть система состоит из п материальных точек, прямо-
угольные координаты которых будем обозначать для удобства
через (xlf х2, х3), (х4, х6, х6),... Эти координаты стеснены
г условиями:
[/» (*1. ^2» ^3» • • •) г = 1. . (23)
где скобка обозначает все г уравнений, получаемых, приписы-
вая i значения от 1 до г. Система находится под действием
сил, имеющих силовую функцию F (xt, х2, х3, х4,...). Пусть
величины m1=m.2 = my, m4 = тпб = m6,‘... обозначают массы
Брашман, Теоретическая механика, Москва 1859, стр. 371.
ТРУДЫ а: Ю. ДАВИДОВА ПО МЕХАНИКЕ
295
точек. Диференциальные уравнения движения представляются
в виде:
<У1
^_dF df df,
* <№ ~ dXi r i dx^ 2 dXi
1» 2,
, (24)
ЗП
где kp kg,... суть некоторые функции времени, определяемые
из уравнений (24) и (23). Назовем через alt а„ а3, ait... зна-
чения координат при равновесии системы и предположим, что
движение, которое нам предстоит исследовать, произошло от
бесконечно [малого уклонения системы от этого положения
равновесия и от сообщения ее точкам некоторых бесконечно
малых скоростей. Мы имеем для положения равновесия:
dF , dfx ,
,44ч
= 0
(25)
где множители р суть постоянные величины, определяемые
из уравнений (25) и из уравнений:
[A(«i,«2,---) = 0]/=l г. (26)
Допускаем, что во время движения
к< = а*+У<=1,...,3и, (27)
где все бесконечно малы. При этом допущении коэфициенты
k„ k2,... будут .бесконечно мало отличаться от v 1г v3,... :
[^ = ^ + Ч=1 г. (28)
Подставляем (27) и (28) в уравнения (24) и преобразуем
на основании уравнений (25). Получаем:
ldt^ ^dat dajj^~ 1да^ da{ ' J *=i,..., зп’
где
^ = F(alt а„ а3, ai} .. •)+ н/1(а1, -а2>- • Э + а2>---).
Кроме уравнений (29) переменные стеснены еще условиями:
44
da.
da^ + da33
(30)
296
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Исключив из уравнений (29) все величины Vj, v2,.. , полу-
чим Зп— г уравнений вида:
Гр S+p §+•• = /’ А+Л А+-1 >(3i)
[i.j dt* 2-з dt i-з 2-з J 3=i,...,-in-r
которые вместе с уравнениями (30) послужат для решения
задачи. Так как уравнения (30) и (31) линейны относительно
неизвестных функций и их производных, то частные инте-
гралы будут:
& = hi-est}i=1 Зй. (32)
Подставляем в уравнения (30) и (31) и определяем вели-
чины s и h из уравнений:
[(/>.,-+ s^.3) А.2+ - • • — 0]j=li . Зга_г, (33)
^ + ^^+...=0
Величина s2 найдется, если приравниваем нулю определитель
этой системы уравнений. Это дает уравнение:
® (s2)==0, (34)
которое будет относительно а2 степени Зп— г, так как s2
входит только в первые Зп — г рядов определителя. Зная s2,
найдем величины h из формул:
’ (35)
где с — постоянное, которому можно приписывать 2(3п—v)
различных значений для различных s.
А. Ю. Давидов доказывает, что все корни а2 действительны,
следующим образом.
Пусть уравнение (34) имеет мнимый корень s2; тогда оно
имеет еще другой ему сопряженный мнимый корень s'2. Под-
ставляя эти значения корней в уравнения (35), найдем при
одинаковом с:
ТРУДЫ А. Ю. ДАВИДОВА ПО МЕХАНИКЕ
297
Составляем частные интегралы:
^i = hie8t 1
.Vl~V es'*Ji=i....зп
и подставляем их поочередно в уравнения (29) и (30):
Умножаем первую систему уравнений (36) соответственно
на Л/, h2 • • и складываем, а вторую систему соответственно
на /ц, h.2, ••• и тоже складываем. Получаем, обращая внима-
ние на уравнения (37):
4=3 — Зп j=3n
i=l «=1 J
i = 3n i = 3n j=3n
- s'3 2 -,wW)= 2
4=1 4=1 J=1 2 J
Вычитая эти уравнения, получаем:
«=3п
(S2_S'2 2 /ИД*42 + ₽42)=О,
4 = 1
откуда заключаем, что s2 — s'2. Это возможно только тогда,
когда мнимые части сопряженных мнимых величин суть нули,
т. е. корни s2 не могут быть мнимы.
Если все корни s2 отрицательны, то общий интеграл, состав-
ленный из частных интегралов вида (32), будет содержать
только тригонометрические функции времени, и равновесие
будет прочное; в противном случае оно будет не прочное.
298
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Умножаем на Ai> Л2, • • • первую группу уравнений (36) и складываем. Получаем: соответственно
i=3«»J=3n 2-1 3=1 г J (39)
при условии ... =0 . даг 11 да2 2 1 (40)
Если бы функция F имела в положении равновесия системы
maximum, то вторая часть уравнения (39) при всяких зна-
чениях h, удовлетворяющих уравнениям (40), была бы отрица-
тельна, а это значит, что тогда бы корни а2 могли бы быть
только отрицательны. Откуда получается известная теорема,
что при максимуме силовой функции положение равновесия
системы устойчиво.
Подобно тому, как первоначальные ученые труды А. Ю. Да-
видова были посвящены механике, некоторые из первых его
лекций были посвящены также этой науке. Он читал курсы
по элементарной статике и по небесной механике. Я не имел
счастья быть его учеником на этих курсах, но не раз слышал
от слушателей их высокую похвалу изложению А. Ю. Дави-
дова. Он всегда становился на самую общую точку зрения,
охватывая вопрос во всей его полноте, и потом прилагал
достигнутые общие результаты к частным случаям, подбирая
их с замечательным умением и разбирая их с полнотой
и ясностью, столь свойственными его изложению.
Настоящая работа входит, как часть, в коллективный труд Н. Е. Жуков-
-ского, П. А. Некрасова и П. М. Покровского „Живиь и труды А. Ю. Да-
видова", напечатанный в „Математическом сборнике", т. XV, 1890.
Прим. ред.
ТРУДЫ С. В. КОВАЛЕВСКОЙ ПО ПРИКЛАДНОЙ
МАТЕМАТИКЕ
С В. КОВАЛЕВСКАЯ
(1850-1891)
ТРУДЫ С. В. КОВАЛЕВСКОЙ ПО ПРИКЛАДНОЙ МАТЕ-
МАТИКЕ
(1891 г.)
С. В. Ковалевская под руководством своего знаменитого
учителя, профессора Вейерштрасса, прошла школу высокого
математического анализа, но самостоятельные работы ее
относятся не к одной чистой математике, а главным образом—
к прикладным наукам.
Она избирала при этом для своего исследования те задачи,
решение которых требовало обширного знания трансцендентных
функций и, вполне обладая этим знанием,
получила результаты, которые составляют
ценный вклад в науку.
Первая работа покойной в рассматри-
ваемой области посвящена трудному во-
просу астрономии: о форме кольца Сатурна.
Она напечатана в 1885 г. в Astronomische
Nachrichten (№ 2643, t. CXI) под назва-
нием: „Zusatze und Bemerkungen zu Lapla-
ce’s Untersuchung uber die Gestalt der Sa-
turnsringe". Лаплас в своей „Небесной
механике" предполагает, что кольцо Са-
турна слагается из нескольких жидких
колец, имеющих форму тел вращения
и симметричных относительно плоско-
сти общего экватора. Вследствие ма-
лости меридионального сечения колец
сравнительно с их диаметром Лаплас пренебрегает взаимо-
действием колец и допускает, что сила притяжения кольца
(фиг. 1) на какую-нибудь точку А его меридионального се-
чения равна силе притяжения на эту точку бесконечно-длин-
302
ХАРАКТЕРИСТИКИ И -БИОГРАФИИ
ного цилиндра ВС, имеющего основанием меридиональное
сечение. При таком допущении Лаплас нашел, что контуры
меридиональных сечений колец суть эллипсы, растянутые
вдоль плоскости экватора, и что плотность колец убывает по
мере удаления от Сатурна.
Анализ Лапласа очень прост и изящен, но он предста-
вляет только первое приближение в решении задачи и обла-
дает тем недостатком, что из него не видно, какого порядка
члены опущены при приближении.
С. В. Ковалевская задалась мыслью исследовать вопрос
о равновесии кольца с большею точностью и повести иссле-
дование так, чтобы по желанию можно было ограничиваться
членами того или другого порядка.
Она выражает потенциал кольца на точку, лежащую на
меридиональном контуре кольца, по формуле Гаусса:
V — р I cos id~, (1)
в которой интеграл распространяется на всю поверхность
кольца, c?S есть элемент этой поверхности, i есть угол внеш -
ней нормали поверхности кольца с радиусом, идущим от при-
тягиваемой точки к элементу а р есть постоянная плот-
ность вещества кольца.
Что касается контура сечения кольца, то С. В. Ковалев-
ская представляет его с помощью уравнений:
х = I (1 — с cos t),
i/ = Za(asin/-|-«'sin2/-|-a'zsin3£-|- .. .), (2)
где I — радиус кольца, a — некоторая малая величина, а t—пе-
ременная величина, которая при изменении от 0 до 2л дает
координатам х, у все последовательные их значения на мери-
диональном сечении кольца. Начало координат берется
в центре Сатурна, ось Оу направляется по оси кольца, а ось
Ох по радиусу кольца.
Подставляя формулы (2) в выражение (1), С. В. Ковалев-
ская представляет его в виде:
ТРУДЫ С. В. КОВАЛЕВСКОЙ
303
О 2г. 2
V = рР f Wdt- 117 = М ( ----+ 7V [ /1-Jt2sin2 6 JO, (3)
J J }/1 —Fsin20 J
2к о О
где коэфициенты М и N при эллиптических интегралах пер-
вого и второго рода зависят от тригонометрических функций
переменных t и t', причем последнее есть значение t для
притягиваемой точки.
Внеся значение W в V, С. В. Ковалевская развертывает
исследуемый потенциал кольца в ряд по косинусам кратных
дуг от t'. Так же поступает она и с потенциалом Сатурна
на рассматриваемую точку меридионального сечения и, на-
писав после этого, что сумма двух найденных потенциалов
на контуре меридионального сечения постоянна, приравни-
вает нулю все коэфициенты при одинаковых косинусах. При
этом выясняется, что коэфициенты [«, ®, « последова-
тельно убывают. Вследствие этого, взяв во второй формуле (2)
надлежащее число членов, мы можем получить решение
задачи с желаемой степенью точности. Решение Лапласа
соответствует только первому члену. Если принять во вни-
мание и второй член, то получается второе приближение.
С. В. Ковалевская показывает, 'что это приближение дает
для меридионального сечения две формы, отклоняющиеся от
эллипса Лапласа так, как изображено на фиг. 2.
304
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Второй работой С. В. Ковалевской по прикладным наукам
является исследование о распространении световой волны
в средах двойной преломляемости. Этот вопрос был теоре-
тически разобран Ляме, который привел его к интегриро-
ванию уравнений:
2_^_ _ А2.А ______
dt- С ду\ду дх/ dz \ dx dz ) ’
d-fj_ 9 d / Э-q_\______ 9 __dig \
dt2 a dz\dz dy / dx \ dy dx / ’
(4)
dt- dx \ dx dz) a dy \ dz dy / ’
e o,
dx dy dz
где E, iQ, С суть весьма малые перемещения точек упругой среды,
выражающиеся функциями координат х, у, z и времени t.
Ляме нашел частное решение этих уравнений в виде формул:
U :Acos2-~7Z ; t]=Fcos2k-^=3; С = Z cos 2^—, (5)
в которых X, Y, Z суть некоторые функции координат, и
показал, что при этом световые волны могут быть построены
с помощью поверхности:
—-——У----1----
г2 — а2‘ г2— Ь2 ' г2— с2
(6)
где г1 = х2 у2 -j- z2. Это есть так называемая поверхность
френелевой волны, состоящая из двух полостей. В частном
случае, при а = Ь или а = с, она приводится {к эллипсоиду
вращения и вписанному или описанному около него шару.
Подставляя в формулу (6) вместо х, у, z величины
х у z
t ’ t ’ t ’
мы получим вид волны по прошествии времени t после
развития колебания в начале координат, а решая найденное
уравнение относительно t, найдем два значения для времени,
в которое та и другая часть поверхности волны пройдут
через точку (х, у, z).
Решение Ляме, по мнению С.1 В. Ковалевской, предста-
вляет то неудобство, что в нем величины X, Y, Z стано-
ТРУДЫ С. В. КОВАЛЕВСКОЙ
305
вятся неопределенными по направлению оптических осей
среды и делаются бесконечно большими в центре колебания.
Ввиду этого, она занялась изысканием общего решения
уравнений (4), которое бы позволило выбрать частное реше-
ние, не обладающее упомянутыми недостатками.
Свои исследования С. В. Ковалевская сообщила в 1883 г.
на VII Съезде русских естествоиспытателей и врачей, бывшем
в Одессе *, и напечатала в Acta Mathematica (6/3) в 1885 г,
под названием „Uber die Brechung des Lichtes in kristal-
linischen Mitteln".
Основанием для решения вопроса послужило ненапечатан-
ное сочинение Вейерштрасса об интегрировании уравнения:
дВ~ дх^ ду^^ dz^ZA ду dz*~
. 2В' + 2 С д1 2*** (п\
dz дх дх ду ’
в котором А, В, С, А', В', С' суть постоянные величины.
Вейерштрасс интегрирует это уравнение подобно тому,
как Коши интегрирует уравнение
^ = ааЛ(Ф),
и пользуется для этого одной новой теоремой о многократ-
ных интегралах, являющейся обобщением теоремы Грина.
Учитель вполне уступил свою работу любимой ученице,
так что статья С. В. Ковалевской начинается изложением
работы Вейерштрасса.
Воспользовавшись способом интегрирования Вейерштрасса,
С. В. Ковалевская находит интегралы уравнений (4) в виде:
6 = (и, v, w) f(x + u,y + v,z + <v)dudvdw,
=иь<
•*1
и, V, w) f(x-}-u,y~\-'v,z-\-w)dudvdw,
(8)
С = J J (и, v, w)f(x + u,y + v,z + w)dudvdw,
1 Протоколы VII Съезда русских естествоиспытателей и врачей, засе-
дание математической секции 22 августа, Одесса 1883.
Зак. 2430. Н. Е. Жуковский. Том IX.
20
306
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
где % суть определенные функции, f—произвольная
функция, интеграция же совершается на объем, заключенный
между двумя поверхностями волны.
Потом она составляет с помощью этих интегралов новое
частное решение задачи, в котором тригонометрические
функции формул (5) заменяются эллиптическими функциями
первого рода. Это частное решение уже не обладает выше-
упомянутыми недостатками. К сожалению решение С. В. Кова-
левской не сопровождается теми ясными геометрическими
иллюстрациями, которыми обставлено изложение свойств
френелевой волны. Я думаю, что подобное геометрическое
исследование решения С. В. Ковалевской дало бы весьма
интересную тему.
Теперь я перехожу к последней работе покойной, которая, по
моему мнению, составляет главным образом ее ученую славу.
На 1888 г. Парижская Академия наук предложила для
соискания премии тему об исследовании вращения твердого
тела около неподвижной точки и в своем заседании 24 декабря
присудила эту премию, увеличенную до 5000 франков, за сочи-
нение, представленное С. В. Ковалевской.
Самостоятельная часть этой работы напечатана в Acta
Mathematica (12/2) в 1889 г. под названием: „Sur le probleme
de la rotation d’un corps solide autour d’un point fixe".
Чтобы яснее выставить на вид, что было прибавлено
С. В. Ковалевской в решении упомянутой трудной задачи,
я напомню коротко результаты, достигнутые при исследовании
этого вопроса другими учеными.
Вопрос о движении тяжелого твердого тела в случае,
когда центр его тяжести находится в точке опоры, аналити-
чески исследован Эйлером, который написал обширный трак-
тат на эту тему; но полное решение его было дано с помощью
изящного геометрического метода Пуансо, показавшим, что
интеграла живых сил и площадей вполне достаточно, чтобы
дать полную картину движений. Второй случай, кото-
рый поддался решению, соответствовал таким обстоятель-
ствам, при которых эллипсоид инерции относительно точки
опоры есть эллипсоид вращения и на оси вращения этого
эллипсоида лежит центр тяжести тела. Задача о движении
ТРУДЫ С. В. КОВАЛЕВСКОЙ
307
такого тела была разрешена Лагранжем, который к интегралу
живых сил и интегралу площадей относительно вертикальной
линии, проходящей через точку опоры, прибавил еще инте-
грал, выражающий постоянство угловой скорости около оси
вращения эллипсоида инерции, и, воспользовавшись этими
тремя интегралами, выразил все искомые величины с помощью
эллиптических трансцендентных. Дальнейшие работы ученых
содержат доказательства различных геометрических и анали-
тических теорем, относящихся в двум упомянутым случаям
движения. Таковы работы: Максвелла, Сильвестра, Мак-Кул-
лаха, Якоби, Сомова, Дарбу и других. При этом из аналити-
ческих исследований выяснилось, что положение тела в про-
странстве в той и другой задаче может быть дано с помощью
Якобиевых функций 6 от линейных функций времени.
С. В. Ковалевская в начале своей статьи задается вопро-
сом: не существует ли еще других случаев движения твер-
дого тела, при которых обстоятельства движения могут быть
выражены с помощью функций времени, аналогичных функ-
циям 6, т. е. имеющих особые точки только в форме полю-
сов. В результате своих изысканий она находит, что подоб-
ными функциями может быть разрешен еще один новый слу-
чай. движения тяжелого твердого тела. В этом случае центр
тяжести тела лежит на плоскости экватора эллипсоида инер-
ции, построенного для неподвижной точки, который должен
быть эллипсоидом вращения и должен удовлетворять условию:
А — В = 2С, (9)
где А, В и С главные моменты инерции. Придя к такому
заключению, С. В. Ковалевская обращается к задаче о дви-
жении твердого тела в упомянутом случае и разрешает ее
вполне. ?Для наглядного сравнения трех случаев движения
тяжелого ^твердого тела, прошу обратить внимание на три
волчка, изображенные на фиг. 3. Первый волчок соответствует
случаю, разрешенному Пуансо, второй представляет случай
Лагранжа, а третий тот случай, который исследован С. В. Кова-
левской. Характерная особенность третьего случая состоит
в том, что с поворотом волчка около оси вращения изме-
няется момент действующей на него силы. в
20*
308
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Весь успех исследования С. В. Ковалевской в рассматри-
ваемой задаче заключается в прибавлении к известным инте-
гралам живых сил и площадей еще одного нового алгебраиче-
ского интеграла. Анализ ее для достижения этой цели настолько
прост, что, по моему мнению, его следует включить в курсы
аналитической механики.
Принимая С = 1, пишем для рассматриваемого случая дифе-
ренциальные уравнения движения твердого тела в виде:
О dp 2Л=’Г> 2д = — Р'—<vf, (10)
dr rff
Tt=n-P1.
где р, (], г суть проекции угловой скорости на главные оси
инерции, у, у', суть углы, образуемые этими осями с напра-
влением силы тяжести, а с0 есть произведение веса тела на
координату х центра тяжести, лежащего на оси Ох.
К трем известным интегралам этих уравнений:
2(р2 + ?2)-4-га = 2сьТ4-6/1,
2(py + 9y') + h" = 2Z,
72 47'24~7"2== 1,
(И)
из которых первый есть интеграл живых сил, второй интеграл
площадей и третий представляет известное соотношение
между косинусами, С. В. Ковалевская прибавляет четвертый
интеграл. Для этого она умножает второе уравнение (10)
на i = V —1 и складывает с первым, потом умножает пятое
на i и складывает с четвертым. Получается:
2 (р 4 qi) = ri (р + qi) — с0 if",
(7 + 7'0 = — ri (i 4- i'O4-t"z (p 4- qi).
'Отсюда по исключении у" находится соотношение:
d Г, , 1 Г 1
27 Цр + дО2 4- со(т 4- 7'0 = — ri (р 4- qi)2 4- с0(7 4- 7'0 . (12)
ТРУДЫ С. В. КОВАЛЕВСКОЙ
309
в котором мы имеем право изменить i на —г, что дает еще
соотношение:
— яФ + с0(т — Л)
= ri
(р —9г)2 + с0(т —Tf'O • (13>
Исключение из уравнений (12) и (13) величины г и интегра-
ция дают искомый интеграл:
[(р+?02+со (т+т'о] [(р—?02+с0(т—/О]=U4)
Когда этот интеграл был найден, то дальнейшее разреше-
ние задачи свелось к совершению вполне определенных ана-
Фиг. 3.
литических операций, которые С. В. Ковалевская выполнила
до конца, сведя отыскание всех обстоятельств движения
к отысканию функций и s2, удовлетворяющих уравнениям:
dsi I
= Л (15)
где /?i(s) есть многочлен пятой степени.
В конце рассматриваемого сочинения С. В. Ковалевская
показывает, что всякое тело, главные моменты инерции кото-
рого > Ci относительно центра тяжести удовлетво-
ряют условию:
Аг = 2 (Bi — Ci),
может быть укреплено в неподвижной точке так, что его дви-
жение будет соответствовать рассмотренному ею случаю. Для
310
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
этого стоит только взять точку опоры на оси, соответствую-
щей моменту А, на расстоянии
|/ м
от центра тяжести.
В 1890 г. в Acta Mathematica (14/1) С. В. Ковалевская
напечатала дополнение к вышеозначенному сочинению под
названием: „Sur une propridte du systeme d’equations differen-
tielles, qui definit la rotation d’un corps solide autour d’un
point fixe“. В этом дополнении она дает подтверждение той
мысли, что случаи Пуансо, Лагранжа и разрешенный ею слу-
чай движения твердого тела суть единственные, обстоятель-
ства движения которых могут быть выражены однозначными
функциями времени, не имеющими иных особых точек, кроме
полюсов.
Вопрос о движении твердого тела, разрешенный С. В. Кова-
левской, несмотря на его частный характер [вследствие соотно-
шения (9)], является ценным прибавлением к имеющимся иссле-
дованиям о движении твердого тела.
Летом 1889 г. я встретил в Париже Пуанкаре, который
передавал мне, что С. В. Ковалевская работает над расшире-
нием рассмотренного случая и имеет надежду разрешить
задачу о движении при центре тяжести, лежащем на плоскости
экватора эллипсоида инерции, который есть какой-нибудь
эллипсоид вращения. К сожалению, ранняя смерть положила
предел всем этим надеждам и лишила нас соотечественницы,
которая немало содействовала прославлению русского имени.
19 февраля 1891 г. в заседании Московского математического общества
автор сделал сообщение „Труды С. В. Ковалевской по прикладной матема-
тике". Работа вошла как часть в коллективный труд А. Г. Столетова,
Н. Е. Жуковского и П. А. Некрасова „С. В. Ковалевская" и была напеча-
тана в „Математическом сборнике", т. XVI, 1891. Прим. ред.
Г. ГЕЛЬМГОЛЬЦ
(1821—1894}
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
(1892 г.)
В своих работах по механике Гельмгольц является одним
из видных представителей той школы ученых, которая, по
выражению Пуансо, поставила себе задачей: „considerer les
choses en elles-memes".
Механика развивалась как глубокомысленными трудами
аналистов, так и остроумными исследованиями геометров.
При этом часто бывало, что сложные аналитические формулы
освещались и представлялись в ясной наглядной форме бла-
годаря удачным геометрическим представлениям. Такие ин-
терпретации захватывали задачу во всей ее полноте и рас-
крывали многие свойства ее, не замеченные при аналитиче-
ском исследовании. Так было с решением задачи о движении
твердого тела около его центра тяжести: решение сперва
было получено Эйлером аналитическим путем, но оставалось
затерянным среди массы формул, и только благодаря простым
и наглядным интерпретациям Пуансо предстало перед глазами
ученых со всей ясностью.
Какая роль выпала на долю Пуансо при разъяснении
вопроса о движении твердого тела, такая же принадлежит
Гельмгольцу в разъяснении вопроса о движении жидкости.
Почти все работы Гельмгольца по механике посвящены
гидродинамике, которой он не перестает заниматься и до
настоящего времени. При этом можно сказать, что современ-
ная гидродинамика своим развитием обязана главным образом
Гельмгольцу. А между тем наиболее замечательная работа
германского ученого в этой области: „Uber Integrale der
hydrodynamischen Gleichungen, welche den Wirbelbewegun-
gen entsprechen" появилась в 1858 г., спустя 43 года после
того как формулы, заключающие в себе принцип сохранения
314
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
вихрей, были найдены Коши. Но Коши рассматривал полу-
ченный им результат только с аналитической стороны и не
предвидел той массы вопросов, которые могут быть решены
при надлежащем геометрическом освещении выводов.
Я постараюсь теперь с возможной простотой выяснить вам
установленное Гельмгольцем понятие о вихре.
Вообразим цилиндрический сосуд конечной высоты (фиг. 1)
с весьма большим основанием, наполненный капельной или
газообразной жидкостью,
и предположим, что эта
жидкость движется так:
центральный цилиндриче-
ский столбик ее некото-
рой толщины вращается,
как твердое тело, около
своей оси, а вся осталь-
ная масса жидкости кру-
тится около этого стол-
бика по кругам со скоро-
Фиг. 1. стями, обратно пропор-
циональными расстоянию
от оси столбика; причем эти скорости, возрастая по мере
приближения к центральному столбику, переходят на его
поверхности в скорость столбика.
Такое движение жидкости и называется вихрем, а харак-
теризующий его цилиндрический столбик — вихревым шнуром.
Быстрота вихревого движения измеряется напряжением ви-
хря,— так называет Гельмгольц произведение из площади
нормального (перпендикулярного) сечения столбика на его
угловую скорость. Можно еще сказать, что напряжение вихря
равно половине произведения скорости жидкости у поверх-
ности вихревого шнура на периметр нормального сечения
шнура. Удвоенную величину этого произведения называют
циркуляцией скорости по нормальному сечению шнура. Во-
обще циркуляция скорости по какому-нибудь замкнутому
контуру внутри движущейся жидкости есть произведение из
длины контура на среднюю из всех составляющих скоростей
точек контура по направлению контура.
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
315
Так как в движении жидкости, изображенном на фиг. 1,
скорости обратно пропорциональны радиусу, то циркуляции
скорости по всем горизонтальным кругам, имеющим центр на
оси столбика и охватывающим его, равны между собой и,
следовательно, равны удвоенному напряжению вихря; а цир-
куляции скорости по контурам, состоящим из отрезков двух
кругов между отрезками двух радиусов и лежащим вне шнура,
равны нулю. Кроме этого легко доказать, что циркуляции
скорости по всяким замкнутым контурам, охватывающим шнур,
равны удвоенному напряжению ви- ----
хря, а циркуляции скорости по вся-
ким замкнутым контурам, его не —— \
охватывающим, равны нулю. X. \
Это замечание позволяет нам ра- / 'к
зыскивать вихревой шнур в данной I
движущейся жидкости. Для этого \
надо провести замкнутый контур и \У ) j
определить для него циркуляцию. /
Если она не равна нулю, то сквозь
контур проходит вихревой шнур. 2
После этого надо уменьшать контур
до тех пор, пока циркуляция не изменяется. Уменьшая его
таким образом, мы можем подойти к поверхности вихревого
шнура.
Если в рассмотренном нами весьма широком сосуде имеется
только один вихрь, обусловленный прямым вихревг’м шнуром,
то шнур будет оставаться неподвижным. Но если бы в этом
сосуде образовалось два таких вихря, крутящихся около па-
раллельных вихревых шнуров, то шнуры стали бы двигаться.
На фиг. 2 изображены в плане два вихревых шнура с раз-
личными напряжениями, вращающиеся в одну сторону. Так
как вихрь, соответствующий левому вихревому шнуру, вра-
щает всю жидкую массу около оси шнура по часовой стрелке,
то он сообщает правому шнуру скорость, направленную пер-
пендикулярно радиусу вниз, а вихрь правого шнура по той же
причине сообщает левому шнуру скорость, направленную
вверх. Вследствие этого происходит то, что оба шнура вра-
щаются по часовой стрелке около некоторой точки; эта точка
316
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
получится, если в центрах двух шнуров мысленно сосредо-
точим массы, пропорциональные напряжению соответственных
вихрей, и отыщем центр тяжести этих двух масс.
Если бы вихри крутились в различные стороны, то вих-
ревые шнуры (фиг. 3) стали бы вращаться около центра,
лежащего со стороны шнура большего напряжения, и враще-
ние совершалось бы в сторону движения вихря большего
напряжения. Если бы при этом оба напряжения были равны,
то этот центр удалился бы в бесконечную даль, и оба шнура
бежали бы вперед (фиг. 4) по направлению, перпендикуляр-
ному к прямой, соединяющей центры.
На фиг. 5 представлены траектории (пути) трех вихревых
шнуров, из которых 7 и 2 вращаются против часовой стрелки,
а 3—по часовой стрелке. На фиг. 6 представлено движение
четырех прямых параллельных вихревых шнуров, равных по
напряжению. При этом шнуры 3 и 4 вращаются по часовой
стрелке, а шнуры 7 и 2— против нее.
Установленное нами понятие о прямом вихревом шнуре,
заключенном в весьма широком цилиндрическом сосуде, рас-
пространяется на вихревые шнуры, зародившиеся в какой
угодно массе жидкости. При этом вихревые шнуры могут
разыскиваться с помощью составления циркуляций по зам-
кнутым контурам, как это было пояснено для случая прямо-
линейного шнура. Если рассматривается идеальная жидкость
без трения, находящаяся под действием сил, удовлетворяющих
закону сохранения энергии, то для нее имеет место следую-
щая замечательная теорема: циркуляция скорости, опреде-
ленная для всякого замкнутого контура в жидкости, не
изменяется с передвижением частичек жидкости, образую-
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
317
образовывать вихревой шнур с тем же напряжением
и никакого нового вихревого шнура в жидкости не
образоваться. Действительно, разыскивая вихревой
с помощью составления циркуляций по замкнутым
щих контур. Из этой теоремы следует, что частицы жидко-
сти, образующие вихревой шнур, во все время движения
будут
вихря,
может
шнур
контурам, мы будем находить по всем контурам, которые
сначала не охватывали шнура, циркуляцию равную нулю,
а для всех контуров, охватывающих шнур,— прежнюю цир-
куляцию; из чего заключим,
вихревой шнур прежнего на-
пряжения.
Из упомянутой теоремы
следует также, что вихревой
что внутри последних проходит
шнур во все время движения либо будет лежать своими концами
на границах жидкости (на стенках сосуда или на свободной
поверхности), либо будет оставаться замкнутым. В самом деле,
для того чтобы сойти со стенок сосуда, основание вихря
должно бы уменьшиться в размерах до нуля; а так как цир-
куляция скорости по контуру основания должна оставаться
неизменной, то схождение потребовало бы, чтобы скорость
крутящейся жидкости при подошве шнура возрасла до беско-
нечности.
Гидродинамическое давление уменьшается прц возрастании
скорости; поэтому, при уменьшении основания вихря на
• 318
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
стенке сосуда, будет быстро уменьшаться давление в этом
месте, и остальная масса жидкости будет надавливать на
частицы конца вихревого шнура и препятствовать их схож-
дению со стенки. Вихревой шнур, так сказать, присасывается
своими концами к стенкам сосуда. Если конец шнура лежит
на свободной поверхности, то подобное присасывание можно
заметить по воронке, образующейся на свободной поверх-
ности у подошвы шнура. Если концы вихревого шнура не
Фиг. 7.
лежат на границах жидкости,
то они должны быть между
собой сомкнуты, и таким об-
разом получается замкнутый
вихревой шнур, — такой, в ко-
тором так сказать, оба конца
присасываются друг к другу.
Самый простой вид замкну-
того вихревого шнура предста-
вляет нам вихревое кольцо,
представленное на фиг. 7. Все
частицы жидкости, лежащие
вне кольца, движутся при этом
по замкнутым кривым, прохо-
дящим сквозь кольцо, так что
циркуляции скорости по всем
этим кривым одинаковы и равны
циркуляции скорости на конту-
ре перпендикулярного сечения
кольца; переходя же во внутрь кольца, мы будем получать
для траекторий его частичек различные циркуляции. Скорости
точек жидкости — самые большие на поверхности кольца; они
уменьшаются по мере удаления от этой поверхности внутрь
кольца и равны нулю на некоторой осевой линии; они умень-
шаются также и по мере удаления от кольца в окружающую
его массу жидкости. Для точек жидкости, значительно уда-
ленных от кольца, скорости обратно пропорциональны кубам
расстояний от кольца.
Мы видели, что зародившиеся в жидкой массе два прямых
параллельных шнура, около которых жидкость крутится
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
319’
с равными напряжениями вихря в противоположные стороны,
будут бежать по направлению, перпендикулярному к прове-
денной через них плоскости. По той же причине вихревое
кольцо не будет оставаться неподвижным, а будет бежать по
направлению, перпендикулярному к плоскости кольца, в ту
сторону, в которую жидкость вытекает из кольца. Мы видим
на фиг. 7, что частицы жидкой массы, движущиеся по верх-
ним замкнутым траекториям, будут надавливать на нижний
край кольца и двигать его вправо, точно так же частицы жид-
кой массы, движущиеся по нижним замкнутым траекториям,
будут надавливать на верхний край кольца и тоже двигать
его вправо. Все кольцо будет передвигаться равномерно
в правую сторону, перенося за собой крутящуюся около него
жидкость. Это движение будет тем быстрее, чем более на-
пряжение вихря и чем менее размер кольца.
Мы сказали, что внутри идеальной жидкой массы зароди-
вшиеся вихревые шнуры должны всегда сохраняться, и новых
шнуров образоваться не может, а между тем в природе мы
часто видим зарождение и погасание вихрей. Это происходит
оттого, что наши вода и воздух обладают некоторой степенью
вязкости, вследствие которой вышеприведенные теоретические
результаты несколько видоизменяются. С одной стороны
вихри могут зарождаться (преимущественно в тех местах,
в которых происходит скольжение друг по другу двух слоев
жидкости с различными скоростями); с другой стороны, за-
родившиеся вихри не сохраняются, а постепенно потухают.
Гельмгольц в своем вышеупомянутом сочинении указывает
простой способ образования вихревых полуколец у поверх-
ности воды. Проведя полупогруженной ложкой в сосуде воды
или веслом с лодки по воде, мы замечаем образование двух
воронок, которые бегут вперед и вращаются в противополож-
ные стороны. Эги воронки суть концы полукругового вихре-
вого шнура, образовавшиеся оттого, что ложка или весло,
унося за собой жидкую массу, заставляют ее скользить по
жидкости, прилегающей с боков. Эта масса трением захваты-
вает прилегающую жидкость и увлекает ее в вихревое движение.
Образование прямых вихрей Гельмгольц демонстрировал
одним прекрасным опытом, описанным в его речи о вихревых
320
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
бурях. Мы здесь повторим этот опыт. В дне цилиндрического
сосуда (фиг. 8) сделано небольшое отверстие, заткнутое
пробкой. Сосуд наполнен водой. Посредством струи воздуха,
направляемой трубкой на один
край свободной поверхности
воды, приводим жидкость в мед-
ленное вращательное движе-
ние. После этого открываем
пробку. Жидкость начинает
истекать из отверстия, подхо-
дя от краев сосуда к его оси.
Так как циркуляции скорости
по окружностям, проведенным
из точки на оси цилиндра че-
рез одни и те же частицы жид-
Фиг. 8. кости, не должны изменяться
со временем, то с уменьшением
радиусов этих окружностей будет возрастать скорость частиц
жидкости. Вращение жидкости по мере приближения к оси
будет становиться все быстрее и быстрее, и мы заметим
Фиг. 9.
резко образовавшийся вихрь, над которым появится воронка,
все более и более углубляющаяся.
Я покажу еще образование вихря посредством быстро
вращающегося диска. На фиг. 9 представлен прибор профес-
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
321
«сора Ф. Н. Щведова. Через дно стеклянного цилиндрического
сосуда проведена в сальнике вертикальная ось, оканчиваю-
щаяся небольшим диском. Эта ось посредством бесконечного
даемня может быть приведена в быстрое вращение. В сосуд
наливается вода и масло, которое всплывает поверх воды.
Вращая диск, мы замечаем, что вода постепенно приходит во
вращение и образует над ди-
ском вихревой шнур, который
замечается по воронке на по-
верхности раздела воды и масла.
Эта воронка заполняется ма-
слом, которое в виде нисходя-
щего смерча спускается к ди-
ску. В тот момент, когда масло
приходит в соприкосновение
с диском, вся его масса разбра-
сывается по воде.
Еще более интересен способ
«образования прямых вихрей,
предложенный Вейером. Воздух,
находящийся над поверхностью
воды, приводят во вращение с
помощью особой быстро вра-
щающейся крылатки, помещен-
ной на некоторой высоте над во-
дой (фиг. 10). Воздушный вихрь
захватывает по своей оси воду
и поднимает ее в виде восходя-
щего смерча до самой крылатки.
Вихревые кольца в воздухе
демонстрируются с помощью
имеющегося здесь прибора Тэта. Он состоит из ящика
(фиг. 11), задняя сторона которого затянута кожей, а в пе-
редней сделано отверстие с острыми краями. Форму отвер-
стия можно по желанию (пользуясь вставными пластинками)
делать круглой, эллиптической, четыреугольной и т. х.’
В ящик ставят два сосуда: в один 'наливают соляной
кислоты, а в другой нашатырного спирта. Вследствие этого
Зак. 2430. Н. Е. ЭКу.ховский. Том IX.
21
322
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
в ящике образуется густой туман от подвешенных частичек
хлористого аммония (нашатыря). Ударяя рукой или деревян-
ным молотком по натянутой коже, мы быстро выталкиваем и»
ящика некоторую массу воздуха вместе с нашатырным тума-
ном. Эта масса, скользя посреди окружающего неподвижного
воздуха, увлекает его в вихревое движение, а сама заверты-
вается в вихревое кольцо, которое будет хорошо заметно по
наполняющему его туману. При этом понятно, что воздух
около кольца будет вращаться так, что наблюдатель, глядя-
ООО
Фиг. 11.
щий на отверстие прибора, видит массу воздуха, выбегающую
к нему из средины кольца. Из этого следует, что образовав-
шееся кольцо должно двигаться из отверстия прибора.
Мы показали на рисунках, каково будет взаимодействие
нескольких прямолинейных вихрей. Следя за кольцами, выбе-
гающими из прибора Тэта, вы можете усмотреть случаи
взаимодействия друг на друга вихревых колец. Вы видите,
что кольца, подбегающие друг к другу боком, взаимно оттал-
киваются и начинают пульсировать; кольца же, идущие одно'
за другим, взаимно притягиваются и проходят одно сквозь,
другое. Этот интересный случай подробно исследован теоре-
тически Гельмгольцем. Он показал, что заднее кольцо должно
уменьшаться в размерах и увеличивать свою скорость, а пе-
реднее кольцо должно увеличиваться в размерах и уменьшать
свою скорость. Это будет продолжаться до тех пор, пока
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
323
заднее кольцо не пройдет сквозь переднее. После того пе-
реднее кольцо делается задним, и явление повторяется. К со-
жалению такую игру двух колец приходится наблюдать редко,
только при особенно удачном их образовании.
То обстоятельство, что кольцо несет быстро крутящийся
около него воздух, мы можем сейчас же обнаружить, напра-
вляя его на зажженную свечу. Вы видите, что свеча, стоящая
на большом расстоянии от прибора, потухает всякий раз, как
пламя ее задевается кольцом. Я помню, что во времена моей
юности я задумался над объяснением причины, вследствие
которой, стреляя пистоном из пистолета, можно тушить свечу
на большом расстоянии. Теперь для меня ясно, отчего это
происходит: из дула пистолета выбегает вихревое кольцо,
которое может перемещаться довольно далеко, не теряясь.
До сих пор кольца выпускались нами из круглого отвер-
стия. Попробуем теперь образовать их, выпуская из отверстия
эллиптического и квадратного. Мы видим, что при этом кольца
не сохраняют формы отверстия, но колеблются, стремясь
перейти в круглое кольцо, которое является таким образом
единственной устойчивой формой замкнутого вихревого шнура.
Рассмотрим теперь влияние на вихревые кольца посторон-
них предметов. Подводя к движущемуся кольцу твердые тела
сбоку, мы видим, что они отталкивают кольцо. Но если кольцо
бежит на параллельную его плоскости неподвижную пло-
скость, то оно, подходя к ней, все более и более увеличи-
вается в размерах, так сказать растекается по плоскости.
Если мы дадим кольцу набежать на нож, плоскость которого
проходит через ось кольца, то последнее разрежется ножом
на два полукольца, концы которых будут скользить по по-
верхности ножа; но, пройдя эту поверхность, концы опять
сомкнутся, и кольцо восстановится.
Неизменяемость и неразрушимость вихревых колец в идеаль-
ной жидкости навела В. Томсона на остроумную гипотезу
вихревых атомов. Предположив, что все пространство все-
ленной наполнено такой жидкостью, он принимает, что в этой
жидкости существует бесчисленное множество бесконечно-
малых замкнутых вихрей, которые представляют вечные и
неизменные атомы вещества. Взаимодействуя друг на друга,
2Г
324
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Фиг. 12.
эти замкнутые вихри соединяются в группы и образуют мо-
лекулы, и т. д.
Кроме дымных колец в воздухе, можно еще наблюдать
воздушные кольца в воде. Эго интересное явление, кажущееся
на первый взгляд парадоксальным, весьма просто объясняется
тем, что вследствие центробежной силы значительно пони-
жается давление на оси вихревого кольца. Если при образо-
вании вихревого кольца мы введем в воду несколько пузырь-
ков воздуха, го они сейчас же заберутся в то место жидкости,
где давление самое малое,
т. е. на ось кольца, и бу-
дут там удерживаться все
время, пока кольцо дви-
жется вдоль имеющейся
массы воды, несмотря на
то, что воздух в 800 раз
легче воды.
Я покажу здесь прибор
для образования воздуш-
ных колец в воде, который
представляет видоизмене-
ние прибора проф. Ос-
борна Рейнольдса. Здесь
имеется (фиг. 12) большая
стеклянная ванна, наполненная водой; в нее погружена изо-
гнутая под прямым угиом широкая стеклянная трубка. На
верхний конец трубки, выходящий из воды, надевают рукав
от резинового шарика, посредством которого можно вгонять
в трубку воздух и выталкивать из нее воду. Быстро сдавливая
шарик, выталкиваем из горизонтального колена трубки стол-
бик воды, и делаем это так, чтобы воздух достиг почти до
нижнего конца трубки, но не вышел из нее в большом ко-
личестве. Колонна воды, выбежав в спокойную окружающую
жидкость, завертывается в вихревое кольцо. При этом, так
как вместе с водой будет вытолкнуто несколько пузырьков
воздуха, то они, разбившись на мелкие пузырьки, располо-
жатся по оси кольца. Вследствие этих пузырьков вихревое
кольцо будет хорошо заметно: оно будет образовано как бы
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
325
из блестящих зерен бисера. Пробегая вдоль всей ванны,
кольца ударяются в противоположную стенку ее и здесь,
расширяясь, пропадают.
Мы можем с помощью нашего прибора отчетливо демон-
стрировать отражение колец от свободной поверхности воды.
Для .этого стоит только повернуть трубку, чтобы она напра-
вилась своим нижним концом немного вверх. Кольцо, подбе-
жав к свободной поверхности жидкости, от нее отражается,
причем угол падения равен углу отражения.
Так как действительные жидкости обладают вязкостью и
трутся о стенки тех сосудов, в которых они движутся, то
они при своем движении постоянно заполняются вихревыми
шнурами. Гельмгольц показал, что жидкую массу во всяком
воображаемом движении можно рассматривать, как непрерывно
заполненную вихревыми шнурами, и дал средства исследовать
движения этих шнуров.
Мы так долго останавливались на первой работе Гельм-
гольца по гидродинамике, потому что она представляет самый
капитальный труд его в этой области. Скажем теперь не-
сколько слов о других его ра-
ботах.
Мы упомянули, что можно
образовать вихревой шнур, про-
водя ложечкой по воде. Пред-
положим, что разрез ложечки
представляет стороны некото-
рого угла (фиг. 13). Вместо того
чтобы двигать ложечку, мож-
но держать ее неподвижно и за-
ставить воду на нее набегать. Фиг- 13.
Вникнем подробнее в причину,
вследствие которой при этом образуются вихревые шнуры.
Струи жидкости, обегая контур начерченного угла, будут
сходить с его углов с некоторой скоростью; жидкость же, ле-
жащая за углом, будет оставаться почти неподвижной. Вслед-
ствие этого образуются поверхности раздела, по которым
будет отделяться бегущая жидкость от неподвижной. На этих
326
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
поверхностях в жидкости, обладающей некоторой степенью
вязкости, зародятся вихревые шнуры, сечения которых от-
мечены на фигуре кружками. Эти шнуры завертываются в те
два вихря, которые мы замечаем за ложечкой в виде двух
воронок.
Эти рассуждения показывают, как важно для гидродина-
мики исследовать движения жидкости, сопровождающиеся об-
разованием поверхностей раздела. Сначала не представлялось
возможным приступиться к этой
трудной задаче. Г ельмгольцу
первому пришла мысль, могу-
щая послужить для разрешения
подобных вопросов. Он пояс-
нил свою идею, определив форт
му струи, вбегающей в про-
странство, заключенное между
двумя стенками, из сосуда, окру-
жающего эти стенки, как это
изображено на фиг. 14. Статья
Гельмгольца об этом предмете
заключает в себе всего деся-
ток страниц. Он, так сказать,
только наметил путь исследова-
ния, по которому пошли Кирх-
гофф, Рэлей, Фохт и многие другие ученые, окончательно
разработавшие решение вопроса. Но таков уж удел великих
ученых, что им всегда приходится стоять во главе научных
открытий. На фиг. 15 изображено соударение двух струй жид-
кости, исследованное по упомянутому способу Фохтом.
Ни время, которым я располагаю, ни специальный характер
предмета, не позволяют мне поговорить с вами о многих дру-
гих работах знаменитого германского ученого по механике.
Он писал и о движении жидкости с трением, и о направляе-
мости воздушных шаров, и о циклических системах и т. Д.
Но я не могу умолчать о последней работе маститого
ученого, совершенной прошлым годом (1890), так сказать
накануне его семидесятилетнего юбилея. Это работа об энер-
гии ветра и взволнованного моря.
РАБОТЫ ГЕЛЬМГОЛЬЦА ПО МЕХАНИКЕ
327
В ней Гельмгольц, как всегда, является перед нами во
всей силе своей оригинальной мысли и своего тонкого анализа.
Вообразим (фиг. 16) поверхность моря, соприкасающуюся
с бегущим над ней слоем воздуха, и предположим, что всей
рассматриваемой системе сообщено поступательное движение
•со скоростью, равной и противоположной скорости распро-
странения волн. Тогда поверхность волн представится нам
неподвижной, а вода и воздух будут течь в стороны, ука-
занные на рисунке стрелками. Проведя две горизонтальные
плоскости, вдоль которых те
чение воздуха и воды совер-
шается почти по горизонталь-
ным прямым, будем считать ко-
Фиг. 16.
личество воздуха, протекшее между верхней плоскостью и по-
верхностью волн, а также и скорость распространения волн,
за данные величины. Для такого течения Гельмгольц дока-
зывает замечательную теорему, которую я сформулирую,
пользуясь понятием об энергии, разъясненным вам в преды-
дущей лекции. Поверхность волн и скорость находящихся
около нее частиц воды и воздуха будут изменяться от дей-
ствия давления ветра на воду так, что разность между по-
тенциальной и кинетической энергией всей системы постоянно
будет уменьшаться.
На основании этой теоремы гладкая поверхность моря при
сильном ветре является неустойчивой поверхностью. Малейшее
ее изменение, произведенное трением ветра о воду, поднимет
большие волны. Это поднятие увеличивает потенциальную
.энергию системы, так как центр тяжести взволнованной воды
выше, нежели невзволнованной. Но рядом с этим, как показал
328
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Гельмгольц, происходит сравнительно еще большее увеличение
кинетической энергии вследствие возрастания скорости воды
у поверхности волн; так что в результате разность двух
энергий уменьшается. Если для данных скоростей ветра и
волны существует поверхность раздела воздуха и воды, при
которой упомянутая разность имеет наименьшее значение, то.
форму этой поверхности и примет по прошествии некоторого
времени поверхность взволнованного моря. Если же такого
минимума нет, то волны рассматриваемой длины не могут уста-
новиться. Гельмгольц показывает, что на поверхности моря
образуется сначала мелкая рябь, в которой длины волн полу-
чаются через разделение скорости ветра на отношение плот-
ностей воды и воздуха (т. е. на 773 при 0°Ц). Эти мелкие
волны интерферируются и постепенно переходят в большие
волны, длина которых пропорциональна скорости ветра. Так
как число волн, пробегающих в секунду через данное место,
равно скорости ветра, разделенной на длину волны и умно-
женной на 60, то это число будет тем более, чем более ско-
рость ветра.
Весной 1890 г. на Антибском мысе (близ Ниццы) Гельм-
гольц производил наблюдения для проверки своей теории.
Он помещался на косе, глубоко выдающейся в море и окан-
чивающейся утесом, и наблюдал скорость ветра и число на-
бегающих волн. Наблюдения подтвердили довольно хорошо
теооию и дали бы, как полагает Гельмгольц, еще более точ-
ные результаты, если бы имелись сведения о состоянии ветра
в прилегающих частях моря.
Этой картиной неустанной научной деятельности масти-
того ученого я и закончу свою лекцию.
Эта работа была сообщена автором 4 апреля 1891 г. в Физической
аудитории Московского университета в серии лекций, прочтенных в пользу
Гельмгольцевского фонда. Работа была напечатана в сборнике „Герман
фон-Гельмгольц“ (1821—1891 гг.), Москва 1892; вторично работа напе-
чатана в книге Дж. Дж. Томсона, Электричество и материя, Гиз, 1928.
Прим. ред.
НЕКРОЛОГ И ОЧЕРК УЧЕНОЙ ДЕЯТЕЛЬНОСТИ
проф. Ф. Е. ОРЛОВА
Ф. Е. ОРЛОВ
(184S—1892)
НЕКРОЛОГ И ОЧЕРК УЧЕНОЙ ДЕЯТЕЛЬНОСТИ
проф. Ф. Е. ОРЛОВА
(1892—1893 и.).
Федор Евплович родился в 1843 г. в селе Великом Нов-
городской губернии, где квартировал тогда полк, в котором
отец покойного, Евпл Григорьевич Орлов, служил врачом.
Вскоре после рождения Федора Евпловича его отец был пе-
реведен на должность лекаря в г. Ставрополь Самарской гу-
бернии, где и протекло раннее детство Ф. Е. под попече-
нием горячо любимой им матери Александры Павловны. Пе-
ред своим замужеством Александра Павловна, урожденная
Лебедева, жила у своих родителей в Москве; там же она по-
знакомилась и с лечившим ее студентом-медиком Московского
университета Орловым и вышла потом за него замуж.
Федору Евпловичу не было еще и восьми лет, когда умер
его отец, и Александра Павловна вместе с семейством, со-
стоявшим из Ф. Е., его брата и сестры, поехала в Москву,
где надеялась личным заработком воспитывать своих детей.
Положение осиротелой семьи ухудшилось еще тем обстоя-
тельством, что небольшой дом, принадлежавший им в Ставро-
поле, вскоре после этого сгорел. Орловы поселились у своих
родственников Соколовых за Москвой рекой. Здесь Ф. Е.
начал свое ученье, поступив в городское училище. Как-то,
(проезжая по Замоскворечью вместе со мной, Ф. Е. показывал
мне это училище и называл его, шутя, своей „академией".
Вскоре по приезде в Москву Александра Павловна по
ходатайству крестного отца Ф- Е., графа Александра Арка-
диевича Суворова (внука знаменитого полководца), получила
место начальницы в Варваринском училище, а Федор Евпло-
вич был определен на казенный счет в Ярославскую гимназию.
Отвозя сына в Ярославль, Александра Павловна надеялась
332
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
на помощь брата ее мужа, Василия Григорьевича Орлова,
о котором знала только, что он живет именно в этом городе..
Василий Григорьевич принял в своем племяннике горячее
участие. К нему Ф. Е. ходил в отпуск по праздникам из дво-
рянского пансиона, в котором был помещен на жительство.
О дяде Федор Евплович сохранил прекрасное воспоминание,
как о человеке, которому он обязан своим нравственным:
воспитанием. Василий Григорьевич Орлов был человек оди-
нокий, сердечный и умный. Он очень полюбил племянника и
внимательно следил за его успехами.
Когда племянник подрос, Василий Григорьевич стал отно-
ситься к нему, как к другу, и часто делился с ним своими
мыслями, толкуя о тех трудностях, которые следует преодо-
левать человеку, чтобы жить честно и справедливо.
Вот как писал Ф. Е. из-за границы по случаю смерти
своего родственника и наставника, последовавшей в 1871 г.г
„Моя любовь к нему и мое безграничное уважение к этому
борцу с тяжелой жизнью возрастали с каждой нашей беседой-
Как рад бы он был увидеть своего Федора, полного сил и
надежд, близкого к цели, на которую он сам указал мне, как
на самую высокую и достойную в жизни, в дни моей первой
молодости, во время наших первых бесед с ним в тихом ма-
леньком кабинете, заваленном книгами, или во время прогу-
лок по берегу широкой Волги".
В гимназии Ф. Е. учился прекрасно, кончил курс с золо-
той медалью и затем шестнадцатилетним юношей приехал
в Москву, где поступил, в 1859 г., на математический фа-
культет.
Еще в Ярославской гимназии Ф. Е. начал давать уроки,
а со второго курса Университета стал посредством уроков
поддерживать свою семью, для которой сделался единствен-
ной опорой, так как матушка его, Александра Павловна, оста-
вила к этому времени Варваринское училище.
Научные занятия Ф. Е. в Университете шли весьма
успешно. Он пользовался особым расположением профессора
механики Н. Д. Брашмана, к которому вместе с несколькими
избранными студентами ходил на дом решать задачи по ме-
ханике. Усердный профессор заставлял этих студентов при-
Ф. Е. ОРЛОВ
333
родить в Университет для упражнений даже по праздникам
и был, по словам Ф. Е., весьма недоволен, когда он вместе
«с товарищами в один из таких весенних праздников ушел на
Воробьевы горы.
По окончании курса в 1863 г. Ф. Е. был оставлен при
Университете по кафедре чистой математики и по выдержа-
нии магистерского экзамена защищал в 1869 г. диссертацию на
степень магистра „О взаимности диференциальных уравнений".
Это сочинение очень понравилось проф. А. Ю. Давидову,
который призывал Федора Евпловича к себе и заставлял
.его рассказывать свою работу, когда она еще печаталась.
К этому времени Совет Московского университета постановил
ходатайствовать в министерстве о посылке одного из моло-
дых ученых за границу для приготовления к занятию кафедры
практической механики, которую, за смертью профессора
А. С. Ершова, временно занимал Д. Н. Лебедев. А. Ю. Да-
видов указал на Ф. Е. как на наиболее желательного канди-
дата для этой цели, причем в том обстоятельстве, что пер-
воначальной специальностью Орлова была чистая математика,
А. Ю. видел только залог, обеспечивающий солидность
практических знаний будущего механика.
Не без внутренней борьбы решился молодой математик
переменить свою специальность. Его воображение манили
к себе некоторые уже намеченные им математические работы.
Но желание скорее стать прочной опорой своей семьи, же-
лание приносить своими знаниями общественную пользу,
в которой Ф. Е. видел цель жизни, заставили его согласиться
на предложение уважаемого профессора.
Ф. Е. поехал в сентябре 1869 г. через Петербург, Берлин,
Франкфурт и Гейдельберг в Цюрих с небольшими останов-
ками по пути. В Петербурге он виделся с И. А. Вышнеград-
ским, П. Л. Чебышевым и Окатовым, которые снабдили его
своими советами и рекомендациями. П. Л. Чебышев толковал
с ним о своих изобретениях в области суставчатых механиз-
мов и впоследствии, проездом чрез Цюрих, заезжал к Ф. Е,
и поручил ему перевод своей статьи о параллелограме Уатта,
.из которой Цейнер пожелал сделать извлечение для журнала
„Ci vilingeni eur ",
334
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
В Цюрихе Ф- Е. провел целый год. Он записался сту-
дентом в политехникуме и прослушал полный курс прикладной
механики у Цейнера, Фейта и Кульмана, а также и курсы
математики у Швартца и Фидлера. Профессором, наиболее
повлиявшим на развитие молодого ученого в области меха-
нических знаний, был знаменитый Цейнер, к которому Ф. Е.
имел рекомендации от Б. Я. Швейцера.
„Преподавание Цейнера, — пишет Федор Евплович к А. Ю.
Давидову, — отличается необыкновенной ясностью и увлека-
тельностью, и в этом отношении он может служить образцом
преподавателя... Труд мой для меня теперь вполне выяснен,,
и я с удовольствием вижу, что он не противоречит моим
склонностям и не превосходит моих сил". Кроме слушания
лекций, Ф. Е. усердно занимался черчением и проектиро-
ванием и в вакационное время, когда политехникум был за-
крыт, чертил в его нижнем подвальном помещении. Из Цю-
риха Ф. Е. делал ряд экскурсий для посещения заводов и
фабрик Швейцарии.
В Цюрихе Ф. Е. получил письмо от А. В. Летникова об
избрании его на кафедру практической механики в Техничес-
ком училище на место выбывшего Ф. Н. Королева. Это
избрание обрадовало молодого ученого, но также и смутила
его, так как он думал сначала посвятить все свои силы пре-
подаванию в Университете.
В своем ответе А. В. Летникову он пишет: „Я очень
счастлив, что успел заслужить доверие и доброе мнение людей,
мною глубоко уважаемых. Мысль, что труд мой оценен прежде,
чем я мог бы заявить себя в нем, служит для меня твердой
нравственной опорой, и я с уверенностью могу сказать, что
Техническое училище найдет во мне добросовестного препо-
давателя... Но так как ближайшая цель моей заграничной
командировки состоит в приготовлении к кафедре прикладной
механики в Университете, то я боюсь: не удалит ли меня
делаемый мной шаг от этой главной цели".
Ф. Е. предполагал сначала переехать летом 1870 г. из
Цюриха в Париж, но возгоревшаяся за это время франко-
прусская война изменила его планы. Хотя Швейцария и
осталась в стороне от грозных событий, но ее они встрево-
Ф. Е. ОРЛОВ
335
жили: явилась опасность, как бы не пришлось позаботиться
о своей самозащите. Проф. Цейнер, по словам Ф. Е., на
вопросы слушателей об экзаменах и дипломах отвечал, что
теперь не до дипломов, когда речь идет о жизни стольких
людей. Сделав несколько прогулок по Швейцарии в сопро-
вождении своих соотечественников Бари и Мессинга, Ф. Е.
в сентябре 1870 г. возвратился опять в Цюрих и оттуда,
запасшись от проф. Цейнера рекомендательным письмом
к проф. Рело, отправился в Берлин, так как быстро идущие
военные события в то время уже приближались к сердцу
Франции.
В Берлине Ф. Е. поступил слушателем в Gewerbe-Akade-
mie и записался на курсы проф. Рело, Вибе, Гросмана, Квинки,
Христофеля и др., кроме того, он посещал лекции математики
в Берлинском университете, где в то время читали Куммер,
Вейерштрасс и Кронекер. Ту выдающуюся роль, которую
играл проф. Цейнер в механическом образовании Ф. Е.
в Цюрихе, занял в Берлине директор Gewerbe-Akademie проф.
Рело. Его курс кинематики Ф. Е. слушал с увлечением и
воспользовался им для своей вступительной лекции в Москов-
ском университете. Вот как писал Федор Евплович о лекциях
Рело А. Ю. Давидову.
„В лекциях своих Рело дает замечательный опыт изложения
кинематики с новой точки зрения. Формулы, которыми он
представляет состав механизма, и открытые им методы иссле-
дований приводят его к самым неожиданным результатам".
Зиму и лето 1870 —1871 гг. Ф. Е. провел в Берлине, усиленно
работая в Gewerbe-Akademie, а во время вакаций делая
поездки по разным городам Германии для осмотра фабрик.
За это время мир с Францией был заключен, и Ф. Е. не
представлялось уже никаких препятствий для переезда в Париж.
Но при этом переезде он заехал в Льеж и в нем зажился.
Он стал посещать Льежский университет и состоящую при
нем специальную школу и с интересом слушал лекции Каталана.
Этот маститый ученый оценил и полюбил молодого рус-
ского математика. Он живо заинтересовался его магистерской
диссертацией и просил Ф. Е. сделать французский перевод
ее, который представил в Бельгийскую академию наук. Ката-
336
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
>лан уговаривал Ф. Е. принять участие в конкурсе на премию
за сочинение, назначенное Бельгийской академией по теории
поверхностей. Но боязнь уклониться от своих прямых обязан-
ностей удержала Ф. Е. от этого заманчивого предложения.
„Я с овеем засиделся в Льеже, — пишет он в своем дневнике, —
и меня начинает мучить угрызение совести, что за последнее
время я покинул практическую механику и исключительно
увлекся своей прежней любимицей — непрактической матема-
тикой". В Льеже и его окрестностях Ф. Е. осмотрел (многие
фабрики. Таким образом протекло время до конца 1871 г.
Заграничная командировка подходила к концу, и надо было
спешить в Париж, куда Федор Евплович^и приехал к новому
году. Он поселился в Латинском квартале и стал посещать
лекции Центральной школы, где слушал Phillips и Haton de
la Gcupilliere, он ходил также в инженерную школу слу-
шать Бресса, посещал Сорбонну и в College de France
слушал Бертрана, Бонне, Пюйзе и Шаля. В Париже
Ф. Е. встретил Н. В. Бугаева и вместе с ним осматри-
вал достопримечательности всемирного города. ’Посеще-
нием фабрик и заводов Франции окончилась заграничная
поездка Ф. Е.
Осенью 1872 г. он был уже в Москве и читал свои всту-
пительные лекции в Московском Университете и в Техниче-
ском училище. Его университетская вступительная лекция
я О машинах" была напечатана в „Математическом сборнике"
и заключает в себе развитие идей Рело о кинематической
паре и цепях, которые у нас в России в то время
являлись новостью. В Техническом училище он читал
вступительную лекцию во втором общем классе по эле-
ментарной механике. Здесь в первый раз мне пришлось
увидеть Ф. Е. Лекция его была составлена прекрасно, но
молодой лектор читал ее робко. В нем еще не было того
спокойствия и уверенности, которые выработались в после-
дующие годы его преподавания.
В этом сказывался характер покойного, в котором не
было самонадеянности, а скорее строгое отношение к сво-
им силам. „Я еще совершенно не приготовлен к своим слу-
жебным обязанностям, — пишет он в своем заграничном
Ф. Е. ОРЛОВ
337
.дневнике. — В голове лежит сырой, еще не обработанный,
не приведенный в систему, материал, в котором придется
долго разбираться; надо составить 'программы и выработать
курсы разом для элементарного и специального преподавания
в Техническом училище и в Университете. Я не теряю,
впрочем, храбрости. Напротив, сердце бьется нетерпеливым
ожиданием этой новой и широкой деятельности после столь-
ких годов терпеливого приготовления. Я уверен, что буду
на своем месте и останусь всегда на уровне современного
«состояния науки". Эта уверенность вполне оправдалась в по-
следующие годы жизни покойного.
Ф. Е. поселился с своей матерью и сестрой около По-
кровки, в Введенском переулке, где и мне пришлось жить
поблизости, а несколько лет спустя мы заняли с ним квар-
тиры на Немецкой улице в одном и том же доме.
Мы сблизились и очень часто видались. Какое отрадное
воспоминание сохранилось у меня о его мирной семейной
.жизни за эти первые годы его служебной деятельности!...
Добрая, хлебосольная хозяйка, Александра Павловна, являлась
центром кружка, состоявшего из родственников и близких
.знакомых. Серьезные разговоры сменялись вечером детской
веселостью и хоровым пением. Важный и сумрачный с виду,
Ф. Е. являлся в своей семье простым и веселым. Остроумная,
безобидная шутка часто оживляла его интересную беседу.
Он так любил все забавное и веселое. Как сейчас слышу
его мягкий смех, причем он обыкновенно снимал очки и
протирал их. Я думаю, что эти годы были самые счастливые
в жизни Ф. Е. Он достиг той цели, о которой мечтал на
берегу Цюрихского озера и о которой писал в своем днев-
нике: „Я остановился на мосту и смотрел на Лиман, в кото-
ром отражались огни города; вдали слышалось чье-то пение.
Судьба ничем не обидела тебя, думал я о себе, она дала
тебе все лучшее в жизни: широкую и славную дорогу, семей-
ную привязанность, родину, для которой ты можешь принести
пэльзу. Все зависит теперь от тебя: последнее усилие воли —
и ты будешь у цели"...
Ф. Е. скоро разобрался в обширном запасе своих научных
«сведений. Лекции его в Техническом училище и Университете
Зак. 2430. Н. Е. Жуковский. Том IX.
22
338
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
пошли успешно. За смертью проф. Д. Н. Лебедева на долю
Ф. Е. выпало чтение самых существенных и ответственных
курсов в Техническом училище, и он повел их на уровне
современного состояния науки. В Московском университете
преподавание практической механики было поставлено Ф. Е.
на ту высоту, на которой оно не стоит ни в одном из рус-
ских университетов. Я помню, как одобрительно отозвался
председатель экзаменационной комиссии В. Г. Имшенецкий,
встретив в ответах студентов по специальным курсам практи-
ческой механики такие обширные знания, которые можно
ожидать только от воспитанников специальных технических
школ. Ф. Е. поощрял студентов заниматься его предметом.
Он устроил в Университете прекрасный механический кабинет,
завел классы черчения и проектирования. Он всегда охотно
сообщал занимавшимся у Него студентам сведения для писа-
ния кандидатских сочинений и наделял их даже книгами из
своей библиотеки. Можно сказать, что почти половина канди-
датских сочинений писалась в Университете по практической
механике.
В 1874 г. Совет Технического училища командировал
Ф. Е. с ученой целью в Московскую, Нижегородскую и Вла-
мирскую губернии для исследования местной фабричной и
заводской промышленности, а в 1876 г. — на Филадельфийскую
выставку для обозрения всех усовершенствований техниче-
ского дела в Соединенных Штатах С. Америки.
В 1878 г. он был командирован с научной целью на Па-
рижскую всемирную выставку, с которой привез обширный
материал, оставшийся, к сожалению, не напечатанным.
В 1883 г. скончалась матушка Ф. Е., Александра Павловна,
и как бы унесла с собой его счастливые дни. В последние
годы жизни Ф. Е. минут веселости у него было все меньше
И меньше. Его сдержанный характер стал еще более замкну-
тым. Надежда его — найти в своей жизни личное счастье,
которого он вполне заслуживал, не сбылась, и он обратил
весь свой интерес на служебные обязанности и, главным об-
разом, на дела Политехнического общества, вице-президентом
которого он был избран в 1886 г. Вот несколько слов из
письма Ф. Е. к двоюродному брату А. П. Соколову (вице-
Ф. Е. ОРЛОВ
339
директору Пулковской обсерватории): „Я принимаю деятель-
ное участие только в одном Политехническом обществе,
где выбран на это трехлетие вице-президентом. Дела после
продолжительного застоя пошли у нас очень оживленно, и
вчера, в годичном собрании Общества, окончившемся това-
рищеским обедом, я был очень растроган торжественным и
лестным для меня признанием моих скромных заслуг на
пользу дорогого мне учреждения". Но и дела Общества
вместе с радостями являлись иногда для Ф. Е. источником
огорчений. Он не всегда был понят и оценен по заслугам.
ОсеньюА1891*г. Ф. Е. вернулся в Москву из Звенигорода,
где провел летние вакации, бодрым и повеселевшим, каким
был в прежние добрые годы. Но в Москве на него опять
нашло мрачное расположение духа, как бы предчувствие
чего-то рокового.
С нового года он захворал инфлуэнцией, перешедшей
в крупозное воспаление легких, и скончался 20 января 1892 г.
на руках своей сестры. Похоронен он в Алексеевском мона-
стыре рядом со своей матерью.
Характер покойного Ф. Е. представлял странное соедине-
ние противоположных свойств: внешней солидности и суро-
вости с простотой и добротой, внешней уравновешенности и
рассудительности с нервностью и впечатлительностью, почти
болезненными. К сожалению, многие, судя по внешности,
не видели его необыкновенной доброты и гуманности, всег-
дашней отзывчивости к судьбе ближних. Быть везде полезным,
устраивать судьбу людей, он как бы считал своей обязан-
ностью. Всегда охотно, с искренним интересом выслушивая
других, вызывая Их к откровенности, он редко открывал
свою душу даже самым близким людям и гордо выносил на
одних своих плечах свои заботы и горе, которого, к сожа-
лению, немало выпало на его долю. Враг всякой фальши и
неискренности, Ф. Е. с уважением относился к чужому до-
стоинству, к самому себе был чрезвычайно строг и не только
никогда не приходилось слышать от него никакой самопо-
хвалы, но он вообще не любил говорить о себе. Чужие
радости всегда возбуждали в нем живую радость, чужое горе
было его горем.
22*
340
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Особенно горячо любил он учащуюся молодежь, к сужде-
ниям ее всегда относился со вниманием, в нравственный ее
смысл и чутье правды глубоко верил. Он часто говорил:
„чуткая к правде молодежь". И эта молодежь умела за внеш-
ней холодностью видеть горячую, благородную душу своего
любимого профессора.
Федор Евплович оставил после себя несколько печатанных
работ, относящихся к чистой и прикладной математике.
В 1866 г. он напечатал во втором томе „Математического
сборника" статью „Доказательство теоремы Эйлера". В этой
статье он делает вывод условия:
ду dx\dy') ‘ dx-\ду" / ' ЛЦЭу/
данного Эйлером для интегрируемости диференциального вы-
ражения f(x, у, у', у",..., yn)dx. Вывод Ф. Е. не зависит от
вариационного исчисления и распространяется как на прямую,
так и на обратную теорему Эйлера.
В 1868 г. была напечатана в третьем томе „Математи-
ческого сборника" диссертация Ф. Е. на степень магистра
чистой математики „О взаимности диференциальных урав-
нений". В этой работе автор предлагает вместе с данным
диференциальным уравнением f(x, у, у') = 0, устанавливаю-
щим связь между ординатой у и абсциссой х, рассматривать
диференциальное уравнение, в котором неизвестной функцией
является отрезок отсекаемый касательной на оси ординат,
а независимым переменным—тангенс р угла наклонения
касательной к оси абсцисс. Это диференциальное уравнение
имеет вид р®' — “, р) = 0 и называется взаимным дан-
ному уравнению, потому что, рассматривая <“ как ординату,
а р как абсциссу и составляя уравнение, взаимное второму
диференциальному уравнению, гмы получим первое диферен-
циальное уравнение. Всякий раз, как интеграл одного из двух
взаимных диференциальных уравнений известен, то известен
и интеграл другого. Автор пользуется этим свойством для инте-
грации диференциальных уравнений различных видов. Потом он
обнаруживает связь между началом взаимности и теорией
Ф. Е. ОРЛОВ
341
последнего множителя. В конце работы идеи взаимности
распространяются на уравнения с частными производными.
В 1869 г. Ф. Е. напечатал в четвертом томе „Математиче-
ского сборника" небольшую заметку „Разыскание интергри-
рующего множителя", которая представляет дальнейшее
развитие идей, высказанных в его магистерской диссертации.
В 1872 г. Ф. Е. прочитал в Московском университете и
напечатал в шестом томе „Математического сборника" свою
вступительную лекцию „О машинах". В ней он изложил новые
в то время воззрения проф. Рело на состав механизма.
В 1883 г. Ф. Е. доложил на VII Съезде русских естество-
испытателей и врачей, собиравшемся в Одессе, и напечатал
в „Трудах Новороссийского общества естествоиспытателей"
статью „Из теории рулет". Эта статья заключает в себе ре-
шение интересной задачи об описании неподвижной и по-
движной полоиды под условием, что одна точка фигуры
описывает прямую линию. Исходя из той теоремы, что в случае
прямолинейного движения одной из точек равномерно враща-
ющейся фигуры все центры ускорений четного порядка лежат
на упомянутой прямой, а все центры ускорений нечетного
порядка лежат на прямой, к ней перпендикулярной, Ф. Е. дает
диференциальное уравнение второго порядка, интеграция
которого при данной зависимости между радиусами кри-
визны полоид позволяет определить эти кривые.
Он разъясняет данный способ решения задачи многими
примерами. Так, он находит, что в случае одинаковости обеих
полоид и их соприкосновения выпуклыми сторонами полоиды
должны быть параболами и точка, описывающая прямую,
будет фокус подвижной параболы. Год спустя, т. е. в 1884 г.,
Ф. Е. напечатал в одиннадцатом томе „Математического сбор-
ника" статью, являющуюся продолжением его исследований
по [теории-[рулет, „О квадратуре [рулет". В этой статье
Ф. Е. определяет площади, заключенные между рулетой
какой-нибудь точки, двумя нормалями, опущенными из концов
рулеты на неподвижную полоиду, и контуром этой, полоиды.
Он обнаруживает, что все точки плоскости подвижной фигуры,
рулеты которых имеют одинаковые площади, лежат на кон-
центрических окружностях, центр которых он называет цент-
342
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ром площадей рулет. При помощи этой точки площади рулет
выражаются простой формулой:
5=4(р2_£°2)’
в которой р есть расстояние точки от центра площадей рулет,
Ео—некоторая постоянная величина, а есть угол, на ко-
торый поворачивается фигура. В предисловии к своей работе
Ф. Е. пишет: „В предлагаемой статье интересные, но мало
известные в нашей литературе предложения относительно
квадратуры рулет выводятся в более общем виде одними
аналитическими методами, в сущности представляющими ра-
звитие простого и изящного метода Дарбу“.
После покойного Ф. Е. остались бумаги, между которыми
имеется ненапечатанное еще сочинение, относящееся к общей
теории рулет. Сочинение это он предназначал для своей
докторской диссертации, но по свойственной ему строгости
к Себе все считал его не вполне оконченным. Две вышеупо-
мянутые статьи о рулетах представляют выдержки из этой
работы. В бумагах Ф. Е. есть много конспектов и заметок,
есть составленные им полные курсы лекций: Цейнера, Вибе
и Каталана. Рассматривая этот материал, видишь наглядно, как
собирались те обширные знания, которыми обладал покойный.
Когда Каталан предлагал Ф. Е. Орлову писать сочинение
на премию Бельгийской академии, то Ф. Е. думал поставить
девизом своей работы: „Travaillez, prenez de la peine, c’est le
fond qui manque le moins“. Я думаю, что это был девиз всей
его жизни.
Н. Е. Жуковский выступал дважды с воспоминаниями об Ф. Е. Ор-
лове: 24 января 1892 г. в заседании Отделения физических наук Общества
любителей естествознания с докладом „Воспоминания о Ф. Е. Орлове" и
3 мая 1892 г. в торжественном заседании Политехнического общества
в Политехническом музее с докладом „Некролог н очерк деятельности
Ф. Е. Орлова как профессора". Работа „Некролог н очерк ученой дея-
тельности Ф. Е. Орлова" была напечатана три раза: 1) в Отчетах Москов-
ского технического училища за 1891—1893 гг., 2) в Отчете Московского
университета за 1893 г., 3) в приложении к книге Ф. Е. Орлова, Днев-
ник заграничной командировки 1869—1872 гг., Москва 1898. Прим. ред.
О ТРУДАХ В. Г. ИМШЕНЕЦКОГО ПО МЕХАНИКЕ
В. Г. ИМШЕНЕЩКИЙ
(1832-1892)
О ТРУДАХ В. Г. ИМШЕНЕЦКОГО ПО МЕХАНИКЕ
(1896 г.)
Многие сочинения покойного Василия Григорьевича Имше-
нецкого относятся к интегрированию уравнений с частными
производными и вследствие этого соприкасаются с вопросами
механики, но непосредственно механике посвящены только
три его работы:
1. Определение силы, движущей по коническому сечению
материальную точку, в функции ее координат.
2. Канонические диференциальные уравнения гибкой не-
растяжимой нити и брахистохроны.
3. Новое аналитическое доказательство параллелограма
сил.
Эти статьи напечатаны в протоколах Математического
общества при Харьковском университете — первая в 1879,
вторая в 1880 и третья в 1890 г.
Первая статья является ответом на задачу, предложенную
академиком Бертраном, и служит, вместе с работами других
авторов на ту же тему1, разъяснением одного интересного
вопроса небесной механики.
Бертран формулировал в „Comp'es rendus" (Avril. 1877
свою задачу так: „Зная, что планеты описывают конические
сечения, и не предполагая ничего более, найги выраже-
ние слагающих действующей на них силы в функции
координат точек ее приложения". При этом он указал для
примера способ решения задачи в случае, когда все кони-
1 D'arboux, „Comptes rendus,“ т. LXXX1V, р. 760, 936. Halphen,.
„Comptes rendus", t.LXXXIV, p. 939. Gia i scher, „Monthly-Notices of the
Astronomical Soeiety", т. XXXIX.
346
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ческие сечения имеют общий фокус. В. Г. Имшенецкий пошел
в своей работе по пути, предложенному Бертраном для
упомянутого частного случая.
Представив уравнение конического сечения в виде:
рх1 + W2 + 2rxy = (ах + by + с)2
и приняв в нем а, Ь, с за произвольные постоянные, он
исключает их с помощью диференцирования по времени, при-
чем вместо вторых производных от координат подставляет
слагающие силы. При этом он обнаружил, что сила должна
быть непременно центральной и должна иметь величину:
(px2~f-2rxy + qy2) 2
Это решение совпало с тем, которое было дано Дарбу,
принявшим наперед, что сила есть центральная1, и прило-
жившим к ее определению формулу Бине. При этом Дарбу
указал еще другое выражение силы:
(ax + fy + с)8 ’
которое получается из предыдущего преобразованием на осно-
вании уравнения траектории, и которое нашлось бы способом
В. Г. Имшенецкого, если бы принять р, q, г за произвольные
постоянные.
Вторая статья В. Г. Имшенецкого по механике относится
к вопросу об аналогиях между задачами о движении мате-
риальной точки и задачами о гибкой нити и о брахисто-
хроне.
Эти аналогии были весьма полно исследованы Клебшем2 и
затронуты в работах некоторых других авторов. Но при этом
1 Найдя простое геометрическое доказательство того, что в предложен-
ной им задаче сила будет центральной, Бертран видоизменил ее задание.
Это видоизменение не было известно В. Г. Имшенецкому, когда он писал
свою работу.
2 Clebsch, „Journal von Crelle“, Bd. 57.
О ТРУДАХ В. Г. ИМШЕНЕЦКОГО ПО МЕХАНИКЕ
347
вопрос по большей части ставился в связи с максимумом и
минимумом некоторых определенных интегралов, играющих
в задачах о гибкой нити и брахистохроне роли, аналогичные
интегралу действия в задаче о движении материальной
точки.
В. Г. Имшенецкий устанавливает аналогии трех упомяну-
тых задач, выражая их диференциальные уравнения в одно-
образной канонической форме.
После такого преобразования уравнений все три задачи
с аналитической стороны становятся тождественны, так что
рассматривание функции Гамильтона позволяет сейчас же
решить, какие механические величины в этих задачах играют
одинаковую роль.
Таким образом выясняется, что любая траектория свобод-
ной материальной точки, описанная под действием сил, имею-
щих силовую функцию, может быть принята за форму
уравновешенной гибкой нити или за форму брахисто-
хроны.
В первом случае надо переменить поле сил, изменяя
знак силовой функции, и считать скорость за натяже-
ние нити; во втором случае следует за силовую функцию U
взять
1
V2(U+h) ’
тде h — постоянное в интеграле живых сил, а за скорость на
брахистохроне принять обратную величину скорости мате-
риальной точки.
Анализ В. Г. Имшенецкого прост (в особенности для сво-
бодной точки) и может быть с удобством введен в курсы
механики.
Изучающий будет при этом видеть в задачах о гибкой нити
и о брахистохроне полную аналогию с знакомыми приемами
решения вопросов о движении материальной точки, тогда как
эти задачи при обыкновенном изложении требуют особого
исследования.
Третья статья содержит аналитическое доказательство
теоремы о параллелограме сил, сходное по основным допу-
348
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
прениям с доказательствами Д’Аламбера и Лапласа, но более
простое в том отношении, что приводит к цели с помощью
одних элементарных средств анализа.
Настоящая работа Н. Е. Жуковского входит, как часть, в коллектив-
ный труд К. А. Андреева, П. А. Некрасова и Н. Е. Жуков-
ского „Жизнь и научная деятельность В. Г. Имшенецкого-, напечатан-
ный в „Математическом сборнике", т. XVIII, 1896. Прим, ред.
ОТТО ЛИЛИЕНТАЛЬ
ОТТО ЛИЛИЕНТАЛЬ
(1847-1896)
ЛЕТАТЕЛЬНЫЙ АППАРАТ ОТТО ЛИЛИЕНТАЛЯ
(1895 г.)
Наиболее выдающееся изобретение за последнее время
в области аэронавтики представляет летательный аппарат не-
мецкого инженера Отто Лилиенталя. Этот аппарат состоит из
неподвижных крыльев, сделанных из ивовых прутьев и пару-
Фиг. 1.
сины и обращенных книзу вогнутой стороной. Крылья имеют
7 м длины и около 2*/2 м ширины (18- м2). Весь аппарат
весит 20 кг и без труда держится на руках, продеваемых до
плеч в отверстия, сделанные в передней части аппарата,
причем руками следует ухватиться за поперечную перекладину
прибора.
Снимок (фиг. 1) представляет Лилиенталя с надетым на
него летательным аппаратом. С таким снаряжением он легко
352
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
может бегать. Первые опыты парения по воздуху Лилиенталь
сделал в 1893 г. в местечке Штеглиц (Steglitz) около Берлина,
где на горе для него была построена башня (10 м). С этой
башни он бросался со своим аппаратом против ветра и дви-
гался в воздухе, ниспадая вниз по отлогому пути. Потом
он перенес свои эксперименты на горы Риновер (Rhinower),
которые представляют конические холмы, дающие во все сто-
роны пологие скаты от 10 до 20°. Эти горы оказались чрез-
Фиг. 2.
вычайно удобными для полетов и позволяли Лилиенталю
впарить против ветра на высоте 20 м над землей на протяже-
нии нескольких сотен метров. Теперь Лилиенталь совершает
свои полеты недалеко от Берлина (вторая станция по Лейп-
цигской дороге) на искусственно устроенной им конической
горе (высота 30 м), в верхней части которой сделана обшир-
ная землянка для хранения его летательных аппаратов.
На следующем снимке (фиг. 2) Отто Лилиенталь пред-
ставлен на вершине своей горы. Установив аппарат против
ЛЕТАТЕЛЬНЫЙ АППАРАТ О. ЛИЛИЕНТАЛЯ
353
Фиг. 3.
ветра, для чего служит ему вертикальный хвост, прикреплен-
ный к задней части прибора, он бежит вниз с горы и, про-
бежав несколько шагов, подхватывается ветром, который под-
держивает крылья подобно змею и позволяет экспериментатору
опускаться вниз по отлогому пути (около 10° к горизонту),
как это изображено на третьей фотографии (фиг. 3).
При этом, вися на руках, Лилиенталь регулирует движение
аппарата перемещением центра тяжести своего тела. Всякий
раз, как аппарат опускается
быстро книзу, Лилиенталь при-
гибает ноги назад, если же ап-
парат забирает вверх, то аэро-
навт продвигает свои ноги впе-
ред; склонение аппарата направо
поправляется передвижением
тела налево и наоборот.
Все эти движения делают-
ся инстинктивно (подобно упра-
влению бициклом), и при ударах
встречного ветра Лилиенталь
сейчас же продвигает ноги впе-
ред, хотя было бы интересно
дать ветру поднять себя вверх. Впрочем, при одном подобном
маневре Лилиенталь было поплатился жизнью за свое стрем-
ление одержать победу над воздухом. Встречным ветром
в 15 м он был поднят на высоту 20 м, причем крылья по-
вернулись передним концом вверх. Вот какими словами опи-
сывает он свое состояние в журнале „Luftschiffahrt": „Я имел
перед своими глазами только голубое небо с белыми обла-
ками и ждал, когда аппарат устремится вниз, и мои опыты над
парением, может быть, навсегда прекратятся". Но обстоя-
тельства сложились благополучно: после нескольких колебаний
в воздухе назад и вперед, подобно падающей пластинке,
аппарат спустился вниз, и воздухоплаватель отделался легкой
раной лица.
Это не уменьшило энергии Отто Лилиенталя. Прикрепив
на ноги резиновые подошвы и резиновые наколенники, он
смело бросается со своей горки и несется, маневрируя в воз-
Зак. 2430. Н. Е, Жуковский. Том IX.
23
354
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
духе и крича сверху наблюдающим его гостям: „О wie
schonl“
А гостей съезжается много. Когда этою осенью я имел
удовольствие воспользоваться любезным приглашением Лилиен-
таля и посетил его гору близ Берлина, то вместе со мной
и еще двумя русскими техниками на полетах присутствовали
немецкий фотограф-любитель, англичанин и американец.
Приезжают гости издалека со своими фотографическими
камерами и развозят по всему свету закрепленные на бумаге
маневры летателя, о которых он сам едва может дать отчет.
Первые три фотографии (фиг. 1, 2, 3} сделаны П. В. Пре-
ображенским во время его пребывания в Берлине этим летом.
Последняя (фиг. 4) представляет один из тех полетов, которые
удалось видеть мне.
Был довольно сильный ветер (от 7 до 9 м), и Лилиенталь
летал на своем маленьком бипланном аппарате, который со-
стоит из двух вогнутых планов, каждый в 9 м2. Этот аппарат
менее громоздкий и лучше управляется.
Возвращаясь с нами на станцию, Лилиенталь развивал свои
взгляды на летание. Он весь проникнут убеждением, что
первое решение воздухоплавательной задачи будет получено
ЛЕТАТЕЛЬНЫЙ АППАРАТ О. ЛИЛИЕНТАЛЯ
355
парением людей наподобие орлов. Для этого, по его мнению,
нужно, чтобы образовался воздухоплавательный спорт, подоб-
ный велосипедному. Нужно, чтобы при больших городах были
устроены конусообразные холмы (около 50 м) с отлогими
скатами (от 10 до 20°), на которых любители спорта могли бы
упражняться в летании. Что касается летательных аппаратов,
то они обойдутся дешевле велосипедов (около 200 марок).
Подъезжая к Берлину, я думал о том направлении, кото-
рое получает теперь разрешение задачи аэронавтики. Стоющая
громадных денег трехсотсильная машина Максима с ее могу-
чими винтовыми пропеллерами отступает перед скромным
ивовым аппаратом остроумного немецкого инженера, потому
что первая, несмотря на ее большую подъемную силу, не
имеет надежного управления, а с прибором Лилиенталя экс-
периментатор, начиная с маленьких полетов, прежде всего
научается правильному управлению своим аппаратом на воз-
духе.
Являясь в форме направляемых шаров или могучих ле-
тательных машин, аэронавтические приборы представляют
секреты правительств, потому что прежде всего преследуют
военные цели. Развиваясь же на почве мирного спорта, воз-
духоплавательная задача призывает к себе любителей всех
национальностей для своего разрешения общим трудом на
пользу всего человечества.
26 октября 1890 г. Н. Е. Жуковский сделал сообщение в Отделении
физических наук Общества любителей естествознания „Об исследованиях
Лилиенталя о летании". Работа „Летательный аппарат О. Лилиенталя"
была напечатана в журнале „Фотографическое обозрение", № 1, 1895.
Прим. ред.
23*
О ГИБЕЛИ ВОЗДУХОПЛАВАТЕЛЯ ОТТО ЛИЛИЕНТАЛЯ
(РЕЧЬ)
(1896 — 1897 и.)
Много раз с этой самой кафедры приходилось мне говорить
перед вами о значительных исследованиях Отто Лилиенталя
над способом летания против ветра наподобие парящих птиц.
Казалось, что за последнее время эти исследования зна-
чительно подвинулись вперед и манили близким разрешением
недоступной до ксих пор задачи о летании без баллонов.
Устройство двупланного летательного аппарата позволило
Лилиенталю получить большую подвижность в воздухе, а особое
приспособление в хвосте прибора дало ему возможность
с большей простотой делать повороты и описывать в воздухе
дуги круга.
И вдруг, 9 августа (н. с.) посреди блестящих эксперимен-
тов, начатых при благоприятном ветре, не превосходящем
6 mJ сек, Лилиенталь был сражен налетевшим на него вихрем
и пал, как воин на поле чести.
Уже три года совершал Лилиенталь свои полеты, которые,
начавшись в 1893 г. небольшими прыжками в воздух с башни
вблизи местечка Штеглиц (St eglitz) (около Берлина), достигли
до полетов на 200 м по горизонту и на 20 м высоты на горах
Риновер (Rhinower).
За это время он совершил множество полетов, которые
оканчивались совершенно благополучно, причем опускание
на землю, по словам Лилиенталя, не представляло ему более
труда, чем соскакивание со стула.
Упражняясь при всякой удобной погоде на конической горе
в 15 м, которую он построил около своей виллы в Лихтерфельде
(Lichterfelde) (вторая станция от Берлина по Лейпцигской
дороге), Лилиенталь достиг такого совершенства в управлении
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
357
летательным аппаратом посредством перемещения своего тела,
что крылья у него оставались всегда горизонтальными.
Только два раза полеты Лилиенталя были неудачны. Первая
неудача произошла вследствие потери аэронавтом надлежа-
щего места в аппарате, который поднялся передним краем
вверх и был заброшен на высоту около 20 м, причем аэронавт
повернулся лицом к небу. „Я имел перед своими глазами
только голубое небо с белыми облаками, — пишет Лилиенталь
в журнале „Luftschifffahrt",— и ждал, когда аппарат устре-
мится вниз, и мои опыты над парением, может быть, навсегда
прекратятся". Но судьба судила иначе: аппарат, совершив
в воздухе несколько колебательных движений наподобие падаю-
щего листа бумаги, плавно опустился, ударившись своим перед-
ним концом о рыхлую почву. При этом аэронавт поплатился
только легкой раной лица, что нисколько не уменьшило его
рвения к продолжению летательных экспериментов.
Вторая неудача была роковой. В воскресенье (9 августа)
Лилиенталь приехал на горы Риновер со своим ассистентом,
который был строителем его летательных аппаратов и всегда
помогал Лилиенталю при его полетах. Первый полет Лилиен-
таль совершил на новом аппарате, имеющем приспособле-
ние для поворотов, и выполнил этот полет вполне удачно.
Второй полет он предпринял на своем двупланном аппа-
рате с парусностью 18 -и2, имея в виду совершить возможно
продолжительное летание (полеты Лилиенталя с его искус-
ственной горы в Лихтерфельде продолжались обыкновенно
от 13 до 15 сек.). Своему ассистенту Лилиенталь передал
секундомер для измерения продолжительности полета. Этот
полет Лилиенталя, по рассказу ассистента, начался плавным
ниспадением под острым углом к горизонту. Аэронавт уже
долетел до подошвы горы, как вдруг быстро поднялся вверх
и повис в воздухе на высоте около 30 м. Подобное обстоя-
тельство не раз случалось с Лилиенталем, и потому ассистент
его не был встревожен и ожидал выполнения обыкновенного
маневра, который при этом делал Лилиенталь, т. е. переме-
щения ног и туловища вперед, причем аппарат обыкновенно
нагибался вниз и скользил по воздуху, опускаясь и двигаясь
навстречу ветру.
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Но в данном случае желаемого результата не получалось,
так что ассистент, бросив секундомер, побежал по направлению
к воздухоплавателю. Вдруг он увидал, что от совершаемого
Лилиенталем маневра летательный аппарат резко нагнулся
передним краем вниз и быстро полетел на землю вместе
с аэронавтом, наклоненным головой вперед. Не успел ассистент
добежать до места катастрофы, как аппарат уже ударился
о землю и, подпрыгнув два раза, остался неподвижным.
Вместе с ним неподвижным лежзл без чувств Отто Лилиенталь,
на первый взгляд не получивший никаких повреждений. Он
Фиг. 1.
был перенесен в ближайшую
гостиницу и через два часа
пришел в чувство.
При этом он не ощущал
боли и выразил даже желание
встать и опять продолжать опы-
ты. Но руки и ноги его были
парализованы, и он скоро впал
опять в обморок.
Ассистент оставил его на
попечение врача и отправился
в город за братом Отто Лилиенталя, Густавом. Брат застал
Отто Лилиенталя в обмороке, от которого знаменитый воз-
духоплаватель уже не очнулся. Он был привезен в Берлин,
в клинику кронпринца, в которой скончался, спустя 24 часа
после своего падения. По определению врачей смерть произо-
шла от перелома спинного хребта.
Смерть знаменитого воздухоплавателя вызвала в немецкой
и иностранной литературе многие статьи и некрологи *. Дава-
лись различные объяснения причины катастрофы, которая,
невидимому, произошла от удара ветра в аппарат сверху.
Я объясняю себе этот несчастный удар ветра так. На воз-
духоплавателя набежал вихрь (фиг. 1) с осью АВ, наклонен-
ной к горизонту. Действием этого вихря аппарат был сначала
приподнят вверх, а потом подвергся удару нисходящего
г. Наибольшего внимания заслуживают статьи Густава Лилиен-
таля (,,Fiir Alle Welt.“, Jahrg. 1897, Heft 5) и Дюбуа-Реймонда
(„Nature", vol. 54, № 1401).
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
359
потока воздуха в свою верхнюю часть. От этого получилась
траектория полета CDE.
Произошло то совпадение опасных условий полета, на
которое указывал покойный Отто Лилиенталь, когда писал:
„Только на короткое время аппарат может получить такое
положение, при котором ветер ударяет в летательную поверх-
ность сверху, тогда весь летательный аппарат устремляется
со скоростью стрелы вниз и может разбиться о землю, прежде
нежели удастся занять такое положение, при котором ветер
опять будет поддерживать аппарат".
Что подобная несчастная случайность представляет исклю-
чительный случай, доказывают многочисленные удачные полеты
Лилиенталя в продолжение трех лет.
Отто Лилиенталь родился 24 мая 1848 г. Еще в раннем
возрасте стал он интересоваться вопросами о летании. С за-
вистью заглядывался он на парящих в небе аистов. Одного
молодого аиста он держал у себя дома, чтобы посмотреть,
как птица начнет свои полеты; но когда она подросла,
то он пустил ее на свободу, не желая лишать ее наслаждения
свободного полета в воздухе.
Будучи мальчиком 13 лет, Лилиенталь устроил себе легкие
крылья, которые он привязывал к спине, и сбегал с ними
с горы. Эти первые детские попытки летания делал он вместе
с своим братом Густавом обыкновенно при лунном свете,
так как боялся насмешек товарищей.
Не обошлись без насмешек и первые серьезные исследо-
вания Отто Лилиенталя в области летания, которые он начал,
окончив курс в Berliner Gewerbe-Akademie. Один из его
профессоров таким образом отзывался о этих исследованиях:
„Не беда, если Лилиенталь на досуге занимается вычисле-
ниями по летательной технике, но пусть он никоим образом
не тратит на это дело денег". Ожидал ли профессор, что его
ученик заплатит за свое любимое дело такой дорогой ценой?
Первые серьезные исследования Лилиенталя в летательной
технике относились к определению силы удара крыльев. Он
устроил крылья клапанной системы, которые приводил в дви-
жение действием ног, и, уменьшив вес экспериментатора
и аппарата до 40 кг посредством противовеса, прикреплен-
360
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ного к веревке, перекинутой через высоко поставленный блок,
поднимался вверх, работая крыльями. При этом приходилось
развивать очень большую работу, на которую человек спосо-
бен только на короткое время. Поэтому такой способ лета-
ния был оставлен Лилиенталем, и он сосредоточил все свое
внимание на действии ветра на кривые поверхности, обращен-
ные вогнутостью вниз. Результаты своих замечательных иссле-
дований, в которых обнаружилось, что при малом угле
наклона к ветру вогнутая поверхность дает подъемную силу,
во много раз превосходящую подъемную силу плоской поверх-
ности (при наклоне 5° в шесть раз большую), Лилиенталь
напечатал в 1889 г. в сочинении „Der Vogelflug, als Grund-
lage der Fliegekunst". В конце этого сочинения Лилиенталь
излагает свои мысли о практическом применении 'найденных
им результатов к летанию человека. Но за осуществление
этих мыслей взялся он только по прошествии четырех лет.
В 1888 г. Отто Лилиенталь женился и занялся устрой-
ством машиностроительного завода. Происхождение этого
завода находится в некоторой связи с летательными иссле-
дованиями Лилиенталя. Придумывая легкие двигатели, Лилиен-
таль изобрел особую систему паровых котлов, в которых
вода поступала в нагретую спиральную трубку и выходила
из другого конца этой трубки в виде пара. Эта система безо-
пасных котлов составила главное производство его фабрики,
которая, начавшись в скромных размерах, достигла через
несколько лет блестящего состояния. Улучшение материаль-
ного положения позволило Отто Лилиенталю перейти к прак-
тическому осуществлению надуманного им способа 'летания-
При этом подготовленный им теоретический материал давал
все расчеты для устройства летательных аппаратов. И вот
в 1893 г. появилось в печати известие, что человек летает
по воздуху, что он совершил не один полет, но делает
эксперименты постоянные, повторяя их по желанию интере-
сующихся летательным делом лиц, и совершает их с вполне
безопасным спуском на землю.,
Я не стдну повторять здесь изложение ^многочисленных
экспериментов Лилиенталя, о которых было так много писано
и говорено. Но я полагаю, что воздам должное памяти покой-
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
361
ного, если заставлю пробежать перед вашими глазами несколь-
ко рисунков, представляющих его замечательный способ ле-
тания.
На фиг. 2 представлен летательный аппарат Отто Лилиен-
таля, который имеется в Московском университете. Аппарат
Фиг. 2.
этот представляет неподвижно соединенные крылья, сделан-
ные из ивовых прутьев и обтянутые голландским полотном.
Вогнутость вниз устанавливается с помощью деревянных дуг,
прикрепленных к верхней поверхности крыльев.
Фиг. 3.
На фиг. 3 можно видеть способ надевания аппарата на руки
и его нижнюю оснастку. Основу аппарата представляет иво-
вое кольцо, к которому приделан хомут для продевания рук
и укрепления ивовых прутьев, образующих каркас крыльев.
362
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
• На фиг. 4 представлен Отто Лилиенталь с надетым на руки
большим летательным аппаратом (7 м длины и 2'/г м ширины).
На этой фигуре виден способ укрепления хвоста прибора.
На фиг. 5 изображен Отто Лилиенталь на вершине его
искусственной горы в Лихтерфельде с аппаратом, расположен-
ным против ветра. Пробежав на небольшое расстояние вниз
горы, он подхватывается встречным ветром и летит по воз-
духу, медленно опускаясь вниз, как это представлено на фиг. 6.
Фиг. 4.
Фотографии (фиг. 4, 5 и 6) сделаны П. В. Преображенским
при его поездке в Берлин весной 1895 г.
Фиг. 7 показывает маневр, который делает аэронавт, что-
бы начать спуск на землю.
На фиг. 8 изображен маневр, которым поправляется подъем
правого крыла вверх. Эта фотография снята с первых поле-
тов Лилиенталя в Штеглице.
Фиг. 9 представляет один из полетов Отто Лилиенталя в
Лихтерфельде на его новом двупланном аппарате. При этих
полетах удалось присутствовать мне во время моей поездки
в Берлин осенью 1895 г. Дул сильный ветер от 8 до 9 м.
Наконец, на фиг. 10 [и 10а] изображен полет Лилиенталя на
(его двупланном аппарате с гор Риновер. Эти горы представ-
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
363
Фиг. 5.
ляют разбросанные по песчаной долине конические холмы,
достигающие высоты в 30 м. По мнению покойного аэронав-
та, они особенно удобны для его способа летания.
В одной из своих статей в жур-
нале ,,Luftschifffahrt“ Лилиенталь
живо описывает чувство страха,
которое сжало его грудь, когда
он в первый раз смотрел с одной
из вершин этих гор на расстилаю-
щуюся у его ног долину. „Мне
думалось,—пишет он,—с этой вы-
си должен ты парить над широко
расстилающейся внизу страной".
Судьба судила, чтобы полет на
Фиг. 6.
этом самом месте унес его в веч-
ность.
Вы видите, что исследования Лилиенталя по аэронавтике
дают нам совершенно выработанный способ летания, который,
364
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
развившись на почве теоретических исследований и многочис-
ленных опытов, перешел в область практического осущест-
вления.
Правда, этот способ дает нам пока движение с горы про-
тив ветра с медленным ниспадением вниз; но при нем воз-
Фиг. 7.
можно и поднятие вверх, когда ветер усиливается, возможны
повороты, а может быть, и движение по кругам наподобие
парящей птицы.
Суждено ли этому способу быть оставленным вследствие
гибели его изобретателя, или ему предстоят дальнейшее раз-
витие и усовершенствование? Я должен сознаться, что в Гер-
мании гибель Отто Лилиенталя произвела панику. Один из
наших московских любителей воздухоплавательного дела,
3. Г. Лесенко, посетил Лихтерфельде в сентябре 1896 г., ког-
да Отто Лилиенталя уже не было в живых. С помощью со-
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
365
Фиг. 9.
366
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
действия Густава Лилиенталя 3. Г. Лесенко удалось проб-
раться на знаменитую горку в сопровождении ассистента по-
койного. Горка была в полном запущении. Показывая лета-
тельные приборы (они хранились в землянке, сделанной в
верхней части горы), ассистент ни под каким видом не сог-
лашался сделать на них полет, говоря, что присутствие при
гибели отважного исследователя произвело на него столь
удручающее впечатление, что ему трудно прикасаться к аппа-
ратам.
Фиг. 10.
Но первое тяжелое впечатление пройдет, и у любителей
воздухоплавания останется в памяти, что был „летающий че-
ловек", который в продолжение трех лет совершил множество
полетов, летая при всякой благоприятной погоде. Они вспом-
нят, что полеты этого летающего человека были обдуманы
теоретически, проверены на практике и при небольшом ровном
ветре являлись вполне безопасными.
И снова неугомонная жажда победы над природой про-
снется в людях, и снова начнут совершаться эксперименты
О ГИБЕЛИ ОТТО ЛИЛИЕНТАЛЯ
367
Лилиенталя, и будет развиваться и совершенствоваться его
способ летания.
А последователи Лилиенталя в Америке: Пилчер и Херинг
(Pilcher u Hering)! Они сейчас имеют летательные аппа-
раты, представляющие видоизменение аппарата Лилиенталя,
на которых совершают самостоятельные полеты. Эти возду-
хоплаватели будут продолжать дело, начатое знаменитым
германским аэротехником •
У же после гибели Лилиенталя американец Шанют (Chanute)
поднялся на змее на высоту около 30 м и показал
этим, что для смелых исследователей воздуха гибель това-
Фиг. 10а.
рища внушает чувство благоговения к почившему, но не
чувство страха.
Не подлежит сомнению, что Лилиенталем сделаны круп-
ные приобретения для разрешения задачи о полете тел, бо-
лее тяжелых, чем воздух. Его имя занесется на страницы
истории воздухоплавания рядом с именами других мучеников
науки, пожертвовавших своей жизнью для разрешения вели-
кой воздухоплавательной задачи, и я убежден, что о Лилиен-
368
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
тале вспомнят, как об ученом, изведавшем этой дорогой це-
ной важные тайны, ревниво охраняемые безбрежным воздуш-
ным океаном.
Эта речь была произнесена Н. Е. Жуковским на годичном заседании
Общества любителей естествозиаиия в Москне 15 октября 1896 г. и напе-
чатана в журнале „Воздухоплавание и исследование атмосферы” (под ред.
М. М. Поморцева), вып. 1, 1897. Прим. ред.
1527
О ДЕЯТЕЛЬНОСТИ А. Г. СТОЛЕТОВА В ОБЩЕСТВЕ
ЛЮБИТЕЛЕЙ ЕСТЕСТВОЗНАНИЯ
Зак. 2130. Н. Е. Жуковский. Том IX.
24
А Г. СТОЛЕТОВ
(1839—1896)
О ДЕЯТЕЛЬНОСТИ А- Г. СТОЛЕТОВА В ОБЩЕСТВЕ
ЛЮБИТЕЛЕЙ ЕСТЕСТВОЗНАНИЯ
(1896—1898гг.)
Я живо вспоминаю квартиру покойного Александра Гри-
горьевича Столетова на Тверской улице, в которую я в первый
раз пришел на заседание физического кружка, устроенного
А. Г. Столетовым. Докладчиками были Умов и я. А. Г. Сто-
летов вместе с В. В. Преображенским и Фишером составляли
слушателей. Компания сидела около маленькой стенной доски.
Александр Григорьевич принимал живое участие в беседе и
подсмеивался со свойственным ему живым юмором над необы-
чайно длинным маятником, о котором говорил я.
Вскоре кружок перенес место своих собраний на квартиру
покойного в университете, а после перешел во вновь устроен-
ную физическую лабораторию. Сюда приходили Зилов, Шил-
лер, Громека, Шапошников, иногда Цингер и другие. А .Г. акку-
ратно посещал собрания и иногда сам делал доклады.
Когда в 1889 году Столетов был избран председателем
физического отделения Общества любителей естествознания,
он перешел туда, так сказать, вместе со своим войском. Все
члены кружка сделались членами физического отделения и
образовали его физико-математическую комиссию. О деятель-
ности этой комиссии свидетельствуют многочисленные рефераты.
Устройство физико-математической комиссии внесло новую
живую струю в деятельность физического отделения, подняв
его научную высоту.
Рядом с физико-математической комиссией А. Г. Столетов
развивал также деятельность прежде существовавшей комис-
сии прикладной физики, которая под его руководством сде-
лалась средоточием электротехников. Здесь показывались но-
вые аппараты и разрешались электротехнические вопросы,
24*
372
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
между прочим вопрос об освещении храма спасителя в Москве.
Под председательством А. Г. Столетова была основана
еще третья комиссия—химическая, которая развилась потом в
самостоятельное отделение.
Но особенное внимание А. Г. Столетовым было обращено
на устройство публичных заседаний. Мы помним эти блестя-
щие заседания: о кипении жидкостей, о статическом электри-
честве, о кометных хвостах, заседание в память столетия
Ньютона и т. д. Александр Григорьевич являлся душой этих
заседаний, и как он умел их устраивать! Все было обдумано,
заранее подготовлено и на своем месте. А. Г. Столетов был
строг к соучастникам заседаний, которым не раз от него
доставалось, но на него никто не обижался, потому что вся-
кий знал, что под его руководством успех был обеспечен.
Александр Григорьевич не упускал случая привлекать для
выступлений на публичных заседаниях общества приезжающих
в Москву ученых; особенно часто выступал на его публичных
заседаниях его друг А. И. Воейков.
В 1889 г. вследствие увеличившихся занятий по универ-
ситету А. Г. Столетов, несмотря на усиленные просьбы чле-
нов общества, покинул звание председателя, но продолжал
посещать заседания общества и принимать в них живое учас-
тие. Особенно любил он наши праздничные заседания, когда
в Москву съезжались иногородние ученые—его ученики: Шил-
лер, Гольдгаммер, Зилов и другие и^заводились живые споры
по различным вопросам физики.
А. Г. не был в прямом смысле основателем физического
отделения общества любителей естествознания. Это отделение
открылось до председательства Столетова. Но тот оживотво-
ряющий дух, которым живет и будет жить физическое отде-
ление, вложен в него А. Г. Столетовым, поэтому, возлагая
венок на преждевременную могилу нашего бывшего предсе-
дателя, мы написали на нем „А. Г. Столетову — созидателю
физического Отделения Общества любителей естествознания".
Эта речь была произнесена Н. Е. Жуковским 15 ноября 1896 г. в сое-
диненном заседании Общества любителей естествознания и его Отделения
физических наук, посвященном памяти А. Г. Столетова, и напечатана в «Трудах
Отделения физических Наук О. Л. Е.“ т. IX, вып. 2, 1898. Прим. ред.
БИОГРАФИЯ И УЧЕНЫЕ ТРУДЫ
ф. А. СЛУДСКОГО
ф. А. СЛУДСКИЙ.
(1841—1897)
БИОГРАФИЯ И УЧЕНЫЕ ТРУДЫ
проф. Ф. А. СЛУДСКОГО
(1898 г.)
Федор Алексеевич Слудский родился 31 января 1841 г.
в г. Ярославле. Он был сын чиновника межевого ведомства.
Матери лишился он еще в раннем возрасте. Средства семьи
Слудских были ограниченные, и воспитание даровитого маль-
чика принял на себя его дядя, который поместил его в семи-
классную ярославскую гимназию.
Учился Федор Алексеевич прекрасно, несмотря на небла-
гоприятные домашние условия, и окончил курс с золотой
медалью в пятнадцатилетием возрасте.
На скудные средства, которые мог ему уделить дядя
Ф. А. перебрался в Москву и поступил на математический
факультет Московского университета. Тяжело было переби-
ваться молодому студенту, тем более, что вскоре по посту-
плении его в университет отец его скончался, и Ф. А. прию-
тил у себя оставшуюся одинокой больную сестру. К ней
относился он с нежностью и заботливостью вплоть до ее смер-
ти, которая наступила тогда, когда счастье улыбнулось
Ф. А. и он получил штатное место.
Время университетского образования Ф. А. Слудского
совпадает со временем обновления преподавания в Москов-
ском университете. Это был канун устава 1863 г. На мате-
матическом факультете читали: Зернов, Брашман, Давидов,
Швейцер, и начинал свою профессорскую деятельность
Ф. А. Бредихин.
Главное внимание Ф. А. Слудского привлекали лекции и
практические занятия у Швейцера и лекции Давидова, у
которого он слушал теорию вероятностей и небесную ме-
ханику. Вот как писал Ф. А. Слудский о лекциях Давидова:
376
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
„покоряющие глубиной мысли и проникнутые чувством меры и
гармонии, эти неподражаемые лекции, можно сказать, очаро-
вывали аудиторию". На четвертом курсе Ф. А. Слудский
стал приготовляться под руководством М. Ф. Хандрикова к
работам по исследованию местной аттракции. С этого вре-
мени между ним и Хандриковым установилась самая тесная
дружба. По окончании в 1860 г. университетского курса со
степенью кандидата Ф. А. был оставлен при университете на
3 года по кафедре астрономии. В это время принимал он уча-
стие в исследованиях Швейцера об отклонении отвеса в Мос-
ковской губернии и производил наблюдения около Нары-Фо-
минской (по Калужской дороге) и около Подольска. По вы-
держании магистерского экзамена Ф. А. защитил в 1863 г.
диссертацию на степень магистра астрономии под названием
„Об уклонении отвесных линий и о притяжении многогранников".
Этот год совпал со введением нового университетского
устава, расширяющего число преподавателей в университете.
Ф. А. Слудскому было предложено чтение лекций по начер-
тательной геометрии и теории чисел в качестве стороннего
преподавателя, а потом с 1864 г. со званием доцента. Мне
пришлось быть в числе первых слушателей молодого доцен-
та. В 1864 г. мы слушали у него начертательную геометрию
на первом курсе. Преподаватель Ф. А. был аккуратный и*тол-
ковый. Все излагаемое им было хорошо обдумано и не ос-
тавляло у слушателя никаких сомнений. В 1865 г. мы собра-
лись в актовую залу на защиту его диссертации на степень
доктора астрономии — „Триангуляция без базиса". Тема была
оригинальная и возбудила горячие прения. В том же^году
Ф. А. Слудский защитил диссертацию по механике „О рав-
новесии и движении капельной жидкости при взаимодействии
ее частиц" и был удостоен степени доктора прикладной ма-
тематики.
В 1866 г. скончался заслуженный профессор Н. Д. Браш-
ман. Он покинул Московский университет еще в сентябре
1864 г., и чтение лекций по механике было временно разде-
лено между А. Ю. Давидовым и В. Я. Цингером. Это чтение
было предложено в 1866 г. Ф. А. Слудскому со званием
экстраординарного профессора механики.
УЧЕНЫЕ ТРУДЫ Ф. А. СЛУДСКОГО
377
Судьба сложилась так, что Ф. А. пришлось переменить
свою специальность и сосредоточиться на новом предмете.
Работа представлялась большая. Н. Д. Брашман значительно
расширил преподавание механики в Московском университете,
стремясь поднять его на высоту, которая дана была этой нау-
ке работами Лагранжа. Но многое еще в деле преподавания
не выяснилось и не уложилось в определенные рамки. Ана-
литические идеи Лагранжа давались студентам с трудом,
и между самими профессорами шли споры о некоторых
теоремах Лагранжа (например, о начале наименьшего
действия).
Ф. А. Слудский выработал стройный курс аналитической
механики, который в 1881 г. был им напечатан под названи-
ем „Курс теоретической механики". В сжатой и ясной форме
излагались в этом курсе основные идеи Лагранжа. Правда,
слушание этого курса казалось нам сначала трудным, но
впоследствии мы оценили в нем единство метода и строй-
ность и дружными аплодисментами благодарили своего про-
фессора на нашей последней лекции четвертого курса.
Экзаменатор Ф. А. Слудский был требовательный, но
непридирчивый. Ему надо было аккуратно написать все со-
держание билета до конца. Даже и на магистерских экзаме-
нах он обыкновенно предлагал вынуть билет по заранее услов-
ленной программе. Но зато экзаменующийся знал, что он из-
бавлен от всяких экзаменных случайностей и что знание его
будет оценено по всей справедливости. К своим профессор-
ским обязанностям Ф. А. относился с чрезвычайной добро-
совестностью. Всякое представленное ему сочинение он про-
читывал с полным вниманием, всякую справку, за которой
к нему обращался ученик, он старался навести, посвящая
иногда несколько часов, чтобы разыскать в своей библиотеке
нужную студенту книжку,
В 1869 г. Ф. А. Слудский был назначен ординарным про-
фессором. В период времени от 1865 г. по 1886 г. ученые
труды Ф. А. Слудского посвящаются главным образом меха-
нике,’ хотя и за это время он нередко делал экскурсии в об-
ласть высшей геодезии, возвращаясь к своей любимой теме —
о силе земного притяжения.
378
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Большинство этих трудов помещено в издании Матема-
тического общества. Ф. А. Слудский был членом-основате-
лем этого общества и одним из его усердных посетителей.
Еще в 1865 г. примкнул он к так называемому „Брашманскому
кружку" и участвовал в первом выпуске „Математического
сборника".
В 1876 г. Федор Алексеевич женился на Александре Ива-
новне Карповой. Мирно протекала его жизнь среди семьи
в кружке нескольких друзей. Ф. А. любил проводить время
дома. Известный ученый охотно занимался преподаванием
элементов математики своим маленьким детям. Гостеприимный
дом Слудских не раз собирал в своих стенах многих членов
Математического общества. Особенно дружественно относил-
ся Ф. А. к председателю этого общества, А. Ю. Давидову.
После смерти Давидова Ф. А. принял на себя заботу о
выработке правил премии, учрежденной женой А. Ю. Дави-
дова, и выполнил это дело со свойственной ему добросовест-
ностью.
В 1886 г., по выслуге 25 лет, Ф. А. Слудский вышел в
отставку и отдался своим любимым занятиям по высшей гео-
дезии. Но университета он не покинул и читал в продолже-
ние четырех лет в качестве приват-доцента специальные кур-
сы „О вращении небесных тел" и „О фигуре земли". В 1890 г.
он был вновь назначен ординарным профессором и утвержден
в звании заслуженного профессора. С этого времени он чи-
тал специальный курс по высшей геодезии, который напеча-
тал в 1894 г. под названием „Лекции по высшей геодезии".
С 1886 г. Ф. А. Слудский состоял вице-президентом Москов-
ского общества испытателей природы и в бюллетенях этого
общества напечатал большинство своих исследований по фигу-
ре Земли и местной аттракции. Не раз, впрочем, приходил
он в Математическое общество, чтобы изложить пред стары-
ми друзьями анализ своих геодезических работ, являющийся
несколько специальным для членов Общества испытателей
природы. В „Математическом сборнике" напечатано и его за-
мечательное сочинение „Общая теория фигуры Земли".
За это сочинение вместе с другими работами по геодезии
Русское географическое общество] присудило в 1890 г.
УЧЕНЫЕ ТРУДЫ Ф. А. СЛУДСКОГО
379
Ф. А. Слудскому высшую награду — константиновскую медаль.
Эта награда принесла Ф. А. большое утешение, так как он
видел в ней справедливую оценку многолетних трудов, соста-
вляющих главный интерес его научной деятельности. Он был
избран в 1891 г. в члены Географического общества и напе-
чатал в его „Известиях" несколько статей. В 1890 г. Ф. А.
был избран председателем Общества испытателей природы.
В продолжение одного года он был деканом физико-мате-
матического факультета (1892—1893) и в продолжение двух
лет (1888—1891) состоял директором Александровского ком-
мерческого училища.
В молодости Ф. А. Слудский был слабого здоровья.
М. Ф. Хандриков вспоминает, что увидел в первый раз Слудско-
го, когда он пришел осенью экзаменоваться за 2-й курс у
Ф. А. Бредихина, отложив свой весенний экзамен по болез-
ни. Потом здоровье Ф. А. окрепло. Живо рисуется в моей
памяти его обычно улыбающееся лицо. Собеседник он был
оживленный и необчайно деликатный: для него было трудно
сказать кому-либо неприятное. Но за последние два года
здоровье Ф. А. пошатнулось, у него обозначалась неизлечи-
мая болезнь, которая постепенно вела к роковому концу.
Терпеливо, безропотно сносил он тяжкий недуг, подтачиваю-
щий его жизнь. Близким его казалось, что он находится в
неведении относительно своего опасного состояния. Но так
ли это было? Может быть, деликатный по природе, Ф. А.
не хотел огорчить дорогих ему людей ропотом на свое поло-
жение.
Последний раз я видел Федора Алексеевича осенью. Он
стал мне рассказывать про письмо генерала Тилло (от 10
сентября 1897 г.), который прислал ему карты французского
ученого Муро и просил заняться определением глубины же-
лезных залежей, производящих магнитную аномалию в Кур-
ской губернии. Ф. А. оживился, излагая соображения, осно-
ванные на его последней статье по этому вопросу. Но за
оживлением вскоре последовал упадок сил. Все чаще и чаще
повторялся такой упадок сил у Ф. А., и в ночь на 13 ноября
1897 г. он тихо отошел в вечность. Похоронили его в Алек-
сеевском монастыре.
380
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Тихо протекла и вся многополезная жизнь Ф. А. Слудского.
Он не любил выставлять на вид свои заслуги, не любил го-
ворить о пользе, которую он приносил окружающим его лю-
дям. Но ученики Ф. А. Слудского высоко ценят эту пользу
и надолго сохранят в своем сердце глубокую благодарность
незабвенному учителю.
Ученые работы Ф. А. Слудского могут быть разделены
на три группы: сочинения по теоретической механике, сочи-
нения критического характера и сочинения по высшей геоде-
зии.
По теоретической механике Ф. А. Слудский написал ряд
небольших статей, относящихся к различным отделам этой
науки, преимущественно к гидростатике и гидродинамике.
Его магистерская диссертация „О равновесии и движении
жидкости при взаимодействии ее частиц" заключает в себе
развитие следствий, вытекающих из той простой мысли, что
для всякого контура, лежащего концами на свободной поверх-
ности, имеет место равенство:
J ds
Сочинение „О свободных движениях свободной капельной
жидкости" и сходная с ним по идее работа „О свободных
движениях гибкой нерастяжимой нити" относятся к изысканию
движений частиц жидкости и гибкой нити, при которых эти
частицы движутся, как свободные материальные точки. Доло-
женная на VI Съезде естествоиспытателей и врачей заметка
„Одно из обобщений теории движения твердых тел в капель-
ной жидкости" заключает в себе указание на случай вихре-
вого движения жидкости, окружающей движущееся в ней твер-
дое тело.
Являясь продолжателем работ Давидова и Брашмана по
равновесию плавающих тел, Ф. А. Слудский предлагает об-
ращение способа Давидова. По способу Давидова между пло-
скостями, отсекающими от тела данный объем, отыскивается
плоскость, перпендикулярная к прямой, соединяющей центр
УЧЕНЫЕ ТРУДЫ Ф. А. СЛУДСКОГО
381
тяжести тела и отсеченного объема; по способу Ф. А. Слуд-
ского следует между плоскостями, перпендикулярными к упо-
мянутой прямой, выбрать плоскость, отсекающую данный
объем. В двух статьях: „О числе положений равновесия пла-
вающей трехгранной призмы" и „К вопросу о числе равно-
весий плавающей трехгранной призмы" Слудский прилагает
свой метод к равновесию трехгранной призмы и пополняет
результаты, найденные Давидовым. Он находит, между про-
чим, что наибольшее число равновесий призмы с прямоуголь-
ным или тупоугольным основанием есть 6 (Давидов дает для
всякой призмы наибольшее число положений равновесия 12).
По общей механике Ф. А. Слудским были написаны три
работы. Статьи: „О начале наименьшего действия" и „За-
метка о начале наименьшего действия" входят в серию не-
скольких сочинений (Сомов, Соколов и др.), написанных в
„Математическом сборнике" по поводу письма Остроград-
ского к Брашману. Ф. А. разъясняет, что различие, представ-
ляющееся в изложении начала наименьшего действия по спо-
собам Остроградского и Лагранжа происходит оттого, что
Остроградский доказывает собственно другую теорему (тео-
рему Гамильтона), отличную от теоремы Лагранжа.
Вторая небольшая работа Ф. А. Слудского по общей ме-
ханике: „О числе условий, выражаемых неравенствами", на-
сколько помню, была вызвана запросом, сделанным покойным
А. В. Летниковым. Она представляет хорошее добавление к
теории связей системы, которое следует ввести в универси-
тетские курсы. По движению твердого тела Ф. А. Слудский
напечатал заметку. „О движении центра тяжести твердого
тела, вращающегося около неподвижной точки , в которой
показал, что центр тяжести тела может двигаться по закону
маятника только в случаях движения Лагранжа и Гесса.
Я отношу к группе работ по механике ;также и три за-
метки Ф. А. Слудского к задаче о многих телах, которые
лежат на границе теоретической механики и астрономии. Они
носят названия: „К задаче о многих телах , „О двух нера-
венствах, имеющих место при движении солнечной системы",
„О движении Земли с Луною вокруг Солнца". Указав на
один интересный частный случай движения многих тел (тела
382
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
находятся все время движения в вершинах правильного мно-
гоугольника или многогранника), автор выводит два неравен-
ства, на основании которых можно доказать, что тела сол-
нечной системы не могут рассыпаться или скучиться. Этими
вопросами Ф. А. Слудский занимался долго и с большим
интересом. В найденные им формулы подставляет он число-
вые величины, имеющие место в нашей солнечной системе
причем вычерчивает графики, дающие наибольшие возможные
расстояния планет [от Солнца. Ф. ‘А. Слудский приходит,
между прочим, к заключению, что Сатурн не мог бы упасть
на Солнце раньше Юпитера.
В своих критических работах, направленных против Кирх-
гоффа („Несколько слов о Kirchhoff’s Vorlesungen fiber ma-
thematische Physik") и Секки („Механика будущего"), Ф. А.
Слудский является охранителем механики Галилея и Ньютона.
Его математическому уму ньютонова идея силы, действую-
щей на расстоянии, представляется более определенной и яс-
ной в своей простоте, чем идея Фарадея силы, действующей
непосредственным прикосновением, которую отстаивает Секки;
также считает он невозможной точку зрения Кирхгоффа на
силу, как на условный термин, служащий для описания на-
блюдаемого движения.
Свой взгляд на значение силы для механики Ф. А. Слуд-
ский выражает следующими словами:
„Механикой называют науку о движении и силе. Понятие
о силе как причине движения физических тел, есть душа
механики; оно оживотворяет сырой научный материал, достав-
ляемый опытами [и наблюдениями, и созидает из него одно
единое целое". Другие критические работы Ф. А. Слудского
относятся к области гидродинамики.
Перехожу к работам Ф. А. Слудского по высшей геоде-
зии. Этими работами начал [он свои ученые занятия, они же
и явились венцом его научной деятельности.
Магистерская диссертация Ф. А. Слудского заключает в
себе изложение методов, определяющих уклонения отвесных
линий, и вывод формул, служащих для определения силы
притяжения тел, ограниченных многогранниками. Вскоре по
защите этой диссертации Ф. А. Слудский напечатал неболь-
УЧЕНЫЕ ТРУДЫ Ф. А. СЛУДСКОГО
38?
шую заметку („Разность долгот Москвы и Подольска")» в ко"
торой показывает, каким образом на основании известного
признака существования силовой функции можно по наблюден-
ным отклонениям отвеса вдоль меридиана сделать суждение
об отклонениях отвеса в ближних точках параллельного круга.
Докторская диссертация Ф. А. Слудского „Триангуляция
без базиса" представляет математическое развитие следую-
щей мысли, высказанной автором во вступлении к его работе:
„Если мы примем базис равным единице, то не получим
только абсолютной величины большой полуоси, не получим
величины ее, выраженной в известной линейной мере. Итак,
измерение базиса нужно исключительно для определения абсо-
лютных размеров Земли; фигура же Земли и положения
точек земной поверхности могут быть определены без базисов".
В заметке „Об определении тела, производящего данное
местное притяжение" Ф. А. Слудский указывает, каким рас-
пределением масс по поверхности Земли можно бы произве-
сти ту местную аттракцию, которую дают залегающие массы
под поверхностью Земли.
К вопросу об определении масс, производящих данную
аномалию тяжести или земного магнетизма, Ф. А. Слудский
возвращается во многих своих последующих работах.
Разрешению его посвящает он статьи: „К вопросу о мест-
ной московской аттракции", „Об исследованиях местных ано-
малий тяжести и земного магнетизма", „Об исследовании
магнитных аномалий". В первой статье автор определяет слой
малой плотности, который производит московскую аномалию
тяжести, в предположении, что слой этот имеет форму тон-
кого горизонтального цилиндра. Во второй дает он более ши-
рокую теоретическую обработку вопроса об аномалии тяжести
и к имеющимся наблюдениям Б. Я. Швейцера прибавляет
наблюдения И. А. Иверонова. Это приводит его к заключе-
нию, что глубина возмущающей разреженной массы имеет вели-
чину около 2,2 км. Последняя из упомянутых работ отно-
сится к разбору исследований Фритче о магнитных ано-
малиях.
Наиболее крупными работами Ф. А. Слудского по геоде-
зии являются: „Probleme principal de la Haute Geodesie%
384
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
„La Figure de la terre d’apres les observations du pendule" и
„Общая теория фигуры Земли".
В первой работе отыскивается та наиболее приближаю-
щаяся к Земле поверхность эллипсоида, к которой должны
быть отнесены все измерения относительно действительной
поверхности Земли и ее поверхностей уровня. Во второй и
третьей работах исследуется потенциальная функция земного
притяжения. В основу этого исследования автор кладет метод
Гаусса, изложенный в его бессмертном творении „Общая тео-
рия земного магнетизма". Развернув потенциальную функцию
в ряд по сферическим функциям, Ф. А. Слудский определяет
коэфициенты членов этого ряда на основании известной ве-
личины напряжения тяжести, получающейся из наблюдений над
качанием маятника» Таким образом является возможным постро-
ить поверхность уровня земного притяжения. Ф. А. Слудский на-
ходит, что эта поверхность для морей лежит выше теоретической
поверхности земли, а для материков по большей части ниже ее.
К работам по теории Земли относится также и прекрас-
ное сочинение Ф. А. Слудского „De la rotation de la terre
supposee fluide a son interieur", в котором он дает теорию
движения жидкого ядра Земли, если бы такое имелось, и де-
лает заключения о влиянии, которое оно бы оказывало на
движение Земли.
Судьба сложилась так, что Ф. А. Слудскому пришлось
переменить свою специальность и перейти от высшей геоде-
зии к механике. Казалось бы, что это обстоятельство могло
отвлечь его от любимого дела. Но вышло иначе. Этот пере-
ход только увеличил научные силы Ф. А. Слудского, раскрыл
ему во всей полноте великие идеи, завещанные Лагранжем,
Якоби, Гауссом. Во всеоружии вернулся “он опять к своим
любимым занятиям по высшей геодезии и написал ряд заме-
чательных исследований, доставивших ему почетную научную
известность.
УЧЕНЫЕ ТРУДЫ Ф. А. СЛУДСКОГО
385
СПИСОК СОЧИНЕНИЙ Ф. А. СЛУДСКОГО
I. Особо напечатанные
1. Об уклонении отвесных линий, 1863.
2. Триангуляция без базиса, 1865.
3. Лекции по высшей геодезии, 1894.
П. В „Московских университетских известиях" и „Ученых записках
Университета"
4. Об основных законах движения физических тел (актовая речь), 1868.
5. Курс теоретической механики, 1881.
Ш. В .Математическом сборнике"
6. О равновесии и движении жидкости при взаимодействии ее час-
тиц, 1865.
7. О начале наименьшего действия, 1866.
8. О разности долгот Москвы и Подольска, 1864.
9. Предмет теории чисел и отношение ее к другим отделам матема-
тики (вступ. лекция), 1864.
10. Заметка о числе и форме простых чисел, 1866.
11. Магнетизм и тяготение, 1868.
12. Заметка о начале наименьшего действия, 1868.
13. Очерк теории весов и взвешивания, 1869.
14. О свойствах степеней двух и трех, 1869.
15. Об определении тела, производящего данное местное притяже-
ние, 1871.
16. О свободных движениях свободной капельной жидкости, 1871.
17. О числе условий, выражаемых неравенствами, 1873.
18. О числе положений равновесия плавающей прямой трехгранной
призмы, 1875.
19. Несколько слов о Kirchhoff’s Vorlesungen fiber mathematische Phy-
sik, 1875.
20. О свободных движениях гибкой нерастяжимой нити, 1877.
21. Механика будущего, 1878.
22. К задаче о многих телах, 1879.
23. Жизнь и труды А. В. Летннкова, 1889.
24. Общая теория фигуры Земли, 1888.
25. Строение земной коры по наблюдениям над маятником, 1891.
26. Определение размеров Земли из градусных измерений по новому
способу, 1892.
27. О движении центра тяжести тяжелого твердого тела, вращающе-
гося около неподвижной точки, 1894.
Зак. 2430. Н. Е. Жуковский. Том IX.
25
386
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
IV. В „Записках С.-Петербургской академии наук“
28 Некоторые дополнения к новым исследованиям по кинетике ка-
пельной жидкости, 1879.
V/B'„Nouvelles Annales de Mathematiques"
29. Note sur le principe de la moindre action.
VI. В „Бюллетене Московского общества испытателей природы"
30. Zur Frage uber das Gleichgewicht schwimmender Korper, 1876.
31. Несколько слов о вихревых атомах В. Томсона, 1879.
32. Новые дополнения к новым исследованиям по гидрокинетике,
статья I, 1881.
33. О двух неравенствах, имеющих место прн движении солнечной
системы, 1882.
34. О движении Земли с Луной около Солнца, 1882.
35. Новые дополнения к новым исследованиям по гидрокннетнке,
статья II, 1883.
36. Probleme principal de la Haute Geodesie, 1884.
37. Essai de solution du probleme geodesique, 1884.
38. La figure de la terre d’apres les observations du pendule, 1886.
39. Note sur la rotation du soleil, 1889.
40. L’influence du frottement dans les mouvements rotatoires des corps
celestes, 1890.
41. Note sur quelques cas particuliers du probleme de plusieurs
corps, 1892.
42. L’emploi de la formule de Bouguer dans la recherche des anomalies
de la pesanteur, 1894.
43. De la rotation de la terre supposee fluide a son interieur, 1896.
tVII. В „Известиях Русского географического общества**
44. К вопросу о местной московской аттракции, 1893.
45. Об исследовании магнитных аномалий, 1894.
46. Об исследовании местных аномалий тяжести н земного магне-
тизма, 1896.
Эта работа была напечатана дважды: 1) в „Трудах Московского обще-
ства испытателен природы" (из речи и отчета Московского университета
ва 1897 г.) и 2) в „Математическом сборнике", т. XX, 1898. Прим. ред.
М. В. ОСТРОГРАДСКИИ
25*
М. В. ОСТРОГРАДСКИЙ
(1801—1861)
М. В. ОСТРОГРАДСКИИ
(РЕЧЬ)
(1901 — 1902 и.)
Московский университет поручил мне почтить память знаме-
нитого русского геометра в его родном городе и приветство-
вать Полтавский физико-математический кружок, устроивший
это славное чествование.
Сто лет назад в деревне Пашенной Кобелякского уезда
родился Михаил Васильевич Остроградский. Харьковскому
университету и его профессору Павловскому обязан он сво-
ими первыми шагами в математике, но силу свою математи-
ческого знания и глубину анализа приобрел он в Париже,
в котором в то время был расцвет математических наук. Коши,
Лаплас, Пуассон, Пуансо, Штурм и Фурье были его учите-
лями, а некоторые из них его покровителями и друзьями. Они
оценили выдающиеся способности русского молодого ученого,
напечатавшего в издании Парижской академии прекрасный
мемуар „О волнообразном движении в цилиндрическом бас-
сейне", и оказали ему нравственную и материальную поддержку..
Вернувшись на родину, Михаил Васильевич вскоре занял
в С.-Петербургской Академии наук кафедру прикладной мате-
матики и явился звеном, соединяющим тогдашний центр мате-
матического знания с нашим отечеством.
Своими глубокими научными исследованиями он пополнял
и расширял идеи французских геометров, а своими прекрас-
ными лекциями он насадил эти идеи среди русских молодых
ученых. Эта двойная заслуга Остроградского была отмечена
Араго и Пуассоном в отзыве, который они дали о лекциях по
„небесной механике", прочитанных Остроградским в С.-Петер-
бургской Академии. Они выразили удовольствие, что русский
ученый привлек многочисленных слушателей к изучению тон-
390
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ких вопросов математики, и отметили плодотворную мысль
автора лекций: „рассматривать вариации координат в выраже-
ниях момента потерянных сил в зависимости от изменения
произвольных постоянных .
Большая часть ученых работ Остроградского относится
к его любимому предмету — аналитической механике. Он писал
по разнообразным вопросам этого предмета: по теории притя-
жения, по колебанию упругого тела, по гидростатике и
гидродинамике, по общей теории удара, по моменту сил при
возможных перемещениях и т. д. Во всех его работах главное
внимание сосредоточивалось не на решении частных задач,
а на установлении общих теорий. Он с особенной любовью
занимался расширением метода Лагранжа о возможных ско-
ростях и установлением на самых общих началах теорем
динамики. Его обширная работа „Об изопериметрах" заклю-
чает в себе, как частные случаи, различные предложения
Лагранжа, Пуассона, Гамильтона и Якоби об интегрировании
уравнений динамики. С именем Остроградского всегда будет
связано распространение способа возможных перемещений на
системы с освобождающими связями и изложение теорем дина-
мики с помощью вариаций координат, происходящих от изме-
нения произвольных постоянных.
Память юношеских лет Остроградского связана с Харьков-
ским университетом, а расцвет его ученой деятельности проте-
кал в С.-Петербурге, но мне приятно здесь отметить также и его-
связь с университетом Московским. Эта связь опиралась на
дружеские отношения Михаила Васильевича к нашему извест-
ному профессору Н. Д. Брашману. Брашман был почитателем
и последователем Остроградского; он переписывался с ним
по разным вопросам механики и излагал на лекциях его
исследования. В первом томе „Математического сборника"
рядом с портретом Брашмана помещены дружеские письма
к нему Остроградского, из которых письмо о начале наимень-
шего действия послужило основанием целому ряду исследова-
ний, напечатанных по рассматриваемому вопросу в „Математи-
ческом сборнике".
Широта анализа Остроградского отразилась на работах
Ю. Давидова, удостоенных премии Демидова. Мой высоко-
М. В. ОСТРОГРАДСКИИ
391
чтимый учитель Ф. А. Слудский был носителем идей Лагранжа
и Остроградского. На лекциях он часто вспоминал Остроград-
ского и с особенным удовольствием излагал в его духе статью
об отрицательных моментах и о начале наименьшего дей-
ствия.
Развитие аналитической механики в недавно истекшем сто-
летии имело, на мой взгляд, три фазы: широкое обобщение
вопросов и их аналитическое исследование, разрешение част-
ных задач механики и их геометрическое толкование, расши-
рение методов исследования и их критика. Михаил Васильевич
явился деятелем в первой фазе развития аналитической меха-
ники. Им сделано в этой области не мало самостоятельного
и ценного. Россия может гордиться именем Остроградского,
и Москва, сердце России, хранит в стенах своего универси-
тета его высокие научные заветы.
Эта речь была произнесена Н. Е. Жуковским 12 сентября 1901 г. на
организованном Полтавским кружком любителей фнзико-математическнх наук
праздновании в Полтаве столетия дня рождения М. В. Остроградского.
Речь напечатана в брошюре П. Трипольского „Остроградский М. В.
Празднование столетня дня его рождения", Полтава 1902, стр. 28. Прим. ред.
НЕКОТОРЫЕ ЧЕРТЫ ИЗ ЖИЗНИ М. В. ОСТРОГРАДСКОГО
(1902 г.)
Совет Московского университета поручил мне почтить па-
мять знаменитого русского математика в его родном городе и
принести приветствие Полтавскому кружку любителей физико-
математических наук, устроившему чествование Остроград-
ского в день столетия от его рождения.
Чествование началось торжественным заседанием Кружка
в Полтавском здании для просветительных целей. На этом
заседании читались адреса и речи от различных учреждений
и лиц и приносились венки, предназначенные для возложения
на могилу Остроградского в деревне Пашенной, Кобеляцкого
уезда. Главным деятелем по устройству славного чествования
был председатель Полтавского кружка любителей физико-
математических наук В. С. Мачуговский.
В достопамятный день чествования Полтава была полна
воспоминаниями о своем знаменитом гражданине. Лица, близко
знавшие покойного математика, и его родственники вспоминали
перед любопытными слушателями характерные черты покой-
ного. На основании этих рассказов и биографических данных,
сообщенных на заседании, в воображении слушателей вставал
как живой наш богатырь-математик.
Михаил Васильевич был большого роста и имел громкий
голос, в особенности когда сердился. Его фигура получала
еще более грозный вид вследствие потери одного глаза. В Пол-
тавском корпусе Остроградского ожидали на экзамены с тре-
петом; ему ставили обыкновенно два стула рядом. В случае
плохих ответов и недостаточных доказательств, предложенных
в курсах, он выговаривал как ученикам, так и учителям, и
голос его гремел по коридору. Но рядом с этим он был
добр и отзывчив к чужой беде и не раз, после неудачного
НЕКОТОРЫЕ ЧЕРТЫ ИЗ ЖИЗНИ ОСТРОГРАДСКОГО
393
экзамена, исправлял дурной балл неуспевшему ученику и на-
зывал его отечески: „душечка моя11. Остроградский умел сразу
оценить понимание и способности учеников, лучших из кото-
рых он называл: „Архимедами11 и „Ньютонами11, а про плохих
говорил, что „им бы в пору не высшую математику изучать,
а пику в руках держать
Лектор он был увлекательный и блестящий; но его живая
мысль обыкновенно опережала его руку, и не раз случалось,
что он переставал писать формулы на доске, а говорил их на
словах. При этом он был чрезвычайно рассеян, и иногда губка
фигурировала в его руках вместо платка.
Фиг. 1.
Родители Остроградского, Василий Ивановичи Ирина Андре-
евна, урожденная Устимович, были зажиточные украинские
помещики. Михаил Васильевич родился в их имении „Пашенная"
в доме, изображенном на фотографии (фиг. 1).
Живой и умный мальчик был отдан в Полтавскую гимна-
зию, где прекрасно учился по математике, но по языкам
шел плохо. Вместе с этим он был по тогдашним порядкам
записан на службу и числился мелким почтамтским чиновни-
ком, причем в 14 лет получил чин коллежского регистратора-
Кто бы подумал, что свидетельство на этот незначительный
394
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
чин будет единственным документом, по которому Остро-
градский, уже прославивший свое имя в Париже, будет иметь
возможность записаться в С.-Петербурге. Сначала Михаил
Васильевич увлекался положением военного и по выходе
из гимназии стремился поступить на военную службу. Но дядя
Михаила Васильевича, Устимович, заметив выдающиеся мате-
матические способности племянника, посоветовал его отцу
определить его в университет. Остроградский был помещен
для предварительного подготовления к адъюнкту военных
наук Робушу и через год был зачислен в число студентов
Харьковского университета по физико-математическому фа-
культету. Здесь под руководством профессоров Павловского
и Осиповского развернулись блестящие математические спо-
собности нашего ученого. Он выдержал через три года
студенческий экзамен, а затем через год экзамен на
кандидата.
Познав силу своих способностей, молодой ученый потянулся
в Париж, в котором был тогда расцвет знаний математических.
Против ожидания Михаила [Васильевича, его отец благо-
склонно отнесся к затеваемой им поездке. Сохранилось письмо
брата Михаила Васильевича, Андрея Васильевича, к отцу, в
котором он пишет, что решимость Мишеля поехать в Париж
свидетельствует его силы и обеспечивает его успех.
Явившись слушателем плеяды знаменитых ученых: Лапласа,
Коши, Ампера, Фурье, Пуансо и др., Остроградский скоро
почувствовал себя не учеником, а товарищем по науке этих
знаменитых геометров. Его первая выдающаяся работа
„Memoire sur la propagation des ondes dans un bassin cylin-
drique" была доложена в Академии и напечатана в „Memoires
presentes par divers savants11 и подняла его авторитет в гла-
зах парижских ученых. Через 2 года пребывания в Париже
Остроградскому было предложено чтение математики в кол-
легиуме Генриха IV.
Вернувшись на родину и заняв место академика в Акаде-
мии наук, Остроградский сделался звеном, соединяющим наше
отечество с тогдашним центром математического мира. Сво-
ими многочисленными учеными работами он расширял и
пополнял идеи французских геометров, а своими блестящими
НЕКОТОРЫЕ ЧЕРТЫ ИЗ ЖИЗНИ ОСТРОГРАДСКОГО
395
лекциями он насаждал эти идеи среди русских молодых
ученых.
Вскоре по возвращении из-за границы, на тридцатом году
от рождения, Остроградский женился на лифляндке Марии
Васильевне Купфер — поэтессе и певице. Он имел трех детей:
сына Виктора и дочерей Марию и Ольгу.
После полных ученой и учебной деятельности зимних
месяцев Остроградский поселялся иногда на вакационное
время в своем имении „Долгое", расположенном недалеко от
„Пашенной". Остроградский любил предаваться полному по-
кою и созерцательной жизни среди широко раскинувшейся
фиг. 2.
перед его глазами украинской степи. На прилагаемой фото-
графии (фиг. 2) изображен дом Остроградского в имении
„Долгом".
Дом этот был прежде двухэтажный; теперь он принад-
лежит новым владельцам, снявшим верхний этаж.
Во время отдыха и бездействия в уме Остроградского
зарождались новые широкие идеи, и когда его математическая
мысль принимала определенное очертание, то он начинал
энергично работать и успокаивался только тогда, когда уче-
396
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ный мемуар был написан. Находясь на верху славы, почтенный
за свои ученые труды во всей Европе, Остроградский держал
себя чрезвычайно просто и не любил говорить о своих лич-
Фиг. 3.
Фиг. 4.
ных заслугах. Рядом с богатырской наружностью Остро-
градский был застенчив и способен был иногда растеряться»
Остроградский скончался в доме Гартман (теперь д. Си-
мон), изображенном на прилагаемой фотографии (фиг. 3).
НЕКОТОРЫЕ ЧЕРТЫ ИЗ ЖИЗНИ ОСТРОГРАДСКОГО
397
Михаил Васильевич был похоронен в том же имении „Па-
шенной", в котором он родился, в семейном склепе Остро-
градских (фиг. 4).
При взгляде на это мирное место успокоения, на широ-
кие поля, убегающие в бесконечную даль, невольно возни-
кает мысль о влиянии природы на человека. В математике
есть тоже своя красота, как в живописи и поэзии. Эта кра-
сота проявляется иногда в отчетливых, ярко очертанных
идеях, где на виду всякая деталь умозаключений, а иногда
поражает она нас в широких замыслах, скрывающих в себе
кое-что недосказанное, но многообещающее.
В творениях Остроградского нас привлекает общность
анализа, основная мысль, столь же широкая, как широк
простор его родных полей.
УЧЕНЫЕ ТРУДЫ М. В. ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
(1902 г.)
Первой научной работой М. В. Остроградского явилось
сочинение по гидродинамике „Memoire sur la propagation des
ondes dans un bassin cylindrique", доложенное в заседании
Парижской академии наук и напечатанное в „Memoires presen-
tes par divers savants". В этом сочинении, примыкающем по
методу исследования к обширному трактату Коши „Theorie
de la propagation des ondes", автор с искусством устанавли-
вает общие выражения для скоростей тяжелой жидкости
в цилиндрическом бассейне и указывает способ определения
этих скоростей по начальному виду свободной поверхности
и начальным значениям скоростей. В дальнейшей ученой
деятельности Остроградского работы по чистой математике
чередуются с работами по механике и математической физике;
но нельзя не заметить, что он занимался аналитической меха-
никой с особенной любовью.
Чтобы яснее изложить в коротком очерке многочисленные
исследования М. В. Остроградского по механике, мы раз-
делим их на три группы: 1) работы по началу возможных
перемещений, 2) работы по диференциальным уравнениям
механики, 3) работы по решению частных механических
задач. Являясь по складу ума склонным к широким обобще-
ниям, Остроградскнй в работах первой группы занялся рас-
ширением анализа принципа возможных перемещений Лагранжа
и начала Даламбера.
В своем мемуаре „Considerations generales sur les moments
des forces" он развивает мысль, высказанную Фурье, о рас-
пространении метода возможных перемещений на системы
с освобождающими связями, поставив условием равновесия
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
399
требование, чтобы полный момент сил был бы равен нулю
или меньше его.
Остроградский удивляется в своем мемуаре, почему Ла-
гранж в новом издании аналитической механики, когда рас-
ширение его методы на системы с освобождающими связями
было уже указано, не рассматривает случаев отрицательного
полного момента сил, несмотря на то, что данное им дока-
зательство начала возможных перемещений (с помощью по-
лиспастов) прямо примыкает к этому случаю.
Прием изложения Остроградского несколько разнится от
теперь общеупотребительных приемов. Остроградский преоб-
разует выражение полного момента сил:
Pdp -|- Q dq-\- R dr~\- ... 1)
с помощью новых переменных в
Ad’i+Bd-^+Cd^ \dL — y.dM— vdN— ..., (2)
где di, dt\, Л,... совершенно произвольны, a dL, dM, dN
произвольны по величине, но стеснены знаком. Для отрица-
тельности выражения (2) необходимо, чтобы
Adi-YBd-^Cd^-\-... =0
и чтобы X, р, v,... имели знаки, одинаковые с dL, dM, dN,...
Сравнение выражений (1) и (2) дает условие равновесия
в виде:
Р dp Q dq -f- R dr -j— ... -j— X dL p- dM -f- v dN • - • ® (3)
при условии одинаковости знаков X, р, с dL, dM, dN,...
Основное уравнение (3) Остроградский применяет к различ-
ным примерам на равновесие систем с освобождающими свя-
зями из области механики точки, гибкой нерастяжимой нити
и несжимаемой жидкости. Мемуар оканчивается рассмотрением
вопроса о движении систем с освобождающими связями, не
зависящими от времени. При этом Остроградский разъясняет,
в какой момент движения произойдет освобождение от связи.
Свои мысли о выводе уравнений динамики при связях, зави-
сящих от времени, М. В. Остроградский коротко формули-
рует в заметке „Sur le principe de vitesses virtuelles et sur la
force d’inertie", являющейся возражением на изложение начала.
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
400
Даламбера в курсе Пуассона. Трактуя о равновесии поте-
рянных сил на движущейся системе, Пуассон, по мнению
Остроградского, только затемняет дело указанием на то, что
конфигурация системы и потерянные силы в моменты времени
t и разнятся на бесконечно малые величины, вследствие
чего можно рассматривать равновесие на конфигурации си-
стемы в момент времени t и условия перемещений Вх, ьуг
iz,.- при связи
L(x, у, Z, х',..., /) = 0 (4)
.писать в виде:
dL" . dL
dL
dz
dL
dx'
= 0.
(5)
Остроградский говорит, что для вывода условия (5) со
всей строгостью „надо считать возможными перемещениями
такие, которые, комбинированные с действительными пере-
мещениями, удовлетворяют связям системы".
Подставляя в условие (3) вместо х, у, z, х'. величины:
он получает:
Но так как действительные перемещения удовлетворяют
уравнению (4) в момент t -J- dt, то
L = 0, JL = 0, d2L = 0
и <5%, ьу, bz, fix',... должны удовлетворять уравнению (5).
Заметка оканчивается возражением против фиктивности сил
инерции, которым Остроградский приписывал реальное
значение.
Свой взгляд на эти силы и на применение методы воз-
можных перемещений для вывода уравнений динамики Остро-
градский подробно развил в прежде напечатанном им большом
сочинении „Memoire sur les deplacements instantanes des
systemes assujettis a des conditions variables". Рассматривая
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
401
сначала движение одной материальной точки т, М. В. Остро-
градский рассуждает нижеуказанным образом.
Пусть (фиг. 1) материальная точка т свободна и по
инерции прошла бы во время dt с постоянной скоростью
путь АВ. От действия силы Р она пройдет путь АС, причем
сила Р направлена по ВС и равна • Сила, имеющая
ту же величину и направленная по СВ, будет силой инер-
ции.
Остроградский пишет: „Материальная точка т, подвер-
женная действию силы Р, следует по АС, так как ничто не
расстраивает этого движения: ни сила действую-
щая, ни сила инерции, ибо эти две силы взаимно /ССоУ?/
уничтожаются". Если же мы заставим нашу ма- В\ /
териальную точку при действии на нее силы Р \ /
описывать путь AD, то сила инерции будет / /
2mDB 2mDC £ \ /
—др—’> и потерянная сила——- будет стре- \ /
миться изменить путь AD и направит его по w
АС. Если путь AD описывает несвободная мате- И
риальная точка, то необходимо, чтобы потерянная фиг. 1.
сила не могла произвести ни одного из пере-
мещений DE, которые, слагаясь с действительным переме-
щением точки, дали бы возможное во время dt при имею-
щихся связях перемещение АЕ.
Такое же рассуждение, перенесенное на систему, приводит
к заключению, что потерянные силы для всех перемещений
os,,. - -, которые, слагаясь с действительными перемеще-
ниями, удовлетворяют связям системы, должны дать полный
момент равным нулю или отрицательной величине.
Так как перемещения 8s, £sj, ... в воззрении Остроград-
ского являются перемещениями, полученными точками системы
от действия потерянных сил в элемент времени dt, то на них
надо в его выводе, по моему мнению, глядеть как на малые
величины порядка dP; при этом после оказывается, что во
всех окончательных результатах эти величины входят однородно
и порядок их малости не имеет значения.
Остроградский пишет условия связей в самом общем виде,
Зак. 2430. Н. Е. Жуковский. Том IX.
26
402
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
допуская что они изменяются со временем и могут предста
влять не интегрируемую форму:
a ds cos 0 + a' ds cos 0' 4“
axds cos 0t + a/ds' cos 6/4-
4- 7 dt^O,
4- T.dt^O,
(7)
где 0, 6', • — углы, образуемые перемещениями ds, ds',...
с проходящими через каждую точку векторами а,
0/...—подобные углы с векторами alt а/,... и т. д.
В случае интегрируемых связей векторы а, а',... суть так
называемые параметры связи.
Для действительных перемещений уравнения (7) обра-
щаются в равенства, и так как они удовлетворены во всякое
время, то коэфициенты их левых частей при dt, dt2, . суть
нули. Мы получаем."
av cos 0 4“ а' v cos 6х 4“ • • •Т— 0,
a}v cos Oj 4- a(v cos 0/ 4~ • -4~ 7^ = 0,
d (v cos R ) , , d (v' cos 6' ) .
G ---77-----;--------------b
dt 1 dt
d(vcos^ , ,d(v' cos 6/) ।
G1 dt dt h
=0,
...4-^ = 0,
(9)
где
d(a cos 6 ) ,d(a' cos O') . d7
M=” dt +” —dt—+•••+*- •
M _ „ d (ci cos 0J । , d (a/ cos 0/) । d 7\
—dt—------dt— + •••+
(8)
(10)
В формулах (9) производные от 0,6'... по времени бе-
рутся в предположении, что векторы а, а',... не изменяются,
а в формулах (10) эти производные берутся в предположе-
нии, что направления скоростей v, v' ... не изменяются.
Если бы в момент времени t система освободилась от
связей, и движение ее точек происходило бы только от при-
обретенных скоростей и действия сил Р, Р', • • •, образующих
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
403
с а, а',... углы a, a', то первые части формул (9) не
были бы, вообще говоря, нулями, а имели бы величины:
— Pcos а -4- -^7 Р cos а' -I-М — — Y,
т т 1
(И)
где на основании формул (9) величины У, У1г... могут
представлены еще в
а
т
d
dt
«1
т
-J-~7 rn' (vi cos 6/) — Pcos 04
m at
таком виде:
(v cos 6 )
т (v1 cos 6j) — Pcos 04 +
1’
быть
(12)
т
a
m
Переходя затем к началу Даламбера и подставляя в фор-
мулы (7) вместо ds, dsit— ds-^8s, ds' -j-fis',.. -, и вместо t
величину t -J- dt, Остроградский находит с точностью до малых
величин второго порядка (относительно dt) условия:
a8s cos -J- a' 8s' cos o' -J-... = 8£,
OjSs cos «4 -]- a/8s'cos о/ = 8LV
(13)
где о, — углы перемещений 8s, 8s ,... с направлением
векторов a, a'; ©lf o/,.. —подобные углы с направлением
векторов an а/,..., а 8L, 8LV..- суть бесконечно малые ве-
личины, стесненные знаками:
8£:==0, SL^O,... (14)
Для всех перемещений 8s, 8sn..., согласных с условиями (14),
должно по принципу Даламбера на основании уравнения (3)
удовлетвориться равенство:
Г „ d(v cos <о) . Г г„ , d(v’ cos о/)] й .
Pcos е — т-------- 8s -р Р cos s — т 8s -{-
4-...+Х8£Н-Х18£1+... =0, (15)
26*
404
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
где е, е', .. суть углы сил Р, Р', ... с перемещениями
8S g/ ..., а “Л • • - суть углы скоростей v, v',... с этими
перемещениями. Что касается множителей X, Хи то они
все должны иметь те же знаки, как 8L, SLj,..., т. е. по на-
шему обозначению должны быть положительны.
Задавшись направлениями перемещений 8$( os', ..., при-
равниваем нулю коэфициенты при величинах этих перемен-
ных в формуле (15), подставив в них 6£, — из фор-
мул (13).
Это дает нам для п точек системы п уравнений дви-
жения:
D J(vcos<o) .
г cos е — т----------1- Ла cos ® K1al cos ... = 0,
rv z rffc/cosw') - , , , . , , , , _ (16)
P coss —m-----у------\-Ka cos®cos®j -f-... = 0,
Взяв еще две группы направлений 8s, 8s', ..., найдем все
Зп уравнений движения, из которых вместе с уравнениями (9)
определим по данным скоростям ускорения точек и все ве-
личины X, Xlt ...
Пользуясь надлежащим выбором упомянутых направлений,
Остроградский дает изящный прием определения величин
X, Хи ... и ускорений.
Предположим, что направления 3s, 8s',... совпадают
с направлением векторов а, а',... и представим уравне-
ния (16) в виде:
d (v cos 6) „ , . . , ,
т-------------Р cos ® = Ха cos (аа) \ar cos (аа,)
d (v' cos 6') , , , . 1/171
m-----~rt-----P cos® =Xa cos(a a )4~X1a/cos(a a/)-f-..., ' '
где {ааг) угол между направлениями векторов а и а1 и т. д.
Умножим уравнения (17) последовательно на —, —, t — ...
т т т" ’
26*
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
405
и сложим, обращая внимание на формулы (12). Получим пер-
вую формулу (18):
Y = Х (а, а) + Х, (a, nJ-}-...,
Л = х («1, а) + х1 (ci»ai)+--->
(18)
где
(ап, ат) = cos (сл)+cos (а/<) + . ..
Что касается второго и последующих уравнений (18), то
они получаются в предположении, что перемещения 8$, 6s',...
направляются по векторам аи а}' и т. д.
Если назовем через 6 функцию X, Xt... вида:
6 = (а, а) Ха-{-2 (a, oj ХХ1 + (а1, ат) X^-j-..,, (19)
то наши ^уравнения (18) могут быть представлены в такой
простой форме:
2У = $-, 2Г, = (20)
оХ ’ 1 оХг ' '
Мы видим теперь, что, задавшись скоростями и определив
Y. Ylf... по формулам (11) и (10), мы найдем из формул (20)
все величины X, Хи ... , а зная эти последние, определим по
формулам (17) ускорения.
Если бы случилось, что некоторые из X вышли отрица-
тельны (имели бы знак, обратный с dL) или нули, то соот-
ветственные связи не могли бы влиять в рассматриваемый
промежуток времени dt на движение системы, и их надо бы
было отбросить.
Изложенный способ, с помощью которого Остроградский
соединяет начало Даламбера с методом возможных переме-
щений, отличается полной строгостью, но надо согласиться,
что этот способ был бы излишне труден в лекционном изло-
жении. Мне не раз случалось слышать от учеников Михаила
Васильевича, как смущало их рассуждение о том, что по
Пуассону „действительные перемещения суть невозможные**.
Я всегда думал, что Остроградский, так же как и Пуассон,
против которого он возражает, затрудняют дело, рассматривая
равновесие потерянных сил на движущейся системе, так как
406
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
через это в исследование перемещений
сится идея о времени, в которое эти
точек системы вно'
перемещения совер
шаются. Изложение
становится
много проще и нагляднее,
когда будем рассуждать нижеследующим
способом. Усмотрев
на фиг. 1,
что направленная по CD сила
2тСР
df2
есть
сила
реакции связей на точку т, мы приходим к заключению, что
каждая из потерянных сил равна и противоположна соответ-
ственной силе реакции связей. Далее надо выставлять на вид,
что силы реакции связей, развившиеся при какой-нибудь
конфигурации системы (при равновесии или при движении),
будучи приложены к точкам системы в обратных направле-
ниях, имеют упомянутую конфигурацию положением равнове-
сия. В силу этого положения применение метода Лагранжа
к началу Даламбера представляет простое изучение равно-
весия системы под действием потерянных сил в конфигура-
ции, соответствующей рассматриваемому моменту времени.
При этом выясняется, что найденные в рассматриваемой за-
даче о равновесии силы натяжений, давлений и т. д. в раз-
личных частях системы будут действительные силы натяже-
ний и давлений при движении системы в рассматриваемый
момент времени t, и что силы инерции суть только образы,
облегчающие наши рассуждения.
Вышеизложенные исследования по началу Даламбера
Остроградский развил еще в статье, напечатанной им в „Comptes
Rendus" (t. XLIV) под заглавием „Sur 1’usage des polynomes
lineaires en dynamique".
Последней работой M. В. Остроградского по расширению
метода Лагранжа является сочинение об ударе неупругих
систем.
В своей „Аналитической механике" Лагранж затронул
почти все вопросы теоретической механики, но вопрос
о явлении удара остался в стороне его анализа.
Распространение метода возможных перемещений на
исследование этого явления принадлежит Остроградскому,
который в сочинении „Memoire sur la theorie generale de la
percussion" исследует удар систем в предположении, что
возникшие в момент удара связи сохраняются и после удара.
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
407
Свой взгляд на весьма быстрое введение в систему новых
связей Остроградский характеризует нижеследующим обра-
зом. Предположив, что на систему сразу наложено условие,
не допускающее уменьшения количества L, несмотря на то,
что скорости точек системы дают dL < 0, он пишет: „Мы
должны заключить, что физические условия, с помощью ко-
торых мы будем стремиться сразу поставить препятствие
уменьшению количества L, невозможны. Это количество бу-
дет уменьшаться до тех пор, пока скорости, изменяясь чрез-
вычайно быстро, удовлетворят условию dL == 0. Это произой-
дет в конце весьма короткого промежутка времени; но в этот
промежуток, как бы он ни был мал, изменение скоростей,
вообще весьма быстрое, будет удовлетворять условию непре-
рывности".
Таким образом явление удара, с точки зрения Остроград-
ского, заключается в введении в систему в момент начала
удара условий, которые, будучи в этот момент согласны со
скоростями точек системы, чрезвычайно быстро изменяются
со временем и в весьма короткий промежуток времени ; про-
изводят конечное изменение скоростей точек системы.
В основу своего анализа М. В. Остроградский берет не
формулу (15), а легко получаемое из нее соотношение:
d (V s \ s ।
I mv cos (00е j — 0 —2--'
+ £Pcos <bos X6L 4“ AjSLj Ц- .. •, (21)
в котором <p, <?' , • • имеют те же значения как е, е', — ,
а ое, ое', ... заменяют os, os', ... и представляют бесконечно
малые векторы, соединяющие одновременные положения то-
чек системы в действительном и в некотором бесконечно
близком воображаемом движении (причем ое, ое', ... — совер-
шенно произвольные функции времени).
Обнаружив, что член, представляющий вариацию живой
силы, за все время удара 6 остается весьма малой величиной
сравнительно с другими членами и положив
Р cos <?ое = mu cos о de j ,
408
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
где и и',. скорости точек системы в предположении, 'что
все эти точки освободились в начальный момент удара от
связей и движутся пОд действием сил Р, Р1г. •., а °, а',... —
углы этих скоростей с векторами Йе, Йе', ... , Остроградский
заменяет уравнение (21) нижеследующим:
mv cos Ш ) = di S ти c°s ° йе j XfiL -f- XjfiLj + ...
Потом он умножает обе части этого уравнения на dt и
совершает интегрирование между пределами t и /Ц-Е, причем
6L, йЛр... как величины, очень мало изменяющиеся за время
удара, выносятся за знаки интеграции.
В результате получается основное уравнение удара:
mv cos йе = cos о 8е v6 £ -|- vx8£j (22)
Если между силами Р, Ри •.. нет мгновенных сил, то все
скорости и, и', ... ничтожно мало отличаются от скоростей
в начальный момент удара, и формула (22) выражает, что
потерянные количества движения уравновешиваются на изме-
ненных связях системы.
С помощью формулы (22) Остроградский получает ряд
интересных соотношений и теорем.
Известная теорема Карно о потерянной живой силе полу-
чилась у Остроградского заменой в формуле (22) векторов
ое, cs'f ... векторами vdt, v'dt, ..., где v, v',...—скорости
точек системы в конце удара. Так как эти скорости по усло-
вию удовлетворяют уравнениям: 8£ = 0, 6£j = 0..., то
cos (и, v),
откуда следует, что
-^-^пги2—= lu2 + u2 — 2uvcos(u, ®)].
Переходим к рассмотрению сочинений Остроградского,
посвященных диференциальным уравнениям динамики. Здесь
прежде всего следует отметить оригинальную мысль М. В. Остро-
градского рассматривать возможные перемещения при дви-
жущейся системе, как происходящие от перехода данного
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
409
движения к другому весьма близкому движению той же си-
стемы, происходящему от изменения постоянных в интегралах
уравнений динамики. Эту мысль Остроградский изложил сна-
чала в своей небольшой статье „Note sur la variation des
constantes arbitraires dans les problemes de mecanique" и потом
положил в основание своего курса „Cours de mecanique celeste",
изданного Янушевским и заслужившего похвальный отзыв
от Араго и Пуассона.
Представив основное уравнение динамики в виде:
П д/ дТ " I дТ - I дТ „ . \ ~
0 “ л аг °х+°s + агог+• • •) -“ ?+‘ v-
Остроградский рассматривает два ряда изменений произволь-
ных постоянных, вызывающие изменения координат: 8х, %у, 8z
и Дх, Ду, Дг, Д%1,...
Вследствие этого он присоединяет к вышена писанному
уравнению еще такое:
и получает из них:
Уравнение (23), обнаруживающее постоянство во времени
выражения, стоящего в скобках, и служит исходным пунктом
рассуждений Остроградского. Он выводит из него основные
теоремы динамики и прилагает его к решению некоторых
вопросов небесной механики о пертурбационной функции.
Вообще М. В. Остроградский приписывал большое значение
рассмотрению полных диференциалов в динамических исследо-
ваниях. В своем письме к Н. Д. Брашману, помещенном в 1-м
томе „Математического сборника", сн указывает на следствие,
вытекающее из вышеупомянутой (формулы (21), в следующих
словах: „Момент движущих сил вместе с моментом сил свя-
зей и вариацией живой силы, выраженные в каких-нибудь
410
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
координатах, представляют полный диференциал. Это самый
простой и самый общий результат, который могут дать урав-
нения динамики. Условие полного диференциала не есть таким
образом специальный случай гидродинамики, а является особен-
ностью всей науки о движении”.
Эту особенность Остроградский положил в основание своего
формулирования начала наименьшего действия, которое в его
изложении представляет собственно начало, указанное несколько
прежде Гамильтоном. Остроградский развил свои идеи об этом
начале и дал обстоятельную обработку вопросов об изопери-
метрах, частным случаем которых являются вопросы динамики,
в своем обширном сочинении „Equations differentielles dans
le probleme des isoperimetres".
Я не стану здесь разбирать это сочинение, так как его
изложение вошло в статью Е. Ф. Сабинина, а перейду к дру-
гой работе М. В. Остроградского по уравнениям динамики
„Sur les integrates des equations generales de la dynamique".
В этом сочинении M. В. Остроградский дает каноническую
форму уравнений динамики и обнаруживает теоремы о харак-
теристической функции, принимая связи системы зависящими
от времени, что тогда являлось существенным добавлением
к напечатанным исследованиям Якоби.
Отделив в выражении V, представляющем сумму живой
силы и силовой функции, члены, не зависящие от скоростей
координатных параметров, члены первого и члены второго
измерения от этих скоростей, он пишет:
1/=г0+к+г2,
= К 4-2Г2 = 14- г0 = И+е, (24)
где
0=14—14 и Pi=^.
Формула (24) дает нам соотношение:
2E<'8p<“S^8'.+8e.
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
411
приводящее к уравнениям динамики в канонической форме:
Что касается характеристической функции, то, представив
ее в форме:
t
S=J Vdt
О
и заметив, что при этом
as
Pi~ ’
Остроградский приходит к уравнению с частными производ-
ными:
л с
^ + 6 = 0 (26)
и обнаруживает предложение Якоби, что полный интеграл
этого уравнения дает все искомые интегралы уравнений дина-
мики в виде:
0.S _ о
Л, Pi’ да, Н’
По своей ясности рассматриваемый мемуар Остроградского
являлся по тогдашнему времени весьма ценным изложением
теории интегрирования уравнений динамики и может с успе-
хом служить для лекционных целей и в настоящее время.
В третью группу отнесены мной многочисленные сочине-
ния М. В. Остроградского по гидростатике, гидродинамике,
теории притяжения, теории упругости и баллистике. Надо,
впрочем, отметить, что и при решении частных задач меха-
ники Остроградский всегда останавливался на самом общем
способе исследования. Свои взгляды на равновесие жидкостей
М. В. Остроградский изложил в мемуаре „Sur un cas singulier
de I’equilibre de fluides incompressibles", в котором он весьма
удачно пользуется данной им обобщенной теоремой Грина
для того, чтобы преобразовывать различные поверхностные
интегралы, встречающиеся в гидростатических задачах, в объ-
емные.
412
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Этот способ изложения гидростатики был введен в курс
Н. Д. Брашмана и до сих пор употребляется при лекционном
изложении в нашем университете. Рассматриваемая статья
Остроградского оканчивается заметкой о движении сфериче-
ского слоя жидкости под действием притягивающего центра,
помещенного в центре слоя, которое М. В. Остроградский
считает невозможным; здесь, повидимому, заключается какой-то
недосмотр.
Небольшая статья Остроградского „Sur le mouvement
des fluides" посвящается рассмотрению поверхностных условий
движущейся жидкости в связи с условием неразрывности.
О статье по волнам мы уже упомянули; присоединим еще
к гидродинамическим работам Остроградского статью, относя-
щуюся собственно к математической физике и трактующую
о распространении теплоты в текущей жидкости. Статья носит
название „Sur I’equation relative a la propagation de la chaleur
dans i’interieur des liquides". Остроградский был наведен Фурье
на упомянутое исследование, который указывал ему, что эта
задача, достойная внимания и трудная' То решение, которое
было дано по этому вопросу Пуассоном, Остроградский
считал недостаточным, так как Пуассон не принимает во вни-
мание [расширение жидкости, с которым следует считаться,
когда речь идет о неравномерно нагретой движущейся массе.
Поставив задачу в самой общей форме и воспользовавшись
своей теоремой о преобразовании поверхностного интеграла
в объемный, Остроградский нашел для основного уравнения
распространения тепла в текущей жидкости следующий вид:
d(kV) d(k()u) . d(kfty) . d(k№) _
,dt dx * dy dz ~
(27)
dx dy dz
где 6— температура, k — теплоемкость и К— коэфициент тепло-
проводности. В частности, когда теплоемкость постоянна
и жидкость несжимаема, тогда формула (27) обращается в фор-
мулу Пуасссна.
ТРУДЫ ОСТРОГРАДСКОГО ПО МЕХАНИКЕ
413
По теории упругости Остроградским была написана большая
работа „Memoire sur [’integration des equations a differences
partielles relatives aux petites vibrations des corps elastiques",
в которой он дает общие выражения для упругих смещений
колеблящегося тела, удовлетворяющие уравнениям упругости
в форме Пуассона. Задача решается с помощью многократных
интегралов и теоремы Фурье в самом общем виде, т. е. при
произвольно заданных начальных данных, но вопрос о поверх-
ностных условиях автором оставляется в стороне.
Теории притяжения посвящена одна из первых работ Остро-
градского „Note sur une integrale qui se rencontre dans le
calcule de 1’attraction des spheroides". Здесь M. В. Остроград-
ский дает вывод теоремы Пуассона о равенстве второго дифе-
ренциального параметра — для точек, лежащих внутри
тела, и трактует также вопрос о том, что будет, если точка
лежит на поверхности. Он пользуется методом ,Коши иссле-
дования многократных интегралов, в которых подинтегральная
функция обращается в бесконечность, и указывает при этом,
что при выводе теоремы он не знал, каким способом она
была доказана Пуассоном.
Я закончу изложение сочинений по механике нашего зна-
менитого математика указанием на его работы по баллистике.
В дни своей ранней юности Остроградский увлекался воен-
ным делом и желал посвятить себя военной службе. Судьба
сложилась так, что он сделался выдающимся математиком;
но в этом положении он принес русскому военному делу
едва ли меньшую пользу своей педагогической деятельностью
в военноучебных заведениях и своими математическими иссле-
дованиями по баллистике. Им было написано три мемуара
в этой области: „Note sur le mouvement des projectiles sph6ri-
ques dans un milieu resistant*1, „Memoire sur le mouvement des
projectiles spheriques dans Fair*1, и „Tables pour faciliter le calcul
de la trajectoire que decrit un mobile dans un milieu resistant".
В двух первых работах Остроградский занимается реше-
нием задачи о движении центра тяжести и о вращении сфери-
ческого снаряда, геометрический центр которого не совпа-
дает с центром тяжести. М. В. дает диференциальные урав-
нения задачи, в которых фигурируют коэфициенты, зависящие
414
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
от сопротивления воздуха, долженствующие, по мнению автора,
быть определенными из артиллерийских опытов. При эксцен-
тричности снаряда, равной нулю, формулы Остроградского
переходят в формулы, данные для этого более простого
случая Пуассоном.
Третье сочинение заключает в себе вычисление таблиц
функции
Ф(0) = 2
J Sin do
которая играет весьма важную роль в баллистике.
Заканчивая этим беглый очерк работ Остроградского по
механике, мы не можем не указать здесь, что эти работы
захватывают собой почти всю область вопросов, на разреше-
нии которых сосредоточивались в то время мысли выдающихся
европейских геометров.
Остроградский, так же как они, чувствовал, какие вопросы
назрели к решению, и разрабатывал их самостоятельно, иногда
отставая от своих европейских товарищей, иногда опережая их.
В тот период расцвета прикладных наук, когда прогресс мате-
матических знаний дал сразу возможность разрешить целый
ряд существенных вопросов естествознания, мы часто встре-
чаемся с однородными работами выдающихся мыслителей.
Нам, русским, отрадно отметить теперь, что в это время
деятельности Фурье, Коши, Пуассона, Якоби и Гаусса мы не
остались в стороне, так как имели Остроградского.
Работы „Некоторые черты из жизни М. В. Остроградского" и „Ученые
труды М. В. Остроградского по механике" были доложены Н. Е. Жуковским
16 октября 1901 г. в заседании Московского математического общества,
посвященном памяти М. В. Остроградского. Работы были напечатаны
в „Математическом сборнике", т. XXII, 1902. Прим. ред.
О РАБОТАХ Д. И. МЕНДЕЛЕЕВА ПО СОПРОТИ-
ВЛЕНИЮ ЖИДКОСТЕЙ И ВОЗДУХОПЛАВАНИЮ
Д. И. МЕНДЕЛЕЕВ
(1834-1897)
О РАБОТАХ Д. И. МЕНДЕЛЕЕВА ПО СОПРОТИВЛЕНИЮ
ЖИДКОСТЕЙ и воздухоплаванию
(1907-1909 п.)
Знаменитый химик, память которого мы ныне чествуем,
не удовлетворялся исследованием вопросов ближайшей спе-
циальности. Он с охотой и успехом занимался во многих
.других областях физических и технических знаний. Русская
литература обязана ему капитальной монографией по сопро-
тивлению жидкостей, которая и теперь может служить основ-
ным руководством для лиц, занимающихся кораблестроением,
воздухоплаванием или баллистикой. „Вопрос о сопротивлении
среды, — пишет он в этой книге, — занял меня сперва только
по, отношению к воздухоплаванию. Приступая к изучению
сопротивления, я, признаться, не ожидал найти такие недо-
статки в теории и опытах, до него касающихся, какие оказа-
лись в действительности". Дмитрий Иванович отмечает эти
недостатки, разбирая ударную теорию Ньютона и Пуассона,
струйную теорию Д. Бернулли и Эйлера, теорию Нордмарка,
волновую теорию Скотт-Роселя и фрикционную Ранкина. Он
приходит к заключению, что имеющихся правильно обста-
вленных наблюдений еще недостаточно для построения рацио-
нальной теории сопротивления жидкостей. „Нужен настоятель-
но, — пишет он, — и будет решать дело разумный и твердый
опыт, а молодое и неопытное умственное построение пойдет
на поводу в ту и другую сторону, пока приученное опытом
.к верной дороге само не станет везти за собой или на себе
всю сущность опытного знания, как обученная на поводу ло-
шадь повезет, куда следует". С этой мыслью Дмитрия Ива-
новича нельзя не согласиться, так как, независимо от труд-
ности интегрирования уравнений гидродинамики с соблюде-
нием тех разнообразных граничных условий, которые пред-
авая. 2430. Н. Е. Жуковский. Том IX.
27
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
ставляет практика, мы не можем без опыта сделать выбора
между различными теоретически возможными течениями, ко-
торые могут образоваться около рассматриваемого тела. Эти
течения могут дать поверхности раздела вследствие образова-
ния застоя жидкости перед носом и кормой, могут дать струн,
сходящие с тела в известных местах, могут образовать вслед-
ствие соприкосновения с телом зарождающиеся вихревые
кольца и т. д. Только прямой и твердый опыт укажет теоре-
тику, с какой задачей гидродинамики он имел дело и в каком
смысле должен он рассматривать явление.
Все разнообразные наблюдения над сопротивлением жид-
костей классифицируются в книге Дмитрия Ивановича по ме-
тодам.
1. Падение тел. Здесь излагаются: наблюдения Галилея»
Торичелли и Мариотта над падением шаров в воздухе, иссле-
дования Ньютона над падением шаров в воздухе и в воде.
Исследования Бенценберга и Рейха над падением шаров в
воздухе с большой высоты, исследования шведских ученых
над падением шаров в воде и собственные исследования
автора над падением шаров в воде, которые он производил
в лаборатории Петербургского университета в сотрудничестве
с М. Л. Гроссман. Числовые результаты всех этих исследований
подвергаются автором математическому анализу, причем
определяется коэфициент к в основной формуле:
R = kDMV\
где R— сила сопротивления, D — плотность жидкости, М—
площадь миделевого сечения и V — скорость. За единицы
меры Дмитрий Иванович везде берет килограмм, метр, секунду
и находит, что для воздуха при скоростях до 30 м сле-
дует в среднем принять
к = 0,027,
а для воды
к = 0,025.
Эта близость коэфициентов при отношении плотностей около
770 оправдывает предположение Ньютона о пропорциональ-
ности силы сопротивления плотности. Заметим здесь, что ив
опытов над шарами-зондами в Аэродинамическом институте
РАБОТЫ МЕНДЕЛЕЕВА ПО ВОЗДУХОПЛАВАНИЮ
419
в Кучине В. В. Кузнецов получает для шаров диаметром 0,8 м
при скорости 3,4 м величину
к = 0,024,
очень близкую к коэфициенту воды. Было бы важно продол-
жать наблюдения, намеченные Кузнецовым, пользуясь при
этом прекрасным расчетом с помощью таблиц ординат кадо-
иды, указанным в книге Менделеева. Собственные опыты
Дмитрия Ивановича над падением шаров в воде позволяли,
изменяя вес шаров, получать при том же радиусе разнообраз-
ные предельные скорости. Из этих опытов получается
к = 0,025. Но цена опытов Менделеева заключается главным
образом в том, что из них ярко выступает закон квадратов
для малых скоростей (от 0,11 до 0,28 м).
На фиг. 1 верхняя линия, близкая к пря-
мой, дает отношение силы р сопроти-
вления к квадрату предельной скоро-
сти с2, а нижняя дает отношение 4р
к скорости.
2. Качание тел. Сюда относятся
опыты Дюбуа над качанием маятников
в воде и Бесселя над их качанием в воз-
духе, опыты Кулона над качанием горизонтальных дисков, пове-
шенных на нити в воде, а равно и теоретические исследования
Пуассона и Стокса. Дмитрий Иванович указывает, что этот
метод с помощью наблюдения времени качания устанавливает
принцип приращенной массы тела в воде, но по отношению
определения величины сопротивления имеет более научный, чем
практический характер. Сам он весьма интересовался этим
методом и видел в точном определении сопротивления воз-
духа качающимся телам средство к наиболее точному опре-
делению абсолютного напряжения тяжести. Члены Съезда,
посетившие Палату мер и весов, имели удовольствие видеть
совершенно законченную установку для определения напря-
жения тяжести с помощью весьма длинных маятников. Над
передним зданием Палаты высится башня, в трубе которой
на проволоке в 22 м длиной вешают шары различных плот-
ностей и диаметров. В основу наблюдений Дмитрий Иванович
420
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
предлагал взять золотой шар весом в 50 кг и диаметром
в 170 мм и сравнивать потухание его амплитуд с потуха-
нием амплитуд равнообъемных шаров из чугуна и из особого
легкого сплава канифоли н воска, которому соответствует
удельный вес 1,05. Таким образом предполагалось выяснить
поправку маятника „на пустоту". На фиг. 2 и 3 даны фото-
графии верхней и нижней частей упомянутой трубы. На фиг. 2
видны подвешенный шар и приспособление под ним, чтобы
Фиг. 2.
Фиг. 3.
наблюдать, не стесняясь явлением Фуко; на фиг. 3 видно
окно, чрез которое подвешивается нить.
3. Полет артиллерийских снарядов дает возможность иссле-
довать сопротивление при скоростях, превышающих 100 м.
Ввиду обстоятельного исследования этого вопроса в курсах
баллистики Д. И. Менделеев его не разбирает. В начале своей
книги, рассуждая о влиянии кормы, Д. И. Менделеев указы-
вает, что коэфициент сопротивления после известной вели-
чины скорости должен возрастать. Здесь приведены по Маев-
скому кривые изменения коэфициента k при скорости, изме-
няющейся от 100 до 600 м (фиг. 4). Мы видим, что между
300 и 350 м при скорости, приближающейся к скорости
звука, происходит быстрое возрастание коэфициента, при ско-
ростях же небольших и очень больших коэфициент мало
изменяется. В недавно появившемся сочинении Н. А. Моро-
зова дана кривая коэфициентов k, указывающая на нх по-
РАБОТЫ МЕНДЕЛЕЕВА ПО ВОЗДУХОПЛАВАНИЮ
421
нижение в пределах от 3 до 15 м, что согласно с наблю-
дениями, производящимися теперь в Московском университете.
4. Наблюдения над пароходами и другими судами.
Д. И. Менделеев высказывается против суммарного определения
сопротивлений судов на основании работы машины, так как при
этом фигурирует много неизвестных факторов. Он предлагает
пользоваться судами для отдельных приспособленных наблю-
дений или для проверки уже установленных законов из пря-
мых опытов. Проект одного нз наблюдений, предлагаемых
Д. И. Менделеевым, дается на фиг. 5. Прибавим к этому, что
в настоящее время при все более совершенствующихся на-
правляемых аэростатах желательно бы было, чтобы данные
наблюдений над ними получались согласно указанию Д. И. Мен-
делеева. Между тем до сих пор производят по большей части
суммарное наблюдение, в котором неизвестно, получился ли
успех от хорошего винта или от хорошей формы аэростата.
5. Способ круговращения. Борда употребил этот способ для
определения сопротивлений на пластинку в воздухе и в воде.
Потом им пользовались многие исследователи: Ванис, Тибо и
Хаген, Рыкачев, Марей, Лилиенталь и Ланглей. Д. И. Мен-
делеев указывает, что этот способ не совсем точен и дает
больший коэфициент сопротивления вследствие эффекта цен-
тробежной силы. Впоследствии из наблюдений Ренара и Лан-
глея выяснилось, что здесь эффект центробежной силы раз-
вивает радиальный поток, который, производя скользящее дви-
жение воздуха по пластинке, увеличивает нормальное давление.
422
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
6. Трубка Пито. Менделеев с особенным вниманием оста-
навливается на исследованиях Дюбуа н Дюшмена, которые
определяли давление на переднюю и „подавление" на заднюю
поверхность тела в потоке жидкости с помощью трубок Пито.
Наблюдения производились при движении тел в спокойной
воде и при ударе воды о неподвижные тела. Для случая
квадратной пластинки получалось при движении пластинки
£ = 0,074 и при движении воды £ = 0,094. Это обстоятельство
дает известный парадокс Дюбуа. Д. И. Менделеев очень за-
интересовался этим явлением и высказал пожелания, чтобы
оно было проверено не только для воды, но и для воздуха.
Многочисленные наблюдения над сопротивлением квадратной
и круглой пластинки, движущейся в воздухе, приводят теперь
к величине £Д = 0,085. Если принять для среднего атмосфер-
ного давления н температуры 15° величину А = 1,2, то надо
положить, что £==0,071. Это дает величину, близкую к той,
которая получается для движения пластинки в спокойной воде-
Но опытов с ударом воздуха на пластинку в галлерее с хо-
рошим однородным потоком воздуха, насколько мне известно,
до сих пор все еще нет, и русским ученым следовало бы вы-
полнить этот завет покойного Дмитрия Ивановича.
7. Способ тяги. Этот способ, начиная с классических наблю-
дений французских академиков Даламбера, Кондорсе н Боссю,
опровергнувших ньютоново положение о пропорциональности
сопротивления кубу синусов, сделался излюбленным для опре-
деления сопротивления воды движущимся телам. С помощью
его были произведены Бофуа обширные опыты над телами
разнообразных форм. Этот способ усовершенствовался через
замену канатной тяги тягой движущейся над бассейном те-
лежки и послужил основанием устройства опытных бассейнов
для исследования моделей судов. В таком бассейне были
произведены Фроудом обширные опыты над сопротивлением
воды доскам, движущимся вдоль своей длины. Здесь сопро-
тивление развивается от трения воды. Оно, как показали на-
блюдения, тоже пропорционально второй степени скорости и
только для весьма гладкой поверхности парафина н колен-
кора соответствует степени п — 1,95 и п = 1,93. Менделеев
полагает, что в этих случаях степень п является заменой
РАБОТЫ МЕНДЕЛЕЕВА ПО ВОЗДУХОПЛАВАНИЮ
423
закона av-\-bv\ который указывает на участие в явлении
трения о стенки и вязкости жидкости. Приняв закон квадра-
тов скорости и положив для силы трения:
F=k^SV%
находим из опытов над потерей напора в трубах, как это
делает Ранкин kt = 0,00018, а из опытов Фроуда kx = 0,00016.
Прибавим сюда, что по недавним опытам Кановетти для воз-
духа &!= 0,0002. Таким образом оказывается, что коэфициент
поверхностного трения’тоже пропорционален плотности жид-
Фиг. 6.
кости. Мы получаем здесь полное подтверждение мысли, вы-
сказанной в начале рассматриваемой нами книги Менделеева.
„Станем ли мы,—пишет он, — производить сопротивление от
инерции жидкости, как это делает Ньютон и его последова-
тели, или будем его считать происходящим преимущественно
от трения, как это признает Ранкин и его последователи, во
всяком случае следует допустить тесную связь между основ-
ными причинами сопротивления и плотностью жидкости, по-
тому что таков результат опытных исследований". 27 лет
прошло после выхода книги Д. И. Менделеева. За это время
появились многочисленные опытные исследования над сопро-
тивлением жидкостей. Появились работы Лилиенталя над со-
противлением вогнутых пластинок, поставленных под различ-
ными углами к ветру. Были произведены обширные работы
424
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
на коловратных машинах: Ланглеем над сопротивлением пла-
стинок и Ренаром над сопротивлением тел различных форм,
причем для хороших форм коэфициент сопротивления пони-
жается до к — 0,0023.
Были в больших размерах произведены исследования со-
противления воздуха методом падения тел: Кальете и Коллардо
и недавно Эйфель воспользовались для этого башней Эйфеля;
Кановетти наблюдал движение крупных моделей по наклонным
проволокам длиной в несколько сот метров. Сделан ряд иссле-
дований над винтовыми пропеллерами Ренаном, Вельнером,
Максимом, Патриком и др. Все это дало ту сумму опытных
данных, которой ждал покойный русский ученый, говоря в
своей книге: „Есть .уверенность в том, что когда-нибудь до-
стигнут полной победы над воздухом, станут управлять поле-
том. Только для этого, очевидно, необходимо точно знать
сопротивление воздуха, хотя бы настолько, чтобы им вос-
пользоваться для первых, пока грубых попыток борьбы с
атмосферой". Не оправдывается ли эта уверенность в совер-
шенных успехах направляемых шаров Цеппелина, Персеваля
Лебоди и Дейча? Не началась ли борьба с атмосферой в.
удачных полетах летательных машин (фиг. 6): братьев Райт,.
Сантос-Дюмона, Блерио и Фармана?
Работа была доложена Н. Е. Жуковским 23 декабря 1907 г. на Перво»
Менделеевском съезде по общей и прикладной химии в Петербурге в 1907 г.
и напечатана в Трудах втого съезда, .Журнал Физико-химического об-
щества", т. XVI, 1909. Прим. ред.
О РАБОТАХ В. Я. ЦИНГЕРА ПО МЕХАНИКЕ
в. Я. ЦИНГЕР
(1836-1907)
О РАБОТАХ В. Я. ЦИНГЕРА ПО МЕХАНИКЕ
(1908 г.)
Сегодня Московское математическое общество чествует
память своего члена-основателя и бывшего президента
общества В. Я. Цингера. Многочисленные ученики покой-
ного собрались сегодня вспомнить дорогого учителя. С этим
воспоминанием воскресают перед нами годы их юности, годы
их первых научных шагов н дружеские беседы с незабвен-
ным Василием Яковлевичем. Не обилием ученых трудов
стяжал проф. Цингер свою известность, а характером этих
трудов.
Все, что он писал, при глубине содержания отличалось
ясностью, законченностью и конкретностью формы. В этом
направлении старались работать и его ученики, как матема-
тики, так и механики.
Недавно Московское математическое общество чествовало
память своего другого президента, знаменитого исследователя
в области прерывных функций н арифмологии, Н. В. Бугаева,
плодотворное влияние которого отразилось в работах наших
аналитиков; теперь мы чествуем память математика, которого
по справедливости можно назвать главой русской геометри-
ческой школы.
Есть математические работы, которые, раз прочитанные,
запоминаются навсегда, подобно тому, как картина зна-
менитого художника, мельком виденная в картинной
галлерее, со всей отчетливостью рисуется потом в вообра-
жении. К такого рода работам относятся сочинения
В. Я. Цингера, из которых четыре посвящены теоретической
механике.
В I томе „Математического сборника” он поместил статью
„Об относительном движении брошенной точки'. В. Я. заме-
428 ХАРАКТЕРИСТИКИ И БИОГРАФИИ
чает, что при обыкновенном приближенном решении этой за-
дачи [с помощью теоремы Кориолиса делают собственно не-
естественное допущение, что точка в своем абсолютном дви-
жении находится под эффектом силы, меняющей направление
в зависимости от перемещения места наблюдения. Он пока-
зывает, что, трактуя задачу, как задачу об абсолютном дви-
жении, мы при указанном предположении именно и получаем
при переходе к относительному движению интегралы дви-
жения в форме Бура. В. Я. Цингер предлагает задачу об
относительном движении брошенной точки решать сначала,
как задачу об абсолютном движении, отбросив от наблюден-
ной силы тяжести центробежную силу, а потом полученное
абсолютное движение преобразовать в относительное. Таким
образом получается без всякого интегрирования полное ре-
шение задачи.
Во II и в III томах „Математического сборника" В. Я Цин-
гер поместил две статьи, которые послужили его докторской
диссертацией: „О движении свободной жидкой массы"
и „Вращательное движение жидкого эллипсоида с измене-
нием вида".
Эти работы примыкают к задаче Дирихле о движении жидкого
эллипсоида, но В. Я. делает из них более общие предполо-
жения о виде действующих на жидкость сил и пользуется
анализом, представляющим значительное упрощение сравни-
тельно с анализом Дирихле. Анализ проф. Цингера сроден
с тем, который употребляется в гидростатике при изыскании
форм равновесия вращающихся жидких масс, и имеет прове-
рочный характер.
Исходя из предположения, что частицы жидкости
движутся, оставаясь на трех семействах деформирую-
щихся поверхностей, из которых одна представляет по-
добные эллипсоиды, и, пользуясь условием несжимаемости,
автор определяет скорости и ускорения точек жидкости.
Когда два другие семейства поверхностей суть параллельные
плоскости, тогда жидкость представляет однородно изменяемую
систему, и мы имеем случай движения Дирихле. Автор ука-
зывает любопытные свойства изменения частицы жидкости
при различных частных случаях этой задачи. Найдя уско-
О РАБОТАХ В. Я. ЦИНГЕРА ПО МЕХАНИКЕ
429
рения, автор ищет силы, действующие на жидкость, под
условием, что они, соединяясь с силами инерции, имеют потен-
циальную функцию и перпендикулярны к свободной поверх-
ности, за которую принимает один из эллипсоидов упомяну-
того семейства.
В первой статье автор останавливается на случае, когда
оси эллипсоидов остаются неподвижными, а во второй — он
рассматривает случай вращения изменяющегося эллипсоида
около одной из своих осей.
Интеграция доводится здесь до конца для случая эллип-
соида вращения.
Мне вспоминается, что при докладе этой работы в Мате-
матическом обществе на замечание В. 'В. Преображенского,
что эта задача разобрана у Дирихле, В. Я. Цингер, шутя,
отвечал: „Но ведь Дирихле получает свои результаты после
нескольких страниц сложных формул".
Четвертая работа В. Я. Цингера по Механике, „Об одном
случае равновесия жидкости", помещена в VI томе „Матема-
тического сборника". Она была вызвана опытной диссер-
тацией Булыгинского по капиллярности. В ближайшем засе-
дании Математического общества, после зищиты диссертации
Булыгинского, В. Я. изложил решение задачи о виде свобод-
ной поверхности жидкости, находящейся под эффектом тя-
жести и силы ньютоновского притяжения погруженной
в жидкость цилиндрической трубки. Получилась поверхность,
характер 'которой такой же, как при капиллярных силах, для
которых, как известно, принимают силу притяжения обратно
пропорциональной расстояниям в степенях значительно выше
второй.
Избрав своей специальностью чистую математику, В. Я. Цин-
гер живо интересовался теоретической механикой. Он
являлся вместе с проф. Ф. А. Слудским, обычным оппонен-
том на диссертациях по механике. В своих спорах он ярко
выдвигал определенное возражение, но зато охотно вникал
в мысли отвечающего. Его возражения обыкновенно отно-
сились к сущности дела и служили для молодого уче-
ного благотворным указанием при дальнейших исследо-
ваниях.
430 ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Своей любовью к образному, геометрическому мышлению
В. Я. Цингер увлекал молодых механиков, направляя их
труды по тому пути, по которому следовали великие геометры
Ньютон, Пуансо, Понселе и Шаль.
Эта речь была произнесена Н. Е. Жуковским 4 апреля 1908 г. в засе-
дании Московского математического общества и напечатана в „Математи-
ческом сборнике", т. XXVIII, 1908. Прим. ред.
Н. А. УМОВ КАК МАТЕМАТИК
Н. А. УМОВ
(1834-1897)
И. А. УМОВ КАК МАТЕМАТИК
(1915— 1916 и.)
Когда чествуется память такого выдающегося ученого
и общественного деятеля, каким был покойный проф. Николай
Алексеевич Умов, тогда многие учреждения стараются при-
соединить к своей области его славное имя. На мою долю
как председателя Московского математического общества
выпала честь сказать о Н. А. Умове как о математике. Об
этом сказать можно многое и независимо от желания привлечь
его нмя к области наук математических. Я всегда думал, что
Н. А. Умов был в душе математический физик, хотя н сни-
скал под конец своей деятельности почетную известность
многими экспериментальными исследованиями.
Уже на университетской скамье изучал он работы Фурье,
Кошн, Пуассона и Ляме и делился своими знаниями с това-
рищами по студенческому кружку математиков, в котором
участвовали Ламовский, Никитин н др. Особенное внимание
было обращено им на труд Ляме, обстоятельное знакомство
с методом криволинейных координат которого послужило
основой для многих физико-математических работ Умова.
Первая из этих работ была доложена в Математическом обще-
стве в 1870 г. и была напечатана в V томе „Математического
сборника" под заглавием „Законы колебаний в неограничен-
ной среде постоянной упругости". Относя среду к системе
ортогональных криволинейных координат, в которых одно нз
семейств координатных поверхностей представляет поверх-
ности волн, и приняв за параметр этого семейства отрезок
длины луча, он доказывает, что при этом соответственный
дцференциальный параметр первого порядка равен единице.
При таком выборе координат, задачи о поперечных колебаниях
по линиям кривизны и о продольных колебаниях разделяются,
Зак. 2430. И. Е. Жукокьский. Том IX
28
434
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
и получается ряд интересных заключений о характере этих
колебаний. Сообщение Н. А. Умова было встречено нашими
учителями с большим одобрением. Через год, т. е. в 1871 г.,
Н. А. Умов напечатал свою магистерскую диссертацию „Тео-
рия термомеханических явлений в твердых упругих телах",
в которой методы термодинамики прилагаются к твердому
телу, причем одновременно с этим рассматривается приток
теплоты вследствие теплопроводности. Эта диссертация была
защищена в Московском университете 1872 г. Я помню, как
декан факультета А. Ю. Давидов, отзываясь в своем резюме
с большой похвалой о работе, объявил, что молодой ученый
уже получил приглашение занять кафедру физики в Одессе.
В Одессе экспериментальную физику тогда читал Шведов,
он же заведывал физическим кабинетом, и Н. А. Умову при-
шлось заниматься исключительно математической физикой.
Результатом этих занятий, кроме блестящих лекций, появился
новый ряд работ Н. А. Умова по математической физике.
В 1872 г. в VI томе „Математического сборника" им напе-
чатана статья „Теория взаимодействий на расстояниях конеч-
ных и ее приложение к выводу электрических и электродина-
мических законов", а в 1873 г. он напечатал в Одессе статью
„Теория простых сред". Обе эти статьи являются подготови-
тельными к его докторской диссертации. По воззрениям
Н. А. Умова потенциальная энергия не может образоваться
в одной простой среде; необходимы, по крайней мере, две
среды, из которых вторая, не подлежащая непосредственно
наблюдению, принимает на себя часть кинетической энергии
и тем создает наше предложение о потенциальной энергии.
В этих статьях у автора вырабатывается взгляд на ток энер-
гии как на ток, подобный тепловому. Этот взгляд лег в основу
его докторской диссертации „Уравнения движения энергии
в телах", которая была напечатана в Одессе в 1874 г., а потом,
в том же году, в Москве было напечатано добавление к этой
работе. При защите своей диссертации Н. А. Умов встретил
горячие возражения профессоров В. Я. Цингера и Ф. А. Слуд-
ского, которым казались слишком своеобразными воззре-
ния Н. А. Но эти воззрения Н. А. Умов отстаивал в продол"
жение всей своей жизни и подобно Фарадею и Максвеллу
Н. А. УМОВ КАК МАТЕМАТИК
435
не считал действие сил на расстоянии и потенциальную энер-
гию физическим объяснением явлений природы. К своим воз-
зрениям обратился он в своей недавней статье, напечатанной
в приложении к „Временнику Леденцовского общества" под
заглавием „Возможный смысл теории квант".
Перехожу к дальнейшим работам Н. А. Умова, прилегаю-
щим к математике. Летом 1875 г. Н. А. был послан в загра-
ничную командировку, в которой слушал лекции Кирхгоффа
и Гельмгольца. Он представил при этом Кирхгоффу статью
о распределении электрического тока в изогнутых пластинках,
которая являлась обобщением исследований знаменитого немец-
кого ученого о движении электричества в плоских пластинках.
Результат, найденный Н. А., был напечатан в „Трудах Берлин-
ской академии наук" с упоминанием его имени, но в видо-
измененном изложении Кирхгоффа, как часть работы послед-
него. Это весьма огорчило Н. А., и он не раз потом жало-
вался своим русским товарищам на такое действие немецкого
ученого. Спустя три года Умов напечатал в IX томе „Мате-
матического сборника" свою статью в том виде, в каком она
была представлена Кирхгоффу, под заглавием „О стационар-
ном движении электричества на проводящих поверхностях
произвольного вида". Результат, найденный Умовым, заклю-
чался в том, что задача о распределении тока в изогнутой
пластинке приводится к задаче о распределении его в плоской
пластинке, которая получается, преобразуя кривую пластинку
конформным преобразованием на плоскость.
В том же 1878 г. Умовым была напечатана в IX томе
„Математического сборника" статья „О фиктивных взаимо-
действиях между телами, погруженными в среду постоянной
упругости". В ней автор подвергает подробному математи-
ческому анализу объяснение кажущегося действия на рас-
стоянии действием упругой среды, в которую погружены
тела и которая вследствие деформации производит на них
давление. Задаваясь видом этой деформации, он получает:
законы ньютонианского и электрического притяжения, закон
взаимодействия магнитных масс и т. Д.
Перехожу к курсам, напечатанным Н. А. Умовым. К сожа-
лению, интересные лекции по математической физике, которыми
28*
436
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
начал Н. А. свою профессорскую деятельность, не были
напечатаны. В печати появились только „Курс математической
физики (введение)", напечатанный в 1878 г. в Одессе, и „Из
лекций математической физики", статья, напечатанная в 1883 г.
там же. Первая статья заключает в себе полную теорию век-
торов, непрерывно распределенных в данном поле, которая
в то время представляла новинку. Вторая же статья содержит
изложение теории малых колебаний системы около положения
равновесия и случай колебания системы с одной степенью
свободы в приложении к явлениям созвучия и абсорбции.
Статья эта представляет обстоятельный анализ явлений коле-
бания с разбором случая равных корней в основном уравне-
нии, изложенном согласно работам Сомова и Вейерштрасса.
Здесь автору удалось ввести в изложение новые приемы.
Я укажу теперь интересный прибор Н. А. Умова для
вычисления интегралов Френеля, который был описан в про-
токолах Новороссийского общества естествоиспытателей
в 1885 г. и демонстрирован Н. А. Умовым в Парижском
физическом обществе при проезде его через Париж на юбилей
Кельвина. Интеграл Френеля, играющий важную роль в тео-
рии света, берется от произведения синуса или косинуса
квадрата дуги на элемент дуги. Для выполнения этой опера-
ции Н. А. навертывает на цилиндр, представленный на фиг. 1,
параболу так, что ось параболы располагается по окружности
основания цилиндра.
Штифт G преобразует с помощью бесконечного шнурка
пройденный путь z во вращение валика В, который повора-
чивается вместе с рамкой М на угол, пропорциональный z2.
Таким образом, стрелка валика А дает интеграл Френеля.
Я окончу мою речь „Умов как математик", рассмотрев
одну из его последних работ, имеющую глубокое математи-
ческое содержание. Эта работа относится к данному им остро-
умному толкованию преобразования Лоренца, лежащего в
основе принципа относительности. Работа называется „Усло-
вия инвариантности волнового уравнения", и напечатана в
1912 г. в „Журнале Физико-химического общества". Содер-
жание ее было доложено в 1911 г. на II Менделеевском
съезде. По моему мнению, она является лучшим математи-
Н. А. УМОВ КАК МАТЕМАТИК
437
ческим толкованием принципа относительности. Подобно тому
как неэвклндовская геометрия и геометрия многих измерений
опираются на инвариантность обобщенного представления об
элементе дуги, принцип относительности по Умову имеет свое
математическое содержание в инвариантности волнового урав-
нения распространения света. Вводя в это уравнение вместо
времени t мнимое переменное x = v>ti, где «> — скорость света,
Умов представляет его в виде равенства'нулю второго диферен-
циального параметра некоторой
функции от координат х, у, z
точки среды и ". Рассматривая
два мира, между величинами х, у,
z, т и х', у', z', х' которых уста-
новлено соответствие, автор под-
бирает это соответствие так, чтобы
волновое уравнение второго мира
выражалось равенством нулю вто-
рого диференциального параметра
от х', у', z', х'. Это устанавли-
вает определенную зависимость
между величинами х', у’, z', t' но-
вого мира и величинами х, у, z, t
старого. Оказывается необходи-
мым, чтобы вторые диференциаль-
ные параметры функций х', у', z'
и т', выраженных чрез х, у, z и т
были равны нулю.
Рассматривая для простоты
случай z = z' = 0, Умов уста-
навливает связь между х', у', х' и х, у, х. При предположении,
что х, у, ~ суть параметры декартовой системы осей коорди-
нат, эта связь требует, чтобы х', у', х' были параметрами изо-
термической системы криволинейных триортогональных коор-
динат. В частном случае можно удовлетворить инвариантно-
сти волнового уравнения в системе обоих миров, принимая,
что х', у', х’ суть тоже параметры прямоугольных декартовых
координат, которые повернуты около оси Оу на некоторый
мнимый угол <pi. Написав при этом обыкновенные фор-
Фиг. 1.
438
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
мулы преобразования координат и положив, что th о = , Умов
находит, что
Эти формулы показывают, что наблюдатель первого мира
видит точки второго мира продвигающимися по оси Ох со
скоростью с и считает всю среду второго мира сжатой по
направлению ее перемещений. Кроме того, на своих часах он
находит время во втором мире, различное в различных его
точках.
Математический факультет предложил на брашманскую
премию будущего года тему „О принципе относительности".
Было бы весьма желательно, чтобы лица, взявшиеся за раз-
работку этой темы, вникли в мысли покойного профессора.
Я начал свою речь, заявив, что Н. А. Умов был в душе ма-
тематическим физиком. Я думаю, что на основании сказанного
могу еще прибавить, что он был математическим философом.
Эта речь была произнесена И. Е. Жуковским 18 апреля 1916 г. в засе-
дании Московского математического общества и напечатана в „Математи-
ческом сборнике*, т. XXX, 1916. Прим. ред.
ВОСПОМИНАНИЯ ОБ А. И. ЛИВЕНЦОВЕ
(1892 г.)
Вы слышали из отчета, что вдова нашего покойного сото-
варища Алевтина Александровна Ливенцова пожертвовала для
начинающейся собираться библиотеки Физического отделения
Общества любителей естествознания книги своего мужа.
Это дает мне повод посвятить несколько слов памяти
покойного Александра Исаевича. Ои окончил курс в Москов-
ском Университете в 1873 г. в выпуске, особенно богатом
хорошими математиками: тут был покойный профессор Гро^
мека, Зилов, Шапошников, Минин и др. За сочинение „Иссле-
дование касательной силы таутохроны" он был удостоен
золотой медали, и сочинение это было напечатано в Математи-
ческом сборнике, в котором печатались впоследствии и все
другие работы покойного. К нашему физико-математическому
кружку Ливенцов примкнул в то время, когда мы собирались
в физической лаборатории, и сделал в нем несколько сооб-
щений по функциональному исчислению и по особым точкам
диференциальных уравнений.
В 1876 г. Александр Исаевич защищал свою магистерскую
диссертацию „Опыт систематического изложения функцио-
нального счисления". В этой работе, вполне новой на русской
почве, автор излагает самостоятельным образом все имею-
щиеся до него исследования в области функционального
исчисления и показывает, что всякое функциональное уравне-
ние может быть сведено к уравнениям с конечными разно-
стями. Вскоре после диссертации появились еще две неболь-
шие статьи автора „О функциональных индексах" и „Об
определении функции через определенный интеграл".
После этого Александр Исаевич был командирован на два
года за границу. Летом 1877 г. я встретился с ним в Париже,
440
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
где нам пришлось жить в одном доме и быть почти всегда
вместе. Здесь я вполне оценил высокие душевные качества
покойного.
Несколько неповоротливый на первый взгляд, он оказался
живым, увлекающим собеседником. Мне так живо вспомина-
ются наши прогулки по окрестностям Парижа, в которых при-
нимали участие Александр Исаевич с женой, профессор
Андреев и я. Кому из нас могло тогда прийти в голову, что
жизнь Александра Исаевича так коротка. Ливенцов слушал
лекции в Коллеже и Сорбонне и очень увлекался чтением
Эрмита. С последним он познакомился, несколько раз бывал
у него и беседовал с ним о своих любимых вопросах по тео-
рии функций и мнимому переменному. Кроме того, он рабо-
тал в Национальной библиотеке, где преимущественно изучал
Коши, находя у великого автора, как он говорит, такие иссле-
дования, о которых нигде не упоминается.
Вернувшись из-за границы, Александр Исаевич привез
с собою несколько работ и напечатал их в „Математическом
сборнике": „О некоторых определенных интегралах", „О ме-
тоде решения Абелевой задачи Летниковым".
Он привез с собой также и материалы для своей доктор-
ской диссертации, которую предполагал писать по теории ло-
гарифмического потенциала в связи с теорией мнимого пере-
менного и исследованием Шварца об особых точках на гра-
ничном контуре.
Математический факультет поручил ему по приезде из-за
границы читать лекции математики естественному отделению.
Но всем этим начинаниям не суждено было осуществиться.
Внезапная болезнь скосила молодую жизнь, столь много обе-
щавшую.
Время ушло, забылось многое. Но на страницах „Мате-
матического сборника" навсегда остались следы глубокой
мысли покинувшего нас товарища.
Н. Е. Жуковский выступил с воспоминаниями об А. И. Ливенцове
11 февраля 1892 г. в заседании Отделения физических наук Общества лю-
бителей естествознания. Воспоминания были напечатаны в «Трудах Отделе-
ления физических паук Общества любителей естествознания", т. V, вып. I.
_______ Прим. ред.
ОТЗЫВ О СОЧИНЕНИИ В. А. МИХЕЛЬСОНА „О НОРМАЛЬ-
НОЙ СКОРОСТИ ВОСПЛАМЕНЕНИЯ ГРЕМУЧИХ ГАЗОВЫХ
СМЕСЕЙ"
(1890 г.)
В рассматриваемом сочинении выставилась на вид с боль-
шой ясностью та симпатичная особенность автора, которую
он проявил и в прежних своих работах. Необычайно простая
мысль кладется в основание остроумных наблюдений и ведет
к богатым результатам. Читатель удивляется, как все заду-
манное и полученное автором не приходило никому в голову
раньше.
В добавление к исследованию других ученых о скорости
распространения взрывной волны, автор в своем сочинении:
„О нормальной скорости воспламенения гремучих газовых
смесей" исследует медленную скорость распространения пла-
м сии при постоянном давлении. Этот процесс по существу
своему не стационарный; автор обращает его в стационарный
тем, что выпускает газ из цилиндрической трубки и подби-
рает скорость его истечения так, чтобы пламя было непо-
движно.
Тогда происходят два движения: с одной стороны, частицы
газа бегут параллельно оси трубки, а с другой — п ламя пере-
мещается по нормалям к поверхности раздела горящего и
негорящего газа. От сложений этих двух движений получается
неподвижное пламя. Очевидно, что при этом произведение
поверхности раздела пламени на скорость его распростране-
ния будет равно секундному объему притекающего газа, так
что весь вопрос об определении искомой скорости сводится
к измерению размеров пламени. Эти измерения тщательно
выполнены автором и привели к весьма согласным результа-
там. С другой стороны задача о движении газа в узкой цилин-
442
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
дрической трубке есть одна из задач гидродинамики, пре-
красно теоретически и опытно исследованная. Имеются
формулы, которые позволяют определить скорость каждой
частицы по секундному объему жидкости и коэфициентам
внутреннего внешнего трения. Зная же эти скорости и ско-
рость распространения пламени, мы сейчас же получаем
диференциальное уравнение меридионального сечения поверх-
ности раздела пламени. Автором это уравнение обинтегриро-
вано и полученная кривая вычерчена. Сравнение ее с дей-
ствительной кривой, взятой с фотографии пламени, дает близ-
кое сходство.
Прибавим к сказанному, что метод исследования автора
дает также возможность определять коэфициенты трения газа.
Мы думаем, что разбираемое сочинение вполне заслужи-
вает премии В. П. Мошнина.
Отзыв о сочинении Михельсона был прочитан Н. Е. Жуковским в за-
крытом заседании Отделения физических наук Общества любителей естество-
знания 29 сентября 1890 г. и напечатай в „Трудах Отделения физических
наук Общества любителей естествознания*, т. III, вып. 2, 1890. Прим. ред.
КРАТКАЯ ХАРАКТЕРИСТИКА ЛИТЕРАТУРНЫХ РАБОТ
А. И. ПЕРМЯКОВА ПО ВОДЯНЫМ ТУРБИНАМ И
РЕАКТИВНЫМ СУДАМ
(1916 г.)
А. И. ПЕРМЯКОВ
Все ниже поименованные 8 работ А. И. Пермякова отно-
сятся к водяным турбинам и к реактивным судам *. А. И. Пер-
мяков имел обширную практику по турбиностроению и напе-
чатал в 1907 г. по этому отделу свой
курс, который, однако уже несколько
устарел ко времени своего появления
в свет в печатном виде. В этом курсе
между прочим изложены мысли автора
об обратных турбинах, которыми он
в то время опытно занимался, делая
испытания над водоподъемниками с осе-
выми турбинами. Работы А. И. Пер-
мякова в этой области направили его
внимание на передвижение судов с по-
мощью реакции выбрасываемой воды.
Этим вопросом он занимался все по-
следние годы своей жизни. В своей
ниже) автор высказывает мнение, что
измеряться величиной т • v, тогда как Буслей
торы измеряют ее величиной тп(г> — и). Величина, принятая
Пермяковым, была бы верна, если бы движущееся судно
несло с собой ту воду, которую оно выбрасывает; но так как
вода забирается из окружающей судно массы воды, то вер-
ным является выражение силы реакции, данное Буслеем.
статье под № 3 (см.
сила реакции должна
и другие ав-
1 См. прилагаемый в конце статьи список работ А. И- Пермякова.
Прим. ред.
444
ХАРАКТЕРИСТИКИ И БИОГРАФИИ
Вследствие ошибочного представления о величине этой силы
А. И. Пермяков переоценивал достоинство реактивных судов,
что и показали его неудачные опыты с судами, испытанными
на р. Каме и на Москве-реке. Несмотря на это, А. И. Пер-
мяков очень упорно держался своего взгляда и отстаивал
его в ряде последующих статей за № 4, 5, 6 и 7. В его
статье под № 5, несмотря на несколько ошибочных формул,
выставлены довольно интересные мысли о возможности по-
строения турбин без направляющего аппарата с высоким коэ-
фициентом полезного действия. Опыты А. И. Пермякова на
Алексеевской водокачке привели его к заключению о том,
что количество воды, протекающей в радиальной турбине без
направляющего аппарата, может быть при ее вращении более
того количества, которое под тем же напором может пройти
через неподвижную турбину, что происходит от действия на
воду центробежной силы. Пользуясь этим свойством, А. И.
Пермяков предполагал осуществить скороходную турбину
низкого давления. Для производства опытов в этом направле-
нии общество имени X. С. Леденцова имело в виду оказать
ему свое содействие. К сожалению, безвременная кончина
А. И. Пермякова не позволила осуществить эти начинания.
В некоторых из своих теоретических соображений А. И.
впадал в ошибки, но в нем нельзя не видеть исследователя,
со всей горячностью преданного разрешению своей задачи;
точно также нельзя не почитать в его лице большого прак-
тика, много поработавшего в области построения турбин и
в свое время немало потрудившегося над их распространением
в России.
КРАТКАЯ ХАРАКТЕРИСТИКА РАБОТ А. И. ПЕРМЯКОВА
445
СПИСОК ЛИТЕРАТУРНЫХ РАБОТ А- И. ПЕРМЯКОВА
1. Неточность формул при расчете радиальных турбин. Заметка, на-
печатанная в „Бюллетенях Политехнического общества" за 1895 —1896,
в № 8.
2. Водяные турбины, их устройство, теория и расчет. Курс, изданный
в 1907 г. т-вом Сытина.
3. Пароходы, приводимые в движение струей воды. Доклад, сделанный
в инженерно-механическом отделе Политехнического общества в сентябре
1908 г. и напечатанный в „Бюллетенях Политехнического общества" в 1908 г.
4. Сила реакции воды в применении к водяным турбинам и к движе-
нию судов. Статья, напечатанная в „Трудах о-ва судоходства" ва 1910 г.
(21/д печатных листа).
5. Водяные турбины без направляющего аппарата. Доклад, сделанный
в инженерно-механическом отделе Политехнического общества в ноябре
1913 г. и в том же году напечатанный в „Бюллетенях Политехнического об-
щества".
6. Суда, приводимые в движение силой реакции воды. Законченная
изложением, но ненапечатанная рукопись, помеченная 15 декабря 1912 г.
7. Энергия вытекающей под напором воды. Законченная изложением,
но ненапечатанная рукопись (29 страниц большого формата), помеченная
20 августа 1915 г. (за 31/2 месяца до смерти автора).
8. Двойная турбина Жонваля на горизонтальном валу, работающая при
Московской городской прачечной. Статья, напечатаииая в „Бюллетенях
Политехнического общества" Кв 7 за 1892—93 г.
„Краткая характеристика литературных работ А. И. Пермякова по
водяным турбинам и реактивным судам* была получена редакцией „Вестника
Политехнического общества" от Н. Е. Жуковского и помещена в коллек-
тивной заметке „А. И. Пермяков", „Вестник Политехнического общества"»
№ 27, 1916. Прим. ред.
ОГЛАВЛЕНИЕ
От редакции.......... 5
Раздел I
Математика
Геометрическое разъяснение
некоторых вопросов теории
уравнений с частными произ-
водными.................... 9
Резюме.................... 16
Заметка по вариационному ис-
числению. . ........... 17
Резюме.......,............ 36
Геометрическое доказательство
первой и второй теорем
С. А. Чаплыгина о диферен-
циальиых неравенствах ... 38
Резюме.................... 48
Упрощенное изложение гауссова
способа определения планет-
ных орбит. ................61
Резюме....................... 82
О графическом решении основ-
ного уравнения при вычисле-
нии планетных орбит .... 86
Резюме....................... 90
Sur une demonstration' nouvelle
du theoreme de Lambert ... 91
О новом доказательстве теоре-
мы Ламберта. (Перевод пре-
дыдущей статьи)........... 97
Резюме......................Ю2
Решение одной задачи из тео-
рии комет.................104
Резюме......................НО
Раздел II
Астрономия и математи-
ческая физика
La deduction des formuies ехас-
tes du mouvement produit par
la force repulsive du soleil • • 53
Вывод точных формул движе-
ния, произведенного отталки-
вающей силой солнца. (Пере-
вод предыдущей статьи). . . 57
Резюме..................... 60
Sur la construction des courbes
syndynamiques et synchroni-
ques........................
О построении синдинамичееких
и синхронических кривых.
(Перевод предыдущей статьи)
Резюме......................
К вопросу о давлена диэлек-
трического газа в электри-
ческом поле.................
Резюме......................
112
133
154
156
177
448
ОГЛАВЛЕНИЕ
Раздел III
Речи и доклады
Характеристики и био-
графии
О значении геометрического
истолкования в теоретической
механике .... .............181
О воздухоплавании.............188
Механика в Московском универ-
ситете аа последнее пяти-
десятилетие ................203
Аэродинамические лаборатории
Московского университета и
Московского технического
училища...................212
Новые научные завоевания в
теории сопротивления жид-
костей......................233
Старая механика в новой фи-
зике .......................245
Ньютон, как основатель теоре-
тической механики...........263
Труды А. Ю. Давидова по ана-
литической механике .... 275
Труды С. В. Ковалевской по
прикладной математике . . . 301
Работы Гельмгольца по меха-
нике .......................313
Некролог и очерк ученой дея-
тельности проф. Ф. Е. Ор-
лова .......................331
О трудах В. Г. Имшенецкого по
механике...................345
Летательный аппарат Отто Ли-
лиенталя ..................351
О гибели воздухоплавателя Отто
Лилиенталя.................356
О деятельности А. Г. Столе-
това в обществе любителей
естествознания.............371
Биография и ученые труды проф.
Ф. А. Слудского............375
М. В. Остроградский..........389
Некоторые черты из жизни
М. В. Остроградского . . . 392
Ученые труды М. В. Остроград-
ского по механике..........398
О работах Д. И. Менделеева
по сопротивлению жидкостей
и воздухоплаванию..........417
О работах В. Я. Циигера по
механике...................427
Н. А. Умов как математик . . 433
Воспоминания об А. И. Ливен-
цове.......................439
Отзыв о сочинении В. А. Ми-
хельсона „О нормальной ско-
рости воспламенения грему-
чих газовых смесей” .... 441
Краткая характеристика литера-
турных работ А. И. Пермя-
кова по водяным турбинам и
реактивным судам.............443
CONTENTS
Editorial................... 5
Section I
Mathematics
Geometrical Elucidation of Some
Questions on Theory of the
Partial Differential Equations. 9
Summary....................... 16
Note on the Calculus of Varia-
tion ......................... 17
Summary....................... 36
Geometrical Proof of S. A. Cha-
plygin’s Theorems on Differen-
tial Inequalities............. 38
Summary..................... 48
Section II
Astronomy and Mathematical
Physics
La deduction des formules exac-
tes du mouvement produit par
la force repulsive du soleil . 53
Deduction of Precise Formulae
of the Motion Produced by
the Repulsive Force of the
Sun (Translation of the above
paper)...................... 57
Summary..................... 60
Simplified Exposition of Gauss’
Method of Determination of
the Planet Orbits............. 61
Summary..................... 82
Зак. 2430- H. E. Жуковский. Том IX
On a Graphical Solution of the
Fundamental Equation in the De-
termination of Planetary Orbits. 86
Summary . ................... 90
Sur une demonstration nouvelle
du theoreme de Lambert. . . 91
On a New Proof of Lambert’s
Theorem (Translation of the
above paper)................. 97
Summary.......................102
Solution of a Problem of Co-
met Theory...................104
Summary..................... 110
Sur la construction des courbes
syndynamiques et synchro-
niques.......................112
On the Construction of Syndy-
namical and Synchronical Curves.
(Translation of the above pa-
per) .........................133
Summary.......................154
To the Question on Pressure of
a Dielectric Gas in an Electric
Field.....................156-
Summary..............• ... 177
Section III
Discourses and Reports
Characteristics and Biographies
On Importance of Geometrical
Interpretation in Theoretic
Mechanics................. . 181
On Aeronautics..................188
Fifty Jears in Mechanics at
Moscow University ... - 203
29
450
CONTENTS
Aerodynamical Laboratories of
Moscow University and Mos-
cow Technical School. .... 212
New-Scientific Achievements In
Theory of Fluid Resistance. . 233
Old Mechanics in New Physics. 245
Newton as Founder of Theoreti-
cal Mechanics..............263
Works of A. U. Davidov on Me-
chanics. .......... 275
Works of S. V. Kowalevski on
Applied Mathematics. .... 301
Works by Helmholtz on Mecha-
nics. *....................313
Obituary and Essay on Scienti-
fic Work of P. E. Orlov . . . 331
On Works of V. S. Imshenetsky
on Mechanics.................345
Flying Machine of O. Lilienthal 351
On the Perishing of the Aero-
naut O. Lilienthal...........356
On the Work of A. G. Stoletov 371
Biography of and Scientific
Works by P. A. Sloodsky. . 375
M. V. Ostrogradsky.............389
Some features from Life of M. V.
Ostrogradsky....................392
Scientific Works on Mechanics
by M. V. Ostrogradsky . . . 398
On Mendeleyev’s Works on Flu-
id Resistance and Aeronautics 417
On Tzlnger’s Works on Mecha-
nics •..........................427
N. A. Umov, as Mathematician . 433
Reminiscences on A. J. Livent-
zov.............................439
Judgement on V. A. Michelson’s
Work „On Normal Speed of
Ignition Fire-Damp Com-
pounds*.........................441
Brief Characteristic of Literatu-
re Works of A. I. Permiakov. 443
Редактор Ф. С. Шаховской.
Техн. ред. А. Н. С а вар и.
Сдано в набор 29!IX 1937 t.
Подписано к неч. 10!ХП 1937 г.
Авторский доювор № 271.
Инд. 10-5-4. Тираж 3000.
Кол. печ. лист. 28'1,^ Бум. л. 141/в
Тип. зн. в 1 бум. листе 89.088.
Учетно-авт. лист. 21,01. Фор-
мат бум.62Х,94’ л. Уполн.Глав-
лита № Б-28205. Заказ № 2430.
2-я тип. ОНТИ им. Евгении
Соколовой, Ленинград, проспект
Красных Командиров, 29.
Опечатки
Стр. Строка Напечатано Должно быть По чьей вине
49 2 сверху non-perpendicular mn perpendicu'ai ред.
76 8 „ tg (o' — = tg(8' —а) = тип.
82 15 снизу 7 Р ред.
103 3 сверху е case In the case ТИП.
287 3 с.шзу + 2)Ф + 2Ф) ТИМ.
Зак. 2430. Жуковский. Полное собрание сочинений, т. IX.